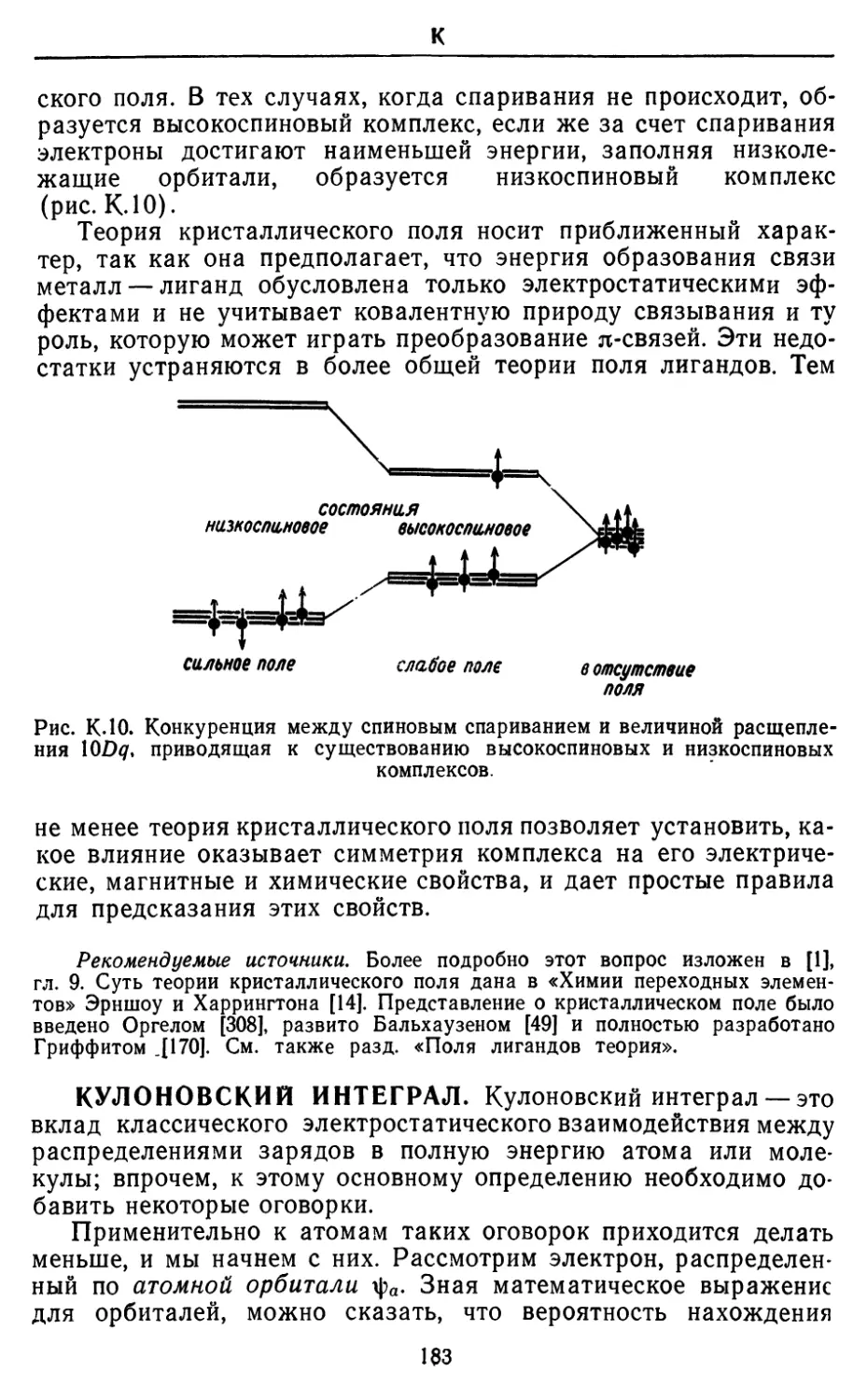
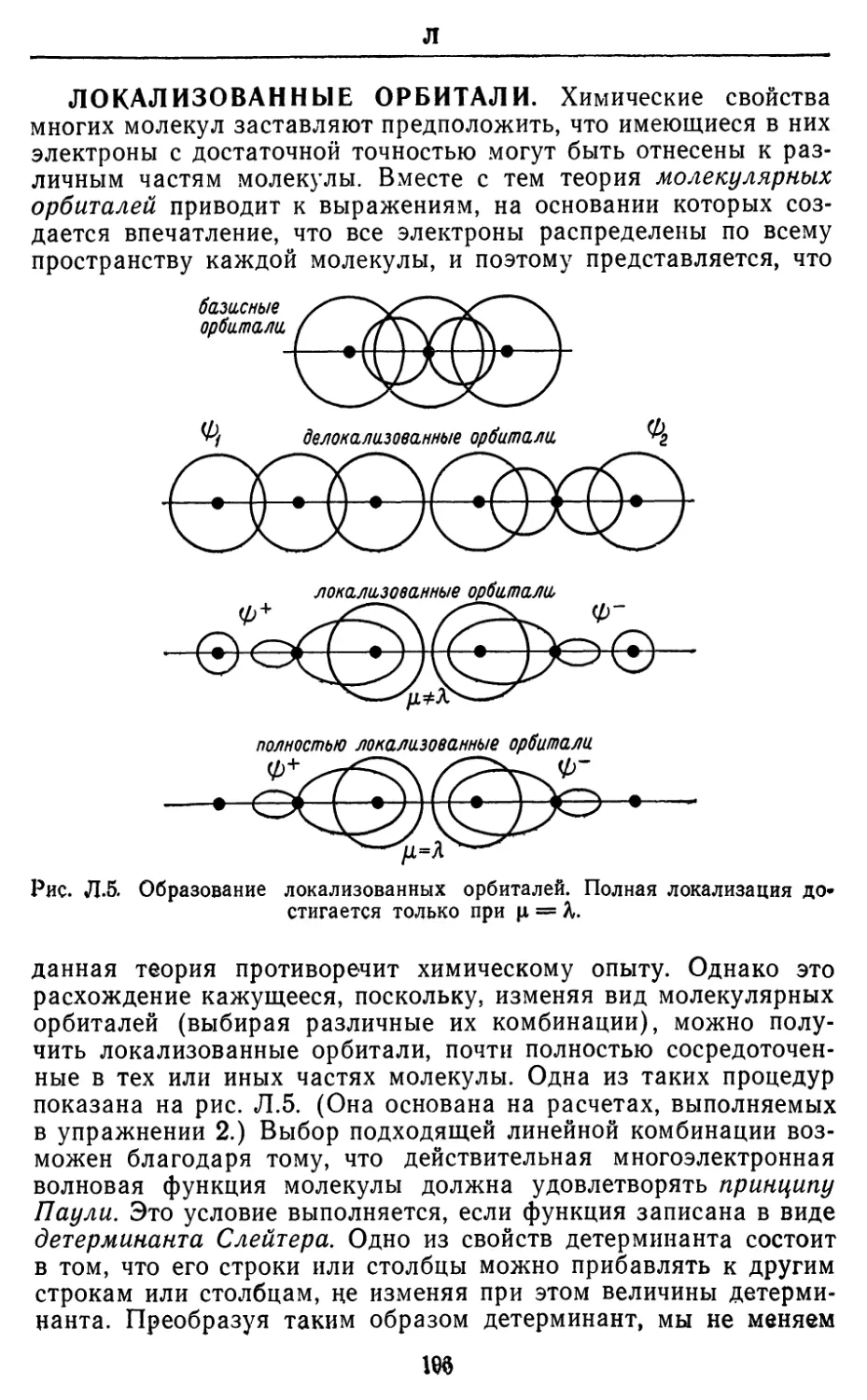
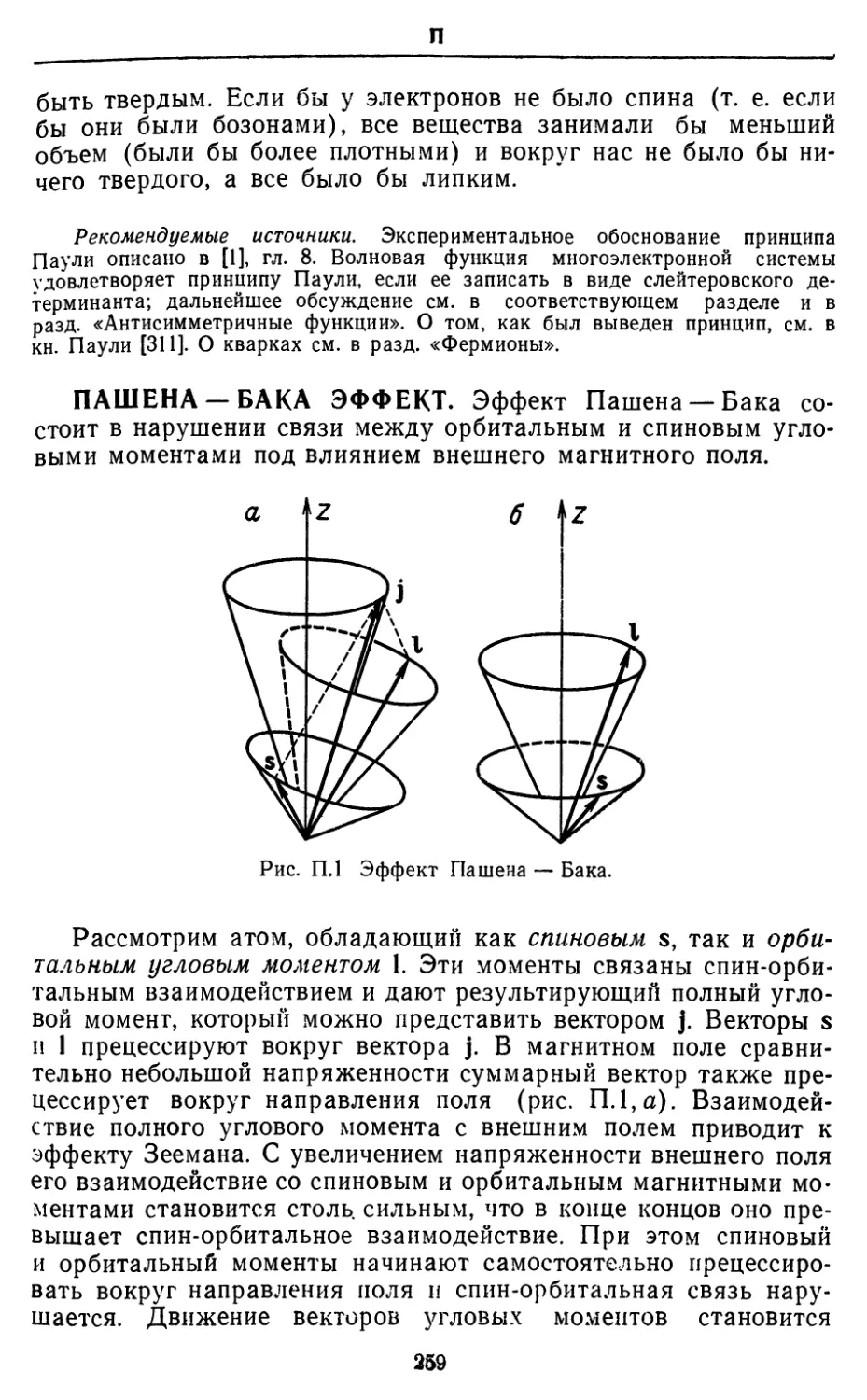
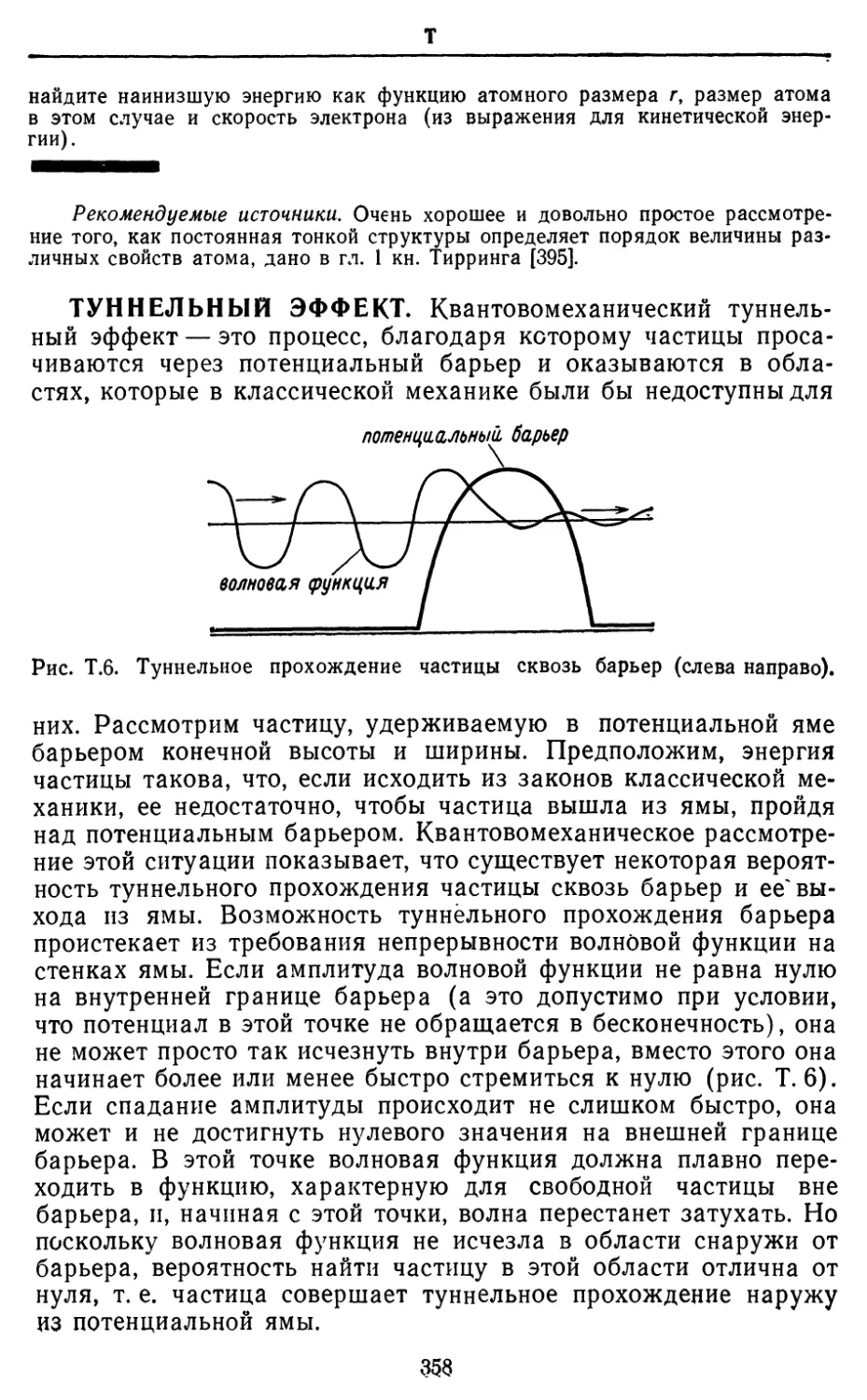
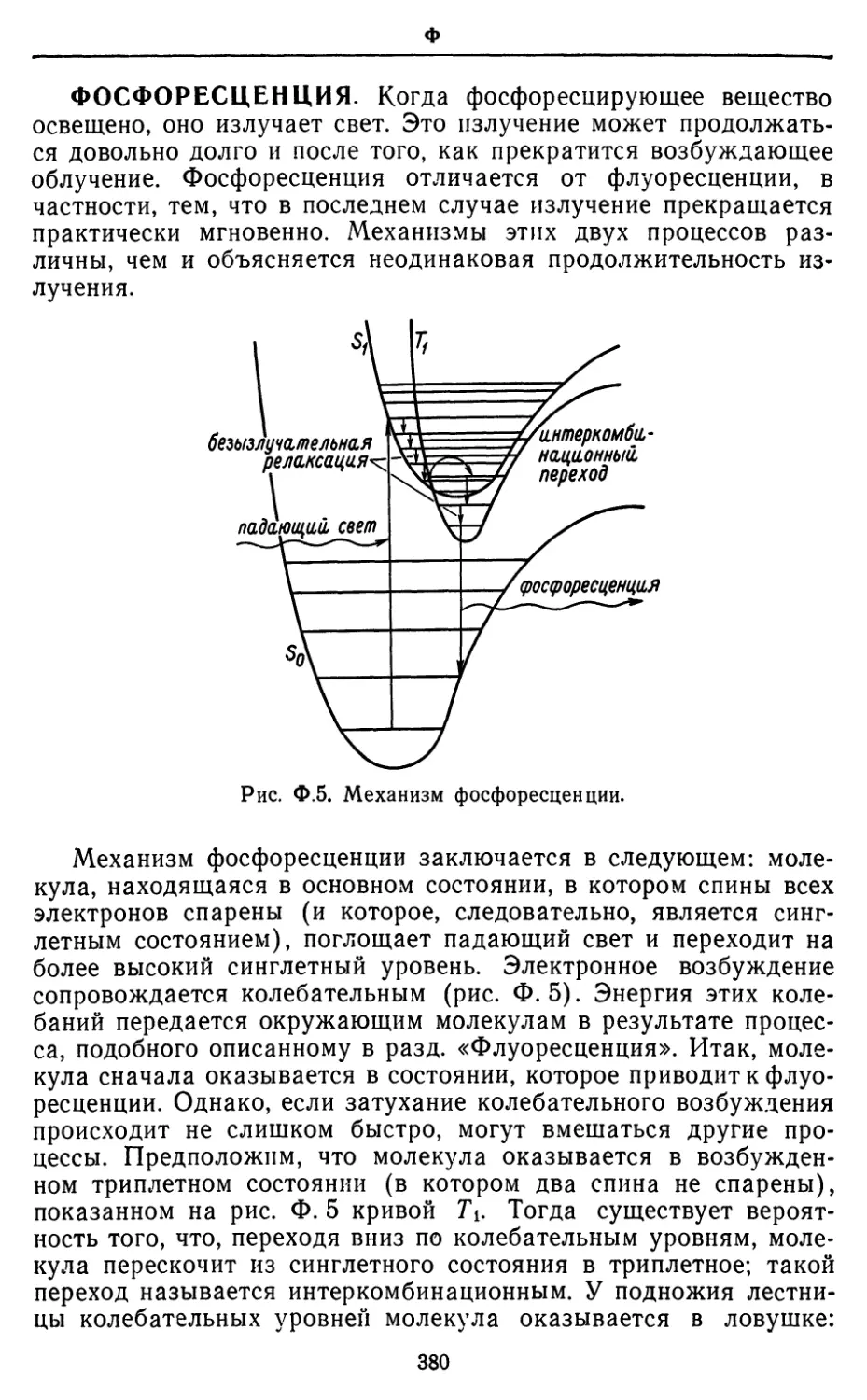
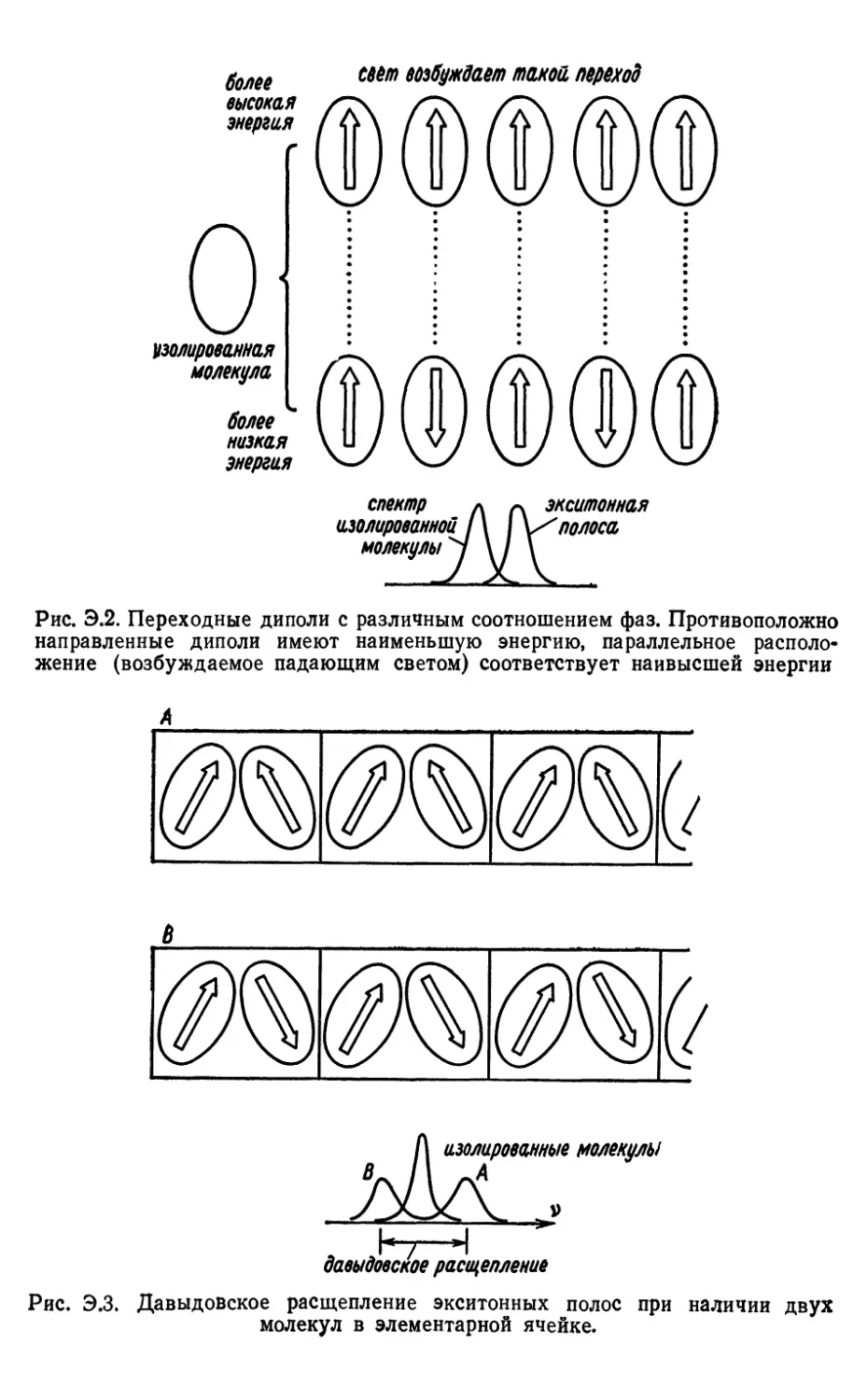
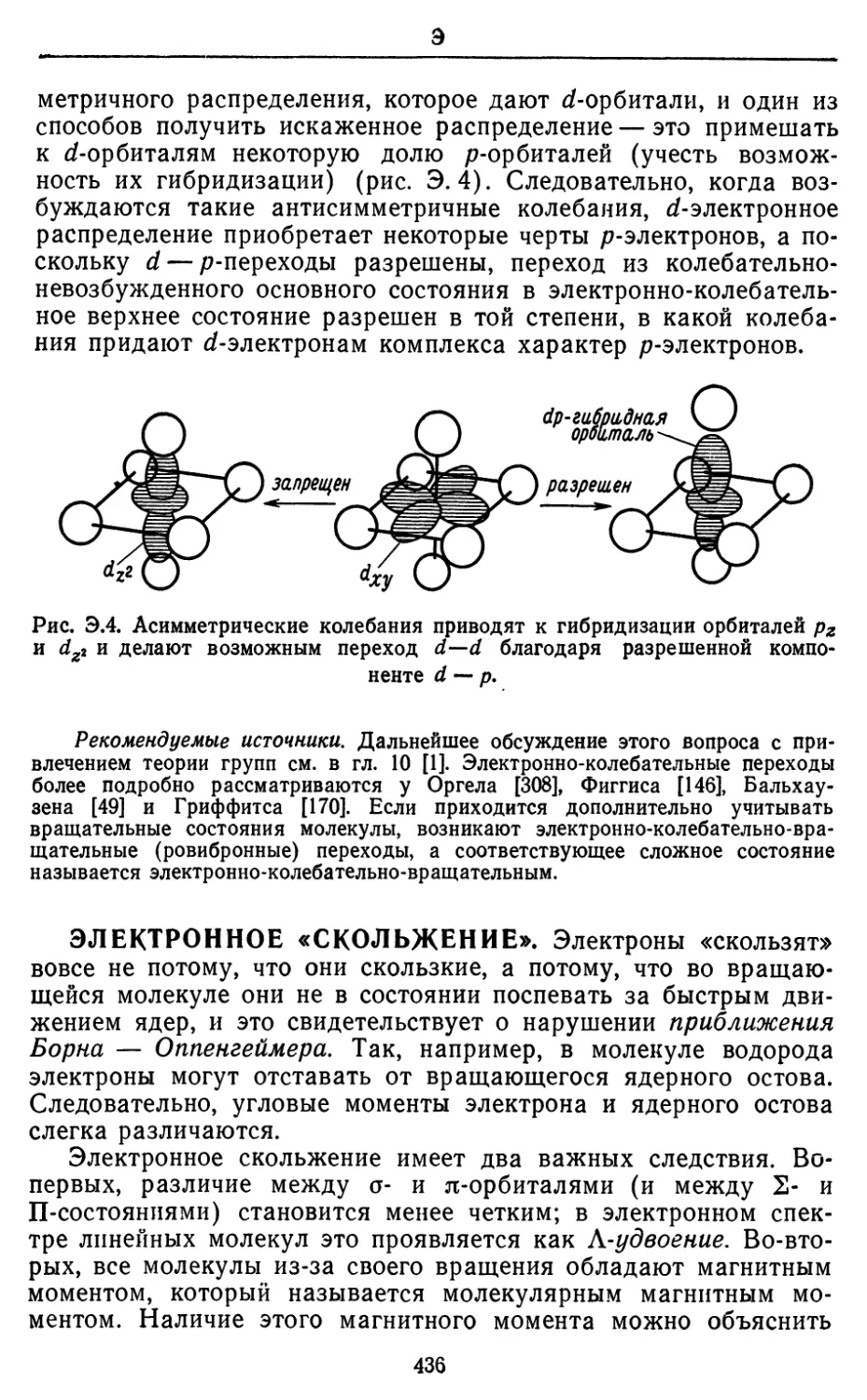
Text
P. W. ATKINS
Fellow of Lincoln College. Oxford
QUANTA
A HANDBOOK OF CONCEPTS
OXFORD
CHEMISTRY SERIES
General Editors
P. W. Atkins, J. S. E. Holker, A. K. Holliday
CLARENDON PRESS OXFORD
1974
п. эткинс
КВАНТЫ
СПРАВОЧНИК КОНЦЕПЦИИ
Перевод с английского
канд. физ.-мат. наук
Е. Л. ЯДРОВСКОГО
Под редакцией
канд. хим. наук
Е. Л. РОЗЕНБЕРГА
ИЗДАТЕЛЬСТВО «МИР»
Москва 1977
УДК 530.145
This translation of Quanta by P. W. Atkins
is published by arrangement with The Oxford
University Press
£) Text —Oxford University Press 1974
g) Illustration —P. W. Atkins 1974
© Перевод на русский язык, «Мир», 1977
Книга представляет собой составленный для химиков
справочник основных понятий квантовой теории атомов и молекул,
дополненный упражнениями. Она дает ясную интерпретацию
основных понятий современной квантовой теории, не допуская их
вульгаризации.
Книга предназначена химикам, преподавателям и студентам
химических специальностей высших учебных заведений, а также
преподавателям и учащимся старших классов средней школы.
Редакция литературы по химии
20503-108
Э 041(01)-77 108-/?
ИБ 654
П. Эткиис
КВАНТЫ. СПРАВОЧНИК КОНЦЕПЦИЙ
Редактор Р. И. Краснова Художник Н Г. Блинов
Технический редактор Г. Б. Алюлина Корректор В. И. Постнова
Сдано в набор 6/IV 1977 г. Подписано к печати 13/Х 1977 г. Бумага № 2 60X90 Vie =-15,50
бум. л. 31,00 печ. л. Уч.-изд. л. 32,32. Изд. № 3/8915. Цена 1 р. 90 к. Зак. 576
Издательство «Мир»
Москва, 1-й Рижский пер., 2
Ордена Трудового Красного Знамени Ленинградская типография № 2 имени Евгении
Соколовой Союзполиграфпрома при Государственном комитете Совета Министров СССР
по делам издательств, полш рафии и книжной торговли. 198052, Ленинград, Л-52,
Измайловский проспект, 29.
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
Предлагаемая вниманию читателей книга представляет
собой адресованный химикам справочник основных понятий
квантовой механики и теории строения атомов и молекул.
Насколько нам известно, это первый опыт такого рода в
литературе, посвященной указанным вопросам, хотя необходимость
появления подобной книги-справочника назрела уже давно.
Квантовая теория надежно завоевала ключевые позиции в
науке и стала рабочим инструментом не только для физиков,
но и для химиков-теоретиков и физико-химиков. Более того,
многие идеи, модельные представления и термины квантовой
теории прочно вошли в обиход современной теоретической
химии и широко используются при обсуждении смысла
процессов, протекающих на атомно-молекулярном уровне. Даже в
школьные учебники теперь включаются сведения о квантах,
строении атома и прцроде химической связи.
Между тем хорошо известно, что интерпретация явлений,
происходящих в мире электронов, атомов и молекул, далеко
не проста и трудна для восприятия. Попытки упростить и даже
популяризировать изложение этих вопросов нередко приводят
к тому, что «вместе с водой выплескивают и ребенка», и в
результате создается выхолощенный образ квантового понятия
или явления, настолько далекий от действительности, что он
не помогает, а, наоборот, мешает понять ее суть.
Разумеется, студентам химических университетов в наше
время дают гораздо более глубокие сведения по основам
квантовой теории и ее применению к изучению строения атомов
и молекул. Однако пробиться сквозь дебри необычных понятий
и выкладок при последовательном изучении квантовой теории
весьма нелегко и, кроме того, это возможно лишь при наличии
хорошей математической подготовки (в частности, в области
теории дифференциальных уравнений). Возможно, именно
поэтому у некоторых вчерашних студентов остается лишь
довольно смутное представление о том, что такое, скажем,
разрыхляющая орбиталь, g-фактор или эффект Штарка или чем,
например, отличаются электрические дипольные переходы от
магнитных и квадрупольных. Однако в практической работе
каждому химику-теоретику, физико-химику и всем, кто
интересуется результатами применения физических методов
исследования в химии, приходится постоянно сталкиваться не
только с хорошо известными понятиями квантовой теории, но и с
5
Предисловие к русскому изданию
такими специальными как «гибридизация», «химический сдвиг
ЯМР», «теория поля лигандов», «ферми-резонанс» и т. п.
Во всех таких случаях книга П. Эткинса должна принести
большую пользу. Ее автор, опытный университетский
профессор, прекрасно знакомый с трудностями преподавания
квантовой механики и ее прикладных аспектов, сумел написать
лаконичные очерки, посвященные приблизительно двумстам
понятиям, которые чаще всего встречаются в обиходе
квантовой теории атомов и молекул.
Какие же темы затронуты в этих очерках-разделах, какова
общая направленность этой книги? Разумеется, в ней прежде
всего обсуждаются важнейшие понятия квантовой механики
(причем это делается с минимальным привлечением
математического аппарата), затем вопросы строения атомов и молекул,
теория химической связи, а также применяемые для
исследования химической связи физические методы (атомная и
молекулярная спектроскопия, электронный парамагнитный и ядерный
магнитный резонансы); наконец, приводится немного сведений из
теории твердого тела. Несомненно, автор книги не затронул
многие интересные темы, например теорию столкновений (лежащую
в основе современной химической кинетики) или теорию
строения атомного ядра (интересующую, в частности,
радиохимиков). Но нельзя объять необъятное, и выбирая из всего
интересного то, что можно было поместить в книгу обычного объема,
автор, естественно, отдал предпочтение лишь наиболее общим
понятиям и прежде всего постарался удовлетворить запросы
как можно более широкой читательской аудитории. Это тем
более понятно, если еще учесть, что данная книга входит в так
называемую «Оксфордскую химическую серию» (одним из
редакторов которой является П. Эткинс), предназначенную для
улучшения постановки общехимического образования в Англии.
Несомненно, направленность книги, равно как и ее стиль,
несут на себе заметный отпечаток научной, педагогической . и
даже литературной индивидуальности автора, уже известного
советским читателям по монографии (написанной совместно
с М. Саймонсом) «Спектры ЭПР и строение неорганических
радикалов» . («Мир», 1970). Опытный педагог, П. Эткинс
мастерски сумел вложить в каждый раздел «Квантов» много
полезной информации, используя для этого разнообразный арсенал
приемов и заботясь прежде всего о четкости изложения
физического смысла обсуждаемых вопросов, а также о простоте
и наглядности их интерпретации.
Каждый раздел начинается с краткого определения
рассматриваемого понятия. Затем следует обсуждение его смысла
с использованием других представлений квантовой теории. При
необходимости выясняются всевозможные следствия рассмат-
6
Предисловие к русскому изданию
риваемого закона, эффекта или явления, его применимость к
исследованию строения атомов и молекул и определяются
взаимосвязи с другими ключевыми понятиями книги. Нередко
приводится дополнительное и довольно необычное толкование
обсуждаемого понятия, и при этом обнаруживается, что многие
простые вещи как бы имеют «второе дно». Особую роль
играют упражнения, помещенные в конце каждого раздела: они
призваны научить читателя думать, связывать различные
понятия и явления.
Путь к более основательному изучению теории указывает
литература, рекомендованная по каждому вопросу. Разумеется,
она подобрана в основном из книг, написанных на английском
языке. Однако можно с удовлетворением отметить, что многие
из наиболее интересных книг переведены на русский язык.
Кроме того, немалую часть библиографического списка
«Квантов» занимают получившие мировое признание книги советских
ученых, среди которых почетное место принадлежит курсу
теоретической физики Л. Ландау и Е. Лифшица и ставшей
классической работе В. Фока.
Все сказанное позволяет надеяться, что настоящая книга
будет с интересом встречена советскими читателями и
принесет пользу как химикам, занимающимся исследовательской
работой, так и преподавателям и учащимся высшей и средней
школы.
Е. Розенберг
ПРЕДИСЛОВИЕ К АНГЛИЙСКОМУ ИЗДАНИЮ
Цель данной книги — попытаться объяснить квантовую
теорию, не прибегая к математике. Вполне понятно, что все
богатство теории в наиболее полном виде можно передать только на
языке математики. Не вызывает сомнения и то, что
существенный вклад в квантовую теорию можно сделать, только прочно
овладев ее математическим аппаратом. Тем не менее я убежден,
что математическая точность — это совсем не то, к чему
стремится каждый, — не всем это интересно, и не все располагают
достаточным временем.
Каждый из нас по-своему представляет основные понятия
квантовой теории. Наше воображение рисует орбитали,
переходы и т. д., и те из нас, кто действительно занимается
научными исследованиями, почти всегда пользуются каким-то
эскизным наброском наблюдаемой системы — ее моделью. Данная
книга, естественно, отражает авторское восприятие основных
представлений квантовой теории. Конечно, рисунки, аналогии
или модели не могут дать полной картины происходящего, и все
же они отражают суть дела и позволяют читателю понять
физический смысл явления.
Я надеюсь, что эта книга принесет пользу широкому кругу
химиков. Работая над ней, я думал и о студентах-химиках,
сталкивающихся на всех этапах обучения с непривычными,
малопонятными или полузабытыми концепциями, и о преподавателях,
которые обязаны отвечать на возникающие у студентов вопросы.
Хотелось бы думать, что приведенной информации будет
достаточно для понимания основных квантовомеханических
представлений. Если же предлагаемое объяснение покажется
неубедительным, помещенная в конце каждого раздела библиография
подскажет, где найти другое толкование.
В каждом разделе книги дается по возможности простое
объяснение физического смысла явления или понятия. Большинство
разделов иллюстрировано примерами, а иногда и
контрпримерами. В каждом разделе курсивом выделены ключевые слова
показывающие, что приведенное объяснение дополняется
материалом, изложенным в другой статье. Выделенное слово не
всегда совпадает с конкретным названием соответствующего
раздела, по достаточно определенно указывает на него.
Там, где представлялось желательным ввести некоторые
математические выкладки (например, если казалось, что полезно
иметь под рукой набор формул, как, скажем, в теории
возмущений), используется система таблиц и списков формул. Каждый
8
Предисловие к английскому изданию
список формул является неотъемлемой частью раздела, он
содержит наиболее употребительные формулы, выделенные, чтобы
не мешать чтению текста. В таблицах (они помещены в конце
книги) дается более детальная информация (иногда
математические выражения, не обязательные для понимания текста),
которую полезно иметь в книге такого типа, чтобы ее можно было
использовать не только при качественном рассмотрении вопроса.
Таблицы содержат также небольшую подборку
экспериментальных данных, которые дают представление о значениях
физических величин и закономерностях их изменения. Эти таблицы ни
в коей мере нельзя рассматривать как источник исчерпывающей
информации, но приведенные в них численные данные
позволяют получить представление об экспериментальных данных.
В конце почти каждого раздела помещены упражнения, они
преследуют двоякую цель. Сначала идут относительно простые
вопросы, помогающие сосредоточить внимание читателя на
ключевых понятиях.
Ответ на них не должен вызывать затруднений, так как его
можно найти в тексте. Более сложные вопросы позволяют
ненавязчиво ввести в книгу хотя бы немного математики: они
заставляют читателя самостоятельно получить математическое
описание материала, изложенного в разделе. Как правило, они
содержат указания и советы. Ответы на вопросы следует искать
в основном тексте, в списках формул и таблицах, приведенных
в книге, и, наконец, в статьях и монографиях, перечисленных в
списках «Рекомендуемые источники». Каждый раздел
заканчивается такой рубрикой; она служит путеводителем по
литературе и содержит ссылки на книги и журналы, где
рассматриваемая тема развивается глубже и с большим привлечением
математического аппарата. Рекомендуемый список литературы
отнюдь нельзя считать исчерпывающим: в него включены лишь те
книги, которые представляются нам наиболее полезными, но из
них читатель сможет узнать и о других источниках. Список книг
составлен в порядке возрастания их сложности, что позволит
читателю продвигаться вперед постепенно, преодолевая все
большие трудности. Сделано, однако, два исключения из этого
правила. Многие из рассмотренных тем более детально обсуждаются
в моей книге «Квантовая механика молекул», и ссылка на
соответствующую часть этой книги включена в начало каждой
рубрики «Рекомендуемые источники». Далее, поскольку «Кванты»
входят в Оксфордскую химическую серию, список книг которой
приведен в начале библиографии, ссылки на книги этой серии
также приводятся в самом начале каждой рубрики «Рекомен
дуемые источники». Число ссылок на Оксфордскую физическую
серию значительно меньше, так как она пока представлена лишь
несколькими томами.
9
Предисловие к английскому изданию
Некоторые разделы книги излагаются на более высоком
уровне, поскольку автор не видел другой возможности дать
удовлетворительное объяснение рассматриваемому явлению.
Впрочем, характерный для книги в целом более низкий уровень
означает лишь, что автор старался не злоупотреблять
математическими выкладками. Однако не приходится сомневаться, что
химику при анализе субмикроскопических явлений в равной
степени нужно и то и другое. Я умышленно не указываю конкретно,
какие статьи написаны на более высоком уровне, полагая, что
читатель разберется и в них. Если же все-таки изложение
материала покажется читателю очень сложным, то здесь ему должны
помочь ключевые слова, о которых говорилось выше.
Необходимо отметить еще два обстоятельства. Во-первых,
следует извиниться перед читателем за качество диаграмм. Дело
в том, что я стремился сделать книгу как можно более дешевой
и все диаграммы выполнил сам. Все это происходило в один из
летних месяцев в Италии, на балконе, где приходилось вести
борьбу с комарами, полчищами муравьев и домашними осами.
Я прошу извинения за дилетантский характер иллюстраций и
прошу не обращать внимания на отдельные неровные линии,
грязные пятна и брызги. Второе замечание адресовано тем, кто
понимает, как можно писать такие статьи, и не удовлетворен
содержанием представленных мною статей или собирается сам
написать что-либо подобное. Предлагаемые вниманию
читателей 200 разделов можно изложить примерно 10300 способами.
Поэтому трудно быть уверенным в том, что ты выбрал наилучший
вариант.
Самая главная и самая приятная задача автора
предисловия— поблагодарить всех, кто принимал участие в издании
книги и облегчил нелегкий авторский труд. Неоценимый вклад,
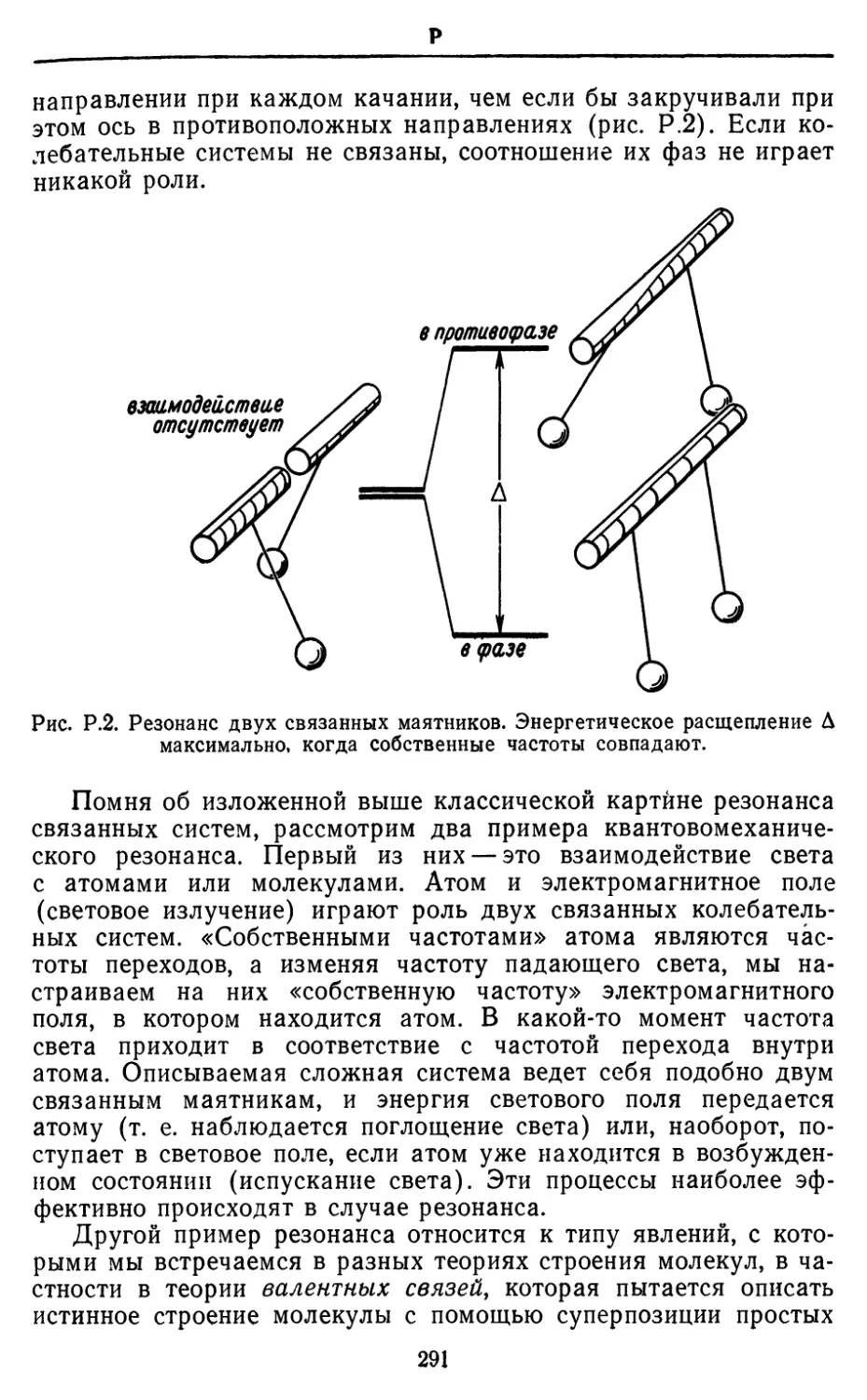
далеко выходящий за рамки обычного чувства долга и
превзошедший всякие ожидания, был сделан Clarendon Press и ее
безымянными служащими. Только благодаря их участию, начи-
ьая с практических советов и содействия в изготовлении
рисунков и кончая детальными продолжительными дискуссиями о
числе авторских экземпляров, эта книга выглядит именно так.
Автор особенно благодарен двум своим студентам-практикантам:
Майклу Клагстону за внимательный просмотр корректуры и
Джону Робертсу, проведшему много часов в беседах с ЭВМ.
Всем остальным я благодарен за то, что их благосклонное
терпение не вылилось в открытое недовольство. Перепечатывание
мало вразумительной рукописи, напечатанной мной самим, было
легко и красиво исполнено г-жой Е. Прайс и г-жой М. Лонг. Они
безусловно заслужили того, чтобы обрести вечность хотя бы на
страницах этой книги.
/7. У. Э.
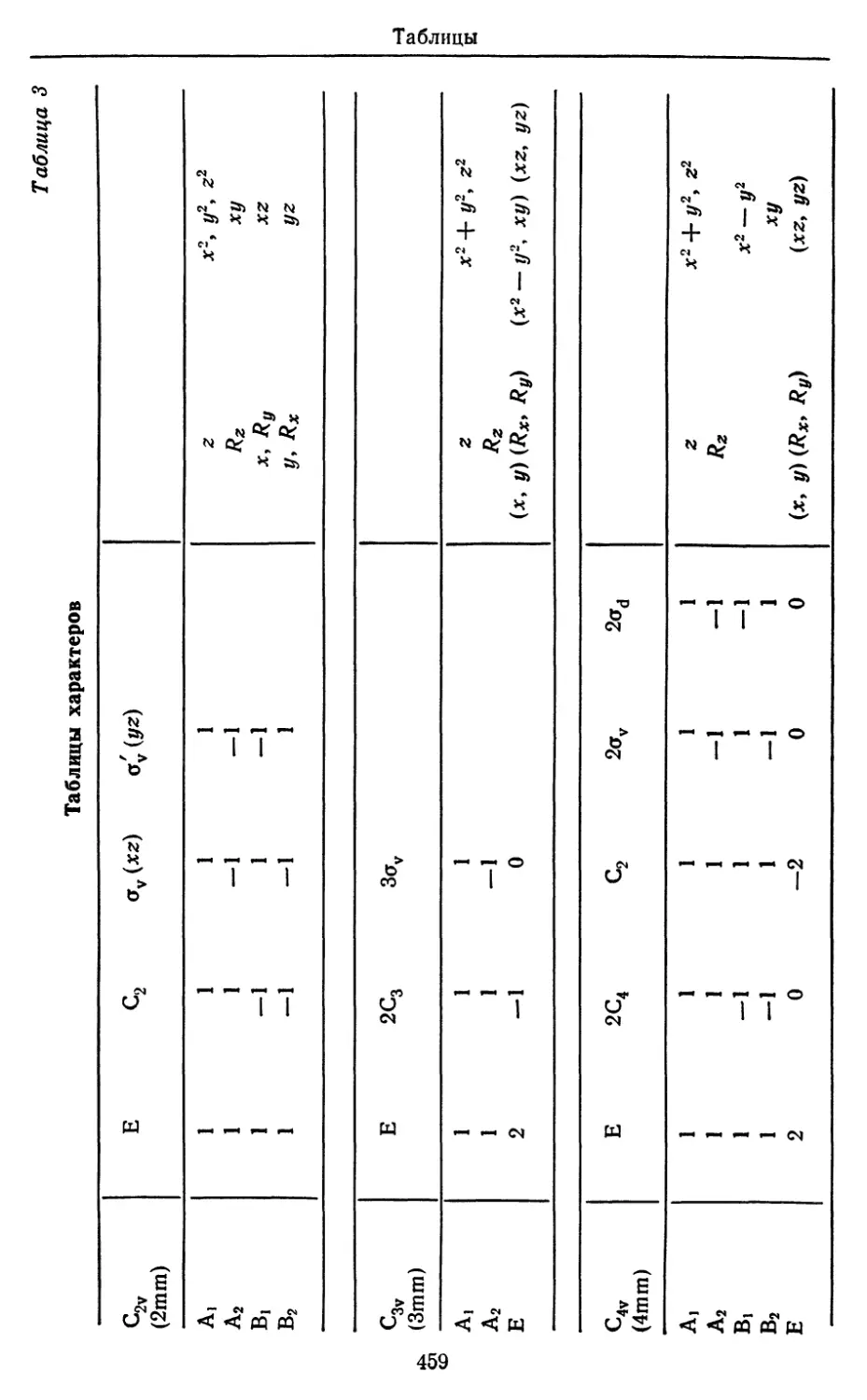
A
Ab initio. Латынь в квантовой химии встречается не часто и
содержит, как правило, заметную долю иронии тех, кто связал
свою судьбу с расчетами на ЭВМ. В вольном переводе ab
initio означает «с самого начала». Этот термин применим к таким
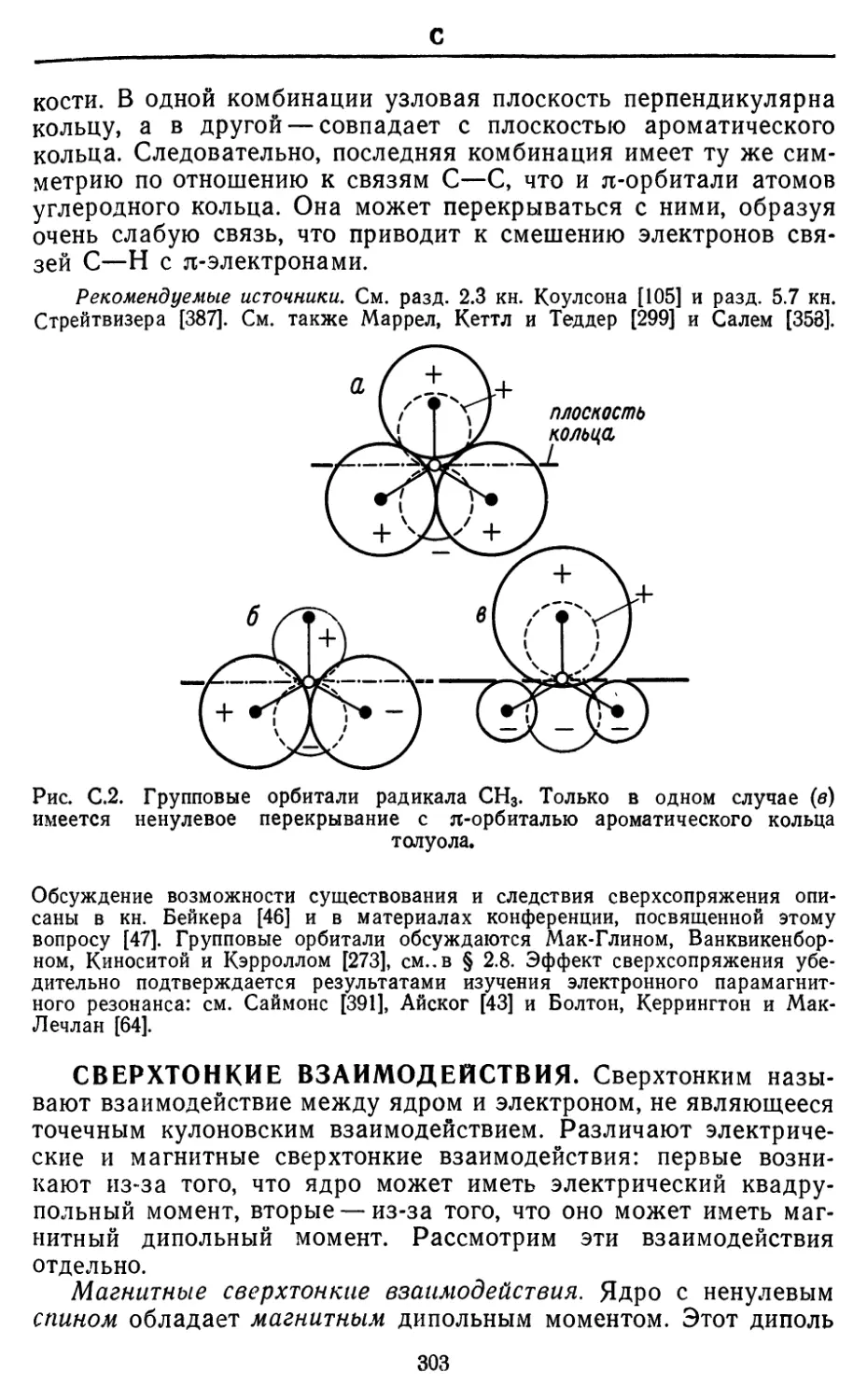
расчетам структуры молекул, которые проводятся только исходя
из первых принципов; включение каких бы то ни было
эмпирических данных на промежуточных этапах расчетов ab initio
рассматривается как нечто неприличное. В данной книге в качестве
первых принципов принимаются уравнение Шредингера и
метод самосогласованного поля.
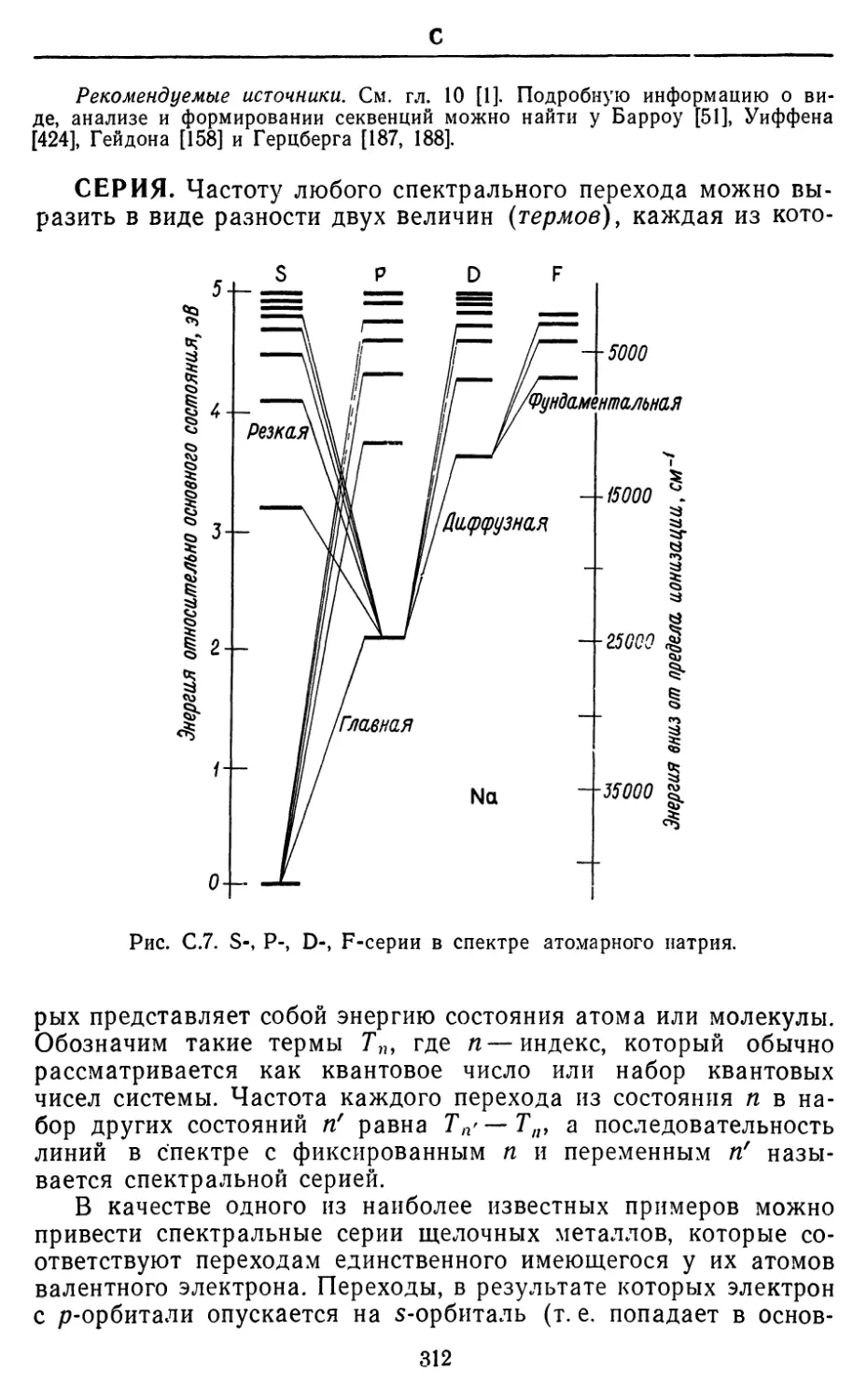
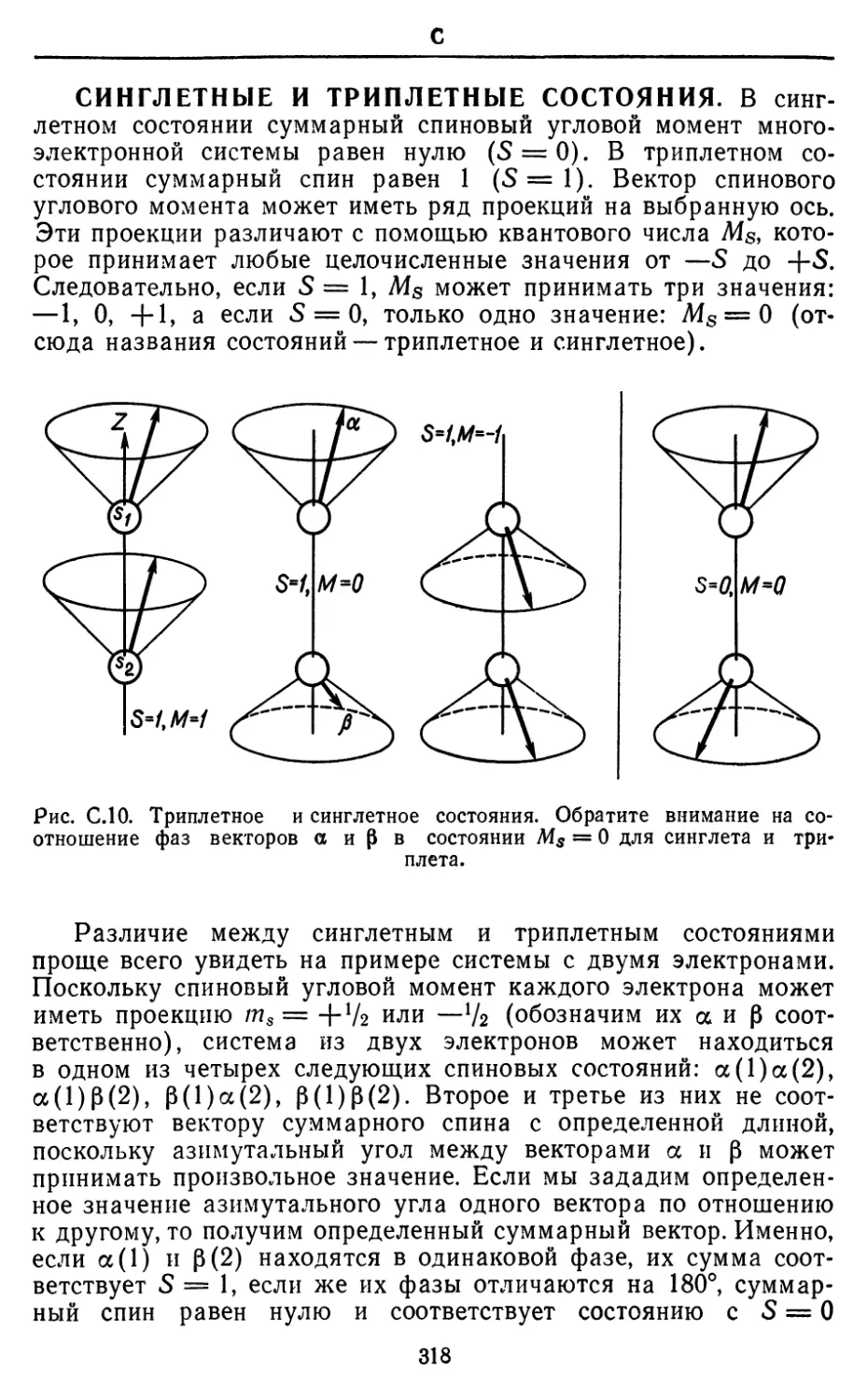
Рекомендуемые источники. Ричарде и Хорсли [336] написали краткое и
доступное руководство по методам расчета ab initio. Их книга содержит
подборку удачных примеров таких расчетов. В ней также сравниваются точные
методы и полуэмпирические подходы, где расчет проводится по методу
самосогласованного поля с использованием некоторых приближений и
эмпирических данных.
АБСОЛЮТНО ЧЕРНОГО ТЕЛА ИЗЛУЧЕНИЕ. Абсолютно
черным телом называется тело, которое поглощает все
падающее на него излучение. Практическим примером является
закрытый контейнер с крошечным отверстием. Это отверстие
ведет себя как абсолютно черное тело, так как весь свет,
падающий на него снаружи, проходит внутрь и, попав туда, не может
выйти наружу через предельно малое отверстие. Внутри
контейнера свет испытывает большое число отражений и в конце
концов поглощается; в результате этого излучение приходит в
тепловое равновесие со стенками. Внутри контейнера распределение
частот электромагнитного поля определяется температурой
стенок. Из-за наличия отверстия небольшая часть равновесного
излучения просачивается наружу и может быть зарегистрирована;
при этом распределение длин волн в излучении абсолютно
черного тела такое же, как и внутри контейнера, так как отверстие
является пренебрежимо малым возмущением. Излучение
абсолютно черного тела — это излучение, находящееся в равновесии
с веществом при определенной температуре.
Основные особенности распределения частот в излучении
абсолютно черного тела известны из повседневного опыта: при
низких температурах отверстие действительно выглядит черным,
хотя чувствительный детектор способен зарегистрировать
небольшое количество длинноволнового излучения. При более вы-
11
A
соких температурах количество испускаемом эперпш
значительно возрастает, п его главная часть лежит в инфракрасной
области. При еще Солее высоких температурах отверстие светится
тускло-красным, затем белым и наконец голубым светом, а
полное количество излучаемой энергии очень резко увеличивается.
Л,нм
синий желтый красный инфракрасный
400 500 600 700
Рис. АЛ. Плотность излучения абсолютно черного тела при различных
частотах и температурах
По мере того как возрастает температура, максимум излучения
проходит через ультрафиолетовую область, хотя температуры,
при которых это происходит, оказываются не легко доступными.
Таким образом, мы установили, что энергия в состоянии
равновесного излучения резко увеличивается с ростом температуры,
при этом его длина волны смещается в сторону голубого света
и далее. Первое наблюдение выражается законом Стефана: пол-
12
A
пая энергия, излучаемая при температуре Т, равна аГ4;
константа а, называемая постоянной Стефана, равна 5,67-10~8 Вт-м-2 X
X К"4. Второе наблюдение формулируется как закон смещения
Вина: длина волны максимума интенсивности излучения обратно
пропорциональна температуре: КтлхТ = 2,9 мм-К.
Исследования излучения абсолютно черного тела нанесли
серьезный удар по позициям классической физики и
способствовали развитию квантовой теории. Результатом применения идей
классической физики к излучению абсолютно черного тела
явился закон Релея — Джинса. Эти исследователи рассчитали число
осцилляторов с определенной длиной волны, которое могло бы
содержаться в полости, а затем применили закон
равнораспределения, приписав каждому типу колебаний энергию, равную kT\
таким образом, было предсказано, что плотность энергии при
длине волны X должна подчиняться закону 8я/еГД4 (рис. АЛ).
Этот вывод не согласуется ни с одним из упомянутых выше
наблюдений, так как предсказывает огромную плотность энергии
излучения в коротковолновой области (ситуация, названная
Эренфестом ультрафиолетовой катастрофой) и бесконечно
большую энергию излучения в любом замкнутом объеме (интеграл
по всем длинам волн расходится). Распределение Релея —
Джинса не имеет максимума, за исключением совершенно
абсурдного— при нулевой длине волны. Согласно классической
теории, даже светлячок опустошил бы все вокруг своим излучением.
Выход из создавшегося положения был найден Планком,
который выдвинул гипотезу о квантах. Исходя из
термодинамических соображений, Планк пришел к выводу, что необходим
такой закон распределения, который воспроизводил бы закон
Релея— Джинса при низких частотах и закон смещения Вина при
высоких частотах. Ему удалось найти такую формулу, которая
при низких и высоких частотах сводилась к этим двум законам
(см. список формул АЛ). Размышляя о смысле полученной
формулы, Планк решил, что излучение любой фиксированной
частоты не может обладать сколь угодно малой энергией:
излучение может быть возбуждено только дискретными порциями
энергии, или квантами. Классический закон утверждает, что»
если в контейнере имеется излучение с частотой v, с ним связана
порция энергии &Г, соответствующая закону
равнораспределения. Квантовый же закон утверждает, что такое излучение
будет возбуждено только в том случае, если при этом выделится
количество энергии, как минимум равное /гv. Константа h
называется постоянной Планка (6,6256-Ю-34 Дж-с). Это означает,
что колебания очень высокой частоты при нормальных
температурах не возбуждаются, так как тепловой энергии стенок
контейнера недостаточно, чтобы сообщить таким колебаниям
13
A
Список формул АЛ
Закон распределения Планка для излучения абсолютно черного тела
Плотность энергии (энергия в единичном объеме) в интервале dX при
длине волны Я:
dU (Я) = р (Я) dX,
_/ЛЧ {8nhc\{ exp(-hc/XkT) )
р W "" VU~) 11 - ехр (-Лс/ЛЛГ) J'
Плотность энергии в интервале dv при частоте v:
dU (v) = р (v) dv,
n M = f 8jt/*v^ ( exp(-hvfkT) \
PW ^ c3 J \\ - exp (-hv/kT) У
Закон Релея — Джинса (длинноволновый и низкочастотный пределы
распределения):
р (Я) « SnkT/X\ X>hc/kT,
р (v) « 8nv2kT/c3. v < £77/г.
Закон Стефана (полная плотность энергии ос Г4):
оо оо I
U = ^Яр (Я) = ^ dvp (v) = (а/с) Т\
о о
а = 5,6697. Ю-8 Вт • м~2 • К"4.
Закон смещения Вина (Xmax Т = const):
^max T = hc/Sk = 6,
6 = 2,8978 • 1СГ3 м . К.
нужную энергию (см. разд. «Квант»). Этот эффект подавляет
рост распределения Релея — Джинса при высоких частотах
(малых длинах волн) и, таким образом, устраняет
ультрафиолетовую катастрофу. Более того, он приводит к появлению максимума
у кривой, описывающей зависимость распределения энергии от
длины волны, и этот максимум в согласии с законом Вина
сдвинут к высоким частотам (постоянная Вина для максимума
оказывается равной hc/5k) Так как высокочастотные колебания
при любой конечной температуре Т не возбуждаются, полная
энергия, излучаемая при температуре Г, тоже конечна; при этом
в согласии с законом Стефана воспроизводится зависимость
энергии излучения от Г4. Таким образом, приходится признать
правильность квантовой гипотезы Планка, а поскольку
взаимодействие вещества и излучения является одним из важнейших
физических процессов, не удивительно, что следствия этой
гипотезы изменили все прежние представления о физической картине
мира.
14
A
Упражнения. 1. Что такое абсолютно черное тело и как оно может быть
реализовано экспериментально? Почему исследованиям излучения,
испускаемого через крошечное отверстие в замкнутой плоскости, придается такое
важное значение? Какие изменения происходят в распределении частот света,
испускаемого абсолютно черным телом, при повышении его температуры?
Сформулируйте законы Стефана и Вина. Какова основа классического
рассмотрения излучения абсолютно черного тела и почему она неприемлема?
В чем заключается гипотеза Планка и как влияет квантование на
высокочастотные осцилляторы? Обсудите различие между возбуждением
классического и квантового гармонического осциллятора. Определите вид
распределения Планка при высоких частотах (см. список формул АЛ), т. е. при
коротких длинах волн. Используя полученное выражение, покажите, что
распределение имеет максимум, причем Хтах « Т~\ и найдите выражение для
постоянной Вина, оценив ее численно. Вычислите плотность энергии,
излучаемой абсолютно черным телом при длинах волн 1 см, 55 нм и 200 нм, когда
оно нагрето до 300, 1000 и 105 К. Полагая, что нить лампы накаливания
излучает, как абсолютно черное тело (это приближение не является
абсурдным), вычислите температуру, до которой она должна быть нагрета, чтобы
излучать свет преимущественно в видимой части спектра.
2. Определение функции распределения включает две стадии: первая
(что мы и проделаем) — учет квантовой гипотезы в распределении Больцмана
и определение средней энергии отдельного колебания, вторая (что мы
делать не будем) — подсчет числа колебаний определенной частоты. Если
энергия осциллятора может принимать только значения nhv, то вероятность того,
что осциллятор имеет энергию nhv, определяется, согласно Больцману, как
оо
ехр(—nhv/kT)/Z, где Z— статистическая сумма, или J] exp (—nhv/kT).
Средняя энергия есть сумма членов вида [(nhv)exp(—nhv/kT)/Z] по всем
значениям п (п = 0, 1, 2, ...). Сначала определяем Z, исходя из того, что
оо
она может быть записана в виде суммы 2^ хп (где х — надлежащим обра-
зом выбранная величина) и является, следовательно, геометрической
прогрессией; после этого вычисляем сумму в числителе, заметив, что ее просто
связать с dZ/dT. Отсюда находим среднюю энергию колебаний с длиной волны
X = с/v. Число колебаний в интервале dX в окрестности X равно 8ndX/X4',
отсюда находим закон распределения Планка. Ответ приведен в списке
формул АЛ.
Рекомендуемые источники. Вывод распределения Планка и определение
числа колебаний в контейнере см. в [1], гл. 1. Другие вопросы этой темы
рассматриваются Гайтлером [180], Пауэром [3241, Бомом [63] и Л ином [2471.
Ретроспективный обзор исследований излучения абсолютно черного тела
выполнен Джеммером [203], а один из последних обзоров по этому вопросу
опубликован Лином [247]. См. также кн. Ингрэма «Излучение и квантовая
физика» [25] и Рейфа [333]. Таблицы распределения Планка в численном
представлении для широкой области температур и длин волн вместе с
интегральными интенсивностями можно найти в кн. Грея [168] «Справочник
Американского института физики» и Абрамовича и Стегуна [30].
АДИАБАТИЧЕСКИЙ ПРОЦЕСС. В квантовой механике
термин «адиабатический» имеет тот же смысл, что и в
термодинамике, где он характеризует процесс, происходящий без обмена
15
A
теплотой с окружающей средой. Поскольку при этом энтропия
системы не меняется, иногда такой процесс называют изоэнтро-
пическим. Последнее означает, что система претерпевает
изменения, которые не могут вызвать ее переход в другие состояния.
В качестве примера представим себе атом водорода с
изменяющимся зарядом ядра. Если вначале атом находился в
основном состоянии и изменение заряда происходит чрезвычайно
медленно, электрон, оставаясь на той же орбите, будет постепенно
приближаться к ядру; при этом, однако, атом будет все время
оставаться в основном состоянии. В некоторый момент времени,
когда заряд ядра станет равным 2, мы будем иметь дело с ионом
Не+ в основном состоянии. Такое изменение системы является
адиабатическим.
И наоборот, если заряд ядра изменится мгновенно (например,
произойдет испускание электрона ядром при |3-распаде),
электрон неожиданно окажется в потенциале нового ядра, сохранив
при этом свое первоначальное пространственное распределение.
Это распределение можно представить в виде разложения по
волновым функциям нового атома. Таким образом, при
мгновенном, или неадиабатическом, переходе система как бы
вклинивается в область состояний конечной системы. Вероятность, с
которой можно обнаружить конечную систему в том или ином
состоянии, определяется интегралом перекрывания волновой
функции этого состояния с волновой функцией основного состояния
первоначального атома. Другим примером адиабатического
процесса может служить медленное сжатие прямоугольной
потенциальной ямы с находящейся в ней частицей. Если вначале
система находилась на n-уровне, она останется на я-уровне
потенциальной ямы меньшего размера при условии, что сжатие было
очень медленным.
Рекомендуемые источники. Этот вопрос более подробно обсуждается в
гл. 7 [1]. Давыдов [119] рассматривает адиабатические переходы методами
теории возмущений и показывает, что процесс можно считать
адиабатическим, если возмущение V(t) меняется настолько медленно, что величина
dVldt оказывается много меньше расстояния между уровнями в области
энергии начального состояния: \dV/dt\ < (\E)2/h. В книге Бома [63J этот
вопрос обсуждается на языке строгих математических формул. Из обзорных
статей, которые были опубликованы в последнее время, следует отметить
работу Колоса [225] и Никитина [306]. См. также правило непересечения
(уровней). Интерпретация термина «адиабатичность» обсуждается в книге Смита
[9]. Связь энтропии с распределением частиц по энергетическим уровням дана
в кн. [19]. Этот вопрос является ключевым в понимании связи между
использованием термина «адиабатический» в термодинамике и квантовой
механике, так как неменяющееся распределение частиц по состояниям
характеризует изоэнтропическое поведение системы.
АНГАРМОНИЧНОСТЬ. Известны два вида
ангармоничности: механическая и электрическая. Механическая ангармонич-
16
A
ность (обычно называется просто «ангармоничность»)
наблюдается у осциллятора, потенциал которого не является точной
параболой и восстанавливающая сила которого не строго
пропорциональна величине смещения. Уровни энергии в этом случае
также отличаются от уровней энергии гармонического
осциллятора. Если природа ангармоничности такова, что потенциал
становится меньше при больших пространственных смещениях,
уровни с большими квантовыми числами сближаются, как это
Рис. Л.2. Ангармонические потенциалы ( ) искажают эквидистантное
расположение уровней гармонического потенциала (—): а — более широкий
потенциал уменьшает расстояния между уровнями (в различной степени для
различных уровней); б — более узкий потенциал увеличивает расстояние
между уровнями; в — сложная ангармоничность, характерная для
химической связи.
показано на рис. А.2. Линии колебательного спектра при
наличии ангармоничности не будут более эквидистантными.
Механическая ангармоничность нарушает правила отбора
гармонического осциллятора. При ангармоническом колебании молекулы
эти правила не выполняются. Поэтому некоторые запрещенные
переходы становятся разрешенными и могут наблюдаться
гармоники основных переходов, отвечающие изменению
колебательного квантового числа на +2, +3 и т. д. Интенсивность таких
переходов растет по мере увеличения ангармоничности
потенциала.
На интенсивность запрещенных переходов и нарушение
правил отбора для гармонического осциллятора влияет также
электрическая ангармоничность. Этот термин связан с нелинейной
зависимостью дипольного момента молекулы от смещения
атомов. Правила отбора обычно устанавливают в предположении,
что дипольный момент молекулы по мере ее растяжения зависит
от расстояния линейно (т.е. изменение дипольного момента
прямо пропорционально растяжению). Если это не так, истинная
зависимость может содержать нелинейный член, в частности
17
A
квадратичный по расстоянию. Это приводит к переходам с Av =
= ±2. Таким образом, электрическая ангармоничность может
привести к изменениям интенсивности в колебательном спектре
молекул, подобным изменениям, вызываемым механической
ангармоничностью, но в отличие от последней электрическая
ангармоничность не влияет на энергии самих уровней.
Кроме того, ангармоничность влияет на интенсивность
колебательного (инфракрасного) спектра молекулы, вызывая
смешение полос, отвечающих колебаниям различной симметрии.
В гармоническом приближении существует набор независимых
колебательных движений молекулы, составляющих так
называемые нормальные колебания. При наличии ангармоничности
нормальные колебания уже не являются независимыми и
энергия одного колебания может переходить к другим колебаниям.
С позиций квантовой механики это можно объяснить смешением
волновых функций колебаний различных типов, в результате
которого смешиваются также характеристики различных
нормальных колебаний. Важным примером ангармонического смешения
нормальных колебаний является резонанс Ферми,
обусловливающий одновременное возбуждение двух нормальных колебаний
(которое вызывает появление в спектре комбинационной полосы)
при условии, что существует разрешенное нормальное колебание
с частотой, близкой к частоте комбинационного перехода.
Ангармоничность внутримолекулярного движения придает
комбинационному колебанию некоторые свойства, присущие
близкому по частоте основному колебанию, и, поскольку
последнее разрешено, это относится и к комбинационному колебанию.
Однако степень разрешения комбинационного колебания
зависит от меры ангармоничности, а также от близости энергий
основного нормального колебания к частоте комбинационного
перехода и максимальна при резонансе этих частот.
Еще одним проявлением ангармоничности является ее
влияние на моменты инерции молекул и вследствие этого на их
вращательные спектры. Молекула, совершающая гармонические
колебания, имеет одинаковые средние размеры независимо от
колебательного состояния, в котором она находится. Молекула,
совершающая ангармонические колебания, постепенно
расширяется и увеличивает свой момент инерции по мере того, как она
возбуждается на все более высокие колебательные уровни (см.
рис. А.2,в). Зависимость моментов инерции от колебательных
состояний влияет на структуру ветвей
колебательно-вращательного спектра.
Упражнения. 1. Какие типы ангармоничности вы знаете, где они
проявляются? Что произойдет при замене потенциала гармонического осциллятора
18
A
на потенциал, близкий к параболическому, но становящийся а) более
широким и б) более узким по мере увеличения смещения? Как проявляется
влияние ангармоничности в случае типичного валентного колебания? Каковы
особенности колебательного потенциала для внеплоскостных колебаний плоской
молекулы (обратите особое внимание на ангармоничность)? Какие
запрещенные переходы становятся разрешенными при наличии ангармоничности?
Какие переходы становятся разрешенными благодаря электрической
ангармоничности? Какое влияние оказывает электрическая ангармоничность на энергию
осциллятора? Каково влияние ангармоничности на правила отбора по
симметрии? Какова теоретико-групповая интерпретация этого влияния? Что
такое комбинационная полоса и как зависит ее интенсивность от резонанса
Ферми? Каким образом изменяется интенсивность колебаний основного типа,
участвующего в резонансе Ферми? Что происходит с энергией последнего?
Какими теоретико-групповыми соображениями можно объяснить особую роль
комбинационной полосы в появлении резонанса Ферми, отличающую ее от
какого-либо другого нормального колебания? (Чтобы ответить на этот
вопрос, исследуйте симметрию ангармонической части энергии молекулы.)
2. Рассмотрите потенциал вида l/2kx2 + clx. Нарисуйте его график,
предположив, что а мало и, используя второй порядок теории возмущений,
рассчитайте влияние линейной ангармоничности на этот потенциал. Покажите,
что зависимость электрического дипольного момента от смещения молекулы
из положения равновесия может быть как линейной, так и квадратичной
(используйте разложение в ряд Тейлора). Покажите также, что
квадратичный член вызовет переходы, запрещенные в случае гармонического
осциллятора. Для решения этой задачи используйте свойства гармонического
осциллятора, указанные в табл. 11.
Рекомендуемые источники. Ангармоничность рассматривается в гл. 10 [1].
Полезное качественное обсуждение этого вопроса дано Вудвордом [433], а
также Брандом и Спикменом [75] и Кингом [229]. См. также кн. Барроу [51],
Уиффена [424], Ганса [1571, Вильсона, Дешиуса и Кросса [431]. Чрезвычайно
большая ангармоничность приводит к диссоциации: экстраполяция
ангармоничности к этому пределу обсуждается в гл. 5 кн. Гейдока [158].
АНТИСИММЕТРИЯ. Функция f(x) является
антисимметричной (или антисимметрической), если /(—х) равно —f(x).
Волновая функция системы, включающей N неразличимых
частиц, является антисимметричной в отношении перестановки
частиц, если она меняет знак, когда частицы любой пары
обмениваются местами, т. е. если \|)(гь г2) = — ф(г2, п). Во избежание
недоразумений не следует путать этот термин с понятием
«асимметрический», означающим отсутствие симметрии. Простейшим
примером антисимметричных функций могут служить функции
а*, так как (—х) = —(х), а также sinx, так как sin(—х) =
= —sinx. Антисимметричной волновой функцией является,
например, функция \|)a(ri)\Mr2)— фа(г2) *Mr0, так как она меняет
знак при перестановке координат Т\ и г2, что эквивалентно
перестановке частиц (рис. А.З).
Важность антисимметризации волновых функций следует из
принципа Паули, который требует, чтобы полная волновая
19
A
функция любой системы электронов была антисимметричной.
Одним из слособов получения антисимметризованиой волновой
функции является построение детерминанта Слейтера. Требование ан-
Рис. А.З. Перестановка частиц 1 и 2 эквивалентна перестановке векторов
г, и г2.
тисимметризации волновых функций приводит к важным
последствиям для энергии системы (см. разд. «Обменная энергия»).
Упражнения. Сформулируйте условие, которому должна удовлетворять
антисимметричная функция f (х). Какие из перечисленных ниже функций
являются антисимметричными: лс2, лс3, Зх2 — 2х3, cos лс, tg xy ехр лс, ехр х2,
cosec лг? Покажите, что любую асимметричную функцию F(x) можно
представить в виде суммы антисимметричной и симметричной функций. Что
понимается под антисимметричной волновой функцией? Какие из
приведенных ниже волновых функций являются антисимметричными:
Фа Ы $>ь Ы, sin [k (ri - r2)h tya fri) tyb (r2) tyc (r3) ~ i>a (Ы ♦& fri) Фс (г3) +
+ Фа (гг) Ф& (Гз) Фс (i*i) — • ••? Покажите, что последнюю функцию можно
записать в виде детерминанта 3X3. Какова роль антисимметрии в
квантовой механике?
Рекомендуемые источники. Причины использования антисимметричных
волновых функций обсуждаются в гл. 8 [1]. Полинг и Вильсон [314], Слейтер
[372], Ричарде и Хорсли [336] рассматривают причины и следствия этого.
Симметрия и антисимметрия функций служат объектом исследования теории
групп: гл. 5 [11, Коттон [99], Тинкхэм [396], Бишоп [59], Олтман [36]. Роль
антисимметризации в статистике рассмотрена Полннгом и Вильсоном [314],
Кондоном и Шортли [96], Хамермешем [173] и Джаддом [212]. Читая эти
книги, можно еще раз убедиться в безграничной сложности математического
описания даже весьма простых физических истин.
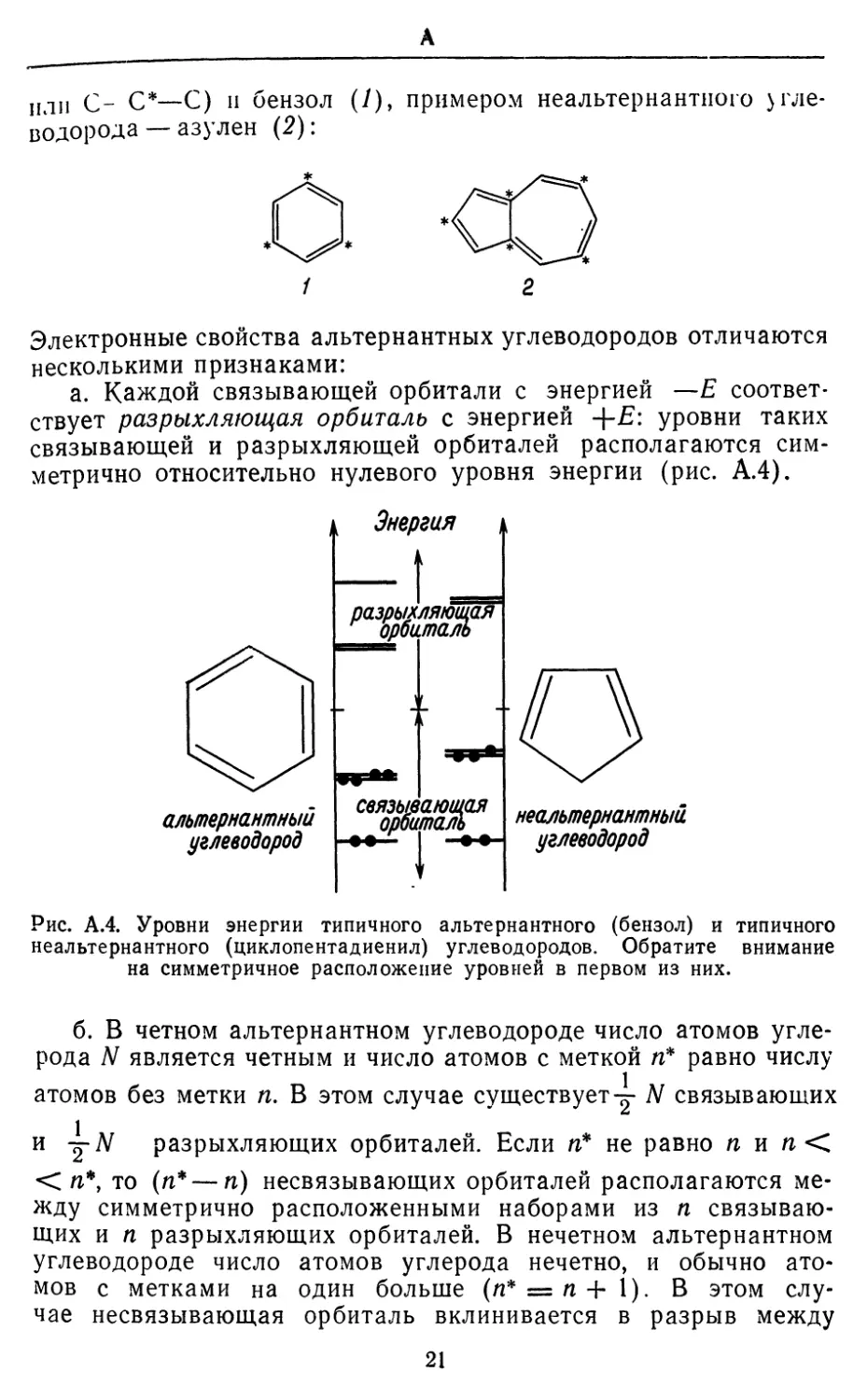
АЛЬТЕРНАНТНЫИ УГЛЕВОДОРОД. Если атомы углерода
в углеводороде пометить через один (есть метка, нет метки,
снова метка и т. д.) и если в результате по соседству не
окажется ни двух атомов с метками, ни двух атомов без меток, то
такой углеводород называется альтернантным. Примерами аль-
тернантных углеводородов могут служить пропилен (С*--С—С*,
20
A
или С- С*—С) и бензол (У), примером неальтернантного
углеводорода —азулен (2):
Электронные свойства альтернантных углеводородов отличаются
несколькими признаками:
а. Каждой связывающей орбитали с энергией —Е
соответствует разрыхляющая орбиталь с энергией +£: уровни таких
связывающей и разрыхляющей орбиталей располагаются
симметрично относительно нулевого уровня энергии (рис. А.4).
Энергия
алыпернантныи
углеводород
связывающая
(фоиталЬ^
\
неальтернантныи
углеводород
Рис. А.4. Уровни энергии типичного альтернантного (бензол) и типичного
неальтернантного (циклопентадиенил) углеводородов. Обратите внимание
на симметричное расположение уровней в первом из них.
б. В четном альтернантном углеводороде число атомов
углерода N является четным и число атомов с меткой rf равно числу
атомов без метки п. В этом случае существует у N связывающих
и yAf разрыхляющих орбиталей. Если я* не равно п и п <.
<. я*, то (я*— п) несвязывающих орбиталей располагаются
между симметрично расположенными наборами из я
связывающих и я разрыхляющих орбиталей. В нечетном альтернантном
углеводороде число атомов углерода нечетно, и обычно
атомов с метками на один больше (я* = я+1). В этом
случае несвязывающая орбиталь вклинивается в разрыв между
21
A
симметричными наборами из я связывающих и п разрыхляющих
орбиталей (я + п* = N).
в. Распределение электронов более однородно в
альтернантных углеводородах, чем в неальтернантных. Количественно это
свойство выражается теоремой Коулсона — Рашбрука, согласно
которой плотность заряда я-электронов на каждом атоме в
основном состоянии альтернантного углеводорода равна единице.
Другими словами, каждому атому углерода принадлежит один
связанный с ним я-электрон.
г. Для нечетных альтернантных углеводородов плотность
электронов соответствующего катиона или аниона определить
весьма просто. Для этого достаточно рассмотреть форму несвя-
зывающей орбитали, потому что как раз при удалении с нее
электрона образуется катион, а при добавлении на нее
электрона — анион; в нейтральном углеводороде заряд
распределяется однородно. Форму несвязывающей орбитали можно
установить путем сопоставления различных факторов. Для этого
пометим атомы таким образом, чтобы число чередующихся
помеченных атомов было максимальным. Тогда амплитуда орбитали
на каждом атоме без метки обратится в нуль. Кроме того,
сумма коэффициентов орбиталей атомов с метками, примыкающих
к данному атому без метки, будет также равна нулю. Отсюда
можно определить относительные значения всех коэффициентов.
Их абсолютные значения находятся нормировкой
несвязывающей орбитали. Плотность заряда на каждом атоме определяется
возведением в квадрат соответствующих коэффициентов.
Стабильность четных альтернантных углеводородов
(например, бензола) можно понять на основе предыдущего
рассмотрения. В частности, в четном Af-атомном альтернантном
углеводороде каждый атом поставляет один я-электрон. На каждую из
-kN связывающих орбиталей можно поместить два электрона
(принцип Паули), и, таким образом, занятыми оказываются
только связывающие орбитали. Стабильность такой структуры
выше, поскольку она лучше защищена от всевозможных
воздействий благодаря однородности распределения заряда, при
которой отсутствуют центры притяжения возможных реагентов.
Упражнения. Чем отличаются альтернантные углеводороды от
неальтернантных? Какие из следующих углеводородов являются альтернантными:
этилен (этен), бутадиен (бутадиен-1,3), циклобутадиен, бензол, нафталин,
антрацен, азулен, циклооктатетраен, бензил (радикал), циклопентадиенил?
Какие свойства вы могли бы предсказать для альтернантных углеводородов из
этого перечня? Сформулируйте теорему Коулсона — Рашбрука.
Воспользуйтесь формой орбиталей молекулы бензола (рис. Б.6), чтобы показать, что
плотность заряда в бензоле однородна и соответствует содержанию этой
теоремы. Определите вид несвязывающей молекулярной орбитали в бензиле, ис-
22
A
пользуя метод, описанный в пункте г. (Вы обнаружите, что коэффициенты
для СНг равны 2/V7, а остальные коэффициенты равны ± 1/Y7 и 0.)
Используя полученные результаты, найдите распределение заряда в катионе
CgH-CHj и в анионе Cgh^CH^. Можете ли вы сделать какие-либо выводы
относительно реакционной способности бензила?
Рекомендуемые источники. См. Коулсон «Форма и структура молекул»-
[10], кн. Робертса [341], Стрейтвизера [387], а также Пилара [318], Салема
[353]. См. также [315]. Спектроскопические свойства обсуждаются Маррелом
[297], а также Холлом и Амосом [171]. Расчеты электронного строения альтер-
нантных углеводородов описаны Парром [3101, Дьюаром [122], а также Поп-
лом и Бевериджем [321], Маррелом и Харгетом [298]. Таблицы коэффициентов
молекулярных орбиталей и их энергий составлены Коулсоном и Стрейтвизе-
ром [ПО]. Доказательство теоремы Коулсона — Рашбрука можно найти в
работах Коулсона и Рашбрука [109] и Коулсона [107].
АРОМАТИЧНОСТЬ. Ароматическая молекула является
циклической, плоской и имеет сопряженную систему связей (т. е.
в ней чередуются двойные и одинарные связи). Стабильность
ароматической молекулы гораздо выше, чем можно было бы
ожидать для молекулы с таким обилием двойных связей. Эта
повышенная стабильность обусловлена резонансом (на языке
теории валентных связей), или делокализацией (на языке теории
молекулярных орбиталей). Дополнительная энергия
стабилизации называется энергией резонанса, или энергией делокализа-
ции. Бензол — прототип ароматических молекул. Установлено,
что такие молекулы имеют 4я + 2 электрона (правило Хюк-
келя), где я— целое число. Для бензола п = 1; простейшей
ароматической молекулой является недавно синтезированный цик-
лопропенильный катион (я = 0). Большая молекула [18]-анну-
лена, содержащая 18 сопряженных атомов углерода, которые
образуют плоский цикл, также относится к разряду
ароматических молекул (я = 4).
Чтобы понять суть правила 4я + 2, рассмотрим
энергетические уровни циклических углеводородов. В системе из N атомов
могут образоваться N молекулярных орбиталей. Самая нижняя
по энергии орбиталь (наиболее сильносвязывающая) не имеет
узлов, все остальные имеют узлы и, быть может, за исключением
самого верхнего уровня, являются дважды вырожденными (см.,
например, рис. А.4). Двукратное вырождение орбиталей можно
рассматривать как следствие того факта, что электрон способен
двигаться вдоль цикла в двух противоположных направлениях.
Когда N — четное число, самый верхний уровень является
невырожденным. На самом нижнем уровне можно разместить два
электрона, а на каждом дважды вырожденном уровне могут
находиться четыре электрона. Поэтому молекула с заполненной
оболочкой содержит 4я + 2 электрона, где я — число полностью
занятых дважды вырожденных уровней.
23
A
Образование заполненной оболочки выгодно в
энергетическом отношении, особенно если электронов ровно столько,
сколько нужно, чтобы занять все связывающие орбитали, и если
незанятыми остаются только разрыхляющие орбитали, заполнение
которых невыгодно в энергетическом отношении.
Установлено также, что некоторые молекулы с сопряженной
системой двойных связей имеют повышенную нестабильность:
они содержат 4п электрона, например циклопропенильный анион
(п = 1). За большую нестабильность эти молекулы называют
антиароматическими.
Рекомендуемые источники. См. [1], гл. 10, Коулсон «Форма и структура
молекул» [101, Коулсон [105], Стрейтвизер [387], Салем [353] и Пилар [318].
Популярный обзор методов получения и свойств разнообразных
ароматических и антиароматических молекул опубликован Бреслоу [76]. Ссылки на
работы, в которых анализируется правило 4п + 2, можно найти в [387]. Там же
обсуждается понятие «псевдоароматичность» и рассматривается критерий
Крейга. Более подробно все эти вопросы освещены в Трудах конференции по
ароматичности, псевдоароматичности и антиароматичности, изданных под ред.
Бергмана и Пюльмана [55].
АТОМНЫЕ ЕДИНИЦЫ. Многие уравнения квантовой
механики принимают более простой вид, когда входящие в них
величины выражены в атомных единицах. За единицу массы
принята масса электрона те\ за единицу заряда выбран заряд
протона е\ расстояние измеряется в радиусах первой боровской
орбиты а0; единицей энергии является удвоенная величина
потенциала ионизации из основного состояния атома водорода.
Общепринято использовать удвоенный потенциал ионизации 27,21 эВ,
или е2/4яеоао, хотя некоторые авторы применяют непосредственно
само значение этого потенциала (13,65 эВ). При таком выборе
единиц Ь = 1. Если за единицу скорости принять скорость света
в вакууме (другими словами, принять с=1), из уравнения
Шредингера можно исключить многие константы. Физические
результаты, выраженные в атомных единицах, можно предста-
Список формул А.2
Атомные единицы (а.е.)
| массы
1 а. с
длины
заряда
энергии
скорости
Следовательно, Ь =
те 9,109 - Ю-"31 кг
а0 5,292-Ю-11 м
е 1,602. 10~19 Кл
е2/4ле0а0 27,2 эВ; 2625 кДж-моль-'
с 2,998-108 м-с-1
= 1; *iB = 72; /?нв,/2
24
A
вить в любой другой общепринятой системе единиц. Для этого
достаточно перевести в эту систему единицы массы, длины,
заряда и энергии, указанные в списке формул А.2.
АТОМНАЯ ОРБИТАЛЬ. Атомная орбиталь описывает
пространственное распределение электрона в атоме и является вол-
новой функцией электрона в атоме. В классической теории Ре-
зерфорда и Бора была сделана попытка построить такую модель
атома водорода: вокруг ядра по одной из орбит-траекторий
движется электрон. Введение квантовых представлений, в частности
принципа неопределенности, показало несостоятельность
понятия траектории в атомных масштабах. Квантовая механика
заменила понятие точной траектории, орбиты, электрона на
понятие пространственного распределения — орбиталь. Атомная
орбиталь \|)(г) является функцией координат электрона. В
соответствии с интерпретацией волновой функции, данной Борном,
вероятность обнаружения электрона в бесконечно малом
объеме dx, окружающем точку г, определяется произведением
\|)*(r)\|)(r)dt. Следовательно, зная вид атомной орбитали, можно
предсказать электронную плотность в любой точке атома.
В основном состоянии атома водорода электрон находится
на атомной орбитали (s-орбитали) вида ехр(—г/а0), где а0 —
константа (радиус первой боровской орбиты, равный 5,29 X
X 10~~п м). Эта орбиталь имеет сферически симметричную форму
(является функцией только радиуса г, но не углов 8 или ф).
Поэтому плотность электронов в любой точке определяется
зависимостью ехр(—2г/а0); она достигает наибольшего значения в
месте нахождения ядра и экспоненциально падает по мере
удаления от него. Такая атомная орбиталь может быть обозначена
сферической граничной поверхностью, внутри которой с
вероятностью, скажем, 90% можно обнаружить электрон. В таком
представлении s-орбиталь изображается в виде сферы
соответствующего радиуса (рис. А.5).
Не следует, однако, забывать, что всегда существует
некоторая небольшая вероятность обнаружить электрон в любой точке
за пределами этой поверхности.
Обычно принято ограничиваться рассмотрением s-, /?-, d- и
в некоторых случаях /-орбиталей. Из них только s-орбиталь
имеет сферически симметричную форму, для остальных
характерна резко выраженная угловая зависимость, которая
соответствует концентрации электронной плотности в отдельных
направлениях в пространстве. Вид этих орбиталей подробно
обсуждается в разд. «Водорода атом».
Величина амплитуды атомной орбитали определяется
удаленностью от ядра. Как и следовало ожидать, на больших
расстояниях от ядра эта амплитуда уменьшается до нуля. При
25
A
больших расстояниях от ядра амплитуда любой орбитали
уменьшается экспоненциально, при малых расстояниях для
большинства орбиталей она имеет осциллирующий характер. Этот вопрос
детально обсуждается в разд. «Водорода атом». Здесь же
следует подчеркнуть следующее: из всех орбиталей только s-орби-
тали не обращаются в нуль на самом ядре (рис. А.5).
Число лепестков (пучностей) атомной орбитали, равное числу
ее угловых узлов, определяется величиной орбитального уело-
вого момента электрона на данной орбитали. Средняя кривизна
орбитали определяется числом радиальных и угловых узлов,
поскольку, чем чаще волна обращается в нуль, тем сильнее она
Рис. А.5. Граничные поверхности,
охватывающие с различной полнотой
электронное распределение атома во-
• • . • дорода в его основном состоянии.
искривляется. Эта кривизна характеризует кинетическую
энергию электрона. Потенциальная энергия электрона в атоме
водорода, а также часть потенциальной энергии, отвечающая
притяжению, в многоэлектронных атомах определяется средней
величиной обратного расстояния электрона от ядра. В
многоэлектронных атомах потенциальная энергия зависит также от
величины межэлектронного отталкивания, приводящего к еще
большему (по сравнению с водородоподобными атомами) искажению
электронной плотности. Эффекты искажения рассчитываются
методами самосогласованного поля. Хотя истинные орбитали
многоэлектронных атомов имеют сложную функциональную
зависимость, их можно довольно просто аппроксимировать орби-
талями, имеющими такую же угловую зависимость, что и в
атоме водорода, и радиальную часть, которая определяется
совокупностью простых правил. Эти аппроксимирующие орбитали,
введенные Слейтером, называются слейтеровскими орбиталями.
Представление атомных орбиталей многоэлектронных атомов
с помощью граничных поверхностей дает весьма упрощенную
картину истинного электронного распределения и, по существу,
служит простым обозначением области пространства, где орби-
таль имеет заметную амплитуду и где с большой вероятностью
можно обнаружить электрон.
26
A
Упражнения. Что такое атомная орбиталь? Какую информацию она
содержит о пространственном распределении и свойствах электрона? В чем
отличие орбитали от орбиты? Что понимается под граничной поверхностью?
Используя вид волновой функции, приведенный в тексте, вычислите радиус
граничной сферы, которая включает 50, 80, 90, 99,99% электронной
плотности для ls-орбитали водорода (а0 = 53 пм, или 0,53 А). Как влияет
отталкивание между электронами в многоэлектронном атоме на форму орбитали
и каким образом его можно учесть? Изобразите граничные поверхности для
/?-, d- и f-орбиталей, а для проверки воспользуйтесь рисунками,
приведенными в разд. «Водорода атом». Каковы доказательства того, что описанное
нами распределение электронов в атомах правильно?
Рекомендуемые источники. См. гл. 8 [1]. Форма атомных орбиталей и их
значение подробно обсуждаются Коулсоном [105], Герцбергом [185], Уайтом
[4251 Полингом и Вильсоном [314] и Козманом [217]. О самосогласованном
поле и слейтеровских орбиталях можно прочесть в соответствующих разделах
данной книги. Заселение атомных орбиталей электронами происходит
согласно принципу заполнения и принципу Паули. Атомные орбитали используются
не только для описания электронной структуры атомов, но и при
исследованиях молекул: см. разд. «Молекулярные орбитали» и «Линейные комбинации
атомных орбиталей». См. также разд. «Волновая функция» и «Радиального
распределения функция». Более детальное обсуждение орбиталей см. в статье
об атоме водорода.
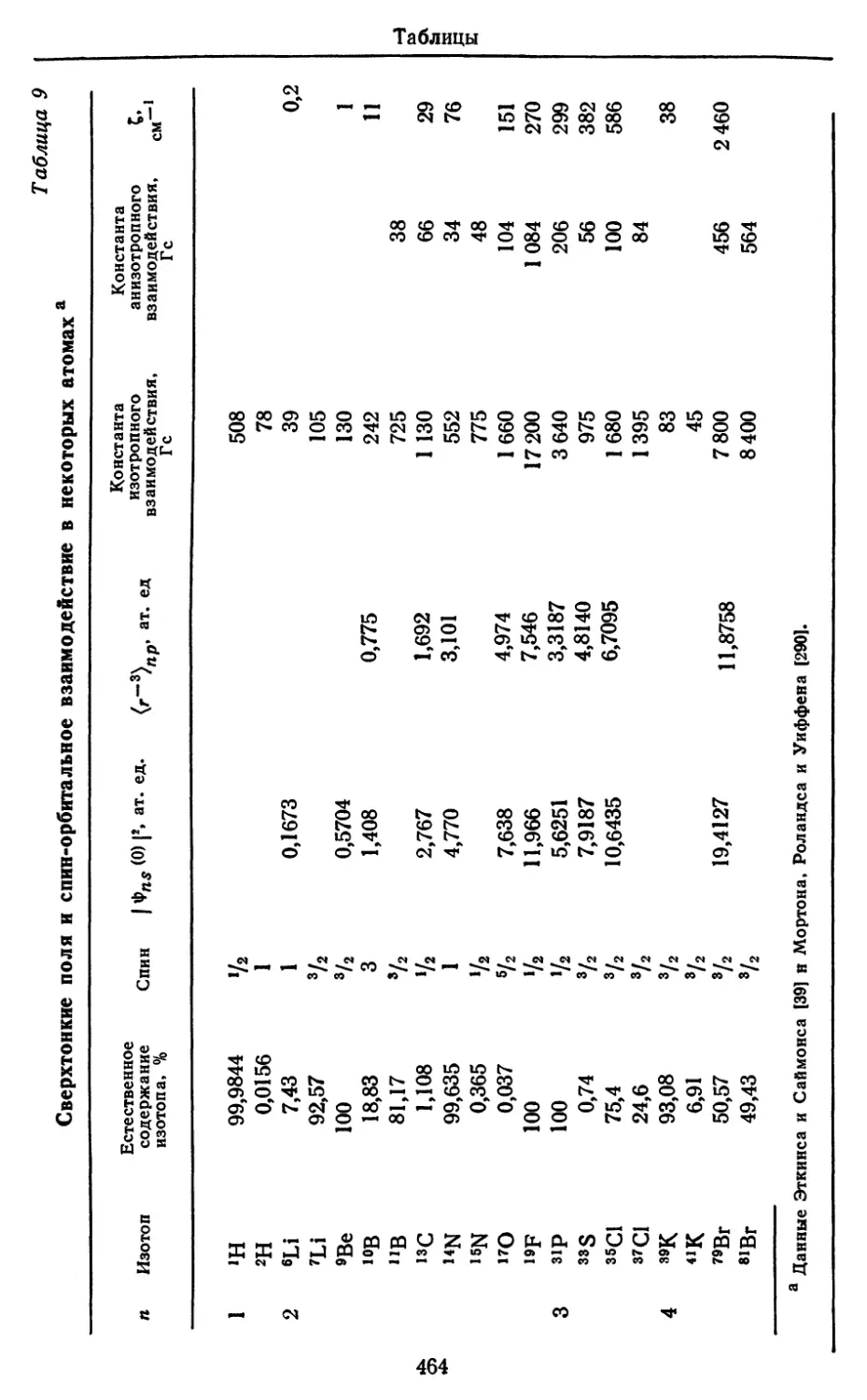
АТОМНЫЕ СПЕКТРЫ (краткий обзор). Спектры
поглощения или испускания атома возникают тогда, когда атом
совершает переход из одного состояния в другое (состояния атома
часто называют термами). В соответствии с комбинационным
принципом каждой линии спектра отвечает разность двух
термов (слово «терм» также применяется для обозначения энергии
терма). Наблюдаемые переходы относятся обычно к
электрическим дипольным переходам, и появление тех или иных линий
в спектре определяется правилами отбора. Интенсивность линии
зависит от величины дипольного момента перехода. Вид спектра
может измениться при наложении сильного внешнего магнитного
поля (эффект Зеемана) или сильного электрического поля
(эффект Штарка), так как они могут привести к небольшим
сдвигам атомных уровней по энергии. В общей структуре спектра
различается тонкая структура, которая интерпретируется как
проявление спин-орбитального взаимодействия, а также видна
более тонкая или сверхтонкая структура, обусловленная
взаимодействием электронов с магнитным дипольным и
электрическим квадрупольным моментами ядра.
Для химии представляет интерес следующая информация,
извлекаемая при изучении атомных спектров:
1. Идентификация веществ. Поскольку каждый элемент имеет
характерный спектр, атомную спектроскопию можно
использовать как метод анализа. В данном случае спектр играет роль
«отпечатков пальцев» элемента.
27
A
2. Доказательство квантования. Исследования спектра атома
водорода оказали глубокое влияние на развитие квантовых
представлений. В результате этих исследований появились
понятие атомной орбитали и все остальные представления квантовой
химии.
3. Принцип Паули. Исследование спектра гелия привело к
неожиданному результату: оказалось, что не все состояния
атома являются разрешенными. Разобраться в этом помог
принцип Паули, открытие которого послужило ключом для
объяснения Периодической системы Менделеева.
4. Атомные уровни энергии. Исследование атомных спектров
дает информацию об энергетических уровнях атомов, оно
позволяет установить, насколько глубоко в атоме расположены
внутренние оболочки и какие электроны и атомные состояния
определяют способность атомов вступать в связь друг с другом (их
валентные возможности и прочность образуемых ими связей).
Зная энергию атомных уровней, можно оценить энергию
валентного состояния и определить роль гибридизации. Данные об
уровнях возбужденных атомов используются также в
фотохимии.
5. Потенциалы ионизации. Атомная спектроскопия позволяет
определить энергию, которая требуется для ионизации атома
(его потенциал ионизации), и энергию сродства к электрону
(правда, сделать это несколько сложнее). Обе эти величины
играют важнейшую роль в исследовании структуры атомов и
молекул и их реакций (см., например, разд. «Электроотрицатель-
иость»).
6. Спин-орбитальное взаимодействие. Из тонкой структуры
спектра можно определить константу спин-орбитального
взаимодействия. Знание этой константы помогает оценить роль три-
плетных состояний в фотохимии (например, влияние тяжелого
атома на затухание фосфоресценции), потому что она
определяет скорость синглет-триплетного интеркомбинационного
перехода. Константа спин-орбитального взаимодействия
используется при расчете ^-факторов в ЭПР и при обсуждении
структуры молекул (см., например, связь Гунда).
7. Константы сверхтонкого взаимодействия. Из сверхтонкой
структуры спектра удается определить силу магнитного и
электрического взаимодействия электронов с ядром, а также спин
ядра.
Эти константы нужны для оценки роли сверхтонкой
структуры в электронном парамагнитном резонансе и спин-спинового
взаимодействия в ядерном магнитном резонансе.
8. Рентгеновские спектры. Исследуя коротковолновую
область рентгеновских спектров, Мозли определил порядковые
номера химических элементов.
28
A
рекомендуемые источники. В гл. 8 [1] обсуждаются взаимодействия,
которые обусловливают структуру атомных спектров, и дается более детальное
описание "этих взаимодействий Введением в теорию атомных спектров могут
сл>жнть кн Уиффена [424], Барроу [51], Герцберга [185], Вудгэйта [432] и
Vain a [425]. Книга Куна [229] рассчитана на несколько более
подготовленного читателя, в ней теория атомных спектров обсуждается более подробно
и приводится много примеров. Детальное рассмотрение вопросов можно
найти в ки. Шора и Мензеля [365], Кандлера [89], где приведено много
экспериментальных данных, Кондона и Шортли [96], Джадда [212, 213] и Вигнера
[427]. Работы Кондона и Шортли [96] и Вигнера [427] являются классическими.
Первая из них была написана до появления удобной техники сложения
углового момента, однако именно эта книга оказала решающее влияние на
развитие данной области пауки. В [427] дается оригинальное изложение
структуры и спектров атома на языке симметрии и теории групп. Обе книги можно
рассматривать в качестве прародителей кн. Гриффита [170], в которой после
обсуждения спектров свободных атомов рассматривается теория спектров
атомов, входящих в комплексы (см. «Теория кристаллического поля»). В [288]
приводятся уровни энергии атомов из данных атомной спектроскопии. В кн.
Вейна [416], Калверта и Питса [88] рассматривается применение теории
атомных спектров в фотохимии.
БАРЬЕРЫ ВНУТРЕННЕГО ВРАЩЕНИЯ. Наиболее
известным примером барьера, препятствующего свободному
внутреннему вращению молекулы, является барьер в этане, где одна
метильная группа не может свободно вращаться вокруг связи
С—С из-за взаимодействия с другой метильной группой. Кон-
формация с минимальной энергией соответствует скрещенному
расположению двух метальных групп (глядя вдоль связи С—С,
гармонический
(косинусои бальный)
потенциал
о
* параболический
потенциал
Рис. Б.1. Барьер внутреннего
вращения в этане. Показано
использование параболического
потенциала вместо
гармонического косинусоидалыюго для
описания малых либрации.
мы видим, что связи С—Н одной группы делят пополам углы
С—Н—С между связями другой группы). Максимальной
энергии соответствует заслоненная конформация (связи С—Н обеих
групп находятся друг против друга). Если одну метальную
группу повернуть на небольшой угол относительно скрещенной кон-
формации, а затем отпустить, молекула начнет совершать
крутильные колебания. Чем больше энергии добавляется к этим
крутильным колебаниям, тем больше становится их амплитуда,
и в конце концов метильная группа оказывается в состоянии
перескочить из одного энергетического минимума в другой. При
наличии достаточной энергии метильная группа вращается почти
свободно. Таким образом, крутильные колебания переходят в
свободное вращение. И наоборот, свободное вращение
становится локализованным и переходит в крутильные колебания по
мере того, как возбужденная молекула теряет энергию.
При квантовомеханическом объяснении этого процесса
система рассматривается как частица с потенциальной энергией,
которая изменяется в зависимости от угла по закону cos (30/2),
30
Б
см. рис. Б.1. Такой потенциал обладает той же периодичностью,
что и потенциал истинной системы, но он лишь приближенно
воспроизводит сложную зависимость последнего от угла
кручения 9. Вблизи минимумов функция косинуса изменяется как 92
(рис. Б.1), и в этих условиях частица ведет себя подобно
гармоническому осциллятору. Отсюда следует, что основным
состоянием внутреннего вращения этана являются нулевые
крутильные колебания метильных групп вокруг связи С—С. Первое
Рис. Б.2. Уровни энергии
свободного ротатора (слева)
изменяются под действием
периодического потенциала и в
случае предельно глубокого
потенциала переходят в уровни
двух независимых
осцилляторов. Обратите внимание на то,
как меняется вырождение.
q = mV/2h2, где V — глубина
ямы.
возбужденное состояние крутильных колебаний в любой из трех
потенциальных ям напоминает поведение гармонического
осциллятора, однако такое соответствие могло бы быть полным
только для бесконечно глубоких потенциальных ям. В реальной
молекуле этана метильная группа может совершать туннельный
переход из одной ямы в другую, поэтому колебательные
волновые функции таких крутильных колебаний не совпадают с
функциями гармонического осциллятора.
При сильном возбуждении колебаний, когда их полная
энергия значительно превышает потенциальный барьер, его
наличием можно пренебречь. В таком предельном случае метильная
группа ведет себя как частица массы Зтр, вращающаяся по
кольцу.
Математическое описание данного явления становится
понятным, если вместо поведения метильной группы рассмотреть
случай, когда имеются только две, а не три ямы (рис. Б.2). В
достаточно глубоких потенциальных ямах каждый уровень энергии
дважды вырожден, поскольку метильная группа, совершающая
свободный,
31
Б
крутильные колебания, может находиться в любой из двух
эквивалентных ям. В предельно мелких ямах каждый уровень, кроме
нижнего, дважды вырожден, поскольку свободный ротатор
может с одной и той же энергией вращаться либо по часовой
стрелке, либо против часовой стрелки; самый нижний уровень,
соответствующий неподвижному ротатору, не вырожден. С
увеличением барьера последний из описанных случаев должен
переходить в первый. Этот переход можно проследить
непосредственно, поскольку уравнение Шредингера с гармоническим по-
Рис. Б.З. Волновые функции крутильных колебаний для низкого и высокого
потенциальных барьеров. Обратите внимание, что функции больше походят
на функции свободного ротатора в первом случае и на функции
независимых осцилляторов — во втором. (/ — высокий барьер, 2 — низкий барьер;
основное состояние волновой функции: 3 — для высокого барьера, 4 — для
низкого барьера).
тенциалом сводится к уравнению Матье, решения которого даны
в табулированном виде. На рис. Б.2 приведены энергии, а на
рис. Б.З — волновые функции для барьеров различной высоты,
иллюстрирующие предыдущие рассуждения, а также
показывающие переход к энергетическим уровням и волновым
функциям свободного ротатора.
Рекомендуемые источники. Хорошее обсуждение проблемы
заторможенного внутреннего вращения приведено в § 8.3 кн. Сагдена и Кениея [388] и в
§ 12.6 кн. Таунса и Шавлова [399]. Решения и свойства уравнения Матье
рассматриваются в § 20 кн. Абрамовича и Стегуна [30], там же приведены
численные данные. В разд. «Инверсионное удвоение» рассматривается ситуация,
близкая к изложенной выше. Обзор по проблеме внутреннего вращения
молекул выполнен Штрауссом [386].
БЕНЗОЛ. Бензол является прототипом ароматических
молекул, в которых кольцо атомов углерода необычно стабильно по
сравнению с другими ненасыщенными системами. Теория
резонанса представляет собой попытку объяснить эту стабильность
32
Б
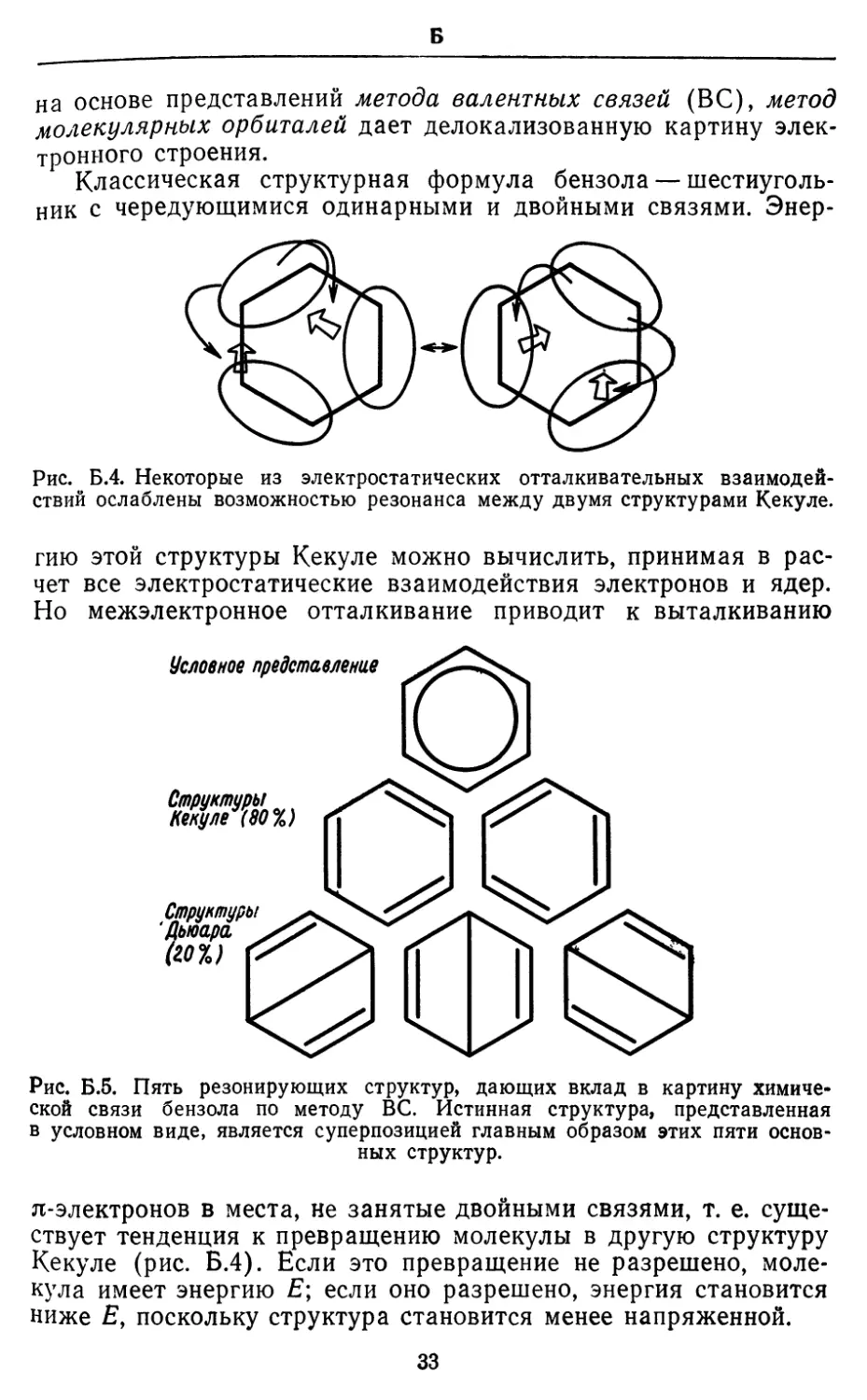
на основе представлений метода валентных связей (ВС), метод
молекулярных орбиталей дает делокализованную картину
электронного строения.
Классическая структурная формула бензола —
шестиугольник с чередующимися одинарными и двойными связями. Энер-
Рис. Б.4. Некоторые из электростатических отталкивательных
взаимодействий ослаблены возможностью резонанса между двумя структурами Кекуле.
гию этой структуры Кекуле можно вычислить, принимая в
расчет все электростатические взаимодействия электронов и ядер.
Но межэлектронное отталкивание приводит к выталкиванию
Рис. Б.5. Пять резонирующих структур, дающих вклад в картину
химической связи бензола по методу ВС. Истинная структура, представленная
в условном виде, является суперпозицией главным образом этих пяти
основных структур.
я-электронов в места, не занятые двойными связями, т. е.
существует тенденция к превращению молекулы в другую структуру
Кекуле (рис. Б.4). Если это превращение не разрешено,
молекула имеет энергию Е; если оно разрешено, энергия становится
ниже £, поскольку структура становится менее напряженной.
33
Б
Следовательно, резонансную стабилизацию структуры можно
объяснить понижением энергии вследствие возможности
резонанса между двумя структурами Кекуле. Такая картина двух
Рис. Б.6. Энергетические уровни и орбитали бензола (по Хюккелю). Числа
являются коэффициентами 2р2-орбитали каждого атома; знак коэффициента
обозначен на орбитали. Необозначенные коэффициенты получаются из
соображений симметрии.
резонирующих структур Кекуле теряет свою простоту, как
только выясняется, что их вклад в истинную полную структуру
бензола (которую можно считать суперпозицией резонирующих
структур) составляет лишь около 80%, а остальные 20%
приходятся на структуры Дьюара (рис. Б.5). Резонансная картина
стабилизации становится при этом менее очевидной, хотя при
надлежащей трактовке остается справедливой и позволяет вы-
34
Б
яснить дополнительные детали электронного строения бензола.
Теория молекулярных орбиталей дает более ясное
объяснение причин стабильности, основанное на том факте, что бензол
является четной альтернантной молекулой, которая может быть
описана путем рассмотрения орбиталей и энергий, показанных
на рис. Б.6. Дополнительную систему я-орбиталей необходимо
заселить шестью электронами, и, поскольку первые три
орбитали являются связывающими, все заселяемые электроны
усиливают стабильность молекулы.
а-Электроны играют важную роль при описании строения
бензола в рамках метода ВС, а также метода МО, потому что
шесть 5/?2-гибридизированных атомов углерода образуют
ненапряженное шестичленное кольцо (с углами 120°). Каждый из
шести атомов углерода в равной мере участвует в
обобществлении своих валентных электронов, и поэтому не возникает
энергии, связанной с неравномерным распределением заряда. В
бензоле нет также центров избыточного положительного или
отрицательного зарядов, способных создать реакционноспособный
участок (см. «Альтернантные углеводороды»). Шестиугольный
цикл атомов углерода — очень хорошо сбалансированная
система.
Упражнения. 1. Почему резонанс двух структур Кекуле придает
стабильность бензольному кольцу? Какие структуры должны быть приняты во
внимание при построении полной картины электронного строения бензола по
методу валентных связей и в какой пропорции они входят в полную структуру?
Должны ли быть включены в рассмотрение также ионные структуры?
Приведите некоторые из них. Какие особенности шестиугольной структуры
бензола делают эту молекулу стабильной в представлении метода молекулярных
орбиталей? Какие характерные черты этого объяснения в равной степени
применимы и к описанию бензола по методу валентных связей?
2. Найдите комбинации трех занятых молекулярных орбиталей бензола,
которые можно интерпретировать как три локализованные связи в одной из
структур Кекуле? (см. разд. «Локализованные орбитали»). Каким образом
из молекулярных орбиталей можно получить другую структуру Кекуле?
Каким образом можно получить структуры Дьюара?
3. Используйте симметрию молекулы бензола для нахождения ее
молекулярных орбиталей и соответствующих энергий в рамках метода Хюккеля.
Найдите энергию резонанса этой молекулы. Экспериментальное значение
равно 150 кДж-моль""1 (подумайте, как можно определить его
экспериментально).
Рекомендуемые источники. В гл. 9 [1] дано простое описание бензола с
помощью метода молекулярных орбиталей. Простое рассмотрение структуры
бензола дано Коулсоном в его кн. «Форма и структура молекул» [101 и в
гл. 9 [105]. Описание бензола в ра*мках метода валентных связей см. также в
кн. Полинга [313] Математические детали расчетов приводятся Мак-Глином.
ранквикенборном, Киноситой и Кэрроллом [273], Салемом [353] и Пиларом
Р18]. Современный обзор спектроскопии бензола дан Маррелом [297], Холлом
35
Б
и Амосом [171]. Другие представляющие интерес разделы данной книги —
резонанс, ароматичность, метод Хюккеля и альтернантные углеводороды.
Некоторые физические свойства бензола представлены в табл. 1*.
БОЗОН. Бозон — это частица, обладающая внутренним
угловым моментом, или спином, который характеризуется
целочисленными значениями спинового квантового числа, включая нуль.
Примеры — дейтерон 2Н(/= 1), ядро 4Не, или а-частица, атом
гелия (/ = 0), а также фотон (I = 1). Бозоны не подчиняются
принципу «запрета» Паули (в отличие от фермионов), и в одном
квантовом состоянии может находиться любое число бозонов.
Они подчиняются общему принципу Паули (принцип
неразличимости одинаковых частиц), который требует, чтобы волновая
функция была симметричной по отношению к перестановке
любой пары одинаковых бозонов. Поскольку одно состояние могут
занимать много бозонов, при низких температурах возникают
такие специфические явления, как сверхтекучесть и
сверхпроводимость (когда пары электронов, т. е. фермионы, ведут себя как
бозоны). Работа лазеров возможна именно потому, что фотон
является бозоном, так как интенсивный монохроматический
пучок света состоит из большого числа фотонов в одном и том же
состоянии.
Рекомендуемые источники. См. разд. «Спин» и «Паули принцип».
Таблица свойств ядер (табл. 1—27) показывает, какие из них являются бозонами,
а какие — фермионами. Принцип заполнения состояний бозонами учитывается
статистикой Бозе— Эйнштейна, она изложена в кн. «Энтропия и
энергетические уровни» [19], в гл. 6 кн. Дэвидсона [116], разд. 9.6 кн. Райфа [333] и в
гл. 22 кн. Хилла [189]. Фундаментальная роль различия между фермионами
и бозонами обсуждается в статье Пайерлса в кн. Салема и Вигнера [352], см.
также кн. Паули [311]. Сверхтекучесть рассматривается в гл. 15 кн. Раиса
[335], а сверхпроводимость — в гл. 11 кн. Киттеля [224], а также в кн. Роуз-
Инса и Родерика [3481 Вопрос о том, может ли фермион 3Не проявлять
свойства сверхтекучести (если два фермиона соединяются вместе), обсуждался
Ошероффом, Галли, Ричардсоном и Ли [309]. Пайерлс (см. выше) обсуждает
также доказательство того, что все частицы являются либо фермионами, либо
бозонами.
БОРА АТОМ. Еще до создания квантовой механики Бор
применил принцип квантования для описания строения атома
водорода. Он постулировал, что:
1) электрон остается в стационарном состоянии до тех пор,
пока не происходит переход;
2) переход из стационарного состояния с энергией Е{ в
состояние с энергией £/ сопровождается испусканием или
поглощением излучения с частотой v, определяемой условием hv ==
= Ef — Et (условие частот Бора);
* Таблицы 1—27 см. в конце книги.
36
Б
3) разрешенные стационарные состояния определяются
условием равенства силы электростатического притяжения электрона
к ядру и центробежной силы, возникающей при движении
электрона по его орбите.
На последнем этапе было наложено квантовое условие, а
именно: Бор постулировал, что
4) единственными разрешенными значениями углового
момента электрона являются те, величина которых кратна й.
Расчет энергетических уровней, основанный на этих
постулатах, привел к выражению вида Е = —R/n2, где R —
постоянная Ридберга, а п — главное квантовое число (я=1, 2, ...).
Это выражение настолько точно согласуется с экспериментом,
что модель атома, предложенная Бором, имела большой успех.
Уточнение этой многообещающей модели проводилось в три
этапа. Прежде всего был учтен тот факт, что орбитальное
движение происходит вокруг центра масс системы, а не вокруг ядра.
Данное обстоятельство легко учесть, заменяя массу электрона
в формуле Бора приведенной массой jli = memp/(me + mp).
Второй шаг был сделан Зоммерфельдом. В атоме Бора — Зоммер-
фельда электрон движется по эллиптическим орбитам, а степень
эллиптичности определяется азимутальным квантовым числом ft,
но энергия орбит не зависит от их эксцентриситета. Третье
уточнение также было внесено Зоммерфельдом. Он учел в рамках
описанной модели релятивистские эффекты и обнаружил, что это
вызывает несовпадение начала каждой из эллиптических орбит
с ее концом, или, другими словами, что электрон движется
вокруг ядра по незамкнутой орбите, которая постоянно
разворачивается и поэтому похожа на розетку. Учет выводов теории
относительности привел к слабой зависимости энергетических
уровней от ft, в результате чего было получено замечательное
согласие с экспериментом (полученные численные данные
совпадают со значениями, которые дает теория атома водорода Дирака).
Несмотря на это согласие, модель атома водорода оказалась
принципиально ошибочной, а согласие ее численных результатов
с экспериментом — удивительным совпадением; это совпадение
связано, вероятно, со специфическими особенностями кулонов-
ского потенциала, которые сохраняются даже в современной
квантовомеханической теории атома. Ошибочность модели Бора
была обнаружена при последующем развитии квантовой теории,
когда выяснилось, что понятие траектории неприменимо в
явлениях атомного масштаба (см. разд. «Принцип
неопределенности»). Следовательно, попытка обсуждать динамику системы в
терминах траектории ее составных частей совершенно
недопустима: орбиты Бора и Бора — Зоммерфельда являются
макроскопическими понятиями, которые не имеют смысла в
масштабах атома водорода. Кроме того, модель Бора неполна в том
37
Б
смысле, что ее постулаты фактически задают строение атома
водорода, а обоснование стационарности состояний и квантования
углового момента отсутствует; эти утверждения обоснованы
значительно позже квантовой механикой. Тем не менее модель
Бора —значительное достижение, так как к механической
проблеме была применена теория, основанная на результатах
исследований свойств излучения, и это явилось одним из первых
свидетельств того, что оптические и механические явления, по
существу, идентичны.
Упражнения. 1. Сформулируйте постулаты боровской модели атома
водорода. Какие из них противоречат требованиям классической механики? Каков
вид выражения для энергии, полученной в рамках этой модели? Выведите
выражения для частот переходов в атоме водорода: согласуются ли они с
известным спектром атома водорода? Как была усовершенствована
первоначальная модель? Каков смысл квантового числа k? Эллиптические орбиты
с k = 0 (прямые линии, проходящие через ядро) были отброшены как
неправдоподобные. Существует ли какая-нибудь связь между этими орбитами
и s-орбиталями в современной теории строения атома? В самом низком
энергетическом состоянии атома, согласно теории Бора, требуется наличие
углового момента, чтобы электрон отталкивался от ядра. Приводит ли квантово-
механическая теория к такому же выводу? В чем причина несостоятельности
теории Бора? Обсудите роль принципа неопределенности в теории Бора.
Почему этой теории придается такое большое значение?
2. Выведите выражение для энергии стационарных состояний атома
водорода на основании теории Бора. Установите выражение для потенциальной
энергии электрона, а затем выразите центробежную силу через угловой
момент. Приравняйте центробежную силу силе притяжения и замените угловой
момент на величину nh. Сравните полученное вами выражение с известным
выражением для постоянной Ридберга. -
Рекомендуемые источники. Расчет атома водорода см. в разд. 1.2 кн.
Герцберга [185] и в гл. 2 кн. Полинга и Вильсона [314]. В кн. Джеммера [203]
дана история вопроса.
БОРНА —ОППЕНГЕЙМЕРА ПРИБЛИЖЕНИЕ. В при-
ближении Борна — Оппенгеймера предполагается, что
электронную плотность в молекуле можно оценивать, считая ядра
неподвижными. Это предположение основано на большом различии
масс электронов и ядер: если ядра сдвигаются, то
распределение электронов мгновенно приспосабливается к новому
потенциалу, а ядра нечувствительны к быстрым флуктуациям
электронов на орбиталях. Практическим следствием такого
предположения является возможность значительно упростить как
обсуждение, так и расчеты электронного строения молекул. Так,
Еместо того чтобы на равных основаниях рассматривать все
частицы, составляющие молекулу, можно исходить из
фиксированной («замороженной») конфигурации ядер и рассчитать энергию
38
Б
и распределение электронов, соответствующие данному
положению ядер. После этого ядра можно сдвинуть в новое положение
и повторить расчет. Таким способом в принципе можно
рассчитать энергию для всех возможных конфигураций ядер и найти
такое их расположение, которое отвечает наименьшей энергии,
т. е. устойчивую конфигурацию молекулы.
Приближение Борна — Оппенгеймера придает кривой
потенциальной энергии молекулы вполне определенный смысл. Если
меняется конфигурация ядер, меняется и энергия молекулы, а
зависимость энергии от их положения и есть кривая
потенциальной энергии молекулы. Для двухатомной молекулы эта кривая
представляет собой график зависимости энергии от длины связи,
а для многоатомной молекулы вместо кривой получается
сложная поверхность. Если нарушить равновесную конфигурацию
молекулы, она вернется в положение равновесия (или по
крайней мере будет колебаться около него), следовательно,
возрастание энергии при изменении равновесной конфигурации
соответствует приобретению молекулой потенциальной энергии.
Приемлемость такого описания зависит от того, насколько
справедливо приближение Борна — Оппенгеймера, так как только при
этом условии можно говорить об энергии молекулы как функции
параметра, определяющего конфигурацию молекулы (длина
свя^и для двухатомной молекулы). Если бы приближение
Борна—Оппенгеймера было неудовлетворительным (так должно
быть в случае легких или быстро движущихся ядер), понятие
поверхности потенциальной энергии, равно как и длины связи и
углов между связями, потеряло бы смысл. На самом деле это
приближение нарушается, но лишь слегка, что вызывает
небольшие спектроскопические эффекты.
Упражнения. Сформулируйте приближение Борна — Оппенгеймера. На
чем оно основано? При каких условиях оно может нарушаться? Какое
упрощение оно вводит? Обсудите понятие кривой потенциальной энергии
молекулы. Вычислите относительные скорости электрона и протона, если каждый
обладает кинетической энергией 100 кДж-моль-1.
Рекомендуемые источники. Краткое обсуждение вопроса см. в [1], гл. 9;
некоторые математические аспекты этого приближения обсуждаются Слей-
тером [372]. Спектральные следствия нарушения этого приближения
освещены Кингом [222].
БРИЛЛЮЭНА ТЕОРЕМА» Однократно возбужденные
состояния молекул с заполненной оболочкой непосредственно не
смешиваются с основным состоянием. (Как и большинство
утверждений, данная теорема может быть выражена более сложным
образом, и для тех, кому это нравится, можно сформулировать
39
в
теорему так: если вычислить матричный элемент
межэлектронного кулоновского взаимодействия между конфигурацией,
соответствующей заполненной оболочке, и конфигурацией,
отличающейся возбуждением одного электрона, то такой матричный
элемент окажется равным нулю.)
Данная теорема упрощает учет конфигурационного
взаимодействия после вычислений по методу самосогласованного поля,
так как она утверждает, что однократно возбужденные
конфигурации не могут непосредственно примешиваться к основному
состоянию системы с заполненной оболочкой. Это вовсе не
означает, что смешение с однократно возбужденными состояниями
не происходит вообще, поскольку они могут смешиваться с ним
косвенным образом, за счет взаимодействия с промежуточными
состояниями. Действительно, в некоторых случаях косвенное
взаимодействие настолько эффективно, что однократно
возбужденные состояния играют важную роль.
Теорема Бриллюэна свидетельствует о стабильности
основного состояния, вычисленного методом самосогласованного поля;
если бы она была неверна, основное состояние могло бы быть
сильно возмущено близлежащими однократно возбужденными
конфигурациями. Однако, поскольку эта теорема верна, прямое
смешение возможно только с относительно далекими по энергии
многократно возбужденными состояниями, а с однократно
возбужденными состояниями допускается только косвенное
смешение.
Рекомендуемые источники. Простое введение и доказательство теоремы
см. в разд. 6.3 кн. Ричардса и Хорсли [336], несколько более подробное
обсуждение и доказательство приводится Слейтером [372]. См. также статью
Бриллюэна [78].
в
ВАЛЕНТНОЕ СОСТОЯНИЕ. Обсудим некоторые свойства
атома углерода, в частности его состояние в молекуле метана.
При описании химического строения метана углерод можно
рассматривать как вр^-гибридизованный атом, который
перекрывается пучностью каждой из его тетраэдрических орбиталеи с орби-
талью одного из четырех окружающих атомов водорода.
Следовательно, связи в метане образуются в результате перекрывания
орбиталеи четырех атомов водорода с четырьмя тетраэдрическими
орбиталями атома углерода в его валентном состоянии
\s22s2px2py2pz. Валентное состояние — это состояние атома,
ответственное за его связь с соседними атомами. Из этого
определения следует, что валентное состояние атома водорода
определяется просто как Is, а валентное состояние атома кислорода
в молекуле воды может быть записано как ls22s22p2x2py2pz.
Важно отметить, что валентное состояние, вообще говоря, не
является реальным спектроскопическим состоянием, т. е. его
нельзя обнаружить по каким-либо спектральным переходам.
Чтобы понять эту особенность валентного состояния, достаточно
напомнить, что образование связи между атомами водорода и
углерода в метане осуществляется в результате спаривания
электронов в каждой отдельной связи, однако это не означает
наличия спаривания спинов, относящихся к разным связям.
Следовательно, валентное состояние углерода характеризуется
произвольной взаимной ориентацией спинов четырех его
электронов. Но состояние с произвольно ориентированными спинами
ие является спектроскопическим, так как предполагается, что в
последнем происходит вполне определенное сложение различных
угловых моментов и, следовательно, достигается строго
определенное распределение взаимных ориентации спинов.
Представляет интерес определение энергии валентных
состояний, особенно для оценки роли гибридизации. Хотя валентное
состояние не является спектроскопическим, его можно
представить в виде смеси (суперпозиции) истинных спектроскопических
состояний и вычислить энергию как среднее энергий
соответствующих состояний. Таким образом можно оценить энергию,
необходимую для перевода электронов из основного состояния
углерода в валентное состояние (7 эВ, 680 кДж-моль"-1).
Возникают ли все же в действительности валентные
состояния? Поскольку это не спектроскопические состояния, ответ
должен быть отрицательным (см., однако, упражнения). Тем не
менее можно считать, что валентное состояние возникает из
41
в
основного состояния атома при приближении соединяющихся с
ним атомов. Еще раз вернемся к метану, но начнем его
рассмотрение с.того, что четыре атома водорода расположены в
вершинах тетраэдра на бесконечно большом расстоянии от
центрального атома углерода, который находится в основном состоянии.
По мере сближения атомов с сохранением их тетраэдрического
расположения поверхность атома углерода начинает
деформироваться, и на короткие промежутки времени его электронная
плотность аккумулируется в направлении к вершинам тетраэдра.
По мере того как атомы сближаются, такие флуктуации
становятся все сильнее и продолжительнее. Когда атомы оказываются
на расстоянии равновесных связей, эти флуктуации становятся
особенно сильными, по существу непрерывными, и приводят к
образованию четырех тетраэдрических а-связей. Только теперь
будет правильным сказать, что центральный атом углерода
находится в своем валентном состоянии, которое образовано из его
основного состояния благодаря присутствию атомов водорода и
наличию энергии связи, которая понижает энергию всей
системы.
Упражнения. Что такое валентное состояние? Почему оно не является
спектроскопическим состоянием? Как можно определить энергию валентного
состояния? Какую роль играют валентные состояния в теории химической
связи и насколько важна их энергия? Валентное состояние можно
представить в виде суперпозиции спектроскопических состояний; представьте себе,
что нам удалось создать состояние атома, которое является такой
суперпозицией спектроскопических состояний, и рассмотрите последовательность
возникновения этого состояния с самого начала его образования.
Рекомендуемые источники. См. гл. 9 [1]. См. также кн. Коулсона «Форма
и структура молекул» [10] и § 8.4 кн. Коулсона [105], где обсуждаются
вопросы, посвященные расчетам валентных состояний, их построению и оценке
энергий со ссылками на Воуга [409], Полинга [312], Моффитта [287] и Скин-
нера [370, 371]. Полезное обсуждение валентных состояний с примерами дано
в § 4.1 кн. Мак-Глина, Ванквикенборна, Киноситы и Кэррола [273].
ВАЛЕНТНЫХ СВЯЗЕЙ МЕТОД. Метод валентных связей
был первой квантовомеханической теорией химической связи,
основанной на химическом толковании связи как образования,
прочность которого зависит от наличия двух спаренных
электронов. Эта теория концентрирует внимание на спаренных
электронах молекулы (приближение идеального спаривания) и исходит
из предположения, что они играют основную роль в образовании
связи. Если несколько структур с идеальным спариванием имеют
близкие энергии, необходимо учесть возможность резонанса
между этими структурами, вследствие чего энергия системы
понижается.
42
в
Наиболее целесообразно пояснить этот метод на примере
самой простой молекулы. Рассмотрим И2— эту наиболее
популярную из молекул. При больших расстояниях между атомами вол-
новая функция системы совпадает с волновой функцией двух
изолированных атомов \|)а(1)фь(2), которую мы для краткости
обозначим как ахЬ2. Если атомы находятся так близко друг к
другу, как это имеет место в молекуле, волновая функция не
должна значительно отличаться от описанной выше.
Единственное различие состоит в том, что теперь каждый электрон
способен удалиться со своего ядра и перейти на другое, электроны
могут обмениваться местами. Таким образом, мы должны
допустить примешивание к состоянию а,\Ъ2 состояния а2Ьи где
электрон 2 занимает орбиталь, на которой до этого находился
электрон 1, и наоборот. Поскольку рассматриваемая система
симметрична, приходится допустить, что ее волновая функция
представляет собой равновероятную смесь обоих состояний, т. е. имеет
вид (a\b2 + a2b\). Теперь, когда физическая картина ясна,
перейдем к математическим выкладкам. Попытаемся вычислить
энергию системы, используя найденную волновую функцию.
Для того чтобы рассчитать потенциальную энергию
молекулы, нам придется вычислить несколько сложных интегралов по
координатам электронов. Эти интегралы представлены на
рис. В.1. Один из них можно интерпретировать как вклад в
полную энергию притяжения /' между электроном одного атома и
ядром другого атома, второй интеграл описывает отталкивание
/ между электронными облаками обоих атомов. Анализ
электронного распределения, описываемого волновой функцией
ахЬ2 + а2Ьи показывает, что в межъядерной области происходит
значительное накопление электронной плотности (на рис. В.1
оно условно показано двумя эллипсами), и эта дополнительная
плотность приводит к дополнительным слагаемым в полной
энергии. Одно из таких слагаемых — энергия отталкивания k между
двумя электронами, заключенными в эллиптических областях,
другое слагаемое — энергия притяжения k' между этими
областями повышенной электронной плотности и ядрами (см. список
формул В.1 и рис. В.2). Численные значения интегралов
показывают, что наиболее важен вклад последнего слагаемого:
согласно теории валентных связей, понижение энергии молекулы по
сравнению с энергией изолированных атомов в основном
обусловлено понижением потенциальной энергии электронов
благодаря их накоплению в межъядерной области, где они могут
притягиваться к обоим ядрам. (Отметим, что строгое объяснение
природы химической связи должно также принимать во
внимание изменение кинетической энергии электронов при
образовании связи и искажение атомных орбиталей вблизи ядер; см.
разд. «Химическая связь» и «Молекулярных орбиталей метод».)
43
j^/drfdT2aff)2(e^e0r/2)b(2)^
j'=/dvfa(02(e*/4jre0r/b)
^т{^а(0Шег/4пе0г,г)а(2)д{2)
/<=fdTfa(f)b(0(e2/4ne0rfa)
Рис. B.l. Вклады в энергию
молекулы Нг в методе валентных
связей.
ей/4яе0Й
Рис. В.2. Зависимость
молекулярных интегралов, дающих вклады
в энергию Нг в методе валентных
связей, от расстояния между
ядрами. Пунктиром показана
кривая полной энергии.
в
Список формул В Л
Молекулярные интегралы и экспериментальные данные для Н2
S^^dxia (1)6(1),
/ — $ dxx dx2a (I)2 (e2/4ne0rl2) b (2)2,
/' - J dxxa (I)2 (e2/4ne0rlb) = J dx2b (2)2 (е2/4яе0г2а),
Л = \dxx dx2a (1) 6 (1) (е2/4яе0г12) fl (2) 6 (2),
W = ^ dTia (1) 6 (1) (в2/4яб0Г1&) = ^ dx2a (2) 6 (2) (е2/4яе0г2а).
Кулоновский интеграл / = (e2/4ttEoR) + / — 2/''
Обменный интеграл К = (е252/4яе0#) + k — 2S&'.
Энергия E± = 2Els (Н) + {у^§г}' (£+ < £"*)-
£is (H) — энергия изолированного атома водорода.
Длина связи в Н2: 74,16 пм (0,7416 А).
Энергия диссоциации D%: 4,476 эВ, 36116 см-1.
Вращательная постоянная: 60,809 см""1.
Частота колебаний: 4395,2 см-1.
Численное значение энергии связи молекулы водорода,
полученное описанным выше образом, составляет 3,14 эВ, что
удовлетворительно согласуется с экспериментальным значением
4,72 эВ. (На самом деле такое согласие нельзя признать
удовлетворительным, но, когда это численное значение было
получено впервые, оно рассматривалось как подтверждение
правильности модели. С тех пор удалось добиться гораздо лучшего
согласия теории с экспериментом без существенного изменения
основных черт модели валентных связей.) Подход,
использованный нами для описания молекулы водорода, получил
дальнейшее развитие, так что с его помощью можно рассматривать
строение более сложных молекул, однако при этом резко
усложняется процедура вычислений. В каждом случае образование
связи приписывается взаимодействию пар электронов, поэтому
задача сводится к выбору пар электронов и расчету энергии их
взаимодействия. На этом этапе проявляется одна из
существенных особенностей теории валентных связей: поскольку в каждом
атоме много электронов и, следовательно, в молекуле много
электронных пар, необходимо учитывать, что электроны,
спаривание которых приводит к образованию различных связей,
45
в
должны электростатически взаимодействовать друг с другом.
Рассмотрим, например, молекулу бензола и одну из его
структур Кекуле. Спаривание спинов в этой структуре приводит к
образованию я-связей, и оценить вклад каждой я-связи в энергию
такой структуры можно точно таким же образом, как это было
показано выше для молекулы водорода. Однако электроны
одной связи взаимодействуют с электронами других связей. Это
приводит к двум следствиям: во-первых, меняется энергия
структуры Кекуле и, во-вторых, электроны проявляют тенденцию к
перераспределению вдоль бензольного кольца (см. рис. Б. 4 и
рис. Р. 3). Одно из таких перераспределений соответствует
другой структуре Кекуле, так что учет взаимодействия между
электронами, принадлежащими к различным связям,
интерпретируется как наличие резонанса между двумя структурами
Кекуле. Это приводит к изменению энергии. Однако истинное
распределение электронов вдоль бензольного кольца не может
быть описано простым резонансом двух структур Кекуле, лучшее
описание и меньшая энергия получаются, если допустить участие
в резонансе других канонических структур (см. разд. «Бензол»).
Соображения, описанные выше, составляют основу общего
подхода метода валентных связей. Сначала выбираются
базисные структуры с идеальным спариванием, удовлетворяющие
определенным правилам (канонам, потому эти структуры и
называются каноническими), рассчитывается энергия каждой
структуры и определяется энергия суперпозиции таких структур в
предположении наличия резонанса между ними.
Теорию валентных связей, несомненно, можно
усовершенствовать. В качестве примера вновь рассмотрим молекулу Н2.
Недостаток приведенного выше простого описания молекулы Н2
связан с присущим методу ВС требованием, что, если один
электрон находится на орбитали одного атома, другой электрон
принадлежит второму атому. На самом же деле мы знаем, что
имеется значительная вероятность найти оба электрона
одновременно на одном из этих атомов, поэтому следует улучшить
волновую функцию, допуская примесь к ней ионных вкладов
ахач (соответствующего структуре Н~Н+) и &i&2
(соответствующего структуре Н+Н~). Согласно вариационному принципу,
улучшение волновой функции ведет к понижению энергии. Так
оно и получается, если учесть примешивание ионной
составляющей к ковалентной волновой функции. В теории валентных
связей такое смешение получило название ионно-ковалентного
резонанса, потому что резонанс между ковалентными и ионными
структурами приводит к понижению энергии.
Обсудим теперь недостатки теории валентных связей,
которые во многом обесценивают достоинство химического
толкования связи, положенное в основу этой теории. Один из недостат-
46
в
ков заключается в том, что число канонических структур,
которые следует включать в расчет, колоссально возрастает с
увеличением числа атомов в молекуле. Например, для молекулы
бензола приходится рассматривать всего 5 таких структур, а для
коронена — уже более 100 000. Поскольку необходимо
учитывать возможность резонанса между всеми такими
каноническими структурами, определение энергии и строения даже
сравнительно небольшой молекулы является уже чрезвычайно
сложной задачей. Другой недостаток теории обусловлен важной
ролью ионных структур, которые должны быть добавлены к
каноническим структурам. Их роль также резко увеличивается
с ростом числа атомов. Современная тенденция, однако,
заключается в пересмотре этих недостатков, и в настоящее время
происходит возрождение теории валентных связей.
Упражнения. 1. В чем заключается основная идея метода валентных
связей? Что такое приближение идеального спаривания? Почему это только
приближение? Что произойдет при наличии нескольких идеально спаренных
структур, имеющих близкие энергии? Как это скажется на энергии системы?
В качестве примеров рассмотрите молекулы Н2 и СбНб. Обсудите описание
молекулы водорода по методу валентных связей. Чем объясняется тот факт,
что энергия молекулы меньше суммы энергий изолированных атомов? Какую
роль играет обмен электронов в Нг? Какую роль играют электронные пары
при образовании химической связи?
2. В обозначениях, использованных в тексте, волновая функция метода
валентных связей для Нг имеет вид (#i&2 + Яг&О- Составьте гамильтониан
молекулы Нг и с помощью этой волновой функции выведите формулу для
энергии молекулы; проверьте, правильно ли записаны интегралы, которые
приведены на рис. В.1 и в списке формул В.1. Покажите, что для другой
комбинации (а^г — агЬ\) энергия определяется теми же интегралами, но
некоторые из них будут иметь иные знаки. Определите, какие знаки будут
у интегралов, и затем покажите, что первой волновой функции соответствует
меньшая энергия. Что, согласно принципу Паули, можно сказать о спинах
электронов, участвующих в образовании связи? Какой вывод мы вынуждены
были бы сделать, если бы спины участвующих в связи электронов были
параллельными (неспаренными). На рис. В.2 графически показано изменение
молекулярных интегралов в зависимости от межъядерного расстояния для Нг-
Используя эти графики, определите энергию и длину связи в молекуле Н2.
3. Что такое каноническая структура? Сколько канонических структур
имеется у бензола? Один из способов определения числа канонических
структур состоит в использовании диаграммы Румера, когда все орбитали,
дающие вклад в образование связей, наносятся на окружность и затем попарно
соединяются, пока не останется ни одной несоединенной пары точек. Число
структур, которые могут быть изображены таким образом при условии
непересечения соединительных линий, определяет число канонических структур
рассматриваемой задачи. Изучите метод составления таких диаграмм на
примере бензола и нафталина. Можно ли вывести общую формулу для числа
канонических структур ароматических молекул? Способ вычисления энергии
каждой структуры и энергии взаимодействия между структурами см. в
списке формул В.2. Каждая каноническая структура поочередно накладывается
на все остальные структуры, включая самое себя, и энергия молекулы
оказывается связанной с числом «островов», образованных замкнувшимися при
47
Список формул В.2
Вековое уравнение метода валентных связей
1. Постройте в приближении идеального спаривания все канонические
структуры молекулы (например, для бензола а — две структуры Ке-
куле и три структуры Дьюара). Если сложность задачи приведет вас
в отчаяние, выберите, основываясь на химической интуиции, несколько
важнейших структур (например, в случае бензола — две структуры
Кекуле).
2. Наложите на каждую структуру сначала такую же точно структуру,
а затем поочередно все остальные структуры и вычислите
соответствующий каждому наложению элемент векового определителя
Нгс — ESrct находящийся на пересечении его /-го столбца и /-ой
строки.
Hrc-ESrc = (j) y-E + AK],
где 2N — полное число электронов; / — число „островов",
образованных замкнутыми линиями при наложении структур; А — число
связанных линиями пар соседей на этих „островах" минус половина числа
пар соседей, оказавшихся на различных „островах". Под соседями
понимаются орбитали, между которыми имеется взаимодействие (и
соседство в обычном геометрическом смысле); / и К —• кулоновский
и обменный интегралы.
Пример. Предположим, что для бензола г соответствует одной из
структур Кекуле, а с — одной из структур Дьюара:
>Ф
Hrc-ESrc=j(J-E + 3K).
3. Постройте полный вековой определитель (размерностью 5 X 5 в
случае бензола) и найдите его корни Е. Минимальный из них отвечает
энергии молекулы. Затем найдите коэффициенты в суперпозиции
структур, которая соответствует этому корню. Квадраты этих
коэффициентов соответствуют вкладам канонических структур в наилучшей
суперпозиции структур для данной молекулы.
: Здесь имеется в виду только я-электронная система бензола.—Прим. ред.
I
i + i
в
наложении структур линиями. Воспользуйтесь формулой из списка
формул В.1, чтобы получить энергию структуры Кекуле для бензола и энергию
взаимодействия двух структур Кекуле для бензола, запишите вековой
определитель, необходимый для определения энергии и состава наилучшей
суперпозиции (т. е. суперпозиции с минимальной энергией), и покажите, что она
содержит по 50% каждой структуры Кекуле и обладает энергией / + 2,4 К и
что, следовательно, энергия резонанса равна 0,9 К. Включите затем в
рассмотрение три структуры Дьюара, запишите волновую функцию молекулы
в виде ck(i|)ki + i|)K2) + £d(i|)di + i|>D2 +i|)ds) (по-видимому, все
обозначения должны быть понятны), получите соответствующий вековой
определитель и найдите выражение для дополнительной энергии стабилизации,
обусловленной учетом структур Дьюара. Какой вклад они вносят в
результирующую структуру молекулы?
Рекомендуемые источники. См. гл. 9 [1]. В кн. Коулсона [105], а также
Маррела, Кеттла и Теддера [299] подробно излагается теория валентных
связей и проводится ее тщательное сравнение с теорией молекулярных орбита-
лей. Детальное обсуждение метода ВС см. также у Эйринга, Уолтера, Ким-
балла [137]. Классическая монография Полинга [313] почти целиком посвящена
рассмотрению описания молекул с помощью метода валентных связей, а
первые издания этой книги представляют собой ни с чем не сравнимый пример
квантовомеханических рассуждений в рамках этой теории. Теории
молекулярных орбиталей и валентных связей обсуждаются в разд. «Валентных связей
и молекулярных орбиталей методы».
ВАЛЕНТНЫХ СВЯЗЕЙ И МОЛЕКУЛЯРНЫХ ОРБИТА-
ЛЕЙ МЕТОДЫ (краткий обзор). Эти два метода рассмотрены
в соответствующих разделах. Цель данного краткого обзора —
попытаться показать их сходство и различие.
1. Обе теории — и метод молекулярных орбиталей (МО), и
метод валентных связей (ВС) — предназначены для описания
строения молекул, их формы, энергии, а также валентностей
атомов, из которых они состоят.
2. Обе теории, по крайней мере в том, что касается
простейшей интерпретации их результатов, достигают цели, так как
приводят к выводу о накоплении электронов в области их наиболее
эффективного взаимодействия с ядрами. Такая область факти-
чески'совпадает с окрестностью межъядерной оси. Эта
общепринятая интерпретация химической связи не учитывает, однако,
роли вклада кинетической энергии в полную энергию. В обеих
теориях значительные вклады как в потенциальную, так и в
кинетическую энергию могут быть приписаны искажению орбита-
лей атомов, составляющих молекулу. При элементарном анализе
рассматриваемых теорий этим важным вкладом часто
пренебрегают, и поэтому в данном разделе мы поступим таким же
образом, а для более детального рассмотрения этого вопроса
отошлем читателя к работам, перечисленным в конце
раздела.
3. Обе теории приводят к выводу о накоплении электронной
плотности в межъядерной области за счет того, что электроны
49
в
не могут локализоваться на отдельном атоме, когда он входит в
состав молекулы. Теория МО утверждает, что, если электрон
может находиться на атоме а и описываться волновой функцией
^Мп) (сокращенно а(1)) либо находиться на атоме Ь и
описываться волновой функцией Ь(1), согласно принципу суперпозиции,
его действительное распределение характеризуется волновой
функцией а(1)±&(1). Если на этой орбитали размещаются два
электрона, их волновая функция имеет вид [a(l)± b(l)][a(2)±
± Ь(2)]. Теория ВС подходит к этой проблеме по-другому. Если
два атома изолированы, то состояние электронов (по одному на
каждом атоме) описывается волновой функцией а(\)Ь(2) (так
описываются две независимые системы в квантовой механике).
Теория ВС предполагает, что, когда два атома окажутся на
расстоянии, допускающем их связывание, все различие в волновой
функции состоит в том, что электрон, первоначально
принадлежавший атому а, может находиться на атоме ft, и наоборот.
Согласно принципу суперпозиции, такое состояние двух электронов
описывается функцией a(\)b(2) ± fe(l)a(2). Анализ выражения
для энергии показывает, что как в теории МО, так и в теории
ВС знак плюс в полученной функции соответствует более низкой
энергии системы. Это означает, что электроны, образующие
связь, обладают спаренными спинами (как того требует принцип
Паули). Таким образом, оба подхода учитывают важную роль
спаривания электронов в образовании химической связи.
4. Хотя оба метода подчеркивают роль спаривания
электронов, они учитывают его различными способами. Теория МО не
интересуется тем, откуда появляется в молекуле электрон, а
занимается вычислением молекулярных орбиталей из подходящих
для этого атомных орбиталей. Полученные молекулярные
орбитали заселяются электронами в соответствии с принципом
заполнения и принципом Паули. Метод ВС с самого начала имеет
дело со спаренными электронами и сводится к вычислению
энергии различных («канонических») структур, учитывающих
всевозможные способы спаривания электронов в молекуле. После того
как получен набор полностью спаренных структур, учитывается
взаимодействие между ними (т. е. истинная волновая функция
выражается как суперпозиция функций, соответствующих
различным структурам) и рассчитывается энергия наилучшей
комбинации. С этой процедурой связано понятие резонанса.
5. Метод МО исходит из того, что электроны распределяются
по всей молекуле, однако делокализованные орбитали могут
быть преобразованы в набор локализованных орбиталей. В
теории ВС с самого начала все внимание сосредоточено на
описании отдельных связей, и эта особенность во многом сохраняется
и в конечной волновой функции, полученной наложением
различных структур. Полная делокализация электронов типа обнару-
50
в
живаемой в бензоле означает существование сильного резонанса
между эквивалентными структурами Кекуле.
6. Хотя оба метода приводят к сходному распределению
электронов, наблюдаются и различия. Из пункта 3 следует, что двух-
электронная МО имеет вид а(1)а(2)+ fe(l)fe(2)± а(1)&(2)±
±&(1)а(2). Она отличается от функции метода ВС
присутствием первых двух членов, которые описывают возможность
расположения обоих электронов на одном из атомов — а либо Ь.
Поскольку эти дополнительные члены имеют тот же вес, что и
другие два члена, приходится сделать вывод, что теория МО не
учитывает эффекта корреляции электронов, т. е. тенденцию
электронов избегать друг друга. Учитывая некоторую вероятность
одновременного обнаружения обоих электронов на атоме а или
fe, следует ожидать, что истинная функция должна иметь вид
a(l)b(2) + b(l)a(2) + Xa(l)a(2)+\ib(l)b(2), где X, \х< 1.
Такая модификация волновой функции осуществляется по методу
конфигурационного взаимодействия. Теория ВС приводит к
другой крайности — запрещает обоим электронам находиться
одновременно на атоме а или Ь и, таким образом, преувеличивает
роль корреляции электронов. Этот недостаток можно исправить
введением ионных членов в первоначальную ковалентную
волновую функцию (ионно-ковалентный резонанс).
7. В расчетах по методу МО электроны вначале распределяют
по приближенным волновым функциям, а затем учитывают
межэлектронное отталкивание, приводящее к изменению
первоначальных орбиталей. Это достигается проведением расчетов по
методу самосогласованного поля (ССП). После этого
учитывается конфигурационное взаимодействие. Численные расчеты
по методу МО получили гораздо большее распространение,
поскольку расчеты по методу ССП легко поддаются
программированию на ЭВМ. Трудность выполнения расчетов по методу ВС
состоит в том, что приходится учитывать огромное число
канонических и ионных структур.
Рекомендуемые источники. См. [1], гл. 9. О методе МО см. кн. Коулсона
[10] «Форма и структура молекул», в которой рассматривается в основном
метод МО, и кн. Полинга [313], где речь идет в основном о методе
валентных связей; см. также кн. Коулсона [105], в которой сравниваются эти
методы. Тщательное исследование природы химической связи проведено Рюден-
бергом [351] и Файнбергом, Рюденбергом и Мехлером [140]. Сравнению
методов посвящена также работа Маррела, Кеттла и Теддера [299]. См. разд.
«Молекулярных орбиталей метод» и «Валентных связей метод».
ВАРИАЦИОННЫЙ МЕТОД, ИЛИ ВАРИАЦИОННЫЙ
ПРИНЦИП. Согласно вариационному принципу, энергия,
вычисленная с использованием произвольной волновой функции, не
может быть меньше истинной минимальной энергии системы»
51
в
Для того чтобы по правилам квантовой теории вычислить
энергию системы, необходимо найти ожидаемое значение ее га-
мильтониана, т. е. вычислить величину Е = \ dx^H^/K йтг|Л|э.
Вариационный принцип утверждает, что если мы выберем
произвольную («пробную») функцию <р, то аналогичная Е величина
йтф*ф, которая называется отношением Релея,
не может быть меньше истинной энергии основного состояния.
Из этого важного результата следует, что если мы выберем ряд
пробных функций различного вида, то та из них, которой будет
отвечать наименьшая энергия, должна лучше других походить
на истинную волновую функцию системы. Если нам повезет и мы
угадаем функцию, которая даст истинную энергию, то получим
истинную функцию основного состояния системы. Однако важно
не полагаться исключительно на интуицию, а разработать метод
выбора лучшей функции. Обычно для этого пользуются
следующими двумя подходами.
В первом из них волновая функция записывается в виде
функции одного или большего числа параметров, которые затем
варьируются, чтобы найти минимум энергии. Так, если пробная
функция зависит от величины параметра /?, дифференцирование
&{р) по р и определение значения /?, при котором достигается
минимум &, дает наилучшее р и, следовательно, лучшую
волновую функцию выбранного вида. Конечно, выбор вида функции
может оказаться неудачным, но найденная указанным способом
функция будет наилучшей функцией этого вида. Например, если
предположить, что основное состояние атома водорода хорошо
описывается функцией ехр(—рг2), то вариационный метод
позволит определить наилучшее значение /?, но даст при этом не
очень хорошее значение энергии. Функции ехр(—/?г), будет
соответствовать другое значение /?, и в этом случае найденная
вариационным методом наилучшая энергия точно совпадет
с энергией основного состояния атома водорода. Следовательно,
вторая пробная функция с найденным значением р
представляет собой точную волновую функцию основного
состояния.
Другой подход развит Ритцем. Он предложил записывать
пробную функцию в виде суммы функций: сами функции не1
варьируются, но их веса в этой смеси являются варьируемыми
параметрами. Пробная функция имеет вид <р = /?it|)i + р2$2 +]
+ ..., и, дифференцируя &{рир2> ...) по всем параметрам /?*,
отыскивают минимум одновременно по всем р{. Эта процедура
лежит в основе метода определения наилучшей смеси в методе
линейных комбинаций атомных орбиталей. И в этом случае
минимальная энергия отличается от истинной, если выбрана недо-
52
в
статочно «гибкая» пробная функция. Минимальная и истинная
энергии также отличаются, если используется приближенный
гамильтониан. В этом случае энергия может получиться даже
меньше истинной, поэтому, чтобы можно было применять
вариационный метод, необходимо использовать точный
гамильтониан.
Очень важно знать, насколько вариационный минимум
энергии, который является верхней границей истинной энергии,
лежит выще последней. Существует метод нахождения нижней
границы (ниже которой не может лежать истинная энергия),
позволяющий получить некоторую информацию о точности
вариационных расчетов, однако этот метод сложен и не находит
широкого применения.
Упражнения. 1. Сформулируйте вариационный принцип. Какую границу
истинной энергии — нижнюю или верхнюю — он дает? Если выбрать
волновую функцию какого-либо вида и с ее помощью вычислить энергию системы,
в чем можно быть уверенным? Каковы два метода определения наилучшей
пробной волновой функции выбранного вида? Почему вычисленная таким
образом энергия может еще значительно превышать истинную энергию
системы? В чем состоит метод Ритца? Что нужно определить для оценки
точности вариационных расчетов?
2. Возьмите пробную функцию вида ехр(—рг) и варьируйте р, с тем
чтобы найти основное состояние атома водорода. (Вид гамильтониана
можно найти в списке формул Г.1, разд. «Гамильтониан», а радиальную часть
лапласиана — в списке формул Л.1 разд. «Лапласиан».) Не забудьте
обеспечить нормированность функции, иными словами, минимизируйте по
параметру р выражение [ dx ф*#ф Д dx ф*ф. Повторите это упражнение с
пробной функцией вида ехр(—рг2). Теперь возьмите функцию вида р{ ехр (— р\г^\ +
+ р2 ехр (— P<2jF) и попытайтесь получить наиболее глубокий минимум.
Дайте графическое изображение вида трех найденных вами наилучших
пробных функций.
3. В методе Ритца выбирают пробную функцию вида J] р$ь и варьи-
руют параметры pi. Покажите, что условие минимума энергии достигается
в том случае, когда определитель \Нц — &Sij\ обращается в нуль (H{j —
интегралы \ dx i^tfify и S^ — интегралы \ dx tyfy). Минимальной энергии
соответствует наименьший корень этого определителя, называемого вековым
определителем (детерминантом). Воспользуйтесь вариационным методом
Ритца, чтобы показать, что в молекуле водорода атомные ls-орбитали дают
равные вклады в связывающую молекулярную орбиталь.
Рекомендуемые источники. Простое доказательство вариационного
принципа и вывод условий минимума см. в гл. 7 [1] и в кн. Коулсона [105J. Эти
же вопросы обсуждаются в кн. Эйринга, Уолтера, Кимбалла [137], Козмана
[217], Пилара [318] и Уилкокса [429]. Способы определения нижних границ
см. в кн. Лёвдина [258] и цитированных им работах.
53
в
ВЕКОВОЙ ОПРЕДЕЛИТЕЛЬ (ДЕТЕРМИНАНТ). При
построении молекулярной орбитали в виде линейной комбинации
атомных орбиталей мы пытаемся представить ее в виде суммы
Catya + Cbtyb + ..., где ф — атомные орбитали атомов a, ft и т. д.,
с — коэффициенты (их необходимо менять до тех пор, пока не
будет получен наилучший набор значений, который даст
наименьшую энергию). Перебирать различные случайные значения
коэффициентов с можно практически до бесконечности, поэтому
необходим метод, позволяющий быстро и точно находить их
оптимальный набор. Использование векового определителя
позволяет решить эту задачу.
В упражнениях, приведенных в конце раздела, мы попросим
вас показать, что наилучшая комбинация орбиталей
определяется одним из решений совместной системы уравнений, в
которые в качестве неизвестных входят коэффициенты с (см.
список формул В.З). Это так называемые вековые уравнения.
Каждое уравнение этой совместной системы уравнений имеет
нетривиальное решение в том случае, когда определитель
системы, составленный из величин, на которые умножаются
неизвестные коэффициенты с> равен нулю (тривиальное решение
соответствует случаю, когда все с сами равны нулю). Этот
определитель (детерминант) называется вековым (секулярным) (см.
список формул В.З). Если в расчет включены N атомных орбиталей,
вековой определитель обращается в нуль столько же раз, что
отвечает N различным значениям энергии системы. Самое
нижнее значение (наименьший корень определителя) можно
идентифицировать как минимальную энергию системы, которая
может быть получена в рамках рассматриваемой модели.
Значения коэффициентов с, которые соответствуют этому корню,
можно найти обычными методами (путем подбора или методом
Крамера, см. список формул В.З) и тем самым получить наилучшую
волновую функцию системы. Остальные N—1 корней отвечают
молекулярным орбиталям с большей энергией. Соответствующие
этим корням коэффициенты с позволяют определить вид
остальных N—1 молекулярных орбиталей.
Вековое уравнение приходится решать во всех тех случаях,
когда несколько орбиталей могут взаимодействовать между
собой. Если имеется возмущение, которое может смешивать одно
состояние с другим, истинное основное состояние системы лучше
всего искать в виде алгебраической суммы двух невозмущенных
состояний. Энергия такой системы определяется наименьшим
корнем векового определителя, а набор коэффициентов,
соответствующий этому корню, дает наилучшую возмущенную
волновую функцию. Подобные ситуации встречаются, например в тех
случаях, когда необходимо учесть взаимодействие
конфигураций, а также в методе Хюккеля для сопряженных молекул.
54
Список формул В.З
Вековой определитель
Прямой подход. Подставим в уравнение Шредингера Яг|э = ^Г-ф
волновую функцию в виде разложения:
N
*-Z«7*r w
Получим
N N
Z */*+/-Z*'/*/-0-
Умножим это равенство слева на -ф^ и проинтегрируем, в результате
получим
N
Z с! [НЦ ~ *Si,) -О С—1-2 Л0- (2)
/=1
где Я£/= \ ^т-ф^Я-ф^ и S^ = Wxfyfy. Выражение (2) представляет
собой систему из N уравнений относительно коэффициентов cf>
имеющую нетривиальные решения при условии, что
A-det|tf,/-*S„|-0. (3)
Раскрывая этот определитель, имеющий размерность N X W» и решая
уравнение (3) относительно <§, получим N собственных значений
гамильтониана Я. Вообще говоря, если N — ограниченное число,
собственные значения являются приближенными.
Каждому корню <8 уравнения (3) соответствует волновая функция
вида (1). Чтобы найти с„ воспользуемся методом Крамера (см. [266]
или [198]). Вводя обозначение k. = cjcy можно придать уравнению (2)
следующий вид:
N
Z */ [НЧ - *Sij\ - (*S,i - Н,х) (/ - 2, 3, ..., N).
/-1
Предположим, что D — определитель размерностью (N — 1) X (Я — 1),
построенный из элементов Я// - $Sih a D'*> (Л) — определитель,
полученный заменой л-го столбца определителя D на (#\S2i — #21,
^S31 — Я31, ..., &SN{— HNl). Тогда согласно правилу Крамера,
k. = D{»(h)/D. (4)
Это позволяет найти отношения с2/су ..., cN/cy Чтобы завершить
определение коэффициентов с,, воспользуемся условием нормировки
*? + <£+...+А-1.
Продолжение списка формул В.З
Описанная процедура позволяет найти коэффициенты с,,
соответствующие корню £Г, и она должна быть проделана для каждого из корней
уравнения (3).
Вариационный подход. Минимизируем & путем варьирования
коэффициентов С£
& = \ сГт-фЯ-фД Ghr-фф
Условие (д&/дсЛ = 0 удовлетворяется, если
Е^(Я(,-^,) = 0' (5)
(Убедитесь в этом, подставляя в выражение для & (1), дифференцируя
его и проводя несложные алгебраические преобразования.) Полученное
выражение тождественно выражению (2), и дальнейшая процедура
аналогична используемой при прямом подходе.
Пример. Для N=^2 вековые уравнения имеют вид
с, (Нп - &Su) + с2 (Я12 - &Sl2) - 0\
С\ (И21 — &S22) + С2 (П22 — &S22) =* О J
а вековой определитель выглядит так:
__ I Н\\ — &S\\ #12 — &S\2 I
I H21 — &S21 H22 — 0S22 I
Корни определителя Л являются корнями уравнения
(S11S22 ~~ 5i2S2l) &2 + (^i2S2l + n2iS\2 — H22S\\ — H\iS22) & +
+ (#11#22-#12tf2i)s==0,
и наименьший из них дает минимальное значение 8. Коэффициенты с
определяются с помощью выражения £ = Я22 — ^522, уравнения (4)
&2 (^22 — &S22) —.— (^21 — ^52l)
и нормировочного соотношения
с?+ 4-1.
В частном случае, когда Sn = S22 = 1; 5i2 = S2i = 0, решение можно
представить в виде
#и> = яп — я12 ctg е, -ф(1) =» -ф, sin e — -ф2 cos e,
#(2)=^22 4^12ctge, V2) = *icosе + -ф2sine,
Где 0 = 1 arctg [2Я12/(Яи - Я22)].
в
Вековой определитель получил такое название по аналогии
с определителями, используемыми в классической механике и
особенно в механике небесных тел. Вековыми изменениями
движения тел, например планетарных орбит, называют такие
изменения, которые нарастают постепенно, в течение долгого
времени (saeculum — по латыни означает «век», «поколение»), в
противоположность изменениям, которые происходят быстро или
периодически и не накапливаются. Какое, однако, все это имеет
отношение к определению строения молекул? Дело в том, что
вариационный метод можно связать с теорией возмущений и что
з вариационном методе рассматриваются как раз те возмущения,
которые накапливаются и дают набор орбиталей с
определенными расстояниями между их энергетическими уровнями.
Особенно четко это видно в теории возмущений для случая
вырожденных состояний, с которой приходится сталкиваться (не
называя это столь сложным образом) в теории молекулярных
орбиталей. Например, если рассматривается гомоядерная
система, метод молекулярных орбиталей эквивалентен теории
возмущений для вырожденных состояний. Действительно, в
отсутствие взаимодействия между атомами все атомные орбитали
с одинаковыми квантовыми числами, комбинации которых дают
затем молекулярные орбитали, соответствуют одному и тому же
вырожденному энергетическому уровню. Влияние межатомного
взаимодействия подобно влиянию возмущения на эту
вырожденную систему. Представим себе, что атомы расположены так же,
как в молекуле, но взаимодействие между ними отсутствует,
а затем будем постепенно включать взаимодействие. По мере
накопления возмущения энергетические уровни различных
линейных комбинаций атомных орбиталей будут расщепляться до
тех пор, пока расстояния между ними не совпадут с
имеющимися в молекуле. Таким образом, в этом случае мы
действительно имеем дело с сильным вековым возмущением атомных
орбиталей, а расстояние между уровнями можно найти с
помощью векового определителя.
В обычной теории возмущений также используется термин
«секулярный». Выражение для энергии, с точностью до второго
порядка по некоторому возмущению состоит из слагаемого, в
которое входит только начальное состояние системы (см. список
формул В.6), и слагаемого, учитывающего виртуальные
переходы в возбужденные состояния. Первое слагаемое соответствует
вкладу секулярной составляющей возмущения, или секулярному
возмущению, тогда как последнее соответствует вкладам несе-
кулярных составляющих.
Упражнения, В вариационном методе система, включающая две орби*
тали, описывается линейной комбинацией этих орбиталей вида \|)=*£ -ф +cbtyb,
57
в
с помощью которой рассчитывается минимальное значение выражения
8 = \d% фЯ'фЛ di \|)i|>. Покажите, что экстремальные значения этого
выражения соответствуют решению системы двух уравнений (Наа — &Saa) ca +
+ (НаЬ - $ Sab) cb - 0 и (Ны - *Sba) са + (Hbb - *SW) ^ - 0, где ЯвЬ
Sa& и т. д. — некоторые интегралы. Получите для этой задачи вековой
определитель и найдите его решения. Найдите выражения для двух
наборов коэффициентов с, соответствующих нижнему и верхнему значениям
энергии. Примените эти расчеты к молекуле Н2, отождествляя t|> и г|).
с ls-орбиталями ядер а и Ь соответственно и полагая Saa = S^ = 1, Наа =
= Нъъ = а и Наь == Нъа = Р- Предположите также, что Sa$ = 0. Теперь
обобщите расчеты на орбитали вида catya + cb$b + ... cNtyN и покажите, что
решение вариационной задачи приводит к определителю размерности N X N.
Обычно для интегралов входящих в вековые определители, используются
приближенные значения. Такой подход характерен для метода Хюккеля и
других аналогичных методов (см. разд. «Хюккеля метод»).
Рекомендуемые источники. См. гл. 7 и 10 [1]. В гл. 7 рассматривается
теория возмущений для вырожденных состояний, а в гл. 10 — применение
метода векового определителя к различным задачам определения строения
молекул. Более подробно этот вопрос обсуждается в кн. Коулсона [105], Стрейт-
визера [387], Полинга и Вильсона [314], Эйринга, Уолтера, Кимбалла [137],
а также Пилара [318] и Мак-Глина, Ванквикенборна, Киноситы и Кэрролла
[273]. См. разд. «Хюккеля метод». «Конфигурационное взаимодействие» и
«Возмущений теория».
ВЕКТОРНАЯ МОДЕЛЬ АТОМА. Векторная модель атома
основана на рассмотрении векторного сложения угловых
моментов электронов в атоме. Согласно этому методу, состояние с
угловым моментом [/i(/i + 1)],/2й изображается вектором ji длиной
t/i(/i +1)]!/*> направленным соответствующим образом. Если
проекция углового момента на некоторую произвольную ось z
точно определена и имеет величину mfi, направление вектора
должно быть таким, чтобы его проекция на эту ось имела длину
т. Поскольку такой угловой момент прецессирует вокруг оси г,
вектор изображают лежащим на конусе при некотором
произвольном, но неопределенном значении азимутального угла
(рис. В.З).
Если имеется и второй вектор j2> полный угловой момент
системы может быть построен в виде суммы двух векторов,
представляющих два момента. Поскольку длина суммарного вектора
должна быть равна [/(/+ 1)]Ч где / выбирается из набора
величин ]\ + /2> h + /2 — 1, ..., | /i — /21 (см. «Угловой момент»),
существует только несколько разрешенных ориентации векторов
ji, J2 и их сумм j. Согласно математической теории углового
момента, векторы ji и j2 прецессируют вокруг своей суммы, а
последняя прецессирует вокруг некоторой произвольной оси г. Эта
58
Рис. В.З. Векторная модель углового
момента.
'классическая
траектория
Рис В.4. Сложение ji и j2 в~
векторной модели.
€FT)
Рис. В.5. Сложение /i=2 и /2 = 1,
приводящее к сумме / = 3, 2, 1
Векторное построение выполнено
сплошными линиями, а приближенная оценка
с использованием отрезков длины /ь
]2> / — пунктирными линиями.
в
прецессия и сложение векторов изображены с помощью
векторных диаграмм на рис. В.4 и В.5. Процесс сложения моментов
позволяет определить все комбинации отдельных спиновых и
орбитальных вкладов, приводящие к полному угловому моменту
атома. К счастью, эта громоздкая задача может быть
существенно упрощена. Во-первых, упрощение связано с тем, что остов
атома (электроны всех оболочек, кроме валентной) имеет
нулевой угловой момент, поскольку спины всех электронов спарены
и оболочки полностью заполнены. Следующее упрощение
основано на предположении о существовании двух идеальных схем
сложения угловых моментов.
1. Схема Рассела—Саундерса, или схема LS-связи, исходит
из предположения, что спин-орбитальное взаимодействие
слишком мало и может учитываться после того, как все орбитальные
моменты слагаются в результирующую сумму L, а все спиновые
моменты — в некоторую сумму S. Орбитальное движение
электронов находится под влиянием электростатического
межэлектронного взаимодействия, которое и является причиной связи
орбитальных угловых моментов. Для двух электронов сложение
li и Ь может быть представлено с помощью диаграммы типа
приведенной на рис. В.6, а. Два спина складываются в
результирующую сумму S; энергия спин-спинового взаимодействия
электронов обусловлена зависящей от спинов обменной энергией,
поэтому такая связь также является электростатической. На
следующем этапе два суммарных момента L и S складываются
вместе и дают в сумме J — полный угловой момент; сила этого
взаимодействия определяется силой спин-орбитальной связи.
2. Если спин-орбитальная связь сильнее, чем
электростатическое взаимодействие, схема Рассела—Саундерса нарушается,
поскольку спиновые и орбитальные моменты отдельных электронов
прежде всего принимают подходящую взаимную
ориентацию. Схема //-связи описывает предельный случай такого рода.
В этой схеме спин каждого электрона складывается с его
орбитальным моментом; например, li и Si дают в сумме ji. Эти два
слагаемых быстро прецессируют вокруг своей суммы, что
характерно для сильно взаимодействующих пар'угловых моментов.
Далее, суммарный момент ji складывается с другим моментом j2
и получается полный угловой момент J; связь моментов на этом
последнем этапе значительно слабее, поскольку она
определяется электростатическим межэлектронным взаимодействием.
Нетрудно видеть, что, хотя полный угловой момент, полученный
указанным образом, может совпадать с полным угловым
моментом, полученным по схеме Рассела — Саундерса, обе схемы
приводят к разным состояниям атома с различными энергиями.
К сожалению, ни одна из рассмотренных схем не дает
точного представления об истинном положении дел, потому что
60
в
всегда существует некоторая конкуренция между различными
типами взаимодействия. Очевидно, что в одном и том же атоме
разные электроны взаимодействуют но разным схемам. Тем не
Рис. В.6. Рассел-саундеровская или LS-связь (а) и //-связь (б).
менее для легких атомов, у которых невелики постоянные спин-
орбитального взаимодействия, схема Рассела — Саундерса
позволяет дать описание поведения валентных электронов. В
тяжелых атомах, у которых постоянные спин-орбитального
взаимодействия значительно больше, часто преобладает //-связь.
Следовательно, волновые функции, соответствующие схеме
Рассела — Саундерса, могут служить хорошим начальным при
ближением для более сложных расчетов легких атомов.
61
в
Угловые моменты, к которым приводит векторная модель,
используются при обозначении состояний атомов символами
термов.
Упражнения. Что представляет собой векторная модель атома? Каковы
основные положения этого метода? Чему равны длины векторов,
изображающих орбитальный угловой момент электрона на S-, р- и d-орбитали
соответственно? Какова длина вектора, изображающего спин электрона? Постройте
векторные диаграммы сложения спинового и орбитального угловых моментов
электрона на р-орбитали. Какова природа их взаимодействия? Какие
предположения можно сделать, чтобы упростить рассмотрение сложения угловых
моментов в атомах? Покажите с помощью векторного построения, что
угловой момент заполненной /(-оболочки (Is2) равен нулю. Что является
причиной взаимодействия между орбитальными моментами электронов? Что
является причиной взаимодействия спинов? При каких условиях следует
использовать схему связи Рассела — Саундерса? При каких условиях вместо
схемы Рассела — Саундерса следует использовать схему //-связи?
Существуют ли еще какие-нибудь возможности? Можно ли использовать символы
термов, основанные на схеме Рассела — Саундерса, если известно, что
преобладает //-связь?
Рекомендуемые источники. Дальнейшее обсуждение векторной модели
атома и двух схем связи см. в гл. 6 и 8 [1]. Хороший обзор дан в § 11.2 кн.
Герцберга [185], гл. V кн. Уайта [425], в § 3.4 кн. Кинга [222] и в гл. 12 кн.
Куна [229]. В кн. Кэндлера [89] основное внимание уделяется описанию
атомов с помощью векторной модели. Применительно к молекулам этот вопрос
обсуждается в разд. «Гунда случаи связи».
ВЕРОЯТНОСТЬ ПЕРЕХОДА. Вероятность перехода —это
вероятность того, что система перейдет из одного состояния в
другое. В частности, вероятность перехода определяет
интенсивность спектральных линий и, следовательно, природу красок.
Квантовомеханическое рассмотрение вероятности перехода
обычно основано на теории возмущений. Действующее на молекулу
осциллирующее электромагнитное поле слегка искажает ее, и
это искажение может быть истолковано как примесь
возбужденных состояний к исходному состоянию молекулы. Поскольку
волновая функция в этом случае содержит компоненты
возбужденных состояний, существует отличная от нуля вероятность
перехода в эти состояния.
Вероятность перехода зависит от силы света (энергии
возмущения), от соответствия между частотами возбуждающего
излучения и возбуждаемого перехода (поскольку взаимодействие
сильнее в случае резонанса) и от силы взаимодействия между
молекулой и электромагнитным полем. Последняя связана с ди-
польным моментом перехода (см. разд. «Электрический диполь-
ный переход»), который, по сути, является мерой смещения
заряда во время перехода: если это смещение велико, сила взаимо-
62
в
действия поля с молекулой тоже велика и спектральная линия
оказывается интенсивной.
В качестве примера рассмотрим возбуждение атома
водорода. При его возбуждении с уровня Is на уровень 2pz
происходит изменение распределения заряда от сферического к
вытянутому вдоль оси г. Указанный переход можно представить себе
как колебания заряда вдоль оси г. Дипольныи момент,
связанный с этим движением, обусловливает появление яркой
спектральной линии. В то же время, хотя переход ls->2s связан со
значительной миграцией заряда, она происходит с сохранением
его исходной сферической симметрии. Следовательно, в данном
случае дипольныи момент, связанный с осцилляциями из одного
состояния в другое, отсутствует, свет не взаимодействует с
атомом и такой переход не проявляется в спектре.
Список формул В А
Вероятность перехода
Золотое правило Ферми:
Скорость перехода (скорость изменения вероятности) для миграции
системы из состояния / в состояние / под действием возмущения V
определяется выражением
*H.|-(2*/»)|Vf/pP(V),
где Vf. = (tyf | V | -фЛ и р (vft.) — плотность энергии падающего
излучения при частоте перехода vfi.
Электрические дипольные переходы:
где В — коэффициент Эйнштейна для вынужденного поглощения или
излучения. Полная скорость излучения определяется выражением
^f^i-^if + Bif9(vfi)t
Ац = 8nh (Vfi/c)3 Bft (в общем случае),
Ац=* (8я2/3е0с3й) v^ | df( |2 (для электрического дипольного перехода)
Дипольныи момент перехода:
йц = \ di^d^i, d= — er.
Математическое выражение для определения вероятности
перехода называется золотым правилом Ферми (см. список
63
в
формул В.4). Это выражение включает произведение квадрата
дипольного момента перехода между состояниями (диполь
вызывает изменения амплитуды волновой функции, а для того чтобы
получить вероятность перехода, надо взять ее квадрат) и
плотности энергии излучения на частоте перехода (чем мощнее
стимулирующее воздействие излучения, тем больше вероятность
перехода). Золотое правило Ферми можно получить с помощью
теории возмущений, зависящих от времени.
Описанный подход к рассмотрению вероятностей переходов
лежит в основе правил отбора, которые позволяют предсказать,
вероятность каких переходов отлична от нуля. Величину
дипольного момента перехода часто оценивают с помощью таких
понятий, как сила осциллятора или коэффициенты Эйнштейна А и В.
Последние удобным образом связаны с коэффициентами экс-
тинкции, которые являются используемой на практике мерой
интенсивности спектральных линий.
Упражнения. 1 Что определяет вероятность перехода? Каким образом
использование теории возмущений, зависящих от времени, позволяет
описывать спектральные переходы? На какой частоте происходит наиболее
сильное поглощение? Что такое дипольный момент перехода? Какому из
следующих переходов соответствует отличный от нуля дипольный момент: ls->2px,
ls->3p*, 2px-+3dXy, 2px-+2pz, 2p2->3p2? Определите моменты переходов
\s-+2px и ls->2py, связанных с излучением света. Можно ли ожидать, что
поляризация света в этих двух случаях будет различной?
2. При переходе из состояния, описываемого функцией г|э* в состояние,
описываемое функцией г|э/, ^-компонента дипольного момента перехода dft
равна интегралу — е \ d% г|^гф£; аналогичными выражениями
определяются его у- и г-компоненты. Вероятность перехода пропорциональна
|d/t|2. Покажите, что для каждого перехода интенсивность вынужденного
поглощения равна интенсивности вынужденного излучения. Рассчитайте
дипольный момент перехода частицы в одномерной прямоугольной яме из
основного в первое возбужденное состояние (воспользуйтесь сведениями,
содержащимися в списке формул. Ч. 1.) Используя данные табл. 11, 14 и 15,
рассчитайте интенсивности переходов из основного состояния одномерного
гармонического осциллятора в его первое и второе возбужденные состояния, а
также интенсивность перехода ls->2/?z в атоме водорода.
Рекомендуемые источники. См. гл. 7 и 11 [1]. Вероятности переходов
описаны в кн. Эйринга, Уолтера, Кимбалла [137], Гайтлера [180], Козмана [217]
И в классических монографиях; по квантовой теории: см. Давыдов [118],
Шифф [356], Мессиа [282]. Вероятности переходов рассматриваются также в
следующих разд.: «Правила отбора». «Сила осциллятора», «Коэффициенты
Эйнштейна А и В», «Поляризуемость», «Межмолекулярные взаимодействия».
Этот вопрос в простой доступной форме обсуждается также Лудоном [256].
64
ВЕТВЬ. Вращательные переходы, происходящие, когда
молекула совершает колебательный переход, вызывают появление
в ее спектре структуры, в которой могут быть выделены
отдельные группы линий. Если вращательное квантовое число
молекулы изменяется от / до /— 1, такие линии составляют Я-ветвь;
если / не меняется, линии образуют Q-ветвь; линии,
соответствующие переходу /->/_+ 1, составляют /?-ветвь. В спектрах
J
4
Рис. В.7. Образование Р-, Q-, /?-
ветвей; #-ветвь имеет кант,
который возникает, когда
вращательная постоянная на верхнем
уровне меньше, чем на нижнем.
2_
*L
р^
i
я
i i
Лд 1 II
^-*-
Til
I
/
-V-*
хпнт
комбинационного рассеяния колебательные переходы могут
сопровождаться изменениями вращательного квантового числа на
±2: получающиеся линии образуют Q- и S-ветвь (для /->/ — 2
и /->/ + 2 соответственно). Q-ветвь
колебательно-вращательных спектров отсутствует, когда молекула не имеет компоненты
углового момента, направленной вдоль ее оси симметрии.
Поэтому в спектрах почти всех двухатомных молекул нет Q-ветви.
Исключение составляют те молекулы (например, N0), которые
имеют составляющую орбитального электронного углового
момента в направлении межъядерной оси. На рис. В.7 показаны
Р-9 Q- и /?-ветви и объяснены причины их появления, а энергии
переходов даны в списке формул В.5.
С5
в
Список формул В.5
Вращательные ветви
Обозначения: У — вращательное квантовое число верхних состояний,
У — вращательное квантовое число нижних состояний
В' — вращательная постоянная верхнего состояния.
В" — вращательная постоянная нижнего состояния.
hv — энергия колебательного перехода
R-ветвь (с более высокой энергией; А/ = + 1; /' = /" + 1):
АЕ = hv + 2В' + (ЗВ' - В") /" + (В' - Вп) Г2 = hv + R (/")•
Q-ветвь (А/ = 0; Г = Г):
А£ = hv + (В7 - В") Г + (В' - В") Г2 = hv + Q (/')
Р-ветвь (с более низкой энергией; Д/ = —1; /' = /" — 1):
AE = hv- (В' + В") /" + (В' - В") Г2 = hv + P (/").
Если В' < В", #-ветвь может образовать кант; если В' > В" Р-ветвь
может образовать кант.
Комбинационные разности:
#(/")-P(/") = 4B'(/" + V2),
# (/" - 1) - Р (/" + 1) = 4В" (/" + V»).
Если верхнее и нижнее колебательные состояния имеют
различные моменты инерции (что особенно вероятно, когда более
высокое колебательное состояние относится к возбужденному
электронному состоянию молекулы), расстояние между линиями
ветви изменяется в зависимости от /. В двухатомных молекулах
момент инерции более высокого колебательного состояния
обычно превосходит момент инерции более низкого состояния, и в
этом случае линии #-ветви с увеличением / сгущаются и могут
даже образовать так называемую голову (или «кант») полосы
при высокой частоте. Причину такого поведения можно
объяснить тем, что при высоких / член (В' — В )Р (см. список
формул В.5) становится больше члена (W' — B")J. В таком случае
о #-ветви говорят, что она «оттенена в красную сторону». Когда
момент инерции в более высоком колебательном состоянии
уменьшен, «голова» (или «кант») полосы появляется у Р-ветви,
и она «оттенена в фиолетовую сторону».
Для определения вращательных постоянных используется
метод комбинирования разностей. Выбрав подходящие пары
линий в R- и Р-ветвях и построив график зависимости разности
их энергий от /", по наклону линии находят 5' или В".
Упражнения. Что называется ветвью колебательного спектра? Какова
классификация ветвей? Каким вращательным переходом они соответствуют?
66
в
При каком условии в спектре имеется Q-ветвь? Почему Q-вегвь должна
состоять из ряда очень близко расположенных линий? Исходя из того, что
энергетические уровни вращающейся двухатомной молекулы определяются
выражением £(v, /) = (v + 1/2)Ь(й + BVJ(J + 1), объясните, почему
вращательная постоянная В должна быть помечена колебательным квантовым
числом v и выведите выражение для энергии переходов Р-, Q-, /?-ветвей
вращающейся молекулы. Какую спектроскопическую информацию можно
получить, изучая структуру ветвей? Предположим, что В зависит от электронного
состояния молекулы. Выведите выражения, приведенные в списке формул В.5
для перехода, включающего электронное, колебательное и вращательное
возбуждение, и найдите такое значение /, при котором может образоваться
«кант» (предположите сначала, что Г > /", а затем, что V < /", где / —
момент инерции).
Рекомендуемые источники. Обсуждение вращательной структуры спектра
см. в [1], гл. 10. Рассмотрение колебательно-вращательных спектров молекул,
примеры структуры ветвей и оценка информации, которую они могут дать,
приведены Уитли [421], Барроу [51], Уиффеном [424], Кингом [222] и Герцбер-
гом [187].
ВИГНЕРА КОЭФФИЦИЕНТЫ. Коэффициенты Вигнера,
Клебша — Гордона, или коэффициенты векторного сложения —
это коэффициенты разложения состояния с суммарным угловым
моментом по состояниям, которые соответствуют
складывающимся угловым моментам.
В качестве примера рассмотрим образование синглетного
состояния при сложении электронных спинов аир. Состояние со
спаренными спинами можно выразить в виде линейной
комбинации произвольных (не имеющих определенного суммарного
момента) состояний, в которых спин 1 имеет ориентацию а, а спин
2 — ориентацию р, и наоборот. Синглетное состояние
представляется в виде (1/д/2) [а (1)Р (2)— р(1) а (2)]. Следовательно,
коэффициент Вигнера для произвольного состояния а(1)р(2) равен
1/д/2, а коэффициент Вигнера для состояния Р(1)а(2) равен
— 1/д/2.Если мы попытаемся построить из этих двух
произвольных состояний одну из компонент триплетного состояния, то,
взяв оба коэффициента равными + 1/д/2, получим при этом
функцию (1 /д/2) [а (1) р (2) + Р(1)а(2)], соответствующую
состоянию триплета с Ms = 0. Коэффициенты Вигнера позволяют
записать все такие линейные комбинации, соответствующие
различным результатам сложения угловых моментов.
Коэффициенты Вигнера для состояния с суммарными
квантовыми числами /, т, построенного из состояний с квантовыми
числами /ь Ш\ и /2, /п«, обозначаются символами (jifn{j2m2\jm).
Модификация этих коэффициентов, которая благодаря большей
симметрии более удобна в использовании, называется З/'-симво-
лами.
67
в
Рекомендуемые источники. Свойства коэффициентов Вигнера см. у
Бринка и Сэтчлера [80], Роуза [347] и Эдмондса [131]. В кн. Хейне [177]
приведена таблица этих коэффициентов Удобные таблицы числовых значений
З/'-символов приведены Ротенбергом, Бивиисом, Метрополисом и Вутеном
[349].
ВИРИАЛА ТЕОРЕМА. В самой простой форме теорема
вириала утверждает, что если потенциальная энергия системы
подчиняется закону 1/г, то средняя кинетическая энергия связана
со средней потенциальной энергией выражением (Т) = —1/2{V).
Из этого в свою очередь следует, что полная энергия системы
равна просто 1/г(1/), или —(Г). В более общей форме теорема
вириала утверждает, что, если потенциальная энергия
изменяется по закону гп, средняя потенциальная энергия и средняя
кинетическая энергия связаны соотношением (Т) = l/2ti{V). Так,
для гармонического осциллятора, у которого потенциальная
энергия является параболической функцией (я = +2), средние
потенциальная и кинетическая энергии связаны соотношением
(Т) = {V), и это равенство является еще одним проявлением
высокой степени симметрии гармонического осциллятора.
Теорема вириала применима к связанным стационарным системам, но
если под средними значениями подразумевать еще и средние во
времени, то она становится применимой и к нестационарным
состояниям.
Термин «вириал» (производное от латинского vis, vires —
сила, силы) заимствован из классической механики, где он
обозначает скорость изменения среднего значения произведения
г.р, здесь г — радиус-вектор положения частицы и р — ее
импульс. Это приводит к уравнению {Т) = —V2(F.r), называемому
вириальной теоремой Клаузиуса (здесь F — действующая сила).
Из этого выражения можно получить в общем виде уравнение
состояния реального газа (между частицами которого действуют
силы); это приводит к вириальному разложению и
термодинамическим вириальным коэффициентам. Теорему вириала можно
также вывести квантовомеханически и применить к обсуждению
строения и свойств атомов и молекул. Например, проверкой того,
насколько точны вычисленные волновые функции, может
служить требование, чтобы ожидаемые значения операторов
потенциальной и кинетической энергии действительно удовлетворяли
теореме вириала. Важно помнить, что теорема вириала
накладывает ограничения на то, каким образом должны изменяться
кинетическая и потенциальная энергии при любом искажении
волновых функций. При некоторых обстоятельствах теорема
вириала может использоваться вместо вариационной теоремы.
Можно провести дальнейшее обобщение теоремы вириала и
получить гипорвириальные теоремы. Так называется набор
теорем, рассматривающих обращение в нуль среднего значения
68
в
коммутатора какого-либо оператора с гамильтонианом системы,
если система находится в собственном состоянии этого
гамильтониана.
Упражнения. Используя волновые функции, приведенные в табл. 11 и 15,
продемонстрируйте справедливость теоремы вириала для основных состояний
гармонического осциллятора и атома водорода. Вернитесь к расчетам
основного состояния атома водорода с помощью вариационного принципа и
выясните, выполняется ли теорема вириала при аппроксимации его волновых
функций с помощью гауссовых орбиталей.
Рекомендуемые источники. Теорема вириала в классической механике
хорошо разобрана Голдстейном [166], который дает вывод теоремы и
рассматривает некоторые примеры ее применения. Вывод законов газового
состояния см. у Линдсея [248]. Вывод квантовомеханической теоремы вириала
приводится Гиршфельдером [191], им же дается вывод и описание гипервириаль-
ных теорем. Применение теоремы вириала к расчетам строения атомов и
молекул описано Коулсоном [106], Дебом [120] и Файнбергом, Рюденбергом и
Мехлером [140].
ВИРТУАЛЬНЫЙ ПЕРЕХОД. Когда на систему действует
возмущение, например внешнее электрическое поле, в ней
происходят изменения. Измененная система может быть описана
суперпозицией волновых функций состояний исходной системы.
Следовательно, система ведет себя так, как будто ей присущи
черты возбужденных состояний; говорят, что она совершает при
этом виртуальные переходы в возбужденные состояния. Когда
световая волна рассеивается на молекуле, искажение, которое
эта волна вызывает, можно рассматривать как ряд виртуальных
переходов в возбужденные молекулярные состояния, вызванных
виртуальным поглощением фотона. Это искажение немедленно
исчезает, и от молекулы отлетает фотон, оставляя ее либо в
исходном состоянии (релеевское рассеяние), либо в одном из
возбужденных состояний, заселенных в результате виртуального
перехода (комбинационное рассеяние).
По мере того как частота падающего света приближается к
частоте одного из молекулярных переходов, переход постепенно
теряет свой виртуальный характер и становится реальным:
молекула действительно возбуждается и фотон действительно
поглощается. В реальных переходах энергия сохраняется, но,
поскольку «виртуальный переход» — это просто название способа
описания искажения и учета влияния возмущения, при
виртуальных переходах энергия не сохраняется.
Упражнения. Что такое виртуальный переход? Чем он отличается от
реального перехода? Когда виртуальный переход приобретает характер
69
в
реального перехода? Сохраняется ли энергия при виртуальном переходе?
Какие виртуальные переходы происходят, когда на атом водорода действует
электрическое поле?
Рекомендуемые источники. Обсуждение теории возмущений и
сопутствующее обсуждение виртуальных переходов см. в гл 7 [1]. При рассмотрении
теории возмущений неизбежно приходится иметь дело с виртуальными
переходами, хотя сам этот термин не всегда используется. См Давыдов [118],
Дирак [123], Ландау и Лифшиц [233], Мессиа [282], Шифф [356]. Вопрос о
трансформации виртуальных переходов в реальные рассматривается в кн. Гайтлера
[180] и Хамеки [172]. См. разд. «Комбинационное рассеяние» и «Штарка
эффект».
ВОЗМУЩЕНИЙ ТЕОРИЯ. Большинство представляющих
интерес квантовомеханических систем описывается уравнением
Шредингера, которое слишком сложно для того, чтобы можно
было получить его точное решение. Однако при тщательном
рассмотрении задачи часто оказывается, что какая-то более
простая, допускающая точное решение система очень похожа на
истинную, для которой не удается получить точное решение. Если
известны волновые функции и энергетические уровни этой более
простой системы, их можно изменить так, чтобы в результате
этого они стали ближе к истинным волновым функциям и
энергиям. Если истинная система очень похожа на простую,
изменения могут быть совсем небольшими и их можно рассматривать
просто как возмущения характеристик простой системы.
Видоизменение волновой функции простой системы достигается
примешиванием к ней в соответствующих пропорциях других
волновых функций той же простой системы. Теория возмущений дает
рецепт такого смешения и позволяет вычислять дополнительные
слагаемые, которые необходимо прибавить к энергии простой
системы, чтобы получить энергию истинной системы.
При расчетах в первом порядке теории возмущений
волновую функцию г|)0 простой системы следует заменить на г|)о +
+ с\^\ + ^2 + • • •, где г|)п — различные волновые функции
модельной системы, которым соответствуют энергии £п, а
коэффициенты сп определяются отношением «силы возмущения» к
разности энергий £о — Еп. «Сила возмущения» представляет собой
разность энергий истинной и простой систем и определяется
матричным элементом гамильтониана возмущения, т. е. разностью
гамильтонианов истинной и модельной систем. Полученная
таким образом волновая функция называется волновой функцией
в первом порядке теории возмущений. Рассмотрим, например,
искажение основного состояния атома водорода внешним
электрическим полем (эффект Штарка). Модельной системой в этом
случае является атом водорода в отсутствие внешнего поля. Его
волновые функции и энергии хорошо известны. Искажение (по-
70
в
ляризацию) атома внешним полем можно учесть, если к
основному состоянию примешать 2/?2-орбиталь, а также 3/?2-орбиталь
и т. д. Коэффициент, сопутствующий каждой примешиваемой
орбитали, определяется отношением энергии возмущения к
разности между энергетическими уровнями (Еи — Е2р, Еи—
— £3р, ...)• Энергией возмущения в данном случае является
энергия электрического взаимодействия ezE, которая получается
из выражения —d.E для энергии диполя d в электрическом поле
напряженностью Е. Вклад каждой орбитали в смесь волновых
функций определяется квадратом сопутствующего ей
коэффициента смешивания (см. разд. «Суперпозиции принцип»),
поэтому ясно, что в смеси будут заметно представлены только те
орбитали, уровни которых лежат достаточно близко к энергии
ls-состояния. Этот результат приводит к общему выводу теории
возмущений: чем больше расстояние между энергетическими
уровнями модельной системы, тем меньше смешивание.
Следовательно, если все уровни энергии модельной системы лежат
значительно выше ее основного состояния, то такая система не
может быть сильно искажена. Поэтому она должна быть очень
похожа на истинную систему. Напротив, если возмущение
слишком велико (т. е. если истинная и модельная системы резко
отличаются), возможно очень сильное смешивание состояний и
теория возмущений первого порядка неприменима. В таком
случае остается выбрать более подходящую модельную систему.
Следует отметить, что метод теории возмущений позволяет
сразу же получить правильный вид истинных волновых функций,
поскольку этот метод указывает правильное направление
искажения простых функций. Совсем иначе обстоит дело при
использовании вариационного метода для приближенного построения
волновых функций, где окончательный вид функции зависит от
исходного выбора формы (и, следовательно, достаточной
«гибкости») пробной функции.
Можно также рассчитать изменение энергии, вызванное
возмущением. Хотя иногда достаточно учесть лишь поправку
первого порядка к энергии, обычно все же необходимо
рассчитывать еще поправку второго порядка. Чтобы вычислить поправку
первого порядка, достаточно найти среднее значение энергии
возмущения по невозмущенным волновым функциям модельной
системы. Поправка второго порядка к энергии вычисляется с
учетом искажения волновых функций модельной системы под
влиянием возмущения: сначала следует определить искажение
волновых функций, а после этого вычислить среднее от энергии
возмущения по этим искаженным волновым функциям. Термин
«второй порядок» как раз и отражает тот факт, что возмущение
учитывается дважды.
71
в
Полезной аналогией, позволяющей понять, как применяется
теория возмущений, является задача об искажении движения
скрипичной струны, вызванном подвешиванием к ней грузиков.
Если грузики прикреплены к струне в узловых точках ее
колебаний, они не влияют ни на ее энергию, ни на движение.
Грузики, прикрепленные к струне в местах пучностей колебаний
(т. е. к точкам, в которых амплитуда колебаний максимальна),
могут оказать значительное влияние на энергию и форму
колебаний струны. Поправку первого порядка к энергии можно
найти, усредняя влияние грузиков (т. е. возмущение) по
«волновой функции» (в данном случае — по смещениям струны при
колебаниях). Грузики искажают также форму колебаний
струны: узловые точки слегка сдвигаются и колебания перестают
быть чисто синусоидальными. Такие искаженные колебания
можно воспроизвести, подобрав подходящую суперпозицию
гармоник ненагруженной струны. Если грузики не слишком велики,
для хорошего описания искаженных колебаний достаточно
включить в суперпозицию всего несколько гармоник. Поправку
второго порядка к энергии колебаний струны можно получить,
усредняя влияние грузиков по искаженным колебаниям. Эту
поправку второго порядка следует прибавить к поправке первого
порядка, а их сумму — к исходной колебательной энергии
ненагруженной струны, и в результате мы получим хорошее
приближение к истинной энергии нагруженной струны.
Величина искажения энергии, обусловленного энергией
возмущения Я, имеет порядок ~Р для поправки первого порядка
и ~Р2/Д для поправки второго порядка, где А — характерное
расстояние между энергетическими уровнями невозмущенной
системы. Часто оказывается, что из-за наличия симметрии у
системы поправка первого порядка к энергии равна нулю. В
поправку первого порядка к волновой функции входят
коэффициенты порядка Р/А, поэтому вклады примешанных состояний
имеют порядок Р2/Д2. Обычно теорией возмущений можно
пользоваться при условии, что Р много меньше Д, т. е. |Р/Д| <С 1.
Важно отметить, что поправку второго порядка к энергии можно
вычислить по волновым функциям, включающим лишь поправку
первого порядка; в общем случае поправку я-го порядка к
энергии вычисляют по теории возмущений с помощью волновых
функций (я— 2)-го порядка. Поэтому, получив хорошее
значение энергии, следует помнить, что волновые функции могут быть
все еще слишком плохими. С другой стороны, можно с
некоторым удовлетворением отметить, что хорошие значения энергии
удается получить с помощью недостаточно точных волновых
функций. Например, волновые функции, точность которых не
превышает 10%, позволяют определить энергию с точностью
до 1%.
72
Список формул В.6
Теория возмущений
Предположим, что нам известны собственные значения и собственные
функции гамильтониана Я<0):
и необходимо определить энергии и собственные функции
гамильтониана Я:
Н=*НМ +Я*1) +Я<2>,
где #W — поправка первого порядка малости (порядка % по
некоторому малому параметру X), а Н® — поправка второго порядка малости
(порядка Я2). Истинные энергии и волновые функции записываются
в виде
*ж-*8» + *й> + 1г8?+....
♦„ =+2?++£>+ **+....
Энергия и волновая функция нулевого приближениях
££> = «> I Я<»> |ф<о>> и *£'
соответственно.
Поправки первого порядка:
^т - /-» Л ' I (£(0) - Ei0)) У
Поправки второго порядка:
Теория возмущений, зависящих от времени:
Предположим, что Н = Н^ + Я(1) (t), и запишем волновые функции
в виде
*т (о = 2>« м ^ о. *<»> w = €> «ф (- 1ф/и).
п
Тогда
еЛ (0 = в„ (0) - (//») £ J ЛЧ (*') Н& (<0 ехр <<о„/,
гдеЯ»>(ОЧ€Ч^')|140)>
в
Продолжение списка формул В.6
При наличии слабого возмущения,
в котором в исходный момент ci (0) =
стояние /), в
Если #<0 (0
cf(t) = \
и если G>f{ -
определяется
pf«)
действующего на
, сЛ0) = 0 (занято
первом порядке теории возмущений имеем
M0 = i,
cf(t) = -
= 2V cos <i>tf
0
т Г 1 ~ ехр [/ (a>fi + 0) t]
f [ Ь (0
-0<0f; +0,
выражением
= |*f(0|2~
/< + »)
вероятность
Г 4Vifvft
|_fi2(0»fi-(D)
(/) exp toftt'.
1 - exp [I (m(i
»(»/*-
найти систему
TJsin22>f(.-
состояние,
только со-
-»)<П 1
»)
В (
.«)
J*
:остоянии /
/.
Математические выкладки теории возмущений приведены в
списке формул В.6. Существует также теория возмущений,
зависящих от времени, которая, в частности, позволяет
рассчитывать такое важное явление, как влияние возмущения,
вызванного световой волной. В этом случае искажения меняются со
временем и примешивание возбужденных состояний системы
можно интерпретировать как переходы из основного состояния
в другие. См. разд. «Вероятность перехода».
Упражнения. 1. Что такое «возмущение»? На что оно влияет? Как можно
учесть эффект возмущения волновых функций? Каков порядок величины
коэффициентов у примешиваемых функций и в какой пропорции они
примешиваются? Как вычислить по теории возмущений поправку первого порядка
к энергии? Как вычислить поправку второго порядка? Чем они отличаются?
Что следует сделать, если окажется, что волновую функцию простой
системы приходится очень сильно видоизменять? Каковы, по порядку величины,
поправки первого и второго порядка к энергии и поправка первого порядка
к волновой функции, если возмущение с энергией, эквивалентной 10 Дж«
•моль-1, действует на систему с расстояниями между уровнями порядка
1 кДж-моль-1? Тело массой 1 кг висит на пружине с упругой постоянной
1Н-М-1. Как изменится движение этого тела, если его массу увеличить еще
на 100 г (g = 9,8 м-с*2)? Рассмотрим теперь аналогичную квантовомехани-
ческую задачу. Представьте, что атом 210Ро колеблется с эффективной
силовой постоянной 40 Н-м-1 и что он находится в основном колебательном
состоянии. Предположим, что этот атом испускает а-частицу. Какова, по
порядку величины, вероятность обнаружить образовавшийся при этом атом
206РЬ в его основном колебательном состоянии?
2. Рассмотрим волновую функцию частицы в одномерной прямоугольной
потенциальной яме и предположим, что на эту систему действует возмуще-
74
в
ние вида —qxy где 0 ^ х ^ L. Найдите в первом порядке теории
возмущений энергии и волновые функции системы. Квантовомеханические выражения
теории возмущений для поправок к энергиям и волновым функциям
приведены в списке формул В.6. Используя ту же самую модельную систему,
будем считать теперь, что потенциал внутри ямы везде постоянен, кроме
маленькой прямоугольной лунки глубиной D и шириной W. Допустим, что центр
этой лунки совпадает с центром ямы и что W <t, L. Рассчитайте поправку
первого порядка к энергии частицы, находящейся в такой потенциальной яме
в основном состоянии (на уровне лг ===== 1) и в первом возбужденном
состоянии (на уровне лг ===== 2). Что можно сказать о величине поправки в каждом
из этих случаев? Отражается ли это различие поправок к энергии на
величине поправки к волновым функциям? Что произойдет, если центр лунки
переместить в точку х = L/3?
3. Оцените величину искажения волновой функции и поправку к
энергии, если к атому водорода в основном состоянии приложено электрическое
поле напряженностью 106 В-м"1.
Рекомендуемые источники. Теория возмущений подробно рассматривается
в [1], гл. 7. Она является одним из наиболее важных методов расчета свойств
атомов и молекул, см., например, [1], гл. 11, кн. Эйринга, Уолтера и Ким-
балла [137], Хамеки [172], Дэвиса [117] и Козмана [217]. Математический
аппарат теории возмущений и ее последующее развитие описаны Гиршфельде-
ром, Байере Брауном и Эпштейном [192], а также Уилкоксом [428]. В этих
двух работах рассматривается также отличие между теорией возмущений
Релея — Шредингера (именно она приведена в списке формул) и теорией
возмущений Вигнера — Бриллюэна. Сходимость ряда теории возмущений
представляет собой нелегкую проблему, однако она несколько упрощается
теоремой Релиха — Като, которая приводится на стр. 6 кн. Уилкокса [428].
Теория возмущений, зависящих от времени, позволяет, в частности,
рассчитывать эволюцию волновой функции во времени. Этот вопрос см. в разд.
«Вероятность перехода», гл. 7 [1] кн. Давыдова [119] и Гайтлера [180].
Изложение теории Гайтлера можно найти у Хамеки [172]. Обзор современного
состояния теории возмущений, зависящих от времени, дан Лангхоффом,
Эпштейном и Карплусом [237].
ВОДОРОДА АТОМ. Теория строения атома водорода —
системы, состоящей из протона и вращающегося вокруг него
электрона,— представляет собой одно из самых замечательных
достижений квантовой механики. Решить эту задачу методами
классической механики оказалось невозможным.
Изучение спектров атома водорода показало, что он
поглощает и испускает свет сериями со строго определенными
частотами (рис. В.8). В 1885 г. Бальмер установил соотношение,
которому удовлетворяют частоты, лежащие в видимой части
спектра. Эта серия Бальмера (рис. В.8) описывается формулой
v = /? (1/22 — l/nf), где rti — целое число, большее 2. Вполне
можно было ожидать, что существуют другие серии линий, в которых
22 заменяется на я*, где п2 — любое целое число. И
действительно, Лайман открыл серию (1914) в ультрафиолетовой части
спектра, соответствующую п2 =1, Пашен (1908) — в
инфракрасной области с яг = 3, Брэкет (1922)—в инфракрасной области
75
mooo A
iooooo-\
95000-\
90000-\
5
moots ooo-\
10000-\
5000-
Л.НМ /?u
A
-97,253-]
-102,572-\
-12tf67->La
серия
Лаамана
-4%,05-\\\r
(видимая
I область)
■656,28-*Ha
-820,4 -j
-Ш -J
-/975./ -I
-2Ш—
-2625,1—
-4051,2—
-7400,0—
серия
брэкета
! серия
I пфунда,
Рис. В.8 Спектр атома водорода.
в
с Пг = 4 и Пфунд (1924)—в далекой инфракрасной области
с п2 = 5.
Предложенная Бором теория строения атома водорода
соединила в себе ядерную модель Резерфорда и квантовую гипотезу,
но она оказалась несовершенной. В 1926 г. Шредингер,
используя им же выведенное уравнение, рассчитал строение атома во*
дорода. Принципиальная особенность этой теории заключается
в том, что энергия атома квантована и ограничена значениями
—Rh/п2, где п — целое положительное число (главное квантовое
число), a Rh — постоянная Ридберга, которая определяется
различными фундаментальными постоянными и равна 109 677 см*-1.
Переход с уровня ri\ на уровень п2 сопровождается изменением
энергии, которое в точности согласуется с экспериментом (см.
«Гротриана диаграмма»).
Строение атома водорода имеет следующие особенности:
1. Электрон распределен вокруг ядра по орбиталям. Каждую
атомную орбиталь можно характеризовать набором из трех
квантовых чисел: главного квантового числа я, орбитального
квантового числа (изредка называемого азимутальным
квантовым числом) / и магнитного квантового числа т*. Главное
квантовое число может принимать любые целые положительные
значения, орбитальное квантовое число принимает целые значения
от нуля до я—1, а магнитное квантовое число — любые целые
значения в интервале от / до —/. Энергия любого состояния
зависит только от главного квантового числа и определяется
выражением —Rh/п2. (Все, что касается постоянной Ридберга, можно
найти в соответствующем разделе.) Орбитальное квантовое
число определяет величину орбитального углового момента
электрона относительно ядра по формуле [/(/+ 1)]|/яй. Магнитное
квантовое число определяет ориентацию этого углового момента
в пространстве, и в соответствии с общими свойствами углового
момента проекция углового момента электрона на выделенную
ось равна mfi.
2. Орбиталь, соответствующая состоянию с квантовыми
числами я, I и ти в общем случае представляет собой функцию
расстояния г электрона от ядра, полярного угла (отсчитываемого
от северного полюса атома) и азимутального угла (долготы
электрона) (рис. В.9). Поэтому ее можно записать как
Ъпш1 (г> ®> ф)- Эту функцию можно выразить в виде
произведения радиальной функции (зависящей только от радиуса) и
угловой функции (зависящей только от углов): г|)„/т/ (г, Э, ф) =
= Rni(r)Yinn(®> ф)- Угловые функции 7/^(9, ф) являются
сферическими гармониками.
2а. Если / = 0, орбиталь изотропна, так как У0о(Э, ф) равна
постоянной '/гл;72 и не зависит от углов. В этом случае орбиталь
77
в
называется s-орбиталью, а занимающей ее электрон
распределен симметрично вокруг ядра (рис. В. 10). Поскольку / = 0,
угловой момент электрона на данной орбитали равен нулю; в
связи с этим важно заметить, что у рассматриваемой орбитали
отсутствуют угловые узлы (число таких узлов определяет
угловой момент).
26. Состоянию с / = 1 соответствует р-орбиталь; ее угловая
зависимость определяется функцией Kim/(8, ф). Она не является
постоянной величиной и имеет максимумы амплитуды вдоль
определенных осей в пространстве. Если mi = 0, р-орбиталь
содержит угловую функцию Ую(Э, ф), которая на первый взгляд
кажется очень сложной, но на самом деле представляет собой
полярный, угол
азимутальный угол-
Рис. В.9. Сферические координаты,
определяющие положение
электрона в атоме водорода
просто cos 9; она имеет экстремумы вдоль оси z при 0 = 0 или
180°. Электрон, который занимает эту орбиталь, с наибольшей
вероятностью находится в областях, сконцентрированных вдоль
оси z (рис. В. 10). Поэтому говорят, что он находится на /?2-ор-
битали. Другими возможными значениями trti (при /= 1)
являются ±1, в обоих случаях зависимость от 9 имеет вид sin 9:
это означает, что обе соответствующие орбитали
сконцентрированы в основном в плоскости ху и всюду на оси z имеют
нулевую амплитуду. Как Y\t i, так и 7i,_i — комплексные функции
(см. табл. 23), но их сумма и разность вещественны, поэтому
эти комбинации легче себе представить. Сумма Y\t\ + ^i,-i
является произведением sin 9 cos ф и, следовательно, является
стоячей волной, сконцентрированной вдоль оси х> поскольку на этой
оси sin 9 и соэф максимальны. Она называется /?х-орбиталью.
Другая комбинация, Y\9\ — Ki,-i, представляет собой функцию
sin 9 sin ф, т. е. стоячую волну, сконцентрированную вдоль оси у.
Она называется /?у-орбиталью. Эти орбитали имеют такую же
форму, как р2-орбиталь, но ориентированы по-другому
(рис. В.10). С каждой р-орбиталью связан угловой момент,
равный [1(1 + 1)],/2й илид/2Й. Ясно, что различные значения
квантового числа т\ соответствуют разным ориентациям
электронных распределений и, следовательно, разным ориентациям орби-
78
fy*2-,
Рис. В. 10. Изображение с помощью граничных поверхностей s-, p-, d- и
/-орбиталей.
в
тального углового момента электрона, занимающего р-орбиталь
(например, если т\ = ±1, электрон находится главным образом
в плоскости ху} а его угловой момент направлен в основном
вдоль оси г).
2в. Следующему значению I отвечают d-орбитали (1 = 2).
Таких орбиталей пять (ш/= 2, 1, 0, —1, —2), и, хотя все пять
функций Y2m}(®> ф) являются комплексными, можно составить
из них пять действительных комбинаций (но выбрать для них
пять геометрически подобных форм невозможно). й^-Орбиталь
концентрируется в направлении г, а символ г2 показывает, что
она имеет более сильную концентрацию вдоль оси г, чем /?-орби-
таль. В соответствии со своим обозначением г/Х2-орбиталь имеет
наибольшую плотность вдоль биссектрис углов, образованных
осями х и г, поэтому у нее имеются четыре лепестка (рис. В. 10).
Орбитали dyz и dxy по форме подобны dxz> но, как показывает
обозначение, сконцентрированы вдоль биссектрис углов,
образованных осями у и z и осями х и у соответственно. Обозначение
пятой d-орбитали — dx*-y> показывает, что ее лепестки похожи
на лепестки трех предыдущих орбиталей, но направлены вдоль
осей х и у.
2г. Семь /-орбиталей, соответствующие / = 3 и большому
угловому моменту Vl2#, 'отвечают сферическим гармоникам
Узт/(6> ф)> а семь возможных вещественных комбинаций
иллюстрируются рис. В. 10. Орбитали с более высоким моментом
встречаются очень редко, но их форму получить довольно
просто, поскольку угловая зависимость всех сферических гармоник
известна.
3. Радиальная зависимость орбиталей выражается функцией
Rni(r)\ она показывает, насколько близко к ядру располагается
электрон, что очень важно при определении потенциальной
энергии электрона и, следовательно, энергии атома. Математическое
выражение этих функций было известно задолго до того, как
было решено уравнение Шредингера, так как, по существу, они
представляют собой присоединенные полиномы Лаггера,
зависящие от г (табл. 14).
Все радиальные функции быстро стремятся к нулю при
больших значениях г: соответственно обнаружить электрон на
больших расстояниях от ядра невозможно. Все функции, за
исключением /?п, о (О, равны нулю в точке, где находится ядро.
Поэтому, если электрон занимает орбиталь с / Ф 0, вероятность
обнаружения электрона в ядре равна нулю. Функции RUt 0(г)
в этом смысле обладают особыми свойствами, поскольку все они
не равны нулю в ядре и поэтому предсказывают конечную
вероятность нахождения там электрона. Поскольку для этих
функций / = 0, мы приходим к выводу, что вероятность обнаружить
80
Рис. В.11. Функции радиального распределения для нескольких состояний
атома водорода (пунктиром показаны вероятности).
в
электрон в ядре отличается от нуля только дляз-орбиталей.
Физическую причину этой особенности можно понять, заметив, что
электрон на s-орбитали имеет нулевой орбитальный угловой
момент и проходит сквозь ядро. В отличие от этого для всех
других орбиталей (/ > 0) угловой момент вызывает наличие
центробежной силы, которая на малых расстояниях от ядра
превосходит кулоновскии потенциал притяжения и отклоняет
электрон от попадания в ядро. Между ядром и бесконечно
удаленной точкой радиальная волновая функция осциллирует
различное число раз: число узлов функции Rni равно п — /— 1.
Радиальное поведение функции изображено на рис. В. 11. Стоит
запомнить,что ls-орбиталь (я = 1, / = 0), т. е. энергетически
самая низкая орбиталь, является просто затухающей
экспоненциальной функцией, которая спадает от конечного значения до
нуля, а на ядре имеет ненулевое значение.
4. Общий вид орбиталей (включая угловую и радиальную
зависимости) изображен для нескольких случаев на рис. В. 12
и представлен в табл. 15. Форма орбиталей и соответствующих
распределений вероятности (которые, согласно интерпретации
Борна, являются квадратами модулей орбитальных функций)
приблизительно одинакова, но зависимость от направления во
втором случае выражена более резко. При обсуждении
различных аспектов строения атомов или молекул пользоваться такими
сложными диаграммами неудобно, и обычно вместо этого
принято изображать граничные поверхности, внутри которых
вероятность нахождения электрона достаточно велика. Именно
такой подход и использован при построении орбиталей на
рис. В. 10. Заметим, что форма поверхности зависит от того, что
стремятся изобразить с ее помощью — основную часть
амплитуды или вероятности. Полезно провести сравнение приведенных
на рис. В. 10 граничных поверхностей с изображением
сферических гармоник на стр. 343. Детальные особенности формы
орбиталей обычно не имеют большого значения, поэтому
изображаемые обычно граничные поверхности не претендуют на высокую
точность (как на рис. В. 11) и служат лишь для
приблизительного указания областей с повышенной амплитудой волновых
функций.
5. Наиболее интересная особенность строения водородного
атома состоит в следующем: энергия зависит только от главного
квантового числа и не зависит от орбитального квантового
числа 1. Это означает, что каждое состояние атома с главным
квантовым числом п имеет одну и ту же энергию независимо от
значений / и trii. Поскольку для данного я значение / может
изменяться от 0 до п — 1, а для каждого / значение т\ может лежать
в интервале от —/ до /, состояние с квантовым числом я
является я2-кратно вырожденным. Это специфическое вырождение,
32
a ^ — ^ б
3d * ~- ^ Iузловаяповерхмость
узловая
поверхность
узловая
поверхность
узловая
поверхность
Рис. В 12 Линии равной
амплитуды некоторых атомных орби-
талей водорода.
в
называехмое случайным, является следствием очень высокой
симметрии центрального кулоновского потенциала. В многоэлек-
трониом атоме оно исчезает, так как симметрия потенциала
понижается из-за присутствия других электронов (см. разд.
«Проникновение электронов и экранирование ядра»).
6. Энергия основного состояния атома водорода заслуживает
подробного обсуждения. Основываясь на законах классической
механики, следует ожидать, что электрон проводит как можно
больше времени в окрестности ядра, поскольку при этом его
потенциальная энергия минимальна. Идеальным положением
электрона с этой точки зрения является контакт с ядром. На самом
же деле в основном состоянии атома водорода электрон,
находящийся на ls-орбитали, хотя и распределен в области, близкой
к ядру, вовсе не ограничен этой областью. Что отталкивает
электрон от ядра? Классический ответ гласит: «Причиной
отталкивания является угловой момент электрона и сопутствующая
центробежная сила». Это предположение и было положено в
основу модели Бора. Однако, поскольку с s-орбиталью не связан
никакой угловой момент, такое объяснение нельзя считать
приемлемым. Правильный ответ можно найти, исследуя форму
радиальной волновой функции и зависимость между ее кривизной
и кинетической энергией.
На рис. В. 13 показаны три возможных распределения
электрона на ls-орбитали. На рис. В.13, в движение электрона
сильно ограничено окрестностью ядра, но это привело бы к сильной
кривизне волновой функции, что соответствует очень большой
составляющей кинетической энергии в радиальном направлении.
Рис. В.13, а демонстрирует такую ситуацию, когда кинетическая
энергия понижена вследствие того, что электрон распределен
в более широкой области. При этом, однако, происходит
повышение потенциальной энергии, когда электрон оказывается на
значительном расстоянии от ядра. В основном состоянии
водородного атома осуществляется промежуточная ситуация
(рис. В.13,б), при которой достигается баланс между
кинетической и потенциальной энергией. Эту ситуацию можно также
интерпретировать с учетом принципа неопределенности (см.
приведенные ниже упражнения).
Главные особенности строения и спектра водородного атома
хорошо объясняются квантовой механикой. Однако
обнаруживаются и некоторые трудности. Тщательное изучение спектра
атомарного водорода показывает, что линии, изображенные на
рис. В.8, в действительности имеют тонкую структуру. Это
явление описано в соответствующем разделе и объясняется
взаимодействием между спиновым и орбитальным моментами, а
энергия взаимодействия и расщепления непосредственно
вычисляются при решении уравнения Дирака. Тем не менее даже при
84
в
применении строгой теории Дирака остается небольшое
расхождение— так называемый лэмбовский сдвиг. Этот сдвиг,
заключающийся в расщеплении уровней 2Sn2 и 2Pi/2 (которые в теории
Дирака вырождены), был объяснен только при рассмотрении
атома водорода с помощью квантовой электродинамики.
Подобно тому как в свое время хорошее совпадение предсказаний
квантовой теории и экспериментальных результатов явилось
слишком малая кривизна
слишком большая кривизна*
Рис. В. 13. Кривизна функции радиального распределения, потенциальная
энергия и компромисс, определяющий основное состояние атома водорода.
триумфом этой теории, так в свою очередь объяснение
крошечного лэмбовского сдвига (остававшееся расхождение составляло
всего 0,033 см-1) стало триумфом современного развития
квантовой теории.
Упражнения. 1. Какие данные дают сведения о строении атома водорода?
Определите переход с наибольшей частотой в каждой из пяти спектральных
серий атома водорода. Лампы уличного освещения, содержащие натрий,
часто поначалу светят красным светом, так как содержат водород. Какому
переходу в атомарном водороде это соответствует? Вычислите потенциал
ионизации атома водорода из частоты линий серии Лаймана (рис. В.8). Каков
смысл квантовых чисел п, / и mi, используемых для обозначения орбиталей
в атоме водорода? Каков общий вид этих орбиталей? Каковы характерные
особенности s-орбиталей? Что отличает их от всех других орбиталей?
Сколько p-t d-, f- и g-орбиталей соответствует значениям главного квантового числа
«=1, 2, 3, 4? Сколько узлов имеет каждая орбиталь? Сколько радиальных,
угловых и общих узлов имеет орбиталь с квантовыми числами п, /, mi?
Каково соотношение между числом узлов и орбитальным угловым моментом?
Что определяется числом радиальных узлов? Что показывают кривые,
которые рисуют, чтобы изобразить атомные орбнтали? Сколько различных
орбиталей атома водорода соответствует энергии —Rh/п2? Зависит ли энергия
85
в
атома водорода от значения т{> Какова физическая интерпретация
основного состояния атома водорода? Каким образом нужно было бы изменить
рассуждения при объяснении строения сходной частицы Не+? Рассмотрите
основное состояние атома водорода с учетом принципа неопределенности:
обсудите, как повлияло бы на импульс и на кинетическую энергию более
сильное ограничение электрона окрестностью ядра. Обсудите влияние на атомные
орбитали изменения заряда ядра. Что произошло бы с орбиталями, если бы
порядковый номер атома увеличился от 1 до 4? Каковы недостатки квантово-
механического описания атома водорода?
2. Используя приведенные в табл. 1—27 данные, изобразите радиальную
волновую функцию для Is-, 2s-, 2p- и З^-орбиталей атома водорода.
Покажите в явном виде, что эти функции нормированы. Начертите кривую
распределения вероятности как функцию г и убедитесь, что наиболее вероятное
положение электрона на s-орбитали совпадает с ядром. Начертите
радиальную функцию распределения для Is- и 25-орбиталей. Вычислите наиболее
вероятный радиус атома как функцию 2. На каком расстоянии от ядра с
наибольшей вероятностью расположен ls-электрон в атомах Не, С, F и U?
Рекомендуемые источники. См. [1], гл. 3. Подробнейшее обсуждение
строения атома водорода см. в кн. Полинга и Вильсона [314], Козмана [217],
Давыдова [119], Мессиа [282] и Шиффа [356]. Этот же вопрос рассматривается
Инфельдом и Халлом [197], Грином [169] и Энглфильдом [135], но с помощью
элегантного метода факторизации уравнения Шредингера. Обсуждение того,
почему вырождения энергетических уровней атома водорода являются не
случайными, см. в [1], гл. 3, в работах Энглфильда [135], Бен дера и Ициксона
[50], Мак-Интоша [274, 275] и Фока [147]. Об изображении орбиталей и их
связи с классическими орбиталями говорится в кн. Уайта [425]. См. также
кн. Герцберга [185]. Обсуждение спектра атома водорода дано в гл. 3 [1],
в кн. Кинга [222], Куна [229], Герцберга [185] и Сирьеса [363]. В статье Мак-
Интоша [275] рассмотрение основано на оригинальном подходе, в котором
затрагиваются случайное вырождение, проекции водородных атомов на
гиперсферы и гипергиперболы, а также четырехмерные и двумерные атомы.
Теоретические и экспериментальные данные касательно атома водорода собраны
в табл. 16.
ВОЛНОВЫЕ ПАКЕТЫ. Если экспериментальное или
теоретическое исследование показывает, что положение частицы
ограничено очень малой областью пространства, то волновая
функция, описывающая такую частицу, должна иметь сильный
максимум в этой области и фактически быть равной нулю в
остальном пространстве. Волновая функция, соответствующая точно
определенному импульсу, имеет точно определенную длину
волны и поэтому распределена по большой области пространства
(фактически по всему пространству). Единственный способ
локализации частицы состоит в том, чтобы взять суперпозицию
функций последнего типа и исследовать их взаимную
интерференцию. Если такая суперпозиция хорошо подобрана,
интерференция приводит к взаимному усилению волн в избранной точке
и ослаблению амплитуды волновой функции во всех остальных
точках (рис. В. 14). Квадрат функции с резким максимумом
также является функцией с резким максимумом, поэтому
вероятность найти частицу отлична от нуля только в ближайшей окре-
86
в
стности рассматриваемой точки. Полученный волновой пакет
описывает локализованную частицу, и, поскольку мы имеем дело
с суперпозицией громадного числа энергетических состояний, это
означает, что импульс частицы не имеет определенного значения.
Волновой пакет находится в движении, так как все
составляющие его волновые функции изменяются во времени, и
поэтому интерференционный максимум перемещается. Можно
показать, что в тех случаях, когда волновые функции являются
а / \ / \
<駧^^
Рис. В. 14. Образование волнового I
пакета: а — состояние со строго I
определенным импульсом, локали- I
зация отсутствует; б — несколько I
состояний небольшая локализация; I
в — много состояний, значительная
локализация; г—бесконечное число I
состояний, полная локализация 2 I
решениями уравнения Шредингера для какого-либо
определенного потенциала, движение волнового пакета очень близко к
предсказываемому для классической частицы при наличии этого
же потенциала. Таким образом, мы видим, что квантовомехани-
ческое описание движения лежит в основе более грубого
описания, которое дает классическая механика. Следует подчеркнуть
важное ^отличие движения волнового пакета от движения
классической частицы: волновой пакет имеет тенденцию
расплываться со временем, но в случае массивных медленно
перемещающихся частиц эта тенденция очень слабо выражена.
Рекомендуемые источники. Образование, роль и движение волновых
пакетов описаны в гл. 3 [1], количественные данные приведены в
приложении 3.1. Хорошее и содержательное рассмотрение можно найти в гл. 3 кн.
Бома [63]; более строгий, но вместе с тем и сложный подход к
рассмотрению этого вопроса дан в кн. Гольдбергера и Ватсона [164], особенно в гл. 3
этой книги.
87
в
ВОЛНОВАЯ ФУНКЦИЯ. Волновая функция системы —это
решение ее уравнения Шредингера. Она содержит всю
информацию о динамических свойствах системы. Если известна
волновая функция, которая описывает состояние системы, все
наблюдаемые характеристики системы в этом состоянии можно
получить путем выполнения соответствующих математических
операций. Волновая функция может зависеть от времени, и в
этом случае ее обычно записывают в виде ^(г, /). Если
волновая функция не зависит от времени (или если зависимость от
времени отделена от нее), она обычно обозначается просто как
if и является функцией всех координат всех частиц, которые
составляют систему. Поскольку волновая функция зависит от
состояния системы, в ее обозначение часто вводят один или
несколько индексов (квантовые числа), которые отличают данное
состояние от других. Таким образом, волновая функция системы
из N частиц, для описания которой необходимо М квантовых
чисел, представляет собой математическую функцию ^п^...
• •• пм(гиг2> •.., Глг). В качестве примера волновой функции
можно привести волновую функцию свободной частицы,
движущейся вдоль оси х с импульсом kb, которая имеет вид exp(ikx),
и волновую функцию основного состояния атома водорода,
имеющую простой вид ехр(—г/а0). Интерпретация волновой
функции, ограничения, которым она подчиняется, и
содержащаяся в ней информация подробно рассматриваются ниже.
1. Интерпретация волновой функции. Рассмотрим систему,
состоящую из одной частицы с координатой х. Борн предложил
интерпретацию функции г|)(х), которая состоит в том, что ty(x)
представляет собой амплитуду распределения вероятностей
положения частицы. Согласно этой интерпретации, вероятность
нахождения частицы в бесконечно малой области dxf
окружающей точку х} пропорциональна ty*(x)ty(x)dx. Следовательно,
плотность этой вероятности пропорциональна произведению
ty*(x)ty(x). Если бы мы имели дело с трехмерной системой,
интерпретация волновой функции \|)(г) была бы следующей:
ij-,*(r)\|)(r)dt представляет собой вероятность нахождения
частицы в бесконечно малом элементе объема dx, окружающем
точку г. Эту интерпретацию можно пояснить, представив себе
детектор, чувствительный к присутствию частицы, который
зондирует в рассматриваемой системе объем dx. При перемещении
детектора в различные точки г показания прибора
пропорциональны объему зонда и величине г|)*(г)\|)(г). Например, волновая
функция основного состояния атома водорода является
убывающей экспоненциальной функцией аргумента г; следовательно,
показания прибора, измеряющего электронную плотность, будут
убывать по закону ехр(—2r/a0)dx, по мере того как зонд
объемом dx удаляется в радиальном направлении от ядра. В системе
88
в
с другой волновой функцией, которая упоминалась выше, а
именно exp(ikx), прибор все время будет давать одни и те же
показания, куда бы ни перемещался зонд, поскольку
[exp(ikx)]*[exp(ikx)] = 1 и не зависит от х. Эта функция
соответствует равномерному распределению частицы во всем
пространстве, тогда как в атоме водорода электронная плотность
выше вблизи ядра.
2. Ограничения, налагаемые на волновую функцию. Чтобы
можно было интерпретировать волновую функцию как
амплитуду плотности вероятности, она должна удовлетворять
некоторым требованиям.
а. Волновая функция должна быть конечной во всем
пространстве, иначе было бы возможно неконтролируемое накопление
плотности вероятности в тех точках, где она обращается в
бесконечность. (На самом деле это требование является слишком
жестким. Вполне достаточно потребовать, чтобы полная
вероятность нахождения частицы во всем пространстве равнялась
единице, т. е. чтобы существовал интеграл \ dx ф* (г) i|> (r); однако
сформулированное выше жесткое требование в большинстве
случаев может приводить к хорошим результатам.)
б. Плотность вероятности должна быть однозначной во всем
пространстве. Действительно, было бы бессмысленно заявить,
что плотность вероятности в некоторой точке равна
одновременно 0,2 и 0,4. Применительно к большинству систем это
требование тождественно требованию однозначности волновой
функции (исключение составляют системы, обладающие спином, но
их волновые функции можно легко привести в соответствие
с этим требованием).
в. Волновая функция должна быть непрерывной, потому что
было бы неразумно, если бы плотность вероятности имела
определенное значение в некоторой точке и отличающееся на конеч*
ную величину значение на бесконечно малом расстоянии от нее.
Указанные ограничения предъявляют строгие требования к
волновой функции, так как вынуждают ее подчиняться
некоторым граничным условиям, что неизбежно приводит к
квантованию (см. разд. «Кванты»), поскольку перечисленным условиям
удовлетворяют далеко не все решения уравнения Шредингера.
3. Информация, содержащаяся в волновой функции. Как было
показано выше, волновая функция содержит информацию о
пространственном распределении частицы. Средний градиент
(наклон, первая производная) волновой функции представляет
собой импульс частицы в данном состоянии; это является
следствием квантовомеханических правил интерпретации
наблюдаемых величин с помощью операторов. Средняя кривизна (вторая
производная) волновой функции определяет кинетическую
89
в
энергию состояния. Значения всех наблюдаемых величин
устанавливают путем вычисления ожидаемых значений
соответствующих им операторов с использованием соответствующих волновых
функций.
4. Волновые функции, зависящие от времени. Если волновая
функция tyn(x) соответствует энергии (собственному значению)
Еп, то зависящая от времени волновая функция Wn(x, t) имеет
вид произведения г|)п(х)ехр (—iEnt/b). Она описывает
стационарное состояние, несмотря на то что в нее входит время /,
потому что плотность вероятности |xFn(x, t)\2 не зависит от
времени.
5. Чистые состояния и суперпозиции. Если известно, что
система находится в состоянии с точно определенными
квантовыми числами, ее волновая функция представляет собой
волновую функцию чистого состояния. Например, если известно, что
атом водорода находится в основном состоянии, то его волновая
функция описывает чистое состояние, частица в состоянии с
определенным импульсом также находится в чистом состоянии и
описывается простой волновой функцией. Если мы полагаем,
что состояние системы принадлежит некоторой области чистых
состояний, например, если импульс системы лежит в интервале
от (k — к)Ъ до (1г-\-к)Ь, то волновая функция системы является
суперпозицией волновых функций чистых состояний,
находящихся в этой области. Итак, если предполагается, что некоторое
состояние принадлежит к области чистых состояний с
волновыми функциями i|)rti (х), урПз (х), ..., то истинное состояние
системы описывается линейной суперпозицией Ф (*) = c,i|)„ (*) +
+ с2$ (х) + Коэффициенты с\ этой суперпозиции
определяют вероятность того, что система находится в одном из
базисных чистых состояний, а именно: вероятность того, что система
находится в состоянии, описываемом волновой функцией tyn(x)f
пропорциональна с*псп>т. е. |сп|2. Эти коэффициенты могут
зависеть от времени. В качестве примера рассмотрим возбуждение
атома водорода падающим на него излучением. Первоначально
атом находится в основном состоянии, описываемом волновой
функцией i|)is(r), но по мере облучения он становится все больше
похожим на атом в состоянии 2pz. Следовательно, в процессе
облучения состояние атома водорода описывается волновой
функцией Ч' (г, t) = cl8 (/) *i, (г) + с2о (/) ty2Pz (г), где cls (0) = 1, c2pz (0) = 0.
Вероятность того, что за время t атом действительно перейдет
в 2/?2-состояние, пропорциональна \c2P(t)\2. Вычисление
подобных коэффициентов является задачей теории возмущений,
примеры приведены в разд. «Вероятность перехода». Примерами
статической суперпозиции волновых функций могут служить
гибридные орбитали или определяемые по методу ЛКАО молеку-
90
в
лярные орбитали (см. разд. «Гибридная орбиталь», «Линейная
комбинация атомных орбиталей», «Молекулярная орбиталь»).
Упражнения. Как получают волновую функцию? Как ее интерпретируют?
В чем различие между вероятностью и плотностью вероятности?
Схематически изобразите показания зонда с детектором, чувствительным к
электронам и погруженным в атом водорода, при перемещении детектора вдоль
радиуса по направлению к ядру. Предположите сначала, что зонд имеет
крошечный объем, в грубом приближении представляет собой куб объемом
dx dy dz% а затем выберите зонд в виде сферического слоя площадью 4яг2
н толщиной dr (r — радиус; заметьте, что объем слоя становится тем меньше,
чем ближе к ядру продвигается зонд; см. разд. «Функция радиального
распределения»). Каковы три ограничения, налагаемые на волновую функцию?
Подходит ли волновая функция ехр(+я*) для описания движения
свободной частицы? Что можно сказать в этом плане о функции x/|x|?. Допустим,
что перемещения частицы ограничены кольцом и в качестве ее волновой
функции предлагается функция exp(imq)). Какие ограничения надо наложить
в этом случае на значения т? Как записывается зависящая от времени
волновая функция стационарного состояния? Предположим, что вместо энергии
Е взята комплексная величина Е — ihT. Что произойдет с амплитудой
состояния, бывшего ранее стационарным, и как это можно интерпретировать?
Каков смысл коэффициентов в суперпозиции волновых функций? Волновая
функция записана- в виде \|?2s + 3l/'2i|)2j>; какова доля s- и р- характера
соответствующего состояния? Постройте $р2-гибридизованную функцию.
Рекомендуемые источники. Решение уравнения Шредингера для
различных систем, а также обсуждение свойств и интерпретации волновых
функций подробно рассматриваются в гл. 1—3 [1]. Интерпретация волновых
функций обсуждается в кн. Полинга и Вильсона [314], Ландау и Лифшица [233]
и Шиффа [356]. Вопросы, возникающие при интерпретации волновой
функции, см. у Бома [63], Джеммера [203], Балантина [48]. См. также разд.
«Нормированные волновые функции» и «Ортогональные волновые функции».
Очень важна интерпретация волновой функции как собственной функции
гамильтониана; см. разд. «Собственные функции» и «Гамильтониан», а также
«Принцип суперпозиции», «Атомные орбитали», «Водорода атом».
ВРАЩЕНИЕ МОЛЕКУЛ. Вращательная энергия молекулы
обусловлена ее угловым моментом, и, поскольку он квантован,
вращательная энергия тоже квантована. Разность энергий
соседних квантов вращательных уровней мала, и переходы между
ними происходят в микроволновом диапазоне спектра (108—
1012 Гц; 102—Ю-2 см-1). Расстояние между уровнями
определяется моментами инерции молекулы, и поэтому микроволновая
спектроскопия позволяет получать информацию о геометрии
молекул. Вращательные переходы наблюдаются также в
колебательных спектрах, электронных спектрах и в спектрах
комбинационного рассеяния, которые дают информацию такого же типа.
При обсуждении вращательных энергетических уровней
молекулы обычно подразделяют на следующие четыре типа:
линейные молекулы, симметричные волчки (молекулы с одной осью
91
в
симметрии), сферические волчки (сферические, тетраэдрические
и октаэдрические молекулы) и асимметричные волчки (все
прочие) .
1. Линейные молекулы. Линейные молекулы обладают только
двумя вращательными степенями свободы, которые
соответствуют вращению молекулы относительно двух взаимно
перпендикулярных осей. Легко понять, почему вопрос о третьей
вращательной степени свободы даже не возникает. В двухатомной
молекуле атомы имеют шесть степеней свободы, три из которых
соответствуют смещению молекулы как целого, одна
ответственна за колебания атомов вдоль линии связи, и, таким образом,
для описания вращения остаются только две степени свободы.
Аналогичные рассуждения применимы к любой линейной
молекуле. В классической механике энергия вращения тела с
моментом инерции / определяется выражением V2/0)2, а поскольку
классический угловой момент равен /со, энергию вращения
можно записать в виде (/со)2/2/. Переход к квантовомеханиче-
скому выражению для энергии вращения не составляет теперь
труда, поскольку из квантовой теории углового момента
известно, что угловой момент тела способен принимать лишь
значения [/(/+ 1)Г/2*> гДе возможные значения / ограничены
числами 0, 1, 2, ... . Следовательно, необходимо просто заменить
/со этим выражением, и в результате для энергии /-го квантового
вращательного уровня получим / (/ + 1) й2/2/. Величину fi2/2/
обычно обозначают буквой В и называют вращательной
постоянной молекулы. Важно отметить, что расстояние между
вращательными уровнями уменьшается с увеличением момента инерции
(так как при этом уменьшается В) и что уровень /
расположен на расстоянии 25(/ + 1) от следующего уровня.
Типичные значения В составляют 60,809 см"1 для Н2, 30,429 см-1 для
D2, 10,5909' см-1 для НС1 и 0,0347 см-1 для 12 (некоторые другие
значения см. в табл. 10).
Согласно теории углового момента, вектор углового момента
вращения молекулы может принимать одну из 2/ -\-1
возможных ориентации. В отсутствие внешних полей ориентация
молекулы не влияет на ее энергию, поэтому все 2/ + 1 ориентации
соответствуют одной и той же энергии (т. е. одному (2/ + 1) -
кратно вырожденному уровню).
Чисто вращательный переход может быть вызван
переменным электромагнитным полем подходящей частоты только в том
случае, если у молекулы имеется постоянный дипольный
момент. Постоянный диполь играет в процессе взаимодействия
молекулы с полем роль «рычага», с помощью которого поле
ускоряет молекулу, создавая вращательный момент. Молекулы, не
обладающие дипольным моментом (например, Н2 и С02), не
дают чисто вращательного спектра. Если у молекулы есть по-
92
в
стоянный дипольный момент, поле может вызывать переходы
только между соседними уровнями. Иными словами, правило
отбора для вращательных переходов заключается в следующем:
Л/ = +1 в случае поглощения и А/ = —1 в случае испускания.
Следовательно, вращательный спектр представляет собой ряд
линий, удаленных друг от друга ,на расстояние 26;
распределение интенсивностей линий определяется первоначальной
тепловой заселенностью уровней и несколько усложненными
правилами отбора, которые зависят от / (рис. В. 15).
J 6-
0—1
0~
/
^—J
J —
4
1 —
Л
А
А
А
"~1 "
А
1 4
и
.ill
111 У-*»
01 23456..,
Рис. В. 15. Чисто вращательный
спектр линейной молекулы,
показывающий заселенность уровней и
распределение интенсивностей
(последнее определяется
заселенностью и величиной дипольного
момента перехода).
Рис. В. 16. Вращение вытянутого
симметричного волчка. Если К
велико, движение происходит
в основном вокруг оси тела, если
К мало — преимущественно вокруг
перпендикулярной оси.
2. Симметричные волчки. Симметричные волчки могут быть
либо продолговатыми (в форме сигары), либо сплюснутыми
(в форме диска); они обладают тремя вращательными
степенями свободы. Поскольку у молекул такой формы имеется два
различных момента инерции (момент инерции /ц, параллельный
оси системы, и два равных между собой момента инерции /j.,
перпендикулярных этой оси), энергия вращения зависит от того,
как распределен угловой момент молекулы относительно трех
ее осей. Если молекула вращается вместе со своей осью
симметрии, энергия определяется лишь одним моментом инерции
1±, но, по мере того как вращение происходит преимущественно
вокруг оси симметрии молекулы, ее энергия начинает все больше
93
в
зависеть от 7 ц. Количественно доля вращения вокруг оси
симметрии молекулы определяется квантовым числом К: КЬ —
компонента углового момента вращения молекулы относительно
этой оси, которая может принимать любые целые значения от
—/ до +/ (всего 2/+ 1) (см. рис. В. 16). Если К равно нулю,
вращение вокруг оси симметрии молекулы отсутствует.
Проследить за тем, как в задаче появляется квантовое число /С, очень
легко. Согласно классической механике, энергия вращения тела
зависит от углового момента относительно каждой из его осей. Если
с осью q связаны компоненты углового момента (1со)я и момент
инерции Iqq, то кинетическая энергия, связанная с вращением
вокруг этой оси, равна 'М^®)2/^?- Следовательно, полная
кинетическая энергия рассматриваемой молекулы определяется
выражением l/2(I®)2xll± + ll2(I®fyll± + 'М/ю)2//,,, где ось z
направлена вдоль оси симметрии молекулы. Если учесть, что (/со)2 +
+ (/со)2 + (/со)2 представляет собой квадрат полного углового
момента молекулы, которому соответствует квантовомеханическое
значение /(/ + 1)й2, то можно представить выражение для
энергии в виде /(/+1)5 V/2(l//||-l//±)(/co)*, где В есть й2/2/х.
Нетрудно видеть, что (/со)г представляет собой компоненту
углового момента относительно оси симметрии молекулы и,
поскольку из квантовой теории углового момента следует, что все
компоненты углового момента квантованы, эта компонента
должна быть кратной величине й. Таким образом, мы
отождествили (/со)2 с КЬ,
Окончательный вид выражения для вращательной энергии
симметричного волчка приведен в списке формул В.7. Это
выражение выглядит именно так, как мы предсказывали. Если Л'
равно нулю, энергия определяется исключительно моментом
инерции /_ь а если Л' = ±/, энергия определяется в основном
(но не исключительно) моментом инерции /ц. Кроме того,
оказывается, что энергия зависит от /С2, а не от /С, и это означает,
что в соответствии со здравым смыслом направление вращения
тела вокруг оси его симметрии че играет никакой роли.
Напомним, что вращающаяся молекула может иметь 2/ + 1 различных
ориентации по отношению к любой фиксированной в
пространстве оси, но в отсутствие внешнего поля все эти ориентации
вырождены.
Спектр симметричного волчка зависит от наличия у него
постоянного дипольного момента, играющего в процессе
взаимодействия молекулы с электромагнитным полем роль «рычага».
Из соображений симметрии этот диполь должен лежать вдоль
оси молекулы, следовательно, световая волна не в состоянии
94
в
Список формул В.7
Вращательные уровни энергии
Двухатомные (и линейные) молекулы'-
£(/) = В/(/ + 1); В = й2/2/
(В измеряется в Дж, если / дано в кг • м2; В = Ь/400лс1 представляет
собой соответствующее выражение позволяющее вычислять В в см"-1).
Энергия перехода: Д£ (/) = Е (J + 1) — Е (/) = 2£ (/ + 1).
Симметричные волчки:
Е (/, К) = BJ (J + 1) + (А - В) /С2,
В = Й22/Х, Л = Й2/2/(|.
Энергия перехода: Д£ (/) = £(/ + 1, К) - Е (/, /С) = 2В (J + 1).
Сферические волчки:
Е (/) = В/ (/ + 1), В = П2/21.
Моменты инерции:
для двухатомной молекулы (массы тА, тв на расстоянии Я)
(ГПлГПа \
^—)R2,
mA + mB /
для линейной трехатомной молекулы (массы тА, тв, тс на
расстояниях #АВ и #вс)
7-тЛ» 4-тА* (тА*АВ-"*С*Вс)2
для пирамидальной молекулы (АВ3. длина связи R, угол ВАВ равен 9)
/,-2mB/?2(l-cos6),
mAmBR2(\ +2 cos 9)
/± = тв/е2(1 -cos6) +
ЗтА + ^в
создать крутящий момент, ускоряющий вращение вокруг этой
оси. Поэтому для симметричного волчка справедливы
следующие правила отбора: Л/С = 0 и Л/ = ± 1.
3. Сферический волчок. Уровни энергии сферического волчка
можно очень легко получить из выражения для энергии
симметричного волчка, приняв /х = 7ц. Соответствующее выражение
приведено в списке формул В.7. Энергия не зависит от /С,
поскольку все оси молекулы эквивалентны. Другими словами, все
(2/+ 1) состояния с разными К при данном / вырождены.
Следовательно, вращательные уровни сферического волчка (2/ +
|+1)2-кратно вырождены (поскольку, кроме вырождения по /С,
существует еще (2/jj-1)-кратное вырождение по квантовому
95
ft
числу Му т. е. пространственной проекции углового момента).
Сферические волчки не удается исследовать с помощью
микроволновой спектроскопии, так как они не обладают постоянным
дипольным моментом и не взаимодействуют с
электромагнитным излучением. Вращательные уровни молекул этого и других
типов могут быть, однако, возбуждены в результате
столкновений с другими молекулами или стенками сосуда, и поэтому при
расчетах свойств газов (например, теплоемкости) необходимо
учитывать возможность возбуждения большого числа
вращательных состояний.
4. Асимметричный волчок. Исследование таких волчков
весьма неудобно, поскольку в этом случае угловой момент не
удается удобно распределить между тремя осями. Сложность
задачи сразу же станет ясна, если мы представим себе
вытянутый симметричный волчок, который имеет сбоку выступ. Если
молекула вращается вокруг своей оси, наличие выступа
приведет к тому, что первоначальное направление вращения молекулы
изменится, т. е. произойдет передача углового момента,
первоначально направленного вдоль оси молекулы, двум другим
осям. Этот процесс продолжается, и, хотя полный угловой
момент вращения молекулы остается постоянным, направление
вращения постоянно изменяется. Уровни энергии асимметричного
волчка можно получить только в результате сложных
вычислений, и вращательные спектры таких молекул чрезвычайно
сложны. Тем не менее тщательный анализ формы спектральных полос
позволяет получать информацию о геометрии молекулы и в этом
случае.
Упражнения. 1. Чем определяется вращательная энергия молекулы?
Почему эта энергия квантована? Может ли быть у молекулы отличная от нуля
вращательная энергия в основном вращательном состоянии? В какой
области спектра происходят вращательные переходы? Как зависят энергии
вращательных переходов от размера молекулы? Какую информацию можно
извлечь из вращательных спектров? Чем должна обладать молекула для того,
чтобы она могла поглотать энергию посредством вращательного перехода?
По каким типам классифицируются молекулы при обсуждении их
вращения? Каков смысл квантового числа /С? В каком случае энергия вращения
молекулы зависит от квантового числа М? Какова кратность вырождения
вращательных состояний линейных молекул и волчков различных типов?
Почему энергия симметричного волчка, хотя и в слабой степени, но зависит от
/_!_> когда К = ±/? При каких условиях можно приписать всю энергию
симметричного волчка вращению вокруг его оси симметрии? Каковы правила
отбора для вращательных переходов? Каким образом все типы вращательного
движения приходят к тепловому равновесию, несмотря на то что в
некоторых случаях электрические дипольные переходы не могут осуществляться?
2. Вычислите расстояние между уровнями (в см-1) для вращательных
переходов в Н2, HD и D2, приняв, что длина связи в каждом случае равна
0,074 нм. Чисто вращательный спектр молекулы HI состоит из ряда
равноотстоящих линий, расстояние между которыми равно 12,8 см-1, вычислите
96
в
длину связи этой молекулы. Почему линии вращательного спектра разделены
равными промежутками? (Нарисуйте схему энергетических уровней и
примените соответствующие правила отбора или просто подумайте о величинах
2BJ и Л/).
3. Вычислите относительные заселенности вращательных уровней
молекул Н2, D2, I2 (В = 0,0374 см-1), СН4 (гсн = 0,1094 нм), NH3 (/„ = 4,437 X
X Ю~47 кг-м2), /х =2,816- 1(Г47 кг-м2) при 300 и 1000 К. Используйте
распределение Больцмана, правильно учтите вырождение уровней, но можете
не учитывать ядерную статистику (даже если вы с ней уже знакомы).
Рекомендуемые источники. Более полное обсуждение вращения молекул
и вращательных спектров дано в гл. 10 [1]. См. также кн. Уиффена [424],
Барроу [51] и Кинга [222]. Сагден и Кенией [388] опубликовали введение
в микроволновую спектроскопию, а Таунс и Шавлов [399] — монографию,
которая сейчас считается классическим трудом; в [388] и [399] приводится
библиография по изученным молекулам. Аллен и Кросс [35] обсуждают
теоретические аспекты проблемы. Теория и практическое применение вопроса
рассматривается Герцбергом [186—188], в книгах которого собраны полезные
данные о молекулах (такие, как длины связей, силовые и вращательные
постоянные). Полезная сводка данных о структуре молекул приведена у Сат-
тона [390]. Вращательные переходы можно также изучать, наблюдая
колебательные и электронные спектры молекул и спектры комбинационного
рассеяния. Теплоемкость молекул зависит от того, насколько легко могут быть
возбуждены вращательные состояния и, следовательно, от их энергии.
Рассмотрение вращения молекул усложняется тем, что заполнение
вращательных уровней ограничено принципом Паули, более подробно об этом см. В
разд. «Ядерная статистика».
ВТОРИЧНОЕ КВАНТОВАНИЕ. Название данного раздела
может смутить тех, для кого даже простое квантование
оказалось достаточно трудной темой; утешить таких читателей можно
только тем, что дальше вторичного квантования дело не зайдет.
Вторичное квантование — это просто элегантный прием,
позволяющий облегчить исследование систем из многих частиц,
включая рассмотрение электромагнитного поля. К введению
вторичного квантования приводят следующие рассуждения: первичное
квантование (которое мы обычно называем квантованием)
заменяет наблюдаемые величины операторами, а поведение систем
и результаты экспериментов рассчитываются как результат
действия этих операторов на волновые функции, полученные
решением уравнения Шредингера для рассматриваемой системы.
Таким образом, динамические функции заменяются операторами,
действующими на функцию ty(x). Предположим теперь по
аналогии, что мы интерпретируем функции г|)(лг) как операторы,
действующие на что-то иное. При этом мы выходим за рамки
привычной процедуры квантования и попадаем в искусственный
мир вторичного квантования, в котором действие оператора
ф*(х) (на нечто иное) порождает частицу в точке х, а действие
оператора ty(x') приводит к уничтожению частицы в точке х\
97
в
Можно понять, что такая возможность порождать и уничтожать
частицы позволяет получить способ вывода уравнений для
расчета квантовомеханических свойств многочастичных систем.
Таким образом, вторичное квантование не приводит к революции
в физике, как это было с первичным квантованием, а лишь
вводит новую технику расчетов и новый язык, в который входят
такие слова, как фотоны, фононы, поляроны, экситоны, магноны,
ротоны.
Рекомендуемые источники. Введение в представления вторичного
квантования излагается в курсе лекций автора [41], в основу которых положена
известная книга Маттука [269]. В качестве введения могут служить также
следующие книги, перечисленные в порядке возрастания сложности: Займан
[438], Роман [343], Давыдов [119], Боголюбов и Ширков [62] и Швебер [358].
См. также кн. Киттеля [223].
ВЫРОЖДЕНИЕ. Если две или несколько различных
волновых функций системы соответствуют одной и той же энергии,
говорят, что они вырождены. Так, три др-орбитали любого
свободного атома образуют трехкратно вырожденную систему
функций, а я-орбитали двухатомных молекул—двукратно
вырожденный набор. Когда определенной энергии соответствует только
одна волновая функция, говорят, что состояние невырожденно
(иногда в этом случае используют термин «однократное
вырождение», но его употребление, по-видимому, неоправданно).
«Снятие вырождения» состояния означает устранение вырождения
(например, в результате наложения на атом электрического
поля).
Вырождение системы тесно связано с ее симметрией, и, если
какая-либо волновая функция действием преобразования
симметрии может быть преобразована в другую волновую
функцию, такие функции образуют вырожденный набор. Так,
вращение свободного атома на 90° вокруг оси z представляет собой
преобразование симметрии, и, поскольку при вращении прх-о$-
биталь переходит в гару-орбиталь, эти орбитали являются
вырожденными. Подобным же образом вращением вокруг другой
оси можно получить Аг/?2-орбиталь, которая вместе с прх (и пру)-
орбиталями образует вырожденный набор. Поскольку Зр-орби-
таль нельзя получить никаким вращением 2/?-орбитали, эти две
орбитали, согласно определению симметрии, не образуют в
атомах общий вырожденный набор, что согласуется с
общепринятыми представлениями.
Когда две волновые функции соответствуют одной и той же
энергии вследствие случайного численного совпадения, а не
потому, что существует определенное преобразование симметрии,
говорят,что эти функции случайно вырождены. Приведем
пример. Может оказаться, что 2sa*- и 2/?я-орбитали какой-нибудь
98
в
двухатомной молекулы имеют одну и ту же энергию с точностью
до нескольких значащих цифр, т. е. они являются случайно
вырожденными. В качестве примера случайного вырождения
нередко приводят атом водорода, в котором все орбитали с
заданным главным квантовым числом (т. е. ns-, np-, nd-орбитали)
имеют одинаковую энергию. Однако этот пример является
ошибочным, поскольку можно найти на первый взгляд скрытое
преобразование симметрии, с помощью которого можно
преобразовать ns-орбиталь в пр-орбиталь и т. д., следовательно,
вырождение является истинным, а не случайным. Такие же «скрытые
преобразования симметрии» можно привлечь для объяснения
явно случайных вырождений состояний частицы в ящике,
размеры которого кратны друг другу (см. упражнение 2), и вообще
все точные «случайные» вырождения можно объяснить с
помощью более глубокого исследования симметрии системы.
Упражнения. 1. В каких случаях имеет место вырождение состояний?
Как связано вырождение с симметрией системы? В какой степени вырождены
основные состояния атома натрия и атома бора (отвечая на этот вопрос,
можно пренебречь спин-орбитальным взаимодействием)? Каково вырождение
состояний электрона в атоме водорода с главным квантовым числом 1, 2, п>
Каково вырождение спинового состояния электрона в нулевом магнитном
поле и чему равно вырождение, когда поле приложено? Что можно сказать
о вырождении состояния электрона в d-оболочке иона переходного металла
при наличии октаэдрического поля лигандов? Обсудите последний вопрос с
точки зрения симметрии.
2 Рассмотрите энергетические уровни частицы в двумерной
прямоугольной яме (см. список формул Ч. 1), размеры которой одинаковы. Покажите,
что наинизшее энергетическое состояние в такой яме не вырождено и что
следующее более высокое состояние двукратно вырождено. Покажите, что
две волновые функции первого возбужденного состояния могут быть
преобразованы одна в другую поворотом квадратной ямы на прямой угол. Может
ли какое-либо состояние частицы в такой яме быть трехкратно
вырожденным? Может ли быть трехкратно вырожденным состояние частицы в
кубическом ящике? Найдите вырожденные Состояния для ямы с размерами а и са,
где с — рациональное число. Являются ли они действительно вырожденными
или вырождение случайно? Возможна ли здесь скрытая симметрия? Что
произойдет, если принять, что с — иррациональное число?
Рекомендуемые источники. Целесообразнее всего проводить обсуждение
вырожденных ситуаций с использованием теории групп; см., в частности, [1]
(гл. 5), кн. Коттона [102], Бишопа [59], Мак-Интоша [274]. Вырождение
водорода обсуждается в [1], кн. Энглфильда [135], Мак-Интоша [274] и Бен-
дера и Ициксона [50]. Снятие вырождения лежит в основе описания ионов
переходных металлов на языке теории кристаллического поля; см., например,
«Химию переходных элементов» Эрншоу и Харрингтона [14], работы [308].
Бальхаузена [49] и Гриффита [170]. Случайное вырождение подробно
обсуждается Мак-Интошем [274, 275].
г
ГАМИЛЬТОНИАН. Имя сэра Вильяма Роуэна Гамильтона
(1805—1865), который стал королевским астрономом Ирландии
еще будучи студентом, увековечено в квантовой механике
потому, что он разработал систему классической механики,
идеально приспособленную к структуре квантовой механики, и
стоял на пороге открытия квантовой механики, т. е. вполне
возможно сделал бы это, если бы того потребовало состояние науки
его времени. Применительно к интересующим нас системам
гамильтониан представляет собой сумму кинетической Т и
потенциальной V энергии (впрочем, как и большинство понятий, его
можно определить более общим и более сложным образом).
Гели обозначить эту функцию символом Н (хотя некоторые
предпочитают Ж), то H=T+V. В квантовой механике
наблюдаемым величинам следует сопоставлять операторы.
Рассматривая Т и V как операторы, мы видим, что оператор
гамильтониана представляет собой оператор полной энергии системы.
Полный гамильтониан любой системы состоит из суммы членов,
соответствующих различным вкладам в полную энергию.
Гамильтонианы различных систем приведены в списке формул ГЛ.
Уравнение Шредингера часто записывается в виде Н\р = £\|),
поэтому его можно интерпретировать как уравнение на
собственные значения, в котором энергия Е системы является
собственным значением гамильтониана, а волновые функции
соответствуют его собственным состояниям.
Упражнения. Что такое гамильтониан? Что такое оператор
гамильтониана? Каким образом можно записать уравнение Шредингера с помощью
гамильтониана и как его можно интерпретировать? Напишите гамильтониан
и проанализируйте смысл каждого члена для свободного электрона, атома
водорода, иона водорода, молекулы водорода, атома гелия, атома углерода,
гармонического осциллятора, гармонически колеблющегося заряда в
электрическом поле, массы на конце пружины, атома водорода в магнитном поле.
Рекомендуемые источники. Простое представление о гамильтониане
вводится в [1], гл. 3, 4. См. также кн. Полинга и Вильсона [314]. Все книги но
квантовой теории содержат обсуждение гамильтонианов, а его классическое
рассмотрение дано Голдстейном [166]. Дополнительную информацию см. в
разд. «Операторы». Большинство гамильтонианов очень сложны, и их
собственные значения нельзя найти точно. Тремя основньши приближенными
методами нахождения собственных значений являются теория возмущений,
вариационный метод и приближение самосогласованного поля. Биографические
сведения о Гамильтоне можно найти в кн. Уиттакера «Американские ученые»
[426].
10Q
г
Список формул Г./
Гамильтониан
Общий вид:
Н=Т + V.
Свободная частица:
H=-(b2l2m)V\
Частица в ящике (одномерная прямоугольная яма):
# = -(fi2/2m)(-J~), 0<*<Д.
Атом водорода:
Я = - (h2/2m) V2 - е2/4яг0г.
Атом гелия:
Н = - (Ь2/2пг) V2 - (П2/2ш) V2 - 2^/inB^ -
— 2е2/4ле0г2 + e2/4ne0ri2.
Молекулярный ион водорода (Н*) при фиксированных ядрах:
Я = — (h2/2m) V2 — е2/4лг0гы — е2/4лв0г1В + е2/4лв0гАВ.
Гармонический осциллятор:
Я--<»»/2«) (£)+■£.
Жесткий ротатор (волчок):
н - - (в»/а/„) 4 - (*72/„) 4 - (*7*U 4
Магнитный дипольный момент ц в поле индукции В:
Я = — ц.В; например, ц = gyes или Yel.
Электрический дипольный момент \i в поле напряженностью Е:
#=-ji.E.
ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР. В классической
механике гармоническими называются такие колебания, когда
возвращающая сила пропорциональна смещению тела из
положения равновесия. Сила —kx, где k — силовая постоянная,
соответствует потенциалу kx2/2 (так как F = —dV/dx).
Гармоническим осциллятором в квантовой механике называется система
с таким параболическим потенциалом, и ее свойства можно
определить, решая уравнение Шредингера с потенциалом kx2/2.
Решение приводит к следующим выводам.
1. Энергия гармонического осциллятора квантована и
принимает значения (v + V2)^o)o, где coo = (k/m)lh и v = 0, 1,2
Это означает существование нулевой энергии, равной ~^%
101
г
когда осциллятор находится в наинизшем состоянии с v = 0,
таким образом, у осциллятора нельзя отнять всю энергию. Нулевую
энергию можно рассматривать на основании принципа
неопределенности: уничтожение всей энергии и, следовательно,
импульса означало бы бесконечную неопределенность для координат,
однако частица пространственно ограничена определенным
потенциалом. Расстояние между энергетическими уровнями равно
йсоо, и энергия колебаний может увеличиться только при
поглощении целого числа колебательных квантов /?ю0.
Следствия этого факта обсуждаются в разд. «Теплоемкость» и
«Квант».
2. Волновыми функциями гармонического осциллятора
являются произведения полиномов (зависящих от смещения) Эр-
мита и гауссовых функций. Некоторые из этих функций
приведены в табл. 11; там же указаны их наиболее важные свойства.
Графическое изображение нескольких функций дано на рис. ГЛ.
В наинизшем состоянии полином Эрмита тождественно равен
единице, поэтому волновая функция представляет собой коло-
колообразную гауссову кривую с максимумом в положении
равновесия. Так как волновая функция характеризует
распределение координат частицы, то, следовательно, в основном состоянии
частица концентрируется вблизи положения равновесия, но
обладает как кинетической, так и потенциальной энергией
благодаря форме волновой функции и наличию потенциала.
Следующий полином пропорционален х, поэтому его произведение на
гауссову функцию представляет собой волну с узлом в центре
(при х = 0). Это соответствует более высокой энергии, так как
волновая функция имеет более резкие изгибы (большая
кинетическая энергия) и глубже проникает за потенциальную кривую
(или, если использовать термины классической механики,
частица раскачивается быстрее и дальше). Следующая функция
опять имеет максимум в центре, но вместе с тем также
значительную величину в областях с более высоким потенциалом. При
дальнейшем возбуждении осциллятора главные максимумы
распределения вероятности оказываются преимущественно на краях
распределения, где при классическом рассмотрении находятся
точки поворота. Это согласуется с классическим результатом,
поскольку в точках поворота кинетическая энергия и,
следовательно, скорость наименьшие, а вероятность нахождения
частицы наибольшая.
3. Когда энергия состояния осциллятора точно не
определена, может сформироваться волновой пакет. Волковой пакет
гауссовой формы движется от одной стороны ямы к другой с
частотой соо таким образом, который напоминает классическое
движение (рис. Г.2); следовательно, расстояние между
квантовыми уровнями соо становится частотой классического осцил-
102
Рис. ГЛ. Энергетические уровни и волновые функции гармонического
осциллятора. Классически доступные области показаны толстыми линиями,
ограниченными потенциалом. Ср. с верхней половиной рис. Ф.8.
Рис. Г.2. Классический предел гармонического осциллятора.
г
лятора. Это хороший пример того, как квантовомеханические
принципы обосновывают классическую механику (см. разд.
«Соответствия принцип». Поведение осциллятора все больше
согласуется с классической механикой по мере того, как
суперпозиция состояний (см. соответствующий раздел) становится более
Оправданной: соответствие увеличивается, когда расстояние
между квантовыми уровнями уменьшается. Отсюда понятно, что
осцилляторы с частотами порядка 1 Гц (или 2я рад-с*-1), такие,
как классические часы, ведут себя в соответствии с законами
классической механики, в то время как периодические процессы
в атомах и молекулах с частотами в интервале 1012—1015 Гц
подчиняются законам квантовой механики.
Важное значение гармонического осциллятора определяется
рядом причин и его характерных особенностей. Во-первых, в
природе колебания часто в хорошем приближении являются
гармоническими, что позволяет использовать теорию гармонического
осциллятора при описании колебаний молекул и атомов в
твердых телах. Поэтому гармонический осциллятор применяется при
рассмотрении теплоемкости и многих свойств твердых тел.
Далее, как и в классической механике, математическое описание
гармонических колебаний тесно связано с описанием
вращательного движения, поэтому не удивительно, что формулы для
гармонического осциллятора используются при обсуждении углового
момента. Описание гармонического осциллятора весьма
несложно: выражение для его энергии симметрично относительно
пространственных и импульсных координат (оба выражения
являются квадратичными функциями). Эта особенность приводит,
например, к равномерному расположению энергетических
уровней гармонического осциллятора. Математическое описание
гармонического осциллятора положено в основу метода вторичного
квантования.
Упражнения. При каких условиях колебания являются гармоническими?
Какому потенциалу это соответствует? Какие значения энергии являются
разрешенными для квантового осциллятора? Каково минимальное значение
его энергии? С чем связано существование нулевой энергии осциллятора?
Каков интервал между любой парой энергетических уровней? Какой вид имеют
волновые функции гармонического осциллятора? Обсудите вид распределения
смещений осциллятора в его основном состоянии и сравните это
распределение с основным состоянием классического осциллятора, а также с
состоянием классического осциллятора, имеющего ту же энергию. Каким образом
изменяется распределение смещений при возбуждении осциллятора? Каким
является движение соответствующего волнового пакета? При каких
условиях может сформироваться такой пакет, как он связан с движением
классического осциллятора с такой же силовой постоянной и массой? Вычислите
энергетический интервал для осциллятора с частотой 1 Гц и 1014 Гц (не
забудьте перевести эти частоты в рад-с1 умножением на 2л). Вычислите
разность энергий между 1 молем осцилляторов каждого типа в основ-
104
г
ном и в возбужденном состоянии и выразите результат в Дж-моль"1
и см'1.
2. Используя свойства полиномов Эрмита (табл. 11), выведите правила
отбора для электрических дипольных переходов гармонического осциллятора.
Дальнейшее развитие этого вопроса см. в разд. «Ангармоничность».
Покажите, что уравнение Шредингера для гармонического осциллятора можно
записать в виде a+aty^ = — (Я — 1) i|^ где а — дифференциальный оператор
(djdy) + у, а+ = (d/dy) — у, у = (тсо0М) Ч*х, х — смещение из положения
равновесия, а Я связано с энергией соотношением Е = Я(Дсо0/2). Наинизшему
уровню соответствует значение X = 1, поэтому a+mpi = 0, а отсюда atyi = 0.
Решите это дифференциальное уравнение первого порядка и покажите, что
его решением действительно является гауссова функция, приведенная в
табл. 11.
Рекомендуемые источники. Обсуждение свойств гармонического
осциллятора и решение уравнения Шредингера для этого случая методом
факторизации (с использованием операторов рождения и уничтожения) см. в гл. 3
[1], решение методом полиномиального разложения см. в кн. Полинга и
Вильсона [314]. Решение уравнения Шредингера для гармонического осциллятора
описано в курсах Ландау и Лифшица [233], Шиффа [356] и Мессиа [282].
Свойства полиномов Эрмита приведены в кн. Абрамовича и Стегуна [30], там
же можно найти численные значения полиномов. Свойства этих полиномов
описаны в справочнике Маргенау и Мэрфи [266]. Связь между
математическими описаниями гармонического осциллятора и углового момента
рассмотрена Липкиным [251], Маттисом [268], Знглфильдом [135] и Швинглером
[360].
ГАУССОВЫ АТОМНЫЕ ОРБИТАЛИ. Трудоемкость
расчетов электронного строения молекул связана со сложностью
вычисления многих интегралов энергии электрон-электронного
взаимодействия. В расчетах по методу самосогласованного поля
многие интегралы включают атомные орбитали, относящиеся
более чем к одному центру; число центров может достигать
четырех. Такие многоцентровые интегралы очень сложны, и на их
вычисление затрачивается много машинного времени. Упростить
эти интегралы можно, в частности выразив атомные орбитали
с помощью гауссовых функций, основная часть которых имеет
вид ехр(—аг2), вместо того чтобы использовать атомные
орбитали слейтеровского типа, которые являются экспоненциальными
функциями вида ехр(—а'г). Преимущество этой замены
заключается в том, что произведение двух гауссовых функций,
относящихся к разным центрам, также является гауссовой функцией,
которая относится к точке, лежащей между этими центрами.
Следовательно, сложный 3- или 4-центровый интеграл можно
выразить как относительно простой 2-центровый интеграл,
который нетрудно вычислить. Недостаток метода заключается в том,
что атомная орбиталь плохо аппроксимируется простой
гауссовой функцией и каждую орбиталь приходится записывать как
сумму нескольких гауссовых функций. Поэтому, хотя каждый
105
г
интеграл становится более простым, приходится вычислять очень
много таких интегралов.
Упражнения. С какими преимуществами и неудобствами связано
использование гауссовых атомных орбиталей? Покажите, что произведение двух
гауссовых функций ехр (— а{г\} и ехр (— a2rfj можно выразить в виде
гауссовой функции, относящейся к точке между двумя исходными центрами,
и выразите положение этой точки через ах и а2. Покажите, что эта процедура
не может быть применена в случае двух экспоненциальных функций. С
помощью вариационного принципа определите наилучшую гауссову орбиталь
для атома водорода; повторите вычисления, выбрав пробную функцию в
виде суммы двух гауссовых орбиталей. Сравните истинную ls-орбиталь с
найденными наилучшими гауссовыми орбиталями, сравнивая их энергии, а также
начертив радиальную зависимость функций.
Рекомендуемые источники. См. Ричарде и Хорсли [336] и Мак-Глин, Ванк-
викенборн, Киносита и Кэррол [273]. Метод использования гауссовых
функций предложен Бойсом [72]. О расчетах, основанных на этом методе, см.
библиографию, собранную Ричардсом, Хинкли и Уокером [337].
ГЕЛЬМАНА —ФЕИНМАНА ТЕОРЕМА. Теорема
утверждает, что градиент энергии по некоторому параметру dE/dP
равен ожидаемому значению градиента гамильтониана по этому
параметру дН/дР. Чтобы вычислить dE/dP (где параметр Р
может быть углом или длиной молекулярной связи, зарядом ядра
или напряженностью внешнего поля), достаточно вычислить
оператор дН/дР, который может оказаться очень простым, а затем
найти его ожидаемое значение. За простотой формулировки
скрывается жесткое ограничение (способное оказаться подвохом
для малопосвященных): волновые функции, используемые при
вычислении ожидаемого значения, должны быть чрезвычайно
точными. Вся трудность как раз и заключается в вычислении
таких функций, а невыполнение этого условия может привести
к значительным ошибкам, даже если волновые функции лишь
слегка отличаются от точных.
В каких случаях используется эта теорема? Она, например,
применяется для вычисления электрической и магнитной
восприимчивости молекул (см. «Поляризуемость»). Другой очень
интересный пример применения теоремы — изучение геометрии
и силовых постоянных молекул. Это применение основывается
на одном из замечательных следствий теоремы, заключающемся
в том, что силу, действующую на ядро какого-либо атома в
молекуле, можно рассчитать как в простых задачах классической
электростатики,' если известно точное (квантовомеханическое)
распределение заряда. Этот вывод из теоремы часто называют
электростатической теоремой Гельмана — Фейнмана. Если из-
10$
г
вестио распределение электронной плотности (а оно известно,
если известна волновая функция), то силу, действующую на
ядро, можно вычислить, рассматривая кулоновскую силу, с
которой такое же классическое распределение заряда действует
на точечное ядро. Это позволяет вычислить для любой
деформации молекулы силовую постоянную, определяя
возвращающую силу, которая действует на ядро при искажении
равновесной геометрии молекулы. Заметим, что такой подход позволяет
рассматривать нахождение равновесной геометрии как задачу
классической электростатики, но это не означает, что учет
обменной энергии и т. п. оказываются в конце концов совершенно
излишними. Все сложности, связанные с учетом обменных
взаимодействий, таятся на самом деле в трудной задаче точного
определения распределения электронной плотности при
фиксированной ядерной конфигурации. Тем не менее эта теорема
позволяет как-то разобраться в форме молекул, так как она сводит
установление их геометрии к рассмотрению баланса
электростатических сил, хотя распределение, ответственное за этот баланс,
определяется законами квантовой механики.
Упражнения. 1. Сформулируйте теорему Гельмана—Фейнмана. При
каких условиях она недействительна? Предложите различные варианты выбора
параметра Р для расчетов тех или иных свойств молекул. Какую пользу
может принести эта теорема при обсуждении структуры молекул? Почему эта
теорема не избавляет от учета обменной энергии, несмотря на то что она
позволяет устанавливать форму молекул путем рассмотрения сил,
действующих на ядра? Какие условия относительно сил, действующих на ядра атомов,
приводят к определению равновесной геометрии молекулы? Что может
представлять собой параметр Р в двухатомной молекуле? Каким образом влияет
обменная энергия на .определение формы молекул с помощью теоремы
Гельмана — Фейнмана?
2. Докажите теорему Гельмана — Фейнмана, рассмотрев выражение
Е(Р) = {ф(Р) | Я(Р)1-ф(Я)), где энергия зависит от параметра Р, так же
как и гамильтониан и точные нормированные волновые функции (т. е.
{ф(Р) \ty(P)) — 0» Продифференцируйте обе стороны выражения по Р и
воспользуйтесь тем, что if (Я)—собственная функция Н(Р) с собственным
значением Е(Р).
Рекомендуемые источники. Простое доказательство теоремы в применении
к электрическим и магнитным явлениям дано в гл. И [1]. О применениях к
молекулярным проблемам см. весьма подробный обзор Деба [120], в котором
можно найти много ссылок. Дополнительные сведения содержатся в кн. Слей-
тера [372]. Оригинальное изложение теоремы см. в работах Гельмана [182] и
Фейнмана [141].
ГИБРИДИЗАЦИЯ. Орбитали, имеющие смешанный s-, /?-,
d-, ... характер, называются гибридными, а процесс их
формирования носит название гибридизации. s/7-Гибридная орбиталь,
107
Рис ГЗ. $/>я-Гибридные орбитали. Рассчитанные линии одинаковой
амплитуды для водородных 2s-, 2р-орбиталей. Узловая поверхность смещена от
ядра.
г
например, имеет равные вклады s- и /?-характера, и можно
считать, что занимающий ее электрон имеет на 50% s-характер и
на 50% —/?-характер.
Как выглядит гибридная орбиталь? Мы знаем, что s-орби-
таль можно рассматривать как сферически симметричную
стоячую волну, а р-орбиталь — тоже как стоячую волну, у которой
в одной из пучностей амплитуда положительна, а в другой —
отрицательна. Гибридная орбиталь является суперпозицией этих
двух стоячих волн. Там, где обе амплитуды положительные,
происходит их сложение, а там, где одна амплитуда
положительная, а другая отрицательная, происходит их вычитание.
Суперпозиция получается асимметричной, как это видно на рис. Г.З.
$/?2-Гибридная орбиталь содержит 33% s-характера, a sp3-op6u-
таль — 25%. Эти орбитали также показаны на рисунке, и видно,
что асимметрия увеличивается при возрастании /^-характера
орбитали. Заметим, что при изменении степени гибридизации
узловая поверхность смещается (в негибридизованной /?-орби-
тали она проходит через ядро, но с появлением s-компоненты
картина меняется).
В чем суть гибридизации? Она происходит при условии, что
ее результатом является понижение энергии молекулы. Но
каким образом понижается энергия молекулы, когда орбитали
в ее атомах гибридизуются? На первый взгляд это непонятно.
Рассмотрим, для примера, атом углерода. В основном состоянии
он имеет конфигурацию s2p2 (мы не учитываем внутренние ls-
электроны), причем 25-электроны имеют несколько меньшую
энергию, чем 2р. Естественно думать, что углерод будет
образовывать связи с помощью 2/?-орбиталей и будет двухвалентным.
Если, однако, мы затратим энергию и переведем один из s-элек-
тронов на р-оболочку, атом приобретает конфигурацию spz.
Каждая из четырех s- и р-орбиталей гибридизуется с образованием
четырех $/?3-гибридных орбиталей, в результате чего каждый
валентный электрон занимает одну из гибридных орбиталей.
Форма этих гибридных орбиталей понятна из рис. Г.З: они являются
сильно направленными, а несложный расчет показывает, что они
направлены к четырем вершинам тетраэдра (рис. Г.4) (см. разд.
«Эквивалентные орбитали»). Теперь следует объяснить, каким
образом можно получить энергию, затраченную для
возбуждения одного из s-электронов. Можно ожидать, что затраченная
энергия будет возмещена в результате образования четырех
связей. Сильно направленные свойства гибридных орбиталей
позволяют им эффективно перекрываться с орбиталями четырех
соседних атомов, и мы можем ожидать появления четырех
сильных связей. Отсюда и получается выигрыш в энергии: за
счет образования четырех сильных (и эквивалентных) связей
с избытком возмещается первоначально затраченная энергия.
109
г
Рассмотрение молекулы аммиака (NH3) помогает понять
другой источник выигрыша в энергии (рис. Г.5). Атом азота
имеет конфигурацию s2/?3, поэтому мы можем ожидать
образования пирамидальной молекулы аммиака в результате
перекрывания ls-орбитали каждого атома водорода с каждой
полузаполненной 2/?-орбиталыо азота. Предположим теперь, что мы
перевели один s-электрон азота на р-оболочку; понизилась ли от
этого энергия молекулы? Затратив энергию на возбуждение
электрона, мы имеем право рассматривать все s- и р-орбитали
на равных основаниях. Мы получаем 5/?3-гибридные орбнтали
Рис. Г.4. Тетраэдрическая spz-
гибридизация (например, в СН4).
с тетраэдрическим расположением и сильными направленными
свойствами. Затем мы расселяем на этих орбиталях пять
электронов и добавляем к ним три электрона от атомов водорода.
Получившаяся структура состоит из трех а-связей,
образованных каждая за счет сильного перекрывания 5/?3-гибридной ор-
битали азота и ls-орбитали водорода (каждая связь образуется
двумя электронами), и еще двух электронов, образующих непо-
деленную пару. Три связи возмещают затраченную энергию
благодаря сильному перекрыванию; частично энергия возмещается
и за счет неподеленной пары, так как^ она локализуется в той
области, где ее электростатическое отталкивание от каждой из
трех а-связей минимально. Кроме того, большие углы между
связями уменьшают отталкивание между атомами водорода.
Истинная структура молекулы аммиака определяется
соотношением между энергией, затрачиваемой для перевода s-электрона
на р-орбиталь, и энергией, которая может быть возмещена за
счет усиления перекрывания и уменьшения несвязывающих
взаимодействий. Структура этой молекулы оказывается
промежуточной (что можно установить, измерив углы между связями:
110
г
в предельном случае связей за счет /?-орбиталей угол Н—N—Н
равен 90°, а в случае образования связей 5/?3-орбиталями он
составляет 109°28'; экспериментальное значение этого угла 103°).
Углерод весьма склонен к гибридизации, ввиду того что
энергия его возбуждения (иногда употребляется термин «промоти-
рование») довольно мала (поскольку промотируемый s-электрон
переходит на пустую р-орбиталь). _
Поэтому у углерода имеется
много вариантов гибридизации,
осуществляемых в зависимости от
условий реакции. В СН4 и его
гомологах наблюдается почти
чистая 5/?3-гибридизация; в алкенах
и ароматических молекулах
возникает плоское треугольное
расположение я/Лгибридных орбита-
лей, а оставшаяся 2/?-орбиталь
этого промотированного
состояния участвует в образовании я-
связи. В ацетиленовых
соединениях (алкинах) сх-связь является
s/7-гибридной, а остальные две
2/?-орбитали образуют я-связи.
Рис. Г.5. Аммиак и гибридизация; не-
поделенная пара электронов
заштрихована, а — энергия промотирования
отсутствует, но зато имеется сильное
отталкивание и умеренное перекрывание;
в —- ослабленные отталкивательные
взаимодействия, сильное перекрывание,
но большая энергия промотирования;
б — промежуточный вариант. Показаны
только две из трех связей.
Перечень структур, образуемых с участием гибридных орби-
талей, дан в табл. 13. Обсуждение формирования гибридных
орбиталей проведено в разд. «Валентное состояние».
Упражнения. 1. Что означает термин «гибридизация»? Нарисуйте
несколько гибридных орбиталей (в частности, sp, sp2, sp3, sd, sd2). Каким
образом гибридизация может понижать энергию молекулы? Опишите
образование СН4, NH3 и Н20 и исследуйте вклады в энергию, которые изменяются
за счет гибридизации центрального атома. Почему гибридизация атома
углерода имеет особенно важное значение?
2. Четыре ярЗ-гибридные орбитали можно записать следующим образом:
S + Px+Py+Рг] S+ Рх — Ру — Рг\ S — рх — ру + Рг\ S — рх + Ру — рг.
Ill
г
Покажите, что они направлены к вершинам тетраэдра и взаимно ортогональны.
Выразите гибридную орбиталь в виде as + $(1рх + тру + npz), где /, т,
п — направляющие косинусы образуемой с ее участием связи и а2 + Р2 = 1.
Возьмите другую эквивалентную орбиталь с направляющими косинусами /',
т\ п' и аналогичным составом. Используя то обстоятельство, что функции
должны быть ортогональны и нормированы, покажите, что а и (5 связаны
с углом 9 между связями соотношениями а2/(52 = — cos 0 и 1/р2 = 2 sin2 l/2Q.
Обсудите форму гибридных орбиталей при 6, равном 180, 90° и углу между
осями тетраэдра. Изобразите графически зависимость s-характера орбитали
от угла 6. Покажите, что эффект гибридизации значителен, только если
используемые орбитали имеют приблизительно одинаковые размеры.
Представьте в предыдущем выражении аир как sin g и cos ^ соответственно (так
что а2 + Р2 = 1 автоматически) и запишите 1рх + тру + прг как р-орби-
таль. Найдите выражение для перекрывания гибридной орбитали с соседней
орбнталью ф через интегралы перекрывания Ss = (s|cp) и Sp = (р\ц>) и
выражение для максимального значения S как функции от g. Ответ таков:
Smax = (S2 + Sp) • Это показывает, что «S заметно отличается от Ss или
SP, только если «S* « SP\ в этом случае перекрывание равно Smax = V2 Ss.
Рекомендуемые источники. См. [1], гл. 9 и особенно приложение 9.2, где
дано более полное обсуждение гибридизации, эквивалентных орбиталей и
локализованных орбиталей, а также дано решение упражнения 2. Зависимость
структуры молекул от гибридизации описана Коулсоном в кн. «Форма и
структура молекул» [10] и в гл. 8 [105]. См. также Маррел, Кеттл и Теддер
[299], Пилар [318], Козман [217] и Мак-Глин, Ванквикенборн, Киносита и Кэр-
рол [273]. В последней книге описываются некоторые детали образования
гибридных орбиталей и вычисляется ряд интегралов перекрывания.
Теоретико-групповые основы формирования гибридных орбиталей описаны в [1].
гл. 9.
ГРОТРИАНА ДИАГРАММА. На диаграмме Гротриана
энергетические уровни атома располагаются- в виде
горизонтальных линий и классифицируются на группы. Спектральные
переходы изображаются линиями, соединяющими термы, между
которыми они происходят, и, если это необходимо, возле них
указываются частоты (или волновые числа) переходов. Иногда
толщиной соединяющих линий указываются относительные
интенсивности переходов. На рис. Г.б показана простейшая
диаграмма Гротриана для атома водорода. Уровни нумеруются
согласно главному квантовому числу и соответствуют различным
значениям орбитального квантового числа I. На диаграмме
указаны переходы, образующие различные серии.
На рис. Г.7 показана диаграмма Гротриана для атома
натрия. Когда имеется более одного электрона, нередко возникает
путаница в обозначении энергетических уровней, так как в одних
случаях для их обозначения используется орбиталь, занятая
возбужденным электроном, а в других — символ терма, т. е.
обозначение состояния атома. Так, в одних случаях наинизшее
состояние атома натрия обозначается 3s, в других — 3s2S или 32S
и, наконец, 12S (последнее означает, что основное состояние яв-
112
г
ляется первым из дублетных состояний; однако такое
обозначение может привести к недоразумениям). Мы будем
использовать предпоследнее обозначение.
Энергия основного состояния атома обычно принимается
равной нулю. Если желательно показать тонкую структуру,
отдельные фрагменты диаграммы можно увеличить.
/2
Ю
чГ 8
4h
2\-
п-1
ч
3
I
20000
40000 g
60000
80000
100000
Рис. Г.6. Диаграмма Гротриана для атома водорода.
Рекомендуемые источники. Дальнейшее обсуждение и примеры см. в [1],
гл. 8. Диаграммы Гротриана обсуждаются Кингом [222], Кэндлером [89],
который приводит много примеров, Куном [229], Кондоном и Шортли [96]
Множество диаграмм представлено в справочнике Американского института
физики [168]. Стандартным сборником данных по энергетическим уровням
атомов является атлас Мур [288]. Другие аспекты использования диаграмм
Гротриана описаны в разд. «Тонкая структура», «Серии», «Водорода атом».
ГРУПП ТЕОРИЯ. Используемая в квантовой механике
теория групп является математической теорией симметрии. Она
ставит на строгую математическую основу наши интуитивные
представления о симметрии объектов и позволяет делать
однозначные выводы о следствиях этой симметрии. Знание симметрии
ИЗ
г
системы уменьшает работу, затрачиваемую на вычисления, и
часто позволяет сделать определенные заключения без сложных
выкладок.
Теорию групп используют, чтобы подобрать подходящую
линейную комбинацию атомных орбиталей для построения
молекулярных орбиталей молекулы, классифицировать атомные и
i 40000
Рис. Г.7. Диаграмма Гротриана для атома натрия.
молекулярные состояния, определять правила отбора для
переходов между этими состояниями и находить нормальные
колебания молекул. Теорию углового момента можно считать одним
из ответвлений теории групп. Аппарат теории групп связан с
преобразованиями симметрии молекул и твердых тел, с их
матричными представлениями, характерами и классами и с
рассмотрением неприводимых представлений.
114
г
Краткая сводка свойств характеров, которые широко
используются в большинстве химических применений теории групп,
дана в списке формул Х.1.
Рекомендуемые источники. Обсуждение основ теории групп см. в [1],
гл. 5; в других разделах книги рассматривается ее применение. Связь теории
групп с теорией углового момента обсуждается в [1], гл. 6. Элементарными
введениями в теорию групп являются кн. Джаффе и Орчина [201] и Коттона
[99]. Более подробное введение в вопрос дано Бишопом [59]. См. также кн.
Тинкхема [396], Сконланда [357] и Мак-Вини [277], а также кн. Вустера [436],
в которой теория групп рассматривается применительно к твердым телам.
Изложение повышенной трудности см. в кн. Вигнера [427], Хамермеша [173],
Вейля [419] и Джадда [212]. Исчерпывающее изложение свойств симметрии
твердых тел приводится Брэдли и Крэкнеллом [74], а небольшой справочник,
содержащий таблицы характеров и групповых свойств и служащий пособием
по теоретико-групповым расчетам, подготовлен Эткинсом, Чайлдом и Филлип-
сом [40]. Популярное изложение теории дано Вейлем [419]. См. также Хох-
штрассер [451] «Молекулярные аспекты симметрии».
ГУНДА ПРАВИЛА. Правила Гунда указывают простой
способ определения последовательности энергий атомных
состояний. Они утверждают следующее:
1) для данной конфигурации терм с наибольшей мультиплет-
ностью имеет наинизший энергетический уровень;
2) для данной конфигурации и мультиплетности терм с
наивысшим орбитальным угловым моментом имеет наинизший
энергетический уровень;
3) для данной конфигурации, мультиплетности и
орбитального углового момента состояние с наименьшим значением
полного углового момента / имеет наинизший энергетический
уровень, если конфигурация соответствует оболочке, заполненной
менее чем наполовину; если оболочка заполнена более чем
наполовину, наинизший энергетический уровень имеет состояние
с наибольшим значением /.
В качестве примера рассмотрим конфигурацию ls22s22p2 и
термы 3D, Ф и 1S, которые возникают из нее. Какова
последовательность их энергетических уровней? В соответствии с
первым правилом 3D <(Ф, *S), а из второго правила вытекает, что
Ф < 1S. Следовательно, термы должны располагаться в
следующем порядке: 3D < Ф < *S. Третье правило позволяет
упорядочить три уровня триплетного терма (3D). Поскольку для 3D
имеем L = 2, a S = 1, возможны состояния с / = 1, 2, 3. Так
как р-оболочка заполнена меньше чем наполовину (она может
содержать 6 электронов), состояния терма 3D должны
располагаться в следующем порядке: 3Di < 3Е>2 < 3D3. Таким образом
устанавливается любая последовательность уровней.
Первые два правила основываются на учете
электростатических взаимодействий, а третье — на учете магнитных
взаимодействий.
115
г
1. В большинстве книг дается упрощенное объяснение
первого правила, но мы постараемся этого избежать. Прежде всего
отметим, что электроны с параллельными спинами должны
располагаться на разных орбиталях (см. «Паули принцип»). Это
даст им возможность находиться дальше друг от друга, а не
«тесниться» на одной орбитали, и в результате межэлектронное
отталкивание ослабляется. Но в конфигурации рхру электроны
находятся на разных орбиталях и могут иметь как
параллельные, так и антипараллельные спины. Какое состояние в этом
случае имеет меньшую энергию и почему? Обычно считают, что
триплетное состояние (с параллельными спинами) лежит ниже,
поскольку электроны с параллельными спинами избегают друг
друга (см. «Спиновая корреляция»), и отталкивание между ними
оказывается слабее, чем в синглетной конфигурации (со
спаренными спинами). Однако детальные расчеты некоторых случаев
показывают, что отталкивание между электронами в триплет-
ных состояниях больше, чем в синглетных, и что на самом деле
понижение энергии обусловлено изменением
электронно-ядерного взаимодействия. Так, в триплетном атоме электронное
распределение оказывается более сжатым, и за счет усиления
ядерного притяжения достигается выигрыш в энергии.
Межэлектронное отталкивание тоже возрастает, но это увеличение не
компенсирует выигрыша в ядерном притяжении. По-видимому,
в результате спиновой корреляции межэлектронное отталкивание
усиливается медленнее, чем ядерное притяжение.
2. Второе правило отражает способность электронов
избегать друг друга, если орбитальные угловые моменты
заставляют их двигаться в одном направлении. В состоянии с
наибольшим суммарным орбитальным моментом все электроны
вращаются в одном направлении и поэтому могут оставаться вдали
друг от друга, если же электроны вращаются в
противоположных направлениях, они будут часто встречаться и,
следовательно, испытывать большее кулоновское отталкивание.
3. Третье правило основано на учете магнитных
взаимодействий, так как последовательность уровней определяется спин-
орбитальным взаимодействием. Когда спиновый магнитный
момент направлен против орбитального момента, магнитная
энергия минимальна, но такая ориентация моментов как раз и
соответствует наименьшему значению полного углового момента (см.
«Тонкая структура», особенно рис. Т.5). Обращение уровней
в том случае, когда оболочка заполнена более4 чем наполовину,
отражает изменение знака постоянной спин-орбитальной связи.
Упражнения. Сформулируйте три правила Гунда. Какие из правил
касаются электростатических взаимодействий, а какие — магнитных? Какое из
правил основано на рассмотрении спин-орбитального взаимодействия? Обос-
116
г
нуйте каждое из трех правил. Почему происходит обращение уровней, когда
оболочка заполнена больше чем наполовину^ Расположите в порядке
возрастания энергии следующие термы. 2S, 2P, 4S. 4D Укажите последовательность
этих термов, предположив, что они соответствуют оболочке, заполненной
более чем наполовину.
Рекомендуемые источники. См. [1], гл. 8. Правила Гунда обсуждаются
Козманом [217], Кингом [222] и Герцбергом [1851. Таблицы термов и
энергетических уровней составлены Мур [288]. Правила Гунда, конечно, не всегда
выполняются. Это может быть обусловлено конфигурационным
взаимодействием, когда присутствие другой конфигурации приводит к понижению терма
ниже того уровня, где он должен находиться, согласно правилам Гунда.
Вывод, что традиционные объяснения (в том числе и приведенное в [1]) первого
правила полностью неправильны, основан на работах Лембергера и Паунца
[241], Кэтриела [215], Колпа и Ислипа [93] О видоизменении правил Гунда
в случае //-связи см. в кн Уокера и Уэбера [413].
ГУНДА СЛУЧАИ СВЯЗИ. В двухатомной молекуле имеется
несколько причин существования углового момента: спин
электронов, их орбитальное движение вокруг оси и вращение
ядерного остова. Полный угловой момент является векторной
суммой всех этих моментов, однако результат сложения зависит от
взаимодействия между ними Случаи Гунда отражают несколько
реальных возможностей установления взаимодействия; мы
рассмотрим четыре простейшие и наиболее общие схемы.
a. При наличии сильного электростатического влияния ядер
только круговое движение электронов относительно направления
аксиального поля (оси молекулы) обусловливает ненулевую
составляющую орбитального углового момента. За счет
спин-орбитального взаимодействия результирующий спиновый момент
электронов тоже связан с сохраняющейся компонентой
орбитального момента; другими словами, спины связаны с осью
молекулы двухступенчатым процессом. Полный электронный
угловой момент направлен вдоль межъядерной оси; следовательно,
орбитальная компонента АЬ и спиновая компонента Sfi дают
полный момент, направленный вдоль оси и равный Qfi, где Q =
= Л+ 2. Однако ядерный остов тоже вращается, и угловой
момент от его вращения можно представить вектором 6,
перпендикулярным оси молекулы (рис. Г.8,а). Следовательно, полный
угловой момент молекулы определяется результирующим
вектором J.
b. Рассмотрим случай, когда связь спинового момента с осью
молекулы исчезает. Это возможно при условии, что
электронный орбитальный момент отсутствует (так что спин-орбитальное
взаимодействие невозможно) или спин-орбитальная связь
слишком слаба, чтобы орбитальный момент мог связать спиновый
момент с осью молекулы Такая ситуация встречается в
двухатомных молекулах, включающих атомы элементов второго
117
г
а
периода, особенно в их гидридах. Орбитальный момент еще
связан электростатически с осью, но спин ориентирован вокруг нее
произвольно. Поэтому электронный орбитальный момент и
момент ядерного остова складываются, образуя результирующий
момент N, и только потом к нему
прибавляется спиновый момент
и получается результирующий
О. s^r\ v^*< | вектор полного момента системы
L^^^j^^l J (см. рис. Г.8,б).
* л~$^4' с- В третьем случае
спин-орбитальная связь настолько
сильна, что независимо от других
условий спиновый и орбитальный
угловые моменты сильно связаны
друг с другом и дают полный
электронный угловой момент Ja.
Этот вектор Ja прецессирует
вокруг межъядерной оси, <и его
ОХу^п /^\] проекция на эту ось равна Qfi.
k^-J^ff j 1 Она взаимодействует с моментом
^\^^=» ядерного остова молекулы, при
этом получается полный момент
всей системы J (рис. Г.8,с).
о
о
Рис. Г.8. Случаи связи Гунда.
В тяжелых атомах с сильным спин-орбитальным
взаимодействием реализуется именно этот случай.
d. И, наконец, в четвертом случае мы рассмотрим
специфическую ситуацию, при которой электроны фактически независимы
от ориентации ядерного остова. Вращение ядер молекулы мало
сказывается на поведении ее самых внешних электронов,
особенно если электрон возбужден на орбиталь, лежащую над
валентной оболочкой (в ридберговское состояние). При этом
электрон удален от ядер настолько далеко, что пара ядер действует
на него как один точечный заряд. В таком случае электронный
орбитальный угловой момент образует с вектором момента
ядерного остова результирующий вектор N, который, складываясь
затем со спиновым моментом (в таких диффузных состояниях
имеется очень слабая спин-орбитальная связь), дает полный
момент молекулы J (см. рис. Г.8, d).
Совершенно очевидно, что четыре рассмотренных случая
составляют лишь малую часть всех возможных вариантов, а если
сами ядра обладают спином, число возможных вариантов воз-
118
г
растает еще больше. Кроме этого, рассмотренные примеры
являются предельными, чистыми случаями. В любой реальной
молекуле возможны различные промежуточные типы
взаимодействия угловых моментов, рассмотрение которых чрезвычайно
затруднено. Переход от одного случая Гунда к другому называют
разрывом связи.
Упражнения. Каковы возможные причины существования углового
момента в двухатомной молекуле? При каких условиях возникает случай Гунда
(а)? Что происходит, если в молекуле отсутствует орбитальный угловой
момент? Какова схема образования связи при слабом спин-орбитальном
взаимодействии? Какая схема возможна при сильной спин-орбитальной связи?
Какова схема образования связи в том случае, когда электрон занимает
диффузную орбиталь? Что означает термин «связывание»? В случае (а)
квантовые числа Л и 2 вполне определены (т. е. являются «хорошими»
квантовыми числами), так ли это в случае (с)? Каким в этом смысле является
квантовое число Q? Что характеризуют эти квантовые числа?
Рекомендуемые источники. Еще один подход к объяснению схем
образования связи см. в гл. 10 [1]. О практическом применении схем связи см. в кн.
Барроу [51], Кинга [222] и Герцберга [187]. Известно еще несколько
интересных схем; все они великолепно изложены Герцбергом [187]. Важный пример
применения схем связи рассмотрен в разд. «Правила отбора» при
обсуждении электронных переходов в двухатомных молекулах.
д
ДВОЙНОЕ ЛУЧЕПРЕЛОМЛЕНИЕ (краткий обзор).
Двойное лучепреломление означает существование различных
показателей преломления для двух компонент поляризации светового
пучка. Двойное лучепреломление может быть естественным
свойством отдельных молекул или определенной кристаллической
формы, кроме того, оно может быть вызвано электрическим,
магнитным или механическим воздействием. Важным примером
естественного двойного лучепреломления является оптическая
активность, т. е. вращение плоскости поляризации света при его
прохождении через среду. Этот эффект представляет собой
круговое двойное лучепреломление, так как он зависит от
различных скоростей прохождения компонент с левой и правой
круговой поляризацией (напомним, что скорость света в среде равна
с/п). Эффект Фарадея заключается в индукции кругового
двойного лучепреломления в образце, не обладающем естественной
активностью, при наложении продольного магнитного поля
(вдоль направления распространения света). Индуцированное
вращение пропорционально напряженности поля, константа
пропорциональности называется постоянной Верде; все молекулы
дают фарадеевское вращение. Поперечное магнитное поле
(перпендикулярное направлению распространения света) индуцирует
линейное двойное лучепреломление, при котором одна плоскопо-
ляризованная компонента распространяется быстрее, чем
другая, что вызывает эллиптичность поляризации луча; это явление
называется эффектом Коттона — Мутона. То же самое явление,
вызванное поперечным электрическим полем, носит название
эффекта Керра. Показатель преломления и коэффициент
поглощения света связаны между собой дисперсионными
соотношениями Крамерса — Кронига, поэтому если показатель
преломления зависит от поляризации, то от нее также зависит и
коэффициент поглощения, и наоборот. Эффекты Керра и Коттона —
Мутона можно наблюдать, варьируя коэффициенты поглощения
для компонент поляризации. Двойное лучепреломление может
вызываться течением жидкости, если ее молекулы достаточно
анизотропны: упорядочение ориентации продолговатых молекул
вносит анизотропию в оптические свойства среды; если
коэффициент преломления зависит от направления поляризации пучка,
наблюдается двойное лучепреломление в потоке.
Рекомендуемые источники. Квантовомеханическое обоснование
естественной оптической активности см. в [1], гл. 11. Простое обсуждение
подробностей дано Козманом [217], а полный обзор по индуцированному двойному
120
д
лучепреломлению — Колдуэллом и Зйрингом [87]. Простое рассмотрение
дихроизма и двойного лучепреломления в электрическом поле, особенно их
применение, см. у Фредерика и Хаусьера [154]. Интересный материал содержат
также статьи Московица [291], Тиноко [397], Масона [267] и Арри [405].
Дальнейшее обсуждение эффектов Фарадея и Коттона — Мутона см. в кн. Бэ-
кингема и Стефенса [84]. Применению индуцированного двойного
лучепреломления на жидких кристаллах в устройствах типа «дисплей» посвящена статья
Эллиотта [133]. Оптические свойства твердых тел рассматриваются в
классическом труде по оптике Борна и Вольфа [70], кн. Ландау и Лифшица [233]
и Вустера [436]. Изучение дисперсии (частотной зависимости) оптической
активности является одним из основных методов исследования стереохимии
молекул; введение в дисперсию оптического вращения дается в [111].
ДЕ БРОИЛЯ СООТНОШЕНИЕ. Согласно соотношению де
Бройля, частица, движущаяся с импульсом /?, имеет связанную
с ним длину волны X = h/p. Когда импульс частицы
увеличивается, длина волны уменьшается. Это соотношение можно
понять, рассматривая волновую функцию частицы и связь между
кривизной этой функции и кинетической энергией частицы. Если
кинетическая энергия частицы увеличивается, кривизна ее
волновой функции возрастает, но увеличение кривизны означает,
что на заданном отрезке длины волна чаще переходит от
положительной амплитуды к отрицательной, т. е. длина волны
уменьшается. Поскольку кинетическая энергия пропорциональна
квадрату импульса, между импульсом и длиной волны существует
обратная зависимость.
Более прямое квантовомеханическое обоснование
соотношения де Бройля можно получить, используя тот факт, что волновая
функция частицы с импульсом р = kb имеет вид exp(ikx). Если
записать ее как cos(2npxjh)-\- isin(2npx/h), то сразу видно, что
функция соответствует суперпозиции реальных волн с длиной
волны h/p.
Упражнения. Что такое соотношение де Бройля? Каким образом erd
можно обосновать квантовомеханически? Почему длина волны частицы
уменьшается, когда ее импульс возрастает? Как можно было бы
экспериментально продемонстрировать существование волны де Бройля? Вычислите
длину волны де Бройля для следующих объектов: электрона, ускоренного из
состояния покоя потенциалом 10 В, 1 кВ и 100 кВ; протона, летящего со
скоростью 1 КМ'С"*1, 1000 км-с~!; частицы массой 1 г, движущейся со скоростью
100 км-ч-1; автомашины массой 1500 кг, движущейся со скоростью 50 км-ч-1.
Какой из этих объектов демонстрирует резко выраженное
квантовомеханическое поведение?
Рекомендуемые источники. См. Фейнман, Лейтон, Сэндс [145] и Бом [63],
гл. 5. В [38] приведено объяснение соотношения де Бройля двумя его
учениками и изложены некоторые оригинальные попытки интерпретировать это
соотношение. Джеммер [203] оценивает вклад де Бройля в квантовую
теорию.
121
д
ДИПОЛЬНЫЙ МОМЕНТ. Положительный (+q) и
отрицательный (—q) заряды, разделенные расстоянием R> представляют
собой электрический диполь, количественной
характеристикой которого является дипольный момент \х = qR. В
молекулярных масштабах типичная величина пространственного
разделения зарядов имеет порядок 1 А (0,1 нм), а типичный заряд —
это заряд электрона (4,80-10"10 ед. СГСЭ; 1,60-10"19 Кл),
поэтому следует ожидать, что дипольные моменты молекул имеют
величину примерно Ю-18 ед. СГСЭ-см (3,3-Ю-30 Кл-м). Во
многих системах диполи действительно имеют такие размеры, а
поэтому для их измерения обычно используется единица дебай
Список формул Ц.1
Дипольный момент
Энергия диполя ц в электрическом поле напряженностью Е:
В = — \х .Е = — \%Е cos G.
Напряженность электрического поля в точке R, создаваемая диполем
в начале координат
R — единичный вектор в направлении R:
R = R/#.
Энергия взаимодействия двух диполей (общий случай):
*— iik) ж[^2 -3 °" -й) <»>*)\.
R — вектор от Hi к ц2.
Энергия взаимодействия двух параллельных диполей:
R образует угол G с \i\ (или \х2).
Средний дипольный момент свободно вращающейся полярной молекулы
в электрическом поле напряженностью Е (функция Ланжевена):
<|1>«|1<?(|1£/ЛГ);
SB (x) = ctg х — 1/х, функция Ланжевена;
(\х) ~ \x2(E/3kT), kT^>\iE.
Молярная ориентационная поляризация (уравнение Ланжевена —
Дебая):
р — плотность, а — поляризуемость, е — относительная проницаемость,
М — молекулярный вес.
122
д
(D) (ID =3,3-Ю-30 Кл-м). Несколько типичных значений
дипольных моментов молекул приведено в табл. 6. Дипольный
момент представляет собой векторную величину, поскольку
положительный заряд локализуется на одном его конце, а
отрицательный— на другом. Направление диполя в молекуле принято
условно обозначать стрелкой, острие которой направлено к
отрицательному заряду: + -*—• Выражения для энергии диполя,
находящегося в электрическом поле, и некоторая другая
информация представлены в списке формул Д.1.
Векторная природа электрических дипольных моментов
принимается во внимание при вычислении полного момента
молекулы. С каждой группой атомов можно связать направленный
дипольный момент, который с хорошей степенью точности не
зависит от остальной части молекулы. Результат векторного
сложения дипольных моментов всех таких групп дает полный
дипольный момент молекулы. Таким образом легко оценить, что
дипольные моменты хлорбензола и о-, м- и п-дихлорбензолов
равны 1,70, 2,25, 1,48D и нулю соответственно (рис. Д.1).
Вычисление дипольных моментов — удивительно сложное
дело, и его успех существенно определяется степенью точности
молекулярных волновых функций. Оценить трудности можно,
рассмотрев простейший возможный подход в таких расчетах.
При этом подходе плотность электронного заряда на каждом
атоме молекулы плюс положительный заряд ядра атома
представляются как точечный заряд, локализованный на каждом
ядре. При этом несложно вычислить дипольный момент
множества точечных зарядов, распределенных в соответствии с
геометрией молекулы. Однако такая модель точечных зарядов
(рис. Д.2, а) дает плохие результаты, так как предположение
о том, что весь электронный заряд локализован в ряде точек,
слишком грубое. Одним из неучтенных факторов является
асимметрический диполь, который возникает из-за
перераспределения заряда, обусловленного перекрыванием орбиталей
неодинаковой протяженности. Рассмотрим такую систему, в которой
заполненная молекулярная орбиталь образована вследствие
перекрывания большой р-орбитали одного атома и маленькой s-op-
битали другого. Область максимального перекрывания лежит
ближе к маленькому атому, и, вместо того чтобы рассматривать
только заряды, локализованные на тех или иных ядрах
молекулы, приходится учитывать значительное накопление заряда
в области перекрывания, расположенной ближе к маленькому
атому (рис. Д.2,б). Асимметрический дипольный момент
представляет собой вклад этого добавочного зарядового
распределения в полный момент. Этот вклад вовсе не мал: он может
достигать ID. Другой важный вклад может давать атомный
диполь, который также называют гибридным диполем и который
123
д
возникает, как видно из названия, в результате того, что
электрон занимает гибридную атомную орбиталь. Когда это имеет
место, центр распределения электронного заряда не обязательно
совпадаете центром ядерного заряда (рис. Д.2,в). Такое
разделение центров зарядов особенно важно, если на гибридной
орбитали находится неподеленная пара электронов; возникающая
Рис. Д.1. Векторное сложение ди- Рис. Д.2. Вклады в дипольный мо-
польных моментов для 1,2-дихлор- мент молекулы Н20: а — модель
бензола. Экспериментальное зна- точечных зарядов, б — асимме-
чение дипольного момента равно трический диполь, в — атомный
2.25D. вклад в диполь, обусловленный
гибридизацией.
при этом асимметрия электронного распределения атома вносит
в полный дипольный момент вклад порядка ID. Различные
вклады в полный момент молекулы воды показаны на рис. Д.2.
Методы измерения дипольных моментов молекул включают
наблюдение эффекта Штарка в молекулярной спектроскопии и
измерение диэлектрической проницаемости постоянных
растворов (см. разд. «Поляризуемость»).
Упражнения, 1. Что характеризует неисчезающий дипольный момент
молекулы? Почему дебай является удобной единицей измерения дипольных
моментов? Почему молекула, имеющая центр симметрии, не обладает диполь-
ным моментом? Используя данные, приведенные в табл. 6, оцените дипольные
моменты для o-t M-t я-дибромбензолов. Каковы недостатки модели точечных
124
д
зарядов? Что такое асимметрический диполь? Каково его направление? Что
такое атомный диполь?
2. Энергия диполя в электрическом поле Е равна — |Л-Е. Вычислите
энергию (в Дж и в Дж-мол-1), необходимую для того, чтобы изменить на
противоположную ориентацию диполя, равного ID (3,3-Ю-3 Кл-м), в поле
100 В-м-1. Какая ориентация имеет наименьшую энергию? Рассчитайте ди-
польный момент свободно вращающейся молекулы; предположите, что
ориентация молекулы в электрическом поле определяется распределением Больцмана,
и покажите, что ее средний дипольный момент не равен нулю. (Покажите,
что средний дипольный момент вращающейся молекулы определяется
функцией Ланжевена; см. список формул Д.1.) Покажите, что при малых
приложенных полях (насколько они должны быть малы?) средний дипольный
момент обратно пропорционален kT. Вычислите степень упорядочения и
энергию оптимальной конфигурации в том случае, когда полярная молекула
находится поблизости от иона. Взяв для примера воду и ион натрия,
проведите расчет для нескольких значений расстояния между ними.
Рекомендуемые источники. Подробное обсуждение вопроса и примеры
расчетов см. в кн. Коулсона [105] и Мак-Глина, Ванквикенборна, Киноситы
и Кэррола [273]. Расчеты дипольных моментов органических молекул см. в
кн. Стрейтвизера [387]. Таблицы моментов, их определение и использование
приведены Смитом [377], Саттоном [389], Мак-Клелланом [270], а также Мин-
киным, Осиповым и др. [283]. Простой вывод выражения Ланжевена см. у
Мур [288] и в кн. Гассера и Ричардса [19] «Энтропия и энергетические
уровни». Уитли [421] дает простое введение в определение и описывает
применение дипольных моментов. Энергия взаимодействия двух диполей, средняя
ориентационная поляризация (дипольный момент ансамбля свободно
вращающихся молекул в присутствии электрического поля, определенный с
помощью функции Ланжевена) и прочая информация приведены в списке
формул — см. также разд. «Поляризуемость».
ДИРАКА УРАВНЕНИЕ. Уравнение Дирака описывает
поведение электрона таким способом, который сочетает в себе
требования квантовой механики и теории относительности.
Недостаток уравнения Шредингера заключается в том, что оно
несимметрично по отношению к пространству и времени (так как
содержит первую производную по времени и вторые
производные по пространственным координатам). Поэтому желательно
было найти уравнение, которое включало бы производные
второго порядка по времени. Однако, к сожалению, решения такого
уравнения (которое было предложено Шредингером и
называется уравнением Клейна — Гордона) обладают тем свойством,
что полная вероятность нахождения частицы где-либо в
пространстве является функцией времени, и поэтому уравнение
допускает, чтобы число частиц в пространстве было переменным.
В свое время это казалось неприемлемым, и Дирак вышел из
положения, взяв уравнение первого порядка по времени и
поставив прокрустовы условия: пространственные производные также
должны быть первого порядка. Однако он не мог сделать этого
произвольно, и возникшие в связи с поставленными
требованиями условия привели к выводу, что волновая функция должна
125
д
быть четырехкомпонентной. Две компоненты соответствовали
отрицательной энергии, что представлялось бессмысленным.
Однако, вместо того чтобы отказаться от этой теории, Дирак
сделал достаточно смелое предположение, что все состояния с
отрицательной энергией целиком заполнены во всей вселенной и
что обычно мы имеем дело с частицами, заполняющими только
верхние состояния с положительной энергией. Допустимость
такого предположения подтвердилась: было экспериментально
показано, что можно возбуждать частицы из состояний с
отрицательной энергией, оставляя в них при этом дырки. Такая
дырка имеет положительный заряд и положительную массу, она
называется позитроном (е+). Дирак показал, что два решения
с положительной энергией имеют одну и ту же энергию, но в
присутствии магнитного поля вырождение снимается, один
уровень повышается, а другой понижается. Эти решения можно
интерпретировать как описывающие существование электрона
с магнитным моментом, способным принимать две ориентации,
другими словами, частицы со спином 7г. Величина расщепления
уровней характерна для заряженной частицы со спином l/2i но
с моментом вдвое большим, чем можно было бы ожидать на
основании классической модели вращающегося заряда. Таким
образом, аномальное значение g-фактора электрона
естественным образом вытекает из уравнения Дирака.
Рекомендуемые источники. В первую очередь работа самого Дирака [123].
Простое обсуждение структуры уравнения Дирака дано Моссом [292] и Бьер-
кеном и Дреллом [60]; см. также Ландау и Лифшиц [233], Шифф [356], Мес-
сиа [282] и Швебер [358]. Последние достижения показаны в работе Салема
и Вигнера [352]
ДИСПЕРСИОННЫЕ СИЛЫ. Составляющая сил
межмолекулярного вандерваальсова взаимодействия, обусловленная
взаимодействием индуцированных диполей, называется лондонов-
ской дисперсионной силой (по имени Лондона). Она является
разновидностью самовозбуждающихся сил и возникает из-за
корреляции во флуктуациях распределения электронной
плотности соседних молекул. Флуктуация электронной плотности в
молекуле А вызывает появление у нее мгновенного дипольного
момента (если молекула полярная, флуктуация вносит
дополнительный мгновенный вклад в постоянный диполь).
Мгновенный диполь поляризует электроны соседней молекулы;
сгущение электронов на молекуле А сдвигает электроны из соседней
области молекулы В и, следовательно, индуцирует там область
положительного заряда (рис. Д.З). Точно так же появлению
области положительного заряда в молекуле А соответствует
появление области отрицательного заряда, индуцируемой в молекуле
В. Такая корреляция зарядовых распределений приводит к по-
126
д
нижению энергии и соответствует наличию связывающей силы.
Заметим, что существенным условием этого эффекта является
наличие корреляции между флуктуациями заряда.
возникшая флуктуация
/(ала отклик)
возникшая флуктуация
(или отклик)
Рис. Д.З. Взаимодействие типа индуцированный диполь — индуцированный
диполь (дисперсионное).
Список формул Д.2
Дисперсионная энергия для молекул сферической формы
Энергия взаимодействия молекул a n b, находящихся на расстоянии /?:
s (R) = " (idv ) (f) £ А™[d (°W d (a)mo] [d {b)on'd (6)"o]'
где Дт/г = (Em — E0)a + (En — E0)b — сумма энергий возбуждения
молекул а и Ь.
d0m (а) = \ dri^ (а) сГфт (а) — переходный диполь молекулы а,
dQ/l (6) = \ rfx^Q (6) di]^ (b) — переходный диполь молекулы Ь.
Формула Лондона:
^--(юА^Я ^ Д/<«) + /<*)>
где а — поляризуемость молекулы, / — потенциал ионизации.
Если а выражается в кубических ангстремах, R — в ангстремах,
а / — в электронвольтах, то
кm ~ ( 3 ^ ra(a)ct(6)4i (_Л£Ш*М эВ
* (Л) ~ \Ш) I *«J U(a) + /(*)J ЭВ'
3/32я2 « 0,0095.
Учег эффекта запаздывания'-
Если RS/bc> 1,
127
д
Энергия дисперсионного взаимодействия характеризуется
зависимостью R-6 [что находит отражение в межмолекулярном
потенциале Леннарда-Джонса (6-12)], причину которой легко
установить в рассмотренной модели. Поле, создаваемое исходным
диполем молекулы А, зависит от расстояния R по закону R~z
(список формул Д.2), а обратное взаимодействие
индуцированного этим полем диполя В на исходный диполь А вносит еще
R~z. Энергия взаимодействия зависит также от поляризуемости
молекул, так как она является не только мерой легкости, с
которой электрическое поле может исказить электронное
распределение молекул, но мерой возможных флуктуации заряда.
Энергия взаимодействия двух сферических молекул, разделенных
расстоянием Rf с поляризуемостями ал и ав и потенциалами
ионизации /А и /в определяется дисперсионной формулой
Лондона, приведенной в списке формул Д.2. Эта энергия имеет
величину порядка нескольких килоджоулей на моль. В формулу
входят потенциалы ионизации молекул, поскольку мера
флуктуации заряда зависит от легкости, с которой можно возбудить
молекулу.
Для больших расстояний эта дисперсионная формула
неприменима, поскольку, чтобы информация о происшедшей
флуктуации распространялась между атомами, необходимо некоторое
время (эффект запаздывания). Если R велико (R^hc/A, где
Л — характерная энергия возбуждения молекулы), зависимость
R-6 заменяется на R~7 и сила взаимодействия уменьшается
значительно быстрее, чем предсказывает формула Лондона.
Упражнения. Что такое дисперсионные силы и почему они возникают?
Какова их зависимость от расстояния между молекулами? Почему энергия
взаимодействия зависит от поляризуемости молекул? От каких других свойств
она зависит? Какой становится зависимость на больших расстояниях и
вследствие чего она изменяется? Чем объясняется летучесть углеводородов?
Почему 12 легко растворяется в жидком аммиаке? Почему гелий трудно
сжижается?
Рекомендуемые источники. Вывод квантового выражения для
дисперсионного взаимодействия и формулы Лондона см. в [1], гл. 11. См. также кн.
Козмана [217], Эйринга, Уолтера и Кимбалла [137], Чу [100], Гиршфельдера,
Кертиса и Берда [193]. Краткий обзор дан Лонге-Хиггинсом [253]; см. также
Роулинсон [350] и Кертис [113]. Межмолекулярные силы рассматриваются в
соответствующем разделе, где указаны другие рекомендуемые источники.
ДОПОЛНИТЕЛЬНОСТИ ПРИНЦИП. Волновые и
корпускулярные свойства «частиц» являются дополнительными в том
смысле, что эксперимент, предназначенный для определения
величины какого-либо волнового свойства частицы, автоматически
128
д
исключает одновременное точное определение какого-либо
корпускулярного свойства (см. разд. «Неопределенности принцип»).
Дополнительность — это взаимоисключение двух типов свойств,
так как невозможно одновременно выявить и волновые, и
корпускулярные свойства частицы.
Рекомендуемые источники. См. разд. «Дуализм», «Неопределенности
принцип», «Волновой пакет». См. кн. Бома [63], Крамерса [227] и Джем-
мера [203].
ДУАЛИЗМ. В классической физике рассматриваются и
волны, и частицы и проводится четкое различие между ними.
Квантовая механика показала двойственную природу вещества
и излучения — корпускулярно-волновой дуализм. Например, те
объекты, которые на протяжении долгого времени было принято
рассматривать как частицы, обнаружили поведение, считавшееся
характерным для волн: Дэвиссон и Джермер открыли, что
электронные пучки могут испытывать дифракцию на
кристаллических решетках, а Томсон показал, что такой же эффект может
наблюдаться при прохождении пучка электронов через тонкую
золотую фольгу. И наоборот, оказалось, что те объекты,
которые было принято рассматривать как волны, демонстрируют
поведение, считавшееся характерным для частиц: объяснения
эффекта Комптона и фотоэффекта требуют, чтобы энергия и
импульс излучения распространялись в локализованных пакетах.
Приходится сделать вывод, что все объекты были разделены на
«волны» и «частицы» потому, что на уровне экспериментов,
выполненных до начала нашего столетия, один тип поведения
всегда доминировал, а другой был замаскирован. Более тщательное
изучение каждого типа объектов выявляет дуализм его
поведения, и поэтому природа вещества и излучения не язляется
взаимоисключающей, она оказывается сочетанием двух
противоположностей. Какой аспект поведения объекта доминирует,
зависит от эксперимента; причем ни один эксперимент не может
выявить обе стороны дуалистической природы объектов
одновременно (см. разд. «Дополнительности принцип»).
Рекомендуемые источники. О возникновении идеи дуализма как
фундаментального свойства материи см. в кн. Джеммера [203], дополнительные
разъяснения см. в кн. Бома [63]. Квантово-механические основы дуализма
можно исследовать, рассматривая волновые пакеты и то, как принцип
неопределенности ограничивает наше познание природы. В данном разделе мы
вкратце рассмотрели корпускулярно-волновой дуализм, др\гие примеры
двойственности природы различных объектов см. в разд. «Экситоны», «Фо-
ноны», «Фотоны» и «Поляроны».
3
ЗАКОН РАВНОРАСПРЕДЕЛЕНИЯ. Средняя энергия, при-
ходящаяся на каждую степень свободы классической системы
при тепловом равновесии, равна -^nkT, где п — число
квадратичных членов (смещения или импульса), входящих в выражение
для ее энергии. Например, энергия свободного атома
определяется его кинетической энергией, которая может быть
выражена в виде суммы трех квадратичных членов р\\2т, рЦ2т и
рЦ2т9 поэтому средняя энергия атома в равновесии при
температуре Т равна -ккТ, а внутренняя энергия одного моля одно-
. з
атомного газа составляет — у RT. У молекулы, способной
вращаться вокруг трех осей, средняя энергия, приходящаяся на
каждую степень свободы, равна -^kT, поэтому средняя враща-
тельная энергия такой молекулы равна у&Г. Гармонический
осциллятор имеет энергию (р2/2пг) + -j kx*9 где х — смещение из
состояния равновесия, поэтому с каждой колебательной степенью
свободы тела связана средняя энергия kT, так как в выражении
для энергии имеется два квадратичных члена.
Закон равнораспределения является следствием из
распределения Больцмана для заселенности энергетических уровней
при тепловом равновесии и предположения, что
рассматриваемые виды движения являются классическими. Когда виды
движения квантованы, закон равнораспределения теряет силу,
поэтому он неприменим ни к колебаниям молекулы, ни к
вращениям небольших молекул при низких температурах.
Упражнения. 1. Сформулируйте закон равнораспределения. Вычислите
полную среднюю энергию двухатомной молекулы, линейной трехатомной
молекулы, изогнутой трехатомной молекулы и метана, исходя из того, что
поступательное и вращательное движение является классическим, а
колебательное движение квантовано и не возбуждено. Выведите выражение для
молярной теплоемкости этих молекул. Основываясь на законе равнораспределения,
обсудите вклад в полную энергию и теплоемкость молекулы от метильнои
группы, которая при высоких температурах может свободно вращаться
вокруг одной оси, а при низких температурах совершает только классические
крутильные колебания вокруг этой оси.
2. Используя распределение Больцмана при температуре Г, покажите,
что компоненты полной энергии вида х2 и р\ дают одинаковый вклад Ч^кТ
130
3
в среднюю полную энергию Что произошло бы с законом
равнораспределения, если бы в выражение для энергии входили члены четвертого порядка
(л:4 и р4)? К какому эффекту приводит ангармоничность вида х и я3?
Рекомендуемые источники. Закон равнораспределения относится к
области статистической механики; некоторые элементарные примеры применения
см. в кн. Гассера и Ричардса [19] «Энтропия и энергетические уровни».
Полезное обсуждение и примеры применения даны Рейфом [333], вывод и
обсуждение— Дэвидсоном [116]. Более глубоко этот вопрос рассматривается
Фаулером и Гуггенгеймом [149] и Ландау и Лифшицем [234]. Глубокое
изложение приведено Фаулером [148] и Толменом [398].
ЗАПОЛНЕНИЯ ПРИНЦИП (aufbau). В квантовой
механике существует правило (так называемый принцип заполнения),
Рис. 3.1. Порядок заполнения уровней энергии в соответствии с принципом
заполнения (aufbau).
в соответствии с которым происходит заполнение электронами
атомных и молекулярных орбиталей. Согласно этому правилу,
электрон заселяет по возможности самое нижнее энергетическое
состояние, если это разрешено принципом Паули.
Следовательно, первый электрон размещается на самом низшем уровне,
второй подселяется к первому (но с противоположной ориентацией
спина), третий приходит на следующую, более высокую орби-
таль, четвертый спаривается с ним и т. д. (рис. 3.1). При
заполнении вырожденных орбиталей (например, р-орбиталей)
наблюдается несколько другая картина: первые электроны
заполняют различные состояния, отвечающие параллельной
ориентации спинов, как этого требует правило Гунда, и только после
того, как на каждой вырожденной орбиталк окажется по
131
3
одному электрону, остальные электроны начнут спариваться с
ними, подселяясь на те же уровни. Перечень орбиталей,
заселенных в соответствии с принципом заполнения, образует
конфигурацию атома.
Упражнения. Что представляет собой принцип заполнения? Каким
образом он зависит от принципа Паули? Как изменился бы принцип заполнения,
если бы орбитали заполнялись бозонами? Каков смысл правила Гунда?
Используя принцип заполнения, рассмотрите электронное строение атомов Не,
Li, Be, С и N, а также молекул Нг, N2, O2, F2 и N0 (в этом вам поможет
разд. «Молекулярные орбитали»). Что может произойти в том случае, когда
два уровня близки по энергии, но не являются вырожденными? При каких
условиях они могут оказаться оба наполовину заполненными прежде, чем
нижний уровень будет полностью заполнен?
Рекомендуемые источники. См. гл. 8 [1], гл. 3 кн. Герцберга [485], кн.
Маррела, Кеттла и Теддера [299]. Принцип заполнения лежит в основе
построения периодической системы, см. Падефат [4] и гл. 2 кн. Филлипса и
Вильямса [317]. Применение принципа заполнения в молекулярных системах
рассматривается в гл. 9 кн. Коулсона [10, 105]. Принцип заполнения имеет
большое значение в химии переходных металлов, так как в комплексных
соединениях ион металла имеет несколько близлежащих уровней и часто
возникает ситуация, подобная рассмотренной в последнем упражнении (см. разд.
«Кристаллического поля теория», «Поля лигандов теория»).
ЗЕЕМАНА ЭФФЕКТ. Эффект Зеемана состоит в
расщеплении спектральных линий на несколько компонент в сильном
магнитном поле. При нормальном эффекте Зеемана, который
наблюдается для атомов, не имеющих спинового момента, каждая
линия расщепляется на три компоненты. Аномальный (хотя
наблюдаемый гораздо чаще) эффект Зеемана, который
обнаруживается для атомов с ненулевым спиновым моментом,
приводит к более сложной картине расщепления спектральных линий,
В отсутствие у атома спинового момента единственным
источником его магнитного момента являются орбитальные угловые
моменты электронов. Приложенное поле, взаимодействуя с
орбитальным моментом атома, изменяет энергию состояния с
проекцией ML от Е до Е + \хвВМь. Вырождение 2L + 1 состояний
терма с орбитальным моментом L снимается, и появляется
несколько энергетических уровней с расстоянием между ними \хвВ.
Например, терм ХР расщепляется на 3 равно отстоящих друг от
друга компоненты. Терм XD расщепляется на 5 компонент с
такой же величиной расщепления. Правило отбора для оптических
переходов указывает, что AML = О, ±1, и поэтому все переходы
подразделяются на три группы. Группа AAfL = 0 дает линию
с той же частотой, что и в отсутствие внешнего поля (рис. 3.2).
Переходы с AAfL = —1 дают линию, смещенную в сторону низ-
132
3
ких частот, а переходы с AML = -\-l—в сторону высоких
частот. Более внимательное рассмотрение теории и эксперимента
показывает, что испускаемый свет поляризован: при наблюдении
в направлении, параллельном магнитному полю, линия,
отвечающая переходу &ML = 0, отсутствует, а линии, отвечающие
переходам с AAfL = ±l, имеют круговую поляризацию (AML =
= —1 имеет левую круговую
поляризацию, AML = +1 —
правую). При наблюдении спектра
в направлении,
перпендикулярном нолю, линия перехода с
AML = 0 присутствует и
поляризована параллельно
направлению поля (она обозначается как
я-линия); линии переходов с
AML = zt:l также плоскополяри-
зованы, но в направлении,
перпендикулярном полю
(обозначаются как а-линии, от
немецкого senkrecht — перпендикуляр). В
магнитном поле напряженностью
Рис. 3.2. Нормальный эффект Зеемана
порядка 30 кГс расщепление составляет около 1,5 см-1, и его
нетрудно обнаружить экспериментально.
При наличии у атома спинового момента он находится в
некотором мультиплетном состоянии, и в этом случае следует
рассматривать влияние магнитного поля на каждый уровень терма.
2/ + 1 состояний с проекцией Мj полного углового момента /
имеют магнитный момент (—gj|Wfi)J, и, следовательно, их
энергия в магнитном поле равна Е + gjiinBMj. Фактор Ланде
(множитель gj) учитывает зависимость магнитного момента
состояния от спинового и орбитального моментов. Поскольку величина
gj зависит от S, L и /, расщепление состояний оказывается
различным для различных термов. Несмотря на существование тех
же правил отбора и той же поляризации, переходы не
распадаются на три четкие группы. Рассмотрим, например, переходы
ZP — 3S. Магнитный момент терма 3S обусловлен исключительно
его спиновым угловым моментом. Поскольку спин S = 1, под
действием магнитного поля происходит расщепление терма на
три состояния с энергией, отличающейся на 2\лвВ (так как
gj = 2, если L = 0, S = 1, / = 1). Терм 3Р имеет три уровня
г
D V
\-
V...
,р / J
\П
1 н&
-■■{
1 i_
м
~~г
в отсутствие поля
при наличии поля I
133
3
3Ль 3Л, 3^2. Ввиду того что L = 1 и S = 1, gj = 0 для / = О,
gj = з/2 для / = 1 и gj = 3/2 для / = 2. Поэтому терм 3Р0 в
магнитном поле не расщепляется, а происходит расщепление
термов 3Л и 3Р2: первый расщепляется на 3 уровня, второй — на
\ д-№
3Р, д-3/i
\д-0
3s/
\
w~
\
1 г
у i м
VI-
Ч
в отсутствие поля
при наличии поля
1
1
Рис. 3.3. Аномальный эффект Зеемана (3Р — 3S).
5 уровней; в обоих случаях величина расщепления между
соседними уровнями равна 3/2\хвВ (рис. 3.3). Используя правила
отбора, можно определить спектр всех переходов 3P->3S,
который, как явствует из рис. 3.3 имеет весьма сложный вид.
Разобраться в таком спектре помогают поляризационные
характеристики линий. При очень больших напряженностях поля все
аномальные эффекты Зеемана становятся нормальными,
поскольку такое поле нарушает связь угловых моментов. Это явле-
134
3
ние известно как эффект Пашена — Бака (см. соответствующий
раздел).
Основное применение эффекта Зеемана связано с
определением мультиплетности термов. Расщепление уровней энергии
в магнитном поле лежит в основе метода магнитного резонанса
(см. разд. «Электронный парамагнитный резонанс» и «Ядерный
магнитный резонанс»).
Упражнения. Что такое эффект Зеемана? При каких условиях он дает
три линии? Когда наблюдается аномальный эффект? Дайте объяснение
нормального эффекта Зеемана. Обсудите проявление эффекта Зеемана для
перехода XD -*■ XF и, чтобы пояснить вид образующегося спектра, постройте
диаграмму, подобную показанной на рис. 3,3. Какова поляризация линий для
перехода xD-^lF при возникновении эффекта Зеемана? Что произойдет с
поляризацией спектральных линий, если изменить направление магнитного поля
на обратное? Какова должна быть величина расщепления при
напряженности магнитного поля в 10 кГс? Почему аномальный эффект зависит от
наличия у атома спинового момента? (Рассмотрите ^-фактор, чтобы убедиться
в зависимости магнитного момента уровня от 5, L и /). Постройте диаграмму
аномального эффекта Зеемана для перехода ZD-*ZF. Укажите поляризацию
спектральных линий. Что произойдет со спектром, если напряженность поля
существенно увеличить (например, до 100 кГс)?
Рекомендуемые источники. Более подробное обсуждение эффекта
Зеемана см. в [1], гл. 8. Эффект Зеемана и его применение рассматривается
Герцбергом [185], Кингом [222], Куном [229], Кондоном и Шортли [96].
ЗОННАЯ ТЕОРИЯ МЕТАЛЛОВ. Теоретическое описание
структуры и свойств металлов основано на представлении о них
как о решетке положительных ионов, связанных между собой
морем окружающих их электронов. Свойства этого моря
электронов определяют типичные характеристики металлов: их
электро- и теплопроводность, отражательную способность, ковкость
и пластичность. Первостепенное значение имеют уровни энергии,
на которых могут располагаться электроны. Эти уровни
объединены в зоны, в промежутках между которыми лежат области,
запрещенные для заселения электронами. Если зона заполнена
электронами не полностью, а лишь частично, электроны могут
двигаться (изменять свое состояние) под действием даже малых
возмущений — это обусловливает высокую проводимость
металлов (см. рис. 3.4,а и в). Если зона заполнена полностью,
движение электронов становится возможным только при получении
ими достаточной энергии, обеспечивающей их возбуждение с
переходом через запрещенную зону в более высокую разрешенную
зону; поскольку энергетически это невыгодно, такие вещества
являются электрическими изоляторами (см. рис. 3.4,6).
135
запрещенные
уровни
ровни
Т
иеннь
ровни
разрешенные
уровни
к Энергия
а
\///Ш//<
.
i
в
занятые
уровш^-
ж
i
1
в
р
■
запрещенные
уровни
+
разрешенные
уровни
Jl
Рис. 3.4. Степень заполнения зон, разделенных щелью, определяет характер
электропроводимости материала (т. е. является он проводником или изо»
лятором).
-<
• •
-е
• • •
-е
Рис. 3.5. По мере образования цепочки из 2, 3, 4, — N атомов уровни
энергии постепенно образуют зону; при очень больших N уровни такой зоны
образуют континуум.
3
При объяснении причин образования энергетических зон в
металлах используется несколько подходов. Мы рассмотрим два
из них. Во-первых, металл можно рассматривать как огромную
молекулу почти бесконечных размеров. Эта молекула состоит
из атомов, расположенных в виде правильной решетки. Орби-
тали соседних атомов перекрываются друг с другом.
Перекрывание орбиталей наблюдается и в обычных молекулах и
используется как основа при описании структуры молекул на языке
метода молекулярных орбиталей. В качестве простого примера
рассмотрим линейный кристалл (т. е. цепочку из N атомов) и
предположим, что в каждом атоме существует единственная
S-орбиталь.
Рассмотрим вначале два соседних атома этой цепочки. Их
орбитали перекрываются и образуют связывающую и
разрыхляющую пару молекулярных орбиталей, и энергетический зазор
(щель) между ними определяется главным образом величиной
перекрывания (рис. 3.5). Добавим в цепочку третий атом, орби-
таль которого перекроется с орбиталью соседнего атома (малым
перекрыванием с орбиталью следующего за ним атома можно
пренебречь). В молекулярных орбиталях при этом произойдут
следующие изменения: вместо двух ранее образовавшихся
орбиталей получится три орбитали — одна связывающая, одна несвя-
зывающая и одна разрыхляющая (см. рис. 3.5). Рассмотренный
процесс составления из атомов линейной цепочки
(напоминающий процесс вычисления на бухгалтерских счетах) можно
продолжать и дальше, и, как показано на рис. 3.5 и рис. 3.6, при
этом будет происходить постепенное накопление энергетических
уровней и при достаточно больших N получится непрерывная
энергетическая зона шириной As. Поскольку эта зона образована
5-орбиталями, она называется s-зоной.
Если каждый атом поставляет один электрон (как натрий),
то поскольку на каждом уровне, согласно принципу Паули,
могут располагаться 2 электрона, только нижняя
половина зоны окажется заполненной электронами, а верхняя ее
часть останется пустой (рис. 3.4,а). То обстоятельство, что
именно нижняя часть зоны заполняется в первую очередь,
определяется принципом заполнения. Наличие наполовину
заполненной зоны наделяет рассмотренную цепочку свойствами
металла. Если каждый из атомов поставляет два электрона,
заполняется вся зона (см. рис. 3.4, б) и внешнее электрическое
поле не вызовет движения электронов, т. е. цепочка таких
атомов ведет себя как изолятор. Ниже более подробно
обсуждается, почему в этом случае не происходит движения
электронов.
Рассмотрение формирования зоны было бы неточным, если бы
мы ограничивались учетом перекрывания только s-орбиталей.
137
3
Если валентная оболочка атомов металла, т. е. самая
внешняя их оболочка, содержит р-орбитали, они также будут
перекрываться. Эффекты экранирования и проникновения в атомах
приводят к тому, что р-орбитали располагаются выше по
энергии, чем s-орбитали, и поэтому /?-зона лежит выше s-зо'ны."
Ширина щели, отделяющей эти зоны друг от друга, зависит от
прочности связи между атомами и от величины s — р-расщепления
в изолированных атомах (рис. 3.7). Приведенный пример
показывает причину появления энергетических зон и запрещенных
областей энергии.
/ 2 3 4 5 6 7 8 9 10 11 11 20
Число атомов в цепочке
Рис. 3.6. Уровни энергии, рассчитанные для цепочки из N атомов, каждый
из которых взаимодействует только со своим ближайшим соседом. Обратите
внимание, что уже при N = 20 зона становится довольно плотной, а ее ширина
практически постоянной.
Такой подход иногда называют приближением сильной связи
(ПСС), так как в нем предполагается, что электроны связаны
с определенными ядрами, и поэтому их поведение хорошо
описывается с помощью атомных орбиталей. Существует другой
подход, который исходит из представления, что достаточно
хорошим первым приближением является предположение о том, что
электроны не испытывают электростатических взаимодействий
и свободно плавают в объеме металла. Влияние периодической
решетки учитывается только для улучшения приближения на
следующем этапе. Этот подход получил название приближения
почти свободных электронов (ПСЭ).
Рассмотрим формирование зон, основываясь на таком
подходе. Вновь воспользуемся моделью одномерного металла, но
будем предполагать, что положительные ионы отсутствуют.
Такая ситуация напоминает случай, рассмотренный в разд.
«Частица в прямоугольной потенциальной яме», а поскольку атомная
цепочка имеет почти бесконечную длину, электроны можно счи-
J38
Рис. 3.7. Образование s- и р-зон со щелью между ними и характер
перекрывания орбиталей на границах каждой зоны: 1 — s — р-расщепление в
атомах 2 — щель между зонами проводимости в металле.
вторая зона
бриллюэна,
мая зона,
оиллюэна,
•2я/а -п/а
л/а 2я/а
Рис. 3.8. а — уровни энергии свободных электронов; б — зонная структура,
обусловленная периодичностью кристаллической решетки.В обоих случаях
число электронов характерно для металлов.
3
тать свободными. Разрешенные энергии для свободных
электронов принимают непрерывный спектр значений и определяются
квадратом импульса ±kh, т. е. величиной k2 (рис. 3.8,а).
Электроны, помещенные в этот континуум уровней, заполняют их до
некоторой энергии £'ф (энергии Ферми), оставляя свободными
все уровни, расположенные выше. Заполненные уровни образуют
Рис. 3.9. Образование энергетической щели, обусловленное периодичностью
решетки, и ее интерпретация в приближении сильной связи (пунктир). Важно
отметить, что самый верхний уровень нижней зоны имеет такую же длину
волны, что и самый низший уровень верхней зоны; различие этих уровней
состоит в том, что одному из них соответствуют узлы на ядрах, а другому—
между ядрами (постоянная решетки здесь обозначена а).
море Ферми с поверхностью Ферми, расположенной при Еф.
Если бы эта простая модель соответствовала действительности,
все кристаллы представляли бы собой металлы, потому что
подобная «зона» не имеет верхнего предела и не может быть
заполнена. Это обстоятельство еще раз подчеркивает, насколько
важную роль играет периодическая решетка, от которой
зависит, является ли вещество металлом или неметаллом.
Чтобы увидеть, каким образом кристаллическая решетка
приводит к появлению зонной структуры, вспомним, что состояния
свободного электрона описываются волнами с определенной
длиной волны (2n/k). В реальных системах можно представить себе
распространение этих волн вдоль периодической решетки. Если
140
3
длины волн больше постоянной решетки а, золны движутся
свободно, но, когда длина волны сравнима с величиной а, решетка
вызывает дифракцию волн. При длине волны, равной удвоенной
величине постоянной решетки, наблюдается формирование
стоячих волн, т. е. волн, которые, многократно отражаясь от
решетки, движутся вперед-назад. Эти стоячие волны с длиной
Рис. 3.10. Когда к материалу с незаполн иной зоной проводимости
прикладывается разность потенциалов, возникает движение электронов с малой
энергией слева направо (из области отрицательных k в область
положительных k).
волны порядка 2а имеют стационарное распределение в
пространстве, причем максимумы амплитуды стоячей волны могут
приходиться на узлы решетки (т. е. на положительные ионы)
либо находиться посередине между узлами. Хотя в модели
свободных электронов такие стоячие волны имеют одинаковые
энергии, в присутствии решетки их потенциальные энергии
различны, что приводит к образованию энергетической щели при k =
= ±п/а (рис. 3.9). Другая щель появится при k = ±2nja и
т. д. Отсюда следует, что наличие периодической решетки
приводит к расщеплению континуума уровней свободных
электронов на серию зон, разделенных интервалами (рис. 3.8). При
заселении этих зон (зоны Бриллюэна) электронами
металлические свойства возникают только в том случае, если в результате
остаются не полностью заполненные зоны.
Связь зон приближения ПСЭ с зонами модели сильной связи
можно установить, сравнив форму орбиталей на границах s- и
/7-зон с видом волн на границах первой и второй зон Бриллюэна.
Из рис. 3.9 можно видеть, что оба подхода дают одинаковую
узловую структуру, электронные распределения отличаются
только в некоторых деталях, особенно в областях,
примыкающих к ядрам.
При энергиях уровней с \k\ «С я/а, т. е. гораздо меньших
верхней границы первой зоны, состояния электронов можно
141
3
представить в виде бегущих волн (в отличие от стоячих волн на
границе зоны). В одномерном случае волны с импульсом -\-kb
распространяются направо и с импульсом —kb — налево.
Поскольку энергия пропорциональна k2, эти две волны оказываются
вырожденными (т. е. имеют одинаковую энергию). Поэтому в
металлах существует равное число электронов, движущихся
направо и налево, и, когда отсутствуют внешние силы,
результирующего тока нет. Если к образцу прилагается разность
потенциалов, энергия электронов, идущих направо, отличается от
энергии электронов, идущих налево (рис. 3.10). В этих
условиях, чтобы занять состояние с минимальной энергией,
электронам приходится изменить свое распределение; например, может
оказаться больше занятых состояний, отвечающих движению
электронов направо, если этим достигается более низкая
энергия, и тогда в состоянии равновесия наблюдается постоянный
электрический ток. Однако, если зона полностью заполнена,
электроны не могут перестроиться, чтобы преимущественно
приобрести выигрышное направление движения (рис. 3.10). В этом
случае ток отсутствует, и, следовательно, материал является
изолятором. В очень сильных полях может произойти большое
смещение зон, так что следующая пустая зона совместится с
заполненной зоной и потечет ток. Но часто этот ток достигается
ценой разрушения материала (пробой диэлектрика).
Зонная теория металлов способна описывать также их
термические свойства. Например, высокую теплопроводность
металлов можно объяснить способностью электронов быстро
переносить тепло по решетке. Нагревая один конец металлического
стержня, можно возбудить колебания решетки, которые в свою
очередь будут возбуждать электроны, расположенные вблизи
поверхности Ферми. Эти электроны, занимая уровни выше
границы Ферми, получают возможность пробегать по решетке с
высокой скоростью. Рано или поздно они «нырнут» обратно под
поверхность Ферми и отдадут избыток энергии решетке, но эта
часть решетки может оказаться удаленной от первоначально
нагретого конца стержня. Так происходит передача тепла вдоль
стержня.
Основоположники теории теплоемкости металлов были
обеспокоены наличием большого моря электронов, каждый из
которых обязан вносить вклад в теплоемкость куска металла.
Зонная теория развеяла это беспокойство, обратив внимание
исследователей на тот факт, что, когда металл возбуждается
тепловым способом, он приобретает энергию порядка kT и что
только часть электронов внутри интервала kT от поверхности
Ферми может при этом возбудиться и занять пустые уровни.
Это означает, что вклад в теплоемкость металла дает очень
малое число электронов.
142
3
Упражнения. 1. Структуру металлов можно представить в виде решетки
положительных ионов, погруженной в море электронов. Каким образом
такое представление объясняет ковкость и пластичность металлов? Какие
другие характеристики металлов должна объяснять любая теория их структуры?
Какое влияние оказывают энергетические зоны на электро- и теплоемкость
металлов? Почему чистая и гладкая поверхность металла обладает высокой
отражательной способностью? Опишите приближение сильной связи и
объясните, как происходит образование зон. В чем состоит различие между s-
и р-зонами? Рассмотрите одномерную решетку металла, в валентной
оболочке которого имеются s- и р-орбитали. Укажите, какое число электронов
определяет наличие у вещества свойств металла или изолятора (рассмотрите
цепочку атомов с рюрбиталями). Чем определяется ширина зон? Какая из
двух зон, s или р, является более широкой? Обсудите теплопроводность
только что рассмотренной вами решетки В чем состоит приближение
свободных электронов? Почему присутствие периодической решетки приводит к
разрывам в зависимости энергии от k? Обсудите связь этих зон с зонами
модели сильной связи. Что такое зона Бриллюэна? Обсудите, каким условиям
в приближении ПСЭ должны удовлетворять металлы. Что означают понятия
«энергия Ферми», «Поверхность Ферми», «море Ферми»? Как объясняет
зонная теория теплоемкость металлов? Допустим, что пустая зона отделена от
полностью заполненной зоны интервалом, меньшим kT. Как электрические
свойства этого полупроводника зависят от температуры?
2. Рассмотрите одномерную цепочку из N атомов в рамках метода Хюк-
келя и покажите, что по мере добавления атомов в цепочку уровни
постепенно образуют непрерывную зону конечной ширины. Для этого постройте
вековой определитель, в котором резонансные интегралы для каждых двух
соседних атомов равны р, для всех прочих равны нулю. Покажите, что
корни уравнения определяются выражением 2(3 cos[mt/ (п + 1) ], п = 1, 2, ..., N,
где iV —число атомов в цепочке. Нарисуйте схему уровней для N = I,
2, ..., 12, оо.
Рекомендуемые источники. В гл. 6 и 7 кн. Солим ара и Уолша [378] и
Дженнингса и Морриса [26] дано простое рассмотрение структуры металлов
и изоляторов и показано, как теория объясняет их разнообразные свойства.
См. также Олтман [36], где количественное описание проводится на
элементарном уровне. Обзор приближений ПСС, ПСЭ и более сложных их
модификаций можно найти в кн. Куина [329]. См. также кн. Киттеля [224], Займана
[438] и Деккера [121]. Простое описание полупроводников дано Солимаром и
Уолшем [378]. Аморфные материалы имеют большое технологическое
значение; краткое изложение этих вопросов дано Моттом и Дэвисом [294].
и
ИНВЕРСИОННОЕ УДВОЕНИЕ. Инверсионное удвоение
уровней можно обсудить на характерном и важном примере
молекулы аммиака. Эта пирамидальная молекула может
совершать симметричные деформационные колебания (подобно тому,
как это происходит с зонтиком, когда с него стряхивают воду).
При этом (как случается и с зонтиком) молекула может
перейти в другую конфигурацию, продолжая в ней совершать
колебания. Исходная и инвертированная конфигурации
молекулы аммиака с физической точки зрения неразличимы, и
колебания в них происходят с одинаковой частотой. Можно
представить себе, что колебания молекулы происходят в одной из
двух потенциальных ям (рис. ИЛ). Наличие некоторой
вероятности инверсии молекулы, т. е. вероятности туннельного
перехода из одной ямы в другую, означает, что волновые функции
колебательных состояний одной ямы, описывающие смещение
ядер молекулы, могут простираться на другую яму. Если бы
волновые функции колебательных состояний были бы
полностью ограничены одной ямой, вероятность инверсии была бы
исключена. Поскольку волновые функции проникают через
потенциальный барьер, их амплитуды перекрываются. Как и при
построении молекулярных орбиталей, для корректного описания
колебательного состояния его следует представить в виде су-
перпозиции функций, относящихся к обеим ямам. Состояния,
соответствующие сумме и разности двух этих функций, имеют
различные энергии: одно из них располагается глубже под
барьером, чем другое. На первый взгляд может показаться, что
более глубокий уровень отвечает состоянию с узлом внутри
барьера, имеющему более низкую потенциальную энергию.
В действительности это не так, и, чтобы понять, в чем здесь
дело, следует учесть кинетическую энергию и рассмотреть
полную энергию молекулы. Когда у функции появляется узел, она
приобретает большую кривизну и ее кинетическая энергия
увеличивается. Это и происходит с туннелирующими состояниями
аммиака. Подробное рассмотрение показывает, что кинетическая
энергия играет при этом доминирующую роль и что менее
изогнутая, не имеющая узлов и симметричная функция
соответствует более низкой полной энергии. (См. также разд. «Барьер
внутреннего вращения».) Таким образом, у молекулы аммиака
вследствие инверсии происходит снятие вырождения
колебательных состояний и каждая пара уровней расщепляется на
два, т. е. каждый уровень удваивается.
144
и
Энергия расщепления определяется разностью амплитуд,
или вероятностью того, что ядра смогут находиться внутри
потенциального барьера. Эта вероятность определяется величиной
перекрывания колебательных волновых функций в двух ямах,
которая в свою очередь зависит от двух факторов: превышения
барьера над взаимодействующими уровнями (чем больше
превышение, тем меньше проницаемость барьера) и массы прохо-
Рис. ИЛ. Инверсионное удвоение в аммиаке.
дящих сквозь барьер частиц (чем больше масса, тем меньше
вероятность прохождения). У молекулы NH3 величина
расщепления, называемая инверсионной частотой, для самого нижнего
уровня равна 23 786 МГц (0,793 см-1). Согласно классической
картине рассмотренного процесса, с такой частотой происходит
инверсия. В квантовой механике такое описание, строго говоря,
неприменимо; считается, что волновой пакет, локализованный
в одной яме (и соответствующий одной из конфигураций
молекулы) может проникнуть через барьер и появиться на другой
его стороне за время, приблизительно определяемое
наблюдаемой «инверсионной частотой».
Упражнения. 1. Почему инверсионное удвоение получило такое название?
Что является причиной этого эффекта? Почему суммарной и разностной ком-
146
и
бинаииям колебательных состояний соответствуют различные энергии?
Какой из этих комбинаций соответствует меньшая энергия? От чего зависит
это расщепление? Рассмотрите зависимость расщепления от высоты барьера
при условии, что барьер уменьшается от бесконечности до нуля. Каким
образом инверсионное удвоение влияет на спектр аммиака? Какие изменения
может вызвать дейтерирование аммиака? Обсудите инверсиснное удвоение в
других гидридах элементов V группы.
2. Рассмотрите двойной прямоугольный потенциал бесконечной глубины
(т. е. V = оо для х < 0 и х > L) с внутренним барьером прямоугольной
формы и высотой В I т. е. V = В для х в интервале -о~£ — b < х <-?r L + b
и V = О для 0 < х <-,rL — b и -^L + bKxKLy Найдите и обсудите
решения уравнения Шредингера для движения частицы с массой т при
таком потенциале. Рассмотрите удвоение уровней, обусловленное уменьшением
высоты барьера, начиная от бесконечного значения. Рассмотрите влияние
изменения массы частицы.
Рекомендуемые источники. См. гл. 10 [1]. Обсуждение роли
инверсионного удвоения в спектроскопии см. в кн. Кинга [222], Сагдена и Кеннея [388],
Герцберга [188] и Таунса и Шавлова [399]. Процесс инверсии положен в
основу принципа действия мазера (лазерное устройство для микроволновой
области спектра) и поэтому исследован весьма детально. О применении
процесса инверсии можно прочесть в разд. «Лазер», а также в кн. Вейлстеке
[412] и Троупа [400].
ИМПУЛЬС. В классической механике понятие «импульс»
играет основополагающую роль, и то же самое можно сказать
о его роли в квантовой механике. Согласно постулатам
квантовой механики, импульсу как наблюдаемой величине должен
соответствовать некоторый оператор. Если известен вид оператора
импульса, то другие наблюдаемые, зависящие от импульса,
также могут быть записаны в операторном виде. Поэтому
выбору оператора импульса придается в квантовой механике
важное значение. Компонента импульса на ось q описывается
дифференциальным оператором (b/i)(d/dq). Отсюда следует, что
импульс системы связан с градиентом волновой функции,
описывающей ее состояние; большие градиенты соответствуют
высоким значениям импульсов. Это свойство волновой функции
согласуется с соотношением де Бройля, согласно которому при
увеличении импульса частицы (р = Ь/Х) длина волны волновой
функции уменьшается. Когда система описывается стоячей
волной, среднее значение ее градиента равно нулю, и это означает,
что в таком состоянии средний импульс также равен нулю.
Например, частица в одномерной прямоугольной яме описывается
стоячей волной и ее средний импульс равен нулю. (На языке
классической механики это можно объяснить многократным
изменением направления импульса при отражении частицы от
стенок, так что его средняя величина равна нулю.) Если импульс
146
и
частицы, движущейся вдоль какой-либо оси, точно известен, то
ее положение на этой оси не определено. Это важное следствие
принципа неопределенности отражает двойственную корпуску-
лярно-волновую природу материи (см. разд. «Дуализм»). Его
можно понять, если принять во внимание, что частица с
определенным импульсом описывается монохроматической волной
бесконечной протяженности; в этом случае, согласно
интерпретации Борна (см. «Волновая функция»), частицу можно
обнаружить с равной вероятностью в любой точке пространства. И
наоборот, при образовании волнового пакета локализация
положения частицы достигается за счет суперпозиции столь большого
числа волн разной длины, что величина импульса оказывается
совершенно неопределенной.
Упражнения. 1. Какое свойство волновой функции определяет величину
импульса? Как это свойство позволяет понять соотношение де Бройля?
В каких случаях импульс частицы равен нулю? Чему равен импульс частицы,
находящейся в основном состоянии одномерной прямоугольной ямы? Почему
кинетическая энергия может быть не равна нулю, хотя импульс равен нулю?
Почему импульс и координаты частицы можно рассматривать как величины,
дополняющие друг друга (см. разд. «Дополнительности принцип»)?
2. Средняя величина градиента определяется его ожидаемым значением.
Вычислите ожидаемое значение импульса частицы, которая описывается
бегущими волнами вида exp ikx или ехр(—ikx). (Обратите внимание на то, что
комплексно сопряженная волновая функция отвечает противоположному
направлению импульса.) Вычислите ожидаемое значение импульса частицы в
одномерной прямоугольной яме (при выборе волновой функции см. разд.
«Частица в прямоугольной потенциальной яме»). Используя свойство эрмитово-
сти оператора импульса, покажите, что ожидаемое значение импульса в
состоянии с вещественной волновой функцией равно нулю.
Рекомендуемые источники. Роль импульса в квантовой механике
обсуждается в [1], гл. 3 и 4. О фундаментальной роли импульса в квантовой
теории см. в кн. Бома [63], Мессиа [282], Шиффа [356], Ландау и Лифшица
[233], Дирака [123], фон Неймана [410] и Джоча [204].
к
КВАДРУПОЛИ И ДРУГИЕ МУЛЬТИПОЛИ. Электриче
ский квадрупольный момент является одним из членов ряда
мультипольных моментов, используемых для описания
распределения электрического заряда по телу. Первый член этого
ряда — электрический монополь, обычно называемый точечным
зарядом. Затем идет электрический дипольный момент, который
можно представить в виде двух противоположных зарядов,
расположенных рядом друг с другом, поэтому у него нулевой
суммарный заряд (отсутствует монопольный момент). Далее
следует электрический квадруполь, который можно представить
состоящим из четырех зарядов, размещенных таким образом, что
они не создают ни суммарного заряда (отсутствует
монопольный момент), ни суммарного дипольного момента. Такое
расположение зарядов показано на рис. К.1. Аналогичным образом
могут быть построены высшие мультиполи. Чтобы получить
мультиполь порядка 2п (я=1: диполь; п = 2: квадруполь;
п = 3: октуполь; п = 4: гексадекаполь), необходимо разместить
2п электрических зарядов так, чтобы они не создавали мульти-
полей низших степеней. Некоторые из таких размещений
представлены на рис. К.1, но возможны и другие размещения
зарядов, обладающие теми же свойствами.
Часто многие мультиполи отсутствуют из-за симметрии
молекулы. Рассмотрим, например, молекулу С02, которая обладает
линейным строением 0 = С = 0. Поскольку суммарный заряд
молекулы равен нулю, электрический монопольный момент у нее
не возникает. Она симметрична относительно атома углерода,
поэтому у нее отсутствует и электрический дипольный момент.
Атомы кислорода более электроотрицательны, чем атом
углерода, и на них плотность заряда больше, чем на центральном
атоме углерода. Таким образом, распределение заряда имеет
вид (б—) — (S + 6+) — (6—). Это распределение типа^ квадру-
польного, поэтому можно ожидать, что квадрупольный момент
молекулы С02 отличен от нуля, что и наблюдается в
действительности.
Потенциал, создаваемый некоторым распределением
зарядов, можно представить в виде суммы потенциалов отдельных
мультиполей, на которые удается разбить это распределение.
Электрический потенциал мультиполя порядка 2п убывает
с расстоянием пропорционально l/rn+1, следовательно,
напряженность электрического поля этого мультиполя уменьшается
с расстоянием как функция 1/гп+2 (напряженность равна произ-
148
к
водной потенциала, взятой со знаком минус). Следовательно,
область действия более высоких мультиполей гораздо меньше,
чем низких: потенциал монополя убывает, согласно закону
Кулона, как 1/г, а потенциал квадруполя — уже как 1/г3. Более
быстрое убывание потенциалов высших мультиполей можно
понять, исходя из следующих рассуждений. Скопление
электрических зарядов типа изображенных на рис. КЛ на больших рас-
О екэ
монополь диполь
квадруполь \+) Оз
квадруполь
октуполь гексадекаполь
Рис. КЛ. Различные электрические мультиполи.
стояниях от них трудно отличить от систем, не содержащих
вообще никаких зарядов, и такая взаимная компенсация действия
отдельных зарядов тем эффективнее, чем выше порядок муль-
типоля.
Мультиполи разных порядков взаимодействуют с
электрическим полем по-разному. Электрический монополь
взаимодействует с любым электрическим потенциалом (см. список
формул КЛ). Электрический диполь испытывает действие поля лишь
при наличии градиента потенциала, иными словами, испытывает
действие напряженности электрического поля. Это легко понять,
если, воспользоваться представлением о диполе как о двух
точечных зарядах, расположенных рядом друг с другом. При
любой ориентации диполя каждый из зарядов противоположного
знака взаимодействует с потенциалом поля в той точке, где он
находится. Только в том случае, когда потенциал в этих двух
точках различен, суммарное взаимодействие отлично от нуля.
Следовательно, взаимодействие возможно только при условии,
149
к
Список формул К J
Характеристики электрического поля мультиполей
Напряженность поля в точке г, создаваемая точечным мультиполем,
находящимся в начале координат:
Еп ос \/гп+2.
Потенциал в точке г:
для диполя: ( 4 ) ( — )cos® (Я* — Я на расстоянии R, \i=sqR);
для линейного квадруполя: -я- [-£-—J ( ~т ) (3 cos2 8—1)
(такой квадруполь образован из двух диполей \i расположенных
навстречу друг другу, так что eQ — 2qR2).
Энергия мультиполя в поле напряженностью Е&
1) для точечного заряда (монополь) & = qy(r), где
Е2 = — dq>/dz)
2) для диполя: # = — jx.E
= — \iEz cos 6 = \i (dcpfdz) cos 8;
3) для квадруполя: & = — eQ (d2y/dz2) (3 cos2 8—1).
о
что в месте нахождения диполя градиент потенциала
отличен от нуля. Квадрупольный момент испытывает действие
поля только при наличии второй производной электрического
потенциала, или, что то же самое, при наличии градиента
напряженности электрического поля. Понять это поможет рис. К.2.
На рис. К.2, а условно изображена такая ситуация, когда
градиент потенциала (напряженность поля) не меняется в области
квадруполя и энергия их взаимодействия не зависит от его
ориентации, поэтому взаимодействие квадруполя с полем равно
нулю. На рис. К.2, б у потенциала имеется кривизна (т. е.
градиент напряженности поля отличен от нуля), энергия зависит
от ориентации квадруполя, и, следовательно, его
взаимодействие с полем отлично от нуля. Математическое описание этого
взаимодействия дано в списке формул К.1.
Типичный молекулярный монополь по порядку величины
равен заряду электрона е (1,6-10"19 Кл). В качестве монополя
такой величины можно рассматривать однозарядный ион.
Величина молекулярного диполя оказывается порядка eR, где
R — диаметр молекулы; если R « 0,1 нм (1 А), величина диполя
составляет примерно 1(Н9 Кл-м (см. дебай в разд. «Дипольный
150
к
момент»). При таком подходе порядок величины электрического
квадрупольного момента можно оценить как eR2, что составляет
приблизительно Ю-39 Кл-м2. Это настолько малое число, что
электрический квадрупольныи момент удобнее записывать в виде
eQy где Q называют «квадрупольным моментом». Эта величина
обычно выражается в квадратных сантиметрах, и тогда
квадрупольныи момент молекулы имеет порядок 10"~16 см2 (1А2),
Рис. К.2. а — энергия квадруполя
в постоянном поле не зависит
от ориентации; б — энергия
квадруполя в поле с отличным от нуля
градиентом зависит от
ориентации. Плотность штриховки
показывает величину потенциала.
а квадрупольныи момент ядра (см. разд. «Сверхтонкие
взаимодействия»)— порядок 10~24 см2.
Упражнения. 1. Покажите графически распределение зарядов,
соответствующее электрическим квадруполю, октуполю, гексадекаполю, 32-полю.
Затем подберите другие размещения зарядов, соответствующие тем же муль-
типолям. Как зависит от расстояния потенциал, создаваемый мультиполем
порядка 2П? Какова зависимость от расстояния напряженности поля,
создаваемого мультиполем порядка 2П? Почему электрический квадрупольныи
момент является самым важным мультипольным моментом молекулы С02?
Каковы первые отличные от нуля мультипольные моменты атома гелия,
молекул метана и воды? Почему потенциал квадруполя убывает с расстоянием
быстрее, чем потенциал, диполя? Каким свойством должно обладать
электрическое поле, чтобы оно взаимодействовало с квадруполем? Почему
электрический квадруполь не взаимодействует с постоянным электрическим полем?
Какое свойство поля обусловливает его взаимодействие с октуполем?
Нарисуйте схему для иллюстрации физической обоснованности вашего ответа. Как
может быть измерен молекулярный квадруполь?
2. На рис. К.1 схематически показаны два квадрупольных размещения
зарядов. Нанесите на каждую из схем точку на расстоянии г от центра
расположения зарядов. Получите выражение для потенциала, создаваемого
мультиполем в этой точке (рассматривая каждую точку мультиполя в
151
к
качествъ источника кулоновского поля). Предположим, что г много больше,
чем расстояние d между зарядами внутри мультиполя. Разложите в этом
случае потенциал по степеням отношения d/r и сохраните лишь главный член
разложения. Определите таким образом потенциал, создаваемый квадрупо-
лем. После этого найдите напряженность поля в точке г. Сравните
полученный ответ с выражениями, приведенными в списке формул К.1.
3. Представьте, что одиночный электрон удален на расстояние г от
центра квадруполя а) молекулярных размеров и б) ядерных размеров. Оцените
энергию, необходимую, чтобы повернуть квадруполь на 90°. Какова величина
кванта энергии, необходимого для инвертирования ядра такого рода? Какой
частоте это соответствует? Такие расчеты лежат в основе теории метода
ядерного квадрупольного резонанса (ЯКР), позволяющего определять
градиенты электрического поля внутри молекулы на основании измерения
энергии, необходимой для изменения ориентации ядер с электрическими квадру-
польными моментами.
Рекомендуемые источники. Простые электростатические расчеты свойств
мультипольных моментов приведены Корсоном и Лоррейном [98], более
сложные—Джексоном [200] и Роузом [346, 347]. Простое изложение, в котором
особое внимание уделено роли квадрупольных моментов в молекулярной
спектроскопии, см. в кн. Сагдена и Кеннея [388]. Расчеты молекулярных
квадрупольных моментов описаны Дэвисом [117], а методы их измерения — Бэ-
кингэмом [81], который рассматривает также роль молекулярных
квадрупольных моментов в межмолекулярном взаимодействии. Лакен [259] обсуждает
методы определения ядерных квадрупольных моментов и дает подробный
обзор спектроскопии ядерного квадрупольного резонанса. По этому же вопросу
см. также статью Дэза и Хана [114]. Обзор современного состояния ЯКР дан
Кихара и Накамура [92]. О роли квадрупольных моментов в магнитном
резонансе см. в кн. Керрингтона и Мак-Лечлана [90]; в гл. 6 кн. Сликтера [374]
дан более глубокий, четко изложенный обзор. Величины ядерных
квадрупольных моментов приведены в § 8 кн. Грея [168], некоторые из них можно найти
в табл. 17.
КВАНТ. Квант энергии — это минимальное количество
энергии, которое система может отдать или получить. В
классической физике отсутствуют ограничения на малость допустимых
изменений энергии системы, но квантовая физика показала, что
энергия может передаваться только порциями вполне
определенной величины, зависящими от системы и от ее состояния.
Простейшим примером является гармонический осциллятор
с собственной частотой v. Согласно классической теории,
собственные колебания осциллятора могут происходить с любой
энергией, и эта энергия может меняться непрерывным образом.
В квантовой теории энергия осциллятора может меняться
только на величину, кратную h\\ где h — постоянная Планка.
Всякие попытки изменить энергию осциллятора на какие-либо
доли hv обречены на провал.
Размеры квантов, соответствующих поведению
макроскопических объектов, столь малы, что изменение их энергии, по
существу, происходит непрерывно, но на микроскопическом уровне
игнорировать квантовый характер изменения энергии нельзя
152
к
Например, величина кванта, необходимого для передачи
энергии маятнику карманных часов (частота v « 0,5 Гц),
составляет всего лишь 3• 10-34 Дж, однако колебания связи в
молекуле происходят с частотой в 1014 раз большей и соответствуют
энергии 6- Ю-20 Дж, т. е. 36 кДж-моль-1.
Когда атом переходит из возбужденного состояния с
энергией Ее в основное — с энергией Eg> разность энергий Ee—Eg
испускается в виде кванта света с частотой v, которая
определяется условием квантования частот Бора hv = Ee — Eg.
Величина испускаемого кванта зависит от того, какие состояния
участвуют в переходе: квантовые переходы с большой энергией
проявляются как высокочастотное излучение, а с малой энергией —
как низкочастотное.
Постоянная Планка имеет размерность действия (Дж-с),
поэтому ее можно рассматривать как элементарный квант
действия. На раннем этапе развития квантовой теории допустимые
значения действия системы ограничивались целыми кратными А.
Условие квантования Бора — Зоммерфельда, которое лежиг
в основе старой квантовой теории, исходит из этой схемы
квантования. Поскольку угловой момент имеет ту же размерность,
что и действие, естественным квантом углового момента также
является постоянная Планка — угловой момент вращающегося
тела может меняться только на величину порядка к (однако
в этом случае величина Ъ = А/2я приводит к лучшим
результатам). Поэтому вращающееся тело не может быть замедлено
постепенно и плавно, оно должно уменьшать свой угловой
момент и энергию дискретными порциями. Для макроскопических
тел кванты углового момента столь ничтожны, что он меняется
у них практически непрерывно, но в атомных масштабах
квантовые эффекты играют важнейшую роль.
Упражнения. Что такое квант энергии? Рассмотрите задачу о
возбуждении колебаний маятника в классическом и квантовом случаях. Какова
энергия кванта, связанного с возбуждением колебаний осциллятора частоты v?
Вычислите величины квантов энергии для периодических процессов с
собственными частотами 1, 1010 и 1015 Гц соответственно. Вычислите энергии
квантов красного, желтого, синего света, ультрафиолетового и рентгеновского
излучения (воспользуйтесь табл. 5).
Рекомендуемые источники. В гл. 1 [1] рассказывается об истории того,
как была понята необходимость введения квантов, в гл. 3 [1] говорится о
некоторых простейших следствиях гипотезы квантования. История вопроса
излагается также Джеммером [203], а Хофман [194], Гайзенберг [179], Андраде-
и-Сильва и Лошак [38] дают подробные обзоры проблемы.
Экспериментальное подтверждение квантования можно найти также у Мелвин-Хьюза [284],
Слейтера [373] и Бома [63] Детальное и наглядное обсуждение проблемы в
целом дано Фейнманом, Лейтоном, Сэндсом [145]. Эффект Джозефсона лежит
153
к
в основе превосходного метода измерения h\ сам эффект описан Лангенбер-
гом, Скалапино и Тейлором [236], а его применения — Тейлором, Лангенбер-
гом и Паркером [393].
КВАНТОВАЯ ТЕОРИЯ (краткий обзор). Представление о
том, что энергия может передаваться от одной системы к
другой только дискретными порциями, а не непрерывно, возникло
на основании наблюдений над взаимодействием вещества с
излучением и над поведением твердых тел при низких
температурах. Экспериментальные доказательства этой точки зрения были
получены при исследовании излучения абсолютно черного тела,
фотоэлектрического эффекта, комптоновского рассеяния, атом-
ных спектров (особенно спектра атомарного водорода) и тепло-
емкостей твердых тел. Первые квантовые расчеты принадлежали
Планку, который вывел закон распределения излучения
абсолютно черного тела. Первыми квантовомеханическими
расчетами, в которых идея квантования была применена к
механическим системам, являются расчеты уровней энергии атома
водорода, выполненные Бором. В 1926 г., когда Шредингер
предложил свое уравнение, а Гайзенберг — матричную механику,
старая квантовая теория была заменена новой квантовой
механикой. За этим последовал полный пересмотр классической
физики, было дано теоретическое обоснование корпускулярно-
волнового дуализма материи. Дирак ввел в квантовую механику
теорию относительности, и в настоящее время релятивистская
квантовая механика является составной частью квантовой
электродинамики и квантовой теории поля.
Рекомендуемые источники. Основные наблюдения, которые привели к
созданию квантовой теории, изложены в гл. 1 [1]. Ознакомиться с историей
вопроса можно по кн. Гайзенберга [179] и Джеммера [203]. Интересное
введение в проблему дано Андраде-и-Сильва и Лошаком [38]. Наиболее важные
ранние работы обобщены Ван-дер-Верденом [406].
КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА. Квантовая
электродинамика представляется нам апофеозом современной
квантовой механики, хотя пока до конца не ясно, существует ли на
самом деле эта теория. По-видимому, действительно существует
лишь единый взгляд на частицы и поля, согласно которому
электрон является проявлением электромагнитного поля. Подобно
призраку отца Гамлета, электрон мгновенно ускользает в
электромагнитное поле, теряет телесность, а затем вновь возникает
в виде опознаваемой частицы. Электрон проводит V137 часть
времени своего существования в виде излучения (что, между
прочим, соответствует четверти того времени, которое призрак
отца Гамлета проводит на сцене), а остальное время в виде
частицы (см. разд. «Постоянная тонкой структуры»). Эта
теснейшая связь между веществом и излучением подчеркивается
154
к
квантовой электродинамикой, в которой поле излучения и
частица рассматриваются как один и тот же объект. Одно из
следствий общности электрона и электромагнитного поля
заключается в том, что в микроскопических масштабах движение
электрона не может быть плавным, и его можно рассматривать
как «подпрыгивание» вдоль траектории; если называть это
«подпрыгивание» по-немецки Zitterbewegung, терминология
приобретет более респектабельный вид.
Для химика важны два проявления этого «подпрыгивания».
Одно из них связано с лэмбовским сдвигом, другое с величиной
g-фактора для свободного электрона. Согласно теории Дирака,
уровни 2Sv2 и 2Ру2 атома водорода должны быть строго
вырожденными, но Лэмб обнаружил для них очень маленькое
расщепление (порядка 1057 МГц). Следовательно, как бы ни была
хороша теория Дирака, она не верна.
Для того чтобы вкратце привести основные положения кван-
тово-электродинамического объяснения лэмбовского сдвига,
необходимо сначала хотя бы весьма приближенно представить
себе, что имеют в виду, когда говорят о вакууме
электромагнитного поля. Представление о световом луче как о
совокупности фотонов основано на том, что энергия возбуждения
колебаний электромагнитного поля с частотой v может быть равна
лишь целому кратному величины /iv. Это аналогично
представлению о том, как возбуждаются колебания гармонического
осциллятора. Если продолжить такую аналогию, можно сказать,
что, когда возбуждение отсутствует (отсутствуют фотоны),
электромагнитное поле все равно обладает энергией нулевых
колебаний. Эта энергия нулевых колебаний связана с
незатухающими флуктуациями электрического и магнитного полей,
которые неуничтожимы точно так же, как не может быть
полностью уничтожено движение гармонического осциллятора.
Такие осцилляции поля подталкивают электрон, поэтому он и
подпрыгивает относительно положения равновесия. Это приводит
к некоторой неопределенности положения электрона, которая
в случае s-орбитали влияет на его энергию немного больше, чем
в случае /7-орбитали, поскольку электрон, находящийся на
s-орбитали, подходит ближе к ядру и там неопределенность его
положения сказывается сильнее. В результате энергии двух орби-
талей изменяются, но по-разному. Соответствующий сдвиг
можно рассчитать, пользуясь представлениями квантовой
электродинамики; результаты расчетов почти полностью
согласуются с экспериментом.
Величина g-фактора электрона определяет его эффективный
магнитный момент, обусловленный спином. В данном случае
тоже можно считать, что во время вращения электрон
подталкивается вакуумным электромагнитным полем и, вместо того
155
к
чтобы вращаться плавно, он одновременно покачивается. Если
представить себе, что электрон совершает колебания в
экваториальной плоскости, то можно рассчитать соответствующий
магнитный момент. Здесь также наблюдается практически
полное согласие с экспериментом.
Рекомендуемые источники. Книги по квантовой электродинамике трудны
для восприятия. См. ки. Гранди [167], Пауэра [324], Фейнмана [142, 143] и
Романа [344] (последняя книга может служить полезным путеводителем),
Бьеркена и Дрелла [61], Хенли и Тирринга [183], Тирринга [395] и Швебера
[358]. Следует также упомянуть сборник важнейших работ Швингера [359].
Существование флуктуации основного состояния вакуума связано также с
силой притяжения между двумя проводящими плоскостями, находящимися
на небольшом расстоянии. Подробнее об этом взаимодействии Казимира —
Польдера см. в кн. Гранди [167], стр. 142, и Пауэра [324], разд. 3.4.
КВАНТОВЫЕ ЧИСЛА. Квантовые числа — это обозначения,
с помощью которых различаются состояния системы. В
простейших случаях, зная квантовые числа, можно даже вычислять
значения наблюдаемых величин. Так, состояния частицы в
трехмерной прямоугольной яме нумеруются квантовым числом я,
которое может принимать все целые значения больше нуля,
и частица в состоянии с номером п имеет энергию n2(A2/8mL2).
Состояние электрона в атоме водорода полностью определено,
если известны значения квантовых чисел я, /, ти s, ms. В этом
случае п — главное квантовое число, которое определяет
энергию состояния Е = —/?н/я2 (#н — постоянная Ридберга); / —
азимутальное квантовое число, т. е. квантовое число
орбитального углового момента, которое определяет величину
орбитального углового момента [/(/+ 1)]'лй и число его возможных
проекций (2/+1); rrii указывает, какую именно проекцию имеет
орбитальный угловой момент и, следовательно, какую из
(2/+ 1) атомных орбиталей с данными п и / занимает электрон.
Квантовое число тг называется магнитным, так как в
магнитном поле электрон обладает энергией mi\xBB, обусловленной его
орбитальным магнитным моментом. Спиновое квантовое число s
определяет величину спинового момента [s(s + 1)]|/ай и для
электрона принимает фиксированное значение 72; ms —магнитное
спиновое квантовое число — определяет ориентацию спинового
углового момента относительно некоторой оси. Если вдоль этой
оси направлено магнитное поле, спин дает дополнительный
вклад в энергию, равный tnsg\xBB.
Из-за эффектов проникновения электронов и экранирования
ядра в атомах, отличных от водорода, энергия орбитали зависит
еще и от /. В этом случае невозможно дать простое
аналитическое выражение, связывающее значения квантовых чисел
с энергией состояния (см., однако, разд. «Квантовый
дефект») .
156
Список формул К-2
Квантовые числа
Заглавные буквы используются для обозначения квантовых чисел,
описывающих системы, которые состоят из нескольких частиц.
F — квантовое число полного углового момента, включающего вклад
спинового момента ядра; интерпретация этого квантового числа
такая же, как для /.
/ — ядерное спиновое квантовое число имеет тот же смысл, что и
число /. / может принимать целые или полуцелые значения,
но каждому изотопу химического элемента присуще
единственное, характерное для пего значение / (см. табл. 17).
/\ / — квантовое число полного углового момента (который, однако,
не включает спинового момента ядра) или обозначение
произвольного углового момента. /, / никогда не бывает
отрицательным и может быть целым или полуцелым в зависимости
от свойств рассматриваемой системы.
Величина углового момента: Ь У/ (/ + 1).
Число проекций на выделенную ось: (2/+ 1).
Величина проекции: см. т.
Если / является суммой }\ и /г, то разрешимы следующие
значения: / = /, + /2, /i + /г — 1. •. •> I /i — /21.
К — проекция углового момента на ось аксиально-симметричной
молекулы, равна КЬ К может принимать (2/+ 1) значение:
/, /-1, ...> -Л
U L — квантовое число орбитального углового момента (его называют
также азимутальным квантовым числом). Интерпретация этого
квантового числа такая же, как для / но / и L могут
принимать только целые значения.
т, М — магнитное квантовое число (часто используются обозначения
mv ms, Mv Ms, Mj Mj и т. д.).
Проекция углового момента на выделенную ось (обычно
ось z): тЬ.
Энергия магнитного момента в магнитном поле В: —тЪу В
п — главное квантовое число; энергия электрона в атоме водорода
равна — Rh/п2 где /г=1, 2 (Заметим, что / не может
превышать /г — 1.) В ряде случаев используется для
обозначения произвольного квантового числа; например для частицы
в прямоугольной яме п = 1 2, ... и энергия равна п2 {h2/&mL2).
N — полный угловой момент (который, однако, не включает
электронного и ядерного спинового моментов). Ограничения и
интерпретация совпадают с указанными для /, L.
s, S — квантовое число спинового углового момента. Значение и
интерпретация совпадают с указанными для /, /. s, S могут
принимать положительные полуцелые значения, s —
однозначная характеристика частицы, определяемая ее свойствами,
а, р — проекции спиновых моментов для частиц со спином 1/2. а
соответствует ms = + V2» a Р соответствует т5 = — 1/2.
Л, Л — проекция орбитального углового момента на ось симметрии
линейной молекулы, равна ЛИ, ЛИ. X и Л ограничены
значениями /, / — 1, .... — / или L, L — 1, ..., — L соответственно.
Уровни, соответствующие значениям Я — X вырождены
в первом приближении.
к
Продолжение списка формул К-2
v — колебательное квантовое число. Энергия гармонического
осциллятора равна (v + V2) Й©о> где v = 0, l, 2, ....
а, 2 — проекция спинового углового момента на ось симметрии
линейной молекулы, равна crfi, 2Й. а может принимать значения
s, s - 1 — s, а 2 - значения S, S — 1, ..., — S.
о, Q — проекция полного электронного углового момента на ось
симметрии линейной молекулы, равна сой, Qfi. Q может принимать
(2/ + 1) значение: /, / — 1, ..., — /.
В списке формул К.2 приведены некоторые часто
встречающиеся квантовые числа и свойства, которые они определяют.
Рекомендуемую литературу можно найти в соответствующих
разделах. Поразмышляйте по поводу того, почему квантовые
числа принимают только целые или полуцелые значения, а не
являются произвольными дробными или иррациональными
числами.
КВАНТОВЫЙ ДЕФЕКТ. Спектр атомарного водорода^
схематически изображенный на рис. В.8, состоит из нескольких
серий линий. Энергии этих линий можно представить в виде
разности двух величин, каждая из которых имеет вид R/n2, где
R— постоянная Ридберга, а п — целое число. Спектры
щелочных металлов также удается сгруппировать в серии, которые
могут быть представлены в виде разности двух членов вида
R'/n2, но тогда вследствие отталкивающего действия электронов
атомного остова число я, называемое эффективным квантовым
числом, уже не является целым. Его можно записать в виде
п' — б, где п' — целое число, а б — поправка, именуемая
квантовым дефектом. Этот дефект уменьшается с увеличением
главного квантового числа электрона, потому что при этом электрон
удаляется от ядра, и оно вместе с окружающими его остовными
электронами все более напоминает единичный положительный
заряд; в результате энергетический спектр становится все более
водородоподобным. Поскольку квантовый дефект очень сильно
зависит от взаимодействия валентного электрона с
электронами атомного остова, не удивительно, что наибольший дефект
наблюдается у электронов на s-орбиталях, которые проникают
к ядру ближе всего. Квантовый дефект позволяет судить о
величине такого проникновения, и этим почти исчерпывается его
теоретическое значение.
Рекомендуемые источники. Квантовый дефект занимает в старой
литературе больше места, чем в современной. Упоминания о нем можно найти в кн.
Кинга [222], Герцберга [185] и Куна [229]; последний автор приводит
некоторые численные значения и объясняет их роль. Кроме того, см. также кн. Хар-
три [175], Кондона и Шортли [96].
158
к
КИНЕТИЧЕСКАЯ ЭНЕРГИЯ. Кинетической энергией
частицы называется энергия, обусловленная ее механическим
движением. В квантовой механике кинетическая энергия связана
с кривизной волновой функции. Когда волновая функция
начинает изгибаться более круто, кинетическая энергия состояния,
которое она представляет, увеличивается. И наоборот, если
состояние описывается почти плоской функцией, оно практически
не имеет кинетической энергии.
Волновая функция свободной частицы неограниченно
простирается в пространстве и имеет тем меньшую длину волны,
чем больше кинетическая энергия. Причину такой зависимости
длины волны легко установить, если рассмотреть связь
кривизны функции и энергии. По мере увеличения кривизны
волновой функции она становится более изогнутой и начинает
быстрее осциллировать между положительным и отрицательным
значениями своей амплитуды, а быстрая смена знака
представляет собой не что иное, как уменьшение длины волны функции.
Рассмотренная связь длины волны и кинетической энергии,
а следовательно, и импульса свободной частицы может служить
пояснением соотношения де Бройля.
Если частица находится в поле с потенциалом, создаваемым
каким-либо центром, ее волновая функция простирается лишь
на сравнительно небольшую область пространства. Поэтому
определить длину волны в таком случае невозможна, и это
понятие теряет смысл. Однако связь между кривизной и
кинетической энергией сохраняется и в этом случае. Примером такой
системы может служить атом водорода. Его основное
состояние определяется балансом кинетической и потенциальной
энергий и описывается простой экспоненциально убывающей
волновой функцией (ls-орбиталь), которая нигде не обращается
в нуль. Наличие у электрона в этом состоянии кинетической
энергии обусловлено экспоненциальным характером функции,
имеющей отличную от нуля среднюю кривизну.
Упражнения. 1. Какие свойства волновой функции определяют
кинетическую энергию системы? Как связана длина волны свободной частицы с ее
кинетической энергией? Каким образом длина волны частицы связана с ее
импульсом? Вычислите длину волны электрона с энергией 1 эВ, 1 кэВ, ! МэВ
(см. разд. «Электронвольт»). Обсудите, как сказывается кривизна волновой
функции на основном состоянии атома водорода. Что произойдет с энергией
этого атома, если уменьшить область локализации электрона вблизи ядра, с
тем чтобы понизить его потенциальную энергию?
2. Кинетическую энергию одномерной системы находят путем
вычисления ожидаемого значения оператора— (h2/2m)(d2/dx2), а для трехмерной
системы — соответствующего оператора — (h2/2m) (&1дх2 + д2/ду2 + д2/дг2),
или— (#2/2ra)V2 (где V2 — лапласиан). Вычислите кинетическую энергию
частицы со следующими волновыми функциями: exp ikx, sin kx, smnkx-sxnmky,
exp(—kx2)t exp(—nr/ao). Изобразите графически зависимость от числа п
159
к
кинетической энергии частицы, вычисленной для последней волновой функции
(при этом вы увидите связь между кривизной водородоподобной
экспоненциальной функции и кинетической энергией).
Рекомендуемые источники. См. гл. 3 и 4 [1]. Связь кривизны и
кинетической энергии рассматривается во всех книгах по квантовой теории: Давыдов
[119], Ландау и Лифшиц [233], Мессиа [282]. Интересный подход, основанный
на аналогии между оптикой и механикой, содержится в гл. 3 кн. Бома [63].
Процесс рассеяния служит прекрасным примером взаимозависимости длины
волны и кинетической энергии. Помимо указанных выше книг, теория
рассеяния подробно рассмотрена в кн. Родберга и Талера [342] и Гольдбергера и
Ватсона [164]. В кн. Левина [244] теория рассеяния применена к
рассмотрению химических реакций. В более наглядном виде этот подход изложен в
кн. Левина и Бернстейна [245].
КОЛЕБАТЕЛЬНАЯ СПЕКТРОСКОПИЯ (краткий обзор).
В первом приближении колебания молекул считаются просто
гармоническими. Частота колебаний зависит от силовой
постоянной и от массы колеблющегося объекта, согласно
выражению со = (^/т),/а, и выражается в радианах в секунду.
Силовые постоянные молекул и колеблющиеся в них массы таковы,
что частоты колебаний попадают в инфракрасную область
спектра, поэтому изучение колебательных спектров является
задачей инфракрасной спектроскопии. Колебательная структура
проявляется также в электронных спектрах молекул, потому что
при электронных переходах могут возбуждаться колебания;
расстояние между линиями колебательной структуры имеет такой
же порядок величины, как частоты инфракрасных спектров.
Частоты колебаний тяжелых атомов, связанных слабыми
связями, находятся в диапазоне нескольких сотен см-1 (связь I—I
в молекуле 12 характеризуется колебаниями с волновым числом
214 см-1, частотой 6,4-1012 Гц, или длиной волны 4,67-104 нм),
а колебания жестких связей между легкими атомами
происходят в диапазоне нескольких тысяч см-1 (связь Н—Н в молекуле
Н2 характеризуется колебаниями с волновым числом 4395 см^1,
частотой 1,3-10м Гц, или длиной волны 2280 нм). Валентные
колебания связей обычно соответствуют более высоким частотам
по сравнению с деформационными колебаниями связей.
Колебательные частоты некоторых двухатомных молекул приведены
в табл. 10, а типичные частоты колебаний отдельных групп
атомов в молекулах даны в табл. 24.
Колебание является активным, т. е. проявляется в
инфракрасном спектре, если оно приводит к изменению дипольного
момента молекулы. Вследствие этого двухатомные молекулы
дают инфракрасные спектры поглощения, только если они по-
лярны. Для того чтобы увидеть, приводят ли совместные
колебания нескольких атомов в более сложных молекулах к появ-
160
к
лению колеблющегося диполя, необходимо тщательно
исследовать форму соответствующего нормального колебания. Иногда
это можно сделать с помощью внимательного изучения
молекулы, однако более надежный способ — учет симметрии системы
с использованием теории групп. Если колебание активно,
правило отбора для перехода состоит в том, что колебательное
квантовое число при этом переходе может меняться на ±1. При
обычных температурах, согласно распределению Больцмана,
почти все молекулы находятся в своих основных колебательных
состояниях. Из этого следует, что спектр поглощения для
каждого типа колебаний молекулы должен состоять всего из одной
линии. Эта линия соответствует возбуждению в молекуле
колебаний данного типа с переходом из основного состояния
молекулы в ее первое возбужденное состояние. Такая линия
называется основным тоном и обозначается (1 <-0).
На самом деле колебания молекулы не являются строго
гармоническими, потому что потенциал, в котором движутся атомы,
не строго параболический; отклонение от нараболичности тем
больше, чем больше смещение из положения равновесия.
Ангармоничность колебаний приводит к нескольким последствиям.
Во-первых, правило отбора для колебательных переходов
оказывается нестрогим в той степени, которая зависит от величины
ангармоничности. Вместо единственной линии для колебаний
каждого типа наблюдается основной тон (1<-0), или первая
гармоника, которая сопровождается более слабыми обертонами,
или, иначе, второй, третьей и т. д. гармониками,
соответствующими прогрессии переходов (2^-0), (Зч-О), ... . Эти
гармоники должны были бы иметь частоты 2со, Зсо, ..., но из-за
ангармоничности колебаний их положение в спектре несколько
смещено. Возможно одновременное возбуждение двух типов
колебаний молекулы, если они не являются совершенно
независимыми, т. е. если имеется ангармоничность, приводящая к-
взаимодействию колебаний этих типов. Поглощение, обусловленное
таким возбуждением, проявляется как комбинационная полоса
спектра. Когда энергия комбинационного уровня лежит близко
к энергии какого-либо невозбужденного колебания (которое
может быть не возбуждено потому, что оно неактивно в
инфракрасном спектре), из-за наличия ангармоничности между этими
колебаниями может возникнуть резонансное взаимодействие.
Оно называется резонансом Ферми и приводит к сдвигу линий,
активные полосы как бы заимствуют интенсивность неактивной,
которая вследствие этого проявляется в спектре (это явление
называется заимствованием интенсивностей, и оно
обусловлено тем, что неактивное колебание приобретает некоторые
свойства активного колебания, см. разд. «Суперпозиции
принцип»).
161
к
Колебательный переход может сопровождаться
вращательным переходом молекулы. Это приводит к появлению структуры
спектра газообразных образцов. В жидкости столкновения
с растворителем делают структуру неразличимой, уменьшая
время жизни вращательных состояний. При электрических ди-
польных переходах вращательное квантовое число / может
меняться на 0 или ±1. Вследствие этого возникают линии,
расположенные там же, где и чисто колебательный переход (А/= 0),
которые составляют Q-ветвь спектра. Возникает также серия
линий с меньшей частотой, соответствующая вращательным
переходам с А/=—1 и образующая Р-ветвь, и еще одна серия
с более высокой частотой (А/= +1), образующая /?-ветвь.
Серия линий, а не единственная линия наблюдается в этих
случаях потому, что, согласно распределению Больцмана, в
начальном колебательном состоянии занят целый ряд вращательных
уровней и каждое из них дает линию определенной ветви. Если
вращательная постоянная верхнего колебательного уровня
значительно отличается от вращательной постоянной нижнего
уровня, ветви могут «оттеняться», образуя кант (см. разд.
«Ветвь»), это особенно важно, когда колебательный переход
сопутствует электронному переходу, потому что в этом случае
вращательные постоянные могут сильно отличаться. Кроме
того, в колебательном спектре может проявляться инверсионное
удвоение (например, в NH3) и удвоение /-типа (в линейных
трехатомных молекулах). (См. разд. «Кориолисово
взаимодействие».)
Основная химическая информация, которую можно получить
при изучении колебательных спектров, сводится к
идентификации веществ путем сравнения их колебательных спектров,
рассматриваемых как своеобразные отпечатки пальцев. Можно
получить и количественную информацию' о жесткости связей
относительно растяжения и изгиба; соответствующие силовые
постоянные являются важными характеристиками химических
связей. Ангармоничность колебаний показывает, насколько
истинный потенциал отличается от идеального параболического.
Вращательная структура колебательных переходов говорит
о геометрии молекулы в различных колебательных состояниях
(зависимость валентных углов и длин связей от колебательного
состояния). Колебательная и вращательная структуры
электронных спектров дают информацию того же типа о
возбужденных электронных состояниях молекул. Эти сведения
позволяют получить полную картину кривых потенциальной энергии
молекул в различных электронных состояниях.
Мы сосредоточили наше внимание на электрических диполь-
ных переходах в колебательных спектрах поглощения, однако
162
к
колебательные переходы могут также наблюдаться и в
спектрах комбинационного рассеяния.
Рекомендуемые источники. Более подробное обсуждение колебательных
и колебательно-вращательных спектров с использованием теории групп см. в
гл. 10 [1]. Введение в проблему колебаний молекул можно найти у Барроу
[51], Уиффена [424] и Кинга [222]. Характеристические частоты многих связей
перечислены Беллами [52, 53], который дает также описание инфракрасной
спектроскопии как метода химического анализа. Более сложные вопросы
рассматриваются в кн. Ганса [157], Герцберга [186], Вильсона, Дешиуса и Кросса
[431] и Аллена и Кросса [35]. См. также кн. Гейдона [158].
КОМБИНАЦИОННОГО РАССЕЯНИЯ СПЕКТРЫ (рама-
новские). Комбинационное рассеяние (КР) —это неупругое
рассеяние света молекулами. Неупругими называются процессы,
в которых происходит передача энергии от одной из
сталкивающихся систем к другой. В случае комбинационного рассеяния
свет может передать энергию молекуле, возбудив один или
несколько типов ее вращательного или колебательного движения,
или, наоборот, может приобрести энергию от молекулы, если эти
виды ее внутреннего движения уже возбуждены. Поскольку
внутренние виды движения квантованы, передача энергии
может происходить лишь определенными порциями, поэтому в
рассеянном от молекулы свете содержатся компоненты, частоты
которых сдвинуты на дискретные величины по отношению к
частоте падающего света. Определение частотного состава
рассеянного света позволяет получить спектр комбинационного
рассеяния исследуемых молекул.
На практике интенсивный монохроматический пучок света
направляют на образец и затем анализируют свет, рассеянный
в перпендикулярном направлении, поскольку компонента,
соответствующая рассеянию вперед, подавляется интенсивным
падающим пучком (см. ниже). Спектр состоит из сильной
компоненты с частотой падающего света, которая называется
компонентой релеевского рассеяния и соответствует упругому
столкновению фотона с молекулой, и из ряда линий с более высокой
и более низкой частотами (рис. К.З). Линии с более низкой
частотой называются стоксовыми линиями и обязаны своим
происхождением неупругим столкновениям, в которых энергия
излучения передается молекуле. Линии с более высокими, чем ре-
леевская компонента, частотами называются антистоксовыми, и
их появление обусловлено неупругими столкновениями, в
которых молекулярное возбуждение передается от молекулы к
излучению. Интенсивность стоксовых линий выше, чем
интенсивность антистоксовых, потому что для появления последних
необходимо, чтобы часть молекул уже находилась в состоянии с
более высокой энергией. Очевидно, что расстояния между
линиями спектра комбинационного рассеяния несут информацию
163
к
о колебательных или вращательных уровнях молекулы, но,
чтобы извлечь ее, необходимо прежде установить природу
различных переходов и их роль в рассеянии.
Комбинационное рассеяние зависит от поляризуемости
молекулы. Это становится понятным, если для описания процесса
рассеяния использовать следующую схему. Падающее
излучение индуцирует у молекулы переменный дипольный момент, а
этот дипольный момент обусловливает испускание
электромагнитного излучения. Эффективность описанного процесса зависит
6-ветвь
J
10
5
С
6В
II
1
г
5
•f*
10
О-ветвь
I
I
I
I ,
15
стоксоеы
линии
релеевская антистоксовы
линия линии
v
чатом падающего
излучения
Рис. К.З. Вращательный спектр комбинационного рассеяния линейной
молекулы.
от того, насколько легко молекула деформируется падающим на
нее излучением, т. е. от ее поляризуемости. Понятно, что
испускаемое молекулой излучение вовсе не обязательно должно
уносить с собой всю энергию, которая требовалась для возбуждения
молекулы, дискретные порции энергии могут поглотиться
молекулой. Итак, молекула должна быть поляризуемой, но одного
этого еще недостаточно.
Для того чтобы у молекулы наблюдался вращательный
спектр комбинационного рассеяния (обусловленный тем, что
неупругие столкновения возбуждают или дезактивируют ее
вращательное движение), ее поляризуемость должна зависеть от
пространственной ориентации. Вращающаяся молекула водорода
активна в отношении комбинационного рассеяния," потому что
в направлениях, параллельном и перпендикулярном связи, у нее
различная поляризуемость. Молекула метана не активна
относительно вращательного комбинационного рассеяния, потому что
из-за высокой симметрии ее поляризуемость не зависит от
ориентации, и поле не может взаимодействовать с ее ядерным
остовом. Требования, предъявляемые к упругому (релеевскому)
рассеянию, гораздо менее жесткие: необходимо только, чтобы мо-
164
к
лекула была поляризуемой. Таким образом, упругое рассеяние
происходит на всех молекулах, но только молекулы с
анизотропной поляризуемостью могут обмениваться с излучением
вращательной энергией.
Для того чтобы у молекулы наблюдался колебательный
спектр комбинационного рассеяния, ее поляризуемость должна
меняться во время колебаний. Колеблющаяся молекула
водорода активна в комбинационном рассеянии, потому что ее
поляризуемость зависит от того, насколько сильно растянута связь.
Антисимметричные
колебания С02, которые можно (
записать в виде 0->-<-С->
-> О з=* О -<- С ->-<-0, не
влияют на поляризуемость
молекулы, так как при этом ее
размеры практически не ме- j
няются, поэтому указанный ^
вид колебаний не активен в
комбинационном рассеянии.
Как и в случае
вращательного комбинационного рас- б
Рис. К.4. Деполяризация релеев-
ских линий и линий спектра
комбинационного рассеяния.
сеяния, изменение поляризуемости является существенным
требованием для возможности передачи энергии и неупругих
столкновений.
Важное правило, называемое правилом альтернативного
запрета, относится к колебательным спектрам комбинационного
рассеяния молекул, имеющих центр симметрии. Если такая
молекула может совершать колебания, активные в обычном
(инфракрасном) спектре, то этот тип колебаний не наблюдается
в колебательном спектре КР, и, наоборот, если колебание не
наблюдается в ИК-спектре, оно активно в спектре КР. Отсюда
видно, что спектры комбинационного рассеяния могут принести
большую пользу при изучении колебаний (и вращений), которые
не поддаются исследованию методом обычной спектроскопии
ИК-поглощения.
Излучение при комбинационном рассеянии поляризовано,
даже если падающее излучение не было поляризовано. На
рис. К.4 показан более простой случай релеевского (упругого)
рассеяния света. Аналогичная, но немного более сложная кар-
165
к
тина имеет место в случае неупругого, комбинационного
рассеяния. Из рис. К.4, а должно быть ясно, что, если молекула
изотропна и падающий свет плоско поляризован, рассеянный свет
также плоско поляризован. Рассеянный свет плоско
поляризован и в том случае, когда падающий свет не поляризован. Если
молекула анизотропна (рис. К.4,б), в рассеянном сзете
присутствуют обе компоненты поляризации, и он не является
плоско поляризованным. Удобной мерой поляризации служит
степень деполяризации р, которая представляет собой отношение
интенсивностей /ц и /±, определение которых ясно из рис. К.4.
В случае изотропной молекулы интенсивность /ц в плоскости
рассеяния нулевая и р = 0. Для анизотропной молекулы
интенсивность отлична от нуля как в плоскости рассеяния, так и в
перпендикулярном направлении и степень деполяризации р
отлична от нуля. Для свободно вращающейся молекулы
максимальное значение р = 6/7 при неполяризованном падающем
свете и р = 3Д при плоско поляризованном падающем свете
(имеются в виду поляризация и схема наблюдения, изображенные на
рис. К.4). При комбинационном рассеянии поляризация
определяется подобным образом, но в этом случае необходимо
рассматривать изотропию или анизотропию изменения поляризуемости
молекулы. Поэтому полносимметричные колебания играют в
комбинационном рассеянии такую же роль, как симметричная
молекула в релеевском рассеянии, следовательно, комбинационное
рассеяние, связанное с таким типом колебаний, полностью
поляризовано и р = 0. Если колебания анизотропны, рассеянный свет
деполяризован и р > 0. Если падающий свет поляризован, р не
может превышать 3/4, а если он не поляризован, р не превышает
6/7. Отсюда следует, что определение поляризации света при
комбинационном рассеянии является ценным методом определения
симметрии активных в рассеянии молекулярных колебаний.
Если не считать качественного замечания о том, что линии
комбинационного рассеяния соответствуют внутренним
движениям молекулы, Ответственным за изменение ее поляризуемости,
мы все еще ничего не знаем, какими переходами обусловлены
линии комбинационных спектров. Правила отбора для
переходов, активных в спектрах комбинационного рассеяния,
указывают, что колебательное квантовое число должно меняться на
±1, а вращательное квантовое число должно меняться на
Д/ = ±2. Требование изменения вращательного квантового
числа сразу на две единицы обусловлено тем, что активные в
КР переходы зависят от поляризуемости, а не от дипольного
момента перехода, который определяет спектры поглощения. Чтобы
понять, почему А/ = ±2, можно представить, будто процесс
рассеяния состоит из двух дипольных переходов — по одному для
падающего и рассеивающего фотонов. Общепринятое объяснение
166
к
того, почем) вращательное квантовое число меняется на ±2, а
колебательное —на ±1, основано на том, что при вращении
молекулы дипольныи момент принимает ориентацию, неотличимую
от исходной, после полного оборота молекулы, а
поляризуемость— дважды за оборот. При колебаниях дипольныи момент
и поляризуемость молекулы принимают исходные значения
одновременно, поэтому и в колебательном спектре
комбинационного рассеяния, и в спектре ИК-поглощения выполняется
правило отбора Av = ± 1.
Вращательные стоксовы и антистоксовы линии связаны с
разными ветвями колебательно-вращательного спектра, и, согласно
обозначениям, используемым в разд. «Ветвь», они образуют 0-
ветвь (А/ = —2, антистоксовы линии) и S-ветвь (А/ = +2, сток-
совы линии). Зная, какие переходы наблюдаются в спектре,
можно связать линии комбинационного рассеяния с энергетическими
уровнями молекулы на основании такого же анализа, как для
соответствующего спектра поглощения, и, таким образом,
извлечь информацию о силовых постоянных, моментах инерции,
геометрии молекулы и идентифицировать исследуемые вещества.
Важным требованием при проведении экспериментов по
спектроскопии КР является наличие интенсивного
монохроматического пучка света. Наиболее полно этим требованиям отвечают
лазеры. Лазерная спектроскопия КР является в настоящее
время основным направлением исследований. Она не только
усовершенствовала технику обычной спектроскопии КР, благодаря
чему стало возможно изучение частот, очень близких к строго
определенной частоте падающего света; кроме того, уникальные
возможности лазерной спектроскопии КР привели к открытию
ряда новых эффектов. К преимуществам лазерной техники,
которые используются в спектроскопии КР, относятся малая
расходимость пучка, позволяющая вести наблюдения вблизи
направления вперед, и исключительно высокая интенсивность.
При наблюдении вынужденного комбинационного рассеяния
интенсивный лазерный пучок света фокусируют на образце и
регистрируют свет, рассеянный вперед или под близкими
направлениями. Рассеянный вперед свет состоит из излучения с частотой
падающего пучка, к которому примешано стоксово
излучение с частотами v, v — v*, v — 2v2- и т. д., где v* — частота
внутреннего движения молекулы, дающего интенсивное
комбинационное рассеяние в обычном эксперименте. Вокруг этого узкого
рассеянного вперед пучка располагается ряд концентрических
колец света с возрастающей частотой: v + v* — в первом кольце,
v + 2vi — во втором, v + 3v» — в третьем и т. д. (рис. К.5, а).
Такой эффект обусловлен следующими причинами. Первичные
стоксовы линии рассеяния настолько интенсивны, что
комбинационное излучение может вновь неупруго рассеиваться, и это
167
к
приводит к появлению следующей стоксовой линии с частотой
v — 2\'г и т. д. Интенсивность антистоксовых линий также
обусловлена многократным рассеянием. Большая интенсивность
первичных антистоксовых линий с частотой v + v* вызвана высокой
интенсивностью лазерного пучка света, делающей возможной
аннигиляцию двух фотонов с частотой v на одной молекуле с
последующим одновременным рождением одного фотона с частотой
v + Vf и другого — с частотой v — v*. Значительная вероятность
Рис. К.5. Вынужденное комбинационное рассеяние (а), гиперкомбинационное
рассеяние (б) и обратное комбинационное рассеяние (в).
того, что два фотона одновременно окажутся в области одной и
той же молекулы, возможна только при чрезвычайно высокой
интенсивности возбуждающего пучка света. Выполнение этого
условия необходимо для того, чтобы появились линии большей и
меньшей частоты. Зависимость частоты рассеянного света от
угла рассеяния является следствием выполнения закона
сохранения импульса при столкновениях.
При наблюдении гиперкомбинационного рассеяния
интенсивный лазерный пучок света с частотой v фокусируют на образце,
и наряду с обычным комбинационным рассеянием в спектре
наблюдаются частоты 2v и 2v ± v< (рис. К.5,б). Таким образом,
гиперкомбинационное рассеяние — это появление некоторой
структуры в спектре неупругого рассеяния от фотонов высокой
частоты, которые рождаются в результате аннигиляции двух
низкочастотных фотонов; в этом процессе участвуют молекула
и два одновременно падающих на нее фотона. Эффективность
гиперкомбинационного рассеяния, как и эффективность вынуж-
168
к
денного комбинационного рассеяния, зависит от интенсивности
лазерного пучка света. Эта разновидность комбинационного
рассеяния применяется, в частности, для измерения гиперполяри-
зуемостей (см. разд. «Поляризуемость»).
При наблюдении обратного комбинационного рассеяния на
образце фокусируют два пучка света. Спектр одного из них
непрерывный, а другой пучок монохроматический, высокой
интенсивности (лазерный). При этом наблюдаются переходы,
которые проявляются как поглощение света с частотами v + vt- из
непрерывного спектра. Этот процесс можно обрисовать
следующим образом. Из пучка с непрерывным спектром на молекулу
попадает фотон с частотой v + v*, одновременно туда же
попадает лазерный фотон с частотой v, который индуцирует
испускание возбужденной молекулой фотона с этой же частотой, и
молекула остается возбужденной с энергией, соответствующей час»
тоте v* (рис. К.5,я).
Упражнения. 1. В чем заключается различие между упругими и
неупругими столкновениями? Какое из них лежит в основе комбинационного
рассеяния? Какова схема эксперимента по спектроскопии КР? Какой выигрыш
дает использование лазера в таких экспериментах? Что такое релеевская
компонента рассеяния? Обсудите вид спектра КР и объясните
происхождение стоксовых и антистоксовых линий. Какими свойствами молекул
обусловлено комбинационное и релеевское рассеяние? Чем вызвана зависимость этих
видов рассеяния от свойств молекул? Каким необходимым свойством
должна характеризоваться молекула, чтобы у нее обнаруживался колебательный
спектр комбинационного рассеяния и соответственно вращательный спектр
комбинационного рассеяния? В чем состоит правило альтернативного
запрета? Какие колебания двуокиси углерода проявляются в спектре КР и
какие — в ИК-спектре? Каковы правила отбора для колебательных и
вращательных спектров КР, почему в последнем случае необходим двухквантовый
переход, а в первом — достаточно одноквантового? Какую информацию
можно извлечь, зная расщепление в О- и S-ветвях вращательного спектра КР?
2. Покажите, что наведенный в классическом поляризуемом ротаторе ди-
польный момент приводит к излучению стоксовых и антистоксовых линий.
При проведении расчетов исходите из того, что поляризуемость молекулы
изменяется гармонически от а — 6а до а + 6а вблизи среднего значения а.
Затем покажите, что молекула обладает наведенным дипольным моментом
вида аЕ + 6а£ cos corf, где Е — напряженность возбуждающего рассеяния
оптического поля. После этого предположите, что Е изменяется во времени по
закону cos coo?, и с помощью простых тригонометрических преобразований
покажите, что в этом случае у наведенного дипольного момента должны быть
компоненты, колеблющиеся с частотами со и со ± со0. Такой расчет приводит
к выводу, что интенсивности стоксовых и антистоксовых линий равны.
Объясните, почему этот вывод неверен.
3. Для того чтобы сформулировать правила отбора для переходов в
колебательном спектре комбинационного рассеяния, можно воспользоваться
методами теории групп. Оператором перехода в данном случае является
тензор поляризуемости молекулы, его главные компоненты преобразуются как
хх, уу, гг. Используя список формул X. 1, покажите, что в молекуле с
центром симметрии правило альтернативного запрета обусловлено разными
свойствами симметрии дипольного момента и поляризуемости относительно
169
к
преобразования инверсии. Используя характеры, приведенные в табл. 3,
убедитесь в том, что колебания А\, Ей Гг наблюдаются в спектрах КР тетра-
эдрической молекулы АВ4. Какие переходы наблюдаются в спектрах КР
молекул воды, двуокиси углерода, аммиака?
Рекомендуемые источники. Ответы на упражнения 2 и 3 и дальнейшее
обсуждение см. гл. 10 [1]. О применениях см. в кн. Вудворда [433], Уиффена
[424] и Барроу [51]. Лазерное комбинационное рассеяние описано Лонгом
[252] и Гилсоном и Хендрой [162]. Этот вопрос подробно рассмотрен Герцбер-
гом [186]. Процессы деполяризации обобщены в гл. 19 кн. Вудворда [433].
КОММУТАТОР. Коммутатором двух операторов А и В
называется разность АВ— ВА\ обычно он обозначается [А, В].
(АВ означает, что сначала выполняется преобразование В, а
затем— преобразование А\ ВА означает, что А предшествует В.)
Два оператора коммутируют, если их коммутатор равен нулю.
Неравенство нулю коммутатора двух операторов указывает на
то, что результат двух преобразований зависит от порядка, в
котором они выполняются:. А после В и В после А приводят к
разным результатам. Например, умножение функции f(x) на х и
последующее дифференцирование не равносильно умножению
после дифференцирования: (dldx)xf(x)=£x(dldx)f(x).
Коммутатор (d/dx) и х, т. е. [d/dxt x], равен 1, так как, согласно
правилам дифференцирования, произведение (d/dx)xf(x) равно
f(x) + x(d/dx)f(x).
Важное значение, придаваемое коммутаторам в квантовой
механике, объясняется большой ролью операторов в этой
теории: квантовомеханические процедуры должны проводиться
с учетом возможной некоммутативности различных операторов;
более того, сам факт, что коммутаторы не всегда исчезают,
является особенностью, определяющей отличия квантовой
механики от классической (см. разд. «Матричная механика»).
В частности, принцип неопределенности применим только к тем
наблюдаемым, операторы которых не коммутируют.
Коммутаторы квантовой теории тесно связаны со скобками
Пуассона классической механики, и установление этой связи
считается одним из самых замечательных достижений Дирака.
Практическое значение коммутаторов связано с тем, что
собственные функции одного оператора являются также
собственными функциями другого оператора, с которым он коммутирует.
Упражнения. Что такое коммутатор? Вычислите коммутатор операторов
(d/dx) и х, d/dx и d/dyy d2/dx2 и *3, а также x(d/dy)— у (d/dx) и z{d/dx) —
— x(dldz). Покажите справедливость приведенных ниже соотношений:
[ДВ] = -[5,4
[А + В, С] = [А, С] + [В, С],
[А, [В, С]] + [В, [С, А]] + [С, [Л, В]] = 0 (тождество Якоби).
170
к
Докажите след>ющее: для того чтобы два оператора имели общие
собственные функции (т. е. чтобы собственные функции одного оператора были
собственными функциями другого), им необходимо и достаточно коммутировать.
Рекомендуемые источники. Обсуждение и доказательство некоторых
следствий некоммутативности операторов см. в [1], гл. 4. Там же приведен ответ
к последнему упражнению. Дальнейшее рассмотрение см. в стандартных
курсах по квантовой теории, например: Давыдов [119], Ландау и Лифшиц [233],
Мессиа [282], Шифф [356] и Дирак [123]. Более глубоко этот вопрос
рассмотрен Джочем [204] и Салемом и Вигнером [352]. Следствия, к которым
приводит некоммутативность экспоненциальных операторов вида exp Q,
получены Уилкоксом [429].
КОМПТОНА ЭФФЕКТ. При рассеянии света электронами
происходит увеличение его длины волны; оно не зависит от
первоначальной длины волны, и определяется только углом, на
который отклоняется свет.
Если исходить из представлений классической теории,
кажется странным, что для определенного угла рассеяния
наблюдается только одно значение сдвига длины волны, и этот
результат наталкивает на мысль о процессе упругого столкновения.
Если предположить, что фотон с энергией hv и импульсом h/K
сталкивается с покоящимся электроном и что при столкновении
двух этих частиц и энергия, и момент сохраняются, нетрудно
вывести выражение 6Я = (h/mec) (1 — cos 0), где 6Я — сдвиг
длины волны (всегда положительный), а 0 — угол рассеяния
света. Это выражение действительно не зависит от
первоначальной длины волны и дает единственное значение 6Я для данного
угла 0. Тем самым подтверждается справедливость модели
столкновения, а это является отличным доказательством того,
что свет состоит из квантов, или фотонов, которые ведут себя
как частицы.
Величина h/mec называется комптоновской длиной волны Яс;
ее численное значение равно 0,024 А, или 2,4 пм (точнее,
2,4263096-10-12 м). Поэтому даже при рассеянии назад (0 =
= 180°)' сдвиг длины волны составляет только 4,8 пм, и малость
этой величины указывает, что для наблюдения эффекта Комп-
тона необходимо использовать рентгеновские или у~лУчи> так
как только тогда сдвиг составляет значительную часть длины
волны; хотя эффект Комптона не зависит от длины волны, в этом
случае его легче зарегистрировать.
Упражнения. 1. Что характерно для комптоновского рассеяния? Какие
особенности этого процесса противоречат его классической трактовке как
взаимодействия заряженной частицы с электромагнитной волной? Почему
эффект Комптона играет незначительную роль при больших длинах волн?
Вычислите комптоновскую длину волны протона.
171
к
2. Выведите формхлу эффекта Комптона. Обозначьте начальную длину
волны фотона как X и конечную — как Я + 6Л; пусть электрон вначале
покоится, а после столкновения приобретает кинетическую энергию mv2/2 и
импульс mv (приведите вывод только для нерелятивистского случая).
Запишите выражение для закона сохранения энергии при столкновении (эго
означает, что столкновение упругое) и то же самое проделайте для импульса,
считая, что свет отклоняется на угол 9. Чтобы получить окончательное
выражение, разложите входящие величины в ряд, ограничиваясь величинами первого
порядка малости по 6Х, и исключите из него v.
Рекомендуемые источники. Обсуждение различий между классическими
и квантовыми явлениями см. в кн. Бома [63], а историю вопроса — в кн.
Джеммера [203]. Оригинальная работа опубликована Комптоном [94]. Более
подробное обсуждение эффекта Комптона приведено в кн. Гайтлера [180],
Джоча и Рёлиха [205] и Швебера [358] Заметим, что нерелятивистский предел
комптоновского рассеяния обычно называется томсоновским рассеянием и что
в результате первого расчета сечения релятивистского фотон-электронного
рассеяния была получена формула Клейна — Нишины. Эти вопросы
обсуждаются в цитированных работах.
КОНТАКТНОЕ ВЗАИМОДЕЙСТВИЕ ФЕРМИ. Контакт
электрона с магнитным ядром приводит к магнитному
взаимодействию, называемому контактным взаимодействием Ферми,
которое является частным случаем сверхтонкого взаимодействия.
Какова природа контактного взаимодействия? Возможны
различные объяснения разной степени сложности; наиболее
наглядным является следующее. Будем считать, что магнитный момент
ядра возникает из-за циркуляции тока, и заменим магнитный
момент эквивалентным кольцевым током. На больших
расстояниях от ядра поле, создаваемое кольцевым током, неотличимо
от поля точечного магнитного диполя, но вблизи ядра, или
кольцевого тока, считать источник поля точечным уже нельзя,
магнитное поле является типичным для кольцевого тока ненулевого
диаметра (рис. К.6). Внесем в это поле электрон со спиновым
магнитным моментом. Вдали от ядра он испытывает действие
чисто дипольного магнитного поля, но, если электрон может
проникнуть в ядро, он попадает в совершенно другую область,
где иоле всюду направлено только в одну сторону. Магнитное
взаимодействие этого недипольного поля и магнитного момента
электрона и представляет собой контактное взаимодействие.
Итак, чтобы возникло это взаимодействие, электрон должен
находиться в контакте с ядром. Возможно ли это? Для
электрона, находящегося на /?-, d- или более высоких орбиталях,
такое взаимодействие не осуществимо, поскольку все эти орбитали
имеют узел в ядре. Узла в ядре нет только у s-орбитали, и у
занимающего эту орбиталь электрона вероятность нахождения на
ядре отлична от нуля. Следовательно, только s-электроны могут
участвовать в контактном взаимодействии Ферми. Поскольку
s-орбитали сферически симметричны, взаимодействие не должно
172
к
иметь преимущественных направлений, и действительно
обнаружено, что оно изотропно.
Насколько сильным является это взаимодействие? О его силе
можно судить по добавочному магнитному полю, которое
действует на электрон из-за его взаимодействия с ядром. Для
ls-орбиталив атоме водорода контактное взаимодействие (с
энергией, соответствующей частоте 1420 МГц) эквивалентно
магнитному полю в 508 Гс; для электрона 2$-орбитали фтора
напряженность добавочного поля составляет примерно 17 кГс. Внут-
Рис. К.6. Интерпретация контактного взаимодействия Ферми: в ядро может
проникать только s-электрон.
ренние электроны в атомах тяжелых элементов могут
испытывать огромные взаимодействия, достигающие миллионов гаусс.
Некоторые типичные величины приведены в табл. 9.
Контактное взаимодействие Ферми играет важную роль
в спектрах электронного парамагнитного резонанса, так как
добавочное локальное поле проявляется в спектре как
сверхтонкая структура. Контактное взаимодействие, будучи изотропным,
не исчезает в жидкой среде. Оно играет также важную роль
в ядерном магнитном резонансе, поскольку вносит вклад в один
из механизмов спин-спинового взаимодействия.
Упражнения. 1. Что такое контактное взаимодействие Ферми? Почему
оно зависит от конечных размеров ядра? Почему контактное взаимодействие
характерно только для s-электрона? Почему оно изотропно? Где это
взаимодействие играет важную роль?
2. Энергия контактного взаимодействия Ферми определяется выражением
— (2iio/S)[yNye\^(0) |2] I-s, где \n и уе — гиромагнитные отношения ядра и
электрона соответственно (см. «Магнитный момент»), 1 и s —их спины, И-о —
173
к
магнитная проницаемость вакуума, а |ф(0)|2 — вероятность того, что
электрон находится в ядре. Покажите, что взаимодействие имеет такой вид, как
если бы ядро создавало магнитное поле (m-o/3)yjv 1^(0) |21, действующее на
магнитный момент электрона, и с помощью выражений для атомных орби-
талей водорода, приведенных в табл. 15, вычислите индукцию магнитного
поля, действующего на электрон, находящийся на Is- и 25-орбитали водорода.
Повторите расчет для различных атомных орбиталей слейтеровского типа
для элементов второго периода. Во всех случаях замените I его
максимальной проекцией mih.
3. Электрон, занимающий орбиталь соседнего с магнитным ядра, может
вступать в контактное взаимодействие, каков бы ни был тип этой орбитали,
при условии что она имеет конечную амплитуду в точке расположения
магнитного ядра (так, 2р-орбиталь на ядре В может иметь ненулевую амплитуду
в точке, где находится соседнее ядро А) Сила вазимодействия в этом случае
определяется выражением, приведенным в упражнении 2, однако множитель
|г|)(0)|2 должен быть заменен на |i|)(R)|2, где R —положение ядра, с
которым взаимодействует электрон, по отношению к ядру, на котором находится
орбиталь. Оцените величину контактного взаимодействия для протона,
приближающегося к атому водорода, пренебрегая возмущением, которое
вызывает присутствие второго протона.
Рекомендуемые источники. Подробное обсуждение контактного
взаимодействия см. в [1], гл. 11. Роль этого взаимодействия рассматривается в кн.
Мак-Лечлана «Магнитный резонанс» [2], Эткинса и Саймонса [39], Керринг-
тона и Мак-Лечлана [90], Сликтера [374], Абрагама и Блини [28]. Величины
контактного взаимодействия для различных ядер приведены Эткинсом и Сай-
монсом [39]. Расчеты, включающие контактное взаимодействие, описаны Ме-
мори [281] и Фрименом и Френкелем [155]. Простой вывод выражения,
описывающего контактное взаимодействие, приведен в [1], гл. 11, и [374]; вывод
из уравнения Дирака дан Гриффитом [170] и Бете и Солпитером [57].
КОНФИГУРАЦИОННОЕ ВЗАИМОДЕЙСТВИЕ.
Конфигурация дает сведения о том, как электроны распределены по
имеющимся атомным или молекулярным орбиталям, и
простейшее описание электронного строения атома или молекулы
сводится к указанию их конфигурации. Например, молекулу
водорода можно описать конфигурацией lsa2. Энергию,
соответствующую такой конфигурации, можно было бы рассматривать как
«молекулярную энергию». Однако такое описание было бы не
вполне правильным, поскольку для точного описания молекулы
необходимо учесть примешивание к данной конфигурации
некоторых других конфигураций. Мы знаем, что по ряду причин
волновая функция молекулы может быть неточной, и однокон-
фигурационное описание ее электронного строения было бы
наверняка ошибочным. Например, одноконфигурационное
описание молекулы водорода ошибочно, поскольку оно позволяет
обоим электронам чрезмерно локализоваться на одном и том же
ядре.
Положение можно улучшить, если изменить волновую
функцию путем учета конфигурационного взаимодействия (KB). Мы
допускаем, что волновая функция молекулы описывается смесью
174
к
(суперпозицией) волновых функций, отвечающих различным
конфигурациям. Примешивание конфигураций некоторых
возбужденных состояний искажает функцию основного состояния, и
если это снижает энергию основного состояния, то, как
утверждает вариационный принцип, мы получаем улучшенное описание
молекулы. В случае Н2 наибольший выигрыш в энергии, и,
следовательно, улучшение волновой функции могут быть
достигнуты примешиванием конфигурации lsa*2. Если
проанализировать влияние этого примешивания (см. приведенные ниже
упражнения), то оказывается, что влияние конфигурационного
взаимодействия заключается в уменьшении вкладов таких
ситуаций, когда оба электрона находятся у одного ядра. Те, кому
знаком язык теории электронной корреляции, поймут, что KB
привело к некоторой зарядовой корреляции; простая теория
молекулярных орбиталей недооценивает электронную корреляцию,
а учет KB позволяет до некоторой степени исправить этот
недостаток.
Какие конфигурации могут смешиваться с основным
состоянием? Первое требование заключается в том, чтобы они имели
ту же симметрию: например, описание Н2 улучшается
примешиванием состояний симметрии *2, а не 32 или 1П. Согласно
второму требованию, вытекающему из теоремы Бриллюэна,
однократно возбужденные состояния не могут взаимодействовать
непосредственно с основным состоянием, если рассматриваются
конфигурации, полученные методом самосогласованного
поля.
Учет KB приводит не только к улучшению молекулярной
энергии. Тот факт, что конфигурации возбужденных состояний
примешиваются к конфигурации основного, означает, что
основное состояние молекулы приобретает некоторые характеристики
возбужденных. Такое примешивание может повлиять, например,
на предсказания, основанные на применении правила Гунда.
Простейший способ учета KB на практике заключается в том,
чтобы вычислить орбитали и их энергии, а затем, заселяя их
электронами, образовать различные конфигурации. Основное
состояние соответствует конфигурации с наименьшей энергией.
Далее искомая волновая функция молекулы выражается в виде
линейной комбинации этих конфигураций (отбор необходимых
конфигураций осуществляется с учетом их симметрии), после
чего вариационным методом определяют наилучшую смесь
конфигураций. Лучшей, но намного более сложной процедурой
является многоконфигурационный расчет, в котором сначала
вычисляется наилучшая структура отдельно для каждой
конфигурации (без использования принципа заполнения единой системы
уровней), а затем к этим оптимизированным конфигурациям
применяется вариационный метод.
175
к
Упражнения. 1. Почему одноконфигурационное описание состояния моле
кулы может оказаться плохим описанием ее истинного электронного
строения? В каком отношении одноконфигурационное описание молекулы водорода
в рамках простой теории молекулярных орбиталей является неправильным?
Что такое конфигурационное взаимодействие, каким образом его учет
исправляет некоторые недостатки одноконфигурационного метода? Как оно влияет
на интерпретацию волновой функции основного состояния Н2? Какие другие
влияния может оказывать учет KB на описание свойств молекул? Установите
влияние учета KB на описание устойчивости, дипольного момента, магнитной
восприимчивости и поляризуемости молекул. Меняет ли учет KB
спектральные правила отбора? Каковы критерии отбора конфигураций, способных
взаимодействовать с основным состоянием?
2. Энергия конфигурации А лежит на Д£ выше энергии Eg конфигурации
основного состояния. Допустим, что между этими конфигурациями
существует взаимодействие (т. е. что матричный элемент V между этими
конфигурациями отличен от нуля). Используя вариационный метод, покажите, что
исправленная с учетом KB энергия основного состояния определяется
меньшим корнем квадратного уравнения (полученного из векового уравнения).
Оцените приближенно Д£ в молекуле Нг и, используя значение V = 1 эВ,
вычислите изменения ее потенциальных кривых из-за учета КВ. Правильно
ли использовать одно и то же значение V при всех межъядерных
расстояниях? Что является причиной взаимодействия, ответственного за
величину V?
3. Используя результаты упр. 2, вычислите волновые функции
рассмотренных там двух состояний. Покажите, что конфигурация сг (где функция а
пропорциональна lsa + lsb) модифицируется примешиванием конфигурации
а*2 (где функция а* пропорциональна \sa + ls/>) таким образом, что это
можно интерпретировать как улучшение распределения электронов. Обсудите,
как влияет учет KB на результаты предсказания продуктов диссоциации Нг-
Рекомендуемые источники. Краткое обсуждение молекулы водорода с
учетом KB см. в [1], а также у Коулсона [105]. Простой практический
подход к обсуждению KB можно найти у Ричардса и Хорсли [336]; несколько
более пространное, но полезное рассмотрение дано Мак-Глином, Ванквикенбор-
ном, Киноситой и Кэрроллом [273]; в обоих работах приводятся примеры.
КОНФИГУРАЦИЯ. Электронная конфигурация атома или
молекулы представляет собой запись распределения электронов
по имеющимся орбиталям. Конфигурации атомов первого и
второго периодов таковы: Н Is; He Is2; Li ls22s; Be ls22s2;
В ls22s22p и так далее вплоть до Ne ls22s22/?6. Иногда
внутренние заполненные оболочки сокращенно обозначаются /С, L, М
и т. д. Например, основную конфигурацию натрия можно
записать так: ls22s22/?63s или [KL]3s. Подобным образом, указывая
занятые орбитали, можно записать и конфигурации молекул.
Так, для Н2 имеем lsa2; для 02—lsa|lsa;22sa22sa;22/7a|2pK42/7Jt*2;
причем последняя запись часто сокращается до ... о2п*ип2.
Если известна электронная конфигурация (ее получают,
используя принцип заполнения), то можно определить
спектроскопические термы и предсказать спектры.
176
к
Упражнения. Что такое конфигурация атома? Если она известна, то
какие выводы можно сделать? Запишите экономным способом конфигурации
атомов Не, В, С, О, F, Al, Si, CI, Cu, Fe, U и Cf. Проделайте то же самое
для молекул Н2, HD, N2, F2, Ne2, FeO и бензола.
Рекомендуемые источники. Стандартный атлас энергетических уровней
атомов, который содержит перечень всех известных конфигураций, составила
]Чур [288]. Классическими работами по строению атомов считаются книги
Герцберга [185] и Кондона и Шортли [96]. Полезен также Кэндлер [89]. См.
•|'акже [1], гл. 8, и разд. «Атомные спектры» и «Принцип заполнения».
КОРИОЛИСОВО ВЗАИМОДЕЙСТВИЕ. Кориолисово
взаимодействие является взаимодействием между вращательным и
колебательным движением молекулы. Рассмотрим сначала
двухатомную молекулу, вращающуюся вокруг оси,
перпендикулярной ее межъядерной оси. Если считать движение молекулы
классическим явлением, можно представить себе, что при колебаниях
связь то удлиняется, то укорачивается и соответственно
меняется момент инерции молекулы.
Угловой момент молекулы сохраняется, т. е. сохраняется
произведение /со (где / — момент инерции, со—-угловая скорость),
поэтому при уменьшении / угловая скорость со увеличивается.
И наоборот, когда связь удлиняется и момент инерции
увеличивается, чтобы угловой момент сохранялся, угловая скорость
должна падать. Поэтому, если связь колеблется, вращение то
ускоряется, то замедляется. (То же наблюдается и при
замедлении или ускорении вращения фигуриста на льду.) Это
показывает, что между вращением и колебанием молекулы
существует взаимосвязь, которая может проявиться в изменениях
спектральных линий.
С существенным влиянием кориолисова взаимодействия мы
сталкиваемся в случае колеблющейся и одновременно
вращающейся линейной трехатомной молекулы. Эта молекула имеет
четыре нормальных типа колебаний', один из них — это
симметричное валентное колебание, при котором обе связи А—В
колеблются в фазе, другой (обозначенный V2)—асимметричное
валентное колебание, при котором одна связь А—В удлиняется,
а другая — укорачивается, а остальные два — деформационные
колебания, которые могут происходить в двух
перпендикулярных плоскостях (см. разд. «Нормальные колебания»).
Рассмотрим эффект взаимодействия колебания v2 с вращением (рис. К.7).
По мере того как связь А—В сокращается, половина молекулы
ускоряет свое движение, поэтому данная связь изгибается
вперед, обгоняя вращение всей молекулы. Тем временем другая
связь становится длиннее, и, поскольку кориолисово
взаимодействие требует, чтобы эта половина молекулы замедлялась при
177
к
вращении, она изгибается назад и отстает от вращения всей
молекулы. Полный эффект заключается в том, что молекула
сгибается в плоскости вращения. Так происходит до тех пор, пока
колебание не достигнет точки поворота и не начнется обратный
процесс: длинная связь укорачивается, а короткая удлиняется.
Опять возникает кориолисово взаимодействие, и в результате
быстрее вращающаяся связь замедляется, и наоборот. Это
заставляет молекулу изгибаться в
обратную сторону. Результатом
такого непрерывного процесса
является то, что совместным
действием антисимметричного
валентного колебания и вращения
молекулы возбуждается
деформационное колебание. Таким
образом, два указанных колебания
не являются независимыми, и,
следовательно, кориолисово вза-
Рис. К.7. Взаимодействие
асимметричного растяжения (помеченного v2) и
вращения молекулы вызывает
деформационное колебание в плоскости
вращения.
имодействие смешивает различные колебания. Это проявляется
в спектре как удвоение /-типа.
Упражнения. Что такое кориолисово взаимодействие? Чем вызвано
взаимодействие между вращательным и колебательным движением молекулы?
Обсудите изменения угловой скорости, частоты, импульса и энергии
вращения молекулы, вызванные изменением ее момента инерции в результате
колебания. Обсудите влияние кориолисова взаимодействия на колебания
линейной трехатомной молекулы. Какие колебания не смешиваются этим
взаимодействием? Как отражается смешение колебаний на спектре? Примените
те же рассуждения к плоской трехугольной молекуле вида АВ3. Какие
колебания этой молекулы способны смешивать ее вращение? Рассмотрите влияние
вращений вокруг оси, перпендикулярной плоскости такой молекулы, и вокруг
оси, лежащей в ее плоскости. Какие другие проявления силы Кориолиса
можно наблюдать в макроскопических явлениях?
Рекомендуемые источники. См. [1], гл. 10. Классические основы
кориолисова взаимодействия, которые касаются поведения механических систем во
вращающихся системах осей (вращающихся системах координат) можно
найти в разд. кн. Голдстейна [166]. Приложения к спектроскопии приводятся
Кингом [222], Герцбергом [186, 188], Сагденом и Кеннеем [388], Вильсоном,
178
к
Дешиусом и Кроссом [431], Таунсом и Шавловым [399]. Полезное
теоретическое обсуждение дано в работе Аллена и Гросса [35].
КОРРЕЛЯЦИОННАЯ ЭНЕРГИЯ. Корректные расчеты
электронного строения атомов или молекул методом
самосогласованного поля по схеме Хартри — Фока обычно приводят к
хорошим результатам, но даже если расчет выполнен с соблюдением
всей строгости, вычисленная энергия отличается от истинной.
Расхождение отчасти обусловлено пренебрежением
релятивистскими эффектами, которые могут быть очень большими для
электронов внутренних оболочек, обладающих высокой
кинетической энергией. Однако, если учесть эти эффекты, некоторое
уточненная
(рункци
Рис. К.8. Действительное
искажение электронного
распределения (а) и хартри-фоковское при-
ближение для его описания (б).
уточненная
хартри,-фокоесмая
функция
расхождение все равно остается. Величина этого остаточного
расхождения представляет собой корреляционную энергию, а
сам факт ее наличия отражает приближенный характер метода
Хартри —Фока. Основное приближение метода Хартри — Фока
заключается в пренебрежении локальным искажением
распределения электронов и в усреднении этого эффекта по всей орби-
тали: вместо того чтобы учесть искажения электронной орби-
тали в окрестности другого электрона, модифицируют некоторым
средним образом всю орбиталь (рис. К.8). Следовательно, в
методе Хартри — Фока пренебрегают локальным
электрон-электронным взаимодействием, т. е. электронной корреляцией.
Пренебрежение электронной корреляцией приводит к тому,
что вычисленная кривая потенциальной энергии молекулы (см.
разд. «Борна — Оппенгеймера приближение») лежит выше
истинной кривой. Однако форма истинной кривой приближенно
воспроизводится, только в области минимума (равновесной
длины связи) она оказывается слишком узкой. Минимум на хартри-
фоковской кривой занимает примерно то же положение, что и
на истинной кривой. Таким образом, равновесная геометрия
предсказывается довольно хорошо, даже если пренебречь
179
к
корреляционными эффектами, но силовые постоянные и,
следовательно, частоты колебаний молекул завышаются.
Упражнения. Даже наилучший расчет по методу Хартри — Фока не дает
точной электронной энергии атома или молекулы. Чем это объясняется? Что
такое корреляционная энергия, почему ее так называют? Каким образом
надо улучшить схему Хартри — Фока, чтобы получить более точные
результаты? Если кривая потенциальной энергии молекулы вычислена по методу
Хартри — Фока, то как равновесные длины связей и частоты колебаний
будут отличаться от их действительных значений? Более или менее важными
становятся эффекты, связанные с пренебрежением электронной корреляцией,
при удлинении связи между двумя атомами? Какие характерные
видоизменения следовало бы ввести в волновую функцию атома гелия, чтобы
отразить тенденцию электронов избегать друг друга?
Рекомендуемые источники. Простое рассмотрение методов расчета
электронного строения атомов и роли корреляционных эффектов дано Ричардсом
и Хорсли [336] и Мак-Глином, Ванквикенборном, Киноситой и Кэрроллом
[273]. Некоторые пути решения проблемы приведены Паунжем [315], Берри
[56], Синаноглу [368], Клементи [101] и Синаноглу и Брукнером [369].
КОЭФФИЦИЕНТЫ ЭЙНШТЕЙНА А и В. Интенсивность
поглощательного перехода между двумя состояниями
пропорциональна плотности излучения на частоте, равной частоте
перехода, а коэффициент пропорциональности представляет собой
коэффициент Эйнштейна для вынужденного поглощения В.
Интенсивность испускания зависит от двух факторов. Вклад одного
из них пропорционален плотности излучения на частоте
перехода, а коэффициент пропорциональности называется
коэффициентом Эйнштейна для вынужденного излучения. Поскольку он
равен /3, его также обозначают /3. Другая компонента
интенсивности перехода не зависит от плотности уже имеющегося
излучения и определяется коэффициентом Эйнштейна для
спонтанного излучения, обозначаемым А. Необходимость введения
этого дополнительного коэффициента А вытекает из условия
равенства скоростей вынужденных переходов вверх и вниз. Если
бы происходили только эти вынужденные процессы,
заселенности верхнего и нижнего состояний в равновесии были бы
одинаковы, в то время как распределение Больцмана требует, чтобы
заселенность верхнего состояния была меньше, чем нижнего.
Процесс спонтанного излучения спасает положение, так как
обеспечивает способ перехода из верхних состояний в нижние со
скоростью, не зависящей от плотности имеющегося излучения.
Таким образом, если п+— равновесная заселенность верхнего
состояния, а п_— нижнего, скорость поглощательных
переходов, т. е. переходов вверх, определяется выражением n_fip(v),
где p(v) —плотность излучения на частоте перехода с энергией
ftv, а скорость переходов вниз — выражением п+А + n+fip(v).
280
к
Если принять, что в соответствии с распределением Больцмана
п+/п- = ехр(—hv/kT)y и приравнять эти две скорости, то
получим выражение для равновесной плотности излучения: p(v) =
= (A/B)[exp(hv/kT)—I]-1, которое свидетельствует, что А не
может быть равно нулю, если равновесная плотность излучения
не равна нулю. Это показывает, насколько существенным
является спонтанный процесс. Можно также найти выражение для
А через S, заметив, что в равновесных условиях плотность
излучения определяется законом излучения абсолютно черного
тела, и поэтому р должно даваться распределением Планка.
Сравнивая написанное выше выражение с приведенным в списке
формул АЛ, легко получить, что А = 8nh(v/c)zB.
Выражение для В можно получить с помощью теории
зависящих от времени возмущений, и для электрических дипольных
переходов В = d2/6eofi2, где d — величина электрического диполя
перехода между интересующими нас состояниями.
Из выражения для отношения А/В следует важный вывод.
Поскольку это соотношение увеличивается пропорционально
третьей степени частоты перехода, спонтанные процессы
становятся очень важными при высоких частотах и могут не
учитываться при низких частотах. Следствием этого являются
принципиальные трудности создания высокочастотных лазеров;
работа лазеров основана на кооперативном эффекте вынужденных
переходов; если спонтанные процессы очень значительны,
возбужденные состояния распадаются слишком быстро и не
принимают действенного участия в кооперативных лазерных
процессах.
Упражнения. Каков смысл коэффициента Эйнштейна В? Чему равна
скорость перехода из основного состояния, занятого N атомами? Чему равна
скорость перехода из верхнего состояния, занятого N' атомами? Покажите,
что, если бы коэффициент А отсутствовал, равновесные заселенности верхнего
и нижнего уровней были бы равны, что противоречило бы распределению
Больцмана. Выведите выражение для коэффициента Эйнштейна Л,
основываясь на больцмановском распределении заселенностей, равенстве скоростей
перехода в состояние равновесия и на распределении Планка для
равновесного излучения. При каких частотах важны процессы спонтанного излучения?
Покажите, что коэффициент В имеет размерность (объем-частота)/(энергия•
• время) и что, поскольку размерность р есть энергия/(частотный диапазон»
•объем), размерность скорости перехода оказывается правильной. Размерность
коэффициента А — время"1. Проверьте справедливость этого
утверждения.
2. На основании распределения Планка (список формул А.1) оцените
плотность излучения с длиной волны 1 см (микроволновое излучение) и
500 нм (видимый свет), испускаемого абсолютно черным телом с
температурой 1000 К; получите значение В, которое соответствует единичной силе
осциллятора, и рассчитайте относительную интенсивность процессов
испускания и поглощения в состоянии равновесия.
181
к
Рекомендуемые источники. См. [1], гл. 7. Коэффициенты А и В
обсуждаются в кн. Дэвидсона [116], Эйринга, Уолтера и Кимбалла [137], Хамеки
[172], Гайтлера [180] и Дирака [123]. Их значение для процессов излучения
лазера отражено в книгах по лазерной технологии; поэтому см. разд. «Лазер».
КРИСТАЛЛИЧЕСКОГО ПОЛЯ ТЕОРИЯ. Пять d-орбиталей
свободного иона переходного металла вырождены (имеют одну
и ту же энергию), но, когда ион входит в комплекс, лиганды
нарушают сферическую симметрию атома и создают поле более
низкой симметрии. Ближайшее окружение иона может быть
октаэдрическим, тетраэдрическим и т. д. Лиганды можно
рассматривать как источник электрического потенциала, так назы-
^У t2g(dxy,dyzJzx)
Рис. К.9. Влияние октаэдрического кристаллического поля на энергию
электрона на d-орбиталях центрального атома.
ваемого кристаллического поля, в котором энергии d-орбиталей
соответствующим образом меняются. В октаэдрическом
комплексе d&- и rf^-^-орбитали направлены прямо к лигандам
(рис. К.9), в то время как другие три d-орбитали ориентированы
в эквивалентных направлениях между лигандами. Отсюда
следует, что первые две обладают одной энергией, а последние
три — другой, так что вырождение орбиталей частично
снимается. Энергетическое расстояние между двумя группами
орбиталей условно обозначается lODq.
Распределение электронов по этим орбиталям в соответствии
с принципом заполнения позволяет обсудить электронное
строение спектра, устойчивость и магнитные свойства комплекса.
Конфигурация иона в комплексе определяется конкуренцией между
стремлением электронов занять орбитали с меньшей энергией
(на которых больше трех электронов может находиться только
в том случае, когда их спины спарены) и стремлением
электронов расположиться на орбиталях так, чтобы их спины были
параллельны (правило Гунда). Какая тенденция побеждает —
определяется главным образом энергетическим расстоянием между
двумя группами орбиталей и, следовательно, силой кристалличе-
182
к
ского поля. В тех случаях, когда спаривания не происходит,
образуется высокоспиновый комплекс, если же за счет спаривания
электроны достигают наименьшей энергии, заполняя низколе-
жащие орбитали, образуется низкоспиновый комплекс
(рис. К. 10).
Теория кристаллического поля носит приближенный
характер, так как она предполагает, что энергия образования связи
металл — лиганд обусловлена только электростатическими
эффектами и не учитывает ковалентную природу связывания и ту
роль, которую может играть преобразование я-связей. Эти
недостатки устраняются в более общей теории поля лигандов. Тем
состояния \ аАа
нимоспановое еысокоспиновое ^Мт
сильное поле слабое поле в отсутствие
поля
Рис. К. 10. Конкуренция между спиновым спариванием и величиной
расщепления WDq* приводящая к существованию высокоспиновых и низкоспиновых
комплексов.
не менее теория кристаллического ноля позволяет установить,
какое влияние оказывает симметрия комплекса на его
электрические, магнитные и химические свойства, и дает простые правила
для предсказания этих свойств.
Рекомендуемые источники. Более подробно этот вопрос изложен в [1],
гл. 9. Суть теории кристаллического поля дана в «Химии переходных
элементов» Эрншоу и Харрингтона [14]. Представление о кристаллическом поле было
введено Оргелом [308], развито Бальхаузеном [49] и полностью разработано
Гриффитом .{170]. См. также разд. «Поля лигандов теория».
КУЛОНОВСКИИ ИНТЕГРАЛ. Кулоновский интеграл— это
вклад классического электростатического взаимодействия между
распределениями зарядов в полную энергию атома или
молекулы; впрочем, к этому основному определению необходимо
добавить некоторые оговорки.
Применительно к атомам таких оговорок приходится делать
меньше, и мы начнем с них. Рассмотрим электрон,
распределенный по атомной орбитали \|)а. Зная математическое выражение
для орбиталей, можно сказать, что вероятность нахождения
183
к
электрона в малом элементе объема dxj, окружающем точку п,
равна |\|)a(ri) \2di\\ поэтому заряд в этой области определяется
выражением dq\ = — e\%(r\) \2dr\. Другой электрон атома
может занимать орбиталь г|)&; если исходить из тех же
соображений, заряд в элементе объема йт2 вблизи точки r2 равен dq2 —
= —в|г|)ь(г2) |2dt2- Если заряды dq\ и dq2 находятся на расстоя-
J=fdztdT21 фаЦг(&4щг1г)\ф(гг)\
внутренние
оболочка
Рис. К.П. Вклады в куло-
новский интеграл в атоме (а).
в двухатомной молекуле
в рамках теории ВС (б) и
в той же молекуле в
рамках теории МО (в).
Стрелки -><- показывают
притяжение, а -«-*■ отталкивание.
нии г12 друг от друга, потенциальная энергия их
взаимодействия определяется выражением для кулоновского потенциала,
а именно dq\dq2IAmorn, Отсюда следует, что два заряда в
точках Г! и г2 дают вклад такого вида в полную энергию атома.
Полный вклад в энергию можно получить суммированием по
всем элементам объема di\ и dx2 или интегрированием по ним,
так как это бесконечно малые элементы объема. Такая
процедура приводит к кулоновскому интегралу /, как показано на
рис. К.П,а. Если знак зарядов одинаков, / положителен и
приводит к увеличению энергии атома. Это свидетельствует, что
кулоновское взаимодействие является отталкивагельным.
Необходимые оговорки к такому описанию касаются присущей
электронам способности коррелировать свое движение; поправка
к кулоновской энергии, возникающая из-за этого эффекта,
носит название обменной энергии.
184
к
В молекулах ситуация усложняется многообразием
взаимодействий, возможных при наличии нескольких ядер.
Дополнительное усложнение возникает из-за того, что имеется два
различных описания химической связи: теория молекулярных ор-
биталей и теория валентных связей. Тем не менее в каждой из
них термин «кулоновский интеграл» обозначает тип энергии,
возникающий из-за классического электростатического
взаимодействия между зарядами.
В теории валентных связей кулоновский интеграл включает
электростатическое отталкивание ядер двух атомов, образующих
связь, отталкивание между распределениями зарядов на
каждом атоме и притяжение между распределением заряда на
одном атоме и противоположным зарядом ядра другого атома
(см. рис. К.11,б). Этот интеграл также обозначается /, но
следует отметить, что он может быть отрицательным, если
последний из трех вкладов превосходит остальные. Кроме того, в него
еще необходимо внести поправку, учитывающую электронный
обмен: подробно этот вопрос рассматривается в разд.
«Валентных связей теория».
В теории молекулярных орбиталей кулоновский интеграл
(который в методе Хюккеля часто обозначается как а) обычно
включает четыре составляющие. Первая составляющая — это
энергия электрона, который предположительно находится на
орбитали изолированного атома (поэтому она учитывает
притяжение электрона к собственному ядру, его отталкивание от
других электронов атома и его кинетическую энергию); вторая
составляющая — это энергия отталкивания ядер, участвующих
в связи; третья — энергия электростатического притяжения
между распределением заряда и ядром соседнего атома и
четвертая — энергия отталкивания электронов, относящихся к двум
соседним ядрам. Эти взаимодействия иллюстрируются
рис. К.11,в и дополнительно обсуждаются в вводной части
разд. «Молекулярных орбиталей теория». Здесь также
необходима поправка на обменные взаимодействия.
Для всех рассмотренных кулоновских интегралов общим
является следующее: из всех возможных внутримолекулярных
взаимодействий выбираются те, которые можно учесть на
основании простой классической электростатической картины
взаимодействий; во всех случаях не учитывается, каким образом
спин электронов коррелирует их движение.
Упражнения. Что такое кулоновский интеграл? Каким образом
кулоновский интеграл появляется в теории атомов? Выведите его выражение'на
основании учета обычных электростатических взаимодействий и покажите, как
это выражение вытекает из гамильтониана многоэлектронного атома.
Выразите энергию атома гелия через кулоновский интеграл /. Может ли / (для
185
к
атомов) быть отрицательным? Какие дополнительные усложнения появляются
в молекулах? Каковы составляющие электростатического взаимодействия,
вводимые при описании химической связи между двумя атомами в теории
валентных связей? Каковы соответствующие вклады, вводимые при описании
той же связи на языке теории молекулярных орбиталеи? Какие детали этих
описаний являются общими? Какие детали специфичны для каждой из
теорий? Могут ли молекулярные кулоновские интегралы быть отрицательными?
Что это означало бы? Какие дополнительные вклады могут возникнуть в
молекуле, содержащей более чем два ядра? Какое максимальное число
различных атомных орбиталеи следует рассматривать в кулоновском интеграле?
Рекомендуемые источники. О роли кулоновского интеграла в расчетах
электронного строения атомов и молекул см. в [1], гл. 8 и 9. См. также кн.
Коулсона [105]. Полезное изложение способов расчетов кулоновского
интеграла можно найти у Мак-Глина, Ванквикенборна, Киноситы и Кэрролла
[273]. Там же, а также у Ричардса и Хорсли [336] содержатся приложения к
определению электронного строения молекул. См. разд. «Обменная энергия»,
«Спиновая корреляция», «Самосогласованное поле», «Молекулярных орбита-
лей теория» и «Валентных связей теория».
КУПМАНСА ТЕОРЕМА. «Теорема» — это довольно громкое
название для приближения, которое часто нарушается, поэтому
лучше было бы называть его «правилом Купманса». Это
правило гласит, что потенциал ионизации электрона равен энергии
орбитали, с которой он удаляется. На первый взгляд оно
является тривиальным утверждением, потому что необходимая
для ионизации атома или молекулы энергия должна
определяться энергией притяжения электронов к ядру и отталкиванием
между электронами, но как раз именно эти факторы и
определяют энергию орбитали.
На самом деле это правило является приближенным, так как
оно предполагает, что остальные электроны не будут
перестраиваться, чтобы воспользоваться отсутствием электрона,
покидающего одну из орбиталеи. Поэтому, если одноэлектронные
энергии определены методом самосогласованного поля Харт-
ри — Фока, потенциал ионизации, найденный по правилу
Купманса, часто оказывается неверным, поскольку это правило
предполагает, что в образующемся ионе электроны занимают
те же орбитали, что и в исходном атоме. Следует отметить
также, что теория Хартри — Фока не учитывает эффекты
корреляции между электронами и является нерелятивистской.
Последнее приближение может оказаться особенно плохим для
сильно связанных электронов, которые испытывают влияние
больших сил взаимодействия.
Упражнения. 1. Сформулируйте правило Купманса. Каким образом оно
обосновывается? Почему это правило является приближенным? Как вы
думаете: приводит ли его использование к переоценке или недооценке потен-
186
к
циалов ионизации? Для каких электронов оно выполняется более точно? Для
каких случаев оно полностью справедливо?
2. Одноэлектронные энергии молекулы СО имеют следующие значения:
4а — 21,87 эВ, 5а—15,09 эВ, 1л—17,40 эВ. Оцените потенциалы ионизации
данной молекулы, соответствующие удалению электрона с каждой указанной
орбитали (экспериментальные значения: 19,72, 14,01 и 16,91 эВ). Обсудите
строение молекулы СО, пользуясь приведенными данными (взятыми из книги
Ричардса и Хорсли [336], стр. 36).
Рекомендуемые источники. Правило Купманса представляет большой
интерес в связи с развитием фотоэлектронной спектроскопии (см. Тернер, Бей-
кер, Бейкер и Брандл [402]). Энергетические уровни различных молекул
приведены в обзоре Ричардса и Хорсли [336].
л
ЛАЗЕР. Слово «лазер» составлено из первых букв полного
названия явления усиления света путем испускания
вынужденного излучения (laser — light amplification by stimulated
emission of radiation). Аналогичным образом, но несколько ранее
появился термин «мазер», где буква «м» взята от слова
«микроволновый». Действие лазера основано на поглощении энергии и
ее испускании в очень узком интервале длин волн в процессе
вынужденного излучения (см. разд. «Эйнштейна коэффициенты
А и 5»). В качестве простого примера рассмотрим образец
вещества, у которого большинство атомов находится в
возбужденном состоянии, и допустим, что этот образец помещен в полость
с отражающими внутренними стенками. При самопроизвольном
переходе одного из атомов в основное состояние произойдет
испускание фотона, который будет двигаться внутри полости,
многократно отражаясь от ее внутренних поверхностей и
стимулировать испускание фотона другим атомом. В результате в
полости появится второй фотон, который станет двигаться в
одинаковой фазе с первым. Пара фотонов будет стимулировать
последующее излучение, и очень скоро наступит каскадное
испускание излучения и внутри полости возникнет интенсивное
световое поле. Этот процесс прекратится, как только заселенность
возбужденного состояния уменьшится до ее равновесного
значения. Если одна из стенок полости полупрозрачна, свет проходит
сквозь нее и можно наблюдать мощную монохроматическую
вспышку света, когерентного по фазе.
Посмотрим, как этот процесс реализуется на практике.
Полости обычно придают форму длинной тонкой трубки, если в
качестве образца используется газ, или изготовляют ее в виде
цилиндра из вещества образца, если им является
кристаллическое твердое тело. При такой конфигурации полости возможно
лишь незначительное отклонение испускаемого излучения от ее
продольной оси, так как только те фотоны, которые отражаются
вперед и назад вдоль оси или в очень близком к ней
направлении, участвуют в каскадном усилении. Остальные фотоны
проходят сквозь боковые стенки полости и покидают систему до того,
как произойдет усиление их интенсивности. Описанная
геометрия системы приводит к очень малой расходимости излучаемого
пучка света.
Перейдем теперь к основной проблеме — получению
инверсной заселенности, необходимой для появления вынужденного
излучения, а следовательно, для работы лазера. Существуют два
188
л
основных способа получения инверсной заселенности. В одном
из них (рис. Л.1,а) в работе лазера участвуют два уровня:
основное и возбужденное состояния. Однако, чтобы эта
простейшая схема работала, необходимо перевести более 50% атомов
из основного состояния в возбужденное. Во втором методе
действие лазера осуществляется на переходах между двумя
возбужденными состояниями. Получить инверсную заселенность таким
способом гораздо легче, особенно если возможна быстрая
релаксация нижнего возбужденного состояния в основное состояние.
В таком трехуровневом лазере (рис. Л. 1,6) атомы или ионы,
I
иакачкас^А
свет
накачка,]
излучение
=а
свет
излучение
i
I тепло
! безызлучательныи
\ переход
а б
Рис. Л.1. Двухуровневый (а) и трехуровневый (б) лазеры.
поглощая интенсивное излучение, возбуждаются на самый верх-
кий уровень Е2. Если этот процесс «накачки» происходит
достаточно эффективно, заселенность уровня Е2 становится
значительно больше заселенности возбужденного уровня с меньшей
энергией Е\. Если исключена утечка заселенности Е2 на более
низкие уровни в результате безызлучательных переходов, лазер
способен работать на переходе Е2->Ег вследствие того, что
фотоны, распространяющиеся в обе стороны между отражающими
стенками полости, вызывают внутреннее излучение на переходе
E2-*Ei. Если на одном конце полости находится
полупрозрачное зеркало, можно получить узконаправленный (слаборасходя-
щийся) монохроматический пучок фотонов с частотой v = (Е2—
— E\)/h. Излучение лазера является, кроме того, когерентным
(все волны находятся в одинаковой фазе, поскольку они
возникают в процессе вынужденного испускания) и поляризованным
(вследствие поляризации квантовых переходов или потому, что
полость имеет поляризующие окна).
В качестве примера лазерного процесса рассмотрим работу
гелий-неонового лазера, активным материалом которого является
189
л
смесь этих двух газов в соотношении 1 :5. Высокочастотный
разряд, на который не распространяются никакие правила
отбора, возбуждает атом гелия, и, хотя многие из его
возбужденных состояний очень быстро релаксируют, первое возбужденное
синглетное состояние является относительно долго живущим
(поскольку s-^s-переходы запрещены). Возбужденный атом
гелия некоторое время двигается в газовой смеси, так как его
переход в основное состояние запрещен; в конце концов он стал-4
кивается с атомом неона, находящимся в основном состоянии.
Нь
№
2'S-
2rS
£7
23S-
радио-
частотный,■—к|
разряд L-*1
/'$-
столкновение
/релаксация
JL
Рис. Л.2. Гелий-неоновый лазер (работающий на длине волны 632,8 нм).
Сочетание газов подобрано таким образом, чтобы энергия
возбуждения атома гелия была почти в точности равна энергии
возбужденного состояния неона. Происходит резонансная
передача энергии, гелий дезактивируется, а неон возбуждается в
состояние с энергией £3 (рис. Л.2). Ниже этого состояния
расположены два незаселенных состояния, не резонирующих с
возбужденным гелием. Получается обычная трехуровневая система,
которая обеспечивает работу лазера на переходах Ez-*E\ с
излучением красного света при 632,82 нм.
Самым известным рабочим веществом лазера является рубин,
который может служить примером трехуровневой системы,
включающей, однако, четыре уровня, но работающей на
переходах в основное состояние подобно двухуровневому лазеру. Эта
особенность работы рубинового лазера становится сразу
понятной, если обратиться к рис. Л.З. Рубин — кристалл весьма
прозаической формулы АЬОз, в котором около 5% ионов А13+
замещено на Сг3+, приводит в восхищение поэтов благодаря двум
своим интенсивным поглощательным переходам: зеленому с энер-
190
л
гией Е2 и фиолетовому с энергией £3- Рубин привлекает
внимание не только поэтов, но и физиков, правда по несколько другой
причине. Содержащиеся в нем ионы хрома способны уменьшать
свою энергию от Е$ и Е2 до Е\. Этот безызлучательный переход
вызывает колебания решетки (которая в результате
нагревается). Интенсивность двух указанных поглощательных
переходов столь велика, что при достаточно интенсивном облучении
образца заселенность уровня Е\ может превысить заселенность
основного состояния, и этим создаются условия для работы ру-
А
накачка
5^
•&,)
Ьллл*
тепло
тепло
и 694,3нм лллт
*(%)
Рис. Л.З. Переходы в рубиновом лазере.
бинового лазера, который дает красное излучение (694,3 нм).
Существуют лазеры непрерывного действия (они испускают
непрерывный поток света в течение всего отрезка времени, пока
осуществляется накачка) и лазеры импульсного действия
(например, рубиновый лазер, который испускает излучение в виде
короткой вспышки в момент появления вынужденного
излучения). Испускание света в виде коротких импульсов позволяет
получить очень большую мощность, правда в течение короткого
времени. В обычном режиме работы рубинового лазера в
качестве накачки используется яркая вспышка с энергией излучения
около 2,5 кДж Рубиновый стержень поглощает большую часть
этой энергии, и, хотя ее значительная часть превращается в
тепло, порядка 25 Дж излучается в результате действия лазера.
Продолжительность лазерного импульса составляет всего 5-
•10~4 с, и поэтому мощность излучения весьма значительна —
50 кВт, но длительность излучения составляет всего 5-Ю""4 с.
Мощность излучения можно увеличить при том же количестве
191
л
энергии излучения, сократив продолжительность импульса.
Такая возможность реализуется на практике путем «модуляции
добротности» лазера. Осуществляется это следующим образом.
Представьте себе, что одно из зеркал полости лазера удалено.
С помощью подсветки осуществляется накачка лазера, и
заселенность верхнего уровня достигает своего максимального
значения, однако стимулированного излучения пока еще нет. Пока
заселенность все еще остается инвертированной, удаленное
ранее зеркало быстро вдвигается на место. При этом возникает
вынужденное излучение, происходит быстрое уменьшение
заселенности верхнего уровня и возникает гигантский импульс
продолжительностью всего 10~8 с. При излучаемой в импульсе
энергии 25 Дж мощность излучения лазера составляет 2,5-109 Вт —
весьма внушительная величина, приблизительно равная мощности
крупной электростанции. (Правда, электростанция работает
на этом уровне мощности круглый год, а не 10~8 с.) В первых
моделях лазеров перемещение зеркал производилось
механическим способом, но сейчас это делается электрооптическим
способом с помощью ячейки Керра или Поккельса. Некоторые
распространенные лазерные материалы и их рабочие длины волн
приведены в табл. 19.
Рекомендуемые источники. Рубиновые лазеры обсуждаются в гл. 10 [1].
Популярные обзоры по лазерам опубликованы Шавловым [355], Вейном [416],
Лендьелом [239], Джонсом [207] (обзор статей) и Хотом [176]. Хот объясняет
смысл терминов «запирание моды» (метод получения коротких пикосекунд-
ных вспышек) и «модуляция добротности», рассматривает различные
лазерные системы и приводит обширн\ю библиографию. Доступный обзор по
жидким лазерам дан Геллером [181]. В качестве возбуждающего источника
(накачки) в лазерах может использоваться не только излучение. Химические
реакции, в которых продуктами реакции являются молекулы в возбужденных
состояниях, также мог>т обеспечить работу лазера. Химический лазер
представляет собой замечательный прибор, позволяющий преобразовать
химическую энергию непосредственно в когерентный свет. См. кн. Хота [176], Левина
и Бернстейна [245]. Применение лазеров в химии обсуждается в кн. Джонса
[207] и Хота [176]. Систематика данных по лазерам дана в кн. Пресли [325]
и Левина и де Мария [243].
ЛАПЛАСИАН. Пьер Симон де Лаплас (1749—1827) был
выдающимся французским математиком, труды которого, в
особенности его внушительная «Небесная механика», и по сей день
пользуются глубоким и заслуженным уважением. На ее
замечательных страницах, исписанных математическими формулами,
находится и уравнение Лапласа (d2f/dx2) + (d2f/dy2) + (d2f/dz2) ==
= 0, где / — некоторая функция. Хотя это уравнение было
получено для описания свойств гравитационных полей, оказалось,
что оно применимо к широкому кругу явлений — например,
позволяет описывать свойства потоков несжимаемых жидкостей,
электромагнитных полей и тепловых потоков. То обстоятельство,
192
л
что столь различные явления описываются одним уравнением,
по-видимому, связано с тенденцией всех существующих в
природе систем к достижению однородных, плавных распределений.
Уравнение Лапласа настолько важно, что входящий в него
дифференциальный оператор (d2/dx2) + (d2/dy2)-{-(d2/dz2) был
обозначен специальным символом V2 (читается «набла-квадрат») и
назван оператором Лапласа, или лапласианом. С введением
этого обозначения уравнение Лапласа принимает простой вид:
V2/ = 0. Применять оператор Лапласа, выраженный в
декартовых координатах, не всегда удобно, а часто заведомо
неправильно. Для систем со сферической или близкой к ней симметрией
удобно использовать выражение для оператора V2 в
сферических координатах (см. список формул Л.1). В этом случае
часть оператора Лапласа, содержащая производные только по
угловым переменным, называется оператором Лежандра и
обозначается символом Л2.
Список формул Л.1
Лапласиан и оператор Лежандра
Лапласиан в декартовых координатах (*, у, г):
дх2 ^ ду2 ^ дг2
Лапласиан в сферических координатах (г, 9, <р):
или
V дг2 ^ г дг^ г2 *
Оператор Лежандра в сферических координатах (г, 9, ф):
д2 _( * V д2 . 1 д__ Q д
А "UinOJ dtp2 + sin9 09 S!nU dQ
или
д2 __/ 1 у J^ . cos 9 д . д2
\ sin 9 ) <V + sin 9 дв + д№ '
Лапласиан в цилиндрических координатах (г, 9, z):
Vo_ 1 д . д2 . 1 д2 д2
г дг~г дг2 ~т~ г2 д№ ■•" дг2 '
Рекомендуемые источники. Оператор Лапласа широко применяется в
квантовой механике, так как является оператором кинетической энергии. Как
одна из компонент гамильтониана он входит в уравнение Шредингера и
образует его дифференциальную часть. Методы перехода от декартовых
координат к сферическим рассмотрены в разд. 6.8 кн. Кирала [231] (быстрые
методы) и в дополнении 5 кн. Мелвин-Хьюза [284] (медленные методы).
Краткая биография Лапласа написана Ньюменом [304].
193
л
ЛИНЕЙНАЯ КОМБИНАЦИЯ АТОМНЫХ ОРБНТАЛЕЙ
(ЛКАО). В методе ЛКАО молекулярная орбиталь,
охватывающая несколько ядер, представляется в виде суммы атомных
орбнталей с центрами на каждом ядре. Например, связывающая
орбиталь молекулы водорода на самом деле является сложной
функцией распределения вокруг обоих ядер. Но поскольку
ожидается, что вблизи каждого ядра она будет походить на его
Рис. Л.4. Метод ЛКАО. Суперпозиция волновых функций атомов ( )
приводит к образованию молекулярных орбнталей ( —).
атомную ls-орбиталь, ее представляют в виде ЛКАО,
образованной суперпозицией двух таких ls-орбиталей (рис. Л.4).
Метод ЛКАО можно было бы считать точным, если бы для
построения истинной молекулярной орбитали использовались все
возможные атомные орбитали. Но, учитывая чрезмерную
сложность такой задачи, обычно в качестве базисного набора
выбирают небольшое число атомных орбнталей, что делает метод
ЛКАО приближенным. Простейшее рассмотрение молекулы
водорода основано на использовании базисного набора из двух
атомных ls-орбиталей. Это позволяет получить вполне
удовлетворительное описание химической связи в молекуле водорода,
которое можно затем уточнить дополнительным включением
в базис 2s-, 2p- и других орбнталей. Использование небольших
194
л
базисных наборов атомных орбиталей является одним из
серьезнейших источников ошибок при описании химической связи в
молекулах по методу ЛКАО. Выбор слишком ограниченного
базисного набора может сделать бессмысленным результаты
любого расчета, безупречного во всех других отношениях.
Использование метода ЛКАО имеет более глубокое
теоретическое обоснование: его можно рассматривать не просто как
математический прием, позволяющий разложить любую функцию
по полному набору более простых функций. Это обоснование
связано с принципом суперпозиции, который в тех случаях, когда
наблюдаемый процесс состоит из нескольких различных
процессов, требует рассмотрения амплитуд вероятностей отдельных
процессов, а не самих вероятностей. Результирующий процесс
при этом описывается полной суммарной амплитудой, расчет
которой является главным объектом внимания и проводится в
первую очередь. Вероятность отдельных процессов можно
определить только в конце расчетов, когда найдена полная амплитуда.
Молекула как раз является примером такой сложной ситуации,
когда существует некоторая вероятность нахождения электрона
на одной из орбиталей каждого атома. Чтобы установить
распределение электрона с учетом всех возможностей его
местонахождения, нужно в соответствии с принципом суперпозиции
определить полную амплитуду вероятности (волновую функцию
молекулярной орбитали) путем комбинации амплитуд отдельных
процессов (волновых функций атомных орбиталей). Именно
такой подход и используется в методе ЛКАО, где молекулярная
орбиталь конструируется из атомных орбиталей.
Упражнения. В чем заключается суть метода ЛКАО? Является ли он
точным методом? Какой из источников ошибок в этом методе самый опасный?
Как можно обосновать этот метод? Каким должен быть базисный набор,
позволяющий дать простейшее описание молекулы кислорода (требуется
указать минимальный базисный набор)? Каким образом можно улучшить
простейшее описание молекулы водорода? Какими физическими соображениями
следует руководствоваться при расширении минимального базисного набора?
(Обдумайте, как принять во внимание энергию, размер и ориентацию орбита-
лей, а также как учесть поляризацию атома, обусловленную соседними
ядрами.)
Рекомендуемые источники. Метод ЛКАО лежит в основе теории
химической связи молекул, он рассматривается в кн. Коулсона [10] и гл. 9 [1], а
также в кн. Коулсона [105], Маррела, Кеттла и Теддера [299], Мак-Глина,
Ванквикенборна, Киноситы и Кэрролла [273]. Простое введение в расчеты
молекул методом самосогласованного поля дано в кн. Ричардса и Хорсли [336].
Построение молекулярных орбиталей из атомных орбиталей должно
осуществляться с учетом свойств симметрии молекулы, большую помощь при этом
оказывает теория групп. См. гл. 5 и 9 [1], Коттон [99], Тинкхэм [396],
Бишоп [59].
195
л
ЛОКАЛИЗОВАННЫЕ ОРБИТАЛИ. Химические свойства
многих молекул заставляют предположить, что имеющиеся в них
электроны с достаточной точностью могут быть отнесены к
различным частям молекулы. Вместе с тем теория молекулярных
орбиталей приводит к выражениям, на основании которых
создается впечатление, что все электроны распределены по всему
пространству каждой молекулы, и поэтому представляется, что
базисные
орбитали
Щ делокализованные орбитали %
QGOGMD
локализованные орбитали
полностью локализованные орбитали
Рис. Л.5. Образование локализованных орбиталей. Полная локализация до»
стигается только при |л = А.
данная теория противоречит химическому опыту. Однако это
расхождение кажущееся, поскольку, изменяя вид молекулярных
орбиталей (выбирая различные их комбинации), можно
получить локализованные орбитали, почти полностью
сосредоточенные в тех или иных частях молекулы. Одна из таких процедур
показана на рис. Л.5. (Она основана на расчетах, выполняемых
в упражнении 2.) Выбор подходящей линейной комбинации
возможен благодаря тому, что действительная многоэлектронная
волновая функция молекулы должна удовлетворять принципу
Паули. Это условие выполняется, если функция записана в виде
детерминанта Слейтера. Одно из свойств детерминанта состоит
в том, что его строки или столбцы можно прибавлять к другим
строкам или столбцам, це изменяя при этом величины
детерминанта. Преобразуя таким образом детерминант, мы не меняем
е»
m
л
полную волновую функцию, и описание молекулы с помощью
локализованных орбиталеи остается математически
эквивалентным первоначальному описанию с помощью делокализованных
орбиталеи. Пример построения локализованных орбиталеи дан
в упражнениях.
Упражнения. 1. Какой из результатов теории молекулярных орбиталеи
представляется противоречащим предсказаниям, основанным на химических
данных? Какие данные подтверждают представление о делокализации
электронов по всей молекуле? Каким образом определяют локализованные орби-
тали? Что достигается при локализации орбиталеи? Каким образом
обосновывается процедура локализации орбиталеи? Почему описания с помощью
делокализованных и локализованных орбиталеи эквивалентны? Предположим, что
одна из орбиталеи молекулы получается суммированием s-орбиталей трех
атомов (а, Ь и с) и имеет следующий вид: -ф± = casa + cbsb + ccsc.
Предположим также, что существует подобная связывающая орбиталь, в которой
центральный атом b участвует своей р-орбиталью: t|>2 = casa + cbpb + c'csc.
Покажите, что комбинации i|?i + -ф2 и i|?i — i|?2 локализованы главным
образом в областях а — Ъ и Ъ — с соответственно, и изобразите графически
полученные локализованные орбитали. Причины выбора именно этих комбинаций
анализируются в следующем более трудном упражнении.
2. Рассмотрим линейную трехатомную молекулу АВ2 (ВАВ), в которой
занятые орбитали имеют вид i|)i = 5 + \i(a + b) и -ф2 = Р + A, (a + b).
(Обозначения должны быть ясны из рис. Л.5). На этих орбиталях находятся
четыре электрона, так что полная волновая функция молекулы описывается
детерминантом Слейтера: ф = (1/4!)1/з | -ф1а (1) г|)1р (2) ф2а (3) ф2р (4) |, где
индексами аир обозначены различные значения спинов. Покажите, что
детерминант может быть преобразован без изменения его величины к виду г|э =^=
= (1/4! ),/а | ♦+ (1) *£ (2) 4£ (3) iff (4) |, где ф± » (i/2)V« (^ ± ^). Образуйте
эти орбитали из первоначальной пары и покажите, что они являются
локализованными и что локализация оказывается полной, если X = \i. Процедура
локализации орбиталеи иллюстрируется рис. Л .5. Обсудите полученные
результаты, используя представления о гибридизации орбиталеи центрального
атома.
Рекомендуемые источники. Рассмотрение локализации орбиталеи и
некоторые примеры см. в [1] (дополнение 9.2). См. также кн. Коулсона «Форма
и структура молекул» [10], Маррела, Кеттла и Теддера [299], Стрейтвизера
[387], Салема [353], Пилара [318]. Хороший обзор литературы по
локализованным орбиталям дан в ст. Леннарда-Джонса и Попла [240], Войза [73] и
Эдмистона и Рюденберга [129, 130].
м
МАГНИТНОЕ ДИПОЛЬНОЕ И ЭЛЕКТРИЧЕСКОЕ КВА-
ДРУПОЛЬНОЕ ИЗЛУЧЕНИЕ. Появление наиболее
интенсивных переходов в спектрах молекул связано с электрическими
дипольными переходами. Однако в тех случаях, когда правила
отбора запрещают электрические дипольные переходы,
проявляются другие механизмы, и переходы все-таки происходят, хотя
и гораздо менее интенсивно. К числу таких механизмов
относятся магнитный дипольный переход, связанный с магнитной
составляющей светового поля, а также электрический квадруполь-
ный переход, имеющий приблизительно такую же интенсивность,
что и магнитный дипольный переход, и связанный с
неоднородностью электрической составляющей светового поля в
пространстве, занимаемом молекулой (другими словами, чтобы мог
произойти квадрупольный переход, должен существовать градиент
поля в молекулярном масштабе).
Магнитный дипольный переход возбуждает магнитную
составляющую светового поля точно так же, как электрический
дипольный переход возбуждает электрическую составляющую
этого поля (разумеется, в каждом из этих случаев возбуждается
и другая составляющая поля). Однако существуют два
принципиальных различия между дипольными магнитными и
электрическими переходами.
Первое различие заключается в слабом взаимодействии
молекулы и светового поля, когда это взаимодейртвие обусловлено
магнитным диполем. Наиболее наглядно это можно
продемонстрировать, исходя из вращательной природы магнитного
дипольного перехода. Если во время перехода заряд перемещается
по изогнутому пути, он создает магнитный диполь перехода
(рис. МЛ). Но кривизна пути перемещения заряда будет
слишком мало заметной в небольшой области, занимаемой
молекулой. Если D — диаметр молекулы, а Я — длина волны,
испускаемого или поглощаемого ею света, разумно предположить, что
эффективность рассматриваемого взаимодействия по порядку
величины равна отношению D/X. Поскольку интенсивность
любого перехода пропорциональна квадрату дипольного момента
перехода, интенсивность магнитного дипольного перехода
должна составлять (D/K)2 от интенсивности электрического
дипольного перехода, никоим образом не связанного с кривизной пути
перемещения заряда. Для молекул типичных размеров и
обычных длин волн величина (D/X)2, характеризующая интенсивность
магнитного дипольного перехода относительно интенсивности
198
м
электрического дипольного перехода, равна ~10~5.
Экспериментально наблюдаемое соотношение интенсивностей имеет такой
же порядок.
Другое различие электрического и магнитного дипольных
переходов заключается в правилах отбора. Как уже отмечалось
выше, магнитный дипольный переход связан с вращательным
перемещением заряда. Поскольку при пространственной
инверсии (повороте вокруг произвольной точки на угол я)
направление вращения не изменяется, магнитный дипольный переход
является четным по
отношению к инверсии (см. разд.
«Четность и нечетность»). В
отличие от электрического
дипольного перехода,
связанного с прямолинейным
перемещением заряда и,
следовательно, нечетного по
отношению к инверсии (что б
приводит к правилам
отбора AL == ±1 и g+-+u) в
магнитном дипольном пере-
Рис. М.1. Смещения заряда при
переходах различного типа.
электрический
дипольный,
переход
магнитный
дипольный.
переход
электрический
кеадрупольныИ
переход
ходе правила отбора имеют вид AL = О и g «-> g, и «*-> и
(четность не меняется). Правило отбора Д/ = ±1 является
общим и для электрического, и для магнитного дипольных
переходов, так как оба они имеют дипольный характер. (О роли
углового момента фотона в правилах отбора см. в разд.
«Электрический дипольный переход» и «Правила отбора».)
Электрический квадрупольный переход происходит благодаря
перемещению заряда квадрупольного типа (показанного на
рис. МЛ), и его интенсивность определяется отношением D2A2,
как и интенсивность магнитного дипольного перехода. Однако
внимательный анализ показывает, что интенсивность квадру-
польных переходов зависит также от квадрата частоты, что еще
на 2 порядка уменьшает их интенсивность в видимом диапазоне.
Поэтому интенсивность электрических квадрупольных переходов
составляет только 10~7 интенсивности электрических дипольных
переходов.
Правила отбора для квадрупольных переходов отличаются
от правил отбора для дипольных переходов. Квадруполь можно
представить себе в виде двух противоположно направленных
199
м
диполей (см. рис. М.1), и, следовательно, он должен быть
четным по отношению к инверсии. Это показывает, что квадруполь-
кые переходы разрешены в тех случаях, когда они происходят
между состояниями одинаковой четности: g->g, u->u. Правила
отбора для углового момента при квадрупольных переходах
имеют следующий вид: AL = 0, ±1, ±2 и Д/=0, ±1, ±2.
Объяснить их, учитывая, что спин фотона равен 1, нельзя,
однако их можно понять путем рассмотрения квадрупольной
природы перехода: при вылете фотона излучающая молекула
приобретает некоторый орбитальный угловой момент вследствие
пространственной распределенности перехода. Поэтому полный
угловой момент фотона может превышать единицу, и это
позволяет понять правило отбора Д/ = ±2, так как оно соответствует
закону сохранения углового момента.
Рекомендуемые источники. Магнитные дипольные переходы удачно
рассмотрены в кн. Куна [229], Гриффита [170] и Хамеки [172]. См. также кн.
Гайтлера [180], Берестецкого, Лифшица и Питаевского [54]. Важная роль ди-
польных магнитных переходов наблюдается в таких явлениях, как
электронный парамагнитный резонанс и ядерный магнитный резонанс, где магнитный
момент взаимодействует с высокочастотным электромагнитным полем.
Молекула, которая может быть возбуждена в одно и то же состояние и
электрическим, и магнитным дипольным переходом, называется оптически активной
(см. разд. «Двойное лучепреломление»).
МАГНИТНЫЕ СВОЙСТВА. Внесение образца в магнитное
поле приводит к явлениям, которые можно понять, рассматривая
искажение силовых линий этого поля (рис. М.2). В
диамагнитном веществе плотность силовых линий становится меньше, что
свидетельствует об уменьшении индукции В внутри образца по
сравнению с ее величиной в свободном пространстве. В
парамагнитном веществе плотность силовых линий и, следовательно,
индукция становятся больше. Если предположить, что под
действием внешнего поля образец намагничивается, можно
объяснить такое поведение различных материалов иным образом.
В диамагнитном веществе создается противоположно
направленное (по отношению к внешнему) поле, и, таким образом,
внешнее поле частично компенсируется. В парамагнитном веществе
картина обратная: направление индуцированного поля совпадает
с направлением внешнего поля, и последнее в результате
усиливается. Простейшее физическое проявление свойств
парамагнетизма и диамагнетизма состоит в том, что под действием
магнитного поля парамагнитный образец втягивается в него, а
диамагнитный образец, наоборот, выталкивается.
Отношение индуцированного магнитного момента к
напряженности внешнего поля называется магнитной
восприимчивостью образца и обычно обозначается %т (см. список формул
МЛ и табл. 20). Магнитная восприимчивость — отрицательная
200
Л!
величина для диамагнитных веществ и положительная для
парамагнитных (в соответствии с различным направлением
намагниченности). Восприимчивость любого вещества можно
представить в виде суммы парамагнитной %рт и диамагнитной у?т
восприимчивостей: %т = хрт + %„- Поскольку для большинства
молекул диамагнитная восприимчивость
преобладает над парамагнитной и %dm < О,
суммарная восприимчивость, как правило,
оказывается отрицательной величиной.
Парамагнитная восприимчивость может
преобладать в таких молекулах, которые
содержат неспаренные электроны. С ростом
температуры х£ уменьшается, причем для
обычных температур она пропорциональна 1/Г
(закон Кюри). В некоторых случаях
парамагнитная восприимчивость может
преобладать над диамагнитной, даже если все
электроны спарены. Такой парамагнетизм
молекул оказывается слабым и не зависит
от температуры. По этой причине его
называют не зависимым от температуры
парамагнетизмом, или высокочастотным
парамагнетизмом.
1. Диамагнетизм. Все молекулы имеют
диамагнитную составляющую магнитной
восприимчивости, которая обусловлена воз-
Рис. М.2. Схематическое изображение магнитной
индукции (плотности магнитного потока) в
магнитных веществах различного типа.
никновением момента вращения электронов под воздействием
внешнего поля. Этот момент вращения вызывает круговое
движение электронов по молекулярным орбиталям (рис. М.З, а), и
возникающий таким образом круговой ток создает магнитный
момент и поле, направленное против внешнего поля. То, что
диамагнитная восприимчивость обусловлена процессами,
происходящими в основном состоянии молекулы, позволило Паскалю
разработать аддитивную схему вкладов в полную диамагнитную
восприимчивость молекул, обусловленных особенностями их
структуры, которые могут сохраняться при переходе от одних
молекул к другим, и представить такие вклады в виде таблиц
Ароматические молекулы, в которых существуют круговые
201
м
Список формул М.1
Магнитные свойства
Намагниченность: М = ХтН,
где %гп — магнитная восприимчивость и Н — напряженность поля.
парамагнитная восприимчивость %^ > О,
диамагнитная восприимчивость /^ < 0.
Магнитная индукция (плотность потока):
В = jioH + д0М = И-о (1 + Xm) H.
Закон Кюри:
Xm = C/Ty C=\ioL\i2/3k,
где \i — магнитный момент; например, для чисто спинового
парамагнетизма \i2 « g2\*%S (S + 1).
Закон Кюри — Вейса:
Xm = C/(T-Q).
Функция Бриллюэна:
M = N\i$J(\iB/kT),
где
Молярная восприимчивость по теории возмущений:
не зависимый от температуры парамагнетизм
~Р - # f «Vo \ V' ( <0Ц|п)-<«|1|0> 1
Хщ 1~к;£ I (*»-£о) г
%^ = — L ( ^ ° ) (г2) (уравнение Ланжевена — Паули). Уравнения
Максвелла приведены в табл. 20.
траектории для я-электронов, обнаруживают аномально большую
восприимчивость, приписываемую кольцевым токам. Эти токи
играют важную роль при определении формы спектра ядерного
магнитного резонанса. (Правда, вопрос о существовании
кольцевых токов является спорным.)
2. Парамагнетизм. Явление спинового парамагнетизма легко
понять, рассматривая магнитные моменты, обусловленные
спиновыми угловыми моментами электронов. В магнитном поле
энергия магнитного момента зависит от его ориентации, что
в случае электронов приводит к двум значениям энергии, свя-
20?
м
занным с двумя возможными ориентациями спина электрона.
Если набор молекул, каждая из которых имеет один неспарен-
ный спин, поместить в магнитное поле, энергия молекул со
спином ms = —V2 (р-спин) уменьшится, а энергия молекул со
спином ms = V2 (а-спин) увеличится на такую же величину. Очень
скоро этот набор молекул придет к тепловому равновесию, и в
образце окажется больше молекул с р-спином, чем с а-спином
(см. рис. М.4). Соотношение между числом различных спинов
определяется распределением Больцмана. Поскольку электрон
имеет отрицательный заряд, направление магнитного спинового
\-поле
Рис. М.З. Диамагнитный (а) и парамагнитный (б) токи. В случае а поле
вызывает токи в пределах атомных орбиталей, в случае б оно приводит к
появлению молекулярных токов за счет примешивания возбужденных состояний.
момента противоположно направлению углового спинового
момента, и, таким образом, в равновесии приобретенный
магнитный момент параллелен внешнему полю. Поле, вызванное этим
моментом, усиливает внешнее поле, и это характеризует образец
как парамагнетик. По мере повышения температуры
распределение Больцмана для двух спиновых ориентации становится
более равномерным, что связано с тепловым движением молекул,
нарушающим упорядоченное расположение спинов, и поэтому
величина наведенного магнитного момента падает. Простые
расчеты, выполненные для комнатных температур (см. упражнение 2),
показывают, что выражение для зависимости парамагнитной
восприимчивости от температуры отвечает закону Кюри. Можно
получить и более общее выражение этой зависимости для любых
температур (однако, таких, при которых вещество не
обращается в ферромагнетик), и такая зависимость называется
функцией Бриллюэна. Оба эти выражения можно обобщить
применительно к молекулам с произвольным спином. (Например,
молекула кислорода является парамагнитной частицей с S = 1,
\поле
203
м
и для нее в магнитном поле существуют три значения энергии,
отвечающие трем ориентациям спина.)
Следует помнить и об орбитальном угловом моменте,
который может играть не последнюю роль в магнитных эффектах.
Во многих молекулах орбитальное движение электронов
подавляется и не дает вклада в магнитную восприимчивость. В этом
случае говорят о чисто спиновом парамагнетизме. Ситуация
усложняется, если полного подавления орбитального движения
U к к к парамагнетш
HttHH ""XT""
ttt*m*tt
парамагнетик
в поле
1 1 1 i . j 1 1 1 i идеальный.
tttttttttt *""*"""*"
, f , t , t . t i ♦ идеальный,
ftft4t444t ытшрерромагнетак
Рис. М.4. Зависимость магнитных свойств различных веществ от
ориентации электронных спинов.
не происходит или если достаточно велика энергия спин-орби-
тального взаимодействия. В этих случаях магнитную
проницаемость нельзя вычислить на основании простого учета величины
спиновых моментов, используя формулу Бриллюэна или Кюри.
Не зависимый от температуры парамагнетизм обусловлен
орбитальным угловым моментом электронов. Когда у молекулы
имеются низко лежащие возбужденные состояния, магнитное
поле использует их, заставляя электроны двигаться по всей
молекуле. Орбитальный угловой момент такого движения приводит
к появлению орбитального магнитного момента. Такое движение
отличается от диамагнитного тока, поскольку оно обусловлено
искажениями электронной плотности внешним полем, тогда как
диамагнитный ток протекает по неискаженным молекулярным
орбиталям. Это различие приводит к появлению тока, который
течет по молекуле в направлении, противоположном
диамагнитному току (рис. М.З), т. е. орбитальный ток создает магнитный
момент, который усиливает внешнее поле. Магнитное поле
определяет характер циркуляции тока и, следовательно, направление
намагниченности. Этим объясняется независимость последнего
204
м
от теплового движения, приводящего к хаотическому
распределению спиновых магнитных моментов, поэтому такой
парамагнетизм является не зависимым от температуры.
3. Ферромагнетизм и антиферромагнетизм. При достаточно
низких температурах многие парамагнитные вещества переходят
в такое состояние, когда все спины в результате взаимодействия
друг с другом ориентированы в одном направлении и тем самым
значительно усиливают магнитные свойства вещества (рис. М.4).
Когда выстраивание спинов в одном направлении происходит
в достаточно протяженной области образца (домене), в нем
возникает сильное намагничение, которое остается и после
выключения внешнего поля, — состояние, называемое ферромагнитной
фазой. Типичными примерами веществ с такой фазой являются
железо (температура перехода, или точка Кюри, 1043 К) и
кобальт (точка Кюри 1403 К). Высокие значения температуры
перехода объясняют, почему постоянные магниты обычно
изготовляют из этих веществ. Их магнитная восприимчивость при
температурах выше точки Кюри следует закону Кюри — Вейсса
(список формул МЛ), но зависимость 1/Г закона Кюри
заменяется на 1/(Тс+Т), где Тс — температура Кюри (в более
точное выражение 1/(90+7") входит величина 0с — парамагнитный
предел, которая несколько больше 7V. 0с = 1100 К для Fe и
9с = 1415 К для Со). В ряде веществ может происходить
переход в антиферромагнитную фазу, где соседние спины
выстраиваются в противоположных направлениях, что приводит к
сильному ослаблению спинового парамагнетизма. Температура
перехода в такое состояние называется точкой Нееля. Известным,
но не единственным примером такого вещества является NiO.
Спин-спиновое взаимодействие, ответственное за выстраивание
спинов в обоих фазовых состояниях, является
электростатическим по природе и связано с обменной энергией (см.
«Рекомендуемые источники»).
Упражнения. 1. Каким образом можно отличить диамагнитное вещество
от парамагнитного? Является ли малой величиной восприимчивость,
обусловленная наведенным моментом? Какова размерность величин Хт? Какую
работу надо затратить, чтобы внести магнитный образец в магнитное поле?
Какое вещество — парамагнитное или диамагнитное — легче внести в магнит*
ное поле? Чем обусловлены парамагнитные свойства вещества? Какова
разность энергий между 1 молем электронов с 6-спином и 1 молем электронов
с а-спином во внешнем поле 5 кГс (0,5 Тс)? Каково различие спиновых засе-
ленностей, если электроны находятся в тепловом равновесии при 300 К?
Какой должна быть намагниченность такого образца и его магнитная
восприимчивость? (Чтобы получить эти величины в правильных единицах, следует
помнить, что намагниченность, как и сила поля, измеряется в А-м-1, магнитная
индукция, или плотность потока, — в Вб-м~2, или кг'С-^А"1, или Тс; см.
табл. 20). В чем состоит различие между токами, обусловливающими
диамагнетизм и не зависимый от температуры парамагнетизм? Каким образом
205
м
можно обосновать аддитивную схему Паскаля? В чем состоит различие
между ферромагнетизмом и антиферромагнетизмом? Что понимается под
температурой перехода в каждом из этих случаев? Какова природа
взаимодействия спинов, приводящего к этим кооперативнььм явлениям
(согласованному выстраиванию спинов)?
2. Выведите закон Кюри, используя следующую схему рассуждений.
Намагниченность образца (магнитный момент) в магнитном поле В равна
магнитному моменту а-спина, умноженному на число а-спииов, плюс момент
Р-спина, умноженный на число Р-спинов. Число а- и Р-спинов определяется
распределением Больцмана при температуре 7\ энергия спина с магнитным
моментом т равна —mzB (предполагается, что поле направлено по оси г).
Когда эта энергия мала, экспоненту в распределении Больцмана можно
разложить в ряд. Полученное выражение должно совпадать с законом Кюри,
приведенным в списке формул Ml.
3. Повторите этот вывод для общего случая частиц со спином S и
найдите температурную зависимость намагниченности при всех температурах,
т. е. функцию Бриллюэна. Ответ дается в списке формул. Изобразите
графически полученную функцию и функцию g\iBB/kT.
Рекомендуемые источники. Классическим трудом по магнитной
восприимчивости считается книга Ван Флека [407], но она написана так давно, что ее
язык устарел. Обзор по расчетам магнитных свойств и их интерпретации с
использованием представлений о токах дан в гл. 11 [1]. Многие из
затронутых в данном разделе вопросов обсуждаются Эрншоу [128], Дэвисом [117] и
Селвудом [362]. Хорошим введением в теорию кооперативных явлений
служат кн. Стенли [381] и Маттиса [268]. Большой интерес представляет
рассмотрение магнитных свойств ионов переходных металлов в рамках теории поля
лигандов. В этом плане представляют интерес книги: Эрншоу и Харрингтон
«Химия переходных элементов» [14], Эрншоу [128], Оргел [308] и Гриффит
[170]. Дополнительную информацию по магнитным свойствам можно найти
в разд. «Электронный парамагнитный резонанс», «Ядерный магнитный
резонанс» и «Химические сдвиги». С полемикой о существовании круговых токов
можно ознакомиться в кн. Машера [300]. Подробная сводка магнитных
свойств всевозможных веществ содержится в § 5 кн. Грея [168]. Уравнения
Максвелла приведены в табл. 20.
МАГНИТНЫЙ МОМЕНТ. Магнитный момент электрона,
обусловленный его орбитальным угловым моментом 1 (т. е.
некоторым круговым током), связан с ним соотношением \iL = уе\9
где коэффициент пропорциональности уе называют
гиромагнитным отношением. Несложные выкладки показывают, что
величина уе равна —е/2пге> где знак минус возникает из-за
отрицательной величины заряда электрона и свидетельствует, что
направление магнитного момента jul противоположно направлению
орбитального момента 1 (рис. М.5).
Спиновый угловой момент также вносит вклад в магнитный
момент электрона (появление которого можно примитивно
объяснить вращением заряда вокруг своей оси). Этот вклад иногда
называют «аномальным», потому что, когда он был впервые
вычислен, его величина вдвое превышала ожидаемую. Чтобы
можно было выразить спиновый угловой момент через
гиромагнитное отношение уе, вводится дополнительный множитель (g-фак-
206
м
тор). В результате jus = gy€s. Эксперимент, а позднее и теория
показали, что g = 2,0023; часто его аппроксимируют значением
g = 2. Спиновый магнитный момент и спиновый угловой момент
коллинеарны, но антипараллельны.
Магнитный момент часто выражается в магнетонах Бора
lxB = eb/2me. Магнетон Бора является положительной величиной
и может рассматриваться как основная единица измерения
магнитных моментов (он равен 9,273-Ю-24 Дж-Т-1, или 9,273»
• 10"28 Дж-Гс-1). Следовательно, уе = — \кв1К откуда \xL =
= — (|W*)1 и jus = — £(|W»)s.
Поскольку электрон является элементарным отрицательным
зарядом и представителем класса легких элементарных частиц
протон
Рис. М.5. Орбитальный и спиновый магнитные моменты.
(так называемых лептонов, к которым относятся электроны,
нейтрино и мюоны), а \хв представляет собой элементарную единицу
магнитного момента, удобно рассматривать протон как
элементарный положительный заряд и представитель класса тяжелых
элементарных частиц (барионов, к которым относятся протоны
и нейтроны, иначе называемые нуклонами). Соответствующей
элементарной единицей магнитного момента является ядерный
магнетон iiN = eb/2mp, равный 5,051-Ю-27 Дж-Т"1, или 5,051 •
•Ю-31 Дж-Гсг"1. Огромное различие в величинах магнетона
Бора и ядерного магнетона обусловлено различием в массах
электрона и протона (тяжелый протон приобретает тот же
самый спиновый угловой момент, что и у электрона, при
значительно меньшей угловой скорости, и, таким образом,
эквивалентному механическому моменту соответствует гораздо меньший
кольцевой ток и меньший магнитный момент). Ядерный
магнетон является удобной единицей выражения магнитных моментов
ядер (а иногда и магнитных моментов вращающихся молекул,
см. разд. «^-Фактор»), Для ядра со спиновым угловым
моментом I магнитный момент равен gn(\iKlti)l, где ядерный
gn-фактор зависит от конкретного ядра; используя это соотношение, его
207
м
можно определить экспериментально (по-видимому, в будущем
его можно будет рассчитать, используя теорию строения ядра).
Установлено, что gn может быть положительной или
отрицательной величиной в зависимости от химического элемента и его
изотопа. Эта величина, несомненно, заслуживает самого глубокого
изучения, так как даже незаряженный нейтрон имеет
магнитный момент. Типичные значения магнитных моментов ядер
некоторых распространенных элементов приведены в табл. 17.
Отметим также, что уп = gn(|W*)«
Рекомендуемые источники. См. [1], гл. 8—10. Классическая
электромагнитная теория магнитных моментов хорошо изложена Корсоном и Лоррай-
ном [98]. Уравнения Максвелла приведены в табл. 20. Квантовомеханическая
теория магнитных моментов рассмотрена в разд. «Спин», «^-Фактор»,
«Магнитные свойства», см. также разд. «Дирака уравнение», «Электронный
парамагнитный резонанс» и «Ядерный магнитный резонанс».
МАТРИЦА. Матрица представляет собой прямоугольную
таблицу, состоящую из чисел, и может рассматриваться как
обобщение понятия числа, поскольку обычное число является
матрицей, состоящей из одной строки и одного столбца (1X0»
т. е. частным случаем матрицы из п строк и m столбцов (n><m).
Числа, образующие матрицу М (матричные элементы),
обозначают порядковыми номерами строки и столбца, в которых
находятся эти числа. Таким образом, каждый элемент матрицы М
можно обозначить как МГСу где первый индекс показывает номер
строки, а второй — номер столбца. В квадратной матрице
п X п число строк равно числу столбцов, и в ней содержится
всего п2 элементов. Квадратные матрицы играют очень важную
роль в квантовой механике (хотя встречаются также
вытянутые матрицы), и в данной статье речь пойдет только
о них.
Существуют простые правила, которым подчиняются
математические операции над матрицами. Если две матрицы имеют
одинаковую размерность (т. е. одинаковое число строк или
столбцов), их можно сложить друг с другом или перемножить.
Правила сложения и умножения матриц даны в списке формул
М.2. Там же приведены некоторые матрицы специального вида.
Особо отметим, что правило перемножения матриц отличается
от умножения обычных чисел (или, как их иногда называют, с-
чисел): в общем случае произведение матриц MN не равно
произведению NM, т. е. матричное произведение не коммутативно.
Разность MN — NM называется коммутатором матриц М и N.
В том, что коммутатор не всегда равен нулю, наиболее ярко
проявляется различие матриц и обычных чисел, и это до
некоторой степени характеризует различие между классической и
квантовой механикой, см. разд. «Матричная механика».
208
Список формул М.2
Матрицы
Квадратная матрица М представляет собой таблицу из п2
элементов Мгс (г — номер строки, с — номер столбца):
Г Ми Ми MiZ ... Мщ
М2\ М22 М2г ... М2п
М= *
LMni Mn2 Мпг ... Мпп
Сложение матриц: М + N = Р, где Prc = Mrc + Nrc.
Умножение матриц: MN = Р, где Prc = ^ MrqNqc.
я
Примеры:
-к:] -»-[; \\
Ld + h c + g}' \de + ch df + cgj
обратите внимание, что
Гае+df Ье+cfl
NM = * . , ,, . It^MN в общем случае.
L ah + dg bh + eg J
Специальные матрицы (и иллюстрации на примере матрицы М,
приведенной выше):
Диагональная матрица
* Га <П
АгС = 0, кроме г—с; например, А = | |.
L0 с J
Единичная матрица
Г все диагональные элементы = 1
1 все недиагональные элементы = 0
[1 01
I. Часто вместо 1ГС используют обозначение 6ГС,
которое называют дельта-символом Кронекера.
Обратная матрица М"1: ММ"1 = М^М = 1 (см. ниже).
Транспонированная матрица
- - ~~ Г a dl
М: МГС = МСГ, например, М = | I.
Комплексно сопряженная матрица:
М*: (М*)ГС = (МГС)\ например, М* - [ ** *]].
Продолжение списка формул М.2
Сопряженная матрица М+ : М+ = М , т. е.
(М+)гс = М*сп например, м+"[^ с»]-
Унитарная матрица М+ = М~1. I
Эрмитова, или самосопряженная, матрица М+ = М.
Детерминант матрицы: | М |, или det М; I
например, | М | = ас — bd\
если Р = MN, | Р | = | М | | N |.
Нахождение обратной матрицы:
1. Находим | М |, если | М | Ф О, обратная матрица существует; если
| М | = 0, матрица сингулярна и не имеет обратной матрицы.
2. Образуем матрицу М.
3. Получаем матрицу NT, элементы которой М'гс являются
алгебраическими дополнениями а (минорами с соответствующими знаками)
элементов (М)гс.
4. Обратная матрица М""1 =М/|М|. I
Например, 1. | М | = ас — bd,
2- ""Ь с}
з. м' = [_^ "*],
*«--Ыт*)[-;-.']-
пр-р««--(-=^г)[; j][_:~:]-
-( l \\ ac~bd -ab + ab]_ *
~~\ac-bd Jlcd-cd - bd + ac J ~" m M
Решение системы линейных алгебраических уравнений:
Систему уравнений для п неизвестных
Muxi + М12х2 + ... М1пхп = сх
М2\Хх + М22х2 + ... М2пхп = с2
9 * * I
• • • I
МщХх + Мп2х2 + ... Мппхп = сп
а Алгебраическим дополнением матричного элемента MfC называется детер- I
мин ант, полученный при вычеркивании в исходной матрице строки г и столбца с I
(минор) и взятый со знаком (—1)г+ .-—Прим. ред. I
I
м
Продолжение списка формул М.2
можно записать в виде Мх = с, где х и с — матрицы /г X Ь
х =
" *\ "
х2
-*«_
с =
-' с\
с2
-Сп_
Тогда, поскольку М~"1М = 1 и 1х = х,
имеем: х = М~1с.
Используя вышеприведенное правило нахождения М""1, можно
определить М"~!с и найти весь набор из п неизвестных хи ..., хп.
Обычная квантовая механика Шредингера может быть
представлена в матричном виде, если интеграл по волновым функ-
циям \ dx i|)*£H»c, где Q — некоторый оператор, обозначить как
Qrc. Тогда набор таких интегралов для г и с, соответствующих
всем состояниям системы, может быть представлен в виде
матрицы Q (см., например, разд. «Теория возмущений»).
Упражнения. Многие операции матричной алгебры можно
проиллюстрировать на примере квадратных матриц второго порядка. Используя три
матрицы
-- -- -- -- "3 2 + 4Г
.5 6
ж Г1 21 » Г5 61 г> Г3 2 + 4/1
Из J' Иг 8J И Иб 6 J'
выполните следующие задания:
1. Найдите элементы Ли, А12, В2и Сц, Ci2.
2. Вычислите А+В, А—В, А + В + С, АВ, ВА, А(ВС), (AB)C, АВ — ВА,
АС — СА.
3. Найдите А, А+, A*, A-1, det А, С*, С+.
4. Вычислите В"1 А В, В1 В, В В-1.
5. Используя правило умножения матриц и обозначая через х матрицу
2 X Ч L запишите систему уравнений х + 2у — 2 и Зх + 4у = Ъ в виде
матричного уравнения. Это уравнение имеет вид Мх = N; покажите, что х и
у можно определить, если можно найти М-1. Решите эту систему,
определив М"1.
Рекомендуемые источники. Общие сведения о матрицах и простых
операциях с ними см. в [1], гл. 6. Несколько более полный обзор по свойствам
матриц дан в гл. 10 кн. Маргенау и Мерфи [266]. Книга Айреса [42] позволит
получить достаточно полное представление о применении матриц для решения
большого круга математических и физических задач. Матрицы служат
211
м
основой современного математического аппарата квантовой механики (см.
«Матричная механика»), и без них невозможно серьезное рассмотрение
теории групп.
МАТРИЦА ПЛОТНОСТИ. В элементарных приложениях
квантовой механики расчеты основываются на использовании
волновой функции «ф, но, какая бы действительная наблюдаемая
ни вычислялась, мы сталкиваемся с формулами, которые
включают квадратичную форму волновой функции или билинейную
комбинацию вида ^*т^п (см., например, разд. «Ожидаемое
значение» или «Вероятность перехода»). Очевидно, имело бы смысл
дать такую формулировку квантовой механики, которая
непосредственно имеет дело с билинейными комбинациями г^г^, а
ие вводит их только при вычислении наблюдаемых. Отметим,
что абсолютная фаза волновой функции несущественна, так как,
если умножить ^>т и г|эп на произвольный фазовый множитель
exp if, произведение ty*„$n не изменится; следовательно, все
наблюдаемые не зависят от абсолютной фазы. (По-видимому,
пользуясь волновыми функциями, мы вынуждены все время
иметь дело и с бесполезной информацией.) И наконец,
отметим, что состояние системы очень редко является чистым.
Обычно реальную систему следует рассматривать как статистический
набор, большой статистический ансамбль подсистем, и
результат эксперимента определяется усредненным (фактически
одним из средних по статистическому ансамблю) значением
произведений ,ф^'фд. Обозначим это статистическое среднее как ф„$п
и будем рассматривать его как я,т-элемент матрицы, а именно
матрицы плотности р. Матрица, состоящая из элементов pmn,
которые определяются как 'ф*^, должна содержать всю инфор-
мацию о системе; она несет всю относящуюся к делу
информацию, содержащуюся в волновой функции, и всю информацию о
роли статистического усреднения. Найти уравнение движения
для матрицы плотности (соответствующее уравнению Шредин-
гера для волновой функции) несложно, но решить его обычно
очень трудно. Тем не менее существуют эффективные методы
работы с матрицей плотности, и ее использование является
обычным подходом при проведении вычислений, касающихся
временной эволюции сложных систем.
Рекомендуемые источники. Несложное введение в вопрос см. у Сликтера
[374]. См. также гл. 4 кн. Займана [438], гл. 1.8 кн. Романа [343] и Фано [138].
Применение матрицы плотности к расчетам электронного строения атомов и
молекул обсуждается Мак-Вини и Сатклифом [279].
МАТРИЧНАЯ МЕХАНИКА. В основе формулировки
квантовой механики, предложенной Гайзенбергом, лежит утвержде-
212
м
ние, что координата частицы q и ее импульс р вдоль этой
координаты должны удовлетворять соотношению qp — pq = ib, где
Ь — постоянная Планка Л, деленная на 2я. Исходя из
предположения, что наблюдаемые значения координаты и импульса
подчиняются этому соотношению, можно получить количественное
согласие со всеми экспериментальными данными. Указанное
соотношение примечательно еще и потому, что оно противоречит
всем представлениям классической физики.
В классической физике можно численно определить
координату частицы (например, расстояние: 4 м от некоторого центра)
и ее импульс (например, 2,5 кг-м-с*1). Произведение этих
чисел, характеризующих наблюдаемые величины, равно 10 Дж-с
и не зависит от того, каким образом проводилось их умножение:
q X Р или р X <7> так что разность qp — pq равна нулю. Согласно
представлениям Гайзенберга, эта разность равна не нулю, а
очень малой мнимой величине ib. Отсюда следует, что р и q
нельзя считать обычными числами. Борн предложил Гайзенбергу
рассматривать их как матрицы, и, поскольку произведение
матриц в общем случае зависит от последовательности
сомножителей, существование разности pq — qp становится обоснованным.
Таким образом, матричная механика основывается на описании
наблюдаемых величин с помощью матриц, или ^-чисел (q —
начальная буква слова «quantum», т. е. квантовый), в отличие от
обычных с-чисел (с — начальная буква слова «classical», т. е.
классический), поскольку ^-числа удовлетворяют правилам
матричного умножения, и в частности соотношению qp — pq = ib.
Если задачи механики решаются с учетом этого требования,
результаты расчетов отлично согласуются с экспериментальными
данными.
Использование неверного соотношения qp — pq = 0, т. е.
рассмотрение величин q и р как с-чисел, влечет за собой ошибку
порядка й. Поэтому результаты расчетов по классическим
законам являются удовлетворительными лишь в том случае, когда
можно пренебречь погрешностью порядка постоянной Планка.
Матричная механика Гайзенберга очень незначительно
опередила волновую механику Шредингера, и очень скоро сам Шре-
дингер установил эквивалентность этих двух математических
теорий. Сегодня их находят одинаково удобными. Формулировка
Гайзенберга, имеющая дело с матрицами или, что то же самое,
с операторами, часто оказывается более удобной в
математическом отношении. Формализм Шредингера, который позволяет
более наглядно представить состояние системы, описывая ее с
помощью волновых функций, чаще используется для конкретных
расчетов энергетических уровней и состояний сложных систем.
Когда в квантовой механике говорят об «описании
Гайзенберга» или «описании Шредингера» (или о соответствующих
213
м
«представлениях», как их принято называть), в эти слова
вкладывают вполне определенный смысл. Различие между этими
двумя подходами связано с неодинаковым учетом зависимости
описания системы от времени. В представлении Гайзенберга
временная зависимость включена в операторы (или матрицы):
состояния остаются постоянными, а операторы, с помощью
которых получают физические величины, изменяются во времени,
поэтому наблюдатель может судить об эволюции системы.
В представлении Шредингера оператор определяемой
величины остается постоянным во времени, а волновая функция
меняется. Различие двух подходов является чисто математическим
и не влияет на физический смысл результатов. Существует
также компромиссное описание, называемое представлением
взаимодействия, или описанием Дирака. Эволюция системы во
времени в этом представлении учитывается как с помощью
операторов, так и с помощью волновых функций. При этом с помощью
операторов учитывают простейшее изменение системы (обычно,
его периодическую составляющую), а с помощью волновой
функции учитывают остальную, более сложную, но зато более
медленную составляющую изменения. Такое описание очень удобно
при использовании методов теории возмущений с зависимостью
от времени.
Рекомендуемые источники. Истолкование квантовой механики, целиком
основанное на представлениях матричной механики, содержится в
небольшой кн. Грина [169]. См. оригинальные статьи Гайзенберга [178], Борна и
Иордана [68], Борна, Гайзенберга и Иордана [67]; переводы этих статей на
английский опубликованы Ван-дер-Верденом [406]. Позиция Борна в этом
вопросе хорошо видна из его переписки с Эйнштейном [65]. Математическая
формулировка матричной механики изложена в кн. Дирака [123], Кембла
[220], Крамерса [227], фон Неймана [410]. Четвертое описание, дополняющее
описания Шредингера, Гайзенберга и Дирака, предложено Маркусом [264].
Математический аппарат первых трех описаний в простой форме изложен
в § 3.2 кн. Займана [438], § 5.4 кн. Сликтера [374] и Романа [343].
МЕЖМОЛЕКУЛЯРНЫЕ СИЛЫ (краткий обзор). В основу
классификации сил межмолекулярного взаимодействия
положена оценка порядка величины их радиуса действия.
Короткодействующие силы являются силами отталкивания, они
обусловлены увеличением энергии, которое происходит при
вынужденном сближении двух электронных облаков и их проникновении
друг в друга. В процессе сближения двух заполненных оболочек
отдельные электроны могут перестроить свое пространственное
распределение таким образом, что займут более выгодные в
энергетическом отношении области. Но в соответствии с
принципом Паули некоторые электроны будут вынуждены занять такие
области, что это приведет к увеличению энергии сближающейся
пары молекул. (В теории молекулярных орбиталей эти области
214
/VI
называются разрыхляющими орбиталями.) Повышение энергии,
обусловленное такими электронами, может преобладать над
понижением энергии, обусловленным электронами, которые
получают более выгодное пространственное распределение, поэтому
энергия пары частиц резко увеличивается при уменьшении
расстояния между ними. Это явление можно приписать действию
некоторых сил отталкивания между молекулами, природа
которых обусловлена принципом Паули.
Наличие дальнодействующих сил притяжения между
молекулами следует по крайней мере из факта существования
конденсированных фаз вещества. Простейшим примером сил
притяжения может служить взаимодействие заряженных частиц (ион-
ионное взаимодействие, ионная связь), при котором кулоновские
силы настолько сближают частицы, насколько это позволяют
сделать силы отталкивания. Хотя большинство молекул не
заряжены, силы притяжения действуют и в этих случаях. В полярных
молекулах появление этих сил может быть обусловлено
наличием у молекул постоянных электрических моментов (диполь-
дипольное взаимодействие или, если одна частица заряжена,
взаимодействие точечного заряда с диполем или взаимодействие
диполя с индуцированным диполем, если только одна из
молекул полярная; в последнем случае сила взаимодействия зависит
от поляризуемости неполярной молекулы). Существуют силы
притяжения и между неполярными молекулами: наиболее
важными из них являются дисперсионные, или лондоновские, силы,
называемые также взаимодействием индуцированный диполь —
индуцированный диполь. Это взаимодействие обусловлено
флуктуацией электронной плотности одной молекулы, приводящей к
появлению у нее мгновенного дипольного момента, который в
свою очередь индуцирует мгновенный дипольный момент в
другой молекуле, два образовавшихся диполя притягиваются друг
к другу. Сила притяжения в этом случае определяется
поляризуемостью обеих молекул, а энергия взаимодействия зависит от
расстояния R между молекулами как /?~6.
Все перечисленные межмолекулярные взаимодействия
получили общее название вандерваальсовых сил.
Силы взаимодействия между полярными молекулами иногда
называют силами Кеезома.
Зависимость вандерваальсовых сил от расстояния и угловую
зависимость взаимодействия несферических частиц обычно
представляют с помощью эмпирических выражений, которые имеют
более или менее правильную качественную форму и включают
минимальное число подгоночных параметров. Некоторые из
наиболее распространенных межмолекулярных потенциалов
графически изображены на рис. М.6 и представлены аналитически в
списке формул М.З. Все эти потенциалы основаны на грубых
215
потенциал
жестких ctpep
i потенциал
\ точечных
i центров
<к
потенциал
прямоугольной.
ямы
R
потенциал
Сюзерленда
потенциал
Меннарда-йжонса
(6J2)
потенциал
бэшнгема
Рис. М.6. Форма некоторых эмпирических потенциалов межмолекулярного
взаимодействия.
Список формул М. 3
Межмолекулярные потенциалы
Потенциал жестких сфер:
Потенциал точечных центров:
V(R) = DR~\
Как правило, 9 < 6 < 15. Для максвелловских молекул 6 = 4.
Потенциал прямоугольной ямы:
/ оо R<(J
V(R) = \ -е <j<R<ro
i 0 R>rv.
Потенциал Сюзерленда:
( оо R<a
V(R)
Потенциал Леннарда-Джонса:
V(R)=*DR-6-CR-\
Частный случай: потенциал (6,12)
Потенциал Бакингема:
V(R) — Be~b* - С/Г6 - С'/?"8.
Модифицированный потенциал Бэкингема (6-ехр):
} = Г [8/(1 - 6/а)] [(6/а) ехр (а - aR/Rm) - /^/Л6]
V(R)- .
Ж Ли
здесь /?w — значение радиуса R, при котором верхнее выражение
для V(R) достигает максимума.
Потенциал Штокмайера:
V(R) = VLJ(R) + &(R, цЬ|12),
где Vц (Л) — потенциал Леннарда-Джонса и 8 (R, |яi, \х2) — энергия
диполь-дипольного взаимодействия, приведенная в списке формул Д. 1.
м
предположениях относительно сил отталкивания, которые в
действительности гораздо более сложны, так как зависят от тонких
особенностей волновых функций молекул и их перекрывания.
Наиболее грубая аппроксимация отталкивательной части
потенциала состоит в представлении ее потенциалом жесткой
непроницаемой сферы. Потенциал Лениарда-Джонса основан на
предположении о быстром возрастании отталкивания на малых
расстояниях, происходящем по закону R~n. Когда из
соображений математического удобства п выбирается равным 12,
получается потенциал Леннарда-Джонса (6, 12); зависимость i?"6 в этом
случае (см. список формул М.З) отражает наличие
дисперсионных сил. Потенциал Бэкингема 6-ехр также учитывает
зависимость i?-6, но основан на предположении об экспоненциальной
зависимости сил отталкивания от расстояния. Потенциал Кеезо-
ма характеризует взаимодействие несферических молекул,
представляя их в виде цилиндров, закрытых полусферами. Потенциал
Штокмайера отличается от потенциала Леннарда-Джонса тем,
что в нем дополнительно учитывается взаимодействие двух
диполей, расположенных в центрах молекул.
Межмолекулярные силы необходимо учитывать в тех
случаях, когда исследуются свойства реальных газов или жидкостей
и необходимо провести точные расчеты. Один из основных
методов расчета термодинамических величин заключается в
использовании вириального уравнения состояния. В этом уравнении
величина PV разлагается в ряд по степеням 1/V; коэффициенты
вириального разложения называются вириальными
коэффициентами. Выражения для них могут быть получены из вида
межмолекулярного потенциала, а эти коэффициенты используются
затем при расчетах свойств газов. Структура жидкостей также
определяется характером межмолекулярных сил. Эти силы
(и соответствующие параметры в эмпирических потенциалах)
можно определить, сравнивая рассчитанные вириальные
коэффициенты и экспериментальные данные, полученные при
изучении транспортных свойств, а еще лучше — при исследовании
рассеяния молекулярных пучков, в которых одни и те же молекулы
используются и как бомбардирующие частицы, и как мишени,
а величина отклонения пучка характеризует межмолекулярное
взаимодействие.
Рекомендуемые источники. Превосходную книгу на данную тему
опубликовали Гиршфельдер, Кертис и Берд [193]; в первых главах книги дается
краткий обзор, а в последующих — детальное изложение вопроса. Об
исследованиях Дебая можно прочесть в кн. Чу [100], квантовомеханический подход
излагается в кн. [1], гл. 11 и кн. Козмана [217], Маргенау и Кестнера [265].
Определение межмолекулярных потенциалов описано Гиршфельдером, Керти-
сом и Бердом [193], Ксртисом [113], Даймондом и Смитом [127]. Описание
молекулярных пучков и методов их применения для нахождения
межмолекулярных потенциалов дано в кн. Левина и Бернштейна [245] и Рамзея [330] и
218
м
в сб. под ред. Росса [345]. Обзор экспериментальных и теоретических
аспектов изучения межмолекулярных сил опубликован Гиршфельдером [190].
МОЛЕКУЛЯРНЫХ ОРБИТАЛЕИ МЕТОД. Метод
молекулярных орбиталеи (МО) является наиболее распространенным
подходом в теории химической связи, в котором понятие
«атомная орбиталь» распространяется на более сложные системы,
содержащие несколько ядер. В молекуле каждый электрон может
быть обнаружен в окрестности любого ядра, поэтому логично
считать, что он распределен с различной плотностью по всему
ядерному остову молекулы. Волновая функция электрона в
молекуле содержит информацию о его распределении, так как,
согласно интерпретации Борна, квадрат волновой функции в
любой точке пропорционален вероятности обнаружения в ней
электрона. Таким образом, волновую функцию электрона в молекуле
можно рассматривать как такую функцию, распределенную по
всему ядерному остову, квадрат которой в любой точке
пропорционален электронной плотности. Эта волновая функция и
представляет собой молекулярную орбиталь.
Распределение электронов на молекулярных орбиталях
позволяет объяснить природу химической связи. В самом деле,
вполне естественно ожидать, что большая амплитуда орбитали
и, следовательно, большая электронная плотность будет
возникать именно там, где такая плотность и должна обнаруживаться,
согласно нашему представлению о химической связи, а именно
в пространстве между ядрами, стягиваемыми за счет
взаимодействия с электроном. Рассмотрим двухатомную молекулу. Для
гомоядерных молекул (с ковалентной связью между двумя
одинаковыми атомами) следует ожидать, что орбиталь равномерно
распределится между двумя ядрами. По мере того как связь
становится более полярной (в гетероядерных молекулах со
связью между различными атомами), следует ожидать
увеличения амплитуды молекулярной орбитали на одном из ядер.
В предельном случае чисто ионной связи молекулярная
орбиталь должна быть полностью локализована на одном из ядер.
При исследовании строения молекул принято применять к
ним такой же подход, основанный на использовании
молекулярных орбиталеи, который применяется при рассмотрении
строения с использованием атомных орбиталеи. В^ частности, при
определении электронного строения молекулы*заселение
молекулярных орбиталеи осуществляется по известному принципу
заполнения. В качестве первого примера применения такого
подхода рассмотрим молекулу водорода. Молекулярная орбиталь,
ответственная за образование связи, симметрично распределена
по обоим ядрам и характеризуется значительным увеличением
плотности в межъядерной области (рис. М.7). Располагая на
219
м
этой орбитали первый, а затем второй электрон, следует
учитывать, что в соответствии с принципом Паули спины электронов
обязаны иметь противоположное направление. Это показывает,
что в теории молекулярных орбиталей естественным образом
учитывается важная роль спинового спаривания в образовании
химической связи. Это следствие принципа заполнения будет
еще не раз обсуждаться в данном разделе.
В принципе нетрудно представить себе, как должно быть
осуществлено обобщение на случай молекулы водорода решения
уравнения Шредингера для атома водорода и даже прямые
расчеты молекулярных орбиталей для многоядерных молекул. Од-
ЯН)—-v у £(Н)
Рис. М.7. Молекулярная орбиталь, отвечающая за образование связи в мо«
лекуле Нг.
нако на практике это чрезвычайно трудно сделать, и такие
расчеты удается довести до конца только для молекулярного иона
водорода (н£), и даже для такой, казалось бы, простой одно-
электронной системы провести расчет совсем не так просто.
Поскольку химиков обычно интересуют молекулы более сложные,
чем HJ, были предложены приближенные схемы расчета
молекулярных орбиталей, включающие приближение Борна—Оппен-
геймера (фиксация определенной геометрии ядерного остова
молекулы) и метод линейных комбинаций атомных орбиталей
(ЛКАО). Более детально эти приближения рассмотрены в
соответствующих разделах, здесь мы вкратце обсудим применение
метода ЛКАО для молекулы водорода и еще одной или двух
простых молекул.
Метод ЛКАО основан на предположении, что истинную
сложную молекулярную орбиталь можно выразить в виде суммы
орбиталей, составляющих молекулу атомов Этот подход является
весьма хорошим приближением, так как позволяет
воспроизвести много существенных особенностей точного решения. В
молекуле Нг наиболее важны ls-орбитали каждого атома, и молеку-
220
м
лярная орбиталь выражается в виде их суммы i|)]Sa + \|)ls^ Такое
простое выражение получается благодаря тому, что ядра
одинаковы и электрон распределяется между ними поровну. Оно
Рис. М.8. Связывающая и разрыхляющая орбитали в молекулярном ионе Н*.
правильно воспроизводит значительное накопление заряда
между ядрами. Действительно, если учесть волновую природу
атомных орбиталей, одна ls-орбиталь может рассматриваться как
стоячая сферическая волна с центром на ядре а, другая — как
стоячая сферическая волна с центром на ядре Ь (рис. М.8). Эти
две волны сильно перекрываются в межъядерной области, что
приводит к их интерференции, и если знаки амплитуд у них
221
м
одинаковы, то полная амплитуда в этой области усиливается, а
следовательно, увеличивается и электронная плотность. При этом
происходит понижение энергии молекулы, вызванное
понижением потенциальной энергии электронов, которые, согласно
рассматриваемому описанию, находятся в межъядерной области и
получают возможность эффективно взаимодействовать с обоими
ядрами. (В действительности энергия связи определяется также
и другими факторами, в частности изменением кинетической
энергии и изменением вида самих атомных орбиталей. Истинная
природа химической связи становится понятной в результате
рассмотрения изменений не только потенциальной, но и
кинетической энергии, и при построении молекулярных орбиталей
необходимо принимать во внимание искажение атомных орбита-
лей при образовании связи. Чтобы не усложнять рассмотрение,
эти факторы не обсуждаются в данном разделе, но им
посвящена последняя часть разд. «Химическая связь».) Нетрудно
понять, что наиболее прочная связь образуется с участием двух
электронов, поскольку принцип Паули разрешает находиться на
связывающей орбитали только двум электронам с
противоположными спинами.
Метод ЛКАО позволяет получить не только связывающие, но
и разрыхляющие молекулярные орбитали. Последние
образуются при противоположных фазах (различных знаках амплитуд)
перекрывающихся атомных орбиталей, когда в результате
интерференции электроны удаляются из межъядерной области
(рис. М.8). Находясь на таких орбиталях, электроны всегда
ослабляют связь. Если в молекулу Нг ввести третий электрон, он
займет разрыхляющую орбиталь, что приведет к ослаблению
связи.
Такой подход легко распространить на более сложные
молекулы. Двухатомная молекула Ог служит весьма интересным и
поучительным примером использования этого метода.
Молекула кислорода состоит из двух ядер и шестнадцати электронов.
Для простоты мы будем рассматривать на каждом ядре только
по одной ls-орбитали, по одной 25-орбитали и по три 2/?-орби-
тали. Это позволяет определить строение молекулы кислорода
на основании следующих рассуждений.
1. Сильнее всего связаны со своими ядрами атомные
ls-орбитали. Если два ядра находятся на расстоянии, характерном для
молекулы Ог, эти две орбитали перекрываются в самой
незначительной степени. Поэтому образуемая ими связывающая
орбиталь приводит к чрезвычайно слабому связыванию, а
разрыхляющая орбиталь — к такому же слабому разрыхлению. Эти
орбитали изображены внизу на рис. М.9.
2. Несколько менее сильно связаны со своими ядрами
атомные 25-орбитали. Как и в Н2, в молекуле Ог эти две орбитали
222
м
перекрываются значительно сильнее и образуют связывающую
и разрыхляющую орбитали приблизительно с такими энергиями,
как это показано на рис. М.9.
3. Для 2/?-орбиталей, еще менее прочно связанных со своими
ядрами, возможны два сильно различающихся варианта пере-
атом А молекула АВ атом В
Рис. М.9. Схематическое изображение энергетических уровней и орбиталей
гомоядерных двухатомных молекул элементов второго периода; показано
заполнение уровней в 02.
крывания: встречное («лобовое») перекрывание и боковое
перекрывание.
а. В первом случае происходит значительное увеличение
электронной плотности на межъядерной оси, и, если орбитали имеют
одинаковую фазу, это приводит к образованию сильной связи,
если же они имеют противоположные фазы, возникает сильное
отталкивание. Существенно, что распределение электронной
плотности на таких молекулярных орбиталях является
цилиндрически симметричным относительно оси, соединяющей ядра
(рис. М.9). Такие орбитали получили название а-орбиталей, а
образующиеся с их участием связи называют а-связями (по
аналогии с s-орбиталями атома, имеющими сферическую симметрию).
223
м
б. В случае бокового сближения р-орбиталей их
перекрывание не слишком велико и в основном происходит не на
межъядерной оси. Тем не менее накопление электронной плотности
в областях перекрывания может вызвать притяжение ядер, что
приводит к возникновению умеренно сильной связи (или
умеренно сильного отталкивания, если перекрывание носит
разрыхляющий характер). Орбитали с таким распределением
электронной плотности называются я-орбиталями, а образующиеся с их
участием связи — я-связями (по аналогии с атомными /?-орби-
талями).
Полный набор построенных таким образом орбиталей
молекулы кислорода показан на рис. М.9. На этих орбиталях в
соответствии с принципом заполнения должны разместиться 16
электронов. Первый электрон помещают на lsa-уровень, к нему
присоединяют второй электрон — с противоположным спином,
следующий электрон помещают на lsa*-ypoBeHb и так далее.
Размещение первых 14 электронов не вызывает затруднений.
(Некоторые сомнения могут появиться при заполнении уровня 2/?я, на
котором могут разместиться 4 электрона, но следует помнить,
что уровню 2рп соответствуют две молекулярные орбитали, одна
из которых образована перекрыванием 2рх-орбиталей, а
другая — перекрыванием 2^-орбиталей.) Пятнадцатый электрон
располагается на разрыхляющей 2/?я*-орбитали. Шестнадцатый
электрон может занять ту же орбиталь, если он обладает
противоположным спином, либо может разместиться на другой
2/?я*-орбитали этой же вырожденной пары и в этом случае
может иметь любое направление спина (принцип Паули
разрешает обе ориентации). Что же получается на самом деле?
Согласно первому правилу Гунда, в этой ситуации более низкой
энергии отвечает параллельная ориентация спинов на
различных орбиталях, поэтому электронная конфигурация молекулы
02 имеет вид lso2lso*22so22so*22po22pnA2pxn*2pyn*. Как
убедиться в достоверности этой конфигурации? Один из наиболее
действенных способов такой проверки — метод электронной
спектроскопии. Однако существует и другой, более быстрый способ,
который основан на том, что можно заметить в молекуле 02
присутствие двух неспаренных спинов, наделяющих 02
парамагнитными свойствами (см. разд. «Магнитные свойства»).
Обнаружение парамагнитных свойств у молекулы кислорода было одним
из первых триумфов теории молекулярных орбиталей.
Как увязать полученные сведения о строении 02 с более
элементарным представлением о ней как о молекуле с двойной
связью 0 = 0? Приведенная на рис. М.9 схема показывает, что
связывающее действие ls-электронов на lsa-орбитали
компенсируется разрыхляющим действием электронов на 1$ст*-орбитали.
То же самое можно сказать и о 2sa- и 2$о*-электронах. Однако,
224
м
поскольку 2/?ст-орбиталь занята, а 2/?а*-орбиталь— пустая, это
означает наличие одной связи. Учитывая, однако, что орбитали
2рхп и 2руп заняты полностью, а 2рхл* и 2рип*— только
наполовину, мы устанавливаем наличие двойной связи 0=0. Каждый
раз, когда современная квантовая теория подтверждает
традиционные представления химии, нельзя не отдать дань уважения
зачинателям химической теории, которые при создании
структурных схем руководствовались интуицией, а не результатами
расчетов. Рассмотренный пример позволяет понять, почему
двойная связь оказывается менее прочной, чем две «простые связи».
Рис. М.10. Образование и два типа представления простых, двойных и
тройных связей. Банановые связи, напоминающие классическое представление
о напряженных связях, получаются соответствующим комбинированием а- и
я-связей.
Казалось бы, простую связь образуют и полностью заполненная
а-орбиталь, и полностью заполненная я-орбиталь, однако
последняя не дает (как мы указывали выше) заметного
увеличения электронной плотности в наиболее эффективной области
связывания. Классики структурной химии объясняли меньшую
прочность двойной связи ее «напряжением», и мы видим,
насколько они оказались правы. Тройная связь (рис. М.10)
образуется одной а- и двумя я-орбиталями.
Теория МО позволяет понять устойчивость двойных связей
к скручиванию. Рассмотрим, например, вращение одной из групп
СН2 этилена относительно другой такой же группы. «Внутреннее
вращение» уменьшает перекрывание между 2/?я-орбиталями, а
это приводит к ослаблению я-связи и увеличению энергии
молекулы (рис. М.11).
Какие орбитали дают наибольший вклад в образование
молекулярных орбиталей? Прежде всего эти атомные орбитали
должны иметь подходящую симметрию; неразумно пытаться
225
м
строить молекулярную орбиталь за счет бокового перекрывания
s- и р-орбиталей, потому что их результирующее перекрывание
окажется равным нулю (однако их встречное перекрывание
вполне возможно). Если этот критерий выполняется, далее
необходимо потребовать, чтобы орбитали имели приблизительно
равную энергию (критерий соответствия энергий) и имели бы
приблизительно одинаковую протяженность (чтобы между ними
осуществлялось хорошее перекрывание). Все эти критерии
рассматриваются в упражнениях. Перекрывание может усилиться,
если допустить возможность гибридизации подходящих атомных
Рис. М.11. Перекрывание при двойной
связи и ее сопротивление
скручиванию.
орбиталей. Изучение характера гибридизации при образовании
молекулярных орбиталей позволяет подойти к обсуждению
структуры молекул на основании метода МО. Все сказанное
выше как будто бы приводит к выводу о полном успехе теории
молекулярных орбиталей. На самом же деле по поводу этой
теории можно сделать много критических замечаний (однако,
если все эти замечания будут учтены, утратится первоначальная
простота ее концепций). Основное замечание заключается в том,
что метод МО недооценивает тенденцию электронов к
отталкиванию. Например, описание молекулы Н2 в рамках простого
варианта теории МО приводит к переоценке роли структур типа
Н+Н~. Этот недостаток можно исправить путем учета
конфигурационного взаимодействия. Метод МО, кроме того, приводит
к плохим результатам для больших межъядерных расстояний;
согласно расчетам, при диссоциации Н2 получаются ионы И+ и
Н~, а не два нейтральных атома водорода (2Н), как должно
быть на самом деле. Впрочем, и этот недостаток удается
преодолеть при учете конфигурационного взаимодействия.
Критическое замечание совсем другого характера состоит в том, что
теория МО не отражает традиционных представлений, согласно ко-
226
м
торым различные области молекулы во многих химических
задачах могут рассматриваться как отдельные, изолированные
образования. Однако сторонники теории МО легко парируют это
замечание, поскольку рассмотренные выше молекулярные орби-
тали, делокализованные по ядерному остову молекулы, нетрудно
преобразовать в набор локализованных орбиталей, относящихся
к различным участкам молекулы. Таким образом, этот
недостаток теории МО преодолевается путем математических
преобразований.
Теорию МО можно приспособить для проведения
количественных расчетов, используя, например, метод самосогласованного
поля.
Использование этого метода расчета атомов для нахождения
точных волновых функций и энергий молекул требует
чрезвычайно трудоемких расчетов (см,, например, разд. «Ab initio»,
«Хюккеля метод» и полуэмпирические методы).
Упраокнения. Что означает термин «молекулярная орбиталь» и какую
информацию он несет? Какими свойствами обладает МО, где ожидается
максимальное значение ее амплитуды и что можно сказать о ее симметрии?
Опишите, как меняется МО при изменении характера описываемой ею связи от
чисто ковалентного до чисто ионного. Как и за счет каких вкладов меняется
при этом энергия связи? Какое приближение используется в обычном методе
построения МО? В чем заключаются недостатки этого метода? Рассмотрите
образование молекулы водорода, используя представления теории МО.
Объясните причины нестабильности молекулы Не2, пользуясь методом МО.
Постройте схемы МО, аналогичные приведенной на рис. М.9, для Ог, для всех
двухатомных молекул элементов второго периода таблицы Менделеева.
Используя полученную схему, расположите в порядке увеличения стабильности
следующие молекулы: С2, С2, С2; Nj, N2, N2; 0£, 02> OJ; F2, F2, F2; Ne2, Ne2, Ne2#
В чем заключается главный недостаток простого варианта метода МО? Каким
образом его можно преодолеть?
2. Рассмотрите молекулярную орбиталь \sa — \sb и покажите, что, когда
она занята электроном, его распределение характеризуется большим вкладом
структуры Н+Н-. (Что можно в таком случае сказать о квадрате амплитуды
волновой функции?) Допустим теперь, что два электрона заселяют орбиталь
lsa + 1^6 и два — орбиталь \sa —* ls&, как в Не* Какой вид имеет
электронное распределение в этой молекуле? Рассмотрите частицу Н2, у которой
орбиталь \sa + ls& заселена одним электроном. Запишите гамильтониан такой
молекулы и выведите выражение для ее энергии через интегралы по
волновым функциям. Некоторые из этих интегралов соответствуют получающимся
при описании атома водорода, поэтому энергию рассматриваемой молекулы
можно выразить через энергию атома водорода и дополнительную энергию,
обусловленную образованием связи. Проанализируйте полученное выражение.
Поместите два электрона на рассматриваемую орбиталь и повторите весь
анализ для полученной молекулы Нг, построив соответствующий
гамильтониан. Очень важно, чтобы при этом вы не забыли учесть антисимметризацию
электронов. Запишите волновую функцию в виде детерминанта Слейтера, и
вы обнаружите, что это даст дополнительный вклад в энергию от
электронного обмена. Проанализируйте этот новый результат.
227
м
3. Рассмотрите орбиталь сра атома а и срб атома b с энергиями Еа и Еь
соответственно. Допустим, они перекрываются и взаимодействуют таким
образом, что величина взаимодействия пропорциональна величине их
перекрывания. Решая вековое уравнение, покажите, что эти две орбитали могут дать
две линейные комбинации, причем энергия одной из них оказывается ниже
исходной, а энергия другой — выше, и изменение энергий тем больше, чем
ближе др>г к другу значения Еа и Еь и чем больше величина перекрывания.
Покажите также, что связывающая орбиталь больше локализована на атоме,
орбиталь которого соответствует более низкой энергии. Эти расчеты
иллюстрируют упомянутые в тексте критерии и показывают, каким образом
полярность связи зависит от относительных энергий орбиталеи, участвующих
в связи.
Рекомендуемые источники. Метод МО описан в гл. 10 [1]. Доступное и
подробное изложение теории МО с примерами ее использования для
химически важных молекул дано Коулсоном в кн. «Форма и структура молекул»
10] и [105]. См. также кн. Маррела, Кеттла и Теддера [299], Стрейтвизера
387], Салема [353], Пилара [318], Слейтера [372] и Доджа [125]. Много
рисунков с изображением молекулярных орбиталеи большого числа молекул
можно найти в кн. Иергенсена и Салема [211]. Описание расчетов
молекулярных орбиталеи дано в разд. «Самосогласованного поля метод», «Ab initio»,
«Хюккеля метод», «Гибридизация», «Эквивалентные орбитали»,
«Разрыхление». Совершенно иной подход к обсуждению строения молекул изложен в
разд. «Валентных связей и молекулярных орбиталеи методы».
МУЛЬТИПЛЕТНОСТЬ. Под мультиплетностью понимается
набор уровней, принадлежащих одному терму, или набор
различных значений квантового числа /, которые могут
соответствовать данному терму. Когда величины квантовых чисел L и >S
таковы, что L ^ S, мультиплетность равна 2S + 1. Именно столько
значений полного момента может получиться при сложении
спина и орбитального момента (/ принимает значения L + S,
L + S—1, ..., \L — S|). Если L < S, число значений / равно
2L+ 1, т.е. мультиплетность в этом случае равна 2L+ 1. При
обозначении терма величина (2S+1) записывается в виде
левого верхнего индекса, но следует еще раз подчеркнуть, что она
равна мультиплетности уровня только в том случае, когда
L^ S. Например, терм 2D («дублет D») состоит из двух
уровней с / = 3/г и / = 5/г, которые записываются 2D /, и 2Do/2.
Мультиплетность терма 3Р (триплет терма Р) равна 3, и его уровни
обозначаются 3Р2, 3Pi, 3Ро- Терм 2S с L = 0 и S = 1/2
рассматривается как дублетный, хотя он имеет только один уровень (/ =
= 1/2). Следует быть осторожным при определении
мультиплетности и всегда помнить об относительной величине S и L.
Упражнения. Что понимается под мультиплетностью терма? Как можно
вычислить ее, зная L и 5? Что означает верхний левый индекс в
обозначении терма? В каких случаях этот индекс свидетельствует о мультиплетно-
сГи? Сколько уровней содержат следующие термы (т. е. какова их мульти-
22S
м
плетность): 2Р, 3Р, 4Р, 'S, 5S, 3D? Определите значения полного момента /
для каждого из уровней.
Рекомендуемые источники. В атомных спектрах мультиплетность термов
проявляется как тонкая структура. Структурные особенности синглетного и
триплетного термов рассмотрены в разд. «Синглетные и триплетные
состояния». Общие понятия даны в разд. «Угловой момент». Более подробно этот
вопрос обсуждается в гл. 8 [1] и в книгах по атомной и молекулярной
спектроскопии: Уиффен [424], Кинг [222], Герцберг [185], Кун [229], Уайт [425],
Кандлер [89] и Кондон и Шортли [96]. Довольно простой и полный
теоретический обзор мультиплетной структуры атомов и молекул дан Стивенсоном
[385]. Калверт и Питтс [88] и Вейн [416] рассматривают связь мультиплетно-
сти различных частиц с их химическими свойствами.
н
НЕОПРЕДЕЛЕННОСТИ ПРИНЦИП. Принцип
неопределенности утверждает, что существуют пары наблюдаемых
величин, которым невозможно одновременно приписать точные
значения: если для одной такой наблюдаемой удается получить
более точное значение, значение второй из нлх становится менее
определенным. Любой эксперимент, целью которого является
одновременное определение двух наблюдаемых величин, позволяет
точно определить одну из них только за счет потери информации
о другой (см. разд. «Дуализм»), а произведение
неопределенностей двух одновременных измерений ни при каких условиях не
может быть меньше, чем малая, но отличная от нуля величина
порядка Ь (соотношение неопределенности).
Наиболее известным примером действия этого принципа
является неопределенность, присущая результатам одновременного
определения координаты частицы вдоль некоторой оси q и
проекции ее импульса на ту же ось pq. Эти две наблюдаемые
связаны между собой в соответствии с принципом
неопределенности. Если мы сможем определить положение частицы с
точностью 8q (здесь под 8q подразумевается среднеквадратичное
отклонение положения частицы от некоторой точки), то принцип
неопределенности требует, чтобы величина рд была
неопределенной в интервале 6pq (это тоже среднеквадратичное отклонение),
причем произведение неопределенностей 8q8pq не может быть
меньше у А. Если положение частицы определяется точнее, т. е.
если 8q уменьшается, неопределенность pq должна увеличиться,
чтобы произведение неопределенностей 8q8pq не стало меньше
у ft. И наоборот, если мы готовы отказаться от любой
информации об импульсе частицы, т. е. если неопределенность 8pq может
быть сколь угодно большой, то неопределенность 8q может стать
бесконечно малой и положение частицы может быть определено
сколь угодно точно. К сожалению, следствием принципа
неопределенности является то, что, хотя мы теперь знаем положение
частицы с любой наперед заданной точностью, невозможно
предсказать, где окажется частица в любой следующий момент
времени, поскольку мы ничего не знаем об импульсе частицы в
момент определения ее положения. Таким образом, принцип
неопределенности исключает возможность использования понятия
«траектория» — центрального понятия в классической механике.
Возможен и другой подход: мы можем измерить ря с любой
230
ft
наперед заданной точностью, но, чтобы произведение
неопределенностей сохранялось постоянным, мы будем вынуждены
отказаться от всей информации о положении q частицы. Однако
такой подход также исключает возможность использования
понятия «траектория».
Следует отметить, что принцип неопределенности для
положения частицы и ее импульса относится к их компонентам вдоль
одной и той же оси и не накладывает никаких ограничений на
одновременные значения этих наблюдаемых вдоль разных осей.
Следовательно, координату вдоль оси х можно измерить
одновременно с импульсом ру вдоль оси у, и принцип
неопределенности не налагает никаких ограничений на точность определения
этих величин. Математическая запись принципа
неопределенностей (см. список формул НЛ) показывает, какие наблюдаемые
Список формул Я. /
Принцип (и соотношение) неопределенности
Пусть А и В — операторы, соответствующие наблюдаемым А и Вк и
пусть ЬА и ЬВ — среднеквадратичные отклонения от их средних
значений:
ЬА = [<Л2> - (Л)2]Ч ЬВ — [(В2) - (В)2]\
Согласно принципу неопределенности, они должны удовлетворять
условию (называемому соотношением неопределенности):
ЬА6В>Ч2\([1В])\,
где [Л, Й\ = АЁ — В А является коммутатором операторов А и В.
К типичным соотношениям неопределенностей относятся следующие:
bpqbg>l/ib. ЫхЫу^12тП, т6Е^у2п.
Что такое т, объясняется в статье.
связаны между собой принципом неопределенности. Чаще всего
одна из таких наблюдаемых включает координату, а другая —
импульс, соответствующий этой координате.
Обсуждение принципа неопределенности часто излагается в
виде рассказа об упрямце, который пытается поставить
эксперимент, опровергающий предсказания этого принципа; в конце кон*
цов он отказывается от этой затеи, потерпев полное поражение.
Гайзенберг, который установил этот принцип, описал такого уп-
рямца, чтобы показать, что все такие мысленные (gedanken)
эксперименты обречены на провал. Его упрямец использует
микроскоп для определения положения частицы и, чтобы делать это
со всевозрастающей точностью, выбирает микроскоп, в
котором частица освещается светом все меньшей длины волны. Но
чем меньше длина волны света, тем больше импульс, который
231
н
несет каждый фотон (в соответствии с соотношением де
Бройля), и, поскольку по крайней мере один фотон должен
отразиться от частицы и попасть в апертуру микроскопа, чтобы
можно было определить ее положение, ясно, что в процессе
наблюдения частица получает импульс. Анализ такого
эксперимента, учитывающий эффекты дифракции света на апертуре
микроскопа и передачу импульса частице при рассеянии на ней света,
показывает, что произведение неопределенностей в самом деле
оказывается не меньше,-чем -^ h {Ь появляется из-за
соотношения де Бройля). В мире законов классической физики упрямец
оказался бы прав, потому что Ь должно обратиться в нуль, и,
следовательно, здесь не должно возникать никаких
принципиальных ограничений на точность одновременного определения
координаты и импульса.
Мысленные эксперименты подобного типа наглядно
иллюстрируют те свойства материи, которые на гораздо более глубоком
уровне описывает принцип неопределенности. Импульс и
координата связаны между собой интерпретацией волновой функции.
Система с точно определенным импульсом описывается плоской
волной определенной длины. Для частицы с импульсом kb
такую волну можно записать в виде exp(ikx), что соответствует
распределению вероятностей, пропорциональному \exp(ikx) |2,
а оно не зависит от х. Следовательно, волна с определенным
импульсом описывает частицу с совершенно неопределенным
положением. Напротив, для того чтобы описать локализованную
частицу, надо сформировать волновой пакет с большой амплитудой
в одной точке и малой во всех остальных точках. Этого можно
добиться путем наложения друг на друга большого числа волн,
имеющих разную длину и, следовательно, различные импульсы.
Поэтому, чем более узкий волновой пакет мы пытаемся
построить, чтобы получить более локализованную частицу, тем
шире диапазон значений импульса частицы.
Другие пары наблюдаемых, связанных соотношением
неопределенности, можно найти, проверяя, не обращается ли в нуль
коммутатор соответствующих им операторов. Если такой
коммутатор отличен от нуля, наблюдаемые не могут быть
одновременно определены с произвольной точностью; если же
коммутатор равен нулю, таких ограничений нет. Некоторые важные пары
наблюдаемых, связанных соотношением неопределенности,
приведены в списке формул Н.1.
Между соотношением неопределенности для энергии и
времени и остальными соотношениями неопределенности имеется
тонкое различие. Дело в том, что в квантовой механике нет
оператора времени (время считается параметром, а не
наблюдаемой), поэтому в данном случае нельзя воспользоваться коммута-
232
н
ционным соотношением. Соотношение неопределенности для
энергии и времени приходится поэтому рассматривать как
следствие некоммутативности операторов положения и импульса или
(что эквивалентно этому) как следствие уравнения Шредингера.
Соотношение неопределенности для энергии и времени зависит
от того, происходит ли эволюция системы за характерное время
т. Если эволюция происходит, уровни энергии системы могут
быть определены лишь с точностью б£, определяемой условием,
чтобы произведение тб£ не было меньше у Н. Для стационарных
состояний, когда т бесконечно, энергия может быть определена
с любой наперед заданной точностью, но, если состояние имеет
конечное время жизни, ее энергию нельзя определить точнее, чем
это позволяет соотношение неопределенности.
В заключение стоит остановиться на вращающихся системах:
с соотношением неопределенности между углом и угловым
моментом следует обращаться с осторожностью, поскольку
неопределенность величиной 2я при определении угла эквивалентна
полной неопределенности. В таких случаях пользуются
специальными формулировками принципа неопределенности.
Упражнения. 1. Сформулируйте принцип неопределенности. Обсудите его
применение к определению координаты х и импульсов рх и ру. Можно ли
одновременно определить координаты частицы (*, у, z) с произвольной
точностью? Могут ли быть определены одновременно кинетическая энергия и
импульс частицы? Каким образом экспериментальное определение
положения частицы связано с ее импульсом? Как объясняется связь между
координатой и импульсом частицы с учетом волновых свойств материи? Как,
основываясь на волновой картине явлений, показать, что х и ру *могут быть
определены с произвольной точностью? Почему представление о траектории
чуждо квантовой механике? С чем связана особенность соотношения
неопределенности для энергии и времени?
2. Координата q частицы определяется с точностью 0,1 мм, 1 мкм, 1 нм,
1 пм; каковы будут соответствующие неопределенности при одновременном
определении импульса? Если рассматриваемая частица — электрон, какой
кинетической энергии соответствует неопределенность импульса? Три состояния
атома обладают временем жизни 0,1 с, 1 мкс, 10~12 с соответственно; какова
неопределенность энергии атома в каждом из этих возбужденных состояний?
Естественная ширина спектральной линии определяется временем жизни
состояния, как это указывается в конце предыдущего вопроса (см. разд.
«Электронный парамагнитный резонанс»).
3. Используйте математическую запись соотношения неопределенности,
приведенную в списке формул Н.1, для исследования ограничений на
одновременное определение следующих пар наблюдаемых: х и рх\ х и ру; рх и
/V, 1Х и ly\ z и lz\ кинетическая энергия и энергия кулоновского потенциала;
полная энергия и х; полная энергия и дипольный момент.
Рекомендуемые источники. Обоснование принципа неопределенности и
его применения см. в гл. 4 [1]. Обсуждение соотношения неопределенности
233
н
см. в кн. Гайзенберга [179], Инграма [25] «Излучение и квантовая физика» и
в классических трудах по квантовой механике: Дирака [123], Мессиа [282],
Шиффа [356], Давыдова [119], а также Ландау и Лифшица [233]. Интересное
изложение вопроса дано у Бома [63]. Один из аспектов соотношения между
энергией и временем рассматривается Салемом и Вигнером [352]; принцип
неопределенности для вращающихся систем обсуждается Каррузерсом и Нето
[91].
НЕПЕРЕСЕЧЕНИЯ ПРАВИЛО. Рассмотрим два состояния
атома или молекулы, энергия которых зависит от некоторого
параметра Р (например, от длины связи). Изменение этого
параметра Р приводит к изменению энергий состояний, и при не-
Рис. Н.1. Правило непересечения. Пунктирными линиями показаны состояния
различной симметрии (которые могут пересекаться), сплошными линиями —
состояния одинаковой симметрии (пересечение которых невозможно).
котором значении Р энергия верхнего уровня может оказаться
меньше энергии более низкого уровня, т. е. энергетические
уровни пересекутся. Правило непересечения утверждает, что если
состояния имеют одинаковую симметрию, то такое пересечение
невозможно. Следовательно, изменение Р приводит к таким
изменениям энергии, которые показаны на рис. Н.1. Это правило
особенно важно учитывать при построении корреляционных
диаграмм (см. разд. «Объединенный атом»), поскольку оно
позволяет проследить за изменением энергии различных состояний
молекул и атомов при образовании связей.
Важно отметить, что поведение уровней, подчиняющихся
правилу непересечения, является примером адиабатического
процесса. Если система вначале находится в состоянии г|)2 и
параметр Р изменяется медленно, то она переходит в состояние г|>1
новой системы (отвечающее другому значению параметра Р —
с правой стороны диаграммы). Если движение слева направо
происходит очень быстро, при конечном значении Р система мо*
234
м
жет остаться в состоянии г|)2, что соответствует возбужденному
состоянию новой системы. Отсюда можно заключить, что
правило непересечения применимо к изменяющимся во времени
системам только при условии, что они изменяются медленно.
Рекомендуемые источники. Диаграмму типа показанной на рис. Н.1
можно получить с помощью теории возмущений решением уравнения Шредин-
гера для двухуровневой системы. Это показано в гл. 7 [1]. -Такой прием
основан на выводе правила непересечения Теллером [394]. Более формальный
вывод осуществлен ранее фон Нейманом и Вигнером [411]. Оба подхода
резко критиковались. Более стролий вывод был дан Накви и Байере Брауном
[303] и распространен на многоатомные системы Накви [302]. В кн. Коулсона
[105] и Герцберга [187] правило непересечения излагается в простой и
доступной форме.
НЕПОДЕЛЕННАЯ ПАРА ЭЛЕКТРОНОВ. Под
неподеленной парой понимается пара электронов валентной оболочки, не
принимающая участия в образовании связи. В качестве примера
рассмотрим тетраэдрическое распределение электронов вокруг
атома кислорода в молекуле НгО: два электрона связывают
с атомом кислорода один протон, два других — другой протон,
а оставшихся четыре электрона образуют две неподеленные пары
(они торчат по обе стороны плоскости молекулы, подобно
кроличьим ушам). Можно считать, что последние четыре электрона
располагаются на локализованных несвязывающих орбиталях.
Неподеленные пары играют важную роль, влияя не только
на структуру молекул, но также и на их химические свойства.
Их влияние на структуру молекул обусловлено сильным
отталкиванием, которое они оказывают на электроны соседних
связей. Например, пирамидальная форма молекулы аммиака
отчасти объясняется влиянием одной неподеленной пары атома
азота, которая оказывает отталкивающее действие на шесть
электронов трех связей N—Н. Анализ структуры молекул с
учетом взаимодействия неподеленных пар лежит в основе правил
Сиджвика — Пауэлла, согласно которым неподеленные пары
являются главным источником отталкивательных взаимодействий
в молекулах. В химии неподеленную пару электронов обычно
рассматривают как нуклеофильный центр, поскольку она легко
образует электронодонорную связь с электроположительным
центром: молекулы с неподеленными парами ведут себя как
основания (по классификации Льюиса).
Если неподеленные пары не окажутся связанными таким
образом с каким-либо ядром, они дают сильный вклад в
электронные спектры. В карбонильных соединениях переход я->я* (где
п обозначает иесвязывающую орбиталь неподеленной пары)
является основным типом возбуждения (см. разд. «Цвет»). При
этом один из электронов неподеленной пары электронов
кислорода переходит со своей орбитали на разрыхляющую я-орбиталь
235
н
карбонильной группы. В результате такого перехода меняется
распределение заряда в карбонильной группе, что сильно
сказывается на растворимости вещества.
Рекомендуемые источники. См. [1], гл. 10. Бадер [44] рассматривает
правила Сиджвика — Пауэлла и их современное развитие. Роль неподеленных
пар в спектрах молекул обсуждается в разд. «Цвет», см. также приведенную
в этом разделе литературу.
НОРМАЛЬНЫЕ КОЛЕБАНИЯ. Вообще говоря, молекула,
содержащая N атомов, может совершать 3N — б колебаний
(3N — 5, если молекула линейная). Такое число колебаний
определяется следующими причинами. Положение атома в
пространстве определяется тремя координатами, и, чтобы задать
положение N атомов, необходимо 3N координат. Изменения этих
координат соответствуют изменению формы молекулы
(изгибанию или растяжению ее связей), перемещению ее в пространстве
или вращению молекулы как единого целого. Из 3N координат
три задают положение центра масс молекулы и соответствуют
ее перемещению в пространстве как единого целого.
Следовательно, 3N— 3 координаты должны определять положение
отдельных атомов относительно центра масс молекулы. Еще три
координаты из этого числа описывают ориентацию молекулы
(если она не является линейной). Остальные 3N— 6 координат
описывают относительное положение всех атомов внутри
молекулы, и их изменение вызывает изгибание или растяжение
связей, другими словами, колебания молекулы. Если молекула
линейна, ее ориентация задается только двумя координатами,
поэтому число ее внутренних координат равно 3N— 5.
Рассмотрим двуокись углерода — линейную трехатомную
молекулу, имеющую 9—5 = 4 внутренние степени свободы
(координаты, необходимые для описания конфигурации молекулы и
пе связанные с ее положением и ориентацией в пространстве).
Допустим, что одна из этих степеней свободы связана с
растяжением одной из связей С—О, и рассмотрим колебание этой
связи. Если возбудить колебания одной связи С—О, их энергия
быстро перейдет к другой эквивалентной связи С—О. Это
вызывается движением атома углерода, участвующего в обеих
связях, и представляет собой резонансную передачу колебаний от
одной связи к другой. Передача колебательного движения от
одной связи к другой будет продолжаться до тех пор, пока
какой-либо внешний процесс не приведет к затуханию
молекулярных колебаний. Допустим теперь, что с самого начала удалось
в равной степени возбудить колебания обеих связей. Тогда
колебания будут происходить равномерно до тех пор, пока не
затухнут. Например, при возбуждении симметричного валентного
колебания 0^-С->0^0->С-^-0 оба атома кислорода при-
236
н
ближаются к атому углерода или удаляются от него равномерно
с обеих сторон, и в отсутствие ангармоничности не может
возникнуть другая комбинация их движений, т. е.
антисимметричное валентное колебание: ч-О — С->-«-0 ^ 0->-«-С — 0->.
Энергия этих колебаний не может перейти и к деформационным
колебаниям, так как для такой передачи необходимы
перпендикулярно направленные силы (обусловленные кориолисовым
взаимодействием, которое возникает при вращении молекулы). Мы
Рис. Н.2. Нормальные координаты в С02 и Н20 (и в других трехатомных
молекулах).
видим, что обоснованный выбор типов молекулярных колебаний
позволяет получить набор независимых движений, которые
называются нормальными колебаниями. Четыре указанных выше
внутренних колебательных типа движения могут быть выбраны
в качестве четырех нормальных колебаний в молекуле С02, и,
поскольку для нее существуют только четыре внутренних типа
движения, любое сколь угодно сложное колебание этой
молекулы можно выразить в виде суперпозиции нормальных
колебаний.
Независимость нормальных колебаний позволяет
использовать для них простое квантовомеханическое описание, в
котором каждое нормальное колебание рассматривается как
отдельный гармонический осциллятор со специально выбранными
массой и силовой постоянной. Этот осциллятор колеблется вдоль
некоторой эквивалентной координаты, которая называется
237
н
нормальной координатой. Поэтому любое нормальное колебание
обладает всеми свойствами осциллятора и подчиняется обычным
правилам отбора для колебательных переходов. В частности,
колебание проявляется в инфракрасной области спектра (т. е.
дает линию в обычном колебательном спектре) только в том
случае, когда изменение нормальной координаты приводит к
изменению дипольного момента, другими словами, если дипольнын
момент молекулы изменяется при ее деформации за счет
рассматриваемого нормального колебания. Некоторые типы
нормальных колебаний в молекулах двуокиси углерода и воды
показаны на рис. Н.2.
Упражнения. Почему нелинейная молекула может совершать ЗЛА — 6
колебаний, а линейная — только 3N — 5 колебаний? Что произойдет с лишним
колебанием в линейной молекуле, если ее согнуть? Что произойдет в
молекулах СОг, Н20 и СН4, если одну связь в них сначала растянуть, а затем
отпустить? Каким образом можно получить стационарные колебания? В каких
случаях нарушается независимость нормальных колебаний? Какие
преимущества связаны с использованием нормальных колебаний? На чем
основываются квантовомеханические расчеты частот нормальных колебаний? Какие
факторы могут влиять на их частоту? Если в СОг заменить 12С на 13С, можно ли
ожидать изменения частот всех нормальных колебаний?
Рекомендуемые источники. См. гл. 10 [1], где рассмотрены свойства
обычных и нормальных колебаний. Доступное изложение классического и кван-
товомеханического описания нормальных колебаний дано в гл. 6 кн. Бранда
и Спикмена [75]. Полезное введение в анализ нормальных колебаний имеется
в кн. Вудворда [433] и в более ранних работах Вильсона, Дешиуса и Кросса
[431], Барроу [51] и Ганса [157]. Все эти книги содержат изложение
теоретико-группового метода анализа нормальных колебаний.
НОРМИРОВАННЫЕ ВОЛНОВЫЕ ФУНКЦИИ. Согласно
интерпретации волновой функции, которую предложил Борн,
величина г|)*(г)«ф(г)йт пропорциональна вероятности обнаружения
частицы в элементе объема dx, окружающем точку г. Когда
константа пропорциональности равна единице, такая волновая
функция называется нормированной (или нормированной на
единицу).
Рассмотрим на примере некоторой волновой функции г|э, как
проводится нормирование. Прежде всего необходимо выяснить,
связана ли эта волновая функция с распределением вероятности
обнаружения частицы: вероятность нахождения частицы во всем
пространстве должна быть равна единице. Эта вероятность
равна сумме вероятностей нахождения частицы в каждом
элементарном объеме пространства йт. Она определяется
интегралом \dTi|n|)*, который и должен равняться единице. Если же
238
н
оказывается, что он равен Ny мы можем нормировать волновые
функции, поделив их на №*. Нормированная функция имеет вид
ЛМп|). Величина N~4* называется нормировочной постоянной.
Если функция не только нормирована, но и принадлежит к
набору ортогональных функций, ее называют ортонормированной
функцией.
Упражнения. Какая волновая функция называется «нормированной»?
Почему в квантовой механике удобно иметь дело с нормированными
функциями? Как проводится нормирование произвольной функции? Отнормируйте
на единицу следующие волновые функции: постоянную ф(дг) = а в
интервале от х = 0 до х = L; функцию sin kx в том же самом интервале;
функцию exp im<p в пространстве, ограниченном кругом; функцию ехр(—г/ао) во
всем трехмерном пространстве.
Рекомендуемые источники. Примеры нормирования волновых функций
даны в гл. 3 [1]. Особая проблема возникает при нормировании функций,
которые слабо убывают на больших расстояниях; например, функция expikx
продолжает осциллировать даже при *->оо. В этих случаях используют
особый прием (нормирование на б-функцию), который описан в кн.
Давыдова [119], Мэндла [262] и Голдбергера и Ватсона [164].
о
ОБЪЕДИНЕННЫЙ АТОМ. Метод объединенного атома,
применяемый для описания строения молекул, является одним
из многих методов, в которых используются корреляционные
диаграммы. Допустим, что известны наборы орбиталей или
состояний системы, соответствующие двум ее различным формам,
и требуется определить, в какие состояния одной формы
превращаются состояния другой формы. Корреляционная диаграмма
состоит из двух схем уровней, соединенных линиями,
показывающими пути (корреляции), по которым одни состояния
превращаются в другие при переходе системы из одной формы в
другую. Наиболее важное правило построения таких диаграмм
состоит в том, что линии, представляющие состояния с той же
симметрией, не должны пересекаться (см. разд. «Правило
непересечения»). Мы рассмотрим использование корреляционных
диаграмм на примере метода объединенного атома, который
является предшественником диаграмм Уолша, показывающих, как
меняются молекулярные орбитали молекул при изменении углов
между связями. Оба эти метода в свою очередь предшествуют
правилам Вудворда — Хоффмана, определяющим изменение
молекулярных орбиталей и состояний при согласованных
перегруппировках молекул.
При составлении корреляционной диаграммы по методу
объединенного атома в качестве одного набора состояний выбирают
орбитали двух изолированных атомов (в данном случае двух
одинаковых атомов А) и рассматривают, как меняются эти
орбитали по мере сближения атомов, пока они не сольются
наконец в один атом с удвоенным зарядом ядра, который и называют
объединенным атомом. Уровни энергии объединенного атома,
как и уровни изолированных атомов, известны; неизвестно лишь
строение промежуточного объекта — двухатомной молекулы
А-А.
Для простейшей иллюстрации метода выберем атомы
водорода; в этом случае объединенный атом представляет собой атом
гелия. (Возможен или невозможен в действительности синтез
двух атомов водорода в один атом гелия — важно для будущего
человечества, но совершенно несущественно для нашего
последующего обсуждения.) Чтобы не усложнять диаграмму,
ограничимся рассмотрением ls-орбиталей изолированных атомов и
посмотрим внимательно, что происходит при их сближении. Если
орбитали имеют одинаковую фазу, они сближаются так, что
положительной амплитуде одной из них соответствует положитель-
240
о
ная амплитуда другой орбитали, процесс объединения атомов в
конце концов приведет к образованию ls-орбитали атома гелия
(рис. 0.1). Если сближающиеся орбитали находятся в противо-
фазе, в промежутке между объединяющимися ядрами образуется
узловая поверхность; когда ядра сливаются, эта поверхность
проходит через объединенное ядро, и, следовательно, слияние
орбиталеи приводит к образованию 2/?-орбитали атома гелия
(рис. 0.1). Известно, что эта орбиталь лежит выше ls-орбитали.
Поэтому можно сделать вывод, что образующиеся на
промежуточной стадии слияния, у молекулы водорода, орбитали, обозна-
0%в
объединенный, молекула изолированные
атом атомы
Рис. 0.1. Объединенный атом Не, образованный из Н + Н, и
промежуточное состояние — молекула Н2.
чаемые о и а*, представляют собой не что иное, как
связывающую и разрыхляющую орбитали теории молекулярных орбита-
лей. К этим орбиталям можно обычным образом применить
принцип заполнения и установить электронное строение
молекулы.
Описанный подход применим и к более сложным парам
атомов и позволяет приближенно оценить электронное строение
образующейся на промежуточной стадии молекулы. При этом,
однако, возникают некоторые затруднения, связанные в основном
с учетом спин-орбитального взаимодействия в тяжелых атомах,
которое усложняет рассмотрение соответствия между
различными уровнями.
Упражнения. Объясните, что такое «корреляционная диаграмма»?
Почему метод объединенного атома можно рассматривать как пример
использования корреляционных диаграмм? Для чего используется метод
объединенного атома? Чем отличается приведенная на рисунке корреляционная
диаграмма и истинная зависимость энергии орбиталеи от расстояния между
ядрами? Насколько важны эти отличия? Какое правило должно учитываться
24!
о
при построении корреляционных диаграмм? Постройте полную
корреляционную диаграмму образования объединенного атома из двух атомов,
обладающих Is-, 2s-, 2р-, 3s- и Зр-орбиталями, и воспользуйтесь этой диаграммой для
обсуждения электронного строения гомоядерных двухатомных молекул,
которые можно построить из атомов элементов второго периода. (Ср. ваш ответ
с рис. 0.2, на котором изображена промежуточная ситуация, описывающая
электронное строение молекулы Оз.)
Рекомендуемые источники. Детальный анализ метода объединенного
атома содержится в § 4.7 кн. Коулсона [105]. Этой же теме посвящена статья
Малликена [295]. Подробное обсуждение того, каким образом метод
объединенного атома используется для анализа электронного строения и спектров
двухатомных молекул, см. в гл. VI кн. Герцберга [187]. Особое значение имеет
правило спиновой корреляции Вигнера — Уитмера, которое указывает, какие
состояния атомов получаются при диссоциации двухатомной молекулы. Этот
вопрос обсуждается также Герцбергом [187], в § 5.2.кн. Вейна [416] и в гл. 3
кн. Гейдона [158]. Применение правил Уолша для рассмотрения электронного
строения молекул описано в его классических статьях [414]. Вопрос о том,
что изображают эти диаграммы, в свое время послужил поводом для
большой дискуссии. Доступное изложение этой проблемы см. в кн. [108]. Правила
Вудворда — Хоффмана описаны Гиллом [159], Вудвордом и Хоффманом [435],
Гиллом и Уиллисом [160], Лонге-Хиггинсом и Абрахамсоном [255]. Обзор
метода со многими примерами применения см. у Вудворда и Хоффмана [434,
435]; полезное рассмотрение дано также Алдером, Бейкером и Брауном [34].
ОБМЕННАЯ ЭНЕРГИЯ. Кулоновское взаимодействие
между двумя электронными распределениями является отталкива-
тельным; его величину можно рассчитать, разделив обе области
распределений на крошечные заряженные объемы, вычислив ку-
лоновскую энергию взаимодействия между каждыми
заряженными элементами объема и просуммировав по всем элементам.
Результат обозначим как / (см. разд. «Кулоновский интеграл»).
К сожалению, эта процедура дает неправильный ответ, так
как она не учитывает эффекта спиновой корреляции, который
заставляет электроны с одинаковым направлением спинов
держаться поодаль друг от друга, а электроны с
противоположными спинами находиться поблизости. Так, если два
электрона имеют одинаковое направление спинов, истинная энергия
отталкивания меньше / из-за присущей таким электронам
тенденции избегать друг друга. Поправка, которую необходимо
внести, меняет среднюю энергию отталкивания на / — /С, где
поправочный член К называется обменной энергией. Это
название отражает происхождение поправки, которая возникает в
соответствии с принципом Паули, и обусловлена поведением
волновых функций при перестановке («обмене») электронов.
Рекомендуемые источники. Более детальное расмотрение и примеры
применения понятия обменной энергии при расмотрении атомов и молекул см. в
гл. 8 и 9 [1]. Хорошее обсуждение дано Бомом [63] и Давыдовым [119].
О применении этого понятия к молекулам см. в кн. Коулсона [105], Ричардса
242
о
и Хорсли [336] и Мак-Глина, Ванквикеиборна, Киноситы и Кэрролла [273],
где содержится руководство к вычислению обменных интегралов.
ОЖЕ ЭФФЕКТ. В литературе встречаются другие названия
этого эффекта: автоионизация и преионизация. Эффект Оже
является безызлучательным переходом из возбужденного
состояния в диссоциативное состояние (при таком переходе не
происходит ни поглощения, ни испускания излучения). На схеме
уровней атома, показанной
на рис. 0.2, можно видеть
следующее. Одна из серий
уровней этого атома имеет
предел ионизации при более
низких энергиях, чем
другая серия. Допустим, что мы
изучаем серию L в
спектре поглощения (на рис. 0.2
показана слева). В таком
спектре будет наблюдаться
ряд узких пиков с
увеличивающейся частотой, однако,
Рис. 0.2. Эффект Оже: уширение
линий спектра (слева) происходит
в том случае, когда атом
совершает безызлучательные переходы
из дискретных состояний (слева)
в несвязанные состояния (справа).
когда частота станет выше предела ионизации для другой
серии (/?), спектр заметно изменится. Пики уже не будут узкими,
например, линии А и В станут широкими. Они могут также
оказаться слегка сдвинутыми. Это происходит вследствие
наличия в атоме какого-либо возмущения (например,
спин-орбитального взаимодействия), приводящего к смешению состояний
серий L и R, в результате чего состояния L становятся несколько
похожими на состояния R. В частности, при энергиях, больших
энергии ионизации для серии /?, состояния L становятся
склонными к ионизации, и эта тенденция усиливается по мере
увеличения смешения. Время жизни состояний А, В ... при этом
уменьшается, а ширина уровней соответственно растет (см. разд.
«Принцип неопределенности»). Смешение состояний R и L
можно охарактеризовать вероятностью перехода атома из
одного состояния (L) в другое (R). При таком подходе эффект
Оже рассматривается просто как безызлучательный переход
в диссоциативное состояние. Термин «преионизация» отражает
ЩШЩ
L-спентр и L-переходы
243
о
тот факт, что ионизация атома из состояний L-серии происходит
раньше, чем это можно ожидать по энергетической оценке
предела ионизации для этой серии уровней. Термин
«автоионизация» отражает «самовозбуждающийся» характер этого
процесса, поскольку возмущение внутри молекулы вызывает ее
ионизацию, превращая связанные состояния в
ионизационные.
Эффект Оже первоначально был обнаружен в рентгеновской
спектроскопии. При бомбардировке твердого образца быстрыми
электронами возбуждаются, скажем, электроны /(-оболочки, а
рентгеновские лучи, которые при этом испускаются,
соответствуют переходам L-электронов на вакантные дырки. Процесс,
конкурирующий с испусканием рентгеновских лучей, обусловлен
эффектом Оже, поскольку возбуждение /(-электронов может
привести к автоионизации, и из атома образца вылетит другой
электрон. Процесс ионизации, конкурируя с испусканием
рентгеновских лучей, уменьшает их интенсивность. Однако эффект
Оже может приносить не только вред, но и пользу. Измеряя
энергии оже-электронов, можно определить энергетические
уровни электронов в твердых телах, что и положено в основу метода
оже-спектроскопии.
Упражнения. Что представляет собой эффект Оже? Каким образом
можно распознать его присутствие в спектре атома? Почему эффект Оже
приводит к уширению спектральной линии? Какие возмущения могут привести к
автоионизации? Опишите вид спектра, который бы свидетельствовал о пре-
ионизации. Как влияет эффект Оже на рентгеновский спектр? В чем состоит
его влияние на линии этого спектра? В каком смысле предиссоциацию
молекул можно рассматривать как эффект Оже? Какие другие процессы можно,
по вашему мнению, рассматривать как хотя бы отдаленное проявление
эффекта Оже?
Рекомендуемые источники. Описание эффекта Оже в атомных спектрах
можно найти в гл. 4.2 кн. Герцберга [185] и в кн. Куна [229]. Влияние его на
рентгеновские спектры рассмотрено в кн. Бурхора [85] и Бурхора и Асада
[86]. Оже-спектроскопия обсуждается в кн. Зигбана [366] и в ссылках к разд.
«Потенциал ионизации». См. также разд. «Предиссоциация».
ОЖИДАЕМОЕ ЗНАЧЕНИЕ. Ожидаемое значение
наблюдаемой величины представляет собой ее среднее значение в
рассматриваемом состоянии системы и является средним
результатом серии экспериментов, предназначенных для определения
значения наблюдаемой в этом состоянии. Так, ожидаемое
значение энергии — это средняя энергия, которая могла бы быть
получена в серии соответствующих экспериментов над набором
одинаковых систем; ожидаемое значение положения — это сред-
244
о
нее значение положения, которое могло бы быть измерено;
ожидаемые значения импульса или углового момента определяются
аналогичным образом.
Если система находится в чистом состоянии по отношению
к одной из наблюдаемых (другими словами, состояние системы
является собственным состоянием оператора, соответствующего
этой наблюдаемой), все идентичные эксперименты дают один
v тот же результат для данной наблюдаемой, так что в этом
случае отсутствует дисперсия. В качестве примера можно
привести определение энергии атома или молекулы, находящихся
в определенном энергетическом состоянии; это энергетическое
состояние является собственным состоянием оператора энергии
системы, а ожидаемое значение данного оператора представляет
собой энергию, которая была бы измерена во всех
экспериментах.
Чаще всего система не находится в чистом состоянии и
гораздо лучше описывается суперпозицией чистых состояний.
Проведя один эксперимент, с тем чтобы измерить какое-либо
свойство такой системы, мы получим результат, который можно
рассматривать как одно из собственных значений оператора,
соответствующего измеряемому свойству, а средний результат
серии одинаковых экспериментов, выполненных над набором
одинаковых систем, является ожидаемым значением наблюдаемой
для данного состояния системы. В качестве примера можно взять
определение импульса системы в состоянии, описываемом
суперпозицией чистых состояний с различными импульсами
(например, если частица описывается волновым пакетом). Если
состояние с импульсом kb входит в суперпозицию с весом |с&|2,
то эксперимент дает значение kb с вероятностью |c/i|2, а также
другие значения с соответствующими вероятностями. Средний
результат всех таких измерений есть ожидаемое значение
импульса, обозначаемое (р).
Если состояние системы описывается волновой функцией г|эп,
то ожидаемое значение (Q) наблюдаемой Q равно интегралу
dx$*nQ$n, где Q — оператор этой наблюдаемой, причем
предполагается, что состояние г|эп нормировано. Поэтому мы можем
предсказать результат серии экспериментов, вычисляя этот
интеграл. Но в одном эксперименте значение, равное величине
интеграла, можно получить, только если состояние г|)Л —
собственное состояние оператора, соответствующего наблюдаемой,
которую мы измеряем. Если оно не является собственным состоянием
этой наблюдаемой, значение интеграла дает нам только средний
результат большого числа экспериментов. Это единственная
информация, которую при таких условиях можно получить;
предсказать точно, какой результат будет получен в отдельном
245
о
эксперименте, не представляется возможным, можно только
указать вероятность получения каждого результата.
Упражнения. Что означает выражение «ожидаемое значение
наблюдаемой величины»? В каком смысле оно определяет результат эксперимента?
Каким образом следует интерпретировать ожидаемое значение в том случае,
когда состояние является смешанным (суперпозицией)? Что имеется в виду
под чистым состоянием? Пучок света состоит из двух плоскополяризованных
ортогональных компонент, результирующий пучок может быть описан как
суперпозиция Cxtyx + суфг, где X и Y характеризуют два направления
поляризации. Обсудите результат эксперимента, поставленного для измерения
поляризации пучка. Используя выражения, приведенные в списке формул 4.1,
вычислите ожидаемые значения кинетической энергии и импульса для
частицы в одномерной прямоугольной яме и обсудите результаты эксперимента
по их определению.
Рекомендуемые источники. Операторы, наблюдаемые и ожидаемые
значения обсуждаются в гл. 4 [1]. См. также курс Фейнмана, Лейтона, Сэндса
[145], а также монографии Козмана [217], Полинга и Вильсона [314] и Бома
[63]. более глубокое обсуждение процесса измерения см. у Дирака [123], фон
Неймана [410] и Джоча [204].
ОПЕРАТОРЫ. Классическая механика имеет дело с
наблюдаемыми величинами типа координаты и импульса либо с
функциями от таких величин, а также от времени, и законы Ньютона
позволяют определить эти функции. В квантовой механике
предполагается, что вся информация о системе содержится в ее
волновой функции, и, чтобы определить значение какой-либо
наблюдаемой величины, эту функцию следует подвергнуть некоторой
математической операции. (Это аналогично необходимости
проведения реального эксперимента над системой для определения
ее состояния.) Гавное внимание в квантовой механике
сосредоточивается на правильном выборе математических операций,
которые соответствуют наблюдаемым величинам.
В обычной квантовой механике (которой в основном
посвящена эта книга) способ определения импульса с помощью
волновой функции заключается в ее дифференцировании и
умножении результата на Ь/L Таким образом, импульс частицы в
определенной точке определяется градиентом ее волновой функции
в этой точке. Оператор, позволяющий определить координату
частицы, представляет собой простое умножение волновой
функции на х, но в действительности осуществить это не так просто.
Поскольку теперь известно, какие операторы отвечают
динамическим переменным координаты и импульса, можно построить
операторы для всех других наблюдаемых величин, представляя
их в виде функций от этих двух основных переменных.
Например, кинетическая энергия в классической механике является
246
о
функцией импульса, а именно р?/2т, где Р2 = Р2Х + Р2У + pl> и
соответствующий оператор можно получить, заменяя р2х на
Й//)2 (д/дх)2 и т. д. Вид этого оператора свидетельствует о связи
кривизны волновой функции с кинетической энергией частицы.
Каким образом устанавливается вид основных операторов р
и х? Прежде всего ясно, что операторы должны приводить к
вещественным значениям наблюдаемых величин, так как
результаты измерения не могут быть комплексными величинами. С
математической точки зрения это означает, что такие операторы
должны обладать свойством эрмитовости (т. е. должны быть
эрмитовыми операторами). Далее искомые операторы должны
удовлетворять условию (хрх — pxx)ijp = itHjp. (Здесь используется
общепринятое обозначение операторов наблюдаемых величин х
и рх как £ и fix.) На языке матричной механики это означает,
что коммутатор от х и рх должен быть равен ib. Последнее
условие является весьмл строгим и имеет глубокий смысл. Из него
можно вывести принцип неопределенности.
Определив вид оператора наблюдаемой величины, можно
найти ее значение в интересующем нас состоянии, вычислив
соответствующее ему собственное значение оператора. Если
система находится в состоянии, которое не является одним из
собственных состояний данного оператора, можно предсказать
результат эксперимента, вычислив ожидаемое значение этого
оператора.
Упражнения. 1. Почему операторы играют важную роль в квантовой
механике? Какие операторы соответствуют компонентам импульса в
направлении осей х и у? Какой оператор позволяет определить положение частицы
вдоль оси г? Какой оператор соответствует кинетической энергии и г-компо-
ненте углового момента? Допустим, что состояние системы описывается
функцией exp ikx\ чему равен импульс этой системы и какова ее кинетическая
энергия? Чему равны импульс и кинетическая энергия системы, описываемой
функцией cos kx?
2. Какими свойствами должны обладать квантовомеханические
операторы? Покажите, что коммутатор от х и (h/i) (d/dx) равен ih. Если бы в
качестве оператора ^-компоненты импульса было выбрано умножение на рх, что
следовало бы взять в этом случае в качестве оператора координаты?
Отвечая на предыдущий вопрос, вы нашли операторы в импульсном
представлении; найдите также соответствующие выражения для кинетической энергии и
для энергии кулоновского взаимодействия двух зарядов, находящихся на
расстоянии г друг от друга.
Рекомендуемые источники. Операторы являются одними из главных
понятий в квантовой механике, поэтому в каждой посвященной ей книге можно
найти достаточно материала по этому вопросу. Доступное изложение основ
квантовой теории дано в гл. 4 [1]. Классическое определение свойств
операторов содержится в книгах Дирака [123], Маккея [261], фон Неймана [410],
Иордана [208], Джоча [204]. Резюме по данному вопросу можно прочесть
з дополнении 1 кн. Романа [343]. Введение в теорию представлений дано
?47
о
в гл. 4 кн. Давыдова [119]. Матричная формулировка квантовой механики (см.
разд. «Матричная механика») основана на непосредственном использовании
свойств операторов и в сжатой форме изложена Грином [169].
ОРБИТАЛЬНОГО УГЛОВОГО МОМЕНТА ПОДАВЛЕНИЕ
(ПОГАШЕНИЕ). Говорят, что угловой момент системы
подавлен (или погашен), когда он уничтожается каким-либо внешним
электростатическим потенциалом. В атоме (а чтобы не
усложнять обсуждение, мы ограничимся атомом водорода) энергия
электрона не зависит от угловых координат — долготы и
широты, поэтому его вращение вокруг ядра может происходить
плавно, без помех. В этом случае орбитальный угловой момент
сохраняется (остается неизменным) и имеет определенное
значение. Когда атом окружен лигандами, энергия электрона
зависит от его угловых координат и на него действуют силы,
которые сложным образом его ускоряют. Пользуясь языком
классической механики, можно сказать, что ускорение непрерывно
меняет направление движения электрона и его средний угловой
момент оказывается равным нулю.
В квантовой механике нельзя использовать такую
аргументацию, поскольку ей чуждо представление о траекториях, но,
рассматривая влияние потенциала поля лигандов на волновую
функцию электрона, можно прийти к тому же заключению.
Влияние потенциала поля лигандов вынуждает электрон дольше
задерживаться в областях высокой вероятности, которые
расположены в направлении лигандов при создании ими
потенциала притяжения и между лигандами при создании ими
потенциала отталкивания. Такое накопление электронной плотности
означает, что первоначальная бегущая волна превратилась в
стоячую (неподвижными пучностями этой волны являются
накопления вероятности), а со стоячей волной не связан никакой
угловой момент. Следовательно, угловой момент погашен
анизотропным потенциалом.
Упражнения. 1. Что означает выражение «подавление (погашение)
углового момента»? Когда происходит такое подавление и чем оно вызывается?
Как можно объяснить это явление с позиций квантовой механики? хМожно
ли той же причиной объяснить тот факт, что в двухатомных молекулах
определенное значение имеет только угловой момент вращения относительно оси,
проходящей через ядро атомов?
2. Волна, бегущая вокруг оси z, описывается функцией exp tmcp. z-Ком-
поненту углового момента можно найти, вычисляя ожидаемое значение
оператора (fi/i)/d/dq>. Покажите, что z-компонента углового момента в этом
состоянии равна mh. Теперь представим себе, что угловой момент подавлен,
заменив бегущую волну, которой соответствует равномерное распределение
вероятности, стоячей волной, в которой происходит накопление вероятности
вблизи ф = 0 и ф = я. Каково ожидаемое значение z-компоненты углового
момента для такой волны?
248
о
3. Используя эрмитовость оператора /2, докажите, что для состоянии,
описываемых вещественными волновыми функциями, его ожидаемое значение
обязательно равно нулю. Таким образом, удается формально показать, что
в состояниях, которым соответствуют вещественные волновые функции,
угловой момент подавлен (погашен).
Рекомендуемые источники. Более подробно подавление (погашение)
углового момента описано в гл. 6 [1], ответ к упражнению 3 можно найти там
же на стр. 417. Это явление сильно влияет на магнитные свойства веществ,
особенно на свойства ионов переходных металлов, потому что, если
орбитальное движение исключено, парамагнетизм обусловлен исключительно
спиновыми магнитными моментами. Эти аспекты описаны также Эрншоу [128],
Бальхаузеном [49], Фиджисом [146], Иоргенсеном [210], Гриффитом [170]. См.
также Дэвис [117] и Ван Флек [407].
ОРБИТАЛЬНЫЙ УГЛОВОЙ МОМЕНТ. Орбитальный
угловой момент является той частью полного углового момента,
которая в классической механике связана с круговым движением
частицы вокруг неподвижного центра. В квантовой механике
орбитальный угловой момент квантуется и характеризуется двумя
особенностями.
1. Величина орбитального углового момента принимает ряд
дискретных значений, определяемых выражением й-у/1(1+1)>
где / — орбитальное (или азимутальное) квантовое число,
принимающее положительные целочисленные значения: / = 0, 1,2, ...
Таким образом, угловой момент любого тела может иметь
значения 0, ft л/2 , ft V^, (Массивные вращающиеся тела,
например велосипедное колесо, имеют угловой момент,
соответствующий значению / порядка 1034.) В некоторых случаях (например,
для атома водорода) максимальное значение / ограничено
величиной других квантовых чисел.
2. Ориентация направления вращения также квантуется (так
называемое пространственное квантование). Ориентация
плоскости вращения определяется величиной магнитного квантового
числа ти которое принимает все целые значения в интервале от
+/ до —/ (всего 21 + 1 таких значений). Плоскость вращения
определяется величиной т/, т. е. при этом проекция
орбитального момента на выделенное направление (обычно ось г) равна
mfi (рис. 0.3). Если, например, величина углового момента
равна ft V^ (т. е. 1 = 2), то проекция углового момента на ось z
может принимать одно из следующих значений: —2й, —й, 0, й,
2й, причем различные знаки отвечают различным направлениям
вращения частицы (в классическом понимании), как это
показано на рис. 0.3,6.
Согласно принципу неопределенности, компонента импульса
на любую из двух других осей (х или у) является неопределен-
249
о
ной величиной. Если изображать угловой момент вектором I
длиной V'('+ 1)> в каждый конкретный момент времени
можно определить его проекцию только на одну ось (например, на
ось г). Одновременное определение других компонент (х или
у) в соответствии с принципом неопределенности невозможно.
Поэтому, изображая угловой
момент вектором, следует
делать это так, чтобы не
создавалось впечатление, будто мы
знаем о его ориентации
больше, чем это позволяет принцип
неопределенности. Правильнее
изображать конус возможных
(но неопределенных)
положений этого вектора (рис. 0.3, б)
длиной h л/1(1+1) с
г-компонентой, пропорциональной mth
(см. разд. «Векторная
модель») . Иногда этот конус
возможных положений
рассматривают как изображение
прецессии углового момента, но,
прежде чем согласиться с
такой интерпретацией, следовало
бы ознакомиться с
соответствующим разделом.
классическая
траектория
Рис. 0.3. а — связь вектора длиной
[/(/+1)]^Й с классической
траекторией; проекция вектора на
ось z равна тЬ\ б — дискретные
ориентации (по отношению к оси г),
разрешенные квантовой теорией для
частицы с / = 2.
Орбитальный угловой момент системы связан с числом узлов
ее волновой функции: полное число угловых узлов равно /, а
число угловых узлов, встречающихся при обходе вокруг оси г,
равно ]ш/|. Таким образом, d-орбиталь имеет два угловых узла,
и этому соответствует / = 2. Оба узла й^-орбитали
располагаются в плоскости ху и встречаются при обходе вокруг оси г,
следовательно, для этой орбитали |ш/| = 2.
Связь между угловым моментом и узловыми свойствами
волновых функций легко понять, если рассмотреть соотношение де
Бройля или, что то же самое, связь кинетической энергии с кри-
250
о
визной волновой функции. Чем меньше длина волны, т. е. чем
более изогнута функция, тем больше образуется узлов на ее
заданном отрезке. Угловой момент можно рассматривать как
импульс при движении по кругу или по сфере, поэтому постоянная
функция (не зависящая от углов <р и 0) не имеет узлов и
характеризуется бесконечной длиной волны, а ее кинетическая энергия
и (угловой) момент равны нулю. (По соотношению де Бройля
это "соответствует импульсу, равному нулю.) Функция с одним
угловым узлом, который проходит по диаметру и рассекает его
круг надвое, соответствует расположению одной длины волны на
длине окружности. Функция с двумя узлами (четыре узловые
Рис. 0.4. Согласованная (а) и
несогласованная (б) волны на круге.
точки на круге) соответствует двум длинам волн на той же
окружности и т. д. Отсюда видно, что по мере увеличения числа
узлов у функции ее длина волны становится все меньше, а
угловой момент, наоборот, возрастает. Представление о
согласовании длины волны с длиной окружности помогает понять причины
квантования углового момента. На окружности должно
укладываться только целое число волн, в противном случае возможно
их ослабление за счет интерференции с волнами, набегающими
при последующих оборотах по окружности (рис. 0.4).
Упражнения. Приведите классическое определение орбитального углового
момента. Как изменится это определение, если к нему подойти с позиций
квантовой механики? Каковы допустимые значения углового момента
твердого тела? Почему нельзя представить угловой момент вектором с
фиксированной ориентацией? В чем заключается связь между числом узлов волновой
функции и ее угловым моментом (и какие узлы имеются здесь в виду)?
Величина \mi\ определяет число узлов по экватору; каков смысл различия
между +mt и — т{> Как объяснить квантование величины и ориентации
орбитального углового момента, пользуясь представлением об укладке целого
числа волн на сферической поверхности? См. также упражнения к разд.
«Угловой момент».
251
Список формул О. /
Орбитальный угловой момент
Классическое определение: 1 = г X Р>
U = УРг — zpy,
ty = zpx — хр2,
lz = xpy - ypx,
Квантовое определение: / = гХр= (Л//) г X 7,
?,=wo(2^-*-|),
В сферических полярных координатах:
?* = — (Л/0 (sin? -gg- + ctg0cosф —J,
ty = (Л/0 (cos ф -щ - Ctg 0 Sin ф -^,
?2 = -/i2A2,
де Л2 — оператор Лежандра (см. список формул Л. 1).
Коммутационные соотношения:
[tx> ty] = ihtZi [tyi tz] = ihtx, [tZi tx] = Ihty,
[P, tq] = 0, q = x, y, z.
Собственные значения и собственные функции:
Htm{Q> Ф) = /(/+1)Л2ф/т(0,ф), / = 0,1,2 ...
tz^im (в, ф) = mh^im (0» Ф)> m = /, / - 1, ..., - /,
где ф, (0, ф) — сферическая гармоника (см. табл. 22).
Матричные элементы. Отличны от нуля лишь следующие матричные
элементы:
(/, m\tz\U m) = mh,
(U m ± 1 | tx | /, m> = (A/2) V/(/+1)-m(m ± 1),
(/, m ± 1 | ty | /, m> = ± (/Л/2) V/ (/ + 1) - m (m ± 1).
Операторы сдвига (поворота): t± = tx ± *?#,
повышающий оператор:
f + | /, m) = Л V/ (/ + 1) - m (m + 1) | /, m + 1>,
понижающий оператор:
U I /, m) = A V/(/ + l)-m(m-l)|/, m - 1).
о
Рекомендуемые источники. См. гл. 2 [1], в которой обсуждается квантово-
механическое поведение частицы на окружности и на сфере, что может
служить введением в квантовую теорию углового момента. Более общие
представления даны в гл. 6 [1]. Основные свойства углового момента
суммированы в списке формул 0.1; следует обратить внимание на то, что волновые
функции системы с заданным орбитальным угловым моментом являются
сферическими гармониками. В этой связи см. кн. Козмана [217]. Детальный
обзор по орбитальному угловому моменту дан Бринком и Сэтчлером [80], Роу-
зом [347] и Эдмондсом [131]. Тинкхэм [396] связал их свойства с симметрией
системы по отношению к вращению. О роли орбитального углового момента
в химических проблемах можно судить по разд. «Атомные орбитали»,
«Водорода атом» и «Атомные спектры».
ОРТОГОНАЛЬНЫЕ ВОЛНОВЫЕ ФУНКЦИИ. Две
функции i|)i и г|)2 являются ортогональными, если интеграл Wt^*^
обращается в нуль или, другими словами, если их интеграл
перекрывания равен нулю. Тривиальным примером
ортогональности функций могут служить ls-орбитали двух атомов водорода,
далеко отстоящих друг от друга. Другими примерами являются
ортогональность Is- и 25-орбиталей одного атома или
ортогональность ls-орбитали одного атома к 2/?я-орбитали соседнего
атома в двухатомной молекуле.
Из правил выполнения математических действий над
операторами следует, что собственные функции эрмитового
оператора, соответствующие различным собственным значениям,
оказываются взаимно ортогональными. Собственные функции,
соответствующие вырожденному собственному значению, не
обязательно должны быть взаимно ортогональными. Однако,
используя процедуру ортогонализации Шмидта, всегда можно
образовать их ортогональные комбинации. На языке теории групп
две функции называются ортогональными, если они принадлежат
различным неприводимым представлениям точечной группы
симметрии системы. Хотя ортогональность функций является
естественным следствием свойств квантовомеханических операторов,
она воспринимается как некое благо, потому что приносит
большую практическую пользу, автоматически избавляя нас от
расчетов огромного числа сложных интегралов.
Упражнения. 1. Какие функции называют ортогональными? Приведите
несколько примеров ортогональных функций. В каком случае можно быть
уверенным, что функции какого-либо набора являются взаимно
ортогональными? Если функции неортогональны, какую процедуру следует использовать
для их ортогонализации? Какое теоретико-групповое свойство гарантирует
ортогональность функций?
2. Рассмотрите функции exp imq> в области 0 ^ ср <; 2л. Покажите, что
функции с различными целыми значениями m взаимно ортогональны.
Покажите, что ls-орбитали атома водорода ортогональны его 2s- и 2/?-орбиталям.
Покажите, что волновые функции частицы в одномерной прямоугольной
яме взаимно ортогональны. Рассмотрите вырожденные волновые функции,
253
о
сосиветствующие самому низкому уровню анергии частицы в двумерной
прямоугольной яме, и покажите, что можно найти как ортогональные, так и
неортогональные линейные комбинации двух вырожденных функций, которые
удовлетворяют уравнению Шредингера с тем же самым собственным
значением. Покажите схематически некоторые из этих комбинаций.
3. Используя процедуру Шмидта, проведите ортогонализацию слейтеров-
ских 2s- и ls-орбиталей атома. Для этого нужно записать сумму ty2s = i|)2s +
+ ctyls и найти величину с из условия ортогональности новой 2з-орбитали
\|)2s к орбитали i|?is. Каким образом слейтеровскую Зя-орбиталь можно еде*
лать ортогональной к орбиталям \|)ls и ф^?
Рекомендуемые источники. В гл. 4 [1] приводится доказательство того,
что невырожденным собственным значениям эрмитовых операторов
соответствуют ортогональные собственные функции, и другие следствия
ортогональности. Теоретико-групповое описание ортогональности см. в [1], гл. 5, и
в кн. Тинкхэма [396], Бишопа [59], Вигнера [427]. С процедурой ортогонали-
зации Шмидта можно ознакомиться в кн. Мак-Глина и др. [272].
ОТБОРА ПРАВИЛА. Если система переходит из одного
состояния в другое состояние с отличающейся энергией, это
обнаруживается по появлению спектральных линий. Все линии
спектра можно сопоставить разностям между энергетическими
состояниями системы (каждую можно представить в виде
комбинации термов), но не все возможные пары состояний приводят
к спектральным переходам: некоторые переходы разрешены, а
другие запрещены. Правила отбора указывают, какие из них
разрешены, а какие запрещены. Обычно правила отбора
выражаются в виде условий для возможных изменений квантовых
чисел, но иногда они представляют собой правила возможных
изменений симметрии состояния. Иногда встречается термин
«общее правило отбора». Этот термин относится к свойству,
которым должна обладать молекула, чтобы подействовали
остальные правила отбора. Правила отбора для различных переходов
приведены в списке формул 0.2.
Существуют различные способы вывода правил отбора.
Общее правило отбора связано с тем, что молекула должна каким-
то образом взаимодействовать с электромагнитным полем.
Например, наличие постоянного дипольного момента означает, что
электрическое поле светового пучка может ускорять молекулу,
создавая действующий на нее момент вращения и таким образом
вызывая вращательные переходы. Другие правила отбора можно
рассматривать как следствие того, что фотон обладает
определенным угловым моментом (так как у фотона имеется спин).
При поглощении фотон аннигилирует, но его угловой момент
должен сохраняться, и этот момент передается электронам или
ядерному остову молекулы. Правила типа Д/ = ± 1 или Д/ = ± 1
254
Список формул 0.2
Правила отбора
Л г в случае LS-связи.
Для атомов:
Электрические дипольные переходы:
А/ = 0, ± 1; но / = ()-/►/ = О,
g-+u; g-fr*g, и-т*и (правило Лапорта),
AL = 0, ±1; но
Магнитные дипольные переходы:
Д/=»0, ±1; но / = 0-^/ = 0,
g -> g, и-+и\ g-t>u,
AL = 0, ±2.
Электрические квадрупольные переходы:
А/ = 0, ±1, ±2; но/ = 0-/*/ = 0,
g -> g, u-+u; g-t+u,
AL = 0, ±1, ±2; но L = 0-/*L = 0.
Для молекул:
Электрические дипольные переходы:
электронные переходы:
А/ = 0, ±1; но / = 0 -^/ = 0,
+ ->-; + -/►+, --/►—,
g -> и; g •¥> g> u-fr>u,
s-+ s, а->а\ s-fr- a;
в случае Гунда (а): ДЛ = 0, ± 1; но для Л = 0->Л = 0:
2+->2+, 2""-* 2~; 2+-/>2~.
AS«0
Д2 = 0
в случаях Гунда (а) и (с): AQ = 0, ± 1; но Q = 0 -/► Q = 0, если А/ = 0;
в случаях Гунда (Ь) и (d): AN = 0, dt 1; но в случае (Ь) Л = 0 -+> Л = 0»
если AN = 0;
колебательные переходы:
поглощение (инфракрасный спектр): должен меняться дипольный момент
вдоль нормальной координаты
Av=±l;
комбинационное рассеяние: во время колебаний должна меняться
поляризуемость
Av = ± 1;
о
Продолжение списка формул О. 2
колебательно-вращатс
Av = ±l; Л/ =
шше переходы:
+ 2 S-ветвь (КРС, стоксовы линии)
+ 1 R-ъетвь (ИК-спектр)
0 Q-ветвь (ИК-спектр) а
— 1 Р-ветвь (ИК-спектр)
— 2 О-ветвь (КРС, антистоксовы линии).
вращательные переходы:
в поглощении (микроволновом): у молекулы должен быть постоянный
дипольный момент
Д/=±1, А/С = 0;
комбинационное рассе
поляризуемость
А/ = ± 2 (стоксовы
а Возникают в том
момента вдоль оси.
яние: у молекулы должна быть анизотропная
линии: +2; антистоксовы: —2).
случае, если у молекулы имеется компонента углового
выражают закон сохранения углового момента в подобных
ситуациях и подробно обсуждаются в разд. «Электрические
дипольные переходы» и в других разделах, посвященных
различным типам спектров (см. варианты этого правила в разд.
«Магнитные дипольные и электрические квадрупольные переходы»).
Все такие правила могут быть получены в результате
изучения дипольного момента перехода (см. разд. «Электрический
дипольный переход»), и один из наиболее удобных способов
такого подхода основан на применении теории групп. Те, кто
знаком с теорией групп и неприводимыми представлениями, должны
знать, что переход не запрещен только в том случае, если
произведение неприводимых представлений начального состояния,
конечного состояния и оператора момента перехода содержит
полностью симметричное представление (см. список формул
Х.1). Те, кто знает теорию групп недостаточно хорошо, чтобы
понять это важное правило, должны как можно скорее
познакомиться с ней.
Рекомендуемые источники. В гл. 5 [1] обсуждаются теоретико-групповые
обоснования правил отбора, в гл. 8 и 10 рассматривается применение правил
отбора ко всем типам атомных и молекулярных переходов. Ссылки на
другие теоретико-групповые рассмотрения можно найти в разд. «Теория групп».
Применения правил отбора к спектрам описаны также в разд. «Электронные
спектры», «Колебательные спектры», «Вращательные спектры» и «Спектры
комбинационного рассеяния», подробное рассмотрение можно найти в кн,
Барроу [51], Уиффена [424], Кинга [222] и Герцберга [185—188].
256
п
ПАУЛИ ПРИНЦИП. Принцип запрета Паули утверждает,
что в каждом состоянии может находиться не более одного
электрона. Следствием этого принципа является принцип
заполнения, который приводит к периодичности свойств химических
элементов, и то, что атомная орбиталь, заданная квантовыми
числами д, /, т/, может быть заселена не более чем двумя
электронами, которые должны иметь различные квантовые числа ms
(т. е. направления спинов должны быть противоположными).
Принцип запрета является частным случаем общего принципа
Паули, относящегося не только к электронам, но вообще ко всем
частицам. В основе принципа Паули лежат следующие
соображения: если две частицы неразличимы, их перестановка не
должна влиять на вычисляемые свойства системы. В частности,
поскольку плотность частиц пропорциональна |\|)|2 (см. разд.
«Волновая функция»), при перестановке двух неразличимых
частиц (когда первая помещается на место второй и наоборот)
плотность частиц и, следовательно, |г|)|2 не должны меняться.
Это означает, что функция г|) при перестановке частиц может
только изменить свой знак (либо не менять его), но никакие
более сложные ее изменения не допустимы. Перемена или
сохранение знака должны происходить при перестановке любой пары
неразличимых частиц, имеющихся в системе. Волновая функция
меняет или сохраняет знак при перестановке двух частиц в
зависимости от того, какие это неразличимые частицы — фермионы
или бозоны. Фермионы — это частицы с полуцелым спином, к
ним относятся, например, электроны, протоны, нейтроны, ядра
13С и 3Не. Бозоны — это частицы с целым спином, такие, как
2Н, 4Не, 12С и фотоны. Если система тождественных частиц
1, 2 ..., п описывается волновой функцией i|)(rb г2, ..., гп),
то, согласно принципу Паули, эта функция должна
удовлетворять следующему строгому условию: при перестановке
координат двух частиц функция меняет знак, если эти две частицы —
фермионы, и не меняет знака, если они бозоны. Другими
словами, полная волновая функция должна быть
антисимметричной относительно перестановки тождественных фермионов и
симметричной относительно перестановки тождественных бозонов.
Этот принцип можно проиллюстрировать, рассматривая
двухчастичную систему в состоянии г|)(гьг2), или, для краткости,
*ф(1, 2). Если частицы являются фермионами, их природа
требует, чтобы выполнялось условие г|)(2, 1) = —г|)(1, 2). Следствия
этого требования для электронов (фермионов) таковы. Предпо-
257
n
ложим, что в состоянии \ра находится электрон 1 и в состоянии
\|)б — электрон 2, тогда система двух электронов описывается
функцией вида iMri)iMr2)> или *М1)Ф&(2). Но данная
функция не удовлетворяет принципу Паули, поскольку она не
является ни симметричной, ни антисимметричной (вообще не
обладает определенной симметрией) относительно перестановки
индексов 1, 2. Однако, если произведение if>a(l)iM2) заменить
на выражение if>a(l)iM2)—*M2)if>b(l), мы получим функцию,
удовлетворяющую принципу Паули, поскольку при перестановке
индексов она меняет знак. Рассмотрение этой функции ясно
показывает, почему в каждом состоянии может находиться только
один электрон. Если бы состояния \|)а и г|)ь совпадали, т. е.
электроны 1 и 2 находились в одном и том же состоянии, волновая
функция, удовлетворяющая принципу Паули, имела бы вид
Ч'аОИа(2)—i|)a(2)i|)a(l) и обращалась бы в нуль. Отсюда видно,
что состояния, занятые более чем одним электроном,
невозможны и что принцип запрета является частным случаем полного
принципа Паули. Если же вместо фермионов мы имеем дело
с бозонами, соответствующая двухчастичная волновая функция
может быть записана как i|)a (1) *\>ь (2) + i|)a (2) фь (1). Эта функция
не обращается в нуль, если принять \ра = $ь, поэтому бозоны не
подчиняются принципу запрета и для них разрешены
многократно заполненные состояния (например, вследствие того что
большое число фотонов может находиться в одном и том же
состоянии, получается интенсивный монохроматический пучок
света). Напомним, что принцип Паули относится к полной
волновой функции системы, а следовательно, г|)а и tyb описывают не
только пространственные (орбитальные), но и спиновые
состояния.
Первоначально принцип Паули был введен для объяснения
спектра гелия, поскольку при изучении этого спектра не были
обнаружены многие термы, присутствие которых предполагалось.
Объяснить это обстоятельство можно было только на основе
предположения, что два электрона не могут заполнять в атоме
одно и то же состояние. Паули обосновал этот принцип
теоретически, применяя релятивистский подход и исходя из требования,
чтобы энергия системы была положительной; таким образом он
показал, что все частицы с полуцелым спином должны
описываться антисимметричными волновыми функциями и вести себя
так, как говорилось выше. Возможным исключением из этого
принципа является поведение кварков — особых частиц, которые
используются в одном из вариантов теории элементарных
частиц. Однако кварки пока экспериментально не наблюдались и
могут оказаться просто игрой воображения, а все обычные
частицы должны подчиняться общему принципу Паули. Если бы
принцип Паули не выполнялся, ни одно вещество не могло бы
258
п
быть твердым. Если бы у электронов не было спина (т. е. если
бы они были бозонами), все вещества занимали бы меньший
объем (были бы более плотными) и вокруг нас не было бы
ничего твердого, а все было бы липким.
Рекомендуемые источники. Экспериментальное обоснование принципа
Паули описано в [1], гл. 8. Волновая функция многоэлектронной системы
удовлетворяет принципу Паули, если ее записать в виде слейтеровского
детерминанта; дальнейшее обсуждение см. в соответствующем разделе и в
разд. «Антисимметричные функции». О том, как был выведен принцип, см. в
кн. Паули [311]. О кварках см. в разд. «Фермионы».
ПАШЕНА — БАКА ЭФФЕКТ. Эффект Пашена —Бака
состоит в нарушении связи между орбитальным и спиновым
угловыми моментами под влиянием внешнего магнитного поля.
Рис. П.1 Эффект Пашена — Бака.
Рассмотрим атом, обладающий как спиновым s, так и
орбитальным угловым моментом 1. Эти моменты связаны
спин-орбитальным взаимодействием и дают результирующий полный
угловой момент, который можно представить вектором j. Векторы s
и I прецессируют вокруг вектора j. В магнитном поле
сравнительно небольшой напряженности суммарный вектор также пре-
цессирует вокруг направления поля (рис. П.1, а).
Взаимодействие полного углового момента с внешним полем приводит к
эффекту Зеемана. С увеличением напряженности внешнего поля
его взаимодействие со спиновым и орбитальным магнитными
моментами становится столь, сильным, что в конце концов оно
превышает спин-орбитальное взаимодействие. При этом спиновый
и орбитальный моменты начинают самостоятельно ирецессиро-
вать вокруг направления поля и спин-орбитальная связь
нарушается. Движение векторов угловых моментов становится
259
п
сложным, поскольку внешнее поле и спин-орбитальное
взаимодействие оказывают конкурирующее влияние на эти два момента.
Если напряженность поля становится достаточно большой
(порядка десятков килогаусс), его влияние превалирует и в атоме
происходит независимая прецессия каждого из угловых
моментов вокруг направления внешнего поля (см. рис. П. 1,6).
Возникает эффект Пашена — Бака, который приводит к нарушению
спин-орбитальной связи.
Спектроскопическое проявление этого эффекта заключается
в том, что при его наличии электронные переходы происходят
более простым образом: поле оптической волны взаимодействует
с орбитальным угловым моментом и вызывает переходы,
которые не зависят от направления спинового момента. Аномальный
эффект Зеемана, зависящий от соотношения между спиновым и
орбитальным моментами, заменяется нормальным эффектом
Зеемана, характерным для бесспиновых систем. Термин «эффект
Пашена — Бака» применяется и в других ситуациях, когда поле
нарушает связь спинового и орбитального моментов. В
качестве примера можно привести действие аксиального ядерного
кулоновского электростатического потенциала на угловые
моменты двухатомной молекулы; его влияние обсуждается в разд.
«Гунда случаи связи».
Упражнения. В чем заключается эффект Пашена — Бака? Рассмотрите
его с использованием векторной модели атома. Каким образом этот эффект
упрощает аномальный эффект Зеемана и заменяет его нормальным? Оцените
напряженность внешнего магнитного поля, необходимого для нарушения
спин-орбитальной связи, если энергия спин-орбитального взаимодействия в
атоме имеет величину порядка 100 см-1.
Рекомендуемые источники. См. разд. «Зеемана эффект» и гл. 8 в [J]. См.
также разд. 11.3 кн. Герцберга [185] и разд. IIIF3 кн. Куна [229], где
подробно обсуждаются спектроскопические следствия эффекта Пашена — Бака.
ПЕРЕКРЫВАНИЕ. Если две волны перекрываются в одной
и той же области пространства, они интерферируют, и в
результате их суперпозиции получается новая волна. Амплитуда этой
волны увеличивается в тех областях, где знаки амплитуд
перекрывающихся волн совпадают, и уменьшается в тех областях,
где амплитуды перекрывающихся волн имеют противоположные
знаки и поэтому погашают друг друга (рис. П.2, а). Поскольку
пространственное распределение электрона определяется
квадратом амплитуды волновой функции, электрон находится в
основном в областях максимумов интерференции и избегает
областей минимумов интерференции. Таким образом, перекрывание
волновых функций может заметно изменить пространственное
260
Рис. П.2. а — интерференция волн ( и ) дает результирующую волну ( ); поскольку у
интерферирующих волн различные длины, мы рассматриваем только малую область интерференции,
б—интерференция волн при перекрывании атомных s- и р-орбиталей. в — области перекрывания,
соответствующие б. Горизонтальной штриховкой показана область, в которой интерференция дает усиление, а
вертикальной штриховкой — область интерференционного ослабления результирующей амплитуды волн.
(/ _ умеренное положительное перекрывание, 2 — сильное положительное перекрывание, 3 — сильное
отрицательное перекрывание, 4 — нулевое суммарное перекрывание.)
п
распределение электрона (или другой частицы). Если s-орби-
таль сближается с р-орбиталью вдоль оси последней (рис. П.2, б),
их интерференция возрастает с уменьшением расстояния. Если
при этом знаки амплитуд совпадают, интерференция приводит
к возрастанию амплитуды результирующей функции, и электрон
заметно локализуется в области перекрывания. По мере
дальнейшего сближения орбиталей размеры области перекрывания
продолжают увеличиваться. Однако суммарный эффект от
перекрывания при этом уменьшается, поскольку s-орбиталь начинает
перекрываться с областью р-орбитали по другую сторону от ее
узла, в которой амплитуда этой орбитали отрицательна. Когда
сба ядра совмещены, s-орбиталь в равной степени
перекрывается с положительной и отрицательной пучностями р-орби-
тали. В результате с одной стороны узла интерференция
приводит к усилению, а с другой — к такому же (количественно)
ослаблению результирующей амплитуды. При дальнейшем
перемещении s-орбитали в том же направлении перекрывание
приводит ко все большему взаимному ослаблению орбиталей, так
как их амплитуды взаимно погашают друг друга. Они и в самом
деле взаимно погашаются на довольно сложной поверхности и
образуют на ней узел новой волны. По мере удаления
s-орбитали от р-орбитали их интерференция ослабевает, поскольку в
области, где велика одна орбиталь, другая — мала, и в конце
концов интерференция прекращается. Если перемещать
s-орбиталь вдоль прямой, перпендикулярной оси р-орбитали, эффекты
ослабления и усиления орбиталей в результате интерференции
равны при любом расстоянии между орбиталями.
Количественной характеристикой суммарного эффекта
перекрывания служит интеграл перекрывания. Он равен нулю, если
суммарный эффект отсутствует (потому что не происходит
перекрывания либо потому, что эффекты интерференционного
усиления и ослабления в областях перекрывания равны), и равен
единице в случае идеального перекрывания (когда орбиталь
перекрывается сама с собой). Орбитали с нулевым интегралом
взаимного перекрывания называются ортогональными. Чтобы
вычислить интеграл перекрывания S, необходимо взять
произведение двух волновых функций в одной и той же точке г
пространства -ф* (г) i|^ 'г) и вычислить интеграл по всему
пространству S= Wti|^ (ii)i|V г). Очевидно, что такое определение
интеграла перекрывании согласуется с оцисанными выше свойствами
перекрывающихся функций.
Упражнения. 1. Что происходит при перекрывании дьух орбиталей?
Рассмотрите, как меняется пространственное распределение электрона по мере
того, как две 1 s-орбитали сближаются, проходят одна сквозь другую и за-
262
п
тем удаляются (допустим, что знаки амплитуд сближающихся орбиталей
совпадают). Изобразите графически величину интеграла перекрывания в
этом случае в зависимости от расстояния между орбиталями. Каковы
эффекты перекрывания, если ls-орбиталь приближается к 3^*2-орбктали:
а) вдоль оси у, б) вдоль оси xl Изобразите форму гибридных орбиталей,
которые получаются в рассмотренных случаях при совмещении атомных ядер.
2. Интеграл перекрывания ls-орбиталей двух атомов водорода,
находящихся на расстоянии R, определяется выражением
S (Is, Is) = (1 + R/a0 + j?73flg) exp (- tf/aQ),
где a0 — боровский радиус (53 пм. или 0,53А). Изобразите графически эту
функцию как функцию R. При каком расстоянии между атомами достигается
максимальное значение S? Интегралы перекрывания ls-орбитали,
сближающейся с 2s- или 2р-орбиталью вдоль их осей, определяются соответственно
выражениями
S (Is, 2s) = (1/2 Уз") (1 + R/a0 + 4R2/3a2Q + R3/3a30) exp (- /?/aQ),
S (Is, 2po) = (R/2a0) (l + R/% + R2!^) exp (- R/aQ).
Изобразите графически эти функции и определите в обоих случаях
расстояния, при которых перекрывание максимально.
3. Предположим, что у одного из атомов имеется гибридная орбиталь
вида a|)2s(r)sin I + i|?2p(r)cos g, где sin g и cos £ — коэффициенты смешения.
Предположим также, что вдоль оси этой орбитали к ней приближается
ls-орбиталь. Обсудите вид соответствующего интеграла перекрывания и
изобразите графически его зависимость от R для такой суперпозиции 2s- и 2/?-орби-
талей, которая соответствует максимальному перекрыванию при любом
расстоянии. Изобразите графически зависимость оптимального значения | от R.
Рекомендуемые источники. Перекрывание играет важную роль при
изучении образования химических связей, поэтому см. гл. 9 [1] и особенно кн.
Коулсона «Форма и строение молекул» [10] и [105], Маррела, Кеттла и Тед-
дера [299]. Метод вычисления интегралов перекрывания описан Эйрингом,
Уолтером, Кимбаллом [137] и более подробно Мак-Глином, Ванквикенборном,
Киноситой и Кэрроллом [273]. Подробные таблицы интегралов перекрывания
опубликованы в ряде изданий: см. библиографию на стр. 421 кн. Мак-Глина
и др. [273]. Перекрывание значительно усиливается, если участвующие в нем
орбитали гибридизованы, прочность образуемых такими орбиталями связей
возрастает. Явление перекрывания и сопутствующие ему интерференционные
эффекты можно рассматривать как проявления принципа суперпозиции —
одного из основных положений квантовой механики.
ПЛОТНОСТЬ ЗАРЯДА. Говоря о плотности заряда,
следует различать два понятия: плотность заряда в определенной
точке атома или молекулы и эффективный заряд, который
ассоциируется с каждым отдельным атомом в молекуле. Плотность
заряда можно определить, если известна волновая функция
атома или молекулы, так как вероятность нахождения
электрона в малом элементе объема dx, окружающем точку г, равна
|г|: (г) |2rfx. Так как электрон несет заряд —е, то количество
заряда в этом объеме равно —е|ф(г) \2d%. Поэтому плотность
заряда (заряд на единицу объема) в данной точке определяется
263
n
как —e|\|)(r)|2. Эту плотность Аможно использовать для
различных целей, например при расчетах кулсновских интегралов или
рассеяния рентгеновских лучей атомами.
Второе понятие предполагает описание молекулы в гораздо
более грубых чертах, при котором не требуется знать все
мельчайшие детали распределения электронов в каждой точке
пространства. Эффективный заряд атома в молекуле понимается
как количество заряда (или плотность электронов за вычетом
числа ядерных зарядов) на каждом атоме в молекуле. Понятно,
что в гомоядернои двухатомной молекуле эффективный заряд
на каждом атоме равен нулю, так как электроны поделены
поровну между атомами и ядерный заряд в точности компенсирует
электронный заряд. В полярной молекуле электроны могут
смещаться ближе к более электроотрицательному атому, тогда
эффективные заряды не одинаковы.
Плотность заряда обычно вычисляется с помощью волновой
функции, записанной в виде линейной комбинации атомных
орбиталей. Если сА — амплитуда атомной орбитали в
молекулярной орбитали, заполненной одним электроном, то вклад такой
атомной орбитали в молекулярную орбиталь равен кл|2, а ее
вклад в плотность заряда на атоме А равен —е|сА[2. Полная
плотность заряда на атоме А вычисляется суммированием таких
членов для всех занятых орбиталей. Плотность заряда можно
использовать для вычисления дипольного момента молекулы,
а также при рассмотрении ее реакционной способности.
Анализ распределения электронов в терминах заселения ими
атомных орбиталей называют анализом заселенностей.
Упражнения. Что понимается под плотностью заряда? Что имеется в виду
под анализом заселенностей? Как рассчитать эффективный заряд на атоме,
если известно электронное строение молекулы? Волновая функция ls-орби-
тали атома имеет вид i|),s (г) = [Xjna^2 exp (— г/а0), какова плотность
заряда в точке г? Что такое полная плотность заряда на атоме? Волновая
функция молекулярного иона водорода имеет вид (\/у2) [i|)is(rai) + i|)is(r&i)],
где ra 1 — расстояние от электрона 1 до ядра а, а гы — расстояние от этого
же электрона до ядра Ь, какова плотность заряда на каждом атоме
водорода? (Заметьте, что молекулярная орбиталь не нормирована. Объясните
почему.) Какова плотность заряда на каждом атоме в молекуле бензола?
Рекомендуемые источники. В разд. «Альтернантные углеводороды» можно
найти сведения о теореме Коулсона — Рашбрука и плотности заряда; о
способе применения данного понятия см. также в разд. «Дипольный момент».
В разд. «Порядок связи» также обсуждаются понятия, связанные с анализом
заселенностей. Обсуждение плотности заряда можно найти у Коулсона [105],
Пилара [318], Мак-Глина, Ванквикенборна, Киноситы и Кэрролла [273]. Коул-
сон и Стрейтвизер [110] составили таблицы параметров молек\лярных
орбиталей. См. также кн. Стрейтвизера [387], Салема [353], Попла и Бевериджа
[321], Маррела и Харгета [298].
264
п
ПОЛЯ ЛИГАНДОВ ТЕОРИЯ (краткий обзор). Теория поля
лигандов применяется для описания строения комплексных
ионов переходных металлов и является обобщением теории
кристаллического поля, учитывающим известную делокализацию
электронов иона на орбитали окружающих лигандов. В то же
время эта теория, как и теория кристаллического поля,
основывается на использовании высокой степени симметрии,
характерной для комплексов. Теория поля лигандов — это, по сути,
теория молекулярных орбиталей комплексов, которая уделяет
основное внимание d-электронам центрального иона. Рассмотрим
для иллюстрации метода октаэдрический комплекс, в котором
центральный ион имеет п d-электронов.
Предположим, что лиганды имеют только а-орбитали и
каждый из них обращен к центральному иону неподеленной парой
электронов (на рис. П.З они обозначены кружками). Из шести
таких а-орбиталей можно образовать шесть комбинаций,
имеющих определенные свойства симметрии. (Тот, кто знаком с
теорией групп, поймет, что выбранные линейные комбинации
должны образовывать неприводимые представления октаэдриче-
ской точечной группы.) Эти шесть комбинаций, показанные на
рис. П.З, подразделяются на три набора. Только один из этих
наборов, обозначенный egi имеет результирующее перекрывание
с d-орбиталями центрального иона, и только эти комбинации
могут образовать с rf-орбиталями связывающие и
разрыхляющие молекулярные орбитали. Полученные молекулярные
орбитали можно представить в виде диаграммы (рис. П.4). Энергии
орбиталей лиганда и иона таковы, что более низкая по энергии
связывающая комбинация близка по свойствам к орбиталям
лигандов, тогда как разрыхляющая комбинация близка по
характеру к орбиталям иона металла.
На рис. П.4 показано одиннадцать орбиталей: дважды
вырожденная связывающая орбиталь (eg), четыре вырожденные,
несвязывающие орбитали, полностью относящиеся к лигандам
(t\u и a\g), три трижды вырожденные несвязывающие орбитали,
полностью относящиеся к иону металла (^), и разрыхляющая
комбинация (e*g). На этих орбиталях нужно разместить 12 +л
электронов (по два от каждого лиганда и п от иона). Следуя
принципу заполнения, можно представить себе, что первые
12 электронов заполнят орбитали eg, t\u, algy имеющие
преимущественно характер орбиталей лигандов. Следующие п
электронов должны бороться за места на t2g- и ejj-орбиталях. Точно
с такой же ситуацией сталкиваются в теории кристаллического
поля (рис. К. 10 и рис. К.11). Поэтому можно сделать
аналогичные выводы. Если энергетическая щель между этими орбита-
лями, обозначаемая как WDq, велика (так называемый случай
сильного поля), электроны заселяют состояния t2g до тех пор,
265
Рис. П.З. Щесть орбиталей лигандов и шесть симметризованных комбинаций
лиганды
комплекс
металл
дополнительные
п электронов
^преобладание
свойств металла
орйтаТа /V преобладание
еа / J свойств лигандов
Рис. П.4. Расщепление уровней в октаэдрическом комплексе, обусловленное
полем лигандов.
п
пока это не запрещается принципом Паули. После этого
электроны начинают заселять верхнее состояние е\. При малой
энергетической щели между орбиталями (случай слабого поля)
энергетически выгоднее такое заселение Ug- и е^-орбиталей,
при котором электроны обладают параллельными спинами
(правила Гунда).
Делая различие между последовательностью заполнения
орбиталей в случаях слабого и сильного полей, которые приводят
к высоко- и низкоспиновым комплексам, теория молекулярных
орбиталей заимствует аналогичный подход из теории
кристаллического поля. Однако причины расщепления орбиталей в этих
Рис. П.5. Двенадцать я-орбиталей октаэдрически расположенных лигэндое.
двух теориях трактуются по-разному. Кроме того, в теории
молекулярных орбиталей е^-орбиталь не принадлежит всецело
иону металла и имеет некоторые признаки орбиталей лигандов,
так как образуется в результате перекрывания орбиталей
металла и лигандов. Это означает, что любой заселяющий ее
электрон может оказаться на лигандах. Доказательство того, что
такой перенос электрона существует, дает спектроскопия, и в
особенности электронный парамагнитный резонанс (в котором
наблюдается сверхтонкая структура, обусловленная лигандами).
Преимущество теории поля лигандов над теорией
кристаллического поля также заключается в том, что она естественным
образом допускает образование я-связей между металлом и
лигандами. Это особенно важно, когда в качестве лигандов
выступают такие группы, как СО или N0. Для того чтобы
увидеть, к чему приводит учет образования я-связей, снова
рассмотрим октаэдрический комплекс и предположим, что каждый
лиганд, помимо а-орбиталей, обладает двумя орбиталями,
направленными перпендикулярно связям металл — лиганд. Из
12 таких орбиталей (рис. П.5) можно построить 12
комбинаций. Три из них имеют ту же симметрию, что и dxy-, dxz-t dyZ-op-
267
n
битали центрального иона (которые до сих пор образовывали
набор несвязывающих ^-орбиталей, относящихся к металлу).
При наличии перекрывания между d-орбиталями и я-орбита-
лями лигандов диаграмма энергетических уровней
молекулярных орбиталей принимает другой вид. Могут возникнуть две
различные ситуации. В первом случае я-орбитали лиганда
полностью заполнены и
расположены ниже а-ор-
биталей. Во втором —
они остаются
незаполненными и находятся выше
а-орбиталей. Оба эти
варианта показаны на рис.
П.6. В первом случае я-
электроны лигандов
занимают все связывающие
комбинации я-орбиталей.
Оставшиеся п электронов
заполняют
разрыхляющие tig и не участвующие
в я-взаимодействии е*ё-
комбинации. Поскольку
несвязывающие до этого
tig -орбитали становятся
Рис. П.6. Влияние я-связыва-
ния на энергию: а — исходные
я-уровни лигандов заполнены
и б- исходные уровни
лигандов не заполнены.
'заполненные
'незаполненные
слабо разрыхляющими, присутствие я-электронов приводит
к уменьшению энергетической щели (т. е. величины \QDq).
Когда я-орбитали лигандов не заселены, возникает
противоположная ситуация: п электронов распределяются на
связывающей ^-комбинации и разрыхляющей ^-комбинации.
Присутствие незаполненных я-орбиталей увеличивает энергетическую
щель между этими группами орбиталей.
Величина расщепления lODq определяет спектроскопические,
магнитные и химические свойства комплексов точно так же, как
и в теории кристаллического поля. Однако делокализация
электронов металла на лиганды заставляет их участвовать в спин-
орбитальном взаимодействии, обусловленном свойствами
лигандов.
268
п
Рекомендуемые источники. Теорию поля лигандов см. в [1] гл. 9.
Простое введение в представления теории поля лигандов дано Эрншоу и Хар-
рнигтоиом [14], этот же вопрос развивается в кн. Коулсона «Форма и
структура молекул» [10]. Объяснение магнитных свойств комплексов с
использованием этих представлений описано Эрншоу [128], а объяснение их
спектральных свойств — Пергенсеном [209, 210]. Простое и хорошее введение в теорию
поля лигандов см. также в кн. Оргела [308], Коулсона [105], Маррела, Кеттла,
Теддера [299]; этот же вопрос, но с большим привлечением математического
аппарата рассматривают Фиджис [146], Бальхаузен [49], Гриффит [170]. См.
также разд. «Кристаллического поля теория» и «Яна — Теллера эффект».
ПОЛЯРИЗУЕМОСТЬ. Если на отдельный атом или
молекулу действует электрическое поле, распределение электронов
и геометрия молекулы искажаются. Поляризуемость
показывает, насколько легко происходит такое искажение. Атомной
поляризуемостью называется вклад геометрического искажения
молекулы в ее полную поляризуемость. Он обычно значительно
меньше, чем вклад электронной поляризуемости, вызываемой
смещением электронов. Есть третья составляющая
поляризуемости объемного образца — это ориентационная поляризация.
Она наблюдается у тех молекул, у которых имеется постоянный
дипольный момент. В этом случае внешнее поле поворачивает
молекулу, и весь образец приобретает суммарную поляризацию.
Молекулы ориентируются вдоль поля не полностью, так как
тепловое движение разупорядочивает их «выстраивание» в
образце. Величину ориентационной поляризации можно
рассчитать, используя распределение Больцмана для определения
среднего дипольного момента образца, в результате получится
ланжевеновскии вклад в полную поляризуемость, приведенный
в списке формул П.1. Этот вклад имеет механическое
происхождение и не будет интересовать нас в дальнейшем, хотя он играет
важную роль в полной поляризуемости. Мы ограничимся
изучением природы электронного вклада.
Сильно поляризуемые молекулы легко откликаются на
внешнее поле; они становятся сильно поляризованными, и центр
распределения отрицательного заряда электронов смещается. Если
первоначально молекула была неполярной, поляризация
приводит к появлению электрического дипольного момента; если она
уже была полярной, появляется дополнительная компонента
дипольного момента. Величина индуцированного дипольного
момента является хорошим показателем поляризуемости
молекулы. Поляризуемость а можно определить как коэффициент
пропорциональности между индуцированным моментом и
напряженностью электрического поля: \х (индуцированное) = аЕ.
Если внешнее поле очень сильное, дипольный момент может не
подчиняться этому соотношению. В этом случае он зависит от Е2
и более высоких степеней £, коэффициенты при £2, £3, ...
называются первой, второй и т. д. гиперполяризуемостью. Ми
269
Список формул П. 1
Поляризуемость
Энергия поляризуемой молекулы в поле напряженностью Е:
&(Е) = Я™-^Е-±аЕ2-±-$Е' + ....
Дипольный момент в поле напряженностью Е:
H = H<0)+a£+i-p£'2+ ....
где fi(0) — постоянный дипольный момент, а —поляризуемость, 0 — первая
гиперполяризуемость. (При описании магнитных свойств а заменяется
на намагничиваемость g.)
Квантовые выражения:
^(0) = <Фо|<М.г|)0>,
a = - (d**/d&)B_0 - f £' A-ViU
где Д^ = Е^ — £^0) — энергия молекулярного возбуждения и d0/l =
= (% I d I i^) — дипольный момент перехода.
Поляризация среды:
Электрическая восприимчивость (%е)' Р — ЪоХеЕ-
Относительная восприимчивость (диэлектрическая проницаемость):
Показатель преломления: пг = е^К
Напряженность лорентцева локального поля: Е< « Е + Р/Зе0 =
= "о"(8г + 2)Е (множитель 7з получен округлением).
Уравнение Лорентца — Лоренца, или Клаузиуса — Мосотти:
/ег- 1 \ f Af \ _ La __
Ur + 2 A p Л Зе0 ~а^
где Af — молекулярный вес, р — плотность, L — число Авогадро.
La/3e0 — молярная поляризуемость, обычно обозначаемая как а^.
Уравнение Дебая (для молярной поляризуемости полярного
диэлектрика):
где аА — атомная поляризуемость,
а£ — электронная (молекулярная) поляризуемость,
aQ — ориентационная поляризуемость, которая для молекулы
с постоянным дипольиым моментом ц (0) определяется ланже-
веновским вкладом
ao-|i<0)2/3M\
Уравнения Максвелла см. в табл. 20.
п
будем пренебрегать этими нелинейными восприимчивостями и
ограничимся рассмотрением линейной восприимчивости, т. е.
рассмотрением поляризуемости а.
Квантовомеханический расчет поляризуемости основан на
вычислении энергии поляризуемой молекулы в электрическом
поле во втором порядке теории возмущений (см. список
формул П.1). Как оказалось, величину поляризуемости а можно
интерпретировать по-разному.
1. Согласно одной из интерпретаций, поляризуемость
усиливается с увеличением размеров атома и числом входящих
в него электронов. Это можно пояснить следующим образом:
когда электроны находятся далеко от ядра или хорошо
экранированы от него другими электронами, внешнее поле легче
изменяет их распределение.
2. Другая интерпретация основана на той точке зрения, что
искажение электронного распределения молекулы можно
представить с помощью соответствующей суперпозиции волновых
функций. В результате выражение для поляризуемости
получается в виде суммы слагаемых, каждое из которых описывает
примесь какого-либо возбужденного состояния к основному
состоянию. Вклад каждого возбужденного состояния зависит от
того, насколько его энергия отличается от основного состояния,
а также от интенсивности оптического (электрического диполь-
ного) перехода между этими состояниями. С увеличением
интенсивности перехода состояние может давать больший вклад,
а с увеличением разности энергий его вклад уменьшается.
Вследствие этого разумно ожидать, что молекулы с большими
интенсивностями переходов в оптической или низкочастотной
областях спектра обладают большой поляризуемостью и что,
следовательно, алифатические углеводороды, для которых
характерны слабые оптические переходы в ультрафиолетовой
области, обладают низкой поляризуемостью.
3. Третья интерпретация основана на том, что выражение
для поляризуемости можно истолковать, рассматривая величину
флуктуации мгновенного электрического дипольного момента
атома или молекулы. Можно представить себе локальные
кратковременные перемещения электронов в молекуле, которые
создают дипольный момент, в среднем равный нулю (для
неполярных молекул); чем больше эти флуктуации, тем больше
поляризуемость, эта интерпретация связана с первой, поскольку
флуктуации сильнее в большой, слабо связанной системе.
Поляризуемость образца зависит от частоты. При низких
частотах (ниже 1012 Гц) молекулы, атомы в молекулах и
электроны этих молекул успевают следовать за изменяющимся
направлением внешнего поля. При более высоких частотах
(выше 1012 Гц, но ниже 1014 Гц) молекулы не успевают
271
п
переориентироваться достаточно быстро, и вклад ориентацион-
ной поляризуемости исчезает. При еще более высоких частотах
атомные ядра не успевают следовать за осциллирующим полем,
и вклад атомной поляризуемости также становится равным нулю.
Отсюда следует, что при высоких частотах (в оптическом
диапазоне частот) единственным вкладом в поляризуемость остается
вклад электронов, но даже он исчезает при очень высоких
частотах. Зависимость поляризуемости от частоты (дисперсия)
позволяет разделять вклады различной природы.
Поляризуемость молекул связана с относительной
восприимчивостью (диэлектрической проницаемостью) образуемой ими
среды (см. список формул П.1) и ее показателем преломления.
Обе эти зависимости позволяют определить поляризуемость
в широком диапазоне частот. (Поскольку показатель
преломления обычно измеряется на оптических частотах, он связан
с электронной поляризуемостью.)
Упражнения. 1. Что произойдет с молекулой, если ее поместить в
электрическое поле? Дайте определение поляризуемости. Какова зависимость
индуцированного дипольного момента от напряженности приложенного поля,
если оно очень сильное? Можно ли ожидать, что поляризуемость молекулы
зависит от ее ориентации по отношению к полю? Почему поляризуемость
должна возрастать по мере того, как молекулы становятся крупнее и их
электроны связаны слабее? Какая частица более поляризуема: Не или Не+?
Каково влияние мгновенных флуктуации дипольного момента атома на
величину его поляризуемости? Можно ли связать поляризуемость с
интенсивностью и частотой оптических переходов? Почему поляризуемость зависит от
примешивания возбужденных состояний к основному состоянию? См. разд.
«Возмущений теория» и «Виртуальные переходы».
2. Воспользуйтесь выражениями из списка формул П.1 и вычислите
поляризуемости заряженного простого гармонического осциллятора, электрона
в одномерной прямоугольной яме и атома водорода. В тех случаях, когда вы
сочтете необходимым, используйте приближение свертки. Рассчитайте
поляризуемость атома углерода, параллельную и перпендикулярную оси 2/?2-орби-
тали, воспользуйтесь для этого слейтеровскими атомными орбиталями и
приближением свертки.
Рекомендуемые источники. Вывод соотношений, приведенных в списке
формул, и дальнейшее обсуждение вопроса см. в гл. 11 [1]. См. также кн.
Ван Флека [407], Дэвиса [117], Бэкингема [81]. Численные значения
поляризуемости приведены у Ландольт-Берштейна. О применении поляризуемости см.
в разд. «Межмолекулярные силы» и «Дисперсионные силы».
Гиперполяризуемость и методы ее определения обсуждаются Бэкингемом и Орром [83]. См.
также Киелих [221].
ПОЛЯРОН. Полярон — это дефект решетки ионного
кристалла, образующийся в том случае, когда избыточный заряд
в какой-либо точке поляризует решетку в окрестности этой
точки. Так, если в кристалле галогенида щелочного металла
272
п
электрон захвачен ионом галогена, то соседние ионы вдоль
решетки металла притягиваются к нему, а другие отрицательные
ионы отталкиваются от него (рис. П.7). Перемещение такого
электрона вызывает ее искажение. То, что электрон перемещает
вместе с собой это искажение, делает его гораздо более
массивной частицей. Искажение решетки, которое движется внутри нее
подобно тяжелой частице, — вот какое содержание вкладывается
в термин «полярон».
ООООФФОФФОООС
ООООффОффОООС
ООООФ
ФОФО
ФФФО
ееое
ООООФ
ооооф
ООООФ
ФОООС
юоос
)ООС
юоос
ФОООС
ФФОООС
ОФФОООС
Рис. П.7. Полярон в простой решетке. Двойной штриховкой показана область
с удвоенным зарядом, одинарной штриховкой — область с единичными
зарядами противоположного знака
Рекомендуемые источники. См. гл. 10 кн. Киттеля [224] и [223]. Хорошее
обсуждение этого вопроса см. в гл. 4 кн. Мотта и Дэвиса [294] и кн. Купера
и Уитфилда [230].
ПОТЕНЦИАЛ ИОНИЗАЦИИ. Потенциалом ионизации
(ПИ) называют энергию, которую необходимо затратить, чтобы
перевести электрон с занимаемой им орбитали атома или
молекулы в бесконечно удаленную точку пространства. Потенциал
ионизации тем больше, чем сильнее связан электрон, а это
зависит от типа занимаемой им орбитали и от состояния
ионизуемого атома. Величина ПИ выражается в электронвольтах
(1 эВ = 96,49 кДж-моль-1). Первый потенциал ионизации
равен энергии, которая требуется для удаления наименее
связанного электрона из нейтрального атома, второй ПИ равен
энергии, требуемой для удаления наименее связанного электрона
из образовавшегося однозарядного иона, и т. д. Потенциалы
273
п
ионизации определяют многие химические свойства элементов и
различные закономерности, наблюдаемые в периодической
системе. Чтобы убедиться в этом, достаточно рассмотреть свойства
и ПИ атомов второго периода периодической системы от Не до
Ne (см. табл. 18). Объяснение свойств этих атомов можно
получить также другим способом, если воспользоваться
представлениями о проникновении электронов и экранировании ядра.
Упражнения. Что называется потенциалом ионизации? Потенциал
ионизации атома натрия составляет 5,14 эВ; какое количество тепла выделится
при образовании 1 моля атомов натрия из газообразных ионов Na+ и
электронов? Может ли атом иметь отрицательный потенциал ионизации?
Объясните закономерности изменения ПИ элементов второго периода, пользуясь
представлениями о проникновении электронов и экранировании ядра.
Рекомендуемые источники. Сведения о потенциалах ионизации можно
найти в таблицах Кайя и Лейби [218] и § 7 сб. Грея [168]. В кн. Падефата
«Периодическая таблица элементов» [4] обсуждается влияние проникновения
электронов и экранирования ядер на свойства элементов. Более детально
этот вопрос рассматривается Филлипсом и Вильямсом [317]. Потенциалы
ионизации используются для вычисления электроотрицательности элементов и
экспериментально устанавливаются для молекул методом фотоэлектронной
спектроскопии (см. «Фотоэффект»).
ПРЕДИССОЦИАЦИЯ. Диссоциация молекулы происходит
обычно в том случае, если она возбуждена в состояние, энергия
которого превышает суммарную энергию изолированных
фрагментов молекулы. Переход с кривой X на кривую А на
рис. П.8, а дает пример такого процесса; начиная с того места,
где верхние колебательные состояния не квантованы' (т. е. где
они на самом деле являются трансляционными состояниями),
спектр становится расплывчатым. Предиссоциация — это
диссоциация, при которой переход с кривой X на кривую А
происходит еще до достижения порога диссоциации.
Рассмотрим переход Х-+А, изображенный на рис. П.8, б.
На электронный переход налагается ряд линий, обусловленных
переходом в колебательные состояния кривой А. При низких
частотах (энергиях) линии резкие, и, казалось бы, такими они
и останутся, пока не поступит достаточное количество энергии,
чтобы возбудить молекулу выше предела диссоциации верхнего
состояния. На рис. П.8, б, видно, что колебательная структура
действительно исчезает при этой энергии. (Ниже этой точки
интенсивности линий колебательной структуры определяются
соответствующими правилами отбора и принципом Франка — Кон-
дона.) В некоторых случаях, однако, колебательная структура
пропадает еще до достижения предела диссоциации. Это
возможно при условии, что какое-либо диссоциативное состояние В
274
Рис. П.8. а — диссациация путем перехода в диссоциативное состояние, б — диссоциация при получении молекулой энергии,
достаточной для разрушения возбужденного состояния, в — предиссоциация, обусловленная наличием диссоциативного
состояния. Слева показано, как выглядят спектры.
п
пересекается с Л и в молекуле существует взаимодействие
(возмущение), способное перевести возбужденную молекулу из
состояния А в состояние В (рис. П.8, б). Возможна другая
интерпретация этого явления: состояния в области Д (рис. П.8, в)
представляют собой смесь состояний, и колебательные
состояния А приобретают в какой-то мере трансляционный характер
состояний В при этой же энергии. Следовательно, состояния
в области Д имеют некоторую склонность к диссоциации, даже
если их энергия много меньше энергии диссоциации
состояния Л. Когда энергия падающего света достаточно велика, чтобы
возбудить колебательное состояние Л, находящееся выше
области Д, спектральные линии опять становятся резкими, так как
в этом случае молекула не может перейти в состояние В. Таким
образом, предиссоциацию можно обнаружить по наличию
области расплывчатых линий в колебательной прогрессии
электронного перехода.
Механизм предиссоциации тесно связан с эффектом Оже\
основное различие их заключается в том, что в первом случае
происходит распад молекулы на фрагменты, а во втором —
выброс электрона. В обоих случаях наблюдаются безызлучатель-
ные переходы из связанного состояния в несвязанное. Предис-
социация подчиняется определенным правилам отбора (см. разд.
«Правила отбора»).
Вынужденная предиссоциация — это предиссоциация,
которая вызвана каким-либо внешним воздействием, в частности
столкновением с молекулой постороннего газа (индуцированная
столкновением предиссоциация) или внешним полем.
Столкновения могут перевести возбужденную молекулу из состояния Л
в состояние 5, а внешнее поле может сделать менее строгими
некоторые из правил отбора, затрудняющих переход A -w> В
(волнистая линия означает безызлучательный переход).
Упражнения. 1. Что означает термин «предиссоциация»? Как можно
обнаружить предиссоциацию в спектре? Как повлияет предиссоциация на вид
спектра излучения молекулы? Что заставляет молекулу переходить с одной
энергетической кривой на другую? Как можно усилить эффективность этого
перехода? В чем предиссоциация сходна с эффектом Оже? Что происходит
с вращательной структурой электронного перехода вблизи области
предиссоциации? Предположим, что реакция диссоциации имеет первый порядок и
что время жизни диссоциативного состояния равно т. Используя принцип
неопределенности, получите выражение, которое в зависимости от т будет
определять, исчезает ли в спектре вращательная структура. Затем получите
аналогичное выражение, определяющее возможное исчезновение
колебательной структуры. Возьмите типичные значения необходимых характеристик
молекул и оцените времена жизни уровней, при которых исчезнут
колебательная и вращательная структуры.
2. В настоящем разделе отмечалось, что вне области Л происходит лишь
несущественное смешение состояний А и В. Обоснуйте такое утверждение.
276
п
Дайте классическую и квантовомеханическую интерпретацию зтого явления;
в последнем случае рассмотрите роль перекрывания таким же образом, как
это делается при обосновании принципов Франка — Кондона.
Рекомендуемые источники. См. гл. 10 [1]. Предиссоциация подробно
рассматривается в кн. Герцберга [187, 188], где приводится множество примеров.
См. также кн. Барроу [31], Гейдона [158] и Кинга [222]. Вынужденная
предиссоциация описана Вейном [416].
ПРЕЛОМЛЕНИЯ ПОКАЗАТЕЛЬ. Отношение скорости
света в вакууме с к его скорости в среде v называется показателем
преломления этой среды: я = c/v.
Величина показателя преломления зависит от степени
взаимодействия между световым полем и средой. Поскольку
электрическая составляющая электромагнитного поля света
взаимодействует со средой сильнее, чем его магнитная составляющая,
следует ожидать, что показатель преломления зависит от
электрической поляризуемости среды. Чем больше ее
поляризуемость, тем сильнее это взаимодействие и тем больше
замедляется прохождение света. Это предположение подтверждается
расчетами; так, в неполярной среде показатель преломления
связан с относительной восприимчивостью (диэлектрической
проницаемостью) соотношением я2 = ег, а диэлектрическая
проницаемость в свою очередь связана с поляризуемостью
соотношением ег = I + Na (со) /ео, где N — концентрация молекул
и а (со)—их поляризуемость. Однако не следует забывать, что
каждая молекула окружена другими поляризуемыми
молекулами. Последние откликаются на электрическое поле света, и их
поляризация усиливает поле, которое действует на центральную
молекулу. Следовательно, необходимо ввести поправку,
учитывающую влияние окружающих молекул. Это влияние учитывает
лоренцева локальная полевая поправка, и с ее введением
напряженность поля увеличивается в 7з(ег + 2) (где ег —
диэлектрическая проницаемость, или я2), а выражение для показателя
преломления становится довольно сложным. Эту поправку ввели
независимо и одновременно Лоренц и Лорентц и получили
формулу Лоренц — Лорентца (я2—1)/(я2 + 2)р = Мх(со)/3рео, где
р — плотность. Поскольку N пропорциональна плотности,
правая часть уравнения от плотности не зависит, поэтому и
выражение в левой части, которое называют преломляемостью среды,
не зависит от р.
Необходимо заметить, что показатель преломления (и
преломляемость) среды зависит от частоты света, так как
поляризуемость зависит от частоты (последняя зависимость описана
в разд. «Поляризуемость»), и при оптических частотах она
обусловлена тем, что высокоэнергетические фотоны более
277
п
способны возбуждать низколежащие электронные состояния
молекул, чем фотоны низких энергий. Следовательно, с ростом
частоты (по мере ее приближения к частоте, на которой происходит
поглощение света молекулой) взаимодействие становится
сильнее и показатель преломления растет. По этой причине
показатель преломления голубого света превышает показатель
преломления красного света, и в результате в преломляющей среде
происходит дисперсия (спектральное разложение) пучка белого
света. Происхождение термина «дисперсия», который
обозначает зависимость какого-либо свойства от частоты, связано
с этой особенностью показателя преломления.
В непосредственной близости к частоте любой полосы
поглощения показатель преломления сильно меняется. Если известно,
как изменяется показатель преломления в соответствующем
диапазоне частот, можно получить спектр поглощения
молекулы, и наоборот. Формула, которая позволяет сделать это,
называется дисперсионным соотношением Крамерса — Кронига.
Дисперсионное соотношение связывает частичную зависимость
дисперсионного свойства (например, такую, как показатель
преломления) с поглощательными свойствами, и наоборот.
Преломляемость сложной молекулы представляет собой
сумму преломляемостей ее составных частей, поскольку
поляризуемость молекулы сама является аддитивным свойством.
Рекомендуемые источники. Более подробное изложение вывода квантово-
механического выражения для показателя преломления молекулы см. в гл. 11
[1]. Вывод лорентцевой локальной полевой поправки с помощью уравнения
Клауаиуса — Моссотти см. у Корсона и Лорана [98]. Этот же вопрос
обсуждается также Ван Флеком [407]. Простое введение в проблемы, связанные
с дисперсионным соотношением Крамерса — Кронига, можно найти в кн.
Сликтера [374] и Романа [343, 344]. Необходимая информация о показателях
преломления содержится в списке формул П.1 (см. «Поляризуемость»).
ПРЕЦЕССИЯ. В векторной модели атома и общей теории
углового момента угловой момент величины [/(/+ 1)]1/2й с z-ком-
понентой mb рассматривают как вектор длиной [/(/+l)]Vl
с проекцией т на ось z. Из принципа неопределенности
известно, что если z-компонента углового момента задана точно, то
х- и ^-компоненты не имеют определенных значений. Эту
ситуацию можно представить с помощью векторной диаграммы, если
множество возможных ориентации углового момента изобразить
в виде конуса (см. рис. П.9, см. также рис. У.1 и У.2). Где бы ни
лежал вектор на этом конусе, его 2-компонента имеет
одинаковую величину, а х- и у-компоненты могут принимать
произвольные значения. Этот конус называют конусом прецессии.
Однако, как можно было заметить, мы не говорили до сих пор, что
угловой момент на самом деле прецессирует вокруг оси z. По-
278
п
верхность конуса представляет собой множество возможных
ориентации углового момента, но на этом этапе мы не хотим
утверждать, что конец вектора движется вокруг отверстия
конуса. В отсутствие магнитного поля вектор покоится в
неопределенном положении на конической поверхности.
Если вдоль оси z направлено магнитное поле, состояния
с различными проекциями т будут иметь различные энергии,
поскольку с угловым моментом связан магнитный момент.
Энергия состояния с проекцией орбитального углового момента т
равна т\1ВВ и 2mixBB— для спинового углового момента. Можно
вычислить частоту, соответствующую этой энергии, если
разделить выражение для энергии на й; в результате получим со =
= т[хв/ВЬ. Векторная диаграмма — это символическое
изображение квантовомеханической картины рассматриваемого
явления, и ее можно немного усложнить, чтобы она позволяла учесть
энергию состояния. Для этого достаточно представить состояние
с энергией т\лвВ вектором, который вращается вокруг оси z
с частотой со (рис. П. 10). Это вращение и называется
прецессией, а его частота со — частотой ларморовской прецессии.
С уменьшением напряженности поля частота прецессии падает,
и в пределе — для нулевого поля — получается статическое,
неопределенное распределение векторов. Состоянию с
максимальной величиной \т\ соответствует самая быстрая прецессия, а
состоянию с т = 0 — полное отсутствие прецессии.
Противоположным знакам т соответствуют противоположные направления
прецессии.
Из изложенного видно, что скорость прецессии вектора
вокруг оси отражает силу его связи с этой осью. Такую точку
зрения можно распространить на случаи, когда энергия прецессии
обусловлена другими источниками, нежели магнитное поле.
Примером может служить случай спин-орбитальной связи:
векторы I и s связаны спин-орбитальным взаимодействием и дают
суммарный вектор j. При сильном спин-орбитальном
взаимодействии схема векторного сложения дает быструю прецессию s
вокруг 1 или, что эквивалентно, быструю прецессию 1 и s вокруг
суммарного вектора j (рис. П.11). В случае слабой связи
прецессия медленная, и связь может быть легко нарушена под
влиянием других факторов.
Рассмотренное графическое изображение прецессии служит
прекрасным примером того, как с помощью диаграмм удается
представить математические концепции квантовой механики.
Каждая деталь диаграммы представляет собой символическое
изображение какого-то аспекта квантовомеханического
описания явления. И это наводит на мысль, что математические
концепции квантовой механики сами являются символическим
языком, позволяющим описывать реальные явления.
279
Рис. П.9. Прецессия. Конус
показывает возможные, но не
поддающиеся определению
ориентации вектора.
Рис. П.10. Ларморовская
прецессия в присутствии
магнитного поля и ее связь с
векторной моделью.
а
Рис. П.11. Две точки зрения
на прецессию связанных
векторов. На рис. (а) наблюдатель
находится на 1 и следит за s
и j, на рис. (б) он находится
на j и следит за s и 1.
п
Упражнения. Что изображает конус прецессии в векторной модели
углового момента в отсутствие внешнего поля? Почему в этой модели
рассматривается именно конус? Как интерпретируется этот конус в том случае,
когда на систему действует магнитное поле? От чего зависит частота
прецессии? Рассчитайте частоту ларморовской прецессии для р-электрона в
магнитных полях напряженностью 1 Гс и 3 кГс. Какова ларморовская частота
прецессии спина электрона в поле напряженностью 3,4 кГс и спина протона
в поле 15 кГс? О чем обычно говорит скорость прецессии? Легко ли
нарушить связь между двумя угловыми моментами, которые быстро прецессируют
друг вокруг друга? Энергия спин-орбитального взаимодействия электрона в
атомах элементов второго периода приблизительно равна 50 см-1, вычислите
соответствующую частоту прецессии, оцените напряженность внешнего
магнитного поля, которое требуется, чтобы заметно нарушилась связь между
спиновым и орбитальным моментами и чтобы отдельные составляющие полного
момента ориентировались вдоль поля. Путем изменения относительной фазы
ориентации двух электронных спинов триплетное состояние может перейти в
синглетное. Так, если один спин прецессирует быстрее другого, его
ориентация сдвигается на 180° по отношению к другому и триплетное состояние
переходит в синглетное (см. разд. «Синглетное и триплетное состояния» и
рис. С.11). Предположим, что два электрона триплетной молекулы находятся
в полях, различающихся на 1 Гс из-за неоднородности поля либо из-за
воздействия на них различных внутренних полей. Определив соответствующие
частоты ларморовской прецессии, рассчитайте, с какой скоростью произойдет
переход молекулы в синглетное состояние. Существует ли, по-вашему, какая-
нибудь связь этого явления с взаимным превращением орто- и параводорода
(см. разд. «Ядерная статистика»)?
Рекомендуемые источники. Математическое описание векторной модели
и ее применение к атомным и молекулярным спектрам рассматриваются в
гл. 6 и 8 [1]. Применение к атомной спектроскопии изложено также Кэндле-
ром [89], Герцбергом [185], Уайтом [425] и Куном [229]. Понятие прецессии
широко используется при обсуждении магнитного резонанса (см., например, кн.
Мак-Лечлана «Магнитный резонанс» [2], Линден-Белла и Харриса [260], Кер-
рингтона и Мак-Лечлана [90], Сликтера [374]). Наглядным примером
нарушения связи двух прецессирующих векторов может служить эффект Пашена —
Бака (см. разд. «Пашена — Бака эффект»).
ПРИБЛИЖЕНИЕ СВЕРТКИ. Выражения, которые
возникают, когда для вычисления свойств молекул используют второй
порядок теории возмущений, обычно содержат суммы по всем
возбужденным состояниям системы, и, чтобы учесть их
надлежащим образом, необходимо знать энергию и волновую
функцию каждого возбужденного состояния. Как правило, ни
энергии возбужденных состояний, ни их волновые функции точно
не известны. Если точный ответ не требуется, например
достаточно оценить лишь порядок физической величины или получить
общее представление о зависимости какого-либо свойства от
различных характеристик молекулы, нередко используется
приближение свертки. Это приближение предполагает, что все
возбужденные состояния, которые смешиваются с основным
состоянием, имеют одну и ту же энергию. Справедливость такого
281
п
приема мы обсудим позднее, пока что укажем только его
преимущество: выражения вида £MQnNn^l(En — £0) (которые, со-
п
гласно списку формул В.6, играют важную роль в теории
возмущений) заменяются на (1/Д) £ MQnNn0, где Д — средняя энергия
п
возбуждения. Это выражение можно переписать по-другому,
если учесть, что оно имеет вид матричного произведения
(см. приведенные ниже упражнения), и поэтому выражение для
поправки второго порядка в теории возмущений сводится
к (AfW)oo/A. Теперь достаточно лишь вычислить среднее по
основному состоянию значение от произведения MN, и никаких
сведений о характере или энергиях возбужденных состояний не
требуется. Переход от суммы по M0nNn0 к (MN)qq представляет
собой математическую операцию свертки, которая и дает
название всему приближению.
Выясним, однако, к чему приводит такой прием. Погрешность
приближения свертки связана с неправомерностью
предположения, что все возбужденные состояния обладают одной
энергией. Когда все они лежат близко друг от друга (что в
некотором смысле имеет место в атоме водорода, см. рис. Г.6), такое
предположение вовсе не является нелепым. В других случаях
этот метод можно в какой-то мере оправдать, если величину Д
рассматривать как параметр, который связывает истинную
сумму с величиной (MN)oo\ параметр затем варьируется так,
чтобы правильно воспроизвести исследуемое свойство молекулы.
Упражнения. В чем трудность использования теории возмущений при
расчетах свойств молекул и каким образом приближение свертки позволяет
обойти эту трудность? При каких условиях это приближение оправдано?
Сумма по возбужденным состояниям не является в действительности
матричной суммой, так как, согласно списку формул В.6, в ней должно быть
пропущено основное состояние. Покажите, что на самом деле приближение
свертки приводит к выражению (MN)o0 — М0о#оо в числителе, но что даже с этой
поправкой необходимо знать только свойства основного состояния. В случае
когда М и N совпадают, рассмотрите, как связан числитель выражения для
поправки второго порядка с флуктуациями свойства М (свяжите числитель
со среднеквадратичным значением этого свойства). Обсудите применение
приближения свертки к вычислению электрической поляризуемости. Покажите, в
частности, что поляризуемость молекулы должна возрастать с увеличением
ее размеров.
Рекомендуемые источники. См. в [1] гл. 10 обсуждение и в гл. 11
применение приближения свертки к расчетам электрических и магнитных свойств
молекул. Другие области применения в общих чертах описаны Дэвисом [117],
который подчеркивает (стр. 47 [117]) замечание, сделанное Мак-Лечланом
[276] о пределах применимости приближения свертки.
282
п
ПРОГРЕССИЯ. В электронных спектрах молекул
возбуждение электрона сопровождается возбуждением колебаний, так
что вместо одной линии в спектре может наблюдаться сложная
полоса переходов. Прогрессия — это серия линий, которые
возникают при переходах с одного и того же колебательного уровня
одного из состояний (основного электронного состояния, если
речь идет о поглощении) на последовательные колебательные
уровни другого состояния. Так, прогрессия v" = 0 — это серия
"переходов, начинающихся с
колебательного уровня основного состояния
с квантовым числом v" = 0 и
кончающихся на колебательных уровнях
верхнего электронного состояния с v' = О,
1, 2 ... (рис. П. 12). Прогрессия v" =
= 1—это аналогичная серия
переходов, начинающихся с колебательного
уровня основного электронного
состояния с v" = 1. Линии в прогрессии
обозначаются (v', v"), следовательно,
прогрессия v" = 0 состоит из
переходов (0, 0), (1, 0), (2, 0) и т. д.
Рис. П.12 Прогрессия в
электронно-колебательном спектре.
Упражнения. Что такое прогрессия? Чем она отличается от секвенции?
Какую информацию можно извлечь из положения линий в прогрессии и
какую информацию можно получить, сравнивая между собой прогрессии с
v" = 0 и с v" = 1. Можно ли ожидать, что интенсивности этих прогрессий
одинаковы? Допустим, что энергия колебательного уровня основного
состояния зависит от v" следующим образом: со" (v" + 7а) + х"®>" (v" + Ч2)2 и
что аналогичное выражение определяет энергию возбужденного состояния;
рассчитайте частоты прогрессий с v" = 0 и v = i.
Рекомендуемые источники. См. гл. 10 [1]. Подробную информацию о виде,
анализе и формировании прогрессий можно найти в кн. Барроу [51], Уиф-
фена [424], Гейдона [158], Кинга [222] и Герцберга [187].
ПРОНИКНОВЕНИЕ ЭЛЕКТРОНОВ И
ЭКРАНИРОВАНИЕ ЯДРА. Проникновение и экранирование кажутся
неразлучными понятиями-близнецами. Действительно, они таковы
в своих проявлениях, но тщательное их изучение говорит о
другом. Рассмотрим ион натрия Na+, в котором ядро с довольно
высоким зарядом (Z=ll) окружено десятью электронами,
1
А
А 1
i
1 1 1
—гтт
!Tj
\\\ -
I 1
II /
II
1 1 П
ы и
II /Г
1 1 О
1 1 Ч
II 0
1 1 А
II
II 7
I i 0
II Л
1 I c
1 1 /
III
LLi—0
anz
«щмгд..
283
п
заполняющими оболочки К и L (конфигурация ls22s22p6).
Поместим теперь на Зэ-орбиталь еще один электрон. Поскольку у всех
s-орбиталей имеется неисчезающая плотность вероятности
вблизи ядра, этот электрон сумеет проникнуть между
окружающими ядро электронами и с малой, но отличной от нуля
вероятностью будет находиться вблизи ядра. Потенциальная энергия
электрона в этой области очень низкая, и поэтому такое
состояние имеет большую устойчивость. Если поместить электрон
вместо Зя-орбитали на Зр-орбиталь, он не сможет проникнуть так
близко к ядру (у любой из р-орбиталей узел совпадает с ядром)
Расстояние от ядра
Рис. П.13. Функции радиального распределения 35- и Зр-орбиталей (———) и
их проникновение в область электронной плотности К- и L-оболочек.
и попасть в область низкой потенциальной энергии (рис. П.13).
Итак, в рассмотренных примерах речь идет о проникновении
электронов. Можно понять, что s-орбитали имеют более низкую
энергию, чем р-9 d-орбитали, поскольку первые находятся ближе
к ядру.
Близость к ядру сама по себе еще недостаточна для того,
чтобы энергия была меньше. Так, в атоме водорода все орби-
тали с одним и тем же значением главного квантового числа
соответствуют одной и той же энергии независимо от того,
являются ли они S-, р- или d-орбиталями. Для того чтобы
проникновение электронов привело к желаемому эффекту, должны
быть нарушены особые свойства чисто кулоновского потенциала
ядра, которые обусловливают уникальные особенности атома
водорода. Это обеспечивается экранированием ядра, которое
создается остальными электронами, имеющимися в
многоэлектронных атомах (рис. П.13). В таких атомах потенциал,
действующий на добавляемый в нашем примере электрон, на малых
расстояниях от ядра представляет собой потенциал ядра с за-
284
п
рядом Ze (Z = 11), но на больших расстояниях, когда
рассматриваемый электрон находится вне атомного остова, потенциал
скорее похож на потенциал ядра с зарядом е, поскольку (Z— 1)
электрон экранируют весь положительный заряд ядра за
вычетом единичного заряда. Поэтому потенциал экранированного
ядра уменьшается с расстоянием гораздо быстрее, чем чисто
кулоновский, и особые свойства кулоновского потенциала
больше не проявляются. В результате s-, p- и d-электроны имеют
различные энергии.
Отсюда должно быть ясно, что различные орбитали имеют
различные энергии из-за эффекта экранирования, а порядок
расположения и расстояния между их энергетическими
уровнями зависит от того, насколько глубоко проникают в атомный
остов находящиеся на них электроны.
Упражнения. Какие орбитали просачиваются ближе всего к ядру? В чем
существенная роль экранирования? Чем объясняется тот факт, что обычно
s-электроны лежат ниже р-электронов, а р-электроны лежат ниже d-элек-
тронов? В каком порядке уменьшаются потенциалы ионизации s-, р- и
^/-электронов?
Рекомендуемые источники. Количественные характеристики и роль
проникновения и экранирования обсуждаются в гл. 8 [1]. Там же и в кн. Уайта
[425] и Герцберга [185] приводятся простые диаграммы для степени
просачивания различных внешних электронов через различные внутренние оболочки.
Константы экранирования рассматриваются в разд. «Слейтеровские атомные
орбитали». Эффекты проникновения и экранирования очень важны для
понимания структуры периодической системы элементов, поскольку они влияют
на свойства элементов. Эти вопросы обсуждают Паддефат [4] в
«Периодической таблице элементов» и Филлипс и Вильяме [317].
p
РАБОТА ВЫХОДА. Работой выхода для металла
называется энергия, необходимая для удаления находящегося в нем
электрона на бесконечность. Следует отметить аналогию этого
понятия с потенциалом ионизации: металлы с малой работой
выхода отдают электроны легче, чем металлы с большой
работой выхода.
Значения работы выхода для некоторых металлов даны
в табл. 25.
Работа выхода играет важную роль в фотоэлектрическом
эффекте и в термоионной эмиссии. Понижение работы выхода
при наложении внешнего электрического поля, обусловленное
суммарным влиянием этого поля и зеркального заряда,
индуцируемого при удалении электрона от поверхности металла,
называется эффектом Шоттки.
Рекомендуемые источники. Этот вопрос вполне доступно излагается
Солим аром и Уолшем [378]. Исчерпывающие таблицы работ выхода даны в § 9
кн. Грея [168]. См. также разд. «Фотоэлектрический эффект».
РАДИАЛЬНОГО РАСПРЕДЕЛЕНИЯ ФУНКЦИЯ.
Функция радиального распределения (р.р. ф.) определяет
вероятность того, что частица находится в каком-то месте сферического
слоя толщиной dr радиусом г. Для волновой функции,
зависящей только от расстояния, функция радиального распределения
Р(г) имеет вид 4rcr2\|)*(r)i|)(r), а вероятность нахождения в слое
радиусом г и толщиной dr — P(r)dr. Вид этой функции можно
установить, если вспомнить интерпретацию волновой функции
и рассмотреть показания зонда, чувствительного к присутствию
частиц. Вероятность нахождения частицы в элементе объемом
с/т, окружающем точку г, равна i|)*(r)i|)(r)dt, и показания зонда
с объемом детектора dx пропорциональны *ф*(г)-ф(г).
Предположим теперь, что детектор имеет форму тонкого сферического
слоя радиусом г и толщиной dr. Этот детектор погружен в атом
таким образом, что ядро совпадает с центром слоя, и показания
прибора отражают полную вероятность нахождения частиц
в любом месте этого слоя. Объем слоя равен 4rcr2dr, поэтому,
если волновая функция изотропна, показания пропорциональны
4яг2г|г* (г) i|> (r) dr, или P(r)dr. Это означает, что Р(г) дает
вероятность нахождения частицы где-либо в слое толщиной dr на
расстоянии г от центра.
Придуманный нами детектор ведет себя странным образом,
потому что его объем уменьшается, когда он зондирует области,
286
p
близкие к ядру (объем слоя пропорционален г2). Показания
прибора падают до нуля у ядра, где детектируемый слой
становится исчезающе малым. Кроме того, показания падают до
нуля на очень больших расстояниях, потому что там исчезающе
малы волновые функции. Поэтому волновая функция атома
водорода, экспоненциально убывающая с расстоянием от ядра,
приводит к р. р. ф., которая обращается в нуль на ядре, затем
возрастает, достигает максимума и в конце концов убывает до
нуля на бесконечном удалении (см. рис. Р.1). Эта кривая
показывает, какова вероятность нахождения электрона на данном
Радиус
Рис. Р.1. Функция радиального распределения для основного состояния атома
водорода.
расстоянии от ядра без учета угловых координат электрона.
Квадрат волновой функции дает вероятность найти электрон
в определенной точке, а число таких точек растет с расстоянием
как 4яг2.
Упражнения. Что такое функция радиального распределения (р.р.ф.)?
Чем отличается интерпретация р.р.ф. и квадрата волновой функции? Как
выглядят р.р.ф. электрона на Is- и 2я-орбиталях атома водорода? Используя
математические выражения для этих двух функций (табл. 15), изобразите
графически соответствующие р.р.ф. Применительно к анизотропным орбита-
лям, например 2р-орбиталям водорода, выведите выражение для наиболее
вероятного радиуса электронного распределения и обсудите природу р.р.ф.
Рекомендуемые источники. Р.р.ф. обсуждаются во всех книгах, где
рассматривается строение атома: Коулсон [105], гл. 2; Герцберг [185], разд. 1.4;
^айт [425], разд. 4.10; Кондон и Шортли [96], разд. V. 2. Функции
радиального распределения позволяют осмыслить многое в неорганической химии,
поскольку они лежат в основе обсуждения явлений проникновения электронов
287
p
и экранирования ядра и их следствий. Разобраться в этом вопросе помогут
кн. Паддерфата «Периодическая таблица элементов» [4], Пасса «Ионы
в растворе» [8], Эрншоу и Харрингтона «Химия переходных элементов» [14],
а также кн. Филлипса и Вильямса [317]. Аналитические выражения и
литературные ссылки для р.р.ф. ряда атомов можно найти у Мак-Глина, Ванкви-
кенборна и Киноситы [273]. См. также [184], где приведены таблицы
численных значений р.р.ф.
РАЗРЫХЛЕНИЕ. Разрыхляющими называются такие орби-
тали, заселение которых способствует диссоциации молекул.
Рассмотрим ls-орбитали двух сближающихся атомов водорода
и предположим, что эти волновые функции имеют
противоположные знаки. При сближении атомов область положительных
амплитуд одной орбитали вторгается в область отрицательных
амплитуд другой. В соответствии с законами волновой механики
интерференция волновых функций приводит к уменьшению
результирующей амплитуды в области перекрывания. Поскольку
квадрат амплитуды волновой функции определяет плотность
вероятности нахождения электронов, это уменьшение касается
и ее. При перекрывании орбиталей будет происходить
уменьшение электронной плотности в межъядерной области. Это
неблагоприятно отражается на энергии молекулы, так как
межъядерная область вносит наибольший вклад в связывающее
взаимодействие электронов с обоими ядрами. Энергия
образовавшейся в результате такого сближения молекулы превышает
энергию двух бесконечно удаленных атомов водорода, и
поэтому эта молекула нестабильна. Орбитали, ответственные за
такую нестабильность, называются разрыхляющими.
Рассмотрим влияние разрыхления еще на одном примере —
на примере двух сближающихся атомов гелия. На малых
расстояниях амплитуды ls-орбиталей одного знака интерферируют
друг с другом таким образом, что в межъядерной области
образуется связывающая молекулярная орбиталь. Амплитуды с
противоположными знаками интерферируют так, что они образуют
другую, разрыхляющую орбиталь. На двух полученных орбита-
лях должны разместиться четыре электрона: два займут
орбиталь с меньшей энергией и будут удерживать ядра вместе,
а два других расположатся на разрыхляющей орбитали и будут
ослаблять эту связь.
Действие двух спаренных электронов на разрыхляющей
орбитали приведет к тому, что отталкивание превысит
притяжение, обусловленное первой парой электронов. Поэтому молекула
Не2 оказывается нестабильной (хотя ион Не? в газовой фазе
имеет небольшую устойчивость). Рассмотренный пример
позволяет понять, почему два атома гелия, сталкиваясь, не
соединяются в молекулу. При их сближении образуются
связывающие и разрыхляющие орбитали, которые заселяются электро-
288
p
нами одновременно, что приводит к увеличению энергии
системы. Это увеличение энергии проявляется как сила
отталкивания. Такой ход рассуждений применим и к более сложным
атомам и молекулам и позволяет понять, почему
конденсированные вещества трудно проницаемы для других тел.
Упражнения. 1. Какое влияние на энергию молекулы оказывает заселение
ее разрыхляющей орбитали? Почему перекрывание атомных орбиталей с
противоположными фазами приводит к образованию разрыхляющих орбита-
лен? Почему частица Не^ менее стабильна, чем Не|+, а молекула Не2
нестабильна? Почему частицы Не|+ не существуют в естественных условиях
в больших количествах? Почему два атома неона не соединяются вместе при
их столкновении в газе? Каким образом следует применять рассмотренный
подход, чтобы ответить на такой же вопрос о метане и N2? Почему
пространство, заполненное конденсированным веществом, непроницаемо для
других тел?
2. Рассмотрите две ls-орбитали, находящиеся на двух протонах, которые
отстоят на расстояние R друг от друга, и, используя математическое
выражение для орбиталей, приведенное в табл. 15, постройте график амплитуды
для молекулярных орбиталей, полученных путем комбинации ls-орбиталей с
фазами одного знака и противоположных знаков. Начертите график
электронной плотности для случая, когда два электрона находятся на
связывающей орбитали, и для случая, когда два электрона находятся на разрыхляющей
орбитали. Постройте кривую разностной плотности, полученной вычитанием
двух плотностей: одна рассчитана для связывающей или разрыхляющей
орбитали, а другая в пренебрежении эффектами интерференции, т. е. в
предположении, что каждый электрон придерживается своего ядра. Проделайте
эти расчеты для трех разумно выбранных расстояний R и попытайтесь
связать полученные результаты с приведенными в данном разделе объяснениями.
В точных расчетах следует использовать нормированные орбитали, однако
для иллюстрации можно ограничиться более простыми вычислениями. Каким
образом отразится нормирование орбиталей на разностных плотностях?
Рекомендуемые источники. Эффекты разрыхления играют важную роль
при определении структуры молекул. См. Коулсон «Форма и структура
молекул» [10], Коулсон [105]. Орчин и Джаффе [307] подробно обсуждают вопрос
о роли перекрывания орбиталей. См. также гл. 9 [1]. Полезные советы по
методам вычисления интегралов перекрывания можно найти в кн. Мак-Глина,
Ванквикенборна, Киноситы, Кэрролла [273]. Подборка данных об энергиях
молекул имеется в кн. Ричардса, Уокера и Хинклея [337]. Карты разностных
плотностей приведены Коулсоном [10] и Дебом [120].
РАМЗАУЭРА ЭФФЕКТ. Когда пучок электронов
пропускают через аргон или другие благородные газы, при некоторых
энергиях электронного пучка рассеивающая способность газов
сильно падает; так называемый резонанс прозрачности
наблюдается при энергии около 0,7 эВ. Этот эффект можно понять,
учитывая волновую природу электрона, если вспомнить, что его
длина волны уменьшается с увеличением энергии (см. разд. «Де
Бройля соотношение»). Рассмотрим такую «электронную
289
p
волну», падающую на атомы. Вблизи атомов возникает
потенциал, отличный от окружающего вакуумного. В областях с
различной потенциальной энергией длина волны электрона
различна, см. разд. «Кинетическая энергия». Точно так же, как
падающий луч света отражается от области, в которой изменяется
показатель преломления, электронная волна отражается от внешней
поверхности атома, на которой потенциал резко меняется, и
отражается от его противоположной внутренней поверхности, где
потенциал опять падает до вакуумного уровня. Если толщина
слоя, в котором происходит изменение потенциала, равна одной
четверти длины волны электрона, волны, отраженные от этих
двух поверхностей, интерферируют, ослабляя друг друга, а
прошедшие волны интерферируют, усиливая друг друга. Отсюда
следует, что интенсивность электронов, отраженных атомами,
уменьшается, а интенсивность прошедших возрастает. (Это
явление аналогично происходящему в тонких пленках, наносимых
на поверхность линз для их просветления.)
Рекомендуемые источники. Полезное обсуждение резонансов прозрачно*
сти проведено Бомом [63], приложения к эффекту Рамзауэра см. в § 11.9 и
в § 21.54 [63], где объяснено, что этот эффект не вполне соответствует
рассмотренному здесь, по существу, случаю прямоугольной ямы. См. также кн.
Давыдова [119] и Мотта и Массе [293].
РЕЗОНАНС. Понятие резонанса заимствовано из
классической механики, поэтому полезно напомнить классическое
толкование этого термина. Если два маятника слабо связаны
между собой (например, если они подвешены на одной и той
же малоупругой оси, как на рис. Р.2), движение одного из них
оказывает влияние на движение другого. Если один маятник
первоначально находится в покое, а другой приводится в
движение, энергия второго маятника передается покоящемуся
маятнику, который тоже начнет колебаться и при этом будет
возвращать часть полученной энергии второму маятнику. Такие
притоки и оттоки энергии в отсутствие сил торможения
продолжаются бесконечно. Обмен энергией наиболее эффективен, если
у маятников одинаковые собственные частоты, и это условие
равенства частот называется резонансом. В таком случае говорят,
что энергия, или амплитуда, резонирует между двумя
связанными системами.
Можно представить себе такой тип связи маятников, когда
энергия системы снижается, если колебания маятников
совпадают по фазе, а самая энергетически невыгодная ситуация
наблюдается, если их колебания имеют противоположные фазы.
Примером такой связи служит гибкая ось: требуется меньше
энергии, чтобы подвесы обоих маятников повернули ее в том же
290
p
направлении при каждом качании, чем если бы закручивали при
этом ось в противоположных направлениях (рис. Р.2). Если
колебательные системы не связаны, соотношение их фаз не играет
никакой роли.
Рис. P.2. Резонанс двух связанных маятников. Энергетическое расщепление Л
максимально, когда собственные частоты совпадают.
Помня об изложенной выше классической картине резонанса
связанных систем, рассмотрим два примера квантовомеханиче-
ского резонанса. Первый из них — это взаимодействие света
с атомами или молекулами. Атом и электромагнитное поле
(световое излучение) играют роль двух связанных
колебательных систем. «Собственными частотами» атома являются
частоты переходов, а изменяя частоту падающего света, мы
настраиваем на них «собственную частоту» электромагнитного
поля, в котором находится атом. В какой-то момент частота
света приходит в соответствие с частотой перехода внутри
атома. Описываемая сложная система ведет себя подобно двум
связанным маятникам, и энергия светового поля передается
атому (т. е. наблюдается поглощение света) или, наоборот,
поступает в световое поле, если атом уже находится в
возбужденном состоянии (испускание света). Эти процессы наиболее
эффективно происходят в случае резонанса.
Другой пример резонанса относится к типу явлений, с
которыми мы встречаемся в разных теориях строения молекул, в
частности в теории валентных связей, которая пытается описать
истинное строение молекулы с помощью суперпозиции простых
291
p
канонических структур. Наиболее известным примером является
бензол. Попытаемся описать его строение суперпозицией двух
структур Кекуле. Предположим, что две структуры Кекуле
связаны, тогда их суперпозиция имеет меньшую энергию, чем
каждая из структур отдельно, если правильно подобраны их фазы
в суперпозиции (вспомните второй аспект классической
концепции резонанса). Каждая структура Кекуле может быть
уподоблена простому маятнику (симметрия этих структур
свидетельствует о том, что им соответствует одинаковая частота),
а наличие связи между ними означает, что их полная энергия
отличается от энергии изолированных структур. Природу связи
противогазе
г
электростатическое
взаимодействие
Рис. Р.З. Резонанс в теории валентных связей (для бензола). Е^ — энергия
резонанса.
между ними можно объяснить тенденцией я-электронов одной
связи С=С выталкивать соседние я-электроны в пространство
между двойными связями, в результате одна структура Кекуле
переходит в другую (рис. Р.З) (см. разд. «Бензол» и рис. Р.З).
Резонанс оказывает стабилизирующее влияние на молекулу
в том смысле, что связанная система обладает меньшей
энергией. Стабилизация сильнее, если собственные частоты
отдельных систем совпадают, и это объясняет, почему резонансная
стабилизация бензола так велика. Ионно-ковалентный резонанс
также оказывает стабилизирующее действие на молекулу, но,
поскольку энергии составляющих его структур различны,
резонанс получается неточным и эффект стабилизации меньше.
Рекомендуемые источники. Обсуждение концепции резонанса в теории
строения молекул см. в кн. Коулсона [105], Полинга [313], а также Эйринга,
Уолтера и Кимбалла [137]. Резонанс при поглощении света обсуждается в
гл. 7 [1]. Другие резонансные явления рассматриваются в разд. «Электронный
парамагнитный резонанс» и «Ядерный магнитный резонанс». Резонанс
прозрачности рассматривается в разд. «Эффект Рамзауэра». См. также
«Бензол», «Валентных связей теория» и «Энергия резонанса».
292
p
РЕЗОНАНСА ЭНЕРГИЯ. Ароматические молекулы
обладают большей стабильностью, чем можно было бы ожидать на
основании наивных представлений о чередовании в них простых
и двойных связей. Разность между истинной энергией, которая
учитывает стабилизацию молекулы в результате резонанса
между различными возможными структурами, и энергией
некоторого состояния системы, которое служит началом отсчета,
называется энергией резонанса (см. рис. Р.З). (При описании
аналогичного явления в теории молекулярных орбиталей
используется термин «энергия делокализации».)
Выбор начала отсчета является сложной проблемой, и
поэтому было выдвинуто несколько предложений. Самое простое
определение Хюккеля: энергия резонанса определяется как
разность энергий истинной молекулы и гипотетической молекулы
с локализованными двойными связями типа этиленовых. Так,
если известно, что я-электронная энергия бензола составляет
За + 4р, а энергия каждой из этиленовых связей равна а + р,
то энергия резонанса бензола должна быть равной р.
Трудности использования определения Хюккеля связаны с
произвольным выбором указанного начала отсчета. Не лучше
ли попытаться найти энергию несопряженной формы конкретной
рассматриваемой молекулы и использовать в качестве начала
отсчета ее? Почему бы не рассмотреть гипотетическую молекулу
циклогексатриена, вычислить его энергию и взять ее в качестве
начала отсчета для бензола? У такой эталонной молекулы
чередуются длинные и короткие связи, и можно считать, что при
ее использовании в качестве начала отсчета полностью
учитывается влияние сопряжения, делокализации или резонанса как
на я-, так и на а-электроны. Такой подход лежит в основе
определения энергии резонанса по Малликену — Парру.
Обычный метод измерения энергии резонанса заключается
в следующем. Определяют теплоту образования молекулы (для
этого, например, измеряют теплоту сгорания молекулы в
калориметрической бомбе и сравнивают ее с известными данными
о теплоте образования продуктов сгорания, которыми чаще
всего оказываются углекислый газ и вода). Затем сравнивают
найденное значение теплоты образования с полученным в
результате приписывания каждой связи в эталонной структуре
определенной энергии связи (энергии связей можно найти в
таблицах). Разность двух результатов дает энергию резонанса.
Например, у структуры Кекуле для бензола шесть связей С—Н,
три связи С—С и три связи С = С, следовательно, энергия этой
структуры равна 6£(С—Н) + 3£(С—С)+ 3£(С = С). Разность
между этой величиной и наблюдаемой теплотой образования
бензола дает резонансную стабилизацию структуры Кекуле
(150 кДж-моль-1). В настоящее время энергию резонанса часто
293
p
определяют по теплоте гидрогенизации, которая уменьшается
при наличии резонансной стабилизации (чем сильнее
стабилизирована молекула, тем ближе ее энергия к энергии полностью
гидрогенизированной молекулы). При таком определении
энергии резонанса теплота гидрогенизации молекулы, содержащей
три (несопряженные) двойные связи, должна быть втрое
больше, чем у циклогексена. Наблюдаемая теплота
гидрогенизации бензола меньше этой величины на 150 кДж-моль-1, и эта
разность рассматривается в качестве энергии резонансной
стабилизации структуры Кекуле.
Упражнения. Что такое энергия резонанса? Приведите два общепринятых
определения. Можете ли вы предложить другие определения? Как определить
энергию резонанса какого-либо углеводорода? Как изменится энергия
резонанса, если вместо ее определения по Хюккелю воспользоваться определением
Малликена — Парра? Экспериментально найденная теплота образования
молекулы нафталина составляет 8623 кДж-моль-1. Из других экспериментов
известны следующие значения энергии связей: С—С, 333 кДж-моль-1; С = С,
593 кДж-моль-1, и С—Н, 418 кДж-моль-1. Вычислите энергию резонанса для
нафталина. Используя метод молекулярных орбиталей Хюккеля, оцените
энергии резонанса для циклобутадиена и бутадиена-1,3.
Рекомендуемые источники. Этот вопрос подробно обсуждается Стрейтви-
зером [387], Салемом [353], Дьюаром [122], Маррелом и Харгетом [298], Мак-
Глином, Ванквикенборном, Киноситой и Кэрроллом [273]. Краткую таблицу
энергий резонанса можно найти в гл. 9 кн. [387] и гл. 4 [298]. Явлению
резонанса в органической химии посвящена кн. Уэланда [423].
РЕННЕРА ЭФФЕКТ. Эффект Реннера, или, правильнее,
эффект Реннера — Теллера, — это снятие вырождения
энергетических уровней в результате взаимодействия между
электронным и колебательным движением линейной молекулы, особенно
оФо
Рис. Р.4. Расщепление я-уровней при наличии эффекта Реннера, три
возможные ситуации.
294
p
трехатомнон линейной молекулы. Рассмотрим 11-состояние
линейной трехатомной молекулы; ее изгиб, приводящий к
треугольной конформации, по-разному влияет на две компоненты
молекулярной орбитали. Предположим для простоты, что я-ор-
биталь молекулы занята только одним электроном. При
линейной конфигурации молекулы орбитали пх и пу вырождены, но,
когда молекула изогнута, их энергии становятся неодинаковыми;
три возможных случая их поведения показаны на рис. Р.4.
Эффект Реннера проявляется в спектре молекул из-за того, что
энергетические уровни деформационных колебаний изменяются
в результате их взаимодействия с электронными уровнями.
Рекомендуемые источники. Эффект Реннера рассмотрен Герцбергом [188],
там же приведен ряд примеров и даны выражения для энергий электронно-
колебательных состояний молекул, в которых проявляется этот эффект. См.
также [222]. Количественное описание эффекта дано Реннером [334], Поплом
и Лонге-Хиггинсом [322] и Лонге-Хиггинсом [253].
РЕНТГЕНОВСКИЙ СПЕКТР. Рентгеновские лучи
представляют собой электромагнитное излучение с длиной волны
приблизительно 0,1 нм (1А). Основным способом их получения
(в земных условиях) является бомбардировка металлов
высокоэнергетическими электронами. Возникающее при этом
излучение имеет две составляющие: непрерывный фон, на котором
выделяется ряд острых пиков, собственно и образующих
рентгеновский спектр.
Непрерывный фон, называемый также тормозным излучением,
образуется в результате торможения бомбардирующих
электронов металлом, поскольку отрицательно заряженный электрон
при замедлении движения излучает электромагнитные волны.
Если его первоначальная энергия достаточно велика, фон может
содержать значительную коротковолновую составляющую.
Дискретные спектральные линии появляются в результате
переходов между уровнями остовных электронов в атомах, из
которых состоит вещество, если энергия бомбардирующего
электрона достаточна для выбивания электрона из глубокой
внутренней оболочки атома. Выбитый электрон может либо совсем
удалиться из атома, либо перейти на какой-то незанятый
верхний уровень. Образовавшуюся в остове дырку может занять
какой-либо другой остовный электрон, а разность энергии этого
электрона и дырки при этом выделится в виде
электромагнитного излучения. Когда выбитый из атома электрон покидает
/(-оболочку (я=1), образуется высокоэнергетическое
(«жесткое») рентгеновское излучение. Если дырку заполняет электрон
из L-оболочки (я = 2), образуется /Са-линия, если электрон из
Л1-оболочки, образуется /Ср-линия и т. д. Более мягкое
рентгеновское излучение (с большей длиной волны) возникает, когда
295
p
электрон выбивается из L-оболочки. При этом заполнению
дырки на L-уровне с переходами электронов из М- и N-оболочек
и т. д. соответствуют линии La и Lp и т. д.
В первом приближении частоту /(-излучения можно
определить по энергиям электронных уровней водородоподобного
атома с эффективным зарядом ядра (Z—1)е, учитывающим
наличие одного электрона, оставшегося в ls-оболочке.
Используя формулу для уровней энергии атома водорода, нетрудно
найти выражение для частоты /(-излучения: (Z—1)2#[(1/12) —
— (1/я2)]. Аналогичные выражения можно записать и для
других линий, но они должны содержать различные константы
экранирования а в выражении для эффективного заряда ядра
(Z — а) е. Из полученного выражения видно, что квадратный
корень из частоты пропорционален Z: эта закономерность
называется законом Мозли. В свое время закон Мозли послужил
основой для однозначного установления последовательности
химических элементов в периодической системе.
Упражнения. Какие виды рентгеновского излучения можно наблюдать
при бомбардировке металла высокоэнергетическими электронами? Что
является источником непрерывного фона излучения? С чем связано появление
острых пиков рентгеновского спектра? Каким переходам соответствуют эти
пики? Что является причиной /(а-излучения? Каким образом частота
рентгеновских лучей зависит от порядкового номера элемента? Почему для
расчета энергии /Са-излучения можно использовать модель водородоподобного
атома с зарядом ядра (Z—\)е? Рассчитайте максимально возможную
частоту непрерывного фона рентгеновского излучения при энергии пучка
бомбардирующих электронов 1 кэВ, 100 кэВ, 1 МэВ.
Ка-излучение меди имеет длину волны 1,541 А (154 пм), молибдена —
0,709 А (70,9 пм), определите порядковые номера этих элементов. Определите
длину волны /Са-излучения алюминия.
Рекомендуемые источники. Обзор по рентгеновским спектрам дан в
гл. XVI кн. Уайта [425], § IVC кн. Куна [229], § IV. 2 кн. Герцберга [185] и
§ 13.9 кн. Кондона и Шортли [96]. Таблицы частот рентгеновских переходов
даны в § 7 кн. Грея [168].
РИДБЕРГА ПОСТОЯННАЯ. Постоянная Ридберга
связывает энергию электрона в атоме водорода с его главным
квантовым числом п: Е = —R/n2. He следует забывать, что эта
постоянная зависит от массы электрона и от массы протона, и, если
вместо водорода рассматривается какой-либо другой одноэлек-
тронный атом (ион), необходимо ввести поправку,
учитывающую массу нового ядра. Поэтому мы будем обозначать
истинную постоянную Ридберга как Roo (см. список формул Р.1).
Постоянная Ридберга для атома водорода с учетом конечной массы
протона равна Rn=Roo/(l +tne/tnp)t Постоянную Ридбергадля
296
p
Список формул P. 1
Постоянная Ридберга
Постоянная Ридберга:
Я'оо = Ho'^V/8/г3 1,097373 • 107 м"1
1,097373-105 см-1
R'^c 3,289842-1015 Гц
Лоо = R'J* = Vf mec2a2 2,17972 • 10~18 Дж
1313 кДж-моль-1
13,60 эВ
Постоянная Ридберга для атома водорода:
#Н = *»/(! + melmp) 1.096776 • Ю7 м-1
1,096776-105 см-1
Величину R^ называют ридбергом (1 ридберг « 13,60 эВ). Заметим, что
1Ри равен половине атомной единицы энергии Хартри (Еа: 1£а = 2Ри).
любого другого ядра можно получить, если заменить в
приведенном выражении массу протона на массу этого ядра. Разные
значения для разных ядер получаются потому, что система
электрон — ядро вращается вокруг центра масс, который слегка
смещен относительно ядра из-за того, что его масса не
бесконечна, а масса электрона не равна нулю.
Рекомендуемые источники. См. разд. «Бора атом», где приводится
первый расчет постоянной Ридберга с использованием фундаментальных
физических постоянных, и разд. «Водорода атом», в котором изложены основы ее
квантовомеханического вывода. См. также литературу, рекомендованную в
этих разделах.
РИДБЕРГОВЫ УРОВНИ. Электронный переход в молекуле
может перевести электрон за пределы орбиталей валентной
оболочки вверх на какую-либо внешнюю орбиталь. Полученное
таким образом состояние называется ридберговым состоянием,
а электрон в этом случае занимает ридбергов уровень.
Примером может служить возбуждение 2/?-электрона атома фтора
в молекуле фтора на Зя-орбиталь или еще более высокий
уровень.
Ридберговы уровни представляют интерес потому, что
занимающий такой уровень электрон находится при этом на очень
диффузной орбитали. Фактически диффузность распределения
электрона так велика, что в двухатомной молекуле оба ядра
297
p
«кажутся» электрону одним. Это означает, что ридбергов
электрон очень слабо связан с ядерным остовом молекулы, который
поэтому способен вращаться, не увлекая за собой электрон;
см. случай связи Гунда (d) в разд. «Гунда случаи связи». Рид-
берговы электроны характеризуются малым квантовым
дефектом: они настолько диффузны, что почти не взаимодействуют
с внутренними электронами, и их волновые функции похожи на
волновые функции атома водорода.
Рекомендуемые источники. Ридберговы уровни и состояния обсуждаются
в § 10.3 кн. Кинга [222] и в § VI. 5 кн. Герцберга [187]. Исчерпывающее
рассмотрение этого вопроса дано Дунканом [126].
с
САМОСОГЛАСОВАННОГО ПОЛЯ МЕТОД. Метод
самосогласованного поля (ССП) для расчетов строения атомов и
молекул первоначально разработан Хартри, усовершенствован
Фоком и используется почти повсеместно. Исходным пунктом
метода является выбор пробных волновых функций для всех
электронов системы. Затем выбирается один электрон и
рассчитывается потенциал, в котором он движется, в предположении,
что распределение всех остальных электронов системы
«заморожено» и создает для рассматриваемого электрона определенный
потенциал. После этого находится решение уравнения Шредин-
гера для электрона, движущегося в поле с таким потенциалом,
и, следовательно, определяется новая волновая функция этого
электрона. Эта процедура повторяется для всех электронов
системы, при этом электроны на «замороженных» орбиталях
играют роль источников потенциала. В результате, когда цикл
завершен (рис. С.1), получается набор орбиталей для всех
электронов системы; как правило, эти орбитали отличаются от
исходного пробного набора. Затем весь цикл вычислений
повторяется, при этом в качестве исходных функций используются
усовершенствованные волновые функции, полученные в первом
цикле. В результате второго цикла получается новый набор
усовершенствованных функций. Эта последовательность
действий (итерационная процедура) продолжается до тех пор, пока
после подстановки очередного набора орбиталей и проведения с
ним цикла вычислений не получится этот же неизмененный набор
орбиталей. Такие орбитали называются самосогласованными.
1. Метод Хартри основан на предположении, что волновая
функция атома или молекулы может быть представлена в виде
произведения орбиталей, по одной для каждого электрона.
Поэтому выбирается некоторый набор функций, и с ними
осуществляется процедура самосогласования; когда после проведения
ряда циклов решение стабилизируется, получается функция
(которая все еще имеет вид произведения одноэлектронных орбита-
лей), описывающая электронное строение системы, а решения
уравнения Шредингера дают орбитальные уровни энергии. На
практике расчеты проводятся с применением уравнений Хартри
(см. список формул С.1), в которых потенциал, действующий
на каждый электрон, представляет собой сумму его
взаимодействий со всеми другими электронами. Считается, что
присутствие рассматриваемого электрона не вносит локального
299
с
искажения в электронное облако и что его влияние состоит в
искажении орбитали как целого. При проведении расчетов не
учитывается, что другие электроны стремятся держаться подальше
от интересующего нас электрона, т. е. не учитываются эффекты
корреляции электронов (см. рис. К.8).
2. В методе Хартри — Фока процедура самосогласования
поля проводится с учетом неразличимости электронов, как того
требует принцип Паули. Это означает, что допускается воз-
Начало цикла
Введение
пробных функций.
ФгФг,.,Фп
/уравнения Шредингера?
. для электрона, _
[описываемого функцией ф\
1 и находящегося в поле 1Г
.электронов е состояниях j
Получение
набора,
ф;, ф*...Фп
Сравнение с исходным набором и повторение цикла
до тех пор, пока отличие не станет несущественным
процесса с целью
пределе ни.
набора
Получение
набора
, Решение ^
/уравнения Шредингера>
для электрона
в состоянию фг
в поле электронов,
{находящихся в состояниях j
ФЖ-Фп
Конец процедуры
самосогласования
Рис. С.1. Цикл процедуры самосогласования.
можность обмена электронов. Для этого в качестве
многоэлектронной волновой функции берется слейтеровский детерминант,
который вводится в цикл самосогласования, изображенный на
рис. С.1. На каждый электрон действует кулоновский
потенциал, модифицированный обменной энергией (представляющей
собой поправку к кулоновской энергии отталкивания, которая
учитывает, что электроны с одинаковыми спинами стремятся
избегать друг друга). Уравнение Шредингера преобразуется
в систему уравнений Хартри — Фока (список формул С.1), в
которых первая часть потенциала соответствует кулоновскому
взаимодействию рассматриваемого электрона со всеми другими
электронами, а вторая часть — поправке, учитывающей энергию
обмена. В методе Хартри — Фока (ХФ) тоже не учитывается
энергия корреляции электронов. Неограниченный метод
Хартри—Фока (НХФ) допускает большую свободу при выборе
формы орбиталей, учитывая, что пространственная часть орби-
300
с
Список формул С.1
Самосогласованное поле
Уравнения Хартри:
[//остова (1) + 2 £ 7/ (1)J ^ (1) = £ е^; (1),
где кулоновский оператор определен следующим образом:
//(1)=J <*т2*/ (2) */ (2) (У/4яе0г12).
Суммирование по / ведется по заполненным орбиталям.
Уравнения Хартри — Фока (для заполненных оболочек)
Г/уостова (1) + 2 £ / (1) - J AT (1)1 t|). (1) = e,4>i (О.
L /=i /=i J
где обменный оператор определен следующим образом:
К, (1) *,(!) = J dT2l|>;(2)*( (2) 02/4яе0г12) ty (1);
*-Е[2е,-2/ +*„],
*. /
где ///-5^^(1)^(1)^.(1)
и
^«/=5^2^(1)^(1)^(0
— кулоновский и обменный интегралы.
тальной волновой функции может зависеть от того, какой у
электрона спин — а или р.
Атомные и молекулярные орбитали, которые используются
в качестве исходных в расчетах по методу ССП, обычно
являются линейными комбинациями атомных орбиталей. Точность
расчетов резко ухудшается, если исходные функции
оказываются недостаточно гибкими. Так может получиться, если их
взяли слишком мало (они образуют слишком малый базисный
набор). Для проведения расчетов принято использовать слей-
теровские атомные орбитали. Вычисление молекулярных
интегралов, однако, значительно упрощается, если используются
гауссовы орбитали, но для хорошего описания атомных
волновых функций необходимо использовать слишком много таких
орбиталей. Если расчеты по методу ССП представляются
слишком громоздкими, вводятся более или менее разумные
приближения. Такие расчеты называются полуэмпирическими
расчетами по методу ССП в отличие от априорных расчетов
301
с
неэмпирическим (ab initio) методом ССП, в которых после
выбора начальных волновых функций не используется никаких
приближений, кроме присущих самому методу Хартри — Фока.
В любом случае точность расчетов повышается, если учесть
конфигурационное взаимодействие.
Упражнения. Какова последовательность расчетов по методу ССП?
Когда прекращается итерационная процедура? Что составляет основу метода
Хартри? Чем пренебрегают при расчетах по методу Хартри? Каковы
основные особенности метода Хартри — Фока, почему он более совершенен, чем
метод Хартри? Почему методом ССП Хартри — Фока нельзя получить
точные атомные волновые функции и энергии? Что такое неограниченный
метод Хартри — Фока ССП? Как расшифровать сокращение ХФ ССП ЛКАО
МО и какую методику расчетов оно обозначает? В чем различие между
расчетом по методу ССП ab initio и полуэмпирическим расчетом? Какие ошибки
вносит использование слишком малого базисного набора, что означает
выражение «базисный набор»? Покажите, что при расчетах методом ССП
необходимо учитывать интегралы отталкивания электронов и обменные
интегралы, в которые входят орбита ли не более чем четырех атомных центров.
Почему в методе Хартри — Фока не нужно разрабатывать способы расчетов
5-центровых интегралов?
Рекомендуемые источники. См. гл. 8 [1]. Простое введение в методы
расчетов энергии атомов и молекул дано Ричардсом и Хорсли [336] и Мак-Гли-
ном, Ванквикенборном, Киноситой и Кэрроллом [273]. Классический обзор
расчетов строения атомов, которые слишком сложны, если не прибегать к
ЭВМ, приведен самим Хартри [175]. В книгах Ричардса и Хорсли и Мак-
Глина и др. рассматриваются примеры таких расчетов. Полуэмпирические
методы описаны в разд. «Хюккеля метод».
СВЕРХСОПРЯЖЕНИЕ. - Перекрывание а- и я-орбиталей,
как, например, перекрывание орбиталей метальных а-связей
С—Н с ароматическими я-орбиталями в толуоле, называется
сверхсопряжением или эффектом Бэйкера — Натана.
Сверхсопряжение с метильной группой, которая выступает в качестве
донора электронов, приводит к увеличению электронной
плотности в орто- и яа/?а-положениях и влияет на реакционную
способность ароматического соединения.
При квантовомеханическом описании три а-связи метильной
группы или, что эквивалентно для наших целей, три ls-орбитали
водорода рассматриваются как набор, из которого можно
сконструировать три групповые орбитали (рис. С.2). Комбинация
этих трех орбиталей с одинаковыми фазами образует орбиталь,
охватывающую все три атома и имеющую цилиндрическую
симметрию относительно направления связи С—С, поэтому она не
дает никакого результирующего перекрывания с ароматической
я-системой. Из трех атомных орбиталей можно образовать еще
две другие комбинации; обе они имеют по одной узловой плос-
302
с
кости. В одной комбинации узловая плоскость перпендикулярна
кольцу, а в другой — совпадает с плоскостью ароматического
кольца. Следовательно, последняя комбинация имеет ту же
симметрию по отношению к связям С—С, что и я-орбитали атомов
углеродного кольца. Она может перекрываться с ними, образуя
очень слабую связь, что приводит к смешению электронов
связей С—Н с я-электронами.
Рекомендуемые источники. См. разд. 2.3 кн. Коулсона [105] и разд. 5.7 кн.
Стрейтвизера [387]. См. также Маррел, Кеттл и Теддер [299] и Салем [358].
Рис. С.2. Групповые орбитали радикала СН3. Только в одном случае (в)
имеется ненулевое перекрывание с я-орбиталью ароматического кольца
толуола.
Обсуждение возможности существования и следствия сверхсопряжения
описаны в кн. Бейкера [46] и в материалах конференции, посвященной этому
вопросу [47]. Групповые орбитали обсуждаются Мак-Глином, Ванквикенбор-
ном, Киноситой и Кэрроллом [273], см.. в § 2.8. Эффект сверхсопряжения
убедительно подтверждается результатами изучения электронного
парамагнитного резонанса: см. Саймоне [391], Айског [43] и Болтон, Керрингтон и Мак-
Лечлан [64].
СВЕРХТОНКИЕ ВЗАИМОДЕЙСТВИЯ. Сверхтонким
называют взаимодействие между ядром и электроном, не являющееся
точечным кулоновским взаимодействием. Различают
электрические и магнитные сверхтонкие взаимодействия: первые
возникают из-за того, что ядро может иметь электрический квадру-
польный момент, вторые — из-за того, что оно может иметь
магнитный дипольный момент. Рассмотрим эти взаимодействия
отдельно.
Магнитные сверхтонкие взаимодействия. Ядро с ненулевым
спином обладает магнитным дипольным моментом. Этот диполь
303
с
создает вокруг себя магнитное поле, с которым могут
взаимодействовать магнитные моменты электронов. Рассмотрим
молекулу, содержащую один неспаренный электрон. Этот электрон
обладает спиновым магнитным моментом, который
взаимодействует с магнитным диполем ядра посредством обычного ди-
поль-дипольного механизма. Энергия взаимодействия зависит
от относительной ориентации спинового магнитного момента
и магнитного диполя ядра (точно так же, как в случае двух
маленьких брусочков-магнитов), а также от относительного
расположения электронного и ядерного спинов.
Предположим, что на рассматриваемую систему
воздействует внешнее магнитное поле (как в экспериментах по
электронному парамагнитному резонансу), которое достаточно
сильно, чтобы удерживать оба интересующих нас магнитных
момента параллельно друг другу. Тогда энергия магнитного
взаимодействия определяется, как в классической задаче о
взаимодействии двух параллельных диполей: она зависит от г как
г-3, а от угла 0 как 1 — 3cos29 (рис. С.З и список формул Д.1).
Если неспаренный электрон занимает s-орбиталь атома с
магнитным ядром, то он распределен вокруг ядра изотропно
(рис. С.4,а); результирующее действие магнитного поля ядра
на электрон равно нулю, и в этом случае диполь-дипольное
взаимодействие отсутствует. Если электрон занимает /?-орби-
таль атома с магнитным ядром, его распределение вокруг ядра
неизотропно и в одних областях магнитного поля ядра электрон
испытывает более сильное воздействие, чем в других (рис. С.4, б).
В этом случае энергия взаимодействия отлична от нуля.
При заданной ориентации спина электрона (определяемой
квантовым числом ms) энергия взаимодействия зависит от
направления ядерного спина, т. е. от /Я/. Так как ядро со спином /
может иметь 2/ + 1 ориентации, электрон может испытывать
влияние одного из 2/ + 1 различных значений локального
магнитного поля. В экспериментах по электронному
парамагнитному резонансу это приводит к расщеплению спектра на 2/ + 1
линий с характерным интервалом, определяемым силой
взаимодействия двух магнитных диполей. Если молекула (радикал)
вращается относительно внешнего магнитного поля, а моменты
сохраняют свои первоначальные проекции ms и тъ электрон
испытывает действие различных областей сверхтонкого поля
ядра, так как /^-орбитальное распределение перемещается,
следуя за вращающимся ядерным остовом молекулы. Отсюда
следует, что диполь-дипольное сверхтонкое взаимодействие
анизотропно (зависит от ориентации молекулы). Если вращение очень
быстрое, как в том случае, когда молекула находится в
жидкости, оно заставляет электронный спин испытывать действие
всевозможных областей сверхтонкого поля ядра: результат такого
304
с
сферического усреднения равен нулю, поэтому сверхтонкая
структура спектра пропадает.
Сверхтонкие поля в месте расположения электрона могут
достигать нескольких десятков гаусс. Типичные значения их на-
пряженностей даны в табл. 9. Приведенные в таблице данные
Рис. С.З. Диполь-дипольное Рис. С.4. Поле магнитного момента ядра:
взаимодействие параллельных а — s-электрон испытывает действие
моментов. положительно и отрицательно
направленного поля в равной степени; б — р-
электрон в большей степени
испытывает влияние положительно
направленного поля, чем отрицательно
направленного (при указанной ориентации).
относятся к /^-электрону, полностью принадлежащему атому
с магнитным ядром. Поэтому если эксперимент дает меньшее
значение, то его отношение к табличному значению позволяет
оценить вклад атомной /7-орбитали в молекулярную орбиталь,
делокализованную по всей молекуле.
Хотя приведенные выше соображения приводят к выводу, что
магнитная сверхтонкая структура спектра электронного
парамагнитного резонанса в жидком растворе исчезает, эксперимент
показывает, что этот вывод далек от истины. Обычно
расщепление сохраняется, и во многих случаях оно значительно больше,
305
с
чем описанная выше анизотропная сверхтонкая структура
(см. рис. Э.7). Ответственно за это расщепление контактное
взаимодействие Ферми. Предшествующее обсуждение
основывалось на приближении, согласно которому ядро создает ди-
польное поле. Это приближение было бы вполне правильным,
если бы ядро имело исчезающе малые размеры или если бы
электрон не мог приблизиться настолько близко к ядру, чтобы
обнаружились конечные размеры последнего. На самом же деле
ядро имеет конечные размеры (его диаметр порядка 10~14 м),
и, если электрон находится на s-орбитали, он может
приблизиться к ядру вплотную. При этом оказывается, что поле ядра
не является чисто дипольным (см. рис. К.7). Будем считать, что
электрон действительно проникает в ядро, и заменим ядерный
магнитный момент эквивалентным круговым током с тем же
радиусом, что и ядро. При сферическом распределении
электрона за пределами кольцевого тока поле, действующее на
электрон, усредняется и обращается в нуль, но внутри
кольцевого тока поле имеет всюду одинаковое направление, никакой
компенсации не происходит, и спиновый магнитный момент
взаимодействует с ненулевым средним значением поля. Это
взаимодействие изотропно, так как не зависит от ориентации
остальной части ядерного остова молекулы. Оно характерно
только для 5-электронов, поскольку все другие орбитали имеют
узел в ядре атома и не могут проникать в ядро.
Контактное взаимодействие Ферми может быть очень
большим. Типичные значения напряженностей магнитных полей,
действующих на электрон посредством этого механизма, также
приведены в табл. 9. Так как контактное взаимодействие
характерно для s-орбитали, величину наблюдаемого изотропного
расщепления можно использовать для определения вклада s-орби-
талей в различные молекулярные орбитали.
Допустим теперь, что внешнее магнитное поле выключено.
При этом в молекуле возникнет конкуренция различных типов
магнитных взаимодействий. Ядерный магнитный момент может
взаимодействовать с магнитными полями различных источников,
имеющихся в молекуле, а в спектре (в частности, во
вращательном) энергия этого взаимодействия будет проявляться как
расщепление линий. Молекулы с разными состояниями ядерного
спина будут давать немного сдвинутые спектры, поэтому
наблюдаемый спектр должен содержать линии всех различных
молекул образца. Другими источниками магнитного момента в
молекуле являются электронный спин (который теперь
взаимодействует с ядром по-другому, так как отсутствует внешнее
магнитное поле, которое удерживало бы его параллельно некоторой
оси в лабораторной системе отсчета), орбитальный магнитный
момент электрона и молекулярный магнитный момент.
306
с
Электрические сверхтонкие взаимодействия. Ядро не может
иметь электрического дипольного момента (это связано с его
свойствами симметрии), но может иметь электрический квад-
рупольный момент, если спиновое квантовое число ядра /
больше или равно 1. Наличие электрического квадрупольного
момента приводит к асимметрии распределения заряда в
молекуле. Два возможных варианта распределения показаны на
рис. С.5. В первом случае в полярных областях ядра (по
отношению к направлению спина) имеется избыток положительного
заряда, а в экваториальной области — компенсирующая зона
отрицательного заряда, и, таким образом, распределение
положительного заряда имеет форму вытянутого эллипсоида
вращения. Во втором случае в полярных областях ядра находится,
©распределение (^п\
положительного Vy
заряда
Рис. С.5. Взаимодействие
электрического
квадрупольного момента ядра с
градиентом электрического ориентация ориентация
поля. с низкой энергией с высокой энергией
наоборот, избыток отрицательного заряда, а распределение
положительного заряда имеет форму сплюснутого эллипсоида
вращения. Электрический квадрупольный момент
взаимодействует не с самим электрическим полем, а с его градиентом.
Поэтому, если в месте нахождения квадрупольного ядра
существует градиент электрического поля, энергия молекулы
зависит от ориентации ядра в молекулярном остове, и возникает
еще одно сверхтонкое взаимодействие.
При каких условиях появляется градиент электрического
поля на каком-либо ядре молекулы? Если окружающие ядро
электроны занимают s-орбитали или образуют заполненную
оболочку, градиента нет. В противном случае возможен очень
сильный градиент поля (см. рис. С.5 и рис. К.2). Следовательно,
спектральные данные о величине электрического квадрупольного
взаимодействия позволяют судить о гибридизации орбиталей,
занятых окружающими ядро электронами (т. е. о величине /?-орби-
тального характера окружающих электронов). Однако при этом
возникают некоторые осложнения. Одно из них заключается
в том, что валентные электроны могут вызывать возмущение во
внутренних заполненных оболочках. Искажение внутренних
оболочек вызывает градиент поля на ядре и поэтому увеличивает
307
с
или уменьшает степень квадрупольного взаимодействия — так
называемые эффекты дезэкранирования или экранирования
Стернхеймера. Изучение квадрупольного взаимодействия
позволяет оценить распределение зарядов в окрестности
квадрупольного ядра в предположении, что молекула состоит из
совокупности точечных зарядов (см. разд. «Дипольный момент»).
Таким путем можно определять степень ионности связей.
Упражнения. Что означает термин «сверхтонкое взаимодействие»? Какие
существуют типы сверхтонких взаимодействий? Какова природа магнитного
взаимодействия между электронным и ядерным спинами? Почему
взаимодействие должно исчезать (при наличии внешнего поля), когда электрон
находится на s-орбитали или когда он находится на р-орбитали, но молекула
быстро вращается в жидкости? Какую информацию можно получить, зная
величину анизотропного сверхтонкого взаимодействия? Почему на самом
деле в жидком растворе вазимодействие не исчезает? О чем свидетельствует
контактное взаимодействие Ферми? В радикале N02 сверхтонкое
взаимодействие с ядром азота составляет 55 Гс для изотропной компоненты и 13 Гс
для максимума анизотропной компоненты; каковы вклады атомных s- и
р-орбиталей азота в молекулярную орбиталь, занятую неспаренным
электроном? (Используйте табл. 9). Что является причиной электрического
сверхтонкого взаимодействия? Какие ядра могут обладать квадрупольным
моментом и что это значит? Какое свойство электронов обусловливает их
взаимодействие с квадрупольным моментом ядра? Какую информацию можно
получить при изучении этого взаимодействия? Что усложняет интерпретацию
опытных данных?
Рекомендуемые источники. Более детальное рассмотрение магнитных
сверхтонких взаимодействий см. в [1], гл. 11. Использование их в методах
электронного парамагнитного резонанса и ядерного магнитного резонанса
(особенно для определения констант спин-спинового взаимодействия)
описано Мак-Лечланом в кн. «Магнитный резонанс» [2]. См. также Линден-Белл
и Харрис [260], Керрингтон и Мак-Лечлан [90], Эткинс и Саймоне [39], Эйс-
ког [43], Сликтер [374] и Абрагам и Блини [28]. Роль сверхтонких
взаимодействий в спектрах и структурная информация, для получения которой они
могут быть использованы, описаны Сагденом и Кеннеем [388], Герцбергом
[187], Таунсом и [Павловым [399]. Основы Еопроса обсуждаются Фрименом и
Франкелем [155]. Магнитные и электрические свойства ядер приведены в
табл. 17.
СВОБОДНАЯ ВАЛЕНТНОСТЬ. Атом может соединяться
со своими соседями связями различного порядка (см. разд.
«Порядок связи»). Свободная валентность представляет собой
разность между максимально возможным полным порядком связи
атома и его полным порядком связи в конкретном соединении и,
следовательно, отражает неполноту насыщения валентных
возможностей данного атома. Если не принимать в расчет тройные
связи, для углерода максимальный полный порядок связи равен
4,73 (или 3 + Уз). Например, в молекуле бензола каждый атом
углерода имеет связь порядка 1 с соседним атомом водорода,
308
с
две а-связи с соседними атомами углерода и две я-связи но-
2
рядка у; поэтому полный порядок связи каждого атома
углерода равен 4,33, а свободная валентность равна 0,40. В
бутадиене порядки связей С—С в цепочке равны 1,89; 1,45 и 1,89,
поэтому свободные валентности равны 0,84 для двух внешних
атомов и 0,39 для каждого атома из внутренней пары.
В ранней теории парциальных валентностей Тиле величина
свободной валентности рассматривалась как количественная
мера, которая позволяет сделать некоторые предсказания об
относительной реакционной способности атомов в сопряженных
цепочках. Тиле полагал, что, поскольку два атома углерода
могут удерживаться вместе одной связью, каждый атом углерода
в цепочке имеет парциальную валентность, которая могла бы
быть использована в реакциях: остающаяся часть двойной связи
является избыточной. Вместе с тем он считал, что парциальные
валентности двух центральных атомов углерода в бутадиене
насыщаются, а свободными остаются только парциальные
валентности внешних атомов. В настоящее время мы судим о
реакционной способности соединений, исходя из представлений о
различных свободных валентностях атомов. Свободные валентности
имеются также на поверхностях металлов, и одним из следствий
этого является существование катализаторов, играющих
исключительно важную роль в химии.
Рекомендуемые источники. См. кн. Коулсона [105] и Стрейтвизера [387],
а также [115, 328]. Таблицы порядков связи даны Коулсоном и Стрейтвизе-
ром [НО]. Обсуждение реакционной способности молекул с использованием
понятия свободной валентности, а также других величин см. в кн.
Стрейтвизера [387]. Каталитическая активность обсуждается Бондом в кн.
«Гетерогенный катализ; принципы и приложения» [18]. Почему максимальный
порядок связи углерода равен 4,73? Ответ на этот вопрос можно найти у Моф-
фита [285].
СВЯЗИ ПОРЯДОК. Порядок связи представляет собой меру
простого, двойного или тройного характера связи. В теории
валентных связей он определяется относительными вкладами
простых, двойных и тройных связей в основные валентные
структуры. В теории молекулярных орбиталей, которая оперирует
более общим определением, понятие порядка связи несколько
усложняется. В основу такого определения (этого достаточно
для качественного понимания) положен учет компенсации
эффектов занятых электронами связывающих и разрыхляющих
орбиталей. Так, в Н2, где полностью занята одна а-связывающая
МО, порядок а-связи равен единице, в Не2, где полностью заняты
а-связывающие МО и соответствующая разрыхляющая орби-
таль, порядок связи равен нулю. В этилене полностью заняты
а- и я-связывающие МО, поэтому порядок связи С—С равен 2
309
с
(двойная связь), а в кислороде действие одной заполненной я-
связывающей орбитали компенсируется действием одной
разрыхляющей я-орбитали (подробности см. в разд. «Теория
молекулярных орбиталей»), и в результате одна а- и одна я-связь
дают порядок 2. Эти представления можно теперь несколько
усложнить и ввести дробные порядки связи.
В приближении ЛКАО теории молекулярных орбиталей
образование связи объясняется тем, что атомные орбитали
соседних атомов перекрываются и, интерферируя, усиливают друг
друга. Если принять, что коэффициент при орбитали атома А
равен 6'а, а при орбитали атома В — ев, то вклад образующейся
молекулярной орбитали в связь пропорционален произведению
сАсв. При этом порядок связи между А и В определяется как
сумма сАсв по всем занятым молекулярным орбиталям. Если
для какой-то отдельной молекулярной орбитали и сА, и ев
большие, ее вклад в полный порядок связи оказывается большим
(но не может превысить единицы), если сА и ев имеют
противоположные знаки, что соответствует разрыхляющему
взаимодействию между А и В, произведение отрицательно; оно
вычитается из общего результата и поэтому уменьшает порядок
связи. Например, в бензоле каждая связь С—С имеет вклад 2/3 от
я-орбиталей и 1 от а-орбиталей, поэтому каждая связь имеет
порядок 12/з. Связь С—С в этане имеет порядок 1, в этилене —
2, а в ацетилене — 3, что согласуется с обычными химическими
представлениями о порядке связи.
Количественное определение порядка связи используется
главным образом для оценки длин связей, особенно между
атомами углерода. Между длиной R и порядком бес связей С—С
установлено приближенное эмпирическое соотношение,
согласно которому Rqc = 1,665 — 0,1398(1 + бес), где Rcc измеряется в
ангстремах (см. табл. 2). При использовании этого соотношения
следует принимать во внимание различную гибридизацию
атомов, образующих связь; в результате такого учета оказывается,
что при фиксированном порядке связи длина ее уменьшается на
0,04 А при переходе от spz- к 5/?2-гибридизованным орбиталям и
еще на 0,04 А при переходе к s/7-гибридизованным орбиталям.
Понятие порядка связи используется также при определении
свободной валентности.
Упражнения. Каково определение порядка связи в теории валентных
связей? Вычислите на основании этого определения порядок связи в бензоле
сначала в предположении, что вклад дают только структуры Кекуле, а
затем в предположении, что 20% общей структуры приходится на долю
структур Дьюара. Каково определение порядка связи в теории молекулярных
орбиталей? Каков порядок связей в Н2 и Не2? Каков порядок связи в Hj? На
основании данных о коэффициентах в молекулярных орбиталях, приведенных
310
с
на рис. Б.6, вычислите порядок связи для бензола, его аниона и катиона.
Оцените длину углерод-углеродных связей в нафталине, где порядки я-связей
имеют следующие значения: 0,725 (С 1—С2); 0,603 (С2—СЗ); 0,554 (С 1—С9) и
0,518 (С9-С10).
Рекомендуемые источники. См. кн. Коулсона «Форма и структура
молекул» [Ю] и [105]. Полезное и подробное обсуждение приведено в разд. 6.7
кн. Стрейтвизера [387]. См. также доклады Коулсона [104] на симпозиуме
памяти Кекуле и кн. Пилара [318].
СЕКВЕНЦИЯ. Прежде всего убедитесь в том, что вы
понимаете смысл выражения «прогрессия колебательной
структуры электронного спектра
молекулы». Секвенцией называется серия
линий, имеющих постоянную разность
значений колебательных квантовых
чисел верхнего и нижнего электронных
состояний. Если верхнее колебательное
квантовое число обозначить v', а
нижнее v", то линия, у которых v7 — v"=0,
составляют одну секвенцию, линии с
v7—v"==—1 другую, линии с v7—v"=
= +1 третью и т. д. (см. рис. С.6).
Если бы колебательные уровни в
обоих электронных состояниях были
1
л»-/
,:
1'
1 !
1
III 1
1 1
i
1
III
||| |
1
III
Pi
г
II;
Г
Г
РЛ>-0
¥.
1
III
1
5»'
4
3
г
/
о
6V"
5
4
J
2
/
Рис. Сб. Две различные секвенции.
жж
эквидистантными, все линии секвенции имели бы одинаковую
частоту. Однако, поскольку ангармоничность колебаний
нарушает эквидистантность состояний чистого гармонического
осциллятора, расстояние между линиями секвенции дает информацию
об отклонении кривой потенциальной энергии молекулы от
идеальной параболической формы.
Упражнения. Что такое секвенция и чем она отличается от прогрессии?
Какую информацию можно извлечь, зная положение линий в секвенции?
В каком случае могут совпасть все линии секвенции? Можно ли ожидать,
что интенсивность всех линий секвенции будет одинаковой? Если этого
ожидать нельзя, то что оказывает определяющее влияние на интенсивность?
Допустим, что колебательная энергия основного состояния зависит от v"
следующим образом: Е (v") = со" (v" + V2) -f x'e®" W + х1^" и что
аналогичное выражение описывает колебательною энергию возбужденного
электронного состояния; рассчитайте частоты секвенций с v' —v" = 0, —1. +1.
311
с
Рекомендуемые источники. См. гл. 10 [1]. Подробную информацию о
виде, анализе и формировании секвенций можно найти у Барроу [51], Уиффена
[424], Гейдона [158] и Герцберга [187, 188].
СЕРИЯ. Частоту любого спектрального перехода можно
выразить в виде разности двух величин (термов), каждая из кото-
Рис. С.7. S-, Р-, D-, F-серии в спектре атомарного натрия.
рых представляет собой энергию состояния атома или молекулы.
Обозначим такие термы Тп, где п—индекс, который обычно
рассматривается как квантовое число или набор квантовых
чисел системы. Частота каждого перехода из состояния п в
набор других состояний пг равна Тп'—Т„, а последовательность
линий в спектре с фиксированным п и переменным п!
называется спектральной серией.
В качестве одного из наиболее известных примеров можно
привести спектральные серии щелочных металлов, которые
соответствуют переходам единственного имеющегося у их атомов
валентного электрона. Переходы, в результате которых электрон
с р-орбитали опускается на s-орбиталь (т. е. попадает в основ-
312
с
ное состояние), дают так называемую главную серию линий
(principal, отсюда латинское р в названии р-орбитали). Серия,
образованная линиями излучения, соответствующими переходам
с высших s-орбиталей на самую нижнюю /?-орбиталь, называется
резкой (sharp, отсюда s в названии s-орбитали). Переходы
электронов с верхних возбужденных d-орбиталей на самую нижнюю
р-орбиталь дают так называемую диффузную серию (diffuse,
отсюда d в названии d-орбитали). Если электроны с /-орбита-
лей переходят на самую нижнюю rf-орбиталь, получается
«фундаментальная» серия (fundamental, отсюда / в названии /-ор-
битали). Эти переходы изображены на рис. С. 7.
Рекомендуемые источники. Дополнительную информацию о сериях
можно найги в гл. 8 [1]. Структуры атомных спектральных серий описаны Уайтом
[425], Кингом [222], Куном [229] и Кондоном и Шортли [96]. Правила отбора,
приводящие к построению рис. С.7, описаны в соответствующем разделе.
Молекулярные серии обсуждаются Кингом [222], Барроу [51], Уиффеном [424] и
Герцбергом [187, 188].
СИЛА ОСЦИЛЛЯТОРА. Сила осциллятора / является
мерой интенсивности перехода и определяется отношением
действительной интенсивности к интенсивности излучения электрона,
рассматриваемого как трехмерный гармонический осциллятор.
Такой идеальный электрон имеет силу осциллятора, равную
единице. Оказывается, что для сильно разрешенных переходов
величина / также приближается к единице. Силы осциллятора
для некоторых типов переходов указаны в табл. 8.
Силу осциллятора можно установить теоретически либо
экспериментально. Важность этого понятия определяется не только
тем, что оно используется для классификации различных
переходов по их интенсивности, но и тем, что оно связывает теорию
с экспериментом.
1. В основе теоретических расчетов силы осциллятора
электрического дипольного перехода лежит выражение / = 4eotnhvB/e2t
где В— коэффициент Эйнштейна, Для электрических диполь-
кых переходов величина В равна d2/6eofi2, где d — дипольный
момент перехода, следовательно, / = (2me/3e2h2) hvd2. Из
полученного выражения видно, что для нахождения величины /
требуется вычислить дипольный момент перехода d.
2. Экспериментальное определение силы осциллятора
основывается на ее связи с коэффициентом экстинкции e(v), а именно
/==4,33 • КГ9 \ dve(v), где v —волновое число. Если
коэффициент затухания известен в определенном интервале волновых
чисел, входящий в это выражение интеграл позволяет
определить экспериментальное значение силы перехода /.
Существует важное теоретическое правило — правило
сумм Куна —Томаса, которое утверждает, что сумма сил
313
с
осциллятора для всех электронов в N-электронной молекуле
равна N. Это означает, например, что атом водорода в целом ведет
себя как идеальный осциллятор, так как для него сумма сил
осциллятора всех переходов из основного состояния равна единице.
Упражнения. 1. Мерой чего служит сила осциллятора трехмерного
гармонического осциллятора? Чему равна сумма сил осцилляторов для всех
возможных переходов из основного состояния атома водорода? Сформулируйте
правило сумм Куна —Томаса для N-электронного атома. Каким образом сила
осциллятора связана с коэффициентом экстинкции перехода? Каким образом
сила осциллятора связана с дипольным моментом перехода?
2. Вычислите силу осциллятора перехода с уровня п на уровень (я + 1)
для электрона в одномерной прямоугольной яме и для одномерного
гармонического осциллятора. Рассчитайте суммарную интенсивность полос
поглощения в соответствующих случаях.
Рекомендуемые источники. Свойства силы осциллятора, ее связь с
коэффициентом экстинкции, а также доказательство правила сумм Куна — Томаса
рассматриваются в гл. 10 [1]. См. также кн. Козмана [217] и Эйринга,
Уолтера и Кимбалла [137]. Применение этого понятия в фотохимии обсуждается
Уэйном [416], Калвертом и Питсом [88].
СИЛОВАЯ ПОСТОЯННАЯ. Силовая постоянная k является
коэффициентом пропорциональности между возвращающей
силой и смещением х простого гармонического осциллятора; сила =
= —kx. Большие силовые постоянные отвечают жестко
связанным системам (возвращающие силы велики даже при малых
отклонениях от положения равновесия). Частота классического
гармонического осциллятора связана с k выражением соо =
= (&/т),/2, где m — масса осциллирующей системы (если k
выражена в ньютонах на метр, а масса в килограммах, частота
имеет размерность радианы в секунду; чтобы перевести ее в
герцы, надо разделить полученную величину на 2я). Из этого
выражения видно, что частота колебаний определяется не
только силовой постоянной, но и массой системы, так как, чем
больше масса, тем менее эффективна возвращающая сила. При
квантовомеханическом описании гармонического осциллятора
энергии уровней выражаются через частоту о>о, вычисленную так
же, как в классическом случае. Энергия n-го квантового уровня
равна (/г+ V2)^coo.
Значение силовой постоянной в квантовой теории
заключается в том, что она является мерой жесткости связей между
атомами и поэтому определяет (наряду с массами атомов)
колебательные частоты молекул.
В табл. 10 приведены типичные значения силовых
постоянных для некоторых молекул, соответствующие частоты и
расстояния между энергетическими уровнями.
314
с
Упражнения. 1. Что такое силовая постоянная? Каков физический смысл
больших силовых постоянных? Можно ли предположить, что силовая
постоянная для связи С—С в алмазе меньше, чем для связи РЬ—РЬ в
металлическом свинце? Тело массой 1 кг подвешено на пружине с силовой
постоянной 1 Н-м-1; чему равна частота колебаний в радианах в секунду и в
герцах? Как нужно изменить массу, чтобы частота колебаний составила
1 МГц? Какая силовая постоянная будет описывать колебания массы, равной
массе протона с частотой, типичной для колебаний молекулярной связи
(~1014 Гц)? Какому волновому числу (см-1) это соответствует в
инфракрасном спектре поглощения? Куда окажется сдвинуто поглощение при
замене протона на дейтерон?
2. Разложив энергию связи в ряд Тейлора вблизи положения
равновесия, покажите, что силовая постоянная пропорциональна кривизне кривой
потенциальной энергии молекулы в точке, соответствующей положению
равновесия.
Рекомендуемые источники. Более полную информацию о молекулярных
колебаниях см. в [1], гл. 10. Наглядное, простое и детальное рассмотрение
дано Вудвордом [433], который показывает, как определять k из данных
колебательных спектров; упомянем классическую монографию Вильсона, Де-
шиуса и Кросса [431]. См. также кн. Кинга [222] и Ганса [157]. Данные о
молекулярных колебаниях обобщены Адамсом [31, 32].
СИММЕТРИИ ПРЕОБРАЗОВАНИЯ. Преобразования, или
операции, симметрии — это преобразования координат системы
(определение пассивного подхода) или преобразования самого
объекта (определение активного подхода), после применения
которых система оказывается в положении, неотличимом от
исходного.
Активный подход к определению операций симметрии более
очевиден, и сначала мы проиллюстрируем его. Представьте
одноцветный квадратный предмет, лежащий на плоскости, на
которую нанесена система координат. Закройте глаза, поверните
этот предмет на 90° в плоскости и посмотрите на него опять.
Никаких признаков, позволяющих заметить, что он был повернут,
вам не удастся обнаружить, поэтому такая операция
представляет собой преобразование симметрии. Если бы поворот был
совершен на угол меньше 90°, мы бы заметили, что у квадрата
изменилась ориентация. Подобно этому, прямоугольный
(продолговатый) предмет поворотом на 180° приводится в
положение, неотличимое от начального; следовательно, такой поворот
является преобразованием симметрии, но поворот данного
предмета на 90° не будет преобразованием симметрии (рис. С.8).
При пассивном подходе на плоскость, где лежит квадратный
предмет, наносится координатная система; если мы сделаем а
единичных шагов вдоль оси х, то придем к краю квадрата
(длина стороны 2а, начало координат в центре квадрата), если
сделаем а шагов вдоль оси у, доберемся до его другого края
315
с
(рис. С.8). Теперь будем поворачивать систему координат, т.е.
поворачивать плоскость, а не предмет, до тех пор пока ось х
Рис. С.8. Активный (а) и пассивный (б) подход к рассмотрению
преобразований симметрии.
Рис. С.9. Преобразования симметрии CfV ov, i н Sn и примеры молекул с сим-
хметрией каждого из этих типов
не совпадет с направлением, которое первоначально занимала
ось у. Отмерив а шагов вдоль новой оси х, мы вновь доберемся
до края предмета; то же самое произойдет, когда мы зашагаем
вдоль новой оси у. Эта система неотличима от исходной: следо-
316
с
вательно, поворот на 90° есть преобразование симметрии. Если
исследуемый предмет — прямоугольник со сторонами 2а и 2fe,
то, проделав а шагов вдоль исходной оси х, мы придем к краю.
Однако, если мы отмерим а шагов вдоль повернутой оси х, то
не окажемся на краю предмета. Это произойдет только при
условии, что а равно Ь. Итак, ситуация, возникающая при
повороте осей, не симметрична исходной, и поворот на 90° в случае
прямоугольника не является преобразованием симметрии.
Мы не можем категорически рекомендовать какой-либо один
из этих подходов — это дело вкуса. Однако, по крайней мере
так представляется автору, пассивный подход предпочтителен,
поскольку манипулировать координатами можно всегда (они
являются удобной математической выдумкой и всегда в нашем
распоряжении), тогда как активные действия могут оказаться
невозможными. Это в особенности справедливо для
преобразований симметрии, отличных от вращения: например, инверсию
относительно какой-либо точки трудно провести активно, хотя
ее, конечно, можно представить себе: то же самое относится
к отражению.
Основными преобразованиями симметрии являются:
трансляции (особенно в периодических системах типа кристаллов
и в свободном пространстве); вращение на 2п/п радиан
(обозначается Сп); отражение в плоскости (обозначается а), причем
индекс v означает, что имеется в виду вертикальная плоскость,
а индекс h — горизонтальная; инверсия относительно какой-либо
точки /; зеркально-поворотное преобразование Sn, которое
состоит из вращения на 2л/п радиан и последующего отражения
в плоскости, перпендикулярной оси вращения (см. рис. С.9).
Изучение следствий преобразований симметрии составляет
основу теории групп.
Упражнения. 1. Что называется преобразованием симметрии? Какие два
подхода используются для их определения? Рассмотрите с помощью
активного и пассивного подходов преобразования, обозначаемые С2, Сз, о\ *\ S4-
Перечислите преобразования симметрии, возможные для следующих
объектов: левая рука, правая рука, человек, стул, куб, треугольник, тетраэдр,
тетрагональная пирамида, молекулы Н20, СО2, CH4, SF6, бензола.
2. Покажите, что определение преобразований симметрии как
преобразований, которые коммутируют с гамильтонианом системы, соответствует
данному в тексте определению.
Рекомендуемые источники. Дальнейшее обсуждение преобразований
симметрии и изложение основ теории групп дано в гл.5 [1]. Простое перечисление
элементов симметрии и некоторые примеры см. у Эткинса, Чайлда и Филлипса
[40]. Другие ссылки см. в разд. «Теория групп». В кн. Вейла [419] дан
увлекательный обзор проявлений симметрии в природе. См. также кн. Хохштрас-
сера [451] «Молекулярные аспекты симметрии».
317
с
СИНГЛЕТНЫЕ И ТРИПЛЕТНЫЕ СОСТОЯНИЯ. В синг-
летном состоянии суммарный спиновый угловой момент
многоэлектронной системы равен нулю (S = 0). В триплетном
состоянии суммарный спин равен 1 (S=l). Вектор спинового
углового момента может иметь ряд проекций на выбранную ось.
Эти проекции различают с помощью квантового числа Ms,
которое принимает любые целочисленные значения от —S до +S.
Следовательно, если S = 1, Ms может принимать три значения:
—1, 0, +1, а если S = О, только одно значение: Afs = 0
(отсюда названия состояний — триплетное и синглетное).
Рис. СЮ. Триплетное и синглетное состояния. Обратите внимание на
соотношение фаз векторов а ир в состоянии М s = О для синглета и
триплета.
Различие между синглетным и триплетным состояниями
проще всего увидеть на примере системы с двумя электронами.
Поскольку спиновый угловой момент каждого электрона может
иметь проекцию ms = +V2 или —1/2 (обозначим их а и р
соответственно), система из двух электронов может находиться
в одном из четырех следующих спиновых состояний: а(1)а(2),
а(1)Р(2), р(1)а(2), р(1)р(2). Второе и третье из них не
соответствуют вектору суммарного спина с определенной длиной,
поскольку азимутальный угол между векторами аир может
принимать произвольное значение. Если мы зададим
определенное значение азимутального угла одного вектора по отношению
к другому, то получим определенный суммарный вектор. Именно,
если а(1) и р(2) находятся в одинаковой фазе, их сумма
соответствует S = 1, если же их фазы отличаются на 180°,
суммарный спин равен нулю и соответствует состоянию с S = 0
318
с
(рис. СЮ). Когда мы говорим, что в сишлетном состоянии
спины спарены, имеем в виду не только то, что у одного
электрона спин а, а у другого р, но и то, что эти спины имеют
противоположное направление (в триплетном состоянии при
j[js = 0 спин одного электрона равен а, а другого р, но их сумма
не равна нулю). На основании квантовомеханического
рассмотрения можно показать, что соответствующая спиновая волновая
функция триплетного состояния (спины находятся в одинаковой
фазе) с Ms = 0 имеют вид а (1) р (2) + р (1) а (2), а спиновая
волновая функция синглетного состояния (спины имеют
противоположные фазы) запишется так: а(1)р(2)—р(1)а(2). Остальным
двум триплетным состояниям с Ms = ±l соответствуют
функции а(1)а(2) и р(1)р(2).
Рис. СП. Изменение относительной
фазы спинов приводит к триплетно-син-
глетному интеркомбинационному
переходу. Штриховкой показана область
с другой величиной спин-орбитального
взаимодействия.
Возможно превращение синглетного терма в триплетный
(и наоборот), если один электрон станет прецессировать быстрее
другого. Это может произойти при условии, что на каждый из
спинов действует неодинаковое магнитное поле, так что лармо-
ровские частоты их прецессии оказываются различными (см.
разд. «Прецессия»); при этом совпадающая по фазе ориентация
спинов постепенно превращается в ориентацию с
противоположными фазами (рис. СП). Поле, создаваемое лабораторным
магнитом, не может привести к такому взаимному превращению
состояний (называемому интеркомбинационным переходом,
ИКП), потому что оно действует на оба спина одинаково —
в молекулярных масштабах это магнитное поле однородно.
Однако магнитные поля, возникающие внутри молекулы, могут
оказаться в состоянии изменить фазовое соотношение между
спинами. Например, спин-орбитальное взаимодействие одного
электрона может отличаться от взаимодействия другого, и,
поскольку это взаимодействие магнитное, возникает ситуация, при
которой ларморовские частоты отличаются. Это объясняет,
почему в молекулах, содержащих тяжелые атомы, для которых
характерно большое спин-орбитальное взаимодействие,
эффективны интеркомбинационные переходы (см. разд.
«Фосфоресценция»),
319
с
Взаимное превращение орто- и параводорода (см. разд.
«Ядерная статистика»), вызываемое парамагнитными ионами,
объясняется тем, что синглетное и триплетное соотношения
между фазами ядерных спинов способны преобразовываться
друг в друга под действием неоднородного поля, которое
создает такой ион, если он находится ближе к одному ядру, чем
к другому.
Рекомендуемые источники. Более подробное обсуждение синглетного и
триплетного состояний и их взаимного превращения см. в гл. 6 и 10 [1].
Роль триплетного состояния в химии и его подробное квантовомеханическое
описание даны Мак-Глином, Азуми и Киноситой [272]; эти авторы приводят
много литературных ссылок. Фотохимические следствия отличия между три-
плетными и синглетными состояниями обсуждаются Уэйном [416] и Калвер-
том и Питтсом [88]. Эти отличия учитываются в правилах Гунда и при
рассмотрении спиновых корреляций (см. соответствующие разделы).
Проявлением синглет-триплетного интеркомбинационного перехода является
фосфоресценция.
СКОБОЧНЫЕ ОБОЗНАЧЕНИЯ; БРА И КЕТ. Введенные
Дираком векторные обозначения «бра» и «кет» получили свои
названия от частей английского слова (bra|c|ket). Состояние
системы, волновая функция которой *фп(^), представляется
кет-вектором |я), а сопряженная волновая функция-ф* (г) — бра-
вектором (п\. Интеграл \ dxty*m(r)tyn(r) обозначается символом
dx ty*m (r) Qtyn (r) — скобкой (m \ Q \ п), где
й — некоторый оператор. Это элегантное обозначение очень ясно
показывает связь между волновой механикой и матричной
механикой и позволяет рассматривать квантовую теорию на более
глубоких основах, так как кет-векторы можно рассматривать
как векторы в особом пространстве (пространстве Гильберта).
Рекомендуемые источники. Относительно использования скобочных
обозначений см. [1], гл. 4. Они изложены в кн. Дирака [123] и обсуждаются Джо-
чем в гл. 9 кн. Салема и Вигнера [352]. Данная тема входит в теорию
преобразований или теорию представлений; см. гл. 4 кн. Давыдова [119], Романа
[343], фон Неймана [410], Каца [216], Кемпфера [214] и Джоча [204].
СЛЕИТЕРОВСКИЕ АТОМНЫЕ ОРБИТАЛИ. Атомные ор-
битали многоэлектронных атомов сложным образом зависят от
координат. Представить эту зависимость точно можно только
численным заданием их амплитуд. Однако для многих целей
желательно иметь аналитическую функцию, а не таблицу чисел.
Слейтеровские атомные орбитали являются аналитическими
функциями, основанными на численных результатах, и
позволяют воспроизводить эти численные результаты с
удовлетворительной точностью. Разработан ряд простых правил, позволяю-
320
с
щих записать выражения для орбиталей слейтеровского типа
(ОСТ) применительно к любому электрону в любом атоме.
Радиальная зависимость слейтеровской орбитали
определяется выражением Nrn*~lex\>(— £г), а ее угловая
зависимость— сферическими гармониками, соответствующими
заданным значениям квантовых чисел / и mt (см. табл. 23). Для
определения эффективного квантового числа п* и показателя
экспоненты £ существуют следующие правила:
1. Эффективное квантовое число п* связано с
соответствующим главным квантовым числом п (я->я*) следующим
образом: 1-И; 2^2; 3-v3; 4-^3,7; 5^4; 6-П,2.
2. Показатель экспоненты £ связан с эффективным
квантовым числом Z0(j) соотношением £ = 2Эф/п*; в свою очередь 1Ъ$
связано с порядковым номером элемента соотношением Z^ =
= Z — а, где а—постоянная экранирования.
3. Постоянная экранирования а вычисляется с помощью
классификации атомных орбиталей по следующим группам:
(15), (2s, 2/7), (35,3р), (3d), (45,4/7), (4d), (4/), (55,5/7),
(5d), .... Постоянная а представляет собой сумму вкладов,
обусловленных каждой из групп, и вычисляется следующим
образом. Предположим, что интересующая нас атомная орбиталь
принадлежит группе X и что ее главное квантовое число равно
п. Вклады, обусловленные присутствием остальных электронов,
таковы:
а) вклад электронов, внешних по отношению к группе X
(т. е. стоящих справа от X в записи электронной конфигурации),
равен нулю;
б) вклад электронов из группы X равен 0,30, если это
ls-электроны, и 0,35 в остальных случаях;
в) если интересующий нас электрон находится на ns- или на
n/7-орбитали,
вклад каждого из электронов с главным квантовым
числом п— 1 равен 0,85,
вклад каждого из электронов с главными квантовыми
числами п — 2, п — 3 ... равен 1,00;
г) если нас интересует электрон на nd- или ^/-орбитали,
вклад каждого электрона из групп, предшествующих X в записи
электронной конфигурации, равен 1,00. Параметры орбиталей
слейтеровского типа для валентных электронов атомов перво-
го — третьего периодов приведены в табл. 21.
Внимательное изучение вида слейтеровских орбиталей
раскрывает их серьезный недостаток: они не имеют радиальных
узлов. Одним из следствий этого является их неортогональность.
Однако они могут быть сделаны ортогональными с помощью
процедуры ортогонализации Шмидта, так что этот недостаток
можно устранить (см. разд. «Ортогональные функции»).
321
с
Упражнения. Получите выражения слейтеровского гипа для орбиталей
Is в Н, 2s в Li, 2s и 2р в С, N, О и F и 3d в Fe2+ и Fe. Найдите в общем
виде нормировочную постоянную для ОСТ. Найдите средний радиус
распределения электронов на каждой из рассмотренных выше орбиталей. Покажите,
что можно выбрать такую сумму Is- и 2s-OCT, чтобы она была ортогональна
к ls-орбитали. Это соответствует процедуре ортогоналнзации Шмидта для
25-орбитали по отношению к ls-орбитали Эту процедуру можно продолжить,
ортогонализуя З&'-орбигали по отношению к Is- и 2$-орбиталям; проделайте
это (см. разд. «Ортогональные функции»). Какое влияние в этом случае
оказывает ортогонализация на число радиальных узлов, а в случае атома С —
на средний радиус 2$-орбитали?
Рекомендуемые источники. Краткое изложение вопроса см. в гл. 8 [1].
Полезное обсуждение орбиталей слейтеровского типа дано в § 11.8 кн. Коул*
сона [105], кн. Маррела, Кеттла и Теддера [299], а также Мак-Глина, Ван-
квикенборна, Киноситы и Кэрролла [273]. В последней из этих книг, в
приложении В, содержится много ссылок на результаты вычисления атомных
орбиталей методом самосогласованного поля в виде суммы ОСТ, а также
таблицы таких орбиталей. Ортогонализация по Шмидту обсуждается в разд.
«Ортогональные функции». Об интегралах перекрывания со слейтеровскими
атомными орбиталями см. в разд. «Перекрывание».
СЛЕИТЕРОВСКИЙ ДЕТЕРМИНАНТ. Согласно принципу
Паули, волновая функция многоэлектронной системы должна
менять знак при перестановке координат любых двух
электронов. Этому принципу, очевидно, не удовлетворяет простое
произведение одноэлектронных волновых функций вида
^20)^(2)11^ (3) ... г|)0 (АО, где электрон 1 занимает орбиталь
фа со спином а и т. д. Однако можно убедиться, что
комбинация произведений такого типа удовлетворяет принципу Паули,
если ее записать в виде детерминанта:
(1/ЛЛ),/2
Раскрывая его согласно правилам обращения с детерминантами,
мы получим N\ слагаемых, половина которых имеет
положительный знак, а другая половина — отрицательный. Множитель
(l/N\)lfi обеспечивает нормированность детерминантной
волновой функции. Слейтеровский детерминант удовлетворяет
принципу Паули, потому что любой детерминант меняет знак при
взаимной перестановке всякой пары строк или столбцов.
Предка) *S(2) *S(3) "• ДО)
*2(D *2(2) +2(3) ... +2W
♦?(1) г|#(2) t£(3) ... tf(N)
* • • ... •
t5(l) tj(2) *S(3) ... *5<*D
322
с
положим, что мы переставляем электроны 1 и 2 и что в
результате перестановки электрон 1 помещается на орбиталь,
занятую до этого электроном 2, и наоборот. В детерминанте этому
соответствует перестановка первого и второго столбцов, которая
приводит к изменению знака детерминанта. То же самое
происходит при перестановке любой другой пары электронов, так что
аетерминант представляет собой подходящую комбинацию одно-
электронных орбиталей.
Можно показать, что детерминантная волновая функция
многоэлектронной системы удовлетворяет также принципу запрета
Паули, потому что детерминант обращается в нуль, если две его
строки или два столбца совпадают. Предположим, что
электрон 1 занимает орбиталь г|)а со спином а и что к нему
присоединяется электрон 2, у которого такой же спин. При этом
первые две строки детерминанта совпадают, и детерминант
обратится в нуль. Следовательно, невозможно получить такое
состояние, в котором на одной орбитали находилось бы более
одного электрона с одним и тем же спином.
Несколько слов об обозначениях. Орбитали с
соответствующими им спиновыми частями называются спин-орбиталями.
Вместо того чтобы записывать спин-орбиталь, соответствующую
спину а в виде i|)£> ее иногда записывают просто как %, а спин
а подразумевается. В таких обозначениях спин-орбиталь со
спином р записывается как tya- Полная запись детерминантной
волновой функции весьма громоздка, поэтому обычно
записывают лишь все диагональные элементы таких функций и не
указывают нормировочную постоянную (но помнят о ней). В этих
обозначениях детерминант, вписанный выше, принимает вид
I Ма^ь ... *фг I-
Следует отметить, что волновую функцию можно представить
в виде одного слейтеровского детерминанта только для
заполненной оболочки. Если оболочка заполнена не полностью,
следует использовать линейную комбинацию детерминантов.
Упражнения. Почему простое произведение орбиталей не является
подходящим описанием состояния многоэлектронной системы? Почему для этой
цели годится слейтеровский детерминант? Запишите слейтеровский
детерминант для атома гелия, раскройте его и убедитесь, что он удовлетворяет
принципу Паули. Проделайте то же самое для четырех электронов в наинизшей
энергетической конфигурации для одномерной прямоугольной ямы.
Убедитесь, что в основном состоянии атома гелия спины должны быть спарены, а
в возбужденном состоянии они могут быть спарены (синглетное состояние)
или не спарены (триплетиое состояние). Проведите такое же рассмотрение
для молекулы водорода. Запишите гамильтониан двухэлектронной системы и
покажите, что простое (недетермииантное) произведение функций приводит
к такому выражению для энергии, в котором взаимодействие электронов
представлено лишь вкладом кулоновского отталкивания. Покажите далее.
323
324
С
что, если использовать слейтеровский детерминант, появляется
дополнительный интеграл (обменный интеграл). Как влияет этог обменный интеграл на
основное состояние атома гелия?
Рекомендуемые источники. См. гл. 8 [1]. Ознакомиться с методами
обращения с детерминантными волновыми функциями можно по кн. Ричардса и
Хорсли [336]; этот же вопрос более подробно излагается Мак-Глином, Ванк-
викенборном, Киноситой и Кэрроллом [273]. Учет принципа Паули при
определении энергии атомов и молекул описан в разд. «Паули принцип», см. также
разделы «Обменная энергия» и «Спиновые корреляции». Используя свойства
слейтеровского детерминанта, можно продемонстрировать локализацию
молекулярных орбиталей в некоторых областях молекулы.
СОБСТВЕННЫЕ ФУНКЦИИ. Если над функцией
совершают некоторую математическую операцию (умножение,
деление, дифференцирование и т. п.), то обычно получают какую-то
другую функцию. Так, дифференцирование функции х2 дает
функцию 2х. Однако некоторые комбинации преобразований
и функций таковы, что в результате операции получается та же
функция, но умноженная на число. Так, дифференцирование
функции ехр 2х дает 2ехр 2х, т. е. исходную функцию, но
умноженную на 2. В таких случаях функция называется собственной
функцией (eigenfunclion) оператора (в данном случае
дифференциального оператора d/dx), а числовой множитель (в
приведенном примере 2) называется собственным значением
(eigenvalue) оператора.
Насколько важны эти понятия в квантовой механике,
нетрудно понять, если вспомнить, что уравнение Шредингера
можно записать как Я-ф = Е$, где Н — дифференциальный
оператор (гамильтониан), и -ф — волновая функция. Оно имеет
форму уравнения на собственные значения, где энергия Е
играет роль собственного значения, а волновая функция — роль
собственной функции. Волновая функция характеризует
состояние системы, поэтому г|) часто именуется собственным
состоянием или, поскольку она обладает некими свойствами векторов,
собственным вектором. Результатом эксперимента,
проделанного над системой в заданном собственном состоянии, является
собственное значение оператора, соответствующего наблюдаемой
величине.
Упражнения. 1. Дайте определение перечисленным терминам:
собственная функция, собственное значение, собственное состояние, собственный
вектор, уравнение на собственные значения. Почему эти термины важны в
квантовой механике? Если бы вы знали состояние системы и математическую
форму оператора, соответствующего наблюдаемой величине, которую вы
хотите определить, как вы могли бы предсказать результат эксперимента?
2. Какая из следующих функций является собственной функцией
оператора d/dx: ах, ах2, ехр ах, ехр ах2, In ax, sin ax? Какие из них являются соб-
324
с
ственнымп функциями оператора d2/dx2? Проекции углового момента на ось
z соответствует оператор (h/i) (д/дф). Если бы вы знали, что состояние
системы описывается функцией f (г, 0)ехр ипф, какой экспериментальный
результат вы могли бы предсказать? Каков будет результат, если состояние
системы описывается ф\нкцией f(r, 0)cos тф'> Сложный и важный вопрос: что
является собственной функцией операции «умножения на к»?
Рекомендуемые источники. Обсуждение операторов и собственных
значений см. в [1], гл. 4. Более глубокое изложение вопроса о собственных
состояниях и объяснения того, почему они называются собственными векторами,
дано Дираком [123], фон Нейманом [410] и Джочем [204]. Полезное резюме
и примеры, включающие последний вопрос упражнений, приведены
Давыдовым [119].
СООТВЕТСТВИЯ ПРИНЦИП. При больших значениях
квантовых чисел среднее поведение системы должно быть идентично
ее поведению, вычисленному на основе законов классической
механики.
Данный принцип предполагает, что законы квантовой
механики сводятся к законам классической механики в том случае,
когда можно пренебречь тонкими деталями явления. В качестве
примера рассмотрим волновой пакет, описывающий движение
свободной частицы, когда ее энергия или импульс не являются
строго определенными: траектория движения пакета совпадает
с траекторией движения частицы той же массы, описываемой
законами классической механики. Но если энергия становится
более точно определенной, так что вклад в нее дает меньшее
число квантовых состояний, характер распределения становится
менее классическим и более квантовым. Другим примером
является распределение Планка для энергии излучения абсолютно
черного тела: когда постоянная Планка стремится к нулю (в
гипотетическом классическом мире), энергетическое
распределение становится распределением классической системы и
согласуется с законом Релея — Джинса. Еще один пример: импульс
фотона (кванта света) передается предмету, который его
поглощает или отражает, и, если в процессе участвует достаточно
большое число фотонов, этот импульс интерпретируется как
постоянное давление излучения в классической электромагнитной
теории.
Принцип соответствия сыграл неоценимую роль в период
становления квантовой теории, так как он требует, чтобы любой
расчет по квантовой теории обязательно соответствовал
результату классической физики, когда мы имеем дело с большими
квантовыми числами, а квантовые флуктуации игнорируются.
В качестве примера рассмотрим излучение, испускаемое
гармонически колеблющимся электроном. Существование у
гармонического осциллятора множества равноотстоящих квантованных
325
с
уровней энергии позволяет предположить, что область
испускаемых частот должна быть очень широкой, поскольку можно
получить бесконечно большое число различных расстояний между
уровнями. Однако классический осциллятор, которому должен
соответствовать квантовый гармонический осциллятор,
испускает только одну частоту, подчиняясь классическим законам
движения. Чтобы воспроизвести этот результат, необходимо
наложить ограничения на переходы квантового осциллятора
с одного уровня на другой; в результате принцип соответствия
приводит к правилу отбора, согласно которому квантовый
осциллятор может совершать переходы только между соседними
уровнями. Такие правила естественным образом следуют из
более поздней квантовой теории, но даже там соответствие в
классическом пределе часто служит хорошей проверкой
правильности расчета. В заключение следует отметить, что чисто
квантовые явления исчезают при переходе к классическому
пределу: в частности, уничтожаются все эффекты, обусловленные
спином.
Рекомендуемые источники. Разнообразные классические пределы
квантовых ситуаций обсуждаются в [1], гл. 3. Историю вопроса, в частности
историю того, как принцип соответствия помог разобраться в старой квантовой
теории и создать новую, см. в кн. Джеммера [203]. Применение принципа
описано Кемблом [220] и Крамерсом [227].
СОХРАНЯЮЩЕЕСЯ СВОЙСТВО. Сохраняющейся
величиной, или свойством, называется величина, не изменяющаяся во
времени. Примерами такой величины являются полная энергия
системы (первый закон термодинамики), угловой момент
электрона в атоме или проекция углового момента на межъядерную
ось в двухатомной молекуле. Примером несохраняющейся
величины служит проекция углового момента на ось,
перпендикулярную межъядерной оси в двухатомной молекуле (в данном
случае дело обстоит так, как будто электрон начинает двигаться
вокруг перпендикулярной оси, но, прежде чем завершится это
путешествие, сталкивается с ядром, и это изменяет проекцию
углового момента относительно перпендикулярной оси,
следовательно, в рассматриваемом случае речь идет о
несохраняющейся величине). Сохраняющаяся величина называется также
интегралом движения.
Можно дать количественное определение сохраняющегося
свойства как наблюдаемой величины, оператор которой
коммутирует с гамильтонианом системы. Например, импульс системы
сохраняется, если оператор импульса коммутирует с
гамильтонианом. В приведенных ниже упражнениях требуется показать,
что коммутатор импульса и гамильтониана пропорционален
градиенту потенциальной энергии системы. Из классической меха-
326
с
ники следует, что градиент потенциала — это сила, и поэтому
можно сделать вывод, что импульс сохраняется только в
отсутствие сил. И наоборот, в присутствии сил импульс не
сохраняется, т. е. изменяется. По существу, это и составляет
содержание второго закона Ньютона.
Упражнения. Что означает термин «сохраняющееся свойство»? Приведите
несколько примеров сохраняющихся величин, помимо тех, о которых
говорилось в тексте. Рассмотрите ожидаемое значение оператора,
соответствующего некоторой наблюдаемой величине Q. Воспользовавшись зависящей от
времени формой уравнения Шредингера, покажите, что скорость изменения
ожидаемого значения d/dt (Q) равна (i/h) ([H, Q]). Это показывает, что, если
коммутатор Н и Q исчезает, ожидаемое значение Q остается постоянным во
времени. Теперь предположим, что Q — оператор импульса в направлении дс,
а Н — оператор, включающий кинетическую энергию и потенциальную
энергию V(x). Выведите выражение для скорости изменения ожидаемого
значения импульса через ожидаемое значение силы. Заметьте, что при этом вы
вывели второй закон движения Ньютона. В свете этого результата можно
сделать вывод, что второй закон Ньютона представляет собой уравнение для
средних значений и что классическая механика оперирует средними
значениями и тем самым игнорирует более тонкие детали движения. Какие
условия должны выполняться для того, чтобы в механических системах
сохранялись энергия, угловой момент и импульс?
Рекомендуемые источники. Краткое обсуждение законов сохранения см.
в [1], гл. 4 и 6. Более подробную информацию можно найти в кн. Романа
[343] и у Фейнмана, Лейтона и Сэндса [145]. В [1] обсуждается также тот
факт, что сохранение энергии, импульса и углового момента связано с
симметрией пространства.
СПАРИВАНИЕ. Если электроны находятся на одной орби-
тали и их спины противоположно направлены, то говорят, что
они спарены. Более того, чтобы два электрона могли находиться
на одной орбитали, они обязательно должны быть спарены —
таково требование принципа Паули.
Электронным парам придается первостепенное значение
в теории химической связи, и при элементарном изложении
этой теории иногда говорят, что образование связей отражает
тенденцию электронов к спариванию. Такое упрощенное
представление основывается на более серьезном соображении, что,
если электроны спарены, они находятся на более низком
энергетическом уровне. В свою очередь причину этого можно понять,
рассматривая образование связей. Предположим, что связь
образуется сначала одним электроном, который находится в
области минимума потенциальной энергии (между двумя ядрами);
второй электрон сможет оказаться в этой области только при
условии, что у него противоположное направление спина, и,
следовательно, он спарен с первым. Согласно принципу Паули,
327
с
третий электрон вообще не может находи/ься ь у топ же области,
поэтому он может играть лишь гораздо меньшую роль в
образовании связи. Основные положения такого подхода можно
проиллюстрировать с помощью теории молекулярных орбиталей.
Для того чтобы сыграть важную роль в образовании связи,
электрон должен находиться на связывающей орбитали,
которая представляет собой распределение вероятностей,
сконцентрированное между двумя участвующими в сзязи ядрами. Два
электрона могут заселить эту орбиталь только при условии, что
их спины противоположно направлены; три или большее число
электронов не могут находиться на этой наиболее выгодной
в энергетическом отношении связывающей орбитали и потому
вынуждены заполнять орбитали с большей энергией, которые
могут оказаться разрыхляющими. Следовательно, важная роль
электронных пар —это отражение того факта, что два электрона
могут заполнять каждую из низкоэнергетических орбиталей
и вносить наибольший вклад в образование связи, при условии
что они спарены и что на наиболее выгодной орбитали не может
находиться более двух электронов. Другими словами, тенденция
электронов к спариванию отражает их тенденцию занимать
уровни с низшей энергией.
Несколько иная ситуация имеет место в атомах, где,
согласно правилу Гунда, электроны самых внешних оболочек не
проявляют тенденции к спариванию. Дело в том, что в атоме
имеется только один центр притяжения, а не два или больше,
и более важную роль играют обменное взаимодействие и
спиновые корреляции.
Рекомендуемые источники. Роль спаривания рассматривается в разд.
«Химическая связь» и «Молекулярных орбиталей метод», а его причины
обсуждаются в разд. «Паули принцип». Теория валентных связей базируется на
важной роли спаривания в образовании химических связей, причем эта точка
зрения количественно обоснована (см. разд. «Валентных связей метод»).
СПЕКТРОСКОПИЧЕСКИЕ ВОЗМУЩЕНИЯ. Наличие
какого-либо возмущения обычно перемешивает и сдвигает уровни
энергии системы и придает ее состояниям в некоторой степени
свойства других состояний. Поскольку спектры обусловлены
переходами между уровнями энергии, возмущения проявляются
как сдвиги и изменения интенсивности спектральных линий.
Наблюдая какую-либо последовательность спектральных
линий, следующих друг за другом с определенными интервалами,
можно обнаружить, как вдруг вблизи какой-то частоты
закономерность их следования нарушается и спектр кажется
искаженным. Это и есть «спектроскопическое возмущение»,
возникшее из-за того, что энергии нескольких состояний оказались
близкими и возмущение привело к их смешению.
328
с
Различают два типа таких возмущений. Гомогенные
возмущения смешивают колебательные и электронные состояния;
в линейной молекуле они смешивают состояния с тем же
значением квантового числа Л. Гетерогенные возмущения — это
электронно-вращательные взаимодействия, как, например, при
Л-удвоении, которые смешивают состояния с квантовыми
числами Л, отличающимися на ±1.
Рекомендуемые источники. См. § 6.19 в кн. Кинга [222] и § V. 4 в кн.
Герцберга [187], а также кн. Герцберга [185], Кронига [228] и Ковача [226].
См. также разд. «Теория возмущений», «Принцип суперпозиции», «Резонанс»
,н «Предиссоциация».
СПИН. Спин — это угловой момент, присущий собственному,
внутреннему движению элементарной частицы. Представление
о том, что спин — это угловой момент, обусловленный вращением
тела вокруг его собственной оси, является очень удобной, хотя
и неверной моделью. Однако такая модель позволяет вспомнить
большинство свойств квантовомеханического волчка, что
особенно важно, чтобы понять (хотя и на примитивном уровне),
почему у заряженных частиц со спином имеется также
внутренний магнитный момент. Квантовомеханическое рассмотрение
спиновых свойств элементарных частиц позволяет сделать
следующие выводы:
1. Величина спинового углового момента частицы
определяется спиновым квантовым числом s, которое принимает
положительное целое или полуцелое значение, однозначно
характеризующее состояние данной частицы. Если значение s известно,
величину спина можно найти из выражения [s(s + 1)]^й.
Например, спин электрона равен 1/2> это означает, что его спиновый
угловой момент равен 3,/2й/2, или 0,91-Ю-34 Дж-с, в каком бы
состоянии и при каких бы условиях ни находился электрон
(спин — это неизменяемая характеристика частицы, такая же,
как ее заряд). У каждого ядра также имеется свой характерный
спин, для обозначения ядерного спинового квантового числа
вместо s используется буква /. Спиновые квантовые числа
некоторых ядер указаны в табл. 17.
2. Ориентация спинового углового момента квантована
(ограничена определенными углами) точно таким же образом,
как и для всех угловых моментов. Эта ориентация определяется
значением спинового магнитного квантового числа ms: величина
msb дает значение проекции спинового углового момента на
произвольную ось в пространстве (обычно в качестве такой оси
выбирают ось г). Например, у электрона возможны два
значения ms (s = l/2), а именно: ms = +l/2 соответствует проекции
спинового момента на ось г величиной {/2Ь и ms = —1/2
соответствует проекции на ось z величиной —1/2Ь. Проекции
329
с
с различными знаками часто называют «спин вверх», или а-спин,
и «спин вниз», или р-спин. Целесообразность такой терминологии
можно понять, рассмотрев векторную модель для этого случая.
3. Спин не является классическим явлением в том смысле,
что, если положить Ь равным нулю, спиновый угловой момент
исчезает. Однако на этом основании не следует делать вывод,
что все угловые моменты не имеют классических аналогов:
несмотря на уменьшение Ь до нуля при переходе к классическому
пределу^орбитальный угловой момент остается конечной
величиной, поскольку / может неограниченно возрастать, так что
произведение [/(/ + 1)]!/«й не обращается в нуль. Однако в
случае спина значение s фиксировано.
4. Спин не является релятивистским явлением в том смысле,
который обычно вкладывают в эти слова. Хотя существование
спина естественным образом следует из релятивистского
уравнения Дирака, к такому же выводу можно прийти, не используя
релятивистских представлений.
5. Спин является таким свойством, которое позволяет
подразделить все элементарные частицы на два класса с
принципиально различным поведением. Частицы с полуцелым спином
называются фермионами и подчиняются статистике Ферми —
Дирака; частицы с целым спином, включая нулевой,
называются бозонами и подчиняются статистике Бозе-—Эйнштейна.
Эти два класса частиц подчиняются различным формам
принципа Паули, что и определяет существенные различия в их
поведении. Возможно, что существует еще третий класс частиц,
куда входят так называемые парафермионы, не являющиеся
ни фермионами, ни бозонами. Парафермионы могут
понадобиться для объяснения свойств кварков, если последние
существуют.
6. Тенденция спинов к спариванию — это выражение, которое
слишком часто неправильно используется при ошибочном
объяснении образования химической связи. Образование
химической связи обусловлено энергетическими соотношениями, и
спаривание спинов происходит, если при этом условии электроны
могут занять низколежащую орбиталь и таким образом сделать
энергию молекулярной системы меньше энергии
изолированных атомов. Электроны вовсе не подвержены какому-то
сверхъестественному взаимному влечению, а, подчиняясь принципу
запрета Паули, вынуждены иметь спаренные спины, чтобы занять
это низкоэнергетическое состояние.
Упражнения. Что такое спин? Что означают квантовые числа s и ms?
Под каким углом к оси z ориентируется вектор спинового момента в а-со-
стоянии электрона? Каково минимальное значение углового момента фотона?
Почему спин является неклассическим свойством частиц? Какие из перечис-
330
с
ленных частиц являются фермионами и какие бозонами: е, р, п, 4Не, 3Не,
2Н+, фотон, Нг, кварк? Почему создается впечатление, что электроны
стремятся иметь спаренные спины?
Рекомендуемые источники. Дополнительные сведения, особенно о
спаривании спинов, см. в гл. 6 [1]. Очень подробное рассмотрение спина дано
Дираком [123], проблема парафермионов обсуждается Салемом и Вигнером
[352]. Спиновый угловой момент обсуждается в разд. «Угловой момент», там
же даны ссылки на другие источники. Обсуждение экспериментальных
проявлений спина см. в кн. Уитли [421], на более серьезном уровне этот вопрос
рассматривается у Мак-Вини [278]. Другие свойства элементарных частиц,
которые ведут себя подобно спину (например, заряд), обсуждаются Липки-
ным [251], Лихтенбергом [246]. Понятие о спине было введено эмпирически
Юленбеком и Гаудсмитом [403, 404] для объяснения некоторых особенностей
атомных спектров, его последовательная теория была разработана Паули, а
затем было показано, что его существование следует из уравнения Дирака.
История вопроса описана в § 3.4 кн. Джеммера [203], который показал, как
рождаются (а иногда и умирают) непривычные понятия. О ранних
экспериментах, доказывающих существование спина, но в свое время не получивших
правильного толкования, см. в разд. «Штерна — Герлаха опыт». Галиндо и
Санчез дел Рио [156] объясняют, почему спин не обязательно является
релятивистским явлением.
СПИНОВЫЕ КОРРЕЛЯЦИИ. Электроны с параллельными
спинами проявляют тенденцию избегать друг друга, а для
электронов с противоположно направленными (антипараллельными)
спинами характерна способность скапливаться вместе. Такое
своеобразное поведение электронов не связано с их зарядом
(хотя он влияет на среднее кулоновское отталкивание двух
электронов и на обменную энергию), но вовсе не является чем-то
сверхъестественным. В этом проявляется внутреннее свойство
электронов, которое следует из принципа Паули. В сказанном
можно убедиться, если рассмотреть волновую функцию системы
двух невзаимодействующих частиц \|)(ri,r2). Такую волновую
функцию можно записать в виде произведения \|)a(ri)*Mr2), где
частица 1 занимает орбиталь а, а частица 2 —орбиталь ft.
Чтобы привести такую волновую функцию в соответствие с
принципом Паули, ее надо несколько изменить; в результате она
примет вид г|)а(Г1)\|)ь(г2) + г|)а(г2)г|)ь(Г1) для спаренных спинов
и г|)а(г0г|)б(г2) — tMr2)*Mri) для параллельных спинов.
Исследуем вероятность нахождения электронов с параллельными
спинами в одной и той же точке пространства. В этом случае
принимают, что т{ и г2 в последней волновой функции
совпадают. В результате функция принимает следующий вид:
^a(ri)t|)b(ri) —\|)a(ri)\|)b(ri), т. е. обращается в нуль.
Следовательно, вероятность того, что электроны с параллельными
спинами находятся в одной и той же точке пространства, равна
нулю.
331
с
Эта ситуация проиллюстрирована на рис. С. 12 для случая,
когда две частицы (электроны, зарядами которых
пренебрегают) находятся в одномерной прямоугольной яме (внутри
тонкой проволоки). Контурные линии показывают вероятность
обнаружить частицы в точках Х\ и х2 внутри проволоки, если одна
из частиц находится в основном состоянии (п = 1, см. разд.
«Частица в прямоугольной яме»), а другая занимает первый
возбужденный уровень (п = 2) Присущее частицам с
параллельными спинами свойство избегать друг друга (рис. С. 12,
параллельные спины антмараллельные спины
Рис. С.12 Образование ферми-дырки. Контурная карта полной волновой
функции двух невзаимодействующих частиц в одномерной прямоугольной
яме. Обратите внимание на то, что в случае параллельных спинов узловая
ПЛОСКОСТЬ Х\ = Х2.
слева) проявляется в том, что вероятность пребывания таких
частиц на линии х\ = х2 равна нулю. Если предположить, что
электрон находится в некоторой точке пространства, то можно
затем представить себе маленький элемент объема, окружающий
эту точку, в который электроны с тем же направлением спина
стремятся не попадать. Эту область называют дыркой Ферми.
Электрон со спином, ангипараллельным спину первого
электрона, описывается другой волновой функцией, и вероятность
его появления в этом маленьком элементе объема усиливается
(однако это не дает повода называть способность
электронов с антипараллельиыми спинами собираться вместе
«уплотнением Ферми»). Итак, мы убедились, что относительное
расположение электронов коррелировано с взаимным направлением
их спинов, и это явление называется спиновой корреляцией.
Рекомендуемые источники. Дальнейшее обсуждение спиновых
корреляций на основании другого подхода приведено в гл. 8 [1]. Краткое изложение
332
с
этом проблемы дано к § IV. 6 кн. Линнета [249]. при рассмотрении гелия
Липнет использ>ет рисунки типа С.12. Роль эффектов спиновой корреляции
в теории химических связей рассматривается этим же автором [250]. К числу
обзоров по проблеме корреляции электронов в атомах и-молекулах относятся
работы Понча [316] и Хиллерааса [196]. Дополнительную информацию можно
найти в разд. «Обменная энергия» и «Самосогласованного поля метод».
СПИН-ОРБИТАЛЬНОЕ ВЗАИМОДЕЙСТВИЕ. Магнитный
момент электрона в атоме состоит из его спинового магнитного
момента и орбитального магнитного момента. Два магнитных
момента, находящиеся вблизи друг от друга, взаимодействуют.
Сила взаимодействия зависит от величины моментов и их
взаимной ориентации, а энергия этого взаимодействия проявляется
в атомных спектрах как тонкая структура.
Происхождение энергии спин-орбитального взаимодействия
можно наглядно представить себе, если вообразить, что
наблюдатель вращается вместе с электроном по орбите вокруг ядра
с зарядом Ze. Такой наблюдатель увидит, что его окружает
положительный ток, вследствие чего в точке, где находится
наблюдатель, возникает магнитный момент. Таким образом, мы
приходим к заключению, что спиновый магнитный момент
электрона находится в магнитном поле, которое обусловлено его
собственным орбитальным движением. На электрон действуют
также магнитные поля, обусловленные орбитальным движением
других электронов атома или молекулы, но такое
взаимодействие спина с другими орбитальными моментами, как правило,
играет менее важную роль. В принципе несложно рассчитать
индукцию В магнитного поля, обусловленного орбитальным
движением электрона, в точке, в которой он находится, а затем,
используя выражение —gyes.B (энергия магнитного
взаимодействия равна —т.В, а спиновый магнитный момент определяется
выражением gyps), получить «магнитную» энергию электрона.
Кроме того, можно ожидать, что индукция В пропорциональна
орбитальному угловому моменту 1 и что поэтому магнитная
энергия должна иметь вид (£/ft2)s.l, где £—постоянная спин-
орбитального взаимодействия. Однако на самом деле
вычисления нельзя проводить столь прямолинейным образом, и первые
физики, которые проводили их именно так, были ошеломлены,
когда обнаружили расхождение с экспериментом.
В процессе такого расчета необходимо найти магнитное поле,
действующее на тело, движущееся с определенной скоростью
в электрическом поле. В данном случае электрическое поле
обусловлено кулоновским потенциалом ядра, а скорость можно
выразить через орбитальный угловой момент, используя
выражение 1 = г X mv. Полученная величина, зависящая от радиуса,
усредняется далее по радиальной части атомной орбитали,
на которой находится электрон, а усредненная константа,
333
с
полученная таким образом, отождествляется с ^/й2. Такой подход
приводит к ответу, который в общих чертах правилен (I сильно
зависит otZ и меняется KaKZ4), но отличается от истинного в два
раза. Из разд. «g-Фактор» мы знаем, что введение множителя 2
осуществляется не произвольно, тем не менее оно должно быть
обосновано. Одно из обоснований введения дополнительного
множителя 2 можно получить из уравнения Дирака, которое
дает правильное значение энергии. Однако желательно найти
не формальное, а физическое наглядное объяснение, и это
удается сделать. Когда мы помещаем наблюдателя на
вращающийся по орбите электрон, чтобы он смог увидеть ток,
вызываемый кажущимся движением ядра, мы должны делать это
с еще большей осмотрительностью, чем Коперник, который, как
известно, поступал противоположным образом. Электрон в атоме
движется так быстро, что его следует рассматривать
релятивистски, и поэтому наблюдение за спином электрона с точки
зрения наблюдателя, находящегося на ядре,— это не то же самое,
что наблюдение за спином ядра с точки зрения наблюдателя,
путешествующего вместе с электроном. Электрон движется
таким образом, что наблюдателю, находящемуся на ядре, он
кажется вращающимся вдвое медленнее, чем путешествующему
с электроном наблюдателю. Такая модификация движения
электрона, называемая томасовской прецессией, дает
дополнительный множитель 1/2 при спин-орбитальных расчетах и, таким
образом, приводит их в согласие с уравнением Дирака и с
экспериментом.
Величина постоянной спин-орбитального взаимодействия
растет с увеличением порядкового номера атома, и тяжелые атомы
имеют большие постоянные спин-орбитального взаимодействия
(некоторые из них приведены в табл. 9). В водородоподобных
атомах зависимость постоянной спин-орбитального
взаимодействия от заряда ядра имеет вид Z4; как уже говорилось выше,
это отражает тот факт, что воздействие поля на электроны в
основном проявляется вблизи ядра, где напряженность поля
велика. С увеличением Z орбиталь сжимается, а напряженность
электрического поля возрастает, оба эти явления приводят
к большому значению £. Внешние электроны расположены
дальше от ядра, и в водородоподобных атомах £ убывает с
ростом п как 1/п3. Эта зависимость также связана с
напряженностью электрического поля, в котором находится электрон.
Рекомендуемые источники. Подробное обсуждение упомянутых выше
проблем, включая вычисление £ для водородоподобных атомов, и дальнейшее
рассмотрение томасовской прецессии см. в гл. 8 [1]. Томасовская прецессия
рассматривается также в кн. Мосса [292] и Хамеки [172]. Роль
экранирующих электронов обсуждается в [1]. Детальное обсуждение проявлений спин-
орбитального взаимодействия, особенно в связи с синглетными и триплет-
334
с
ными состояниями и фосфоресценцией, можно найти у Мак-Глина, Азуми и
Киноситы [272]; в этой книге объясняется, как проводить расчеты с учетом
спин-орбитального взаимодействия, и приведены табулированные данные
таких расчетов. О проявлении спин орбитального взаимодействия в атомной
спектроскопии см. в разд. «Тонкая структура». Некоторые данные о
постоянных спин-орбитального взаимодействия приведены в табл. 9.
СПИН-СПИНОВОЕ ВЗАИМОДЕЙСТВИЕ. Взаимодействие
между ядрами, которое в методе ядерного магнитного резонанса
(ЯМР) приводит к расщеплению, известному под названием
тонкой структуры, называется спин-спиновым взаимодействием.
Его величина обычно обозначается буквой / и измеряется в
герцах (Гц, циклы в секунду). На рис. Я. 12 показан спектр ЯМР,
в котором проявляется тонкая структура.
Спин-спиновое взаимодействие протонов в большинстве
случаев имеет величину от —20 до +40 Гц, хотя обычно
наблюдаемая область значений охватывает от 0 до 10 Гц. Это
чрезвычайно малые энергии, они соответствуют магнитному полю,
которое действует на одно ядро в результате присутствия
и определенной ориентации другого ядра.
Одним из возможных механизмов этого взаимодействия
является прямое диполь-дипольное взаимодействие между двумя
ядерными спиновыми магнитными моментами. Однако при
усреднении по углам такое взаимодействие оказывается равным
нулю, поэтому оно не может давать вклада в тонкую структуру,
если молекулы свободно вращаются в жидкости.
Другой механизм взаимодействия основан на передаче
взаимодействия между ядрами через связывающие электроны
молекулы. Этот механизм можно проиллюстрировать на примере
молекулы водорода. Необходимо объяснить, почему энергия
молекулы с параллельными ядерными спинами отличается от
энергии молекулы с антипараллельными ядерными спинами.
Ключевым явлением в этом механизме является сверхтонкое
взаимодействие между ядрами и электронами. Рассмотрим
случай, когда а-электрон находится вблизи ядра А. Вследствие
контактного взаимодействия Ферми между электронным и
ядерным магнитными моментами конфигурации с меньшей энергией
соответствуют антипараллельные спины ядра и соседнего с ним
электрона, т. е. параллельная ориентация их магнитных
моментов (рис. С. 13). Но принцип Паули требует, чтобы спин второго
связывающего электрона был антипараллелен спину первого
электрона, а электростатическое отталкивание между
электронами приводит к тому, что второй электрон со спином р
находится в основном вблизи ядра В. Из-за контактного
взаимодействия Ферми у второго электрона также возникает сверхтонкое
взаимодействие с ядром В, так что конфигурация с
наинизшей энергией достигается при наличии у ядра В спинового
335
с
магнитного момента, ориентированного, как у р-электрона. Итак,
если у одного из ядер в двухатомной молекуле имеется
определенный спин, то другое находится на низшем уровне энергии, если
у него противоположный спин. Отсюда следует, что энергия
молекулы с параллельными ядерными спинами немного выше,
чем у молекулы с антипараллельными спинами, поэтому, чтобы
повернуть спины и сделать их параллельными друг другу,
требуется затратить энергию.
Величина этого эффекта определяется силой участвующих
в нем сверхтонких взаимодействий и поляризуемостью
электронов, участвующих в образовании связи, от которой зависит их
Рис. С. 13. Спин-спиновое взаимодействие протонов.
способность двигаться преимущественно вблизи ядра с
подходящим направлением спинового момента. Последнее зависит от
средней энергии возбуждения связи, и, поскольку при этом
необходимо учитывать тенденцию электронных спинов к
распариванию, оказывается, что искомая средняя энергия —это
средняя энергия возбуждения триплетной конфигурации связи
(см. разд. «Синглетные и триплетные состояния»). Описываемое
взаимодействие не обращается в нуль при усреднении по
вращению молекулы, поскольку контактные взаимодействия
изотропны и их среднее не равно нулю.
При рассмотрении этого механизма совершенно не
учитывается внешнее магнитное поле, поэтому следует ожидать, как
это и есть на самом деле, что спин-спиновое взаимодействие не
зависит от напряженности приложенного внешнего поля.
Мы показали, что энергия взаимодействия двух ядерных
спинов зависит от их относительной ориентации. Следовательно,
вполне резонно ожидать, что энергия этого взаимодействия
пропорциональна скалярному произведению 1д-1в. Детальные
расчеты подтверждают такой вывод, а коэффициент
пропорциональности в этом произведении как раз и является константой
спин-спинового взаимодействия Jib. Если J положительна, более
336
с
устойчивой оказывается антипараллельная ориентация спинов,
потому что в этом случае (//fi)IA-IB дает отрицательный вклад
в полную энергию.
Пример, который мы рассмотрели, нереалистичен только
в одном отношении: спин-спиновое взаимодействие может быть
обнаружено в спектре ЯМР только при условии, что
взаимодействующие ядра находятся в различном химическом
окружении (т. е. если сигналы ЯМР от них имеют различный
химический сдвиг). Поэтому, хотя между протонами в Н2 имеется
взаимодействие (величиной 280 Гц), спектр ЯМР этой молекулы
состоит из одной линии, поскольку все разрешенные переходы
происходят при одной и той же энергии (см. разд. «Ядерный
магнитный резонанс»). Рассматривая протонное взаимодействие
в более сложных молекулах, мы получим более реалистическую
картину. Описанный выше механизм можно простым образом
обобщить, рассматривая цепочку взаимодействий через связи,
а также учитывая возможность прямого взаимодействия в
результате перекрывания, вызванного тем, что два несвязанных
ядра оказались неподалеку друг от друга.
Используя большие и малые стрелки для обозначения спинов
электрона и протона соответственно, взаимодействие в Н2 можно
представить схемой {аЦ*} для ориентации с меньшей энергией
и схемой {а||а} Для ориентации с большей энергией.
Аналогично для группы СН2 подобная схема имеет вид {аЦЧПа},
где параллельная ориентация средней электронной пары
обусловлена правилом Гунда о максимальной мультиплетности
состояний атомов (согласно этому правилу, параллельная
ориентация спинов в атоме оказывается предпочтительной).
Ориентации ядерных спинов с более высокой энергией для этой
группы описывается схемой {*it!ti*}- Важно отметить, что
в этом случае из-за включения атома в цепочку взаимодействий
параллельная ориентация ядерных спинов оказывается более
выгодной (имеет меньшую энергию) по сравнению с
антипараллельной (соответствующей отрицательному /). Такие цепочки
взаимодействий могут быть очень большими, и соответствующие
значения констант попадают в диапазон —21,5 Гц <С / <
< 42,4 Гц. Так, в НСНО константа спин-спинового
взаимодействия равна 42,4 Гц. Взаимодействие между двумя протонами,
которые разделены тремя связями, осуществляется по схеме
{aJtltlUf4-} и приводит к антипараллельному расположению
ядерных спинов в состоянии с низшей „энергией (/
положительно). В цепочках, состоящих из большого числа связей,
взаимодействие заметно ослаблено, и это обстоятельство является
весьма благоприятным, так как в противном случае спектры
ЯМР были бы усложнены настолько, что в них невозможно
было бы разобраться.
337
с
Спин-спиновое взаимодействие между протонами, которые
разделены несколькими связями, зависит от конформации
молекулы. Связано это с тем, что эффективность выстраивания
электронных спинов в промежуточных атомах зависит от
относительной ориентации связей. Например, предпочтительность схемы
{ fit } по сравнению со схемой {-—Щ-—} зависит от
таких факторов, как гибридизация атомов. Например, константа
траяс-взаимодействия в этилене равна 19,1 Гц, тогда как
константа цис-взаимодействия составляет 11,6 Гц.
Хотя мы отвергли механизм прямого диполь-дипольного
взаимодействия для молекул в жидкостях, электронно-ядерное
дипольное сверхтонкое взаимодействие может давать вклад
в спин-спиновое взаимодействие. Мы видели, что в механизме
передачи взаимодействия через спины участвуют два
сверхтонких взаимодействия, по одному на каждом конце цепочки.
Поскольку результат усреднения произведения двух дипольных
взаимодействий по всевозможным ориентациям не обращается
в нуль, два электронно-ядерных дипольных взаимодействия, по
одному у каждого протона, могут давать вклад в спин-спиновое
взаимодействие. Такой тип взаимодействия важен в атомах,
отличных от водорода, в которых химическая связь образуется
с участием валентных /?-орбиталей.
Упражнения. Что означает термин «спин-спиновое взаимодействие» в
спектрах ЯМР? При каких условиях это взаимодействие не проявляется в
спектре, даже если оно отлично от нуля? Каков диапазон изменения
константы спин-спинового взаимодействия протонов в ЯМР? Как зависит эта
константа от напряженности внешнего поля? Почему прямое, диполь-дипольное
взаимодействие между двумя спинами не играет роли, если молекула
находится в жидкости? Важно ли оно в твердом теле? Какова характерная
величина прямого дипольного взаимодействия между двумя протонами в
молекуле воды? Исследуйте, как это взаимодействие зависит от ориентации
молекулы по отношению к внешнему полю (предположите, что протонные
моменты выстраиваются вдоль этого поля, и найдите нужные формулы в
списке формул Д.1). Какую информацию о структуре молекул можно надеяться
получить из изучения прямого взаимодействия? Каково происхождение спин-
спинового взаимодействия протонов молекул, находящихся в жидкости?
Объясните, какая последовательность взаимодействий передает информацию об
ориентации протона его соседу. Что происходит со спин-спиновым
взаимодействием, когда протоны разделены 3, 4 и 5 связями? Какие возбужденные
состояния должны быть примешаны к основному состоянию, чтобы возникла
спиновая поляризация связи? Может ли дипольное взаимодействие играть
какую-либо роль в жидкостях? Что означают отрицательные значения /?
Рекомендуемые источники. Подробное обсуждение механизма
спин-спинового взаимодействия см. в гл. 11 [1]. Роль, которую оно играет в ЯМР,
описана Мак-Лечланом в кн. «Магнитный резонанс» [2]. Этот же вопрос
подробно рассматривается Линден-Беллом и Харрисом [260], Керрингтоном и Мак-
Лечланом [90], Сликтером [374], Мемори [281] и Абрагамом [27]. Анализ спек-
338
с
тров ЯМР с целью извлечения данных о спин-спиновом взаимодействии и
вопросы их использования описаны перечисленными авторами, а также Роберт-
сом [340], Абрахамом [29], Эмсли, Финеем и Сатклифом [134], Поплом, Шней-
дером и Бернстейном [323], Корио [97]. Причину того, почему в спектре
проявляется взаимодействие лишь между неэквивалентными ядрами, можно
понять на основании рассмотрения математических выкладок, приведенных Кер-
рингтоном и Мак-Лечланом [90]. Таблицы величин / приведены Эмсли,
Финеем и Сатклифом [134].
СРОДСТВО К ЭЛЕКТРОНУ. Сродство к электрону
изолированного атома — это энергия, выделяющаяся, если к этому
атому из бесконечности приближается электрон и образуется
анион. Следовательно, сродство к электрону представляет собой
разность энергий нейтрального атома и его отрицательного иона:
Е'С(Х) = Е(Х) — £(Х~~). Положительное сродство означает, что
анион более стабилен, чем нейтральный атом. Поскольку, чтобы
вновь получить из иона X" нейтральный атом и удаленный на
бесконечность электрон, необходимо проделать некоторую
работу Е'С(Х), очевидно, что £"(Х) представляет собой не что
иное, как потенциал ионизации /(Х-) аниона: £'(Х) =/(Х-).
Определить сродство к электрону часто довольно сложно.
Один из прямых методов — это измерение потенциала ионизации
аниона. Применяются также такие методы, как
1) электронный удар, при котором пытаются установить
потенциал появления отрицательного иона в реакции
XY + *?->X- + Y;
2) исследования прилипания электрона к атомам (так
называемая спектроскопия сродства к электрону);
3) полярография;
4) расчет цикла Борна — Габера для энергии решетки
ионного кристалла.
Одним из примеров использования данных о сродстве атомов
к электрону является построение шкалы
электроотрицательности Малликена, полезной в тех случаях, когда необходимо
оценить устойчивость анионов.
Рекомендуемые источники. Обзор методов определения сродства к
электрону дан Мак-Дауэллом [271]. Другие сведения и таблицы значений
сродства можно найти в кн. Причарда [326], Веденеева, Гуревича, Кондратьева,
Медведева и Франкевича [408] и Бриглеба [77]. Применение этого понятия в
химии рассматривается Падефаттом в кн. «Периодическая система
элементов» и Филлипсом и Вильямсом [317].
СУПЕРПОЗИЦИИ ПРИНЦИП. Принцип суперпозиции
утверждает, что, если некоторое событие состоит из нескольких
более простых событий, его амплитуда является суперпозицией
амплитуд простых событий. Значение этого принципа, который
339
с
является одним из основных в квантовой механике и приводит
к важнейшим различиям между классической и квантовой
механикой, можно пояснить, рассмотрев следующий пример.
Предположим, что некоторое событие можно разделить на
ряд составляющих. Например, рассматриваемым событием
может быть путешествие из пункта р[ в пункт рг, а элементарными
событиями могут быть путешествия по различным путям,
проходящим через пункты ра или рь. Классическая теория
приписывает вероятность Р(а) пути, проходящему через точку ра, и ве-
Шссическое
представление
Р(а)
Р(Ь)
<4——0
Рис. С. 14. Принцип суперпозиции.
Р(а)+Р(Ь)
Квантово-
механическое
представление
Р(а)=ф*(а)ф(а)
Р(Ь)=ф*(Ь)ф(Ь)
\ф(а)+ф(Ь)\г
роятность Р(Ь) —пути, проходящему через рь. Далее, в
классической теории утверждается, что полная вероятность совершить
путешествие из pi в р2 равна сумме вероятностей путешествий
по отдельным путям Р = Р(а)+ Р(Ь) (рис. С. 14). Такие
рассуждения могут показаться тривиальными, но в квантовой теории
они неверны. Принцип суперпозиции признает, что существует
вероятность совершить путешествие через точку ра и что она
равна Р(а), аналогичное утверждение справедливо в отношении
пути через точку рь. Однако принцип суперпозиции отвергает
утверждение, что полная вероятность равна сумме вероятностей
составляющих событий. Согласно принципу суперпозиции, для
вычисления полной вероятности необходимо сначала найти
амплитуды вероятностей (волновые функции) для каждого пути,
затем найти амплитуду вероятности суммарного события и с ее
помощью определить искомую вероятность (рис. С. 14). Пусть
амплитуда вероятности для путешествия через точку ра есть
г|)(а), это означает, что сама вероятность равна *1у|у, соответ-
340
с
ствующая амплитуда вероятности путешествия через точку рь
есть у^(Ь). Принцип суперпозиции утверждает, что амплитуда г|)
результирующего процесса равна сумме \];(а)+г|)(6). Отсюда
следует, что вероятность результирующего процесса равна tj?*i|).
В развернутом виде это выражение можно записать так:
Р(а)+ P(b) + $*(a)y$>(b)+ \$)(a)ty*(b). Таким образом, полная
вероятность события отличается от суммы вероятностей
отдельных событий интерференционным слагаемым ^*(a)*|)(fe) +
-f- г|?(а)\|;*(Ь)- Заметим, что, если бы один из путей был
запрещен, амплитуда вероятности его осуществления равнялась бы
нулю и окончательная вероятность путешествия свелась бы к
р = Р(а) (если путь запрещен через точку ръ). Кроме того,
заметим, что интерференционные слагаемые не возникают в
классическом случае, они характерны для квантовых процессов и
обусловлены требованием принципа суперпозиции, чтобы все
основные манипуляции производились с амплитудами.
Если принцип суперпозиции соответствует истинным законам
природы, значит, должны обнаруживаться какие-то его прямые
физические следствия. По-видимому, должны были бы
наблюдаться эффекты интерференции частиц, которые летят из пушки,
находящейся в точке pi к мишени в точке рч сквозь экран, в
котором проделаны два отверстия. И действительно, наблюдаются
такие интерференционные эффекты для частиц, соответствующие
интерференции света в аналогичных обстоятельствах.
Принцип суперпозиции применяется ко всем процессам
квантовой механики. При рассмотрении любого сложного события
вычисления необходимо проводить с волновыми функциями
(амплитудами состояний). Поэтому уравнение Шредингера играет
центральную роль в квантовой механике — оно позволяет
вычислять амплитуду состояния и показывает, как определить ее
эволюцию во времени.
Примером использования принципа суперпозиции является
метод ЛКАО. Будем рассуждать таким образом. Вероятность
найти электрон в определенной точке молекулы зависит от
вероятности того, что он находится на одной из атомных орбиталей
составляющих молекулу атомов. Следовательно, чтобы найти
вероятность обнаружения электрона в точке г, нужно прежде
всего знать амплитуды вероятностей того, что электрон
находится в этой точке, если он принадлежит каждому из атомов в
отдельности. Эти амплитуды вероятностей как раз и являются
волновыми функциями атомных орбиталей, каждую из которых
надо вычислить в точке г. В результате полная амплитуда
вероятности обнаружить электрон в точке г равна сумме атомных
орбиталей в этой точке, а полная вероятность равна квадрату
этой амплитуды. Такова интерпретация молекулярных орбита-
лей при использовании приближения ЛКАО.
341
с
Упражнения. Сформулируйте принцип суперпозиции Допустим, что
путешествие из одного пункта в другой можно совершить по двум дорогам;
учтите в рамках законов классической, а также квантовой механики
возможность того, что ворота, установленные на этих дорогах, могут быть закрыты.
Обсудите на основе принципа суперпозиции аналогию между
распространением частиц и света. Обсудите на этой же основе дифракцию частиц. Каково
обоснование метода ЛКАО, применяемого для расчетов строения молекул, с
учетом принципа суперпозиции? Обсудите также с этой точки зрения
представления о гибридизации.
Рекомендуемые источники. См. курс лекций Фейнмана, Лейтона, Сэндса
[145], § 9.2 кн. Бома [63], гл. 1 кн. Дирака [123]. Простое рассмотрение
оптических аналогий дано в гл. 2 [1]. Историю вопроса см. у Джеммера [203].
Построение квантовой механики на основе принципа суперпозиции см. в кн.
Фейнмана и Гиббса [144].
СФЕРИЧЕСКИЕ ГАРМОНИКИ. Сферические гармоники —
это набор функций угловых координат 8 и ф (определение
которых показано на рис. С. 15), удовлетворяющих
дифференциальному уравнению Л2У;т(8, ф) =—/(/+ 1)У;т(8, ф), где Л2
—оператор Лежандра (см. разд. «Лапласиан»). Их можно выразить
в виде полиномов от sin 8, cos 8, sin ф, cos ф или в виде
полиномов от переменных х, у, z (табл. 22 и 23) и можно наглядно
представить себе как различные типы колебаний сферической
оболочки.
Эти функции нумеруются числами / и т, причем / может
принимать любое положительное целое значение, включая нуль, а
m при заданном значении / может меняться через единицу от —/
до /. Допустимые значения / и m аналогичны квантовым числам
орбитального углового момента и его проекции, что не случайно,
так как сферические гармоники являются волновыми
функциями, соответствующими состояниям с определенными значениями
углового момента / и его проекции m на выделенное
направление.
Функция У0,о(8, ф) равна постоянной (1/2 Vя) и>
следовательно, имеет одно и то же значение во всех точках на поверхности
сферы. Поэтому ее можно представить в виде функции,
изображенной на рис. С. 16, а, где Уо,о — поверхность, всюду отстоящая
на одинаковое расстояние от сферической поверхности. Удобный
способ изображения изотропии этой функции, т. е. ее сферической
симметрии, состоит в том, что значение функции в каждой точке
откладывается вдоль радиуса сферы от ее центра; это приводит
к появлению вспомогательной функции, которая сама является
сферой радиуса Уо, о и содержит всю информацию о форме
сферической гармоники Уо, о. Следует отметить связь между этой
вспомогательной функцией и графическими изображениями
атомной ls-орбитали (см. стр. 83). Гармоника У0, о не имеет
узлов ни при каких углах, поэтому она соответствует волне с
нулевым орбитальным угловым моментом.
342
полярный угол
азимутальный уюл\
Рис. С.15. Сферические полярные координаты.
сферическая
гармоника
вспомогательная
г—_ функция
Рис. С.16. Функции (а) К0>0 (Э, ф), (б) К!>0 (9, ф) и (в) К2>0 (Э, ф),
соответствующие вспомогательные функции и проекции поперечного сечения^
с
Функция Vi, о(в, ф) пропорциональна cos 9 и не зависит от ср.
Она принимает экстремальные значения на полюсах и равна
нулю на экваторе; ее можно изобразить так, как это сделано на
рис. С. 16,6. Вспомогательную функцию можно построить таким
же образом, как и в первом случае. Заметим, что в северном
полушарии амплитуда волны положительна (и это отмечено
знаком + у вспомогательной функции), а в южном
полушарии — отрицательна. Следует отметить сходство полученной
вспомогательной функции с граничной поверхностью /?2-орбита-
ли. Поскольку у этой функции имеется один угловой узел, такая
волна соответствует состоянию с угловым моментом 1=1. Если
смотреть вдоль оси г, экваториальный узел не будет виден, и,
следовательно, проекция углового момента на ось z равна нулю
(а это, как следует напомнить, и означает, что квантовое
число т равно нулю).
Другие сферические гармоники, соответствующие /=1, имеют
проекции т = 1 и —1. Обе эти функции комплексные, они
соответствуют волнам, бегущим вокруг оси z с амплитудами,
которые принимают максимальные значения в экваториальной
области. Можно построить такие комбинации этих двух функций,
которые будут действительными и будут соответствовать
стоячим волнам. Одна из этих комбинаций имеет вид Yif i + Yi} _i,
она пропорциональна cos qp (см. табл. 23). Эта функция имеет
ту же форму, что и У4, о, но она ориентирована вдоль оси х.
Комбинация У4,1—У4, _1, которая пропорциональна sin ф, также
имеет ту же форму, но ориентирована вдоль оси у. Следует
обратить внимание на связь этих комбинаций с рх- и /v-орбиталями.
Дальнейшее рассмотрение включает пять функций с / = 2.
Получающиеся вспомогательные функции очень похожи на
атомные d-орбитали (рис. С. 16 и рис. В. 10). В любом случае число
угловых узлов равно / (мы считаем узлом каждую плоскую
поверхность, на которой У;,т(Э, ф)=0). Связь между числом узлов
и угловым моментом является следствием соотношения де Брой-
ля и связи между кинетической энергией состояний и его
волновой функцией. Следует отметить, что угловые зависимости
сферических гармоник и граничные поверхности атомных орбиталей
не вполне идентичны, поскольку последние определяются как
границы областей пространства, заключающих в себе
определенные значения амплитуды или плотности, и зависимость этих
характеристик от радиуса (а не только от углов) искажает
форму сферических гармоник.
Если требуется найти угловое распределение частицы,
скользящей с определенным угловым моментом по поверхности
сферы, то, согласно интерпретации Борна (см. разд. «Волновая
функция»), его можно вычислить как квадрат соответствующей
сферической функции. Частица с нулевым угловым моментом
344
с
(/ = 0) равномерно распределяется по сферической
поверхности; частица с / = 1 в основном сконцентрирована либо в
полярных областях (т = 0), либо в экваториальных (т = ±1);
частица с / = 2 сильно локализована в полярных областях, но,
кроме того, у нее имеется заметная равномерно распределенная
плотность вблизи экватора (т = 0), или же она локализована
в двух зонах, сосредоточенных вблизи 45° северной широты и 45°
южной шпроты (т = ±1), либо сильно сконцентрирована в
зоне, находящейся вблизи экватора (т = ±2).
Упражнения. 1. Какова роль сферических гармоник в классической
теории и в квантовой теории? Какие значения могут принимать индексы / и т
и сколько значений т возможно при заданном значении /? Какова форма
функции Ко, о, и почему она соответствует состоянию с нулевым угловым
моментом? Каким колебаниям сферической поверхности она соответствует?
Постройте вспомогательные функции для рх-, dz2- и d^-орбиталей. Для
каждой из этих орбиталей изобразите форму функции, которая определяет
распределение вероятности обнаружения на ней частицы Каким колебаниям
сферической поверхности сотвегствуют эти орбитали? Как можно возбудить
каждое из этих колебаний? Рассмотрите таким же образом /-орбитали (/ = 3).
Сравните полученные ответы с изображением атомных орбиталей водорода,,
приведенных на рис. ВЛО. Почему приведенные там контурные диаграммы
должны быть сходными (но не должны совпадать) с изображенными вами
вспомогательными функциями? Предположим, что в каждой точке
сферической поверхности, описанной вокруг протона в атоме водорода, отложены
значения волновых функций для различных орбитальных состояний. Можно
ли ожидать, что полученные таким образом функции совпадут с функциями,
изображенными вами ранее? Обоснуйте свой ответ. Найдите широты,
отвечающие максимальным концентрациям электронных плотностей для орбита-
лей dXy, dxz, fxyz-
2. Убедитесь, что функции Y0,0, Y\,\t У4, з действительно удовлетворяют
дифференциальному уравнению, которое определяет сферические гармоники.
Воспользуйтесь для этого оператором Лежандра из списка формул Л.1.
Подействуйте оператором 1г (см список формул 0.1) на явное выражение
сферической гармоники общего вида и убедитесь, что Yim — собственная
функция оператора /2, соответствующая собственному значению mh. Докажите,
что решения в виде стоячих волн Yi, m ± Yi, _w являются собственными
функциями оператора длины углового момента, но соответствуют состояниям с
нулевой проекцией углового момента на ось z (как и следует ожидать для
стоячих волн) и не являются собственными функциями оператора 1г (см.
разд. «Подавление орбитального углового момента»).
Рекомендуемые источники. Дальнейшее обсуждение сферических
гармоник и их связи с угловым моментом, а также метода их иллюстрации с
помощью вспомогательных функций см. в гл. 3 [1]. Рассмотрение свойств
сферических гармоник и их связи с состояниями с определенным угловым мо*
ментом, с волнами на затопленной планете, с приливными явлениями и с
колебаниями сферы дано Козманом [217]. Там же рассматривается решение
дифференциальных уравнений для сферических гармоник; см. также кн. По-
линга и Вильсона [314]. Другие подходы изложены в гл. 6 [1], в кн. Роуза
[347], Бринка и Сэтчлера [80] и Эдмондса [131]. Математические свойства
сферических гармоник и входящих в них присоединенных функций Лежандра
подробно изложены Абрамовичем и Стегуном [30].
345
т
ТЕНЗОР. Для математика тензор — это величина,
преобразующаяся вполне определенным образом при преобразованиях
координат, которые математик использует для описания задачи.
Скалярная величина, которую можно считать тензором нулевого
ранга, не меняется при преобразованиях координат. Вектор
изменяется при преобразованиях координат (хотя его величина
остается неизменной, ее описание в новых координатах отлично
от описания в исходных координатах) и представляет собой
тензор первого ранга. В качестве примеров тензоров высших
рангов можно привести более сложные величины, например такие,
как гг, где г — вектор, который представляет собой тензор
второго ранга. Математики различают контравариантные и кова-
риантные тензоры. Например, набор координат вектора [х, yt z]
преобразуется как контравариантный тензор первого ранга, а
набор величин [df/dx, df/ду, df/dz], где / — скалярная функция,
преобразуется как ковариантный тензор первого ранга.
Тензорное исчисление занимается общими преобразованиями
координат и является эффективным методом изучения неэвклидовой
геометрии, например в общей теории относительности. Если речь
идет только об ортогональных преобразованиях координат при
сохраняющихся углах между осями (типа простого вращения
осей), требования, которым должны удовлетворять величины,
чтобы быть тензорами, менее жестки. Величины, которые
удовлетворяют этим требованиям, называются декартовыми
тензорами. Если такие величины преобразуются при вращениях
системы координатных осей некоторым особым образом, мы
имеем дело с неприводимыми сферическими тензорами, которые
играют важную роль при обсуждении молекулярных и атомных
свойств.
Для химика тензор — это величина, которая выражает
зависимость свойств молекул и твердых тел от направления. Как
правило, химик не совершает ошибки, используя этот термин,
поскольку обычно (но не всегда) исследуемые характеристики
преобразуются тем же образом, что и тензоры, а следовательно,
и являются тензорами. В качестве примера рассмотрим влияние
электрического поля на молекулу. Предположим, что поле
направлено вдоль некоторой оси Z, что оно поляризует молекулу
и индуцирует дипольный момент. Обычно главная компонента
индуцированного диполя лежит в том же направлении, что и
поле, но, как правило, поле и индуцированный момент не совсем
параллельны, поскольку имеются еще Х- и У-компоненты диполя
346
т
(рис. Т. 1). Величины этих компонент пропорциональны
напряженности приложенного электрического поля EZl поэтому они
равны aXzEz, ayzEz и aZ2£z, где olqq> — коэффициенты
пропорциональности, характеризующие поляризуемость молекулы. Если
поле направлено вдоль осей X или У, для описания
индуцированного диполя можно использовать аналогичные выражения.
Если молекула анизотропна, соответствующие коэффициенты
пропорциональности имеют неодинаковые значения, всего мы
получим девять коэффициентов вида aQQ<. Напомним, что
величина гг с девятью компонентами ХХУ XY, XZ, ..., ZZ является
Рис. Т.1. Роль недиагональных элементов
тензора поляризуемости. Когда вектор
напряженности поля Е направлен вдоль
произвольной оси, оно может
индуцировать дипольный момент, не обязательно
направленный параллельно Е. Дипольный
момент параллелен вектору напряженности
поля Я, если оно направлено вдоль главной
оси (одной из выделенных осей) молекулы.
тензором второго ранга. Следовательно, можно по аналогии
назвать совокупность девяти величин olqq', которые являются
компонентами тензора второго ранга а, тензором поляризуемости.
Если известен тензор а, то при любом направлении
приложенного поля можно предсказать поляризацию молекулы в любом
направлении.
Подобно тензорам ведут себя в частности, те физические
величины, которые описывают связь между деформациями и
напряжениями упругих тел и другие подобные соотношения;
отсюда произошел и сам термин «тензор» (tense — натянутый,
напряженный). В рассмотренном выше примере «напряжение»
создается приложенным полем, а «деформацией» является
-результирующая поляризация молекулы. Магнитная восприимчивость
принадлежит к числу характеристик этого же типа и может
быть выражена в виде тензора второго ранга. К этому же типу
свойств принадлежит упругость тела, ее также можно
представить в виде тензора. По некоторым причинам g-тензор, с
которым мы встречаемся при обсуждении парамагнитного резонанса,
не является истинным тензором, поэтому мы называли его
^-фактором (см. соответствующий раздел), но если не подходить
столь строго, то его тоже можно назвать тензором, и в
некоторых случаях он им почти является.
347
т
Спинор — это величина, которая напоминает тензор, но имеет
следующее особое свойство: при вращении осей координат на
360° она меняет знак. Следовательно, чтобы вернуть спинор к
исходному виду, необходимо произвести вращение осей
координат на угол 4тт. Величины, обладающие свойствами спиноров,
используются при математическом описании спина, этим и
объясняется происхождение самого термина «спинор».
Рекомендуемые источники. Превосходное и достаточно простое введение
в общую математическую теорию тензоров можно найти в кн. Синга и Шил-
да [392], Кирала [231] и Джеффриса [206]. Роль тензоров в обсуждении
физических свойств материи описана Бринком и Сэтчлером [80], Роузом [347] и
Эндмондсом [131]. Общее обсуждение вопроса дано Фано и Рака [139].
В § 15.6 кн. Абрагама и Блини [28] объясняется, почему ^-фактор не
является тензором.
ТЕПЛОЕМКОСТЬ. Теория теплоемкости кристаллических
твердых тел началась установлением Дюлонгом и Пти закона,
утверждавшего, что теплоемкость всех металлов равна
6 кал-град-1-моль-1 (25 Дж-К^-моль-1). К сожалению,
большинство металлов не подчиняется этому «закону», а при низких
температурах он вообще не выполняется ни для одного металла.
Тем не менее полезно разобраться в рассуждениях, которые
«подтверждают» закон Дюлонга и Пти, так как тогда легче
понять квантовую теорию теплоемкости. Предположим, что кусок
металла содержит N атомов, каждый из которых может
колебаться в трех перпендикулярных направлениях; следовательно,
металл ведет себя как система из 3N осцилляторов. Согласно
закону равнораспределения, в состоянии теплового равновесия
каждому колебанию соответствует энергия kT\ поэтому полная
энергия металла при температуре Т равна 3NkT, или 3RT в
расчете на 1 моль металла. Термодинамика утверждает, что
теплоемкость при постоянном объеме равна (dU/dT)v, где U —
внутренняя энергия образца. В нашем случае U = 3RT, поэтому
теплоемкость равна Су = 3R, а численное значение этой
величины согласуется с законом Дюлонга и Пти.
Квантовая теория предупреждает нас, что закон
равнораспределения, применимый к классическим системам, может
нарушаться для систем, которые, подобно колебаниям атомов в
кристалле, необходимо рассматривать в рамках квантовой
механики. Причина несоответствия этому закону связана с
неспособностью квантового осциллятора поглотить меньше, чем его
полный квант энергии. Это уменьшает эффективность осцилляторов,
входящих в состав образца, и, следовательно, снижает его
теплоемкость.
Простейшим приближением к реальной картине является
модель Эйнштейна, основанная на предположении, что каждый
348
т
осциллятор в образце имеет одну и ту же собственную частоту
ye- Предположим, что источник тепла с температурой Т
находится в контакте с системой осцилляторов, обладающих одной
и той же частотой. Если бы эти осцилляторы подчинялись
законам классической физики, то каждый из них был бы возбужден
и каждый из них колебался бы со своей частотой, но с такой
амплитудой, которая соответствовала бы средней энергии kT. Но
поскольку осциллятор подчиняется законам квантовой механики,
то при передаче тепла металлу при низкой температуре оно
может быть использовано для возбуждения только небольшого
числа осцилляторов, так как ни один возбужденный осциллятор
не может обладать энергией, меньшей чем /ive- Небольшое число
осцилляторов должно обладать некоторой энергией, а остальные
должны оставаться в покое. Эти соображения приводят к
выводу об эффективном уменьшении числа осцилляторов в
образце и, следовательно, об уменьшении его теплоемкости. При
высоких температурах энергия может быть распределена по очень
многим осцилляторам, т. е. большее их число может поглотить
энергию; поэтому теплоемкость оказывается больше, чем при
низких температурах. При очень высоких температурах, когда
энергия образца намного превосходит энергию возбуждения
осцилляторов, все осцилляторы способны поглощать энергию и
могут быть возбуждены на высокие уровни, а теплоемкость
образца достигает своего классического значения 3R. В списке
Список формул ТА
Теплоемкость твердого тела
Закон Дюлонеа и Пти:
Cv = 3Lk = 3#.
Модель Эйнштейна:
Модель Дебая:
I C^94v)3 J ^Mtt^^I^o^^w1,8-r<^
GD = /*vD/*.
vD и 0D можно связать со скоростью звука v:
vl = 3NvV4nV,
где N/V — плотность числа атомов в образце.
349
т
формул Т. 1 Дана формула Эйнштейна для теплоемкости, а на
рис. Т. 2 показана предсказываемая ею температурная
зависимость теплоемкости.
Модель Дебая, которая представляет собой модификацию
модели Эйнштейна, учитывает то обстоятельство, что интервал
собственных частот осцилляторов простирается от нуля до
некоторого предельного значения vD. Наличие предельной частоты
колебания можно обосновать двумя способами. Во-первых, можно
рассматривать твердое тело как континуум (своеобразный
студень). Студень может колебаться с любыми частотами от нуля
§
Рис. Т.2. Расчетные кривые теплоемкости.
до очень высокого значения, и число типов колебаний, которые
имеют данную частоту, вычисляется очень просто. Но суммарное
число типов колебаний студня не может превосходить общего
числа колебаний всех атомов, которые образуют студень. Это
число равно 3jV; следовательно, должен существовать верхний
предел частоты колебаний студня, чтобы общее число
осцилляторов было равно 3N. (Если бы студень был настоящим
континуумом, как вакуум, верхнего частотного предела не
существовало бы, так как континуум соответствует системе с
бесконечным числом осциллирующих компонент; именно по этой причине
в вакууме может распространяться свет всех частот.)
Доказать существование верхнего предела частот можно и
другим способом. Рассмотрим с этой целью рис. Т. 3, где
показана цепочка атомов в кристалле, колеблющихся относительно
друг друга. Если мы ограничимся только поперечными
колебаниями (которые перпендикулярны цепочке атомов), то нам
нетрудно будет установить, что наибольшей возвращающей силой
характеризуются те колебания, при которых соседние атомы
35Q
т
смещаются в противоположных направлениях, а наименьшей
возвращающей силой — те, при которых все атомы смещаются
в одном направлении (но в разной степени; если бы все атомы
» -ооееядоо-
Рис. Т.З. Колебания в цепочке атомов с наименьшей частотой (а),
промежуточной частотой (б) и наибольшей Частотой (в).
£
2
Рис. Т.4. Распределение числа осцилляторов Af (v) с частотой v согласно
моделям Эйнштейна и Дебая, а также экспериментальные данные (для Си).
смещались на одно расстояние, мы получили бы трансляцию
Цепочки). Существуют также промежуточные типы смещения,
поэтому можно ожидать, что имеется интервал значений
возвращающей силы и соответственно интервал собственных
колебаний цепочки частот. Однако этот интервал должен быть
ограничен максимальной частотой, так как невозможно получить воз-
351
т
вращающую силу, большую, чем в случае противоположных
смещений соседних атомов. Этот случай иллюстрируется на
рис. Т. 4.
Модель Дебая учитывает распределение частот колебаний
посредством определения числа собственных колебаний каждой
частоты v в интервале от 0 до vd и вычисления общего вклада
в теплоемкость (см. список формул Т. 1 и рис. Т. 2). Поскольку
модель Дебая допускает наличие осцилляторов с частотой
более низкой, чем единственная частота в модели Эйнштейна,
теплоемкость в модели Дебая превосходит теплоемкость в
последней, но при высоких температурах, когда поведение
осцилляторов приближается к классическому, различие между этими
моделями пропадает. Теплоемкость зависит от температуры и
характеристической постоянной, называемой температурой Дебая
6d = /ivd/&; так как предельная частота колебаний в
высокоупругих веществах выше, для них соответственно выше и
температура Дебая. Некоторые характерные значения 8d приведены
в табл. 12. При заданной температуре высокая температура
Дебая означает меньшую теплоемкость. При низких температурах,
согласно модели Дебая, теплоемкость должна быть
пропорциональна (ГДЬ)3; это соотношение часто используется при
вычислениях энтропии.
Рекомендуемые источники. В гл. 1 [1] приводятся подробности вывода
формулы теплоемкости Эйнштейна и основные моменты вывода формулы
теплоемкости Дебая. Изложение вывода формулы Эйнштейна и обсуждение
модели Дебая см в кн. Гассера и Ричардса «Энтропия и энергетические
уровни» [19]. Очень хорошее обсуждение теплоемкостей со всеми
выкладками дается в кн. Киттеля [224] и Деккера [121]. См. также кн. Дэвиц-
сона [116]. Подборку числовых данных, включая численные значения функций
Дебая и Эйнштейна и температур Дебая для многих веществ, можно найти
в кн. Грея [168]. Функция Дебая рассматривается также Абрамовичем и
Стегуном [30]. Температуры Дебая для некоторых веществ приведены также
и в других упомянутых книгах.
ТЕРМ. Слово «терм» (term — член математического
выражения, слагаемое) появилось вначале в жаргоне спектроскопистов,
которые тогда не вкладывали в его понятие конкретный смысл.
В начале развития атомной спектроскопии было обнаружено,
что можно описание спектров значительно упростить, если
выражать частоту каждой линии в виде разности двух членов —
термов. Поскольку каждый терм дает вклад в несколько
спектральных линий, оказывается возможным перечислять гораздо
меньше энергий термов, чем энергий переходов. Правило такого
описания спектров известно под названием комбинационного
принципа Ритца (вычисление частот или энергий переходов
осуществляется путем вычитания друг из друга различных
комбинаций термов). Итак, первоначально спектральные термы были
352
т
просто набором чисел, с помощью которых удавалось
предсказать спектр. Однако, как это ни странно, оказалось, что не все
комбинации Т[ — Т2 соответствуют наблюдаемым переходам.
Квантовая теория дала естественное толкование этому
понятию; оказалось, что терм — это энергетическое состояние атома.
Комбинационный принцип был частично объяснен постулатом
Бора, а позднее квантовомеханическими расчетами, которые
показали, что спектральная линия соответствует переходу атома
из одного стационарного энергетического состояния в другое и
что частота перехода определяется выражением hv = 7\ — Г2.
Квантовая механика позволила также получить правила отбора,
которые указывают, какие из комбинаций термов можно
наблюдать.
В настоящее время понятие «терм» используется для
указания энергетического состояния атома. Символ терма,
используемый для обозначения энергетического состояния, образуется из
квантовых чисел, определяющих это состояние. Типичные
символы термов имеют вид 2S или 3Р, но часто, чтобы задать
состояние более полно, вводят и другие индексы. Символ терма,
приведенный со всеми подробностями в списке формул,
образуется следующим образом:
Список формул Т.2
Символы термов
Мультиплетность-> (25 + 1) М. <- состояние
X
Значение L-> /««-уровень
L = 0, 1, 2, 3, 4,....
X = 5, Р, Д F, G.
1. Буквенное обозначение терма связано.с величиной L, т.е.
со значением квантового числа полного орбитального углового
момента, согласно следующему правилу: L = О, 1, 2, 3, 4, ... *-+
++S,P,D,F9G9 ... .
2. Индекс слева вверху указывает величину (25 + 1), где
5 — квантовое число полного спинового углового момента атома
(отличить это S от 5, соответствующего L = 0, легко). Величина
25 + 1 часто называется мультиплетностью терма, ее свойства и
значение описаны в соответствующем разделе. Добавим, что 2S
читается как дублетный терм 5, 3Р — как трнплетный терм Р.
3. Уровни определенного терма различаются с помощью
правого нижнего индекса, которым определяется значение /. На-
353
т
пример, у дублетного терма с L = 1, т. е. 2Р, имеются два
уровня: один с / = 7г и другой с / = %> эти уровни обозначаются
как 2А, и 2P~i, соответственно и читаются как «дублет Р одна
вторая» и «дублет Р три вторых».
4. Состояние атома можно описать еще подробнее, если
задать значение MJy т. е. величину проекции / на какую-либо ось.
Это значение указывает правый верхний индекс. Например,
состояние уровня / = 2 триплетного терма с L = 2 и Mj = —1
обозначается 3Dj\ и по этому символу мы можем определить
значения всех квантовых чисел S, L, / и Mj (см. список
формул Т.2).
Перечисление термов и их энергий позволяет установить
спектр атома, но сделать это можно, только если известно, какие
комбинации разрешены. Разрешенные комбинации термов
определяются правилами отбора, которые обычно выражаются в виде
значений AS, AL, A/, AiWj, допустимых при переходах.
Информация, содержащаяся в символе терма, совместно с этими
правилами позволяет ясно увидеть, какие переходы разрешены.
Символы термов встречаются также в молекулярной
спектроскопии, но, поскольку в этом случае L не является точным
квантовым числом, индексы молекулярных термов обычно
связаны лишь с их теоретико-групповой классификацией.
Рекомендуемые источники. Атомные спектры обсуждаются в гл. 8 [1],
молекулярные спектры — в гл. 10, в обеих главах показано использование
символов термов. См. также разд. «Атомные спектры», «Правила отбора», «Тон*
кая структура», «Мультиплетность».
ТОНКАЯ СТРУКТУРА. Тонкой структурой атомного спектра
называется система близких линий, возникающая в результате
расщепления уровней (определенного терма с различными
значениями /). В атоме натрия энергия уровня 2А/2 отличается от
энергии 2Р*/,У поэтому излучения при переходах 2Pi/2-> 2Sy2 и
/У2 -> 2Si/2 слегка отличаются по частоте (возникают две близко
расположенные желтые D-линии спектра натрия); это и есть
проявление тонкой структуры.
Тонкая структура является проявлением спин-орбитальной
связи. Лучше всего рассмотреть это явление на примере одно-
электронного атома. Предположим, что орбитальный угловой
момент электрона равен 1. Поскольку электрон имеет заряд, он
обладает также магнитным моментом, который, согласно закону
Ампера, можно рассматривать как диполь в центре орбиты. Этот
магнитный момент создает магнитное поле, взаимодействующее
со спиновым магнитным моментом электрона, а энергия
взаимодействия зависит от относительной ориентации спинового и
орбитального магнитных моментов. Это означает, что энергия
зависит от относительной ориентации угловых моментов 1 и S
354
т
(рис. Т. 5). Низкоэнергетическая относительная ориентация
достигается при противоположных по знаку проекциях \хь и \is и
поэтому соответствует противоположному направлению векторов
1 и s. Таким образом, меньшее значение полного углового
момента j (j = 1 + s) отвечает меньшей энергии.
Итак, различные значения /' (а в многоэлектронных
атомах /) вследствие магнитного спин-орбитального
взаимодействия соответствуют различным энергиям. Это обстоятельство и
лежит в основе третьего правила Гунда, согласно которому, если
электронная оболочка за-
высокая энергия,
большее значение J
полнена меньше чем
наполовину, малые значения /
отвечают более низким
энергиям, чем большие значения
/ (если оболочка заполнена
более чем наполовину,
наблюдается обратное
соотношение). Термы, в которых
Рис. Т.5. Магнитное
взаимодействие, приводящее к появлению
тонкой структуры. Большее
значение полного углового момента
соответствует параллельному
расположению моментов и,
следовательно, большей энергии.
уровни с большими значениями / имеют более высокую
энергию, чем уровни с меньшими /, называются нормальными, а те
термы, в которых уровни с меньшими / оказываются наиболее
высокими, называются обращенными. Терм с несколькими
значениями / (например, терм 2Р, который имеет два уровня 2Р*Ь и
2Р*,\) называется мультиплетным термом, и это объясняет
названия «нормальный мультиплет» и «обращенный мультиплет».
В пределах данного мультиплета расстояния между уровнями
подчиняются правилу интервалов Ланде, которое устанавливает,
что интервалы между парами соседних уровней относятся как
значения / верхнего уровня каждой пары. Так, отношение
интервала 3Рг — ZP\ к интервалу 3Л — 3Р0 равно 2:1.
Спнн-орбнтальная связь увеличивается с ростом порядкового
номера элемента, поэтому можно ожидать, что тонкая структура
оказывает большое влияние на спектры тяжелых атомов, что и
наблюдается в действительности.
Рекомендуемые источники. Более подробно тонкая структура
обсуждается в [1], гл. 8. См. кн. Куна [229], где довольно просто представлен матема-
355
т
тический аппарат для ее описания; в этой же работе рассматриваются и
многоэлектронные атомы, которые подчиняются тем же принципам, .что и
водород. См. особенно гл. 2 кн. Герцберга [185]. Мультиплетная структура и
тонкая структура атома описана достаточно подробно Вудгейтом [433], Кон-
доном и Шортли [96], Гриффитом [170] и Шором и Мензелом [365].
ТОНКОЙ СТРУКТУРЫ ПОСТОЯННАЯ. Постоянная тонкой
структуры является мерой взаимодействия между заряженной
частицей и электромагнитным полем. Она определяется
выражением а = е2/4леоЬс, является безразмерной величиной и имеет
численное значение 1/137,03602 или приближенно 1/137. То
обстоятельство, что постоянная очень мала, представляется
чрезвычайно важным, поскольку она определяет размер атомов и
устойчивость вещества. Если бы постоянная а была значительно
больше, различие между веществом и излучением было бы
намного менее четким, если бы она была много меньше, вещество
фактически не могло бы взаимодействовать с электромагнитным
полем.
Эти рассуждения можно понять, рассмотрев, каким образом
постоянная тонкой структуры (т. е. мера взаимодействия между
заряженным веществом и электромагнитным полем) определяет
размер атомов и порядок величины некоторых их свойств.
Рассмотрим атом радиуса г; порядок величины потенциальной
энергии электрона в таком атоме определяется выражением Ze2l4neor.
Его нетрудно выразить через а и получить Zabc/r. Кинетическая
энергия атома определяется вкладами вида р2/2те; чтобы
оценить порядок величины этого выражения, воспользуемся
принципом неопределенности и тем, что электрон занимает область
радиуса г. Тогда р ~ h/r. В результате можно выразить полную
энергию атома через параметр г, его приближенный размер, и
найти г, минимизируя полную энергию (определяя значение г,
для которого dE/dr = 0). В результате мы получим г ~ кк/Za,
где Як — комптоновская длина волны электрона (Як = h\cme «
«2,4-Ю-12 м). Такая грубая оценка показывает, что размер
атома в 137 раз больше этого характерного для электрона
«размера». Интересно отметить, что боровский радиус можно
выразить как Кк/4па или как ге/а2, где ге — классический радиус
электрона. Если бы постоянная а была намного меньше, атом
был бы намного больше, а при значительно большем значении а,
сравнимом по величине со значением аналогичной постоянной
ядерного взаимодействия («сильного взаимодействия» в отличие
от «слабого» электромагнитного), атомы имели бы
приблизительно такие же размеры, как их ядра. Минимальную энергию
можно найти, подставив размер атома в выражение для его
энергии. В результате такой подстановки получаем
~-1/<2%2а2(гПеС2), где тес2 — релятивистское выражение для
энергии покоя частицы массой те. Следовательно, энергия атома от-
356
т
личается от ее значения Z2/1372. Этот множитель мал при
малых Z, но может достигать единицы, когда Z становится
большим (в тяжелых атомах). Это означает, что обычная нереляти-
внстская квантовая механика вполне применима, пока речь идет
о легких атомах, но становится все более и более неприменимой
по мере продвижения к концу периодической таблицы. Другой
интересный вывод касается порядка величины скорости
электрона в атоме или молекуле. Из приведенного выше выражения
для энергии следует (см. упражнения), что v ~ Zac, а
поскольку постоянная а мала, электроны движутся с
нерелятивистскими скоростями, исключение составляют только тяжелые атомы.
Постоянная тонкой структуры входит также в выражение спин-
орбитального взаимодействия, которое определяет тонкую
структуру спектров (этим и объясняется название постоянной а).
В водородоподобных атомах взаимодействие пропорционально
oPRy где R — постоянная Ридберга.
Устойчивость атомов определяется малой величиной а по
нескольким причинам. Одна из них заключается в том, что
вероятность перехода для электрического дипольного излучения
(главный механизм, посредством которого атом излучает или
поглощает фотоны) зависит от а. Рассмотрение этой зависимости
показывает, что электрон должен совершить примерно l/a(aZ)2
колебаний, прежде чем испустит фотон. Это объясняет метаста-
бильный характер возбужденных состояний атомов и молекул.
Вероятность того, что возбужденный атом одновременно
испустит два фотона, пропорциональна квадрату вероятности
испускания одного фотона, поэтому такой процесс имеет очень
малую вероятность и действительно наблюдается очень редко. Но
вещество может также распадаться с излучением энергии:
вещество может аннигилировать и превращаться в
электромагнитное излучение. Вероятность такого способа исчезновения
электрона пропорциональна мере его взаимодействия с
электромагнитным полем и, следовательно, зависит от а. Другими словами,
величина а характеризует часть времени, которое электрон
проводит в виде электромагнитного излучения. Как известно,
величина а мала, но, если бы она была близка к единице, вещество
и излучение были бы неразличимы.
Упражнения. Мерой чего является постоянная тонкой структуры? К
каким последствиям привело бы равенство этой величины нулю? Оцените
величину постоянной тонкой структуры, исходя из значений фундаментальных
постоянных, и докажите, что она безразмерна. Какие особенности атомной и
молекулярной структуры определяет а? Выразите постоянную
спин-орбитального взаимодействия, боровский радиус, постоянную Ридберга и
коэффициенты Эйнштейна через а и попытайтесь интерпретировать эти выражения.
Проведите расчет энергии атома водорода так, как описано в тексте, т. е.
357
т
найдите наинизшую энергию как функцию атомного размера г, размер атома
в этом случае и скорость электрона (из выражения для кинетической
энергии).
Рекомендуемые источники. Очень хорошее и довольно простое
рассмотрение того, как постоянная тонкой структуры определяет порядок величины
различных свойств атома, дано в гл. 1 кн. Тирринга [395].
ТУННЕЛЬНЫЙ ЭФФЕКТ. Квантовомеханический
туннельный эффект — это процесс, благодаря которому частицы
просачиваются через потенциальный барьер и оказываются в
областях, которые в классической механике были бы недоступны для
потенциальный, барьер
Рис. Т.6. Туннельное прохождение частицы сквозь барьер (слева направо).
них. Рассмотрим частицу, удерживаемую в потенциальной яме
барьером конечной высоты и ширины. Предположим, энергия
частицы такова, что, если исходить из законов классической
механики, ее недостаточно, чтобы частица вышла из ямы, пройдя
над потенциальным барьером. Квантовомеханическое
рассмотрение этой ситуации показывает, что существует некоторая
вероятность туннельного прохождения частицы сквозь барьер и ее^
выхода из ямы. Возможность туннельного прохождения барьера
проистекает из требования непрерывности волновой функции на
стенках ямы. Если амплитуда волновой функции не равна нулю
на внутренней границе барьера (а это допустимо при условии,
что потенциал в этой точке не обращается в бесконечность), она
не может просто так исчезнуть внутри барьера, вместо этого она
начинает более или менее быстро стремиться к нулю (рис. Т. 6).
Если спадание амплитуды происходит не слишком быстро, она
может и не достигнуть нулевого значения на внешней границе
барьера. В этой точке волновая функция должна плавно
переходить в функцию, характерную для свободной частицы вне
барьера, и, начиная с этой точки, волна перестанет затухать. Но
поскольку волновая функция не исчезла в области снаружи от
барьера, вероятность найти частицу в этой области отлична от
нуля, т. е. частица совершает туннельное прохождение наружу
из потенциальной ямы.
353
т
Амплитуда волновой функции внутри барьера убывает тем
быстрее, чем выше барьер относительно энергии падающей на
него частицы, поэтому амплитуда волновой функции с внешней
стороны барьера тоже оказывается тем меньше, чем больше
относительная высота барьера. В результате с увеличением
высоты барьера быстро уменьшается вероятность туннельного
прохождения. Амплитуда быстро убывает также с возрастанием
массы частицы; следовательно, вероятность туннельного
эффекта уменьшается, если масса проходящей через барьер частицы
увеличивается. Важную роль играет также форма потенциала,
поскольку резко меняющиеся («крутые») потенциалы
эффективнее отражают частицы, чем медленно меняющиеся («плавные»)
потенциалы (аналогичная ситуация имеет место при
прохождении света: свет сильнее отражается от тех областей, в которых
резко меняется показатель преломления). Следовательно,
наиболее благоприятна для туннельного эффекта такая ситуация,
когда легкая частица подходит к медленно меняющемуся
потенциальному барьеру. Очень эффективно совершают туннельное
прохождение электроны, хуже, но еще заметно, — протоны и
совсем слабо — дейтероны.
Часто высказывается некоторая озабоченность по поводу
кажущегося бессмысленным наличия у частицы отрицательной
кинетической энергии в областях пространства, запрещенных с
точки зрения классической физики, где потенциальная энергия
явно больше полной энергии. Наличие отрицательной
кинетической энергии в классической механике в самом деле служит
основанием того, что частицы не могут попасть в такие области.
В квантовой механике такая проблема не возникает, поскольку
в качестве кинетической энергии частицы следует рассматривать
среднее значение, вычисленное по всей волновой функции. То,
что кинетическая энергия в отдельных местах принимает
отрицательные значения, не противоречит факту, что наблюдаемая
кинетическая энергия (т. е. ее среднее значение) положительна.
Более того, предположим, что мы попытались ограничить
местонахождение частицы исключительно областью барьера, чтобы
получить отрицательную кинетическую энергию. Разумный
выход из такой искусственной ситуации указывает принцип
неопределенности: попытка удержать частицу в ограниченной области
приводит к неопределенности в ее энергии, и этой
неопределенности достаточно, чтобы предохранить нас от вывода, что у
частицы отрицательная кинетическая энергия.
Упражнения. 1. Что называется туннельным эффектом? Каковы наиболее
благоприятные условия туннельного прохождения. Каково его квантовомеха-
ническое объяснение? Почему нет смысла беспокоиться по поводу появления
отрицательной кинетической энергии? Обсудите вероятность туннельного эф*
359
т
фекта для частиц, которыми стреляют в прямоугольный потенциальный
барьер, постепенно повышая их кинетическую энергию. Что произойдет, когда
кинетическая энергия частиц достигнет такого значения, которого будет
достаточно, чтобы в соответствии с законами классической механики частицы
свободно проходили над барьером?
2. Рассмотрите прямоугольный барьер высоты V и ширины W, с обеих
сторон которого во всем остальном пространстве потенциал равен нулю.
Запишите и решите уравнение Шредингера для этой системы; затем с учетом
требования непрерывности волновой функции определите приемлемые
решения. Покажите, что вероятность туннельного эффекта сильно зависит от V,
W и от массы частицы. Рассчитайте относительные вероятности туннельного
прохождения электрона, протона и дейтерона сквозь такой барьер.
Рекомендуемые источники. Расчеты явлений туннельного прохождения
описаны в гл. 11 кн. Бома [63], в § 26 кн. Давыдова [119], кн. Мессиа [282],
Шиффа [356] и др. Задачи с подробными решениями можно найти у Гольд-
мана и Кривчеикова [165]. Важные проявления туннельного эффекта имеются
в фотоэлектрическом эффекте (см. соответствующий раздел), в химических
реакциях (обзор этого вопроса дан Хармони [174]) и в электродных
процессах (см. кн. Элбери [15] «Кинетика электродных процессов»).
У
УГЛОВОЙ МОМЕНТ. В классической механике угловой
момент тела определяется произведением /со, где / — момент
инерции тела и со — его угловая скорость (рад/с). Большое тело,
имеющее большой момент инерции, при медленном вращении
(с небольшой угловой скоростью) может иметь такой же
угловой момент, что и быстро вращающееся маленькое тело. В
классической механике угловой момент может принимать любые
значения; в квантовой теории величина углового момента любого
тела квантуется и может принимать только значения [/(/+1)]1/ай,
где / — неотрицательное целое или полуцелое число (О, */г,
1, ...). Только одна компонента квантованного углового
момента может иметь определенное значение (т. е. можно определять
угловой момент тела только относительно одной оси); величина
этой компоненты углового момента может принимать
квантованные значения mb, где m = /, / — 1, ..., —/. Это означает, что
в отличие от классической физики в квантовой механике
вращающееся тело может иметь только дискретную
последовательность ориентации по отношению к любой выбранной оси.
Квантование ориентации называют также пространственным
квантованием.
Угловой момент удобно представлять в виде вектора длиной
[/(/+1)]1/а (рис. У. 1). Дискретный набор ориентации, которые
может принимать момент / = 2, показан на рис. У. 2.
Изображение углового момента вектором положено в основу векторной
модели атома.
Поскольку определить можно только одну компоненту
вектора углового момента (обычно это ^-компонента), а две другие
(связанные с его ориентацией в плоскости ху) не известны,
угловой момент как бы совершает прецессию на поверхности
соответствующего телесного угла.
Угловой момент, обусловленный пространственным
движением частицы, называется ее орбитальным угловым моментом.
Квантовые числа орбитального углового момента, обозначаемые
обычно I, принимают целочисленные неотрицательные значения.
Угловой момент внутреннего движения частицы, ее спин, может
принимать как целые, так и полуцелые значения, обозначают
его обычно s (или / для ядер).
Если частица или система частиц обладает двумя
независимыми угловыми моментами, ее полный угловой момент также
квантуется и его величина [/(/.+ 1)]1/зй находится в пределах,
определяемых пределами квантового числа /: /1+/2, /1+/2—1, ...
361
У
... |/i — /21, где /i и /2 — квантовые числа каждого исходного
углового момента. Эта последовательность чисел называется
рядом Клебша — Гордона. Электрон со спином 5 = 1/2,
находящийся на орбитали с орбитальным угловым моментом /= 1,
является одним из примером системы с двумя слагаемыми
углового момента. Полный угловой момент такого электрона может
принимать значения: / = 1/2 + 1, 7г + 1 — 1, или % и 4/2, в
зависимости от относительной ориентации спина и орбитального мо-
Рис. УЛ. Классический угловой Рис. У.2. Угловой момент / = 2, со-
момент и его представление век- гласно законам квантовой механики,
мотором с заданной проекцией на жет принимать только пять (2/ + 1)
ось z. ориентации в пространстве (в
соответствии с законами классической механики
он может иметь любое направление).
мента / = 1. Если они параллельны, / = 3/2, если антипараллель-
ны, / = 7г. Когда система содержит несколько слагаемых
углового момента, суммарный момент также квантуется и
определяется последовательным сложением /i + /2, полученная
величина прибавляется к /з и т. д. На каждом этапе суммарный
момент определяется рядом Клебша — Гордона.
В квантовой механике угловой момент определяется также с
помощью характерных коммутационных соотношений для
соответствующих операторов. Любой набор операторов,
удовлетворяющий коммутационным соотношениям типа [/ж, jy]=i1*jz,
можно рассматривать как операторы углового момента, свойства
которого были вкратце определены выше. Таким путем можно
прийти к обобщению теории углового момента и описанию с ее
помощью внутренних свойств систем, например их спинов и
зарядов.
363
У
Упражнения. Сформулируйте правила квантования углового момента.
Какие величины углового момента отвечают квантовым числам: 72, 1, 2, 1034?
Изобразите на рисунке угловой момент в виде вектора и примите / = 1,
т = 1, 0, —1; изобразите также классическое движение частицы,
отвечающее этим трем значениям т. Рассмотрите векторное представление углового
момента колеса велосипеда: можно ли ехать таким образом, чтобы
велосипед оставался строго перпендикулярным дороге? При каких скоростях такое
движение станет невозможным? Спин фотона равен 1, какова величина его
внутреннего углового момента? Какие угловые моменты могут возникнуть при
сложении спина электрона с его орбитальным моментом, когда электрон
находится на d-орбитали (/ = 2)? Какие состояния полного орбитального
момента получатся при сложении моментов двух р-электронов, двух d-электро-
нов, р- и ^-электронов, трех р-электронов?
Рекомендуемые источники. Теория углового момента детально
рассматривается в гл. 6 [1]. Интересные сведения приведены в книге Козмана [217], где
особое внимание уделяется связи классических и квантовых представлений
об угловом моменте. Ряд книг специально посвящен квантовой теории
углового момента: Бринк и Сэтчлер [80], Роуз [347], Эдмондс [131], Джадд [212],
Биденхарн и ван Дам [58]. В последней обсуждается несколько важных
оригинальных статей. В гл. 6 [1] и кн. Тинкхэма [396]* дана зависимость
углового момента от способа изменения системы в процессе ее вращения. Эта
книга знакомит также со свойствами симметрии системы и зависимостью
углового момента от симметрии системы. Волновую функцию состояния со
связанными угловыми моментами можно представить в виде линейной
комбинации волновых функций состояний с несвязанными угловыми моментами.
Коэффициенты этой линейной комбинации называются коэффициентами
векторного сложения или коэффициентами Вигнера. Формальная связь углового
момента с другими свойствами системы, такими, как заряд, рассмотрена в
книгах Липкина [251] и Лихтенберга [246] *.
УДВОЕНИЕ. В спектроскопии термином «удвоение»
называют такую ситуацию, когда вырождение какого-либо уровня
снимается таким взаимодействием, которым до тех пор
пренебрегали; каждый дважды вырожденный уровень расщепляется
на два отдельных уровня, т. е. происходит «удвоение». Оно
проявляется в спектре либо как действительное удвоение числа
линий, когда становятся возможными переходы на разделенные
уровни с других состояний (рис. У. 3, а), либо когда некоторые
состояния комбинируют (т. е. связаны переходами) только с
одной из компонент дублета, а другие состояния комбинируют с
другой его компонентой (рис. У. 3, б).
Примером удвоения в атомной спектроскопии является
тонкая структура спектра щелочных металлов. Возьмем в качестве
примера натрий и рассмотрим возбужденную конфигурацию, в
которой валентный электрон занимает Зр-орбиталь, а затем
переходит на Зз-орбиталь, причем этот переход сопровождается
испусканием характерного желтого света (589 нм). Тщательное
* См. также [444, 445]. — Прим. перев.
363
У
изучение спектра показывает, что желтый свет фактически
включает две компоненты, одна из которых соответствует длине
волны 588,99 нм, а другая — 589,59 нм; это расщепление можно
приписать удвоению возбужденных уровней. Подробно данный
вопрос рассматривается в разд. «Тонкая структура»; здесь же
/ S
а
1
V"
6\
тт
т_
Рис. У.З. Различные типы удвоения
в спектре: а — первоначально
вырожденный уровень взаимодействует с одним
уровнем; б — первоначально
вырожденный уровень взаимодействует с двумя
различными уровнями. Пунктиром
показаны невозмущенные уровни
мы заметим только, что возбужденное состояние натрия 2Р имеет
два уровня 2Pi/2 и 2P*j2t которые можно считать вырожденными,
если не учитывать спин-орбитальное взаимодействие, но которые
на самом деле отличаются по энергии, если оно принимается во
Рис. У.4. Механизм Л-удвоения в двухатомной молекуле.
внимание. Переходы с этих двух уровней в основное состояние
2Si/0 дают две спектральные линии, отстоящие друг от друга на
17,2 см-1.
Примером удвоения в молекулярной спектроскопии является
Л-удвоение (лямбда-удвоение), при котором вращение линейной
молекулы снимает вырождение двух компонент П-терма (или,
хотя это менее важно, А- или Ф-терма). Определить
взаимодействие, ответственное за такое удвоение, можно, рассмотрев
двухатомную молекулу, в которой один валентный электрон
занимает я-орбиталь. На рис. У. 4 показаны два возможных вариан-
364
У
J
4
<
III
Рис. У.5. Правила отбора и вид
спектра при наличии Л-удвоения-
Выбрано большое Л-удвоение
верхнего состояния. Сравните с рис. В.7,
где используются те же параметры.
I+JL
П
р ГГ
V
№
та; электрон занимает либо я+-, либо я~-орбиталь, где верхний
индекс связан с поведением знака орбиталей при их отражении
в плоскости вращения молекулы. Если бы электроны могли
точно следовать за вращением ядер, не запаздывая и не опережая
их, две я-орбитали имели бы в точности одну и ту же энергию,
как это известно из теории
химической связи, где
рассматривается неподвижная
молекула. Но электроны не
следуют точно за движением ядра
(см. разд. «Электронное
скольжение» и «Борна — Оппенгей-
мера приближение»), и
существует тенденция к отставанию
электронов относительно
движения ядра. В случае
я-орбитали запаздывание фактически
не оказывает влияния,
поскольку в простейшем
приближении ядро скользит немного
вперед в плоскости узла орби-
тали, и поэтому электронная
плотность вокруг ядра
остается примерно такой же, что и в
t*
статическом случае. Но одновременно ядро выскальзывает из
вертикальной узловой плоскости я+-орбитали в область
ненулевой электронной плотности, и поэтому вполне понятно, что
энергия я+-орбитали в результате вращения изменяется. Отсюда
следует, что две орбитали приобретают различную энергию и что
их энергетическое разделение, или удвоение, зависит от скорости
вращения.
Влияние Л-удвоения на спектр можно увидеть, рассмотрев
вращательную структуру электронного перехода, при котором
двухатомная молекула переходит из 2- в П-состояние (точнее,
мы рассматриваем переход 12+->1П). Л-Удвоение верхнего
состояния показано на рис. У. 5: расстояние между компонентами
растет с увеличением вращательного квантового числа /,
согласно правилу qJ(J+l)f где q — константа. Для Р- и R-ветвей
365
У
спектра разрешены переходы из вращательных состояний
нижнего электронного состояния только на одну из компонент
(помечена знаком плюс) верхнего электронного состояния, а для
Q-ветви переходы могут совершаться только на другую
компоненту. Из анализа сдвига Q-ветви относительно центра Р- и
Я-ветвей можно извлечь значение параметра q (см. приведенное
ниже упражнение) и связать это значение с расстоянием между
электронными состояниями в молекуле.
Приведем еще два важных примера удвоения. Первым из
них является Z-удвоение, при котором вырождение
колебательного уровня линейной трехатомной молекулы, связанного с
деформационным колебанием, снимается эффектами
молекулярного вращения (см. «Кориолисово взаимодействие»). Второй
пример — это инверсионное удвоение, при котором способность
молекулы переходить путем инверсии из одной конфигурации в
другую удваивает ее колебательный спектр. Q-Удвоение (омега-
удвоение) является аналогом Л-удвоения при условии, что
соответствующей схемой связи является случай (в) правил Гунда.
Упражнения. 1. Что означает термин «удвоение»? Каким образом его
наличие сказывается на спектре атома или молекулы? Обсудите удвоение,
которое возникает в спектре щелочных металлов: какое взаимодействие
ответственно за удвоение; как меняется удвоение при переходе от Na к Cs;
приемлемы ли для его объяснения правила отбора? Если имеются две линии —
588,99 и 589,59 нм, каково их расщепление (в см-1)? Определите на
основании этих даных значение постоянной спин-орбитального взаимодействия в Na.
Что является причиной Л-удвоения? Почему удвоение должно увеличиваться
с возрастанием вращательного квантового числа? Изучив рис. У.4, покажите,
что в результате вращения молекулы с я+-орбиталью смешивается
а-орбиталь. Является ли эта а-орбиталь связывающей или разрыхляющей? Какое
смешение должно произойти в случае разрыхляющей я-орбитали? (Следует
подчеркнуть, что строгий расчет эффектов Л-удвоения должен проводиться
с учетом полных состояний, а не одноэлектронных орбиталей.)
2. Л-Удвоение изменяется как ^/(/+1); покажите, что в спектре
двухатомной молекулы /?- и Я-ветви соответствуют двухатомной молекуле с
кажущейся вращательной постоянной В + 6, где В — истинная вращательная
постоянная, а Q-ветвь соответствует молекуле с кажущейся вращательной
постоянной В + У. Выразите b и У через q и покажите, как можно
использовать смещение ветвей для определения истинной величины В. Постройте
несколько первых линий вращательной структуры электронного перехода, в
котором молекула переходит из состояния !2+ в 41, полагая, что в нижнем
состоянии В = 6,020 см"1, в верхнем состоянии В = 6,00 см-1 и в верхнем
состоянии q = 0,008 см-1.
Рекомендуемые источника. Более детальное обсуждение вопроса см. в
[1], гл. 10, а также в кн. Уиффена [424] и Барроу [51]. Удвоение подробно
рассматривается в кн. Герцберга [185], Сагден и Кенией [388] обсуждают
/-удвоение, Кинг [222] приводит полезное рассмотрение Л-удвоения, /-удвоения и
инверсионного удвоения. Расчеты Л-удвоения подробно описаны Ковачем [226].
См. также ки. Таунса и Шавлова [399].
366
У
УЗЕЛ ВОЛНОВОЙ ФУНКЦИИ. Узлом называется место
пространства, где амплитуда волновой функции обращается в
нуль. Узлом может быть точка, линия или поверхность.
Волновая функция частицы, находящейся в одномерной
прямоугольной яме бесконечной глубины, имеет узлы на стенках ямы и в
ряде регулярно расположенных точек внутри ямы. Более
высокой энергии частицы (или более высокой гармонике основных
колебаний) соответствует большее число узлов ее волновой
функции. У ls-орбитали атома водорода нет узлов, кроме
довольно специфической узловой поверхности на бесконечности
(см. «Атомная орбиталь»); у 25-орбитали — один узел, который
можно представить в виде сферической поверхности,
окружающей ядро. Поскольку положение этого узла зависит только от
радиуса и поскольку он сферически симметричен, его называют
радиальным узлом. 2/?-орбиталь не имеет радиальных узлов
(кроме узла на бесконечности), но она делится на два лепестка
угловым узлом, который представляет собой плоскость,
проходящую через ядро. Для других атомных орбиталей характерна
более сложная узловая структура, но у s-орбитали никогда не
бывает угловых узлов, у р-орбитали всегда имеется один узел,
а у d-орбитали — два угловых узла.
Важная роль узловой структуры волновой функции
обусловлена ее связью с импульсом и кинетической энергией системы:
чем больше узлов в данной области, тем больше величина
кинетической энергии. Объясняется это следующим. Узел появляется
там, где волновая функция меняет знак, а чем чаще функция
меняет знак в данной области пространства, тем меньше ее
длина волны. Принимая во внимание соотношение де Бройля,
можно связать уменьшение длины волны с ростом импульса.
Следовательно, чем больше узлов, тем больше импульс и тем больше
кинетическая энергия. Эту связь демонстрирует приведенный
выше пример с частицей в прямоугольной потенциальной яме.
В случае угловых узлов роль импульса играет орбитальный
момент, величина которого растет по мере увеличения числа
угловых узлов. Данный вывод подтверждается тем, что число
угловых узлов численно равно величине орбитального
квантового числа /, а сама величина углового момента
пропорциональна д//(/+ 1). Поэтому орбитальный момент d-электрона (2
угловых узла) больше величины орбитального момента р-электро-
на (1 угловой узел).
Упражнения. Что такое узел? Какой вид он может иметь? Может ли для
частицы в двумерной яме существовать узловая точка или в таком случае
возможна только узловая линия? Каким образом классифицируются узлы в
атомной системе? Сколько узлов имеет волновая функция атома водорода
с главным квантовым числом п> Зависит ли число узлов от п и /? Влияет
367
У
ли величина mi на сделанные выводы? Чем обусловлена связь между числом
угловых узлов и орбитальным угловым моментом состояния? Рассмотрите
узловую структуру орбиталей двухатомной молекулы и объясните ее
физический смысл.
Рекомендуемые источники. В гл. 3 [1] рассмотрены различные системы
с узлами всевозможных типов. Поскольку узел функции представляет собой
место пространства, где она обращается в нуль, могут представлять интерес
таблицы нулей математических функций, приведенные, в частности,
Абрамовичем и Стегуном [30]. Общая теорема об узлах утверждает, что наиболее
низкое энергетическое состояние системы не имеет узлов; см. кн. Ландау и
Лифшица [233]. Эта теорема не выполняется, если в системе много частиц,
так как в этом случае вследствие спиновой корреляции в волновой функции
образуются дырки Ферми.
УРОВЕНЬ. В теории строения атома и атомной
спектроскопии понятие уровня тесно связано с определенным значением
полного углового момента /. Например, конфигурации ls22s22p
соответствует дублетный терм Р, который обозначается 2Р. Два
уровня этого дублета отвечают значениям полного момента / =
= 3/2 и / = 7г, так как только такие значения можно получить,
складывая L=l и S = 7г (см. «Угловой момент»). Эти два
уровня терма обозначаются как 2Рч2 и 2Рз/2.
Число уровней каждого терма определяет его мультиплет-
ность. Например, терму 2Р отвечают два уровня; терму ZD —
три уровня (3Z?i, 3D2, 3D3) и т. д. Вследствие спин-орбитального
взаимодействия эти уровни имеют различные энергии, и их
последовательность определяется правилами Гунда. Угловой
момент / может иметь (2/+1) различных проекций на какую-
либо ось, значения которых принято обозначать Mj. С учетом
этих проекций состояние, соответствующее какому-либо уровню
терма, записывается как 2Р^7.
Упражнения. Поясните смысл термина «уровень» в атомной
спектроскопии. Выпишите уровни, которые могут появиться у следующих термов: Ф,
з/7, 3S, 4D, 6D. В каких случаях верхний индекс не служит обозначением муль-
типлетности? (См. разд. «Термы».)
Рекомендуемые источники. Детальное описание атомных спектров см. в
гл. 8 [1]. Уровни, мультиплетность и тонкая структура обсуждаются в кн.
Куна [229] и Герцберга [185]. См. также разд. «Атомные спектры» и «Тонкая
структура».
ф
g-ФАКТОР. Магнитный момент электрона, который
возникает из-за наличия орбитального углового момента, равен уе\,
где Ye — гиромагнитное отношение, а магнитный момент
электрона, обусловленный спиновым угловым моментом, равен gyes,
где g— дополнительный «аномальный» множитель, который,
как экспериментально установлено, равен 2,0023 (часто
принимается равным 2). Как и большинство «аномалий», это значение
^-фактора удалось объяснить благодаря последовательному
усовершенствованию квантовой теории. Оказалось, что наличие
связанного со спином дополнительного множителя 2 не
представляет собой ничего удивительного. Напомним, что спин не имеет
классического аналога и характеризуется как целыми, так и
полуцелыми квантовыми числами. Эти представления были
развиты в теории Дирака. Его релятивистская квантовая механика
естественным образом приводит к выводу, что g = 2, но,
согласно этой теории, g должно быть равно целому числу 2. В этом
проявляется несовершенство теории Дирака. Добавка 0,0023,
требуемая для совпадения с наблюдаемым значением, может
быть найдена с помощью еще более совершенной теории —
квантовой электродинамики. В этой теории электрон непрерывно
взаимодействует с электромагнитным полем, которое всегда
существует, даже в идеальном вакууме. Это поле действует на
спин электрона таким образом, что магнитный момент его
несколько увеличивается по сравнению с дираковским значением.
Вычисление точного значения ^-фактора для свободного
электрона явилось одним из триумфов квантовой электродинамики.
Рассматриваемый здесь g-фактор тесно связан с ^-фактором
Ланде; действительно, они совпадают в предельном случае,
когда орбитальный угловой момент электрона обращается в
нуль. ^-Фактор Ланде определяет эффективный магнитный
момент электрона или атома, обладающего как спином, так и
угловым орбитальным моментом, которые слагаются в полный
угловой момент /. Для атома, описываемого квантовыми числами S,
L и /, g-фактор Ланде равен gj = 1 + xk{U(/ + 1) + S (S + 1) —
—L(L + l)]//(/+ 1)}. Если L = 0, мы получаем gj == 2, так как
тогда / оказывается равным S, если же S = 0, мы получаем
gj=l, что является нормальным значением для бесспиновой
системы. Используя ^-фактор Ланде, магнитный момент
системы с угловым моментом J можно записать как gj\eJ.
Выражение для gj обусловлено следующими соображениями.
На рис. Ф. I показана схема векторной связи для системы со
369
ф
спиновым моментом S и орбитальным моментом L,
складывающимися в результирующий момент J. Векторы L и S прецессируют
вокруг J, a J прецессирует вокруг некоторой оси г, Антипарал-
лельно к L и S можно провести векторы, которые изображают
соответствующие магнитные моменты, причем вектор спинового
магнитного момента должен быть вдвое больше, чем вектор
орбитального момента из-за наличия множителя g = 2. Сумма
Рис. Ф.1. Слева показано, как возникает g-фактор Ланде; справа —
гипотетическая ситуация при ge = 1.
векторов \xL и fis, обозначенная \i'p не располагается вдоль
направления / (как это было бы при g=l, см. рис. Ф. 1, б), а
прецессирует вокруг него из-за прецессии L и S вокруг J. Во время
прецессии не усредняется до нуля только компонента магнитного
момента, направленная вдоль J, поэтому эффективный
магнитный момент, соответствующий J (который мы обозначим \xj),
зависит от этой компоненты и, следовательно, от значений L и S.
Если L^$> S или S ^> L, компонента \л) направлена почти точно
вдоль J, a gj равен примерно 1 или 2 соответственно, так как
доминирует либо орбитальный, либо спиновый момент, но, если
L и 5 близки, эффективная часть магнитного момента \ij может
быть намного меньше, чем его истинное значение. Поскольку /
прецессирует вокруг направления z, так же ведет себя \ij.
Поэтому, если Jz — проекция / на z, gjyeh — проекция [ij на z
(gj — множитель, который определяется из геометрических сооб-
370
ф
ражений в соответствии с рис. Ф. 1,а). Этим множителем и
является упомянутый выше ^-фактор Ланде.
g-Фактор, измеряемый в электронном парамагнитном
резонансе (ЭПР), связан с обоими этими ^-факторами. В методе
ЭПР, подробно описанном в соответствующем разделе, быстро-
переменное поле частоты v приводится в резонанс со спиновой
системой, помещенной в магнитное поле с индукцией В. Энергия
быстропеременного поля равна /iv, а энергетическое
расщепление электронных спиновых уровней (а именно энергетический
интервал между уровнями с т8 = ^ и ms=—"2") Равно ё\*>вВу
поэтому условие резонанса имеет вид hv = g\iifB. g-Фактор в
этом выражении имел бы значение ge для свободного электрона,
если бы рассматриваемые электроны были свободными, или
^/-фактора Ланде, если бы они были связаны в атоме. На самом
деле исследуемые электроны обычно являются частью
молекулярной системы, поэтому ни один из этих случаев не
соответствует действительности. В очень хорошем приближении
(исключение составляют ионы переходных металлов) можно считать,
что электрон в молекуле не обладает орбитальным угловым
моментом, следовательно, и в радикалах ^-фактор должен быть
очень близок к 2,0023. Однако ввиду наличия спин-орбитального
взаимодействия орбитальный угловой момент не полностью
подавлен. Обычно спин-орбитальная связь вполне достаточна по
величине, чтобы наличие спинового углового момента приводило
к появлению небольшого орбитального углового момента.
Поэтому следует ожидать, что ^-фактор окажется немного меньше
2,0023, поскольку значение, которое имелось бы, если бы момент
был чисто орбитальным, а не спиновым, должно быть равно 1.
Это действительно наблюдается, и часто встречаются значения
g-факторов, приближающиеся к 2,0000. Кроме того, установлено,
что отклонения ^-фактора от его значения для свободного
электрона возрастают с увеличением постоянной спин-орбитального
взаимодействия, и это согласуется с нашими рассуждениями.
Для грубой оценки порядка величины этого эффекта можно
записать отклонение от значения 2,0023 как £/Д, где % —
постоянная спин-орбитального взаимодействия, а А — типичная энергия
возбуждения радикала (см. разд. «Теория возмущений» и
«Тонкая структура»; некоторые значения % приведены в табл. 9).
Этим механизмом можно .объяснить также существование
^-факторов, превосходящих значение для свободного спина, которые
наблюдаются, когда электрон входит в оболочку, заполненную
более чем наполовину, но при этом требуется немного более
сложная аргументация. В основном увеличение ^-фактора
связано с обращением последовательности уровней при переходе от
заполненной менее чем наполовину оболочки к заполненной
371
ф
больше чем наполовину. Согласно правилу Гунда,
последовательность уровней обращается (уровни с меньшими /
оказываются выше, чем уровни с большими /) при изменении знака
постоянной спин-орбитального взаимодействия. Это можно
объяснить, рассматривая вместо системы, в которой по орбиталям
движутся электроны, систему, в заполненой оболочке которой
движутся дырки. Дырка несет заряд, противоположный заряду
электрона, что и объясняет инверсию /-уровней, а также
отклонение ^-фактора в сторону значений, больших чем для
свободного спина.
Наконец, рассмотрим еще молекулярный ^-фактор, который
связывает вращательный угловой момент всей молекулы с
магнитным моментом, возникающим из-за ее вращения. Даже
молекула с заполненной оболочкой, такая, как Нг или метан,
обладает магнитным моментом из-за вращательного движения. Он
возникает потому, что электронное скольжение и вызванная им
несогласованность движения положительных и отрицательных
вращающихся зарядов приводят к появлению кругового тока,
следовательно, и магнитного момента. Если вращательное
движение ускоряется, несогласованность усиливается, поэтому
магнитный момент пропорционален J — вращательному угловому
моменту. Обычно записывают \х = gy^J, где g — молекулярный
g-фактор, который зависит от особенностей электронного
строения молекулы. Заметим, что для определения величины
молекулярного g-фактора принято использовать ядерный магнетон
(fjijv = еЪ/2тр). Молекулярные магнитные моменты настолько
малы, что для их выражения удобнее пользоваться величиной
fijv, а не магнетоном Бора (в единицах \\n g имеет порядок 1).
Для аммиака g ~ 0,53, поэтому величина [i в состоянии
молекулы с моментом / = 10 составляет примерно 5,3 \xn.
Упражнения. 1. Какое свойство электрона определяет g-фактор? В атоме
g-фактор имеет индекс /. Почему атомный магнитный момент зависит от /,
L и 5? Оцените g-фактор Ланде для атомов с S = 0, L = 1; S = 7г> L = \;
S = 0, L = 2. Вычислите его для всех возможных значений / в каждом
случае. Энергия магнитного момента с z-компонентой \iz в магнитном поле с
индукцией В, направленном вдоль оси z, равна —\izB\ вычислите энергии
атомных состояний, для которых вы определили ^-факторы Ланде. Повторите
расчет при допущении, что g-фактор для свободного электрона равен 1, а не 2.
Чтобы увидеть, как связь L и S изменяет магнитные свойства системы,
представьте ваши результаты графически на диаграмме энергетических уровней.
Дальнейшее рассмотрение этого вопроса см. в разд. «Эффект Зеемана». Что
характеризует g-фактор в экспериментах по электронному парамагнитному
резонансу? Почему g-фактор может отличаться от 2, когда электрон входит
в состав радикала? Какую информацию об электронном строении радикала
дает значение ^-фактора? Вычислите напряженность магнитного поля для
резонансного поглощения излучения частотой 9 ГГц (а) свободным
электроном, (б) радикалом eg — 2,0057, (в) радикалом с g = 1,9980. Выразите ре-
372
ф
зультаты в гауссах (Гс). Каково влияние спин-орбитального взаимодействия
на величину ^-фактора молекулы? Почему в некоторых случаях значение g
больше, чем для свободного спина? Что такое молекулярный g-фактор и чем
он обусловлен?
2. В этом упражнении предлагается вывести выражение для ^-фактора
Ланде. Рассмотрим систему, геометрия которой представлена на рис. Ф.1,а,
с магнитным полем вдоль оси z. Попытаемся выразить энергию системы как
—gjye3b, в то время как на самом деле магнитная энергия равна —yeL-b—
— 2y*S-B (т. е. сумма взаимодействий орбитального и спинового моментов
с полем). Мы знаем также, что J = L + S. Рассмотрим L. Этот вектор пре-
цессирует вокруг J, и единственная не зависящая от времени и поэтому ^е
равная нулю его компонента параллельна J; она имеет значение L-J/|J|.
Эта компонента ведет себя подобно вектору [(L-J)/|J|](J/|J|),
вращающемуся вокруг оси z, когда сам J прецессирует вокруг нее (J/|J| -—единичный
вектор, направленный вдоль J). Такой вектор имеет проекцию на направление
магнитного поля, которую можно записать как [(L-J)/|J|][J-B/|J|], поэтому
—Ye[L-J/|J|2]J-В — единственная не зависящая от времени компонента
величины —y*L-B. Она имеет вид — gjyeJ-B который и требовалось
установить. Подобное выражение для —2y*SB можно записать как "~^/YeJ* В
(проделайте это сами), поэтому мы теперь должны показать, что gj + g" =
= g/, т. е. фактору Ланде. Сделайте это, использовав выражение —2L-J =
= (J — L)2-—J2—L2 = S2 —J2 — L2 и аналогично для S-J и заменив
операторы типа J2 на их квантовомеханические значения /(/+ 1)Я2. Найдите
более точное выражение для фактора Ланде, используя ge = 2,0023 вместо
ge ~ 2.
Рекомендуемые источники. Вывод выражения для ^-фактора Ланде
можно найти в [1], гл. 8, а дальнейшее обсуждение дано в кн. Герцберга [188],
Куна [229]. ^-Фактор играет важную роль в интерпретации эффекта Зеемана
и магнитных свойств ионов переходных металлов. Литературу по последнему
вопросу см. в разд. «Кристаллического поля теория» и «Поля лигандов
теория». Подробно он рассматривается в кн. Гриффита [170], а также Абрагама
и Блини [28]. О роли ^-фактора при исследованиях электронного
парамагнитного резонанса см. [1], гл. 11, где более детально обсуждается превышение
величины ^-фактора над значением 2,0023 и рассматривается вычисление
^-факторов для молекул. Этот вопрос рассматривается также в кн. Эткинса
и Саймонса [39], Керрингтона и Мак-Лечлана [90], Сликтера [374] и Гриффита
[170]. Мак-Лечлан описывает зависимость спектра электронного
парамагнитного резонанса от ^-фактора в кн. «Магнитный резонанс» [2]. Молекулярные
магнитные моменты обсуждаются в кн. Таунса и Шавлова [399].
ФЕРМИОН. Фермион — это частица, обладающая
собственным спиновым угловым моментом, характеризуемым
полуцелым спиновым квантовым числом (s или /). Примеры: электрон
(5 = 72), протон (/ = V2), нейтрон (/ = V2), нейтрино (s = V2),
ядра 35С1 (/ = 3/2), 13С (/= 72) и 170 (/ = 5/2). Фермионы
подчиняются принципу запрета Паули, поэтому в одном квантовом
состоянии может находиться не более одного фермиона. Это
делает их поведение исключительно своеобразным и резко
отличает их от бозонов, любое число которых может занимать
данное состояние. Принцип Паули требует, чтобы волновая функ-
373
ф
ция была антисимметричной при перестановке любой пары
тождественных фермионов.
Рекомендуемые источники. См. разд. «Спин» и «Паули принцип». При
рассмотрении больших ансамблей фермионов ограничение на заполнение
состояний учитывается статистикой Ферми— Дирака. Этот вопрос рассмотрен
Гассером и Ричардсом в кн. «Энтропия и энергетические уровни» [19], Де-
видсоном [116] и Рейфом [333].
ФЛУОРЕСЦЕНЦИЯ. Свет, поглощенный молекулой, может
превращаться в тепловое движение или вновь излучаться ею.
Испускание света возбужденной молекулой называется
флуоресценцией или фосфоресценцией. Эти два типа излучения
отличаются по механизму; существует, правда, менее точное
определение их различия: флуоресценция прекращается сразу же, как
только исчезает действие источника возбуждения, а
фосфоресценция при этом еще может продолжаться. О механизме
последней см. в разд. «Фосфоресценция».
Механизм флуоресценции схематически показан на рис. Ф. 2.
Падающий свет возбуждает молекулу из основного состояния в
состояние, которое мы обозначим Si; если- предположить, что
основное состояние является синглетным (обычно в молекулах
все электроны спарены), а начальное поглощение сильное, то
верхнее состояние также должно быть синглетным. Во время
перехода в молекуле возбуждаются также колебания атомов (см.
разд. «Франка — Кондона принцип»). Столкновения с
частицами окружающей среды — газа, растворителя или твердого
тела — вызывают колебательные переходы, так как к
окружающим молекулам могут переходить сравнительно малые порции
колебательной энергии молекулы. В результате возбужденная
молекула постепенно опускается по ступенькам колебательных
уровней верхнего электронного состояния. Когда молекула
достигнет своего наинизшего колебательного состояния, может
произойти следующее. Во-первых, растворитель может унести
электронную энергию и таким путем дезактивировать молекулу.
Для этого необходимо, чтобы энергетический уровень молекул
растворителя соответствовал энергии возбужденной молекулы.
Если указанное условие выполняется, происходит резонансная
передача излучения растворителю, который затем растрачивает
свое возбуждение на тепловое движение. Второй возможный
путь дезактивации (который нас собственно и интересует)—это
флуоресценция из возбужденного электронного состояния. В
данном случае молекула дезактивируется в результате испускания
фотона и переходит в более низкое электронное состояние.
Испускаемое при таком переходе излучение называется
флуоресцентным. Вероятность флуоресцентного перехода зависит от
конкуренции между безызлучательной дезактивацией, включающей
374
ф
перенос энергии к окружающей среде, и испусканием излучения.
В газовой фазе молекула испытывает примерно 1010
столкновений в секунду, а в жидкой фазе число столкновений с
молекулами растворителя составляет примерно 1012—1013 в секунду.
Наблюдаемые времена жизни флуоресцентного излучения
составляют примерно Ю-8 с, следовательно, в газе за это время
происходит приблизительно 100 столкновений, а в
растворителе— 104—105. Если эти столкновения «сильны», т.е.
приводят к эффективной передаче энергии, то дезактивация молекулы
безызлучательный,
I переход
Рис. Ф.2. Процессы, ведущие к флуоресценции, и «зеркальное отражение»
спектров поглощения и флуоресценции. Обратите внимание на сдвиг
последнего в сторону больших длин волн.
протекает как безызлучательный процесс, особенно когда
молекулы находятся в жидкости. Если столкновения не
сопровождаются значительной передачей энергии, то даже в растворителе
будет происходить только постепенное снижение энергии
электронно-возбужденной молекулы по ступенькам колебательных
уровней, но не будет происходить передачи электронного
возбуждения. В этом случае преобладает излучательная дезактивация
и молекула флуоресцирует.
Необходимо отметить две характерные особенности
флуоресценции. Во-первых, частота флуоресцентного излучения ниже,
чем частота возбуждающего света. Это видно из рис. Ф. 2,
который показывает, что энергия испускаемого фотона отличается
от энергии поглощенного на величину колебательной энергии,
переданной окружающей среде. Поэтому можно ожидать, что
область флуоресцентного излучения объекта, облученного голу-
375
ф
бым или ультрафиолетовым светом, сдвинута к красному краю
спектра. (Именно этим обстоятельством объясняется
ярко-красная флуоресцирующая окраска многих современных тканей). Во-
вторых, в спектре флуоресцентного излучения может
наблюдаться колебательная структура, которая представляет собой
прогрессию, возникающую при дезактивации основного
колебательного состояния верхнего электронного уровня путем переходов
на различные колебательные уровни более низкого электронного
уровня. Изучение этой структуры может дать информацию о
силовой постоянной молекулы в основном состоянии, тогда как
обычный электронный спектр характеризует жесткость связей в
верхнем электронном состоянии. Следовательно, спектр
поглощения и спектр флуоресценции молекулы должны походить друг на
друга. Обычно говорят, что один спектр является «зеркальным
отражением» другого (см. рис. Ф. 2), но это не следует понимать
буквально, так как колебательные расщепления и интенсивности
обоих спектров не одинаковы.
К этому описанию можно добавить ряд деталей. Прежде
всего в результате начального поглощения молекула не
обязательно переходит в наинизшее возбужденное синглетное
состояние. В этом случае происходит внутренняя конверсия, при
которой из возбужденных вначале более высоких синглетных
состояний 52, S3 и т. д. вследствие столкновений происходит безызлу-
чательный переход в наинизшее синглетное состояние, которое
затем дает флуоресценцию (см. разд. «Оже-эффект»). Эта
ситуация описывается известным правилом Каши:
«Флуоресцентный уровень является наинизшим уровнем данной мультиплет-
ности (например, наинизший возбужденный синглетный
уровень)». Интенсивность флуоресценции сильно зависит от
физического состояния образца, поскольку с флуоресценцией
конкурируют дезактивирующие столкновения. Чистые, неразбавленные
жидкости обычно имеют очень низкую флуоресцентную
способность, так как возбуждение может передаваться от одной
молекулы к идентичной соседней посредством резонансного процесса
(об аналогичном эффекте в твердых телах см. в разд. «Экси-
тон»). Наоборот, флуоресценцию можно усилить, если ввести
молекулу, которая может поглощать падающее излучение и
затем передавать его (при столкновении из-за совпадения
уровней) молекуле, которая далее может флуоресцировать. Это так
называемая сенсибилизированная флуоресценция, она
используется в некоторых типах лазеров. Другой часто встречающийся
термин — «резонансная флуоресценция» — означает
флуоресцентное излучение, имеющее ту же частоту, что и падающее
излучение. В этом случае флуоресценция может быть ярче, так
как переход является вынужденным. Резонансная
флуоресценция наблюдается редко, поскольку наличие растворителя не-
376
ф
много сдвигает энергетические кривые. Поэтому колебательный
(О — 0)-переход вверх (переход с наинизшего колебательного
уровня одного состояния на наинизший уровень другого) может
отличаться по энергии ,от (0 — 0)-перехода вниз: сольватация
молекулы в верхнем состоянии растворителем может успеть
измениться, прежде чем произойдет флуоресценция. Флуоресценция
обычно гаснет, как только прекращается возбуждающее
облучение. Объясняется это следующим: все рассматриваемые
переходы разрешены и, следовательно, происходят очень быстро. Тем
не менее известна и запаздывающая флуоресценция (не следует
путать ее с фосфоресценцией), которая может продолжаться в
течение нескольких миллисекунд. Механизм этого явления
заключается в следующем: молекула возбуждается из основного
состояния So в синглет Sb после чего мигрирует к другой
молекуле и прилипает к ней, обмениваясь энергией возбуждения.
Таким образом, происходит реакция Sv) + S?->(S0Si)*- Этот экси-
мер (если две молекулы одинаковы) или эксиплекс (если
молекулы разные) вскоре распадается с испусканием
флуоресцентного излучения.
Упражнения. Каковы характеристики флуоресцентного излучения? Как
можно отличить его от фосфоресцентного излучения? Какие электронные
процессы ответственны за флуоресценцию? Какие другие пути понижения
энергии возможны для возбужденных атомов и молекул в газах и растворах?
Какие свойства растворителя определяют скорость безызлучательной
дезактивации возбужденных состояний? Чем отличается флуоресценция молекулы,
растворенной в сильно взаимодействующем растворителе с высокочастотными
валентными и деформационными колебаниями, например в воде, от
флуоресценции молекулы, растворенной в слабо взаимодействующем растворителе со
слабыми связями, например в хлорокиси селена? Какую информацию дает
флуоресцентный спектр молекулы? Как она дополняет информацию,
полученную из спектра поглощения? В каком смысле спектр флуоресценции
является зеркальным отражением спектра поглощения? Каким образом
принцип Франка — Кондона позволяет объяснить структуру спектра
флуоресценции? Что означает термин «внутренняя конверсия», каково ее значение при
изучении флуоресценции? В каком смысле флуоресценцию можно
рассматривать как процесс Оже? Почему флуоресценция сильно гасится в
неразбавленной жидкости? Каким образом можно усилить флуоресценцию? Что такое
резонансная флуоресценция? Каким образом действие некоторых типов
лазеров зависит от описанных здесь механизмов? Почему в спектре
флуоресценции имеется сдвиг относительно положения спектра поглощения, даже
если они имеют зеркальную симметрию? Чтобы ответить на этот вопрос,
рассмотрите молекулу, окруженную полярным растворителем и возбужденную
переходом, который изменяет полярность молекулы (например, электрический
дипольный п ->я*-переход). Рассмотрите энергию эмиссионного перехода,
предположив, что полярный растворитель приходит в равновесие с
возбужденным состоянием. Что означают термины «эксимер» и «эксиплекс» и
каковы следствия их образования? Каким образом можно отличить
запаздывающую флуоресценцию от фосфоресценции?
377
ф
Рекомендуемые источники. Более полное обсуждение см. в [1] гл. 10.
Простое рассмотрение некоторых процессов релаксации в связи с
обсуждением жидких лазеров проведено Геллером [181]. См. также кн. Гаухта [176].
Хорошее рассмотрение флуоресценции и связанных с ней процессов дано Боу-
эном [71], Вейном [416], Калвертом и Питтсом [88]. Генерация света при
химических реакциях (хемилюмкнесценция) — явление, связанное с
флуоресценцией, различие между ним заключается в том, что в первом случае
возбужденное состояние излучающей молекулы образуется в результате
химической реакции. Этот вопрос см. в [416]. О процессах переноса энергии,
определяющих флуоресцентную способность вещества, см. в кн. Левина и Берн-
стейна [245].
ФОНОНЫ. Аналогично тому как фотоны являются
квантованными колебаниями электромагнитного поля, фононы — это
поперечные колебания /.Энергия hv
ООрШОООСЩОО Ч-а=-
' ^^-^ 1 \^^^ f ни одного (ронона
ооооосххххюоо °'г1
продольные колебания
Рис. Ф.З. Поперечные и продольные колебания одинаковой длины волны;
степень возбуждения можно описать числом имеющихся фононов.
квантованные колебания кристаллической решетки. Для начала
представим себе линейную цепочку атомов, которая совершает
низкочастотные колебания (рис. Ф.З). Эти колебания
квантованы и могут обладать только дискретными значениями энергии.
Если частота колебаний равна v, их энергия должна быть
кратна целому числу квантов hv. Вместо того чтобы рассматривать
возбуждение колебаний какого-либо типа как последовательные
переходы системы вверх по ее равноотстоящим квантовым
уровням, можно считать, что энергия системы возрастает в
результате добавления к исходному состоянию гипотетических частиц.
Если п таких частиц появляются в состоянии с собственной
частотой v, энергия системы возрастает на nhv. Именно такое
представление о возбуждении колебаний как о возникновении неких
частиц и лежит в основе концепции фонона. Фонон — это квант
возбуждения определенной частоты, и его можно рассматривать
как возникающую в системе частицу с энергией hv.
В твердых веществах сложного состава могут существовать
фононы разных частот (так же как в световом
электромагнитном поле имеются фотоны разной частоты). Как и фотоны в пуч-
378
ф
ке света, фононы в твердом теле могут быгь поляризованы.
Однако в отличие от фотонов бывают как поперечные фононы,
которым соответствует смещение атомов решетки в направлении,
перпендикулярном направлению распространения (рис. Ф.З,а),
так и продольные фононы, в которых смещение происходит вдоль
направления распространения, аналогично тому как это имеет
место у звуковой волны в жидкости (рис. Ф.З, б). Дальнейшее
усложнение этих простых представлений можно
проиллюстрировать на примере ионной решетки, содержащей положительные и
акустическая ветвь
0 0 0 0 0 ©
0 ф 0 -(+> 0- Ф
ОО €Х>ШП>
оптическая ветвь
Фиг. Ф.4. Акустическая и оптическая ветви колебаний одинаковой длины
волны. Обратите внимание, что дипольный момент меняется только в
последней.
отрицательные ионы. Предположим сначала, что колебания двух
взаимопроникающих решеток независимы, и рассмотрим при
этом предположении всю систему в целом. Возможны две
ситуации (рис. Ф. 4). Если фазы движения решеток
положительных и отрицательных ионов совпадают, возникает акустическая
ветвь фононного спектра. Если же фазы смещений двух решеток
противоположны, возникает оптическая ветвь спектра.
Последнее название обязано своим происхождением изменениям ди-
польного момента кристалла в том случае, когда две его подре-
шетки движутся не в одинаковой фазе — луч света может
взаимодействовать с таким осциллирующим диполем и способен
возбуждать эту частотную ветвь колебаний решетки.
Рекомендуемые источники. Хорошее введение в теорию колебаний
решетки дано у Киттеля [224], более сложные вопросы рассматриваются в кн.
Киттеля [223] и Займана [439, 440]. В этих книгах обсуждается, каким
образом фононы определяют электрические, оптические и тепловые свойства
твердых тел. Простое изложение этих вопросов дано в кн. Дженниса и Морриса
[26].
379
ф
ФОСФОРЕСЦЕНЦИЯ. Когда фосфоресцирующее вещество
освещено, оно излучает свет. Это излучение может
продолжаться довольно долго и после того, как прекратится возбуждающее
облучение. Фосфоресценция отличается от флуоресценции, в
частности, тем, что в последнем случае излучение прекращается
практически мгновенно. Механизмы этих двух процессов
различны, чем и объясняется неодинаковая продолжительность
излучения.
безызлуштельная
релаксация*^]
фосфоресценция
Рис. Ф.5. Механизм фосфоресценции.
Механизм фосфоресценции заключается в следующем:
молекула, находящаяся в основном состоянии, в котором спины всех
электронов спарены (и которое, следовательно, является синг-
летным состоянием), поглощает падающий свет и переходит на
более высокий синглетный уровень. Электронное возбуждение
сопровождается колебательным (рис. Ф. 5). Энергия этих
колебаний передается окружающим молекулам в результате
процесса, подобного описанному в разд. «Флуоресценция». Итак,
молекула сначала оказывается в состоянии, которое приводит к
флуоресценции. Однако, если затухание колебательного возбуждения
происходит не слишком быстро, могут вмешаться другие
процессы. Предположим, что молекула оказывается в
возбужденном триплетном состоянии (в котором два спина не спарены),
показанном на рис. Ф. 5 кривой 7\. Тогда существует
вероятность того, что, переходя вниз по колебательным уровням,
молекула перескочит из синглетного состояния в триплетное; такой
переход называется интеркомбинационным. У подножия
лестницы колебательных уровней молекула оказывается в ловушке:
380
ф
она не может испустить энергию электронного возбуждения и
опуститься в основное состояние, так как переход из триплет-
ного состояния в синглетное запрещен правилами отбора, и не
может подняться вверх до точки пересечения синглетного и три-
плетного состояний и затем спуститься вниз по лестнице
колебательных уровней синглетного состояния, потому что столкновения
с решеткой не передают ей достаточной для этого энергии. Она
не может передать энергию электронного возбуждения
окружающим молекулам и с помощью безызлучательного перехода,
поскольку мы предположили, что даже колебательное затухание
возбуждения происходит недостаточно эффективно, а ведь оно
осуществляется потерей меньших порций энергии, которые легче
отдавать. Если бы все сказанное выше было справедливо,
молекула застряла бы в верхнем триплетном состоянии. Однако
сделанные выше замечания, как и вообще большинство замечаний,
не совсем строги, и самым большим заблуждением является
утверждение, что переходы между триплетным и синглетным
состояниями строго запрещены. В самом деле, если бы они были
строго запрещены, молекула не могла бы перейти в начале
описанного процесса из синглетного состояния в триплетное. Если
же такой переход все же произошел, то это означает, что сппи-
орбитальное взаимодействие достаточно сильно, чтобы это
правило отбора нарушалось и чтобы подобный переход был слабо
разрешен. Но если переход Ti-+Sq разрешен только слабо, он
осуществляется медленно и может происходить даже после того,
как прекратилось возбуждающее облучение.
В процессе фосфоресценции происходит изменение мультп-
плетности состояния (происходит «распаривание» спинов), в
этом принципиальное различие механизмов фосфоресценции и
флуоресценции. Следовательно, фосфоресценция возможна при
условии, что вблизи синглетного состояния молекулы имеется
подходящее триплетное состояние и что спин-орбитальное
взаимодействие достаточно сильно для осуществления
интеркомбинационного перехода. Присутствие тяжелого атома повышает
вероятность такого перехода. Далее, у молекулы должно быть
достаточно времени, чтобы она могла перейти с одной кривой на
другую. Это означает, что колебательное затухание возбуждения
не должно проходить настолько быстро, чтобы молекула
«успокоилась» и оказалось ниже точки пересечения кривых до того,
как произойдет интеркомбинацнонный переход. По эгой причине
многие молекулы, флуоресцирующие в жидких растворах,
фосфоресцируют, если они закреплены в твердой решетке такой, как
гель или стекло. Из рис. Ф. 5 видно также, что длина волны
излучаемого при фосфоресценции света должна быть больше (т. е.
он сдвинут в красную сторону спектра), чем при
флуоресцентном излучении, поскольку нижний колебательный уровень три-
381
ф
плетного состояния имеет меньшую энергию, чем нижний
колебательный уровень возбужденного синглетного состояни. И
наконец, некоторые молекулы все-таки способны вскарабкаться
опять в синглетное состояние Si, из которого они уже переходят
в основное состояние, и этот переход сопровождается
флуоресцентным излучением (так называемая замедленная
флуоресценция). В этом случае триплетное состояние всего лишь играет
роль резервуара.
Каковы экспериментальные подтверждения того, что в
фосфоресценции участвует триплетное состояние? Первое
непосредственное подтверждение было получено при определении
магнитной восприимчивости освещенного и неосвещенного
фосфоресцирующего образца: освещенный образец приобретает
парамагнитные свойства. Наиболее чувствительным способом обнаружения
триплетного состояния является применение к
фосфоресцирующим молекулам метода электронного парамагнитного резонанса;
результаты не оставляют никаких сомнений в отношении
участия в фосфоресценции триплетного состояния.
Упражнения. Каково наблюдаемое отличие фосфоресценции от
флуоресценции? Изобразите схему образования флуоресцентного состояния и
сравните ее с такой же схемой для фосфоресцентного состояния. Конкуренция
между какими процессами определяет этот механизм излучения? Каким
образом может быть усилена фосфоресценция по сравнению с флуоресценцией и
безызлучательными переходами? Объясните термин «интеркомбинационный
переход». Чем он отличается от внутренней конверсии? Почему
фосфоресценция является медленным процессом? Какое возмущение ответственно за
интеркомбинационный переход и за фосфоресцентное излучение? Как может
быть усилено это возмущение? Что такое замедленная флуоресценция и как
ее отличить от фосфоресценции? Как ее можно отличить теоретически и
экспериментально от обычной флуоресценции с большим временем жизни? Как
можно экспериментально доказать, что в процессе фосфоресценции участвует
триплетное состояние? Обсудите причины, по которым следует считать, что
интеркомбинационный переход происходит в точке пересечения двух
потенциальных кривых.
Рекомендуемые источники. См. [1], гл. 10, а также разд. «Флуоресценция»
и «Лазеры». См. кн. Боуэна [71], Вейна [416], Калверта и Питса [88],
Мак-Глина, Адзуми, Киноситы [272]. Использование электронного парамагнитного
резонанса для изучения роли триплетного состояния в процессе фосфоресценции
описано Хатчисоном и Мангамом [195] и Керрингтоном и Мак-Лечланом [90];
этот же вопрос подробно обсуждается Мак-Глином и др. [272].
ФОТОНЫ. Свет частоты v может передавать энергию только
дискретными порциями (квантами) величины /iv, где h —
постоянная Планка. Следовательно, энергия пучка света частоты v
может равняться только целому числу квантов hv. Поэтому
естественно представлять себе последовательное возбуждение
какого-либо типа световых колебаний с определенной частотой как
382
ф
результат появления в том или ином состоянии нескольких
гипотетических частиц. Таким образом, пучок света частоты v с
энергией nhv можно считать состоящим из п световых
корпускул. Эти кванты возбуждения, или гипотетические корпускулы,
и называются фотонами. Каждый фотон с длиной волны X = c/v
несет энергию hv и, согласно соотношению де Бройля, импульс
hv/c. Низкочастотные фотоны несут малую энергию и малый
импульс, фотоны высокой частоты — большую энергию и
большой импульс.
Проявляет ли свет корпускулярные свойства, которые
должны следовать из такого описания? Безусловно, проявляет, так
как фотоэлектрический эффект подтверждает, что энергия
может передаваться только дискретными порциями
(соответствующими аннигиляции фотона), а эффект Комптона показывает, что
каждый фотон несет определенный импульс, соответствующий
его частоте. При таком подходе давление излучения можно
рассматривать как давление, оказываемое на поверхность тела
стационарным пучком падающих фотонов.
Фотоны могут быть поляризованы так, что их электрическая
компонента лежит в одной плоскости (шюскополяризованный
свет) или совершает движение по кругу или эллипсу, но в любом
случае электрическая компонента обязательно перпендикулярна
направлению распространения. У фотона имеется собственный
угловой момент (спин), и проявлением именно этого свойства
является левая или правая круговая поляризация света. Спин
фотона равен единице. Одно значение его проекции
(соответствующее правовинтовому вращению относительно направления
движения) отвечает свету с левой круговой поляризацией,
другое (соответствующее левовинтовому вращению)—свету с
правой круговой поляризацией, третье значение (напомним, что для
спина 1 возможны три проекции на выделенную ось) запрещено
для частиц, движущихся со скоростью света, к числу которых
относится фотон.
Наличие спина у фотона лежит в основе установления
правил отбора для электрических дипольных переходов. Поскольку
спин фотона равен единице, он относится к бозонам. Согласно
принципу Паули, каждое состояние может заполняться
бесконечным числом фотонов, и это позволяет получать интенсивные
монохроматические пучки света (см. разд. «Лазер»).
Упражнения. Что означает термин «фотон»? Какова энергия фотона в
пучке света частоты v и какой импульс он несет? Какова энергия фотона в
пучке света, соответствующего микроволновой области- спектра (1 см-1),
инфракрасной (500 см*1), видимой (~550 нм) и ультрафиолетовой (300 нм)
областям спектра и диапазону у-лучей (Ю-11 м)?" Сколько фотонов излучает
за импульс с энергией 1 мДж азотный газовый лазер с длиной волны 337 нм?
383
ф
Сколько фотонов в секунду излучает электрическая лампочка с
вольфрамовой нитью, если ее мощность равна 100 Вт, а длина волны излучения равна
450 нм? Какова минимальная частота света, с помощью которого можно
разорвать молекулярную связь с энергией 100 кДж-моль-1? Каковы
экспериментальные доказательства корпускулярной природы света? Как можно
согласовать описанный корпускулярный подход с существованием такого
типично волнового явления, как дифракция света?
Рекомендуемые источники. Квантовая механика фотонов очень сложна,
но в настоящее время благодаря возрастающей роли лазеров она играет
очень важную роль. Если этот вопрос действительно интересует вас, см. Гран-
ди [167], Луизелл [257], Берестецкий, Лифшиц и Питаевский [54], Ахиезер и
Берестецкий [33], Левич, Мямлин и Вдовин [242], Джоч и Рорлих [204], Кемп-
фер [214]. Соотношение неопределенности между фазой фотонов и их числом
корректно (что является редкостью) рассмотрено Каррузерсом и Нето [91].
Концепция фотона играет важную роль при интерпретации квантовой
механики, см. Дирак [123] и Фейнман, Лейтон, Сэндс [145]. Квантовая оптика —
это область оптики, в которой преобладает квантовый, т е. фотонный,
аспект. Обзор вопроса см. в кн. Глаубера [163], современное состояние
проблемы изложено Лоудоном [256] и Лойзеллом [257]. Являются ли фотоны
частицами? По этому вопросу см. кн. Борна и Бейма [66]. Полезное
рассмотрение разложения плоской волны на круговые компоненты дано на стр. 9 кн.
Уиттейкера «Стереохимия и механизмы реакций» [426].
ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ. Когда свет с короткой
длиной волны падает на поверхность металла, с нее вылетают
электроны. Очень важными являются три следующих
экспериментальных наблюдения:
1) испускание электронов возможно только при условии, что
длина волны падающего света меньше некоторого порогового
значения, характерного для данного металла;
2) испускание электронов происходит даже при очень
низких интенсивностях падающего света, если выполняется первое
условие. Каким бы тусклым ни был падающий свет, между его
попаданием на поверхность и появлением фотоэлектронов нет
задержки во времени;
3) если частота падающего света превышает пороговое
значение, кинетическая энергия фотоэлектронов линейно зависит от
нее.
Из первого наблюдения следует, что энергия, которая
должна быть передана поверхности металла, чтобы она выбросила
электрон, связана с частотой света и что поверхность металла
не может постепенно накапливать энергию, необходимую для
выброса электрона. Такое поведение не согласуется с
представлениями классической физики, в соответствии с которыми
следовало бы ожидать, что электромагнитная световая волна будет
передавать свою энергию металлу независимо от ее частоты.
Квантовая теория, используя представления о фотонах,
позволяет объяснить все особенности этого явления простым и
381
ф
естественным образом. Согласно квантовой теории, световую
волну частотой v можно рассматривать как совокупность
фотонов, каждый из которых несет энергию /iv. Поэтому все три
описанные выше экспериментальные закономерности можно
объяснить следующим образом:
1. Когда фотон ударяется о поверхность металла, он может
выбить электрон, передав ему всю свою энергию. Но это
произойдет только в том случае, если переданная энергия hv
превышает энергию связи электрона с металлом (работу выхода ф).
Если частота фотона мала и его энергия меньше работы выхода,
испускания электрона не происходит и фотон вылетает с
поверхности в составе отраженного пучка. Так объясняется наличие
пороговой частоты фотоэлектрического эффекта.
2. Возникновение фотоэффекта при любой интенсивности
падающего света и отсутствие у него запаздывания объясняется
теми же причинами: если частота фотона превышает пороговую,
он в состоянии выбить электрон. Фотоэлектрический эффект
определяется индивидуальными фотон-электронными столкнове-
ниями, а вовсе не накоплением энергии, поступающей от
проходящего волнового фронта. При низких интенсивностях
излучения, когда фотонов мало, число столкновений также невелико,
но каждый фотон несет такую же энергию /iv, как и фотоны
сильно заселенного интенсивного пучка той же частоты.
3. Третье наблюдение можно объяснить, исходя из того, что
обладающий достаточно большой частотой фотон аннигилирует
при столкновении, которое приводит к испусканию электрона.
Согласно закону сохранения энергии, вся энергия фотона при
этом должна перейти к электрону. Часть этой энергии, равная
работе выхода, расходуется на вырывание электрона из
металла, остальная энергия hv—ф должна перейти в кинетическую
энергию выбрасываемого электрона xl2tnev2- Отсюда следует, что
кинетическая энергия электрона, вылетающего с поверхности
металла, пропорциональна частоте падающего света.
Значение фотоэлектрического эффекта не ограничивается его
техническим применением в светочувствительных приборах.
Фотоэлектрический эффект сыграл исторически важную роль в
развитии представлений о квантовании излучения. Кроме того,
фотоэлектрический эффект применяется для определения работы
выхода металлов (по пороговой частоте фотоэффекта).
Примером современного применения фотоэффекта является
фотоэлектронная спектроскопия, при которой электроны выбиваются из
молекул с помощью высокоэнергетическнх фотонов из
коротковолнового источника. «Работой выхода» в этом случае является
энергия, необходимая для удаления электрона с орбитали,
которую он занимает в молекуле. Поэтому появление электронов
с различными значениями кинетической энергии под действием
385
ф
монохроматического пучка света означает, что эти электроны
удалены с соответствующего набора орбиталей с различными
энергиями связей (рис. Ф. 6). Анализ спектра кинетических
энергий испускаемых электронов дает подробную информацию
об энергетических уровнях молекулы. Когда падающие фотоны
принадлежат рентгеновскому диапазону, каждый из них несет
достаточно энергии, чтобы выбивать электроны с самых
внутренних оболочек атомов, таким образом можно изучать и их
Рис. Ф.6. Возникновение фото- Рис. Ф.7. Вырывание электронов
электронного спектра. из различных областей атома.
энергии (рис. Ф. 7). Основанный на этом метод рентгеноэлек-
тронной спектроскопии известен также под названием
«электронная спектроскопия для химического анализа». См. также разд.
«Оже-эффект».
Упражнения. Перечислите основные закономерности фотоэлектрического
эффекта. Почему классическая волновая теория света не способна объяснить
их? Как объясняется фотоэлектрический эффект и какую роль при этом
играют фотоны? Каково значение работы выхода при фотоэлектрическом
эффекте? Свет с длиной волны 750, 500 и 200 нм падает на поверхность одного
из следующих металлов: Na (2,3 эВ), К (2,2 эВ), Cs (2,1 эВ), W (4,5 эВ);
числа в скобках обозначают работы выхода для соответствующего металла.
Какой должна быть кинетическая энергия испускаемого электрона в тех
случаях, когда такое испускание возможно? Измерена кинетическая энергия
испускаемых электронов в зависимости от частоты падающего света: при длине
волны 625 нм кинетическая энергия равна 0,2 эВ, при 416 нм —равна 1,2 эВ,
386
ф
при 312 нм — равна 2,2 эВ; рассчитайте работу выхода для такого металла.
Как связана фотоэлектронная спектроскопия с фотоэлектрическим эффектом?
Рекомендуемые источники. Анализ фотоэлектрического эффекта дается в
гл. 2 кн. Бома [63] и в § 1.3 кн. Джеммера [203]. Значение этого явления для
развития представления о фотонах описано Борном и Беймом [66].
Фотоэлектронная спектроскопия рассматривается в кн. Тернера, Бейкера и Брандла
[402], Бейкера и Беттериджа [45] и Зигбана и др. [367]. В кн. Зигбана [366]
дано введение в рентгеноэлектронную спектроскопию, а в кн. Тернера [401] —
введение в фотоэлектронную спектроскопию.
ФРАНКА—ГЕРЦА ОПЫТ. В опыте Франка —Герца пучок
электронов пропускали через газ при низком давлении и
регистрировали проходящий сквозь газ ток; в последующих
экспериментах регистрировалась также энергия проходящих газ
электронов. В результате этого опыта было обнаружено, что при
возрастании энергии влетающих в газ электронов сила
регистрируемого тока резко уменьшается каждый раз, когда их энергия
оказывается равной энергии возбуждения атома или молекулы.
Кроме того, было обнаружено, что газ одновременно испускает
излучение, частота которого соответствует энергии электронного
пучка. Объяснить это явление можно, исходя из принципа
квантования энергии. Электроны отдают свою кинетическую энергию
атому только при условии, что атом может быть возбужден этой
порцией энергии. Следовательно, сила регистрируемого тока
будет уменьшаться каждый раз, когда энергия может быть
передана этой квантованной системе. Такой вывод подтверждается
следующим: атомы газа испускают излучение соответствующей
частоты (/iv = A£). Значение опыта Франка — Герца
заключается в том, что он показывает квантованный характер энергии
даже в том случае, когда она относится к механическому
движению, а не к электромагнитному излучению.
Рекомендуемые источники. Введение в вопрос см. в кн. Уайта [425].
Логически последовательное изложение вопроса дано Бомом [63] и Джеммером
[203]. См. также оригинальные статьи Франка и Герца [151—153].
ФРАНКА—КОНДОНА ПРИНЦИП. Интенсивность спект-
тральных переходов между колебательными уровнями
различных электронных состояний молекул подчиняется принципу
Франка — Кондона, который гласит, что вследствие большой
разницы в массах между ядерным остовом и возбуждаемым
электроном электронный переход происходит так быстро, что во
время него ядра можно считать неподвижными. При
электронном возбуждении молекулы происходит вертикальный переход,
т. е. расположение ядер в верхнем электронном состоянии
оказывается таким же, как в нижнем. Но так как кривые
молекулярной энергии могут быть смещены (рис. Ф. 8), такое располо-
387
ф
жение ядер может соответствовать сильно сжатому или
растянутому состоянию возбужденной молекулы, поэтому молекула
немедленно начинает колебаться. Отсюда следует, что
электронный переход обычно сопровождается колебательным
возбуждением молекулы.
Какой из колебательных уровней более всего заселяется в
результате перехода — определяется относительным положением
верхней и нижней энергетических кривых. Если бы кривые были
AZ3TZ
тШЮ -ЖЮ ЧШЮ
Рис. Ф.8. Классическое обоснование принципа Франка — Кондона. В процессе
возбуждения грузик остается неподвижным, а величина колебательной
энергии зависит от относительного положения кривых потенциальной энергии.
строго одинаковой формы и лежали точно одна над другой
(рис. Ф. 8, а), то это соответствовало бы переходу с основного
колебательного уровня одного состояния на основной
колебательный уровень другого состояния и переход не сопровождался
бы колебательным возбуждением. Вообще говоря, можно
считать, что переход происходит из наиболее вероятной конформа-
ции основного состояния молекулы, которой соответствует
неподвижное равновесное расположение ядер. В процессе
электронного перехода ядра не меняют своего расположения. После
завершения перехода ядра еще неподвижны, но находятся в новом
силовом поле, соответствующем новому электронному
распределению. Поэтому они начинают двигаться, т. е. попеременно
отклоняться и возвращаться назад в первоначальное
расположение по закону гармонических колебаний (рис. Ф. 8, б и в).
Отсюда следует, что первоначальное расположение ядер
возбужденной молекулы представляет собой точку поворота нового ко-
заа
ф
лебательного движения, а возбужденная молекула приобретает
колебательную энергию. Линия, проведенная вертикально из
начального основного состояния, пересекает верхнюю кривую
потенциальной энергии в точке, которая является точкой поворота
колебательного движения в возбужденном состоянии и которая
Рис. Ф.9. Квантовое обоснование принципа Франка — Кондона. Самый
сильный переход происходит в состояние, с которым наинизший колебательный
уровень нижнего состояния имеет наибольшее перекрывание; он показан
жирной линией. Слева дан соответствующий спектр.
показывает, сколько энергии поглощается при переходе.
(Напомним, что энергия гармонического осциллятора постоянна:
потенциальная энергия, теряемая при разжатии пружины,
превращается в кинетическую энергию, которая расходуется на
повторное сжатие. Поэтому потенциальная энергия в точке
поворота (£КОл на Рпс- Ф- 8) определяет энергию возбуждаемых
колебаний при всех смещениях.)
Квантовомеханическое обоснование принципа Франка —
Кондона связано с рассмотрением перекрывания колебательных
волновых функций двух электронных состояний. Наиболее
интенсивные переходы происходят между теми колебательными
состояниями, которые перекрываются наиболее сильно, так как та-
389
ф
кие состояния имеют близкие характеристики. Волновая
функция основного колебательного состояния имеет вид колоколооб-
разной кривой с максимумом, соответствующим равновесному
расположению ядер (рис. Ф.9). С этой функцией перекрывается
много колебательных волновых функций возбужденных
электронных состояний, но наибольшее перекрывание характерно
для функций с максимумом в той же области пространства.
Если энергетические кривые смещены, наибольшее
перекрывание осуществляется с максимумами, которые располагаются на
краю потенциальной ямы (см. рис. Ф.9), поэтому возбуждаться
будут те колебания, которые соответствуют точке пересечения
вертикальной черты, проведенной из равновесного положения в
основном состоянии (наиболее вероятной конфигурации,
отвечающей максимуму колебательной волновой функции), с
верхней потенциальной кривой. В окрестности точки пересечения
колебательные волновые функции имеют сравнительно большие
амплитуды, и поэтому перекрывание с основным колебательным
состоянием наиболее велико. Наблюдаемое распределение ин-
тенсивностей колебаний отражает различное перекрывание
волновых функций основного и возбужденных колебательных
состояний.
Упражнения. 1. Сформулируйте принцип Франка — Кондона. При каких
условиях он должен выполняться? Каково «классическое» объяснение этого
принципа? Каково его квантовомеханическое объяснение и как оно связано
с классическим? Что такое вертикальный переход? Постройте диаграмму,
подобную рис. Ф.9, с помощью которой принцип Франка — Кондона может
быть применен для определения распределения интенсивностей
флуоресцентных переходов (с основного колебательного уровня верхнего электронного
состояния на различные колебательные уровни нижнего электронного
состояния).
2. Дайте квантовомеханическое обоснование принципа Франка —
Кондона, рассмотрев дипольный момент перехода между двумя состояниями. При
этом предположите, что состояние молекулы может быть записано в виде
произведения колебательного v и электронного е состояний, и рассмотрите
переходный момент (е*, v*|d|e, v). Покажите, что его можно
аппроксимировать выражением (e*|d|£) (v*|v), где явно выделен интеграл перекрывания
между колебательными функциями двух электронных состояний. Вычислите
интеграл перекрывания между основными состояниями двух гармонических
осцилляторов, чьи положения равновесия отстоят на расстояние R, и
начертите график зависимости интенсивности (0—0) -перехода (переход с v = 0 на
v* = 0) от R.
Рекомендуемые источники. Дальнейшее обсуждение и обоснование
принципа Франка — Кондона см. в [1], гл. 10. См. также работы Кинга [222], Уиф-
фена [424], Барроу [51]. Тщательное обсуждение обоснования этого принципа
дано Герцбергом в 1950 г. [187], более детально развито в 1966 г. [188].
Первоначально принцип был сформулирован Франком [150], а его математическое
описание выполнено Кондоном [95]. Полезный обзор современных работ,
включающих рассмотрение принципа Франка — Кондона, опубликован Николсом
[305].
390
ХАРАКТЕР. В химических приложениях теории групп
преобразование симметрии обычно представляется матрицей.
Характер %(R) преобразования R — это сумма диагональных
элементов (след, или шпур) его матрицы. Для тех, кто в общих чертах
знаком с теорией групп, напомним следующее:
1. В любом неприводимом представлении группы
преобразования симметрии, принадлежащие одному и тому же классу,
имеют один и тот же характер.
2. Характеры различных неприводимых представлений груп^
пы ортогональны (п. 2 списка формул X. 1).
3. Характер преобразования инвариантен относительно пре^
образования подобия.
4. Характер приводимого представления группы равен сумме
характеров неприводимых представлений, на которые оно
разлагается (п. 3 списка формул X. 1).
Список формул XJ
Характер
1. Определение: %{i) (#)^Sp D{i) (R)^ £ D^ (R).
у}1) (R) является характером преобразования R в представлении Т^\ \
в котором преобразование R представляется матрицей D^ (/?).
2. Ортогональность: £ %{i) (R)* %^] (R) = hdiff
R
h — порядок (число элементов) группы.
3. Разложение представлении Г:
Г - X а^> at =* ОМ) И %m(R)*x(R).
i R
4. Проекционный оператор P^l) проектирует произвольную функцию f
на базис /(t) представления Г(1):
p(i)f = f«\ p«-(/,/*) £jcf)(/})4
R
U — размерность представления Г'1).
5. Правила отбора. Интеграл \ dxf^ *QM/W равен нулю, если Г(^ не
входит в разложение произведения Г*'* X Г***.
5. Характеры можно комбинировать в виде проекционного
оператора, который, будучи применен к произвольной функции,
391
X
выделяет из нее компоненту, являющуюся базисом
неприводимого представления группы.
6. Характер тождественного преобразования конкретного
неприводимого представления равен размерности этого
представления; размерность представления равна степени вырождения
базиса представления.
Эти свойства суммированы в списке формул X. 1, несколько
полезных таблиц характеров приведены в табл. 3, а более
подробно ознакомиться с этим вопросом можно по работам,
приведенным в списке рекомендованной литературы.
Рекомендуемые источники. Ознакомиться в общих чертах с теорией групп
можно, прочитав статью под соответствующим заголовком; подробное
содержание теории, метод и применение даны в [1], гл. 6, а примеры ее
применения к изучению структуры и свойств молекул —в гл. 9—11. Эткинс, Чайлд и
Филлипс [40] составили таблицы характеров для всех простых точечных и
некоторых непростых групп, сопроводив таблицы замечаниями относитель*
но их применения. Тщательный анализ см. в работах Коттона [102], Бишопа
[59], Тинкхэма [396] и Брэдли и Крэкнелла [74], в которых, в частности,
рассматривается теория групп применительно к твердым телам. См. также кн.
Хохштрассера [451].
ХИМИЧЕСКАЯ СВЯЗЬ. Природа химической связи
(причина, по которой атомы соединяются вместе и образуют
молекулы определенной формы и с определенной энергией) является
одной из центральных областей естествознания, где применение
квантовой теории оказалось наиболее успешным. Элементарная
химия различает три типа связи между атомами: ионную
(электроны переходят от одного атома к другому, и связь
обусловлена электростатическим взаимодействием между ионами), кова-
лентную (электроны поставляются обоими атомами и
обобществляются ими в более или менее равной степени) и донорно-ак-
цепторную (один атом поставляет оба электрона, которые затем
обобществляются обоими партнерами). Современная квантовая
химия показывает, что эти три типа можно рассматривать как
частные случаи общей теории. Элементарная химия
приписывает тенденцию к образованию связи стремлению атомов
«образовать октет» или «достигнуть конфигурации инертного газа».
Современная квантовая химия объясняет эти эмпирические
правила квантовомеханическими свойствами электронов и
ядер.
Атомы группируются вместе и образуют молекулы, если тем
самым достигается более выгодное состояние с меньшей
энергией; поэтому мы должны искать причину, по которой при
образовании молекулы происходит уменьшение энергии. Как
правило, различные пространственные конфигурации атомов сильно
отличаются по энергии, поэтому форма молекулы обычно
является вполне определенной и соответствует такому простран-
392
X
ственному расположению атомов, которое позволяет системе
достичь наименьшей энергии. И наоборот, молекула распадается
на исходные атомы или группы атомов, если она приобретает
достаточную энергию (в результате столкновения с другой
молекулой или стенкой сосуда или поглощения света), чтобы полная
энергия молекулы превзошла суммарную энергию ее
изолированных фрагментов. Энергия определяет все: установить форму
и устойчивость молекулы можно, только исследуя ее энергию.
Чтобы определить отдельные вклады, вызывающие
понижение энергии, мы должны помнить, что полная энергия состоит
из двух частей — кинетической и потенциальной. Тщательный
анализ вкладов, которые они вносят, очень труден, и очень часто
вкладом кинетической энергии пренебрегают, полагая, что
главным вкладом в энергию связи является понижение
потенциальной энергии при достаточном сближении электронов с
несколькими ядрами. Пренебрежение ролью кинетической энергии —
опасный шаг, так как при этом описание химической связи
выглядит проще, чем оно есть на самом деле. Тем не менее мы
также прибегнем к такому упрощению, поскольку полный
анализ ситуации проведен только в одном случае, к которому мы
вернемся позднее.
Представим себе систему, состоящую из двух протонов и
одного электрона. Куда нужно поместить электрон, чтобы
получить стабильную молекулу (н£)? Обычный ход рассуждения
таков: из соображений электростатики следует, что электрон
следует поместить в межъядерную область. Тогда межъядерное ку-
лоновское отталкивание компенсируется притяжением между
электроном и каждым из ядер, и за счет этого Н$ достигнет
стабильности. Естественно, что электрон не занимает какое-то
фиксированное положение посередине между ядрами.
Электронный заряд распределен вокруг двух ядер так, что плотность
заряда в межъядерной области повышена. Добавление второго
электрона (с образованием Нг) в ту же самую область
пространства приведет к усилению связи: ядра будут удерживаться
притяжением к двум электронам.
Основываясь на проведенном выше рассмотрении, строение
молекулы водорода можно представить себе следующим
образом: два ядра окружены облаком заряда двух электронов с
повышенной плотностью в межъядерной области, называемой
связывающей областью. Характеристическая длина связи в Нг
определяется положением равновесия между отталкиванием
самих ядер, которое усиливается при укорочении связи, и
притяжением ядер к находящимся между ними электронам; при
слишком малых межъядерных расстояниях электроны не могут
скапливаться в связывающей области и отталкивание преобла-
393
X
дает. Если в молекуле Нг добавляется третий электрон, он
стремится разместиться поближе к ядрам, но не может проникнуть
в связывающую область из-за наличия первоначальной пары
электронов (это запрещается принципом Паули). Поэтому
третий электрон увеличивает плотность заряда межъядерной
области. Его воздействие на ядра разъединяет их, и в результате
присутствие третьего электрона приводит к удлинению и
ослаблению связи. Добавление четвертого электрона приводит к
полному разрыву связи.
При таком описании ковалентной связи (когда электроны,
образующие связь, поставляются в равной степени двумя
атомами) становится ясно, что наиболее прочную связь дают два
электрона. Образование прочных связей энергетически выгодно, и
поэтому атомы стремятся образовать по возможности больше
связей, насколько это возможно без привлечения внутренних,
крепко связанных электронов. Именно это и имеется в виду,
когда говорят, что «атомы обобществляют свои электроны,
чтобы иметь завершенные октеты». Заметим также следующее:
чтобы связь была эффективной, два обобществляемых электрона
должны занимать одну и ту же область пространства, а для
этого их спины должны иметь противоположное направление
(это требование является следствием принципа Паули).
Сказанное объясняет важную роль понятия электронной пары в теории
химической связи. Электроны оказываются спаренными вовсе
не по какой-то таинственной причине и не потому, что энергия
их отталкивания уменьшается в результате спаривания.
Наоборот, чтобы поместить два электрона на одну и ту же орбиталь,
необходимо затратить энергию. Они образуют пару, чтобы
создать такое распределение заряда, которое могло бы как можно
сильнее понизить энергию всей системы, и одно из множества
таких распределений способно привести к образованию
молекулы. Такое описание роли электронной пары ясно
просматривается как в теории молекулярных орбиталей, так и в теории
валентных связей.
В гетероядерных молекулах (где осуществляется связь
между двумя различными атомами) мы сталкиваемся с аналогичной
ситуацией. Она лишь видоизменяется из-за того, что энергия
такой системы окажется ниже, если связывающая пара электронов
расположится ближе к одному атому, чем к другому:
электроны в большей мере смещаются в сторону более
электроотрицательного атома. Такую ситуацию можно рассматривать как
отталкивание одного из валентных электронов менее
электроотрицательного атома (с меньшим потенциалом ионизации) и
смещение его к атому с большим сродством к электрону. Этот процесс
ведет к образованию полярной связи, и, пользуясь
терминологией теории валентных связей, можно сказать, что к чисто кова-
394
X
лентной связи примешивается ионная составляющая. Другими
словами, молекулярная волновая функция оказывается
суперпозицией ковалентной и ионной волновых функций. Атомы с
наибольшей электроотрицательностью, как правило, имеют
электронную конфигурацию, которой недостает до конфигурации
заполненной оболочки только одного или двух электронов; таким
образом, мы еще раз убеждаемся, что тенденцию к образованию
октета можно рассматривать как тенденцию к распределению
электронов с наинизшей энергией.
Когда электроотрицательности двух атомов в гетероядерной
молекуле (или связи) сильно различаются, как, например, в том
случае, когда атом с низким потенциалом ионизации (из левой
части периодической системы) находится рядом с атомом с
высоким сродством к электрону (из правой части периодической
системы), устойчивость, достигаемая полным переносом
электрона от одного атома к другому, может быть очень большой.
Сближение двух таких атомов приводит к тому, что по соседству
располагаются положительный и отрицательный ионы; они
удерживают друг друга за счет кулоновского взаимодействия между
разноименными зарядами. Этот предельный случай полярной
связи и есть ионная связь. Важно отметить, что потенциалы
ионизации всегда больше, чем сродство любых атомов к
электрону, и поэтому энергию, необходимую для образования ионных
связей, обеспечивает кулоновское притяжение между ионами.
Самое главное различие между ионной и ковалентной связью,
не считая полярности, — это направленные свойства последней
при отсутствии таковых у первой. Дело в том, что кулоновское
взаимодействие между двумя зарядами изотропно (одинаково
во всех направлениях) и образующиеся структуры, нередко
обладающие большой протяженностью, зависят главным образом
от стерических условий пространственной упаковки ионов
различных размеров. Поэтому ионная связь приводит к
образованию прочных и протяженных кристаллических решеток с
характерными типами упаковки.. В случае чисто ковалентной связи
взаимодействие вовсе не изотропно, так как его сила зависит от
способности атома поставлять электроны в межъядерную
область между собой и своим партнером по связи. Для
двухатомных молекул в принципе никаких проблем при этом не
возникает, но, если рассматриваются хотя бы три атома, приходится
объяснить, почему геометрия ковалентно связанных структур
определяется электронным строением атомов, а не
геометрической проблемой их упаковки. Так, например, атомы кислорода и
водорода могут образовать молекулу НО, если каждый из них
поставит по одному электрону для образования полярной связи,'
а затем второй атом водорода образует с кислородом вторую
связь, так что получается молекула НОН. В конфигурации с
395
X
наименьшей энергией вторая связь должна быть направлена под
углом 104,5° к первой, потому что под таким углом атом
кислорода может образовать самые прочные связи (см. разд.
«Гибридизация»). В молекуле воды кислородный октет завершен, и
добавление еще одного атома водорода приводит к нестабильной
молекуле Н30 (так как НзО обладает большей энергией, чем
изолированные частицы НгО и Н). Однако молекула воды
способна еще вступать в донорно-акцепториую связь, поставляя для
этого сразу два электрона, как это происходит при образовании
иона гидроксония НзО+ (в котором .неподеленная пара
электронов кислорода акцептируется протоном) или акво-комплексных
ионов. Все сказанное свидетельствует, что молекула воды
является вполне обособленной дискретной частицей конечных
размеров. Валентность атома, т. е. число связей, которые он может
образовать в большинстве ковалентных соединений,
определяется сравнительно просто, а стереохимия этих соединений
обусловлена способностью атомов поставлять электроны для
достижения такой валентности. Это четко видно как в теории
молекулярных орбиталей, так и в теории гибридизации.
Все предшествующее обсуждение основывается на
традиционном подходе, изложенном в четвертом абзаце; однако, хотя
все сказанное и представляется разумным, на самом деле оно
оказывается совершеннейшим заблуждением. Молекулярная
структура лишь в очень немногих случаях изучена настолько
детально, чтобы можно было тщательно проанализировать
истинную природу химической связи, но для Н£ можно сделать такие
выводы, и они не согласуются с упомянутой выше точкой
зрения. Эти выводы противоречат большинству простых объяснений
природы химической связи и, насколько известно автору книги,
всему, что можно найти в учебниках. По-видимому, в Н£ связь
обусловлена сложным соотношением между кинетической и
потенциальной энергией электронов. Точная волновая функция
показывает, что, когда Н+ и Н сближаются, электрон
действительно смещается в межъядерную область, но это приводит к
увеличению потенциальной энергии системы вопреки
предположению, что она уменьшилась бы, если бы электрон мог
принадлежать сразу обоим ядрам. Подумав, мы, конечно, должны
согласиться с тем, что увеличение потенциальной энергии более
правдоподобно, чем уменьшение, поскольку наинизшая
потенциальная энергия достигается в том случае, когда электрон
находится как можно ближе к одному из ядер. Чем же в таком
случае определяется энергия связи? Прежде всего следует учесть,
что, двигаясь в окрестности двух протонов, электрон
приобретает большую свободу и в результате его кинетическая энергия
при движении вдоль связи уменьшается; однако дело обстоит
396
X
не совсем так просто. Из-за сжатия атомных орбиталей на
каждом ядре энергия системы еще больше понижается
(увеличивается энергия связи). Сжатие атомных орбиталей позволяет
электрону сильнее приближаться к ядрам, что приводит к
понижению потенциальной энергии, и именно это обстоятельство
определяет основное изменение потенциальной энергии. Однако
орбитальное сжатие вызывает и противоположный эффект,
поскольку, когда движение электрона ограничивается меньшей
областью, его кинетическая энергия возрастает, и это почти
компенсирует уменьшение потециальной энергии. Но компенсация
оказывается не полной, и указанное выше уменьшение
кинетической энергии за счет движения электрона вдоль межъядерной
оси позволяет получить необходимое изменение. Наконец, форма
волновой функции свидетельствует о сдвиге электронной
плотности из областей за ядрами в область связи за счет поляризации
атомных орбиталей, из-за этого потенциальная энергия тоже
понижается, а кинетическая немного увеличивается. Суммарным
эффектом является большое понижение потенциальной энергии,
главным образом обусловленное орбитальным сжатием, и почти
такое же большое увеличение кинетической энергии,
обусловленной в основном тем же явлением; однако преобладающим
оказывается понижение потенциальной энергии. В результате Нг
имеет более низкую полную энергию, чем Н+ + Н, и поэтому
оказывается устойчивой частицей. Эта сложная картина была
выяснена на основании тщательного изучения волновой
функции Hj, а в более сложных случаях могут потребоваться
уточнения. Рассмотренный случай является примером того, как
устойчивы сложившиеся в химии точки зрения, и показывает,
какую роль играют тщательные и точные вычисления для
установления истинной природы химической связи.
Упражнения. Что определяет, соединятся ли атомы вместе с
образованием молекулы или нет? Какая термодинамическая величина является мерой
силы химической связи? Что происходит, когда молекула получает извне
большое количество энергии? Каким образом может быть передана ей
энергия? Какая особенность распределения электрона в молекуле водорода
проще всего объясняет ее устойчивость? Какой вклад в полную энергию не
учитывается при таком объяснении? Почему молекула водорода более устойчива,
чем Н^, а Щ менее устойчива, чем Н2 и Н2? Можно ли, рассуждая
подобным образом, объяснить, почему два атома гелия не образуют
устойчивой молекулы? Применим ли такой подход к обсуждению устойчивости
связей между любыми частицами с заполненными оболочками, например, в
случае инертных газов? Как изменяется распределение электронов при переходе
от гомоядерной связи к гетероядерной? Появляется ли при этом
дополнительный вклад в энергию связи? Что определяет степень поляризации связи?
При каких условиях образуется почти чисто ионная связь? Чем объясняется
устойчивость ионного кристалла? Почему кристалл обычной поваренной соли
397
X
не превращается в газ, состоящий из атомов натрия и хлора? Почему
кристаллы имеют определенную структуру? Почему при возникновении ковалент-
ных связей образуются отдельные молекулы, а при возникновении ионных
связей — протяженные структуры? Что определяет форму соединений с ко-
валентным и ионным характером связи? Чем определяется валентность
атомов в ионных и ковалентных соединениях? Какой не рассматривавшийся
здесь тип связи также приводит к образованию протяженных структур, в ко*
торых расположение атомов определяется главным образом требованиями
упаковки? Обсудите наиболее вероятную причину образования связи в Щ.
Рекомендуемые источники. Детальное изложение квантовой теории
химической связи см. в [1], гл. 10. Простое объяснение структуры молекул см. в
кн. Коулсона «Форма и структура молекул» [10], а также [105]. См. также
Маррел, Кеттл и Теддер [299]. Классический вводный курс, где обсуждается
применение квантовой механики к реальным химическим проблемам, — это
кн. Полинга [313]. Тщательный анализ причин уменьшения энергии при
образовании связи дан Рюденбергом [351], а глубокое изучение этого вопроса
с подробным обсуждением структуры Н£ проведено Файнбергом,
Рюденбергом, Мехлером [140]; особый интерес представляет обсуждение, приведенное
на стр. 54 этой работы. О том, как упомянутые здесь концепции развивались
в квантовой механике, в результате чего стали возможны количественные
расчеты, см. в разд. «Теория молекулярных орбиталей», «Теория валентных
связей, разрыхление, электроотрицательность, гибридизация». Отметим, что здесь
совершенно не рассматривался один из типов связи, ответственный за
структуру металлов (см. «Зонная теория металлов»),
ХИМИЧЕСКИЙ СДВИГ. В экспериментах по ядерному маг-
нитному резонансу (ЯМР) внешнее магнитное поле плавно
изменяют до тех пор, пока энергия, необходимая для
инвертирования спина ядра (обращения его магнитного момента), не станет
равной энергии фотонов электромагнитного поля, в котором
находится образец. Обмен энергией, происходящий при этом,
наиболее эффективен, когда энергетические уровни ядра
оказываются в резонансе с полем излучения. Магнитная энергия ядра
зависит от локального магнитного поля, а не приложенного
внешнего поля, а они могут отличаться, поскольку внешнее поле
может индуцировать дополнительные локальные поля в
окрестности ядра. Находясь в заданном внешнем поле, ядра с
различным химическим окружением испытывают действие различных,
но характерных локальных полей и поэтому приходят в
резонанс с излучением при различных напряженностях внешнего
поля. В связи с этим разные группы ядер вызывают появление
линий поглощения вмагнитных полях различной напряженности,
и, так как спектр ЯМР представляет собой график зависимости
поглощения от напряженности приложенного поля, различные
молекулы, и даже различные группы одной и той же молекулы,
вызывают поглощение в разных частях спектра (рис. X. 1).
Расстояние между линиями поглощения и представляет собой
химический сдвиг.
398
X
Рассмотрим сначала шкалы, в которых измеряются
химические сдвиги. Интервалы между резонансами измеряются в
герцах (Гц, число периодов в секунду), но, так как локальное поле
зависит от напряженности приложенного поля, указать эти
интервалы недостаточно. Поэтому указанные интервалы делят на
среднюю частоту или, что практически то же самое, на частоту
слабое экранирование
сальное
экранирование
9,806"
слабое поле
от
б-шкала\ 2,20&- О
сильное поле
•| х-шкала | 7,80т 10,00v
Рис. Х.1. Спектр ЯМР (при 60 МГц) ацетальдегида и ТМС, используемого
в качестве стандарта. Для определения химического сдвига групп СНО и
СНз использованы 6- и т-шкалы. Обратите внимание на тонкую
структуру спектра.
вынуждающего поля vo. Если один протон резонирует при
частоте V/, а другой —при частоте Vj, величина 6*j = (v2- — vj)/vo
представляет собой химический сдвиг в б-шкале. Поскольку
обычно интервалы между резонансами не превышают примерно
1 кГц, а рабочая частота спектрометра имеет порядок 100 МГц,
масштаб химических сдвигов составляет ~ 10~5. Поэтому
химические сдвиги удобно выражать в миллионных долях (м. д.).
Следовательно, если говорят, что сдвиг равен 1 м. д., это
означает, что две линии разделены интервалом в 100 Гц при
использовании спектрометра, работающего на частоте 100 МГц, и
интервалом в 60 Гц, если спектрометр работает на частоте 60 МГц.
Абсолютный химический сдвиг, т. е. сдвиг резонанса протона в
молекуле по отношению к резонансной частоте изолированного
399
X
протона, не представляет большого практического интереса;
чаще используется шкала, где за начало отсчета принимается
химический сдвиг протонов тетраметилсилана Si(CH3)4 (TMC),
для которого по определению 6 = 0. Сильно экранированные
протоны имеют малые сдвиги 6, и их резонансы находятся
вблизи линии ТМС; слабо экранированные протоны имеют большие
сдвиги 6, и их резонансы сдвинуты далеко от линии ТМС в
сторону слабого поля. Применяется и другая шкала отсчета
сдвигов — так называемая т-шкала, в которой линия ТМС находится
при т = 10; таким образом, обе шкалы связаны соотношением
т= Ю — 6. Если значение т большое, ядра сильно
экранированы. Для некоторых характерных случаев сдвиги в т-шкале
приведены в табл. 4.
Какими причинами определяется химическое экранирование
протона? Все вклады в этот эффект могут быть приписаны
токам, индуцированным внешним полем на самом атоме, либо
токам, индуцированным в соседних группах. Токи,
индуцированные внешним полем на атоме, могут быть парамагнитными или
диамагнитными (см. разд. «Магнитные свойства»), и они
соответственно усиливают приложенное поле (деэкранируют ядро,
сдвигают резонанс в область малых т) или ослабляют его
(экранируют ядро, сдвигают резонанс в область больших т). Общее
рассмотрение магнитных свойств показывает, что
парамагнитные токи малы, когда возбужденные состояния атома
расположены высоко по энергии; так обстоит дело в случае атома
водорода. Для других атомов, входящих в молекулы, существует
несколько состояний, лежащих почти вплотную к основному, и
в них парамагнитные эффекты могут преобладать над
диамагнитными. Диамагнитные токи не зависят от наличия
возбужденных состояний и поэтому всегда дают вклад в экранирование
(хотя этот вклад не всегда является определяющим).
Когда токи индуцируются в соседней группе, протон
испытывает влияние дополнительного поля, которое может быть
приписано индуцированному в ней магнитному дипольному моменту.
Так, если восприимчивость соседней группы в направлении
приложенного поля равна %т, последнее индуцирут магнитный
момент %тВ, который является источником дополнительного поля
для протона. Обусловленное диполем поле характеризуется
зависимостью (1 — 3 cos2 8)/Я3 (см. рис. X. 2), и поэтому от
взаимной ориентации протона и индуцированного момента зависит,
будет взаимодействие экранирующим пли деэкранпрующим;
знак сдвига зависит также от знака восприимчивости Учитывая
возможность вращения молекулы, нетрудно понять, что такая
локальная поправка исчезает, если магнитная восприимчивость
соседней группы не является анизотропной, поэтому сдвиг
пропорционален степени анизотропии. На рис. Х.2 проиллюстрированы
400
X
два хорошо известных примера, когда резонанс на протонах,
находящихся вблизи двойной связи С = С определяется главным
образом магнитным моментом, индуцируемым за счет
электронов я-связей. В первом примере действие поля, создаваемого
этим моментом, заключается в экранировании или деэкраниро-
вании протонов в зависимости от того, оказываются ли
протоны соответственно внутри или снаружи двойного конуса с
полууглом при вершине 54° 44' (при котором 1—3 cos2 8 = 0). Во
Рис. Х.2. а — области
положительного и отрицательного
химического сдвига в окрестности
двойной связи Если ТС л и %х — маг"
нитные восприимчивости в
направлениях параллельном и
перпендикулярном связи, константа
экранирования изменяется в
зависимости от расстояния R и от угла 9
как а « (ТС|| — %х) 0 — cos2 8)/3#3;
б — вклад кольцевого тока в
химический сдвиг протонов в
бензоле.
втором примере сдвиг протонного резонанса в сторону слабого
поля возникает в основном из-за того, что молекула бензола
способна создавать кольцевой ток под действием внешнего поля,
когда оно направлено перпендикулярно плоскости молекулы.
Расчеты химических сдвигов обычно сводятся к вычислению
константы экранирования а. Она связывает индукцию
локального поля с индукцией приложенного поля В следующим
образом: В (локальное) = (1—а)5. Если а — отрицательная
величина, локальное поле сильнее приложенного (деэкранирование)
и ядро резонирует при более низкой напряженности поля; когда
а—положительная величина, локальное поле слабее, чем
приложенное, ядро экранируется и резонанс наступает при более
высокой напряженности поля. Положительную или
отрицательную константу экранирования можно связать с диамагнитным
или парамагнитным током, поскольку влияние соседней группы,
как мы уже знаем, зависит от ориентации молекулы, и в
зависимости от ориентации тот или иной знак константы определяется
тем или иным знаком тока.
^экранирование
экранирование
экранирование
^экранирование
В индуцированный
кольцевой ток
деэкранированныи
протон
401
X
Упражнения. 1. Что означает термин «химический сдвиг»? Зависит ли
химический сдвиг от силы приложенного поля? Большим или меньшим
оказывается в сильном поле сдвиг резонанса, связанный с разным химическим
окружением протонов, чем в слабом поле? Что происходит со сдвигом, когда
поле меняется от 14 до 50 кГс? Обладает ли каким-либо преимуществом
наблюдение резонансов в сильных магнитных полях? Что означают выражения
«протоны резонируют при 6т мс = 2» и «протоны резонируют при 2т»?
Укажите, в каком порядке (в сторону усиления поля) должны наблюдаться
протонные резонансы в следующих молекулах: СбНб, СН31, СНзОН, CeHi2 (см.
табл. 4). Что является причиной различия между локальным и приложенным
полем? Каковы условия возникновения деэкранирующего эффекта? Какова
роль соседней с протоном группы? Почему возможен и положительный, и
отрицательный химический сдвиг как от парамагнитного, так и от
диамагнитного токов в окружающей группе? Магнитная восприимчивость бензольного
кольца в "направлении, перпендикулярном его плоскости, составляет — 9,5-10~5,
а в направлении, параллельном кольцу, равна —3,5-10~5; вычислите
химический сдвиг на протонах в бензоле, используя формулу, приведенную в
подписи к рис. Х.2; вычислите сдвиг протона в точке, расположенной на
расстоянии 3 А над центром кольца. Какова константа экранирования в каждом
случае?
2. Выведите выражение для химического сдвига протонов в бензоле, в
котором учтены анизотропия магнитной восприимчивости кольца и свободное
вращение молекулы, и покажите, что влияние кольцевого тока исчезло бы,
если бы анизотропия была равна нулю. Воспользуйтесь предположением, что
поле индуцирует магнитный дипольный момент в центре кольца.
Рекомендуемые источники. Подробное рассмотрение процедуры
вычисления химического сдвига молекул с учетом полей и токов, наведенных
приложенным полем, см. в [1], гл. 11. О роли химического сдвига в ЯМР см. в кн.
Мак-Лечлана «Магнитный резонанс» [2]. Дополнительные детали можно найти
у Линден-Белла и Харриса [260], Керрингтона и Мак-Лечлана [90], Попла,
Шнейдера и Бернстейна [323], Мемори [281], Эмсли, Финнея и Сатклифа [134]
и Абрагама [27]. Во всех этих книгах приводятся расчеты и интерпретация
спектров ЯМР в терминах химических сдвигов. См. также рекомендуемую
литературу к разд. «Ядерный магнитный резонанс». Требуемый в
упражнении 2 расчет проделан Керрингтоном и Мак-Лечланом [90]. Природа
кольцевого тока обсуждается как этими авторами, так и Дэвисом [117].
ХЮККЕЛЯ МЕТОД. Принимая очень грубые
предположения, но зато учитывая симметрию молекулы, Хюккель развил
простую схему вычисления энергии я-электронов в сопряженных
системах. Использованные Хюккелем приближения (они
приведены ниже) являются крайне упрощенными, так как не
учитывают любой сколько-нибудь сложный аспект реальных задач.
1. Пренебрежение а-электронами; неявно они учитываются,
поскольку в значительной степени ответственны за форму
молекулы, но их взаимодействием с я-электронами пренебрегают.
2. Совершенно не учитывается перекрывание. Несмотря на
то что интеграл перекрывания между я-орбнталямн соседних
атомов углерода приблизительно равен 0,25, правомочность
этого приближения вполне обоснована. (Оказывается, что пере-
402
X
крывание можно довольно просто включить в рассмотрение,
однако это не очень сильно влияет на результаты.)
А как поступают со всеми сложными интегралами, которые
встречаются при точном решении задачи? Вычислять их
действительно очень трудно, но избавиться от всех интегралов
означало бы вообще не решать задачу. Поэтому поступают
следующим образом:
3. Все интегралы, относящиеся только к одному атому (они
приблизительно соответствуют энергии электрона, занимающего
2р-орбиталь углерода), полагаются равными а. Эта величина
называется кулоновским интегралом.
4. Все интегралы, относящиеся к атомам, разделенным более
чем одной связью, не учитывают, так как они слишком сложны
для вычисления.
5. Все интегралы, относящиеся к соседним атомам,
полагаются равными одной и той же величине р, называемой
резонансным интегралом.
6. После всех этих приближений едва ли стоит проводить
антисимметризацию волновой функции, и этого не делают. (В
каком-то смысле эффект антисимметризации — роль обменной
энергии — учитывается параметрами а и р.)
Основываясь на этих приближениях, применяют
вариационный метод, чтобы определить наилучшую линейную комбинацию
атомных п-орбиталей> которая позволяет описать структуру
молекулы. Вариационный метод приводит к вековому
определителю, корни которого дают энергии орбиталей. (Каждый
диагональный элемент определителя равен а — £, а все
недиагональные элементы равны нулю, за исключением тех, которые
соответствуют соседним атомам и равны р). После того, как решено
вековое уравнение и найдены энергии молекулярных орбиталей,
можно определить коэффициенты при атомных орбиталях.
В этом и состоит все решение задачи в приближении Хюккеля,
после чего можно определить ряд свойств молекулы. Например,
можно оценить энергию делокализации или резонанса, энергии
переходов в я-электронной системе, плотность заряда на атомах
углерода, вклад я-электронов в дипольный момент, порядок
связи и свободную валентность. При расчетах энергии делока-
лизации рекомендуется пользоваться значением р, равным
—0,69 эВ (—67 кДж-моль-1), но для спектральных переходов
более приемлема величина —2,71 эВ (—21900 см-1). Пример
расчета приведен в списке формул X. 2.
Метод Хюккеля можно рассматривать как
удовлетворительный, поскольку в его основу положен учет симметрии молекулы.
Орбитали классифицируются по типу их симметрии, после чего
путем рассмотрения коэффициента при р подсчитывается число
связывающих и разрыхляющих комбинаций перекрывающихся
403
X
Список формул X, 2
Расчет по методу Хюккеля (пример)
Общий случай:
1. Запишите МО в виде -ф = ^ с.у..
i
2. Постройте вековой определитель | И.. — ES.. |, где
Г !, если / = /,
I 0, если гф].
Г а, если i = f,
Hij = I р, если / ф /, но / и / — соседние атомы,
I 0 в остальных случаях
3. Решите вековое уравнение / Нц — ESij | = 0 относительно
энергии Е.
Для бутадиена: i|> = ^ф! + с2фг + ^зфз + ^4ф4, где <рь ... ф4 — 2ря-
орбитали на атомах углерода в молекуле СН2СНСНСН2. Вековое
уравнение имеет вид:
а —£ р О О
р а—Е р О
О р а — Е р
О 0 р а—Е
Если хр = а — Е, уравнение сводится к виду л:4 — Зх2 +1=0. Корни
этого уравнения
/:=a±l,6P и £ = а±0,бр
дают энергии четырех молекулярных орбиталей бутадиена. Обычно
вековой определитель можно упростить (факторизовать), используя
свойства симметрии. См. „Рекомендуемые источники".
= 0
я-орбиталей. Таким путем определяют последовательность всех
энергетических уровней молекулы.
Существует много возможностей улучшения метода Хюккеля,
и в этом направлении проделана очень большая работа.
Простейшее усовершенствование заключается в учете перекрывания
между соседними атомами: это сближает нижние, связывающие
орбитали и раздвигает верхние, разрыхляющие уровни, однако
не оказывает заметного влияния на их последовательность.
Следующее усовершенствование, часто используемое в простых
расчетах, заключается в учете того обстоятельства, что энергия
электрона в атоме углерода, измеряемая величиной а, зависит
от плотности заряда на этом атоме. Метод Хюккеля игнорирует
такую зависимость и приписывает одно и то же значение а
всем атомам независимо от локального увеличения электронной
404
X
плотности (в связи с этим см. разд. «Альтернантные
углеводороды»). Попытка исправить этот недостаток, вводя с помощью
коэффициента пропорциональности со зависимость а от
плотности заряда, применяется в варианте метода Хюккеля,
называемом «оз-техникой». Этот вариант представляет собой простой
пример самосогласованного расчета: вначале выполняется
расчет простым методом Хюккеля (находится плотность заряда),
затем в каждое значение а вносят соответствующую поправку,
и расчет повторяется с новым набором величин а. Процедура
повторяется до тех пор, пока плотность заряда не перестает
изменяться.
Помимо всех этих тривиальных модификаций
первоначальной теории, используются полуэмпирические методы, которые
находятся в центре внимания большинства современных
исследований. С их помощью пытаются смягчить грубые предположе1
ния метода Хюккеля и приблизиться по точности к строгим
расчетам. В них пренебрегают большей или меньшей частью
интегралов электронного отталкивания и выражают значение
оставшихся молекулярных интегралов через некоторую эмпирическую
величину или через величины, вычисленные для атомов, либо
оставляют их в качестве подгоночных параметров. Фактически
во всех этих методах имеют дело только с валентными
электронами, а влияние внутренних электронов учитывается лишь при
окончательном выборе параметров. В большинстве методов не
делается различия между а- и я-электронами, если не считать
учета их симметрии, поэтому такие методы можно применять к
молекулам, не обладающим плоскостью симметрии. Одно время
пользовался популярностью метод Паризера — Парра — Попла
(ППП), который представляет собой лишь незначительно
усовершенствованный метод Хюккеля и пренебрегает фактически
всеми интегралами электронного отталкивания между атомами.
Метод ППДП (полное пренебрежение дифференциальным
перекрыванием) не учитывает меньшее число интегралов и является
основой многих современных расчетов. Методы ЧПДП
(частичное пренебрежение дифференциальным перекрыванием) и
МЧПДП (модифицированный ЧПДП)—это схемы расчетов, в
которых одни интегралы не учитываются, а значения других
подбираются определенным образом. Детально ознакомиться с
существующими вариантами выбора интегралов и
приближениями, используемыми в этих схемах, можно по работам,
приведенным в списке рекомендуемых литературных источников.
Упражнения. 1. Перечислите приближения метода Хюккеля, применяемого
Для расчета энергии я-электронов. Каков смысл параметров аир? Почему
параметр а должен зависеть от заряда на атоме? Какие свойства молекул
Можно рассчитать по методу Хюккеля? Какие усовершенствования этого ме-
405
X
тода можно сделать достаточно просто? Какое улучшение значительно груд,
нее внести? Что главным образом ограничивает точность полуэмпирических
методов? Почему они хуже точных расчетов по методу самосогласованного
поля Хартри — Фока?
2. Используя схему расчета, приведенную в списке формул, составьте и
решите уравнения метода Хюккеля для молекул СН2=СН—СН=СН2,
СН2=С = СН2, циклопропена и бензола, вычислите энергию делокализации и
распределение разрядов в каждой из них. Исследуйте влияние учета
перекрывания между соседними атомами для молекулы циклобутадиена, считая,
что интеграл перекрывания во всех случаях равен S (на завершающей
стадии расчета примите 5 = 0,25).
3. В варианте метода Хюккеля с использованием со-техники
предполагается, что кулоновский интеграл на атоме г связан с плотностью заряда qT
формулой <Хг = а+(1—<7г)соР, где коэффициент со приблизительно равен
1,4. Примените эту схему расчета к аллильному катиону, начав с
приближения Хюккеля и выполнив три цикла уточнения с использованием со-техники.
К чему должно привести использование со-техники в случае альтернантных
углеводородов?
Рекомендуемые источники. См. [1], гл. 9. Метод Хюккеля детально описан
во многих книгах, где обычно приводится много примеров. См. кн. Коулсона
«Форма и структура молекул» [10] и [105], а также кн. Маррела, Кеттла и
Теддера [299], Стрейтвизера [387], Пилара [318], Салема [353], Мак-Глина,
Ванквикенборна, Киноситы и Кэрролла [273] и Дьюара [122]. Вопросы
развития метода рассматриваются в кн. Попла и Бевериджа [321], Доджа [125],
Маррела и Харгетта [298]. Результаты таких расчетов обобщены Коулсоном
и Стрейтвизером [ПО]. Стрейтвизер [387] выполнил много расчетов
органических молекул и показал, как эти результаты можно применить для
предсказания химических свойств. Роберте [341] критически проанализировал основы
метода. Парр [310] опубликовал обзор современных теорий молекулярной
структуры, в его книге цитируется много ценных оригинальных работ.
ц
ЦВЕТ. Вещество имеет цвет (окраску), если оно способно
поглощать в какой-либо области длин волн падающего белого
света или рассеивать свет одной частоты более эффективно, чем
другой. Если оставить в стороне голубой цвет неба, то первый
из этих механизмов является наиболее распространенным.
Видимый свет охватывает область от 700 (красный цвет) до 420 нм
(фиолетовый цвет), в которую входят желтый (~580 нм),
зеленый (530 нм) и голубой цвет (470 нм). Указанному интервалу
соответствуют энергии фотонов от 1,7 до 3,0 эВ, и, чтобы
система поглощала в видимой области, она должна обладать
возбужденными состояниями, отстоящими от основного в пределах это-
го интервала энергий. Если поглощается красный свет (из-за
наличия низколежащих возбужденных состояний), предмет
оказывается голубым; если поглощается голубой или фиолетовый
свет, предмет оказывается красным. Живые системы редко
обладают низколежащими уровнями энергии, и поэтому цвета
существующих в природе организмов в основном сдвинуты к
красной области спектра: никто не встречает пурпурных коров или
ярко-голубых собак, редко встречаются синие растения и т. д.
Более того, если бы в живых системах имелись низколежащие
возбужденные состояния, они были бы подвержены фотолизу.
В то же время хлорофилл специально приспособлен к такой
ситуации, и поэтому зеленый цвет является широко
распространенным.
Наиболее интенсивная окраска предметов обусловливается
электрическими дипольными переходами. Группа атомов,
которая придает молекуле цвет, называется хромофором. Важным
органическим хромофором является двойная связь С = С, в
которой соответствующим переходом является переход электрона
со связывающей я-орбитали на рызрыхляющую п*-орбиталь
(я->я*-переход). Карбонильная группа (С = 0) также играет
важную роль; однако соответствующий переход с несвязываю-
щей свободной пары кислорода на я*-орбиталь (д-*я*-переход)
является запрещенным электрическим дипольным переходом
(см. разд. «Правила отбора» и «Сила осциллятора») и поэтому
обычно слабее, чем я—*я*-переход.
Комплексы переходных металлов, как правило, окрашены,
что объясняется наличием у них d-электронов, энергетические
уровни которых подвергаются небольшому расщеплению под
влиянием кристаллического поля окружающих лигандов. Интея-
407
ц
сивность окраски невелика, так как d -> d-переходы запрещены
правилами отбора и окраска определяется
электронно-колебательными переходами. Более интенсивная окраска таких систем
(как, например, характерный интенсивный пурпурный цвет пер-
манганат-иона MnOI) часто обусловлена переходами с переносом
заряда, при которых электроны перемещаются от иона металла
к лиганду или наоборот. Такие переходы характеризуются
большим переходным дипольным моментом.
Изоляторы обычно бесцветны, а если это кристаллические
вещества, то и прозрачны (вспомните алмаз). Электроны в
изоляторах прочно связаны с атомами и не способны обеспечить
ни проводимость, ни поглощение света (чтобы электроны могли
достигнуть зоны проводимости алмаза, их энергия должна быть
повышена на 5,3 эВ). Те соединения, в которых связь менее
прочна или зона проводимости расположена ближе к
заполненной зоне, оказываются окрашенными. Так, расстояние между
зонами в CdS2 равно 2,42 эВ, и поэтому этот кристалл имеет
желто-оранжевый цвет (поглощение в голубой области); кремний,
где расстояние между зонами составляет только 1,14 эВ,
поглощает свет всех частот и имеет металлический блеск.
Металлы характеризуются блестящей поверхностью на
свежем срезе. На первый взгляд это трудно согласовать с тем, что
они поглощают весь падающий свет. Ответ заключается в том,
что они и излучают весь падающий свет. Это можно объяснить
высокой подвижностью электронов в металле. Когда
осциллирующая световая волна достигает поверхности металла, ее
электрическое поле раскачивает поверхностные электроны и
падающий свет гаснет. Но осциллирующие поверхностные электроны
сами вызывают поле излучения, и поэтому почти весь свет
отражается. У некоторых металлов (например, меди и золота)
существуют настоящие зоны поглощения в видимой области, и оба
эти металла до некоторой степени поглощают голубой свет (и
при этом нагреваются).
Приведем теперь два примера, когда появление окраски
обусловлено рассеянием. Небо имеет голубую окраску потому, что
голубой свет рассеивается сильнее, чем красный, и вниз
рассеивается больше голубого солнечного света, чем красного (на
закате солнце становится кроваво-красным именно потому, что
дальше от нас на запад небо в это время приобретает дневной
голубой цвет). Облака видны также из-за рассеяния падающего
света, белый цвет их объясняется размером рассеивающих
частиц (см. рекомендуемую литературу). Другим примером
является известный способ окрашивания стекла осаждением в нем
коллоидального золота; крошечные частицы золота рассеивают
голубую компоненту проходящего света, а стеклу придают
глубокий рубиновый оттенок.
408
Ц
Рекомендуемые источники. Электронные спектры органических молекул
см. в кн. Маррела [297], а хороший обзор оптических свойств изоляторов
дается Киттелем [224]. Наиболее убедительное изложение физических основ
цветности содержится в простой работе Вайскопфа [417]. Фотохимические
аспекты поглощения света описаны Вейном [416] и Калвертом и Питтсом [88];
на основании этих работ составлена табл. 5. Химические аспекты светового
воздействия описаны также Боуэном [71]. Интенсивность поглощения света
зависит от силы осциллятора электрических дипольных переходов, а
экспериментально выражается с помощью коэффициента экстинкции; см. [1], [416].
Понятия, методы и данные, имеющие отношение к свету, описаны Вишецким
и Стайлсом [437].
ч
ЧАСТИЦА В ПРЯМОУГОЛЬНОЙ ПОТЕНЦИАЛЬНОЙ
ЯМЕ. Если область пространства, в которой находится частица,
строго ограничена и всякое просачивание частицы через
границы этой области невозможно, говорят, что частица находится в
прямоугольной потенциальной яме. Такая терминология
объясняется тем, что можно ограничить область локализации
частицы, если положить, что потенциал в области ее свободного
движения равен нулю, а на границах области обращается в
бесконечность перпендикулярно дну потенциальной ямы. Геометриче*
екая форма подобной области может быть различной;
простейшим примером является одномерная прямоугольная яма, или
ящик, в которой частица может свободно перемещаться вдоль
оси х между точками от 0 до L, и этим интервалом
исчерпываются ее допустимые координаты. Двумерная прямоугольная яма
может иметь форму любой фигуры на плоскости, в частности
форму прямоугольника или квадрата. В качестве трехмерных
прямоугольных ям обычно рассматриваются куб и шар; в
последнем случае часто говорят (не задумываясь о парадоксаль-
ности такого словосочетания), что частица находится в
«сферической прямоугольной яме».
В любой такой яме энергия частицы обусловлена
исключительно ее кинетической энергией, поскольку частица не может
проникнуть в те области пространства, где потенциальная
энергия отлична от нуля. Частица находится в ограниченной
области пространства, поэтому ее энергия квантована, и
разрешенные уровни энергии (приведенные для ям различного вида в
списке формул Ч. 1) получаются решением уравнения Шредин-
гера с учетом граничных условий для соответствующей
прямоугольной ямы. Поскольку вероятность обнаружить частицу за
пределами ямы должна быть равна нулю, требование
непрерывности волновой функции приводит к тому, что эта функция
должна обращаться в нуль на границах разрешенной области.
Отсюда следует, что, хотя волновые функции частицы внутри
ямы совпадают с функциями свободно движущейся частицы, их
длины волн должны удовлетворять условию nl/2 = L, где п —
целое положительное число, в противном случае узлы волновых
функций не смогут оказаться одновременно на обеих стенках
ямы. Согласно соотношению де Бройля, длина волны
определяет импульс частицы, который в свою очередь определяет ее
кинетическую энергию, поэтому разрешенные значения энергий
ограничены значениями n2/L2. Это решение является хорошей
410
ч
Список формул Ч. 1
Частица в прямоугольной потенциальной яме
Линейная (одномерная) прямоугольная яма длиной L:
Е«=п2{-шт)> +»w-(T),/,e,n(iTL)'
/г=1, 2, ....
Трехмерный прямоугольный ящик со сторонами Lb L2, Lz:
Еп1п2п3==\['ц) +(тт) "Нт9 )Ш'
я, = 1, 2, ...; /г2 = 1, 2, ...; /г3 = 1, 2, ....
Сферическая прямоугольная яма радиусом R:
f10 = 3,142, fu= 4,493, f i2 —5,763,
f20 = 6,283, /,3 = 6,988, f21 =7,725 ....
k = f/#; /^ — сферическая функция Бесселя. См. § 36 в кн. Давыдова
[119].
иллюстрацией связи кинетической энергии и кривизны волновой
функции в квантовой механике. Дело в том, что, чем больше
волн мы пытаемся уложить на заданном отрезке прямой, тем
более волнистой становится функция и тем более возрастает ее
кривизна. Такие функции имеют вид обычных синусоид с
уменьшающейся длиной волны, некоторые из них изображены на
рис. Ч. 1.
Сформулируем основные данные о свойствах частицы в
прямоугольной яме.
1. В одномерной потенциальной яме разрешенные значения
энергии определяются единственным квантовым числом п и
пропорциональны n2/L2 (см. список формул). Это число может
принимать значения 1, 2, 3, ... , и, поскольку значение п — О
запрещено (волновая функция с п = 0 всюду равна нулю),
нижний уровень энергии больше нуля, т. е. у частицы в яме имеется
неустранимая «нулевая» энергия. Все состояния частицы в
одномерной потенциальной яме не вырождены.
2. В трехмерной яме разрешенные значения энергии зависят
от трех квантовых чисел, и в прямоугольном ящике со
сторонами Li, L2, L3 они пропорциональны (пУL]) + (nilLf) + (ni/LlJ>
411
ц
где пи п>2, пз могут принимать любые целые положительные
значения. «Нулевая» энергия основного состояния соответствует
щ = я2 = п3= 1.
3. Волновые функции являются простыми синусоидальными
функциями различной длины волны, и, следовательно, им
соответствует различная кинетическая энергия. «Нулевая» энергия
Рис. 4.1 Энергетические уровни и волновые функции частицы в
одномерной прямоугольной потенциальной яме.
соответствует состоянию, в котором частица с наибольшей
вероятностью находится в центре ящика, как можно дальше от его
стенок. При больших значениях квантовых чисел плотность
вероятности равномернее распределена по ограниченной области
пространства ямы.
4. При сближении стенок ямы уровни энергии раздвигаются:
целое число полуволн при этом должно уместиться на меньшем
участке, поэтому длина волны уменьшается, кинетическая
энергия возрастает. При раздвигании стенок ямы расстояние между
энергетическими уровнями уменьшается, в предельном случае
бесконечно широкой ямы уровни образуют непрерывную
последовательность (континуум) и система перестает быть квантовой.
5. Увеличение массы частицы приводит к такому же
эффекту, что и увеличение размеров ямы. Поведение частицы большей
412
ч
массы в яме заданного размера в большей степени определяется
законами классической механики, чем поведение частицы малой*
массы.
6. Локализованную частицу можно получить, сформировав
подходящую суперпозицию, соответствующую волновому пакету
в точке, где находится частица. Пакет, сформированный таким
образом, движется в полном согласии с законами классической
механики для частицы, которая находится в области
пространства, ограниченной бесконечно жесткими и идеально
отражающими стенками.
Упражнения. 1. Объясните термин «прямоугольная потенциальная яма». Как
сказывается присутствие непроницаемых стенок на разрешенных
энергетических уровнях частицы в потенциальной яме? Почему энергия частицы в яме
пропорциональна n2/L2} Используя классическое выражение для
кинетической энергии как функции импульса и соотношение де Бройля для импульса
как функции длины волны, получите выражение для энергии частицы в
одномерной прямоугольной потенциальной яме. Сравните полученный ответ с
выражением, приведенным в списке формул. Какова минимальная допустимая
энергия частицы в потенциальном ящике и как она зависит от размеров
ящика? Как можно интерпретировать энергию основного состояния с
учетом принципа неопределенности? Чему равен средний импульс частицы,
находящейся на каком-либо энергетическом уровне в потенциальном ящике?
В каком предельном случае частица ведет себя согласно законам
классической физики? Вычислите минимальную энергию электрона в потенциальном
ящике размером 1 м, 1 нм, 0,1 нм, 10~15 м. Какая энергия требуется для
перехода на первый возбужденный уровень в каждом из этих случаев? Почему,
муха, летающая в комнате, является во всех смыслах классической
частицей? Электрон в сопряженном полиене можно рассматривать как частицу в
одномерном потенциальном ящике. Оцените энергию перехода электрона с
/г-го уровня на п-\~ 1-й уровень в полиеновой цепочке из N атомов углерода.
2. Уравнение Шредингера для одномерного ящика имеет следующий вид:
— (h2/2m) (d2ldx2)^ = £\|э. Найдите решение этого уравнения в виде функции
типа Л sin kx -f- В cos kx и потребуйте выполнения следующих граничных
условий: функция должна обращаться в нуль при х = 0 и х = L, т. е. на
стенках ящика. Покажите, что коэффициент А можно определить из условия нор-
мированности функции и что функции, соответствующие состояниям с
различной энергией, ортогональны. Покажите, что задачу о двумерной
прямоугольной яме методом разделения переменных можно свести к задаче о двух
одномерных ямах прямоугольной формы (см. разд. «Шредингера уравнение»).
Рекомендуемые источники. Подробную информацию о решении
уравнения Шредингера для частицы в прямоугольных ямах см. в гл. 3 fll. Задача
о сферической яме сложнее, ее решение описано в кн. Козмана [217].
Поскольку такая задача является хорошим приближением для описания
поведения электрона в жидком аммиаке (металлоаммиачные растворы), см. Ле-
Путье и Сиенко [238] и Лаговский и Сиенко [232], где обсуждаются
применения и особенности этой модели. В случае непрямоугольного бесконечного
барьера частица может просачиваться в глубь стенки, а если потенциал
снаружи падает до некоторого конечного значения, частица может за счет
туннельного эффекта (см. соответствующий раздел) проходить сквозь барьер.
Такого рода задачи обсуждаются и решаются в § 32 кн. Давыдова [119], см.
413
ч
также кн. Шиффа [356], Мессиа [282], Ландау и Лифшица [233]. Гольдман и
Кривченков [165] приводят ряд задач для различных барьеров. Хорошее
обсуждение случая прямоугольного потенциала дано также в гл. 11 кн. Бома [63].
ЧЕТНОСТЬ И НЕЧЕТНОСТЬ (g и и). Немецкие слова
gerade (четный) и ungerade (нечетный) используются для
обозначения (символами g и и) различных состояний и волновых
функций, чтобы указать их поведение относительно инверсии
г/т грп
Рис. 4.2. Четная и нечетная симметрия.
(четность или нечетность). Простым примером является
классификация орбиталей молекулы водорода, где центр инверсии
располагается в середине связи. Рассмотрим амплитуду
связывающей lsa-орбитали в произвольной точке молекулы и проведем
прямую линию от этой точки через центр инверсии, затем
отложим равное расстояние по другую сторону от него (рис. Ч. 2).
Знак и величина амплитуды a-связывающей орбитали в новой
точке оказываются такими же, как в исходной точке, поэтому
орбиталь является четной (g) по отношению к этому
преобразованию симметрии и обозначается og. Начав с той же исходной
точки для разрыхляющей орбитали (lsa*), мы перейдем от
области с положительной амплитудой через узел и окажемся в
точке с отрицательной амплитудой. Следовательно, такая
орбиталь нечетна и обозначается а*. 2ра-Орбитали ведут себя
аналогичным образом, а поведение я-орбиталей отличается (см.
414
ч
рис. 4.2); связывающая я-орбиталь ведет себя как нечетная (и),
а разрыхляющая — как четная (g).
Классификация на четные и нечетные (g или и) применима
и к состояниям. При этом рассматривается произведение четно-
стей всех компонент состояния. Так/ основное состояние
молекулы Н2(а|) является четным (g), так как (четный) X
(четный) = (четный), а возбужденная конфигурация в о*и является
нечетной (и), поскольку g X и = и.
Если центр инверсии отсутствует, классификация по четности
неприменима, поэтому индексы gnu могут быть добавлены к
состояниям и орбиталям гомоядерных двухатомных молекул и
центросимметричных октаэдрических комплексов, но не гетеро-
ядерных двухатомных молекул или тетраэдрических комплексов.
Классификация по четности полезна при обсуждении правил
отбора, так как разрешенные электрические дипольные
переходы происходят только с изменением четности; таким образом,
g-+u- и и -*^-переходы разрешены, a g-*g- и и'-> ^-переходы
запрещены.
Упражнения. В чем смысл индексов g и и> Почему они неприменимы К
гетероядерным двухатомным молекулам? Какие из перечисленных молекул
могли бы иметь орбитали и состояния, различаемые индексами g и и: 02,
NO, N02, C02, CH4, He, NH3? Классифицируйте типом симметрии по g и и
следующие орбитали: s-, p-, d-t /-орбитали свободных атомов и lsa-, 2ря*-,
3do-, 3dn-, Зая*-, З^б-орбитали гомоядерных двухатомных молекул.
Классифицируйте таким же образом основные состояния Не, Н2 и 02. Какие элек*
трические дипольные переходы разрешены при g, «-классификации?
Рекомендуемые источники. Обозначения g и и — это теоретико-групповая
классификация четности состояния; см. [1], гл. 5, кн. Коттона [99], Бишопа
[59], Тинкхэма [396]. См. также книги, посвященные обсуждению структуры
молекул, такие, как кн. Коулсона [10] «Форма и структура молекул», Коул-
сона [105], и Маррела, Кеттла и Теддера [299]. В кн. Кинга [222] и Герц*
берга [187] обсуждена роль ^«-классификации при рассмотрении
электронных спектров молекул.
ш
ШРЕДИНГЕРА УРАВНЕНИЕ. Уравнение Шредингера
(в силу одного из редких совпадений оно названо по имени
человека, действительно открывшего его *) является
дифференциальным уравнением, решение которого позволяет найти
волновую функцию интересующей нас системы. Это показывает,
сколь важное значение придается уравнению Шредингера в
квантовой теории. Если получена волновая функция системы,
можно в принципе предсказать все ее свойства, так как при этом
условии квантовая механика имеет готовые рецепты для
извлечения необходимой информации. Поэтому применение квантово-
механического подхода к рассмотрению физических систем
сводится к решению соответствующего уравнения Шредингера. Этот
подход основан на представлении, что полученная в качестве
решения уравнения Шредингера математическая функция
представляет собой волновую функцию рассматриваемой системы.
К сожалению, уравнение Шредингера является не простым
алгебраическим уравнением (наподобие уравнения х2 = 2), а,
как говорилось выше, дифференциальным уравнением. За
исключением весьма небольшого числа случаев, решать такие
уравнения очень трудно. Однако это не имеет существенного
значения, и самое главное заключается в том, что, по-видимому, мы
получили уравнение, которое в принципе позволяет точно
описывать происходящие в природе явления. (В действительности это
не совсем верно, так как уравнение Шредингера не учитывает
релятивистских эффектов, обнаруживающихся при больших
скоростях частиц, близких к скорости света. Поэтому оно является
приближенным и относится к точному описанию так же, как
механика Ньютона к теории Эйнштейна. Это несовершенство
уравнения Шредингера было частично исправлено его заменой
уравнением Дирака, но остаются и другие, менее значительные
трудности, которые тем не менее приводили в прошлом к заметным
потрясениям в этой области.)
* Во время пребывания в Париже Виктор Генри получил от Ланжевена
экземпляр «замечательной диссертации де Бройля». Возвратясь в Цюрих и
лишь поверхностно ознакомившись с нею, он передал ее Шредингеру,
который недели через две вернул ее Генри со словами: «Возьмите обратно,
все это вздор». Во время следующего визита к Ланжевену Генри передал
ему эти слова Шредингера. Ланжевен ответил на это: «Я думаю, Шредингер
неправ. Ему следовало бы посмотреть эту работу еще раз». Когда Генри
вернулся в Цюрих, он сказал Шредингеру: «Вам следует прочитать работу
де Бройля снова, Ланжевен считает, что это очень хорошая работа».
Шредингер так и сделал и начал свою работу... (Макс Джеммер [203]).
416
ш
Список формул Ш. 1
Уравнение Шредингера
Зависящее от времени: HW = lh (dW/dt), где Н — гамильтониан.
Не зависящее от времени: если И не зависит от времени, ¥ =
= ф ехр (— iEt/h), где ф не зависит от t и удовлетворяет уравнению
Типичная форма уравнения:
для одномерной системы с массой m в поле с потенциалом V(x)
-(&)(-S-) + yw*w-B*w
или
|i*+(|L)tE_WHW_„;
для трехмерной системы с массой m в поле с потенциалом V(r)
~(~ш) V2*(r)+К(г) +(г)=£*(г)'
где V2 — лапласиан (см. соотв. раздел).
Разделение переменных. Запишем *F —-фЭ, где ф является функцией
координат, а 6 — функция времени. Пусть Н не зависит от времени.
Тогда уравнение HW^ihW принимает вида
е#ф = *7И|>е или (1/ф) Яф = (//г/9) 9.
Левая часть является функцией только координат, а правая — не
зависит от переменной х. Поэтому обе части последнего уравнения должны
быть равны одной и той же постоянной:
(1/ф)#ф = £ = (*7*/9)ё.
Следовательно,
е = ехр(~Ш/Л) и #ф = £ф.
Точка над символом функции означает дифференцирование по времени.
Уравнение Шредингера — это линейное дифференциальное
уравнение второго порядка по отношению к пространственным
координатам (оно содержит члены вида d2/dx2) и первого
порядка по отношению к времени. Различные виды его записи
показаны в списке формул Ш. 1. Посмотрев на его запись в
полном виде, можно заметить, что оно не является волновым
уравнением: в такие уравнения обычно входит вторая производная
по времени. Правильнее рассматривать его как разновидность
уравнения диффузии, и это не лишено смысла, поскольку
эволюция «волновой функции» во времени должна походить на
процесс диффузии. Это замечание представляет большой интерес,
417
ш
так как диффузионная форма уравнения Шредингера означает,
что волновую функцию можно интерпретировать как функцию,
указывающую вероятность обнаружения частицы в различных
областях пространства (см. интерпретацию Борна в разд.
«Волновая функция»). Если бы это уравнение было истинным
волновым уравнением, такая интерпретация была бы несостоятельна.
Его зависимость от времени часто устраняется путем
использования метода разделения переменных (см. упражнения, пункт 2
и список формул Ш. 1), при этом
получается не зависящее от вре*
мени уравнение Шредингера,
которое имеет тот же вид, что
и уравнение для стоячих волн.
Вид последнего уравнения как
s~\
^х
ф>0
—1
\ф>0
\ф<0
1 £<К
\J
Г\
Е>У
Г\
\У
>ф~о
Ф<0
ф~0
Ф^О
Рис. Ш.1. Кривизна волновой функ- Рис. Ш. 2. Распространение волны
ции в зависимости от знаков ф при Е > V.
nE-V.
раз и послужил поводом к возникновению термина «волновая
механика».
Не зависящее от времени уравнение Шредингера можно
рассматривать как уравнение, определяющее кривизну волновой
функции, что позволяет предвидеть некоторые особенности его
решений. Вторые производные д2^/дх2 и т. д., согласно обычным
представлениям, описывают кривизну функции. Воспользуемся
этим понятием дифференциального исчисления и заметим, что,
когда г|/' (так мы будем обозначать вторую производную)
положительна, кривизна функции \|э придает ей вид w, а когда г|/'
отрицательна, функция -ф имеет вид г\. Существенно, что
величина производной (крутизна изгиба) увеличивается по мере
того, как полная энергия Е системы превышает ее потенциаль-
ную'энергию V(x). Разность Е— V(x) в точности соответствует
классической кинетической энергии системы в точке х, и, таким
образом, мы видим, что кинетическая энергия и кривизна
волновой функции пропорциональны друг другу. Заметим также, что
знак второй производной (направление кривизны) зависит от
418
ш
знака самой функции г|>: если Е— везде больше V, кривизна
имеет в каждой точке знак, противоположный знаку самой
функции г|) (—1|?) (рис. Ш. 1). Интересно проследить за тем, как этот
подход применяется к описанию поведения свободной частицы
при условии, что V — постоянно и что Е > V. Предположим,
что мы выбрали точку, где г|)> 0; кривизна в этой точке
отрицательна, и, следовательно, функция -ф стремится к нулю как
кривая вида ^ (рис. Ш. 2). Рано или поздно она пройдет через
нуль и станет отрицательной. Но при этом изменится знак ее
второй производной. То, что функция имеет теперь
положительную кривизну (так как по-прежнему Е > К, но г|) < 0), приведет
к ее изгибанию вверх, приближению снова к нулю, переходу в
область положительных значений, снова к отклонению вниз
и т. д. Зависимость кривизны функции от ее знака будет
заставлять функцию колебаться вверх и вниз, то и дело пересекая ось
абсцисс, т. е. вести себя как гармоническая волна. Следует
также отметить, что быстрота, с которой колеблется функция,
возрастает с увеличением кинетической энергии (см. разд.
«Кинетическая энергия» и «Соотношение де Бройля»). Если потенциал
зависит от координат, длина волны больше не является
постоянной (и, по существу, перестает быть определенной величиной),
но рассмотренный выше простой подход тем не менее может
оказаться полезным для качественного выяснения вида
волновой функции электронов в атомах и молекулах.
Единственный точный способ количественного определения
вида волновой функции для атомов и молекул заключается в
математическом решении уравнения Шредингера. Однако, как
только мы приступим к его решению, сразу же столкнемся со
следующей проблемой — дифференциальное уравнение второго
порядка имеет неограниченное число решений. Однако очень
важно то, что лишь некоторые из этих решений будут
удовлетворять строгим требованиям, вытекающим из интерпретации
волновой функции, предложенной Борном. Если установлено, каким
условиям должна удовлетворять функция в некоторых точках
пространства (т. е. если налагаются определенные граничные
условия), приемлемыми оказываются только несколько решений.
Отсюда сразу же следует, что связанные состояния систем
должны быть квантованными.
Очень часто вообще не представляется возможным найти
аналитическое решение уравнений Шредингера, а тем более
такое, которое было бы не слишком сложным для дальнейшего
использования. Эти трудности, встречающиеся, как правило, при
исследовании строения атомов и молекул, заставляют
обращаться к приближенным методам: теории возмущений, вариационной
теории и методу самосогласованного поля. Теория возмущений,
зависящих от времени, также является одним из способов реше-
419
ш
ния уравнения Шредингера. Некоторые решения этого
уравнения обсуждаются в соответствующих разделах (см. разд.
«Частица в прямоугольной потенциальной яме», «Гармонический
осциллятор», «Угловой момент» и «Атом водорода»).
То, что уравнение Шредингера является линейным
дифференциальным уравнением, означает обоснованность принципа
суперпозиции и всего того, что с ним связано.
Упражнения. Почему уравнению Шредингера придается столь важное
значение? Почему зависящее от времени уравнение Шредингера не является
истинным волновым уравнением и как его следовало бы видоизменить, чтобы
оно действительно выглядело как волновое уравнение? Какие важные
локальные свойства волновой функции определяет это уравнение? Покажите
сначала качественно, а затем количественно, что волновая функция
свободной частицы является волной постоянной длины. Какова связь между
длиной этой волны, а также импульсом и кинетической энергией частицы,
которая описывается этой волной? Изобразите волновую функцию для частицы
с энергией Е в поле, потенциал которого линейно убывает с расстоянием.
Может ли частица описываться волной, если в некоторой точке ее энергия Е
меньше потенциальной энергии в той же точке? Изобразите волновую
функцию частицы в поле, потенциал которого растет линейно с расстоянием и
пересекает точку V(x) = Е. Изобразите несколько возможных волновых
функций для частицы в прямоугольной потенциальной яме и для частицы с
потенциалом гармонического осциллятора (попробуйте сделать это, не
заглядывая в ответ, который можно отыскать в соответствующих разделах; если же
вы затрудняетесь это сделать, попытайтесь дать интерпретацию вида
волновых функций, основываясь на рассмотрении ее кривизны).
2. Используя метод разделения переменных, покажите, что зависящее от
времени уравнение Шредингера можно разделить на два уравнения, одно из
которых зависит только от времени, а другое только от пространственных
координат; решите первое уравнение. Для этого представьте функцию ^(х, t)
в виде 6(/)ф(*) и подставьте ее в уравнение Шредингера, зависящее от
времени. Разделив его (осторожно) на 0-ф, вы убедитесь, что одна часть
членов зависит только от ху а другая только от t. Каждый из этих членов в
отдельности должен быть равен некоторой константе, обозначьте ее Е (на том
основании, что она имеет размерность энергии). После этого решите
уравнение относительно времени и сравните ответ с приведенным в списке формул
Рекомендуемые источники. Один из способов вывода уравнения
Шредингера дан в [1] гл. 2; в гл. 3 рассмотрен метод получения некоторых его
решений для ряда важных частных случаев. Полезное обсуждение содержится
в кн. Полинга и Вильсона [314] и Козмана [217]. Уравнение Шредингера
упоминается во всех книгах, относящихся к квантовой теории, за исключением
наиболее сложных. Смотрите также оригинальную работу Шредингера [361] и
чудесный комментарий в гл. 5 кн. Джеммера [203] или у Шерера и Динса
[364]. Уравнение Шредингера является лишь одной из нескольких
возможных эквивалентных формулировок квантовой механики и отнюдь не самой
простой, особенно в математическом отношении. О другой формулировке см.
разд. «Матричная механика».
ШТАРКА ЭФФЕКТ. Изменение уровней энергии атомов и
молекул и, следовательно, изменение их спектров под действием
420
ш
электрического поля известно под названием эффекта Штарка.
Различают эффекты Штарка первого и второго порядка,
которые имеют соответственно линейную и квадратичную
зависимость от напряженности приложенного поля, а также атомный и
молекулярный эффекты Штарка.
Атомный эффект Штарка первого порядка значителен по
величине, но встречается редко, потому что он зависит от наличия
вырождения, которое позволяет атому активно откликаться на
приложенное поле. Такая ситуация имеет место в атоме
водорода: поскольку 25- и 2/7-орбитали вырождены, после приложе-
в отсутствие поля
при наличии поля
Рис. Ш.З. Линейный эффект Штарка в атомарном водороде.
ния поля электрон может легко перестроиться путем
гибридизации орбиталей. Так, комбинация г|)25 + ^2Рг Дает распределение,
сильно смещенное в'направлении области с низким потенциалом,
а другая возможная комбинация, т. е. г|)25 — 'Фг^,
сконцентрирована с той стороны ядра, где потенциал высок (рис. Ш. 3).
Следовательно, переходы, в которых участвует атомная оболочка с
п = 2, больше не вырождены и происходят на различных
частотах. Орбитали рх и ру не затрагиваются внешним полем,
направленным вдоль оси 2.
Как и в случае эффекта Зеемана, возникающие переходы
поляризованы. Из обсуждения электрических дипольных
переходов (см. соотв. раздел) следуют два вывода:
1. Если mi не изменяется, излученный свет (дающий я-линии
в спектре) поляризован параллельно направлению
приложенного поля (и поэтому он не будет виден, если смотреть вдоль
421
ш
направления поля, он излучается в поясе вблизи
перпендикулярного направления).
2. Если mi меняется на ±1, излученный свет (дающий а-ли-
нии в спектре) поляризован в поперечном направлении. При
наблюдении в направлении, перпендикулярном полю, компонента
с Дт* = +1 будет обладать правой круговой поляризацией, а
компонента с Ami = —1 — левой круговой поляризацией. Если
смотреть вдоль направления поля, свет не будет поляризован,
потому что переходы с Ami = +1 и —1 происходят на одной и
той же частоте, и свет, излученный различными атомами, дает
некогерентную суперпозицию обоих поляризованных по кругу
состояний.
Рис. Ш.4. Дополнительные
проявления эффекта Штар-
ка в атомарном водороде
(1 — потенциал
приложенного поля, 2 — полный
потенциал, 3 — истинный ПИ,
4 — кажущийся ПИ, 5 — ку-
лоновский потенциал ядра).
Эффект Штарка приводит не только к расщеплению линий,
он также вызывает их небольшое уширение и сдвигает пределы
серий в направлении меньшей частоты. Оба последних явления
связаны с наличием области с меньшим потенциалом с одной
стороны атома, поскольку она облегчает удаление от него
электрона (рис. Ш.4). Электрон, находящийся в состоянии, близком
к пределу ионизации, может просочиться через оставшийся
потенциальный барьер и очутиться в области, где приложенное
внешнее поле оторвет его от атома. Время жизни электрона в
возбужденном состоянии уменьшается, и, согласно принципу
неопределенности, энергия такого состояния становится менее
точно определенной. Эта неопределенность энергии проявляется в
спектре в виде уширения соответствующих линий. Чтобы
произошла ионизация, при наличии внешнего поля не требуется
столь большой энергии возбуждения электрона, как в отсутствие
поля, поэтому поле уменьшает также энергию пределов
ионизации спектральных серий (рис Ш. 4)ч
422
ш
В атомах, в которых нет такого вырождения, как у водорода,
эффект первого порядка отсутствует, вместо него наблюдается
гораздо более слабый эффект второго порядка. Его можно
представить себе как сочетание двух эффектов первого порядка:
сначала нарушение сферической симметрии атома (т. е. его
поляризация), а затем взаимодействие поля с дипольным моментом
искаженного атома, приводящее к расщеплению его
энергетических уровней. Поскольку обычные поля могут лишь
незначительно поляризовать атом, индуцированный ими дипольный
момент атома невелик и слабо взаимодействует с полем.
Следовательно, энергетические сдвиги при эффекте Штарка второго
порядка малы и для их наблюдения необходимо использовать поля
с огромными напряженностями (~ 105 В/см).
Существует также молекулярный эффект Штарка первого и
второго порядка. Эффект первого порядка наблюдается у молекул
типа симметричного волчка с постоянным дипольным
моментом. Внешнее поле приводит к тому, что вращательные
состояния с одинаковыми квантовыми числами 7, но различными М
приобретают различные энергии (в отсутствие поля они
вырождены). Как будет показано ниже, возникающее расщепление
уровней пропорционально постоянному дипольному моменту
молекулы [I. Поскольку поля порядка 50 кВ/см дают расщепления
~20 МГц, которые легко и точно регистрируются в
микроволновой спектроскопии, на этом эффекте основан эффективный метод
определения дипольных моментов.
Интересно и совсем не трудно разобраться в том, почему
поле напряженностью Е сдвигает энергию состояния с
квантовыми числами /, К и М на величину —[iMKE/J(J + 1). Из
теории вращения молекул типа симметричного волчка мы знаем,
что К — это проекция углового момента J на ось молекулы и
что J прецессирует вокруг этой оси. Возможна и другая точка
зрения: будем считать, что вектор J фиксирован, а ось молекулы
прецессирует вокруг него. Поскольку молекулярный диполь
направлен вдоль ее оси, движение усредняет все его компоненты,
кроме одной, направленной вдоль J и равной \х cos 9 (см.
рис. Ш.5). Но вектор J в свою очередь прецессирует вокруг
направления поля, так что компонента диполя, параллельная полю,
должна быть равна [г cos 9 cos 9', следовательно, энергия их
взаимодействия равна —\хЕ cos 9 cos 9'. Используя простые
тригонометрические соотношения, с помощью рис. Ш.5 мы можем
выразить cos 9 как /(/[/(/ + 1)],/з и cos 9' как M/[J(J + l)]l/f.
Комбинируя эти результаты, мы получим энергию в виде
—lxMKE/J(J + 1), как и требовалось показать. Использование
правил отбора Д/ = ±1, Д/С = 0 и AM = 0, ±1 позволяет
предсказывать спектр, а по изменению М можно установить
поляризацию линий.
423
ш
В тех случаях, когда угловой момент линейной молекулы
перпендикулярен дипольному моменту, а также если молекула
представляет собой асимметрический волчок и из-за отсутствия
симметрии происходит очень сложное движение, линейный
эффект отсутствует. Однако и в этих случаях ориентирующее
действие поля (которое, если воспользоваться классическими
понятиями, искажает траекторию вращения молекулы) изменяет
энергии состояний и приводит к
энергетическим сдвигам типа |i22?2(i4i-f-'
+ А2М*).
Молекулярный эффект Штарка
используется при изучении постоянных
дипольных моментов молекул с
помощью микроволновой спектроскопии.
Он также играет важную роль в самом
методе микроволновой спектроскопии,
поскольку осциллирующее
электрическое поле (обычно с напряженностью в
несколько десятков кВ/см)
непрерывно изменяет положение спектральных
Рис. Ш. 5. Молекулярный эффект Штарка.
линий и, следовательно, интенсивность поглощения или
излучения на заданной частоте. Детекторы, основанные на регистрации
этих осцилляции интенсивности, называются спектрометрами со
штарковской модуляцией.
Упражнения, Что такое эффект Штарка? Каковы его разновидности?
Почему атомный эффект первого порядка бывает только у водородоподобных
атомов? Можно ли ожидать, что он проявится у гелия в
высоковозбужденном состоянии? Какая поляризация наблюдается при наличии эффекта
Штарка для разрешенных переходов в атомах водорода? Измените схему
уровней энергии водорода (рис. Г.б) таким образом, чтобы учесть влияние
электрического поля, и обсудите вид возникающего при этом спектра. Сдвиг
энергии электрона в оболочке с п = 2 приводит к расщеплению уровней
величиной 6еа0Е, где #о — боровский радиус. Вычислите это расщепление для
внешнего поля напряженностью 20 кВ-см-1 и 100 кВ-см-1. Какое
расщепление можно ожидать для Не+ в том же состоянии и в полях с такими же
напряженностями? К каким другим эффектам приводит действие сильного
поля? Каково действие поля на атомы, в которых нет водородоподобного
вырождения? Почему эффект Штарка второго порядка невелик? Какие
разновидности эффекта Штарка проявляются в молекулах? Постоянный диполь-
ный момент аммиака равен 1,47D, определите величину расщепления
состояний с / = 0, 1, 2 во внешнем поле напряженностью 50 кВ-см-1,
схематически изобразите вид возникающего спектра и укажите поляризацию линий (не
учитывайте эффекты ядерной статистики, если вы вообще знаете о них).
424
ш
2. Используя явные выражения для орбиталей, приведенные в табл. 15,
получите систему двух вековых уравнений для определения влияния
электрического поля, приложенного вдоль оси z, на энергии 2s- и 2р-орбиталей
атома водорода. Решите эти уравнения для определения энергий и волновых
функций, вычислите все необходимые интегралы. Расщепление 2s- и 2р-орби-
талей, как было укаазно в предыдущем упражнении, равно 6еа0Е, это и
должно получиться в ответе.
Рекомендуемые источники. См. гл. 8 [1]. Обсуждение роли эффекта Штар-
ка в атомных спектрах изложено в гл. 17 кн. Кондона и Шортли [96], см.
также § III A4 кн. Куна [229], гл. 20 кн. Уайта [425] и § 11.3 кн. Герцберга
[185]. Молекулярный эффект Штарка, методика определения дипольных
моментов молекул и принципы конструирования спектрометров, основанных на
использовании штарковской модуляции, описаны в гл. 7 кн. Сагдена и Кен-
нея [388] и в гл. 10 кн. Таунса и Шавлова [399].
ШТЕРНА И ГЕРЛАХА ЭКСПЕРИМЕНТ. Эксперимент,
проведенный Штерном и Герлахом, заключался в пропускании
узкого пучка атомов (атомы серебра, испаряемые с горячего
металла сквозь щель в вакуум) через неоднородное магнитное
поле и в изучении распределения атомов после того, как пучок
осаждается на стеклянной пластинке. Если у атомов есть
магнитный момент, влияние неоднородного магнитного поля
приводит к тому, что все атомы с одной ориентацией магнитного
момента отклоняются в одну сторону, а все атомы с
противоположной ориентацией — в противоположную; все атомы с
промежуточной ориентацией, согласно представлениям классической
физики, должны оказаться на пластинке в промежуточной
области. Для этого эффекта существенна неоднородность магнитного
поля, поскольку однородное поле не будет расщеплять пучок,
так как в нем не содержится информации о каком-либо
выделенном направлении. Неоднородное поле с отличным от нуля
градиентом дает атомам возможность «почувствовать»
выделенное направление.
В первом варианте эксперимента Штерн и Герлах наблюдали
этот результат, предсказываемый классической физикой. Во
втором варианте эксперимента, где было уделено больше
внимания созданию низкого давления и длительной экспозиции,
обнаружилось, что полоса осажденных на пластинку атомов
состоит из двух близко расположенных компонент, между
которыми остается чистая область. Этот результат совершенно не
согласуется с предсказаниями классической физики, но зато
полностью согласуется с квантовой теорией, потому что у каждого
атома серебра есть неспаренный электрон, у электрона есть спин
и, следовательно, магнитный момент. Квантовая теория
предсказывает, что частицы со спином г/2 могут принимать лишь две
ориентации в магнитном поле, и эксперимент Штерна — Герлаха
самым поразительным образом подтверждает это положение.
425
ш
Важно отметить, что он послужил первым
экспериментальным подтверждением квантовой теории, которое не должно было
основываться на каких-либо термодинамических данных или
результатах экспериментов с участием излучения. Этот эсперимент
дал чисто механическую демонстрацию квантования
(свидетельствуя о пространственном квантовании — так называется
ограничение числа возможных ориентации углового момента). Его
первоначальное объяснение не связывало магнитный момент
атома с внутренним спином электрона, это истолкование
появилось позже (1925 г.), когда Юленбек и Гаудсмит в результате
изучения атомных спектров ввели представление о спине
электрона. Эксперимент Штерна и Герлаха был также одним из
первых применений молекулярных пучков; это направление
исследования атомов и молекул сейчас быстро развивается.
Упражнения. Нарисуйте схему эксперимента Штерна и Герлаха. Почему
для его проведения необходимо создать в установке низкое давление? Какой
результат эксперимента предсказывается классической физикой? Что
получается на самом деле? Как этот результат согласуется с квантовой теорией?
Предположим, что одна часть пучка пропущена через еще одно неоднородное
поле; рассмотрите случаи, когда направление этого поля совпадает с
направлением первого и когда оно повернуто на 90° относительно направления
пучка; опишите результаты такого эксперимента.
Рекомендуемые источники. Эксперимент Штерна и Герлаха в
историческом плане рассматривается в § 3.4 кн. Джеммера [203]. Детально он
обсуждается в кн. Рихтмейера, Кеннарда и Лауристена [338] и в § VI. 2 кн. Рам-
зея [330], см. также работы самого Штерна [383] и Штерна и Герлаха [384].
Анализ этого эксперимента дается Бомом [63]. Философская дискуссия,
начальным толчком для которой послужил результат эксперимента Штерна —
Герлаха, описана Эйнштейном и Эренфестом [132] и Джеммером [203].
Современное состояние метода молекулярных пучков см. в кн. Росса [345] и
Рамзея [330], а также Левина и Бернстейна [245].
э
ЭКВИВАЛЕНТНАЯ ОРБИТАЛЬ. Молекулярная орбиталь
входит в набор эквивалентных орбиталей, если операция
симметрии, примененная к молекуле, преобразует эту орбиталь в
другую орбиталь этого набора. В качестве примера рассмотрим
одну из связей С—Н в метане. Эта а-связь образуется
перекрыванием 5/?3-гибридной орбитали углерода и ls-орбитали
водорода. Если тетраэдрическую молекулу метана повернуть в
другое эквивалентное положение, другая sp*—ls-связь займет
положение рассматриваемой нами связи. Таким образом, четыре
а-связи С—Н в метане образуют набор эквивалентных орбита-
лей. Понятие эквивалентной орбитали тесно связано с
гибридизацией и локализованными орбиталями.
Рекомендуемые источники. См. приложение 9.2 в [1] и гл. 8 в кн. Коул-
сона [105]. См. также разд. «Локализованные орбитали».
ЭКС ИТОН. Представим себе ряд одинаковых молекул в
кристалле и допустим, что одна из них возбуждена. Это
возбуждение переходит с молекулы на молекулу и перемещается по
кристаллу, пока не затухнет. Возбуждение перемещается
подобно частице, и это явление описывается термином «экситон»,
который означает распространяющееся возбуждение. Если
возбуждение вызвано переходом электрона с одной орбитали молекулы
(атома или иона) на более высокую орбиталь, то возбуженное
состояние молекулы можно рассматривать как сосуществование
электрона и дырки. Перемещение пары электрон — дырка от
молекулы к молекуле и есть миграция экситона. Если электрон и
дырка перемещаются вместе от молекулы к молекуле, то это
называется случаем сильной связи, а мигрирующее возбуждение —
экситоном Френкеля. Электрон и дырка могут находиться на
разных молекулах, но в непосредственной близости друг от
друга; такая ситуация характерна для случая слабой связи, а
мигрирующее возбуждение, охватывающее при этом несколько
молекул (чаще всего ионов), называется экситоном Ванье. В
молекулярных кристаллах чаще встречается экситон Френкеля, о нем
и пойдет р.ечь дальше.
Образование экситона влияет на спектр молекул в твердом
теле. Это не удивительно, так как миграция экситона означает,
что между молекулами, образующими кристалл, имеется
взаимодействие (в противном случае возбуждение не могло бы
распространяться), которое, несомненно, должно влиять на их
энергетические уровни. Сила взаимодействия определяет скорость, с
427
э
которой экситон движется по кристаллу. Сильное
взаимодействие приводит к быстрому перемещению; отсутствие
взаимодействия приводит к тому, что экситон локализуется на исходной
молекуле, и в этом случае имеется обычное возбуждение
«изолированной» молекулы. Образование экситона вызывает сдвиг и
расщепление спектральных линий и изменение их интенсивности.
Причины этого станут ясны после того, как мы объясним
характер взаимодействия между молекулами.
Электронный переход в молекуле приводит к смещению
заряда (см. разд. «Вероятность перехода» и «Электрический ди-
польный переход»). Смещение заряда на одной молекуле в свою
очередь может вызвать сдвиг заряда на соседней молекуле.
Такой процесс взаимодействия переходных диполей может
продолжаться и далее, в результате чего возбуждение
распространяется по кристаллу (рис. Э. 1).
эоеееа
Рис. Э.1. Миграция возбуждения через кристалл в виде экситона.
К этому процессу можно подойти несколько иначе, если
рассмотреть все возможные относительные ориентации переходных
дипольных моментов молекул кристалла, а затем выяснить,
какую их комбинацию может возбудить световая волна.
Рассмотрим линейную цепочку молекул с переходными моментами,
перпендикулярными линии расположения (стрелки указывают
эффективное направление движения заряда при возбуждении
молекулы). Согласно законам обычной электростатики, энергия
цепочки с параллельными переходными диполями выше, чем при
любой их другой ориентации (рис. Э. 2), поэтому переход к
такому расположению диполей во всем кристалле происходит при
более высокой энергии, чем переход к любому другому
расположению, и, конечно, более высокой, чем переход в отдельных
молекулах. Но указанное расположение — единственное, которое в
состоянии возбудить падающий свет. Длина волны света
настолько велика по сравнению с межмолекулярным расстоянием,
что ее электрическое поле имеет одну и ту же фазу для большого
числа молекул, поэтому она вынуждает целую область
переходных диполей двигаться в одинаковой фазе. Это означает, что
наличие экситонной связи должно проявляться в спектре как
сдвиг полосы поглощения в сторону большей энергии. Если бы
переходные дипольные моменты были направлены вдоль цепоч-
428
более
высокая
teem возбуждает такой, переход
более
низкая
энергия
спектр
изолированной
молекулы"
л /ч эксит
1й1 \ \ \^ПОЛС
экситонная
полоса
Рис. Э.2. Переходные диполи с различным соотношением фаз. Противоположно
направленные диполи имеют наименьшую энергию, параллельное
расположение (возбуждаемое падающим светом) соответствует наивысшей энергии
изолированные молекулы
давыдовское расщепление
Рис. Э.З. Давыдовское расщепление экситонных полос при наличии двух
молекул в элементарной ячейке.
э
ки молекул, должен был бы наблюдаться обратный сдвиг. В
самом деле, такое синфазное возбуждение переходных диполей
даст цепочку молекул с переходными диполями,
расположенными друг за другом (голова к хвосту), что соответствует низкой
энергии.
Если в элементарной ячейке кристалла находится больше
одной молекулы, можно получить несколько полос; N молекул в
ячейке дают N линий поглощения, или экситонных полос.
Расщепление таких полос называется давыдовским расщеплением.
Предположим, что N = 2 и молекулы расположены так, как
показано на рис. Э. 3, а переходные диполи расположены вдоль
большей оси продолговатых молекул. Поле световой волны
стимулирует синфазное возбуждение переходных диполей, но они
должны быть синфазны только с аналогично расположенными
диполями в соседних ячейках. Внутри каждой элементарной
ячейки переходные диполи могут быть расположены так, как
показано на рис. Э. 3 (А или В), и иметь разные энергии
взаимодействия. Это должно приводить к появлению в спектре двух
полос, расщепление между которыми соответствует энергии
взаимодействия переходных диполей в пределах элементарной
ячейки.
Упражнения. 1. Объясните термин «экситон»? В чем различие между
экситоном Френкеля и экситоном Ванье? Вносят ли экситоны вклад в
электропроводность среды? Каким образом можно обнаружить экситоны
спектроскопически? Почему имеет смысл рассматривать только синфазное
возбуждение переходных диполей? Что бы произошло со спектром, если бы такое
приближение стало неприменимым? Оцените длину волны, при которой можно
ожидать значительной ошибки для полосы антрацена (380 нм)?
2. Оцените энергию взаимодействия между двумя переходными диполями
величиной ID (3,3-10~30 Кл-м), расположенными на расстоянии 0,3 нм.
Допустим, что сила осциллятора этого перехода в свободной молекуле / = 0,2;
оцените экситонный сдвиг. Что является причиной давыдовского
расщепления? Какова поляризация расщепленных полос?
Рекомендуемые источники. Простое рассмотрение образования
молекулярных экситонов можно найти у Маррела [297], который обсуждает также
гипохромный (уменьшение интенсивности поглощения) и гиперхромный
(увеличение интенсивности) эффекты. (Некоторая путаница может быть вызвана
терминами «гипсохромный эффект», что означает ослабление окраски, и «ба-
тохромный эффект», т. е. насыщение (углубление) окраски.) Введение в
математическую теорию экситонов дано Крейгом и Уолмсли [112] и Киттелем
[224], а болое детально рассмотрено Давыдовым [118, 119].
ЭКСТИНКЦИИ КОЭФФИЦИЕНТ. При прохождении пучка
света через поглощающую среду его интенсивность уменьшается.
Поскольку количество света, поглощаемое каждой молекулой,
пропорционально интенсивности дошедшего до нее света, при
прохождении через поглощающую среду интенсивность света па-
430
э
дает экспоненциально. Скорость уменьшения интенсивности
определяется коэффициентом экстинкции. Интенсивность
определяется законом Ламберта — Бера / = /оехр(—eel), где /0 —
начальная интенсивность, с — молярная концентрация
поглощающих частиц, / — длина пути света (которая обычно
выражается в сантиметрах), а е — коэффициент экстинкции
(погашения). Коэффициент экстинкции зависит от частоты падающего
света и обычно записывается в виде функции e(v), где
v—соответствующее волновое число в cmw1.
Коэффициент экстинкции является мерой вероятности
перехода с данной частотой и поэтому мерой переходного диполя и
силы осциллятора перехода, а следовательно, связан с
коэффициентом Эйнштейна для вынужденного поглощения. Молярные
коэффициенты экстинкции для некоторых веществ приведены в
табл. 8. Произведение ce(v)l называется оптической плотностью
вещества при заданной частоте.
Рекомендуемые источники. Связь между коэффициентом экстинкции и
силой осциллятора рассматривается в [1], гл. 10 и приложении 10.2; см. также
разд. «Сила осциллятора». Обсуждение закона Ламберта — Бера, его
применения и пределов применимости можно найти у Вейна [416]. В кн. Меллона
[280] обобщены данные по коэффициентам экстинкции и обсуждено их
аналитическое применение.
ЭЛЕКТРИЧЕСКИЙ ДИПОЛЬНЫИ ПЕРЕХОД. Наиболее
интенсивные переходы атомов и молекул вызываются
взаимодействием электрической компоненты электромагнитного поля с
электрическим дипольным моментом системы. В качестве
примера можно указать взаимодействие постоянного дипольного
момента какой-нибудь молекулы со световым пучком; при
наличии такого взаимодействия вращательное движение молекулы
ускоряется, и она совершает переход между двумя вращатель-
ними уровнями. И наоборот, вращающийся электрический ди-
польный момент ведет себя как осциллирующий электрический
заряд, поэтому такая вращающаяся система порождает
электромагнитную волну. Волна уносит энергию, поэтому молекула
спускается вниз по лестнице вращательных энергетических уровней.
Тот же тип электрических дипольных переходов наблюдается в
колеблющихся системах, если колебание сопровождается
движением заряда. Так, электрические дипольные переходы могут
происходить между колебательными уровнями энергии полярной
молекулы НС1, поскольку наблюдатель, находящийся рядом с
молекулой, увидит изменение зарядового распределения в
процессе колебания. Тот же наблюдатель, следящий за молекулой
СЬ, не зарегистрирует такого изменения, следовательно,
молекулы указанного типа не могут взаимодействовать с
электромагнитным полем посредством электрического дипольного механиз-
43}
э
ма; они не могут ни получать энергию за счет поглощения, ни
отдавать энергию полю за счет испускания.
Электрические дипольные переходы могут также происходить
между электронными состояниями атомов, и в этом случае опять
необходимо определить, сопровождается ли переход движением
заряда, которое можно интерпретировать как осцилляцию ди:
поля. Совершенно ясно, что переход со сферически
симметричной ls-орбитали на сферически симметричную 25-орбиталь
сопровождается симметричным перераспределением заряда, и с
таким переходом нельзя связать никакого дипольного момента.
Поэтому указанный переход не может происходит за счет
электрического дипольного механизма. Если же мы наблюдаем
s — /7-переход, его можно идентифицировать как дипольный.
Если переход происходит с s-орбитали на /?2-орбиталь,
осциллирующий диполь располагается вдоль оси z и, следовательно,
испускаемое излучение является плоскополяризованным с
электрическим вектором в 2-направлении (наибольшая
интенсивность наблюдается в плоскости ху). В случае перехода s-»px
(или s-*py) излучение поляризовано в направлении х (или у), а
испускается главным образом в плоскости yz (или zx).
Если переходы совершаются между орбиталями с
определенными значениями квантового числа Ши излучение имеет
круговую поляризацию. Излучение имеет левую круговую
поляризацию, если ш\ уменьшается на единицу, и правую круговую
поляризацию, если mi увеличивается на единицу; когда гп\ не
меняется, свет плоскополяризован. (Относительно наблюдателя, по
направлению к которому распространяется свет, электрический
вектор света с левой круговой поляризацией вращается против
часовой стрелки.) Такое поведение можно понять, рассмотрев
s — /7-переходы; рх и ру можно выразить в виде суперпозиций
состояний с различными т/, и поэтому испущенное излучение
является соответствующей суперпозицией плоскополяризован-
ного излучения, которое описано выше.
Правила отбора для электрического дипольного излучения
могут быть разъяснены либо на основе проведенного выше
обсуждения, либо с учетом того, что фотон обладает собственным
спиновым угловым моментом. Первая точка зрения приводит к
правилу отбора Лапорта, которое утверждает, что при диполь-
ном электрическом переходе должна меняться четность орбита-
ли (см. разд. «Четность и нечетность»). Так s — /7-переход
связывает четную орбиталь (четную относительно инверсии, центр
которой — атомное ядро) с нечетной. То же самое справедливо и
для d — /7-переходов. Правило отбора запрещает переходы s — s,
р — /7, d — dy так как они не имеют дипольного момента
перехода. Существование углового момента фотона в сочетании с
законом сохранения углового момента позволяют обсудить вопрос
432
э
о правилах отбора с другой точки зрения, поскольку символы s,
pud означают, что электроны на соответствующих орбиталях
обладают различными угловыми моментами, и, когда
происходит испускание или поглощение фотона, угловой момент чатома
должен измениться так, чтобы полный момент системы остался
неизменным. Фотон, взаимодействующий с электроном на s-op-
битали, должен перевести его на /7-орбиталь и не способен
обеспечить переход на d-орбиталь, поскольку имеет недостаточный
для этого угловой момент. Когда падающий фотон
взаимодействует с электроном на /7-орбитали, это может привести к
переходу, как на d-, так и на 5-орбиталь в зависимости от
относительной ориентации угловых моментов при столкновении.
Связь между изменением значения mi и поляризацией света
также можно понять с учетом спина фотона, так как свет с
левой круговой поляризацией соответствует одной ориентации
спина относительно направления распространения, а свет с
правой круговой поляризацией — другой. Поэтому, чтобы
сохранялась проекция полного углового момента всей системы на
выделенное направление, при поглощении или испускании света mi
должно изменяться соответствующим образом. Если свет
приближается к атому вдоль отрицательной оси z (из точки z =
=—оо) и^имеет левую круговую поляризацию (проекция спина
фотона на направление распространения равна +1, и он
движется подобно правовращающему буравчику), при его
поглощении атом должен перейти из состояния mi в состояние т*+ 1,
чтобы сохранился полный момент системы относительно оси г.
Те же аргументы применимы и к испусканию.
Если оптический переход все же наблюдается, хотя
изложенные выше правила его запрещают, объясняться это может тем,
что атом из-за своего окружения теряет центр симметрии, или
тем, что между электронными и колебательными видами
движения существует связь (см. «Электронно-колебательные
переходы»). Может также оказаться, что переход обусловлен
магнитным дипольным или электрическим квадрупольным моментом.
Можно утверждать с очень большой точностью, что
электрическое поле света не способно взимодействовать непосредственно
со спином электрона, поскольку спин — это внутренний вид
движения и при электрических дипольных переходах он
сохраняется; однако это правило может нарушаться в результате
спин-орбитального взаимодействия.
Упражнения. Чем обусловлены наиболее интенсивные оптические
переходы? Почему электромагнитное поле способно ускорить вращающуюся
молекулу? Чем должна обладать для этого молекула? Может ли электрический
дипольный переход увеличить значение углового момента относительно
геометрической оси (оси симметрии) цилиндрической или дисковидной молеку-
433
э
лы? Поляризован ли свет при вращательных электрических дипольных
переходах? При каких условиях колеблющаяся молекула может поглощать или
испускать свет в результате электрических дипольных переходов? Какие типы
колебаний двуокиси углерода могут взаимодействовать с электромагнитным
полем и какие не могут? (Отвечая на этот вопрос, полезно просмотреть разд.
«Нормальные колебания» и «Колебательный спектр».) Почему можно
считать, что переходы между состояниями атома вызывают электрический ди-
польный момент? Как называется такой момент? Как связана с ориентацией
электрического диполя поляризация света, участвующего в переходе?
Обсудите поляризацию переходов s — pZy s — рх, s — (px + ipy), где под (рх +
+ ipv) имеется в виду р-орбиталь с mi = 1. Рассмотрите действие магнитного
поля на атом (эффект Зеемана)\ какую поляризацию света зафиксировал бы
детектор, чувствительный к трем переходам, s — pz> s —p+i, s — p-i,
двигаясь по поверхности окружающей атом сферы во всех направлениях?
Сформулируйте правило отбора Лапорта. При каких условиях оно справедливо и
когда нарушается? Какую роль играет спин фотона в установлении правил
отбора для электрических дипольных переходов? Каким образом можно
установить соответствие такого описания с правилом Лапорта? Рассмотрите
поляризацию при указанных выше переходах, учитывая угловой момент фотона
и закон сохранения полного углового момента? Почему при поглощении или
испускании фотона угловой момент атома может либо увеличиваться, либо
уменьшаться? Чем можно объяснить наблюдаемую интенсивность перехода,
когда электрический дипольный переход запрещен?
2. Обсудите смысл фразы: «Электрический диполь перехода осциллирует
с частотой, равной частоте излучения, которое он испускает». (Принцип
соответствия утверждает, что некоторый смысл в этом должен быть.)
Рассмотрите зависимость дипольного момента перехода от времени, выразив
матричный элемент перехода \ dx *F* d4fg (где 4% — возбужденное состояние,
4g — основное состояние системы, ad — оператор электрического дипольного
момента) с учетом явного вида зависимости состояний от времени, т. е.
запишите: Ч^ = yfpg exp(—iEgt/h). Выведите правило отбора Лапорта,
применив к этому матричному элементу теорию групп (см. разд. «Характер»).
Рекомендуемые источники. Обсуждение электрических дипольных
переходов см. в [1], гл. 8. Применение в органической химии см. в кн. Маррела [297]
и Сандорфи [354]; о применении в неорганической химии, особенно в
электронных спектрах соединений переходных металлов, говорится в кн. Оргела
[308], Бальхаузена [49] и Гриффита [170]. Обоснованием правил отбора
являются расчеты вероятностей переходов по теории зависящих от времени
возмущений: см. [1], гл. 7, Герцберг [185], Эйринг, Уолтер и Кимбалл [137].
ЭЛЕКТРОНВОЛЬТ. Электронвольт (эВ) —это энергия,
приобретаемая электроном, когда он ускоряется разностью
потенциалов 1В. Заряд электрона равен —1,602-10~19 Кл,
следовательно, эта энергия эквивалентна 1,602-10"19 Дж, или
96,49 кДж-моль"1. Приведем еще одно полезное соотношение:
1 эВ « 8023 см-1.
ЭЛЕКТРОННО-КОЛЕБАТЕЛЬНЫЙ (ВИБРОННЫИ)
ПЕРЕХОД. Слово «вибронный» является сокращением слов
«вибрационный» (колебательный) и «электронный» и указывает на
то, что в переходе одновременно участвуют оба типа возбужде-
434
э
ния. Электронно-колебательным называют состояние молекулы,
в котором нельзя считать электронное и колебательное состояния
независимыми.
Чтобы пояснить такое описание, рассмотрим электронный
переход d-электрона в октаэдрическом комплексном ионе. В
теории кристаллического поля и в теории поля лигандов показано,
что d-орбитали комплексных ионов переходных металлов
расщепляются на две группы, несколько отличающиеся по энергии.
Поэтому появляется искушение приписать наличие окраски
у комплексных ионов переходных металлов электронным
переходам с одного набора d-орбиталей на другой. Однако при этом
мы сразу же сталкиваемся с необходимостью учета правила
отбора Лапорта, которое запрещает d — d-переходы, потому что
они являются переходами без изменения четности (g— g).
Однако большинство законов можно обойти, и одно из правил
поиска путей обхода закона состоит в том, что надо найти
приближение, которое может лежать в основе этого закона, а затем
подправить это приближение. Правило Лапорта основано на
предположении о существовании у комплексного иона центра
симметрии, поэтому это правило должно точно соблюдаться
только при условии, что комплекс имеет строго октаэдрическое
строение. Но комплекс может колебаться, и некоторые типы его
колебаний нарушают его центральную симметрию. Рассмотрим
теперь колебательно-невозбужденный комплекс и
приближающийся к нему фотон. Допустим, фотон одновременно возбуждает
d-электрон и колебания комплекса. Тогда, если возбуждаемый
тип колебаний принадлежит к числу тех, которые нарушают
центральную симметрию комплекса, правило Лапорта будет
слегка, но вполне достаточно нарушено, потому что у комплекса
больше нет центра инверсии в конечном состоянии.
Переход разрешен только в том случае, если справедливо
предположение, что колебательное и электронное движение
связаны и совместно определяют симметрию объекта, с которым
взаимодействует свет. Следовательно, переход является
электронно-колебательным и состояния комплекса следует считать
электронно-колебательными состояниями. Такая точка зрения
приводит к другому возможному подходу к рассмотрению
электронно-колебательных переходов. При таком подходе мы
рассматриваем возможность перехода с d-орбитали на р-орбиталь;
этот переход является g — ^-переходом и потому разрешен. Но
почему верхний уровень может оказаться р-орбиталью или, по
меньшей мере, откуда у него возьмутся какие-то свойства /?-ор-
битали? Если электрон следует за ядерными колебаниями,
электронное распределение в верхнем состоянии должно
следовать за ядерным распределением. Для того чтобы это
произошло, оно должно быть искажено относительно центрально-сим-
435
a
метричного распределения, которое дают d-орбитали, и один из
способов получить искаженное распределение — это примешать
к d-орбиталям некоторую долю /?-орбиталей (учесть
возможность их гибридизации) (рис. Э. 4). Следовательно, когда
возбуждаются такие антисимметричные колебания, d-электронное
распределение приобретает некоторые черты р-электронов, а
поскольку d — р-переходы разрешены, переход из колебательно-
невозбужденного основного состояния в
электронно-колебательное верхнее состояние разрешен в той степени, в какой
колебания придают d-электронам комплекса характер р-электронов.
Рис. Э.4. Асимметрические колебания приводят к гибридизации орбиталей рг
и dZ2 и делают возможным переход d—d благодаря разрешенной
компоненте d--p.
Рекомендуемые источники. Дальнейшее обсуждение этого вопроса с
привлечением теории групп см. в гл. 10 [1]. Электронно-колебательные переходы
более подробно рассматриваются у Оргела [308], Фиггиса [146], Бальхау-
зена [49] и Гриффитса [170]. Если приходится дополнительно учитывать
вращательные состояния молекулы, возникают
электронно-колебательно-вращательные (ровибронные) переходы, а соответствующее сложное состояние
называется электронно-колебательно-вращательным.
ЭЛЕКТРОННОЕ «СКОЛЬЖЕНИЕ». Электроны «скользят»
вовсе не потому, что они скользкие, а потому, что во
вращающейся молекуле они не в состоянии поспевать за быстрым
движением ядер, и это свидетельствует о нарушении приближения
Борна — Оппенгеймера. Так, например, в молекуле водорода
электроны могут отставать от вращающегося ядерного остова.
Следовательно, угловые моменты электрона и ядерного остова
слегка различаются.
Электронное скольжение имеет два важных следствия. Во-
первых, различие между а- и я-орбиталями (и между 2- и
П-состояниями) становится менее четким; в электронном
спектре линейных молекул это проявляется как А-удвоение.
Во-вторых, все молекулы из-за своего вращения обладают магнитным
моментом, который называется молекулярным магнитным
моментом. Наличие этого магнитного момента можно объяснить
436
a
различными скоростями вращения положительно заряженного
ядерного остова и отрицательно заряженного электронного
облака молекулы. Это означает, что имеется результирующий ток,
а следовательно, и магнитный момент. Величина его возрастает
с увеличением вращательного квантового числа J молекулы.
Рекомендуемые источники, В гл. 10 [1] более подробно обсуждается
вопрос о том, почему электронное «скольжение» вызывает смешение 2- и П-со-
стояний; см. также рис. У.5. Количественное рассмотрение дано в кн. Кинга
[222], Герцберга [187] и Ковача [226] О молекулярных магнитных моментах
см. разд. «g-Фактор» и кн. Таунса и Швлова [399] и Герцберга [187].
ЭЛЕКТРОННЫЕ СПЕКТРЫ МОЛЕКУЛ (краткий обзор).
Электронные спектры молекул обычно подразделяют по степени
сложности на спектры двухатомных молекул, спектры
многоатомных молекул, спектры хромофорных групп в сложных
молекулах и, наконец, спектры молекул в твердых телах.
Электронный спектр двухатомной молекулы содержит ряд
полос, каждая из которых появляется в результате перехода из
основного электронного состояния (X) в одно из возбужденных
электронных состояний (А, В, ...); структура этих полос
обусловлена одновременным возбуждением колебаний, а
интенсивность прогрессий стуктуры определяется принципом Франка —
Кондона и другими правилами отбора. На колебательную
структуру накладывается дополнительная структура, обусловленная
возбуждением вращательного движения, при этом наблюдаются
главным образом Р- и R-ветви, а в некоторых случаях и Q-ветви.
Поскольку в основном и возбужденных электронных состояниях
момент инерции отличается, ветви могут образовывать кант (см.
рис. В. 7). Если момент инерции в верхнем состоянии больше,
чем в нижнем, кант имеет #-ветвь, т. е. ветвь с большей
частотой. Колебательные линии сгущаются в сторону большей
энергии, так как колебательные уровни сходятся по направлению к
пределу диссоциации. Энергию диссоциации можно определить,
наблюдая диссоциационный предел или с помощью тщательной
экстраполяции от более низких частот (часто используется
экстраполяция Берджа — Спонера). В некоторых случаях
колебательная и вращательная структуры исчезают и вновь
появляются, прежде чем достигается предел диссоциации, — это
проявление предиссоциации. Из спектра можно определить силовые
постоянные, энергию диссоциации и ангармоничность электронных
состояний молекулы, а также параметры кривых потенциальной
энергии молекулы.
Электронный спектр многоатомной молекулы значительно
сложнее, однако для его интерпретации используют те же
принципы и получают аналогичную информацию. В многоатомных
молекулах дополнительный интерес представляет обратный пе-
437
э
реход из возбужденного состояния в основное, особенно если
молекула теряет свою энергию в процессе флуоресценции или
фосфоресценции. В конденсированных фазах вращательная
структура спектра теряется, а колебательный спектр становится
настолько диффузным, что спектр поглощения часто
представляет собой последовательность широких полос. Особый интерес
вызывают электронные спектры комплексов переходных
металлов, где переходы часто можно связать с расщеплением уровней
d-электронов кристаллическим полем (см. разд.
«Кристаллического поля теория», «Поля лигандов теория».) В других случаях
наблюдаются переходы с переносом заряда от ионов металла
к лигандам (см. «Цвет»). В органических молекулах поглощение
часто связано с наличием хромофора, как, например,
карбонильная группа (электрический диполный переход я->я*) или
двойная связь (переход я->я*; см. разд. «Цвет»).
Если молекула входит в состав кристаллической решетки,
могут наблюдаться другие эффекты; один из наиболее важных
эффектов — образование экситона, посредством которого
возбуждение распространяется по кристаллической решетке.
Рекомендуемые источники. Обсуждение электронных спектров молекул см.
в [1], гл. 10. Применение электронных спектров для изучения структуры
молекул рассматривается в кн. Барроу [511, Уиффена [424], Диксона [124], Кинга
[222], Джаффе и Орчина [201], Рао [332], Стерна и Тиммонса [382], Герцберга
[187, 188], Маррела [297], Гейдона [158]. Дополнительные сведения по
затронутым вопросам можно найти в соответствующих разделах. Интерпретация
электронных спектров малых молекул и примеры извлечения данных о
кривых потенциальной энергии и энергии диссоциации даны Гейдоном [158]. В кн.
Маррела [297] речь идет о больших органических молекулах и
рассматриваются отдельные хромофоры и их взаимодействие в твердых телах. Богатым
источником подробнейшей информации и блестящим примером применения
теоретических концепций к детальному анализу свойств молекул являются кн.
Герцберга [187, 188].
ЭЛЕКТРОННЫЙ ПАРАМАГНИТНЫЙ РЕЗОНАНС
(краткий обзор). Экспериментальное наблюдение явления
электронного парамагнитного резонанса (ЭПР) заключается в
регистрации энергии, необходимой для «перевертывания» электронного
спина в присутствии магнитного поля. Электрон обладает
спиновым магнитным моментом и при наличии приложенного поля
две разрешенные ориентации спина (а и р) имеют различные
энергии (в поле 3 кГс а-состояние лежит на 0,3 см-1 выше, чем
р-состояние). Можно заставить электрон обратить направление
спина (совершить переход из рв а), если наложить
электромагнитное поле подходящей частоты; для магнитного поля 3 кГс
излучение с волновым числом 0,3 см-1 (длина волны 3 см,
частота 9 ГГц) лежит в микроволновой области спектра.
Установка для наблюдения ЭПР состоит из магнита, обеспечивающего
однородное поле напряженностью порядка 3 кГс, источника трех-
438
э
сантиметровых волн (клистрон) и детектора, регистрирующего
поглощение падающего излучения. При наблюдении ЭПР
частота микроволнового излучения поддерживается постоянной, а
напряженность магнитного поля изменяется до тех пор, пока не
происходит поглощения падающего излучения (рис. Э. 5); при
этой напряженности поля расстояние между энергетическими
уровнями а- и р-ориентации точно совпадает (находится в резо-
Рис. Э.5. Переход при электронном парамагнитном резонансе и
соответствующий спектр.
нансе) с частотой излучения. Образец парамагнитного вещества
может представлять собой твердое тело, жидкость или (в более
редких случаях) газ.
Эксперимент позволяет получить информацию трех типов:
1. Положение спектра. Магнитное поле, действующее на
электрон, может отличаться от приложенного поля, ввиду того что
последнее индуцирует локальные поля. При заданной частоте
микроволнового излучения условие резонанса выполняется при
одной и той же величине локального поля, и, следовательно, для
различных молекул необходимы слегка отличающиеся внешние
поля. Если частота микроволнового излучения равна v, так что
каждый фотон несет энергию hvf а индукция приложенного поля
равна 5, то условие резонанса имеет вид g\xeB = /iv, где
множитель g (который называется g-фактором) учитывает возмож-
439
э
ность того, что индукция локального поля не в точности равна В.
Измерение положения спектра позволяет определить g-фактор,
а так как он зависит от электронного строения парамагнитных
частиц, можно сделать о нем некоторые выводы. Характерные
значения ^-фактора у органических и неорганических радикалов
позволяют проводить идентификацию этих частиц; у ионов пере-
Рис. Э.6. Причина сверхтонкого расщепления в радикале, содержащем одно
ядро со спином 7г (обозначено большим кружочком).
ходных металлов обнаружены более широкие вариации
значения ^-фактора, однако и там он может дать полезную
структурную информацию, особенно о расстояниях между
энергетическими уровнями лигандов и о делокализации электронов на лигаи-
ды. ^-Фактор может быть анизотропным, и в этом случае
положение спектра зависит от ориентации парамагнитных частиц
(когда такая частица удерживается в кристалле, а кристалл
поворачивается, положение резонанса изменяется).
2. Сверхтонкая структура спектра. Как правило, спектр ЭПР
состоит не из одной линии. Его структура обусловлена
сверхтонким взаимодействием электрона и магнитных ядер, входящих в
состав молекулы. Магнитное ядро (например, протон) создает
440
П0Л6
ф)
г
j
г
LJ
ГТТ
Рис. Э.7. Типичный спектр электронного парамагнитного резонанса радикала
(с одним ядром со спином 1), удерживаемого в кристалле. Показаны две
ориентации кристалла: обратите внимание на сдвиг центра спектра
(анизотропия g-фактора) и изменение величины расщепления (анизотропные сверх*
тонкие взаимодействия).
спины протона;
• а
oft
Рис. Э.8. Типичный спектр электронного парамагнитного резонанса в
растворе (содержащем анион-радикалы бензола) и его интерпретация.
э
локальное магнитное поле, которое в зависимости от
относительной ориентации ядерного спина и приложенного поля может
увеличивать или уменьшать локальное поле, действующее на
электронный спин. Это означает, что радикалы с различными
ориентациями ядерного спина резонируют при разных напряжен-
ностях приложенного магнитного поля, и спектр образца, куда
входит много различных радикалов, состоит из линий,
соответствующих всем этим напряженностям приложенного поля
(рис. Э. 6). Например, N радикалов, каждый из которых
содержит один протон, создают ансамбль, состоящий из N/2
радикалов, у которых спин протона направлен вдоль внешнего
магнитного поля, и N/2 радикалов, у которых спин протона направлен
против магнитного поля. Электроны одной группы радикалов
испытывают действие одного локального поля и резонируют при
соответствующей напряженности приложенного поля, а
электроны другой группы резонируют при другой напряженности
приложенного поля. Поэтому спектр состоит из двух линий,
удаленных друг от друга на несколько гаусс. Наблюдаемая
сверхтонкая структура (СТС) спектра может использоваться для
характеристики вероятности пребывания неспаренного электрона в
окрестности каждого магнитного ядра, поэтому изучение СТС
позволяет определить картину распределения электронов в
молекуле. СТС имеет изотропную и анизотропную компоненты
(рис. Э. 7). Первая обусловлена контактным взаимодействием
Ферми и характерна для электрона, находящегося на s-орбита-
ли, вторая обусловлена диполь-дипольным взаимодействием и
характерна для электрона р-орбитали. Поэтому изучение
угловой зависимости СТС позволяет получить сведения о
гибридизации орбитали неспаренного электрона, а это в свою очередь
может быть использовано для определения формы радикала
(например, таким образом установлено, что метальный радикал
является плоским). В растворах наблюдается только изотропная
СТС (см., например, рис. Э. 8), и ее изучение применяется
главным образом для того, чтобы определить распределение
спиновой плотности в радикалах. В ароматических радикалах СТС
обусловлена механизмом спиновой поляризации вдоль связи
С—Н, как показано на рис. Э. 9. Если я-электрон имеет спин а,
то электрон со спином а в а-связи С—Н расположен
преимущественно в окрестности атома углерода, т. е. ближе к я-элек-
трону (потому что в атомах электроны стремятся иметь
параллельные спины, см. правила Гунда)\ таким образом, в
окрестности протона преимущественно находится электрон со спином р.
Поэтому, хотя электроны, образующие связи С—Н имеют
спаренные спины, вблизи протона оказывается преимущественно
только один спин, что и приводит к сверхтонкому взаимодей*
ствию.
442
э
3. Форма спектральных линий. Форма линий зависит от
характера движения радикалов, так как она определяется
процессами релаксации. Различают два типа релаксации:
спин-решеточную и спин-спиновую. Первая возникает из-за движения
радикала, приводящего к флуктуациям магнитного поля, которое
действует на неспаренный электрон. Если эти флуктуации имеют
компоненту, осциллирующую с частотой, равной частоте
перехода, то из-за этого может возникнуть переход. Время жизни
верхнего состояния уменьшается, и в соответствии с принципом
неопределенности энергетический уровень этого состояния
уширяется. Если хаотическое движение молекулы происходит медленно,
спин-решеточная
релаксация ничтожна (поскольку в
флуктуирующем поле нет
осцилляции с необходимой
частотой 1010 с"1); она
становится максимальной,
когда характерное время мо-
Рис. Э.9. Механизм спиновой
поляризации в радикале СН.
лекулярного движения составляет 10"10 с, после чего опять
падает; последнее наблюдается в предельно текучих жидкостях, где
большинство флуктуации происходит с очень высокими
частотами (рис. Э. 10). Время жизни спинового состояния,
обусловленное этим механизмом, обозначается 7\ и называется временем
спин-решеточной или продольной релаксации. Чем больше Ти
тем уже линия.
Другой тип релаксации представляет собой спин-спиновый
процесс. В жидком, но вязком растворе каждый радикал
находится в специфическом магнитном окружении и имеет
определенную ориентацию, поэтому все локальные поля немного
отличаются. Соответственно радикалы резонируют при несколько
различных приложенных полях, и спектр представляет собой
совокупность уширенных линий. Если подвижность молекул
увеличивается, различия в магнитных окружениях, или
анизотропные взаимодействия, усредняются и линии сужаются. Эффект
процесса уширения характеризуется временем спин-спиновой,
или поперечной, релаксации 7V чем больше Г2, тем уже линия.
Эффект уширения исчезает с увеличением подвижности
радикалов (в результате повышения температуры или уменьшения
вязкости).
обменное
/спаривание
сверхтонкое
взаимодействие
} электронная
корреляция
443
:3
s
I
преобладание анизотропии
Подвижность ладикалов
Рис. Э.10. Зависимость времени релаксации от быстроты молекулярного
движения.
Рис. Э.П. Процессы релаксации, характеризуемые временами Т\ и Г2.
э
Отметим, что только 7\-процесс уменьшает число радикалов
в верхнем спиновом состоянии, поэтому только он является
настоящим механизмом релаксации энергии (направление потока
энергии — от спиновой системы к решетке или к окружению —
определяется термодинамикой системы; при наличии теплового
потока от небольшой спиновой системы к фактически
бесконечной решетке энтропия увеличивается). Гг-Процесс — это процесс
релаксации другого типа; он разупорядочивает относительную
фазу прецессирующих электронных спинов (рис. Э.11).
Изучение ширины линий и насыщения (уменьшения
интенсивности сигнала ЭПР при высоких мощностях микроволнового
излучения в результате выравнивания заселенностей состояний
аир) спектра дают информацию о движении молекул в
жидкостях, поскольку из формы линий можно извлечь сведения о
скорости движения. Можно получить также сведения о скорости
химических процессов, например таутомерии, так как они также
изменяют окружение электронных спинов.
Рекомендуемые источники. См. кн. Мак-Лечлана [2] «Магнитный
резонанс», где дано простое изложение принципов и применений ЭПР. См. также
кн. Линден-Белла и Харриса [260], Керрингтона и Мак-Лечлана [90], Вертца и
Болтона [418], Сликтера [374], Абрагама и Б лини [28]. Аппаратура описана
Пулом [319]. В этих работах, а также в работе Эйскога [43] описано
применение ЭПР к органическим системам; применение к соединениям переходных
металлов описано Эткинсом и Саймонсом [39]; применение к ионам
переходных металлов рассмотрено Керрингтоном и Мак-Лечланом [90], Вертцем и
Болтоном [418], Сликтером [374], вычисление ^-фактора для простых систем
проведено в [1], гл. 11. См. также Мемори [281]. Процессы релаксации
описаны Мак-Лечланом и Керрингтоном [90], Пулом и Фарачем [320] и Стендли
и Воганом [380]; ряд важных работ опубликован Маненковым и Орбахом [263].
Подробное теоретическое описание можно найти у Мууса и Эткинса [301].
ЭЛЕКТРООТРИЦАТЕЛЬНОСТЬ. Электроотрицательность
элемента в молекуле является мерой его способности
притягивать электроны; чем больше электроотрицательность элемента,
тем больше его способность притягивать электроны. Наиболее
употребительны два определения электроотрицательности,
введенные Полингом и Малликеном.
Шкала электроотрицательности Полинга основывается на
рассмотрении понижения вычисленной энергии двухатомной
молекулы при учете в ее описании вклада ионных структур.
Предположим, что энергия молекулы АВ в действительности равна
£(АВ), а вычисления, основанные на чисто ковалентных
структурах, дали £Ков(АВ), тогда неучтенный вклад ионных структур
равен £Ион(АВ) = £(АВ)—£КОв(АВ). Полинг обнаружил, что
квадратный корень из £Ион(АВ) пропорционален разности двух
чисел, одно из которых характеризует элемент А, а другое —
элемент В, и что выражение [£ион (АВ)],/г == | х" — Хв | справед-
445
9
ливо в широком интервале сочетаний элементов. Чтобы
построить шкалу электроотрицательностей, необходимо оценить
^ковСАВ). Полинг предположил, что разумным приближением
является среднее значение энергий молекул Аг и В2. Такое
приближение вполне оправдано, поскольку эти молекулы заведомо
неполярные, и, следовательно, энергии А2, AB и Вг должны
образовывать простую последовательность, если в АВ исключены
полярные структуры. Для составления таблицы
электроотрицательностей (см. табл. 7) Полинг использовал оценку £КОв(АВ)
как среднего арифметического, либо среднего. геометрического
значения величин Е(А2) и £(В2).
Установив шкалу электроотрицательностей, можно
определить ряд свойств молекул. Во-первых, она позволяет оценить
энергии связи, если известны энергии связи молекул А2 и Вг.
Хотя эта оценка основана на обращении определения
электроотрицательности, таким путем можно предсказать энергии связи
для молекул, отличающихся от использованных для построения
шкалы. Во-вторых, шкала электроотрицательностей позволяет
предсказать ионность связи (т. е. процент ионного характера
связи); для шкалы, выраженной в электронвольтах, ионность
связи определяется выражением 161 х" — 5Св | + 3,515С^ — Хв |2-
Если известна длина связи, то, зная ее ионность, можно
приближенно оценить дипольный момент связи.
Более обосновано применение шкалы Малликена, так как
при ее составлении пользуются уже не оцениваемыми
величинами (как в шкале Полинга), а измеряемыми — средним между
потенциалом ионизации атома и его сродством к электрону.
Таким образом, шкала Малликена основывается на выражении
^а = V2 U (А) + Ес (А)]. Дополнительным преимуществом этой
схемы является то, что она может учитывать различия в элек-
троотрицательностях различных орбиталей одного и того же
атома или зависимость электроотрицательности от гибридизации.
Не удивительно, что эти две шкалы связаны: численно
величине Хд ~~ Хв соответствует величина 2,78 (х£ — х")- Более
глубокое рассмотрение позволяет показать, что в хорошем
приближении величина £Ион(АВ) определяется энергией,
необходимой для перемещения электрона от А к В, которая равна
£C(B) — /(А), и энергией, необходимой для перемещения его от
В к А, т.е. ЕС(А)—/(В), и что для неполярной молекулы эти
величины равны (так как ни одна тенденция не превосходит
другую). В этом последнем случае, т. е. когда
электроотрицательности не отличаются, легко установить, что £С(А)+/(А) =
= £С(В) + /(В). Следовательно, разность этих двух величин
должна быть пропорциональна разности электроотрицательно*
стей двух атомов.
446
э
Упражнения. Мерой чего является электроотрицательность элементов?
Почему вполне допустимо считать, что £Ков(АВ) представляет собой среднее
двух величин £(А2) и £(В2)? Исходя из того, что энергии связи галогенов Хг
равны 2,17 эВ для F2, 2,475 эВ для С12 и 1,971 эВ для Вг2, энергия Н2 равна
4,476 эВ, а энергия 02 —5,080 эВ, оцените энергии связи различных гетеро-
ядерных двухатомных молекул, которые можно образовать из указанных
элементов. Оцените ионный характер каждой молекулы. Выведите выражение
для дипольного момента двухатомной молекулы через
электроотрицательности ее атомов. Почему оценка с помощью этого выражения дипольных
моментов должна давать плохое согласие с экспериментальными данными (даже
если получено правильное выражение)? В чем заключается определение
электроотрицательности по Малликечу? В чем принципиальное отличие шкалы
Малликена от шкалы Полинга? Почему можно считать, что шкалы Полинга
и Малликена связаны между собой? Какие вклады в энергию молекулы при
этом не учитываются?
Рекомендуемые источники. См. разд. 5.8 в кн. Коулсона [105] и разд. 2.11
в кн. Полинга [313], где детально обсуждаются роль и определение электро-
отрицательностей. Анализ Малликена см. в работах Малликена [296] и Моф-
фитта [285].
ЭРМИТОВЫ ОПЕРАТОРЫ. Оператор Q является
эрмитовым, если интеграл \ dxf*Qg равен интегралу \ dx(Qf)* g. В ди-
раковских скобочных обозначениях это требование имеет вид
(/|Q|g) = (g|Q|/)*. Эрмитовы операторы важны в квантовой
теории потому, что их собственные значения вещественны;
операторы, соответствующие наблюдаемым физическим величинам,
должны быть эрмитовыми. Другим следствием эрмитовости
является ортогональность собственных функций, соответствующих
различным собственным значениям эрмитовых операторов.
Упражнения. 1. Что означает термин «эрмитовость»? Какие свойства
вытекают из эрмитовости оператора и почему эрмитовы операторы важны в
квантовой механике? Является ли эрмитовым оператор «умножение на х»и
оператор d/dx, оператор (ft/i)(d/dx)? (При исследовании эрмитовости
оператора d/dx используйте интегрирование по частям и то свойство, что функции
/ и g на достаточно больших расстояниях обращаются в нуль.) Какие из
этих операторов могут соответствовать наблюдаемым физическим величинам
и каким?
2. Докажите, что собственные значения эрмитовых операторов
вещественны и что собственные функции, соответствующие различным собственным
значениям, ортогональны. Докажите справедливость этих выводов применительно
к оператору tz = (h/i)(d/d(p)> используемому в теории углового момента.
Рекомендуемые источники. Обсуждение эрмитовости операторов, ее
следствий и доказательство отмеченных свойств см. в [1], гл. 4. См. также
монографии Дирака [123], фон Неймана [410], Иордана [208] и Джоча [204], где
подробно излагаются квантовомеханические аспекты эрмитовости.
447
я
ЯДЕРНАЯ СТАТИСТИКА. Ядра, как и электроны, и другие
частицы, должны удовлетворять принципу Паули; всякий раз,
когда два эквивалентных ядра меняются местами, знак полной
волновой функции меняется, если эти ядра являются фермиона-
мн, и остается неизменным, если ядра являются бозонами. Это
требование оказывает сильное влияние на вращательные уровни
молекулы, так как вращение молекулы является таким видом
движения, при котором происходит перестановка ядер. Правда,
молекула, вращаясь, увлекает за собой электроны, поэтому
приходится затрачивать много усилий, чтобы отличить эффект
перестановки ядер от других эффектов, сопутствующих вращению
молекулы. Чтобы не усложнять описание, мы обратимся к
молекуле водорода, тем более что на ее примере можно также
увидеть влияние ядерной статистики на термодинамические
свойства газообразного водорода.
Итак, представим себе, что молекула водорода повернулась
на 180°. Ядра при этом поменялись местами, кроме того,
изменились ориентация молекулы и расположение электронов. Из
рис. Я. 1 видно, что вернуть электроны в первоначальное
положение можно просто путем их инверсии относительно центра
молекулы (знак электронной волновой функции основного
состояния Нг при этом не меняется) и последующего отражения их
относительно плоскости вращения молекулы (что также не
меняет знак волновой функции основного состояния Нг).
Взглянув на рисунок, можно убедиться, что такая перестановка
меняет положения ядер, но не меняет состояния электронов.
Теперь проанализируем влияние каждой из рассмотренных
выше операций на волновую функцию молекулы. Эту функцию
можно представить в виде произведения волновых функций
электронного состояния молекулы г|)еь ее колебательного состояния
\|)vib, вращательного состояния \prot и состояния ядер -фпис, о
котором речь пойдет несколько позднее. При повороте молекулы
на 180° вращательная волновая функция меняет знак, если
вращательное квантовое число / является нечетным, и не меняет
знак, если это число является четным (подобно поведению орби-
талей s, /?, d, f, ...). Таким образом, поворот молекулы
приводит к появлению в ее волновой функции множителя (—1)J. На
двух последующих этапах — инверсии и отражения
электронов — в волновой функции молекулы Нг не происходит никаких
изменений (хотя волновые функции других молекул,
находящихся в состояниях, отличных от Sj, могут изменить знак), и
448
я
в результате на стадии Г (рис. ЯЛ) волновая функция меняет
знак как (—1)J. На конечной стадии ориентация спинов ядер
меняется на обратную, что соответствует переходу от Г к Д. Это
означает, что получена первоначальная молекула, у которой
просто изменены обозначения ядер.
Когда происходит перестановка двух протонов, принцип
Паули требует изменения знака полной волновой функции.
Следовательно, цепочка операций А — Б — В — Г — Д должна приво-
Рис. ЯЛ. Операции симметрии, затрагивающие ядра и электроны
двухатомной гомоядерной молекулы.
дить к изменению знака полной волновой функции молекулы.
Пока что было установлено лишь появление множителя (—l)J.
Однако стадия Г -* Д может также менять знак функции, что
связано с возможными спиновыми состояниями двух
эквивалентных протонов: их спины могут быть параллельны либо анти-
параллельны (как и у двух электронов). Волновая функция при
антипараллельной ориентации ядерных спинов имеет следующий
вид: an{a)$n{b)— $n(a)an(b) (см. разд. «Синглетные и триплет-
ные состояния»), и, если ее компоненты ап и рп переставить, она
изменит знак. Параллельной ориентации спинов (ядерный
триплет) отвечают три состояния: ал(а)ап(&)> ап(а)$п(Ь)-\-
+$п(а)ап(Ь), рп(я)Рп(&)> которые при изменении ориентации
не изменяют знака.
Если предположить, что спины протонов в Нг антипараллель-
ны, то стадии Г-> Д отвечает множитель (—1), а полной цепоч-
449
я
ке операций А —Д множитель (—1)/+1. Но поскольку протоны
являются фермионами и волновая функция при переходе от А
к Д должна менять знак, следует заключить, что, если ядерные
спины антипараллельны, молекула может занимать
вращательные состояния только с четными вращательными квантовыми
числами /. При параллельной ориентации ядерных спинов
переход от Г к Д не меняет знака и фактор (—l)J отвечает всей
цепочке переходов от Л к Д. Молекула с параллельными
протонными спинами может занимать состояния только с нечетными
значениями /.
Ограничение на квантовые числа вращательных состояний
молекулы приводят к двум важным эффектам. Во-первых, оно
влияет на вид спектра молекулы: в состоянии теплового
равновесия состояний с нечетными / занято в три раза больше, чем
состояний с четными /, так как возможны гри варианта
взаимной ориентации ядерных спинов в случае нечетных / и только
один вариант их взаимной ориентации для четных значений /.
Возникающее в результате этого чередование интенсивности
линий характерно для вращательной структуры спектра молекул,
содержащих одинаковые ядра. Молекулы водорода в состоянии
со спаренными ядерными спинами (и поэтому четными
значениями /) называют параводородом, а в состоянии с
параллельными ядерными спинами (и соответственно с нечетными
значениями /) — ортоводородом. В условиях теплового равновесия
ортоводорода в любом образце газа в три раза больше, чем
параводорода. Только при самых низких температурах, когда все
молекулы газа стремятся занять самый нижний вращательный
уровень с / = 0, в условиях теплового равновесия образец
содержит исключительно параводород. Различия в
термодинамических свойствах орто- и параводорода, наблюдаемые при низких
температурах, обусловлены различиями в доступных для их
молекул вращательных уровнях энергии.
Установление теплового равновесия может происходить
весьма медленно, так как оно связано с изменением относительной
ориентации ядерных спинов. Чистый параводород при
комнатной температуре очень медленно переходит в смесь орто- и
параводорода, поскольку при этом большому числу спинов придется
изменить свою ориентацию по отношению к спинам их
партнеров с антипараллельной на параллельную. Пара — орто-конвер-
сия водорода ускоряется в присутствии поверхностных
катализаторов, на которых может происходить диссоциация молекул и
последующая рекомбинация атомов со случайными партнерами.
Переход в равновесное состояние ускоряется также в
присутствии парамагнитной молекулы (например кислорода или иона
переходного металла), когда магнитное поле молекулы может
взаимодействовать с протоном, имеющим одну спиновую ориен-
450
я
тацию, сильнее, чем с другим протоном (см. рис. С. 11), что
приводит к изменению взаимной ориентации их спинов.
Ядерные статистические эффекты исчезают при переходе к
изотопически замещенным молекулам, которые уже не имеют
эквивалентных ядер. Молекула HD не проявляет ни одного из
рассмотренных выше свойств. В молекуле D2 мы опять имеем
дело с эквивалентными ядрами, но, поскольку дейтероны
являются бозонами, это накладывает свой отпечаток на
распределение интенсивностей (см. упражнения). Влияние ядерной
статистики на спектры и термодинамические свойства проявляется и
у других молекул, содержащих эквивалентные ядра, например
у О2, HCCH, Н20, СНзСНз, СН4. Хотя анализ этих молекул
сложнее, но в нем используются те же понятия, что и при анализе H2.
Упражнения. 1. На чем основано влияние относительной ориентации
ядерных спинов на вращательные уровни энергии молекул? Влияют ли ядра на
молекулярные энергетические уровни или только на их заселенности? Чем
вызвана необходимость рассмотрения схемы, приведенной на рис. ЯЛ?
Почему, если ядра являются фермионами, состояния с четными / связаны с
антипараллельной ориентацией ядерных спинов, а состояния с нечетными J
связаны с параллельной ориентацией спинов? Как проявляется зависимость
спектральных и термических свойств водорода от ядерной статистики? В чем
состоит смысл классификации молекул водорода на орто- и парасостояния?
Какой из этих двух модификаций при повышенных температурах
соответствует более высокая концентрация в тепловом равновесии? Почему
изменение ориентации ядерных спинов — медленный процесс, можно ли его
ускорить?
2. Рассмотрите молекулу D2 и, учитывая, что спин дейтерона равен 1,
определите, какие ядерные состояния этой молекулы могут быть описаны
четным и нечетным значениями /. Какое состояние этой молекулы является
более устойчивым? Покажите, что при повышенных температурах отношение
числа состояний с четными и нечетными У равно 2:1.
3. Покажите, что отношение числа состояний с четным и нечетным
ядерными спинами в молекуле, содержащей два эквивалентных ядра со спином
/, равно (7+1):/. Предварительно найдите число всевозможных четных и
нечетных комбинаций состояний 1та1ть.
Рекомендуемые источники. Дальнейшее обсуждение и вывод общего
правила см. в [1], гл. 10. Этот же вопрос в доступной форме изложен в кн. Саг-
дена и Кеннея [388] и Кинга [222], где рассматривается также влияние
ядерной статистики. Влияние на термодинамические свойства описано
Дэвидсоном [116]. Обсуждение эффектов ядерной статистики в случае более
сложных молекул проведено Таунсом и [Павловым [399].
ЯДЕРНЫЙ МАГНИТНЫЙ РЕЗОНАНС (краткий обзор).
Спектроскопия ядерного магнитного резонанса (ЯМР) основана
на наблюдении поглощения электромагнитного излучения
магнитными ядрами молекул (в частности, протонами) в
присутствии приложенного внешнего магнитного поля.
451
я
В магнитном поле двум ориентациям спина протона отвечают
различные энергии (ориентация а имеет более низкую энергию,
чем р). Переходы, отвечающие изменению ориентации спина,
могут быть вызваны электромагнитным полем соответствующей
резонансной частоты. Типичные спектрометры дают магнитное
поле напряженностью 15 кГс, которое вызывает расщепление
энергетических уровней, соответствующее частоте 60 МГц.
Новейшие приборы дают магнитное поле напряженностью 50 кГс,
которому соответствует частота излучения порядка 200 МГц. Эти
цифры показывают, что ЯМР является разновидностью
радиоспектроскопии. Обычно при проведении эксперимента на
образец воздействуют излучением с фиксированной радиочастотой, а
напряженность магнитного поля изменяют до тех пор, пока не
наступит наиболее сильное поглощение высокочастотного
излучения. Это и есть условие резонанса. Типичный спектр показан
на рис. Я.2.
Из спектров ЯМР извлекают следующую информацию.
1. Положение резонанса. Протоны в различном химическом
окружении резонируют при различных напряженностях
приложенного магнитного поля — это называется химическим сдвигом
резонанса. Внешнее поле индуцирует в молекуле локальные
поля, и ядра испытывают влияние результирующего поля.
Внешнее поле индуцирует различные поля в химических группах
разного типа, и при фиксированной радиочастоте резонанс протонов
в этих группах наблюдается при различных значениях
напряженности приложенного поля. Более подробно об этом сказано
в разд. «Химический сдвиг». Простейший пример использования
данных о химических сдвигах — распознавание групп различных
типов в неизвестных молекулах (см. рис. Я. 2).
2. Тонкая структура спектра. При высоком разрешении
наблюдается тонкая структура линий в спектре ЯМР. Она
обусловлена спин-спиновым взаимодействием магнитных ядер. В
первом приближении можно считать, что влияние магнитных
моментов других ядер приводит к изменению локального
магнитного поля интересующего нас ядра. Спектроскопически это
проявляется как зависимость резонансного значения
приложенного поля от ориентации спинов соседних ядер. Спин-спиновое
взаимодействие в группе магнитно-эквивалентных ядер (т. е. в
группе ядер с одинаковым химическим сдвигом) может быть
большим, хотя из-за наличия определенных правил отбора это
и не проявляется в спектре. Если спин-спиновое взаимодействие
и химический сдвиг сравнимы по величине, спектр может
принимать очень сложный вид, если же они заметно отличаются друг
от друга, интерпретация спектра оказывается довольно простой
(рис. Я. 2). Исследование тонкой структуры спектров ЯМР яв-
452
я
ляется превосходным средством идентификации неизвестных
молекул и исследования молекулярной структуры.
3. Ширина и форма линий. Форма линий и особенно их
ширина при исследованиях растворов определяются процессами
релаксации. Эти процессы рассмотрены в разд. «Электронный
парамагнитный резонанс». Те же эффекты возникают и в ЯМР, но,
поскольку ядерный магнитный момент приблизительно в 2000 раз
Рис. Я.2. Структура спектра ЯМР (ацетальдегида). Звездочками помечены
протоны, ответственные за возникновение резонансных линий.
меньше, чем электронный спиновый магнитный момент, его
взаимодействие с окружающей средой оказывается весьма слабым,
а время релаксации соответственно очень большим (и это
определяет значительно меньшую ширину линий). Тем не менее
определение ширины линий ЯМР и времени релаксации играет
важную роль в исследовании молекулярного движения в жидких
растворах. Важную роль играет оно и в исследованиях таких
явлений, как таутомерия и протонный обмен. Форма линии
сильно зависит от процессов, происходящих за время, характерное
для переходов в ЯМР. Если какой-либо процесс изменяет
химический сдвиг ядра (например, если протон колеблется между
двумя неэквивалентными окружениями), линия имеет
наибольшую ширину в том случае, когда частота этого движения
453
я
оказывается сопоставимой с разностью частот двух
резонансных положений.
Рекомендуемые источники. См. разд. «Химический сдвиг» и
«Спин-спиновое взаимодействие». Магнитные моменты ядер приведены в табл. 17.
Описание метода ЯМР и его применений можно найти в кн. Мак-Лечлана
«Магнитный резонанс» [2]. Этот же вопрос, но в более доступной форме
излагается в кн. Линден-Белла и Харриса [260], Джекмана [199], Робертса [339],
Керрингтона и Мак-Лечлана [90]. Гораздо более детально он рассмотрен в
кн. Попла, Шнейдера и Бернстейна [323], Эмсли, Финнея и Сатклиффа [134],
Сликтера [376] и Абрагама [27]. Последние достижения в области ЯМР
освещаются в сборниках «Advances in magnetic resonance», «Progress in nuclear
magnetic resonance spectroscopy», «Annual review of n. m. r. spectroscopy» и
в «Specialist periodical reports of the Chemical Society». Исследование
кинетических процессов с помощью ЯМР описано, в частности, в гл. 12 кн.
Керрингтона и Мак-Лечлана [90].
ЯНА —ТЕЛЛЕРА ЭФФЕКТ. Для тех, кто уверен, что
природа стремится к состояниям с высшей симметрией, теорема
Яна — Теллера покажется горькой пилюлей. Она утверждает,
что в ряде случаев молекулам с высокой симметрией присуща
внутренняя неустойчивость и они способны понизить свою
энергию, переходя в конфигурацию с более низкой симметрией. В
более точной формулировке теорема утверждает, что вырожденное
электронное состояние нелинейной молекулы не может быть
устойчивым. Поэтому если результаты расчетов показывают, что
основное состояние молекулы вырождено, то рассматриваемая
форма этой молекулы является неустойчивой, а ее естественное
состояние — менее симметричная форма, в которой отсутствует
вырождение. Эта теорема не распространяется на линейные
молекулы, которые могут существовать в симметричных
вырожденных состояниях, однако для них существует аналогичный эффект
более высокого порядка, называемый эффектом Реннера —
Теллера.
Рассмотрим эффект Яна — Теллера на примере комплексного
иона Си2+ с октаэдрическим расположением лигандов.
Исследование его электронного строения в рамках теории
кристаллического поля показывает, что он имеет конфигурацию t*e6. Эта
конфигурация является вырожденной, так как состояние dl*dx*-y* и
d%-ytdZi характеризуются одинаковой энергией. Поскольку
комплексный ион имеет нелинейное строение, согласно теореме
Яна — Теллера, вырождение должно сниматься в результате
искажения координационного многогранника.
Чтобы понять физические причины этого явления, следует
рассмотреть силы, действующие на лиганды. В состоянии
d%dx*-y* электронная плотность в направлении оси z выше, чем
в экваториальной плоскости, а в состоянии dx*-y*dzi наоборот.
В первом случае лиганды, расположенные вдоль оси г, стре-
454
я
мятся сместиться от центрального иона, а экваториальные ли-
ганды стремятся сместиться к центру*. Во втором случае
направления смещения противоположны. Если же комплекс
деформируется, вытянувшись вдоль оси г, электронная конфигурация
dlidxt-yt будет иметь более низкую энергию, чем другая
электронная конфигурация при том же расположении лигандов
(рис. Я. 3, а). Если же произойдет сжатие комплекса вдоль
Рис. Я.З. Влияние растяжения (а) и сжатия (б) октаэдра на энергию
электронов на dZi- и ^..^-орбиталях
оси г, то более низкая энергия будет соответствовать второй
конфигурации (рис. Я. 3, б). Следовательно, как мы сами убедились,
возможны такие искажения молекулы, которые снимают
вырождение электронных состояний, поэтому следует ожидать, что
молекула окажется либо вытянутой, либо сжатой. (Что произойдет
в действительности, предсказать трудно.)
Можно заранее указать несколько электронных
конфигураций, способных привести к искажениям ян-теллеровского типа в
октаэдрических комплексах. Чтобы найти их, следует просто
отобрать такие случаи, когда могут возникнуть вырожденные
конфигурации. Вырожденными являются высокоспиновая
конфигурация dk (t3el)f низкоспиновая конфигурация d7 (/6е*), а также
* Имеются в виду отрицательно заряженные лиганды, иначе картина
оказывается противоположной. — Прим. ред.
455
я
конфигурация d? (t6e6), в которых один электрон либо дырка
должны занимать одну из двух вырожденных е-орбиталей (dz*
или djt*-*/*). В качестве примеров можно привести ионы Cu2+(d9)
и Cr2+(d4), соединения которых часто имеют близко родственные
искаженные структуры; Mn3+ (d4), Co2+ (d7, редко
встречающаяся низкоспиновая конфигурация); Ni3+ (d7, низкоспиновая
конфигурация) и Ag2+ (d9). Искажений ян-теллеровского типа не
следует ожидать для конфигураций d3, d5 (высокоспиновая), d6
(низкоспиновая) или d8. Эффект Яна — Теллера мог бы
проявиться для конфигураций с вырождением на /-орбиталях, таких,
как d1, d2, d6 (высокоспиновая) и d7 (высокоспиновая). Однако в
действительности /-орбитали направлены между осями связей
металл — лиганд, а не вдоль этих осей, и поэтому их неравное
заселение электронами не приводит к заметным искажениям.
Конфигурацию d8 необходимо рассмотреть особо. В этом
случае малых искажений ожидать не следует: или их нет вообще,
или они большие. Объясняется это следующим. Чтобы спины
электронов в соответствии с правилом Гунда были
параллельными, один электрон должен занимать d^-орбиталь, другой —
djc«_r/2. При малых искажениях энергия одного электрона
возрастает, а другого — убывает, так что в целом энергия иона не
меняется. Однако при большом искажении разность энергий
d2a- и d^-r/2-орбиталей может превысить энергию, которую
требуется затратить, чтобы поместить оба электрона на одну из этих
орбиталей (т.е. нарушить первое правило Гунда). Строго
говоря, этот эффект не является эффектом Яна — Теллера,
поскольку он не снимает вырождение системы.
Анализ эффекта Яна — Теллера усложняется присутствием
двух других эффектов. Один из них, динамический эффект
Яна — Теллера, обусловлен движением молекулы; вырождение
может наступить при определенных конформациях ядер. Второй
связан со спин-орбитальным взаимодействием, которое, как
правило, уменьшает величину эффекта Яна — Теллера.
Экспериментальное определение искажения Яна — Теллера в чистом виде —
весьма трудная задача, так как существуют и другие причины,
приводящие к искажению комплексов. Одна из таких трудностей
связана с учетом искажений, обусловленных требованиями
упаковки при образовании кристалла.
Упражнения. О чем говорит теорема Яна —Теллера? На какие молекулы
она не распространяется? Что следует из нее в том случае, когда расчет
предсказывает существование молекулы в вырожденном состоянии?
Объясните содержание теоремы в рамках представлений теории кристаллического
поля для комплексов переходных металлов. Почему искажение октаэдриче-
ского комплекса может приводить к уменьшению его энергии? Каким числом
электронов должен обладать такой комплекс, чтобы к нему можно было при-
456
я
менить рассматриваемый подход? Почему эффект Яна — Теллера играет
гораздо менее важную роль в тетраэдрических комплексах? В чем состоит
особенность конфигурации центрального иона dbJ Какие существуют методы
обнаружения эффекта Яна — Теллера и с чем связаны возникающие при этом
затруднения? При каких условиях необходимо учитывать динамический
эффект Яна — Теллера? Как объясняется эффект Яна — Теллера в рамках
теории поля лигандов (теории молекулярных орбиталей)?
Рекомендуемые источники. См. гл. 10 [1]. Популярное объяснение эффекта
Яна —Теллера см. в разд. 4.2 кн. Оргела [308] и кн. Коулсона [105].
Несложное математическое описание эффекта приведено в разд. 8 кн. Бальхаузена
[49], полное и интересное обсуждение спектроскопических явлений, связанных
с эффектом, дано в разд. 1.2 кн. Герцберга [188]. Оба эффекта —
статистический и динамический — обсуждаются в кн. Энглмана [136]. Простые примеры
даны на стр. 45 кн. Герцберга [188] и на стр. 194 кн. Бальхаузена [49].
J
Буква / используется в квантовой теории для обозначения
самых разнообразных величин, но обычно благодаря контексту
это не приводит к недоразумениям. Буквами / и / обозначаются
квантовые числа полного углового момента системы: заглавная
применяется для многоэлектронных систем или для описания
вращения молекулы как единого целого, а строчная—для
описания отдельных частиц. Буквами / и / обозначают термы и их
энергетические уровни. Буква / используется также для
обозначения констант спин-спинового взаимодействия в ЯМР и, кроме
того, для обозначения кулоновских интегралов
электростатического взаимодействия электронов. Наконец, буквы / и /
используют для обозначения всевозможных токов, будь это
электронные токи, индуцируемые внешними полями в металлах, атомах
и молекулах, или потоки вещества, тепла и энтропии.
457
Таблицы
Таблица 1
Физические свойства бензола
Длина связи С—С
Длина связи С—Н
Энтальпия образования
Энергия резонанса
Первый потенциал
ионизации
Поляризуемость
Показатель преломления
(20 °С, D-линия)
Относительная
диэлектрическая проницаемость
(20 °С)
Магнитная восприимчивость
Полосы поглощения
139,7 пм (1.397А)
108,4 пм (1.084А)
AHf. 83,2 кДж-моль-1 (19,820 ккал-моль-1)
150 кДж'Моль-1 (36.0 ккал-моль-1)
9,24 эВ
а„ = 6,35-10~24 см3 (6,67-10"41 Ф-м~2)
ах = 12,31 • Ю-24 см3 (10,89.10""41 Ф • м~2)
аау = 10,32.10"24 см3 (9,13 • 1<Г41 Ф. м"2)
1,5011
е, = 2,284
%ц 3,49. JO"5
Xj. = -9,46.10-S
Xav = ^7,47.10-S
6,8 эВ (Alg->Elu); 6,0 эВ (Alg->E2g)
6,0 эВ (Alg->Blu?); 4,9 эВ (Alg~>B2u)
Корреляции порядка и длины связи а
Таблица 2
Углеводород
Связь
Порядок
л-связи
Длина связи,
пм
Этилен
Бензол
Нафталин
Антрацен
Графит
1,2
2,3
1,9
9,10
1,2
2,3
1,9а
9,9а
4а, 9а
1,0
0,667
0,725
.0,603
0,554
0,518
0,738
0,586
0,535
0,606
0,485
0,535
133.5
139,7
136,5
140,4
142,5
139,3
137,0
140,8
142,3
139,6
143,6
142,1
Более полную информацию по этому вопросу можно найти в кн. Стрейт-
визера 1387] и Доделя, Лефевра и Мозера [115].
458
Таблицы
5s> Н Н ^
О
о*
&
а
X
ч
8,
d*
ш
I I
I I
S
" N - N
< < п п
ь
со
О
щ
Е
> Е
и S2
n с.
5Si
+
О?
Н
~* О
I
< < w
Ь
Ь
и*
О
Щ
-• о
I
,- Р-И О
I I
Ё
*!
< <С Я OQ Щ
459
Таблицы
о
со
О
I
счю
и
сч
и"
сч
Щ
,$
О
°i. ^
N ТГ *
N
N ^ N* 1
^ * ?S>
+ н|
* ч
а>
Of
* 1
*
N*S
S>
* 1
*
~ *т О О
1
S: &
2 ^
•^ —• ,л «°
Я о
о
сч <*
"~8§
о
<* сч
~ ~ сч сч
-* е* ~ м
1 < < w ы I
8
00
00
То
о
со
>
ь
со
О
6°
сч
СО
СЧ
Ш
^
l US
N
+
| | |
1 1
| , |
1
""I
1
< < с5
,
|
i
т
!
-
0Q
1з>
N 1
*
S
^
£
о о
о о
сч сч
1
1 1
1
сч сч
щ Щ 1
и
сч
Щ
+
N
* I
N С£
?с£
5fc
— —. О
I
О О
8-8-8-
ГГсч со
— ~ сч сч сч
г* 5» -« w «
< < ы ы ы
460
Таблицы
*8
si
I
сч
U
со
<NCO
и
rt*
о"
щ
1 "~**
со
1 н^
+
м
+
с»
_^
•^
-
-
<
^^
М
5fc
1
н
1
м
5fc
1
м
<-* »-^
% »
• ъ
—
W
'n4
^
N
5s>
is
QC
r-m 1
1
О
о
со
H 1
Си
х
и
со
те
CD
J*
со
со
00
Щ
Зт)
1 Г4 >w*
сч " |
I
1
N * М
4- *Ч
5Л | Н \
CN,
3
*iS
~707~
i i
i i
^ ^ ^ о о
1
- - <N СО СО
< < ы н н 1
ч с^
CD
те
CD
со
1 со
00
щ
со
1 OS
"-^ 1
^
+ * *
"^ Ч* **> \
* 7 М
CN
3
^
£>
^
^
^
iS
~7°7 ~
_ ^ о ~ —
1 1
^ ^ ^
1 1
~ -« ~ о о
1
~ ~ см со со
< < Ы Н Н |
461
Таблицы
Таблица 4
Химические сдвиги в т-шкале для некоторых молекул
сн3со2н*
сн3сн*о
СбНб
п-сбн;(сн3)2
с8н8
С2Н4
Н2О(0°С)
н2
сбн5осн;
-1,37
0,20
2,73
3,05
4,31
4,68
4,68
5,66
6,27
сн3*он
CfiHeCHnCHe
С6Н5СН3
сн*сно
СН31
СНзСОСНз
сн*со2н
CHgCN
С2Н2
6,62
7,38
7,66
7,80
7,84
7,91
7,93
8,03
8,51
C6Hi2
СгНб
Н20 (пар)
сн4
Si(CH3)4
HCI
НВг
HI
8,56
9,11
9,26
9,86
10,00
10,31
14,21
23,11
Цвет, частота и энергия света'
Таблица 5
Цвет
Длина
волны,
нм
Частота,
Гц
Волновое
число,
см"'
Энергия
эВ кДж'Моль ккал'моль
Инфракрасный
Красный
Оранжевый
Желтый
Зеленый
Синий
Фиолетовый
Близкий
ультрафиолетовый
Далекий
ультрафиолетовый
1000
700
620
580
530
470
420
300
200
3,00-1014
4,28
4,84
5,17
5,66
6,38
7,14
1,00-1015
1,50
1,00 -104
1,43
1,61
1,72
1,89
2,13
2,38
3,33
5,00
1,23
1,77
2,00
2,14
2,34
2,63
2,95
4,15
6,22
120
171
193
206
226
254
285
400
600
28,5
40,8
46,1
49,3
53,9
60,8
68,1
95,7
143
Переработка данных из книги Калверта и Питса [88].
Дипольные моменты (D)
Таблица 6
NH3
Н20
HF
НС1
НВг
HI
HCN
N02
N20
S02
СО
1,47
1,85
1,91
1,08
0,80
0,42
3,0
0,32
0,17
1,59
0,10
СНС13
CH2CI2
СН3С1
СНзОН
СНдСНО
СНзОСНз
СН3СН2ОН
СбНбСНз
о-СбН4(СНз)г
СбН5С1
СбН5Вг
0-C6H4CI2
,w-C6H4Cl2
1,01
1,57
1,87
1,71
2,72
1,30
1,68
0,36
0,62
1,57
1,70
2,25
1,72
Н
Li
Na
К
2,1
1,0
0,9
0
462
Таблицы
Таблица 7
Электроотрицательность по Полингуа
н
2,1
Li
1,0
Na
0,9
К
0,8
Rb
0,8
Cs
0,8
Be
1,5
Mg
1,3
В
2,0
Al
1,6
С
2,6
Si
1,9
Ge
2,0
N
3,0
P
2,2
As
2,2
О
3,4
S
2,6
Se
2,6
F
4,0
CI
3,2
Br
3,0
I
2,7
Дипольный момент, D: М-ав^5Сд "" 5Св*
Ионный характер связи, %: 16 | %к — %в | + 3,5 | %А — %в [2.
Энергия ионно-ковалентного резонанса, эВ: Д«0СА — %в)2.
Шкала Малликена МА — Мв = 2,78 (%А — %в),
Ма = '/2(/а + £а)-
а Полная сводка значений электроотрицательности по Полингу
и Малликену дана в книге Коттона и Уилкинсона [102].
Таблица 8
Силы осциллятора и молярные коэффициенты
экстинкции
ПеРеходы f сы-'.дГ'.моль-1
Разрешенные электрические дипольные
Разрешенные магнитные дипольные
Разрешенные электрические
польные
Запрещенные по спину
Запрещенные по четности
Примеры:
я->я* С=С
С=С—С=С
п -> я* С=0
N=N
с=с—с=о
N=0
эльные 1
:ые 10"5
квадру- 10"7
ю-5
ю-1
^макс> нм
180
220
280
350
320
660
10<-105
Ю-2-10
кг^-кг1
Ю-"2-10
103
е,
— 1 3
см • дм «моль
10000
20000
20
100
100
10
463
Таблица 9
Сверхтонкие поля и спин-орбитальное взаимодействие в некоторых атомах а
&
п
1
2
3
4
Изотоп
2Н
6Li
7Li
9Ве
юв
ПВ
1зс
14N
15N
17Q
19р
Зф
33S
35Cl
37С1
39К
4,К
79Вг
81Вг
Естественное
содержание
изотопа, %
99,9844
0,0156
7,43
92,57
100
18,83
81,17
1,108
99,635
0,365
0,037
100
100
0,74
75,4
24,6
93,08
6,91
50,57
49,43
Спин
Vt
1
1
72
3/2
3
8/2
!/2
1
V2
5/2
Vt
Vt
3/2
3/2
3/2
3/2
8/2
8/2
3/2
1 *ns <0) I2' ат* еЛ*
0,1673
0,5704
1,408
2,767
4,770
7,638
11,966
5,6251
7,9187
10,6435
19,4127
<г~\р' ат- ед
0,775
1,692
3,101
4,974
7,546
3,3187
4,8140
6,7095
11,8758
Константа
изотропного
взаимодействия,
Гс
508
78
39
105
130
242
725
ИЗО
552
775
1660
17200
3 640
975
1680
1395
83
45
7800
8400
Константа
анизотропного
взаимодействия,
Гс
38
66
34
48
104
1084
206
56
100
84
456
564
смЬ
0,2
1
11
29
76
151
270
299
382
586
38
2 460
1 Данные Эткинса и Саймонса [39] н Мортона, Роландса и Уиффена [290].
Таблицы
Таблица 10
Свойства некоторых двухатомных молекул'
Молекула
Частота
колебаний»
Длина связи,
пм
Вращательная
постоянная,
см~"
Энергия
диссоциации,
эВ
Силовая
постоянная»
Н-м-1
Вг2 (79Вг81Вг)
12С2
35С12
12C16Q
19F2
lH2
2Н2
JHBr
ХН38С1
lH19p
1H127J
l27I2
"N2
,602
a Эти молеку
берга [187].
323,2
1641,35
564,9
2170,21
892,1
4395,2
3118,4
2649,67
2989,74
4138,52
2309,5
214,57
2359,61
1580,361
лы отобраны из
228,3
131,17
198,8
112,81
143,5
74,16
74,16
141,3
127,460
91,71
160,4
266,6
109,4
0,08091
1,6326
0,2438
1,9313
60,809
30,429
8,473
10,5909
20,939
6,551
0,03735
2,010
120,739 1,44566
более подробного списка,
1,971
3,6
2,475
11,108 (?)
<2,75
4,476
4,553
3,75
4,430
<6,40
3,056
1,5417
' 9,756
5,080
приведенного в
245,8
952,1
328,6
1902
718,6
573,4
576,8
411,6
515,7
965,5
314,1
172,1
2296
1177
книге Герц-
Таблица 11
Полиномы Эрмита и волновые функций осциллятора
Гармонический осциллятор: масса т, силовая постоянная k
Уравнение Шредингера
1
энергии
- (Ъ2/2пг) d2 ф (x)/dx* + у кхЦ (х) = £<ф (*);
волновые функции
*W-(2^)**(»ep(-tW'
рде а ==*moo/fi, £ = V(w<*>o/fi) x =*a^xf #v (£) — полиномы Эрмита.
465
Таблицы
Таблица II (продолжение)
Свойства полиномов Эрмита:
#v(£) удовлетворяет соотношению
#;'($)-2Stf;(?) + 2v#v(?) = 0.
Формула Родригеса
#v(S) = (-l)vexp?2-^exp (-?*).
Рекуррентные соотношения
Я;(?) = 2гЯ^1(?),
2yyv(t)-tfv+i(t) + 2vtfv-i(».
Интегралы
оо
если v Ф v'
если v = v ,
В явном виде:
Я0(?) = 1
Я,(?)-»2?
Я2(?) = 4?2-2
Я3(?) = 8?'-12?
Я«(?) = 16?*-48?2 + 12
Я5(?) = 32?«-160?* + 120?
Яв (?) =■ 64?в - 480?< + 720?2 - 120
Я7 (?) = 128?' - 1 344?* + 3 360?3 - 1 680?
Я, (?) — 256?8 - 3 584?» + 13 440?« - 13 440?2 + 1 680
Таблица 12
Температура Дебая
eD. к
Li
Na
К
Rb
Cs
С (алмаз)
NaCl
КС1
KBr
CaF2
344
156
91,1
55,5
39,5
2230
321
230
177
570
для некоторых твердых веществ
eD, к
Си
Ar
Аи
343
226
162
eD. к
А1
Ti
Hg
428
420
71,9
466
Таблицы
Таблица 13
Гибридные орбитали
национное
число
Форма молекулы
Гибридизация
Линейная
Изогнутая
Треугольная плоская
Несимметричная плоская
Тригональная пирамидальная
Тетраэдрическая
Неправильный тетраэдр
Тетрагональная пирамида
Бипирамидальная
Тетрагональная пирамида
Плоская пентагональная
Пентагональная пирамида
Октаэдрическая
Тригональная призма
Тригональная антипризма
sp, dp
р2, ds, d2
sp2, dp2, ds2, d%
dsp
p\ d2p
sp8, d*s
d2sp, dp\ d%p
d*
dsp3, d*sp
d2sp2, d*s, d2p%, d*p
dzp2
d*
d2sp*
d4sp, dbp
d*p*
Таблица 14
Присоединенные полиномы и функции Лагерра
Дифференциальное уравнение Лагерра имеет следующий вид:
х (d2f/dx2) + (1 - х) (df/dx) + nf « О,
где п — неотрицательное целое число. Решениями этого уравнения являются
полиномы Лагерра Ln (х),
п
Ln (,) - (-1)» £ (■*=}£) ( (^7Г)2 *""' - е* WW Л-.
Присоединенные полиномы Лагерра и величины Ln (x) связаны процедурой
дифференцирования:
L*(x)-dhLn(x)ld*
и удовлетворяют уравнению
х (d2f/dx2) + (k + 1 - х) (df/dx) + (ц - *) f - 0.
Присоединенные функции Лагерра связаны с величинами L%(x) следующим
соотношением: t , ^ % t
S\ (x) = е" VaVA^-^L* (x)
и удовлетворяют уравнению
х (d'f/dx2) + 2(df/dx) + [п - «/я (k - 1) - 'Л* - (k2 - 1)/4*1 f = 0.
Нормированная радиальная часть волновой функции атома водорода имеет вид
«-и-{(£)'(*йт*)}*«»,<*
где p = 2Zr/na0. ^ ,„
Эти волновые функции приведены в табл. 16.
467
Таблицы
Волновые функции атома водорода
Таблица 15
Общий вид:
+»/m^^V)-J?(|l(r)K|lI,(ftq.).
где часть Rni(r) пропорциональна присоединенным функциям Лагерра (см.
табл. 14) и Yim(Q, <p) — сферические гармоники (см. табл. 23).
Конкретный вид радиальных волновых функций (p = 2Zr/na0)
,2е-Р/2
Is:
2s:
2р:
3s:
Зр:
3d:
4s:
4р:
Ad:
4f:
R,o(r) = (Z/a0)
Ri0 (r) = (Z/a0)'
*„(r)-.(Z/a,)'
Язо (r) = (Z/a„)!
*«(»*)-(Z/аоУ
Rsi (r) — (Z/ao)
R,o (r) = (Z/a0)3'
#41 (r) = (Z/a0j
#42 (r) = (Z/a0)
/?43(r)-(Z/a0y
41/eV3)(6-6p + p2)e-Pe
4'/9V6)(4-p)pe-B'2
(•/eV3^)pV/2
4,/e6)(24-36p+12p2-p3)e-P/2
'* (7з2 VT5") (20 - Юр + p2) pe-P'2
''(VoeVsKe-pjpV/2
('/e6V35)p3e-p/2
Атом водорода
Таблица 16
Серия Бальмера:
Серия Пашена:
Серия Брэккета:
Серия Пфунда:
Серия Хэмфри:
Экспериментальные данные
Спектральные линии (К, нм):
Серия Лаймана: 121,567 (а). 102,572 (р), 97,253 (у), ..., 91,15
656,28(а), 486,13 (Р), 434,05 (у), ..., 364.6
1875.1, 1281,8, 1093,8, ..., 820,4
4051.2, 2625,1, ..., 1458,4
7451,2, ..., 2278,8
12 368, ..., 3281,4
Потенциал ионизации: 1,097 • 105 см"1, 13,60 эВ.
Сродство к электрону: 0,77 эВ.
Лэмбовский сдвиг (2S1/2 — 2Р1/г): 1,058 ГГц
Сверхтонкое взаимодействие (контактное взаимодействие
1420,4 МГц
Поляризуемость (основное состояние): 4,5aJ, 8,7 «10""31 м3
Диамагнитная восприимчивость (основное состояние): —3,97 • 10~в
Ковалентный радиус: 30 пм (0,30 А)
Электроотрицательность (по Полингу): %\
Ферми):
468
Таблицы
Таблица 16 (продолжение)
Теоретические данные
Гамильтониан атома: # = — (Ь2/2ц) V2 — е2/4яеоГ.
Энергия состояния с квантовыми числами nt U m.
п1щ~ \~&ЯфГ)1?—Т
где «el, 2, 3, .•.; /==0, 1, 2, ..., л — 1; m^U I — 1. .••, — J. ц
(приведенная масса) = rnempj{me + тр) и #н — постоянная Ридберга.
Степень вырождения состояний с энергией — /?н/я2 : п2
Волновые функции %lm (г, 9, ф) -■ Rnl (г) Yы (9, ф).
Угловые функции — сферические гармоники, показаны в табл. 23;
радиальные функции являются присоединенными функциями Лагерра
Kl(r)tte-oloplL»Zt{p\
где р s=s 2Zr/na0 и L (р) — присоединенный полином Лагерра. Аналитический
вид радиальных функций и их нормировка приведены в табл. 14 и 15.
Ожидаемые величины и прочие данные
Средние радиусы:
w-(eie./z){i+i(i-iiy^)}
(r-l)=*Z/a0n2
<r-3> _(Z/oo)e/A (/+!)(/ + !)
Наиболее вероятный радиус (основное состояние): а0 (боровский радиус
5,2917715- КГ11 м).
Параметр спин-орбитальной связи:
П-2г ш( zV V * V, a2^/?M»-2
"' V 8ne0mlc*al J \ n3l (I + •/,) (J + 1) J A (I + >/,) (/ + 1)'
где о — постоянная тонкой структуры.
Вероятность нахождения электрона в ядре:
Изотоп Естественное
(* радиоактивный) содержание, %
1П*
'Н
2Н
зн*
6Li
7Li
9Ве
юв
"В
13£
$ ,4N
О 15N
17Q
wp
22Na*
23Na
Зф
33 s
35S*
35CI
36(31*
37CI
39K
40K*
4,K
48 Ca
7*>Br
8,Br
99,9844
1,56-10*"2
7,43
92,57
100
18,83
81,17
1,108
99,635
0,365
3,7-10-2
100
100
100
0,74
75,4
24,6
93,08
1,19-10-2
6,91
0,13
50,57
49,43
Спиновые свойства некоторых ядер
Таблица 17
Спин
Магнитный
момент (им)
Электрический
квадрупольный момент
Частота ЯМР
при 10 кГс, МГц
Чг
Чг
1
1
Чг
"/2
3/2
3/2
2
3/2
4
3/2
У2
3/2
-1,9130
2,79270
0,85738
2,9788
0,82191
3,2560
-1,1774
1,8006
2,6880
0,70216
0,40357
—0,28304
—1,8930
2,6273
1,745
2,2161
1,1305
0,64274
1,00
0,82089
1,2838
0,68329
0,39094
-1,294
0,21453
-1,3153
2,0990
2,2626
2,77.10*"
4,6-10*"
—4,2.10**
2.10"
0,111
3,55.10""
2.10*"2
—4-10
-3
?
0,1
-6,4-10"
4,5-10"
-7,97-10"
-1,68.10"
—6,21 • 10"
?
?
?
?
0,33
0,28
29,165
42,577
6,536
45,414
6,265
16,547
5,983
4,575
13,660
10,705
3,076
4,315
5,772
40,055
4,434
11,262
17,235
3,266
5,08
4,172
4,893
3,472
1,987
2,470
1,092
2,865
10,667
11,498
Таблицы
Первый и второй потенциалы ионизации (в эВ)
для некоторых элементов
Таблица 18
н
13.599
—
Li
5,392
75,641
Na
5,139
47,29
К
4,341
31,81
Be
9,323
18,211
Mg
7,646
15,035
Са
6,113
11,872
В
8,298
25,156
А1
5,986
18,828
С
11,260
24,383
Si
8,152
16,346
N
14,53
29,602
Р
10,487
19,72
О
13,618
35,118
S
10,360
23,4
F
17,423
34,98
С1
12,967
23,80
Вг
11.814
21,6
Не
24,588
54,418
Ne
21.565
40,964
Аг
15.760
27,62
Кг
14,000
24,56
Некоторые лазерные системы
Таблица 19
К, нм
Мощность
Тип действия и продолжительность
импульса
Газовые лазеры
He-Ne
Ne
Ar
Кг
Хе
Н2
N2
со2
Твердотельные
лазеры
Рубиновый
Nd3+ : YAQ
GaAs
InAs
632,8
1084
1 152
3 391
540,1
488,0
514,5
457,9
465,8
472,7
476,5
496,5
647,1
568,2
520,8
476,2
170,0
116,0
337 1
10 600 (10,6 мкм)
694,3
100 мВт
10 мВт
20 мВт
10 мВт
10 кВт
10 Вт
500 мВт
40 мВт
100 мВт
100 мВт
5 Вт
50 мВт
50 мВт
25 мВт
0,2 МВт
1 кВт
400 кВт
1бГВт
0600
905,0
845,0
3150
16ГВТ
300 Вт
10 МВт
10 МВт
60 Вт
1 Вт
50 мВт
Непрерывный
Импульсный (3 не)
Непрерывный
»
»
»
»
»
»
Импульсный (10 не)
Непрерывный
В обычном импульсном
режиме (1 мс)
С модуляцией добротности
(10-20 не)
В режиме «запирания моды» (Юпс)
Непрерывный
В режиме «запирания моды» (1 пс)
С модуляцией добротности (10 не)
Импульсный (200 не)
Импульсный (2 мке)
Импульсный (2 не)
471
Таблицу
Уравнения Максвелла
Таблица 20
Обозначения:
•).
Е — напряженность электрического поля (В • м-
Н — напряженность магнитного поля (А -м-1)»
D — электрическое смещение (Кл • м-2),
В — магнитная индукция, плотность потока (Т или Вб • м~2),
р — плотность заряда (Кл • м~3),
J — плотность тока (А • м~2).
Величины D и В могут быть связаны с Е и Н с помощью поляризации Р и
намагниченности М:
D = 60Е + Р,
Уравнения Максвелла
В «в ц0И + \х0М 0А0ео = с-2).
V.D==p
V.B = 0
V X Е — - dB/dt
VXH=J + dD/d*.
Потенциалы
А — векторный потенциал, ф — скалярный потенциал
B = VXA
Е = - дХ/dt - Vq>
Калибровочное преобразование: если заменить А -> А + V/ и ф -> <р — %jdt
где х — любая дифференцируемая функция, Е и В не изменятся. Когда %
выбирается так, чтобы V.A = 0, получаем кулоновскую калибровку, а если
V.A + (1/c2) (dq>/dt) = 0, получаем калибровку Лоренца.
Атомные слейтеровские орбитали
Таблица 21
Величины 2Эфф я Z — о для s- и р-орбиталей нейтральных атомов элементов
первого, второго и третьего периодов
Н Не
Is 1 1,70
Is
2s, 2р
Is
2s, 2p
3s, 3p
Li
2,70
1,30
Na
10,70
6,85
2,20
Be
3,70
1,95
Mg
11,70
7,85
2,85
В
4,70
2,60
Al
12,70
8,85
3,50
С
5,70
3,25
Si
13,70
9,85
4,15
N
6,70
3,90
P
14,70
10,85
4,80
Сферические гармоники и функции
0
7,70
4,55
S
15,70
11,85
5,45
Лежандра
F Ne
8,70 9,70
5,20 5,85
CI Ar
16,70 17 JO
12,85 13,85
6,10 6,75
Таблица 22
Сферические гармоники Ущ (9. ф) удовлетворяют уравнению
Л2Гш = -/(/+1)У/т ' = 0, Ь 2...
472
Таблицы
Таблица 22 (продолжение)
Разделение переменных:
УшФ. Ф) — В/т (в) Фт (<р)
""'*'-VIST'"*
ft, fffl-f IV» f (2/+l)(/-m)! V/, m
Присоединенные функции Лежандра Pf:
FT w - [(i - «Т/Л.] (-£^r) (*2 - 0'=(i - tf* JL Pl ix).
Функции Лежандра Pf.
P/(*)-(I/t,/l)(-£r)(*,-D'.
Свойства Yim
симметрия:
Ytm (я - в. ф + Я) = (-1)' Ytm (в. ф),
У?т(в.Ч>)-(-,)",1Г|,-т(в.ф).
ортогональность:
я 2я
J dB sin в J <*фУ^ (в, Ф) Yrm> (в, Ф) = bn,bmm,
о о
(6/гбтот/ = 1, если / = /'ит = т'и0в противном случае)
Рекуррентные соотношения для Pf:
(l-m+ \)Pf_x (x) - (2/ + 1) xPf (x) + {l+ m)p;»_, (x) - 0
xP,m(*)-(/- m + I) (1 - х2)'1' P?~X (x) - Pf_x (x) = 0
ЯД., (x) - xPf (x) - (/ + m) (1 - x2)"2 p,""1 (x) = 0
(/ - m + 1) РД., (x) + (1 - x2)''' P^1 (x) - (/ + m + 1) xP,w (x) = 0
(1 - x2)''* РГ+1 (x) - 2/nxP/» (x) + (/ + m) (/ - m + 1) (l - x2)'1' Pf-1 (x) = 0
(1 - xT' (■£-) P? (*) = (* + D xPf (x) - (/ - /n + 1) P?>+1 (x) .
= (l + m)pf_l(x)-lxPf(x).
Интегралы от Pf:
l
J dxP? (x) Pj* (x) - M„, [(/ + m)!/(2/ + 1)(/ - m)!]
-l
r ( Pf(x)Pf(x) 1
3 rf* \ (1-х») } "И/ + '«)'/'«(/-m)l]
473
Таблица 23
Сферические гармоники в декартовых и сферических (полярных) координатах Y 1т
1
0
1
2
3
т
0
0
±1
0
±1
±2
0
±1
±2
±3
Декартовы координаты
1/2я'/«
■^Ш^Ш
=Ру(3/2я)'/8(*±#)/г
i-(5/«)%(22* _ ** - J,*)/,-*
=Р-^(15/2Я)'/*г(л:±/9)/г2
1(15/2я)'/*(*±#)7г2
-i- (7/я)''* 2 (2г2 - Зх2 - Зу2)/^
=F j (21/я)'/г (х ± #) (4г2 - ж2 - у2)/^
•i- (105/2я)% г (х ± ty)2/r3
±-|-(35/я)'/'(*±^)7г3
Сферические координаты
1/2я1/2
y(3ji)1/2cose
=Fi-(3/2ji)1/2sinee±iq>
-j (5/я)!/« (3 cos2 6 - t)
cos 6 sin Ge* *ф
1(15/2^* sin2 Ge±2f*
~ (7/я),/2 (2 cos3 0 — 3 cos в sin2 6)
=F 4- (21M),/2 (4 cos2 6 sin 6 - sin3 6) e± f<p
о
■j (105/2я)'/« cos 6 sin2 Qe±2lv
О
Таблицы
Таблица 24
Частота колебаний, см""1
сн
сн
с—с
с=с
о=с
О—Н
валентные
деформационные
2850-2960
1340-1465
деформационные и валентные 700—1250
валентные
валентные
валентные
Н-связи
с=о
N—Н
C=N
C=N
N=N
Р—Н
С—F
С—С1
С—Вг
С—I
coj-
Ш8~
NO-
soj-
валентные
валентные
валентные
валентные
валентные
валентные
валентные
валентные
валентные
валентные
Силикаты
Более
1620-1680
2100-2260
3590-3650
3200-3570
1640-1780
3200-3500
2215-2275
1480-1690
1575-1630
2350-2440
1000-1400
600-800
500-600
500
1410-1450
1350-1420
1230-1250
1080-1130
900-1100
подробные сведения см. в кн. Беллами [52, 53].
Таблица 25
Фотоэлектрические (и термоиоииые) значения
работы выхода для различных металлов (эВ)
Li
2,42
Na
2,3
К
2,25
Rb
2,09
Cs
2,14
(1.86)
Си
4.8
(4,5)
Ag
4.3
(4.3)
Аи
5.4
(4,3)
Be
3,9
(3.67)
Mg
3,7
Ca
3,2
(2,2)
475
Таблицы
Элемент
Н
С—
с=
С=5
С— (бензол)
0-
0=
N— (аминогруппа)
Свойства
Ковалентный
/?, пм
30
77
67
60
69,5
66
57
70
векторов и
радиус
Элемент
N— (нитрогруппа)
N=
S—
S= (сульфогруппа)
С1—
Вг—
I—
операции над векторами
Таблица 26
R, пм
70
65
104
95
99
114
133
Таблица 27
Рассмотрим векторы F и G, где
F-Fx\ + Fyl+P*
G = Gx\ + Gy\ + Gzk
Скалярное произведение
F.G^FxGx + FyGy + FzQz
Векторное произведение
И J k I
FXG= Fx Fy Fg U-GXF
I Gx Gy Gz I
Произведение трех и четырех векторов
F.(GXH)=G.(HXF) = H.(FXG) = (FXG).H
FX(GXH)=G(F.H)-H(F.G)
(F X G).(H X I) = (F.H) (G.I) - (F.I) (G.H)
градиент
grad U — W =» (-^-) ' + (lty~) i + \~dy~) k' BeKT°PHa« величина
дивергенция
(dFz
*'-«-(£)+(£)+(£>
ротор
rotF = VXF«
i J k
д/дх д/ду д/dz
F* Fv F2
скалярная величина
векторная величина
ГХ Гу
дифференцирование произведений:
V.(UF) = UV.F+F.W
VX(UF) = U(VXF)+(VU)XF
V.(F X О)« G.(V X F) - F.(V X О)
V X (V X F) — V (V.F) - V2F
V X (F X G) — F (V.G) - (V.F) G + (G.V) F - (F.V) G
V(F.G) = (F.V) G + (G.V) F + F X (V X O) + G X (VX F)
V2tf«V.V£/
VX(Vtf)0
476
СПИСОК ЛИТЕРАТУРЫ
I. Atkins P. №.. Molecular quantum mechanics, Clarendon Press, Oxford,
1970.
Книги оксфордской химической серии (OCS),
в которых подробно рассматриваются многие из вопросов,
затронутых в данном справочнике
2. McLauchlan К. A., Magnetic resonance, 1972.
3. Robbins /, Ions in solution (2): an introduction to electrochemistry, 1972.
4. Puddephatt R. /., The periodic table of the elements, 1972.
5. Jackson R. Лм Mechanism: an introduction to the study of organic
reactions, 1972.
6. Whittaker D., Stereochemistry and mechanism, 1973.
7. Hughes G., Radiation chemistry, 1973.
8. Pass G., Ions in solution (3): inorganic properties, 1973,
9. Smith £. £., Basic chemical thermodinamics, 1973.
10. Coulson С. Л., The shape and structure of molecules, 1973.
II. Wormald /., Diffraction methods, 1973.
12. Shorter /., Correlation analysis in organic chemistry: an introduction to
linear free-energy relationships, 1973.
13. Stern E. S. (Ed.), The chemist in industry (1): fine chemicals for
polymers, 1973.
14. Earnshaw Л., Harrington T. /., The chemistry of the transition elements,
1973.
15. Albery W. /., Electrode kinetics, 1974.
16. Fyfe W. S., Geochemistry, 1974.
17. Stern E. S. (Ed.), The chemist in industry (2): human health and plant
protection, 1974.
18. Bond G. C, Heterogeneous catalysis: principles and applications, 1974.
19. Gasser R. P. #., Richards W. G., Entropy and energy levels, 1974.
20. Spedding D. /., Air pollution, 1974.
21. Atkins P. W.y Quanta: a handbook of concepts, 1974.
22. Pilling M. /., Reaction kinetics, 1974.
Книги оксфордской серии (OPS)
23. Robinson F. N. H., Electromagnetism, 1973.
24. Lancaster G., D. с and a. c. circuits, 1973.
25. Ingram D. J. E., Radiation and quantum physics, 1973.
26. Jennings B. R.t Morris V. /., Atoms in contact, 1974.
Общий список
27. Абрагам Л., Ядерный магнетизм, «Мир», 1963.
28. Абрагам Л., Блини Б., Электронный парамагнитный резонанс переходных
ионов, т. 1, 2, «Мир», 1972.
29. Abraham R. /., The analysis of high resolution n. m. r. spectra, Elsevier,
Amsterdam, 1971.
477
Литература
30. Abramowitz М., Stegun I. Л., Handbook of mathematical functions, Dover,
New York, 1965.
31. Adams D. M., Metal-ligand and related vibrations, Arnold, London, 1967.
32. Adams D. M., Inorganic vibrational spectroscopy, A. Rep. Chem. Soc, 47
(1971).
33. Ахиезер А. И., Берестецкий В. В., Квантовая электродинамика, «Наука»,
1969.
34. Alder R. W., Baker R., Brown J. M., Mechanism in organic chemistry,
Wiley, London, 1971.
35. Allen H. C, Cross P. C, Molecular vib-rotors, Wiley, New York, 1963.
36. Altmann S. L., Group theory. In: Quantum theory (Ed. D. R. Bates),
Vol. 2, p. 87, 1962.
37. Altmann S. L., Band theory of metals, Pergamon Press, Oxford, 1970.
38. Andrade e Silva /., Lochak 0., Quanta, Weidenfeld and Nicholson,
London, 1969.
39. Эткинс П., Саймоне Af., Спектры ЭПР и строение неорганических
радикалов, «Мир», 1970.
40. Atkins P. W., Child M. S.t Phillips С. S. С, Tables for group theory,
Clarendon Press, Oxford, 1970.
41. Atkins P. W.t Diagrammatic perturbation theory. University of Oxford,
Department of Theoretical Chemistry, Lecture Note Series, 1973.
42. Ayres F.% Theory and problems of matrices. (Schaum Outline series),
McGraw-Hill, New York, 1962.
43. Auscough P. B.t Electron spin resonance in chemistry, Methuen, London,
1967.
44. Bader R. /., Molecular geometry, Van Nostrand, New York, 1972.
45. Baker A. />., Betteridge D., Photoelectron spectroscopy: chemical and
analytical aspects, Pergamon Press, Oxford, 1972.
46. Baker J. W., Hyperconjugation, Clarendon Press, Oxford, 1952.
47. Baker J. W., Conference in hyperconjugation, Pergamon Press, 1958. (See
also Tetrahedron, 5, 105 et seq. (1959).
48. Ballantine L. E., The statistical interpretation of quantum mechanics, Rev.
mod. Phys., 42, 358 (1970).
49. Бальхаузен /С., Введение в теорию поля лигандов, «Мир», 1964.
50. Bander M., Itzykson С, Group theory and the hydrogen atom, Rev. mod.
Phys., 38, 330 (Part I), 346 (Part II) (1966).
51. Barrow G. M., Introduction to molecular spectroscopy, McGraw-Hill, New
York, 1962.
52. Беллами Л., Инфракрасные спектры молекул, «Мир», 1963.
53. Беллами Л., Новые данные по ИК-спектрам сложных молекул, «Мир»,
1971.
54. Берестецкий В. Б., Лифшиц Е. Л1, Питаевский Л. Я., Релятивистская
квантовая теория, «Наука», 1968.
55. Bergmann Е. /)., Pullman В., Aromaticity, pseudoaromaticity, anti-aroma-
ticity, Israel Academy of Sciences, Jerusalem, 1971.
56. Berry R. S., Atomic orbitals, J. chem. Educ, 43, 283 (1966).
57. Бете Г., Солпитер «9., Квантовая механика атомов с одним и двумя
электронами, Физматгиз, 1960.
58. Biedenharn L. С, Van Dam H. (Eds), Quantum theory of angular mo*
mentum, Academic Press, New York, 1965.
59. Bishop £>., Group theory and chemistry, Clarendon Press, Oxford, 1973.
60. Bjorken J. £>., Drell S. D., Relativistic quantum mechanics, McGraw-Hill,
New York, 1964.
61. Bjorken J. £>., Drell S. D., Relativistic quantum fields, McGraw-Hill, New
York, 1965.
62. Боголюбов Н. #., Ширков Д. В., Введение в теорию квантованных
полей, «Наука», 1973.
478
Литература
63. Бом Д., Квантовая теория, «Наука», 1965.
64. Bolton J. R.y Carrington A., McLachlan A. XX, Electron spin resonance
studies of hyperconjugation in aromatic ions, Mol. Phys., 5, 31 (1962).
65. Born M., The Born-Einstein letters, Walker, New York, 1970.
66. Born M., Beim W., Dualism in quantum theory, Phys. Today, August,
p. 51 (1968).
67. Born AT, Heisenberg W., Jordan P., Zur Quantenmechanik, Z. Phys., 35,
557 (1926).
68. Born M., Jordan P., Zur Quantenmechanick, Z. Phys., 34, 858 (1925).
69. Born M., Oppenheimer J. R., Zur Quantentheorie der Molekulen, Annln
Phys., 84, 457 (1927), Sec. 1—2, Appendix 2.
70. Born Af., Wolf E., Principles of optics, Pergamon Press, Oxford, 1970.
71. Bowen E. /., Chemical aspects of light, Clarendon Press, Oxford, 1946.
72. Boys S. F., Electronic wavefunctions. I. A general method of calculation
for the stationary states of any molecular system, Proc. R. Soc, A200,
542 (1950).
73. Boys S. F., Construction of some molecular orbitals to be approximately
invariant for changes from one molecule to another, Rev. mod. Phys., 32,
296 (1960).
74. Bradley C. /., Cracknell A. P., The mathematical theory of symmetry in
solids, Clarendon Press, Oxford, 1972.
75. Brand J. C. D.t Speakman J. C, Molecular structure: the physical
approach, Arnold, London, 1960.
76. Breslow R., The nature of aromatic molecules, Scient. Am., 227, 32
(1972).
77. Briegleb G., Electron affinity of organic molecules, Angew. Chem., Int.
Ed. Engl., 3,617 (1964).
78. Brillouin L., La methode du champ self-consistent, Actualites sci. indust,
71 (1933).
79. Brillouin Z,., Les champs self-consistent de Hartree et de Fock, Actualites
sci. indust., 159 (1934).
80. Brink D. M., Satchler G. R., Angular momentum, Clarendon Press, Oxford,
1968.
81. Buckingam A. £)., Optical, electrical and magnetic properties of
molecules, A. Rep. chem. Soc, 57, 53 (1960).
82. Buckingam A. D., Experiments with oriented molecules, Chem. Brit., 1,
54 (1965).
83. Buckingam A. £>., Orr B. /., Molecular hyperpolarizabilities, Q. Rev. chem.
Soc, 21, 195 (1967).
84. Buckingam A. £)., Stephens P. /., Magnetic optical activity, Adv. chem.
phys., 17, 399 (1966).
85. Burhop E. H. S.y The Auger effect and other radiationless transitions,
Cambridge University Press, 1952.
86. Burhop E. H. S., Asaad W. N., The Auger effect, Adv. at. mol. Phys., 8,
164 (1972).
87. Caldwell D. /., Eyring #., The theory of optical activity, Wiley-Inter-
science, New York, 1971.
88. Калверт Дж., Питтс Дж., Фотохимия, «Мир», 1968.
89. Candler С., Atomic spectra and the vector model, Hilger and Watts,
London, 1964.
90. Керрингтон Л., Мак-Лечлан Э., Магнитный резонанс и его применение в
химии, «Мир», 1970.
91. Carruthers P., Nieto M. M., Phase and angle variables in quantum
mechanics, Rev. mod. Phys., 40, 411 (1968).
92. Chihara #., Nakamura N.y Nuclear quadrupole resonance spectroscopy,
MTP int. Rev. Sci., Phys. Chem. Ser., 1, 4, 125 (1972).
479
Литература
93. Colpa J. P., /slip M. F. /., Hund's rule and Z expansion for the energy,
electron repulsion, and electron-nuclear attraction, Mol. Phys., 25, 701
(1973).
94. Compton A. //., A quantum theory of the scattering of X-rays by light
elements, Phys. Rev., 21, 483 (1923).
95. Condon E. V.y Nuclear motions associated with electron transitions in
diatomic molecules, Phys. Rev., 32, 858 (1928).
96. Condon E. U., Shortley G., The theory of atomic spectra, Cambridge
University Press, 1963 (см. перевод первого издания: Кондон £., Шорт ли Р.,
Теория атомных спектров, ИЛ, 1949).
97. Corio P., The structure of high resolution n. m. r. spectra, Academic Press,
New York, 1966.
98. Corson />., Lorrain P., Introduction to electro-magnetic fields and waves,
Freeman, San Francisco, 1970.
99. Cotton F. A.y Chemical applications of group theory, Wiley, New York,
1963.
100. Chu £., Molecular forces, Wiley-Interscience, New York, 1967.
101. Clementi £., Ab initio computations in atoms and molecules, IBM JI.
Res. Dev., 9, 2 (1965).
102. Cotton F. A., Wilkinson G.y Advanced inorganic chemistry, Interscience,
New York, 1972. (См. перевод первого издания: Коттон Ф., Уилкин-
сон Дж.у Современная неорганическая химия, «Мир», 1969.)
103. Coulson С. Л., The electronic structure of some polymers and aromatic
molecules. VII. Bonds of fractional order by the molecular orbital method,
Proc. R. Soc, A169, 413 (1939).
104. Coulson С. Л., Molecular geometry and steric deformation. In Kekule
symposium (IUPAC and the Chemical Society), p. 49, Butterworth, London,
1959.
105. Коулсон Ч.у Валентность, «Мир», 1965.
106. Coulson С. A.f The use of commutator relationships in determining Schr5-
dinger wave functions, Q. JI Math., 16, 279 (1965).
107. Coulson С. Л., я-bonds. In: Physical Chemistry, an advanced treatise
(Eds H. Eyring, D. Henderson, W. Jost), Vol. 5, p. 369, Academic Press,
New York, 1970.
108. Coulson С. Л., Deb В. M., On the theoretical foundation of Walsh's
rules of molecular geometry in terms of the Hellmann-Feynman theorem,
Int. J. Quantum Chem., 5, 411 (1971).
109. Coulson С. A., Rushbrook G. S., Note on the method of molecular orbi-
tals, Proc. Camb. Phil. Soc, 36, 193 (1940).
110. Coulson С. Л., Streitweiser Л., Dictionary of я-electron calculations, Per-
gamon Press, Oxford, 1965.
111. Crabbe P., Optical rotatory dispersion and circular dichroism in organic
chemistry, Holden-Day, San Francisco, 1965.
112. Craig D. P., Walmsley S. #., Excitons in molecular crystals, Benjamin,
New York, 1968.
113. Curtiss C. P., Real gases In: Physical chemistry, an advanced treatise
(Eds H. Eyring, D. Henderson, W. Jost), Vol. 2, p. 286, Academic Press,
New York, 1967.
114. Das T. P., Hahn E. L., Nuclear quadrupole resonance spectroscopy, Solid
State Phys., Suppl. 1, 1958.
115. Daudel R., Lefebvre #., Moser C, Quantum chemistry; methods and
applications, Interscience, New York, 1959.
11.6. Davidson N., Statistical mechanics, McGraw-Hill, New York, 1962.
117. Davies D. W., The theory of the electric and magnetic properties of
molecules, Wiley, London, 1967.
118. Давыдов А. С, Теория молекулярных экситонов, «Наука», 1968.
119. Давыдов А. С, Квантовая механика, ГИФМЛ, 1963.
480
Литература
120. Deb В. М., The force concept in chemistry, Rev. mod. Phys., 45, 22 (1973).
121. Dekker A. /., Solid state physics, Macmillan, London, I960.
122. Дьюар М., Теория молекулярных орбиталей в органической химии,
«Мир», 1972.
123. Дирак П. А. М., Принципы квантовой механики, ИЛ, 1960.
124. Dixon R. N., Spectroscopy and structure, Methuen, London, 1965.
125. Doggett G., The electronic structure of molecules: theory and
applications to inorganic molecules, Pergamon Press, Oxford, 1972.
126. Duncan A. B. F.f Rydberg series in atoms and molecules, Academic Press,
New York, 1971.
127. Dymond J. #., Smith E. £., The virial coefficients of gases; a critical
complication, Clarendon Press, Oxford, 1969.
128. Earnshaw Л., Introduction to magnetochemistry, Academic Press, New
York, 1968.
129. Edmiston C, Reudenberg /(., Localized atomic and molecular orbitals, Rev.
mod. Phys., 35, 457 (1963).
130. Edmiston C., Ruedenberg /(., Localized atomic and molecular orbitals. II,
J. Chem. Phys., 43, 597 (1965).
131. Эдмондс Л., Угловые моменты в квантовой механике, в кн.
«Деформация атомных ядер», ИЛ, 1958.
132. Einstein Л., Ehrenfest P., Quantentheoretische Bemerkungen zum
Experiment von Stern und Gerlach, Z. Phys., 11, 31 (1922).
133. Elliott G., Liquid crystals for electro-optical displays, Chem. Brit., 9, 213
(1973).
134. Эмсли Дж., Финей Дж.у Сатклиф «/7., Спектроскопия ядерного магнитного
резонанса высокого разрешения, т. 1, «Мир», 1968; т. 2, «Мир», 1969.
135. Englefield М. /., Group theory and the Coulomb problem, Wiley-Interscien-
ce, New York, 1972.
136. Englman /?., The Jahn-Teller effect in molecules and crystals Wiley, New
York, 1972.
137. Эйринг Г., Уолтер Дж.у Кимбалл Дж.у Квантовая химия, ИЛ, 1948.
138. Fano £/., Description of states in quantum mechanics by density matrix
and operator techniques, Rev. mod. Phys., 29, 74 (1957).
139. Fano U., Racah G., Irreducible tensorial sets, Academic Press, New York,
1959.
140. Feinberg M. /., Ruedenberg /(., Mehler E. L.y The origin of binding and
antibinding in the hydrogen molecule-ion, Adv. Quantum Chem., 5, 21
(1970).
141. Feynman R. P., Forces in molecules, Phys. Rev., 56, 340 (1939).
142. Фейнман P., Квантовая электродинамика, «Мир», 1964.
143. Feynman R. P., The theory of fundamental processes, Addison-Wesley-
Benjamin, Reading, Mass, 1962.
144. Фейнман Р., Хибс Л., Квантовая механика и интегралы по траекториям,
«Мир», 1968.
145. Фейнман Р., Лейтон Р., Сэндс AL, Фейнмановские лекции по физике,
«Мир», 1969.
146. Figgis В. N., Introduction to ligand fields, Wiley, New York, 1966.
147. Fock V., Zur Theorie des Wasserstoffatoms, Z. Phys., 98, 145 (1935).
148. Fowler R. #., Statistical mechanics, Cambridge University Press, 1936.
149. Фаулер Р., Гуггенгейм «9., Статистическая термодинамика, ИЛ, 1949.
150. Frank /., Elementary processes of photochemical reactions, Trans.
Faraday Soc, 21, 536 (1925).
151. Franck /., Hertz G., Uber Zusammenstofie zwischen Electronen und den
Molekulen des Quecksiberdampfes und die Ionisierungspannung desselben,
Verh. dt. phys. Ges., 16, 457 (1914).
152. Franck /., Hertz C, Uber Kinetik von Elektronen und Ionen in Gasen,
Phys. Z., 17, 409 (1916).
481
Литература
153. Franck /., Hertz G., Die Bestatigung der Bohrschen Atomtheorie in optis-
chen Spektrum durch Untersuchungen der inelastischen Zusammenstofie
langsamer Elektronen mit Gasmolekulen, Phys. Z., 20, 132 (1919).
154. Frederico £., Houssier C, Electric dichroism and electric birefringence,
Clarendon Press, Oxford, 1973.
155. Freeman A. /., Frankel R. В., Hyperfine interactions, Academic Press,
New York, 1967.
156. Galindo Л., Sanchez del Rio C, Intrinsic magnetic moment as a nonrela-
tivistic phenomenon, Am. J. Phys., 29, 582 (1961).
157. Gans P., Vibrating molecules, Chapman and Hall, 1971.
158. Гейдон Л., Энергии диссоциации и спектры двухатомных молекул, ИЛ,
1949.
159. Gill G. В., The Woodward-Hoffman orbital symmetry rules. In Essays in
chemistry (Eds J. N. Bradley, R. D. Gillard, R. F. Hudson), Vol. 1, p. 43,
Academic Press, New York and London, 1970.
160. Gill G. B.y Willis M. R., The conservation of orbital symmetry, Methuen,
London, 1969.
161. Гиллеспи Р., Геометрия молекул, «Мир», 1975.
162. Гилсон Т., Хендра #., Лазерная спектроскопия КР в химии, «Мир», 1973.
163. Glauber R. /. (Ed.), Quantum electronics, Academic Press, New York,
1969.
164. Гольдбергер Af., Ватсон /С., Теория столкновений, «Мир», 1967.
165. GoVdman I. /., Krivchenkov V, £>., Problems in quantum mechanics, Per-
gamon Press, Oxford, 1961.
166. Голдстейн Г., Классическая механика, «Наука», 1975.
167. Grandy W. Т., Introduction to electrodynamics and radiation, Academic
Press, New York, 1970.
168. Gray D. E. (Ed.), American Institute of Physics handbook. McGraw-Hill,
New York, 1972.
169. Грин Х.у Матричная квантовая механика, «Мир», 1968.
170. Griffith J. S., The theory of transition metal ions, Cambridge University
Press, 1964.
171. Hall G. G., Amos А. 7\, Pi electron theory of the spectra of conjugated
molecules. In: Physical chemistry, an advanced treatise (Eds H. Eyring,
D. Henderson, W. Jost), Vol. 3, p. 447, Academic Press, New York, 1969.
172. Hameka H. F.y Advanced quantum chemistry, Addison-Wesley Reading,
Mass, 1965.
173. Хамермеш Af., Теория групп и ее применение к физическим проблемам,
«Мир», 1966.
174. Harmony M. D., Quantum mechanical tunneling in chemistry, Chem. Soc.
Rev., 1,211 (1972).
175. Хартри Д., Расчеты атомных структур, ИЛ, 1960.
176. Нaught A. F., Lasers and their applications to physical chemistry, A. Rev.
phys. Chem., 19,343 (1968).
177. Heine V., Group theory, Pergamon Press, Oxford, 1960.
178. Heisenberg №., Uber quantentheoretische Undentung kinematischer und
mechanischer Beziehungen, Z. Phys., 33, 879 (1925).
179. Heisenberg W., The physical principles of quantum theory, Dover, New
York, 1930.
180. Гайтлер В., Квантовая теория излучения, ИЛ, 1956.
181. Heller Л., Laser action in liquids, Phys. Today, 20 (No 11), 34 (1967).
182. Hellmann #., Einfuhrung in die Quantenchemie, Denticke, Leipzig, 1937
183. Henley E. Af., Thirring W. E., Elementary quantum field theory, McGraw-
Hill, New York, 1962.
184. Herman F., Skillman S., Atomic structure calculations, Prentice-Hall, Eng-
lewood Cliffs, New Jersey, 1963.
185. Герцберг Г., Атомные спектры и строение атомов, ИЛ, 1948.
482
Литература
186. Герцберг Г., Колебательные и вращательные спектры многоатомных
молекул, ИЛ, 1949.
187. Герцберг Г., Спектры и строение двухатомных молекул, ИЛ, 1949.
188. Герцберг Г., Электронные спектры и строение многоатомных молекул,
«Мир», 1969.
189. Hill Т. L., An introduction to statistical thermodynamics, Addison-Wesley,
Reading, Mass, 1960.
190. Hirschfelder J. 0., Advances in chemical physics, Vol. 12, Intermolecular
forces, Wiley, New York, 1967.
191. Hirschfelder J. 0. (Ed.), Classical and quantum mechanical hypervirial
theorems, J. Chem. Phys., 33, 1462 (I960).
192. Hirschfelder J. 0., Byers Brown W., Epstein S. Т., Recent developments
in perturbation theory, Adv. Quantum Chem., 1, 256 (1964).
193. Гиршфельдер Дж., Кертис 4.t Берд Р., Молекулярная теория газов и
жидкостей, ИЛ, 1961.
194. Hoffman B.y The strange story of the quantum, Dover, New York, 1959.
195. Hutchison C. A., Mangum B. W.f Paramagnetic resonance absorption in
naphthalene in its phosphorescent state, J. chem Phys., 29, 952 (1958).
196. Hylleraas E. A., The Schrodinger two-electron problem, Adv. quantum
Chem., 1, 1 (1964).
197. Infeld L, Hull T. £., The factorization method, Rev. mod.. Phys., 23, 21
(1951).
198. Irving /., Mullineux N.y Mathematics in physics and engineering,
Academic Press, New York, 1959.
199. Jackman L. M., Nuclear resonance spectroscopy, Pergamon Press, Oxford,
1959.
200. Джексон Дж., Классическая электродинамика, «Мир», 1965.
201. Jaffe H. Я., Or chin Af., Theory and applications of ultraviolet
spectroscopy, Wiley, New York, 1962.
202. Джаффе Г., Орчин М., Симметрия в химии, «Мир», 1967.
203. Jammer M., The conceptual development of quantum mechanics, McGraw-
Hill, New York, 1966.
204. Jauch J. M., Foundations of quantum mechanics, Addison-Wesley,
Reading, Mass, 1968.
205. Jauch J. M., Rohlich F.y The theory of photons and electrons
Addison-Wesley, Reading, Mass., 1955.
206. Jeffreys //., Cartesian tensors, Cambridge University Press, 1931.
207. Jones W. /., Lasers, Q. Rev. Chem. Soc, 23, 73 (1969).
208. Jordan T. F., Linear operators for quantum mechanics, Wiley, New York,
1969.
209. Jergensen C. /(., Absorption spectra and chemical bonding in complexes,
Pergamon Press, Oxford, 1962.
210. Jergensen C. K„ Modern aspects of ligand field theory, North-Holland,
Amsterdam, 1971.
211. Jergensen W. L., Salem L., The organic chemists book of orbitals,
Academic Press, New York, 1973.
212. Judd B. /?., Operator techniques in atomic spectroscopy, McGraw-Hill, New
York, 1963.
213. Джадд Б., Вторичное квантование и атомная спектроскопия, «Мир», 1970.
214. Кемпфер Ф., Основные положения квантовой механики, «Мир», 1967.
215. Katriel /., A study of the interpretation of Hund's rule, Theor. Chim. Acta,
23, 309 (1972).
216. Katz A., Classical mechanics, quantum mechanics, field theory, Academic
Press, New York and London, 1965.
217. Козман У, Введение в квантовую химию, ИЛ, 1960.
218. Кауе G. W. С, Laby Т. Я., Tables of physical and chemical constants.
Longmas, London, 1956.
483
Литература
219. Kekule Symposium. Theoretical organic chemistry, Butterworths, London,
1959.
220. Kemble E. C, The fundamental principles of quantum mechanics, Dover,
New York, 1958.
221. Kiellch S., Optical harmonic generation and laser light frequency mixing
processes in nonlinear media, Opto-electronics, 2, 125 1970.
222. King G. W., Spectroscopy an molecular structure, Holt Reinhardt and
Winston, New York, 1964.
223. Kittel C, Quantum theory of solids, Wiley, New York, 1963.
224. Кил ель Ч., Введение в физику твердого тела, ГИФМЛ, 1963.
225. Kolos W., Adiabatic approximation and its accuracy, Adv. Quantum Chem.,
5, 99, Academic Press, New York, 1970.
226. Kovacs /., Rotational structure in the spectra of diatomic molecules, Hil-
ger, London, 1959.
227. Kramers H. A.y Quantum mechanics, Dover, New York, 1964.
228. Kronig R. L., Band spectra and molecular structure, Cambridge
University Press, 1930.
229. Kuhn #., Atomic spectra, Longmans, London, 1962.
230. Kuper С G., Whitfield G. D. (Eds), Polarons and excitons, Plenum, New
York, 1963.
231. Kyrala Л., Theoretical physics: applications of vectors, matrices, and
quaternions, Saunders, Philadelphia, 1967.
232. Lagowski J. /., Sienko M. /., Metal-ammonia solutions, Butterworths,
London, 1970.
233. Ландау Л. Д., Лифшиц Е. Af., Квантовая механика, «Наука», 1974.
234. Ландау Л. Д., Лифшиц Е. М., Статистическая физика, «Наука», 1964.
235. Ландау Л. Д., Лифшиц Е. М., Электродинамика сплошных сред,
ГИФМЛ, 1959.
236. Langenberg D. N., Scalapino D. /., Taylor В. N., The Josephson effects,
Sci. Am., 214 (May), 30 (1966).
237. Langhoff P. W., Epstein S. Т., Karplus Af., Aspects of time-dependent
perturbation theory, Rev. mod. Phys., 44, 602 (1972).
238. Lepoutre G., Sienko M. J. (Eds), Metal-ammonia solutions, Benjamin, New
York, 1964.
239. Лендьел Б., Лазеры, «Мир», 1964.
240. Lennard-Jones /., Pople J. A., The molecular orbital theory of chemical
valency. IV. The significance of equivalent orbitals, Proc. R. Soc, A202, 166
(1950).
241. Lemberger Л., Pauncz R.y The theoretical interpretation of Hund's rule,
Acta Phys., hung., 27, 169 (1970).
242. Левин В. Г., Вдовин Ю. Л., Мямлин В. Л., Курс теоретической физики,
ГИФМЛ, 1962.
243. Levine A. /(., DeMaria A. /., Lasers; a series of advances, Marcel Dekker,
New York (1966 et seq.).
244. Levine /?. D., The quantum mechanics of molecular rate processes,
Clarendon Press, Oxford, 1969.
245. Levine R. D., Bernstein R. В., Molecular reaction dynamics, Clarendon
Press, Oxford, 1974.
246. Lichtenberg D. В., Unitary symmetry and elementary particles, Academic
Press, New York, 1970.
247. Lin S. #., Crystal and blackbody radiation. In Physical chemistry; an
advanced treatise (Eds H. Eyring, D. Henderson, W. Jost), Vol. 2, Academic
Press, New York, 1967.
248. Lindsay R. В., Introduction to physical statistics, Wiley, New York, 1941.
249. Linnet J. W., Wave mechanics and valency, Methuen, London, 1960.
250. Linnet J. W., The electronic structure of molecules. A new approach, Wb
ley, New York, 1964.
484
Литература
251. Lipkin H. У., Lie groups for pedestrains, North-Holland, Amsterdam, 1965.
252. Long D. Л., Spectroscopy in a new light, Chem. Brit., 7, 108 (1971).
253. Longuet-Higgins H. C, Adv. Spectrosc, 2, 429 (1961).
254. Longuet-Higgins H. C, Intermolecular forces, Discuss. Faraday Soc, 40,
7 (1965).
255. Longuet-Higgins H. C, Abrahamson E. W., The electronic mechanism of
electrocyclic reactions, J. Am. Chem. Soc, 87, 2045 (1965).
256. Loudon R., The quantum theory of light, Clarendon Press, Oxford, 1973.
257. Louisetl W. //., Quantum statistical properties of radiation, Wiley, New
York, 1973.
258. Lowdin P. 0., The calculation of upper and lower bounds of energy
eigenvalues in perturbation theory by means of partitioning techniques. In Per*
turbation theory and its applications in quantum mechanics (Ed. С. Н.
Wilcox), p. 255, Wiley, New York, 1966.
259. Lucken E. A. C, Nuclear quadrupole coupling constants, Academic Press,
New York, 1969.
260. Lynden-Bell R. Af., Harris R. /(., Nuclear magnetic resonance spectroscopy,
Nelson, London, 1969.
261. Маки Г., Лекции по математическим основам квантовой механики,
«Мир», 1965.
262. Mandt F., Quantum mechanics, Butterworths, London, 1957.
263. Manenkov A. A, Orbach R. (Eds), Spin-lattice relaxation in ionic solids,
Harper and Row, New York, 1966.
264. Marcus R. A.y Fourth picture in quantum mechanics, J. chem. Phys., 53,
1349 (1970).
265. Margenau H., Kestner N. /?., Theory of intermolecular forces, Pergamon
Press, Oxford, 1969.
266. Margenau #., Murphy G. Af., The mathematics in physics and chemistry,
Vol. 1, Van Nostrand, New York, 1956.
267. Mason S. F., Optical rotatory power, Q. Rev. Chem. Soc, 17, 20 (1963).
268. Маттис Д., Теория магнетизма, «Мир», 1967.
269. Маттук Р., Фейнмановские диаграммы в проблеме многих тел, «Мир»,
1969.
270. McClellan A. L., Tables of experimental dipole moments, Freeman, San
Francisco, 1963.
271. McDowell C. A.f Ionization potentials and electron affinities. In: Physical
chemistry, an advanced treatise (Eds H. Eyring, D. Henderson, W. Jost),
Vol. 3, p. 496, Academic Press, New York, 1969.
272. Мак-Глин С, Адзуми Г., Киносита Af., Молекулярная спектроскопия три-
плетного состояния, «Мир», 1972.
273. McGlynn S. P., Vanquickenborne L. С, Kinoshita M., Carroll D. G.,
Introduction to applied quantum chemistry, Holt, Reinhardt and Winston,
New York, 1972.
274. Mcintosh H. V.y On accidental degeneracy in classical and quantum
mechanics. Am. J. Phys., 27, 620 (1959).
275. Mcintosh H. V., Symmetry and degeneracy. In: Group theory and its
applications (Ed. E. M. Loebl), Vol. 2, p. 75, 1971.
276. McLachlan A. /)., Dangers and «average energy approximation» in
perturbation theory, J. chem. Phys., 32, 1263 (1960).
277. McWeeny /?., Symmetry, Pergamon Press, Oxford, 1963.
278. McWeeny R„ Spins in chemistry, Academic Press, New York, 1970.
279. Мак-Вини Р., Сатклиф Б., Квантовая механика молекул, «Мир», 1972.
280. Mellon M. G, Analytical absorption spectroscopy, Wiley, New York,
1950.
281. Memory J. /)., Quantum theory of magnetic resonance parameters, McGraw-
Hill, New York, 1968.
282. Messiah Л., Quantum mechanics, Wiley, New York, 1961.
485
Литература
283. Минкин В. #., Осипов О. Л., Гарповский А. Д., Справочник по диполь-
ным моментам, «Высшая школа», 1971.
284. Мелвин-Хьюз Э., Физическая химия, кн. 1, ИЛ, 1961; кн. 2, ИЛ, 1962.
285. Moffitt W.y The residual affinity of conjugated and resonanting
hydrocarbons, Trans. Faraday Soc, 45, 373 (1949).
286. Moffitt W., Molecular orbitals and the Hartree field, Proc. R. Soc, A196,
510 (1949).
287. Moffitt W„ Term values in hybrid states, Proc. R. Soc, A202, 534
(1950).
288. Moore С £., Atomic energy levels, Vol. 1 (1949); Vol. 2 (1952); Vol. 3
(1958); National Bureau of Standards Circular 467, Washington D. C.
289. Moore W. /., Physical chemistry, Longmans, London and Prentice-Hall,
Englewood Cliffs, 1972.
290. Morton J. /?., Rowlands /. R., Whiffen D. #., NPL, Gr. Brit. Circular No.
BPR 13, 1962.
291. Moscowitz A., Theoretical aspects of optical activity. I. Small molecules,
Adv. chem. Phys., 4, 67 (1962).
292. Moss R. £., Advanced molecular quantum mechanics, Chapman and Hall,
London, 1973.
293. Мотт #., Месси Г., Теория атомных столкновений, «Мир», 1969.
294. Мотт //., Дэвис Э., Электронные процессы в некристаллических
веществах, «Мир», 1974.
295. Mulliken R. S., The interpretation of band spectra. III. Electron quantum
numbers and states of molecules and their atoms, Rev. mod. Phys., 4, 1
(1932).
296. Mulliken R. S., A new electronegativity scale; together with data on
valence states and on valence ionization potentials and electron affinities, J.
chem. Phys., 2, 782 (1934).
297. Murrell J. N.y The theory of the electronic spectra of organic molecules,
Chapman and Hall, London, 1971.
298. Murrell J. N., Harget A. /., Semi-empirical self-consistent-field molecular
orbital theory of molecules, Wiley-Interscience, New York, 1972.
299. Маррел Дж., Кеттл С, Теддер Дж., Теория валентности, «Мир», 1968.
300. Musher J. /., Theory of the chemical shift, Adv. magn. Reson., 2, 177
(1966).
301. Muus L. 7\, Atkins P. W„ Electron spin relafation in liquids, Plenum,
New York, 1972.
302. Naqvi R. /(., On the noncrossing rule for potential energy surfaces of
polyatomic molecules, Chem. Phys. Lett., 15, 634 (1972).
303. Naqvi R. /(., Byers Brown W., The noncrossing rule in molecular
quantum mechanics, Int. J. Quantum Chem., 6, 271 (1972).
304. Newman J. R„ Laplace. In: Mathematics in the modern world. Readings
from Scientific American (Ed. M. Kline), p. 45, Freeman, San Francisco,
1954.
305. Nicholls R. W.y Electronic spectra of diatomic molecules. In: Physical
chemistry, an advanced treatise (Eds H. Eyring, D. Henderson, W. Jost),
Vol. 3, p. 325, Academic Press, New York, 1969.
306. Nikitin E. £., The theory of nonadiabatic transitions: recent developments
with exponential models, Adv. Quantum Chem., 5, 135 (1970).
307. Орчин Af., Джаффе Г., Разрыхляющие орбитали, «Мир», 1969.
308. Оргел Л., Введение в химию переходных металлов, «Мир», 1964.
309. Osheroff D. D., Gully W. /., Richardson R. С, Lee D. M., New magnetic
phenomena in liquid 3He below 3 mK, Phys. Rev. Lett., 29, 920 (1972).
(See the account in Phys. Today, November 1972, p. 17.)
310. Parr R. (7., Quantum theory of molecular electronic structure, Benjamin,
New York, 1963.
311. Pauli W., The connection between spin and statistics, Phys, Rev., 58,
486
Литература
716 (1940). (This paper is included in the selection edited by Schwinger
[1958].)
312. Pauling L. The valence-state energy of the bivalent oxygen atom, Proc.
Natn. Acad. Sci. U. S, A., 35, 229 (1949).
313. Pauling L., Nature of the chemical bond, Cornell University Press, I960.
314. Pauling L., Wilson E. B.y Introduction to quantum mechanics, McGraw-
Hill, New York, 1935 (см. перевод первого издания: Паулинг Л.у
«Природа химической связи», Госхимиздат, 1947).
315. Pauncz R.y Alternant molecular orbital method, Saunders Philadelphia,
1967.
316. Pauncz R., Electron correlation in atoms and molecules. In: Physical
chemistry, and advanced treatise (Eds H. Eyring, D. Henderson, W. Jost).
Vol. 3, p. 185. Academic Press, New York, 1969.
317. Phillips С S. G.y Williams R. J. P., Inorganic chemistry, Clarendon Press,
Oxford, 1965.
318. Pilar F.y Elementary quantum chemistry, McGraw-Hill, New York, 1968.
319. Poole C. P., Electron spin resonance, Wiley-Interscience, New York,
1967.
320. Poole С P.y Farach H. A., Relaxation in magnetic resonance, Academic
Press, New York, 1971.
321. Pople J. A., Beveridge D. L., Approximate molecular orbital theory,
McGraw-Hill, New York, 1970.
322. Pople /. A.t Longuet-Higgins H. C, Theory of the Renner effect in the
NH2 radical, Mol. Phys., 1, 372 (1958).
323. Попл Дж., Шнейдер В., Бернстейн Г., Спектры ядерного магнитного
резонанса высокого разрешения, ИЛ, 1962.
324. Power Е. Л., Introductory quantum electrodynamics, Longmans London,
1964.
325. Pressley R. /., Handbook of lasers, Chemical Rubber Co., Cleveland, Ohio,
1971.
326. Prichard H. 0., The determination of electron affinities, Chem. Rev., 52,
529 (1953).
327. Prigogine /., Adv. chem. Phys., 1958 et seq. (10 (1966) —is devoted to
molecular beams.)
328. Pullman B.y Pullman A.y Free valence in conjugated organic molecules,
Prog. org. Chem., 4, 31 (1958).
329. Quinn С. M.y An introduction to the quantum chemistry of solids,
Clarendon Press, Oxford, 1973.
330. Рамзей #., Молекулярные пучки, ИЛ, 1960.
331. Rao С. N. R.y Chemical applications of infrared spectroscopy, Academic
Press, New York, 1963.
332. Rao С N. /?., Ultraviolet and visible spectroscopy, Butterworths, London,
1967 (см. перевод первого издания: Рао Ч.у Электронные спектры в
химии, «Мир», 1964).
333. Reif F., Fundamentals of statistical and thermal physics, McGraw-Hill,
New York, 1965.
334. Renner £., Z. Phys., 92, 172 (1934).
335. Rice O. K.y Statistical mechanics, thermodynamics and kinetics, Freeman,
San Francisco, 1967.
336. Richards W. G., Horsley J. A.y Ab initio molecular orbital calculations for
chemists, Clarendon Press, Oxford, 1970.
337. Richards W. G.y Walker Т. Е. #., Hinkley R. /(., A bibliography of ab
initio molecular wave functions, Oxford Science Research Papers,
Clarendon Press, Oxford, 1971.
338. Richtmeyr F. /(., Kennard E. //., Lauristen Г., Introduction to modern
physics, McGraw-Hill, New York, 1955.
339. Роберте Дж.у Ядерный магнитный резонанс, ИЛ, 1961.
487
Литература
340. Роберте Дж., Введение в анализ спектров ЯМР высокого разрешения
(спин-спиновое взаимодействие), ИЛ, 1963.
341. Роберте Дж., Расчеты по методу молекулярных орбиталей, ИЛ, 1963.
342. Rodberg L. S., Thaler R. M.y Introduction to the quantum theory of
scattering, Academic Press, New York, 1967.
343. Roman P., Advanced quantum theory, Addison-Wesley, Reading Mass,
1965.
344. Roman P., Introduction to quantum field theory, Wiley, New York, 1969.
345. Ross J. (Ed.), Adv. chem. Phys., 10 (on molecular beams) (1966).
346. Роуз Af., Поля мультиполей, ИЛ, 1957.
347. Rose M. £., Elementary theory of angular momentum, Wiley, New York,
1957.
348. Роуз-Инс Л., Родерик £., Введение в физику сверхпроводимости, «Мир»,
1972.
349. Rotenberg М., Bivins R.y Metropolis N.y Wooten J. /(., The 3j and 6j
symbols, Technology Press, MIT, 1959.
350. Rowlinson /. S., Liquids and liquid mixtures, Butterworths, London, 1969.
351. Рюденберг /(., Физическая природа химической связи, «Мир», 1964.
352. Salem Л., Wigner E. P., Aspects of quantum theory, Cambridge
University Press, 1972.
353. Salem L., The molecular orbital theory of conjugated systems, Benjamin,
New York, 1966.
354. Sandorfy C, Electronic spectra and quantum chemistry, Prentice-Hall,
Englewood Cliffs, New Jersey, 1964.
355. Schawlow A, L, Lasers and light, Freeman, San Francisco, 1969.
356. Шифф Л., Квантовая механика, ИЛ, 1959.
357. Schonland D. S., Molecular symmetry, Van Nostrand-Reinhold, New York,
1965.
358. Швебер С, Введение в релятивистскую квантовую теорию поля, ИЛ,
1963.
359. Schwinger J. (Ed.), Quantum electrodynamics, Dover, New York, 1958.
360. Schwinger /., On angular momentum. In Quantum theory of angular
momentum (eds L. C. Beidenharn, H. van Dam), p. 229, Academic Press, New
York, 1965.
361. Schrodinger £., Quantisierung als Eigenwertproblem, Annln. Phys., 79,
361; 79, 489; 80, 437; 81, 109 (1926).
362. Селвуд Я., Магнитохимия, ИЛ, 1958.
363. Series С. W., The spectrum of atomic hydrogen, Clarendon Press, Oxford,
1957.
364. Shearer /., Deans W. M., Collected papers on wave mechanics
(translation of Abhandlungen zur Wellenmechanik). (Ed. J. Barth), Blackie,
Glasgow, 1928.
365. Shore B. VP\, Menzel D. #., Principles of atomic spectra, Wiley, New York,
1968.
366. Siegbahn /(., Electron spectroscopy — a new way of looking into matter,
Endeavour 32, 51, 1973.
367. Siegbahn /(., Nordling C, Johansson G.y Hedman /., Heden P. F.y Ham-
rin /(., Gelvius U., Bergmark Г., Werne L. O., Manne /?., Baer У., ESCA
applied to free molecules, Horth-Holland, Amsterdan, 1969.
368. Синаноглу О., Многоэлектронная теория атомов, молекул и их
взаимодействий, «Мир», 1966.
369. Sinanoglu О., Brueckner /С. Л., Three approaches to electron correlations
in atoms, Yale University Press, New Haven and London, 1970.
370. Skinner H. Л., Valence states of some elements from groups 2, 3 and 4;
configurations containing d-orbitals, Trans. Faraday Soc, 51, 1036 (1955).
371. Skinner H. Л., Printchard H. O., The measure of electronegativity, Trans.
Faraday Soc, 49, 1254 (1953).
488
Литература
372. Слэтер Дж., Электронная структура молекул, «Мир», 1965.
373. Slater /. С, Introduction to chemical physics, McGraw-Hill, New York,
1968.
374. Сликтер V., Основы теории магнитного резонанса, «Мир», 1967.
375. Smith J. W., Electric dipole moments, Buttgerworths, London, 1955.
376. Smith R. A., Wave mechanics of crystalline solids, Chapman and Hall,
London, 1969.
377. Smyth C. P., Dielectric behaviour and structure, McGraw-Hill, New York,
1955.
378. Solymar L., Walsh £>., Lectures on the electrical properties of materials,
Clarendon Press, Oxford, 1970.
379. Sommerfeld A., Wave mechanics (translation from Atombau und Spektral-
linien: Wellenmechanischer Ergazungsband, 1928), Methuen, London, 1930.
380. Standley K. /., Vaughan R. Л., Electron spin relaxation phenomena in
solids, Hilger, London, 1969.
381. Стенли Г., Фазовые переходы и критические явления, «Мир», 1973.
382. Stern E. S., Timmons С. /., Electronic absorption spectroscopy in organic
chemistry, Arnold, London, 1970.
383. Stern 0., Ein Weg zur experimentellen Prufung der Richtungsquantelung
im Magnetfeld, Z. Phys., 7, 249, 1921.
384. Stern O., Gerlach W.y Der experimented Nachweis des magnetischen
moments des silberatoms, Z. Phys., 8, 110 (1922).
385. Stevenson /?., Multiplet structure of atoms and molecules, Saunders,
Philadelphia, 1965.
386. Strauss H. £., Vibrational spectroscopy, A. Rep. phys. Chem., 19, 419
(1968).
387. Стрейтвизер Э., Теория молекулярных орбит для химиков-органиков,
«Мир», 1965.
388. Sugden Т. М., Кеппеу С. #., Microwave spectroscopy of gases, Van Nos-
trand, London, 1965.
389. Sutton L. £., Dipole moments. In «Determination of organic structures
by physical methods» (Eds E. A. Brande, F. С Machod), Vol. 1, p. 373,
Academic Press, New York, 1955.
390. Sutton L. E., Tables of interatomic distences and configuration of
molecules, Chem. Soc. Spec. Publ. No. 11 (1958) (Suppl. 1965; Spec. Publ.
No. 18).
391. Symons M. C. R.y The identification of organic free radicals by electron
spin resonance, Adv phys. ord. Chem., 1, 284 (1963).
392. Synge J. L.y Schild Л., Tensor calculus, Toronto University Press, 1949.
393. Taylor B. N., Langenberg D. N„ Parker W. N., The fundamental physical
constants, Sci. Am., 223 (October), 62 (1970).
394. Teller £., The crossing of potential surfaces, J. phys. Chem., 41, 109
(1937).
395. Thirring W. £., Principles of quantum electrodynamics, Academic Press,
New York, 1958.
396. Tinkham Af., Group theory and quantum mechanics, McGraw-Hill, New
York, 1964.
397. Tinoco /., Theoretical aspects of optical activity. II. Polymers, Adv. chem.
Phys., 4, 113 (1962).
398. Tolman R. C, The principles of statistical mechanics, Clarendon Press,
Oxford, 1938.
399. Townes C. #., Schawlow A. L., Microwave spectroscopy, McGraw-Hill,
New York, 1955.
400. Troup G., Masers and lasers, Methuen, London, 1963.
401. Turner D. W., Photoelectron spectroscopy, Chem. Brit., 4, 435, 1968.
402. Turner D. W\, Baker C, Baker A. £>., Brundle С R.> Molecular photo-
electron spectroscopy, Wiley-Interscience, New York, 1970.
489
Литература
403. Uhlenbeck G. £., Goudsmit S., Ersetzung der Hypothese vom unmechanis-
chen Zwang durch eine Forderung bezuglich des inneren Verhaltens jedes
einzelnen Elektrons, Naturwissenschaften, 13, 953 (1925).
404. Uhlenbeck G. E., Goudsmit S., Spinning electrons and the structure
spectra, Nature, 117,264 (1926).
405. Urry D. W.t Optical rotation, Adv. phys. Chem., 19, 477 (1968).
406. Van der Waerden B. L., Sources of quantum mechanics, North-Holland,
Amsterdam, 1968.
407. Van Vleck /, Я., The theory of electric and magnetic susceptibilities,
Clarendon Press, Oxford, 1932.
408. Vedeneyev V. /., Gurvich L. V., Kondrat'yev V. N., Medaredev V. Л.,
Frankevich Y. L., Bond energies, ionization potentials, and electron
affinities, Arnold, London, 1966.
409. Voge Я. #., Relation of the states of the carbon atom to its valence in
methane, J. chem. Phys., 4, 581 (1936).
410. фон Нейман И., Математические основы квантовой механики, «Наука»,
1964.
411. von Neumann /., Wigner E. P., Ober das Verhalten von Eigenwerten bei
adiabatischen Prozessen, Phys. Z., 30, 467 (1929).
412. Вейлстеке Л., Основы теории квантовых усилителей и генераторов, ИЛ,
1963.
413. Walker Т. Е. Я., Weber /. 7\, Modified Hund's rule for jj-coupling, Phys.
Rev., 7, 1218 (1973).
414. Walsh A. D., The electronic orbitals, shapes, and spectra of polyatomic
molecules, J. chem. Soc, 1953, 2266, et seq.
415. Waugh J. S., (Ed.), Adv. magn. Reson, 1966 et Seq.
416. Wayne R. P., Photochemistry, Butterworth, London, 1970.
417. Weisskopf V, F., How light interactions with matter, Scient. Am. 219, No.
3, 60 (1968).
418. Вертц Дж., Болтон Дж., Теория и практические приложения метода
ЭПР, «Мир», 1975.
419. Weyl Я., The theory of groups and quantum mechanics, Dover, New York,
1930.
420. Вейль Г.у Симметрия, «Наука», 1968.
421. Уитли Я., Определение молекулярной структуры, «Мир», 1970.
422. Wheatley P., The chemical comsequences of nuclear spin, North-Holland,
Amsterdam, 1970.
423. Уэланд Дж. Ч., Теория резонанса и ее применение в органической химии,
ИЛ, 1948.
424. Whiffen D. Я., Spectroscopy, Longmans, London, 1972.
425. White Я. £., Introduction to atomic spectra, McGraw-Hill, New York,
1934.
426. Whittaker E., William Roman Hamilton. In Mathematics in the modern
world, Readings from Scientific American (Ed. M. Klinel), Freeman, San
Francisco, 1954.
427. Вигнер £., Теория групп, ИЛ, 1961.
428. Wilcox D. Я., Perturbation theory and its applications in quantum
mechanics, Wiley, New York, 1966.
429. Wilcox R. M.t Expotential operators and parameter differentiation in
quantum physics, J. math. Phys., 8, 962 (1967).
430. Wilson А. Я., Thermodynamics and statistical mechanics, Cambridge
University Press, 1957.
431. Вильсон £., Дешиус Дж., Кросс П., Теория колебательных спектров
молекул, ИЛ, 1960.
432. Woodgate G. К., Elementary atomic structure, McGraw-Hill, London, 1970.
433. Woodward L. A.y Introduction to the theory of molecular vibrations and
vibrational spectroscopy, Clarendon Press, Oxford, 1972.
490
Литература
434. Вудворд Р., Хоффман Р., Сохранение орбитальной симметрии, «Мир»,
435. Woodward R. В., Hoffman P., The conservation of orbital symmetry, Ver-
lag Chemie, Gmbh., Academic Press, New York.
436. Wooster W. Л., Tensors and group theory for the physical properties of
crystals, Clarendon Press, Oxford, 1973.
437. Wyszecki G., Stiles W. S., Color science, Wiley, New York, 1967.
438. Займан Дж., Современная квантовая теория, «Мир», 1971.
439. Займан Дж., Электроны и фононы, «Мир», 1963.
440. Займан Дж., Принципы теории твердого тела, «Мир», 1966.
Список дополнительной литературы*
441. Хигаси /С., Баба X., Рембаум А., Квантовая органическая химия, «Мир»,
1967.
442. Хюккель В., Теоретические основы органической химии, ИЛ, т. 1, 1955,
т. 2, 1958.
443. Хюккель В., Химическая связь, ИЛ, 1960.
444. Херберхольд Af., я-Комплексы металлов, «Мир», 1975.
445. Пиментел Дж., Мак-Клеллан А., Водородная связь, «Мир», 1964.
446. Пиментел Г., Спратли Р., Как квантовая механика объясняет химическую
связь, «Мир», 1973.
447. Дьюар М., Сверхсопряжение, «Мир», 1965.
448. Грей Г.у Электроны и химическая связь, «Мир», 1965.
449. Берсукер И. Б., Строение и свойства координационных соединений,
«Химия», 1971.
450. Мелешина А. М.у Курс квантовой механики для химиков, Воронежский
университет, 1974.
451. Хохштрассер Р., Молекулярные аспекты симметрии, «Мир», 1968.
* Составлен переводчиком и редактором.
СОДЕРЖАНИЕ
Предисловие к русскому изданию 5
Предисловие к английскому изданию 8
Ab initio 11
Абсолютно черного тела излучение 11
Адиабатический процесс 15
Ангармоничность 16
Антисимметрия 19
Альтернантный углеводород 20
Ароматичность 23
Атомные единицы 24
Атомная орбиталь 25
Атомные спектры 27
Барьеры внутреннего вращения 30
Бензол 32
Бозон 36
Бора атом 36
Борна — Оппенгеймера приближение 38
Бриллюэна теорема 39
Валентное состояние . . . . • 41
Валентных связей метод 42
Валентных связей и молекулярных орбиталей методы 49
Вариационный метод, или вариационный принцип 51
Вековой определитель (детерминант) 54
Векторная модель атома 58
Вероятность перехода 62
Ветвь 65
Вигнера коэффициенты 67
Вириала теорема 68
Виртуальный переход 69
Возмущений теория 70
Водорода атом 75
Волновые пакеты 86
Волновая функция 88
Вращение молекул 91
Вторичное квантование 97
Вырождение 98
Гамильтониан 100
Гармонический осциллятор . 101
492
Содержание
Гауссовы атомные орбитали 105
Гельмана —- Фейнмана теорема 106
Гибридизация 107
Гротриана диаграмма 112
Групп теория 113
Гунда правила 115
Гунда случаи связи 117
Двойное лучепреломление 120
де Бройля соотношение 121
Дипольный момент 122
Дирака уравнение 125
Дисперсионные силы 126
Дополнительности принцип 128
Дуализм 129
Закон равнораспределения 130
Заполнения принцип (aufbau) 131
Зеемана эффект 132
Зонная теория металлов 135
Инверсионное удвоение 144
Импульс 146
Квадруполи и другие мультиполи 148
Квант 152
Квантовая теория 154
Квантовая электродинамика 154
Квантовые числа 156
Квантовый дефект 158
Кинетическая энергия 159
Колебательная спектроскопия 160
Комбинационного рассеяния спектры 163
Коммутатор 170
Комптона эффект 171
Контактное взаимодействие Ферми . 172
Конфигурационное взаимодействие 174
Конфигурация 176
Кориолнсово взаимодействие . . , 177
Корреляционная энергия 170
Коэффициенты Эйнштейна А и В 180
Кристаллического поля теория 182
Кулоновский интеграл 183
Купманса теорема 186
Лазер 188
Лапласиан 192
493
Содержание
Линейная комбинация атомных орбиталей (ЛКАО) 194
Локализованные орбитали 196
Магнитное дипольное и электрическое квадрупольное излучение .... 198
Магнитные свойства 200
Магнитный момент 206
Матрица 208
Матрица плотности 212
Матричная механика 212
Межмолекулярные силы 214
Молекулярных орбиталей метод 219
Мультиплетность 228
Неопределенности принцип 230
Непересечения правило 234
Неподеленная пара электронов 235
Нормальные колебания 236
Нормированные волновые функции 238
Объединенный атом 240
Обменная энергия 242
Оже эффект 243
Ожидаемое значение 244
Операторы 246
Орбитального углового момента подавление (погашение) 248
Орбитальный угловой момент 249
Ортогональные волновые функции 253
Отбора правила 254
Паули принцип 267
Пашена — Бака эффект 259
Перекрывание 260
Плотность заряда 263
Поля лигандов теория 265
Поляризуемость 269
Полярон 272
Потенциал ионизации 273
Предиссоциация 274
Преломления показатель 277
Прецессия 278
Приближение свертки 281
Прогрессия 283
Проникновение электронов и экранирование ядра 283
Работа выхода 286
Радиального распределения функция 286
Разрыхление 288
494
Содержание
Рамзауэра эффект 289
Резонанс 291
Резонанса энергия 293
Реннера эффект 294
Рентгеновский спектр 295
Ридберга постоянная 296
Ридберговы уровни 297
Самосогласованного поля метод 299
Сверхсопряжение 302
Сверхтонкие взаимодействия 303
Свободная валентность 308
Связи порядок 309
Секвенция 311
Серия 312
Сила осциллятора 313
Силовая постоянная 314
Симметрии преобразования 315
Синглетные и триплетные состояния 318
Скобочные обозначения; бра и кет 320
Слейтеровские атомные орбитали 320
Слейтеровский детерминант 322
Собственные функции 324
Соответствия принцип 325
Сохраняющееся свойство 326
Спаривание 327
Спектроскопические возмущения 328
Спин 329
Спиновые корреляции 331
Спин-орбитальное взаимодействие 333
Спин-спиновое взаимодействие 335
Сродство к электрону 339
Суперпозиции принцип 339
Сферические гармоники 342
Тензор 346
Теплоемкость 348
Терм 352
Тонкая структура 354
Тонкой структуры постоянная 356
Туннельный эффект 358
Угловой момент 361
Удвоение 363
Узел волновой функции 367
Уровень 368
495
Содержание
g-Фактор 369
Фермион 373
Флуоресценция 374
Фононы 378
Фосфоресценция 380
Фотоны 382
Фотоэлектрический эффект 384
Франка — Герца опыт 387
Франка — Кондона принцип 387
Характер 391
Химическая связь 392
Химический сдвиг 398
Хюккеля метод 402
Цвет 407
Частица в прямоугольной потенциальной яме 410
Четность и нечетность 414
Шредингера уравнение 416
Штарка эффект 420
Штерна и Герлаха эксперимент 425
Эквивалентная орбиталь 427
Экситон 427
Экстинкции коэффициент 430
Электрический дипольный переход 431
Электронвольт 434
Электронно-колебательный (вибронныи) переход 434
Электронное «скольжение» 436
Электронные спектры молекул 437
Электронный парамагнитный резонанс 438
Электроотрицательность 445
Эрмитовы операторы 447
Ядерная статистика ♦ 448
Ядерный магнитный резонанс 451
Яна — Теллера эффект 454
J 457
Таблицы 458
Список литературы 477
. т
»
СПРАВОЧНИК КОНЦЕПЦИ *