Author: Башмаков М.И.
Tags: математика геометрия алгебра курс математики учебное пособие издательство высшая школа профтехобразование
Year: 1987
Text
М. И. Башмаков
МАТЕМАТИКА
ПРОФ
ТЕХ
ОБРАЗОВАНИЕ
Учебное
пособие
МАТЕМАТИКА
М. И. Башмаков
М. И. Башмаков
МАТЕМАТИ КА
Одобрено
Ученым советом Государственного комитета СССР
по профессионально-техническому образованию
в качестве экспериментального учебного пособия
для средних профессионально-технических училищ
МОСКВА «ВЫСШАЯ ШКОЛА» 1987
ББК 22.1
БЗЗ
УДК 51
Рецензенты: лаборатория математики (НИИ профтехпедагогики
АПН СССР); д-р физ.-мат. наук, проф. С. В. Востоков (Ленин¬
градский государственный университет им. А. А. Жданова)
Башмаков М. И.
БЗЗ Математика: Эксперимент, учеб. пособие для
СПТУ. — М.: Высш. шк., 1987. — 463 с.: ил.
Пособие написано в соответствии с программой единого курса
математики, разработанной группой ленинградских математиков.
Алгебра, начала анализа и геометрия излагаются как один учеб¬
ный предмет «Математика». Изложение материала сопровождается
большим количеством примеров.
Для учащихся и преподавателей средних профтехучилищ.
„ 4306020400—270 _ ББК 22.1
Б 145—87
052(01)—87 51
@ Издательство «Высшая школа», 1987
ОГЛАВЛЕНИЕ
Предисловие 5
Вступительное слово автора 6
\ Числа, функции и графики 7
§ 1 Числовая ось 7
§ 2 Декартовы координаты на плоскости 12
§ 3 Понятие функции 19
§ 4 Уравнения и неравенства 35
Задачи и вопросы 42
2 Производная и ее применение 51
§ 5 Введение производной 51
§ 6 Вычисление производной 60
§ 7 Исследование функции с помощью производной 69
§ 8 Приложения производной 85
§ 9 Дифференциал 91
§ 10 Задачи на максимум и минимум 98
Задачи и вопросы 104
3 Параллельность прямых и плоскостей 114
§ 11 Взаимное расположение прямых и плоскостей Н4
§ 12 Признаки параллельности 122
§ 13 Аксиоматическое построение геометрии 130
Задачи и вопросы 134
4 Векторы 1^7
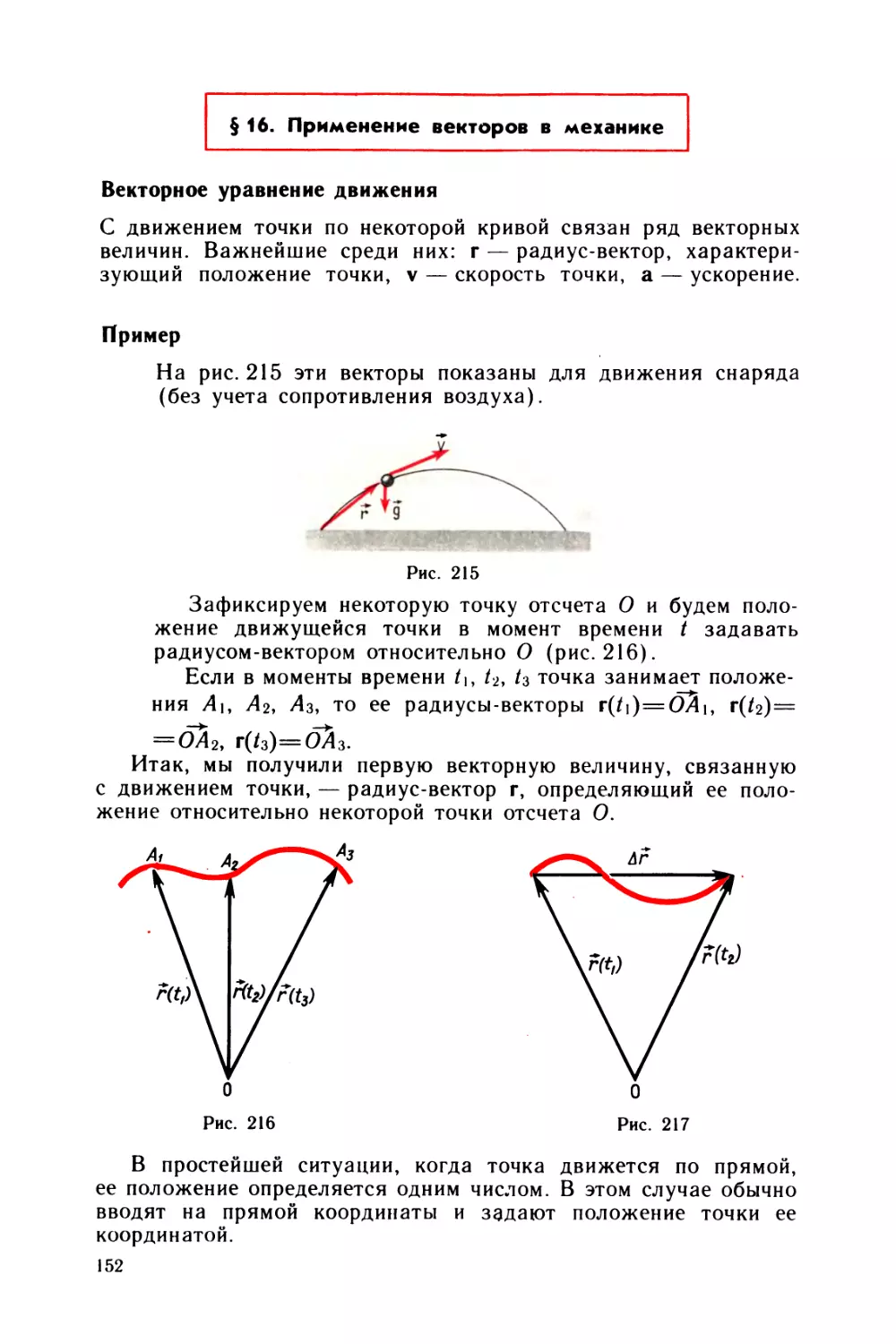
§ 14 Направленные отрезки 137
§ 15 Координаты вектора 1*7
§ 16 Применение векторов в механике 152
§ 17 Векторное пространство 157
Задачи и вопросы 159
5 Тригонометрические функции 166
§ 18 Углы и повороты 166
§ 19 Определение тригонометрических функций 175
§ 20 Исследование синуса и косинуса 185
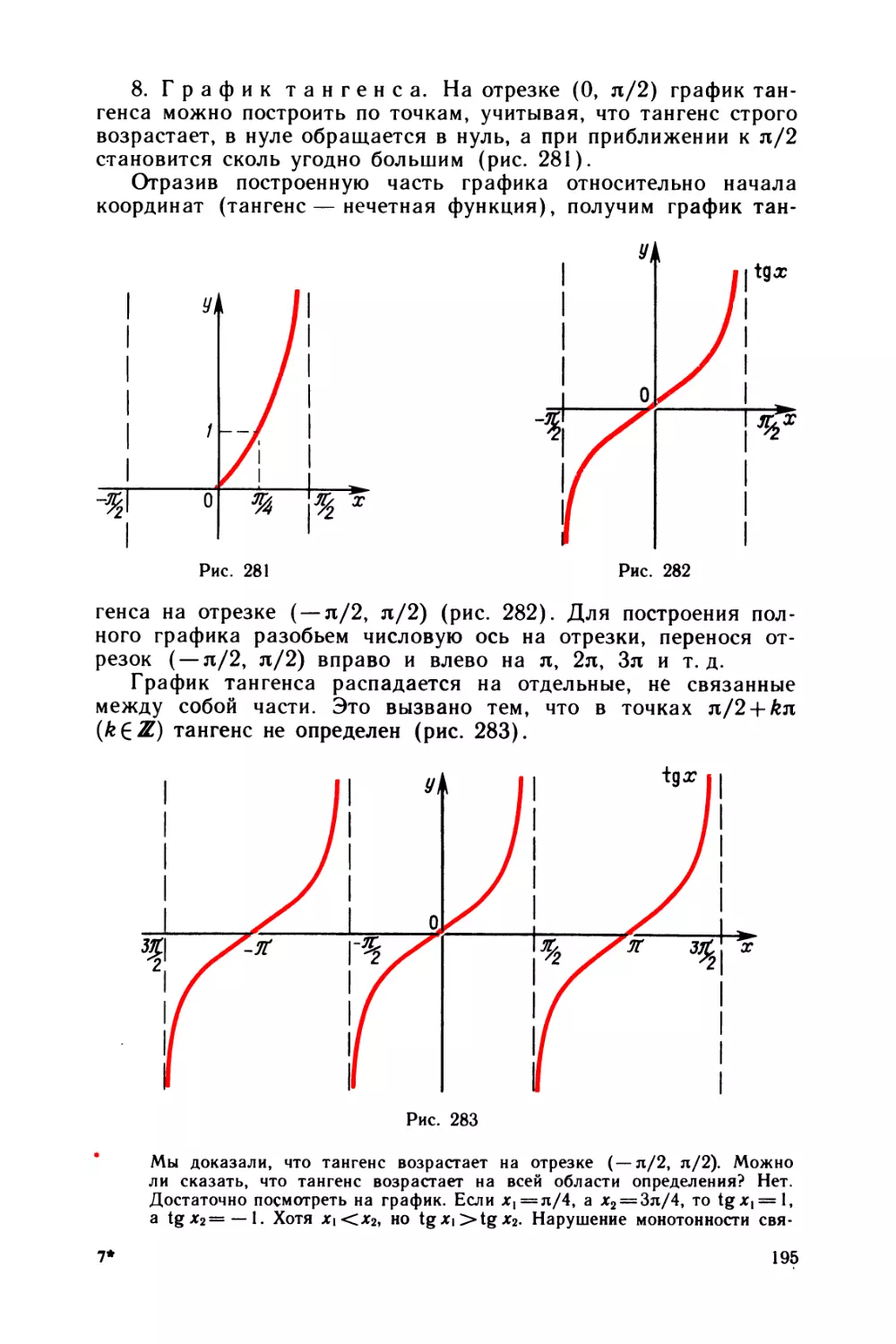
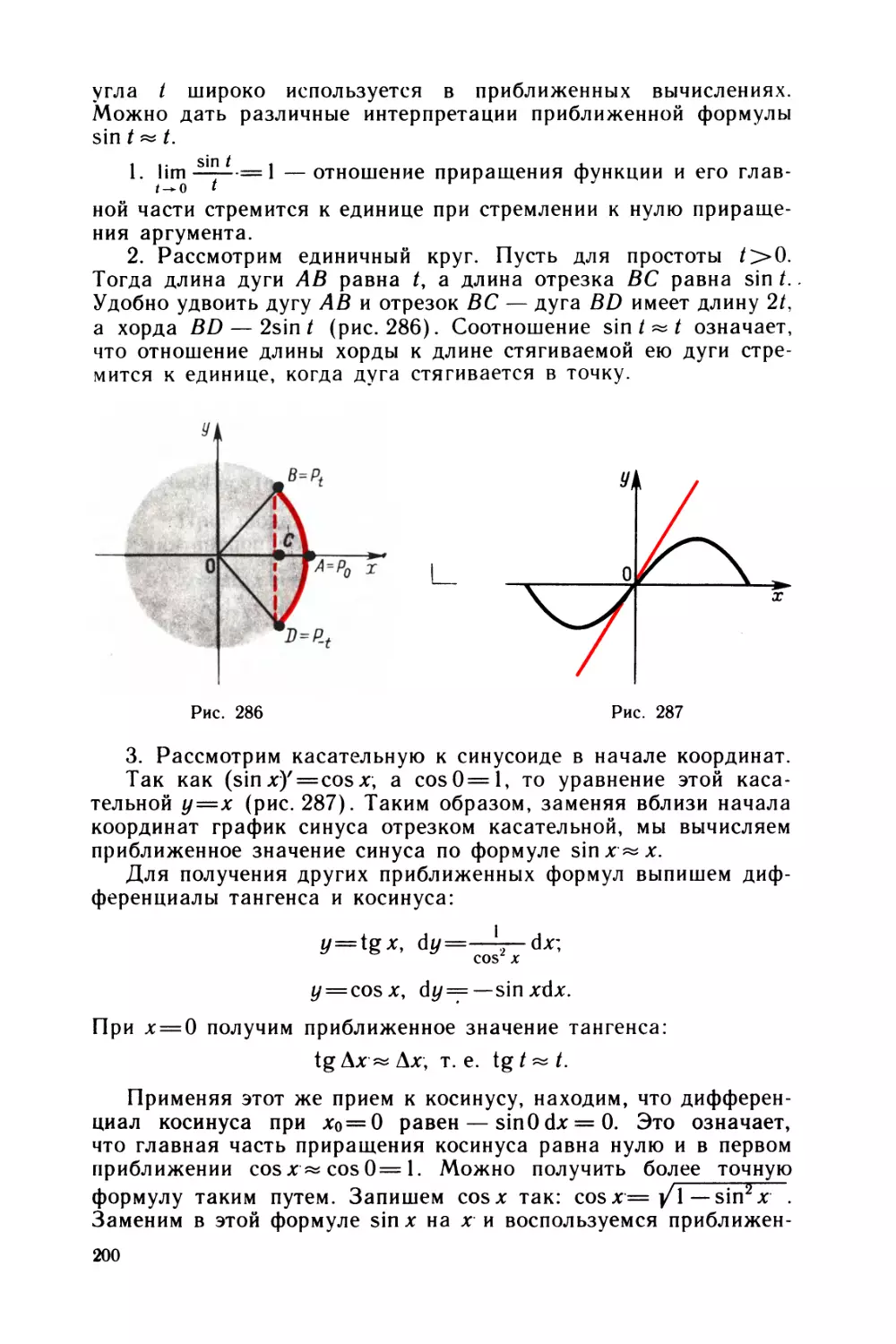
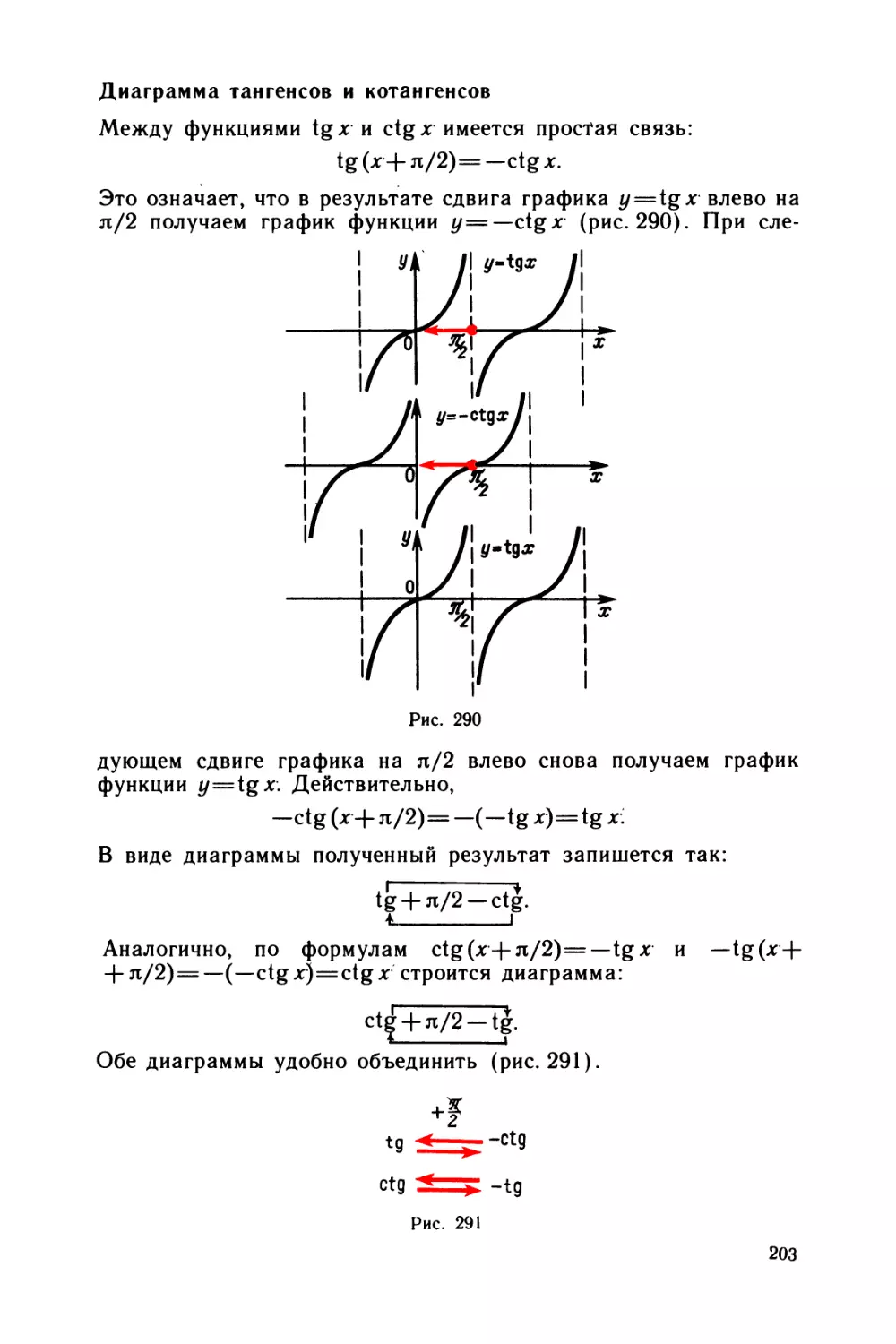
§ 21 Тангенс и котангенс 193
§ 22 Производные тригонометрических функций 197
§ 23 Диаграммы приведения 201
Задачи и вопросы 205
6 Скалярное произведение 210
§ 24 Проекция вектора 210
§ 25 Свойства скалярного произведения 213
Задачи и вопросы 220
7 Тригонометрические тождества и уравнения 222
26 Формулы сложения 222
27 Простейшие тригонометрические уравнения 230
§ 28 Решение тригонометрических уравнений 237
§ 29 Обратные функции 242
Задачи и вопросы 252
8 Перпендикулярность прямых и плоскостей 259
§ 30 Векторное задание прямой 259
§ 31 Векторное задание плоскости 265
§ 32 Двугранные углы 274
Задачи и вопросы 278
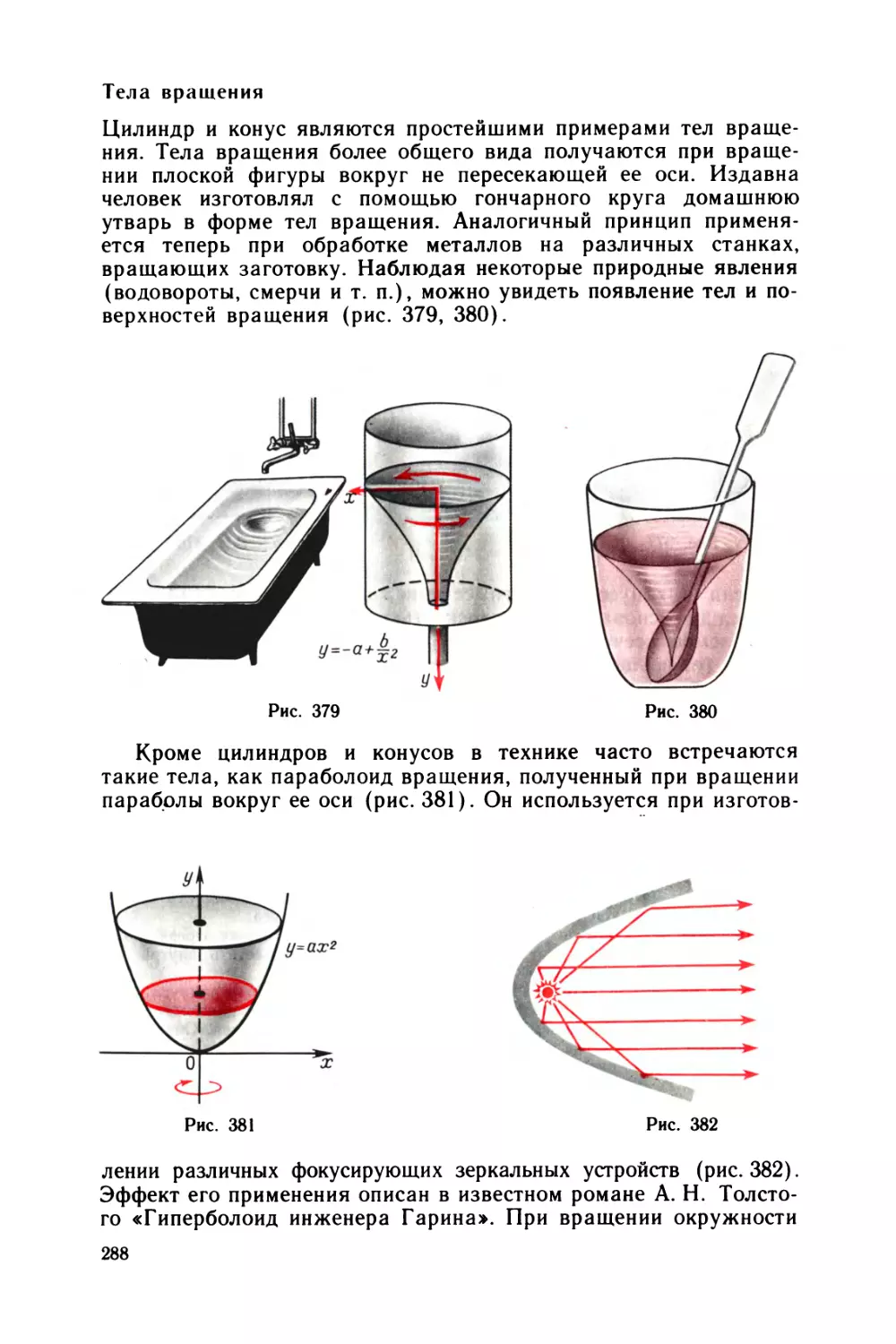
9 Пространственные тела 283
§ 33 Цилиндры и конусы 283
§ 34 Шар и сфера 291
§ 35 Призмы и пирамиды 295
§ 36 Многогранники 303
Задачи и вопросы 310
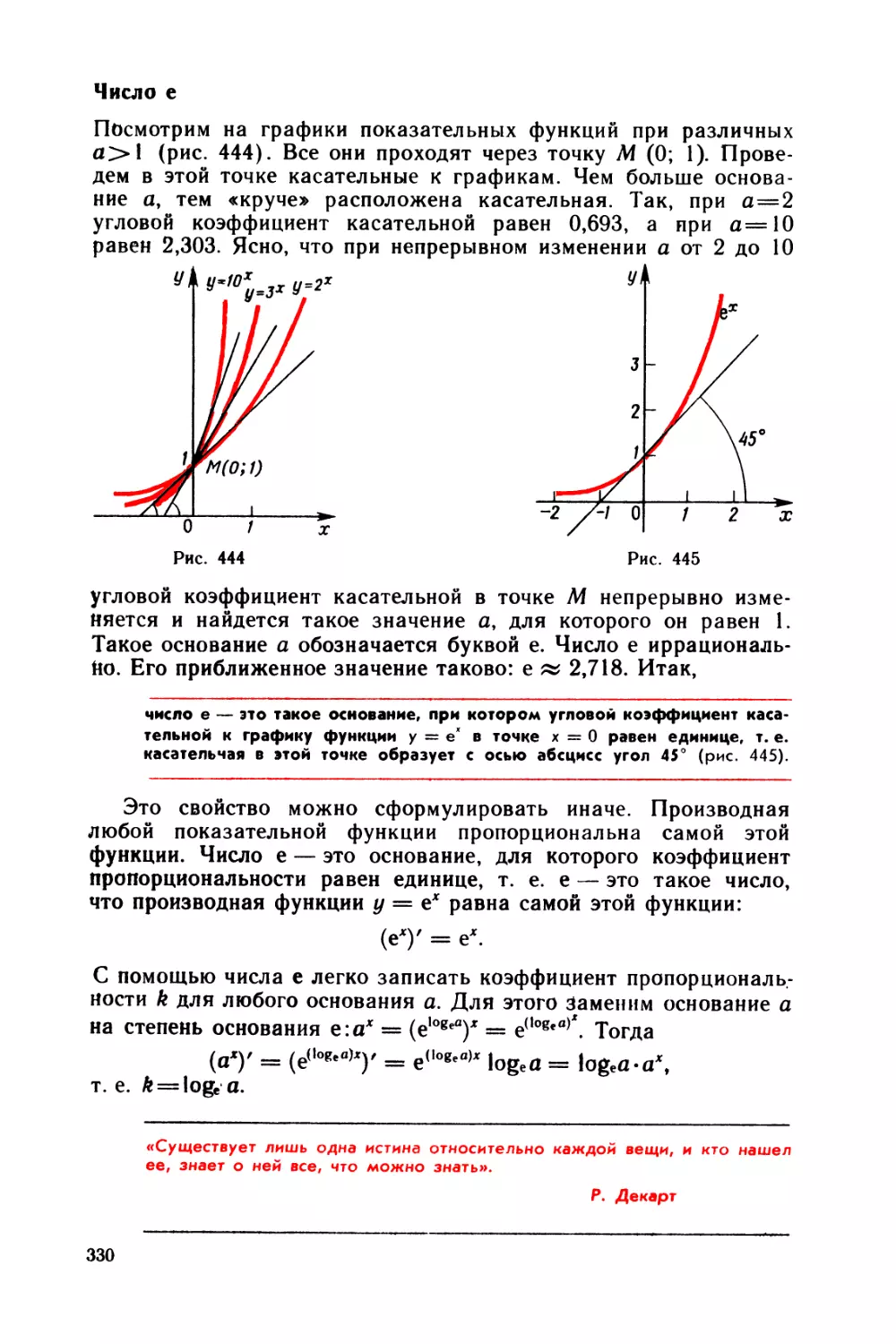
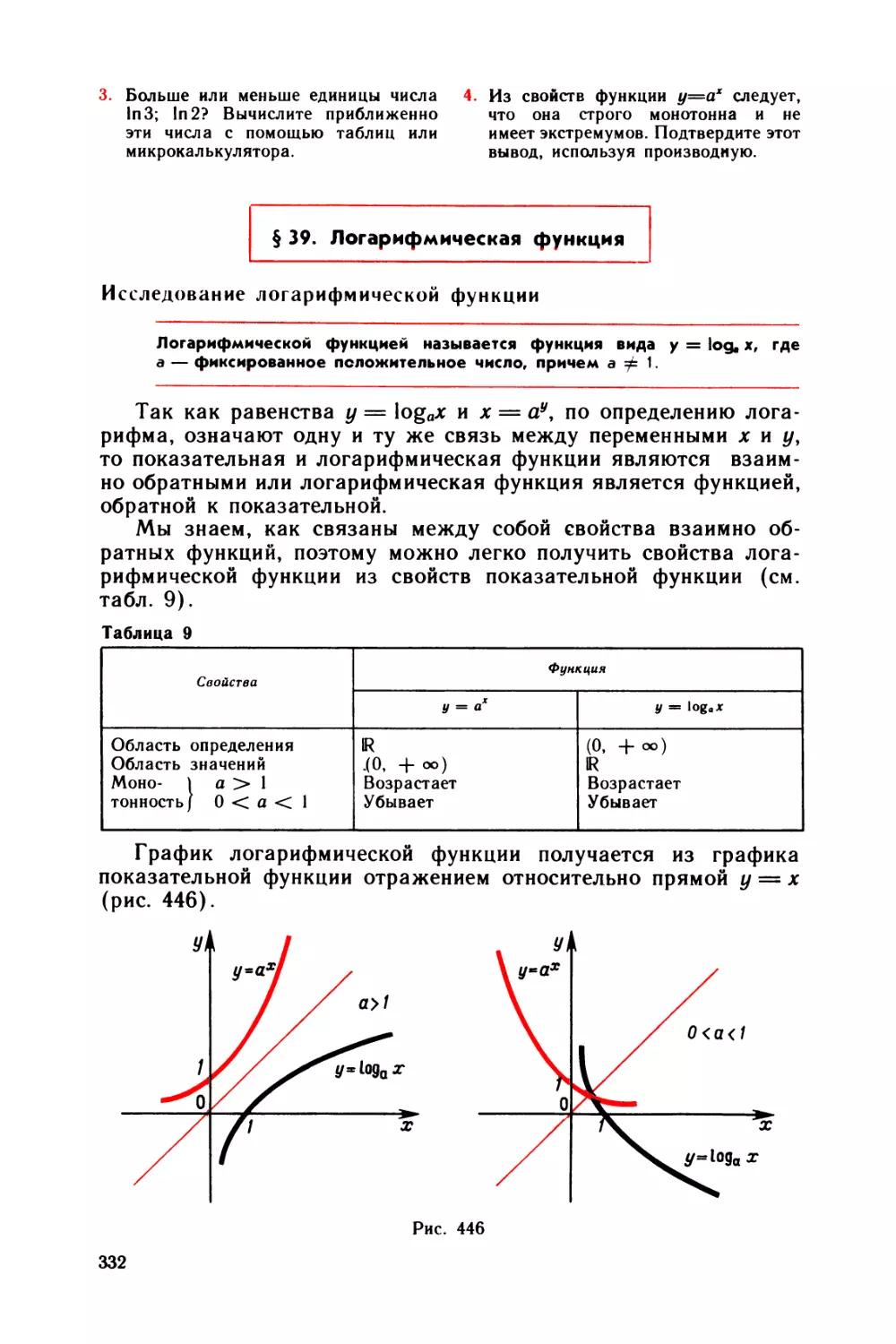
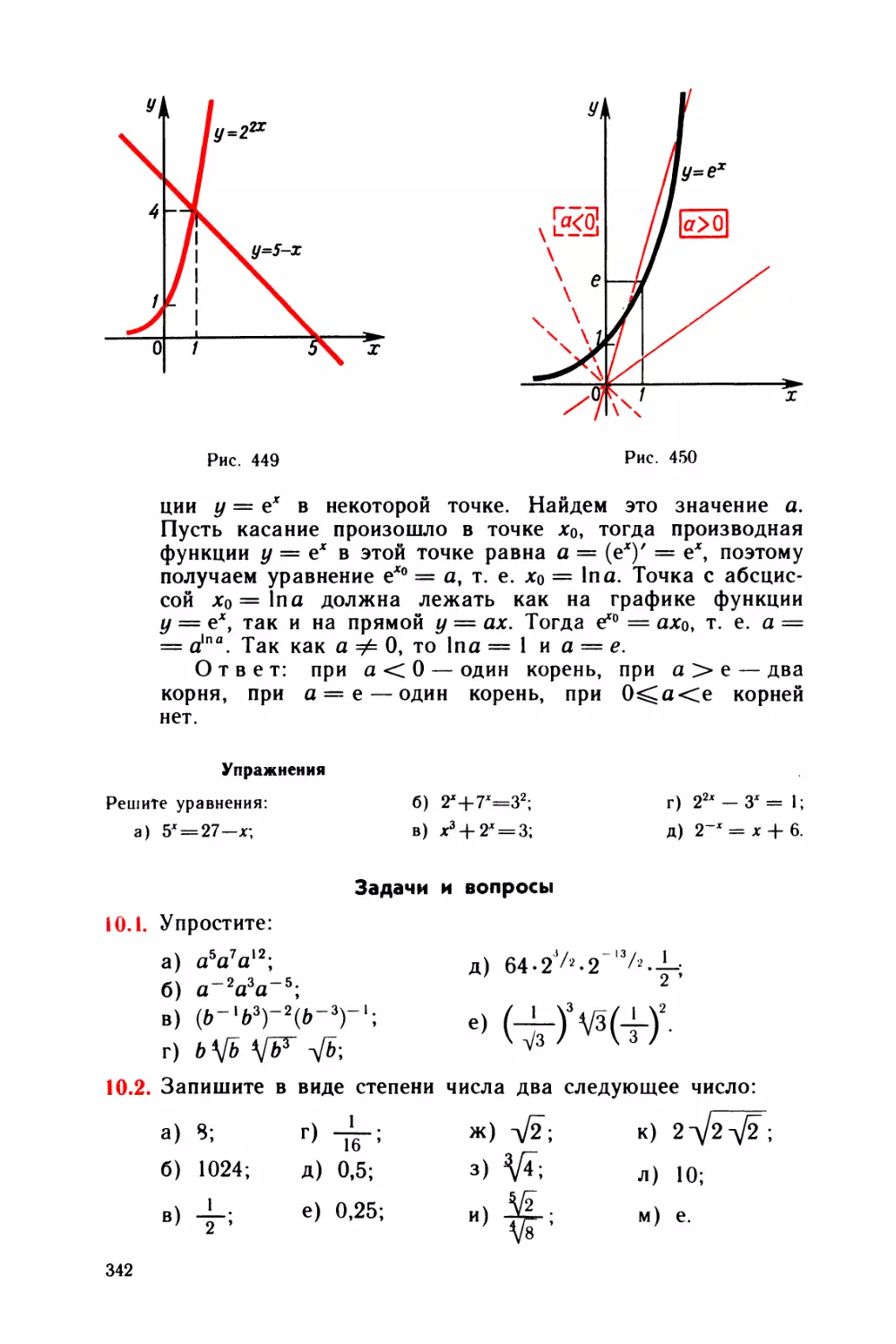
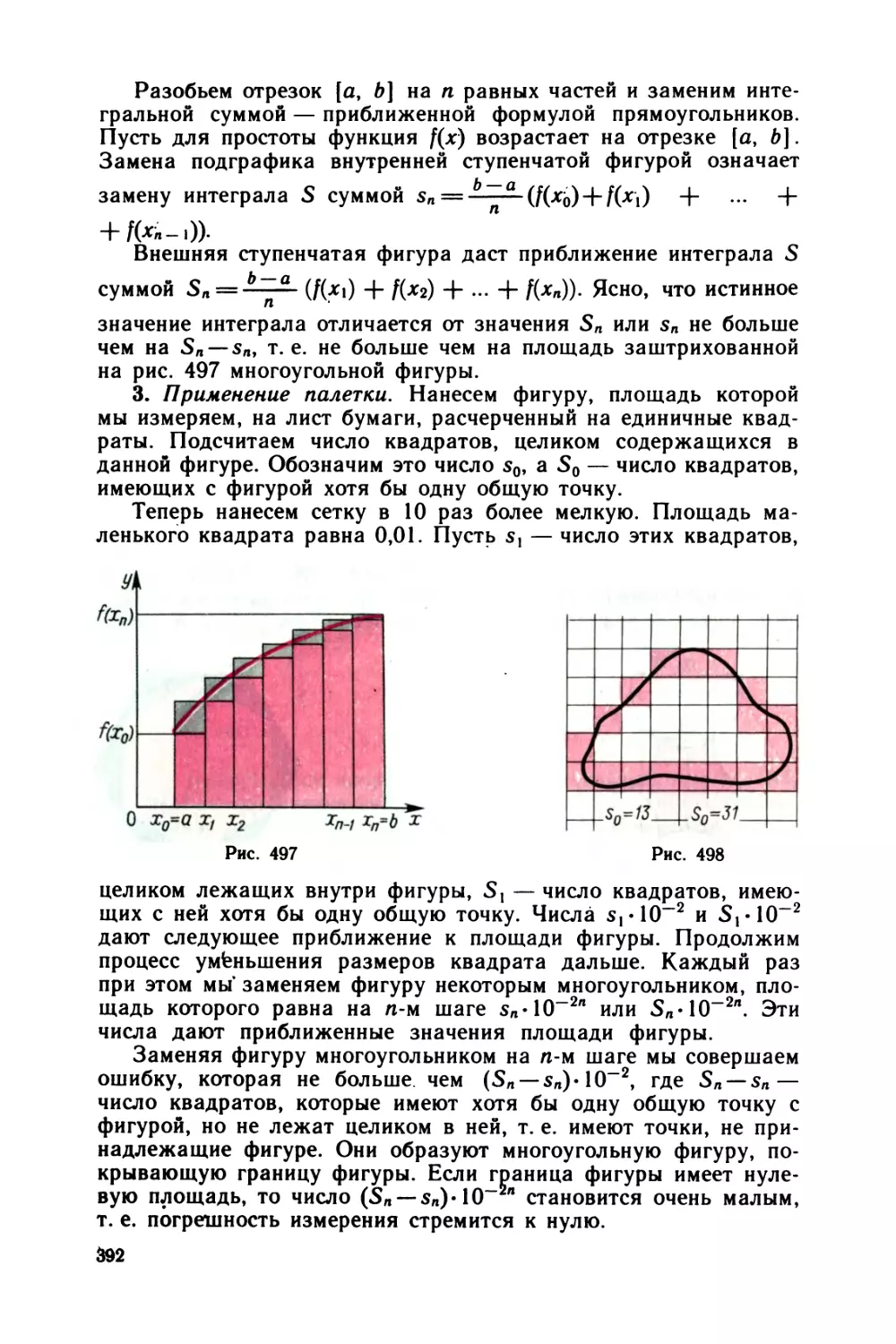
ю Показательная и логарифмическая функции 320
§ 37 Степени и логарифмы 320
§ 38 Показательная функция 327
§ 39 Логарифмическая функция 332
§ 40 Показательные и логарифмические уравнения и неравенства . . . 336
Задачи и вопросы 342
1 1 Интеграл и его приложения 348
£ 41 Определение интеграла 348
§ 42 Вычисление интеграла 356
§ 43 Приложения интеграла 362
§ 44 Дифференциальные уравнения 371
Задачи и вопросы 379
12 Площади и объемы 384
§ 45 Площади плоских фигур 384
§ 46 Объемы пространственных тел 393
§ 47 Площадь поверхности 399
Задачи и вопросы 401
13 Уравнения и неравенства 407
§ 48 Решение уравнений и неравенств с одним неизвестным 407
§ 49 Системы уравнений 418
§ 50 Составление уравнений 424
Задачи и вопросы 434
Послесловие 435
Приложение 441
Ответы 448
Предметный указатель 460
Предисловие
Книга представляет собой экспериментальный курс математики,
соответствующий программе старших классов общеобразовательной
школы, без традиционного деления на различные дисциплины — ал¬
гебра и начала анализа, геометрия. Настоящее издание составлено
на основе «Экспериментальных учебных материалов» (М., Высшая
школа, 1982) и пособия «Математика» (М., Просвещение, 1983).
В ходе преподавания экспериментального курса математики
в средних профтехучилищах г. Ленинграда и некоторых других
регионов страны в 1974—1985 гг. нашла подтверждение правиль¬
ность выбора основных методических принципов, заложенных в
программе единого курса математики. Главные идеи этого курса
оказались хорошо согласованными с основными направлениями
реформы общеобразовательной и профессиональной школы и спо¬
собствуют практической ее реализации. Программа такого курса
была разработана группой ленинградских ученых в рамках научных
исследований НИИ профтехпедагогики АПН СССР.
В подготовке книги принимал участие коллектив сотрудников
кафедры высшей математики Ленинградского электротехнического
института им. В. И. Ульянова (Ленина). Всем им, а также своим
многочисленным коллегам в институтах, школах и профтехучилищах
г. Ленинграда автор выражает искреннюю признательность.
Вступительное слово автора
Уважаемый читатель!
Перед вами экспериментальное учебное пособие по математике.
Математика за 2500 лет своего существования накопила богатейший
инструмент для исследования окружающего нас мира. Однако, как
заметил выдающийся русский математик и кораблестроитель акаде¬
мик А. Н. Крылов, человек обращается к математике «не затем,
чтобы любоваться неисчислимыми сокровищами». Ему прежде всего
нужно ознакомиться со «столетиями испытанными инструментами
и научиться ими правильно и искусно владеть».
Данная книга научит вас обращаться с такими математическими
инстоументами, как функции и их графики, геометрические фигуры,
векторы и координаты, производная и интеграл. Хотя первое озна¬
комление с большинством из этих понятий состоялось у вас раньше,
книга представляет их вам заново. Это удобно для тех, кто забыл
изучавшийся ранее материал, и полезно всем, так как даже в зна¬
комых вещах обнаружатся новые стороны и связи.
Для облегчения работы с пособием самые важные положения
и формулировки выделены. Большую роль играют иллюстрации:
если вы не до конца поняли учебный текст, внимательно рассмотрите
относящийся к нему чертеж. Еще в древности использовали этот
способ изучения математики — рисовали чертеж и говорили: смотри!
Каждый параграф книги разделен на пункты. В конце пунктов
помещены упражнения. Этих упражнений, конечно, недостаточно,
чтобы овладеть нужными навыками. Их цель — показать главное
направление усилий, необходимых для овладения соответствующим
материалом.
Достаточно полный набор задач и упражнений помещен в конце
каждой главы.
1
ЧИСЛА, ФУНКЦИИ И ГРАФИКИ
§ 1. Числовая ось
Изображение чисел точками числовой оси
Прямая с указанной начальной точкой, выбранным положительным на¬
правлением отсчета и фиксированным отрезком (единицей масштаба)
называется числовой осью (рис. 1).
Каждое число можно изобразить точкой числовой оси.
Наоборот, каждая точка оси изображает какое-нибудь число.
Если число х изображается точкой Af, то это число называ¬
ется координатой точки Af. Запись М(х) означает: точка М имеет
координату х (рис. 2).
Соответствие между числами и точками настолько естествен¬
но, что часто не различают число и изображающую его точку.
Говорят, например, «точка 2», «точка —0,5», «нулевая точка».
«Все есть число.»
Пифагор
Пифагор — греческий математик и философ VI века до н. э. Сведения
о нем легендарны. Школе Пифагора приписывается доказательство со¬
отношения между сторонами прямоугольного треугольника и открытие
иррациональных чисел (например, V2).
7
Рис. 1
Рис. 2
Число является одним из основных понятий математики.
Представление о числе развивалось в течение многих тысячеле¬
тий одновременно с потребностями в счете и измерении.
Мы используем различные числа — натуральные (1; 2; 3; ...),
з
целые (0; 1; —1; 2; —2;...), рациональные (3; —; —0,5;...),
иррациональные (-у[2 \^[Ъ \ п = 3,1415 ...; ...). Все числа вместе
называются вещественными (действительными).
На шкалы различных измерительных приборов нанесены чис¬
ла. Этим они похожи на отрезки числовой оси. При этом исполь¬
зуют не только прямолинейные шкалы, но и круговые (рис. 3).
Рис. 3
Сре^и числовых множеств особенно часто встречаются мно¬
жества чисел, лежащих между двумя точками числовой оси.
Эти множества называют числовыми промежутками. В книгах
используют различные термины для их обозначения — отрезок,
сегмент, интервал, промежуток. Мы не будем делать различия
между этими словами, считая их синонимами. Чаще всего мы будем
применять слово «отрезок», реже — «интервал». Обозначаются
отрезки с помощью скобок. При этом квадратная скобка указы¬
вает на то, что соответствующий конец отрезка включается в
рассматриваемое множество, а круглая — на то, что не вклю¬
чается.
Бесконечные промежутки (множества чисел, лежащих справа
или слева от некоторой точки) называются также отрезками или
интервалами.
Упражнения
1. На числовой оси буквами А, В, С, D
12
показаны числа 2,2; /3”; ——;
—■4+ /1Г (рис. 4). Определите,
какое число соответствует каждой
букве.
2. На числовой оси указаны точки
А, Ву С, D (рис. 5). Определите
приближенно их координаты.
3 Нанесите на числовую ось точки
Л(2,5); В(-3); С(— 11 /3).
4. Даны координаты двух точек: А(а) и
В(Ь). Докажите, что середина отрез¬
ка АВ имеет координату (а+Ь)/2.
8
Рис. 4
Рис. 5
Модуль числа
Модулем числа х называется расстояние от начала отсчета до точки,
изображающей число х. Модуль числа х обозначается так: | х |.
Модуль разности двух чисел равен расстоянию между точками, изоб¬
ражающими эти числа.
* Нанесем на числовую ось числа а, b, и их разность а — Ь. Обозначим
получившиеся точки через Л, В и С. Из рис. 6 ясно, что \АВ\ = |0С|.
По определению модуля, \а — Ь\ = |ОС|, т. е. (а — Ь) — расстояние
между точками А и В, изображающими числа а и Ь.
Зная, что модуль обозначает расстояние, можно легко на¬
учиться решать простые уравнения и неравенства с модулем.
Рис. 6
Прочтем условие \х\ ^ 2: расстояние от точки х до точки О
больше или равно 2. Нанесем на ось точки А и А\ для которых
это расстояние равно 2, и объединим точки, лежащие вне от¬
резка А'А.
Полученное числовое множество состоит из чисел, удовлетво¬
ряющих одному из неравенств х <1 —2 или х ^ 2.
* При решении уравнений и неравенств с модулем полезно, используя свойст¬
ва модуля, преобразовать условие так, чтобы был явно выражен модуль
разности неизвестного и какого-либо числа.
Примеры
1. |3 — х\ = \х — 3|.
2. \2х + 5| = \2(х + 5/2)\=2\х - (-5/2)1-
3. 16 — 3*1 = |3дс —6| = 3|jc —2|.
При записи решения неравенства в виде отрезков типа (а, 6),
[а, Ь) и т. п. следите за тем, чтобы левый конец отрезка был
меньше правого. Нельзя допускать ответы вида (5, —1). То же
самое относится и к записи решения в виде двойных нера¬
венств — их нужно приводить к такому виду, чтобы числа шли
в возрастающем порядке, например —-2 < дс < 0; —1
Модуль числа х можно определить следующим образом.
. . __ г л:, если х ^ 0;
\—х, если * <0.
9
Возьмем число х и изобразим его точкой М на числовой оси (рис. 7). Если
х ^ О, то расстояние |ОЛ4| равно х. Если х < 0, то это расстояние рав¬
но (—л:):
{х, если х > О,
— х, если х < 0.
Так как \х\ есть, по определению, расстояние |ОМ|, то мы и получаем тре¬
буемую формулу. Она позволяет «раскрывать» модуль, т. е. записывать
выражения без знака модуля.
Примеры
1. | —2| = 2; | + л| = л;
| —V2I = л/2; 12 - л/51 = л/5 - 2.
2. Раскроем модули в выражении у = \х-+ 2| + I*-- 2|.
Корнями выражений, стоящих под знаком модуля, являют¬
ся числа Х\ = —2; Х2 = 2. Они разбивают числовую ось
на три области: /, //, /// (рис. 8). Указываем знаки выра¬
жений х + 2 и х — 2 в каждой из этих областей и осво¬
бождаемся от знака модуля:
I) х < — 2, */= —(дс + 2) — (лс — 2) = —х — 2 — лс+
+ 2 = —2х;
II) —2 ^ лт ^ 2, у = (лт -f- 2) — (х — 2) = х -f- 2 — лг -f~
+ 2 = 4;
III) х > 2, у = {х + 2) + (х ^ 2) = 2х.
Упражнения
1. Нанесите на числовую ось числа,
модуль которых равен трем.
2. Нанесите на числовую ось точки,
расстояние от которых до точки 1
равно трем.
3. Запишите с помощью модуля ут¬
верждение: «расстояние от точки х
до точки 5 равно 2». Найдите все
такие точки х.
4. Докажите, что \х\ = |—х\. Дайте
геометрическое объяснение.
10
Рис. 7
Рис. 8
5. Решите уравнения:
а) 1*1=5; в) |х+5| = 2;
б) к—3|=1; г) |3—2*| = */2.
6. Решите неравенства:
а) |*i<3; г) |*+2|>3;
б) 1*0 2; д) |1—2*|<4;
в) |*|<1; е) |3(5-*)|<6.
7. Придумайте уравнение или неравен¬
ство с модулем, решение которого
составило бы данное множество
чисел:
а) *=±3;
б) х\ = —2, jc*2 = 4;
в)
г) *<2, *i>6;
•Д) (-1; 5);
е) [2, 8].
8 Решите уравнения:
а) U-1| + |jc+1| = 2;
б) U+2I —|х—1|=3;
в) N-31=1;
г) |W + 3|=5.
9. Раскройте модуль в следующих
выражениях:
|-1,1|, |3— /ТО|, |л2—10|, |23—32|.
10. Выражение \х—2| равно jc—2,
если *^2, и равно 2—*, если *<2.
Аналогично раскройте модуль в
следующих выражениях:
|*+1|, |2дг—3|, |4-3jc|, |3+jc/2|.
11. Раскройте модуль в следующих
выражениях:
а) у=I*f+I*+3|;
б) у= |*+5| — |*—2|;
в) (/=|jc-3| + 2|jc+2| + 3jc-1;
г) у= \2—Зх\ — 2\х— 11 — jc;
д) у=\х—1| + |*| + |*+1|;
е) */=(*+1*0/2.
Округление чисел
В вычислениях практического характера используют округлен¬
ные числа. Обычно числа округляют до единицы какого-либо раз¬
ряда в десятичной записи. Так, округление числа а = 264,783
с точностью до сотен дает число 300, с точностью до единиц —
число 265, с точностью до 0,1 — число 264,8 и т. п.
Если мы нанесем на числовую ось (рис. 9) точное значение и
округленное значение, то легко будет оценивать, насколько близ¬
ки между собой эти числа. Так, ясно, что расстояние между
взятым ранее числом а и его округлением до единиц меньше по¬
ловины. Так как расстояние между точками числовой оси вычис-
ляетс?я с помощью модуля, то
Iа - 265| < 0,5.
На практике используют разные обозначения для записи
округленных чисел: а « 265 или а = 265 ± 0,5.
Пример
С помощью амперметра, градуированного через 2А, можно
измерить приближенное значение силы тока с точностью
11
Рис. 9
до 1 А (рис. 10) Если показание амперметра 12 А, то это
означает, что сила тока / отличается от 12 не более чем
на 1. Это можно записать по-разному: / ж 12 А или, точнее,
I = (12 zb 1 )А или с помощью знака модуля |/ — 121 <1 1,
или с помощью неравенств (в амперах) 11 ^ ^ 13.
Рис. 10
Упражнения
1. Деления омметра идут через 10 кОм.
Какие записи результата измерения
сопротивления (в килоомах) вы счи¬
таете правильными:
а) /? = 33; г) /?« 33,5;
б) R « 30; д) г = 30±5;
в) /? = 30; е) R = 30±10?
Запишите с ломощью модуля пра¬
вильную оценку результата изме¬
рения.
2. Нанесите на числовую ось все
числа, округление которых с точно¬
стью до 1 равно 3.
3. Округлите с точностью до 10 сле¬
дующие числа: 387,12; 498,36;
100,19; 99,91. Эти же числа округли¬
те с точностью до 0,1.
§ 2. Декартовы координаты на плоскости
Задание точек плоскости координатами
Декартова система координат на плоскости — это две взаимно перпенди¬
кулярные числовые оси с общим началом.
Декартова система координат позволяет совершать две операции: каж¬
дой точке плоскости сопоставлять пару чисел — координаты этой точки;
обратно: по данной паре чисел строить точку плоскости с этими коорди¬
натами.
Если на прямой выбрать начало отсчета, положительное на¬
правление и единицу масштаба, то можно определить всякую
точку этой прямой с помощью числа — координаты этой точки.
Оказывается:
с помощью чисел можно задавать не только точки прямой, но также
точки плоскости или пространства.
Эта идея принадлежит французскому математику Рене Де¬
карту (XVII в.).
12
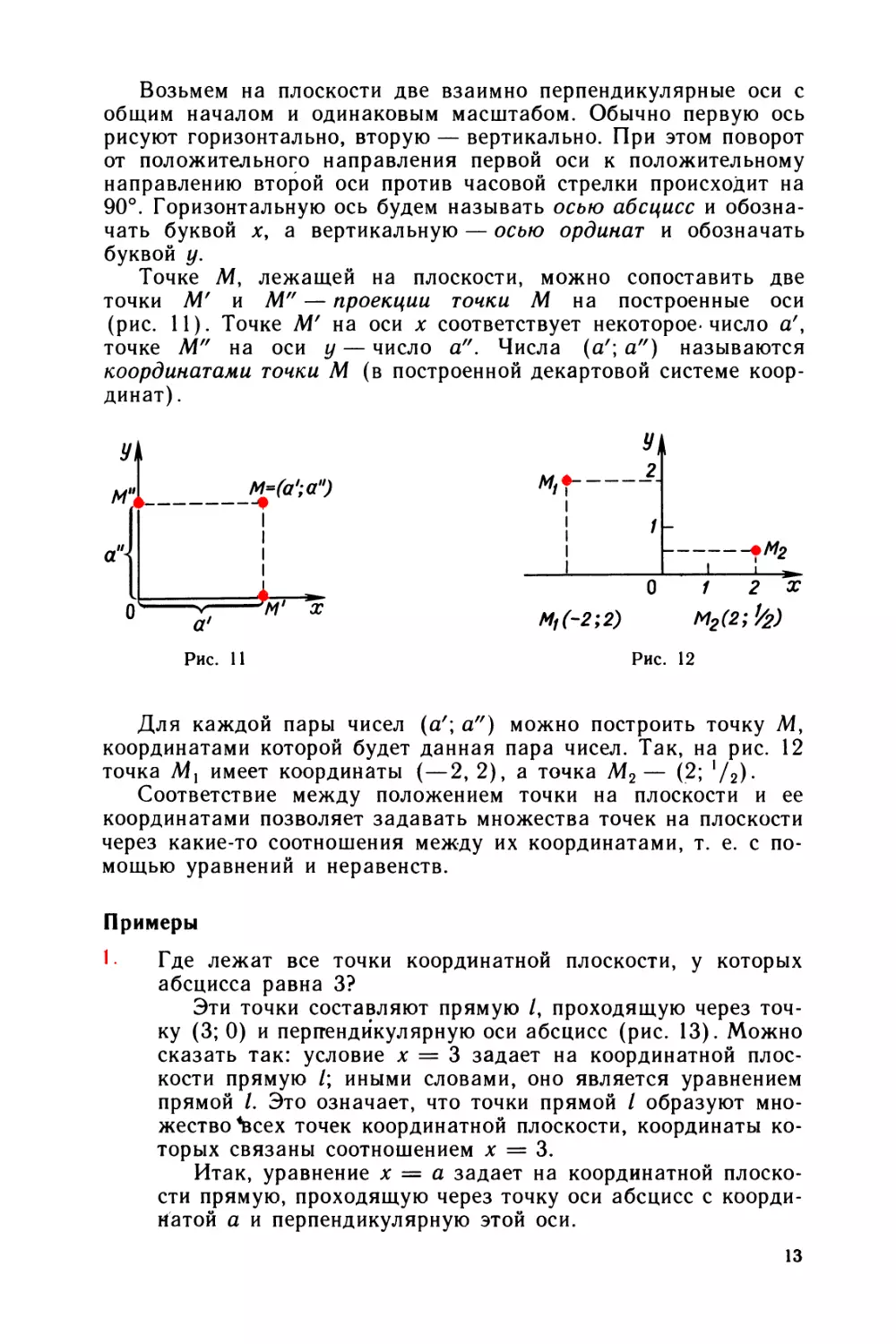
Возьмем на плоскости две взаимно перпендикулярные оси с
общим началом и одинаковым масштабом. Обычно первую ось
рисуют горизонтально, вторую — вертикально. При этом поворот
от положительного направления первой оси к положительному
направлению второй оси против часовой стрелки происходит на
90°. Горизонтальную ось будем называть осью абсцисс и обозна¬
чать буквой xf а вертикальную — осью ординат и обозначать
буквой у.
Точке М, лежащей на плоскости, можно сопоставить две
точки М' и М” — проекции тонки М на построенные оси
(рис. И). Точке М' на оси х соответствует некоторое-число а',
точке М" на оси у — число а". Числа (а'; а") называются
координатами тонки М (в построенной декартовой системе коор¬
динат).
Для каждой пары чисел (а'; а") можно построить точку М,
координатами которой будет данная пара чисел. Так, на рис. 12
точка М} имеет координаты (—2, 2), а точка М2— (2; 1 /2).
Соответствие между положением точки на плоскости и ее
координатами позволяет задавать множества точек на плоскости
через какие-то соотношения между их координатами, т. е. с по¬
мощью уравнений и неравенств.
Примеры
1 Где лежат все точки координатной плоскости, у которых
абсцисса равна 3?
Эти точки составляют прямую /, проходящую через точ¬
ку (3; 0) и перпендикулярную оси абсцисс (рис. 13). Можно
сказать так: условие х = 3 задает на координатной плос¬
кости прямую /; иными словами, оно является уравнением
прямой /. Это означает, что точки прямой / образуют мно¬
жество Ъсех точек координатной плоскости, координаты ко¬
торых связаны соотношением х = 3.
Итак, уравнение х = а задает на координатной плоско¬
сти прямую, проходящую через точку оси абсцисс с коорди¬
натой а и перпендикулярную этой оси.
13
Рис. 11
Рис. 12
2. Как изображается множество всех точек, у которых по¬
стоянной является ордината?
Точки координатной плоскости, у которых у = — 1,
лежат на прямой, перпендикулярной оси ординат и прохо¬
дящей через точку (0; — 1).
Уравнение у = Ь задает на координатной плоскости
прямую, проходящую через точку оси ординат с координа¬
той b и перпендикулярную этой оси.
Рассмотрим координатные четверти. В каждой из чет¬
вертей координаты имеют определенные знаки. Так, напри¬
мер, у точек четвертой четверти абсцисса положительна,
а ордината отрицательна (рис. 14). Можно сказать, что
точки четвертой четверти задаются системой нера¬
венств (х > 0,
[у < о.
Идея задавать геометрические объекты числами получила
со времен Декарта большое развитие. Кроме декартовых (пря¬
моугольных) координат стали использоваться различные другие
системы, например географическая система координат (рис. 15),
8
7
6
S
Ч
J
г
1
Рис. 16
Рис. 13
Рис. 14
Рис. 15
в которой положение точки на земном шаре задается двумя
числами: широтой и долготой. Аналогом системы координат
является шахматная нотация — известная запись положения фи¬
гур на шахматной доске (рис. 16).
Упражнения
1. На рис. 17 изображены точки А, В,
С, D. Определите приближенно их
координаты.
2. Постройте точки с указанными
координатами
А (1;2), В(0; -3), С (-5; 0),
D (2; -7).
3. Изобразите на координатной пло¬
скости точки, координаты которых
связаны соотношениями:
Уравнения простейших кривых
В математике и ее приложениях часто встречаются следующие
два типа задач. В первом из них даны геометрические свойства
кривой и нужно перевести их на алгебраический язык — соста¬
вить уравнение кривой, получить зависимость между координа¬
тами точек. Второй тип задач таков: дано уравнение кривой,
т. е. известна зависимость между координатами, а надо постро¬
ить кривую, график, представить себе геометрические ее свой¬
ства.
Пример
Составим уравнение оружности.
Для этого прежде всего надо знать ее центр и радиус.
Пусть центр окружности — точка М (а; 6), а радиус равен R.
Затем надо испо^зовать условие того, что точка А лежит
на данной окружности. Это означает, что расстояние \АМ\
15
Рис. 17
равно R (рис. 18). Обозначим координаты точки А через
(х\ у) и запишем формулу расстояния между двумя точ¬
ками:
\АМ\ = У(дс — df + Jy — bf .
Подставляя это выражение в условие \АМ\ — R, получаем
уравнение окружности: "д/(лг — а)2 + (и — 6)2 = /? или,
возводя в квадрат, (х — а)2 + (у — bf = R2.
Важно отметить следующее (рис. 19).
1. Координаты всякой точки окружности связаны соотношением
(х — af + (у — bf = R2.
2. Всякая точка плоскости А(х;и), координаты которой удов¬
летворяют соотношению (л: — af + {У ^)2 — #2> лежит на
рассматриваемой окружности.
В общем виде, когда говорят, что некоторое соотношение
между координатами есть уравнение кривой С, надо быть уве¬
ренным в двух положениях: 1) координаты любой точки С свя¬
заны данным уравнением; 2) всякая точка плоскости, коорди¬
наты которой удовлетворяют уравнению, лежит на кривой С.
Пусть соотношение между координатами записано символи-
«Арифметические знаки — это записанные геометрические фигуры, а ге¬
ометрические фигуры — это нарисованные формулы.»
Д. Гильберт
Гильберт Давид (1862—1943 гг.) — немецкий математик, основатель
Геттингенской математической школы. Гильберт завершил начатое Евкли¬
дом. Ему принадлежит глубокое обобщение евклидовой геометрии (гиль¬
бертовы пространства), он получил важнейшие результаты в математи¬
ческой логике, являющиеся основой современных взглядов на логический
фундамент математики.
16
Рис. 18
Рис. 19
Рис. 22
Рис. 20
Рис. 21
Рис. 23
Рис. 24
чески в виде f (х% у) = 0. То, что / (х, у) = 0 есть уравнение кри¬
вой С, можно записать так:
f(Xy у) = 0 о А(х, у) <ЕЕ С.
Кроме уравнения окружности полезно запомнить следующие
уравнения:
у = kx + b — уравнение прямой с угловым коэф¬
фициентом (рис. 20);
Ах + By + С = 0 — уравнение прямой в общем виде;
(х — а)2 + (у — Ь)2 = R2 — уравнение окружности;
ху = с —уравнение гиперболы (рис. 21).
Примеры
1. Цепная линия — линия, по которой провисает тяжелая цепь
при ее креплении за два конца (рис. 22). Ее уравнение
y = a{\0kx+l0-kx).
2. Астроида — кривая, по которой движется точка на колесе,
катящемся внутри обода вчетверо большего радиуса
(рис. 23). Ее уравнение
XV3 + у2/Ъ = а2/3
3. Логарифмическая спираль — кривая, определяющая форму
спиральных галактик (рис. 24). Уравнение этой спирали в
декартовых координатах написать можно, но оно будет
громоздким.
Вывести уравнения этих кривых исходя из их физического
смысла — достаточно трудная задача.
Упражнения торых до начала координат вдвое
болБше расстояния до оси х.
4. На рис. 25 изображено пять пря-
1. Напишите уравнение окружности с мых. Их уравнения даны в пере-
центром в начале координат и ра- путанном порядке:
диусом 3.
2. Напишите уравнение окружности,
а) X—2; г) у = 3;
проходящей через начало коорди- б) у—1=0; д) х-\-у—3=0.
нат, с центром в точке М (3; 4). в) х + у=0;
3*. Выведите уравнение геометриче- Определите, какое уравнение имеет
ского места точек, расстояние ко- каждая из прямых.
Рис. 25
Рис. 26
5. На рис. 26 изображено пять кри¬
вых. Их уравнения:
а) х+у=\; б) дг2+«/2=1;
в) ху= — 1; г) jq/=2;
д) г+2г+(/2=0.
Найдите уравнение каждой кривой.
§ 3. Понятие функции
Переменные и зависимость между ними
Понятие переменной является одним из важнейших в математи¬
ке. Ф. Энгельс писал, что благодаря переменной в математику
вошли движение и диалектика.
Изучение какого-либо процесса приводит к выявлению тех
или иных его характеристик, которые обычно могут меняться
и потому называются переменными. Например, состояние газа в
замкнутом объеме можно описывать его параметрами: темпе¬
ратурой Г, объемом V и давлением р (переменные).
Свободное падение тела можно описывать с помощью пере¬
менных: пути 5, пройденного телом за время /, скоростью v в
момент времени t, кинетической энергией Е в момент времени t
и т. д.
Различные переменные, описывающие какой-либо процесс,
обычно связаны между собой. Изучение этих связей является
одной из основных задач экспериментальных наук. Так, основ¬
ные законы физики обычно записываются как связи, т. е. зави¬
симости между теми или иными переменными. Например, закон
Клапейрона — Менделеева .утверждает, что давление р, объем V
и термодинамическая температура Т ~ идеального газа связаны
соотношением
Реальные процессы обычно связаны с большим числом пере¬
менных и зависимостей между ними. В то же время можно от¬
влечься от каких-то частных деталей, сосредоточив свое внима¬
ние лишь на некоторых сторонах процесса, идеализировав ус¬
ловия, в которых он протекает. Тогда удается построить мате¬
матическую модель процесса, описывающую основные характе-
= const .
19
ристики и связи между ними. Например, вводя понятие идеаль¬
ного газа, т. е. пренебрегая взаимодействием между молекула¬
ми газа и их размером, с помощью основных характеристик /?,
V и Т получаем газовые законы.
При изучении свободного падения материального тела можно
пренебречь сопротивлением воздуха, изменением силы тяжести
и т. п. и считать, что движение происходит по прямой с по¬
стоянным ускорением g. Положение тела в любой момент вре¬
мени t можно найти, зная его начальное положение и начальную
скорость.
Соотношения между переменными математической модели
часто имеют вид уравнения, и можно попытаться построить
геометрический образ этих соотношений. Как правило, измеряе¬
мых величин бывает несколько. В том случае, когда их две, связь
между ними удобно изобразить на координатной плоскости.
Так, зависимость между давлением и объемом реального газа
при условии постоянства температуры Т может быть записана
уравнением рV = С, где С — константа (закон Бойля — Ма-
риотта). Эта зависимость на плоскости с декартовыми коорди¬
натами (р; V) изображается частью гиперболы (рис. 27). Физи¬
ческие условия обычно задают границы значений р и I/, в кото¬
рых действует данная связь между величинами.
20
Рис. 27
Рис. 28
Кинетическая энергия Е тела массы т, движущегося в мо¬
мент времени t со скоростью v, равна mv2/2. Зависимость между
кинетической энергией и временем в случае свободного падения
тела с нулевой начальной скоростью (и при тех физических
предположениях, которые были сделаны вьиие) выражается
формулой
Ее графическое изображение на плоскости (£, t) приведено на
рис. 28.
Для изображения зависимости между тремя величинами
нужно переходить от координат в плоскости к координатам в
пространстве, т. е. от рисунка в плоскости к рисунку в простран¬
стве. Одновременное изучение большего числа величин потребо¬
вало от математиков построения многомерных пространств —
таких пространств, в которых положение точки определяется
не обязательно одним, двумя или тремя числами, как на пря¬
мой, плоскости, или в пространстве, а любым числом координат.
Нашей главной задачей будет изучение зависимостей между
двумя величинами. Для этого вводится известное вам понятие
функции.
Задания
1. Представим полет космической ра¬
кеты. Введем переменные величины,
характеризующие этот полет: t —
время, прошедшее с момента старта;
s — расстояние от Земли до ракеты;
v, а и т — скорость, ускорение и
масса ракеты соответственно. Какие
значения могут принимать эти пере¬
менные? Выделите какие-либо пары
переменных и придумайте зависи¬
мости между ними. Попробуйте
изобразить эти зависимости на
графике.
2. Рассмотрите какой-либо производ¬
ственный процесс, связанный с ва¬
шей будущей специальностью. Вы¬
делите переменные, которыми мож¬
но охарактеризовать процесс. Какие
значения могут принимать эти пе¬
ременные? Связаны ли переменные
между собой? Какие переменные вы
можете менять по своему усмотре¬
нию в ходе процесса, а какие будут
меняться независимо от вас? По¬
пробуйте менять одну из перемен¬
ных и опишите, как будут при этом
меняться другие.
3. На рис. 29, а—е даны шесть зави¬
симостей между переменными х и у.
Для каждой из них укажите, какие
значения могут принимать пере¬
менные. В каких случаях зависи¬
мость позволяет выразить у через jc?
Рис. 29
21
Функция и ее график
Пусть даны две переменные хну.
Переменная у называется функцией от переменной х, если каждое зна-
чение х однозначно определяет некоторое значение у.
Примеры
1) у = kx + Ь\ 3) у = х2\
2) у = |*|; 4) у = 1/х (х > 0).
Графики этих функций приведены на рис. 30, 31.
Для того чтобы задать функцию, нужно указать: .
1) множество чисел D — всех возможных значений перемен¬
ной х. Множество D называют областью определения функции;
Рис. 31
2) правило, по которому каждому числу х из множества D
сопоставляется число у. Это число у называется значением
функции в точке х (рис. 32).
Функция обычно обозначается одной буквой, например /,
а ее значение в точке х — f (jc).
Итак, если задана функция /, то задано множество чисел D
и каждому числу х е D сопоставлено число у = f (х). Буква,
которая обозначает число из области задания функции, назы¬
вается аргументом или независимой переменной, D — это об¬
ласть значений аргумента.
22
Рис. 30
Рис. 32
Пусть задана функция / с областью определения D. Рассмот¬
рим плоскость с декартовой системой координат. По оси абсцисс
будем откладывать значение аргумента, а по оси ординат —
значение функции. Для каждого числа х е D вычислим
у = f (х) и построим точку М с координатами (х; у). Множество
всех таких точек образует кривую — график функции f в задан¬
ной системе координат.
Графиком функции f называется множество точек плоскости с координа¬
тами (х; f(x)), где х пробегает область определения функции f.
Понятие функции включает в себя, во-первых, задание об¬
ласти определения функции и, во-вторых, указание правила вы¬
числения значений. Начнем с обсуждения того, как задается
правило вычисления значений.
Обучаясь математике, мы ознакомились с различными дей¬
ствиями, операциями над числами. Например, используя только
сложение и умножение, можно из числа х получить новые чис¬
ла, скажем, Зле, Зх + 5, лс2, 2х3 — 1 и т. п. Уже такого рода вы¬
ражения могут служить для построения довольно богатого клас¬
са функций.
Появление деления сильно расширило запас функций. Теперь
1 х 4- 1 2х
можно образовать выражения вида ^^^ - и т. п.
Операция деления отличается от сложения и умножения тем, что
она не всегда определена — в знаменателе дроби нельзя ста¬
вить нуль. Поэтому в выражение 7 можно подставить лю¬
бые числа, кроме х = 1 и х = — 1, при которых знаменатель
равен нулю.
Появление новых операций и введение специальных знаков
для их обозначения приводит к дальнейшему расширению до¬
ступного нам математического аппарата — извлечению корня,
взятию синуса, переходу к модулю числа и т. п.
Пример
Пусть
— 1, если х < О,
f (х) = - 0, если х = О,
1, если х> 0.
Мы описали правило вычисления, применимое к любому
числу. Обозначим число / (дс), найденное по этому правилу,
через sgnx (sgn — от лат. signum — зАак). Теперь получим
символ для обозначения новой операции и построим новые
формулы,* например
f(x) = \ + Sgn(x - 1).
График функции у = sgn jc изображен на рис. 33.
Запись -д/sin х совершенно ясна — сначала надо взять синус
числа х, а затем извлечь квадратный корень. Трудность состоит
в том, что некоторые из производимых операций имеют огра¬
ниченную область применимости (так, квадратный корень вы¬
числяется только для положительных чисел). В то же время
для всех введенных нами знаков математических операций
имеется твердая договоренность о том, к каким числам их можно
применять.
Поэтому, когда функция задана формулой, ее областью оп¬
ределения считается множество всех дс, над которыми можно
выполнить операции, участвующие в этой формуле. Иногда
это множество называют естественной областью определения
данной функции.
Итак, правила вычисления значений функции могут зада¬
ваться формулами, выражениями, полученными с помощью из¬
вестных нам действий над числами.
Другим важным способом задания значений функции явля¬
ется табличный. В таблице указываются значения функции,
однако лишь для конечного набора значений аргумента.
Наконец, часто функцию задают с помощью ее графика. Этот
способ очень удобен — он позволяет наглядно представить свой¬
ства функции.
На рис. 34 изображены вольт-амперные характеристики не¬
которых электрических элементов, которые графически задают
зависимости напряжения от силы тока. Они получены не по го¬
товой формуле, а экспериментально.
Упражнения б) Р(4;-2), /(х)=уТ;
1. Найдите область определения еле- ^(~5;5), f(*)=|*|;
дующих функций: г) ^(5; —5), f(x)=\x\.
а\ и =—- в\ и= i/l—x ■ 3- Постройте график функции y = f(x)t
х ’ > у v ’ где
х
2. Лежит ли данная точка Р на гра- [—1 » jO>1.
фике функции f:
4. Запишите с помощью формул функ-
а) Р( 12) f(x) • цию’ гРаФик которой изображен на
24
Рис. 33
Рис. 34
Чтение графика
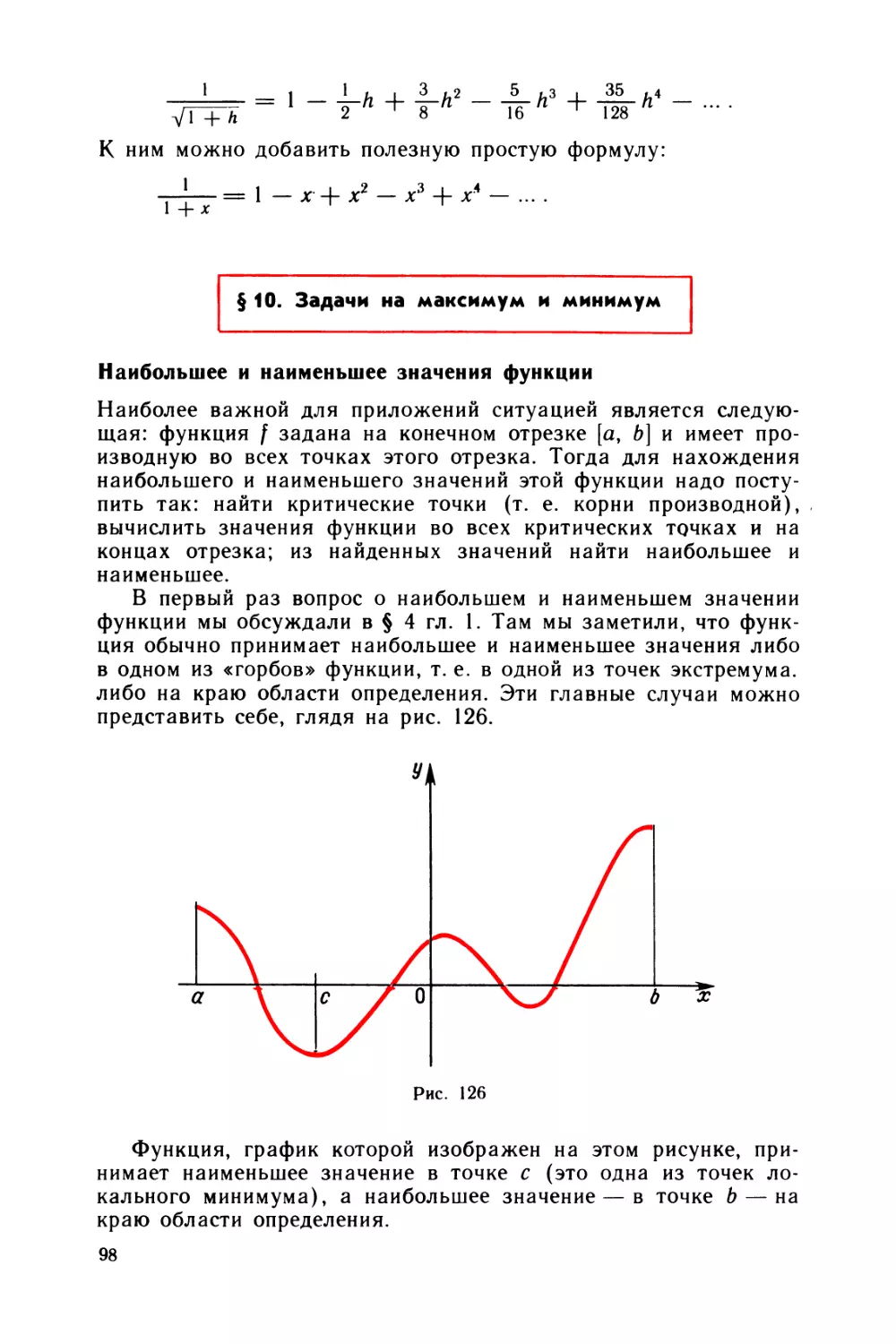
Рассмотрим функцию /, график которой показан на рис. 36.
О каких свойствах функции f можно сказать, глядя на график?
1. Спроектируем точки графика на ось х. Мы получим отре¬
зок [а{1а9]. Он является областью определения функции. Каж¬
дая прямая, параллельная оси у и проходящая через точку
этого отрезка, пересекает график в одной точке. Вертикальные
прямые, проходящие через точки х вне отрезка [ах, а9], график
не пересекают.
2. Рассмотрим точки пересечения графика с осью х. На чер¬
теже это а2, а4, а6, а8. В этих точках функция обращается в нуль.
Числа а2, а4, а6, а8 являются корнями уравнения f (х) = 0. Итак,
множество чисел {а2, а4, а6, а8} представляет собой множество
решений уравнения f (х) = 0. Указанные числа называются кор¬
нями функции (или нулями функции).
3. Корни функции f разбивают отрезок [аь а9] на интервалы,
в каждом из которых f сохраняет постоянный знак. Функция
положительна на интервалах (аь а2), (а4, а6), (а8, а9) и отрицатель¬
на на интервалах (а2, а4), (а6, а8).
Объединение интервалов (аь а2) U (а4> ав) U (а8> аэ) представ¬
ляет собой решение неравенства f (х) > 0.
4. Из чертежа видно, какую роль для определения формы
графика играют «горбы» функции f. Они соответствуют точкам
а3, а5, а7. Выясним, какие свойства функции характеризуют
«горбы» и «впадины».
Точка а3 замечательна тем, что если мы рассмотрим ход
изменения функции f вблизи нее, то значение f в этой точке будет
наименьшим. Отметим еще раз: f (а3) не является самым ма¬
леньким значением функции f (на чертеже легко найти точки,
в которых значение f меньше, чем f (а3), f (а5)). Это наименьшее
значение среди значений в точках, близких к аз. Точно так же в
точке а5 функция принимает значение, наибольшее среди зна¬
чений в точках, близких к а5.
25
Рис. 35
Рис. 36
Точку а3 называют тонкой локального минимума, а точку а5 —
точкой локального максимума. Слово «локальный» означает
«местный» и подчеркивает, что, скажем, f (а3) — наименьшее зна¬
чение вблизи точки а3.
Итак, в точках а3 и а7 функция f имеет локальный минимум,
а в точкеа5— локальный максимум.
5. Наибольшее значение функции f принимает в точке а9, a
наименьшее — в точке а7. На этот раз речь идет о самом боль¬
шом и самом малом значениях функции на всей области опре¬
деления.
Латинские слова «максимум» и «минимум» соответствуют русским словам
«наибольшее значение» и «наименьшее значение». Иногда латинские слова
оставляют для обозначения «горбов» (и даже опускают слово «локаль¬
ный») и просто говорят: точки максимумов и минимумов функции, а рус¬
ские слова — для обозначения общего, глобального, абсолютного макси¬
мума и минимума. Часто используют еще одно латинские слово —
«экстремум», которое объединяет оба понятия: максимум и минимум.
6. Что можно сказать о поведении функции f на отрезках
между точками экстремумов?
Из графика ясно, что на отрезке [аь а3] функция f убывает,
затем на отрезке [а3, а5] она возрастает, далее на отрезке
[а5, а7] функция f убывает и, наконец, на отрезке [а7, а9] снова
возрастает.
7. Спроектируем точки графика на ось у. Мы получим отре¬
зок [Ьь Ь2]у являющийся областью значений функции f. Он
состоит из всех точек у, являющихся значениями функции /
при каком-либо (не обязательно одном) значении х.
Задания
1. Составьте таблицу долготы дня в
вашей местности, отметив ее в
24 точках — по две точки на каж¬
дый месяц (если вы будете опреде¬
лять долготу дня по печатному ка¬
лендарю, то учтите, что он дает
данные для широты Москвы). Вы¬
числите в каждой точке превыше¬
ние h долготы дня над 12 часами
(вычисления ведите в часах с точ¬
ностью до 0,1 ч; для нахождения h
вычтите из долготы дня число 12).
Постройте график функции h = h(t)
по точкам. Повторите для функ¬
ции h исследование, проведенное
в этом пункте. Постарайтесь объяс¬
нить смысл каждого пункта иссле¬
дования. Ответьте дополнительно на
следующий вопрос: когда долгота
дня возрастает быстрее всего?
2 Проведите исследование функций
по графику (рис. 37). Если край¬
ние точки кривых не отмечены, то
считайте, что кривые могут быть
продолжены бесконечно.
26
Рис. 37
Словесное и графическое исследование функций приведено в
табл. 1.
Таблица 1
Область определения, т. е. множество
значений аргумента, при которых за¬
дана функция
Корни, т. е. точки, в которых функ¬
ция обращается в нуль, или, иначе,
решения уравнения f(x) = О
Участки знакопостоянства, т. е. интер¬
валы, на которых функция положи¬
тельна или отрицательна, или, иначе,
решения неравенств f(x) >0 и
«*) < о
Точки экстремума, т. е. точки, лежа¬
щие внутри области определения, в
которых функция принимает самое
большое (максимум) или самое малое
(минимум) значение по сравнению со
значениями в близких точках
Участки возрастания и убивания, т. е.
интервалы, на которых функция или
возрастает, или убывает
Наибольшее и наименьшее значения
функции (по сравнению со всеми воз¬
можными в отличие от экстремумов,
где сравнение ведется только с близ¬
кими точками)
Область значений функции, т. е.
множество чисел, состоящее из всех
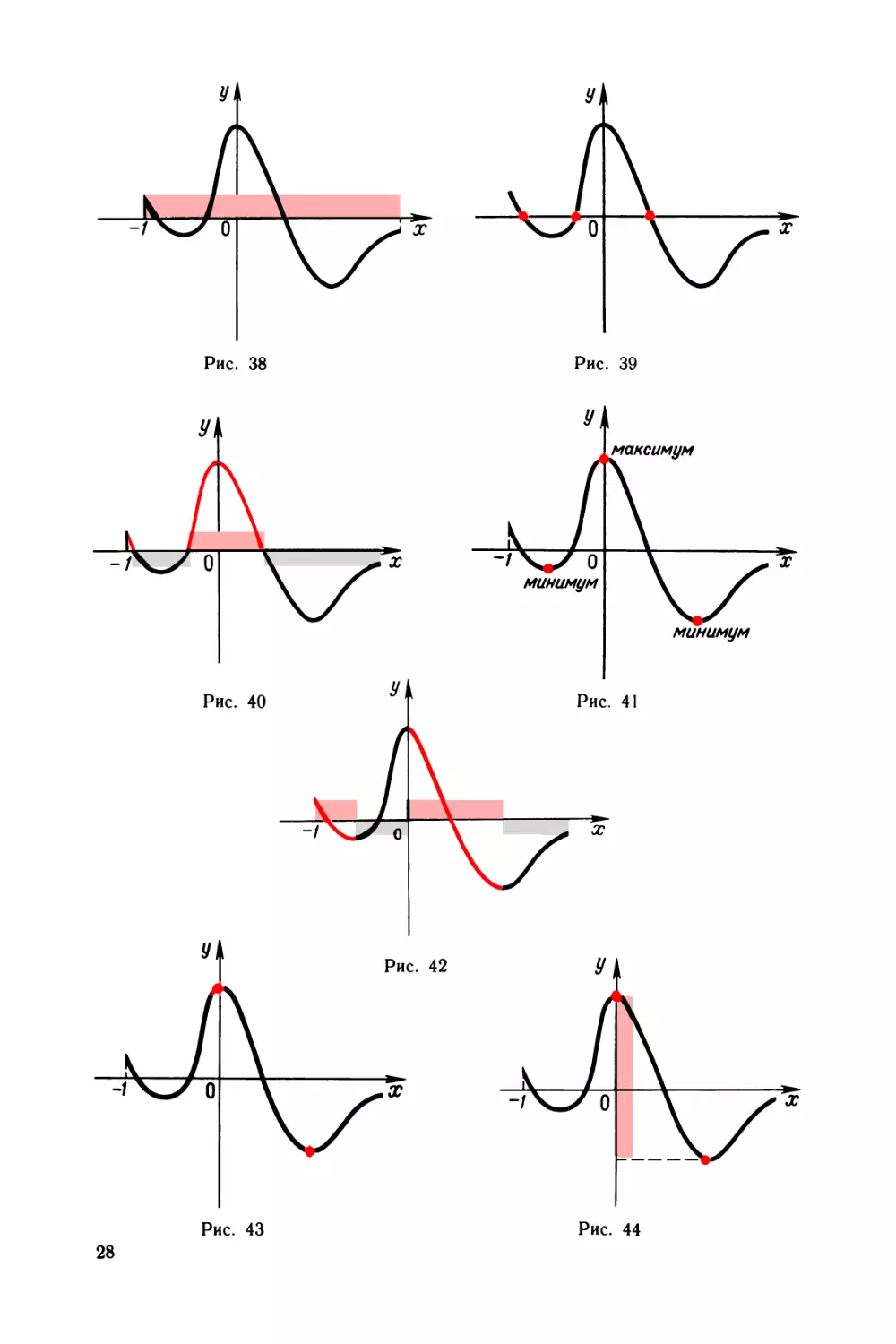
значений функции
Проекция графика на ось х (рис. 38)
Точки пересечения графика с осью х
(рис. 39)
Участки оси х, соответствующие точ¬
кам графика, лежащим выше (ниже)
оси (рис. 40)
Точки экстремума (рис. 41)
Участки оси х, где график идет вверх
или вниз (рис. 42)
Самая высокая и самая низкая точки
графика (рис. 43)
Проекция графика на ось у (рис. 44)
1. Если функция задана формулой, то имеется в виду ее естественная
область определения, т. е. множество чисел, к которым применима дан¬
ная формула. Ответ можно привести, записывая отрезок числовой оси, не¬
равенства или указывая «исключительные» значения аргумента (т. е. та¬
кие значения, которые не входят в область определения функции).
х
Например: 1) у = g . область определения#?;
1
2) У = — —область определения: хфО, или (— оо; 0)(J(0; + оо);
3) у = V*~ — область определения: [0; оо] или х ^ 0.
2. Участки знакопостоянства функции, рассмотренной на с. 25, определя¬
лись ее корнями (см. рис. 36). Однако из этого правила бывают исклю¬
чения. Такие графики показаны на рис. 45, а — в.
В случаях а и 6 на рис. 45 функция изменила свой знак, но в нуль
не обратилась. Это бывает тогда, когда график функции оказывается
разорванным. Особенно характерным является случай а, здесь в точке
х — 0 функция просто не определена. Случай в показывает, что функция
может обратиться в нуль, но знака при этом не изменяет.
27
Рис. 38
Рис. 39
Рис. 40
Рис. 41
Рис. 43
Рис. 44
Рис. 42
3. В простейших случаях точки экстремума находятся непосредственно.
Нахождение точек экстремума более сложных функций делается с по¬
мощью производной (см. с. 73).
4. Слова «возрастание» и «убывание» функции иногда заменяют одним
СЛОВОМ — МОНОТОННОСТЬ функции V.
Мы говорим о монотонности функции лишь на отрезках, целиком
входящих в область определения функции. Рассмотрим, например,
функцию у = , заданную при всех х, кроме нуля (рис. 45, а). Эта
функция возрастает на каждом интервале, не содержащем нуля, однако
о ней нельзя говорить как о возрастающей на всей числовой оси.
Рис. 45
5. В примере, рассмотренном на с. 25 (см. рис. 36), областью значений
функции был отрезок [bx,b2], где Ьх и Ь2 — наименьшее и наибольшее
значения функции. Так бывает не всегда. Если график функции имеет
разрыв, то некоторые промежуточные значения функции могут пропускать¬
ся (рис. 45, б)
Простейшие зависимости
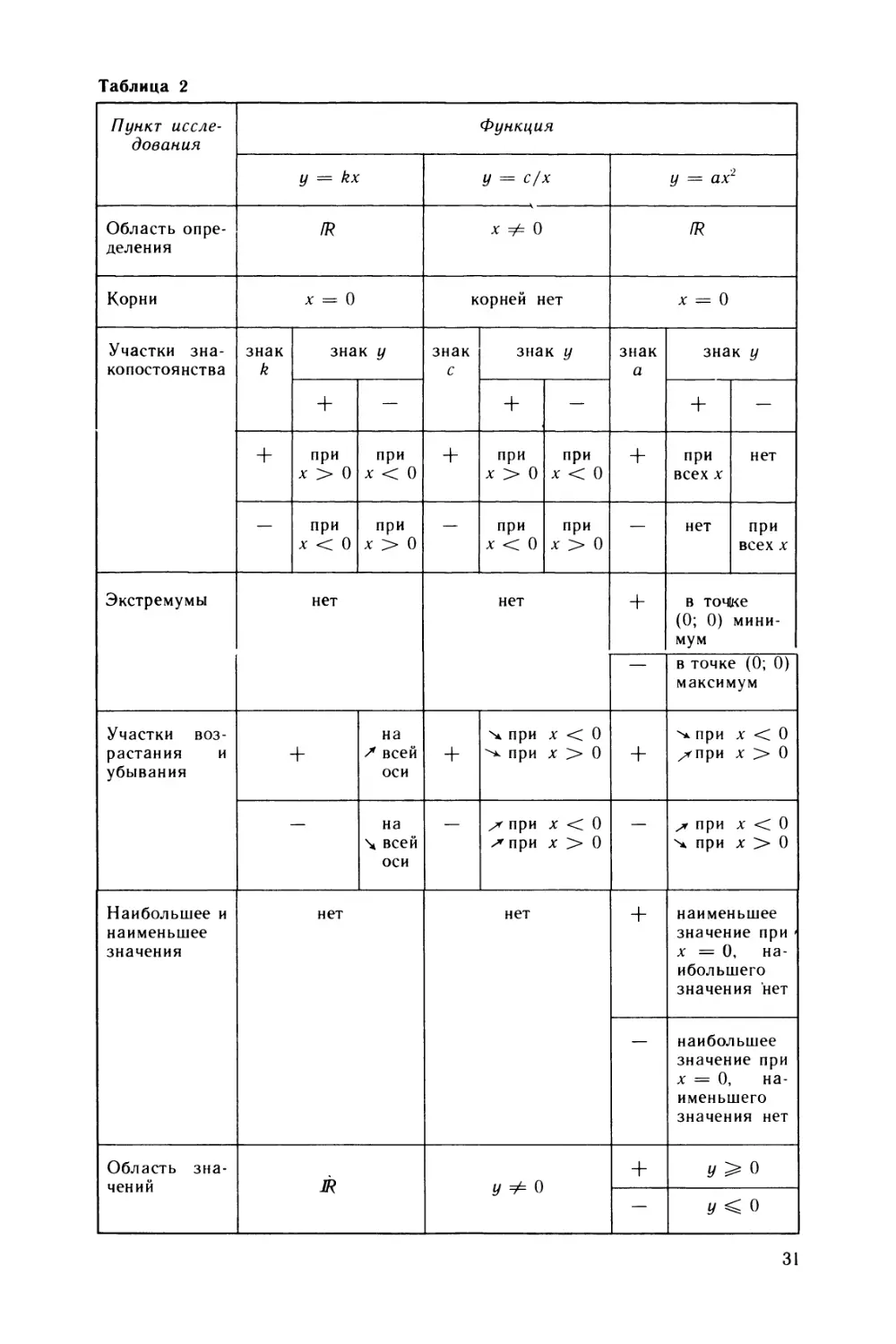
Рассмотрим следующие простые зависимости.
1. Прямая пропорциональность у = kx (рис. 46).
Q
2. Обратная пропорциональность у = — (рис. 47)
Рис. 46
Рис. 48
3. Квадратичный закон у = ах2 (рис. 48).
Проведем кратко по известным графикам исследование про¬
стейших зависимостей (считаем, что константы k, с, а отличны
от нуля, табл. 2).
Примеры
1. I — ~б закон Ома, где / — сила тока в цепи, U — напря-
д
жение на участке цепи, R — сопротивление резистора.
Встречаются электрические цепи, в которых одна из этих
трех переменных постоянна, а две другие связаны по закону
Ома прямой или обратной пропорциональной зависимостью.
2. pV = RT — закон Клапейрона — Менделеева, где р — дав¬
ление, V — объем, Т — термодинамическая температура,
R — молярная газовая постоянная.
3. s — vt — закон равномерного прямолинейного движения,
где s — путь, пройденный телом, / — время, в течение кото¬
рого пройден путь, v — скорость тела.
4. s = 4^ закон свободного падения, где s — путь, t — вре¬
мя, g — ускорение свободного падения.
30
Рис 47
Таблица 2
Пункт иссле¬
дования
Функция
II
*
II
у = ах2
Область опре¬
деления
[R
х =/= 0
[R
Корни
х = 0
корней нет
х = 0
Участки зна-
копостоянства
знак
k
знак у
знак
с
знак у
знак
а
знак у
+
—
+
-
+
-
+
при
X > 0
при
X < 0
+
при
х > 0
при
X < 0
+
при
всех х
нет
-
при
JC < 0
при
X > 0
-
при
х < 0
при
X > 0
-
нет
при
всех х
Экстремумы
нет
нет
+
в точке
(0; 0) мини¬
мум
в точке (0; 0)
максимум
Участки воз¬
растания и
убывания
+
на
всей
оси
+
>4 при х < 0
^ при х > 0
+
при х < 0
/<при х > 0
—
на
\ всей
оси
—
S при х < 0
s при х > 0
—
s при х < 0
N. при X >» 0
Наибольшее и
наименьшее
значения
нет
нет
+
наименьшее
значение при «
х = 0, на¬
ибольшего
значения нет
наибольшее
значение при
х = 0, на¬
именьшего
значения нет
Область зна¬
чений
1R
уф о
+
у> о
-
У<0
31
5. Q = CU — уравнение конденсатора, где Q — заряд конден¬
сатора, С — его электроемкость, U — напряжение на об¬
кладках конденсатора.
2
6. £=-^ кинетическая энергия движущейся материаль¬
ной точки, где т — масса точки, и — ее скорость.
Упражнения
1 Как меняется наклон графика ли¬
нейной функции y = kx при измене¬
нии коэффициента k?
2. Выразите из закона Ома зависи¬
мость силы тока, даваемого акку¬
муляторной батареей постоянного
напряжения U = 6 В, от сопротив¬
ления резистора, включенного в
цепь. Постройте график этой зави¬
симости.
3. В каком случае потребуется меньше
времени: если путь пройден с по¬
стоянной скоростью или если первую
половину пути идти вдвое быстрее,
а вторую — вдвое медленнее?
4. Когда будет больше пройденный
путь: при движении с постоянной
скоростью или если одну половину
времени идти вдвое быстрее, а дру¬
гую — вдвое медленнее?
5. Приведите примеры квадратичной
зависимости переменных.
Преобразования графиков
Чтобы легче ориентироваться в огромном мире зависимостей
между величинами, полезно ознакомиться с некоторыми преоб¬
разованиями, с помощью которых из одних функций получаются
другие. К числу простейших преобразований такого рода отно¬
сятся линейные преобразования переменных. Физически они
соответствуют параллельным переносам, изменениям масштаба,
зеркальным отражениям.
График функции y=f(x — а) получается из графика функции y=f(х) па¬
раллельным переносом вдоль оси х (вправо) на а единиц масштаба
(рис. 49, а).
Доказательство. Пусть точка Р(х о; уо) графика функции
y = f(x — a) соответствует конкретному значению аргумента
х = х0 (рис. 50). Это же самое значение у о будет значением
Рис. 49
32
исходной функции y = f(x) при х = хо — а. Значит, точка (х0 — а;
уо) графика исходной функции перешла в точку (х0; уо) новой
функции.
Построим обе точки: (х0 — а; у0) и (х0; уо). Вторая из них по¬
лучается из первой параллельным переносом вдоль оси х на а
единиц масштаба.
Аналогично можно получить следующие правила преобразо¬
вания графиков.
График функции у = f(x) + b получается из графика функции у = f(х)
параллельным переносом вдоль оси у (вверх) на b единиц масштаба
(рис. 49, б).
График функции у=—f(x) симметричен графику функции
у = f(x) относительно оси х (рис. 49, в).
Графики функций y = f(kx) и у = kf(x) получаются из графика
функции y = f(x) изменением масштаба по осям х и у соответ¬
ственно (рис. 51, 52).
Рис. 52
33
Рис. 50
Рис. 51
Примеры
1. График функции у = kx + Ъ можно построить, сделав па¬
раллельный перенос графика функции у = kx вдоль оси у.
Значит, ее график — прямая, параллельная прямой у = kx
и проходящая через точку (0; Ь) (рис. 53). Графики пря¬
мых у = kx и y=—kx симметричны друг другу относи¬
тельно оси х.
2. График функции у=—^— получается из графика обратно
пропорциональной зависимости y=j~ (гипербола) парал¬
лельным переносом вдоль оси х (рис. 54). Линейными пре¬
образованиями из функции у = y можно получить произ¬
вольную дробно-линейную функцию у = ^ ^ • Возьмем,
например, функцию у= Преобразуем выражение
X 1
X ш X X -f 1 — 1 | 1
JC+l* JC+1 х+1 х + 1 '
Итак, надо сдвинуть исходный график по оси х на — 1,
симметрично отразить его относительно этой оси и затем
сдвинуть по оси у на 1.
3. График квадратной функции у = ах2 + Ъх + с получается
из графика функции у = ах2 параллельным переносом. Вы¬
полним преобразования:
ах2 + Ьх + с = ах2 + 2 ах + ~ — +с =
2а 4а 4а2
= а(х + ±-
V ’ 2а ) 4а
Можно произвести два переноса вдоль координатных осей,
а можно их заменить одним параллельным переносом, при
Рис. 53
Рис. 54
котором вершина параболы у = ах2, т. е. точка (0; 0), пере-
/ гг\ / b Ь2 — 4ас \
ходит в точку (рис. 55) (— — ; — — ).
Полезно запомнить формулу для абсциссы вершины параболы
у = ах2 + Ьх + с: Хо==~т^1- Ординату вершины у0 всегда мож¬
но найти, вычислив значение функции у = ах2 + Ьх + с при
х == Xq.
§ 4. Уравнения и неравенства
Числовые неравенства
Числа можно сравнивать — из двух различных чисел одно всегда больше
другого.
То, что число а больше числа ft, записывается следующим
образом: а > Ь. Так, 3 > 1; 7 > л; — 3,1 > —3,2 и т. п. Вместо
неравенства а> Ь можно писать имеющее тот же смысл неравен¬
ство Ь<а (ft меньше а).
Числа, большие нуля, — это положительные числа, а меньшие нуля —
отрицательные.
Свойства неравенств:
1. a>b, Ь > с=>а> с.
2. а ^> Ь=>а -}- с Ь -|- с.
3. а > ft, т > 0 =>ас > Ьс.
4. а>Ьу с <0=>ас с Ьс.
5. а ft, с d=>a —|— с ft -d.
6. а > ft, с < — О b — d.
Свойства 4—6 можно вывести из свойств 1—3.
Числа а и ft часто соединяют знаком > (или <) еще до
2*
35
Рис 55
того, как проверено, действительно ли а больше Ь. В этом случае
о неравенстве а>Ь говорят как о высказывании, которое может
оказаться как верным, так и неверным. Например, неравенство
З2 > 23 верно, а неравенство 53 > З5 неверно, в чем можно убе¬
диться, вычислив написанные степени.
Неравенство а^Ь считают верным, если верно одно из двух:
а больше b или а равно Ь. Поэтому, по определению, верны такие
неравенства: 5 ^ 3, 3 ^ 3, 1 ^ 2, но неверны такие: 5^7, 5 >• 5,
5<3.
* Из двух неравенств а < b и а ^ b всегда верно одно. Это помогает строить
«отрицание неравенств»: если неверно, что а <Ь, то верно, что а ^ Ь
(iи наоборот).
Некоторые неравенства выполняются тождественно, т. е.
при всех допустимых значениях входящих букв.
Примеры
1. а2> 0.
2. (а - bf > 0.
3- x2 + y2 + z2^ 0.
4. Уа ^ 0 при а ^ 0.
Справедливость написанных неравенств очевидна.
Иногда возникает задача доказательства неравенства. Для
этого неравенство преобразуется так, чтобы оно стало оче¬
видным.
Пример
Доказать неравенство a -^b ^ ab.
Оно может быть сведено к виду а2 -\- Ь2 — 2ab ^ 0, т. е.
(iа — ft)2 ^ 0. Мы пришли к очевидному неравенству. Так как
из него обратными преобразованиями можно получить
исходное неравенство, то доказательство закончено.
При таком способе доказательства неравенств надо следить за тем, чтобы
в процессе преобразований мы не нарушили справедливость неравенств,
т. е. чтобы из последнего полученного неравенства можно было вернуться
к тому, которое надо было доказать.
Упражнения 3. Известно, что:
, „ а) 0<Cci<Cb. Что больше: —b или
1- Выясните, какое из чисел больше: | |
а) 0,429 или 0,432; ~а; Т ИЛ" Т’ “* ИЛИ ^
б) —12,0027 или —12,003; б) а<Ь<0. Что больше: —а или
в) л или 3,14; _ь. _!_ или а2 или Ь2. a3 или ьз?
г) 5/7 или 8/11;
д) —3/5 или —5
е) 0,54 или 7/15.
д) 3/5 или —5/8; 4. Используя неравенство а ~
4. Используя неравенство —-—^ab,
доказать:
2. Укажите какое-нибудь число, заклю- х-\-у /—
ченное между числами: а) —о—^ УХУ (х>
ченное между числами: d) —cj-
1) 0,373 и 0,374; 2) -1/13 и 0,01; б) 1
3) 10/7 и 17/12. JC " ^>UJ-
36
Выражения х~^у и л[ху называются средним арифметиче¬
ским и средним геометрическим чисел х и у. Соотношение между
ними можно сформулировать так:
среднее геометрическое не больше среднего арифметического (для
неотрицательных чисел).
Решение уравнений и неравенств
Решение (корень) уравнения с одним неизвестным — это число, при под¬
становке которого уравнение превращается в верное числовое равенство.
Решить уравнение — это значит найти множество всех его корней.
Аналогичные определения даются для решения неравенств с
одним неизвестным.
Два уравнения (неравенства) называются равносильными, если множества
их решений совпадают, т. е. если каждое решение одного из них явля¬
ется решением другого, и наоборот.
Линейное уравнение вида ах-\-Ь = О (а Ф 0) имеет один
Ь
корень х = — — .
Линейное неравенство вида ах-\-Ь> 0 можно решить, пре¬
образовав его к равносильному неравенству х> —(при
а>0) или хС — Ь— (при а < о).
Решения квадратного уравнения ах2-\-Ьх + с = 0 можно
найти по формуле
— bdt л]ь2 — Аас
*1,2 = о >
2 а
которая дает два корня, если дискриминант D = Ь2— 4ас>0у
один корень х= —> если D = 0. Если D < 0, то квадратное
уравнение решений не имеет.
Квадратное неравенство решают по графику или с помощью метода
интервалов.
Примеры
1. Зх + 4 = ОоЗх = —4ох = —4/3.
2. (х — 4)(х + 1) = 0^>jci = 4, JC2 = — 1.
3. х2 — 4 = Оох2 = 4ox\t2 = ±2.
37
4.
5.
6.
7.
8.
х2 + 2х + 1 =0о(х+ I)2 = Оох = -1.
х2 + х — 6 = Оох\ = — 3, *2 = 2 (корни подобраны с по¬
мощью теоремы Виета).
х2 + х + 6 = 0, корней нет, так как D = 1 — 4 • 6 С 0.
х2 + 2х — 1 = 0^jci,2 = — 1 =Ь л/2.
Зх2 + 2х — 5 = 0ох\ = 1, Хъ = — 5/3 (один корень очевиден,
а другой найден по теореме Виета).
_ -1 ± Уб1
9. Зх -}- х — 5 — 0, -Х|,2 —
10. Зх2 + 4х - 5 = 0, jci.2 = ~2±^9 •
Решения уравнений и неравенств можно найти, используя
графики. Проводя прямую у = а (параллельно оси абсцисс) и
рассматривая точки ее пересечения с графиком функции y = f(x),
получим корни уравнения f(x) = a при различных значениях а
(рис. 56).
Очевидно, что уравнение f{x)= 1 имеет пять корней, f(x) =
= 3 — два корня, а уравнение f(x)= —4 — ни одного.
Решение неравенств с помощью графика проиллюстрируем
квадратными неравенствами. На рис. 57, а—г изображены реше¬
ния неравенства у = ах2Ьх-\-с> 0 в различных случаях.
38
Рис. 57
Рис. 56
Упражнения
1. Решите уравнения:
а) 3—х—2дс+2;
б) *0Н-2) = л:2—3;
в) х2—х—2 = 0;
г) 5л:2—jc—4 = 0;
д) х2Ч-*+ 1 =0;
е) 2х2+х—1=0;
ж) х3—х = 0\
з) л;4—16 = 0.
3.
2. По графику функции y=f(х) (рис. 58)
ответьте на следующие вопросы:
а) Сколько корней имеет уравне¬
ние f(x)= 0?
б) Каковы (приближенно) корни
уравнения /(*)=*= — 1?
в) При каких а уравнение f(x)=a
имеет хотя бы один корень?
г) При каких а уравнение f(x)=a
имеет ровно один корень?
д) Сколько корней имеет уравнение
f(x) = x2?
Разложите на множители:
2; д) 2х2-\-х—3;
3jc2+4jc—7;
а)
б)
х2+х-
х2—2;
в) х'+х;
г) jc2+2jc—3;
Д)
е)
ж) jc2+4jc+4;
з) х2+4х+3.
Метод интервалов
Метод интервалов — это метод решения неравенств вида f(x) > 0, когда
функцию f(х) можно представить в виде произведения линейных мно¬
жителей.
Сущность этого метода заключается в том, что надо:
1) разложить f(x) на линейные множители;
2) найти корень каждого множителя и нанести все корни на
числовую ось;
3) исследовать знак произведения на каждом из получив¬
шихся интервалов числовой оси.
Если все линейные множители различны (f(x) имеет разные
корни), то произведение будет менять знак при переходе от
каждого интервала числовой оси к соседнему (знаки чередуют¬
ся). Поэтому достаточно определить знак на одном каком-нибудь
интервале (обычно это крайний правый интервал).
Как применяется этот метод, видно из следующих примеров.
39
Рис. 58
Примеры
1. Решить неравенство (х — 1) (х — 3) >> 0.
Нанесем на числовую ось точки х\ = 1, х2 = 3 (корни линей¬
ных функций у = х^-\ и у = х — 3), разбивающие число¬
вую ось на три интервала: (— оо; 1); (1; 3); (3; +°°)*
На каждом из этих интервалов каждый множитель сохра¬
няет постоянный знак, а при переходе через корень меняет
знак один из множителей. Начнем с крайнего правого
интервала (3; +оо). На нем оба множителя положительны.
При переходе (справа налево) через точку х2 = 3 множи¬
тель х — 3 стал отрицательным и все произведение стало
отрицательным. При переходе через точку Х\ = 1 изменил
знак первый множитель и все произведение стало положи¬
тельным. Результат исследования знаков записывают в виде
схемы, показанной на. рис. 59.
Ответ: (— оо ; 1) (J (3; + оо), т. е. х < 1 ил и х> 3.
Рис. 59
2. Решить неравенство < 0.
Нанесем на числовую ось корни всех линейных выраже¬
ний, с помощью которых образована дробь (*+ ОС* — .5,)
х(х-\)
Точки х\ = — 1; *2=0; *з=1; *4=5 разбили числовую ось
на пять интервалов. Распределение знаков дроби на этих
интервалах изображено на рис. 60.
Ответ: (—1; 0) U (1; 5), т. е. — 1 < jc < 0;1 < jc < 5.
+ I ~ I + ■ - 1+
-/0 1 5 X
Рис. 60
Иногда для применения метода интервалов приходится,
раскладывая многочлены на множители, выносить число¬
вые множители для того, чтобы записать левую часть в
стандартной форме как произведение или частное функций
вида x — xk.
у2 о
3. Решить неравенство 5 — 2л: > °*
Разложив числитель на множители, имеем х2-\-х — 2 =
= (х + 2)(х — 1). Тогда
■|,+2НГ')>о~|-,+211Г')<о-
5-2л: 2(*-7,(
40
Находим корни линейных множителей, входящих в числи¬
тель и знаменатель: Х\ = —2; x<i — 1; Хъ = 5/2 (рис. 61).
Ответ: (— оо ; — 2) U (1; 5/г)’ т* е- х < ~~ 2; 1 С х < 5/2.
При решении нестрогих неравенств вида f(x)7^ 0 или
f{x)^ 0 надо включать в множество решений точки, являю¬
щиеся корнями линейных множителей, стоящих в числителе.
^2 х}х
4. Решить неравенство (2jc 5) (2^ + з) > °-
Перепишем неравенство в равносильной форме:
Ах-2)
-<0.
2(* + 5/г) ‘ 2(дс + /г)
Нанесем на числовую ось точки х\ = —5/2, *2 = —3/2» *3 =
= 0, х4 = 2 (рис. 62).
Ответ: (— 5/2; —3/г)U[0,2].
Рис. 62
Существенной чертой метода интервалов является разбиение
числовой оси на участки и рассмотрение данной функции отдель¬
но на каждом участке. Это же обычно приходится делать, когда
нужно «раскрыть модули».
Пример
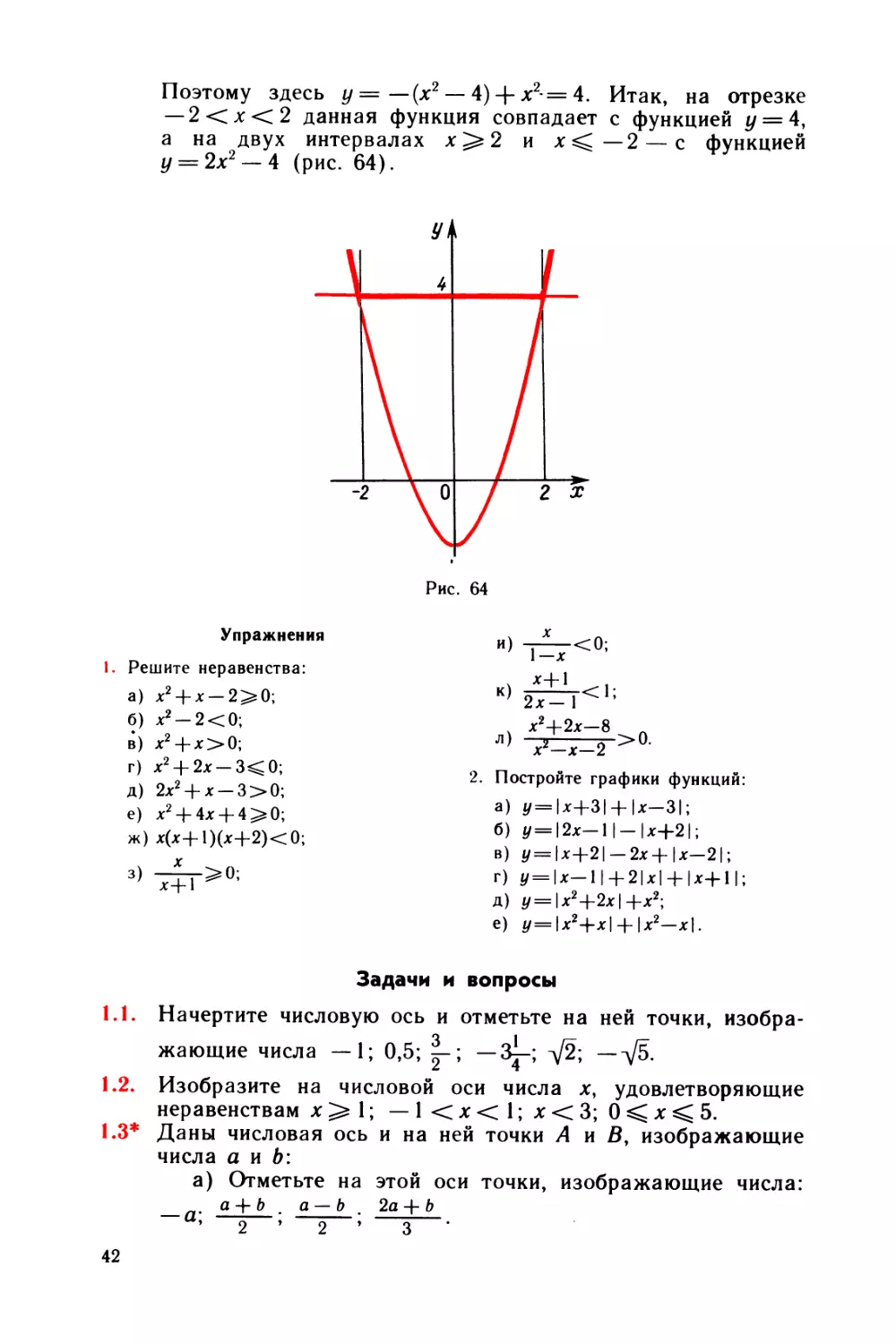
Построить график функции у—\х2-А\-\-х2.
Выясним, при каких х выполняется неравенство х2 —
— 4^0. Решая его с помощью метода интервалов, получим
два интервала: х^2 и х<-2 (рис. 63).
При этих х выражение под знаком модуля не отрица¬
тельно, поэтому, раскрывая модуль, находим, что при этих
х у = х2 — 4 + х — 2.x2 — 4. При остальных jc, т. е. при
-2<х<2, выражение под знаком модуля отрицательно.
41
Рис. 61
Рис. 63
Поэтому здесь у=—(х2— 4) + х2 = 4. Итак, на отрезке
— 2<х<2 данная функция совпадает с функцией у = 4,
а на двух интервалах х>2 и * < — 2 — с функцией
у = 2х2 — 4 (рис. 64).
Рис. 64
Упражнения
Решите неравенства:
х2 + х — 2^0;
х2 — 2 < 0;
*2 + *>0;
jc2 + 2jc-3<0
2jc2 + jc-3>0
х2 -|- 4х + 4 ^ 0
а)
в)
г)
Д)
е)
ж) *(*+1)(*+2)<0;
х
3)
Х+1
■>0;
и)
1 —х
<0;
\ х-\-1 t
к) 2l=T<1;
jc2+2jc—8
jc—2
л)
>0.
2. Постройте графики функций:
а) у=\х-\-3\-\-\х—31;
б) у= \2x—l I — |лг+2|;
в) У=\х+2| —2jc+|jc—2|;
г) y=|jc-l| + 2|jc1 + |jc-fЦ;
Д) У=\х2+2х\+х2;
е) У=\х2+х\ + \х2—х].
Задачи и вопросы
1.1. Начертите числовую ось и отметьте на ней точки, изобра-
жающие числа —1; 0,5; ; — 3^-; л[2\ — ^5.
1.2. Изобразите на числовой оси числа х, удовлетворяющие
неравенствам jc^I; — 1<jc<1;jc<3;0<jc<5.
1.3* Даны числовая ось и на ней точки А и В, изображающие
числа а и Ь:
а) Отметьте на этой оси точки, изображающие числа:
а + 6 . a — b 2 а-\- b
2 ’ 2 ’ 3
б) Какое число изображает точка С, симметричная
точке В относительно точки А?
в) Какое число изображает точка D, симметричная
середине отрезка АВ относительно точки В?
г) Какое число изображает точка £, которая получается
из точки А при гомотетии с центром О и коэффициентом
-3/2?
д) Какое число изображает точка F, которая получается
из точки В при гомотетии с центром А и коэффициентом 2?
1.4. Вычислите:
|2,3|; |-1,7|; |л-4|;
|3 —s/T|; V(1 —л/2)2; Ул2- Юл+ 25. -
1.5. Раскройте знак модуля:
|2-У5|; ls- + g--^- | •
1.6. Запишите без знака модуля:
\х — 31; U + 4I; |3 —jc|.
1.7. Докажите тождество
\х + у\2 + \х — у\2=2(\х\‘2 + \у\2).
1-8. Решите уравнения:
а) |* — 1| = 2;
б) Iдс —|— 31 = 1;
в) |2*+1| =4;
г) |3*-2| = 6;
д) |5* + 2| = -2;
е)* ||*| — 1|=2;
1.9. Решите неравенства:
а) 1*1 ^ 1;
б) |* - 1| <5;
в) |* + 2|>2;
г) |* + 5| < 1;
д) |2 — *| > 3;
е) |3 + *|<1;
1.10. Составьте уравнение или неравенство с модулем по данному
множеству решений:
а) *i = —2, *2 = 0; в) — 1 ^ ^ 5;
б) *1 = 2, *2 = 3; г) * < — 2, * > 2.
ж)* |*| + |*-3| =5;
з)* |*- 1| + |*-5| = 3
и)* |*+ И + |* + 2| = 1
к)* |* — 5| — |*- !| =2
л)* |* + 3| - |* — 2| = 5
М)* \Х— и = 2|*-4|.
ж) |2* — 3| < 5;
з) 11 + 2*| > 1;
и)* |*| + \х— 11 < 1;
к)* ||*| — 2| < 1;
л)* |*+ 1| < I*—3|;
м)* |*| — |* — 11 < 2.
1.11. Изобразите на координатной плоскости точки с координата¬
ми А( 1; 2); Я( —1;3); С(3; -1); D(-2;-2); ДО; 0) f(.l;0);
G(0; —3). Найдите расстояние между точками А и В, А и
С, D и £, F и G, Л и G.
1.12. ABCD — прямоугольник. Найдите координаты точки D,
если:
а) у4(0; 0), Я(0; 3), С(2; 0);
б) Л(0; 0), Я(0; -2), С(1; 0);
в) А( — 2; -3), В( — 2; 0), С(0; -3);
г) Л(— 1; 4), В(-1; 2), С(3; 4).
1.13. Даны координаты точки Л. Найдите координаты точки,
симметричной точке А относительно оси абсцисс; оси орди¬
нат; начала координат:
а) А(2; 3); в) Л(-1; -2);
б) А( — 2; 1); г) А{-3; 0).
1.14. Даны координаты точек А и В. Найдите координаты сере¬
дины отрезка АВ и координаты точки, симметричной точ¬
ке А относительно точки В:
а) А(2; 1), В(2; 5); в) Л(1; 1), В(3; 3);
б) Л(— 1; -3), В(3; -3); г) Л(-2;4),Я(1; -3).
1.15. Изобразите на плоскости точки, координаты которых удов¬
летворяют следующим уравнениям и неравенствам:
а) х = 5; е) |у + 11 > 2;
■> (!
б) У = 2; ж1 /|дг| < 2,
в) U — 2| = 3
г) If/ + 11 = 5
д) \х- И <2
\у + 1;
+ И=3,
1^-2| = 1.
1.16. Поля шахматной доски 8X8 занумерованы координата¬
ми— парами целых чисел (a; ft), где 1 ^ а, ft <18. Как
распределены клетки доски, сумма координат которых чет¬
на? Докажите, что конь с клетки (1; 1) в клетку (8; 8) не
может попасть, сделав 9 шагов.
1.17. На координатной плоскости ху изобразите множество точек,
удовлетворяющих условию:
а) ху = 0; ж) х2 + у2 = 0;
б) (х- 1)(</ + 2) = 0; з) х2 -\- у2 — 2у -\- 1 =0;
в) х2 = 1; и) у = х\
г) х2 — \х -{- 3 = 0; к) у= — х;
д) — = 0; л) у = 2х;
у
е) 7ГТ = 0;5; м) у = т;
44
и) у = — Зх;
о) У = х + 1;
п) у = — х — 2;
р) у = — 2л:+ 3;
с) х + у = 1;
т) х — у = 2.
1.18. Изобразите на координатной плоскости ху множество точек,
удовлетворяющих условию:
а) у ^х; к) х2 + у2> 1;
б) у<х\ л) (х — З)2 + у2 < 9;
в) 2jc + i/^1; м) х2 + 4х + у2 ^ 5;
г) *0 < 0; , (2х - у < 1,
д) (* + 1) (у — 2) > 0; н)\х-2у>3;
е) х2 > у2; гх2-1-«2
ж) ху>2\ °)
з)х{/<-3; , JJf’-iVsM,
и) 2*у+1>0; п) ((x _ 2)2(у _ 2)2 < 8.
1.19. На рис. 65 изображено пять прямых. Найдите уравнение
каждой из них: у = 2х; х -\- у = 0; у = — 2х + 1; у = 2х — 2;
у = х.
Рис. 65
Рис. 66
1.20. На рис. 66 изображено четыре окружности. Найдите урав¬
нение каждой из них:
а) *2 + у2 = 9; в) х'2 + (у + 2)2 = 9;
б) (х — 2)2 + у2 = 9; г) (х + I)2 + (у — I)2 = 1.
1.21. Даны зависимости между переменными. Выразите, если
можно, каждую из них как функцию другой:
а)' Зх + 5у = 2; в) 2у + 3\х\ = 0;
б) 2х — 7у + 3 = 0; г) |у | + 4х = 1;
д) s2 = v3;
е) 10^—1 = /3;
s + 2
Ж) (.+/*) " 2 •
з) (s + \)(t— 1) = t.
1.22. Вычислите значения f( 1); f( — 2); К'/2) + К3/4); f(2t),
f(x -f- 1); f(x— 1); f(2x— 1); 5/(jc/5) для следующих функций:
а) f(x) = x + 1;
б) f(x) = Ul;
в) f(x) = l/x;
r) f(x) = x2\
Д) f(x) = X + \/x\
е) f(x) =
ж) f{x) =
0 при x ^ 0,
1 при x > 0;
0 при x ^ 0,
1 при x > 0.
1.23. Даны точки P,(l, 1), Л>(-1; 1), Я3(1; -1), Р4(-1; -1).
Проверьте, будут ли они лежать на графиках функций
y = f(x) задачи 1.22.
1.24. Проведите исследование функций, изображенных на рис. 67,
а—в.
Рис. 67
1.25. Найдите области определения функций:
3 V 1
а) У =
1
б> * = ^-+7^1-;
в) У = У* + V2 — х ;
г) У =
Д) У =
уг- 1 ’
х
хг+Т+ 1 ’
?) у = -л/х2 — Х+ 1 .
1.26. С помощью графика функции у = f(x) (рис. 68) решите
•.неравенства:
a) f(x) > 0;
б) f(x)< 0;
в) f(x) > 1.
1.27. По графику функции y = f(x) (рис. 69) найдите значения jt,
при которых \у \ ^ 1.
46
1.28. Как связаны между собой точки экстремума функций
у — /(•*)> у= —/W?
1.29. Начертите график функции, область определения которой
была бы отрезком [0, 5], а область значений — отрезком
[-1, 2].
1.30. К условию задачи 1.29 добавьте условие, чтобы функция
возрастала на отрезке [0, 3] и убывала на отрезке [3, 5],
была отрицательной на отрезке [0, 2] и положительной на
отрезке [2, 5].
1.31. Постройте графики:
а) У = х/*х\
б) у = 4*;
в) у = — '/4*;
г) У = —4х;
д) у = 2/х;
е) у = х2;
ж) у = 'Л*2;
з) у = 2*2;
и) у = — х2.
1.32. Проведите исследование функций, построив их график:
а) у = —2х; в) у = х2 — 4; д) у = — дг2 — 1;
б)у=—3/*; г) у — 9 — х2; е)у = (х + I)2.
1.33. Известно, что зависимость u = f(x) имеет вид либо y = kxy
либо у = С/х, либо у = ах . Найдите вид зависимости и
постройте ее график, если известно, что /(2) = 2 и /(4)= 1.
1.34. На рис. 70 изображен график функции /. Постройте графи¬
ки следующих функций:
а) У = f(x)+ 1;
б) У = Я*) — 1;
в) у = 2f(x)\
г) У = l/2f(x);
Д) У = —f(x)\
е) У= \f(x)\;
ж) дг = —2f(x);
з) У = 1 - f(x);
и) У = If{x)— 1|;
к) у = \f(x)\ — 1;
л) У = Я* + 1);
м) У = Я* ^ 2);
н) y = f(-x);-
°) у — Я2*);
п) у = Я*/5);
Р) У = К~х/2);
с) у = Я1 — *);
т) у = 2/(дг — 1).
1.35*. Постройте графики дробно-линейных функций:
*+1
б) У = —
в) «/ =
*+1
47
Рис. 68
Рис. 69
Рис. 71
Г) У =
х — 2
Д) У =
3-х
е) У =
2х
2х— 1
* + 3 ’ 57 2* + 1 ’
1.36. Постройте графики квадратичных функций:
а) у = х2 + х + I; г) у = 2х2 + 4х — 3;
б) у = х2 — 2х\ д) £/ = 2 Н- (jc — 1 )2;
в) у = 6 — х — х2\ е) у = — 3 + (х+ I)2.
1.37. Дан график функции y = f(x) (рис. 71). Постройте графики
функций:
а) У = /(jc — 2);
б) у = /(х)+1;
в) У = Я2*); е) у
1.38. Решите уравнения:
а) 2х + 3 = 5л: — 1;
б)
г) у = 2f(x);
Д) У = f(x/2);
= 'ЛЯ*);
ж) У — —f(x).
з) у = /(—■*);
И) t/ = 1Я*)1-
в)
г)
Д)
е)
ж)
'/2х + 2 = 0;
— 2[1 — jc — 3(лг + 2)] = лг;
1 + а* = Ь\
X + 1
X - 1
2-х
- 2;
к)
Л)
м)
Н)
о)
п)
Зх + 5 4
х + 2 2х — 1
х — 3 — 2* -f 1
з) х2 — 5jc = 0;
и) jc2 — 3 = 0;
х — х — 12 = 0;
л:2 + jc — 20 = 0;
jc2 + Зх — 4 = 0;
jc2 - 3* - 10 = 0
jc2 + 3jc — 18 = 0
p) 2дг2 — Зх — 5 = 0
с) л:2 + 2jc — 4 = 0;
т) л:2 + 7jc + 10 = 0;
у) х2 + 7х+ 12 = 0;
ф) х2 — 5х + 6== 0.
1.39. Разложите на множители левые части уравнений з)—ф)
примера 1.38.
1.40. Разложите на множители:
-3 ~ в) 4л:4-25; д) jc3 + 8;
г) х3 + х2 + х + 1; е) х* — 3jc2 — 4.
а) х“ — jc;
б) jc4 — 1;
Рис. 70
1.41 Решите неравенства:
а) 2х-\-7>0; д) — 3(2 — х)^х; ж) —-—0;
б) 3-х<0;
в) 2 + 5*<0: е) ТТГ>0: з) —-—>0
г) 7х+3>х — 2; Зх+1"
1.42. Решите неравенства:
а) (х - 1)(х + 1) > 0; к) -JL-r- < 0;
б) х(х + 7) 0;
в) (х + 2)(3 - х) < 0; л) £~_Х‘25 > 0;
г) х(х— 1)(х + 2Хх + 3) > 0;
д) j£ + - 3> < о-
Я) (х + ЗХ* - 2) ^ и’ ,
н) Г-^" ^ ' -
ч (5 - 2х)(х + 3) ^ n. X + 2
) {2х _ 7Х6 _ бдс) ^ U’ , __5_
ж) х2 + 2х < 0; °' х х + 2
< 2.
з) х2 -|- х — 6 ^ 0: . х
и) 2х2 + х — 3 < 0; П' * + I
1.43. Докажите следующие свойства неравенств:
а) а > Ь, с > d, Ь > 0 =>- ас > bd\
б) а > Ь > 0 =>- /а” > /Ь~;
в) а>6>0=^ —
а b
1.44. Равносильны ли неравенства:
а) х < 1 и х2 < 1; в) х < 1 и —> 1;
X
г) д/х — 1 ^ дг и
х — I < х2?
1.45. Докажите неравенства:
а) с 0 + ь. • г) ?£ < I ■
’ 1/а + 1/ft 2 ’ ' 1 + а2 ^ ’
(а, Ь > 0); д) аб = 1 =>- а2 + 62 ^ 2;
б) 2 < Jab- е) а + Ь = 1 ^ аб < >/4;
l/а + 1/й » ’ ж) ab = 1 =>-
(а>& >0); . =►(! + а2Х1 + Ь2) > 4.
в) ^
1.46. Найдите область определения и область значений функции,
описывающей зависимость площади квадрата от длины его
стороны.
1.47. Из железа изготовлен кубик. Найдите зависимость массы
кубика: а) от длины ребра кубика, б) от его объема; в) от
его полной поверхности. Запишите эти зависимости, считая,
что 1 см3 железа имеет массу 7,8 г.
1.48. В окружность радиуса R вписан прямоугольник, длины
сторон которого равны х и у. Выразите у как функцию от
х. При каких значениях х определено это выражение?
Во что превратится прямоугольник, если х — 2/?? Выразите
площадь прямоугольника как функцию от х.
1.49. Выразите площадь равностороннего треугольника через
длину х его стороны. Выразите эту же площадь через ради¬
ус г вписанной окружности.
1.50. Выразите площадь прямоугольника, вписанного в круг
радиуса 1, через основание х прямоугольника.
1.51. Выразите площадь круга через его диаметр.
Выразите эту же площадь через длину окружности.
1.52. Найдите зависимость площади квадрата от длины его
диагонали; от радиуса вписанной окружности; от радиуса
описанной окружности.
2
ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
§ 5. Введение производной
Механический смысл производной
Производная — это скорость.
Представим себе, что мы едем в кабине автомашины по
прямолинейному шоссе. Посмотрим на счетчик километража.
Запомнив показания счетчика в начальный момент, можно опре¬
делить проделанный путь в любой момент времени. Посмотрим
на стрелку спидометра. Она покажет скорость движения в дан¬
ный момент (рис. 72). Так с нашим движением связаны две вели¬
чины — путь 5 и скорость vy которые являются функциями вре¬
мени /: s = s(t\ v = v(t).
Рис. 72
Ясно, что функции s и v связаны между собой. В конце
XVII в. великий английский ученый Исаак Ньютон открыл общий
способ вычисления скорости по заданному пути. С помощью
этого способа для каждой функции 5 можно построить новую
функцию и. Эту функцию называют производной функции s,
а сам переход от функции s к функции v — дифференцированием.
Открытие Ньютона явилось поворотным пунктом в истории
естествознания. Оказалось, что количественные характеристики
51
самых различных процессов, исследуемых в физике, химии, био¬
логии, в технических дисциплинах, могут быть выражены на
языке математического анализа, изучающего связи между функ¬
циями и их производными.
Самой важной и самой простой моделью для построения
производной остается изученная еще Ньютоном модель механи¬
ческого движения. В этой модели исходной функцией является
путь, ее производной — скорость. Вот почему самым простым и
коротким ответом на вопрос, что такое производная, является
такой: производная — это скорость.
А что такое скорость? Оказывается, на этот простой вопрос ответить не так
просто. Прочтите диалог между водителем (женщиной) и полицейским, оста¬
новившим автомобиль за превышение скорости. Он взят из знаменитых «Фейн-
мановских лекций по физике»:
— Мадам, Вы нарушили правила уличного движения. Вы ехали со ско¬
ростью 90 км/ч.
— Простите, это невозможно. Как я могла проехать 90 километров за час,
если я еду всего лишь 7 минут!
— Я имею в виду, мадам, что, если бы Вы продолжили ехать таким же
образом, то через час Вы бы проехали 90 километров.
— Если бы я продолжала ехать, как ехала, еще час, то налетела бы на
стенку в конце улицы!
— Ваш спидометр показывал 90 км/ч.
— Мой спидометр сломан и давно не работает.
Вот видите, что полицейский не смог объяснить, что такое скорость 90 км/ч.
А вы смогли бы?
Попробуйте объяснить, что такое скорость равномерного движения и как ее
можно измерить.
Геометрический смысл производной
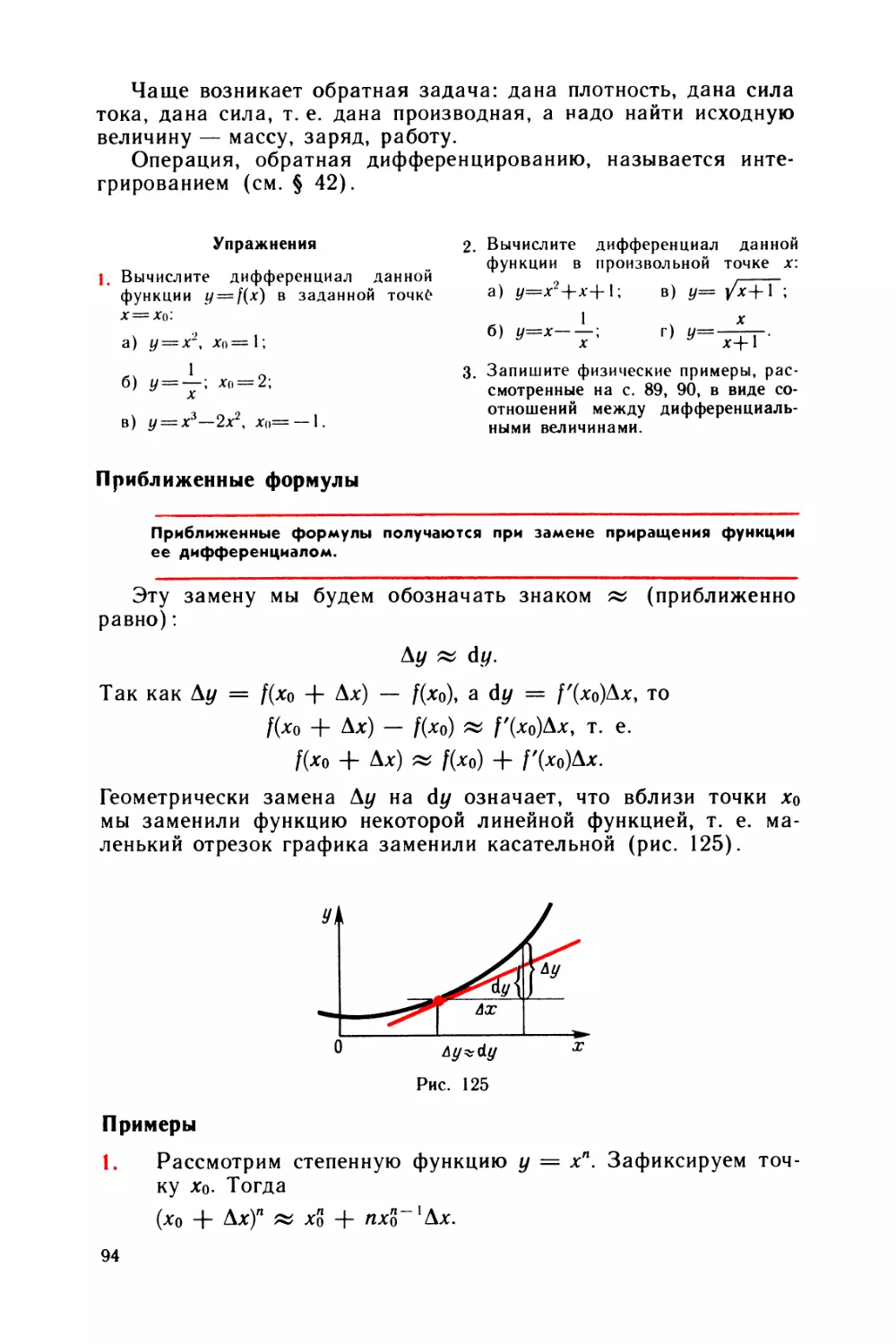
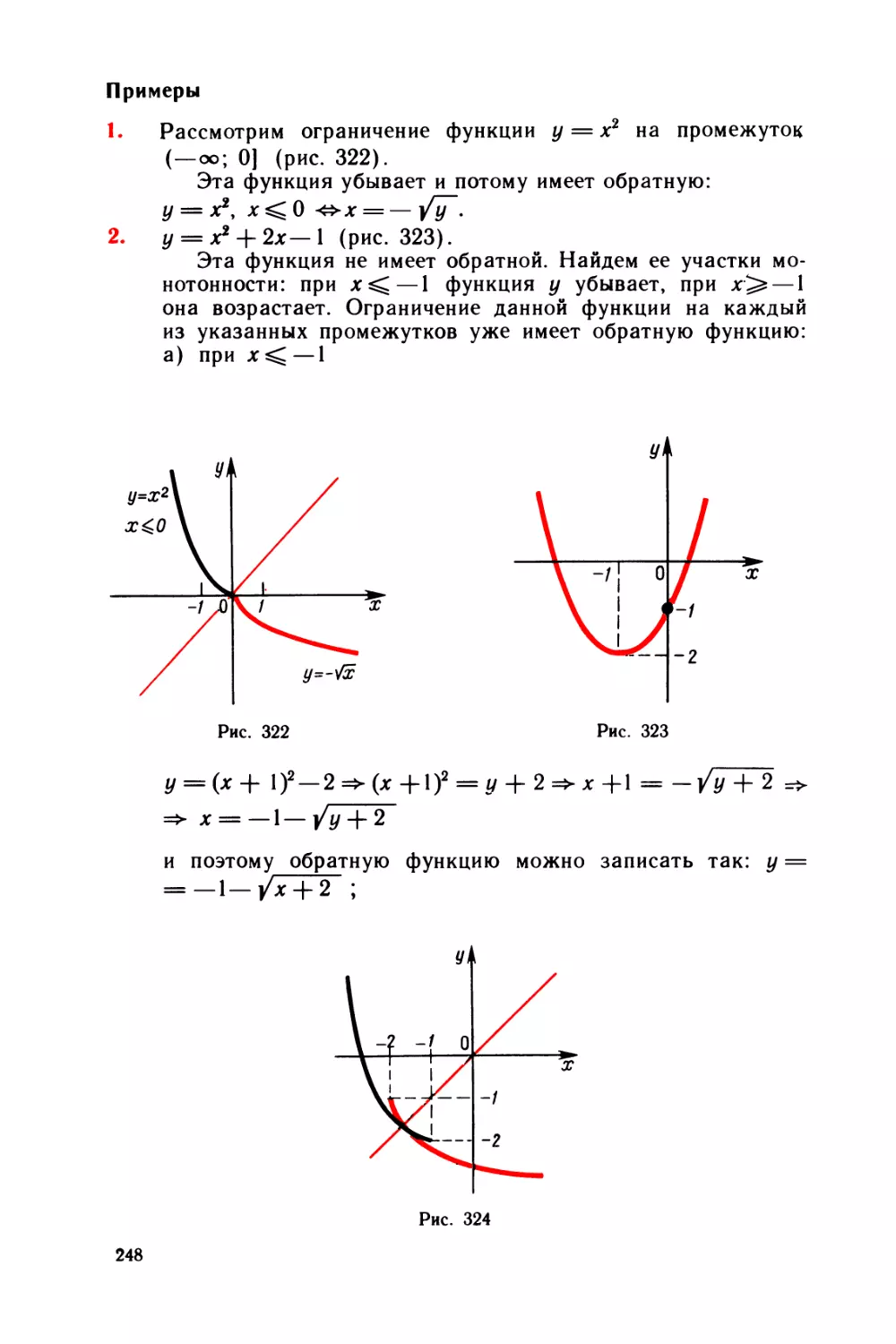
Производная — это угловой коэффициент касательной.
Одновременно с Ньютоном к задаче нахождения производной
пришел немецкий математик Г. Лейбниц, изучая касательные к
произвольным кривым.
Геометрически, чтобы провести касательную, надо к графику
кривой приставить линейку так, чтобы она коснулась графика в
выбранной точке (рис. 73).
Как связаны между собой задачи нахождения скорости и
проведения касательной? Начертим график зависимости пути 5
от времени t. Предположим сначала, что в течение какого-то
промежутка времени движение равномерно. Тогда соответствую¬
щий участок изобразится отрезком некоторой прямой /. Скорость
при этом постоянна. Она равна угловому коэффициенту прямой /.
С другой стороны, прямая / и будет касательной к графику пути
в точках рассматриваемого отрезка.
' В общем случае представим себе кривую — график пути 5 —
в виде ломаной с очень большим числом маленьких звеньев.
Именно так представляли себе кривую создатели дифференци¬
ального исчисления. В первом учебнике по математическому
52
анализу, написанном триста лет назад учеником Лейбница мар¬
кизом Лопиталем, было сказано: если продолжить одно из ма¬
леньких звеньев MN ломаной, составляющей кривую линию, то
продолженная таким образом сторона будет называться каса¬
тельной к кривой в точке М или N (рис. 74).
На этом маленьком отрезке скорость движения постоянна и,
как мы выяснили, равна угловому коэффициенту прямой MN.
Таким образом, скорость равна угловому коэффициенту каса¬
тельной к графику пути.
Итак, надо научиться находить скорость по заданному пути,
или, что то же самое, угловой коэффициент касательной. Эту
операцию называют дифференцированием, а ее результат —
производной.
Дифференцирование, или нахождение производной, — это
новая математическая операция, которая в механике имеет тот
же смысл, что и нахождение скорости, а в геометрии — вычис¬
ление углового коэффициента касательной.
Для нахождения производной надо рассмотреть маленький
участок изменения аргумента. Средняя скорость на этом отрезке
(на языке механики), или угловой коэффициент секущей (на
языке геометрии), приближенно равна производной. Для точного
вычисления производной надо совершать предельный переход —
стянуть отрезок изменения аргумента в точку. Тогда средняя
скорость превратится в мгновенную скорость в данной точке,
а секущая — в касательную, и мы вычислим производную.
Задание
Перечертите (лучше всего на мил¬
лиметровую бумагу) график функ¬
ции, изображенной на рис. 75.
Выберите 3—4 точки графика, про¬
ведите касательные к графику в
этих точках и вычислите прибли¬
женно их угловые коэффициенты.
Найдите точку, в которой каса¬
тельная проходит круче всего, —
в этой точке производная будет
самой большой. В какой точке
касательная параллельна оси х?
53
Рис. 73
Рис. 74
Что можно сказать о скорости в от времени)? По найденным зна-
этой точке (если считать, что гра- чениям начертите график скорости,
фик изображает зависимость пути расположив его под графиком ис¬
ходной функции.
Поведение в малом
Основная идея Ньютона состояла в следующем. Скорость равно¬
мерного движения постоянна и легко вычисляется. За малый
промежуток времени неравномерное движение приблизительно
можно считать равномерным. Так, стрелка спидометра автома¬
шины колеблется при движении, однако этим колебанием можно
пренебречь, если взять достаточно малый промежуток времени.
Примерно так же рассуждал Лейбниц. Прямая имеет посто¬
янный наклон. Касательная к ней в каждой точке совпадает с
ней самой. Если мы хотим провести касательную к кривой в точ¬
ке Р, надо немного отступить от нее и провести секущую через
две точки Р и Pi (рис. 76). Чем ближе точка Pi к точке Р, тем
точнее совпадает секущая РР\ с касательной в точке Р.
Обе точки зрения — механическая и геометрическая — очень
сходны между собой. На малом отрезке, или, как говорят мате¬
матики, в малом, всякое движение равномерно и прямолинейно
и всякая кривая мало отличается от прямой. Это наглядно видно
на рис. 77, где показаны части одной и той же параболы, но в
Рис. 77
54
Рис. 75
Рис. 76
разных масштабах, и взята одна и та же точка М(1; 1). На
рис. 77, а ясно видно, что парабола искривлена. На рис. 77, б
это искривление уже менее заметно, а на рис. 77, в график функ¬
ции почти неотличим от прямой линии.
Упражнение
По графику движения (рис. 78) опре- дующих отрезках времени: [0,2],
делите скорости движения на еле- [2,5], [5,9], [9,10].
Средняя и мгновенная скорости
Пусть точка движется по прямой и задан закон, по которому
можно вычислить путь 5 как функцию времени t:
s = s(t).
Например, если точка движется равномерно со скоростью у,
то s = vt (считаем, что при t = 0 путь 5 = 0). Если точка движет¬
ся под действием силы тяжести с нулевой начальной скоростью,
то s = gt2/2 (мы считаем, что g — ускорение свободного паде¬
ния— постоянно). Возможны и другие законы движения. Так,
тело, запущенное с поверхности Земли вертикально вверх с
начальной скоростью, позволяющей полностью преодолеть зем¬
ное притяжение (вторая космическая скорость), удаляется от
центра Земли по закону s = A(t -f- С)2/з, где А и С — некоторые
константы.
Определим среднюю скорость точки за промежуток времени
[/i, /г] как отношение пройденного пути ко времени движения
(рис. 79):
Определим скорость точки в момент времени t (ее в механике
называют мгновенной скоростью; рис. 80). Для этого вычислим
среднюю скорость за промежуток времени [/|, t2\. Уменьшая
отрезок [/|, /г], т. е. приближая U к t\y мы заметим, что значение
средней скорости при этом практически не меняется, а вернее,
55
Рис. 78
Рис. 79
Рис. 80
приближается к некоторому числу, которое и считается значени¬
ем скорости в момент времени /.
Пример
Длина пути задается функцией 5 = gt2/2. Зафиксируем
произвольный момент времени и вычислим среднюю ско¬
рость на отрезке [/, /1]:
s(/i) — s(t) gt'j/2 — gt2/2 _g t] — t2
cp U—t /,-/ 2 /,
■(t i + t).
Если стягивать отрезок [/, t\] к точке /, т. е. брать значения
t\ все ближе и ближе к /, то сумма t\ 1 будет приближать¬
ся к / + t = 2/, а все выражение (g/2) (/i + /) — к (g/2)• 2t =
= gt. Это и есть мгновенная скорость в точке t:
v = gt.
Переход от средней скорости на отрезке [/, t\] к мгновенной
скорости в точке t при стягивании отрезка [/, t\] к точке t
называется предельным переходом. Обычно говорят так:
при стремлении t\ к / выражение (g/2)(t\1) стремится
к gt. Запишем это:
Hm f (tt +t) = gt.
Используя слово «предел», можно сказать, что мгновенная ско¬
рость в точке t — это предел средней скорости при стягивании
отрезка, на котором измеряется эта скорость, к точке t.
1. Средняя скорость вычисляется для каждого отрезка времени, мгновен¬
ная скорость вычисляется в каждый момент времени.
2. Средняя скорость является приближением к мгновенной, и это при-
ближгние тем точнее, чем меньше отрезок.
Скорость роста функции
Мы рассматривали движение точки по прямой. Путь задавался
как функция времени s = s(t), и мы строили новую функцию —
скорость v = v(t). Аналогично можно поступить с произвольной
функцией.
56
Рассмотрим некоторую функцию /: у = f(x). Зафиксируем
какую-либо точку х на отрезке [jc, х\\ целиком входящем в об¬
ласть определения /. Найдем среднюю скорость роста / на отрез¬
ке [jc, jti]:
Начнем стягивать отрезок [jc, х\\ к точке х, т. е. приближать х\ к
х. Тогда значения средней скорости будут близки друг к другу.
Обычно удается определить новую функцию g, для которой при
стягиваний отрезка к точке х значения средней скорости станут
приближаться к значению функции g в точке х. Эта функция gy
играющая роль скорости роста функции, называется производ¬
ной от функции и обозначается g = f' (читается «/-штрих»).
Примеры
1. f(x) = ax-\-b.
На отрезке [х, Х\] средняя скорость / равна
Уср[х> Х||= («*■ + »)-(«* +Ь) =Ф1-х1 = а
FL J Х\ — X Х\ — X
Мы видим, что средняя скорость линейной функции одна и
та же на любом отрезке и равна коэффициенту при х.
Ясно, что в качестве скорости роста / надо взять посто¬
янную функцию g(x) = a. Значения средней скорости просто
равны значениям функции gy и g(x) = a есть производная
линейной функции. Итак, (ах + Ь)' = а.
В частности, если а = 0, то f(x) = Ь постоянна и ее произ¬
водная /' = 0. Итак,
производная постоянной равна нулю.
2. у = х1.
Вычислим среднюю скорость на отрезке:
г 1 Х[ — х2 .
vcp[x, Х\\ = = Х\+Х.
Kl J Х\ — X
Теперь уже средняя скорость не является одной и той же
на каждом отрезке. Рассуждая, как в примере вычисления
скорости равноускоренного движения, мы получаем, что
при приближении х\ к х средняя скорость, равная Jti+Jt,
будет приближаться к х-\-х = 2х. Поэтому, если взять функ¬
цию g (jc) = 2jc, то она и будет производной от /. Итак,
(jc2)' = 2jc.
Как же теперь ответить на вопрос, что такое производная?
Производная — это скорость роста функции.
57
Математический анализ, созданный Ньютоном и Лейбницем,
долго развивался на основе интуитивного понятия производной
как скорости роста функции. Во второй половине XIX в. были
уточнены те основные понятия, на которых строится математи¬
ческий анализ, — понятия вещественного числа, функции, преде¬
ла. С их помощью можно дать точное определение того, что
такое скорость роста функции. В следующих параграфах мы
продолжим ознакомление с этим понятием.
Переход к пределу
Опишем еще раз, как следует поступать, чтобы найти скорость
роста функции /, т. е. ее производную.
1. Нужно зафиксировать точку х и взять отрезок [ху х\\ где
точка х\ находится на некотором расстоянии от х, и аычислить
среднюю скорость на отрезке [*, *|]:
2. Нужно представить, что точка х\ приближается к точке ху
и догадаться, что получается «в пределе», т. е. к какому значе¬
нию приближается средняя скорость при приближении х\ к х.
Из приведенного описания видно, что основная часть нахож¬
дения производной — вычисление предела средней скорости —
не формализована, требует догадки. Из этого затруднения мож¬
но выйти следующим образом: сначала найдем производную для
самых простых функций (например, линейных), затем изучим
правила для вычисления производных функций, которые нахо¬
дятся из известных функций с помощью простых операций —
сложения, умножения, деления, возведения в степень. Это позво¬
лит научиться вычислять производные многочленов, рациональ¬
ных дробей и некоторых других несложных функций. Рассмотре¬
ние новых функций (тригонометрических, показательных, лога-
«Скорости, с которыми каждая величина увеличивается, я буду изобра¬
жать теми же буквами с точкой: v, х, у, г.»
И. Ньютон
Ньютон Исаак (1643—1727 гг.) —английский физик и математик.
Создал современную механику (законы Ньютона) и открыл закон все¬
мирного тяготения. В его главном сочинении «Математические начала
натуральной философии» дал математический вывод основных фактов о
движении небесных тел. Один из создателей дифференциального и
интегрального исчисления, определивший пути развития математического
анализа на долгое время.
Потомки по достоинству оценили гений Ньютона.
«Был этот мир глубокой тьмой окутан.
Да будет свет! — и вот явился Ньютон», — сказал о нем поэт А. Поп.
58
рифмических) каждый раз потребует от нас вывода правил их
дифференцирования.
Сделаем первый шаг в нахождении производной — вычисле¬
ние средней скорости функции y = f(х) (рис. 81, а—в). Мы фик¬
сируем точку х и отступаем от нее — берем точку х\. Часто раз¬
ность Х\ — х обозначают Ал: (дельта икс) и называют прираще¬
нием аргумента. В этих обозначениях точка х\ запишется как
х + Ал:, а отрезок [ху х\] — как [х. х-\- Ах].
* Отступить от точки х можно как вправо, так и влево, поэтому Х\ может
быть как больше, так и меньше х, а Дх соответственно может быть как
больше, так и меньше 0.
Затем мы вычисляем разность значений /(xi) — f(x) = f(x +
-|- Алг) — f(x). Эту разность называют приращением функции и
обозначают Ау. Итак,
Кратко можно сказать так:
средняя скорость есть отношение приращения функции к приращению
аргумента.
Итак, в качестве первого шага в нахождении производной
мы составляем отношение приращения функции к приращению
аргумента.
На втором шаге надо приближать точку х\ к х, т. е. умень¬
шать приращение аргумента Ах. Далее надо проследить за тем,
что происходит с отношением - при уменьшении Ах. При этом
видно, что это отношение стремится к некоторому числу, которое
Рис. 81
59
Наконец, составляем выражение для средней скорости:
и называют производной функции у в точке х. Нахождение того
числа, к которому приближается при стремлении Ах к нулю,
называется нахождением предела. Поэтому можно окончательно
сформулировать следующее правило:
производная есть предел отношения приращения функции к при¬
ращению аргумента, когда приращение аргумента стремится к нулю.
Символически это правило записывается так:
У'=
Длс_^0 &Х
Изучение поведения отношения когда Ах приближается
к нулю, т. е. нахождение lim в общем виде является слож-
ной задачей. Для ее решения в математике построена общая
теория пределов. Трудность этой теории заключается в том, что
она обслуживает все встречающиеся в математике функции,
а они могут быть весьма сложными и запутанными. Для тех
функций, которые мы будем изучать, можно вычислить произ¬
водные, не прибегая к построению общей теории пределов.
§ 6. Вычисление производной
Схема вычисления производной
Производные вычисляем по следующей схеме:
1. Находим приращение функции y = f(x) на промежутке
[л:; х + Ах]:
Лу = fix + Ьх) — f(x).
2. Делим приращение функции на приращение аргумента,
т. е. находим среднюю скорость роста функции / на отрезке
[ху X + Ах]:
7. _ __ f(x + &х) - f(x)
Vcp ~~ Л* ~~ \х
3. Переходим к пределу, т. е. стараемся преобразовать сред¬
нюю скорость так, чтобы было легко угадать мгновенную
скорость — функцию, значение которой в точке х близко к
при малых Ах. В этих преобразованиях часто удается сокра¬
тить Ах.
Примеры
1. Производная постоянной функции у=С.
Функция определена на всей вещественной оси IR и
принимает постоянное значение С в каждой точке, поэтому
ее приращение
Ау = С — С = 0=^уср = 0.
Так как отношение постоянно и равно нулю, то про-
изводная у тоже равна нулю: у' = 0. Итак, производная
постоянной равна нулю.
2. Производная линейной функции у = ах -+- Ь.
Функция определена на всей вещественной оси IR, и ее
приращение равно
Ау = а(х + Ах) + b — (ах + b) = ах + аАх -+- Ь — ах — Ь =
а /\и аАх
— аАх= —— = а.
S.x S.X
Отношение является постоянным. Поэтому в качест¬
ве производной надо взять функцию, принимающую это
постоянное значение а: у'= а. Итак,
производная линейной функции равна коэффициенту при переменной
Полученный результат неудивителен — линейная функция
соответствует равномерному движению, скорость которого посто¬
янна.
3. Производная функции у = х3.
Вычислим Ау:
Ау = (х + Ах)3 — х3 = Зх2Ах + Зх(Ах)2 + (Ах)3.
Найдем отношение: = Зх2 -f- ЗхАх -f- (Ах)2.
Ясно, что при малых значениях Ах дробь опреде¬
ляется только первым слагаемым. В качестве производной
надо взять функцию g(x) = Зх2. Получаем у'= Зх2.
4. Производная функции у=^—.
Эта функция определена при всех jc, кроме Jt = 0. Най¬
дем отношение приращения функции к приращению аргу¬
мента:
Д« = —! -= - ; &-= ! .
х + Ajc х х(х -|- Дх) Дх х(х -|- Дх)
Ясно, что при малых значениях Ах выражение хАх
близко к х, а вся дробь — мало отличается от
дроби — -^-= — Следовательно, у'= —
* Эти примеры затрагивали только многочлены и дроби — рациональные
функции. При вычислении производной рациональной функции дробь
всегда сократится на Ах. После этого можно просто положить Ах ;= О
и получить производную.
5. Производная функции у = ^/х. Эта функция определена при
всех х^О:
Лу = л/х + Ах — д/х; = Дх ~
Для того чтобы сократить дробь на Дх, умножим ее
числитель и знаменатель на сумму радикалов:
Д«/ Vjc -f- Ajc — Ух У* + Ajc + Vjc x Ajc — x
Д* Ад: -л/л: + Ajc + У* A*(V* + A* + V* )
Ax 1
Ах(У* Ax + yi) ^x Ax + Vi
При малых Дл: значение корня -\jx -f- Дл: приближается к
У*. Поэтому при переходе к пределу надо заменить
-\Jx -f- Дх в знаменателе на
1 1
1/ — = •
л[х-\-л[х 2-у/х
Производные, вычисленные в этих примерах, полезно запом¬
нить:
С' = 0;
(ах + by = а;
(х2)' = 2лг;
Упражнения
Тело движется прямолинейно по
закону s(t)=t2—2t. Найдите сред¬
нюю скорость тела на отрезках
времени [0,1]; [1,2]; [0,2].
2. Для функции у = х2—х вычислите
у( 3), у{ 3+АдО, Ьу=у(3+/±х)—у(3),
&У it
Чему равна производная у
в точке л:=3?
3. Дан график пути s как функция
времени t (рис. 82). Вычислите
62
Рис. 82
Рис. 83
приближенно значения скорости в 4. На рис. 83, а—е изображено шесть
нескольких точках. Постройте гра- графиков. Объедините их в пары
фик скорости. «функция — ее производная».
Правила дифференцирования
1. Производная суммы.
Производная суммы двух функций равна сумме их производных:
(и -f- v)' = и' -f- v'.
2. Вынесение постоянной за знак производной.
Если функцию умножить на постоянное число, то и производная умно¬
жится на это число:
(Су)' = Су'.
3. Производная произведения:
(UVУ = u'v -f- uv'.
4. Производная частного:
(и \ u'v — uv'
ГУ Р •
63
Доказательство.
1. Пусть функция w равна сумме функций и и v, т. е. w(x) =
= и(х) + v(x). Вычислим Aw:
Aw = w(x -f- Ах) — w(x) = и(х -f- Ах) -f- v(x -f- Ах) — [w(jc) -f- у(х)] =
= и(х -f- А*) — и(х) -f- y(jc -f- Ах) — v(x) = Аи-\- Av.
Составим дробь
Адо Аы + Ду Aw , At;
Ax Ax Ax Ax
Мы видим, что средняя скорость роста суммы двух функций
равна сумме средних скоростей слагаемых. При переходе к пре¬
делу это соотношение должно сохраниться: если близко к
и\ а близко к v' то + близко к и'4-v'. Итак,
Ах Ах Ах
—>и' + v\ т. е. (u + v)' = и' -\- v'.
2. Вычислим приращение функции Су:
НС у) = Су(х + Ах) — Су(х) = СЬу, = С .
Мы видим, что при умножении функции на постоянное число
средняя скорость также умножится на это число. Это соотноше¬
ние сохранится и в пределе, т. е. если близко к у', то
С-~- близко к Су'. Итак, —*Су\ т. е. (Су)' = Су'.
3. Вычислим среднюю скорость изменения произведения:
A(uv) и(х + Ах)* v(x Ах) — u(x)v(x)
Ах Ах
«Лейбниц... сразу же задумался над вопросом, верно ли что d(ху) —
= dxdy, ответил на него отрицательно и постепенно пришел к верному
правилу. Ньютону уже за десять лет до того было известно, что если
z = ху, то z = ху + ху, но он не дает себе труда говорить об этом.»
Н. Бурбаки
Лейбниц Готфрид Вильгельм (1646—1716 гг.) — немецкий математик,
физик, философ, создатель Берлинской Академии наук. Основоположник
дифференциального и интегрального исчисления, ввел большую часть
современной символики математического анализа. В работах Лейбница
впервые появились идеи теории алгоритмов.
Н. Винер писал о нем:
«После Лейбница, быть может, уже не было человека, который бы
полностью охватывал всю интеллектуальную жизнь своего времени».
64
В числителе прибавим и вычтем произведение u(x)v(x -f- Ах):
&(uv) и(х + Ах) - v(x + Ах) — и(х)у(х + Ах) + u(x)v(x + Ах) — u{x)v(x)
Ах
[и(х + Ах) — u(x)]v(x + Ах) . и(х) [у{х + Ах) — у(х)|
Ах “т Ах
-+ху то и v(x-\- Ax)^v(x). В итоге получим ^ -—>u'v -|- uv',
т. е. (uv)' = u'v + uv'.
Правило 2 можно получить как следствие правила 3, считая, что Су есть
произведение постоянной функции и— С на v = у:
Переход к пределу, который совершается при доказательстве правила
2, гораздо проще того, который нужен для правила 3, поэтому мы дали
отдельное доказательство важного правила дифференцирования — выне¬
сение постоянного числа за знак производной.
4. Вычисления можно провести по стандартной схеме, находя
среднюю скорость частного. Мы поступим иначе. Обозначим u/v
через А. Получим u/v = hy u = vh. Найдем производную функ¬
цию и по правилу дифференцирования произведения:
Выразим из этой формулы А', а вместо h подставим его зна¬
чения u/v:
(СуУ = (С)'У + С(у)' = 0-£/ + С£/' = Су'.
и' = v'h + vh'.
и' — v'h и' — у*(и/у) и' у — у'и
У У у2
Окончательно
*
Производную функции У = — можно получить, пользуясь правилом 4.
Представим У=~~ как частное функций и= 1 и у = х. Тогда
1 V (1 )'(х) — 1(х)'
X. ) X2
О- 1
X
Упражнения
1. Вычислите производные:
а) у=3хг\
2
д) у=—<
3
и) у—-
2. Вычислите производные:
а) у = 2х2-Зх-\-5\
б) у=2 — у—х2-,
О
в) У = —з Зх2+6х— 1;
г) у = хА—х2С~
Производная степенной функции
Производную любой степени с натуральным показателем можно
получить, пользуясь правилом дифференцирования произведения.
Пример
Найдем производную функции у = х4.
Представим х4 как х3х. Зная производные от у = х3 и
у = х, вычислим производную от произведения:
(х4)' — (х3)'х + х3(х)' = Зх2х + х3 • 1 = 4л:3.
Сопоставим друг с другом формулы х'=\; (л:2)' = 2х\
(х3)'= 3х2; (хА)' = Ах3. Найдем общую закономерность:
(хпу = пхп-\
* Проверить это можно так. Предположим, что (хп~1)' = (п — \)хп~2. Пред¬
ставив хп = хп~[х, найдем
(хп)' = (хп~ 1)'х + хп~ \х)' = (п— \)хп~2х + хп~х =(п— 1 )хп — 1 хп~1 =
= пхп~\
Таким образом, если формула (xk)' = kxk~x верна при k = n — 1,
то она верна и при k = ti. Нам эта формула уже известна, напри¬
мер, при k = 2. Тогда она верна и при k = 3, а следовательно,
и при k = 4, k = 5 и т. д., т. е. при любом натуральном к.
Рассуждение, которое мы здесь провели, называется матема¬
тической индукцией.
Теперь найдем производную функции у = -^г :
У (*л)2 х2п-(п-\) хп+\
Если дробь у =-^j- записать как у = хк, где k= — n (т. е. как степень с
отрицательным показателем), то у' = ( — п)х~п~’. Заменив ( — п) на k,
получим у' = kxk~ \ т. е. формула дифференцирования степени, выведенная
дг —1
3> »=7+р
и) У~~х^Т
3. Выведите формулу для произведе¬
ния трех функций:
(wvw)' = u'vw -)- uv'w uvw'.
нами для натуральных показателей, остается верной и для целых отрица¬
тельных показателей:
(**)' =
где k — любое целое число, кроме нуля. На самом деле выведенная форму¬
ла остается верной и для дробных показателей, которые мы будем изучать
позже.
Примеры
1. у = 2х3 + Зх+1.
у' = (2 X3)' + (ЗхУ + Г =6х2 + 3.
2х2 — 1
2.
X
Преобразуем исходную функцию к сумме, выполним по-
2х2 1 1
членное деление: и = =2х-\ .
X X
Теперь производная вычисляется аналогично предыдущему
случаю:
*'' = <2->'+(-г)' = 2-(-7)=2 + Т =
2х*+ 1
3. у = л/Зх + 1.
у' = (л/3^)' = -^
2 ух
4. у
х*+1 '
(>+ I)2 “ (*2+1)2 _(*2+1)2
, MX*2 + 1) — х(х2 +1)' х2 + 1 — х-2х 1 — х2
У
JC200 — 1
5. У = „,оо
. ^юо х~ 100
у'= 1 ООдг" 100*-101 = 100 *200+ ■ .
Упражнения ч л:4+3л:2— 1
г) У = zn
1, Вычислите производные:
х4 х2
а) у- — -f3x3 ^—h 5jc — 1; х /— , 1
* 4 2 7 д) у= /х Н
х5-\-2х3—2х-}-5
б) у = >
2 \ x-j-3
в) е) у- — :
3. Какова производная квадратной
функдии?
з) у—3]/2х^.
4. Какую степень имеет производная
многочлена п-й степени?
2. Чему равна производная линейной
функции?
5. Что можно сказать о функции,
если ее производная — многочлен
второй степени?
Изменение производной при линейной замене аргумента
Новое правило дифференцирования:
Допустим, что надо взять производную функции (/= (2х + I)3.
Можно раскрыть куб суммы и продифференцировать:
Можно поступить иначе. Обозначим выражение 2х+1 через /.
Тогда зависимость у от t выразится формулой y = t3. Можно
сказать, что мы сделали линейную замену аргумента: / = 2х1.
Такая замена имеет простой геометрический смысл — прибавле¬
ние константы означает параллельный перенос, изменение нача¬
ла отсчета. Умножение на константу означает изменение масшта¬
ба. Из физических представлений (производная — это скорость)
ясно, что начало отсчета не может повлиять на производную,
а изменение масштаба вызывает изменение производной в этом
же отношении. Это похоже на изменение системы единиц — при
уменьшении единицы времени в k раз скорость в новой единице
увеличится в k раз. Так, например, 30 км/ч = 30-60 км/мин.
Приведем соответствующие выкладки в общем виде. Пусть
y = f(kx-\-b). Обозначим t = kx + b, тогда y = f(t). Вычислим
производную у (считая х аргументом). Для этого запишем сред¬
нюю скорость у: уср=-^-. Заметим, что A/ = feAjt, так как t —
линейная функция от х. Подставим Дх = -у- в выражение для
средней скорости: уср=-^-. Если у рассматривать как функ¬
цию от /, то выражение -^у- есть ее средняя скорость. При
Дх-^0 будет стремиться к нулю и Д/ = £Дх. Поэтому -^у- бу¬
дет приближаться к производной у как функции от /. Но y = f(t\
поэтому -|у--^Г(0> а -|—= k kf'(t)- Подставляя t=kx-\-b
в /'(/), получаем
\f(kx + b)Y = kr(bx + b).
(2х+ 1 )3 = 8а:3 + 12х2 + 6х + 1; у' = 24а:2 + 24а: + 6.
I^-+kf'{kx + b), т. е. [f(kx + b)}' = kf'(kx + b),
что и требовалось доказать.
68
В рассмотренном выше примере / = 2х+1, y = t3, поэтому
1/'=2(/3)'=2-3/2 = 6(2дсЧ- 1 )2 = 24дс2 + 24г + 6, что мы получили
другим способом.
Примеры
1. ,, = (*+I)5, у' = 5(лг+I)4.
2. у = (5х-I)4, у' = 5-4(5х-I)3.
3- у-^гт- »'=-2 '
2* + 3 ’ * (2х + З)2
1
4. у = Уб*—Т, f/' = 6- .
2л/блг - 1 л/^ - 1
При дифференцировании функций вида y = (kх)п выведенной
формулой пользоваться не рационально. Лучше вынести кон¬
станту за знак производной.
Пример
((За:)5)' = 35(jc5)' = З5 • 5л:4.
Упражнения 2* Выведите формулу [f(x2)]' = 2xf'(x2)
4 п и вычислите по ней производные:
J. Вычислите производные: г
а) у=(х—З)7; в) у = (3х—4)9; а) у = (х2+1)|(>; в) у= 5 .
б) у=(\-хГ, г) у=-{з^т. б) у = рз-;
§ 7. Исследование функции с помощью производной
Связь свойств функции и ее производной
Как сказывается поведение функции на свойствах производной?
Функция возрастает ^ производная положительна.
Функция убывает ==>производная отрицательна.
Функция достигла максимума или минимума ==> производная обрати¬
лась в нуль.
Объясним эту связь, исходя из механического смысла производ¬
ной. Будем считать данную функцию законом движения точки.
Тогда производная данной функции будет скоростью движения
точки.
Разберем это более подробно. Представим себе материаль¬
ную точку Af, движущуюся по прямой. Положение точки на
прямой задается координатой у. Зависимость координаты (поло-
69
жения точки) от времени х — это и есть то, что в механике
называют законом движения точки, а в математике — функцией,
которую мы, как обычно, обозначим /, т. е.
У = f(x).
Что означает возрастание функции с точки зрения механики?
Точка движется по оси у. Возрастание координаты у означает,
что точка движется в направлении, совпадающем с положитель¬
ным направлением оси у. Аналогично, убывание координаты у
означает, что точка движется в противоположном направлении.
Итак, возрастание и убывание функции y = f(x), задающей
закон движения точки, зависит от направления движения точки.
Эта зависимость изображена на оис. 84.
Как связано направление движения точки с ее скоростью?
Посмотрите еще раз на рис. 84. Ясно, что движение вверх проис¬
ходит с положительной скоростью, а вниз — с отрицательной.
Знак скорости, т. е. направление вектора скорости, совпадает с
направлением перемещения.
Итак, если функция возрастает (точка движется в положи¬
тельном направлении), то ее скорость положительна (f'^0).
Если функция убывает (точка движется в отрицательном направ¬
лении), то ее скорость отрицательна (f'^.0).
Как перевести на язык механики то, что функция достигла
максимума или минимума? Представьте себе, что вы подбросили
кверху мяч. В тот момент, когда он будет находиться в самой
высокой точке, его скорость равна нулю. Точки экстремума (мак¬
симума или минимума) функции соответствуют моментам ее
остановки, т. е. в точках экстремума производная обращается
в нуль (рис. 85).
Воспользуемся геометрическим смыслом производной. Вспом¬
ним, в чем состоит геометрический смысл производной. Рассмот¬
рим график функции y = f(x) и проведем через точку (х; у) графи¬
ка касательную к нему (рис. 86). Производная — это угловой
70
Рис. 84
Рис. 85
коэффициент касательной, т. е. f/(x) = tga, где a — угол наклона
касательной к оси абсцисс. Как же связано возрастание или
убывание функции с углом наклона касательной? Из рис. 87, а, б
ясно видно, что для возрастающей функции угол а острый, т. е.
f'(x) = tg a > 0, а для убывающей — тупой, т. е. /'(*) = tga<0.
Посмотрим на рис. 88. Он показывает, что касательные, про¬
веденные в точках экстремума, параллельны оси абсцисс. Угол
между такой касательной и осью абсцисс равен нулю, поэтому и
тангенс этого угла равен нулю. Это означает, что в точках эк¬
стремума производная равна нулю.
71
Рис. 86
Рис. 87
Рис. 88
В этом пункте мы рассуждали так: нам было известно пове¬
дение функции, и мы получали свойства производной, т. е. дока¬
зывали такие утверждения: если функция f возрастает, то /' ^ О,
если в точке х функция f достигла максимума, то /'(х) = 0:
0, 0.
В точке х функция имеет максимум или минимум; следовательно,
f'(x) = 0.
Можно сказать, что мы нашли необходимые условия возра¬
стания и убывания функции, необходимое условие экстремума.
Являются ли эти условия достаточными — это мы обсудим
позже.
Упражнения
1. Шарик прикреплен к концу пружи¬
ны. Пружину немного растянули и
отпустили. Шарик начал совершать
колебания, график которых изобра¬
жен на рис. 89. На графике по
оси / откладывается время, по
оси х—смещение шарика. За нуль
выбрано положение равновесия. На
каких отрезках времени скорость
шарика положительна и на каких -
отрицательна? В какие моменты
времени скорость шарика равна
нулю? Что можно сказать об ампли¬
туде колебания?
2. Рассмотрим движение мяча, отска¬
кивающего от пола (рис. 90). Раз¬
бейте время / движения на отрезки,
на которых скорость мяча положи¬
тельна и на которых — отрицатель¬
на. В какие моменты времени мяч
останавливается (его скорость рав¬
на нулю)? В какие моменты смеще¬
ние было максимальным и мини¬
мальным?
Если вы правильно выполнили это упражнение, то, наверное, заметили,
что в рассмотренном примере движения мяча нарушается сформулиро¬
ванное выше правило (необходимое условие экстремума). Когда мяч ка¬
сался пола, его положение достигло минимума, однако его скорость не
была равна нулю. Это нарушение связано с тем, что в те моменты, когда
мяч отскакивает от пола, его направление движения и скорость меняются
резко, рывком. В моменты касания пола вообще нельзя точно сказать,
чему равна скорость мяча. В эти моменты времени функция, задающая
положение мяча, не имеет производной, или, как говорят, недифферен¬
цируема. Следовательно, в выведенном нами правиле надо было сделать
оговорку о том, что мы рассматриваем только дифференцируемые функции.
72
Рис. 89
Рис. 90
Определение свойств функции но поведению ее производной
Как поведение производной влияет на свойства функции?
Производная положительна =#*функция возрастает.
Производная отрицательна =#»функция убывает.
Производная в точке х обратилась в нуль Ф> ничего определенного о ее
поведении сказать нельзя и надо посмотреть на изменение знака про¬
изводной при прохождении через точку х. Если производная изменила
свой знак с « + » на «— »г то в точке х максимум, если знак изменила
с «—» на «+»г то в этой точке минимум, если производная свой знак
не изменяла, то экстремума в точке х нет.
Воспользуемся механическим смыслом экстремума. Как всег¬
да, будем понимать функцию y — f(х) как закон движения точки
по оси у в зависимости от времени х. Знак производной, т. е. ско¬
рости, указывает на направление движения точки: если v =
= f'(x) ^ 0, то точка движется в положительном направлении и
ее координата у увеличивается, а функция f(x) возрастает; если
v = /'(х)^0, то координата уменьшается и функция f(x) убывает.
Если скорость точки обратилась в некоторый момент времени
в нуль, то в это мгновение точка остановилась. После этого она
может изменить направление движения (рис. 91, а, б), а может
Рис. 91
продолжать движение в том же направлении (рис. 92, а, б).
Ясно, что во втором случае никакого экстремума нет, так как
координата точки будет по-прежнему возрастать или убывать.
Если же точка сменила направление движения, то будет экстре¬
мум; если же она шла в положительном направлении и сменила
его на отрицательное (производная изменила знак с « + » на
«—»), то точка достигла максимума, если наоборот, то мини¬
мума.
Обратимся к геометрическому смыслу экстремума. То, что на
графике участки возрастания (убывания) функции и участки,
где ее производная положительна (отрицательна), совпадают,
мы уже видели и раньше. Возможное поведение функции в зави-
73
Рис. 92
симости от знака производной вблизи точки, где эта производная
обратилась в нуль, показано на рис. 93.
Таким образом, мы нашли достаточные условия монотонно¬
сти функции и наличия экстремума. Для возрастания (убыва¬
ния) функции эти условия совпали с необходимыми условиями.
Можно сказать теперь так:
для того чтобы функция f(x) возрастала, необходимо и достаточно, чтобы
ее производная Г(х) была > 0.
Аналогично формулируется условие убывания.
По-другому обстоит дело с точками экстремума. Необходи¬
мое условие экстремума — обращение производной в нуль —
не является достаточным. Достаточным будет более сильное
условие — вместе с обращением производной в нуль необходима
смена ее знака. Не является ли это более сильное достаточное
условие экстремума одновременно и необходимым, т. е. всегда ли
в точке экстремума производная меняет свой знак? На всех
изображенных нами графиках это так. Однако существуют такие
функции, для которых это неверно — они бесконечно много раз
74
Рис. 93
колеблются около точки экстремума. Построить такие функции
трудно, и в прикладных задачах они встречаются редко.
Точки, в которых производная обращается в нуль, называются критиче¬
скими точками функции.
Если дифференцируемая функция в точке имеет экстремум, то
эта точка — критическая. Обратное не всегда верно — если точка
является критической, то в ней экстремум может быть, а может и
не быть.
Эти правила относятся к «хорошим» функциям, не имеющим особенно¬
стей, подобных тем, что были в упражнении 2 на с. 72 . Исследование
функций с особенностями требует всегда дополнительных усилий.
Примеры
1.
f(x) = x3- Зх.
Вычисляем производную: f'(x) = Зх — 3 = 3(х — 1) =
= 3(х + 1)(jc — 1). С помощью метода интервалов устанав¬
ливаем распределение ее знаков (рис. 94). На промежутках
(—оо, —1] и [1, +оо) функция возрастает, а на отрезке
[—1, 1]—убывает. Производная f' имеет две точки смены
знака. В точке х= —1 производная меняет знак с « + » на
«—», а в точке л: = 1 —с «—» на « + ». Поэтому х\ =
= —1 —точка максимума, а лгг = 1 —точка минимума.
Полученную картину возрастания, убывания и экстрему¬
мов функции f можно символически представить так, как
показано на рис. 95. График функции изображен на рис. 96.
Рис. 96
76
Рис. 97
2. f(x) = *3.
Здесь производная f'{x) = 3x^0 для всех x и, значит,
f' не имеет точек смены знака. Эта функция возрастает на
всей числовой оси, экстремумов не имеет (рис. 97).
Упражнения
1. Исследуйте монотонность и нали¬
чие точек экстремума у функции
вида у — хп, где п — натуральное
число. Начните с конкретных зна¬
чений п= 1,2, 3,4. Сформулируйте
общий результат в зависимости
от п.
2. Сколько точек экстремума может
иметь квадратная функция? куби-
• ческая функция?
3.*Исслед>йте вопрос о числе точек
экстремума кубической функции у —
= х -\-px-\-q.
4. Найдите критические точки функ¬
ции у = х4—4хл+10. Все ли они
будут точками экстремума?
5. Точка движется по закону s=tA-f
-}-4/ll-f 4t2—7. В какие моменты вре¬
мени точка останавливается? Изме¬
няется ли при этом направление
движения?
Схема исследования функции с помощью производной
Дана функция y = f(x).
1. Уточняем область определения.
2. Находим корни, т. е. решаем уравнение f(x) = 0. Наносим
значения корней на числовую ось. Если можно, раскладываем
f(x) на множители.
3. Определяем знаки функции, т. е. решаем неравенство
f(x) > 0 методом интервалов.
4. Исследуем монотонность и находим экстремумы. Вычисля¬
ем производную, находим ее корни (критические точки), наносим
их на числовую ось, определяем знаки производной, определяем
характер поведения функции.
5. Вычисляем значения функции: в критических точках, при
х = 0у на концах области определения (если она представляет
собой отрезок или луч). Исследуем поведение функции вблизи
«особых точек», например там, где знаменатель обращается в
нуль.
6. Наносим «опорные точки» и строим график.
Примеры
1. Исследуем функцию f(x) = х3 — Зх.
Ее область определения — вся числовая ось Щ. Пред¬
ставляя функцию f в виде у = х(х2 — 3) = х(х — УЗ) (х + У§),
видим, что она обращается в 0 в трех точках: —УЗ, 0, УЗ;
ее знаки распределены, как показано на рис. 98. Картину
возрастания и убывания этой функции мы уже получили в
76
Рис. 98
примере 1 на с. 75. В точке л: = — 1 —максимум, в точке
х = I—минимум. Вычислим значения функции в точках
f(—1) = 2, f(l)=— 2. Теперь строим график (рис. 99).
Остается заметить, что область значений функции — вся
ось IR, и ни наибольшего, ни наименьшего значений у нее
поэтому нет.
Рис. 99
2. Исследовать функцию у = Г •
Эта функция определена на всей оси IR, кроме точки
х = 1, где знаменатель обращается в нуль. Поскольку
х2^0 для всех ху имеем х2-[-3^3, поэтому корней наша
функция не имеет и ее знак определяется знаком знаменате¬
ля х — 1 (рис. 100).
Рис. 100
Около точки х = 1 значения функции сколь угодно ведики по модулю,
и поэтому «кусок» графика (рис. 101) можно построить сразу же.
Рис. 101
77
Вычисляем производную:
2х(х - 1) - (х2 + 3)
У'
х2-2х — 3
(x-lf
(х- I)2
Рис. 103
Теперь можно указать участки монотонности и точки
максимума и минимума (рис. 103). Вычисляем значения
в точках экстремума:
у(-1)=4ггг=-2. у(3)=|if=6.
Теперь можно дополнить рис. 101 до полного графика
функции (рис. 104).
Очевидно, что ни наибольшего, ни наименьшего значе¬
ния функция не имеет, а ее область значений — объедине¬
ние двух лучей: (—оо. —2] и [6, +оо), т. е. —2
и (/>6
78
Рис. 104
Рис. 102
Решая квадратное уравнение х2 — 2х — 3=0, находим
его корни *1 = 3, х2= — 1. Поэтому производную можно
представить в виде у' = -- • Распределение ее
знаков показано на рис. 102.
При переходе через точку х = 1 производная знака не меняет!
Образец краткой записи исследования функции
Исследовать функцию у = х4 — 5х2 -}- 4 и построить ее график.
1. Область определения: IR.
2. Корни у. Решим уравнения: х4 — Ъх2 + 4 = 0, х2 = /, /2 — 5/-f 4 = О,
t\ = 1, /2 = 4, Х|,2 = ±1, *3.4 = d= 2.
Разложим функцию на сомножители:
У = ((— >)(< — 4) = (х2— 1)(л-2 — 4) = (х — 1)(дг + 1) (х — 2) (х + 2).
3. Знаки у показаны на рис. 105.
4. Корни у'. Найдем производную: ц' = 4х3 — 10х. Решим уравнение:
4хл — IOjc = 0ох(2х2 — 5) = = 0, х2,з = =tл/2,5 ~ ± 1,6.
5. Знаки у' показаны на рис. 106.
7. График у (рис. 107).
Изучение свойств функции и построение ее графика — одно из самых заме¬
чательных приложений производной. Этот способ исследования функции, откры¬
тый более трехсот лет назад, неоднократно подвергался тщательному анализу.
Основная причина, заставляющая вновь и вновь возвращаться к простому,
казалось бы, вопросу о связи свойств функции и ее производной, состоит в том,
-гг о в ходе развития математики явления описывались все более и более слож¬
ными функциями. Скажем, появились функции, не имеющие ни в одной точке
производной. Трудно представить себе движение, при котором ни в один момент
времени нельзя вычислить скорость. Однако изучение броуновского движения
мельчайших частиц привело к построению как раз такой математической модели.
Рис. 107
79
Рис. 105
Рис. 10Ь
Наши методы доказательства, основанные на простых механических и геометри¬
ческих соображениях, близки к тем, которые были созданы еще Ньютоном и
Лейбницем. Они уже непригодны в более сложных ситуациях и требуют уточ¬
нений.
Новые теоремы в математике доказывают путем логического рассуждения
(вывода) с использованием ранее доказанных теорем или некоторых исходных
простых утверждений (аксиом), принимаемых без доказательства. В наших рас¬
суждениях такие исходные утверждения механики были приняты без доказа¬
тельства'. В частности, мы приняли за очевидное то, что при прямолинейном
движении направление скорости совпадает с направлением перемещения.
Использование модели (интерпретации) для проведения математического
доказательства требует также умения переводить математические понятия на
язык этой модели (или знать правила перевода). Так, при использовании меха¬
нической модели мы рассматривали функцию у = f(x) как закон движения точки
по прямой (х—время, у—координата точки). При этом надо знать (или при¬
нять по определению), что производная функция /—это скорость движения
точки.
Преимущество проведенного доказательства состоит в том, что оно позволи¬
ло получить нам новое содержательное утверждение (о связи монотонности
функции и ее производной) исходя из более простых и более очевидных утвер¬
ждений механики. Недостатком его является то, что перевод теоремы на ялик
механической модели сделан описательно, без формулировки точных определений
и аксиом, исходя из индивидуальных представлений о механическом движении
и его характеристиках.
То же самое относится и к пояснению теоремы с помощью геометрической
модели о расположении касательной.
Однако в приложениях математики стремятся как раз к обратному. Для ис¬
следования какого-либо реального процесса или явления (например, механиче¬
ского движения) переводят основные понятия и свойства этого явления на язык
математики. Затем проводят математические рассуждения — выводят новые
формулы, связывающие введенные величины, доказывают их новые свойства
и т. п. Наконец возвращаются к исходному явлению и смотрят на то, что дакл
для его изучения полученные математические теоремы. Такой подход требует
развитой математической теории. Усилиями великих математиков XIX в. О. Коши
(1789—1857) и К. Вейерштрасса (1815—1897) была построена строгая теория
математического анализа, основанная на понятии предела. Ознакомиться с этой
теорией можно с помощью любого учебника по математике, предназначенного
для высших учебных заведений.
Дополнительные вопросы исследования функции
Симметрия графика
Графики функций, изображенные на рис. 108, а—г, имеют
различную симметрию. Попробуйте определить ее самостоятель¬
но. Симметрия графика проявляется в записи функции с по¬
мощью формул.
Функция у = f(х) называется четной, если верно тождество f(—х) = f(x).
График четной функции симметричен относительно оси у, так
как вместе с точкой (а; b), где b = f(a), он содержит и точ¬
ку ( — а; Ь), так как f( — a)= /(а), а точки (а; Ь) и ( — а; Ь) симмет¬
ричны друг другу относительно оси у (рис. 109). Заметим, что
область определения четной функции должна быть симметрична
относительно начала координат.
80
Рис. 108
Функция у = f(х) называется нечетной, если верно тождество f(—х) =
= -'(х).
График нечетной функции симметричен относительно начала
координат. Вместе с точкой (а; Ь)у где b = f{a), он содержит
точку (— а; —Ь), так как f( — b)= —а, а точки (а; Ь) и (— а; —Ь)
симметричны друг другу относительно начала координат.
Примеры
1. Четные функции:
у—\\ У = *2; г/ = лг4 + 5лг2 + 4; у = 2х + 2~х; у ---- ~ | .
Рис. 109
2. Нечетные функции:
У = х; у = х + -Ь
У = х* — Зх; у = 2х — 2~х.
Большинство функций не являются ни четными, ни нечетными.
Упражнения
1. Проверьте четность или нечетность
функций в примерах 1, 2.
2. Докажите, что сумма четных функ¬
ций есть четная функция, произве¬
дение четной и нечетной функций
есть нечетная функция. Сформули¬
руйте и докажите аналогичные
свойства для различных операций
над функциями.
3* Пусть y = j(x) — произвольная
функция с областью определения,
симметричной относительно начала.
Докажите, что функция y=g(x) =
—j(x)-\-((—x) является четной, а
функция y = h(x) = f(x) — /(—х) —
нечетной. Докажите, что любую
функцию f можно представить в
виде суммы четной и нечетной функ¬
ций.
Наибольшее и наименьшее значения функции
Как вы уже знаете, надо различать максимумы-минимумы от
наибольшего-наименьшего значений функции. Напомним еще раз
о принятой нами терминологии.
Точка экстремума — это точка, лежащая внутри области определения,
в которой функция принимает самое большое или самое малое значение
по сравнению со значениями в близких точках. Если функция дифферен¬
цируема, то в точке экстремума производная равна нулю. Найти экстре¬
мумы функции — значит найти точки экстремума (значения аргумента)
и значения функции в этих точках (экстремальные значения).
Наибольшее (наименьшее) значение функции — это самое большое
(малое) значение по сравнению со значениями во всей области опреде¬
ления функции. Функция может принимать свое наибольшее (наимень¬
шее) значение в одной точке, в нескольких разных точках, а может и
вообще не принимать такого значения.
Посмотрите на графики, изображенные на рис. 110, а—д.
В случае а наибольшее значение функции достигается на од¬
ном из «горбов» (в одной из точек локального максимума); в слу¬
чае б — наибольшее значение функции в крайней точке области
определения; в случаях в—д функция не имеет наибольшего
значения. Последние случаи несколько отличаются друг от друга.
В случаях виг функция не ограничена: среди ее значений есть
сколь угодно большие числа. Случай г показывает, что неограни¬
ченной может быть функция, заданная на конечном отрезке.
В случае д все значения функции лежат на конечном отрезке,
т. е. функция ограничена, но нет такой точки, значение в которой
превышало бы значение во всех других точках.
82
Рис. 110
Область значений функции
Если начерчен график функции, то область ее значений найти
легко — надо спроецировать точки графика на ось у (рис. 111).
Число а входит в область значений функции /, если найдется
такое число ху что f(x) = a. Следовательно, область значений
состоит из тех чисел а, для которых разрешимо уравнение f(x) =
= а. Это правило хорошо иллюстрируется графически: а при¬
надлежит области значений тогда и только тогда, когда прямая
у=а пересекает график. Графический способ — это основной
способ нахождения области значений, однако иногда рациональ¬
но исследовать разрешимость уравнения f(x) = a.
Примеры
1. у = 2х + 3.
Рис. 111
83
Так как линейное уравнение 2х + 3 = а разрешимо при
любом а, то областью значений является вся числовая
ось IR.
у = х2 + х.
Квадратное уравнение х2 + х = аох2 + х — а — 0 разре¬
шимо тогда и только тогда, когда его дискриминант D =
= 1 + 4а ^ Ооа ^ . Область значений: луч а ^ .
* + 2 *
Уравнение
*+ 1
х + 2
а равносильно линеиному уравнению
(а — 1 )лг = 1 — 2а. Оно разрешимо, когда коэффициент при х
отличен от нуля. Область значений: аф 1.
Упражнение
Найти области значений функции, ре¬
шая уравнение у = а:
а) у — Ъ—Ьх\
б) у — 2—х—х2’,
2х-\
в)
Особые точки функции
На рис. 112 изображены функции, имеющие различные особен¬
ности при х = 0. В случае а функция в точке О имеет конечный
скачок. Такую особенность имеет график зависимости напряже¬
ния при включении какого-либо прибора в электрическую сеть.
Ук
в)
84
Рис. 112
В случае б в нуле функция имеет излом — производной в
этой точке нет. Так ведет себя, например, график скорости тела,
которое покоилось при jc^O, а затем стало свободно падать.
В случае в в нуле бесконечный разрыв. Около э;гой точки
функция не ограничена. Реализовать физически такой процесс
трудно. В каком-то приближении такие графики возникают при
изучении явлений типа взрыва.
В случае г при приближении к нулю бесконечно растет про¬
изводная. Касательная в нуле совпадает с осью у.
Такие функции встречаются в механике. Попробуйте, напри¬
мер, нарисовать траекторию движения некоторой точки, нахо¬
дящейся на ободе велосипедного колеса.
§ 8. Приложения производной
Скорость
Понятие производной возникло как математическое описание
скорости движения. Поэтому важнейшим приложением произ¬
водной является вычисление скорости. Скорость произвольно
движущейся точки является векторной величиной, так как она
определяется с помощью вектора — перемещения точки за про¬
межуток времени, в течение которого это перемещение произо¬
шло. Рассмотрим простейший случай — движение точки по пря¬
мой. При прямолинейном движении точки ее перемещение,
скорость, ускорение и другие характеристики, которые, вообще
говоря, имеют векторный смысл, можно считать скалярными
величинами.
Пусть на прямой выбраны начало отсчета, масштаб и на¬
правление. Это позволяет задать положение точки на прямой
одним числом — координатой этой точки. Пусть положение дви¬
жущейся точки в момент времени t определяется функцией
X = x(t).
Перемещением точки за промежуток времени [Л, /2] будет
разность x(t2) — x(t 1). Средней скоростью на этом отрезке времени
- JC(/2) — *(/|) о /
будет число , а мгновенной скоростью (или просто
скоростью) — производная функции х, т. е. производная коорди¬
наты точки по времени: v(t) = x'(t) (рис. 113).
85
Рис. 113
Примеры
1. Пусть точка движется по прямой по линейному закону
x(t) = kt-\-b. Тогда скорость равна u(t) = x'(t) = ky т. е. ко¬
эффициенту при t. Это случай движения с постоянной
скоростью.
2. Пусть закон движения квадратичен: x(t) = At2 + Bt + С.
Тогда скорость равна v(t) = x'(t) = 2At + В и является ли¬
нейной функцией от времени. Мы увидим, что в этом случае
ускорение постоянно.
3. Пусть закон движения задается функцией x(t) = .
t с
Скорость такого движения v(t) = x'(t) = — —^- .
Задачи
1. Высота камня, брошенного вертикально вверх со скоростью
vo с начальной высоты Л0 от земли, изменяется по закону
х = ho + vot — где £«10м/с2 — ускорение свободного
падения.
а) Найдите зависимость скорости камня от времени.
б) При Л0=20 м, vo=S м/с найдите скорость камня
через 2 с. Зачем указано значение ho? Через какое время
камень упадет на землю?
в) На какой высоте скорость обратится в О?
г) Покажите, что энергия камня Е ='/2mv2 -f- mgx
(т — масса камня) не зависит от времени.
2. Тело удаляется от Земли по закону s = A(t + С)2/з. Найдите
закон, по которому изменяется его скорость.
Ускорение
Ускорение по своему смыслу есть скорость изменения скорости.
Если функция v = v(t) задает скорость движения точки по
прямой, то производная этой функции есть ускорение: a(t)=v'(t).
Если задана координата x = x(t) точки, то, чтобы найти
ускорение, надо сначала продифференцировать функцию х и полу¬
чить скорость у, а затем еще раз продифференцировать и полу¬
чить ускорение. Поэтому ускорение называют второй производ¬
ной пути (перемещения) по времени и обозначают так:
a(t) = x"(t).
Примеры
1. x(t) = kty v(t) = x'{t) = ky a(t) = x"(t) = 0.
Такое движение называется равномерным, ускорение в этом
случае равно нулю.
86
2. x(t) = At2 + Bt + C, v(t) = x'(t) = 2At + В, a(t) = x"(t) = 2A.
Ускорение движения, когда координата х зависит от
времени квадратично, постоянно и равно удвоенному
коэффициенту при t2. Из механики известно и обратное —
если ускорение постоянно, то перемещение зависит от /
по квадратичному закону. Если ускорение равно а, скорость
при / = 0 равна у0, а положение точки в начальный момент
есть хь, то путь задается формулой x{t)=x / 2at2vot-\-xo.
Это объясняет смысл коэффициента в квадратичном законе
движения.
3. X(t) = —j-rr, v(t) - x'(t) - — — ~ , a(t) - x"(t)
t + С ’ w (t + C)2 ’ w w (t + cf ’
Мы видим, что направление ускорения противоположно
направлению движения, а модуль ускорения убывает очень
быстро.
С помощью второго закона Ньютона, зная ускорение,
можно узнать, как изменяется со временем сила F = та.
Задачи
1. Докажите, что движение по кубическому закону s = at3 +
+ bt2 + ct + d происходит ;c ускорением, меняющимся
линейно.
2. Вычислите ускорение, с которым движется тело, удаляю¬
щееся от Земли по закону s = A(t + С)2/з (см. задачу 2 на
с. 86). Проверьте, что сила, которая при этом действует
на тело, меняется обратно пропорционально квадрату рас¬
стояния s.
Другие приложения производной
Так как производная есть скорость роста функции, то всюду,
где мы сталкиваемся с какой-либо переменной величиной, полез¬
но рассматривать и ее производную — скорость ее изменения.
Примеры
1. Работа. Если работа А есть функция времени А = A(t\ то
* дл
средняя скорость изменения работы есть средняя мощ¬
ность, а производная работы по времени есть мощность
(мгновенная).
2. Масса тонкого стержня. Пусть есть неоднородный тонкий
стержень. Если ввести координаты так, как показано на
рис. 114, то можно рассмотреть функцию m = m(l) — массу
куска стержня от точки О до точки /. «Средняя скорость»
изменения массы на отрезке [Л, /г] равна . Ее на-
12 — *1
зывают в физике средней линейной плотностью. Линейная
плотность есть производная функции т, т. е. производная
массы тонкого стержня по длине.
3. Заряд. Пусть q = q(t) — заряд, переносимый электрическим
током через поперечное сечение проводника за время t.
Средняя скорость переноса заряда есть (рис. 115) и
называется средней силой тока. Если ток постоянный, то
постоянная величина (и заряд q линейно зависит от
времени). В общем случае производная от заряда по вре¬
мени есть сила тока:
I(t)=q'(t)-
4. Снова работа. В первом примере мы рассматривали работу
как функцию времени и ее производной по времени была
мощность. В ряде физических задач работа вычисляется
как функция перемещения — пути, на котором она вычисля¬
ется. Так обстоит дело с вычислением работы в поле тяготе¬
ния, в электромагнитном поле. Приращение работы ДЛ
на маленьком участке перемещения Ах можно представить
как произведение силы F(x\ которая хотя и зависит от х,
но ее можно считать постоянной на маленьком отрезке,
на перемещение Ах: А А = FAx.
г АЛ
Следовательно, среднее значение силы есть а са¬
ма сила — производная работы по перемещению
(рис. 116).
Рис. 116
5. Теплота. Рассмотрим процесс нагревания какого-нибудь
вещества и вычислим количество теплоты Q(t)y которое не¬
обходимо для нагревания 1 кг этого вещества от 0°С до t.
Зависимость Q = Q(t) очень сложна и определяется экспери-
88
Рис. 114
Рис 115
ментально. Для многих веществ она получена с хорошей
степенью точности. Так, для воды Q(t) = 0,396/ + 2,081 X
X Ю-3/2 — 5,024-Ю-7/3 (1°С 5^ / ^ 95°С); для железа Q(t) =
= 440,86/ + 297,2• 10-3/2 (0°С < / < 200°С).
Что представляет собой скорость изменения теплоты?
Если мы вычислим количество теплоты, расходуемое на
нагревание от температуры / до / + А/, и разделим AQ на
А/, то получим среднюю теплоемкость вещества Сср =
= Ы В диапазоне изменения температуры [/, / + А/].
Уменьшая А/, мы найдем в пределе настоящую теплоем¬
кость c(t) как производную Q по /. Итак, теплоемкость —
это производная количества теплоты по температуре: c(t) =
= Q (t) (рис. 117).
Рис. 117
Давление. Мы привыкли под этим термином понимать
отношение сил к площади поверхности, на которую эта сила
действует. Для точности надо говорить о нормальной
составляющей силы и тогда давление представляется как
р = 4тг- (рис. 118), где AFn — скаляр, представляющий
До
собой силу, действующую на площадь AS. Однако сила
давления зависит не только от площади AS, но и от ее
местоположения — мы слышим по радио, что давление
воздуха сегодня в Москве 760 мм рт. ст., а в Ленинграде —
Рис. 118
всего 735 мм рт. ст. Давление можно понимать как произ¬
водную силы по площади.
7. Движение ракеты.' Возможность использования реактивного
движения для полета в космос исследовал К. Э. Циолков¬
ский, который вывел формулу скорости одноступенчатой
ракеты в зависимости от ее массы и скорости истечения
продуктов сгорания. Эта формула основана на нахождении
скорости изменения массы ракеты, т. е. производной массы
по времени (рис. 119).
8. Площадь круга. Как быстро изменяется площадь круга при
изменении радиуса? Зная производную, на этот вопрос
ответить легко:
S = л/?2, S' = 2nR.
Выражение 2nR нам известно — это длина окружности
радиуса R. Что означает полученный нами результат на
геометрическом языке? Рассмотрим приращение площади
AS круга. Это площадь кольца между двумя концентриче¬
скими окружностями радиусов R и R-\-AR. Отношение
этой площади к AR близко к длине окружности. Поэтому
производной площади круга по радиусу будет длина окруж¬
ности (рис. 120).
9. Производительность труда. Важнейшей экономической
характеристикой производства является рост производи-
Рис. 119
Рис. 120
Рис. 121
тельности труда. Темпы роста производительности труда —
это производная производительности труда по времени.
10 Успехи в учебе. Обсуждая успехи своего ученика, учитель
математики так отозвался о нем: он очень мало знает, но у
него положительная производная. Все поняли, что хотел
сказать учитель: скорость приращения знаний у ученика
положительная, а это есть залог того, что его знания воз¬
растут. Подумайте, как вы могли бы охарактеризовать три
разные кривые роста знаний, изображенные на рис. 121.
$9. Дифференциал
Определение дифференциала
Дифференциал функции — это линейная часть ее приращения.
Возьмем произвольную функцию y — f{x)> построим ее график
и зафиксируем на нем какую-либо точку (хо; */о). Рассмотрим
приращение аргумента Ах и соответствующее ему приращение
функции А у. Зависимость приращения функции А у от прираще¬
ния аргумента Ах может оказаться достаточно сложной. Если
график вблизи точки (хо, уо)—отрезок прямой, то эта зависи¬
мость линейная: Ay—kAx (рис. 122). В общем случае график не
является отрезком прямой, но на маленьком участке он очень
близок к прямой — касательной в точке (лг0; уо)• Если рассмотреть
линейную функцию от Ах, заданную формулой feAx, где k — f\xо),
то ее значения будут близки к А у. Эту функцию (от Ах) называ¬
ют дифференциалом функции f (в точке хо) и обозначают dу.
Итак, можно сказать, что, по определению, дифференциал функ¬
ции f в точке хо равен f\xо)Ах.
91
Рис. 122
Дифференциал есть функция от Ах, а не от х. То, что независимая пере¬
менная обозначена двойной буквой Ах, конечно, вносит неудобства, и во
избежание путаницы можно было бы обозначить Ах одной буквой, напри¬
мер h, и тогда дифференциал записался бы так: z — kh, 'где k = f'(x0).
Однако мы сохраним обозначение Ах, особенно распространенное в при¬
ложениях.
Рассмотрим функцию у = х. Так как производная этой функ¬
ции постоянна и равна единице, то дифференциал этой функции
равен Ах, т. е. для независимой переменной верно равенство
djc = Ajc. Поэтому дифференциал произвольной функции записы¬
вают обычно в виде
di/ = f'(x)dx.
Заметим, что значение производной f'(xо) можно получить,
составляя отношение дифференциалов: f'(x0) = -^-.
С этим связано классическое обозначение производной функ¬
ции у как (читается «дэ-игрек по дэ-икс»).
Дифференциал функции — это главная часть ее приращения.
Сравним приращение функции Ау и ее дифференциал Ау
(рис. 123). На рисунке видно, что чем меньше Ах, тем ближе
Ау к Ау. Действительно, разность Ау — Ау преобразуем так:
Ау-Ау = Ау- f'(xо)Ах = Ах(^~ /'(*,)).
По определению производной, при стремлении Ах к нулю раз¬
ность — f'(xо) тоже стремится к нулю. При умножении на
Ах мы получим выражение, еще быстрее приближающееся к
нулю. Таким образом, приращение функции отличается от ее
«Предупреждаю, чтобы остерегались отбрасывать dx — ошибка, которую
часто допускают и которая препятствует продвижению вперед.»
Г. В. Лейбниц
92
Рис. 123
дифференциала на такую функцию, которая стремится к нулю
еще быстрее, чем Ах. Поэтому и говорят, что дифференциал есть
главная часть приращения функции.
Дифференциал в физике
Первоначально понятие дифференциала появилось в работах
Лейбница, а лишь затем была введена производная как коэффи¬
циент пропорциональности в соотношении
d у == kdx.
В физических приложениях последнее равенство появляется
следующим образом. Рассматривается приращение величины у как
функция от приращения величины х. При упрощающих предпо¬
ложениях эту зависимость можно считать прямой пропорцио¬
нальностью (линейной). Так получают дифференциал, который
еще иначе называют «элементом величины у».
Примеры
1. Работа. Рассмотрим работу А как функцию перемещения
при заданной силе F(x). Предположим, что на малом отрез¬
ке сила F постоянная. Вычисляем элемент работы:
cL4 = Fd)с, или = F, или А'(х) = F.
2. Масса тонкого стержня. На маленьком отрезке считаем ли¬
нейную плотность постоянной. Тогда dm = pd/ (рис. 124).
Ряс. 124
3. Заряд. На малом отрезке времени силу тока можно считать
постоянной, поэтому dq = Idt.
4. Выделение теплоты при нагревании. На малом интервале
изменения температуры теплоемкость можно считать по¬
стоянной. Тогда dQ = cdt.
5. Линейное расширение тела при нагревании: относительное
удлинение тела при нагревании пропорционально измене-
A J.
нию температуры: -у- = adt.
Важнейшие соотношения между физическими величинами
обычно удается записать в виде некоторого соотношения между
их дифференциалами. Эти соотношения служат для вычисления
производной, например плотности как производной массы по
длине, силы тока — как производной заряда по времени и т. д.
93
Чаще возникает обратная задача: дана плотность, дана сила
тока, дана сила, т. е. дана производная, а надо найти исходную
величину — массу, заряд, работу.
Операция, обратная дифференцированию, называется инте¬
грированием (см. § 42).
Упражнения
I. Вычислите дифференциал данной
функции y = f(x) в заданной точкС
х = хо:
а) у — х2, лго=1;
б) у = — \ *о = 2;
х
в) у = х3—2х2, Х(,= — 1.
2. Вычислите дифференциал данной
функции в произвольной точке х:
а) у=х2-М-Н;
б) у=х-\-\
г) У
у= /х+Г;
х
Х+\
3. Запишите физические примеры, рас¬
смотренные на с. 89, 90, в виде со¬
отношений между дифференциаль¬
ными величинами.
Приближенные формулы
Приближенные формулы получаются при замене приращения функции
ее дифференциалом.
Эту замену мы будем обозначать знаком « (приближенно
равно):
А у « d у.
Так как А у = /(х о + Ajc) — f(x о), ad у = f'(xo)Axy то
f(xо + Ах) — f(xо) « f'(xо)Ах, т. е.
f(xо + Ах) « f(xо) + f'(xо)Ах.
Геометрически замена А у на dу означает, что вблизи точки хо
мы заменили функцию некоторой линейной функцией, т. е. ма¬
ленький отрезок графика заменили касательной (рис. 125).
Рис. 125
Примеры
1. Рассмотрим степенную функцию у = хп. Зафиксируем точ¬
ку Хо. Тогда
(х0 + Ах)" » хо + яхо-1Ах.
Например, (1.0003)5 = (1 + 0.0003)5 = 1 + 5-0,0003 =
= 1,0015; (2,0001)7 = (2 + 0.0001)7 = 27 + 7-26.0,0001 =
— 128 + 0,0448 = 128,0448 = 128,05 ± 0;01.
При хо = 1 эта формула имеет вид
(1 + Ах)п ж 1 + пАх.
2 Рассмотрим функцию у =
Получаем приближенную формулу:
_J ~ J La,
а ^ n—lAX.
Хо + &Х Хо Хо
При хо = 1 найдем формулу, удобную для вычислений:
3. Вычислить приближенно значение функции у = х в
точке х = 3,02.
Находим дифференциал функции у:
= (тгтУdx = - (7ТГГ
cl JC
Выбираем начальную точку хо = 3. Тогда Ау = 2 =
т1)
= -^-dx\ х = 3,02 = хо + 0,02; Ах = 0,02;
1о
\у ж Ay = « 0,001; /(х) да f(xо) + dу w 0,751.
На практике вычисляемая величина обычно зависит от не¬
скольких аргументов, значения которых известны приближен¬
но. В этом случае общий дифференциал (главная часть прира¬
щения) складывается из частных дифференциалов, получающих¬
ся при изменении одной переменной.
Пример
JC2
Вычислить приближенно значение функции z = , если
х = 2,04; у = 1,03.
Выберем начальные значения: хо = 2, уо = Г, zо =
= = 4. Тогда
Уо
Az « dz= dz(x) + dz(y) = — dx — ^ Ay.
У У
дг да -2*2-0,04 - 4-0,03 - 0,16 - 0,12 - 0,04,
Уо Уо
Az ж 4,04.
Упражнения
i- Даны функция y = f(x) и точка х.
Вычистите приближенно значение
у в точке х:
2. Вычислите приближенно:
а) (1,002)6; г) у^984 ;
б) (0.997)3; д) 1/1,021;
а) у — 2х5, х= 1,003;
б) у = Л-4 + л:2+1. * = 2,04;
в) у = х2-{-~, х = 1,97;
г) у = 5 /лГ, х = 4,02.
3. Вычислить приближенно:
а) (2,003)5; б) /15,92; в)
г) (3.996)3; д) V49.012.
Погрешности
На практике часто приходится вычислять значения функций в
точках, которые известны лишь с некоторой точностью. Так,
измеряя диаметр заготовки штангенциркулем, можно найти его
значение в такой форме: D = (10 ±1)мм.
Нам нужно вычислить площадь круга диаметром D по фор-
jiD*
муле S = —— Возникает вопрос: с какой точностью получит¬
ся результат, если в эту формулу подставить D=10? Можно
считать, что мы вычисляем функцию S в точке Do + AD, где
Do = 10, а | AD | ^ 1. Отклонение S(Do + AD) от S(D0), т. е.
AS, мы заменяем дифференциалом: dS = n-2D0AD = 5nAD.
Так как |AD|^1, то |dSK5n»16, т. е. погрешность вычис¬
лений площади порядка 16 (мм2). Итак, взяв за Ах погрешность
вычисления аргумента, мы найдем погрешность вычисления
функции y = f(x) по формуле |Ау| ж |/'(х0)| Ах.
Наиболее употребительные формулы:
У = У\+У2\ |A(/|<|A(/il + |Af/2|;
У = У1 — У2\ А у = Ai/i — Af/2, но \Ау\ < I Af/i | + \Ау2\;
у = уху2\ \Ау\ ж \ух\ \Ау2\ + \у2\ IAt/i|
У _ _У}_ . ~ \У2\ IA*/il ~Ь \уЛ lAj/zl
Пусть у\ = 10± 1, у2= 15±2. Тогда \А(у\ =h(/2)<3; |A(f/if/2)l«
ж35; \А(У]/У2)\ъОЛ<э.
Заменяя А*/ на &у, мы вносим некоторую погрешность. Нельзя
ли ее уменьшить? Иными словами, если нас не устраивает точ¬
ность вычислений, получаемая при замене А у на Ау, как увели¬
чить эту точность?
Надо вычислить УГО. Возьмем за начальное приближение
число 3 = -д/9. Сделаем простые преобразования:
Ау ж п\х0\пп ‘Ах;
Пример
Vlo = V9^M = Зд/1 + 'Л-
96
Первое приближение корня по известной нам формуле дает
лДО * з(1 + 3 + 1-» 3,15.
Как получить лучшее приближение? Нужно вычислить V 1 + /г
(для удобства мы пишем h вместо х. В нашем примере h = 1/9).
Увеличения точности можно достичь, прибавляя последовательно
к начальному значению 1 члены, пропорциональные /г, /г2, /г3
и т. д., т. е. представляя У 1 + h в виде У 1 + h = 1 + k\h +
k2h2k3h3k4h4... Как из этого равенства найти коэф¬
фициенты k\y k2, k3,... ? Для этого есть замечательный способ,
открытый вслед за созданием в XVII в. дифференциального ис¬
числения. Продифференцируем обе части (по переменной /г):
— = ft, + 2kih + 3k3h2 + 4 k4h3 + ...
2^/T+h
Положим в этом равенстве h = 0. Тогда fe1 = 1/2. Точно так же
можно найти и коэффициенты fe2, k3y.... Продифференцируем
еще раз:
-L(J ! V = _L\ » =
2 V 2 VI+ Л / 2 V 2 /(1 + Л)VI + h
= 2k2 + 6k3h + 12kAh2 + ... .
Положим h— 0. Тогда — 1 /4 = 2Л2, откуда fe2= — !/8. Мы полу¬
чили гораздо более точную формулу:
VTTA« 1 +-Lh--Lh2.
Возвратимся к вычислению УТО:
/то-з[1+±.1-;.^]«3.,7.
и мы уже имеем точность порядка 0,01. Замечательно, что точ¬
ность можно повышать этим приемом столько раз, сколько мы
захотим. Еще раз продифференцируем:
~2"(“ 2~) ((1 +л)VT + Л ) _
_ _L ( -3/2УПм~ _ Ц_1_\ (_ АЛ 1 =
2 \ 2 ) (1-h/i)3 2\ 2 / \ 2 / (l+fcfVT+I
= 6fe3 -h 24&4/z + ... •
Полагая h = 0, имеем k3 = !/16, и новая добавка равна
0,0625/г3. При /г = 1 /9 это слагаемое имеет уже порядок 0,001.
Формулы, получаемые этим методом, названы именем Б. Тей¬
лора (1685—1731) — английского математика, ученика Ньютона.
Приведем несколько формул Тейлора:
vm =, + i_„ _ _ _|_А. + ^ f
4—1681
97
! = 1 —h + — h2 — h3 + --3-5 h4 —
^JT+Th 2 8 16 ^ 128
К ним можно добавить полезную простую формулу:
=1 — X + х2 — X3 + X* — ... .
§ 10. Задачи на максимум и минимум
Наибольшее и наименьшее значения функции
Наиболее важной для приложений ситуацией является следую¬
щая: функция f задана на конечном отрезке [а, Ь] и имеет про¬
изводную во всех точках этого отрезка. Тогда для нахождения
наибольшего и наименьшего значений этой функции надо посту¬
пить так: найти критические точки (т. е. корни производной),
вычислить значения функции во всех критических точках и на
концах отрезка; из найденных значений найти наибольшее и
наименьшее.
В первый раз вопрос о наибольшем и наименьшем значении
функции мы обсуждали в § 4 гл. 1. Там мы заметили, что функ¬
ция обычно принимает наибольшее и наименьшее значения либо
в одном из «горбов» функции, т. е. в одной из точек экстремума,
либо на краю области определения. Эти главные случаи можно
представить себе, глядя на рис. 126.
Функция, график которой изображен на этом рисунке, при¬
нимает наименьшее значение в точке с (это одна из точек ло¬
кального минимума), а наибольшее значение — в точке b — на
краю области определения.
98
Рис. 126
На самом деле возможны и другие случаи, которые можно
представить себе по рис. 127, а — в. Предлагаем вам самостоя¬
тельно подумать над тем, что происходит с наибольшими
и наименьшими значениями функций изображенных на гра¬
фиках.
Примеры
1. Найти наибольшее и наименьшее значения функции у =
= \ — 2х — х2, заданной на [ — 2, 2].
Находим производную: у' = — 2 — 2х; у' = 0 о х = — 1.
Вычисляем значения у в точках —2; —1; 2:
Получаем: унаиб = 2, унаим = — 7. При этом наибольшее
значение функция принимает в точке локального максиму¬
ма, а наименьшее — на правом конце отрезка (рис. 128).
2. Найти наибольшее и наименьшее значения функции
у = sin2 jc + 4 sin jc + 2.
В этом примере полезно сделать замену sin jc = z и рас¬
смотреть функцию у = z2 + 4г + 2. Ее область опреде¬
ления— отрезок [—1, 1], совпадающий с множеством зна¬
чений функции z = sin jc. Находим производную у как
функцию от z: f/' = 2z + 4. у' = 0о z= — 2. Заметим,
что критическая точка не принадлежит отрезку [—1, 1],
4*
99
Рис. 127
Рис. 128
поэтому надо сравнить значения у только на концах от¬
резка:
X
+ 1
1
У
-1
7
Итак, (/наиб — 7, t/иаим 1*
Упражнения
1. Найдите наибольшее и наимень¬
шее значения функции y = f(x) на
указанном отрезке:
а) у = хъ—6*2+1 (— 1<х^2);
б) {/ = 7+4*3—х4 (-1<х<3);
. 2х2—9х—2 /Л ^ гх
в> р—5дс—6 (0<^5);
Г) У=^ +Y
2. Найдите наименьший член последо¬
вательности {а„}:
а) ап=п2—7/г+1;
« б) ап=п4—5/г3—3/г2.
3. Докажите, что если 1*1^2, то
|x3-3*]<2.
Прикладные задачи
Многие прикладные задачи сводятся к нахождению наибольших
и наименьших значений функций, заданных на конечном отрезке.
Такие задачи часто называют задачами на максимум-минимум.
100
Задачи
1. Из прямоугольного листа жести размером 5X8 надо изго¬
товить открытую коробку наибольшего объема, вырезая
квадратные уголки так, как показано на рис. 129, а — в.
Рис. 129
Обозначим через х длину стороны вырезаемого квад¬
рата. Длины сторон уменьшатся на 2х и объем коробки бу¬
дет равен
V = х(8 — 2х\Ъ — 2х) = 4х3 — 26л:2 + 40*.
При этом х может меняться в следующих пределах:
0 ^ х ^ 2,5; заметим сразу, что в крайних точках объем
равен нулю. Находим критические точки:
V' = \2х2 - 52* + 40, V' = 0 о х = 1, х = '%•
Заметим, что значение х = ,0/3 не принадлежит области
определения. При х = 1 объем максимален: Vmax = 18
(рис. 130).
2. В данный шар вписать цилиндр наибольшего объема.
Обозначим R радиус шара, а г и А — соответственно
радиус основания и высоту вписанного цилиндра. Как видно
из рис. 131, выполняется соотношение Л2/4 + г2 = R2.
Будем считать h переменным. Тогда
V = nr2h = п(R2 - = nR2h -
101
Рис. 130
Рис. 131
Заметим, что h меняется в пределах от 0 до 2/?, причем
на концах цилиндр вырождается и объем его равен нулю.
Находим критические точки:
V' = л/?2 - |-лЛ2; V = О^Л2 = 4-^-^Л = Щг.
4 з уз
При этом значении h объем будет максимальным:
1/ _ пЗ 2 2 4л D3
•'max — П.К — К •
3 д/3 Зл/З
1. Если переменной считать не Л, а г, то /i = 2^jR2 — г2 и К =
= 2лг2 V/?2 — г2. Находить производную К как функцию от г в этом
случае труднее. Но очевидно, что функции К и К2 принимают наиболь¬
шее значение одновременно. Тогда рассматривается новая функция
W = К2 = 4л V(/?2 — г) и без труда находятся ее критические
точки.
2. Функции К, > 0), V + С принимают наибольшее значение одно¬
временно. Это значение позволяет при вычислении производных убирать
постоянные множители и слагаемые.
3*. Над центром круглого стола радиуса г висит лампа
(рис. 132). На какой высоте следует подвесить эту лампу,
чтобы на краях стола получить наибольшую освещен¬
ность?
Известно, что освещенность обратно пропорциональна
квадрату расстояния до источника света и пропорциональна
синусу угла наклона освещаемой маленькой площадки к
лучу света. Иными словами,
р и sin ф
^“л2 + г2 ’
где Е — освещенность на краю стола; sin ф = Л/УЛ2 + г2;
h — расстояние от лампы до стола.
н
Вместо функции Е = k рассмотрим функцию
102
Рис. 132
Т = Дг£'2 = —. При этом вместо h можно взять пере-
k2 (h + г2)3 к к
менную z = h2 и найти критические точки Т как функции
от z:
Т = z j, = (z + г2)3 —z-3(z + r2)2
(2 +Г2)3 ’ (2 +Г2)6
г == 0^(z + r2)2(z + г2 - 3г) = 0o2z = r2oz = г2/2,
т. е. А2 = г2/2 и Л = гД/2.
Итак, освещенность максимальна при h = r/^J2, т. е.
если
Л , 1
Задачи
1. Какую наименьшую площадь полной поверхности может
иметь цилиндр, если его объем равен V (рис. 133)?
2. Параболическим сегментом называется фигура, ограничен¬
ная параболой и прямой, перпендикулярной ее оси. Расстоя¬
ние от вершины параболы до этой прямой называется высо¬
той сегмента, а длина отрезка прямой, отсекаемого парабо¬
лой, — основанием сегмента. Какую наибольшую площадь
может иметь прямоугольник, вписанный в параболиче¬
ский сегмент с основанием а и высотой Я? (Одна из
сторон прямоугольника параллельна оси параболы;
рис. 134.)
3. Из пункта Л, находящегося в лесу в 5 км от прямолинейной
дороги, пешеходу нужно попасть в пункт В, расположен¬
ный на этой дороге в 13 км от пункта А (рис. 135). По доро¬
ге пешеход может двигаться с максимальной скоростью
103
Рис. 133
Рис. 134
5 км/ч, а по лесу — с максималь¬
ной скоростью 3 км/ч. За какое ми¬
нимальное время пешеход сможет
добраться из пункта А в пункт В?
4. Тело представляет собой прямой круговой цилиндр, завер¬
шенный сверху полушаром (рис. 136). Какую наименьшую
площадь полной поверхности может иметь это тело, если его
объем равен V?
Задачи и вопросы
Каково механическое истолкование производной?
Каков геометрический смысл производной?
Что такое средняя скорость роста функции?
Чем отличается мгновенная скорость от средней скорости?
Для функции f(x) = Зх 2 найдите А у, если:
а) л: = 1 и Ал: = 0,1; в) х = 1 и Ах = 0,02;
б) х = 6 и Ах = 0,1; г) х = 6 и Ах = 0,02.
Для функции f(x) = x2 — x найдите Ауу если:
а) х = 1,5 и xi = 2,5; в) х = 4 и хх = 3.
б) х = 1,5 и х\ = 3,5;
Найдите /fe+A*)~/М , если:
Ах
а) f(x) = ах + Ь\ в) /(х) = х3.
б) f(x) = ах2 + Ьх + с;
2.8. Точка движется прямолинейно по закону f(t) = 3t—l.
Найдите:
а) среднюю скорость на отрезках [2; 2,2]; [2; 2,02];
[3; 4]; [3; 3,3);
б) мгновенную скорость при t = 2\ t = 3.
104
2.1.
2.2.
2.3.
2.4.
2.5.
2.6.
Й.7.
Рис. 135
Рис. 136
2.9. Точка движется прямолинейно по закону f(t) = t2. Найдите:
а) среднюю скорость на отрезках [1; 2]; [1; 1,2];
[1; 1,02]; [2; 2,02];
б) мгновенную скорость при / = 1; t = 2.
2.10. Точка движется прямолинейно по закону s(/) = 2/2-f1.
Найдите среднюю скорость движения на отрезках [1; 2],
[1; 3/2], [1; 1,1], [1; 1,01]. Чему равна мгновенная ско¬
рость в момент времени t = \ с?
2.11. Найдите среднюю скорость роста функции f(x)=x2—x на
отрезках [0; 1], [0; 72], [0; 0,1], [0; 0,01]. Чему равна
производная этой функции в точке х = 0?
2.12. Зависимость пути от времени s(t) задана графиком
(рис. 137). Найдите среднюю скорость движения тела для
отрезков времени: [0; 4], [2; 4], [3; 4], [3,5; 4]. Чему
равна мгновенная скорость в момент времени / = 4 с?
Рис. 137
2.13. По заданному графику функции (рис. 138, а—в) постройте
график производной.
2.14* Рис. 139 изображает алгоритм построения графика ско¬
рости по графику пути. Разберите этот алгоритм по рисунку
Рис. 138
105
Рис. 139
и примените его для построения графиков производной для
функций, изображенных на рис. 140, а—в. Попробуйте дать
обоснование алгоритма.
2.15. На рис. 141 изображена зависимость перемещения тела
от времени в случае упругого удара. Постройте график за¬
висимости скорости от времени.
2.16. По заданному графику производной (рис. 142, а—в) вос¬
становите примерный график функции.
106
Рис. 140
Рис. 141
Рис. 142
Рис. 143
2.17. На каждом из рисунков (рис. 143, а—в) изображены гра¬
фики двух функций на одном и том же отрезке. У какой
из этих функций средняя скорость роста на этом отрезке
больше?
2.18. На каждом из рисунков (рис. 144, а—е) изображен график
функции. Выясните, что больше: средняя скорость роста
этой функции на отрезке [а; Ь] или на отрезке [Ь; с] ?
2.19. Для функции у = -у- найдите А у и если:
в) х = 5,06; А* = —0,03;
г) х = 6; Дх = —0,02.
а) х = 9; Ajc = 0,06;
б) х = 4,02; А* = 0,02;
2.20. Используя схему вычисления производной, найдите произ¬
водные функций:
2 г Уу = -$г\
1 д) У =
а> У = -х
б) у = —
в) у = X3;
2х2
е) У =
1
X
X + 1
Найдите значения этих производных при х=\ и при х = 2.
Рис. 144
107
2.21. Вычислите производные:
а) у = Зх4; з) у = (х2 — 1)(х2 + 1);
б) y = JT’ и) у = ■?')Х
3 X (З*2 -\- х — 8);
в) у = —;
г) у = — V3x; к) {/ = (х+~Г + ~?')х
^ 1 X (*2 + х + 1);
д) У = ^г; _ *2
е) у = 5х4 - 7х2 - х; л) У ~ Т+Т'
ж) у = х5 + 2х3- м) у = 2
2л: ’ 7 * 2л:2- 1 '
2.22 Вычислите значения производных в данных точках:
а) f(x) = х3 — jc + 2, вычислите Г(2);
б) /О) == ^ 2 . вычислите /'(0);
в* } + зх ’ найдите /'(*). Г(0);
2^ з
г) f(x)= {_3х , найдите /'(а) для а = 1 и а = 0.
Что больше: f'(l) или /'(0)?
2.23. В какой точке функция у = Зх2 растет быстрее: а) в точке
х = 1 или в точке jc = 0; б) в точке х=\ или в точке х = 2;
в) в точке х=1 или в точке jc =1 /2?
2.24 Функции х\ л[х\ х2; хъ расположите в порядке скорости их
роста в области х> 1.
2.25. Вычислите производные:
а) у = (х + I)2 — Зх; е) у = ^[х + 2 — V* — 2;
б) у = (2х+ 1)3 + 5(Зх-2)2; ж) у = (1-х2)5;
ч 1 \ 2
в) У = 3) У = 77-гтт-—‘
(Зх+ I)3 ’ ' * (*+ 1)2 + 1 ’
г) у — д/бх — 1 ; и) у = (х—1)4(х+I)3.
д) у =
2.26* Выведите формулу (/2(jc))' = 2/(jc)-/'(jc) и вычислите с ее по¬
мощью производные:
а) У = (V* + I)2; в) «/ = (* + ^ л/^)2;
б) У = (-*3 + X2 — 2х+ I)2; г) г/ = (угу) ’
108
2.27, Найдите промежутки монотонности для функций:
а) У = *2; к) у =
б) у = 2х2 — х;
в) у = 6 — х — х2; л) У = ;
2
г) у = х3 + х; х2-х +
д) у = х3 — 2х2 + Зх + \ ; м ^ У х2 + X + 1 ’
е) у = Зх-х3; „ = _! !_•
ж) у = х4 — 2х3 + х2 — 2; (*+l)2 -г2 ’
з) I/ = Зх5 — 5*3 — ЗОх; о) у=х — -у]х;
и)У = х+±; П)у = ^=1.
2.28. Исследуйте на экстремумы следующие функции:
а) у = 3 — х2; и) у = х4 — х2;
б) у = х2 -\- 4х; к) у = х4 2х2 + 1;
в) у = \ — х — х2, л) у = х4 — х3;
г) у — 2х2 — х + 5; м) у = (х + I)3 — 27(х + 1);
д.) у = 12х — х3; ч ,1
[ з^2 н) У = х-\ ;
е) у = х3 — 6х2; *
ж) у = ^+х2-4х + 5; о) у =
з) у= 2х3 — 9л:2 — 60* + 1; п) у = х^[х — д/х.
2.29. Найдите точки остановки тела, движущегося по следую¬
щему закону:
а) s(0 = 1- ~<г+2 (t > 0); Д) s(/) = + -р-
б) s(/) = 2/ — 1 + y-J-p (0 < t < 2);
('>0)li »> »(')= ,> + ;, + , (<>0);
") s(() = 7-Г7- (< > I); ж) s(/) — 2i‘ — 61 — I;
. 3) s(t) = 2/* - I5i! +
r) s(0 t2 _|_ 4 . +36/ — 13.
2.30. Проведите исследование функции и постройте ее график:
а) у = х2 — х; ж) у = Зх-х3;
б) у = х2 + 2х; з) у = 2х3 + Зх2 — 2;
в) у = \ — х2; и) у = 2х3 — 9х2 + 12х- 3;
г) у = 2х2 + х + 1; к) у = + -у- — х;
Д) У — 2 — х — х2; Л) у = (* — 1 )3 — 3(дс — I);
е) у = х3- Зх2+1; м) у = Зх4 - 4х3 - 12х2-г 10;
Н) У =
4х3 •
о) г/ = jc+ —;
п) У = *~Т'
Р) У = -Г^г;
") У = тЬ^;
т) у = х — 2л/х.
2.31. Найдите число корней уравнения:
а) х3 — Зх2 + 6* — 1 = 0; в) 12х4 — 12дс3 -+- Зх2 —
б) 5х3 — 5х — 3 = 0; —5 = 0.
2.32. Исследуйте функции на максимум-минимум. Разберите от¬
дельно случаи а> 0 и а< 0:
а) у — ах2;
б) у = х + а/х\
в) у = х4 + ах2 + 6;
г) У = х3 + ах + 1.
2.33. По графикам функций (рис. 145, а—з) постройте графики
их производных.
2.34. Разбейте графики функций (рис. 146, а—м) на пары «функ¬
ция — ее производная».
Рис. 145
110
Рис. 146
2*3с Выберите из следующего списка формулу, задающую каж¬
дую из функций, изображенных на рис. 146:
а) у = х3+ 1;
б) у = 4х — х2;
в) у = 2jT;
г) у = Зх2;
д) у = л[х\
е)
Ж) y = x + -t-;
з) у = х + 5;
и) У = -у- + 5х + -2-;
к) у = — 2х + 4;
л) г/ = — 2* — 4;
м) у = —2.
2-36?Докажите, что если функция четна, то ее производная
нечетна, и, наоборот, если функция нечетна, то ее производ¬
ная четна.
2-37. Какие степени переменной х могут входить в многочлен
f(x)y если известно, что функция y = f(x) четна? нечетна?
2.38. Точка движется по закону x(t) = 2-\-20t — 5/2. Найдите
мгновенную скорость в момент / = 0, /= 1, t = 2. Постройте
график зависимости мгновенной скорости от времени.
2.39. Рассмотрите движение точки по оси ху заданное законом
x(t)= \0/t. Найдите мгновенную скорость в момент t— \ с,
/ = 2с, / = 3 с. Обратите внимание на знак скорости.
2.40. х0ЧКа движется прямолинейно по закону x(t) = /3 + 3/2.
Найдите скорость и ускорение точки в момент времени /= 1 с.
2.41. Точка движется прямолинейно по закону x(t) = -^ft. Дока¬
жите, что движение замедленное и что ускорение а пропор¬
ционально кубу скорости и.
2.42. Тело массой 5 кг движется прямолинейно по закону x(t) =
= t2 — 3/ + 2, где t выражается в секундах. Найдите кине¬
тическую энергию тела через 10 с после начала движения.
111
2.43 В какой момент времени тело, движущееся прямолинейно
по закону x(t) = t + \/t (t > 0), будет иметь минимальную
кинетическую энергию?
2.44. При равномерном движении тела по окружности угловой
скоростью называется величина, равная отношению угла
поворота к интервалу времени, в течение которого произо¬
шел поворот. Дайте определение угловой скорости для
неравномерного движения.
2.45. Если бы процесс радиоактивного распада протекал равно¬
мерно, то под скоростью распада следовало бы понимать
массу вещества, распавшегося в 1 с. На самом деле про¬
цесс неравномерен. Дайте определение скорости радиоак¬
тивного распада.
2.46. Величина, численно равная количеству электричества, про¬
ходящего через поперечное сечение проводника в 1 с, назы¬
вается силой тока. Дайте определение силы тока в общем
случае.
2.47. Количество электричества, протекающее через проводник
начиная с момента t = 0, задается формулой q(t) = 3t2-\-
+ / + 2. Найдите силу тока в момент времени / = 3.
2.48. В какие моменты времени сила тока в цепи равна нулю,
если количество электричества, протекающее через провод¬
ник, задается формулой
a) q(t) = t+l/t, б) q(t) = t-^l +1 (/>0)?
2.49. Длина стержня меняется в зависимости от температуры
по закону / =/0( 1 + 0,00It + 0,000It2). Найдите коэффициент
линейного расширения при / = 5°С.
2.50. Вычислите дифференциалы функций:
а) у = х2 + 5х; в) E(r) = kr2 ■
б) s(R) = л/?2; г) W(t) = 3/3 - 2Ц2.
2.51. Найдите указанные значения, пользуясь приближенными
формулами:
ч 1 ч 2
Д/ 1 ПП1 » Ж/ 1 ПЛОЗ
а) 2,012; в) 9,998*; ' ’ 7
б) 5,043; г) V0,999; , 1 ■ з) 5
0,9972 ’ -у/9,004 '
2.52. Приближенное значение л[2 можно вычислить по формуле
Vi +х ~ 1 -\-х/2 двумя способами: а) 2 = 4(1 — 1/2) >
б) 2=1 + 1. Какое из двух приближений более точное?
2.53, Докажите неравенства:
а) 1 + ~2 g-< |/1 + х < 1 + — (х > 0);
б) 1 — X < 1 — х + X2.
112
2.54. Найдите наибольшее и наименьшее значения функции на
указанном отрезке:
а) у = 2хъ + Зх2, [—1; 1]; д) у = 1хъ + 9х2 — Зх + 6,
2.55?Объем правильной четырехугольной призмы 8 см3. Какую
длину должны иметь сторона основания и высота призмы,
чтобы площадь ее поверхности была наименьшей?
2.56. В основании пирамиды прямоугольный треугольник с гипо¬
тенузой 2 см. Высота пирамиды 6 см. Найдите наибольший
объем пирамиды.
2.57. Найдите наибольший объем правильной треугольной приз¬
мы, у которой периметр боковой грани равен 6 см.
2.58. В прямоугольном параллелепипеде ABCDA'B'C'D' рас¬
стояние АС равно 2-^2 см, А'А=1 см. Найдите площадь
боковой поверхности параллелепипеда, имеющего наиболь¬
ший объем при данных условиях.
2.59. Найдите число, которое, сложенное со своим квадратом,
дает наименьшую сумму.
2.60. Найдите положительное число, которое, сложенное с обрат¬
ным ему числом, дает наименьшую сумму.
2.61. Найдите положительное число так, чтобы разность между
ним и его кубом была наибольшей.
2.62. Требуется изготовить ящик (без крышки) с прямоуголь¬
ным основанием и заданным объемом V> отношение сторон
основания которого равно k. Каковы должны быть размеры
ящика, чтобы его поверхность была наименьшей? Вычис¬
лить размеры ящика при: a) k=\t V = 32; б) k = 2,
V = 36.
2.63. Бак цилиндрической формы должен вмещать V литров
воды. Каковы должны быть его размеры, чтобы поверхность
(без крышки) была наименьшей?
2.64? Периметр равнобедренного треугольника равен 2р. Какой
длины должны быть его стороны, чтобы объем тела, обра¬
зованного вращением этого треугольника вокруг его осно¬
вания, был наибольшим?
б) у = 5* - !~*3, [0; 2]; [-1;!];
е) у — 2хг — 15х2 + 36* —
- 13, [-'Л; 3].
3
ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ
И ПЛОСКОСТЕЙ
§11. Взаимное расположение прямых и плоскостей
Прямые в пространстве
Точка, прямая, плоскость — с этими словами у нас связаны
определенные представления. Мы говорим: «прямой, как натяну¬
тая струна», «пересечь улицу по прямой», «луч света движется
по прямой». Линии пересечения стен и потолков, траектории
свободно падающих тел служат наглядными примерами прямых
линий.
Со словом «плоскость» у нас ассоциируется поверхность сто¬
ла, стены, пола. Плоской в нашем представлении является по¬
верхность озера в безветренный день или гладь хорошо залитого
катка.
Дотронемся мелом до доски. Останется след — точка. По¬
смотрим на ночное небо — звезда нам кажется светящейся точ¬
кой. Взглянем на угол комнаты — это тоже точка.
Не будем пока задумываться над тем, что же такое точка,
прямая, плоскость. Наша ближайшая цель — уточнить привыч¬
ные представления о взаимном расположении точек, прямых и
плоскостей.
Две прямые, которые не лежат в одной плоскости, называются скрещи¬
вающимися.
Две прямые называются параллельными, если они лежат в одной плос¬
кости и не имеют общих точек (не пересекаются).
Две прямые, имеющие ровно одну общую точку, называются пересе¬
кающимися (рис. 147).
Для пары прямых в пространстве имеются две возможности:
либо через них можно провести плоскость, либо нельзя. Если
плоскость провести нельзя, то прямые — скрещивающиеся. Рас¬
смотрим первую возможность.
114
Рис. 147
Пусть прямые лежат в одной плоскости. Тогда они либо
имеют общую точку (пересекаются), либо нет (параллельны).
Обратим внимание на логику рассуждений, которые мы при¬
меняли при разборе вариантов расположения двух прямых в
пространстве. Сначала мы разбили пары прямых на типы по та¬
кому признаку: прямые лежат или не лежат в одной плоскости.
Ясно, что это два взаимно исключающие друг друга случая,
исчерпывающие все мыслимые возможности. Затем мы рассмот¬
рели пары прямых, лежащих в одной плоскости, и прибегли к
дополнительному признаку: прямые не имеют общих точек или
прямые имеют одну общую точку.
Сколько общих точек могут иметь две прямые? Из планимет¬
рии нам известно, что через две (различные) точки можно про¬
вести только одну прямую, поэтому две (различные) прямые не
могут иметь более одной общей точки. Это доказывает, что две
различные прямые могут быть либо скрещивающимися, либо
параллельными, либо пересекающимися.
Проведите самостоятельно классификацию расположения
пары прямых в пространстве, начиная с признака: прямые имеют
общие точки или прямые не имеют общих точек.
Примеры
1. На рис. 148 изображен разрез обычной комнаты. Плоскости
стен, пола и потолка пересекаются по прямым. Три из этих
прямых выделены и обозначены а, b и с. Прямые а и b пере-
Рис. 148
115
секаются, прямые а и с парал¬
лельны, прямые b и с скрещива¬
ются. Укажите на этом рисунке
другие пары параллельных, пе¬
ресекающихся и скрещиваю¬
щихся прямых.
2. На рис. 149 изображен токар¬
ный резец. Его кромки — отрез¬
ки прямых линий. Разберите
самостоятельно расположение
этих прямых.
3. Выберем четыре произвольные точки Л, В, С и Д не лежа¬
щие в одной плоскости (рис. 150). Проведем прямые АВ
и CD. Они скрещиваются, так как, если бы они лежали в
одной плоскости, то и все данные точки лежали бы в одной
плоскости, что противоречит условию. Точки Л, В, С и D
определяют три пары скрещивающихся прямых AB \\ CD,
АС и SD, AD и ВС. На этих прямых лежат ребра треуголь¬
ной пирамиды ABCD.
Рис. 150
Рис. 151
Упражнения
1* На рис. 151 изображена треуголь¬
ная призма. Перечислите все пря¬
мые, которые пересекаются, парал¬
лельны и скрещиваются с выделен¬
ным ребром основания.
2- Сколько всего пар прямых можно
образовать с помощью ребер тре¬
угольной призмы? Сколько из них
пересекающихся? параллельных?
скрещивающихся?
3. Приведите пример трех прямых,
каждые две из которых скрещива¬
ются. Сколько можно построить
прямых, каждые две из которых
будут скрещиваться?
Каких пар прямых больше — параллельных, пересекающихся
или скрещивающихся? Вопрос поставлен неточно — разумеется,
есть бесконечно много пар и параллельных, и пересекающихся,
и скрещивающихся прямых. Однако он все же имеет смысл.
Две наугад взятые прямые скорее всего не будут лежать в одной
плоскости, а значит, будут скрещиваться. Пересечение или па¬
раллельность двух прямых в пространстве — это в каком-то
смысле специальный, частный случай их расположения, а скре¬
щивание — общий. Про скрещивающиеся прямые говорят иног¬
да, что они находятся в общем положении.
116
Рис. 149
Признак скрещивающихся прямых
Теорема
Пусть даны две прямые а и Ь. Если можно найти такую плоскость а, ко¬
торая содержит прямую а и пересекает прямую Ь в точке, не лежащей
на прямой а, то прямые а и b скрещиваются (рис. 152).
Рис. 152
Доказательство. Будем доказывать теорему от про¬
тивного. Прямые скрещиваются — это означает, что они не ле¬
жат в одной плоскости. Противоположное утверждение означает,
что прямые а и Ь лежат в одной плоскости. Эта плоскость долж¬
на совпадать с плоскостью а. Действительно, в ней лежат пря¬
мая а и вся прямая Ьу а значит, та точка А прямой Ь, о которой
говорилось в условии теоремы. Однако ясно, что прямая а и не
лежащая на ней точка А однозначно определяют плоскость.
Значит, вся прямая Ь должна лежать в плоскости а, что про¬
тиворечит условию. Следовательно, исходное предположение о
том, что прямые а и Ь лежат в одной плоскости, неверно. Теорема
доказана.
С помощью условных знаков теорему 1 можно записать так:
Объекты Взаимное расположение
прямые а, b а £ а
плоскость а А £ bt A = b (] а
точка А А <1 а
Доказать: а — Ь.
«Легче найти доказательство, приобретя сначала некоторое понятие о
том, что мы ищем, чем искать такое доказательство без всякого предва¬
рительного знания.»
Архимед
Архимед (ок. 287—212 г.г. до н. э.) — греческий физик и математик.
Ему принадлежит метод нахождения длин и площадей, предвосхитивший
интегральное исчисление. Закон Архимеда — один из фундаментальных
законов механики.
«Внимательно читая сочинения Архимеда, перестаешь удивляться всем
новейшим открытиям геометров», сказал о нем Лейбниц.
117
* Признак скрещивающихся прямых является первой доказанной нами тео¬
ремой стереометрии. Откуда получается первая теорема, на что опирается
ее доказательство, какие аргументы мы привели в защиту доказываемого
утверждения? Во-первых, нам помогает логика. Мы понимаем, что две
прямые либо лежат в одной плоскости, либо нет. Если мы привели к проти¬
воречию предположение о том, что они лежат в одной плоскости, значит,
они не лежат в одной плоскости, т. е. скрещиваются (по определению
скрещивающихся прямых). Однако одной логики нам было мало. В дока¬
зательстве использованы некоторые дополнительные свойства прямых и
плоскостей, которые мы никак не аргументировали, так как они хорошо
соответствуют нашим представлениям о расположении прямых и плоско¬
стей в пространстве. В рассуждении использовано, что прямая и не ле¬
жащая на ней точка однозначно задают плоскость.
Ясно, что нельзя доказать все на свете — какие-то свойства
рассматриваемых объектов должны быть приняты без доказа¬
тельств, в качестве исходных, первичных утверждений — ак¬
сиом.
Сформулируем более полно свойство пространства, использо¬
ванное в теореме 1.
Свойство 1
Через прямую и не лежащую на ней точку можно провести плоскость
и притом только одну.
Пример
Представим себе, что на стене проведена прямая (рис. 153),
а мы стреляем в стену (считаем, что пуля полетит по пря¬
мой). При попадании в прямую траектория пули будет пере¬
секать ее, а при промахе — скрещиваться с ней (примене-
Рис. 153
ние признака требует, чтобы пуля при промахе все-таки
попала в стену). Ясно, что промахнуться неизмеримо легче,
чем попасть в тонкую линию. Это еще раз подчеркивает,
насколько скрещивающихся прямых больше, чем пересе¬
кающихся.
118
Упражнения
1- На рис. 154 изображен куб. Дока¬
жите, что прямая АВ скрещивается
с прямыми A'D', В'С', A'D, В'С,
DC', D'C.
утверждать, что все три прямые
лежат в одной плоскости?
4- Даны три точки А, В и С, не ле¬
жащие на одной прямой. Где ле¬
жат все точки D такие, что прямые
АВ и CD скрещиваются?
Рис. 154
2. Выполните упражнения 1 и 3 на
с. 116, используя признак скрещи¬
вающихся прямых.
3. Нарисуйте три прямые, первые две
из которых пересекаются, а третья
скрещивается:
а) с каждой из двух первых;
б) только с первой из них;
в) ни с одной из них.
В случае б) можно ли утверждать,
что третья прямая пересекается со
второй? В случае в) можно ли
5* Прямая а скрещивается с прямой b,
прямая b скрещивается с прямой с.
Что можно сказать о взаимном рас¬
положении прямых а и с?
6* Прямые а и b параллельны. Пря¬
мая а скрещивается с прямой с. Что
можно сказать о взаимном распо¬
ложении прямых а и с?
7- Прямые а и b пересекаются. Пря¬
мая а скрещивается с прямой с. Что
можно сказать о взаимном распо¬
ложении прямых b н с?
Прямая и плоскость
Прямая и плоскость называются пересекающимися, если у них только
одна общая точка.
Прямая и плоскость называются параллельными, если они не имеют
общих точек (рис. 155).
Начнем классификацию пар, состоящих из плоскости и пря¬
мой, лежащей вне этой плоскости, со следующего признака: пря¬
мая и плоскость имеют общие точки или прямая и плоскость не
имеют общих точек. Во втором случае прямую и плоскость мы
назвали параллельными. Вернемся к первому случаю. Сколько
может быть общих точек у прямой и плоскости? Наши наглядные
представления подсказывают, что если у прямой и плоскости
более одной общей точки, то вся прямая целиком лежит в данной
плоскости (если ровную линейку в двух точках приложить к
хорошо отшлифованной плоской поверхности, то линейка цели¬
ком ляжет на эту поверхность). Таким образом, наша классифи¬
кация взаимных расположений прямой и плоскости опирается на
119
Рис. 155
Рис. 156
следующее свойство пространства, которое мы примем без дока¬
зательства, считая его аксиомой.
Свойство 2
Если две различные точки прямой лежат в некоторой плоскости, то вся
прямая лежит в этой плоскости (рис. 156).
Плоскости в пространстве
Две плоскости называются параллельными, если они не имеют общих
точек (рис. 157, а).
Две плоскости называются пересекающимися, если множество их об¬
щих точек есть прямая (рис. 157, б).
Снова рассмотрим возможные варианты. Две плоскости либо
не имеют общих точек (параллельны), либо имеют общие точки.
Наглядно ясно, что если две различные плоскости имеют общие
точки, то общие точки заполняют целую прямую. Поступим с
этим свойством так же, как и в предыдущих пунктах, — сформу¬
лируем его без доказательства, считая это свойство аксиомой.
Свойство 3
Если две различные плоскости имеют хотя бы одну общую точку, то
они пересекаются по прямой, т. е. множество их общих точек есть пря¬
мая (рис. 158).
Рис. 157
120
На рис. 159 изображена комната. Плоскость пола обозначена
через а. Из выделенных трех прямых прямая а лежит в плоско¬
сти а, прямая Ь пересекается с плоскостью а, прямая с парал¬
лельна плоскости а. Как расположены по отношению к плоско¬
сти а другие прямые, изображенные на рис. 159?
Возьмем наугад плоскость и прямую в пространстве. Какое их
взаимное расположение будет более вероятным? Скорее всего
прямая и плоскость будут пересекаться. Про пересекающиеся
плоскости и прямую говорят, что они находятся в общем поло¬
жении. Другие случаи взаимного расположения плоскости и пря¬
мой в пространстве являются более частными, специальными.
Плоскости пола и потолка на рис. 159 параллельны друг дру¬
гу. Плоскости стен пересекают плоскость пола. Как расположены
между собой плоскости стен?
Упражнения
1. Нарисуйте две пересекающиеся пря¬
мые, лежащие в одной плоскости, и
прямую, не лежащую в этой пл'ос-
кости, но пересекающую обе прямые.
2. Нарисуйте прямую, лежащую в пло¬
скости, и две прямые, не лежащие
в этой плоскости, но пересекающие
эту прямую.
3. На рис. 160 изображена треуголь¬
ная призма с выделенной плоско¬
стью боковой грани. Укажите ребра
призмы, лежащие в этой грани,
параллельные ей и пересекающие
эту грань.
4. Даны две параллельные плоскости
и прямая, лежащая в одной из них.
Докажите, что эта прямая парал¬
лельна другой плоскости.
5. Две параллельные плоскости пере¬
сечены третьей плоскостью. Дока¬
жите, что линии пересечения па¬
раллельны.
6. Сколько пар параллельных и пере¬
секающихся плоскостей вы видите
на рис. 159?
7. Могут ли две плоскости иметь
ровно одну? ровно две общие точки?
одну общую прямую? две общие
прямые?
8. Перечислите и покажите схематиче¬
скими рисунками взаимное распо¬
ложение трех плоскостей.
121
Рис. 158
Рис. 159
Рис. 160
§ 12. Признаки параллельности
Признак параллельности прямой и плоскости
Теорема 2
Если прямая, не лежащая в плоскости, параллельна прямой на плоско¬
сти, то исходная прямая параллельна плоскости.
Более подробно эта теорема может быть сформулирована
следующим образом.
Пусть прямая а не лежит в плоскости а. Если в плоско¬
сти а есть прямая, параллельная прямой а, то прямая а парал¬
лельна плоскости а (рис. 161).
Остановимся на логической структуре доказательства теоре¬
мы 2. В условии теоремы указано расположение прямых а и b от¬
носительно плоскости а (а^а, Ь 6 а). Сама теорема представляет
собой условное утверждение: если а\\Ь, то а ||а. При доказатель¬
стве строится отрицание заключения: пусть неверно, что а ||а.
С учетом условия а это означает, что прямая а и плоскость а
пересекаются. Это утверждение приводится к противоречию
с условием а || Ь. Такой тип доказательства называют «доказатель¬
ством от противного».
Запишем кратко условие теоремы.
Объекты Взаимное расположение
прямая а а £ а
плоскость а b 6 а
прямая b а || 6
Доказать: а || а
Доказательство. Каковы логически возможные случаи
расположения прямой а и плоскости а ? Мы знаем, что либо а
лежит в плоскости а, либо а пересекает плоскость а, либо а па¬
раллельна а. Первая возможность отвергнута условием. Доста¬
точно отвергнуть вторую возможность.
122
Рис. 161
Проведем через параллельные прямые а и Ь плоскость. Обо¬
значим ее р. Если прямая а пересекает плоскость а в некоторой
точке С, то эта точка — общая для плоскостей р и а. Но все об¬
щие точки различных плоскостей аир лежат на прямой Ь. Сле¬
довательно, точка С лежит на прямой bf но это противоречит
параллельности прямых а и Ь. Теорема доказана.
Упражнения
1. На рис. 162 изображен куб. Укажи¬
те все его ребра, лежащие на пря¬
мых, параллельных основанию.
2. Докажите, что диагональ верхнего
основания куба параллельна пло¬
скости нижнего основания (рис. 162).
3. Даны правильный шестиугольник и
плоскость, параллельная одной из
4 На рис. 163 изображена призма,
в основании которой — правиль¬
ный шестиугольник. Какие ребра
призмы параллельны выделенной
боковой грани? Какие грани парал¬
лельны выделенному боковому реб¬
ру ВВ'? стороне основания ВС?
его сторон. Как эта плоскость
может быть расположена по отно¬
шению к другим сторонам шести¬
угольника?
5. Дана произвольная пирамида. До¬
кажите, что прямые, соединяющие
середины двух боковых ребер, па¬
раллельны основанию.
Признак параллельности двух прямых
Теорема 3
Если плоскость проходит через прямую, параллельную другой плоско¬
сти, и пересекает эту плоскость, то линия пересечения параллельна
исходной прямой.
Введем обозначения и более подробно сформулируем теорему.
Нам даны некоторая прямая а и параллельная ей плоскость р.
Другая плоскость а проходит через прямую а и пересекает плос¬
кость р по некоторой прямой Ь. Теорема утверждает, что пря¬
мые а и Ь параллельны.
Запишем кратко условие теоремы.
Объекты
прямые а, b
плоскости а, р
Доказать: а \\Ь
Взаимное расположение
аба
а||0
*> = аПР
123
Рис. 162
Рис. 163
Доказательство. По условию, прямые а и Ь (рис. 164)
лежат в одной плоскости а. Следовательно, они либо параллель¬
ны, либо пересекаются (вспомним классификацию пар прямых).
Если бы они пересекались, то их общая точка С лежала бы одно¬
временно на прямой айв плоскости р (так как прямая b лежит
в плоскости Р). Это противоречит тому, что прямая а параллель¬
на плоскости р. Теорема доказана.
Задача
Даны две скрещивающиеся прямые. Провести через одну из них
плоскость, параллельную другой (рис. 165).
Обозначим данные скрещивающиеся прямые через а и Ь.
Возьмем на прямой а произвольную точку А и проведем плос¬
кость а через прямую Ь и точку А.
Проведем в плоскости а через точку А прямую с, параллель¬
ную прямой Ь. Через эти две пересекающиеся прямые awe
проведем плоскость р. Эта плоскость будет параллельна пря¬
мой Ь. Почему? Как вы думаете, сколько есть плоскостей, про¬
ходящих через прямую а и параллельных прямой b?
Упражнения
1. В кубе проведено сечение через
нижнюю сторону основания, пере¬
секающее верхнее основание. Какая
фигура получится в сечении?
2. В основании четырехугольной пи¬
рамиды лежит параллелограмм
ABCD. Через сторону основания АВ
проводится плоскость. Какая фигура
может получиться в сечении?
3. Даны две параллельные прямые а
и b, не лежащие в плоскости а.
Докажите, что если а || а, то и Ь\\а.
Признак параллельности двух плоскостей
Теорема 4
Если каждая из двух пересекающихся прямых одной плоскости парал¬
лельна другой плоскости, то эти плоскости параллельны (рис. 166).
124
Рис. 164
Рис. 165
Запишем кратко условие теоремы.
Объекты Взаимное расположение
плоскости а, р а £ а, b 6 а
прямые а, b а X Ь, а || р, b || р
Доказать: а || р
Доказательство. Будем рассуждать от противного.
Пусть плоскости а и р не параллельны. Тогда они пересекаются
по некоторой прямой, обозначим ее с. Все три прямые а, b и с
лежат в плоскости а.
Так как прямые а и Ь параллельны плоскости р, то, по тео¬
реме 2, прямая с, как линия пересечения плоскостей аир, парал¬
лельна прямым а и Ь.
Итак, через точку пересечения прямых а и b в плоскости а
проходят две прямые (а и 6), параллельные прямой с. Это про¬
тиворечит аксиоме о параллельных из планиметрии. Полученное
противоречие доказывает теорему.
При решении задач часто используют другую формулировку
теоремы 4:
Если две пересекающиеся прямые одной плоскости соответственно па¬
раллельны двум прямым другой плоскости, то эти плоскости параллель¬
ны (рис. 167).
Иными словами, если в двух плоскостях можно найти по углу
с соответственно параллельными сторонами, то эти плоскости па¬
раллельны. Выведите самостоятельно сформулированное утверж¬
дение из теоремы 4, используя признак параллельности прямой
и плоскости.
Упражнения
1. В треугольной пирамиде SABC
точки К, L, М — середины боковых
сторон SA, SB и SC. Докажите,
что плоскость треугольника KLM
параллельна плоскости основания
пирамиды.
2. Докажите, что в кубе ABCDA'В'С'D'
плоскости АВ'С и A'C'D парал¬
лельны.
3. Линии пересечения плоскостей ои и
125
Рис. 166
Рис. 167
d2 с плоскостью а параллельны
между собой. Параллельны ли плос¬
кости СИ И 02?
4. При установке нивелира на гори¬
зонтальность инструмент проверяют
обычно только по двум непарал¬
лельным направлениям. Достаточна
ли такая проверка?
Параллельность трех прямых
Теорема 5—
Если две прямые параллельны третьей, то они параллельны между
собой (рис. 168).
Запишем кратко условие теоремы.
Объекты Взаимное расположение
прямые: а, Ь, с а || с и b \\а
Доказать: с\\ b
Доказательство. Если все прямые а, b и с лежат в
одной плоскости, то получается известная в планиметрии тео¬
рема.
Рис. 168
Пусть прямые а, b и с не лежат в одной плоскости. Нам
нужно доказать, что прямые с и b параллельны, т. е. лежат в од¬
ной плоскости и не имеют общих точек.
Как доказать, что с и b лежат в одной плоскости? Здесь
никакое применение доказанных ранее теорем не поможет, так
«Нет царского пути в геометрию.»
Евклид — Птоломею I
Евклид — греческий математик III века до н. э., автор знаменитых
«Начал», которые до сих пор являются основой всех учебников гео¬
метрии.
126
как ни одна из них не содержит вывода, что прямые по каким-то
причинам лежат в одной плоскости. Однако плоскость можно
провести через прямую и не лежащую на ней точку (свойство 1).
Поэтому поступим так. Возьмем на прямой Ь произвольную точ¬
ку и проведем плоскость через нее и прямую с. Остается доказать,
что пересечение плоскости р с плоскостью а, проведенной через
прямые Ь и а, есть прямая Ь.
Прямая а не лежит в плоскости р и параллельна прямой с,
лежащей в плоскости р. Согласно теореме 3, прямая а парал¬
лельна плоскости р. Из этой же теоремы следует, что линия
пересечения Ь' плоскостей аир параллельна прямой а. По¬
скольку же 6, Ь\ а лежат в одной плоскости и прямая 6, имею¬
щая с b' общую точку, тоже параллельна а, получаем б = Ь'.
Теорема доказана.
Задача
Даны две скрещивающиеся прямые. Провести через каждую из
них по плоскости так, чтобы эти плоскости получились парал¬
лельными (рис. 169).
Рис. 169
Мы уже умеем проводить через одну из скрещивающихся
прямых плоскость, параллельную другой (см. задачу на с. 124).
Пусть даны две скрещивающиеся прямые а и Ь. Проведем через
прямую а плоскость а, параллельную Ьу а через b — плоскость (3,
параллельную а.
Докажем, что плоскости аир параллельны. Если бы они
пересекались, то линия их пересечения — прямая с — была бы
параллельна каждой из прямых а и b (дайте обоснование). По
теореме 5, прямые а и b должны были бы быть параллельными,
но известно, что они скрещиваются. Задача решена.
Упражнение дины сторон AS, DS, AD, SBy АВ
соответственно. Докажите:
SABCD — пирамида с квадратным ос- а) КМ\\ВС\ б) PRWMN.
нованием, /С, М, N, Р, R — сере-
127
Построение сечений многогранников
Признаки параллельности применяются для построения сечений
кубов, призм, пирамид и других многогранников. Для задания
секущей плоскости можно использовать следующие элементы:
1) три точки, не лежащие на одной прямой;
2) прямая и не лежащая на ней точка;
3) пара пересекающихся прямых;
4) пара параллельных прямых.
Каждый из этих случаев определяет ровно одну плоскость.
Плоскость сечения пересекает грани многогранника по отрез¬
кам прямых. Обычно для изображения сечения достаточно
построить все эти отрезки. Иногда полезно построить пересече¬
ние с диагональными плоскостями (в призме) или другими выде¬
ленными плоскостями.
Задача
Построить сечение куба плоскостью, проходящей через середины
двух смежных сторон основания и через центр куба.
Дано: куб ABCDA'B'C'D', К — середина АВУ L — середина
ADy О — центр куба. Указанные три точки однозначно опреде¬
ляют плоскость сечения.
Соединим точки К и L отрезком. Проведем диагональное се¬
чение B'D'DB (рис. 170). Центр куба О является центром пря¬
моугольника B'D'DB. Плоскость сечения проходит через KL и
пересекает плоскость диагонального сечения. KL параллельна
с
плоскости диагонального сечения, так как KL || BD (как средняя
линия треугольника ABD) — признак параллельности прямой и
плоскости. Линия пересечения должна быть параллельна пря¬
мой KL (признак параллельности двух, прямых) и, следователь¬
но, параллельна BD (по теореме о параллельности трех прямых).
Проводим через точку О прямую MN || BD. Мы получим точки
сечения, расположенные на ребрах ВВ' и DD'.
Рассмотрим второе диагональное сечение АА'С'С (рис. 171).
Оно пересекает отрезок KL в точке Р (его середина) и проходит
Рис. 170
128
Рис. 171
через центр О. Плоскость сечения пересекает эту диагональную
плоскость по прямой РО. Пусть Q — точка пересечения этой пря¬
мой с верхним основанием (с отрезком А'С'). Рассмотрим, как
пересекает искомая плоскость сечения плоскость верхнего осно¬
вания. Так как прямая KL || BD, BD || B'D', то KL параллельна
плоскости этого основания и линия пересечения будет тоже па¬
раллельна всем этим прямым. Проводя через точку Q прямую
/?S||B'D', получим недостающие точки сечения (рис. 172).
В сечении получился шестиугольник. Вторую половину по¬
строения можно было сократить, заметив, что сечение должно
быть симметрично относительно центра. Равны ли между собой
стороны построенного шестиугольника? Будет ли этот шести¬
угольник правильным?
Плоскость сечения может быть задана условиями параллель¬
ности некоторым прямым или плоскостям.
1. Даны прямая и плоскость. Ставится задача провести
плоскость через данную прямую параллельно данной плоскости.
Эта задача разрешима только в том случае, когда данная прямая
и плоскость параллельны. В этом случае решение единственно.
2. Даны плоскость и точка вне ее. Всегда можно провести
плоскость через данную точку параллельно данной плоскости.
Решение единственно.
3. Даны две скрещивающиеся прямые. Провести плоскость
через одну из них параллельно другой. Эту задачу мы рассматри¬
вали на с. 1°4.
4. Даны две прямые и точка. Требуется построить плоскость,
проходящую через заданную точку, параллельную обеим пря¬
мым. Исследуйте самостоятельно разрешимость этой задачи.
Задача
В четырехугольной пирамиде SABCD провести сечение через
точки Р и Q, лежащие на боковых ребрах SA и SC, параллель¬
но диагонали основания BD.
Проведем диагональные сечения SAC и SBD. Они пересе¬
каются по прямой SO, где О — точка пересечения диагоналей
основания'(рис. 173).
5—1681
129
Рис. 172
Рис. 173
Соединим точки Р и Q. Отрезок PQ пересекает SO в неко¬
торой точке R. Плоскость сечения, по условию, должна быть
параллельна прямой BD. Поэтому она пересекает плоскость SBD
по прямой, параллельной BD (признак параллельности двух пря¬
мых). Проведем через точку R в плоскости SBD прямую, парал¬
лельную BD. Получим недостающие точки М и N сечения. За¬
дача решена.
Упражнения
1. Постройте сечения куба
ABCDA'B'C'D':
а') через сторону АВ и произволь¬
ную точку Р грани CDD'C'\
б) через три произвольные точки на
ребрах АА\ ВВ\ DD'.
2. Дана четырехугольная пирамида
SABCD, в основании которой —
квадрат ABCD. Постройте сечение
пирамиды:
а) через сторону АВ и точку Р на
противолежащей боковой грани;
б) через середины сторон АВ и AD
и точку Р на боковом ребре SC.
3. В кубе ABCDA' В'С' D' через две
точки Р и Q, расположенные на
ребрах А А' и СС\ пр9вести сече¬
ние параллельно диагонали BD.
4. Через точку, расположенную на
ребре треугольной пирамиды, про¬
вести сечение параллельно одной
из граней.
5. В тетраэдре ABCD точка М лежит
на ребре ADy а точки К и L — на
ребрах А С и ВС так, что:
а) KL не параллельна АВ;
б) KL \\АВ
Постройте для каждого из случаев
сечение тетраэдра-плоскостью KLM.
6. Постройте сечение куба
ABCDA'B'C'D' плоскостью, прохо¬
дящей через середины ребер:
а) AD и вершины А', С';
б) д'С' и вершины А, А';
в) АА', СС' и вершину В';
г) АА\ А'В', В'С'.
§13. Аксиоматическое построение геометрии
Основные понятия
Основные понятия стереометрии: точка, прямая, плоскость.
Рассмотрим какую-нибудь геометрическую фигуру, например
квадрат. Попробуем ответить на вопрос, что же такое квадрат.
Квадрат — это прямоугольник, у которого все стороны равны.
Прямоугольник — это четырехугольник, у которого все углы пря¬
мые. Четырехугольник — это фигура, которая состоит из четырех
точек и четырех отрезков, последовательно соединяющих эти
точки.
А что такое фигура, что такое отрезок, что такое точка?
Отрезок АВ — это часть прямой, состоящая из точек, лежа¬
щих между точками Л и В, а фигура составлена из точек. Итак,
мы пришли к простейшим понятиям—точка, прямая, которые
считаются основными геометрическими понятиями и принима¬
ются без определения. Любая теория обычно начинается с пере¬
числения основных понятий, поясняемых примерами, наглядными
образами; точных определений этим понятиям не дают, так как
130
в определениях снова участвовали бы какие-то понятия, требую¬
щие объяснений. При этом стараются по возможности умень¬
шить число понятий, вводимых без определения. Выбор этих
основных (неопределяемых) понятий в значительной степени
произволен. По традиции, идущей от Евклида, в стереометрии
таковыми являются точка, прямая и плоскость. Кроме того, мы
пользуемся понятием множества, которому тоже не даем опре¬
деления.
Аксиомы
Простейшие связи между основными понятиями описываются утвержде¬
ниями, которые принимаются без доказательства. Они называются
аксиомами.
Вы уже знакомы с аксиомами планиметрии. Выбор аксиом
для любого раздела науки — трудное и ответственное дело.
Прежде всего надо, чтобы аксиомы отражали действительно про¬
стейшие, основные связи между понятиями, которые не вызывают
сомнений и которые можно положить в фундамент строящейся
теории. Аксиом не должно быть очень много — теория всегда
выглядит более привлекательной, если она получает новые инте¬
ресные выводы из малого числа исходных предпосылок (аксиом).
В то же время число аксиом должно быть достаточным для того,
чтобы выводить из них новые содержательные утверждения.
Наконец, аксиомы не должны приводить к противоречивым
утверждениям. В середине XIX в. русский ученый Н. И. Лобачев¬
ский и венгерский ученый Я. Больяи, анализируя аксиомы гео¬
метрии, предложенные еще Евклидом в III в. до н. э., пришли к
заключению, что одна из них — знаменитая аксиома о парал¬
лельных прямых — не может быть выведена из остальных. Они
поняли, что вместо этой аксиомы можно ввести другую, по
смыслу ей противоположную, и, исходя из новой системы аксиом,
развить новую геометрию.
Такие разделы математики, как планиметрия, стереометрия,
учение о числе, теория площадей и объемов, учение о функциях
«Первые понятия, с которых начинается какая-нибудь наука, должны быть
ясны и приведены к самому меньшему числу. Тогда только они могут
служить прочным и достаточным основанием учения.»
Н. И. Лобачевский
Лобачевский Николай Иванович (1792—1856 г.г.) — русский математик,
профессор и ректор Казанского университета. Создатель неевклидовой
геометрии. Работы Лобачевского печатались в 1826—1838 г.г. и были не
поняты современниками. Признание неевклидовой геометрии и понима¬
ние ее места в математике пришло лишь в 70-х годах XIX века.
5*
131
и другие, многократно подвергались анализу с целью введения
основных понятий и аксиом и вывода из них важнейших резуль¬
татов.
Аксиомы стереометрии
1. Каждая прямая содержит по меньшей мере две точки.
2. Через любые две точки проходит одна и только одна прямая.
3. Каждая плоскость содержит по меньшей мере три точки.
4. Через любые три точки, не лежащие на одной прямой, проходит одна
и только одна плоскость.
5. Если две точки прямой принадлежат некоторой плоскости, то вся
прямая содержится в этой плоскости.
6. Если две плоскости имеют общую точку, то множество всех их об¬
щих точек есть прямая (т. е. плоскости пересекаются по прямой).
7. Через любую точку, не лежащую на данной прямой, проходит одна
и только одна прямая, параллельная данной.
Будем считать, что пространство состоит из точек. При этом
в пространстве выделены множества двух типов —“^прямые и
плоскости, удовлетворяющие перечисленным аксиомам. Этих
аксиом достаточно для того, чтобы развить теорию параллельно¬
сти (прямых и плоскостей) в полном соответствии с положе¬
ниями, изложенными в § 2. В то же время они не охватывают
такие понятия, как отрезок, длина, перемещение и т. д. Приведем
доказательство уже известных нам теорем с помощью аксиом.
1. Расположение прямых и плоскостей в
пространстве.
Из аксиом 1—6 непосредственно следует, что пара прямых
всегда имеет одно из следующих расположений (сравните с тем,
что было установлено в § 12):
прямые не лежат в одной плоскости (скрещивающиеся прямые);
прямые лежат в одной плоскости и при этом: а) совпадают; б) не имеют
общих точек; в) имеют ровно одну общую точку.
Здесь исчерпаны все возможные случаи, так как, если прямые
имеют более одной общей точки, то, согласно аксиоме 2, они
совпадают.
В случае б) прямые называются параллельными, в случае
в) — пересекающимися.
Докажите самостоятельно, что возможны лишь три случая
расположения прямой и плоскости (см. с. 119; в доказательстве
использована аксиома 5) и что возможны лишь три случая рас¬
положения двух плоскостей (см. с. 120; в доказательстве исполь¬
зована аксиома 6).
2. Проведение плоскости.
▲. Через прямую и не принадлежащую ей точку проходит одна и только
одна плоскость.
132
Доказательство. Даны прямая а и точка Л, не лежа¬
щая на прямой а. На прямой а есть по меньшей мере две (раз¬
личные) точки, скажем, В и С. Точки Л, В и С не лежат на одной
прямой, так как иначе эта прямая, проходящая через В и С,
должна была бы совпадать с а (аксиома 2) и точка А должна
была бы принадлежать прямой а. Через точки А, В и С прохо¬
дит некоторая плоскость а (аксиома 3), содержащая прямую а,
так как ей принадлежат две точки этой прямой (аксиома 5).
Если а —другая плоскость, содержащая прямую а и точку Л,
то она содержит точки Л, В и С; следовательно, совпадает с а
(аксиома 4).
Б. Через две пересекающиеся прямые проходит одна и только одна
плоскость.
В. Через две различные параллельные прямые проходит одна и только
одна плоскость.
Случаи Б и В доказываются аналогично А.
3. Признаки параллельности.
Все теоремы § 12 можно вывести из аксиом 1—7. Докажем,
например, теорему 5. Сначала разберем случай, когда прямые а,
b и с лежат в одной плоскости.
1. Предположим, что прямые 6, с не параллельны. Тогда они
пересекаются.
2. Прямые 6, с имеют общую точку и параллельны прямой а.
Следовательно, Ь = с (аксиома 7).
3. Совпадение прямых b и с противоречит условию теоремы.
Таким образом, прямые b w с параллельны.
Теперь разберем случай, когда прямые а, Ь и с не лежат в
одной плоскости. Обозначим аир плоскости, проходящие через
прямые а, b и а, с соответственно.
1. По построению плоскости аир содержат прямую а и не
совпадают.
2. Пересечение плоскостей аир есть прямая а (аксиома 6).
3. Прямые b и с не имеют общих точек, поскольку они лежат
в плоскостях аир соответственно и не имеют общих точек с пря¬
мой а (условие теоремы).
4. Возьмем на прямой Ь произвольную точку Р (аксиома 1).
5. Через прямую с и точку Р проведем плоскость и обозна¬
чим ее у
6. Плоскость у пересекается с плоскостью р по прямой с
и с плоскостью а по некоторой прямой Ь' (аксиома 6).
7. Так как а и с не пересекаются, то из А.6 следует, что у и а
тоже не пересекаются.
8. Из аксиомы 7 следует, что Ь' и а не пересекаются.
9. Так как прямые bub' имеют общую точку, лежат в одной
плоскости с прямой а и не пересекаются а, то b = b' (аксиома 7).
10. Так как b = b\ то 6, как и с, лежит в плоскости у.
11. Из п. 3 и 10 следует, что прямые b и с параллельны.
133
Упражнения
1. Что представляют собой свойства 2
и 3 (см. с. 120) по отношению к
выбранной нами системе аксиом?
Являются они аксиомами или теоре¬
мами?
2. Свойство 1 не взято нами в каче¬
стве аксиомы. Мы его вывели, ис¬
пользуя аксиому 4. Можно ли по¬
менять местами аксиому 4 и свой¬
ство 1, т. е. принять свойство 1 за
аксиому, а утверждение 4 вывести
из остальных аксиом и свойства 1?
3. Выведите из аксиом признак парал¬
лельности прямой и плоскости.
Задачи и вопросы
3.1. Какие прямые называются скрещивающимися?
3.2. Перечислите все возможные случаи расположения в про¬
странстве двух прямых.
3.3. На двух скрещивающихся прямых /, и /2 взяты четыре точ¬
ки — Л и В на прямой /,, С и D — на прямой /2. Что можно
сказать о расположении прямых АС и BD?
3.4. Как с помощью двух нитей определить, будет ли стол с че¬
тырьмя ножками стоять на ровном полу устойчиво?
3.5. На рис. 174 изображен куб ABCDA'B'C'D', на поверх¬
ности которого отмечены точки К, L, Af, N. Установите:
а) пересекаются ли отрезки [AD'] и [А'В] \ б) пересека¬
ются ли прямые AD' и А'В; в) лежат ли в одной плоскости
точки Af, N, ’В; г) лежат ли в одной плоскости точки А, В,
В', Af; д) лежат ли в одной плоскости точки А\ D\ С', К;
е) лежат ли в одной плоскости точки А\ D\ С', L.
S
3.6. На рис. 175 изображена четырехугольная пирамида SABCD
и отмечены точки /С, Ly Af. Установите: а) л^жат ли точ¬
ки Ку L, Af на одной прямой; б) пересекаются ли пря¬
мые CD и SB; в) пересекаются ли прямые ’CD и SA.
3.7. Существуют ли две параллельные прямые, каждая из кото¬
рых пересекает две данные скрещивающиеся прямые?
3.8. Можно ли провести прямую, пересекающую две данные
скрещивающиеся прямые и проходящую через данную
точку?
3.9. Некоторое множество прямых таково, что любые две пря¬
мые из этого множества пересекаются. Докажите, что все
134
Рис. 174
Рис. 175
прямые либо лежат в одной плоскости, либо проходят
через одну точку.
3.10. Прямые /, и /2 параллельны плоскости а. Верно ли, что
/ill /2?
3.11. Прямая АВ параллельна плоскости а. Верно ли, что любая
прямая, проходящая через точку плоскости а и параллель¬
ная прямой АВ, лежит в плоскости а?
3.12. а, р — параллельные плоскости, Р£ а. Докажите, что вся¬
кая прямая, проходящая через точку Р и параллельная
плоскости р, лежит в плоскости а.
3.13. Плоскость р пересекает Некоторую прямую, параллельную
плоскости а. Докажите, что плоскости аир пересекаются.
3.14. Даны две непараллельные прямые а и 6, лежащие в одной
плоскости, и точка Р, не лежащая в этой плоскости. Про¬
ведите линию пересечения плоскостей, одна из которых
проходит через а и Р, а другая — через b и Р.
3.15. Сколько существует плоскостей, которые проходят через
одну из двух данных скрещивающихся прямых и: а) пере¬
секают вторую прямую? б) параллельны второй прямой?
3.16. Плоскости си и (Х2 пересекаются по прямой АВ. Прямая CD
лежит в плоскости си и пересекает прямую АВ. Можно ли
в плоскости аг провести прямую, параллельную прямой CD?
3.17. В основании четырехугольной пирамиды SABCD лежит
прямоугольник ABCD. На ребре SA взята точка К. Про¬
вести через точку К прямую, параллельную двум плоско¬
стям — плоскости основания и плоскости боковой грани
SCD.
3.18. ABCDA'B'C'D'— куб. Докажите, что плоскости A'BD и
B'CD' параллельны.
3.19. В кубе ABCDA'B'C'D' проведено сечение АА'СС'. Парал¬
лельна ли плоскости сечения прямая, проходящая через:
а) центры граней ADD'А' и CDD'C'; б) середины ребер
A'D' и DC; в) середину ребра AD и центр грани CDD'C'?.
3.20. Найдите множество середин отрезков, концы которых при¬
надлежат двум данным параллельным плоскостям.
3.21. Точки М и N лежат на сторонах АА' и СС' куба
ABCDA'B'C'D'. Докажите, что прямая, соединяющая точки
М и УУ, пересекает плоскость BB'DD'. Постройте точку пере¬
сечения.
3.22. В тетраэдре ABCD даны точки Му N на грани ADB и К на
грани ABC. Провести через них сечение.
3.23. В кубе ABCDA'B'C'D' даны точки Л4, N на грани ВВ'С'С.
Провести сечение через эти точки и центр нижней грани.
3.24. Какую форму имеет сечение параллелепипеда ABCDA'B'C'D'
плоскостью, проходящей через точки В' и С и через точ¬
ку Л4, лежащую на ребре А А'? Постройте это сечение.
3.25. В тетраэдре ABCD провести через середину ребра DC сече¬
ние, параллельное грани ABD.
135
3.26. В прямоугольном параллелепипеде ABCDA'B'C'D' дана
точка М на отрезке [ЛС]. Провести через нее сечение, парал¬
лельное плоскости BB'D'D.
3.27. В правильной шестиугольной призме ABC...D'E'F' дана
точка М на ребре АВ. Провести через нее сечение, парал¬
лельное грани СВВ'С'.
3.28. Какие многоугольники могут получиться при сечении куба
плоскостью?
3.29. Каким многоугольником может быть тень куба на плоскость?
3.30. Какое наибольшее число сторон может иметь многоугольник,
получающийся в сечении 10-угольной призмы плоскостью?
Сколько у него может быть пар параллельных сторон?
3.31. На сколько частей делят пространство три пары параллель¬
ных плоскостей?
3.32. На какое наибольшее число частей могут разделить про¬
странство четыре плоскости?
3.33. На сколько частей делят пространство четыре плоскости,
проходящие через одну точку?
3.34. Сколько параллельных прямых может получиться при пере¬
сечении четырех плоскостей?
4.
ВЕКТОРЫ
§ 14. Направленные отрезки
Примеры векторных величин
Появление многих математических понятий связано с задачей
измерения величин. Для таких величин, как длина, температура,
работа, масса, в результате измерения получается число, причем
в этих случаях результат измерения служит полным описанием
измеряемой величины. Об этих величинах говорят, что они явля¬
ются скалярными. Значения скалярной величины можно распо¬
ложить на координатной прямой, шкале.
Слова «скаляр» и «шкала» имеют одинаковое происхожде¬
ние. Само понятие «шкала» возникло из задачи измерения ска¬
лярных величин.
Понятие «вектор» охватывает более широкий класс величин.
В этот класс входят такие величины, как,скажем, сила, скорость,
напряженность электрического поля и т. д.
Конечно, последние величины также можно измерять какими-
нибудь числовыми характеристиками, однако для полного описа¬
ния этих величин одной числовой характеристики недостаточно.
Так, выражая силу в ньютонах, мы еще не получаем полного
описания силы. Действительно, зная только, что к телу приложе¬
ны две силы, каждая по 1 Н, мы даже не в состоянии определить,
сколькими ньютонами измеряется результирующая сила
(рис. 176). Причина кроется в том, что сила имеет еще такую
характеристику, как направление. Для описания такого рода
величин вводят понятие вектора.
Рис. 176
137
Вектор — это величина, которая задается своей длиной и направле
нием.
Вектор изображается направленным отрезком, длина которого равна длине
вектора. Вектор обозначается обычно прямой полужирной буквой или
буквой, над которой ставится Грелка: а, Хв. Длина вектора обозна¬
чается той же светлой буквой или буквой со знаком модуля. Длину век¬
тора часто называют модулем.
Примеры
1. На рис. 177 изображены силы, приложенные к саням, кото¬
рые тянут за веревку.
Точкой О обозначены сани (точка приложения сил),
mg — сила тяжести, N — сила нормального давления (ре¬
акция опоры), F — сила натяжения веревки, FTp — сила
трения.
2. Движение мяча (рис. 178) описывается следующими век¬
торными величинами: г — перемещение мяча, v — ско¬
рость, mg — сила тяжести, действующая на мяч, ю —угло¬
вая скорость вращения мяча вокруг оси.
138
Рис. 178
Рис. 177
Рассмотрим параллельный перенос пространства. Выбе¬
рем в пространстве направленный отрезок АВ и сопоставим
ему параллельный перенос, т. е. преобразование простран¬
ства, при котором точка М переходит в такую точку ЛГ,
что отрезки ММ' и АВ имеют одинаковую длину, парал-
Рис. 179
лельны и одинаково направлены. Параллельный перенос —
это вектор. Он определяется не только длиной отрезка АВ, но
и его направлением (рис. 179).
Упражнения
1. Вспомните басню И. А. Крылова
«Лебедь, рак и щука» и изобразите
направленными отрезками силы,
приложенные к «возу с поклажей».
Как математически записать со¬
бытие, изложенное в басне: «а воз
и ныне там»?
2. Ракета движется в космическом
пространстве. Какие векторные ве¬
личины характеризуют ее полет?
Изобразите эти векторы направ¬
ленными отрезками.
Изображение векторов направленными отрезками
Векторные величины задаются длиной и направлением. Другой
важной характеристикой векторных величин является то, что их
можно складывать и умножать на числа. Как проявляются эти
свойства векторных величин при изображении их направленными
отрезками? Сформулируем соответствующие правила.
Правила изображения векторов
1. От любой точки можно отложить направленный отрезок, изобра¬
жающий данный вектор (рис. 180).
Можно сказать короче:
вектор можно отложить от любой точки.
139
Рис. 180
Рис. 181
Рис. 182
2. Условие равенства. Направленные отрезки изображают один
и тот же вектор в том и только в том случае, когда отрезки равны
по длине, параллельны и одинаково направлены (рис. 181).
3. Правило трех точек. Если отрезок АВ изображает вектор аг
отрезок ВС — вектор Ьг то отрезок АС изображает сумму а + b
(рис. 182).
4. Растяжение. Если отрезок АВ изображает вектор аг то вектор ка мож¬
но изобразить как отрезок АС, лежащий на прямой АВ, с длиной
|ACI =_^кI АВ и с направлением, совпадающим с направлением от¬
резка АВ, если к > О, и противоположным ему, если к < 0 (рис. 183).
5. Правило параллелограмма. Пусть ОА, = а и ОА2 = Ь.
Тогда диагональ ОА3 параллелограмма ОА,А2А3 со сторонами ОА,, ОА2
изображает сумму векторов а и Ь (рис. 184).
6. Изображение противоположного вектора. Пусть
АВ = а и точка С симметрична В относительно А. Тогда отрезки АС и
ВА изображают вектор (—а), направленный противоположно вектору а
(рис 185).
Рис. 186
вектора. Нулевой вектор О
у которого начало и конец совпа-
7. Изображение нулевого
изображается точкой, т. е. отрезком
дают (рис. 186).
8. Правило многоугольника. Если несколько векторов изоб¬
ражены тар, что начало второго есть конец первого, начало третьего —
конец второго и т. д., то отрезок, соединяющий начало первого с кон¬
цом последнего, изображает сумму этих векторов (рис. 187).
Рис. 187
140
Рис. 183
Рис. 184
Рис. 185
Рис. 188
9. Изображение разности. Если два вектора а и Ь отложены
от одной точки О. О А = а, ОВ = Ь, — то разность их b — а изображает¬
ся отрезком АВ, соединяющим концы (рис. 188). Полезно также запом¬
нить, что диагонали параллелограмма изображают векторную сумму и
разность сторон этого параллелограмма.
10. Правило параллелепипеда. Если ОА, = а, ОА2 = b и
О Аз с, то диагональ О А параллелепипеда со сторонами ОА,, ОАг, ОА3
изображает сумму векторов а + Ь + с (рис. 189).
Первые четыре из сформулированных правил являются основ¬
ными, принимаемыми без доказательства. Остальные правила
можно из них вывести.
Докажем, например, правило параллелограмма.
Действительно, из свойств параллелограмма и из правил трех
точек следует: А\Аз = ОА2, ОА\ -\-A\A$ = OAz. Таким образом,
О А1 -f О А 2 = О Аз.
Докажите самостоятельно правило изображения разности.
Упражнения в) Постройте векторы а—b+с, а—
-b-с, 2а+72Ь—2с.
1. Даны три вектора а, b и с (рис. 190). 2. В параллелограмме ABCD выра-
а) Выберите произвольно точку О зите: ^ ^ ^
и отложите от нее векторы а, Ь, с. а) СЛ, BD, DB через АВ и AD\
б) Постройте сумму a+b+с. б) ЛТЗ, D?, ТГВ через ЕЛ и AS.
«Математическая символика — самый надежный язык; избежать ее мож-
410 только ценой длинных перефраз, которые все равно не будут понятны
профану и которые поймет лишь подготовленный читатель, переведя их
обратно в символы.»
Н. Винер
Винер Норберт (1894—1964 г.г.) — американский математик, создатель
кибернетики как «науки об управлении и связи в живём организме и
машине». Работы Винера являются основополагающими для применения
вычислительных машин в различных сферах человеческой деятельности.
Норберту Винеру принадлежит высказывание: «Вычислительная машина
ценна ровно настолько, насколько ценен использующий ее человек».
141
Рис. 189
Рис. 190
Применение векторов к решению геометрических задач
Пусть О — фиксированная точка. Тогда радиусом-вектором точ¬
ки Р (относительно точки О) называют вектор ОР.
Использование векторов при решении геометрических задач
основано на том, что:
1] каждую точку можно задавать радиусом-вектором (рис. 191).
2) каждую пару точек А, В можно считать началом и концом век¬
тора АВ.
Выведем формулу для радиуса-вектора середины отрезка.
Теорема
Пусть точка С — середина отрезка АВ. Тогда радиус-вектор точки С есть
полусумма радиусов-векторов точек А и В,
т. е. ОС='/2 (ОА + ОВ), где О — произвольно выбранная точка
(рис. 192).
Доказательство. Согласно правилу трех точек, ОС—
= о\ + а£\ 0£=0^ + в£. Складывая эти равенства, мы
получаем 2бЪ=(?А + ОВ + АС + ВС, ОС=°Л + °В + АС + ВЯ
Но, поскольку АС=—ВС (правило 4), сумма АС + ВС
равна 0. Следовательно,
О А 4" О В
Задачи
1. Доказать, что середины сторон четырехугольника образуют
параллелограмм (рис. 193).
Пусть /С, L, Af, N — середины сторон АВУ ВС, CD, AD че¬
тырехугольника ABCD. Если K*L=N%1, то точки /С, L, Af, N
Рис. 191
Рис. 192
образуют параллелограмм. Докажем, что KL = N%i. Cg-
гласнотеореме, примененной к серединам сторон ЛВ, ВС,
CD, DA:
0%='/2(б% + Ш), Ш = х/ 2(о£+ об),
б1 = '/2(бВ + ОС), 6n=x/2(OD + OA).
Вычитая из второго равенства первое и из третьего
четвертое, мы получаем (правило 9):
^1=72(ос,_ол), nm='/2(6c-6a) и kl=nm.
Заметим, что в этой задаче четырехугольник мог быть
не плоским и самопеоесекающимся.
Рис. 193
2. Пусть G — точка пересечения медиан треугольника ABC.
Доказать, что аЬ + вЬ-\-СЬ = 0 (рис. 194).
Обозначим А', В', С' середины сторон ВС, СА и АВ.
Согласно известному свойству точки пересечения медиан,
AG = 2/3AA'; BG = 2/3BB'; CG = 2/3CC/.
Складывая эти равенства, получаем
AG + BG 4- CG = 2/3(А*А' + ВЪ' + с£').
По теореме (см. с. 142), примененной к серединам отрез¬
ков ВС, АС и АВ, имеем:
АЛ' = 1/2(АВ + АС)\ В"В' = 72(ВЛ+В"С); СС'=х / 2{СА + СВ).
Такдм дбразом, АА^-{-ВВ'-{-CC' = xJ^(ABj^AC-\-BA +
4-/^ + С^+СВ)=0, и так как AG-\-ВЪ-\-CG=2/Ъ{АА'-\-
+ ВВ' + СС')> то
AG + BG + CG = 0.
Полученное в этой задаче равенство можно переписать так:
GA + бЬ GC=0. Это свойство точки пересечения медиан имеет
физический смысл. Оно означает, что в том случае, когда точки
А, В, С имеют одинаковые массы, центр масс системы Л, В, С
находится в точке пересечения медиан треугольника ABC. Дело в
Рис. 194
том, что центр масс системы точек Ау В, С имеющих массы пц,
тв, тс, определяется равенством
mAGA + mBGB + mcGC = 0.
Упражнения
В параллелограмме ABCD точ¬
ка О — точка пересечения диагона¬
лей. Выразите через^ векторы ДЗ и
AD векторы АО, ВО, Сб, DO.
2. Каждая из сторон треугольника
ABC разделена на три равные
части (рис. 195). Докажите:
а) Mrf/^ + WP=0,
б) RM=PL + KNt
в) LN=KP.
3. О — точка пересечения медиан тре¬
угольника ABC, О — произвольная
точка. Докажите, что UG= /3 (ОА-\-
+ 0/5 + 0?).
4. В каком случае существует тре¬
угольник, стороны которого были бы
равны и параллельны данным трем
направленным отрезкам а, b и с?
Можно ли построить треугольник,
стороны которого были бы равны и
параллельны медианам данного тре¬
угольника?
Разложение векторов на составляющие
Построение в плоскости. Пусть в некоторой плоскости
даны вектор а и две непараллельные прямыд. Возьмем произ¬
вольную точку О, отложим от нее вектор а = ОА. Проведем через
точки О и А прямые, параллельные дв^м данным прямым. Полу-
чдм падалледограмм ОВАС. Вектор ОА можно представить так:
ОА = ОВ-j-OC. Полученное представление называется разложе¬
нием вектора по двум данным направлениям в плоскости
(рис. 196):
Построение в пространстве. Пусть даны век¬
тор а и три прямые, попарно не параллельные и не лежащие все
три в одной плоскости. Возьмем произвольную точку О, отложим
от нее вектор а = ОА. Проведем через точку О прямые /1, /2, /3,
Рис. 195
Рис. 196
Рис. 197
параллельные данным трем прямым. Построим параллелепипед
с ребрами, параллельными /1, /2, /3, и с диагональю CML По пра¬
вилу параллелепипеда получим разложение ОА = ОВ-\-ОС +
+ OD, которое называется разложением вектора по трем данным
направлениям в пространстве (рис. 197).
Представим себе, что мы тянем сани за веревку с некоторой
силой F. Нас может интересовать, какой эффект производит
эта сила в двух направлениях: горизонтальном и вертикальном.
Для этого надо представить вектор F в виде суммы векторов
F| и F2, направленных по вертикали и горизонтали (рис. 198).
Направления, по которым приходится раскладывать вектор,
не обязательно совпадают с горизонтальным и вертикальным.
Например, силу тяжести груза (рис. 199) нужно разложить
по направлениям удерживающих тросов, чтобы узнать, выдержат
ли тросы этот груз.
Упражнения
1. Найдите силы, действующие на
стержни, на которых укреплен гру*
массой 10 кг. Определите, какие из
этих сил производят растяжение, а
какие — сжатие (рис. 200). ^
2. Разложите графически вектор ОС
Размерность
Сравнивая разложение векторов на прямой, в плоскости и в
пространстве, можно заметить некоторые общие закономерности.
Так, на прямой можно выбрать один, на плоскости — два, в
пространстве — три вектора, по которым можно разложить лю¬
бой вектор (прямой, плоскости, пространства). С другой сторо¬
ны, если взять на прямой два, на плоскости — три, в простран¬
стве — четыре вектора, то всегда один из них будет расклады¬
ваться по о гальным. Последнее свойство прямой, плоскости и
по векторам ОЛ и ОЁ (рис. 201).
3. Разложите графически силу тяже¬
сти котла по направлениям опор
(рис. 202).
4. Разложите графически силу mg по
направлениям стержней АС и ВС
(рис. 203—205).
Рис. 198
145
Рис. 199
Рис. 200
Рис. 201
Рис. 203
146
Рис. 202
Рис. 204
Рис. 205
пространства мы не доказываем, считая его очевидным. Эти
свойства обычно принимают в качестве аксиом, указывающих
размерность прямой, плоскости и пространства. Размерность
прямой считается равной единице, плоскости *—двум и простран¬
ства — трем. Это соответствует нашим представлениям о числе
«измерений» прямой, плоскости и пространства.
§15. Координаты вектора
Декартова система координат
Введем координаты в пространстве по аналогии с координатами
на прямой и на плоскости (см. § 1,2). Для этого выберем произ¬
вольную начальную точку О и проведем через нее три взаимно
перпендикулярные оси с общим началом О. Обозначим эти оси
Ох, Оу, Oz (рис. 206).
Плоскость, натянутую на Оу и Ozy обозначим yOz, плоскость,
натянутую на Ох и Оу, — хОу и плоскость, натянутую на Oz и
Ох, — zOx.
Пусть М — произвольная точка. Проведем через нее плоско¬
сти, параллельные плоскостям хОуу yOz, zOx. Они вместе с
координатными плоскостями (хОу, yOz, zOx) образуют паралле¬
лепипед. В нем три ребра ОМх, ОМу, 0М2 расположены на осях
координат и ОМ является диагональю. Положение точек на осях
Ох, Оу, Oz определяется координатами точек. Обозначим коор¬
динаты точек МХу Муу Мг через х, у, z соответственно и назовем
их координатами точки М (рис. 207).
Каждой точке пространства сопоставим набор из трех
чисел — координат этой точки. Ясно, что при этом для любой
тройки чисел (х; у\ г) в пространстве найдется точка с координа¬
тами (х; у; z). Таким образом, мы установили взаимно однознач¬
ное соответствие между точками пространства и тройками чисел.
В дальнейшем пространство, снабженное декартовой систе¬
147
Рис. 206
Рис. 207
мой координат, мы будем называть координатным простран¬
ством.
Нам известна важнейшая математическая идея (связываемая
с именами французских математиков XVII в. Декарта и Ферма)
задавать точки числами, координатами. Теперь выясним, как,
следуя этой идее, задавать векторы. Это расширит наши возмож¬
ности в действиях с векторами, а также приведет к интересным
обобщениям.
Произвольный вектор а отложим от начала координат. Тогда он изобра¬
зится направленным отрезком ОА. Координаты его конца, т. е. точки А,
называются координатами вектора а (рис. 208).
Это определение имеет смысл как на координатной прямой,
координатной плоскости, так и в координатном пространстве.
Итак, чтобы найти координаты вектора, надо отложить его
от начала координат и взять координаты конца построенного
отрезка.
Координаты вектора обозначаются так же, как и координаты
точек, т. е. наборами чисел, записанными в скобках.
Упражнения
1. Постройте на числовой оси точки
с данными координатами: Л (1,5);
В (-1); С (-2,5); D(JT).
2. Постройте на координатной плос¬
кости точки с данными коорди¬
натами: А (1; — 1); В (0; 5); С(-3; 2);
D (—1,5; 0).
3. Постройте в ’ координатном про¬
странстве точки с данными коор¬
динатами: А (1; 2; 1); В (—2; 0; 1);
С (0; 0; 3); D (0; 1;3).
4. Где лежат точки координатного про¬
странства, которые удовлетворяют
следующим условиям:
а) все координаты положительные;
б) первая координата равна нулю;
в) первая и вторая координаты рав¬
ны нулю;
г) все координаты равны;
д) первая координата равна еди¬
нице;
е) произведение координат равно
нулю;
ж) модули каждой из координат не
больше единицы?
5. Постройте в координатной плоско¬
сти векторы с заданными коорди¬
натами: ai(l, —3); аг(0; 5);
а3(—1; 4); а4(2; 0).
6. Постройте в координатном про¬
странстве векторы с заданными ко¬
ординатами: ai (1; 2; —3); а2 (0; 3; 1);
а3 (-2; 0; 2).
148
Рис. 208
Действия над векторами в координатах
Рассмотрим на плоскости декартову систему координат. Единич¬
ные векторы, направленные по осям координат х и уу обозначим
соответственно 1 и j и назовем ортами координатных осей
(рис. 209).
Возьмем произвольный вектор а. Изобразим его направлен¬
ным отрезком ОЛ. Разложим ОА по направлениям координатных
осей:
ОА = ОА \ + ОЛ2.
Пусть (jc; у) —координаты точки Л, т. е. х — координата
точки Ах на оси абсцисс, у — координата точки А2 на оси орди¬
нат. На векторном языке это означает, что OAi = xi и ОА2 = у\-
Получаем
а = О А = О А1 -f“ О А 2 = х\ -f- у j.
Разложение a = jri-f-t/j называется разложением вектора по
ортам координатных осей. Числа х и у в этом разложении явля¬
ются координатами точки Л, а следовательно, по определению
координат вектора, координатами вектора а. Итак,
координаты вектора а равны коэффициентам его разложения по ортам
координатных осей.
Аналогичное построение делается в пространстве.
Рассмотрим координатное пространство и обозначим i, j, k
единичные векторы, направленные по осям координат (орты).
Возьмем произвольный вектор а, отложим его от начала
координат: а= 6Й. Если точка А имеет координаты {х\ у\ ^), то
вектор а представляется в виде а=ОЛ = ОА\ + ОЛ2 + СМз =
==Jti + J/j + zk (рис. 210), т. е. коэффициенты разложения вектора
по ортам являются координатами этого вектора.
Следующие правила показывают, как выполнять действия с
векторами на языке координат.
Правило f
При умножении вектора на число его координаты умножаются на это
число.
149
Рис. 209
Доказательство. Согласно условию, &=х\-{-у). Сле¬
довательно, Ха = Х(х\-\-у\) и Ха=(Ajc)i-|-(Ал/)j. Последнее равен¬
ство означает, что вектор А,а имеет координаты (Хх\ Ху). На
рис. 211 приведена иллюстрация этого правила.
Правило 2
При сложении векторов их координаты складываются.
Доказательство. Согласно условию, ai=*ii + */ij,
a2=JC2i + (/2j- Складывая эти равенства, получаем
ai +a2=Oi +x2)i + (yi +1/2)|.
Это равенство означает, что вектор ai + a2 имеет координаты
(Х\ Х'2у у\ +1/2).
Иллюстрацией к этому правилу служит рис. 212. На нем
векторы ai, а2 показаны радиусами-векторами точек Аи А2.
Сумма векторов ai, а2 изображается радиусом-вектором
точки Л3 — вершины параллелограмма, построенного на СМ, и
ОА2. На рисунке видно, что координаты точки Аъ равны суммам
координат точек Л, и Л2.
Для векторов в пространстве сформулированные правила
действий сохраняются.
1. Если вектор а имеет координаты (х; у; z), то вектор А,а, где X€R,
имеет координаты (Ах; Ху; Xz).
Рис. 210
Рис. 211
Рис. 212
I. Если вектор а имеет координаты (х,; у,; z,), а вектор а имеет коор¬
динаты (х у ; г.), то вектор a, -f а имеет координаты (х, + х у, + у,;
Z, + Z,).
Для нахождения координат вектора у нас есть два правила.
Согласно первому правилу (принятому за определение), надо
вектор отложить от начала координат и взять обычные декарто¬
вы координаты точки — конца построенного отрезка. Согласно
второму правилу, вектор надо разложить по ортам координат¬
ных осей и взять коэффициенты этого разложения. Есть еще
третье правило — надо изобразить вектор произвольным направ¬
ленным отрезком и взять разности координат конца и начала.
Докажем это правило.
Пусть вектор а с координатами (х\ у) изображен направ¬
ленным отрезком Ah. Представим вектод^а ка^ разность радиу¬
сов-векторов конца и начала: а=АЁ = ОВ — ОА. Пусть (ха, ул)
и (Хв\ ув) — координаты точек А и В. Эти же числа являются
координатами векторов ОА и ОВ. Учитывая правила 1 и 2,
получаем
х—Хв — Ха у У=Ув — Уа,
Координаты вектора равны разностям координат конца и начала нэпраз
ленного отрезка, изображающего этот вектор (рис. 213).
Упражнения
1. Найдите координаты векторов,
изображенных ца рис. 214.
2. Даны векторы а (1; —3); b (0; 2);
с(—3; 2). Вычислите координаты
векторов d=a+b-fc, l=2a—b,
=а—1 /2Ь—2с и постройте эти век¬
торы.
3. Даны точки Л (1; 0; —2), В (—2; 3;
— 1), С (2; —1;3). Найдите коорди¬
наты векторов /Г5, а£, сВ, л§,
-At.
151
Рис. 213
Рис. 214
§16. Применение векторов в механике
Векторное уравнение движения
С движением точки по некоторой кривой связан ряд векторных
величин. Важнейшие среди них: г — радиус-вектор, характери¬
зующий положение точки, v — скорость точки, а — ускорение.
Пример
На рис. 215 эти векторы показаны для движения снаряда
(без учета сопротивления воздуха).
Рис. 215
Зафиксируем некоторую точку отсчета О и будем поло¬
жение движущейся точки в момент времени t задавать
радиусом-вектором относительно О (рис. 216).
Если в моменты времени Л, /з точка занимает положе¬
ния А\у Л2, Аз, то ее радиусы-векторы v(t\)=6%\y г(/2)=
= ОЛг, г(/з)=ОЛз.
Итак, мы получили первую векторную величину, связанную
с движением точки, — радиус-вектор г, определяющий ее поло¬
жение относительно некоторой точки отсчета О.
В простейшей ситуации, когда точка движется по прямой,
ее положение определяется одним числом. В этом случае обычно
вводят на прямой координаты и задают положение точки ее
координатой.
Рис. 216
Рис. 217
Часто в механике важно знать не положение точки, а ее
перемещение за интервал времени [t 1, /2]. Перемещение является
вектором и изображается направленным отрезком, начало и
конец которого совпадают с положениями точки в моменты t\ и
/2. Перемещение обозначают Лг. Вектор Лг связан с радиусами-
векторами, характеризующими положение точки: Лг = г(/г) —
— r(/i). Про перемещение можно сказать, что оно является при¬
ращением вектора г за отрезок времени [t\, /2] (рис. 217).
В простейшем случае, когда точка движется по прямой, ско¬
рость направлена по этой же прямой. В общем случае скорость
направлена по касательной к траектории движения (рис. 218).
Ускорение — это скорость изменения скорости.
Между вектором ускорения а и вектором силы F, действую¬
щей на точку массой т, есть соотношение, являющееся одним
из основных в механике Ньютона: ma = F (второй закон Нью¬
тона).
Если мы вспомним, что ускорение является второй производ¬
ной положения точки, то на соотношение ma = F можно посмот¬
реть как на дифференциальное уравнение движения. В простых
случаях мы из него можем получить зависимость вектора г от вре¬
мени /.
Если равнодействующая F всех сил, действующих на точку,
равна нулю, то ускорение а тоже равно нулю и точка движется
с постоянной скоростью v. В этом случае радиус-вектор г точки
линейно зависит от времени: r = ro + v/, где t — время и го —
начальное положение точки, т. е. го=г(0) (рис. 219). Если на
точку действует постоянная сила F, то ускорение а постоянно
и точка совершает движение по квадратичному закону г = Го +
+ vo/ + 1/2gf2 (рис. 220), где v0 — начальная скорость точки.
Скорость точки в этом случае меняется линейно:
V = Vo + g t.
Рассмотрим, например, движение снаряда, начальная ско¬
рость v0 которого была направлена под углом а к горизонту.
Выберем в качестве начальной точки О положение снаряда в
момент времени / = 0, тогда мы получаем соотношение r = vo/ +
+ 1/2g^2- (Здесь мы, конечно, имеем в виду идеальную ситуацию,
153
Рис. 218
Рис. 219
когда сила тяжести, действующая на снаряд, постоянна и другие
силы на снаряд не действуют.)
При решении задач от векторных уравнений переходят к
координатным.
Выберем оси координат так, как показано на рис. 221. Век¬
торное равенство г=Уо/+1/г£*2 запишем в координатном виде.
Сначала разложим векторы vo и g по горизонтальному и верти¬
кальному направлениям. Проекция вектора vo на ось х равна
uocosa, а на ось у — uosina; проекция ускорения на ось х равна
нулю, а на ось у равна — g. Таким образом,
х= tv0 cosa, у= tvo sina—1 /2gt2,
где x, у — координаты вектора г. Такая система позволяет решить
ряд задач.
Задачи
1. Найти время движения снаряда.
Снаряд касается земли в момент />0, когда у = 0. Прирав¬
ниваем к нулю выражение для у:
tv о sin a—l/2 gt2 = 0.
Решая это квадратное уравнение относительно /, получаем
/1=0; /2= 2р° e|n a . Ясно, что t\ соответствует моменту
вылета снаряда, а t2 — моменту его падения.
2. Найти расстояние по горизонтали, которое пролетит снаряд.
Известно время движения снаряда. Подставляя его в
формулу для г, получаем
2i>o sin a 2vl sin a cos a
x— vo cos a=— .
g g
Найдите самостоятельно, на какую максимальную высо¬
ту поднимается снаряд.
Рис. 220
Рис. 221
Координаты вектора скорости
Если положение точки задается вектором г = r(t), имеющим координаты
х = x(t) и у = у(t), то вектор скорости v = v(t) имеет координаты
y'(t), равные производным координат вектора г:
Пусть точка А движется по криволинейной траектории. Обо¬
значим координаты точки А в момент времени t через x(t) и y(t)
(рис. 222). Эти координаты зависят от времени t и являются
функциями от t. Рассмотрим мгновенную скорость v движущей¬
ся точки А в момент времени t. Вектор мгновенной скорости v
направлен по касательной к траектории в точке А. Координаты
вектора v тоже зависят от времени t и меняются, вообще говоря,
при переходе от одной точки траектории к другой.
Пусть координаты точки А в момент времени t равны
(*(/), y(t)). Покажем, что координаты вектора скорости v точки А
равны х (t) и y'(t)y где x'(t) и y'(t) — производные функций х и у
в точке t.
За время Л/ точка А переместится в точку В с координата¬
ми x(t + At) и y(t-{-At) (рис. 223). Рассмотрим вектор перемеще¬
ния Он является разностью векторов оЁ и Ш , и его ко¬
ординаты поэтому будут разностями координат этих векторов.
Следовательно, координаты вектора АВ
Напомним, что средней скоростью называется отношение
перемещение ко времени. Таким образом, вектор средней скоро¬
сти равен ЛВ/Л/, поэтому его координаты
Вектор средней скорости при уменьшении Л/ приближается
к вектору мгновенной скорости в момент времени t. (Это значит,
что разность между вектором мгновенной скорости и средней
скоростью может быть сделана сколь угодно малой за счет выбо¬
ра М.)
г(х; у), v(x'; у').
Рис. 222
Рис. 223
155
По определению производной, при уменьшении At величина
приближается к *'(/), a — к */'(/).
Таким образом,
координаты вектора мгновенной скорости в момент времени t равны
х'(0 И у'(О-
Рассмотрим снова, движение снаряда, выпущенного под
углом а к горизонту с начальной скоростью Vo (рис. 224).
Снаряд, если пренебречь сопротивлением воздуха, будет
двигаться по параболе. Вектор скорости v направлен . по
касательной к ней. Известное соотношение v=vo + g/ полу¬
чается дифференцированием соотношения r=vo/+1/2&^2
(векторы vo и g постоянны). Можно вычислить и координа¬
ты вектора скорости, зная координаты вектора г(х; у):
х (t) = Mcosa.
y(t)=vot sin a — */2gt2.
Известно, что вектор скорости v имеет координаты
(x'(t\ y'(t)). Вычислим производные: x' = i;ocosa; у'=
= aosin a — gt.
Эти же равенства можно получить, спроектировав
известную заранее векторную формулу v = vo + g* на оси
координат (рис. 225).
Пример
Рис. 224
Упражнения
5. Как вычисляются координаты век¬
тора скорости?
1. Какие векторные величины харак-
6. В следующих задачах дан закон
теризуют движение точки?
2. Как направлена скорость?
3. Что такое ускорение?
4. Как в векторной форме записать
движения в координатах:
а) г (3/; 4/-1);
б) г (2/; t2—<);
закон движения с постоянным уско¬
рением?
156
Рис. 225
г) r(/2-l; <(/2-1)).
Найдите координаты вектора ско¬
рости.
8*. Что можно сказать о скорости дви¬
жения точки в примере 6 а)? Чему
равен ее модуль? Что можно ска¬
зать об ускорении* точки в примере
6 6)? Как оно направлено? Чему
равен модуль скорости в примере
6 в) ?
7*. Нарисуйте траектории, по которым
движутся точки в задаче 6.
§17. Векторное пространство
Новые примеры векторных величин
До сих пор мы рассматривали вектор как направленный отрезок,
т. е. задавали его длиной и направлением. Введение координат
позволяет задавать векторы наборами чисел. Так, вектор плоско¬
сти определяется парой чисел, вектор пространства — тройкой
чисел. Для того чтобы не противопоставлять скалярные величи¬
ны векторным, можно считать, что скалярные величины изобра¬
жаются на прямой и задаются модулем (абсолютным значением)
и направлением (знаком). Задание векторов наборами чисел
позволяет рассматривать новые векторные величины.
Допустим, цех выпускает изделия четырех наименований.
Выпуск продукции за месяц можно охарактеризовать строчкой
из четырех чисел: (а\, a<i, аз, 04), где а\ — число выпускаемых
изделий первого вида, аг, аз, а\ — аналогичные числа для изде¬
лий остальных видов. Полностью определить выпуск продукции
с помощью одного числа невозможно. Строчка (а(, а2, а3, аД
характеризующая выпуск продукции по ассортименту, является
векторной величиной.
Рассмотрим множество квадратных трехчленов ах2+ Ьх -\-с,
где а, 6, с — произвольные действительные числа (мы допускаем
обращение в нуль любого из коэффициентов а, 6, с). Например,
тройка чисел (1, 0, 0) задает трехчлен вида х2-\- Ox -f- 0=jc2,
а тройка чисел (2, —1, —1) — трехчлен 2х2 — х—1. Квадратный
трехчлен мы можем тоже рассматривать как вектор.
Векторное пространство
Примеры, рассмотренные на с. 138, не похожи друг на друга, в то
же время в каждом из них речь шла о векторной величине. Как
же выделить какие-то общие свойства векторных величин? Важ¬
ным свойством, объединяющим все векторные величины, являет¬
ся возможность совершать с ними две операции: сложение и
умножение на число.
Сложение параллельных переносов и умножение их на чиоло
известно из геометрии, сложение сил — из механики.
Если рассматривать строки из четырех чисел (ai, a2, аз, а4),
157
задающих выпуск фиксированных четырех видов продукции,
то естественно складывать их следующим образом:
(аь а2, а3, a4) + (6i, b2, Ь3, 64)=
= (я 1 4“ & 1, ^2 + ^2, аз+ 63, 04 + 64)-
Это делается при суммировании выпуска продукции за не¬
сколько месяцев или определении выпуска продукции несколь¬
кими предприятиями, имеющими одинаковый ассортимент
изделий.
Аналогично складываются и умножаются на число квадрат¬
ные трехчлены.
Обратим внимание на важную особенность разобранных
примеров. Мы говорили о квадратных трехчленах, но при этом не
фиксировали внимание на каком-то одном из них, а брали сразу
множество всех квадратных трехчленов. При изучении парал¬
лельных переносов полезно рассматривать все параллельные
переносы; лишь тогда можно складывать их и умножать на
число.
Таким образом, мы каждый раз имеем дело с множеством
значений векторной величины, причем эти значения можно скла¬
дывать и умножать на число. Во всех примерах эти две операции
удовлетворяют всем законам векторной алгебры. Эти правила
мы уже фактически использовали в доказательствах, но не
обращали на это внимания.
В математике множество объектов, которые можно склады¬
вать и умножать на число, называют векторным пространством,
если для ^тих операций выполнены законы векторной алгебры.
Размерность
Мы начали изучение векторов с того, что указали величины,
которые нельзя задавать одним числом. Оказалось возможным
задавать эти величины несколькими числами, их координатами.
Так, силу, действующую на точку в пространстве, можно
задавать тремя числами — проекциями силы на оси координат.
Выпуск продукции цехом, изготовляющим четыре вида изделий,
задается четырьмя числами — количеством выпускаемых изде¬
лий по каждому виду отдельно. Квадратный трехчлен ах2-{-Ьх-{-
+ с задается тремя числами — коэффициентами a, b и с. Таким
образом, векторные величины различаются тем, сколько чисел
требуется вычислить для их задания (конечно, речь идет о наи¬
меньшем количестве чисел, нужных для вычислений векторной
величины).
Если для задания векторной величины нужно задать п чисел,
то говорят, что она является л-мерной векторной величиной,
а про векторное пространство, образованное значениями этой
величины, говорят, что оно имеет размерность /г, или /г-мерно.
Так, сила, действующая в пространстве, есть трехмерная
векторная величина, размерность пространства параллельных
158
переносов в плоскости равна двум, квадратные трехчлены запол¬
няют трехмерное пространство, а выпуск продукции четырех
видов изображается элементом такого пространства, для которо¬
го п = 4. Скалярные величины задаются одним числом. Их можно
рассматривать как одномерные векторные величины.
Примером я-мерного пространства при любом п является
множество строчек длины п: Rn={(ai; а2; ап)}.
Сложение строчек и умножение их на число производится, по
следующим правилам:
(ai, a2, аз, щ, ...» an)-\-{bi, ft2, йз, ..., Ьп)=
=(ai -\-b\, a2-|-ft2, ..., cLh-\-bn)\
к(а\, а2, ..., а„)=(А,аь А,а2, ..., А,а„).
Размерность векторной величины является ее основной харак-
теристикой. Все векторные величины одной и той же размерно¬
сти похожи друг на друга, например, тем, что каждую из них
можно задавать строчкой из такого же количества чисел. Это
сходство проявляется и в геометрическом изображении векторов.
Все двумерные векторные величины можно изобразить на пло¬
скости; все трехмерные — в пространстве. Прибавим к этому, что
все одномерные векторные величины — скаляры — изображают¬
ся на числовой прямой.
Многие теоретические и прикладные дисциплины (физика,
экономика, радиотехника и др.) используют я-мерные векторные
пространства с п>3.
Упражнения
1. Каковы общие свойства векторных
величин?
2. Сформулируйте свойства сложения
векторов и умножения вектора на
число.
3. Приведите примеры величин, задаю¬
щихся наборами чисел.
4. Приведите пример четырехмерного
пространства.
Задачи и вопросы
4.1. Приведите примеры скалярных и векторных величин.
4.2. Как изображаются векторы?
4.3. Как обозначаются векторы?
4.4. Как изображается сумма векторов?
4.5. Какими векторными равенствами связаны диагонали парал¬
лелограмма с его сторонами?
4.6. На точку О действуют три силы, расположенные в одной
плоскости (рис. 226). Модуль каждой силы один и тот же и
равен 1. Постройте результирующую силу F. Чему равен ее
модуль |F|?
4.7. Груз опускается на парашюте с высоты 120 м с постоянной
вертикальной скоростью 3 м/с. Ветер, дующий горизонталь¬
но со скоростью 2 м/с, относит его в сторону. Какой путь
пролетает груз? Вычислите ответ с точностью до 1 м.
159
Рис. 226
4.8 Параллельные переносы плоскости а и b задаются направ¬
ленными отрезками АЪ и АС (рис. 227). Постройте направ¬
ленный отрезок, задающий параллельный перенос а + Ь,
так чтобы начало отрезка совпадало с точкой Л, с точкой В,
с точкой С. Постройте направленные отрезки (с произволь¬
но выбранным началом), задающие параллельные переносы
а —b и а + 2Ь.
Рис. 227
4.9. А, В, С, D — точки. Докажите, что аЪ-\-15Ъ=аЪ + ЪЬ.
4.10. Дан тетраэдр ABCD. Найдите сумму векторов: a) ЛВ-|-
+вЬ+1>£\ б) a5+c£+d£; в)
4.11. Дан параллелепипед ABCDA'B'C'D'. Найдите сумму векто-
ров: а) АЁ + Ш' + В7?', б) Ct} + WX' + A6'\ в) Тб+
+ 1у% + Ш'-, г) Wb+iX' + сЬ+с7Е.
4.12. Л, В, С, D — произвольные точки пространства. Докажите,
что аЗ + вТ:=вЬ+а£.
4.13. А, В, С, D, Е, F — точки. Докажите, что А3-}-ВЙ-}-СЙ=
=а£+вР+сЗ.
4.14. Докажите, что сумма радиусов-векторов вершин треуголь¬
ника равна сумме радиусов-векторов середин его сторон.
4.15. В произвольном шестиугольнике отмечены середины его
сторон — Л' В', С', D', £', F'. Докажите, что А
-\=C'D'-\ WP'=0.
4.16. Известно, что центр масс G треугольника ABC обладает
таким свойством: G^ + GS+GC=0. Какой физический
смысл можно придать точке Af, такой, что МА-\-2МЬ-\-
+ ЗЛ4&=0?
4.17. Mi и М2— точки пересечения медиан треугольников A\BiC\
и А2В2С2. Докажите, что M\ld2=xU(A\A2 + В\Ё2 + С\д2).
4.18. А, В, С, D — точки, Е и F — середины отрезков АВ и CD.
160
Докажите, что: а) ЁР=1/2(В^-\-ХЗ)\ б) \ЕР\^ !/2(|В?| +
+ \ЛЪ\); в) если \^\ = х / 2(\вЪ\ + \аЬ\)у то BC\\AD.
4.19? ABCD— четырехугольник, М— точка. Докажите, что
точки, симметричные точке Af, относительно середин сторон
четырехугольника ABCD, являются вершинами параллело¬
грамма.
4.20. ABCDE — пятиугольник. КУ Ly Му N — середины сторон АВ,
ВСУ CD и DE, Р и Q — середины отрезков КМ и LN соот¬
ветственно. Докажите, что PQWAE и \PQ\ = X / а\АЕ\.
4.21. ABCDEF— шестиугольник, /С, Ly Му N— центры масс тре¬
угольников АВСУ BCDy DEFy EFA. Докажите, что KLMN —
параллелограмм.
4.22. На сторонах АВУ ВСУ СА треугольника ABC выбраны такие
точки С', АВ', что ^=JM1=J£§14 Докажите, что
центры масс треугольников ABC и А'В'С' совпадают.
4.23. Ау Ву С, D — точки. Выразите АЁ через: а) Л&, DC,
б) D%, сЬ, вЬ\ в) аЪ, вЬ, Ш.
4.24. ABCD — параллелограмм. Точка Е на стороне ВС такова,
что |5Ё1=з|ё£|, а точка F на стороне AD такова, что
2\Ap\ = 5\D*F\. Выразите ЁР через Л?} и
4.25. ABCD — параллелограмм, О — точка пересечения его диа¬
гоналей. Выразите А&у Tifcy сЪу через ОА и OS.
4.26. ABCD — параллелограмм, М — середина его диагоналей.
Выразите АСУ АЙУ сЪу м£ через АЁ и АЗ. ^
4.27. Точка С на отрезке АВ такова, что \АС\ = 2\ВС\. Вырази¬
те: а) АЬ и ВС через А§; б) О? через 0% и оЬ (О —
произвольная точка).
4.28. Дан правильный шестиугольник ABCDEF, О — его центр,
А&=р и XP=q. Выразите сД ХЬу Wfcy Л75, АСУ АЕУ
Вру через р и q. Постройте векторы, равные: а) АЁ +
+ б) АЁ + СЬ; в) Ah + DF; г) A& + d£; д) Л? +
+ Z)t; е) АЁ + АР.
4.29. ABCDEF — правильный шестиугольник. Выразите: a) DEy
ЁРУ СЬУ F% через А% и вЬ\ б) в£у сЪу Шу Ё?, че¬
рез АЁ и fiS.
4.30. ABCD — параллелограмм, Е — середина стороны ВСУ а
точка F на стороне CD такова, что \CF\ = 2\Dp\. Вырази¬
те Хв и ВЬ через А*Е и A*F.
4.31. В тетраэдре ABCD точка О — центр масс треугольни¬
ка BCD. Выразите ЛЬ через АЪУ АЬ и AD.
4.32. Дан параллелепипед ABCDA'B'C'D'. Му Ny Р — середины
отрезков DD' СС'У ВС' соответственно. Разложите по век¬
торам р = АВ'У q=Aby г=А*А' векторы: а) А*В'\ б)АС
6—1681
161
в) Ш\ г) Ttfi-, д) Jр- е) Л$, где Q^D'C' и Wt}: D'C'=
5:11.
4.33. Вне плоскости параллелограмма ABCD взята точка О. Раз¬
ложите по векторам а = 0%, Ъ = 0&у с = од векторы:
а) 0%1, где М — точка пересечения АС и BD\ б) OD\ в)
О*, где /С — середина Л£.
4.34. Что называется координатами вектора?
4.35. Как меняются координаты вектора при умножении его на
число?
4.36. Как по координатам двух векторов найти координаты век¬
тора их суммы?
4.37. Как связаны координаты радиуса-вектора с координатами
его конца?
4.38. Как по координатам начала и конца направленного отрезка
найти координаты вектора, изображаемого этим отрезком?
4.39. Чем отличаются действия с координатами векторов на плос¬
кости и в пространстве?
4.40. Дан нулевой вектор ОА. Отложите от точки О векторы:
а) '/2бЙ; б) -20?; в) -2/30%; г) 20Й; д) -ЗОЙ.
4.41.0 — точка пересечения диагоналей параллелограмма ABCD.
Найдите х, если: a) Ah =хСЪ\ б) АС=хАО\ в) ОВ=хЁЪ\
г) ($C=xCD.
4.42. В треугольнике ABC медианы ЛЛ', ВВ\ СС' пересекаются
в точке М. Найдите множитель k> если: a) A*C=feffC;
б) AC = k(?X'\ в) Ш = г) C^’=kCtl\ д) мЖ'=
= kWb\ е) Ш = кАХ'.
4.43. Разложите по ортам координатных осей _^на плоскости или
в пространстве) следующие векторы: а) ОА, где Л (—1; 2);
б) ЛЬ, где /1(0; 1), В(1; 0); в) Ш, где А( 1; 2; -3);
г)ЛЬ, где А (—1; 2; 1), В (0; 2; 3).
4.44. Выразите: а) ш — 5п через а и Ь, если ш = а + Ь, п = а — Ь;
б) Зш —2п через а и b и а и b через шип, если т = 2а—ЗЬ,
п='/2а + 2Ь; в) а, Ь, с через т, п, р, если m = a-fb + c,
n = a + b — с, р = а — b — с.
4.45. Выразите вектор с через векторы а и Ь:
а) a = 4i — 2j, b = 3i + 3j, с = i — 7j,
б) a = 5i + 4j, b = —3i, c=19i + 8j,
в) a =—6i + 2j, b = 4i + 7j, c —9i 3j.
4.46. Выясните, при каком значении к вектор а + AJb коллинеарен
вектору с:
а) а = i + 5j, b = 2i + 3j, с = i — 2j,
б) а = 4i — 3j, b = i — 4j, c = 2i + 5j,
в) a = 4i + 6j, b==2i — 6j, c = i + 3j.
162
4.47. Постройте в пространстве точки (—1; 1; 2), (—2; 3; 1).
4.48. Как узнать по координатам точки, лежащие: а) в плоско¬
сти Оху, б) на оси х\ в) на оси z?
4.49. Где лежат точки пространства с координатами (х; у\ z),
у которых Jt^O?
4.50. Какую фигуру заполняют точки пространства с координа¬
тами (х\ у\ z), если: а) |х|<1; б) |х|<1, li/Kl, |z|< 1 (все
неравенства выполняются одновременно)?
4.51. Произведите указанные действия над радиусами-векторами
точек А (1; 1; 1), В (0; 1; —1), С (2; 0; —3): а) Ш + Ш+
+ о£; б) о%—Ш—оЕ-. в) 20Й+зб£—о£.
4.52. Даны точки: А (ха\ Уа \ za) и В (хв, ув, zB). Докажите, что
точка С (середина отрезка АВ) имеет координаты: Хс =
— /^ХА+Хв), Ус = 1/АУа+Ув), Zc = 1/2(za+zb).
4.53. Найдите середины сторон треугольника ABC для точек за¬
дачи 4.51.
4.54. Найдите координаты вектора АВ: а) Л(2; 1; 0), В(1; —2; 3);
б) Л(1; 2; 3), В(3; 0; -Ч); в) А(3У -1; 4), В(0; 2; -3).
4.55. От точки А отложен вектор АВ = а. Найдите координаты
точки В: а) А (0; 0; 0), a=2i + j — к; б) Л (3; 1; —2), а=
= i-3j + k; в) Л (1; -1; 0), a=3i-2j.
4.56. Найдите координаты середины отрезка АВ: а) Л(2; 1; 2),
В (—1; 4; 0); б) А (3; -1; 2), В (—3; 1; -2); в) Л (4; 2;
-2), В (2; -1; 2).
4.57. Найдите координаты центра масс треугольника: а) Л (1; 1; 1),
В (—1; 0; 2), С(1; 2; 4); б) Л (-1; 2; 4), В (0; 3; -1),
С (—1; -1; 2); в) Л( 1; 3; -2), В (0; 0; 4), С (3; 9; -10).
4.58. Найдите координаты вершины D и координаты точки пере¬
сечения диагоналей параллелограмма ABCD: а) Л (0; 0; 0),
6(1; 2; 3), С (—1; 1; -2); б) Л (—1; 2; 1), В (0; 4; 4),
С(-2; 3; -1); в) Л(—1; 1; 2), fl(0; 3; 5), С(-2; 2; 0).
4.59. Каким вектором задается положение точки?
4.60 Как связан вектор перемещения с векторами положения
точки?
4.61 Верно ли, что векторы скорости и перемещения коллине-
арны? Почему?
4.62. Точка движется по прямой с постоянной скоростью. Через
2 с после начала движения она имела координаты (—1; 3),
а через 5 с— (5; 0). а) Найдите вектор скорости. Разло¬
жите его по ортам координатных осей, б) Какие координа¬
ты имела точка в начальный момент? в) Напишите вектор¬
ное уравнение движения точки, г) Напишите уравнение
движения точки в координатах, д) Напишите уравнение
прямой, по которой движется точка.
4.63. К концу кронштейна приложена сила mg = 20 Н. Найдите
силу растяжения стержня АВ и силу сжатия стержня ВС
(рис. 228).
4.64. К концу кронштейна приложена сила mg = 42H. Найдите
6*
163
силу сжатия стержня ВС и силу растяжения стержня АВ
(рис. 229).
4.65. Проволока закреплена в точках Л и С, а в точке В прило¬
жена сила mg = 45 Н. Найдите усилия на участках АВ и ВС
(АВ горизонтально, рис. 230).
4.66. Проволока закреплена в точках Л и В, а в точке С прило¬
жена сила mg = 45H. Найдите усилия на участках АС и
ВС, если Л и В — на одном уровне (рис. 231).
4.67. Мачтовый кран состоит из стрелы АС и цепи ВС. К концу
стрелы приложена сила mg. Разложите mg по направле¬
ниям АС и ВС (рис. 232).
Рис. 230
Рис. 231
4.68. Сани тянут по снегу за веревку. Какие силы действуют на
сани? Разложите силу натяжения веревки на горизонталь¬
ную и вертикальную составляющие.
4.69 Какие действия определены в векторном пространстве?
4.70 Напишите два противоположных квадратных трехчлена.
4.71. Образуют ли скалярные величины векторное пространство?
4.72 Дайте определение размерности.
4.73 Какие векторы называются линейно зависимыми?
4.74. В чем состоит переместительный закон сложения векторов?
Какой геометрический смысл он имеет?
164
Рис. 228
Рис. 229
4.75. Как формулируется сочетательный закон сложения век¬
торов?
4.76. Какие другие (кроме переместительного и сочетательного)
законы сложения векторов вам известны?
4.77. Сформулируйте законы умножения вектора на число.
Рис. 232
4.78. Нарисуйте все векторы, связанные с прямолинейным равно¬
замедленным движением точки.
4.79. Как в векторной форме записать движение точки с постоян¬
ным ускорением?
4.80. Сложите квадратные трехчлены \х=2х2—х+1 и f2 =
= — х2-\-х. Вычислите 2/,— f2. Какой квадратный трехчлен
будет противоположным трехчлену f{?
4.81. В строчке Л, =(500, 190, 160, 210) указана зарплата че¬
тырех рабочих за первый месяц (руб.), а в строчке Л2=
= (170, 190, 150, 230)—аналогичные данные за второй
месяц. Составьте строчку, указывающую среднюю зарплату
рабочих за два месяца. Как выразить строчку А через
строчки Л, и Л2?
4.82.* Образуют ли векторное пространство: а) линейные функ¬
ции у=ах-\-Ь по отношению к обычным операциям сложе¬
ния и умножения на число; б) линейные функции, обра¬
щающиеся в нуль при х = 0; в) линейные функции, обра¬
щающиеся в единицу при jc = 0?
5
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Тригонометрия треугольника
Тригонометрия возникла как наука об измерении треугольников
в связи с необходимостью производить астрономические вычис¬
ления и долгое время была частью астрономии. В средние века
она отделилась от астрономии и стала самостоятельной частью
математики. Последовательное изучение тригонометрических
функций как функций произвольного числового аргумента связа¬
но с именем замечательного математика XVIII в. Леонарда Эйле¬
ра. Оно открыло до[югу самым широким применениям тригоно¬
метрических функций и вместе с тем соединило их изучение
с изучением других функций, покончив с изолированным поло¬
жением тригонометрии внутри математики.
Вычисления в треугольниках — это истоки тригонометриче¬
ских функций. Значение этих вычислений сохраняется до наших
дней. Поэтому мы начнем изучение тригонометрии с того, что
вспомним, как применяются синус, косинус, тангенс и котангенс
для решения треугольников.
В треугольнике три угла. Их можно измерять в градусах.
Сумма углов треугольника равна 180° (рис. 233). Угол 90° на¬
зывается прямым, меньший 90° — острым, больший 90° — тупым
(рис. 234).
§18. Углы и повороты
Рис. 234
166
Рис. 233
Рис. 235
В прямоугольном треугольнике отношения сторон не зависят
от их длин, а зависят только от углов треугольника (рис. 235).
Эти отношения называются синусом, косинусом, тангенсом и ко¬
тангенсом.
Пусть а— острый угол прямоугольного треугольника. Отношение про¬
тиволежащего ему катета к гипотенузе называется синусом угла а, от¬
ношение прилежащего катета к гипотенузе называется косинусом
угла а. Отношение противолежащего катета к прилежащему называется
тангенсом, прилежащего катета к противолежащему — котангенсом.
Основные соотношения для прямоугольного треугольника
(рис. 236):
sina = —; tga = -£-;
с ’ Б Ь ’
Ь , ь
cos a = —; ctga = —;
с s a ’
sin2 a + cos2 a = 1 (теорема Пифагора);
I sin a i cos a
& cos a e sin a
tgactga= 1; tgp = ctga;
sin p = cos a;
о • P = tg a.
cos p = sin a; & к &
Рассмотрим частные случаи приведенных соотношений.
1. Равнобедренный прямоугольный треугольник. Его острые
углы а = р=45° (рис. 237). Оба катета в таком треугольнике
Рис. 236
Рис. 237
Рис. 238
равны и если их длины принять равными 1, то по теореме Пифа¬
гора длина гипотенузы равна /Т. Поэтому
sin 45°= cos 45° = Щ- ; tg45° = ctg 45° = 1.
2. Прямоугольный треугольник, у которого гипотенуза вдвое
больше одного из катетов. Его острые углы — 30° и 60° (рис. 238).
Катет, лежащий против угла 30° в таком треугольнике, в два раза
меньше гипотенузы. Если его длину принять равной за 1 (т. е. ги¬
потенуза равна 2), то другой катет по теореме Пифагора ра¬
вен /37. Поэтому
sin 30° = cos 60° = -Ь tg 30° = ctg 60° = JL = ;
sin 60° = cos 30°= ctg 30° = tg 60° = /3".
В общем случае знание одной из сторон и одной из тригоно¬
метрических функций острого угла достаточно для вычисления
всех элементов прямоугольного треугольника. Знание двух сто¬
рон (а значит, и третьей по теореме Пифагора) достаточно для
вычисления тригонометрических функций углов прямоугольного
треугольника.
Упражнения
1. Даны катеты а и Ь. Вычислите
гипотенузу и тригонометрические
функции углов, если:
а) а=3, Ь=4; б) а=5, Ь=12;
в) а= 1, Ь—2.
2. Даны катет а и гипотенуза с. Вы¬
числить другой катет и тригоно¬
метрические функции углов, если:
а) а=3, с=5; б) а= 15, с= 17;
в) а= 1, с=Ъ.
3. Даны катет а (или гипотенуза с)
и одна из функций противолежа¬
щего угла а или прилежащего
угла р. Вычислить неизвестные сто¬
роны.
4. Найдите неизвестные величины в
треугольниках:
а) а=5, sina=3/5;
б) а—5, cosa=0,6;
в) a=5, tga=2;
г) a=5, ctga=0,l;
д) a=5, sin|}=0,8;
е) а=Ь, tgp=10;
ж) с= 10, sina=0,5;
з) с=10, cosa= 12/13;
и) с=10, tga=l;
к) с= 10, ctga=0,75.
5. Какие значения могут принимать
синус, косинус, тангенс и котангенс
углов прямоугольного треугольника?
6. Для каких углов синус меньше
косинуса?
7. Для каких углов синус больше по¬
ловины?
8. Для каких углов котангенс меньше
единицы?
9. Что больше: синус или тангенс угла
треугольника?
10. Заставим в прямоугольном тре¬
угольнике угол а приближаться
к нулю. Как будут вести себя
тригонометрические функции угла
а? тригонометрические функции дру¬
гого острого угла р?
168
Углы и их измерение
Геометрически угол — это часть плоскости, ограниченная двумя лучами,
выходящими из одной точки. Эти лучи называются сторонами угла, а
точка, из которой они выходят, — вершиной (рис. 239).
Как измеряют углы? В качестве единицы геометрических
углов принят градус, т. е. ^зво полного угла. Конкретные углы
удобно измерять в градусах с помощью транспортира (рис. 240).
На практике часто приходится иметь дело с углами, которые
получаются в результате вращения одной стороны относительно
другой (рис. 241).
Во многих оптических приборах также используют градусную
неру угла. Углы, получающиеся при непрерывном вращении,
удобно измерять не в градусах, а с помощью таких чисел,
которые отражали бы процесс построения угла, т. е. вра¬
щение.
Представим себе, что зафиксирована не только вершина угла,
но и один из образующих его лучей (рис. 241). Другой луч вра¬
щается вокруг вершины. Получающиеся углы будут зависеть от
угловой скорости вращения и времени. Можно считать, что вра¬
щение происходит равномерно (с постоянной угловой ско¬
ростью). Тогда угол поворота определяется длиной дуги, по ко¬
торой проходит какая-либо фиксированная точка подвиж¬
ного луча.
Если расстояние от точки до вершины равно /?, то при вра¬
щении точка движется по окружности радиуса R. В простейшем
Рис. 239
Рис. 240
Рис. 241
169
случае при /? = 1 угол — это путь, который пройдет точка по
окружности единичного радиуса.
Чему равен полный угол? Ясно, что величина полного угла
равна длине единичной окружности, т. е. числу 2л (где л — отно¬
шение длины окружности к ее диаметру). Число л было известно
людям с глубокой древности и с довольно большой точностью.
Первые десятичные знаки этого числа таковы: л = 3,14159265358...
Итак, полный угол равен 2л, развернутый — л, а прямой —
л/2. Угол величины 1 называют радианом (рад), а введенную
меру угла — радианной.
Радианную меру легко связать с градусной. Достаточно срав¬
нить меры одного и того же угла, например прямого: л/2 рад=
= 90°, откуда
1° = л/180° «0,017 рад.
Обратно: можно выразить 1 рад в градусной мере, т. е.
1 Рад = — .90° = — • 1° = ... = 57°,296.
Я Я
В географии, астрономии и других прикладных науках ис¬
пользуют доли градуса — минуту (') и секунду ("). Минута —
это 1/60°, а секунда— 1/60'. Запишем соотношения между раз¬
личными единицами углов:
1° = 0,017 рад;
1,=(w),=0’0003 рад;
'"“(^'-(w)-0’000005
1 рад = 57°,296 = 57° 17'45".
Градусный и радианный способы измерения углов равно¬
правны и используются достаточно широко. Так, широту и дол¬
готу точки на земном шаре обычно задают в градусах и минутах.
При проведении приближенных вычислений обычно заменяют
sin а на а (при малых углах а), но это можно делать только
тогда, когда угол выражен в радианах.
Заметим еще, что обозначение градуса (минуты, секунды)
записывают, а обозначение радиана, как правило, пропускают
(так как с физической точки зрения угол — безразмерная вели¬
чина, например а = 0,23; а = 3,14; а = 0,01).
Во многих случаях радианную меру угла удобно записать
в виде доли угла л:а = л/3 (вместо а=1,05), а=2/5л (вместо
а= 1,26) и т. п.
Рассмотрим равномерное движение точки окружности единич¬
ного радиуса со скоростью v = l в зависимости от времени t.
Надо указать, в каком направлении происходит движение.
В качестве положительного направления движения по традиции
170
Рис. 242
выбирается направление движения против часовой стрелки
(рис. 242).
Представим себе маленький шарик, который равномерно дви¬
жется по окружности в положительном направлении. Будем счи¬
тать, что в момент времени / = О шарик находился в положении А
и за время t= 1 прошел по окружности расстояние, равное 1.
Тогда за время, равное л, он пройдет расстояние, равное я, т. е.
половину окружности.
Обозначим Pt точку на окружности, в которой шарик нахо¬
дится в момент времени t. Для того чтобы найти положение этой
точки, надо отложить от точки Р0=А по окружности путь дли¬
ны |/| в положительном направлении, если />0, и в отрицатель¬
ном направлении (т. е. по часовой стрелке), если /<0.
Примеры
1. Пусть /=я/4. Отложим от точки Ро в положительном
направлении путь длины я/4. Так как длина всей окруж¬
ности равна 2я, то точка Ря/4 является серединой дуги АВ
(рис. 243).
2. Пусть / = 9л/4. Отложим от точки Р0 путь длины 9л/4.
Заметим, что 9я/4 = 2я + л/4. Пройдя путь 2л, точка опять
171
Рис. 243
Рис. 244
попадает в А. Пройдя оставшийся путь, она попадает в
середину дуги АВ. Таким образом, точка Р9л/4 совпадает
с точкой Рл/4.
3. Найдем теперь точку Р-л/з. Для этого точке необхо¬
димо пройти в отрицательном направлении путь л/3
(рис. 244).
Таким образом, мы для каждого значения t построили точ¬
ку Pty а значит, и угол. До сих пор у нас были только геометриче¬
ские углы. Их значения изменялись от 0 до 2л (или от 0 до 360°).
Иногда обобщают понятие угла и говорят об угле t для любого
значения /, понимая под этим угол, строящийся с помощью вра¬
щательного движения за время t. Теперь можно говорить об
угле, равном 5л; —11 л/2; 10,1; —5 и т. п.
Оси координат делят плоскость на четыре четверти. В зависи¬
мости от того, в какую часть плоскости попадает точка Р/,
говорят о том, в какую четверть попадает угол t. При этом по¬
лезно помнить, что 1 рад чуть меньше 60°, т. е. трети разверну¬
того угла.
Упражнения
I Переведите углы из радианной меры
в градусную: ‘/„я, 7„я, 7/6я, 2/3я,
/г", /е"-
Переведите углы из градусной меры
в радианную: 60, 135, 150, 210, 230,
270, 300, 320°.
3. В какой четверти лежат углы 2; 3;
3,5; п/4л; 5?
4. Постройте точки Р:. соответствую¬
щие следующим значениям t: 1; 2;
3; 4; 5; —3; —4; 10; 100л; —12%л;
—7/6л; п/2п.
Свойства вращательного движения
Свойство 1
Для всякого целого числа к точка Р, совпадает с точкой Р, + 2 кл.
(если моменты времени отличаются на целое кратное число 2лг то точка
в эти моменты времени занимает одно и то же положение (рис. 245).
Это свойство выражает периодичность вращательного дви¬
жения.
Действительно, в разные моменты времени точка может за¬
нимать на окружности одно и то же положение. Так, в примере 2
(см. с. 171) мы убедились, что Ря/4=Р9л/4. Это произошло из-за
того, что числа 9л/4 и л/4 отличаются друг от друга на 2л, а
за время / = 2л точка проходит всю окружность и возвращается
в исходное положение. Аналогично, если разность tx — t2 равна
4л, 6л, 8л или —2л, —4л и т.д., то Ptl=Pt2y т. е. в моменты
времени /,±2л, /!±4л, ... точка занимает одно и то же поло¬
жение на окружности.
Свойство 2
Если Р,, = Р,2, то найдется такое целое число к, что f, — t.2 + 2лк
(рис. 246).
172
Рис. 245
Рис. 246
Действительно, если в два каких-то момента времени поло¬
жения точки совпали, то между этими двумя моментами точка
прошла целое число раз всю окружность.
Свойство 3
Для всякого значения t точки Р, и Р, + л диаметрально противоположны
(рис. 247).
Действительно, за время я точка проходит половину окруж¬
ности и занимает положение, диаметрально противоположное
исходному.
Свойство 4
Для всякого значения t точки Р, и Р_, симметричны друг другу относи¬
тельно оси абсцисс (рис. 248).
173
Рис. 247
Рис. 248
Действительно, для построения точек Pt и P-t надо отложить
от точки Р0 дуги, равные |/|, но в противоположных направ¬
лениях.
Свойство 5
Для всякого значения t точки Р# и Р_, + л симметричны относительно оси
ординат (рис. 249—251).
Это свойство выводится из свойств 4, 3.
Свойство 6 ——
Для всякого значения t точки Pf и Pfy-t симметричны друг другу относи¬
тельно биссектрисы первого и третьего координатных углов (рис. 252).
Возьмем две точки: Р0 и Рл/2. Они симметричны друг другу
относительно биссектрисы первого и третьего координатных
углов. Точка Pt получится при перемещении на расстояние |/| в
одном каком-то направлении от Р0, а точка Pn/2-t — при пере¬
мещении на такое же расстояние от точки Рл/2, но в противопо¬
ложном направлении.
Ясно, что в этом случае точки Pt и Pn/2-t при всяком t будут
оставаться симметричными друг другу относительно указанной
прямой.
174
Рис. 249
Рис. 250
Рис. 251
Рис. 252
Упражнение
противоположны; симметричны от¬
носительно:
а) оси абсцисс;
б) оси ординат;
в) биссектрисы первого и третьего
координатных углов;
г) биссектрисы второго и четвер-
укажите такое значение при кото¬
ром точки Pt и Pf: диаметрально того координатных углов.
§ 19. Определение тригонометрических функций
Координаты вращающейся точки
Первоначально тригонометрические функции — синус, косинус,
тангенс и котангенс — были введены нами для острых углов —
углов прямоугольного треугольника. Определим эти функции для
произвольного числового значения аргумента, который пока обо¬
значим буквой /, так как тригонометрические функции связаны
с некоторым движением, зависящим от времени t.
Пусть дано произвольное число t. Как построить угол t? Надо
представить себе шарик, вращающийся по единичной окружно¬
сти с единичной скоростью (рис. 253). Пусть в начальный мо¬
мент времени t = 0 он находится в точке Л (1; 0). В момент вре¬
мени t он будет находиться в некоторой точке Pt. Угол t — это
угол, образованный лучами ОА и ОР/.
Точку Pt можно построить геометрически, отложив от точки А
по окружности путь, равный |/|, в положительном или отрица¬
тельном направлении в зависимости от знака t.
Возьмем произвольное число t. Построим угол, задаваемый
точкой Pt на единичной окружности. Пусть, (х; у) — координаты
+очки Pt.
Синусом числа t называется ордината точки Р,: sin f = у.
Косинусом числа t называется абсцисса точки Р,: cos f = x (рис. 253).
Тангенсом числа t называется отношение ординаты точки Р, к ее абсциссе:
tgf = y/x.
Котангенсом числа t называется отношение абсциссы точки Р, к ее орди¬
нате: ctg f = х/у.
Если угол t лежит в первой четверти, то абсцисса и ордината
точки Pt являются длинами катетов треугольника OPtQ (рис. 254).
В этом случае определения тригонометрических функций явля¬
ются теми же самыми, какими они были для углов прямоуголь-
«Латынь Эйлера проста и обозначения почти современны — лучше было
бы сказать, что современные обозначения почти Эйлеровы.»
Д: Я. Стройк
175
Рис. 253 Рис. 254
ного треугольника. В остальных четвертях значения тригоно¬
метрических функций также могут быть определены из треуголь¬
ников, только при этом надо учитывать знаки координат точ¬
ки Pt и связь угла t с острыми углами треугольника (см. с. 180).
Упражнения ось * Если точка Pt имеет коорди¬
наты (х\у), как записать через х
1. По какой оси откладываются зна- и у длины катетов треугольника
чения синуса? OP,Q?
2. По какой оси откладываются зна- 5. Как записать теорему Пифагора для
чения косинуса? треугольника OPtQ? Какое соотно-
3. Точка Pt на единичной окружности шение мы получаем для синуса и
имеет координаты (—3/5; 4/5). косинуса произвольного числа /?
Вычислите sin/, cos/, tg/, ctg/. 6. Как выражаются тангенс и котан-
4. Пусть Q — проекция точки Pt на гене через синус и косинус?
Периодичность
При изучении вращательного движения в качестве первого его
свойства мы назвали периодичность; пройдя полный оборот,
вращающаяся точка займет то же положение, что и вначале:
Rt + 2nk = Pt (k£Z).
Тригонометрические функции определены с помощью координат
вращающейся точки. Поэтому раз для двух чисел t и /-\-2nk по¬
ложения вращающейся точки совпадают, то совпадают и значе¬
ния всех тригонометрических функций от этих чисел:
sin (/ + 2nk) = sin t\ tg (t + 2nk) = tg t\
cos (t + 2nk) = cos t\ ctg (t + 2nk) = ctg t.
Функции, значения которых не изменяются при прибавлении к аргументу
какого-либо постоянного числаг называются периодическими функциями.
Синус, косинус, тангенс и котангенс являются периодическими функциями.
Равенство s\n(t-\-2n)=s\n t верно при всех значениях t. Это
означает, что число 2л является периодом синуса. Подставляя
в это равенство вместо / число / + 2л, получаем цепочку равенств
176
sin(/ + 2n + 2n)=sin(/ + 2n)=sin t, т. e. равенство siri(/4-4n)=
= sin/ также верно при всех значениях /. Аналогично; подстав¬
ляя вместо t число / — 2я, получаем тождество sin (/—^2n)=sin t.
Так как 2л — период синуса, то и 2*2я, —2 л,..;, тайже явля¬
ются его периодами. Точно так же всякое число вида 2nk(k£Z)
является периодом синуса.
Однако 2л выделяется тем, что это наименьший положитель¬
ный период синуса. Аналогично, 2л — наименьший положитель¬
ный период косинуса. В отличие от них 2л хотя и является
периодом тангенса и котангенса, однако не наименьшим среди
положительных периодов этих функций (см. с. 193). Более под¬
робно свойства периодичности рассмотрены в § 20.
Упражнения
1- Выясните, какие из написанных
ниже равенств являются тождест¬
вами и почему:
а) sin/ = sin(f—4л);
б) sin(f—n)=sin(/+n);
в) cos(/ — 3/2n) = cos(/ + n/2);
г) cos/ = cos(/+3n).
2. Даны точки t\ = 2n/3; /2=— л/6;
/з=7л/2; *4 = 4я/3; *«=19л/6; /6 =
= —10л/3; ti— — л/6; /в = 5л/3.
В каждом из указанных ниже интер¬
валов длины 2л найдите точки,
отличающиеся от данных на целое
кратное 2л (на полное число обо¬
ротов):
а) [0, 2л]; б) [—л, л]; в) [л, Зл].
Знаки тригонометрических функций
Знаки тригонометрических функций определяются в зависимости от
того, в какой четверти лежит рассматриваемый угол.
Синус числа t есть ордината точки Pt. Поэтому синус положи¬
телен в первой и второй четвертях и отрицателен в третьей и
четвертой (рис. 255).
Аналогично, косинус числа t как абсцисса точки Pt положи¬
телен в первой и четвертой четвертях и отрицателен во второй
и третьей (рис. 256).
знаки
синуса
знаки
косинуса
Рис. 255
Рис. 256
177
Рис. 257
Тангенс и котангенс являются отношениями координат. По¬
этому они положительны тогда, когда эти координаты имеют
одинаковые знаки (первая и третья четверти), и отрицательны,
когда разные знаки (вторая и четвертая четверти; рис. 257).
Упражнение
Определите знаки следующих значе¬
ний тригонометрических функций:
a) sin(7n/6); б) sin2;
в) sin(—5л/3); з) cos(5n/4);
г) sin(7n/4); и) tg(—Зя/4);
д) cos(5л/6); к) ctg(10n/3);
е) cos3; л) tg(2n/3);
ж) cos(—4я/3); м) ctg(l 1 jx/6).
Четность
Синус — нечетная функция: при всех t выполнено равенство sin (—t) =
= —sin t (рис. 258).
Косинус — четная функция: при всех f выполнено равенство cos ( f) =
= COS t.
Действительно, для всякого значения t точки Pt и P-t сим¬
метричны друг другу относительно оси абсцисс (свойство 4 вра¬
178
Рис. 258
щательного движения). У точек Pt и P-t совпадают абсциссы
(cos(—/) = cost), а ординаты противоположны (sin(—/)= —sin/).
Тангенс и котангенс — нечетные функции.
Действительно, известно, как эти функции выражаются через
синус и косинус:
tg< = JL = !iHi( ctg* = ^- = ^f.
° х cost ° у sin /
Зная поведение синуса и косинуса при замене t ма — /, получаем
доказательство нечетности тангенса (и аналогично, котангенса):
t ы-t) = 5^-~0. = ~sinf = _ let
^ 4 cos(—/) COS / ё
Упражнения
Выясните четность следующих функ¬
ций:
а) z = —sin/;
б) z = —cos /;
в) z=sin2/;
г) z — cos3/;
д) z = sin/cos/;
е) z = sin3/;
ж) z = sin2/ — cos2/;
з) z = sin/ + cost.
Простейшие тождества
Тригонометрические функции связаны между собой рядом
тождеств.
Основные тождества:
3. ctg t =
COS 1
COS /
sin /
4. tg f-ctg t = 1.
5. 1 + tg21 = 1
6. 1 + ctg21 =
cos2 /
1
sin2 /
Тождество 1 как следствие теоремы Пифагора получено нами
в упражнении на с. 176. Тождества 2 и 3 — это другая запись
определения тангенса и котангенса, которую мы уже использо¬
вали раньше. Тождество 4 получается перемножением тож¬
деств 2 и 3. Покажем вывод одного из тождеств:
1 + tg2<=1 +
sin2/
cos2/
cos2 / + sin2/
cos2/
1
cos2/
Упражнение 6) cos4 / — sin4 / = cos2 / — sin2/;
Выведите с помощью основных тож- * 1 -|-ctg2a 2
деств следующие тождества: в' tgza-|-ctg2a С ^
а) tg/ + ctg/=^-j! Г) ‘g2P-si"2P=tg2psin2p.
6 6 sin/cos/
179
Формулы приведения
Значения тригонометрических функций острых углов можно вы¬
числить по таблицам или с помощью прямоугольного треуголь¬
ника. Их вычисление для любого значения аргумента можно
привести к вычислению значений для аргумента t ^ [0, л/2].
Соответствующие формулы так и называются — формулы при¬
ведения. Они основаны на симметрии вращательного движения.
Основные формулы:
1. sin(/ + л) = — sin t. 4. cos(t -|- л) = — cos t.
2. sin (л — t) = sin t. 5. С08(л — t) = — cos t.
3. sin(V2 — 0 = cos t. 6. cos(V2 — t) = sin t.
Формула 1—это запись в координатной форме свойства 3
вращательного движения, формулы 2 — свойства 5, а форму¬
лы 3 — свойства 6. Для их уяснения полезно еще раз посмотреть
на рис. 247, 249—252.
Используя свойства периодичности, четности и формулы 1—3,
можно привести вычисление синуса и косинуса любого числа к
значению /, лежащему между 0 и л/2, т. е. к 0 < / < л/2. Поэто¬
му формулы 1—3 называют формулами приведения.
Можно вывести и другие формулы приведения:
sin^/2 + 0 = cos/; соэ(л/2 + /) = — sin/.
Доказательство: s\n(n/2 + t) = s\n(n/2 — (—/)) =
= cos (—/) = cost; cos(n/2-\-t) = соз(л/2 — (—/)) = sin(— /) =
= — sin(/).
Аналогично выведем формулы
8т(Зл/2 + 0= — cos/; со8(Зл/24-/) = — sin t.
Формулы приведения для тангенса и котангенса получаются
как следствие полученных формул для синуса и косинуса, на¬
пример:
Формулы приведения:
sin (я/2 — /) = cos t\ sin ("/2 +0 — — cos sin(/ — n/2) = cos<;
cos (я/2 — 0 = sin /; cos (“/2 + 0 = sin /; cos(/ — n/2) = sin /;
tg (V2 0 = ctg t\ tg(n/2 + /) = -ctgt; tg(/-V2) = ctg/;
ctgfA — 0 = tg/; ctg(*/2-f/)=—tg/; ctg(/ — 72) = tg/;
sin (я — /) = sin/; sin(H-f-/) =—sin/; sin(/ — я)=—sin/;
cos (я — /) = — cos /; cos (n-\-t)=—cost; cos (/— я)=— cos/;
эт(Зя/2 —/) = —cos/; зт(Зя/2 + /) = — cos/; sin(/ —Зя/2) = со5/;
соз(Зя/2 —/)= — sin/; cos(3H/2 + /) = sin/; cos(/ —Зя/2) = —sin/.
180
Название функции не меняется, если к аргументу левой части добавля¬
ется —л или +л, и меняется, если добавляются числа ± л/2 или ± Зл/2.
Знак в правой части определяется знаком левой при 0<f<n/2.
Примеры
1. Вычислить sin
о
Представим —так: -^-=6л + -|-л. Далее, sin =
bob b
= sin (бл + -|-л) = sin -|-л = sin (л — sin -|-= тг-
9 82л (оа I 4л Ч 4 л / , л \ 1
l- cos -J— = cos (26л + — 1 = cos — = cos 1л + —1= Y ■
Л 82л /ос 2л \
А можно иначе: cos —= cos 128л — I =
(2л \ 2л / л \ л
t )=cos — = с°8(л-—)=-c°s— =
= Т'
Значения тригонометрических функций
Вычисление значений тригонометрических функций имеет длин¬
ную историю. Потребности точных астрономических наблюдений
вызвали к жизни появление огромных таблиц, позволяющих про¬
изводить вычисления с четырьмя, пятью и даже семью (и более)
знаками. На составление этих таблиц было потрачено много уси¬
лий. Сейчас, нажав кнопку микрокалькулятора, можно момен¬
тально получить требуемое значение величины с очень высокой
точностью. С помощью ЭВМ нетрудно найти значения тригоно¬
метрических функций с еще большей степенью точности.
Известные нам свойства тригонометрических функций облег¬
чают вычисления и позволяют разумно использовать вычисли¬
тельные устройства.
1. С помощью формул приведения вычисление значения три¬
гонометрической функции любого числа можно свести к вычисле¬
нию функции от угла, лежащего в первой четверти.
2. Достаточно знать значение лишь одной из тригонометри¬
ческих функций. С помощью основных тождеств и зная четверть,
в которой лежат значения аргумента, легко найти значения
остальных функций.
Примеры
Пусть sin/= — — и t лежит в третьей четверти. Тогда
о
cos21 = 1 — sin2/ = -jjjr и cost = — у-, так как косинус в
181
третьей четверти отрицателен. Получаем tg/ = -j- и
2. cos/ = —/£ > 2л J. Получаем: sin/ = — ^ 1 —i- =
*g<--2/T, 018/ = -^=--^.
3. tg/= —10 и / лежит во второй четверти. Получаем: cos2t=
1 4 1
и cos t =
101 f/ТоГ
sin/ = tg/cos/ = —7==r-; ctg/ =
Полезно помнить значения тригонометрических функций
для углов двух прямоугольных треугольников: равнобед¬
ренного и треугольника с углами 30° (л/6) и 60° (л/3).
Эти значения обычно записывают с помощью радикалов
и при необходимости эти радикалы заменяют их прибли¬
женными значениями ( /2~ = 1,414..., /3~ = 1,7...). Сведем
их в таблицу, дополнив ее значениями тригонометрических
функций аргументов / = 0 и / = л/2.
Таблица 3
t
sin t
COS t
•g'
ctg t
0
0
1
0
—
л
1/2
V3/2
i V3
V3
Т
л
1 У2
1 V2
1
\
т
У2 “ 2
л/2 “ 2
л
т
V3
2
1/2
л/3
1 л/з
vr=~
л
т
1
0
—
0
Упражнения
1. Зная значение одной из функций и
четверть, в которой лежит угол,
вычислите значения трех других
тригонометрических функций:
а) sin/ = 12/13, /€=[я/2,я];
б) cos/ = — 1/5, л</<Зя/2;
в) ctg/ = 5/2, л</<Зл/2.
2. Используя формулы приведения и
таблицу значений, вычислите сле¬
дующие значения тригонометриче¬
ских функций:
х 2л
а) sin—;
/сч 5л .
б) cos-^-;
о
V * 7я
в) tg—;
г) ctg
4л
182
Решение простейших уравнений
Мы рассмотрели вопрос о вычислении значений тригонометри¬
ческих функций. Решение уравнений приводит к обратной зада¬
че — по значению функции найти угол. Для полного решения
этой задачи необходимо ввести обратные тригонометрические
функции, изучение которых мы отложим на будущее.
Для решения некоторых особенно простых, но важных урав¬
нений достаточно вспомнить определение тригонометрических
функций с помощью координат точек единичной окружности.
Примеры
1. sin/ = 0. Вращающаяся точка Pt имеет нулевую ординату
в моменты времени * = 0,я, 2я, ..., а также /==—я,
— 2я, ... . В общем виде множество этих значений можно
записать в виде t = nk (JeZ). Таким образом, решением
уравнения sin/ = 0 будут числа t = nk (рис. 259).
Рис. 260
Запишем кратко ответы для решения еще нескольких
уравнений, которые вам предлагаются для самостоятельной
проверки (k£Z):
2. sin/=l, /=я/2 + 2яЛ (рис. 260).
Рис. 261
Рис. 259
Рис. 262
3. sin/=— 1, t =—n/22nk (рис. 261).
4. cos/ = 0, t = n/2-\-nk (рис. 262).
5. cos / = 1, t = 2nk (рис. 263).
6. cos/ = — 1, / = я + 2nk (рис. 264).
Заметим, что все рассмотренные уравнения имеют бесчислен¬
ное множество решений. Они записываются в виде бесконечных
серий с помощью переменной (в наших примерах — &)> которая
может принимать любые целые значения.
Часто приходится искать не все решения тригонометрического
Рис. 263 рис 264
уравнения, а только те, которые лежат в определенном проме¬
жутке. Тогда решений обычно бывает конечное число (часто
просто одно) и их можно перечислить.
Примеры
1. cos / = 0, / ^ [я, 2я].
В указанном промежутке уравнение cos / = 0 имеет одно
решение t = Зл/2.
184
Рис. 265
2.
sin/ = 1/2, t e jj-, я].
Из рис. 265 видно, что решение единственно: / = л — л/6 =
= 5 л/6.
Упражнения
Напишите все решения уравнений:
а) tg/ = 0; в) sin2/ = 1;
б) ctg/ = 0; г) cos21 = 1.
Найдите решения следующих урав¬
нений в указанных промежутках:
а) sin/ == — 1, /е[0, 4л];
б) cos/ = 1, /е[—я, Зя];
в) tg/ = 1, 0</<л/2;
г) cost — —0</<2л;
д) sin/= —
/3”
/е=[0, 2л].
§ 20. Исследование синуса и косинуса
Периодические функции
Важнейшей особенностью тригонометрических функций является
их периодичность. Приведем общее определение периодической
функции.
Функция у = f(x) называется периодической, если существует такое
число Т, называемое периодом, что для всех х выполняется равенство
f(x + Т) = f(x).
Периодичность тригонометрических функций связана с тем,
что эти функции определены с помощью вращательного дви¬
жения точки, а положение этой точки периодически повто¬
ряется.
С помощью периодических функций описываются различные
периодические процессы. Периодичность вращения Земли вокруг
Солн-ца, периодичность движения других небесных тел порожда¬
ют многие известные нам повторяющиеся явления — смену вре¬
мен года, изменение долготы дня, изменение фаз Луны и т. д.
В технике периодические процессы возникают при изучении раз¬
личных колебаний — от колебаний простейшей пружины до коле¬
баний, связанных с электрическим током.
Синус и косинус описывают простейшие периодические про¬
цессы, но из них, как из кирпичиков, можно составить более
сложные колебания. С этим явлением наверняка сталкивались
те, кто наблюдал сложение сигналов на экране осциллографа или
интересовался принципом устройства и работы звуковых коло¬
нок. Поэтому важно как следует изучить свойства синуса и ко¬
синуса.
185
Для исследования периодических функций надо знать их на¬
именьший положительный период Т. Тогда можно сосредоточить
внимание на изучении свойств этих функций на промежутке дли¬
ны Т. Эти свойства будут затем повторяться периодически.
2л — наименьший положительный период синуса и косинуса.
Докажем это утверждение для синуса. Пусть число Т>О
такое, что равенство sin(x + r) = sinx выполняется тождествен¬
но. При х = 0 получим sin Г = sin0 = 0. Есть лишь одно поло¬
жительное число Г, меньшее 2л, для которого sin Т = 0 — это
число Т = л. Следовательно, единственно возможным положи¬
тельным периодом синуса, меньшим 2л, является число л. Одна¬
ко оно не является периодом, так как sin(xл) = — sinjc (по
формуле приведения), а (—sinx) не может быть равным тождест¬
венно sinx: Утверждение,доказано.
л— наименьший положительный период тангенса и котангенса.
Проверим сначала, что л вообще является периодом этих
функций:
tgfx4- л) = з1п(дг+я) = ~sinr = tsx
-Г п) C0S(r + Л) -cosr g
Для котангенса доказательство проводится аналогично.
То, что л — наименьший период, доказывается легко: из тож¬
дества tg(x + f) = tgx при х = 0 следует, что tgT=0, а л —
наименьший положительный корень тангенса. Так как ctgx =
1
= -—г, то аналогичное утверждение верно и для котангенса,
igjt
Упражнения
1. Докажите, что если Т — период
функции /, то числа 2Т, 37\ — Г,
—2Т и т. п. являются ее периодами.
Обратите внимание на то, что при
этом вам Надо уметь вычислять
значения f в точках дг, хЦ-Т, х—7\
г+27\ х—2Т и т. п. Как бы вы
смогли сформулировать требования
к области определения функции f?
2. Найдите наименьший положитель¬
ный период следующих функций:
а) y = s\n2xi в) t/=|cosr1;
б) у — sin3jr, г) y = \tgx + ctgx}.
3. Всякое число х можно представить
в виде суммы целого числа и неотри¬
цательного числа, меньшего единицы.
Например, 3,14=3+0,14; —2,3=
= — 3+0,7; 0,96=0+0,96. Первое
слагаемое в таком разложении на¬
зывают целой частью х и обозна¬
чают [г], а второе — дробной ча¬
стью (иногда майтиссой) и обозна¬
чают {*). Получаем лг= [г] + {*},
причем [х\^Ж, а 0<{дс}<1. Рас¬
смотрим функцию у={х). Докажи¬
те, что эта функция периодична,
найдите ее наименьший положи¬
тельный период и постройте ее
график.
186
Основные свойства синуса и косинуса
При введении тригонометрических функций мы аргумент обозна¬
чали буквой /, так как буквы х и у обозначали координаты вра¬
щающейся точки Pt. Сейчас при исследовании тригонометриче¬
ских функций мы вернемся к обычным обозначениям: х — аргу¬
мент, у — функция.
Рассмотрим свойства функции у = sin г и у = cos*.
1. Область определения. Синус и косинус числа х
задаются как координаты точки Рх> получающейся из точки
(1, 0) поворотом на угол х. Так как поворот возможен на любой
угол, то
областью определения синуса и косинуса является множество всех ве¬
щественных чисел, т. е. D = [R.
2. Участки монотонности. Проследим за характе¬
ром изменения координат точки, движущейся по окружности.
При х = 0 точка занимает положение Ро (1, 0) (рис. 266). Пока
она движется по окружности, оставаясь в первой четверти, ее
абсцисса уменьшается, а ордината увеличивается. При х = я/2
точка займет положение Рл/2 (0, 1). Итак,
в первой четверти синус (ордината) возрастает от 0 до 1, а косинус
(абсцисса) убывает от 1 до 0.
Когда точка переходит во вторую четверть (рис. 267), ордина¬
та начинает убывать и меняется от 1 до 0. Абсцисса становится
отрицательной и растет по абсолютной величине — значит, коси¬
нус продолжает убывать от 0 до —1.
В третьей четверти синус становится отрицательным и убы¬
вает от 0 до —1 (рис. 268), а косинус начинает возрастать и
изменяется от —1 до 0.
187
Рис. 266
Рис. 267
Наконец, в четвертой четверти синус возрастает от —1 до О
и косинус возрастает от 0 до 1 (рис. 269).
Составим таблицу для определения монотонности синуса и
косинуса по четвертям:
Таблица 4
3. Точки экстремума. Координаты вращающейся точ¬
ки меняются между —1 и +1. Эти числа являются наименьшим
и наибольшим значениями синуса и косинуса. Если требуется
указать абсциссы точек экстремума, то надо решить уравнения
sinx=zbl и cosjc=zbl (см. § 19).
4. Участки знакопостоянства и точки обра¬
щения в нуль. Эти вопросы были нами также изучены
в § 19. Мы повторим их еще раз при построении графика.
5. Множество значений. Синус и косинус принима¬
ют любые значения от — 1 до +1, так как являются координа¬
тами точки, движущейся по единичной окружности.
«Высшее назначение математики состоит в том, чтобы находить скрытый
порядок в хаосе, который нас окружает.»
Н. Винер
188
Рис. 268
Рис. 269
Функция
sin
COS
Четверть
Упражнения
1. Как определяются синус и косинус
числа х?
2. Какова область определения синуса
и косинуса?
3. В каких точках синус и косинус
обращаются в нуль?
4. Как меняются знаки синуса и коси¬
нуса?
5. Каковы наименьшее и наибольшее
значения синуса и косинуса?
6. Являются ли точки, в которых си¬
нус (или косинус) принимает наи¬
большее или наименьшее значение,
точками экстремума?
Графики синуса и косинуса
Как выглядит график синуса — синусоида, вы, наверное, себе
представляете. Для приближенного построения синусоиды можно
поступить так. Разделим первую четверть на восемь равных
частей и на столько же частей разделим отрезок [0; я/2] =
= [0; 1,57...] оси абсцисс. Удобно при этом сместить окружность
влево (рис. 270). Перенесем проекции на ось у точек деления
окружности (значения синуса) к соответствующим точкам деле¬
ния отрезка (0; л/2). Получим точки, лежащие на синусоиде, ко¬
торые нужно плавно соединить и продолжить кривую дальше,
пользуясь симметрией.
Сопоставим график со свойствами синуса.
Функция у = sinjc имеет период 2л.
На графике это свойство отражается следующим образом:
если мы разобьем ось х на отрезки длиной 2л, например точка¬
ми ... —4л, —2л, 0, 2л, 4л, ..., то весь график разобьется на «оди¬
наковые» части, получающиеся друг из друга параллельным пе¬
реносом вдоль оси (рис. 271).
Функция у = sin г нечетна.
На графике это свойство проявляется так — синусоида сим¬
метрична относительно начала координат (рис. 272).
7. Сколько точек экстремума имеет
синус (косинус)?
8. Сколько раз принимает свое наи¬
большее (наименьшее) значение
синус (косинус)? Чему оно равно?
9. Какому неравенству удовлетворяют
все значения синуса (косинуса)?
10. Каково множество значений синуса
(косинуса)?
11. Можно ли сказать, что синус (ко¬
синус) является монотонной функ¬
цией?
12. На каких промежутках (в каких
четвертях) синус (косинус) возра¬
стает (убывает)?
189
Рис. 270
У
Функция у = sinх обращается в нуль при х = kn (k е Ж).
На графике — это точки пересечения синусоиды с осью
абсцисс.
Функция у= sinx положительна при 2kn<x<.(2k + 1)я
и отрицательна при (2k+l)n<x<(2k + 2)n(k^Z). Указан¬
ные отрезки соответствуют тем значениям угла х, которые лежат
в первой — второй (где sinr>0) или третьей — четвертой чет¬
вертях (где sin* < 0) (рис. 273).
190
рис. 273
Рис. 271
Рис. 272
Функция у = sin* возрастает при —• д/2 + 2яЛ<лг<я/2 +
+ 2kn и убывает при л/2 + 2kn ^ х ^ Зл/2 2&л.
Точно так же указанные отрезки соответствуют четвертой —
первой и второй — третьей четвертям.
Множеством значений функции у = sin х является отрезок [—1, 1].
Действительно, проекции движущейся точки Р на ось у за¬
полняют отрезок [—1; 1] (рис. 274). Следовательно, синусоида
расположена в полосе —1 ^ sinjc ^ 1 и при этом проекции точек
графика целиком заполняют отрезок [—1, 1] (рис. 275).
График косинуса можно построить так же, как и график си¬
нуса (рис. 276). Но возможен и другой путь. Формулы приве¬
дения показывают, что синус и косинус связаны между собой
простыми соотношениями. Воспользуемся, например, формулой
cosx = sin(x + л/2). Эта формула показывает, что график коси¬
нуса получается сдвигом синусоиды на л/2 влево по оси х
(рис. 277).
Если аргумент умножать на число, то синусоида будет сжи¬
маться или стягиваться по оси х (рис. 278). Если значения си¬
нуса умножить на число, то произойдет растяжение (сжатие)
синусоиды по оси у (рис. 279).
Функции вида y = Asm((dx-\-a) при различных А, со, а имеют
графики в виде синусоид.
Эти функции описывают гармонические колебания — движение проекции
вращающегося шарика ла ось или колебания конца упругой пружины.
Постоянные величины Л,о>, а, задающие колебание, имеют
наглядный физический смысл: А — амплитуда колебания, со —
его частота, а — начальная фаза.
Рис. 274
Рис. 275
191
192
Рис. 276
Рис. 277
Рис. 279
Рис. 278
Упражнения
Постройте графики следующих
функций:
а) у = 2sin3jc;
б) у— — sinjt = sin(jt+ji);
в) t/ = cos2jc = sin(2jc-|-n/2)=
= sin 2(х+л/4);
г) у= sin(2x4- л/4).
Отметьте на графике функции у =
= sin jc точки, для которых:
а) sinjc= 1;
б) sin* = ‘/2;
в) sin jc = — 1 /3;
г) sinjoO;
Д) sinjt>y2;
е)*—rJ— <2.
§21. Тангенс и котангенс
Исследование тангенса
Если свойства синуса и косинуса мы получили, рассматривая
свойства движения точки по окружности, то для исследования
тангенса и котангенса поступим иначе.
По определению, тангенс числа х задается как отношение
sin г к cos х. Рассмотрим свойства тангенса.
1. Область определения. Областью определения
функции
i sin х
v cos x
является множество всех действительных чисел, за исключением
тех, в, которых косинус обращается в нуль. Запишем это мно¬
жество:
[х л/2 7ik (& £2?)}.
2. Периодичность. Тангенс — периодическая функция
с периодом л.
3. Нечетность. Тангенс — нечетная функция, т. е.
tg (-*)=—tg*.
4. Нахождение корней. Функция у=igx обращается
в нуль одновременно с синусом, т. е. для x=kn (k£Z).
5. Знаки. Функция у=tgx положительна в первой и
третьей четвертях и отрицательна во второй и четвертой
(см. рис. 255).
Выберем для дальнейшего изучения тангенса какой-либо от¬
резок числовой оси с длиной, равной периоду, т. е. числу л.
Можно было бы использовать отрезок от 0 до л, но это неудобно,
так как внутри этого отрезка есть точка х = л/2, в которой тан¬
генс не определен. Лучше выбрать отрезок (—л/2, л/2).
6. Монотонность. Тангенс возрастает в первой четвер
ти. Действительно, пусть 0^дг1Сх2Сл/2. Тогда sinx,Csinx2
(возрастание синуса) и cosx,>cosx2 (убывание косинуса). Так
7—1681
193
как значения косинуса положительны, то по свойству неравенств
имеем
COS JC, COS х2
Умножив это неравенство на неравенство sin х\ <sin х2 с по¬
ложительными членами, получим tgx\<Ctgx2. Тангенс возрастает
также и в четвертой четверти. Действительно, пусть —л/2<г,<
<*2^0. Тогда 0<1 — *2< — *,<я/2. Теперь числа (—хх) и
(—х2) лежат в первой четверти и можно воспользоваться тем,
что в первой четверти тангенс возрастает: tg(—*^)<tg(— х\).
Но так как тангенс — нечетная функция, то
tg(— *2)<tg( — *l)^ — tg*2< — tgr.OtgjqCtg.Xj.
От —л/2 до 0 тангенс отрицателен и возрастает. Затем от 0
до л/2 тангенс положителен и возрастает. Итак, тангенс воз¬
растает на отрезке (—л/2г п/2).
7. Область значений. Какие же значения принимает
тангенс? Когда х возрастает от 0 до л/2, тангенс возрастает.
При этом, когда х приближается к л/2, значение sin jc близко
к единице, а значение cos* близко к нулю. Поэтому отношение
становится сколь угодно большим. То, что любое действи¬
тельное число может быть значением тангенса, видно из рис. 280.
Построим ось, параллельную оси ординат с началом в точ¬
ке Р0. Возьмем на этой оси точку, соответствующую произвольно
выбранному числу а (рис. 279). Соединим Оса. Получим точ¬
ку Р на окружности. Пусть х — число, лежащее на отрезке
( — л/2, л/2) и такое, что (cos г, sin г) —координаты Р. Тогда
tg х = sinr =-^- = а. Мы показали, что областью значений
® COS X 1
тангенса является вся числовая ось Ж.
194
Рис. 280
8. График тангенса. На отрезке (0, л/2) график тан¬
генса можно построить по точкам, учитывая, что тангенс строго
возрастает, в нуле обращается в нуль, а при приближении к л/2
становится сколь угодно большим (рис. 281).
Отразив построенную часть графика относительно начала
координат (тангенс — нечетная функция), получим график тан¬
генса на отрезке ( — л/2, л/2) (рис. 282). Для построения пол¬
ного графика разобьем числовую ось на отрезки, перенося от¬
резок ( — л/2, л/2) вправо и влево на л, 2л, Зл и т.д.
График тангенса распадается на отдельные, не связанные
между собой части. Это вызвано тем, что в точках n/2 + kn
(k£Z) тангенс не определен (рис. 283).
Мы доказали, что тангенс возрастает на отрезке (—я/2, я/2). Можно
ли сказать, что тангенс возрастает на всей области определения? Нет.
Достаточно посмотреть на график. Если лс, = я/4, а дс2 = Зя/4, то tgx,= l,
a tgx2= — 1. Хотя ххсх2у но tg *i > tg х2. Нарушение монотонности свя¬
7*
195
Рис. 281
Рис. 282
Рис. 283
зано с тем, что между точками хх и х2 лежала точка х — п/2, в которой
тангенс не определен.
Однако верно, что тангенс возрастает на каждом отрезке, который
целиком попадает в его область определения.
Котангенс
Свойства котангенса получаются так же, как и свойства тан¬
генса. Перечислим кратко эти свойства, оставляя их доказатель¬
ство для самостоятельной работы.
1. Функция у=ctgjc= С^~ определена при хфкп (k£Z).
2. Функция у=ctgx периодична. Ее периодом является чис¬
ло л : ctg(r+ л)=ctgx:.
3. Функция у=ctgx нечетна: ctg(—х)=— ctgx.
4. Функция у=ctgx обращается в нуль одновременно с коси¬
нусом, т. е. для х—л/2 + Лл (1г£Ж).
5. Функция у=ctgx положительна в первой и третьей чет¬
вертях и отрицательна во второй и четвертой (см. рис. 255).
6. Функция у = ctgx убывает на отрезке (0, л). Перенося
этот отрезок на йл, получаем, что котангенс убывает на каждом
отрезке (£л, /гл + л)(k£X).
7. Область значений котангенса — множество Щ всех действи¬
тельных чисел.
8. График котангенса изображен на рис. 284.
Упражнения
1. Какова область определения тан¬
генса (котангенса)?
2. Каков период тангенса (котан¬
генса)?
3. В каких точках тангенс (котангенс)
обращается в нуль?
4. Как меняются знаки тангенса (ко¬
тангенса)?
5. Что можно сказать о монотонности
тангенса (котангенса)?
6. Имеет ли тангенс (котангенс) точки
экстремума?
7. Принимает ли тангенс (котангенс)
Г96
Рис. 284
наибольшее (наименьшее) значе- jq На графике тангенса (котангенса)
ния? указать точки, в которых:
a) tg*=l; г) tgx>
Какова область значений тангенса
(котангенса)?
9. Сколько раз принимает каждое свое б) ctg* = 2; д) ctgjc<c
значение тангенс (котангенс)? х . 0 .
' в) tgjc= —3; e)*ctgjt = x.
§ 22. Производные тригонометрических функций
Производные синуса и косинуса
Пусть точка А движется с единичной скоростью по окружности
радиуса 1 с центром в начале координат в положительном на¬
правлении. Координаты точки A=Pt в момент времени t рав¬
ны cos t и sin t.
Вектор мгновенной скорости точки А в момент времени t на¬
правлен по касательной к окружности в точке А (рис. 285), и,
Рис. 285
по теореме о перпендикулярности касательной к радиусу, прове¬
денному в точку касания, вектор v перпендикулярен радиусу-
вектору ОА.
Вычислим координаты вектора v. Отложив от точки О век¬
тор v, мы получим вектор ОВ, координаты которого равны ко¬
ординатам вектора v. Так как движение точки А по окружности
происходит с единйчной скоростью, то длина вектора равна 1
и поэтому длина вектора ОВ также равна 1. Следовательно,
точка В лежит на окружности.
Вектор ОВ перпендикулярен вектору ОЛ, поэтому если Л=Р/,
то В=Я/ + л/2. Таким образом, координаты вектора v = OB равны
cos(/ + л/2)= — sin t и sin(/ + n/2) = cos/.
Найденные значения координат вектора v являются производ-
ными от координат радиуса-вектора точки А, равных sin/, cos/.
Следовательно,
(sin t)' = cos /, (cos /)' = — sin /.
Перейдя к обозначениям sinx, cos г, получим таблицу произ¬
водных синуса и косинуса:
У
У'
s\nx
COSJC
COSJC
— sinjc
Пример
Найти производную функции:
а) у = A sin(co/ + a);
у' = A cos (со/ + а) со = А со cos (со/ + а).
Производная содержит множитель со (скорость колеба¬
ния пропорциональна его частоте).
б) у = sinxcosx:
у' = (sinx)'cosx + sinx(cosx)' = cos2x — sin2x;
в) y = sin5x:
у' = 5cos5x;
г) y = cosj-:
f 1 X
у =--sm-;
д) у = 2sin(3x — л/6):
у' = 2 • 3 • cos (Зх— л/6)=6 cos (Зх —- л/6);
е) у = 5соз(л/3 — х):
у' = 5-(—1)-(—l)sin^/3 — х) = 5sin^/3 — х).
Производные тангенса и котангенса
Вычислим теперь производную функции у = tgx. Так как tgx =
sinx
= --s^., то по теореме о производной частного получаем
/х у sin'* cosjc — cos'jc sinjc cos2r-|- sin2jc 1
' cos2* COS2JC cos2r ’
Следовательно,
(tgx)' = —V-
V & ' COS2JC
198
Аналогично,
<cos х Y (cos jc/sin jc —(sin jc/cos x —sin2 jc — cos2 jc
sin2 jc
1
Таким образом,
(ctgr)' =
sinA JC
Полученные значения производных тангенса и котангенса
сведем в таблицу:
Примеры
I- У=tgx + ctgx.
, 1 1 sin2 jc —cos2 jc
У о " 2 " 2 2 *
COS JC sin JC sin JCCOS JC
2. f/=2tg3r.
y' = 2'S Cos23r = cos23* '
3. ..sctgg-f).
( 1 \_ 3
^ 2 \sin2(jc/2 —л/4) / 2sin2 (jc/2 — л/4)
Приближенные формулы
Главная приближенная формула: вблизи нуля sin / « t.
Доказательство. Найдем дифференциал функции у=
= sin jc при х=0; dy = cosxdx. Так как cosO=l, то при * = 0,
d sinаг= djc. Так как A(/«dy, то A(/=sinAjc«d(/ = djc = Ajc.
Вместо Аг возьмем t и получим sin/«/ или х и получим sin jc «
«х. Необходимо помнить, что во всех этих приближенных
формулах аргумент выбирается близким к нулю.
Эта формула дает тем точнее значение синуса, чем ближе t
к нулю. Возможность заменять sin t на t при малых значениях
199
угла t широко используется в приближенных вычислениях.
Можно дать различные интерпретации приближенной формулы
sin t^t.
1. lim-^-^=l —отношение приращения функции и его глав¬
но t
ной части стремится к единице при стремлении к нулю прираще¬
ния аргумента.
2. Рассмотрим единичный круг. Пусть для простоты t>0.
Тогда длина дуги АВ равна t, а длина отрезка ВС равна sin/.
Удобно удвоить дугу АВ и отрезок ВС — дуга BD имеет длину 2/,
а хорда BD — 2sin / (рис. 286). Соотношение sin t^t означает,
что отношение длины хорды к длине стягиваемой ею дуги стре¬
мится к единице, когда дуга стягивается в точку.
3. Рассмотрим касательную к синусоиде в начале координат.
Так как (sin x)'=cosг, a cos0=1, то уравнение этой каса¬
тельной у=х (рис. 287). Таким образом, заменяя вблизи начала
координат график синуса отрезком касательной, мы вычисляем
приближенное значение синуса по формуле sinjt^jt.
Для получения других приближенных формул выпишем диф¬
ференциалы тангенса и косинуса:
y=tgx, dy=—^—dx:
COS X
у = cos X, dy=— sin xdx.
При x = 0 получим приближенное значение тангенса:
tgAx^Ajc, т. е. tgt^t.
Применяя этот же прием к косинусу, находим, что дифферен¬
циал косинуса при *о=0 равен — sin0djt = 0. Это означает,
что главная часть приращения косинуса равна нулю и в первом
приближении cosr^cos0=l. Можно получить более точную
формулу таким путем. Запишем cosx так: cos х= /1 — sin2х .
Заменим в этой формуле sin jc на х и воспользуемся приближен¬
но
Рис. 286
Рис. 287
ной формулой для корня: cosr= |/1 — sin2jc« /1 — х1 « 1 —
—1 /2-^2- Эта формула для косинуса вблизи точки агь = 0 весьма
точна.
Более точные приближения можно получить с помощью
формулы Тейлора (см. § 9). Для синуса и косинуса формула
Тейлора имеет вид
Примеры
Вычислить приближенно:
а) sin 0,03-tg0,12; sin 0,03 « 0,03; tg 0,12 « 0,12;
sin 0,03 • tg 0,12 « 0,0036 « 0,004.
б) sin 2°. Переводим 2° в радианную меру: 2°«0,034,
поэтому sin 2° « 0,034.
в) sin 32°. Выберем исходное «хорошее» значение аргу¬
мента: хь=30°. Представляем х—32° = 30° + 2°=jt + cU.
При подстановке заменяем в dr градусную меру на радиан¬
ную: sin 32° « 0,5 + /З-/2 • 0,034 « 0,529.
Диаграмма синусов и косинусов
В § 19 были получены различные формулы приведения. Все их
легко запомнить, если связать с преобразованиями графиков.
Для этого заметим, что формула приведения sin (х-\-я/2)=
§ 23. Диаграммы приведения
Рис. 288
201
=cosr означает: сдвиг графика функции y=s'mx влево по
оси х на я/2 дает график функции у=cos г (рис. 288).
При сдвиге графика еще на я/2 получим график функции
у=—sinr, так как со5(г+я/2)=— sin г. Следующий сдвиг на
я/2 влево дает график функции у=— cos г. Действительно,
—sin (лг+я/2)=—cos х. Наконец, последний сдвиг влево на я/2
возвращает нас снова к графику синуса: —cos (г+я/2)=
= —(—sin х)=sin х.
Последующие сдвиги графика sin д: приведут к повторению
тех же графиков. Полученные выводы сведем в диаграмму, пока¬
занную на рис. 289 (каждая стрелка обозначает добавление к
аргументу числа я/2).
Примеры
1. Привести выражение 5т(г+Зя/2) к аргументу х.
К аргументу г прибавим три раза по я/2; следовательно,
начиная с sin* нужно трижды пройти в направлении стре¬
лок, тогда получаем —cos г. Таким образом, sin (х + Зя/2)=
= —cos х.
2. Привести выражение cos(2jc —я) к аргументу 2х\
От аргумента 2х вычитается два раза по я/2; следова¬
тельно, от cos г нужно дважды пройти против направления
стрелок; получаем —cos2r. Таким образом, cos(2r—я)=
= —cos 2х.
3. Привести выражение 5т(5я/2 — /) к аргументу /.
Изменим порядок слагаемых в скобках, чтобы первым
стоял аргумент (—/): sin(—/ + 5я/2). Начиная с sin(—/)
нужно пять раз пройти в направлении стрелок, тогда полу¬
чаем cos(—/). Используем четность косинуса: cos(—/)=
=cos t. Окончательно 5т(5я/2 — /)=cos t.
Упражнение
Упростите выражения:
a) cos(z-+-3n/2); б) sin(/—Зл/2);
в) cos(2r1f л/2); д) sin(a+5ji/2);
г) cos(z—Зл/2); е) sin(3n/2—х).
202
Рис. 289
Диаграмма тангенсов и котангенсов
Между функциями tgx и ctg г имеется простая связь:
tg (*'+ л/2)= —ctg х.
Это означает, что в результате сдвига графика у = tgx влево на
л/2 получаем график функции у=— ctg г (рис. 290). При сле-
Рис. 290
дующем сдвиге графика на л/2 влево снова получаем график
функции у=tgx. Действительно,
—ctg (* + я/2)=—(—tg r)=tg X.
В виде диаграммы полученный результат запишется так:
tg + n/2 — ctg.
t I
Аналогично, по формулам ctg(r+ л/2)=— tg х и —tg(r+
+ л/2)=— (—ctgx)=ctgх строится диаграмма:
ctg + я/2 — tg.
Обе диаграммы удобно объединить (рис. 291).
Рис. 291
Примеры
1.
Привести *ё(?г+?г) к аргументу
Начиная с tg^- проходим один раз в направлении стрел-
ки, получаем —ctg|-. Итак, tg (|-+5-)= —ctgy .
2. Упростить ctg 05—
Преобразуем выражение, поменяв порядок слагаемых
в скобках: ctg 05—/)=ctg < + Начиная с
ctg(—t) проходим трижды в направлении стрелок и полу¬
чаем —tg(—t). Так как тангенс — нечетная функция, то
—tg(—<)=—(—tg 0—tg<- Окончательно, ctg 05—1^=
= tgt.
3. Вычислить sin-^-я.
О
Преобразуем -у-л, выделив целую часть: л = 6л + -у-.
Начиная с 5т-|-л проходим 12 раз по направлению
стрелок на диаграмме синусов-косинусов и получаем
5 п - 5 л 5 2 . 3
sin-g-л. Преобразуем —пу выделив —л=—л + — л=
=у + у, sin(y + y) получается из siny переходом один
раз по направлению стрелки начиная с sin^-, поэтому
имеем cos5“> что равно Окончательно получим
. 41 1
8|П-гя=г-
Упражнения 100 5
в) tg^—л; г> tg-^-л;
1. Упростите выражения: ° °
19 / 23 \
а) ^(у— ‘У’ б) ctg(7jf+n); д> е> ctg( б“л}-
ft Зл V 3. Чему равны sin(a + 3n)
^\2 2 / cos (4рл — аесли sina=y?
2. Вычислите:
* • 17 82
а) sin-^-л; б) cos-^-л;
204
Задачи и вопросы
5.1. В равнобедренном треугольнике угол при вершине равен а,
угол при основании р, основание а, боковая сторона Ь.
В следующих задачах указываются данные элементы тре¬
угольника и те, которые надо выразить через них.
а) Дано: а, а. Вычислите: р, 6, высоты, радиус г впи¬
санного круга.
б) Дано: Ьу р. Вычислите: а, а, высоты, г.
в) Дано: высота, опущенная на основание, а. Вычисли¬
те: а, Ьу р, г.
5.2. а — сторона равностороннего треугольника. Вычислите его
высоту, радиусы вписанного и описанного кругов, площадь.
5.3. Выразите в радианах: 1, 10, 15, 30, 45, 60, 90, 120, 225, 240,
330°.
1 1 2 117
5.4. Выразите в градусах: -jg-л; -у^л; g-л; -^-л; ^-л; 6,28.
5.5. Найдите в радианной мере дополнение до прямого угла
1 1 7
следующих острых углов: — л; -уул; -^л, 0,6; 0,7321.
5.6. Для данных в радианной мере углов найдите их смежные
, V 2 И 7
углы (в градусной мере): — л; -о^л; — л.
О ZU У
5.7. Зубчатое колесо имеет 72 зубца. Выразите в градусах угол,
на который повернется колесо при повороте на 1 зубец,
30 зубцов, 144 зубца*, 300 зубцов.
5.8. Постройте угол —а, если угол а имеет следующее значение:
10°; 180°; л/2; -30°; -л/2; -л; 270°, -3/2л, 1.
5.9. а) Вектор ОМ повернут в отрицательном направлении на
(—45°) относительно начальной стороны *04. Какие углы
соответствуют такому положению вектора ОМ?
б) Выразите в градусах 1,5.
в) Выразите в радианах —135°.
г) Шкив скоростного электродвигателя делает 120 000 обо¬
ротов в минуту. Определите угловую скорость вращения
этого шкива: 1) в град/с; 2) в рад/с.
5.10. Вычислите:
а) sin 135°;
б) cos 120°;
в) cos 135°;
г) tg 150°;
Д) ctg 225°;
е) sin 1110°;
\ • 2
ж) 8ШуЛ;
з) cos у я;
Ч * 3
и) tg —л;
к) ctg -|- л;
л) sin л;
м) cos л;
Н) tg-5-л;
о) ctg -jjr- я;
\ 11
п) sin —я;
р) sin 420°;
с) sin 480°;
т) tg2 225°.
205
5.1). Упростите:
а) sin4 а + 2sin2acos2a + ж) (tg а + ctg а? —
+ cos4 а; — (tg а — ctg а)2;
б) (sin а + cos а)2 + v /_1 l ctea W
+ (sin а - cos а)2; > bin а + CleaJ Х
в) sin4 а — cos4 а + cos2 а; X Г ctgaY
г) cos4 а + sin4 а + \sina /’
+ sin2 a cos2 а; , tg а 1 - ctg2 а .
ч cos a tg a i 1 ~ tg2 a ctg а
Д) —г-г* ctg a cos а;
sin21 а & j j
к) тттхг +
е) sin а — cos a(tg а + 1 + tg2 а 1 + ctg2 а
+ ctg а);
5.12. Докажите тождества:
а) cos4 a —sin4 a-—cos2 a —sin2 а;
б) ! = |+1е2а .
w / 2 • 2 i j. 2 »
cos a —sin a 1-tg a
в) ctg2 a — cos2 a=ctg2 a cos2 a;
r) 3sin4 a —2sin6 a= 1 — 3cos4 a + 2cos6 a;
ч tga + ctgp _ tgn .
Д; ctga + tgP ctgp ’
e) ,l_+ctg2a =ctg2a.
tg2 a + ctg2 a ®
,2 I /1 I + 2
ж) (1— tga)2 + (l + tga):
ч 1 — sin4 a — cos4 a 2
з) 4 =2tg a;
cos a
и) (sin a + tga)(cos a + ctga)=(l + sin a)(l + cos a);
к) -г—37^ =sin2a;
tga + ctga
л) sin4 a + sin2 a cos2 a + cos2 a=l;
м) (sin a + sin p) (sin a — sin p) + (cos a + cos p) X
X(cos a — cos P)=0;
и) l~ctg-7 = —ctg-y.
1 — tg V
5.13 Выясните, существует ли число, удовлетворяющее условию:
ч • 7 . 24
а)s.na = ir, cosa = —;
б) sin а = —0,7; cos а = —0,3;
в) sin а = cos а = — 4-;
5 о
206
г) tg а = |-; ctg а = — е) tg а = 2 + -\/3;
д) tg а = у-; ctg а = j-; ctg а = 2 — -\/з.
5.14. Найдите:
a) sin a, cos а, ctg а, если tga=/5”, «6 (о,
»
)=
г) sin a, cos a, tga, если ctga= — и аб^ул, 2я).
5.15. Упростите:
v cos2(2a— я/2) + ctg2(n/2 + 2а) + 1 .
sin2 (2а — 3/2п) + tg\3/2n + 2а) + 1
sin2(n/2 + а) ~ cos2 (а — я/2) .
tg2 (я/2 + а) — ctg2 (а — я/2)
в\ ctg2 (а + я/2) cos2 (а — я/2) ,
ctgfta—я/2)— cos^a+я/2)
ctg (3/2я — a) ctg2 (2я — а)- I .
1 — tg2(a — n)ctg(n + a)
д) sin (100° - а) + cos (90° + а) - tg (360° - а) +
+ ctg (270°-а);
е) sin (л/2 — а) — cos (л — а)+tg (л — 2) — ctg (3/2л + а);
v tg (270° - a) sin 130° cos 320° sin 270° .
Ж' ctg(180°-a)cos 50° sin 220° cos 360° ’
з) tg2 (a - 360°) sin2 (a - 270°) + cos2 (360° + a);
и) sin (л/5 — a) ctg (4/5л + a) cos (9/5л + a)+ctg (я + 0) X
X ctg (3/ 2я — p);
к) tg(113° + a)ctg(67° ^a)+sin2(26°-i-a) + sin2 (244° — a).
б) sin a, tga, ctg а, если cosa=—— и a€(jr>
5 / 3
в) sin a, tga, ctg а, если cosa = —— и af (л, —л
5.16. Найдите период функций:
а) у = 3 + 5sin х\ д) у = tg За:;
б) у = 2sin(* + е) у = tg(4x -
в) у = cos 2х; ж) у = tg(x/3 + 7е);
г) у = sin '/5; з) у = tg(3n/4 — х).
207
5.17. Постройте графики функций:
а) У = 1 + sin х;
б) у = cos х — 2;
в) у = 2sin х;
г) у = — 3cos х;
jx) у = sin 2х;
е) у = cos у- ;
ж) t/ = sin(x + J-);
5.18 Выясните, является ли функция четной, нечетной:
а) у = sin 2*; з) у = sjn / + я\
б) и = sin -4- 1: V 4 /
3)
У =
COS^X —
■H
и)
У =
—tg(*
+ f>
К)
У =
2tgf;
л)
У =
ctg(f-
— 2x^;
м)
У =
sin x +
I sin x\
Н)
У =
cos x +
|cos X
О)
У =
1 tg 2x\.
и) г/ = tg Зх sin 2х;
К) </ =
б) «/ = sin 2х + 1;
в) у = cos (дс + J-);
г) у = tg 2jc cos 4л:; » j
д) у = sin 5jc; л) y = ^-L-
v . Sin JC
е) у = sin x + cos *; , ,,_sin;c + tg*
ж) У = tg * + ctg x; м) У x •
5.19. Найдите множество значений функций:
а) у = sin Здс; г) у = tg2*;
б) у = — 3cos2x — 1; д) у = (cosдс + I)2;
в) </ = sin2*; е) у = 1 — ctg2х.
5.20. Решите уравнения:
a)
sin x=0;
ж)
tgx = 0;
H)
sinx = 1 /2;
6)
sin x = 1;
3)
tg* = 1;
0)
cos x = -V2/;
в)
sin x = — 1;
И)
Ctgx = — 1;
n)
tgx = V3;
r)
4^2 cosx = 0
; к)
ctg x — 0;
p)
sin x = 2;
Д)
cos x = 1;
л)
sin x = cos x;
0
cosx = — 3;
e)
cos jc=— 1;
м)
sin x = — cosx;
T)
tg* = -v3/.,
5.21. Решите уравнения:
а) 2 sin х — -yfe = 0; е) 4cos2(2jc — я/3) — 3 = 0;
б) cos(2x — л/е) — 1=0; ж) cos п / 2 ~\~ cos х = 1;
в) 2cos(jc + л/4) — -у/з = 0; з) sin 30° + cos х = 1;
г) 3 tg(3jc - ЛД) - УЗ = 0; и) 3 ctg(jc + 17°) + -у/з = 0;
д) 4sin23x= 1; к) Isinxl = 1;
л) |cos jc| = ^/2; H) sin(f“* — *) +
м) -\j2 sin 2x = 1; + 2 cos(2n — x) = 3;
o) tg(x + л) = tg(y- - x)
5.22 Вычислите производную функции:
а) у = 2 sin jc; к) у = sin5jt;
1 — 3cos* 4 x
б) у = g ; л) У = cos-g-;
в) у — 3tg* + 2ctgx; м) у = tg(2x + 1);
г) у = sinxcosx; ч Л . / „ \
ч 2 н) у = 2s n(3* — -£-) +
д) у = cos^x; ' 9 \ 6 / T
е) y = *2sinAr; +3cos + |-),
у — sinjc о) у = sin2(* +
3)«/ = ^; XCOS^^.
X
И) У =
= iEJ
SinJC — COS*
5.23 Найдите приближенно: sin31°; cos44°. sin29°; cos46°;
tg48°; ctg 63°.
6
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
§ 24. Проекция вектора
Проектирование на прямую
Пусть в пространстве задана прямая /. Возьмем произвольную
точку Р. Как найти ее проекцию на прямую /? Сначала надо
через точку Р и прямую / провести плоскость. Затем в этой
плоскости надо опустить перпендикуляр из Р на прямую /. Основа¬
ние этого перпендикуляра и будет проекцией точки Р на пря¬
мую /. В этом построении предполагалось, что точка Р лежит вне
прямой / — тогда есть единственная плоскость, проходящая
через Р и /. Если Я£/, то точка Р совпадает со своей проекцией.
Проекцией точки Р на прямую I называется такая точка Q прямой I, что
PQ L I. Если P6I, то проекцией точки Р на прямую I является сама точ¬
ка Р (рис. 292).
Слово «проекция» употребляется в математике в разных смыслах. Описан¬
ное нами построение называют ортогональным проектированием, если
нужно его отличить от другого вида проектирования, например параллель¬
ного.
Пусть теперь на прямой / выбраны положительное направле¬
ние, начальная точка и указан масштаб, т. е. прямая / превраще¬
на в числовую ось. Тогда каждая точка Q прямой / однозначно
Рис. 292
210
определяется числом — координатой этой точки. Поэтому часто
проекцией точки Р на ось / называют не только точку Q, но и
число — координату точки Q на оси / (рис. 293).
Проекция вектора
Как найти проекцию вектора а на ось /? Изобразим вектор а
направленным отрезком Ah и спроектируем его концы на ось /.
Проекцией вектора на ось называется число, равное разности координат
проекций на эту ось конца и начала этого вектора.
Иными словами, если а=А§, то проекция вектора а на ось /
равна числу В/— Л/, где В/ и Л/ — координаты проекций точек В
и Л на ось /. Обозначим проекцию вектора а на ось / через а/.
Получим равенство (рис. 294)
а / = В/ — Л/.
Если этот же вектор а показать другим направленным отрез¬
ком СД то проекция вектора а на ось / не изменится, т. е. если
л1? = С\б, то D/ —С/=В/ — Л/. Это наглядно видно из рис. 295.
Свойства проекции вектора на ось
Проекция вектора на ось равна длине этого вектора, умноженной на
косинус угла между вектором и осью.
Пусть ф — угол между вектором а и осью / (рис. 296). Тогда
свойство можно записать в виде формулы
а/= |а| cos ф.
211
Рис. 293
Рис. 294
Рис. 295
Рис. 296
Д q к азательство. Отложим вектор а от начала О оси /:
а = СМ. Пусть Ai — проекция точки А на ось /. По определению,
проекция вектора а на ось / равна координате точки Л/, так как
координата начала О равна нулю. Координата точки Л/ равна
длине отрезка ОЛ, умноженной на coscp, т. е. а/= \ОА\cos ф=
= |a|coscp, что и требовалось доказать.
Проекция суммы векторов равна сумме проекций:
(а + Ь)/ = а/ + Ь/.
Доказа тельство. Изобразим вектор а направленным
отрезком АВ. Отложим вектор Ь от точки В: b = jB6. Вектор Аб
равен сумме векторов а и Ь: а + Ь=АС. Рассмотрим проекции
точек Л, В и С на ось / (рис. 297). Получим
3.1=Вi — Ai\ Ь/=С/ — В/.
Сложим эти равенства: a/ + b/=B/ — А/ + С/ — В/= С/ — At. Мы
получим проекцию вектора Afc = а + Ь, что и требовалось до¬
казать.
При умножении вектора на число его проекция тоже умножается на
это число:
(аа); = «а,.
Дока з а)т е л ь с т в о. Изобразим вектор а направленным
отрезком О А. Отложим вектор аа от точки О: аа=ОВ
(рис. 298). Найдем проекции точек А и В на ось /. Из свойств
Рис. 297
Рис. 298
пропорциональных отрезков имеем OBi=aOAiy т. е. проекция
вектора аа = ОЁ равна проекции вектора а = ОЛу умноженной
на число а, что и требовалось доказать.
Упражнения
1. Где лежат все точки пространства,
проектирующиеся в данную точку Q
прямой /?
2. Используя рис. 299, найдите проек¬
ции векторов AS, ВС и СА на оси
х и у.
3. Правильный шестиугольник ABCDEF
расположен так, что его центр
совпадает с началом оси /, а вер¬
212
шина А — с единичной точкой этой
оси. Постройте проекции на ось /
всех вершин шестиугольника и вы¬
числите проекции на эту ось векто-
ров Ш, е%, dP, оЬ, of, Ш, Те.
^•На поршень действуют две силы Fi
и F2, равные 5/2~Н и 6 Н и направ¬
ленные так, как показано на
рис. 300, а, б. Вычислите суммарную
силу давления на поршень.
Цан треугольник ABC. Начертите
ось / так, чтобы:
a) (Xb)i = 0; б) (Ab)i = \аЬ\;
в) (ДЬ)/ = - \АВ\; г) (ХЬи = $С)1;
д) A = 2(^)/; е) (AB)t =
= -T(AC)h
§ 25. Свойства скалярного произведения
Определение скалярного произведения
Скалярным произведением двух векторов называется произведение их
длин на косинус угла между ними.
Если обозначить векторы а и Ь, а угол между ними — <р, то
определение скалярного произведения можно записать в виде
формулы
а - Ь = |а| • |Ь| cos <р.
Знак скалярного умножения будет обозначаться точкой, как
и обычное умножение чисел.
Рис. 299
Рис. 300
1. Если хотя бы один из векторов а или b нулевой, то угол между вектора-
3* ми не определен. В этом случае, по определению, считается, что скалярное
произведение а*Ь равно нулю.
2. Важно помнить, что в результате скалярного умножения двух векторов
получается число, скаляр, поэтому произведение и названо скалярным.
Пример
Представим себе, что мы тянем за веревку сани с постоян¬
ной силой F (рис. 301). Какую работу мы совершим, пере¬
местив сани на s?
Если мы разложим силу F по горизонтальному и верти¬
кальному направлениям, то станет ясно, что работу по пере¬
мещению выполняет лишь горизонтальная составляю1
щая F/:
i4 = |F/Ms| = |F| cos <p|s| = F*s,
где <р — угол между направлениями силы тяги и переме¬
щения.
Формула для скалярного произведения через проекции
Разбирая • пример вычисления работы, мы выяснили, что эту
работу совершает лишь горизонтальная составляющая силы,
т. е. ее проекция на направление перемещения. Поэтому скаляр¬
ное произведение можно вычислить через проекцию одного векто¬
ра на направление другого.
«Обобщение понятия часто бывает полезно для постижения его сущ¬
ности».
А. Н. Колмогоров
Колмогоров Андрей Николаевич (род. в 1903 г.) — советский мате¬
матик, один из создателей и автор общепринятой системы аксиом совре¬
менной теории вероятностей. Вместе с А. Я. Хинчиным и одновременно
с Н. Винером развивал теорию случайных процессов, которая легла
в основу кибернетики. Автор глубоких идей и результатов в топологии,
математической логике, гидродинамике и небесной механике.
214
Рис. 301
Рис. 3Q2
Пусть а и b — два вектора, причем Ь=^0. Проведем прямую /,
параллельную вектору Ь. Положительное направление оси / опре¬
деляем по направлению Ь. Проекцией вектора а на направление
вектора b называют проекцию а на построенную ось /. Обозна¬
чают эту проекцию так: аь. Пусть угол ф— угол между вектора¬
ми а и Ь. Ясно, что это то же самое, что угол между вектором а
и осью / (рис. 302). Из свойств проекции следует, что аь =
= |а|созф. Сравнивая эту формулу с определением скалярного
произведения, получаем
а-Ь = аь. |Ь|,
т. е. скалярное произведение двух векторов равно проекции одно¬
го из них на направление другого, умноженной на длину этого
второго вектора.
В примере механической работы получаем
i4 = F-s = Fs • |s|,
где Fs — горизонтальная составляющая силы, т. е. ее проекция
на направление вектора s.
Заметим, что мы на самом деле получили две формулы, так
как можно проектировать а на Ь, а можно, наоборот, b на а:
а-Ь = аь • |b| = ba • |а|.
Отметим еще, что во всех этих формулах надо считать, что
векторы а и b ненулевые.
Упражнения
1. Дан правильный шестиугольник
ABCDEF, сторона которого равна а.
Вычислите скалярные произведения:
а) аЬ-ЛР\ в) Ар-Ар, д) аЪ-£)Р;
б) It-Ар; г) е) АЁ-М.
Свойства скалярного произведения
Перечислим некоторые свойства скалярного произведения векто¬
ров, вытекающие непосредственно из его определения.
Скалярный квадрат вектора равен квадрату его длины:
аа = а2 = | а| .
В самом деле,
а2 = |а|2cos Z_(a, а)=|а|2.
так как Z_(а, а)=0, a cos 0=1.
Скалярное умножение векторов перестановочно:
ab = Ьа.
2. Груз тянут за две веревки, обра¬
зующие с направлением движения
углы 45° и 30°. Какую работу надо
совершить для перемещения груза
на 25 м, если к каждой веревке
прикладывается постоянная сила
200 Н?
215
В самом деле,
Z(a, b)=Z(b, а) и ab=|a|-|b|coszl(a, b)=ba.
Скалярное умножение векторов линейно:
а(Ь + с) = а • Ь + а «с и a(ub) = </ (а • Ь).
Для доказательства воспользуемся сначала формулой для
скалярного произведения через проекции, а затем свойствами
проекции:
a(b + c)=|a| •(b + c)t = |a| *Ьа + |а| •са = а*Ь + а-с;
a(ab)= |а| • (ab)t = |а|а(Ьа)=а|а| • (Ьа)=а(а • Ь).
Первые два свойства позволяют обращаться со скалярным умно¬
жением векторов как с умножением чисел. Например,
(а + Ь) (а — Ь)=а2 — Ь2;
(а + Ь)2=а2 + Ь2 + 2аЬ;
(а — Ь)2 != а2 + Ь2 — 2аЬ.
Последнее тождество имеет важные применения в геометрии.
Рассмотримдреугодьник ABC (рис. 303). В векторных обозначе¬
ниях ВС=АС — АВ и поэтому
|ВС|2 = |АВ|2 + \АС\2- 2\АВ\ • \АС\ cos /-{АВ, АС\
т. е. в обычных геометрических обозначениях
a2=b2 -\-с2 — 2bc cos /LA.
Полученное соотношение называют теоремой косинусов. Если
угол А прямой, то cos Z_i4=0 и теорема косинусов превращается
в теорему Пифагора:
а2 = Ь2 + с2.
Упражнения
1* Докажите формулу | а+Ы2 + I а—
—b|2 = 2( |а|2 -f-1 b|^). Постройте на
лекторах а и b параллелограмм и
дайте геометрическую формулиров¬
ку доказанного тождества.
2. ABCDEF — правильный шести¬
угольник со стороной 2р. Точка К —
середина стороны ВС. Вычислите:
а) л1(-А5\ б) ffi-ffi, в) АК • ЕК.
Перед вычислением скалярных про¬
изведений разложите указанные век¬
торы по векторам Д2*=а и аР=Ъ.
3. В треугольнике ABC найдите длину
стороны АС, если известно:
а) \АВ\=4, IВС 1=5, ААВС=60°\
216
Рис. 303
б) |ЛВ|=3, |ВС|=7, ААВС= 120°;
в) IЛЯ|=5, |ВС|=2, ААВС=\ЗЬ°.
4. На тело действуют две силы Fi=2H
и F2=3H под углом 120°. Найдите
равнодействующую силу.
5. Выведите формулу
(а+Ь+с)2=|а|2+ |Ь|2+ |с|2+
+2(ab+ac+bc).
5. Силы F|=2H, F2=3H, F3=3H дей¬
ствуют так, как показано на рис. 304.
С помощью предыдущей формулы
вычислите равнодействующую силу.
Условие перпендикулярности
Теорема
Два ненулевых вектора перпендикулярны тогда и только тогда, когда
их скалярное произведение равно нулю.
Доказательство. Пусть а и b — данные векторы, ф —
угол между ними. Если a_Lb, то cos<p=0 и а-Ь = 0. Обратно:
если а*Ь=0 и при этом а=^0, то cosq)=0 и a_Lb. Теорема
доказана.
Эта теорема имеет геометрические применения, так как, вы¬
числяя скалярное произведение, легко проверять перпендикуляр¬
ность и неперпендикулярность векторов, а значит, и прямых.
Пример
Рассмотрим четырехугольник ABCD (рис. 305). Пусть /(,
L, Му N — середины соответствующих сторон. Доказать,
что если \KL\ = \MN\, то диагонали АС и BD перпендику
лярны между собой
Доказательство. В векторных обозначениях
АК=1 /2А8, aL = xMAC-\-Au) и поэтому KL = '/2(Л£ +
+ аЬ — АВ)2 =1 ]2{АС + Ви). Аналогично, MW =
— АС). Склащвая почленно, получаем BD = f\L-h MN.
Аналогично. АС = KL — MN. Перемножая, получаем
&D-A£={l{L + M)(tL-l^) = fo2-AfN2 = 0. Значит,
А*С _L вЪ, что и требовалось доказать.
217
Рис. 304
Рис. 305
Упражнения
1. В треугольнике одна сторона вдвое
больше другой, а угол между
ними 60°. Докажите, что треуголь¬
ник — прямоугольный.
2. ABCD — пирамида, все грани кото¬
рой правильные треугольники. До¬
кажите, что скрещивающиеся ребра
взаимно перпендикулярны.
Выражение скалярного произведения в координатах
Введем на плоскости декартову систему координат. Пусть i и
j — орты координатных осей. Так как i_Lj, а длины их равны
единице, то i =j2=l, a ij=ji=0 (рис. 306).
yk
Рис. 306
Возьмем теперь два вектора ai и а2 на плоскости и разложим
их по ортам:
ai=rii + (/ij; a2=r2i + (/2j.
Вычислим скалярное произведение векторов ai и а2. При этом
вычислении будем учитывать линейность скалярного произведе¬
ния, а также правило умножения ортов:
aia2 = (x\i + y\l) (*2i + (/2j) =
= (*ii) (x2i) + (x,i) Ы) + Ы) (x2i) + (г/ij) Ы) = х{х2+у\у2.
Сформулируем правило вычисления скалярного произведения
в координатах:
скалярное произведение двух векторов плоскости равно сумме произ¬
ведений их одноименных координат:
а1а2 = Х1Х2 + У\У2'
Из этой формулы можно вывести ряд следствий.
1. Длина вектора а с координатами (х; у):
|а| = /аа= /*2 + гД
2. Условие перпендикулярности:
а> _La2^aia2 = 0^jciJc2 + (/i(/2=0.
218
3. Формула для угла ф между векторами:
aia2 х\х2 + у\у2
C°s ф |а,|.|а*| - M + rfM + A '
Аналогичные формулы верны и в пространстве. Если i, j, k —
орты координатных осей в пространстве, то их скалярные квад¬
раты равны 1, а скалярные произведения различных ортов равны
нулю:
i2=j2=k2= 1, ij=jk=ki=0.
Все рассуждения теперь проведем точно так же. Разложим
векторы ai и аг по их ортам:
ai=rii + (/ij + zik; a2=x2i + yj + z.2k.
Вычислим aia2, используя линейность скалярного произведе¬
ния и правило умножения ортов:
а\&2 = Х\Х2 + У1У2 + Z\z2i
т. е. скалярное произведение двух векторов равно сумме произве¬
дений их одноименных координат.
Запишем несколько полезных формул.
1. Длина вектора а с координатами (х; у\ г) |а|2=аа=х2 +
+ (/2 + z2, откуда
la|= \/x* + y2 + z2.
2. Расстояние между двумя точками в пространстве. Пусть
даны две точки: А\(х\\ у\\ z\) и А2(х2\ у2\ z<i). Рдсстояние между
ними мождо вычислить как длину вектора А Иг. Координаты
вектора А\А2 таковы: (х2 — х\\ у2 — у\\ 22 — 21). Тогда
\Л\А2\ = / (*2 — X\f + (у2 — у\У + (22 — Zl)2.
3. Условие перпендикулярности двух векторов в простран¬
стве:
ai _La2^aia2 = 0^riJc2 + (/i(/2 + 2iZ2=0.
Упражнения
1. ABCD — квадрат со стороной 1.
Точки /Си М — середины сторон ВС
и CD. Введите систему координат
и вычислите скалярные произведе¬
ния: _а) ЛЁ-аХ; б^аХ-аЬ;
в) г) Afo•d’K; д) АК.-[ГК..
2. Дан единичный куб ABCDA'B'C'D'.
Введя систему координат, вычис¬
лите указанные скалярные произведе¬
ния: а) АЙ-ХЬ, б) АВ-Л?,
в) а%-а£, г) ДЬ.Д£, д) А%-вЪ,
е) AD-BD, ж) BD-AC.
Рис. 307
3. На листе в клетку нарисована фи- 4. Найдите расстояние между точками
гура (рис. 307). Докажите, что Л i (1; 0; —3) и Л2 (—1; 2; —4).
J_]w 5. Вычислите угол между диагоналями
А'С и DB' куба ABCDA'B'C'D
Задачи и вопросы
6.1. Дан прямоугольный ДЛВС, у которого угол при вершине С
прямой, а при вершину В равен 40^. Найдите углы между
парами векторов: а) СА и Со; б) СА и Аа\ в) АВ и СВ.
6.2. ABCDE — правильный ш^тиугрльни^Найдите углы меж¬
ду парами^вектород: а)_АВ и Лг; б)Лв и Ау\ в) АВ и Ёил
г) ВС и EF\ д) Ad и ВС\ е) АС и AF\ ж) АС и А§; з) АВ
и AF.
6.3. Известны проекции векторов а и b на ось /: а/= —1, Ь/ = 3*
Вычислите проекции следующих векторов:
а) (а + b)/; г) (а — Ь),;
б) (а + 2Ь),; д) (За-'ДЬ),.
в) — (а + 2Ь),;
6.4. Вектор а образует с осью / угол <р. Найдите проекцию век-
тора на ось / и поясните это на рисунке:
а) ф = 0°, |а| = 3; г) <р = 45°, |а| = 1;
б) ф = 90°, |а|=2; д) ф = 60°, |а|=2;
в) ф= 180°, |а|=3/2; е) Ф — 120°, |а|=2.
6.5. Дана ось /. Начертите дЛВС такой, что:
а) (ЛБ), = 0; в) (Ab)t = (cb)r,
б) (ЛВ),= \Ab\- г) (ЛЬ),= -(СЬ),.
6.6. Радиус-вектор точки М образует с осью х угол 60°. Расстоя¬
ние от точки М до начала координат равно 2/3”. Найдите
проекцию радиуса-вектора на ось у.
6.7. Вектор а образует с осью х угол 105°. Найдите проекцию
этого вектора на биссектрису первого координатного угла,
если |а|=4.
6.8. Дан ромб ABCD со стордной2 и острым углом >4=60°.
Найдите: а) АЁ-ВС\ б) ВС-CD; в) AB-CD.
6.9. В прямоугольном треугольнике ABC углы при вершина^ С
и Л^ращы 90° и 60° соответственно. Вычислите (Ао +
+ СВ)-ЛС, если длина гипотенузы 2.
6.10. ABCD — параллелограмм, ZLBy4D=60°, |ЛВ|=3, \ВС\=е£.
Точка К_+- середина стороны ВС. Вычислите: а) Аа*АС\
б) AC-KD.
6.11. В параллелограмме ABCD угол при вершине А равен 60°.
Длины стород Афи AD соответственно равны 3 и 1,5. Дока¬
жите, что BDJ-Ли.
220
6.12. Точка О лежит внутридЛВС на расстоянии 1 от вершины
4_^так, что Z.ВАО=\Ъ°у Z.ОАС=45°. Докажите, что
BO-LA£, если \Хв\=уТ.
6.13. ABCDEF — правильный шестиугольник со стороной, рав¬
ной 4^Точка К и М — середины сторон ВС и КС. Докажите,
что AK-LDM.
6.14. В тредгольнике_^4ВС проведены высоты CF_q BE. Покажите,
что AB-AF=AC-А1Е=Ъ-с, если АВ = Ь, АС=с.
6.15. ABCDEF — правильный шестиугольник, вписанный в еди¬
ничную окружность, К — середина стороны ВС. Найдите
\АС\ и \АК\.
6.16. В аАВС угол при вершине А равен 60°, \АВ\ = 4У |>4С| = 5.
Найдите длину медианы, проведенной из вершины А.
6.17. Докажите с помощью скалярного произведения, что диаго¬
нали ромба перпендикулярны.
6.18. Стороны АВ и ВС единичного квадрата продолжены и на
них взяты точки Ки М^так, что \ВК\=2\АВ\, \СМ\ = 2\ВС\.
Докажите, что AM_LD/C.
6.19. Из спичек выложена фигура (рис. 308). Докажите, что
AC±BD.
6.20. AJ^CDA'JB'C'iy — куб. Докажите, введя координаты, что
AD'±DC и AB'^tft.
6.21. ABCDA'B'C'D' — единичный куб. Точки К и М — середины
ребер АА' и D'C', О — пересечение_^диаг^нале01 грани
A'B'C'D'. Вычислите длины векторов КС\ DO и Км.
6.22. ABCDA'B'C'D' — куб. Найдите угол между векторами AD'
и АВ\ введя систему координат.
6.23. В кубе ABCDA'B'C'D' точки К, М и N — середины ребер
D'A\ ВВ' и DC. Докажите, что Z-KMN = 60°.
6.24. В кубе ABCDA'B'C'D' найдите /-АСА', используя тригоно¬
метрические таблицы.
6.25. ABCD — квадрат. Точки К и М — середины сторон АВ и
ВС. Найдите Z.MKD, используя таблицы.
221
Рис. 308
7
ТРИГОНОМЕТРИЧЕСКИЕ
ТОЖДЕСТВА И УРАВНЕНИЯ
§ 26. Формулы сложения
Основная формула
Тригонометрические функции связаны между собой многочислен¬
ными соотношениями. Одна их часть объясняется связью между
координатами точки окружности (основные соотношения).
Вторая часть тригонометрических соотношений связана с раз¬
личными видами симметрии и периодичности в движении точки
по окружности (формулы приведения). Третья часть тригономе¬
трических формул, к изучению которой мы приходим, объясня¬
ется тем обстоятельством, что поворот точки на угол а + р можно
составить из двух поворотов: на угол а и на угол р. Простые
формулы, связывающие координаты точек Рау Р$ и Яа + р, назы¬
ваются формулами сложения.
Выведем формулы, связывающие sin(a±p), cos(a±P),
tg(a±p), ctg(a±P) с тригонометрическими функциями углов
аир. Оказывается, что достаточно вывести формулу для косину¬
са разности. Остальные формулы получатся как ее следствия.
Теорема ——
Косинус разности двух углов равен произведению косинусов этих углов,
сложенному с произведением синусов:
cos (a — Р) = cosa cos|3 -t- sina sinf.
Доказательство. Построим углы аире помощью
единичной окружности, т._£.. нанесем точки Ра и Р$ такие, что их
радиусы-векторы ОРа и ОРр образуют углы аире положитель¬
ном направлением оси абсцисс. Угол между векторами ОРа и
0Р$ равен а —р (рис. 309). Вычислим скалярное произведение
этих векторов. По определению скалярного произведения, имеем
oTv loKl ■ 10^1 cos(a-Р) = cos(a-р), так как векторы
бРа и ОРр имеют единичную длину. Теперь вычисли^ это же
скалярное произведение с помощью координат: дРа-ОРр=
222
Синус суммы
Воспользуемся одной из формул приведения:
sin(a + p)=cos (у — (a + P))=cos ((у — «)— Р)-
Теперь используем формулу для косинуса разности:
cos — a)— p)=cos (у — a)cos p + sin (у — a)sin p.
Окончательно
sin (a-f P)=sin a cos p + cos a sin p.
Синус разности
sin (a — p)=sin (a + (—P))=sin a cos (—p) + cos a sin (—p)=
= sin a cos p — cos a sin p,
или окончательно
sin (a — §) = sin a cos P — cos a sin p .
223
Рис. 309
=cos a cos p + sin a sin p. Сравнивая результаты вычислений,
получаем
cos (a —р)=cos a cos p + sina sin p.
Косинус суммы
Сумму a + p запишем как разность a —(—р) и подставим в
формулу для косинуса разности:
cos (a + p)=cos (a — (—p))=cos a cos (—P) + sin a sin (—p).
Воспользуемся тем, что cos(—p)=cosp (четность косинуса),
a sin (—Р)=—sin р (нечетность синуса) Тогда
cos(a+p) = cos a cos р —sin a sin р.
Пример
Вычислим sin 15°.
Представим 15° как разность 45° — 30°. Тогда sin 15° =
= sin (45° — 30°) = sin45° *cos30° — cos45°-sin30° =
_ VL. VL_ VL.1= n
— 2 2 2 2 4
Тангенс суммы и разности
По определению, tg(a + Р) = ^(а + р) •
По формулам синуса и косинуса суммы имеем
. , , sin a cos p + cos a sin ft
cos a cos p — sin a sin p
Разделив числитель и знаменатель этой дроби на cosacosp,
найдем
. о\ tga + tgp
tg(a + p)- ,_tgatgp •
Заменяя р на — р и пользуясь нечетностью тангенса, получаем
te (a — 6) = tgg ~ tgp
tgia PJ i+tgatgp'
Упражнения
1. Выведите самостоятельно формулу
сложения для котангенса: •
ctg(a+p)= etspcyp-i
ctga + ctgP
2. С помощью формул сложения вы¬
числите: cos 15°; sin 75°; tgl05°;
cos 165°.
3. Формула для тангенса суммы не 5.
имеет смысла, когда не определено
хотя бы одно из чисел tga, tgfi.
tg(a-j-p). В знаменателе этой форм\
лы стоит выражение 1—tgatgp.
Докажите, что если tga, tgp,
tg(a--j-р) имеют смысл, то это выра¬
жение не обращается в нуль.
пу-
4. Вычислите a + р, если sina = —-—,
/ТЗ
cosр = —, причем а лежит в
первой четверти, а р — во второй.
Вычислите tg(a—р), если sina =
= 4/5, cosp = 5/13, причем аир —
углы первой четверти.
Тригонометрические функции двойных углов
Формулы сложения являются одними из основных формул, свя¬
зывающих тригонометрические функции. Из них можно вывести
различные следствия. Полагая a = р, получим тригонометриче¬
ские функции двойных углов:
1. sin 2a = sin (a -(- a) = sin a cos a + cos a sin a = 2sina cos a;
sin 2a = 2sina cosa.
2. cos 2a = cos (a + a) = cos a cos a — sin a sin a = cos2a — sin2a;
cos 2a = cos2a — sin2a .
Заметим, что в формуле для cos2а можно заменить cos2а
на 1 —sin2a или sin2a на 1—cos2а. Получим две новые фор¬
мулы:
cos 2а = 1 — 2 sin2a,
cos 2а = 2cos2a — 1.
з. tg 2а = tg (а + а) = = , 2t^ ;
& 1—tga tga 1 — tg2a ’
tg 2a =
K 1 - tg2a
Упражнения
1. Вычислите sin2a, cos2a, tg2a, если
4
sina=— и a—угол первой чет¬
верти.
2. Докажите тождества:
а) sin4a — cos4a = — cos2a;
б) sin4 a+ cos4a = 1 sin2 2a;
Тригонометрические функции половинного угла
Из формул двойных углов cos 2a = 2cos2a —1 = 1— 2sin2a
можно получить формулы для синуса и косинуса половинного
угла.
Сначала запишем
cos2a = -^-(1 +cos2a), sin2a = -^-(1 —cos2a).
Затем в этих формулах подставим вместо а:
cos2y=-i-(l + cos a), sin2y =-l-(i — cosa),
а . ч/1 — cosa а , ,/1 4- cosa
Sin—=± У ^ ’ cos— = ± V—2 •
Для того чтобы правильно выбрать знак перед корнем, надо
определить, в какой четверти лежит угол а/2.
Тангенс половинного угла
Обилие тригонометрических формул связано с тем, что между
основными тригонометрическими функциями — синусом, косину¬
сом, тангенсом и котангенсом — есть соотношения, которые поз¬
воляют по-разному записать одно и то же выражение. Так,
cos2а можно выразить через cosa и sina: cos2a = cos2a—
— sin2a, а можно* только через cosa или только через sina:
cos 2a = 2cos2a — 1, cos 2a = 1 — 2sin2a. Нетрудно при желании
выразить cos 2a через tga (эту формулу мы получим ниже).
в) tga + ctga
г) tga
sin 2a
sin 2a
l-|-cos2a
3. Записав 3a как 2a -|- a, выведите
формулы для sin 3a и cos3a.
8—1681
225
Нельзя ли выбрать одну какую-то функцию и через нее вы¬
ражать все остальные? Если в качестве такой функции взять
синус, то во многих формулах появятся квадратные корни. Так,
выражая sin 2а через sin а, находим
sin 2а = 2sin а cos а = 2sin а(± ]/1 — sin2a).
Такие формулы неудобны.
Оказывается, что все тригонометрические функции от аргу¬
мента (и от кратных этого аргумента) выражаются через тан¬
генс половинного угла рационально, без квадратных корней.
Выведем эти полезные формулы.
Напишем формулы двойного угла для исходного угла у :
sinx = 2sin-|-cos-y-, cos x = cos2-^ sin2-^-.
Представим число 1 в виде 1 = sin2-|- + cos2-|- и поделим на
1 правые части последних формул:
cin Г — 2sin(72)c°s(72) cos2(72) - sin2(72)
sin2(72) + cosj(72) ’ sin2(72) + COSJ(72) '
Разделим числитель и знаменатель каждой дроби на cos2 у и за¬
меним smна tg-|-;
cos(7j) s 2
sin;c_ 2tg(7.) Cosx = »-tg»(V»)
l + tg*(7*) ’ 1+ tg*(7*) '
Пользуясь этими формулами, функцию вида y = asinx +
+ b cosx + с можно представить в виде рациональной функции
от tg-£-.
Пример
Преобразовать функцию у = 2 sinх + 3 cosx — 1 к функции
от tgy:
2 sin х -1-3 cosx - I - о 2tg(V*> I 3 1 ~ 1 =
2 sin x + о cos x l + tg*(72) + l + tg2(7j)
4tg(7«) + 3 - 3tg*(7«) - I -tg2(72)
i + tg*(7*)
- 4tg*(7«) + 4tg(7«) + 2 _
1 + tg*(7*)
^ 2tg*(7i) -2tg(72)- 1
— 1 ’ i+tg*(7 2)
226
Упражнения
1. Вычислите s*n-7jr и cos“?T’ если
24 г л и
5'П“=25И “SL0'TJ-
2. Что изменится в ответе на преды¬
дущий вопрос, если в его условии
заменить на *а ПРИ'
надлежит первой четверти»? Заметь-
7л
те, что про угол а= — можно ска¬
зать, что он лежит в первой чет¬
верти, но нельзя сказать, что
«[*т}
3. Выразите следующие функции в
виде функций от tg-?f:
а) £/ = sinjc — 2cosjt,
б) £/=a sin jc -|- bcosx\
3sinr+cosjt—1
в) и = ; .
sin * +cos*
Преобразование суммы тригонометрических функций в
произведение
Преобразуем сумму sin а + sin р. Сделаем следующий искусст¬
венный прием. Напишем тождества а = а Р + а ~ Р и р =
а -|- Р а — Р о
= —j-s- заменим аир выражениями, стоящими спра¬
ва, в формулах для синуса суммы и разности:
sin а + sin р = Sin(^±± + -^-)+ sin(i±£- - -s4J-) =
= sin “ + р cos ° ~ Р + cos а + Р sin ° ~ р +
+ sin а ^ Р cos а ~ ^— cos ° ^ sin ° ~ ^ =
= 2sin а + Р cos Р ;
sin а + sin р = 2sin
a + P
2
COS
a - p
2
sin а — sin р = 2sin-
a — p
2
COS
a + P
2
cos а + cos р = 2 cos
a + P
2
- COS
a — p
2
cos а — cos p = 2 sin
a + P
2
-sin
P-a
2
Преобразование произведения тригонометрических функций в
сумму
Выпишем формулы сложения:
1. sin (а + р) = sin а cos р + cos а sin р .
2. sin (а — р) = sin а cos р — cos а sin р .
3. cos (a + p) = cos a cos p — sin a sin p .
4. cos (a — p) = cos a cos p + sin a sin p .
Вычтем почленно равенство 3 из 4:
sin a sin р = -^-(cos (a — p) — cos (a + p)).
Сложим третье и четвертое равенства:
cos a cos p = у (cos (a — p) + cos (a + p)).
Сложим два первых равенства:
sin a cos a = у (sin (a + p) + sin (a — p)).
В этом параграфе рассмотрены различные тождества, свя¬
зывающие тригонометрические функции. Все их запомнить
трудно, и приходится обращаться к справочникам. Однако не¬
которые формулы, например для синуса и косинуса двойного
угла, вообще говоря, запомнить полезно.
Преобразование суммы тригонометрических функций в произ¬
ведение связано с возможностью вычислять эти суммы с по¬
мощью логарифмических таблиц. Для компьютерных вычислений
такие преобразования не обязательны.
Необходимость преобразования произведения в сумму объяс¬
няется иначе. С помощью этого преобразования можно объяс¬
нить явление модуляции в радиотехнике. В математике эти
формулы нужны для интегрирования произведений тригономет¬
рических функций.
Упражнения
1. Докажите тождества:
sin a + sin ft a+ft .
cosa + cosfl ^ 2
6) sina + cosa= /2~sin
2. Пусть a, p, у — углы треугольника.
Докажите, что cos a + cos 0 +cos у =
a В V
= l+4sinysin^-siny.
3. Преобразуйте в произведение 1 +
+ cos a + cos 2a -+■ cos 3a.
4. Преобразуйте в сумму:
а) sin a sin 8a;
б) sin 2rsin 7x'— sin 4rsin 5дг,
в) sin*sin я*.
Сложение гармонических колебаний
При движении точки по окружности ее проекция на ось коорди¬
нат совершает гармонические колебания. В простейшем случае,
когда радиус окружности равен 1, угловая скорость точки рав¬
на 1 и точка начинает движение из положения Р0 (1; 0), коорди¬
наты точки Pt задаются синусом и косинусом (рис. 310): х =
= cos ty у = sin t (это определение синуса и косинуса).
228
Ограничимся колебанием ординаты. В простейшем случае
оно описывается формулой у = sin /. Если движение происходит
по окружности радиуса R (говорят, что амплитуда колебания
равна /?), то формула принимает вид у = Rs’xnt. Если точка
движется с угловой скоростью со, то это скажется на коэффи¬
циенте при аргументе /: £/ = /? sin со/ (со/ — длина дуги, прой¬
денной за время / с угловой скоростью со). Если при / = О
(т. е. в начальный момент) точка находилась не в положении Р0,
а в положении Ра, то в формуле колебаний произошло бы еще
одно изменение: у = R sin (со/ + а). Таким образом, гармониче¬
ское колебание общего вида определяется тремя параметрами:
Рис. 310
амплитудой /?, угловой скоростью со и начальной фазой а. Часто
вместо угловой скорости со говорят о частоте колебания v, кото¬
рая связана с угловой скоростью со (круговой частотой) фор¬
мулой со = 2nv.
Необходимо научиться складывать колебания. В механике это
связано с тем, что на точку может действовать несколько сил,
каждая из которых вызывает гармоническое колебание. В элек-
тро- и радиотехнике сложение колебаний также является одной
из важнейших операций. Оказывается, что при сложении гармо¬
нических колебаний одной и той же частоты получается снова
гармоническое колебание той же частоты. На математическом
языке это означает, что сумма двух функций
y=R\ sin (со/ + ai) и y=R2 sin (со/ + аг)
есть функция того же вида:
y=Rz sin (co/ + a3).
Достаточно научиться складывать функции вида у = /?i sin со/
и y=R2 cos со/. Для их сложения применяется прием введения
вспомогательного угла. Итак, рассмотрим выражение у=
=/?i sin со/ + /?2 cos со/. Оно похоже на формулу синуса суммы:
229
sin (o)/-(-a) = sin (о/cos а + cos (о/sin а. Числа R\ и R2 нельзя
считать косинусом и синусом, однако можно их разделить на
число у R2\ + R\ и тогда это будет возможно. Введем угол а с по-
и R1 . R‘2 'T-
МОЩЬЮ соотношении: cosa=—====, sin «= . Так как
/Ж+Ж /яТ+Ж
(/?i/УЖЧ-Ж)2 + (/?2//^Т-рЖ)2= 1, то это возможно. Тогда
/?1 sin О)/ /?2 COS ti>t= //??-+-/?2 ( ;-f' г S'n +
' /Ж+Ж
Н—7^==r cos о)/)=/?3 sin (ш/ + а), где /?з= /Я2 + #2-
у/?|+/?2 7
Упражнения 2. Каково наибольшее значение функ¬
ции y = asmx-\- bcosx?
1. Найдите амплитуду колебания у= 3 Найдите амплитуду колебания у =
= 3 sin 2/+ 4 cos 2/. = sin(x + л/3) + sinjc>
§ 27. Простейшие тригонометрические уравнения
Уравнение sinr=a
Простейшими тригонометрическими уравнениями считают урав¬
нения вида sinr=a, cos x = a, tg x = a, ctg x—a.
Как уже известно, область значений синуса — отрезок
[—1, 1]. Если |а|>1, то уравнение sinx=a решений не имеет.
Пусть теперь |а|^1. Построим на одном рисунке графики у=а
и у=sinx.
«И чем труднее доказательство, тем больше будут удовольствия тому,
кто доказательство найдет.»
Р. Декарт
Дехарт Рене (1596 —1650 г.г.) — французским философ и математик.
Одновременно с Ферма заложил основы аналитической геометрии и
разработал теорию алгебраических уравнений. Историк математики
Д. Я. Стройк написал о нем:
«Заслуги Декарта прежде всего в том, что он применил хорошо разви¬
тую алгебру начала семнадцатого века к геометрическому анализу
древних».
230
По рис. 311 видно, что прямая у=а пересекает синусоиду
бесконечно много раз. Это означает, что при |а|^1 уравнение
sin х=а имеет бесконечно много корней. Так как синус имеет
период 2л, то достаточно найти все решения в пределах одного
периода. По графику (рис. 312) видно, что при |а|<1 на отрезке
[О, 2л] есть два числа, синус которых равен а.
То же самое можно получить, рассматривая движение точки
по окружности: в пределах одного оборота найдутся два угла с
одинаковыми значениями синуса.
Если один из таких углов а, то другой я —а. Все другие
решения уравнения sin* = а (|а|<1) получаются из двух найден¬
ных прибавлением периода.
Рис. 312
Итак, пусть а — какое-либо решение уравнения sin*=a,
(|а|<1). Тогда все решения этого уравнения получаются по
формулам (рис. 313)
*=а + 2Ал, х = л — a-\-2kn (&£Z).
Рис. 311
Рис. 313
Эти две серии решений указаны на графике и иногда запи¬
сываются одной формулой
х=(— 1)ла-(-пп (n£Z).
Пример
Решить уравнение sinx=y.
Одно решение этого уравнения: х—. Все остальные
решения получаются по формулам
х=^ + 2кп и х=л-^ + 2кл=^+2кл (k£X).
Арксинус
Пусть число а по модулю не превосходит единицы. Арксинусом числа а
называется угол х, лежащий на отрезке I— -у, -3- I, синус которого
равен а.
Обозначение: х=arcsina.
Итак, равенство r=arcsina равносильно двум условиям:
sinr=a и —Обратим внимание на то, что arcsina
существует лишь если |at<Jl.
Примеры
1. arcsin0=0. Действительно, 06^— у, yj и sin0=0.
г» -1л
2. arcsiny=—.
3. arcsin ( у )= —-^-.
Теперь решения уравнения sinx=а (при |а|^1) можно пред¬
ставить формулами
х=arcsin а -\-2nk и х—п — arcsin a-\-2nk (££Z)
или в виде одной формулы
х=(—1)* arcsin a-\-nk (£gZ).
Отметим некоторые тождества:
1. sin (arcsin a)=a. Действительно, согласно определению,
arcsina — это такой угол х\ что sinx=a, т. е. sin (arcsin a)=a.
Здесь не использовано условие arcsin а 6 Ит]
2. arcsin (sinjc)=r, если xg . Действительно, обо¬
значим sin г через а. Тогда тождество превратится в определение
арксинуса: arcsin а=х\ если х£ И 1] и sinx=a. Заметим,
что выражение arcsin (sin л:) имеет смысл при любом ху однако
при х£ Г-тт] оно не равно х.
3. arcsin (—а)=— arcsin а. Действительно, синусы от правой
и левой частей равны sin (arcsin (—а))=—а и sin (—arcsin а)=
= —sin (arcsin а)= — а. В то же время правая часть — это угол,
лежащий в пределах Поэтому левая и правая
части равны между собой.
Упражнения
1 Решите уравнения:
ч • /2"
а) sinr=
^ • 1
б) sinr=—;
4
Ч ■ 2 1
в) sin jc=—;
2
г) sin2r=—;
д) sinT=—IF:
е) sin (* + |)=А.
2. Вычислите:
a) arcsin-
1
/2";
б) arcsin(—1);
\ \
в) arcsin I — у
г) arcsin 1;
д) arcsin 2;
е) arcsin — .
3. Вычислите:
а) sin ^arcsin
б) arcsin (siny>
в) arcsin ^sin-^p-
г) arcsin (sin*); хе
Уравнение cos х=а
Так же как и в предыдущем случае, получаем, что при |а|>1
уравнение cosx=a решения не имеет, при |а|^1 решений беско¬
нечно много.
Если а — какое-либо решение уравнения cos х=а, то —а
также является решением (cos a = -(-cos (—а)). По графику
(рис. 314) или на тригонометрическом круге видно, что в преде¬
лах одного периода уравнение cos х=а имеет два решения при
laid. '
233
Если а — одно решение уравнения cos х—ау то все решения
исчерпываются двумя сериями:
x=a-\-2kn9 х=— а-(-2лЛ (k£Z).
Эти серии обычно записывают в виде одной формулы
x—±a-\-2nk (££Z).
Пример
Решить уравнение cosjc=—у.
о
Одно решение находится легко: х=ул. Все остальные
решения уравнения cosjt=— у: х=±уЛ + 2Лл (&6Z).
Арккосинус
Так же как и для синуса, выделяется одно определенное решение
уравнения cos х=ау которое называется арккосинусом.
Пусть а — число, по модулю не превосходящее единицы. Арккосинусом
числа а называется угол хг лежащий на отрезке [0, л], косинус которого
равен а.
Обозначение: х=arccos а.
Равенство x=arccosa равносильно двум условиям: cosх=а
и О^дг^л. Арккосинус числа а существует лишь при — 1.
Примеры
arccosO=y, arccosy=y, arccos л.
Решение уравнения cos х—а |а|^1 можно записать в общем
виде: х— ±arccos а + 2лй (k£Z).
По каким причинам для значений арксинуса был выбран
отрезок [-т-т]- а для арккосинуса — [0, л]? Выбраны эти
отрезки, так как на них, во-первых, синус и косинус принимают
все возможные значения от —1 до 1 и, во-вторых, каждое значение
Рис. 314
принимается ровно один раз. Отрезков, удовлетворяющих этим
условиям, бесконечное множество, но при этом выбраны отрезки,
«наиболее близкие к нулю».
Для арккосинуса можно вывести ряд тождеств:
1. cos (arccos а)=а. Это часть определения арккосинуса.
2. arccos (cosх)=х\ если л:£[0, я]. Обозначим cosх—а.
Получим определение арккосинуса: arccosа=х, если rg[0, я] и
cos х=а.
3. arccos (—а)=л — arccos а.
Вычислим косинус от обеих частей этого равенства, используя
первое тождество:
cos (arccos (—а))=—а,
cos (я —arccos а)=—cos (arccos а)=—а.
Если равны косинусы двух чисел, то это еще не означает, что
равны сами числа. Проверим, что правая часть лежит на отрезке
[О, я]. Так как левая часть тоже лежит на этом отрезке, то из
равенства косинусов двух чисел теперь уже будет следовать
равенство самих чисел, так как на отрезке [0, я] косинус прини¬
мает каждое значение ровно один раз.
Итак, надо доказать, что я — arccos а 6 [0, я]. Действительно,
arccos а 6 [0, я], —arccos а 6 [—я, 0], я — arccos а 6 [0, я], что и
требовалось доказать.
Упражнения
1- Решите уравнения:
a) cosх =-
б) cosдс =——;
и
2 1
в) cos л=—;
г) cos2jc=—;
4
д) Cos*=—
ч X 1
е) cosT=-y.
2. Вычислите:
__1
/г
б) arccos (—1);
a) arccos Г- V, г) arccos 1;
д) arccos (—3);
е) arccosO.
/3"
в) arccos—2~;
3 Вычислите:
а) cosarccos4~;
5
( Зл \
б) a rccos I cos -g- I
в) arccos (cos (-т))
\ / 6jl \
r) arccos ^cos-g-^.
4. Докажите тождества:
a) arcsinjc-j-arccosjc=y;
б) sinarccosjt= /1 — x* ;
в) cosarcsinjc= /1— x* .
Решение уравнений tgx=a и ctgx—a
Область значений тангенса (котангенса) — вся числовая ось IR.
Поэтому уравнения tgr=a и ctgx=a имеют решения при
любом а. В пределах одного периода (а он равен я) тангенс и
котангенс принимают каждое значение ровно один раз. Поэтому
235
если известно одно решение уравнения tg х—а или ctgx—а,
то все остальные получаются прибавлением периода:
tgх=а=>х—а-\-kny ctgx—a=>x—a-\-kn (££Z),
где a — какое-либо решение соответствующего уравнения.
Примеры
Решите уравнения:
1. tg х'= 1, x—^ + kn (k£Z).
2. ctgx=-£-, х=-± + кл (keZ).
Арктангенс и арккотангенс
Определения арктангенса и арккотангенса аналогичны определе¬
ниям арксинуса и арккосинуса.
Арктангенсом числа а называется угол х s ^ Т' ~7 /’ тангенс кото"
рого равен а.
Арккотангенсом числа а называется угол x^i (0, л ), котангенс которо¬
го равен а.
Обозначения: х=arctga, х=arcctg a.
Примеры
arctgO = 0, arcctgO = у-, arctg(—1) = —arcctg(—1) =
Зл_
— Т"*
При решении уравнений функции arctgx, arcctgx ис¬
пользуются так:
tgx = ао х = arctga + kn (k^Z)\
ctgx = a -о x = arcctga -(- kn (k^ Z).
Основные тождества
1) tg arctga = a, ctg arcctga = a;
2) arctg (tgx) = x, если xe(-p |-);
arcctg (ctgx) = x; если x e (0, л);
3) arctg (—x) = —arctgx,
arcctg (—x) = я—arcctgx.
Упражнения
1. Решите уравнения:
а) tgr= —;
✓з-
б) tg2х= 1;
в) ctg2r=3;
г) ctgr= —0,1;
д) tg3r=-y;
е> ‘«(г—J-)=-3-
2. Вычислите:
а) arctg /3";
б) arcctg( )‘,
в) arctg 1;
г) arcctg/3";
д) arctg(—у-);
е) arcctg(— /Т).
3. Вычислите:
а) tgarctg2;
б) ctgarcctg(—2);
в) arctg (tg-j^p);
г) arctg (tg-^-)-
4. Докажите тождества:
а) arctg* + arcctgr=y;
б) ctgarctgr=-^;
в) sinarctgr=—т— -•
VI+х*
§ 28. Решение тригонометрических уравнений
Общие сведения
Тригонометрические уравнения встречаются в задачах, в которых
из соотношений между тригонометрическими функциями требует¬
ся найти неизвестные углы. Следует отметить, что простейшие
тригонометрические уравнения обычна имеют бесконечные серии
решений, задаваемые с помощью параметра, принимающего це¬
лые значения. Так, например, уравнение sinx=имеет реше-
ния, задаваемые двумя сериями:
х = arcsin-^—\- 2Лл, х = л—arcsin-^—\- 2kn (k ^ Z).
Более сложные тригонометрические уравнения обычно ре¬
шаются сведением их к простейшим с помощью различных алгеб¬
раических и тригонометрических формул и преобразований.
В этом параграфе рассматриваются некоторые приемы решения
тригонометрических уравнений.
237
Уравнения, алгебраические относительно одной из тригонометри¬
ческих функций
Примеры
1. Решить уравнение 2sin2x -(- 3 sin jc — 2 = 0.
Это уравнение является квадратным относительно sin*.
Его корни: sinx = y-, sinr=—2. Второе из полученных
простейших уравнений не имеет решений, так как Isinxj^l,
решения первого можно записать так:
х = —\-2kn, х = л——\- 2nk = (- 2nk
Если в уравнении встречаются разные тригонометрические функции, то
надо пытаться заменить их bee на какую-нибудь одну, используя три¬
гонометрические тождества.
2. Решить уравнение 2sin2jc — 5cosx—5 = 0.
Так как квадрат синуса легко выражается через косинус,
то, заменяя sin2jc на 1—cos2* и приводя уравнение к квадрат¬
ному относительно cos*, получим 2(1—cos2*)—5cos*—5 =
= 0, т. е. квадратное уравнение 2cos2* + 5cos* + 3 = 0,
з
корни которого cos* = —1, cos* =—2”. Уравнение cos* =
= —-|- решений не имеет. Решения уравнения cos* = —1
запишем в виде
х = л + 2kn (teZ).
3. Решить уравнение tg jc + 3ctg* = 4.
Заменяя ctg* на — и приводя выражение к общему
tg X
знаменателю, получаем квадратное уравнение tg2*—4tg*-|-
+ 3 = 0, корни которого tgjc = 1, tg* = 3, откуда х =
= —(- Лл, х = arctg 3 -(- kn (£^Z).
4. Решить уравнение 2sin* + cos* = 2.
Если в этом уравнении заменим косинус на синус (по
аналогии с предыдущими примерами) или наоборот, то по¬
лучим уравнение с радикалами. Чтобы избежать этого, ис¬
пользуем формулы, выражающие синус и косинус через
тангенс половинного угла:
sin r=_2.tgfr/2) и CQSJC== 1-У.(*/2)_
1 + tg2(x/2) И C°S* l+tg2^) ‘
Делая замену, получаем уравнение относительно tgy-:
4tg -f- + 1 - tg2^- = 2(l + tg2-f-)
238
Квадратное уравнение Stg2-^—4tgJ—|- 1 =0 имеет корни
tg-f-= 1, tg-|- = откуда
-y = JT + kn' x = Jt + 2кл< IT = arct& “Г + кл’
х = 2arctg-i-+ 2nk (fceZ).
Это же уравнение можно решить другим способом, вводя
вспомогательный угол (см. § 26):
2sinx -)- cos* = /5~(-^sinjc +-^=cosjc)
2
Пусть a = arccos—T=. Тогда можно продолжить преобра-
/5
зование: 2sinjt + cosjc = /5~sin(jt + а). Получаем простей¬
шее уравнение /б” sin(jc + а) = 2, т. е. sin(jt -+- а) =
2 2
= —=> откуда х + а = arcsin —= + 2Лл, или
/5 /5
2
х + а = я — arcsin—— -)- 2Лл.
/5
Ответ получился в другом виде, однако можно проверить,
что решения на самом деле совпадают.
Упражнения б) sinjc + /3~cosjc= 1;
Решите уравнения: в) s*n* — 2cos*=2;
a) 2sinJ* + cosr-l=0; г> 2tg*-3ctg*~ 1 =0.
Понижение порядка уравнения
Формулы удвоения
sin2x = 2sinxcosjt, cos2jc = cos2* — sin2*,
cos2* = у (1 + cos2jc), sin2x = у (1—cos2x).
позволяют квадраты синуса, косинуса и их произведения заме¬
нять линейными функциями от синуса и косинуса двойного угла.
Такие замены делать выгодно, так как они понижают порядок
уравнения.
Примеры
1. Решить уравнение cos2xcos2r■'=
Можно заменить cos2x на 2cos2jc—1 и получить квад¬
ратное уравнение относительно cosx, но проще заменить
cos2* на у(1 -|-cos2jt) и получить линейное уравнение отно¬
сительно cos2x.
65
2. Решить уравнение sin4* -(- cos4* = —
Подставляя вместо sin2jc; cos2x их выражения через
cos 2л:, получаем:
cos2*)2 + +1 + cos 2х)2 = -|у-,
1 —2cos2x + cos22jc + 1 + 2cos2jc-)-cos22jc = 4*-gy-,
cos22x = 2--gy— 1, cos22x = -|y-, cos2* = ± -g-,
2x = ±arccos-^- + kn, x = ±-|~агссоз-|- + -^- (AeZ).
Упражнения 6) 4sin2* — cos2* = 5;
Решите уравнения: B) sin4*-|-cos22.K=2;
a) 4cos2x + cos2*=5; r) 3 j « 3 J_
2 2 /5~
Использование тригонометрических формул сложения и след¬
ствий из них
Иногда в уравнениях встречаются тригонометрические функции
кратных углов. В таких случаях нужно использовать формулы
сложения.
Примеры
1. Решить уравнение sin* + sin2x + sin3jc = 0.
Сложим два крайних слагаемых: (sin* + sin3x) +
+ sin2jc = 0, откуда 2sin2jccosx + sin2jc = 0, sin2jc(2cosjc-(-
-j- 1) = 0. Тогда sin2x = 0, 2x = kn, x = —kn или 2cosx =
— — 1, x = 4h узт —|— 2kn (k g Z).
2. Решить уравнение sin3jcsin5jc = sinx sin7x.
Преобразуем произведение синусов в сумму:
у- (cos2*—cos8jc) = -^-(cos6jc—cos8x),
откуда cos2jc = cos6jc. Полученное уравнение можно ре¬
шить разными способами: 1) воспользоваться формулами
сложения; 2) преобразовать cos6x — cos2x в произведение.
Удобнее воспользоваться условием равенства косинусов
240
двух углов 2х и блг: 6x=±2x-\-2nk (£^Z). Получаем два
уравнения:
Проверьте, что решения второй серии содержат в себе все
решения первой серии. Учитывая это, ответ можно записать
короче:
Однородные уравнения
Рассмотрим уравнение sin2jc — 5sinjtcosjt + 6cos2x = 0. Если
считать, что sinx и cos* — члены первой степени, то каждое сла¬
гаемое имеет степень 2.
Уравнение, в котором каждое слагаемое имеет одну и ту же степень,
называется однородным.
Его можно решить, выполнив деление на старшую степень синуса
(или косинуса). Делим наше уравнение на cosх: Заметим: если
в данное уравнение подставить cosjc = 0, то получим sinjc = 0,
что невозможно, значит, в результате деления на cos2* не будет
потери корней. Продолжая решение, находим:
tgx = 3, х = arctg2 + kn, х = arctg3 + kn
Так как 1 = sin2jc-(-cos2x, то постоянные слагаемые можно счи¬
тать членами второй степени.
6х = 2х + 2nk, 4х = 2nk, х = у Л л,
6jc = — 2х + 2kn, 8х = 2kn, х = kn.
х = -^~ (fteZ).
Упражнения
Решите уравнения:
a) cos2jcsin4r=cosjcsin5jc;
б) sinдс -|- sin 3jc -|- sin 5jc = 0;
в) cos2* +cos4* — cos3jc=0;
r) cos6jc —cos8jc= 1 — cos2jc.
+ 6 = 0, tg2x—5tg* + 6 = 0, tgx = 2,
Пример
5sin2jt + 3sinjc cosjc = 4.
Заменяя 4 на 4 (sin2* + cos2*), получаем:
sin2x + 3siruccosjc — 4cos2jc = 0, tg2x + 3tgx —4 = 0,
tgx = 1, tgx = — 4, x = ~—b kn, x = — arctg4 + kn
(k<=2).
241
Упражнения
Решите уравнения:
a) 7 sin2* = 8 sin* cos* — cos2*;
б) 3sin2*-|-2sin*cos* = 2;
в) 6 sin2 * + 3 sin* cos* — 2cos2* = 3.
§29. Обратные функции
Взаимно обратные функции
Напишем формулу для вычисления площади круга по его ра¬
диусу:
S = я/?2.
Эта формула задает площадь S круга как функцию от его радиу¬
са /?, т. е. для каждого (положительного) числа R по этой фор¬
муле вычисляется площадь S круга. Представим себе, что надо
решить обратную задачу: по данной площади S круга вычислить
его радиус. Для этого выразим R через S:
R =
У л
Новая формула задает радиус R круга как функцию от его
площади S. Полученные две функции S = S(/?) и R = R(S)
являются взаимно обратными функциями.
Примеры
1. у = 2х + 5 и х = \
2. у = х? (х>0) и х = Уу~ (у>0).
3. у = 10х и х = \gy.
Соответствие между переменными величинами в этих приме¬
рах, задаваемое взаимно обратными функциями, одно и то же.
В самом деле, зависимость между радиусом и площадью круга
остается одной и той же, записывается ли она в виде S = яR2
или же в виде R = / . Точно так же функции у = 2х + 5 и
у ^
х = ——задают одну и ту же зависимость между перемен¬
ными х и у. Эту зависимость можно записать и так: 2х—у-|-5=0.
Из последней формулы видно, что можно выразить у как функ¬
цию от xt а можно выразить х как функцию от у.
Две функции у = f(x) и х = g(у) называются взаимно обратными, если
между переменными х и у выполняются соотношения у = f(x) и х = д(у)
одновременно:
У=Чх) <=>■ *=g(y).
242
При этом область значений функции f является областью
определения функции g, и наоборот. Подставляя равенства
у = f(x) и х = g(y) одно в другое, получаем тождества
f(g(y)) = У и g(f(x)) = х.
Упражнения
Из соотношения между переменными х
и у выразите каждую из перемен¬
ных как функцию от другой:
Обратная функция и ее график
Пусть дана функция у — f(x). Если это соотношение между переменными
позволяет однозначно выразить х как функцию от у, то эту функцию
называют обратной по отношению к исходной.
Таким образом, если из соотношения у = f(x) можно выра¬
зить х в виде х = g(y), то тогда говорят, что х = g(y) есть функ¬
ция, обратная к функции у= f(x). Так как соотношения у = f(x)
и х = g(y) выполняются одновременно, то исходная функция и
обратная к ней образуют пару взаимно обратных функций.
Можно сказать и наоборот: если у = f(x) и х = g(y) — взаим¬
но обратные функции, то каждую из них можно рассматривать
как обратную функцию по отношению к другой.
Аргумент функции и ее значения можно обозначать какими
угодно буквами. Так, формулы у = 2х + 5, S = 2/-(-5, х =
= 2у + 5, а = 2Ь + 5 и т. д. определяют одну и ту же функцию.
В записи пар взаимно обратных функций у = f(x) и х = g(y)
удобно обозначать аргумент одной из них так же, как значение
другой. При такой записи видно, что переменные х и у связаны
одной и той же зависимостью. Однако иногда удобно аргумент
каждой встречающейся функции обозначать одной и той же бук¬
вой, например буквой х.
Пары функций:
1) у = 2*+ 5 и у = \—
2) у = х3, х^О и у — УГ (х^О);
3) у = 10х и y = lgx
— также являются взаимно обратными функциями.
Разница в обозначениях наглядно иллюстрируется на графике
(рис. 315). Две взаимно обратные функции у = f(x) и х = g(y)
на плоскости с координатами (х; у) будут иметь один и тот же
график, так как зависимость между координатами точек у = f(x)
и х = g(y), по определению взаимно обратных функций, одна
и та же.
а) 3* + 5i/= 4;
б) *2+02=1, (*>0, </>0);
в) (л:—2)(£/+3)= 1
243
В то же время если аргумент каждой функции обозначать
(как это обычно принято) одной переменной ху то графики вза¬
имно обратных функций будут симметричны друг другу отно¬
сительно прямой у = х.
Это связано со следующим обстоятельством. Возьмем два
числа а и Ь. Если мы откладываем число а на оси абсцисс,
а число Ь — на оси ординат, то получаем точку Р(а, Ь) (рис. 316).
Если же, наоборот, мы откладываем число а на оси ординат,
а число Ь — на оси абсцисс, то получаем точку Q(fe, а). Точки
Р и Q симметричны друг другу относительно прямой у = х
(рис. 317).
Упражнение v х /—
а) у=— — \\ б) у= /Г;
Для данной функции найдите обрат¬
ную и постройте графики обеих 3
функций, откладывая аргумент каж- в' У
дой из них по оси абсцисс:
Условие существования обратной функции
Вернемся снова к площади S круга как функции радиуса
/?: S = л/?2. Эта функция имеет обратную потому, что можно
однозначно выразить R через S, т. е. R = . То же самое
было верно и для других функций, рассмотренных на с. 242. При-
Рис. 315
Рис. 316
Рис. 317
ведем примеры функций, для которых нельзя однозначно выра¬
зить аргумент через заданное значение функции.
Примеры
1. у = \х\ (рис. 318, а). Для данного положительного чис¬
ла у найдутся два значения аргумента х такие, что \х\ =
= у. Допустим, что у = 2, тогда х = —2 или х — 2. Вы¬
разить однозначно х через у нельзя.
2. у = х2. Ситуация здесь такая же, как в примере 1: х = 1/у~
или х= —л[у (рис. 318,6).
3. у = sin*. При заданном значении у (\у\ ^ 1) найдется не
по два, как в предыдущих примерах, а бесконечно много
таких значений *, что y = sin*. Здесь также нельзя одно¬
значно выразить х через у (рис. 318, в).
Сравним на графике эти примеры с примерами, данными на
с. 242. Возьмем число у0 из области значений функции f и прове¬
дем прямую у = г/0, параллельную оси абсцисс. В первых трех
случаях эта прямая пересекает график в одной точке, т. е. можно
по заданному значению однозначно найти значение *. В послед¬
них трех случаях при некоторых у0 прямая пересекает график
более чем в одной точке: для этого у0 нельзя однозначно найти *.
В первых трех случаях функции имеют обратные, а в послед¬
них — нет.
Как же сформулировать условие того, что функция f имеет
обратную? Это можно сделать одним из следующих равно¬
значных способов.
Функция у = f(x) имеет обратную, если:
1) из соотношения у = f(x) можно однозначно выразить х через у;
2) всякая прямая у = у0 пересекает график функции у = f(x) не более
чем в одной точке (она может совсем не пересекать график, если у0
не принадлежит области значений функции f);
3) уравнение yQ = f(x) при каждом у0 имеет не более одного решения;
4) при разных значениях аргумента функция принимает разные значе¬
ния, Т. е. X, j=. х2 => f(x,) Ф f(x2) или
f(x i) = f(x2) =► X, = х2.
245
Рис. 318
Монотонные функции
Условие того, что функция имеет обратную, заведомо выполняет¬
ся, если функция строго возрастает или строго убывает. Действи¬
тельно, если / возрастает, то при двух различных значениях
аргумента она принимает различные значения, так как большему
значению аргумента соответствует большее значение функции.
В примерах, изображенных на рис. 146, три функции (б, д, и)
были возрастающими, поэтому они имели обратные.
Условие строгой монотонности функции / достаточно для
того, чтобы функция / имела обратную.
Условие монотонности не является необходимым условием для того, чтобы
функция имела обратную, т. е. не только монотонные функции имеют
обратные.
Пример
Изображенная на рис. 319 функция, заданная формулами
У =
-L (х<0),
Рис. 319
х (х^О),
имеет обратйую, хотя и не является монотонной.
Упражнение
На рис. 320, а—е изображены графики
шести функций. Определите по гра¬
фику, какая функция имеет обрат¬
ную, а какая — нет.
Сужение области определения
Сравним две функции: функцию S = я/?2, где R — радиус круга
и R> 0, и функцию у = пх2 (xei?). Эти две функции выра¬
жают одну и ту же зависимость, однако первая из них имеет
обратную, а вторая — нет. Дело в том, что первая функция опре-
246
делена только при положительных значениях аргумента (радиус
круга положителен), а вторая — при любых его значениях.
При положительных значениях аргумента из соотношения
у = лх2 можно однозначно выразить х через у, а при rfe#? этого
сделать нельзя. Сравним графики этих функций.
На графике (рис. 321) видно, что условие существования об¬
ратной функции выполнено для первой функции и не выполнено
для второй. Связь между функциями у = лх2 (х^О) и у =
= лх2 (x^IR) проста: первая функция является ограничением
(сужением) второй из них на отрезок [0; +оо).
Если функция не имеет обратной, то обычно можно умень¬
шить ее область определения так, чтобы новая функция прини¬
мала каждое свое значение ровно один раз. Эта новая функция
уже будет иметь обратную.
247
Рис. 320
Рис. 321
Примеры
1. Рассмотрим ограничение функции у = х2 на промежуток
(—оо; 0] (рис. 322).
Эта функция убывает и потому имеет обратную:
у = jc2, jc^O ох = —/у~.
2. у = х* + 2х— 1 (рис. 323).
Эта функция не имеет обратной. Найдем ее участки мо¬
нотонности: при —1 функция у убывает, при х^ — 1
она возрастает. Ограничение данной функции на каждый
из указанных промежутков уже имеет обратную функцию:
а) при х < —1
у = (х + If—2=> (х +1)2 = у + 2=>х +\ = —/у + 2 =*.
=> х = — 1— |/у + 2
и поэтому обратную функцию можно записать так: у =
= -1-1/7+У ;
248
Рис. 324
Рис. 322
Рис. 323
б) при X > —1
у = (х+ I)2—2 =»• (х+ 1)2 = у + 2=>х+1= |/ у 2 =>
=*■ Г = — 1 + /у + 2 .
Приведем графики полученных функций (рис. 324).
Свойства взаимно обратных функций
Свойства взаимно обратных функций тесно связаны между со¬
бой. Пусть даны две взаимно обратные функции у = f(x) и
У = &(*)> т- е* условия у = f(x) и х = g(y) равносильны (рис. 325).
1. Область определения функции f совпадает с областью
значений функции gy и, наоборот, область значений функции /
совпадает с областью определения функции g (рис. 326):
D(f) = E(g) и E(f) = D(g).
2. Если функция f возрастает, то и функция g возрастает.
Если функция f убывает, то и функция g убывает.
Обратные тригонометрические функции
Тригонометрические функции y = s\nx> у = cosx, у = tgx,
у = ctg X' не имеют обратных—из приведенных соотношений
нельзя однозначно выразить г через у. На языке уравнений это
означает, что простейшие тригонометрические уравнения (типа
sinjt = a) никогда не имеют единственного решения.
Однако мы знаем, что если уменьшить область значений х\
то можно добиться того, чтобы простейшее уравнение имело ров¬
но одно решение. Так, уравнения sinх = у, cosх = уу tgх = у,
ctgx = у, имеют единственные решения на промежутках
х е= [—J-; -|-] , X е [0, я] ,х «= ^х е (0; л) соот-
ветственно. Эти решения: arcsine, arccos у, arctg у, arcctg у.
249
Рис. 325
Рис. 326
С помощью этих обозначений можно определить обратные
тригонометрические функции.
Арксинус. Возьмем число *е [—1, 1]. Арксинусом числа
х (arcsin*) является угол уу лежащий на отрезке [-Г- f]
синус которого равен х. Это правило определяет функцию
у = arcsin*. Она будет обратной к функции у = sin*,
*te £—у-; J (рис. 327). Свойства функции arcsin* выведем
из соответствующих свойств функции sin* (табл. 5).
Таблица 5
Арккосинус. Возьмем число *е[ — 1, 1]. Арккосинусом числа
х (arccosjc) является угол у, лежащий на отрезке [0, л], косинус
которого равен х. Это правило определяет функцию у = arccos*.
Она будет обратной к функции у = cos*, *е[0, я] (рис. 328).
Свойства арккосинуса указаны в табл. 6.
Свойства
Функция
Область определения
Область значений
Монотонность
Четность
Возрастает
Нечетная
sin( — х) = — sinx
Возрастает
Нечетная
arcsin(—х) = — arcsinx
Рис. 327
Рис. 328
Таблица 6
Свойства
Функция
у == COS X,
х е [0, л]
у = arccos*
Область определения
|0, л]
[-1. ч
Область значений
[-1. 11
[0, л]
Монотонность
Убывает
Убывает
Четность
В таблице свойств арккосинуса в графе «четность> стоит прочерк. Дело
в том, что арккосинус не является ни четной, ни нечетной функций.
Между arccosx и arccos(—х) есть соотношение, доказанное в § 27:
arccos(—х) = я—arccosjt.
Арктангенс. Возьмем любое число х. По определению, арк¬
тангенсом числа х (arcctgx) является угол у, лежащий на от¬
резке ^тангенс которого равен х. Это правило вы¬
числения арктангенса определяет функцию у = arctgjc. Она будет
обратной к функции у = tgr, х (рис. 329).
Простейшие свойства тангенса и арктангенса приведены в
табл. 7.
Таблица 7
251
Рис. 329
Свойства
Функция
Область определения
Область значений
Монотонность
Четность
Возрастает
Нечетная
Возрастает
Нечетная
Функция у = arcctgjc используется редко, однако и ее не¬
трудно определить, рассматривая решения уравнения ctgy = х,
лежащие на отрезке (0, я).
Мы определили обратные тригонометрические функции, вос¬
пользовавшись данными ранее определениями арксинуса, аркко¬
синуса и арктангенса как решений тригонометрических уравне¬
ний, лежащих на определенном отрезке. На языке функций мож¬
но сказать, что, уменьшив области определения синуса, косинуса
и тангенса, мы добились того, что они стали строго монотонны¬
ми и, следовательно, стали иметь обратные функции.
Упражнения
!• Какова область определения функ¬
ции у=arcsin*?
2. Какова область значения этой функ¬
ции?
3. Какими тождествами связаны меж¬
ду собой синус и арксинус?
4. Какая функция будет обратной к
функции у=arcsin г? Ответьте на
аналогичные вопросы для арккоси¬
нуса и арктангенса?
5. Принимает ли арктангенс наиболь¬
шее и наименьшее значения?
Задачи и вопросы
7.1. Вычислите:
a)
sin 13° cos 17° +
e)
cos 71° cos 26° +
+ sin 17° cos 13°;
+ sin 71° sin 26°;
6)
sin 16° cos 29° +
Ж)
cos 20° cos 25° —
+ sin 29° cos 16°;
— sin 20° sin 25°;
в)
sin 78° cos 18° —
з)
cos 87° cos 33° —
— sin 18° cos 78°;
— sin 87° sin 33°;
r)
sin 63° cos 33° —
и)
cos 8° cos 37° —
— sin 33° cos 63°;
— cos 82° cos53°;
Д)
cos 66° cos 6°
к)
sin 64° sin 34° —
+ sin 66° sin 6°;
— sin 56° cos 116°.
7.2. Упростите:
а) sin За cos 2а —
— cos За sin 2а;
б) sin(a — p)cos р +
+ cos(a — P)sin Р;
7.3. Вычислите:
а) cos215° — sin215°;
б) cos2|---sin21-;
в)
г)
sin(a + Р) + sin(a — ft) .
sin(a + р) — sin(a — р) ’
sin(a + р) — 2 sin a cos p
cos(a + p) — 2 cos a cos p
в) 2cos’-^-- 1;
r) 1 — 2 sin2-|-;
252
д) sin 15° COS 15°; ж\ Sin 25° sin 65°
ч sin 20° cos 20° . C0S 40
' cos 50° ’
7.4. Упростите:
a) (sin a -j- cos а)2 v cos 2a
1 + sin 2a ’ sin a + cos a *
1 — sin 2a r) sin3 a cos a — sina cos3a.
(cos a — sin a)2 *
7.5. Докажите тождества:
а) cos4a — sin4a = в) tga + ctea = —-—;
„„„ о ■ & sin 2 .
= cos 2a;
б) cos4 a + sin4 a = r) sin2a/(l + cos 2a) = tga.
= 1 — y-sin2 2a;
7.6. Найдите:
а) sin-i-; в) tg£; д) cos-^;
б) cos^-; r) sin -2-; e) tg-|-.
7.7. Найдите:
а) sin + если sina=y, аб(о, у);
б) sin(y + a), если sina=y, аб(у, я);
в) cos (у —а), если cosa=-^-, аб(о, у);
\ а 2
г) cos а, если cos—=— ;
Z ч5
д) sin а, если siny = —у, «6 (—у. о);
е) sin а, если siny=—у а 6 (—я, 0).
7.8. Вычислите:
tg 10° + tg35° . tg72° + ctg 48° .
’ 1 -tgl0°tg35o ’ 4 1 + tg42°ctg 18'
6) tg73° — tg 13° . ^ 2tg(V,)
l+tg73°tgl3° ’ 1 - tg2(7e) *
!0° + tg25° . . tgf/,«)
ctg65°ctg70° ’ 1 - tgif/„) •
253
7.9. Докажите тождества:
•>*«(7--“)-пп£< ■> **(-Г + “)-
Г) tg(-5- - а) =
cos 2а
1 — sin 2а ’
cosa — sina
cosa + sina
7.10. Найдите:
а) 4§(т —“)’ если tga=2;
б) tga, tgp, если tga + tgp=2tg(a + p)=4.
7.11. Вычислите:
ях 2tg(y6) , . 1 - tg2(78) .
' 1 + tg2(78) ’ l + tg*r/.) ’
ti\ tg15” • r\ I + tg215°
' 1 + tg215° ’ ; 1 - tg215° *
7.12. Найдите:
а) sina, cosa, tga, если tgy=3;
б) sina, cosa, tga, если ctgy=y-
7.13 Докажите тождества:
v sina + sinp _■ a + p .
cos a + cos p ® 2 ’
г-ч sin a + sin ft cos ((a— ft)/2)
' sin a cos p + cos a sin 0 cos ((a + P)/2) ’
в) sin a + cos a =/Т cos ^a—
r) sin a —cos a= /2~sin ^a —
Д) cos a + 2cos 2a + cos 3a=4cos2 у cos 2a.
7.14. Преобразуйте сумму тригонометрических функций в произ
веденйе и упростите:
а) sin75° + sin 15°; г) cos48° — cos 12°;
б) sin78° - sin42°; sin25° + sin 15° .
в) cos 152° + cos28°; sin25° — sinl5
254
е) sin20° + cos40°; л) cos-| cos-j^;
ж) cos20° — sin20°;
v . , . 2„ M) sin4a + sin2a;
3 ; „) sin(40. + a)_
и) cos a cos P; - sin <40° - a);
к) sin -Jq sin ; o) sina + sin2a +
+ sin3a + sin4a.
7.15. Преобразуйте произведение тригонометрических функций
в сумму:
а) cos 45° cos 15°; ж) sin 5a sin 3a;
б) sin cos —; з) sin 4a cos 2a;
» cos 20" cos 10"; “> sl" 2« »М«+ Ю:
r) cosf-cos-?-; K C,°SCtC0S<“ + W'
10 5 л) 2 sin a sin 2a sin 3a;
д) sinsinm) 8 cos (a — p) cos (a — у) X
5 8
e) sin JL- cos
X COS (y — P).
7.16. Найдите амплитуду и начальную фазу гармонических коле¬
баний:
а) sin2< + cos2<; ж) cos/^_ & \ +
б) sin/ — cos/; V 3 /
в) 2cos/ + 3sin/; +cos(^ + ^lV
г) 12cos3< — 5sin3/; ' 3 '
д) 16sin2n/ + 2cos2n<; 3) cosco< + cos(a>< + f-).
е) sin2< + 2cos (2t —
7.17. Решите уравнения:
а) sin3jc = 0; л) ctgЗл: = — 1;
б) = м) sin + -§-) =
в) sin2* = — 1;
и) sin22x= 1;
о) cos(-f--f-) = -f-;
г) cos = 0;
д) cos2**= 1;
е) cos -|- = 2; п) cos2-^- =
ж) tg = 0;
р) tg(2x + -|-) = —л/З;
с) tg2x = 3;
к) ctg -у- = 1; т) ctg(-|- + -2-) = -f-.
255
з) tg2л: = — 1;
и) ctg4jc = 0; с) tg2x = 3;
7.18. Вычислите:
а) arcsinO; ж) arctg ( — 1); л) arctg^-;
б) arccosO; з) arcctgl;
в) arctgO; м> ^csin(-l);
г) arcctgO; и) arcsin/ н> arccos(-l);
l ' аГС81Ч 2 )' о) arctg(—V3);
д) arcsin
/ i \ к) arccos^-; n) arcctgf 1=).
е) arccos (—^-1; 1 \ V-* /
7.19. Вычислите:
а) sin (arcsin в) tg (arctg ( — -i-));
б) cos (arccos-i-); r) ctg (arctg
7.20. Вычислите:
а) sin (arccos в) tg (arccos-^-); д) cos(arctg3);
б) cos (arcsinr) tg (arcsin e) s,n (arctg—
7.21. Вычислите:
а) arcsin (sin-i-) ; в) arccos(cos—\ e) arcctgtg3;
\ 3 / \ 5 /’ . хх.
. „ ж) arcctgctgl;
,, . / . Зл \ r) arccos cos2; &
б) arcsin (sin —); ... юол
V 4 / , , . 2л з) arcsin sin —.
д) arctg tg—; 7
7.22. Вычислите:
1 1 5 / 5 \
a) arcsin-g-+arccos-g-; 6) arccos-—arcsinf — —1
7.23. Решите уравнения:
а) 2sin2jc — 3sinje +1=0; д) 4cos2jc — 3sinx = 3;
б) 2sin2je — 2sinx = 1; e) 2cos2 2x = 8cosx— 1;
в) 2cos2jc + cosjc =1; ж) 6tg2x + tg jc — 1=0;
r) 2sin2x -f- 5cosjc — 4 = 0; з) 3tg2x + ctg2* = 4.
7.24. Решите уравнения:
а) 3sinjc = cosoc; = 2cos(*
б) 2sin* + 3cosjc = 0; \ 4 у
r) cos2* — 3sin*cos* +
в) 3sin (x + = -f- 2cos2jc = 0.
256
7.25. Решите уравнение:
а) sin4л: — sin7л: = 0;
б) cos3* + cos5* = 0;
в) cos4* = cos5*;
г) sin 15л: = sin 7л:;
д) cos (Зх =
= cos(* + -J-);
е) cos (2х + -2-) =
*
= — cos —;
7.26. Решите уравнение:
а) cos * +cos 2* +cos 3* +cos 4*=0;
б) 1 + cos Зх + cos 7*+ cos 10*=0;
в) sin x + sin 3* + sin 5* +sin 7x—0;
г) cos2 x + cos2 2л: + cos2 3*=y ;
д) sin2 3* + sin2 4* +sin2 6* +sin2 7*=2;
е) sin 2л: cos 4л:—sin 7* cos 9л:;
ж) cos 7x cos 1 Ox=cos 2x cos 15*;
з) sin 5* sin 3* + cos 7*cos*=0.
7.27. Решите уравнение:
а) asin* + bcosx = 0;
б) -^sin* _|_ cosx ^2;
ж) cos3* = sin Юл:;
з) sin7х = cos 13л:;
и) tg3* = tg5*;
к) ctg5* = ctg*;
л) 1 — cos 7л: = 2cos29*;
м) (cos 5л: + sin 5л:)2 =
= 2sin26*;
н) sin4* — cos4* = sin5*;
о) tg2*tg7* = 1.
в) sin*cos* =
sin*
+
г) ^/2cos2* = cos* + sin*;
д) cos4* + cos2* +
+ cos* = 0;
е) cos* — cos2* = sin2*.
+
cos*
7.28. Решите уравнение:
7
а) sin* = -r-cos*;
о
б) 3sin2* = cos2*;
в) 3sin2* + 4cos2* =
= 13sin*cos*;
r) sin2* + 2 sin* cos* =
= 3cos2*;
9—1681
д) 1 — 3cos2* = 2sin*cos*;
е) 6sin2* — 3sin*cos* —
— cos2* = 1;
ж) 3cos2* + 2sin*cos* +
+ 5sin2* = 2;
з) 3sin*cos* + 4cos2* = 0.
257
7.29. Найдите функцию, обратную к функции у:
а) у = 2х\ в) У = -\ 3;
е) у = х3- 1.
7.30. Из формулы /=/0(1+аО выразите t как функцию от /.
7.31. Из формулы t=t0+ выразите v как функцию от t.
7.32. Для данной функции найдите промежутки ее возрастания и
постройте на этом промежутке обратную функцию:
7.33. Для пар взаимно обратных функций, найденных в приме¬
рах 7.29 (а—е) и 7.23 (а — е), постройте графики, откла¬
дывая значения аргумента на оси х, а затем значения
функции на оси у.
7.34. Постройте график функции:
а) у = sinarcsinx; в) у = cosarccosx;
б) у = arcsin(sinjt); г) у = arccos(cosx).
б) у = *+^-(*>0),
в) у = (х — I)2 + 1;
г) у = X' — (•*'>0);
а) у = х2— 1;
я) у — X2 + 4Л",
е) У = V1 — *2-
8
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ
И ПЛОСКОСТЕЙ
§ 30. Векторное задание прямой
Направляющий вектор прямой
Направляющим вектором прямой называется любой ненулевой вектор,
который лежит на этой прямой.
Рассмотрим в пространстве прямую /. Выберем на ней две
точки: А и В. Вектор Ав является* направляющим вектором
прямой /. Направляющий вектор прямой определен неоднознач¬
но. Любой ненулевой вектор, коллинеарный АВ, также будет
направляющим вектором прямой /.
На рис. 330 изображены различные направленные отрезки,
которые можно принять за направляющий вектор прямой /.
Обозначим направляющий вектор прямой одной буквой, напри¬
мер v (рис. 331). Такое обозначение принято в курсе физики:
если точка равномерно движется по прямой /, то ее скорость v
может быть взята за направляющий вектор этой прямой. Отме¬
тим, что если vi и V2 — направляющие векторы одной и той же
прямой /, то они коллинеарны, т. е. найдется такое число /=^=0,
что v2 = t\\. Это означает, что если две точки движутся по одной
Рис. 330
Рис. 331
9*
259
и той же прямой или по параллельным прямым, то их скорости
являются коллинеарными векторами.
Чтобы однозначно определить прямую, нужно кроме ее на¬
правляющего вектора v задать положение какой-либо ее точки.
Пусть в пространстве зафиксирована начальная точка О, дана
точка Ро своим радиусом-вектором г0 и дан вектор v^O. Прове¬
дем через точку Я0 прямую / с направляющим вектором v.
Пусть^г — радиус-вектор ее произвольной точки Р. Тогда
вектор РоР, как один из направляющих векторов прямой^, кол-
линеарен вектору v,_t. е. найдется такое число t, что PQP = tv.
Записывая вектор Р0Р как разность векторов г и го, получаем:
г — r0 = /v или r = r0 + /v.
Обратно: если радиус-вектор г какой-либо точки Р удовлетво¬
ряет такому уравнению при некотором /£/?, то вектор РоР
коллинеарен v и точка Р лежит на прямой /. Поэтому это уравне¬
ние называют уравнением прямой (в векторной форме). Оно
описывает траекторию точки, движущейся с постоянной ско¬
ростью v и имеющей положение Р0 в момент времени t=/=0.
Векторное уравнение прямой r = r0 + /v, или г — r0=/v, можно
переписать в координатной форме. Рассмотрим для простоты
прямую, лежащую в плоскости с декартовыми координатами
(jc; у). Пусть (jc; у) — координаты переменного вектора г,
(лгь; уо) — координаты точки Я0; (т; п)— направляющего векто¬
ра v. Векторное равенство означает равенство соответствующих
координат:
х — хо = tm,
y — yo=tn.
Мы воспользовались правилом действий над векторами в
координатах. От системы уравнений можно перейти к одному
уравнению, связывающему х и уу если исключить параметр t.
Для этого надо умножить первое уравнение на п и вычесть из
«Ферма... раньше Декарта понял принцип аналитической геометрии... и
установил основной принцип, по которому уравнение первого порядка
на плоскости представляет прямую».
Н. Бурбаки
Ферма Пьер (1605—1665 г.г.) — французский математик, один из
создателей аналитической геометрии и дифференциального исчисления.
Открыл правило нахождения экстремума с помощью производной.
Автор многих теорем теории чисел. Знаменитая теорема Ферма из
теории чисел, которую Ферма сформулировал без доказательства, не
доказана и до сих пор. Формулировка Ферма гласит: «Разделить куб
на два других куба и вообще какую-нибудь степень выше второй на две
степени с тем же обозначением невозможно, и я нашел воистину заме¬
чательное доказательство этого, но поля слишком узки, чтобы вместить его».
260
него второе, умноженное на т. Получится уравнение прямой на
плоскости в координатной форме:
п(х — х'о) — т(у — у о) = 0.
Если раскрыть скобки и обозначить п=А, —т = В, — пхо-\-
-\-туо=С, то мы получим уравнение прямой Ах-\-Ву+С = 0.
Пример
Пусть прямая / на координатной плоскости (х\ у) проходит
через точки А (3; —2) и В (4; 1). Построим точки А и В и
проведем через них прямую /. В качестве направляющего
вектора прямой / можно взять вектор Ad. Он имеет коорди¬
наты (1; 3), которые находятся как разности координат
конца и начала. За направляющий^вектор прямой / можно
взять и другие^ векторы —ВА, АС (точка С — середина
отрезка АВ), OD (точка D выбрана так, что OD\\AB).
В качестве начальной точки можно взять точку А. Тогда
векторное уравнение прямой / можно записать в виде г =
= г0 + t\, где г(х; у) — радиус-вектор переменной точки
прямой /, г0(3; — 2) =0/1, v(l; 3) = Хв. В координатах
уравнение прямой / имеет вид
\x = 3 + t,
| У=—2 + 3/.
Умножая первое уравнение на 3 и вычитая из него вто¬
рое, получаем уравнение Зх — у=\\, или Зх — у— 11=0.
Это же уравнение можно записать в виде у = Зх — 11, от¬
куда следует, что угловой коэффициент прямой / равен 3.
Упражнения
1. Что такое направляющий вектор
прямой?
2. Что нужно задать, чтобы опреде¬
лить положение прямой? Достаточно
ли для этого только направляю¬
щего вектора?
3. Найдите координаты направляю¬
щего вектора прямой, проходящей
через точки А и В:
а) А (2; 1; 3); Я (-1; 0; 1), б) А (-2;
1; 1); Я (1; 1; -1).
4. Найдите направляющий вектор пря¬
мой на плоскости, если заданы две
точки прямой: Л (3; 1) и В (2; — 1).
Выведите координатное уравнение
этой прямой. Чему равен угловой
коэффициент этой прямой?
5. Точка движется по прямой. В мо¬
мент времени / = 0 она занимала
положение Ро(1;1;2), а в момент
времени t= I — положение Р\ (2;
2; 5). Какое положение она будет
занимать в момент времени / = 3,
/ = 4,'*/= — 1?
Параллельность и перпендикулярность прямых
Если две прямые параллельны, то их направляющие векторы колли-
неарны.
Коллинеарность векторов геометрически означает, что изобра¬
жающие их направленные отрезки лежат на параллельных
прямых. Можно сказать, что направляющий вектор прямой /
261
является одновременно направляющим вектором любой прямой,
параллельной /.
Запишем условия параллельности прямых /1 и /2 с направляю¬
щими векторами vi и v2 (рис. 332):
l\ II I2OV| || V2^V|=XV2.
Рассмотрим теперь перпендикулярные прямые. Возьмем две
пересекающиеся прямые /1 и /2 с направляющими векторами
Vi и V2. Прямая 1\ перпендикулярна прямой /2 тогда и только
тогда, когда векторы vi и V2 ортогональны (рис. 333).
Не обязательно брать только пересекающиеся прямые. Две
прямые в пространстве называются перпендикулярными, если
ортогональны их направляющие векторы (рис. 334).
Запишем условие перпендикулярности прямых 1\ и /2 с на¬
правляющими векторами vi и v2:
Примеры
1. Найдите по рис. 335 к^орд^наты^точек С и D, вычислите
координаты векторов В А, А£ и OD и убедитесь в том, что
они коллинеарны вектору АВ.
2. В кубе ABCDA'B'C'D' (рис. 336) ребро АВ перпендикуляр¬
но восьми ребрам: АА\ ВВ', СС\ DD', AD, AfD\ В'С' и
ВС. Проверим, что диагонали АС и B'D' тоже перпендику¬
лярны. Докажем, что AC-B'D'=0.
262
Рис. 332
Рис. 333
Рис. 334
Рис. 335
Рис. 336
Сначала заменим вектор B'D' на равный ему вектор BD.
Затем разложим: А£=аЬ-{-АЬ, вЪ=аЪ — АЬ. Получим
А£-в^о'=а£-1&=(аЬ+аЬ)-1аЬ-аё) =аЪ-ЛЁ2=о,
так как длины векторов ХЪ и АВ равны как длины сторон
квадрата.
3. На следящем устройстве отмечаются координаты двух
самолетов, летящих по прямолинейным траекториям. Пер¬
вый самолет находился при двух наблюдениях в точках
Л|(3; 17; 10)иЛ2(8; 11; 11), второй — в точках В\(2; 29; 11)
и В2(7; 33; 10). Докажем, что их траектории перпендику¬
лярны.
Векторы А\А2 и В\В2 можно принять за направляющие
векторы траекторий. Вычислим координаты этих векторов
А\А2{5; — (>; 1), В\В2{Ъ\ 4; —1) и составим скалярное произ¬
ведение: _£\А2-В?В2 = 5-5 + (—6)-4 -f 1-(— 1) = 0, т. е.
А \А2 _L В\В2.
Предлагаем трудный вопрос: пересекаются ли траекто¬
рии самолетов?
Упражнения
1. Три прямые имеют направляющие
•векторы vi (I; 0; 2), V2 (—2; 1; 1) и
Уз (2; 0; 4). Что можно сказать о
параллельности или перпендикуляр¬
ности каждой пары из этих пря¬
мых?
2. Запишите условие перпендикуляр-
Угол между прямыми
Углом между двумя прямыми в пространстве называется угол между
их направляющими векторами (рис. 33/).
Направляющий вектор прямой определен неоднозначно. Как
сказывается эта неоднозначность на определении угла между
прямыми? Заменим вектор vi на коллинеарный ему вектор v'i.
Пусть \\ = Х\\. Если А,>0, то углы между векторами (vi; v2) и
ности двух прямых с направляю¬
щими векторами vi (mi; ti\) и V2 (тг;
по) в координатной форме.
3. Напишите векторное уравнение пря¬
мой, проходящей через точку Л (1; 1)
и параллельной прямой, проходящей
через точки В (2\ — 1) и С (0; 3).
Выведите координатное уравнение
этой прямой.
263
Рис. 337
(Xvi; V2) равны (рис. 338). Если А,<0, то направление вектора
изменится на противоположное и угол также изменится
(рис. 339).
Таким образом, направляющие векторы двух прямых при
различном выборе этих векторов могут образовывать два разных
угла, дающих в сумме развернутый угол. Если нужно уточнить,
какой из углов имеется в виду, то часто указывают, например,
«острый угол между двумя прямыми» или «тупой угол».
Углы между прямыми можно вычислить с помощью скалярно¬
го произведения, так как формула для угла между векторами
известна. Пусть прямые 1\ и /2 имеют направляющие векторы Vi
и V2. Косинус угла между прямыми 1{ и /2 вычисляется по фор¬
муле
cosZ(vi, v2)=
•v2
|V|| |v2|
Заметим, что косинусы двух различных углов между прямыми
имеют одинаковый модуль и разные знаки, так как cos (я — а)=
= —cos а. По знаку косинуса можно узнать, острый или тупой
угол образуют выбранные направляющие векторы прямых.
Упражнения
1. Даны три точки на плоскости:
А (— 1; 2), В(3;-1) и С (-1;-1).
Найдите углы треугольника ABC.
2. Треугольная пирамида ABCD зада¬
на кординатами своих вершин:
А (2; 0; 0), В (—3; 2; 5), С( 1;1;5),
О (— 1; 4; 7). Найдите угол между
ребрами АС и BD.
264
Рис. 338
Рис. 339
§31. Векторное задание плоскости
Нормаль к плоскости
Прямая называется перпендикулярной плоскости, если она перпендику¬
лярна любой прямой на этой плоскости (рис. 340).
Нормалью к плоскости называется ненулевой вектор, который лежит на
прямой, перпендикулярной данной плоскости.
Нормаль к плоскости определена неоднозначно (рис. 341).
Любой ненулевой вектор, коллинеарный нормали, также являет¬
ся нормально к этой плоскости. Обозначим п нормаль к плоско¬
сти. Для однозначного задания плоскости кроме нормали доста¬
точно задать положение какой-либо ее точки.
Рис. 340 Рис. 341
Пусть ос — некоторая плоскость, п — ее нормаль, г0 — радиус-
вектор какой-либо точки Ро плоскости д, г — радиус-вектор ее
произвольной точки Р. Так как вектор PqP лежит в плоскости а,
то он ортогонален нормали az, т. е. PqP-п = 0 (рис. 342).
_^Обратно: если^для некоторой точки Р выполняется условие
Р0Р-п = 0, т. е. PqP _L п, то точка Р лежит в плоскости а. Таким
образом, условие того, что точка Р лежит в плоскости а, имеет
вид
265
Рис. 342
Это условие можно переписать в координатах, зная коорди¬
наты точки Р0(х0; уо; zo) и вектора нормали п(Л; В\ С): (х —
— Xo)A+(y — yo)B+(z — zo)C = 0. Если раскрыть скобки и обо¬
значить — Axo — Byo — Czo через D, то получим уравнение плоско¬
сти в координатах:
Ax-\-By-\-Cz-\-D=0.
Если обозначить радиусы-векторы точек Ро и Р через Го и г,
то векторное уравнение плоскости таково:
(г — Го)-II = 0.
* Полезно запомнить, что при задании уравнения плоскости в виде Ах-\-
Ву-\- Cz-\- D = 0 коэффициенты (Л, В, С) являются координатами
вектора нормали к плоскости.
Пример
Прямая / проходит через точки Pi(l; 2; —5) и Р2(6; —2;
—3). Рассмотрим различные плоскости, перпендикулярные
прямой /. В качестве нормали любой из них можно взять
вектор Я1Я2, т. е. направляющий вектор прямой /. Вектор
Р|Т*2 имеет координаты (5; —4; 2). Напишем координат¬
ное уравнение плоскости, проходящей через точку Р\ и пер¬
пендикулярной прямой /:
5(jc-1)-4(*/-2) + 2(z + 5)=0,
или
5х — 4 у -f- 2 z -f-13 = 0.
Уравнение плоскости, проходящей через точку Р2 и пер¬
пендикулярной прямой /, имеет вид
5(д. _ 6) - 4 (у + 2) + 2(2 + 3)=0,
или
5х — 4у + 2z — 32 = 0.
Упражнения
1. Дайте определение прямой, перпен¬
дикулярной плоскости.
2. Что такое нормаль к плоскости?
3. Что нужно задать, чтобы опреде¬
лить положение плоскости? Доста¬
точно ли для этого, чтобы была
задана нормаль?
4. Плоскость а задана векторным
уравнением (г—г0)Хп = 0, где г0(1;
— 1; 0), n(2; 1; —1). Определить, ле¬
жат ли следующие точки в плос¬
кости а: Р| (2; 1; 4), Р2О; 1; 1),
Рз(0; -1; -4), Р4 (0; 0; 0).
5. Дана прямая /, проходящая через
точку Ро (2; — I; 3) и имеющая на¬
правляющий вектор v (0; 1; 2). На¬
пишите координатное уравнение
плоскости, проходящей через точ¬
ку Ро и перпендикулярной пря¬
мой /.
6. Даны две точки: Р|(1;3;— 2) и
Рг(0;1;5). Напишите координатное
уравнение плоскости, проходящей
через точку Р\ и перпендикулярной
прямой Р\Р2.
266
Признак перпендикулярности прямой и плоскости
В определении прямой, перпендикулярной плоскости, содержится
требование того, чтобы эта прямая была перпендикулярна каж¬
дой прямой данной плоскости. Прямых в плоскости бесконечно
много, и поэтому непосредственно пользоваться этим определе¬
нием нельзя. Оказывается, что если данная прямая перпен¬
дикулярна всего двум пересекающимся прямым в плоскости,
то она уже перпендикулярна любой другой прямой в этой плос¬
кости.
Теорема
Если прямая перпендикулярна двум пересекающимся прямым некото¬
рой плоскости, то она перпендикулярна этой плоскости.
Запишем кратко условие теоремы:
Объекты Взаимное расположение
плоскость а 1\ 6 а, h 6 а
прямые /, /,, /2 /i X ^2
П /I / _L /, / ± /2
Доказать: /1а 1 £
Доказательство. По определению, прямая / перпен¬
дикулярна плоскости а, если она перпендикулярна любой прямой
этс7й плоскости. Выберем произвольную прямую т£а и пока¬
жем, что 11. т.
Прямая Направляющий вектор
/ v
h V,
/2 v2
m u
Так как прямые 1\ и h пересекаются (рис. 343), то векторы
vi и V2 не коллинеарны и поэтому вектор и, лежащий в плоско¬
сти а, можно разложить по этим векторам: u = lk\W\ +X2V2.
Рис. 343
267
Для проверки того, что /J_m, вычислим скалярное произве¬
дение векторов v и и:
VU = v (к\\\ + A,2v2)=A,i(vvi) +A,2(vv2).
Так как / _L Л и /_1_/2, то vvi = vv2 = 0, поэтому vu = 0 и /_1_т.
Теорема доказана.
Упражнения
1. В прямоугольном параллелепипеде
все грани — прямоугольники. Дока¬
жите, что каждое боковое ребро
перпендикулярно плоскости осно¬
вания.
2. Прямая / перпендикулярна двум
параллельным прямым в плоско¬
сти а. Приведите пример, когда
прямая / не перпендикулярна пло¬
скости.
3. Даны два произвольных вектора:
vi (mi; п\\ р|) и v2 (m2; п2\ р2). Дока¬
жите, что вектор п с координатами
(fl\P2 — П2р\\ Р\П%2—р2т\\ Ш\П2 — ГП2П\)
ортогонален каждому из векторов
vi, V2. Указанная формула позво¬
ляет находить координаты нормали
к плоскости, в которой задано два
вектора.
4. В плоскости известны три точки:
Л (1; 2, 3), £(-1;0; 2) и С (2; 5; -1).
Найдите координаты нормали к пло¬
скости, проходящей через точки .4,
В и С (используйте формулу пре¬
дыдущей задачи).
Условия параллельности и перпендикулярности прямой
и плоскости
Векторное задание прямых и плоскостей позволяет легко опре¬
делять их параллельность и перпендикулярность. Пусть даны
прямая / с направляющим ветором v и плоскость а с нормалью
п (рис. 344).
Прямая / перпендикулярна плоскости а — это означает, что
ее направляющий вектор v коллинеарен нормали п:
/ _La^v||n.
Если прямая / лежит в плоскости а, то ее направляющий
вектор v ортогонален нормали п. Если прямая / параллельна
плоскости а (рис. 345), то в этой плоскости всегда есть прямая /',
Рис. 344
268
Рис. 345
параллельная /. Направляющие векторы v и v' прямых / и Г
коллинеарны, поэтому если v'_Ln, то и v_Ln (рис. 346). Итак,
/6 а или /||a<^v_Ln.
Выведенные условия позволяют доказывать различные теоре¬
мы о параллельности и перпендикулярности прямых и плоскостей.
Пример
Плоскость а и прямая /, перпендикулярные прямой т,
параллельны.
Запишем кратко условие примера.
Объекты
плоскость a
прямые /, m
Доказать: 11| a
Взаимное расположение
a _L m
I _L m
Рис. 346
а
Рис. 347
Доказательство. Пусть п — нормаль к плос¬
кости a, v и и — направляющие векторы прямых / и т.
По условию (рис. 347).
a_Lm=^u||n;
I _Lm=^v_Lu.
Если v_Lu, а n||v, то и n ± и, т. е. а||/ (или на самом
деле еще может быть, что I 6 а).
Отметим два важных свойства векторов, которые часто
используются при доказательствах:
1. а||Ь, Ь||с=^а||с.
2. а||b, bJ_c=^a_Lc.
Упражнения 2. Векторы, а, b и с связаны соотно¬
шениями a_Lb, b_Lc. Верно ли,
1. /, m — прямые, а—плоскость. До- что а||с?
кажите: /1| a, m_La=^/_Lm.
269
Наклонная к плоскости
Если прямая I не параллельна и не перпендикулярна плоскости а, то ее
называют наклонной к этой плоскости.
Чтобы определить угол между наклонной и плоскостью, надо
спроектировать прямую / на плоскость а. Для этого выбирают
точку Р на прямой /, отличную от точки Ро пересечения наклон¬
ной и плоскости. Затем, проектируя точку Р на плоскость а,
получают точку Q. Прямая PoQ и является проекцией прямой /
на плоскость а.
Углом между наклонной и плоскостью называется угол между наклон¬
ной и ее проекцией на эту плоскость (рис. 348).
Пусть v — направляющий вектор прямой /, ап — нормаль к
плоскости а. Из рис. 349 ясно, как связаны между собой угол
между прямой / и плоскостью а и угол между векторами v и п.
Рис. 349
Всегда можно так согласовать направление нормали с направле¬
нием вектора v, что угол между ними будет острым. Если обозна¬
чить острый угол между / и а через <р, то <p + ^_(v, п) =
=л/2. С помощью скалярного произведения можно определить
угол ф:
sin <p=sin(n/2— Z-(vn))=cos Z.(vn) =
Теорема о трех перпендикулярах
lv| |п|
Теорема ——
Если наклонная к плоскости перпендикулярна какой-нибудь прямой
в этой плоскости, то и проекция наклонной перпендикулярна этой пря¬
мой. Обратно: если проекция наклонной перпендикулярна прямой в
плоскости, то и сама наклонная перпендикулярна этой прямой.
Запишем кратко условие теоремы.
Объекты
плоскость а
прямые /, /' и m
Доказать (рис. 350):
1)
2) /' JL m =* / J_ m.
Взаимное расположение
I — наклонная к а
V — проекция / на а
m 6 а
270
Рис. 348
Доказательство. Пусть Ро — точка пересечения на¬
клонной / и плоскости а, РфРо— произвольная точ^а прямой
/, Q — ее проекция на плоскость а. Тогда вектор PQ-La, т. е.
является нормалью к плоскости а. Вектор Р^Р является направ¬
ляющим вектором прямой /, а вектор PoQ — направляющим
вектором прямой /'. Эти векторы связаны соотношением Р0Р +
+ PQ = PoQ. Кроме того, v — направляющий вектор прямой т.
Докажем первое из двух утверждений теоремы.
Пусть /1т. Тогда Po^-Lv. Для проверки того, что /'JLm,
вычислим скалярное произведение направляющих векторов этих
прямых:
PoQ • v=(РоР + PQ) v = РоР • v + PQ • v.
Первое слагаемое равно нулю по условию, а второе — из-за
того, что v, как вектор в плоскости а, перпендикулярен нормали
PQ к этой плоскости.
Второе утверждение доказывается аналогично. Проведите
доказательство самостоятельно.
Теорема о трех перпендикулярах показывает, что проектиро¬
вание точки на прямую можно осуществить так: сначала про¬
ектируют точку на плоскость, содержащую эту прямую, а затем,
оставаясь в плоскости, проектируют точку на прямую (рис. 351).
Это подтверждает еще один способ нахождения координат тонки
Рис. 352
271
Рис. 350
Рис. 351
в декартовой системе координат: чтобы спроектировать точку Р,
например на ось х\ можно сначала ее спроектировать на плос¬
кость хОу, получить точку Рху,
спроектировать точку Рху на ось
Упражнения
Прямая I задана точкой Ро, направ¬
ляющим вектором v. Плоскость а
задана в координатной форме:
х — 2у + 3z + 2 = 0. Определите вза¬
имное расположение прямой / и
плоскости а(/||а, /JLа, /£а, / —
наклонная к а):
а) Ро (0; 0; 0), v (1; -1; 1);
б) Р0(1; 1; 1), v(1; -1; 1);
а затем уже в этой плоскости
и получить точку Рх (рис. 352).
в) Ро(0; 1; 2), v (1; —2; 3);
г) Р0(0;0;0), v (1; 2; -3);
д) Ро(0;0;0), v (1; 1; 1);
е) Р0(0; 1; 0), v (1; 1; 1).
В основании четырехугольной пира¬
миды лежит квадрат, а вершина
пирамиды проектируется в центр
этого квадрата. Докажите, что боко¬
вое ребро пирамиды перпендикуляр¬
но не смежной с ним диагонали
основания.
Ортогональное проектирование
При построении проекции наклонной мы использовали проекти¬
рование на плоскость. Рассмотрим это преобразование более
подробно.
Пусть дана плоскость а. Ортогональной проекцией точки Р
на плоскость а называется такая точка Q плоскости а, что
прямая PQ перпендикулярна а (рис. 353). Если точка Р лежит
в плоскости а, то она и считается своей проекцией.
Пусть даны плоскость а и точка Q £а. Проведем через точ¬
ку Q прямую /, перпендикулярную плоскости а. Тогда точки
прямой / — это все точки, проектирующиеся в точку Q (рис. 354).
Рис. 353
Рис. 354
При проектировании на прямую / все пространство представ¬
ляется как бы расслоенным на параллельные плоскости, перпен¬
дикулярные прямой /, а при проектировании на плоскость а
пространство расслаивается на параллельные прямые, перпенди¬
кулярные плоскости а (рис. 355).
Ортогональное проектирование на плоскость широко приме¬
няется в техническом черчении — детали на чертеже изобража¬
ются своими ортогональными проекциями на разные плоскости.
Рис. 355
Рассмотрим прямоугольный треугольник ABC, у которого
угол В — прямой, сторона ВС лежит в плоскости а, а вершина А
находится вне ее. Спроектируем вершину А на плоскость а, по¬
лучим точку О. Полученная конфигурация часто встречается $
различных задачах (рис. 356).
Рис. 356
Сначала заметим, что ОВ является проекцией наклонной АВ
и поэтому OB_LBC, т. е. треугольник ОВС тоже прямоугольный.
Вычислим соотношения между элементами треугольника ABC
и его проекции. Для удобства введем следующие обозначения:
\АС\=Ь, |СВ|=а, |ОС| = d>/-ACB = a, АОСВ = р, ААСО=у,
ААВО = 8.
Вычислим косинусы углов а, р и у:
cosa=a/fe, cosp=a/d, cosy = d/b.
Перемножая последние два равенства, получаем первое:
cos a = cos р cos 7.
Следствие
Угол V меньше угла а, т. е. угол между наклонной и ее проекцией мень¬
ше любого угла, образуемого этой наклонной с прямой на плоскости.
Действительно, так как 0<cosp<l, то cos р cos у < cos у,
т. е. cos a<cosy, а тогда а>у, так как косинус убывает в первой
четверти. Аналогично доказывается, что а>р.
Вычислим площади треугольников ABC и ОВС:
Sabc = x/2о\АВ\, Sobc = х/2о\ОВ\.
773
с
Видим, что отношение площадей °в--, равно отношению
Ълвс
i2|L=cos6, т. е. Sobc=Sabc cos б.
Упражнения
1. Дан куб ABCDA'B'C'D':
а) спроектируйте на плоскость
АА'С'С ребра AD\ ВС, диаго¬
наль B'D\
б) спроектируйте на плоскость
A'B'CD ребра В'С' > C'D\
грань ABCD.
2. Какой формы тень может отбрасы¬
вать пакет с кефиром в форме
треугольной пирамиды?
3. На рис. 357 изображены проекции
на три координатные плоскости
некоторой детали. Изобразите ее
внешний вид.
4. Для конфигурации, изображенной
на рис. 356, мы доказали, что угол а
больше своей проекции. Приведите
пример угла, который увеличивается
при проектировании.
§ 32. Двугранные углы
Линейный угол двугранного угла
Две непараллельные плоскости пересекаются по прямой и делят все
пространство на четыре части, называемые двугранными углами.
Двугранный угол — это фигура, ограниченная двумя полуплоскостями с
общим ребром (рис. 358).
Рис. 358 Рис. 359
Четыре двугранных угла, образованных двумя пересекающи¬
мися плоскостями, распадаются на две пары равных между
собой двугранных углов, что аналогично равенству вертикальных
углов, образующихся при пересечении двух прямых (рис. 359).
Двугранные углы можно измерять с помощью линейных углов.
Рис. 357
274
Построение линейного угла
Возьмем на ребре двугранного угла точку и восставим в гранях
по перпендикуляру к этому ребру. Угол, образованный построен¬
ными перпендикулярами, называется линейным углом двугранно¬
го угла (рис. 360).
Рис. 360 Рис. 361
В качестве вершины линейного угла можно взять любую точ¬
ку на ребре двугранного угла. Все такие углы будут равны между
собой как углы с соответственно параллельными сторонами.
Равные двугранные углы имеют равные линейные углыг и, наоборот,
двугранные углы с равными линейными углами равны между собой
(рис. 361).
Плоскость, проходящая через стороны линейного угла, перпендикулярна
ребру двугранного угла, так как это ребро перпендикулярно двум пере¬
секающимся прямым (сторонам угла), лежащим в этой плоскости.
Обратно: если мы проведем плоскость, перпендикулярную
ребру двугранного угла, то в сечении получится линейный угол
(рис. 362). Действительно, ребро перпендикулярно плоскости
Рис. 362
сечения; следовательно, перпендикулярно прямым, по которым
эта плоскбсть пересекает грани двугранного угла. Эти прямые
образуют, по определению, линейный угол.
Упражнения углов, образуемых основанием и
боковыми гранями.
I. В четырехугольной пирамиде по- 2. Предложите способ измерения угла
стройте линейные углы двугранных деревянного клина.
275
3. Квадрат повернули вокруг его сто- 4.
роны. Как, измеряя расстояния,
узнать угол, на который его по¬
вернули?
Пересечем двугранный угол плоско¬
стью, не перпендикулярной ребру.
Какой получится в сечении угол —
больший или меньший линейного?
Перпендикулярные плоскости
Две плоскости называются перпендикулярными, если, пересекаясь, они
образуют равные двугранные углы.
Перпендикулярные плоскости образуют двугранные углы по 90° (рис. 363).
Рис. 363
Теорема (признак перпендикулярности двух плоскостей)
Если плоскость проходит через прямую, перпендикулярную другой
плоскости, то эти плоскости перпендикулярны (рис. 364).
Запишем кратко условие теоремы.
Объекты Взаимное расположение
плоскости а, р / £ а
прямая I I _|_ р
Доказать: a _L р
Доказательство. Пусть Р — точка пересечения пря¬
мой / с плоскостью р. Плоскости аир пересекаются (Р£а, Р£Р)
по прямой т. Прямые / и т перпендикулярны (определение
перпендикуляра к плоскости). Проведем в плоскости р через
точку Р прямую /', перпендикулярную т. Прямые / и /' образуют
линейный угол двугранного угла с ребром т, так как обе они
перпендикулярны ребру. Но /_!_/' (по определению перпендику¬
ляра к плоскости). Следовательно, линейный угол прямой, т. е.
плоскости аир перпендикулярны. Теорема доказана.
Если плоскости заданы векторными уравнениями, то их пер¬
пендикулярность легко проверить, вычисляя скалярное произве¬
дение их нормалей. Очевидно, что если плоскости перпендикуляр¬
ны, то и нормали к ним перпендикулярны и их скалярное произ¬
ведение равно нулю.
Это позволяет доказывать новые теоремы о перпендикулярно¬
сти прямых и плоскостей.
276
Рис. 364 Рис. 365
Пример
Если прямая / параллельна плоскости а и перпендикулярна
плоскости р, то плоскости аир перпендикулярны (рис. 365).
Запишем кратко условие примера.
Объекты Взаимное расположение
прямая b I || а
плоскости а, р / _L р
Доказать: а _1_ р
Пусть v — направляющий вектор прямой /, ш и п — нормали
к плоскостям а и р. По условию,
/||a=^v_Lm, /J_p=^v||n.
Если п||v, a v_Lm, то и nlm, т. е. a_Lp.
Упражнения
1. Докажите, что в основании четырех¬
угольной пирамиды лежит квадрат,
причем вершина пирамиды проекти¬
руется в его центр. Диагональное
сечение пирамиды перпендикулярно
основанию.
2. В кубе имеются перпендикулярные
сечения, найдите их.
3. Докажите, что если прямая перпен¬
дикулярна одной из двух взаимно
перпендикулярных плоскостей, то
она параллельна другой (или лежит
в ней).
Угол между плоскостями
Пусть даны две пересекающиеся плоскости. Они образуют между
собой два угла, сумма которых равна 180°. Выберем один из дву¬
гранных углов, образованных этими плоскостями. Обозначим
его ф. Проведем к плоскостям нормали так, чтобы они были на-
277
правлены внутрь двугранного угла. Из рис. 366 ясно, что сумма
угла ф и угла между нормалями тоже равна 180°. Поэтому вы¬
числение угла между плоскостями можно заменить вычислением
угла между нормалями.
Пусть tij и п2 — нормали к данным плоскостям. Косинус
угла между двумя векторами определяется по известной фор¬
муле:
cos ф = П| "2 .
|П|| Insl
По этой же формуле находится и угол между плоскостями.
При этом надо помнить, что если скалярное произведение полу¬
чится отрицательным, то это означает, что найден косинус боль¬
шего (тупого) угла из двух углов, образованных плоскостями.
Упражнения
1. Найдите угол между плоскостями:
а) x+y+z=0 и х—у—2+2=0;
б) x—y+2z=\ и 2х-\-у—2+1=0.
2, Какой угол образует плоскость с
осью z, если она образует с пло¬
скостью хОу угол 30°?
3. Угол между плоскостью и осью х
равен 50°. Какие углы она образует
с плоскостью yOz>
Задачи и вопросы
8.1. Найдите какой-либо направляющий вектор прямой /, ле¬
жащей в координатной плоскости, если:
а) / — биссектриса первого и третьего координатных
углов;
б) / задана уравнением у = 2х;
в) / проходит через точки Р, (1; 0) и Р2 (2; 3) ;
г) / образует с осью х угол 30°;
д) / перпендикулярна прямой у = 2х.
8.2. Найдите направляющий вектор прямой, зная две точки
Я, и Р2у лежащие на этой прямой:
а) Р,(0; 1), Р2( 1; 0); в) Р,(1; 2; 0); Р2(-1; 0; 1);
б) />i(l; 2), Р2(3; -5); г) Р,(0; 0; 1), Р2(1; 1; 0).
278
8.3. Найдите направляющий вектор прямой на плоскости, зная
ее уравнение в координатах:
а) у = 2х\ в) х + у = 1;
б) у = Зх + 2; г) 2х — Зу + 5 = 0.
8.4. Точка движется по прямой по закону г = г0 + W, где
г0 (1; 0; 2), v (2; 1; 1). Определите:
а) каковы ее координаты в момент времени t = 2, t = 5;
б) в какой момент времени радиус-вектор точки ортого¬
нален вектору w (1; —4; 1).
8.5. Дан вектор а. Найдите такое число х, при котором вектор b
коллинеарен вектору а:
а) а(1; 3), Ь(2; х); в) а(2; 0), Ь(5; х);
б) а(2; -1), b(x; 1); г) а(4; 2; 1), Ь(—2; -1; х).
8.6. Дан вектор а. Найдите такое число х, при котором векто¬
ры а и b ортогональны:
а) а(2; 1), Ь(1; х); в) а(—1; 1; 5), Ь(1; 1; х);
б) а(1; 0; 3), Ь(х; 3; 1); г) а(1; 2; 3), Ь(х; х; х).
8.7. Лежит ли точка Р на прямой АВ, если:
а) А (—2; 1), В (2; 5), Я(-Ю;7);
б) А (— 1; 2; 3), Я(4;-1; 1), Р (0;-2;-3)?
8.8. Будет ли четырехугольник ABCD параллелограммом, если:
а) А (1; 2; 3), Я(-1;0;1), С (2;-2; 5), D (0;-4;3);
б) А (0; 0; 0), В (1; 2; 5), С (—1; —2; 4). D (0; 0; 8)?
Если ответ отрицателен, то измените координаты точки D
так, чтобы ABCD стал параллелограммом.
8.9. Будут ли перпендикулярны прямые АВ и CD, если:
а) А (—2; 0), В (0;3), С (3; 1), D (1; 0);
б) А (—1; 0; 1), В (0; 1; —2), С (1; —3; 0), D (0; —2; 5)?
8.10. Будет ли четырехугольник ABCD прямоугольником, если:
а) А (1; 1), В (2; 3), С (2;-1), D (3; 1); .
б) А (1; 2; — 1), В (— 1; 1; 2), С (2; 3; —4), D (0; 2; — 1)?
8.11. Найдите углы между прямыми /, и /2, выбрав на них на¬
правляющие векторы, если:
а) 1Х проходит через точки Я, (1; 2; 3) и Р2 (2; 0;—1),
а /2 через точки Ръ (1; 0; 5) и Р4(— 1; 4; 13);
б) /, задана уравнением # = Зх + 5, а /2 — уравнением
х -f- Зу — 2 = 0;
в) /, проходит через точки Р, (1; 1;—1) и Р2 (2; 1;0),
а /2 параллельна оси Ох.
8.12. В координатном пространстве дана прямая /, проходящая
через точки Рх (1; 1; 1) и Р2 (2; —1; 3). Какие углы обра¬
зует эта прямая с осями координат?
8.13. Вычислите угол между прямыми АВ и CD:
а) А (—1; 0), В (3; 2), С (—4; 1), D (0; -1);
б) А (—2; 1; 0), В (0; -2; 1), С(1; 0; -2), D( 1; 1; 0).
8.14. Дан куб ABCDA'B'C'D', /С, L — середины сторон ВС и
В'С'. Найдите углы между:
a) B'D' и АС; б) ЛО' и C'D; в) АК и CL.
8.15. Напишите координатные уравнения плоскостей, проходящих
через точку А (1; 2; 3) и перпендикулярных каждой из коор¬
динатных осей.
8.16. Найдите нормаль к плоскостй а, зная, что:
а) плоскость а перпендикулярна оси Оу и проходит
через точку (1; 2; 1);
б) координатное уравнение плоскости а: х + у +
+ z=0, 2r— (/ + 3z + 5=0, Зх — 5z — 8=0;
в) плоскость а параллельна плоскости 2х — (/ + 3z=0
и проходит через точку Р( 1; 1; —1).
Даны две скрещивающиеся прямые / и т. А и В — точки
прямой /, С — точка прямой т. Докажите, что если прямые
АС и ВС перпендикулярны прямой т, то прямые / и т
перпендикулярны.
Предложите, как проверить перпендикулярность прямой и
плоскости, если можно измерять расстояния между любыми
двумя точками.
SABCD — пирамида, в основании которой — прямоуголь¬
ник с центром О. Известно, что |Si4| = |SB| = |SC| = |SD|.
Докажите, что SO перпендикулярно плоскости основания.
Как использовать эту конструкцию для того, чтобы устано¬
вить шест с помощью тросов вертикально?
SABC — пирамида, в основании которой лежит правильный
треугольник с центром О. Известно, что .|Si4| = |SB| = |SC|.
Докажите, что SO перпендикулярно плоскости основа¬
ния.
В плоскости а лежит квадрат со стороной 1. Точка Р не
лежит в плоскости а и удалена от его вершин на одно и то
же расстояние 5. Чему равно расстояние от точки Р до
плоскости а?
Наклонная образует равные углы с двумя прямыми, лежа¬
щими в плоскости а. Докажите, что ее проекция также
образует равные углы с этими прямыми (рис. 367).
ABCDA'B'C'D' — куб, О — центр грани ABCD. Объясните,
почему:
а) В'0±АС, б) B'D±AC, в) A'C±BD, г) B'D-LCD'.
Какие диагонали граней перпендикулярны АС'?
. Может ли длина отрезка быть равной длине своей проекции
на плоскость? больше нее? меньше нее?
280
Рис. 367 Рис. 368
8.25. В плоскости а лежит равнобедренный треугольник ABC.
Прямая В'В перпендикулярна плоскости а (рис. 368):
а) объясните, почему ААВС является проекцией АЛВ'С;
б) докажите, что треугольник АВ'С равнобедренный;
в) что происходит с площадью А АВ'С при движении точ¬
ки В' по перпендикуляру к плоскости?
8.26. Прямая проходит через точки А{ 1; —1; 2) и В (0; —2; 1).
Какой угол она образует с плоскостями:
а) х — Зу + z — 1 = 0; в) х + z = 0;
б) —2х + Зу — 2 = 0; г) z = — 1.
8.27. Как вычислить двугранные углы треугольной пирамиды с
равными ребрами?
8.28. Через ребро двугранного угла проведена плоскость, деля¬
щая двугранный угол пополам. Докажите, что точки этой
плоскости равноудалены от граней угла.
8.29. Найдите углы между плоскостями, заданными уравне¬
ниями:
а) Зх — y + 2z — 2 = 0; 6х —2*/ + 42 + 3 = 0;
б) х + у — 2 + 2 = 0; 2х — 3у — 2+1=0;
в) x-+y + z=0; x + y — z= 1.
8.30. Докажите, что прямая, лежащая в одной из двух взаимно
перпендикулярных плоскостей и перпендикулярная их линии
пересечения, перпендикулярна другой плоскости.
8.31. Докажите, что прямая, имеющая общую точку с одной из
двух перпендикулярных плоскостей и перпендикулярная
другой плоскости, целиком лежит в первой из них.
8.32. Докажите, что линия пересечения двух плоскостей, перпен¬
дикулярных третьей плоскости, перпендикулярна этой пло¬
скости.
8.33. Найдите геометрическое место точек пространства, равно¬
удаленных от:
а) трех вершин данного треугольника;
б) двух данных точек;
281
в) двух данных пересекающихся прямых;
г) двух данных параллельных прямых.
8.34. Найдите геометрическое место оснований наклонных, про¬
веденных из данной точки к плоскости и имеющих одну и ту
же данную длину.
8.35. Точки А и В лежат по одну сторону от плоскости а. Найди¬
те в этой плоскости такую точку М, чтобы сумма расстоя¬
ний \АМ\ -f- \ВМ\ была наименьшей.
8.36. Центр нижнего основания куба соединен прямыми с че¬
тырьмя вершинами верхнего основания. Найдите углы меж¬
ду этими прямыми.
8.37. При каком условии проекция прямого угла на горизонталь¬
ную плоскость будет снова прямым углом?
8.38. Из точки в пространстве проведены три луча, не лежащие
в одной плоскости. Через каждый луч и биссектрису угла
между двумя другими проведена плоскость. Докажите, что
эти три плоскости пересекаются по одной прямой /. Дока¬
жите, что если на данных лучах от точки О отложить оди¬
наковые по длине векторы, то их сумма направлена по той
же прямой.
8.39. Из вершин А и В треугольной пирамиды ABCD опущены
высоты — прямые, перпендикулярные противоположным
граням. Докажите, что они пересекаются в том и только
в том случае, если ребра АВ и CD перпендикулярны.
8.40. Докажите, что если одна высота треугольной пирамиды
попадает в точку пересечения высот противоположной гра¬
ни, то все четыре высоты пересекаются в одной точке.
9
ПРОСТРАНСТВЕННЫЕ ТЕЛА
§ 33. Цилиндры и конусы
Прямой круговой цилиндр
Форма тел обычно сложна. Однако, как правило, тело можно
разбить на части, имеющие более простую форму. На рис. 369
изображен древнегреческий храм — акрополь. В его структуре
ясно выделяются цилиндрические колонны, основной корпус в
виде коробки — параллелепипеда, увенчанного треугольным
фронтоном. Как из тел простой формы — параллелепипедов,
призм, пирамид, шаров, цилиндров — создать прекрасное зда¬
ние — это секрет искусства, архитектуры. Однако основа этого
секрета кроется в геометрии, в использовании различных
свойств симметрии тел и их сочетаний.
Нашей задачей является изучение геометрических свойств
простейших тел. Эти тела — многогранники, тела вращения, ко¬
нусы, цилиндры.
Цилиндр — одно из самых распространенных тел. Простей¬
шим цилиндром является прямой круговой цилиндр.
Прямым круговым цилиндром называется тело, образованное вращением
прямоугольника вокруг одной из его сторон (рис. 370).
В цилиндре можно выделить два основания, лежащие в па¬
раллельных плоскостях и представляющие собой круги одинако¬
вого радиуса. Прямая, проходящая через центры оснований,
называется осью цилиндра.
Границу цилиндра составляют два основания и боковая
поверхность цилиндра. Ее можно представлять себе образован¬
ной вращением отрезка вокруг оси цилиндра.
Сечением цилиндра плоскостью, параллельной основанию,
будет круг того же радиуса, что и основание (рис. 371).
Высота цилиндра — это расстояние между основаниями, т. е.
длина отрезка оси между центрами оснований. Обычно цилиндр
задают двумя числовыми данными: радиусом основания и вы¬
сотой.
Боковую поверхность цилиндра можно развернуть на плос¬
кость. Если представить себе эту поверхность сделанной из бума¬
ги и разрезать ее параллельно оси цилиндра, то она развернется
в форме прямоугольника, одна из сторон которого равна высоте
цилиндра, а другая — длине окружности основания (рис. 372).
Рис. 370
Рис. 371
Упражнения
1. Приведите примеры тел цилиндри¬
ческой формы.
2. Какая фигура получится в сечении
цилиндра плоскостью, проходящей
через его ось (это сечение называют
осевым сечением цилиндра)? Како¬
вы размеры этой фигуры?
6. Высота цилиндра равна //, радиус
основания R. Вычислите:
а) площадь осевого сечения;
б) площадь боковой поверхности
цилиндра;
в) наибольшую длину ребра куба,
который можно поместить внутрь
цилиндра;
г) наибольшую длину отрезка, ко-
3. Какие фигуры будут получаться в
сечении цилиндра плоскостью, па¬
раллельной его оси? Как будут
меняться размеры этой фигуры?
4. Нарисуйте различные по форме
сечения цилиндра.
5. Цилиндр катится по плоскости. Ка¬
кая фигура получается при движе¬
нии его оси?
торый можно поместить внутрь
цилиндра.
7* Три одинаковых цилиндра с ра¬
диусом основания R касаются друг
друга (рис. 373). Цилиндр какого
радиуса может находиться в отвер¬
стии между ними?
8. Найдите геометрическое место точек
пространства, удаленных на рас¬
стояние R от данной прямой.
Прямой круговой конус
Коническая форма, так же как и цилиндрическая, широко рас¬
пространена в окружающем нас мире. В форме конуса делают
колпаки и кульки, различные втулки и емкости, коническую фор¬
му принимают насыпанная куча песка (рис. 374) и воронка от
взрыва. Прожектор освещает часть пространства в форме
конуса.
Прямым круговым конусом называется телог образованное вращением
прямоугольного треугольника вокруг одного из его катетов (рис. 375).
В конусе можно выделить основание в форме круга и верши¬
ну. Прямая, проходящая через вершину и центр основания, на¬
зывается осью конуса.
Боковая поверхность конуса образована вращением вокруг
оси отрезка, один конец которого совпадает с вершиной конуса.
Сечением конуса плоскостью, параллельной основанию, будет
круг (рис. 376).
285
Рис. 373
Рис. 374
Рис. 375
Рис. 376
Высота конуса — это расстояние от его вершины до основа¬
ния, т. е. длина отрезка оси, соединяющего вершину и центр
основания. Конус можно задать двумя числовыми данными:
радиусом основания и высотой.
286
Радиус основания и высота — это катеты того прямоугольно¬
го треугольника, вращением которого был образован конус.
Гипотенуза этого треугольника называется образующей конуса.
Так же как и у цилиндра, боковую поверхность конуса можно
развернуть на плоскость. Если разрез сделать по образующей,
то разверткой будет круговой сектор (рис. 377).
Если в конусе провести сечение, параллельное основанию,
то между основанием и плоскостью сечения получится тело,
называемое усеченным конусом (рис. 378). Оставшаяся часть
конуса (от вершины до плоскости сечения) будет также конусом,
подобным исходному. Коэффициент подобия равен отношению
высот (или отношению радиусов оснований).
Упражнения
1. Приведите примеры тел конической
формы.
2. Какая фигура получится в сечении
конуса плоскостью, проходящей че¬
рез его ось (это сечение называют
осевым сечением конуса)?
3. Нарисуйте различные по форме се¬
чения конуса.
4. Конус катится по плоскости так,
что его вершина остается неподвиж¬
ной. Какую фигуру опишет центр
основания конуса? Какая фигура
получится при движении оси конуса?
5. Высота конуса равна //, радиус
основания R. Вычислите:
а) длину образующей;
б)' площадь осевого сечения;
в) угол наклона образующей к пло¬
скости основания;
г) угол при вершине осевого сече¬
ния (угол раствора конуса);
6. В конусе высотой Н и радиусом
основания R проведено сечение,
параллельное основанию на рас¬
стоянии h от него. Вычислите:
а) радиус верхнего основания;
б) площадь осевого сечения;
в) наибольшую длину ребра куба,
который можно поместить внутрь
усеченного конуса;
г) наибольшую длину отрезка, кото¬
рый можно поместить внутрь усе¬
ченного конуса.
7. Конус высоты Н и радиуса осно¬
вания R лежит на плоскости, каса¬
ясь ее по образующей. Определите:
а) какой угол образует с этой пло¬
скостью основание конуса;
б) на какой максимальной высоте
от плоскости лежат точки конуса.
8. Из полукруга радиуса г склеили
боковую поверхность конуса. Наиди-
те его радиус основания, длину
образующей и высоту.
9. Нарисуйте развертку усеченного ко¬
нуса.
287
Рис. 377
Рис. 378
Тела вращения
Цилиндр и конус являются простейшими примерами тел враще¬
ния. Тела вращения более общего вида получаются при враще¬
нии плоской фигуры вокруг не пересекающей ее оси. Издавна
человек изготовлял с помощью гончарного круга домашнюю
утварь в форме тел вращения. Аналогичный принцип применя¬
ется теперь при обработке металлов на различных станках,
вращающих заготовку. Наблюдая некоторые природные явления
(водовороты, смерчи и т. п.), можно увидеть появление тел и по¬
верхностей вращения (рис. 379, 380).
Кроме цилиндров и конусов в технике часто встречаются
такие тела, как параболоид вращения, полученный при вращении
параболы вокруг ее оси (рис. 381). Он используется при изготов¬
лении различных фокусирующих зеркальных устройств (рис. 382).
Эффект его применения описан в известном романе А. Н. Толсто¬
го «Гиперболоид инженера Гарина». При вращении окружности
288
Рис. 379
Рис. 380
Рис. 381
Рис. 382
Рис. 383
вокруг не пересекающей ее оси получается тело в форме баранки.
В математике это тело называют тором (рис. 383).
Упражнение
Какое тело образуется при вращении:
а) треугольника вокруг одной из
его сторон;
б) прямоугольного треугольника во¬
круг оси, параллельной одному из
его катетов;
в) прямоугольника вокруг оси, па¬
раллельной одной из его сторон;
г) трапеции вокруг оси, перпенди¬
кулярной основаниям?
Общее представление о цилиндре и конусе
Прямой круговой цилиндр и прямой круговой крнус были нами
определены с помощью операции вращения. Это привело нас к
одному обобщению — к понятию тела вращения. Однако цилиндр
и конус можно получить иначе, используя другие свойства этих
тел.
Обычный, т. е. прямой, круговой цилиндр можно получить
так: взять круг и сделать его параллельный перенос на вектор,
ортогональный плоскости этого круга; затем соединить отрезком
каждую точку исходного круга с соответствующей точкой нового,
передвинутого круга. Цилиндр получится как объединение всех
этих отрезков. Это построение можно обобщить: выбрать в каче¬
стве исходной фигуры не обязательно круг, а произвольную
плоскую фигуру, и совершать параллельный перенос на произ¬
вольный вектор.
Пусть даны плоская фигура F и вектор аг не лежащий в плоскости фи¬
гуры. Цилиндром называется телог образованное отрезками, соединяю¬
щими точки фигуры F, с точками, получающимися из них при параллель¬
ном переносе на вектор а (рис. 384).
Фигура F и равная ей фигура, получающаяся при параллель¬
ном переносе F на вектор а, называются основаниями цилиндра.
Расстояние между плоскостями оснований называется высотой
цилиндра. Если вектор а ортогонален плоскости основания, то
цилиндр прямой (рис. 385).
10—1681
289
Рис. 384 Рис. 385
В сечении цилиндра плоскостью, параллельной основанию,
получается фигура, равная основанию. Вообще, если цилиндр
получен с помощью фигуры F и параллельного переноса на
вектор а, то сечение этого цилиндра плоскостями, параллель¬
ными основанию, можнб получать при параллельном переносе
фигуры F на векторы вида А,а, где
Обычный, т. е. прямой, круговой конус можно получить так:
взять круг, выбрать точку, проектирующуюся в центр этого круга,
и соединить ее со всеми точками круга. Конус получится как
объединение всех этих отрезков. Обобщим это построение, взяв
в качестве основания произвольную плоскую фигуру, а в каче¬
стве вершины — произвольную точку.
Пусть даны плоская фигура F и точка О вне плоскости фигуры. Конусом
называется телог образованное отрезками, соединяющими точку О со
всеми точками фигуры F (рис. 386).
Точка О называется вершиной конуса, фигура F — его осно¬
ванием, расстояние от вершины до плоскости основания — вы¬
сотой.
В сечении конуса плоскостью, параллельной основанию, полу¬
чается фигура, подобная фигуре F. Коэффициент подобия равен
290
Рис. 386
отношению расстояния от вершины до плоскости сечения к высо¬
те конуса. Преобразование подобия осуществляется как раз с
помощью тех отрезков, которые соединяют вершину конуса с
точками основания.
В отличие от цилиндра мы не даем определения прямого конуса. Такое
определение имело бы смысл, если бы основание конуса имело центр сим¬
метрии. Подумайте, как в этом случае дать определение прямого конуса.
§ 34. Шар и сфера
Определения
Сферой радиуса R (где R > 0) с центром в точке О называется множест¬
во точек пространства, удаленных от точки О на расстояние R (рис. 387).
Рис. 387
Сфера разбивает пространство на две части: внутреннюю,
составленную из точек, удаленных от точки О на расстояние,
меньшее /?, и внешнюю, составленную из точек, удаленных от
точки О на расстояние, большее R. Внутренняя часть простран¬
ства вместе со сферой называется шаром радиуса R с центром
в точке О. Таким образом, шар — множество точек пространства,
удаленных от точки О на расстояние, меньшее или равное R.
Сфера и шар радиуса R с центром в точке О получаются при
вращении соответственно окружности и круга вокруг диаметра.
Отрезки, соединяющие точки сферы с центром, называются
радиусами сферы. Они же называются радиусами соответствую¬
щего шара. Диаметрами шара и сферы называются отрезки, по
которым шар пересекается с прямыми, проходящими через центр.
Этими же словами — «радиус» и «диаметр» — обозначают не
только указанные отрезки, но и их длины.
«Из фигур он считал прекраснейшими среди плоских — круг, а среди
объемных — шар».
Диоген Лаэртский о Пифагоре
10*
291
Сечение шара плоскостью
Теорема
Пусть даны шар радиуса R и плоскость, расстояние которой до центра
шара равно d.
1. Если d - R, то у шара и плоскости нет общих точек (рис. 388, а).
2. Если d = R, то у шара и плоскости одна общая точка — проекция
центра шара на плоскость (рис. 388, б).
3. Если d < R. то пересечение шара и плоскости является кругом радиуса
г = V R—d: (рис. 388, в).
Доказательство. Даны шар S с центром О и пло¬
скостью а. Спроектируем точку О на плоскость а. Получим точку
Р£а. Дано, что \OP\ = d (рис. 389).
Пусть X — произвольная точка плоскости а. Вычислим рас¬
стояние от нее до центра шара: |ОЛ]2=|ЯЛ12 + ^2.
Рис. 389
1. d>R. Тогда |ОХ|2>|Я*|2 + /?2>/?2, т. е. |ОХ|>/?. Это
означает, что расстояние от точки X до центра шара больше
радиуса, значит, точка X лежит вне шара. Это верно для любой
точки X плоскости а. Следовательно, все точки плоскости а ле¬
жат вне шара и шар с плоскостью не пересекаются.
2. d = R и точка X принадлежит шару. Тогда \OX\^.R. Под¬
ставив d=R и \OX\^R в формулу \OX\'z=\PX\2 + d2y получим
\PX\2 + R2^R2t т. е. |ЯХ|2<0.
292
Рис. 388
Это возможно лишь в том случае, когда |РЛП = 0, т. е. когда
точки Р и X совпадают. Вспомним, что Р — однозначно опреде¬
ленная точка, проекция центра шара на плоскость а. Итак, мы
доказали, что общая точка у шара и плоскости одна — проекция
центра шара на плоскость.
3. d<R и точка X принадлежит шару. Тогда \OX\^.R. Вве¬
дем обозначения: г= //?2 — с?1. Из АОРХ (рис. 389) |РЛ12=
= \OX\2 — d2^.R2 — d2 = r2y т. е. |РЛГ|^г. Мы получили, что рас¬
стояние от точки X до точки Р не превосходит г. Это означает,
что точка X лежит в круге с центром в точке Р и радиусом г.
Заметим, что все точки этого круга лежат в сечении шара и
плоскости. Действительно, если х£а и лежит в круге с центром Р
и радиусом г, то |РХ|<г. Тогда \ОХ\2 = \РХ\2+ d^ = \PX\2 + R2 —
— r2^r2 + R2 — г2 = /?2, т. е. \OX\^Ry откуда следует, что X£S,
т. е. ^gSf|a. Теорема доказана.
Аналогично можно рассмотреть пересечение плоскости и сфе¬
ры. Сформулируйте самостоятельно теорему о пересечении пло¬
скости и сферы.
В сечении шара радиуса R плоскостью (если они пересекают¬
ся) получается круг некоторого радиуса r= ^R? — d2, где d —
расстояние от центра шара до плоскости. Так как это расстояние
может изменяться от 0 до /?, то и г как функция от d может
изменяться в этих же пределах.
При d=0 (в том случае, когда плоскость проходит через
центр шара) в сечении получаются круги максимального ра¬
диуса R. Они называются большими кругами шара.
Касательная плоскость
Теорема о пересечении плоскости и шара показывает, что воз¬
можны три случая расположения шара и плоскости: шар и плос¬
кость не имеют общих точек, шар и плоскость имеют одну общую
точку, общие точки шара и плоскости заполняют круг.
Плоскость называется касательной к шару, если она имеет с ним одну
общую точку (рис. 390).
Аналогично определяется касательная плоскость к сфере.
При доказательстве теоремы о пересечении плоскости и шара
мы выяснили, что одна общая точка у них будет в том случае,
когда радиус шара равен расстоянию от центра шара до плоско¬
сти. При этом единственная общая точка (точка касания) будет
проекцией центра шара на плоскость. Это свойство можно сфор¬
мулировать следующим образом:
Радиус шара, проведенный в точку касания шара с плоскостью, является
перпендикуляром к этой плоскости.
293
Теорема
Пусть Р — общая точка плоскости а и шара. Если радиус шара, прове¬
денный в точку Р, перпендикулярен плоскости а, то эта плоскость а явля¬
ется касательной к шару, а точка Р — точка касания.
Доказательство. Пусть О — центр шара. По условию,
OPJLa и \0Р\ = R, где R — радиус шара. Пусть X — любая
другая точка плоскости а. Тогда |ОЛ]>|ОЯ|, так как перпенди¬
куляр к плоскости короче наклонной. Следовательно, у шара и
плоскости а есть единственная общая точка Р и, по определению,
плоскость а касается шара. Теорема доказана.
Рис. 390
Рис. 391
Шар нельзя развернуть на плоскость. Каждый из нас сталки¬
вался с тем, что бумагой, не сминая ее, нельзя оклеить шар
(рис. 391), как нельзя скроить круглую шляпу из нерастяжимой
материи. Это замечательное свойство шара, отличающее его
от конусов и цилиндров, кажется нам вполне очевидным, однако
получить его математическое доказательство очень трудно.
Упражнения
1. Где лежат точки пространства, рас¬
стояния от которых до данной
точки О удовлетворяют неравен¬
ству 1 ^ | ОХ | ^ 2?
2 Дан шар радиуса R. Точка Q
удалена от центра шара на рас¬
стояние acR. Каким может быть
радиус круга, получающегося в се¬
чении шара • плоскостью, проходя¬
щей через точку Q? Когда этот
радиус будет наибольшим и когда —-
наименьшим?
3. Сколько точек пересечения могут
иметь две окружности, расположен¬
ные на сфере?
4. Сколько касательных плоскостей к
шару можно провести через точку,
лежащую вне этого шара?
5. Сколько общих касательных пло¬
скостей, проходящих через данную
точку, можно провести к двум непе-
ресекающимся шарам?
6. Какое наибольшее число общих
касательных плоскостей можно про¬
вести к трем шарам?
7. Ось прямого кругового цилиндра
проходит через центр сферы. Что
может получиться в пересечении
цилиндра и сферы?
8. Три шара радиуса R касаются друг
друга. Вычислите:
а) стороны треугольника, образо¬
ванного центрами этих шаров;
б)* радиусы шаров, касающихся
этих трех шаров внутренним и
внешним образом.
9.* На плоскости лежит шар радиу¬
са R. Он касается плоскости в
точке Р. Диаметрально противопо¬
ложная точка шара обозначена Q.
На плоскости с центром с точке Р
проводится круг радиуса х. Его точ¬
ки соединяются с точкой Q. При
этом получается конус, пересекаю¬
щий шар по кругу радиуса г. Вы¬
числите зависимость г от г'
294
§ 35. Призмы и пирамиды
пР измы
Призмой называется цилиндр, в основании которого лежит многоуголь
ник (рис. 392).
По определению цилиндра получаем следующий способ по¬
строения призмы. Берем многоугольник F и вектор а, не лежа¬
щий в плоскости этого многоугольника. Каждую точку много¬
угольника F переносим на вектор а. Соединяем полученные точки
отрезками и объединяем вместе все отрезки.
Исходный многоугольник F удобно называть нижним основа¬
нием призмы, а многоугольник, полученный из F параллельным
переносом на вектор а, — верхним основанием. Отрезки, соеди¬
няющие соответствующие вершины верхнего и нижнего основа¬
ний, называются боковыми ребрами призмы.
Теорема
Все боковые ребра призмы параллельны друг другу и равны между
собой (рис. 393).
Доказательство. Пусть А и В — две вершины нижне¬
го основания призмы, Л' и В' — соответствующие им вершины
верхнего основания. Так как точки А' и В' получены из точек
A_j\ В параллельным переносом на один и тот же вектор а, то
АА' = ВВ'=ау а это и означает, что АА'\\ВВ'и \АА'\ = \ВВ'\, что
и требовалось доказать.
Следствие
Боковые грани призмы являются параллелограммами.
Действительно, они являются четырехугольниками, имеющи¬
ми пару равных и параллельных сторон.
295
Рис. 392
Рис. 393
Введем определения.
Треугольная, четырехугольная, ..., п-угольная призма — в основании
призмы лежит треугольник, четырехугольник, n-угольник (рис. 394—
395).
Прямая призма — боковые ребра призмы перпендикулярны основанию
(рис. 396).
Рис. 395
Определение прямой призмы совпадает с общим определением
прямого цилиндра.
Наклонная призма, т. е. не прямая, ее боковые ребра не перпендикуляр¬
ны основанию.
Правильная призма — прямая и в ее основании лежит правильный много¬
угольник.
Рис. 396
Диагональ призмы — это отрезок, соединяющий вершины
двух оснований призмы и лежащий внутри ее (не лежащий в
боковой грани) (рис. 397).
296
Упражнения
1. Приведите примеры тел, имеющих
форму призмы.
2. Докажите, что боковые грани пря¬
мой призмы являются прямоуголь-.
никами.
3. Докажите, что грани прямой приз¬
мы перпендикулярны основаниям.
4. Нарисуйте различный по форме
сечения треугольной призмы.
5. В правильной четырехугольной приз¬
ме проводится сечение через сторону
основания под углом а к нему. Сто¬
рона основания равна а. Вычислите
площадь сечения.
6. -В основании наклонной призмы ле¬
жит правильный треугольник. Изве¬
стно, что боковое ребро образует
равные углы с двумя смежными
сторонами основания. Докажите,
что это боковое ребро перпендику¬
лярно не смежной с ним стороне
основания.
7. В правильной шестиугольной приз¬
ме сторона основания равна а,
высота — h. Вычислите углы накло¬
на диагоналей призмы к плоскости
основания.
Пирамиды
Пирамидой называется конусг в основании которого лежит много¬
угольник.
Вспоминая определение конуса, получаем следующий способ
построения пирамиды. Берем многоугольник F и точку О, не ле¬
жащую в его плоскости. Соединяем точку О с каждой точкой
многоугольника F и объединяем все построенные отрезки
(рис. 398).
Отрезки, соединяющие вершину пирамиды с вершинами осно¬
вания, называются боковыми ребрами пирамиды.
Рис. 398
297
Рис. 397
Введем определения.
Треугольная, четырехугольная, ..., n-угольная пирамида — в основании
лежит треугольник, четырехугольник, n-угольник (рис. 399). Треуголь¬
ную пирамиду еще иначе называют тетраэдром.
Правильная пирамида — в основании лежит правильный многоугольник,
а вершина пирамиды проектируется в центр этого многоугольника
(рис. 400).
Усеченная пирамида — часть пирамиды, отсекаемая плоскостью, парал¬
лельной основанию (рис. 401).
Напомним, что, как и для всякого конуса, в сечении пирами¬
ды плоскостью, параллельной основанию, получается фигура,
подобная основанию. Поэтому, например, в таких сечениях пра¬
вильной 'пирамиды будут получаться правильные многоуголь¬
ники.
Теорема
В правильной пирамиде боковые ребра равны и одинаково наклонены
к плоскости основания (рис. 402).
Доказательство. Пусть S — вершина пирамиды, А и
В — две произвольные вершины основания, О — его центр. По
условию, отрезок SO перпендикулярен основанию (вершина пра-
Рис. 399
Рис. 400
Рис. 401
298
вильной пирамиды проектируется в его центр); \ОА\ = \ОВ\ как
радиусы круга, описанного около основания. Следовательно,
прямоугольные треугольники OS/1 и OSB равны, так как имеют
по два равных катета. Отсюда вытекает, что |Sj4| = |SB| и
/-SAO = Z.SBO, что и требовалось доказать.
Упражнения
1. Приведите примеры тел, имеющих
форму пирамиды.
2. Площадь основания пирамиды рав¬
на S, а периметр — р. Высоту пи¬
рамиды разделили на четыре равные
части и через точки деления про¬
вели плоскости, параллельные осно-
5. В треугольной пирамиде, боковые
ребра равны. Докажите, что вер¬
шина пирамиды проектируется в
центр круга, описанного около осно¬
вания. Обобщите результат задачи.
6. В основании треугольной пирамиды
лежит правильный треугольник.
Одно боковое ребро образует рав¬
ные углы со смежными сторонами
ваниям. Найдите площади и пери¬
метры получившихся сечений.
3. В правильной четырехугольной пи¬
рамиде сторона основания равна а,
угол при вершине (в боковой грани)
равен а (рис. 403). Вычислите:
а) апофему пирамиды (высоту бо¬
ковой грани, проведенную из вер¬
шины) ;
б) высоту пирамиды;
в) угол наклона боковой грани к
плоскости основания;
г) угол наклона бокового ребра
к плоскости основания.
4. Нарисуйте различные по форме се¬
чения треугольной пирамиды.
основания. Докажите, что оно пер¬
пендикулярно не смежной с ним
стороне основания.
7 В основании треугольной пира¬
миды SABC лежит равнобедренный
треугольник (АВ=АС). Вершина 5
проектируется в середину основа¬
ния ВС (рис. 404). Докажите:
a) Sy4_L£C; б) боковые грани SAC
и SBC равны между собой.
8. Вычислите длины всех ребер пира¬
миды (рис. 404), если а — угол
наклона ребра S/4 к плоскости осно¬
вания, h — высота пирамиды и
\ВС\ = а — основание.
Параллелепипеды
Параллелепипедом называется призма, в основании которой лежит па¬
раллелограмм (рис. 405).
Боковые грани параллелепипеда, как у всякой призмы, явля¬
ются параллелограммами. Поэтому в отличие от произвольной
299
Рис. 402
Рис. 403
Рис. 404
с
Рис. 405
призмы у параллелепипеда нельзя однозначно выделить основа¬
ния. В качестве оснований можно взять любую из трех пар про¬
тивоположных граней.
Если продолжить все грани параллелепипеда, то они образу¬
ют три пары параллельных плоскостей. Вспомним, параллело¬
грамм можно получить, рассматривая пересечение двух пар
параллельных прямых. Аналогично, и параллелепипед получается
с помощью пересечения трех пар параллельных плоскостей
(рис. 406).
В параллелепипеде можно провести четыре диагонали.
Теорема
Четыре диагонали параллелепипеда пересекаются в одной точке, являю¬
щейся серединой каждой диагонали (рис. 407).
Доказательство. Возьмем две любые диагонали. Они
лежат в одном из диагональных сечений. Это сечение является
параллелограммом. Выбранные диагонали параллелепипеда
будут диагоналями этого параллелограмма. По свойству парал¬
лелограмма
диагонали в точке пересечения делятся пополам.
Это верно для любой пары диагоналей, т. е. середины любых
двух диагоналей совпадают, значит, они совпадают у всех четы¬
рех диагоналей. Эта точка и есть точка пересечения всех диаго¬
налей. Теорема доказана.
Рис. 406
300
Рис. 407
Параллелепипед, у которого все грани — прямоугольники, называется
прямоугольным (рис. 408).
Пространственная теорема Пифагора
Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадра
тов катетов (рис. 409):
а2 + Ь2 = d2.
Рис. 409
О
Рис. 410
Вместо прямоугольного треугольника можно рассматривать
прямоугольник и дать теореме Пифагора равносильную форму¬
лировку:
В прямоугольнике квадрат диагонали равен сумме квадратов сторон,
исходящих из одной вершины (рис. 410).
301
Рис. 408
В такой формулировке теорема Пифагора обобщается на
пространственный случай. Прямоугольник теперь заменяется
прямоугольным параллелепипедом.
Теорема
Квадрат диагонали прямоугольного параллелепипеда равен сумме квад¬
ратов сторон, исходящих из одной вершины (рис. 410):
d2 = а2 + Ь2 + с2.
Доказательство. Возьмем диагональ А'С. Треугольник
АА'С прямоугольный, так как в прямоугольном параллелепипеде
боковые ребра перпендикулярны основанию. По теореме Пифаго¬
ра, на плоскости
\А'С\2 = \АА'\2 + |ЛС|2 = \АА'\2 + \AD\2 + \АВ\2,
что и требовалось доказать.
Пространственная теорема Пифагора на самом деле мало
чем отличается от формулы расстояния между двумя точками
в декартовых координатах.
Рис. 411
Пусть_£fi(*i; у\\ z\) и М^х2; у2\ z2) — две точки (рис. 411).
Вектор М1М2 имеет координаты (х2—*i; у2—уи z2—zi). Квадрат
его длины равен
|M|Af2|2 = (X5 — Х\ )2 + (1/2 — yi)2 + (z2 — 2i)2.
Отрезок М\М2 можно представить как диагональ прямоуголь¬
ного параллелепипеда с ребрами, параллельными координатным
осям. Длины сторон (измерения) этого параллелепипеда равны
1*2— *il, \у2 — У\L \z2 — z\\, откуда видно совпадение двух указан¬
ных выше формул.
Упражнения
1. Приведите примеры тел, имеющих
форму параллелепипеда.
2. Сколько граней, являющихся пря
моугольниками, может быть в па
раллелепипеде? Сколько из них мо
жет быть квадратами?
302
3. Нарисуйте различные по форме се¬
чения параллелепипеда.
4. В параллелепипеде все грани —
равные ромбы.
а) Докажите:
все ребра параллелепипеда равны
между собой;
одно из диагональных сечений пер¬
пендикулярно плоскости основания;
другое диагональное сечение — пря¬
моугольник.
б) Найдите проекции вершин одно¬
го основания на плоскость дру¬
гого.
в) Вычислите высоту параллелепи¬
педа, длины его диагоналей и диа¬
гоналей основания, если острый
угол ромба равен 60°, сторона
основания равна а.
5. В прямоугольном параллелепипеде
стороны равны 1, 1 и 2. Вычислите:
а) диагонали параллелепипеда;
б) угол между диагоналями.
§ 36. Многогранники
Примеры многогранников
Многогранник — это тело, ограниченное многоугольниками (рис. 412).
Данное определение многогранника еще не вполне отвечает
обычным представлениям о многограннике. Так, все простран¬
ство, кроме fo4eK некоторого куба (т.е. вне точек некоторого
куба), тоже можно считать телом, ограниченным многоугольни¬
ками. Мы же представляем себе многогранник ограниченным
телом.
Рис. 412
Рассмотрим тела, ограниченные конечным числом многоуголь¬
ников, и изучим конкретные типы многогранников, которые легко
себе представить и модели которых нетрудно изготовить.
Призмы и пирамиды являются простейшими примерами мно¬
гогранников.
зоз
Среди всех тел многогранники выделяются тем, что их по¬
верхность состоит из кусков плоскостей, являющихся много¬
угольниками. Эти многоугольники называются гранями, их сто¬
роны — ребрами, а вершины — вершинами многогранника. Так,
треугольная пирамида имеет четыре грани, каждая из которых
представляет собой треугольник. Всего у треугольной пирамиды
шесть ребер и четыре вершины, в каждой из которых сходится
по три ребра.
У куба 6 граней, 12 ребер и 8 вершин, каждая грань является
квадратом. В каждой вершине сходится по 3 ребра.
Может ли многогранник иметь любое количество граней,
ребер и вершин? Оказывается, нет. Давно было замечено, что
между числом граней, ребер и вершин многогранника есть про¬
стое соотношение. Попробуйте заметить его сами, посмотрев на
табл. 8, в которой указано число граней, ребер и вершин для
шести многогранников (рис. 412).
Таблица 8
Номер многогранника
Число
граней
ребер
вершин
1
8
14
8
2
13
24
13
3
8
18
12
4
60
90
32
5
5
9
6
6
8
12
6
Легко заметить, что сумма числа граней и числа вершин
всегда на 2 больше числа ребер. Это наблюдение верно для лю¬
бого выпуклого многогранника и составляет содержание знаме¬
нитой теоремы, доказанной впервые Леонардом Эйлером (1707—
1783).
«Математика, вероятно, никогда не достигла бы такой высокой степени
совершенства, если бы древние не приложили столько усилий для изуче¬
ния вопросов, которыми сегодня многие пренебрегают из-за их мнимой
бесплодности».
Л. Эйлер
Эйлер Леонард (1707—1783 г.г.) — швейцарский математик и механик,
академик Петербургской Академии Наук, автор огромного количества
глубоких результатов во всех областях математики. Полное собрание
сочинений Эйлера — 72 тома — не вышло целиком и до сих пор.
Эйлер первым применил средства математического анализа в теории чи¬
сел, положил начало топологии. Современное школьное изложение три¬
гонометрии почти точно повторяет Эйлера. Э. Т. Белл писал о нем:
«Эйлер не проглядел ничего в современной ему математике, хотя
последние семнадцать лет своей жизни был совершенно слеп».
304
Теорема Эйлера
Пусть Г обозначает число граней, Р — число ребер, В — число вершин
выпуклого многогранника. Тогда
Г + В = Р + 2.
Полное доказательство теоремы Эйлера довольно трудоемко,
и мы его приводить не будем. Проверить же эту теорему для
частных случаев многогранников достаточно просто.
К многогранникам надо отнести и такие необычные конфигурации, которые
изображены на рис. 413. Все они невыпуклые, однако для некоторых из них
Рис. 413
соотношение Эйлера Г-\-В = Р-\-2 выполнено, а для некоторых — нет.
На самом деле еро справедливость связана не с выпуклостью многогран¬
ника, а скорее с другими его свойствами, например наличием или отсут¬
ствием «дырок».
Упражнение пирамиды и проверьте для этих
многогранников справедливость тео-
Подсчитайте число вершин, ребер и ремы Эйлера,
граней п — угольной призмы и
Правильные многогранники
Куб — параллелепипед, у которого все грани — квадраты. Все ребра
куба имеют одинаковую длину, поскольку все стороны квадрата имеют
одинаковую длину. Ребра, выходящие из одной вершины, попарно пер¬
пендикулярны. Соседние грани куба перпендикулярны друг другу, по¬
скольку каждая из них содержит ребро, перпендикулярное другой.
Куб имеет девять плоскостей симметрии (рис. 414), девять
осей симметрии (рис. 415) и центр симметрии (рис. 416). Кроме
Рис. 414
305
Рис. 415
того, при повороте на углы, кратные 90°, вокруг осей а\9 ач, аз
и при повороте на углы, кратные 120°, вокруг диагоналей куба
куб в целом сохраняет свое положение (при этом некоторые
вершины, ребра и грани, конечно, меняются местами). Всего
существует 48 перемещений, включая 24 поворота, при которых
куб сохраняет свое положение. С помощью поворотов можно
осуществить перестановку диагоналей куба. В частности, эти
повороты позволяют поменять местами любые два трехгранных
угла куба. И с этой точки зрения все трехгранные углы куба
одинаковые.
Правильный тетраэдр — это тетраэдр, у которого все грани — правильные
треугольники.
Примером правильного тетраэдра служит тетраэдр, образо¬
ванный попарно не смежными вершинами куба (рис. 417). Более
того, всякий правильный тетраэдр можно, таким образом, впи¬
сать в подходящий куб. Перемещения, при которых тетраэдр
сохраняет свое положение, составляют часть тех перемещений,
при которых сохраняет свое положение куб. Всего существует
24 таких перемещения, среди них — три поворота на 90°, четы¬
ре— на 120°, четыре — на 240°, шесть симметрий относительно
плоскости (рис. 418). Эти перемещения позволяют отождествить
все трехгранные углы правильного тетраэдра.
306
Рис. 416
Рис. 417
Следующий правильный многогранник — это октаэдр. Его вершинами
служат центры граней куба; октаэдр является объединением двух че¬
тырехугольных пирамид (рис. 419).
Перемещения, которые не меняют положения куба, сохраняют
и положение октаэдра. Более того, ими исчерпываются все пере¬
мещения, при которых октаэдр сохраняет свое положение.
Существует еще два типа многогранников, у которых пере¬
мещениями, сохраняющими многогранник в целом, можно поме¬
нять местами любые две вершины, любые два ребра и любые две
грани. Это икосаэдр (рис. 420) и додекаэдр.
Рис. 419 Рис. 420
Икосаэдр имеет 12 вершин, 30 ребер и 20 граней (являющих¬
ся правильными треугольниками). Додекаэдр имеет 20 вершин,
30 ребер и 12 граней (являющихся правильными пятиугольника¬
ми; рис. 421). Эти два типа многогранников тесно связаны между
собой: центры граней икосаэдра служат вершинами додекаэдра,
а центры граней додекаэдра служат вершинами икосаэдра.
Икосаэдр и додекаэдр обладают 120 перемещениями (среди них
60 поворотов), сохраняющими положение этих тел.
Рис. 421
Итак, мы познакомились с пятью многогранниками, которые
мы назвали правильными. Это правильный тетраэдр, куб, окта¬
эдр, икосаэдр и додекаэдр. Можно по-разному определить «пра¬
вильность» многогранника, например, заметив, что их грани —
правильные многоугольники. Однако существует много других
многогранников, грани которых являются правильными много¬
угольниками. Некоторые из них изображены на рис. 422. Обычно
определяют правильность многогранника так.
Рис. 418
307
Рис. 422
Выпуклый многогранник называется правильным, если его грани — равные
правильные многоугольники и о каждой его вершине сходится одинако¬
вое число граней.
Оказывается, что этому определению «правильности» уже ни¬
какие другие многогранники, кроме указанных выше пяти, не
удовлетворяют. Это можно строго доказать с помощью теоремы
Эйлера. Проведем это доказательство.
Доказательство. Пусть в каждой вершине правильно¬
го многогранника сходятся т ребер и каждая грань — много¬
угольник с п ребрами. Пусть у многогранника всего В вершин,
Р ребер и Г граней. Подсчитаем разными способами число ребер.
Всего есть Г граней, в каждой — п ребер, всего Гп ребер, но
каждое сосчитано два раза, так как оно принадлежит двум гра¬
ням. Итак, Гп = 2Р.
С другой стороны, всего есть В вершин, в каждой сходится
т ребер, но снова каждое ребро засчитано дважды, так как оно
соединяет две вершины. Итак, Вт = 2Р.
Подставим в соотношение Эйлера Г + В = Р-\-2 вместо Г и В
их выражения через т, п и Р:
— +—=Р + 2.
т п
Нам достаточно даже неравенства Сокращая его
на 2Р, получаем Числа тип больше или равны
трем. Оба они не могут быть больше трех, так как уже
1.1 1 ^ „ l.l^lc
__ , и при т, 4 получим: —+ —. есть возмож¬
ности т\ = п\ =3; Ш2 = 3, п2 =4; тз=4, Яз=3; т4 = 5, м4 = 3;
т5 = 3, пъ = Ъ. Если же одно из чисел равно трем, а другое боль¬
ше или равно шести, то
m л 3 6 2
Итак, у неравенства только пять решений. Они соответствуют
известным нам пяти типам правильных многогранников.
308
Многогранные углы и многогранники
В этом параграфе мы уже не раз рассматривали многогранные
углы: трехгранные углы — это углы, образованные сходящимися
в одной вершине гранями тетраэдра, параллелепипеда, доде¬
каэдра; четырехгранные углы — это углы, образованные сходя¬
щимися в одной вершине гранями октаэдра; пятигранные углы —
это углы, образованные сходящимися в одной вершине гранями
додекаэдра; наконец, угол при вершине л-угольной пирамиды
(образованной гранями пирамиды) — это пример п-гранного
угла. Последний пример дает нам я-гранные углы с любым п^З.
Вспоминая определение пирамиды, мы приходим к следую¬
щей конструкции многогранного угла: пусть даны я-угольник и
точка О, не лежащая в. плоскости n-угольника; тогда объедине¬
ние лучей, соединяющих точку О с точками л-угольника, являет¬
ся я-гранным углом. Эта конструкция (называемая конической)
еще не исчерпывает всего запаса многогранных углов — она не
охватывает двугранные углы и некоторые я-гранные углы сп>2,
однако объединения углов, получающихся с помощью этой кон¬
струкции и имеющих общую вершину, уже дают все возможные
многогранные углы (на рис. 423 изображен многогранный угол,
который не получается конической конструкцией; на рисунке он
представлен как объединение трех углов, строящихся с помощью
конической конструкции).
Рис. 423 Рис. 424
Наиболее простой тип многогранника — это выпуклые много¬
гранники. Пусть задано несколько плоскостей в пространстве;
они разбивают пространство на части, и те из частей, которые
ограничены, называются выпуклыми многогранниками (напри¬
мер, тетраэдр, параллелепипед, правильные многогранники).
Чтобы убедиться в их выпуклости, достаточно провести плоско¬
сти, в которых лежат грани этих многогранников. Часто наиболее
удобным способом проверки выпуклости служит следующий кри¬
терий: многогранник выпуклый тогда и только тогда, когда он
вместе с любыми своими двумя точками содержит целиком весь
отрезок, соединяющий эти точки. С помощью этого критерия
легко убедиться в том, что призма, изображенная на рис. 424,
не выпуклая.
309
2. Можно ли все1 пространство раз¬
бить на одинаковые правильные
тетраэдры? октаэдры?
3. Вычислите угол между двумя сосед¬
ними гранями октаэдра.
Задачи и вопросы
9.1. Высота цилиндра равна 3, радиус основания — 2. Найдите
пару точек цилиндра, наиболее удаленных друг от друга.
Вычислите расстояние между ними. Сколько таких
пар?
9.2. Диаметр основания цилиндра равен 12, высота — 20. Рас¬
смотрим точки на боковой поверхности, удаленные от цент¬
ра нижнего основания на расстояние 10. На какой высоте
они находятся? Сколько их? Какую фигуру они обра¬
зуют?
9.3. Основание цилиндрической бочки радиуса 0,6 м и высотой
1,6 м находится на полу в помещении высотой 1,9 м. Можно
ли выкатить бочку из этого помещения?
9.4. Радиус основания и высота цилиндра равны 5. В цилиндре
проведены два сечения, параллельные между собой и парал¬
лельные оси. Площади этих сечений 40 и 30 см2. Найдите
расстояние между сечениями.
9.5. Дан цилиндр с радиусом 2 и высотой 4. Параллельно его
оси проводится сечение на расстоянии 1 см от оси. Найдите
площадь и периметр сечения (рис. 426).
9.6. Развертка боковой поверхности цилиндра — квадрат ABCD
со стороной 6; О — центр квадрата, К — середина CD.
Найдите расстояние между точками О, К, С на развертке
и на цилиндре (рис. 427).
9.7. В цилиндре диаметром 15 сделано цилиндрическое отвер¬
стие диаметром 5. Оси обоих цилиндров совпадают. Затем
цилиндр разрезали пополам плоскостью, проходящей через
Итак, выпуклые многогранники не исчерпывают всего за¬
паса многогранников. Однако любой многогранник можно
сложить, как из кирпичей, из выпуклых многогранников
(рис. 425).
Упражнения
1 Два равных правильных тетраэдра
приложены друг к другу одной
гранью. Будет ли правильным полу¬
ченный многогранник?
Рис. 426
Рис. 427
ось (рис. 428). Нарисовать и указать размеры получившего¬
ся тела.
9.8. В цилиндре общая площадь оснований равна площади бо¬
ковой поверхности. Что можно сказать о соотношении меж¬
ду высотой и радиусом основания цилиндра?
9.9. В прямоугольном треугольнике гипотенуза равна 6, а один
из острых углов 30°. Конус получается вращением этого
треугольника относительно одного из катетов. Найдите для
обоих конусов: а) высоту; б) радиус основания; в) площадь
осевого сечения; г) угол при вершине осевого сечения;
е) угол между образующей и основанием.
9.10. Радиусы оснований усеченного конуса равны 1 и 2, высо¬
та— 3 (рис. 429). Найдите: а) длину образующей; б) тан¬
генс угла наклона (коэффициент наклона) образующей к
основанию; в) площадь осевого сечения; г) наибольшее
расстояние между точками конуса; д) высоту конуса, из
которого получен усеченный конус, и угол при его вершине.
9.11. В усеченном конусе радиусы оснований 1 и 4, а длина обра¬
зующей 5. Найдите: а) высоту конуса; б) угол наклона
образующей к основанию; в) площадь сечения, проходяще¬
го через середину высоты параллельно основаниям; г) дли¬
ну наибольшего отрезка, который помещается внутри кону¬
са, и угол его наклона к основанию.
s
Рис. 428
Рис. 429
Рис. 430
311
9.12. Угол между образующей конуса и основанием а, диаметр
основания D. Найдите: а) высоту конуса; б) образующую;
в) угол при вершине осевого сечения.
9.13 В конусе проведены два сечения, параллельные основанию.
Они делят высоту конуса на три равные части. Вычислите
отношение их площадей.
9.14. В конусе, у которого R = H= 1, проводятся сечения, парал¬
лельные основанию. Выразите площади этих сечений как
функции от ху где х — это расстояние от центра основания
до сечения (рис. 430).
9.15. Через вершину конуса проводятся сечения. Найдите пло¬
щадь наибольшего из них, если высота конуса 3, а радиус
основания 5 (рис. 431).
При решении задачи нужно: а) нарисовать несколько сечений и убедиться
в наличии максимума; б) найти площадь сечения, обозначив г расстояние
от центра основания до нижней стороны треугольника в сечении; в) возвести
площадь в квадрат, чтобы избавиться от радикалов (максимальное
значение площади и ее квадрата достигается при одном значении х)\
г) найти производную получившейся функции, приравнять ее к нулю и
решить соответствующее уравнение; д) получившийся корень подставить
в формулу для площади.
9.16. При вращении отрезка параболы получается параболоид с
радиусом основания R и высотой Н (рис. 432). Проведите
через середину высоты сечение параллельно основанию.
Найдите: а) уравнение параболы; б) радиус получившегося
в сечении круга и площадь сечения.
9.17 В параболоиде, радиус основания и высота которого равны
1, проведено сечение, параллельное основанию и удаленное
от него на расстояние х (рис. 433). Найдите зависимость
расстояния от вершины до точек границы сечения (окруж¬
ности) от х.
312
Рис. 431
Рис. 432
9.18. Какими фигурами являются сечения произвольного цилинд¬
ра плоскостями, параллельными образующей цилиндра?
9.19. Какими фигурами являются сечения произвольного конуса
плоскостями, проходящими через его вершину?
9.20. Нарисуйте цилиндры, все сечения которого плоскостями,
параллельными основанию, — квадраты.
9.21. Нарисуйте конус, все сечения которого плоскостями, парал¬
лельными основанию, — правильные треугольники.
9.22. Докажите, что тело не может быть и цилиндром и конусом
одновременно.
9.23. В основании цилиндра лежит круг. Образующая цилиндра
равна 8 и наклонена к основанию под углом 30°. Найдите
высоту цилиндра (перпендикуляр, опущенный из точки
одного основания на другое). Можно ли по этим данным
найти радиус основания? Сделайте рисунок.
9.24. В основании конуса лежит круг радиуса 3. Высота конуса
падает на одну из точек окружности и равна 8. Найдите
длину наибольшей образующей конуса. Найдите зависи¬
мость длины образующей от угла ее наклона к основанию.
Сделайте рисунок.
9.25. Радиус шара равен 5. Плоскость проходит на расстоянии 3
от центра ш&ра. Найдите радиус круга в сечении, площадь
сечения.
9.26. Шар радиуса 15 пересечен плоскостью. Радиус сечения 12.
На каком расстоянии от центра шара находится эта плос¬
кость?
9.27. Два шара радиуса 5 расположены так, что расстояние
между их центрами равно 6. Найдите радиус круга, явля¬
ющегося пересечением шаров (рис. 434) .
9.28. Две одинаковые сферы пересекаются по окружности диа¬
метра 12. Расстояние между их центрами равно 16. Найдите
радиусы сфер.
9.29. Шар радиуса 2 пересекается с другим шаром по кругу
радиуса /3”. Найдите радиус второго шара, если расстоя¬
ние между центрами шаров равно 3.
313
Рис. 433
Рис. 434
9.30. Точка А лежит на касательной к шару плоскости на рас¬
стоянии, равном 12 от точки касания. Радиус шара равен 5.
Найдите расстояние от точки А до центра шара. ;
9.31. К шару радиуса 1 проведены две касательные плоскости,
перпендикулярные между собой. Определите расстояние от
центра шара до ребра двугранного угла, образованного
плоскостями (рис. 435).
Рис. 435
9.32. Через точку на поверхности шара проведены диаметр и
сечение, образующие угол 60°. Найдите радиус шара, если
радиус сечения равен 5 (рис. 436).
9.33. Через точку вне шара проведены касательная плоскость и
плоскость, проходящая через центр шара. Угол между ними
равен 30°, а расстояние от центра шара до прямой пересе¬
чения плоскостей равно 20. Найдите радиус шара.
9.34. Футбольный мяч (/?=15см) лежит: а) у стены; б) в углу.
Уместится ли в образовавшемся зазоре шарик от настоль¬
ного тенниса (г=1,5см)?
314
Рис. 436
9.35. На плоскости лежат два шара радиусов 1 и 2 м. Они имеют
единственную общую точку. Определите:
а) на каком расстоянии друг от друга находятся общие
точки этих шаров и плоскости;
б) на какой высоте от плоскости находится их общая
точка.
9.36. Три шара (рис. 437) лежат на плоскости, и каждые два из
них имеют единственную общую точку (касаются). Назовем
эти точки Л, В, С: \АВ\=3, |ЛС|=3, |ВС|=4. Какой из
этих шаров наибольший? наименьший?
Рис. 437
9.37. В цилиндр вписан шар (он касается оснований и боковой
поверхности). Во сколько раз высота цилиндра больше его
радиуса?
9.38. В усеченный конус вписан шар. Радиус верхнего основания
конуса равен 3, радиус нижнего основания — 5. Найдите
длину образующей и высоту усеченного конуса (рис. 438).
9.39. В конус с углом 60° при вершине осевого сечения вписан
шар. Определите радиус:
а) шара, если длина образующей равна 4;
б) основания конуса, если радиус шара равен 1.
315
9.40. Рассмотрите произвольный прямой круговой конус (сами
выберите Н и R) и ответьте на вопросы: чему равна обра¬
зующая конуса? Чему равен радиус вписанного шара?
9.41. В полусферу радиуса 5 вписан цилиндр с диаметром осно¬
вания 6. Найдите высоту цилиндра (рис. 439).
Рис. 438
Рис. 439
9.42. Цилиндр радиуса R и с высотой Н (рис. 440) накрыт полу¬
сферой. Определите наименьший радиус полусферы.
9.43. В цилиндр вписан шар радиуса R. Найти радиус шара,
описанного около цилиндра.
9.44. Угол при вершине осевого сечения конуса 120°. Радиус
основания равен 3. Найдите:
а) длину образующей; б) высоту конуса; в) радиус вписан¬
ного шара; г) радиус описанного шара.
Рис. 440
9.45. Угол при вершине осевого сечения конуса равен 90°. Обра¬
зующая равна 2. Найдите радиус шара, вписанного в конус.
9.46. В шаре радиуса R находится цилиндр с наибольшим по
площади осевым сечением. Каковы размеры этого цилинд¬
ра? Обозначив х — радиус цилиндра, исследуйте с помощью
производной зависимость площади осевого сечения вписан¬
ного цилиндра от х:
9.47. В шаре радиуса 2 находится конус с наибольшим по пло¬
щади осевым сечением. Каковы размеры этого конуса?
9.48. Из всех конусов с заданной образующей L найдите радиус
того, у которого площадь осевого сечения наибольшая.
9.49. В конусе угол между образующей и основанием равен а.
Диаметр основания D. Найдите: а) радиус основания;
б) длину образующей конуса; в) высоту конуса; г) площадь
316
осевого сечения; д) угол при вершине осевого сечения;
е) радиус вписанного шара; ж) расстояние от одного из
концов диаметра основания до противоположной образую¬
щей; з) площадь сечения, проходящего через вершину и
хорду основания длины /.
9.50. В конусе угол при вершине осевого сечения равен а. Длина
образующей /. Ответьте на вопросы задачи 9.49.
9.51. В прямой треугольной призме боковое ребро равно 3. В ос¬
новании призмы лежит равносторонний треугольник ABC,
\АС\ = \АВ\ = \ВС\=4. Найдите: а) длины диагоналей боко¬
вых граней; б) угол между А'С и плоскостью основания,
между В'С и плоскостью основания; в) двугранный угол
между СА'В и ABC; г) площадь сечения СА'В.
9.52. В условии предыдущей задачи К и М — середины сторон
А'С' и А'В'. Найдите:
а) площадь сечения КМВС\
б) угол между КС и основанием;
в) угол между сечением и основанием.
9.53. В правильной пирамиде ABCD все ребра равны 2. Вычисли¬
те: а) высоту пирамиды; б) апофему; в) площадь сечения,
проходящего через боковое ребро, и высоту; г) углы между
боковыми гранями и основанием.
9.54. В пирамиде SABC: SAJ-ABC, |y4S| = 3, |ЛЯ| = |ЛС|=4,
/.ВАС=90°. Вычислите:
а) длины всех ребер;
б) площади всех граней;
в) углы боковых ребер с основанием;
г) углы боковых граней с основанием.
9.55. В правильной шестиугольной пирамиде сторона основания
равна а, боковое ребро 2а (рис. 441). Найдите: а) площадь
каждого диагонального сечения; б) угол между боковым
ребром и основанием.
9.56. Основание пирамиды — равнобедренный треугольник, у
которого основание равно 12, а боковая сторона — 10. Бо¬
ковые грани образуют с основанием двугранные углы,
равные 45°. Найдите высоту пирамиды.
317
Тис. 441
9.57. В правильной шестиугольной пирамиде SABCDEF сторона
основания равна 6, а боковое ребро — 10. Через середину
высоты проведено сечение, перпендикулярное высоте. Дока¬
жите: a) SAA-BF\ б) будет ли SA.LDE? Вычислите: а) вы¬
соту пирамиды; б) угол между SA и плоскостью основания;
в) угол при ребре АВ\ г) площадь сечения; д) угол между
ребрами SA и SE\ е) угол между плоскостями ABS и EDC.
9.58. Высота правильной четырехугольной усеченной пирамиды
равна 7. Стороны основания 10 и 2.. Найдите: а) апофему;
б) длину бокового ребра; в) угол наклона боковых ребер
к основанию; г) площадь сечения, проходящего через сере¬
дину высоты параллельно основанию.
9.59. В прямоугольном параллелепипеде ABCDA'B'C'D' в осно¬
вании лежит квадрат. Докажите, что плоскости A'C'D' и
BB'D' перпендикулярны. Найдите: а) угол между плоско¬
стью A'C'D и основанием; б) угол между прямой B'D и
основанием, между B'D и сечением DD'C С\ в) угол между
плоскостями AA'D' и DD'C'.
9.60. ABCDA'B'C'D' — куб, длина ребра которого равна 1. Най¬
дите: а) угол /-CAD\ б) угол между прямыми AD' и В'С\
в) угол между прямыми AD' и DC'\ г) угол между прямыми
АС' и DB'\ д) расстояние между прямыми BD и A'D'\
е) расстояние между прямыми СА и D'B'\ ж) расстояние
между прямыми ВС и DB'\ з) площадь сечения, проходя¬
щего через середины ребер АВ, ВВ\ В'С\ C'D\ D'D, AD.
Докажите: а) плоскости AD'B' и DC'B параллельны;
б) каждая из плоскостей AD'B' и DC'B перпендикулярна
прямой Л'С; в) плоскости AD'B' и DC'B делят диагональ
А'С куба на три равные части.
9.61. Найдите: а) длину диагонали прямоугольного параллеле¬
пипеда, ребра которого равны 3, 4 и 12; б) площадь поверх¬
ности прямоугольного параллелепипеда, диагональ которого
равна 3, а два из трех смежных ребер равны 1 и 2.
9.62. Для условия задачи 9.60 вычислите:
а) угол между B'D и основанием; б) AB'AD\ в) угол меж¬
ду диагоналями; г) угол между плоскостями A'C'D и ЛВС;
д) угол между диагональными сечениями; е) длину Л/С,
где К — середина С'С.
9.63. Приведите пример многогранника такого, что: а) из каждой
вершины его выходят три ребра; б) из каждой вершины
выходят четыре ребра; в) общее число ребер равно 100;
г) общее число ребер равно 33. Какое наименьшее число
ребер может иметь.многогранник? Известно, что некоторый
многогранник имеет 16 вершин и из каждой его вершины
выходит 5 ребер. Найдите число ребер этого многогранника.
Существует ли многогранник, у которого 23 вершины, из
каждой из которых выходит 5 ребер?
9.64. На какое наименьшее число треугольных пирамид можно
разбить пирамиду? куб?
318
9.65. Постройте сечение: а) треугольной пирамиды плоскостью
так, чтобы в сечении получился треугольник; б) треуголь¬
ной пирамиды плоскостью так, чтобы в сечении получился
четырехугольник; в) правильного тетраэдра плоскостью так,
чтобы в сечении получился ромб. Какие многоугольники
могут получиться в сечении призмы плоскостью?
9.66. Существует ли пирамида: а) треугольная, у которой две
боковые грани перпендикулярны плоскости основания;
б) треугольная, у которой все боковые грани перпендику¬
лярны плоскости основания; в) четырехугольная, у которой
две боковые грани перпендикулярны плоскости основания;
г) четырехугольная, у которой три боковые грани перпен¬
дикулярны плоскости основания; д) четырехугольная, у ко¬
торой две противоположные грани перпендикулярны плос¬
кости основания?
9.67. Докажите, что в правильном октаэдре противоположные
ребра параллельны.
9.68. Сколько граней, вершин и ребер у пирамиды: а) четырех¬
угольной; б) пятиугольной; в) стоугольной; г) п-угольной?
9.69. Сколько граней, вершин и ребер у призмы: а) треугольной;
б) четырехугольной; в) пятиугольной; г) стоугольной;
д) п-угольной?
9.70. Нарисуйте многогранники, получаемые срезанием вершин
куба: а) через точки на расстоянии трети длины ребер от
вершины; б) через середины ребер.
9.71. Решите задачу 9.70 для тетраэдра.
ю
ПОКАЗАТЕЛЬНАЯ
И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
§ 37. Степени и логарифмы
Корни
Извлечение корня — это операция, обратная операции возведения в
степень.
Корнем п-й степени из числа а называется такое число Ь, n-я степень
которого равна а : b— корень n-й степени из а Ь" = а.
Примеры
1. Так как 26 = 64, то число 2 является корнем 6-й степени
из числа 64.
2. Равенства (—З)3 = —27, (—5)4 = 625 можно прочесть так:
число —3 является кубическим корнем из —27, —5 являет¬
ся корнем четвертой степени из 625.
Если число п четно, то равенство Ьп = а возможно лишь
при а ^ О, так как любое число в четной степени положительно.
Это означает, что корней четной степени из отрицательных чисел
не существует.
Если Ьп = а, то (—Ь)п = а, так как четная степень «минус
единицы» равна «плюс единице». Это означает, что если Ь —
корень четной степени из числа а, то и (—Ь) есть корень той же
степени из числа а.
Если п нечетно, то корень n-й степени можно извлечь из лю¬
бого числа. В равенстве Ьп = а при нечетном п числа а и Ь
имеют Одинаковые знаки, поэтому корень нечетной степени из
положительного .числа положителен, а из отрицательного —
отрицателен.
При нечетном п корень п-й степени из числа а извлекается
единственным способом. Он и обозначается с помощью радикала:
Ьп = аоЬ = Уа~.
320
Можно записать: У—27 = —3, У32 = 2, ^—1 =—1,
Уо" = 0. При четном п корень n-й степени можно извлечь толь¬
ко из положительного числа, но при этом есть два корня п-и сте¬
пени из а: положительный и отрицательный. С помощью ради¬
кала четной степени обозначается положительный корень.
if (>Н if
VT6 = 2, |ЛТ = 1, /(2— /5“)* = /5~~—2, Уо~ = 0.
Итак, корней четной степени из положительного числа а су¬
ществует два: один (положительный) Уа~, а другой (отрица¬
тельный) — у^г.
Положительный корень n-й степени из положительного чис¬
ла а, т. е. V5-. называют арифметическим корнем п-й степени.
Свойства радикалов:
(УГ)--*
2. Уаб = - (Vo-)* = V?.
3. "У? = Ya ; VVT = nk/^~
Если показатель n радикала четный, то считается, что под знаком ради¬
кала стоит положительное число. Доказательство всех свойств радикалов
проводится по одной и той же схеме
Примеры
1. Уа/?=п|/я_ Vb . Вспомним, что такое n\fab. По определе¬
нию, это такое число, п-я степень которого равна числу aby
причем если п четно, то это число положительно. Проверим,
что этим свойством обладает правая часть. Возведем в сте¬
пень число п/сГ n/b~, пользуясь известным свойством сте¬
пени:
(Уа~ УГ)" = (Уа~)п (УЬ~У = ab-
При четном п каждый множитель "/а” и п/Ь~ положителен,
поэтому и п/сГпуГЬ~ положительно.
2. У Vo" = "Уа". Возведем число УУа" в степень nk, поль¬
зуясь известным свойством степени;
(УУ^Т-)1* = = (WY = а.
Полученное равенство означает, что число У является
корнем степени мй из числа а. Если число пй четно, то, по
условию, число а положительно, а тогда являются положи-
тельными числа Va и п^к/сГ
Преобразования радикалов приходится делать над выражениями, которые
содержат отрицательные числа. При этом надо соблюдать осторожность,
в частности следить за знаками перед радикалами четной степени.
Примеры
1. Выражение Уа2 имеет смысл при любом значении а, так
как под корнем стоит число а2^ 0. Однако при сокращении
показателей надо учесть знак а: если а ^ 0, то У<? =3/а_,
если же д<СО, то У? ——Уо~. В частности, У(3—я)2 =
* У(#—3) (им —уз—я).
2. Вырэдеение У^ При четном п имеет смысл при любом зна¬
чении а. При этом если 0# то Уа" =а, если же а<0,
то Уа* =5» —а. Можно использовать знак модуля и записать
(при четном п)
Уо* = \а\.
Извлечение корня /t-й степени всегда считалось трудной вы¬
числительной задачей — уже алгоритм извлечения квадратного
корня,вручную достаточно сложен и плохо запоминается. На со¬
временных микрокалькуляторах обычно есть операция извлече¬
ния квадратного корня. Корни более высокой степени вычисляют¬
ся как значения показательной функции у = ах при рациональ¬
ных значениях х.
Упражнения
1. Вычислите;
i}) У27; б) Увй ») V76-2S;
Г) Щ, a) VW; е) угу»'
2. Вцнеснте циржителн за знак корня
(буквами везде обозначены положи¬
тельные числа):
а) |/9?Р"; б) yi6a468c® ;
щ) V7&F; г) ;
д) V0,027a,5b9; е) ЩЩа^.
Степени
Наша> задача — определить степень аь при любом значении Ь.
Будём считать, что основание степени — число а> 0.
Понятие степени строится постепенно. Сначала надо вепом-
3. Внесите множитель под знак корня:
а) 2/5~; б) —; в) a3/a~; г) —%-.
V3- V?
4. Сравните числа (не проводя при¬
ближенных вычислений):
а) /2~ и УЗ~; б) 5/То и УТ";
в) УГ и у/зуГ;
г) /Г— /.Г и i/6~- /Г.
5. При каких значениях х определена
функция у— /jc2—jc4 ? При каких
значениях х справедливо тождество
— X* — —X /1 — X2 ?
нить, что такое степень с натуральным показателем, т. е. рас¬
смотреть случай, когда b — натуральное число. Запись 210 мы
понимаем как произведение десяти одинаковых множителей,
каждый из которых равен 2. В общем виде, если b = п — на¬
туральное число, запись ап означает произведение п множите¬
лей, каждый из которых равен а:
ап = аа...а.
п раз
Если b — отрицательное целое число, то его можно записать в
виде b = —п, где п — натуральное число. Тогда
a~n=if-
Если b = 0, то аь принимается равным единице:
а°=1.
Итак, мы определили степень с произвольным целым пока¬
зателем. Рассмотрим случай, когда b — рациональное число. Его
можно записать в виде дроби b = т/п, где т — целое число,
п — натуральное число. Определим степень аь с помощью корня:
ат/п =
Так, fh=y¥= У9~- (-f-f'* = j/Cff5"» V
Степень с произвольным вещественным показателем Ь опре¬
деляется следующим образом. Для числа b выбирается последо¬
вательность рациональных чисел Ьь Ь2, Ьп, задающая
приближение числа b с любой степенью точности. Строится
последовательность степеней с рациональными показателями:
сР2у ..., сРп, ... . Оказывается, эта последовательность задает
приближение некоторого числа с с любой степенью точности.
Это число с называется степенью аь.
Таким образом, мы определили степень аь положительного
основания а с любым показателем Ь.
1. Степень числа с натуральным показателем имеет смысл не только для
положительного, но и для любого основания, так как эта степень опреде¬
ляется с помощью операции умножения, а умножать можно любые числа.
Поэтому имеют смысл равенства (—З)3 = (—3)*(—3)*(—3)= — 27,
(—1),о° = 1, (-
тельным показателем может быть определена для любого числа, кроме
нуля, так как ее вычисление сводится к операциям умножения и деления.
Определение же степени с рациональным показателем требует операции
извлечения корня, которая выполнима, как правило, только для положи¬
тельных чисел. Поэтому мы с самого начала считаем основание положи¬
тельным числом.
2. Определение степени с рациональным показателем основано на понятии
корня п-й степени из числа: = Из-за того, что одно и то же
рациональное число может быть записано в виде различных дробей (на-
У = — 0й =0 и т. п. Степень с целым отрица-
11
323
2 4 6
пример, —=—=— и т.д.), может показаться, что будет различным определе¬
ние степени (a2/3=Va*", а/в = 6|/а^и т.д.). Однако, по свойству корней,пк^а™к —
= у а, поэтому на самом деле определение степени с рациональным показателем
не зависит от того, в виде какой дроби записан этот показатель.
3. Вычисление степени с иррациональным показателем делается приближенно.
Сначала мы задаем приближения к числу b с помощью рациональных чисел,
затем вычисляем степени с рациональным показателем. У нас остался невыяс¬
ненным вопрос: зная погрешность приближения числа b с помощью рациональ¬
ного числа Ьку как оценить погрешность приближения аЬк к числу аь?
Свойства степеней
1. d’'c/’2=ct'+b\
2. —=сР'~ь\
3. =
Для рациональных значений показателя эти свойства сводят¬
ся к свойствам радикалов. Докажем, например, первое свойство
для рациональных положительных показателей.
Пусть b\=Ь2==~~~. Приведем эти дроби к общему зна¬
менателю, а затем их сложим:
t т\П2 и гп2П\ , . i тхПчЛ-т^Пх
01= , 0 2= , 01+02 = •
П\П<2. ПъП\ П\1%2
Тогда
т\П2 тгП\
ct'ct2 =аПхП2 а П2Пх —п'пу‘ат'П2 п'П2-^сГ2П' —/К|П2|/дт1П2—
т I ti2 “Ь |
П|П2^/дУЯ|Д2+^гП| д Л| п2 Д&1+&2
Упражнения в) */=г/г; д) у = 3* 3;
1. Запишите с помощью степеней с v \, -*/7
дробным показателем: ^ ’ е' У /7х 7-
а) Va5^' в) |/^5 • д) 3. Запищите с помощью степеней с
* b ' дробным показателем и вычислите
с помощью микрокалькулятора
б) 1 ; Г) У&Ж; е) аЬ2Уа*Ь. <с ДВУМЯ знаками после запятой):
угт ’ о,— 1 yio
3)ViO; в)-^=; Л)1—
, 5) УТОО ; г )-L=
/г Vl25^
2. Выразите дг как степень у с дробным * ’ 7j/T2*
показателем:
а) у=х3-, 6)1/=—; 6)Vl00; г)-|=; е)
Логарифмы
Пусть числа a, ft и с связаны соотношением аь = с. Можно ска¬
зать, что число с является степенью числа а (основания) с пока¬
зателем Ь. Если числа а и с фиксированы, а нужно выразить
через них Ь, то используют понятие логарифма. Будем считать,
что в качестве основания взято положительное число а, отличное
от единицы (если а = 1, то \b = 1 при любом Ь).
Логарифмом числа с по основанию а называется такое число Ь, что аь = с,
т. е. показатель степени, в которую надо возвести основание, чтобы по¬
лучить число с:
Ь = 1од.с.
Логарифмы по основанию а= 10 используются чаще других,
и для них принято сокращенное обозначение: lg.
Равенства аь = с и b = 1од.с выражают одну и ту же связь между числа¬
ми а, b и с.
Подставляя в равенство аь=с запись числа b в виде лога¬
рифма, получаем основное логарифмическое тождество:
cl°** = c.
Подставляя в равенство b = logo с выражение в виде степени,
получаем еще одно тождество:
loga аь=Ь.
Свойства степеней и логарифмов тесно связаны между собой.
Они фактически выражают одно и то же, только один раз мы
обращаем внимание на поведение самих степеней, а другой — на
поведение показателей. Запишем свойства логарифмов, соответ¬
ствующие свойствам степеней:
ab'ab2 — a*1'1"'’2; log„(ciC2) = log„Ci + log„c2;
_^_=ab,-h. = loS°C| — ,0g«c2;
(ab)k = abk; log„c* = k\ogac\
= a /»; logo = “logaC.
Свойства степеней отражают свойства умножения чисел.
Соответствующие свойства логарифмов выводятся из свойств
степеней с помощью основного логарифмического тождества,
выражающего определение логарифма.
Выведем первое свойство:
loga (С\С2)= loga С\ + loga С2.
Логарифм произведения равен сумме логарифмов.
Обозначим loga С\== Ь1, log,, £2=62. По основному логарифми¬
ческому тождеству имеем
ct' =С\, С?2=С2.
Перемножим эти равенства: c£'d2 = c\c2. По свойству степеней,
ct,'a}2 = d,l+b\ т. е. ас2=с/}1+ь\ По определению логарифма, Ь\ +
+ /?2 = loga(ClC2), тогда
loga (CiC2)= loga С\ + loga С2,
что и требовалось доказать.
Первые три свойства показывали поведение степеней и их
показателей при умножении, делении и возведении в степень.
Извлечение корня п-й степени можно понимать как возведение в
степень 1/п.
В вычислениях в качестве основания а часто берется число
а= 10. В то же время возникает необходимость проводить вы¬
числения степеней и логарифмов с разными основаниями. Как же
связать между собой степени и логарифмы с разными основани¬
ями?
Пусть дана степень (с основанием а) с = аь. Для перехода
к новому основанию d запишем число с=аь в виде dx при неко¬
тором х:
c = ab=dx.
Прологарифмируем эти два равенства по основанию а:
loga C = b=x \oga a,
откуда
logo с
logad *
Прологарифмировав по основанию dy получим
logd с=х.
Сравнивая эти выражения, находим
logdc=-!^.
6 loga d
Это формула перехода от одного основания к другому. Таким
образом, при изменении основания значения логарифмов изменя¬
ются линейно. Коэффициент пропорциональности часто
называют модулем перехода.
Отметим простые следствия формулы перехода:
1о^а=1^Т(с=а);
2) logs* с=———~ (d=Q^y,
3) logj_JE = — loga* (fc= —1).
a
326
Упражнения
1. Вычислите логарифмы:
а) log„e, iog„l, |og„a5, log„-i-,
loga/ci, logaV^i
б) log7iy, log,/t2, !og,/f8, logVi fl.
2. Замените следующие логарифмы
логарифмами по основанию 2:
log,/2a, log8a, log,/ О, log^a, log3a.
3. Докажите тождества:
•)
6) lo gabX = .
l/logflx+l/lag**
4. Запишите число в виде степени 10:
а) 10000; 6)0,001; в) 10-Ю; г) I;
2; е) 3,2.
5. Найдите целую часть (характери¬
стику) числа lg*:
а) *=101; в) *=0,13;
б) *=6378; г) *=0,00051.
6. Прологарифмируйте выражение:
б) Л = 0,1*1+31«\
7. Найдите выражение Л по его лога¬
рифму (эту операции иногда назы¬
вают потенцированием):
а) lg/l=2lgr— Vslg(*— I):
б) Ig4=3lg3 + 2jg5-72lg4+l;
в) Ig4=2lgsin2x — '/jlgcos*;
г) lg^ = 2 + jclgx;
д) lg/4 =3 — Ig(Igx).
$38. Показательная функция
Исследование показательной функции
Локазвтельной функцией называется функция вида у = а’, где а — фикси
рованное положительное число.
При исследовании показательной функции будем считать, что
основание аф 1, так как при а=1 функция получается посто¬
янной.
Основные свойства показательной функции:
Г Область определения; множество всех вещественных чисел №.
2. Монотонность: при а > 1 функция у ~ а* возрастает, при
0 < а < 1 функция у = а* убызает.
3. Положительность: значения функции у = а* строго положи¬
тельны (при любом основании а > 0).
4. Область значений: множество всех положительных чисел, т. е.
интервал (0, + оо).
Доказательство свойств 2 и 3. Эти свойства проверя¬
ются последовательно для натуральных, целых, рациональных
показателей, а затем уже переносятся на произвольные действи¬
тельные показатели.
327
Рис. 442
Свойства показательной функции позволяют построить ее
график. Графики показательных функций при различных осно¬
ваниях а приведены на рис. 442.
Пример
Рассмотрим показательную функцию у = 2х. С ростом х
значения этой функции возрастают очень быстро. Так,
2,0« 103, 2I00« 10*° и т. д. Если лг<0, то 2х быстро прибли¬
жается к нулю: 2-,0« 0,001, 2“100« 10“30 и т.д. Это свой¬
ство экспоненты — быстро увеличиваться, с одной стороны,
и быстро приближаться к нулю — с другой, — хорошо вид¬
но на графике.
Вместе с функцией у = ах показательной функцией счи¬
тают и функцию вида у=Сах, где С — постоянная. К тако¬
му виду можно привести, например, функцию у=2х+'2,
сделав преобразование:
2*+2 = 2*-22=4 -2\
Упражнения
1. Укажите, какие из следующих пока
зательных функций возрастают, а
какие убывают:
а) у = 5ж;
б) у=С/,оУ;
в) у=2~х;
г) </=('/зГ':
д) (/ = 3—
е) </=('/
ж) о=Зх-4
з) у= —2';
и) у= 2*(7з)*.
2. Покажите, что графики функций
у=2х и у=(1/2у симметричны отно¬
сительно оси ординат.
3. По графику ответьте на следующие
вопросы:
а) Сколько решений имеет уравне
ние 2Ж=2, 2*=3, 2А=-2, 2х=0?
б) Сформулируйте общий результат
о числе решений уравнения 2x=k
в зависимости от числа k.
в) При каких х функция у=2х при¬
нимает значения, большие единицы?
большие четырех? меньше чем 1 /2?
4. Постройте на одном чертеже графи¬
ки функций у=2х, у=2х~\ у=2х+|.
Почему графики этих функций не
пересекаются? Какие общие свой¬
ства можно назвать у всех этих
функций?
328
Производная показательной функции
Возьмем показательную функцию у=ах. Вычислим сред¬
нюю скорость роста этой функции на отрезке [х\ х + Ах]:
Ау ах+&х — а* х аЛ* — 1
Ах Ах а Ах
Мы видим, что средняя скорость роста показательной функ¬
ции в точке х равна значению этой функции в точке г, умножен¬
ному на число gA^~! . Исследуем, как ведет себя эта дробь при
малых значениях Лг. Так как а°= 1, то сР* при малых значениях
Лг близко к 1. Если провести секущую на графике функции, про¬
ходящую через точки (0; 1) и (Лх; a*x), то ее угловой коэффи-
дЛ* j
циент будет равен —(рис. 443). При Лх->0 секущая при¬
ближается к касательной к графику функции в точке (0; 1). Это
означает, что приближается к произведению ах на значение
производной при х=0. Итак, для нахождения производной функ¬
ции у—ах надо знать только значение этой производной в нуле.
Обозначим его через Л, тогда
(axy=ka\
т. е. производная показательной функции пропорциональна самой
функции.
Как же найти коэффициент пропорциональности k? Мы
знаем, что он равен угловому коэффициенту касательной, прове¬
денной в точке (0; 1). Можно приближенно по графику вычис¬
лить этот коэффициент. Так, известно, что для а= 10 его значе¬
ние k « 2,3, поэтому (10х)'« 2,3-10х.
Рис. 443
Число е
Посмотрим на графики показательных функций при различных
а> 1 (рис. 444). Все они проходят через точку М (0; 1). Прове¬
дем в этой точке касательные к графикам. Чем больше основа¬
ние а, тем «круче» расположена касательная. Так, при а=2
угловой коэффициент касательной равен 0,693, а при а=10
равен 2,303. Ясно, что при непрерывном изменении а от 2 до 10
угловой коэффициент касательной в точке М непрерывно изме¬
няется и найдется такое значение а, для которого он равен 1.
Такое основание а обозначается буквой е. Число е иррациональ¬
но. Его приближенное значение таково: е « 2,718. Итак,
число е — это такое основание, при котором угловой коэффициент каса¬
тельной к графику функции у = е* в точке х = 0 равен единице, т. е.
касательная в этой точке образует с осью абсцисс угол 45° (рис. 445).
Это свойство можно сформулировать иначе. Производная
любой показательной функции пропорциональна самой этой
функции. Число е — это основание, для которого коэффициент
пропорциональности равен единице, т. е. е — это такое число,
что производная функции у = ех равна самой этой функции:
(е*)' = е\
С помощью числа е легко записать коэффициент пропорциональ¬
ности k для любого основания а. Для этого Заменим основание а
на степень основания е:ах = (eIogea)x = e(,ogea)\ Тогда
(а*)' = (е<|ок*°>')' = е(|0в'0)* logea = logea-a\
т. е. k = \ogе a.
«Существует лишь одна истина относительно каждой вещи, и кто нашел
ее, знает о ней все, что можно знать».
Р. Декарт
330
Рис. 444
Рис. 445
С помощью символа lim коэффициент k можно записать следую¬
щим образом:
и 1* 0^ — 1
k= lim — .
Дх -*■ О
Мы выяснили, что число k есть логарифм а по некоторому осно¬
ванию е. Для а = е число k = 1, тогда
г 1 !
lim —т = 1.
Лх—о А*
Это предельное соотношение часто служит определением числа е.
Пользуясь приближенными равенствами, находим ^
~ 1 « 1 =>- еЛх — 1 « \х =>- еЛ* « 1 + Л* =► е « (1 + Дх) ^
Ajc
т. е. j
е= lim (1 + Дх)Л\
А* — О
Если в качестве стандартной переменной Ах, стремящейся к
нулю, взять последовательность Ах = = 1, 2, 3, ...), то
е = lim (l + —) .
П —*■ оо \ п /
Число е играет исключительно важную роль. При нахождении
производной произвольной показательной функции мы пришли к
необходимости рассматривать логарифмы по основанию е. Эти
логарифмы получили название натуральных. Натуральные лога¬
рифмы были введены шотландским математиком Дж. Непером
в начале XVII в., фактически раньше, чем логарифмы по другим
основаниям. Натуральный логарифм обозначается In.
Теперь можно записать:
ах = ех1па, (аху = 1па-а\
При переходе от десятичных логарифмов к натуральным мож¬
но пользоваться модулем перехода:
1«*-TO“w=0-434,n*
In х = = In 10 lg jc = 2,303 Ig jc.
Упражнения
1. Вычислите производные следующих
функций:
а) I/ = е2‘; г) у= 3‘;
б) д) у=3'+';
в) у=3е2*—е*; е) i/=101-'.
2. Приведите каждую из следующих
показательных функций к виду
у=Секх и найдите после этого ее
производную:
а) у= 10х; в) i/=3-2х;
б) у= 10,-х; г) у=32x+I.
331
3. Больше или меньше единицы числа
1пЗ; In2? Вычислите приближенно
эти числа с помощью таблиц или
микрокалькулятора.
4. Из свойств функции у=ах следует,
что она строго монотонна и не
имеет экстремумов. Подтвердите этот
вывод, используя производную.
§ 39. Логарифмическая функция
Исследование логарифмической функции
Логарифмической функцией называется функция вида у = log. х, где
а — фиксированное положительное число, причем а ф 1.
Так как равенства у = \ogax и х = ау, по определению лога¬
рифма, означают одну и ту же связь между переменными хну,
то показательная и логарифмическая функции являются взаим¬
но обратными или логарифмическая функция является функцией,
обратной к показательной.
Мы знаем, как связаны между собой свойства взаимно об¬
ратных функций, поэтому можно легко получить свойства лога¬
рифмической функции из свойств показательной функции (см.
табл. 9).
Таблица 9
Свойства
Функция
у = а
у = log аХ
Область определения
IR
(0, + оо)
Область значений
-(0, + оо)
IR
Моно- \ а > 1
Возрастает
Возрастает
тонность/ 0 < а < 1
Убывает
Убывает
График логарифмической функции получается из графика
показательной функции отражением относительно прямой и = х
(рис. 446).
332
Рис. 446
Упражнения
В) у= log./,*; Г) y=log2—.
1. Укажите область определения сле¬
дующих функций:
a) y=\ogax\ б) y=logafxl;
в) y=\oga(x+\); г) у = !oga( Jf).
3. Начертите графики следующих
функций:
а) у=\пх; б) у=\п^~;
в) 1/=1п(—дс); г) (/=lnU|.
2. Определите монотонность следую¬
щих функций:
a) y=\gx\ б) у = 1пх;
Производная логарифмической функции
Докажем следующие формулы для производной:
у = In *=► у' =1;
y=\ogaX=>y'
In а х
Логарифмическая функция, по определению, является обрат¬
ной к показательной функции. Это означает, что равенства
у = In х и х = еу выполняются одновременно.
Зная производную показательной функции, легко найти про¬
изводную обратной ее функции.
Средние скорости роста функций у = 1пх и х = еу взаимно
обратны по величине. Действительно, • Все дейст¬
вия над дробями можно выполнять без всяких оговорок, так
как у и х—,возрастающие функции и их приращения Ау и Ах
не могут обратиться в нуль, если не обратится в нуль прираще¬
ние аргумента.
Так как производной функции х = еу будет та же Самая
Ах
функция х’ = еу (у— аргумент, а х — функция), то еу,
У
но у = In*, a elnjf=*, и поэтому = • Итак, произ¬
водная натурального логарифма равна т. е. (1п*)'=у . Так
1. Вычислите производные следующих . lnfx—ПГх+П
функций (до вычисления производ- ' ' А “г
ных полезно сделать преобразова- 2. Из свойств функции у—In jc ясно,
как loga* =ТО (logflx)' =-^ (Injc)
In a x
Упражнения
ния, используя свойства логариф¬
мов) :
что она возрастает и не имеет
экстремумов. Подтвердите этот вы¬
вод' с помощью производной.,
а) у= In2*;
оид v iiuiuulu,uiv пригииидиип. t
3. Постройте график функции у=х —
— In X.
б) у=\п(—х); г) у= In/Г;
333
Формулы для производной сложной и обратной функции
Выведем новые правила для вычисления производных:
Если f и g — взаимно обратные функции, то
g'W= f'(g(x)) •
Приведем краткие обоснования. Если у = /(Л), а Л = Л(г),
то y = f(h(x)) называется сложной функцией. Представим сред-
&у
нюю скорость в виде
А у А у A h
Ajc АЛ Ajc
Первую дробь можно рассматривать как среднюю ско¬
рость роста у как функции от Л, а вторую — как среднюю ско¬
рость роста А как функции от х: Переходя к пределу, получаем
у'(х) = y'(h) h'(x) = y'(h(x)) h'(x).
Для вывода второй формулы повторим рассуждения, сделан¬
ные при выводе производной логарифма.
Если функции fug — взаимно обратные, то соотношения
y = g(x) и x = f(y) выполняются одновременно. Между сред¬
ними скоростями роста функций f и g простая связь: ^ =
1 Отсюда ясно, что g'(x) = ■?;!- . Следует понимать,
Ах/А у * ’ S ' f'(У)
что аргументы в правой и левой частях этого равенства разные,
поэтому надо подставить вместо у его значение у = g(x):
g' (х) = ! .
* f'(gW)
Проведенное рассуждение имеет наглядный геометрический
смысл. Пусть даны две взаимно обратные функции у = g(x) и
y = f(х). (Обозначим теперь у обеих функций аргумент одной
буквой х.)
Их графики (в обычной системе координат, когда по оси абс¬
цисс откладывается значение аргумента обеих функций) сим¬
метричны друг другу относительно биссектрисы I первого и
третьего координатных углов (рис. 447).
Возьмем какую-нибудь точку х = а и вычислим значение
одной из функций в этой точке: f(a) = b. Тогда, по определению
обратной функции, имеем g(b) = а.
Точки (а, f(a)) = (а, Ь) и (fr, g(b)) = (ft, а) симметричны друг
другу относительно указанной прямой /. Так как кривые сим¬
метричны, то и касательные к ним симметричны относительно
334
Рис. 447
Рис. 448
прямой / (рис. 448). Осталось выяснить, как связаны между
собой угловые коэффициенты прямых, симметричных относи¬
тельно прямой /.
Из симметрии ясно, что угол одной из этих прямых с осью X
равен углу другой прямой с осью у. Если первая прямая образует
с осью х угол а, то ее угловой коэффициент равен Л, = tga*
тогда вторая прямая имеет угловой коэффициент k2 —
мых, симметричных относительно прямой /, взаимно обратны:
Переходя к производным и вспоминая, что угловой коэффи¬
циент касательной является значением производной, получаем,
что значения производных взаимно обратных функций в соот¬
ветствующих точках взаимно обратны:
Напомним еще раз, что b — f(a) и а = g(b).
В проведенных выше рассуждениях предполагалось, что k Ф О, т. е. ка¬
сательные к кривым не параллельны осям координат.
Примеры
1. у = е^7, у' = е^ -^i=-. Здесь y = eh, h = V*~-
2. у = sine*, у' = (cose*)ex. Здесь у — sin A, h — е*.
3. у = sin (sinдг), у' = (cos(sinjt))cosx. Здесь у = sin/», Л =
4. у = (2х - З)5, у' = 5(2* - З)4 • 2. Здесь у = Л5, h = 2x-3.
5. у = f(x) = х3. Обратной функцией будет функция у =
— ё(х) == VF. Найдем производную функции g(*). Возьмем
— a
)=ctga = -jp. Таким образом, угловые коэффициенты пря-
= Sin JC.
335
точку х = х0. Обозначим g(x0) через у0. Тогда f(y0) = дс0,
т. е. yl = Хд. Тогда
а'( х Л = 1 — 1 — 1
g(XoJ гм Wo зу*г ’
т.е. (V57 = ^
в. t/ = f(x) = smx, X 6 [—j-.y ]. Обратной функцией будет
у = g(х) = arcsin х.
Найдем производную арксинуса:
а'(х)= - 1 -= 1 1
f'(g(x)) cos arcsin* д/1 — jc2 ‘
Итак,
(arcsinjc)' = —=L==.
'У/Х — xr
Аналогично вычисляются производные функций у =
= arccosx, у = arctgx:
(arccos xf = — ^=L= ; (arctgAr)' = •
Упражнения в) у = ln(ex + 1);
Вычислите производные: г) i/ = (ех — In jc)
а) |/= /1пдс ; д) i/=arctg/F;
б) i/=sin**; е) 1/=1п1п*.
1/,
§ 40. Показательные н логарифмические
уравнения и неравенства
Простейшие уравнения
Уравнение ах = Ь при Ь > 0 имеет один корень и не имеет кор¬
ней, если 6^0. Корень уравнения ах = Ь можно записать с
помощью логарифмов по разным основаниям, например
X=\ogab ИЛИ X = — .
6 logea
Часто встречаются уравнения, полученные приравниванием
степеней с одинаковым основанием, например 2х = 22х~1. В этом
случае приравнивают показатели степеней, т. е. переходят к
уравнению х = 2х — 1. Это то же самое, что логарифмирова-
ние (в нашем примере — по основанию 2), но оно делается без
использования знака логарифма. Итак, от уравнения вида
d{x) = a*(r) мы переходим к уравнению f(x) = g(x).
Во многих случаях приходится применять свойства степе¬
ней, чтобы привести обе части уравнения к степени с одним и
тем же основанием.
Примеры
1. 2х=\о2х = 2°ох = 0.
2. 2х = 8 о 2х = 23 о л; = 3.
3. 9х = -о- 32х = З-3 -о- 2* = — 3 о- х = —.
4. 3.4'_2.3’-~£ = 4^(4f = 4~2,= l,,=.'..
5. 2.5* = 3*+,^2-5' = 3-3*^(|-)X = A^jclg|- =
2 5 Ig5 - Ig3
g 3
Из примера 5 видно, что если исходное уравнение не удается
привести к равенству одинаковых степеней с «хорошими» показа¬
телями, то его лучше сразу логарифмировать. Если требуется
дать числовой ответ, то удобнее применять в качестве основа¬
ния число 10 или число е и использовать таблицы или калькуля¬
тор. Тогда
2.5х = Зх+1 о In 2 + л; In 5 = (jc + 1) In 3 о
о jc(ln5 — 1пЗ) = 1пЗ — \п2 о х = lnf ~ 1п^ .
4 ' 1п5 — In 3
Решение уравнения типа logaJC = Ь находится операцией, об¬
ратной логарифмированию: х = аь.
Примеры:
1. log2х = 0, х = 2°/х = 1.
2. log3jc = 1, х = 3.
log,/2х = — 1, х= (у)-1 =2.
4. log8x = у, x = 81/3, х = 2.
logi/з* =-±^х= (1 У'2 = 3|/2 = УЗ".
В заключение обратим внимание на то, что происходит с
множеством корней уравнения при логарифмировании и возведе¬
нии в степень.
Если в уравнении ах = Ь основание аф 1, а > 0, b > 0, то
уравнение имеет ровно один корень, так как показательная
337
функция вследствие монотонности принимает каждое свое зна¬
чение ровно один раз. Поэтому при логарифмировании нужно
внимательно следить за тем, чтобы основание было отлично от
единицы и чтобы обе части уравнения были положительны. При
Ь ^ 0 уравнение ах = Ь корней не имеет.
При возведении в степень ситуация аналогична, уравнение
logах = Ь имеет ровно один корень, но так как loga* имеет
смысл только при х > 0, то при возведении в степень более
сложных выражений нужно следить за тем, чтобы под знаком
логарифма были положительные числа. Так, переходя от равенст¬
ва lg(jc — 5) = lg (3 — jc) к равенству jc — 5 = 3 — jc, т. e. x = 4,
мы получаем значение jc, при котором lg (3 — х) не существует,
поэтому исходное уравнение корней не имеет.
Упражнения
Решите уравнения:
а) 3х = 81;
«» (т)'=*
в) 5'-"= 125;
* г'Н-кГ-
Простейшие неравенства
Простейшими показательными неравенствами можно считать не¬
равенства вида а* < Ь или ах > Ь. Запись их решений зависит
от того, будет ли основание а больше или меньше единицы. Если
а> 1, то решением неравенства ах <Ь являются все числа
х < loga6, а при 0 < а < 1 — jc> logab.
Указанное правило является следствием монотонности пока¬
зательной и логарифмической функции: при jc = loga6 левая
часть равна правой; при всех jc, меньших logab, выполняется
неравенство одного знака, а при всех х, больших logab> — про¬
тивоположное.
Примеры
1. 2х < 1 ^ jc < 0.
2.
3- (т)*>4^(тУ>(т)~2^*<-2-
4. 5* < 3 • 2* о- (у У < 3 лс < logs/г 3.
Итак, при решении простейших показательных неравенств
надо пытаться получить неравенство, в обеих частях которого
д) 3х = 4;
е)
ж) \gx=— 3;
з) lg(2jt+l)=l;
и) lg(JC-l)=lg(5*-7);
к) log3(x2—х+1)=0;
л) log2(3x+l)=2;
м) log2(3x+l)=2.
стояли бы степени с одинаковыми основаниями. Тогда это не¬
равенство заменяется неравенством между показателями сте¬
пеней. Если это не удается сделать, не вводя сложных показа¬
телей, то можно логарифмировать обе части неравенства, при¬
чем лучше использовать одно из оснований (10 или е). Так, при
решении примера 4 можно поступать следующим образом:
5* < 3• 2х о х lg5 < lg3 + Jt \g2 о x (lg5 - lg2) < lg3 ^
lg3
о x <C
Ig5 — Ig2
(заметим, что число lg5 — lg2 положительное).
Неравенство вида logajc < Ь решается так: если a > 1, то
решением будут числа 0<х <аь, если же 0<a< 1, то чис¬
ла * > а6.
Как и ранее, обратим внимание на то, что происходит с не¬
равенством при его логарифмировании и обратной операции.
Пусть для определенности основание а > 1. Неравенства ах < b
и jc < logab равносильны. Однако следует иметь в виду, что
второе неравенство имеет смысл лишь при Ь > 0. Поэтому если
встречаются неравенства вида ах < Ь при 6^0, то их нельзя
логарифмировать. Решением неравенства ах>Ь при Ь^О бу¬
дут все действительные числа, а неравенство ах <Z b при b ^ 0
решений не имеет.
Аналогично, освобождаясь от логарифма в обеих частях
при решении неравенств, следует помнить, что под знаком лога¬
рифма должны стоять положительные числа. Так, решая не¬
равенство log2(jc — 3) < 2, нельзя записать только х — 3 < 22,
нужно добавить условие х — 3 > 0. Это существенно влияет на
окончательный результат: решениями неравенства будут числа
3 < х < 7, т. е. промежуток (3, 7), но не х < 7.
Упражнения е) 5х* <625;
Решите неравенства: ж) lgx^>l;
а) Зх>1; з) lgr<0;
_1_. и) log2(x+3)>3;
< 5 ’ к) log2(3—Jt)< 1;
в) 2Х<3Х; л) log2(jt+lKlog2(3jt-5);
г) 7,-х>49; м) log2jc>log4(JC— 1).
Д) 4х >5;
Введение новой неизвестной
Многие показательные уравнения и неравенства сводятся к
обычным алгебраическим с помощью введения новой неизвест¬
ной. Для того чтобы догадаться до нужной замены, нужно
внимательно посмотреть на все степени, входящие в уравнение.
339
Примеры
1. 3-4* — 2*+3 + 8 = 22х+| — (у)-'”*
В уравнение входят такие степени: 4х, 2*+3, 22jf+1,
(1 \~1 ~х
— \ . Все их можно представить как степени 2: 4х =
= 22\ (у) =2Jf+1. Постоянные слагаемые в показате¬
лях степеней играют роль коэффициентов, т. е. по свойствам
степеней имеем:
22*+1 = 22*• 2 = 2• 22\ 2*+3 = 23• 2х = 8• 2х, 2х+1 = 2-2х.
Теперь видно, что у основания 2 имеются показатели х и 2х.
Если обозначить 2х = у, то 22х = (2х)2 = у2. Поэтому, сде¬
лав указанную замену, получим квадратное уравнение отно¬
сительно у:
Зу2 — 8у + 8 = 2у2 - 2уо у2 - 6у + 8 = О,
откуда у\ =4, у2 = 2. Возвращаясь к первоначальной не¬
известной jc, получаем простейшие уравнения 2х = 4 и
2х = 2, откуда х\ = 2, лгг = 1 -
* Если а* = у, то а2х = у2, а~х = -Jp Аналогичные замены производятся и
У
при решении логарифмических уравнений. Например, в уравнении
——^ 1- -—г—; =1 полезна замена: Igjc — у. Тогда алгебраиче-
5 — Igx 1 Igjc
1 . 2
ское уравнение — 1- -у—j-—= 1 сводится к квадратному относи¬
тельно у. Иногда приходится делать преобразования логарифмов, приво¬
дя их к одному основанию.
2- log3x log9JC log27x log8, x = 2/з-
Перейдем к основанию 3, заменяя log9x = у log3*,
log27jc = у log3JC, log8jjc = -^- log3*, а затем уже* полагая
\og3x = y, получим у'Т *Т ^ = У ’ откУда У4=16,
у = ±2. Далее log3* = 2, х = 9 и log3* = — 2, х=\/9.
Ответ: Х\ = 9, Х2 = 1/9.
Логарифмы в качестве новых неизвестных появляются при
логарифмировании выражений, имеющих неизвестную как в
основании, так и в показателе степени.
340
Пример
Решите уравнение №х~2 = 1000.
Логарифмируя, получаем IgOt16*”2) = lg 1000, (lgjt—2)lgjt=
= 3. Делая замену lgjc = у, имеем квадратное уравне¬
ние у2 — 2у — 3 = 0, откуда у\ = 3, у2 = — 1. Находим х:
lgjc = 3, х = 1000, lg-С = —1, X =
Ответ: Х\ = 1000, х2 = 1/10.
Упражнения г) (log2*)2 + 31og2Jt = 4;
1. Решите уравнения: д) (lg 10x)lg(100x) = 6;
а) З2-—2-3^=3; е) 1024.
б) 2X+I-J-2_X=3; 1)е!11ите неравенства:
р) 4х+6х=2-9*; а) 32х—2*3*<3;
б) (10g2JC)9 + 310g2JC>4.
Использование свойства монотонности функций при решении
показательных уравнений
Показательная функция монотонна: либо убывает, либо возрастает.
Это позволяет определить число корней уравнений, а
иногда и найти их значения.
Примеры
1. Решить уравнение 22х = 5 — х.
В левой части уравнения имеем возрастающую функцию,
а в правой — убывающую (рис. 449). Следовательно, урав¬
нение не может иметь более одного корня. Один корень
можно угадать: х— 1. Это число после проверки и оказы¬
вается окончательным ответом.
2. Решить уравнение 4х — 3х = 1.
Одно решение х = 1 легко найти подбором. Докажем,
что других корней нет. Перепишем уравнение так: 4х =
= 3х + 1 ^ 1 = 0-) В правой части последнего
уравнения сумма убывающих функций. Следовательно, зна¬
чение у = 1 эта сумма может принять только один раз.
О т в е т х = 1.
3. Сколько решений имеет уравнение ех = ах в зависимости
от параметра а (рис. 450)?
Изобразим графики функций у = ех и у = ах. При а < 0
графики имеют одну точку пересечения. При а > 0 графики
могут не пересекаться, касаться друг^руга или пересекать¬
ся в двух точках. Граничным значением параметра а, при
котором происходит разделение основных случаев (две точ¬
ки пересечения или ни одной), является значение а, при ко¬
тором прямая у = ах будет касательной к графику функ-
341
ции у = е* в некоторой точке. Найдем это значение а.
Пусть касание произошло в точке Jto, тогда производная
функции у = ех в этой точке равна а = (е*)' = е*, поэтому
получаем уравнение ех° = а, т. е. Jto = In а. Точка с абсцис¬
сой jt0 = In а должна лежать как на графике функции
у = ех, так и на прямой у = ах. Тогда е*° = ajco, т. е. а =
= a,na. Так как аФ 0, то lna =1 и а = е.
Ответ: при а С 0 — один корень, при а > е — два
корня, при а = е — один корень, при 0<а<е корней
нет.
Упражнения
Решите уравнения:
а) 5х = 27-х;
б) 2Х+7*=32;
в) *3+2* = 3;
г) 22'-3'= 1;
д) 2“'= * + 6.
Задачи и вопросы
10.1. Упростите:
а) a5a7a12;
б) a-2a3a-5;
в)
г) b\[bW V*; 4 V3
10.2. Запишите в виде степени числа два следующее число:
д) 64-2Л/*.2~,3/г-Ь
а) S;
б) 1024;
342
Рис. 449
Рис. 450
10.3. Вычислите:
а) log327;
б) log3-J-;
в) log9-^-;
г) log2 д/2;
д) i°g2^2-;
е) logs5V5;
10.4. Вычислите:
a) 2log23;
10.5. Вычислите:
а) log62 + log63;
б) log62 — log6 j;
10.6 Вычислите:
a) logs 12 + log'/83;
6) 4log23; в) 2log<3;
ж) logV22V2;
з) logty2 4;
и) Vl25-
г) 27logv3V4.
6)
log932 .
log94 ’
B) log'/53 + log'/55;
r) log1/^312 - log'/V34.
д) log349 + log751og2527;
log35
е) 6 ‘+'0832 ;
log37
в) ,l0^52r7- ;
IOg25 л/3
ж) 25 logV5 5
г) log451og561og671og78;
10.7 Найдите:
а) log89, если log12 18 = a;
б) log9 15, если logfy45 25 = a.
10.8 Выясните, какое из чисел больи^
3\ bgz 18 logs 9
log36 2 log72 2 '
а) V-£- ИЛИ лДй Г> (т)'/б ИЛИ (f),/s;
б) V0.44 или
в) V3 или У(5; е) 23""’ или З2
10.9. Постройте графики следующих функций:
д) 1714 или 31";
,150
а) y=(-LY- в) у = 2ех; д) у = Зе х;
г) у = —5ех; е) у = е3х.
б) у = е
10.10. Что больше:
а) log32 или 0;
б) logi/53 или 0;
в) logi/s3 или 0;
г) log у3у- или 0;
343
д) log34 или 1; л) logy53 или —1;
е) logi/j-^-или 1; м) log>/53 или logy, 5;
ж) log23 или log25; н) loge2 или logs2;
з) log2 или log2-g-; о) logy73 или logy,3;
и) logy37 или log'/310; п) log32 или
к) |об'/.1-|_или Р) log27 или log38?
10.11. Вычислите производную:
а) у = 2е*\ г) у = х?е л; ж) у = е~х cos*
б) у = ех -+- е”*; д) t^e'sinx; з) 1/ = 5*+|.
в) у = хех\ е) у = х/ех;
10.12. Исследуйте функцию и постройте ее график:
\ е' + е-' ,. г л ч х
а) У = —2 : б) У = хе ; в) у = ех — х.
10.13. Найдите наибольшее и наименьшее значения функции:
а) у = 2х, х е [—1; 1]; в) у = х + ех, х «= [— 1, 1];
б) у = 3~х, х е [0, 2]; г) у — e'sinx, х е [0, я].
10.14. Найдите области определения функций:
а) У — log2(5 — 2х)\ в) у = log2(9 — х2);
б) У = log2(3 — д:) + г) у = lnlnx.
+ log2(A: + 3);
10.15. Вычислите производную:
а) у = In2лг; в) у = д) у = In5л:;
IV tv COSJC 7 *
б) t/ = jclnjc; г) у = ех\пх; е) у = \п-^[х.
10.16. Исследуйте функцию и постройте ее график:
а) у = Зх б) у — ех 2х.
10.17. Найдите наибольшее и наименьшее значения функции:
а) у = 1пдс, в) у = х — In дс,
* е [f. .]; * <= [f. e}
б) у = 31gjc + 2, г) у = 2ЛС2 — lnx,
дс <= [1, 100]; * e= [-p l].
10.18. Вычислите производную:
а) г/ = 3 sin Зле; ж) г/ = sinjc2; н) у = е х -,
б) у = cosx; з) y = (sinjt)2; о) у = sin(3x + а):
в) u = te—- и) и = tg—• п) У = &2*'
У ® 5 ’ ’ У g X ' р) y = ecos2.t;
г) у = е~х/2\ к) у = е3х+2; е) у = In lnx;
п.) у = 22а; л) y = lncosjc; т) у = ее\
е) у = \nkx\ м) t/ = cos In л:;
10.19. Найдите область значений функции:
а) у = esinx; д) у =
1 + е* ’
б) у = е_со*Л; е) у = хъ~х (х ^ 0);
£* I g'
в) у = In sin jc; ж) у — —^ ;
2
г) у = e~xsin* (х ^ 0); з) у = е~х .
10.20. Постройте график функции:
а) у = е~х , в) # = exsinx; д) «/=|1пл:|;
б) у = хе~'\ г) у = е~х cosx, е) у = ем.
10:21. Решите уравнения:
а)
2х = 4;
е)
5х = 1;
Л)
7х = 72~х ■
б)
2х = 16;
ж)
3х - 3 = 0;
м)
25х = 53_х;
в)
3х = - 1;
з)
32х = 81;
Н)
2х.Зх+| =81;
г)
2х = 3;
и)
23х = 5;
О)
Зх-52х_3 = 45;
Д)
О
II
со
к)
у»-5,+ 8 =9;
п)
2Х-3Х~ 1 *52х = 3 -104
10.22. Решите уравнения:
а) 2х + 2Х+1 + 2Х+2 + г) З2* —2-3* = 3;
+ 2Х+3 = 30; у + з- =
б) 7.5х 4 90 = 5Х+2; } У - 3“х
в) 4Х+3 4- 22х+2 = 51; е) 2-Зх+| - б-Э^2 = 81.
10.23. Решите уравнения:
3* = Зх+2 - 4я; г) 4х + 6х = 2-9*;
д) 2-4* - 5-6х + 3-9* = 0;
е) 4х-52х+' = 6- 10х.
в) 18 • 4х + 2 • 9х =
= 36-4Х+1 - З2х+3;
345
10.24. Решите уравнения:
а) log2* = 3;
б) log,3 = 2;
в) lgx = 0;
г) log,/2(2x — 3) = —2;
10.25. Решите уравнения:
a) log2 х — 31og3 ж+ 2 = 0;
1 . I
д) log*3 = 2;
е) log* 5 = 0;
ж) loge-,* = 2;
з) log7log3log2* = 0.
6)
l;
3 — lg дс 1 H- Ig jc
в) logl x + log3 x2 = 8;
r) lg3jt2 = 81gjt;
Д) log2 X log4 x logg x\ogl6X= 2/з;
е) log2 x-|-logy2 x-f-log'/j x=6;
o
ж) log3, —+ log§*= 1.
10.26. Решите неравенство:
а) T > 1;
б) 2*>-b
в) 3* > 0;
> 9;
3 — jc
* Ш*
< 3;
*) (f)
е) (f) < 4;
ж) 32jr_1 — Э*-' > 2;
10.27. Решите неравенство:
а) lgx> 1;
б) lgx < 2;
в) log2x < — 1;
r) logo,5* > 2;
д) lg(l — x) > 2;
е) In jc2 < 1;
ж) log2(2* — 3) < 3;
з) logo.sC* + 5) < —2;
и) \gx + lg(x — 3)<1;
к) (log2*)2 < 4;
л) lg(2jc + 3) < lg(* — 1)
m) 21g(jc — 2)> lg(x -|- 4).
10.28. Решите уравнение, используя графики:
а) 5х = 7 - 2х; в) 32(-±-)* = х3;
г) 2 = 1 + \gx.
346
10.29. При радиоактивном распаде вещества через t мин от т мг
осталось п мг. Найдите его период полураспада, т. е. через
сколько минут останется 0,5 мг вещества.
10.30. К началу радиоактивного распада имели 1 г полония-218.
Через сколько минут останется 0,125 г полония, если его
период полураспада 3 мин?
10.31. Период полураспада вещества равен 1 ч. Через сколько
часов его масса уменьшится в 10 раз? Вычислите, какая
доля вещества останется через 1000 лет, если период его
полураспада 1550 лет.
11
ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
§41. Определение интеграла
Задача интегрирования
Математика изучает различные связи между величинами. Важ¬
нейшие примеры таких связей дает механическое движение.
Мы уже много раз обращались к примеру движения материаль¬
ной точки на оси. Между положением (координатой) точки и ее
скоростью есть известная связь, лежащая в основе математиче¬
ского анализа: скорость является производной от координаты
по времени. Операция нахождения производной называется диф¬
ференцированием. Обратная задача — нахождение положения
точки по ее скорости — решается с помощью другой математи¬
ческой операции — интегрирования.
Мы знаем много пар величин, которые связаны между со¬
бой так же, как положение точки и ее скорость. Нахождение
одной из этих величин, если известна другая, сводится к опера¬
ции дифференцирования. Так, линейная плотность тонкого
стержня есть производная его массы по длине, мощность есть
производная работы по времени, сила тока есть производная
заряда по времени и т. д. С помощью обратной операции, интег¬
рирования, мы научимся вычислять массу по заданной плот¬
ности, работу по известной мощности, заряд по заданной силе
тока и т. д.
Прежде чем учиться вычислять интегралы, рассмотрим
их геометрический смысл. Начнем по-прежнему с задачи о меха¬
ническом движении. Пусть точка движется с постоянной ско¬
ростью v = Vo. Графиком скорости в системе координат (/; v)
будет прямая v = v0, параллельная оси времени t. Если считать,
что в начальный момент времени / = О точка находилась в на¬
чале координат, то ее положение х в момент времени t запишется
формулой х = vt. Величина vt представляет собой площадь пря¬
моугольника, ограниченного графиком скорости, осью абсцисс
и двумя вертикальными прямыми, т. е. путь (положение точки)
можно вычислить как площадь под графиком скорости. Анало¬
348
гичная связь между величинами сохраняется и при движении
точки с непостоянной скоростью. Так, мы знаем, что в случае
движения с ускорением а и начальной скоростью vo = 0 скорость
изменяется по закону v = а/, а положение точки (считая, что она
находилась при / = О в начале координат) —по закону х =
= -^-. График скорости — прямая, а площадь под ней вычис-
. с at-1 at2
ляется по формуле площади треугольника: S = —— = -^—,
т. е., как и прежде, путь можно найти, как площадь под графи¬
ком скорости.
Таким образом, задача интегрирования тесно связана с за¬
дачей вычисления площади.
Геометрический смысл интеграла
Интеграл — это площадь.
Способ вычисления площади, о котором пойдет речь в этой
главе, уходит корнями в глубокую древность. Так, в III в. до н. э.
великий Архимед вычислил площадь параболического сегмента
с помощью изобретенного им «метода исчерпывания», который
через две тысячи лет преобразовался в метод интегрирования,
применяемый к вычислению многих других величин.
Метод интегрирования для вычисления площади плоской фи¬
гуры требует, чтобы граница этой фигуры была задана аналити¬
чески, т. е. чтобы на плоскости была введена система координат,
а граница была задана уравнением, связывающим координаты
ее точек. Простейшими фигурами такого рода являются криво¬
линейные трапеции.
Пусть на координатной плоскости дан график неотрицательной функции f,
заданной на отрезке [а, Ь]. Криволинейной трапецией называется фигура,
ограниченная графиком функции f, прямыми х = а и х = b и осью
абсцисс (рис. 451).
«Сближение теории с практикой дает самые благотворные результаты,
и не одна только практика от этого выигрывает, сами науки развиваются
под влиянием ее, она открывает им новые предметы ддя исследования,
или новые стороны в предметах давно известных.»
П. Л. Чебышев
Чебышев Пафнутий Львович (1821 — 1894 г.г.) — русский математик,
основатель Петербургской математической школы. Создал современную
теорию приближений, получил глубокие результаты в теории чисел и
теории вероятностей. Чебышев придавал очень большое значение
прикладным задачам и занимался теорией механизмов.
349
Рис. 451
Можно образовать криволинейные трапеции с помощью раз¬
личных известных вам функций. Некоторые примеры представле¬
ны на рис. 452, а, б, в.
Рис. 452
Криволинейную трапецию, построенную с помощью графика
неотрицательной функции fy будем сокращенно называть под-
графиком функции f. Определим интеграл.
Пусть дана неотрицательная функция f, определенная на конечном от¬
резке [а, Ь]. Интегралом от функции f называется площадь ее под-
графика.
Итак, интеграл — это площадь. Если мы научимся вычислять
площади, то сумеем вычислить и интегралы, а значит, и многие
физические величины.
Прямое вычисление площадей различных фигур (интегралов
от некоторых функций) провел еще Архимед. Однако лишь
в XVII в. Ньютону и Лейбницу удалось открыть общий способ
вычисления интегралов.
Интегральные суммы
Метод исчерпывания Архимеда хотя и не дал общего способа вы¬
числения площади, однако сыграл очень большую роль в матема¬
350
тике, так как с его помощью удалось объединить самые разные
задачи — вычисление площади, объема, массы, работы, давле¬
ния, электрического заряда, светового потока и многие, многие
другие.
Проиллюстрируем этот метод на простом примере. Предполо¬
жим, что нам надо вычислить объем лимона. Он имеет непра¬
вильную форму, и применить какую-либо известную формулу
нельзя. С помощью взвешивания найти объем также трудно,
так как плотность лимона в разных частях его разная. Поступим
следующим образом. Нарежем лимон на тонкие дольки. Каждую
дольку приближенно можно считать цилиндриком, в основании
его — круг, радиус которого можно измерить. Объем такого ци¬
линдра вычислить легко по готовой формуле. Сложив объемы
маленьких цилиндров, мы получим приближенное значение объе¬
ма всего лимона. Приближение будет тем точнее, чем на более
тонкие части мы сможем нарезать лимон.
Объясним более точно эту процедуру для вычисления площади
подграфика. Рассмотрим подграфик функции /, заданной на от¬
резке [а, Ь\. Разобьем этот отрезок на несколько частей. Пло¬
щадь всего подграфика разобьется на сумму площадей более
мелких криволинейных трапеций. Каждую такую трапецию мож¬
но приближенно считать прямоугольником. Сумма площадей этих
прямоугольников дает приближенное представление о всей пло¬
щади подграфика. Чем мельче, мы разобьем отрезок [а, 6], тем
точнее вычислим площадь.
Запишем проведенное рассуждение в виде формул.
Разделим отрезок [а, Ь] на п частей х0 = a, xh ... , xn = b.
Длину /-го отрезка обозначим через Ах, = xt — x,_i. Составим
сумму: Sn = f(x\)Ax! + ... + f(xn)Axn. Геометрически эта сумма
представляет собой площадь ступенчатой фигуры, заштрихован¬
ной на рис. 453.
Суммы вида Sn = f(x\)Ах\ + ...+ f(xn)Axn называются ин¬
тегральными суммами для функции /.
Интегральные суммы дают приближенное значение площади.
Рис. 453
Точное значение получается при помощи предельного перехода.
Представим себе, что мы измельчаем разбиение отрезка [а, Ь]
так, что длины всех маленьких отрезков стремятся к нулю (т. е.
Ах,->-0). Тогда площадь ступенчатой фигуры будет приближать¬
ся к площади подграфика S. Можно сказать, что площадь под-
графика равна пределу интегральных сумм, т. е.
S = limS„.
Интеграл можно определить так.
Интеграл — это предел интегральных сумм.
С помощью интегральных сумм можно приближенно вычис¬
лять самые различные величины.
Примеры
1. Объем лимона. Обозначим АЛ, толщину i-й дольки (не обя¬
зательно резать лимон на дольки одинаковой толщины),
гi (i = 1, ..., п — число долек) — ее радиус. Объем лимона
приближенно представится интегральной суммой:
S„ = яг? ДА, + ... + яГпАА,,.
2. Работа. Предположим, что на точку, движущуюся по оси х\
действует некоторая сила F, направленная по той же оси.
Если сила F постоянна, то работа равна Fsy где 5 — путь,
пройденный точкой. Предположим, что F изменяется от точ¬
ки к точке и ее значение в каждой точке некоторого проме¬
жутка [а, Ь] равно F(x). Как найти работу А по перемеще¬
нию точки из а в Ь?
Разобьем отрезок [а, Ь\ на п отрезков. Будем приближенно
считать, что на каждом малом отрезке сила постоянна. Если
/-Й отрезок образован точками i, х, то в качестве силы
можно взять значение функции F в одной из точек этого отрезка,
например в xt. Работа на i-м отрезке пути приближенно предста¬
вится как произведение F(xi)Axi, а на всем отрезке — интеграль¬
ной суммой:
Ап = F(x{) Ах, + ... + F(xn)Axn.
Точное значение работы А получим, переходя к пределу:
А = lim Ап.
Вычислять интегралы через пределы соответствующих интег¬
ральных сумм очень трудно. Архимед сумел найти некоторые
площади, объемы фактически через пределы интегральных сумм
для квадратичных функций. Однако этот результат стоял особня¬
ком в математике до конца XVII в., когда было выяснено, что
нахождение площади является обратной задачей к задаче на¬
хождения скорости.
Скорость роста площади
Рассмотрим неотрицательную функцию f, заданную на конечном
отрезке [а, Ь]. Представим себе «переменную» криволинейную
трапецию, полученную следующим образом: закрепим левую
стенку х■= а, а правую начнем перемещать вдоль оси абсцисс.
Такая трапеция изображена на рис. 454. Ее можно считать под-
графиком функции fy область определения которой ограничена
отрезком [а, х].
Обозначая площадь переменной трапеции, т. е. площадь под-
графика функции /, заданной на отрезке [а, х], через S(jc),
получаем новую функцию S (переменная площадь): S = S,(jc).
Перечислим свойства функции S. Она определена для всех
*е[а, Ь], ее значение при х = а равно нулю (трапеция вы¬
рождается в отрезок, и ее площадь равна нулю), эта функция
возрастает, и при х = Ь ее значение равно площади всего под-
графика, т. е. интегралу от функции f.
Найдем скорость роста функции S и результат запишем в
виде теоремы.
Теорема о скорости роста площади
Пусть f — неотрицательная функция, S — переменная площадь ее под-
графика, тогда производная функции S равна функции f, т. е. S (x) = f(x).
Теорема утверждает, что производная переменной площади
подграфика функции f равна самой функции f. Для доказатель¬
ства теоремы поступим так, как всегда поступают при вычисле¬
нии производной.
Зафиксируем значение аргумента х и придадим аргументу
приращение Ajc. Вычислим приращение функции: AS =
= S(jc + Ajc) — S(jc). По рис. 455 видно, что приращение площади
есть площадь подграфика функции /, определенной на отрезке
[х, х + Ajc).
Если Ajc достаточно мало, то площадь криволинейной трапе¬
ции мало отличается от площади прямоугольника со сторонами
/(jc) и Ajc, т. е. можно записать приближенное равенство AS «
12—1681
353
Рис. 454
Рис. 455
«/(jc)-Ajc. Следовательно, « f(x), т. e. производная функ¬
ции S равна функции /, что и утверждалось в теореме.
В доказательстве теоремы мы использовали такую идею: если отрезок
[jc, х-\-Ах] достаточно мал, то площадь подграфика функции f на этом
отрезке мало отличается от произведения f{jc)Ajc. Но если в точке х функ¬
ция f имеет разрыв, то это неверно, как хорошо видно из рис. 456. Поэто¬
му в формулировку теоремы о скорости роста площади надо добавить
требование непрерывности функции f.
Итак, для функции / мы получили новую функцию S — пере¬
менную площадь подграфика. Связь между функциями f и S
такова:
S — интеграл от функции f,
f — производная функции S.
Из этого сравнения видно, что нахождение интеграла (интег¬
рирование) и нахождение производной (дифференцирование) яв¬
ляются взаимно обратными операциями. Если известна функ¬
ция /, то нахождение функции S (площади подграфика функ¬
ции f) есть задача интегрирования функции /. Если же задана
функция S, то нахождение функции f (скорости роста площади)
есть задача дифференцирования функции S.
Обозначение интеграла
Интеграл от функции у = f(x) на отрезке [а, Ь] обозначается
так:
ь
$/(*) dx.
а
Эта традиция имеет исторические корни. Интегральные сум¬
мы, с помощью которых приближенно вычисляется интеграл,
составляются из слагаемых вида f(x)Ax. Приближенное равенство
354
Рис. 456
AS « f(x)Ax может быть заменено точным равенством дифферен¬
циалов dS = f(x)dx. Интеграл можно представить как сумму
«бесконечного числа дифференциалов». Знак интеграла и есть
стилизованная форма буквы S — первой буквы слова summa
(лат.). Запись ь
S = S/(x)d*
а
напоминает, что площадь S можно получить суммированием
слагаемых вида f(x)dx. Около знака интеграла ставят пределы
интегрирования — концы отрезка [а, Ь], на котором задана
функция f.
Переменная площадь S(x) (площадь подграфика функции f
на отрезке [а, х]) запишется в виде интеграла с переменным
верхним пределом:
X
50) = $/(*) dx.
а
Связь между функциями / и S, установленную в теореме о
скорости роста площади, можно записать так:
ф(х)Ах) = Кх).
Отсюда видно, что операции интегрирования и дифференци¬
рования являются взаимно обратными.
Определение интеграла и полученные для него результаты не¬
трудно распространить на произвольную функцию /, отказавшись
от требования ее неотрицательности. Рассмотрим произвольную
функцию, заданную на отрезке [а, 6], и ее подграфик, т. е. часть
плоскости, ограниченную графиком f, прямыми х = а, х = Ь
и осью абсцисс (рис. 457).
Интегралом от функции называется сумма площадей частей ее подгра-
фикаг взятых со знаком «-]-» для частей, расположенных выше оси
абсцисс, и со знаком «—» — ниже ее.
12*
355
Рис. 457
Упражнения
1. Что такое подграфик функции?
2. Постройте на клетчатой бумаге гра¬
фики следующих функций в масш¬
табе «две клетки — единица длины».
в) i/ = 5sin-pp *<=[0, 10].
3- Для функций, указанных на с. 350,
вычислите интегральные суммы с
помощью микрокалькулятора, взяв
§ 42. Вычисление интеграла
Первообразная
В § 41 мы установили, что интегрирование является операцией,
в определенном смысле обратной дифференцированию. Вычисле¬
ние интегралов сводится к нахождению функции, производная
которой равна заданной функции. Эту операцию мы рассмотрим
отдельно.
Первообразной для функции f называется такая функция F, производная
которой равна данной функции.
Иными словами, равенство
F' = f
можно прочесть двояко: / — производная функции /\ или F —
первообразная для функции f. Для обозначения первообразной
используют знак «неопределенного интеграла», т. е. интеграла
без указания пределов интегрирования:
F = V(x) dx.
356
Вычисляя число клеток, дайте при¬
ближенные значения для интегра¬
лов от этих функций на указанных
промежутках:
а) у = 0,Ijc2, хе[0, 10];
б) *<=[!, 10];
Ах=1 и вычисляя значение функ¬
ции на правом конце отрезков
[г, х+Дг].
4. Для функций, графики которых
изображены на рис. 458, а, б, по¬
стройте графики функций S=S(x),
задающих переменную площадь
подграфика.
Рис. 458
Свойства первообразной
1. Если F — первообразная для функции f, то F \ С, где С — константа,
также первообразная для той же функции f.
Действительно, (F + С)' — F' + С' = f + 0 = /.
2. Обратно: если F. и F, — две первообразные для одной и той же функ¬
ции f, то они отличаются на постоянное слагаемое.
Действительно, из F\ = / и F2 = f следует (F{ — F^)'=
= F\ — F'2 = f — f = 0. Функция, производная которой тождест¬
венно равна нулю, является постоянной. Это свойство производ¬
ной очевидно из ее механического смысла: если скорость точки
равна нулю, то она стоит на месте и ее координата постоянна.
Итак, F\ — F2 = С. Все первообразные для функции f получают¬
ся из одной из них прибавлением к ней произвольной постоянной.
Надо помнить, что знак $ является «неопределенным» в том
смысле, что он обозначает какую-либо первообразную.
3- \(f(x) + g(x))dx = \f(x)dx + \g(x)dx.
Действительно, пусть F и G — первообразные для функций /
и g соответственно. Тогда F + G является первообразной для
функции f + g: (F + G)' = F' + G' = f + g.
4. $c/(jt)djt = c^f(x)dx.
Доказывается аналогично.
Таблицу первообразных получают с помощью таблицы произ¬
водных. Проверить табл. 10 можно, делая обратную операцию,
т. е. вычисляя производные.
Таблица 10
357
Линейная замена переменной
Пусть F — первообразная для функции f. Тогда
tf(kx + b) Ах — -j-F{kx + Ь).
Действительно, вычислим производную от F(kx + b): (F{kx +
+ Ь)У = kF'(kx + b) = kf(kx + b). Отсюда -j-F(kx + Ь) является
первообразной для функции f(kx-\-b).
Следовательно, таблица первообразных может быть дополне¬
на (табл. 11).
Таблица 11
Операция дифференцирования совершается формально — нужно запом¬
нить несколько правил и их будет достаточно для нахождения производ¬
ных. Не так обстоит дело с интегрированием: например, нет формулы для
интегрирования произведения и частного функций. Поэтому составлены
обширные таблицы интегралов (первообразных) и появляется новая за¬
дача — научиться преобразовывать вычисляемые интегралы к табличным.
Пример
Вычислить \s\n2xdx.
В таблице интегралов нет интеграла от sin2*. Однако можно
воспользоваться формулой sin2* = !/2 (1 — cos 2х). Для cos 2*
интеграл известен, поэтому
$ sin2*d* = $ ‘/2(1 “ cos 2х) Ах = ‘/2 ($ dx — $ cos 2х dx) =
= ■/,<*—'/, sin 2*)—§--
Упражнения
Для следующих функций вычислите
первообразную:
а) у—х3-{-2х2 — 5r+ 1;
358
X*— 1
y — sm2xc°s4x\
и) j/ = cos5jt,
н) у=
е* + е
е — е
е> У~Т+Т' .2
ж) y = s\nx-\-cosxm, о) у
П) У
2
3) «/ = sin(3* + |); 1
7+Т’
к) */ = 2sinrcosх; р) у=—J .
л) i/ = sinjcsinЗлг;
Теорема Ньютона — Лейбница
Знаменитая теорема, названная именами основоположников ма¬
тематического анализа, гласит:
интеграл равен приращению первообразной.
Запишем формулировку более подробно.
Теорема Ньютона — Лейбница
Пусть f — данная функция, F — ее первообразная. Тогда
Jf(x)dx^F(b)-F(a).
Доказательство. Одна первообразная для функции f
известна — это S(jc) — переменная площадь подграфика функ-
ъ
ции f. По определению интеграла, ^f(x)dx = S(b) — S(a) =
а
= S (b)y так как S (а) = 0. Пусть F — произвольная первооб¬
разная для функции f. Тогда она отличается от S на константу,
но приращение функций F и S будет одним и тем же:
S(x) = F(x) + С,
ь
S f (*) dx = S(b) - S(a) = (F(b) + С) - (F{a) + С) =
= F(b)-F(a),
что и требовалось доказать. Разность F (b) — F (а) сокращенно
записывается в виде F (х) |£•
Теорема Ньютона — Лейбница сводит вычисления интегралов
к вычислению первообразных.
Примеры
1
1. Вычислить 5 х2 dx.
о
0SJf2dx = xlo=T-°=T-
я/2
2. Вычислить J sin 2jc djc.
0
я/2
5 sin 2xdx = — 1 / 2 cos 2jc l^2 = — l/2 cos л + ‘/2 cos0 = 1.
о
Свойства интеграла
Формула Ньютона — Лейбница сводит свойства интеграла к
свойствам первообразной, которые, в свою очередь, опираются
на свойства производной:
ь ъ ъ
1- S (f + g)d* = S /d* + S g dx.
a a a
b b
2. $cfdx = c$fdx.
a a
Доказательство (первого свойства). Пусть F и G —
первообразные для функций fug соответственно. Тогда функ¬
ция F-f G — одна из первообразных функций f -+■ g- По теоре¬
ме Ньютона — Лейбница,
ь
Uf + g)dx = (F+G)\ba = F (b) + G (Ь) - F (а) - G (а) =
а
Ь Ь
= F(b)-F(a)+G(b) - G (а) = $ fdx + $ gdx.
а а
Второе свойство доказывается аналогично.
Отметим следствия свойств 1 и 2:
ь ь ь
$ (f - g)dx = S / dx — $ gdx,
a a a
b b b
$ (a/ + Pg) dx = a $ fdx + P $ gdx.
a a a
Некрторые свойства интеграла являются следствием свойств
площади, лежащей в определении интеграла.
Ь с Ь
3. $fdx= $fdx + $ fdx .
а а с
Докажем это. Площадь всей криволинейной трапеции с ос¬
нованием [а, Ь] (рис. 459) есть сумма площадей трапеций с
основаниями [а, с] и [с, Ь].
Это же свойство можно получить и вычислением. Пусть
F — первообразная для функции fc. Тогда
с Ь
$ fdx = F(c) - F(a), S fdx = F(b) - F(c).
a с
Складывая почленно последние равенства, получаем
ь
F(c) - F(а) + F(b) - F(c) = F(b) - F(a) = $ fdx .
a
Доказанное свойство интеграла называют его аддитивностью
(от лат. addo — складываю).
а
Полезно отметить, что § /dx = 0, так как F(a) — F(a) = 0.
а
4. Если f(x)^g(x), то
$ f(x)dx> Sf(x)dx.
а а
Действительно, функция / (jc) = / (л) — g (jc), по условию,
не отрицательна. Следовательно, не отрицателен от нее и интег¬
рал, являющийся, по определению, площадью подграфика:
ъ
$(/(*) —“ ^ 0. Раскрывая левую часть этого неравенства
ъ ь
по свойствам 1 и 2, получаем > 0, т. е.
а а
Ь Ь
$g(*)dx, что и требовалось доказать.
а а
Рис. 459
Примеры
я/2
1. Вычислите J (jc — sin jc) djc.
о
я/2
5 (jc — sin jc) djc = J jcdjc — § sin jc djc =
O 0 0
+ -4-1=0.23.
Ji±*±Lix_j(i+± + ^)dJ[ =
= jcf + lnjcf-^|2=2-l + ln2-0--2-+l =
= ±. + In 2 « 2,19.
Упражнения
Вычислите интегралы:
i
a)
0
0
б) $ x3dx-,
-I
1
в) 5 X?&X-,
D S djC
x+\ ’
д) 5 e dr;
0
2л
е) J sin jcdx;
о
ж) j sin2jtdjr,
-я/4
я/2
з) J sin2xtix;
о
и) ^ -yj4xdx;
к) ( (1 — x)&x\
о
л) j (* — l)3dJt;
-l
м
) (cos(*-JL)d*;
h) j
jcdx
£ *+1 ’
o) ^ -^4 — xdx.
§ 43. Приложения интеграла
Площадь
Пусть надо вычислить площадь какой-либо плоской фигуры Ф.
Введем на плоскости декартову систему координат. Тогда от¬
дельные куски границы фигуры Ф можно задать в виде графи¬
ков некоторых функций. Сравнительно простой случай изображен
на рис. 460. Площадь фигуры Ф можно получить сложением
и вычитанием площадей подграфиков функций, задающих гра¬
ницу. Так, в типичном случае площадь фигуры Ф (рис. 461)
получается как разность подграфиков функций f и g, т. е. вы¬
ражается через интегралы:
362
Рис. 460
Рис. 461
Примеры
1. Найти площадь одной арки синусоиды (рис. 462).
я
S = ^ sin х dx = — cos х I” = 1 + 1 = 2.
0 'о
2. Найти площадь между дугами парабол у = х2 и у = У*~
(рис. 463).
Рис. 462
Данная фигура ограничена графиками двух функций:
f(x) = ^/T и g(x) = x2. Искомая площадь равна
1 1
5=5 VF dx — 5 *2dx =
о о
_ хт |1 X3 и 2_ J_ _ J_
3/2 *о з 10 — з 3 - 3 *
То, что площадь вычисляется с помощью интеграла — это
не удивительно, так как понятие интеграла с самого начала у нас
вводилось через понятие площади. Вычисление других физиче¬
ских величин с помощью интеграла потребует дополнительных
рассуждений.
Упражнения
Вычислите площади фигур, ограни¬
ченных следующими кривыми:
а) у=х—х2 и у=х2—х\
363,
Рис. 463
2. На рис. 464 изображено несколько
фигур. Введите на плоскости систе¬
му координат, разбейте границу
каждой фигуры так, чтобы куски
могли быть графиками каких-либо
функций, обозначьте эти функции и
выразите площади фигур через
интегралы от этих функций.
Схема применения интеграла
При ознакомлении с понятием интеграла мы выделили три
его характеристики:
1) интеграл от функции f есть площадь ее подграфика (с уче¬
том знака);
2) интеграл есть предел интегральных сумм;
3) интеграл от функции / есть приращение ее первообразной.
Любая из этих характеристик интеграла может служить
основой для его приложений. Наиболее стандартным путем вы¬
ражения какой-либо физической величины в виде интеграла от
другой является использование третьей характеристики интегра¬
ла как приращения первообразной. Однако и две первые харак¬
теристики очень важны в приложениях, так как позволяют полу¬
чить геометрический смысл связи между физическими величина¬
ми и дать простой способ приближенного вычисления.
Вернемся еще раз к величинам, которые вычисляются с по¬
мощью интеграла (например, такие физические понятия, как
перемещение, работа, масса, электрический заряд, давление,
теплота). К ним можно добавить геометрические величины —
длину, площадь, объем. Все эти величины обладают некоторыми
общими свойствами.
1. Величины можно рассматривать как функции отрезка.
Перемещение вычисляется в зависимости от отрезка времени
движения. Работа переменной силы при движении по прямой
364
зависит от пройденного отрезка пути. Массу тонкого неодно¬
родного стержня можно рассматривать как функцию от отрезков
этого стержня. Электрический заряд, протекающий через попе¬
речное сечение проводника, зависит от отрезка времени, за ко¬
торый производится измерение.
Функции отрезка часто можно представить как приращение
обычной функции. Так, при движении точки по прямой можно
рассматривать эту прямую как числовую ось и ввести функцию
времени — координату точки. Тогда перемещение на данном от¬
резке времени запишем как приращение координаты:
х = х(/), s = Ах = х(t2) — х (/,).
При вычислении массы стержня можно считать, что стер¬
жень расположен на числовой оси х и занимает положение от
О до / (/ — длина стержня). Теперь введем функцию т = т(х) —
массу стержня с концами в начальной точке и в точке х. Тогда
масСа отрезка стержня с концами в точках х{ и х2 равна прира¬
щению функции т(х) на этом отрезке:
Am = т (х2) — т (х,).
Для вычисления площади подграфика мы вводили перемен¬
ную площадь S = S(x)—площадь под графиком функции от
начальной точки до точки х. Площадь криволинейной трапе¬
ции с основанием [хьх2\ равна приращению функции S на
этом отрезке.
Заметим, что так как мы вычисляли приращение функции,
а оно не изменится, если функцию изменить на постоянное
слагаемое, то при определении переменных массы, работы или
площади не важно, какое значение мы выбираем для этой функ¬
ции в начальной точке или от какой точки начинаем вычислять
ее значения.
2. Известна скорость изменения величины.
Так, скоростью изменения перемещения будет скорость в
обычном смысле этого слова. Скоростью изменения работы в
зависимости от времени является мощность, а скоростью изме¬
нения работы в зависимости от перемещения является сила. Ско¬
рость изменения массы — это плотность. Само слово «плотность»
имеет такой же универсальный характер, как слово «скорость»,
и им широко пользуются. Например, плотность тока, плотность
заряда.
Если величину записать как приращение некоторой обычной
функции, то ее скорость (или плотность) равна производной
этой функции.
Примеры
I. Скорость механического движения
365
2. Линейная плотность стержня
dm
Р dx
3. Мощность
4. Сила при перемещении по прямой
г d А
F==-лГ-
Интеграл применяется тогда, когда известна скорость или плотность f
искомой величины. Если искомая величина представлена в виде прираще¬
ния некоторой функции F, то f является производной F, a F — первообраз¬
ной для функции f, т, е. интегралом от функции f.
Запишем этот вывод с помощью формул. Независимый аргу¬
мент обозначим /, а искомую величину — F. Рассмотрим зна¬
чение F на малом отрезке [/, t-\-dt]. Пусть f — скорость из¬
менения F. Запишем связь между F и / в дифференциальной
форме:
dF = f(t)dt.
Следовательно,
ь
F=
а
Итак, схема применения интеграла сводится к следующему.
1. Записываем главную часть изменения искомой величины с
помощью дифференциалов: dF = f(t)dt.
2. Запишем F в виде интеграла:
а
3. Находим первообразную для функции f и вычисляем F как
разность значений первообразной на концах отрезка.
1. Отметим вольность в выборе обозначений, которая часто допускается
в приложениях. Мы ищем некоторую величину, например массу стержня.
Обозначаем ее какой-то буквой, скажем, m. В данном случае m — масса
конкретного стержня, т. е. просто число. Однако для нахождения m
надо рассматривать массу произвольного отрезка стержня. Ее снова
обозначаем ш, хотя сейчас понимаем m как функцию отрезка. Затем мы
вводим переменную массу — массу стержня от начальной точки до точ¬
ки jc — и эту функцию от х тоже удобно обозначать той же буквой m,
чтобы записать соотношение для плотности: р=—:—, или dm == pdjc.
dx
Мы употребляем везде одну и ту же букву (хотя речь идет о разных
понятиях, для обозначения используется одна и та же буква).
366
2. Рассмотренные нами величины были функциями отрезка. Часто встре¬
чаются аналогичные величины, но зависящие от других областей. Так,
масса произвольного тела зависит не от отрезка, как это мы идеализи¬
ровали для тонкого стержня, а от области пространства. Существуют
более сложные интегралы, которые позволяют вычислить величины, за¬
висящие от частей кривой линии (криволинейные интегралы), от частей
поверхности (поверхностные интегралы), от частей объема (объемные,
или тройные, интегралы). В некоторых простых случаях искомые величины
удается рассмотреть как функции отрезка и свести их нахождение к
вычислению обычных интегралов. С такими примерами мы ознакомимся
при вычислении объемов и при решении прикладных задач.
Работа
Пусть точка движется по оси х, в каждой точке которой прило¬
жена некоторая сила F = F (х). Вычислим работу, которую надо
совершить при перемещении из точки а в точку Ь. На малом от¬
резке пути от точки х до точки х dx можно считать силу
постоянной и равной F (х). Тогда дифференциал работы dА =
= F(x)dx. Отсюда получаем, что вся работа на отрезке [а, Ь\
равна ь
А=^(х) dx.
а
Эта формула позволяет вычислить работу при прямолиней¬
ном движении. Перемещение по криволинейным траекториям
требует другого, так называемого криволинейного интеграла,
однако запись работы в виде интеграла осталась бы прежней.
В этом случае сила была бы векторной величиной F, перемеще¬
ние совершалось бы не обязательно по прямой, и на малом от¬
резке, его можно было бы записать dr. Главная часть работы
есть скалярное произведение dA = F dr, а вся работа — кри¬
волинейный интеграл $ F d г, где Г — кривая, по которой проис-
г
ходит перемещение точки.
Пример
Предположим, что в точке О помещен единичный элект¬
рический заряд. Он создает электрическое поле. На другой
единичный заряД, помещенный в точку х, действует сила /\
обратно пропорциональная квадрату расстояния, т. е.
k
F(x) = —г. Найти работу электрического поля по переме¬
щению единичного заряда из точки хх в точку х2.
Применяя формулу для работы, получаем
Для функции F(*)==—g- первообразную и(х) можно
найти по таблице: и(х) = — k/x. Тогда А = и(х) \ хх\ =
= (— k/x) | *2 = k/xx — k/x2.
367
Функция и(х) = — k(x) называется потенциалом электриче¬
ского поля. Работа А равна приращению функции и, т. е. раз¬
ности потенциалов на концах отрезка.
Поскольку геометрический смысл интеграла — это площадь,
работу можно представить как площадь подграфика для функ¬
ции F(x). Изобразим этот график для разобранного примера
(рис. 465).
Перемещение
Предположим, что точка движется по прямой (по оси х) с из¬
вестной скоростью. Положение точки на оси будем считать
функцией времени: х = x(t). Как найти перемещение точки за
промежуток времени [tlyt2]?
Если скорость точки постоянна и равна vy то перемещение
s = v(t2 — /1). Пусть теперь , скорость меняется по закону
v = v (t). За промежуток времени [/, t + At] главную часть
перемещения As мы получим, если будем считать, что на этом
промежутке скорость постоянна и равна v(t). Тогда ds = u(t)dty
h
следовательно, s = §i/(/)d/.
Если изобразить график скорости, то перемещение будет за¬
даваться площадью подграфика (рис. 466).
Масса
Масса произвольного тела является величиной, для вычисле¬
ния которой нужно тоже понятие интеграла, только более слож¬
ное. Мы сможем написать формулу для вычисления массы тон¬
кого стержня, т. е. такого тела, в котором плотность изменяется
вдоль одного направления и его можно представить как отрезок
тонкой проволоки с изменяющейся плотностью.
Если стержень однороден, то его масса m пропорциональна
длине /, т. е. m = р/, где р—коэффициент пропорциональ¬
ности, называемый линейной плотностью. Вычислим массу неод¬
нородного стержня, если известно, как меняется плотность р.
Представим себе, что стержень расположен вдоль оси х так,
368
Рис. 465
Рис. 466
что занимает положение [0, /]. Его линейную плотность р можно
считать функцией от х р = р(лг), заданной на этом отрезке.
Считая на отрезке [jc, х + djc] плотность постоянной, получаем
dm = p(jt)djt, следовательно,
/
m = § р (jc) djt.
о
Таким образом, масса стержня является интегралом от его
линейной плотности.
Электрический заряд
Представим себе переменный ток, текущий по проводнику. Как
вычислить заряд q, переносимый за интервал времени [а, Ь]
через сечение проводника? Если сила тока / не изменяется со
временем, то изменение заряда q равно / (Ь — а). Пусть задан
закон изменения / = /(t) в зависимости от времени. На малом
интервале времени [t, t -f dt] можно считать силу тока постоян¬
ной и равной I(t\ тогда dq = I(t)dt и, следовательно,
ъ
<7= S^Od*-
а
Сравним эти примеры с физическими примерами, обсуждав¬
шимися в связи с производной. Фактически рассматриваются
одни и те же соотношения вида dF = f(x)dx, но в первом случае
дана величина F и нужно найти f (f выступает как производ¬
ная F), а во втором случае известна величина f и надо найти F
(F является интегралом от f).
Составим из наших примеров табл. 12.
Таблица 12
369
Величина
Соотношение в диф¬
ференциалах
Производная
Интеграл
А — работа
N — мощность
F — сила
m — масса тонкого
стержня
р—линейная плот¬
ность
q — электрический
заряд
I — сила тока
s — перемещение
v — скорость
Прикладные задачи
Пирамида Хеопса представляет собой правильную четырехуголь¬
ную пирамиду высотой 147 м, в основании которой квадрат со
стороной 232 м. Она построена из камня, плотность которого
2,5 г/см3. Найти работу против силы тяжести, затраченную при
постройке.
Проведем вертикально вверх ось х с началом у основания
пирамиды. По этой оси будем измерять высоту подъема камней.
Сначала решим задачу в общем виде. Обозначим Н — высоту
пирамиды, а — сторону основания, р — плотность камня, А(х) —
работу, выполненную при возведении пирамиды от основания до
высоты х. Найдем сначала сторону у квадрата, получающегося
в горизонтальном сечении пирамиды на высоте х. Из подобия
треугольников получаем Н откуда у = -- (Я — х)
(рис. 467). Рассмотрим тонкий слой пирамиды, расположенный
на расстоянии х от основания. Пусть толщина слоя равна dx.
Рис. 467
Слой можно приблизительно считать параллелепипедом. Его мас-
2
са dm = py2dx = p-jp-(H — x)2dx. При подъеме этого слоя на
высоту х была выполнена работа dA = dmgx, где g — ускорение
2
свободного падения, т. е. dA = pg -jp- х(Н — x)2dx.
Отсюда
Подставляя числовые данные, получаем А= 2,37 • 1012 Дж.
р ga2H2
12
Упражнения
1. Из цистерны, имеющей форму пря¬
мого кругового конуса с радиусом
основания R = Зм и высотой Н —
=5 м, выкачивают воду через вер¬
шину конуса. Найдите совершаемую
при этом работу.
2. Вычислите давление воды на квад¬
ратную пластину со стороной а,
погруженную в воду перпендикуляр¬
но ее поверхности, считая, что верх¬
нее основание пластины находится
на расстоянии h от поверхности
воды.
3. Найдите работу, совершенную при
постройке египетской пирамиды Хеф-
рена, имеющей высоту 143,5 м и сто¬
рону основания 215 м.
§ 44. Дифференциальные уравнения
Составление дифференциального уравнения
Вернемся к задаче на с. 370. Для вычисления произведенной
работы мы ввели две переменные величины: х — высоту от земли,
на которую подняты камни, и А — работу, совершенную при воз¬
ведении пирамиды до высоты х. Дальнейшие рассуждения дали
соотношение между дифференциалами этих величин d А =
2
= F(x)dx, где F(x) = х(Н — х)2. Полученное соотношение
назовем дифференциальным уравнением для нахождения А =
= А(х). Запишем его с помощью производной: = F(x) или
А' = F(x). Это уравнение очень простое — в нем производная не¬
известной функции выражена через аргумент х. Отыскание самой
функции А сводится к интегрированию:
х
А(х) = $ F(x)dx.
о
Дифференциальные уравнения — это уравнения, связывающие неизвест¬
ную функцию и ее производные.
Многие физические законы имеют вид дифференциальных
уравнений, т. е. соотношений между функциями и их производ¬
ными. Задача интегрирования этих уравнений — важнейшая за¬
дача математики. Одни дифференциальные уравнения удается
проинтегрировать в явном виде, т. е. записать искомую функцию
в виде формул. Для решения других до сих пор не удается найти
достаточно удобных формул. В этих случаях можно найти при¬
371
ближенные решения с помощью вычислительных машин. Мы не
будем подробно изучать методы интегрирования дифференциаль¬
ных уравнений, а только рассмотрим несколько примеров.
Примеры
1. Уравнение механического движения. Пусть материальная
точка массы т движется под действием силы F по оси х.
Обозначим t время ее движения, v — скорость, а — ускоре¬
ние. Второй закон Ньютона а = F/m примет вид дифферен¬
циального уравнения, если записать ускорение а как вторую
производную:
Уравнение тх" — F называют уравнением механическо¬
го движения, где х = x{t) — неизвестная функция, т и F —
известные величины. В зависимости от условий задачи по-
разному и записываются различные дифференциальные
уравнения.
Например:
а) сила постоянна (F = const). Уравнение движения
Р
х" = —= а (где а — const);
б) сила периодически изменяется со временем, например
по закону F = fosinco/. Уравнение движения
х" = sin а)/;
т
в) сила пропорциональна смещению (движение идеально
упругой пружины): F = — kx (k >0), знак «—» указывает
на то, что направление силы противоположно направлению
смещения. Уравнение движения
г) сила, обратно пропорциональная квадрату расстоя¬
ния: F =—(свободный полет). Уравнение движения
д) постоянная сила тяжести F\ =—mg и сила трения
F2 = —kx\ пропорциональная скорости, действующие од¬
новременно (падение с трением). Уравнение движения
Во всех уравнениях движения вторая производная неиз¬
вестной функции х выражена через время /, положение х
372
точки и ее скорость v. Такое уравнение называют уравне¬
нием второго порядка, так как в него входит вторая произ¬
водная. Дифференциальное уравнение для работы по по¬
стройке пирамиды Хеопса является уравнением первого
порядка, так как в нем имеется только первая производ¬
ная.
2. Радиоактивный распад. Масса m радиоактивного вещества
изменяется со временем: m = m(t). Экспериментальные дан¬
ные дают основание считать, что скорость изменения массы
пропорциональна массе вещества в данный момент:
где k — коэффициент пропорциональности (знак «—» пока¬
зывает, что масса вещества убывает).
3. Народонаселение. Представим число жителей страны в мо¬
мент времени t как функцию L = L(t). Допустим, что за
единицу времени народонаселение увеличивается на опреде¬
ленный процент. Если в момент времени t число жителей
равно Ц/), то за период времени [/, t + появится при¬
мерно kL(t)dt новых жителей, т. е. AL « kL(t)dt. Хотя ве¬
личина L принимает целые значения, обычно интересуются
приближенными значениями L. Заменяя функцию L функ¬
цией, принимающей значения непрерывно и удовлетворяю¬
щей соотношению dL = kLdt, мы не сделаем большой
ошибки. Таким образом, скорость роста функции L рав¬
на kL и она удовлетворяет дифференциальному уравне¬
нию
4. Электрическая цепь. Пусть электрическая цепь состоит из
последовательно соединенных резистора и конденсатора
(рис. 468). В цепи произошло короткое замыкание и кон-
Рис. 468
денсатор, имевший начальный заряд, начинает разряжать¬
ся. Напряжение на конденсаторе в момент времени t обо¬
значим U = U(t). Заряд q = q(t) связан с напряжением U
формулой q = CU, где С — емкость конденсатора. Через
сопротивление пойдет ток I = — , где R — сопротивление
резистора, а знак «—» связан с направлением тока. Сила
тока — это производная заряда по времени; учитывая, что
/= a q = CU, получаем
и
п dU U dU 1 г,
СЖ=~— или ЧГ=~Иси-
Многие явления природы и техники описываются дифферен¬
циальными уравнениями, т. е. уравнениями, связывающими не¬
известные величины и их производные. Вывод дифференциаль¬
ных уравнений основан на знании законов изучаемых явле¬
ний.
Решение дифференциального уравнения
Дифференциальное и интегральное исчисления позволили запи¬
сать на математическом языке в виде дифференциальных уравне¬
ний различные законы и явления. За триста лет существования
этого раздела математики появились многие тысячи дифферен¬
циальных уравнений. Однако замечательно то, что многие урав¬
нения похожи друг на друга. Сравним, например, три уравнения,
полученных в примерах 2—4 на с. 373:
— hm dL — hi dU — if
dt ’ d t ' d t RC
Все они имеют один и тот же вид — скорость изменения
искомой функции пропорциональна значению этой функции. Ре¬
шения всех трех уравнений сводятся к решению одного:
dx
w = ax
(при разных значениях коэффициента пропорциональности а).
Здесь мы наблюдаем удивительное могущество математики — со¬
вершенно разные процессы приводят к одной и той же математи¬
ческой модели. Ее исследование дает нам ответ как в разобран¬
ных задачах, так и во многих других, которые приводят к такому
же уравнению.
Математики научились объединять вместе похожие уравне¬
ния, классифицировать их. Так же как в случае простых алгебра¬
ических уравнений были найдены в свое время формулы для их
корней, так и в случае некоторых стандартных дифференциаль¬
ных уравнений были получены формулы для их решений.
Решение дифференциального уравнения — это функция, при
подстановке которой в уравнение оно превращается в тождество.
Так как операция дифференцирования выполняется просто, то
всегда нетрудно проверить, является ли данная функция реше¬
нием дифференциального уравнения или нет.
374
Примеры
1. Функция х = -у- + v0t + jc0, где у0, х0 — произвольные
числа, является решением уравнения х" = а. Действитель¬
но, вычисляя производные, получаем
х* = at + Уо, х" = а.
4. Функция m = Ce~kt, где С — произвольная постоянная,
является решением уравнения m' = —km.
Однако не для всех уравнений решения записываются так
просто. Уже для уравнения свободного космического полета на¬
писать формулу решения довольно трудно. Часто удается иссле¬
довать решение дифференциального уравнения, не находя само¬
го решения.
Уравнение показательного роста
Известно много процессов, в которых скорость изменения какой-
либо величины пропорциональна ее значению. К числу таких
процессов относят радиоактивный распад, остывание тела, раз¬
ряд емкости через сопротивление, изменение народонаселения
и т. д.
Эти процессы описываются дифференциальным уравнением
первого порядка х' = ах при различных значениях коэффи¬
циента а.
Как же решить уравнение х/ = аг?
Мы знаем, что показательная функция обладает тем свойст¬
вом, что ее производная пропорциональна ей самой. Таким обра¬
зом, функция х/ = еа/ является одним из решений уравнения
х/ = ах. Как найти все решения? Пусть z — произвольное реше¬
ние, т. е. zr = az. Запишем z = уе , где у — новая неизвестная
функция. Тогда
р
2. Функция х = sincot -f vot + Хо является решением
Р
уравнения, хп = sin со/.
т
3. Функция
А и а — произ¬
вольные числа, является решением уравнения х" = ——х.
т
1. Проверьте, что функции в приме¬
рах 2—4 действительно являются
решениями соответствующих диф¬
ференциальных уравнений.
Упражнения
2. Найдите такое число а, при котором
функция х'—а{/г будет решением
уравнения х" —
х
3. При каком значении к степенная
функция х = ctk может быть ре¬
шением уравнения х" = ах3?
(уеа‘У = а(уеа1).
375
Вычислим производную левой части:
(yeaty = y'eat + а уеы.
Приравнивая правые части уравнений, находим eaty' = 0, т. е.
у' = 0. Таким образом, производная функция равна нулю и
у = С. Итак, любое решение уравнения х' = ах имеет вид х =
= Сеа/, где С — константа.
Получаем решения для рассмотренных выше уравнений.
Значение константы С определяем, зная начальное значение
искомой величины. Если в качестве начального момента времени
взято / = 0, то значение С как раз и равно значению искомой
величины при t = 0. Так, если начальное напряжение на конден¬
саторе Uо, то конденсатор разряжается по экспоненциальному
закону: (J = Uое-//(/?С). При больших t значения U приближаются
к нулю. Графики показательных функций при разных а приведе¬
ны на рис. 469.
Упражнение
Численность народонаселения в двух
странах подчиняется одному и
тому же дифференциальному урав¬
нению L' — aL, но с разными коэф¬
фициентами а. Для первой страны
а = 0,005,, для второй а = 0,02.
В настоящий момент численность
первой страны равна 10 млн., а вто¬
рой — 5 млн. Через сколько лет чис¬
ленность народонаселения во вто¬
рой стране будет больше, чем в
первой?
Уравнение гармонических колебаний
Напомним уравнение движения материальной точки, прикреплен¬
ной к концу упругой пружины: mx" = —kx. Оказывается, ёсть
много задач, приводящих к аналогичным уравнениям второго
порядка.
Пример
Рассмотрим электрическую цепь, состоящую из последова¬
тельно соединенных конденсатора емкостью С и катушки
индуктивностью L (рис. 470). На конденсаторе есть начальное
376
Рис. 469
Рис. 470
напряжение. В начальный момент времени цепь замкнули
накоротко и через катушку пошел ток. Обозначим U = U(t)
напряжение на конденсаторе в момент времени t. Напря¬
жение U(t) на катушке (при выбранном направлении тока)
пропорционально скорости изменения силы тока /, проходя¬
щего через катушку: U = — Подставляя в это выра¬
жение / = где q = CU, получаем
d 2U
U = -L^-=—L^r=—LC
d t dr dr
Окончательно приходим к уравнению второго порядка отно¬
сительно напряжения:
d2U _ 1 ,,
~dF~~TF
Итак, две разные на первый взгляд задачи физики — колеба¬
ние упругой пружины и разряд конденсатора через катушку —
привели к одному и тому же дифференциальному уравнению
второго порядка, только записанному в разных обозначе¬
ниях:
х" = -±-х и U" = - и.
т L С
Разберем первое из них, обозначив —со2 константу, стоящую
перед искомой функцией хп = —со2*. Это уравнение называется
уравнением свободных гармонических колебаний.
Проверим, что функция х = Acos(a)/ + а), где А и а — кон¬
станты, является решением уравнения х" = — со2*. Действи¬
тельно,
х* = — ^o)sin(a)/ + a),
x,f = —Ao>2cos (со/ + a) = —ы2х.
Оказывается, что, изменяя А и а, мы получаем все решения урав¬
нения гармонических колебаний. Константы А и а имеют нагляд¬
ный смысл: А — это амплитуда колебаний, a — начальная
фаза. Значения А и а находятся из начальных условий — значе¬
ний х и х' в начальный момент времени. Графики гармонических
колебаний при различных значениях Л, со и а приведены на
рис. 471.
377
Рис. 471
Уравнение гармонических колебаний получено нами при пред¬
положениях, которые реально не выполняются. Так, при описа¬
нии колебания пружины надо учитывать трение, а при описании
разряда конденсатора — внутреннее сопротивление. При этом
в уравнении колебаний появляется дополнительное слагаемое,
зависящее от первой производной (скорости).
Решения такого уравнения зависят от соотношения между
параметрами L, R, С.
Мы рассматривали свободные колебания. Такие колебания
будут наблюдаться в электрической цепи, если в ней сделать ко¬
роткое замыкание и считать, что ток идет только за счет началь¬
ного заряда конденсатора. Если к цепи подключить источ¬
ник ЭДС, то колебания тока в ней будут описываться новым
уравнением, которое нетрудно вывести. Решения такого уравне¬
ния описывают вынужденные колебания, зависящие от подавае¬
мого напряжения.
Пример
Уравнение для силы тока / в цепи (рис. 472)
Рис. 472
378
В этом параграфе были рассмотрены некоторые примеры дифференциаль¬
ных уравнений. Решения этих уравнений — предмет специального раздела
математики, теории дифференциальных уравнений, которая изучается в
высшей школе. Нам важно понять, что с помощью основных операций
анализа (дифференцирования и интегрирования) можно строить матема¬
тические модели (дифференциальные уравнения) достаточно сложных
и важных процессов. Полезно иметь в виду и то, что разные задачи мо¬
гут приводить к одной и той же модели. К числу наиболее часто встре¬
чающихся уравнений относятся уравнение показательного роста, уравне¬
ния свободных и вынужденных колебаний.
Задачи и вопросы
11.1. Запишите выражения для площадей фигур, изображенных
на рис. 473, а—д в виде интегралов.
Рис. 473
11.2. Нарисуйте фигуры, площади которых задаются следующи¬
ми интегралами:
11.3, Найдите первообразные функций:
а) У = 1; и) у = У*;
б) у = х; ,
в) у = Зх;
г) у — х9; j
д) у = Зх3 - 5х2 + х - 2; л) У = * “ '
е) у = ‘/зх3 — 1;
■ м) у =
ж) у == -7-; л/х
2 yjx ’
jc 1
2jc2 - 1
1
JC2 ’
3
3) У =
л
11.4. Найдите первообразные функций:
а) у — 3sinjc;
б) у — 2cosjc;
в) у = sin2jc;
г) у = Лcosto*;
я) у — 2ех\
е) у = cos2 -j-;
ж) у — 2ех\
з) у = е~х\
и) . = -4^;
к) у = 2х;
11.5. Вычислите интегралы:
2
а) $ dx;
-1
3
б) \ 5dx;
0
5
в) \ хАх\
-2
1
г) \ x2dx;
о
4
д) 5 (3 — 2x)dx;
л) у = е3х+1;
м) у = 10~х;
н) у = 4-;
о) у =
1
Р> * = -Г+7^
jc3 + jc2 + Jt + 1
с) У =
т) (/ =
л
1
е) S(*2+l)d*;
О
О
ж) $ (*2 + 2x)dx;
- 1
2
з) 5 (2л:3 — JC — l)djc;
0
1
и) j (2х2 - 5х - 7)djc;
-1
«> 1
380
2 ■ я/4
л) S ^г; с) | sin-y-cos-^-dx;
4 л/2
м) \ s[xdx\ т) \ cos2-£-dJc;
1 -л/2 1
1 л/2
н) SV?“dx; у)
О л/4
л/4
djc
COS2*
\ f dx п/‘
0) * vr; Ф) S
о
8 л/4
п) S 7* +--dx; х) 5 tg2jcdjc;
1 \Х о
л/2 2
р) J sinjcdjc; ц) \ \х — l\dx.
о о
11.6. Найдите площади фигур, ограниченных линиями:
а) прямыми х = — 1, х = —2, # = 0 и кривой у = х2 + 1;
б) прямой у =0 и параболой i/ = 1—х2\
в) прямыми х = 1, jc = 2, у = 0 w кривой у = х2 -\- 1;
г) кривой у = х2—х—5 и прямой у = х—2;
д) .кривыми у = х2-\-х—4 и у = 6—jc2;
е) у = —х2 + 4 и у = 2—х\
ж) у = sinx, * = у-, х = л, г/ = 0;
з) 1/ = * = 1, х = 3, # = 0;
и) У = —х2 + Зх, £/ = 0;
к) у = 2х, * = —1, х = 1, £/ = 0;
л) £/ = 4—х2, х = 0, у = 0;
м) У = 9—х*> х = 0, 1/ = 0, jc = —2;
н) у = х2-\-4, х = 0, х = —1, £/ = 0;
о) */ = *2 и у = Ух~.
11.7. Найдите площадь фигуры, заданной на координатной плос¬
кости условием: а) у ^ jc2, х^у2; б) 15—7х^у2 ^7—3jc.
11.8. Укажите на рис. 474,а—е, какой функции соответствует
график какой первообразной.
11.9. Найдите количество теплоты, выделяемое переменным сину¬
соидальным током I(t) = /Osin((o/ + ф) в течение одного пе¬
риода колебаний в проводнике с сопротивлением R.
381
Рис. 474
11.10. Два точечных электрических заряда +104 и —104 К л на¬
ходятся на расстоянии 10 см друг от друга. Найдите рабо-
боту, необходимую для того, чтобы их развести на рас¬
стояние 10 км.
11.11. Точка движется по оси абсцисс так, что скорость ее в
произвольный момент времени , t задается формулой
v(t) = cos (/ + л/4). Найдите положение точки в момент
времени л/2, если в момент времени t = л/4 она имела
абсциссу —1.
382
11.12. Найдите силу гравитационного взаимодействия между
расположенными на одной прямой материальной точкой
массы т и однородным стержнем длины / и массы М.
Расстояние от точки до ближайшего конца стержня
равно с.
11.13. Скорость электрона в линейном ускорителе изменяется
по закону v =~где U — ускоряющее напряжение, /—
длина ускорителя. За какое время электрон пролетит весь
ускоритель и какую максимальную скорость он приобре¬
тает?
11.14. Найдите функцию ^.удовлетворяющую условию:
а) Пх) = х2, /(2)=1;
б) /'(*) = в"', № = -2;
В) ГМ = -£-(*> 0), /(е) = е;
г) Г« = |(*< 0), /(-1)= 1;
Д) /'(*) = ^> Де2) = 2(х > 0).
11.15. Найдите все решения дифференциального уравнения
11.16. Решите дифференциальные уравнения:
а) у' — 2у\ б) у' = у, в) 2у' = Ъу.
11.17. Период полураспада радиоактивного вещества равен
4,4-109 лет. Через сколько лет останется 99,99% исходной
массы радиоактивного вещества?
11.18. Напишите закон радиоактивного распада, если известно,
что при t = t0 масса вещества m(t0) = т0.
11.19. Скорость роста дрожжей пропорциональна их массе. Най¬
дите зависимость массы дрожжей от времени, если извест¬
но, что при t = 0 их масса равна т.
11.20. Найдите коэффициент пропорциональности в задаче 11.19,
если известно, что прирост дрожжей через 2 ч больше, чем
прирост за первый час, на 11 кг, а начальная масса дрож¬
жей 100 кг.
11.21. При прохождении света через линзу теряется 10% све¬
тового потока. Какое максимальное число линз можно
вставить в конструкции сложного объектива, чтобы на
выходе иметь не менее 50% начального светового потока?
11.22. За счет специальной обработки линз (просветление опти¬
ки) потери светового потока для каждой линзы удалось
снизить до 2%. Какая часть светового потока будет на
выходе сложного объектива в условиях задачи 11.20?
11.23. Какой должен быть среднегодовой рост производства, что¬
бы за 10 лет объем производства удвоился?
383
12
ПЛОЩАДИ И ОБЪЕМЫ
§ 45. Площади плоских фигур
Аксиомы площади
Площадь — это положительная скалярная величина. Если за¬
фиксировать единицу площади, то площадь каждой измеряемой
фигуры будет неотрицательным числом. Отметим это в качестве
первой аксиомы площади.
Аксиома S, (неотрицательность площади)
Площадь каждой измеряемой плоской фигуры есть неотрицательное
число.
Обозначим фигуру F, ее площадь S(F). Тогда аксиому Sj
можно записать в виде неравенства S(F)^ 0.
На самом деле аксиома Sj подразумевает несколько больше,
чем просто утверждение о неотрицательности площади. В ней
неявно говорится о том, что всякой измеряемой фигуре можно
сопоставить некоторое неотрицательное число, т. е. о задании
отображения S множества измеряемых фигур во множество не¬
отрицательных чисел. Следующие аксиомы фиксируют основные
свойства этого отображения.
Аксиома S2 (аддитивность площади)
Пусть фигура F разбита на две части F, и Р2, не имеющие общих точек
(рис. 475). Тогда площадь фигуры F равна сумме площадей фигур F, и F2.
Используя теоретико-множественную символику, можно за¬
писать вторую аксиому площади так: если F=FX[}F2 (причем
F\ П F2 = 0), то S(F{) + S(F2) = S(F).
Аксиома S< (нормированность площади)
Площадь прямоугольника равна произведению длин сторон.
Если F — прямоугольник со сторонами а и Ь, то S(F) = ab.
Аксиома S4 (инвариантность площади) —
Равные фигуры имеют равные площади.
Если фигуры Fx и F2 равны, т. е. совмещаются при перемеще¬
нии, то их площади равны.
Остальные свойства площади можно вывести из аксиом
Si—S4. Для примера докажем свойство монотонности площади.
Теорема
Площадь части фигуры не больше площади всей фигуры.
Доказательство. Пусть фигура Fx является частью
фигуры F (рис. 476). Обозначим F2 ту часть фигуры F, которая
состоит из точек, не входящих в Fx. Тогда фигура F разбивается
Рис. 475 Рис. 476
на две части Fx и F2, не имеющие общих точек. По аксиоме S2
имеем S(F) = S(FX) + S(F2). Слагаемое S(F2) не отрицательно по
аксиоме следовательно, S(F)'^S(Fl), что и составляет
утверждение этой теоремы.
Обратите внимание на неточность рис. 475, иллюстрирующего аксиому
S2. Фигура F разбита на две части: F, и F2. Условие аксиомы требует, что¬
бы F, и F2 не имели общих точек. Но как быть с границей между F, и F2?
Конечно, ее можно искусственно приписать одной из частей, т. е. считать,
например, что кривая, разделяющая F, и F2, принадлежит Z7,, а множество
Рг в этой стороне «открыто», не имеет границы. Однако это условно:
почему границу надо относить именно к п, а не к F2? На самом де¬
ле все это несущественно, так как граница имеет площадь, равную
нулю, и поэтому ее можно рассматривать отдельно, а можно приписывать
к любой области. С этой оговоркой в аксиоме S, можно не требовать, чтобы
фигуры F, и F2 не имели общих точек, а фиксировать наличие общих
точек (границы), так чтобы площадь этой общей части была равна нулю.
Все это связано с тем, что в математике принято считать,
что точка, отрезок, кривая имеют нулевую площадь. Данное ут¬
верждение можно пояснить исходя из аксиом.
Пример
Пусть площадь некоторой точки А равна S(y4). Докажем,
что S(A) = 0. Возьмем произвольное положительное число а
13—1681 385
и изобразим квадрат со стороной а так, чтобы точка А была
внутри этого квадрата (например, в его центре; рис. 477).
Обозначим построенный квадрат Ка. По аксиоме S3,
S(/Ca) = аа = а2. По теореме о монотонности площади,
Рис. 477
S(j4) = S ^ S(Ka) = а2. Итак, при любом положительном а
получаем неравенство O^S^a2. Так как число а произ¬
вольно, то а2 можно взять как угодно малым, поэтому S
равно нулю, что и требовалось доказать.
В дальнейшем при вычислении площадей мы уже не будем обращать
внимание на то, включена граница в рассматриваемую фигуру или нет:
у всех рассматриваемых фигур площадь границы считается равной нулю.
Упражнения
1. Докажите, что площадь круга боль¬
ше площади вписанного в него
квадрата.
2. Пусть фигуры F| и F2 пересекаются,
F — их общая часть, т. е. F=Fi[)F2-
Докажите формулу для площади
объединения фигур F\ и F2:
S(F, U F2)=S(Fi) + S(F2) - S(F).
3. Вычислите площади фигур, изобра¬
женных на рис. 478, а—в. Необхо¬
димые размеры указаны на чертеже.
Рис. 478
Важные формулы планиметрии
Напомним различные формулы для вычисления площадей много¬
угольников:
1. Площадь прямоугольного треугольника (рис. 479)
S = {/2аЬ.
Для доказательства формулы достроим треугольник до пря-
386
Рис. 479 Рис. 480
моугольника (рис. 480). По аксиоме S4, площади полученных
треугольников равны, а в сумме (по аксиоме S2) они равны пло¬
щади прямоугольника, которая, по аксиоме S3, равна ab. Итак,
площадь прямоугольного треугольника равна половине произве¬
дения длин катетов, т. е. S = х/2ab, что и требовалось доказать.
Рис. 481
2. Площадь произвольного треугольника (рис. 481, а, б)
S = 7 2 ah.
Предлагаем вам самостоятельно провести доказательство
этой формулы, используя рис. 482.
Напомним известные вам из планиметрии формулы для вы¬
числения площадей многоугольников.
Рис. 482 Рис. 483 Рис. 484
3. Площадь параллелограмма (рис. 483)
S = ah = absina, S = ‘/2 dicksinp.
4. Площадь треугольника (рис. 484)
5 = y26csina, S = rp, S = S = /p(p — a)(p — b)(p — cj,
где r — радиус вписанного круга, R — радиус описанного круга,
р — полупериметр.
Рис. 485 Рис. 486 Рис. 487
5. Площадь равнобедренного треугольника (рис. 485)
S = Х/2Ь2sina = 72Ь2sin2p, S = -£tgp.
6. Площадь правильного треугольника (рис. 486)
5 = а2 /3~ s _ 3R2 |/3~
4 ’ 4 ’
где a — R |/3~, R — радиус описанного круга.
7. Площадь правильного многоугольника с п сторонами
(рис. 487)
S„ = l/2nah, Sn = 1/2nR2sin^L,
где A — апофема, p — полупериметр. При n = 4
S = a2 = R2/2;
при n = 6
S = 3R2 yT/2 = 3a2 |/T/2.
Упражнения 2. Вычислите площади фигур, изобра¬
женных на рис. 489, а—в. Необхо-
1. Вычислите площади фигур, изобра- димые размеры выберите самостоя-
женных на рис. 488, а—е. тельно.
Выражение площади через интеграл
Приведенные в предыдущем пункте формулы позволили найти
площади некоторых специальных многоугольников. Площадь
произвольной фигуры может быть выражена через интеграл.
388
Рис. 488
1. Площадь подграфика
S(F)= \f(x)dx,
а
где f(x)^ 0 (рис. 490). Эта формула является определением
интеграла.
2. Площадь произвольной фигуры (рис. 491). Введем систему
координат так, чтобы границу фигуры F можно было разбить на
графики двух функций (рис. 492).
389
Рис. 489
Рис. 490
Рис. 491
Из аксиомы S2 следует, что площадь подграфика функции f
определяется суммой площадей фигуры F и подграфика функ¬
ции /2. Тогда
(эта формула получена в § 43, там же даны примеры вычисления
площадей с помощью интеграла).
Теперь определим площадь фигуры с использованием интегра¬
ла в том случае, когда надо самостоятельно вводить систему
координат.
Вычислите площадь фигуры, изображенной на рис. 493,
если известно, что закругление выполнено в форме квадра¬
тичной параболы.
Выберем оси координат так, как показано на рис. 494.
Найдем уравнение квадратичной параболы. Так как ее вер¬
шина лежит на оси у, то у = ахг + Ь. Коэффициенты а
и b вычислим, зная указанные на чертеже размеры: подста¬
вив в уравнение х = 0, найдем 6 = 4, подставив у = 0, по¬
лучим ах2 + 4 = 0, но из чертежа х = 8, поэтому а*82 +
+ 4 = 0, откуда а = —1/16/ Итак, уравнение параболы
у = j^-jc2 + 4. Разобьем фигуру на треугольник и под-
график параболы. Площадь треугольника равна !/2* 16-8 =
= 64. Площадь подграфика вычисляем с помощью интег¬
рала:
Пример
Рис. 493
Рис. 494
Общая площадь: 64 + 43=107.
390
Упражнение
веден вырез из правильного шести¬
угольника со стороной 12, сделаны
в форме одинаковых квадратичных
парабол. Какова площадь вырезан¬
ной части?
Вычислите площадь фигуры, изобра¬
женной на рис. 495, если известно,
что закругления, по которым произ-
Приближение площадей фигур многоугольниками
Со времен Архимеда (а возможно, и раньше) в геометрии ис¬
пользовалась следующая идея: для вычисления площади криво¬
линейной фигуры ее заменяли приближенно многоугольником и
пользовались формулами площади многоугольника.
Примеры использования этой идеи.
1. Площадь круга. Впишем в круг радиуса R и опишем около
него правильные м-угольники. Пусть рп и Рп — периметры
л-угольников, 5/t и Sn — их площади, hn — апофема вписанного
м-угольника. Получаем две последовательности sn = l /2hnpn и
Sn=l /2RPny задающие приближения (с недостатком и с избыт¬
ком) площади круга. Как, зная, что длина окружности равна
2л/?, получить площадь круга, равную яR2? Можно проследить,
к какому числу приближаются последовательности Sn и sn. В по¬
следовательности Sn = l/2RPn числа Рп приближаются к 2я/?,
а все произведение — к числу 1 /2R>2nR=nR2. Аналогично, в
последовательности sn = l/2hnpn числа hn приближаются к чис¬
лу R, числа рп — к 2я/?, а все произведение — к */2R*2nR=nR2.
Так как круг лежит между вписанным и описанным много¬
угольниками, то, по свойству монотонности площади, 5n<S<Sn.
Ясно, что площадь круга отличается от площади правильного
вписанного или описанного многоугольника меньше чем на
Sn — sn (площадь заштрихованной на рис. 496 многоугольной
фигуры).
2. Приближенное вычисление интеграла. Запишем формулу
площади подграфика положительной функции.
п=6
Рис. 496
Рис. 495
391
Разобьем отрезок [а, Ъ] на п равных частей и заменим инте¬
гральной суммой — приближенной формулой прямоугольников.
Пусть для простоты функция f(x) возрастает на отрезке [а, Ь].
Замена подграфика внутренней ступенчатой фигурой означает
замену интеграла S суммой sn = ^—^(Кхо) + /(ri) + ••• +
+ /W.-0).
Внешняя ступенчатая фигура даст приближение интеграла S
суммой Sn = Ъ~~ (f(xi) + f(x2) + ... + f{xn)). Ясно, что истинное
значение интеграла отличается от значения Sn или sn не больше
чем на Sn — Sn, т. е. не больше чем на площадь заштрихованной
на рис. 497 многоугольной фигуры.
3. Применение палетки. Нанесем фигуру, площадь которой
мы измеряем, на лист бумаги, расчерченный на единичные квад¬
раты. Подсчитаем число квадратов, целиком содержащихся в
данной фигуре. Обозначим это число s0, a S0 — число квадратов,
имеющих с фигурой хотя бы одну общую точку.
Теперь нанесем сетку в 10 раз более мелкую. Площадь ма¬
ленького квадрата равна 0,01. Пусть s, — число этих квадратов,
целиком лежащих внутри фигуры, Sj — число квадратов, имею¬
щих с ней хотя бы одну общую точку. Числа s,*10“2 и S,-10“2
дают следующее приближение к площади фигуры. Продолжим
процесс умёньшения размеров квадрата дальше. Каждый раз
при этом мы’ заменяем фигуру некоторым многоугольником, пло¬
щадь которого равна на п-м шаге sn-10“2/I или Sn-10_2n. Эти
числа дают приближенные значения площади фигуры.
Заменяя фигуру многоугольником на п-м шаге мы совершаем
ошибку, которая не больше чем (S„ — sn)« 10-2, где Sn — sn —
число квадратов, которые имеют хотя бы одну общую точку с
фигурой, но не лежат целиком в ней, т. е. имеют точки, не при¬
надлежащие фигуре. Они образуют многоугольную фигуру, по¬
крывающую границу фигуры. Если граница фигуры имеет нуле¬
вую площадь, то число (S„ — sn)e10 становится очень малым,
т. е. погрешность измерения стремится к нулю.
392
Рис. 497
Рис. 498
Квадратную сетку, с помощью которой происходит измерение, называют
палеткой (рис. 498).
Во всех трех рассмотренных случаях вычисления площади
некоторой фигуры F мы поступали следующим образом: строили
(способы построения были различными) две последовательности
многоугольников: одну, составленную из многоугольников, це¬
ликом лежащих внутри фигуры Z7, другую — из многоугольни¬
ков, покрывающих F. Измеряя площади этих многоугольников,
мы получали две последовательности чисел, задающих прибли¬
жения (с недостатком и с избытком) площади фигуры F. Раз¬
ность этих приближений на п-м шаге дает оценку для ошибки
измерения. Геометрически эта оценка совпадала с площадью
многоугольной фигуры, которой можно покрыть границу фи¬
гуры F. Так как граница фигуры имеет нулевую площадь, то
ошибку можно сделать сколь угодно малой.
Упражнение
Найдите приближенно (с точностью до
трех знаков после запятой) с по¬
мощью формулы прямоугольников
площадь под кривой на
отрезке [0, 10], разбив его на де¬
сять равных частей. Зная первооб-
разную S In(**+!)>
сравните полученный результат с
точным.
§ 46. Объемы пространственных тел
Аксиомы объема
Изучение объемов мы проведем точно так же, как изучение
площадей.
Аксиома V, (неотрицательность объема)
Объем V каждого измеряемого тела F есть неотрицательное число:
V (F) > 0.
Аксиома V2 (аддитивность объема)
Если тело F разбито на две части F, и Р2, не имеющие общих точек, то
объем тела есть сумма объемов тела F, и Р2:
V(F) = V(Ft) + V(F2).
Аксиома V3 (нормированность объема)
Объем прямого цилиндра равен произведению площади основания на
высоту (рис. 499).
В частности, объем единичного куба равен единице.
Аксиома V4 (инвариантность объема)
Равные тепа имеют равные объемы.
Эта аксиома утверждает, что при перемещении тела его
объем не изменяется.
Теорема о монотонности объема доказывается аналогично
соответствующей теореме о площади.
Теорема — — —
Объем части тепа не больше объема всего тела (рис. 500):
V(F,) < V(F).
Так же как и в случае площадей, можно доказать, что точка,
кривая, поверхность имеют объем, равный нулю. Это позволяет
при использовании аддитивности объема разбивать тело на две
части некоторой поверхностью и не заботиться о том, какой час¬
ти приписать эту поверхность — границу, так как она имеет ну¬
левой объем.
Упражнения 2. Пусть F — общая часть (пересе-
, Л . чение) тел Fi и F2. Докажите фор-
I. Оконный переплет изготовлен из мулу Д-ПЯ объема объединения:
бруса, поперечное сечение которо¬
го— прямоугольник размера 3x5. U^2)= V(Fi)+ V^Fi) — V(F).
Размер окна 50x120. Вычислите
объем переплета.
Интегральная формула для объема
Вспомним, как мы вычислили объем лимона (см. с. 352) в главе,
посвященной интегралу. Лимон резался на дольки с параллель¬
ными краями. Очень важно, что каждая долька настолько тонка,
что ее можно считать цилиндром (с одинаковыми по площади
«Строгие методы являются в то же время простейшими и наиболее до¬
ступными».
Д. Гильберт
394
Рис. 499
Рис. 500
основаниями). Правда, для разных долек эта площадь будет
разной. Однако, зная, как меняется эта площадь в зависимости
от того, где, в какой части лимона, вырезана долька, можно
написать интегральную формулу для объема.
Рассмотрим тело F, выберем в пространстве некоторую ось х
и будем рассекать тело F плоскостями, перпендикулярными
оси jc-
Проекция тела F на ось jc представляет некоторый отрезок,
концы которого обозначим а и Ь. Плоскость сечения будем за¬
давать точкой х на оси: а^х^Ь. Площадь сечения, проведен¬
ного через точку jc, обозначим S(jc) (рис. 501). Таким образом,
мы построили функцию — площадь переменного сечения S = S(jc),
определенную при jc 6 [а, Ь\
Рис. 501 Рис. 502
Из всего тела выделим маленькую часть, заключенную между
сечениями, проведенными через точки jc и jc+djc (рис. 502). Эту
маленькую часть тела можно приближенно считать цилиндром
с основанием S(jc) и высотой djc. Объем такого цилиндра, по
аксиоме V3, равен S(jc)djc. Следовательно, dK=S(jc)djc, откуда
ь
Jswdx
а
Это и есть интегральная формула для объема:
объем равен интегралу от площади переменного сечения.
* При вычислении объема тела с помощью интегральной формулы направ¬
ление, в котором проводятся плоские сечения, может быть произвольным.
Его обычно выбирают так, чтобы формула для площади переменного
сечения была возможно более простой. Мы убедимся в этом, вычисляя
объемы пирамиды, конуса и шара.
Объем наклонного цилиндра
Рассмотрим наклонный цилиндр. Сечения этого цилиндра плос¬
костями, параллельными основаниям, имеют постоянную пло¬
щадь S (рис. 503), поэтому ось х проведем перпендикулярно
плоскостям оснований. Выберем начало О на оси х в точке пере¬
сечения оси с нижним основанием цилиндра, а направление оси
укажем снизу вверх. Тогда плоскость верхнего основания пере¬
секает ось х в точке Я, где Н — высота цилиндра. Итак,
н н
S(x)=S и V=$Sdx=S$dx=SH.
Мы получили, что для объема наклонного цилиндра справедлива
та же формула, что и для объема прямого цилиндра.
Объем пирамиды
Рассмотрим пирамиду (рис. 504). Ось х проведем перпендику¬
лярно плоскости основания. Тогда в сечениях пирамиды плоскос¬
тями, параллельными основанию (а. значит, перпендикулярными
оси х), будут многоугольники, подобные основанию. Выберем
начало О на оси х в точке пересечения оси с сечением, проходя¬
щим через вершину пирамиды, а направление — сверху вниз
(рис. 504). Тогда плоскость основания пересекает ось в точке
х=#, где Н — высота пирамиды.
Вычислим площадь переменного сечения S(x). В сечении по¬
лучается многоугольник, подобный основанию. Коэффициент по¬
добия равен отношению расстояний секущих плоскостей от вер¬
шины: х/Н. Обозначим площадь основания S. По теореме об
отношении площадей подобных многоугольников имеем
^s~= (тг)2’ те‘ =
Площадь переменного сечения представлена квадратичной
функцией от х. Интеграл от нее вычисляется просто:
3%
Рис. 503
Рис. 504
Объем пирамиды равен одной трети произведения площади основания
на высоту.
Объем конуса
Формула для объема конуса получается аналогично формуле
для объема пирамиды (рис. 505):
S(x) = ~lrx\ V = ±-SH.
Объем любого конуса равен одной трети произведения площади основа¬
ния на высоту.
В частности, объем кругового конуса с радиусом основания R
и высотой Н равен
V = Уз nR2H.
Объем шара
В сечении шара любой плоскостью получается круг. Поэтому
ось х можно выбрать произвольно, а начало О взять в точке пе¬
ресечения плоскости, проходящей через центр шара (рис. 506).
Вычислим площадь круга, получающегося в сечении плоскостью,
проходящей через точку х. По теореме Пифагора, r2-|-jc2 = /?2
(рис. 507), откуда
S(x) = яг2 = n(R2 — х2).
Вследствие симметрии шара весь его объем V равен удвоен¬
ному объему его верхней половины, который получится при ин-
397
Рис. 505
Рис. 506 Рис. 507
тегрировании переменной площади от 0 до R:
R R R R
V = 2 $ S(x) dx = 2 $ n(R2 — х2) dx = 2я(R2 $ dr— § x2 dx) =
0 0 0 0
_ 2»(я* - 4 £ ) = 2я(л> - £) = 2я ^ = -1. яЛ».
Итак, объем шара радиуса R равен
V = 4/,nR\
Объем тела вращения
Кроме шара существует и много других тел, в сечениях которых
получаются круги. Представим себе тело, образованное враще¬
нием некоторой плоской фигуры относительно оси. Сечение этого
тела, перпендикулярное оси вращения, — круг.
Пусть фигура представляет собой подграфик функции y=f(x)y
заданной на отрезке [а, Ь] (/(*)>0). При вращении этого под-
графика относительно оси х получим тело вращения (рис. 508).
Сечение, проведенное через точку х перпендикулярно оси, будет
Рис. 508
398
кругом радиуса r=f(x). Площадь сечения S=nr2=nf2(x). По
интегральной формуле, объем тела вращения
ь
V = я \ f2(x) dx.
а
Примеры
1. Найти объем тела, полученного при вращении отрезка ги¬
перболы у=—, г£[1/2, 2], вокруг оси х.
= Р/2==я-“Г = Т-'
1/2
2. Найти объемы тел, образованных вращением отрезка па¬
раболы у=хг6[0, 1], вокруг оси х и вокруг оси у.
Объем тела вращения относительно оси х вычисляется
по формуле
1 1
V = я J (jc2)2 dx— я J х4 dr = -у- ж 0,63.
0 о
Для нахождения объема тела вращения относительно
оси у зависимость у(х)=х2 заменяется на зависимость
х(у)= где f/б[0, 1]:
1 1
К = я$(/у")2 &у = л §t/di/ = -g-« 1,05.
о о
§ 47. Площадь поверхности
Тела с плоскими развертками
Общая формула площади поверхности достаточно сложна. Мы
ограничимся лишь простыми частными случаями.
Выведем формулу площади поверхности тела, когда его по¬
верхность развертывается на плоскость. Простейшими приме¬
рами таких тел являются многогранники. Поверхность таких тел
состоит из многоугольников, площади которых мы уже умеем
вычислять, а площадь всей поверхности равна сумме площадей
всех граней, исходя из свойства аддитивности площадей.
Другим примером тел, допускающих развертку, являются ци¬
линдры и конусы. Приведем формулы для площадей боковых
поверхностей некоторых тел:
399
1) правильная п-угольная призма со стороной основания а
и высотой Н
5бок — па Н,
2) правильная п-угольная пирамида со стороной основания а
и апофемой h
S6oK = ' /2nah;
3) прямой круговой цилиндр с радиусом основания R и вы¬
сотой Н
5бок = 2л/?#;
4) прямой круговой конус с радиусом R и образующей I
•^бок TiR I.
Выведем последнюю формулу.
Разверткой боковой поверхности прямого кругового конуса
является круговой сектор, радиус которого равен длине образую¬
щей /, а длина дуги равна длине окружности основания конуса,
т. е. 2nR (рис. 509). Используя формулу для площади кругового
сектора, получаем
5б0к =1 /22л Rl=nRl.
Нетрудно представить себе и другие тела, поверхности кото¬
рых получены изгибанием плоских фигур. В этих случаях вычис-
Рис. 509 Рис. 510
ление площади поверхности можно свести к вычислению пло¬
щадей плоских фигур-разверток (рис. 510).
Поверхность шара
Далеко не всякое тело можно развернуть на плоскость. Про¬
стейшим примером может служить шар. Как же тогда измеря¬
ется площадь его поверхности?
Размер площади кривой поверхности можно определить по
количеству краски, которую нужно потратить на равномерное
покрытие поверхности. Предположим, что краска нанесена рав¬
номерно слоем толщины е только на одну сторону поверхности.
Масса краски пропорциональна объему AV тонкой пленки, ко¬
торый можно приближенно оценить как произведение искомой
400
площади S на толщину е слоя: Al/ = Se. Чем меньше в, тем точ¬
нее формула. Можно вычислить площадь S* приближенно как
отношение AV/г при малом е, т. е. за площадь поверхности тела
принять предел отношения объема слоя к его толщине при стрем¬
лении толщины этого слоя к нулю.
Применим указанную идею для вычисления площади поверх¬
ности шара. Пусть шар имеет радиус /?. Тонкая пленка предста¬
вит собой тело, заключенное между двумя концентрическими
шарами радиусов R и /? + d/?, где d R — толщина пленки
(рис. 511).
Если V(x) — объем шара радиуса ху то объем пленки равен
V(R-\-dR)—V(R)=AV, т. е. приращению объема как функции
радиуса.
Предел отношения AV/AR есть производная объема шара по
радиусу: S(/?) = -|j^-. Зная формулу объема шара, дифференци¬
рованием получаем формулу для площади поверхности:
V(R) = 4/3 л/?3 =► S(R) = (4/3 л/?3)' = ‘4/3л• 3 R2 = 4 л/?2.
Итак, площадь поверхности шара радиуса R равна 4л/?2.
Интересно заметить, что аналогично поверхности шара мож¬
но получить формулы для длин кривых исходя из площадей.
Так, длина окружности С получается дифференцированием фор¬
мулы для площади круга:
5=л/?2 =>- C = S'=(nR2)' = 2nR.
Задачи и вопросы
12.1. Разделите данный отрезок а на две, три, пять равных час-
г-т о я 2л Зл 7л 20л _ л |-т
теи. Построите углы , —, —, —, —— радиан. Пе¬
реведите из градусной меры в радианную следующие углы:
75, 120, 135, 210, 240, 270, 300, 400°. Переведите из ра-
дианной меры в градусную следующие углы:—, —,
4 6
7л 19л 11л
Т’ 6 ■
12.2. Радиус окружности равен 5. Вычислите с точностью до
14 — 1681 401
Рис. 511
0,1 длины дуг, соответствующих углам
о о 4 ^
12.3. Круговой сектор имеет угол 10° и периметр 5. Найдите
радиус сектора с точностью до 0,1.
12.4. Длина окружности равна 6• 103. Ее радиус увеличили на 1.
На сколько увеличилась ее длина?
12.5. Как изменится длина дуги окружности, если радиус ок¬
ружности уменьшится вдвое, а угол вдвое увеличится?
если и радиус, и угол увеличатся в два раза?
12.6. Докажите: а) отрезок имеет нулевую площадь; б) окруж¬
ность имеет нулевую площадь.
12.7. Стороны двух участков земли квадратной формы равны 10
и 15 м. Определите сторону квадратного участка, равнове¬
ликого им.
12.8. Как изменится площадь квадрата, если его сторону увели¬
чить в 4 раза? уменьшить в 3 раза?
12.9. Во сколько раз надо увеличить сторону квадрата, чтобы
его площадь увеличилась в 36 раз? уменьшилась в 25 раз?
12.10. Найдите стороны прямоугольника, если его стороны от¬
носятся как 3:5, а площадь равна 240.
12.11. Параллелограмм и прямоугольник имеют одинаковые сто¬
роны. Найдите острый угол параллелограмма, если пло¬
щадь его равна половине площади прямоугольника.
12.12. Что имеет большую площадь; квадрат или ромб? Объясни¬
те ответ.
12.13. Найдите площадь треугольника по трем сторонам: а) 15;
13 и 4 см; б) 35; 29 и 8 см.
12.14. Найдите меньшую высоту треугольника со сторонами 4, 5
и 7 см.
12.15. Боковая сторона равнобедренного треугольника 6 см, вы¬
сота 4 см. Найдите радиус описанной окружности.
12.16. Во сколько раз увеличится площадь круга, если его
диаметр увеличить в п раз?
12.17. В прямоугольном треугольнике через а, Ь обозначены ка¬
теты, с — гипотенуза, а — острый угол, А — высота, опу¬
щенная из вершины прямого угла. Вычислите площадь по
следующим данным: а) а, с\ б) а, а; в) с, а; г) А, а;
д) а, А.
12.18. В равнобедренном треугольнике через а обозначено осно¬
вание, b — боковая сторона, а — угол при вершине, р —
угол при основании, г — радиус вписанного круга. Вычис¬
лите площадь S треугольника по следующим данным:
а) а, Ь\ б) а, а; в) а, 0; г) 6, а; д) Ьу 0; е) г, d\ ж) г, р.
12.19. В равнобочной трапеции а — большее основание, b —
меньшее основание, а — угол при большем основании,
А — высота, с — боковая сторона. Вычислите площадь S
по следующим данным: а) а, Ьу с; б) а, b, а; в) а, с, а;
г) а, А, а; д) ft, А, а.
402
12.20. В круговом секторе R — радиус, а — угол, / — длина
дуги, г — радиус круга, вписанного в сектор. Вычислите
площадь сектора по следующим данным: а) /?, а; б) /?, /;
в) /, а; г) г, а.
12.21. Найдите отношение площади круга, описанного около квад¬
рата, к площади круга, вписанного в квадрат.
12.22. Найдите отношение площади квадрата, описанного около
круга, к площади квадрата, вписанного в этот круг.
12.23. Во сколько раз площадь круга, описанного около шести¬
угольника, больше площади круга, вписанного в этот
шестиугольник?
12.24. Во сколько раз площадь правильного треугольника, опи¬
санного около круга, больше площади правильного тре¬
угольника, вписанного в него?
12.25. Докажите, что если два треугольника имеют общий угол,
то отношение их площадей равно отношению произведе¬
ний сторон, заключающих этот угол.
12.26. Докажите, что площадь трапеции равна произведению
одной из боковых сторон на длину перпендикуляра, опу¬
щенного на нее из середины другой боковой стороны.
12.27. Через точку, взятую на диагонали АС параллелограмма
ABCD, проведены прямые, параллельные его сторонам.
Параллелограмм делится ими на четыре параллелограмма.
Два из них пересекаются диагональю АС. Докажите, что
два других параллелограмма равновелики.
12.28. Через каждую, вершину выпуклого четырехугольника про¬
ведена прямая, параллельная его диагонали. Докажите,
что полученный четырехугольник имеет площадь, вдвое
большую площади исходного четырехугольника.
12.29. Докажите, что площадь многоугольника, описанного
около окружности, разна половине произведения радиуса
этой окружности на периметр многоугольника.
12.30. Найдите площадь, заключенную между графиками:
а) у=х и у=х2\ б) у=х2 и у= 1.
12.31. Вычислите с точностью до 0,01 интегралы:
\ ТТ?-; S tgxdx.
о о
12.32. Найдите объем цилиндра, получаемого вращением прямо¬
угольника со сторонами а и b (а>Ь) вокруг прямой, про¬
ходящей через большую сторону.
12.33. Прямоугольник со сторонами а и b двумя способами сво¬
рачивают в цилиндр. Найдите объемы этих цилиндров.
12.34. Найдите объем конуса, получаемого вращением равно¬
бедренного треугольника с основанием а и высотой h во¬
круг высоты.
12.35. Из круга радиуса г вырезали сектор с центральным
углом а и из оставшейся части свернули воронку. Найди¬
те вместимость полученной воронки.
14*
403
12.36. Найдите объем тела, получаемого вращением равнобоч¬
ной трапеции с основаниями а и Ь (а>Ь) и высотой А
вокруг большего основания.
12.37. По полуокружности радиуса R скользит фигура так, что
ее плоскость перпендикулярна диаметру этой полуокруж¬
ности. Изобразить получающееся тело и найти его объем,
если фигура является: а) квадратом со стороной а;
б) правильным треугольником со стороной а; в) окруж¬
ностью радиуса г.
12.38. Найдите объем правильных тетраэдра и октаэдра с реб¬
ром а.
12.39. Основание прямого параллелепипеда — ромб, площадь
которого 1 м2. Площади диагональных сечений 3 и 6 см2.
Найдите объем параллелепипеда.
12.40. Деревянная плитка в форме правильного восьмиугольника
со стороной 3,2 см и толщиной 0,7 см сделана из дерева
с плотностью 0,5 г/см3. Найдите массу деревянной плитки.
12.41. Сколько бочек длиной 1,5 м и диаметром 0,8 м нужно,
чтобы разлить в них содержимое цистерны длиной 4,5 м
и диаметром 1,6 м?
12.42. Как измерить объем воды в цилиндрической цистерне с
помощью вертикального прута?
12.43. Почему струя воды, текущая из крана, сужается книзу?
12.44. В правильной я-угольной пирамиде а — сторона основа¬
ния, Ь — боковое ребро, А — высота, а — плоский угол при
вершине,, р — угол наклона боковой грани к плоскости
основания, у — угол наклона бокового ребра к плоскости
основания. Вычислите объем пирамиды по следующим
данным:
I. п = 3:
а) а, А; б) а, Ь\ в) by А; г) а, а; д) А, Р; е) а, Р;
ж) 6, у; з) А, у\
II. п=4:
а) а, А; б) а, Ь\ в) Ьу А; г) а, а; д) А, Р; е) Ьу у\
ж) А, у;
III. п=6:
a) а, Р; б) A, y; в) fe, а.
12.45. Найдите объем шара, вписанного: а) в куб с ребром а;
б) в цилиндр радиуса /?; в) в правильную четырехуголь¬
ную пирамиду со стороной основания а и высотой А;
г) в правильную четырехугольную пирамиду со стороной
основания а и углом а между боковой гранью и плоско¬
стью основания.
12.46. Найдите отношение объема шара, описанного около куба,
к объему шара, вписанного в куб.
12.47. Найдите отношение объема куба, описанного около шара,
к объему куба, вписанного в шар.
12.48. Два одинаковых конуса расположены так, что верши¬
на одного лежит в центре основания другого. Какую
404
часть составляет объем их общей части от объема всего
конуса?
12.49. Металлический шар радиуса 1 м переплавили в шары ра¬
диусов 10 см. Один из них переплавили в шарики радиу¬
сов 1 см. Каких шаров теперь больше?
12.50. Что бы вы предпочли: съесть арбуз радиуса 15 см вчетве¬
ром или арбуз радиуса 20 см восьмером?
12.51. Одно цилиндрическое бревно вдвое длиннее, но вдвое
тоньше другого. Из какого бревна выйдет больше по¬
леньев?
12.52. Найдите объем тела вращения, полученного вращением
вокруг гипотенузы прямоугольного треугольника с углом 30°
и гипотенузой 6 см.
12.53. Найдите объем цилиндра, вписанного в куб со стороной а.
12.54. Найдите объем цилиндра, описанного около шара ра¬
диуса R.
12.55. Найдите объем конуса, вписанного в куб со стороной а.
12.56. Найдите цилиндр наибольшего объема, вписанный в шар
радиуса R.
12.57. Найдите конус наибольшего объема, вписанный в шар
радиуса R.
12.58. Найдите цилиндр наибольшего объема, вписанный в конус
с радиусом основания /?, у которого угол наклона обра¬
зующей к плоскости основания равен 45°.
12.59. Найдите площадь поверхности правильного тетраэдра со
стороной а.
12.60. Найдите площадь боковой поверхности правильной че-
тырехугольной пирамиды со стороной основания а и
плоским углом а при вершине.
12.61. Найдите отношение площади поверхности шара, описан¬
ного около куба, к площади поверхности шара, вписан¬
ного в куб.
12.62. Найдите отношение площади поверхности куба, описан¬
ного около шара, к площади поверхности куба, вписан¬
ного в шар.
12.63. Прямоугольник со сторонами а и Ь двумя способами сво¬
рачивают в цилиндр. Найдите площадь боковых и полных
поверхностей этих цилиндров.
12.64. Найдите боковую и полную поверхности конуса, получен¬
ного вращением вокруг высоты равнобедренного треуголь¬
ника с основанием а и высотой Н.
12.65. Воронка имеет вид конуса, свернутого из кругового сек¬
тора радиусом R и центральным углом а. Найдите площа¬
ди боковой и полной поверхностей конуса.
12.66. В правильной я-угольной пирамиде (п=3, 4, 6) а — сто¬
рона основания, а — плоский угол при вершине, Ь — бо¬
ковое ребро, h — высота, р — угол наклона боковых гра¬
ней к основанию, у — угол наклона боковых ребер к осно¬
ванию. Вычислите площадь боковой поверхности по сле-
405
дующим данным: а) а, А; б) а, Ь\ в) b, А; г) а, а;
д) А, Р; е) а, Р; ж) 6, у; з) А, у-
12.67. Найдите площади сфер, вписанных: а) в куб с ребром а;
б) в цилиндр радиуса R и высоты 2R\ в) в правильную
четырехугольную пирамиду со стороной основания а и
высотой Н\ г) в правильную треугольную пирамиду со
стороной основания а и высотой Н.
12.68. Как относятся площади сфер, описанной около правиль¬
ного тетраэдра и вписанной в этот тетраэдр?
12.69. Образующая конуса равна 1 м. Каковы наибольшее и
наименьшее значения его боковой поверхности?
12.70. Сколько листового железа требуется для изготовления
цилиндрической цистерны объемом 20 м3?
13
УРАВНЕНИЯ И НЕРАВЕНСТВА
§ 48. Решение уравнении и неравенств
с одним неизвестным
Основные определения
Вспомним основные понятия, связанные с решением уравнений
и неравенств.
Уравнение — это два буквенных выражения, соединенных знаком ра¬
венства.
Неравенство — это два буквенных выражения, соединенных одним из
знаков неравенства (>, >, <, <).
Величины, входящие в состав уравнения (неравенства), на¬
зываются неизвестными.
Решение уравнения (неравенства) — это набор значений не¬
известных, при подстановке которых получается верное числовое
равенство (неравенство).
Решить уравнение (неравенство) — это значит найти все его решения.
Решение уравнения с одним неизвестным обычно называют
корнем уравнения. Поэтому можно сказать, что решить уравне-
нение — это значит найти все его корни.
В этом параграфе рассмотрены только уравнения и неравен¬
ства с одним неизвестным.
Примеры
1. *(jc+1)(* + 2)(jc + 3)=120.
Это уравнение с одним неизвестным х. Число х = 2 является
его корнем, так как 2-3-4-5=120— верное равенство. Чис¬
ло х=\ не является корнем этого уравнения, так как ра¬
венство 1-2-3-4= 120 неверно.
407
/х^2>1.
Это неравенство с одним неизвестным х. Число х = 11 —
его решение, так как числовое неравенство -д/11—2 > 1
верно. Число х = 9/л не является решением, так как неравен¬
ство У9Л-2>1 неверно (левая часть равна 1 /2) - Число
х= 1 также не решение неравенства, так как его нельзя под¬
ставлять в левую часть: -\х—2 имеет смысл лишь при
Область допустимых значений уравнения (неравенства) ОДЗ — это мно¬
жество всех знаний неизвестного, при которых определены все выраже¬
ния, входящие в состав уравнения (неравенства).
Область допустимых значений уравнения в примере 1 —
множество всех действительных чисел IR. Область допусти¬
мых значений во втором примере х^2.
х 2х — 1
х+ 1 X— 1
Область допустимых значений этого уравнения — все
числа, кроме х= 1 и х= — 1 или ОДЗ: хф-fcl.
]/х — 3 + /5 — х = 2.
Область допустимых значений этого уравнения нахо¬
дится из двух условий: х — 3^0 и 5 — х^О. Откладывая
решения этих неравенств на числовую ось, получаем ОДЗ:
3<*<[5.
1. Слово «решение» применяется в двух смыслах. Можно сказать о ре¬
шении уравнения как его корне. В этом случае справедливы такие фразы,
как «уравнение имеет одно решение», «уравнение имеет три решения»,
«уравнение не имеет решений». В речи часто используют словосочетание
«решение уравнения» как процесс нахождения его корней (решений).
Можно сказать так: «уравнение имеет сложное решение», «я не смог най¬
ти путь решения этого уравнения». В процессе решения уравнения может
обнаружиться, что оно совсем не имеет корней (решений). В этом случае
мы скажем, что уравнение решили: доказали, что у него решений нет.
2. Что означает найти корни уравнения?
В школьной практике при решении уравнений принято записывать
ответ как результат операций над числами, например:
*=/2-, * = УГТ7Г,
log35
х — sin , x = 2/J.
5
В то же время при решении прикладных задач бывает необходимо
представить ответ в десятичной записи с определенным числом знаков
после запятой. Такой ответ можно получить, используя микрокалькулятор.
3. Мы условились областью допустимых значений считать множество всех
значений неизвестного, которые имеет смысл подставить в данное урав¬
нение (неравенство), иначе говоря, общую область определения всех
входящих в уравнение функций. Однако часто область допустимых зна¬
чений бывает меньше за счет дополнительных ограничений, возникающих
тогда, когда уравнение (неравенство) появилось из прикладной задачи,
в которой неизвестные не могут принимать какие угодно значения.
Так, если неизвестное х — расстояние, пройденное поездом, то надо
считать, что jc>0; если х — неизвестное число землекопов, то надо счи¬
тать, что х — натуральное число, и не допускать, чтобы в ответе получа¬
лось «два землекопа и две трети».
Упражнения
1. Найдите целые корни уравнения
х4—Зх3+х2—х—6=0. Указание.
Целыми корнями могут быть только
делители свободного члена, т. е.
числа ±1, ±2, ±3, ±6.
2. Найдите целые решения неравен¬
ства 4х2—4х—3<0.
3. Найдите области допустимых значе
ний следующих уравнений и нера
венств:
а) log2(jc-l)= /х+Т\
б) log2(jt—5)+ log3(10—х)^х\
в) /log7j дс > 1;
г) ^х—4 + /2—х =3.
Равносильность
Два уравнения называются равносильными, если каждый корень первого
уравнения является корнем второго и, обратно, каждый корень второго
уравнения является корнем первого.
Два неравенства называются равносильными, если всякое решение пер¬
вого является решением второго и, обратно, всякое решение второго не¬
равенства является решением первого.
Переход от одного уравнения (неравенства) к другому, ему
равносильному, является основным приемом в процессе решения.
Можно сказать, что равносильные уравнения имеют одни и
те же корни, или, иначе, множества корней равносильных урав¬
нений совпадают. Поэтому, заменяя уравнение' ему равносиль¬
ным, мы получаем уравнение с теми же корнями, но решение
его может оказаться проще..
Чаще всего приходится делать следующие алгебраические
преобразования уравнения: перенос членов из одной части в
другую; раскрытие скобок; приведение к общему знаменателю;
преобразования, использующие свойства логарифмов, корней,
тригонометрических функций, и т. п.
При этом надо следить, не происходит ли при совершаемом
преобразовании нарушение равносильности. Особенно надо
быть внимательным к таким преобразованиям как умножение
обеих частей уравнения на одно и то же выражение, возведение
в квадрат, освобождение от логарифмов (потенцирование).
в) y/F> 1 и log2*>0;
г) \х\<2 и jc2<4;
д) х* = 4 и х—2 = 0.
2. Могла ли нарушиться равносиль¬
ность уравнений при переходе от
Упражнения
1. Равносильны ли следующие уравне¬
ния и неравенства:
а) 2*—3=1 и х2—4х-|— 4=0;
б) я—3=0 и (jc-2)(jc-3)=0;
одного уравнения к другому и если
могла, то за счет чего:
б) /(*)=!
и f(x) = x— 1;
и (/«)2= 1;
в) log2/(*)=0 и f(x)= 1;
Г) log2/W=log2^W и f(x) = g(x)\
Д) /Кх) =1 _ и /(*)= 1;
е) v7W~= и f(x)=g(x).
Общие приемы решения уравнений
1. Разложение на множители. Если с помощью
алгебраическйх преобразований удается привести уравнение к
такому виду, когда в одной части будет произведение нескольких
множителей, а в другой — нуль, то надо приравнять нулю
каждый из множителей, решить полученные уравнения, а затем
объединить полученные корни .
Примеры
1. jt(*+l)(jt + 2)(* + 3)=120;
х(х-\- 1)(х2 + 5л: + 6)= 120;
r4 + 6*3+ 1l*2 + 6* + 1 - 121 =0;
(*2 + 3*+1)2-112=0;
(х2 + Зх+12)(х2 + Зх-1 0)=0.
Уравнение jc2 + 3x+12=0 корней не имеет, а уравнение
х2-\-Зх— 10=0 имеет корни Х\=2 и х2 =—5.
Нельзя сокращать общие множители в уравнении, а надо перенести все
члены в одну часть и разложить на множители.
2. sin2 x=sin х cos х,
sin х (sin x — cos x)=0.
Решаем каждое уравнение отдельно:
sin х = 0; х = nk (k 6 2Z)\
sinx=cosjt:, tgx=l; x=n/4-\-nk.
Затем объединяем корни: x=nky х=л/A-\-nk.
2. Введение нового неизвестного. Посмотрите,
не решая, на следующий набор уравнений:
В каждом из них отметим присутствие выражения х2-\-Зх.
Если заменить его буквой у (у=х2 -\-Зх)у то получим более про¬
стые уравнения относительно у:
1) (х2 + Зх)2 + 2(х2 + Зх) — 120=0;
1) у2 + 2у — 120 = 0;
2) л[у + л/у + 1 = 1;
3) 2у - 2У~1 =
4) log\у — log2у — 2 = 0.
3. Графический метод. Рассмотрим уравнение с од¬
ним неизвестным
Мх)=Мх).
Изобразим на одном рис. 512 графики функций i/|=/i(jt) и
y2 = f2(x). Точкам пересечения графиков этих функций соответ¬
ствуют те значения аргумента ху при которых совпадают значе¬
ния функций, т. е. корни данного уравнения.
Итак, абсциссы точек пересечения графиков функций у\ =
= f\(x) и y2 = f2(x) являются корнями уравнения /1(*)=/2(л;).
Например, для уравнения хг=х-\-2 такими точками будут
Р,=(-1; 1) и Р2=(2; 4) (рис. 513).
«В основе большинства математических открытий лежит какая-либо
простая идея... поэтому нет непроходимой стены между оригинальными
математическими исследованиями и решением задач, доступных способ¬
ному и достаточно упорному начинающему математику.»
А. Н. Колмогоров
411
Рис. 512
Рис. 513
Если уравнение имеет вид /(х)=0, то в качестве функции,
стоящей в правой части, выступает функция у=0. Графиком ее
будет ось Ох, поэтому корни уравнения /(*)=0 — абсциссы точек
пересечения графика функции y=f(x) с осью Ох (рис. 514).
Графическая иллюстрация решения уравнения указывает на
первый взгляд и способ решения уравнения: строят в системе
координат две кривые и находят их точки пересечения. Действи¬
тельно, если выбрать масштаб и построить графики достаточно
аккуратно, то можно приближенно найти точки пересечения и их
абсциссы — корни уравнения. Но для того чтобы найти коорди¬
наты точей пересечения точно, как раз и нужно решить соответ¬
ствующее уравнение! В то же время графическая иллюстрация
часто дает некоторые качественные ответы: число корней и
указывает отрезки на числовой оси, где они могут находиться.
Примеры
1. Определить графически интервалы, в которых лежат корни
уравнения (л: — I)2 = -у[х~.
Построим графики функций, стоящих в левой и правой
частях (рис. 515).
Из рисунка можно заключить, что уравнение имеет два
действительных корня, один из них находится в интервале
(0; 1), а другой — в интервале (2; 3). Можно указать эти
412
Рис. 514
Рис. 515
Рис. 516
интервалы и более точно: (0; 0,5) и (2; 2,5); еще более точ¬
но: (0,2; 0,3) и (2,2; 2,3). Действительно, нетрудно прове¬
рить, что при х = 0,2 имеем -у]х < (jc — 1 )2, а при х = 0,3 —
уже -д/х ;>(* — I)2, точно так же при х = 2,2 левая часть
уравнения больше правой, а при х = 2,3 — меньше.
Вычисляя и сравнивая значения правой и левой частей
уравнения, можно найти корни с любой степенью точности.
2. Корни уравнения пятой степени хъ — Зх+1=0 нельзя запи¬
сать с помощью радикалов, но, построив достаточно точный
график функции у=хъ — Зх-\-1 (рис. 516), можно опреде¬
лить, что уравнение имеет три корня в интервалах (—1,5;
— 1,3), (0; 0,5) и (1; 1,3).
Упражнения
1. С помощью разложения на множи¬
тели приведите решение данного
уравнения к решению более простых
уравнений (не решая уравнения):
а) 3sirt2л: — 2cosjc = 0;
б) log3z+log3(z—2)=log3(z3—2);
в) sin3jc — 2 sin2jc + 5 sin л:— 10 = 0.
2. С помощью замены неизвестного
приведите уравнение к более просто¬
му виду (не решая получившегося
уравнения):
Классификация уравнений и неравенств
Уравнения и неравенства часто классифицируют в зависимости
от того, какие функции входят в их состав. Так, выделяют рацио-
нальные уравнения и неравенства, образованные рациональными
функциями, т. е. дробями, в числителе и знаменателе которых
стоят многочлены.
Примеры
1. (х* — х)2 — 3(х2— *) + 2 = 0.
3 * I ^ сСГ ^
Jf+ 1 ~ * + 3 JC + 2 '
4. jjc2 -|- лс — 6|^4дг.
Уравнения и неравенства, в которые входят неизвестные под радикалом,
называются иррациональными.
а) sin(х2-|-1)sin2(j«r2-|-1)=2;
б) 3',+ ,-3',+2 = -2;
в) 3 уФ+1 -хг=2\
г) ъы?+о+1ок§(*41>=1-
3. Определите по графику число кор¬
ней уравнения:
а) 2х = 3-2х-х2;
б) log2* = Jt2+*--2;
в) siru = 1/2*—W
413
Примеры
1. /7+2=X.
2. V~h~+2 V/£±-!-=3.
r x +1 r X
3. }/jc + 2>x.
Классификация уравнений и неравенств (показательное
уравнение, логарифмическое уравнение, тригонометрическое
уравнение и т. п.) является, конечно, условной, так как на самом
деле в одно уравнение могут входить функции самых различных
типов.
Среди уравнений (неравенств) обычно выделяют простейшие,
решения которых находят по готовым формулам.
Примеры
Решите уравнения и неравенства:
1. (х2 — х)2 — 3(х2 — *) + 2 = 0.
Делаем замену неизвестного: х2 — х = у, у2 — Зу 2 =
= 0, у\ = 2, у2 = 1.
Решаем уравнения относительно х: х2 — х = 2, х2 — х —
— 2=0, *1=2, х2 = — 1; х2 — х=1, х2 — х— 1 =0, *3,4 =
= ~2^~ ' Уединяем корни: ' х\=2, jc2 —— 1, *з,4=
1 ± /5~
2
2. -5—-=(* — \f-\-x2.
х — х 1 v } 1
Преобразуем правую часть: (х— \)2-{-х2 = х2 — 2х-\-1 +
-\-х2 = 2(х2 — *)+ 1). Делаем замену: х2 — х = у, -~y==2t/+ 1-
Умножаем обе части на у-\-1: 15=(г/ -|-\){2у-\-1),
2«/2 + 3«/—14 = 0, t/i =2, у2 = —7/г-
Проверяем, что при найденных значениях у множитель
у+ 1 не обращается в нуль. Находим х: х2 — х=2, х\ = 2у
Х2 = — 1; х2 — х=—1 /2, х — л: + 7/2 = 0. Корней нет.
Ответ: *i = 2, Х2 = — 1.
3 1 I 2 - 3
JC+ 1 ' Jt + 3 ^ * + 2 *
Перенесем правую часть неравенства в левую, приведем
к общему знаменателю и разложим числитель на множи¬
тели:
— 1— -—<0
х+ 1 ~ JC + 3 х + 2 ^ ’
дс8 -|- 5дс + 6 -|- 2(дсг -f- Зле -|- 2) — 3(дсг -f- 4дс -|- 3) п
(х+1)(х + 2)(х + 3) ^U’
^-±-! <о,
(х+1)(* + 2)(* + 3)
£nJ >0
(х+1)(* + 2)(* + 3) "'и-
Применяя метод интервалов, находим (рис. 517) решение
неравенства.
Ответ: х<С —3, —2<х< — 1, х>\.
4. |лг^ jc — 6| ^ 4jc.
Раскрываем модуль. Для этого наносим на числовую ось
корни Х\ = —3; Х2=2 (рис. 518) квадратного трехчлена
х2 + х-6.
I. В области 3 или х^2 исходное неравенство
имеет вид х2 + х — 6^4х, х2 — Зх — 6<10.
Находим корни трехчлена х2 — Зх — 6: х\ = 3~ ^ , х2=
о I ,/7^
= 2—' Заносим их на числовую ось (рис. 519) и выпи¬
сываем решения в области I: 3+ ^
II. В области —3<jcC2 исходное неравенство имеет
вид —(jc2 +jc —6)^4дг, х2-\-5х — 6^0. Наносим на число-
Рис. 520
вую ось корни трехчлена х2-{-5х — 6 (рис. 520): jci = —6,
*2=1. Находим решения в области II: 1^дс^2.
Объединяем ответы: 1 (рис. 521).
Рис. 521
415
Рис. 517
Рис. 518
Рис. 519
5. \/х-\-2 = х.
Возводим уравнение в квадрат и для сохранения равно¬
сильности пишем дополнительное условие х^О: x-j-2 = x2,
х>0, х2 — х — 2 = 0, х\ = — 1, JC2=2. Первый корень не
удовлетворяет условию х^О.
Ответ: х=2.
в. |^Г+2 |/нг=з.
r ЛГ + 1 г X
4 /
Делаем замену: K^q7[-=*/» тогДа */ + 2у = 3, у2 —
— Зу-\-2 = 0 (у = 0 не является корнем этого уравнения,
поэтому умножение на у не привело к появлению посторонних
корней): у\ =2, r/2 = 1 - Возвращаясь к переменной х, находим
у—=2, 1/—=1. Возводя обе части этих уравнений
f х+\ ¥ х+\
в четвертую степень, находим ^ ^ =16, ^^ - = 1, \6x-\-
16 = х, х = х+1, х= — ,6/15, корней нет.
Ответ: х= — ,6/,5.
7. /*+'2>*.
ОДЗ: х-\-2^0ох^ —2 (рис. 522).
Если иррациональное уравнение мы смело возводили в
квадрат, так как всегда можно было проверить нарушение
равносильности, подставляя корни полученного уравнения,
то при решении неравенства нужно поступать аккуратнее.
Переход a>b=^a2>b2 является верным при Ь>0. Если
6<0, то этот переход может быть как верным, так и невер¬
ным, в чем легко убедиться на примерах: 3> — 2=>9>4 —
верный переход; 3>—5=^9>25 — неверный переход.
Неравенство а>Ь, где а>0, Ь<С0, является всегда верным, какие бы значе¬
ния указанных знаков ни подставляли вместо а и Ь. Поэтому если х<0, то
неравенство ^х-\-2>х верное. Итак, все отрицательные числа, входящие
в ОДЗ, будут решениями неравенства. Нанесем их на числовую ось. Пусть
х^О. Возведение в квадрат теперь не нарушает равносильности: х + 2>
>х2охг — х — 2<0. Корни квадратного трехчлена х\ = — 1, лг2 = 2 наносим
на числовую ось; решением будут числа 0^х<2 (рис. 532).
Ответ: — 2<х<2.
Рис. 523
416
8. log2(x — 1) + log2 (x -|- 5) —4.
Потенцируя уравнение, находим (x— l)(x + 5) = 24.
При этом переходе увеличилась область допустимых значе¬
ний. Можно либо решать уравнение до конца и проверять,
лежат ли найденные корни в ОДЗ, либо с самого начала
выписать ОДЗ. Первый путь в этом примере проще: х2 +
+ 4х —21=0, xi=3, Х2=—7. Первый корень попадает в
ОДЗ, а второй — нет.
Ответ: х = 3.
9. 22х+1 -2х- 1<0.
Делаем замену: 2х = у, тогда 2у2 — у— 1^0. Находим
корни квадратного трехчлена: г/, = —1 /2; (/2=1. Решаем не¬
равенство относительно у: —Возвращаемся к
переменной х и решаем два простейших показательных нера¬
венства:
1. 2х^ — ‘/2 верно при любых х, так как 2х>-0.
2. 2*^1 зерно при х^О.
Ответ: х^О.
IQ sin3 х cos х — sin х cos'1 х ^ ^
cos 4х ®
Преобразуем числитель левой части:
sin3 х cos х — sin х cos3 х = sin х cos x(sin2 x — cos2 x) =
=1 /2 sin 2x(—cos 2x)= —1 /2 sin 2x cos 2x = — !/4 sin 4x.
Левая часть равна ~4~ cos'H = ~T ^ ^x. Переходим к
tg2x и делаем замену ig2x=y:
_1 2tg 2х _fc.or 1 У У о.. п
у (3y~-f )=о>у,=о’ ^з=± /F-
tg 2аг = 0, 2x = nk, х = -у- (k £Z),
tg2x=±]/|^, 2x=±arctg У^+kn,
*=±± arctg (k£Z).
Ответ: x=^~, *=±yarctg }/| + -y-.
11. Найдите решения неравенства —2, лежащие между
0 и 2л.
Если cos*;>0, то неравенство —!—> —2 верно, так как
r cos X Г
слева стоит положительное число, которое больше, чем —2.
417
Если cosx<0, то неравенство можно переписать так:
cos х <С —1 /2»
Обращаемся к тригонометрическому кругу (рис. 524).
Значения х, при которых cosx= — l/2 для *6 [0, 2л], таковы:
*1=2л/3, *2=4л/3. Необходимо выписать все значения
х 6 [0, 2л], где cos х либо положителен, либо меньше —1 /2.
Ответ. 0<*<л/2, 2л/3<л:<4л/3, Зл/2<х<2л.
§ 49. Системы уравнений
Способ подстановки
Системы уравнений появляются при решении задач, где неизвест¬
ной является не одна величина, а несколько. Эти величины связаны
определенными зависимостями, которые записываются в виде
уравнений.
Если система имеет хотя быть одно решение, она называется совмест
ной. Если решений у системы нет, она называется несовместной.
Слово «несовместность» наглядно показывает, что разные
уравнения системы накладывают несовместимые друг с другом
условия, которым должны удовлетворять неизвестные.
Одним из основных способов решения систем является способ
подстановки. Рассмотрим, например, систему двух уравнений с
двумя неизвестными х и у. Часто удается одно уравнение преоб¬
разовать так, чтобы одно неизвестное явно выражалось как
функция другого. Тогда, подставляя его во второе уравнение, мы
получим уравнение с одним неизвестным.
418
Рис. 524
Примеры
х2-\-у2 = 25, 2. | х2-\-у2=Ъ,
х — у= 1. | х2 + у=3.
Т-+у=2, 4. | 2х-\-Зу=4ху,
ху= 3. \х + У=3/2*У.
В каждой из четырех систем второе уравнение системы
можно, рёшить относительно у, т. е. преобразовать его к ви-
ду у = f(x), а именно:
1. х—у=\оу=х—\.
2. x2 + y=3oy=3 — x2
3. Ху=3^у=^-.
4. х + у=~ху^у (l —^-x')=—xoy=TjJ—^-.
Подставляя у = f(x) в первое уравнение системы, полу¬
чаем уравнение с одним неизвестным:
1. *2 + (х - I)2 = 25.
2. х2 (3 — jc2)2 = 5.
3. \/х + х = 2.
4. 2л+ 3* —=4х - * — .
3/2х—\ 3/2Х—1
Решая получившиеся уравнения с одним неизвестным,
находим его корни — значения неизвестного, а затем для
каждого из них находим соответствующее значение по фор¬
муле у = f{x):
1. х2 -\-(х — 1)2=25-Ф>-2дс2 — 2х — 24=0-ф>-л:2 — х— 12=0^-
-ojci =4, Х2=— 3, у| =jci — 1 =3, t/2=—3—1 = —4.
Решения системы:
[ х\ =4, 1х2=— 3,
,'/|=3 " 11/2 = —4.
2. jc2 + (3 — ■х2)2=5о-.х4— 5дс2 + 4=0, (jc2)i = 1, (х2)г=4. Урав¬
нение имеет четыре корня, а система — четыре решения:
( *1 = 1, (Х2 = — 1, (Хз = 2, (х4=— 2,
I «/1=2; (4/2=2; |«/з= — 1; |у4 = —1.
3. х-\-1/х = 2ох2 — 2дс + 1 = 0 jc = 1.
Решение одно: J дг=1,
U=3.
419
Ответ:
Способ подстановки возможен не всегда, а кроме того, не
всегда выгоден и тогда, когда возможен. Часто из уравнений
системы, удается получить новое уравнение — их следствие —
более простого вида. Так, в четвертом из рассматривавшихся
выше примеров можно исключить произведение хуу стоящее
справа:
Последнее соотношение является линейным, и из него легче
находится связь между хну: у=2х.
Важным приемом, часто позволяющим упростить систему,
является замена неизвестных. Так, во втором примере полезно
заменить х2 на z и получить более простую систему:
Системы с двумя неизвестными и их решения можно изобра¬
зить графически на координатной плоскости. На рис. 525—528
показаны кривые уравнений для написанных выше систем.
Точки пересечения кривых (а точнее, их координаты) — реше¬
ния систем.
Z + у2 = 5 ,
z + у = 3 .
Рис. 525
420
Рис. 526
Рис. 527
Рис. >28
Есть некоторые типы систем, для которых известны стандарт¬
ные методы решения. Рассмотрим два из них: симметричные
системы и линейные системы.
Симметричные системы
Симметричными называются системы, составленные из выражений,
являющихся симметричными относительно всех неизвестных.
Приведем примеры различных симметричных выражений для
двух неизвестных х и у:
1. их = х + у. 2. и<2 = ху. 3. иг = Х3-\-у3.
4. и4= — + —. 5. иъ = х2 + у2. 6. и6 = - ~ 1 + у ~ 1 .
* х у ь 1 у у X
Решение простейшей симметричной системы (х + у = а, ое-
I *У= Р
новано на теореме, обратной теореме Виета: хну, удовлетворяю¬
щие указанной системе, являются корнями квадратного уравне¬
ния г — at + р = 0. Этот вывод можно получить, подставив
из первого уравнения во второе у = а — х.
Итак, дл-я решения простейшей симметричной системы надо
составить квадратное уравнение с заданными суммой и произ¬
ведением корней и решить его. Найденные корни будут значе¬
ниями х и у.
Примеры
,*• }Х + у = 3,
1 ху =— 4.
421
Составляем квадратное уравнение: t2 — 3/ — 4 = 0, откуда
/i = 4, /2 = — 1. Решения систем: fxx = 4, и глг2 = — 1,
\У\ = — 1 1*/2 = 4.
Решение других симметричных систем основано на том, что
всякое симметричное выражение относительно х и у можно пред¬
ставить через и = х -\- у и v = xy. Например,
х2 + У2 = х2 + 2 ху + у2 — 2 ху = (х + у)2 — 2 ху = и2 — 2и,
у + * _ w
х у ху V
jc3 + £/3 = (х + £/) (л:2 + J/2 — *1/) = и (и2 — 2и — и) = и (и2 — Зи),
х — 1 | j/ — 1 х2 -j- у2 — х — у и2 — 2v — и
у X ху V
Делая в симметричной системе замену х + у = и, ху = v,
получаем более простую систему относительно и и и, а затем,
найдя числовые значения и и и, приходим к решению простей¬
ших симметричных систем
(X + у= и ,
1 xy=v.
2. j*2 + £/2 = 25, (и2 — 2и = 25, \и = 7,
х + у = 7-, (и = 7; ^ (и = '/2(ы2 - 25) = 12.
Решаем систему ( х + у — 7,
*</ = 12.
*3 + У3 = 7,
JC2 + 3.U/ + I/2 = — 1.
Воспользуемся найденным выше выражением хъ + уъ
через и и v:
( и(и2 — Зи) = 7,
\и2 — 2и + 3и = — 1.
Из второго уравнения находим и = — и2 — 1. Тогда
и3 + Зи(и2 + \) = 7о4и3 + Зи-7 = 0о(и - 1) (4 и2 +
+ 4и + 7) = 0, и, = 1, у = — и2 — 1 = — 2 и 4и2 + 4и +
+ 7 = 0 — корней нет. Решаем систему
\х + у = 1,
\ху = 2.
Линейные системы
Раньше вы изучали системы двух линейных уравнений с двумя
неизвестными вида
\ах + by = ky
j сх + dy = l.
В практике встречаются системы линейных уравнений с
большим количеством неизвестных. Так, в задачах математиче-
ской экономики существуют системы, состоящие из нескольких
сотен уравнений с таким же примерно числом неизвестных. Для
их решения разработаны мощные машинные методы. Эти методы
в основном имитируют знакомый вам метод подстановки, кото¬
рым, в принципе, можно решить любую такую систему. Основ¬
ную роль при этом играют компактные способы записи систем
и их преобразований. Представьте только себе — система из ты¬
сячи уравнений с тысячью неизвестными содержит миллион
коэффициентов.
Рассмотрим более простой пример — систему трех линейных
уравнений с тремя неизвестными.
Пример
х + 2у + 3z = 2,
2х + Зу — 4z = — 5,
3* + у + z = 3.
Будем решать систему методом исключения неизвестных.'
Чтобы исключить х из второго и третьего уравнений, надо
вычесть из них первое, умноженное соответственно на 2 и
на 3:
f х + 2у 3z = 2,
| — у — 10z = — 9,
( — by — 8z = — 3.
Удобно умножить второе и третье уравнение на — 1,
а затем из третьего уравнения вычесть второе, умноженное
на 5. Получим «треугольную» систему
х + 2у 3z = 2,
у + 10z = 9,
42z = 42.
Из третьего уравнения системы находим z = 1. Под¬
ставляя это значение во второе уравнение, находим
у = 9 — 10 = — 1.
Подставляя z = 1у у = — I в первое уравнение, нахо¬
дим х = 1.
Ответ: х = \у у = — 1, z = 1.
Показанный на этом примере способ решения линейной сис¬
темы называется методом Гаусса, по имени великого немецкого
математика, жившего в первой половине XIX в. Метод Гаусса с
различными модификациями используется при решении линейных
систем с помощью вычислительных машин.
423
§ 50. Составление уравнений
Рассмотрим несколько задач, приводящих к уравнениям.
Вспомним задачу, знакомую нам с детских лет: «Из городов
А и Б, расстояние между которыми 150 км, одновременно
вышли навстречу друг другу два поезда. Скорость первого
поезда 60 км/ч, второго — 40 км/ч. Какое расстояние
прошел первый поезд до встречи?». Решая задачу, мы обо¬
значаем через * искомое расстояние, составляем уравнение
относительно х и находим корень этого уравнения. Таким
образом, задача распадается на две части: составление
уравнения и его решение. Рассмотрим эти две части под¬
робно.
В примере идет речь о равномерном движении по пря¬
мой. Основные величины, характеризующие такое движе¬
ние (путь 5, скорость v и время /), связаны соотношением
5 = vt. Приравнивая время движения обоих поездов до
встречи (рис. 529), получаем уравнение для нахождения
искомого расстояния *:
х 150 — х
60"“ 40 ■
То, что мы делали до сих пор, не является на самом
деле чисто математической задачей. Связи и соотноше¬
ния между величинами, нужные для составления уравне¬
ния.
берутся нами из физики, из специальных дисциплин, дру¬
гими словами, из тех областей, в которых применяется
математика.
Наша задача свелась к нахождению корней уравне¬
ния.
х 150 — х
60~ 40 ‘
Теперь можно применить наши математические знания.
Сделаем преобразования: 40лг=60( 150 — л:), 40л:=60• 150 —
— 60*, 40* + 60* = 9 000, 100* = 9 000, * = 90.
Мы рассмотрели очень простой случай — для составле¬
ния уравнения использовались самые элементарные сведе¬
ния из механики, для решения уравнения понадобилось
умение делать несложные преобразования над алгебраи¬
ческими выражениями. Однако и в этом случае наглядно
Рис. 529
видны две стороны приложений математики: построение
математической модели изучаемого! явления (составление
уравнения) и исследование этой модели (нахождение кор¬
ней уравнения).
В прямоугольной планке размером аУ^Ь надо вырубить
прямоугольное отверстие площади S так, чтобы стороны
отверстия были равноудалены от краев планки (рис. 530).
Какими должны быть размеры этого отверстия?
Рис. 530
В этой задаче большая часть перевода на математиче¬
ский язык уже проделана: определено, что данная планка
имеет вид прямоугольника, сказано, что искомое отверстие
тоже имеет вид прямоугольника, причем его стороны равно¬
удалены от краев. планки, а значит, им параллельны.
Осталось обозначить искомые величины и записать связи
между ними в виде уравнений. Можно было бы ввести два
неизвестных — размеры отверстия. Одно связывающее их
соотношение — это формула площади прямоугольника, а
другое — условие равноудаленности от краев. Так как пер¬
вое из этих соотношений очень простое, то можно обой¬
тись одним неизвестным. Обозначим через х длину той
стороны отверстия, которая параллельна краю планки дли¬
ны а. Тогда вторая сторона равна S/x. Удвоенные рас¬
стояния до краев планки равны а — х и b — S/x соответ¬
ственно. Приравнивая эти величины, получаем
а — х — b — S/x.
Анализ задачи привел нас к уравнению. Теперь надо
решить это уравнение. Преобразуем его:
а — х = b — S/x, х2 — (а — b)x — S = 0.
Получили квадратное уравнение, корни которого находятся
. (а - Ь) ± У(а - Ь)2 + 45 п
по формуле jti,2 = - — — . Решили ли мы
исходное уравнение? Да. Два найденных числа дают реше¬
ние квадратного уравнения х2 — (а — b)x — S = 0. Эти же
числа образуют решение и исходного уравнения. Решили
ли мы исходную задачу? Нет. Во-первых, мы получили два
числа, а по смыслу задачи ясно, что размеры отверстия
определяются однозначно. Во-вторых, подставим конкрет-
425
ные значения а = 2, 6=1, S = 6 в формулу. Тогда
1 ± V25” 1 ± 5 0 0 ~
*i,2 = —— = —2— ; х\ = 3; х2 = — 2. Ясно, что нужно
взять положительное значение * = 3. Второй размер от¬
верстия равен S/* = 6/3 = 2. Итак, отверстие должно
иметь размер 3X2, т. е. больший, чем размер 2X1 самой
планки. Понятно, за счет чего это произошло — заданная
площадь S = 6 отверстия превышает площадь планки.
Таким образом, для решения исходной задачи надо не
просто найти корни полученного уравнения, но и исследо¬
вать их.
По шоссе едут два автомобиля с постоянными скоростями.
В пункте А первый автомобиль был на час раньше второго,
а в пункт В, отстоящий от пункта А на 400 км, автомобили
прибыли одновременно. Через 3 ч после того, как первый
автомобиль прошел пункт Л, он опережал второй автомо¬
биль на 40 км. Найти скорости автомобилей.
Обозначим скорости автомобилей (км/ч) и, и v2. Пер¬
вое соотношение между этими неизвестными получим, срав¬
нивая время движения автомобилей между пунктами А и В:
400 _ 400 = J
vx v2 ~
При составлении уравнения надо следить за тем, чтобы
единицы величин были согласованы.
Второе уравнение мы найдем, сравнивая расстояния,
пройденные автомобилями через 3 ч (для второго автомо¬
биля) после пункта А:
Зи, — 2v2 = 40.
Полученные два соотношения составляют систему урав¬
нений для нахождения неизвестных vx и v2:
[ 400 400 .
I Зи, — 2v2 = 40.
При ее решении можно из второго уравнения выра¬
зить v2 через и, и подставить его в первое, предварительно
упростив первое уравнение:
400^3р12 40 и,^= Uj 3Ul 2 40 о 400(3uj — 40 — 2и,) =
= vl(3vl — 40) о 400uj — 16 000 = 3v\ — 40^ о 3v\ —
- 440у, + 16 000 = 0.
Получаем vx= 80, v\ = и иг= 100, = 80.
Таким образом, ответом в задаче являются две возмож-
ные пары скоростей автомобилей: (80; 100) и 80^.
4. По шоссе едут два автомобиля с постоянными скоростями.
Пункт А они проехали с интервалом в 1 ч, в пункт В при¬
были одновременно, а пункт С, равноотстоящий от Л и Б,
проехали с интервалом в 20 мин. Каковы скорости автомо¬
билей?
Обозначим v\ и скорости автомобилей (км/ч), а
5 — расстояние между А и В (км). Получим два уравнения:
5 S j
V\ V2
S S 1
2v\ 2v2 3
Эта система несовместна, так как второе уравнение
s s 2
можно записать так: = —- но одна и та же
V\ V2 3
величина — — не может одновременно быть равной 1
И 2/з.
Задачи и вопросы
13.1. Равносильны ли следующие уравнения:
а) х8 — 2х4 + х = 1 и 4л:8 — 8л:4 + 4л: = 4;
б) (х — 1 Х4х5 — 1) = х — 1 и 4л:5 —1 = 1;
в) хв + Зх2 + 5 = х и х6 + Зх2 — х + 5 = 0;
г) * + 3-тЬ-=1-7Т2 »* * + 3=1;
д) дс = 1 и х2 = 1;
е) х2 + 4х + 4 = 9 и х + 2 = 3;
Ж>т5т=-гЬ- идг-2-1;
«Не считать ничего сделанным, если еще кое-что осталось сделать.»
К. Ф. Гаусс
Гаусс Карл Фридрих (1777—1855 г.г.) — немецкий математик, астро¬
ном и физик. Еще студентом написал «Арифметические исследования»,
определившие развитие теории чисел до нашего времени. В 19 лет опре¬
делил, какие правильные многоугольники можно построить циркулем и
линейкой. Занимался геодезией и вычислительной астрономией. Создал
теорию кривых поверхностей. Один из создателей неевклидовой геомет¬
рии.
«Гаусс в полном смысле этого слова создал современную теорию чисел
и предопределил все ее дальнейшее развитие до нынешнего дня», писал
о нем Ф. Клейн.
427
з) (х2 + 1)* = X2 + 1
и) ~\[х — 1 = 1 — х
к) X2 + \gx = * + lg*
13.2. Решите уравнения:
3 6
а)
5х + 2
б> ТТТ +
в> 6+7=7
8
л:2 _ 9 "
л: — 2
15 — х
х2 + Зх
З-jc
+
3
Х>-4 —
13.3. Решите уравнения:
а) |2* - 1| = 3;
б) |* + 11 + I* — 3|
в) ||* — 21 — 5|=4;
13.4. Решите уравнения:
а) *4 - 13*2 + 36 = 0;
б) З*4 - *2 - 2 = 0;
в) 2*6 — II*3 — 40 = 0;
г) 3(2*2 + * - 2)2 =
= 8*2 + 4* - 9;
д) (*2 - 16*)2 -
- 2(*2 - 16*) - 63 = 0;
13.5. Решите неравенства:
и * = 1;
и * — 1 = (1 — jc)2;
и *2 = *?
V х + 6 . х — 5
' х — 5 ~ х + 6
= 5;
а)
2*2 + 5* - 7
<
0;
б)
З*2 - 4* + 1
>
0;
в)
х4 — 5*2 + 4
>
0;
г)
(*2 + * + I)2
<
5л:2 +
+ 5* — 1;
д)
* ~3 > о-
х + 2 ’
е)
х2 + 6х + 15 .— q
х — 4
Д)
е)
2х2 + 23х + 61
х2 + х - 30
2 х — 5
х — 3
9
1
+
х2 - 9 '
2
х+\
х2-\ ’
5
Ж) 1 _-L = ^L=JL
х Ьх Ьх
г) 2(* ~ 2,5) — 3 =
1.
х — 3
е) (*2 + 3* - 4)2 +
“h (х2 —|— Злг —|— 2)2 — 36 = 0
*> (4-+ 2)’ + f = Ю;
з) _ 1—L _
3; VI + х) 1 + х
- 20 = 0.
ж) * + f + I > -3;
' х — 4х + 3
о\ * ~ 10 1 •
5 + х2 < 2 ’
(«■ + у -л
' х + 3
к) -Ц-^- < 0.
' * + 1
428
13.6. Найдите области определения функций:
а) у = У5*2 — 6* + 1; в) у =
б) у = V4 + 8дс — 5*2;
13.7. Докажите, что следующие иррациональные уравнения не
имеют решения:
COS*
е) tg3* = tg*;
ж) cosxtgjc = 0;
з) sinjc( 1 — cosx) = 0;
13.11.. Решите уравнения:
а) 7х = 343;
6> (ож)' - 128;
е)
а) У2* — 3 + У5*~—~1 = У* + 1;
б) УЗ* — 5 + 4 = 3.
13.8. Решите уравнения:
а) УЗ** - 5* — 12 = 10;
б) У*2 — 5 = У* + 1;
в) У* + 1 = х — 1;
г) Уб — х — х2 = х + 1;
13.9. Решите неравенства:
а) У2* -f 7 < х + 2;
б) У* + 4 ^ х - 2;
13.10. Решите уравнения:
а) 2cos(3* — 1) = 0,5;
б) 3sm(f+ f) - f;
в) '/isin(2, - f) = -
Г) '/2tg(3* + 1) = -7;
д) 2 + 2tg*cos* =
+ tg*;
Д) У* + 2 - У2* - 3 = 1;
* + 2 _
2УТ+Т - 3
У* ~ь i ~ь i
+ 4.
в) У* + 4 < * — 2;
г) У* + 9 > x — 3.
и) cos2* — 2 sin2* = — 3;
к) tg(-^- + *) +
+ ctg(n — *) = —3;
л) 4 — cos2*= 13sin*cos*;
м) 1 + cos* = 2sin2*;
h) cos* — cos3* = sin2*;
o) sin 6* = sin 8*;
n) 2sin2* + 5cos* — 4 = 0;
p) 1 + 2cos2* = 8cos*;
c) 2sin* + 5cos* = 0;
t) cos2* — 3sin*cos* +
+ 2 sin2* = 0.
в) 25 = фг;
У 2х
г) 11*~7 = 177"*;
429
д) 2Х+3 — 2х = 112;
е) 3х = 81;
ж) З2*-2 + 32х = 30;
з) 4х = У64;
и) 2*+' + 4х = 8;
к) 5* = 0,008;
л) 3*+2 = 9х+|;
м) С/ь)3х~' = (5/<)2х~9-,
н) 4-3х - 9-2* = 5-б'/2;
13.12. Решите уравнения:
а) (е*)2 = е4;
б) е* — е~х — 2;
в) Зе~х - 2ех = 0;
г) \ех-\\ = ({-)*;
Д) \2Х - \ \ +
+ 12х - 2| = 1;
13.13 Решите уравнения:
а) logy2( - 7-) = 4;
б) log3(x — 12) = 2;
в) lg(x — 5) — lg2 =
= flg(3* - 20);
г) lg(2*+14) +
+ lg(jc + 12) = 3;
Д) lg(7* — 9)2 +
+ \g(3x — 4)2 = 1;
е) log2* — 31og3x + 2 = 0;
ж) lg2x — lg*3 + 2 = 0;
3)
17 — lg jc _
4 lg jc
4 lgjc;
13.14. Решите уравнения:
a) log*2 — log4Jc + |-= 0;
6) log2log3(jc2 — 16) —
1
0) 2-25"-5-10" +
+ 2-4* = 0;
n) 6* + 9* = 22x+';
p) (л/7 +л/48)х +
+ (У7 - = 14;
■> Ш+' =<'-•
т> 1ГГТ =
е) 2e3jt + 3e2x - 8e* +
+ 3 = 0;
ж) 12ел - 1| = 'A;
з) (ex - e3Xe* - e) = 0;
и) e2jt_l + ex = 1 + f;
к) 4e~3x - 5e~x + e* = 0.
и) 1 + — ]) 1
H> 1 - lg‘(* - l) +
+
1;
log|/2 logi/3
л - 16
= 2;
1 - lg(* - 1)
к) 21ogi/3(jc + 1) =
= logy3(2*2 + 1);
л) lg(3*-24-*) =
= 2 + -fig 16 -
M) log4log2* +
+ log2log2* = 2;
h) 21og3(* — 2) +
+ log3(x — 4)2 = 0;
o) log3Jclog9xlog27xlog8,x =
2_
— 3 ’
B) 31og)25x log^x = 2;
r) lg(* + s/3) =
= - lg(jc - V3);
Д) lg(* + 5) +
+ \g(x — 5) = 2;
430
е) lg(5 — х) +
+ 21ёл/З^Т = 0;
ж) lg(152 + л:3) -
- 3lg(x + 2) = 0;
1
з)
5 -
+
l0g2*
2
+
и) logsinx COSX +
+ logcosxSinx = 2;
к) logsinx(sinx —
— -^-cosx) = 3.
= 1;
1 + log2JC
13.15. Решите неравенства:
а) T > 4;
б) 9* > 3;
в) 2“ < '/2;
г) С/з)3~х < 9;
д) 32x~' —3х-' > 2;
е) log2(x — 1) > 1;
ж) log5(x + 1) < 2;
з) logi/3(l — 2x) > — 1;
и) log3x + log3(x — 2)> 1;
л)
m)
H)
O)
n)
log* 2 < 2;
X —3
<
1
3
3x — 5
(3 - x)3~x < 1;
l°g8(*2 + 4* + 3) < 1;
iog2iog34:=14- > — •;
к» ш
ч /1 \
p) (-)
2 - jc
Зх— 1
1 \'°g,/2^ > j
13.16. Решите уравнения графически:
а) У* + 1 = 2x — 8;
б) l°g2(x + •) = x2 — 7;
в) lgx = -фс — 1;
13.17. Решите системы уравнений:
a) j Зх + Ъу = 4,
I 7х — Зу = 24;
б) j 4х + 6у — 3,
1 6х + 9у = 4,5;
в) I 2х — 3у = 4,
I 4х — 6у = 5;
г) ( 2дг2 - Зу2 = 24,
\ 2х = Зу;
г)
д)
е)
= 4
х;
2х = х2 - 1;
х2 + 4 > 10
— х.
д)
Зу;
* + 2у = 7,
Зх — у = 14,
2* + у = 12;
е)
ж)
з)
и)
к)
10
х + 2
1
+
У -
2_.
*
</
5,
X — 1
: х + ху = з,
I ху2 + ху3 = 12;
х2 + у2 = 29,
ху = 10;
х — у + ху = 5,
х — у — ху = —7;
х2 - 2ху + у2 = 25,
2х2 — 2 ху — у2 = 11;
431
о) \ 2х — Зу — 6z = 10,
х + у + 2z = 0У
Зх + 2у — 4z = — 2;
н) х + Ъу — 2z = 5,
5х — у -+- 2z = 31;
7х — Зу — 4z = —9,
13.18. При каких значениях т система^^.
(т + 3)лг + 2у = 2т,
2х + ту = 1
имеет единственное решение?
13.19. При каких значениях а прямые
а) пересекаются; б) параллельны; в) сливаются?
13.20. При каких т система уравнений имеет единственное ре¬
шение, бесконечное множество решений, не имеет ре¬
шений:
13.21. Два пешехода вышли одновременно из пунктов А и В
навстречу друг другу и встретились через 3 ч. За какое
время пройдет все расстояние каждый, если первый при¬
шел в В на 2,5 ч позже, чем второй пришел в Л?
13.22. Один сплав состоит из двух металлов, входящих в него в
в отношении 1:2, а другой сплав содержит те же металлы
в отношении 2:3. Из скольких частей обоих сплавов можно
получить новый сплав, содержащий те же металлы в отно¬
шении 17:27?
13.23. Совхозом было заготовлено на зиму т тонн кормов для
скота, но п голов скота отправили в соседнюю область и
вследствие этого норма кормов на голову скота увеличи¬
лась на с тонн. Сколько тонн кормов предполагалось рас¬
ходовать на голову скота раньше?
13.24. Открытая с обоих концов цилиндрическая трубка дли¬
ной /, (/ в мм), наполовину погружена в ртуть. Закрыв
верхний конец трубки, ее вынимают, при этом часть ртути
вытекает. Какой длины столбик ртути останется в трубке,
если во время этого опыта атмосферное давление равно Н
(величина Н выражена в мм рт. ст.).
13.25. Между освещенным предметом и находящимся на рассто¬
янии d от него экраном требуется поместить выпуклую
432
линзу, чтобы получить на экране четкое изображение этого
предмета. Фокусное расстояние линзы равно F. На каком
расстоянии от предмета следует поместить линзу?
13.26. Производительность станка-автомата А составляет 10 еди¬
ниц продукции в час. Конструируются еще два станка-
автомата того же назначения: станок В и станок С, при¬
чем поставлено требование, чтобы производительность
станка В составляла не менее 75% суммарной производи¬
тельности станков Л и С, производительность станка С —
не менее 50% суммарной производительности станков А
и В. Найдите производительность станков В и С.
13.27. Найдите область значений функции:
а) /(*) = ** + * + 1, D(f) = (— °°> + °°);
б) /(*) = ** + * + 1, D(f) = [0; +оо);
в) Д*) = *2 + * + 1D(f) = (—оо, —1);
г) /(*) = ** + * + 1, D(f) = [— 1, 1];
д) /(*) = ** + * + 1, D(f) = [ 1, 2];
е) f(x) = X* + X2 + 1, D(f) = (— оо, + оо) .
13.30. Какую наибольшую площадь может иметь прямоугольник
с периметром 4 см?
13.31. Из круга радиуса г требуется вырезать прямоугольник на¬
ибольшей площади. Найдите стороны такого прямоуголь¬
ника.
13.32. Какую наименьшую площадь полной поверхности может
иметь цилиндр, если его объем равен 1 дм ?
13.33. Докажите, что объем шара, вписанного в конус, не превос¬
ходит половины объема того конуса.
13.34. Какой сектор надо вырезать из круга радиуса /?, чтобы
из него можно было свернуть воронку наибольшей вмести¬
мости?
13.35. Из пункта А, находящегося в лесу в 5 км от прямолинейной
дороги, пешеходу нужно попасть в пункт В, расположен¬
ный на этой дороге в 13 км от пункта А, по прямой. По до¬
роге пешеход может двигаться с максимальной скоростью
5 км/ч, а по лесу — с максимальной скоростью 3 км/ч.
За какое минимальное время пешеход сможет добраться
из пункта А в пункт В?
13.28. Найдите область значения функций:
а) f(x) = 1 + 3sin2jc; в) f(x) = sinx + cosjc;
б) f(x) = cos(2x + 5); r) f(x) = sin2x + sinx + 1.
13.29. Постройте графики функций:
в) f{x) = sin
д) f(x) = sin* + cos*;
е) /(*) = sin 2* — cos 2*.
15—1681
Послесловие
Изучением этой книги заканчивается общеобразовательный курс математики.
Этот курс очень богат. На нем лежит печать истории нашей культуры и цивили¬
зации. Войдя с арифметикой во «врата учености», как говорил М. В. Ломоносов,
вы прошли путь, достойный самого высокого уважения. Овладев геометрией
Евклида, вы подошли к тем вершинам человеческой мысли, к которым, как го¬
ворили древние, «нет царской дороги». Научившись векторам и координатному
методу, вы получили возможность решать такие задачи, с которыми в средние
века не справлялись самые лучшие умы. Освоив начала математического
анализа, вы ознакомились с мощным математическим инструментом познания
мира, который еще недавно считался доступным лишь избранным.
Но не нужно обольщаться. Не все математические премудрости вы прев¬
зошли, не все нужное узнали, не все доступное унесли с собой. Вам предстоит
учиться всю вашу жизнь, и, хотя роль и место математики в ней будут зависеть
от выбранного пути, подавляющее большинство из вас еще встретится с этой
наукой.
Прежде всего она будет заложена в бурно развивающейся новой технике —
от компьютеров и станков с программным управлением до современных бытовых
приборов. Вы всегда будете ощущать нехватку математических знаний в кон¬
кретной профессиональной деятельности, при чтении научно-популярных (а иног¬
да и художественных) книг, в попытках самостоятельной творческой работы.
Здесь на помощь вам придут испытанные друзья — книги. Научные библио¬
теки накопили колоссальный запас математических книг на любой вкус и на лю¬
бую потребность. Посоветуйтесь с опытными людьми, и вам подскажут, в какой
книге можно отыскать нужный вам материал. Сейчас было бы трудно указать
одну (или даже десять) книгу, которую можно рекомендовать для дальнейшего
изучения математики всем, без указания целей и возможностей читателя.
Однако может быть стоит указать некоторые разделы математики, которых нет
в общеобразовательном курсе и которые стоят на пороге включения в него, а зна¬
чит, наверняка будут полезны подавляющему большинству читателей: теория
вероятностей, математическая статистика, теория алгоритмов и математическая
логика, дифференциальные уравнения, комплексные числа, основные алгебра¬
ические системы, теория графов и комбинаторика, методы приближенных
вычислений.
СПРАВОЧНЫЙ МАТЕРИАЛ
Основные обозначения, используемые в книге
Числовые множества
R — множество всех вещественных (действительных) чисел
TL — множество всех целых чисел
Множество чисел х, удовлетворяющих неравенствам:
[а, Ь] — а < х < b
(а, Ь] — а < х ^ b
[а, Ь) — а ^ х < b
(а, Ь) — а С х с b
[а, + с») — х ^ а
(а, + оо) — * > а
(— оо, а] — х ^ а
(— оо, а) — х <С а
Специальные знаки, используемые для сокращения записи
/, \, -► — возрастает, убывает, стремится к пределу (о функции)
е, — принадлежит, не принадлежит (лежит, не лежит — о числах, точках^
прямых, плоскостях и т. п.)
П — пересечение, общая часть (о прямых, плоскостях, множествах чисел,
точек и т. п.)*
U — объединение (множеств корней, решений и других множеств)
II, _L — параллельны, перпендикулярны (о прямых, плоскостях)
/ — скрещиваются (о прямых)
=^, о — следовательно, равносильно (если... то, тогда и только тогда в форму¬
лировках теорем, свойств при решении уравнений и неравенств)
Функциональные знаки
D(/) — область определения функции f
X — пересекаются (о прямых, плоскостях)
А/ — приращение функции f
d/ — дифференциал функции f
f' — производная функции f
ь
5 f(x)dx — интеграл от функции f на отрезке [а, Ь].
Функции и графики
1) Линейная функция у = kx + Ь. График — прямая линия.
2) Квадратичная функция: у = ах2 + Ьх + с.
г . * - ( Ь Ь2 — \ас \
График— парабола с вершинои в точке 1 —, — I.
3) Степенная функция: у = хп, п — натуральное число.
4) Степенная функция с положительным рациональным показателем:
у = = х1/2\ у = 3j/jT~ = х*/3 и т. п.
-v гж ^ ^ 1 1 * 1 1
5) Дробно-лине иная функция: у = — , у = , у = — — = 1 . .
X XX j I X | 1
* Не следует использовать этот знак в смысле «пересекается» для утвержде¬
ния о том, что прямые и плоскости пересекаются, т. е. имеют хотя бы одну общую
точку.
15*
435
6) Рациональная функция: у = х , у = , у = - --- и т. п.
7) Показательная функция: у = а*.
8) Логарифмическая функция: у — logfljc.
9) Тригонометрические функции: у = sin сох, у = coswjc, у — tgcojc, 1/=
= CtgtoJC.
10) Обратные тригонометрические функции: и = arcsinjc, и = arccosх,
у == arctgjc, I/ = arcctgjc.
11) Уравнение прямой: Ах + By -f С = 0.
12) Уравнение окружности радиуса R с центром в точке (а, 6): (jc — а)2 +
+ (у - by — R2.
13) Равнобочная гипербола: ху—\ (см. дробно-линейную функцию
У = \/х).
Преобразование выражений
1) Алгебраические выражения:
a2-fc2 = (a + Ь\а - 6),
а3 — Ь3 = (а — Ь\а2 + ab + b2),
а3 + Ь3 = (а + 6Ха2 - аЬ + *2),
(а =Ь Ь)2 = а2 ± 2а6 + b2,
(д it ft)3 == fl3 it 3a2ft -f- 3ab2 it ft3*
(a ± ft)4 = a4 ± 4a3ft + 6a2ft2 di 4aft3 + ft4,
1 - xT = (1 - jcXI + * + ** + ... + J*"1).
b2 — \ac
ax1 + bx + с = a [(r+ -A-J - ^ ],
ad — be
ac
2) Экспоненты и логарифмы:
a°gaX = x, logojci/ = log0jt + log„y,
a' = e*1"0, log0 = >ogaX — log„y,
logbX = l^gTT ’ logfl**= k logaXy
logaV*7 = lQg<?X , loga Ь :
1
log* a
3) Тригонометрические функции.
Основные соотношения:
sin2jc + cos2jc =1, cos — x ^=
sinjc,
. sin x . /я \ . cos jc . /л \
tgJC = , Sin I— X 1= COSJC, CtgJC = —: , tg I— X 1= CtgJC,
s cosr \2 / K sin jc \2 / *
l + tg2jr=-ji7’ctg(T_J!)=tgJt
Формулы сложения и следствия из них:
sin (а ± Р) = sin a cos 0 ± cos a sin р,
cos (a d= Р) = cos a cos 0 =F sin a sin р,
436
sin 2a = 2 sin a cos a,
cos2a = cos2a — sin2a = 2cos2a —1 = 1— 2sin2a,
1 + cosa = 2cos2 , 1 — cosa = 2sin2
sin 3a = 3 sin a cos2 a — sin3 a, cos 3a = cos3 a — 3 sin2 a cos a.
sin a + sin p = 2 sin a ^ cos a ^ ^ ,
cos a + cos P = 2 cos a ^ cos ^ ,
a о • a — P a“f“P
sin a — sin p = 2sm —cos —,
_ a + P a — 8
cos a — cos p = — 2 sin sin 7~—,
sin a cos p =-i- [sin (a + p)+ sin (a — p)],
sin a sin p=-^- [cos (a — p) — cos (a + p)].
cos a cos p=-i- [cos (a + p) + cos (a — p)],
2tg|- 1 — tg2 J- 2tgJ-
sin a= , cos a= , tga = .
'+‘g2J- 1 + tg2|- i—tg2f-
4) Обратные тригонометрические функции:
sin (arcsin x)=x, arcsin (—*)= —arcsin x,
cos (arccos x)=x, arccos (—x)=л— arccos x,
tg (arctg arctg (—x)= — arctg x,
cos (arcsin x) = /1 — x*, arcctg (— x)= — arcctg x,
sin (arccos x)— /1 — x*, arcsin * + arccos x = ~^ »
sin (arctg x)=—-rJL===., tg (arcsin х)=---Л__~
y 1 + x£ у \—xl
Векторы
Правило треугольника: Afe + BC = AC.
Координаты вектора: аЬ=(хи — хА, Ув~Уа, zB — zA),
где (хЛ, уАу za), (хв, ув, zB) — координаты точек А и В.
Проекция вектора на ось: а/= |а|*cos Z.(a, /), (а + Ь)/ = а<> + Ь/, (А,а)/ = А,*а/.
Скалярное произведение: а-Ь = |а|• |b|-cos Z(a, Ь)=|а|*Ьа = |Ь|*аь.
Скалярное произведение в координатах: а-Ъ = а\Ь\ + а2Ь2 + азЬз, где (а(, а2,
аз), (Ь1, Ь2, Ьз)— координаты векторов а и Ь.
Ортогональность векторов: a_Lboa*b = 0.
Коллинеарность векторов a||boa = A,b.
Длина вектора: |а|= /а*а = |/х2 yi -Ь г2, где (х, у, г) — координаты век¬
тора а.
437
Векторное уравнение прямой: r = ro + W.
Векторное уравнение плоскости: (г — Го)п = 0, где (А, В, С)=п — вектор
нормали.
Измерения
1) Соотношения в треугольнике.
Прямоугольный треугольник:
а2 + Ь2 = с2.
b = c s\nB = ccosA = atgB = a ctg А,
S=\ab.
Произвольный треугольник.
Теорема синусов: 0 л =——„ = 2R.
sin A sin В sin С
Теорема косинусов: a2 = b2-{-c2 — 2bc cos А,
S=y a/i„ = rp=-^-=y Ьс sin А= ^р(р-а)(р-Ь)(р-с).
Правильный треугольник:
а /Т а /Т 3 R
R=~Т~' н=^~=—'
R а /3~ с а2 /3”
2) Соотношения в круге.
Длина дуги: l = Ra.
Длина окружности: l = 2nR.
Площадь сектора: S1 /2/?2сь.
Площадь круга: S = nR2
Сторона ап правильного вписанного я-угольника при п = 3, 4, 6'.
а3 = R /Т, а4 = /?/5~, a6 = R.
3) Объемы тел и площади поверхностей.
Призма: V = SH.
Пирамида: К='/зSH.
Цилиндр: V = SH.
Конус: V =' /3SH.
Шар: V = 4/3nR3.
ь
Интегральная формула: S(jc)djc.
а
Ь
Объем тела вращения: V = n^b2(x)dx.
а
Площадь боковой поверхности кругового конуса:
S = nRl.
Площадь поверхности шара: S = 4nR2.
Производные и интегралы
Правила дифференцирования:
(и + v)' = u' + v\ и(ах)'= аи'(ах),
(ХиУ = Хи', (и")' = пип~1и',
(vu)' = v'u + vu', (u(v))f = u'(v)x/,
( U Y u'v — uvf
w= V2
Таблица 1
Функция у
Производная у'
Первообразная § У&х
xn
nx"'
xfl+1
, , , n Ф 1
n + 1
— , JC>0
JC
1
X2
Inx
sinx
COSJC
— COSX
COSJC
— Sinjc
sinx
sin (DJC
(DCOS(DX
1
COS (DX
(D
COS (DJC
— (D Sin (DJC
1 .
Sin (DX
(D
tgx
e*
1
2
COS X
ex
ex
ax
ax In а
1
а
lna
arcsin x
1
✓i - /
Формулы для приближенных вычислений
/Г+7-1+т—г.
п ГГ~Х— . . 1 Я— 1 о
О +•*)*« • +fe-t+ ^ X2, Sin X = X ,
^ О
X2 X3
cos д: 1 tg *«* + —,
e*-!+*+-£, ln(l+x)-x—
Корни уравнения
ах + b = 0 (а Ф 0), х = —,
ах2+ 6х + с = 0 (афО), Х|,2 =—4*аС
2а
если 62 —4ас<0, то корней нет.
ax=b, x=loga6, loga* =6, x=ab.
sinx = a, x = arcsin a + 2/гл, х = л — arcsin а + 2/гл,
cos x=a, x = ±arccos а + 2/гл,
tgx = a, x = arctg а + /гл,
ctgx=a, x = arcctg a-\- /гл,
sinx = 0, x = kn, cosx = 0, jc = 4|- + /гл,
tgx=0, х = /гл, ctgx = 0, х = у + /гл.
439
Значения обратных тригонометрических функций:
л л
arcsin0 = 0, arctg 0=0, arccos 0 = — , arcctg 0 = —,
1 л . /<Г л 1 л
arcs,n_=_, arctg—=т, arccos —= — ,
arcctg — 31
3 ’
arcsin — “p» arctg 1 = i, arccos , arcctg 1 = -j-,
/5" л л /3" л . /7T-
arcsm ^ = — , arctg/3=—, arccos ^ = — , arcctg /3 =
arcsin 1=-^-, arccos 1=0.
ПРИЛОЖЕНИЯ
Задачи для подготовки к олимпиаде
Вступление
Математические задачи можно решать по обязанности, а
можно это делать ради удовольствия. Если считать постоянным
число задач, которое человек должен решить за всю свою жизнь
(скажем, 10000), то чем большую часть из них он решит, получая
при этом удовольствие, тем больше радости будет ему отпущено.
Однако многие постоянные трудоемкие занятия (спортивные тре¬
нировки, музыкальные упражнения, работа в мастерской) не
доставляют удовольствия, если человек никогда не ощущал удов¬
летворения от самостоятельно выполненного дела (победа на
соревновании, исполнение хорошей музыки, изготовление краси¬
вой детали).
Попробуйте порешать нестандартные, иногда шуточные зада¬
чи. Решения придут вам в голову часто неожиданным, непредви¬
денным путем — и это доставит вам большую радость. И тогда
вам, возможно, не покажутся скучными и обычные школьные за¬
дачи, так как вы почувствуете, что владение математической
техникой, как всяким мастерством, сильно расширит ваши воз¬
можности.
Испытанным путем приобщения к радостям, которые может
дать математика, является решение олимпиадных задач. В на¬
шей стране по традиции ежегодно проводятся математические
олимпиады. В них могут принять участие все учащиеся. Собран¬
ные здесь задачи помогут вам проверить свои силы и подгото¬
виться к олимпиаде.
Задачи на смекалку
1. Яйцо варится 9 мин. Как отсчитать это время с помощью
двух песочных часов по 5 и 7 мин?
2. Разделите диферблат часов (с арабскими цифрами) на три
части так, чтобы суммы цифр в каждой части были одина¬
ковы.
3. Могут ли три человека, имея один двухместный мотоцикл,
преодолеть за три часа 80 км, если скорость мотоцикла
70 км/ч, а человека 5 км/ч? Тот же вопрос для 83 км.
4. Можно ли, перекатывая кубик по плоскости, вернуть его на
прежнее место так, чтобы нижняя и верхняя грани поменя¬
441
лись местами? Можно ли добиться, чтобы левая грань при
этом: а) вернулась на свое место? б) стала передней
гранью? в) стала правой гранью?
5. В январе было четыре пятницы и четыре понедельника. Ка¬
кой день недели был 1 января?
6. 11 шестеренок зацеплены по кругу (первая со второй, вто¬
рая с третьей,..., одиннадцатая с первой). Может ли полу¬
ченная система вращаться?
7. Дама сдавала в багаж: рюкзак, чемодан, саквояж и кор¬
зину. Чемодан весит больше, чем рюкзак, саквояж и рюкзак
вместе весят больше, чем две остальные вещи, а корзина
и саквояж весят вместе столько же, сколько чемодан и
рюкзак. Какая из вещей самая тяжелая, а какая самая
легкая?
8. В шахматном турнире участвовали восемь человек. Каждый
из участников сыграл по одному разу с остальными, и все
шахматисты набрали разное количество очков. Шахматист,
занявший второе место, набрал столько же очков, сколько
четыре последних вместе. Как сыграли между собой шахма¬
тисты, занявшие третье и седьмое места?
9. Несколько человек в течение 5 ч наблюдали за улиткой.
Каждый наблюдал за ней ровно 1 ч и заметил, что за этот
час улитка проползла ровно 1 м. Без наблюдений улитка не
оставалась. Могла ли улитка за эти 5 ч проползти 6 м?
10. 200 человек выстроены прямоугольником —по десять чело¬
век в каждом продольном и по двадцать человек в каждом
поперечном ряду. В каждом продольном ряду выбирается
самый высокий человек и из получившихся 20 человек выби¬
рается самый низкий. В каждом поперечном ряду выби¬
рается самый низкий человек и из получившихся 10 человек
выбирается самый высокий. Кто выше — самый низкий из
самых высоких илй самый высокий из самых низких?
Задачи на автоматы
11. Автомат выполняет две операции: возводит данное число
в куб или делит данное число на 8. Можно ли, начиная с
числа 2, получить на этом автомате числа: а) 64, б) 1000,
в) 218, г) 2 , д) 21987?
12. Автомат разменивает десятикопеечную монету на три трех¬
копеечные и копейку. Кассир может обменять любое коли¬
чество денег на десятикопеечные монеты, если обмен можно
произвести без сдачи. Как, имея бумажный рубль, выменять
наибольшее число однокопеечных монет, пользуясь услугами
кассира и автомата?
13. На микрокалькуляторе разрешается выполнять четыре
арифметических действия и вычислять тангенс. Как с его
помощью вычислить sin(a — p)/sin(a + р)?
14. В стоэтажном доме установлен лифт, в котором действуют
442
лишь две кнопки. Если нажать на первую кнопку, то лифт
поднимется на семь этажей вверх, если нажать на вторую
кнопку, то лифт опустится на девять этажей вниз. Можно
ли, пользуясь этим лифтом, попасть с 1-го этажа на 72-й?
15. Автомат Л за 10 коп. умножает заданное число на 3. Авто¬
мат В за 1 коп. прибавляет к заданному ему числу 2. С по¬
мощью автоматов А и В превратить число 0 в число 1980,
израсходовав при этом не более 56 коп.
16. В трех вершинах квадрата находятся три кузнечика. Они
играют в чехарду, т. е. перепрыгивают друг через друга.
При этом если кузнечик А прыгает через кузнечика В, то
после прыжка он оказывается от В на том же расстоянии,
что и до прыжка,и, естественно, настой же прямой. Может
ли один из них попасть в четвертую вершину квадрата?
17. На доске написаны числа 34 и 21. Разрешается за один
шаг приписать к имеющемся числам разность между ка¬
кими-нибудь двумя из них. Как получить число 27?
18. Первый член последовательности равен З1987. Каждый сле¬
дующий равен сумме цифр предыдущего. Найти десятый
член.
19. Имеются два сосуда. В первом находится 1 л воды, а дру¬
гой — пустой. Из первого сосуда переливают половину
имеющейся в нем воды во второй, затем из второго перели¬
вают треть имеющейся в нем воды в первый, затем из пер¬
вого переливают четверть имеющейся в нем воды во вто¬
рой и т. д. Сколько воды окажется в первом сосуде после
101 переливания?
20. Имеется 20 камешков. Можно брать 1, 2 или 5. Двое ходят
по очереди. Кто выигрывает при правильной игре, если
надо взять последний камень?
Задачи на составление фигур
21. Задача простая: деревья в саду.
Девять деревьев. По три в ряду.
Их посадить нужно в десять рядов.
Задача простая — ответ ваш готов?
22. Радиус шара, описанного около правильной пирамиды, ра¬
вен 1 м. С помощью провода длиной меньше 4 м соедините
все вершины пирамиды между собой.
23. Можно ли в произвольный прямоугольник площади, рав-
1
ной 1987 , поместить несколько непересекающихся кругов,
сумма радиусов которых равнялась бы 1987?
24. Расположите на плоскости шесть точек так, чтобы любые
три из них образовывали равнобедренный треугольник.
25. Замкнутая ломаная пересекает Каждое свое звено ровно
один раз. Постройте шестизвенную ломаную с таким свойст¬
443
вом. При-каких n существуют я-звенные ломаные с таким
свойством?
26. Может ли пересечение треугольника и четырехугольника
быть восьмиугольником?
27. Докажите, что при любом k > 7 существует многогранник,
имеющий k ребер.
28 Какое наибольшее число пакетов молока можно приставить
друг к другу так, чтобы все они имели общее ребро?
29. Как расположить на плоскости четыре треугольника так,
чтобы любые два из них имели общий участок границы и не
имели других общих точек?
30. Можно ли из трех стержней и нескольких ниток изготовить
жесткую пространственную конструкцию так, чтобы стерж¬
ни не соприкасались между собой, а были только связаны
нитками, прикрепленными к их концам?
Задачи на модели
31. Пакет молока — тетраэдр с длинами ребер по 16,3 см —
можно протащить через петлю, сделанную из веревки дли¬
ной 48,9 см. На сколько можно уменьшить петлю, чтобы че¬
рез нее еще протаскивался пакет?
32. Имеются лист бумаги, карандаш, измерительная линейка и
спичечный коробок. Найдите, ничего не вычисляя, длину
диагонали, соединяющей противоположные вершины ко¬
робка.
33. Как вычислить радиус металлического шарика, используя
линейку и прозрачный цилиндрический сосуд с водой?
34. Стальную плитку размером 60X85 см обвели карандашом
на бумаге. Найти центр полученного прямоугольника, имея
лишь эту плитку и карандаш.
35. Плитку в форме прямоугольного треугольника со сторона¬
ми 3, 4, 5 см обвели карандашом на бумаге. Построить
центр вписанной окружности, имея лишь эту плитку и ка¬
рандаш.
36. Разрешается делать две операции — проводить прямые и
из точки на прямой восстанавливать к ней перпендикуляр.
Дана прямая и точка вне ее. Опустите из этой точки
перпендикуляр на прямую, используя лишь разрешенные
операции.
37. Можно ли кубик с ребром 1 см завернуть в квадратный пла¬
ток со стороной 3 см?
38. Можно ли на планете, имеющей форму шара диаметром 1,
расположить восемь станций слежения так, чтобы любое
тело, находящееся на высоте 1 над поверхностью планеты,
было видно по меньшей мере с двух станций?
39. Постройте с помощью линейки с делениями через 1 см бис¬
сектрису данного угла.
40. ABCDA'B'C'D' — правильная призма, АА' = ЗАВ. Точ-
ка Р лежит на ребре АА' и РА = АВ. Нарисуйте кратчай¬
ший путь по поверхности призмы от точки Р до точки С'.
Задачи на исследование функций
41. При каких а функция у = — х3 + 3 ах + 1 и функция
у = х2 + (а + 1)* имеют минимум в одной и той же точке?
42. Функция у = (х — а)(х2 — 1) имеет минимум при х= 1/9.
В какой точке у нее максимум?
43. Найти квадратный трехчлен у = /(*), если известно, что
/'(*) + /(*) = 2х2 -Зх - 1.
44. Известно, что парабола у = х2 + рх + q касается пря¬
мой у = х в точке (1,1). Найти р и q.
45. Построить график функции у = т\п{х2 — 2ху 2 — х).
46. Доказать, что четыре точки пересечения парабол у =
= х2 -\- х — 40 и х = у2 -\- у — 41 лежат на одной окруж¬
ности.
47. Сколько корней имеет уравнение х2 + ах + Ь = 0, если
известно, что 100 + 10а + b < 0?
48. Пусть /(1 + \/х) = х2 — 1. Найдите f(x).
49. Докажите, что уравнение (х — а)(х — Ь) + (х — Ь)(х — с) +
+ (х — с)(х — а) = 0 имеет вещественные корни.
50. Среди всех квадратных функций со старшим коэффициен¬
том 1 найдите ту, для которой на промежутке [ — 1,1] на¬
ибольшее по модулю значение минимально.
Задачи на экстремум
51. При скорости v (км/ч) автомобиль расходует 10^Jv/100—v
литров бензина в час. Найдите минимальный запас бензина,
позволяющий проехать 100 км.
52. На двух стройплощадках возводятся два одноэтажных
склада, общая площадь 600 м2. Стоимость постройки скла¬
да прямо пропорциональна квадрату его площади. Кроме
того, известно, что строительство на второй площадке об¬
ходится на 40% дороже, чем на первой. Какой должна
быть площадка каждого склада, чтобы общая стоимость
строительства была наименьшей?
53. Каково должно быть отношение высоты консервной банки
к радиусу ее основания, чтобы при данном объеме расход
металла был минимальным?
54. В трапеции ABCD длины сторон АВУ ВС и CD равны 1 см.
Каким должен быть угол при вершине D, чтобы площадь
трапеции была наибольшей?
55. Турист находится в поле в точке А на расстоянии d от бли¬
жайшей точки В прямой дороги. В какую точку дороги он
должен направиться до прямой, чтобы скорее попасть в
удаленный пункт D на этой дороге, если известно, что ско¬
рость по полю v, а по дороге и(и > v).
445
56. Несколько одинаковых ящиков весят вместе 10 т, причем
каждый из них весит не больше 1 т. Какое наименьшее ко¬
личество трехтонок заведомо достаточно, чтоб увезти за
один раз весь этот груз?
57. У грузового автомобиля передние покрышки стираются че¬
рез 15000 км пути, а задние — через 25000 км (на задних
колесах по две покрышки, а на передних — по одной). Как
нужно менять покрышки на колесах, чтобы проехать На
одних и тех же покрышках наибольшее возможное расстоя¬
ние? Найдите это расстояние.
58. Малыш может съесть торт за 10 мин, банку варенья — за
8 мин и выпить кастрюлю молока — за 15 мин, а Карлсон
может сделать это за 2, 3 и 4 мин (соответственно). За ка¬
кое наименьшее время они могут вместе покончить с зав¬
траком, состоящим из торта, банки варенья и кастрюли
молока?
59. Человек стоит на заснеженном поле на расстоянии h от
асфальтированного шоссе. Его скорость при движении по
снегу вдвое меньше скорости на асфальте. Какое расстояние
человек должен пробежать по снегу так, чтобы как можно
быстрее добраться до некоторой (достаточно удаленной)
точки на шоссе?
60. На странице книги печатный текст занимает 150 см2. Верх¬
нее и нижнее поле страницы — по 3 см, правое и левое —
по 2 см. Если принимать во внимание только экономию
бумаги, то каковы должны быть наиболее выгодные разме¬
ры страницы?
Задачи на неравенства
61. Какое из двух чисел больше:
а) У0,999 или 0,999; б) sin 1 или sin4; в) У 1986 + У 1988
или 2 Vl987; г) 8х или 5* + 6* при х ^ 2; д) 1/1,00003
или 0,99997?
62. ап = У я +I — У я . Доказать, что ап < 1 /2 У я .
63. Пусть S — площадь фигуры, ограниченной отрезком [0, я]
оси абсцисс и графиком функции у = ysin х . Доказать,
что S > 2.
64. Докажите, что хотя бы одно из значений функции у =
= х2 + рх + q в точках —1,0, 1 по модулю не меньше 1/2.
65. 9 одинаковых авторучек стоят 11 руб. с копейками, а 13 таких
же авторучек— 15 руб. с копейками. Сколько стоит одна
авторучка?
66. Каждое из двух квадратных уравнений х2 + ах + b = 0
и х2 + сх + d = 0 не имеет корней. Докажите, что уравнение
2х2 + (а + с)х + b + d = 0 также не имеет корней.
67. В квадрате со стороной 1 произвольным образом отметили
51 точку. Докажите, что какие-нибудь три из них можно
покрыть кругом радиуса 1/7.
446
68. Одна треугольная пирамида расположена внутри другой
треугольной пирамиды. Может ли сумма длин всех ребер
внутренней пирамиды быть больше суммы длин всех ребер
внешней пирамиды?
69. Верно ли, что при всех х £ [0, я] справедливо неравенство
. sin2* . sin3jt _
Sin X Н ^ 1 2
70. Верно ли следующее утверждение: для любой точки, лежа¬
щей внутри выпуклого четырехугольника, сумма расстояний
от нее до всех вершин четырехугольника меньше его пе¬
риметра?
Задачи на развитие пространственного воображения
71. Могут ли две противоположные грани четырехугольной пи¬
рамиды бьГгь перпендикулярны плоскости основания?
72. Какой угол образуют две диагонали смежных граней куба,
выходящие из одной вершины?
73. Найдите геометрическое место середин отрезков, концы
которых расположены на двух данных скрещивающихся
прямых.
74. Два отрезка постоянной длины скользят по двум скрещиваю¬
щимся прямым. Докажите, что объем тетраэдра с вершинами
в концах отрезков является постоянным.
75. Три зеркала образуют трехгранный угол со взаимно пер¬
пендикулярными гранями. Докажите, что луч света, отразив¬
шись от всех трех граней, будет идти в направлении, парал¬
лельном исходному.
76. Докажите, что сумма расстояний любой точки внутри пра¬
вильного тетраэдра до его граней постоянна.
77. Вершины треугольника ABC расположены на ребрах трех¬
гранного угла. Найдите геометрическое место центров тя¬
жести треугольников, если две вершины закреплены, а
третья скользит по ребру трехгранного угла.
78. Пусть в условии предыдущей задачи закреплена только одна
вершина треугольника, а две другие независимо скользят по
ребрам трехгранного угла. Найдите геометрическое место
центров тяжести.
79. Тело S состоит из всех точек пространства, расстояние кото¬
рых до данного отрезка длины h не превосходит R. Найдите
объем тела S.
80. Тело Т состоит из всех точек пространства, расстояние ко¬
торых до квадрата со стороной а не превосходит R. Найдите
объем тела Т.
ОТВЕТЫ
1.3. б) С (2а — Ь)\ в) D г) Е (~Та); д> F (2Ь~аУ 1Л-
1,7; 2/3; 4 — л; 2; 2; */2“— 1; 5-я. 1.5. /5“-2; 2; 0. 1.6. |jc-3| = F_^
|х— 3 (д:<3);
(х + 4, (jc>—4), (х — 3 (jc>3),
|jc + 4| = т . v |3_х)= ' -- '• , 8 а) *=_!, * = 3; б) * =
I—дс —4 (дс< —4); I 3 — х (х<3).
= —4, jc= —2; в) jc = —5/2. jc = 3/2; г) дс = —4/3, дс = 8/3; д) решений нет;
е) дс=— 3, лс = 3; ж) х= — 1, дс = 4; з) решений нет; и) —2<!х<; —1; к) х = 2;
л) *5»2; м) х = 3, х = 7. 1.9. а) (— оо, —1 ](J[ 1. +°°); б) [—4, 6]; в) (—оо, —4](J
U[0, +оо); г) (—6, —4); д) (— оо, 1)U(5, +оо); е) [—4, —2]; ж) (—1, 4);
3) (— оо, -1)U(0, +оо); и) [0, 1]; к) (-3, -1)U(1, 3); л) (-оо, 1); м) (—ОО,
+ оо). 1.10. а) |х+1|=1;б) |дг — 5/2| = 1/2; в) \х—2|<3; г) М>2. 1.11. \АВ\ =
= /5~, |ЛС|=/Т3, \DE\=2y/T, \FG\= /ГО, \AG\= 1.12. а) (2; 3); б) (1;
-2); в) (0; 0); г) (3; 2). 1.13. а) (2; —3), (—2; 3), (—2; —3); б) (—2; —1),
(2; 1), (2; —1); в) (—1; 2), (1; —2), (1; 2); г) (—3; 0), (3; 0), (3; 0). 1.14. а) (2;
3), (2; 9); б) (1; -3), (7; -3); в) (2; 2), (5; 5); г) (-1/2; 1/2), (4; -10).
. v 2 — Зх 2 — 5у ^ 2х + 3 7у — 3 , ...
1.21. а) у=—=—, х=—; б) у=—=—, х=—»—; в) у=— 3W;
г) х-
з) S-
1 — li/1 v 3 /~т \ f3 -|- 1
—j2— -, д) v= ys2 ; е)
<= y'lOs— 1; ж) s=
(i + o2
—2;
Ю ’ ' r ” 2
t_{-, /=у+1. 1.22. a) 2, —1, 3-i-, /+1, 2/+1, y+ 1, jc + 2, jc, 2jc,
1
jc+5, j^-hl, (лг-hl)2, *+2; 6) 1, 2, 1-i, \t\, 2|/|,
\x\,
1
2 I r \ , 1 Q 1 1 1
x. W; в) 1, -T,3T,T,
13
U—1
1
jc+1 ’ jc— 1 ’ 2л:.— 1
1
u-fll,
1
^2-, *; г) 1, 4, t\ 4—, (x+ l)2, (x-\)2, (2x 1), —
_9_L 55
2 ’ 12
1
/+T’ 2/+1Г"Т + Т’ *+1+*+1
*-1 +
X+\
+
25
1
Yic—T
, * + , *Ч-V, ^-h-V + 2, * + —+
JC JT JT JC
7+T
; e) 1, 0, 2,
Г0(/<0), |0(<<0), Г0(х<-1), |0(x<l),
\l (<>0); \l (<>0); U (x > —1); \l (jc > 1);
I 0 (*-0), r
I 1 (JC 0); I
{
|2jc-1|,
_25 1_
x ' x1 ’
x\ Д) 2,
2x-l +
0 («0),
1 (/>0);
0 (x < 0),
5 (x > 0);
0 (x < 0),
1 (x > 0)
, Г0 (*<0). 5 Г 0 (t<0)
; \ 1 (x > 0); Ж)1' T’ \ /
I, / 0 (/ < 0),
; I 2/ (/ > 0);
0 (t < 0),
Y«>°);
{
0 (JC< -1),
jc-h 1 (JC > — 1);
{ 0 (x< 1),
1 JC - 1 (JC > 1);
с
(JC < 0). xt
0 (jc < 0),
(t > 0);
2x-1 (*>y) ;
Г 0 (*<0). r
1 JC2 (jc > 0); 1 JC (jc > 0).
1.23. а) нет; 6) Pi, P2; в) Pi, P4; r) Pi, P2; д) нет; e) Pi; ж) Pi. 1.25.
a) (-00; — 1)U(—1; 1)U(1; +00); 6) (-00; 0)U(0; 1)U(1; +00); в) [0; 2]; г) (0; 1)U
(x>0);
448
U(l; +°°); +<»); e) (—00; +00). 1.38. a) *=4/3; 6) —4; в) *=—10/7; r) *=
= —; Д) 3; c) jc==13/7; ж) jc= 1/12; з) *=0, *=5; и) *=±-\/3 ; к) *=2, *=—3;
л) * = 4, x = —3; m) * = 4, x = —5; h) x= \, x=—4; o) * = 5, x——2; n) x = 3,
x = — 6; p) x= — l, * = 5/2; c) x= —1 ± y^5 ; t) x=— 2, x = —5; y) x=— 3,
x= —4; ф) * = — 1/3, *=1/4. 1.39. з) *(* — 5); и) (* — fe~)(x+ yT");
к) (* —2)(* + 3); л) (* — 4)(* + 3); m) (* —4)(* + 5); н) (дс— l)(* + 4); o) (* —5)X
X (•* + 2); п) (* —3)(* + 6); p) (*+l)(2* —5); c) (* + 1 + у1Г)(* + 1 — );
т) (* + 2)(* + 5); у) (* + 3)(* + 4); ф) 12 + (* + т) ' ,‘40, a) *(*—OX
X(*+l); 6) (* — 1)(* + 1)(*2+ 1); в) (2хг + 5)(уТх— /5")(у^'* + ,/IT); r) (* +
+ 1)(**+1); д) (* + 2)(хг-2х + 4); e) (хг+ 1)(*-2)(* + 2). 1.41. a) *>-7/2;
б) х^З; в) x<C— 2/5; r) x^ — 5/6; д) x^3\ e) x>—5; ж) х>2; з) x> — 1/3.
1.42. a) (—oo, — 1)U(1, +«>); 6) (—7, 0); в) (—00, —2)(J(3, +00); r) (—00, — 3)U
U(-2, -1)U(0, +00); д) (-3, -2)U(2, 3); e) [-3, 6/5)U[5/2, 7/2); ж) (-2, 0);
з) решений нет; и) (-3/2, 1); к) (—00, — 1)U[0, 1); л) [-3, -5/2)U(5/2, 3];
м) [-5, 0]; н) (—оо, — 2)U[1» +оо); о) (-00, —2)U(—1/3, 0); п) (-00, —2]U
U(— 1 > + °°)- 1*44. а) нет; б) да; в) нет; г) нет. 1.46. D(/)=(0, +00); £(/)=(0,
/ \ 3/2
+ оо). 1.47. а) /п = 7,8а3; б) т = 7,8V; в) т = 7,8 / —) . 1.48. у= /4Я2-*2 ;
S =* |/4/?2 — jc2. 1.49. s=Sfx*, S=3/3~y2. 1.50. S=x /4 - х\
2.5. а) 0,3; б) 0,3; в) 0,06; г) 0,06. 2.6. а) 3; б) 9; в) 6. 2.7. а) а; б) 2ах + Ь +
+ аД*; в) 3** + 3*&*+(Д*)2. 2.8. а-) оср = 3; б) 1>мгн = 3. 2.9. а) 3; 2,2; 2,02; 4,02;
б) 2; 4. 2.10. 7; 6; 5,2; 5,02; u„r„=5. 2.11. 0; —1/2; —0,9; —0,99; Д0)=—1. 2.12. 1;
3/2; 2; 2. 2.19. а) —0,7-10“3; — 1,226-10-2;. б) —1,23-10-3; —6,15-Ю-2;
в) +1,17-10-3; -3,928-10~2; г) +5,574-10"4; -2, 787-10“2. 2.20. а) у' = ? ;
X
б) </'=-3-; в) у'=3х2\ г) у' = А; д) у' = — 1 ; е) у' 1
*» ’ ' ’ • ' ' X4 ‘ Л' ' 2хГх ’ ' * “Cx+if*
а) —2; —1/2; б) 1; 1/8; в) 3,12; г) —3; -3/16; д) —1/2; — 1/4^/2 ; е) 1/4; 1/9.
2.21. а) у'=12х3; б) yf =З*8; в) i/'=--А; г) yf = -}/3“-1/2*^1/2; д) у’=
= — 3/2дг_5/2; е) у'=20хг— 14*— 1; ж) (//=5*4 + 6** + -^-; з) (/' = 4*3;
И) г/'=(1 —1/2*-3/2 + 2*-3)(3*2 + * — 8) + (х+1/уТ—1/*2)(6*+1); к) у' =
=(1-7") ^+JC+1)+(-t+““+~r)(2jt+0; *> у'=1—
М) 1 • 2'22‘ а) б) 0; В) ^)=-(1+3*)"2; к°>
Г) /'(•)= -7/4; Д0)=-7. 2.23. а) *=1; б) * = 2; в) *=1. 2.24. Vi, А х3.
2.25. а) у'=.2*-1; б) у'= 12**+ 102* — 57; в) у? = -9(3*+ 1)“4; г) у' =
=|-(5*-1Г'/2; д) у' = 1/Ж\—х)-3/2; е) ?='/;/—±— -J—V ж) <^ =
\УГ+2 л[Т^2'
=10*(1—*2)4; з) у’=- (лД^+2)2 Г И) J/'=(*~1)3 (*+02(7*+0- 2.26. а) / =
—(>''*’ + 1)1//х ; б) (/, = 2(*г + **-2*+1)(3*2 + 2*-2); в) у' = 2(*+ 1/* —
/*”)(! — I/*2— 1/2/*”); г) /—4 (*+‘)3 . 2.27. а) (-оо, 0]\, [0, +»)/;
449
б) (—оо, 1/4]\, [1/4, +оо)/; в) (— оо, —1/2]/, [—1/2, +оо)\; г) (—оо, +оо)/;
д) (—оо, -|-оо)/; е) (—оо, —1]/, [—1, 1]\, [1, +оо)/; Ж) (— оо, 0]\, [0, +00)/;
з) (—оо, - /Г]/, [-/S', /5>, [/2", + оо)/; и) (-00, -1]/, [-1, 0)\, (0, 1]\,
[1, -|-оо)/; к) (—оо, 0)/, (0, +оо)/; л) ( — оо, 0)\, (0, 1]\, [1, +оо)/; м) (— оо,
-1]Л ]+1, 1]\. [1. +00)/; Н) ( —оо, -1>/, (-1, 0)\, (0, +оо)/; О) [О, 1 /4]\,
[1/4, -J-oo)/; п) (0, +оо)/. 2.28. а) jc = 0 — максимум; б) jc= —2—минимум;
в) х = —1/2 — максимум; г) jc = 1 /4 — минимум; д) jc = —2 — минимум; х —
= 2 —максимум; е) jc = 0 — максимум, х = 4 — минимум; ж) х~ — \— /5~ —
максимум, jc = -1 + /5~—минимум; з) jc=—2 — максимум, jc = 5—минимум;
и) jc = 0 — максимум, jc = ±1//5" —минимум; к) jc = 0 — минимум; л) х =
= 3/4 — минимум; м) jc=—4 — максимум, jc = 2 — минимум; н) х= — \ —
максимум, jc= 1 — минимум; о) jc= —/5" — минимум, х= /5" — максимум;
п) jc= 1/3 — минимум. 2.31. а) 1; 6} 1; в) 2. 2.32. а) а>0, jc=0 — минимум, а<0,
jc = 0—максимум; б) а<сО, нет экстремумов, а>0, jc = -|-/а”— минимум, х —
= —/а” — максимум; в) а>0, jc = 0 — минимум, а<0, х=± — мини¬
мум , jc = 0 — максимум; г) а>0, нет экстремумов, а<0, х = + мини¬
мум, x=-~\J-^ максимум. 2.37. Четные, нечетные. 2.38. i/(0) = 20; i/(l)=10;
у(2) = 0; 1/(0 = $)-Ю/. 2.39. и(1)=-10, и(2)=-5/2; и(3)=-10/9. 2.40. и(1) = 9,
а(1) = 12. 2.42. 722,5 Дж. 2.43. /= 1. 2.47. /(3) = 19. 2.48. а) /=±1; б) /=1/4.
. 2.49. 0,002. 2.50. а) Лу = (2jc + 5)djc; б) dS = 2nRdR\ в) d£ = 2fcrdr + \dr\
г) dw = (9t2 + 4/-3)d/. 2.54. а) утш =y(0) = 0, yma* = y( 1) = 5; 6) ymin = y(2) =
=— Ю/3, Утах = У( 1) = Ю/3, B) J/min==*/(4)= 2, Утах—У{ 1 /4) = /a\ г) ym\n = У{ 1) =
— — 1; Утах=у{9)=3\ д) ут\п—у{ 1 )= 1 1» Цтах=у( 1)= 19; е) ут\п=у{ 1/2)= 35,
J/max = J/(3)=14. 2.55. a = h = У24. 2.56.^max = 6. 2.57. Утах = л/3. 2.58. S6oK=16.
2.59.-1/2. 2.60. 1.2.61. 1/У3.2.62.а=л/35Щ^-. 6=V*(M:W с=
3 i— ft V(*+0
2.63. R = h= 2.64. 3/4p, 3Лр, 'АР-
¥ Я
3.2. a) Совпадают; б) пересекаются; в) параллельны; г) скрещиваются.
3.3. Скрещиваются. 3.4. Достаточно натянуть нити, соединив основания ножек
по диагоналям. Стол будет стоять устойчиво только в том случае, когда нити
соприкасаются, причем без излома. 3.5. а) нет; б) нет; в) да; г) да; д) да; е) нет.
3.6. а) нет; б) нет; в) нет. 3.7. Нет. 3.8. Если плоскость, проходящая через одну
из прямых и точку, параллельна другой прямой, то нельзя. В противном случае
можно. 3.10. Возможны оба случая: /ill/г и /1^/2. 3.11. Да. 3.14. Эта линия —
прямая, соединяющая точку пересечения прямых а и b с точкой Р. 3.15. а) Бес¬
конечно много; б) одна. 3.16. Нет. 3.17. Эта прямая лежит в плоскости ABS и
параллельна прямой АВ. 3.19. а) Да; б) да; в) да. 3.20. Плоскость, парал¬
лельная данным и равноудаленная от них. 3.21. Эта точка лежит на пересечении
прямой MN со средней линией четырехугольника АА'СС', параллельной сторо¬
нам АА' и СС'. 3.24. Сечение является трапецией, в которой В'С — одна из
параллельных сторон. 3.25. Сечение проходит через середины ребер АС', ВС и
DC. 3.26. Сечение является прямоугольником, основание которого параллельно
отрезку BD. 3.27. Сечение является прямоугольником, основание которого па¬
раллельно отрезку СВ.
4.6. V2 —1. 4.7. 144 м. 4.10. а) I?; б) АЙ\ в) 0. 4.11. а) I?,; б) сб{\
в) аВ\; г) D^B. 4.16. Точка М-центр масс системы точек Л, В, С, массы которых
находятся в отношении 3:2:1 соответственно. 4.23. а) Х5= Л?— D? — 5S;
б) Хё= -в£-сБ-Ш\ в) АЁ^Ш-BD* 4.24. EF= -АВ^\/28ВС. 4.25. АВ=
450
= ОЁ-ОА\ в£=—Ш—Ш\ с15 = О А — (ЭЙ; Ш=оА+Ш. 4.26. Д7Г= Ш+
+ J5; AM = '/2aS+'/2a5-, Ш= -л5; Ш = У2л£ + ‘/2Ж 4.27. Л?= 7зЖ
4.28. С/5 = g; ЦЁ=— р; A/5=2(q+p); B?=q+p; Л(5=д+р; Jf=2p+q;
= 2q + p; EF=2q, £?=p—q. 4.29. a) dE=-JS; ТХ=М—~вЕ\ £?= —B?;
сд=Ш-Ш, б) в?=72в^+72л^, сЬ=— '/2аЙ+'/М>, ЦЁ=—аЁ,
£?=-72Ж—'/2вЗ; Ft=[/2jS-'/2BS. 4.30. М=6/5а?—3/5аЙ, в£ =
= 75Л7Г-2/5Л?:. 4.31. Л<5='/зЛ£+7зЖ?+Уз;475. 4.32. а) р; б) q+p; в) q +
+ 72Г; г) q+p— 7гг; Д) 72Q+P —7гг; е) ^‘Р+Ч + 'П'1'- 4-33- а) ОЙ— 7*а+
+ 7гс, б) 0/5=а+с-Ь, в) 0#=а+72(с-Ь). 4.41. а) -1; б) 2; в) -1/2; г) 0.
4.42. а) 72;б) 0; в) 2; г) —2; д) — 1 /3; е) —2/3. 4.43. а) —i+2j, б) I—j, в) i+2j-
—Зк, г) i+2k. 4.44. а) 6Ь—4а; б) 5а— 13b, а=4/пП1-|-6/пп> Ь=4/цп —‘/ит;
в) а=|/2т + ,/2Р, Ь=1 /2п—1 /2Р, с= ‘/2т—1 /2п. 4.45. а) с=4Да— 13/эЬ; б) с =
= 2а—ЗЬ; в) с= — 3/2а. 4.46. а) —1; б) —2; в) —1/2. 4.48. а) (х\ у\ 0); б) (jc;
0; 0); в) (0; 0; z)\ 4.50. б) Внутренность куба с центром в точке О (0; 0; 0) и вер¬
шинами в точках с координатами: (1; 1; 1), (—1; 1; 1), (—1; —1; 1), (1; —1; 1),
(1; 1; —1), (—1; 1; —1), (—1; —1; 1), (1; —1; —1). 4.51. а) (3; 2; —3); б) ( —1;
0; 5); в) (0; 5; 2). 4.53. (1/2; 1; 0); (1; 1/2; —2); (3/2; 1/2; —1). 4.54. а) ( —1;
—3; 3); б) (2;—2;—3), в) (—3; 3; 7). 4.55. а) (2; 1; —1); б) (4;—2; —1);
в) (4; — 3; 0). 4.56. а) (1/2; 5/2; 1); б) (0; 0; 0); в) (3; 1 /2; 0). 4.57. а) (1/3; 1;
7/3); б) (—2/3; 4/3; 5/3); в) (4/3; 4; —8/3). 4.58. а) (—2; —1; —5), (—1/2;
1/2; —1); б) (—3; 1; —4), (—3/2; 5/2; 0); в) (—3; 0; —3), (—3/2; 3/2; 2/3).
4.62. a) v = (2; ~1); б) (—5; 5); в) r=r0+W; г) лг= —5+2/, y=b—t\ д) х-\-2у—
20 42
-5=0. 4.63. 20tg50°«23,8 (Н); -^-«31,1 (Н). 4.64. « 60,0 (Н);
42 - 73,2 (Н). 4.65. 15УЗ « 26Д ЗОл/З « 52,0. 4.66, 45 «35,0 (Н),
sin35° ~ v '• v ’ ’ v ’ ’ 2 sin40°
45
2 sin 40° ~ 35,0 (H)' 4‘80‘ *2 + 1; X + 2’ “ + * “ 1- 4-81- (335> 190'
155, 220). 4.82. а) Да; б) да; в) нет.
*> 90‘-f-; isiHiwW' f I■ SA ”/l80' ”/18i
я/12; я/6; я/4; я/3; я/2; 2я/3; 1,25я; 4я/3; ЗЗя/18. 5.4. 12°; 15°; 72°; 99°; 140°
360°. 5.5. я/4; 5я/12; Зя/20; 0,97; 0,84. 5.6. 108°; 81°; 40°. 5.7. 5°; 150°; 720°
1500°. 5.9. б) 270°; в) —0,75я; г) 720 000 град/с; 4000я с-1. 5.10. а) У2/2
б) 1/2; в) ^2 /2; г) —УЗ /3. 5.11. а) 1; б) 2; в) sin2 а; г) 1 — ^-sin2 2а; д) sin а
е) —cos2 а/sin а; ж) 4; з) 1; и) —4ctg 4а; к) 1. 5.13. а), в), д), е) существует
б), г) не существует. 5.14._а) ctg a=^2 /2j_ cos a= 1Д/3 ; sina=V2/V3
в) sin a= —^11/6; tga=yil/5; ctga=5/yil; r) tga=—15/8; cosa=8/17
sin a= —15/17. 5.16. а) 2я; б) 2я; в) я; г) 10я; д) я/3; е) я/4; ж) Зя; з) 4я/3.
5.18. а) Нечетная; б) не является; в) не является; г) нечетная; д) нечетная; е) не
является; ж) нечетная; з) не является; и) четная; к) нечетная; л) четная; м) не
является; н) нечетная. 5.19. а) [ — 1, 1); б) [—4, —1]; в) [0, 1]; г) [0, +оо);
д) [0, 41; е) (—оо, 1]. 5.20. a) x=nk\ б) x=n/2-\-2nk\ в) х= — n/2-\-2nk\
г) *=я/2 + яЛ; д) x = 2nk\ е) *=я + 2яЛ; ж) х=пк\ з) х= я/4 + яЛ; и) х =
= Зя/4-|-яЛ; к) x=n/2-\-nk\ л) x=n/4-\-nk\ м) х= Зя/4 + яЛ; н) х = (— 1)*Х
Хя/6 + яЛ; о) х— =ьЗя/4-|-2яЛ; п) * = я/3-|-яЛ; р) 0; с) 0. 5.21. а) х =
= (— 1)*я/4-|-яЛ; б) х= я/12 + яЛ; в) *= ±я/6 —я/4 + яЛ; г) х= я/9-|-яЛ/3;
д) х= ±я/18 + я£/3; е) х= ±я/12-|-я/6 + яЛ/3; ж) x=2nk\ з) *=±я/3 +
451
+ 2л/г; и) х= — л/3— 17л/180-|-л£; к) x—n/2-\-nk\ л) х= ±л/6+ лЛ; м) х =
3
= (— 1 )лл/8 -|- лЛ/2; н) 0; о) * = л/4-f л£/2. 5.22. a) 2cos *; б) — sin*;
3 2 2cos jc
в) г =—; г) cos 2*; д) —sin 2jc; е) 2х sin х — х2 cos х\ ж) ^—;
cos х sin х sin х
л!2 sin (f л/4) _ уg cos я 4) tgjc .
ч jccosjc—sin* v cos'* v r np rv. „ч 1 w
a, -3 ; » 2sln. ■ «) to»5'- "> TX
xsinl- “> ,os'(L+l) ; B) (3,~г)~|Мп(г'+т): 01 2'"S(2' +
+£)“* (т-г);-у”" (f-T )sl" (2'+f )• Ml5; 0J№
0,485; 0,695; 1,111; 0,51.
6.1. a). 90°; 6) 130°; в) 40°. 6.2. a) 120°; 6) 60°; в) 0°; г) 180°; д) 60°; e) 90°;
ж) 30°; з) 120°. 6.3. a) 2; б) 5; в) —5; г) —4; д) —4^-. 6.4. а) 3; б) 0; в) —3/2
г) -у/2 /2; д) 1; е) —6д/2 /2; ж) —д/з ■ 6.6. 3. 6.7. 2. 6.8. а)_ 2; б) —2; в)_—
6.9. 1. 6.10. а) 15; б) -5. 6.15. |Л£|=УЗ; \Ш\ = ^7/2. 6.16. т/61/2
6.21. |/С?'| = 3/2; \Ш>\ = А1г /2; \кй\ = л/з/2- в.22. 60°. 6.24. 35,3°. 6.25. 71,6°
7Л. а) 1 /2; б) л/2/2; в) л/3/2; г) '/2; д) '/2; е) л/2/2; ж) л/2/2; з) —‘/2
и) л/2 /2; к) V 3 /2. 7.2. a) sin а; б) cos 2а; в) sin а; г) tgactg($; д) tg(a— ($)
7.3. а) л/3 /2; б) л/2 /2; в) л/3 /2; г) л/2 /2; д) '/<; е) 'Л; ж) 'Л- 7.4. а) 1; б) 1
, . т/2-л/3 , л/2 + л/3 1
в) cosa— sinсс; г) — /4sin4a. 7.6. а) ^ ; б) ^2 + ^3
ч -д/2 —л/2 . л/2 + л/2 ,1 7л/2 л/2
r)-V-:a) 2-;e)TTvT- 7-7- а) ^ ; б) "10-
в) 5"^26^ ; г) “4s Д) е) ±_^2Г“- 7'8' а) 1: б) в) 1/л/5
г) 1; д) 1/л/З^е) 1; ж) 1/л/З. 7.10. а) —1/3; б) 1йа=1±л/2/2. 7.11. а) л/2/2
б) 1/4; в)_ л/2 /2; г) 2/л/З . 7.12. а) 3/5, —4/5, —3/4; б) 4/5, —3/5, —4/3
7.14. а) V6 /2; б) sin 18°; в) 0; г) —sin 18°; д) tg 20° ctg 5°; е) 2sin 35° cos 15
ж) У2 sin 25°; з) sin (a—р) sin (a-fp); и) —sin (a— p) sin (a+p); к) 2sin-j^- X
X cos —; л) —2sin sin ; м) 2sin3acosa; h) 2sinacos40G
1 zU 144 144 _ _ _
o) 4cos у cos a sin -^y-. 7.15. a) —; 6) ~ ; B) y~ "bcos^° )
r\ 1 / Зл л \ \ \ ( Зл 13л \ 1 / . 9л л \
r)rVcosT6 + cosTo/’ д)г VCOS40“COS-40“> e) rVs,n40“s,nT0>)
ж) -у (cos 2a — cos 8a); з) у (sin 2a-f sin 6a); и) y(cos (a—p) —cos (3a+p))
к) y(cos (2a-f p)-|-cos p); л) у (sin 2a-f sin 4a—sin 6a); m) 2(cos2(a—p) +
+ cos 2(a —y)+ cos 2(y —p) + 1). 7.16. а) л]2 ; —л/4; б) У2 ; —Зл/4; в) УТЗ;
—arctg у; г) 13; arctg ~; д) 2^65; —arctg 8; е) ^5+2^3, — arctg (1+УЗ );
452
ж) 1, л; з) 1, л/3. 7.17. a) jc= л/г/3; б) х= 2л(1 + 4/г); в) jc=—л/4 + л/г; г) х =
= Зя/2 + Зл/г; д) x=nk; е) jc=4n£; ж) JC=2л/г; з) jc = — л/8 + л/г/2; и) jc =
= я/8 -h я/г/4; к) * = л/2 + 2л/г; л) jc = л/4 -J- л/г/3; м) jc = —л/8 -|-
-|- (— 1)*л/6 -|- л/г; н) jc = л/4 + л/г/2; о) jc = =fc л/3 + 2л/7 + 4л/г; п) jc =
= я -J- 2я/г; р) jc = — 4я/15 -J- л/г/2; с) jc = zh я/3 -J- т) jc = л/2 Зл/г.
7.18. а) 0; б) л/2; в) 0; г) л/2; д) л/6; е) 2л/3; ж) — л/4; з) л/4; и) — л/4
к) я/6; л) л/6; м) —я/2; н) л; о) —л/3; п) 2я/3. 7.19. а) 2/3; б) 1/7
в) —1/3; г) 4/3. 7.20. а) УИГ/З; б) У1Г/3; в) УН~; г) 1/(2УБ~); д) 1 /У 1 0 :
е) 1 /У 1 7 . 7.21. а) 1/3; б) я/4; в) л/5; г) 2; д) 2я/5; е) 3 — л; ж) 1; з) 2я/7.
7.22. а) л/2; б) я/2. 7.23. a) jc = л/2 + 2/гл, jc = (— 1)*л/6 -J- л/г; б) jc =
j уз~
= (— l)*arcsin Ь л/г; в) jc = л + 2л/г, jc = =h л/3 + 2л/г; г) jc =
= zt я/3 -|- 2л/г; д) jc = — я/2 -f 2л/г, jc = (— 1)*arcsin — -|- л/г; е) jc =
= ± arccos ^1 ж) х — — arctg -|- л&, jc = arctg -i- + л/г;
з) jc = ± л/4 -f л/г, jc = zh я/6 + я/г. 7.24. a) jc = arctg -i- + л/г; б) jc =
3 2 У2Г ЗУЗ~
= — arctg у + я*; в) х = arctg —jZTfyT •" пк* г) * = п/4 + пк’ * =
= arctg 4- + пк. 7.25. а) х = 2л*/3, х = (2fe + 1)л ■ б) х = + ‘)п; „) * =
1 11 О
2 л/s jrJfe
= —д-; Г) JC = —, х = я/22 + л/г/11; д) jc = - л/48 + л/г/2, jc = 5л/24 +
+ л/г; е) jc = Зл/10 + 4л/г/5, jc = л/2 + 4я/г/3; ж) jc = л/14 -f 2л/г/7, jc =
= л/26 -f 2я/г/13; з) jc = л/40 + я/г/10, jc = — л/12 + л/г/3; и) jc = л/г/2;
\ ч (2/г + 1)л (2/г -J- 1)я . ,
к) jc = я/г/4; л) jc = ——-—, jc =-г —"» м) х = я/4 + х —
= —л/44-|-я/г/11; н) jc = л/6 + 2л/г/3, jc = л/14-f 2я/г/7; о) jc=n/18 +
+ я/г/9. 7.26. a) jc = л/5 -J- 2я/г/5, jc = л/2 -J- л£; б) jc = л/3 + 2я/г/3, jc =
= л/10 -f я/г/5, jc = л/7 + 2я/г/7; в) jc = л/г/4; r) jc = я/8 -h я/г/4, jc =
= ± я/3 + 2л/г; д) jc = я/20 + л/г/10, jc = л/6 -J- я/г/3; е) jc = л/г/5, jc =
= я/22 + л/г/11; ж) jc = я/г/5, jc = лЛ/8; з) jc = я/8 + л/г/4. 7.27. a) jc =
= — arctg + я/j; б) jc = — л/6 + (— 1)*л/4 -|- л/г; в) jc = Зл/4 +/гл;
r) jc = — я/4 -(-я/г, х = я/4 + (— 1)*+| л/6 -f я/г; д) jc = л/2 -f /гл, jc = л/4 +
+ /гя/2; е) jc = л/2 -|- /гя, jc = ± 2л/9 + 2л/г/3; ж) jc = 2я/г/3, jc = л + 4л£.
7
7.28. a) jc = arctg — -J- л/г; б) jc = zh я/6 -f л/г; в) jc = arctg4 -f я/г, jc =
о
= arctg —|- я/г; r) jc =—arctg 3-f я/г, jc = л/4 -h я/г; д) jc = arctg (1 zb
2
d= У3~) + я/г; e) jc = л/г/4, jc =— arctg — + я/г; ж) решений нет; з) х =
О
= -arctgi- + пк. 7.29. а) «/= у; б) j/=-£±1; в) 1/=2(л: + 3); г) у =
Д) *-Н*: e)y=W+T 7.30. /= 1/2(///0- 1). 7.31.
» = “о + -Г—Г- 7,32- а) [0, +оо), 1/ = б) [1,оо), у= 1/2(х +
L го
+ V^2 — 4)» в) +°°), = 1 + V* — 1; г) [0, +оо), j/= 1/2(х -h Vx2-f4);
Д) [— 2, + оо), (/ = — 2 + У* + 4; е) [— 1; 0], у == — ^ 1 — х2
8.1. а) (1; 1), а также (Я,; Я,) с любым кфО; б) (1; 2)._а также (Я,; 2Я,) с любым
А, =^=0; в) (1; 3), а также (X; ЗЯ,) с любым Я=^0; г) (л/З ; 1), а также (Я,УЗ ; Я,)
453
с любым кф 0; д) (2; —1), а также (2А,; —А,) с любым кф 0. 8.2. а) (1; —1) и
(—1; 1) и др.; б) (2; —7) и (—2; 7) и др; в) (—2; —2; 1) и (2; 2; —1) и др.;
г) (1; 1; —1) и (—1; —1; 1) и др.. 8.3. а) (1; 2), а также (А,; 2А,) с А,=^=0; б) (1;
3), а также (А,; ЗХ) с кфО; в) (1; —1), а также (к; —А,) с кфО; г) (3; 2), а также
(ЗА,; 2А,) с кфО. 8.4. а) (5; 2; 4) при / = 2 и (11; 5; 7) при t= 5; б) t= 3. 8.5. а) 6;
б) —2; в) 0; г) —1/2; д) решений нет. 8.6. а) —2; б) —3; в) 0; г) 0; д) при
любом х. 8.7. а)Нет; б) нет. 8.8. а)Да; б) нет; а при D (0; 0; 9), D (—2; —4; —1),
D (2; 4; 1) — да. 8.9. а) Нет; б) нет. 8.10. а)Нет; б) нет. 8.11. а) 0; б) я/2; в) л/4.
1 2 2 3 1
8.12. arccos — , arccos— и arccos — . 8.13. a) arccos — ; б) arccos ■ .
6 о о о /U
8.14. а) я/2; б) я/3; в) arccos-^-. 8.15. *=1, у= 2 и 2 = 3. 8.16. а) (0; 1; 0);
U
б) (1; 1; 1), (2; —1; 3), (3; 0; —5); в) (2; —1; 3). 8.18. На окружности, имеющей
центр в точке пересечения прямой с плоскостью и лежащей в этой плоскости,
взять три точки так, чтобы никакие две не лежали на одном диаметре. Кроме того,
отметить на прямой точку, не лежащую в плоскости. Если эта точка равноудалена
от выделенных точек окружности, то прямая и плоскость перпендикулярны.
В противном* случае они не перпендикулярны. 8.19. Построить в горизонтальной
плоскости прямоугольник с центром с точке О. Установить основание шеста в
точке О и соединить тросами верхний конец шеста с вершинами прямоугольника.
Выравнивая тросы, установить шест вертикально. 8.21. 7-^2 /2. 8.23. а) Так как
В'В и ВО перпендикулярны АС; б) так как DD' и D’B перпендикулярны АС;
в) аналогично б); г) аналогично б) ив), все диагонали, которые не проходят
через А и С'. 8.24. а) Да; б) да; в) нет. 8.25. а) Проекциями точек Ау В' и С
на плоскость а служат соответственно А, В и С; в) увеличивается при удалении
1 1 2
точки В' от плоскости а. 8.26. a) arcsin———; б) arcsin—в) arcsin—— ;
У 33 V 39 л/6
г) arcsin——. 8.27. Применить теорему косинусов к треугольнику АВЕ, где Е
Уз
середина ребра CD. 8.29. а) 0; б) я/2; в) arccos — . 8.33. а) Прямая, проходящая
о
через центр окружности, описанной вокруг треугольника, и перпендикулярная
плоскости треугольника; б) плоскость, проходящая через середину отрезка,
соединяющего данные точки, и перпендикулярная этому отрезку; в) две плоско¬
сти, перпендикулярные плоскости прямых и проходящие через биссектрисы углов,
образованных прямыми; г) плоскость, перпендикулярная плоскости прямых и
проходящая через среднюю линию полосы, образованной прямыми. 8.34. Окруж¬
ность, центром которой^служит проекция данной точки на плоскость. Радиус
окружности равен -yl2 — d2, где / — длина наклонных и d — расстояние от дан¬
ной точки до плоскости.
9.1. 5, бесконечно много. 9.2. 8, бесконечно много, окружность. 9.3. Можно.
9.4. 7 или 1. 9.5. S = 8V3, р = 2(2л/3 +4). 9.6. На развертке: |0/С| = tC/CI = 3;
|ОС| = ЗУ2 ; на цилиндре: \СК\ = 3, |0/(| = —, |ОС| = —л/4+л2 9.8. R = H.
Я я
9.9. а) ЗУЗ, 3; б) 3, ЗУЗ ; в) г) 60°, 120°; д) 60°, 30°. 9.10. а) УЙ);
б) 3; в) 9; г) 3-^2; д) 6, 2arctg-^-. 9.11. а) 4; б) arccos ; в) 6,25л; г) 8, 0°,-
О о
9.12. a) -^-tga; б) ^ ; в) л — 2а. 9.13. 1 : 4. 9.14. S(x) = я(1 -xf. 9.15. 17.
9.16. а) y = JLx2\ б) S='/2HR2. 9.17. l=^jx2-Зх+2. 9.23. Л = 4, нет.
R -у/2
9.24. 10, —4—. 9.25. 4, 16я. 9.26. 9. 9.27. 4. 9.28. 10. 9.29. -J7 . 9.30. 13. 9.31. У2 .
sin a * v
4 Л
9.32. 10. 9.33. 10. 9.34. Да, да. 9.35. а) У8; б) 4/3. 9.37. В 2 раза. 9.38. 8; л/60.
9.39. a) -jL-; б) УЗ . 9.40. 1=^Ih2 + R2; r = 4r(^H2 + R2-R). 9.41. 4.
V з н
9.42. "^4R2+^-~9.43. Ял/2. 9.44. а) 2л/3; б) УЗ; в) 3(2-У3); г) 2л/3.
9.45. 2-V2. 9.46. r = -^r-, H=R^2 . 9.47. /?УЗ , Я=3. 9.48. .
V2 ^ V2
9.49. а) А; б),-^-; в) yPtg«; г) -g-tgcg д) я-2а; е) £-tgf-;
ж) D sin а; з) ~ "Д/— /2. 9.50. a) L sin; б) L; в) Lcos^-; г) ^-L2X
4 * cos а 1 11
XSi"P; Д) P; e) 20+SsjlnP(P/2)) : Ж> LSi"P; 3> \l^ALi~P- 9-5,‘ a> ^
б) arctg-?-; в) arctg^y-; r) 2-\/21. 9.52. a) &УЗ ; 6) arctg?-; в)
9.53. a) 2 V-т; 6> V3; в) У§ ; r) arcsin^-. 9.54. а) |ВС| = 4л/2, |SB| =
o <5
= |5C| = 5; 6) 5^ = 5,450 = 6, 5лся = 8; 5Sflc = 2V34; в) ; arctg r) ,
arctg —9.55. a) a2^3 f ,fl У^9 ; 6) £ • 9.57. a) 8; 6) arcsin i- ;
2V2 _ ♦_
в) arctg—^=-; г) ; д) 2aresin-5^-; e) arctg—^=-. 9.58. a) -v/65;
зуз 2 10 зуз
б) 9; в) arcsin-^-; д) 36. 9.60. а) ; б) ; в) ; г) 2arctg —^=- .
У 4 2 d у2
9.61. а) 13; б) 16. 9.63. а) Куб; б) октаэдр; в) пирамида, в основании которой
50-угольник; г) призма, в основании которой 11-угольник; 6; 40; нет. 9.66. а) Да;
б) нет; в) да; г) нет. Нет. 9.68. г) Г =п\-1, В = п+ 1, Р— 2(л+1). 9.69. д) Г =
= п-1-2, В = 2пу Р = 3п.
10.1. а) а24; б) а~4; в) Ь~'; г) b2^jb ; д) 1; е) З-325. 10.2. a) 23; б) 210; в) 2“';
г) 2~4; д) 2“'; е) 2-2; ж) 2|/2; з) 22/3; и) 2-0-55; к) 21-75; л) 23’3219; м) 2-2-3219.
10.3. а) 3; б) —2; в) —1,5; г) 0,5; д) —0,5; е) 1,5; ж) 3; з) 6; и) —1,5. 10.4. а) 3;
б) 9; в) 3; г) 16. 10.5. а) 1; б) 1; в) 1; г) —2. 10.6. а) 2/3; б) 2,5; в) 36; г) 1,5;
д) 6; е) 5; ж) 7; з) 2. 10.7. a) Ь) ■ 10.8. а) У9/Гэ<У Й/гЗ;
б) У0Д4<У2/~3; в) V3>V6; г) (1/6)1/6>( 1/5)1/5; д) 1714>31“; е) 23'00>
>32'М. 10.10. a) log3 2>0; б) log3y<0; в) logi/53<0; г) log,/3l/2>0;
Д) log3 4> 1; е) log,/7 1/8> 1; ж) log23<log25; з) log2 l/7>log2 1/9;
и) log,/з 7>log,/з 10; к) log,/3 l/5<log,/3 1/7; л) log,/53>—1; м) log,/53>
>log,/55; н) log6 2<log5 2; o) log,/7 3<log,/8 3; n) log32<2/3; p) log27>
>log38. 10.11. a) 2ех; б) ex — e~x\ в) еж( 1 дс); г) xee~x 0 1^; д) e*(sinjt-|-
-|-cos*); е) е—дс( 1 — дс); ж) —e-JC(sin х -J-cosjc); з) 5X+I In 5. 10.12. а) Убывает на
( —оо, 0), возрастает на (0, в точке jc = 0 минимум у= 2; б) у убывает на
4
( —оо, 0), у{ 0) = 0, возрастает на (0, 2), у{2) = —— « 0,5413; убывает на (2, -foo),
е^
455
стремясь к 0; в) убывает на ( — оо, 0), 1/(0) = 1, возрастает на (0, + оо).
10.13. a) J/min=l/2, Утах == 2; б) J/min=l/9, У max == 1 '■> в) i/m in == */(0) = 1, Утах =
= j/(-l) = e-l ~ 1,72; г) </m.x = </ (-^)=е3”'4, -А-«7,46, «/mln = 1/(0) = </(л) =
= 0. 10.14. а) *<2,5; б) —Зле<jc<3; в) —3<jc<3; г) jc> 1. 10.15. а) 1/*
, ,1ч cosjc + jcln jcsin jc , 1 0,4343
б) lnx+1; в) j ; г) е'(1пл:+1Д); д) « —
JC COS JC X in I и X
10.16. а) Убывает на (0, 1/9), #(1/9) = 1/3+ 1/3In9 « 1,066, возрастает на
(1/9, +оо); б) монотонно возрастает на всей оси, у= 0 при jc » — 0,35.
10.17. а) J/min — 1» Утах == 11 б) Ут\п == 2, Утах == 8; в) J/min = 1» Утах = е 1;
г) #min=#(l/2) = 1 /2+1п2 « 1,193, утах=у(\)=2. 10.18. a) 9cos3jc; б) — cosincojc;
в) 1/5 _! ; г) 1/2е-х/2; д) 22х+| In 2; е) 1 /jc; ж) 2jccosjc2; з) 2sinjccos*;
cos2 (jc/5)
и) 2 -т-г-; к) Зе3х+2; л) —tg*; м) — S*n ; н) —2*е * ; о) 3cos (3* +
jrcos'(l/jc) /в х
+ а); п) 6tg23jc \ ; р) —2ecos 2дс sin 2jc; с) —р—; т) eV\ 10.19. a) [1/е,
cos 3jc s_ х In *
е]; б) [1/е, е]; в) (-оо, 0]; г) — 1/2е”гЯ, 1/2е-я/4; д) (0, 1); е) (0, 1/е];
ж) [1, +оо); з) (0; 1]. 10.21. a) jc=2; б) jc = 4;‘ в) нет решений; г) jc =
= !? ^ ; д) нет решений; е) jc = 0; ж) jc= 1; з) jc = 2; и) jc= ^ -- ; к) Х\ — 2,
lg I olg I
jc2 = 3; л) jc = 1; м) jc = 1; н) jc = ; °) x = 2; n) x=4. 10.22. a) x= I;
б) jc = 1; в) jc = -[§_?—1; r) jc = 1; д) x=2; e) X\ = 4 —rMr • Ю.23. a) x =
Ig 4 lg о
- "g2 ■ б) lg7 —lg6 . lg 7 +lg 18 —lg 29 .
“ 21g2-lg3 ’ 6) * lg 5 —lg 2 lg 9 — lg_4 ’Г) * U’A)
= 0, jc2 = — 1; e) jc=lg 6 — lg 5. 10.24. a) jc = 8; 6) jc = ^3 ; в) jc = 1; r) jc=3,5;
д) jc = ^3 ; e) нет решений; ж) jc = 4; з) jc = 8; и) нет решений. 10.25. a) jci = 3,
jc2 = 9; б) jc= 10; в) jc = 9; г) jci = 1; jc2= 10; JC3 = 1/10; д) jc = 4; е) jc = 8; ж) jci =
= 1, jc2 = 3, JC3= 1/9. 10.26. a) jc>0; 6) jc> —1; в) —oo<jc<oo; r) jc> —1;
д) jc<— 2; e) jc<5; ж) jc>1; 3) jc^—1. 10.27. a) jc>10; 6) 0<jc< 100; в) 0<
<jc< 1/2; r) 0<jc<0,25; д) jc<—99; e) —л\е <jcC^Je (хфО); ж) 1,5<jc<
<5,5; з) jc> —1; и) 3<jc<5; к) 1/4<jc<4; л) нет решений; м) jc>5.
10.28. a) jc= 1; б) jc= 1;«.в) jc = 2; г) jc= 1; д) jc= 1. 10.29. 7=//(log2 m — log2 я).
10.30. Через 9 мин. 10.31. Через 3,32 часа; 0,64.
5 4 2л 1
11.1. a) J —-—djc; б) J (b + 2jc — jc2) djc; в) J sin jcdjc; г) J ~\J 1 — jc2 djc;
l 2 -1 л -1
3 4
д) J djc + J (4 — jc)djc. 11.3. a) jc; 6%) jc2/2; b) jc3; r) jc10/ 10; д) 3jc4/4 — 5jc3/3 +
0 6 3
+jc2/2 — 2jc; e) ^4/12—jc; ж) — 1 /jc; 3) — 1 /jc3; и) 2/з*3/2; к) -yjx ; л) *2+l/*;
м) 4/5jc5/2 — 2^/jc . 11.4. a) —3cosjc; 6) 2sinjc; в) — ‘/гсоБ 2jc; r) (A/w) sincojc;
д) tg jc; e) jc/2 + sin jc/2; ж) 2ex; з) —e-x; и) ex — e-jr; к) 2x/ln2; л) /зе3х+|;
м) — 10-JC/ln 10 = — 10-xlge; H)21njc; o) ln(jc+l); n) In jc + jc2/2; p) lnjc +
+ 2 In (jc — 1); c) jc — In (jc + 1); t) jc2/2 + jc + in |x| — 1 /jc. 11.5. a) 3; 6) 15;
в) 10,5; r) 1/3; д) -6; e) 4/3; ж) —2/3; з) 4; и) —12-|-; к) 5/14; л) 31/480;
456
м) 14/3; н) 3/5; о) 2^/2 ; п) 384; р) 1; с) -^2 ‘ ; т) л/2+1; у) 1; ф) 1;
х) 1 — л/4; ц) 1. 11.6. а) 6; б) 4/3; в) 3-|-; г) 10-§-; д) 30-^-; е) 4,5; ж) 1;
ООО
з) In3; и) 4,5; к) 3; л) 5у; м) 15у; н) 4у, о) 5/12. 11.7. а) 1/3; б) 16/63.
11.8. (1-3), (2 — 6), (3-1), (4 — 2), (5 — 5), (6 — 4). 11.9. Rll/2. 11.10.
450 Дж. 11.11. л]2/2— 2. 11.12. G ^ ^ , где G — гравитационная постоян-
, jt3 — S
ная. 11.13. t = I |/21 (k U), итах = y^2kU . 11.14. а) - ; б) — е~х — 1-
О
в) lnjc + e— 1; г) 1 + In |jc|; д) In |jc| — 1. 11.15. In (/jc), с > 0 произвольно.
11.16. a) y — ce2x; б) y = ce~x; в) y = ce25x. 11.17. 635 420 лет. 11.18. m =
= m02~^Tl/2, где 7*1/2 — период полураспада. 11.19. m = m0ex/, если m' = km.
11.20. A, = 0,0953 4"‘. 11.21. 6 линз. 11.22. 88,58%. 11.23. 7.18%.
12.1. 5л/12; 2л/3; Зл/4; 7л/6; 4л/3; Зл/2; 5л/3; 20л/9; 45°; 150°; 420°;
1140°; 330^. 12.3. 2,28. 12.4. 2л. 12.5. Не изменится; увеличится в 4 раза.
12.7. 5V 1 3 . 12.8. Возрастет в 16 раз; уменьшится в 9 раз. 12.9. Увеличится
в 6 и 1/5 раза соответственно. 12.10. 12 и 20. 12.11. 30°. 12.13. а) 48; б) 84.
12.14. у Уб. 12.15. 4у. 12.16. п2. 12.17. а) а /с2 - а2/2; б) а2 ctg а/2; в)
(с/2)2 sin 2а; г) ft2/sin 2а; д) у —^==f-,2-18. а) у ]Л2 — (у^2 ; б)
(|)*с1вТ: В) (т)2‘8Р; Г) */«** sin а; д) '/Ф2 sin 20; е) ctg[a/2) (l +
+ sin '(a/2) ) ; Ж) Ctg2 T~tgp- 12J9- 3) -Ч1 6)
a2 — b2
tga; в) с sin a (a — с cos a); r) h(a — h ctg a); д) h(b + h ctga).
12.20. а) а/?г/2; 6) Rt/2; в) l2/(2а); r) -y~ (l + — (a/2)')2' ,2'22' 2' ,2-23'
4/3. 12.24. 4. 12.30. a) 1/6; 6) 4/3. 12.31. 0,79; 0,345. 12.32. nab. 12.33. ab2/(4я);
a2b/{4n). 12.34. na2h/\2. 12.35. |я|| - y^V \ \ - (l - -^-)2 • 12.36.
(t + T~)' l2-37- a) 2/?q2; 6) 2~Ra2; b) 2nRf2’ ,2-38'
12.39. Зм3. 12.40. 3,5 r. 12.41. 12. 12.44. 1. a) a2h\ 6) Щ-a2 \/б2 -
лЛ2(-^-+-^-). 12.37. a) 2Ra2\ 6) — j- /?а2; в) 2nRr2. 12.38. а3 и a3.
4 - 4-»’ 1^3
B) iiL/t (fe2-ft2); r) -^-a3 ~V'4coSV/2f ~ T; Д) 3V3cos2pft3;e) a3/(8cosP);
ж) y^-cos2 v sin yft3; з) -5-^3 Л3 ctg2 у. II- a) |o*A; б) у a2 ~\Jb2 — у ;
в) А Л (ft2-Л3); г) yfl3V 4sin2 (ot/2~j F ’ Д) в) T со^ sin ^
III. a) -5-a3tg P; 6) ctg2?/*3; в) 2УЗ sin2-^-"^ 1 — 4sin2~63. 12.45. а) ла3/6;
4 _,o . 4 / а/i \3 v 4 / osina \3
б) -^-лR ; в) —л( ) ; г) —л( —г ) . 12.46. ЗУЗ. 12.47.
3 3 V а + 2Уа2 + И2 ' 3 V cosa + 2 /
457
Зл/З. 12.48. 1/4. 12.49. 1см. 12.50. '2.52. -^-см3. 12.53. яа3/4.
12.54. 2nR\ 12.55. ла3/12. 12.56. -^-л/ЗяЯ3. 12.57. 32лЯ3/27. 12.58. 4яЯ3/27.
12.59. УЗа2. 12.61. 3. 12.62. 3. 12.63. аЬ\ аЬ + Ьг/(2л) или aft + а2/(2л).
12.64. яаА/2; яоЛ/2 + лаг/4. 12.65. а/?2/2; аЯ2/(4я) + <х/?2/2. 12.66.
а) -|а^\/А2 + |2; б) Ь2 - в) d^-^~h2 У&2 + ЗЛ2;
“• Зл/3_ ctgp ,2. УЗ а2 . . л/3
г) ^2ctg^; д) 4"iftpЛ2; е>"г1^ЙГ *>^Wl+»7;
з) *~4cos^y^S'n^ ^2' 2ад/л2+а2/4 ; б) 2a-yjb2—a2/4 ; в) 2-\Jb4—h* ;
г) a2ctga; д) 4Л2 cos p/sin2 Р; е) a2/cosP; ж) 262^ 1 — sin4v ; з) 2/i2^/l/sin4v— 1 .
111. а) Зад/Л2+За2/4 ; б) 3ад/&2-а2/4 ; в) 3У&2-Л2 Уй2+3»2/4 ; г) —;
д)2л/32А2^|;е) 3V3yCOsp; ж) 3b2cosy~\] I _£2!_V ; з) ^h2ctgy^J 1 + ^ту-
12.67. а) ла2; б) 4яЯ2; в) ^(я + л/^ + ХТ; г> 4,-f, _■
4 \ V 4 / (а + Уа2+12Я2)2
13.1. а) да; б) нет; в) да; г) нет; д) нет; е) нет; ж) нет; з) да; и) нет;
к) нет. 13.2. а) —1, 38/7; б) 5; в) 1, —,7/7; г) 0; д) —11; е) —5/п; ж) а = 5 или
в = 0 — нет решений, иначе—jt=(a—Ъ)/Ь. 13.3. а) —1,2; б) 7/2, —3/2; в) —7, 1,
3, 11; г) нет решений. 13.4. а) —2, 2, —3, 3; б) —1, 1; б) 2, —VF/2 ; г) 1, —3/г,
; д) 8±У73, 8±У57; е) -1, -2, -4, 1; ж) 1-'/6; з) -2/3, -5/з-
13.5. а) (-7/2> Г); б) (-оо, l/3] U[ Ь °°). в) (-оо, -2]U[-1; 1]U[2, +оо);
г) (~2, ~‘7V5 )U(- 1+2^5 , l); д)( оо, —2) U (3, +оо); е)’ (4, +оо);
ж) ( —оо, 1)U(3, -foo); з) ( —оо, -foo); и) (—3, —2)(J(2, +00); к) ( — 00, 1)(J
U(5/7» -foo). 13.6. а) (—ОО, y5]U[l, +00); б) [—Vs, 2]; в) (-00, 1)U(1, +00);
г) (-1, 1] U(2, -foo). 13.8. а) 7, — ,6/3; б) 3; в) 3; г) 1; д) 2; е) 3,440. 13.9. а) [1,
-foo); б) [—4, 5]; в) [5, -foo); г) [—9, 7). 13.10. а) у arccos-^- -f 2nk -f 1
6) 2(-l)*arcsin-^ +2я*-у; в) у у+я*); г) у (-arctgy+kn-
— 1^; д) я+2я£, ±y-\-2nk\ e) nk, + ж) 3) (2£+1)я; и) -^-+я£;
к) arctgy-f лЛ; л) arctg3-fnfc, arctg-^--f nk\ м) n+2nk\ ±y + 2kn\ h) nk/2,
я/6+2л£, 5я/6+ 2kn\ o) kn, + н)±я/3+2nk\ p)dtarccos^ 1 —^y^-f
5 1 •
+ 2nk\ c) — arctgy-f nk\ t) я/4-f яЛ, arctgy-f nk. 13.11. a) 3; б) 7/з‘, в) —16;
г) 7; д) 4; е) 4; ж) х/2\ з) —3; и) 1; к) —3; л) 0; м) 2; н) 4; o)±log2/52; п) 0;
р) ±2; с) 1/7; м) log35. 13.12. а) 2; б) 1п(У2 +1); в) у,.пу; г) ,П (~"2~" )
д) [0, 1]; е) —1п2, 0; ж) —1п4, 1п-|-; з) 3, 1; и) 0; к) 0, yln4. 13.13. а) у;
458
б) 21; в) 11 ± л/14; д) 2; е) 3,9; ж) 10, 100; з) 10, 10* /,6; и) Hej реше-
ний; к) х= 0, х= 2; л) 3; м) г2*'3; н) 3,3 + У§ ; о) 9, у. 13.14. а) 8, 2_2/3;
б) ±5; в) 25; г) 2; д) УТ25; е) 4 —л/2; ж) 4; з) нет решений; и) */\-\-я/г;
к) "/«"Ья/г. 13.15. а) (2; -Ь°°); б) ( ‘/г, + 00); в) ( — 00, —1); г) (—оо, 5);
д) (1, +оо);е) (3;+оо);ж) (-1,24);з) (-1, ‘/2); и) [3, +оо); к) (-00, —*/*)U
U(5, +оо); Л) (V2^ + oo)U(0; 1); м) (2/з. 5А); н) (-оо, 5/3)U(2, 3); о) (-5, —3)U
и(-'-1); (wf'2); Р» пл1' ■» »-
= —1; б) у= (3 — 4*)/6; в) решений нет; г) решений нет; д) х=6, у=4;е)л:=3,
у= 4; дс= —0,6, (/=—3,2; ж) лг= 1, у=2; у=—2, х= —3; з) *=+5, (/= 4=2;
*=±2, */= zh5; и) *=2, (/=3; лг= —3, у= —2; к) х= + 18, £/= ±13; х= ±2,
(/= ±3; л) решений нет; м) х= ±5, у= =ЬЗ; н) х=4, у= 3, 2=7; о) х=2, у= —3,
2=0,5; п) х= — 1, у=2, 2=0; р) х=1/2, У= —1 /з, 2=‘Л. 13.18. при тф—4; 1.
13.19. а) а^=—5; б) а= — 5; в) никогда. 12.20. а) т^—5/з; никогда; т= —5/3;
б) тф1\ 2тф\\ т=2. 13.21. 5г и 7,5 г. 13.22. 9:35. 13.23. 2тС
-\/с п -\-4птссп
13.24. i±^-_iyT+TF. 13.25. у±^^-Fd . 13.26. *„„„=18, </min=14
(jc — для В, у — для С). 13.27. а) [3/4, оо]; б) [1, +оо]; в) [ 1_, +оо]; г) [3/4, 3);
д) [3, 7]; е) [1, +оо]. 13.28. а) [-2, 4]; б) [-1, 1]; в) [ —л/2 , л/2 ]; г) [3/4, 3].
13.30. 1. 13.31. 752, 7й2. 13.32. r = V”/2, S = 7' + 2nr2. 13.34. 2лУ*ТГ.
13.35. 3 ч 44 мин.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
А
Аддитивность 361
Аксиома 118, 131
Аксиомы стереометрии 132
Аргумент 22
Арккосинус 234, 250
Арккотангенс 236, 251
Арксинус 232, 233, 250
Арктангенс 236, 251
В
Вектор 137, 138, 149, 150, 157
— нулевой 140
Векторы коллинеарные 260, 262
Г
График функции 23, 32, 33
Д
Давление 89
Диаграммы приведения 201—203
Дифференциал функции 91, 92
Дифференцирование 51, 53, 348, 355
Длина окружности 401
3
Заряд электрический 88, 93, 368
Значение функции наибольшее 98
— — наименьшее 98
И
Интеграл 348—350, 352, 354, 366
К
Касательная к кривой 53
Квадрат 130
Колебания гармонические 191, 22£
Конус 285, 289, 290
— усеченный 287
Координаты вектора 148, 149, 151
— точки 7, 13, 147
— — вращающейся 175
Корни арифметические 321
— уравнения 25
— функции 25
Косинус 175, 178, 186—189, 191, 197
Котангенс 175, 179, 186, 193, 196, 199,
203
Куб 305
J1
Логарифм 325
— натуральный 331
М
Масса 368
— стержня 87, 93
Мера угла градусная 169
— — радианная 170
Метод Гаусса 423
460
— интервалов 39
Многогранник 303, 308
Модуль 138
— перехода 326
— числа 9
Монотонность функции 29
Н
Направляющий вектор прямой 259
Неравенства иррациональные 413
— равносильные 409
— рациональные 413
Неравенство 35, 407
— квадратное 37
— простейшее 339
О
Область значений допустимых 409
— — функции 83
— определения функции 24, 246
Объем 393, 394
— куба 393
— цилиндра 393, 395
Октаэдр 307
Орты осей 149
Ось числовая 7
П
Палетка 393
Параллелепипед 299, 300
Первообразная 356
Параллельность прямых 126
Переменные 19
Перемещение 368
Переход предельный 56
Период 185
Периодичность 176, 185
Пирамида 297, 298
Плоскости параллельные 120, 124, 125
— пересекающиеся 120
— перпендикулярные 276
Плоскость 114, 119, 130
— касательная 293
Площадь 362
— конуса 400
— круга 90
— многоугольника 388
— параллелограмма 387
— подграфика 389
— призмы 400
— треугольника 386—388
— фигуры произвольной 389
— цилиндра 400
Плотность линейная 87
Поверхность шара 400
Погрешность 96
Правила изображения векторов 139—
141
Правило многоугольника 140
— параллелепипеда 141
— параллелограмма 140, 141
— трех точек 140
Призма 295, 296
Признак параллельности двух плоско¬
стей 124
— — — прямых 123
— перпендикулярности прямой и плос¬
кости 267
— скрещивающихся прямых 117
Признаки параллельности 122
Приращение аргумента 59
— функции 59
•Проекция вектора 211
— ортогональная 272
— точки 210
Произведение скалярное 210, 213—216
Производительность труда 90
Производная 51—53, 57, 60—63, 69
Промежуток числовой 8
Пространство векторное 157
Прямая 114, 119, 130
Прямые параллельные 114, 132
— пересекающиеся 114, 132
— скрещивающиеся 114, 126, 132
Р
Работа 87, 88, 93, 367
Равенство векторное 260
Радиан 170
Радиус-вектор 142, 153
Разложение вектора 145, 147
Размерность 145, 158, 159
Растяжение 140
Расширение тела линейное 83
Решение уравнения 37
461
с
Свойства движения вращательного
172—174
— интеграла 360
— неравенств 35
— радикалов 321
— степеней 324
Сегмент параболический 103
Сечение конуса осевое 287
Синус 175, 178, 186, 187-189, 191, 197
Система координат географическая 14
— — декартова 12, 147
— несовместная 419
— совместная 419
Системы линейные 422
— симметричные 421
Скорость 85, 155, 365
— мгновенная 55, 60, 156
— роста функции 56
— средняя 55, 59
— угловая 229
Соотношения для треугольника 167
Среднее арифметическое 37
— геометрическое 37
Степень 323
Суммы интегральные 350, 351
Сфера 291
Т
Тангенс 175, 179, 186, 193—195, 198,
203
Тела вращения 288
Теорема косинусов 216
— Ньютона — Лейбница 358
— о трех перпендикулярах 270
— Пифагора 167
— — пространственная 301, 302
— Эйлера 305, 308
Теплоемкость 89
Теплота 88
Точка 114, 130
— критическая 75
— локального максимума 26
— — минимума 26
— особая 84
— экстремума 82
Тригонометрические тождества 179,
236
— уравнения 230, 237
— формулы двойных углов 224
— — сложения 240
— функции 249—251
— — половинного угл& 225
У
Угловой коэффициент касательной 52
Углы 116, 169, 170
— двугранные 274, 275
— линейные 275
— многогранные 309
Угол раствора конуса 287
Уравнение 407
— движения 372
векторное 152
— дифференциальное 371, 374
— иррациональное 413
— колебаний гармонических 376, 377
— логарифмическое 336
— порядка второго 373
— — первого 373
— показательное 337
— прямой 18, 260
— рациональное 413
Уравнения однородные 241
— простейшие 183
— равносильные 37, 409
Ускорение 86, 153
Условие параллельности прямой и
плоскости 268
— — прямых 262
— перпендикулярности векторов 217—
219
— — прямой и плоскости 268
— — прямых 262
— равенства 140
Ф
Формулы приближения 94, 199, 200
— приведения 180, 222
— сложения 222—224
— тригонометрические двойных углов
224
Функции взаимно обратные 242, 243,
249
— монотонные 246
— обратные 243, 244, 245
— периодические 176, 185
462
— показательные 327, 329, 341, 375
— тригонометрические 175, 177, 181
Функция 22, 70
— логарифмическая 332, 333
— нечетная 81
— четная 80
Ц
Цилиндр 283, 284, 289
Ч
Четырехугольник 130
Четность 178
Число 7
— действительное 8
— е 330
— иррациональное 324
— натуральное 8
— отрицательное 35
— положительное 35
— рациональное 8,323
Ш
Шар 291, 292
Учебное издание
Марк Иванович Башмаков
МАТЕМАТИКА
Зав. редакцией Е. С. Гридасова
Научный редактор А. Г. Мордкович
Редактор Г. Н. Чернышева
Мл. редакторы Н. П. Майкова, Г. В. Вятоха
Художественный редактор В. И. Пономаренко
Оформление художника Ю. Д. Федичкина
Технический редактор Т. Д. Гарина
Корректор Г. И. Кострикова
ИБ № 6590
Изд. № ФМ-880. Сдано в набор 26.11.86. Подп. в печать 06.04.87. Формат 60X90‘/i6-
Бум. офсетная № 1. Гарнитура литературная. Печать офсетная. Объем 29 уел. печ. л.
58,25 уел. кр.-отт. 24,96 уч.-изд. л. Тираж 100 000 экз. Зак. № 1681. Цена 80 коп.
Издательство «Высшая школа», 1Q1430, Москва, ГСП-4, Неглинная ул., д. 29/14.
Ярославский полиграфкомбинат Союзполиграфпрома при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговли. 150014, Ярославль, ул. Свободы, 97
80 К.