О.Ф.Кабардин, В.А.Орлов, А.Р.Зильберман
ФИЗИКА. ЗАДАЧНИК. 9—11 КЛ
В сборник вошли задачи, соответствующие программе общеобразовательных учебных заведений. Многие из них были представлены на российских и международных олимпиадах по физике. Ко всем задачам даны полные решения с краткими теоретическими комментариями.
ОГЛАВЛЕНИЕ
Введение	3
Г лава 1. Кинематика	6
Глава 2. Динамика	28
Глава 3. Статика	52
Глава 4. Закон всемирного тяготения	73
Г лава 5. Законы сохранения в механике	94
Глава 6. Механические колебания	117
Глава 7. Молекулярная физика	139
Глава 8. Термодинамика	163
Глава 9. Электрическое поле	186
Глава 10. Магнитное поле	206
Г лава 11. Постоянный ток	226
Глава 12. Переменный ток	245
Глава 13. Электромагнитные волны	273
Глава 14. Геометрическая оптика	303
Глава 15. Квантовая физика	334
ВВЕДЕНИЕ
В настоящее время наше общество переживает период быстрых и глубоких изменений. Эти изменения в значительной мере обусловлены попытками использовать западные модели в экономике, в политике и даже в культуре и в образовании. На трудном пути преобразования общества очень важно правильно выбрать направление изменений.
Это утверждение имеет особое значение для нашей общеобразовательной школы.
В работе с одаренными школьниками мы прежде всего ориентировались на развитие их интереса к занятиям, на организацию самостоятельного познавательного процесса и самостоятельной практической деятельности.
Поэтому данная книга предназначена в первую очередь школьникам, желающим самостоятельно повысить свой уровень подготовки по физике. В книге представлена система задач постепенно возрастающей сложности по всем основным темам курса физики средней школы. Применение теоретических знаний при решении этой системы задач обеспечивает свободное владение основным содержанием курса физики средней школы развитых стран мира.
При самостоятельной работе целесообразно каждую задачу пытаться решить, не заглядывая в решение. Если задача слишком сложна, можно бегло просмотреть решение для понимания его основной идеи и вновь попытаться решить задачу самостоятельно. Решать задачи целесообразно в том порядке, в каком они расположены в книге.
Книга может быть использована учителем физики для занятий с группой учащихся, проявляющих повышенный интерес к физике.
Особенностью занятия по решению теоретических задач может быть использование задачи в качестве стимула к изучению нового материала, выходящего за рамки основного школьного курса, чтобы дать школьникам подготовку по физике на уровне высших мировых стандартов, расширить круг изучаемых физических явлений и законов. Введение нового теоретического материала непосредственно в процессе решения конкретных задач во многих случаях оказывается более эффективным, чем при проведении лекционных и практических занятий.
3
Кроме того занятия по решению теоретических задач дают возможность обеспечить учащихся материалами для самостоятельной домашней работы. С этой целью после разбора двух-трех ключевых задач на занятии в классе целесообразно дать комплект из 5—10 задач по данной теме для самостоятельной домашней работы с обязательным полным письменным оформлением. Разумеется, количество решаемых задач определяется желанием школьника, но общее число предлагаемых задач должно быть достаточным для удовлетворения потребностей наиболее способных и настойчивых учащихся.
В конце изучения каждой темы целесообразно проведение занятия в форме тура физической олимпиады. В этом случае все учащиеся получают одинаковые комплекты из трех задач. Это задание выполняется за два или четыре часа, в зависимости от сложности задач, без какой-либо посторонней помощи и без обсуждения возникающих проблем с другими участниками. Итогом работы должен быть письменный отчет, содержащий полное теоретическое решение.
Оценка решений задач по физике в школах системы Международного Бакалавриата или на Международных физических олимпиадах производится по заранее согласованным критериям. Эти критерии неизвестны школьникам.
Для знакомства с возможными вариантами критериев оценки работы можно в конце занятия выдавать участникам занятий заранее подготовленные критерии и предлагать им выполнить самооценку своих результатов. Затем учитель выполняет контроль произведенной самооценки и выставляет окончательную оценку.
В том случае, если большинство участников получило очень низкие оценки, выполнение задания целесообразно повторить на следующем занятии.
Проведение занятий в форме олимпиады во многих отношениях предпочтительнее других форм, но и она не является абсолютно лучшей. Прежде всего, любая форма занятий при длительном употреблении становится все менее эффективной из-за однообразия, надоедания. Возможных замен несколько. Например, «мозговой штурм», когда одна задача предлагается всем учащимся и совместно обсуждаются различные варианты ее решения.
Очень интересны для учащихся игровые формы организации занятий по решению задач.
В качестве примера опишем игру «Кто больше?».
Класс разбивается на группы, в каждой из которых должен быть ♦ генератор идей», «физик», «математик», «скептик» и т. д.
4
На доске или на отдельных листочках записываются условия задач, предлагаемых для решения. Группа, которая решила какую-либо задачу первой (после проверки правильности полученного ответа преподавателем), получает 10 баллов. Группы, которые решили эту задачу позже, получают соответственно 9, 8, 7 и т. д. баллов. Выигрывает та команда, которая набрала большее число баллов.
При такой организации занятий в процессе решения задач участвуют все учащиеся, а главное, он сопровождается эмоциональным подъемом.
Разновидность этой игры — «Поле чудес». Выделенные группы школьников решают предложенные учителем задачи. Затем разыгрывается (с помощью вертушки) номер задачи, решение которой надо объяснить классу (если это решение получено).
При проверке выполнения домашнего задания по решению трудных задач полезна методика, используемая при проведении турнира физиков. Одна группа рассказывает решение задач, вторая является оппонентом, третья — рецензентом. При объяснении решения другой задачи группы меняются таким образом, чтобы каждая выступила и докладчиком, и оппонентом, и рецензентом.
Особенностью этой формы проведения занятий является обоснование решения задачи в устном выступлении. Оценка выставляется с учетом убедительности аргументов при отстаивании правильности полученного решения (максимальная оценка — 10 баллов), а также при оппонировании (5 баллов) и рецензировании выступлений докладчика и оппонента (3 балла).
Игровые формы проведения занятий — это коллективные соревнования школьников в умении решать задачи. Они являются хорошим дополнением к традиционным формам проведения занятий по решению задач, описанных нами выше.
Желаем вам успеха в освоении предложенной системы теорети
ческих задач.
& Будем рады получить ваши предложения и замечания по адресу: 142432, п. Черноголовка Московской обл., а/я 95.
Авторы
Глава 1
КИНЕМАТИКА
Задача 1.1. График зависимости проекции скорости иа ось Ох прямолинейно движущегося тела от времени изображен на рисунке 1.1, а. Постройте график зависимости проекции ускорения на ось Ох и координаты X от времени.
Решение. За начало отсчета координаты х примем точку, в которой тело находилось в момент времени, равный нулю. Тогда начальные условия можно записать следующим образом:
п	о м
хо - 0, °ох ~	•
с
График проекции скорости на участке t е(0;7) — прямая, не параллельная оси времени, следовательно, движение тела равноускоренное. Проекция ускорения на этом участке равна:
График проекции скорости их на участке ie(7;10) — прямая, параллельная оси времени, следовательно, проекция ускорения ах на этом участке равна а2х = 0.
На участке fe(10;16) проекция скорости тела их уменьшается и проекция ускорения ах отрицательна:
у16х _ Г10х , м
“Зх = ----—----- - - 1 -2 •
Л^З	с2
Этих данных достаточно для построения графика проекции ускорения ах (рис. 1.1, б).
6
Для построения графика зависимости координаты тела х от времени необходимо написать уравнение зависимости координаты х от времени. На участке t е(0;7) это уравнение имеет вид:
t2
х = х0 + vOxt + —^—;	х = - 8t +12.
В конце седьмой секунды координата х7 = - 7м.
На участке te(7;10) уравнение зависимости координаты х от времени имеет вид:
х = х7 + t>7x(i - 7), х = -7 + 6(t - 7).
В конце десятой секунды координата Хц> = 11 м.
На участке te(10;16) уравнение зависимости координаты х от времени имеет вид:
(\2 t - 10)
Л - 3-10 -г о10х^ - IV) -г	-	,
, \ -10)2 х = и + e(t - ю) -	.
Используя полученные уравнения, составим таблицу зависимости координат от времени. Поскольку эта зависимость нелинейная, то для точного построения графика потребуется большое число точек.
t, с	0	1	2	3	4	5	6	7	8
X, м	0	-7	-12	-15	-16	-15	-12	-7	-1
t, с	9	10	11	12	13	14	15	16	
X, м	5	11	16,5	21	24,5	27	28,5	29	
С помощью полученной таблицы построим график зависимости координаты х от времени (рис. 1.1, в).
Задача 1.2. Зависимость от времени координаты груза, подвешенного на пружине и совершающего свободные колебания, выражается кривой, представленной на рисунке 1.2. Используя этот график, укажите моменты времени, в которые скорость тела равна нулю и в которые проекция скорости тела их максимальна.
Решение. Проекция мгновенной скорости на ось Ох определяется кх	,	„
отношением их =---- при условии At —> 0.
At
На графике зависимости координаты х от времени это отношение определяет тангенс угла наклона касательной к оси Of в точке кривой, соответствующей данному моменту времени (рис. 1.3).
7
Касательная к графику x(t) параллельна оси Ot в моменты времени 1 с и 3 с (рис. 1.2). Следовательно, в эти моменты времени скорость тела равна нулю, так как тангенс угла наклона равен нулю.
Максимальные значения угол наклона касательной, а следовательно, и проекция скорости движения тела их имеют в моменты времени О, 2 и 4 с.
Рис. 1.2.	Рис. 1.3.
Задача 1.3. Два автомобиля приближаются к перекрестку по взаимно перпендикулярным дорогам с постоянными скоростями и . В момент времени, когда первый автомобиль достиг перекрестка, второй находился от него на расстоянии 1д- Определите минимальное расстояние между автомобилями в процессе их движения.
Возможные способы решения задачи.
Первый способ. В качестве тела отсчета выберем Землю. Движение автомобилей по поверхности Земли на малых по сравнению с радиусом Земли расстояниях можно считать происходящим на плоскости. В этом случае положение каждого из них можно задать двумя координатами. Оси координат Ох и Оу направим вдоль дорог в направлении движения автомобилей (рис. 1.4). За начало отсчета расстояний выберем перекресток, за начало отсчета времени — момент времени пересечения перекрестка первой машиной.
Начальные условия движения автомобилей запишем в виде:
= 0, и1у = щ, xoi = 0, 1/01 = 0;
С»2Х = t>2> и2у = 0, Хо2 = -	У02 = 0-
Координаты машин в любой произвольный момент времени определяются уравнениями:
Х1 = х01 +	х2 = XQ2 +
У1 = 1/01 + Olyt,	У2 = У02 + »2yt-
С учетом начальных условий получим:
X! = 0, х2 = - 10 + v2t, У1 = t>it, у2 = 0.
8
Как видно из рисунка 1.5, расстояние между точками на плоскости можно выразить через их координаты следующим способом:
1 = \(х1-х2)2 +(У1 -У2}2 
Отсюда расстояние I между автомобилями в любой момент времени равно:
= 1/уО ~	
Для нахождения минимального значения расстояния I найдем производную Г и приравняем ее к нулю:
—	+ f2^ +	— 0.
Отсюда найдем время t =
г0и2
fl +02
а затем значение Zrrljn:
^min
,2
/ » г°°2
10 ~ ° 2 ~5-2
fj+f^
J^O
fl +f2
Второй способ. В качестве тела отсчета выберем второй автомобиль, направление координатных осей и начальный момент отсчета времени примем такими же, как и в первом способе решения задачи. В системе отсчета, связанной со вторым автомобилем, первый автомобиль движется со скоростью о12, равной:
fl2 = fl ~ ^2>	у12 =	+ у2 •
9
по которой движется первый авто-
Эта скорость направлена под углом а к прямой, соединяющей автомобили в начальный момент времени t = О (рис. 1.6).
Кратчайшее расстояние между автомобилями равно длине отрезка перпендикуляра, опущенного из начала координат, в котором находится второй автомобиль, на прямую, мобиль.
Из рисунка 1.6 видно, что
/min - lo sin a, sin а =
_Е1_	1 - lovi
’ ^min /-------------- •
Задача 1.4. Ракета, движущаяся равномерно и прямолинейно со скоростью и в системе координат, связанной с «неподвижными» звездами, имеет два двигателя, рассчитанные на работу в течение интервалов времени tj и ig- Двигатели сообщают ракете постоянные ускорения и ag, причем > ag. Включаться они могут только последовательно. Скорость ракеты может быть уменьшена до нуля при любом порядке включения двигателей после полной их отработки. Какой порядок включения двигателей следует избрать для того, чтобы путь, пройденный ракетой к моменту окончания работы двигателей, был минимальным?
Возможные способы решения задачи.
Аналитическое решение. Поскольку движение происходит вдоль одной прямой, положение ракеты в пространстве можно определить одной координатой. Для этого ось Ох системы координат направим вдоль вектора скорости ракеты, а за начало отсчета координат примем точку, в которой находится центр массы ракеты в момент включения двигателя. Момент включения двигателя примем за начало отсчета времени.
При этом начальные условия движения ракеты
Хо = о, РОх = о.
Для того чтобы путь торможения ракеты был минимальным, она должна быть ориентирована в пространстве так, чтобы вектор ускорения при включении двигателя был противоположен вектору скорости ракеты. При этом путь будет равен проекции перемещения s на ось Ох:
/ = sx.
Если включить сначала первый двигатель, а затем второй, то путь, пройденный ракетой за время работы первого и второго двигателей, будет равен:
.2	.2
®1х = у0х*1 +	+ р1х*2 +
10
Подставляя в уравнение значения проекций скоростей и ускорений на ось Ох:
Ц)х =	^1х ~ ^Ох + Л1х*1 ~ у —	’ а1х = ~ а1> а2х = ~ Л2>
получаем:
.2	.2	+2	.2
Л1Г1 /	\ cintfj /	\ dy Ci	ЛоГо
«1х = -Чг- + (°“аАГ2 “Чг" = ”01 +М ---------------7—«1^2-
z	A	A Zl
Повторив аналогичные рассуждения для случая включения сначала второго двигателя, а затем первого, получим, что ракета за то же время t = 1± + t2 пройдет путь
.2	.2	м2 .2
Cinto /	\	Лу *1	/	\ fli»i Л9Г9
s2x = &2 - ~~ +(” - «2*2/1 -	= ”01 +*2)-Ч-------^~«2*1*2-
Л	А	л А
Сравним пройденные пути:
s2x - six = *1*г(«1 - а2)-
Так как > а2, то S2X - «ix > 0, т.е. s2x > six-
Итак, ракета пройдет меньший путь, если сначала включить двигатель, создающий большее ускорение.
Эту задачу можно решить и графическим способом.
Графическое решение. Построим график зависимости проекции скорости ракеты ох от времени при различном порядке включения двигателей. В начальный момент времени t = 0 проекция скорости ракеты 1>х в обоих случаях равна и (точка А), в момент окончания работы двигателей i = ti + i2 проекция скорости ракеты в обоих случаях равна нулю (точка С). Графики зависимости проекций скорости от времени для двух различных способов включения двигателей соединяют точки А и С ломаными линиями АВС и ADC (рис. 1.7).
Углы наклона отрезков ломаных линий к оси времени cq и а2 можно определить из выражений:
tga1=a1, tga2 = a2, так как тангенс угла наклона графика проекции скорости к оси време-ни равен ускорению: tga =  =а.
Д2
При включении сначала первого двигателя, а затем второго график проекции скорости ракеты изобразится ломаной линией АВС. При включении сначала второго двигателя, а затем первого график проекции скорости изобразится ломаной линией ADC. Поскольку ракета движется прямолинейно вдоль оси Ох и не изменяет направления ско-
11
рости, площадь фигуры, образованной графиком проекции скорости осями координат и ординатами, соответствующими начальному и конечному значениям проекций скорости, пропорциональна пройденному пути. Сравнивая площади фигур ОАВС и OADC, приходим к выводу о том, что для получения меньшей величины пути торможения необходимо сначала включить двигатель, создающий большее ускорение, т.е. первый.
Задача 1.5. Ракета стартовала с поверхности Земли и двигалась верти-м
кально вверх с ускорением 5-- в течение 10 с, пока работали ее двигатели.
с2
Сколько времени пройдет с момента прекращения работы двигателей до момента падения ракеты на Землю (рис. 1.8)? Сопротивлением воздуха пренебречь. Уско-м рение свободного падения принять равным 10-.
с2
Решение.	t = t2 + t3,
l>10 ati	/ 2/г3
t2= --- = ----, t2 = oc, t3 - -------,
g g	N g
h3 =	+ h2,
at? h} = —/ij = 250 m, 2 gt? h2 =	----’	^2 = 125 m,
= 250 м + 125 м = 375 m, t3 ® 8,7 c, 5 c + 8,7 c ® 13,7 c.
Задача 1.6. Два камня падают с одинаковой высоты 80 м, причем второй камень начал падать на 2 с позже первого. Постройте график зависимости проекции скорости первого камня на вертикальную ось в системе отсчета, связанной м со вторым камнем. Ускорение свободного падения принять равным 10-. Пос-
с2
ле столкновения с поверхностью Земли камень неподвижен.
12
Возможные способы решения задачи.
Первый способ. Выберем за начало отсчета положение камней в начальный момент времени, ось Оу направим вертикально вниз.
Время t падения каждого камня с высоты 77 = 80 м определим из выражения:
тт gt2	[2Н	12-80
Н = —, t= --------, t = .------с = 4 с.
2	V g	V 10
В течение первых двух секунд (0 с < t < 2 с) первый камень падает с ускорением g, а второй покоится.
В течение последующих двух секунд (2 с < t < 4 с) оба камня находятся в свободном падении. Затем в интервал времени 4 с < t < 6 с падает только второй камень, а при t > 6 с оба камня неподвижно лежат на земле.
Запишем зависимость Oy(t) в системе отсчета, связанной с Землей, в указанные промежутки времени:
а)	0	с	<	t	<	2	с,	oYy = gt,	и2у - 0;
б)	2	с	<	7	<	4	с,	Dly = gt,	o2y = g(t-2);
в)	4	с	<	t	<	6	с,	у1у = 0,	о2у = g(t-	2);
г)	t	> 6	с,	oYy = 0, р2г/ =	0-
Следовательно, относительная скорость первого камня в системе отсчета, связанной со вторым камнем, в соответствующие интервалы времени будет равна:
a)	0c<t<2c, vY2 = gt-0 = gt;
б)	2 с < t < 4 с, о12 = gt - g(t - 2) = 2g;
в)	4 с < t < 6 с, i>12 = 0 ~	~ 2) = g(2 - f);
г)	t > 6 с, у12 = 0-0 = 0.
График Oy(t) для указанных интервалов времени показан на рисунке 1.9.
Второй способ. При выборе системы отсчета, связанной со вторым камнем, в промежуток времени 0 с < t < 2 с проекция скорости первого камня определяется выражением и = gt, так как второй камень в этот промежуток времени покоится.
В промежуток времени 2 с < t < 4 с второй камень свободно падает с таким же ускорением, как и первый. Следовательно, скорость первого камня относительно второго не изменяется и равна скорости, достигнутой первым камнем за 2 с: о = 2g.
13
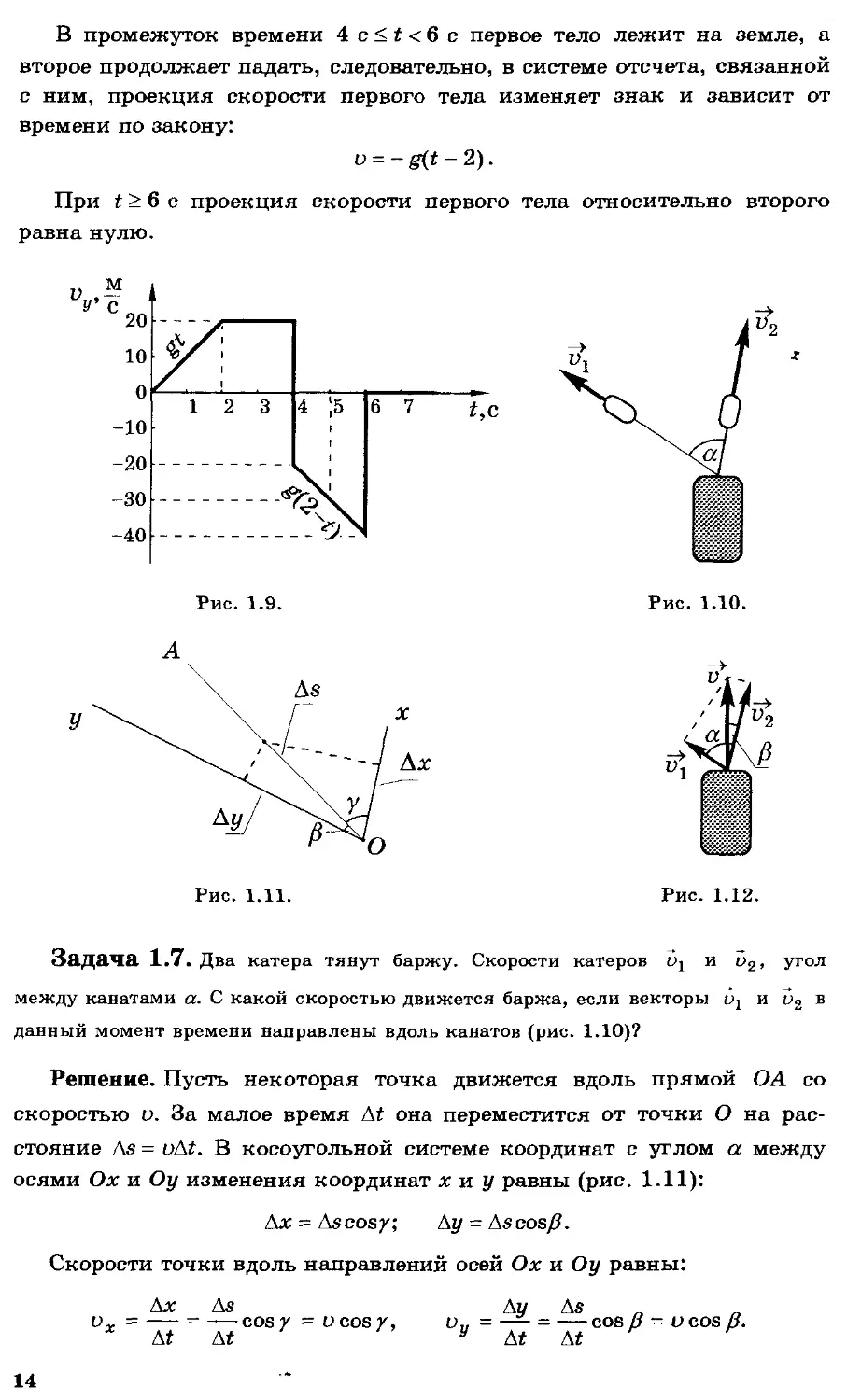
В промежуток времени 4 с < t < 6 с первое тело лежит на земле, а второе продолжает падать, следовательно, в системе отсчета, связанной с ним, проекция скорости первого тела изменяет знак и зависит от времени по закону:
u = -g(t-2).
При t > 6 с проекция скорости первого тела относительно второго равна нулю.
Рис. 1.10.
Рис. 1.9.
Рис. 1.12.
Задача 1.7. Два катера тянут баржу. Скорости катеров Oj и о2, угол между канатами а. С какой скоростью движется баржа, если векторы и в данный момент времени направлены вдоль канатов (рис. 1.10)?
Решение. Пусть некоторая точка движется вдоль прямой ОА со скоростью о. За малое время А? она переместится от точки О на расстояние As = иМ. В косоугольной системе координат с углом а между осями Ох и Оу изменения координат х и у равны (рис. 1.11):
Ax = Ascosy; Ap = Ascos/7.
Скорости точки вдоль направлений осей Ох и Оу равны:
Ах As	Ар As
= = -— cos у = и cos у,	= — cos В = и cos В.
ММ	УММ
14
Отсюда следует, что проекции искомого вектора и на направления канатов должны быть равны скоростям катеров и и2 (рис. 1.12). Следовательно, вектор и не является суммой векторов Uj и о2, если а *90°.
= и cos(а - р}, о2 = ° cos А cos ft	cos ft
cos (а - /?) cos a cos ft + sin a sin ft ’ 1	„	1 ('l
	= —=> tgft =-------- —— -cos a =-------±----ctga, cos а + sin atgft---------------------------------------------о г	sin a \ u2 ) v2 sin a
и =	= o271 + tg2^-
cos ft
Задача 1.8. На ленту транспортера перпендикулярно направлению ее движения соскальзывают консервные банки. Путь банки по ленте до остановки м
0,5 м. Скорость банки ui перед ее выходом на ленту транспортера 0,9 —, ско-с
м
рость ленты транспортера равна 0,45 —. Для снятия банки с ленты наиболее с
удобна точка, в которой скорость банки относительно Земли минимальна. Определите минимальное значение скорости банки относительно неподвижного наблюдателя на Земле. Определите координаты точки А, в которой находится банка в момент, когда ее скорость минимальна относительно Земли. За начало отсчета примите точку О вхождения банки на ленту транспортера, ось Ох параллельна скорости t>Y , ось Оу — вектору скорости и2 (рис. 1.13).
Решение. В системе отсчета, связанной с лентой транспортера, скорость банки о3 в момент соприкосновения с лентой транспортера равна (рис. 1.14):
-	—	—	/ 9	9~	I	~~Г" М _ М
Од = О^ —	Од = л/О^ + О 2 ,	Од — \ 0,81 + 0,2 — ~ 1 — .
С с
15
Вектор силы трения F направлен против вектора скорости и, ектория банки в системе отсчета «лента транспортера» прямолине движение равноускоренное.
Ускорение банки а определяется через значения начальной скс ти о3 и пути s до остановки:
Do	1 м , м
а = -2-, а »------------= 1----.
2s	2  0,5 с2 с2
Найдем сначала минимальное значение omjn скорости банки отн< тельно Земли. Скорость банки о4 относительно Земли является ( мой скорости банки о3 относительно ленты транспортера и скорс ленты транспортера и2 (рис. 1.15).
Скорость о3 в процессе торможения уменьшается до нуля, скорс о2 остается постоянной. Вектор 64 (сумма векторов о3 и о2) иа няет свой модуль и направление до остановки банки относительно i ты.
Построим годограф скоростей банки о4 (рис. 1.16).
Конец вектора й4 перемещается по стороне параллелограмма, пс роенного векторами Б3 и о2. Модуль вектора о4 имеет минималы значение в случае, когда вектор б4 перпендикулярен вектору о3.
Следовательно,
р, DnD-, 0,45 • 0,9 м „ . м fmin = р2 sm а = р2 —t- =--i- =----------« 0,4 —.
i>3	i>3 i2 с с
16
Отыскав нужное значение скорости о 4 в системе отсчета «Земля», найдем скорость банки о5 относительно ленты в этот момент времени:
у 5 =	~ у/0,2 - 0,16 — = 0,2 —.
с с
По изменению скорости До относительно ленты и ускорению а найдем время движения банки до искомой точки А:
Au = aAt, At = — =	°5 , At = 1-0,2 = 0,8 c.
a a	1
За время At перемещение s, банки по ленте равно:
= t>3At
a At2 4”
1(0,8)
s, = 10,8 м----i--1—
2
м = 0,8 м - 0,32 м = 0,48 m.
Найдем проекции slx и sly этого перемещения на оси Ох и Оу
(рис. 1.17):
Pi	Р2
slx = si sm а = «1 —sly = Sj cos« = «4 — Уз	Уз
09
slx = 0,48 • -у- м » 0,43
м,
ХА = six = °,43 м,
*1!/
0,45
= 0,48------м ~ 0,22 м,
1
У А ~ s2 ~ sly = t>2^t - Siy = 0,45 • 0,8 м - 0,22 м = 0,14 м.
17
Задача 1.9. На рисунке 1.18 представлен график зависимости скорости движения точки от времени, имеющий форму полуокружности. Определите путь, пройденный точкой за интервал времени от tj до t2.
Решение. Путь пропорционален площади под графиком v(t).
Площадь круга равна:
SK = л/?2, где R — его радиус.
Площадь заданной фигуры равна:
_ дй2 о —----.
3
Отсюда пройденный путь s равен:
nut	л 10 -2
s =----; s -----------м » 21 м.
3	3
Задача 1.10. Расстояние между двумя станциями 22,5 км поезд проходит за 25 минут. Сначала он идет в течение 5 минут равноускоренно, а затем равнозамедленно до полной остановки. Определите максимальное значение скорости поезда.
Возможные способы решения задачи.
Аналитическое решение.
„ _ „ . „ _ а1*1 , „ t а2*2 _ а1*1 f f a2f2
s - s1+s2 - —— + O02t2	+ аР1г2 „ >
Л	A	A	la
«1*1 = «2*2 = fmaX = t>,
oii	uio	о	о	о /	\
S=~5- + t,i2-— = -*1+7*2 =7(*l+*2> La	La	La	la	La
2s	45 IO3 м „ м
0=-------,	0 =----------= 30—.
+12	25-60 с c
Графическое решение. Построим график зависимости скорости от времени для движения поезда (рис. 1.19).
Учитывая, что площадь под графиком u(t) численно равна расстоянию s между станциями, получим:
у1мх*
откуда отах
2s _ 2-22,5-103 м ~ 3() м t 25-60 с с
18
Задача 1.11. Тело брошено под углом «о = 45° к горизонту со скоростью м
«о = 20—. Определите скорость и координаты тела через t = lc после начала с
движения.
Решение. В качестве тела отсчета выберем Землю. Начало отсчета системы координат поместим в точку, из которой тело начало двигаться. Ось Оу направим вертикально вверх, а ось Ох расположим так, чтобы вектор скорости лежал в плоскости хОу (рис. 1.20). В этом случае движение будет происходить в указанной плоскости и для определения положения тела нужно знать лишь две координаты. Движение
„	~ тМ3
тела происходит только под действием силы тяготения F = G---------—,
где М3— масса Земли, R3 — расстояние между телом и центром Земли. Поскольку радиус Земли значительно больше высоты тела над поверх-
п	г-	у, М3
ностью Земли, то, обозначив G—— = g, можно записать:
F = mg.
За начало отсчета времени примем момент бросания тела. Запишем начальные условия:
*о = 0, у0 = 0, о0х = 1>0 cos «о, о0у = °о sin «о, ах = 0, ау = - g.
Проекции скорости на оси координат равны:
= и0х +
<->у = °0у + ау*-
19
Используя начальные условия, получим:
их = d0 cosa0, иу = d0 sin «о - St.
Отсюда можно определить модуль и направление вектора скорости в любой момент времени t:
D =	C°S2 а0 + (°0 sin а0 ~ &t)2 ’
°у _ t>0 sin а0 - gt их i>o cos ао
где а — угол наклона вектора скорости тела к горизонтальной плоскости в момент t.
Подставив числовые данные, получим:
I	1 (	,/9
d = ,400 -+ 20 —-10 1
V	2	2
2
М , . - м — ® 14,7 —
с	с
tga
20 —-101 2
20 —
2
~ 0,3;
a « 17°.
Координаты тела
в любой момент
времени равны:
х = Xq
art2 + vOxt +
у = Уо + VQyt +
Используя начальные условия, можно записать:
X = Dq COS O()t,
у = Do sin aot
gt2
2
Подставляя числовые данные, получим:
Jo х = 20-----1 м = 14 м.
2
Jo и = 20 — 1 2
101
м-----
2
м = 9 м.
Задача 1.12. Камень бросили под углом 60° к горизонту со скоростью м
10—. Определите радиус кривизны его траектории в верхней точке и в момент с
падения на Землю.
20
Решение. Ускорение камня в каждой точке траектории его движения равно ускорению свободного падения g. В верхней точке траектории касательная направлена горизонтально (рис. 1.21). Так как ускорение свободного падения направлено по вертикали, проекция его на касательную равна нулю, а центростремительное ускорение равно ускорению свободного падения:
(i>0 cos а]2
“цс = Rr = 8'
Отсюда радиус кривизны, т.е. радиус окружности, дуга которой является участком параболы в верхней точке, равен:
2	2
_ (?о cos а
В момент падения на Землю горизонтальная составляющая скорости остается такой же, как и в момент бросания, вертикальная составляющая по модулю становится равной начальному значению, а по направлению изменяется на 180°. Поэтому вектор скорости камня в момент падения направлен под углом (360° - а) к горизонту и равен по модулю начальному значению о0. Центростремительное ускорение ацс направлено к центру окружности, дугой которой является участок параболы в данный момент. Его можно нейти как проекцию ускорения свободного падения g на перпендикуляр к вектору скорости в момент падения, так как вектор скорости направлен по касательной к траектории:
ацс = g cos а = —— .
/?2
Отсюда получим:
“2 -geos а
Подставив численные значения физических величин, получим:
102 1
=-----— м = 2,5 м,
10
102 Нп =----м = 20 м.
1
10-2
21
Рис. 1.21.
Рис. 1.22.
Задача 1.13. Метатель молота бросил свой снаряд на 72,9 м. Определите касательное и центростремительное ускорения молота перед моментом его освобождения, приняв, что бросок совершен под углом 45° к горизонту от поверхности Земли, а раскручивание молота происходило с постоянным касательным ускорением в течение 6 оборотов по окружности радиуса 2,1 м.
Решение. Касательное ускорение можно рассчитать, зная скорость вылета молота и и путь I, пройденный молотом за время разгона t. Путь, пройденный молотом за время раскручивания, определим из выражения:
l = 2nRn, I = 2л • 2,1 • 6 м = 80 м.
Скорость молота в момент освобождения можно определить по дальности его полета S. В качестве тела отсчета выберем Землю, ось Оу направим вертикально вверх, а горизонтальную ось Ох расположим так, чтобы вектор скорости лежал в плоскости хОу (рис. 1.22).
При таком выборе системы координат движение молота происходит в плоскости хОу, и для определения положения молота нужно знать лишь две координаты.
За начало координат примем точку вылета молота, считая ее находящейся на поверхности Земли. Координаты молота в любой момент времени будут равны:
х = х0 + uOxt, у = Уо + vOyt +	.
Используя начальные условия х0 = 0, l>qx = Up cos а, Уо = 0 , Lpy = Uo sin а, a.y = ~g, получим:
^.2
х = Op c°s a t, у = t>p sin а • t-.
22
В момент падения молота его координата у равна нулю, отсюда:
Лу 2	.	gt%
0 =	O = uosmat- —.
•n	x 2и0у	x 2uosina
Время полета молота t =-----— или t = —-------
ay	«
Дальность полета I можно определить из выражения:
2u0 sin a 2t>o .
s = uOxt, s = t>o cos a —~~ sm a cos a  g g
Следовательно, начальная скорость Up вылета молота равна:
sg
u0 = J—-----------
V 2 sm a cos a
72,9  9,8 м 27 м
Jz Jz с c
2-——• — 2	2
fo =
Вычислим касательное ускорение а,
молота:
a u20	272
K 21 ±xRn ~ 160
м
7
. « М
’ ~7‘
Его центростремительное ускорение:
_ uq _ 272 M “ц° " 7_ 7Г ”7
м
7
» 350
Задача 1.14. Самолет выполняет «мертвую петлю» в вертикальной плос-кости, двигаясь с постоянной по модулю скоростью. Определите минимальное значение скорости движения самолета при заданном радиусе «петли» (2?о = 90 м) и максимальное значение радиуса «петли» при заданной скорости движения са-( , молета vQ = 100— . \	с/
О2
Решение. Центростремительное ускорение самолета ацо = —. R
В верхней части «мертвой петли» это ускорение не может быть
меньше ускорения свободного падения: ацс>£. Следовательно, g< —. R
При заданном радиусе петли Rq скорость самолета должна быть больше некоторого минимального значения
и ^min = 7^0 ’
^min =710-90^ = 30^-. с с
23
При заданной скорости движения самолета радиус петли должен быть меньше некоторого максимального значения Ятах:
2	2
R ятах, _Rmax = -^ = м = 1000 м.
g Ю
Задача 1.15. На крышу дома высотой h с расстояния I от него мальчик хочет забросить мяч (рис. 1.23). Каково минимальное значение начальной скорости мяча для такого броска?
Решение. Выберем систему отсчета, показанную на рисунке 1.24.
•	2	2
gsmai t	. ,	. geostp t
---------, у = и0 sm(a - <p)t-------,
&	л
х = 1>0 cos|
У = Sin|
+ h2,
хв
У в = °,
uq sm|
9
gcosfftB = 0
2t>0 sinja - <p\
fB =---------------
gcos<p
B 2
z \ 2onsin(a-<3)
хв = и0 cost a -	------------—
'	’ g cos <р
gsin <p 4oq sin2(« - tp) _ 2 g2 cos2 <p
2
2 geos (p
cos <р - sin <д[1 - cos|
2 ^0
2 g COS (p
sin <p
+ h2.
"0
yjl2 + h2  geos2 (р sin(2a - - sin <p ’
It (p
2
2	_
^Omin ~
o	2
+ h ' g COS (p _
+ h2  gl2
1 - sin <p
gl2
+ h2 -h
- g\yl2 +h2 +h ,
^Omin
I2 +h2 +h .
1-- * = . Л2+12
24
X
Рис. 1.23.
Рис. 1.24.
Задача 1.16. Самолет движется прямолинейно со скоростью и, . Его преследует ракета с постоянной по модулю скоростью . Ракета автоматически ориентируется на самолет. С каким ускорением движется ракета в тот момент времени, когда ее вектор скорости перпендикулярен вектору скорости самолета, а расстояние между ними 11
Решение. За очень короткий промежуток времени At самолет пройдет расстояние , ракета— u2 \t. Траекторию ракеты за этот интервал времени можно рассматривать как дугу окружности радиуса R (рис. 1.25):
= R0,	= 10,
Рис. 1.25.
Рис. 1.26.
25
Задача 1.17. Стержень длиной I одним концом опирается на вертикальную стену, другим на горизонтальную поверхность пола. Нижиий конец стержня (точка А на рис. 1.26) движется в горизонтальной плоскости от стены со скоростью Uq . Какая точка стержня при угле а с горизонтальной плоскостью движется с минимальной скоростью? Чему равна эта скорость?
Решение. Скорость верхнего конца стержня (точка В, рис. 1.27) относительно точки А есть:
ив = ° в “ ^0’ или
ив = 0)1,
ив = —— = col, sin а
со=-^.
I sin а
Найдем положение мгновенного центра О вращения стержня. Для этого через точку А проведем прямую, перпендикулярную вектору и0, и через точку В — прямую, перпендикулярную вектору йв (рис. 1.28).
Центр вращения О есть точка пересечения этих прямых.
Произвольная точка М стержня движется вокруг мгновенного центра вращения О со скоростью:
им = <о  ОМ, oniin = со  ОМ0,
где OMq — перпендикуляр из точки О на стержень.
OMq = I sin a cos a, yniin = ® si11 а cos а = u0 cos а-
Рис. 1.27.
Рис. 1.28.
26
З&Д&ча 1.18. На диск радиуса R намотаны две нерастяжимые нити, закрепленные в двух разных точках (рис. 1.29). При отпускании диск вращается. Когда угол между нитями у диска а, угловая скорость вращения диска ш. С какой скоростью в этот момент движется центр диска? Нити остаются натянутыми.
Рис. 1.30.
Рис. 1.29.
Решение. Нити нерастяжимы, поэтому векторы скоростей точек А и В перпендикулярны нитям (рис. 1.30). Мгновенный центр вращения находится в точке пересечения перпендикуляров к скоростям и А и и В, т. е. в точке О.
Вектор скорости центра диска С перпендикулярен ОС и равен по модулю:
= cor - со  ОС =-.
cos — 2
Глава 2
ДИНАМИКА
Задача 2.1. На горизонтальной доске длиной I лежит груз массой т (рис. 2.1). Коэффициент трения между грузом и доской равен д . Через какое
время груз соскользнет с доски, если доска движется с ускорением а, направленным вправо?
Решение. Выберем в качестве системы отсчета доску. Поскольку доска движется с ускорением относительно Земли, эта система отсчета является неинерциальной. Для того чтобы в ней можно было пользоваться законами Ньютона, необходимо к грузу, кроме сил взаимодействия mg, N и FTp, приложить силу инерции Fm,, равную
Fm = -та (рис. 2.2).
Применив второй закон Ньютона в проекциях на координатные оси, получим:
(таг = Fral ~ FTp = та- FTp,
[о = mg - N,
где аг — ускорение груза относительно доски.
Сила трения скольжения равна:
=PN,
28
поэтому ускорение груза равно:
pmg
аг = а- —— = а - pg. т
Время движения груза по доске равно:
t =
21
a-pg
Из полученного выражения следует, что при а < pg груз никогда не соскользнет с доски. Груз движется по доске при выполнении условия а > pg-
Задача 2.2. Какую силу F должен приложить человек массой т, чтобы сдвинуть с места ящик массой М? Коэффициенты трения о пол человека и ящика одинаковы и равны р. Считать М > т.
Решение. Рассмотрим случай, когда человек тянет ящик. Для того чтобы сдвинуть ящик, не скользя по полу, человек должен приложить
к ящику силу F, горизонтальная проекция которой по абсолютному значению больше или равна силе трения покоя ящика о пол и меньше силы трения покоя человека о пол:
F cos а > p(Mg - F sin а),
F cos а < p(mg + F sin а), где а — угол между приложенной к ящику силой и горизонтом (рис. 2.3). Отсюда
pF sin а > pMg - F cos а,
pF sin a > F cos a - pmg.
Решая эту систему уравнений относительно Г sin а и F cos а, по-
лучаем:
F cos a > i p{M + mjg.
Следовательно, F > — gJ^M - mj2 + p2[M + m}2 .
Задача 2.3. Длинная доска массой М лежит на гладком горизонтальном столе. На доске находится брусок массой т. Коэффициент трения между бруском и доской р. К бруску приложена сила, параллельная доске, зависящая от времени по закону F = at. Исследуйте зависимости проекций на горизонтальную ось ускорений бруска и доски от времени действия силы. Начертите графики этих зависимостей.
29
Рис. 2.4.
Решение. Относительно инерциальной системы отсчета, связанной с Землей, на брусок действуют две силы: внешняя сила F и сила трения Д со стороны доски, направленная в сторону, противоположную направлению внешней силы F. На доску действует только одна неуравновешенная сила сила трения со стороны бруска (рис. 2.4). Силы тяжести доски и бруска уравновешиваются упругими силами реакции опор.
Уравнения второго закона Ньютона в проекции на ось Ох, направленную параллельно вектору силы F, можно записать в виде (рис. 2.5):
Fx + 1\х = таУх, f2x = Ма2х.
По третьему закону Ньютона
А=-/2,	|/1х| = |/2х| = Л
Следовательно, уравнение можно записать в виде:
Fx-f = maVx, f = Ма2х.
Эти уравнения имеют смысл только при значениях а1х > а2х, так как по условию задачи доска не может двигаться быстрее бруска.
В начале движения ускорения бруска и доски равны между собой:
F-f _ f
“lx - а2х> ------ - ~ 
т М
Предельное значение силы Fq, при котором ускорения доски и
с	Fq - 4>	4>
бруска еще равны, можно определить из условия —----------— = —,
т. М
где /о — максимальное значение силы трения покоя, равное силе тре-
ния скольжения: 4> = FmS-
30
Отсюда
Fo - nmg = /img т М
„	(, т\
Fo = firng 1 + — , к MJ
т.е. при F < Fo
F
а1х - а2х -т + М
лг fjmg\ 1 + — Fc,	к	М)
Таким образом, до момента времени t0 = —— =------------------- проек-
а
а
ции ускорения обоих тел одинаковы и
растут по линейному закону:
а1х - а2х
at
т + М
= kyt,
где kY =
При доски и
а
т + М
t > проекции ускорения бруска будут разными. Про-
екция ускорения доски, достигнув ве-[img
личины а9„ =------, останется далее с
2 М
течением времени неизменной, в то время как проекция ускорения бруска будет увеличиваться со временем по закону:
Рис. 2.6.
at - pmg а	,	, а
а1ж =-------= — t - ng = k2t - ng, где k2 = — .
m m	m
Графически зависимости ускорений бруска и доски от времени показаны на рисунке 2.6.
Задача 2.4. Доска наклонена под таким углом а к горизонтальной плоскости, что для коэффициента трения скольжения п монеты выполняется соотношение п - tga (рис. 2.7). Монете сообщается начальная скорость и0. Вектор и0 направлен под углом <р0 к горизонтальной оси Ох в плоскости доски. Каково значение установившейся (постоянной) скорости движения монеты на доске?
Решение. Вдоль направления вектора скорости и (рис. 2.8) действуют сила трения
F^ = ~nmg cos а = -mg sin a
31
и проекция вектора силы тяжести на направление вектора скорости
Fgr = -mg sin a cosl — - <р\,
р = р + р  х г х тр ' х gr ’
Fr = -mgsina(l + sin^).
Рис. 2.9.	Рис. 2.10.
Ускорение dr равно (рис. 2.9):
ar = -g'sina^l + sin^j.
Изменение скорости dur за dt равно:
dur = -g sin a(l + sin <pjdt.
Вдоль оси Оу действуют проекция силы трения F^ и проекция силы тяжести Fgy (рис. 2.10):
= Fgy +	’
32
1 + cos---(0
\2	,
Fv = mg sin a + mg sin a cos\-<p
Fy = mg sin a
Fy = mg sin a(l + sin <p}.
Отсюда проекция ускорения на ось Оу равна: ау = gsin a(l + sin ip).
При движении монеты вдоль оси Ох действует только сила трения, поэтому через некоторое время t эта составляющая станет равной нулю их = О. В результате монета будет двигаться только вдоль оси Оу. Скорость ее станет постоянной, так как в любой момент
dvr = ~dVy.
Найдем конечное значение скорости ис :
fd^r=- / dlJy, VC-VQ = -Vc-U0sinq>Q, '<o	-u0sin(o0
1 - sin cm
= ”0-----•
Задача 2.5. Бруску сообщили скорость v0 = 3,8 м/с, направленную вверх по наклонной плоскости. Угол а наклона плоскости к горизонту равен 30°. Найдите путь, пройденный бруском за t=l с, если коэффициент трения бруска о плоскость равен у. = 0,3.
Решение. При движении бруска вверх по наклонной плоскости (рис. 2.11) модуль его ускорения равен:
F + Ртр	mg sin а + umg cos a t .
щ =------— =----------------------= glsin a + у cos a
m	m	'
Подставляя числовые данные, получим:
щ = 10 • (0,5 + 0,3 • 0,87)	« 7,6	.
с2 с2
Время движения бруска вверх равно:
р0	3,8
ii = -2-,	t-, ~---с = 0,5 с.
а/	7,6
33
Путь, пройденный за время tlt равен:
а, л2
S1 = <V1 - Чг ’ Л
7,6 • (0,б)2
s, « 3,8  0,5 м---м = 0,95 м.
2
При движении бруска вниз по наклонной плоскости (рис. 2.12) модуль его ускорения равен:
F - F,	mg sin а - umg cos a	z .	\
a2 --------- =------------sin а - /л cos a),
m	m	x
a2 « 10 -(0,5-0,3 0,87)^- = 2,4^-. cz c
Путь, пройденный за время t2 - t = 1 c - 0,5 c = 0,5 с, равен:
a2t2 2,4 • 0,25
s2 =	®	--— м = 0,3 m.
2	2
Общий путь, пройденный бруском за 1 с, будет равен:
s = Sj + s2 ~ 0,95 м + 0,3 м = 1,25 м.
Рис. 2.11.
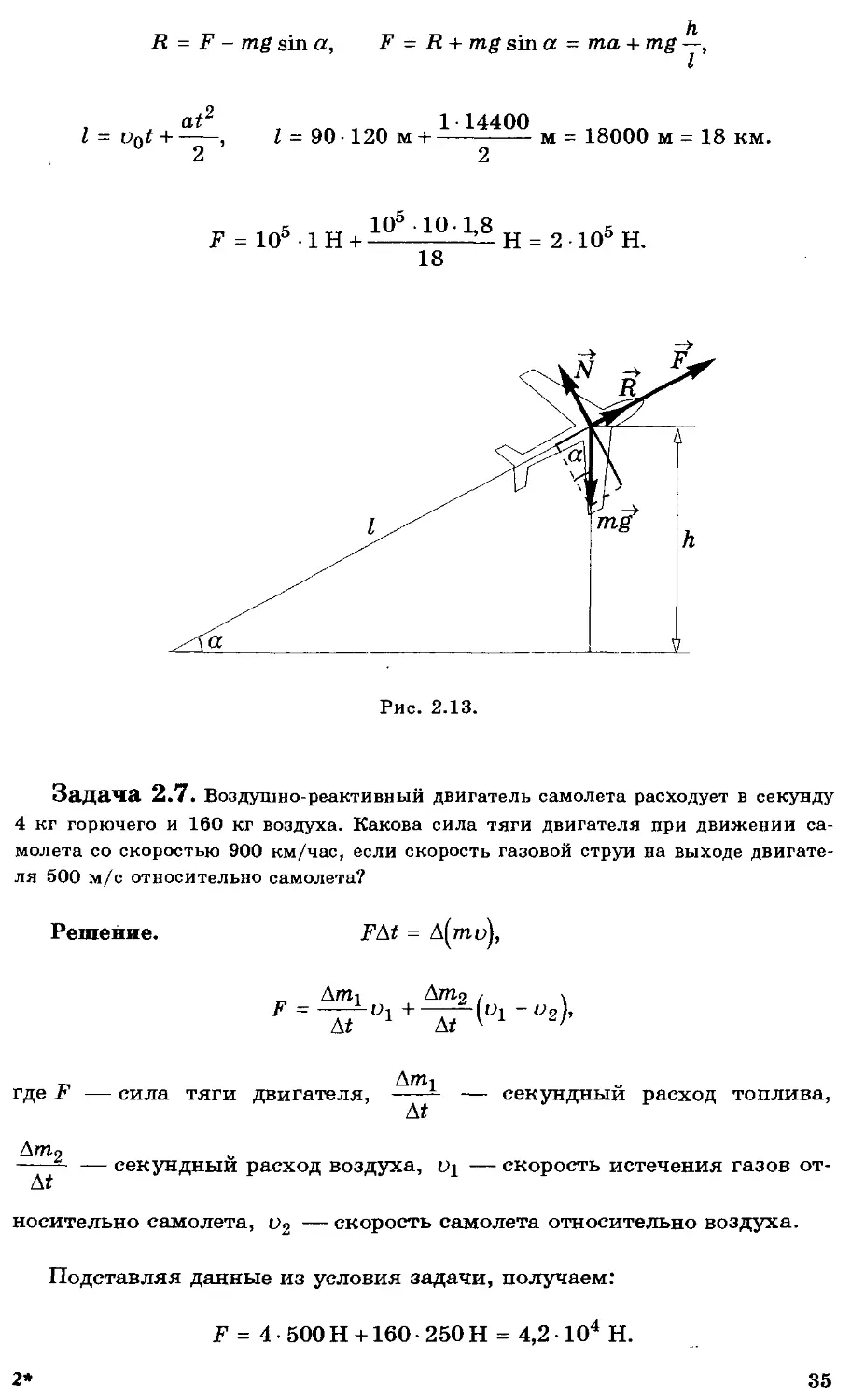
Задача 2.6. Самолет массой 100 тонн после отрыва от взлетной полосы при скорости 90 м/с движется равноускоренно прямолинейно с ускорением 1 м/с2 и через 2 минуты оказывается на высоте Л = 1,8 км над поверхностью Земли. Определите силу тяги двигателей самолета. Сопротивлением воздуха в расчетах пренебречь.
Решение. При движении самолета на него действуют сила тяги F, сила тяжести mg и подъемная сила N, равнодействующая R направлена вдоль траектории движения самолета (рис. 2.13):
R = F + mg + N; R = та, N + mg cos а = 0,
34
R = F - mg sin a, F = R + mg sin a = ma + mg
2
l = vot +	i = 90 • 120 м + 1 14400	_ |gQQQ м = 18 km.
2	2
F = 105 • 1 H+-——--^8 H = 2 • 105 H.
18
Рис. 2.13.
Задача 2.7. Воздушно-реактивный двигатель самолета расходует в секунду 4 кг горючего и 160 кг воздуха. Какова сила тяги двигателя при движении самолета со скоростью 900 км/час, если скорость газовой струи на выходе двигателя 500 м/с относительно самолета?
Решение.	FAt = Д(игр),
„ Дт, Дти2 ,	,
F ------От Ч-----(tli —	/’
Д? 1 Д£ 1 1	2/
„	Атх
где t — сила тяги двигателя, ------- — секундный расход топлива,
At
Ат2
---— — секундный расход воздуха, с>х — скорость истечения газов от-At
носительно самолета, с>2 — скорость самолета относительно воздуха.
Подставляя данные из условия задачи, получаем:
F = 4-500Н +160 -250Н = 4,2104 Н.
2*
35
Задача 2.8. В трубе течет вода со скоростью 5 м/с. Как изменится давление воды в трубе у заслонки, если течение воды резко остановить заслонкой?
Скорость звука в воде 1500 м/с.
Решение. Изменения давления в воде распространяются в ней со скоростью звука с. При остановке воды давление возрастает. Изменение давления распространяется за время А? на расстояние
Л/ = сД/.
Масса остановившейся воды равна:
Дпг = pAV = pSAl = pScAt, грр р — плотность воды, S — площадь поперечного сечения трубы у заслонки.
При этом происходит изменение импульса mV воды:
Д(игУ) = ДигУ, FAt = Д(тпУ), F =	= pgcV.
At
Отсюда следует, что давление р равно:
F Р = — = рсу-
р= 103 1500-5 Па= 7,5-106 Па.
Задача 2.9. Модель вертолета в 1/8 натуральной величины удерживается в воздухе двигателем мощностью 50 Вт. Какой мощности двигатель нужен для настоящего вертолета? В модели использованы те же материалы, что и в настоящем вертолете.
Решение. Вертолет удерживается в воздухе реактивной силой струи воздуха, отбрасываемой винтом.
Если плотность воздуха р, площадь, захватываемая винтом, S и скорость струи воздуха t>, то за время At масса отбрасываемого воздуха равна:
Ат = pSuAt.
При этом изменение импульса воздуха равно:
А(ти) = Amu = pSu2 At, а сила действия винта на воздух равна:
At
Соответственно воздух действует на винт силой:
pSv2 = Mg,	(1)
где М — масса вертолета.
36
Для создания такой струи вертолет должен иметь мощность:
ЛЕ _ Дтпр2
М ~ 2М
Отсюда
N =
Anw2
2 At
= >,Л
и, как следует из (1),
Поэтому
1 iMg N = —Mgl----.
2 у pS
Масса М вертолета пропорциональна L3, S ~ L2, N - L7/2, где L — линейный размер вертолета.
N
N
модели
\7/2
= 87/2
'модели/
АГ = ^модели • 87/2 -72,4 кВт.
Задача 2.10. Чему равен секундный расход топлива в момент старта ракеты массой 106 кг, если она стартует вертикально с ускорением 0,б£? Скорость истечения газов принять равной 2 км/с.
Решение. В момент старта на ракету действует сила тяжести F = mg и реактивная сила Ер.
Выбрав систему отсчета, связанную с Землей, запишем уравнение для проекций векторов сил и ускорений на вертикальную ось:
та = Ер - mg, отсюда:
Ер = т[а + £).
„	„	Дпг
Подставляя в это выражение модуль реактивной силы Еп =----и,
At получим:
Am / ч
— u=m(a + 4
37
Следовательно, секундный расход топлива будет равен:
Am _ m(a + g) AZ и
Am 106 1,5 10 кг „ „„ кг
At 2000 с	с
Задача 2.11. Мальчик вращает в вертикальной плоскости камень на нити длиной 1,2 м. После обрыва нити камень летит вертикально вверх. На какую максимальную высоту поднимется камень, если в момент отрыва полное ускорение камня было направлено под углом 45° к вертикали?
Решение. На камень действует сила упругости Т и сила тяжести mg. Камень летит вертикально вверх, следовательно, обрыв нити произошел в точке А (рис. 2.14). В этой точке векторы Т и mg взаимно перпендикулярны. Так как равнодействующая направлена под углом 45°, то модули силы тяжести и силы натяжения нити равны:
mv2 mg = Т, -----= Т = mg,
R
v2
~r=8'
и = y[Rg,
2g
— = 0,6 м. 2
Задача 2.12. Обруч радиуса R, вращающийся с угловой скоростью £Уо, начинает движение вверх по наклонной плоскости, угол наклона в (рис. 2.15). Начальная линейная скорость равна нулю. Определите время движения обруча вверх по наклонной плоскости до остановки.
Решение.	fimg cos 0 - mg sin в = ma,	(1)
fimgR cos 0 = Jaj,	(2)
где Oi — угловое ускорение обруча, I — его момент инерции относительно центра обруча (рис. 2.16).
Я1?1 = (ю0 - ajZijl?,	(3)
а1 = g(fi cos 0 -
sin 0)
a-[R = fig cos#
t a>0R	__________
+ aiR g{2/i cos 0 - sin #)

38
В интервале времени линейная скорость возрастает от О до t/p в интервале времени t2 убывает от до О. Поэтому = a2t2,
mg sin 0 -	= та2
F^R = Ia2, a2 = a2R
gsin 0
g\u cos в - sin 0)	-------v
f _ “1*1 _ '	g(2/7cos0- sin0J
2 a2	gsin «
2
co0R 2(/7Cos 0 - sin 0) g sin 0(2/7 cos 0 - sin 0) ’
t —	4- ^2 ~
cdqR sin0 + 2/^ cos0-2sin0 g sin 0(2/7 cos 0 - sin 0)
a>0R gsin 0
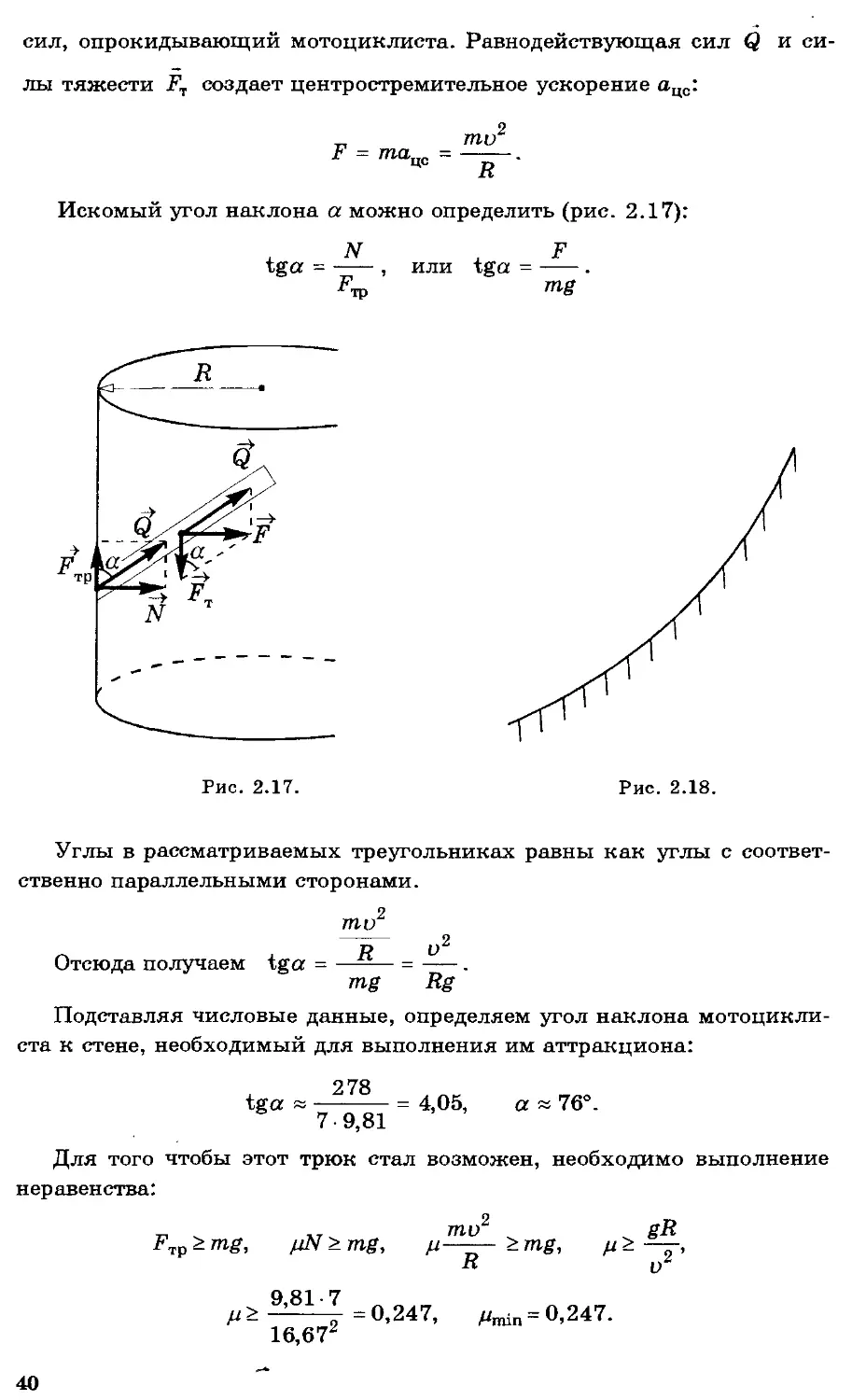
Задача 2.13. Мотоциклист, участвуя в аттракционе «гонки на мотоциклах по вертикальной стене», развивает скорость 60 км/ч. Определите угол наклона мотоциклиста к стене, если радиус закругления стены аттракциона равен 7 м. При каком минимальном коэффициенте трения возможен этот трюк?
Решение. На мотоциклиста, совершающего движение по вертикальной стене, действует сила тяжести, сила трения покоя и сила реакции опоры N (рис. 2.17). Силой трения качения, направленной против скорости мотоциклиста, пренебрегаем. Равнодействующая Q сил трения и реакции опоры при правильном наклоне мотоциклиста проходит через его центр масс. В противном случае возникает момент
39
сил, опрокидывающий мотоциклиста. Равнодействующая сил Q и силы тяжести Гт создает центростремительное ускорение ацс:
nw2
F = та,,. =-----.
цс R
Искомый угол наклона а можно определить (рис. 2.17):
W	F
tga =----, или tga =------.
Ftp	mg
Углы в рассматриваемых треугольниках равны как углы с соответственно параллельными сторонами.
то2
R Р2
Отсюда получаем tga = ——— =------.
mg Rg
Подставляя числовые данные, определяем угол наклона мотоциклиста к стене, необходимый для выполнения им аттракциона:
2 78 tga =-------= 4,05, a » 76°.
7-9,81
Для того чтобы этот трюк стал возможен, необходимо выполнение неравенства:
„ .	mu2	gR
FTp>mg, /jN> mg,	^mg, ц> —,
R	l>
9,81-7
Zz- — -0,247, Цт1п = 0,247.
16,672
40
Проверим, чему равен коэффициент трения в условиях данной задачи:
ц- ctga = ctg 76° = 0,249.
Видим, что А > Amin, т- е- условие задачи корректно.
Задача 2.14. Конькобежец на ледяной дорожке старается пройти вираж как можно ближе к внутренней бровке. Велосипедист же на велотреке проходит вираж возможно дальше от внутренней бровки. Как объяснить это различие в движении конькобежца и велосипедиста на вираже? Профиль трека изображен на рисунке 2.18.
Решение. Конькобежцу сообщает центростремительное ускорение максимальная сила трения покоя о лед
Яф = /JN,
где N — сила нормальной реакции льда (рис. 2.19, а). Силой трения скольжения, направленной против скорости конькобежца, пренебрегаем.
Так как конькобежец не перемещается в вертикальном направлении, то сила N равна по модулю действующей на конькобежца силе тяжести Mg. Поэтому
F-rp = vmg, = nmg.
41
Отсюда и = JggR .
Делая поворот, конькобежец проходит расстояние s = лЕ за время
(1)
Чем больше радиус окружности, по которой движется конькобежец, тем больше это время. Хотя с увеличением радиуса поворота растет максимальная скорость конькобежца, еще больше увеличивается проходимое им расстояние: в то время как скорость пропорциональна Jr, пройденное расстояние пропорционально R. Именно поэтому конькобежец и старается пройти поворот как можно ближе к внутренней бровке.
Теперь рассмотрим движение велосипедиста на наклонном треке. Ему центростремительное ускорение сообщает равнодействующая силы трения Еф и силы N реакции опоры (рис. 2.19, б). Спроектировав эти силы на ось X, получаем:
ти2
F.„, cos а + N sin а =-.	(2)
тр	R
Так как в вертикальном направлении велосипедист не перемещается, то сумма проекций на ось У всех сил, действующих на велосипедиста, равна нулю:
N cos а - Еф sin а - mg = О.	(3)
Учитывая, что Ец, = jliN, найдем из уравнений (2) и (3) максимальную скорость, с которой может двигаться велосипедист:
]	1 - /ztga
Эта скорость зависит не только от радиуса окружности, но и от угла наклона трека к горизонту. При профиле трека, показанном на рисунке 2.19, б, угол наклона не меняется. Если а = Яд = arctg|—], то мак-
VA/
симальная скорость движения велосипедиста принимает бесконечное значение. Это значит, что скорость велосипедиста может быть любой.
Время, необходимое велосипедисту для того, чтобы пройти поворот радиуса R, определяется так:
, nR |Е 1 - zztga R , г Г
i =---= л--------------- л—tgia0 - а).
и \ g /и + tga \g	’
42
Если велосипедист проходит поворот дальше от бровки, то меняется не только радиус поворота, но и угол а наклона трека к горизонту. Благодаря этому уменьшается время прохождения поворота.
Задача 2.15. Сфера радиуса R = 0,5 м вращается вокруг своего вертикального диаметра с постоянной угловой скоростью <у = 5 рад/с (рис. 2.20). Вместе со сферой на ее внутренней поверхности вращается небольшое тело, находящееся на высоте, равной половине радиуса.
Определите минимальное значение коэффициента трения, при котором это состояние возможно.
Определите минимальное значение коэффициента трения, если угловая скорость сферы равна а> = 8 рад/с.
Рис. 2.20.
Рис. 2.21.
Решение. На рисунке 2.21 показаны силы, действующие на тело: сила тяжести mg, сила реакции со стороны сферы N и сила трения FTp. Сила трения перпендикулярна силе реакции, но направление ее неизвестно: она может быть направлена так, как показано на рисунке 2.21, или в противоположную сторону.
43
Равнодействующая FR этих трех сил FR = mg + N + F^ сообщает 2 2n 
телу центростремительное ускорение ацс = о г = со Я sin а, где а — угол между радиусом ОС и вертикалью.
Следовательно, вектор FR направлен к оси вращения и перпендикулярен ей. Модуль этой силы равен:
Fr = mco2Rsina.
В зависимости от направления вектора силы трения ЕТр модуль силы Fr будет иметь разные значения. Это хорошо видно из рисунков 2.22 и 2.23.
Так как угол между векторами mg и N равен а, получим:
FR=mgtg(a-p\	(1)
если сила трения направлена так, как показано на рисунке 2.21.
Если сила трения направлена в противоположную сторону, то
Fr = mgtg(a + Р)	(2)
где р = arctg g.
ч	. „ -^тр	pN
Это ясно из соотношения tg В = —— --= и.
Н	N	N
Следовательно, для равновесия тела на сфере должно выполняться условие
/z>tgA	(3)
Значение tg/? нетрудно найти из выражений (1) и (2). Учитывая,
/	_\	tg а ± tg р
что tg(а ± Р\ -------— , получим:
1	’ l + igaigp
gtga-02_Rsina sin a g - co2R cos a\
ЧР = J1	1---5----Г~ '
g+ tg a  co R sin a g cos a + co Rsm a
При условии co =	= 5 рад/с выполняется неравенство g > ccPR cos a,
тогда
sin alg - co2R cos a)
Pl min =-----*--5----T2 « °’23-	(4)
geos a +0 .Rsm a
44
При условии о = <z>2 = 8 рад/с выполняется неравенство g < aPR cos а, тогда
sin ala>2R cos a -gj
^2 min = ----*---5-----« 0,18.	(5)
g cos a + a> R sin a
Переход от Д1га1п до ,u2min происходит при такой угловой скорости Оо, что = 0, а следовательно, р= 0 (рис. 2.24).
При этом в соответствии со вторым законом Ньютона
m.<ao/?sina = mg tga,
а угловая скорость <э0 вращения сферы равна:
Рис. 2.24.
Рис. 2.25.
Задача 2.16. Вследствие действия приливов продолжительность суток на Земле увеличивается за 100 лет на 0,001 с. Определите приливную силу трения. Землю считать однородным шаром массой 6 1024 кг и радиусом 6,4 10® м.
Решение. Из основного уравнения динамики вращательного движения изменение момента импульса Земли	равно произведению
момента приливной силы М на время его действия AZ:
Д(1о) = МД*.
Момент инерции Земли I = 0,4mR2. Изменение угловой скорости Земли равно:
А 2л 2л	2 л АГ	2 л АГ
До =------------= —г и-----------— .
Т Т + ДГ Т\Т + ДТ) Т2
Момент приливной силы трения М = F^R.
45
Подставив значение момента инерции Земли I, изменения угловой скорости До и момента приливной силы трения М в основное уравнение динамики вращательного движения, получим:
О MUSI 0,4mR2	= F^Rbt,
0,8лтИЛТ T2\t
Произведя вычисления, получим:
Гтр «6 109 Н.
Задача 2.17. Стержень массой 3 кг подвешен за концы на двух нитях, длина нитей мала по сравнению с длиной стержня. Одна нить перерезается. При каком значении угла поворота 0 стержня оборвется вторая нить, если она выдерживает максимальную нагрузку 20 Н? Принять, что g » 10 м/с2. Считать вторую точку подвеса практически неподвижной.
Решение. На рисунке 2.25 изображены силы, действующие на стержень.
mg cos 0 - Т„ = ma,, а, = а — , у i	2
где а — угловое ускорение, I — длина стержня.
2 I Тх - mg sin 0 = ma2, а2 = о — .
Запишем основное уравнение динамики вращательного движения для стержня:
М = 1а, где М — момент силы тяжести, I — момент инерции стержня.
„ I 1 ,9	3 gc.cs 0
mg cos 0 — = — ml а => а =----------.
2	3	2 Z
Запишем закон сохранения энергии для малого изменения высоты ДА конца стержня:
1	2
mg\h = — Iсо . Отсюда
I . „	1 1	,2 2	2 3g sin 0
mg —sm0 =-------ml со => о =-------
2	2 3	I
3	3
aj = — g cos 0,	02 = —g sin 0,
46
3	1
mg cos 0-Tu = m—g cos 0 => Tu = — mg cos 0, *	4	y 4
3	5
Tx - mg sin 0 = — mg sin 0 => Tx = — mg sin 0, 2	2
m [^2 ^7 П77 25. о „ у 9 9 sm2 0 + 1
T = JTX + T„ = mg J— cos2 0 + — sm2 0 = mg -----------
’	’ V16	4	4
„ 2	V99sin2 0 + 1	2
T = — mg, mg---------------= — mg,
3	4	3
99sin20 + l = — => sin0 = —; 0-14°. 9	9
Задача 2.18. Цилиндр массой M - 3 кг и радиусом R = 5 см установлен на горизонтальной поверхности стола. На цилиндре имеется шкив радиусом г < R. На шкив намотана нить, на втором конце нити имеется груз массой т — 0,1 кг. Нить перекинута через блок и расположена горизонтально (рис. 2.26). Определите ускорение а поступательного движения цилиндра. Исследуйте зависимость силы трения FTp от радиуса г шкива. Силы трения качения цилиндра и на оси блока считать пренебрежимо малыми, момент инерции блока значительно меньше момента инерции цилиндра.
Решение. Запишем уравнения второго закона Ньютона для поступательного движения цилиндра и груза:
mg + Т = тат,
T + F^=MaM,
(1)
(2)
где Т — сила упругости нити.
47
Для груза тп направления силы тяжести и силы упругости противоположны, поэтому для модулей сил и ускорений имеем:
mg-T = тат.
(3)
Для цилиндра направление вектора силы трения неизвестно, примем его условно противоположным направлению вектора Т силы упругости:
Т ~ ^тр = Мам-	(4)
Если при решении значение Т будет положительным (Т > О), то наше предположение верно, в противном случае (Т < О) направление вектора Етр совпадает с направлением вектора Т.
Установим связь ускорения ат движения груза с ускорением ау цилиндра. Смещение цилиндра происходит при его повороте на угол л ^ХМ R
В результате такого поворота со шкива сматывается нить на
Ах = Л<,9 • г.
Смещение Лг/т груза при этом равно:
R г
Лут = AXftf + hx =	+ г) = Ахм ——
Из уравнения (5) следует:
ат - аМ\ 1 +— • \ XI/
(5)
(6)
Из уравнений (3), (4) и (6) получаем:
- тат - Еф = Мам,
I г I
Етр = mg - тат - Мам = mg - там\ 1 + — - Мам = \ RJ
= mg -
...	г
ЛзГ + т\ 1 ч-------в-м •
(7)
Запишем уравнение динамики вращательного движения цилиндра относительно его оси:
Тг + ЕфД = 1е,
(8)
48
I = — MR2, 2
(9)
где I — момент инерции цилиндра, £ — угловое ускорение его вращения,
_ ам R
(10)
Tr + F^R = ^MRaM.
(И)
Подставим в (11) значения Т из (3) и FTp из (7):
( г\	( г ।	1
mgr - там\ 1 + — г + mgR - MaMR - maMR\ 1 + — = — MRaM, \ RJ	\ RJ 2
ам 3RM + 2Rm 1 + — + 2mr 1 + — I RJ I R,
= 2mgr + 2mgR,
aMRM
,	х 2
3 + 2 —11+—I RJ
= 2mgR\ 1ч-,
I R)
m
M
2 mg ам - —гг~ М
______R
з + 221Г1 + гУ
Ml RJ
(12)
Подставляя (12) в (7), находим выражение, устанавливающее силы трения с радиусом г шкива:
связь
F^ = mg--
М + т 1 + —
I R,
 2mg\ 1 + — \	-Rz
\2>
M 3 + 2 — 1 + — I Ml RJ \
Z -.2	Z X	Z x2
3mgM +2m2g|1 + — I - 2mMg 1 + — I - 2m2g 1 + — I k	RJ	\	RJ	k	RJ
/	\2’
3 + 2 — fl + —1 Ml RJ
mg - 2mg —
----------- = mg
3+2 — fl + -l
Ml RJ
1-2 — R
/ \2 m L. r I — 1 + — m\. rj
(13)
M
49
Из уравнения (13) следует, что при условии г = — сила трения
„ R
равна нулю. При г < — ее значения положительны, т.е. направление
вектора F^ соответствует нашему выбору, сделанному при переходе от записи уравнений динамики в векторной форме к алгебраической.
R —
При г > — сила F^ приобретает отрицательные значения, т.е. ее
направление противоположно сделанному нами выбору.
Используя условие т « М , получим из (12) и (13):
_.М1+Д 3 М I RJ
тр 3 ( r)
(14)
(15)
Из уравнения (15) следует, что связь силы трения FTp с радиусом г шкива приблизительно линейная.
Найдем приближенные значения ускорения и силы трения по формулам (14) и (15), £=10 м/с2, для значений г = 1 см, 2 см, 3 см, 4 см.
г, м	0,01	0,02	0,03	0,04
«М> М/с2	0,77	0,31	0,36	0,40
FTp,H	0,2	0,067	-0,067	-0,2
Зависимость представлена графически на рисунке 2.27.
Рис. 2.27.
Рис. 2.28.
50
Задача 2.19. На горизонтальную плоскость вертикально падает шар, вращающийся вокруг горизонтальной оси с угловой скоростью qjq. Коэффициент трения шара о поверхность стола ц. Под каким максимальным углом а к вертикали может начать движение шар после упругого удара?
Решение. Угол а можно найти, определив проекции скорости и шара после удара на вертикальную оу и горизонтальную ох оси (рис. 2.28):
tga = —. иу
При упругом ударе вертикальная проекция скорости не изменяется по модулю, а лишь изменяет свой знак:
т-ЛОу = FAt = 2vym,
где F — среднее значение силы нормального давления, At — время столкновения.
Горизонтальная составляющая скорости в конце столкновения определяется соотношением pFAt = пгих:
/iFAt
их =------.	(2)
т
Из (1) и (2) следует:
tga = — = 2ц, a = arctg2/z. °у
Глава 3
СТАТИКА
Задача 3.1. Лестница длиной I и массой т прислонена к стене. Чему ра вен минимальный угол <р между лестницей и полом, при котором лестница еще находится в равновесии, если коэффициент трения между лестницей и стенкой равен а между лестницей и полом ufl Определите силы реакции опор и силы трения между лестницей, полом и стенкой.
Рис. 3.1.	Рис. 3.2.
Решение. На лестницу действуют пять сил: mg, N^, N2, F^, FTyi2 (рис. 3.1). Число уравнений равновесия равно трем, так как все силы лежат в одной плоскости, а число неизвестных равно пяти: N}, N2, Ftpi, F^p2, <р. Но задача решается, так как между силами трения FTpl и F^2 и силами нормального давления JVj и Ng существуют соотношения
Frpl =	F^2 = f*2N2
при условии предельного угла <р. При этом угле силы трения покоя достигают максимума, равного силам трения скольжения.
52
Запишем условия равновесия:
YFX = O,	N1-/j2N2=O,
Y.Fy = 0,		+ N2-mg = О,
[Е-Л^А - 0,	cos tp +/j2N21 sin. tp - mg—cos <p = 0.
2
Решение этих трех уравнений равновесия позволяет найти все искомые параметры:
Nl = ^те ,	n2= --^-8 ,
1 + 1 + №
- аЛ =	. -Л™-,
1 +	1 + №^2
tgp = mg-2^NL = 1-^2 , у =	1-Д1Д2
2^2Я2	2^2	2№
Задача 3.2. В гладком цилиндрическом стакане лежит стержень массой т = 0,1кг (рис. 3.2). Определите силы реакции опор, если угол между стержнем и дном стакана равен (р = 45°.
Решение. На стержень со стороны стакана действуют три неизвестные силы:	N2 и ^3 (рис. 3.3), следовательно, для их определения
нужно использовать все возможные уравнения равновесия:
Е^ =0,
=0,
ЕМа. =0.
Выбор оси, проходящей через точку А, определяется тем соображением, что моменты двух сил Ny и N2 относительно этой оси равны нулю. Это облегчает решение задачи:
Nr - Ns = 0,
• jV2 “ т& ~ °’
mg cos (р - NA sin <р = 0, где I — длина стержня.
53
N2 = mg = 0,1  10 H = 1 H.
= — mg cig ip = i  0,1  10 -1 H = 0,5 H. 2	2
N3 = Xj = 0,5 H.
Задача 3.3. Два человека одинакового роста держат за концы в горизонтальном положении трубу длиной 1 = 2 м и массой znx = 10 кг (рис. 3.4). На расстоянии d = 0,5 м от первого человека к трубе подвешен груз массой тп2 = 100 кг. Определите силы, с которыми труба давит на плечи первого и второго человека.
Рис. 3.4.	Рис. 3.5.
Решение. В рассматриваемой задаче все силы параллельны, поэтому уравнения равновесия имеют вид:
=0,
= 0.
Укажем на чертеже силы, действующие на трубу, и запишем условия ее равновесия, выбрав ось, проходящую через точку А, для записи уравнения моментов сил (рис. 3.5):
Ni + N2 - m.xg - m2g = 0,
m2g^AC\ + тjАО| - N2|ав| = 0.
Отсюда найдем:
пг2^|ЛС1+zrai^lAOl ЮО 10 0,5 + 10101 тт тт
No = -------;---;----- = -------------------Н = о00 Н,
|ав|	2
= (m1+m2)g- N2 = (100 +10) 10 - 300 H = 800 H.
54
Для проверки полученного ответа модуль силы Ni можно определить, применив правило моментов относительно точки В:
xJabI - m2g\CB\ -	= о,
m2g\CB\+m1g\OB\ ЮО 10 • 1,5 + 10 10 1 „	„
iVi = -----:--i------=---------------------Н = oUU н.
|ab|	2
В соответствии с третьим законом Ньютона труба давит на плечи с силами Fi и F2 , равными по модулю, но противоположно направленными силам Ni и N2 :
Fi = -Ni, F2 = -N2. Fi = 800 H, F2 = 300 H.
Задача 3.4. Груз массой m = 10 кг висит на двух нерастяжимых тросах, составляющих между собой угол 2<р - 120° (рис. 3.6). Чему равны силы натяжения тросов?
Решение. Так как все три силы Л^, N2, mg, действующие на груз, пересекаются в одной точке, то условие равновесия определяется двумя уравнениями:
X Fxi = 0,	Ni sin ср - N2 sin ср = 0,
Y Fyi = 0,	Ni cos cp + N2 cos cp - mg = 0.
После математических преобразований получим:
^1 = n2,	10 10
Ni = N2 = g = --- - - H = 100 H.
ЗЛ^сов^ = mg,	2 cos <P 2 • 0,5
Рис. 3.6.
Рис. 3.7, а.	Рис. 3.7, б.
55
Задача 3.5. Балка длиной I и массой 120 кг висит на трех шнурах одинаковой жесткости (рис. 3.7, а). Центр масс балки отстоит от первого шнура на I расстоянии —. Определите силы натяжения шнуров. Растяжения малы. 4
Решение. На балку действуют сила тяжести mg и силы натяжения нитей Ni, N2, Я3 (рис. 3.7, а). Поскольку все эти силы параллельны, уравнений равновесия только два:
Xi + N2 + Ns - mg = 0,	(1)
N2~ + N3l-mg^ = °	(2)
(относительно оси, проходящей через левый конец балки).
Так как общее число сил реакции больше числа уравнений, содержащих эти силы, то данная система является статически неопределимой. В этом случае модель абсолютно твердого тела оказывается непригодной и при решении задачи необходимо учитывать деформацию тел, применив закон Гука.
Обозначив растяжения шнуров Д11; Л12, Л^з и используя закон Гука:
ЛГ1 =	2V2 ~ h&l2, Ng — kkl%,	(3)
получим третье условие равновесия (рис. 3.7, б):
Л11	=1 = 2.	(4)
Л12 - Л/3 I
2
Из выражений (3) и (4) следует:
N1+Ns=2N2.	(5)
Решая уравнения (1) — (5), получим:
7	7
N, = — mg =-----120 10 Н = 700 Н,
1	12	12
N2 = - mg = 1  120 10 Н = 400 Н, 3	3
ЛГ3 = — mg = -1 • 120 • 10 Н = 100 Н. л 12	12
Задача 3.6. Груз массой 10 кг подвешен на трех одинаковых упругих тросах разной длины. Точки подвеса тросов лежат на одной прямой, средний трос расположен вертикально, а два других составляют с ним равные углы 60°. Чему равны силы натяжения тросов, если при их деформации выполняется закон Гука?
56
Рис. 3.9.
Решение. На рисунке 3.8 указаны силы, действующие на груз. Запишем условия равновесия груза:
Е Fx = О,	F3 sin а - FY sin а = О,
'hFy = 0,	Fy cos a +F2 + F$ cos a - mg = 0.
Из полученных уравнений следует:
Fl = F3,	(1)
F2 + 2FY cos a = mg.	(2)
Поскольку в двух уравнениях содержится три неизвестных, то задача статически не определена. Условие Y.M0 = 0 ничего не добавляет, так как плечи всех сил относительно точки О равны нулю.
На рисунке 3.9 видно, что между удлинениями тросов AZj и AZ2 существует зависимость:
AZ1 = AZ2 cos «1 » AZ2 cos a.
В соответствии с законом Гука модули сил Fy и F2 равны:
Fx ~ fe^AZ^, F2 — Z?2AZ2, где ky и k2 — жесткости тросов, которые обратно пропорциональны их длинам:
, 1 , 1
«1 —; -----------•
1 Zi	z2
57
Отсюда следует, что
Fy	ZzjAZj	ZgAZ^
F2	^2^2	^1^2
Так как Z2 = lr cos а, то отношение сил равно:
— = cos2a.	(3)
^2
Используя уравнения (1), (2) и (3), получаем выражения для вычисления всех трех неизвестных сил:
2	,
„	cos а	1
Fl = Fs = mg----------, F2 = mg--------------.
2 cos a + 1	2 cos a + 1
Подставив численные значения, получим:
Fr = Fs = 20 H, F2 = 80 H.
Задача 3.7. По деревянным сходням, образующим угол а с горизонтом, втаскивают ящик с помощью веревки (рис. 3.10). Под каким углом <р к горизонту следует тянуть веревку, чтобы с наименьшим усилием равномерно втаскивать ящик? Коэффициент трения ящика о сходни ц.
Решение. При равномерном движении ящика векторная сумма всех сил, действующих на ящик, равна нулю. Заменим силу реакции опоры N и силу трения FTp = цЛГ) их равнодействующей Q.
Как видно из рисунка 3.10, угол 8 между векторами сил Q и N определяется из выражения:
FTO gN tg 8 = — = — = g, 8 = aretg/z.
N N
58
Силы mg, F и Q должны образовывать замкнутый треугольник. Направления сил mg и Q известны. Вектор Q с вертикалью составляет угол (а + <$j.
Модуль вектора силы F, соединяющего конец вектора силы Q с началом вектора силы mg, будет минимальным, если сила F будет перпендикулярна к направлению действия силы Q (рис. 3.11).
Из конца вектора mg под углом (а + проводим прямую, вдоль которой направлена сила Q.
Из рисунка 3.11 ясно, что искомый угол ср и угол (а + <5) равны как углы со взаимно перпендикулярными сторонами:
<р = а + arctg ц.
Задача 3.8. Цилиндр радиусом R имеет цилиндрическое отверстие радиу-R
сом г = —, ось отверстия параллельна оси цилиндра. Центр отверстия находит-
ся на расстоянии г от оси цилиндра (рис. 3.12). Каково максимальное значение угла а наклона плоскости, при котором цилиндр не будет скатываться по ней?
Решение. При максимальном значении угла а цилиндр располагается на наклонной плоскости так, как представлено на рисунке 3.13. Представим действие отверстия в цилиндре как действие цилиндра радиусом г с отрицательной массой, находящегося в сплошном цилиндре:
_ -.	/	\	_	771
Mgx - mgl г + х) = 0 => х =-------г,
v ’	М - т
59
<>	•> M R2
М-лВ2, тп~лг2,	— = ^- = 4,
m г2
1	1 г R
х = —------г =----г = — = —,
4-1 3 6
пг
x = Rsina =— => sina=—;	а»9,6”.
6	6
Задача 3.9. Крыша с наклоном 30° была покрыта металлическими листами. Обнаружилось, что эти листы постепенно сдвигаются вниз. Объясните это явление и вычислите смещение листа длиной 1 м за 1000 дней, если коэффициент линейного расширения металла 28 • 10 6 °C-1, среднее значение разности дневной и ночной температур 11°С.
Как добиться самостоятельного подъема листа вверх по крыше?
Решение. Явление спуска металлического листа на крыше объясняется неодинаковым положением неподвижной линии на листе при расширении и сжатии в результате суточных колебаний температуры.
Рассмотрим сначала процесс расширения листа при нагревании. При нагревании в результате теплового расширения верхний край листа будет двигаться вверх, а нижний вниз. Неподвижными будут точки, лежащие на некотором расстоянии х^ от верхнего края листа.
Сумма проекций сил тяжести и сил трения на направление оси ОХ для двух частей листа длиной Лц и I - х-^ равна нулю (рис. 3.14):
60
umgx, cos <p /ung(l - хЛ cos <p mg sm cp +------±--------------i;-----------= 0,
I
_ /i cos <р - sin <р 2/1 cos ср
Смещение нижнего края листа при нагревании на ДТ равно:
AZ^ = ——----------где Д1 = 21&.Т.
При понижении температуры листа на ДТ верхний край листа будет двигаться вниз, а нижний — вверх. Расстояние х2 до неподвижной линии определяется аналогично с учетом изменения направлений векторов сил трения (рис. 3.15):
umgx<> cos <р /img(l - х2)cos (р mg sm ср - —-------— +-----1----------= 0,
/I cos (р + sin <р
#2 ~ ------------------
2/7 cos <р
t\ln
Смещение нижнего края листа вверх при охлаждении на ДТ равно:
Z -х2 I
В результате за сутки нижний край сместится вниз на расстояние:
«I л; дг(х2 - х1) AZtgp	aZAT-tg^
Д‘1 _ -“2 =---------=---------=------------
Z	/I	/I
61
За п дней смещение равно:
л г	л, \ nalATigtp
/\L — al AZj — AZ2) —-----•
A
Подставляя числовые значения, получим:
. к 1000 28 10"6 1 11 0,58
AL = ----------------------— м =s 0,3 m.
0,6
Для осуществления подъема листа нужно сделать поверхность крыши зубчатой, с наклоном зубцов вверх. На краях листа нужно иметь два зубца с обратным наклоном (рис. 3.16). Тогда при нагревании нижний край листа будет опираться на нижний зубец и будет неподвижным, верхний будет двигаться вверх. При охлаждении верхний край листа будет неподвижным благодаря верхнему зубцу, нижний край будет подтягиваться вверх. Для движения листа вверх расстояние а между зубцами на крыше должно быть меньше суточного изменения длины листа AZ :
а < Л1 = а1ЛТ,
а < 28-10 6 1 11 м « 3 10“4 м = 0,3 мм.
Задача 3.10. Автомобиль массой т = 1000 кг движется прямолинейно и начинает тормозить с ускорением а = 2 м/с2. Расстояние L между осями автомобиля равно 2 м, высота Н центра масс над поверхностью Земли равна 1 м, жесткость каждой из двух рессор автомобиля k = 104Н/м. Считайте, что центр масс находится посередине автомобиля. Найдите деформации рессор.
Решение. Выберем систему отсчета, связанную с автомобилем. Так как при торможении автомобиля она является неинерциальной, то, кроме сил тяжести mg и реакций опор и ZV2, на автомобиль будет
действовать сила инерции Fm = -та, приложенная к его центру тяжести (рис. 3.17). Эта сила создает вращающий момент, в результате
62
чего автомобиль наклоняется передней частью вниз, при этом передняя рессора сжимается на Д/р а деформация задней рессоры уменьшается на Д/2. Это приводит к изменению сил реакций опоры на Д?^ и Д?/2:
^=#-1-^!, N2=N + zW2,
где N — модуль реакции опоры до начала торможения. Из условия равновесия сил можно записать:
N± + ^2 ~ т8 = О,
2N +	+ zW2 - mg = 0.
Так как центр масс находится посередине автомобиля, то 2N = mg, Л/Vl = —zW2, т-е- модули изменений сил реакции ДДТ опоры одинаковы. Жесткости рессор равны, поэтому, используя закон Гука, запишем:
йД/j + &Д/2 — 0,
т.е. AZ± = —Д/2, модули деформации Д/ обоих рессор одинаковы. Запишем условия равновесия моментов сил относительно точки А (точки касания переднего колеса и Земли), получим (моменты сил трения относительно точки А равны нулю):
таН +(N - AN= mg .
С учетом условий mg=2N и AN = k,M запишем:
maH - ANl = 0, maH = kAl  L,
, maH	103-21
AZ =----, Al =-----------м = 0,1 m.
Lk	2 IO4
Задача 3.11. Через неподвижное горизонтально закрепленное бревно переброшена веревка. Для того чтобы удерживать груз массой т = 6 кг, подвешенный на этой веревке, необходимо тянуть второй конец веревки с минимальной силой f) = 40 Н. С какой минимальной силой F2 наД° тянуть веревку, чтобы груз начал подниматься?
Решение. Вес груза Р = mg = 60 Н существенно больше силы Flt с которой надо тянуть веревку. Такая ситуация нам хорошо знакома из жизни и связана с наличием трения между веревкой и бревном.
В первом случае (веревка неподвижна) силы трения направлены против действия веса груза и помогают удерживать веревку с грузом.
63
Полный расчет распределения сил трения довольно сложен, так как абсолютное значение силы натяжения веревки (которая определяет силу реакции в точках соприкосновения веревки с бревном) меняется от 2*1 (условие равновесия левого конца веревки) до Р = mg (условие равновесия правого конца). Однако для решения задачи нам достаточно заметить, что максимальная сила трения, пропорциональная в каждой точке силе реакции опоры, будет пропорциональна силе натяжения веревки; для определенности будем считать, что пропорци-
ональна большей силе натяжения, т.е. = kP. Это означает, что
Fi = Р - kP и отношение большей силы натяжения Р к меньшей есть величина постоянная:
Р 1
— =------= const.
Fi 1-k
Во втором случае, когда мы хотим поднять груз, концы веревки как бы меняются местами. Сила трения оказывается направленной против действия силы F2 и Уже не помогает, а мешает.
Отношение большей силы натяжения F2 к меньшей Р должно быть таким же, как и в первом случае:
Р F/
Р2 F2=----= 90 Н.
*1
Задача 3.12. В цилиндрический стакан наливают воду. При высоте уровня воды а = 4 см центр масс системы «стакан + вода» занимает самое низкое положение. Масса воды в стакане в этом случае равна массе стакана. На какой высоте находится центр масс стакана?
Рис. 3.18, а.
Рис. 3.19.
Решение. Положение центра тяжести стакана с водой будет наи-низшим в том случае, когда оно совпадает с уровнем воды в стакане.
64
Действительно, если центр тяжести О системы находится выше уровня воды в стакане (рис. 3.18, а), то он понизится при доливании в стакан воды. Если же центр тяжести системы лежит ниже уровня воды (рис. 3.18, б), то он понизится, если вылить часть воды, находящейся выше центра тяжести.
Выполним мысленный эксперимент. «Отвердим» воду, повернем стакан на 90° вокруг горизонтальной оси и подвесим на нити, опоясывающей его по уровню воды (рис. 3.19). Так как линия подвеса проходит через центр масс О системы, система находится в равновесии. Обозначив C>i и С>2 положения центров масс стакана и воды, можно записать условие равновесия:
m.]g|OOi| = m2g\OO2], тп1 = тп2,
jOOjJ = |ОО2| = —,	b = jOO^ + а = —а, Ъ = 6 см.
2	2
Задача ЗЛЗ. Имеется подвеска, состоящая из стержней, соединенных шарнирно (рис. 3.20). Стержни АО, ВС, DE и СН сплошные. Между точками О и М натянута нить. Определить силу Т натяжения нити ОМ, если масса всей системы равна т.
Рис. 3.20.
Рис. 3.21.
Решение. Чтобы система с идеальными связями оставалась в равновесии, необходимо и достаточно, чтобы сумма элементарных работ всех внешних сил, действующих на систему на любом возможном перемещении ее, равнялась нулю (принцип возможных перемещений). Применение принципа возможных перемещений приводит к выражению
' mg^x2 = 0.
(1)
65
Связь между перемещениями и Дх2 устанавливается легко. Действительно, при бесконечно малом уменьшении длины нити на величину Дд^ точка М подвески поднимается на высоту 3Ajq, а центр тяжести подвески на высоту
Дх2 = -Дхр	(2)
Л
Из выражений (1) и (2) получаем: F,™ = mg^~^~ = — mg.
Д*!	2
Задача 3.14. Из двух одинаковых кусков стальной проволоки свили две пружины. Диаметр витков одной из них d, другой — 2d. Первая пружина под
действием груза растянулась на своей длины. На какую часть своей длины растянется под действием того же груза вторая пружина? Проволока тонкая.
Решение. Удлинение Д/ пружины можно выразить так:
сс
Al = n2d sin — , 2
где п — число витков пружины, а а — угол, на который разворачивается виток пружины (рис. 3.21). Так как общее удлинение пружины мало, то этот угол мал и
Следовательно,
Угол а пропорционален моментам сил Fj и F2, которые растягивают виток:
a~Fd, где F = |Д| = |f2|. Так как силы F\ и F2 по модулю равны весу Р груза, подвешенного к пружине, то
Д/ - nd2P.
Диаметр витков второй пружины вдвое больше, а число витков у нее вдвое меньше; следовательно, абсолютное удлинение второй пружины вдвое больше, чем первой. Таким образом, вторая пружина рас-2 тянется на — своей длины.
sin— » —
2	2
Д.1 = nda.
66
Задача 3.15. Найти давление в центре жидкой планеты радиуса R, если жидкость несжимаема и имеет плотность р. Выполнить расчет для R = 6,4 • 10® м, р = 1,7 • 103 кг/м3.
Решение. Разобьем объем планеты на тонкие сферические слои толщиной Аг . Легко показать, что равнодействующая гравитационных сил, действующих со стороны слоя на частицу внутри этого слоя, равна нулю. Действительно, рассмотрим для этого конус с малым углом при вершине, в которую помещена частица массой т. Конус вырезает из слоя участки площадями Si и S2 (рис. 3.22).
Если масса вещества, приходящегося на единицу поверхности слоя, равна ц, то гравитационные силы, действующие на массу т со стороны участков Si и S2 , равны:
р r m/jSi	_ mpS2
Т	г£
67
-ycosaj = —j*-cosa2 = Ф
Г1	г2
где Q — телесный угол при вершине О конуса. По построению ОМ у = OAi и ОМ2 = ОА2. Поэтому
AOA^i = АОА2М2.
Кроме того, ZOAjBi = АОА2В2 (как углы, опирающиеся на одну и ту же дугу).
Так как = АОА^Вг - ZOAjMj, а2 = АОА2В2 - АОА2М2, то «1 = а2 и, следовательно,
2	2 ‘
П Г2
Благодаря этому F± = F2, и эти силы взаимно уравновешивают друг друга. Проведя аналогичное рассмотрение для других участков слоя, мы и докажем сделанное утверждение.
Сила, с которой притягивается элемент слоя объема ASAr к центру планеты, равна:
где г — расстояние от этого элемента до центра планеты. Отсюда найдем, что увеличение давления на участке толщиной Аг равно:
F 4	2
Ар =----- — nGp г Аг.
AS 3
Отсюда давление на расстоянии г0 от центра планеты будет равно:
Р = Ро + ~лСр2^.гАг. О
Так как сумма Y,rAr равна площади фигуры, ограниченной графи-
„ .	(^ + r0)(7?-r0) Я2-г2
ком у = г и осью г, то У г Аг =  -——----=--------—.
2	2
Поэтому
р = Ро +|л-вр2(/г2 — 7*0 j.
Приняв давление р0 на поверхности планеты равным нулю, получаем:
р = ~^Gp2^R2 -т*02).
68
В центре планеты (г0 = О) давление равно р = — nGp2R2.
3
Подставляя численные данные для р и Я3, получим:
р «1,6.ю9 4--м
Задача 3.16. В стакане с водой плавает деревянная шайба с цилиндрическим сквозным отверстием. Оси шайбы и отверстия параллельны. Площадь дна стакана S, площадь сечения отверстия Sj. Отверстие осторожно заполняют доверху маслом. На какую высоту поднимется шайба, если в начале ее выступающая из воды часть имела высоту Л?
Плотность масла р, плотность воды ро- Известно, что все масло осталось в отверстии.
Решение. Нетрудно понять, что при осторожном наполнении отверстия маслом шайба будет постепенно подниматься, пока отверстие не окажется заполненным доверху. Если при этом уровень воды вне шайбы в стакане поднимется на величину х, то ровно настолько поднимется и шайба. Пусть высота слоя воды внутри отверстия будет при этом равна у. Если высота шайбы равна d, то остальную часть отверстия, высоту (d - у}, будет заполнять масло. Тогда из условия равенства давлений внешнего столба воды высотой (d - h} и давления, создаваемого водой и маслом внутри отверстия, получим:
р0£р - й) = POgy + Pg{d -у), у = d- р •
Так как масса масла, находящегося в отверстии, равна:
Дтп = pS-^d - р),
то сила давления на дно стакана после добавления масла должна возрасти на величину t\F = Kmg. С другой стороны, из-за поднятия уровня воды в стакане на величину х давление на дно стакана возрастает на величину ДР = poxg, откуда
pS][d - y)g = poxgS,
pos[ y>-(p0-p)s-
Шайба поднимется на высоту ДЛ = х, следовательно,
ДЛ = 7—Л.
(Ро “Pl)®
69
Задача 3.17. Гирю, подвешенную к динамометру, опускают в воду, пока уровень воды в сосуде не поднимется на ДА = 5 см. Показание динамометра при этом изменилось на ДР = 0,5 Н. Определить площадь дна сосуда. Плотность воды р0 = 1000 кг • м“3.
Решение. Так как сила, действующая на гирю со стороны пружины динамометра, уменьшается, а гиря находится в равновесии, то на соответствующую величину возрастает сила, действующая со стороны воды на гирю (по закону Архимеда). По третьему закону Ньютона ровно на эту величину возрастает сила давления на воду со стороны гири, а следовательно, и сила давления воды на дно сосуда, которая возрастает на величину Д^ддвл = p0St±hg, где S — площадь поперечного сечения сосуда.
Следовательно,
&F	9
W = Д^вл = P0SMg, S = —— = 10 см2.
PMlg
Задача 3.18. Цилиндрический сосуд с жидкостью вращается вокруг вертикальной оси, проходящей через центр сосуда, с частотой v. Какую форму примет поверхность жидкости в сосуде? Зависит ли эта форма от плотности жидкости?
Возможные способы решения задачи.
Первый способ. В системе отсчета, связанной с сосудом, на каждый элемент жидкости массой т будут действовать сила тяжести mg и центробежная сила инерции Fw = -mdCD (рис. 3.23), где dOjO — уско-
Рис. 3.23.
Рис. 3.24.
70
Вектор равнодействующей этих сил составляет с вертикалью угол а, определяемый соотношением:
•^ин	пг4л-2у2х	4л2у2х
tga =----=---------=---------,
mg mg	g
т.е. с увеличением расстояния х от оси вращения угол а увеличивается.
Поверхность жидкости устанавливается перпендикулярно направлению этой равнодействующей. Для определения вида кривой, являющейся сечением поверхности жидкости в плоскости чертежа, рассмотрим на ней произвольную точку А с координатами (х,у) (рис. 3.24). Вследствие вращения жидкости давление в точке В будет больше атмосферного давления в точке О на величину
АР = Рв-Ро-
Выделим цилиндрический слой жидкости сечением площадью S и рассмотрим центробежную силу инерции, действующую на малый элемент жидкости массой Лиг этого слоя с координатами его краев х{ и
xi+1:
^ин = Лпг4л-21/2хср , где- хор = Xi +*i+1 , Am = pS(xi+1 - x;).
Отсюда
^ин = 2^2pSv2(xf+1 - xf).
Следовательно, перепад давлений между точками с координатами xi и xi+1 равен:
Ар, = 2л2pv2(x2+1 - xf).
Суммируя все перепады давлений на участке ОВ, получим, что перепад давления между точкой В и точкой О равен:
&рв = 2л2ру2х2.
Высота подъема жидкости у связана с изменением давления выражением
Ар = pgy.
Отсюда следует, что
Это уравнение параболы, следовательно, форма поверхности жидкости — параболоид вращения. Так как в полученное уравнение не вхо
71
дит плотность жидкости р, то форма поверхности жидкости не зависит от нее, а определяется только частотой вращения.
Второй способ. Эту задачу проще решить в инерциальной системе отсчета.
На малый элемент жидкости на ее поверхности действует сила реакции жидкости N (сила Архимеда) и сила тяжести mg (рис. 3.23).
Равнодействующая этих сил сообщает элементу жидкости центрост-
2 ремительное ускорение а = а> х.
Запишем выражения второго закона Ньютона в проекциях на коор-
динатные оси Ох и Оу.	f\r •	2 a sin а = то х, N cos a = mg.,
2 ,	(О tga =	х, g Отсюда следует, что	j	2	2 du О	1 О	, —= — x, dy =	x dx. dx g	g
2 о у = 	 2g	..	2л2 v2 2	. 4- Const = 	X + const, g
т.е. поверхность вращающейся жидкости — параболоид вращения.
Из полученного уравнения видно, что форма поверхности жидкости не зависит от ее плотности, а определяется лишь частотой вращения сосуда с жидкостью.
Глава 4
ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ
Задача 4.1. Каким должен быть радиус круговой орбиты искусственного спутника Земли для того, чтобы он все время находился над одной и той же точкой земной поверхности на экваторе?
Решение. Для того чтобы спутник, двигаясь по круговой орбите, находился все время над одной и той же точкой земной поверхности на экваторе, необходимо, чтобы период обращения спутника вокруг Земли Тс был равен периоду обращения Земли вокруг своей оси Т3.
В качестве тела отсчета выберем Солнце. Так как масса спутника много меньше массы Земли, ускорение Земли можно считать пренебрежимо малым. В этом случае для определения ускорения спутника можно применять второй закон Ньютона. Центростремительное ускорение спутника создается силой притяжения его к Земле:
F
а = —.
пг
Подставляя значения ускорения и силы тяготения
/	\ 2
2лй | и2 а = — R
„ „ пгМ F = G—^-,
R2
R Т2 ’
где R — радиус орбиты; М — масса Земли, получим:
4л2 „	_ тМ
m — R = G-~
R2
=	= Jgmt;2
V 4л2 У 4л-2
Расчеты дают следующий результат:
, 6,67-ПГ11 -бЮ24 • 864002
Л — у)—-----------------------
I	4л2
м = 4,2 • 107 м.
73
Задача 4.2. Определите ускорение свободного падения на Солнце по следующим данным: расстояние от Земли до Солнца 1,496 -ДОЧ м; угол, под которым видно Солнце с Земли, равен 32', период обращения Земли вокруг Солнца 3,1557 107 с.
Решение. Ускорение свободного падения на Солнце равно:
^c=G-^,	(1)
где Л1С и Дс — соответственно масса и радиус Солнца.
Радиус Солнца Яс можно определить из геометрического соотношения
„ D R sin а
где R — расстояние от Земли до Солнца, а — угол, под которым виден диаметр Солнца с Земли.
Массу Солнца определим, применив второй закон Ньютона к движению Земли вокруг Солнца:
F = М3а,
М3МС
4я2Д Т32
Мс =
4л-2Д3 GT32
(3)
= м3
Из выражений (1), (2) и (3) получим:
4л-2Д3-4	_ 16л-2Д
GT2R2 sin2a	Г2 sin2 а'
16я2 149,6 109 м	м
--------------------------» 274 — (з,1557-107)2 sin232' с*--с*
Задача 4.3. Рассчитайте вторую космическую скорость. Сравните ее с первой космической скоростью.
Решение. Вторая космическая скорость — это скорость, необходимая кораблю для того, чтобы удалиться от Земли на бесконечно большое расстояние, т.е. покинуть поле тяготения Земли. Эту же скорость приобретает у Земли космический корабль, который на бесконечно большом расстоянии покоился, а затем стал падать на Землю под действием силы тяготения. В этом случае работа силы тяготения является
74
мерой увеличения кинетической энергии корабля и одновременно мерой уменьшения его потенциальной энергии: А = АЕк = ~^Ер .
2	2
= де =-g^-o = -g^.
2	2 ’ P R	R
m	* г mun a mM
Так как &Ek = -ЛЕр, то --— = G----, откуда
2 R
2GM 2GM „	г-—:
= v—= J2gR 
I R У r2
Подставляя числовые значения, получим:
vn = 1,12 IO4 —. c
Первая космическая скорость определяется уравнением:
[GM г-
Сравнивая эти выражения, получим:
Vfj = Vj-fe.
Задача 4.4. Рассчитайте третью космическую скорость, т.е. минимальную скорость, которую надо сообщить космическому кораблю, стартующему с Земли, чтобы он смог покинуть пределы Солнечной системы.
Решение. Для того чтобы покинуть пределы Солнечной системы, космический корабль массой т должен обладать скоростью 1>с относительно Солнца, определяемой законом сохранения энергии:
muj с тМс = 0
2 Rc
где Мс = 2 • Ю30 ной орбиты. Из тельно Солнца:
кг — масса Солнца, Rq = 1,5-1011 м — радиус зем-этого выражения найдем скорость корабля относи-
i?c -
= 4,22 -104
Rc.	с
Корабль, вследствие движения вместе с Землей по орбите вокруг Солнца, уже обладает скоростью ц>, которую можно найти, применив второй закон Ньютона:
сМст = щцр
Л3 " Яс
75
Отсюда
и0 = I^C = 2,98-Ю4 Ос
м
с
Следовательно, при разгоне корабля по орбите вокруг Солнца в направлении вектора скорости движения Земли его скорость относительно Земли для выхода за пределы Солнечной системы должна быть равна:
икз = Uq - i?o = 1>0	= 1,24 • 104 —.
Для того чтобы удалить корабль из поля тяготения Земли, ему надо сообщить вторую космическую скорость (ее мы рассчитали в предыдущей задаче):
I2GM3
Un 1 R3 ’
где М3 = 6 1024 кг — масса Земли, В3 =* 6,4-10® м — радиус Земли, ии = 1,12-104 -.
с
Следовательно, кинетическая энергия Ek, которую надо сообщить космическому кораблю для того, чтобы он покинул Солнечную систему, складывается из кинетической энергии ЕА], необходимой для того, чтобы его удалить из поля тяготения Земли, и кинетической энергии Efe2, необходимой для того, чтобы он с орбиты Земли ушел в космическое пространство:
о	О	2
„	„	, „	mvlll	токЗ
Еъ — Еьу + Ek9, или ------—--------1-----.
* 2	2 2
Отсюда
иш =	+ °кЗ
иш = Jl,122 IO8 +1,242 108 — = 1,67 • 104 —. с	с
Задача 4.5. С Южного и Северного полюсов Земли одновременно стартуют две ракеты с одинаковыми начальными скоростями, направленными горизонтально. Через время г= 3 ч 20 мин ракеты оказались на максимальном удалении друг от друга. Определить максимальное расстояние между ракетами. Ускорение свободного падения на Земле считать известным. Радиус Земли Нд = 6400 км.
Решение. Ракеты движутся по эллипсам. Точка их старта соответствует минимальному расстоянию от центра Земли, а точка орбиты,
76
лежащая над диаметрально противоположной точкой Земли, — апогею орбиты. В этих точках скорость ракеты перпендикулярна прямой, проведенной из центра Земли к орбите.
Обозначим через L длину большой оси орбиты. Тогда максимальное расстояние s между ракетами (рис. 4.1) равно:
s = 2L - 27?3.
Рис. 4.1.
Период Т обращения ракеты по орбите равен 2 г. Если период обращения по круговой орбите радиуса R3 обозначить через Ту, то согласно III закону Кеплера
2^2 т/
Лз
/	\2
( т] L = 2Я3? —
Так как центростремительное ускорение спутника, движущегося по круговой орбите радиуса Я3, равно g, то g = <o2R3.
„ 2л Ir3
7i = — = 2 л М-.
о V g
Поэтому
I 4т2д-	.
L = 2Д33 о » 5,6Я3, s = 9,2Я3 « 5,9 • 104 км.
77
Задача 4.6. Космический корабль движется по круговой орбите вокруг Земли в плоскости орбиты Луны с угловой скоростью, равной угловой скорости вращения Луны вокруг Земли. Во время движения корабль находится между Землей и Луной на прямой, соединяющей их центры. Расстояние от корабля до Земли таково, что силы притяжения, действующие на корабль со стороны Земли и Луны, равны друг другу. Работают ли двигатели корабля? Каков вес космонавта, находящегося на корабле?
Масса космонавта 70 кг, период обращения Луны вокруг Земли 27,3 сут. Масса Земли в 81 раз больше массы Луны, а расстояние от Земли до Луны равно 60 земным радиусам. Радиус Земли принять равным 6400 км.
Решение. Поскольку во время движения корабль находится на прямой, соединяющей центры Луны и Земли, то период его обращения вокруг Земли равен периоду обращения Луны вокруг Земли, а его центростремительное ускорение равно:
а = a>2R = ^-R,
где R — расстояние от космического корабля до центра Земли. Для нахождения веса космонавта, находящегося на корабле, т.е. для решения обратной задачи механики, следует воспользоваться вторым законом Ньютона: сумма всех сил, действующих на космонавта, равна произведению массы космонавта на ускорение (рис. 4.2):
2*^ + 7*2 4- 2*3 = тгш,
где Г] — сила притяжения космонавта Землей
„ тМ?
?1=G---
R2
F2 -
сила притяжения космонавта Луной
Е2 = G-----------
(6ОЯО - Rj
Rq — ради-
ус Земли, F3 — сила, с которой корабль действует на космонавта.
Если за положительное направление выбрать направление от Луны к Земле, то можно записать:
R (бО2?о - 2?) Т2
Из условия, что силы притяжения космонавта Землей и Луной равны друг другу, получим:
2R2 - 243R0R + 7290 = 0;
78
243Д0 ±д/59О49Яо - 58320Bq _ 243 R0 ±277?0
R} = 67,52?o; R2 = 54Д0.
Первый корень не удовлетворяет условию задачи, так как расстояние Ri больше расстояния между Землей и Луной 6О7?о- Итак, космический корабль находится на расстоянии 54R0 от центра Земли, а следовательно, сила F3, с которой корабль действует на космонавта, равна:
4л-2	4-10	а
F3 = R2m =------------------54 • 6,4  106 • 70 Н = 0,17 Н.
Т2 (27,3 86400)2
Эта сила сообщает космонавту центростремительное ускорение, следовательно, она направлена к Земле. Для этого реактивные двигатели корабля должны работать, выбрасывая газы в направлении от Земли к Луне. Вес космонавта, т.е. сила, с которой он давит на стенку корабля, равен 0,17 Н и направлен по прямой, соединяющей центры Земли и Луны, в сторону Луны.
Задача 4.7. Искусственный спутник Земли массой тп, равной 100 кг, движущийся по круговой орбите в высоких слоях атмосферы, испытывает сопротивление разреженного воздуха. Сила сопротивления F = 5 10-4Н. Определить, на сколько изменится скорость спутника за один оборот вокруг Земли. Высота полета спутника над поверхностью Земли мала по сравнению с радиусом Земли.
Решение. Потенциальная энергия спутника равна:
где М — масса Земли, R — ее радиус.
„	mu2 _ Mm
Кинетическая энергия спутника — учитывая, что -----= G —— —
R R2 равна:
Е т°2 _ сМт
*2 2R ‘
Таким образом, общая механическая энергия есть
Е = Ек + Ер = -G-.
* р 2R
В результате действия силы сопротивления энергия спутника меняется, следовательно, меняется радиус орбиты. Изменение энергии спутника за один оборот численно равно работе силы сопротивления:
/ХЕ = -2xRF.
79
С другой стороны:
. „	Мт „ Мт „ Мт „
ДЕ = - G-,---г + G--« G---- АЛ.
2(Я + AR) 2R 2R* 2 * *
„	_ М
Учитывая, что G—- = g, получаем:
R2
-2nRF = — ЛЯ, 2
mg
. С М	1м	1 1м AR
До = , G---. G— » —. G----
у R + AR V R	2 V R R
Изменение скорости спутника в результате его торможения в атмосфере Земли имеет положительный знак, т.е. в результате торможения скорость спутника возрастает. Увеличение кинетической энергии спутника при его торможении происходит в результате уменьшения потенциальной энергии при переходе на орбиту меньшего радиуса.
Задача 4.8. Метеорит, скорость которого равна ио = 2360 м/с, летит в сторону Луны, радиус которой Яд = 1,74 • 106 м (рис. 4.3). Определите минимальное прицельное расстояние I, при котором метеорит не упадет на поверхность Луны. Ускорение свободного падения на Луне gл = 1,6 м/с2.
Решение. Запишем выражения законов сохранения механической энергии и момента импульса для метеорита (для бесконечно удаленной точки от Луны и ближайшей к ней). Это возможно, так как на метеорит действует консервативная сила тяготения, момент которой относительно центра Луны равен нулю:
лп>о mu2 GmMft ~2~ = ~2	R^~
mtjol = muRji,
(1)
(2)
где и — скорость метеорита вблизи поверхности Луны в момент време-
ни, когда O-LEji , Мл — масса Луны.
80
м
Из выражений (1) и (2) с учетом того, что G—— = gj}, получим:
° = 7°0 + 2#Л#Л ’ lmin -	+
N ”0
^min
1,74 IO6 1 +
2 1,6 1,74 IO6
(2,36)2 • 106
м « 2,45 IO6 m.
Задача 4.9. Космический корабль массой 400 кг двигался вокруг Земли радиусом 6370 км по круговой орбите на высоте hi - 200 км от ее поверхности. В результате включения ракетного двигателя на короткое время At скорость космического корабля увеличилась на Ди =10 м/с, а траектория движения стала эллипсом с минимальным удалением от поверхности Земли h} = 200 км и максимальным удалением от поверхности Земли Л2=234 км. С какой скоростью ь>2 движется космический корабль в точке максимального удаления от поверхности Земли? Чему равны сила тяги F ракетного двигателя, время At его работы, масса израсходованного топлива Ат?
Изменением массы корабля пренебречь. Массу Земли М считать равной 6 • 1024 кг, гравитационную постоянную G= 6,67 • 10"11 Н -м2/кг2, секундный рас-Дтп
ход топлива т. =---= 1 кг/с, скорость истечения газов и = 4000 м/с, удельную
At
теплоту сгорания горючего и окислителя q = 1,2  107 Дж/кг.
Решение. Скорость и, космического корабля в точке минимального удаления от поверхности Земли равна:
Di = dq + До.
Скорость и0 движения по круговой орбите можно найти из уравнения
tnoo Мт
где #1 = R + Й1 = 6,57 • 106 м, отсюда
IGM
Подставив числовые значения, найдем:
6,67 Ю”11 - 61024
°о = J-----------«----
V 6,37 106
— = 7,805-103 —, С	с
81
= 7,805 • 103 + 10 — = 7,815 • 103 —. c	c
По закону сохранения момента импульса для космического корабля выполняется равенство
muiRi = mu2R2,
поэтому скорость i>2 в точке максимального удаления равна:
,, «Л
где R2 = R + h2 = 6,604 • 106 м.
Подставив числовые значения, получим:
U2 = Z;8-151£3- 6’57O:io6 “ = 7,775. ю3 “.
6,604 106 с	с
Силу тяги F ракетного двигателя найдем из уравнения:
F\t = Лти,
где Azn — масса газов, выброшенных ракетным двигателем за интервал времени \t, и — скорость истечения газовой струи. Перепишем это уравнение в виде:
_ \т
F =----и = тм.
М
Подставив числовые данные, найдем:
Г=1 4000 = 4-103 Н.
Время работы двигателя можно найти по изменению импульса космического корабля:
FAi = тЛи,
где т — масса космического корабля, Ди — изменение его скорости,
Массу Лот- израсходованного топлива и окислителя можно найти по закону сохранения импульса для системы «корабль — горючее»:
л ,	. тЛи „	4000 10
таи = От и, ат =-------, ат =------------кг = 10 кг.
и	400
Коэффициент полезного действия ракетного двигателя определяется выражением:
82
Qc = mcq, то КПД ракеты равен:
и2 (41°3)2
= — = --------= 0,67.
где N — мощность двигателя, Qc — мощность, выделяющаяся при сжигании топлива.
Так как N = m<:U ,
2
7 '±<1	2 1,2 10‘
Существенно иной результат можно получить, если найти КПД ракетного двигателя как отношение изменения кинетической энергии корабля к количеству теплоты, выделившейся при сжигании топлива:
Изменение кинетической энергии корабля равно работе силы тяги на участке разгона:
ЛЕа = FS = Fu0St = тсии0М.
Отсюда КПД равен:
, _ mciw0A? _ ии0 _ 7,8 • 103 • 4  103 _ g
77 mcq\t q	1,2 107
Мы получили парадоксальный результат: КПД ракетного двигателя равен 260%! Никакой ошибки в расчетах здесь нет. Парадокс объясняется тем, что при работе двигателя в ракете, летящей с большой скоростью, часть кинетической энергии топлива, двигавшегося вместе с ракетой, передается ракете.
Задача 4.10. Космический корабль массы М = 12 т движется вокруг Луны по круговой орбите на высоте Л =100 км. Для перехода на орбиту прилунения на короткое время включается двигатель. Скорость вылетающих из сопла ракеты газов и= 104 м/с. Радиус Луны и ускорение свободного падения у ее поверхности Ял = 1,7 • 10® м, ga = 1,7м/с2.
1. Какое количество топлива необходимо израсходовать для того, чтобы при включении тормозного двигателя в точке А траектории корабль опустился на Луну в точке В (рис. 4.4)?
2. Во втором варианте прилунения кораблю в точке А сообщается импульс в направлении на центр Луны, чтобы перевести корабль на орбиту, касающуюся Луйы в точке С (рис. 4.5). Какое количество топлива необходимо израсходовать в этом случае?
83
Рис. 4.4.	Рис. 4.5.
Решение. 1. При движении корабля по круговой орбите его центростремительное ускорение создается силой тяготения к Луне:
ММ л	Ми20
где R = Яд + h — радиус первоначальной орбиты, с>о — скорость корабля на круговой орбите:
- С Мл и°-Г~Г-
7VT тт
Так как = G —~, то «л
^0
р I Sjl
— Лп. ----
}Rn+h
(1)
После включения тормозного двигателя, сообщающего кораблю импульс, касательный к траектории, скорость корабля останется перпендикулярной к радиус-вектору ОА (рис. 4.4). Корабль при этом начинает двигаться по эллипсу с фокусом в центре Луны.
Обозначив через Цд и ив скорости корабля в точках А и В, запишем уравнения законов сохранения энергии и момента импульса:
ММЛ Ми2в „ММЛ	„
--------(д.--- —-------Ст------ I 1
2	R 2 Лл
MvAR = MvBRn-	(3)
Решая уравнения (2) и (3) совместно, находим:

I2C
R(R + #л)
84
С учетом выражения (1) получим:
2ЯЛ
Уд = и0. ----
°\R + Rji
Следовательно, изменение скорости Ду корабля в точке А должно быть равно:
1-11 2 Яд
Ду = у0 - уа = Ур 1 -	‘
\ V к J
2*л
\2Rn+h.
= 24—. с
Так как двигатель включается на короткое время, закон сохранения импульса для системы «корабль — топливо» можно записать в виде:
(М - тп^Ду = т\и,
гце тп-! — масса сгоревшего топлива. Отсюда получаем:
Др
т1 =------М.
и + Ду
С учетом того что Ду «и , находим:
т1 и М = 29 кг. и
2. Во втором случае вектор Ду2 направлен перпендикулярно векто
ру у0, поэтому
и л ~ Ур +ДУг>	у а - уУр + Ду1 -
На основании закона сохранения энергии в этом случае можно писать уравнение:
Л*(ур +Ду2) _ ОММЛ _ Ми2с _ ОММЛ
R	2 Rjj
2
а на основании закона сохранения момента импульса — уравнение
М VqR — ЛГус-Нд.
Решая уравнения (4) и (5) совместно и учитывая выражение (1), ходим:
Ди2 =
Sn к 97 м , Яд + h с
за-
(4)
(5)
на-
Используя закон сохранения импульса, получим:
т2 = —— М и 116 кг. и
85
Задача 4.11. Космический корабль движется по круговой орбите на расстоянии 400 км от поверхности Земли. На сколько нужно увеличить скорость корабля для перевода его на эллиптическую орбиту с расстоянием 400 км от поверхности Земли в перигее и 40000 км в апогее? Каким будет новый период обращения корабля?
Решение. Определим начальную скорость корабля: mV() _ GMm	_ I GM
^=(Л + л)2’
На основании закона сохранения энергии (рис. 4.6):
muf GmM _ nwf GmM
2 R + h 2	2? + h
На основании закона сохранения момента импульса:
mvx(R + h) = mu2(R + 2?).
(2)
Из (1) и (2) следует:
I 2GM R + H
V 2R + Н + h R + h 1
Ли =	~ и0 - 2461 —.
с
По закону Кеплера:
а
—— = const, /р2
tV (2R+H+hf Го7 8(2? + hf
2д(2? + h\
То =-----------
Оо
т /о тт 1Л /22? + Н + h
Т = m2R + H + hY.------
v 'V 2GM
T « 4,4-104 с = 12 ч.
Задача 4.12. Космический корабль движется вокруг Земли по круговой орбите радиусом Я= 6570 км. Сколько топлива потребуется израсходовать для вывода корабля за пределы солнечной системы?
Сведения о космическом корабле и его двигательной установке: масса корабля с двигательной установкой и топливом т-о — 40000 кг; скорость истечения газов и = 4000 м/с.
Сведения о Земле и Солнце: радиус орбиты Земли Ко = 1,5 10Ч м; масса Земли Л23 = 6 • 1024 кг; масса Солнца Мс = 2 • 1О80 кг; гравитационная постоянная G = 6,67 10 11 Н-м2/кг2.
86
Рис. 4.7.
Решение. Для выхода космического корабля за пределы солнечной системы из точки на расстоянии Rq от центра Солнца по закону сохранения энергии сумма его кинетической энергии Ek и потенциальной энергии Ер должна быть равна нулю:
Ek + Ер = О-	(1)
Обозначим начальную скорость космического корабля (третья космическая скорость).
Ее значение можно получить из уравнения (1):
Z^3_G^=0,	(2)
2	Йо
|2GMC Йо
(3)
2  6,67-10"11 • 2  1О30
}	1,5 • 1011
м с
— « 42,2 • 103 с
Минимальным расход топлива будет в том случае, если двигатель
включается в момент времени, когда вектор Uj скорости движения корабля по круговой орбите вокруг Земли совпадает по направлению с вектором 5Т движения Земли вокруг Солнца (рис. 4.7). В этом случае начальная скорость космического корабля относительно Солнца ин максимальна и равна ин = Uj +ит.
87
Кораблю необходимо сообщить дополнительную скорость Цц или дополнительную кинетическую энергию £кр
2
WWK1
'-’к! = ^3 ~	-®к1 =	-	•
Вычислим значения скоростей он и ик1:
nwj тМ3	/GM3
k67.10--.8 igf
У 6,57 106 с	с
тли2 _ q тМс	_ 1^МС
кГ’
От= &ПЕЕИЕмя29>8.10зм5 у 1,5 1011 с	с
ин = 7,8103 — + 29,8 103 — = 37,6-Ю3 —. с	с	с
Отсюда получаем, что для выхода за пределы поля тяготения Солнца космическому кораблю на орбите спутника Земли нужно сообщить дополнительную скорость:
ок1 = 42,2  103 — - 37,6 • 103 — = 4,6  103 —. с	с	с
Однако если сообщить такую начальную скорость космическому кораблю, находящемуся не только в гравитационном поле Солнца, но и в гравитационном поле Земли, то его кинетическая энергия окажется недостаточной для выхода за пределы сферы действия гравитационных полей Солнца и Земли.
Вычислим, какое изменение скорости корабля необходимо для вывода его из сферы гравитационного притяжения Земли. Для этого вычислим вторую космическую скорость и2 для орбиты космического корабля и найдем разность ик2 = и2 ~ и1-
ти2 _ М3тл	l2GM3
---- = (j	. Do = J- , 2 R--------------------------} R
12 -6,6710 11 - 6 IO24 м „ л м
o2 = ---------------------= 11,0 IO3 —,
У 6,57-106 с	c
88
Q М	о М	о М
ик2 = 11,0 103 —-7,8103 — = 3,2103 —. с	с	с
Следовательно, для преодоления сил тяготения Земли кораблю нужно сообщить дополнительную кинетическую энергию
пги2к2
Е.2 = "у- •
Для преодоления действия сил притяжения Земли и Солнца кораблю нужно передать дополнительную кинетическую энергию _ЕК, равную сумме значений энергии £к1 и £к2:
Ек =	+ Ек.2 
Отсюда получим значение необходимого увеличения скорости корабля ск: <>2	2
тик2 2	2	2
vK = ^4,6 IO3 j2 + (з,2 • 103)2 — = 5,6 103 —.
Найдем массу топлива m, необходимого для сообщения кораблю скорости цк, выбрав систему отсчета, связанную с центром масс космического корабля, и используя формулу Циолковского:
/ 2	2
С к = -иик1 + ик2
т0 - т
где е — основание натурального логарифма.
Отсюда следует:
' 5600
т = 4  104 1-е 4000
кг = 3  104 кг.
Задача 4.13. в космическом исследовательском проекте запуска космического корабля за пределы Солнечной системы обсуждаются две возможности:
1. Аппарат запускается со скоростью, достаточной для выхода за пределы Солнечной системы, непосредственно с орбиты Земли.
2. Аппарат приближается к одной из внешних планет, с ее помощью изменяет направление движения и приобретает скорость, необходимую для выхода за пределы Солнечной системы.
Можно считать, что во всех случаях корабль движется под действием гравитационного поля только Солнца или планеты, в зависимости от того, чье поле сильнее в данной точке.
Определите:
а)	Минимальную скорость корабля ь>а и ее направление относительно вектора орбитальной скорости Земли для реализации проекта 1.
89
б)	Скорость аппарата, когда он пересекает орбиту Марса, предположив, что корабль запущен в направлении, определенном в пункте а), но с другой скоростью относительно Земли (т.е. найдите параллельную и перпендикулярную составляющие этой скорости относительно орбиты Марса), при условии, что в этот момент Марс находится далеко от аппарата.
в)	Минимальную стартовую скорость аппарата ив с орбиты Земли, необходимую для выхода из Солнечной системы после воздействия на него гравитационного поля Марса, предположив, что аппарат вошел в его гравитационное поле. (Вас не должно интересовать точное положение Марса во время взаимодействия с аппаратом.)
Подсказка: из результата, определенного в а), вы знаете оптимальную величину и направление скорости аппарата, необходимой для выхода за пределы Солнечной системы. Найдите связь между этой скоростью и компонентами скорости до вхождения аппарата в гравитационное поле Марса, т.е. компонентами, определенными вами в б). Будет ли сохраняться энергия аппарата?
г)	Максимально возможную часть сбереженной энергии в проекте 2 по сравнению с проектом 1.
Примечания: можно считать, что все планеты вращаются вокруг Солнца по окружностям в одном направлении и в одной плоскости. Сопротивлением воздуха, вращением Земли вокруг своей оси и энергией, затраченной при выходе из гравитационного поля Земли, пренебречь.
Численные данные: скорость Земли вокруг Солнца равна о0 = 30 км/с, отно-
2 шение расстояний от Земли и Марса до Солнца равно —.
3
Решение, а) Если принять потенциальную энергию аппарата в поле тяготения Солнца равной нулю при бесконечном удалении от Солнца, то для выхода космического аппарата за пределы Солнечной системы с орбиты Земли необходимо, чтобы в момент старта его полная энергия была больше или равна нулю:
£ = Z^_GZ^>o,	о2>^,	(1)
2 и	г)
где т — масса аппарата, rj — радиус земной орбиты, М — масса Солнца, и — скорость аппарата относительно Солнца. Орбитальная скорость Земли и0 ‘определяется из второго закона Ньютона:
^.8*	(2)
П О	г,
Из выражений (1) и (2) получаем: и2 > 2ь>о, и S у/2и0.
С другой стороны, между стартовой скоростью иа и скоростями и и и0 существует соотношение и = Од + йа (рис. 4.8). Из рисунка 4.8 ясно, что и < и0 + иа , т.е.
90
иа > и-о0 > V2 -lb0.
(3)
Следовательно, минимальное значение искомой скорости
ua = L’ol'V2 - 1) ~ 12,4 -— достигается при угле (р между векторами и и
Oq, равном нулю = О).
б)	Для нахождения параллельной рц и перпендикулярной и । составляющих скорости аппарата и в момент пересечения орбиты Марса (рис. 4.9) воспользуемся законами сохранения момента импульса и энергии:
ш(оо + Ц>)п = тицг2,
т(^о+иб)2 „тМ т[и1+с>2) тМ -----------(г----- =-----------(j-----,
2	rj	2	г2
где г2 — радиус орбиты Марса. Отсюда находим:
V|| = — (vo + ^б)> г2
, (ио + о6)2| 1 - -^| - 2t>ofl - —
V	{	г2)	\	г2,
(4)
(5)
в)	Перейдем в систему отсчета, связанную с Марсом. Из потенциальности гравитационного поля следует, что в этой системе аппарат, выйдя из гравитационного поля Марса, имеет тот же модуль скорости, что и при входе в поле: о' = ps, направление же скорости изменяется (рис. 4.10). Для того чтобы после облета Марса корабль покинул Сол
91
нечную систему, необходимо, чтобы его скорость u's удовлетворяла неравенству, аналогичному неравенству (3):
и* * (V2 -1)ом,	(6)
где 1>м — орбитальная скорость Марса, равная
Рис. 4.11.
При входе в гравитационное поле Марса корабль имеет скорость
us, которую можно определить из выражения (рис. 4.11):
Из соотношений (6), (7) и (8), условия (/, = и значений цц и
из пункта б) получаем выражение для стартовой скорости корабля и относительно Солнца:
3/2
+ 2-2у[2 —
Г2
Отсюда минимальная скорость запуска ц, относительно Земли равна:
Чв = ик - ”о>
+ 2-2л/2 — -1
Г2
~ 0,1851>0 » 5,5 —М .
С
92
Энергия аппарата в системе отсчета, связанной с Солнцем, при таком способе запуска не сохраняется — она возрастает за счет изменения кинетической энергии Марса.
г)	Сбереженную часть энергии можно определить по формуле:
а = El ~ Ez = и»-~ив м 0 8 = 80% .
Однако для практических целей более важно другое отношение:
THj - т2 mi
где ту и m2 — массы топлива, необходимые для разгона аппарата в первом и втором случаях. В соответствии с формулой Циолковского
т = ту, е и - 1
(то — полезная масса аппарата, и — скорость истечения газов относительно аппарата) получаем:
ца ив р и _ р и
, иа
е и -1
т.е. ответ перестает быть однозначным и зависит от величины и. Для км
современных ракет — у которых и » 5---- — fl » 0,81.
с
Глава 5
ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ
Задача 5.1. Существует метод определения скорости пули методом баллистического маятника. Пуля массой т попадает в ящик с песком массой М, подвешенный на тросе. Максимальное отклонение ящика от положения равновесия после попадания пули таково, что его центр тяжести поднимается на высоту h от первоначального уровня. Определите скорость пули.
Возможные способы решения задачи.
Первый способ. Применив закон сохранения механической энергии к системе тел «пуля — ящик», получим:
/пу2 ,	.	l2(M+m)gh
2	'	'	\ т
Второй способ. Применим закон сохранения импульса к системе тел «пуля — ящик»:
ти = (М + т]и..
Отсюда скорость и системы тел равна:
ти и =------.
М + т
Согласно закону сохранения энергии
(М + т)и2 .	.	9
i— = (М + m}gh, и2 = 2gh,
т2о2 „ ,	М + т [-—г
------------------ = 2gh, о =	-J2gh. (М + иг)---------------т
Какое из двух решений правильное?
В первом способе решения встречается весьма распространенная ошибка, связанная с некорректным применением закона сохранения механической энергии за пределами границ его применимости. Закон сохранения механической энергии можно применять для замкнутых
94
систем, если нет превращения механической энергии в другие виды энергии.
Удар пули в ящик с песком является неупругим, при этом происходит превращение части механической энергии пули во внутреннюю энергию системы тел (в тепло). Поэтому первый способ решения ошибочен. Во втором способе решения закон сохранения импульса применяется корректно, так как система тел «пуля — ящик» замкнута, а большего для выполнения закона сохранения импульса не требуется. Для получившейся после кратковременного удара системы тел можно применять закон сохранения механической энергии, так как на ящик с пулей после ее остановки действует сила тяжести, являющаяся консервативной.
Задача 5.2. Пуля массой т движется со скоростью и и попадает в платформу с песком, движущуюся со скоростью й в том же направлении, и застревает в ней. В системе отсчета, связанной с Землей, изменение кинетической энергии пули равно:
а в системе отсчета, связанной с платформой, . „ т /	\2
^2	'
Считая, что количество теплоты, выделившееся при столкновении, равно изменению кинетической энергии Q = -ЛЕ^, получаем парадоксальный результат, противоречащий принципу относительности: будто возможно, что в одной системе отсчета пуля расплавится, а в другой не расплавится. Объясните этот парадокс.
Решение. Изменения кинетической энергии пули в выбранных системах отсчета действительно различны, так как изменение кинетической энергии в незамкнутой системе тел является величиной относительной.
Часть этой энергии в обоих случаях расходуется на увеличение кинетической энергии платформы ЛЕпл.
В системе отсчета, в которой платформа была неподвижной, изменением ее кинетической энергии можно пренебречь по сравнению с энергией пули, так как
ml и - и) где Ди — изменение скорости платформы, а выражение Ди = —*--------
М легко получить, применив закон сохранения импульса.
95
Отсюда
2 М
При т«М ЛЕПЛ«ЕА1, следовательно,
Q2 = -ЛЕА2 =у(и~м) •
В системе отсчета «Земля» платформа до взаимодействия двигалась со скоростью й и изменением ее энергии пренебречь нельзя, так как
М(и + Ди)2 Ми2	MtSu2
ДЕ’ = —i-------- — = Mu.Au + —-— « Мики.
2	2	2
ml и - и)
Подставив значение Ли = —------- (оно инвариантно во всех инер-
М
циальных системах отсчета), получим:
mfo-u)
ДЕ' = Ми —-------- = тщ о - и).
С учетом этого изменения энергии платформы запишем:
что согласуется с результатом, полученным в системе отсчета «платформа».
Известен так называемый парадокс «большого» тела. Суть этого парадокса сводится к тому, что при взаимодействии тел с существенно разными массами (т«М} изменением энергии тела большой массы М можно пренебречь только в тех системах отсчета, в которых «большое» тело до взаимодействия покоилось. Действительно, в этих системах отсчета изменение кинетической энергии тела большой массы пренебрежимо мало:
. „ ММ>2 „ МДо2
2	2
В системах отсчета, в которых тело большой массы до взаимодействия двигалось со скоростью о0, изменением его кинетической энергии пренебречь уже нельзя:
М(и0+Ло)2	МДо2
AEL = —i--------------— =	+------,
2	2	2
так как ЛГо0Ло не является малой величиной.
96
Задача 5.3. На концах и в середине невесомого стержня длины Z расположены одинаковые шарики. Стержень ставят вертикально и отпускают. Считая, что трение между плоскостью и нижним шариком отсутствует, найти скорость верхнего шарика в момент удара о горизонтальную поверхность. Как изменится ответ, если нижний шарик шарнирно закреплен?
Решение. Так как в горизонтальном направлении на систему не действуют никакие внешние силы, то центр масс системы (средний шарик) движется вертикально. Это означает, что в тот момент, когда верхний шарик касается плоскости, скорость нижнего шарика равна нулю, а скорость верхнего шарика направлена вертикально и по модулю вдвое больше скорости среднего шарика. Заметим, что, хотя движение системы в том случае, когда нижний шарик закреплен, и отличается от случая, когда он не закреплен, полученный вывод об отношении скоростей шариков остается справедливым. Поэтому в обоих случаях согласно закону сохранения энергии
I , ти2 пг mg —I- mgl =----I--
2	2	2
где т — масса каждого из шариков.
Отсюда
Задача 5.4. «Парадокс спутника» заключается в том, что при торможении спутника в атмосфере его скорость не уменьшается, а увеличивается. Объясните механизм этого явления и рассчитайте ускорение спускаемого аппарата космического корабля «Восток» массой 2,4 10s кг, движущегося на высоте 100 км над поверхностью Земли, если диаметр аппарата 2,3 м, а плотность воздуха на этой высоте 5,6 • 10"7 кг/м3. Массу Земли принять равной 6  1024 кг.
Решение. При торможении спутника траектория его движения отличается от окружности и становится похожей на спираль. При этом направление вектора скорости составляет с направлением силы тяжести острый угол и составляющая силы тяжести создает положительное
До ускорение а =----, т.е. скорость спутника увеличивается.
А?
Кинетическая энергия спутника увеличивается, но его полная механическая энергия Е уменьшается. Покажем это. Будем считать, что спутник движется по круговой траектории. Его полная энергия Е равна:
E = Ek+Ep	(1)
* р 2 R
где М® — масса Земли, R — радиус орбиты спутника.
97
По второму закону Ньютона
тМ9
то2
R
(2)
Из выражений (1) и (2) получаем:
2	2
_ то о т^>
Е =------то =--------
2	2
Изменение полной механической энергии спутника равно:
. „ т /	4 ,2 т о
ЛЕ = - —(о + До)----о
2	2
= -тпоДо- —До2 » -тлоДо.
2
(3)
Следовательно, при увеличении скорости спутника полная его энергия уменьшается: если До > 0, то ЛЕ < 0.
Это уменьшение связано с соударениями молекул о спутник, движущийся со скоростью о. За время Д< произойдет столкновение корабля с молекулами, находящимися в объеме SoAi. Если удары молекул о корабль упругие, скорость каждой из них увеличивается на 2 о, следовательно, увеличение кинетической энергии всех молекул равно:
2
kEk =	= 2pSo3Ai .
(4)
Так как изменение полной энергии спутника равно изменению кинетической энергии молекул, взятому с обратным знаком: ДЕ = -ДЕА, то из выражений (3) и (4) получаем:
„ о Зл, л Ao 2pS 2 npd2 2
-2pSo Д£ - - токо, ---= —о = —— о .
kt т 2т
„	2 л
С учетом равенства и = G-^-
получаем искомое ускорение спутни-
ko лр<12 GM
К fl Cl-i — - = ---•-----.
kt 2т R
Однако, строго говоря, взаимодействие молекул нельзя считать упругим.
Рассмотрим другой предельный случай — неупругое соударение молекул. При этом изменение энергии молекул будет равно pSo2kt, а
*	pS 2 npd2 GM
ускорение спутника а2 = -— о = —--------.
т 4т R Реальное значение ускорения спутника будет лежать в пределах
U-2 < л < а 1.
Подставив численные значения, получим:
1,5  10-2 м/с2 < а < з . 10-2 м/с2.
98
ЗАДАЧА 5.5. Считая Солнце однородным шаром, оцените его минимальный радиус при сжатии под действием сил тяготения при исчерпании внутренних источников энергии, поддерживающих высокую температуру газа. Радиус Солнца 7 • 108 м, период вращения вокруг своей оси 2,2 • 10е с. С какой частотой вращался бы такой «солнечный пульсар»?
Решение. Моменты сил тяготения, под действием которых происходит сжатие, равны нулю. Поэтому на основании закона сохранения момента импульса
Л40! = I2CO21
где 1у тл 12 — моменты инерции до и после сжатия Солнца, <У] и а>2 — угяовые скорости. Момент инерции однородного шара равен:
I = 0,4mR2, поэтому 0,4mR2	= 0,4mR%	;
Т1	т2
Для удержания вещества Солнца необходимо, чтобы на его экваторе сила тяготения обеспечила необходимое центростремительное ускорение:
тМ	4л2
Г = ща6;	G—-- = т —— R2;
' R2	^2
2 _ 4л2В3
2	GM
Из выражений (1) и (2) получаем:
Я2 = Дшп =	= 1,5 104 м;
GMT2
?2=7if—1 = Ю-3 с.
«Солнечный пульсар» имел бы радиус всего 15 км и вращался бы с частотой 1000 оборотов в секунду!
Задача 5.6. Автомобиль массой т, мощность которого N, движется по горизонтальному участку дороги с коэффициентом трения ц. Через какой минимальный промежуток времени скорость автомобиля может достигнуть значения п?
Решение. Максимальная сила тяги автомобиля равна силе трения. Если обе оси автомобиля ведущие, т® = fjmg.
99
Время, в течение которого скорость автомобиля станет равной и, определится из выражения:
Однако такое решение может оказаться ошибочным, так как оно найдено в предположении, что автомобиль разгоняется под действием постоянной силы, равной максимальному значению силы трения покоя F л max •
Такое предположение не противоречит условию задачи до тех пор, пока выполняется условие:
^тах^’ NAt,
где N — максимальная полезная мощность двигателя.
Преобразовав это выражение, получим:
Дд
•^тах — N, •^тахи — N,
N N
=> о <-----=-----.
^тах
Следовательно, если и < о0 =----, то минимальное время разгона
цтё
автомобиля до скорости и равно:
и =  не
„	*	N
После достижения автомобилем скорости и > и0 =------ движение
цтё
его с постоянным ускорением а = pg при постоянной мощности двигателя становится невозможным, так как изменение кинетической энергии автомобиля не может превышать работы, совершенной двигателем.
Если пренебречь потерями, то согласно теореме о кинетической энергии можно записать:
А = ДК,
_ mu2 ttWq
fiftf) —---------,	—
2	2	2
77l(U2 - t>o) => Tn = --------- .
2 2N
100
Таким образом, если после достижения автомобилем скорости Uq мощность двигателя начинает использоваться полностью, то время, необходимое для достижения скорости и, большей Ц), будет складываться из времени, необходимого для достижения скорости Ц), и времени, которое нужно для увеличения скорости от значения Vq до и:
т(и2 - cig)
Hg 2N
„	N
Подставляя в это выражение значение скорости	, полу-
чим:
х N mu2 N mu2 N
£ _ -.... —    —	— — _ - -}- . — — - - . _
m^g2 2N 2mn2g2	2m^g2
Следовательно, скорость автомобиля может возрастать пропорцио-
нально времени в первой степени до значения о0 =---, а дальнейшее
приращение скорости будет увеличиваться пропорционально времени в 1 степени — .
2
Задача 5.7. Автомобиль движется равноускоренно по горизонтальной до-роге и достигает скорости D. Одинакова ли работа, совершаемая двигателем при
разгоне до скорости — (участок О;—) и от скорости — до и (— ;и)?
Решение. Будем считать, что работа, совершаемая двигателем, идет только на увеличение кинетической энергии автомобиля А = АЕ*-
~	л О 1
Следовательно, на участке разгона 10; — I двигатель совершит рабо-
Z \2
I т —	„
.	. А „	\2j	л mir
ту Aj, равную Ai = ДЕА1 =------------0 =-----
2	8
На участке ; oj работа А2 равна:
Z х2
I f)
9 т ~ а _ ЛГ _ ти2
А2 ~	~  -----" 
3	2
= — то .
8
101
Отношение работ на указанных участках разгона равно:
А = 1
3
т.е. чем больше скорость, тем большую работу должен совершить двигатель, чтобы поддерживать ускорение движения постоянным.
Тот же результат можно получить и другим путем. При равноуско-
ренном движении изменение скорости на — происходит за равные ин-
2
тервалы времени. Отношение же путей, пройденных за последовательные равные промежутки времени, при равноускоренном движении с
нулевой начальной скоростью равно —- = —.
A] Fs1	1
Отсюда —- = —- =	= —.
-^2	^s2 s2 ®
Задача 5.8. Пушка, жестко скрепленная с самолетом, находящимся в по-ти2 кое, сообщает снаряду массой т кинетическую энергию —-—. Определите энер-
гию снаряда относительно Земли, если выстрел будет произведен из самолета, летящего горизонтально со скоростью и, в направлении его полета. Ученики дали на вопрос задачи разные ответы.
1-й ученик: До выстрела снаряд вместе с самолетом летел со скоростью и от-о	с	- с	mL>2
носительно Земли и, следовательно, обладал кинетической энергией = —-—.
При выстреле из пушки летящего самолета кинетическая энергия снаряда изменилась так, как и при выстреле из самолета, находящегося в покое, т.е.
следовательно, кинетическая энергия снаряда относительно Земли после выстре-
ла из летящего самолета составляет:
E'k лсв
= Еь 4- ДЕь «сн
9	9
ти -----1----
2	2
= ти2.
2-й ученик: Скорость движения снаряда до выстрела в летящем самолете была равна и относительно Земли. После выстрела скорость снаряда увеличилась на и.
Согласно закону сложения скоростей скорость снаряда после выстрела относительно Земли равна 2 о, и, следовательно, его кинетическая энергия равна:
/п(2п)2
2
Е'к
СИ
= 2ти2.
Какое рассуждение правильно?
102
Решение. Прав второй ученик, который основывает свои рассуждения на законе сложения скоростей.
Ошибка первого ученика заключается в необоснованном предположении о равенстве изменений кинетической энергии снаряда при выстреле из пушки покоящегося и летящего самолетов. Хотя наблюдения производятся в одной и той же инерциальной системе отсчета, связанной с Землей, равенство изменений кинетической энергии снаряда не следует из каких-либо физических законов, так как начальные условия опытов различны.
Покажем, что последовательное решение задачи на основе использования законов сохранения в механике приводит к тому же результату, который получен на основе использования закона сложения скоростей.
На основании закона сохранения энергии в системе «самолет — снаряд» сумма изменений потенциальной и кинетической энергии равна нулю. Отсюда можно найти изменение потенциальной энергии АЕр
пороховых газов при выстреле из пушки самолета, находившегося в покое:
Л/j? +	4- A/j?L — О,
Р\' «сам "сн ’
— А/? п — А/?ь +. А/?ь г «сам «сн
М{&и)2
2	2
На основании закона сохранения импульса для модулей проекций на направление полета самолета МЛи = ти, откуда
. ти
Ли =--
М
Аналогично для второго случая получим:
ЛЕ~ + AEL + AEL — О, Р "сам "сн ’
откуда изменение кинетической энергии снаряда ЛЕ£сн равно:
AEL = - АЕ' - &Е'к « сн	Р « сам
Так как второй случай эквивалентен переходу наблюдателя в инерциальную систему отсчета, движущуюся со скоростью - и относительно первой, при выстреле из пушки самолета, летящего со скоростью и относительно Земли, изменение потенциальной энергии газов ДЕ'р и изменение скорости снаряда и’ и самолета Ли' остаются такими же, как и в первом случае:
ДЕр = ДЕр, и' - и, Ди' = Ди.
103
Поэтому получаем:
&E'k = - АЕ „ - AEL дсн	Р *сам
М(До)2 тр2
2	+ 2
М(у - До)2 Ми2
2	2~
М(&и\ mv2	ЛГ(До) ти2
- —*—— +----+ М iAu----—— =----
2	2	2	2
Используя последнее выражение и значение До =----, находим:
М
ти2 2	3	2
&E’k =------+ ти = — ти .
сн о	9
Отсюда кинетическая энергия снаряда, выпущенного из пушки летящего самолета, относительно Земли равна:
ти2 3 о 9
E'k = Ek + AEL =------+ — ти=2ти.
*сн ясн дсн 2	2
Задача 5.9. Ракета массой М ускоряется за счет выбрасывания газов массой т, М » т . Если ракета первоначально неподвижна, то она при выбрасывании газов массой т приобретает кинетическую энергию 10"4 Дж. На сколько изменится кинетическая энергия той же ракеты при таком же срабатывании ее двигателей, если ракета двигалась с кинетической энергией 1О10 Дж?
Решение.	ти = МАи, Аи =-----.
М
Изменение скорости ракеты До одинаково в первом и втором случаях.
м(До)2	М(о + До)2 Ми2 . МАи2
2	2	2	2	2
До «о, ДЕ2 s МоДо,
(Л£2)2 = 4^^- • МЛц2 = 4£2Л£!,	Л£2 = З^Д^,
2	2
ДЯ2 = 2х/1О10 104 Дж = 2  107 Дж.
Парадоксальный результат А£2 = 2ОООД2?! объясняется тем, что во втором случае ракете передается не только энергия, выделяющаяся при сжигании топлива, но и кинетическая энергия горючего.
104
Задача 5.10. Частица массой т испытывает прямое упругое столкновение с неподвижной частицей массой М. Вычислите потерю энергии частицей при таком столкновении.
Решение. Обозначим начальную скорость первой частицы й0, ее скорость после столкновения и, скорость второй частицы после столкновения и. Тогда на основании законов сохранения и импульса имеем:
1 о 1 , о 1	9
— тип = —Ми -I—ти , 2	2	2
(1)
	тип	= Mu	+ mu.	(2)
Для прямого столкновения из		уравнения (2) следует:		
	ти0 = Ми + то, или ть>0 = Ми - то.			(3)
Пусть k =	м т — . Тогда из (1) следует: т			
	4	-и2 =	ku2.	(4)
Из (3):	L>0 ~ L> = ku,	ИЛИ	u0 + t> = ku.	(5)
Из (4):		JXU0 +	L>j = ku2.	(6)
Из (5) и (6):				
	+ и) =	ku2 -	+ и = u,	(7)
ИЛИ	feu^L>0 - l>) =	ku2 -	O0 - D = U.	(8)
Из (6), (7)	и (8):			
	L>0 - D = ku t>o + u -u	или	V0 + D = ku Dq - U = U	
	2u0 = (k + lju,		2u0 = (k + lju.	
	2	Mu2	= 4ft^._1 , 2 (fe + 1)2	
	A + l ’	2		
	p "WO 0	2	E =	Eo	2 • (*+i)	
При А->0	и A->oo E-»0, при k =		1 E = E0.	
105
Задача 5.11. Метеорит массой т=1кг движется со скоростью |Б| = 2 • 103 м/с относительно Земли и попадает в спутник массой М = 100 кг, движущийся со скоростью |й| = 8  10s м/с относительно Земли навстречу метеориту. После неупругого столкновения спутник и метеорит движутся вместе. Определите количество теплоты Q, выделившееся при столкновении.
Решение. Перейдем в систему отсчета, связанную с центром масс системы «метеорит — спутник». Центр масс системы движется относительно Земли со скоростью:
Ми - ти и =--------,
М + т
поэтому скорости метеорита и спутника в новой системе отсчета равны соответственно:
Ми - ти М(и + и\ = у +------- = —-----,
М + т М + т
Ми - ти иг = -и +-------=----i.
М + т М + т
В системе отсчета, связанной с центром масс системы «метеорит — спутник», сумма кинетических энергий двух тел до столкновения равна выделившемуся количеству теплоты:
,,	ти2	Ми?
Q = W, + W9 =--- +---Ь- =
2	2	2
тМ2(у + и)2 Мт2(у + и^ тМ(у + и)2 2(М + mf 2{М + mf	2(м + т)
1 100108
2 101
Дж » 5 • 107 Дж.
Рис. 5.1.
Задача 5.12. Два тела малых размеров массой т каждое соединены стержнем пренебрежимо малой массы длиной I. Система из начального вертикального положения у вертикальной гладкой стены приходит в движение. Нижнее тело скользит без трения по горизонтальной поверхности, верхнее — по вертикальной (рис. 5.1). Найдите значение скорости нижнего тела, при котором верхнее оторвется от вертикальной стенки.
106
Решение. В системе выполняется закон сохранения механической энергии.
2	2
ти ти А _	\
----+----= mgAh = mgll 1 - cos а),
2	2
и2 + и2 = 2gZ(l - cos а).
Так как расстояние между телами неизменно, то о cos а = и sin а.
Из (1) и (2) следует:
и2 = 2gl(cos2a - cos3a) = 2gl\x2 - х3
(1)
(2)
если х = cos а.
При отрыве верхнего тела от вертикальной стены действие силы реакции стены прекращается и ускорение нижнего тела становится равным нулю:
du	d\u j „du
dt	dt dt
у = x2 - x3 => у' = 2x -3x2 =0 => x = — ,
u
з
2 cos a = — ,
3
2 max
= 2g?
3j
2 ПГТ
Задача 5.13. Частица массой M, движущаяся со скоростью и, сталкивается с неподвижной частицей массой т. Каков максимальный угол в отклонения направления движения первой частицы после столкновения (рис. 5.2)? Столкновение упругое.
Решение. Выберем систему отсчета, связанную с центром масс системы из двух частиц. Скорость центра масс V равна:
М + т
Импульс первой частицы до столкновения в системе отсчета, связанной с центром масс:
Мти Рм = М и - V = —----.
'	' М + т
При упругом столкновении в системе «центр масс» импульс и кинетическая энергия системы сохраняются (рис. 5.3).
107
Рм + Pm = 0, p'M + p'm = 0,
2	2	,2	,2	/ii\	/ л -1 \
Pm ,Pm_ Pm , Pm n2 I 1 4- 1 I - n'2l 1 + 1 I In I - I n' I 7-Г7 + -—’ Pm ~ +— - Pm ~	, Pm - Pm 
2M 2m 2M 2m	\M mJ \M mJ 1	1 1	1
Следовательно, скорость первой частицы йм после столкновения в системе центра масс по абсолютной величине остается постоянной:
I,- | Рм т^> 1 М	М + т
Направление вектора йм может быть любым (рис. 5.4).
Возвратимся в первоначальную систему отсчета. В этой системе скорость и'м первой частицы после столкновения равна:
5' = V + йм.
Вектор и' при постоянном по абсолютной величине значении вектора йм отклоняется на максимальный угол при условии перпендикулярности вектору йм. Это направление касательной из начала вектора V к окружности, образованной концами векторов и (рис. 5.5):
108
Максимальный угол отклонения образуется при М > т. Так, если М = 2т, то втвх = 30°. При М < т угол в может быть любым.
Задача 5.14. Два стальных шара падают на стальную плиту большой массы с высоты Н= 1 м. Масса М первого шара значительно больше массы т второго шара, М» т, второй шар движется точно по прямой за первым на небольшом расстоянии. На какую высоту поднимется второй шар после столкновения? Удары шара о плиту и соударение шаров считать абсолютно упругими.
Решение. При упругом ударе о плиту первый шар будет двигаться вверх со скоростью, равной по модулю конечной скорости падения:
(?! = yl2gH.
С такой же скоростью навстречу ему летит второй шар. В системе отсчета, связанной с первым шаром, скорость второго шара равна:
и'2 = 2иу.
После удара она изменяет направление на противоположное, модуль ее остается практически неизменным, так как М »т.
В системе отсчета «Земля» скорость второго шара и2 равна:
2 = и2 +	= 301-
Отсюда высота подъема h второго шара:
и22 9uf_92gH п — — —----—--------— ул .
2g 2g 2g
h = 9 м.
Задача 5.15. Масса ракеты с топливом т0 = 106 кг. Сколько топлива Am потребуется израсходовать для достижения ракетой первой космической скорости о = 8 10® м/с, если скорость истечения газовой струи относительно ракеты равна и = 4 • 10® м/с?
Влияние сопротивления воздуха и силы тяжести на процесс разгона ракеты не учитывать.
Решение. По закону сохранения импульса
	udm + mdb = 0,
dm т	dv	J dm _ 1 и	„ т	и то и	°
, т	d In	= —, и	= е и,	т = тое и zn0
109
т = 10V2 « 1,35 105 кг.
Am = m0 - m, /\т и 8,65-105 кг.
Этот результат показывает, что одноступенчатой ракетой очень трудно осуществить запуск спутника, так как более 80% массы ракеты должно быть в виде горючего.
Задача 5.16. «Миллисекундный пульсар» — источник излучения во Вселенной, испускающий очень короткие импульсы с периодом от одной до нескольких миллисекунд. Поскольку частота этого излучения находится в радиодиапазоне, хорошим радиоприемником можно принимать его отдельные импульсы и очень точно определять период колебаний.
Радиоимпульсы возникают от поверхности особого типа звезды, так называемой нейтронной. Такие звезды представляют собой очень плотные звездные образования, имеющие радиус несколько десятков километров, массу, приблизительно равную массе Солнца, и быстро вращающиеся вокруг своей оси. Из-за этого вращения нейтронная звезда немножко расплющивается.
Предположим, что гр — расстояние от центра звезды до ее поверхности у полюса вращения, а ге — расстояние от того же центра до поверхности у экватора.
ге - г п
Тогда коэффициент сплющивания звезды можно выразить так: е =-------. Рас-
ГР
смотрим нейтронную звезду, имеющую массу 2,0 • 1О80 кг, средний радиус 1,0 104 м, период вращения 2,0 10 2 с.
1. Вычислите коэффициент сплющивания, если гравитационная постоянная равна 6,67 -10-11 Нм2/кг2.
Из-за потерь энергии вращение звезды постепенно замедляется, поэтому сплющивание будет уменьшаться. Однако звезда имеет твердую кору, которая «плавает» на поверхности жидкой сердцевины (ядра). Время от времени в коре происходят сотрясения, что приводит к скачкообразному изменению ее формы. Обнаружено, что во угловая скорость коры изменяется. Это изоб
ражено на рисунке 5.6, где по горизонтальной оси отложено время (в сутках), а по вертикальной — угловая скорость коры (в радианах в секунду).
2. Вычислите радиус жидкого ядра 7?я на основе данных рисунка 5.6. Считайте, что плотности коры и ядра одинаковы, а изменением формы ядра можно пренебречь.
314.164-
314.163
314.162
314.161
314.160
314.159
314.158
-1,0 0,0 1,0 2,0 3,0 4,0	5,0
Рис. 5.6. время и после такого сотрясения
Решение. 1. Представим себе цилиндр с площадью поперечного сечения S от поверхности нейтронной звезды до ее центра. Этот цилиндр содержит вещество звезды массой т1 = pSr.
110
Вещество в этом цилиндре при отсутствии вращения находится в гидростатическом равновесии при равенстве полярного гр и экваториального ге радиусов.
При вращении звезды с угловой скоростью в) в системе отсчета, связанной с вращающейся звездой, на вещество в цилиндре действует сила инерции
= mYa>2 * ,	(1)
Г
где — — расстояние до центра масс цилиндра в случае постоянной
плотности вещества р. Цилиндр не будет двигаться от центра звезды в том случае, если на него сверху, в направлении к центру звезды, действует равная по модулю сила F2, обусловленная весом избыточного слоя вещества толщиной h на экваторе:
F2 = m2g,	(2)
^L = pShG^-, 2	г2
ffl2r4 * * * * * *
Л =------,
2Gm
(314Д6)2 (104)4
2 -6,67 IO'11 2 IO30
(3)
« 3,7 (м).
e = -, e = —= 3,710*. г	104
2. Для определения радиуса жидкого ядра используем закон сохра-
нения момента импульса. В момент времени t = 0 твердая кора враща-
ется с угловой скоростью O>i, жидкое ядро вращается с угловой скорос-
тью (Oq. В результате взаимодействия коры с ядром угловая скорость
вращения коры и ядра становится одинаковой и равной а>2. Угловая
скорость вращения коры уменьшается на Л«эк = а>2 - а угловая
скорость вращения ядра увеличивается на Л«эя = (02 - а>0.
По закону сохранения момента импульса:
7-Да>_ + -LAfti =0,	1=1- 1Я,
л	л	IV	tv	'	IV	л*
111
°^тягя (®2 - ®о) + 0,4\тг2 - тяг2}(®2 - <yj = О, тяг2(а>} -®о) = тг2^ -а>2), j^pr2(co1 - о>0) = -|лгг3рг2(®1 -®2)>
Гя
= 10<^
V 0,0047
м « 9,8 103
м.
Задача 5.17. Ученик наблюдает падение камня с высоты h над поверхностью Земли в системе отсчета, связанной с Землей. В начальный момент времени камень покоился, следовательно, его кинетическая энергия была равна нулю:
= о-
Потенциальная энергия системы «Земля — камень»:
Epi = mgh.
К поверхности Земли камень подлетает со скоростью у, которую можно рассчитать из выражений:
2
и = gt, откуда о = yj2gh.
Следовательно, его кинетическая энергия у поверхности Земли
„ my2 m2gh
= — = —= mgh.
Потенциальная энергия системы «Земля — камень» в этом положении равна нулю:
= 0.
Таким образом, ученик убедился, что в его системе отсчета закон сохранения механической энергии выполняется:
Следовательно,
+ Ер1 =	0 + mgh = mgh,
Ek2 + Ер2 -	mgh + 0 = mgh.
Ekl + Ер1	= Ек2 + £p2.
112
Второй ученик наблюдает падение этого же камня в системе отсчета, связанной с лифтом, движущимся вертикально вниз со скоростью и относительно поверхности Земли. В начальный момент времени камень в системе отсчета, связанной с лифтом, имеет скорость и, направленную вертикально вверх, следовательно, его кинетическая энергия
р, kl 2
При этом камень находится на высоте h над поверхностью Земли, поэтому потенциальная энергия взаимодействия системы «Земля — камень» Е'р^ = mgh.
У поверхности Земли кинетическая энергия камня в этой системе отсчета равна нулю, так как скорость камня относительно Земли становится равной скорости лифта: Ej2 = О.
Потенциальная энергия системы «Земля — камень» в этом положении также равна нулю: Е'р2 - 0.
Так как
2
E'ki + ^1 = —~— + mSh, E'k2 + Е'р2 = О, второй ученик приходит к выводу, что механическая энергия системы «Земля — камень» не сохраняется. Каким образом можно разрешить возникший парадокс?
Рис. 5.7.
a«g
		
	1	
		
Решение. Для разрешения и объяснения парадокса выполним расчеты в двух инерциальных системах отсчета. Первая из них связана с центром масс системы «Земля — камень» (рис. 5.7), вторая движется с постоянной скоростью V относительно первой по направлению к Земле.
113
В первой системе отсчета начальные значения кинетических энергий камня и Земли были равны нулю:
= 0.
Начальное значение потенциальной энергии системы тел «Земля — камень»:
Ер1 = mgh.
В момент подлета камня к поверхности Земли потенциальная энергия взаимодействия системы тел «Земля — камень» будет равна нулю:
Ер2 0.
Под действием сил тяготения камень при подлете к поверхности Земли приобретет скорость l>1; а Земля — скорость Up Следовательно, сумма значений кинетических энергий камня и Земли в этот момент составит:
„ тпр? Мил
Ek2 =---- +------ >
2	2
где М — масса Земли.
Из третьего закона Ньютона следует, что модули сил, действующих на камень и Землю, равны между собой:
*i =f2.
Применяя второй закон Ньютона, получим:
mg = Ма,
где g и а — ускорения камня и Земли, получаемые ими при взаимодействии.
Следовательно, скорости камня и Земли в момент подлета камня к поверхности Земли будут иметь следующие значения:
где hi и Л2 — пути, пройденные камнем и Землей до столкновения.
Сумма кинетических энергий камня и Земли в этот момент:
m2ghi M2ah2 ,	.. ,
Ек2 ~-------*-------— mghi +
2	2
Учитывая, что Ma = mg, a + h2 = h, получим:
Ек2 = mg(fii + h2) = mgh.
Таким образом, закон сохранения механической энергии в первой инерциальной системе отсчета выполняется:
Ек\ + Ер1 = 0 + mgh, Ek2 + Ер2 = mgh + 0,
114
следовательно,
Ekl + Epl = Ek2 + Ер2-
В инерциальной системе отсчета, связанной с лифтом (рис. 5.8), в начальный момент времени камень и Земля имеют одинаковую скорость и, следовательно, сумма их кинетических энергий
ти2 Ми2
Е^у =----+------
2	2
Потенциальная энергия системы тел «Земля — камень» в этот момент равна:
Epi = mgh.
В момент подлета камня к Земле потенциальная энергия взаимодействия системы «Земля — камень» равна нулю: Е'р2 - 0. Сумма кинетических энергий Земли и камня в этот момент £^2-
ТПРп MUo ~ ----------
Скорости камня и2 и Земли и2 в этот момент времени можно оп-
ределить из выражений:
Ну = ut - и2 = Ju2 -2gHy,
t>2 = O-gt,
rr	at2
H9 = ut -i---,
2	2
u2 = и + at, u2 = у u2 + 2aH2 ,
где Ну и H2 — пути, пройденные камнем и Землей до столкновения, а g и а — ускорения, приобретаемые камнем и Землей за время движения.
Подставим значения и2 и и2 в выражение для кинетической энергии Е'к2 :
E'k2
и2 + 2aH2j = ~~ о2 t-и2 + {МаН2 -mgHyj.
Учитывая, что соотношение между ускорениями камня и Земли остается прежним [mg = Maj, так как силы и ускорения инвариантны относительно инерциальных систем отсчета, а Н2 - Ну - h, получим:
ти2 Ми2
Ek2 = —g-+—g- + mSh-Л z
115
Таким образом, закон сохранения механической энергии и во второй инерциальной системе отсчета:
ти2 Ми2
Eki + Epi ~ —g— + —~
А л
то2 Ми2	.
Ек2 + Ер2 - —-— 4-~+ О,
Л	и
следовательно,
-Ек + Е'р1 = Е'к2 + Е'р2-
Суть парадокса можно уяснить лучше, если провести нений кинетической энергии Земли в двух инерциальных счета:
выполняется
расчет изме-системах от-
- А’
АЕ*2 - -А-2’
i\Eky = Mah2,
&Ek2 = МаН2.
Учитывая, что Ma = mg, получим:
. „	, at2	( at2
AEkl = mgh2 = mg-, ^Ek2 = mS\ & +-
2	12
Сравнивая полученные выражения изменений кинетической энергии Земли, приходим к выводу, что изменение кинетической энергии Земли во второй системе отсчета больше изменения кинетической энергии в первой системе отсчета на величину, равную:
ЛР л г	(	at2\	at2
^Еь2 -	= mg\ ut +---- - mg------= mgut.
\	2 /	2
Учитывая, что gt = l>, получим:
AE*2 -	= m-v2-
Это выражение показывает, что изменение кинетической энергии Земли в системе отсчета, движущейся со скоростью о, в два раза превосходит изменение кинетической или потенциальной энергии камня. Если в первой системе отсчета, как показал расчет, изменением кинетической энергии Земли можно пренебречь, то во второй системе отсчета, в которой Земля движется, изменением ее кинетической энергии пренебречь нельзя!
Глава 6
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Задача 6.1. Точка подвеса математического маятника длины L совершает горизонтальные колебания; при этом ее координата х меняется со временем t по закону х = а • cos tut. Считая колебания малыми, найти амплитуду и фазу вынужденных колебаний маятника.
Решение. Рассмотрим математический маятник, частота малых колебаний которого равна to. Из формулы
находим длину L такого маятника:
При малых колебаниях можно считать, что все точки маятника движутся по горизонтальным прямым. Пусть амплитуда колебаний груза маятника такова, что точка А, находящаяся на расстоянии L от груза, колеблется с амплитудой а.
Колебания маятника, очевидно, не изменятся, если мы сделаем точкой подвеса маятника точку А и будем поддерживать ее колебания такими, чтобы ее смещения остались прежними в каждый момент времени.
g
При этом если 1<L (или 1<——), то, как видно из рисунка 6.1, а: а2
Ь L	ag
~ = ~Г—7 ’	Ь =-----Г •
a L - I	g -
Фаза колебаний маятника в этом случае равна at.
Если l> L (рис. 6.1, б), то
L - L ь - ag я I - L	1а2 - g
В этом случае фаза колебаний равна at + л.
117
Рис. 6.2.
Рис. 6.3.
Задача 6.2. При слабом ударе футбольного мяча о стенку он деформируется, как показано на рисунке 6.2. При этом деформация X мяча много меньше его радиуса, и можно с хорошим приближением считать, что давление р воздуха в мяче в процессе удара не меняется. Пренебрегая упругостью покрышки, оценить время соударения мяча со стеной. Провести числовой расчет этого времени для случая, когда масса мяча т = 0,5 кг, давление в нем р = 2 • 10s Па и радиус мяча R = 12,5 см.
Решение. Во время удара на мяч действуют сила реакции N со стороны стенки и сила атмосферного давления Fa.
Согласно третьему закону Ньютона сила N равна по модулю силе давления FK мяча на стенку. Так как упругость покрышки не учитывается, то
N = Гд = pS = рлг2,
118
где S = яг2 — площадь соприкосновения мяча со стенкой. Направлена сила N перпендикулярно к стенке, т.е. по горизонтали вправо (рис. 6.3).
Для того чтобы найти силу атмосферного давления, разобьем поверхность мяча на малые участки площадью AS;. На каждый участок действует сила атмосферного давления (рис. 6.3), направленная перпендикулярно к поверхности и равная по модулю
Ft =
где р0 — атмосферное давление. Из соображений симметрии можно утверждать, что сумма проекций всех сил Ft на вертикальное направление равна нулю.
Поэтому равнодействующая Fa = X-f; направлена горизонтально и равна по модулю:
Fa = X Ff cos а = р0 X AS; cos а.
Но AS; cos а — это площадь проекции i-ro участка на вертикальную плоскость, а X AS/ cos а — сумма площадей таких проекций, равная площади проекции поверхности мяча:
X AS; cos а = яг2.
Следовательно,
F& = Ро^г2.
Найдем теперь модуль равнодействующей F сил N и Fa:
1^1 = Н “ l*°I = (р ~ р°Уг2 = я(р ~ Ро)[д2 - (л - х)2] =
=	- Ро)(2Ях - х2).
Поскольку деформация х мяча мала по сравнению с его радиусом, то величиной х2 можно пренебречь по сравнению с величиной 2Rx. Поэтому
|р| » 2яЯх(р - р0).
Так как сила F направлена противоположно деформации, можно записать:
F = -kx,
119
где h = 2лЛ[р - Po). Таким образом, модуль силы F пропорционален деформации х. Под действием такой силы тело совершает колебания с периодом:
где т — масса тела.
Очевидно, что время г соударения мяча со стенкой равно половине периода колебаний:
Т 1™ I	о ш-3
г = — = л.— « л ---г я 8 • 10 с.
2 V h у 2лН(р - р0)
Задача 6.3. Громкоговоритель имеет диффузор с лобовой площадью S = ЗООсм2 и массой т= 5 г. Резонансная частота диффузора v0 = 50 Гц. Какой окажется его резонансная частота, если поместить громкоговоритель на стенке закрытого ящика объемом Vo =40 л, как показано на рисунке 6.4? Расчет вести в предположении, что температура воздуха внутри ящика не изменяется при колебании диффузора.
Решение. Диффузор представляет собой пружинный маятник, и его резонансная циклическая частота равна:
®о =	,	(1)
V т
где k0 — жесткость упругой системы диффузора. Отсюда
k0 = OJ^m.	(2)
Когда громкоговоритель помещают в ящик, то при смещении диффузора от положения равновесия на него действует дополнительная сила
F=(p-p0)S,	(3)
где р — давление воздуха в ящике, а р0 — атмосферное давление вне ящика. Так как температура воздуха в ящике не меняется, то по закону Бойля — Мариотта
pV = PoVo, р = ^-.
Подставляя это выражение в формулу (3), получаем:
Vn-V
F = p0S-^—.	(4)
Так как Vo - V = Sx, где х — смещение диффузора, то
120
Vo
(5)
(ввиду того, что изменение объема мало, принимаем в знаменателе V = Vo). Из этой формулы следует, что воздух в ящике действует по-
добно пружине с жесткостью
1 v0
Общая жесткость упругой системы равна:
s2
k ~ Jiq + hy — (Dqtti ч——
а резонансная частота v диффузора:
Pf2 «115 Гц. 4л-2Т07п
Рис. 6.4.	Рис. 6.5.
Задача 6.4. Два шара, массой т каждый, соединенные пружиной жесткости k, находятся на гладкой горизонтальной поверхности. Определите период собственных колебаний этой системы.
Возможные способы решения задачи.
Первый способ. Оба шара будут совершать колебания около центра масс системы — точки О, являющейся центром симметрии. Поэтому можно считать, что каждый шар колеблется независимо от другого около точки О на пружине, имеющей меньшую длину (рис. 6.5). Жесткость fei такой укороченной пружины в два раза больше жесткости всей пружины.
121
Записав выражение второго закона Ньютона для колебаний каждого шара, получим:
-kyX = тх", х --------х, a>Q = —,
т	т
Х" = ~O)qX, 	„ р
Т = 2л, —.
V 2k
Второй способ. При энергетическом подходе напишем выражение закона сохранения энергии:
ти2 ти2 k(2x)
-----+-----+ —-—— = const.
2	2	2
Продифференцируем обе части полученного уравнения:
2mw' + 4йхх' = 0, 2тх'х" + 4kxx' = О,
х"
2k — х.
т
Из последнего уравнения следует:
Т = 2л.
Задача 6.5. Два шара массами mj и m2 соединены между собой пружиной жесткости k. Каков период колебаний этой системы на гладкой горизонтальной поверхности после деформации пружины? Массой пружины пренебречь.
Решение. Центр масс системы при колебаниях находится в покое. Найдем положение центра масс. Выберем ось Ох проходящей через
Рис. 6.6.
периода независимых
центры шаров, начало координат в центре первого шара (рис. 6.6). Тогда для координаты хц м центра масс выполняется равенство:
т21 хц.м =	•
7П1 + т2
Решение задачи сводится к определению колебаний одного из шаров (любого) относитель-
но центра масс системы.
где fej и k2 — жесткости частей пружины от шаров до центра масс.
122
Жесткость пружины обратно пропорциональна ее длине, поэтому: kl = k^ = knn^t
*ц.м	™2
k2=k~L~ = kn±^'
I - *ц.м
Период колебаний шаров равен:
Т = 2л& = 2лЕ^З,
у kr V klmi + т?)
г=2 Б = 2^Г ..т
у k2 у klm^ + т2\
Выражение тппр = -	— называют приведенной массой системы
+ пг2
тел, поэтому:
Задача 6.6. Невесомая штанга длиной L одним концом закреплена в идеальном шарнире, другим опирается на пружину жесткостью k. На штанге находится груз массой т. Определите зависимость периода колебаний штанги с грузом от расстояния I до центра масс груза от шарнира (рис. 6.7).
Рис. 6.7.
Рис. 6.8.
Возможные способы решения задачи.
Первый способ. Запишем закон сохранения для произвольного момента времени t, в который деформация пружины равна х:
йх2 то2
	1	= const, 2-------2
где и — скорость груза.
(1)
123
Из рисунка 6.7 видно, что
I и = —х'.
L
(2)
Подставим (2) в (1) и продифференцируем:
kx2 т I2 о , 2kxx’ т I2 _ , „ -----1-----z-x = const,--------------1------2х х = О,
2	2 ь2	2	2 L2
kL2
ml2
(3)
2 kL2
®о = —Г’
ml2
2я „1т
--= 2л—J—
®0 L V k
Второй способ. Рассмотрим силы, действующие на штангу (рис. 6.8), и запишем условие равновесия
(1)
При смещении
^-^£=0.
груза на х по вертикали деформация х^ пружины
равна х1 = х—, а
сила упругости равна:
^упр = kxl = kx — 
(2)
Подставив (2) в
(1), получим:
кг kL2
N = —— х,	тх'
I2
kL2
Т
х" = -а>ох,
Рис. 6.9.
2 kL2
®о = —г,
ml2
_ 2л „ I
Т =--= 2л—
®о L
Задача 6.7. Вычислите скорость звука в воздухе при давлении 2 10s Па и плотности 2,6 кг/м8, считая колебания давления воздуха адиабатическими.
Решение. Рассмотрим процесс возникновения звуковой волны в воздухе. В результате быстрого смещения пластины (рис. 6.9) у ее поверхности происходит повышение давления воздуха на величину Др и повышение его плотности на величину Др. Сжатый воз-
124
дух расширяется и вызывает сжатие прилегающего к нему слоя воздуха. Этот процесс распространяется дальше. При распространении волны сжатия масса Дтп воздуха, проходящего за время At через площадку S перпендикулярно направлению распространения волны, может быть выражена так:
Дтп = ApSvAt,	(1)
где р — плотность воздуха и и — скорость распространения волны сжатия.
Отсюда следует, что изменение импульса равно:
Amv = ApSvI 2 * At.	(2)
Это изменение импульса вызвано избыточным давлением Др и равно импульсу силы F за тот же интервал времени At:
FAt = Amv,	. .
ApSAt = ApSv2At.	(3)
Отсюда для скорости распространения волны сжатия находим следующее выражение:
<4> V Др
Связь между давлением и объемом газа в адиабатном процессе определяется соотношением:
pVr = const,	(5)
где у—постоянная величина, равная для воздуха 1,4.
Из уравнения т = pV при условии т = const следует:
Дтп = ApV + AVp = О,
Др = -^р.	(6)
Из уравнения (5) следует:
ApV7 + Д(Ух)р = О,
«Г)£=	мк.	7
V7	V
Подставляя (6) и (7) в (4), получаем:
I р	. 2 • 10б м м
t>= r—, ст = .1,4----------»328—.
Y р V 2,6 с с
125
Задача 6.8. В трубу органа вдувается воздух при температуре 17 °C, и при этом труба издает звук с частотой 440 Гц. При какой температуре вдуваемого воздуха эта же труба будет издавать звук с частотой 466 Гц?
Решение. Резонансная частота трубы при изменении температуры воздуха изменяется потому, что длина резонансной звуковой волны для трубы остается неизменной, но резонансная частота с изменением температуры изменяется, так как изменяется скорость звука:
1 =	=	(1)
П v2
=	(2)
^2 и2
Найдем выражение, связывающее скорость звука в воздухе с температурой.
Используем известное соотношение:
и уравнение состояния идеального газа:
pV = — RT.
М
Из (1) и (2) следует:
£L= К
«2 УГг'
Из (2) и (6) следует:
т2=4г1’
(46б)2
Т2 = ---^290 К = 317 К.
(440)2
(3)
(4)
(б)
(6)
(7)
Задача 6.9« Найдите частоту звука, регистрируемого приемником при частоте источника звука 450 Гц, скорости звука в воздухе 340 м/с для следующих случаев:
1.	Источник звука движется в воздухе со скоростью 34 м/с к неподвижному приемнику.
2.	Приемник звука движется в воздухе со скоростью 34 м/с к неподвижному источнику звука.
126
3.	Источник и приемник звука движутся навстречу друг другу, скорость каждого из них относительно воздуха 17 м/с.
Решение. 1. Рассмотрим случай движения источника колебаний со скоростью о; меньшей скорости распространения волн в среде и: и<и (рис. 6.10).
Точки О, О15 О2, Оз показывают положение источника колебаний через интервалы времени, равные периоду колебаний Т. В тот момент, когда источник находится в точке Оз, фронты волн, испущенных источником в точках О, О1, О2, будут сферическими с радиусами ЗиТ, 2иТ, иТ.
Рис. 6.10.
На рисунке 6.10 видно, что фронт каждой последующей волны находится внутри фронта предыдущей. В этом случае длина излученных волн, равная расстоянию между фронтами волн, различна в разных направлениях и отличается от длины волны неподвижного источника:
127
Ло = иТ. Длина волны Я^, излученной источником по направлению его движения, меньше длины волны Яд на величину иТ (рис. 6.11).
Длина волны Я2, излученной в направлении, противоположном движению источника, больше Яо на величину иТ (рис. 6.12). Тогда:
/	\ и - и
Л-1 = Яо - иТ = Т\и - и) =-,
И)
, и + и Я2 = Яр 4-	= TI и 4~ и I — - ,
И)
где Vq — частота излучения.
Рис. 6.11.
Неподвижные приемники, регистрирующие эти волны в точках А и 5, будут регистрировать волны с частотами V] и v2, отличными от v0:
и
(1)
V - “ -
Vo —   — -----.
Л2	, о
л	1 4- -
U
Например, при приближении источника звуковых колебаний тон звука повышается. Это легко заметить, слушая звук сирены приближающегося поезда. При удалении источника звука высота тона понижается .
2. Изменение частоты волн наблюдается и при движении приемника относительно неподвижного источника звуковых волн. В этом случае длина волны в среде остается неизменной:
и
= Л2 — Aq = и?1 = —, но скорость распространения волны относительно приемника изменяется.
128
В случае приближения приемника к источнику колебания со скоростью w скорость волны будет равна: и + ю, в случае удаления приемника со скоростью w скорость волны равна: и - w.
Частота колебаний, регистрируемая приемником, равна соответственно:
, U+W	U + W	(	оЛ
П = ~	= И) =	1+~ >
Ло и	\	uj
(2) и - w и - ш f ш
г2 = —-— =	Vo = vo 1	•
Лп и	\ uj
Сравнивая выражения (1) и (2), приходим к выводу: и движение источника, и движение приемника приводят к изменению частоты, но эти изменения различны.
3. Если источник колебаний и приемник движутся навстречу друг другу со скоростями о и w относительно среды, то приемником регистрируют волны с частотой:
1 + -
V = И)---.	(3)
1--и
Подставляя данные задачи в формулы (1), (2) и (3), получим:
У! = 500 Гц, у2 = 495 Гц, рз = 497Гц.
Задача 6.10. При подвешивании груза массой 10 кг стальная струна длиной 2 м с площадью поперечного сечения 0,1 мм2 удлиняется на 1 см. Плотность стали 7,8 108 кг/м8. Какова скорость звука в стали?
Решение. При ударе по стальному стержню под действием силы F происходит деформация стержня (рис. 6.13). Увеличение деформации прекращается, когда сила упругости Fynp становится равной внешней действующей силе F:
где Е — модуль Юнга, S — площадь поперечного сечения, Л/ — удлинение, I — длина образца. Если средняя скорость перемещения ударяющего тела и, а скорость распространения деформации (скорость звука) с, то:
AZ = uAt, I = c\t, — = — , Г =	.
I c	с
129
Рис. 6.13
Под действием силы F за время At пришли в движение со скоростью V атомы в объеме
ДР = SI = ScAt, их масса
Am = pAV = pScAt.
Следовательно:
FAt = &(mu) = Amu,
At = pScAtu, с
Модуль Юнга Е стали определяем по данным задачи для струны:
„ Fl hi =---,
SAI
Е =
10-9,8-2
10 7•102
Па « 1,96-1011 Па.
Отсюда получаем:
1,96-1011 м з м
5	О «5 10	.
У 7,8-103 с	с
Задача 6.11. Дана проволочная вешалка, которая качается с маленькой амплитудой в плоскости чертежа относительно заданных положений равновесия (рис. 6.14). В положениях а и б длинная сторона расположена горизонтально. Две другие стороны равны между собой. Во всех трех случаях (а — в) возникают колебания с одинаковыми периодами. Где лежит центр масс и каков период колебаний?
Из эскизов не могут быть сняты другие данные, кроме размеров. В частности, распределение массы вешалки в деталях нам неизвестно.
Решение. Как видно из рисунка 6.15, центр масс вешалки лежит на прямой, которая одновременно является высотой, медианой и биссектрисой равнобедренного треугольника. Обозначим Sa, Sg, SB расстояния от центра масс до точек подвеса в случаях, изображенных на рисунке 6.15.
Так как во всех трех случаях колеблющаяся вешалка является физическим маятником, то период колебаний этого маятника (вешалки) можно определить как
Т = 2 л,---,
V mgS
(1)
130
где I — момент инерции вешалки относительно оси колебаний. Согласно теореме Штейнера
I = I0+mS2,	(2)
где 10 — момент инерции вешалки относительно ее центра масс, S — расстояние от центра масс до оси колебаний.
Из выражений (1) и (2) получаем:
m „ I0+mS2
Т = 2л, —----
У mgS
2
Io + mS2
S2-W—1 + ^ = 0.
V 2л7 m
(3)
Так как по условию периоды колебаний вешалки во всех трех случаях равны, то уравнение (3) имеет не более двух корней. Другими словами, два значения из трех — Sa, S6, SB — равны между собой.
Учитывая соотношение SB > Sa + S6, получаем, что равными могут быть только расстояния Sa и S6.
Рис. 6.15.
Рис. 6.14.
Из условий Sa = Sg и Sa + S6 = 10 см получаем:
Sa = Sg = 5 см, SB = д/212 + б2 см = 21,6 см.
Зная два разных корня Si и S2 уравнения (3), из теоремы Виета можно получить:
Si + S2 = £ — \ /
Si + &2 о I *^а + -------  = 2 л, —------S-
g V g
Подстановка числовых данных приводит к результату: Т = 1,03 с.
131
Примечание. Формулу (1) нетрудно вывести. При отклонении вешалки на малый угол а от положения равновесия на нее будет действовать момент сил М, возвращающий ее к первоначальному положению:
М = -mgSa.
Используя второй закон динамики для вращательного движения
М = Is = la", получим дифференциальное уравнение „ mgS а =-----------------------------------а.
I
Решением этого уравнения является гармоническая функция с периодом
Т = 2 л-,/——.
у mgS
Доказать теорему Штейнера попробуйте сами.
Задача 6.12. Частица движется вдоль положительной полуоси Ох под действием силы F, проекция Fx которой на ось Ох представлена на рисунке 6.16 (F2 = Fy = О).
Одновременно на частицу действует сила трения, модуль которой равен FTp=l,00 Н. В начале координат установлена идеально отражающая стенка, перпендикулярная оси Ох. Частица стартует из точки х0 = 1,00 м с кинетической энергией F^ = 10,0 Дж.
Выполните следующие задания:
1.	Определите путь, пройденный частицей до ее полной остановки.
2.	Представьте графически зависимость потенциальной энергии частицы в поле силы Fx от координаты х.
3.	Постройте качественный график зависимости проекции скорости их от координаты х.
Рнс. 6.16.
Рис. 6.17.
Решение. 1. В поле силы Fx можно ввести потенциальную энергию Ер (аналогично потенциальной энергии в поле силы тяжести).
Работа силы трения является мерой изменения механической энергии частицы:
Ар =	+Ер)-
Так как остановиться частица может только у стенки (в других случаях равновесие невозможно), то перемещение ее происходит из х0 до О:
-РтрЗ = -Ek - Fxx0,
S = Ek + Fxx0 = 2() м
F тр
2. Так как зависимость потенциальной энергии частицы от координаты выражается соотношением
Ер - Еро + Fxx,
то график Ер(х} является линейной функцией. При Ер() = О прямая проходит через начало координат (рис. 6.17).
Рис. 6.18.
133
3. При движении частицы к стенке ее ускорение равно
F -F	F +F
* тр	х X ' х тр
а1х =------а при движении от стенки а2х =-----------.
т	т
График зависимости	для обоих случаев (и0х>0,	бу-
дет состоять из половинок разных парабол. Это следует из выражений:
2	9	9 ^х ~ ^тр	2	9	9 ^х + ^тр
»xk = 2а1хх = 2-----х,	. = 2а2хх = 2----- х.
т	х\ь+1]	т
Отсюда °2хк _ Fx ~ -Ртр _ 9 и2, ч Fx + ?тр 11
Следовательно, отношение последовательных отрезков по оси Ох равно:
_ 11
В зависимости от направления вектора начальной скорости графики будут иметь вид, представленный на рисунке 6.18 или 6.19.
Рис. 6.19.
134
Задача 6.13. В начале этого века была предложена модель Земли, в которой предполагалось, что Земля представляет собой шар радиусом R, состоящий из однородной изотропной твердой оболочки и жидкого ядра радиусом Rc (рис. 6.20). Скорости Dp ти vs сейсмических продольных и поперечных волн, так называемых волн р н S, внутри оболочки постоянны. В ядре продольные волны имеют скорость иср, а поперечные волны не распространяются. Землетрясение в точке Е на поверхности Землн образует сейсмические волны, которые пробегают сквозь Землю и регистрируются на поверхности наблюдателем, который может установить свой сейсмограф в любой точке X земной поверхности. Угловое расстояние между точками Е и X равно Z ЕОХ = 20, где О — центр Землн.
Выполните следующие задания:
1.	Покажите, что сейсмические волны, распространяющиеся только в оболочке по прямой, достигнут точки X за время t (время пробега волн после землетрясения), определяемое по формуле:
где v = vp для волн р и v = vs для волн S.
( R
2.	Если положение точки X такое, что 0 > arccos —— , то сейсмические вол-k R)
ны р достигают наблюдателя после двух преломлений на границе между оболочкой и ядром. Начертите траекторию распространения такой сейсмической волны. Получите соотношение между углом 0 и углом падения i сейсмической волны р на границу между оболочкой и ядром.
3.	Используя данные R= 6370 км, Rc = 3470 км, ц, = 10,85 км с-1, us = 6,31 км с-1, иср = 9,02 км с-1 и результат, полученный в задании 2, начертите качественный график зависимости 0 от г. Прокомментируйте физические последствия формы этой зависимости для наблюдателей, находящихся в различных точках земной поверхности. Нарисуйте графики зависимости времени пробега волн р и S от угла 0 для 0 < 0 < 90°.
4.	После землетрясения наблюдатель измеряет задержку по времени между прибытием волны S вслед за волной р, равную 2 мин 11 с. Определите угловое расстояние, измеренное от центра Земли, между точкой землетрясения и наблюдателем, используя данные задания 3.
5.	Наблюдатель, который сделал измерение в задании 4, замечает, что через некоторое время после прибытия волн р и S последовали еще два отсчета на сейсмографе, причем промежуток времени между ними равен 6 мин 37 с. Объясните этот результат и проверьте, что он действительно связан с угловым расстоянием, определенным в предыдущем пункте.
135
Рис. 6.22, б.
Рис. 6.22, а.
Решение. 1. Прямолинейное распространение волн возможно, если отрезок ЕХ весь лежит в оболочке (рис. 6.21). При этом время распространения волн, имеющих скорость о, равно:
EX 2R sin в „	(Rc
t =---=--------- для в < arccos -- .
и и	\R)
( R У
2.	Возможные пути волн р в случае 0 > arccos —— показаны на \ R J
рисунках 6.22, а и 6.22, б (в обоих случаях АВ || ЕХ). Если i — угол падения волны на границу «ядро — оболочка», аг — угол преломления, то по закону преломления
sini _ ир sin г и.„ ср
136
Тогда из треугольника АОЕ по теореме синусов для угла в получим (в случае а):
л лло f • ° ср sin i	. Rc sin
О = 90 - i + arcsm —----F arcsm — ---- .
I	R )
В случае б получим:
„ „„„ f . уср si11 *	. Rr sin i'l
0 = 90 + i - arcsm------+ arcsm —-----
I °P	R )
(i может меняться от О до 90°).
3.	Графики зависимости 0 от i приведены на рисунке 6.23 (для каждого значения t мы имеем два возможных значения в). Видим, что существуют минимальное и максимальное значения в: 0min = 75°35' и 0тах = Ю4°25' при 1=55°. Поэтому преломленные волны смогут зарегистрировать только наблюдатели, находящиеся в зоне М2М2 (рис. 6.24), а «прямые» волны — на участках М^Е и ЕМ^. Так как
0а = arccos = 57° < 0min = 75°35', V	11L1I1
существуют зоны (М3М4 и	где землетрясение чувствуется
очень слабо — туда волны могут дойти только после отражения от одной из границ ядра или оболочки.
Рис. 6.23.
Рис. 6.24.
137
Рис. 6.25.
График зависимости времени пробега волн р и S от угла в дан на рисунке 6.25. Для О < в < 0О время определяется выражением:
_ 27? sin#
и
(и = Up ИЛИ U = Us), в зону 0О < в < волны практически не попадают, в зону #т;п < 0 < 90° попадают только преломленные волны.
4.	Учитывая, что время распространения волны по прямой равно
t =-------- (и = и„ или и = Us), получим, что задержка волны S рав-
»1	г
на At12 = ts - tp = 2R I—-— sin 6* (для Us<up).
V>S Up)
Отсюда угловое расстояние
UsUnAt
ЛЕОХ = 20 = 2 arcsin--------------r « 17’84'.
2-R(l>p - 4s)
Это соответствует 0 = 8,92° < 0O = 57° , т.е. волны действительно доходят до наблюдателя без преломления.
5.	Два последних отсчета вызваны отражениями волн на границе между оболочкой и ядром. Промежуток времени между этими отсчетами
.	„ /	\	2RRr cos 0
^34 = 2(ь>р - t>s)V-R + ЛС----------.
Подставив 0 = 8,92°, находим Д?34 «396,7 с « 6 мин 37 с, т.е. наше предположение подтверждается.
Глава 7
МОЛЕКУЛЯРНАЯ ФИЗИКА
Задача 7.1. Оболочка аэростата частично заполнена гелием, поэтому при подъеме в земной атмосфере давление газа внутри аэростата все время равно внешнему атмосферному давлению. Подъем происходит медленно, поэтому температура газа в аэростате одинакова с температурой атмосферного воздуха.
Как изменяется подъемная сила аэростата с высотой подъема, если температура линейно убывает с увеличением высоты?
Решение. Подъемная сила F аэростата объемом V определяется формулой
F = (Pi~P2)gV^	(!)
где pi — плотность атмосферного воздуха на той высоте, на которой находится аэростат, и р2 — плотность наполняющего аэростат газа.
Из уравнения Менделеева — Клапейрона следует, что между плот-
ностью газа и его давлением имеется соотношение р = RT.
М
Так как давление внутри аэростата равно давлению снаружи, то:
Pl
-^-RT = ММ2

P^=P^-.	(2)
мг M2
TT	m2	T-T
Ho p2 = i где m2 — масса наполняющего аэростат газа. Поэтому
соотношение (2) можно записать так:
PiK = ^i-zn2.	(3)
Подставив выражение (3) в формулу (1), получим:
(М, F = • \М2	)
Отсюда видно, что подъемная сила аэростата не зависит от высоты.
139
Задача 7.2. До какой температуры нужно нагреть воздух внутри оболочки воздушного шара объемом 500 м8, чтобы он мог поднять человека массой 70 кг? Масса оболочки шара равна 30 кг.
Решение. Для подъема человека архимедова сила, действующая на воздушный шар, должна превышать равнодействующую сил тяжести человека, оболочки шара и горячего воздуха в шаре:
РА > ("11 +
Сила Архимеда равна весу воздуха, вытесненного шаром: FA = m4g, где T/i4 — масса вытесненного воздуха, поэтому получаем уравнение
7П4 > TTlj + 77l2 + 772g .
Значения массы тп3 воздуха в шаре и массы 77i4 воздуха, вытес-
ненного шаром, определяются из уравнения состояния идеального газа:
pVM тл = ——, R7\
pVM mv =----,
RT2
pVM	pVM
-----> 771, + m2 -I-----,
RT\	RT2
n	pVM
2 > pVM I ------------1771,
T, ' 1
Примем, что атмосферное давление равно примерно 105 Па, температура атмосферного воздуха 300 К, молярная масса воздуха 29  10-3кг/моль. Подставляя числовые данные, получим:
Т2
____105 500 29 1° 3___к K 362 K; t2 > 89 °C. 10^500,29,101 10()
300
Задача 7.3. Дан воздушный шар с постоянным объемом V = 1,10 м3. Масса оболочки (объемом оболочки пренебречь) составляет ша = 0,187 кг. Шар должен стартовать прн окружающей температуре воздуха tj = 20 °C и нормальном атмосферном давлении р0 = 1,013  10s Па. Плотность воздуха при этих условиях Ру = 1,2 кг/м3.
Выполните следующие задания:
1.	Вычислите температуру t2, которую должен иметь нагретый воздух внутри шара, чтобы он мог свободно парить в воздухе.
2.	Воздух внутри привязанного на тросе шара нагревается до постоянной температуры ts = ПО °C. Вычислите силу, действующую на трос.
140
3.	Примем, что отверстие снизу шара завязано (плотность воздуха в нем остается тогда постоянной). Шар поднимается с постоянной температурой внутреннего воздуха ts = 110 °C в изотермической атмосфере при 20 °C и давлении на уровне Земли р0 = 1,013  10s Па. Вычислите высоту Л, которой достигнет шар при этих условиях.
4.	Шар, находящийся на высоте h (задание 3), смещается на высоту, приблизительно равную ЛЛ=10 м, из положения равновесия и затем отпускается. Опишите качественно, как он движется.
Решение. 1. Условие равновесия шара в воздухе запишем в виде
р. =р
где Fa — архимедова сила, равная F& = piVg, a FT — сила тяжести шара с воздухом: FT = p2Vg + m$g (pi и p2 — плотности окружающего воздуха при температуре Ту и воздуха в шаре при температуре Т2).
Тогда условие равновесия шара в воздухе можно записать как
fiVg = p2Vg + mQg, откуда
= (Pl -P2)v-	(!)
Из уравнения газового состояния
pV = — RT, р = -2-ЯТ, М	М
рМ	рМ
следует, что	Р1 = ——,	р2 = ——.
Отсюда
— = • (2)
Р2 Д
Из выражений (1) и (2) получаем:
Т2 = —-	(3)
рИ
Подстановка числовых данных приводит к результату Т2 = 341 К, или t2 = 68 °C.
2.	Если воздух в шаре нагреть до температуры Т2 = 383 К, то новое значение силы тяжести Е, , действующей на шар, равно:
FT =mag+p2Vg.
141
Для удержания шара в положении равновесия необходимо, чтобы сила F, действующая на трос, привязанный к шару, была равна:
F = Fa-Ft = piVg -(/no + p3Vg) = [(pi ~Рз)у -	(4)
Аналогично выражению (2) записываем:
Р1 = 2k
Рз Л
Из выражений (4) и (5) получаем:
F =
Г т А
Pi !--4- У-Шо
V '37
g = 1,2 Н.
(5)
(6)
3.	Из условия равновесия шара на искомой высоте h получаем:
phVg = mQg+p^Vg, Ph = m° у?--,	(7)
где р^ — плотность воздуха на высоте h.
С другой стороны, плотности воздуха рЛ и р^ в изотермической атмосфере связаны барометрической формулой:
Plgh
Ph = Р1е Р° .	(8)
откуда	h = In ,
Pig Ph
а с учетом выражений (5) и (7) запишем:
= Аь	.	(9)
Pig	+ р3 V Pig + P-J\v
гз
Подстановкой численных значений получаем: h « 843 м.
4.	При небольшой разности высот Л/г = 10 м по сравнению с высотой h = 843 м барометрическую формулу (8) можно представить в виде линейной функции:
Р1Я(й+АА)	pjgAA
РО	РО	I 1 PigM J
Ph+\h = Ple	= Phe ° х Ph 1-----------•
I Ро )
Следовательно, для шара, у которого отверстие закрыто, архимедова сила, действующая на него, равна:
Fa = Ph^hvg-
142
Изменение этой силы при малых изменениях высоты АЛ нетрудно
рассчитать:
AFa
ДА
PhPvS Vg, Ро
2 др = -PhPi^_VAfl_
Ро
Так как сила, действующая на шар, прямо пропорциональна смещению шара, то он совершает гармонические колебания, период которых равен:
Т = 2л
(m0 + р3У)р0 _ 2л (m0 + Р3У)Ро _ phprg2V g \ (mo + р3^)Р1
_ 2я 1ро_ и jgg с и з мин.
g у Pi
При получении этого результата мы не учитывали сопротивление воздуха, которое, с одной стороны, приведет к тому, что колебания будут затухающими, а с другой стороны, период реальных колебаний будет несколько больше рассчитанного.
Отметим, что в связи с большим периодом колебаний шара (около 3 минут) указанные поправки к полученному значению будут незначительными, так как сила сопротивления, зависящая от скорости, будет невелика.
Примечание. При решении этой части задачи мы не учитывали эффекта «присоединенной массы» воздуха.
Задача 7.4. В камеру сгорания реактивного двигателя (рис. 7.1) поступает в секунду масса т водорода и необходимое для полного сгорания количество кислорода. Площадь сечения выходного отверстия сопла двигателя S, давление в этом сечении р, абсолютная температура Т. Определить силу тяги двигателя.
Решение. Найдем массу водяных паров, образующихся при сгорании массы тп водорода. Из уравнения реакции горения водорода
2Н2 + О2 = 2Н2О
видно, что две молекулы водорода соединяются с одной молекулой
кислорода.
В результате получаются две
молекулы водяного пара.
Это
означает, что для сгорания одного киломоля водорода необходима половина киломоля кислорода и в результате реакции получается один кило-
т-г	m
моль воды. При сгорании v =-------
мв
киломолей водорода получится столько же киломолей водяного пара
Рис. 7.1.
143
(здесь Мв = 2 кг/кмоль). Поэтому при сгорании массы тп водорода получается масса ту водяного пара:
18
т1 = vMn = — т = 9т,
где М„ = 18 кг-кмоль-1.
Эта масса водяных паров вылетает из сопла двигателя за 1 с. Так как площадь выходного сопла двигателя известна, можно найти скорость и газа, выходящего из сопла. За 1 с из сопла двигателя будет выброшен объем пара V = uS. Если плотность пара равна р, то масса этого объема пара будет равна:
mr = pvS-
Отсюда
т, 9т и =---=----.
pS pS
Из уравнения Менделеева — Клапейрона
pV =
Мл находим неизвестную плотность пара: _ рмп V RT '
Так как за время At из сопла ракеты выбрасывается масса пара m,At с импульсом TTijAft), то на газ действует сила
- m, Atu
Fl =	1	=
At
Такая же по модулю сила, но направленная в противоположную сторону, действует на двигатель. Полная сила, действующая на двигатель (сила тяги двигателя), равна сумме реактивной силы Fx и силы статического давления F2 = pS, т.е.
F = пг}и + pS.
Обычно сопла ракетных двигателей устроены так, что давление р газа, выходящего из сопла, мало. Поэтому второй член в выражении для силы тяги двигателя мал по сравнению с первым и при расчетах им можно пренебречь:
144
Задача 7.5. Оцените, сколько литров воздуха расходует автомобильный двигатель при сжигании 1 кг бензина. Используйте при расчетах формулу С6Н14 как формулу бензина. Известно, что продуктами сжигания бензина являются соединения СО2, Н2О и СО.
Решение. Составим химическое уравнение:
С6Н14 + а  О2 —> b  СО2 + с  Н2О + d  СО.
Приняв с = 7 и d = 1 (по количеству атомов водорода и требованию четности атомов кислорода), получаем Ь = 5 и а = 9:
С6Н14 +9О2 —> 5СО2 + 7Н2О + СО.
Таким образом, на одну молекулу бензина при сжигании расходуется девять молекул кислорода.
Отношение массы кислорода тк к массе бензина mg Равно:
тк _ 9МК «б мб
Кислорода в воздухе по массе 23%, поэтому отношение массы израсходованного воздуха тк к массе бензина nig равно:
тв 9МК 9 • 32
ш6 ” 0,23М6 ” 0,23  86
Следовательно, на 1 кг бензина двигатель расходует минимум 15 кг воздуха. Вычислим объем 15 кг воздуха при нормальных условиях. Приняв М » 29 г/моль, получаем:
тп	т RT
— RT, У =-----------,
М	М р
15-8,31-300 з
-------ч--Г м
29-10-10"
«13 м?» 1,3-104 л.
Задача 7.6. Изготовлена модель парового реактивного двигателя. Водяной котел нагревается спиртовкой, мощность теплопередачи котлу 100 Вт. Пар из котла выходит через отверстие площадью 0,2 мм2. Определите силу тяги реактивного двигателя.
Решение.
FAt- \{ти\,	F-—'U,
'	!	At
„	Am
где F — реактивная сила, -- — секундный расход, и — скорость ис-
At
течения пара.
NAt = &тг,
Am N
At г
где N — мощность теплопередачи, г— удельная теплота испарения.
145
AV и = —- ,
AtS
где AV — объем пара, выходящий за t секунд, S — площадь сечения отверстия.
pAV = — RT, М
,r Am RT
AV =------,
M p
_ NMnRT _ N2RT rM\tSp r2MSp
F =
IO4 - 8,31- 373
XI £ XU XI.
(2,25б)2 • 1012 • 18  10 3 • 2 • 10 7 • 105
Задача 7.7. Основываясь на представлениях молекулярно-кинетической теории, оцените давление и температуру внутри Солнца. Масса Солнца 2 1О80 кг, радиус 7 • 1О8 м. В расчетах можно принять, что Солнце состоит в основном из атомарного водорода.
Решение. Согласно молекулярно-кинетической теории давление газа р связано с его температурой Т и концентрацией молекул п соотношением р = nkT, отсюда
Т = nk
Поскольку Солнце не расширяется и не сжимается, давление его внутренних слоев на любой глубине равно давлению вышележащих слоев, создаваемому действием силы тяжести F:
F
Р ~ s'
Отсюда следует, что для определения температуры на какой-то глубине внутри Солнца необходимо определить концентрацию атомов п на этой глубине и давление вышележащих слоев р.
Для упрощения зададимся целью определить температуру на рас-R
стоянии — от центра Солнца, где концентрацию атомов водорода можно считать приближенно равной среднему значению для Солнца:
- N . МС^А ... McNa PNa cp V MV „4	3 M
M nR
3
Выделив вертикальный столб газа с площадью основания S, давление верхних слоев на лежащие ниже можно оценить, пренебрегая зависимостью плотности р газа от глубины. Примем расстояние до цент-
146
ра масс верхней половины столба газа равным — R и произведем рас-4
чет силы тяготения, пренебрегая отличием формы тяготеющих тел от точечных и шарообразных тел:
„ „ -мс SM?
F = G--= G—------
^7? Ш R2
rpSMc
— <’----
9r
8
Тогда давление будет равно:
p = L = gpmv
S
— R 8
м2с
— R—xR3 8 3
= G
М2
2
а температура:
т = Р = GpMcM nk 9 „	,
- RpNAk
О
GMCM о -RNAk 8
Подставив числовые значения, получим оценку давления и температуры:
6,67 io 11 (21030)2 р =------------------—
3
2
Па « 2 • 1015 Па;
Т - 6^6710~11 2 1Озо1О 3
- • 7 • 108  6 • 1023 • 1,38 • 10 23 8
К « 2 • 107 К.
Задача 7.8. Два баллона одинакового объема соединены длинной тонкой трубкой. При одинаковой температуре 300 К давление газа в баллонах 3 • 105 Па. Каким станет давление при нагревании газа в первом баллоне до 600 К, если температура газа во втором баллоне не изменяется?
Решение. До нагревания:
m	mRTi
— R1\, Р1 =---------3-.
М 1	1 2MV
После нагревания:
m^RT^ RT^ ш-2	7^
P2 ~ MV ~ MV ’ Hl! ~ T2’
147
+ т2 = т,
Т\ ту + m-i = т, Т2
m-i =
т
Я
т2
mRT\
MV 1 + Ш
I т2)
2 pi	То
7—= 2рг----*— .
fl+	Г1+У2
I т2)
р2 = 2•3•105 Па = 4 • 105 Па.
900
Задача 7.9. Для улучшения теплоизоляции в колбе термоса между двойными стеклянными стенками газ находится при таком низком давлении, что длина свободного пробега молекул значительно больше расстояния между стенками колбы. Оцените давление газа в колбе термоса, если известно, что 1 кг горячей воды в нем остывает от 100 °C до 94 °C за 1 час. Между стенками колбы находится гелий.
Решение. Давление газа р можно определить, зная концентрацию п его молекул и температуру Т-.
р = nkT.
Температуру можно принять равной
Тс„ = 97 °C = 370 К. up
Концентрацию молекул можно найти по известной скорости теплопередачи. Выберем ось Ох перпендикулярной стенке баллона термоса. На одну степень свободы молекулы приходится энергия:
Так как к одной стенке колбы летит половина молекул, то число V ударов молекул о стенку колбы площадью S в единицу времени равно:
При каждом столкновении со стенкой кинетическая энергия молекулы становится равной среднему значению энергии теплового движения молекул стенки. При перелете от горячей стенки к холодной молекула переносит энергию:
где ATj — разность температур двух стенок колбы.
148
За время t переносится количество теплоты Q:
О
Q = i\Evt = — k(l\ - Т2
где Т «
Т1+Т2
2
По известным значениям Q, S, Т, m и t можно найти концентрацию п:
а затем найти р'.
4Q-jmT р = nkT =------->
3S,\7\t^k
где Q = спг/\Т2 и AT2 — изменение температуры воды в термосе.
Q = 4,2 • 103 • 1 • 6 Дж = 4,2 • 104 Дж.
ТП = — = 41°1 КГ « 6,66  10-27 кг.
Na 6 1023
Представим термос объемом 1 л в виде цилиндра радиусом г и длиной I.
S = 2лг1, V = лг21 = 10 3 м3, S = —,
Г
г = 0,05 м, S =	Ю— м2 = 4-10 2 м2.
0,05
Если комнатная температура 22 °C, то ЛТ\ = 75 К.
Р =
4-4,2 1041/б,66 10"27 -370
3 • 4 • 10 2^1,38 -10 23 - 75 - 36 00
Па ® 2,2 Па.
Задача 7.10. В баллоне объемом 3 м8 находится разреженная смесь газов водорода и кислорода при температуре 27 °C, масса водорода равна массе кислорода. Через какое время при открывании отверстия площадью 1 см2 давление ' смеси газов уменьшится на 1%? Баллон находится в вакууме. Каково отношение концентраций молекул водорода и кислорода в выходящей струе газа?
Примечание. Значения величин, относящиеся к водороду, отмечены индексом «1», к кислороду —индексом «2».
149
Решение. p = Py + p2 = HykT + n2hT = (^ + n2}hT, Ap = (Awj + An2jkT = 0,01p,
An-i =
Nyt riySijyt
N2t n2Su2t	3kT
Alli) — 1 '	— ------- , U — а |------
V V	V m
*p_^
P
n.2>jV1jm1m2
t = —
P
2(ny + n2^V-Jmym2
•Mj .T	-Л^2	ЯЛ-
= —-Na,	n2 = ——N^,	Mx = M2,
P2
my =	, m2 = -^-,
Nx	Nx
t^ P
2 — +1
VAl P2
Sy/3kT
l -“1	-“2 J
= &p' %(ру + p2)v<JPyP2
( 3 .	3>
10 2 • 2 • (2 + 32) • IO"3 • 3 • 72 -32 • 10'3
t = -
IO4 • ^3  8,31 300 •
c =
3,2 IO’4 2 + (0,4 IO'4 2
6,8 10 3 - 3 -8
-----------------------c « 320 c » 5,3 мин. 86,5 (5,7 + 0,25) IO6
3kT
Azij n-ySDytV
Дп-2 Vn^Su^tt fi2d2
n-1 V ml n2 l3kT
]
^ = 16, тп1
= 4Zh
ДП-2 Tty
150
Задача 7.11. Спускаемый аппарат космического корабля опускается вертикально на поверхность планеты с постоянной скоростью, передавая на борт корабля данные о наружном давлении. График зависимости давления (в условных единицах) от времени приведен на рисунке 7.2.
Оказавшись на поверхности планеты, аппарат измерил и передал на борт данные о температуре 7’= 700 К и ускорении свободного падения £=10 м/с2. Атмосфера планеты состоит из углекислого газа (СО2). Определить скорость спуска аппарата и температуру атмосферы на высоте 15 км над поверхностью планеты.
Решение. Определим сначала скорость спускаемого аппарата. Изменение давления /\р с изменением высоты АЛ связано выражением:
Ар = - pg Ah,	(1)
где р — плотность газа. Из закона Менделеева — Клапейрона следует,
что р = RT (здесь Т — температура газа именно в той точке, вблизи М
которой мы интересуемся изменением давления). Учитывая, что Ah = - и At, где и — скорость спуска аппарата, At — время спуска, можно записать выражение (1) в виде:
=	(2)
р RT
Зная отношение ----, т.е. тангенс угла наклона касательной в ко-
At
нечной точке А графика (рис. 7.2), с помощью соотношения (2) найдем скорость и (отметим, что, поскольку в левой части (2) стоит отношение Др
---, нам безразлично, каков масштаб графика по оси ординат). Опре-Р
деляя с помощью графика и подставляя М = 44 г/моль для СО2, pAt
получим, что скорость спуска аппарата космического корабля равна:
ВТ Ар 8,3  7 -102 м ,, м и =--------=-------------------~ 11,5	.
gM pAt 10• 44• IO-3 • 1150 с с
Перейдем теперь к решению второй части задачи. Учитывая, что
м скорость аппарата о = 11,5 —, на высоте п = 15 км над поверхностью с
планеты он был за 1300 с до посадки, т.е. этому соответствует время
t = 2350 с. Зная значения в этой точке графика, из выражения pAt
(2) найдем искомую температуру Th:
= gMofpA?| 430К.
R VAp)t
151
Задача 7.12. На улице целый день моросит холодный осенний дождь. В кухне развесили много выстиранного белья. Быстрее ли высохнет белье, если открыть форточку?
Решение. Пар как на улице, так и при закрытой форточке в кухне насыщен. Однако температура на улице ниже, чем в помещении. Значит, давление пара на улице меньше, чем в комнате. Поэтому при открывании форточки пар из кухни будет выходить на улицу, благодаря чему пар в кухне будет все время ненасыщенным. Белье будет сохнуть быстрее.
Задача 7.13. В цилиндре объемом 10 л, закрытом поршнем и помещенном в термостат с температурой 40 °C, находится по 0,05 моль двух вещестн. Определить массу жидкости в цилиндре после изотермического сжатия, вследствие которого объем под поршнем уменьшается в 3 раза. При температуре 40 °C давление насыщенных паров первой жидкости = 7 кПа, давление насыщенных паров второй жидкости при той же температуре рВ2=17 кПа. Начертить изотерму сжатия. Молярная масса первой жидкости составляет =1,8 10~2 кг/моль, а второй — М2 = 4,6 • 10 2 кг/моль.
Решение. Определим давление 0,05 моль идеального газа объемом 10-2 м3 ПрИ температуре 313 К:
pV = vRT, р =
0,05 8,31 313 iQiMn р &--—---Па « 1,3 • 10 Па.
102
Таким образом, р > рн1 и р <ри%. Следовательно, второе вещество находится в газообразном состоянии и его парциальное давление вначале равно Р2', первое же вещество частично сконденсировано, и его парциальное давление равно рп\. Давление же в сосуде вначале равно:
Ро = Рн1 +Р2 «2 -104 Па.
152
При сжатии газов давление первого газа будет оставаться неизменным и равным p„i- Давление же второго газа при изотермическом сжатии будет расти до тех пор, пока не станет равным рн2. Это произойдет при объеме сосуда V\, удовлетворяющем уравнению Менделеева — Клапейрона:
Рн2^1 = v2RT, т.е. при
v2RT
V1 = —---» 7,6 л.
Рн2
Следовательно, давление в сосуде изотермически увеличивается при уменьшении объема сосуда до 7,6 л. В дальнейшем давление в сосуде остается постоянным, равным:
Р' =Рн1 +Рн2 = 2,4  104 Па.
График зависимости р(Г) приведен на рисунке 7.3.
Найдем массу жидкости, когда объем сосуда равен:
V2 =	= 3^ л.
3 0	3
Так как объемы жидкостей малы по сравнению с объемами газов, то числа молей веществ, находящихся в газообразном состоянии, равны соответственно:
=	= 9.10-3 м	V1 = АЛ = 2 2.10-2 моль
RT	7?Т
Следовательно, в жидком состоянии находится
- vj = 4,1 • 10-2 моль первого вещества и
v2 - Vg = 2,8-10 2 моль
второго вещества. Поэтому масса жидкости в сосуде равна:
т = (i/j -	+(v2 - v2)M2 » 2,03 г.
Задача 7.14. Два цилиндра А и В одинаковых диаметров имеют свободно передвигающиеся поршни малой массы с общим стержнем. Стержень представляет собой короткую трубку, снабженную краном, который вначале закрыт. Цилиндр А вместе с поршнем теплоизолирован, а цилиндр В находится в термостате, имеющем температуру t=27 °C (рис. 7.4).
153
Рис. 7.4.
Вначале поршень цилиндра А закреплен и внутри цилиндра находится т = 32 кг аргона под давлением выше атмосферного. Цилиндр В объемом VB = 5,54 м3 содержит некоторое количество кислорода.
После освобождения поршень цилиндра А движется достаточно медленно (квазистатически). В состоянии равновесия объем аргона увеличился в 8 раз, а плотность кислорода в цилиндре В увеличилась в 2 раза. Известно количество теплоты Q = 747,9 • 104 Дж, переданное термостату. Молярная масса аргона М = 40 • 10~3 кг/моль.
Выполните следующие задания:
1.	Докажите на основании кинетической теории газов, учитывая упругие столкновения молекул с поршнем, что процесс в цилиндре А описывается урав-2
нением TV3 = const.
2.	Определите параметры р, V, Т аргона в начальном и конечном состояниях.
3.	Вычислите конечное давление смеси газов, получающейся после открытия крана, соединяющего два цилиндра.
Решение. 1. Обозначим о — скорость молекулы в системе отсчета xyz, а их— ее проекцию на ось Ох, перпендикулярную поршню (рис. 7.5).
В системе отсчета х'у'г' (рис. 7.6), движущейся со скоростью поршня и, скорость молекулы равна и1 = и - и. Проекция скорости молекулы на ось О'х' равна и'х: = их - и, а после упругого взаимодействия молекулы с поршнем становится равной:
= ~(ох-и) = и- их.
154
В неподвижной системе координат xyz проекция скорости молекулы, отлетающей от поршня, на ось Ох равна их = 2и- и х.
Поскольку все направления движения молекул равновероятны, то модуль скорости подлетающих к поршню молекул будет равен:
Р0 = у/^х+^у +
а модуль скорости отлетающих от поршня молекул равен:
Изменение кинетической энергии молекулы после столкновения с поршнем равно:
2 2г	-1
ДЕа =	---таР° = —[(2и - о Л2 + 2их - Зих 1 = 2ти2 - 2mui) . (1)
«	2	2	2 L' х х j	х '
Так как скорость теплового движения молекул их намного больше скорости движения поршня и (их » и), то AEk ~ -2тиих. За время Л£ с поршнем площадью S сталкивается Z молекул:
Z = — п
2 1
- ujSAi,
(2)
где п — концентрация молекул, - и — среднее значение модуля
разности скоростей их и и.
Следовательно, за время AZ внутренняя энергия всего газа изменяется на величину:
— п|и 2 1 '
А17 = AEkZ = - 2тиих
- u|SA£ = - nmSuxuAt.
1	~~9
AU =---nmSu uAt.
3
(3)
Полная энергия молекул газа в объеме V равна:
u = nVm^L.
2
(4)
Из выражений (3) и (4) получим =
2 SuAt
3 V
Так как изменение объема AV = SuAt,
то
АП
U
2 AV ----, или
3 V
AU 2 ДУ
----1----— 0.
и 3 V
(5)
155
Перейдем к бесконечно малым приращениям и проинтегрируем выражение (5):
rdU 2 rdV
----I—  = const,
U 3 V
2
2	О
In U -I—In V = const, или UVA = const.
3
Так как U - T f U = — — RT j, to I 2 M )
2
TV3 = const,	(6)
что и требовалось доказать.
2. Обозначим начальные параметры состояния аргона в цилиндре Pl, V\, Ту, а конечные параметры р2, V2, Т2- По условию V2 = 8Vj.
Так как плотность кислорода в цилиндре В увеличилась в 2 раза, то
Vn при той же массе объем кислорода V уменьшился в 2 раза: V =-, где
2
VB — его начальный объем.
Так как сумма объемов газов в двух цилиндрах остается неизменной (VA + VB = const), то
V, + VB = V, +^B_= 8V, +^~ .
2	2
Отсюда
Vi =^-, Vx = 0,396 m3; V2 = 8Vb V2 = 3,166 m3.
Как мы доказали в пункте 1, процесс в цилиндре А описывается уравнением
2	2
W = W-
Из этого уравнения следует:
ZL = fM3
Т2 W
-	2
8V 13	-
—L = 83 = 4,
. V1J
т.е. при адиабатном увеличении объема в 8 раз температура уменьшается в 4 раза.
За счет уменьшения внутренней энергии аргона совершается работа:
А = - АС/ = - — Eh} - Т2)
2 М V 1	21
156
(Q/Y = О, так как нет теплообмена). При этом в сосуде В выделяется и передается термостату количество теплоты Q=A (MJ в =0, так как процесс изотермический), следовательно,
q = - да = 3^LR(T -т2\.
2 М ' 1	1
По условию задачи = 4Т2, поэтому
	Т .	т * QM 1	9 mR ’	2	9 mR '
Подставив данные значения, получим 1\ = 1000 К, Т2 = 250 К.
Из уравнения Менделеева — Клапейрона найдем искомые значения
Pl пр2:	,^=8^=112^ VYM 9 Vi 9 VB mT2R 2 Q 7 Q , in6rr Do 			— =	=	= 5,25 105 Па. V2M 9 V2 18 VB
3. После открывания кранов в обоих сосудах устанавливается температура t = 27 °C (Т = 300 К).
Суммарное давление смеси газов по закону Дальтона будет равно сумме парциальных давлений аргона и кислорода:
Р = РАг + Ро2.
mRT	mRT 14 mRT	,
рАг = —--------г = —т-------V =--------« 3,36 105 Па
М VS + VB) VB А 15 MVB 114 B)
Кислород расширился, но его температура в конце процесса та же, что и в начале, поэтому запишем: /тг . тг \	[ тг ,
/>2	- РО2 (VB +V1) - Ро2 + 7ГГ = 77 Ро2 -
2	2	’	2 V 14)	14	2
При равновесии начальное давление кислорода было равно конечному давлению аргона р2:
Ро2 = ^7/>2 = 2,45 105 Па. X о
Окончательно получаем:
р= 5,81 105 Па.
157
Задача 7.15. При относительной влажности воздуха Г) = 50% вода, налитая в блюдце, испарилась на открытом воздухе за время q = 40 мин. За какое время Г2 испарилась бы вода при г 2 = 80% ?
Решение. Наряду с процессом испарения жидкости идет и процесс конденсации пара. Скорость испарения в обоих случаях (и при rj = 50% и при г2 = 80% ) одна и та же — она зависит только от температуры жидкости. Скорость же конденсации пропорциональна концентрации молекул пара в воздухе, т.е. она пропорциональна относительной влажности и во втором случае выше, чем в первом.
Ясно, что скорость убывания уровня воды
V = V - V * у у исп ' конд •
При 100% влажности воздуха Уисп = Уконд. Учитывая все это, можно записать:
при rj = 50 /q Vyj = Уисп — Уконд! = 0,5Уисп,
при г2 = 80% Уу1 = Уиоп - Уконд2 = 0,2Уисп.
Тогда
У1 5
г2 = fi ~ fi = ЮО мин.
Уу2 2
Важно отметить, что цифра эта занижена — при недостаточной конвекции воздуха у самой поверхности воды образуется тонкий слой насыщенного пара, который сильно замедляет испарение.
Задача 7.16. Подвижный поршень делит цилиндр на две равные части объемом Vq = 10~3 м3. В одной части находится сухой воздух, в другой — водяной пар и тп = 4 г воды. При медленном нагревании цилиндра поршень приходит в движение. После смещения поршня на — часть длины цилиндра движение 4
прекратилось. Каковы масса воздуха /по и водяных паров тпп, находившихся в сосуде до нагревания? Какова была начальная температура и при какой температуре поршень перестал двигаться? Зависимость давления насыщенных паров pH(t) воды от температуры:
t, °C	100	120	133	152	180
pH(t), кПа	100	200	300	500	1000
Решение. Движение поршня прекратится, когда вся вода испарится; при этом слева и справа от поршня будут газы (воздух и водяной пар), состояния которых описываются уравнением Менделеева — Клапейрона. Легко понять, что до этого при движении поршня уменыпал-
158
ся объем воздуха от Vo до ——, а водяной пар все время оставался на-2
сыщенным.
Пусть начальные температура и давление — То и р0, конечные —
и Тогда можно записать уравнения для воздуха
Povo = PiFo	(1)
То 271 ’
для пара в начальный момент времени
Ро=ра(М,	(2)
м
и для пара в конце процесса
Pl t v0 =	р = р (#1);	(3)
2 М
где М — молярная масса водяного пара. Решая совместно уравнения
(1) — (3), находим массу водяного пара до нагревания:
Пользуясь приведенными в условии данными, построим график зависимости pH(t) для водяного пара (рис. 7.7). Тогда температура То определяется из условия пересечения этого графика с прямой
а Ту — с прямой
/Пл +то 2 R т Р М 3 Го
Используя графический метод решения, находим:
t0 = 140 °C, ty = 170 °C, р0 » 3,8-105 Па.
Зная температуру То = 413 К и величину р0 из уравнения Менделеева — Клапейрона для воздуха, находим массу воздуха Мд'.
М = PoYqMb х 3 2
° ЯТЬ
где Мв = 29 г/моль.
159
Рис. 7.7.
Рис. 7.8.
Задача 7.17. Смесь газов, состоящую из т1 = 100 г азота и неизвестного количества кислорода, подвергают изотермическому сжатию при температуре Т = 74,4 К. График зависимости давления смеси газов от ее объема приведен на рисунке 7.8 (в условных единицах). Определите массу кислорода Д1о2- Рассчитайте давление насыщенных паров кислорода рОа при этой температуре.
Примечание. Т - 74,4 К — это температура кипения жидкого азота при нормальном давлении; кислород кипит при более высокой температуре.
Решение. Обозначим характерные точки на графике, как показано на рисунке 7.8. При V < давление смеси газов не меняется — это означает, что и кислород, и азот конденсируются и давление равно сумме давлений насыщенных паров кислорода />H,O2 и азота pH,N2 при температуре Т = 74,4 К. Так как данная температура является температурой кипения жидкого азота, то рн>м2 = Ро (атмосферному давлению, 105 Па). Изломы на графике в точках У)} и (Р2> vz) свидетельствуют о фазовых переходах — конденсации газов: если при V < Vj конденсируются оба газа, то при У; < V < У2 лишь один, а при V > У2 конденсации нет. Предположим, что в данной точке У)) начал конденсироваться азот, тогда кислород сконденсировался в точке (р2>^г)’ и мы можем записать систему уравнений:
Р1 = Рн,О2 + То>
(1)
Р2 = Рн,О2 + Pn2>
160
где Pn2 — парциальное давление азота в точке	Поскольку на
участке азот находится лишь в газообразном состоянии, то из за-
V2
кона Войля — Мариотта следует, что ркг =	. Подставляя это
2 *i
значение в (1) и поделив уравнения (1) друг на друга (используя соот-
Р1 7	1
ношения -£— = — и —- = — ), находим
Р2 4 V2 2
Рн,о2 = и !7 кПа.
О
Предположив, что в точке (.PpVi) конденсируется кислород, мы получили бы, как нетрудно проверить, рн,О2 ~6Ро- ®то противоречит тому, что кислород кипит при более высокой температуре — давление насыщенных паров кислорода при Т = 74 К должно быть меньше Pq.
Найдем теперь массу кислорода т02- Точка (р2,К2) соответствует началу конденсации кислорода, т.е. его давление равно рн о2 и весь кислород при этом находится в газообразном состоянии. В соответствии с законом Менделеева — Клапейрона
Ра,o2V2 = —^RT,	(2)
М02
где Mq2 — молярная масса кислорода. Для азота конденсация начинается в точке (pi, Vj), значит,
Povi = -—2-RT, mn2
О)
где MN2 — молярная
MN2 7
тывая, что --— = —
Mq2 8
масса азота. Поделив уравнение (2) на (3) и учи-
1
и Рн.Оо =~~Ро> определим массу кислорода: 2	6
8 mO2 =^7™N2 “38 г. Li J.
Задача 7.18. Мыльная пленка обладает коэффициентом поверхностного натяжения 40 мН/м. Каково избыточное давление &р воздуха в мыльном пузыре радиусом 8 см?
161
Решение. Пузырь обладает таким радиусом R, при котором работа газа при увеличении объема на малую величину ЛУ равна увеличению поверхностной энергии пленки:
\p\V = crAS,
4
+ Лг)3 - лт3
3	2
Пренебрегая малыми величинами, содержащими Дг и Дг , получаем:
Дрят2Дг = сг2лтЛг,
. 2сг „	2 4 10"z
Др =----, Др =-----------—
г	8 10 2
Глава 8
ТЕРМОДИНАМИКА
Задача 8.1. В стакан с водой опустили нагреватель и сняли зависимость температуры воды от времени:
Г, мин	0	1	2	3	4	5
t, °C	20	26,2	31,8	36,8	41,4	45,6
Г, мин	6	7	8	9	10	
t, °C	49,3	52,7	55,8	58,5	61,1	
1) На сколько остынет вода за 1 мин, если нагреватель отключить от сети при температуре = 50 °C?
2) Закипит ли вода, если нагреватель не выключать достаточно долго? Мощность нагревателя считать неизменной.
Решение. Будем считать, что температура воды увеличивается неравномерно за счет увеличения теплоотдачи с ростом температуры. Чтобы учесть влияние теплоотдачи, проследим, как меняется приращение А? температуры за Аг = 1 мин работы нагревателя в зависимости от температуры воды (температуру будем брать среднюю между ее значениями в начале и в конце каждой минуты). Построим до данным ус-
ловиям график зависимости ------- от
Аг
t, °C. Как видно из графика (рис. 8.1), все точки хорошо ложатся на прямую, пересекающую ось температур в точке ?кр = 85 °C. Ясно, что если даже закон теплоотдачи не изменится (а с ростом температуры испарение должно увеличиться, что увеличит теплоотдачу), вода нагреется только до 85 °C и, следовательно, при нормальных условиях не закипит.
Из этого же графика видно, что при
Рис. 8.1.
163
температуре t\ = 50 °C вода за одну минуту нагрелась на 3,5 °C, а без теплоотдачи она нагрелась бы на 6,5 °C (температура окружающей среды 20 °C). Значит, если при температуре 50 °C отключить нагреватель, то за 1 минуту вода остынет на 3 °C.
Задача 8.2. Имеются два теплоизолированных сосуда. В первом из них находится 5 л воды при температуре tj = 60 °C, во втором — 1 л воды при температуре t2 = 20 °C. Вначале часть воды перелили из первого сосуда во второй. Затем, когда во втором сосуде установилось тепловое равновесие, из него в первый сосуд отлили столько воды, чтобы ее объемы в сосудах стали равны первоначальным. После этих операций температура воды в первом сосуде стала равной t = 59 °C. Сколько воды переливали из первого сосуда во второй и обратно?
Решение. В результате двух переливаний масса воды в первом сосуде осталась прежней, а ее температура уменьшилась на = 1 °C. Следовательно, энергия воды в первом сосуде уменьшилась на
AQ = CgWjAi,
где св— теплоемкость воды,	— масса воды в первом сосуде.
Энергия воды во втором сосуде увеличилась на AQ, поэтому
AQ = свт2А?2,
(т-2 — первоначальная масса воды во втором сосуде). Следовательно,
Cgin^t-L = cBm2f\t2, => At2 = —— Atj = 5 °C.
m2
Температура воды во втором сосуде t2 = t2 + Д?2 = 25 °C. Этого значения она достигла после переливания из первого сосуда во второй некоторой массы воды Ат, имеющей температуру Запишем уравнение теплового баланса:
cBAm(tj -12) = cBm2(t2 - t2), Am = m2 ——— » 0,14 кг. ?! -t2
Задача 8.3. В теплоизолированном цилиндре объемом V идеальный газ сжимается поршнем. Как изменится температура газа при изменении его объема на ДУ? Скорость движения поршня и. После изменения объема газа на ДУ поршень останавливается и в газе устанавливается тепловое равновесие. Теплоемкостью поршня и стенок цилиндра в расчетах пренебречь.
Решение. Если молекула движется навстречу поршню со скоростью ь>, то при упругом столкновении с поршнем направление ее движения
164
меняется на противоположное, а модуль скорости изменяется от о до и + 2и. Кинетическая энергия молекулы при этом увеличивается на
. „ пг(и + 2и)2 ти2	, _	2	,, ч
ЛЕь = —--------------= 2тии + 2ти ,	(1)
к 2	2
где пг — масса молекулы. Рассмотрим два крайних случая в зависимости от скорости и движения поршня по сравнению со средней скоростью и теплового движения молекул.
Случай 1: и « и.
В этом случае 2тии»2ти2, поэтому из (1) следует:
AEk ~ 2mvu.	(2)
Если считать, что навстречу поршню летит примерно 1 всех моле-6
кул, то число Z столкновений молекул с поршнем в единицу времени равно:
Z = —nvS,	(3)
6
где п — концентрация молекул, S — площадь поршня. Изменение внутренней энергии газа за время Д£ равно:
1	1	о
ДЕ7 = AEkZAt = 2muu — nuSAt = — nmirSuAt = - pAV. (4) 6	3
Знак минус в последнем равенстве показывает, что объем газа в этом процессе уменьшается при увеличении энергии газа. Мы получили первый закон термодинамики для адиабатного процесса: ДЕ7 + рАУ = О.	(5)
Для одного моля газа Д17 = СуАТ, следовательно:
Су АТ = - pAV.	(6)
Из уравнения состояния идеального газа
pV = RT	(7)
следует:
*/ rzx	pAV + VAp pAV + VAp
A(pV) = RAT, AT = —-------— = —------— .	(8)
R	Cp — Cy
165
Подставляя (8) в (6), получаем:
рАУ + - Сг (ДрУ + рДУ) = О, Ср - Су
Ср
—— p&V + ДрУ = о. Су
Обозначим
2р.
Cv
О)
и получим:
урДУ + ДрУ = О,
ДУ	Др
у — =-------•	(10)
У	р
При переходе к бесконечно малым изменениям объема и давления получим:
сГУ	dp
y— =-------	(10, а)
У	р
Из (10, а) следует: рУх = const.	(11)
Это уравнение адиабатного процесса (уравнение Пуассона). Из (11) и (7) следует:
TVr 1 = const.
(12)
Используем уравнение (12) для определения изменения температуры газа:
Мы получили, что изменение температуры газа при медленном сжатии не зависит от скорости движения поршня и определяется только относительным изменением объема газа.
Случай 2: и » и.
В этом случае 2mvu « 2тиг. Из (1) в этом случае следует:
® 2ти2.
(14)
1в6
Учтя, что в этом случае число столкновений молекул с поршнем в единицу времени равно Z = nuS, получим:
NU = NEhZbt = nuS  2mu2At = - 2пти2ЛУ.	(15)
Если масса газа М и удельная теплоемкость при постоянном объеме Су, то изменение температуры газа после остановки поршня и установления теплового равновесия в газе равно:
AlCy	AlCy
Мы получили, что если скорость движения поршня и значительно превосходит скорость и теплового движения молекул газа, то изменение температуры газа пропорционально квадрату скорости и поршня и первой степени изменения ДУ объема газа.
Задача 8.4. Вертикальный теплоизолированный сосуд, в котором находится одноатомный газ, закрыт поршнем массы М. В сосуде включают нагреватель мощностью N, и поршень начинает медленно сдвигаться вверх. За какое время т он поднимется на высоту Н относительно начального положения? Теплоемкостью поршня и трением пренебречь. Атмосферное давление отсутствует.
Решение. За искомое время г к газу подводится количество теплоты Q = Nt. Оно расходуется на работу по расширению газа при постоянном давлении, равную работе по равномерному поднятию поршня
А = p,\V = vRNT = MgH, и на увеличение внутренней энергии v (моль) одноатомного газа
All = - vRNT = — MgH, NT = MgH+~MgH, г = - MgH .
2	2	2	2 N
Задача 8.5. В вертикальном цилиндре высотой h0 = 2 м с теплоизолированными стенками находится 0,08 моль гелия при температуре У = 300 К. На какой высоте h окончательно установится поршень массой т — 40 кг, отпущенный сверху цилиндра и движущийся в нем свободно, если над поршнем вакуум?
3	3
Решение.	mgNh = — А(рУ) = — vRNT,
2 mg/\h	mg vR(T() + NT) vR(T + AT)
ду =-------п =--------=------------=----------
3 vR	S	V	Sh2
,	(	2 mgNiX	vRT 2,	,
mgh = vR\T +--------, h =------+ — (h() - h),
k 3 vR J	mg 3V u '
167
5 , vRT 2 ,	,	2 ,	3 vRT
— h- + — ho, h~—h0+— 3 mg 3	5	5 mg
h = 1,1 m.
Это решение верно в том случае, если есть небольшое трение, но все тепло, выделяющееся при трении, передается газу.
Задача 8.6. Горизонтально расположенный цилиндрический теплоизолированный сосуд объема Vo = 100 л, заполненный гелием, разделен на две части теплонепроницаемым поршнем, который может перемещаться без трения. Газу, находящемуся в левой части сосуда, сообщают количество тепла &Q = 100 Дж. Найти изменение давления в сосуде к тому моменту, когда поршень перестанет двигаться.
Решение. После подведения тепла AQ газ в левой части сосуда расширяется, совершая работу ДА. Эта работа целиком идет на увеличение энергии газа в правой части сосуда. Таким образом,
AQ = Alli + ДА = Alli +Л172 = — й|—Д71+—-^-ДТ2 |.	(1)
2 \М М )
Условие равновесия поршня до нагревания р\ = р2 = р, уравнения состояния в левой и правой частях сосуда:
pV^^RT^ pV2=^RT2, м	м
где У1+У2 = Уо- После нагревания, когда поршень уже не будет двигаться, давления в левой и правой частях уравниваются. Обозначим увеличение давления в сосуде Др; тогда
(р + Др)(У! + ДУ) =	+ А^1),
(р + Др)(У2 - ДУ) = ^я(т2 + ЛГ2).
После простых преобразований получаем:
Лр(У, + У2) = яГ^-дт, + -^ДтЛ v 1 27 1м 1 м 2)
или, с учетом (1):
о Друо =-де. о
168
Отсюда находим Др:
2 AQ	Н
Др =-----« 667 —-.
3V0	м2
Задача 8.7. В цилиндре тепловой машины заключен 1 моль одноатомного идеального газа. Определите КПД тепловой машины, если изменение состояния газа в цилиндре осуществляется по циклу, представленному на рисунке 8.2.
^4
Решение.	л = —.	(1)
Qi
А=р0У0.	(2)
Qac - лилс+А' = — ИЛТлс + 2poVo.
^ТАС = Тс~Та = 4ГА - ТА = ЗГА-
Q = — ВТа + 2p0V0.
Учтя, что рдУо = ЛТд, получим:
Qac=^-PoVo.	(3)
Из выражений (1), (2), (3) следует:
т] = — «0,15.
13
Рис. 8.2.
Рис. 8.3.
169
Задача 8.8. Карбюраторный двигатель внутреннего сгорания работает по циклу, состоящему из четырех последовательно происходящих процессов: адиабатного сжатия из состояния А в состояние В, изохорного перехода из состояния В в состояние С в результате нагревания воздуха при сжигании горючей смеси, адиабатного расширения из состояния С в состояние D и изохорного перехода из состояния D в исходное состояние А (рис. 8.3). Вычислите КПД двигателя для случая, если бы воздух был идеальным одноатомным газом при значениях температуры в состояниях А, В, С и D соответственно Тд = 300 К, Тд=524 К, Тс = 786 К и 7/) = 450 К.
Решение. Значение КПД теплового двигателя определяется соотно-
Qi - Qn	„
шением г/ = —4---— , где Qj — количество теплоты, переданное за
Q1
цикл рабочему телу от нагревателя, Q2 — количество теплоты, полученное за цикл холодильником от рабочего тела.
Во время осуществления адиабатных процессов расширения и сжатия нет теплообмена рабочего тела ни с холодильником, ни с нагревателем. Следовательно, весь процесс теплоотдачи количества теплоты Qj от нагревателя осуществляется при переходе газа из состояния В в состояние С, а процесс передачи количества теплоты Q2 холодильнику — при переходе газа из состояния D в состояние А. При изохорном переходе газа из состояния В в состояние С работа внешних сил равна нулю: А = 0, так как поршень неподвижен. Из первого закона термодинамики для этого процесса следует:
ВС = Qi + -А, А = 0,
Таким образом, количество теплоты, полученное газом от нагревателя за весь цикл, равно изменению внутренней энергии газа при переходе из состояния В в состояние С:
Qi = AUBC =UC-UB = ~ — RTc-- — RTB = - —(Tc - TB). 1	C 2M 2M 2M B
Аналогично количество теплоты переданное холодильнику при изохорном переходе газа из состояния D в состояние А, равно:
Q2 = bUDA = UD — UA =	~ ta)-
Подставляя полученные выражения для Qj и Q2 в уравнение для определения КПД, получаем:
п п S~R(TC-TB)-~ — R(TD-ТА) „ т т
= Qi ~Q2 = 2 М	2 М А/ = TC-TB-TD + ТА
~ — R(T.с-Тв)	ТС~ТВ
2 М с в>
170
Найдем численное значение КПД:
Л =
786 - 524 - 450 + 300
786 - 524
« 0,43.
Задача 8.9. На рисунке 8.4 представлена диаграмма цикла, осуществленного с 0,2 моль одноатомного идеального газа. Участки ВС и DA — адиабаты. Вычислите коэффициент полезного действия тепловой машины, работающей по этому циклу. Определите работу, совершенную газом на участке ВС. Найдите максимальное значение КПД тепловой машины с использованием нагревателя и холодильника, с которыми осуществлен данный цикл, если в точке В газ находился в тепловом равновесии с нагревателем, а в точке D — в тепловом равновесии с холодильником.
рх10 , Па
11
10
9
8
7
6
5
4
3
2
1
0 J 2	3	4	5	6	7	8	9 ТЛ -з 3
Vх!0 , М
Рис. 8.4.
Решение. Так как участки ВС и DA являются адиабатами, то передача количества теплоты Qj от нагревателя осуществляется только при изохорном процессе А—В, а передача количества теплоты холодильнику — только при изохорном процессе С—D.
171
При изохорных процессах работа равна нулю, поэтому из первого закона термодинамики следует:
Qi = Af7|, Q2 = AUg.
Изменение внутренней энергии Д17 идеального газа при изохорном процессе равно:
AL7 = — ийАГ = — VAp, 2	2
следовательно,
Ql = — VA‘^PAB’ Q2 - ^vc^Pcd-
Работа А', совершенная за цикл, равна:
3
А! - Qi _ Q2 = ~ <Уа^Рав ~ Vc^Pcj))-
КПД цикла равен:
_ Q1 - #2 _ КаДрав ~ Ус^ВСР Qi	vaaPab
Подставим числовые данные величин из диаграммы на рисунке 8.4:
ЗЮ'3 -8105 -610"3 -2,5 105
р =-----------------------------= 0,375.
310 -8 10й
Работа газа при адиабатном расширении из состояния В в состояние С равна изменению внутренней энергии газа с противоположным знаком:
АВС - ~ ЛС7вс, - А17вс - ~уК(ТВ ~ Тс)-
Используя уравнение состояния температуры в точках В и С:
идеального газа, найдем значение
т Pbvb
т РсУс
1г — ----
с vR
ТВ =
11 105-3 10~3 „	„
--------------К = 1986 К, 0,2  8,31
3,5105-6 Ю-Зк = 126зк. с 0,2 8,31
Тв - Тс = 723 К.
3	q
АВС = - • °,2 • 8,31 • 723 Дж « 1,8 • 103 Дж.
172
Задача 8.10. Отношение £ максимального и минимального объемов цилиндра четырехтактного двигателя равно 9,5. рУ-диаграмма работы двигателя показана на рисунке 8.5. В двигатель поступает наружный воздух при температуре t] = 27 °C и давлении р± = 105 Па. В момент зажигания горючей смеси давление в цилиндре возрастает в два раза.
Ответьте на следующие вопросы и выполните задания:
1.	Какие процессы происходят с газом между точками О—1, 2—3, 4—1 и 1—О? Процессы 1—2 и 3—4 — адиабатные (у = 1,4).
2.	Определите параметры р и Т газа в точках 1, 2, 3 и 4.
3.	Вычислите КПД цикла теплового двигателя.
4.	Оцените реальность полученных результатов.
Рис. 8.5.
Решение. 1. Участок О—1 характеризует изобарное всасывание смеси, 1—2 — ее адиабатное сжатие, 2—3 — изохорное увеличение давления при зажигании смеси, 3—4 — адиабатное расширение — «рабочий ход», 4—1 — изохорный выпуск газов, 1—0 — изобарное удаление смеси из цилиндра.
2.	Ti = Tq = 300 К, =ро = 105 Па. Так как процесс 1—2 адиабатный, воспользуемся уравнением Пуассона:
P1V2 = P2V1 >	(1)
Рг = Pif“) = Pi^ = 2.34 МПа,	(2)
к nJ
V2 где £ =-- — степень сжатия.
173
Из уравнения Клапейрона
PlV2 _ Р2^1 т _ т P2_Yl =	?2
Л ^2	Pl ^2	£ Pl
С учетом (2) находим:
Т2 = 71Z"1 = 740 К.
По условию при зажигании свечи давление возрастает в 2 раза, т.е.
ps = 2 р2 = 4,68 МПа.
Для изохорного процесса 2—3 имеем:
т3 = Т2 = 2Т2 = 1480 К.
Р2 ^2	Р2
Процесс 3—4 адиабатный, поэтому записываем:
P2vl = P4V2 ’ Pi = Рз[тг) = Рз£~г = °>2 МПа-
р3^ Pi^2
Из уравнения Клапейрона ——— = ——— получим: Л
Ti=T3^^- = Т2е Г£ = Т3еГ~7 = 600 К.
Рз V1
Процесс 4—1 изохорный, поэтому
= Д-, г/ = Т4 = 300 К.
Pl Т\	Pi
t
Как и следовало ожидать, Т\ = 7р
3.	КПД цикла теплового двигателя по определению равен:
=	= Qi ~ Q2
Qi Qi
где Ап — полезная работа, совершенная двигателем за цикл, Qj — количество теплоты, подведенное от нагревателя, Q2 — количество теплоты, отданное холодильнику. Так как процессы 1—2 и 3—4 происходят без теплообмена, то подвод и отвод тепла осуществляется только на участках 2—3 и 4—1:
Qi = cvm(T3 - Т2), Q2 = cvm(7\ - 7i),
где Су — удельная теплоемкость газа при постоянном объеме,
174
Cv^[(T3-7-2)-(7-4-T1)]_i ут, t Tt t 1 _Q6 cvm(T:i - T2)	T;i - T2 T2	1
4.	Полученные в результате идеализации значения максимального давления р3 = 4,68 МПа и КПД р « 60% превышают значения максимального давления ро и КПД реальных карбюраторных двигателей внутреннего сгорания.
Задача 8.11. Горный хребет обтекается аднабатно влажным воздухом (рис. 8.6). Метеорологические станции Mq и Мз фиксируют давление воздуха ро = 100 кПа, станция М2 фиксирует давление р%- 70 кПа. Температура воздуха в точке Mq tQ = 20 °C. Когда воздух поднимается, при давлении рх = 84,5 кПа начинается образование облаков. При дальнейшем поднятии воздух, в котором происходит конденсация водяного пара (масса этого воздуха над каждым квадратным метром поверхности равна 2000 кг), достигает вершины хребта (станция М2) через 1500 с. При этом он отдает, в расчете на один килограмм воздуха, т = 2,45 г воды в качестве осадков (дождя).
Ответьте на следующие вопросы и выполните задания:
1.	Какова температура на уровне нижней границы облаков?
2.	На какой высоте hi над станцией Мо расположена нижняя граница облаков, если допустить, что плотность воздуха убывает с высотой линейно?
3.	Какая температура Т2 будет измерена на вершине хребта?
4.	Какой высоты достигает столб воды (высота осадков на единицу площади), выпадающий из потока воздуха в течение 3 часов? Условия конденсации пара считать одинаковыми на участке от Mi до М2.
5.	Какова температура Т3 на задней стороне хребта у станции М$1 Обсудите состояние воздуха у станции М3 по сравнению с его состоянием у станции Mq.
Указания и данные.
Воздух следует рассматривать как идеальный газ.
Влиянием присутствия водяного пара на удельную теплоемкость и на плотность воздуха, а также зависимостью удельной теплоты испарения от температуры следует пренебречь. Температуры следует указать с точностью до 1 К, высоту нижней границы облаков — с точностью до 10 м, высоту осадков — с точностью до 0,1 мм.
Удельная теплоемкость воздуха в интересующем нас интервале температур равна Ср =1005 Дж/(кг • К); плотность воздуха у станции Мо при ро и То равна ро = 1,189 кг/м3; удельная теплота испарения воды в области облака
CD
qv = 2500 кДж/кг; -= у = 1,4; g = 9,81 м/с2.
cv'
Решение. Установим связь между температурой Г, объемом V и давлением р идеального газа в адиабатном процессе.
175
При адиабатном процессе для идеального газа имеем:
Q = О, А = - ДГ/,
ДГ/ = СутЛТ, А = рДУ, рДУ = - СутЛТ.	(1)
Используем уравнение состояния идеального газа:
pV = — RT,	Д(рУ) = — ДДТ,	Д(рУ) » ДрУ + ДГр,
м	м
Из (1) и (2) следует:
Так как
(ДрУ + ДУр)М mRAT
рДУ + —^-~~(ЛрУ + ДУр). R
ср - Су
(2)
(3)
(4)
R ч--,
м
R ~м~Ср Су
Q &U+A рДУ М™Т R
' п — - — ----- — Су Ч--— Су Ч-----— Су ч--,
р тпДТ тАГ v m\T v mAT v М
Су
то из (3) следует:	рДУ ч----------(ДрУ + ДУр) = О,
Ср - Су
Ср CV p\V + ДрУ + ДУр = 0, рЛГ + ДрИ = 0. Су	Су
р
С учетом того что —— = у:
Су
ypAV + ДрГ = 0.	(5)
Равенство (5) выполняется, если выполняется условие:
pVr = const.	(6)
Это уравнение адиабаты, или Пуассона (вывод этого уравнения дан в решении задачи 8.3).
dfpV7) = dpVr +yVr-1dVp = 0,	(7)
dpV + ypdV = 0.
(8)
176
Используя уравнение адиабаты, получим:
состояния идеального газа и уравнение (6)
,, пт pV = — RT, м
mRT	mRTVr
p =----,	------= const,
MV MV
TVr 1 = const.
(9)
Аналогично:
P -----= const.
(Ю)
1. Применим уравнение адиабаты для решения задачи:
Po P{
To " T{
™ т й Г
Ч - J0 ---
\Ро)
(И)
0,4
| 04 к.1 n3 I 1,4
T, = 293 —-------_ к = 279,2 К.
I 105 )
2. Используем уравнение состояния идеального газа для ния плотности р\ воздуха на высоте
определе-
Й1:
PqVq _ P1Y1
То
?1 ’
Ро _ Р1
РоТо Р1Т1
Р17'о
Ро?! ’
Р1 = 1,189 • 0,845 • 1,05	= 1,054
м3	м3
Pi = Po - (P° o'P1) ghi’
2
h = 2(Р0 -pQ
1 (Po+Pl)^’
2(1-0,845) 10s
Ai ~	’--------------м = 1408 m.
(1,189 +1,054) • 9,81
3. Температура воздуха при перемещении от М1 до М2 уменьшается в результате адиабатного расширения от Ti до Т2 по закону (11):
r-1
T2 = Tr fe| 7 \P1)
0,4
То = 279,21-^-11,4 К « 264,6 К
\84,5у
177
и повышается на АТ за счет теплоты конденсации пара:
ЛТ = ^, СР
2,5 106 -2,45 10~3
1005
К ~ 6,1 К.
В результате температура в точке М2 принимает значение:
Т2 = Т2+ЛТ, Т2 = 264,8 К +6,1 К = 270,9 К.
тг иг	2000mt2
pV = М, pSh =------------,
,	2000znt2	,	2000 2,45 10 3 3600 3	„ л2
Л =-------Л =-------------Ц---------------м «3,53 10 2 м.
pSh	1О3 1 1500
5.
= Т2

0,4
Т3 = 270,9 f1--)1’4
<7 J
К « 300 к.
Рис. 8.6.
Рис. 8.7.
Задача 8.12. Стенки цилиндра, поршень и внутренняя перегородка площадью 1 дм2 изготовлены из теплоизоляционного материала (рис. 8.7). Клапан в перегородке открывается в том случае, если давление справа больше давления слева. В начальном состоянии в левой части цилиндра длиной Iq - 11,2 дм находится 12 г гелия, в правой части, имеющей ту же длину, — 2 г гелия, с обеих сторон температура газа равна 0° С. Внешнее давление 105 Па. Удельная теплоемкость гелия при постоянном объеме cv = 3,15 • 103 Дж/(кг • К), а при постоянном давлении ср = 5,25 • 103 Дж/(кг • К).
Медленно передвигаем поршень по направлению к перегородке (с небольшой остановкой в момент открытия клапана) и осторожно доводим поршень до перегородки. Чему равна произведенная нами работа?
178
Решение. Для теплоизолированной системы первый закон термодинамики можно записать в виде:
А = AU.	(1)
Полная работа А совершается над газом силой, которой мы действовали на поршень, и силой атмосферного давления:
А = Aj + p0Sl0.	(2)
Изменение внутренней энергии гелия определяется как
Ш = cv(mi+m2)(T-T0),	(3)
где cv— удельная теплоемкость гелия при постоянном объеме, Т — конечная температура газа.
Из выражений (1) — (3) получаем формулу для расчета искомой работы А,:
Ах = Су(тп1 + т2)(Т -То)~ PoSIq,	(4)
в которой неизвестна лишь конечная температура Т.
Для ее нахождения рассмотрим последовательно все этапы процесса сжатия гелия.
Начальные значения давления гелия в левой и правой частях цилиндра (рис. 8.7) определим из уравнения Менделеева — Клапейрона:
Так как т1 > т2, то р01 > р02.
При движении поршня к перегородке газ в правой части будет сжиматься до тех пор, пока его давление не станет равным р01. В этот момент открывается клапан.
Так как сосуд с газом теплоизолирован, то процесс в нем будет адиабатным и описывается уравнением Пуассона: pV7 = const,
СР где у = -.
cv
Запишем уравнение Пуассона для гелия в правой части цилиндра:
Poi^Y = Р02^() ’
где V7! — объем газа в правой части цилиндра в момент открывания клапана:
Vi=Vof-^V.	(6)
VPoi/
179
Подставляя значения Poi и Р02 в выражение (6), найдем:
УТПу)
(7)
Vi « O,34Vo.
Температуру Ti, которую будет иметь газ в правой части цилиндра в момент открытия клапана, найдем из уравнения Клапейрона:
РоЛ Po2Vo
откуда
71	10
71 =Т0“^--Р02 V2
С учетом выражений (5) и (7) получим:
Л Л1 Л	'
=ТоЫГ = 2,О5То.
771-2 772-1 J	\ 771 j /
(8)
После открывания клапана газы перемешиваются и происходит теплообмен при постоянном объеме. Из уравнения теплового баланса Сутщ^О - 7’0) = с1/тп2(71 _ в) находим в = т^'(> +.ГП2^1. ~ 1Д5Т0.
После перемешивания весь газ массой m = m-i + m2 сжимается адиа-батно от объема Vj + Vq до объема Vq, а его температура увеличивается от 0 до Т в соответствии с уравнением Пуассона:
pVr = const => TV'7' = const,
7^’ =0(r1+Vof1,
T = 0pl±Zoy =/1+11Г «l,4T0.
I Vo ) I Vo)
Подставляя значение конечной температуры Т смеси газов в выражение (4), найдем искомую работу, совершенную при сжатии:
Ах = 4816 Дж - 1120 Дж = 3696 Дж ~ 3,7 кДж.
Задача 8.13. На рисунке 8.8 представлен цикл, проведенный с идеальным одноатомным газом. Определите КПД этого цикла.
Решение. КПД цикла определяется по формуле:
п = —, Q
180
где А — работа газа за цикл, Q — количество теплоты, полученное за цикл от нагревателя.
Работа газа пропорциональна площади треугольника АВС:
А = |'6Ро -6Ро = 18рого-
Передача теплоты Q от нагревателя осуществляется в изохорном процессе АВ и в некоторой части BD процесса ВС: Q = Qab + Qbd (рис. 8.9).
В изохорном процессе количество переданной теплоты равно изменению внутренней энергии газа:
Qab = Qab = ~^APV = ®Povo-
Для нахождения второй части переданного количества теплоты нужно найти положение точки D на участке ВС. Точка D является точкой касания адиабаты к отрезку ВС. На участке BD в этом случае происходит передача теплоты газу от нагревателя, на участке DC — передача теплоты от газа холодильнику.
Запишем уравнение прямой ВС:
(1)
Для этой прямой выполняется условие:
dp _ _ Ро dV Го ’
(2)
Для адиабаты, проходящей через точку D на прямой ВС, выполняются равенства:
pVr = a,	(3)
a = Pdvd ’ a	(4)
p = —, v:'	(5)
dp	a dV ~ Г yr A ‘	(6)
Из (6), (2) и (4) для точки D следует:
Ро _ PdVD Рр _ Ро
V0 V£+1 ’ VD Vo ’
181
Рис. 8.8.
Рис. 8.9.
Из (1) и (7) для точки D следует при у = —:
3
POVD	о _ f •> VD 1 v	>0 _ sv	_ 8Po _ о
—, vd  ----------------------7 - &v0’	Pd - г -'’Po-
YV0 v 8p0J	r + 1	У+1
На участке BD цикла количество переданной теплоты Qbd равно:
Qbd = Ш + А = UD-UB + PA±PJL(vd-Va) =
- ~Pdvd -~7Povo + P° (rD -IZa) -
= |3pO5Vo -~7p0V0 + 7Po+3Po^y-o _	= 32povO'
П-±-________A— =	. 0,44.
Q Qab + Qbd ЭРо^о + 82p0V0
Задача 8.14. Нагревая воздух в комнате с помощью электронагревателя, мы всю энергию электрического тока переводим в тепло. А нельзя ли предложить прибор, который, затратив некоторую энергию, выдал бы тепла в несколько раз больше, и тем самым сэкономить расходы на отопление?
Решение. Тепловые машины можно с помощью другого двигателя, например, электромотора, заставить совершать цикл в обратном направлении. В обратных процессах (циклах) холодильником по-прежнему называют тело с более низкой температурой, хотя оно теперь отдает тепло, а нагревателем — тело, имеющее более высокую температуру, хотя теперь оно его получает. При этом рабочее тело будет получать за один цикл от холодильника количество теплоты Q2, отдавая
182
нагревателю количество теплоты Q1; которое больше Q2 на величину работы А, совершаемой электромотором:
Q1 - Q2 +-А-
Можно сказать, что в данном случае тепловая машина производит отрицательную работу: Q2 - Qy = - А.
В результате проведения обратного цикла увеличивается разность температур между нагревателем и холодильником. В этих условиях тепловая машина работает как «тепловой насос». За счет работы, совершаемой электромотором, машина переносит количество теплоты Q2 от холодного тела к горячему.
Важнейшей характеристикой холодильной машины является холодильный коэффициент, равный:
£ - ^2 _ Q2
А ~ Q^Q2 '
Холодильный коэффициент показывает, какое количество теплоты отнимается от охлаждаемого тела при совершении единицы работы.
В идеальной холодильной машине максимальное значение холодильного коэффициента может быть равно:
/ = _А_
Х 71 -Т2'
Можно использовать холодильник для отапливания помещения в холодное время года. Для этого холодильную камеру надо вынести на улицу, а все остальные части «агрегата» оставить в комнате. Тогда, совершив работу (отобрав энергию у электрической сети) и забрав с улицы количество теплоты Q2, мы передаем в комнату количество теплоты Q1=A + Q2>A. Понятно, что никакого противоречия с законом сохранения энергии нет — дополнительная энергия в виде тепла отбирается от холодного наружного воздуха.
Холодильная машина, работающая таким образом, и называется «тепловым насосом», поскольку тепло «перекачивается» снаружи внутрь комнаты. В результате работы теплового насоса в помещении становится теплее, а на улице — еще холоднее (последний эффект конечно же незаметен). КПД теплового насоса (отопительный коэффициент) гот определяется отношением получаемого помещением количества теплоты к необходимой для этого внешней работе. В идеальном случае он равен:
е = = 1 =
A Qi - Q2	7 max	- Т2
и всегда больше единицы.
183
В качестве примера рассмотрим случай, когда температура наружного воздуха Т2 = - 20 °C = 253 К, а внутри дома необходимо поддер-
293
живать температуру Ту = 20 °C = 293 К. Тогда	« 7,3, т.е., ис-
40
пользуя электрическую энергию для работы теплового насоса, мы можем получить в 7 раз больше тепла, чем пользуясь электронагревательным прибором. Разумеется, реальный КПД всегда ниже, к тому же двигатель теплового насоса также превращает в работу не всю потребляемую энергию.
Задача 8.15. Давление насыщенного водяного пара при температуре 100 °C равно 105 Па. Каково давление насыщенного водяного пара при температуре 105 °C? Удельная теплота испарения воды при 100 °C равна 2,3  106 Дж/кг.
Решение. Представим изотермы насыщенного водяного пара при температурах 100 °C и 105 °C (рис. 8.10). Рассмотрим цикл Карно 1— 2—3—4, в котором на участке цикла 1—2 один моль воды при температуре Т + ДТ испаряется при изотермическом расширении, затем на участке цикла 2—3 охлаждается до температуры Т в результате адиабатного расширения, на участке цикла 3—4 превращается из пара в жидкость в результате изотермического сжатия и на участке 4—1 воз
184
вращается в исходное состояние в результате адиабатного сжатия. Для цикла Карно можно записать:
А АГ
Q1 ~	’
(1)
где А — работа за цикл, Q — количество теплоты, полученное за цикл от нагревателя, ДТ — разность температур нагревателя и холодильника, Tj — температура нагревателя.
От нагревателя при испарении одного моля воды получено количество теплоты
Q1 = гМ,	(2)
где г — удельная теплота парообразования, М — масса одного моля воды.
Работа пара за цикл определяется по площади цикла на pV-диаграмме:
А = ДрДИ.	(3)
Из (1), (2) и (3) следует:
Др гМ ---=------	(4) ДТ Т\АУ
Пренебрегая объемом жидкости по сравнению с объемом пара, изменение объема пара AV при переходе из жидкого в газообразное состояние можно принять равным объему пара ДИ « Vn.
Тогда
Др гМ гМ гМр
ДТ = ПК = T1RH =	’
1 р
Используем данные задачи:
Др * 2,3  10^18  10~3  Ю5 Па.й 4>4.103 Па.
ДТ	8,31 • 3732
По условию задачи ДТ = 5 К. Тогда
Др » 4,4 • 103 • 5 Па « 2,2 • 104 Па, Р1 =р + Др » 1,2 • 105 Па.
Глава 9
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
Задача 9.1. На расстоянии а от центра незаряженного металлического шара находится точечный заряд q. Определить потенциал шара.
Решение. Так как напряженность поля внутри шара равна нулю, то потенциал всех точек внутри шара одинаков и равен потенциалу точек, лежащих на его поверхности. Поэтому достаточно определить потенциал поля в любой точке внутри шара, например в его центре. Он равен:
у-' —	' 7.	5
4яг£0а 4яг«-ог
где Алд — заряды, индуцированные на поверхности шара, г — радиус
шара. Так как полный заряд шара <2 = ЕДф равен нулю, то второе i
слагаемое равно нулю. В результате находим:
Ц/ —-------.
4яаб-оа
Задача 9.2. Заряженная металлическая сфера радиуса R разрезана на две части по плоскости, отстоящей на расстоянии h от центра (рис. 9.1). Найти силу, с которой отталкиваются эти части. Полный заряд сферы Q.
Решение. Так как сфера металлическая, то заряд Q распределится равномерно по ее внешней поверхности. Для того чтобы определить силу, действующую, например, на верхнюю часть сферы со стороны нижней, разобьем мысленно эту часть сферы на элементарные участки. Сила F, действующая на один из таких участков (рис. 9.2), определяется формулой:
Fs = qF,
где q — заряд выделенного участка, Е — напряженность поля, созданного всей остальной частью сферы. Очевидно, что
186
QS
Ч =----Г’
4яй2
где S — площадь выделенного участка.
Рис. 9.1.
Рис. 9.2.
Как известно, напряженность поля вне заряженной сферы у ее поверхности определяется формулой:
Е 1 Q
"С .	9 ’
4жг0 R2
а напряженность поля внутри такой сферы равна нулю.
Согласно принципу суперпозиции напряженность поля как внутри, так и вне сферы складывается из напряженности поля выделенного участка заряженной сферы и напряженности поля остальной части сферы. Будем считать, что выделенный участок настолько мал, что его можно считать плоским. Тогда напряженности поля этого участка как внутри, так и вне сферы равны по модулю и направлены перпендикулярно площадке в противоположные стороны, т.е.
Еу - - Е2.
Пусть для определенности заряд сферы положителен. Тогда векторы £j и Е2 направлены так, как показано на рисунке 9.2.
Поскольку напряженность поля внутри сферы равна нулю, то сумма вектора Е2 и вектора Е напряженности поля остальной части сферы равна нулю. Следовательно,
Е2 + Е — О, Еу — — Е2 = Е.
Тогда для напряженности поля вне сферы можно записать:
Ес = Ё + Ёу
Е = -Ес
2
1____±
&леое R2
187
Следовательно, для модуля силы Fg, действующей на выделенный участок сферы, можно записать:
Fg ~ Fq —
q2s
32я2е0Я*
Теперь найдем силу F, действующую на всю верхнюю часть сферы. Для этого нужно найти сумму сил Fg, действующих на элементарные участки «верхушки» сферы, т.е. поверхности сферического сегмента. Из соображений симметрии очевидно, что сумма горизонтальных составляющих сил Fg равна нулю. Поэтому
Q2
F = Х^Хверт = ZFg cosas =---------XScosa,
32лЛ.0Я4
где а — угол между вектором Fg и вертикалью. Так как S cos а — это проекция площади участка на горизонтальную плоскость, то сумма £ S cos а равна площади S основания сферического сегмента:
S = да-2,
где г — радиус основания сферического сегмента. Следовательно,
32л2£0В4	32да0В2 < R2
Задача 9.3. Согласно одной из первых моделей (модель Томсона), атом водорода представляет собой равномерно заряженный положительным электричеством шар, в центре которого находится электрон. В целом атом нейтрален. Найти радиус такого атома, если известно, что минимальная энергия, которую нужно сообщить электрону для его удаления из атома на большое расстояние, равна W[. Заряд электрона е.
Указание. Принять во внимание, что равномерно заряженный шаровой слой в своей внутренней полости электрического поля не создает.
Решение. Величина W равна работе, которую необходимо затратить для того, чтобы удалить из атома электрон.
Легко найти работу, которую необходимо затратить для того, чтобы удалить электрон с поверхности атома «на бесконечность» (бесконечно далеко от него). Эта работа равна потенциальной энергии электрона у поверхности положительно заряженного шара. Так как потенциал электрического поля на поверхности шара равен:
е
<р =------
188
(где е — заряд шара и В — его радиус), то работа
Чтобы найти работу, которую необходимо затратить для перемещения электрона из центра атома на его поверхность, мысленно разобьем шар на тонкие шаровые слои толщиной ДВ. На протяжении каждого из таких слоев можно силу, действующую на заряд, считать постоянной. Напряженность поля, создаваемого зарядами каждого из слоев в полости, ограниченной этим слоем, как известно, равна нулю, а вне слоя напряженность такая же, какой она была бы, если бы весь заряд слоя был сосредоточен в центре шара. Это означает, что напряженность электрического поля внутри атома на расстоянии г от его центра определяется формулой:
4жог2
а сила, действующая в этом поле на электрон, выражается формулой:
F = еЕ = ——- , 4жог2
где q — заряд, который находится внутри сферы радиуса г.
Так как заряд е распределен в объеме шара равномерно, то в еди-
е нице объема сосредоточен заряд р =----.
^R* 3
Значит, внутри шара с радиусом г будет находиться заряд
3 е
4 4лй3
4 з
— яг
4яг02?3
3
Для того чтобы вычислить работу, которая совершается при перемещении электрона в атоме, умножим среднее значение силы на перемещение R электрона. Так как сила, действующая на электрон, пропорциональна расстоянию электрона до центра атома, то среднее значение силы равно половине модуля силы, действующей на электрон, находящийся на поверхности атома:
F 1	е2	л = F It
СР - 2 4^0Я3 ” 8^0К2 ’	2 -	- 8ягод •
Следовательно,
4яг0Д 8xs0R 8k£qR
189
Искомое значение R равно:
R Зе2
87ze0W£
е+
Рис. 9.3.
Р
Задача 9.4. Два протона и два позитрона, первоначально покоившиеся в вершинах квадрата (рис. 9.3), раз-М летаются. Отношение их масс --= 2000, а заряды оди-
т
наковы. Найти отношение скоростей протонов и позитронов после разлета (на бесконечности). Сторона квадрата а.
Решение. Вначале на все частицы действуют одинаковые по модулю силы. Но массы протонов в 2000 раз превышают массы позитронов. Это означает, что ускорения позитронов будут в 2000 раз
больше ускорения протонов. Поэтому позитроны быстро разлетятся на бесконечность, а затем протоны будут разлетаться, уже только взаимодействуя друг с другом. Это дает возможность при вычислении скоростей позитронов протоны считать неподвижными.
Найдем полную потенциальную энергию позитронов до разлета. Если бы протонов не было, то потенциальная энергия взаимодействия двух позитронов была бы равна:
Это работа, которую нужно затратить для сближения двух позитронов. Потенциал поля, которое создает каждый из протонов в точке, где находится позитрон, очевидно, равен:
е «Р = -- •
4л£0а
Поэтому полная потенциальная энергия позитронов будет равна:
е2	е	е	1 (	1 е2
Wr =------= + 2-----е + 2-----е =---- 4 + —j= — .
4жгоа72	4я£0а	4л£0а	4жг0 V	<27 «
Вся эта потенциальная энергия перейдет в кинетическую энергию позитронов при их разлете. Поэтому
е2 (	1	ти2
----- 4 + —== = 2---, или
4яг0а V	V27	2
ти2 =|4+—1—--------- (1)
k yl2J 4ж0а
(скорости обоих позитронов на бесконечности одинаковы).
190
Теперь рассмотрим разлет протонов. Их потенциальная энергия до разлета, очевидно, равна:
е2
W2 - -----
Эта энергия переходит в разлета:
кинетическую энергию протонов после их
в2 г = Ми2, 4ж.0а>/2
(2)
т 1 Л -----;=--- = 0,01.
М 4у2 +1
где и — скорость протона.
Разделив теперь уравнение (2) на уравнение (1), получим:
/ \ 2 1 | U | U 4-^2 +1	т VLv ’ и
Задача 9.5. Заряженные шарики с одинаковой массой, расположенные на расстоянии I друг от друга, отпустили без начальной скорости. Через время t расстояние между ними удвоилось. Через какое время удвоится расстояние между этими шариками, если их отпустить с начального расстояния 3Z?
Решение. Шарики удаляются друг от друга под действием силы электрического отталкивания:
где q — заряд каждого шарика, г — расстояние между шариками и
4яг0
Эта сила и, следовательно, ускорения шариков меняются по модулю по мере изменения расстояния между шариками. Поэтому движение шариков не будет равноускоренным.
Разобьем перемещения шариков в первом и во втором случаях на одинаковое число участков, таких, чтобы относительные перемещения в обоих случаях были одинаковыми. Обозначим расстояние между шариками в начальный момент через 2х0, а в некоторый последующий
х
момент времени — через 2х. Величина £ = — есть относительное пе-х0
ремещение шариков.
Пусть £ изменилось на величину Д£. Тогда перемещение каждого шарика в первом случае (когда 2xq = Г) равно:
Л«1 = А^,
191
а во втором случае (когда 2х0 = 31) равно:
Л*2 =	-
При изменении на величину Д£ средние скорости шариков будут отличаться тоже в у/з раз:
^ср.2
Промежутки времени, за которые шарики перемещаются на Дх; в первом случае и на Дх2 во втором случае, равны соответственно:
Л. AXi	Лх2	\t2 Лх2 ucp.i /-
^ср.1	^ср.2	ДХ| t^cp.2
Следовательно, при любом изменении величины £ время движения в первом случае больше времени движения во втором случае в Зу/з раза. Когда расстояния между шариками удвоятся, полное время t2 будет больше времени ty тоже в Зу/з раза:
t2 =	= 3y/3t.
Когда же расстояние между шариками станет равным 2х, их потенциальная энергия примет значение
2 W = h^—, 2х
а значение кинетической энергии станет равным:
9 Wk = 2^— = то2, *	2
где т — масса шарика. По закону сохранения энергии
k-^-—= k—+ то2, =>
2х0 2х	у 2х0т4
Таким образом, при одном и том же значении относительного перемещения скорость шарика в первом случае больше, чем во втором, в
Д:Д£ = ^раза.
V ml У 3ml
192
Задача 9.6. У поверхности Земли напряженность электрического поля Ei = 120 В/м, на высоте Л = 1,5 км Е% = 25 В/м. Определите электрический заряд в атмосфере от поверхности Земли до высоты Л. Плотность электрических зарядов в атмосфере примите постоянной. Вектор напряженности направлен к Земле.
Решение. Обозначим заряд Земли q^, заряд слоя атмосферы от поверхности Земли до высоты h =1,5 км обозначим д2. Радиус Земли R « 6,4 106 м.
В этом случае имеем:
E!=k^-,	(1)
R2
E2=k(qx+q2l .	(2)
(R + h)
Так как h « R,
(3) R2
Из (1) и (3) следует:
*	9•109
?! = - 5,5  105 Кл,
_ 25-(6,4)2
42 -
• 1012
------Кл + 5,5 • 105 Кл = 4,4 • 105 Кл.
9 10®
Задача 9.7. В шаре распределен электрический заряд с постоянной плотностью р. В шаре имеется сферическая полость радиусом г. Центр полости находится на расстоянии I от центра заряженного шара. Определите напряженность электрического поля в точке А внутри сферической полости. Точка А находится на расстоянии а от центра заряженной сферы и на расстоянии Ь от центра полости (рис. 9.4).
Решение.
ООХ = I, ОА = а, О{А = Ъ, ЁА = Д - Ё2,
193
Рис. 9.4.
4 з	4 з
— ла р	~ лЪ р .,
91	, 3	±Ьрл	q2 з	±kpn
—— = д-----— =----а	= д —— = д------------
а2 а2 3	б2 ь2 3
тр /» — = /ОАО, = /ВАС, е2 ъ
еа _
I а
ЕА=^-1,
3
BClIOOj,
EaIIoOj.
Вывод: ЕА не зависит от а и Ъ,
внутри полости электрическое поле
однородное.
Задача 9.8. Три металлические пластины площадью S каждая расположены параллельно на расстояниях d друг от друга (рис. 9.5). На первой пластине имеется положительный электрический заряд qi, между первоначально незаря-
женными второй я третьей пластинами включена батарея с ЭДС £. Найдите заряды Qa и q% на пластинах 2 и 3.
Решение. Заряды q2 и д3 в сумме равны нулю (по закону сохранения электрического заряда):
92 + 93 = 0,	92 = - 9з = 9-
194
Напряжение U между пластинами равно ЭДС батареи:
U = £.
Так как векторы напряженности Е электрических полей, создаваемых зарядами qlt q2 и 9з, имеют между пластинами 2 и 3 одинаковое направление, то
_X_+_9_ + _J_L
2SfQ 2SfQ 2ScqJ
Рис. 9.5.
Рис. 9.6.
_ s0S£ 9i
4 J 2
d
Задача 9.9. Два шара одинакового радиуса Но с одноименными зарядами Q1 и 9г находятся на расстоянии г друг от друга. Если их соединить на короткое время проводником, то заряды станут равными:
а' -а> - 91 + 92
91-92-	2	
Сравните энергию электростатического взаимодействия шаров до и после опыта. Объясните полученный результат.
Решение. Потенциальная энергия взаимодействия заряженных шаров сначала равна:
Лр1 - 9i9>2 - «--------,
затем становится равной:
91 +<12
Е = q&'2 = 91±92_к_2_ = k(9i+9?)2 р2 1 2	2 г	4г
7*
195
Для сравнения величин Ер1 и Ер2 наймем их разность АЕр.
ь
ЬЕр = Ер2-Ер1=-
'	\2
91 + 92 |
, 2 J
-9192
I. (91 - 92)2 = к-----------
Г
Следовательно, при любых значениях зарядов Qj и ?2 энергия электростатического взаимодействия заряженных шаров после перераспределения зарядов возрастает! Этот результат кажется еще более парадоксальным, если учесть, что при перераспределении зарядов должно выделиться некоторое количество теплоты в проводнике, через который протекал электрический ток.
Объяснение полученного результата возможно лишь при учете «собственной энергии» заряженных шаров, т.е. потенциальной энергии взаимодействия зарядов на каждом из них.
Действительно, потенциальная энергия взаимодействия зарядов на шарах до перераспределения зарядов равна:
1	1	, Qi2 , q%
ЕР1 =^91<Р1 +-92<Р2	+
После перераспределения зарядов эта энергия становится равной:
\2
91 + 92 |
2 ) (оч 4- q2)
Л’2 = — q\m\ + — q2<p'9 = Zft-----= k—------.
р2 2 1 1 2 z 2	22?	42?
Изменение потенциальной энергии ДЕ' равно:
~ Е'р2 - Ер1 =	[(91 + 9г)2 _2(9i + 9г)] = “77(91 “ 92)2 < °>
4xv L	J 4л
т.е. потенциальная энергия взаимодействия зарядов на шарах уменьшилась. Так как R<r, то увеличение энергии электростатического взаимодействия шаров всегда меньше, чем уменьшение потенциальной энергии взаимодействия заряженных шаров.
Задача 9.10. Плоский заряженный конденсатор с прямоугольными пластинами установлен в вертикальном положении так, что его пластины соприкасаются с диэлектрической жидкостью. Расстояние между пластинами гораздо меньше линейных размеров пластин. Известны: напряженность начального электрического поля Е заряженного конденсатора, плотность р и диэлектрическая проницаемость е жидкости, высота пластин конденсатора Н.
Определите высоту поднятия жидкости между пластинами и объясните это явление. Капиллярностью пренебречь.
Решение. Причиной возникновения силы, поднимающей жидкость в зазоре между пластинами конденсатора, является неоднородность электростатического поля у края пластин конденсатора. Жидкость по
196
ляризуется, и на каждый ее диполь действует сила, втягивающая его в область более сильного поля, т.е. внутрь конденсатора. Конденсатор отключен от источника тока, заряд на его пластинах не изменяется:
Qo = C0U0.
При поднятии жидкости на высоту h (рис. 9.6) общий заряд пластин сохраняется, а емкость С полученного конденсатора станет равной:
х,	„ h „ H-h
С - CY +С2 - Сое — + с0 —
где Н — высота пластин конденсатора. Энергия электрического поля такого конденсатора вместе с потенциальной энергией поднятой жидкости равна:
w= Ql+mgh
2С 2 ’
W =
2С0
Qo
Eh (Н - h)
Н+ Н
pHhdgh
2
QqH pgHdh2
2C0 [И + h(s -1)]	2
где d — расстояние между пластинами, Н — ширина каждой пластины конденсатора (считаем их для простоты квадратными).
Условие равновесия — минимальное значение энергии W(h).
Для исследования функции W(h) на минимум берем производную W'(h) и приравниваем ее нулю. При этом высоту подъема жидкости обозначим hi'.
W'(h) = ---ОоЩе-Л)-----+ pgHdh^ = 0> или
2С0[Н + М*-1)]
Ь[Н + h^E - I)]2
Qo(g-I) 2Copdg
Введем обозначения:
=	Qq(£~1) 1 = wo(e - i) = Wp g-1
H	2C0pg dH3 pgdH2	2
где Жщах — потенциальная энергия жидкости, заполняющей весь конденсатор.
Подставляя эти обозначения в последнее уравнение, получаем кубическое уравнение относительно а:
ajl + а(е - l)j = А.
197
При небольших значениях а и £ приближенное решение этого уравнения а = А, откуда
h _ rr жо £ - 1 _ (* “ 1)го£о Нл — rl---------------------.
Wmax 2 2pg
Нет смысла вычислять это значение более строго, так как даже для воды (г = 81), приняв Eq = 104 В/м, получим:
(81-1)-8,85 10 12 Ю8	.
hr = 1--------—----------м = 4 • 10 м,
2103 10
что явно меньше влияния капиллярности и других эффектов. Видно также, что конденсатор не заполняется жидкостью целиком.
Задача 9.11. Внутри тонкостенной металлической сферы радиуса Я=20см находится металлический шар радиуса г=10см, имеющий общий центр со сферой. Шар через отверстие в сфере соединен с помощью очень длинного провода с Землей (рис. 9.7). На внешнюю сферу помещен заряд Q= 10 8 Кл. Вычислите потенциал этой сферы, электрическую емкость полученной системы проводящих тел и начертите эквивалентную электрическую схему.
Рис. 9.8.
Решение. Потенциал сферы в случае отсутствия заряда на шаре равен:
1 Q
(Рое =----— = 450 В.
4я£0 R
При соединении шара, находящегося внутри сферы, с Землей потенциал шара равен нулю, между ним и сферой существует электрическое поле, под действием которого на шар с Земли перетечет некоторый заряд q. Заряд Q, равномерно распределенный на сфере, не создает
198
поля внутри нее, поэтому поле внутри сферы определяется только зарядом шара q, и разность потенциалов между шаром и сферой равна:
&<Р = Vm - <Рс
1 j Ч
4дао кг
—1
R)
(1)
Поле вне сферы такое, как если бы все заряды были расположены в центре сферы. Поэтому потенциал сферы <рс после соединения шара с Землей равен:
1 g + Q
<РС = ~л------„
R
(2)
Следовательно, потенциал шара
<дш = <д0 + А<д =
\ R
1 f g + Q , g g
R,
1(Q g 1 -----=о,	(3) 4лг0 R г)
откуда следует, что
(4)
Подставляя выражение (4) в (2), тенциала сферы:
получим
искомое значение для по-
д =
-Q—.
R
<Ра
1 Q “ Q —
1 R
4да0 R
l_^zr)=225B.
4да0 я2
Электрическая емкость полученной системы проводящих тел равна:
С = — = 4ж'°Д = 4,4 • 10 11 Ф = 44 пФ.
<рс R-r
Эквивалентная электрическая система состоит из двух параллельно соединенных конденсаторов: сферического с зарядами на обкладках +q и -g и конденсатора «сфера — Земля» с зарядами на обкладках +(Q - g) и -(Q - g) (рис. 9.8).
Задача 9.12. Имеется электрическая цепь, содержащая 20 контактов. Каждая пара соединена конденсатором электроемкостью 1 мкФ. Какая электроемкость будет обнаружена при измерении между двумя любыми контактами?
Решение. Будем соединять конденсаторами последовательно 2, 3, 4 и т. д. контактов. Принципиальная электрическая схема такого соединения представлена на рисунке 9.9.
199
В силу симметрии схемы относительно точек 3, 4, 5, ... потенциалы этих точек при подключении контактов 1 и 2 к источнику напряжения одинаковы, конденсаторы 3—4, 4—5, 3—5, ... не заряжаются. Следовательно, схема рисунка 9.9 эквивалентна более простой схеме рисунка 9.10.
В этом случае (для п контактов) к одному конденсатору емкостью С мы имеем (п - 2) параллельно включенных пар из последовательно соединенных конденсаторов емкостью С каждый. Общая электроемкость Сп между контактами 1—2 определяется выражением
Сп = С + (п-2)~ = ±пС (п>2). Л &
По условию задачи п = 20, С = 10 6 Ф.
Следовательно, Сп = 1СГ5 Ф.
Рис. 9.9.
Рис. 9.10.
Задача 9.13. Ускоряющее напряжение в электронно-лучевой трубке £/а=1,5 кВ, расстояние от отклоняющих пластин до экрана L = 30 см. На какое расстояние сместится пятно на экране осциллографа при подаче на отклоняющие пластины напряжения Uy = 20 В? Расстояние между пластинами d = 0,5 см, длина пластин / = 2,5 см.
Решение. Выберем систему координат с осью Ох, направленной вдоль оси трубки, по направлению вектора скорости электронов до входа в пространство между отклоняющими пластинами. Ось Оу выберем направленной противоположно вектору напряженности электрического поля между отклоняющими пластинами (рис. 9.11).
Пренебрегая малым смещением электронов между пластинами, отклонение у электронного луча можно найти, зная проекцию скорости электрона на ось Оу после прохождения между отклоняющими пластинами и время t2 движения электрона от отклоняющих пластин до экрана:
У = oyt2 .	(1)
200
Время Z2 равно:
Z2=—•	(2)
»х
Проекцию скорости электрона на ось Оу можно найти по проекции
ускорения ау и времени Zj движения электрона между пластинами:
= ауЬ, где	(3)
F	еЕ eU„
а„ =  = = -------- (е — заряд электрона; т — его масса), а (4)
v т	т	md
4= — .	(5)
»х
Рис. 9.11.
Так как кинетическая энергия электрона равна работе сил ускоряющего электрического поля, проекцию скорости электрона их можно тт т°2х наити из выражения eUa = —:
(6)
Используя выражения (1) —
(6), получим:
eUylL eUylLm UylL
У — Vj.t? — dj.tytn —
y y mdoxux md2eUa 2dUt
Подставляя данные из условия задачи, находим смещение луча:
20 2,5 10“2 0,30
У =---sм = 10
2 5 -10 -1,5 Ю3
м.
и
2eCZa т
201
Задача 9.14. Две пересекающиеся плоскости равномерно заряжены отрицательным зарядом. В некоторой точке между плоскостями помещен радиоактивный источник. Начертить примерный вид траектории движения положительно и отрицательно заряженных частиц, испускаемых источником. Что это за кривые?
Решение. Заряды каждой из плоскостей создают однородное электростатическое поле с напряженностью Е, направленной перпендикулярно плоскости. Модуль напряженности определяется формулой
Е = —, 2е0
где ст — плотность зарядов. Согласно принципу суперпозиции поле обеих плоскостей будет тоже однородно, а его напряженность будет равна векторной сумме напряженностей полей пластин; результирующая будет направлена параллельно биссектрисе угла, образованного плоскостями. В таком поле заряженные частицы будут двигаться так же, как и тела в поле силы тяжести, — по параболам с осями симметрии, параллельными биссектрисе угла, образованного плоскостями.
Задача 9.15. В цилиндрический конденсатор в точке А впускается слегка расходящийся пучок положительных ионов с малым углом раствора а (рис. 9.12). Все ионы в пучке имеют одинаковую энергию. Те ионы, у которых вектор скорости в точке А направлен перпендикулярно к отрезку ОА, движутся по окружности радиуса г - ОА, концентрической с обкладками конденсатора. До-
Л казать, что пучок ионов будет фокусироваться в точке В такой, что ZAOB = —.
V2
Определить максимальную ширину пучка.
Решение. Применив теорему Гаусса, найдем, что в цилиндрическом конденсаторе напряженность электрического поля убывает обратно пропорционально расстоянию R до оси цилиндра:
ES =
£0
„ ст  2яг/
Е  2яЯ/ =-------
£о
EqR R
(1)
В этом поле на заряд q действует сила
„ kq
F = — . Ускорение заряда
равно:
kq а = —— . Rm
(2)
202
При отклонении на малое расстояние х от основной круговой траектории радиуса Rq ион движется с ускорением:
а,—.	(3)
пЦЯо + х)
В системе отсчета, вращающейся вокруг оси цилиндрического конденсатора с угловой скоростью to, ускорение иона равно:
= а + ац,
«1 = X - ®2(Яо + 4
(4)
По закону сохранения момента импульса для иона в точке Айв любой другой точке траектории имеем:
mjRoa>o = m(Ro + х)2®,
(5)
где ©о — угловая скорость иона в точке А.
с°о^о = —~’ jnltQ
2 k9
®0 = —“7 mRfi
(6)
Из (4), (5) и (6) следует:
«1 =
kq
«о
9
7 mfa+x) m^R^+x'j3
kq(- 2Лох - х2) аг = —i------------
(7)
з
При условии х « Ro*.
2kq
«1 = —V mRo
(8)
Уравнение (8) есть уравнение гармонических колебаний с периодом:
Т = 2
у 2kq
(9)
Все ионы будут пересекать основную круговую траекторию через Т интервалы времени, кратные половине периода колебаний: tn = п—.
2
203
Угловое расстояние между соседними точками фокусировки пучка
Т л
Найдем максимальную ширину пучка <imax:
Рис. 9.12.
Рис. 9.13.
Задача 9.16. Направленный поток электронов вылетает из тонкой длинной щели со скоростью и = 10s м/с (рис. 9.13). Концентрация электронов в потоке л = 1О10 частиц/м3. На каком расстоянии от щели толщина пучка увеличилась в 2 раза? Масса электрона m = 9  10~31 кг, заряд электрона е = 1,6 • 10 19 Кл, электрическая постоянная £0 = 8,85 • 10-12 Ф/м.
Решение. Будем считать, что щель настолько узка, что расстояние, на котором толщина пучка заметно меняется (например, в два раза), много больше ширины щели d^. В этом случае можно считать, что пучок представляет собой плоскопараллельную заряженную пластину, создающую электрическое поле с напряженностью
Е = — ,
2₽о
204
где а — плотность заряда на пластине, равная отношению заряда Q участка пластины к площади S этого участка. Так как
Q = enSdQ, то
<т= endQ.
Следовательно,
Е _ endp 2^0
В этом поле на электрон у края пучка действует сила:
F = eE, сообщающая ему в направлении, перпендикулярном к пучку, ускорение
F _ e2ndp
т 2т.£0
Ширина пучка удвоится, когда электрон пройдет с этим ускорением do расстояние , т.е. через промежуток времени
. _ ро" _ 12£0т
V а У е2п
Вдоль направления пучка электрон за это время удалится от щели на расстояние ,	2£пт
I - ut = о —« 2,5 см.
V е2п
Глава 10
МАГНИТНОЕ ПОЛЕ
Задача 10.1. По проводнику, имеющему форму окружности радиусом R, проходит ток I. Используя закон Био — Савара — Лапласа, вычислите индукцию магнитного поля в центре окружности.
Решение. Выбирая элемент проводника Д^ малым, можно считать его прямолинейным и перпендикулярным к прямой, соединяющей его с центром окружности (рис. 10.1). При этом условии угол а равен 90°. Получаем:
п Ро
Й1 = 1----9~ ‘
4л д2
Аналогичные выражения определяют индукцию магнитного поля, создаваемого в центре окружности другими элементами проводника: Д12,
Д/3, ..., Д/п. Индукцию магнитного поля В, создаваемого всем круговым током, можно найти суммированием векторов индукции отдельных элементов проводника с током Д^, Д/2, ..., Д/п • Все эти векторы параллельны, поэтому модуль вектора индукции кругового тока определяется выражением:
В — By + В2
+ ...+Вп = -^-?--(Д/1+Д/2 + ...+Д/п) = 4л R2 '	1
Ро
4л
-4-2лй =
R2
Ро
2
I
R
206
Мы получили, что индукция магнитного поля в центре кругового тока прямо пропорциональна силе тока в проводнике и обратно пропорциональна радиусу окружности.
Задача 10.2. в проводящем кольце радиуса 40 см течет постоянный ток 20 А. Найдите магнитную индукцию на оси кольца на расстоянии 30 см от центра кольца.
Решение. Для решения задачи используем закон Био — Савара — Лапласа:
Afxr,	(1)
4л г3
где АВ — вектор индукции магнитного поля, создаваемого малым элементом AZ тока I на расстоянии г от этого элемента тока до точки наблюдения, AZ х г — векторное произведение вектора AZ длины элемента тока и радиус-вектора г от элемента тока до точки наблюдения.
Найдем магнитную индукцию dB, создаваемую элементом AZ тока в кольце в точке А (рис. 10.2).
Рис. 10.2.
Так как радиус-вектор г перпендикулярен элементу тока AZ, получаем:
dB = £o£.
4л- R2 + Z2
Не производя интегрирования, можно получить значение вектора В.
207
Компоненты вектора dB, перпендикулярные оси ОА от симметричных относительно точки О элементов тока, компенсируют друг друга. Поэтому результирующий вектор В определяется из пропорции:
В _ 2лй & _ йв 2^Rsing _ HqIR2
dB sin a dl ’	dl I 2 ,2\3^2
zi a + l i
Подставив данные задачи, получаем:
12,566 10~7 -20 0,16
2 0,125
Тл « 1,6 10 5
Тл.
Задача 10•3. Определите магнитную индукцию в центре квадратной рамки со стороной I при силе тока I.
Решение. Найдем магнитную индукцию тока I на расстоянии — от
прямолинейного проводника длиной I.
По закону Био — Савара — Лапласа для участка проводника длиной .AZ имеем (рис. 10.3):
й д01 AZ х г	I
4л ГА	2 cos а
д, r,Aa ZAg
AZ -	-	- .
cos a 2cos2g
Рис. 10.3.
д01 Z Ag  4 cos 2 g  sin(90°-g)	ApI cos g  A g
4л	2 cos2g • Z2	2^Z
208
By = jdB = fcosa da = -^^-(sinai +sina2). 2/rZ	2^1
Так как а1 = а2 = 45° (рис. 10.4), то = ——
2я7
Для четырех сторон квадрата
В4 = 4Bj =
Задача 10.4. Определите магнитную индукцию на расстоянии 2 м от длинного прямолинейного провода при силе тока в нем 10 А.
Решение. Применим закон полного тока к контуру, представляющему собой окружность радиуса R с цен-
тром на оси проводника и лежащую в плоскости, перпендикулярной проводнику (рис. 10.5):
fBdf = доХЛ-
В силу симметрии вектор В магнитной индукции в любой точке на окружности должен иметь одно значение и направлен по касательной к окружности.
Следовательно,
В • 2лЯ = п0/, В =	.
2nR
12,6 10 7 10 2-3,14-2
Тл ® 10 6 Тл.
Задача 10.5. Электроны ускоряются в электронной пушке электрическим полем, проходя отрезок пути, напряжение на концах которого U = 103 В. Вылетев из пушки в точке Т, электроны движутся затем по прямой ТТ' (рис. 10.6). В точке М на расстоянии d = 5,0 см от точки Т находится мишень, причем прямая ТМ образует угол а - 60° с прямой ТТ'.
1. Какой должна быть индукция В однородного магнитного поля, перпендикулярного плоскости рисунка, чтобы электроны, вылетевшие из пушки, попадали в мишень?
2. Какой должна быть индукция Bt однородного магнитного поля, параллельного прямой ТМ, чтобы электроны попадали в мишень?
Считать, что модули векторов индукции В и В1 не превышают 0,03 Тл.
209
Решение. 1. Электроны попадают в магнитное поле, имея скорость и, которую они приобрели, ускоряясь в электрическом поле:
тт m°2 l2eU	/п
eU = --, u = J-------,	(1)
2	V rn
где е и т — заряд и масса электрона.
В случае, когда вектор индукции магнитного поля В перпендикулярен плоскости рисунка (рис. 10.6), электроны движутся в этом поле по окружности, которая касается прямой ТТ' в точке Т, и попадают в точку М мишени.
Центростремительное ускорение электронов создается силой Лоренца Fjj = еиВ:
и2 еиВ
R ш
Искомая индукция магнитного поля равна:
В = — eR
Подставляя в эту формулу выражение (1), получим:
1 2mU
В = —J--
R\ e
Из рисунка 10.7 видно, что
R=-*-
2 sin а
(2)
(3)
(4)
210
Подставив (4) в (3), получим ответ задачи в общем виде:
В =
2 sin a 2mU dye
(5)
Числовое значение индукции: В = 3,7 • 10 3 Тл.
2. В этом случае электроны влетают в магнитное поле под углом а к вектору индукции магнитного поля Bj и движутся по спирали. Это сложное движение можно представить как результат двух движений: равномерного движения со скоростью = о cos а в направлении линий индукции магнитного поля и равномерного движения по окружности со скоростью и2 = и sin а в плоскости, перпендикулярной прямой ТМ (рис. 10.8).
, * 2яй1
Сделав целый оборот вокруг оси спирали за время t =-, элект-
U2
роны пересекут прямую ТМ на расстоянии I = u^t от точки Т. Чтобы электроны попали в мишень М, им необходимо сделать целое число оборотов, т.е. чтобы расстояние ТМ = d содержало целое число отрезков Т.
d = nl = ni>i = 2^/?^— = 2flR1nctga.	(6)
При движении электронов по окружности под действием силы Ло-„„2 — ТТЮо ренца	,
Й1
Д1=».	(7)
еВ]
Учитывая, что и2 = и sin а, и используя полученное выражение (1) для скорости электрона и, получим:
„	1 2mU .
Ri = —,----sm a.
В V e
(8)
Из (6) и (8) получаем:
, „ п l2mU d - 2л—,-----cos a
Bj V e
к находим искомое значение индукции Bj магнитного поля:
Bi = 2£ncosa 2иг£=п 67 10_3 Тд d V е
211
По условию задачи By <3 10 2 Тл, поэтому возможны такие значения модуля индукции при п=1, 2, 3, 4: By = 6,7 10-3Тл; В{ = 1,34 • 10“2 Тл; Bf = 2,01 • 10~2 Тл; В{"= 2,68 • 102 Тл.
При больших п значения В > 3 • 10~2 Тл.
Задача 10.6. Из точки Q в одной плоскости испускается пучок положительных однозарядных ионов (заряд +е) одинаковой и постоянной массы т. Ионы, ускоренные напряжением U, отклоняются однородным магнитным полем, которое направлено перпендикулярно к плоскости распространения ионов. Индукция магнитного поля равна В. Границы магнитного поля должны быть такими, чтобы пучок ионов сходился в одной точке A (QA = 2а). Траектории ионов должны быть симметричными относительно линии, перпендикулярной к отрезку QA и проходящей через его середину. Из возможных границ магнитного поля следует выбрать такие, которые находились бы в окрестностях линии, перпендикулярной к середине отрезка QA, но не захватывали точек Q и А. Область должна быть односвязной, т.е. без дыр и разрывов.
1.	Выразите радиус кривизны R траектории частиц в магнитном поле как функцию напряжения U и индукции В.
2.	Укажите характерные свойства траектории частиц в описанной установке.
3.	Найдите границы магнитного поля путем геометрического построения для случаев: R<a, R = a и R>a.
4.	Найдите математическое выражение для границы магнитного поля.
Решение. 1. Изменение кинетической энергии положительных ионов происходит вследствие совершения работы силами электростатического поля:
А = AEk,
ТТ т°2 l2eU
eU = -—, u = J---------.	(1)
2	v т
На ион в магнитном поле действует сила Лоренца: F = еиВ. Эта сила сообщает иону центростремительное ускорение. Применив второй закон Ньютона, можно записать следующее равенство:
_ ти2 „ ти
еиВ =---- => R =-------,	(2)
R	еВ
где R — радиус окружности, по которой движется ион в поперечном магнитном поле.
Подставив выражение (1) в (2), получим:
„ 1 l2mU
— —Л1---- .
В Ц е
2гк
2.	Ионы движутся по прямым до пересечения с областью магнитного поля, в магнитном поле их траектории искривляются и становятся дугами окружностей. После выхода из магнитного поля ионы снова движутся по прямым (рис. 10.9). Ясно, что прямые являются касательными к дугам окружностей, и следовательно, радиусы, проведенные к границе магнитного поля, перпендикулярны к этим прямым.
Так как траектории ионов должны быть симметричными относительно перпендикуляра ОО', проходящего через середину отрезка QA, то траектории ионов пересекают прямую ОО' под прямым углом, причем центры окружностей лежат на этой прямой.
Рис. 10.10.
Рис. 10.9.
Рис. 10.12.
213
3.	В зависимости от соотношения между R и а границы магнитного поля будут иметь различный вид.
Для R < а границы магнитного поля имеют вид, представленный на рисунке 10.9, для R = а — на рисунке 10.10, для R > а — на рисунке 10.11.
4.	На рисунке 10.12 показана одна из траекторий иона. Точка Р(х,у) принадлежит границе магнитного поля. Обозначим а — угол между осью Оу и радиусом, проведенным в точку Р. Так как радиус перпендикулярен касательной АР, то угол , А тоже равен а (как углы со взаимно перпендикулярными сторонами). Из рисунка 10.12 видно, что
(а - х)х
х = Rsma, y = la-x)tga, у = ;	/ — .
v ’	Jr2-*2
Задача 10.7. Заряженная частица попадает в среду, где на нее действует сила сопротивления, пропорциональная скорости. До полной остановки частица проходит путь S = 10 см. Если в среде имеется магнитное поле, перпендикулярное скорости частицы, то она при той же начальной скорости остановится на расстоянии = 6 см от точки входа в среду.
На каком расстоянии I2 от точки входа в среду остановилась бы частица, если бы поле было в два раза меньше?
Решение. На частицу в среде при наличии магнитного поля действуют две взаимно перпендикулярные пропорциональные скорости частицы силы, сила трения и сила Лоренца:
F	Fji =qB —
тр	At л At
(рис. 10.13). Сила трения перпендикулярна силе Лоренца.
Поэтому приращение импульса гпДй за время At есть векторная сумма импульса силы трения /г| Дг| и перпендикулярного ему импульса силы Лоренца qB\ Дг|. Три упомянутых вектора образуют прямоугольный треугольник (рис. 10.13, а). Подобный треугольник образуют и соответствующие векторы за все время движения частицы (рис. 10.13, б), где I — расстояние от точки входа в среду до точки остановки, а 1>0 — начальная скорость частицы. В отсутствии поля прямоугольный треугольник вырождается в прямую и ти0 = kS. В магнитном поле В, используя теорему Пифагора, можем записать:
77WO = 5/(^i)2 +(?-BZ1)2 ;
214
в
в поле —:
2
Из этих трех соотношений легко находим, что
и 8,33 см.
Рис. 10.13, а.
Рис. 10.13, б.
Задача 10.8. В длинном бруске, имеющем форму разностороннего параллелепипеда (а>Ъ»с) и сделанном из полупроводникового материала InSb, течет ток I в направлении ребра а. Брусок находится в магнитном поле, направление вектора индукции В которого совпадает с ребром с. Переносчики тока в InSb — электроны, которые движутся в электрическом поле с напряженностью Е со средней скоростью и = иЕ (коэффициент и называется подвижностью электронов). При наличии магнитного поля необходимо учитывать действие силы Лоренца на электроны — направление вектора напряженности в этом случае не будет параллельно электрическому току. Этот феномен известен как «эффект Холла».
Выполните следующие задания:
1.	Определите модуль и направление вектора напряженности электрического поля в бруске.
215
2.	Вычислите разность потенциалов между противоположными точками на поверхности бруска в направлении ребра Ь.
3.	Получите аналитическое выражение для прстоянной компоненты разности потенциалов, найденной в пункте 2, если сила тока и индукция магиитното поля меняются по законам:
I = Io sinart, В = Во sin^art + р).
Решение. 1. Под действием силы Лоренца происходит перераспределение электронов по поверхности бруска. Электроны движутся до тех пор, пока сила F', действующая на них со стороны электрического поля с напряженностью Е', которое создается возникшими поверхностными зарядами, не уравновесит силу Лоренца (рис. 10.14):
Fji = F', еиВ = еЕ', Е' = иВ.
Рис. 10.14.
Рис. 10.15.
Полная напряженность (рис. 10.15):
электрического поля в бруске равна
Так как сила тока I в бруске равна I = пеисЬ, то
— Е + Е'.
I и = ———, necb
Е' = 1>В =------
necb
„и 1
Е — — — —-
и песЬи
216
Тогда
£п = Je2 +Е'2 = —— ,Р- + В2 « 4,1 В/м, песЬ у и2
а = arctg|—] = arctg(Bu) « 38°.
2. В направлении ребра Ъ возникнет напряжение:
и = Е'Ь = — = 2,5  10“2 В.
пес
3. Разность потенциалов U будет изменяться по закону:
— _ IB 1 -	. /	\
и =-----=----10 sin <ot  Во sin( a>t + <р I =
пес пес		7
_ £оД) cos _ IqBo <,^/2^ + 0,1 2nec 2nec '	7
Таким образом, напряжение имеет постоянную составляющую:
Uo =	- cos <р.
2пес
Задача 10.9. Определите индуктивность цилиндрической катушки длиной 50 см из 1000 витков с площадью витка 10 см2.
Решение. Индуктивность L катушки можно найти, зная магнитный поток Ф, создаваемый в ней током I:
Ф
Ф = LI, L = — .
I
Идеализируем задачу. Найдем магнитную индукцию в очень длинной катушке с площадью витка S и числом витков п на единицу длины при силе тока I.
У очень длинной катушки магнитная индукция вдали от ее концов очень мала, внутри катушки вектор В магнитной индукции параллелен оси катушки (рис. 10.16). Для нахождения модуля вектора В выделим прямоугольный контур ABCD с длиной стороны АВ, равной I. Расположим сторону АВ параллельно вектору В внутри катушки, а сторону DC вне катушки. Контур ABCD охватывает ток
IK = 1пМ,
где I — сила тока в катушке,
п — число витков катушки на единицу длины,
— длина стороны АВ контура, параллельной оси катушки.
217
I
м
Рис. 10.16.
По закону полного тока для контура ABCD выполняется равенство \Bdi = ^it,
т.е. интеграл от произведения вектора магнитной индукции на бесконечно малый элемент контура вдоль контура равен произведению д0 на алгебраическую сумму токов, охватываемых контуром.
В нашей задаче отличен от нуля интеграл по контуру лишь на стороне АВ и равен В1. На сторонах AD и ВС произведение Bdl внутри катушки равно нулю вследствии взаимной перпендикулярности векторов В и dl, вне катушки В = 0.
Следовательно:
ВЫ = РоЛ< =	В = Воп1-
Магнитный поток Ф через катушку из .У витков с площадью S равен:
Ф = BSN = ponISN.
Отсюда индуктивность длинной катушки равна:
, Ф скт fj0N2S
L = y = WiSN =	,
где I — длина катушки, W — число витков, S — площадь сечения витка.
Подставим числовые значения из условия задачи:
L = 12,6  10 7 • 106 • 10 3 • 2 Гн » 2,5 • 10~3 Гн.
Задача 10.10. Две катушки из сверхпроводящего провода индуктивностью 2 • 10 Гн и 4 • 10 Гн соединены параллельно. Каковы максимальные значения силы тока в катушках при соединении их концов с конденсатором электроемкостью 3 мкФ, заряженным до напряжения 100 В?
218
Решение. По закону сохранения энергии:
brf । JLgZf	U2C
2	2	2
Изменения напряжения на катушках одинаковы, поэтому:
- L2	- L2^2-
st	st
Из (1) и (2) следует:
I2=^J	^!2 + Ф1 = и2с
L2 1	l2
(2)
' I CL2
] ^1(^2 + -Ч)
г 3 1(Г6 4 10’2
IY = iooJ---------------
V 2 - 10-z - 6 - 10-z
I2 =0,5 A.
Задача 10.11. Контур из сверхпроводника индуктивностью L и площадью S вносится в однородное магнитное поле с индукцией В, плоскость контура перпендикулярна вектору В. Какова сила тока, возникающего при этом в контуре?
Решение. Ток в сверхпроводящем контуре возрастает до полной компенсации изменения магнитного потока через контур:
Ф = BS, Ф = LI, I = —.
L
Задача 10.12. Два одинаковых полосовых магнита соединены противоположными полюсами. Для их разъединения оказывается необходимым приложить силу 100 Н. Какова индукция магнитного поля в небольшом зазоре между полюсами магнита? Площадь поперечного сечения магнита 2,5 см2.
Решение. При разделении полюсов магнита работа внешних сил затрачивается на увеличение энергии магнитного поля:
А = SE. .
При небольшом зазоре Ad между полюсами магнита можно считать, что все изменения магнитного поля происходят только в пространстве между полюсами магнитов, поле в зазоре между полюсами магнитов однородное. Плотность энергии однородного магнитного поля равна:
В2
<о =----.
2До
219
Изменение энергии магнитного поля при раздвижении полюсов на малое расстояние d равно:
2До 2ц0
Работа силы F при этом равна:
A = Fd;
d d
Следовательно:
2ц0 ’ V S ’
(2-12,6-10'7-100
В = J--------------- 1 Л и 1 1 Л.
V 2 • 10"4
Задача 10.13. На сверхпроводящий образец массой т, парящий над постоянным магнитом, кладут груз точно такой же массы. Во сколько раз необходимо увеличить индукцию поля, создаваемого магнитом, чтобы сверхпроводник с грузом парил на прежнем расстоянии от магнита?
Решение. Магнитное поле, созданное постоянным магнитом, не проникает в сверхпроводящий образец. Это происходит потому, что в поверхностном слое сверхпроводника индуцируется ток, который создает свое собственное поле, компенсирующее внешнее.
Этот ток I должен быть пропорционален магнитной индукции В внешнего поля: I ~ В. Согласно закону Ампера взаимодействие электрического тока с магнитным полем характеризуется силой F, пропорциональной и силе тока /, и магнитной индукции В. В нашем случае
F-IB-B2.
Эта сила и уравновешивает силу тяжести сверхпроводящего образца. Если масса образца с грузом удвоилась, для сохранения равновесия магнитная индукция поля постоянного магнита должна быть увеличена в д/з раз.
Задача 10.14. По длинному сверхпроводящему соленоиду с индуктивностью Lq = 1 Гн, содержащему N = 200 витков, течет ток Го = 0,1 А. Издали к соленоиду подносят замкнутый проводящий виток того же радиуса, что и витки соленоида; индуктивность витка Lj = 1 • 10~3 Гн. Виток вставляют между витками соленоида соосно с ними. Как изменится ток, текущий по соленоиду? Каким будет ток витка?
220
Решение. Вначале магнитный поток через катушку равен:
Ф = LoIq.
Число витков можно считать достаточно большим и не учитывать «неравноправное» положение крайних витков катушки. Тогда каждый из витков катушки «пронизан» потоком
С другой стороны, каждый из витков катушки создает поле, пронизывающее все витки, и его вклад в созданный катушкой поток состав-
Ф ляет тоже — = ®о (это не случайное совпадение — так и должно
А
быть!).
После внесения в катушку замкнутого витка в нем возникнет ток (обозначим его Ji), изменится и ток через катушку (обозначим его /2)-Виток не имеет сопротивления, поэтому магнитный поток через него должен остаться равным нулю:
Ljlj + — LqI2 = 0.
Аналогично (с учетом вклада поля внесенного витка) для катушки:
Мо = L0I2 + — L0Il.
Решая систему, получим:
Д = -	---—----7 « - 0,5 А, 12 =--------«0,1 А.
-М	1-Аг
I ьА
Задача 10.15. Для того чтобы получить две совершенно одинаковые катушки, их наматывают на немагнитный сердечник одновременно, используя сложенные вместе провода (рис. 10.17). Одну из катушек подключают через ключ К к батарейке с напряжением UQ, вторую — к резистору R. Ключ замыкают. Рассчитайте мощность тока на резисторе.
Решение. При расчете ЭДС индукции в цепи каждой катушки нужно учитывать полный магнитный поток через нее, т.е. сумму потоков, создаваемых токами обеих катушек.
После замыкания ключа в обеих цепях возникают одинаковые ЭДС = £2 = Uq и мощность, выделяющаяся на резисторе, равна:
R R
221
Ток, текущий через вторую катушку, 12 =	. Магнитный поток,
R
пронизывающий первую катушку,
Ф1 = Lly + LI2,
где Jj — ток через первую катушку и через батарейку (поток через каждую катушку, создаваемый током 12, один и тот же — катушки намотаны вместе).
Следовательно,
£j _ С10 _
б/ф 1 dt
L^L + L^2 dt dt
dlr
(так как I2 = const). Отсюда
r Uo U0 It =---1--
R L
График I^t) приведен на рисунке 10.18. Скачок тока в первый момент связан с тем, что полный поток через катушки не должен меняться скачком, и сразу после включения возникает добавочный поток, направленный против потока, создаваемого первой катушкой.
Рис. 10.18.
К моменту размыкания ключа полный поток через вторую катушку
Ф2г - ~LI2 +LIlr - L —Q-r — Uot. Lj
Сразу после размыкания ключа в этой катушке возникнет ток:
г  иог
р L ’
222
поскольку поток через катушку не должен меняться скачком. Тепло, которое выделится на резисторе с момента размыкания, —
W = -LI2
2 р
и&2
2L
Задача 10.16. Металлическая рамка в форме буквы «П» расположена вертикально в однородном магнитном поле, вектор индукции В направлен перпендикулярно плоскости рамки (рис. 10.19). Вертикально вниз из состояния покоя начинает движение металлический стержень АВ. Стержень находится в электрическом контакте с вертикальными сторонами рамки, но движется вдоль них без трения. Определите скорость и движения стержня через t секунд после начала движения. Масса стержня т, электрическое сопротивление стержня 7?, расстояние между точками контактов стержня с рамкой I. Электрическое сопротивление рамки и ее индуктивность пренебрежимо малы. Самоиндукцией пренебречь.
Рис. 10.19.
Решение. На стержень действуют сила тяжести и сила Ампера. По
второму закону Ньютона для стержня запишем:				
	du т — dt	= mg - IBl,		(1)
	du dt	= g~	IBl m	(2)
Так как	4 1= -	p иинд R	_ Blu^ R ’	(3)
то из (2) и (3) следует:	du	= g-	B2l2u	(4)
	dt		mR	
При условии		du dt	= 0	(5)
скорость перемычки перестает увеличиваться. Из (4) и (5) скорость и
установившегося движения равна:
mgR
В212 '
(6)
223
Если о « vK, то влиянием силы Ампера можно пренебречь и определять скорость движения перемычки из уравнения:
О « gt.	(7)
Более полный и строгий ответ на вопрос задачи может быть найден путем решения дифференциального уравнения (4). Как известно, решение дифференциального неоднородного уравнения типа
= W + A	(8)
dx
может быть найдено как сумма общего решения однородного уравнения вида
и какого-либо частного решения неоднородного уравнения (8). Общее решение однородного уравнения (9) хорошо известно:
у = Серх .	(10)
Частное решение неоднородного уравнения (8) найдем для случая
у = В = const.	(11)
В этом случае
— = рВ + А = 0, dx
В = -—~.	(12)
Р
Следовательно, общее решение уравнения (8) имеет вид:
У = - — + Серх.	(13)
Р
Из (4), (6) и (8) для нашей задачи следует:
В^1^ и = у, t = х, А = g, р =------------, или
mR
Поэтому решение уравнения (13) приобретает вид:
gt	gt
i) = —g + Ce °к =ок+Се °к.	(14)
g
224
При условии t —> О получаем:
_ Л
о —> О,	е Uk -> е° = 1,
О = ок + С, С = — ик.
Из (14) и (15) следует:
' _ л'
и = ик 1-е "к .
I 7
(15)
(16)
Из (16) можно определить условия применимости приближенных решений (6) и (7).
ТТ	,	<4
При условии t » —— g
При условии t « —— g
mR
——— имеем: о -> ок. В212
mR
—— имеем: о » gt. В2!2
Последнее следует из известного соотношения е х = 1 - х, при ма-
лых х.
Тогда
gt
»К и i _ St , «к ’
и = «к

= gt.
Глава 11
ПОСТОЯННЫЙ ТОК
Задача 11.1. Из одинаковых резисторов с электрическим сопротивлением 1 Ом каждого составлена электрическая цепь (рис. 11.1). Каким будет электрическое сопротивление цепи между точками А и В при неограниченном увеличении числа звеньев цепи?
Решение. Электрическое сопротивление цепи из одного звена равно 2 Ом, подключение каждого следующего звена уменьшает общее сопротивление цепи, так как сопротивление 2 Ом включается параллельно части цепи. Обозначим общее сопротивление цепи при очень большом числе п звеньев R. Тогда общее сопротивление цепи при добавлении еще одного звена также равно R (рис. 11.2).
г + —^- = Л,	Rr + r2 + Rr ~ R2 - Rr = О, R2 - Rr - г2 = О,
R + г
R =
г ± 1/г2 + 4г2
2
2
Электрическое сопротивление цепи имеет только положительное
значение, поэтому:
2
R « 1,62 Ом.
Рис. 11.1.
Рис. 11.2.
R =
г R
226
Задача 11.2. Двадцать точек соединены резисторами по г = 10 Ом, причем каждая точка соединена с любой другой одним резистором. Каково сопротивление R между любыми двумя точками?
Решение. Составим эквивалентную электрическую схему данной цепи. Сначала соединим резистором точки 1 и 2. Затем точку 3 соединим резисторами с точками 1 и 2, точку 4 соединим резисторами с точками 1, 2 и 3 и так далее. На рисунке 11.3 представлена схема соединения пяти точек. Рисунок показывает, что при измерении сопротивления между точками 1 и 2 (т.е. при подключении внешнего источника к этим точкам) резисторы Л;)4,	5 и Яз5 не влияют на резуль-
таты измерений, так как они включены между точками с одинаковыми потенциалами и электрический ток через эти резисторы не идет. Следовательно, эквивалентная схема соединения резисторов для п точек может быть представлена рисунком 11.4.
Для п элементов имеем:
1	1 п - 2	п	„2т
— = — +-= — , R = — .
R	г	2т	2г	п
Задача 11.3. На рисунке 11.5 представлен график зависимости силы тока от напряжения на нелинейном резисторе. Определите силу тока в цепи при подключении этого резистора к источнику тока с ЭДС 10 В и внутренним сопротивлением 100 Ом.
Решение. При подключении резистора с электрическим сопротивлением R к источнику тока с ЭДС £ и внутренним сопротивлением г сила тока I в цепи равна:
1 = ^-.
R + r
8*
227
Напряжение U на резисторе равно:
U = £ - 1т.
При любых изменениях электрического сопротивления R на внешнем участке сила тока I в цепи связана с напряжением U на внешнем участке цепи и внутренним сопротивлением г источника уравнением:
г
Это уравнение прямой, пересекающей ось абсцисс в точке I = О,
£ U = £ и ось ординат в точке U = О, I = — .
г
Проведем эту прямую (рис. 11.6). Точка пересечения прямой с графиком I(U) для резистора дает значения силы тока Iq в цепи и напряжения Uy на резисторе:
£
I = — = 0,1 А, и = £ = 10 В, 10 ~ 0,06 А, и0 * 4 В.
Задача 11.4. Рабочее напряжение лампочки, вольтамперная характеристика которой приведена на рисунке 11.7, равно 3,5 В (кривая обрывается при напряжении 4 В — лампочка перегорает). Две такие лампочки соединяют последовательно и подключают к мощному источнику напряжения 5 В.
Чему равна сила тока в цепи? Какой резистор И нужно подключить параллельно одной из лампочек, чтобы напряжение на другой составило 3,5 В? Перегорит ли какая-нибудь из лампочек, если этот резистор заменить еще одной такой же лампочкой?
Решение. При последовательном подключении двух одинаковых лампочек напряжения на них будут одинаковы, а так как суммарное
228
напряжение равно 5 В (напряжение мощного источника не меняется при подключении к нему нагрузки), то на каждой из лампочек окажется 2,5 В.
Во втором случае напряжение на лампочке, которая горит полным накалом, равно 3,5 В, значит, на второй (и на подключенном к ней резисторе) напряжение составляет 5 В - 3,5В = 1,5В. По вольтамперной характеристике находим токи через лампочки при напряжениях 3,5 В и 1,5 В — они составляют 0,28 А и 0,22 А. Значит, ток через резистор равен 0,06 А (разность токов лампочек) и по закону Ома можно найти сопротивление R резистора:
1 5
R = —-— Ом = 25 Ом.
0,06
Теперь посмотрим, перегорит ли лампочка в последнем случае (рис. 11.8) — ясно, что речь может идти об «одиночной» лампочке. Пусть напряжение на ней составит 4 В (предельное значение). Сила тока I при этом примерно равна 0,28 А. При силе тока
/1 = 0,14 A I L =-|
I 2.)
напряжение на лампочках, включенных параллельно, составило бы 0,7 В, т.е. предельного значения 4 В напряжение на одиночной лампочке достигло бы при напряжении источника 4,7 В. Значит, при напряжении источника 5 В лампочка должна перегореть.
Задача 11.5. При конструировании лампы-вспышки применили нелинейный конденсатор (он заполнен диэлектриком, у которого диэлектрическая проницаемость зависит от напряженности поля). График зависимости напряжения U от заряда q конденсатора приведен на рисунке 11.9. Конденсатор заряжают от батареи с Ug = 300 В через резистор с сопротивлением R = 10 кОм. Найти максимальную энергию вспышки. Оценить максимальное число вспышек за одну ми-
229
путу. Считать, что при вспышке конденсатор полностью разряжается. Минимальное начальное напряжение вспышки !7i = 250B.
Решение. Максимальная энергия вспышки численно равна площади под графиком кривой U(q), ограниченной значением U = Uo = = 300 В. По графику (рис. 11.9) определяем, что при этом q » 0,3 Кл. Чтобы определить эту площадь, разделим кривую U(q) на участки, на каждом из которых зависимость U(q) можно приближенно считать линейной. Под каждым таким участком площадь численно равна AqiUcp. Таким образом, максимальная энергия вспышки
140
W а------0,05 Дж +
2
140+200	200 + 300
--------0,075 Дж +---------
2	2
0,175 Дж » 60 Дж.
Удобный способ определения времени заряда
250 В подсказывает формула I\t = \q, откуда At =
^общ ” Е
конденсатора от 0 до
Aq —- и
I
Начертим график зависимости
от q (рис. 11.10). Силу тока при
(Пр — п)
заданном значении q находим по графику I = ------------ . Площадь под
7?
графиком кривой, ограниченной значениями I 1 = 200 А \ q = 0,2 Кл, численно равна времени заряда конденсатора:
33 + 100 „, г 100 + 200 „„„
to6... ~----------0,125 с +--------------0,075 с ~ 20 с.
щ 2	2
Итак, вспышки можно производить примерно три раза в минуту.
230
Задача 11.6. На рисунке 11.11 приведен график зависимости напряжения на разрядном промежутке дугового разряда от тока. Дугу подключают к источнику постоянного напряжения последовательно с резистором. При каком максимальном значении сопротивления резистора дуга может гореть при напряжении источника Uo = 85 В?
Решение. Напряжение U на «дуге» при включении ее последовательно с балластным резистором сопротивлением R определяется формулой:
U = Uо - IR,
где I — сила тока в цепи.
Это уравнение можно решать графически, сопоставляя вычерченные на одной координатной плоскости вольтамперную характеристику дуги U = U(I) и нагрузочную прямую U = Uo - IR (рис. 11.12).
Точки а и б пересечения нагрузочной прямой с вольтамперной характеристикой дуги U(I) (точка а соответствует неустойчивому, а точка б — устойчивому горению дуги) определяют возможные значения силы тока и напряжения на дуге. Если у нагрузочной прямой нет общей точки с вольтамперной характеристикой дуги, то горение дуги невозможно. Следовательно, максимально возможному сопротивлению R соответствует касательная к графику U(I), чем и определяется максимальное значение сопротивления резистора:
R =
---= 5 Ом.
М
Рис. 11.11.
Рис. 11.12.
231
Задача 11.7. При увеличении силы тока напряжение на разрядном промежутке дугового разряда уменьшается, стремясь при больших значениях силы тока к некоторому постоянному значению. Электрическую дугу включили в сеть последовательно с некоторым балластным резистором. Вольтамперная характеристика зависимости напряжения от тока такой цепи — на рисунке 11.13.
Выполните следующие задания:
1. Постройте вольтамперную характеристику дуги без балластного резистора.
2. Используя полученную вольтамперную характеристику дуги, определите максимальное сопротивление балластного резистора, при котором дуга может гореть при напряжении источника Ug = 85 В.
Решение. 1. Напряжение Uo на входе системы равно сумме напряжения U на дуге и напряжения EZj на резисторе. Так как U\ = IR, где I — ток в цепи и R — сопротивление резистора, то
U0(I)= U(I) + IR.
Напряжение U на дуге убывает при увеличении I и при больших токах стремится к постоянному значению с. Это означает, что при больших токах зависимость U0(I) должна стать линейной:
U0 = IR + c,
причем тангенс угла наклона графика U = U(I) равен R, т.е. ——— = R.
Из рисунка 11.14 видно, что при I > 15 А график представляет собой практически прямую. Из рисунка находим:
25 R =-----Ом « 1,4 Ом.
17,5
Для того чтобы построить вольтамперную характеристику дуги U(I), надо, как показано на рисунке 11.14, из значений Ug(I) вычитать соответствующие значения UR = IR.
232
2. Далее задача решается так же, как задача 11.6. Для максимального значения сопротивления резистора находим:
лтах * 5 Ом-
Задача 11.8. Зависимость напряжения от силы тока для некоторого источника электрической энергии показана на рисунке 11.15. Определите силу тока I и напряжение (7Н при подключении резистора R к выходу источника.
Решение. Подключим к источнику резистор с сопротивлением R. Напряжение на нем связано с силой тока простым соотношением — UH = RI. Там же, где изображена зависимость U(I), начертим прямую UH = RI. Точка пересечения графика U(I) и прямой UH = RI даст нам искомые значения силы тока и напряжения. Для обычного источника, у которого напряжение на зажимах тем меньше, чем больше сила тока, никаких проблем больше не возникает — точка пересечения одна и результат определяется однозначно. А вот для необычного источника тока, у которого на некотором участке напряжение растет с ростом силы тока, есть область значения R, при которых точек пересечения три. Понятно, что сила тока не может иметь одновременно три значения; значит, с этой областью нужно разбираться отдельно — удобный графический способ определения тока в цепи тут явно не подходит.
Подключим к источнику сначала резистор с очень большим сопротивлением, а затем будем постепенно уменьшать сопротивление. Первоначальный ток в цепи будет очень малым, и при уменьшении сопротивления он будет возрастать. На рисунке 11.16, а такому режиму соответствует участок аЬ, на котором значения U и I(U) меняются от Ua = 20 В, 1а = 0 до Ub к 10 В, 1Ь ® 120 мА. Каждая точка этого участка соответствует устойчивому состоянию (малые изменения тока в цепи приводят к изменениям напряжения, которые стремятся компенсировать изменения тока, это характерно для всех «нормальных» цепей).
Рис. 11.15.
Рис. 11.16, а.
Рис. 11.16, б.
233
При дальнейшем уменьшении R режим меняется скачком — от Ub, Ib до Uc » 22 В, 1С « 260 мА, а затем — снова «устойчивый» режим (справа от точки с по кривой 17(1)).
Если мы начнем с малых сопротивлений резистора, то при увеличении R дойдем до точки d (рис. 11.16, б), затем — скачок от
® 23 В, 1(1 « 210 мА до Ue « 8 В, 1е « 80 мА и снова по кривой 17(1) до точки а.
А. что, если взять резистор, сопротивление которого лежит в области 80 Ом < R < 100 Ом, и подключить его к источнику (значению R« 80 Ом соответствуют точки Ь и с на рисунке 11.16, а, значению R ~ 100 Ом — точки е и d на рисунке 11.16, б)? Каковы будут напряжение и сила тока в цепи?
Чтобы ответить на этот вопрос, надо знать такие параметры цепи, как индуктивность проводов, емкость между выводами резистора. Если, например, индуктивность проводов большая (длинные провода), а емкость между проводами маленькая, то в момент подключения резистора к источнику сила тока будет малой (влияние индуктивности), а затем будет нарастать — режим в цепи будет устанавливаться в соответствии с рисунком 11.16, а. Если велика емкость между подключаемыми к источнику проводами, а индуктивность проводов маленькая, то в первый момент сила тока будет большой и станет уменьшаться по мере зарядки емкости — случай, соответствующий рисунку 11.16, б.
Задача 11.9. На рисунке 11.17 приведена зависимость напряжения источника питания от силы тока нагрузки. Найти максимальную мощность Щд, которую можно получить в нагрузке. При каком сопротивлении нагрузки она достигается? Для чего может понадобиться такой источник питания и как практически осуществить такую зависимость [/(/)?
Рис. 11.17.
Рис. 11.18.
234
Решение. Наклон прямой вольтамперной характеристики определяется внутренним сопротивлением источника. Данный источник питания как бы состоит из двух источников с разными ЭДС и внутренними сопротивлениями, которые «работают» только в определенных диапазонах значений U и I. Из графика на рисунке 11.17 определяем, что:
на участке I
на участке II
<?! = (7Д0) = 6 В,
л = —— Ом = 20 Ом;
0,3
S2 = и2(0) = 3 в,
з
Гп =----Ом = 5 Ом.
0,6
Мощность, выделяющаяся на нагрузке
с сопротивлением R, равна:
WR
= i2r =
s2r
(R + rf
Из условия WR = 0 найдем, при каком R максимальна WR :
г2
Wk = ~^~ К
2S2R „	, 2R
-----— = 0 или 1---------= 0,
Р 4- Г
откуда получаем R = г.
Итак, на участках I и II максимальные мощности выделяются на нагрузках, сопротивления которых равны, соответственно,
7?! = rj = 20 Ом, Т?2 = г2 = 5 Ом.
Соответственно силы токов в цепи должны быть равны:
Ij =	— = 0,15 А, 12 = —— = 0,3 А.
7?1 + Д	R2 + г2
Обе рабочие точки попадают на соответствующие участки, и, следовательно, на каждом из них действительно обеспечивается максимальная мощность в нагрузке.
Соответствующая максимальная мощность:
Wr = I2R^ = 0,45 Вт, W2 = I2R2 = 0,45 Вт.
На рисунке 11.18 приведена простая схема, обеспечивающая зависимость 17(1) в цепи, подобную изображенной на рисунке 11.17 (диод считаем идеальным). Интересно отметить, что при значительных изменениях нагрузочного сопротивления мощность в нагрузке почти не изменяется. Это может оказаться очень удобным для калориметрических опытов.
235
Задача 11.10. Определите заряд конденсатора СЗ, включенного в электрическую цепь, представленную на рисунке 11.19, если внутреннее сопротивление батареи можно считать бесконечно малым.
Решение. Для нахождения заряда на обкладках конденсатора СЗ необходимо найти напряжение на конденсаторе UBB. Так как внутреннее сопротивление батареи пренебрежимо мало, то по закону Ома для
полной цепи можно записать уравнение для цепи £АВС£:
£
Я] + r2
Отсюда
и АВ = RJ = ---1£ , ивс = r2i = —
1 Rt + R2 ВС 2 R} + R2
В замкнутом контуре £АВС£ ЭДС батареи равна сумме напряжений на конденсаторах С1 и С2‘.
£ = UV +U2	+
С, с2
Отсюда
qi=£C1-^L
1 С2
По закону сохранения заряда сумма зарядов трех обкладок конденсаторов Cl, С2 и СЗ, соединенных в точке D, равна нулю. Обозначив заряды верхних (по схеме) обкладок конденсаторов С1 и С2 соответственно через qi и q2, а заряд правой обкладки конденсатора СЗ через <7з, получим:
91 ” 92 ~ 9з = °-
В замкнутом контуре BCDB нет источника ЭДС, напряжение на резисторе R2 равно сумме напряжений на обкладках конденсаторов СЗ и С2:
UBc = UBD + UDC.
Напряжение между точками В и С равно:
Отсюда
92 = UBcC2 + д'з	= £Q - UBCC1 - qs 
<-з	сз
236
Подставляя в уравнение qi= q2 + qs найденные выражения для q± и q2, получим:
С	С
£Ci - UgcCi - q3 = UBCC2 + q3 + q2, с3	Ч}
?з[~ + ~ +1) -	- и вссх - ивсс2,
\С3 Сз у
гсх (Cj + с2)
~Ubc(^i + Q) __Д1 + Д2
Ci Си -I	^2 л
+	+ l	—L+-^- + l
С3 С3	С3 С3
Рис. 11.19.
Задача 11.11. Определите, какой заряд Дд протечет через ключ К при его замыкании (рис. 11.20).
Решение. До включения:
1L+‘£L = _^^,	|?1| = |?2| = ?,
С2 Ri+R2 11 11	Ci С2 R1+R2
£R2CyC2
q~ (С1+С2)(Я1+Я2)’
После замыкания ключа:
СД1 п, _	_ £RiC2
” G •	—•	•	(J \ ~ С> '-'1 •	Qo	__ *
Ci	С2 R]_+R2	Rt+R2
237
Заряды q{ и q2 одноименные, заряды qx и q2 разноименные и одинаковые по модулю. Следовательно, при замыкании ключа протечет заряд:
£RYC2 £С1(7?1 + Я2) + £ R1C2
= q{ + q2 = £CX + ---=--*------------
1*1 + л2
7?j + Т?2
Задача 11.12. Аккумулятор с ЭДС, равной 9 В, и внутренним сопротивлением 0,2 Ом заряжается от генератора с ЭДС 12 В и внутренним сопротивлением 0,1 Ом. Параллельно аккумулятору включена электрическая лампа сопротивлением 2 Ом. Определите силу тока в цепи генератора и в цепи лампы.
Решение. Схема включения генератора, аккумулятора и лампы представлена на рисунке 11.21, где — ЭДС генератора, rj — его внутреннее сопротивление, £2 — ЭДС аккумулятора, г2 — его внутреннее сопротивление, R — сопротивление лампы.
Предположим, что токи в цепи имеют направления, указанные на рисунке 11.21. Сумма ЭДС источников в любом замкнутом контуре равна сумме падений напряжения на элементах этой цепи. На этом основании с учетом направления токов и полярности включения источников можно составить уравнения:
- 6"2 =	+ 12Г2,	б-! = I3R + IjFp
По первому правилу Кирхгофа сумма сил токов в узле должна быть равной нулю, или
Л = -^ 2 + -^ з •
Решая систему уравнений, получаем:
£j ~ ^2 = АГ1 +(Л ~1з)г2 , h =—1	1 1 ’
£1 - ^2 ~ ЛГ1 + 11г2 ~{£1 “
11
- £2) + 6"1Г2 л(п + П>) + гР2
2-3 + 12 0,2
2 0,3 + 0,02
А » 13,55 А,
12-13,55 0,1 2
А » 5,32 А.

11
238
Рис. 11.22.
Задача 11.13. Схема, изображенная на рисунке 11.22, состоит из двух одинаковых резисторов R2 и R3 сопротивлением R каждый и двух одинаковых нелинейных резисторов R1 и R4, вольтамперная характеристика которых имеет вид U = al2 (где а — известный постоянный коэффициент). При каком напряжении источника питания Uq сила тока через гальванометр равна нулю?
Решение. Моет будет сбалансирован, и через гальванометр не будет идти ток, если между напряжениями на резисторах выполняется соотношение
Так как
Щ = al2, U2 = IR, U3 = IR,	U 4 = al2,
то условие (1) можно записать так:
al2 IR
IR~ al2'
Отсюда
1 = ~.	(2)
а
Следовательно,
р2
170 = Щ +U2 = al2 +RI = 2—.
а
Задача 11.14. Для получения напряжения, значение которого мало зависит от температуры, собрана схема по рисунку 11.23. Вольтамперные характеристики диода Д при трех различных температурах окружающей среды tj = 125 °C,
239
t2 = 25 °C, <з = -60 °C приведены на рисунке 11.24. Напряжение источника 17 = 6 В при температуре 25 °C и с увеличением температуры возрастает на 25 10-3 В/°С. Найти напряжение между зажимами А и В при t= 25 °C и зависимость этого напряжения от температуры.
Рис. 11.23.
Рис. 11.24.
Решение. Диод подключен к источнику последовательно с резисторами, сопротивление которых равно:
Яо6щ = 5,2 103 ом
Следовательно, в любой момент времени (при любой температуре) сила тока в цепи равна:
^общ
где U, — значения напряжения на источнике и на диоде в данный момент.
Построим на рисунке 11.25 графики зависимости 1(17д) для трех различных температур:
8,5 - Un 12б
^ = 125°С, П12б = 8,5В,	/125=-------—~ мА;
5,2
6 — 17гт об t2 = 25 °C,	U25 = 6 В, 125 =-------мА;
5,2
3,875 — U д —бо
73 = -6О°С,	17_60 = 3,875 В, /_60 =------------мА.
5,2
Точки пересечения этих графиков с вольтамперными характеристиками диода (для соответствующих температур) определяют напряжение на диоде и сила тока в цепи при данной температуре.
240
Из рисунка 11.25 находим (разумеется, приближенно): ЦцД25 = 0,77 В, /125 = 1,48 мА;
^Д,25 = 0,8 В, I25 = 1 мА," 17д _бо — 3,88 В,	— 0,58 мА.
Соответствующие значения напряжения Uдд = 17д +1  0,2 между
зажимами А и В:
АВ, 125 - 1>07 В, ^ЛЛ,25 --1В,	6() - 0,94 В.
Таким образом, температурный коэффициент, характеризующий относительное (относительно U АВ, 2б ) изменение напряжения UАд при изменении температуры от - 60 °C до 125 °C, равен:
= _^Еав_и7.1о~4 (°с)~1
UАВ, 25 -
По сравнению с исходным температурным коэффициентом
• lu	/	\—1
<Zq =--------~ 4  10 (°C) полученное значение а примерно в 6 раз
Рис. 11.25.
241
Задача 11.15. Электродвигатель постоянного тока с независимым возбуждением (или с постоянным магнитом) поднимает груз со скоростью t>i при помощи нити, наматывающейся на вал двигателя. В отсутствие груза невесомая нить поднимается со скоростью С какой скоростью будет опускаться тот же груз, если в цепи якоря произойдет замыкание, в результате которого обмотка якоря окажется замкнутой накоротко? Трением в подшипниках пренебречь.
Решение. После того как обмотка окажется замкнутой накоротко, электродвигатель превращается в генератор, причем ток в якоре генератора будет таким же, каким он был, когда машина работала как электродвигатель. Действительно, в обоих случаях один и тот же груз движется (поднимается или опускается) равномерно. Поэтому момент сил, действующих на якорь со стороны магнитного поля индуктора и пропорциональных силе тока, равен моменту силы тяжести, действующей на груз.
При подъеме невесомой нити (в режиме холостого хода) момент нагрузки равен нулю. В этом случае равна нулю и сила тока 10 в якоре. Запишем закон Ома для всех трех случаев.
При подъеме груза с помощью электродвигателя закон Ома запишется так:
U-SU = IR,	(1)
где I — сила тока в якоре, U — напряжение на зажимах электродвигателя и 8и — индуцируемая в якоре ЭДС.
При опускании груза, когда электродвигатель работает как генератор, закон Ома принимает вид:
£ = IR.	(2)
Когда же электродвигатель работает на холостом ходу, сила тока равна нулю и напряжение на зажимах равно ЭДС, индуцирующейся в якоре:
U-£'u=0.	(3)
Так как ЭДС индукции пропорциональна скорости изменения магнитного потока, т.е. угловой скорости а> вращения якоря, а со ~ о, то
£и=Й1Д,	£ = kv2, £'u=kv0,	(4)
где k — коэффициент пропорциональности. Из равенств (1) — (4) получаем:
и2 = и0 ~ t?! •
242
Задача 11.16. При движении трамвая по горизонтальному участку пути с некоторой скоростью его двигатель потребляет ток Ц = 100 А. КПД двигателя г] = 0,9. При движении трамвая по наклонному участку пути вниз с той же скоростью двигатель тока не потребляет. Какой ток будет потреблять двигатель при движении трамвая по тому же участку пути вверх с той же скоростью? При решении задачи учесть, что КПД двигателя зависит от потребляемого тока.
Решение. Обозначим через t/0 напряжение в контактной сети. При движении трамвая по горизонтальному участку дороги мощность, потребляемая двигателем от сети, равна U^Iy. Часть этой мощности теряется, т.е. идет на нагрев обмотки двигателя и контактных проводов. Эта часть мощности равна if Д (где R — общее сопротивление цепи). Поэтому КПД равен:
ад-^ = 1адк ад и0
Так как трамвай движется с постоянной скоростью, то полезная мощность г/UqIi равна абсолютному значению мощности сил сопротивления Fcix.
= Fc»>	(2)
где и—скорость трамвая.
При движении вниз по наклонному участку с постоянной скоростью и двигатель выключен и абсолютное значение мощности сил сопротивления Fcd равно мощности силы тяжести (рис. 11.26):
Fcu = mgu sin а,	(3)
где а — угол наклона горы.
Сопоставляя равенства (2) и (3), получаем:
myosin а = т/ПоА •	(4)
При движении вверх по этому же участку горы энергия, потребляемая из сети, расходуется на нагрев проводов и совершение работы против сил сопротивления и силы тяжести. Поэтому
И012 =	+ Fcu+ Rusina.	(5)
Учитывая (2) и (4), можно это уравнение записать так:
Ц)А = ^2 F + 7^0 А + 7^оА>
if — - А + 2т)А = 0.
и0
243
Найдя из равенства (1) отношение —— и подставив его в последнее ио
уравнение, получаем:
=0.	(6)
Далее решаем это квадратное уравнение относительно 12‘.
_ ^±^-8^1-^
Подставляя сюда численные значения всех величин, находим два возможных значения для силы тока 12:
12 = 765 А, 12 = 235 А.
Неоднозначность ответа связана с тем, что одна и та же мощность потребляется двигателями при двух различных механических нагрузках и соответственно при двух значениях скорости вращения якоря. С помощью редукторных передач эта скорость выбирается так, чтобы сила тока, потребляемого двигателем из сети, была наименьшей из возможных.
Рис. 11.26.
Глава 12
ПЕРЕМЕННЫЙ ТОК
Задача 12.1. Цепь состоит из последовательно соединенных конденсатора электроемкостью С = 2 мкФ, катушки индуктивностью L - 0,51 Гн и электрическим сопротивлением R = 100 Ом. Определите действующее значение силы тока в цепи, если к ней подводится переменное напряжение U — 220 В (действующее значение) с частотой v- 50 Гц. Определите действующие значения напряжения на отдельных элементах цепи, силу тока в цепи и cos (р, где <р — сдвиг по фазе между колебаниями силы тока и напряжения. Рассчитайте, при какой электроемкости конденсатора наступил бы резонанс напряжений. Определите волновое сопротивление и добротность.
Решение. В любой момент времени сумма напряжений на последовательно включенных элементах цепи равна мгновенному значению приложенного напряжения (рис. 12.1):
U=UR+UL+UC.	(1)
Рис. 12.1.
Рис. 12.2.
Во всех последовательно включенных элементах этой цепи сила тока изменяется практически одинаково, так как распространение электромагнитных взаимодействий происходит со скоростью света. Поэто
245
му можно считать, что колебания силы тока во всех элементах последовательной цепи происходят по одному закону:
i - Im cos tot.	(2)
Колебания напряжения на активном сопротивлении совпадают по фазе с колебаниями силы тока, колебания напряжения на конденсаторе отстают по фазе на от колебаний силы тока, а колебания напря-
жения на катушке опережают по фазе колебания силы тока на . Поэтому уравнение (1) можно записать так:
и = UR cos IDt + Uс cos I tot - — + Ut cos tot + — ,	(3)
nm	I 2y L‘m I 2 7	7
где URm, UCm и U Lm — амплитуды колебаний напряжения на активном сопротивлении, конденсаторе и катушке.
Амплитуду колебаний напряжения в цепи переменного тока можно выразить через амплитудные значения напряжения на отдельных ее элементах, воспользовавшись методом векторных диаграмм.
При построении векторной диаграммы необходимо учитывать, что колебания напряжения на активном сопротивлении совпадают по фазе с колебаниями силы тока, вектор напряжения URm совпадает по направлению с вектором силы тока 1т. Колебания напряжения на кон-денсаторе отстают по фазе на — от колебании силы тока, поэтому век-
тор напряжения ^ст отстает от вектора силы тока 1т на угол 90°. Колебания напряжения на катушке опережают по фазе колебания си-
п
лы тока на — , поэтому вектор напряжения Uопережает вектор
силы тока 1т на угол 90°.
На векторной диаграмме (рис. 12.2) напряжения на резисторе, конденсаторе и катушке определяются проекциями на горизонтальную ось векторов URm, UCm и вращающихся с одинаковой угловой скоростью (о против часовой стрелки. Общее мгновенное напряжение и равно сумме мгновенных напряжений uR, ис и uL на отдельных элементах цепи, т.е. сумме проекций векторов URm, UCm, U-[,m на горизонтальную ось. Так как сумма проекций векторов на произвольную ось равна проекции суммы этих векторов на ту же ось, то амплитуду полного напряжения можно найти как модуль суммы векторов:
246
U=UR +UC +UL .	(4)
Из рисунка 12.2 видно, что
Um=}lUnm +(ULm ~иСт)2 ’ ИЛИ	<5>
Um=^ImR)2 +(lmXL-ImXc)2 =
i------------ I 1 TV
= Im^R2+(XL-Xc)2 ^1 \R2+\(0L------- ,
V \	69C//
отсюда:
Л, ;	.	(6)
. R2 + ®L--— у I (oCJ
Действующие значения силы тока I и напряжения U связаны аналогичным выражением.
Так как колебания напряжения на конденсаторе и катушке индуктивности при их последовательном включении происходят в противофазе, а ток через все элементы цепи протекает один и тот же, то при равенстве индуктивного и емкостного сопротивлений напряжения на них в любой момент времени одинаковы по модулю, но имеют противоположные знаки:
= -ис.	(7)
Такой вид резонанса в электрической цепи переменного тока называют резонансом напряжений.
При резонансе напряжение на активном сопротивлении оказывается равным напряжению на всех трех элементах цепи:
и = uR +	+ ис - uR.
Отсюда можно найти мгновенные и
тока в цепи при наступлении резонанса:
_uR и
действующие значения силы
(8)
рез R ~ R
Условие резонанса позволяет определить резонансную частоту а>о по известным значениям индуктивности катушки L и электроемкости конденсатора С:
г 1	1
-	—, а>о - ,—•
®ос	VLC
247
Резонанс наступает при совпадении частоты переменного тока (о с частотой свободных колебаний в контуре. Индуктивное сопротивление катушки Х^ и емкостное сопротивление конденсатора Хр при резонансе можно выразить через величины L и С:
XL=a>0L = -±=L=&, XC.J-^.K у/1с УС’ С Ш()С С \с
Величину называют волновым сопротивлением колебательного контура и обозначают буквой р:
<9)
Отношение амплитуды напряжения на катушке (или на конденсаторе) при наступлении резонанса к амплитуде приложенного напряжения равно отношению волнового сопротивления контура к его активному сопротивлению:
_ UCm __ Imp _ р	(10)
um ~ Um ~ImR'R
Это отношение называют добротностью контура и обозначают буквой Q:
Q = <	(11)
Л
Сдвиг фазы (р также может быть определен из векторной диаграммы:
cos <р =	=----г. ImR == = — .	(12)
ит ( Tv z
Im,R2 + a>L---
\ I <oCj
Так как
XL = 2nvL = 2л•50 0,51 Ом и 160 Ом,
—-— =-------------Ом к 1600 Ом,
2лиС 2л-50-210“6
то из (6) следует:
________220________ ^1002 +(1600-160)2
А к 0,152 А.
248
Из (12) следует:
100
COS Ср =  .. ....
^lOO2 +(1600-160)2
« 0,069.
Применяя закон Ома для отдельных элементов цепи, получим:
Ur=IR = 0,152 100 В = 15,2 В,
UL = IXL = °Д52 160 В = 24,3 В, Uc = 1ХС = 0,152 • 1600 В = 243 В.
Резонанс
1 „ , -----= 2лиь.
2луС
напряжений возникает при выполнении условия
Отсюда
12
--— = —---Ф = 2 • 10 ° Ф = 20 мкФ. 4л2у2Л 4л2-2500 0,51
При возникновении резонанса напряжений сила тока достигает максимального значения:
U 220
— =-----А = 2,2 А.
R 100
Волновое сопротивление р контура находим так:
[L _ / 0,51
Р \С ^20-106
Ом = 160 Ом.
С =

Зная волновое сопротивление, определим добротность контура Q:
Q =
Р
R
160
100
= 1,6.
Задача 12.2. Конденсатор электроемкостью 100 мкФ, катушка индуктивностью 10 мГн и резистор активным сопротивлением 10 кОм соединены параллельно. Найдите значения амплитуд колебаний силы тока в общей цепи и в цепи катушки при наступлении резонанса, если амплитуда колебаний переменного напряжения 100 В. Активное сопротивление катушки пренебрежимо мало.
Решение. При параллельном соединении резистора, конденсатора и катушки (рис. 12.3) напряжение на всех этих элементах электрической цепи изменяется по одному и тому же закону:
и = Um cos cot.
С учетом возникновения сдвига фазы между током и напряжением на реактивных элементах электрической цепи сила тока в ветвях определяется формулами:
i т> =	= cos cot.
R
ic = UmcoCcosl cot + — I,
Um (	л
iT = ——cos cot-
L coL I	2,
249
Полный ток в цепи в любой момент времени равен сумме токов в параллельных ветвях:
i - iR +tc +iL.
Для нахождения полного тока построим векторную диаграмму (рис. 12.4).
Из нее видно, что суммарный ток можно найти по формуле:
I = Im cos^cot +
(1)
где 1т — амплитуда колебаний тока в общей цепи, — сдвиг между током и напряжением.
Амплитуда тока выражается так:
фазы
1 f 1 у
—— + <»С	-
R2 k a>LJ
(2)
Действующие значения силы тока I и напряжения U связаны аналогичным выражением:
1 (	1 у
I = U,------+ \а>С------
У RI 2 к <оь)
Из векторной диаграммы можно найти сдвиг по фазе между баниями силы тока и напряжения:
1
1
cos (р = ——
Im hr 1 V I г 1 V ®С--~ Jl + Я2 а>С--=
V R2 к a>IJ U к a>Lj
(3)
коле-
(4)
250
Полное сопротивление электрической цепи переменному току определяется следующим выражением:
7 ит U
Im I
(5)
При равенстве индуктивного и емкостного сопротивлений токи через катушку и конденсатор в любой момент времени равны друг другу по модулю и противоположны по направлению (или по фазе колебания), т.е.
ю0С = —<6) (DqL	\ LC
Сумма токов и в этом случае равна нулю, а сила тока в общей цепи равна силе тока через активное сопротивление:
i =iR+iL+iC = ^R’	
Этот же результат можно получить формально подстановкой выражения (6) в выражение (2).
При выполнении условия (6) полное сопротивление электрической цепи принимает максимальное значение Z = R. Максимальному значению полного сопротивления такой электрической цепи
соответствует минимальное значение си-	рис 5
лы тока. Следовательно, при выполнении
условия (6), называемого условием резонанса токов в колебательном контуре, сила тока в общей цепи минимальна.
Зависимость амплитуды колебаний силы тока от частоты приложенного напряжения при постоянной его амплитуде в общем участке цепи при параллельном соединении катушки, конденсатора и элемента с активным сопротивлением представлена на рисунке 12.5.
Найдем амплитуду колебаний силы тока в общей цепи:
^А.ИГ’
104
А.
Найдем резонансную частоту:
®о -
----------- с"1 = 103 с’1
10 2  10"4
251
Найдем амплитуду колебаний силы тока в цепи катушки:

100
10310 2
А = 10 А.
Задача 12.3. В цепь из последовательно соединенных резистора сопротивлением R, конденсатора электроемкостью С и катушки индуктивностью L включен источник синусоидального переменного напряжения. При каких частотах достигаются максимальные значения амплитуд колебаний силы тока и напряжения на обкладках конденсатора?
Решение. Из закона Ома для цепи переменного тока
2 < 1
Я2 + «L -
\	соС)
следует, что сила тока достигает максимального значения при выполнении условия:
т 1
®0L =----7? >
а>0С
откуда искомая частота (о$ равна:
1
®0 - I—-y/LC
Напряжение на обкладках конденсатора UCm равно:
Uc =	=----- С	.
m шС ( Г?2
а>.IR2 +1 a>L- 1
у к шС)
Исследуя полученное выражение на максимум, получим условие
[	Гч	vc
“ ^>01 1----= р---------т , гДе Q ~ ------добротность контура.
V 2L у 2Q2	R
Таким образом, только для контуров с высокой добротностью максимум амплитуды колебаний напряжения на конденсаторе достигается при резонансной частоте
252
Задача 12.4. Два конденсатора одинаковой электроемкости Ci = Сг = С и катушка индуктивностью L соединены так, как показано на рисунке 12.6. В начальный момент времени ключ разомкнут, конденсатор С1 заряжен до разности потенциалов U, а конденсатор С2 не заряжен и сила тока в катушке равна нулю. Определите максимальное значение силы тока в катушке после замыкания цепи и период электромагнитных колебаний в цепи.
Рис. 12.6.
Решение. После замыкания ключа в первый момент времени происходит перераспределение заряда между конденсаторами. Это связано с тем, что цепь С1—С2 можно считать колебательным контуром с очень малой индуктивностью проводов, и следовательно, большой собственной частотой. Заряды конденсаторов С1 и С2 станут равными по си ---, а полная их энергия будет равна: 2
си2 си2 _ си2
8	8 ~ 4
CV2 TT
Это вдвое меньше энергии первого конденсатора ----. Половина
2
энергии электрического поля диссипирует (рассеивается) в другие виды энергии, чятце всего в тепло.
После перераспределения заряда возникают электромагнитные колебания с периодом
Т = 2л^2ЬС.
Максимальную силу тока в катушке можно найти, используя закон сохранения энергии:
4	2 ’ m \2L
Задача 12.5. Как зависит напряжение между точками А и В (рис. 12.7) от сопротивления резистора fi?
Решение. Построим векторную диаграмму для цепи (рис. 12.8). Токи, текущие через конденсатор С и резистор R, одинаковы, значит, векторы и UmC перпендикулярны. Сумма их равна вектору UM, и через концы этих векторов можно провести окружность, диаметр которой равен |ЙМ|. Напряжение [7д на резисторе с сопротивлением R равно ^mR . Следовательно, искомое напряжение [/„дд численно равно
253
радиусу построенной окружности, т.е. UmAB =—— и не зависит от ве-2
личины R.
При изменении R меняется угол сдвига фаз между векторами UM и
так что предложенная схема может служить фазовращателем.
Рис. 12.7.
Рис. 12.8.
Задача 12.6. В обычной схеме однополупериодного выпрямителя (рис. 12.9) С= 1000 мкФ, R = 500 Ом, частота сети v= 50 Гц. Считая диод идеальным, найти:
1. Коэффициент пульсаций напряжения k = на резисторе R.
2. Во сколько раз уменьшится коэффициент к, если последовательно с резистором включить катушку индуктивности L= 1ОО Гн?
Решение. 1. При выбранных параметрах С и R заряд конденсатора меняется незначительно, поэтому ток разрядки конденсатора можно считать постоянным. Тогда:
Arr Ад /А? UAt	AU	At
С С	RC	и	RC
Если конденсатор разряжается мало, то он подзаряжается в моменты максимального положительного напряжения в сети (рис. 12.10), т.е.
At = Т = -, k = —= 0,04. v	vRC
2. При подсоединении катушки индуктивности коэффициент пульсаций станет еще меньше (индуктивность большая: 2kvL » R). Ток нагрузки тем более можно считать постоянным; значит, напряжение на
254
конденсаторе будет меняться по тому же закону, что и в первом случае. При этом напряжение на катушке будет почти компенсировать изменения напряжения на конденсаторе. Ток через катушку в течение периода будет меняться по параболическому закону (ЭДС индукции меняется по линейному закону), причем максимальное значение тока будет в середине периода:
£ = ^-t при t е \пТ, (п + 1)7’], I = 10 -	• —  — 72.
Т	L '	! j	° Т L 2
Пульсации в этом случае определяются изменениями тока:
AUi = BAI.
Поскольку
AZ = I,
__ 1_ АП Г2 _ 2 UT2 max mi" 2 114 - 8 LRC ’
UT
а АП =---, окончательно получаем:
ВС
, AU1 к = —-U
111 = 5.10-4
8 LC
Итак, при подсоединении
4 10"2 уменьшатся в -------= 80 раз.
5- IO"4
катушки индуктивности пульсации
Задача 12.7. На рисунке 12.11 приведена вольтамперная характеристика лампы накаливания, номинальное напряжение которой Us = 220 В, номинальная мощность Рн = 100 Вт. Лампу подключают к сети переменного тока (220 В, 50 Гц) последовательно с конденсатором емкости С = 10 мкФ. Определить силу тока в лампе и напряжение на ней. Считать, что в течение периода сетевого напряжения температура нити практически не меняется.
255
Рис. 12.11.
Решение. Поскольку температура нити в течение периода остается неизменной, в рабочей точке лампу можно считать обычным резистором.
На рисунке 12.12, а приведена векторная диаграмма для цепи с последовательно включенными резистором и конденсатором. Из диаграммы находим:
U0C + Ugft - Ug.
Подставляя
и'ос -
т-
10
м ’
(О с
найдем связь между напряжением 170д
на лампе и током I через нее:
/0 = (oC^Ug - U?)R = 314 • 10’5  ^48400 - UgR А.
Построим график этой зависимости на том же рисунке 12.12, б, на котором задана вольтамперная характеристика лампы. Точка пересечения графиков и определяет рабочую точку: 17л = 180 В, /л « 0,4 А.
Задача 12.8. В схеме, приведенной на рисунке 12.13, трансформатор идеальный. Параметры схемы указаны на рисунке. Найти амплитуду тока и сдвиг фаз в первичной цепи.
Решение. Напряжения обмоток трансформатора связаны соотношением:
^1 _ 2LL
[72 п2
256
Поскольку трансформатор идеальный, мгновенная мощность во вторичной цепи равна мощности первичной. Значит, токи обмоток связаны соотношением:
Л п2
12	П-!
71
Ток /2 и напряжение U% сдвинуты по фазе на —; такой же сдвиг 2
будет и между Ту и U}. Отсюда видно, что трансформатор с подключенным к нему конденсатором емкости С можно заменить конденсатором, емкость которого равна:
( Л2
С1=сЫ = 410~6Ф.
\пг)
После такого преобразования наша схема представляет собой обычную цепь, содержащую сопротивление R и емкость Ср Амплитуда тока в цепи равна:
п-1 л 2 2 4 zi2 4л v п-2 С
0,17 А.
Сдвиг фаз равен:
7?	71
tp = arctg----= arctg 2лт—^-/?С « 0,9 рад.
_l_. I nf )
2nv(\
Рис. 12.13.
Рис. 12.14.
Задача 12.9. Обмотки трансформатора содержат гц = 1000 и л2 = 2000 витков и намотаны на сердечник с большой магнитной проницаемостью. Соединим обмотки параллельно и подключим их к сети напряжением 220 вольт последовательно с резистором R = 1000 Ом. Какие токи потекут по обмоткам?
257
Решение. При таком странном подключении трансформатора и результат получится необычным — напряжение на каждой из обмоток будет равно нулю (рис. 12.14). В самом деле, обмотки соединены параллельно, значит, их напряжения одинаковы. Магнитный поток не рассеивается (сердечник имеет большую магнитную проницаемость), значит, поток Ф через любой из витков один и тот же, т.е.
njC>' = п2Ф', т.е. Ф' = 0.
Это может выполняться только в том случае, когда поля обмоток в сердечнике компенсируются. Поле каждого из витков пропорционально его току, т.е.
AljJl ± п212 = 0.	(1)
«Плюс» или «минус» в формуле получаются при различных подключениях обмоток друг относительно друга (если одну из обмоток переключить наоборот, то ее поле в сердечнике изменит направление на противоположное).
Так как напряжение источника приложено к резистору R, то:
Л + ^2 = Т7 	(2)
11
Решая эту систему (1) и (2) (точнее — две системы из двух уравнений каждая), получим:
Д « 0,147 A,	f/i = 0,44 А,
12 « 0,073 А;	[12 « 0,22 А.
Задача 12.10. Число витков вторичной обмотки трансформатора вдвое больше числа витков первичной обмотки. Активное сопротивление первичной обмотки равно 20 Ом, а ее индуктивное сопротивление — 200 Ом. На первичную обмотку подали переменное напряжение 100 В. Определите напряжение на вторичной обмотке в режиме холостого хода. Как изменится напряжение на вторичной обмотке, если сердечник трансформатора заменить другим того же размера, но сделанным из материала с магнитной проницаемостью в 10 раз меньшей? Рассеянием магнитного потока и потерями в сердечнике пренебрегите.
Решение. Если бы не было потерь на активном сопротивлении первичной обмотки, напряжение на вторичной обмотке было бы равно:
U2 = 2Ui.
Вследствие же потерь на нагревание первичной обмотки напряжение на вторичной обмотке определяется формулой:
U2 = 2UlL,
где UlL = Цсо!^.
258
Напряжение же на первичной обмотке U\ определяется формулой:
- >IU1R +U1L-
Следовательно,
U1L X1L
U2
2Ur
При замене сердечника индуктивное сопротивление уменьшается в 10 раз:
X{L =	= 20 Ом.
10
В этом случае напряжение
на вторичной обмотке станет равным:
щ =
2Щ
2 100
В « 140 В.
Таким образом, необходимым
условием для нормальной работы
трансформатора является выполнение соотношения XL » R.
Задача 12.11. Два одинаковых трансформатора имеют по две обмотки, отношение числа витков в первой обмотке к числу витков во второй обмотке равно 2. Первая обмотка одного трансформатора и вторая обмотка второго трансформатора соединены последовательно и включены в сеть переменного тока с напряжением 100 В. Какое напряжение будет на концах двух других катушек трансформаторов при последовательном их включении? Трансформаторы считать идеальными.
Решение. Напряжения на катушках при одинаковых значениях силы тока пропорциональны их индуктивностям:
Uy — a) 9 U=
Индуктивности катушек пропорциональны квадрату числа витков: иг = (Dan^I, U2 = соап^Т-
и2 nl
259
U1+U2 = 100 В, U, = 80 В, и2 = 20 В.
Напряжение U' на выходах двух других обмоток равно сумме напряжений U{ и U2 (рис. 12.15):
U' = Щ + Щ.
Так как у первого трансформатора в сеть включена обмотка с вдвое большим числом витков, то на второй его обмотке напряжение равно половине напряжения на первой обмотке:
U,
U', = и\ = 40 В.
1	2	1
У второго трансформатора в сеть включена обмотка с меньшим числом витков, на второй обмотке напряжение в два раза больше, чем на первой:
U'2 = 2U2,	tZ£=40B.
Сумма напряжений U' =	+ U2 равна 80 В или
0 В в зависимости
от того, как соединены начала и концы обмоток.
Рис. 12.15.
Рис. 12.16.
Задача 12.12. Трансформатор имеет две катушки. Отношение числа витков в первой катушке к числу витков во второй катушке равно 0,115. Ток холостого хода при напряжении Щ = 1 В на первой катушке 1$ = 3,5 мА. Электрическое сопротивление 7*1 провода первой катушки равно 9 Ом, сопротивление Г2 провода второй катушки равно 730 Ом. Каково электрическое сопротивление R2 нагрузки в цепи второй катушки, если сила тока 1% во вторичной цепи 5 мА? Какова сила тока при этом в первичной цепи?
Напряжение на концах первичной катушки Ui равно 1,5 В.
Решение. При подключении нагрузки R2 к выводам второй обмотки во вторичной цепи возникают колебания силы тока с амплитудой 12- По закону Ленца индукционный ток во второй обмотке создает магнитный поток, компенсирующий те изменения магнитного потока, которые вызывают возникновение ЭДС индукции во второй обмотке.
260
Уменьшение изменений магнитного потока вызывает уменьшение ЭДС самоиндукции в первой обмотке и возрастание амплитуды колебаний силы тока в ней на такую величину ЛЦ, при которой амплитуда колебаний магнитного потока восстанавливается до первоначального значения. Обозначим индуктивность одного витка катушки трансформатора L, тогда изменение магнитного потока через него равно:
АФ = LAI.
Условие работы трансформатора в режиме нагрузки:
ДФ1 = -ДФ2, [tIjLAZjI = |п2ЬД12|,	= — = k,
Д/i = /j - /0,	Л12 = /2, Vj =	.
к
Если /0 « /j, то выполняется приближенное равенство:
h « ЛГр
В этом случае:
А = Л = 510 А « 43,5  10'3 А. k	0,115
Для нахождения сопротивления нагрузки R2 представим эквивалентную электрическую схему трансформатора (рис. 12.16), где Г] и г2 — сопротивления проводов первой и второй катушек, R2 — сопротивление внешней нагрузки в цепи второй катушки, £^ — ЭДС самоин-
дукции в первой катушке, £2 — ЭДС индукции во второй катушке.
По известным значениям силы тока в первичной цепи и напряжения Ui на концах катушки найдем ЭДС самоиндукции в первичной цепи:
Z] = U1 £1 ,	£1 = Ul-I1rl, £r = 1,5-43,5 10 3-9 В = 1,11В.
ri
Так как через первую и вторую катушки проходит один и тот же магнитный поток, его изменения вызывают одинаковые значения ЭДС индукции е в каждом витке первой и второй катушек. Поэтому отно-
шение ЭДС самоиндукции в первой катушке £} к ЭДС индукции во
второй катушке £2 равно отношению числа витков п1 в первой катушке к числу витков п2 во второй катушке:
£i п^е f 2	п2е п2
261
Найдем ЭДС индукции £2 во второй катушке:
£9=^-, Е2 = -УД В = 9,65 В.
2	k 2	0,115
Сила тока 12 во второй катушке определяется из уравнения:
где R2 — сопротивление нагрузки, г2 — сопротивление провода катушки.
Отсюда следует:
R2 =	- r2, R2 = 9,65 Ом - 730 Ом = 1200 Ом.
I2	5 10"3
ЭДС самоиндукции в первой катушке равна по модулю напряжению на индуктивном сопротивлении:
Ы = Ы-
Так как это напряжение примерно равно 1 В, то значение холостого тока 10 можно считать примерно равным данному в условии задачи значению 3,5 мА. Отсюда более точное значение силы тока в первой катушке:
Д = Alj +10,	= 43,5 • 10"3 А + 3,5 • 10 3 А = 47  10"3 А.
Задача 12.13. Цепь переменного тока (рис. 12.17) состоит из идеальных катушек индуктивностью Lj = 10 мГн, L% = 20 мГн, резистора с сопротивлением R = 100 кОм и конденсаторов емкостью Cj = 10 нФ, Сг= 5 нФ. При замкнутой цепи амплитуда силы переменного тока остается постоянной при изменении частоты генератора синусоидального напряжения (генератор тока с постоянной амплитудой).
Цепь размыкается. Известно, что в момент времени to после размыкания цепи силы тока в катушках L1 и L2 имеют значения: toi = ОД А и to2 = ОД А (на рисунке 12.17 показаны направления токов), а напряжение на конденсаторе С1 равно Uо = 40 В.
Определите:
1.	Отношение частоты vmax, при которой активная мощность Ршах, выделяемая в замкнутой цепи, максимальна, к разности частот Дг =	, где v. и
v_ — частоту, при которых активная мощность равна половине максимальной мощности Ртах-
2.	Частоту свободных электромагнитных колебаний в цепи L1C1C2L2 после размыкания.
3.	Силу тока на участке контура АВ.
4.	Амплитуду колебаний силы тока в катушке L1.
Указание. Взаимной индукцией катушек L1 и L2 пренебречь.
262
LI
С7 	II	,	^*01 А
II	
С2 II	В
I!	
	102
R	
	1	1	,	
	
Рис. 12.17.
Рис. 12.18.
Решение. 1. Вычислим силу тока I, протекающего через источник тока, воспользовавшись методом векторных диаграмм (рис. 12.18):
I ~ Jl/i +(^LJ +Il2 ~ Ici ~ 1сг) =	—у + ~~— + ~~Z----®С1 ~ юС2
По условию задачи амплитуда этого тока поддерживается постоянной при любой частоте генератора: I = 1д.
Введя эквивалентную индуктивность двух параллельно соединен-
111
ных катушек — =---1--и эквивалентную емкость двух параллельно
L Li L2
соединенных конденсаторов С = С± + С2 , получим:
lo-R
Средняя активная мощность Р за период равна:
1
СI 2 _____________________
2R~ 2 ’	7 х А2 '
1 + В2 — --соС\ \a>L J
Отсюда ясно, что активная мощность, передаваемая цепи от источника тока, максимальна при выполнении условия:
-------^тах^ = О,
®тах-^
263
1
1
= 10б с
Условие, при котором активная мощность Р(й>±) равна половине
максимальной мощности Ртах Р(й>±) = тах (рис. 12.19), можно за
писать в виде:
1 ) л--------а>С\ = 1.
\a>L J
Отсюда получаем уравнение:
4	2(2,1)	1
й) — 6У I-1-Ч----
Ilc Rzc2) l2c2
Согласно теореме Виета
(D2 +С02
2	1
LC + r2c2 ’
+ cd2 - 2а>+а>
1 ДС'
Рис. 12.19.
Рис. 12.20.
Следовательно, искомое значение отношения —равно: Av
Ртах = Дтах =	= R [С = R	+ L2) =
Av Аа> у/Zc и У ^1^2
264
2.	Представив контур L1C1C2L2 в виде эквивалентного контура LC,
где
L =	, С = С!+С2,
Li+b, получим, что частота свободных электромагнитных колебаний в нем равна:
v0 = 1.—  1	= = 15,9 кГц.
2л
V ^(а+ь2)
Этот же результат можно получить, используя результаты первого задания: максимальная активная мощность выделяется при совпадении частоты vmax колебаний приложенного напряжения с собственной частотой колебаний.
Заметим, что, так как IqCx = L2C2 (10 мГн -10 нФ = 20 мГн - 5 нФ), то частоты свободных колебаний контуров L1C1 и L2C2 совпадают:
1 1
И = Г2 = -г== = -----7= ,
2k^L}Ci 2л^Г2С2
т.е. колебания в них происходят независимо друг от друга.
Вместе с тем этот факт не препятствует существованию кольцевого тока I, который может без затухания течь через катушки L1 и L2. Причиной его возникновения могло быть, например, изменение внешнего магнитного поля.
3.	Если ток на участке цепи АВ существует, то он как раз и является постоянным кольцевым током 1дя, протекающим через катушки L1 и L2. Для постоянного тока достаточно найти одно значение в момент времени t^.
Рассмотрим цепь, изображенную на рисунке 12.20. Из первого закона Кирхгофа следует, что
1дв - *01 +iCl - _ *С2 ~ Ч)2>
+ iC2 - ~ (’О! +*02)-
Учтя, что
dQ dU . dU
1С1 ~ "77 ~	’	1С2 - С2 -3—,
dt dt	dt
получим:
i-ci =
iC2 С-2
265
Отсюда с помощью математических преобразований можно получить:
гс/ = (ici +iC2)	1	= ”(Zo1 + Z°2)'r Jr '
Из последнего выражения и формулы (*):
1 АВ = *01 + 1С1 = г01 “ (*01 + *02)7;
С1 + с2
1ав=- 0,1 А.
Следовательно, ток течет от точки В к точке А и равен -Гва = 0,1 А.
4.	Поскольку колебания в контурах L1C1 и L2C2 не зависят друг от друга, вычислим амплитуду колебаний силы тока 101 в катушке L1, применив закон сохранения энергии к первому контуру для момента времени t(t.
Учтем также, что вследствие линейности уравнений U(t), I(t), Q(t) колебания не зависят и от наличия кольцевого тока в цепи L1L2, нужно только вычесть его из 101, чтобы получить мгновенное значение колебания силы тока в катушке L1:
i - i	I	Al-^Ol - L1 (i I I2 + C]U®
4 - J01 1AB^ 2  _	+—“
Отсюда для амплитуды колебаний силы тока в катушке L1 получаем:
I	2
Л)1 = -»/(г01 “ Iab) + 1 ° “ °,2 А-V	-Ч
Задача 12.14. Дана люминесцентная лампа, включенная по схеме рисунка 12.21, частота приложенного переменного напряжения составляет 50 Гц. Измеряются следующие величины: общее (сетевое) напряжение U = 228,5 В, сила тока I = 0,60 А. Напряжение на люминесцентной лампе U' = 84 В, омическое сопротивление балластного дросселя Rd = 26,3 Ом. Люминесцентная лампа должна рассматриваться как омическое сопротивление.
Ответьте на следующие вопросы и выполните задания:
1.	Какой индуктивностью L обладает дроссель?
2.	Определить значение сдвига фазы <р между напряжением и током.
3.	Какая активная мощность Р выделяется в цепи?
4,	Дроссель, кроме ограничения тока, имеет еще одну важную функцию. Назовите и объясните ее.
266
Указание. Стартер S имеет контакт, который вскоре после включения замыкается, затем открывается и остается открытым.
5.	Нарисуйте кривую зависимости испущенного лампой светового потока от времени (с количественной шкалой по оси времени).
6.	Почему лампа горит все время, хотя приложенное переменное напряжение через определенные промежутки времени проходит через нуль?
7.	У люминесцентных ламп описанного типа к дросселю может быть последовательно подключен конденсатор емкостью приблизительно 4,7 мкФ. Как это действует на работу лампы и для какой цели предусмотрена эта возможность?
Решение. 1. Когда лампа находится в рабочем режиме, эквивалентную схему цепи можно представить так, как показано на рисунке 12.22.
Полное сопротивление такой цепи равно:
Z = у(Вл + Hd) + (2^vL) , откуда искомая индуктивность дросселя
L = ~Jz2 -(Лл+Яа)2.
Подставляя в последнее уравнение Z =— и _Кд = ^—, получим:
1 U2 (	U'\
L =----- я +_	« 1,09 Гн.
2лу V j2 \	IJ 
Дроссель
Рис. 12.21.
Рис. 12.22.
2. Как видно из векторной диаграммы для данной цепи на рисунке 12.23, сдвиг фазы между колебаниями напряжения и силы тока определяется из выражения:
UL _ 2луЬ _ 2nvL иЛ + ud ^+Rd и' , n
tg^>=2,06; <p~64,l°.
267
3.	Среднюю мощность, выделяемую в цепи за период, можно рассчитать по одной из нижеприведенных формул:
Р = IU cos <р,
где I и U — действующие значения силы тока и напряжения, или
—	9	U'}
Р = I2R = I2 Rd +-1
k l)
(1)
(2)
Подстановка числовых данных в любую из этих формул приводит к
результату: Р ~ 60 Вт.
4.	Сетевое напряжение ниже напряжения зажигания люминесцентной лампы. При замыкании контактов стартера через дроссельную катушку течет ток. При размыкании контактов стартера возникает ЭДС самоиндукции, пропорциональная индуктивности катушки и скорости изменения тока:
т	г-
£ — — L — — — Li .
At
Характерное время г, в течение которого изменяется сила тока в катушке, зависит от емкости С схемы, включенной параллельно дросселю:
г - VEc.
Если емкость С мала, то ЭДС самоиндукции может достигать значения, достаточного для зажигания газового разряда в лампе.
Примечание. Для зажигания лампы необходимо, чтобы момент размыкания контактов стартера не совпал с моментом, когда мгновенное значение силы тока равно нулю.
5.	В стационарном режиме световой поток Ф лампы пропорционален выделяемой в ней электрической мощности Р:
268
Ф - Р = sin2 =	+ cos 2a>tj = i®M(l + cos 2art),
где 1до и Фм — амплитудные значения силы тока и светового потока. Из полученного выражения видно, что частота колебаний Ф и Р равна 2v= 100 Гц. График зависимости мощности Р лампы от времени t показан на рисунке 12.24 штриховой линией.
График зависимости Ф(1) не полностью совпадает с графиком P(t). В моменты времени, когда Р = 0, Ф ф 0, так как свечение плазмы в лампе полностью не прекращается. Приблизительный график Ф(1) представлен на рисунке 12.24 сплошной линией.
6.	Несмотря на то что напряжение на лампе в определенные промежутки времени равно нулю, в лампе остаются свободные носители заряда — ионы ртути и электроны. Время их рекомбинации достаточно велико по сравнению со временем, в течение которого отсутствует подвод энергии.
7.	Подключение последовательно с дросселем конденсатора Со практически не отразится на зажигании лампы, так как емкость конденсатора Со = 4,7 мкФ много больше емкости С, образуемой электродами лампы и стартера, и их совместная емкость С мало отличается от С:
г, сос С
Со+С 1 + _С ~ со
Поэтому при размыкании контактов стартера напряжение на лампе значительно больше напряжения на конденсаторе:
Ел = Со » 1 и с
Таким образом, принцип зажигания лампы останется прежним.
Рассмотрим теперь, изменится ли сила тока, протекающего через лампу в стационарном режиме.
Схема новой цепи представлена на рисунке 12.25. Полное сопротивление этой цепи равно:
—— I	11/	\2
Z' = JI (oL - —— I +(1?л+.йсг) .
Так как
XL = coL ® 342 Ом,	Xq = —— ~ 677 Ом, т.е.
СйС
269
|o>l| ®
a>L-------
<oC
получаем:
Z' » 374 Ом (Z' » Z).
Следовательно, сила тока в цепи изменится мало: Г = 0,61 А. Мало изменится и напряжение на лампе: U' = 85,5 В.
Мало изменится также модуль сдвига фаз — этот угол лишь изменит знак, что хорошо видно из векторной диаграммы (рис. 12.26):
,01;	<р' = -63,6° (|^'| » |<р|).
r 1 coL-----
а>С
При параллельном включении большого количества люминесцентных ламп увеличивается сдвиг фаз между током и напряжением, и для получения той же мощности на каждой лампе нужна большая сила тока.
Рассмотрим это на примере. При двух параллельно включенных лампах без конденсаторов сила тока равна:
I = Io cos (cot + <р)+ Io cos(art + <р) = 2I0 cos (art +
Если же включить параллельно такой лампе лампу с конденсатором Со, то
I = 70 cos (art + <р( + Io cos (art - <р( = 2I0 cos <p cos cat.
Из полученных выражений видно, что сила тока во втором случае меньше в 2,3 раза, так как cos^> ® 0,44.
Таким образом, конденсаторы нужны для компенсации сдвига фаз.
Рис. 12.25.
Рис. 12.26.
Рис. 12.27.
270
Задача 12.15. Катушка индуктивностью 10 2 Гн соединена параллельно с резистором R электрическим сопротивлением 1 кОм. Активное сопротивление катушки пренебрежимо мало. Катушка и резистор подключаются к источнику тока с ЭДС 10 В и внутренним сопротивлением г, равным 10 Ом. Какой заряд протечет через резистор Л за 1 секунду (рис. 12.27)?
Решение. При замыкании ключа К в цепи возникает ток I, изменение тока в цепи приводит к возникновению ЭДС самоиндукции в катушке LI'. Пренебрегая влиянием резистора R на переходный процесс, запишем уравнение:
£ = HL+/r.	(1)
При замыкании ключа ЭДС самоиндукции в катушке имеет максимальное значение, затем убывает со временем. Для нахождения зависимости силы тока I в цепи от времени попробуем отыскать решение для напряжения на катушке Uj(t~) в форме
t
UL = Uoe\	(2)
где v— некоторая постоянная.
t
Так как UL = LI', I' =	е 1, то
L L
1 =	(3)
L
Подставим (2) и (3) в (1):
_ I	*
8 = Uoe - ~^Uoe	(4)
Продифференцируем части уравнения (4):
£ _ 1
О = -^-е * + — Uoe т L
lr	L
— = —, т - — .
т L	г
(5)
Следовательно, сила тока I в цепи
изменяется со временем по зако-
ну:
£-Uoe
t
(6)
271
£
При t —> oo I —> —, при t - 0 I = 0 и
u0 = £.
Подставляя (7) в (6), получаем:
I = — 1-е
Из (7), (5) и (2) следует:
t	tr
UL= £е г = £е L .
Сила тока через резистор R равна:
Ir
tr
UL
= — е L .
R R
(7)
(8)
(9)
(Ю)
t
Постоянная времени iJL-цепи равна:
£/ 10-2	Л* —
г = —=----= 10 3 с, dQ=IRdt = —e тdt,
г 10	н R
1
Q = jdQ = о
р 1 —
— fe 'dt = -Ro
£L
Rr
-1
t = 1 c, r=103c, e 1000 —> 0,
PT
Q=——,	$ = 105Кл.
Rr
Глава 13
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
Задача 13.1. Электрический заряд </ совершает гармонические колебания с частотой со вдоль прямой Ох. Какова напряженность электрического поля излучаемой электромагнитной волны в точке А на расстоянии г от заряда в направлении под углом 0 к оси Ох? Как изменится мощность излучения электромагнитных волн при увеличении частоты колебаний заряда в 100 раз?
Решение. Пусть точечный электрический заряд g движется по прямой MN сначала с постоянной скоростью 5 (рис. 13.1), а затем в течение времени г замедленно до остановки в точке О.
Выясним, какой вид имеет картина силовых линий электрического поля спустя время t после остановки заряда в точке О, если изменения в электрическом поле распространяются со скоростью с.
Так как с момента начала торможения заряда прошло время t + г, то возмущение электрического поля распространилось на расстояние:
г2 = с(?+г).	(1)
За пределами сферы радиусом г2 поле должно иметь такой вид, какой оно имело бы, если бы заряд q продолжал двигаться равномерно со скоростью и- Но если бы заряд действительно двигался после точки О со скоростью D, он к моменту t + г находился бы в точке Oj на расстоянии OOj = ut от точки О. Следовательно, силовые линии электрического поля за пределами сферы радиусом г2 являются прямыми, проходящими через точку Ор Но на самом деле в течение времени t заряд q неподвижен и находится в точке О. За время t электрическое поле неподвижного заряда устанавливается в пределах сферы радиусом:
rj = г = ct.	(2)
Чтобы установить, какие изменения происходят в электрическом поле при движении заряда с ускорением в течение времени г, найдем за пределами сферы радиусом г2 продолжение каждой силовой линии электрического поля, выходящей из сферы радиусом г, и соединим их.
273
Рисунок 13.1 показывает, что на всех силовых линиях, кроме линий, совпадающих по направлению с вектором скорости движения заряда, образуется изгиб.
Таким образом, воспользовавшись представлениями Фарадея о силовых линиях электрического поля, мы получили, что торможение электрического заряда, двигавшегося со скоростью D, приводит к возникновению изгиба на силовых линиях и перемещению этого изгиба вдоль силовых линий со скоростью с.
Изгиб силовой линии (линии напряженности) электрического поля свидетельствует о том, что при ускоренном движении электрического заряда возникает составляющая вектора напряженности Е электрического поля, направленная перпендикулярно прямой, соединяющей данную точку поля с электрическим зарядом. Найдем значение этой составляющей вектора напряженности на расстоянии г от заряда q в направлении под углом 0 к вектору скорости б движения заряда. Приближенный вывод, приводимый далее, основан на использовании того факта, что кулоновская составляющая Е вектора напряженности электрического поля, направленная вдоль прямой ОА (рис. 13.2), соединяющей заряд с данной точкой поля А, остается неизменной при ускоренном движении заряда и равной:
Этот факт можно доказать, используя теорему Гаусса.
Как видно из рисунка 13.2,
£±=KKtga, где	(4)
Так как отрезок AD = ОуЕ и BD ~АЕ, то
О]Е ОО} .	• а
tg а ~ 4— = - sm 0 = — sm 0.	(5)
AF AF тс
Подставляя в выражение (4) выражения (3), (5) и (2), получим:
„	1 Qtu - л 1 ЯР • о
Ej_=--------—sm0 =---------------srntf.	(6)
4л£0 глст	teor гт
274
Если движение заряда в течение времени г было равноускоренным, то модуль а его ускорения равен:
Подставляя выражение (7) в выражение (6), получим:
= —- • S?- sin в.	(8)
4л£0с г
Таким образом, при движении электрического заряда с ускорением а в произвольной точке А пространства возникает нормальная составляющая Ек вектора напряженности Е электрического поля, модуль которой прямо пропорционален модулю ускорения а заряда, обратно пропорционален первой степени расстояния г от заряда и зависит от угла 0 между прямой ОА, соединяющей заряд с данной точкой А и вектором ускорения а.
Если электрический заряд q совершает колебания вдоль оси ОХ по гармоническому закону
х = хт cos cot,	(9)
то модуль ускорения движения заряда также изменяется со временем по гармоническому закону:
а = хта>2 cos cot.	(10)
Подставляя выражение (10) в формулу (8), получим:
1	2
Еу =------—  sin 0 cos cot.	(11)
4леос2 r
Следовательно, при гармоническом колебании электрического заряда вдоль прямой Ох с амплитудой хт и частотой со в произвольной точке А на расстоянии г от заряда возникает переменная составляющая Еу напряженности электрического поля, направленная перпендикулярно прямой ОА, модуль которой изменяется со временем по гармоническому закону. Амплитуда колебаний нормальной составляющей Е, прямо пропорциональна квадрату частоты колебаний со.
При всяком изменении электрического поля возникает вихревое магнитное поле. Поэтому возникновение электрического поля с нормальной составляющей Еу напряженности при ускоренном движении заряда обязательно сопровождается возникновением магнитного поля.
275
Вектор магнитной индукции В этого поля направлен перпендикулярно вектору Е> и прямой ОА.
Таким образом, при гармоническом колебании электрического заряда q в пространстве вокруг него возникают изменяющиеся по гармоническому закону взаимосвязанные электрическое поле и магнитное поле, или единое электромагнитное поле.
Так как плотность энергии электрического поля прямо пропорциональна квадрату напряженности Е электрического поля, то энергия электромагнитного поля, излучаемая электрическим зарядом при гармонических колебаниях, оказывается пропорциональной четвертой степени частоты ю:
W ~ El ~а>4.
Следовательно, с увеличением частоты колебаний заряда в 100 раз мощность излучения электромагнитных волн увеличивается в 108 раз.
Рис. 13.1.
Рис. 13.2.
Задача 13.2. Приемник радиоволн радиоастрономической обсерватории расположен на берегу моря на высоте h- 2 м над уровнем моря. При восходе над горизонтом радиозвезды, излучающей электромагнитные волны длиной волны Л =21 см, приемник регистрирует чередующиеся максимумы и минимумы. Регистрируемый сигнал прямо пропорционален интенсивности попадающих в приемник электромагнитных волн, электрический вектор которых колеблется в направлении, параллельном водной поверхности.
276
Выполните следующие задания и ответьте на вопросы:
в
1.	Определите высоты звезды над гори-	\
зонтом, измеренные в углах по небесной сфе-	''
ре, при которых регистрируются максимумы т	4
и минимумы (в общем виде).	ь	' । о
\ \ 1
2.	Будет ли сигнал в приемнике возрас-тать или уменьшаться непосредственно после	~С~	~~
восхода радиозвезды?
3.	Найдите отношение сигналов в первом	рис jg 3
максимуме и следующем за ним минимуме.
При отражении электромагнитной волны от воды отношение амплитуд напряженностей электрического поля отраженной (Ег) и падающей (Ei) волн описывается законом:
Er п — cos (р
Et п + cos ф
где п — показатель преломления, а <р— угол падения электромагнитной волны. Для границы «воздух — вода» при Л = 21 см п - 9.
4.	Будет ли возрастать или уменьшаться отношение интенсивностей сигналов, принимаемых в соседних максимумах и минимумах, с восхождением звезды над горизонтом?
Указание. При решении задачи считать морскую поверхность гладкой.
Решение. 1. Сигнал, регистрируемый приемником А, определяется интерференцией прямого луча 1 и луча 2, отраженного от поверхности воды (рис. 13.3). Так как луч 2 отражается от оптически более плотной среды, фаза колебаний изменяется на тт, при этом разность хода Д лучей 1 и 2 равна:
Л. [ h ] п Я Л / О\
Д = AC -I----------АВ ~ —— -I------------------------- cos 2а - — н—;------------ 1 - cos 2а).
9	о it-, rv 9 I о it-, zv /	9 cin zv '	'
Л = — + 2h sin а.
2
Запишем условие интерференционных максимумов:
— + 2Л sin amax = kA., или
sinamax
(1)
(2)
где k = 1, 2, 3,	19 (разность хода не может превышать Л, следова-
тельно, k не превышает 19).
277
Условия интерференционных минимумов определяются из выражения:
Я п1.  - + 2Asrnami
min =(2fe + l)4, отсюда
Ы sin a„in = — , mm 2h
(3)
где k = 0, 1, 2, 3,	19.
2.	Так как при восходе угловая высота а радиозвезды равна нулю, то выполняется условие минимума. Поэтому непосредственно после ее восхода интенсивность принимаемого сигнала будет возрастать.
3.	При выполнении условия интерференционного максимума в приемник попадает электромагнитная волна, амплитуда электрического поля £тах которой равна сумме амплитуд электрического поля Е( падающей волны прямого луча и отраженной волны Er: Етах = Е,- + Ег.
„ п. - cos q>
1 ак как по условию задачи Ег = E,l-----, то
п + cos <р
р р , п cos <ртах Лтах - -^1 1 +-------------
< п + cos ^тах
Поскольку
CL max ’
получим
Е 2-'тах
n-sin^max"l = 2п _ zi + sinpmaxJ !n + sinpmax
(4)
При интерференционном минимуме амплитуда результирующей волны равна:
Emin = Et - Е г - Et 2sin^ -	(5)
n +srn^min
Интенсивность I пропорциональна квадрату амплитуды E, поэтому отношение интенсивностей в соответствующих максимумах и минимумах равно:
I	(Е V п2 (п + sinfi>„:n)2
2max _ -^max _	_____\_____y min/
Anin V -^min ) sin2 ^min (n -b sill ^max)2
Подставляя в выражение (6) условия (2) и (3) для sin<pmin и sin^>max, получим:
278
г л-,21,2 П + fe — ^max _
Anin /г2я2 n+^2fe-l)A
(7)
Из этой общей формулы, справедливой для любого k, получим выражение для частного случая k = 1, соответствующего первому максимуму и следующему за ним минимуму:
Агпах
^min
4л.2 Л2
Я2
2h _Я_ 4/г,
= 3 104.
4.	Так как п » —, то из соотношения (7) получаем:
Лпах , 4п2/г2 /min " Й2Я2 ’
т.е. с восхождением радиозвезды над горизонтом в связи с ростом чис-
ла k отношение интенсивностей сигналов ^гпах , принимаемых в сосед-Ашп
них максимумах и минимумах, уменьшается.
Задача 13.3. Юный радиолюбитель поддерживает радиосвязь с двумя девушками, проживающими в разных городах. Он намерен сконструировать такую систему антенн, которая позволила бы ему разговаривать с одной из девушек (живущей в городе В) с оптимальным качеством связи, но таким образом, чтобы вторая девушка (живущая в городе А) их разговор слышать не могла, и наоборот. Система антенн собирается из двух вертикальных антенн, излучающих с одинаковой интенсивностью во всех горизонтальных направлениях.
Определите расстояние г между антеннами, угол между плоскостью, проходящей через обе антенны, и направлением на север, и разность фаз Др электрических сигналов, излучаемых антеннами. Расстояние между антеннами должно быть минимальным.
Найдите численное решение в случае, если юноша имеет радиостанцию, работающую на частоте г= 27 МГц.
Примечание. Используя карту, юноша выяснил, что углы между направлением на север и направлениями на города А и В составляют i/i = 72° и у/2 = 157° соответственно.
Решение. На рисунке 13.4 показаны положения антенн 1 и 2 (расстояние между которыми г) и направления на города А и В (угол между которыми ip). Полные фазовые сдвиги колебаний, возбуждае
279
мых обеими антеннами в некоторой точке, в направлениях А и В равны:
л/	П rCOS а А	/14
А) = 2л--------1- А<р,	(1)
Я
, . rcos(\i/-a\
Д(В) = 2л------+ /\<р,	(2)
Л
где Я — длина волны передатчика, :\(р — разность фаз колебаний в антеннах, а — угол между плоскостью, проходящей через обе антенны, и направлением на город А.
Запишем условия минимума интенсивности в городе А и максимума интенсивности в городе В:
Д(А) = (2п + 1)л,	(3)
Л(В) = 2яй,	(4)
где кип — целые числа. Из выражений (1) — (4) следует:
Л(В) - Л(А) = 2fl--^-(cos(y< - а) - cos а) = (2(/г - п) - 1)л, откуда
Я 2(fe - п) -1 . . (уЛ . (	\if\
4 sin — sin а - — <27 I	2)
Расстояние
г между антеннами минимально, если k - п и
этом случае
Я
Г .	— -----------
' min	/
А . I у/
4 Sin —
<2.
у/ - л
(5)
(6)
2
плоскости, проходящей через антенны, является бис-
т.е. нормаль к сектрисой угла I//. Из выражений (1), (3), (5) и (6) найдем:
, л
1\<р= —.
2
Изменение знака i\cp (от — до ~ ~ ) приводит к противоположному эффекту: максимальная интенсивность излучения будет в направлении 280
А, а минимальная — в направлении В. На рисунке 13.5 показаны положения антенн, направление на север N, а также направления на данные города А и В. Из этого рисунка видно, что
У'=^2- V'l = 85°>
Я

------—— к 4,1 м,
. • I W 1 4vsm ~
\2)
Задача 13.4. На экран А (рис. 13.6) от точечного источника, находящегося от него на большом расстоянии, падает свет с длиной волны 560 нм. В экране имеются две параллельные щели на расстоянии 10’4 м одна от другой. Определите расстояние между двумя соседними полосами интерференционных максимумов, наблюдаемых на экране В, расположенном параллельно экрану А на расстоянии 1 м от него.
Решение. В произвольной точке С экрана В (рис. 13.6) будет наблюдаться интерференционный максимум при выполнении условия
Zg — /1 — /гЯ.
281
Из рисунка видно, что
г	.Л1
l[ =12+ й £
I	2J

4 = I2
Отсюда следует, что:
Z22 - zf = 2hkd, (Z2 - Zi)(Z2 + Zx) = 2hkd,
l2 ~ k
2hkd
I2 + Zj
В случае, когда hk «l, можно считать справедливым приближен-
ное равенство Z2 +	» 21. Тогда:
г2 11
hkd
Приравнивая первое и последнее выражения для разности Z2 - Zj, получаем:
М Z
= АЛ,
, ЫА. hb=~r d
Искомое расстояние ДА между соседними интерференционными полосами найдем так:
Л , г г ^-Z - ^fe+1 ~^k = — d
Подставляя значения величин, получаем:
ДА = 5,6 10-3 м.
282
Задача 13.5. Стеклянная линза, у которой одна поверхность сферическая радиусом Я = 8,6 м, а вторая плоская, положена выпуклой стороной на плоскую стеклянную пластину. При освещении сверху параллельным пучком монохроматического света, падающим перпендикулярно плоской пластине, в отраженном свете наблюдается интерференционная картина в виде чередующихся темных и светлых колец (кольца Ньютона). Определите длину световой волны, если радиус четвертого темного кольца равен г = 4,5 мм.
Решение. Волны, отраженные от поверхности линзы в точке В и от поверхности пластины в точке А, имеют разность хода 2АВ (рис. 13.7). При отражении от поверхности пластины в точке А происходит потеря X „ — . Следовательно, условие минимума 2
2АВ+ — = (2Л + 1)— , 2АВ = Ы.
2 V ’ 2
г2
АВ = ОЕ = — .
2R
г2	г2
2—= Ы, Я = —, 2R	Rk
(4,5 -нт3)2
Л = -i------м = 0,589 • 10 6 м.
8,6 4
Задача 13.6. Прямоугольная проволочная рамка погружается в мыльную воду, благодаря чему на ней образуется мыльная пленка. При наблюдении в отраженном свете, угол падения которого а = 30°, пленка кажется зеленой (Ло = 500 нм). Размеры сторон рамки а = 0,020 м и Ъ - 0,30 м. Плотность мыльного раствора р — 103 кг/м3, показатель преломления пленки п~ 1,33.
Выполните следующие задания и ответьте на вопросы:
1. Можно ли найти массу этой пленки с помощью весов, чувствительность которых 0,1 мг?
2. Какого цвета будет казаться самая тонкая из пленок, удовлетворяющих условию задачи, если свет будет падать на нее н затем отражаться перпендикулярно пленке?
Решение. 1. Для ответа на первый вопрос задачи нужно рассчитать минимальную массу пленки и сравнить ее с чувствительностью весов Дтп = 0,1 мг:
TMjnin —
где dmin — толщина самой тонкой пленки, при которой возможен интерференционный максимум для света с длиной волны Яд.
283
Интерференция происходит между лучами 1 и 2 (рис. 13.8). Оптическая разность хода этих лучей равна:
Д = (АВ + BC)n - DC = 2-^—- 2d tg/?sina.
'	1	COS p
„	sin a
Согласно закону преломления n =-------, поэтому
sin/?
A =	(1 - sin2 /?) = 2dn cos /?.
COS P \	/
(1)
Известно, что при отражении луча 2 в точке С происходит изменение фазы волны на я, т.е. «теряется» половина волны. Поэтому оптическая разность хода волн в точке наблюдения равна:
Запишем условие интерференционного максимума:
Яр
Д' = 2k——,
2
где k — целое число. Тогда
2dncosp — = 2k ——, или 2dn cos р = (2k + 1) —— .	(3)
2	2	2
Из выражения (3) найдем толщину мыльной пленки d*.
(2k + 1)Я0	(2k + 1)Я0	(2k + 1)Я0 (2fe + l)A0
d =	~	.	— =	= ~	. (4)
4n COS В	Л /i - 2 г>	-2 Л 2	.2
и 4nVl-sin В „	, sin а 4\п -sin а
V	4n 1----—
V п
Толщину самой тонкой пленки ^п1;п можно определить при k = 0:
^min
Я-о 1
'2	.2
п - sin
» 10 7 м. •
Минимальная масса пленки равна:
mmin = abdminp =6 10 8 кг = 0,06 мг < 0,1 мг,
следовательно, массу этой пленки измерить на наших весах нельзя.
2.	При нормальном падении и отражении света (а = 0) выражение (4) запишем в виде:
284
При k = О
2k + 1 Л d =--------
п 4
(5)
(6)
^min
А
4n ’
Отсюда получаем, что длина волны Л излучения, для которой выполняется условие интерференционного максимума для самой тонкой мыльной пленки, равна Л = iLndn^n ® 5,32 • 10 7 м, что соответствует зеленому цвету. Значит, при освещении белым светом пленка будет казаться зеленой.
Рис. 13.9.
Рис. 13.8.
Задача 13.7. Над стеклянным отшлифованным кубиком, длина ребра которого 2 см, помещена стеклянная отшлифованная пластинка так, что в пространстве между ней и кубиком возникает тонкий воздушный слой. Если пластинку осветить сверху под прямым углом к ее поверхности излучением с длинами волн от 400 до 1150 нм, для которых пластинка прозрачна, то в отраженном свете выполняется условие максимума интенсивности только для двух длин волн: Ло = 400 нм и еще для одной длины волны. Определите эту длину волны. Вычислите, насколько нужно повысить температуру кубика, чтобы он прикоснулся к пластине. Коэффициент линейного расширения стекла а - 8 • 10-6 К-1, показатель преломления воздуха п = 1. Расстояние от основания кубика до пластинки во время нагревания не меняется.
Решение. Запишем условие интерференционного максимума для отраженного света:
Д = пЯ,	(1)
где n = 1, 2, 3, ..., Л — длина волны, Д — разность хода лучей 1 и 2 (рис. 13.9). Луч 1, отразившийся от верхней грани кубика, пройдет
285
расстояние на 2d большее, чем луч 2, отразившийся от нижней грани пластинки, если угол падения близок к нулю. Кроме того, луч 1 отражается от оптически более плотной среды, при этом происходит сдвиг Л
по фазе на л (потеря — ), а луч 2 отражается от оптически менее плот-2
ной среды и его фаза не изменяется. Таким образом, условие (1) можно записать в виде:
Л	(2п - 1U
2d 4— = пЛ , или 2d = -----— .	(2)
2	2
Условие (2) должно выполняться для двух длин волн: при п = k + 1 для = 400 нм и при п = k для Л1, находящейся между 400 и 1150 нм, т.е.
Отсюда получаем, что
2 = j-+1 Ао.
1 2k - 1 0
Но по условию Л] < 1150 нм, следовательно:
2k +1 ------400 нм < 1150 нм.
2k - 1
Это неравенство выполняется при k > 1.
Третья длина волны Л2 (при п = k - 1) должна быть уже больше 1150 нм:
— • 400 нм > 1150 нм.
2k - 3
Это неравенство выполняется при k < 3. Следовательно, 1 < k < 3, т.е. k = 2. Тогда
Л] =	-- + 1	Лг, = — Ло = 666,7 нм,
1	2Л-1	3	и
,	2 k 4-1	.	5	_ _
d =-----Ло = — Ло = 500 нм.
4	4
Теперь можно найти изменение температуры, при котором за счет теплового расширения ребро куба удлинится на толщину зазора d = ааАТ, откуда
ДТ = —, ДТ = 3,1 К. аа
286
Задача 13.8. На расстоянии 4 м от точечного источника света с длиной волны 6-10 7 м расположена диафрагма с круглым отверстием. При каком радиусе отверстия центральная часть дифракционной картины на расстоянии 6 м от отверстия будет наиболее светлая и при каком радиусе наиболее темная?
Решение. Если источник света А точечный и монохроматический, а среда, в которой распространяется свет, изотропна, волновой фронт в произвольный момент времени будет иметь форму сферы радиусом г = ct. Каждая точка на этой сферической поверхности является вторичным источником волн. Колебания во всех точках волновой поверхности происходят с одинаковой частотой и в одинаковой фазе. Следовательно, все эти вторичные источники волн когерентны. Для нахождения амплитуды колебаний в точке О необходимо произвести сложение когерентных колебаний от всех вторичных источников на волновой поверхности. Так как расстояния от точки О до различных участков волновой поверхности не одинаковы, то колебания от них в точку О будут приходить в различных фазах.
Для нахождения результата интерференции колебаний от вторичных источников Френель предложил метод разбиения волнового фронта на зоны, называемые теперь зонами Френеля.
Обозначим расстояние от точки О до ближайшей точки волновой поверхности В через г0 (рис. 13.10).
Первая зона Френеля ограничивается точками волновой поверхности, расстояние от которых до точки О равно:
Л ri = го + г ’ Л
где Л — длина световой волны. Эти точки располагаются на окружности. Вторая зона находится между краем первой зоны и точками волновой поверхности, расстояние от которых до точки О равно:
Л .
^2 = Гг + — = г0 + Л.
&
Аналогично определяются границы третьей, четвертой и последующих зон.
Расчеты показывают, что площади зон Френеля одинаковы. Поэтому одинаковыми должны быть и амплитуды колебаний, возбужденных каждой из зон. Но так как разность хода от двух соседних зон равна Л	г-	,
— , то колебания от них приходят в точку О в противоположных фа-2
зах.
Пока радиус отверстия меньше радиуса первой зоны Френеля, его увеличение приводит к увеличению амплитуды колебаний в точке О (так как разность хода для колебаний, пришедших от различных то
287
чек первой зоны, не превышает — ). Максимального значения амплитуда колебаний в точке А достигает при равенстве радиуса отверстия радиусу первой зоны Френеля.
При дальнейшем увеличении радиуса отверстия амплитуда колебаний в точке О уменьшается в результате интерференции колебаний, приходящих от первой и второй зон; она становится минимальной при равенстве радиуса отверстия радиусу второй зоны. При дальнейшем увеличении радиуса отверстия амплитуда колебаний принимает минимальные значения, когда в отверстии укладывается четное число зон Френеля, и максимальные значения при нечетном их числе.
Рис. 13.10.
Рассчитаем радиус rj первой зоны. Обозначим а — расстояние от источника А до экрана, b — расстояние от экрана до точки наблюдения В, лежащей на прямой, проходящей через источник А и центр отверстия О (рис. 13.11).
Для радиуса Г; первой зоны выполняется условие:
288
AC + СВ = AB + — , 2
Ja2 + rf + ^b2 + r2 = a + b + , A
2	2	2
av1+^2 +N1+^ -a~b = -^’ \ a2 \ b2	2
(1)
rt « а, л} « b,
n2
a2
« 1,
fl
b2
« 1,
поэтому выполняются приближенные равенства:
(2)
(3)
Из (1), (2) и (3) следует:
г2
а+ — + & + — - а - b = —
2а 2Ь	2
2Ь

г2 (а + b) = ЛаЬ,
(4)
Рис. 13.11.
289
Аналогично можно получить:
2ЛаЬ а + Ь
(5)
ЗЯлб а + Ъ
И Т. д.
(6)
Если источник находится очень далеко от экрана (а » Ъ), формулы (4), (5), (6) превращаются соответственно в формулы:
q = д/яК,
г2 = yl2Ab,
= yjsAb.
(7)
(8)
(9)
Из формулы (4) найдем радиусы первой и второй зон по условию задачи:
» 1,2 • 10 3 м,
г2 ® 1,7 10~3 м.
Задача 13.9. На пути параллельного когерентного монохроматического пучка света с длиной волны 5 • 10 7 м установлен экран с круглым отверстием радиусом 5 мм. На каком минимальном расстоянии от экрана интенсивность света в центре экрана будет близкой к нулю?
Решение. Интенсивность света за экраном будет близкой к нулю в той точке, для которой на отверстии в экране укладывается две зоны Френеля. Следовательно, радиус отверстия г должен быть равен радиусу г2 второй зоны Френеля:
г=г2-
Для случая параллельного пучка света а —> ас,
г2
2ЛаЬ а + Ъ
~у12М,
2 Я.	2Я ’
Подставляя значения г и Л из условия задачи, получаем:
b » 25 м.
290
Задача 13.10. На пути монохроматического когерентного параллельного светового пучка поставлен экран с круглым отверстием. На некотором расстоянии за экраном Э в точке А измерена интенсивность света (рис. 13.12). Как изменится интенсивность света в точке А при закрывании половины площади отверстия в экране?
Решение. На поставленный в задаче вопрос нельзя дать однозначный ответ без сведений о длине световой волны Л, диаметре отверстия d, расстоянии ОА и способе закрывания отверстия.
Рассмотрим два возможных случая.
Первый случай — радиус отверстия в экране меньше или равен радиусу первой зоны Френеля для точки А. В этом слу
чае при закрывании половины площади
отверстия интенсивность света в точке А	Рис. 13.12.
уменьшится при любом способе закрыва-
ния отверстия. Однако уменьшение интенсивности будет зависеть от
способа закрывания отверстия. Интенсивность уменьшится наполовину при закрывании отверстия сегментом в половину круга (рис. 13.13), так как разности хода для различных лучей до точки А останутся та
кими же, как при полностью открытом отверстии, но их число уменьшится вдвое.
Если закрыть только центральную (рис. 13.14) или только внешнюю (рис. 13.15) часть кругового отверстия, то интенсивность света уменьшится менее чем вдвое, так как у оставшихся лучей будет меньшая разность хода.
Если же закрыть кольцевую зону между центральной и внешней частью отверстия (рис. 13.16), то интенсивность света уменьшится более чем вдвое из-за увеличения разности хода для оставшихся лучей.
Второй случай — радиус отверстия больше радиуса первой зоны Френеля для точки А. В этом случае в зависимости от способа закрывания половины площади отверстия в точке А возможно как уменьшение, так и увеличение интенсивности света.
Если на пути когерентного светового пучка, проходящего через отверстие, в котором укладывается п зон Френеля для точки наблюдения А, поместить пластинку, на которой в месте расположения всех четных зон нанесены концентрические кольца из непрозрачного материала, то в точку А будут приходить колебания только от нечетных зон, происходящие в одной и той же фазе. Эти колебания в результате интерференции должны усиливать друг друга. Освещенность в точке А должна значительно возрасти после того, как половина площади отверстия будет закрыта непрозрачным экраном.
291
Рис. 13.13.
Рис. 13.14.
Рис. 13.15.
Рис. 13.16.
Задача 13.11. На пути параллельного когерентного пучка света с длиной волны 6 • 10~7 м находится непрозрачный экран с отверстием в форме щели шириной 0,1 мм. С помощью линзы с фокусным расстоянием 1 м получено действительное изображение щели. Каково расстояние между нулевым и четвертым дифракционными максимумами?
Решение. Выясним, от чего зависит освещенность в произвольно выбранной на экране точке А, в которую линза собирает параллельный пучок лучей, идущих в результате дифракции в некотором произвольном направлении (рис. 13.17).
Рис. 13.17.
292
Во всех точках волновой поверхности, достигшей щели, совершаются колебания в одинаковой фазе. Но в точку А на экране волны приходят с неодинаковыми фазами, так как оптические пути их различны. Поскольку линза не изменяет длины оптического пути, разность хода света от точек В и С щели можно определить, опустив перпендикуляр из точки С на направление распространения света, проходящего через
Л
точку В. Если разность хода BD = —, то расстояние ВС = х является 2
шириной зоны Френеля.
Разобьем щель на зоны шириной, равной ширине зоны Френеля. Все зоны ориентированы относительно выбранного направления одинаково, но колебания, приходящие от двух соседних зон в точку А,
А ГТ
имеют разность хода —. Поэтому если на щели укладывается четное 2
число зон, то в точке А происходит полное взаимное гашение колебаний и освещенность будет равна нулю. Если же число зон нечетно, то колебания от одной из зон останутся непогашенными и в точке А будет наблюдаться некоторая освещенность (максимум освещенности).
Итак, освещенность в точке А зависит от числа зон Френеля, которые укладываются на щели. Найдем количественное выражение этой зависимости.
Пусть х — ширина зоны. Учитывая, что разность хода между лу-
2
чами, исходящими от краев зоны, равна —, можно записать:
2
BD 2
---= — = srnft отсюда:
ВС 2х
Л	.
х = — •	(D
2 sin (р
Если а — ширина щели, то легко определить число п укладывающихся на ней зон:
a 2as>m(p
п = - =----—.	(2)
х Л
Из выражения (1) видно, как зависит число зон, укладывающихся на щели, от угла <р, ширины щели а и длины волны А. Если число зон является четным (п = 2/г), то можно записать следующее равенство:
2а sirup
2в =-------, или
А
as,ixi<p = kX.	(3)
293
Это условие, при выполнении которого наблюдается минимум освещенности от одной щели.
Условием наблюдения максимума освещенности является условие нечетности числа зон: n = 2k + 1. Тогда:
2fe+l = ^^ Л
или
л
a sin <р = (2 k + 1) — .
2
(4)
(5)
Для четвертого максимума
,	.	9 ,	9Л
k - 4, asm<p = — Л, sma> = —
2	2а
Расстояние b от нулевого максимума до четвертого определяется выражением:
b = F tg q> .
Так как угол (р очень мал,
9z
tg<p ~ sin $7 = —- ,
2а
ь 9FA
Ь =----
2а
Подставим значения F, а и Л из условия задачи:
1-9 6 10~7
2 10 4
м = 2,7 10 2
м.
Задача 13.12. На пути когерентного параллельного пучка света длиной волны 2 поставлен непрозрачный экран с двумя параллельными щелями. Ширина каждой щели а, расстояние между щелями Ъ. Под какими углами к первоначальному направлению распространения света будут наблюдаться дифракционные максимумы и минимумы?
Решение. Пусть плоский фронт монохроматической волны достиг положения, совпадающего с плоскостью пары щелей. С помощью линзы соберем все параллельные группы дифракционных параллельных лучей на экране MN. Выберем на экране произвольную точку А, в которой собирается пучок параллельных лучей, идущих в некотором направлении, как показано на рисунке 13.18, и определим, от чего зависит получение максимума или минимума освещенности в этой точке.
294
Пусть выбранное направление таково, что выполняется условие получения минимума света от одной щели:
asin^ = kA.	(1)
Так как в этом направлении каждая щель в отдельности на экране света не дает, значит, и при наличии двух щелей в этом направлении не будет наблюдаться света.
Условие (1) в применении к двум щелям называют условием прежних минимумов. Ясно, что оно справедливо для любого числа щелей, так как независимо от числа щелей минимумы наблюдаются в тех же местах на экране, что и в случае одной щели.
Рис. 13.18.
Теперь выберем такое направление, в котором каждая щель в отдельности дает на экране свет. Для случая двух щелей могут предста
виться две возможности, в зависимости от разности хода слагаемых колебаний: 1) интерференция света от двух щелей приводит к усилению света на экране; 2) происходит взаимное гашение. Назовем точки щелей, расположенных на расстоянии d = а + Ъ, соответственными точками. Очевидно, что усиление света будет происходить тогда, когда разность хода А от соответственных точек равна четному числу полуволн. Как видно из рисунка 13.18, эта разность хода определяется формулой:
А = rising.	(2)
При выполнении условия
Л
d sin <р = 2k— = kA	(3)
свет от соответственных точек будет при интерференции в точке А давать максимум освещенности. Выражение (3) называют выражением для главных максимумов. Выражение для главных максимумов так же, как и выражение для прежних минимумов, справедливо при любом количестве щелей.
В направлении, для которого разность хода от соответственных точек щелей равна нечетному числу полуволн, наблюдается интерференционный минимум на экране. Поэтому в направлениях, в которых каждая щель в отдельности дает на экране свет, при совместном действии щелей света наблюдаться не будет, если выполняется условие:
d sin <р = (2k +
(4)
295
Это справедливо для любого четного числа щелей. Направления, определяемые выражением (4), называют направлениями на дополнительные минимумы. Такое название происходит от того, что в случае одной щели в этих направлениях на экране будет свет.
Задача 13.13. При наблюдении дифракции от двух параллельных щелей шириной а каждая на расстоянии Ь одна от другой интенсивность света в первом главном максимуме оказалась равной Яр Какой будет интенсивность света в первом главном максимуме при использовании того же источника света и дифракционной решетки, содержащей 200 таких же параллельных щелей, как в первом эксперименте? Постоянная решетки d = а + Ь.
Решение. С увеличением числа щелей главные максимумы и прежние минимумы, направления на которые определяются выражениями
d sin^j = k/. и	(1)
a An. ср = /гЛ,	(2)
справедливыми для любого числа щелей, остаются на прежних местах, но максимумы становятся ярче, а промежутки между ними все темнее. Дело в том, что с увеличением числа щелей увеличивается число дополнительных минимумов
и интенсивность света в промежутке между максимумами уменьшается до исчезающе малого фона. С увеличением числа щелей энергия световых колебаний в главных максимумах возрастает пропорционально квадрату числа щелей.
Действительно, результирующая амплитуда А в главном максимуме равна сумме амплитуд колебаний а, присылаемых каждой щелью, так как в главных максимумах интерферируют колебания в одинаковых фазах. Если число щелей N, то
A = Na.
Но поскольку энергия колебаний пропорциональна квадрату амплитуды, то
Е - А2 = W2a2 - N2.
Е2 _ N22
-El wf ’
(200)2
E2 = ~T-El = 2--T-Ej = ЮОООЯр
Nl (2)2
296
Задача 13.14. Оцените разрешающую способность человеческого глаза.
Решение. Разрешающая способность любых оптических систем ограничивается явлением дифракции. При освещении отверстия радиусом И светом длиной волны Л с плоским волновым фронтом во всех точках отверстия колебания происходят в одной фазе. При построении изображения отверстия с помощью линзы для волн, собранных линзой в точке О2 (рис. 13.19), разность хода равна нулю. Поэтому в точке О2 наблюдается максимум. Световой пучок, распространяющийся в результате дифракции под углом а к направлению прямолинейного распространения света, собирается линзой в точку Ор И в этом случае от любой точки на плоскости, перпендикулярной направлению распространения света, например, на плоскости АВ, длина оптического пути до фокуса Oj одинакова. Однако к плоскости АВ световые волны от разных точек отверстия приходят в разных фазах, так как проходят различные пути.
Вычислим разность хода для волн, идущих от центра отверстия и от его краев. Как видно из рисунка 13.19, эта разность хода равна:
AZ = DC - AD • sina= R • sina.	(1)
Можно принять, что граница центрального светлого пятна, или, точнее, положение первого темного кольца, определяется условием:
AZ = В • sina = —.	(2)
2
297
Таким образом, в результате дифракции света малое отверстие в экране радиусом Я воспринимается как светлое пятно с угловым радиусом, приблизительно равным:
a = sina =
Л _ Л
2R ~ D
(3)
Длину волны света Л примем равной 5,6 10 7 м. Тогда угловой радиус а центрального светлого дифракционного пятна при попадании на зрачок глаза параллельного пучка света может быть определен по формуле (3), где D х 2  10 3 м:
а = — a 2,8 • 10 4 рад® 1'.
D
Таким образом, в результате дифракции бесконечно удаленный точечный источник воспринимается глазом как светлое пятно с угловым радиусом, равным примерно одной угловой минуте. Две светящиеся точки могут восприниматься глазом как отдельные источники света при условии, если угловое расстояние между ними превышает угловой радиус центрального дифракционного светлого пятна от одного точечного источника (рис. 13.20). Следовательно, разрешающая способность человеческого глаза равна примерно одной угловой минуте.
Рис. 13.20.
Задача 13.15. Оцените минимальное расстояние между двумя точками, при котором они могут быть различимы отдельно при наблюдении в микроскоп.
Решение. Если в изображении, построенном объективом микроскопа, две светящиеся точки становятся неразличимыми в результате на
298
ложения их дифракционных изображений, то дальнейшее увеличение изображения с помощью окуляра не может сделать их различимыми. Следовательно, как и в случае определения разрешающей способности глаза, минимальное угловое расстояние между точками, которые могут быть разрешены как отдельные источники света, приблизительно равно угловому радиусу а центрального светлого дифракционного пятна.
Угол а выражается через диаметр объектива D и длину световой волны Л:
Обозначив расстояние от предмета до объектива микроскопа через d (рис. 13.21), получим для минимального линейного расстояния у между двумя светящимися точками А и В, на котором они могут быть разрешены при наблюдении в микроскоп, следующее выражение:
л Ad у я ad —
D
Отсюда видно, что разрешающая способность микроскопа возрастает с увеличением диаметра объектива микроскопа, с уменьшением длины световой волны и расстояния от объектива до объекта.
Так как объектив микроскопа должен построить действительное изображение, то d > F.
Следовательно, для уменьшения расстояния d необходимо использовать возможно более короткофокусные линзы. Увеличение разрешающей способности объектива микроскопа при заданном фокусном расстоянии путем увеличения диаметра D объектива ограничено естественным пределом:
D = 2R,
где R — радиус кривизны линзы. Это означает, что плосковыпуклая линза, обычно применяемая в качестве первой линзы объектива микроскопа, должна быть полушаровой.
Так как фокусное расстояние плосковыпуклой линзы определяется формулой:
то для объектива микроскопа можно записать соотношение:
299
Учитывая это, можно минимальное расстояние, на котором могут находиться две светящиеся точки, различимые с помощью микроскопа, выразить так:
~ ЯЛ AF _ ЛЯ _ Я
У ~ D > 2Я ~ 2Я(п -1) ~ 2(п - 1) ’
Принимая показатель преломления стекла, из которого сделана линза объектива, п = 1,5, получаем: у ~ Л.
Таким образом, минимальное расстояние, на котором с помощью микроскопа могут быть разрешены две светящиеся точки при оптимальной конструкции объектива, приблизительно равно длине световой волны.
Задача 13.16. В советско-французском эксперименте по оптической локации Луны импульсное излучение рубинового лазера на длине волны Л = 0,69 мкм направлялось с помощью телескопа, имеющего диаметр зеркала D = 2,6 м, на лунную поверхность. На Луне был установлен отражатель, который работал как идеальное зеркало диаметром d = 20 см, отражающее свет точно в обратном направлении. Отраженный свет улавливался тем же телескопом и фокусировался на фотоприемник.
Выполните следующие задания и ответьте на вопросы:
1.	С какой точностью должна быть установлена оптическая ось телескопа в этом эксперименте?
2.	Пренебрегая потерями света в атмосфере Земли и в телескопе, оцените, какая доля световой энергии лазера будет после отражения от Луны зарегистрирована фотоприемником.
300
3.	Можно ли отраженный световой импульс увидеть невооруженным глазом, если пороговую чувствительность глаза принять равной п = 100 световых квантов, а энергию, излучаемую лазером в течение импульса, равной Е= 1 Дж?
4.	Оцените выигрыш, который дает применение отражателя. Считать, что поверхность Луны рассеивает а = 10% падающего света равномерно в телесный угол 2л стерадиан.
Примечания. Расстояние от Земли до Луны L = 380 тыс. км. Диаметр зрачка глаза принять равным d3p=5 мм.
Постоянная Планка Л = 6,6 10~84 Дж  с.
Решение. 1. Точность установки оптической оси телескопа определяется расходимостью светового пучка вследствие дифракции на угол 8<р:
^«А-2,610-7 рад® 0,05".
2.	Долю световой энергии лазера Ку, попавшей на отражатель, с	(с nd2}
можно наити по отношению площади oj отражателя =--------------- к
I )
LA, площади S2 светового пятна на Луне (S2 = пг2, где г = L8<p L —
расстояние от Земли до Луны):
St _ d2 _ d2P2
1	S2 (2r)2	4Л2Ь2 ’
Отраженный световой пучок тоже расходится и образует на поверхности Земли световое пятно радиусом R.
о	о
R =----, так как г « R.
d
Поэтому доля К2 отраженной энергии, попавшей в телескоп, составляет:
Р2 P2d2
2	~ (2R)2 ” 4Л2Ь2 ’
Доля Ку энергии лазера, попавшей в телескоп после отражения света от отражателя на Луне, равна:
301
3. В зрачок невооруженного глаза попадает во столько раз меньшая доля светового потока по сравнению с телескопом, во сколько раз площадь зрачка S3p меньше площади зеркала телескопа ST:
^зр = ко^- = Ко « 3,7 • Ю18.
ST D
Поэтому число фотонов 7V, попавших в зрачок, равно:
Е
N =	= 12.
hv зр
Так как N < п, то невооруженным глазом зафиксировать отраженный импульс невозможно.
4. В отсутствие отражателя а = 10% энергии лазерного излучения, попавшего на Луну, рассеивается лунной поверхностью в телесном угле
= 2л ср.
Телесный угол, в котором видно с Луны зеркало телескопа, составляет:
Q =^ = ^L.
2 L2 4L2
Поэтому в телескоп попадает доля К энергии, равная
К = а^- = а~ « 0,5 • 10~18.
8I2
Таким образом, выигрыш Д который дает применение отражателя, равен:
Р = ^2- » 2 • 106.
К
Примечание. Полученный результат Является лишь оценочным, так как световой поток внутри угла распределяется неравномерно.
Глава 14
ГЕОМЕТРИЧЕСКАЯ ОПТИКА
Задача 14.1. На плоскую поверхность стеклянного полуцилиндра падают световые лучи под углом а = 45°. Лучи проходят в плоскости, перпендикулярной оси полуцилиндра. Из какой части боковой поверхности полуцилиндра будут выходить лучи света? Показатель преломления стекла п = ^2.
Решение. Найдем угол Р преломления на плоской поверхности полуцилиндра. По законам преломления
sin а	. „ sin а sin 45°
-----= п, sm р =---------=--т=— = 0,5.
sin Р	п ^2
Отсюда р = arcsin 0,5 = 30°.
На цилиндрическую поверхность полуцилиндра лучи падают под разными углами. Из полуцилиндра выйдут лишь лучи, не испытавшие внутреннего отражения. Условие выхода луча:
1 sm у < —.
п
Критический угол падения луча на цилиндрическую поверхность равен:
 1 . 1
у = arcsm— = arcsm—j=;	у = 45 .
п V2
Из рисунка 14.1 видно, что из полуцилиндра выйдут лучи, точки падения которых на цилиндрическую поверхность определяются углами (р, лежащими в пределах:
< ^ <	= (180° - (fa],
при которых у = 45°. Найдем углы <р± и <р%. Из &ОАВ получим:
<рх = 180° - у - (90° - р) = 90° - у + р = 90° - 45° + 30° = 75°.
Из &OCD найдем <р% = у + (90°+/?) = 165°.
303
Рис. 14.1.
Таким образом, свет будет выходить из части боковой поверхности цилиндра, ограниченной дугой BD, отсекающей углы <р, лежащие в пределах:
75° < <р < 165°.
Примечание. Лучи, которые падают под углами (р <75° или <р > 165°, потерпят многократное внутреннее отражение и тоже выйдут из полуцилиндра, но через его плоскую поверхность. Попробуйте это доказать.
Задача 14.2. Две призмы с преломляющими углами Aj = 60°, Ag = 30° склеены так, как показано на рисунке 14.2 (угол С = 90°). Показатели преломления призм выражаются соотношениями:
1	1 Л2 * 2	2 Л2
где aj = 1,1 нм2, &! = 105 нм2, а2 = 1,3 нм2, Ь2 - 5  104 нм2.
Выполните следующие задания и ответьте на вопросы:
1. Определите длину волны Aq излучения, падающего на систему призм, если волна распространяется без преломления на границе АС при любом угле падения ее на грань AD. Определите также значения показателей преломления и п2 для этой длины волны.
2. Нарисуйте ход лучей в системе призм для трех различных длин волн Лер > Ль Л>> Лф < Ль если угол падения для всех трех волн на грань АО одинаков.
304
3. Определите угол наименьшего отклонения системой призм света с длиной волны Я<).
4. Определите длину волны излучения, падающего на систему призм параллельно основанию DC и выходящего из нее также параллельно основанию DC.
Решение. 1. Для того, чтобы пучок света с длиной волны не преломлялся на границе АС при любом угле падения на грань AD, показатели преломления должны быть равны: П[ = п2, следовательно,
Л о = ——— = 500 нм.
J &2 - П]
При этом
Ь1 т к
Пу = п2 = n0 = а, +	= 1,5.
4
2.	Приняв длину волны красного цвета Ак[) = 800 нм, а фиолетового Лф = 400 нм, получим:
п1кР = а1 +	= 1,26; п2кр = а2 + —— = 1,38.
Л'кр	Л к р
Аналогично найдем:
п1ф = 1ДЗ, п2ф = 1,61.
Полученные результаты говорят о том, что показатель преломления второй призмы для красного цвета больше, чем для первой, а для фиолетовой — наоборот. Учтя это, нарисуем качественно ход лучей в призме (рис. 14.3).
305
3.	При длине волны падающего света, для которой выполняется условие zij = п2, две призмы эквивалентны одной призме с преломляющим углом Ар = 30°.
Легко видеть, что угол отклонения луча 0 такой призмой будет минимальным, если угол, под которым луч падает на переднюю грань призмы AD, равен углу, под которым он выходит из задней грани ВС (рис. 14.4), т.е.
Л и min
sin а по ~ ~----
sin/
sin А° +gmin
I 2
= 2 arcsin
- Ар = 15°40'.
4.	На рисунке 14.5 показан ход луча, удовлетворяющего условиям задачи. Запишем законы преломления для этого луча:
sin 30° _	sin(60°-;g) _ n2
sin Р J’	sin 30°	nj
Рис. 14.5.
Подставляя выражения для показателей преломления, данные по
Ъ2
условию задачи: = «1 +—п2 = а2 + —т-, получаем уравнение: А2	А2
306
Л4^3а2 - al - а2 - 1) + ^(бл^ - 2a2b2 - б2) + (3bf ~ Ь2 ) = °>
0,36Л4 - 4,8-105 Л2 - 2,75 • 1О10 = О.
Решение этого биквадратного уравнения дает ответ задачи: Л ® 1200 нм.
Задача 14.3. На плоскопараллельную пластинку (рис. 14.6) в точке А с координатой х = 0 перпендикулярно к пластинке падает узкий пучок света. По-
П0 казатель преломления вещества пластинки меняется по формуле пх =-----,
1--
R
где п0 и R — постоянные величины. Пучок покидает пластинку в точке В под углом а к начальному направлению.
Выполните следующие задания и ответьте на вопросы:
1.	Определите показатель преломления в точке В, в которой пучок покидает пластинку.
2.	Определите координату хв точки В.
3.	Определите толщину пластинки d.
Указания. Принять п0 = 1,2, R = 13 см, а = 30°.
Решение. 1. Разобьем мысленно пластинку на очень тонкие слои, перпендикулярные оси Ах. Внутри каждого слоя показатель преломления будем считать постоянным. При переходе из одного слоя в другой луч испытывает преломление (рис. 14.7). Ввиду различных флуктуаций реальный световой пучок нельзя направить на эти слои абсолютно точно под углом падения 90°, поэтому пучок будет преломляться (это ясно и из обратимости лучей).
Запишем закон преломления для перехода луча из слоя (i - 1) в слой i:
sin#i _ щ sinA	’
Записав такие же отношения для соседних слоев между сечениями А и В и перемножив их, получим:
nA sin/?A = пв sin/Зв.
По условию задачи пА = п0, flA = 90°, откуда найдем:
п0 = пв sin ffB.
(1)
Рис. 14.6.
307
Рассмотрим преломление на границе «стекло — воздух» в точке В (рис. 14.7):
sin/ 1
sina
где у = fiА - Рв = ~ _ Рв • Следовательно, sin у = cos Рв = SU1 °

откуда
. п , sin2 а sm рв = 1 -

Из (1) и (2) получаем:
, sin2 а по=пвл1----или
V “в
(2)
+ sin2
Пд
Подставив числовые данные, найдем пв = 1,3.
2. По условию задачи пв = ———, тогда 1_£в
R
Хв =R 1-^0. . \ пв/
хв = 0,01 м.
3. Как было показано в пункте 1, в точке С с координатами х и у (рис. 14.8) выполняется равенство:
nc sin/?c = nosin/?A = n0.
Следовательно,
sin^ = ^.	(3)
nc
Пп
Подставив условие	"— в выражение (3), получим:
1-	—
R
sin/?c = 1--|.	(4)
Проведем ряд математических преобразований, чтобы получить зависимость Аг/ (Дх):
sin Рс = -г=^= 	(5)
•Jax2 + Дг/2
308
Из (4) и (5) получаем:
R - х
R
sin/?c
^Лх2 + Al/2
= 1--
R
(6)
Из равенства (6) следует:
ДУ R~x tgPc = — = ~г==-^R2 - (7? - х)2
Отсюда находим зависимость Ду (Ах
ч	7? - х
Ду = .	Ах.
Jr2 -[R- xf
Для бесконечно малых значений Дх и At/ получим:
dy = -j-	-..— dx.
y/R2 -(R- x)2
Проинтегрировав выражение (7) в пределах от 0 до хв, получим:
Рис. 14.7.
Рис. 14.8.
309
Задача 14.4. Выполните следующие задания и ответьте на вопросы:
1.	На рисунке 14.9 показан ход луча через плоскопараллельную прозрачную пластинку, коэффициент преломления которой изменяется с расстоянием z от нижней поверхности пластинки. Докажите, что n^sintz = n5sin/7.
2.	Представьте, что вы стоите посередине широкой плоской пустыни. Вдали вы видите нечто похожее на водную поверхность. Когда вы приближаетесь к «воде», она постепенно удаляется от вас, так что расстояние до нее все время остается равным 250 м. Объясните этот феномен.
3.	Вычислите температуру Т у поверхности Земли для предыдущего пункта задачи, предположив, что ваши глаза находятся на высоте 1,6 м от поверхности. Известно, что показатель преломления воздуха п0 при температуре То = 15 °C и нормальном атмосферном давлении равен 1,000276. Температуру воздуха на высоте, большей 1 м, считать постоянной и равной 7^ = 30 °C. Давление нормальное (0,1013 МПа). Принять, что (п - 1) пропорционально плотности частиц в газе.
Решение. 1. Разбиваем пластинку на большое число параллельных слоев, каждому слою соответствует свой показатель преломления: п15 п2, п3, ...
Записывая закон преломления для каждой последовательной пары слоев (рис. 14.10), получим:
sin а	sintzj	n2	sina2 _ Лз
smtZi	пА sina2	Л1	sina3 п2
откуда
пА sin а - nj sin tzj = n2 sin tz2 = n3 sin tz3 = ... = sin p.
Рис. 14.9.
Рис. 14.10.
310
Рис. 14.11.
Рис. 14.12.
2. Лучи света, идущие от неба, отражаются от околоземных слоев воздуха, имеющих большую температуру и соответственно меньший показатель преломления. При выполнении условия полного отражения виден мираж —кажущаяся «водная поверхность», отражающая небо.
При смещении наблюдателя на расстояние AS вся картина смещается так, что расстояние до «воды» остается одинаковым. Это видно из рисунка 14.11. Граница «водной поверхности» представляет собой окружность с центром в точке нахождения наблюдателя.
3. Рассмотрим ход луча, который кажется нам исходящим от границы водной поверхности (рис. 14.12). Обозначим показатель преломления воздуха у поверхности Земли п, в точке наблюдения — щ. Как было показано в п.1:
nsin J3 = Пу sinaK.
Так как sin /? = sin 90°= 1, то щ sinaK = п, где ак — критический угол, при котором наблюдатель начинает видеть «водную» поверхность.
311
Из формулы
sin а =
L
Jb2+h2
можно рассчитать показатель преломления воздуха п:
п =
L
>Il2 + h2
Так как по условию задачи (п - 1) = hp,
(1)
т РаМ
— =	, то
V RT
Р
п0 - 1 = h
рам ВТ0 ’
РАМ RT
«.j - 1 = h
РАМ RTX ’
п - 1 = k
где То = 15 °C = 288 К, Tj = 30 °C = 303 К, а Г — искомая температура воздуха у поверхности Земли.
Из полученных выражений, считая атмосферное давление постоянным, находим:
71
п = 1+у-(п°-1)’
71
П1 =1 + ^г(п0~1)-
(2)
(3)
Подставляя в (3) числовые значения, находим: = 1,0002623. Зная
Пр с помощью формулы (1) рассчитываем п:
п =	п, = 1,0002418.
l/lf+h2
Из выражения (2) получаем формулу для расчета искомой температуры Т:
Т = Т0 П9~— = 329 К = 56 °C.
JI -1
Можно оценить поправку, вносимую изменением давления воздуха с высотой:
< P18h = ~RT\-8h’
ЛР Mgh
РАС Kb”
Видно, что изменением давления с высотой можно пренебречь по сравнению с изменением показателя преломления воздуха.
312
Задача 14.5. Перед вертикально расположенным плоским зеркалом находится наполненный водой аквариум шарообразной формы из тонкого стекла. Радиус аквариума R, расстояние между его центром и зеркалом составляет ЗЯ. Наблюдатель, находящийся на большом расстоянии от аквариума и зеркала, смотрит по направлению, проходящему через центр аквариума, перпендикулярно зеркалу. В диаметрально противоположной от наблюдателя точке аквариума находится маленькая рыбка, которая начинает перемещаться вдоль стенки аквариума со скоростью и. С какой относительной скоростью ц„н будут расходиться изображения рыбки, видимые наблюдателем? Показатель преломления воды 4 п = —.
3
Решение. При рассматривании рыбки будут видны два ее изображения. Первое изображение получается в результате прохождения световых лучей от рыбки к наблюдателю через одну преломляющую поверхность «вода — воздух» (преломлением в стекле по условию задачи пренебрегаем). Второе изображение получается в результате прохождения через аквариум световых лучей, отраженных плоским зеркалом. В этом случае аквариум можно считать шаровой линзой, через которую рассматривается изображение рыбки, даваемое плоским зеркалом. Найдем скорость перемещения первого изображения. Пусть рыбка за малый интервал времени Д? переместилась вдоль стенки аквариума из точки А в точку В (рис. 14.13). Найдем перемещение ее изображения. Для этого найдем положение изображения рыбки.
Рис. 14.13.	Рис. 14.14.
Выберем луч 1 света, выходящий из точки В и проходящий через центр О сферического аквариума. Этот луч выйдет из аквариума без преломления. Луч 2 — это такой луч, который после преломления на границе «аквариум — воздух» идет параллельно прямой, проходящей через точки О и А. Когда рыбка находится в точке В, ее изображение находится на пересечении продолжений лучей 1 и 2 в точке Bj. Найдем скорость и1 перемещения изображения рыбки из точки Aj в точку Вр
Aj Bj ц, = — 1 At
313
Перемещение A^j изображения можно выразить через действительное перемещение АВ рыбки и затем через ее действительную скорость и:
АВ	u-i	А, В,
и =-----,	—	=	——-.
At	и	АВ
Для малых углов (р и а из рисунка 14.14 следует, что АВ » R(p, AjBj = DC я Ra, где R — радиус сферического аквариума. Следовательно,
Uj _ Aj-Bj _ а и АВ (р
Как видно из рисунка 14.13, угол у = 180° - 2/7 = 180° - а - <р. Отсюда следует, что ср = 2/7 - а и
I а I £1 = а = и	2/3-а 2 _ f
тт	„	a sin«
Для малых углов а и /3 запишем: — я-----= п, откуда
/3 sin /3
Uj _ п и 2 - п
При п = — получаем — = 2, т.е. = 2tj, вектор О] скорости пе-3	и
ремещения изображения рыбки направлен в ту же сторону, что и вектор скорости и рыбки.
Найдем теперь скорость и2 перемещения второго изображения. Сначала определим фокусное расстояние аквариума как шаровой линзы.
Рассмотрим ход произвольного луча света, проходящего на небольшом расстоянии от центра О сферического аквариума (рис. 14.14). После преломления на двух границах раздела «воздух — вода» (в точке С) и «вода — воздух» (в точке А) луч отклоняется от первоначального направления распространения и пересекает прямую, проходящую через центр О и параллельную первоначальному направлению луча в некоторой точке F. Найдем расстояние BF, которое обозначим a (BP = а).
314
Для малых углов у и 8 можно записать приближенные равенства:
АВ » BF -8 и АВ&ОВ  у.
Так как ОВ = R, из этих равенств следует:
аЗ = Яг, или а = —!—
8
Остается выразить а через величины углов у и 8. Для углов AAOF можно записать равенство:
8 = а - у.
Так как угол у = 2р - а, получим:
3= 2а- 2р.
Подставляя полученные значения для углов у и 8 в выражение для а, находим:
Углы а и р являются соответственно углами падения и преломления световых лучей на границе «воздух — вода». Для малых углов « и „	a sin а
Р запишем: — ®------= п. Отсюда
р sin р
2 - п а = R-.----г-.
2(п -1)
„	4
Подставив значение показателя преломления п = —, получаем:
3
а = Я.
Следовательно, фокус шарового аквариума с водой находится на расстоянии Я от его поверхности или на расстоянии 2Я от его центра.
Рассматривая изображение рыбки в плоском зеркале как действительный объект, найдем его изображение после прохождения лучей через аквариум.
Для нахождения положения изображения точки Bi выберем два луча, один из которых проходит через центр О сферы, второй — через фокус F на прямой ОА (рис. 14.15). Луч 1 пройдет через аквариум без
315
изменения направления, луч 2 после прохождения аквариума пойдет параллельно прямой ОА. Изображение точки Bj получится в точке В3 пересечения этих лучей.
Используя рисунок 14.15, можно установить соотношение между действительным перемещением АВ рыбки в аквариуме и перемещением А3В3 ее изображения перед аквариумом.
При отражении в плоском зеркале выполняется равенство:
AjBj = АВ.
Из подобия треугольников FA9B9 и FA]Bj следует:
AgB2	Bl	ALjFJj	АВ
	 = - = —, Ал/Эо = ——— = ------. Ai-Bj--------------------------------37? 3	3	3
Расчеты, аналогичные проведенным для первого случая, показывают, что
AqTJq _
—-—— = 2, следовательно, а2в2
А3В3 - 2А2В2 - — АВ.
Таким образом, скорость второго изображения рыбки
А3В3 2 (2
U 9 = —2—- = — - = — и
At 3 I At J 3
направлена в сторону, противоположную направлению скорости рыб
ки:
Рис. 14.15.
316
Относительная скорость, с которой будут расходиться два изображения рыбки, равна:
„	2	8
Ц>тн _ и1 ^2» Ц>тн —	' К — С.
О о
Задача 14.6. Постройте изображение предмета, находящегося на расстоянии d от сферического зеркала радиуса R.
Решение. Для построения изображения используем любые из трех лучей, ход которых легко предсказать, исходя из основных свойств сферического зеркала, не проводя строгих геометрических построений:
1.	Луч, падающий на зеркало параллельно главной оптической оси, после отражения проходит через фокус, находящийся на расстоянии
R
— от полюса зеркала.
2.	Луч, падающий на зеркало через главный фокус, вследствие принципа обратимости световых лучей после отражения идет параллельно главной оптической оси.
3.	Луч, проходящий через оптический центр зеркала, падает перпендикулярно поверхности зеркала и после отражения идет по этой же прямой.
В зависимости от соотношения между d и R, а также от вида зеркала (вогнутое или выпуклое) изменяются характер изображения и его размер. Например, построение изображения для вогнутого зеркала при условии d > R представлено на рисунке 14.16. В этом случае изображение действительное, уменьшенное, перевернутое.
Выпуклое зеркало всегда дает изображение мнимое, прямое, уменьшенное (рис. 14.17).
Рис. 14.17.
Рис. 14.16.
317
Рис. 14.18.
Задача 14.7. Какую форму должна иметь поверхность зеркала, способного собирать параллельный пучок световых лучей в одну точку?
Решение. Пусть пучок параллельных лучей падает на зеркальную поверхность, фокусирующую все лучи в одной точке F (рис. 14.18). Рассмотрим два параллельных луча: центральный, идущий вдоль оси Оу, и произвольный, падающий на зеркало в точке А с координатами (х, у).
На основании принципа Ферма запишем:
Так как
по теореме Пифагора
СА + AF = ВО + OF.
ВО = СА + у,
где F — фокусное расстояние зеркала. Тогда
= У + F,
x2+(F-yf = (у+ F)2,
Мы получили уравнение параболы. Следовательно, если сделать зеркало с параболической поверхностью, то все параллельные лучи соберутся в одной точке.
Задача 14.8. В телескопе установлено сферическое зеркало, поперечный диаметр которого равен D- 0,5 м и радиус кривизны 7?= 2 м. В главном фокусе зеркала F помещен приемник излучения в виде круглого диска. Диск расположен перпендикулярно оптической оси зеркала (рис. 14.19). Каким должен быть радиус г приемника, чтобы он мог принимать весь поток излучения, отраженного зеркалом? Во сколько раз уменьшится поток излучения, принимаемый приемником, если его размеры уменьшить в 8 раз?
Указания. При. расчетах для малых значений а, где а « 1, можно произво-
дить замену
дифракцию не учитывать.
318
Решение. Как известно, лучи, параллельные главной оптической оси сферического зеркала и проходящие на небольших расстояниях от нее, после отражения сходятся в главном фокусе зеркала F, находя-
R
щемся на расстоянии — от центра О сферической поверхности. Рас-
смотрим теперь ход луча, отраженного у края сферического зеркала большого диаметра D (рис. 14.20). Угол падения луча на поверхность зеркала а равен углу отражения. Поэтому угол ОАВ в треугольнике, образованном радиусом О А сферы, проведенным в точку падения луча, отраженным лучом АВ и отрезком ВО главной оптической оси, равен а. Углы ВОА и МАО равны, т.е. угол ВОА равен а.
Следовательно, треугольник АОВ равнобедренный, сторона АВ в нем равна стороне ВО. Так как сумма длин двух любых сторон в треуголь-
R нике больше длины его третьей стороны, АВ + ВО > ОА = R, то ВО > —.
2
Это означает, что луч, параллельный главной оптической оси сферического зеркала и проходящий не очень близко от нее, после отражения пересекает главную оптическую ось в точке В, расположенной между фокусом F и зеркалом (заметим, что BF«OF). Фокальную плоскость этот луч пересекает в точке С, удаленной от главного фокуса на некоторое расстояние CF = г.
Таким образом, при отражении параллельного пучка лучей от сферического зеркала конечных размеров он не сходится в фокусе зеркала, а образует в фокальной плоскости пучок радиуса г.
Рис. 14.19.
Рис. 14.20.
319
Из i\BFC записываем:
г = BF tg/3 = BF  tg2a,
где a — максимальный угол
падения крайнего луча, падающего на
D зеркало, причем sm а =----:
2R
BF = ВО- OF ----------
2 cos а 2
R 1 - cos а
2 cos а
,,	R 1 - cos a sin2«
Следовательно, г =--------------------.
2 cos a cos 2«
Выразим значения cos«,
sin2a, cos2a через sin а, учитывая малость угла «:
L . 2	, sm а . „	„ .
cos а = \/1 - sm а » 1-----, sm 2а = 2 sm a cos а,
v	2
о	2	.2	1 П • 2
cos 2а = cos а - sm а = 1 - 2 sm а.
Тогда
R sin3a	R	з D3
г  ------------~ — sin а ®.
2 l-2sin2a	2	16Я2
Подставляя числовые данные, получим: г ~ 1,95 10 3 м ~ 2 мм.
Из выражения D = \16R2r видно, что если радиус приемника уменьшить в 8 раз, то поперечный диаметр D' зеркала, с которого падает свет на приемник, уменьшится в 2 раза, а, следовательно, «рабочая» площадь зеркала уменьшится в 4 раза.
Во столько же раз уменьшится поток излучения Ф, попадающий в зеркало и принимаемый приемником, так как Ф - S.
Задача 14.9. На рисунке 14.21 показана главная оптическая ось линзы OjOg. Линза дает изображение точки А в точке В. Найдите построением хода лучей положение оптического центра линзы и ее главных фокусов.
Решение. При прохождении через линзу один из всех лучей, выходящих из точки А, попадает в точку В по прямой без изменения направления распространения. Это луч, проходящий через оптический центр линзы. Следовательно, оптический центр лежит на главной оптической оси О}О2 и на прямой АВ, поэтому точка О пересечения прямой АВ и главной оптической оси ОуО2 и является оптическим центром линзы О (рис. 14.22).
320
Чтобы найти положение главных фокусов линзы, проведем через точку О прямую, перпендикулярную главной оптической оси и отмечающую положение линзы. Так как предмет и его изображение находятся по разные стороны от линзы, изображение действительное. Следовательно, линза собирающая.
Для нахождения положения главного фокуса собирающей линзы выберем луч, идущий из точки А параллельно главной оптической оси. Этот луч после преломления в линзе попадает в точку В, как и все остальные лучи, выходящие из точки А. Вместе с тем луч, параллельный главной оптической оси, при выходе из линзы проходит через ее главный фокус, лежащий на главной оптической оси. Следовательно, точка пересечения этого луча с главной оптической осью является главным фокусом линзы. Второй главный фокус расположен на главной оптической оси по другую сторону от оптического центра на таком же расстоянии, как и первый.
Задача 14.10. Найдите построением хода лучей изображение точки А, лежащей на главной оптической оси собирающей линзы. Положение главных фокусов линзы указано на рисунке 14.23.
Решение. Для нахождения изображения точки А выберем произвольно направленный луч АВ. Чтобы найти направление его распространения после прохождения линзы, проведем через оптический центр линзы побочную ось, параллельную лучу АВ (рис. 14.24). Лучи, параллельные побочной оси, собираются в одну точку, находящуюся в фокальной плоскости линзы. Отметим на рисунке положение этой плоскости прямой FE.
Луч АВ после преломления в линзе проходит через точку С пересечения побочной оси с фокальной плоскостью. Прямая, проходящая через точки В и С, отмечает направление распространения луча АВ после преломления в линзе. Точка D пересечения луча с главной оптической осью и является изображением точки А.
321
Рис. 14.25.	Рис. 14.26.
Задача 14.11. Экспериментально установлено, что линза из прозрачного материала, ограниченная двумя сферическими поверхностями радиусов Щ и /i2, способна собирать в одну точку узкий пучок света, испускаемый точечным источником. Используя этот опытный факт и принцип Ферма, установите связь фокусного расстояния линзы с коэффициентом преломления п стекла и радиусами кривизны и R2.
Решение. На рисунке 14.25 источник света обозначен Sj, его изображение S2. Согласно принципу Ферма, оптические пути для всех лучей, выходящих из источника Sj и попадающих в его изображение S2, должны быть одинаковыми. Обозначив расстояние от источника Sj до линзы через d, а от изображения до линзы через f, получим:
d +	+ x2~j + f =	+ S2A,	(1)
где n — показатель преломления вещества линзы.
Отрезки SjA и S2A найдем из прямоугольных треугольников S\AO и AOS2 по теореме Пифагора:
322
Si A = ^(d +^i)2 + h2 = (d + xj 1 +------,
У (<* + *i)
>82 A = J(f + X2) + h2 = (f + x2} 11 ч--.
V	(/ + X2)
Из курса математики известно, что для любой малой величины а « 1 можно записать:
г,--- , а
VI	ч- а « 1ч—. 2
Тогда при выполнении условий
Л2	h2
	- «1 и 	- « 1 (d + *i)---------------(/ + *2)
(т.е. для узкого пучка лучей) можно записать:
$1A as d Ч- Xi Ч-------,	1S2 А & f Ч- Х2 ч---	.
2 d ч- х,	2 f ч- х2
Подставив приближенные значения SiA и S2A в выражение (1),
получим:
(п - 1)(х, ч- х2) = — f——— Ч- —-—1. v Л1	7	2 U+X! /ч-х2;
Если линза тонкая, т.е. х-^ « d и х2 « f, то выполняется равен
ство:
(2)
Выразим значения х1 и х2 через радиусы кривизны Я] и П2 сферических поверхностей линзы (рис. 14.26). Точки Ci и С2 — центры сферических поверхностей линзы.
Из рисунка 14.26 видно, что
11*
323
Xj = B2 — 5/-B2 ~
R2
,2
\	*2
h2
2R2
Подставив значения Xj и x2
в выражение (2), получим:
1 1 ---1-.
d f
(3)
Это выражение называют формулой тонкой линзы. Из нее следует, что при условии d —> 00
1 , J 1	1
t Xri r2J
(4)
Это значит, что параллельный пучок лучей собирается тонкой линзой в точку, находящуюся на расстоянии f от линзы. Это расстояние определяется из выражения (4). Его называют фокусным расстоянием F:
- = (п-1)[— + — .
F Vi R2)
(5)
Задача 14.12. В микроскопе объектив с фокусным расстоянием 1 см находится на расстоянии 15 см от окуляра с фокусным расстоянием 3 см. Определите увеличение микроскопа.
Решение. Предмет АВ помещают на расстояние dj, немного большее фокусного расстояния F] от первой линзы — объектива (dj » Ер). Действительное перевернутое увеличенное изображение предмета А'В' рассматривают с помощью второй линзы — окуляра, используемой как лупа (d2 ~ F2). Мнимое увеличенное изображение А!'В" рассматривают глазом (рис. 14.27).
Увеличение микроскопа равно произведению увеличений объектива и окуляра:
к = кхк2 = di d2
Так как dj « d2 « F2, то
fi”l-F2,
где I — расстояние между объективом и окуляром.
324
Принимая расстояние /2 Д° изображения равным расстоянию наилучшего зрения « 25 см), получим формулу для увеличения микроскопа:
„ 25(1 ~F2)
К _ 25(15-3) _ 100
1-3
Рис. 14.27.
Задача 14.13. Имеется две собирающие линзы с фокусными расстояниями 1 м и 5 см. На каком расстоянии нужно установить друг от друга эти линзы для изготовления зрительной трубы Кеплера? Какое угловое увеличение дает труба с этими линзами?
Решение. В трубе Кеплера (рис. 14.28) объектив и окуляр являются собирающими линзами, расположенными на расстоянии, равном сумме фокусных расстояний объектива и окуляра. Изображение предмета в
325
фокальной плоскости объектива находится одновременно и в фокальной плоскости окуляра. Поэтому после окуляра лучи идут параллельным пучком и рассматриваются ненапряженным глазом (без его аккомодации). Увеличение такой трубы равно:
[ а ]
<р f F2 W
где a — размер действительного изображения в фокальной плоскости.
Для получения большого увеличения используют длиннофокусный объектив и короткофокусный окуляр.
а = F-, + F2, а = 1 м + 0,05 м = 1,05 м, К = —-— = 20. 0,05
Задача 14.14. Телескоп состоит из объектива с фокусным расстоянием = 50 см и рассеивающей линзы с фокусным расстоянием F2 = — 5 см, используемой в качестве окуляра. Окуляр находится на расстоянии Z = 45 см от объектива. На каком расстоянии f2 от окуляра нужно установить экран для получения изображения Солнца?
Решение. Объектив строит изображение Солнца в фокальной плоскости, изображение на экране строит окуляр. Так как расстояние от объектива до окуляра меньше фокусного расстояния объектива, в формуле линзы для окуляра нужно поставить знак минус перед слагаемым обратного расстояния до предмета:
+	d-F-1	/ d2F2 №-0*2
d2 f2 F2	d2+F2 F1-l + F2
(0,50 м - 0,45 m)(- 0,05 m) fo =------------------—---= 0,2 M.
0,50 м - 0,45 м - 0,05 м
Задача 14.15. Объектив проекционного аппарата состоит из двух линз с фокусными расстояниями 20 см и 10 см, расстояние между оптическими центрами линз 5 см. Какое увеличение дает объектив при проектировании изображения на экран на расстоянии 5 м?
Решение. Обозначим dj расстояние от первой линзы до предмета, — расстояние до изображения от первой линзы, F± — фокусное расстояние первой линзы, аналогично для второй линзы соответственно d2, f2 и F2, расстояние между линзами а. По формуле линзы имеем:
326
1 1 _ 1 di + fi ~ -fi ’
(1)
1	1 _J
<^2 /2	^2
(2)
T=-J-,	(3)
“1
где Г — линейное увеличение.
По условию задачи
fi = 0,2 м, F2 = 0,1 м, = 5 м, а = 0,05 м.
Для второй линзы «предметом» является изображение, построенное первой линзой. Это изображение находится на расстоянии (д - а) от второй линзы. Так как «предмет» для второй линзы находится по ту же сторону от оптического центра, что и изображение, в формуле (2) нужно перед первым слагаемым сменить знак плюс на минус:
__1^ £_J_	1
<^2	/2 F2 fl ~ а /2 F2
fi~ а =
f2F2
F2 ~ 12
(4)
1	F2~f2
fl f2^2 + я(-₽2 ~ /2)
Из (5) и (1) следует:
1	1	F2-f2
di	-fi /2^2 + °{F2 - /2)
(5)
(6)
Из (3) и (6) получаем:
г = г2
F2 - /2	_ 12_________F2 - /2	.
f2F2 + °{f2 - f2)J	Fr p a + a'F2
f2
5 м	0,1 м - 5 м
0,2 м n0,05 м * 0,1 м ’	0,1 м - 0,05 м + —--
5 м
1
Л
327
Рис. 14.30.
Задача 14.16. Фотоаппаратом, сфокусированным на бесконечность, сделали фотоснимок. Фокусное расстояние объектива 5 см, отношение диаметра D
объектива к фокусному расстоянию F равно — = 0,5. На каком минимальном F
расстоянии d от фотоаппарата предметы на снимке будут достаточно резкими, если считать, что допустимое размытие изображения равно 0,1 мм?
Решение. Если объектив фотоаппарата установлен на бесконечность, то фотопленку размещают в его фокальной плоскости (рис. 14.29).
Точечный источник света S на фотопленке будет изображаться в виде кружка диаметром х.
Из подобия треугольников запишем:
D f х f-F
F
Из условия задачи D = — и формулы линзы следует:
2х 2 • 10“4 м
328
Задача 14.17. Труба Кеилера наведена на Солнце. Фокусное расстояние объектива равно /-) = 50 см, окуляра F2 = 5 см. На расстоянии / = 15 см от окуляра расположен экран. При каком расстоянии L между объективом и окуляром на экране получится четкое изображение Солнца? Чему равен диаметр D этого изображения? Угловой диаметр Солнца а = 30'.
Решение. Объектив трубы Кеплера в фокальной плоскости дает изображение Солнца диаметром х = aFi- Это изображение служит предметом для окуляра (рис. 14.30).
Из формулы линзы для окуляра запишем:
1 1 1	, fP2
---1— = , а —	. d f F2	f-F2
Из рисунка 14.30 видно, что
т	т „ fF2	15 см -5 см
L = Ji + d, L = F +------— = 50 см ч-----------= 57,5 см.
f - F2	10 cm
Диаметр изображения D можно найти из подобия треугольников АО В и MON:
D _ f х L- Fx'
0,5
.	„ .	-----50 см • 15 см
=	-------------. о,88 см.
L- Fy L - Fi	7,5 см
Задача 14.18. Сферическое зеркало собирает узкий параллельный пучок света, проходящий через центр сферической поверхности, в точке на расстоянии 60 см от поверхности зеркала. В зеркало налили прозрачную жидкость, в результате свет оказался сфокусированным на расстоянии 40 см от поверхности зеркала. Каков показатель преломления жидкости?
Решение. Для зеркала без жидкости:
1 _ 2
Ji ” R
Для зеркала и линзы из жидкости:
329
Множитель 2 во втором слагаемом получается вследствие того, что свет проходит через линзу дважды.
Подставляем числовые значения F^ и F2:
0,6 Г К п =----= 1,5.
0,4
Задача 14.19. Для толстой стеклянной линзы с радиусами кривизны Tj и г2 и толщиной d (рис. 14.31), находящейся в воздухе, фокусное расстояние F определяется следующим выражением:
р = __________пг1г2_________
(а-1)[а(г2 - rj + d(n - 1)] ’ где п — показатель преломления (воздух — стекло).
Указание: г( > 0 означает, что центр кривизны О( лежит с правой стороны от точки St; rf < О означает, что центр кривизны Ot лежит с левой стороны от точки Si (i = 1, 2).
Для определенных целей желательно, чтобы фокусное расстояние не зависело от длины волны света 2.
Выполните следующие задания и ответьте на вопросы:
1.	Для скольких различных длин волн можно добиться одного и того же значения фокусного расстояния?
2.	Найдите соотношение между г(, d и показателями преломления, при котором фокусное расстояние линзы не зависит от длины волны света (см. предыдущий вопрос), и обсудите это соотношение. Нарисуйте возможные формы линзы. Укажите положения центров кривизны О] и О2.
3.	Покажите, что для плосковыпуклой линзы определенное фокусное расстояние можно получить только для одной длины волны света.
4.	Укажите еще случаи, когда при определенных параметрах толстой линзы можно реализовать заданное фокусное расстояние только для одной длины волны.
Рис. 14.31.
Решение. 1. Уравнение зависимости фокусного расстояния F линзы от показателя преломления стекла относительно воздуха п квадратное, следовательно, одно и то же значение F возможно только при двух значениях п, а значит, и при двух значениях длины волны А, так как
п = п.(л)
— монотонная функция.
330
Рис. 14.32.
Рис. 14.33.
Рис. 14.34.
d
Рис. 14.35.
2.	Запишем выражение F\n-^ = F(n2), используя условие задачи:
____________П1Г1Г2_________=_____________п2т\г2__________
(«1 - l)^ (г2 - 7i) 4- d(n, - 1)]	(n2 - l)[n2(r2 - rl) + d(n2 - 1)]
Проведя преобразования, получим:
П1П2(П2 - гцХгг - 7i + d) = (n2 - njd.
Если Пу *n2, то r\ -r2 = d (1----------------------— |.	(1)
\	п\П,2)
Так как п} > 1 и п2 > 1, то
О < Г1 - r2 < d,	(2)
где d — толщина линзы (d > О).
Возможны следующие случаи:
а)	Г] >0, г2 > 0, т.е. центры кривизны обеих линз лежат справа от точек S] и iS2, причем г2 < т\ < r2 + dr. При этом OjO2 < S^S2 (рис. 14.32);
331
б)	Г] >0, г2 < 0, при этом 0 < |ri| + |г2| < ^2 (рис- 14.33);
в)	Г1<0, г2 < о, при этом О < |г2| - |ri| < d2, т.е. |ri| < |r2| < d3 + |п.| (рис. 14.34). Ясно, что и в этом случае О}О2 < SlS2.
Примечание. Случай т\ < 0, г2 > 0 не удовлетворяет условию (2), так как при этом г\ - г2 < 0.
3.	Для плосковыпуклой линзы г2 —> оо. Фокусное расстояние такой линзы будет стремиться к значению F}:
При заданном значении F получаем для п линейное уравнение
т.е. определенное фокусное расстояние можно получить только при одном значении п (или Л).
4.	Преобразовав исходное уравнение -Р(п), получим:
F(r2 - Г1 + d)n2 - J(r2 - t\)F + 2dF +	+ Fd = 0.
Введем для удобства рассмотрения следующие обозначения:
А = (г2 - Г1 + d}F;
В = -[(r2 - f\)F + 2dF + Г]Г2];
С = Fd. Переписав наше уравнение с учетом введенных обозначений, получим квадратное уравнение:
Ап2 + Вп + С = 0.
Это квадратное уравнение имеет только одно положительное действительное решение при выполнении одного из следующих условий:
-С а) А = 0, тогда п =---> 1. При этом
Fd	„	Fd
-----Г	>1, п =	> 1. г2 - Г] I + 2Fd + Г;Г2--------Fd + i\r2
332
Отсюда следует, что г\г2 < 0, т.е. г2 < 0, г\ > 0, d = |7i| + |г2|. Этот случай представлен на рисунке 14.35.
6) Дискриминант уравнения равен нулю: В2 - 4АС = 0, тогда
-В ,
п. =--> 1. При этом
2А
[г(г2 - п) +Г!Г2]2 + 4Fdr\r2 = О,
п = F(2ri + r2 - rj + гхг2 > х 2F(d + r2 - rj
2 -С „
в) В = 0, тогда п =------> 1. При этом
А
F(r2 — 71 + 2d) + Г[Г2 = О,
| г2 - Г1 + d
г) Возможен также случай, когда один из двух корней уравнения отрицательный или меньше единицы. Тогда значение п > 1 будет только одно, и заданное фокусное расстояние можно реализовать только для одной длины волны.
Глава 15
КВАНТОВАЯ ФИЗИКА
Задача 15.1. Определите температуру поверхности Солнца, если известно, что на границе земной атмосферы плотность потока солнечного излучения равна и>0 = 1,37 • 103 Вт/м2. Излучение Солнца считайте близким к излучению черного тела.
Решение. Плотность потока теплового излучения, испускаемого единицей поверхности черного тела, определяется законом Стефана — Больцмана:
w = сгТ4,
_	« Вт
где сг = 5,67 10 ------. Отсюда
м2 К4
Для определения значения плотности потока w надо полную мощность W излучения Солнца разделить на площадь его поверхности:
W W w = — =------—,
>Si	4 л Я2
где 1?! — радиус Солнца.
Полную мощность излучения Солнца определим из выражения:
W = w0S,
где S — поверхность сферы, имеющей радиус R2, равный расстоянию
от Солнца до Земли. Так как S = 4 лR2, то
W = w04^R2.
Следовательно, w04kR2 u>0R2 т = 1-------------------------v - v—г-
у сг4лВ2 | aRf
334
Подставляя значения входящих в эту формулу величин, получим:
Т = 4
1,37 103(1,5 1 0п)2 j 5,67- 10“8(б,95-108)2
К = 5800 К.
Задача 15.2. Какой была бы температура поверхности тела человека, если бы он обладал массой, равной массе Солнца? Считать, что плотность тела такого большого человека и удельная мощность выделения энергии такие же, как и у обычного человека.
Решение. Масса Солнца 2 • 1030 кг, удельная мощность выделения энергии в теле человека примерно 1,5 Вт/кг. Следовательно, общая мощность выделения энергии в теле «большого человека» равна:
W = mq, W = 2- Ю30 • 1,5 Вт = 3  Ю30 Вт.
Для определения площади поверхности «большого человека» представим его шарообразным. Тогда его радиус равен:
4	о	13m
m = Vp = — jtR?p, R = 3------;
3	]4тгр
л = з12^м = 8.108 м.
V 4л 1000
Площадь поверхности равна:
5 = 4лВ2,	S^8 1018m2.
По закону Стефана — Больцмана мощность излучения с единицы поверхности равна:
w = ~ = оТ4, Т = S
I Я 1 п^о
Т = 2----7S--------5- К = 5 • 104 К.
V81018 •5,67 10~8
ЗАДАЧА 15.3. До какой температуры нагреются излучением Солнца малые черные шары из вещества с хорошей теплопроводностью, находящиеся на орбитах Венеры, Земли, Марса?
335
Решение. Мощность излучения Солнца равна:
Wc = 4n:RI 2 *crT4,
где R — радиус Солнца, Т — температура его поверхности, ст — постоянная Стефана — Больцмана.
На шар радиуса г на расстоянии I от Солнца попадает излучение мощностью:
Мощность излучения шара:
Wm=<jT^r2.
Так как Win равно , то
4nR2<jT4nr2
4л12
= сгТ4  4лт2,
Подставляя значения I для Венеры, Земли и Марса, получим:
J 6 95•Ю8
—!--------- = 329 К « 56 °C;
2 1,08-1011
I 6 95•108
Тш3 = 5800 I ’	,, = 279 К ~ 6 °C;
V 2 1,5 1011
^шМ
= 5800 I 6’95 108
|2 2,28 10й
= 226 К ® - 46,6 °C.
Задача 15.4. Металлический шар радиусом 10 см облучают светом с длиной волны 2 10 7 м. Определите установившийся заряд шара, если работа выхода электрона с его поверхности равна 7,2 10-19 Дж.
Решение. Заряд на шаре будет установившимся при условии, что самые быстрые электроны, покидающие поверхность шара вследствие фотоэффекта, возвращаются на шар под действием электростатического поля. В этом случае выполняется равенство:
336
титях , еЯ	,	1
----max_ = fe_i, где k = --
2 R	4лг0
= 9-10*^ Кл2
mp2
Используя уравнение Эйнштейна -^n-— = hv~A, получим:
I с	I
/,	\h---АВ
keq	(hv-A\R V A	J
—- = hv - A, q = -i-----— =----------
R	he	he
Подставив значения величин, найдем:
q =
6,6 • 10 34 —10— - 7,2  1019 | • 0,1 ._______2  10~7____J
9 109 1,6 10 19
Кл «1,9 10"11 Кл.
Задача 15.5. Две плоские заряженные металлические пластины расположены параллельно на расстоянии 1 см в вакууме. Напряжение между пластинами 10 В. Отрицательно заряженная пластина освещается узким пучком света, длина волны которого 1,3 10 7 м. Определите радиус окружности на поверхности положительно заряженной пластины, ограничивающей область попадания фотоэлектронов. Красная граница фотоэффекта с поверхности пластины равна 3,3 10'7 м.
Решение. Выберем начало координат (точку О) на поверхности пластины, в которую попадает пучок света. Ось Ох направим перпендикулярно к плоскости пластины, а ось Оу пусть лежит в плоскости пластины.
В этом случае радиус R искомой окружности равен максимальному значению координаты у фотоэлектрона при достижении им положительно заряженной пластины:
= Утах ~ 4,Утах^тах*
Двигаясь между пластинами, фотоэлектрон удаляется от оси Ох на максимальное расстояние в том случае, когда модуль составляющей скорости иу имеет максимальное значение, а модуль составляющей ох — минимальное (так как при этом время t движения электрона между пластинами становится максимальным). Максимальное значение модуля составляющей скорости иу равно максимальному значению начальной скорости фотоэлектрона:
U!/max = 1?тях ’
337
Максимальную скорость найдем из уравнения Эйнштейна:
OTI^max
2
^тах
2 (hv-A) _ m
2 Л —
т
Работу выхода определим по известной красной границе фотоэффекта:
А = hv,
he
^гр
^тах
С С
2 h~-h---
л
пг
2hc (Я
тЯ„,Я
Максимальное время определится так:
движения фотоэлектрона между пластинами
.2
^тах _
2	“ ’
^тах
2d2m Ue
Тогда для искомого радиуса окружности имеем:
phe^A^ - Aj-2d2m fic^A^-/ = ^max^max = д	, TT	~	' J ~
11	~1	1 TT"	" Я„.Я Ue
Подставляя в это выражение значения величин, получим:
R = 2 10“2
6,6 10“34 - З Ю8 2 10 7
„	„	,r m«1,6102m.
3,3 • 10“7 1,3 • 10 7 • 10 1,6 • 10“19
Задача 15.6. Докажите, что свободный электрон не может поглотить квант света.
Решение. Предположим, что электрон, покоящийся в данной системе отсчета, цоглотил световой квант с энергией s = hv. В этом слу-
чае его скорость можно определить, применив закон сохранения энергии:
о	2
, ти л ти hv -------о =-----
2	2
С другой стороны, при поглощении подняться закон сохранения импульса.
светового кванта должен вы-Вычисления, выполненные на
znAppA Ue
О =
338
основе использования этого закона, дают другое значение для скорости электрона:
hv	hv
— = ти-О = ти, и-----.
с	тс
Следовательно, свободный электрон не может поглотить световой квант, так как в этом случае не могут одновременно выполняться закон сохранения импульса и закон сохранения энергии.
Мы рассмотрели нерелятивистский случай. Рассмотрим теперь релятивистский случай (у —> с).
Применим закон сохранения энергии и импульса для фотона и электрона:
fy + £q — (1;2)
Ру = Ро-
Е.,
Учтя, что р =—L-, получим: ' с
Е = ^S^+p2C2 = у £ () + Е2 .	(3)
Итак, из (1) и (3) получаем:
Г~2 Г
£у + &0 ~ у ^0 £у >
= 0,
чего быть не может. Следовательно, свободный электрон не может поглотить световой квант.
Задача 15.7. Неподвижный атом водорода излучил квант света, соответствующий головной линии серии Лаймана (серия Лаймана соответствует переходам на уровень п = 1). Определите относительное изменение частоты фотона вследствие отдачи атома. Какую скорость приобрел атом за счет энергии отдачи?
Решение. Для явления излучения фотона запишем законы сохранения энергии и импульса:
hv0 = Е21 = hv + ~-,	(1)
— = Ми.	(2)
С
Мы предположили, что v « с, т.е. рассмотрели нерелятивистский случай.
339
Из уравнений (1) и (2) следует:
hv
о =---
Мс
h (V° ’ = ^U’
|ZO - V _ Cl
v 2c ’
(3)
„ Av и = 2c--.
Из выражений (1) и (2) следует и другое равенство:
h (И) “ v) =
h2v2
2Мс2 ’
Av hv v 2Мс2 '
(4)
Запишем выражение полной энергии для атома водорода:
то2 е2 Е =-------------.
2	4леог
Из второго закона Ньютона можно записать:
2	2
ти	в
Г	4леог2
(5)
(6)
Из выражений (5) и (6) получим:
е2
£ = -------.	(7)
8ле0г
Из условия квантования орбит mvr = nh и выражения (7) найдем радиус орбиты и полную энергию:
Й2п.2	те4	А
гп = 4лс0---Еп = —------------------— =------
те	(4^0) -2Га2
4
где А =------—--------, А « 2,17 • 10 18 Дж.
(4л£0) -2Й2
На основании постулата Бора запишем:
11	II	( 1А Я
Av0 = Е2 - Ег = -А —---- = А 1 - — I = — А.
Uf п\)	< 47 4
(8)
Проведя преобразования выражений (4) и (8), получим:
Av _ ftv0 _ Б21 _ ЗА v _ 2Мс2 2Мс2 8Мс2 ’
340
Av 3	2,17 10 18	_ 1(. 9
---=-----------------------------« 5,4 • 10
V 8 1840 • 9,1 • 10 31 • 9 • 1016
Подставим полученное значение ---- в выражение (3), найдем ско-
V
рость:
Ду	я	п М	М
и = 2с---= 2  3 • 108  5,4  10 9 — = 3,24 —.
V	с	с
Действительно, v « с, т.е. наше предположение справедливо.
Задача 15.8. При бомбардировке быстрыми электронами металлического антикатода рентгеновской трубки возникает рентгеновское тормозное излучение. Определите коротковолновую границу спектра рентгеновского излучения при скорости электронов 150000 км/с.
Решение. Коротковолновая граница спектра рентгеновского излучения определяется условием равенства кинетической энергии электрона энергии фотона:
Ek = Av0 =---, откуда получаем:
Яо
Яо
he
(1)
Так как скорость электрона о сравнима со скоростью света, то его кинетическую энергию следует рассчитывать по релятивистской формуле:
Ek = (m-m0)c2
zn0c2
- wipe2.
В этом случае выражение (1) можно записать:
341
При условии и = —
6,62 • 10“34
Яо -
"4>с
9,1 10-31 ЗЮ8 0,155
м » 1,56 1011
м.
Рис. 15.1.
Задача 15.9. Рентгеновский фотон с частотой 7,5 1018Гц испытывает рассеяние на 90° на свободном электроне. Определите частоту фотона после столкновения, импульс и энергию электрона отдачи.
Решение. Длина волны фотона увеличится на ЛА:
ЛА = -—(1 - cos	= 0,24  1011 м.
тс  'тс
Частота фотона уменьшится и станет равной vf.
ЛА = —
V1
Vj =——— = 4,7 1018 Гц. с + vAv
Применив закон сохранения импульса, найдем импульс (р =
электрона отдачи:
hv,
= —- + ти.
Из рисунка 15.1 следует:
Р
2
h v
с с
с
V
р = -~\jv2 + v2 = 2 1 0 23 кг м/с,
Ek =	= 0,22  1015 Дж.
2т
342
Задача 15.10. При прямом комптон-эффекте фотон отдает часть своей энергии покоящемуся электрону. При обратном комптон-эффекте фотон получает часть энергии от движущегося электрона. Оцените энергию фотона, испускаемого в результате обратного комптон-эффекта при лобовом столкновении «оптического фотона» (Л ~ 0,63 мкм) с электроном, обладающим кинетической энергией 500 МэВ. Фотон движется вдоль траектории электрона.
Решение. Запишем законы сохранения импульса и энергии:
hv + Е = hv-, + E-i
Учтем, что Из (1) и (3) следует:	Е2 = р2е2 + m-QC4 ,	(3) Ек=Е-т0с2.	(4)
1 т2 4 У Е2 Так как ttIqC2 = 0,51 МэВ р то?4 2Е Из (6) и (2) следует: „2„4	^4 -hv = E1l--^-+hv1.	(5) « Ек0 = 500 МэВ, то 2 4 hv = Ег -^- + hvx.	(6) ~2 4	т
2hv + —^— = —— =>	= Е---——
2Е 2Е,	, ±Ehv
Из (7) и (2) при условии hv « Е следует: .	,	4Е2	t 4Е2 hv1 » hv		г- ® hv	= 2-4|, 4ЕЙУ ]	т^с4 тос i + к тмос 7 hvi ® 1,3 • 10-12 Дж « 8 МэВ.	he 4Ef т^с4
343
Задача 15.11. Фотон с длиной волны At рассеялся на движущемся свободном электроне. В результате электрон остановился, а фотон с длиной волны Ад отклонился от направления движения первоначального фотона на угол в = 60°. Рассеянный фотон испытал новое рассеяние на другом неподвижном свободном электроне. В результате последнего рассеяния фотон с длиной волны А{ = 1,25 1О-10 м отклонился от направления движения фотона с длиной волны Ад опять на угол 9= 60°.
Определите длину волны де Бройля электрона, взаимодействовавшего с исходным фотоном. Известны следующие величины: постоянная Планка h = 6,6 • 10 ’34 Дж с, масса покоя электрона тд = 9,1  10 31 кг, скорость света с = 3,0 108 м/с.
Решение. Длина волны де Бройля для электрона, взаимодействующего с исходным фотоном, равна:
Л
Ре ’
где ре — импульс электрона — связан с его кинетической энергией
Eh следующим образом:
+ 2ш-оС2
Ре = --:
Эта формула получается из выражений, следующих из специальной
теории относительности:
Eh = тс2 - т^с2;
2 2	2 4	2 4
р с‘ - т с - т^с.
Кинетическую энергию Ек можно найти из закона сохранения энергии:
о he 2 he
тос -I------ тс -I---, откуда
Л о	Л/
2	2 he he
Ек = тс - т$с =---------.
Ао /Ц
Итак, для определения искомой длины волны де Бройля Ле надо найти длину волны фотона Ло.
344
Рассчитаем изменение длины волны фотона при рассеянии на неподвижном электроне, применив законы сохранения энергии и импульса:
о he 2 he тос +— = тс -I---------,
Ло	P-f
„2
Ре2 ~
h£
- 2------cos#.
Проведя несложные математические преобразования, получим:
Xf ~ 'Ц = —(1 - cos#).	(1)
тос '
Величина ----- называется комптоновской длиной волны. Для
тос
электрона она равна 2,4- 1СГ12 м. Следовательно,
Ло = Л, - -^-(1 - cos 60°) = 1,24 • 10 10 м.
"гос
Записав аналогичные уравнения для первого рассеяния (на движущемся свободном электроне), получим:
he
Ло
he _ р ~ - -^1»
Л,-
/	\2	/ х2
22	Л о \ I ЛС I ( he I
Peic =+ 2rnc ) = -—	+ —
V	'	\М)
,2 2 2^-
Л0Я(-
cos #,
\2 о
Л] Л
— -2--------cos#, откуда
Ao -	= ——-(1 - cos #).
me '	’
(2)
Сравнивая выражения (1) и (2), находим, что Л(- = Лу, рл = ре2 •
Равенства = Лу и ре1 = ре2 можно было бы получить сразу, заметив, что оба рассеяния фотонов на электронах — одинаковые процессы, обращенные во времени (рис. 15.2).
345
Z X 2
9 I h | Pel = Г
Так как кинетическая энергия электрона
he
Ek = — Ло
— = 1,6-Ю17 Дж » 100 эВ
Л,-
много меньше его энергии
покоя
то формула
ГПоС2
8,1 • 10 14 Дж « 0,5 МэВ,
упрощается: ре = yl2m0Ek,
Ре
искомая длина волны
де Бройля для
и
электрона равна:
2	___________
/t-g —	—	<---------
Ре
h И 1,24 10 10 м.
Задачу можно было решить следующим простым приближенным
способом. Выяснив, что Д1 «Л,-
это следует из того, что
ЛЛ » 10’12 м, Лг =10 10 м — получаем, что импульсы фотонов Pi и />0 приблизительно равны между собой, а так как угол между ними равен 60°, то из рисунка 15.3 видно, что импульс электрона ре = Др равен по
модулю pi = —. Отсюда следует, что длина волны де Бройля электро-
П П	>л
на равна Ле = — = — = Л; » 1,25 • 10 и м. Ре Pi
Рис. 15.2.
Рис. 15.3.
346
Задача 15.12. С неподвижным атомом водорода, находящимся в основном энергетическом состоянии, сталкивается такой же атом водорода, движущийся со скоростью и. Пользуясь моделью Бора и зная, что энергия ионизации атома водорода составляет £и, а масса атома равна т, определить предельную скорость и0, ниже которой столкновения атомов являются упругими.
После достижения скорости t>0 столкновения между атомами могут стать неупругими, что вызывает излучение. Определите процентное отношение разности частот излучений, наблюдаемых в направлении, совпадающем с направлением начальной скорости налетающего атома, и в противоположном направлении, к среднему арифметическому этих частот.
Известно, что Еи = 13,6 эВ = 2,18 • 10 18 Дж; т = 1,67 • 10 27 кг.
Решение. Согласно модели атома Бора излучение (или поглощение) кванта электромагнитной энергии возможно при переходе из одного стационарного состояния в другое:
Ek - Еп = hvkn = hR
где R — постоянная Ридберга, h — постоянная Планка. Энергия ионизации атома водорода равна энергии перехода из основного состояния п = 1 в состояние k = со:
Е„ = о) = hR.	(1)
Так как по условию атомы водорода находятся в основном состоянии, то минимальная энергия возбуждения Ев равна:
(	1>	3
Ев . = Е2 - Е, = hR 1 - - = - hR.
Bnun z 1 V 4/	4
Учитывая выражение (1), получим:
Е . = —Е.	(2)
вт.ш 4И
В системе отсчета, связанной с центром масс атомов, оба атома во-и дорода имеют скорости, равные —,
2
Применим закон сохранения энергии
/ \2	2
2— — = Ек + Е, или = Ек+Ев,	(3)
2 Ы	4	*
где Ек — кинетическая энергия атомов после соударения (Ек > О), Ев — энергия возбуждения атома водорода.
1_______1_
.2 fc2
347
Соударение будет упругим, если
^<ЕВ . = ~Е . 4 Brmn 4 и
Следовательно, из равенства
предельная скорость и0, ниже которой столкновения атомов являются упругими, будет
‘'.-Ж V тп
Подставив числовые значения, получим с>0 = 6,26  104 м/с.
Заметим, что мы рассмотрели нерелятивистский случай (v0 « с).
Пусть и0 — скорость налетающего атома. Тогда после неупругого столкновения система будет двигаться со скоростью и, модуль которой можно определить из закона сохранения импульса:
тип = 2тпм; и =
2
Частоты излучения и г2, наблюдаемые в направлении движения и в противоположном направлении, согласно эффекту Доплера, можно определить как
(л
И1 « V0 1+- ,
\ с}
Il и
v2 ~ v0 1-------
\ С,
где v0 — частота излучения неподвижного атома, с — скорость света.
Отсюда
vcp V! + V2
Ду = 2 n ~ v2
2u _ u0 c c
Подставляя числовые данные, получим:
— = 2•104 ^ор
----100% = 0,02% . ^ср
348
Задача 15.13. В экспериментах с электронами и другими частицами было установлено, что любая частица массой т при движении со скоростью и обладает волновыми свойствами. Длина волны Л частицы (волны де Бройля) равна:
ти
где h = 6,63  10 34 Дж с — постоянная Планка.
Исходя из этого факта, установите связь неопределенности Дх координаты частицы с неопределенностью Др ее импульса.
Решение. Рассмотрим явление дифракции моноэнергетического параллельного пучка частиц на щели шириной d (рис. 15.4). На экране, находящемся на расстоянии L, в результате явления дифракции частиц образуется размытая полоса с максимумом против центра отверстия (рис. 15.4). Можно приблизительно принять, что все частицы после прохождения отверстия попадут на экран в области между центральным максимумом и первыми минимумами по обе стороны от него. Положение первого минимума на экране определяется обычным условием дифракционного минимума от щели:
d sin <р = Л.
Частица с импульсом р обладает длиной волны:
поэтому условие первого минимума можно представить в виде:
, . Л
d sin <р = —, или Р
dp sin <р = h.
(1)
349
Отклонение частицы в результате дифракции от первоначального направления движения свидетельствует об изменении ее импульса. По углу отклонения <р можно определить изменение импульса частицы
(рис. 15.5):
sinp = —(2) Р
Подставляя выражение (2) в условие первого минимума (1), получаем:
d •	= Л.	(3)
Таким образом, если известно, что частица с первоначальным точно известным значением импульса р прошла через щель шириной d и тем самым положение частицы в пространстве, ее координата х были определены с точностью до Дх = d, то сведения об импульсе частицы становятся менее определенными. Неопределенность импульса Држ частицы определяется полученным соотношением:
ДхДрж = h,	(4)
где h — постоянная Планка. Смысл полученного соотношения, называемого соотношением неопределенностей, заключается в следующем. При любой попытке все более точного определения положения частицы в пространстве (ее координаты) обязательно будут все менее определенными сведения об импульсе частицы. Если же каким-либо способом более точно определять значение импульса частицы, то сведения о координатах будут все менее точными. Более точное выражение для соотношения неопределенностей
Ах/\рх > fi,
где Й = 1,05 • 10“34 Дж • с.
Задача 15.14. Предположим, что нам удалось измерить радиус пятой круговой орбиты электрона в атоме водорода с точностью -10%:
г6 = 13,2 10-10м ± 1Ю10м.
С какой точностью нам стала известна при этом скорость электрона?
Решение. Возможности одновременного определения координаты и скорости любого материального объекта ограничиваются соотношением неопределенностей:
ЛрхЛх > ft,	(1)
350
где Држ — неопределенность значения проекции импульса на ось х, l\x — неопределенность значения координаты х, Й = 1,05- 10-34 Дж с — постоянная Планка.
По известным значениям массы электрона тп = 9,110 31 кг и неопределенности координаты Дх = Ю10м найдем неопределенность значения проекции скорости Дцж из (1), если ось Ох направлена по радиусу:
й
Ди„ >-----,
Дхт-
1,05 10~34 м ~	6 м
10 10 • 9,1 • 10 31 с с
Для определения относительной погрешности определения скорости найдем значение скорости кругового движения электрона по пятой воровской орбите:
пй	5 1,05-10 34 м , м
	’	^5 -	if.------77Г----4 10 —. тгп----------------------------------9,1 10“31-13,2 Ю10 с	с
Мы получили, что неопределенность Дцж значения скорости электрона превосходит значение их скорости в 2,5 раза:
^ = ^- = 2,5.
4-ю5
Другими словами, неопределенность Дцж значения скорости электрона превосходит значение на 250%!
ОГЛАВЛЕНИЕ
Введение.........................................     3
Глава 1.	Кинематика ................................. 6
Глава 2.	Динамика .................................. 28
Глава 3.	Статика ................................    52
Глава 4. Закон всемирного тяготения ................ 73
Глава 5. Законы сохранения в механике .............. 94
Глава 6. Механические колебания ................... 117
Глава 7. Молекулярная физика ...................... 139
Глава 8. Термодинамика ............................ 163
Глава 9. Электрическое поле ....................... 186
Глава 10. Магнитное поле .......................... 206
Глава 11. Постоянный ток .......................... 226
Глава 12. Переменный ток .......................... 245
Глава 13. Электромагнитные волны .................. 273
Глава 14. Геометрическая оптика ................... 303
Глава 15. Квантовая физика ....................     334