Author: Паншина А.В. Розенблат Г.М. Козлова З.П.
Tags: механика теоретическая механика
ISBN: 978-5-397-00350-6
Year: 2009
Text
3. П. Козлова
А. В. Паншина
Г. М. Розенблат
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
В РЕШЕНИЯХ ЗАДАЧ
ИЗ СБОРНИКА
И. В. МЕЩЕРСКОГО
Динамика
материальной системы
Допущено Министерством образования и науки
Российской Федерации
в качестве учебного пособия
по теоретической механике
для студентов высших учебных заведений
Под редакцией
кандидата физико-математических наук
Г. М. Розенблата
Издание второе
LCRSS
МОСКВА
ББК 22.21 22.1я73
Козлова Зоя Павловна,
Паншина Алла Викторовна,
Розенблат Григорий Маркович
Теоретическая механика в решениях задач из сборника И. В. Мещер-
ского: Динамика материальной системы: Учебное пособие / Под ред.
Г. М. Розенблата. Изд. 2-е. — М.: Книжный дом «ЛИБРОКОМ», 2009. —
432 с.
Учебное пособие содержит решения всех задач из главы X «Динамика мате-
риальной системы» книги И. В. Мещерского «Задачи по теоретической механи-
ке». Решения задач сопровождаются замечаниями и комментариями, касающими-
ся постановок задач и ответов к ним.
Предназначено для студентов вузов, изучающих теоретическую механику,
преподавателей механики, а также для лиц, интересующихся теоретической меха-
никой.
Рецензенты:
заведующий кафедрой теоретической механики Московского
физико-технического института (МФТИ), академик РАН В. Ф. Журавлев;
заведующий кафедрой теоретической механики и мехатроники
Московского государственного университета им. М. В. Ломоносова,
заместитель директора Математического института им. В. А. Стеклова,
член-корреспондент РАН Д. В. Трещёв
Издательство «Книжный дом “ЛИБРОКОМ”».
117312, Москва, пр-т Шестидесятилетия Октября, 9.
Формат 60x90/16. Псч. л. 27. Зак. № 1984.
Отпечатано в ООО «ЛЕИАНД».
117312, Москва, пр-т Шестидесятилетия Октября 11А, стр. 11.
ISBN 978-5-397-00350-6
© Книжный дом «ЛИБРОКОМ», 2008
НАУЧНАЯ И УЧЕБНАЯ ЛИТЕРАТУРА
E-mail URSS@URSS.nj
Каталог изданий в Интернете:
http://URSS.ru
Тел /факс 7 (499) 135-42-16
5693 ID 72414
URSS Тел./факс 7(499)135-42-46
Hill
9 785397 003506
Все права защищены. Никакая часть настоящей книги не может быть воспроизведена или
передана в какой бы то ни было форме и какими бы то ни было средствами, будь то элек-
тронные или механические, включая фотокопирование и запись на магнитный носитель,
а также размещение в Интернете, если на то нет письменного разрешения владельца.
Оглавление
Введение ...................................................... 5
1. Геометрия масс: центр масс материальной системы,
моменты инерции твердых тел (§34, [10]) ...................... 6
2. Теорема о движении центра масс материальной
системы (§35, [10]).......................................... 37
3. Теорема об изменении главного вектора количеств движения
материальной системы. Приложение к сплошным
средам (§ 36, [10]).......................................... 68
4. Теорема об изменении главного момента количеств движения
материальной системы. Дифференциальное уравнение вращения
твердого тела вокруг неподвижной оси (§37, [10])............. 82
5. Теорема об изменении кинетической энергии материальной
системы (§38, [10])..........................................151
6. Плоскопараллельное (плоское) движение твердого
тела (§39, [10]).............................................224
7. Приближенная теория гироскопов (§40, [10])...............257
8. Метод кинетостатики (§41, [10])..........................273
9. Давление вращающегося твердого тела
на ось вращения (§42, [10])................................305
10. Смешанные задачи (§43, [10])..............................343
11. Удар (§44, [10])..........................................368
12. Динамика точки и системы переменной массы
(переменного состава) (§45, [10])..........................396
Литература....................................................425
Приведена соответствующая нумерация параграфов из задачника
И. В. Мещерского [10].
Полезно решать
дифференциальные уравнения.
И. Ньютон
При изучении движения полезно
исследовать силы, его вызывающие.
Введение
Настоящее пособие является продолжением работы авторов [6] и со-
держит решения всех задач из главы X «Динамика материальной системы»
сборника [10]. Нумерация задач соответствует изданиям сборника [10]
1986-2006 гг. Эта нумерация двойная: первое число означает номер пара-
графа, второе — номер задачи в этом параграфе. В скобках указывается
номер, который имела задача в 32-34 изданиях сборника [10].
Отметим, что некоторые условия задач и ответы к ним не являются
достаточно полными. В этих случаях авторы настоящего пособия позво-
лили себе сделать соответствующие замечания и дополнения. Кроме того,
в части задач ответы, полученные авторами, не совпадают (или не совсем
совпадают) с ответами сборника [10]. Это связано либо с точностью вычис-
лений, либо с использованием других (более современных) обозначений,
либо с иными обстоятельствами, ответственность за которые лежит на
авторах настоящего пособия. В основном это относится к задачам с одно-
сторонними связями, где возникают неожиданные эффекты. Изложенные
соображения и результаты были доложены авторами в декабре 2006 года
на заседании Научно-методического совета по теоретической механике
при Министерстве образования и науки РФ (председатель: академик МАН
ВШ, профессор Ю. Г. Мартыненко). Тем не менее, ответственность за эти
замечания и дополнения целиком лежит на авторах настоящего пособия.
Авторы надеются, что предлагаемое пособие окажется полезным для
студентов вузов, изучающих механику, так как суть этой науки (и ее при-
влекательность) можно ощутить только на решениях конкретных задач
или примеров. Кроме того, пособие может оказаться также полезным
и для преподавателей механики, которым, возможно, оно сократит время
подготовки к занятиям.
Пользуясь случаем, авторы хотели бы выразить благодарность уважае-
мым рецензентам: академику РАН В. Ф. Журавлеву и члену-корреспонден-
ту РАН Д. В.Трещёву за полезные обсуждения и критические замечания,
которые способствовали улучшению настоящего пособия. Кроме того,
авторы выражают свою признательность Доминго Марину Рикою и всем
сотрудникам издательства URSS, принявшим участие в реализации дан-
ного проекта.
3. П. Козлова, А. В. Паншина, Г. М. Розенблат
г. Москва, май 2007 г.
1. Геометрия масс: центр масс материальной системы,
моменты инерции твердых тел (§ 34, [10])
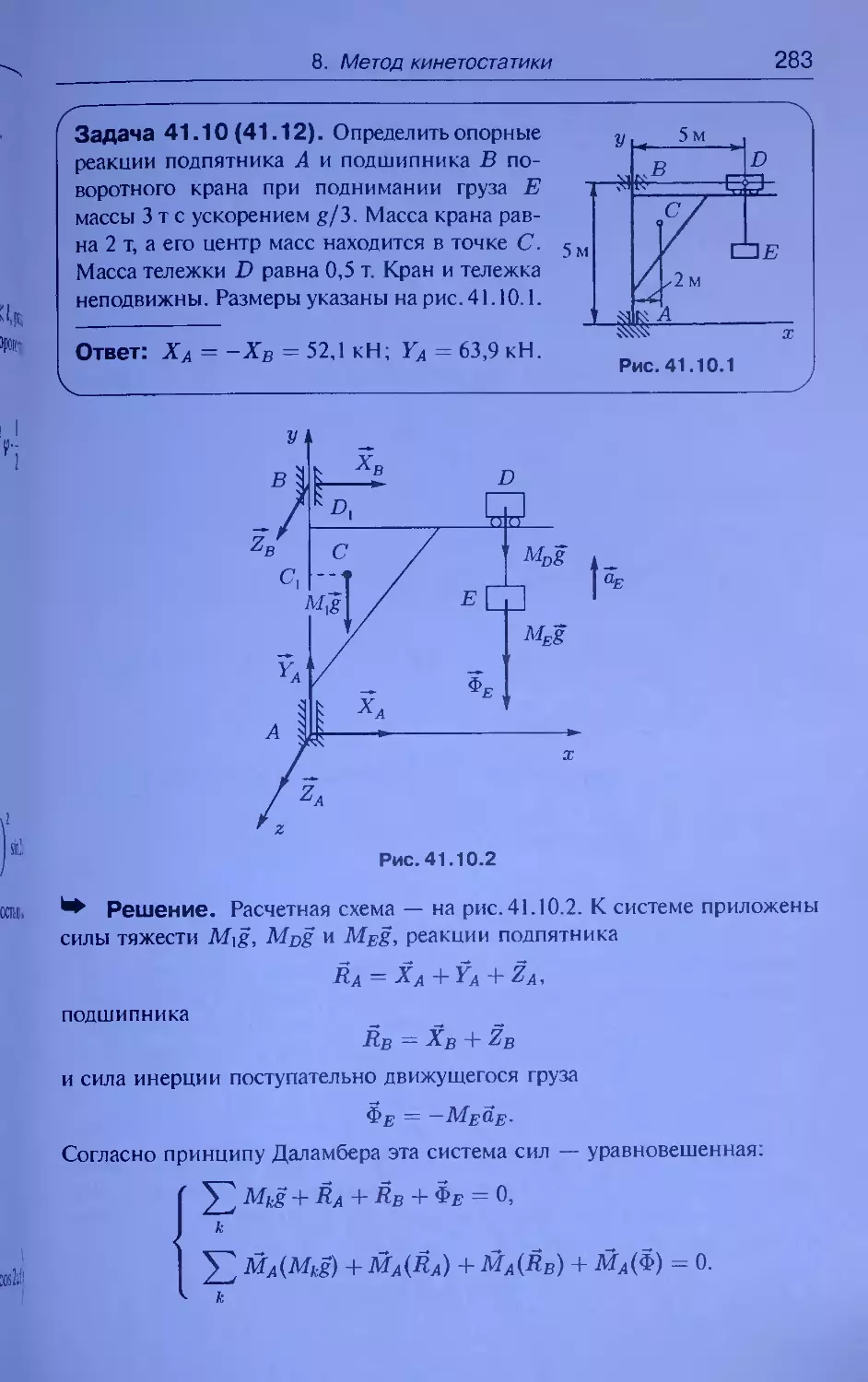
Задача 34.1 (34.1). Коленчатый вал трехцилиндрового двигателя,
изображенный на рисунке, состоит из трех колен, расположенных под
углом 120 друг к другу. Определить положение центра масс колен-
чатого вала, считая, что массы колен сосредоточены в точках А, В
и D, причем тпа = тпв = тп — т, и пренебрегая массами остальных
частей вала. Размеры указаны на рис. 34.1.1.
Ответ: Центр масс совпадает с начадим координат О.
Решение. Расчетная
точек А, В и D;
схема — на рис. 34.1.2. Запишем координаты
ха = d sin 30°, уА = dcos 30°, zA = -(a + b);
xB=dcos60°, ув = -d cos 30е, zB — 0;
xp — -d, yD = 0, zd = a + b.
Формулы координат центра масс С коленчатого вала
1 " ] п । п
ХС = —ГИ ткхк, УС = ^^ ткУк, mkZ^
fc=l fc=l
A = 1
в данном случае примут вид:
хс —---------;--(тА d sin 30° + тпв d cos 60° - mD d) =
mA + mB +m.D ’
1. Геометрия масс
7
1
Зтп
md - + md — md
2 2
Ус =-------------------(тпд d cos 30° - тв d cos 30° + mD 0) =
tn A + mB + mD
zc ---------------(~mA(a + b) + mB • 0 + mD(a + fc)) =
4- mB + mo
= -— (-m(a + b) + m(a + b)) = 0.
Значит, центр масс С совпадает с началом координат.
Задача 34.2(34.2). Найти уравнения дви-
жения центра масс шарнирного параллело-
грамма ОАВО\, а также уравнение траекто-
рии его центра масс при вращении кривоши-
па О А с постоянной угловой скоростью О).
Звенья параллелограмма — однородные стерж-
ни, причем ОА = О\В = АВ/2 = а (рис. 34.2.1).
Рис. 34.2.1
3 3
Ответ: хс — a + -acoswt, ус = -asincvf; уравнение траектории
з V з
-а ) — окружность радиуса -а с центром в точке К
4 ) 4
(Хс-О^ + Ус =
с координатами (о, 0).
Решение. Расчетная схема — на рис. 34.2.2. В состав материаль-
ной системы входят три однородных стержня ОА, АВ и О^В. Их центры
8
1. Геометрия масс
Рис. 34.2.2
масс — точки С|, С2 и Су. Причем ОС\ = CtA, АСг = С2В, ВСз — CjOi.
Запишем координаты этих точек в зависимости от угла поворота криво-
шипа ОА ip — iot:
1
Ж1 = -a cosot,
х2 = a cos iot + a,
y\ — -a sin lot;
y2 = asinot;
I
Уз = -a sin lot.
xy = la + ^a cosot,
Формулы координат центра масс материальной системы принимают
вид:
хс =----------(т] • а?1 + т2 • ж2 + тз хз),
гп\ + тп2 + m3
ус=^4+™/"“ »'+“> й+“э »>
Учитывая выписанные выше зависимости координат и т, = тз = т,
гпз = 1т, получим:
2
2
хс ~ -— m-a cos о t + lm(a cos wt + a) + ml la + -a cos lot
4m [2 \ 2
« 3
= - (4 + 3 cos iot) = a + -a cos lot,
1
Ус = т—
4m
1 1 \ 3
m-a sin iot + Ima sin lot + m-a sin lot] = -a sin iot.
1 1/4
Следовательно, уравнения движения центра масс имеют вид:
3
хс = а + -a cos iot,
4
3
Ус = -a sin iot.
4
Исключив из них параметр времени t с помощью тригонометрического
соотношения
sin2 iot + cos2 iot = 1,
1. Геометрия масс
9
получим уравнение траектории центра масс:
(хс — о)2 + Ус —
Это окружность радиуса -а с центром в точке К = (а, 0).
Задача 34.3(34.3). К ползуну I массы М\ посредством тонкой не-
весомой нити прикреплен груз II массы Mi- При колебаниях груза
по закону <р = 9?0 sin wt ползун скользит по неподвижной горизон-
тальной гладкой поверхности. Найти уравнение движения ползуна
X] = f(t) считая, что в начальный момент (t = 0) ползун находился
в начале отсчета О оси х. Длина нити равна I.
Mi
Ответ: xt =-----— I sin (w0 sin ivt).
M\+Mi
Решение. Расчетная схема — на рис. 34.3.1.
Ползун скользит по гладкой поверхности, поэто-
му на механическую систему «ползун 4- стержень
+ груз» не действуют силы вдоль оси х. Следо-
вательно, центр масс С системы не перемещается
вдоль оси х:
xc(t) = МО)-
77777
Рис. 34.3.1
Распишем формулу для координаты Хс в произвольный момент времени:
Хс^ = м -г м ’ х'^ + +1 sin V5)] =
-f- IVi}
= । ЛГ| • Xi(t) + Mi(xi(/) +1 sin (y>0 sin
Согласно условию задачи,
M°) = M 1 A# • 0 + M2 • 0) = 0.
/VI i -f- IVLy
Приравняв выражение для xc(t) нулю, решим полученное уравнение
относительно Х|(£). Откуда
Mil
Х1 (0 = -т, , sin (<Ро sinwf)-
1V11 -f- JV12
10
1. Геометрия масс
Задача 34.4 (34.4). Определить положение центра масс центро-
бежного регулятора, изображенного на рисунке, если масса каждого
из шаров А и В равна Mt масса муфты D равна М2. Шары А и В
считать точечными массами. Массой стержней пренебречь.
_ М\ + М2
Ответ: хс = Ус =
Решение. Расчетная схема — на рис. 34.4.1. За-
пишем координаты точек А, В и D:
Ха = —I sin 9?, Уа = 1 cos <р;
Хв — I sin 9?, ув =1 cos 9?;
Хв — 0, yD — 21 cos 9?
Отсюда
Хс = 1 sin <г> + Mil sin tp + M2 0) = 0,
2.1V1 1 + -М2
1 /
Ус= (M|Zcosy>+M|Z cosy+M2-2Z cosy?) =
21V1\ + IVZ2
= 2Й^Й;''С“’’<2М'+2М2) =
м} +м2
= 2-------1 cos с?.
2М'+М2 *
Задача 34.5(34.5). Определить траекторию центра масс механизма
эллипсографа, состоящего из муфт Л и В массы М{ каждая, криво-
шипа ОС массы М2 и линейки АВ массы 2М2; дано: ОС = АС =
= СВ = Z. Считать, что линейка и кривошип представляют однород-
ные стержни, а муфты — точечные массы.
Ответ: Окружность с центром в точке О и радиусом, равным
4М| + 5Мг I
2М\ 4-ЗМ2 ’ 2‘
Решение. Расчетная схема — на рис. 34.5.1. В состав материальной
системы входят: муфты А и В, кривошип ОС (точка D — его центр масс)
и линейка АВ (точка С — центр масс линейки).
1. Геометрия масс
11
Запишем координаты точек А, В, D и С в произвольном положении
механизма, задаваемом углом 92:
уА = 21 sin 92,
хв = 21 cos 9?, ув = О,
хА = О,
1
хв = -I cos 92,
Обозначим точку, в которой находится центр масс системы через Е.
Распишем формулы для координат Хе и уЕ'-
Уе = sin
хс = I cos <р, ус — I sin 92.
ХЕ = ^7---Г7--ттт- (М}хА + МХХВ + M2XD + 2М2гес) =
2М\ + М2 + 2М2
1
= 2М} + ЗМ2
= 2M,LмЛ,(W|+5M1)COS1,,’
М\ • 21 cos 92 + М2 -I cos 9? + 2M2I cos 9?
Уе = - д эГГ{мГУа + Мхув + М2ув + 1М2ус) -
2-lVL\ + Ла 2 +
1
“ 2М} + ЗМ2
М] • 21 sin 9? + М2 • -I sin 9? + 2M2I sin 92
=------------ -Z(4Mi + 57И2) sin 92.
2Mi + 3M2 2 V ' *
Найдем уравнение траектории центра масс Е, исключив из получен-
ных выражений угол 92:
4Mi + 5М2 I\2
2М\ + ЗМ2 2.)
Это окружность с центром в точке О и радиусом
4М} + 5М2 I
2 . 2
XE + УЕ —
2Mi + ЗМ2 2
12
1. Геометрия масс
Задача 34.6. К вертикальному валу АВ прикреплены два одина-
ковых груза Е и D с помощью двух перпендикулярных оси АВ и
притом взаимно перпендикулярных стержней ОЕ — OD = г. Масса-
ми стержней и вала пренебречь. Грузы считать точечными массами.
Найти положение центра масс С системы, а также центробежные
моменты инерции Jxz, Jyz, Jxy.
Ответ: С\ -г, -г, 0 , Jx~ = J„, — Jxv —Q
Решение. Расчетная схема
— на рис. 34.6.1. Выпишем координаты
точек Е и D:
хЕ = г, Уе- 0, ze = 0;
xD = 0, yD = г, zD = 0.
Обозначим их массы через т.
Z д Распишем формулы координат центра масс С системы: I г хс = —(т г + т • 0) = 2т 2
Or D V / / V Е / У х 0 I Т Ус = — (m-0 + m-r) = 2т 2 zc = 0 + т • 0) = 0. 2т
Вычислим центробежные моменты инер-
Рис. 34.6.1 ции системы:
п
Jiz = >7 • xkzk = m xEzE + m • xDzD - 0.
fc=i
n
Jyz = У V ’ Укгк — m yEzE + m ' yDzD — 0,
fc=l
n
Jxy = х,:Ук = m хеУе + тп xDyD = 0.
fc=i
Задача 34.7 (34.8). Вычислить момент инерции стального вала ра-
диуса 5 см и массы 100 кг относительно его образующей. Вал считать
однородным сплошным цилиндром.
Ответ: 3750 кг-см3.
1. Геометрия масс
13
Решение. Момент инерции вала относительно продольной оси, про-
ходящей через его центр масс, вычисляется по формуле:
mr2
Jcz =
Тогда согласно теореме Штейнера, момент инерции относительно обра-
зующей будет равен
2
ТПГ
J -------1- mr = -mr
2 2
п 3 п 3 т 2\
- =-• 100-5 = 3750 (кг-см2).
2 2 '
Задача 34.8(34.9). Вычислить момент инерции тонкого однород-
ного полудиска массы М и радиуса г относительно оси, проходящей
вдоль диаметра, ограничивающего полудиск.
Ответ: Мт2/4.
Решение. Для тонкого однородного круглого диска массы тп мо-
мент инерции относительно оси х, проходящей через диаметр, равен
Jx = mr2/^. Момент инерции половины диска в силу симметрии в два раза
меньше, но так как М = т/2, то искомый момент инерции Jx = Мт /4.
Задача 34.9(34.10). Вычислить осевые Jx
и Jy моменты инерции изображенной на
рис. 34.9.1 однородной прямоугольной пла-
стинки массы М относительно осей х и у.
4 , 4 2
Ответ: Jx = -Ma , Jy = ~Mb .
Рис. 34.9.1
Решение. Расчетная схема — на рис. 34.9.2. Определим момент инер-
ции пластинки относительно оси х, т. е. Jx. Для этого выделим бесконечно
Рис. 34.9.2
14
1. Геометрия масс
тонкую полоску, параллельную оси х. Длина полоски 26, ширина полос-
ки dy. Полоска находится на расстоянии у от оси х. Площадь полоски
26 • dy. Масса полоски
М М ,
dm = -—— • 2bdy = —- dy.
la • 26 2а
Момент инерции полоски относительно оси х равен
2 М 2
dJx = у dm = —у dy.
2a
Момент инерции всей пластинки
2а
Г м 2 м .
/ dy = ^'
J 2a 2а 3
о
2a _ M(2a)2
3
= 5мо2.
I 3
X
О
Для
полоску,
получим
(М)
нахождения момента инерции Jy выделим бесконечно тонкую
параллельную оси у, и, проделав аналогичные вычисления,
M(26)2 4 2
г = V ' = -Mb2.
y 3 3
Задача 34.10 (34.11). Вычислить моменты инерции изображенно-
го на рисунке однородного прямоугольного параллелепипеда массы М
относительно осей х, у и z.
Мэ, Mil М Т т
Ответ: Jx = —(a2 + 4с2), Jy = — (b2 +4с2), Jz = у (a + b2).
Решение. Расчетная схема — на рис. 34.10.1. Воспользуемся опре-
делением момента инерции при непрерывном распределении масс мате-
риальных точек в твердом
теле:
Здесь
J M , M
dm — — dV = -—— dx dy dz =
V 2a-lb-2c 12
М
— dx dy dz.
Babe
Поэтому
2с a b
J’ = ^f f +
0 -a -b
1. Геометрия масс
15
2c a
0 -a
2c / a
0 4 -a
2c
M Г/1
= -z~r \z- 2by
8abc J \3
о
2c
M [ (2b- 2a3
8abc J \ 3
3
b \
I dy dz =
6 /
a \
I 2bz2 dy\dz —
-в
a
7
+ 2bz у
-a
+ 2b 2az2
a
—а
о
(2b-2a3-2c : 2b-2a-(2c)3
\ 3
M
8abc
= y(a +4c).
Используя симметрию, запишем момент инерции
Л = у-(Ь2+4с2).
Вычислим момент инерции
3
(М)
2c a b
= ГЗГ [ [ Л®2 + dx dy dz =
8abc J J J
0 -a -b
2c a
О -а
2с
— [(
8abc J \
о
2b3 -2a-2с 2b- 2a3 2с
3 + 3
26 3\
• 2a Ч---- 2a I dz =
3 J
М
8abc
-у 2
= у (а + b )
16
1. Гюметрия масс
Рис. 34.11.1
Задача 34.11 (34.12). В тонком однородном
круглом диске радиуса R высверлено концен-
трическое отверстие радиуса г (рис. 34.11.1). Вы-
числить момент инерции этого диска массы М
относительно оси z, проходящей через его центр
масс перпендикулярно плоскости диска.
М , 7 7
Ответ: Jz = —(R2 + г2).
Решение. Расчетная схема — на рис. 34.11.2. Ось Oz перпендику-
лярна плоскости диска. Выделим бесконечно тонкий слой, представляю-
щий собой концентрическую окружность. Все точки этого слоя находятся
на расстоянии х от оси Oz. Толщина слоя dx.
Площадь слоя равна 2тггг • dx. Масса выделен-
ного слоя
М j 2М
,„7---• 2тГГГ dx = —z---~ х dx.
tt(R2 - г2) R2 - г2
Момент инерции этого слоя относительно оси z
равен
Рис. 34.11.2
dm =
dJz = х2 dm =
2М з
—----тх dx.
R2-r2
Момент инерции
диска
z
R
Г 2M
' R2 — r2
2М
(М)
1
2 '
х3 dx = - .
4 А2-г2
^2.^-r4) = ^(R2 + r2).
• X
,4
R
Задача 34.12(34.13). Вычислить момент инер-
ции тонкой однородной пластинки массы М, име-
ющей форму равнобедренного треугольника с вы-
сотой h, относительно оси, проходящей через ее
центр масс С параллельно основанию (рис. 34.12.1).
1 2
Ответ: —Mh.
18
Решение. Расчетная схема — на рис. 34.12.2. AB = AD, точка С —
центр масс треугольника. Из планиметрии известно, что АС = (2/3)Л.
1. Геометрия масс
17
Пусть сторона BD — а. Выделим бесконечно
тонкую полоску, параллельную оси х. Полоска
находится на расстоянии |у| от оси х. Ширина
полоски dy. Используя подобие треугольников
САК и С\АК[ и тот факт, что
2 2
СК = -ED = -
3 3
а
2’
получим, что длина выделенной полоски равна
«Р _ _ Р _у_
2 \3 h) -\3 h
Площадь полоски равна
ds = а
у\
h )
dy.
Масса полоски равна
М /2 у\ 2М /2 \ J
dm = 'y -d.s= —a - - - I dy = \-h-y]dy.
1 \ 3 hl he \ 3 /
-ha '
2
Момент инерции полоски относительно оси х равен
2 2М /2 \ 2 л
dJx = у dm= — { -h-y \ у dy.
he \ 3 /
h2
Момент инерции всей пластинки относительно оси х равен
18
1. Геометрия масс
Задача 34.13. Однородная металлическая пластинка выполнена в
виде равностороннего треугольника (рис. 34.13.1). Масса пластинки
Рис. 34.13.1
равна М, I — длина ее стороны. Вычислить момент
инерции пластинки относительно оси z, проходящей
через ее вершину параллельно основанию.
Ответ: Iz — -Ml1.
8
А
В I D
Рис. 34.13.2
Решение. Расчетная схема — на рис. 34.13.2.
Точка С — центр масс треугольника. По теореме
Штейнера
Jz = Jx + М • AC1 = Jx + М
Воспользуемся результатом, полученным в задаче
34.12. Момент инерции
Поэтому
Задача 34.14. Однородная равносторонняя треугольная пластина
имеет массу М и длину стороны I (рис. 34.14.1). Вычислить момент
инерции пластины относительно оси z, проходящей
через вершину пластины перпендикулярно ее плоско-
сти.
Рис. 34.14.1
Ответ: Iz = —Ml2.
12
Рис. 34.14.2
*" Решение. Расчетная схема — на рис. 34.14.2. Ось
Az перендикулярна плоскости пластины. Выделим бес-
конечно тонкую полоску, параллельную основанию
треугольника. Полоска находится на расстоянии х от
оси Az. Ширина полоски равна dx. Длина полоски Ъ
находится из подобия треугольников:
b х
I
1. Геометрия масс
19
Поэтому длина полоски равна
2 2
Ъ = —=х. Площадь полоски as = —рх dx.
Уз УЗ
Масса полоски
М
dm = у • ds =
2 8М
• ——х dx = -~ггх dx.
\/3 3 I2
2 2
Введем вспомогательную ось C'z , параллельную Az и проходящую
через центр масс выделенной тонкой полоски. Момент инерции полоски
относительно этой оси равен
/ 2 \2
<'т1;75а9 8м,_
dJc'?' ~------------—-----гХ ах.
Сг 12 27 I2
По теореме Штейнера момент инерции полоски относительно оси Az
равен
, 8 М , 8 7W 2 8O7W з ,
dJz = dJC'z' + dm {AC) = — -yx dx + -—^x dx • x = ——x dx.
Z / t JI Z / t
Следовательно, момент инерции всей пластины относительно оси Az
вычисляется по формуле:
1УЗ/2
Г 80 М Г з 80 М
Jz = J dJz==27~l2 J Х dX=2712
(М) о
1 4
4
0
Задача 34.15(34.16). Вычислить момен-
ты инерции относительно трех взаимно пер-
пендикулярных осей х, у и z тонкой одно-
родной эллиптической пластинки массы М,
ограниченной контуром
/J3/2
5 2
= —Ml2
12
х2 у2
М 2 М 2 М , 1 2'
Ответ: Jx = —Ь, Jv = —а , Jz = —{а +Ь ).
4 у 4 4
Решение. Расчетная схема — на рис. 34.15.2. Вычислим момент инер-
ции пластины относительно оси х, т. е. Jx. Для этого выделим беско-
нечно тонкую полоску, параллельную оси х. Полоска находится на рас-
стоянии у от оси х. Ширина полоски равна dy. Длина полоски равна
20
1. Геометрия масс
а* 1 2, так как концы полоски — это точки, принадлежащие
ж2 у2 / у2
эллипсу — Н—- — 1. Пл -щадь полоски ds — 2a\ 1 — —г dy. Масса по-
а2 Ъ2 у о2
лоски равна
М
dm = yds =-------- 2а
7гао
у2 2М ------------7
1 “ dy = dy-
Ь2 тго2
Момент инерции полоски относительно оси х равен
2 27Vf г-.----— т
ddx =у dm = -^b2 -у2 у dy.
Момент инерции всей пластины относительно оси х вычисляется по фор-
Используя симметрию, выпишем момент инерции пластины относи-
тельно оси у.
М 2
а •
Вычислим момент инерции пластины относительно оси z.
1. Геометрия масс
21
где
По определению
х2 dm +
(М)
у2 dm,
Поэтому
так как
dm =---------dx dy.
тг ab
М 2 М J М 2 »2\
Jz = Л + Jy = — ь2 + — а2 = —(а2 + Ь2),
Ч Ч
Jx ~ J у2 dm, Jy = J х2 dm
(М) (М)
(по определению).
Задача 34.16 (34.17). Определить момент инерции однородного
полого шара массы М относительно оси, проходящей через его центр
тяжести. Внешний и внутренний радиусы соответственно равны Янг.
2 R5 - г5
Ответ: -М—------г.
5 R3 - г3
Решение. Искомый момент инерции есть раз-
ность между моментом инерции сплошного шара ра-
диуса R и шара радиуса г (см. рис. 34.16.1). Пусть
р — плотность материала. Тогда
2 2 2 2
J = Jr-Jt = -Mr-R2 - -Мт • г2,
где
Рис. 34.16.1
4 о 4 з
MR = р- -irR , Мт = р - -7гг .
Кроме того,
М
Р = 4 ’ 4 з
— ТГ-Тс---7Гг
3 3
Подставляя эти формулы, получим:
2 [ М
5 Я3 - г3
(Я5 - г5)
= -М
5
R5-r5
R3 - г3
22
1. Геометрия масс
Задача 34.17(34.18). Вычислить момент инерции однородной тон-
кой оболочки, выполненной в виде полусферы радиуса R, относи-
Рис. 34.17.1
тельно оси, проходящей через центр полусферы
перпендикулярно к ограничивающей ее плос-
кости (рис. 34.17.1). Масса М оболочки равно-
мерно распределена по поверхности полусферы.
2 ?
Ответ: -MR .
3
Решение. Искомый момент инерции (в силу симметрии) равен
половине соответствующего момента инерции полной сферической обо-
лочки массы 2М. Чтобы вычислить эту величину, устремим г —> R в ответе
предыдущей задачи 34.16. Имеем
1 1/2 R5 - г5
«^полусферы — ~ lim J = — lim I — (27W)—- -
2 t-»r 2 г >r \ 5 R3 - r3
= -А2М) lim I 5 г-»я ( „2 , r\R2 - r2)\ 1 Л -Ь . Q I R3 - r3 J
= 7<2М) lim 1 5 r-fR (r2 (r + r^3 R2 + Rr + r2
1 / 2 \ 2
= -(2M)\R2 + -R2} = -MR2.
Задача 34.18(34.19). Вычислить радиус
инерции сплошного однородного цилиндра
относительно оси z, перпендикулярной оси
цилиндра и отстоящей от его центра масс С
на расстоянии 10 см, если радиус цилиндра
равен 4 см, а высота 40 см.
Ответ: 15,4 см.
Решение. Пусть М — масса цилиндра. Тогда момент инерции от-
носительно указанной оси, проходящей через центр масс,
Jc = ~^M{3>R2 + Л2),
1. Геометрия масс
23
где R = 4 см — радиус, h = 40 см — высота. Согласно теореме Штейнера
для искомого радиуса инеонии имеем:
р2 = ^{Jc + М-^ = ^3R2 + + /2’
где I = 10 см — расстояние между осями. Отсюда р = 15,405 см.
Задача 34.19(34.21). Маятник состоит из тонкого
однородного стержня АВ массы М\, к концу которо-
го прикреплен однородный диск С массы М2. Длина
стержня равна 4г, где г — радиус диска. Вычислить
момент инерции маятника относительно его оси при-
веса О, перпендикулярной плоскости маятника и от-
стоящей на расстоянии г от конца стержня.
Ответ:
4М| + 99М2 2
Решение. Для стержня имеем:
jZ = «+« = s + =
I 27\ 2 28 ,7
= — + — ) = M\T — = M}r2
у12 12/ 12 3
4L = ^ис’ка + M2 • (4Г)2 = M2y + M2 16Г = M2T^.
Искомый момент инерции:
1 33\ r2 ,
Jo = г21 Mi • - + M2 • — ) = — • (14M| + 997W2).
Замечание к задаче 34.19. В ответе к этой задаче, приведенном в сборнике [Ю],
допущена опечатка: вместо числа 14 указано 4.
Задача 34.20 (34.23). Тонкий однородный стержень АВ длины 21
и массы М прикреплен в центре О к вертикальной оси, образуя с ней
угол а. Вычислить моменты инерции стержня Jx, Jy и центробежный
момент инерции Jxy. Оси координат показаны на рис. 34.20.1. * 3
Л Ml1 2 Ml2 2 Ml1
Ответ: Jx —-----cos a, Jy =----sin a, Jxv = —— sin 2a.
3 y 3 y 6
24
1. Геометрия масс
Решение. Расчетная схема — на рис. 34.20.2, где Oxyz — исходная
система координат, Ох$, уо, zq — главные оси инерции. Имеем:
JXll = 0 (для тонкого стержня);
Ло = А, = = Х-М1г.
Используем известную формулу:
Л = Л cos2 a + Jy cos2 f3 + Jz cos2 7 -
- 2 Jxy cos a cos /5 - 2JXZ cos a cos 7 - 2 Jyz cos /3 cos 7,
где u — любое направление, cos a, cos/3, cos7 — направляющие косинусы
этого направления с осями x,y,z соответственно. Возьмем в качестве
х, у, z главные оси ж0, у0, zq. Тогда
Л = (sin о)2 + Jyn (- cos о)2 + J2|) • 0 = |м/2 cos2 a,
Jy = Jx„ • (cos a)2 + Jyn (sin a)2 + JZi. 0 = ^Ml2 ' s*n2 a’
Jz = JZo = [-mi2.
Теперь применим эту формулу, взяв оси х, у, z, а в качестве и возь-
мем xq. Тогда
Л = Л„ = 0 = Jx • (sin a)2 + Jy (cos a)2 + Jz • 0 -
- 2 Jxy sin a cos a - 2 Jxz sin a 0 - 2 Jyz cos a 0 =>
7 1 (Ml- , . , Ml2 2 , \ Ml2
Jxy = --------I —z~ cos" a sin" a -I—— sin a cos a =---------sin 2a.
y 2 sin a cos a \ 3 3 /6
1. Геометрия масс
25
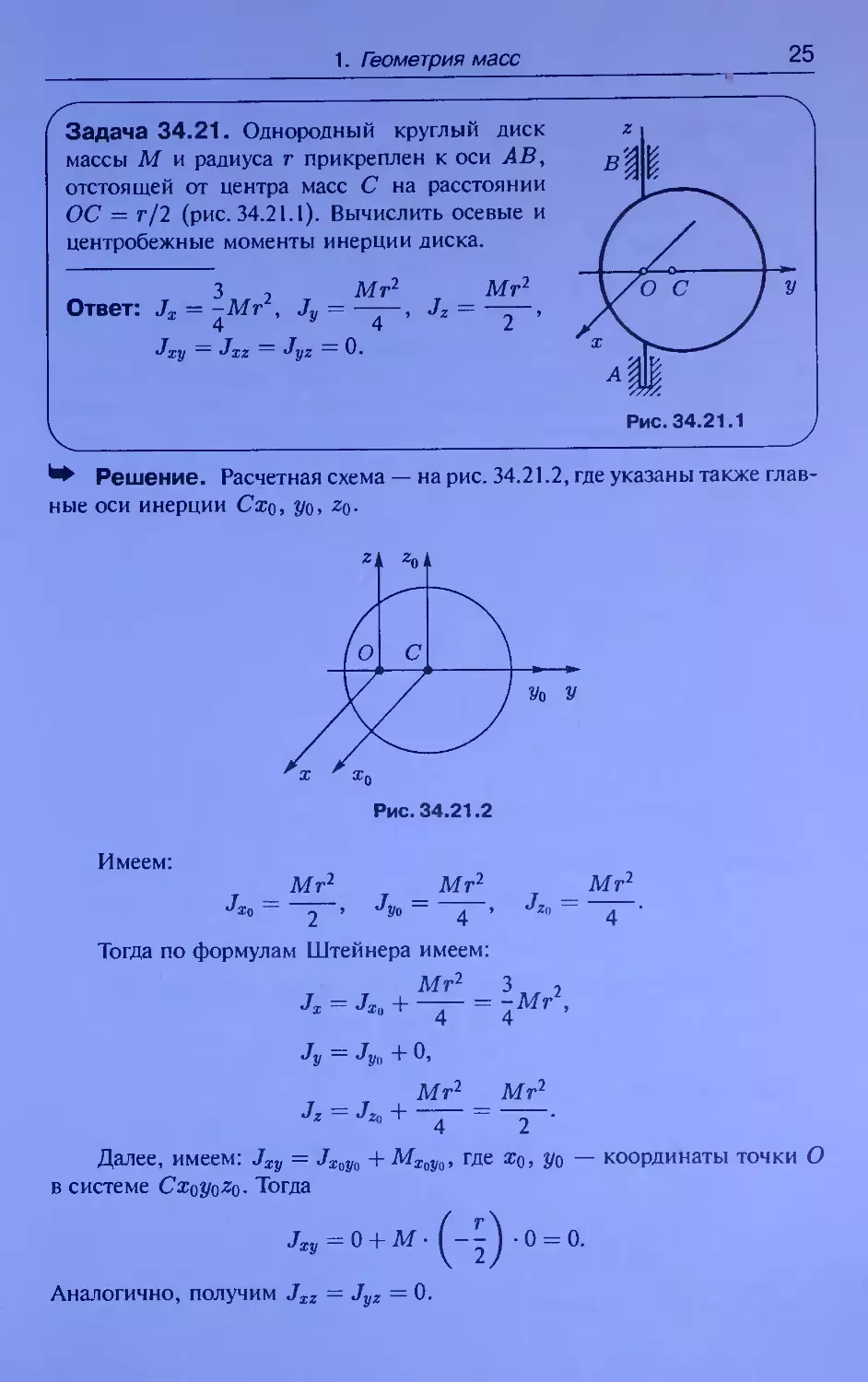
Задача 34.21. Однородный круглый диск
массы М и радиуса г прикреплен к оси АВ,
отстоящей от центра масс С на расстоянии
ОС = г/2 (рис. 34.21.1). Вычислить осевые и
центробежные моменты инерции диска.
3 2 Mr Mr2
Ответ: Jx = -Mr , Jv =------, Jz = ——
x 4 y 4 2
Jxy — JXZ — Jyz = 0.
Рис. 34.21.1
Решение. Расчетная схема — на рис. 34.21.2, где указаны также глав-
ные оси инерции Схо, уо, zq.
Имеем:
Рис. 34.21.2
Mr2
г _ ------
3-0 2 ’
_ Mr2
Тогда по формулам Штейнера имеем:
т Mr2
=
— Jy« +
Mr2
- Ло +
гоУо + МХоУп, где х0, Уо — координаты точки О
Mr2
'z" - “Т"
3 2
= -Mr2,
4
.2
Mr2
~2~
х
У
z
Далее, имеем: Jxy =
в системе Cxcy^ZQ. Тогда
Jxy — от М •
•0 = 0.
Аналогично, получим Jxz = Jyz = 0.
26
1. Геометрия масс
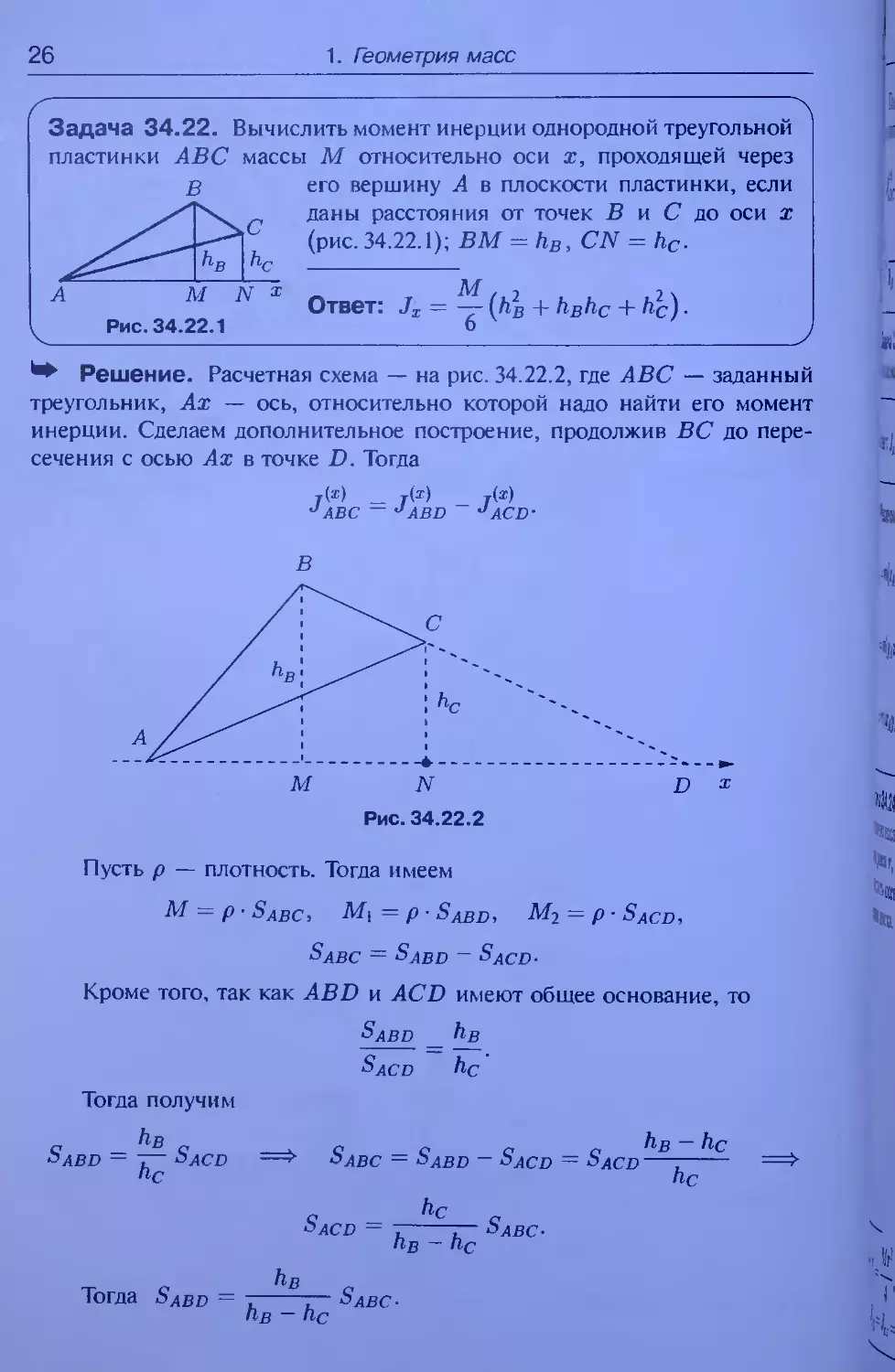
Задача 34.22. Вычислить момент инерции однородной треугольной
пластинки АВС
В
массы М относительно оси х, проходящей через
его вершину А в плоскости пластинки, если
даны расстояния от точек В и С по оси х
(рис. 34.22.1); ВМ = hB, CN = hC-
С
h,
hB
А М~ N х
Рис. 34.22.1
At у j т \
Ответ: Jx = — (Лд + hBhc + hc)-
о
Решение. Расчетная схема — на рис. 34.22.2, где АВС — заданный
треугольник, Ах — ось, относительно которой надо найти его момент
инерции. Сделаем дополнительное построение, продолжив ВС до пере-
сечения с осью Ах в точке D. Тогда
гС3*) __ т(-0 __ т(3)
АВС — JABD JACD-
Пусть р — плотность. Тогда имеем
М — р 8дВс, М\ — р - Sabd, М2 — р Sacd,
Sabc = Sabd — Sacd-
Кроме того, так как ABD и ACD имеют общее основание, то
Sabd _ hB
Sacd he
Тогда получим
hB
Sabd = ~r~ Sacd
he
Sabc — Sabd - Sacd = Sacd —7——
he
Sacd — 7 Sabc-
hB - he
Тогда Sabd = 7-----— Sabc-
hB — he
1. Геометрия масс
27
Подставляя полученные соотношения в формулы для моментов инер-
ции, получим:
тСО 1 п 1.2 1 г. 12 1 hB 2
JaBC — 6? ^ABD &ACD 'Рс-^Р' h _ ^АВС ' "-В
- cP' 7—^~7Г $АВС — гР $авс • —т~ = 7^1(Лв + h2c + hB hc).
о hB — he 6 hB — he 6
Задача 34.23 (34.24). По данным задачи 34.1 определить центро-
бежные моменты инерции Jxz, Jyz, Jxy коленчатого вала.
3 \/3
Ответ: Jxz — -~md(a + b), Jyz =——md(a + b), Jxy = Q.
к___________________________________________________________
Решение. Имеем (см. рис. 34.1.1 к задаче 34.1):
3
Jxz = fn(xAZA + XBZB + xDzD) = - -md (о + &),
\/3
Jyz = rn(yAzA + VbZB + yDZD) = —Ymd^a + b)’
f 2з/3 \
Jxy = m{xAyA + xByB + xDyD) = m I d — - d — + (~d) -01 =0.
Задача 34.24 (34.25). Однородный круглый диск массы М экс-
центрично насажен на ось z, перпендикулярную его плоскости. Радиус
диска равен г, эксцентриситет ОС = а, где С — центр масс диска.
Вычислить осевые Jx,Jy,Jz и центробежные Jxy, Jxz, Jyz моменты
инерции диска. Оси координат показаны на рис. 34.24.1.
Ответ:
28
1. Геометрия масс
Решение. Эта задача аналогична задаче 34.21 с небольшим измене-
нием наименований осей. Получим:
_ Mr2
Jx — JхС — »
4
, Mr2 7
Jy — Jyc З- Ma — ——— -f- TVffl ,
, Mr2 ,
Jz — JzC 4- Ma~ — ———|- Ma ;
Jxy = 0 4“ = 0-
Аналогично получим Jxz — Jyz = 0.
Задача 34.25 (34.27). По данным задачи 34.24 вычислить момент
инерции диска относительно оси Z\, лежащей в вертикальной плос-
кости xz и образующей с осью z угол у? (см. рис. 34.25.1).
"* Решение. Пусть и — единичный вектор направления оси Ozt. Ис-
пользуем известную формулу:
Ju = Jz, = Jx C°S2 Ct + Jy COS2 /3 + Jz COS2 7 -
- 2 JXy cos a cos /3 — 2 Jxz cos a cos 7 — 2 Jyz cos /3 cos 7,
где cos о, cos /3, cos 7 — направляющие косинусы оси Oz} в системе Oxyz.
Ясно, что cos a = sin ip, cos /3 = 0, cos 7 = cos ip. Тогда получим:
Mr2 . 2 (Mr2 Л (Mr2 ?\ 2
Ju - Jz, = —— sin <p + I —— + Ma 1-0+1 —— + Ma 1 cos <p =
Mr2 2 (т1 t\ i
= —— sin ip + MI у + a I cos p
(Здесь использованы результаты задачи 34.24!)
1. Геометрия масс
29
Задача 34.26(34.28). Однородный круглый диск массы М наса-
жен на ось z, проходящую через его центр масс С. Ось симметрии дис-
ка Z\ лежит в вертикальной плоскости симметрии xz и образует с осью z
угол а. Радиус диска равен г. Вычислить центробежные моменты инер-
ции диска Jxz, Jyz, Jxy. Оси координат показаны на рис. 34.26.1.
Ответ. JXy — JZy — 0, Jxz
sin 2а
2
Mr2
—— sin 2а.
О
Решение. Используем таблицу углов между главными осями Х\, у\,
Z\ и осями x,y,z: Xi yi Zi
X «1 Pi 7i
У a2 02 72
z «3 /Зз 7з
Для условия задачи 34.26 имеем:
7Г 7Г
01=0, о2 = а-i---а\
7Г 7Г
/31 = 2’ /32 = О’ Л=2;
7Г 7Г
7i = j+a, 72=2’ '>3 = о-
Для вычисления центробежных моментов инерции используем из-
вестные формулы (см. [11]):
Jxz =(JZl - Jz,)cOSO!3COSai + (JZ1 - J,,,) cos cos/3] =
Mr2 Mr2\ (Mr2 Mr2\ 7Г 7Г Mr2
---sin a coso + I-cos — cos — —-sin 2a,
2 4/ \2 4/228
30
1. Геометрия масс
Jxy = (Л1 - Л,) cos a, cos а2 + (Л, - Jy,) cos/3] cos fa = 0,
Jyz - {Jz, - Ja-I)cosa2cosa3 + (JZ| - Jyi)cosfacosfa =0.
Задача 34.27(34.29). Решить предыдущую задачу в предположе-
нии, что диск эксцентрично насажен на ось z (рис. 34.27.1), причем
эксцентриситет ОС = а.
Решение. По формулам преобразования центробежных моментов
инерции относительно параллельных осей имеем:
Jrj^ — Jyz 7176с,
J— Jzz 4~ TVTca,
J^z] = Jxy 4~ AJab,
где x, у, z проходят через центр масс тела, £, у, £ — параллельные им оси,
проходящие через точку А с координатами (а, 6, с) В условиях нашей за-
дачи проведем через центр масс С диска оси х2, у2, z2, параллельные осям
х, у, z. Тогда координаты точки О в системе {х2, у2, z2) будут (о cos о, 0,
a sin а). Причем центробежные моменты инерции в осях х2, у2, z2 извест-
ны нам из предыдущей задачи 34.26. Тогда получим:
Jxy = Jx2y2 4- м • (a cos а) 0 = 0,
= Jy2z2 4- М 0 (а sin а) = 0,
Jxz = Jx2z2 + М - {a cos а) • (а sin а) =
Mr2 . Ма2
= —т— sin 2а -|---— sin 2а =
8 2
М/г2 Л
= — I — 4- a I sin 2а.
2 \ 4 /
1. Геометрия масс
31
Задача 34.28 (34.30). Однородный круглый диск радиуса R наса-
жен на ось вращения z, проходящую через точку О и составляющую
с осью симметрии диска Cz\ угол а (рис. 34.28.1). Масса диска
равна М. Определить момент инерции Jz диска относительно оси
вращения z и центробежные моменты инерции Jxz и Jyz, если OL —
проекция оси z на плоскость диска, ОЕ — а, ОК = Ъ.
Рис. 34.28.1
Ответ: Jz = М
7 1 7 1 7 1 7 7 7
а + -R I cos а + -R sin а + Ь ,
2 / 4
Jxz = M{-R2 + a2
\4
sin a cos a, Jyz = Mab sin а.
Решение. Эта задача отличается от задачи 34.27 лишь тем, что точка
крепления О оси z смещена вдоль главной оси Су\ влево на расстояние
ОК = СЕ = b (если смотреть с конца главной оси Cz\, см. рис. 34.28.2).
Возьмем в точке С оси CxzyzZz, параллельные осям Oxyz. Мы при-
дем к условию задачи 34.28, т. е.
Mr2
Jx2y2 — Jy2z2 — 0, JX2z2 — g sin 2a.
Рис. 34.28.2
32
1. Геоь.етрия масс
Далее, координаты точки О в системе Cxyyyzy суть следующие:
хо — a cos a,
Уо = b,
zq — a sin a.
Тогда по формулам параллельного переноса осей:
Jxy = JX2y2 + МхоУо = Mabcosa,
Mr2 2
Jxz = Jx2z2 + ™ozo = q sin la + Ma sin a cos a,
О
Jj/jj = Jy2z2 + Myozo = Mob sin a.
Далее, чтобы найти Jz, возьмем в точке О оси Oxyyyzy, параллельные
главным осям Cx\y\Z\. По формулам параллельного переноса имеем:
/г2 \
Jx2 — Jx\ т Mb — МI ——и ь I,
\ 4 /
/г2 \
Jy3 = Jy, + Mq1 = м ( + b2 J ,
/г2 \
JZ} =JZl + M(a2 4-b2) — М (—+ a2 + b2 j;
Jx2y2 = Jx\y\ T M^ab — Mab,
Jx}z2 — Jx\z\ T Ma -0 = 0,
Jyjz2 = JyiZi 4" Mb -0 = 0.
Направляющие косинусы оси z с осями xy,yy,zy:
cos (z, xy) = sin a,
cos (z, yy) = 0,
cos (z, zy) — cos a.
Поэтому по известной формуле имеем:
Jz = JX1 • (sin a)2 + Jyj (0)2 + JZ3 (cos a)2 -
- Ux,y3 sin a • 0 - 2JXjZ3 sin a cos a - 2Jy3Z} • 0 • cos a =
(r2 2
= M —+62
\ 4
sin a + MI — + a + b
cos2 a =
4
4i
’^(1
= M
r2 A r2
* 2 12 ' 2 7
— + a cos ad---sin a + b
2 J 4
1. Геометрия масс
33
Задача 34.29. Однородная прямоугольная пла-
стинка OABD массы М со сторонами а и b при-
креплена стороной О А к оси ОЕ (рис. 34.29.1).
Вычислить центробежные моменты инерции пла-
стинки Jxz, Jyz и Jxy.
« Mab
OtBGT. J^z ~ *^ху ~ Os Jyz ~ ~~
Решение. Расчетная схема — на рис. 34.29.2. Возьмем в точке С (цен-
тре масс пластины) главные оси инерции Cx\y\Z\, которые параллельны
осям х, у, z. В главных осях имеем:
~ ^1*1 = Л/iZi = 0-
По формулам параллельного переноса,
учитывая, что координаты точки О в систе-
ме Cx\y\Z\ суть:
Ь а
®о = 0, уо = -~, zo = -~,
получим:
Jxy ~ J%iyi Мх^уо ~ 0.
Jxz ~ JxiZj 4" AfX()Zo = 0s
Рис. 34.29.2
, ab
r!/12| 4-W)Z0 = M —.
Задача 34.30(34.31). Однородная прямоугольная пластинка мас-
сы М со сторонами длины а и b прикреплена к оси z, проходящей
через одну из ее диагоналей. Вычислить центробежный момент инер-
ции JyZ пластинки относительно осей у и z,
лежащих вместе с пластинкой в плоскости
рисунка. Начало координат совмещено с цен-
тром масс пластинки.
Ответ: Jyz =
М ab(a2 - Ь2)
12 ’ а2 + Ь2 ’
Рис. 34.30.1
34
1. Геометрия масс
Рис. 34.30.2
Решение. Возьмем в точке О (центре масс пластины, см. рис. 34.30.2)
главные оси Ox\y\Z\. Таблица углов:
Xt У1 Z\
X «1 /31 7i
У «2 /32 72
z «3 /Зз 73
Для случая, изображенного на рис. 34.30.2, имеем:
ct| = 0.
7Г
7Г
71 = 2’
7Г 7Г
“г = Р “3=Г
ft = а, ft - у + а;
7Г
72 = - - а, ъ = <*-
Для вычисления центробежного момента инерции Jyz используем
известную формулу (см. [11]):
jyz = (Л| — Jxt) = COS &2 COS О3 + (Jz> — Jy] ) COS /?2 COS /З3 =
= (J2| — Jyi) cos о sin a — ЗИа2 — —cos ° s*n °’
но так как
2 1 1 ft2
cos a =-------3— =----------—- =--------
1 + tg2 a \+a2/b2 a2 + b2'
tgo a/b a
sin a = —-— — — = ...
V 1 + tg2 a 1 + aJ/b2 Va2 + ft2 ’
1. Гэометрия масс
35
TO ab
cos ct sin ct — - -, a2 + ft2
t. e. JW n 7 ab J = _(a2 _ ft2). —— y 12v ’ a1 E b2
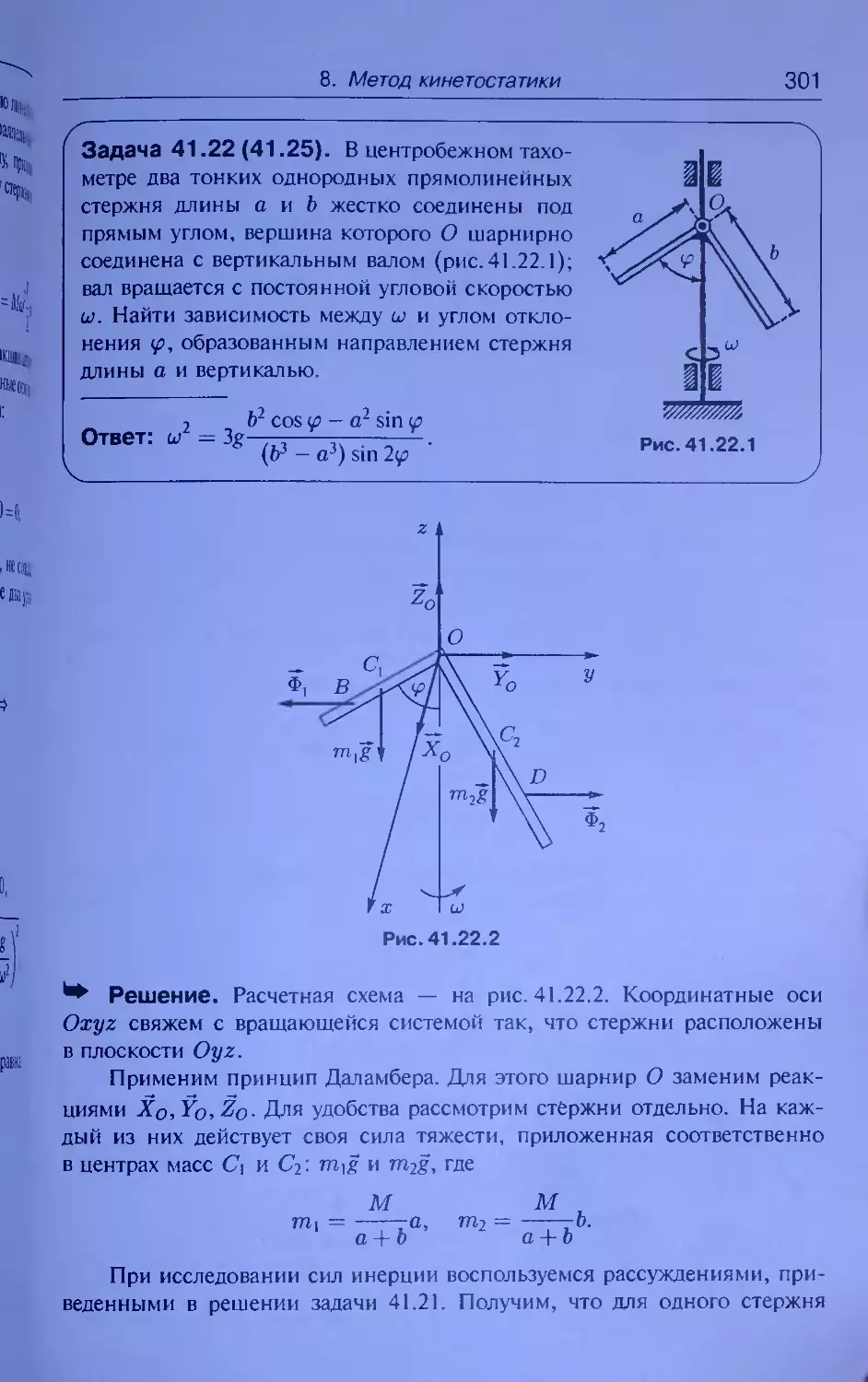
Задача 34.31 (34.34). Вращающаяся часть подъемного крана со-
стоит из стрелы CD длины L и массы М\, противовеса Е массы М2
и груза К массы Му. Рассматривая стрелу как однородную тонкую бал-
ку, а противовес Е и круг К как точечные массы, определить момент
инерции Jz крана относительно вертикальной оси вращения z и цен-
тробежные моменты инерции относительно осей координат x,y,z,
связанных с краном. Центр масс всей системы находится на оси z;
стрела CD расположена в плоскости yz.
Ответ: Jz = М2а2 +
1
Му + -мх
2 2
L sin a,
Vz —
1 / ’
-1 My + -My
2\ 3
L2 sin 2a — MyLl sin a,
Рис. 34.31.1
Решение.
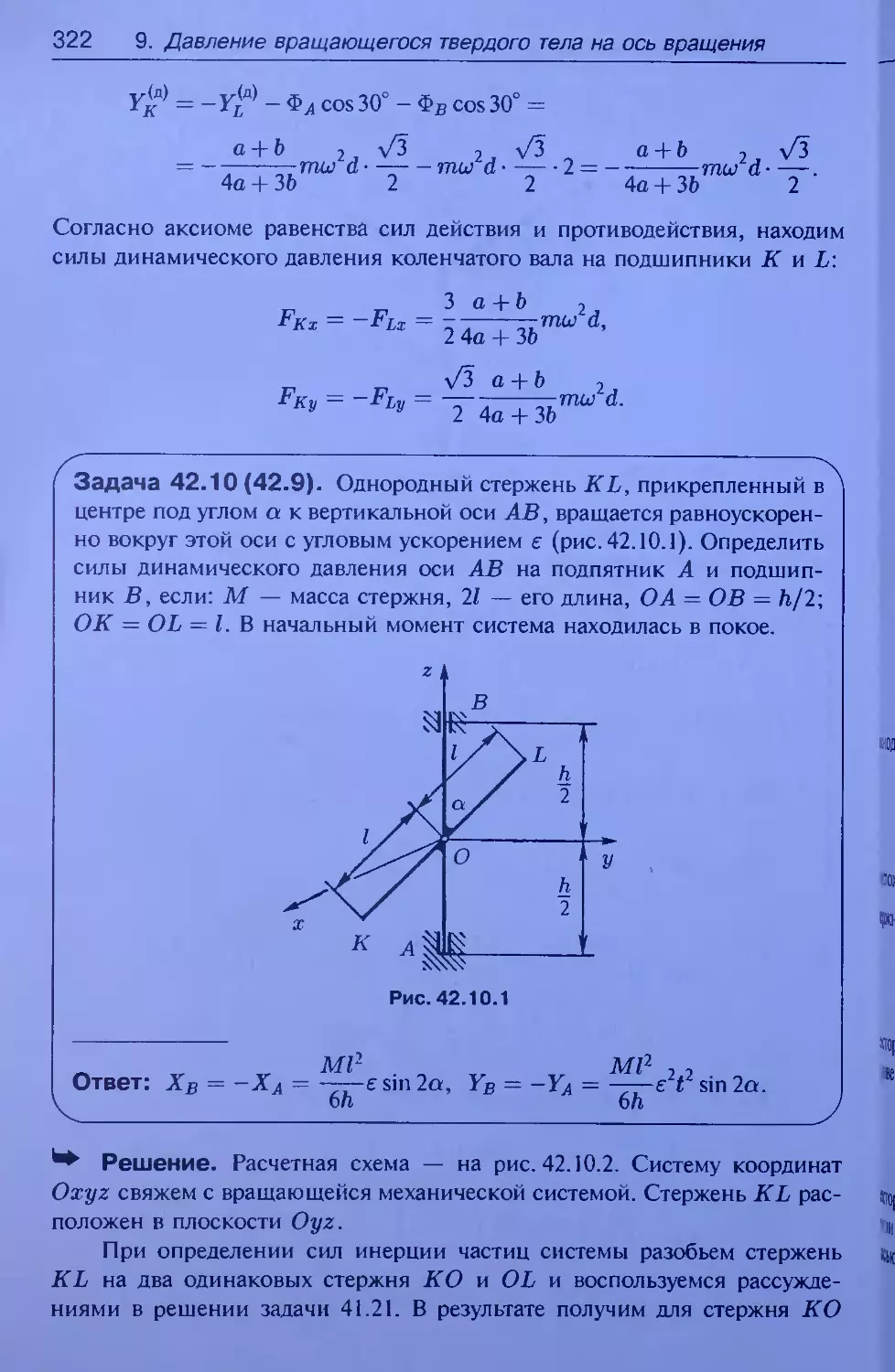
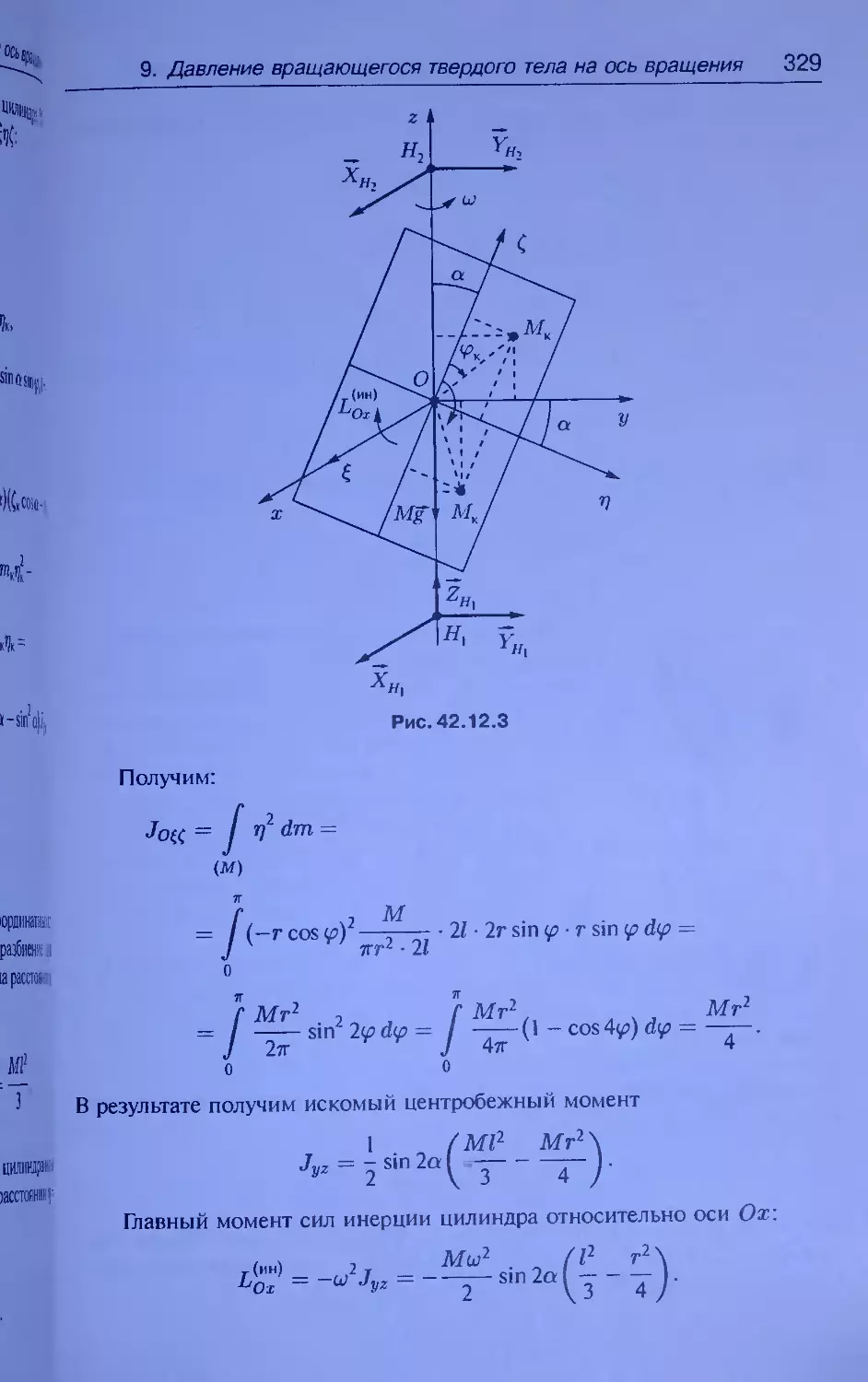
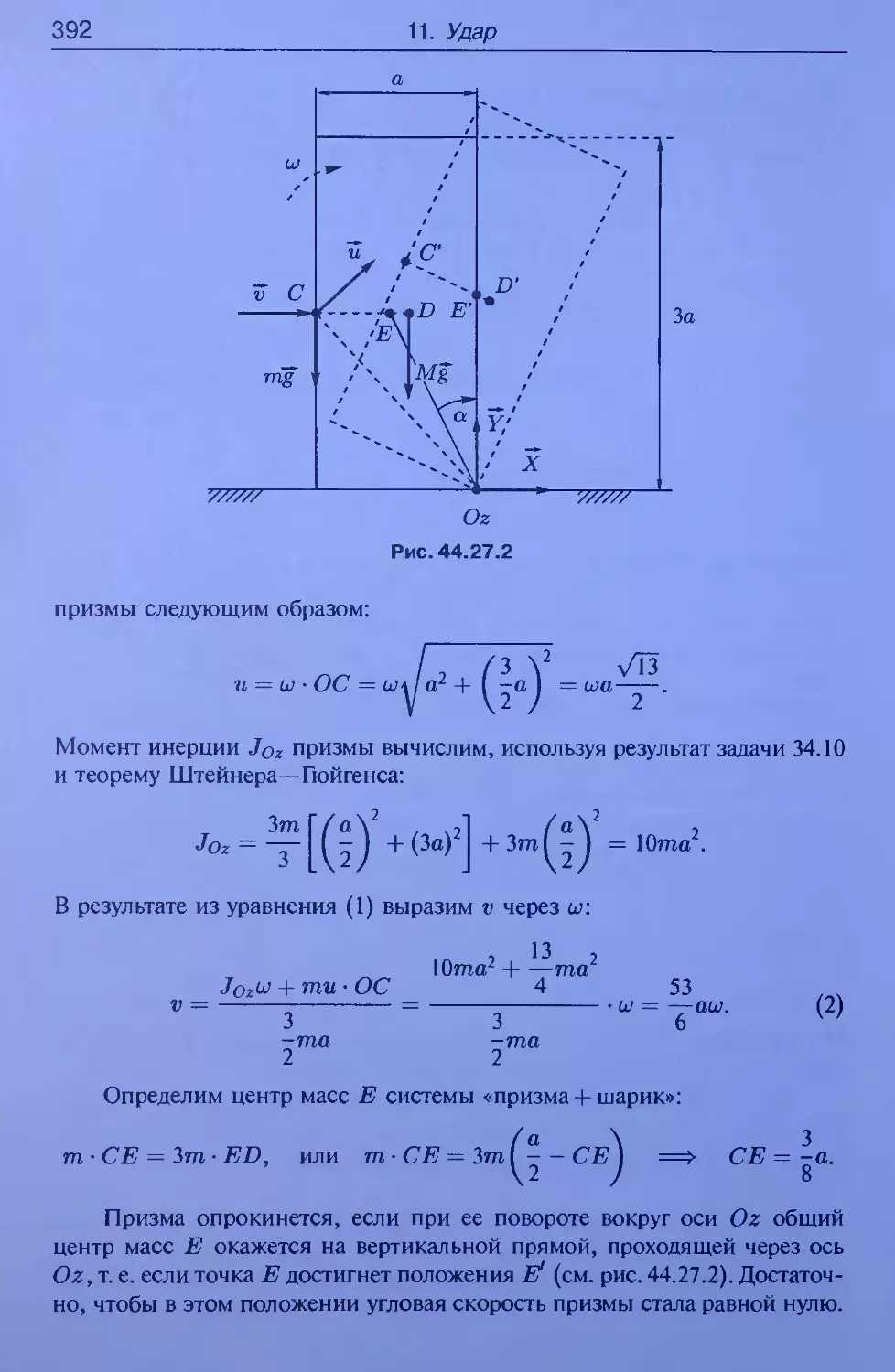
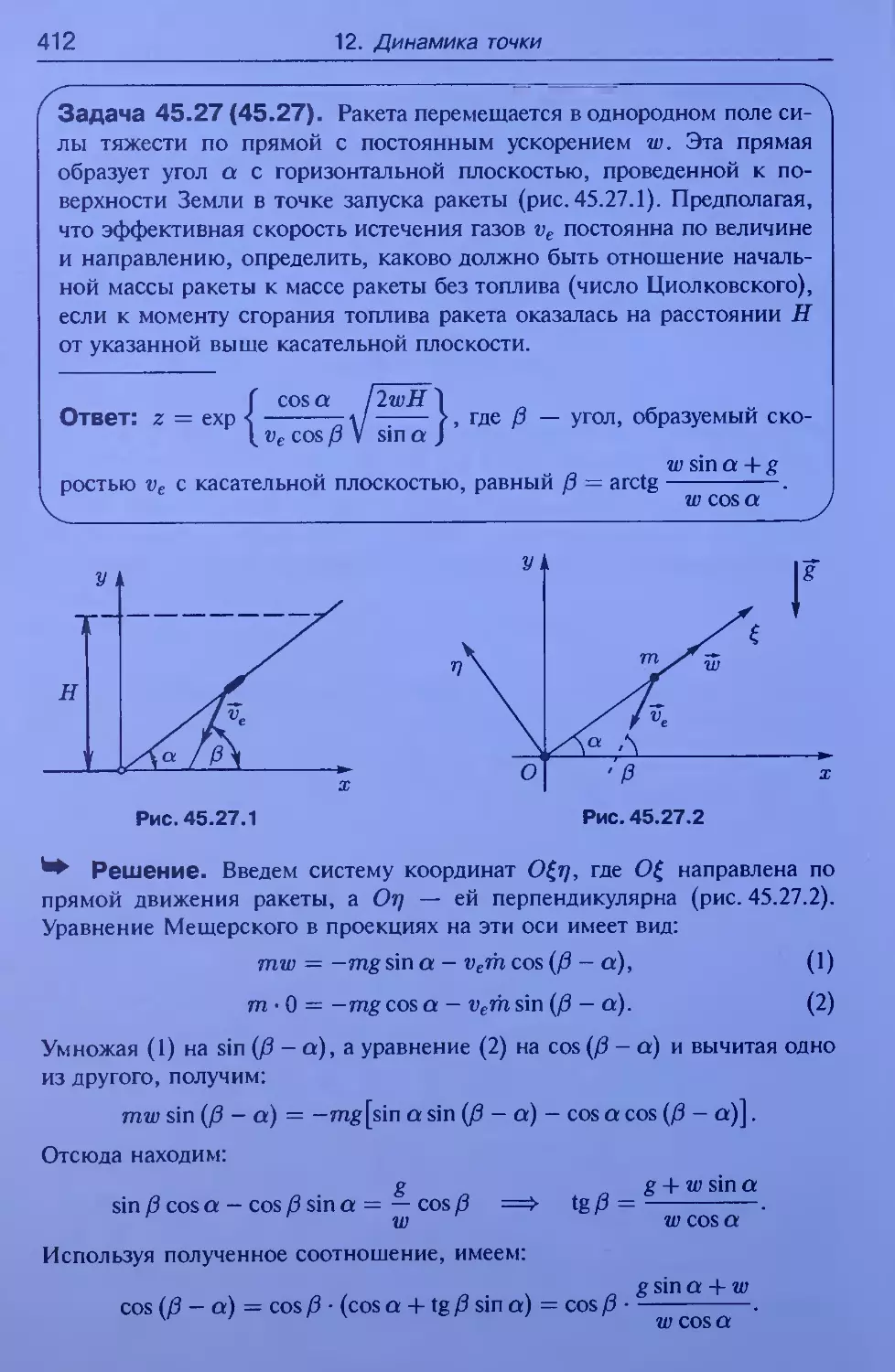
= My (L sin а)2 (см. рис. 34.31.2),
rd
CD
xt
+ Jyi (cos ct)2 + JZl (sin ct)2 =
M{L2
3
sin2 a,
J(E} = M2a2,
36
1. Геометрия масс
Jz = M2a2 + L2 sin2 a yMi + -Mx J ,
J^.z> = (L sin a) • (h + L cos a - I),
J(f} = M2 • (-a) • h = -M2ah.
Центробежный момент инерции стержня проще всего подсчи-
тать непосредственно:
L
^cd — j (h + S cos a) S sin a =
о
L2 L3
= ph sin a -------h p sin a cos a • —
2 3
hL sin a cos a • L2'
— sin a +
2
= M\
3
Суммируя полученные результаты и используя тот факт, что центр
масс системы находится на оси z, т. е.
L
М2а = М\ • — sin а + M2L sin a,
получим:
(Lh sin a + L2 sin a cos a - LI sin a) -
hL MXL2
- M2ah + Mx — sin a 4----— sin a cos a =
= Mi (Lh sin a + L2 sin a cos a - LI sin a) - Mx — sin a -
hL L2
- MihL sin a + Mx — sin a + Mx — sin a cos a =
> L2
= М3 (£" sin a cos a - LI sin a) + Mx — sin a cos a =
1 / 1 \ ,
= - I Mi + -M| I L~ sin 2a - MiLl sin a.
Jxy = Jxz — так как ж-координаты всех точек системы равны нулю!
2. Теорема о движении центра
масс материальной системы (§ 35, [10])
Задача 35.1 (35.1). Определить главный
вектор внешних сил, действующих на ма-
ховик М, вращающийся вокруг оси АВ
(рис. 35.1.1). Ось АВ, укрепленная в кру-
говой раме, в свою очередь вращается вокруг
оси DE. Центр масс С маховика находится
в точке пересечения осей АВ и DE.
Рис. 35.1.1
Ответ: Главный вектор внешних сил равен нулю.
Решение. Воспользуемся теоремой о движении центра масс махо-
вика:
тас = ^€)-
к
Так как центр масс С маховика, находясь в точке пересечения осей вра-
щения, не движется, то главный вектор внешних сил
R^> = 22 *ке) = °-
к
Задача 35.2 (35.2). Определить главный
вектор внешних сил, приложенных к ли-
нейке АВ эллипсографа, изображенного на
рис. 35.2.1. Кривошип ОС вращается с посто-
янной угловой скоростью ы, масса линейки
АВ равна М; ОС = АС = ВС = I.
Ответ: Главный вектор внешних сил парал-
лелен СО и равен по модулю Mlw2.
Рис. 35.2.1
Решение. Расчетная схема — на рис. 35.2.2. Для определения глав-
ного вектора внешних сил, приложенных к линейке АВ, в соответствии
с теоремой о движении центра масс
к
определим ускорение точки С.
38
2. Теорема о движении центра масс материальной системы
х
Рис 35.2.2
Точка С, с другой стороны, принадлежит кривошипу ОС, кото-
рый вращается с постоянной угловой скоростью ш. Поэтому ускорение
«с = «с = и направлено к точке О. Следовательно, главный вектор
внешних сил — Mac = Mw2l и направлен от точки С к точке О.
Задача 35.3(35.3). Определить главный век-
тор внешних сил, действующих на колесо мас-
сы М, скатывающееся с наклонной плоскости
вниз, если его центр масс С движется по закону
Хс = at2/2.
Ответ: Главный вектор внешних сил параллелен
оси х, направлен в сторону движения и равен
по модулю Ma.
Решение. Расчетная схема представлена на рис. 35.3.2. Воспользу-
емся теоремой о движении центра масс С в проекциях на оси х и у.
к к
Так как центр масс С движется вдоль оси х
по закону хс = at2/2, то главный вектор внеш-
них сил имеет следующие проекции на оси ко-
ординат:
№ = ^^ = Мхс = Ма,
к
Ry} = £ FS = м$с = °-
Значит главный вектор внешних сил параллелен оси х, направлен
в сторону движения и равен по модулю Ma.
2. Теорема о движении центра масс материальной системы 39
Задача 35.4(35.4). Колесо катится со скольжением по горизон-
тальной прямой под действием силы F. Найти закон движения цен-
тра масс С колеса, если коэффициент трения скольжения равен /,
a F = 5fP, где Р — вес колеса. В начальный момент колесо находи-
лось в покое.
Ответ: xc = 2fgt2.
Рис. 35.4.1
Решение. Расчетная схема — на рис. 35.4.1, где С — центр масс
колеса, vc — его скорость, ш — угловая скорость колеса, К — точка ка-
сания колеса с плоскостью, vk — скорость точки К, Frp — сила трения
скольжения в точке К, причем согласно закону Кулона
FrP = -fN-^~, vK^0,
где N — модуль нормальной реакции. Для ситуации, рассматриваемой
в задаче, имеем N = Р.
Пусть в начальный момент колесо находилось в покое, т. е. «с(О) = О,
ш(0) = 0. Выясним, как будет направлена скорость точки К в последую-
щие моменты времени. Запишем уравнение движения центра масс колеса:
mvc = F - Frp
(О
и уравнение моментов количеств движения относительно центра масс
колеса:
Jw = F^ • г
тпг2
(2)
40
2. Теорема о движении центра масс материальной системы
(3)
так как
Для точки касания К имеем кинематическую связь:
Vr = Vc - ыг => Vk = i>c - в)г.
Используя соотношения (1), (2), получим:
F-Frp т\ F — F7p 2 _F-3-FTp
— т FTp — F^ —
mJ mm m
Отметим, что в (3), FTp > 0, если vK > 0 (см. рис 35.4.1), FTp < О,
если vk < 0 (знак vr выбираем так же, как и знак Vc, т.е. в соответствии
с направлением оси х). Рассмотрим два случая:
Г. F > 3|FrPmjx| = 3/F. Тогда формула (3) дает vk > О
vk(0) = 0, получим z’x(t) > 0 при t > 0, и ситуация в точности такая,
как это показано на рис. 35.4.1.
2°. О < F < 3|FTPmax| = 3fP. Пусть в этой ситуации при t > +0 началось
скольжение, т.е. vk /= 0. Предположим, что vr > 0, т.е. ^к(+0) > 0
(см. рис. 35.4.1). Тогда из (3) получаем при FTp — FTPmjx — fP > 0:
. . F - 3fP
Vk(+0) = --------- < 0, т. e. противоречие! Пусть vK < 0 (т. e.
тп
®к(+0) < 0 и FtP < 0). Тогда из (3) получаем при FTp = -fP:
F + 3fP
Vr(+0) = --------- > 0, т. е. опять противоречие! Единственная
m
ситуация, таким образом, которая непротиворечиво реализуется, это:
vr — 0 —> Vx(t) = 0 при всех t, т.е. чистое качение. В этом случае
в точке контакта К возникает сила трения покоя, которая зависит
от величины силы F € [0, З/F). В этом случае имеем уравнения
динамики:
— F FTp покоя >
= FTp ПОКОЯ ’ Т >
(4)
(5)
«II
-л
ИЙ
Иц»
«и
2В1
Ч=-
и кинематическую связь:
vK = vc - ыт = 0.
Из этих уравнений мы получим, по аналогии с (3):
F - 3 • F 1
0 = = -___ ^тр. покоя р _ 1
u 7 ^тр покоя — 3 ’
причем направление силы трения покоя FTp покоя такое же, как и у FTp
на рис. 35.4.1.
Таким образом, мы получаем следующий ответ:
I. F € (3fP, оо) (т е. случай нашей задачи, где F = 5/F > 3fP). Тогда
для движения реализуется схема, указанная на рис. 35.4.1, и, в соот-
ветствии с (1), имеем:
mic = F- FTPnux = F-fP = 4fP
2. Теорема о движении центра масс материальной системы 41
(при F = 5fP), т. е. хс = 4fg=> при а?с(О) = хс(0) = 0 получаем:
t2 2
®с(0 = 4fg~ = 2/gf
(ответ задачи).
И. F G (О, 3/Р). Тогда движение с проскальзыванием не реализуется,
а из (4) имеем:
1 2
mvc = F — Frp покоя — F — -F
Причем реализуется схема с чистым качением, т. е. так, как указано
на рис. 35.4.1, где Vk = 0. В предложении F — const, получим:
2 Ft2 Ft2
Xc{t) = Z-----•
3m 2 3m
Замечание к задаче 35.4. Мы решили задачу для произвольного значения силы F.
Это решение показывает, почему в условии задачи выбрано значение силы F = 5 fP,
которое соответствует случаю 1 полученного ответа.
Задача 35.5(35.5). Колесо катится со скольжением по горизон-
тальной прямой под действием приложенного к нему вращающего
момента. Найти закон движения центра масс С колеса, если коэф-
фициент трения скольжения равен f. В начальный момент колесо
находилось в покое.
Ответ: хс = ——.
_________ 2 ____________________________________________________J
Решение. Расчетная схема — на рис. 35.5.1, где обозначения такие же,
как в предыдущей задаче. Однако вместо силы F к колесу приложена
Рис. 35.5.1
42 2. Теорема о движении центра масс материальной системы
пара сил с моментом М. Пусть vk 0. Уравнения движения центра масс
С и моментов количеств движения относительно точки С будут такими:
_ „ _ mv1
т
mvc = -Ртр, J<v = M + PTp • r,
(О
Для точки К имеем кинематическую связь:
vk = Vc - => Vk — Vc - шг.
Используя (1), отсюда получаем:
h =-^-7(м + Ртр.г) = -^-Ртру
m J v m v J
= -^(1+2)---- = -1(зРтр + —Y
m m r m\ r /
г
- -М =
(2)
Отметим, что в (2) Ртр > 0, если vK > 0 (см. рис. 35.5.1) и Ртр < 0,
если vk < 0 (знак Vk соответствует знаку Vc^). Рассмотрим два случая:
о 2М . 3
1 • > 3|PTPmax| = 3/Р ==> М > -fPr. Тогда из (2) следует, что
^к(+0) < 0 => г>/<(+0) < 0, т.е. точка К начнет скользить в сторону,
противоположную vc (см. рис. 35.5.1, где Ртр и vk следует поменять
местами). Таким образом, здесь
^тр = -РТРтах = ~fP => vc — fg => Хс = fg =>
"I
' |ф
И
"ЗЛЬ
‘аян
лк
Xc(t) = -у- при а?с(0) = ±с(0) = 0.
2М 3
2°. — < 3|PT₽max | = 3fP => M < -fPr. Тогда, в соответствии с (2),
мы получим vk < 0, т.е. реализуется схема скольжения при Ртр =
^Pnux = ~fp (см- рис. 35.5.1, где vk и Ртр следует поменять местами!).
Из формулы (2) мы имеем:
vK =--I -3/P 4--
m \ r
2 /3
--I ~fPv ~ ТП
mr \ 2
т. е. мы пришли к противоречию! Следовательно, в этом случае
скольжение точки К невозможно, т.е. реализуется чистое качение.
Таким образом, vk = 0 ==> v#(i) = 0, а в точке касания возникает
сила трения покоя, величина которой определяется из соотношения
кинематической связи в случае чистого качения:
1
vK =-----
m
2т
Зт*тр покоя Н
г
= 0
fp —________________
Л TD. ПОКОЯ — ~
Зг
'М,
к
ч
ц
ч
Ч|
%
2. Теорема о движении центра масс материальной системы 43
Тогда уравнение для движения центра масс будет таким:
2
mvc = —М => при М — const и хс(0) = ±с(0) - О,
Зг
получим:
2М t2 _ Mt2
Хс^ Зтпг 2 Зтг
Как видим, здесь закон движения зависит от приложенного момента.
Таким образом, мы получаем следующий ответ:
3
I. При М > -fPr (т. е. при достаточно большом внешнем момен-
те, или достаточно малом коэффициенте трения), движение колеса
происходит с проскальзыванием, реализуется схема рис. 35.5.1, где
Др и Vk следует поменять местами, а закон движения не зависит
от величины М и определяется формулой:
®с(0 =
при жс(0) = ±с(0) = 0.
3
II. При М < -fPr (т. е. при малом внешнем моменте, или большом
коэффициенте трения), движение колеса происходит без проскаль-
зывания, т. е. реализуется чистое качение (см. схему на рис. 35.5.1, где
следует положить vk = 0, а силу Др — Frp покоя направить по оси х).
Тогда закон движения уже зависит от величины М = const:
/ х Mt2
Zc(t) =
5тпг
при 2?с(0) = ±с(0) = 0.
Замечание к задаче 35.5. Вопросы, рассматриваемые в задачах 35.4,35.5, изуча-
лись в известной монографии П.Пэнлеве «Лекции о трении» [12].
Задача 35.6 (35.6). Вагон трамвая совершает вертикальные гармо-
нические колебания на рессорах амплитуды 2,5 см и периода Т = 0,5 с.
Масса кузова с нагрузкой 10 т, масса тележки и колес 1 т. Определить
силу давления вагона на рельсы.
Ответ: от 68,0 до 147,6 кН.
\_______________________________________________________________
Решение. Расчетная схема — на рис. 35.6.1. Механическая система
состоит из кузова (с центром масс в точке С\) и тележки с колесами
(с центром масс в точке Сг). На систему действуют внешние силы: силы
тяжести m\g и m2g, нормальные реакции N\ и N2, силы трения ДР1 и Др2.
44
2. Теорема о движении центра масс материальной системы
Рис. 35.6.1
Запишем теорему о движении центра масс механической системы
в проекции на вертикальную ось у.
*
Используя определение центра масс системы, получим:
‘ГП\У\ + ТП2У1 = Nt+N2- m{g - m2g.
Так как по условию
У2 = const => 3/2=0
И
3/1 = A sin kt => yt = -Ak2 sin kt,
где
л n me i 27Г 27Г , АРад\
A — 0,025 м, к — — = — = 4тг I ---------- I
T 0,5 \ c /'
Сила давления вагона на рельсы, в соответствии с законом Ньютона,
равна
^давл — Ni + N2 = mig + m2g + miyl = m}g + m^g - ттцAk2 sin kt,
^давл min — mig + m2g - m\Ak2 =
= 11 000 • 9,8 - 10 000 • 0,025 • (4тг)2 к 68 322 (H),
^давл max — t7l|g + Tflig T ТП[Ак =
= 11 000 • 9,8 + 10 000 • 0,025 (4д)2 к 147 278 (Н).
2. Теорема о движении центра масс материальной системы 45
Значит, сила давления вагона на рельсы меняется в пределах от 68,3 кН
до 147,3 кН. Направлена эта сила вертикально вниз.
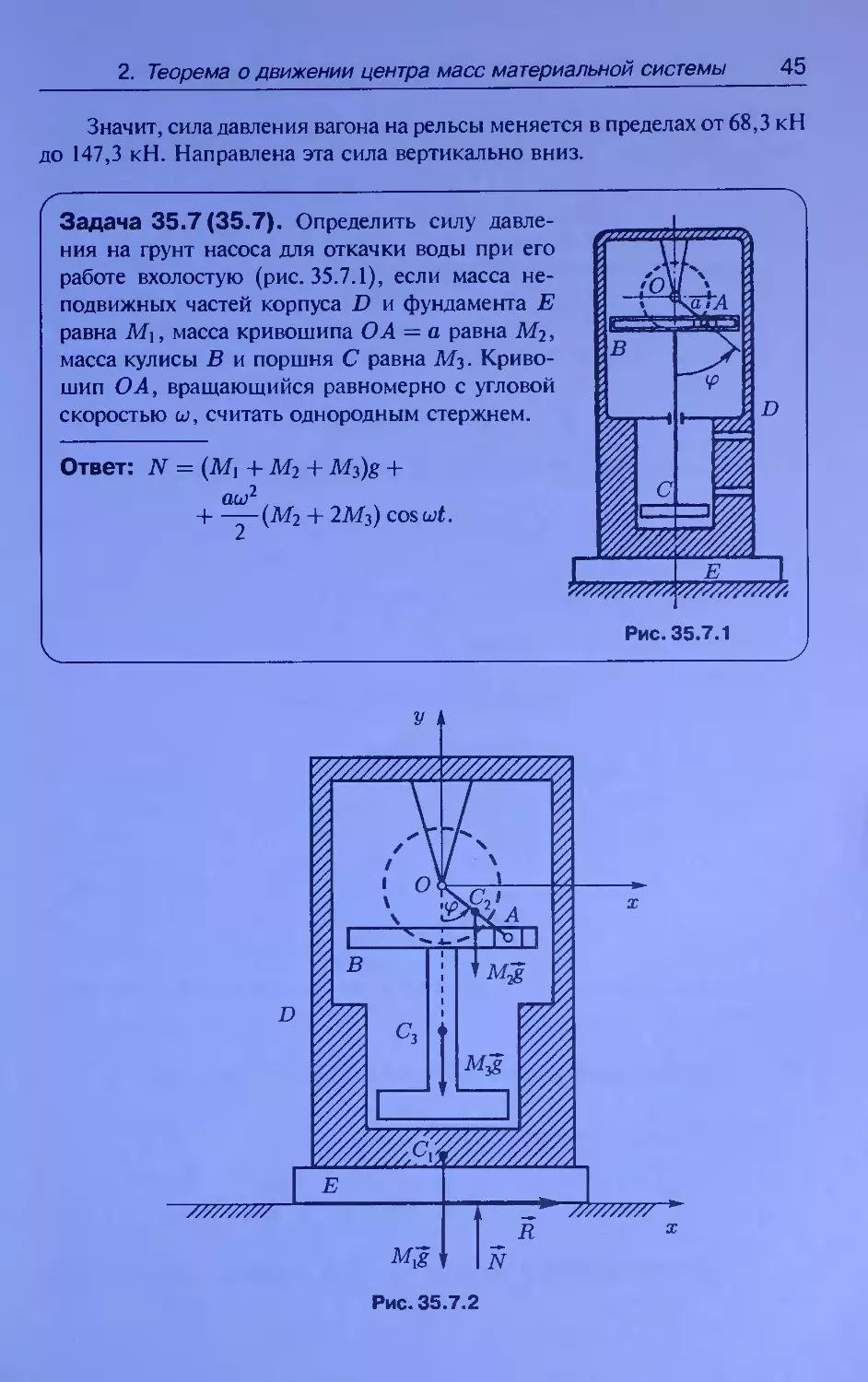
Задача 35.7 (35.7). Определить силу давле-
ния на грунт насоса для откачки воды при его
работе вхолостую (рис. 35.7.1), если масса не-
подвижных частей корпуса D и фундамента Е
равна М\, масса кривошипа О А = а равна М2,
масса кулисы В и поршня С равна М3. Криво-
шип О А, вращающийся равномерно с угловой
скоростью си, считать однородным стержнем.
Ответ: N = (Mi + М2 + M3)g +
aw2,
Ч——(М2 + 2Мз) cos art.
У
Рис. 35.7.2
46 2. Теорема о движении центра масс материальной системы
Решение. Расчетная схема — на рис. 35.7.2. Направим ось х гори-
зонтально направо и ось у вертикально вверх. Система состоит из не-
подвижных частей корпуса D и фундамента Е (центр масс в точке Cj),
кривошипа О А (центр масс в точке С2, причем OCi = CiA = а/2) и
поршня С с кулисой В (центр масс в точке Сз).
К системе приложены внешние силы: силы тяжести Mtg, Mig, M3g,
приложенные к соответствующим центрам масс; суммарная нормальная
реакция фундамента N и суммарная горизонтальная реакция фундамента R.
Согласно теореме о движении центра масс системы в проекции на
ось у имеем:
Муц = N - Mig - Mig - M3g.
Используя определение центра масс системы, запишем
Муи = mkyk = Miух + Miyi + М3у3.
к
Распишем координаты центров масс Cj, Ci и С3.
yi — const,
a a
yi = -- cos ip -- - - cos cut
Уз = const - a cos wt.
Следовательно,
У\ = 0,
a 2
yi = cosatf,
Уз = aw2 cos cot.
Внося полученные соотношения в теорему о движении центра масс,
получим:
a
М2-
ш2 cos wt + М3аы2 cos cut = N - Mtg — Mig - M3g.
Отсюда нормальная реакция
N — Mtg + Mig + M3g + aw2 cos wt
Mi
-~+M3
Искомая сила давления на грунт .Рдавл = N и направлена вертикально
вниз.
2. Теорема о движении центра масс материальной системы
47
Задача 35.8(35.8). Использовав данные предыдущей задачи, счи-
тать, что насос установлен на упругом основании, коэффициент упру-
гости которого равен с. Найти закон движения оси О кривошипа О А
по вертикали, если в начальный момент ось О находилась в положе-
нии статического равновесия и ей была сообщена по вертикали вниз
скорость г>0- Взять начало отсчета оси х, направленной вертикально
вниз, в положении статического равновесия оси О. Силами сопро-
тивления пренебречь.
Ответ: 1) При —--------ш2
М\ + Л?2 + Мз
h Vo h
хо = —х-------т cos kt + — sin kt -|—r----r cos wt,
kz — w1 к к1 — ы1
где
I с My + 2Мз aw1
к — * / ' , h ——
у М\ Т ЛТ -Мз М{ + Му -Ь Мз 2
, с >
2) При -----------------= ы
’ Ml + Му + М3
Vo h
хо = — sin wt + —t sin uit.
w 2ь)
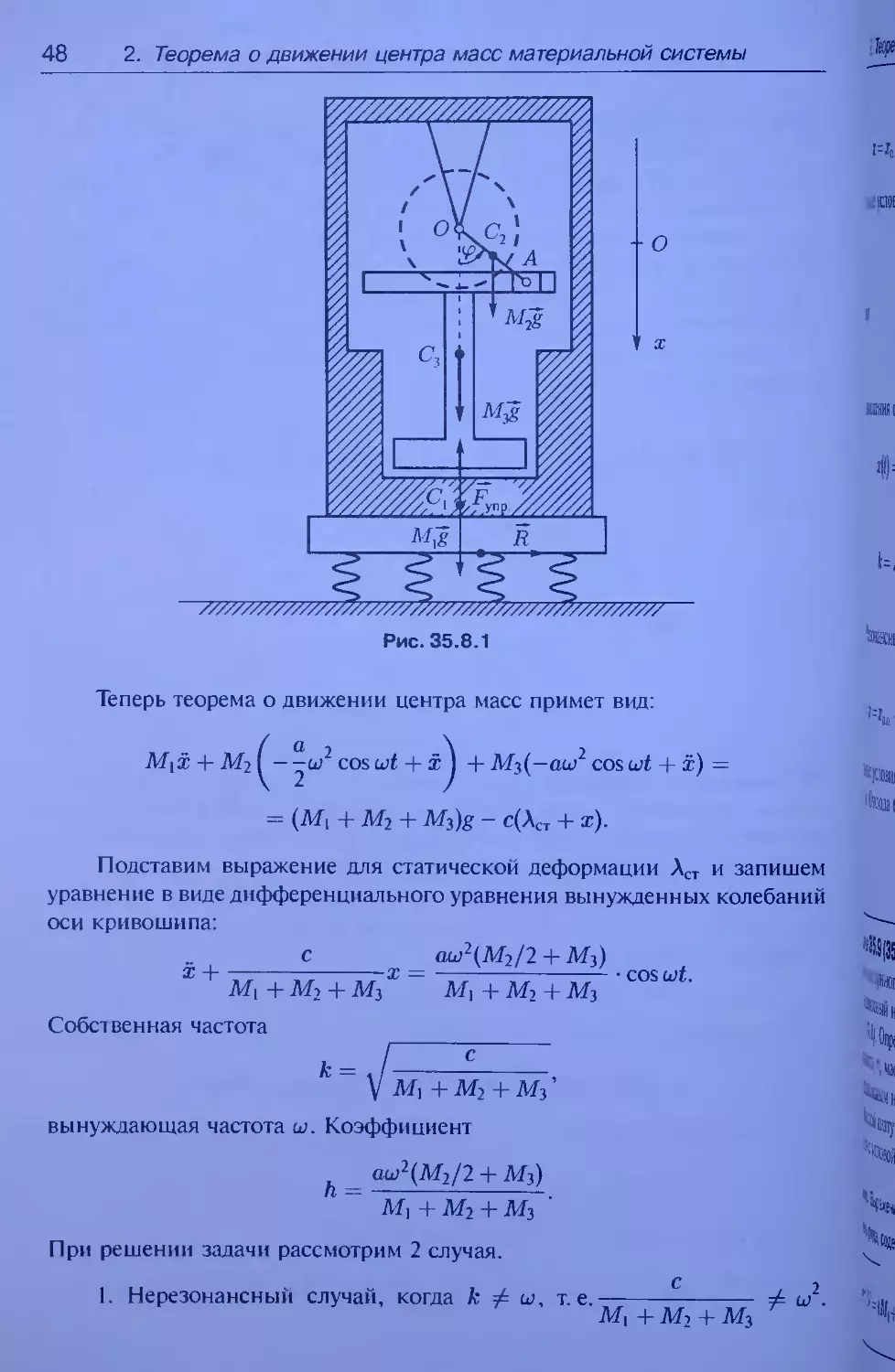
Решение. Расчетная схема — на рис. 35.8.1. Введем ось х, направ-
ленную вертикально вниз. Начало отсчета оси в положении т. О при
равновесии системы, когда с - Аст = (М\ + Му + My)g. Воспользуемся
результатами из задачи 35.7. Теперь на систему вместо нормальной ре-
акции N действует сила упругости Тупр упругого основания. Величина
^упр = с(Аст + а:). где х — координата оси О. Воспользуемся теоремой
о движении центра масс системы:
Mxu = (Mi + Му + M3)g - Fynp.
Распишем координаты центров масс С|, Су и Су:
a
Х\ = х, Ху — — cos bit + х, Хз = a cos wt + х.
Ускорения этих точек:
О 2 2
Xi = х, Ху — —ш coswt + x, хз = —аы cosbjt + x.
Распишем ускорение центра масс системы:
Е( ^2
mjtS/t = М\х + Му I cosu^ + ^
+ Мз(—аш2 cos bit + х).
к
48 2. Теорема о движении центра масс матеоиальной системы
Рис. 35.8.1
Теперь теорема о движении центра масс примет вид:
(Д Т у
— -w cos wt + х j + Mj(-aa) cos wt + x) =
= (M, + M2 + M2)g - c(ACT + x).
Подставим выражение ддя статической деформации Аст и запишем
уравнение в виде дифференциального уравнения вынужденных колебаний
оси кривошипа:
с аал(7И2/2 + 7И3)
Х + М! + М2 + Mj х м}+м2 + м3 cosut-
Собе I венная частота
к = J----- ° —,
V М\ + м2 + м2
вынуждающая частота ш. Коэффициент
ош2(М2/2 + М2)
М\ + м2 + м2
При решении задачи рассмотрим 2 случая.
1. Нерезонансный случай, когда к т. е.------------- ш2.
М\ + М2 + М2
2. Теорема о движении центра масс материальной системы 49
Тогда
® -- З-О-О.
h
= C[ sin kt + C2 cos kt H—z-- cos kt.
k2 - w2
Начальные условия: to = 0, x(0) = 0, я:(0) = v0. Отсюда имеем:
h
0 = Су + 75----7, ^0 — C\k + 0
k2 - w2
Поэтому
Vn h
Cl = ~, ^ = -77—
к к2 — w2
Закон движения оси кривошипа
Vo h h
x(t) = — sin kt-у----- cos kt + —--7 cos kt,
к к2 — w2 к2 — w2
где
h _ aw2(M2/2 + My)
M\ 4- M3 + My M\ T My T My
c
2. Резонансный случай, когда к = ш, т. е. —-—---—
М\ + М2 + Му
h /
= С sin kt + C2 cos kt -1-1 cos I wt-
2w X 2
Ж — X — Xqq
= w2. Тогда
7Г
с
2
Начальные условия: <о = 0, ®(0) = 0, i(0) = vq дают уравнения: 0 = Cj,
v0 = Ci Л. Отсюда С, = v0/k = v0/w, C2 = 0. Закон движения оси криво-
шипа
Vo h
x(t) — — sin wt 4----1 sin wt.
w 2w
Задача 35.9 (35.9). Ножницы для резки металла состоят из криво-
шипно-ползунного механизма О АВ, к ползуну В которого прикреп-
лен подвижный нож. Неподвижный нож укреплен на фундаменте С
(рис. 35.9.1). Определить давление фундамента на грунт, если длина
кривошипа г, масса кривошипа М\, длина шатуна I, масса ползуна
В с подвижным ножом М2, масса фундамента С и корпуса D равна
Му. Массой шатуна пренебречь. Кривошип О А, равномерно враща-
ющийся с угловой скоростью w, считать однородным стержнем.
Указание. Выражение у 1 - (г/Г)2 sin2 wt следует разложить в ряд и отбросить
все члены ряда, содержащие отношение т/l в степени выше второй.
2
rw
Ответ: N = (Mi+My+Myjg^——
(M\+2M2) coswt+2M2~ cos 2wt .
50 2. Теорема о движении центра масс материальной системы
lie
Рис. 35.9.1
"1ГО
(И:
й
Решение. Расчетная схема — на рис. 35.9.2. Введем ось х, направ-
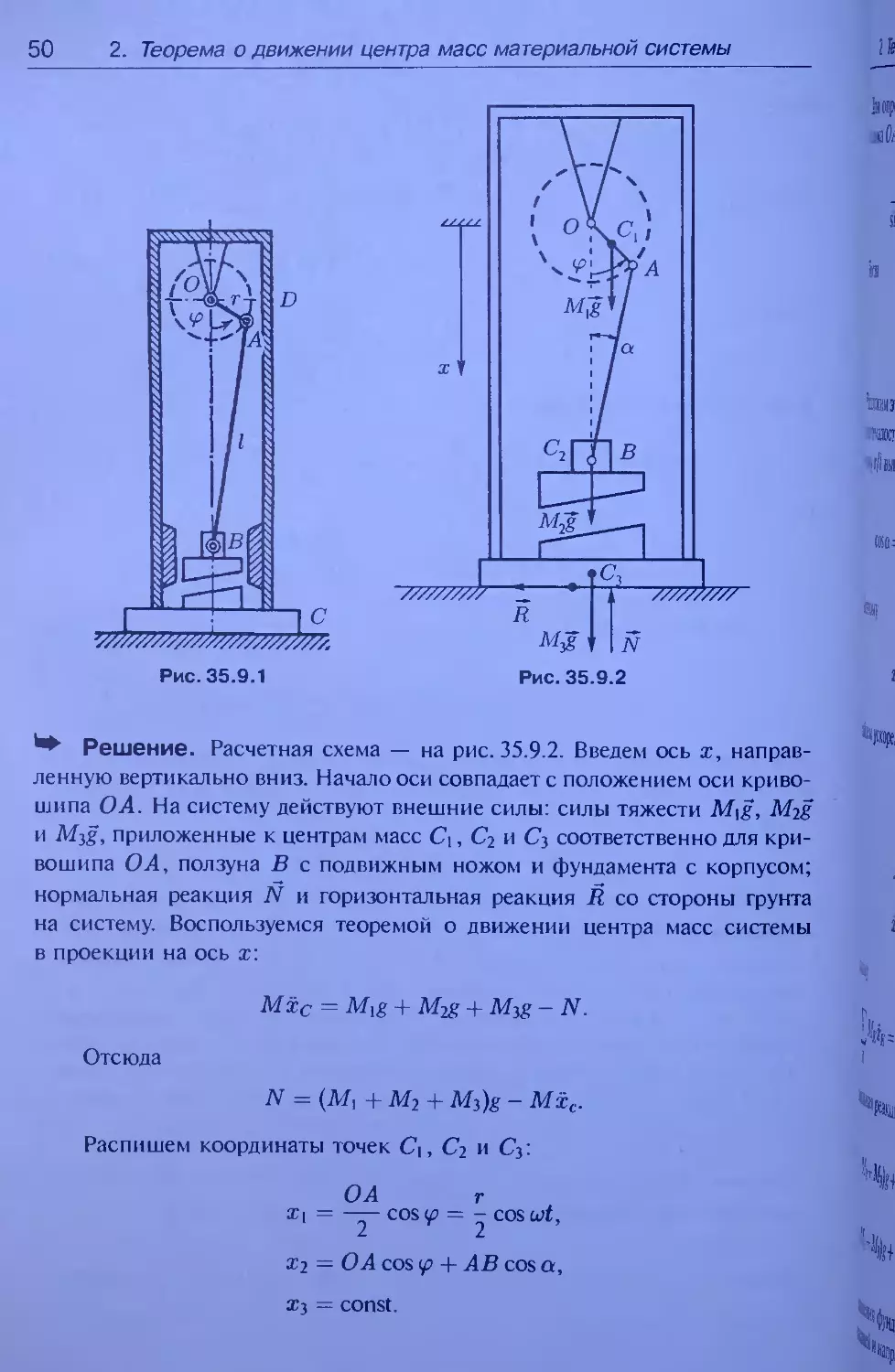
ленную вертикально вниз. Начало оси совпадаете положением оси криво-
шипа ОА. На систему действуют внешние силы: силы тяжести Myg, M2g
и M2g, приложенные к центрам масс Су, С2 и С$ соответственно для кри-
вошипа О А, ползуна В с подвижным ножом и фундамента с корпусом;
нормальная реакция N и горизонтальная реакция R со стороны грунта
на систему. Воспользуемся теоремой о движении центра масс системы
в проекции на ось х:
Mie = Myg + M2g + M2g - N.
Отсюда
N — (Му + М2 + M2)g - Мхс.
Распишем координаты точек Cj, С2 и Су.
Ча
О А г
Ху = cos = - cos wt,
х2 = О A cos + АВ cos а,
х2 — const.
ч
2. Теорема о движении центра масс материальной системы
51
Для определения угла а воспользуемся теоремой синусов для тре-
угольника ОАВ-.
r I
sin a sin 92
г т
sin a — - sin 92 = - sin ut.
I I
Тогда
cos a = 1 — sin2 a =
T2
1 - — sin2 ut.
Разложим это выражение в ряд. учитывая предположение в указании
к задаче о малости отношения т/1,и отбросим все члены ряда, содержащие
величину т/l выше второй степени:
1
2
cos а =
1 -
2 -11/2
sin2 ut
)2
2
sin ut.
Поэтому
Г i ( r
x2 = r cos ut +1 1 - - I -
2 -1
2
I sin ut .
Найдем ускорения центров масс С\, С2 и Су.
Г 2
Ж1 =-----U COS ut,
1
г2
х2 = -ru cos ut —-u cos lut,
I
х2 = 0.
Поэтому
Мхс = ^2
г 2 э г2 2
MrXk = -Mi-u cosut-M2ru cosut — М2—u coslut,
к 2 1
Нормальная реакция со стороны грунта, следовательно, равна
г 2 2 г2 2
N = (Mj + М2 + M2)g+Mi ~U COSUt + M2TU coswf + M2~u coslut —
r
ru2 Г r
= (Mi +M2 + Mi)g+ (Mi+lM2)cosut + lM2~ coslut .
I
Сила давления фундамента на грунт совпадает по величине с нор-
мальной реакцией и направлена вертикально вниз.
52
2. Теорема о движении центра масс материальной системы
Задача 35.10(35.10). Электрический мотор массы М\ установлен
без креплений на гладком горизонтальном фундаменте; на валу мотора
Рис. 35.10.1
под прямым углом закреплен одним концом
однородный стержень длины 21 и массы М2,
на другой конец стержня насажен точечный
груз массы Му, угловая скорость вала равна ш
(рис. 35.10.1).
Определить: 1) горизонтальное движение
мотора; 2) наибольшее горизонтальное уси-
лие R, действующее на болты, если ими будет
закреплен кожух электромотора на фунда-
менте.
Ответ: 1) Гармонические колебания с амплитудой
и периодом 2тг/а>;
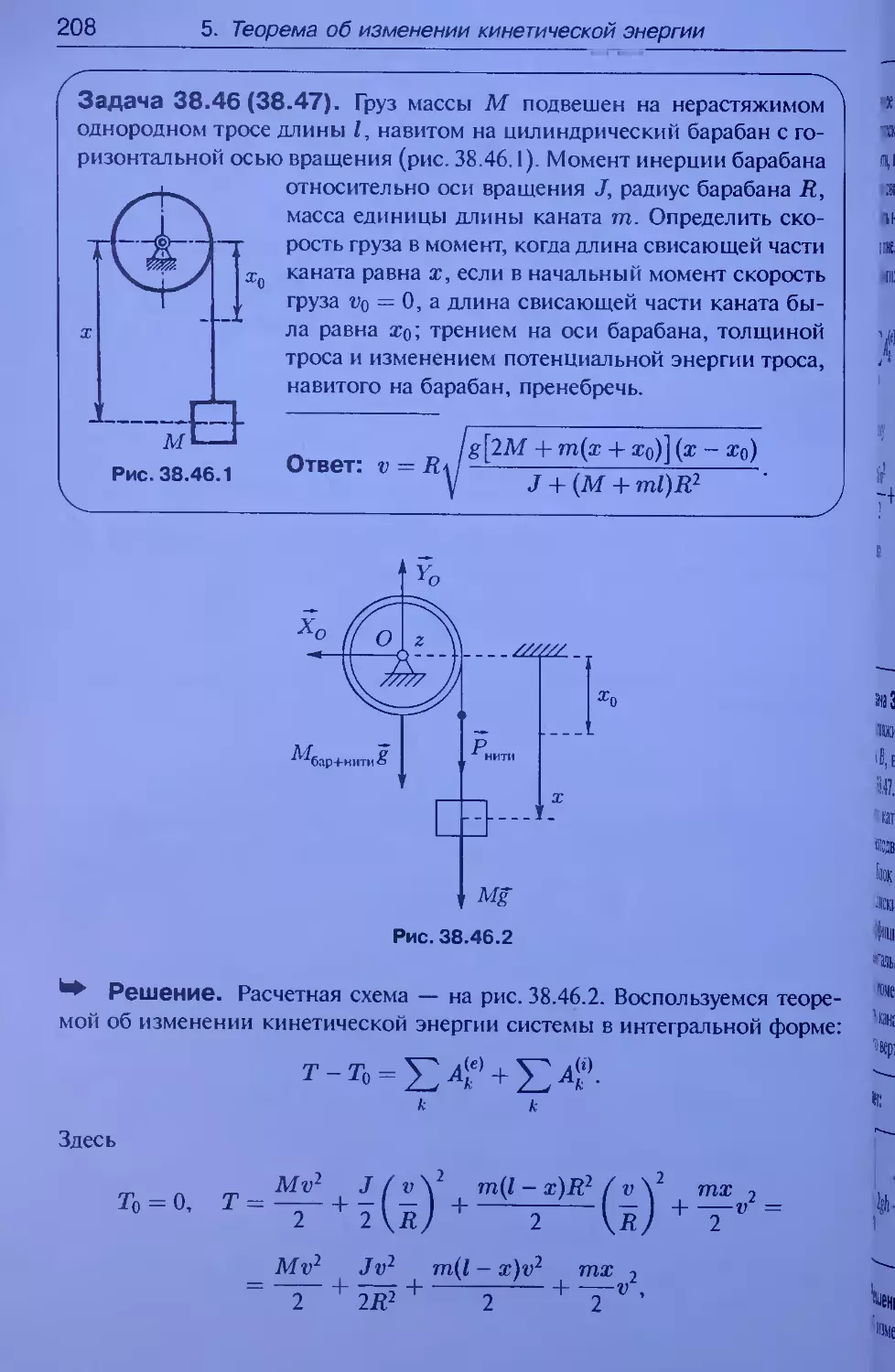
2) R = (М2 + 2М1)1ы2.
1(М2 + 2М3)
М\ + м2 + м3
Решение. Рассмотрим часть 1. Расчетная схема — на рис. 35.10.2.
Мотор установлен на гладком фундаменте без креплений. На механиче-
скую систему действуют внешние силы: силы тяжести Mig, Mig и M3g,
приложенные в центрах масс мотора (т. Cj), стержня (т. С'2) и точечно-
го груза (т. Сз), а также нормальная реакция гладкого фундамента N.
Введем оси координат х и у. Начало этой системы координат выберем
У
Wi
Ч
'ш
Ч
Рис. 35.10.2
2. Теорема о движении центра масс материальной системы
53
в положении центра масс мотора (точка Cj) в момент t — 0, когда угол
— ait|<=о = 0. Воспользуемся теоремой о движении центра масс системы
в проекции на горизонтальную ось х:
к
Так как
V Fkx = °’
к
то Мхе = 0. Отсюда Mie = const, т. е. скорость центра масс системы
вдоль оси х постоянна. Пусть в начальный момент времени система
покоилась, тогда Mie = 0- Отсюда Мхц = const. Значит центр масс
системы не перемещается вдоль оси х при движении отдельных ее частей.
Выпишем координаты центров масс С], С2 и Сз как функции вре-
мени:
= Xi,
Xi(t) = Х[ + АС2 cos <р = Ж| + Z cos art,
X)(t) = х\ + AC) cos ip = S| 4- 21 cos ait.
Поэтому
Mxc(t) = m^x^t) = M\X\ + М2(34 + I cos ait) + M)(xi + 21 cosait).
к
Так как Mxc(t) = const, то Mxc(t) = Mxc(0). Поэтому
M\Xi -I- М2(з;| +1 cosait) + Мз(;Г1 + 21 cosait) = M2I + M)2l.
Отсюда получаем, что горизонтальное движение мотора осуществля-
ется по закону
x\(t) =
1(М2 + 2М3)
+ М2 + М)
cos ait,
т. е. представляет собой гармонические колебания.
Рассмотрим часть 2. Расчетная схема — на рис. 35.10.3. Кожух мотора
закреплен на фундаменте болтами. Тогда внешними силами будут: силы
тяжести, вертикальная результирующая реакция со стороны болтов и фун-
дамента R' и горизонтальная результирующая сила со стороны болтов R.
Систему координат свяжем с неподвижным кожухом электромотора. Тео-
рема о движении центра масс системы в проекции на ось х принимает
вид: Мхе = R- В этом случае
Мхс = AffcXfe = М\ • 0 + M2l cos ait + M)2l cos ait = ЦМ2 + 27Из) cos ait.
k
54 2. Теорема о движении центра масс материальной системы
Рис. 35.10.3
Поэтому Мхе = + 2M3)u)2 cos art. Значит горизонтальная ре-
акция R — —l(M2+2M3)u2 cos ut. По такому же закону меняется горизон-
тальное усилие на болты со стороны кожуха мотора. Поэтому наибольшее
горизонтальное усилие на болты равно (М2 4-2Мз)/ш2.
Задача 35.11 (35.11). По условиям предыдущей задачи вычислить
ту угловую скорость и вала электромотора, при которой электромотор
будет подпрыгивать над фундаментом, не будучи к нему прикреплен
болтами.
Ответ: и >
(M\ + М2 + A/3)g
(M2 + 2M3)l
Решение. Расчетная схема — на рис. 35.10.2. Запишем теорему о дви-
жении центра масс системы в проекции на вертикальную ось у:
Мус => Мус = N - Myg - M2g - M3g.
к
Распишем координаты у}, у2 и у3 центров масс С2 и Ср
У\=®, Ут = ЛС| + I sinwZ, уз = ACi + 21 sin ut.
Поэтому
Мус — У М^Ук = -M2lu2 sin ut - M32lu2 sin ut.
к
Подставим это выражение в теорему о движении центра масс и вы-
разим нормальную реакцию
N = (М| + М2 + M3)g — ЦМ2 4- 2M3)u2 sin ut.
2. Теорема о движении центра масс материальной системы
55
Условие подпрыгивания мотора: 7Vmin < 0, т.е.
(Mi + М2 + M3)g - 1(М2 + 2М3)о>2 • 1 < 0.
Отсюда w >
(Ml + М2 + M3)g
1(М2 + 2М3)
Задача 35.12 (35.12). При сборке электромотора его ротор В был
эксцентрично насажен на ось вращения С) на расстоянии С\С2 = а,
где С\ — центр масс статора .4, а С2 — центр масс ротора В. Ротор
равномерно вращается с угловой скоростью w (рис. 35.12.1). Электро-
мотор установлен посередине упругой балки,
статический прогиб которой равен А; М\ —
масса статора, М2 — масса ротора.
Найти уравнение движения точки С\ по
вертикали, если в начальный момент она на-
ходилась в покое в положении статического
равновесия. Силами сопротивления прене-
бречь. Начало отсчета оси х взять в положе-
нии статического равновесия точки Gj.
Рис. 35.12.1
Ответ: 1) При y/g/b. w
w h h
Xi =-----z----z sin kt -|—z--z sin wt,
к к2 - w2 к2 - w2
где к = \/g/A, h
M2 2
-------aw .
Mi + M2
h h
x\ = —z- sin wt---1 cos wt.
2w2 2w
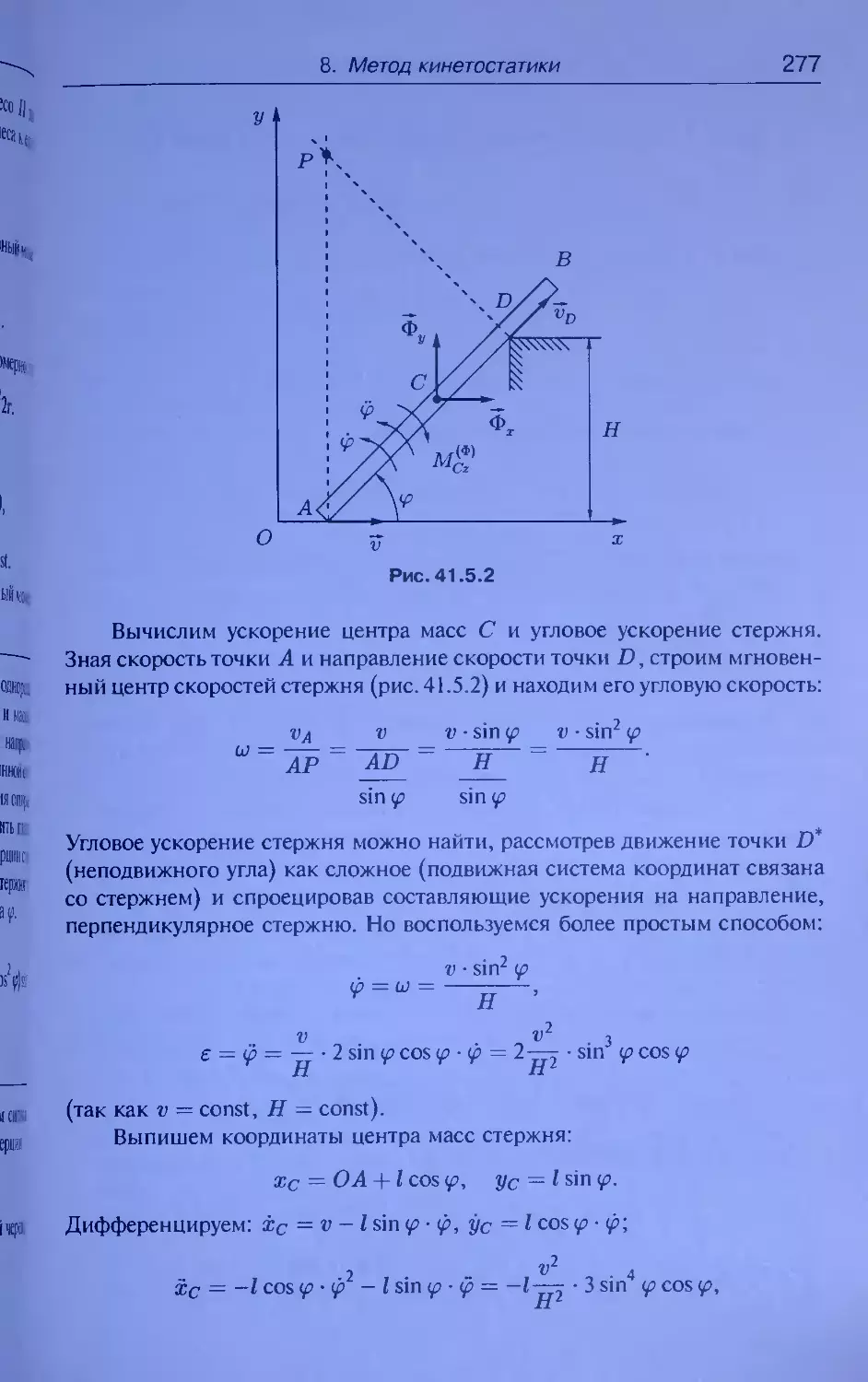
Решение. Расчетная схема представлена
на рис. 35.12.2, где х — вертикальная коор-
дината точки G], отсчитываемая от положения
статического равновесия. На систему вдоль оси
х действуют три внешние силы: Mig, М^, Fynp.
Пусть х — смещение (вниз) точки Ci от ста-
тического равновесия. Тогда Fynp = —с(А + ж),
где А — статический прогиб балки. Причем,
по условию сА = (Mi + M2)g (статическое рав-
Рис. 35.12.2
56 2. Теорема о движении центра масс материальной системы
новесие). Отсюда II®
(М, + M2)g
С~ А
Запишем уравнение для движения центра масс системы вдоль оси х. Ко-
ордината по х центра масс системы дается выражением:
хс — —-------Га: • М] + (х + a sin wt) М21.
Mi + М2 де
Уравнение движения центра масс по оси х:
(Мх + М2)хс = (М] + M2)g - с(Д + х). ___
Из этих уравнений получим, учитывая, что W
Mil
(М,+М2)г = сд „ W
А 3.1!)
А .ли
g М2 2
=> х + —х = —--------—aw sin wt. e
А М| + М2 *
2 S , M2aw2
Обозначая к = —, п = ~м + м ’ ®Удем искать решение в стандарт- в1=
ном виде:
x(t) = A sin wt + В sin kt + С cos kt, при k w.
Jim
n h
Подставляя в уравнение, получим А = —--------- Константы В и С
к1 - w1
выбираем так, чтобы удовлетворить начальным условиям х(0) = ж(0) = 0.
w h
Тогда получим С = 0, В = -- • —------- Итак: ih
к к2 - w2 Ш
ш h • ., h
х(ч — --г • уз----у sin kt + —----- sin wt.
к к1 -w1 k2 - w2
-®1)4
Посмотрим теперь, что будет при к —> ш. Положим к — w + с. Тогда
получим:
,, х w h h
x(i^ ---------;----;—т sin (w + £)« + ---------- sin wt =
w + € 2wc + £2 2we + c2
_ -uh sin + £)£] + h(w + £) sin wt %
(2wc + £-2)(w + £)
2. Теорема о движении центра масс материальной системы 57
Используя правило Лопиталя, получим:
-wht cos |(w + e)fj + h sin wt
x(t) = lim x(t, c) = lim —---:--------—— , . —
V 7 r->0 ' 7 r->0 2wc + €2 + (w + f)(2w + 2c)
-wht cos wt + h sin wt
~ 2w2 ’
Таким образом, при к = w, т.е. \/g/A = w, имеем резонансное ре-
шение, представляемое формулой:
, ч h ht
x(t) = —=• sin wt - — cos wt.
v ' 2w2 2w
Задача 35.13(35.13). Электрический мо-
тор массы М\ установлен на балке, жесткость
которой равна с. На вал мотора насажен груз
массы М2 на расстоянии I от оси вала. Уг-
ловая скорость мотора w = const. Определить
амплитуду вынужденных колебаний мотора
и критическое число его оборотов в минуту,
пренебрегая массой балки и сопротивлением
Рис. 35.13.1
движению.
M2lw2 30 / с
Ответ: a =--------------г, пКГ1 = —. /-------
С - (М, + M2)w2 Р 7Г V Ml + М2
Решение. Воспользуемся результатом предыдущей задачи 35.12, из
которой возьмем только вынужденную компоненту:
h
72-----2 sin
к2 - w2
M2lw 2 S . „ , к
где h =-------, к = —, А — статический прогиб балки, причем:
М| + М2 А
сД = (Mi + M2)g к2 =
Mi + М2
Тогда получим:
M2lw2 1 M2lw2
Лвын ~ Mi +М2 ’ g J _ с - (Mi + M2)w2 ’
M] +м2
Критические обороты мотора получаются тогда, когда знаменатель
обращается в нуль, т.е. 4ВЬ|Н -> оо. Таким образом,
/ с а?кр • 60 30шкр
Шкр“ УМ.+М/ Пкр“ 2л “ 7Г '
58
2. Теорема о движении центра масс материальной системы
Задача 35.14 (35.15). На рис. 35.14.1 изображена крановая тележка
А массы М\, которая заторможена посередине балки BD. В центре
масс С\ тележки подвешен трос длины I с привязанным к нему грузом
С2 массы М2. Трос с грузом совершает гармонические колебания
в вертикальной плоскости. Определить: I) суммарную вертикальную
реакцию балки BD, считая ее жесткой; 2) закон движения точки С|
в вертикальном направлении, считая балку упругой с коэффициентом
упругости, равным с.
В начальный момент балка, будучи недеформированной, находи-
лась в покое в горизонтальном положении. Считая колебания троса
малыми, принять: sin 92 ~ у>, cosy? « I. Начало отсчета оси у взять
в положении статического равновесия точки Cj. Массой троса и раз-
мерами тележки по сравнению с длиной балки пренебречь.
Ответ: I) Ry = (Mt + M2)g; 2) точка С\ совершает свободные коле-
(М} + M2)g / ~
бания по закону щ =----------cos . /------- t.
У с V Mt+M-i
Решение. Расчетная схема — на рис. 35.14.2, где ось у направлена
вертикально вниз, ось х — по горизонтали вправо. Начало отсчета оси у
размещаем в положении статического равновесия точки Ct, при этом
деформация балки будет Д, причем: с-Д = (Mt + M2)g. Далее пусть у{ —
координата точки Ct, отсчитываемая вниз от ее статического равновесия.
Тогда на систему (тележка + маятник) по оси у действуют силы: M\g,
M2g, Fylip. Далее имеем: ус, = yt, Ус. = У\ -Hcosy>. Применяем теорему
Рис. 35.14.2
2. Теорема о движении центра масс материальной системы 59
о движении центра масс этой системы вдоль оси у:
(Mi + М2)ус = Mig + M2g - с(Д + yi),
где
Miyi + M2(yi +1 cos tp)
Ус = Mi +M2 '
Подставляя ус и учитывая соотношение с- Д = (Mi + M2)g, получим:
Miy{ +M2yi + M2l(cos tp)" = -cyi =>
•• 2 M2l .
где уг = C .
Mi + M2
Так как в начальный момент балка была недеформирована, то
yi(0) = -& =--------------.
Кроме того, если движение началось из состояния покоя, то t/i(0) = 0.
Далее имеем
(cos р)~ — —(sin <р • ф + cos tp • ф2) ~ 0,
если колебания маятника малы. В результате получим уравнения:
.. । 2 п /пх + M2)g . „
У1 + w yi = 0, 2/1(0) =----------, 2/1(0) = 0,
решение которого ищем в виде:
yi (t) = A sin wt + В cos wt.
(Mi + M2)g
Учитывая начальные условия, получим: А = 0, В =------------. Тогда
с
решение:
(Mi + M2)g f I с \
yi(t) =------------cos A/ —-----— • t ).
c \\ Mi+M2 J
Теперь положим, что балка абсолютно жесткая. Тогда уравнение (1)
для движения центра масс системы «тележка + маятник» примет вид:
(Mi + М2)ус = Mig + M2g - Ny,
где
—Mi Д + М2(—Д +1 cos <р)
Ус ~ 7И, +М2 ’
Ny — нормальная реакция балки, равная, очевидно, сумме нормальных
реакций в шарнирах В и D.
60
2. Теорема о движении центра масс материальной системы
Тогда получим:
Ny = (Mi + M2)g - M2Z(cos у)"
Предполагая колебания малыми, опять получим (cos^)”~ 0, т.е.
Ny = (М( + M2)g.
^Задача 35.15(35.16). Сохранив данные предыдущей задачи и счи-
тая балку BD жесткой, определить: I) суммарную горизонтальную
реакцию рельсов; 2) в предположении, что тележка не заторможена,
закон движения центра масс С\ тележки А вдоль оси х.
В начальный момент точка С\ находилась в покое в начале отсчета
оси х. Трос совершает колебания по закону <р — cosotf.
Ответ: 1) Rx = -M2l(pow2 cosotf; 2) точка G совершает колебания
М2
с амплитудой —---—Z^o и круговой частотой ш по закону
м2
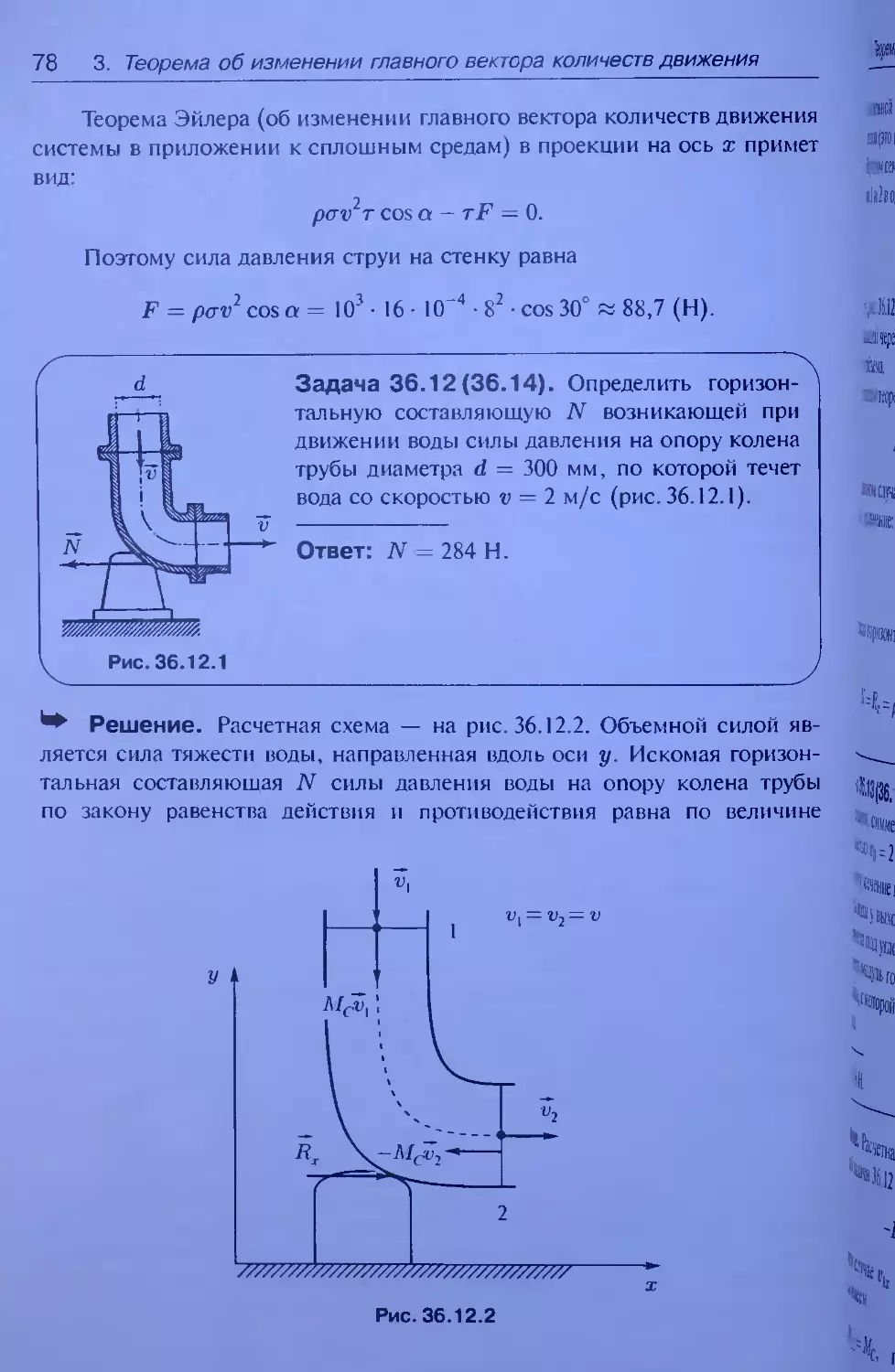
Решение. Используем схему и результаты решения предыдущей
задачи 35.14. Если тележка заторможена, то координата центра масс
системы «тележка 4- маятник», отсчитанная от точки С\, будет:
М2 М21<р
Хс =----------• I sin ~--------.
+ М2 Mt + М2
Тогда теорема о движении центра масс этой системы вдоль оси х дает:
/., , ит\- яг I ’ М2 W2M2l<Po cos ut
(Ml + М2)хс = NX => Nx = —----------=------------2-™------,
Mt + M2 Mi + M2
где Nx — суммарная горизонтальная реакция шарниров В и D.
Пусть тележка не заторможена, а х, — координата точки С\, отсчи-
танная от начального ее положения Тогда
Хс = Mi + м2 + М^Х[ +1 sin ‘
Предполагая, что вдоль оси х отсутствуют силы сопротивления,
получим из теоремы о центре масс вдоль оси х, что
~ I ЛТ 1Х1®1 + ^2(®1 + 1ф cos ^)] = const =
ivl 1 “Г 1V12
2. Теорема о движении центра масс материальной системы 61
= ®с(0) = 77---7Г [Л/|± 1 (°) + (°) + W) cos Ро)] =
М\ ~г М.2
Ml
=--------- l(-wow sin wt
Mi + Mi v
• cos — 0 =>
<=o
ад
а"(', = -ЙГйй*’с“*’
Mil
xl(t)-xl(0) = - (sin <p - sin po) =
1VL । -J- 1V12
Mil r , x •.
= “ nzf ЛТ l.sir cos “ Sin ^°J ~
1V1\ “Г 1VL2
Mil M2l<p0
~ —------— (v’o “ Pocos ut) = —-------— (1 - cos wt).
M\ + М2 M\ + М2
А так как Ж|(0) = 0, то получим ответ
Milipti
Задача 35.16(35.17). На средней скамейке лодки, находившейся
в покое, сидели два человека. Один из них, массы М\ = 50 кг, пе-
реместился вправо на нос лодки. В каком направлении и на какое
расстояние должен переместиться второй человек массы Mi — 70 кг
для того, чтобы лодка осталась в покое? Длина лодки 4 м. Сопротив-
лением воды движению лодки пренебречь.
Ответ: Влево на корму лодки на расстояние 1,43 м.
Решение. Расчетная схема — на рис. 35.16.1. Пусть в начале центр
масс системы находился в точке О (где в начальный момент находились
оба человека). В данном случае под системой мы имеем в виду систему
Рис. 35.16.1
62
2. Теорема о движении центра масс материальной системы
«лодка 4- человек М\ + человек М2». Так как горизонтальных внешних
сил, по предположению, нет, то при любых перемещениях людей в лодке
центр масс этой системы останется в точке О. Пусть — координата
центра масс лодки до перемещения. По условию центр масс лодки должен
остаться в точке х0 и после перемещения
i лт i тПГ Солодки ‘ + Mi 0 + М2 ‘ О —
Млодки + Ml + М2
1 / ч
ТТ П йТ i и/г Солодки ' "Т Mi • 7. + М2 • х),
-^юдки + Ml + М2 4
где Млодки — масса лодки, х — искомое перемещение второго человека
массы М2. Отсюда:
„Mi 50 10
х = -2 • — = —2— =---= -1,428 (м).
М2 70 7 v '
Знак «минус» говорит о том, что перемещаться надо влево (если, ко-
нечно, человек массы Mt пошел вправо).
Задача 35.17(35.18). На однородную призму А, лежащую на го-
ризонтальной плоскости, положена однородная призма В\ попереч-
ные сечения призм — прямоугольные треугольники, масса призмы А
Рис. 35.17.1
втрое больше массы призмы В. Предполагая,
что призмы и горизонтальная плоскость иде-
ально гладкие, определить длину I, на кото-
рую передвинется призма А, когда призма В,
спускаясь по А дойдет до горизонтальной
плоскости.
_ a - Ь
Ответ: I =----
4
Решение. Так как вдоль горизонтали х на систему А + В не дей-
ствует внешних горизонтальных сил, то центр масс этой системы не пе-
ремещается вдоль оси х. Пусть жл(0), жв(0) — начальные ж-координаты
центров масс призм. Тогда ж-координата центра масс системы Л+В будет:
Жс.(0) =--------[тлжд0) + твжв(0)].
шд + тв
Пусть хо — перемещение призмы А, когда В достигла горизонталь-
ной плоскости. При этом вдоль х относительно призмы А, эта призма В
переместится на расстояние с = а — Ь. Абсолютное перемещение призмы В
2. Теорема о движении центра масс материальной системы 63
составит Ад = a - b + Xq. Таким образом новая координата по х центра
масс системы А + В будет:
х*с = ---!---[тА (агл(О) + х0) + тв (zB(0) + а - Ь + х0)] •
+ тв
Приравнивая Жс(0) = Хс, получим:
тпл;гд(0) + тпвхв(0) — тАхА(0) + тАхо + твхв(0) + тв(а - b + хо) =>
=> О = тАхо + тв(а-Ь + хо) =>
а - b а - Ь
(тл + тв)х„=.-тг(«-6) =>• '
Задача 35.18(35.19). По горизонтальной товарной платформе дли- I
ны 6 м и массы 2700 кг, находившейся в начальный момент в покое,
двое рабочих перекатывают тяжелую отливку из левого конца плат-
формы в правый. В какую сторону и насколько переместится при этом
платформа, если общая масса груза и рабочих равна 1800 кг? Силами
сопротивления движению платформы пренебречь.
Ответ: Налево на 2,4 м.
Решение. Расчетная схема — на рис. 35.18.1. Пусть L = 6 — длина
платформы. Центр масс системы «М + т» остается на месте вдоль оси х,
так как отсутствуют внешние силы вдоль горизонтали х, а движение нача-
лось из состояния покоя. Пусть xm(fi), хм(0) — начальные х-координаты
центров масс людей с отливкой и платформы. Тогда а?-координаты центра
масс в начальный момент:
М0) = —Г77[тХт(°) + Мхм(°)1
т + М
Пусть 2?о — перемещение платформы после того, как т перемести-
лось относительно платформы на расстояние L. Тогда абсолютное пере-
М (платформа)
Рис. 35.18.1
64 2. Теорема о движении центра масс материальной системы
мешение массы т составит Д = L + хц. Новая координата центра масс
системы будет:
Х*с = М~+т +L + Xo) +м(МО) + ж0)].
Приравнивая хс(0) и Хс, получим:
тхт(0) + Мхм (0) = тхт(0) + mL + тхо + MxM(G) + Мх0 =>
=> 0 = mL + Хо(т + М) =>
т 1800 „ 2
=> хо =----------L --------6 =-----6 = -2,4 м.
т + М 4500 5
Знак «минус» говорит о том, что перемещение платформы пойдет
влево (если т перемещается вправо относительно платформы!).
A
M,
90е
30°
—| W
Рис. 35.19.1
Задача 35.19(35.20). Два груза М\ и М2,
соответственно массы М\ и М2, соединенные
нерастяжимой нитью, переброшенной через
блок А, скользят по гладким боковым сто-
ронам прямоугольного клина, опирающего-
ся основанием ВС на гладкую горизонталь-
ную плоскость. Найти перемещение клина
по горизонтальной плоскости при опускании груза М\ на высоту
h = 10 см. Масса клина М = 4ЛД = I6M2; массой нити и блока
пренебречь.
Ответ: Клин переместится вправо на 3,77 см.
Решение. Расчетная схема — на рис. 35.19.2. Пусть перемещение
клина АВС по оси х составляет zq. Относительное перемещение грузов
М\ и М2 по оси х (относительно клина) составляет:
Aix = -h • etg 30°,
Дгх = ~h2 • ctg60°.
Рис. 35.19.2
2. Теорема о движении центра масс материальной системы 65
Кроме того, так как нить нерастяжима, то
h h2 sin 60°, z—
Д5 =-------=-----— => h2 =------------h = V3 h.
sin 30° sin 60° sin 30°
Абсолютные перемещения грузов Mi и M2 по оси х будут:
Xi — Д1Х + х0 = -h- etg 30° + xQ,
Отсюда
Х\ = -h • V3 + Xq,
3
Смещение центра масс по оси х таково:
1
.. nr nr [Mxo + Mt(-h-V3 + xQ) +M2(-h + x0)] = Дх.
M + Mi + M2 L
Но так как по горизонтали на систему не действуют внешние силы, то
Mi \/3 + М2 4М2 х/з + М2
М + Mi + М2 \6М2 + 4Л42 "Г М2
4v/3 + l .
=--------h = 3,775 (см).
21 V 7
Дж = О
Задаче. 35.20(35.21). Три груза массы М\ = 20 кг, М2 = 15 кг
и М2 = 10 кг соединены нерастяжимой нитью, переброшенной че-
рез неподвижные блоки L и N. При опускании груза Mi вниз груз
М2 перемещается по верхнему основанию четырехугольной усеченной
пирамиды ABCD массы М = 100 кг вправо, а груз М2 поднимается
по боковой грани АВ вверх (рис. 35.20.1). Пре-
небрегая трением между усеченной пирамидой
ABCD и полом, определить перемещение усе-
ченной пирамиды ABCD относительно пола,
если груз Mi опустится вниз на 1 м. Массой
нити пренебречь.
L A/W\ М, N —д
с :зм' D
Рис. 35.20.1
Ответ: Влево на 14 см.
Решение. Расчетная схема — на рис. 35.20.2. Определяем отно-
сительные s-перемещения грузов Mi, М2, М2 (относительно пирамиды
ABCD). Имеем Д13; = 0, &2х = hi, Дзж = hi cos60. Пусть xq — переме-
щение пирамиды. Тогда абсолютные смещения по х грузов Mi, М2, Му.
hi
Xi — 0 + xq, х2 — hi + а?о, х3 — xq Ч—
66
2. Теорема о движении центра масс материальной системы
Рис. 35.20.2
Тогда перемещение центра масс этой системы по оси х составит:
1
Лг =----------------
М + М\ + м2 + м3
Mxq + М}Х0 + M2(h\ + жо) + М3
Но так как внешних горизонтальных сил, действующих на систему
«М + М} 4- М2 + М3», нет, то Az = 0 =>
1 / , М3\ 15 + 5
ж(| =----------------- Ат2 Ч---I hi =------------------ I -
М + Mi + М2 + М3 \ 2 ) 20+15+10+100
20 4
= — = — = 0,1379 (м) » 14 (см).
1 Л Ч л(1 ' ' ' '
Задача 35.21 (35.21). Подвижной поворотный кран для ремонта
Рис. 35.21.1
уличной электросети установлен на автомашине массы I т. Люлька
К крана, укрепленная на стержне L, может поворачиваться вокруг
горизонтальной оси О, перпендикулярной плоскости рисунка. В на-
чальный момент кран, занимавший горизон-
тальное положение, и автомашина находи-
лись в покое. Определить перемещение неза-
торможенной автомашины, если кран повер-
нулся на 60°. Масса однородного стержня L
длины 3 м равна I00 кг, а люльки К — 200 кг.
Центр масс С люльки К отстоит от оси О
на расстоянии ОС = 3,5 м. Сопротивлением
движению пренебречь.
Ответ: Направо на 32,7 см.
Решение. Расчетная схема — на рис. 35.21.2. Пусть жо — перемеще-
ния машины (по ж). Относительные (по ж) перемещения (относительно
машины) точек С\ и С2:
Ас, = -ОС} • (1 - cos а), Дс2 = -ОС2 (1 - cos а).
2. Теорема о движении центра масс материальной системы
67
Рис. 35.21.2
Тогда абсолютные перемещения:
хС1 = а?о “ ОС\ • (1 - cos а), хСг = х0 - ОС2 • (1 - cos а).
Перемещение центра масс системы по оси х:
= «л- , ----+Г 1маХо + Мк (®0 - ОС2 (1 - cos а)) +
МА + Мк + ML L
+ ML(x0 - ОСХ (1 - cosa))].
Но так как на систему в горизонтальном направлении не действуют
внешние силы, то
Дж = О
1 - cos a , ___ _________,
Х° = ~мт—Г~мт—I ЛТ ’ + ‘ ~
Ма + мк + ML
1-0/2)
1000 + 200+ 100
-(200-3,5+ 100- 1,5) =
0,5 • 850
1300
425
1300
= 0,3269 (м) = 32,69 (см).
3. Теорема об изменении главного вектора
количеств движения материальной системы. Приложение
к сплошным средам (§ 36, [10])
Задача 36.1 (36.1). Определить главный век-
тор количеств движения работающего редуктора
скоростей, изображенного на рис. 36.1.1, если
центры тяжести каждого из четырех вращаю-
щихся зубчатых колес лежат на осях вращения.
Ответ: Главный вектор количеств движения
равен нулю.
Рис. 36.1.1
Решение. По определению главный вектор количеств движения ре-
дуктора скоростей
4
Q = 52
Л=1
где — скорость центра масс зубчатого колеса под номером к (к = 1,4).
Но центры масс колес лежат на их неподвижных осях вращения. Поэтому
vk = 0. Отсюда Q — 0.
Задача 36.2(36.2). Определить сумму импульсов внешних сил, при-
ложенных к редуктору, рассмотренному в предыдущей задаче, за про-
извольный конечный промежуток времени.
Ответ: Сумма импульсов внешних сил равна нулю.
Решение. По теореме об изменении главного вектора количеств
движения системы в интегральной форме
=Е
к
Но так как
Q — const = 0,
то сумма импульсов внешних сил равна нулю.
3. Теорема об изменении главного вектора количеств движения 69
Задача 36.3 (36.3). Определить главный век-
тор количеств движения маятника, состоящего
из однородного стержня О А массы М\, длины
4г и однородного диска В массы Mi, радиу-
са г, если угловая скорость маятника в данный
момент равна oj (рис. 36.3.1).
Ответ: Главный вектор количеств движения на-
правлен перпендикулярно стержню О А и по мо-
дулю равен (2Л1| + 5Mi)rw.
Решение. Расчетная схема — на рис. 36.3.2. Главный вектор коли-
честв движения системы
Q = MiVc, + M2vc,,
vct = w - OC\ = ш -2т,
Vc2= (в • OCi = o>(4r + r) = 5wr.
Так как vct || Vc2, to
Q = Mi • 2o?r + M2 5wr = (2M, + 5M2)wr.
Направлен вектор Q перпендикулярно стержню
О А по направлению движения.
Задача 36.4 (36.4). Определить модуль и направление главного век-
тора количеств движения механизма эллипсографа, если масса криво-
шипа равна Mi, масса линейки АВ эллипсографа равна 2М\, масса
каждой из муфт А и В равна Му, даны разме-
ры: ОС = АС = СВ = I. Центры масс криво-
шипа и линейки расположены в их серединах.
Кривошип вращается с угловой скоростью w
(рис. 36.4.1).
Ответ: Модуль главного вектора равен
wl
<2 = у(5М( +4М2);
Рис. 36.4.1
вление главного вектора перпендикулярно кривошипу.
Решение. Расчетная схема — на рис. 36.4.2. Центр масс кривошипа
в точке Ci (OCi = CiCi), центр масс линейки в точке С2 (ЛС2 = С2В),
70 3. Теорема об изменении главного вектора количеств движения
т. А и В — центры масс муфт. Главный вектор количеств движения си-
стемы:
Q = MjVCl + 2Mtvc2 + M2vA + M2vB.
Скорости vc, = ool/'I, Vc2 = wl, так как точки С] и C2 принадлежат
кривошипу. Найдем скорости точек Ан Б. Для этого построим мгновен-
ный центр скоростей линейки АВ (т. Р). Угловая скорость
Vc2
СОап — ---- — --- — О).
АВ С2Р I
Поэтому
VA = ^АВ • АР — w 'll cos wt,
VB = ^AB • BP = w 11 sin wt.
Вычислим вектор Q. Для этого представим его в виде проекций на оси
координат х и у.
Q = Qx + Qy;
k
I
-M\w- sin wt - 2M]W I sin wt —
— M2 Iwl sin wt = —wl
+ 1M2
sin wt,
Qy — У mkvky — MiW- cos wt + M{wl cos wt +
+ M2 • Iwl cos wt = wl
3
~M\ + 1M2
cos wt.
3. Теорема об изменении главного вектора количеств движения 71
Величина
Q = yjQl + Ql = ш1р-мх + 2М2
Для выяснения направления Q заметим, что скалярное произведение
Q • е = 0, где е = (cos ut, sin ut) — единичный вектор вдоль кривошипа.
Действительно,
Q • ё — Qx • cos ut + Qy sin ut =
= ul f -M\ + IM2 j (-sin ut cos ut + cos ut sin ut) = 0.
Следовательно, вектор Q направлен перпендикулярно кривошипу.
Задача 36.5(36.5). Определить главный вектор
количеств движения центробежного регулятора,
ускоренно вращающегося вокруг вертикальной оси
(рис. 36.5.1). При этом углы <р изменяются по за-
кону tp = <p(t) и верхние стержни, поворачива-
ясь, поднимают шары А и В. Длины стержней:
О А = OB = AD = BD = I. Центр масс муфты D
массы М2 лежит на оси z. Шары А и В счи-
тать точечными массами массы М\ каждый. Массой
стержней пренебречь.
Ответ: Qx = Qy = О, Qz = -2{М\ + М2)1<р sin <р,
где Q — главный вектор количеств движения; плос-
кость yz совпадает с плоскостью расположения
устержней регулятора.
Решение. Расчетная схема — на рис. 36.5.2. Длины стержней рав-
ны I. Главный вектор количеств движения центробежного регулятора
Q = M\vA + М\ёБ + M2vD.
Вычислим скорости точек А, В и D: vA = vB = ф1', точка Р — мгно-
венный центр скоростей стержня BD. Отсюда
vb
ubd - BP’
DP sin ADBP sin 2p
VD = uBD • DP = vB——= vB . = ф1 . —-- = 21ф sin <p.
BP sin Z.BDP sin (90° - ip)
72 3. Теорема об изменении главного вектора количеств движения
Рис. 36.5.2
Рис. 36.6.1
Система координат Oxyz вращается вме-
сте с регулятором, плоскость Gyz совпадает
с плоскостью расположения стержней регу-
лятора. Найдем проекции вектора Q на оси
координат.
Qx = = о,
к
Qv = -M\Va cos <р + M\vB cos <p = 0,
Qz = —M\Va cos (90° - 9?) —
-MtVB cos (90° - 9?) - M2VD =
= —2М[1ф sin <p — М2 1ф sin <p =
= — 2(M\ + М2УФ sin tp.
Задача 36.6 (36.7). В механизме, изображенном на рис. 36.6.1, дви-
жущееся колесо радиуса г имеет массу М, причем центр масс колеса
находится в точке Ot, центр масс прямоли-
нейного стержня АВ массы кМ находится
в его середине. Кривошип ОО\ вращается
вокруг оси О с постоянной угловой скоро-
стью ш. Определить главный вектор коли-
честв движения системы, пренебрегая массой
кривошипа.
Ответ: Проекции главного вектора коли-
честв движения системы на оси координат:
1) на ось Ох: -Mrw coswt;
2) на ось Оу: Mrw(l + 2/г) sin wt.
Решение. Расчетная схема — на рис. 36.6.2. Пусть кривошип OOi
вращается по часовой стрелке. Тогда скорость Vot — шт и направлена как
указано на рис. 36.6.2.
Считаем, что колесо катится без проскальзывания, тогда точка ка-
сания Р — это мгновенный центр скоростей копеса. Скорость точки А
Vq
колеса va = АР. Заметим, что угол РАО — это вписанный в окруж-
ность угол, опирающийся на диаметр. Поэтому АРАО = 90° для любого
значения угла <р. Скорость точки А колеса направлена всегда вертикально
вверх (при принятом направлении вращения кривошипа 00]).
3. Теорема об изменении главного вектора количеств движения
73
Теперь рассмотрим точку А, принадлежа-
щую стержню АВ. Ее движение можно пред-
ставить как сложное: переносное (вместе с ко-
лесом) и относительное (относительно колеса).
Поэтому абсолютная скорость этой точки лежит
вдоль стержня АВ, который может двигать-
ся только поступательно. Относительная ско-
рость — вдоль касательной к колесу, переносная
скорость — это найденная выше скорость точки
А колеса, направленная вертикально вверх. От-
сюда следует, что относительная скорость равна
нулю и абсолютная скорость точки А стерж-
ня равна скорости точки А колеса. Причем это
имеет место при любом значении угла <р. То есть
Рис. 36.6.2
данный механизм преобразует вращательные движения кривошипа OOi
в возвратно-поступательные движения стержня АВ. Точка А колеса
и стержня при этом всегда одна и та же.
Итак, скорость центра масс Ci стержня АВ при его поступальном
движении равна скорости точки А:
Vo. ЫГ
vc = va = — • АР = — • 2r sin <p = 2wr sin wt.
r r
Вычислим проекции главного вектора количеств движения механизма
на оси х и у:
Qx = тп^Хк = —М • vox cos <р + kM • 0 = -Мыт cos wt;
к
Qy = ^ ткУК =м -Vo, sin <р + kM Vc2 =
к
= Мыт sin wt + kM 2шт sin wt = Мыт(1 + 2fc) sin wt.
Задача 36.7 (36.8). Масса ствола орудия равна 11 т. Масса снаряда
равна 54 кг. Скорость снаряда у дульного среза vq = 900 м/с. Опре-
делить скорость свободного отката ствола орудия в момент вылета
снаряда.
Ответ: Скорость отката ствола орудия равна 4,42 м/с и направлена
в сторону, противоположную движению снаряда.
Решение. Расчетная схема — на рис. 36.7.1. На систему «ствол ору-
дия + снаряд» не действуют внешние силы вдоль горизонтальной оси х.
Поэтому главный вектор количеств движения этой системы в проекции
74 3. Теорема об изменении главного вектора количеств движения
Рис. 36.7.1
на ось х системы сохраняется: Qx — const. Так как в начальный момент
части системы покоились, то Qx — 0. Отсюда получаем, что
+ M2V2 = 0.
Поэтому в момент вылета снаряда
М} 54
M2v2 = -M\V\ ==> V2 =--------=------------ 900 и -4,42
М2 11 000
Скорость отката ствола направлена противоположно движению сна-
ряда.
Задача 36.8(36.9). Граната массы 12 кг, летевшая со скоростью
15 м/с, разорвалась в воздухе на две части. Скорость осколка массы
8 кг возросла в направлении движения до 25 м/с. Определить скорость
второго осколка.
Ответ: 5 м/с в направлении, противоположном движению первого
осколка.
тп
(до взрыва)
(после взрыва)
Рис. 36.8.1
Решение. Расчетная схема — на рис. 36.8.1. Применим закон сохра-
нения количества движения вдоль оси х (направления движения гранаты
п?о), так как вдоль оси х никаких внешних сил нет. Тогда получим:
т0г>0 = 7П| Д| + т2г>2 =?►
3. Теорема об изменении главного вектора количеств движения 75
той) _ mtVi 12 • 15 - 8 • 25 180 — 200 / м
==> mo - m\ 12 — 8 4 \с
где знак «минус» указывает направление против оси х.
Задача 36.9(36.11). По горизонтальной платформе А, движущей-
ся по инерции со скоростью vq, перемещается тележка В с посто-
янной относительной скоростью uq. В некоторый момент времени
тележка была заторможена. Определить об-
щую скорость v платформы с тележкой после
ее остановки, если М — масса платформы,
ат — масса тележки.
А Jfr
Рис. 36.9.1
m
Ответ: v = v0 + —-u0.
М + m
Решение. Используем теорему о сохранении количества движения
вдоль оси х (так как вдоль этой оси нет внешних (по отношению к системе
«М + т») сил). До торможения количество движения (см. рис. 36.9.2.)
будет: Mvo + m(vo + щ). После торможения тележки, обозначив через
v — искомую общую скорость системы вдоль оси х, имеем: (М + m)v.
Приравнивая эти выражения, получим:
Mv0 + mvo + muo m
v =-----77-------= «о + —----u0.
M + m M + m
Рис. 36.9.2
Задача 36.10(36.12). Сохранив условие предыдущей задачи, опре-
делить путь s, который пройдет тележка В по платформе А с момента
начала торможения до полной остановки, и время торможения т, если
считать, что при торможении возникает постоянная по величине сила
сопротивления F.
Указание. В дифференциальном уравнении движения тележки использовать
соотношение Mv +m(u 4-1>) = const, где и и v — переменные скорости.
1 mM Ып тМ ио
Ответ: s —----------, т =---------.
2M + m f т + МF
76 3. Теорема об изменении главного вектора количеств движения
Решение. Пусть u(t) — относительная скорость тележки после на-
чала торможения, v(t) — абсолютная скорость платформы для этого t.
Тогда имеем закон сохранения количества движения (аналогично реше-
нию предыдущей задачи 36.9):
Mvq + т(г>о + «о) = Mv(t) + m[u(£) + «(<)],
дифференцируя получим:
(М + m)v + mil = 0.
Запишем уравнение Ньютона вдоль оси х для одной только тележки:
m(u + v) = -F.
(2)
Из (1) и (2) получим:
[ m
mil + m I---------it
\ M + m
= —F
Ft(M + m)
U(t) — Uo —---—---
mM
mM
=> ------= -F
М + т
Пусть t — г, когда и(т) = 0. Тогда
Ft(M + m)
-Un =--------=
mM
u^mM
F(M + m) ’
Пройденный путь определяется интегралом:
s
= U0T -
О
F(M + m) т2 1 u^mM
mM 2 2 F(M + m) ’
Задача 36.11 (36.13). Из наконечника пожарного рукава с попе-
речным сечением 16 см2 бьет струя воды под углом a — 30° к горизонту
со скоростью 8 м/с. Определить силу давления струи на вертикаль-
Рис. 36.11.1
ную стену, пренебрегая действием силы тяжести
на форму струи и считая, что частицы жидкости
после встречи со стеною приобретут скорости,
направленные вдоль стены.
Ответ: 88,8 Н.
Решение. Расчетная схема — на рис. 36.11.2. Будем считать, что сила
давления струи воды на стенку FflaBJ1 направлена перпендикулярно стенке.
По закону Ньютона о равенстве действия и противодействия, со стороны
стенки на частицы воды действует реакция стенки F (рис. 36.11.2).
3. Теорема об изменении главного вектора количеств движения
77
Рис. 36.11.2
Воспользуемся теоремой Эйлера, которая говорит о том, что сумма
главных векторов объемных FoC и поверхностных сил Fn0B, а также
секундных количеств движения среды, протекающей через два поперечных
сечения трубы, равна нулю, если векторы секундных количеств движения
направить внутрь выделенного сечениями объема:
Дб + ^пов + Mcv} - Mcv2 = 0.
Выделим отрезок струи АВ = vr, движение которого будем рас-
сматривать. Здесь v — скорость струи воды, т — малый промежуток
времени, для которого и применим теорему Эйлера к рассматриваемому
объему воды.
В начальный момент времени t\ количество движения рассматрива-
емого объема воды в проекции на ось х равно
QX} = УЗ mkvkXl = УЗ mkv cos а = v cos а УЗ = Mucosa,
А А А
где М — масса воды в выделенном объеме струи, М = pavr (р — плот-
ность воды, <т — площадь поперечного сечения струи, которая не меняется
вдоль струи). Поэтому
QX] = Mv cos a = pav2 т cos a.
Так как скорости частиц воды после встречи со стеной направлены
вдоль стены, то в момент времени = t\ + т vkX2 = 0 и количество
движения этого объема воды в проекции на ось х:
Qx2 = mkvkx2=0-
fc
На выделенную часть струи действуют внешние силы: объемная сила
тяжести, действующая по вертикали, реакция стенки F (поверхностная
сила) и сила давления со стороны массы воды, не входящей в выделен-
ный объем. Этой силой пренебрегаем, так как она мала по сравнению
с реакцией стенки.
78 3. Теорема об изменении главного вектора количеств движения
Теорема Эйлера (об изменении главного вектора количеств движения
системы в приложении к сплошным средам) в проекции на ось х примет
вид:
pcrv^T cos a - tF — 0.
Поэтому сила давления струи на стенку равна
F = pcrv2 cos a = 103 • 16 • 10 4 • 82 • cos 30° ~ 88,7 (H).
Рис. 36.12.1
Задача 36.12 (36.14). Определить горизон-
тальную составляющую N возникающей при
движении воды силы давления на опору колена
трубы диаметра d = 300 мм, по которой течет
вода со скоростью v = 2 м/с (рис. 36.12.1).
Ответ: N = 284 H.
Решение. Расчетная схема — на рис. 36.12.2. Объемной силой яв-
ляется сила тяжести воды, направленная вдоль оси у. Искомая горизон-
тальная составляющая N силы давления воды на опору колена трубы
по закону равенства действия и противодействия равна по величине
х
Рис. 36.12.2
3. Теорема об изменении главного вектора количеств движения 79
горизонтальной реакции опоры на воду Rx и противоположна ей по на-
правлению (это поверхностная сила).
Выразим секундную массу воды, т.е. массу воды, протекающей через
сечения 1 и 2 в одну секунду:
7ИС = p(TV = /97Г
I - I V
\2/
На рис. 36.12.2 изобразим секундные количества движения воды,
протекающей через сечения трубы 1 и 2, направив их внутрь рассматри-
ваемого объема.
Запишем теорему Эйлера в проекции на ось х:
Т'об.т 4“ Т'пов.гг 4“ McV[x MqV2x — 0.
В данном случае FnfiT = 0, Fn0B2. = Rx, V\x = 0, v2x = v, поэтому
получим уравнение:
/d\2 2
Rx — ръ I ~ ) v = 0-
Отсюда горизонтальная составляющая силы давления воды равна
N = Rx = pir( - \ д2 = 103-я-(0,15)2 • 22 й 283 (Н).
Задача 36.13(36.15). Вода входит в неподвижный канал перемен-
ного сечения, симметричный относительно вертикальной плоскости,
со скоростью до = 2 м/с под углом «о = 90°
к горизонту; сечение канала при входе 0,02 м2;
скорость воды у выхода из канала vt — 4 м/с
и направлена под углом О| = 30° к горизонту.
Определить модуль горизонтальной составля-
ющей силы, с которой вода действует на стен-
ки канала.
(Ответ: 138 Н.
Рис. 36.13.1
Решение. Расчетная схема — на рис. 36.13.2 Аналогично решению
предыдущей задачи 36.12 теорема Эйлера в проекции на ось х имеет вид:
Rx 4“ ^^x^lx ^^х^2х — 0.
(1)
В данном случае v\x = 0, v2x = — ^2cos30°. Согласно закону сохра-
нения массы имеем
МС1 = МС2 = мс, где МС\ = p<T\V\ = p(T]VQ, МС2 = pc2v2.
80 3. Теорема об изменении главного вектора количеств движения
Рис. 36.13.2
Подставим эти выражения в (I). Получим:
-Rx + cos 30° = 0.
Отсюда горизонтальная составляющая силы давления воды на стенки
сосуда
Уз
R'x = RX = pa^w cos 30° = 103 • 0,02 • 2 • 4 • — ss 138,5 (H).
Рис. 36.14.1
Задача 36.14(36.17). Определить модуль горизон-
тальной составляющей силы давления струи воды на не-
подвижную лопатку турбинного колеса, если объемный
расход воды Q, плотность 7, скорость подачи воды
на лопатку г>| горизонтальна, скорость схода воды v2
образует угол а с горизонтом.
Ответ: N = 7Q(vt + v2 cos a).
Решение. Расчетная схема — на рис. 36.14.2. Аналогично решению
задачи 36.12 запишем теорему Эйлера в проекции на ось х:
Rx + McV\x — MqVix = 0.
В данном случае
vi« = -«1 a v2x = v2 cos a, Mc = Q-y-
Поэтому уравнение принимает вид:
Rx + Й7(-г,1) ~ Qtv2 coso = 0.
3. Теорема об изменении главного вектора количеств движения
81
Горизонтальная составляющая силы давления струи воды на непо-
движную лопатку турбинного колеса согласно закону равенства действия
и противодействия равна
Rx ~ + ^2 cos «)•
4. Теорема об изменении главного момента
количеств движения материальной системы.
Дифференциальное уравнение вращения твердого тела
вокруг неподвижной оси (§ 37, [10])
Задача 37.1 (37.1). Однородный круглый диск массы М = 50 кг
и радиуса R = 30 см катится без скольжения по горизонтальной плос-
кости, делая вокруг своей оси 60 об/мин. Вычислить главный момент
количеств движения диска относительно осей: 1) проходящей через
центр диска перпендикулярно плоскости движения; 2) относительно
мгновенной оси.
Ответ: 1) 14,1 кг-м* 2/с; 2)42,3 кг-м2/с.
Решение. Расчетная схема — на рис. 37.1.1. Угловая скорость диска
2тг • 60 / рад
Ш — 77— = 27Г I ।----
60 \ с
Так как диск катится без скольжения, то
точка касания Р с неподвижной поверхностью
есть мгновенный центр скоростей. Поэтому
vc = bjR.
Главный момент количеств движения дис-
ка относительно оси Cz, перпендикулярной
плоскости движения диска вычисляется по
формуле
MR2 50 • (0,3)2 /кг-м2
Kez — Jcz^z = —-—и — ---------------- • 2тг ~ 14,1 ( -----
2 2 \ с
Главный момент количеств движения диска относительно мгновенной
оси Pz равен
Кр2 — Kez + 7V/p.(Q) = Jcz^z + R • Mvc =
MR2 3 ,
---a) + RMwR — -MRa; =
2 2
= | • 50 • (0,3)2 • 27Г « 42,4 f IS2LA
2 v \ c )
4. Теорема об изменении главного момента
83
Задача 37.2(37.2). Вычислить главный момент количеств движе-
ния линейки АВ эллипсографа в абсолютном движении относительно
оси z, совпадающей с осью вращения кривошипа ОС, а также в от-
носительном движении по отношению к оси, проходящей через центр
масс С линейки параллельно оси z. Кривошип вращается с угло-
вой скоростью, проекция которой на ось z равна и>2; масса линейки
равна т; ОС = АС = ВС = I (см. рисунок к задаче 34.5).
2 2 т^2
Ответ: KOz = -ml wz, KCz = -—wz.
Решение. Расчетная схема — на рис. 37.2.1. Оси Oz и Cz перпенди-
кулярны плоскости движения эллипсографа. Вычислим главный момент
количеств движения линейки АВ в абсолютном движении относительно
оси Oz-.
KOz = К{£ + MOz(mvc).
Moz(mvc) — это момент относительно оси Oz количеств движения
линейки.
Moz(mvc) — I ‘ mvc = lmu>zl = ma>zl2.
(г)
KCz — главный момент количеств движения линейки в относитель-
ном движении по отношению к оси Cz.
/г) m(2l)2 ml1
Kez = Jcz^abz =-----——vz = —~uz.
Покажем, что cuABz = ~wz- Для этого построим мгновенный центр
скоростей линейки — точку Р. Тогда
«с ^Ocl
84
4. Теорема об изменении главного момента
То есть модули угловых скоростей кривошипа и линейки равны. На-
правление ujabz, как видно из рис. 37.2.1 противоположно угловой скоро-
сти кривошипа Теперь вернемся к вычислению Kqz\
(г) ТП1^ 2^2
KOz = К'с' + MOz(ttwc) = - ~uz + m-wzl = - ml wz.
Задача 37.3(37.3). Вычислить главный момент количеств движе-
ния планетарной передачи относительно неподвижной оси z, совпа-
дающей с осью вращения кривошипа ОСу. Неподвижное колесо 1
и подвижное колесо 3 — одинакового радиуса т (рис. 37.3.1). Масса
колеса 3 равна т. Колесо 2 массы имеет радиус т2. Кривошип вра-
щается с угловой скоростью, проекция которой на ось z равна wz. Мас-
сой кривошипа пренебречь. Колеса считать однородными дисками.
m2(2r + 3r2) + 8m(r + г2)
Ответ: KOz =------------------------(г + r2)w.
Решение. Расчетная схема — на рис. 37.3.2. Зададим для опреде-
ленности направление угловой скорости кривошипа ljz как на рис. 37.3.2.
Распишем главный момент количеств движения планетарной передачи
относительно оси Oz:
П-Oz — h-Oz + ^Oz-
Рис. 37.3.2
4. Теорема об изменении главного момента
85
Кривошип не имеет кинетического момента, так как его массой прене-
брегаем. Рассмотрим
К(£=К{£Г + Modm2Vc2).
Кинетический момент колеса 2 в относительном его движении по от-
ношению к оси C2Z, перпендикулярной плоскости рисунка, вычисляется
по формуле:
Е-(2).г т(2) т(2) m2r2
Kc2z = Jc2zu2z, где JCjZ =
Для определения угловой скорости tzpz воспользуемся тем, что коле-
со 1 неподвижное, и точка касания колес 2 и 1 — это мгновенный центр
скоростей 2-го колеса:
Vc2 V • (г + г2)
U>2 — --- — ----------.
Т2 Г2
Учитывая направления, получим проекцию на ось z;
г + г2
^2z = ^z------
Г2
Итак,
„(2), г ™2rl Г + Г2 ТП2Г2. , .
KC2z = = ~^Г +
Величина
MO2(m2f>c2) = (г + T2^m2Vc2 = m2 (г + г2)2о>2.
Поэтому
(2) m2l'2 / , / ,2 , / 3 \
K'oz = ~Y~V + r2)uz + m2(r + r2) bJz =rn2(r + r2)lr + -r2 \uz-
Вычислим кинетический момент колеса 3:
К% = К^ + MOz(m3vc2).
Рассмотрим кинематику колеса 3 (рис. 37.3.3).
Построим мгновенный центр скоростей колеса
3 — т. Р3. Скорость
= lvc2 = 2w(r + r2).
Скорость ТОЧКИ Сз
Vc2 = и • (2r + 2r2) = 2w(r + r2).
Так как vc} — vr, to МЦС не существует, колесо 3 движется поступа-
тельно, а?з = 0 (рис. 37.3.2).
86
4. Теорема об изменении главного момента
Поэтому
фг=о,
KqI = = 2(r 4- r2) m • 2w(r + r2) = 4(r 4- r2)2nwz.
Суммарный кинетический момент
KOz = m2(r 4- r2) (t 4- |r2) uz 4- 4(r 4- r2)2mw, =
m2(2r + 3r2) 4- 8m(r 4- r2) . .
= —i---------------------(r + r2)wz.
Задача 37.4(37.4). Натяжения ведущей и ведомой ветвей ремня,
приводящего во вращение шкив радиуса г = 20 см, массы М = 3,27 кг,
соответственно равны: Т\ = 100 Н, Т2 = 50 Н. Чему должен быть
равен момент сил сопротивления для того, чтобы шкив вращался с уг-
ловым ускорением е = 1,5 рад/с2? Шкив считать однородным диском.
Ответ: 9,8 Нм.
Рис. 37.4.1
Решение. Расчетная схема — на рис. 37.4.1.
Применим теорему об изменении главного момен-
та количеств движения шкива относительно непо-
движной оси Oz\
Так как
Мт1
Koz — Joz^z = —— Uz,
то уравнение принимает вид:
Mr2
= Tlr-T2r- Мс.
Искомый момент сил сопротивления
, ч Mr2
Мс = (Т( - т2)г - —EZ =
, ч 3,27 • 0,22
= (100 - 50) • 0,2 -
1,5 й 9,9 (Н-м).
4. Теорема об изменении главного момента
87
Задача 37.5(37.5). Для определения момента трения в цапфах на
вал насажен маховик массы 500 кг; радиус инерции маховика р = 1,5 м.
Маховику сообщена угловая скорость, соответствующая п = 240 об/мин;
предоставленный самому себе, он остановился через 10 мин. Опреде-
лить момент трения, считая его постоянным.
Ответ: 47,1 Н -м.
Решение. Запишем дифференциальное уравнение движения махо-
вика с помощью теоремы об изменении главного момента количеств
движения относительно неподвижной оси его вращения Oz:
Joz^z — Л7тр.
Так как
Joz = tnp2, ez = wz,
то уравнение принимает вид
mp — = -Мтр.
Так как Mjp = const, то интегрирование приводит к результату:
1° |й
= -Mpd .
Iwo Io
mp2wz
Поэтому момент трения
тр2и>о тр22.тгп
МТп — ------- = --------
р Д tt • 60
500 • 1,52 • 2тг • 240
-----------------« 47,1 (Н • м .
10-60-60 ' '
Задача 37.6 (37.7). Для быстрого торможения больших маховиков
применяется электрический тормоз, состоящий из двух диаметрально
расположенных полюсов, несущий на себе обмотку, питаемую посто-
янным током. Токи, индуцируемые в массе маховика при его движении
мимо полюсов, создают тормозящий момент М\, пропорциональный
скорости v на ободе маховика: М\ = kv, где к — коэффициент,
зависящий от магнитного потока и размеров маховика. Момент М2
от трения в подшипниках можно считать постоянным; диаметр махо-
вика D, момент инерции его относительно оси вращения J. Найти,
через какой промежуток времени остановится маховик, вращающийся
с угловой скоростью о>о-
Ответ: Т = — In
kD
88
4. Теорема об изменении главного момента
UeOpSUi
Решение. Воспользуемся теоремой об изменении главного момента
количеств движения маховика относительно неподвижной оси его враще-
ния, чтобы составить дифференциальное уравнение вращения:
Jw = -М2 - kv,
где М2 — постоянный момент трения в подшипниках, М\ = kv — тор-
мозящий момент, индуцируемый токами.
D
Скорость точек обода маховика v = wR — Поэтому уравнение
можно переписать в виде:
I
= -1л1
Интегрируем
Jdw
kD ( 2М2
Jdw
kD~
М2 +---w
2
= -dt
= -dt.
2J
kD
In
2М2
~kD
Wo
Ч»раск]
-'ШС.10В
Жми
2 \ kD
о
2J (
время до остановки Т = —— In I 1
KU \
kDwo
2М>
Задача 37.7 (37.8). Твердое тело, находившееся в покое, приводит-
ся во вращение вокруг неподвижной вертикальной оси постоянным
моментом, равным М: при этом возникает момент сил сопротивления
М\ пропорциональный квадрату угловой скорости вращения твердого
тела: М\ = aw2. Найти закон изменения угловой скорости; момент
инерции твердого тела относительно оси вращения равен J.
•IM). Рец
'Лротнще
дтиа: Л
Ответ: w =
М - 1
а е&1 + 1
%1ввд:
2
Решение. Согласно теореме об изменении главного момента коли-
честв движения тела имеем дифференциальное уравнение вращательного ^".постоя
движения относительно его неподвижной оси:
dw 2 й’Лен|
J dt~M
где M — вращающий момент, М\ = aw2 — момент сил сопротивления. |
Для интегрирования уравнения разделим переменные
Jdw
—7Т7-----\“ = dt.
(М 2\
а I----w I ip,
\ а }
4. Теорема об изменении главного момента
89
Получим:
J 1 ЛсГ
а'2\м'П
у/М/a + о?
у/М/о. - ш
( у/М/a + аА 2y/at
In —. ---- I = —=
\ у/M/а - wj Jу/М
Заметим, что при раскрытии знака модуля был выбран знак «+», что
следует из начальных условий (to = 0, о>о = 0).
Для этого надо рассмотреть выражение
j , + п
—. • In I ±—. - I = 0.
2jaM \ y/M/a-Oj
Задача 37.8(37.9). Решить предыдущую задачу в предположении,
что момент сил сопротивления М\ пропорционален угловой скорости
вращения твердого тела: М\ = aw.
Ответ: ш = —(1-е
а
Решение. Дифференциальное уравнение вращения тела вокруг его
неподвижной оси имеет вид:
dw
J — = М - аш,
dt
где М — вращающий постоянный момент, М\ = aw — момент сил со-
противления.
Проинтегрируем уравнение, учитывая нулевые начальные условия,
и получим закон изменения угловой скорости:
In
(М/а) - w
(М/а)
о? = — (1 - e~o</J).
а
90
4. Теорема об изменении главного момента
Заметим, что при раскрытии модуля надо учитывать начальные усло-
вия. Действительно, рассмотрим
In ±
(М/а) - оА
(М/а) )
Подставим начальные условия: при to = 0, о?о = 0- Получим
In ±
М/а\ _о
М/а
Видно, что модуль следует раскрывать со знаком «+».
Задача 37.9(37.10). Шарик А, находящийся в сосуде с жидко-
стью и прикрепленный к концу стержня АВ длины I, приводится
во вращение вокруг вертикальной оси 0,0? с начальной угловой
скоростью а?о- Сила сопротивления жидкости пропорциональна уг-
ловой скорости вращения: R — аттш, где m — масса шарика, а —
коэффициент пропорциональности. Опреде-
лить, через какой промежуток времени уг-
ловая скорость вращения станет в два раза
меньше начальной, а также число оборотов п,
которое сделает стержень с шариком за этот
промежуток времени. Массу шарика считать
сосредоточенной в его центре, массой стерж-
ня пренебречь.
_ I 1(^0
Ответ: Т = — In 2, п =--------.
а 4тга
Решение. Расчетная схема — на рис. 37.9.2. На механическую си-
стему, состоящую из шарика А, невесомого стержня АВ и невесомого ва-
ла О [О, действуют следующие внешние силы: сила
тяжести шарика mg, сила сопротивления R — amw
(направлена противоположно линейной скорости
шарика 4), силы реакции подшипника О и под-
пятника 01 (Ro и RO]).
Воспользовавшисьтеоремой об изменении глав-
ного момента количеств движения системы отно-
сительно неподвижной оси вращения z, составим
дифференциальное уравнение вращения системы:
Рис. 37.9.2
4. Теорема об изменении главного момента
91
ml2w = —arrw I
a
ш =
т
Проинтегрируем полученное уравнение:
М>/2
Г dw
Wo
о
J
(d()
Отсюда искомое время
W0 О!
In — - In Wo = -yT.
£- v
2
Т = - In 2 (с).
a
Чтобы найти число оборотов п, которое сделает стержень с шариком
за время Т, перепишем полученное дифференциальное уравнение в виде:
a
(р = --ф.
Отсюда получим
dip
ФЛр =
2тгп
Шо/2
а
y-w0 = -j-27rn
ZWo
П = -—
4тга
а
~тф
а
7
О
Задача 37.10(37.11). Определить, с какой
угловой скоростью w упадет на землю спи-
ленное дерево массы М, если его центр масс
С расположен на расстоянии h от основания,
а силы сопротивления воздуха создают момент
.2
сопротивления тпс, причем тс = —аф , где
а = const. Момент инерции дерева относи-
тельно оси z, совпадающей с осью, вокруг
которой поворачивается дерево при падении,
равен J.
Рис. 37.10.1
Ответ: w =
IMghJ
J2 + 4а2
Решение. Расчетная схема — на рис. 37.10.2. Составим дифферен-
циальное уравнение движения дерева:
) => Jip = Mgh sin ip — аф1.
it а \
e-tt7r/j + 2- ).
92 4. Теорема об изменении главного момента
Mg
Рис. 37.10.2
Проинтегрируем уравнение:
&ф (1ф 2
J-----— Mgh sin p — ap
dt dp
dp 2
=> Jtp— = Mgh sin p — atp
dp
1 dtp* 2 2
=> J -------= Mgh sin p — atp .
2 dp
.2
Сделав замену переменных u ~ ф , получим
J du . __
----= Mgh sin p — au =>
2 dp
, 2a 2Mgh
u 4---u =------sin p.
Решим уравнение как линейное неоднородное с постоянными коэффи-
циентами: и — и00. 4-иЧц.- Решение u00 = се 2q^/J. Частное решение
ищем в виде u4 н = A sin р + В cos р. С помощью метода неопределенных
коэффициентов вычислим А и В:
2a z ч 2Mgh
A cos р - В sin р + — (4 sin р + В cos р) = —-— sin р ==>
2a 2a t 2Mgh
А + —В = 0, -В + —А = —-2-
2MghJ
J2 + 4а2 ’
4Mgh a 2Mgh J
J2 + 4a2 J2 + 4a2'
Используя нулевые начальные условия (pq = 0, u0 = pl = 0), соста-
вим уравнение для коэффициента С:
2MghJ
0 = С - —г => С =
J2 + 4а2
Закон изменения
.2 z х 2MghJ _2qv/j 2MghJ .
=u^= j2 + 4Q2e + JTT^^sin^- Jcosp).
Поэтому угловая скорость дерева в момент падения
7 7Г
<Р = 2
2Mgh J , ...2Mgh z
e~2air/(2J) + * (2a - J • 0) =
J2 + 4a2 J2 + 4o2 ’
2Mgh J ( .. a
---°---I g-an/J , 2 —
j2 + 4a2\ J
4. Теорема об изменении главного момента
93
Задача 37.11 (37.12). Вал радиуса г приводится во вращательное
движение вокруг горизонтальной оси гирей, подвешенной посред-
ством троса. Для того чтобы угловая скорость вала через некоторое вре-
мя после начала движения имела величину, близкую к постоянной, с ва-
лом соединены п одинаковых пластин; сопротивление воздуха, испыты-
ваемое пластиной, приводится к силе, нормальной к пластине, прило-
женной на расстоянии R от оси вала и пропорциональной квадрату ее уг-
ловой скорости, причем коэффициент пропорциональности равен к.
Масса гири т, момент инерции всех вращающихся частей относитель-
но оси вращения равен J; массой троса и трением в опорах пренебречь.
Определить угловую скорость ы вала, предполагая, что в началь-
ный момент она равна нулю.
Ответ: w =
mgr eat - I 2 t---------——
-------- , где a = ^\/mgnkrR\ при доста-
knR eat + 1---------J + mr* 2 * * * v 6
точно большом значении t угловая скорость w близка к постоянной
величине
Рис. 37.11.1
Решение. Расчетная схема — на рис. 37.11.1.
Составим дифференциальное уравнение движения
системы, используя теорему об изменении главного
момента количеств движения относительно непо-
движной оси вращения Oz.
dKOz
dt
—(Jw + rmv) — mgr - nF R
dt
d
—(Ju + mwr ) = mgr - nF • R
dt
2 du
=> (J + mr )— - mgr - nF • R,
dt
где сила сопротивления F = ku1.
Проинтегрируем уравнение:
dw
(J 4- mr2)---------— = dt
(mgr t\
nkRl ~^~w2 I
\ nkR /
t
J + mr2 Г dw
nkR J 2 = J
0 nkR 0
94
4. Теорема об изменении главного момента
где
J + mr* 2
nkR
nkR
mgr
- О!
(В
— In 1
M'
mgr
\------Ь w
, V nkR
ln i
mgr
\ /-----0?
V nkR
у/mgrnkR
J + mr2
еы - 1
w = а~т>-----,
еы + Г
mgr
nkR’
Заметим, что при t —> oo
a --
2 ,------
b = ———,,- • v mgnkrR.
J + mr
mgr
----— const.
nkR
Задача 37.12(37.15). Упругую проволоку, на которой подвешен
однородный шар с радиусом г и массой т, закручивают на угол ^о,
а затем предоставляют ей свободно раскручиваться. Момент, необхо-
димый для закручивания проволоки на один радиан, равен с. Опреде-
лить движение, пренебрегая сопротивлением воздуха и считая момент
силы упругости закрученной проволоки пропорциональным углу кру-
чения р.
•яй
ICH
Звдо
«шика
w
«ifei
Ответ: p = 9?0 cos
5c
£---7-t.
2mrz
a + ы ы
----= e
a — w
= t
= 2
e
Решение. Расчетная схема — на рис. 37.12.1. Угол поворота шара р
вокруг неподвижной вертикальной оси Cz отсчитывается в горизонталь-
ной плоскости Сху.
На шар действуют внешние силы: сила тяжести mg, сила натяжения
проволоки Т, момент упругости проволоки Мупр. Дифференциальное
уравнение вращения шара вокруг оси z имеет вид:
2 ,
Jp = -Мупр, где 7Иупр = ср, J = -mr
®1Н
,wjp
Ф+2mr^ °'
Решение уравнения
p — A sin
5с
2тпг2
Mb
I
4. Теорема об изменении главного момента
95
Начальные условия:
«о = 0, 9?(0) = ^о, У>(0) = 0.
Отсюда имеем уравнения относительно Лиа:
/ 5с
<£>о = Л sin а, 0 = Лд/---rcosa.
V Тлпг1
Поэтому а = 7г/2, Л =
/ 5с
Закон движения шара: a? = со0 cos \ -т t.
V 2mr2
mg
Рис. 37.12.1
Задача 37.13(37.16). Часовой балансир Л может Л
вращаться вокруг оси, перпендикулярной его плос- /У И
кости и проходящей через центр тяжести О, имея //
относительно этой оси момент инерции J. Балансир II II
приводится в движение спиральной пружиной, один / J
конец которой с ним скреплен, а другой присоеди-
нен к неподвижному корпусу часов. При повороте p^c 37 13 1
балансира возникает момент сил упругости пружи-
ны, пропорциональный углу поворота. Момент, необходимый для
закручивания пружины на один радиан, равен с. Определить закон
движения балансира, если в начальный момент в условиях отсутствия
сил упругости балансиру сообщили начальную угловую скорость ш0.
Ответ:
Решение. Расчетная схема — на рис. 37.13.2.
Ось вращения Oz перпендикулярна плоскости ри-
сунка.
Дифференциальное уравнение вращения ча-
сового балансира вокруг оси Oz\
— МуПр, где -IWynp — ср.
Рис. 37.13.2
Поэтому ф -I—р = 0. Решение
G/rM-
Начальные условия:
<о = 0, у>(0) = 0, у>(0) = w0-
с
<р — A sin
96
4. Теорема об изменении главного момента
Поэтому о = 0, А = о?о
Закон движения белансира: <р = Wo
t.
Задача 37.14(37.17). Для определения момента инерции Jz тела
А относительно вертикальной оси Oz его прикрепили к упругому вер-
тикальному стержню 001, закрутили этот стер-
жень, повернув тело А вокруг оси Oz на малый
угол <р0, и отпустили; период возникших колеба-
ний оказался равным Т\, момент сил упругости
относительно оси Oz равен mz = —ap. Для опре-
деления коэффициента с проделали второй опыт;
на стержень в точке О был надет однородный
круглый диск радиуса г массы М, и тогда период
колебаний оказался равным Т^. Определить мо-
мент инерции тела Jz.
Ответ:
Mr2 ТТЛ2
~Т~ Vib /
Решение. Расчетная схема — на рис. 37.14.2. Составим дифферен-
циальное уравнение вращения тела вокруг оси z:
=> Jz<p = —ap, так как mz = —ap =>
с
=> Ф + ~г<Р - 0.
Jz
Поэтому период
Рис. 37.14.2
Это дифференциальное уравнение описывает
колебания тела вокруг оси Oz с частотой
Отсюда момент инерции тела
Jz = сТ21
1
4л-2'
4. Теорема об изменении главного момента
97
Для выяснения величины коэффициента с запишем уравнение движения
однородного круглого диска:
Мт2 1с
=> ф + —^ = 0.
Частота колебаний диска
Период его колебаний
Поэтому
1тг2Мг2
с=~тГ'
Следовательно, момент инерции
Тп2Мт2 2 1 Mr2 ТТЛ2
г — ___________ т12_ _ ___I _ I
2 1 47Г2 2 \Т2) ’
Задача 37.15(37.18). Решить предыдущую задачу в предположе-
нии, что для определения коэффициента с второй опыт проделывают
иначе: однородный круглый диск массы Ми радиуса г прикрепляется
к телу, момент инерции которого требуется определить. Найти момент
инерции тела Jz, если период колебаний тела rt, а период колебаний
тела с прикрепленным к нему диском т2.
Mr2 г.2
Ответ: Jz = —----2-----
2 7-2 - Т\
Решение. Воспользуемся результатами предыдущей задачи (37.14).
Дифференциальное уравнение вращения системы двух тел имеет вид:
ф + с<р = 0.
Поэтому частота колебаний системы
Mr2'
~Г
98
4. Теорема об изменении главного момента
4.
Период колебаний
2тг
72 = -----
Ц}
Mr2
с
Отсюда
Мг2\ 4тг2
2 / т2 ’
2 1
Найденный коэффициент с подставим в выражение Jz = CTj Полу-
чим уравнение относительно момента инерции
4тг2
_2
Mr2
~т~
.2
4тг2
Следовательно,
с =
Mr2 т2
2 т,2 -
.2 '
ИЙ
!'!!. По
Рис. 37.16.1
Задача 37.16 (37.19). Бифилярный подвес со-
стоит из однородного стержня АВ длины 2а,
подвешенного горизонтально посредством двух
вертикальных нитей длины I, отстоящих друг от
друга на расстоянии 2Ь. Определить период кру-
тильных колебаний стержня, полагая, что стер-
жень в течение всего времени движения остается
в горизонтальном положении и натяжение каж-
дой из нитей равно половине веса стержня.
Указание. При определении горизонтальной составляющей натяжения каждой
из нитей, считая колебания бифиляра малыми, заменить синус угла между на-
правлением нити и вертикалью самим углом.
Решение. Расчетная схема движения бифилярного подвеса пред-
ставлена на рис. 37.16.2. Угол поворота стержня вокруг вертикальной оси
Cz — угол <р. Будем считать угол <р малым, т. е. <р ~ 0. Силы натя-
жения нитей F\ = Fj = mg/2 (по условию задачи). При составлении
дифференциального уравнения движения стержня АВ учтем, что момент
относительно оси Cz создают лишь горизонтальные составляющие сил
«!1
-ip
1
' I
“^1
4. Теорема об изменении главного момента
99
Рис. 37.16.2
1
натяжения нитей, которые равны Q = F\ sin а = -mg sin а. По условию
задачи a ~ 0. Поэтому
1 1
Q « -mga к -mgtga.
Из геометрических соображений нетрудно увидеть, что
2dsin(y>/2) 2b(<p/2) b
180 =-----7---к~Г' = 7’’-
Окончательно получаем, что
1 Ь
Q ~ 2т8
Уравнение движения стержня:
V
Jz<p =-2.-Q-bcos - =>
m(2a)2 Id, <p
==> ———ф = 2 • -mgjtp b • 1, так как cos — и 1 =>
'5 + 7^^ = o-
Поэтому период крутильных колебаний стержня
100
4. теорема об изменении главного момента
Задача 37.17 (37.20). Диск, подвешенный к упругой проволоке,
совершает крутильные колебания в жидкости. Момент инерции дис-
ка относительно оси проволоки равен J. Момент, необходимый для
закручивания проволоки на один радиан, равен с. Момент сопро-
тивления движению равен aSw, где a — коэффициент вязкости
жидкости, S — сумма площадей верхнего и нижнего оснований дис-
ка, iv — угловая скорость диска. Определить период колебаний диска
в жидкости.
4тг7
Ответ: Т = .
\?4cJ - a2S2
;;лри(
t,n-
IBip
татя
фт.
Решение. Составим дифференциальное уравнение крутильных ко-
лебаний диска. Для этого введем угол поворота диска в горизонтальной
плоскости — угол <р. Получим
Jz<p = -Мупр - Мс, ®.(ад
’йл;
где момент инерции
Л = J, 7
момент упругости , .
ЛДпр — Су>,
момент сопротивления ’ Й
Мс = aSui = aS<p.
Отсюда имеем ’®(л‘
= -с<р - aS<p =>
aS с
=> Ф+ —ф + -<р = 0.
<J <Lf
Полученное уравнение — это уравнение малых колебаний диска
с учетом вязкого сопротивления. Причем движения носят характер зату-
хающих колебаний только при условии, когда
aS Гс
2J < у 7’ '^то
т.е. при малом сопротивлении. В этом случае частота затухающих коле-
баний
, Гс (aS\2 I /-------------— Д.
= \ у ~ ( ту ) =57 Г4с j - a1 S2 ц/
и условный период
Т 2тг 4?rJ j/c
fc, y/4cJ - a2S2' Ц ‘
4. Теорема об изменении главного момента
101
Задача 37.18(37.22). Твердое тедо, подвешенное на упругой про-
волоке, совершает крутильные колебания под действием внешнего
момента тв, причем mez = m\ sin иЛ + m3 sin Зо>£, где тп\, m3 и ш —
постоянные, az — ось, направленная вдоль проволоки. Момент сил
упругости проволоки равен тупр, причем mynpz = -ср, где с — ко-
эффициент упругости, a р — угол закручивания. Определить закон
вынужденных крутильных колебаний твердого тела, если его момент
инерции относительно оси z равен Jz. Силами сопротивления дви-
жению пренебречь. Считать, что у/с/ Jz 7^ iv и х/ё/Л £ За/.
h\ hi 2 с тп\
Ответ: р — —7----- sinut Ч—:----? sin где А = —, h\ — ——,
Ar - о/2 к1 - 9or Jz Jz
m3
hi~T'
______Jz_______________________________________________________J
Решение. Составим дифференциальное уравнение вынужденных кру-
тильных колебаний тела вокруг неподвижной оси z:
Jz$ = гпупрг Ч- m/,2 —т*
=> Jzp = — ср Ч- m\ sin u>t + my sin 3wt =>
c m\ m3
=> p + —p = — sin wt 4- — sin 3wt.
Jz Jz Jz
Собственная частота колебаний
к = у/т-
Коэффициенты в правой части уравнения
mi m3
hi = — и й2 = —.
Jz Jz
Так как возбуждающий момент равен сумме двух гармонических функций,
причем собственная частота по условию не равна частотам возбуждения
(х/C/Jz 7^ д/c/Jz Зо>), то вынужденные колебания описываются
законом
Л1 . , ^2 .
s,n +
mi m3
=------------г- sin wf Ч---------— sin 3ut.
JД — - w ) J J — - 9w )
\^Z / \Jz /
102
4. Теорема об изменении главного момента
Задача 37.19(37.23). Решить предыдущую задачу с учетом мо-
мента сил сопротивления тпс, пропорционального угловой скорости
твердого тела, причем mcz — —[Зф, где /3 — постоянный коэффициент.
S|37
лшкг
Ответ: р = Л1 sin (w£ - fj) + А3 sin (3wt - £3), где
Л,
1 у/(к2 - <х>2)2 + 4п2ш2 ’
Лз
yj, -__ -
у/(к2 - 9ш2)2 + 36п2ш2 ’
2пш
£1 = arctg -5-г >
к2 - ш2
бпш /3
tJ = arct8F^’ "=2Л
jpm
Ж1Н
'г
Решение. В рамках предыдущей задачи следует учесть момент сил -—
сопротивления
fTtcZ г
cz ш
В результате получим дифференциальное уравнение движения тела:
/3 С ТП\ ТП3
р -I---р -I----р — — sin ut + — sin 3ut.
Jz Jz Jz Jz
Поэтому вынужденные крутильные колебания тела описываются за-
коном:
Л|
У’вын =-====== Sin (ut - £,) +
(к2 - u2)2 + 4n2w2
Wu
'Won
I
где
Лэ
-I 7—- ~ = sin (3ut —
\/(k2 - 9w2)2 + 36nw2
. m3
Л| — —, «2 = —,
Jz Jz
т I3
к = . / —, n = —,
V Jz 2J;
2nu 6nw
£,=arc,8Srr^- £! = ага«7тт^
U$Hll
4. Теорема об изменении главного момента
103
Задача 37.20(37.20). Диск D, радиус которого ра-
вен R, а масса — М, подвешен на упругом стержне АВ,
имеющем жесткость на кручение с (рис. 37.20.1). Конец
стержня В вращается по закону рв — wof + $ sinpZ, где
w0, Ф, р — постоянные величины. Пренебрегая силами
сопротивления, определить движение диска D: 1) при
отсутствии резонанса, 2) при резонансе. В начальный
момент диск был неподвижен, а стержень — недефор-
мирован.
Ct?O
Ответ: 1) pA(t) = bJot-------sin kt +
к
h
Рис. 37.20.1
P \
- . sin pt - - sin kt I, где fc =
Ar — p1 \ к /
. w0 h
2) <pA(t) = b>ot- -Г Sinfcf-b —
К Z.K
2c k 2сФ
MR2’ = MR2 ’
— sin kt — t cos kt).
Решение. Составим дифференциальное уравнение движения диска,
используя теорему об изменении главного момента количеств движения
относительно вертикальной неподвижной оси вращения z:
Jz<p = -с(р - рв).
Здесь р — угол поворота диска (абсолютный), р-рв — угол закручивания
стержня, Jz = MR?/2 — момент инерции диска относительно оси z,
проходящей через его центр масс.
Поэтому
MR2
—р = -Ср + c(wol + Ф sin pt),
2с 2сФ 2с
Это есть дифференциальное уравнение вынужденных крутильных ко-
лебаний диска без сопротивления. Собственная частота
2с
MR2’
коэффициент
2сФ
h ~ MR2'
Решение уравнения р — ро.о. + рчн.- Собственные колебания
<Ро.о. = G sin kt + С2 cos kt.
104
4. Теорема об изменении главного момента
Вынужденная часть колебаний зависит от соотношения собственной к
и вынуждающей р частот. Рассмотрим два случая.
1. Отсутствие резонанса ( к фр, т.е.
2c \
MR2 P) ’
h
<p = Ci sin kt + Cj cos kt + —т---r- sin pt + wot.
|fc2 -p2|
Начальные условия: при to = 0 y>(0) = 0, ф(0) = 0, дают уравнения
относительно Ci и Ср.
„ hp
0 = Сг, 0 = Cifc + —j--------jr + шо-
I*2 “P l
Отсюда находим:
C1 = “T
hp
Ф2-Р2Г C1 °'
Поэтому движение диска определяется законом
й?0 Л
v = W0(-Tsin«+jF-7i
Р \
sin pt------sin kt I,
fc J
где к =
2c 2сФ
MR2’ h ~ MR2'
2. Явление резонанса
к = р,т. е.
2c A
——г- — p I. Тогда
MR2
h ( тг\
<р = Cj sin kt + С2 cos kt 4-1 sin I pt-I + Wot.
2p \ 2 /
Из начальных условий определяем С| и Cj:
„ „ h ( тг\
0 — Cj, 0 = С\к Н- — sin I —— j Tu?o z
2р \ 2 /
__. Г - h - h W° Г’-П
1 2pk к 2k2 к’ 2
Поэтому движение диска определяется законом:
(h Шо\ h
—7 —— I sin kt-------1 cos kt —
2k2 к J 2k
wq h
= u)Ot- — sin kt + —
К .
— W()£ +
-1 — sin kt — t cos kt |.
2k \k J
4. Теорема об изменении главного момента
105
Задача 37.21 (37.21). Твердое тело, подвешенное к упругой прово-
локе, совершает крутильные колебания в жидкости. Момент инерции
тела относительно оси проволоки z равен Jz. Момент сил упругости
проволоки mynpz = -ap, где с — коэффициент упругости, а р — угол
закручивания; момент сопротивления движению mcz = -(Зф, где ф —
угловая скорость твердого тела, а /3 > 0. В начальный момент твердое
тело было закручено на угол <р$ и отпущено без начальной скорости.
Наити уравнение движения твердого тела, если -— <
_____________
Ответ: Затухающие крутильные колебания по закону
Ф =
cos (\/к2 - п2t) -I—sin (д/к2 — п2 f)
\/к2-п2
.2 с I3'
где Л- = —, п - —
^Z *-Jz
Решение. Дифференциальное уравнение движения тела имеет вид:
= -ap - /Зф,
где <р — угол закручивания. Отсюда имеем
/3 с
ф+ -гф+ —<р = 0.
Лг Jz
Это дифференциальное уравнение свободных движений тела с учетом
вязкого сопротивления. Коэффициент затухания п = (3/(2Jz), собствен-
ная частота к = x/c/Jz.
Характеристическое уравнение, соответствующее полученному урав-
нению, следующее:
А2 + 2пА + к2 = 0.
Его решение
Ai,2 = — п ± \/п2 — к2 = —п ± k\i,
где
так как по условию
Поэтому
i = а/-Т,
/3
2JZ
малого сопротивления, п
<к).
<р — е nt(C] sin 4-С2 cos
106
4. Теорема об изменении главного момента
Начальные условия: при to — 0 ^(0) = ^>(0) = 0. Вычислив производ-
ную
^(t) — -~п€ 71 sin k[t + С*2 cos t^t) Ч- е (C^fe] cos k\t (Фк\ sin fcjt),
найдем постоянные интегрирования: Ci = n<po/ki, C2 = У’о- Закон дви-
жения тела принимает вид-
(Т1 \
— sin k\t -|- cos k]t I, где k\ —
k\ /
тело совершает затухающие крутильные колебания.
/"с
Задача 37.22 (37.22). Однородный круглый диск массы М и ра-
диуса R, подвешенный к упругой проволоке, может совершать кру-
тильные колебания в жидкости. Момент сил упругости проволоки
mynpz = —ар, где ось z проведена вдоль проволоки, с — коэффи-
циент упругости, а — угол закручивания; момент сопротивления
движению mcz = —(Зф, где ф — угловая скорость диска, а (3 > 0.
В начальный момент диск был закручен на угол и отпущен без
начальной скорости. Найти уравнение движения диска, если:
ч /3 / 2с х (3 / 2с
11 ——— — а /-- 2) ——— > л /----
' MR2 V MR2' 1 MR2 V MR2’
Ответ: Апериодическое движение по закону
/3 / 2с _nt /3
= v = v°e 11+ "'’' где "=щр-
2) Г(Л/^-Р-п)»-'/?=111 -1-
7 MR2 V MR2 * 2-фп2 - к2 L'v '
+ (\4^+п)<.-^«]> где «? = ^,
Решение. Дифференциальное уравнение движения диска:
Jz$ = -су> - /Зф,
где Jz = MR1 /2. Отсюда
2/3 2с
Коэффициент затухания п
/3
MR2’
собственная частота к =
2с
MR2'
Начальные условия: при to = 0 у>(0) = у>о, ^>(0) = 0.
4. Теорема об изменении главного момента
107
Рассмотрим случай 1, когда
/3 / 2с
MR2 ~ У MR2 ’
Это случай критического сопротивления (п = к). Характеристическое урав-
нение имеет вид
А2 + 2пХ + к2 = 0.
Его корни
А|,2 = ~п ± W - к2 = -п.
Поэтому решение
ур(О = е-п<(С, + C2t).
Скорость меняется по закону
= -ne~nt(Ci + C2t) + e~ntC2.
Используя начальные условия, получаем постоянные интегрирования:
Ci = <ро, С2 = п<ро.
Следовательно, закон движения диска имеет вид:
^ = ¥,e-W(^)(1+n0>
апериодическое затухающее движение.
Рассмотрим случай 2, когда
/3 / 2с
MR2 > V MR2'
Это случай большого сопротивления (п > к). Здесь характеристическое
уравнение имеет два действительных решения
Ai,2 — — п ± у/п2 — к2.
Поэтому закон движения диска следующий:
„ „-nt (/-< -у/п'-к11 , „у/гг-к-
= е I C|C 4- C2e I.
Скорость
<p(t) = - ne~nt + C2e'/"IZFt) +
+ e~nt (-C, Vn2 - k2e-yf^t 4- C2y/n2 - k2e'/^t^.
108
4. Теорема об изменении главного момента
Используя начальные условия, получаем, что
tpo y/n2 - k2 - n tpo Vn2- k2 + n
2 y/n2 — k2 2 \/n2 — k2
Следовательно, диск совершает апериодическое затухающее движение по
закону
V = ^/=
2y/nz — к1 L
.j । Vn2-k2t
kz + n)e
Задача 37.23(37.23). Твердое тело, подвешенное на упругой про-
волоке, совершает крутильные колебания под действием внешнего
момента ты = mo cos pt, где то и р — положительные постоянные,
az — ось, направленная вдоль проволоки. Момент сил упругости про-
волоки mynpz = -су>, где с — коэффициент упругости, а р — угол за-
кручивания. Момент инерции твердого тела относительно оси z равен
Jz. Силами сопротивления движению пренебречь. Определить урав-
нение движения твердого зела в случаях: 1) -Jc/Jz^p, 2) у/ с/ Jz —р,
если в начальный момент при ненапряженной проволоке твердому
телу была сообщена угловая скорость Wq-
^Р,
о>о h
р — — sin kt + —--------(cospt - cos kt), где
к к1 — p1
, mo
ti = —
= Р<
Wo h
p = — sin kt 4-----1 sin kt, где
к 2k
. m0
= P, h = —
Решение. Дифференциальное уравнение вынужденных крутильных
колебаний тела без учета сопротивления имеет вид:
c mo
p + —p = — cos pt.
Jz Jz
Здесь <р — угол закручивания упругой проволоки, определяющий
положение тела при его вращении вокруг вертикальной оси z.
Собственные колебания описываются законом
p00 = C\ sin kt + C, cos kt,
4. Теорема об изменении главного момента
109
где к = y/c/Jz. Начальные условия: при to = 0 9?(0) = 0, ^(0) = wq.
Вынужденные колебания зависят от соотношения частот к и р.
1. Рассмотрим нерезонансный случай к р, т.е. c/Jz р. Ищем
частное решение в виде Bcospt. С помощью метода неопределенных
то
коэффициентов находим В = —------г-. Поэтому закон колебаний тела
Jz(k2-p2)
будет
то
w = С, sin kt 4- Ci cos kt 4-cos pt.
Jz(k2-p2)
Найдем скорость
mop
ф(1) = С\к cos kt - Cik sin kt —----=- sin kt.
Jzik* - p1)
Использование начальных условий позволяет вычислить постоянные ин-
тегрирования С|, Ст,. Итак,
* к' С2 Jz(k>-P2y
Поэтому в нерезонансном случае закон крутильных колебаний диска
имеет вид:
т0
У> =
wo mo
— sin kt 4- — ------t-(cospt — cos kt),
к Jz\k — p )
где к = у с/ Jz.
2. Рассмотрим
Воспользуемся решением, полученным выше, при р —> к. Введем новую
переменную £ по формуле р = к + £. Вычислим
случай резонанса, когда к = р, т. е. \/с/ Jz = р.
lim
f->0
Wo
— sin kt +
Ft
то
(cos ((Л + £)t) — cos kt)
Wo Шо
= — sin kt 4------lim
— ii.>i , • (cos kt cos et — sin kt sin st — cos kt) .
Jz e-t0\_—2k£ — £2 ' J
w0
к
Так как при £ —> 0 и числитель, и знаменатель стремятся к нулю, то
воспользуемся правилом Лопиталя:
- cos kt t sin £t - sin kt t cos £t
й>0 Шй
— sin kt 4- — lim
/с £~
mo — t • sin kt
-(2fc + 2e)
wq mo — t sin kt wo mo
= — sin kt 4---------------= — sin kt 4------— t sin kt.
к Jz -2k к Jz -2k
Следовательно, при резонансе закон крутильных колебаний диска имеет
вид:
ц> = — sin kt 4--------- t sin kt, к =
* к Jz-2k
110
4 Теорема об изменении главного момента
' Задача 37.24(37.24). Однородный круглый диск массы М и ра-
диуса R, подвешенный на упругой проволоке, совершает резонансные
крутильные колебания в жидкости под действием внешнего момента
mBZ = mo sin pi, где и р — положительные постоянные, a z —
ось, направленная вдоль проволоки; момент сил упругости проволоки
wynpz = -ср, где с — коэффициент упругости, а р — угол закручива-
ния; момент сопротивления движению mcz = -0ф, где ф — угловая
скорость диска, а /3 > 0. Найти уравнение вынужденных резонансных
колебаний диска.
/ 2С
Ответ: При р = \ ---г
Р Р V МВ?
h 2mo 0
р = -~—COS pi, где ft = ,, , П = .
r 2np MR2 MR2
Решение. Дифференциальное уравнение вынужденных колебаний
диска имеет вид:
Ъф — -ср - 0ф + mo sin pi.
Момент инерции Jz = MR?/2. Перепишем уравнение в каноническом
виде:
.. , 2/3 с 2т0
ф Ч----Ч-----р =-----т sin pi.
* MR2 * Jz MR2 Р
Коэффициент затухания
0
П — ---г,
MR?
собственная частота диска
137.25(3
iw
iSH
дина
,;жт
ЯКИ
moi
taai
д
й
«Е.Дн<]
•I М(
Wk
(по условию задачи имеет место случай резонанса), коэффициент
2m0
ft =---т-
MR?
Закон вынужденных резонансных крутильных колебаний диска имеет
вид:
ft ( 7Г\
у/(к2 - р2)2 Ч- 4п2р2 \ 2 )
2mo-(MR2)2 Jz ± m0MR2Jz / Г^с~ \
“------СХР‘ =------------------С“ (V 7'
3«(31
Ч,
ч
Ч(
Ч
'V11
4. Теорема об изменении главного момента
111
Задача 37.25 (37.24). Для определения коэффициента вязкости
жидкости наблюдают колебания диска, подвешенного к упругой про-
волоке в жидкости. К диску приложен внешний момент, равный
Afosinpf (Mo = const), при котором наблюдается явление резонанса.
Момент сопротивления движению диска в жидкости равен aSw, где
a — коэффициент вязкости жидкости, S — сумма площадей верхнего
и нижнего оснований диска, w — угловая скорость диска. Определить
коэффициент а вязкости жидкости, если амплитуда вынужденных
колебаний диска при резонансе равна 9?0.
” ~ Мо
Ответ: a =------.
___________¥>о$Р_____________________________________ /
Решение. Дифференциальное уравнение вынужденных колебаний
диска с учетом вязкого сопротивления:
<р + 2пр + А*2^ = h sin pt,
где
aS
п=тг к=
к
Т‘
Jz
По условию наблюдается явление резонанса, значит к = р и ампли-
туда вынужденных колебаний
в _ h
2пр
h
С другой стороны, В = у?(). Поэтому приравняв -— = или
2пр
h
2-(aS/(2Jz))P~V>0’
получаем коэффициент вязкости жидкости
h Jz 2MqJz Mt,
Q — ---- = --------- — -----
25^o Jz-'ISiptfP Sipop
Задача 37.26 (37.26). При полете снаряда вращение его вокруг оси
симметрии замедляется действием момента силы сопротивления воз-
духа, равного кш, где w — угловая скорость вращения снаряда, к —
постоянный коэффициент пропорциональности. Определить закон
убывания угловой скорости, если начальная угловая скорость равна о>о,
а момент инерции снаряда относительно оси симметрии равен J.
Ответ: ш = а?()е ktiJ
112 4 Теорема об изменении главного момента
Решение. Записав теорему об изменении главного момента коли-
честв движения снаряда относительно его оси симметрии, движущейся
поступательно, получим дифференциальное уравнение движения снаряда:
Jw = —kw.
Проинтегрируем это уравнение, учитывая начальные условия:
t
dw
J— = — kw
dt
dw
J— = -kdt
w
= -к
0)()
о
w
Jin — = — kt
w0
-kt/j
w = woe
Это и есть закон убывания угловой скорости с течением времени.
Задача 37.27 (37.27). Для определения ускорения силы тяжести
пользуются оборотным маятником, который представляет собой стер-
жень, снабженный двумя трехгранными ножами А и В.
Т Один из ножей неподвижен, а второй может переме-
г щаться вдоль стержня (рис. 37.27.1). Подвешивая стер-
i жень то на один, то на другой нож и меняя расстояние
I АВ между ними, можно добиться равенства периодов
| качаний маятника вокруг каждого из ножей. Чему рав-
: но ускорение силы тяжести, если расстояние между
f В ножами, при котором периоды качаний маятника рав-
Ij| ны, АВ = I, а период качаний равен Т?
Рис. 37.27.1 Ответ: g = 4п21/Т2.
Рис. 37.27.2
Решение. Запишем дифференциальное уравнение
колебаний системы, подвешенной за один из ножей:
J(p = -mgl sin
Размерами ножей пренебрегаем, длину I считаем дли-
ной приведенного физического маятника. Предполагаем
угол малым. Поэтому уравнение принимает вид:
тп12ф + mgltp — 0.
Частота колебаний к = \/g]l, период колебаний Т = 1тг/к.
Отсюда находим ускорение силы тяжести
4ТГ2/
уг-
4. Теорема об изменении главного момента
113
Задача 37.28(37.28). Два твердых тела могут качаться вокруг од-
ной и той же горизонтальной оси как отдельно друг от друга, так
и скрепленные вместе. Определить приведенную длину сложного ма-
ятника, если массы твердых тел М\ и М2, расстояния от их центров
тяжести до общей оси вращения а\ и аг, а приведенные длины при
отдельном качании каждого и h-
+ Л/гОг^г
Ответ: /пр = —----------—--------
M\Q,\ -|- M2G2
Решение. Расчетная схема — на рис. 37.28.1, где — переменный
угол качания сложного маятника, у?о — постоянный угол между осями
OCi и ОС2 (Ci,Cz — центры масс исходных маятников). Пусть J\, J2
моменты инерции маятников относительно точки подвеса О. Так как
ОС\ = а(, ОС2 = аг, то имеем для приведенных длин I], 12'
Jx , Ji
71 ’ ’ л г
Для приведенной длины сложного маятника имеем:
J] -(- J2 + Л/гаг^г
+ М2)а (Mi + М2)а ’
где а — расстояние нового центра масс С до точки подвеса О. Чтобы
вычислить это расстояние поступим следующим образом. Введем систему
координат Оху, где ось Ох направлена по линии OCi, а ось Оу — пер-
пендикуляр к ней (см. рис. 37.28.1). В этой системе имеем для координат
ХС’ Ус нового центра масс С:
Хс = л# 1 лт (Xc>Ml + хЬМд = .,1л, (oiAfi + а2 cosуг0 • М2),
lvi\ + JVi2 1v1\ ~г 1V12
114
4. Теорема об изменении главного момента
а = г/^ + ^ = _
— у а\М2 + а^М2 + la\a2M\M2 cos ^о-
Ус =---------+ VcsM?) =----------—~ ' «2 sin w>o • М2.
ус Mt+M2 ' 2 Mt+M2 r
Тогда получим:
1
i +
Тогда получаем ответ:
М2(1212
yja2M2 + + 2а\а2М\М2 cos
Заметим, что при <ро = 0 (маятники соосны), мы получим ответ, приве-
денный в задачнике [10].
Задача 37.29 (37.29). Часть прибора представляет собой однород-
ный стержень длины L, свободно подвешенный одним концом на го-
ризонтальной оси О. Для регистрации качаний стержня к его нижнему
концу приклеивается небольшое зеркало массы тп. При этом, чтобы
частота колебаний стержня не изменилась, на нем в другом месте
укрепляется груз А. Рассматривая зеркало и груз как материальные
точки, найти минимальную массу, которую должен иметь груз А.
На каком расстоянии от оси О его следует прикрепить?
Ответ: mA = 3m, О А = -L.
Решение. Расчетная схема — на рис. 37.29.1, где то — масса стерж-
ня, а С — его центр масс, m, тА — дополнительные массы. Пусть
Рис. 37.29.1
Jo = тоД2/3 — момент инерции стержня относи-
тельно точки О. Начальная приведенная обратная
длина:
1 m^L/l
lo Jo
Новая обратная приведенная длина:
1 _ (moJ/2) + mL + тАх
I Jo + тАх2 + mL2
Приравнивая эти выражения, получаем:
э™г _ 1 2 , ™ 2 , ™А L
— Зж -|-------L ----=------------—
тпд т 2xL - Зх2
4. Теорема об изменении главного момента
115
тл =
-----J ТП.
х\
l
2
- - 3
L /
Минимум Шу] по х б (О, L) соответствует максимуму знаменателя, т. е.:
\ 21
L
К
11
й
ti
!
/ х
max 2 —
и достигается при 2 - 3 2 A = 0 A* = 1/3. Таким образом,
I * 1
si = A* • L --- -L, mA = ——m — 3m.
3 1/3
= max [2А - ЗА2] = -
o^x^i 3
-3
^Задача 37.30(37.29). Для регулирования хода часов к маятнику
массы Mi приведенной длины I с расстоянием а отего центра тяжести
до оси подвеса прикрепляют добавочный груз массы Mi на расстоя-
нии х от оси подвеса. Принимая добавочный груз за материальную
точку, определить изменение AZ приведенной длины маятника при
данных значениях и х и значение х = ®j, при котором заданное
изменение AZ приведенной длины маятника достигается при помощи
добавочного груза наименьшей массы.
Ответ: Приведенную длину маятника надо уменьшить на
М2х(х -I) * 1 * * *
AZ —----------, х \ — (Z Т AZ).
Mia + M^x 2V * * * * '
U
н
р
Решение. Расчетная схема — на рис. 37.30.1, где а — расстояние
от центра масс Со исходного маятника до точки подвеса О, ОМ\ = I —
длина соответствующего приведенного матема-
тического маятника. Имеем, по определению:
I = —
Mia
где Ji — момент инерции исходного маятника
относительно подвеса О. Пусть теперь на оси
OCqMi разместили добавочный груз М2, при-
чем ОМ2 = х. Тогда имеем новый момент инер-
ции относительно точки О:
J2 = <71 Т ZV/i х ,
а новое расстояние аг от точки О до нового положения центра масс:
°2 = w (M|Q + М^ХУ
М1+М2
116
4. Теорема об изменении главного момента
Новая приведенная длина (по определению):
J2 Jj+MiZ2 M^al + М2х2
^2 (M\+M2)a2 М}а + М2х M\a + M2x'
Изменение приведенной длины:
I I М\0,1 + М2х2 М2х2 - М2х1 М2х(х-Г)
M]d + M2x M\a + M2x M\a + M2x
Фиксируем AZ, х и находим из этого соотношения М2.
M\a-Al М|О-Д/
^2 х(х -Г) - х • Al х(х - I - АГ)
Рассмотрим два случая:
Г. А1 = -е < 0. Тогда согласно (1), имеем х € (0,I). Формула (2) при-
обретает вид:
, , М\ • a • е
М2(х) = ’ х 6 (°>1 ~
Х[1 — Е - X)
Отсюда следует, что min М2(х) соответствует
х 6 (0,I-е)
max [z(Z -£--z)] =------ при х< = ——-
4 2
Для корректности необходимо еще показать, что 0 < е < I. Это сле-
дует из формулы (1), которая при А1 = -е имеет вид:
М2х(1 - х)
М}а + М2х
е <1, т. е.
М2х(1 - х) (М}а + М2х) <=>
—М2х2 < M]dl.
Последнее неравенство уже очевидно. Итак, для уменьшения при-
веденной длины дополнительная минимальная масса должна быть
размещена на расстоянии от точки подвеса, равном половине новой
приведенной длины.
2°. А1 = е > 0. Тогда согласно (1), имеем х G (Z, оо). Формула (2) при-
обретает вид:
М2х(1 - х)
М\ а + М2х
, М\й-Е
М2(х) = ---Г, X е(1 + Е, оо).
х(х -1-е)
Из последнего выражения следует, что min М2(х) — 0 и достигается
этот минимум при х = оо. Итак, увеличение приведенной длины
может быть осуществлено как угодно малой дополнительной массой,
помещаемой на достаточно большом расстоянии от точки подвеса.
4. Теорема об изменении главного момента
117
Задача 37.31 (37.30). Для определения момента инерции J дан-
ного тела относительно некоторой оси АВ, проходящей через центр
масс G тела, его подвесили жестко скрепленными с ним стержнями
AD и БЕ, свободно насаженными на неподвижную горизонталь-
ную ось DE, так, что ось АВ параллельна
DE (рис. 37.31.1); приведя затем тело в ко-
лебательное движение, определили продол-
жительность Т одного размаха. Как велик
момент инерции J, если масса тела М и рас-
стояние между осями АВ и DE равно Л?
Массами стержней пренебречь.
/72 h
Ответ: J = hMg —7-------
\7Г2 g
Решение. Согласно условию задачи мо-
мент инерции тела относительно оси вращения
DE (см. рис. 37.31.2), с использованием теоремы
Штейнера—Гюйгенса, есть:
Jde — Jab + Mh1.
Тогда приведенная длина, по определению, есть:
Jab + Mh2
Mh
где h — расстояние центра масс G до оси вращения DE. Согласно фор-
муле для полупериода математического маятника, имеем:
г=^
Jab + Mh2
Mh
T2g
Jab = Mgh
h
g
Задача 37.32(37.31). Решить предыдущую задачу с учетом массы
тонких однородных прямолинейных стержней AD и BE, если масса
каждого из них равна М\.
Ответ: J h
(М vMx)gT2 ЗМ + 2М' '
------- h .
3
7Г2
Решение. С учетом массы стержней AD и BE имеем (рис. 37.31.2)
для момента инерции всей системы относительно оси вращения DE:
M\h2 . 2 2
J = Jde + 2 • ——— = Jab + Mh + -^M\h .
118
4. Теорема об изменении главного момента
Расстояние от нового центра масс до оси вращения DE:
1 / h h\ М + М}
a =-----( Mh + Mx • - + • - = h • ————
M + 2М} \ 2 2 J M + 2M\
Приведенная длина в этом случае:
I =
□ 2 ,
Jab+ML —M\h
h(M +М^
так как Т = я
получим:
Jab = h
~(M + Mi)gt2 3M + 2Mi ‘
--------------------------- h .
3
7Г2
Задача 37.33 (37.32). Для определения момента инерции шатуна
его заставляют качаться вокруг горизонтальной оси (рис. 37.33.1), про-
дев через втулку цапфы крейцкопфа тонкий цилиндрический стер-
жень. Продолжительность ста размахов 100Z = 100 с, где Т — по-
ловина периода. Затем для определения расстояния АС = h центра
масс С от центра А отверстия шатун положили горизонтально, под-
весив его в точке А к талям и оперев точкой В на платформу деся-
тичных весов; давление на нее оказалось при этом равным Р. Опре-
делить центральный момент инерции J шатуна относительно оси, пер-
пендикулярной плоскости рисунка, имея следующие данные: масса
шатуна М, расстояние между вертикалями, проведенными через точ-
ки А и В (см. правый рисунок) равно I, радиус цапфы крейцкопфа г.
Ответ: J =
Pl + Mgr
Рис. 37.33.1
4. Теорема об изменении главного момента
119
Рис. 37.33.2 Рис. 37.33.3
Решение. Прежде всего определим расстояние АС = Л из схемы
рис. 37.33.2, составляя уравнение моментов относительно точки А:
Р
P-AB-Mg-AC = 0 => h=-—-l,
Mg
Приведенная длина шатуна (см. рис. 37.33.3)
. _ Ja _ Jc + Mh2
1 = Mh[ = Mh\ '
где hi = h+r — расстояние от центра масс до точки подвеса. Полупериод
Т = 1 (с). С другой стороны Т = TT\/l\/g =>
Т2 _ Jc + Mh2
1 7г2^ Mhi
г л.г (Т^ Pl A Pl + Mgr(T2g Pl \
=> Jc = мhl I - — - т =-----------------I —у - —- - г I.
\ 7Г2 Mg / g \ 7Г2 Mg /
Задача 37.34(37.33). Маятник состоит из стержня
АВ с прикрепленным к нему шаром массы m и ра-
диуса г, центр которого С находится на продолжении
стержня (рис. 37.34.1). Определить, пренебрегая мас-
сой стержня, в какой точке стержня нужно поместить
ось подвеса для того, чтобы продолжительность одного
размаха при малых качаниях имела данную величину Т.
Ответ: ОС = — (gT2 + у/gT4 - 1,6тг4г2).
2тг2
Так как должно быть ОС г, то решение возможно, если
Т2 l,4(7r2/g)r; решение, соответствующее знаку «минус»
перед радикалом, невозможно.
А
О*
Рис. 37.34.1
120
4. Теорема об изменении главного момента
Решение. Расчетная схема — на рис. 37.34.2. Имеем
2 2 , 2
Jo — Jc + mx — -mr 4- mx .
Приведенная длина
2 2 . -2
т ~~т
i = - = i-
mx
квадратное уравнение
2
х-----тх
7Г~
7Г2
.2
g2T4 _ ^7Г4Г2
Исследуем теперь формулы (1). Прежде всего ясно, что для существования
решения необходима положительность подкоренного выражения в (1), т. е.
24,2 =
(О
2m4 . 8 42
g T > -7Г r
Кроме того, из физических соображений следует неравенство х > г
Рассмотрим знак «минус» в (1). Имеем:
7Г2Г.
(2)
х2 =
8 . 1
-7Г4Г2 1 = -----v
5 J 2тг2
8 4~?
~7Г Г
8 4 „2
-7Г Г
5
)1П,Т
миобеч
МИЭТ(
фк(
137.35(37
зешенфи
и!
'Настоя
0,цм»
Или.
«•, [fycii
'"«PUlffl
’Wiyno
J
®инерщ
х
2 2
5 = °
Используя неравенство (2), получим:
8 4 2 8 4 2
1 5 . 1 ~тг г 1 /8 2 1 /8 ЛГ
2яI 2 gT2 2тг2 /8 2тг2 V 5 Я Г 2 V 5 Г ~ \ 20 Г < Г'
V 5 Г
Следовательно, х2 < г и знак «минус» в (1) не подходит для решения.
Рассмотрим знак «плюс» и найдем те значения Т, для которых соблюдено
неравенство Ж| > г, т. е.:
I 8
g2T4 _ _7г4г2 > 27Г2Г - gT2.
4. Теорема об изменении главного момента 121
Если gT2 > 2тг2г, то неравенство заведомо выполнено. Пусть gT2 < 2л2т.
Тогда возводя обе части в квадрат, получаем:
g2T4-^7r4r2>47r4r2+g2T4-47r2rg7’2 => 4?r2rgT2 > у7г4г2 ==>
? 28 7 22
=> gT2 > —я г <=> gT2 > 1,4тг г.
20
При выполнении этого неравенства заведомо соблюдается неравенство (2)
и корень Х\ физически реализуем.
Ответ: ОС = xt = -Дг (gT2 + \ g2T4 - -тг4г2 ) при gT2 > 1,4тг2г.
2тг \ V 5 j
Задача 37.35(37.34). На каком расстоянии от центра масс должен
быть подвешен физический маятник, чтобы период его качаний был
наименьшим?
Ответ: На расстоянии, равном радиусу инерции маятника относи-
тельно оси, проходящей через его центр масс перпендикулярно плос-
кости качаний.____________________________________
Решение. Пусть х — расстояние точки подвеса до центра масс,
J — момент инерции тела относительно центра масс. Тогда приведенная
длина дается формулой:
J + ms2 ( J \ 1 2 1
I =-------= | — I - + х = р---1- х,
тпх \т/ х х
где р — радиус инерции тела относительно центра масс. Период вычис-
ляется по формуле:
Д’ 2тг Г\ 1
Т = 2л л - — —\ р2 • - + х .
V g V х
Ищем минимум функции
/(я) = Р2~ + х’
при х & (0, оо). Имеем
fx = ~ Р ' j +1—0 ---< +run = Pi
X1
а так как
/"=> °>
то это — точка минимума. Таким образом, подвешивать надо на расстоя-
нии от центра масс, равном радиусу инерции тела.
122
4. Теорема об изменении главного момента
Задача 37.36 (37.35). Маятник состоит из стержня с двумя за-
крепленными на нем грузами, расстояние между которыми равно /;
верхний груз имеет массу mt, нижний — массу m2- Определить,
на каком расстоянии хот нижнего груза нужно поместить ось подвеса
для того, чтобы период малых качаний маятника был наименьшим;
массой стержня пренебречь и грузы считать материальными точками.
— v/m7+v™2
Ответ: х = IJrrti-------
тщ 4- m2
Решение. Расчетная схема изображена на
рис. 37.36.1, где О — искомая точка подвеса.
Ось х направляем по стержню АВ, начало ее —
в точке О, а положительный отсчет — в сторону
нижней массы m2. Тогда х-координаты точек
Ш| и m2 таковы:
Яго, — (J •&), •Em? — •£•
Считаем х — координату центра масс:
хс = а =
----; (mia;mi + rn2xm,) =---[-mi(Z - х) 4- m2x].
mi 4-m2--------------------------------’ wi| 4m2
Будем предполагать, что a > 0. Это соответствует нижнему (устойчивому)
положению приведенного маятника. Случай а < 0 соответствует верхнему
(неустойчивому) положению маятника и поворотом на 180° сводится
к случаю a > 0. В предположении a > 0 мы имеем область изменения х
из неравенства:
- х) + m2X = a(m,i + m2) > 0 <=> х > ———I.
mi 4- m2
Запишем формулу для приведенной длины:
Jo mi(l - х)2 + т2х2 mi
<0 — т--:---г- =-----г.----г-----, х > ---------1.
(mi+m2)a -mi (4 - х) + т2х mi+m2
Квадрат периода вычисляется по формуле:
2 21о 47Г2 mi(l - х)2 + т2х2
1 = 47Г — =-----------------------------.
g g -mi(l — х) + т2х
Для вычисления минимума обозначим:
-mi(l - х) 4- т2х = у
mil + у
х —--------
mi + m2 ’
4. Теорема об изменении главного момента
123
Тогда получим:
2 4тг2 1
т\у) = — ----------
(m2l-y)2
g (m, + т2)2 [у У
4тг2 ( 1
= ---------(y+-mim2l , у 0.
g(m, +т2)\ у )
Ясно, что минимум Т2 (у) при у 0 достигается в точке у» = 1у/т\т2,
т. е.
I , ,____ч
ж* =--------(т, + у/т\т2).
ту + т2
Причем это минимальное значение дается выражением:
2 8тг2/ ут}т2 8тг2/ I
-Дпт — Т г-
g т{+т2 g mi
8тг2/
g
4тг2/
g
1
2
Ясно, что полученное х, удовлетворяет неравенству ж, > ------------1.
гп\ + т2
Отметим, что случай a < 0 приводит к тому же результату, если допу-
стить поворот маятника на 180° (массы т,\ и т2 во всех формулах нужно
поменять местами!).
Задача 37.37(37.36). На каком расстоянии от оси подвеса должен
быть присоединен к физическому маятнику добавочный груз, чтобы
период качаний маятника не изменился?
Ответ: На расстоянии приведенной длины физического маятника.
Решение. Расчетная схема — на рис. 37.37.1, где С\ — центр масс
исходного физического маятника, причем ОС\ = aj, а в точке С2 раз-
мещена добавочная масса т2. Пусть ОС2 = х и угол между ОС\ и ОС2
Рис. 37.37.1
124 4. Теорема об изменении главного момента
равен 9?0- Пусть масса исходного маятника т\, а его момент инерции
относительно подвеса О равен J. Тогда начальная приведенная длина:
т\О,\ ’
а после добавления массы m2'.
ТП2Х2 4- J
(т! + т2) • а2 ’
где а2 = ОС, С — новый центр масс. Чтобы вычислить а2, введем систему
координат Оху, где ось Ох направим по ОС\, а ось Оу — перпендику-
лярно к ней. В этой системе имеем:
1
хс =---------(miOi + m2a;coso0),
mi + m2
Ус =---------(mi • 0 + m2x sin ip0).
mi + m2
Отсюда
a2 = yJ^c+Ус = m --------yjm2a2 4- m^x2 4- 2mim2aix cos<po .
Подставляя эту формулу в выражение для 12 и приравнивая Ц и /2,
получим уравнение:
J т2ж2 + J
m'ai yjт2а2 4- т$х2 + 2т[т2а1Ж cos <р0
Подставляя сюда J — miaj], получим уравнение:
l2\(m2ia2i+т]х2 + 2mim2aixcos(p0) = (т2ж2 + ттца,/,)2. (1)
Проще всего решить это уравнение при у>0 = 0 (т. е. когда дополнительная
масса размещается на оси 0С|). Тогда имеем:
/2(т|О| + т2ж)2 = (т2ж2 4-пца^2 ==>
==> li(mtai+т2х) — (т2х2-I-miaili) =>
==> Цт2х = т2х2 => xi = 0, х2 = 1\,
т. е. приведенная длина, а значит, и период, не изменяются, если доба-
вочную массу разместить либо в точке подвеса, либо в центре качаний,
т. е. на расстоянии приведенной длины по оси 0С\\ Причем это решение
не зависит от величины добавочной массы т2! Этот ответ приведен в сбор-
нике [10].
Ь.Тгорема
.--------
Лмравн!
'•-и
яЗкиор»
’чржние (
M^i/li-
гарема i
M(ICOS|
яует о н
Wnpei
аф,
illл рщцуса
Л.1), перг
Ь вмени
Шить
Шуюм,
^ЙЩНИЙ
^добавлена
Ж+(2()!
4. Теорема об изменении главного момента
125
Если ^>о / 0, то уравнение (1) приобретает вид:
х3 + x(2Xailt - Zi) - 2Aa(Z? cos 920 = 0, (2)
где А = mi/mj — отношение масс. Любое положительное (х > 0) решение
уравнения (2) удовлетворяет условию задачи. Введем новое переменное
z = х/1\. Тогда уравнение (2) примет вид:
/(z) — z3 + z(2Xp - 1) - 2Хр cos 920 = 0, (3)
где А = т[/т2, р = Q\/l\. Пусть у?0 £ [-тг/2,тг/2]. Тогда уравнение (3)
заведомо имеет корень на интервале z 6 [0, 1]. Действительно:
/(0) = -2A//cos9?o < 0, /(1) — 2A/z( 1 - cos 920) > 0.
Это и свидетельствует о наличии корня, однако величина этого корня
будет уже определяться тремя параметрами: А, р, 920!
Задача 37.38(37.37). Круглый цилиндр мас-
сы М, длины 2/ и радиуса г = 7/6 качается около
оси О (рис. 37.38.1), перпендикулярной плоско-
сти рисунка. Как изменится период качаний ци-
линдра, если прикрепить к нему на расстоянии
ОК = 827/72 точечную массу т?
Ответ: Период качаний не изменится, так как
точечная масса добавлена в центре качаний ци-
линдра.
Решение. Вычислим момент инерции цилиндра относительно точ-
ки подвеса О (см. рис. 37.38.2)
Jo — Jc + М
1 г 2 , Ml
= иМ[Зг2 + (2/)!] + —=
12
Ml2
+ —
= — м
Mi1 mi2 mi2 _
I44 + + -
Ml2 7M12 85M12
"iK4" 12 “ 144
126
4. Теорема об изменении главного момента
Приведенная длина этого физического маятника вычисляется по формуле:
Jo 85MZ2 2 _ 85
пр ” М1/2 ~ 144 ' Ml ~ 72 ’1 ~ К’
т. е., в соответствии с результатом предыдущей задачи 37.37, прикрепление
груза в точке К (центре качания) не изменяет периода колебаний.
Задача 37.39 (37.38). Найти уравнение малых колебаний однород-
ного диска массы М и радиуса г, совершающего колебания вокруг
Ответ: 1) При р
горизонтальной оси Oz, перпендикулярной его
плоскости и отстоящей от центра масс С диска
на расстоянии ОС = г/2 (рис. 37.39.1). К. дис-
ку приложен вращающий момент тпвр, причем
— mo sin pt, где m0 и р — постоянные. В на-
чальный момент диску, находившемуся в нижнем
положении, была сообщена угловая скорость (До-
Силами сопротивления пренебречь. Считая ко-
лебания малыми, принять sin « <р.
if hp \ h
<P — T I wo ~ уз-г I sin kt + -z-у sin , где k =
k\ k2—p2J k2-p2
4т0
ЗМг2’
1 ( . Л \ h , 4т0
<р = - (д0 + — I smpZ - — t cospt, где h =----
Р\ 2р] р 2р г ЗМг2
Решение. Расчетная схема — на рис. 37.39.2, Составим уравнение
изменения кинетического момента относительно точки подвеса О:
т
= mBp - Mg- sin <p,
где
.2
T T ,, f r\2 mr2 mr4 3 ->
Jo — Jc + мI - ) = —— -|------= -Mr.
\2 J 2 4 4
Полагая sin ss <p, получим:
3. _ 2.. . , Mgr
-Mr <p = m0 smpt------—p ==>
4. Теорема об изменении главного момента
127
.. , 2g 4m0 .
=> ф + k <р = hsinpt,
.2 2г л.
где k = —, п —
Зг
4т0
ЗМг2'
Г. Пусть к р. Тогда решение ищем в стандартной форме:
p(t) — A sin kt + В cos kt 4- С sin pt.
Константу С находим простой подстановкой этого решения в урав-
нение; получим после сокращений:
-Ср2 sin pt + к2С sin pt = h sin pt => C = -5--------7.
- jr
Константы А и В находим из начальных условий: у?(0), 0(0) = w0.
Тогда получим:
1 1 / ph \
0 = В, м0 = кА + Ср => А = -(w0 - Ср) = - I w0 - — I
nJ Л» \ Kj р j
Таким образом, получаем решение:
1 h ( Р \
<p(t) = -w0 sin kt + -т-т I sin pt - - sin kt I. (1)
к к2 - p2 \ к J
2°. Пусть к = p. Устремим в выражении (1) к —> р. Получим, используя
правило Лопиталя:
lim <p(t) = -Wo sin pt 4- lim — I — • t cos kt 4- 75 sin kt
ic—p к—2k у к к
= -Wq sinpf 4--I -t cos pt 4- - sinpf
P Ip \ P
1 ( h\ h
= - I Wo 4- — ) sin - — t cos pt.
p\ 2p J 2p
Задача 37.40(37.39). В сейсмографах — приборах для регистра-
ции землетрясений — применяется физический маятник, ось подвеса
которого образует угол а с вертикалью. Расстояние от оси подвеса до
центра масс маятника равно а, момент инерции маятника относитель-
но оси, проходящей через его центр масс параллельно оси подвеса, равен
Jc, масса маятника равна М. Определить период колебаний маятника.
Ответ: Т = 2тг
Jc + Ma2
Mag sin a
4. Теорема об изменении главного момента
128
Решение. Расчетная схема представлена
на рис. 37 40.1, где АВ — ось подвеса, образую-
щая угол а с вертикалью Колебания маятника
в этом случае — это обычные колебания около
«новой» вертикали DE, которая перпендику-
лярна оси АВ и лежит в плоскости, образуемой
осью АВ и «старой» вертикалью. В результате,
колебания маятника происходят в плоскости,
перпендикулярной плоскости рис. 37.40.1, в по-
ле силы тяжести, которое является проекцией
ускорения g на ось DE, т. е. g| — g sin а. Тогда
приведенная длина дается формулой:
4. Ге
я; йен
W
_ Jc + Ma2
rip " Ma
T = 2тг
где Jc — момент инерции маятника относительно оси, проходящей через
центр масс С и параллельной оси подвеса АВ.
’Лте,а
глнух
Ми
®прав
Рис. 37.41.1
коэффициент
Задача 37.41 (37.40). В вибрографе для записи го-
ризонтальных колебаний фундаментов машин маят-
ник ОА, состоящий из рычага с грузом на конце,
может качаться вокруг своей горизонтальной оси О,
удерживаясь в вертикальном положении устойчивого
равновесия собственной массой и спиральной пру-
жиной (рис. 37.41.1). Определить период собственных
колебаний маятника при малых углах отклонения, ес-
ли максимальный статический момент силы тяжести
маятника относительно его оси вращения равен Mgh,
момент инерции относительно той же оси равен Jz,
жесткости пружины, сопротивление которой пропор-
йрекод
“Ml! ВВОДЯ
•®ас
Ц=-
ционально углу закручивания, равен с; при равновесном положении
маятника пружина находится в ненапряженном состоянии. Сопротив-
лениями пренебречь.
Ответ: Т = 2тг
с + Mgh
Решение. Составляя уравнение изменения кинетического момента
относительно оси вращения маятника, получим:
4’WlX к
‘Ммп
Jz<p — -c<p - Mgh sin tp.
4. Теорема об изменении главного момента
129
При малых <р имеем sin <р к <р, тогда:
Jz<p — -с<р - Mghip =>
.. /C + Mgh\
V + ----z--- I = 0-
z
Таким образом, малые колебания происходят с частотой
<v0 =
С + Mgh
и периодом Т = 2ti/wq.
Задача 37.42 (37.41). Виброграф (см. предыдущую задачу) закреп-
лен на фундаменте, совершающем горизонтальные гармонические ко-
лебания по закону х — asinutf. Определить амплитуду а колебаний
фундамента, если амплитуда вынужденных колебаний маятника виб-
рографа оказалась равной у?0-
Ответ: a =
<р0(с Т Mgh - Jzw* 2)
Mhw2
Решение. Переходя в подвижную систему координат, связанную
с фундаментом, и вводя силу инерции — Мх, мы получим уравнение
кинетического момента относительно оси маятника:
Jz<p = —с<р - Mgh sin <р - Мх h cos (р.
Подставляя сюда х = -aw1 sin wt и принимая sin у? ~ <р, cos<p ~ 1,
получим:
Jztp 4- у?(с + Mgh) = Maw2h sinaii =>
2 Maw2h
Ср + <p • Wq =---sin wt,
Jz
где
2 Ст Mgh
w0 = 7 •
Jz
Уравнение вынужденных колебаний <p = <po sin wt. Подставим <p в урав-
нение:
2 2 Maw2h
— <p0- w sin wt T wtfp® sin wt =---sin wt
Jz
a =
MwAh
Mw2h
130
4. Теорема об изменении главного момента
Задача 37.43 (37.42). При пуске в ход электрической лебедки к ба-
рабану А приложен вращающий момент твр, пропорциональный вре-
Рис. 37.43.1
мени, причем твр = at, где a — постоянная. Груз В
массы М\ поднимается посредством каната, навитого
на барабан А радиуса г и массы Mi (рис. 37.43.1).
Определить угловую скорость барабана, считая его
сплошным цилиндром. В начальный момент лебед-
ка находилась в покое.
Ответ: ш =
(at - 2Migr)t
r2(2Mi + М2)'
-Т
Рис. 37.43.2
Решение. Расчетная схема — на рис. 37.43.2.
Применяя теорему об изменении кинетического
момента относительно точки О, получим:
d
—(Jam + M\VB г) = mBp - Mxg г.
dt
Используя кинематическую связь vB =wr, получим:
М2Г2 i
—-—w + М\Г w = at — M\gr =>
I / ai2 \
“(i) - = м,г + м2г>/1 (т - M'grt) =
= (2М,+М^<°‘2-2М'^-
Задача 37.44(37.43). Для определения момента
инерции J махового колеса А радиуса R относитель-
но оси, проходящей через центр масс, колесо обмотали
тонкой проволокой, к которой привязали гирю В мас-
сы Mi и наблюдали продолжительность Т опускания
гири с высоты h (рис. 37.44.1). Для исключения трения
в подшипниках проделали второй опыт с гирей массы
Мз, причем продолжительность опускания оказалась
равной Ti при прежней высоте. Считая момент силы
трения постоянным и не зависящим от массы гири,
вычислить момент инерции J.
g
Ответ: J — R2 —
(Ml - Mi) - [(Mi/T?) - (Mi/т})]
(\/т2)-(\/т2)
4. Теорема об изменении главного момента
131
Решение. Расчетная схема — на рис. 37.44.2.
Составим уравнение для изменения кинетиче-
ского момента относительно точки О системы
«Л + В»'.
(jAw + Mi• R) = Mig • 7? - mTp,
где mTp = const — момент сил трения. Используя
(О г>
кинематическую связь vB = wR, мы получим для
ускорения точки В\
Рис. 37.44.2
v^(~+MiR
\ к
= MigR - ттр
. (i> R^MigR-myp)
<Z] = Vr = -=---. , -7,-".
JA Т MiR
Аналогично для груза М2:
д(2)
VB
= MygR - m,p
,(2) R(MygR — тпТр
= = Ja + M2R2
(JA \
\ /
С другой стороны постоянные ускорения
матических формул:
oi и ay можно найти из кине-
(рТ2 o-iTy
п —-------; п =----------
2 2
2h lh
°’ - «2 -
Таким образом, получим систему двух уравнений:
R(MxgR - mTp) = ~ (JA + MXR2),
R(M2gR - m-rp) = ~y(Ja + MyR ).
12
Вычитая одно уравнение из другого получим:
? / 1 1 \ yf Mi
R\Mi - My)g = JA • 2h - -yj + 2hR2 -
Mi
М\ — М2
IL
1 1
2^ t!
My
T2
12
M2
T1
132
4. Теорема об изменении главного момента
ГГШ» 2 3’ Задача 37.45 (37.44). К валу I присоеди-^
Г л 4- йен электрический мотор, вращающий мо мент которого равен (рис. 37.45.1). По- гтт средством редуктора скоростей, 'остоящего
* ' KffWX m, P никаез 1 ис. 37. при с тп, из четырех зубчатых колес 1, 2, 3 и 4, этот вращающий момент передается на шпиндель 45.1 jjp токарного станка, к которому приложен момент сопротивления т2 (этот момент воз- :нятии резцом стружки с обтачиваемого изделия). Опре-
делить угловое ускорение шпинделя III, если моменты инерции всех
вращающихся деталей, насаженных на валы I, II и III, соответствен-
но равны Jj, Ju, Jin- Радиусы колес равны Г|, гг, гз и г4.
ТЩ к\ 2 ‘ &3 4 — ^2
Ответ: е1П — -—--------------------,
(//^12 + Jn)ky4 + Jjjj
Г2 Г4
где к} 2 = —, ку 4 = —
г, Гз
Рис. 37.45.2
Решение. Расчетная схема — на рис. 37.45.2. Пусть ш,, ш2, шз. ^’4 —
угловые скорости вращения колес 1, 2, 3, 4. Причем, так как 2 и 3 —
на общем валу, то д>2 = шз- Так как линейные скорости в точках контакта
А и В равны, то имеем кинематические связи:
Ш I Г] = ДЭТ2, <Д2Гз = Ш4Г4 =>
Г 4 Г2
г <*>2 — Ufy — kyAU>4, — —ку 4Ш4 = к\ 2 ’ &3 4 ’ Д24.
г3 Г|
Теперь, используя полученные соотношения, составим уравнения для из-
менения кинетического момента относительно осей I, III и П-1Г.
d . .
— (JiwJ =ml+SA-ri,
d , .
— (-/2^2) = SA-r2 + SB ry,
(T3W4) = -m2 + SB r4,
4. Теорема об изменении главного момента
133
где Sa, Sb — силы касательного взаимодействия в точках сцепления колес
А и В, причем знак «минус» в кинетическом моменте относительно оси
II-II появляется потому, что вращение колес 2, 3 противоположно
вращению колес 1 и 4! Исключая Sa и Sb, получим соотношение:
/ 7П| (?|
- J2W2 = Г2---------И J\
\ Г, Г,
(mi олА
+ —+ /з—
г 4 Г 4 )
1 1
— .Л^З 4^4 — —Tn\-ki2~l~J\-k\2'k\2'^3 4^4 + Т-" m2 + «^ЗТ ' ^4,
«3,4 «3,4
й>4 (~Ь>^2 ‘ ^3,4 3~ J\ " ^-1,2 ’ ^-3,4 "Ь *^з) ~ ^1 ^1,2^3,4 — ^2
031^1,2^3,4 — т2
=> £4 — Ш4 =
^2^3,4 + Jl ’ ^1,2 ’ М,4 + ^3
Задача 37.46 (37.45). Барабан А массы Му и радиуса г приво-
дится во вращение посредством груза С массы М2, привязанного
к концу нерастяжимого троса. Трос переброшен через блок В и на-
мотан на барабан А (рис. 37.46.1). К барабану А приложен момент
сопротивления тпс, пропорциональный угло-
вой скорости барабана; коэффициент пропор-
циональности равен а. Определить угловую
скорость барабана, если в начальный момент
система находилась в покое. Массами кана-
та и блока В пренебречь. Барабан считать
сплошным однородным цилиндром.
Ответ: = У2 —(| - е где /3 =
а
.. ^2gr
lim ш —------= const.
t-юо а
2а
r2(Mi + 2М2) ’
Решение. Расчетная схема — на рис. 37.46.2. Разобьем систему на
две части: первая часть состоит из блока В с грузом С, вторая часть —
это барабан А.
Изобразим внешние силы, приложенные к каждой из двух частей.
Это силы тяжести груза M2g и барабана M\g, составляющие реакций
отброшенных подшипников в осях блока В и барабана А (Хв, Yb, Xq, Yq),
момент сопротивления тс = а<р, силы натяжения троса Т2 и Tlt которые
равны по величине в силу равенства действия и противодействия.
Пусть </> — угол поворота барабана А.
Составим уравнения движения выделенных частей системы с по-
мощью теоремы об изменении главного момента количеств движения
134
4. Теорема об изменении главного момента
Рис. 37.46.2
относительно соответствующих неподвижных осей Bz и Oz. Так как блок
В невесомый, то уравнение для первой части принимает вид:
d
—(гв M2v2) = M2grB - T2rB.
dt
В силу нерастяжимости троса v2 = фт. Поэтому получаем
гвМ2гф = M2grB - Т2тв.
Отсюда сила натяжения
Та = M2g — М2гф.
Уравнение движения второй части системы:
d (М\г2 \
dt \ 2 /
= Т]Г — аф.
Используя тот факт, что Tt = Т2 = M2g — М2гф, перепишем уравнение
движения в виде:
М,г2
2
ф = M2gr - М2г2ф - аф,
или
, т~ dd>
(Л7| + 2М2) — ~— — M2gr - аф.
2 dt
Интегрируем уравнение по частям, используя нулевые начальные условия;
(М|+2М2)у [ - -----= [ dt =>
2 J (M2gr \ J
о а|-------Т> I о
= t
2а
M2gr/a
f, аш \ -2at
\ Migr) r1(M\+2M2)'
4. Теорема об изменении главного момента
135
Поэтому угловая скорость барабана равна
M2gr ( ( -lot
W = ------ I 1 ~ еХР > .
а \ ( г3(Л1] + 2Л72)
Заметим, что
M2gr
hm w(i) =------= const.
<->oo a
Задача 37.47 (37.46). Определить угловое ускорение ведущего ко-
леса автомашины массы М и радиуса г, если к колесу приложен
вращающий момент твр. Момент инерции колеса относительно оси,
проходящей через центр масс С перпендикулярно плоскости мате-
риальной симметрии, равен Jc ', /к — коэффициент трения качения,
— сила трения. Найти также значение вращающего момента, при
котором колесо катится с постоянной угловой скоростью.
_ ?п,вр — MgfK — Fipr
Ответ: е = —-----------------, mBp = MgfK + FTpr.
____ ______________1с____________________'_______________________J
Решение. Расчетная схема — на рис. 37.47.1. При решении задачи
следует рассмотреть два случая:
Г. Колесо движется вначале без проскальзывания, т. е. = О (/Г — точка
контакта колеса с дорогой; см. рис. 37.47.1), а затем прикладывается
внешний момент твр. В частности колесо находится в покое, а затем
включается момент твр.
2°. Колесо движется вначале с проскальзыванием, т. е. Vk £ 0, а затем
прикладывается момент твр. Причем здесь ответ зависит от знака
Рис. 37.47.1
136
4. Теорема об изменении главного момента
Рассмотрим эти случаи в отдельности.
Г. Запишем уравнения для движения центра масс С колеса, и уравнение
для изменения кинетического момента относительно центра масс С:
Mi)C = -Fip, 0 = N - Mg, Ju = mBp + FTp-r - fKN, (I)
где F(p = Fo sgn vK, а знак vK соответствует знаку vc по направлению
оси x. Кроме того, при Vr £ 0, |FTp| = fN, а при Vk = 0 _FTp С fN.
Пусть Vjt(O) = 0. Выясним, что будет при t > 0. Имеем кинематиче-
скую связь:
vk = vc - ur ==> vK — vc - йг.
Используя уравнения (1), отсюда получим:
F т
= ~ j(msp + Ftp ’ Г ~ =
= 7 [--Ртр(г2 + р2) - твр • г + fKrMg],
где р — радиус инерции колеса.
Обозначим G = fKrMg - тпер г, тогда (2) примет вид:
Ак = у [_FTp(r2 + р2) + G]. (3)
Пусть началось скольжение так, что vK (0) > 0, т. е. Vk > 0 (так как Vk (0) = 0).
Тогда Flp — Jq = fMg, и выполнено, согласно (3), неравенство:
-F0(r2 + p2) + G>0 => <4>
N + р2
Если началось скольжение так, что vK < 0, т. е. Vk < 0 (так как
?'я(0) = 0)- Тогда Fyp = -Fq = - fMg, и выполнено, согласно (3), нера-
венство:
F0(r2 + р2) + G < 0 => (5)
т1 + р-
Из формул (4) и (5) следует, что при G > 0 скольжение точки К будет
вправо, если соблюдено (4), а при G < 0 скольжение точки К будет
влево, если соблюдено (5). Таким образом, объединяя эти условия, можно
утверждать, что при
F^ = fMg<-^-^\G\ = -r~3\fprMg-mep-r\ (6)
будет скольжение с качением. А если
Fo = fMg> _|G| = -J—-\fKrMg-mBp-r\, (7)
то будет чистое качение при гд = 0.
4. Теорема об изменении главного момента
137
Физический смысл условий (6) и (7) таков: при малом трении (/ С 1)
будет скольжение с качением, а при большом трении (/ }> 1) — чистое
качение будет сохраняться.
Теперь легко получить ответы к поставленной задаче.
1) Если выполнено (6) и G = r(fKMg — тпвр) > 0, то будет качение
со скольжением так, что vK > 0. и при этом из (1) следует:
й = е = у (гтр - ^g) = Г (fMg-^GX <0,
J \ г- J J \ г- /
так как из (6) следует:
fMG < |G| =
г2 + p1 г + p- r~
Ясно, что этот случай реализуется для уже двигавшегося колеса.
Если колесо покоилось, то движения не будет в силу неравенства
G > 0 <=> fKMg > твр (т. е. очень большой момент трения качения!).
2) Если выполнено (6) и G = r(fKMg - твр) < 0, то будет качение
со скольжением так, что Vk < 0, и при этом из (1) следует:
г ( \ \ г ( тв0 f,Mg\
й = е = - -fMg - -G = - -fMg + > 0,
J у г2 J J \ г г J
так как из (6) следует
1 , , G G
fMg < -----у G = -------у < —у.
г2 + р2 г2 + р- г2
Ясно, что в этом случае движение будет происходить и из состояния
покоя также! Здесь моменту твр удается преодолеть момент трения
качения. Отметим, что именно этот ответ приведен в сборнике [10].
3) Если выполнено (7), то будет чистое качение (или останется чистое
качение, если движение колеса с чистым качением уже было!). В этом
случае уравнения (1) имеют вид:
Мгй = -Fw, Ju; — Flp-r----G, (8)
г
причем FTp — это сила трения покоя, для которой должно соблю-
даться условие: |FTP| < fMg. Из уравнения (8) имеем:
w(J + Mr2) = --G = ~(fKMg - mBp),
г
Mr , MG
F7T. = -|----tUkM# - mBD) =--------yG = ----y.
p J + Mr1 p' J + Mr2 r2 + p2
138 4. Теорема об изменении главного момента Ь-Тец
В силу неравенства (7) эта сила удовлетворяет неравенству для силы 3748(37,
трения покоя: |FTp| < fMg. Таким образом, здесь угловое ускорение: ' ' ’
1U1V fiv.'lvv
твр и по гор
_ - _ твр - fJ^g _ ~М~ ~ «ГОРИЗОНТ,
£ W J + Mr2 т2 + р2 л С. Мог
[М плос
Разберем теперь вопрос о выборе тпвр, обеспечивающем постоянство енттрения
ш, т. е. е = w = 0. Положим жм. В н
mnp = fKMg ==> G = 0.
•НЛ
Тогда уравнение (3) примет вид:
Fjp(r2 + р2) F0(r2 + р2)
VK =------Е—-------=---------------sgn VK.
Из полученного уравнения следует, что Vk = 0 (vk > 0 влечет Vk > 0
и vk < 0, т. е. противоречие, аналогично приводит к противоречию
предположение Vk < 0). Итак, Vk = 0 => Frp = 0- Тогда из по-
следнего уравнения системы (1) получим w = е = 0. Таким образом,
если колесо катилось без проскальзывания, то прикладывая момент
mBp = fKMg, мы также получим качение без проскальзывания, но уже
с постоянной угловой скоростью.
2° Пусть колесо двигалось с проскальзыванием, т. е. Vk(0) 7^ 0. В этом
случае последнее уравнение системы (1) имеет вид:
Jw = mBp - fKMg -1- fMgr, если J6j = mBp - fyMg - fMgr, если vK > 0,
vk < 0,
а постоянство ш обеспечивает тпвр, выбираемый из соотношений: Расчет
mBp = fKMg - fMg г при vK > 0, к пред сила i
mBp = fKMg + fMg г при vK < 0. "’ОТТОГО
‘^“'Мзанс
Соответственно, равенство (3) имеет вид: 'Wccm
vK = 7 [-Fo(r2 + P2) + fMg r2] = -yfMgp2 J J < 0 при vK > 0, ’Я=0. но 1 добыло
vk = 7 [+F0(r2 + p ) - fMg r2] = +y fMgp2 d J > 0 при vK < 0- ^1р + f Ч,р0=
Эти соотношения показывают, что через конечное время будет vK = 0, '^чеа
и мы приходим к случаю, рассмотренному в пункте Г.
4. Теорема об изменении главного момента
139
Задача 37.48(37.47). Определить угловую скорость ведомого ав-
томобильного колеса массы М и радиуса г. Колесо, катящееся со
скольжением по горизонтальному шоссе, приводится в движение по-
средством горизонтально направленной силы, приложенной в его
центре масс С. Момент инерции колеса относительно оси С, пер-
пендикулярной плоскости материальной симметрии, равен Jc', —
коэффициент трения качения, f — коэффициент трения при качении
со скольжением. В начальный момент колесо находилось в покое.
Mg,
Ответ: ш = — (fr-fK)t.
Решение. Расчетная схема представлена на рис. 37.48.1, где в отли-
чие от рис. 37.47.1 к предыдущей задаче к колесу приложена в центре масс
С горизонтальная сила F вместо вращающего момента твр Здесь также
решение зависит от того, скользит точка контакта К или нет Но так как
в условии задачи указано, что качение происходит со скольжением из со-
стояния покоя, то рассмотрим лишь этот случай. Итак, пусть г>к(0) = О,
ш(0) = 0, г>с(0) = 0, но 1>а (0) 0. Запишем уравнения движения анало-
гично тому, как это было сделано при решении задачи 37.47:
Мvc = + F, 0 = N — Mg, J(j = Fjp-r- fK-N, (1)
где Frp = Fo sgn vK, Fo = fMg при vK 0.
Имеем кинематическую связь
vK=vc-ur
( 1 г2
vK = i>c - г = - FTP1 — -I- у
/ F fKr \
U+W <2>
140
4. Теорема об изменении главного момента
Из соотношения (2) сразу следует, что при
(1 т2 \ F f т
m + 7)>m + -TMs- (3)
качение со скольжением нереализуемо (предположение Vk > 0 => Vk > 0
(так как г>к(0) = 0) и предположение < 0 => vk < 0, приводят
к противоречиям!). Таким образом, скольжение будет при:
F fKr / 1 г2\
(4)
Предполагая неравенство (4) выполненным, из (2) получаем, что Vk > 0,
т.е. vk > 0, и реализуется схема, указанная на рис. 37.47.1. В этом случае
из последнего уравнения системы (1) получим:
Jw = fMgr - fKMg = Mg(fr - /к) => o>(0 = —Ll
•J
(это ответ, приведенный в сборнике [10]). Отметим, что для корректности
рассуждений необходимо еще полагать, что fr > /к. Это условие обеспе-
чивает w > 0 о> > 0 (см. последнее уравнение системы (1), где следует
положить FTp — fMg, ввиду предполагаемого проскальзывания!). Для
реальных колес коэффициент трения качения (вернее, отношение fK/r)
достаточно мал, так что условие (5) оправдано! Нетрудно показать, что
условие (4) при наличии неравенства (5) влечет неравенство F > fMg, т. е.
из первого уравнения системы (1) следует vc > 0. Таким образом, к ответу,
приведенному в сборнике [10] необходимо добавить неравенства (4) и (5),
которые обеспечивают реализуемость качения со скольжением. А если не-
равенство (4) нарушено (т. е. выполнено (3)), то при условии (5) и условии
Fr > fKMg реализуется чистое качение (гд- = 0, = 0). При этом в точ-
ке контакта возникает сила трения покоя Fir, которая зависит от силы F:
F = г | гЛЛЛ:
,р + Г +
где р1 = J/М — квадрат радиуса инерции колеса. При этом угловое уско-
рение е дается формулой:
е = d,_ Fr ~ f*Mg
М (р2 + г2) ’
т. е. угловое ускорение уже зависит от силы F!
Замечание к задаче 37.48. Вопросы о качении, рассматриваемые в задачах 37.47
и 37.48, изучались в монографии П. Пэнлеве «Лекции о трении» [12].
4. Теорема об изменении главного момента
141
Задача 37.49 (37.48). Изменится ли угловая скорость колеса, рас-
смотренного в предыдущей задаче, если модуль силы, приложенной
в его центре масс С, увеличится в два раза?
Ответ: Не изменится.
Решение. Пусть для силы F выполнено условие (4) из решения
предыдущей задачи 37.48 (условие (5), естественно, предполагаем выпол-
ненным!). Тогда угловое ускорение дается формулой:
Е = й = fj.
Если силу F увеличить в два раза, то условие (4) сохранится заведомо,
и ответ останется прежним, так как он не зависит от величины силы F!
Задача 37.50 (37.49). Через блок, массой которого
пренебрегаем, перекинут канат (рис. 37.50.1); за точку А
каната ухватился человек, к точке В подвязан груз оди-
наковой массы с человеком. Что произойдет с грузом,
если человек станет подниматься по канату со скоро-
стью v относительно каната?
Ответ: Груз будет подниматься с канатом
со скоростью v/2.
Рис. 37.50.1
’ Решение. Расчетная схема — на рис. 37.50.2. Применим к системе
«Л + В» теорему об изменении кинетического момента относительно
точки О. Ясно, что сумма моментов всех внешних сил, приложенных
к этой системе, относительно этой точки равна нулю. Для силы реакции,
приложенной в точке О, это очевидно. А силы
тяжести в точках А и В дают моменты, рав-
ные по модулю, но противоположные по знаку!
Пусть vb — скорость движения груза В, на-
правленная вверх. Тогда имеем кинетический
момент относительно точки О:
тппв • г + m(vB — v) - г = 0 ==>
v
vB = ~.
Замечание к задаче 37.50. Отметим, что при реше-
нии данной задачи делается (в условии задачи это
не указано) допущение о невесомости каната. Если
канат имеет вес, то решение существенно изменится.
Рис. 37.50.2
142
4. Теорема об изменении главного момента
В частности, вся система на рис. 37.50.2 будет двигаться с ускорением. Кроме того,
так как контакт каната с блоком — это, вообще говоря, неудерживающая связь, то
небезынтересен вопрос о знаке вертикальной (нормальной) реакции, действую-
щей в точке контакта каната с блоком. В частности, можно показать, что при массе
каната в 5 раз большей массы человека, в определенный момент будет наблюдать-
ся отрыв каната от блока. Доказательство этого факта основано на применении
теоремы о движении центра масс системы вдоль вертикали и здесь не приводится.
Задача 37.51 (37.50). Решить предыдущую задачу, принимая во
внимание массу блока, которая в четыре раза меньше массы человека.
Считать, что масса блока равномерно распределена по его ободу.
Ответ: Груз будет подниматься со скоростью 4г,/9.
Решение. Здесь надо добавить кинетический момент блока, кото-
рый равен Ju>, где J = тт2 /4, ш — угловая его скорость. Если веревка
не скользит по блоку, то имеем кинематическую связь: ыг = vb- Тогда
получим для общего кинетического момента:
. х т 2
mvB • г + m(vB - V) • г + —г ш = О
vB г + (ув - v) + =0 =4
4
= -V.
Задача 37.52(37.51). Круглая горизонтальная платформа может
вращаться без трения вокруг неподвижной оси Oz, проходящей через
ее центр О', по платформе на неизменном расстоянии от оси Oz,
равном г, идет с постоянной относительной скоростью и человек,
масса которого равна М\. С какой угловой скоростью ш будет при
этом вращаться платформа вокруг оси, если массу ее М2 можно
считать равномерно распределенной по площади круга радиуса R,
а в начальный момент платформа и человек имели скорость, равную
нулю?
Л 2М,г
Ответ: щ =-------------- и.
M2R2 + 2Mir2
Решение. Расчетная схема — на рис. 37.52.1. Кинетический момент
системы ^платформа 4- человек» относительно вертикальной оси враще-
ния АВ сохраняется, так как внешние силы не создают момента относи-
тельно этой оси (они либо параллельны АВ, как силы тяжести M\g, Mig,
либо ее пересекают, как силы реакции в точках А и В!). Поэтому имеем:
Ja> + Mi (щг - и) • г = О,
4. Теорема об изменении главного момента
143
где J = M2R2/2 — момент инерции платформы относительно оси АВ,
uj — ее угловая скорость. Отсюда получаем:
2Mtur
ш =-----г-------г.
M2R2 + 2М\Г2
Задача 37.53 (37.52). Круглая горизонтальная платформа враща-
ется без трения вокруг вертикальной оси, проходящей через ее центр
масс (рис. 37.53.1), с постоянной угловой скоростью о>о, при этом
на платформе стоят четыре человека одинаковой массы: два — на краю
платформы, а два — на расстояниях от оси вращения, равных полови-
не радиуса платформы. Как изменится угловая скорость платформы,
если люди, стоящие на краю, будут двигаться по окружности в сторону
вращения с относительной линейной скоростью и, а люди, стоящие
на расстоянии половины радиуса от оси вращения, будут двигаться
по окружности в противоположную сторону с относительной линей-
ной скоростью 2и? Людей считать точечными массами, а платформу —
круглым однородным диском.
Ответ: Платформа будет вращаться с той же угловой скоростью.
144
4. Теорема об изменении главного момента
Решение. Решение здесь аналогично решению предыдущей задачи
с использованием сохранения кинетического момента системы относи-
тельно оси вращения. Пусть wq — начальная угловая скорость платформы.
До движения людей кинетический момент:
2
Ко = Jwq + 2mujoR
+ 2тпй?о
Пусть w — угловая скорость при указанном в задаче движении людей.
Тогда'
К = Jw + 2mR(ijjR + и) + 2m—
2
= Jw + 2mwR + 2mw
Но так как К — Ко, то получим w = o/q.
Задача 37.54(37.53). Решить предыдущую задачу в предположе-
нии, что все люди двигаются в сторону вращения платформы. Радиус
платформы R, ее масса в четыре раза больше массы каждого из людей
и равномерно распределена по всей ее площади. Выяснить также,
чему должна быть равна относительная линейная скорость и для того,
чтобы платформа перестала вращаться.
8 и 9
Ответ: о?! = ~ —, и = -Ruo-
7 -К О
Решение. В новых условиях имеем:
2
К = Ju + 2mR(uR + и) + 2m— + 2uJ =
4mR* 2 * * * * * * 9 2 R2
= —-—+ 2mR и + 2m—и + 4mRu = Ko =
4m ji 2 R2
= -т-R + 2mu)oR + 2mujo —
2 4
9 2 9 ,
==> -mR и + 4mRu — -mR u0
8 и
U) — й/п —--
9R
и для обнуления a> получаем:
9
и = -w0R.
О
4. Теорема об изменении главного момента
145
Задача 37.55 (37.54). Человеку, стоящему на скамейке Жуковско-
го, в то время, когда он протянул руки в стороны, сообщают на-
чальную угловую скорость, соответствующую 15 об/мин; при этом
момент инерции человека и скамейки относительно оси вращения ра-
вен 0,8 кг-м2. С какой угловой скоростью начнет вращаться скамейка
с человеком, если, приблизив руки к туловищу, он уменьшит момент
инерции системы до 0,12 кг - м2?
Ответ: 100 об/мин.
Решение. Расчетная схема движения человека на
скамейке Жуковского — на рис. 37.55.1. Так как внеш-
ние силы, приложенные к системе «человек + скамей-
ка» либо параллельны оси вращения Oz (силы тяжести),
либо пересекают ось (силы реакции гладких подшип-
ников), то
к
Следовательно, имеет место закон сохранения главного
момента количеств движения системы в проекции на
ось Ozi KOz = const. Поэтому = J^2- Отсюда
Рис. 37.55.1
й?2 = й?]—.
Аналогичная зависимость между числами оборотов системы:
об \
°.8
n2 = nl — = 15- —— = 100
J2 U,12
МИН
в®
М
D
Задача 37.56 (37.56). Горизонтальная трубка CD может свободно
вращаться вокруг вертикальной оси АВ. Внутри трубки на расстоя-
нии МС = а от оси находится шарик М (рис. 37.56.1). В некоторый
момент времени трубке сообщается началь-
ная угловая скорость wq. Определить угловую
скорость w трубки в момент, когда шарик
вылетит из трубки. Момент инерции трубки
относительно оси вращения равен J; L — ее
длина; трением пренебречь, шарик считать
материальной точкой массы т.
С
J + ma2
Ответ: о> = -----т д>о-
J + mL2
Рис. 37.56.1
146
4. Теорема об изменении главного момента
Решение. Расчетная схема представлена
на рис. 37.56.2. Воспользуемся теоремой об из-
менении главного момента количеств движения
системы
«трубка CD + вал АВ + шарик М»
относительно неподвижной оси Az. Так как все
силы либо пересекают ось Az, либо ей парал-
лельны, то
Следовательно,
Az
dt
= 0.
К Az = const.
Имеет место закон сохранения главного момента количеств движения
системы в проекции на ось Az. Выпишем выражение для Kaz, выбрав
положительным направление по дуговой стрелке угловой скорости ы:
I fepi
------
ж
чгокьег
зига
иврашате.
.-««и с у
enirfr
жмет
иирми
«рассто
Йнить
1'
ериои
МрЫ!
шиты
Т<г _ ^(трубки) тАМ)
Kaz-B-az + KAz ’
к£рубк,,) = Ju,
К{^} = прЛ2 [СМ х m(vc + дг)] =
= bVazCM х mve + npAzCM х mvr —
= CM • m • u CM + 0 — mu x2,
так как
CM x mvr = 6, CM = x.
Поэтому
К az = Ju + mu • x2 = + mx2).
Так как Kaz = const, то приравняем значение этой величины в начальный
момент, когда х = а, и в конечный момент, когда х = L:
+ ma2) = u, (J + mL2).
Поэтому угловая скорость трубки в момент вылета из нее шарика равна
J + та2
Ш1 —ту-
J + mL1
< Расчет
''Шим
aoiiiaf
Мести, ।
’Ли on
Лающи
i
Л=с
когда I
Цкоц
w
4iio>
Заметим, что угловая скорость уменьшается при увеличении момента
инерции системы относительно оси Az.
4. Теорема об изменении главного момента
147
1
и
Л/,
М2 В
Рис. 37.57.1
Задача 37.57 (37.57). Однородный стержень АВ длины 2L = 180 см
и массы М\ = 2 кг подвешен в устойчивом положении равновесия на
острие так, что ось его горизонтальна (рис. 37.57.1). Вдоль стержня мо-
гут перемещаться два шара массы М2 = 5 кг каждый, прикрепленные
к концам двух одинаковых пружин. Стержню
сообщается вращательное движение вокруг
вертикальной оси с угловой скоростью, соот-
ветствующей П\ = 64 об/мин, причем шары
расположены симметрично относительно оси
вращения и центры их с помощью нити удер-
живаются на расстоянии 2/, = 72 см друг
от друга. Затем нить пережигается, и шары, совершив некоторое чис-
ло колебаний, устанавливаются под действием пружин и сил трения
в положение равновесия на расстоянии 212 — 108 см друг от друга.
Рассматривая шары как материальные точки и пренебрегая массами
пружин, определить новое число п2 оборотов стержня в минуту.
Л 6M2Z? + MjL2
Ответ: п2 =-----5-------- щ = 34 об/мин.
6M2l2 + M{L2
Решение. Расчетная схема представлена
на рис. 37.57.2. Внешние силы, приложенные
к системе
«стержень 4- стойка + 2 шара + 2 пружины»
— это силы тяжести, параллельные оси вра-
щения z, и реакция опоры с составляющими
Ri и R2, пересекающими ось z. Поэтому
к
Следовательно, Kz = const. Приравняем зна-
чение кинетического момента системы в мо-
мент времени, когда I = Ц, к его значению
в момент времени, когда I = 12:
М'^ -ХЭ ЛТР _^1(W
---—----СД) 4“ 2 • Л12/]й?] — —
Отсюда получаем, что угловая скорость
Рис. 37.57.2
7
й>2 И- 2 •
12
2 M2l]
—----Н 2 • М212
148
4. Теорема об изменении главного момента
Так как ш — 2irn, то новое число оборотов
3
M\L 2 2 • 0,92 2
-у- 4- 2 • М21\ —+ 2 • 5 • 0,362
п? = П1 • -------------= 64-------2—5---------------= 34
M'L ЛЛ- ,2 2 • 0,92 2
——- + 2 • М212 —-— + 2 • 5 • 0,542
J 3
об
мин
Задача 37.58(37.58). Тележка поворотного подъемного крана дви-
жется с постоянной скоростью v относительно стрелы (рис. 37.58.1).
Мотор, вращающий кран, создает в период раз-
гона постоянный момент, равный то- Определить
угловую скорость ш вращения крана в зависимо-
сти от расстояния х тележки до оси вращения АВ,
если масса тележки с грузом равна М; J — мо-
мент инерции крана (без тележки) относительно оси
вращения; вращение начинается в момент, когда те-
лежка находится на расстоянии а?о от оси АВ.
Рис. 37.58.1
m0 х-хо
Ответ: ш =-----------
J + Мх2 v
8
Решение. Расчетная схема представлена на
рис. 37.58.2. Так как кинетический момент систе-
мы относительно оси АВ (т.е. z) равен:
Kz = Jw + Mujx х («кран + тележка»)
(ve — шх и относительная составляющая скоро-
сти момента относительно оси z не дает, так как
пересекает ее!). Следовательно, теорема об изме-
нении кинетического момента системы «кран +
тележка» относительно вертикали z дает:
d э
— (Ju+Mljx ) = mo
Jw+Мшх2 = mot
Так как относительная скорость тележки постоянна и равна v, то
х - а?о = vt
X - Хо
V
Таким образом, получаем:
тп0(х - х0)
(jJ ZZZ ---------
(J + Mx2)v
4. Теорема об изменении главного момента
149
Задача 37.59 (37.59). Сохранив условие предыдущей задачи, опре-
делить угловую скорость ш вращения крана, если мотор создает вра-
щающий момент, равный т0 — aw, где т0 и а — положительные
постоянные.
Ответ: w = , [ еряк1б{х/к} dx,
v(J + Мх2) J
i a
гцек=\-,ц = -
V M vx
а / —— (ось х направлена вправо вдоль стрелы).
V «7 -1W
Решение. Уравнение для изменения кинетического момента систе-
мы, полученное в предыдущей задаче, здесь имеет вид:
d , 2ч
—(Ju; + Mwx ) = mo — aw.
Перейдем к независимой переменной х. Имеем:
d г dx
— w(J + Мх )\ — = тп0 - aw =>
dx J dt
d r z mo_ dx
=> — lw(J + Mx ) =---------, где v = — = const
dxL J v dt
dw, m0 —
=> — (J + Mx2) + w-2Mx = —-------- =>
dx v
dw Г 2Mx a "I mo
=’> dx _J + Mx2 v(J + Mx2)_ v(J + Mx2)'
Решим сначала однородное уравнение:
dw Г 2Мх а
dx Ш J + Мх2 v(J + Мх2)
dw 2Mxdx adx
w J + Mx2 v(J + Mx2)
интегрируем:
1 ( \
arctg I у —x I
Inw = - \n(J + Mx )--,
V y/jM
1 f a f Ж
= c -——5 exp <--------7= arctg \ —x >.
J + Mx2 H ( vy/TM \ V J J J
150
4. Теорема об изменении главного момента
Пользуясь методом вариации постоянной, получим частное решение не-
однородного уравнения:
х ^аобизм
ц, = Ш° . e-/-arctg(x/fc) . f emWk)d^
Vi J I 1W X ) J
xa ------
где обозначено к =
a
u = —7=
vy/JM
»й.1(38.1)
остояще
цист
шарнир
лов ci
•Л|Ж<
«(
Л)Ж>ЙСК<
j
Whcik
^=2
^кает(
Чу
5. Теорема об изменении кинетической энергии
материальной системы (§ 38, [10])
Задача 38.1 (38.1). Вычислить кинетическую энергию плоского
механизма, состоящего из трех стержней АВ, ВС и CD, прикреплен-
ных цилиндрическими шарнирами А и D к потолку и соединенных
между собой шарнирами В и С (рис.38.I.1).
Масса каждого из стержней АВ и CD дли-
ны I равна М\, масса стержня ВС равна М2,
причем ВС = AD. Стержни АВ и DC вра-
щаются с угловой скоростью bJ.
2ЛГ| + ЗМ2 2 1
Ответ: Т =------—------12ш2.
6
Рис. 38.1.2
Решение. Расчетная схема — на рис. 38.1.2. Кинетическая энергия
механизма
Т = Тдв + Тос + Твс-
Так как стержни АВ и DC одинаковые и вращаются с равными угловыми
скоростями вокруг неподвижных осей вращения, то
ш1 М\12 2
Tab = Tdc = Jaz~ =
Mil2 2
6 “
Стержень ВС движется поступательно,
так как все время движения
ВС || AD. Поэтому
_ М2у2вс _ M2v2B _ М2(ыГ)2
ВС 2 2 2
Суммарная кинетическая энергия
Mil2u2 М212ш2
г=2—+—
2ЛТ1 + ЗМ2 2 2
I W .
6
152
5. Теорема об изменении кинетической энергии
Задача 38.2(38.2).
опирается на угол В и
Рис. 38.2.1
Однородный тонкий стержень АВ массы М
концом А скользит по горизонтальной направ-
ляющей (рис 38.2.1). Упор Е перемещается
вправо с постоянной скоростью v. Опреде-
лить кинетическую энергию стержня в зави-
симости от угла если длина стержня равна
21, а превышение угла В над горизонтальной
направляющей равно Н.
Ответ: Т =
I . з 4 I2 . 4 \
-2—sin ^ + -—ysin .
11 J 11^ /
Решение. Расчетная схема движения стержня АВ — на рис. 38.2.2.
Кинетическая энергия стержня, движущегося плоскопараллельно, вычис-
ляется по формуле Кёнига:
Рис. 38.2.2
m 1 2 1 2
Т — -Mvc + ~Jcz^
Скорость Va = Ve — v. Скорость точки В
стержня направлена вдоль стержня, иначе про-
изошло бы нарушение связи.
Построим мгновенный центр скоростей
стержня в точке Р пересечения перпендикуля-
ров в т. А и D к их скоростям. Угловая скорость
VA
стержня о) — ,
скорость vc — ш • PC. Най-
дем расстояния РА и PC. Для этого рассмот-
рим прямоуголные треугольники APD и СРВ.
В /ХАРВ ЛАРВ = у>, ЛАВР = 90°, АВ =
sin </>
Поэтому
РА =
АВ
sin
Н
sin2 <р
Сторона
sin2 <р
Н
В /\СРВ сторона < D = АВ — АС = —------------I, поэтому гипотенуза
sin <р
PC = \/PD2 + СВ2 =
Н2 cos2 w ( Н \2
- 4 + --------------И
sin4^ \sin^ /
5. Теорема об изменении кинетической энергии
153
H2 cos2 p
sin4 p
Н2 HI
——5----I2 — 2 ——
Sin7 (f> sin
H
sin2 p
VA
Следовательно, ш = —-
РА
I2 21
—2 sin4 p - — sin3 p .
v sin2 ip
---— v------,
PA H
H
vc = w • PC = v —z— x
sin7 p
sin2 u>
x -----
H
I2 . 21 . .
+ —J sin4 - — sin3 ip = V
I2 21
1 + д2 sin4 " д sin’ ’
Поэтому
1
T = -Mv
2
Mv2
1 M(2Z)2 2 sin4 92
2 12 V H2
2
Р 4 21 з \ 1
1 + -^ sin <р - — sin + 2
I з 4 Г- 4 \
1 - 2— sin + - — sin <р j .
Задача 38.3(38.3). Вычислить кинетическую энергию кулисного
механизма, если момент инерции кривошипа ОА относительно оси
вращения, перпендикулярной плоскости рис. 38.3.1, равен Jo; длина
кривошипа равна а, масса кулисы равна т, массой камня А прене-
бречь. Кривошип О А вращается с угловой скоростью ш. При каких
положениях механизма кинетическая энергия достигает наибольшего
и наименьшего значений?
Ответ: Т = - (Jo + ma2 sin2 .
Наименьшая кинетическая энергия — при крайних положениях ку-
лисы, наибольшая — при прохождении кулисой среднего положения^/
154
5. Теооема об изменении кинетической энергии
Решение. Расчетная схема кулисного механизма — на рис. 38.3.2.
Кинетическая энергия Т = Т\ + Тт, где I — кривошип, 2 — кулиса.
Кривошип вращается вокруг неподвижной оси, поэтому Т\ = Jqu /2.
Кулиса движется поступательно, поэтому Ti = mvj/2.
Для определения Vb рассмотрим движение точки А как сложное:
vA = vr + ve. Абсолютная скорость va = wa, относительная скорость vr
направлена вертикально (относительно кулисы), переносная скорость ve
направлена горизонтально (вместе с кулисой). Построим треугольник
скоростей (рис. 38.3.2). Из него находим
ve — уА sin ip = w • a • sin <p.
А это и есть скорость поступательного движения кулисы V}.
Следовательно,
Т = Т} +Т2 = - Jqw2 + -mw2c? sin2 <р = -(J + ma2 sin2 <р)ш2-
Из вида функции T(ip) ясно, что Tmm при sin ip = 0, т.е. при <р = 0°, 180°
и т. д. (при крайних положениях кулисы). Ттах при sin ip = ±1, т.е. при
<р = 90°, 270° и т. д. (при прохождении кулисой среднего положения).
Рис. 38.4.1
Задача 38.4 (38.4). Вычислить кинетиче-
скую энергию гусеницы трактора, движуще-
гося со скоростью vq. Расстояние между ося-
ми колес равно I, радиусы колес равны г,
масса одного погонного метра гусеничной
цепи равна 7 (рис. 38.4.1).
Ответ: Т = 2||/ + лт)^.
Решение. Расчетная схема — на рис. 38.4.2. Разобьем гусеницу трак-
тора на 4 части: АВ, ВС, CD и AD.
Т — Tab + Твс + Ico + Tad-
5. Теорема об изменении кинетической энергии
155
Так как участок гусеницы AD неподвижен (трактор движется без сколь-
жения), то Tad = 0- Участок ВС движется поступательно со скоростью
2г;0. Поэтому
mBC(2«i0)2 з
Твс =------------ = 7/2^
В силу симметрии ТАв = TCD. Вычислим ТАв- Для этого разобьем участок
АВ на элементарные дуги длиной ds = г dp. Масса этого элемента
dm — 7Г dtp.
Скорость этого элемента
Vq tp tp
v — юр = — 2r sin — = 2ro sin —.
г 2 2
Кинетическая энергия
этого выделенного бесконечно
малого элемента
dT =
dm • v2
2
2
р \ 2
2«0 sin — J = 2yrvo
. 1Ч> ,
sin — dp.
Поэтому
7Г 7Г
ТАВ = У* 27ГГ0 sin2 у dp = 2yrv^ J -(! - cos p) dp =
о 0
1
= 27Г«о
7Г
I’0
- sin p
2
= 7г«о • тт.
Суммарная кинетическая энергия равна
Т = 2 • ТАв + ?вс = 27™^ + 27/^0 = 27(г7г + l)vl.
156 5. Теорема об изменении кинетической энергии
Задача 38.5(38.5). Вычислить кинетическую энергию кривошип-
но-ползунного механизма, если масса кривошипа mj, длина кри-
вошипа г, масса ползуна т2, длина шатуна I (рис. 38.5.1). Массой
шатуна пренебречь. Кривошип считать однородным стержнем. Угло-
вая скорость вращения кривошипа ед.
J я|о+?)
=Кйсо$р+
Ответ:
г Z \ 2 п
11 I т sin 2р \
Т = - -mi + m? I sin <z> + — —. „ .. 1
2 [з \ 21 — (r/l)2 sin2 ip/ .
!МЮ1,
ч ।
2
Рис. 38.5.1
Решение. Расчетная схема движения кривошипно-ползунного ме-
ханизма — на рис. 38.5.2. Кинетическая энергия механизма Т = Tqa+Tb-
Кривошип ОА вращается вокруг неподвижной оси. Поэтому
W|. Реш
Шперле
1 7
Тод =
1 т\Г2 2
- • ---W
2 3
2 2
Г W .
I
Для ползуна Тв = т^Вв^. Чтобы определить скорость точки В, рассмот-
рим кинематику шатуна АВ. Построим мгновенный центр скоростей
шатуна (точка F) и запишем соотношения: /ц
vA иг Г РВ '\q,
Va —шг, сдав — — -т—; Vb — ^дв РВ = w -. п
РА РА РА
Рассмотрим /ХАРВ. Нетрудно увидеть, что
/.АРВ = 90° - <р, ЛРАВ — tp + a, AABP = 90°-ot. ^^йеляя.
Угол а определяется с помощью теоремы синусов для /\ОАВ:
т
sin a = - sin <р.
Теперь применим теорему синусов для 2ХАРВ:
РА РВ
sin (90 - a) sin (a + <p)
То
IUlWni
-’hopoq
5. Теорема об изменении кинетической энергии 157
РВ sin(o + ^) sin a cos p + cos a sin ip
PA sin (90° - a) cos a
(r/l) sin p
= tg a cos p + sin p = —. _ — • cos p + sm p.
* * Ф - (r/l? sin^
Поэтому
PB ( r sin p cos p \
Vb = iVT~—- = fjJT I - —. . • + sin p .
PA V \/1 - (r/l)2 sin2 p /
Окончательно имеем,
1 2 2 1 2 2 ( r S*n V
T = -Ш\Г ш + -Ш2Г w I ——. - + sin p 1 =
6 2 \2Z ^/1 - (r/Z)2 sin2 p /
1 2 2 Г I ( T Sill V
= -r tv -mt + m21 — p- n + sin pl .
2 L3 \2Z -у/1 - (r/Z)2 sin2 p ) .
Задача 38.6(38.6). Решить предыдущую задачу для положения,
когда кривошип О А перпендикулярен направляющей ползуна; учесть
массу шатуна m3.
I / I 12 2
Ответ: Т = -1 -mi + m2 + m3 1 г ш .
Решение. Расчетная схема — на рис. 38.6.1. Угол р = 90°. Теперь
кинетическая энергия
Т = Тоа + Tab + Тв,
1 2 1 2 2
Тоа = 2Jbj = ^TOir ш •
Рассмотрим кинематику шатуна АВ. Для положения, когда р = 90'
мгновенный центр скоростей не существует. Значит шатун АВ движется
мгновенно-поступательно. Поэтому в данном положении vb — va = ivr.
158
5. Теорема об изменении кинетической энергии
i Георема (
Кинетическая энергия
1 2 * 2 1 2 2
Tab = T^-iVAB = -^n3vA = -m3w г .
Для ползуна
1 2 । 2 2
Тв = = -m2w г .
Поэтому суммарная кинетическая энергия
1 э2 1 2 2 1 22 1/1
Т = -mjW г + -тпзиГг + -m2w г = -1
6 2 2 2 < 5
-т\ + т2 + тп3 Iы2г2
Рис. 38.7.1
Задача 38.7(38.7). Планетарный механизм,
расположенный в горизонтальной плоскости,
приводится в движение кривошипом О А, со-
единяющим оси трех одинаковых колес I, II
и III (рис. 38.7.1). Колесо I неподвижно; кри-
вошип вращается с угловой скоростью ш. Мас-
са каждого из колес равна М\, радиус каждого
из колес равен г, масса кривошипа равна М2. Вычислить кинети-
ческую энергию механизма, считая колеса однородными дисками,
а кривошип — однородным стержнем. Чему равна работа пары сил,
приложенной к колесу III?
Ответ: Т = - (ЗЗЛД +8Л/2); работа равна нулю. **
** Решение. Расчетная схема — на рис. 38.7.2. Кинетическая энергия
механизма Т = Тоа + Ти + Тш. Для кривошипа О А, который вращается
вокруг неподвижной оси,
«ику к
j. Так как
1.Т0Ви:
.tpujr
, lii К при
и,
иШлрило
1
Ш).
МккСГ
’У|; масса
^Полп
*.чец
*Ию3
'йвд
ЭД пои
Приваты
:*бе[унс
ii.
^‘OCMCj
‘•i=2rn=
•«и В
"Шк
,n;
Рис. 38.7.2
5. Теорема об изменении кинетической энергии
159
Рассмотри кинематику колес II и III Скорость точки В равна vB =
— w • lr = lair. Так как колесо I неподвижно и нет проскальзывания
между колесами, то ац = vB/r = la. Скорость точки зацепления колес
II и III равна vK = ац lr — 4ar. Скорость точки A vA = a • О А = 4ar.
Так как точки А и К принадлежат колесу III, то видно, что оно движется
поступательно (иш — 0). Поэтому
I 7 1 7 1 7 7 1 Al I Г ) 7 7
Тп — -M\VB 4- = -M\4a г + -—-— • 4a = ЗМ\Г a .
Тщ = — M\v\ = 8Л/|Г2<д2.
Следовательно,
T = jM2r2a2 + 3-MirV + Ш,г2ш2 = + 8М2)
Если к колесу III приложить пару сил с моментом L, то работа
А(Ь) = 0, так как dA = Ld<p — L • am dt = 0.
Задача 38.8(38.8). Мельничные бегуны А и В насажены на го-
ризонтальную ось CD, которая вращается вокруг вертикальной оси
EF (рис. 38.8.1); масса каждого бегуна 200 кг;
диаметры бегунов одинаковы, каждый равен
1 м, расстояние между ними CD равно 1 м.
Найти кинетическую энергию бегунов, когда
ось CD совершает 20 об/мин, допуская, что
при вычислении моментов инерции бегуны
можно рассматривать как однородные тонкие
диски. Качение бегунов по опорной плоско-
сти происходит без скольжения.
Ответ: 383 Н м.
Рис. 38.8.1
Решение. Расчетная схема — на рис. 38.8.2.
Угловая скорость оси CD равна
20 2 / рад
= шсо = 2тгп = 2тг — = -тг [ -----
60 3 \ с
Так как бегуны А и В одинаковые и движения
их совпадают, то рассмотрим бегун В. Скорость
его центра масс
CD
vB — —— — W| • OD.
Рис. 38.8.2
160 5. Теорема об изменении кинетической энергии
Так как бегуны катятся без проскальзывания, то шг = vi)/r — u\OD/r —
угловая скорость бегуна относительно собственной оси вращения (ось CD).
Бегуны вращаются вокруг неподвижной точки О. Введем систему
координат Oxyz, связанную с бегуном В. Угол а между осью Oz и не-
подвижной вертикалью — это угол поворота бегуна В в своей плоскости.
Кинетическая энергия бегуна вычисляется по известной формуле:
Т — ~(,Jx^x + ~~ ^-Jyz^y^z 2JZXUJZUJX 2JXylt)xU)y>)
где шх = sin а, izy = о>2, wz = -oleosa — проекции мгновенной
угловой скорости w = а)[ + а)2 на соответствующие оси координат.
Так как оси х, у, z — главные оси инерции бегуна в точке О, то цен-
тробежные моменты инерции Jxy = Jxz = Jyz — 0. Осевые моменты инер-
ции выражаются формулами:
тпг2 mr2
Jx — Jz =-----h fn • OD , Jy —--.
4 y 2
Поэтому
(mr2 „ -Д -> -> mr2 ->
———F m • OD' I • o)] sin a 4—-— • o)J +
(7 \ /7 \ 7
mr2 _ 2 \ 7 7 ( WT 7 \ 7 ТП/i 1
——F m OD I • o)j cos a = I —-—F m • OD' I • o)] -|—— o;j —
— ma)2
+ OD' + r--
2
a 383 (Нм).
Задача 38.9(38.9). В кулисном механизме
при качании рычага ОС вокруг оси О, пер-
пендикулярной плоскости рис. 38.9.1, ползун
А, перемещаясь вдоль рычага ОС, приво-
дит в движение стержень АВ, движущий-
ся в вертикальных направляющих К. Рычаг
ОС длины R считать однородным стержнем
Рис 38 9 1 с массою TOi масса ползуна равна mi, масса
стержня АВ равна ту, ОК — I. Выразить
кинетическую энергию механизма в функции от угловой скорости
и угла поворота рычага ОС. Ползун считать точечной массой.
Ответ: Т =
О)2
6 cos4 9?
[miY?’ cos4 -F 3Z2(m2 -F m3)].
5. Теорема об изменении кинетической энергии
161
Решение. Расчетная схема представлена на
рис. 38-9.2. Кинетическая энергия механизма
Т = Тос + Та t- Tab-
Для вращающегося вокруг неподвижной оси Oz
кривошипа ОС
рим 38.9.2
I 2 1 тщЕ2 г
г ОС — ~ш
Для определения скорости ползуна А рассмот-
рим его движение как сложное, выбрав подвиж-
ную систему координат, связанную с кривошипом ОС. Абсолютная ско-
рость vA направлена по вертикали, так как точка А двигается вместе
со стержнем АВ. Переносная скорость ve — это скорость соответствую-
щей точки А', принадлежащей кривошипу. Поэтому
Ve = о; • О А = и---.
cos <р
Относительная скорость vr точки А направлена вдоль кривошипа. Изоб-
разив треугольник скоростей, найдем из него
ve I
vA =------= <•>—— .
cos <p
В результате имеем
1 2
ТА = -тп2 vA =
Для поступательно перемещающегося стержня АВ кинетическая энергия
1 2 1ЩШ212
Tab = -m3 v~A = ----—.
2 2 cos4
cos-
m2 w2l2
2 cos4 w
Поэтому кинетическая энергия механизма
1 , 9 m2 v2l2 m.) ш212
Т = -mxR2J + =
6 2 cos4 2 cos4 <р
-----z— [miТ2 cos4 + 3Z2(m2 -I- m3)].
6 cos4
162
5. Теорема об изменении кинетической энергии
F, Р2
Рис. 38.10.2
гаи
^.11(31
Ж
звщ
'ошаэро
4/
- йфор»
•Wo
Решение. Расчетная схема — на рис. 38.10.2. Кинетическая энергия
системы
Т — 2Тколеса + То,о2 + Tab-
Так как колеса катятся без проскальзывания, то мгновенный центр ско-
ростей каждого колеса находится в точке касания с рельсом. Отсюда
находим угловую скорость каждого из колес: w = vq/t.
I э 1 •> 1 э ' 2 (1^0 2
^колеса ~ + ~JOiZ^ ~ ~zAl}V(j -Т —М\Т I I =- М\ Vq.
2 2 2 2 \ г /
Кинетическая энергия стержня OiO2> движущегося поступательно со
ростью «о, равна
ско-
khp
рв
"“ене
,дша
"М
'Гл
ТО1О2 = ~М2 vq.
Спарник АВ движется также поступательно. Поэтому
1 » 1 >
Tab = ~М, Ц = -М2(ш • РА)2 =
5. Теорема об изменении кинетической энергии
163
= ш2
= -Mi
2 *
Ур
г
!+G
2 /
1 /
• Г I
2 г
— 2г • - cos (90° 4- g>)
5
- + sin <р
= -Ml v(}
5 \
- + sin (р I .
4 J
Суммарная кинетическая энергия
1 1 1 1 2/5
Т — 2A/|?1q 4- ~Л/2^о 4- -Miv^, I ~ 4- sin р
V2
= — [16М1 + ЛЬ (9 + 4 sin 92)].
8
Задача 38.11 (38.11). Автомобиль массы М движется прямоли-
нейно по горизонтальной дороге со скоростью V. Коэффициент тре-
ния качения между колесами автомобиля и дорогой равен /к, радиус
колес г, сила аэродинамического сопротивления Rc воздуха пропор-
циональна квадрату скорости: Rc = pMgv где р — коэффициент,
зависящий от формы автомобиля. Определить мощность N двигателя,
передаваемую на оси ведущих колес, в установившемся режиме.
( fк Л
Ответ: N = Mg I------h uv ш
\ r )
Решение. Расчетная схема движения ав-
томобиля — на рис. 38.11.I. Воспользуемся
теоремой об изменении кинетической энер-
гии в дифференциальной форме:
ТР|
к2
Рис. 38.11.1
A, ,
J Mg N2
M..
dT = 2_
к
к
В установившемся режиме v = const, поэтому
dT — 0. Считаем автомобиль абсолютно твер-
дым телом и пренебрегаем силами внутреннего трения. Поэтому сумма
элементарных работ внутренних сил равна нулю. А момент двигателя со-
вершает работу
<М$11Г / 0.
Рассмотрим сумму элементарных работ внешних сил:
ft!? = dA(Mg) + dA(Rc) 4- 2 dA(Nt) + 2 dA(Ni) 4- 2 <L4(FTp,) +
к
+ 2 <M(FTP2) + 2 dA(MK[) + 2 dA(MK2).
(1)
164
5. Теорема об изменении кинетической энергии
Отметим, что нормальные реакции и N2, силы трения скольжения
FT₽| и FTP2 и моменты трения качения МК| и МК2 изображены на рис. 38.11.1
для видимых колес задней ведомой и передней ведущей пар колес.
Так как по условию автомобиль движется по горизонтальной дороге,
то вертикальное перемещение центра масс С, к которому приложена
сила тяжести, равна нулю, поэтому dA(Mg) = 0. При качении колес
без скольжения их мгновенные центры скоростей Р3 находятся в точках
касания. Силы трения скольжения приложены к этим точкам. Поэтому
<M(FTP)) = FTp? • dfPj =0 (j = 1, 2, 3, 4).
По этой же причине
dA(Nt) + dA(N2) = 0.
Вычислим сумму элементарных работ моментов трения качения. Так
как размеры колес и коэффициенты трения качения для всех колес
одинаковы, то вычисление приведем к одному колесу, считая нормальную
реакцию равной Mg. Действительно,
2 <М(МК1) + 2 (ЛТК?) = —2/K2V, dp - 2fKN2 dp =
= -А(2^ + 2N2) dp = -fKMgdp.
Работа отрицательна, так как направление момента трения качения
противоположно направлению угла поворота колес р.
Элементарная работа силы аэродинамического сопротивления
dA(Rc) = -Rc ds = -pMgv2 ds.
Работа отрицательна, так как сила Rc противоположна перемещению ав-
томобиля.
Перепишем уравнение (1) с учетом произведенных вычислений:
0 = -pMgv2 ds - fKMg dp + (Мдаиг.
По определению, мощность
поэтому искомая мощность двигателя, передаваемая на оси ведущих колес,
равна
^Ддвиг 7 ds dp >
TV = = pMgv — + fKMg— = pMgv V + fKMgu =
dt dt dt
j v ( 7 f K \
= pMgv + fKMg- = Mgv pv + — ).
r \ r /
5. Теорема об изменении кинетической энергии
165
Задача 38.12(38.12). Машина массы М для шлифовки льда дви-
жется равномерно и прямолинейно со скоростью v по горизонтальной
плоскости катка. Положение центра масс С указано на рис. 38.12.1.
Вычислить мощность N двигателя, передаваемую на оси колес радиу-
са г, если /к — коэффициент трения качения
между колесами автомашины и льдом, a f —
коэффициент трения скольжения между шли-
фующей кромкой А и льдом. Колеса катятся
без скольжения.
Mg
Ответ: N = —
3
Решение. Расчетная схема — на рис. 38.12.2. Воспользуемся теоре-
мой об изменении кинетической энергии системы в дифференциальной
форме:
dT = ^dAf + ^dA^- <’)
к к
Так как машина движется равномерно (у = const), то dT — 0. Счита-
ем, что машина является абсолютно твердым телом, пренебрегаем силами
внутреннего трения. Поэтому сумма элементарных работ внутренних сил
равна нулю, кроме момента двигателя; т. е.
<М$11Г £ 0.
Рассмотрим сумму элементарных работ внешних сил:
dA{? = dA(Mg) + 2 dA(Fjpi) + 2 (Ы(ГТР2) + <M(FTP3) +
к
+ 2 dA(Nx) + 2 dA(N2) + dA(N3) + 2 <M(MK1) + 2 dA(MKJ.
166
5. Теорема об изменении кинетической энергии
Так как колеса машины катятся без проскальзывания, то их мгновенные
центры скоростей находятся в точках касания. Поэтому силы трения
скольжения колес и нормальные реакции, приложенные в МЦС колес,
не совершают работу. Нормальная реакция N3 также не совершает ра-
боту в силу того, что элементарное перемещение точки ее приложения
(имеется в виду равнодействующая нормальная реакция со стороны льда
на шлифующую кромку) направлено горизонтально и dfA ± N3.
dA(Mg) = 0, так как элементарное перемещение центра масс С
направлено все время горизонтально.
Элементарная работа силы трения скольжения шлифующей кромки
<L4(FT₽3) = FTP3 • drA = -FTp3 • dsA = -fN3v dt.
Вычислим сумму элементарных работ моментов трения качения
2 <М(МК|) + 2 dA(MKJ = -2fKNt d<p - 2fKN2 d<p =
= -2/K(JV, + N2) d<p = -2fK(Ni + N2)u> dt,
где a; = v/r. Осталось вычислить величины и 2(7V| -|- N2). Так как
машина движется равномерно и прямолинейно, то справедливы уравне-
ния равновесия сил, приложенных к твердому телу. Составим уравнение
моментов для сил относительно оси, проходящей через точки касания
с поверхностью передних колес:
I 2
-N3- + N!,-l-fKN{-fKN^0. где М = 2ЛГЬ ^ = 2^.
Мы рассматриваем плоский случай. В силу малости коэффициента /к
в уравнении можно пренебречь моментами трения качения. Поэтому по-
лучим:
Z ,2
-N3- + N^-l = 0.
Теперь составим уравнение для суммы проекций сил на вертикальную
ось:
X + N2 + N3-Mg = O.
Можно считать, что наибольшая нагрузка приходится на крайние опоры,
т. е. на шлифующую кромку и на задние колеса. Тогда 7V,' « 0. Поэтому
из составленных уравнений равновесия получаем, что
1 2
N'2 = ~Mg, N3 — -Mg.
С учетом вышеперечисленного, уравнение (1) примет вид:
0 = -f~Mgv dt - fJ-Mgu dt + (М^1Г.
5. Теорема об изменении кинетической энергии
167
Подставим сюда ш = v/r и все члены поделим на dt. В результате перейдем
к мощности:
2 1 v
О = --fMgv - -fKMg- + W.
Поэтому мощность двигателя, передаваемая на оси колес, равна
М%(-ч , /Л
W =---- 2 f Ч---V.
3 \ г 7
Замечание к задаче 38.12. Рассматриваемая система является, вообше говоря,
статически неопределимой, так как нормальные реакции ?V|, ТЛ невозможно
определить из двух уравнений (моментов и проекций на вертикальную ось). По-
этому в решении и было принято упрощающее предположение Nt ss 0. Более
строгое решение задачи возможно, если предполагать грунт линейно упругим
при абсолютной жесткости автомобиля (или наоборот). Тогда решение становится
однозначным, так как можно записать третье уравнение, являющееся кинемати-
ческим и отображающим тот факт, что точки контакта опор при деформациях
грунта всегда лежат на одной прямой.
Задача 38.13(38.12). На вал диаметра 60 мм насажен маховик диа-
метра 50 см, делающий 180 об/мин. Определить коэффициент трения
скольжения f между валом и подшипниками, если после выключения
привода маховик сделал 90 оборотов до остановки. Массу маховика
считать равномерно распределенной по его ободу. Массой вала пре-
небречь.
Ответ: f = 0,07.
Решение. Расчетная схема — на рис. 38.13.1. Воспользуемся тео-
ремой об изменении кинетической энергии в интегральной форме для
системы, состоящей из вала и маховика:
Рис. 38.13.1
168
5. Теорема об изменении кинетической энергии
Работу совершают лишь силы трения скольжения между валом и под-
шипниками:
/d С d
(FTP, + FTP2)- d<p = - J (fNt + fN2)- dip =
о о
v>. v* , ,
T d f d d
= ~ f(Ni + N2)-d<p = - J fMg- dp = -fMg-<pt =
о о
d
= - fMg- 18Отг = —90fMgTrd,
ш
я
так как система до остановки повернулась на угол ipt = 2тгп = 180тг.
Кинетическая энергия системы в начальный момент времени:
Я
rj.
Тй = ~Г
1 /£>\2 /2тг- 180\2 9 2 2
= -Ml — ) ( -------) =
2 \ 2 7 V 60 7 2
В конечный момент Т = 0. Поэтому
9 2 7
— -MD2ir = —90fMgird.
Отсюда коэффициент трения скольжения равен:
Г>2тг (0,5)2тг
f ~ 20gd ~ 20 • 9,8 • 0,06
0,07.
IK.
II
61
<1
Й!
№
•И
*
Задача 38.14(38.13). Цилиндрический вал диаметра 10 см и массы
0,5 т, на который насажено маховое колесо диаметра 2 м и массы 3 т,
вращается в данный момент с угловой скоростью 60 об/мин, а затем
он предоставлен самому себе. Сколько оборотов еще сделает вал
до остановки, если коэффициент трения в подшипниках равен 0,05?
Массу маховика считать равномерно распределенной по его ободу.
Ответ: 109,8 об.
Решение. Воспользуемся расчетной схемой на рис. 38.13.1. Началь-
ное значение кинетической энергии
1 \m(d/2)2
2
2п
+ М —
2 \ 2
2
Конечное значение Т — 0.
5. Теорема об изменении кинетической энергии
169
По аналогии с решением задачи 38.13
р.
С d d
A(Fip) = - f(m + M)g— dip = -f(m + M)g- 2тгп,
о
где п — искомое число оборотов вала до остановки. Приравняв изменение
кинетической энергии системы работе сил, получим уравнение:
—-(md2 + 2MD2)4ir2 = -f(m + M)gdim.
16
Отсюда
(md2 + 2M D2)4tt2
\6f(m+M)gdir
n =
(500-0,01+2-3000-4)-4тг2
16-0,05(500+3000)-9,8-0,1-%
Задача 38.15(38.14). Однородный стержень О А
длины I и массы М может вращаться вокруг гори-
зонтальной неподвижной оси О, проходящей через
его конец перпендикулярно плоскости рис. 38.15.1.
Спиральная пружина, коэффициент упругости кото-
рой равен с, одним концом скреплена с неподвиж-
ной осью О, а другим — со стержнем. Стержень на-
ходится в покое в вертикальном положении, причем
пружина при этом не деформирована. Какую ско-
рость надо сообщить концу А стержня для того, что-
бы он отклонился от вертикали на угол, равный 60е?
Л 9Mgl + 2ir2c
Ответ: v = \ ------——-----
V 67И
Решение. Расчетная схема — на рис. 38.15.2. Со-
гласно теореме об изменении кинетической энергии
для стержня имеем:
1 , I
0--Joz^ = -Mg-(\ -cosy?) + Л(Мупр).
Работа момента упругости спиральной пружины
^(Л^упр) = ~"^Р
Момент инерции стержня
Ml2
Joz — 3
109,8 (оборотов).
Рис. 38.15.1
Рис. 38.15.2
170 5. Теорема об изменении кинетической энергии
Отсюда угловая скорость, с которой стержень начинает вращение,
чтобы отклониться на угол = л/3, равна
W =
I С 7Г2
С7Г2
ЗЛЯ2'
Поэтому концу А стержня надо сообщить скорость
V = wl =
3 тг2с / 9Mgl + 2тг2с
2gl + ЗМ~ V 6М
Задача 38.16(38.16). К концам гибкой нерастяжимой нити, пе-
реброшенной через ничтожно малый блок А, подвешены два груза
(рис. 38.16.1). Груз массы М\ может скользить
вдоль гладкого вертикального стержня CD,
отстоящего от оси блока на расстоянии а;
центр тяжести этого груза в начальный мо-
мент находился на одном уровне с осью блока;
под действием силы тяжести этот груз начина-
ет опускаться без начальной скорости. Найти
зависимость между скоростью первого груза
и высотой его опускания h. Масса второго
груза равна М.
Ответ: v2 = 2g(a2 + Л2)
Mth-M(Va2 + fi‘-a)
M}(a2 + h2) + Mh2
Решение. Расчетная схема — на рис. 38.16.2. Применим теорему об
изменении кинетической энергии в интегральной форме для механиче-
ской системы, включающей в себя два груза В и С, соединенных гибкой
нерастяжимой невесомой нитью, и невесомый блок А.
Рис. 38.16.2
5. Теорема об изменении кинетической энергии 171
Так как движение начинается из состояния покоя, то = 0. Текущее
значение кинетической энергии системы равно
Выразим величину Vb через скорость vc- Для этого запишем геометриче-
ское соотношение:
АС2 = у2с + а2,
где длина участка нити АС = I — ув- Здесь длину всей нити обозначили
через I, координаты грузов В и С обозначили соответственно через у в
и ус, и воспользовались условием ничтожной малости размеров блока А.
Тогда
G - Ув)2 = Ус + °2 =>
=> У в = I - yjо.2 + Ус =>
2усУс Ус^с
=> vB = У в =------г — =-------, ----
2у/а2 + у2с у]а2 + у2с
В момент, когда груз С опустился на высоту h,
hvc
VB ~~ y/a2 + hy
Поэтому
М (hvc)2 Mxv2c v2c\Mh2 + M|(a2 + Л2)]
т = T (a2 + Л2) + 2 = 2(a2 + Л2) ‘
Работу при опускании груза С на высоту h совершат лишь силы
тяжести грузов:
A{M\g) + A(Mg) = M}gh - Mg[(l -a)-(I- Va2 + /*2)] =
- M\gh - Mg(\/a2 + h2 - a).
Приравняем изменение кинетической энергии системы работе этих сил:
Mh2 + М\(а2 + h2) , / 2 ’ 2 \
о-------т 2 7------L = M'Sh ~ Mg(Va2 + h2- a),
2 (a2 + h1)
отсюда
2 _ 0 z 2 , .2, M}h-M(Va2 + h2-a)
vc 2g(a + h ) + Л2) + Mh2
172 5. Теорема об изменении кинетической энергии
Задача 38.17(38.17). Груз Р массы М с наложенным на него до-
полнительным грузом массы М{ посредством шнура, перекинутого
через блок, приводит в движение из состояния покоя тело А мас-
сы М2, находящееся на негладкой горизонтальной плоскости ВС
(рис. 38.17.1). Опустившись на расстояние Sj, груз М проходит через
кольцо D, которое снимает дополнительный груз М\, после чего
груз М, опустившись на расстояние «2, приходит в состояние покоя.
Определить коэффициент трения f между телом А и плоскостью, пре-
небрегая массой шнура и блока и трением в блоке; дано М2 = 0,8 кг,
М = Mi =0,1 кг, S| = 50 см, = 30 см.
Ответ. _ Si(Mi + М)(М + М2) + s7M(M + Mi+ М2)
М2 [s, (ЛГ + М2) + S2^M + М\ + Л/г)]
= 0,2.
Решение. Расчетная схема — на рис. 38.17.2. Рассмотрим первый этап
движения системы грузов, соединенных нерастяжимым шнуром, когда
груз Р\ принадлежит системе. Воспользуемся теоремой об изменении ки-
нетической энергии в интегральной форме. Так как движение начинается
из состояния покоя, то То = 0. Конечное значение кинетической энергии
{МM\)v2 M2V2. v2
т = = -(М + Ml + м2),
так как скорости грузов, соединенных нерастяжимым шнуром, совпадают.
Рис. 38.17.2
5. Теорема об изменении кинетической энергии 173
При опускании грузов Р и Pi на расстояние 5| работу совершат толь-
ко сила тяжести совокупности этих грузов Р и Р, и сила трения тела А:
А((М + M})g) + Л(Ар) = (М + Mt)g • Si - Ртр • S1,
где
FTp = fN = fMig
(так как тело А движется по горизонтальной поверхности). Приравняем
изменение кинетической энергии сумме работ сил:
V2
—(М + М} + М2) = (М + M\)g- s, - fMigSy.
Отсюда получим
2 М + М}- fM2
v _ 2gs ।-----------.
6 М + Ml + м2
С такой скоростью груз Р проходит через кольцо D. Пренебрежем удар-
ными явлениями, происходящими в момент, когда груз Р\ остается на
кольце D, что возможно из-за небольшой скорости v.
Рассмотрим второй этап движения, когда груз Р\ уже не принадлежит
системе. Теперь
Mv2 Мру. v2, , „
т0 = —+ -^ = у(м + м2), т = о.
Суммарная работа сил
A (Mg) + Л(Гтр) = Mg s2 - fM2g s2.
По теореме об изменении кинетической энергии имеем
V2
~—(М + М2) = Mg Si- fM2g s2.
Подставим сюда найденное выше выражение для скорости v:
м +Mi- fMi,
~gм+м,+м,( + М1} = Mg 12 ~ fM2g S2-
Определим из полученного уравнения коэффициент трения f между
телом А и плоскостью:
S\(M + Mi)(M + М2) + s2M(M + Mi + М2)
f ~ M2 [«1 (M + Mi) + s2{M +Ml + M2)] ”
_ 0,5(0,1 + 0,l)(0,1 + 0,8) + 0,3 • 0,1(0,1 + 0,1 + 0,8) _
0,8[0,5(0,1 + 0,8) + 0,3(0,1 + 0,1 + 0,8)]
174
5. Теорема об изменении кинетической энергии
Задача 38.18(38.18). Однородная нить длины L, часть которой
лежит на гладком горизонтальном столе, движется под влиянием
силы тяжести другой части, которая свешивается со стола. Определить
промежуток времени Т, по истечении которого нить покинет стол,
если известно, что в начальный момент длина свешивающейся части
равна I, а начальная скорость равна нулю.
Ответ: Т —
L + VL2 — I2
I
Решение. Расчетная схема — на рис. 38.18.1. где х — координата
нижнего конца В нити, отсчитываемая вертикально вниз от угла А стола.
Тогда я(0) = I, а нить целиком движется со скоростью х. Применим
Рис. 38.18.1
теорему об изменении кинетической энергии в
конечной форме для промежутка времени [0, £]:
тх2
внешних сил*
Ясно, что в работу Лвнешних сил дают вклад только
силы тяжести, приложенные к вертикальной части
АВ нити, т.е. изменению потенциальной энергии
нити:
х
причем П(ж) = -mAB(x)g-,
если за нулевой уровень принять точку А. Таким образом:
mi2 I / х\ I х
= -TnAB(l)g- - \-mAB(x)g- I - -pig- +pxg-,
где тп = pL — масса всей нити, ар — линейная плотность нити. Произ-
водя сокращения, получим дифференциальное уравнение:
Li2 = -gl2 +gx2 => = а у/х2 -I2 =>
at у L
dx
Vx^T2
dt
5. Теорема об изменении кинетической энергии
175
Подставляя в последнее соотношение х = L, получим ответ:
Замечание к задаче 38.18. Заметим, что рассматриваемая в задаче система явля-
ется системой с односторонней связью. Этот факт существенно влияет на решение
задачи. Именно, можно показать, что в процессе «сползания» нити со стола всегда
существует такой момент t < Т(!), при котором реакция стола в точке А становит-
ся нулевой, а впоследствии отрицательной. Дальнейшее движение нити становится
очень сложным и не сохраняет простой формы, представленной на рис. 38.18.1.
Чтобы сохранить корректность условия и решения задачи необходимо предпола-
гать, что движение нити происходит в канале, повторяющем угол стола.
Задача 38.19 (38.19). Однородная нить длины 2а, висевшая на
гладком штифте и находившаяся в покое, начинает двигаться с на-
чальной скоростью До. Определить скорость нити в тот момент, когда
она сойдет со штифта.
Ответ: v = \Jag + v%.
Решение. Расчетная схема — на рис. 38.19.1, где показаны началь-
ное и конечное состояния нити. Применяя теорему об изменении кине-
тической энергии к этим состояниям, получим:
mv2
~Г
mv?.
— = mg
= y/a? + vl-
Рис. 38.19.1
176
5. Теорема об изменении кинетической энергии
Замечание к задаче 38.19. Система, рассматриваемая в настоящей задаче, яв-
ляется системой с односторонней (в точке контакта со штифтом) связью. Можно
показать, что при Vq > x^S нить сразу же (т. е. в начальный момент движения')
перестает контактировать со штифтом (нормальная реакция становится отрица-
тельной). Если же о < Vo < \/ag, то контакт со штифтом прекращается при
„ « A
X = —7=1/ *----,
V2 V аё
где х — перемещение конца нити, отсчитываемое от начального его положения.
Дальнейшее движение нити становится достаточно сложным, но поддается ана-
литическому исследованию (подробности см. [8]). Для сохранения корректности
условия и решения задачи, необходимо предполагать, что в окрестности штифта
нить движется в канале, обеспечивающем двустороннюю связь.
Задача 38.20 (38.20). Транспортер приводится в движение из со-
стояния покоя приводом, присоединенным к нижнему шкиву В.
Привод сообщает этому шкиву постоянный вращающий момент М
(рис. 38.20.1). Определить скорость ленты транспортера v в зависимо-
сти от ее перемещения s, если масса поднимаемого груза А равна Mi,
а шкивы В и С радиуса г и массы М2 каждый представляют собой
однородные круглые цилиндры. Лента транспортера, массой которой
следует пренебречь, образует с горизонтом угол а. Скольжение ленты
по шкивам отсутствует.
Ответ: v =
2(М — Migr sin а)
-----------——-- S.
r(M\ + М2)
Рис. 38.20.2
Решение. Расчетная схема — на рис. 38.20.2. Пусть груз А вместе
с лентой транспортера прошел расстояние s, тогда он поднялся на высоту
h = s • sin а,
и сила тяжести совершит отрицательную работу
Л1 — —M\g • s • sin а.
5. Теорема об изменении кинетической энергии
177
Кроме того, совершит работу (положительную) момент М, т.е.:
s
Ам = М<р = М-.
г
Осталось применить теорему об изменении кинетической энергии:
v
Mt- + 2 •
M2r2
2
s
= M----M\g • s • sin a.
r
Задача 38.21 (38.21). Горизонтальная трубка CD может свободно
вращаться вокруг вертикальной оси АВ (см. рис. 37.56.1 к задаче 37.56).
Внутри трубки на расстоянии МС = Жо от оси лежит тело М. В некото-
рый момент времени трубке сообщена начальная угловая скорость Wq.
Определить скорость v тела М относительно трубки в момент,
когда тело вылетит из трубки. Момент инерции трубки относительно
оси вращения равен J, L — длина трубки; трением пренебречь. Тело
считать материальной точкой массы тп.
Указание. Воспользоваться ответом к задаче 37.56.
Ответ: v = wq
J + mxl
J + mL2
(L2-x2}.
Решение. Расчетная схема — на рис. 37.56.2. Воспользуемся тео-
ремой об изменении кинетической энергии в интегральной форме для
системы, состоящей из тела М, трубки CD и невесомого вала АВ.
Кинетическая энергия системы в начальный момент времени:
ro = ^ + MopV = i(J+miM
Кинетическая энергия системы в момент вылета тела М из трубки
Jw2 m[(bjL)2 + г?2] 1 2 2
Т - — + ------ = -U + mL2)w2 + —.
Воспользуемся ответом, полученным в задаче 37.56, где находилось зна-
чение угловой скорости трубки в момент вылета из нее тела М:
J + mxl
Поэтому
1 (J + mx0)2 2 mv2
Т = 2 J + + ~
178
5. Теорема об изменении кинетической энергии
Так как трубка горизонтальная и трением пренебрегаем, то работа всех
внешних и внутренних сил равна нулю. Отсюда Т = 7q, т. е.
1 (J + тж0)* 2
2 J + mL2
j mv2
% Н——
(j + mxl
2
По-
следовательно, скорость тела М относительно трубки в момент вылета
из нее равна
V =
J + mxl
J + mL2
• (L2-x2).
Задача 38.22 (38.22). По горизонтальной платформе А, движу-
щейся при отсутствии трения, перемещается тело В с постоянной
относительной скоростью щ (см. рис. 36.9.1 к задаче 36.9). При за-
тормаживании тела В между ним и платформой А возникают силы
трения. Определить работу внутренних сил трения между телом В
и платформой А от момента начала торможения до полной остановки
тела В относительно платформы А, если их массы соответственно
равны m и М.
Указание. Воспользоваться ответом задачи 36.9.
Ответ: А = -
1 тМ ,
tZfi.
2 М + т
Решение. Воспользуемся расчетной схемой на рис. 36.9.2. Запишем
для системы «платформа А + тело В» теорему об изменении кинетической
энергии в интегральной форме. Для этого выпишем начальное и конечное
значения кинетической энергии системы:
Mvl m(v0 + u0)2 (М + m)v2
То = —- +--------’ Т=--------------2----
2
Из решения задачи 36.9 возьмем величину общей скорости v платформы
А и тела В после его остановки относительно платформы:
V = То +
т
-------«о
М + т
В результате, изменение кинетической энергии системы равно
2
Т-То =
М + т / т
—з— ( v°+ ту—
2 \ М + т
тт2 т 2
— - у(по + по) =
ГЛ2 2 т 2 Мт 2
2(M + m)U° ~ ~2U° ~ ~2(M + m)U°'
5. Теорема об изменении кинетической энергии
179
Так как горизонтальная платформа А движется по гладкой горизон-
тальной поверхности, то работу совершают лишь внутренние силы трения
скольжения между телом В и платформой’
Е4‘’+Е4'’=аАр)=л.
к к
Поэтому
Т-Т0 = А
Мт 2
Л ~--------Wn.
2(М + т) °
Задача 38.23(38.23). С помощью электромотора лебедки к валу
барабана Л радиуса г и массы М\ приложен вращающий момент твр,
пропорциональный углу поворота у? барабана, причем коэффициент
пропорциональности равен а (см. рис. 37.43.1 к задаче 37.43). Опреде-
лить скорость поднимаемого груза В массы М2 в зависимости от вы-
соты его подъема h. Барабан Л считать сплошным цилиндром. Массой
троса пренебречь. В начальный момент система находилась в покое.
Ответ: v —
2h(ah - 2M2gr1 2)
r2(Mi+2M2)
Решение. Воспользуемся рис. 37.43.2. Запишем теорему об измене-
нии кинетической энергии для системы рассматриваемых тел.
Го = О,
т _ Jzu2 M2v2
2 2
M\r2 f v2^ M2v2
4 у г ) 2
М, \
-у+М2),
2
где v2 — скорость груза В.
<р
j dtp dtp
о
1 2 1 Л2
- M2gh = -dtp - M2gh = -d - M2gh,
2 2 rz
так как tp — h/г. Следовательно,
vifMi \ 1 h2
V Hr + M?1 = ^a~2 ~ M^h-
2 \ 2 / 2 Г
Отсюда получаем зависимость скорости поднимаемого груза от вы-
соты подъема h:
v =
2h(dh — 2M2gr2)
(Mi + 2M2)r2
180
5. Теорема об изменении кинетической энергии
Задача 38.24(38.24). На рис. 38.24.1 изоб-
ражен подъемный механизм лебедки. Груз Л
массы Mi поднимается посредством троса, пе-
реброшенного через блок С и навитого на
барабан В радиуса г и массы Mi. К бара-
бану приложен вращающий момент, который
Рис. 38.24.1 с момента включения пропорционален квад-
2
рату угла поворота tp барабана: mBp = atp , где
a — постоянный коэффициент. Определить скорость груза Л в мо-
мент, когда он поднимается на высоту Л. Массу барабана В считать
равномерно распределенной по его ободу. Блок С — сплошной диск
массы М2. Массой троса пренебречь. В начальный момент система
находилась в покое.
Ответ: v =
4h(ah1 2 - 3M]gr3)
Зг3(2М] + 2М2 + М3)'
Рис. 38.24.2
Решение. Расчетная схема — на рис. 38.24.2. Воспользуемся теоре-
мой об изменении кинетической энергии системы в интегральной форме:
т0 = о, т-тл+т„ + тс^
Miv2
2
M2rl
)2 ?
= 4(2М,+2М2+М3).
4
52 } + IS = +
k k
V
A(Mig) = J atp2 dp - M]gh =
о
1 3 t 1 h3 h
= -atp - M\gh = -a — — Migh, так как tp = -.
3 Зг-* г
5. Теорема об изменении кинетической энергии
181
Приравняем изменение кинетической энергии системы работе сил:
w? I Л3
-L(2M, + 2М2 + Му) = -a -у - M\gh.
4 3 г3
Получим из уравнения скорость груза А:
W, =
4Л(аЛ2 - 3M,gr3)
Зг3(2М, + 2М2 + М3) ’
Задача 38.25 (38.25). Какую начальную скорость, параллельную
линии наибольшего ската наклонной плоскости, надо сообщить оси
колеса радиуса г для того, чтобы оно, катясь без скольжения, под-
нялось на высоту h по наклонной плоскости, образующей угол а
с горизонтом? Коэффициент трения качения равен /к. Колесо счи-
тать однородным диском.
2 / / /к \
Ответ: v = - < / 3gh I 1 ч-ctg а I.
3 V \ г )
8
Решение. Расчетная схема — на рис. 38.25.1. Применим теорему
об изменении кинетической энергии на участке от начала движения
до момента его остановки, т. е. когда v = 0. Пусть пройденный центром
путь вдоль плоскости есть s, тогда s = 7i/(sina). Угол, на который
повернется колесо при качении без проскальзывания будет
s h
¥> = - = —:—•
г г sin а
Тогда теорема кинетической энергии дает:
0 “2TW — Т Атр.качеНцЯ,
где: Amg = -mgh — работа силы тяжести, Атр.качения = ~Мк<р — работа
момента трения качения. Нормальная реакция N и сила сцепления F
182
5. Теорема об изменении кинетической энергии
работы не совершают, так как скорость точки контакта, в которой они
приложены, равна 0 (отсутствие проскальзывания!). Используя формулу
для а и равенство Мк — fKN = fKmgcosa, получим:
2 , г * 11
-mv — mgh + fKmg cos a -----------
4 r sin a
2
v —
V3
gh( 1 + — ctg a ].
\ r /
Замечание к задаче 38.25. Выясним условия, при которых может быть реализо-
вано чистое качение колеса, которое предполагается в условии задачи. Несложные
рассуждения приводят к неравенству:
3
I
И
t
El
и
II
и
I
1 2 А
- tg a - - —
3 3 г
где f — коэффициент трения скольжения. Именно при этом условии возможно
качение колеса без проскальзывания!!!
Задача 38.26 (38.26). Два цилиндра одинаковой массы и радиуса
скатываются без скольжения по наклонной плоскости. Первый ци-
линдр сплошной, массу второго цилиндра можно считать равномерно
распределенной по его ободу. Найти зависимость между скоростями
центров масс цилиндров при опускании их на одну и ту же высоту.
В начальный момент цилиндры находились в покое.
_ v2 V3
Ответ: — = —
v, 2
Решение. Запишем теорему об изменении кинетической энергии
длч каждого из цилиндров:
mv? Jiw? л mv?
—' + —1 _ 0 = mgA, ~^ +
В силу условий непроскальзывания, имеем:
V?
а>2 == —
R
-----0 = mgh.
«1
Wi = —,
R
Моменты инерции цилиндров.
mR1
J' = ~
J2 = mR1.
41
II
Тогда
-mv? = mgh, mv2 = mgh ==>
3 2 2
=> = V2
^1-11
Щ ~ 2
’.I
5. Теорема об изменении кинетической энергии
183
Задача 38.27(38.27). Эпициклический механизм, расположенный
в горизонтальной плоскости, приводится в движение из состояния по-
коя посредством постоянного вращающего момента L, приложенного
к кривошипу О А (рис. 38.27.1). Определить угловую скорость криво-
шлпа в зависимости от его угла поворота, если неподвижное
имеет радиус Г|, подвижное колесо II — радиус
г2 и массу М\, а кривошип О А — массу М^.
Колесо II считать однородным диском, а кри-
вошип — однородным стержнем.
2
Ответ: ш =---------
Г1 + г2
колесо I
II
Рис. 38.27.1
А
3L<p
9М} + 2М2 ’
Решение. Расчетная схема — на рис. 38.27.2. Применим теорему об
изменении кинетической энергии в дифференциальной форме:
±(T) = We+Wr, (1)
at
где We — мощность внешних сил, к которым в данном случае относится
лишь момент L, a W, — мощность внутренних сил, которая в отсутствии
проскальзывания и трения будет равна нулю. Имеем
1 7 M]V2. JfT-Uj
Т = ТОА+ТИ, Toa = -(JOa№2, = + We = I4>.
Кроме того, из кинематических соображений, получим:
VA
Va = О А • ф = (Г1 + Т1)ф, Wi = —
Г2
184 5. Теорема об изменении кинетической энергии
(так как В — МЦС колеса II). Тогда, учитывая, что
M2(ri+r2)2 т М\т22
Jo а = ---у-----> - ~2—’
получаем:
„ 1М2(п+г2)2 ,2 М\ 2.2 \Мхг2(г\+г2)2Ф2
т = ------------Ф + у(П + Г2) ф + -----------2---
2 3 Z z z ' 2
Ф2 ГМ2(Г1 + г2)2 2 , . \2
= У ------------- + М,(п + г2) + — (п + г2) =
ф2 М2 31. .2
= — — + -Ml (ri + r2)2.
Подстановка вычисленных величин в (1) дает:
^21М2 3 \ .. 6-1
ФФ(Г1 + r2) + -MJ -Вф => ф- +Г2)2(2М2 + 9М,)’
Представляя
. ^Ф 1 d(tp)2
ф = ф — =-------,
d<p 2 dtp
получим:
d&)2 __________12-Т_________
dp (ri + г2)2(2М2 + 9М1)
.2 12-Т-у? . 2 Г Lp
= (ri + г2)2(2М2 + 9М{) V~ rt+r2 \ 2М2 + 9Mi'
Задача 38.28(38.28). В кулачковом меха-
низме, расположенном в горизонтальной плос-
кости, эксцентрик Л приводит в возвратно-
поступательное движение ролик В со штан-
гой D (рис. 38.28.1). Пружина Е, соединен-
ная со штангой, обеспечивает постоянный
контакт ролика с эксцентриком. Масса эксцентрика равна М, экс-
центриситет е равен половине его радиуса; коэффициент упругости
пружины равен с. При крайнем левом положении штанги пружина не
напряжена. Какую угловую скорость надо сообщить эксцентрику для
того, чтобы он переместил штангу D из крайнего левого в крайнее
правое положение? Массой ролика, штанги и пружины пренебречь.
Эксцентрик считать однородным круглым диском.
Ответ: ш = 2yJс/(ЗМ).
°ешение. Расчетная схема — на рис. 38.28.2, где представлены два
крайних положения штока D. В соответствии с теоремой об изменении
кинетической энергии, вся сообщенная в крайнем правом положении ки-
нетическая энергия перейдет в потенциальную энергию пружины. Имеем:
2 2
где А — сжатие пружины, которое, очевидно, равно г (см. рис. 38.28.2).
По теореме Штейнера—Гюйгенса имеем:
Mr2 Mr2
3 2
= -Mr .
4
Тогда получим:
1 2 3 э С 7
-и -Mr2 ~ -г2
2 4 2
ш = 2
Задача 38.29(38.29). Какой путь проедет велосипедист не вращая
педалями до остановки, если в начальный момент он двигался со ско-
ростью 9 км/ч? Общая масса велосипеда и велосипедиста равна 80 кг.
Масса каждого из колес равна 5 кг; массу каждого из колес считать
равномерно распределенной по окружности радиуса 50 см. Коэффи-
циент трения качения колес о землю равен 0,5 см.
Ответ: 35,6 м.
Решение. Пусть s — путь, который проехал велосипедист до полной
остановки, тогда а = s/R — угол поворота колес. По теореме об измене-
186
5. Теорема об изменении кинетической энергии
нии кинетической энергии имеем:
/ mc/vl 1 , s
О - ( —+ 2 - Jwo = ~MKa = -fKmog—,
\ 2 2 1 л
где т0 — общая масса системы, J = m}R2 — момент инерции колеса,
mi — масса колеса. Используя кинематическую связь w0R — v0, получим:
2 / mo \ . s
Vol —+2mi ] =mofKg— =+
\ 2 / л
9 / Ш0 \
/9-103\2 40 + 2-5
fKgmo = \ 3600 ) ' °’5 ’ 0,5-10-2-9,81-80
1 2 1 50 1 4 5 . .
—102 --------------------= —10 -------~ 39 (м)
16 2 (1/2)-10-2-9,81-80 16 8-9,81
Задача 38.30 (38.31). Груз А массы М\ опускаясь вниз, при помо-
щи троса, перекинутого через неподвижный блок D, поднимает вверх
груз В массы М2, прикрепленный к оси подвижного блока С. Блоки С
и D считать однородными сплошными дисками мас-
сы Мз каждый (рис. 38.30.1). Определить скорость
груза Л в момент, когда он опустится на высоту h.
Массой троса, проскальзыванием по ободам блоков
и силами сопротивления пренебречь. В начальный
момент система находилась в покое.
/ 2МХ - Мз - Мз
Ответ: v — 2» 2gh--------------
V 8М, + 2М2 + 7М3
Рис. 38.30.2
Решение. Расчетная схема представлена
на рис. 38.30.2, где v — скорость опускания
груза Л. Запишем кинетическую энергию си-
стемы:
T = TA+TB+TC+TD.
Согласно схеме, используя теорему Кёнига,
имеем:
М,«2 M2v2
Тл = —. Ъ = —
Й,
f!
7
in
Д
5. Теорема об изменении кинетической энергии 187
Кинематические соотношения получим из условия нерастяжимости нитей:
V = «1 = Ш1Г2, Ш2Г2 = • 2гз, О>зГз = «3, V2 = Vc}-
Отсюда получим
ш2 = 1 1 V V VC3 = -, V2 = -.
— V, W3 = V,
Г2 7Г3
Кроме того, т3 2 Jy = ~^т3> M3r\ J2= 2
Тогда получим:
Mi г»2 М2 v2 М3 v2 M3 2 । 2 , 1 2
Т = —ь 1 1
2 V2 ( 2 4 2 4 М3 м3 М3 4 4г\ 4 г2 М3\
+ т)"
v2 /8М, +2М2 + 7Мз
8
По теореме об изменении кинетической энергии эта величина Т
должна быть равна работе сил тяжести на описанном в задаче перемеще-
нии, т. е.
Amg = Migh - (M2g + ,
где h\ — высота подъема грузов В и С. Но так как
1
vc3 =
1
fii — -h.
2
Следовательно,
v2 /8Л7] + 2M2 + 7M3\ . «л- \ ’ 1,
Т = — ------------------ = Migh - (M2g + M3g)-h
2 у о / 2
=> V2 =-----------!-------Г \6Migh - 8Л(М2 + M3)g\ =>
8Mi + 2М2 + ТМ3 L * V J
=> v = — ___ 2gh(2Mi — Mi — M3),
x/SMi + 2M2 + 7M3 V v i2’
ясно, что для корректности необходимо потребовать неравенства
2Mi > М2 + М3.
188
5. Теорема об изменении кинетической энергии
Задача 38.31 (38.32). К ведущему колесу — барабану А — снего-
очистителя приложен постоянный вращающий момент m (рис. 38.31.1).
Массу барабана А можно считать равномерно распределенной по его
Рис. 38.31.1
ободу. Суммарная масса снега D, щита В
и всех прочих поступательно движущихся ча-
стей постоянна и равна М2- Коэффициент
трения скольжения снега и щита о землю ра-
вен /, коэффициент трения качения барабана
о землю равен /к. Масса барабана равна М\,
его радиус г.
Определить зависимость между путем s, пройденным щитом В
снегоочистителя, и модулем его скорости v, если в начальный момент
система находилась в покое.
2М\ + М2
Г -f- m2 2
Ответ: s =----------------------— v .
2 m - (Mi/K + fM2r)g
Рис. 38.31.2
Решение. Расчетная схема — на рис. 38.31.2. Подсчитаем кинетиче-
скую энергию системы, предполагая, что А катится без скольжения (д* — 0)
/ПЛ' 1 , , 1 ->
Т —---------h -М\г ш2 + -M2V2.
2 2 2
Используя кинематическую связь wr = v (так как К — МЦС колеса),
получим:
V2
Т - у(М] + М\ +М2).
По теореме об изменении кинетической энергии в дифференциальной
форме имеем:
dT
— = mw - MKw - FTP2 v,
at
где F1P2 — сила трения скольжения, приложенная к В и D, сила трения
FTP1 мощности не создает при отсутствии проскальзывания. Тогда получим,
5. Теорема об изменении кинетической энергии
189
используя кинематическую связь ш — v/r и равенства
мк = А • Mxg, FTP2 = fN2 = fM2g:
д v
vv(Mx + Mx + M2) = m------fK- M\g •----fM2gv
r r
1 / m
=> vi =----------v —
2Mi + M2 \r
f.Mjg
r
-fMgg
Интегрируем это равенство от нуля до текущего момента времени £:
1 2 1
1 rfr^Mi + М2)
s - .
2m- fKMxg - frM2g
Замечание к задаче 38.31. Из-за невесомости стержня СЕ сила реакции между
барабаном Л и щитом В направлена горизонтально вдоль стержня. Поэтому в
силу отсутствия движения центров масс барабана и щчта В со снегом D вдоль
вертикали нормальные реакции:
N2 = M2g, N\ = Mtg.
Задача 38.32(38.33). Скорость автомашины, движущейся по пря-
мой горизонтальной дороге, возросла от до v2 за счет увеличения
мощности мотора. При этом был пройден путь s. Вычислить работу,
совершенную мотором на этом перемещении автомашины, если Мх —
масса каждого из четырех колес, М2 — масса кузова, г — радиус колес,
А — коэффициент трения качения колес о шоссе. Колеса, катящиеся
без скольжения, считать однородными сплошными дисками. Кинети-
ческой энергией всех деталей, кроме колес и кузова, пренебречь.
6Mi + М2
Ответ: А =----------
2
(«2 - v?) +
Решение. Воспользуемся теоремой об изменении кинетической
энергии в интегральной форме для автомашины:
- Т, = £ 4’+£ 4°-
к к
(1)
Кинетическая энергия
Т — Аузова 4“ ^Тколеса
M-gv1
2
MjV1 Jcz^2
2 + 2
4
Здесь v — скорость кузова автомашины, равная скорости центров масс
колес; угловая скорость колес w = v/r, так как нет скольжения у колес;
190
5. Теорема об изменении кинетической энергии
моменты инерции колес
W2
Jcz — 2 ’
Отсюда
M2v2 [MiV2 Mir2fv\7'] 2/1., олт А
2 [2 4 \r J \2 /
Поэтому изменение кинетической энергии равно
Т2 - Т\ = (v2 - vf) Qm2 + ЗМ,)
Из внешних сил работу совершают лишь моменты трения качения:
J24e) = -(2MK1^ + 2MK2^),
k
где Мк1 — момент трения качения передних колес, Мк2 — момент трения
качения задних колес, угол поворота колес <р = s/г. Так как
ЛА, = AM, МК2 = AM,
то
4е) = -(2AM +2АМ)’ | = - А ^(2М + 2М) = - A J(4M, +M2)g.
Последнее равенство следует из теоремы о движении центра масс
автомашины в проекции на вертикальную ось:
0 = 2М + 2М - 4M|g - M2g.
Силы трения скольжения не совершают работу, так как колеса катятся
без скольжения. Силы тяжести не совершают работу, так как движение
происходит по горизонтальной дороге.
Работа внутренних сил сводится к работе мотора:
Г 4’ = л.
к
Подставим найденные выражения в (1):
( \м2 + ЗМ, ) = - А -(4М, + M2)g + А.
\ 2 / Г
Отсюда работа, совершенная мотором, равна
А = (д2 ~ (^2^2 + “*• — s(4Mt + M2)g =
= (^22 - V?) |(6М, + М2) + ~ (4М, + M2)gs.
5. Теорема об изменении кинетической энергии
191
Задача 38.33 (38.34). Стремянка АВС с шарниром В стоит на глад-
ком горизонтальном полу, длина АВ = ВС = 21, центры масс нахо-
дятся в серединах D и Е стержней, радиус инерции каждой лестницы
относительно оси, проходящей через центр масс,
равен р, расстояние шарнира В от пола равно h
(рис. 38.33.1). В некоторый момент времени стре-
мянка начинает падать вследствие разрыва стержня
FG. Пренебрегая трением в шарнире, определить:
1) скорость точки В в момент удара ее о пол;
2) скорость точки В в тот момент, когда расстоя-
ние ее от пола будет равно h/2.
Рис. 38.33.1
Л . I ~gh ч 1 I I6Z2 - h* 1
Ответ: 1) v — 2l\-:-2) v=-Jgh—1--------—.
I ’ \l2 + p2 ’ 2\S 2(l2 + р2)
Решение. Расчетная схема — на рис. 38.33.2. Так как пол гладкий
(нет сил трения), то центр масс стремянки не будет перемещаться вдоль
горизонтального направления. Лестницы АВ и ВС одинаковые. Поэтому
центр масс стремянки все время будет находиться на середине отрезка
DE, т. е. на оси у. Поэтому и точка В все время будет находиться на оси у.
Применим теорему об изменении кинетической энергии.
(nw р 3е?.^ \ ? ? 7
= mvE + тД’
Выразим скорость центра масс стержня ВС Ve и его угловую скорость ш
через скорость точки В. Для этого запишем геометрические соотношения:
ув = 21 cos <р, Хе = 1^\г\<р, уЕ = 1 cos <р.
Продифференцируем их по времени:
Ув = -21 sin <р • ф, хе = I costp • <р, Уе = —I sin <р • <р.
192
5. Теорема об изменении кинетической энергии
Следовательно,
Ув
tp —----------,
21 sin tp
I -1 vb
a) = <3 = ---------,
2Zsin</
2 .2 -2 2 2 -2
vE = xE + yE = I cos tp • ф
+I2 sin2 tp-ф2 = 12ф2 =
у2в
4 sin2 tp
Поэтому
VB
V D ~)
T = m------z---F mp , ,
4 sin2 tp 4Z2 sin2 tp
Работу совершают только силы тяжести:
mv2B
4 sin2 tp
l2 + p2
I1
2A(mg) = 2mg{yE(tp0)-yE(tp)) = 2mg[ I
h
— - Z cos у?
Из теоремы об изменении кинетической
энергии имеем:
4 sin2 tp
Z2 + p2
—— = mg(h - 21 cos 9?)
Vb = 21 sin <р
g(h - 21 cos tp)
P+7
1) Скорость точки В в момент удара ее о пол, когда tp = 90°,
vB = 21
gh
l2 + p2'
2) Скорость точки В в тот момент, когда расстояние ее от пола равно
h h
— и cos tp = —, sin tp =
2 * 41 *
h2
1----—г, будет равна
16Z2
vB = 21
h2 h- 2lh/(4l) 1 / 16Z2 - h2
16Z2 ‘ у 8 I2 + p2 ~ 2y8h2(l2+p2Y
Замечание к задаче 38.33. Отметим, что в этой задаче рассматривается система
с односторонней связью в точках А и С! Этот факт накладывает определенные
ограничения на решение и ответ задачи. Подсчитаем нормальные реакции в точках
Л и С. В силу симметрии ясно, что NA = N, = N. Тогда теорема о движении
центра масс по оси у дает:
2тпуЕ — -2т1(ф2 cos tp + <р sin tp) = -2mg + 2N.
Нетрудно получить из решения данной задачи формулы:
^2 = ^Тр(л-2/С0^)>
Тогда получим выражение для нормальной реакции:
N 12 2 h р2\
— = ~Г7~п I 3 cos tp - - cos tp + — ,
mg p2 +12 \ p I2 J
7Г \
<f> € V’o, j ) •
5. Теорема об изменении кинетической энергии
193
Отсюда следует, что для безотрывного движения (N 0) при всех <р € [^0, тг/2),
необходимо и достаточно соблюдения неравенства:
р2^ь2- О
Именно это неравенство н следует добавить к ответу задачи 13.33. Если же вы-
полнено неравенство
то до падения точки В на пол произойдет отрыв точек Л и С от пола, и задачу
следует решать по-другому. Причем, отрыв происходит при р — ip, таком, что:
л h / / h
0 < cos^t = — I 1 4- з /1 - 12 — ) < cos tp0 =
Ы \ V п,L ) 21
Отметим, что в случае однородных стержней АВ и ВС мы имеем р2 = Z2/3
и неравенство безотрывности (I) выполнено всегда, так как
/2 I
рг = - ^Л2 <=> h2 4Z2 <=^ h 21,
а это неравенство выполнено заведомо.
Задача 38.34 (38.35). Стержень АВ длины 2а
падает, скользя концом А по гладкому горизон-
тальному полу (рис. 38.34.1). В начальный момент
стержень занимал вертикальное положение и на-
ходился в покое. Определить скорость центра масс
стержня в зависимости от его высоты h над полом.
Рис. 38.34.1
Ответ: v — (а - Л)
6g(a + h)
4а2 - 3h2’
Решение. Расчетная схема — на рис. 38.34.2.
Так как пол гладкий, то согласно теореме о движе-
нии центра масс середина С стержня перемещается
только вдоль неподвижной оси у.
Воспользуемся теоремой об изменении кине-
тической энергии стержня:
к к
Рис. 38.34.2
mv\ Jcz^2 mvi m4a2 7
Т0 = 0, Г = _?£+_ = ^ + ^!.
Запишем координату точки С:
УС = О, cos <р.
194
5. Теорема об изменении кинетической энергии
Скорость
Ус = -a sin р р.
Угловая скорость
i -I Vc
ш = М = —:--------------
a sin p
Поэтому
mv2r
гр _ __С
2
vlc
sin2 р
Работа силы тяжести
m
6~
mvy
~6~
I \ mv}c 4a2 - 3y^
1~(Ус/а)2) 6 a2 ~ Ус
g
A(mg) = mg(a - a cos p) = mg(a - yc).
Теорема об изменении кинетической энергии дает уравнение:
mv^ 4a2 - Зур
~~ —-------F = mg(a - ус),
6 а2 - у2с
из которого находим скорость
6g(a + ус) . ,.
4+^7 =(^"’
Замечание к задаче 38.34. Связь в точке А стержня является односторонней
и поэтому для корректности решения необходимо проверить неотрицательность
нормальной реакции N в точке А в течение всего интервала падения. Используя
результаты решения задачи, мы можем получить:
2 2(g/a) .. fe/a)sin^ /4 2 \
= ТТЛ—- cosy5)- Т = ТГР,--------------—77 7 + cos V ~ 2 cos и ).
1/3 4- sin2 р' г' г (1/3 +sin2 р)2 \3 J
Применяя (например) теорему об изменении кинетического момента относитель-
но центра масс, мы получаем:
хг т8 (4 2
N = -1/, /1 , 2 42 I - + cos р - 2 cos р
3(1/3 + sin2 ру \3
Последнее неравенство следует из тождества:
4 2 I 7
- + cos р - 2 cos р = - + (1 - cos р) > 0.
Можно показать справедливость следующего более общего утверждения. Пусть
стержень начинает движение при произвольных начальных условиях:
У’(О) = Ф^>) =
(р и р мы отсчитываем по часовой стрелке). Тогда:
vc = (a - Ус)
6g(a + h)
—5——-г, так как yc = h.
4a2 - 3h2
7Г
> 0 при р Е 0, — .
Г. Если a>0 > 0, то безотрывное движение будет при < ———. Если
a cos ро
2 . S г
u>o > ------. то будет отрыв и произойдет он в начальный момент,
a cos
Я
ж
2
2
II
111
а
KI
И
не
«I
4ц
5. Теорема об изменении кинетической энергии
195
2°. Если ш0 < 0, то безотрывное движение будет при
2 2 _ g (7/3 - 2 cos у?о)
шо w0| — — . . z
a (4/3 - cos2
Если > o>oi, то будет отрыв. Причем, если , то отрыв
a cos
произойдет не сразу, а в точке € (у50, тг/2), а если ш0 > ----, то отрыв
acos^o
происходит сразу (т.е. в начальный момент).
Задача 38.35(38.36). В дифференциальном вороте два жестко со-
единенных вала К\ и К2 с радиусами г, и г2 и моментами инерции
относительно оси О|О2 соответственно J\ и J2 приводятся во вра-
щение рукояткой АВ. Подвижный блок С подвешен на невесомой
нерастяжимой нити, левая ветвь которой навита на вал К\, а пра-
вая ветвь — на вал К2 (рис. 38.35.1). При вращении рукоятки АВ
левая ветвь нити сматывается с вала К\, а правая ветвь наматыва-
ется на вал К2. К рукоятке АВ приложен постоянный вращающий
момент тп. К блоку С подвешен груз D массы М. Найти угловую
скорость вращения рукоятки в момент, соответствующий концу подъ-
ема груза D на высоту s. В начальный момент система находилась
в покое. Массами рукоятки и блока пренебречь.
Рис. 38.35.1
Ответ: w = 24 2s
2m - Mg(r2 - ri)
(r2 - ~ ri)2 + 4(J] + J2)]
Решение. Расчетная схема — на рис. 38.35.2 (вид сбоку). Распишем
теорему об изменении кинетической энергии системы:
Mv2d (J, + J2)a>2
2 2
= m<p - Mg • s.
(1)
196
5. Теорема об изменении кинетической энергии
Из кинематики плоского движения блока С
видно, что
- ^Г1
и
ф W
VD = 8 = -(Г2 - Г1) = у(г2 - Г,).
Подставим в уравнение (1) выражения для vp
и Получим
М[ш I2 (Ji + J2)w2 2s
+-------------------------=m— -Mgs
Отсюда угловая скорость
2 Ils 2Ш ~ Mg^2 ~ Г‘)
у S(r2-r1)[M(r2-ri)2 + 4(J1 + J2)]
Задача 38.36(38.37). Ворот приводится в движение посредством
ременной передачи, соединяющей шкив II, сидящий на валу ворота,
со шкивом I, сидящим на валу мотора. К шкиву I массы М\ и ра-
диуса т приложен постоянный вращающий момент тп (рис. 38.36.1).
Масса шкива II равна М2, радиус его R. Масса барабана ворота
Мз, радиус его г, масса поднимаемого груза Мд. Ворот приводится
в движение из состояния покоя. Найти скорость груза в момент, ко-
гда он поднимается на высоту Л. Массами ремня, каната и трением
в подшипниках пренебречь. Шкивы и барабан считать однородными
круглыми цилиндрами.
Рис. 38.36.1
Ответ: v — 2
h(mR/r2 - Mig)
M^R/r)2 + M2(R/r)2 + M3 + 2Mi ‘
ь
Решение. Расчетная схема — на рис. 38.36.2. Чтобы применить тео-
Vr
— рему об изменении кинетической энергии системы, запишем выражения
сре для кинетической энергии и работы внешних и внутренних сил.
C.MJ
навр
То = О,
т = т,+т2 + т3 + т4 =
, M4V4
2~ 2
Выразим все кинематические характеристики через скорость груза V4 = v:
2
2
pi®. v v R R
ш = w3 = wi = w2- = v~.
flip
Осевые моменты инерции тел:
opoir
Mir2 M2R2 М3т2
Jzt = — , Jz3 = —3 Jz3 = —•
Итак,
М\т2 2 R2 M2R2 v2 M3r2 v2 M4V2
T = ~v '74+~T" V V + T“
V2
T
R2
Mi-j- +M2^- +
Мз + 2M4 .
Работа всех сил сводится к двум слагаемым:
R
A(m) + A(M4g) = m<f>\ - M4gh = m!t- - M4gft.
r2
Теорема об изменении кинетической энергии системы дает уравнение:
v2 / R2 R2
— \ М\ — + M2—z- + М3 + 2.М4
/| \
R
= mh— — M4gh.
rL
198
5. Теорема об изменении кинетической энергии
Из уравнения получаем скорость груза в момент, когда он поднимется
на высоту h:
v = 2
h(mR/r2 — M4g)
Mi(R2/r2) + M2(R2/r2) + M3 + 2M4
Задача 38.37(38.38). Решить предыдущую задачу, принимая во вни-
мание массу каната, к которому привязан груз. Длина каната I, масса
единицы длины каната М. В начальный момент с вала барабана ворота
свисала часть каната длиной 2h.
Ответ: v = 2
h(mR/r2 — M4g - (3/2)Afg/i)
M^R/r)2 + M2(R/r)2 + M3 + 2M4 + 2MI'
Решение. Воспользуемся решением задачи 38.36. Принимая во вни-
мание массу каната, к которому подвешен груз, добавим в кинетическую
энергию слагаемое Тканата и в работу слагаемое Д(РКаната)- Вычислим их
(см. рис. 38.37.1)
_ М(1 - h)r2 Mhv2 M(l - h)r2 v2 Mhv2 Mlv2
2 каната — 7 4 ~ “ T 4 “ — ~ J
2 2 2 2 2
h
ЖАаната) = ~ f Mg(h + y) dy = - ^Mgh2 + '-Mgh2^ = -|м^Л2.
0
Теорема об изменении кинетической энергии примет вид:
v2 ( R2 R2 \ R 3 2
— ( М| — + М2 — + М3 + 2М4 + 2М1 ) = mh— - M4gh-----------Mgh .
\ j y**- 2
Скорость груза
I h(mR/r2 - M4g - (3/2)Mgh)
V~ \ Mi(R2/r2) + M2(R2/r2) + M3 + 2M4 + 2МГ
5. Теорема об изменении кинетической энергии
199
Задача 38.38(38.39). Постоянный враща-
ющий момент L приложен к барабану ворота
радиуса г и массы М\. К концу А намо-
танного на барабан троса привязан груз мас-
сы Mi, который поднимается по наклонной
плоскости, расположенной под углом а к го-
ризонту (рис. 38.38.1). Какую угловую ско-
рость приобретет барабан ворота, повернув-
шись на угол 9?? Коэффициент трения сколь-
жения груза о наклонную плоскость равен f. Массой троса пренебречь,
барабан считать однородным круглым цилиндром. В начальный мо-
мент система была в покое.
Рис. 38.38.1
Ответ:
2 L - M2gr(sinа + /cos а)
г у М\ + 2Mi
Рис. 38.38.2
Решение. Расчетная схема — на рис. 38.38.2. Применим теорему об
изменении кинетической энергии:
Т-Т0 = ^А^ + ^А^.
к к
(1)
Здесь
JozV2 М\Г2 i
То = О, Т = Т, + Т2, Т, = ы2,
MiV2 Mi, ) 1 9 i,
Ti = = -y(ur)2 => T = -u2t\mx + 2M2).
J2 4> + A® = A(L) + A(M2g) + Л(/тр) =
к к
— L<p — Migx sin a — Fyp x —
= Ltp — Migrtp sin a — fMigrtp cos a =
200
5. Теорема об изменении кинетической энергии
— Lip - M-igr 9?(sin a 4- f cos a),
так как
Ftp = fN, N = M2g cos a.
Подставив полученные соотношения в (1), будем иметь уравнение:
1 2 2
-a) г (Mt 4- 2М2) = Lip - M2grip(sm a + f cos a).
Отсюда угловая скорость барабана ворота равна
2
Ш — -
г
L - M2gr(sin a 4~ f cos a)
•92.
М\ + 2М2
Задача 38.39 (38.40). Решить предыдущую задачу с учетом массы
троса, к которому привязан груз. Длина троса равна I, масса единицы
длины троса равна М. В начальный момент с барабана ворота свисала
часть троса длиной а. Изменением потенциальной энергии троса,
намотанного на барабан, пренебречь.
Л 1
Ответ: us = -
r
2.L- 2Af2gr(sin а 4- f cos a) - Mgr (2 а - пр) sin a
2-------------------------—-------—----------------------ip.
М । + 2М2 + 2МI
Решение. Воспользуемся решением задачи 38.38. При учете массы
троса в уравнении (1) добавятся следующие слагаемые: Тороса и Ж Ароса)-
В момент времени, когда барабан повернулся на угол ip,
_ M(l-a + np)r2 2 M(a — rip) 2 Ml 2 2
2троса — 2 ^4-------------(шт) = U) r .
Работа силы тяжести троса при повороте барабана на угол ip:
rtp
Ж-Ароса) — ~ J Mg(a - х) sin ads = -Mg sin a (anp - ^r2ip2
о
(1) => ^u2r2(Mi + 2М2) + ^“2r2 =
= L<p - M2gr 9?(sin a 4- f cos a) - Mg sin a ]-np(2a - rip) =>
а) = -
г
2Д — 2M2gr(sin а + f cos а) — Mgr sin а(2а - пр)
2-----------------гт----—------—---------------------ip.
Mi + 2М2 + 2М1
5. Теорема об изменении кинетической энергии
201
Задача 38.40 (38.41). К барабану ворота
радиуса Г1 и массы М\ приложен постоян-
ный вращающий момент L. К концу троса,
намотанного на барабан, прикреплена ось С
колеса массы М2 (рис. 38.40.1). Колесо ка-
тится без скольжения вверх по наклонной
плоскости, расположенной под углом а к го-
ризонту. Какую угловую скорость приобретет
барабан, сделав п оборотов? Барабан и колесо считать однородны-
ми круглыми цилиндрами. В начальный момент система находилась
в покое. Массой троса и трением пренебречь.
Рис. 38.40.1
Ответ: о> = —
О
L — M2grx since
27Г71-------------
M\ + 3M2
Решение. Расчетная схема — на рис. 38.40.2. Воспользуемся теоре-
мой об изменении кинетической энергии в интегральной форме.
Движение начинается из состояния покоя,
поэтому То = 0. Через п оборотов барабана
Т1 Т _1_ Т M2Vq Jcz^2
1 — i \ +12 —
Рис. 38.40.2
2 2 2 '
Так как колесо катится без скольжения, то
в точке его касания с плоскостью находится
мгновенный центр скоростей. Поэтому
«С UJiTi
U)2 — -- — -----.
Г2 Г2
2
Отсюда
-> M2rl 2 M2rl r? , 9 r?, . ,
T = —- — (Д] -I----— U| -I--------2 wl = W1 + ЗМ2).
4 2 4 r2 4
Работа всех внешних и внутренних сил для системы сводится к двум сла-
гаемым:
A(L) + Л(М^) = Lupx ~ M2ghc = L • 2т п - M2gr\(2irri) sin a.
Составим уравнение:
г2
Wi -^-(Мх + ЗМ2) = L 2тгп - M2gTx(2irn) sin a.
Отсюда, угловая скорость барабана
2
= —
О
L — M2gr\ sin a
27Г71-------------
Mx + 3M2
202
5. Теорема об изменении кинетической энергии
Задача 38.41 (38.42). Решить предыдущую задачу с учетом массы
троса и трения качения колеса о наклонную плоскость, если I —
длина троса, М — масса его единицы длины, a — длина части троса,
не намотанной на барабан в начальный момент /к — коэффициент
трения качения, г2 — радиус колеса. Изменением потенциальной
энергии троса, намотанного на барабан, пренебречь.
Ответ:
2
о) = —А 2тгп
п 5
L - rig М2 sin a + — cos a | + M (a - 7ГПГ1 k r2 / sin a
Ml + ЗМ2 + 2М1
Рис. 38.41.1
Решение. Расчетная схема изображена
на рис. 38.41.1. Воспользуемся решением за-
дачи 38.40.:
г2
То = 0, Т = (М, + ЗМ2) + Ттроса,
где Ттроса складывается из кинетической энер-
гии части троса, намотанного на барабан, и
части троса, не намотанного на барабан, через
п его оборотов.
/0)^2 m^v2
^троса = « I «
= -М(1 - а 4- 2ттпГ1)Г| • w2 + -M(a - 2тгпт])г1 oj, = -^Mlrjcdf.
Отсюда
г2
Т = w? -±(Mi + ЗМ2 + 2М1).
К работе всех внешних и внутренних сил системы добавятся работа
момента трения качения колеса о наклонную поверхность:
V2
Л(тк) = - J mKd<f>2 =
о
<Р2
Г Г1
/ fKN d<p2 = -fKM2g cos a • 2тгп—
J r2
о
и работа силы тяжести той части троса, которая в начальный момент не
была намотана на барабан:
2яПГ|
о
5. Теорема об изменении кинетической энергии
203
1 2
-Mg sin a 27rnria --(2тгпг|)
= -2Mg sin a 1гпт\(а - тгпг ।).
Уравнение примет вид:
w?^-(Ml+3M2 + 2MZ) =
Г]
= 2imL - 2тпМ^Т\ sina - 2тт/кMtgcc&a-27rnMgsina: • rt(a - 7ГПГ1).
Т1
Угловая скорость барабана после п оборотов будет равна
2
a?i = -
L - r\g М21 sin a + — cos a + M sin a • (a - -ппт\)
27ГП
Г2 /
Mi + 3M2 + 2MZ
Задача 38.42(38.43). Колесо А скатыва-
ется без скольжения по наклонной плоско-
сти ОК, поднимая посредством нерастяжи-
мого троса колесо В, которое катится без
скольжения по наклонной плоскости ON.
Трос переброшен через блок С, вращаю- Рис. 38.42.1
щийся вокруг неподвижной горизонтальной
оси О (рис. 38.42.1). Найти скорость оси колеса А при ее перемеще-
нии параллельно линии ОК на расстояние s. В начальный момент
система была в покое. Оба колеса и блок считать однородными дис-
ками одинаковой массы и радиуса. Массой троса пренебречь.
Ответ: v —
Рис. 38.42.2
Решение. Расчетная схема — на рис. 38.42.2. Применим теорему об
изменении кинетической энергии.
204
5. Теорема об изменении кинетической энергии
То = О,
Т = ТА+Тв + Тс =
MAv2 , JAz^A MBV2 Jbz^b , Jcz^c
2 2 2 2 2
Mv2 Mr2 /гА2 Mv2
^~ + ~4~\r) + ~Г~
Mr2 (v\ Mr2 f v\ 7 )
4----I - I 4--1 - I = -Mv ,
4 \r / 4 \r/ 4
так как колеса А и Б и блок С — одинаковые однородные диски, и колеса
катятся без скольжения; v — скорость оси колеса А.
В силу отсутствия скольжения колес работу совершают лишь силы
тяжести колес А и В:
м!
!«Н
JJ
#1
а
лри
MAgs sin a - MBgs sin /3 = Mgs(sin a — sin /3).
Из теоремы получаем уравнение для скорости v:
-Mv = Mgs(sin a — sin /3)
-gs(sina - sin/3).
Задача 38.43(38.44). Решить предыдущую задачу, принимая во вни-
мание трение качения колес о наклонные плоскости. Коэффициент
трения качения равен /к, радиусы колес равны г.
Ответ: v = 2
1 J к
-gs sin a - sin /3--------(cos a + cos /3) .
7 r
7'
Решение. При наличии трения качения колес надо учесть работу
моментов трения качения. В результате из теоремы об изменении кине-
тической энергии получим уравнение:
да
й
иок
1)1
Ши
?;tn
v = 2
1
у
-Mv* 2 = Mgs(sin a — sin /3) - тпкА <pA - mvB • <рв-
Здесь моменты трения качения колес равны соответственно
! и»
ткА = fKNA = fKMg cos а и ткВ = fJ^B = f*Mg cos /3.
Углы поворота колес:
$
Фа = <Рв = -.
т
Поэтому скорость
1
v = 2
-gs sin a - sin /3------ (cos a + cos /3)
7 r
7
5. Теорема об изменении кинетической энергии
205
Задача 38.44(38.45). К грузу А массы Mt прикреплена нерастя-
жимая нить, переброшенная через блок D массы М-> и намотанная
на боковую поверхность цилиндрического катка В массы Му. При
движении груза А вниз по наклонной плоскости, расположенной
под углом а к горизонту, вращается блок D, а каток В катится без
скольжения вверх по наклонной плоскости, образующей с горизонтом
угол /3 (рис. 38.44.1).
Определить скорость груза А в зависимости от пройденного им
пути s, если в начальный момент система находилась в покое. Блок
D и каток В считать однородными круглыми цилиндрами. Силами
трения и массой нити пренебречь.
/ 2М] sin a - Му sin В
Ответ: v = 2* 2gs-----------------
У 8М, + 4М2 + ЗМу
Решение. Расчетная схема — на рис. 38.44.2. Воспользуемся теоре-
мой об изменении кинетической энергии системы в интегральной форме:
= £ 4’+ £><".
fc к
Согласно тому, что в начальный момент времени система покоилась,
То — 0. В момент времени, когда груз пройдет расстояние s, кинетическая
Рис. 38.44.2
206
5. Теорема об изменении кинетической энергии
энергия системы
Т = 7, + Т2 + Т3 =
M{v2 JDZu2 t MyVc Jcz^}
2 + 2 + 2 + 2
Mxv2
2
М2Г2 ( v\ М3 (v\2 Мзг1 ( v \2
4 +~2\2/ + 4 \2r7y
v2 ( M, 3 \
- + Л ,
Z \ Z о /
так как каток В катится без скольжения и потому в точке его касания
с наклонной поверхностью находится мгновенный центр скоростей. Нить
нерастяжимая, поэтому
Е4’ = &
к
Сумма работ внешних сил
Е * = A(M\g) + А(Мзё) = Migs sin a - M3g | sin /3,
так как каток В катится без скольжения. Приравнивая изменение кине-
тической энергии системы сумме работ, получим уравнение для скорости
груза V.
V2
~2
М2 3
Mj -I- — + -М3
Z о
S
— M\gs sin a — M3g - sin /3.
Отсюда
v = 2
2gs
2M} sin a - М3 sin /3
8M1 + 4Л/2 + 3M3
Задача 38.45 (38.46). Решить предыдущую задачу в предположе-
нии, что коэффициенты трения скольжения и качения соответственно
равны f и Д. Радиус катка В равен г.
Ответ: u> = 2
2М} (sin a - f cos о) - М3 ( sin (5 + — cos /3
9 .____________________________\_________r
gS 8M1 + 4M2 + ЗМ3
Решение. Расчетная схема — на рис. 38.45.1. Воспользуемся реше-
нием задачи 38.44. С учетом шероховатой поверхности для груза Л работа
ч
I:
5. Теорема об изменении кинетической энергии
207
силы трения FTP| будет равна
Л(АР1) = --Ftp, • s = —fNi • s = -fMigcos a s.
Здесь нормальная реакция TV, определяется из условия отсутствия движе-
ния груза вдоль нормали к наклонной поверхности:
0 = TV, — M}g cos a.
С учетом трения качения катка В работа момента трения качения Мк
будет равна
S S
А(МК) = -Мк <р = -fKN3 — = -ДЖ? cos/3 • —.
Здесь нормальная реакция N3 определяется из условия отсутствия движе-
ния центра масс катка вдоль нормали к наклонной поверхности:
О = N3 — M3g cos /3.
Уравнение движения системы принимает вид:
V2
7
м2 з
м,+ -/ + -м3
L о
S S
= M\gs sin a - M3g - sin (3 - fM\g cos a • s - fKM3g cos /3 • —
2 2т
Отсюда
v = 2
/ J
2Afi(sin a — f cos a) — M31 sin /3 4--cos /3
\ J'
2gs------------------------------------------------
s + 4M2 + 3M3
208
5. Теорема об изменении кинетической энергии
Задача 38.46 (38.47). Груз массы М подвешен на нерастяжимом
однородном тросе длины I, навитом на цилиндрический барабан с го-
ризонтальной осью вращения (рис. 38.46.1). Момент инерции барабана
относительно оси вращения J, радиус барабана R,
масса единицы длины каната т. Определить ско-
рость груза в момент, когда длина свисающей части
каната равна х, если в начальный момент скорость
груза Vo — 0, а длина свисающей части каната бы-
ла равна а?о; трением на оси барабана, толщиной
троса и изменением потенциальной энергии троса,
навитого на барабан, пренебречь.
Ответ: v = R
g[2M + m(x + ж0)] - хо)
J + (М + ml)R2
Mg-
Рис. 38.46.2
Решение. Расчетная схема — на рис. 38.46.2. Воспользуемся теоре-
мой об изменении кинетической энергии системы в интегральной форме:
т-1о = £л<'| + ^4>.
k к
Здесь
То = О,
Mv2
Т- —
2
2
г> \
r) +
m(Z - x)R2 / v\2 mx 2
' I I -|- ---D ~
2 \RJ 2
Mv2
IT
Jv2 m(l - x)v2 mx >
1R2 + 2 + ~TV
5. Теорема об изменении кинетической энергии
209
где первое слагаемое — кинетическая энергия груза, второе слагаемое —
кинетическая энергия барабана, третье слагаемое — кинетическая энер-
гия нити, намотанной на барабан, четвертое слагаемое — кинетическая
энергия свисающей части нити.
Нить нерастяжимая, поэтому внутренние силы не совершают работу.
Работа внешних сил сводится к работе сил тяжести груза и свисающей
части нити:
X
А^} = Mg(x - So) + / mgx dx = Mg(x - s0) + (s2 - x%).
k Xo
Поэтому
Mv2 Jv2 m(l - x)v2 mx -> , , mg, ,
— + ^2 + 2 + = Mg(x - So) + y{x2- xl).
Отсюда
g[2M + m(s + so)] (s - s0)
v = R \ —----------z----—----.
V j + MR2 + mlR2
Задача 38.47(38.48). Груз А массы Mt подвешен к однородному
нерастяжимому канату длины L и массы М2. Канат переброшен через
блок В, вращающийся вокруг оси О, перпендикулярной плоскости
рис. 38.47.1. Второй конец каната прикреплен
к оси катка С, катящегося без скольжения ' 7ТО
по неподвижной плоскости. л
Блок В и каток С — однородные круг- | I
лые диски радиуса г и массы Му каждый. %QA
Коэффициент трения качения катка С о го- Рис. 38.47.1
ризонтальную плоскость равен /к. В началь-
ный момент, когда система находилась в покое, с блока В свисала
часть каната длины I. Определить скорость груза А в зависимости
от его вертикального перемещения h.
Ответ:
М2, , /к Г /1 I 1гг h \
M1 + _(a+2r+4-L Мэ+мг(-------)
V = \ 2gh--------------------------------
Решение. Расчетная схема — на рис. 38.47.2. Воспользуемся теоре-
мой об изменении кинетической энергии системы в дифференциальной
210
5. Теорема об изменении кинетической энергии
Рис. 38.47.2
форме:
к к
Кинетическая энергия системы
Т = ТА + Тв + ТС + Тканата =
_ M\V2 МуГ2 f v\2 MyV2 МуГ2 fv~\2 M2V2
+ +-T + T2vj +~2“ =
г?
= y(Mi + M2 + 2My).
В вычислениях учли отсутствие скольжения катка С (точка касания
Р — мгновенный центр скоростей катка).
Дифференциал кинетической энергии
dT = (М] + М2 + 2My)v dv.
Суммарная элементарная работа внутренних и внешних сил сводится
к работе силы тяжести груза А:
dA(M}g) = M^gdy;
работе силы тяжести каната:
М-,
dA(M2g) = —^(1 + г + y)g dy
L
5. Теорема об изменении кинетической энергии
211
и работе момента трения качения катка С:
dA(MK) = -Мк dp = -fKN(y) — .
Г
В результате уравнение принимает вид
du
(М\ + М2 + 2Mj)v dv = M}gdy + — (Z 4- г + y)gdy - fKN(y) —. (1)
L r
Для определения нормальной реакции катка N(y) воспользуемся тео-
ремой об изменении кинетического момента всей системы относительно
оси вращения блока В:
± (41’+4? + +47"”’) = Е (??’) =*
к
d Г Mgr2 v ( M2r2 v\
=> — Mgvr -I--— • - + Mgvr -I------ - + M2vr
dt L 2 г \ 2 г /
7Г
= Migr + M22gr + M22g BS2 cos - - M2lg S}K -
- M2g 2SXK + N 2S{K - Mk.
Здесь масса горизонтального участка каната
М2 ( иг
Mix^~\L-l-y- —
масса участка каната, облегающего блок В,
М2 7ГГ
м22 = — —;
L 2
масса вертикального участка каната
Мз,
М2з = -Al + y).
1J
Центр масс горизонтального участка каната — точка S\, причем
1
SiK = -
L-l-y—
Центр масс каната, облегающего блок В — точка S2, такая, что
г sin (я/4) 2\/2г
В52 =-------=------------
7Г/4 7Г
212
5. Теорема об изменении кинетической энергии
После преобразований получим:
dv, 4 M2 ,
— (Mi + M2 + 27Из) = Myg H——g (I + r + y)—
dt L
M2 1 / 7rr\2 1 T ТГГ
- (L-l-y- — - M3g- [L-l-y-—
L 2r\ 2 / r \ 2
(2)
1 ( 7гг\ /к
+ N-{L-l-y- — \ -N-.
г \ 2 ) г
Из полученного уравнения (2) выразим N(y):
М2 М2 £
var- Migr---—g br + — g — + M3gc
N(y) =------------~-----------------
К
где
7ГГ
a — M\ T M^2 -|~ ЗА/3, b = I у г ч c — L — I — у —
Подставим N(y) в уравнение (1):
ЛЬ /к var Migr
av dv = Mig dy + —bg dy-------— dy + -------— dy +
L r c- fK r c- fK
fK M2gbr fK M2gc* fK M3gc
+ — у;---yr dy------—----— dy----------- dy.
r L(c - fK) r L(c - /к)2 r c - fK
Разделим левую и правую части на dt и сократим все слагаемые на v.
Далее после несложных преобразований и умножения левой и правой
частей на (с — /к), получим:
,, , M2gfK ( c1 bc\ fKc
L \ lr fKJ r
Сокращаем на с, расписываем выражения a, b и с, группируем члены.
В результате получаем:
, ч ЛЬ, ч ЛГ? А (1 I
v(Mi+M2 + 2M3)=g Mi + -^(2l + 2r)-^^(-- — ~ —
2L г \2 2L 4L
fK T \
- M3— +M2—l — +---- t/
r - » or Г t I
г \2L LfK
Так как
dv dy dv
— — — v—,
dt dy dy
5. Теорема об изменении кинетической энергии
213
то разделяем переменные в дифференциальном уравнении и берем инте-
грал:
V
о
М / 1
г \ 2
ft /к / 1 Г \
- М3— +М2—[— + —]у dy.
h
Г г м2,
= / g М} + -Ч21 + 2г)-
О
I 1ГГ\ /к /к ( 1 г \ ‘
2£-4ь)-М’7 + М^(2£ + ЬА>]^
Из полученного выражения получаем величину скорости груза А при
его опускании на высоту h;
f 2gh.
М2/
мх + -/(2Z 4- 2г + Л) -
v =
7Vf| -|- TVf2 -Ь 2Л/з
- — м3 + м2
г
I I тгг
2 “ 2L ~ 4L
Задача 38.48(38.49). Механизм эллипсографа, расположенный в
горизонтальной плоскости, приводится в движение посредством по-
стоянного вращающего момента то, приложенного к кривошипу ОС
(рис. 38.48.1). В начальный момент при <р = 0 механизм находился
в покое. Найти угловую скорость кривошипа ОС в момент, когда он
сделал четверть оборота. Дано: М — масса
стержня АВ, гпа = тпв = тп — массы пол-
зунов А и В, ОС = АС = ВС = I; массой
кривошипа ОС и силами сопротивления пре-
небречь.
Ответ:
1 / Зтгт0
се — — \ ----------.
21 V М + Зт
Решение. Расчетная схема — на рис. 38.48.2. Воспользуемся теоре-
мой об изменении кинетической энергии системы в интегральной форме:
т-^Е^+Е^0-
к к
В силу условия задачи То = 0. Определим кинетическую энергию системы
для конечного ее положения:
Т = ТАВ+ТА + ТВ,
где
Mv2 Jcz^ab mAv2A mv2A mBv2B mv2B
1AB — —-— + --------, -IA — ---2-- — ’ ±B ~ ----2-- ~
214
5. Теорема об изменении кинетической энергии
Выразим все кинематические параметры системы через искомую
угловую скорость кривошипа шо- Для этого построим мгновенный центр
скоростей стержня АВ (точку Р) и запишем:
= Wo • ОС — wqI
(так как точка С принадлежит кривошипу ОС),
Vc = ШАВ • СР = &ав1
(так как точка С принадлежит стержню АВ),
Ылв —
va = ^ав АР = • 21 cos Ы = О,
1(Р=тг/2
Vb = Мав ВР = Шо-21 sin 92 = • 21.
\ip=ir/2
Поэтому
Т =
Мм212
2
М^1У U+n-L тй?°24/2
-|2-2“»+0+^—
= 2шцГ ( — + m J .
Сумма работ внутренних сил системы
Е4’=о.
к
так как абсолютно твердые тела соединены гладкими шарнирами. Из внеш-
них сил работу совершает лишь постоянный по величине вращающий
момент то:
— Л(то) = то • Д92 -- то<£>|
, 1^=тг/2
то7г
~~2~
5. Теорема об изменении кинетической энергии
215
Подставив все найденные величины в исходное уравнение, получим:
□ .2,2 (м , \ "io*-
2 °Z + / = ~2~'
Отсюда угловая скорость кривошипа
1 / Зтгто
Шп = “ Л /-------.
21V М + Зт
Задача 38.49 (38.50). Решить предыдущую задачу с учетом посто-
янного момента сопротивления тс в шарнире С.
Ответ: w = —
21
Зтг(т0 - 2тс)
М + Зт
Решение. Воспользуемся решением задачи 38.48. Теперь, с учетом
действующего в шарнире С постоянного момента сопротивления тс,
где чр — угол между кривошипом и стержнем (Z.OCB) равен чр = тг -2<р.
Поэтому чр = -2ф. Отсюда
t
А(тс) = -тс J
о
тг/2
—тстг,
так как ф не меняет знак на заданном участке движения и \чр\ = 2|у>| = 2ф.
Теорема об изменении кинетической энергии примет вид:
-тс I
о
7 7 ( ТО
2wnZ । — Т т
и V з
то7г
—-----тС7г.
Я Отсюда угловая скорость кривошипа
1
Шл — —
21
Зтг(то - 2тс)
М + Зт
216
5. Теорема об изменении кинетической энергии
Рис. 38.50.1
Задача 38.50 (38.51). К кривошипу OOt
эпициклического механизма, расположенно-
го в горизонтальной плоскости (рис. 38.50.1),
приложен вращающий момент 7Ивр = Mq - otw,
где Мо и а — положительные постоянные,
а w — угловая скорость кривошипа. Масса
кривошипа равна тп, М — масса сателли-
та (подвижного колеса). Считая кривошип
тонким однородным стержнем, а сателлит —
однородным круглым диском радиуса г, опре-
делить угловую скорость w кривошипа как функцию времени. В на-
чальный момент система находилась в покое. Радиус неподвижной
шестерни равен /?; силами сопротивления пренебречь.
Указание. Применить теорему об измененный кинетической энергии в диффе-
ренциальной форме.
Ответ: ш — (1 - е , где Jnp =
(тп 3 \
у+ -М)(Л + г)2.
Решение. Расчетная схема — на рис. 38.50.2. Воспользуемся теоре-
мой об изменении кинетической энергии системы в дифференциальной
форме
к к
Кинетическая энергия системы Т = Т\ +2г- Кинетическая энергия кри-
вошипа OOi
JOz i 1 m(R + г)2 2
ii =---и? =------------ш .
2 2 3
Кинетическая энергия сателлита (подвижного колеса)
5. Теорема об изменении кинетической энергии
217
Скорость центра масс сателлита
vO] = w • ОС), — ш • (/? + г);
момент инерции
Mr1 2 3
Joiz — ;
угловая скорость
vo, R + r
Wl — — = w-------,
г г
так как предполагаем качение сателлита без проскальзывания и потому
в точке его касания с неподвижной шестерней находится мгновенный
центр скоростей. Итак,
Т = ^m(R + r)2w2 + + г)2 + -Мг2ш-— + г^ =
6 2 4 г2
— -m(R + r)2w2 + ~-M(R + r)2w2 = -w2(j? + r)2 (-m + -M^ .
6 4 2 \3 2 /
Дифференциал кинетической энергии
(1 3 \
-m + -M |dw.
3 2 J
Так как абсолютно твердые тела системы соединены гладким шарниром,
то
Е «4*=о-
к
Так как механизм расположен в горизонтальной плоскости, то
dA^ = dA(MBp) = Мвр dp = (Mo - aw) dtp.
k
Подставив найденные выражения в теорему об изменении кинетиче-
ской энергии, получим дифференциальное уравнение для w:
w(fl + г)2
1 3 \
-тп + -М dw —
3 2 /
Мз - aw 1 dp.
Разделим левую и правую части уравнения на dt'.
u(R + г)2
1 3 \ dw dw
-m + -М — = (Мо - aw) —
3 2 J dt dt
(R + r)2
1 3
-m + -M
3 2
dw
Mo - aw
= dt.
218
5. Теорема об изменении кинетической энергии
Проинтегрируем уравнение:
--------( -т+ —М ) In I----w I = <
а \3 2 / \ а ) о Io
(Я + г)2
а
1 3 \
-тп + -М In
3 2 /
(М0/а)-а>\
М0/а )
= t.
Введем обозначение
/I 3 \ ,
ЛР = I ~тп + -М HR + r) .
Перепишем результат интегрирования в виде
Отсюда, потенцируя, получим угловую скорость кривошипа
ш = — (1 - где Jnp = (\тп + + г)2.
а \3 2 /
Задача 38.51 (38.52). Решить предыдущую задачу с учетом посто-
янного момента трения Мтр на оси О\ сателлита.
Л/о -Л^тр / m 3 \
Ответ: ы =--------—(l, где Jnp = ( — + -ЛМ(Я + г) .
Решение. Воспользуемся решением задачи 38.50. С учетом посто-
янного момента трения Mjp на оси О] имеем
dA^ = d4(MTP) = —Мтр sign чр dip = -Мтр sign чр чр dt — -7Итр|^| dt.
к
Здесь чр = <pi-чр — угол поворота сателлита относительно кривошипа.
Распишем
R + г .
г ‘
|^| = |^, - у>| =
• ЛГ1 R-
Р-Р =-М = -р,
так как ф не меняет знак. Поэтому
R R
dA(Mjp) = -Мтр • —ф dt = -MTp— dp.
Используя теорему об изменении кинетической энергии, получим (см. ре-
шение задачи 38.50):
X R
o>Jnp dw = (Mo - aw) dp - MTP — dp,
5. Теорема об изменении кинетической энергии
219
где
2
dw
Jmdw , , R
= (Мо - aw) -Мхр- => /лр —----- ----= dt
dt г Мо - MyP(R/r) - aw
------ In I Мо - Му
о \
r R
тр Cm?
Г
о
a
—^In
a
M0-MyP(R/r)“) 1
R
М-0 М^р
т
0) = -------
a
где
Задача 38.52(38.53). Кривошип ОО\ гипоциклического механиз-
ма, расположенного в горизонтальной плоскости
щается с постоянной угловой скоростью а>о-
В некоторый момент времени двигатель был
отключен и под действием постоянного мо-
мента Мтр сил трения на оси сателлита (по-
движного колеса) механизм остановился.
Определить время т торможения и угол tp
поворота кривошипа за это время, если его
масса равна М\, М^ — масса сателлита, R
и г — радиусы большого и малого колес.
Кривошип принять за однородный тонкий
стержень, а сателлит — за однородный диск.
Указание. Применить теорему об изменении кинетической энергии в диффе-
ренциальной форме.
(рис. 38.52.1), вра-
Рис. 38.52.1
Ответ: T = -^E-w0
RMyp
1 ^'Aip 9 т
• гае J™=
Решение. Расчетная схема — на рис. 38.52.2. Применим теорему об
изменении кинетической энергии в дифференциальной форме:
к
к
220
5. Теорема об изменении кинетической энергии
Поэтому
MAR -г)2 2 М2(Я-г)2 , M2r2(R-r)2 2
Т = 6- + 2 =
. \2 f М\ 3 \ /Лр 2
= у (R - r) ^у + 2М2 J = у WI ’
где приведенный момент инерции
^пр —
(у + |м2)(Я-г)2.
Дифференциал
dT — 7пра>| dw\
Так как механизм расположен в горизонтальной плоскости и шар-
нир О гладкий, то
Ed4e) = °-
к
Из-за наличия постоянного момента М1р сил трения на оси сателлита О]
dA^ = <L4(MTp) = —Mrp sign ip dip — -Mjp sign ip ip dt = -Мтр|^| dt,
к
где угол ip = +^2 — Угол поворота сателлита относительно кривошипа.
|V>| = l^i +0г| =
R-r
+----&
Г
R,-l R-
= 71^1 = 7^’
так как не меняет знак при движении механизма.
R . R
dA{Alsp) — dt — 7WTp~ d(fi\.
5. Теорема об изменении кинетической энергии
221
Уравнение движения механизма принимает вид:
г R
dw, = -Мтр — dtf>\. (1)
г
Проинтегрируем уравнение (1):
О (Pi
У ЛрО?! dw\ = - У М1р^ dipi =>
О
угол поворота кривошипа
I ~> / 71Д 3 \
*’, = 2йй;“6- ™
Для определения времени торможения кривошипа т перепишем уравне-
ние (1) в виде:
г R
Длро>1 dw} = -Мтр—о;, dt.
г
Отсюда
О т
/R rJn
Л^тр Г — СДц.
Г RMlp
о»о О
Задача 38.53(38.54). Крестовина С приво-
дится во вращение вокруг неподвижной оси О\
посредством однородного стержня АВ, враща-
ющегося вокруг неподвижной оси О (оси О
и О| перпендикулярны плоскости рис. 38.53.1).
При этом ползуны А и В, соединенные при
помощи шарниров со стержнем АВ, сколь-
зят вдоль взаимно перпендикулярных прорезей
крестовины С. Вращение стержня происходит
под действием постоянного вращающего мо-
мента твр. Определить угловую скорость стержня АВ в момент, когда
он сделает четверть оборота, если в начальный момент при <р = 0 он
имел угловую скорость Шо- Величина момента сопротивления, возни-
кающего в каждом из шарниров ползунов А и В, в два раза меньше
твр. Прочими силами сопротивления пренебречь. Масса стержня рав-
на т; момент инерции крестовины С относительно оси равен J;
ОО\ =ОА = ОВ = 1.
Рис. 38.53.1
Ответ: w =
6тГ7ПВр 2
4m/2 + 3J +Ш°’
222
5. Теорема об изменении кинетической энергии
Рис. 38.53.2
Решение. Расчетная схема — на рис. 38.53.2. Центры масс кресто-
вины С и стержня АВ находятся в неподвижных точках О\ и О. Поэтому
расположение плоскости механизма непринципиально. Применим теоре-
му об изменении кинетической энергии в интегральной форме
t-To = E4’+Z4’-
к к
Для вычисления кинетической энергии определим скорости звеньев си-
стемы.
Если w — угловая скорость стержня АВ, то Vb — w • OB — wl.
Рассмотрим теперь сложное движение точки В (ползуна В). Подвиж-
ную систему координат свяжем с крестовиной С. Тогда Vb = ^Вг + ^Ве
(см. рис. 38.53.2). Из треугольника скоростей получаем, что Vb£ = Vb cos^i ,
так как угол между векторами vB и &ве равен <р>\. Это следует из того, что
АО — О\О = О В и, следовательно, ДО, ОД — равнобедренный. Кроме
того, Vb -L О В и ± О\В.
С другой стороны, переносная скорость точки В равна
VBe = • О\В = 0?! • 2 • О]О COS^I = 2wtl cos^>|.
Приравнивая два выписанных выражения для vBe, получим угловую ско-
рость крестовины
vb wl w
OJl — - = - — —.
2/2/2
В дальнейшем понадобится соотношение между углами поворота
стержня АВ и крестовины С. Из геометрических соображений нетрудно
увидеть, что <р । = <р/2.
Теперь выпишем кинетическую энергию системы:
Jo-w2 m(2/)2 w2 ml2w2
T = TAB+Tc, ТАв = ——^^-- = ——,
2. 12 2 о
5. Теорема об изменении кинетической энергии
223
JO]Zw] J f w\2 J 2
=8" =*
-> i ml2 J\ w2, ,
> Т = ш -------+ - )=— (4mr + 3J).
\ 6 8J 24' '
В начальный момент движения
То = g(4mZ2 + 3J).
Работа внешних сил
тг/2
У^ = А(твр) = / твр • dtp = m,
* о
^вр
тА = тв = —
Работа внутренних сил
Лдг> = А(тА) + Л(тв), где
к
— моменты сопротивления, возникающие в шарнирах ползунов А и В.
Воспользуемся при вычислении работы моментов сопротивления рассуж-
дениями, приведенными в решениях задач 38.49 и 38.51. Получим
pi Pi
к
Pio
тг/2
(₽В>
тг/2
твр7г
4
О
О
Окончательно имеем уравнение:
—(4ml2 + 3J) - ^~(4тГ + 3.7) = т:
Отсюда получаем угловую скорость стержня АВ:
7Г 7ПВр7Г
вр2 “
/ 6тгшВр
ш = \ -----г------ь ал;.
V 4ml2 + 3J
6. Плоскопараллельное (плоское) движение
твердого тела (§ 39, [10])
в
м2
11
Рис. 39.1.1
Задача 39.1 (39.1). Тяжелое тело состоит из стержня
АВ длины 80 см и массы 1 кг и прикрепленного к нему
диска радиуса 20 см и массы 2 кг (рис. 39.1.1). В началь-
ный момент при вертикальном положении стержня телу
сообщено такое движение, что скорость центра масс М}
стержня равна нулю, а скорость центра масс Mi диска
равна 360 см/с и направлена по горизонтали вправо. Най-
ти последующее движение тела, принимая во внимание
только действие силы тяжести.
Ответ: Тело равномерно вращается с угловой скоростью 6 рад/с во-
круг своего центра масс, который описывает параболу у1 = 117,5а;;
(начало координат — в точке В, ось у направлена по горизонтали
вправо, ось х — вниз).
Решение. Расчетная схема — на рис. 39.1.2. Найдем центр масс С
тела, считая стержень и диск однородными. Введем вертикальную ось Ах.
Очевидно, центр масс С расположен на этой оси:
к
Хс =
У2гпкхк
40 • 1 + (80 + 20) • 2
= 80 (см).
I +2
KI
W!
tel
tl
к
Следовательно, центр масс С расположен в точке В.
Удобно неподвижную систему координат с осями
х и у выбрать с началом в исходном положении точки
В (т. е. точки С).
Так как начальная скорость точки М2 и един-
ственная действующая сила — сила тяжести mg —
расположены в вертикальной плоскости Вху, то дви-
жение тела будет происходить в этой же плоско-
сти (плоское движение тела). Поэтому целесообразно
общие теоремы динамики системы: теорему о движении
k=
ЦК
*3!
применить две
центра масс и теорему об изменении главного момента количеств движе-
ния системы в относительном движении по отношению к системе коорди-
Si)’
6. Плоскопараллельное (плоское) движение твердого тела 225
нат, движущейся поступательно с центром масс С (система осей Кёнига):
Аг Аг Аг
В итоге получаем дифференциальные уравнения плоского движения
тела:
r m^c =
к
< =
к
JC^ = ^MCZ(F^,
- к
которые в нашем случае принимают вид
{mxc — mg,
тус = О,
JCzu = 0.
Интегрируем уравнения:
Хс — -gt~ + C\t + Cj, ус — Cyt + Сд, w — С$.
Константы интегрирования определим из начальных условий:
при <о = 0, жсо = Усъ = 0, хСо = 0, усе = vc, о>0 = w*.
Для определения Vc и ш* воспользуемся тем, что в начальном положении
тела Vmi = 0 и, следовательно, точка М\ является мгновенным цен-
тром скоростей тела. Строим диаграмму распределения скоростей точек
(см. рис. 39.1.2) и получаем, что
ВМ] 40 / см\ Vc ~ м Vm> " ал ’ 360 = 240 г- ) ’ МэМ\ 60 \ с / vc 240 (рад\ ВМ\ 40 \ с )
Итак, Ci = 240, Ci = Ci = Сд = 0, С5 = 6.
Поэтому хс = ~gt2, Ус = 240f, ш = 6.
226
6. Плоскопараллельное (плоское) движение твердого тела
Ус \
240/
Видно, что тело равномерно вращается с угловой скоростью w = 6 —
с
1
вокруг своего центра масс, который описывает параболу Хс = -g
или ус = 117,5жс (см).
Задача 39.2(39.2). Диск падает в вертикальной плоскости под дей-
ствием силы тяжести. В начальный момент диску была сообщена
угловая скорость wo, а его центр масс С, находившийся в начале ко-
ординат, имел горизонтально направленную ско-
рость VQ. Найти уравнения движения диска. Оси
х, у изображены на рис. 39.2.1. Силами сопро-
тивления пренебречь.
Ответ: хс = vot, ус = gt1/2, <р = wot, где <р —
угол поворота диска, образованный осью х и диа-
метром, занимавшим в началный момент гори-
зонтальное положение.
Решение. Расчетная схема — на рис. 39.2.2. Составим дифферен-
циальные уравнения плоскопараллельного движения диска:
' mic - 52 FS’
k
k
JCz<p = ^MCz(F^.
Имеем:
mxc = 0,
myc = mg,
JCzV> = 0.
Интегрируя уравнение, получим
— Git + С2, Ус — = + Сб-
Выпишем начальные условия:
при to = 0 жсо = усо = <Ро — 0, Хсо = vo, усо = 0, р0 = w0-
6. Плоскопараллельное (плоское) движение твердого тела 227
Используя начальные условия, составим уравнения относительно посто-
янных интегрирования:
о = с2, о = с4, о = с6,
^о = С(, 0 = Сз, wo = С5.
Отсюда имеем:
С\ = Vo, С2 — Сз = С4 = Cf, = О, С5 — По-
следовательно, диск движется по следующему закону:
1 2
ХС = Ус = -jgt , <f> = u>ot.
Задача 39.3(39.3). Решить предыдущую задачу, считая, что момент
тс сопротивления движению относительно подвижной горизонталь-
ной оси, проходящей через центр масс С диска перпендикулярно
плоскости движения его, пропорционален первой степени угловой
скорости диска ф, причем коэффициент пропорциональности ра-
вен /3. Момент инерции диска отнросительно этой оси равен Jc.
gt2
Ответ: хс = vot, ус=—,(р =
Jc&0 /. -Bt/JcX
——— (1 - е р , где <р — угол
г*
ворота диска, образованный осью х и диаметром, занимавшим в
по-
на-
чальный момент горизонтальное положение.
Решение. Воспользуемся решением задачи 39.2. С учетом момента
сопротивления дифференциальные уравнения движения диска примут
228 6. Плоскопараллельное (плоское) движение твердого тела
вид- иф
Г т£с = °’ ®н
< тус = mg,
I JcP = ~РФ-
Так как начальные условия не изменились, то уравнения движения центра |
масс сохраняются:
, 1 .2 н(2)
Хс = vot, Ус = 2^ •
Проинтегрируем третье дифференциальное уравнение
dtp в , , В
Jc~=-pV => -±- = -^dt \n\tp\ =--^-t + С5.
dt tp Jc Jc
Используем начальные условия: 1пш0 = С5. Запишем:
правнс
1^1 Р , ________ . -pt/jc ________ Jc -yt/JC Г'
In— = => <р = шоер/с => tp =-щ— е р ' с + С6.
W0 Jc Р
Из начальных условий получаем:
Ct, —
Следовательно, уравнение поворота диска
лен
(Ml
ш
цегоь
i
Задача 39.4 (39.4). Ведущее колесо автомашины радиуса г и массы
М движется горизонтально и прямолинейно. К колесу приложен вра-
щающий момент т. Радиус инерции колеса относительно оси, прохо-
дящей через центр масс перпендикулярно его плоскости, равен р. Ко-
эффициент трения скольжения колеса о землю равен /. Какому уело- Кли
вию должен удовлятворять вращающий момент для того, чтобы колесо
катилось без скольжения? Сопротивлением качения пренебречь. Ниц
г2 + р2
Ответ: m^fMg-------------.
, г / „
Ч______________________._______________________________________У чи pt
Решение. Расчетная схема движения колеса — на рис. 39.4.1. Bj
Пусть колесо катится без скольжения. Тогда мгновенный центр ско-
ростей Р находится в точке касания с неподвижной поверхностью. Ки-
нематические соотношения для колеса следующие:
хс = фг, Ус —г. (1)
<ЙТ[
6. Плоскопараллельное (плоское) движение твердого тела 229
Составим дифференциальные уравнения пло-
скопараллельного движения колеса:
Мхс = ДР,
Мус = N - Mg, (2)
JCz<p = m- F-грГ.
Уравнения (2) с учетом (1) принимают вид:
Afxc — Fp,
Q = N -Mg,
2 XC
Mp — —m - F7pr, так как
г
JCz = Mp1.
Решим уравнения относительно нормальной реакции N и силы трения
скольжения Fjp:
mr
N = Mg, FTp = —
Условие качения колеса без скольжения имеет вид: |FTp| < Fnpe;1, где пре-
дельная сила трения скольжения Fnpep = fN.
Расписав это условие, получим неравенство для искомой величины
вращающего момента т:
тт
р2 + г2
^fMg.
Отсюда
р2 + г2
т fMg---------
г
Задача 39.5(39.5). Решить предыдущую задачу с учетом трения ка-
чения, если коэффициент трения качения равен fK.
г2 + р2
Ответ: т У fMg---------\-Mgf*.
г у
Решение. Расчетная схема движения колеса — на рис. 39.5.1. Вос-
пользуемся решением задачи 39.4. Дифференциальные уравнения движе-
ния колеса в данном случае имеют вид
Мхс = FTP,
Мус = N - Mg,
Mp2ip = т- Fjpr - тк,
где момент трения качения mK = fKN.
230 6. Плоскопараллельное (плоское) движение твердого тела
С учетом соотношений (1) из решения
задачи 39.4 получаем уравнения для опреде-
ления сил N и FTP:
Мхс = F,p,
0 = TV — Mg,
Mp2^ = m-FKr- fKN.
Г
Отсюда
N = Mg, F^tm-fxMgy-^—i.
р + г2
Условие качения колеса без скольжения |FTp | < fN принимает вид
Отсюда
(m - fKMg) Г < fMg.
р + г2
о2 + г2
т fMg----------+ fKMg.
т
Задача 39.6(39.6). Ось ведомого колеса автомашины движется го-
ризонтально и прямолинейно. Коси колеса приложена горизонтально
направленная движущая сила F. Радиус инерции колеса относительно
оси, проходящей через центр масс перпендикулярно его плоскости,
равен р. Коэффициент трения скольжения колеса о землю равен /.
Радиус колеса равен г, масса колеса равна М. Какому условию должна
удовлетворять величина силы F для того, чтобы колесо катилось без
скольжения? Сопротивлением качения пренебречь.
Ответ: F fMg
г2 + р2
Р1
Решение. Расчетная схема движения колеса — на рис. 39.6.1.
По условию колесо катится без скольжения. Поэтому в точке касания
с землей находится мгновенный центр скоро-
стей колеса и потому Хс = <рт. А также ус = г.
Составим дифференциальные уравнения плос-
кого движения колеса:
Мхс = F - FTp,
Мус =N - Mg,
Mp2ip = FTpr.
6. Плоскопараллельное (плоское) движение твердого тела 231
С учетом кинематических соотношений имеем:
Мхс = F - FTp,
О = N - Mg,
Mp2—=Fjpr.
г
Отсюда
о2
N = Mg, Fip = F-^—2.
р1 + г1
Динамическое условие качения без скольжения |FTp| принимает вид:
о2
f^—2 fMg.
р1 + т1
Отсюда
р2 + т2
F fMg^-.
Задача 39.7 (39.7). Решить предыдущую задачу с учетом трения ка-
чения, если коэффициент трения качения равен /к.
_ „ , fMg(r2 + р2) - MgfK г
Ответ: F -------------т---------.
< - __________________Р __________-___________________________/
Решение. Воспользуемся решением задачи 39.6. С учетом трения
качения дифференциальные уравнения качения колеса без скольжения
принимают вид:
Мхс = F- Fip,
< 0 - N - Mg,
2%С
Мр — = Frpr - mK,
г
где момент трения качения mK = fKN. Решим уравнения относительно
нормальной реакции N и силы трения скольжения:
N = Mg, FTp = (Fp2 + fKrMg) ,
p + r
Условие отсутствия скольжения при качении |FTp| fN принимает вид
неравенства для F:
232 6. Плоскопараллельное (плоское) движение твердого тела
6
Отсюда движущая сила
fMg(p2 + г2) - fprMg
Р1
Задача 39.8(39.8). Автомобильный прицеп движется замедленно
с ускорением Wo до остановки (рис. 39.8.1). При этом тормоз в од-
ном из его колес не включается. Давление колеса на дорогу равно
Рис. 39.8.1
N. Коэффициент трения колеса с дорогой равен f.
Дано: г — радиус колеса, тп — его масса, р —
радиус инерции. Определить силу горизонтального
давления S колеса на его ось.
ч fN г2 ( р2
Ответ: I) wq —----~, S — micol 1 +
m pz \ г1
ч fN г2
2) w0 > ---т, S = mwv + fN.
m р1
Решение. Расчетная схема — на рис. 39.8.2. Согласно закону ра-
и противодействия нормальная реакция на колесо
венства сил действия
Рис. 39.8.2
со стороны дороги равна N и горизонтальная
реакция на колесо со стороны оси равна S.
Пусть вертикальная реакция со стороны оси
на колесо равна Q. Запишем дифференциаль-
ные уравнения движения колеса:
fj
«у
mxc — Sx И- FTp,
< O = -Mg + N + Sy,
k тр2ф = —Fjpr.
По условию задачи Хд = -Wo- Для дальнейших рассуждений пона-
добятся первое и третье уравнения:
' -mwo = Sx+ FTp,
„ тр~ф = -Fjpr.
‘I.
J?
I
Следует рассмотреть два случая.
Г. Колесо катится без проскальзывания, т. е. точка Р — мгновенный
центр скоростей и Хд — фт. Значит ф — -w$/r. Поэтому
-mw0 = Sx + FTp>
2^0 „
-mp — = -Fjpr.
r
a
sm
6. Плоскопараллельное (плоское) движение твердого тела 233
Отсюда получаем, что
тр2
Ftp = -^-w0
г
и
р2 ( р2\
Sx — -mwo - FTV = -mwo - = -mwo I 1 -b —, J.
7*^ \ 7*^ J
Выясним, когда возможно качение без скольжения. Условие Кулона
движения без скольжения:
IF^I < fN,
т. е.
р2
m-w^ fN.
г2
Следовательно,
1С0
fN г2
т р2
При таком ускорении гео сила
( Р2\
|5г| = micol 1 + )•
\ Г /
2°. Колесо катится с проскальзыванием, т.е. хр 0. В этом случае
Frpx = - fN sign Xp = -fN sign (xc - фг).
Поэтому уравнения движения приобретают вид:
тхс = Sx- fN sign (хс - фг),
2 0
тр Ф = fN sign (±с — фг) г.
Возможны две ситуации:
2°.1. хР > 0;
2°.2. хР < 0.
Рассмотрим их.
2°,1. хр = хс - фг > 0. Тогда из (1) получим:
тхс = Sx- fN,
2
тР Ф = fNr.
Согласно условию задачи хс = -wo (^о > 0)- Тогда из (2) получим:
-mwo = Sx- fN,
fNr
<p(t) = 92(0) + -—yf, xc(t) = ±c(0) - wot.
234 6. Плоскопараллельное (плоское) движение твердого тела
Для скорости точки Р имеем:
fNr2
xP(t) = ±c(0) - wot - ф(0)г----Tt =
mp1
j'Nr2\
Wo H-----г 11.
mp1 J
= [±с(0) - 9?(0)г
Отсюда видно, что при
ip(0) = ±с(0) - ^>(0)r 0 имеем Xp(t) < 0 (£ ^ 0).
Этот случай должен быть отброшен. А если
жР(0) = жс(0) - 9?(0)г > 0,
то эта ситуация продолжается в течение времени
±Р(0)
1 fNr2 ’
w0 +-------г
mp1
При этом имеем Sx = fN - mw$. Остановка колеса (т.е. точка xc(t) = 0)
®с(0)
произойдет в момент г* =------Ясно, что
Wo
жс(0) жс(0) - <£(0)r fNr2
так как ----->----------—где А=-—г-.
Wo Wo + A mp2
Поэтому при t € [<!,<*) процесс пойдет либо с чистым качением (при
fN г2. fN г2
w0 < либ° с проскальзыванием жР(0) < 0 (при w0 > 4
А это есть ситуация 2.°2.
2°.2. хР = х - фг < 0. Тогда из (1) получим:
{mxc = Sx + fN,
тпр2ф = —fNr.
Так как хс — — Wo, то из (3) следует:
-mw0 = Sx + fN,
fNr
<p(t) = ф(0)----Tt, xc(t) = ®c(0) - wot,
mpz
Sx = -(mw0 + fN).
Тогда для скорости точки Р имеем:
тп р2
(3)
.2
1С0 -
6. Плоскопараллельное (плоское) движение твердого тела 235
fNr2
Пусть wo > -----5-. Тогда, если жс(0) - у>(0)г < 0, то ip(f) < 0 при всех
тр2
t Е [0,£»), т.е. происходит торможение со скольжением точки Р влево.
И здесь Sx = -(mwo + fN). А если xc(ty - ф(0)г > 0, то xP(t) > 0 при
достаточно малых t, т. е. ситуация не реализуется.
fN г2
Пусть wo <--------т = Л. Тогда, если xc(f>) - Ф(0)т 0, то iP(t) < 0
m р1
в течение времени
_ ~(М°) - у(°)г) _ У’(О)^ ~ МО)
-(гс0 - Л) А - wo
Посмотрим, когда tt < £? (т.е. скольжение будет продолжаться весь ин-
тервал торможения):
МО) < у(°)г - МО)
wo A-wo
=> Л±с(0) - woXC(O) < ^(O)rwo - xc(O)wo =>
ir(0)
=> Axc(ty C <p(O)rwo => Wo > A——.
®с(0)
Итак, при ±с(0) ^(0)г и при А С к?о А будет торможение
9?(0)г
со скольжением точки Р влево. При этом Sx = -(mwo + fN).
t ®с(0)
Если 0 < wo < А- . . -, то такое движение будет продолжаться в те-
9?(0)г
чение времени
y>(0)r - xc(0)
Q = ------Л------’
A - wo
а затем уже будет чистое качение вплоть до остановки (хс = 0).
Если же ±с(0) > 9?(0)г, то при wq А будем иметь iP(t) > 0 при
достаточно малых t, т. е. ситуация не реализуется.
Итак, результат и ответ таковы:
1) ±р(0) = ±с(0) - <p(Q)r > 0.
fN г2
1.1 wo> -------7;
m р1
жр(0)
при 0 < t t\ — ----------7 происходит качение со скольжением
fNr
Wo +-----т
mp1
в точке Р вправо, причем Sx = fN — mwo, xP(tf) = 0;
236 6. Плоскопараллельное (плоское) движение твердого тела
1.2.
±с(0)
при £] < t < t* =----происходит качение со скольжением точки Р
Wo
влево, причем Sx = -(fN + mwo).
fN г2
wo -------,;
m pz
2)
2.1.
2.2.
sp(0)
при 0 < t < i| = ----- 2 происходит качение co скольжением
fNr
Wo -I---z-
mpz
точки P вправо, причем Sx = fN — mwo, xP(ti) = 0;
±c(0)
при t] <t =---------происходит чистое
Wo
/ p2\
Sx = -mwo I 1 + -г I.
\ '7
±p(0) = xc(0) - ф(0)г < 0.
±c(0) fN r2
m p2 ’
®c(0)
при 0 < г < =------происходит качение co
Wo
влево вплоть до остановки (хс = 0), причем Sx = -(fN 4- mwo).
®с(0)
W° ф(0)г
качение (хр = 0), причем
W° " ф(0)г
fN r2
m p2 ’
скольжением точки Р
при 0 < t
ф(0)г - ±c(0)
——r- 2---- (здесь Xp(t,2) — 0) происходит
f In r
-----2 - Wo
m pz
качение co скольжением точки P влево вплоть до остановки, причем
Sx = ~(fN + mwo);
( Р2\
при £2 С С происходит чистое качение, причем Sx = -mwo I 1 + —г ).
\ '/
3) ip(0) — ±с(0) - 9?(0)г = 0 (то, что предполагается, наверное, в усло-
вии задачи).
3.1.
fN г2
при 0 t tt происходит качение со скольжением влево, причем
Sx = -(fN + mwo).
3.2. w0
fN t2
m p2 ’
6. Плоскопараллельное (плоское) движение твердого тела 237
при 0 tt происходит чистое качение, причем Sx = -mwo
^с(О)
wo
где tt =
— время торможения вплоть до остановки.
Замечание к задаче 39.8. Мы видим, что решение и ответ к данной задаче
существенно зависят от начальных условий движения колеса, в момент начала
торможения всего прицепа. Кроме того, сама сила Sx может принимать значе-
ние Sx = fN — w0, которое отсутствует в ответе, приведенном в задачнике [10].
Отметим, что значение силы Sx принципиально влияет на движение прицепа
в горизонтальной плоскости, определяя его курсовую устойчивость.
Задача 39.9(39.9). Колесо радиуса г катится по прямолинейному
горизонтальному рельсу под действием приложенного вращающего
момента mBp = -fMgr, где f — коэффициент трения скольжения,
М — масса колеса. Определить скорость точки колеса, соприкаса-
ющейся с рельсом (скорость проскальзывания). Масса колеса рав-
номерно распределена по его ободу. Трением качения пренебречь.
В начальный момент колесо находилось в покое.
_ fs.
Ответ: — t.
Решение. Расчетная схема движения ко-
леса — на рис. 39.9.1. Составим дифференци-
альные уравнения плоского движения колеса:
Fix с — Т^р,
0 = N - Mg,
Mr2(f> = mBp - FTp • г.
(О
Проверим, будет ли при заданных вращающем
моменте
"'-вр = -^fMgr
Рис. 39.9.1
и коэффициенте трения скольжения f проскальзывание. Для этого пред-
положим отсутствие проскальзывания, учтем в уравнениях (I) связь
хс = фг и выразим из них N и FTp. Получим:
Мхс = Fip,
N = Mg,
Хс 5
Mr — - - fMgr - FTp • г
г 2
=> N = Mg, FTP = 5-f Mg.
238 6. Плоскопараллельное (плоское) движение твердого тела
1>
Составим условие отсутствия скольжения
грим
|FTP|^PV, т.е. ,[£=J
4 J'=l
Видно, что это условие не выполняется, следовательно колесо катится
со скольжением. Поэтому FTP = fN = fMg.
Вернемся к уравнениям (1), учитывая скольжение: г
Мхс = fMg,
N = Mg,
2 5
Мт ф = - fMgr — fMgr.
Интегрируя первое и третье уравнения, получим:
3 g
xc = fgt + Ci, ф = ~f~t + C2.
2 г
Так как в начальный момент колесо находилось в покое (±со = фо = 0),
то Ci = С2 = 0. Поэтому
хс = fgt, ф = l-f-t.
2 г
При нахождении скорости точки А (точки касания колеса с рельсом)
воспользуемся теоремой о скоростях точек тела при плоском движении:
vA = vc + vac-
Спроецируем векторное соотношение на ось х:
3 g 1
хА = хс-фт => vA = xA = fgt- -f-t-r = --fgt.
2 г 2
Знак « —» говорит о том, что скорость точки А направлена влево, т.е.
против оси х.
Задача 39.10(39.10). Решить предыдущую задачу с учетом трения |
качения, если коэффициент трения качения fK =
Ответ: ^fgt.
Решение. Воспользуемся решением задачи 39.9. С учетом трения
качения дифференциальные уравнения примут вид:
Мхс = FTp,
0 = N - Mg,
2 5 1
Mr ф - - fMgr - -fr • N - F,pr.
Ж0
1ЖТ(
t^pei
[Jfi(
p
i
^1104
•roe
•Я
№
"Ml
Ki»
lil®
•»!НД
6. Плоскопараллельное (плоское) движение твердого тела 239
Проверим, будет ли скольжение колеса:
Мхо — -^тр'
N = Mg,
?хс 5 1
Mr — = -fMgr - -fMgr - FTpr
г 2 4
9
TV = Mg, FTp = -fMg.
О
Условие отсутствия скольжения
\fMg fMg
О
не выполняется. Значит колесо проскальзывает.
Дифференциальные уравнения движения при проскальзывании ко-
леса:
' Мхс = fMg,
2 5 1
Mr ф — -jfMgr - -frMg — fMgr
Хс = fg,
.. 5 fg
ip =--------
Y 4 r
Интегрируем дифференциальные уравнения с учетом нулевых начальных
условий:
. , 5 fg
Хс = fgt,
4 г
Скорость точки А касания колеса с рельсом:
5 fg ।
va = хА = хс - фг = fgt - -~t г = ~~fgt.
4 г 4
Знак «—» говорит о том, что скорость точки А направлена против оси х.
Задача 39.11 (39.11). Однородный цилиндр с горизонтальной осью
скатывается под действием силы тяжести по наклонной шероховатой
плоскости с коэффициентом трения /. Определить угол наклона
плоскости к горизонту и ускорение оси цилиндра, предполагая, что
при движении цилиндра скольжение отсутствует. Сопротивлением
качения пренебречь.
Ответ: a^arctg3/.
2
w — -g sin a.
3
Решение. Расчетная схема движения цилиндра — на рис. 39. 111.
Так как скольжение отсутствует, то точка Р — мгновенный центр скоро-
стей цилиндра, и, значит, Хс — фг. Запишем дифференциальные уравне-
240 6. Плоскопараллельное (плоское) движение твердого тела
Рис. 39.11.1
ния плоскопараллельного движения цилиндра с учетом отсутствия сколь-
жения:
mic -- mg sin a - Fip,
0 = N - mg cos a,
Jcz—=FK, JCz = ~
r 2
Отсюда имеем:
N — mg cos a, = -mg sin a.
Составим условие отсутствия скольжения |FTp| < fN:
-mg sin a fmg cos a.
Решим полученное неравенство относительно угла а:
tgo^3/ ==> <r^arctg3/.
Это означает, что при угле наклона a $ arctg 3/ возможно качение ци-
линдра без скольжения. Теперь из первого уравнения системы (I) найдем
ускорение оси цилиндра:
^тр 1 . 2
ас = хс = g sin a----= g sin a--g sin a = -g sin o.
m 3 3
Задача 39.12 (39.13). Однородный сплошной круглый диск катит-
ся без скольжения по наклонной плоскости, расположенной под углом
а к горизонту. Ось диска образует угол /3 с линией наибольшего ската.
Определить ускорение центра масс диска, считая, что его качение
происходит в одной вертикальной плоскости.
Ответ: wc = -g sin a sin /3.
6. Плоскопараллельное (плоское) движение твердого тела 241
Решение. Расчетная схема — на рис. 39.12.1, изображен вид сверху
на наклонную плоскость и катящийся диск. Введены две системы коорди-
нат: Pxyz, PCriC', где Р — точка касания диска с наклонной плоскостью,
Ру — по линии наибольшего ската наклонной плоскости, Рх ± Ру,
Pz ± Ру, причем, Рх лежит в наклонной плоскости, a Pz — ей перпен-
дикулярна и направлена вверх {Pxyz — правая система координат), Ру —
проекция плоскости диска на наклонную плоскость, т.е. плоскость каче-
ния диска, которая по условию задачи неизменна. PC, ± Ру, PC, ± Ру,
причем PC, лежит в наклонной плоскости, а PC, — ей перпендикулярна
и направлена вверх {РСуС — правая система координат). Ясно, что PC,
параллельна оси диска, поэтому (по условию задачи) (Ру — /3.
На диск при его качении действуют две силы: R — сила реакции
плоскости, приложенная в точке Р, mg — сила тяжести, приложенная
в центре масс диска. Пусть R^, R^, R( — проекции силы R на оси £, у, С-
Чтобы найти проекции силы mg на оси С, у, С, разложим сначала mg
по осям х, у, z. В силу построения системы Pxyz, имеем:
mgx — 0, mgy — mg sin a, mgz — -mg cos a.
Тогда (см. рис. 39.12.1) получим:
mg£ = mg sin a cos (3, mgv = mg sin a sin /3, mg^ = -mg cos a.
Пусть vc — вектор скорости центра масс диска, — вектор его угловой
скорости. Уравнения движения центра масс диска в проекциях на оси
mvct = mg sin a cos fi + R$,
mvcrj = mg sin a sin (3 + RV, (1)
mvc^ = —mg cos a + R^.
Уравнения изменения кинетического момента диска относительно кени-
товых осей С^у'С', которые являются главными центральными осями
242 6. Плоскопараллельное (плоское) движение твердого тела
инерции (£, г/, С’ параллельны осям %, т], £), имеют вид:
Jcp^p = R^-r, JcrfUrf ~ -Щ г, JCpWp = 0, (2)
где
mr1 mr2
Jср = Jср = Jср = — •
Так как диск катится без скольжения в неизменной плоскости rjC,, то
имеем следующие кинематические соотношения:
vcv
<Др = ——, Wrj' = bJC = О, VC(1 = vci = 0.
Подставляя формулы (3) в (1) и (2), получим:
(3)
= —mg sin a cos (3 0, (4) Mf COCK(
Rrj = mvcrj - mg sin a sin (3, (5) ЖЯС
R( = mg cos a, (6)
mr2 vCri _ — Rji 2 r 0 = -R^ • r, (7) (8) aonpe, eenpej «нал
= 0.
(9)
Из (5) и (7) получим
/2\
V&) = ( - ]g Sin a sin fi,
что совпадает с ответом к задаче.
Однако уравнения (4) и (8) противоречат друг другу. Чтобы устранить Ж
это противоречие, необходимо принять существование дополнительного inaoa
реактивного момента в точке Р, направленного вдоль оси Т]. Тогда Кии,
второе уравнение из (2) принимает вид JcpWp = -R< г + Mv, а уравне-
ние (8) будет таким:
0=^-R^-r + Mv => Mjj = R^ • г — -mgr sin a cos (3.
Физически реализация такой связи может быть осуществлена при помощи
дорожки с углублением, вдоль которой движется диск.
Задача 39.13 (39.14). Однородный цилиндр с горизонтальной осью
скатывается под действием силы тяжести со скольжением по наклон-
ной плоскости при коэффициенте трения скольжения /. Определить
угол наклона плоскости к горизонту и ускорение оси цилиндра.
Ответ: а > arctg3/, w =g(sina - /cosо).
Шот
истеч
Ч)е. и
6. Плоскопараллельное (плоское) движение твердого тела 243
Рис. 39.13.1
Решение. Расчетная схема — на рис. 39.13.1. По условию цилиндр
катится со скольжением. Значит точка Р касания цилиндра с поверхно-
стью не является мгновенным центром скоростей и vp 0. Поэтому
хс £ фг.
Для определения угла наклона а воспользуемся решением задачи
39.11 и получим, что скольжение будет при a > arctg 3/.
Для определения ускорения оси цилиндра (т. е. точки С) составим
дифференциальные уравнения движения:
mxc = mg sin a - Fjp,
< 0 = N-mgcosa,
mr2
—Ф = FJP • r.
jjj. Здесь предположили, что скольжение точки Р происходит вниз по на-
клонной плоскости, поэтому сила трения скольжения Fip направлена
;iql против оси х. Величина FTp = fN.
f mxc = mg sin a — fmg cos a,
I N = mg cos a,
() ^ ) 2
I mr
м ( —Ф = fmg cos ar
__ => ac = xc =g(sina - /cos a).
Ай Замечание к задаче 39.13. Отметим, что ответ и решение данной задачи должны
Wi зависеть от начальных условий'. Если начальные условия таковы, что vP направлена
вверх по наклонной плоскости (ф(0) очень большая), то
ра. ас =g(sinа 4- /cosа).
Однако, по истечении конечного интервала времени скольжение сменится на про-
тивоположное, и мы получим ответ из задачника [10].
244 6. Плоскопараллельное (плоское) движение твердого тела
Задача 39.14(39.15). Однородное колесо радиуса г скатывается
без скольжения по наклонной плоскости, образующей угол а с гори-
зонтом. При каком значении коэффициента трения качения /к центр
масс колеса будет двигаться равномерно, а колесо при этом будет
равномерно вращаться вокруг оси, проходящей через центр масс пер-
пендикулярно его плоскости?
Ответ: /K = rtgci.
Рис. 39.14.1
Решение. Расчетная схема — на рис. 39.14.1. Колесо катится без
скольжения. Поэтому точка Р (точка касания) — мгновенный центр ско-
ростей. Значит,
хс = фг.
По условию
Vc = Хс = const и ф — const.
Дифференциальные уравнения движения колеса принимают вид:
О = mg sin a - Frp,
О — N - mg cos o ,
0 = FTpr - MK,
где момент трения качения
Мк = Д/V.
Решаем уравнения:
F-tp = mg sin a, N = mg cos a.
Из третьего уравнения получаем:
= F7pr ==> fymg cos a = mg sin ar => = r tg a.
6. Плоскопараллельное (плоское) движение твердого тела 245
Задача 39.15 (39.16). На барабан одно-
родного катка массы М и радиуса г, лежа-
щего на горизонтальном шероховатом полу,
намотана нить, к которой приложена сила Т
под углом а к горизонту (рис. 39.15.1). Радиус
барабана о, радиус инерции катка р. Опреде-
лить закон движения оси катка О. В началь-
ный момент каток находился в покое, затем
катился без скольжения.
Рис. 39.15.1
Т r(rcosa — о) 2
Ответ: х =-------z-----г-—t , причем ось х направлена слева направо.
М 2(р2 + г2)
' Мх0 = Т cos а - FTp,
Mp2— =Fypr-T-a
г
Frp =Т cos а - тпхо,
Р .. °
тп у.Т() — Fyp Т
т- г
r(r cos а — а)
Х° = Т М(р2 + г2) ’
Интегрируя с учетом нулевых начальных условий, получим закон движе-
ния оси катка:
r(r cos а — а) <2
Х° = ' 2Vi(p2+r2) 1 '
246 6. Плоскопараллельное (плоское) движение твердого тела
Задача 39.16(39.17). Однородный стержень АВ массы М гори-
зонтально подвешен к потолку посредством двух вертикальных нитей,
прикрепленных к концам стержня (рис. 39.16.1). Найти натяжение
одной из нитей в момент обрыва другой.
А В
Рис. 39.16.1
Указание. Составить дифференциальные уравнения дви-
жения стержня для весьма малого промежутка времени,
следующего за моментом обрыва нити, пренебрегая из-
менением направления стержня и изменением расстояния
центра масс стержня от другой нити.
Mg
Ответ: Т = —
4
Рис. 39.16.2
Решение. На рис. 39.16.2 изображен стержень в момент обрыва пра-
вой нити. Пользуясь указанием к задаче, составим дифференциальные
уравнения плоского движения стержня для малого промежутка времени,
следующего за моментом обрыва нити, пренебрегая изменением направ-
ления стержня и изменением расстояния центра масс стержня С от левой
нити. Имеем:
Мхс = О,
Мус = -Т + Mg,
М (АВ)2 .. АВ
12 ~
При указанных предположениях
Ус 2
АВ
(заметим, что скорости равны нулю). Поэтому
Мус = Т - Mg,
АВ АВ
М----ус = Т --
6 2
6. Плоскопараллельное (плоское) движение твердого тела 247
Мус = -Т 4- Mg,
Мус = 37
4
Рис. 39.17.2
(1)
Решение. На рис. 39.17.2 изображен стержень в момент обрыва пра-
вой нити. Воспользуемся указанием к задаче 39.16. Получим дифференци-
альные уравнения плоского движения стержня сразу после обрыва нити;
{Мхс = -Т cos 60°,
Мус — Mg - Т sin 60°,
М (AB)2 „ АВ .
(р — Т sin 60 .
12--------------2
В момент обрыва нити угловая скорость стержня w = 0, а угловое уско-
рение е 0. Скорость точки A va = 0, а ее ускорение ал будет отлично
V2
от нуля и направлено -L О А (так как ее нормальное ускорение —- = 0).
Следовательно,
—* —♦ —*т
чс = аА + аСА + асл-
Причем
АВ
а^л = = 0 (так как w — О),
АВ
Чса— £^2~’ ^саААС
248 6. Плоскопараллельное (плоское) движение твердого тела
Поэтому можно записать
' Хс — ~aA sin 60°,
< - АВ (2)
Ус = «Л cos 60 +£~^-
С учетом (2) из системы (1) получим три уравнения для трех неизвестных
(ал, £, Т):
' -МаА sin 60° = —Т cos 60°,
/ лв\
< Л/(ал cos 60° + е-^-J = Mg - Т sin 60°, ,
М (АВ)2 АВ
----—Е = Т-------sin 60
12 2
МаА
МаА + МеАВ = 2Mg - Тх/З,
МеАВ = Т3х/3
2Mg
2y/lMg
----------7= - - ~ 0,266Mg.
V3/3 ) + 4х/3 13
Задача 39.18(39.19). Однородный тонкий стержень длины 21 и
массы М лежит на двух опорах А и В; центр масс С стержня на-
ходится на одинаковых расстояниях от опор (рис. 39.18.1), причем
СА = СВ — а; давление на каждую опору равно Р/2. Как изменится
давление на опору А в тот момент, когда опора В будет мгновенно
удалена? (См. указание к задаче 30.16.)
А С В
-у- * -
Ответ: Давление на опору А получит прираще-
/2 —За2
Mg.
Рис. 39.18.1
ние, равное —т—------г-
2(/2 + За2)
У
Рис. 39.18.2
6. • ваапацвмнэммж лвляаше «ацмого аанэ
* Ре_-е- <•-- На рис.39.И. ? кюбражи стсряЕнь а момсап. копи опо-
ра В мгвоееиво ул»»-— Пользуясь указанием к зигк Э9.16. зааянЕМ
> _* = - -. е т-u-t - ; : ••ait- и ж- х'; иажмэ .. -«
енецроимвза ймввжм KUUHHH опоры:
Мжс=9,
Uic = Ug-NA,
(I)
В «owcnr уписано оторва риопм сж|яюь к Еацваяв * пцраа нмн
гзсркто равны «гуаво Мжаретое точен Л равна куш Угаорсиие тона С:
— —л । -^ ...,._ j» 2 .
— Л -Сл» ’ ‘ — *• - —
ьсл - =• = лг. - *
laaTCKy из : » (1J ->игл- •»
Мгь = - JVa,
---:=в- —
3
I' гсп:>1^ е
г2
.^=хг—
Лж азк знвовзвве при лд* авцркк ® зове Л раню тж ^ьг. сак
и ® waae то плсж уаизяин дичртд ® ючвк В лакюже ® свкрс Л
нг. HcJti"- '
й2 В - Зет
-V. = М-^ТЗГ -= -тту-т "ft-
~?,т,эч„-. 'з- ~~ 1- 1; “ - 1
io аввпапв зовдсзние авиай пвзмв ааикзи
j?:-‘ г - - - . :
5ез ^.Х'.с- г..;-.-.---"; ?-ч. 7
CrmaiCTiTi >. XJ-.X - < эта
ВПЬзэтустр-зя 1й£ ?•: <?- Й1.,Ш -;а»" ' • к л~ '. л’- '
в
»=^ ЗГ>
Ь-ИЕ ВТ • :
250 6. Плоскопараллельное (плоское) движение твердого тела
Решение. Расчетная схема — на рис. 39.19.2. Так как конец В нити
закреплен неподвижно, то точка Р схода нити с цилиндра является мгно-
венным центром скоростей. Поэтому
хА = фг
ХА — Фг-
Составим уравнения плоскопараллельного движения
цилиндра:
{тпха = mg - Т,
mr2
—Ф = Тг.
Уравнения (2) с учетом (1) принимают вид:
(2)
тпха = mg - Т,
mr2 ха
------ = Тг.
2 г
Решим эти два уравнения с двумя неизвестными хА и Т:
2 ГТ. 1
ХА = -g; т = -mg.
Для определения скорости оси цилиндра проинтегрируем дифференци-
2
альное уравнение хА = -g:
dx 2
~dt~ 3g
dx 2
=> x— = -g =>
dx 3
1 2 2
=> 2X = 3gX + C'
Постоянная интегрирования С = 0, так как цилиндр
скорости. Итак,
падает без начальной
vA = x =
После того, как ось опустится на высоту h,
2 ,----
vA = -jVlgh-
Сила натяжения нити постоянна и равна
6. Плоскопараллельное (плоа ое) движение твердого тела 251
Задача 39.20(39.21). Две гибкие нити об-
мотаны вокруг однородного круглого цилиндра
массы М и радиуса г так, что завитки их
расположены симметрично относительно сред-
ней плоскости, параллельной основаниям. Ци-
линдр помещен на наклонной плоскости АВ
так, что его образующие перпендикулярны ли-
нии наибольшего ската, а концы С нитей
закреплены симметрично относительно выше- Рис. 39.20.1
указанной средней плоскости на расстоянии
2г от плоскости АВ (рис. 39.20.1). Цилиндр начинает двигаться без
начальной скорости под действием силы тяжести, преодолевая тре-
ние о наклонную плоскость, причем коэффициент трения равен f.
Определить путь s, пройденный цен iром масс цилиндра за время t,
и натяжение Т нитей, предполагая, что в течение рассматриваемого
промежутка времени ни одна из нитей не сматывается до конца.
1 2 1
Ответ: s = -g(sin a-2f cos a)t , T = -A4g(sin a + f cos a).
3 6
Цилиндр остается в покое, если tg a < 2f.
Решение. Расчетная схема изображена
на рис. 39.20.2. Силы натяжения нитей, нор-
мальные реакции и силы трения — это си-
стемы параллельных сил, равномерно рас-
пределенных (в силу симметрии) вдоль об-
разующих цилиндра. Поэтому изображенная
на рис. 39.20.2 сила f — это равнодейству-
ющая двух сил натяжения нитей, сила N —
равнодействующая нормальная реакция, сила
F — равнодействующая сила трения сколь-
Рис. 39.20.2
жения.
Составим дифференциальные уравнения плоского движения цилиндра:
' Мхо — Mg sin a - Т - _FTp,
0 = N - Mg cos a,
Mr2
(1)
(p = Tr- Fipr.
Выясним, при каком соотношении параметров будет происходить
качение (со скольжением) цилиндра. Для этого предположим, что цилиндр
остается в покое (и значит нет скольжения).
252 6. Плоскопараллельное (плоское) движение твердого тела
(1)
' 0 = Mg sin а -Т - FTp,
< N = Mg cos a,
. T = Fip
{N = Mg cos a,
1
F-jp = -Mg sin a.
Запишем условие отсутствия скольжения (в состоянии равновесия):
1
-Mg sin a < fMg cos a.
Отсюда получаем, что цилиндр остается в покое при tga < If.
Предполагая выполнение условия tga > 2/, перепишем уравне-
ния (1), учитывая, что FTp = /TV:
{Мхо — Mg sin a — Т — fMg cos a,
N - Mg cos a,
Mr2
ф = Tr - fMg cos a • r.
Воспользуемся тем, что точка Р схода нити с цилиндра — мгновенный
центр скоростей: ±о = фг => х$ = фг.
{Мх0 = Mg sin a - Т - fMg cos a,
Mr2 xq —
——- — = Tr - fMg cos a • r
2 r
(2)
{Т = —(Mg sin ct + fMg cos a),
.. 2 .
x0 = -g(sin « - If cos a).
Так как T — равнодействующая двух сил натяжения нитей, которые
равны в силу симметрии, то
Ti = T2 = -T — -Mg(sin a + f cos a).
2 6
Для определения пути s, пройденного центром масс цилиндра, проинте-
грируем дифференциальное уравнение для координаты Жо с учетом нуле-
вых начальных условий. Получим:
s = xo(t) = -g(sin a - If cosa)t2.
7. Приближенная теория гироскопов
265
Приравнивая величины векторных произведений, получим
sin в = ОС • F sin 6.
Отсюда
F= ОС = ОС
1200 • 0,16 • 4тг2
оЗ
« 15 159,7 (Н).
В результате, сила давления бегуна на горизонтальное дно чаши склады-
вается из силы гироскопического давления F и силы тяжести бегуна Mg:
^давл = F + Mg = 15 159,7 + 1200 • 9,8 « 26 900 (Н)
или Гдавл « 26,9 (кН).
Направлен вектор вниз.
Задача 40.8 (40.8). Колесный скат массы М = 1400 кг, радиуса
о = 75 см и с радиусом инерции относительно своей оси р = \/0,55а
движется равномерно со скоростью v = 20 м/с по закруглению радиуса
R = 200 м, лежащему в горизонтальной плос-
кости (рис. 40.8.1). Определить силу давления
ската на рельсы, если расстояние между рель-
сами Z = 1,5 м.
ч»---------
{ОДВМЫЯШЖЖилШиА
_________J
Ответ: N = (6,87 ± 0,77) кН.
I
Рис. 40.8.1
Решение. Расчетная схема — на рис. 40.8.2. Ось прецессии направ-
лена перпендикулярно рисунку, собственный кинетический момент Н ко-
лесного ската (гироскопа) направлен по его оси влево по ходу движения.
Рис. 40.8.2
266
7. Приближенная теория гироскопов
В соответствии с формулой (4) в этом случае возникает гироскопический
момент Му, стремящийся совместить векторы Н и &2 и направленный
перпендикулярно оси колесного ската, вперед по ходу ее движения. Этот
момент нагружает внешний и разгружает внутренний рельсы (по отно-
шению к траектории движения ската). Этот момент реализуется как пара
сил давления, приложенных к рельсам.
Запишем: F\l = Hu>2 sin 90°.
Отсюда
HU>2 Мр2Ш\Ш2
Fi =-----=---------.
I I
Угловая скорость вращения колес о?| = v/a, угловая скорость вынуж-
денной прецессии от искривления пути W2 = v/R.
Поэтому
, V2
Mp2---М-0,55a2—
aR aR 1400 0,55 • 0,75 • 400
F, =--------=-------------=-------------’-----= 770 (H).
I I 200-1,5 v '
Так как у ската два колеса, то сила давления его на рельсы следующая:
на внутренний рельс сила давления равна
Mg
- F2 = 700 • 9,8 - 770 « 6860 - 770 ~ 6090 (Н),
а на внешний рельс —
Mg
+ F, = 700 • 9,8 + 770 « 6860 + 770 к 7630 (Н).
Задача 40.9 (40.9). Нарис. 40.9.1 изобра-
жен узел поворотной части разводного мо-
ста. Вал АВ с шарнирно прикрепленными
к нему под углом а стержнями CD и СЕ
вращается с угловой скоростью о?о- При этом
конические шестерни К и L, свободно на-
саженные на стержни CD и СЕ, катятся без
скольжения по неподвижной плоской гори-
зонтальной шестерне. Определить силу до-
полнительного динамического давления ше-
стерен К и L массы М каждая на неподвижную горизонтальную
шестерню, если радиусы всех шестерен равны г. Подвижные шестер-
ни считать сплошными однородными дисками.
Mrwn sin a
Ответ: ---------
2
7. Приближенная теория гироскопов
267
Решение. Расчетная схема — на рис. 40.9.2. Рассмотрим одну из ше-
стерен. Так как она катится без скольжения, то вектор ее мгновенной
угловой скорости (д лежит на прямой СР.
Причем
Ы — (До + (Д|,
где (д0 — переносная угловая скорость (угловая скорость прецессии), (д, —
угловая скорость собственного вращения шестерни, направленная по ее
оси симметрии (вдоль стержня СЕ). Величину (д1 найдем из векторного
параллелограмма угловых скоростей. Нетрудно убедиться, что полученный
параллелограмм есть ромб. Поэтому = (До-
В соответствии с формулой (4) за счет вынужденной прецессии с уг-
ловой скоростью о>о возникает гироскопический момент
Mv — Н х (д0,
который реализуется в виде момента дополнительной реакции F (силы ги-
роскопического давления) в точке Р относительно неподвижной точки С:
Нш0 sin a = Fr
Mr2
Hwosina 2 W|<v° s’n a Mrwl sin a
Ь =---------— =
r r r
268
7. Приближенная теория гироскопов
Задача 40.10(40.10). Квадратная рама со сто-
роной а = 20 см вращается вокруг вертикальной
оси АВ с угловой скоростью о?| = 2 рад/с. Вокруг
оси ED, совмещенной с диагональю рамы, враща-
ется диск М радиуса т — Ю см с угловой скоро-
стью w = 300 рад/с (рис. 40.10.1). Определить от-
ношение дополнительных сил бокового давления
на опоры А и В к соответствующим статическим
давлениям. Массой рамы пренебречь. Массу диска
считать равномерно распределенной по ободу.
Ответ: 4,32.
Решение. Расчетная схема — на рис. 40.10.2. Зададим для опреде-
ленности направления вращения рамки с угловой скоростью а?| и диска
с угловой скоростью О) (рис. 40.10.2). По условию о? й?(. Поэтому диск
рассматриваем как гироскоп, ось £ которого прецессирует вокруг верти-
кальной оси у. Собственный кинетический момент
Н = Jw = Мг2ш.
Гироскопический момент Мр в соответствии с формулой (4) стремится
совместить векторы Н и :
Mr = н X Ш|,
Вектор Мг направлен перпендикулярно рамке противоположно ее дви-
жению. Mf есть момент пары сил дополнительного бокового давления
на опоры А и В за счет вращения с угловой скоростью о?|:
Мг — АВ х F\ = BA х F.
Поэтому имеем соотношение
Mr2u)bjf sin 45 ’ = АВ F.
Отсюда
Мг2ш<л\ sin 45°
F = F, =-------------
АВ
Определим теперь статические боковые давления в опорах А и В. Для
этого составим уравнения равновесия системы (при отсутствии вращения
рамки и диска);
к
<
52 маМ) = о.
- к
7. Приближенная теория гироскопов
269
Получим:
Заметим, что
Рис. 40.10.2
FT ~ F'b = О,
+ =0.
77СТ Z?СТ fpCT fiCT
— -Г А у * В ~ ~*В •
Силы со штрихом — это реакции со стороны подшипников на систему.
Следовател ьно,
трСТ _ трСТ
Г А —
Mga
2 АВ'
Получим отношение дополнительных сил бокового давления к соответ-
ствующим статическим давлениям в опорах А и В;
F _ Ft
F1CT Z7CT
А *В
sin 45° • 2 • АВ
АВ Mga
V2
(0,1)2 - 300 • 2-2
-2----~ 4д
9,8-0,2
270
7. Приближенная теория гироскопов
Задача 40.11 (40.12). Колесо радиуса а и массы 2М вращается во-
круг горизонтальной оси АВ с постоянной угловой скоростью wq; ось
АВ вращается вокруг вертикальной оси OD, проходящей через центр
колеса, с постоянной угловой скоростью направления вращений
показаны стрелками (рис. 40.12.1). Найти си-
лы давления Na и Nb на подшипники А
и В, если АО = О В = h; масса колеса рав-
номерно распределена по его ободу.
Ответ: NA = Мg 1 +-— ,
\ gh J
(2 \
1----р •
gh /
Решение. Расчетная схема — на рис. 40.11.2. Собственный кинети-
ческий момент колеса (гироскопа) равен
Н — = 2Ма?М\.
Ось колеса £ прецессирует с угловой скоростью вокруг неподвижной
вертикальной оси z. Возникает гироскопический момент Му = Н х о/2,
перпендикулярный плоскости O(z и направленный на нас (см. рис. 40.11.2).
В результате в подшипниках А и В возникает пара дополнительных сил
Рис. 40.11.2
it
j
:
к
о
к
|Р
и
’I
*4.
If
7. Приближенная теория гироскопов
271
гироскопического давления F и F\. Определим их:
2Ма2Ш]Ш2 sin 90° = F АВ =>
2Ма2Ш1Ш2 2Ма21Л\1Л2 Ма2Ш}Ш2
> F — FI = ——--------—-----------— 1 --
АВ 2h h
Найдем силы статического давления на подшипники. Для этого составим
уравнения равновесия системы (вращения отсутствуют):
Ел« = 0’
< k
MOy(Fk) = 0.
< k
Заметим, что на рис. 40.11.2 в точках А и В изображены силы давления
на подшипники А и В. В уравнения равновесия войдут силы реакции,
действующие на вал АВ со стороны подшипников, которые удовлетво-
ряют условиям: Fa = -Fa, Fb = -Fb1. Итак, уравнения равновесия:
' F'a + F™ - 2Mg = 0,
-F'a -h + F'^ h = 0.
Из них получаем, что Fa — FB = Mg. Выпишем суммарные силы давле-
ния на подшипники А и В:
„ Ма2ш\1Л2 / а2ш\М2\
Na—F + Fa =--------^+Mg = Mg( 1 +--------— ,
h \ gh /
„ Ма21Л\1л2 ,r ,r( a2wiW2\
NB = - Fi + Fb =------+ Mg = Mg 1------------— .
h \ gh )
Задача 40.12(40.13). Простейший гиротахометр состоит из гиро-
скопа, рамка которого соединена двумя пружинами, прикрепленными к
корпусу прибора (рис.40.12.1). Момент инерции гироскопа относительно
оси собственного вращения равен J, угловая
скорость гироскопа равна ш. Определить угол а,
на который повернется ось гироскопа вместе с
его рамкой, если прибор установлен на плат-
форме, вращающейся с угловой скоростью
вокруг оси х, перпендикулярной оси у враще-
ния рамки. Коэффициенты жесткости пружин
равны с; угол а считать малым; расстояние от
оси вращения рамки до пружин равно а.
Jw
Ответ: a = -—wj.
2ca
Рис. 40.12.1
272
7. Приближенная теория гироскопов
Рис. 40.12.2
Решение. Расчетная схема — на рис. 40.12.2. Ось гироскопа z пре-
цессирует с угловой скоростью а>| вокруг вертикальной оси х. Согласно
правилу Жуковского, вынужденная прецессия вызывает гироскопический
момент Mr = Hxuji, стремящийся сделать ось гироскопа z параллельной
оси прецессии х, т.е. поворачивающий рамку гироскопа вокруг оси у
против часовой стрелки. В данном случае гироскопический момент ре-
ализуется в виде момента, противодействующего моменту сил упругости
двух одинаковых пружин. Поэтому
sin 90° = 2Fynp • a.
Сила упругости каждой пружины Fyiip = сД, где Д = аа — деформация
при малых а. Поэтому стрелка (ось z) отклоняется вверх на угол
7fcj|Sin90° Ja;a;|
а =------------=------—
2аЛ 2са2
Замечание к задаче 40.12. В ответе, приведенном в сборнике [10]. вероятно, опе-
чатка.
8. Метод кинетостатики (§ 41, [10])
Задача 41.1 (41.1). Определить силу тяжести, действующую на круг-
лый однородный диск радиуса 20 см, вращающийся вокруг оси по за-
кону = 3t2. Ось проходит через центр диска перпендикулярно его
плоскости; главный момент сил инерции диска относительно оси вра-
щения равен 4 Н • см.
Ответ: 3,27 Н.
Решение. Расчетная схема изображена
на рис. 41.1.1. Главный момент сил инерции
диска
= -Jcz^z = -JczV-
Момент инерции Jcz — mr2/2. Угловое уско-
рение ez = ф = 6. Отсюда масса диска
т =
2|£<g| _ 2 -4- 10~2
г2е (0,2)2 • 6
« 0,33 (кг).
Поэтому сила тяжести диска Р = mg = 3,27 Н.
Задача 41.2(41.2). Тонкий прямолинейный однородный стержень I
длины I и массы М вращается вокруг оси, проходящей перпендику-
лярно стержню через его конец, по закону = at2. Найти величины
и направления равнодействующих Jn и JT центробежных и враща-
тельных сил инерции частиц стержня.
Ответ: Равнодействующая вращательных сил инерции JT = Mai
направлена перпендикулярно стержню на расстоянии 2Z/3 от оси вра-
щения; равнодействующая центробежных сил инерции Jn = 2Ma2lt2
направлена вдоль стержня от оси вращения.
Решение. Расчетная схема — на рис. 41.2.1. Угловая скорость стерж-
ня ы = ф = 2at, угловое ускорение стержня е — ф — 2а. Заметим, что вра-
щение стержня ускоренное.
Разобьем стержень на элементарные участки одинаковой длины.
Ускорения середин этих участков складываются из нормальных и каса-
тельных составляющих:
ак = аТк 4- аь где ак = ehk, ак = w2hk.
274
8. Метод кинетостатики
•де
ап
кк
.«
,1П
ЯН
И
лар;
яне|
tai
< Ф"
Рис. 41.2.1
hk — расстояние от середины к-го элементарного участка до оси вращения -и
(т. О). Касательные ускорения распределяются вдоль стержня по линей- ®
ному закону, нормальные ускорения лежат вдоль стержня.
Сила инерции к-го участка, принимаемого за точку, равна
и
= ~mkai = -mkaTk - ткак = Фк + ф£. ®pi
Касательные силы инерции ф£ распределяются так же, как и касательные
ускорения, по линейному закону, образуя треугольник. Распределенные ,|й
так параллельные силы имеют равнодействующую силу, линия действия
которой проходит через точку, находящуюся на расстоянии 21/3 от вер-
шины треугольника. Равнодействующая равна главному вектору распре-
деленных по треугольнику сил. Поэтому
Фт = -Матс, ,а
где точка С — центр масс стержня. Величина
№
Нормальные силы инерции ф£ лежат на одной прямой (вдоль стерж- ин
ня) и направлены в одну сторону (от оси вращения). Равнодействующая й
равна главному вектору такой системы сил -С
11
Фп = —Мас- ад.
Величина равна
Фп = Мш2- = 2Ма2И2.
2
epi
*нт
Вектор направлен вдоль оси стержня от оси вращения
8. Метод кинетостатики
275
Задача 41.3(41.3). Колесо массы М и радиуса г катится без сколь-
жения по прямолинейному горизонтальному рельсу. Определить глав-
ный вектор и главный момент сил инерции относительно оси, прохо-
дящей через центр масс колеса перпендикулярно плоскости движения.
Колесо считать сплошным однородным диском. Центр масс С дви-
жется по закону хс = at2/2, где a — постоянная положительная
величина. Ось х направлена вдоль рельса.
Ответ: Главный вектор сил инерции равен по модулю Маи направ-
лен параллельно оси в отрицательном направлении; главный момент
сил инерции равен по абсолютной величине (2/3)Маг.
Решение. Расчетная схема — на рис. 41.3.1. Силы инерции частиц
колеса, движущегося плоскопараллельно, приводим к центру масс колеса.
Получаем главный вектор сил инерции
Ф = -Мас,
приложенный к точке С, и главный момент
сил инерции
= -Jcztz.
Величина ускорения
ас = = °-
= а/т. Величина главного
Колесо катится без скольжения, поэтому е
вектора сил инерции
Ф = Ма,
величина главного момента сил инерции
|МЙ,|=*1г =
Mr2 а
2 т
Маг
2
Задача 41.4(41.4). Определить главный вектор и главный момент
сил инерции подвижного колеса II планетарного механизма от-
носительно оси, проходящей через его центр
масс С перпендикулярно плоскости движения
(рис. 41.4.1). Кривошип ОС вращается с посто-
янной угловой скоростью ш. Масса колеса II
равна М. Радиусы колес равны г.
Ответ: Главный вектор сил инерции паралле-
лен кривошипу ОС и равен 2Мгш2; главный
момент сил инерции равен нулю.
276
8. Метод кинетостатики
Рис. 41.4.2
Решение. Расчетная схема — на рис. 41.4.2. Колесо II движется
плоскопараллельно. Приведем силы инерции частиц колеса к его центру
масс С. Получим главный вектор сил инерции
Ф = -Мас,
приложенный к точке С, и главный момент сил
инерции относительно оси Cz
M^cz = -Jcz^IIz-
Кривошип вращается равномерно, поэтому
о-с = вс, ас = ш 2г.
Угловое ускорение колеса II
d d f vc\ d (w -2r
dC ’ dt\r J dt\ r
так как колесо II катится без проскальзывания и ш = const.
Итак, главный вектор сил инерции Ф = 2Мш2г, главный момент сил
инерции равен нулю.
Рис. 41.5.1
ня относительно оси,
Задача 41.5(41.5). Конец А однородного
тонкого стержня АВ длины 21 и массы М
перемешается по горизонтальной направляю-
щей с помощью упора Е с постоянной скоро-
стью v, причем стержень все время опирается
на угол D (рис. 41.5.1). Определить главный
вектор и главный момент сил инерции стерж-
проходящей через центр масс С стержня пер-
в
j
пендикулярно плоскости движения, в зависимости от угла <р.
Ответ: = ЗМ—l sin4 cosy?, = M^~l(l - 3cos2 sin3 <p,
Hz n hz
(j\ 2 2 V2 3
mCz =—Ml —у sin y?cosy?.
__________________3_______________________ ________________________у
Решение. Расчетная схема — на рис. 41.5.2. Приводим силы инер-
ции точек стержня к центру масс С. Главный вектор сил инерции
Ф = -Мас,
главный момент сил инерции относительно оси, проходящей через центр
масс перпендикулярно плоскости движения.
-Jcz^z-
8. Метод кинетостатики
277
Рис. 41.5.2
Вычислим ускорение центра масс С и угловое ускорение стержня.
Зная скорость точки А и направление скорости точки D, строим мгновен-
ный центр скоростей стержня (рис. 41.5.2) и находим его угловую скорость:
va v v • sin <р v sin2 <p
“=AP = ~AD = = H ’
sin <p sin <p
Угловое ускорение стержня можно найти, рассмотрев движение точки D*
(неподвижного угла) как сложное (подвижная система координат связана
со стержнем) и спроецировав составляющие ускорения на направление,
перпендикулярное стержню. Но воспользуемся более простым способом:
v sin2 <р
ф = IV =-------------,
Н
3
е — ф = — • 2 sin <р cos -ф = 2^ • sin <р cos
(так как v = const, Н — const).
Выпишем координаты центра масс стержня:
хс = О А +1 cos <р, ус = 1 sin <р.
Дифференцируем: ±с = v — I sin ф • ф, ус = 1 cos ф • ф',
2 г’2 - . 4
хс = -1со&<р-ф - Z sin • ф = —I—у • 3sin 9?cos9>,
Н1
278
8. Метсд кинетостатики
v2
Ус = —Z sin у? • ф2 +1 cos р • ф = -Z^y (sin5 у? - 2 cos2 у? sin3 у?) —
v2
= — I-—r sin3 p • (1 — 3 cos2 y?).
Главный вектор сил инерции стержня:
д2 4
Фг = — Мхс = 3M-—^l sin у? cos у?,
^2
Фу = —Мус = Мj^jZ(l ~ 3 cos2 у?) sin3 у?.
Главный момент сил инерции стержня:
(Ф) М{11)2 2 2 д2 3
MCz = -Jcz^z = —Ф = --Ml sin у? cos у?.
Задача 41.6(41.6). По данным предыдущей задачи определить ди-
намическое давление Nd стержня на угол D.
8 v2l2
Ответ: Л'п =----sir4 у? cos у?.
3 Н3
Решение. Воспользуемся результатами задачи 41.5. Для определе-
ния динамического давления ND стержня на угол D применим принцип
Даламбера для системы материальных точек. К центру масс стержня при-
ложены сила тяжести Mg и главный вектор сил инерции Ф, в точках А
и V приложены реакции опор и Rd, вдоль оси Cz, перпендикулярной
плоскости движения, приложен главный момент сил инерции стержня
M^z . Так как требуется определить не полное давление, а динамическое,
то не будем учитывать силу тяжести. Опору в точке D предполагаем
гладкой. Поэтому вектор Rd направлен перпендикулярно стержню АВ
вверх. Система сил, приложенных к стержню — плоская.
Достаточно записать одно уравнение: сумма моментов перечисленных
сил относительно точки А равна нулю (см. рис. 41.5.2):
Н
------= 0.
sin у?
S-
~ia
w J
cn
’ча
ff
IB
WK
ITp
и
ID I
ПО
1Й
151
IK 1
-Фз-Z sin p + Ф^ cosy? + M^ + Rd —
Динамическая реакция опоры D равна:
Rd = Фх~ sin2 р - Фу^- sin р cosy? - М^
Н Н
2 4 / э \ 2 i 4
— М—^1 sin y?cos^(l — 3cos^) +-7И/ * sin (pcos92 =
Д* 2 6
= 3M~^l sin у?cosy?-
Wh
..B(
-ива
Me
'0
•hi
8. Метод кинетостатики
279
> V~
=м1'н*
2 V2 4 /2
= Ml sin <р cos <р I - - 1 4- 3
-»-6 -4 _ . д л
3sin ^>cos^>-sin cos ^> + 3 sin cos <р + - sin y>cos^
8 э v2 4
—-МГ—г sin <р cos <р.
3 Я3 * У
Согласно закону равенства сил действия и противодействия дина-
мическое давление стержня на угол D равно по величине динамической
реакции силы: ND = RD.
Задача 41.7(41.9). Для экспериментального определения замед-
ления троллейбуса применяется жидкостный акселерометр, состоя-
щий из изогнутой трубки, наполненной маслом и расположенной
в вертикальной плоскости (рис. 41.7.1). Определить величину замед-
ления троллейбуса при торможении, если при этом уровень жидкости
в конце трубки, расположенном в направлении движения, повыша-
ется до величины h2, а в противоположном
конце понижается до hi. Положение акселе-
рометра указано на рисунке: Q| = «2 = 45°,
h\ — 25 мм, Лг = 75 мм.
Ответ: w = g
(h2 - hi) tga, tga2
hi tg Л + /i2tg«i
= 0,5g.
Решение. Расчетная схема — на рис. 41.7.2. Соединим уровни жид-
кости в левой и правой трубках прямой АВ. Ясно, что прямая АВ парал-
лельна уровню жидкости, который устанавливается в процессе движения
(сообщающиеся сосуды). Уровень жидкости на свободной поверхности
устанавливается в соответствии с уравнением кинетостатики для частицы
жидкости (см. рис. 41.7.3):
Am • wT = Am • g + (-Am • wt) + Ap,
(О
где wr — относительное ускорение частицы относительно троллейбуса,
которое в положении равновесия равно 0, we — переносное ускорение,
280
8. Метод кинетостатики
Рис. 41.7.3
которое равно w, Ар — сила нормального давления
в жидкости, которая перпендикулярна к свободной
поверхности.
Проецируя уравнение (1) на ось т (направление
свободной поверхности), получим: g sin (3 = w cos (3,
где /3 — угол, образуемый свободной поверхностью
с горизонталью х. Тогда w =g-tg^. Найдем tg(3
из геометрических соображений (см. рис. 41.7.2):
tg/3 =
h2 — h\
CD ’
Из прямоугольных треугольников АОС и BOD получим:
CD = СО + OD =
hi h2
tga, tga2’
Тогда
h2- hi
tgp =-------------------,
hi • ctgQ] + h2 • ctga2
w =g-tg/3
g(h2~ hi)tgaitga2
hi • tga2 + h2 • tgai ’
Задача 41.8(41.10). С каким ускорением должна двигаться по го-
ризонтальной плоскости призма, боковая грань которой образует угол
а с горизонтом, чтобы груз, лежащий на боковой грани, не переме-
щался относительно призмы?
Ответ: w=gtgo.
Рис. 41.8.1
Решение. Расчетная схема —на рис. 41.8.1.
Применим к грузу принцип Даламбера. Груз дви-
жется поступательно, поэтому силы инерции ча-
стиц груза приводятся к равнодействующей
Ф = -ma,
которая приложена к центру масс груза.
На груз, кроме того, действуют сила тяжести
mg и нормальная реакция со стороны гладкой
поверхности призмы N. Составим уравнение равновесия, приравняв нулю
сумму проекций всех сил на ось х, направленную вдоль наклонной по-
верхности призмы:
mg sin a - Ф cos a = 0.
8. Метод кинетостатики
281
Так как Ф = ma, то
mg sin a - ma cos a = 0.
Поэтому искомое ускорение призмы
a = g tg a.
Задача 41.9 (41.11). Для исследования влияния быст-
ро чередующихся растягивающих и сжимающих сил на
металлический брусок (испытание на усталость) испыту-
емый брусок А прикрепляют за верхний конец к ползуну
В кривошипного механизма ВСО, а к нижнему концу
подвешивают груз массы М (рис. 41.9.1). Найти силу,
растягивающую брусок, в том случае, когда кривошип
ОС вращается вокруг оси О с постоянной угловой ско-
ростью ш.
Указание. Выражение у I — (т/1)г sin2 ip следует разложить в ряд
и отбросить все члены ряда, содержащие отношение г/l в степени
выше второй.
Рис. 41.9.1
2 1 Г
Ответ: Mg + Мты I cos wt + - cos
Решение. Расчетная схема — на рис. 41.9.2. Применим принцип
Даламбера к бруску А. Брусок движется поступательно и прямолинейно,
поэтому силы инерции его частиц приводятся к равнодействующей, линия
действия которой направлена вдоль бруска. Согласно принципу Даламбера
приложенные к нему силы уравновешены:
RB + Mg + $ = 0. (1)
Вектор Ф = -Ma. Реакция RB со стороны пол-
зуна и есть искомая растягивающая сила.
Определим ускорение бруса а, которое сов-
падает с ускорением ползуна В. Введем ось х
вдоль направляющей ползуна В и запишем его
координату:
хв = г cos +1 cos a.
Угол а найдем по теореме синусов из треуголь-
ника ОС В:
г I
sin a sin <р
г
sin а = - sin <р
Рис. 41.9.2
282
8. Метод кинетостатики
cos a = у/1 — sin2 a =
2
I sin2 <р.
Координата
Хв = r cos <р +1
г
1
1 -
Воспользуемся указанием к задаче и, предположив, что г <£1, разложим
второе слагаемое в степенной ряд и отбросим члены выше второго порядка
малости:
Я
л
и
213
Ь,а
шт
"
к
r\2 z
у j sin2 <р - у/\ - z ~ 1 - - = 1 -
Л2 . 2 1
МП ^у
Выпишем
Хв ~ т cos <р — I
1
Продифференцируем:
Хв = -г sin <р • ф - I
sin <р cos <р ф =
/ г
-г sin р • ф - ZI у
2
XB = -rcos^-y> — г sin92 — I
2
cos 2р> ф2
sin 2<р ф.
Кривошип ОС вращается равномерно с угловой скоростью По-
этому |Щ|
<р = wt, ф — w, ф = О
2 / Г \
Хв — -TW I COS Wt + у cos Iwt J .
Спроецируем уравнение (1) на ось х:
-RB + Mg + Ф = 0.
ч
и»
J0
Растягивающая сила
RB = Mg + Ф = Mg + Ma — Mg + Мты2
т
COS wt + у cos 2wt
21
I у sin 2^-9?,
и
8. Метод кинетостатики
283
Задача 41.10(41.12). Определить опорные
реакции подпятника А и подшипника В по-
воротного крана при поднимании груза Е
массы 3 т с ускорением g/З. Масса крана рав-
на 2 т, а его центр масс находится в точке С.
Масса тележки D равна 0,5 т. Кран и тележка
неподвижны. Размеры указаны на рис. 41. Ю. I.
Ответ: ХА = -Хв = 52,1 кН; Уд = 63,9 кН.
Решение. Расчетная схема — на рис. 41.10.2. К системе приложены
силы тяжести M\g, MDg и MEg, реакции подпятника
Ra = Ха + Уд + Уд,
подшипника
Rb — Хв +• Уд
и сила инерции поступательно движущегося груза
Фе = -МЕаЕ-
Согласно принципу Даламбера эта система сил — уравновешенная:
Mkg + Ra + RB + Фе = 0,
к
<
У2 Ма(МтЯ) + Ma(Ra) + Ma(Rb) + МА(Ф) — 0.
< к
284
8. Метод кинетостатики
Спроецируем векторные уравнения на оси координат:
' хА + хЕ = О,
Ya ~ - MDg - MEg - Ф = О,
ZA + %в = О,
<
ZB • AB = 0,
0 = 0,
, - XB AB — M\g • CiC — MEg D\D — MEg • D\D — ФЕ • D\D = 0,
где
1
Фе = MEaE — ME-g.
Решая уравнения, получаем опорные реакции подпятника А и под-
шипника В:
Ха = -Хв = 7в
g с 1 \
= |( 2000-2 + 500-5 + 3000-5Ч-ЗООО---5J w51 940 Н,
или ХА — -Хв ~ 52 кН;
Ya = Mig + MDg + MEg , Ф — g (^Mt + MD + ME + —ME
2000 + 500 + 3000 + - • 3000) = 63 700 H,
3 ' il
или Ya ~ 63,7 кН; ZA = ZB = 0.
£
Mig-CiC + MDg-DiD + MEg-DiD Me--DiD
?s9,8-
Задача 41.11 (41.13). Определить опорные реакции подпятника А
и подшипника В поворотного крана, рассмотренного в предыдущей
задаче, при перемещении тележки влево с ускорением 0,5g при отсут-
ствии груза Е. Центр масс тележки находится на уровне опоры В.
Ответ: ХА = 12,8 кН, Хв = -15,2 кН; YA = 24,5 кН.
Решение. Расчетная схема — на рис. 41.11.1. Воспользуемся реше-
нием задачи 41.10. Система (согласно принципу Даламбера) находится
в равновесии под действием плоской системы сил: силы тяжести, равно-
действующая сил инерции поступательно движущейся тележки
фе — —МЕ dE
8. Метод кинетостатики
285
и ненулевые составляющие реакций в опорах Л и В, расположенные
в той же плоскости Аху.
Поэтому составим три уравнения равновесия: суммы проекций всех
сил на оси координат х и у равны нулю и сумма алгебраических моментов
всех сил относительно точки А равна нулю:
А-/ + Хв + Фо = О,
< Ya - M{g - MDg = о,
. -Хв АВ - M\g • CtC - MDg • BD - Ф АВ — 0.
Решая эти уравнения, получим опорные реакции:
Ya I M}g + MDg = g(Mi + Мд) к 9,8(2000 + 500) = 24 500 (H),
или Ya = 24,5 кН;
1 / ч
Хв = —ттг (M\g • С] С + Mpg BD + Фд ’ АВ) =
АВ
= \ • С\С + Mog BD + MD-g АВ J =
АВ \ 2 /
= —— ( Mi -С\С + md-bd + \md- АВ ) и
АВ \ 2 J
9 8/ 1 \
и—-I 2000-2 + 500-5 +--500-5 = —15 190 (Н),
5 \ 2 / '
или ХБ ~ -15,2 кН;
ХА = -ХБ - Фд = 15,2 - 0,5 • | • 9,8 = 12,75 (кН).
286
8. Метод кинетостатики
Задача 41.12(41.14). На паром, привязанный к берегу двумя па-
раллельными канатами, въезжает грузовик массы 7 т со скоростью
12 км/ч; тормоза останавливают грузовик на протяжении 3 м. Пред-
полагая, что сила трения колес о настил парома постоянна, определить
натяжение канатов. Массой и ускорением парома пренебречь.
Ответ: Т = 6,48 кН.
Рис. 41.12.1
Решение. Расчетная схема — на рис. 41.12.1. Сила Т — сила натя-
жения канатов, FApx — сила Архимеда, Ф = —Ma — равнодействующая
сил инерции точек грузовика, движущегося поступательно. Используя
принцип Даламбера, составим уравнение равновесия всех сил системы
в виде суммы проекций сил на горизонтальную ось х;
Ф - Т = 0, или Ma - Т — 0.
Отсюда Т = Ma.
Определим ускорение грузовика а. Так как по условию сила трения
колес о настил парома постоянна, то ускорение замедления при тормо-
жении грузовика а = const.
Поэтому
Суммарная сила натяжения канатов
Т = Ма —
2s ’
8. Метод кинетостатики
287
В силу симметрии сила натяжения каждого каната
/ 12 000\2
, , 7000 ------
1 Mvl \ 3600 J х
Т{ = -Т =-----=---------------й 6481 (Н).
2 4s 4-3 V ’
Замечание к задаче 41.12. В [4] подобная задача под номером 26 24 из [Ю] ре-
шалась другим методом.
Задача 41.13(41.15). Автомобиль массы М движется прямоли-
нейно с ускорением w. Определить вертикальное давление передних
и задних колес автомобиля, если его центр масс С находится на вы-
соте А от поверхности грунта. Расстояния передней и задней осей ав-
томобиля от вертикали, проходящей через центр масс, соответственно
равны а и Ь. Массами колес пренебречь. Как должен двигаться авто-
мобиль, чтобы давления передних и задних колес оказались равными?
М (gb — wh) М (ga + wh)
Ответ: N\ = ------------, = -----—------; при торможении ав-
a + b a + b
a - b
томобиля с замедлением w =g • .
zh
Решение. Расчетная схема движения автомобиля — на рис. 41.13.1.
К автомобилю приложены сила тяжести, нормальные реакции со стороны
поверхности дороги, силы трения скольжения колес и равнодействующая
сил инерции частиц поступательно движущегося автомобиля (массами
колес по условию пренебрегаем).
Причем
Ф = -Mw,
N\, N2 — суммарные нормальные реакции соответственно передних и зад-
них колес, FTp , FTP2 — суммарные силы трения скольжения соответствен-
Рис. 41.13.1
288
8. Метод кинетостатики
но передних и задних колес. Предполагаем систему сил плоской Приме-
няя принцип Даламбера, составим уравнения:
' $2^ = 0,
к
< УЗ Гьу = 0’
к
Е MCz(Fk) = 0,
• к
т. е.
Г FTP1 + FT₽2 - Ф = 0,
\ N\ + N2 — Mg = 0,
L TV] о + FTP1 h — TV26 + FTP2 h — 0.
Решаем полученные уравнения:
f FTp + FTP2 = Ф,
Ni+N2 = Mg,
< TV] + N2 = Mg, => =>
N\a - N2b + h$ = 0
\ — N2b + hfJF-tp' + FTP2) = 0
Mgb — h$ Mgb-hMw M(gb — wh)
TV] —--------—--------------=------------,
a+b a+b a+b
M (ga + wh)
N2 = Mg — N\ =
a -p b
Заметим, что силы TV] и TV2 — это реакции, действующие на авто-
мобиль со стороны дороги. Силы давления колес автомобиля на дорогу
согласно закону равенства сил действия и противодействия будут таки-
ми же по величине, но направлены вниз.
Найдем, при каком условии TV] = TV2:
М(gb — wh) М(ga + wh) a - b
— => w = —g .
a + b-------------------------------------a + b-2h
Это означает, что автомобиль движется с замедлением, если a > b,
и ускоренно, если a < b.
,, M(gb — wh)
Замечание к задаче 41.13. Из полученного выражения TVt = ----- сле-
a + Ъ
дует, что при w > g • b/h реакция TV] < 0, т. е. происходит отрыв передних
М (ga + wh)
колес. Аналогично из выражения N, =----;---следует, что при замедлении
a + b
с w < -g - a/h реакция TV2 < 0 и происходит отрыв задних колес.
8. Метод кинетостатики
289
Задача 41.14(41.16). С каким ускорением w опус-
кается груз массы , поднимая груз массы Mi с помо-
щью полиспаста, изображенного на рис. 41.14.1? Како-
во условие равномерного движения груза Mt ? Массами
блоков и троса пренебречь.
Указание. Ускорение груза
ния груза М\.
в четыре раза меньше ускоре-
4Mi - М2
Ответ: w = 4g——----—,
1 6М [ + М2
Л/,
М2
Рис. 41.14.1
Ml _ 1
Л^2 “ 4
Решение. Расчетная схема — на рис. 41.14.2. Система совершает
одномерное движение вдоль вертикали (на рис. 41.14.2 ось х направлена
вдоль вертикали вниз). Подвижный блок О2 перемещается прямолинейно
вдоль оси х (вращаясь при этом) в том и только в том случае, если
его мгновенный центр скоростей Р находится строго вертикально под
точкой 01 (центром неподвижного блока). Найдем положение точки
Р. Установим связь между перемещениями точек М\ и М2. Пусть Mt
переместилась на х{ вниз, тогда в силу нерастяжимости нити точка К
переместится на Х\ вверх. Пусть х2 — перемещение груза М2 и, значит,
точки 02 — центра блока. Тогда точка О4 — центр подвижного блочка —
переместится также вверх на х2, а так как точка Р4 — МЦС маленького
блочка Од (нить Р4О3 имеет нулевую скорость), то перемещение точки L
подвижной нити равно 2х2 и направлено вниз. МЦС блока 02 находится
на пересечении прямой, проходящей через концы перемещений точек 02,
L и К с горизонтальным диаметром блока. Тогда
1 2
Р02 — -г, LP = -г.
3 3
Из подобия треугольников получим:
Xi РК Х[ О]
— =------ => — =4 ==> — =4,
х2 Р02 х2 а2
где О] и а2 — ускорения грузов М\ и М2. Вводя силы инерции Ф1 = — Midi
и Ф2 = -М2а2 и составляя уравнения моментов сил {Фь Ф2, Р\, Р2, Rot}
относительно точки О,, получим:
(Mig - M}ai)R - (TW2g - М2а2) • = О
290
8. Метод кинетостатики
Рис. 41.14.2
и, воспользовавшись равенствами R = 4г/3, «2 = di/4, получим
а, = w =
4g(47W| - М2)
16Л/| — М2
Если М\ = М2/4, то w = 0.
8. Метод кинетостатики
291
Рис. 41.15.1
Задача 41.15(41.17). Гладкий клин массы М и с углом 2а при вер-
шине раздвигает две пластины массы М\ каждая, лежащие в покое на
гладком горизонтальном столе (рис. 41.15.1).
Написать уравнения движения клина и пла-
стин и определить силу давления клина на
каждую из пластин.
Ответ: Уравнение движения клина:
wt2 М ctg a
s =----, где w = е-------------------;
2 М ctg a + 2Mj tg a
уравнение движения пластин:
W\t2
где W\=wtga;
сила давления
MiWi
=
cos a
Решение. Расчетная схема — на рис. 41.15.2. Расчленим систему
и исследуем движение клина и левой пластины отдельно. Заметим, что
в силу симметрии правая пластина движется так же, как и левая (только
в другую сторону: направо).
Согласно принципу Даламбера пластина находится в равновесии
под действием силы тяжести M\g, нормальной реакции гладкого гори-
зонтального стола N\, силы давления со стороны клина перпен-
дикулярной боковой поверхности пластины, и равнодействующей силы
инерции Ф1 = поступательно движущейся пластины с ускоре-
нием Й] (см. рис. 41.15.2). Клин находится в равновесии под действием
292
8. Метод кинетостатики
силы тяжести Mg, сил реакций со стороны пластин (F\ = —и F2)
и равнодействующей силы инерции Ф = —Ma (см. рис. 41.15.2).
Составим уравнения движения пластины и клина в форме принципа
Даламбера, записав суммы проекций перечисленных выше сил на оси
координат х и у:
№
и
F'i cos а - Ф] = 0.
Mig + F{ sin a — ЛГ| = 0
!-Fi cos a + F2 cos a = 0,
(1)
Mg — Ф — F\ sin a - F2 sin a = 0,
где Ф] = Miai, Ф = Ma.
Найдем связь между ускорениями пластины а, и клина а. Для этого
рассмотрим движение точки А клина как сложное. Подвижные оси £ и у
Рис. 41.15.3
свяжем с поступательно движущейся пластиной
(см. рис. 41.15.3).
Абсолютное ускорение точки А, равное уско-
рению клина, можно представить как сумму от-
носительного аг и переносного ае ускорений:
а — ат —|— ае.
Ускорение Кориолиса равно нулю. Переносное ускорение ае равно уско-
рению пластины Й|. Из треугольника ускорений имеем соотношение:
ла
fill
Ж
sft
Ki
аол
Нас
G] = a tga.
Перепишем уравнения (1) в виде:
' F\ cos а - М{аща = 0,
Р
Mig + Ft sin a - Ni = 0,
-F\ cos а + F2 cos а = 0, Ш(
, Mg - Ma - F\ sin a - F2 sin a = 0. щя
Решая их, получим:
tga
Fi = F2 = M\a--—,
< cos a =>
k Mg — Ma — 2F| sin a — 0
M M cig a
%M + 2ЛД tg2 a &M ctga + 2M\ tga’
Fi = F2 = F{ = Mia^- = Mt
cos a cos a
Клин и пластина движутся с постоянными ускорениями:
М ctga
а = g----------------, fli = a tg a.
kM ctga + 2M, tga’ 1 K
8. Метод кинетостатики
293
Сила давления клина на каждую из пластин:
fli
N = Г, = Г2 = М,——.
cos а
Уравнение движения клина получим, интегрируя дифференциальное урав-
нение у = а с нулевыми начальными условиями:
at2
Уравнение движения пластины получим, интегрируя дифференциальное
уравнение х = at с нулевыми начальными условиями
att2
Х ~ ~2~
Задача 41.16(41.18). Груз А массы М\ опускаясь вниз, приво-
дит в движение посредством нерастяжимой
через неподвижный блок С, груз В массы
Mi (рис 41.16.1). Определить силу давления
стола D на пол, если масса стола равна М3.
Массой нити пренебречь.
Ответ: N — I М} + М2 + ЛД -
М2 А
Mt+M2)8
нити, переброшенной
Решение. Расчетная схема — на рис. 41.16.2. Применим принцип
Даламбера для всей системы. Согласно принципу, внешние для системы
силы (силы тяжести Mtg, M2g, M3g; нормальная реакция пола N, силы
трения со стороны пола) и силы инерции грузов Ф] = -М\ d\, Ф2 = — М2а2
Рис. 41.16.2
294
8. Метод кинетостатики
образуют уравновешенную систему сил. Заметим, что ускорения грузов
О| и а2 равны по величине в силу нерастяжимости нити.
Приравняем нулю сумму проекций всех сил на вертикальную ось у:
-N + M\g + M2g + M3g - Ф, = 0.
Отсюда
TV = M\g + M2g + M3g - Mia|.
Для определения ускорения а, применим принцип Даламбера для
каждого из грузов, записав сумму проекций сил для 1-го груза на верти-
кальную ось у, а для 2-го груза — на горизонтальную ось х:
Mlg - Ф, - т, = О, Т2 - Ф2 = о,
где
Ф| = М\а ।, Ф2 = М2а2 = М2аь
силы натяжения нити Т\ = Т2 (так как нить невесомая и блок С непо-
движен).
Итак,
Мх
d\ =--------g,
М\+М2
и, следовательно, нормальная реакция со стороны пола, а значит и сила
давления стола на пол, равна величине
, X -W1
N =g(M{ +М2 + М3) - М} -r—-—g =
JvL\ + Jvi2
f Ml \
= g [Mx + M2 + M3 - ----- .
\ M\ + M2 J
Задача 41.17(41.19). Груз А массы Mx, опускаясь вниз по на-
клонной плоскости D, образующей угол а с горизонтом, приводит
Рис. 41.17.1
в движение посредством нерастяжимой ни-
ти, переброшенной через неподвижный блок
С, груз В массы М2 (рис. 41.17.1). Опреде-
лить горизонтальную составляющую давления
наклонной плоскости D на выступ пола Е.
Массой нити пренебречь.
Мх sin а - М->
Ответ: N = Mxg---------------- cos а.
М^х т М^2
Решение. Применяя принцип Даламбера для всей системы, запи-
шем уравнение в виде суммы проекций сил на ось х (см рис. 41.17.2):
RT - Ф| cosa = 0.
8. Метод кинетостатики
295
M2g
$2
Рис. 41.17.3
Горизонтальная реакция, действующая на клин D со стороны выступа Е,
равна Rx = Ф| cos a = Mta\ cos a.
Согласно закону равенства сил действия и противодействия с такой же
по величине силой клин D действует на выступ Е вдоль горизонтали.
Найдем ускорение груза А. Заметим, что в силу нерастяжимости нити
ускорения грузов А и В равны по величине:
О,\ = О2-
Применим принцип Даламбера отдельно для груза А и отдельно для
груза В. Сумма проекций всех сил, с учетом равнодействующей силы
инерции поступательно движущегося груза А, на ось S вдоль наклонной
плоскости клина равна нулю:
Mig sin a - Ф] - Т\ — 0.
Аналогично, для груза В сумма проекций сил на вертикальную ось у
равна нулю:
Т2 - M2g - Ф2 = 0.
Силы натяжения нитей Т\ и Т2 равны по величине, так как нить невесома
и блок С неподвижен.
Перепишем последние два уравнения с учетом того, что
Т\—Т2, Ф\=М\а\, Ф2 — М2а2 = M2at:
Migsin а - М\а\ - Т\ = О,
Т\ - M2g - M2at = 0.
Из полученной системы уравнений определяем ускорение
М\ sin а - М2
а' = 8 М\+М2
Поэтому искомая сила давления
М\ sin а — М2
Fm^R. = M,s- cost,.
296
8. Метод кинетостатики
Задача 41.18(41.21). Однородный стержень массы М и длины I
вращается с постоянной угловой скоростью и вокруг неподвижной
вертикальной оси, перпендикулярной стержню и проходящей через
его конец. Определить растягивающую силу в поперечном сечении
стержня, отстоящем от оси вращения на расстоянии а.
а>2
Ответ: F = M(Z2 - а2) —.
Рис. 41.18.1
Решение. Расчетная схема — на рис. 41.18.1. «Разрежем» стержень
на расстоянии а от его оси вращения и отбросим правую часть, заменив ее
действие силами реакции вдоль осей координат Rx,Ry,Rx и моментами
МХ,МУ, Mz.
К оставшейся части стержня применим принцип Даламбера. Для
этого добавим к силе тяжести mg, реакциям Aq, Yo, Zq,Mox, Моу, Mqz
в точке О на оси вращения и реакциям на правом конце силы инерции
частиц стержня.
Стержень вращается равномерно. Поэтому частицы стержня име-
ют лишь нормальные ускорения, направленные вдоль стержня к оси
вращения. Силы инерции частиц стержня направлены вдоль стержня
противоположно ускорениям. Такая система сил приводится к равнодей-
ствующеи силе инерции Ф1 = -ni\aC], линия действия которой проходит
через центр масс Ci вдоль стержня. Величина
„ а о у а2
Ф| = т,аС| =М-м~- = Мы —
Дй
в
]ред(
«.J
ь-1
а
и
жу
пь
W
1ПИ
я»
91.1
<В1
и, в
tone
Л|.
sipai
;Йр
1ВЦ
«си
Ц
All
«ИН
8. Метод кинетостатики
297
Приравняем нулю сумму проекций всех перечисленных сил на ось у,
направленную вдоль стержня:
То + -Ry + Ф । = 0. (I)
Для определения реакции Ко применим принцип Даламбера для всего
стержня. Запишем уравнение равновесия в виде суммы проекций сил на
ось у:
Yo + $ = 0, (2)
где Ф — —Ma1}; — равнодействующая сил инерции частиц целого стержня.
Величина
,1
Ф = Мы-.
2
Решаем уравнение (2):
71
Yo = -$ = -Мы2-.
2
Полученную величину Yo подставляем в (1) и выражаем
') Д т I I Q
Rv — —Ф] - Yo = -Мш~-----h Mbi - = Мы2--------.
у 1 и 21 2 21
Это и есть сила, растягивающая стержень в поперечном направлении.
Задача 41.19(41.22). Однородная прямоуголь-
ная пластинка массы М равномерно вращается
вокруг вертикальной оси с угловой скоростью
(рис. 41.19.1). Определить силу, разрывающую пла-
стину в направлении, перпендикулярном оси вра-
щения, в сечении, проходящем через ось вращения.
Ответ:
Maw2
4
Решение. Расчетная схема изображена
на рис. 41.19.2. Система координат Oxyz свя-
зана с вращающейся пластиной.
«Отбросим» правую половину пластины
и вал вдоль вертикальной оси. Их действие
на оставшуюся половину заменим составля-
ющими силы и момента реакции Хо, Yo, Yo
и МОх, Моу, MOz.
Применим принцип Даламбера. Для это-
го добавим силы инерции частиц полупласти-
ны. Так как вращение равномерное, то частицы
298
8. Метод кинетостатики
имеют лишь нормальные ускорения, направленные параллельно оси Ох
к оси вращения Oz. Поэтому их силы инерции также параллельны оси Ох
и направлены от оси вращения Oz (толщиной пластины пренебрегаем).
Так как пластина однородная, то такая система сил инерции имеет рав-
нодействующую, линия действия которой проходит через центр масс С|:
Ф = -771)0^1 • Величина
n М ,а
Ф = m}aCt = —ш -
Маш2
4
Приравняем нулю сумму проекций всех сил на ось Ох:
Xq + Ф — 0.
Отсюда Xq = -Маш1 /4. Следовательно, искомая сила, разрывающая
пластину, равна Маш1 /4.
Рис. 41.20.1
Задача 41.20 (41.23). Однородный круглый диск
радиуса R и массы М вращается с постоянной уг-
ловой скоростью ш вокруг своего вертикального диа-
метра (рис. 41.20.1). Определить силу, разрывающую
диск по диаметру.
Ответ:
2МКш2
Зя
Решение. Расчетная схема — на рис. 41.20.2. Система координат
Oxyz связана с вращающимся диском. «Разрежем» диск вдоль вертикаль-
ного диаметра и «отбросим» левую половину.
Действие отброшенной части и вертикально-
го вала на оставшуюся часть диска заменим
реакциями XO,YO,ZO и МОх, МОу, МОг.
Центр масс С\ половины диска опреде-
ляется соотношением [4, 11]:
2 sin а 2 sin (я/2)
ОС\ = -R-= -R—V-2
За 3 я/2
4R
Зя ’
Чтобы воспользоваться принципом Даламбе-
ра, добавим силы инерции частиц полудиска.
Приведем силы инерции к точке О. Так как
система вращается равномерно и все три оси являются главными осями
инерции для точки О, то главный момент сил инерции полудиска отно-
сительно точки О равен нулю (L^ — 0). Главный вектор сил инерции
8. Метод кинетостатики
299
(равнодействующая сила инерции): Ф — —тщете,. Линия действия прохо-
дит через центр масс Ct. Величина
_ М
Ф = = и? ‘ ОС\ —
2Mu2R
ЗТГ
Составим уравнение равновесия сил для полудиска в проекции на ось Оу:
YO + ® = Q.
Получим
2 Mu2R
Yo = -$ = --------.
3 7Г
2Mu2R
Сила, разрывающая диск по диаметру, равна --
Зтг
Задача 41.21 (41.24). Тонкий прямолинейный однородный стер-
жень длины I и массы М вращается с постоянной угловой скоростью ш
около неподвижной точки О (шаровой шар-
нир), описывая коническую поверхность с
осью О А и вершиной в точке О (рис. 41.21.1).
Вычислить угол отклонения стержня от вер-
тикального направления, а также величину N
давления стержня на шарнир О.
_ 3g
Ответ: = arccos —,
г 21ш2
1 э
N = -М1ш
2
Рис. 41.21.1
412а>4 ’
Решение. Расчетная схема изображена
на рис. 41.21.2. Применим принцип Даламбе-
ра. На стержень действуют сила тяжести Mg
и сила реакции шарового шарнира О с соста-
вляющими Xo,Yo,Zo (рис. 41.21.2).
Разобьем стержень на элементарные участ-
ки одинаковой длины (рис. 41.21.3). Ускоре-
ния средних точек этих участков распределят-
ся вдоль стержня по линейному закону, так
как w = const и Ofc = w2/ifc, где h* — рассто-
яние от средней точки элементарного участка
до оси вращения Oz. Силы инерции элемен-
тарных участков стержня (которые принимаем
300
8. Метод кинетостатики
Рис. 41.21.3
за точки), тоже распределятся по линейному за-
кону. Распределенные так параллельные силы
имеют равнодействующую силу, приложенную
к точке D, которая делит длину стержня в отно-
шении 2 : 1 [4,11].
Поэтому
2 ,1
OD = -I, Ф = —Мас, Ф = Мш2 *-sin 92.
Составим уравнения равновесия силы тяжести, сил реакции шарнира О
и силы инерции в виде суммы проекций их на координатные оси и суммы
моментов их относительно координатных осей. Получим:
Хо — 0, Yq + Ф — 0, Zq — Mg — 0,
I 2
— Mg- sin <р + Ф • -I cos <p = 0, 0 = 0,
0 = 0.
Заметим, что указанные силы, приложенные к стержню, не создают мо-
менты относительно осей Оу и Oz, поэтому последние два уравнения
обращаются в нулевые тождества.
Решаем четвертое уравнение системы:
I 21 2
-Mg- sin <р + Mu - sin tp-l cos tp = 0
3g
COS^=2V
sin ip 0
3g
w — arccos------т.
2/oj2
Из первых трех уравнений системы получаем, что Xq = 0,
2 I э /
Yn — —Ф = -Mu — sin о? = -Ми -
2 2
2
i-Г—
Zq — Mg.
Поэтому величина силы давления стержня на шарнир О равна
2V = V/x2+y(2 + Z2 =
I2 9
М2ш4--------M2g2 +M2g2 =
4 16
7g2
4/V
8. Метод кинетостатики
301
Задача 41.22(41.25). В центробежном тахо-
метре два тонких однородных прямолинейных
стержня длины а и Ь жестко соединены под
прямым углом, вершина которого О шарнирно
соединена с вертикальным валом (рис. 41.22.1);
вал вращается с постоянной угловой скоростью
ед. Найти зависимость между ш и углом откло-
нения <р, образованным направлением стержня
длины а и вертикалью.
-> b2 cos <р — a2 sin <р
Ответ: w = з^—----------———
(b3 — a3) sin
Решение. Расчетная схема — на рис. 41.22.2. Координатные оси
Oxyz свяжем с вращающейся системой так, что стержни расположены
в плоскости Oyz.
Применим принцип Даламбера. Для этого шарнир О заменим реак-
циями Xo,Yo, Zo- Для удобства рассмотрим стержни отдельно. На каж-
дый из них действует своя сила тяжести, приложенная соответственно
в центрах масс С\ и Су. m^g и myg, где
М
т' = —ГТО’
а + о
ТП2 =
м
(z -J- Ъ
При исследовании сил инерции воспользуемся рассуждениями, при-
веденными в решении задачи 41.21. Получим, что для одного стержня
302
8. Метод кинетостатики
равнодействующая сила инерции
Ф1 = -miSc,
приложена к точке В (ОВ — 2а/3), причем величина
ж п М 2° -
Ф1 = т\ас, =-----аш - sin w;
1 a+b 2 Y
а для другого стержня равнодействующая сила инерции
Ф2 = ~т2апС1
приложена к точке D (QD = 2Ь/3), причем величина
П М t 2b
Ф2 = т2аС1 = —-j—^осд 2 C°S
Запишем уравнение равновесия всех перечисленных сил изогнутого
стержня в виде суммы моментов сил относительно оси Ох:
а b 2 2
Triig- sin ip - m2g- cos p - Ф]-асо5 ip + Фг-fcsin p = 0.
Расписав величины, получим:
b2 М а2 ,2
—g cos ip--—- —w -a sin ip cos ip +
CL I C) 2 S
b2 22
—сд —b sin ip cos ip = 0.
М а2
—— -gsin^-
а + о 2
М
M
4------
a T b
После несложных преобразований выразим зависимость между угловой
скоростью <д и углом отклонения р:
2 Ъ2 cos <р - a2 sin р
w ----з\ • п—•
(tr — <r) sin 2р
Рис. 41.23.1
Задача 41.23(41.26). Тонкий однородный прямо-
линейный стержень АВ шарнирно соединен с верти-
кальным валом в точке О (рис. 41.23.1). Вал вращается
с постоянной скоростью <д. Определить угол отклоне-
ния р стержня от вертикали, если ОА = а и ОВ — Ь.
3 g a-b
Ответ: cos ip = —- —z------r.
2 сд2 a2 — ab + b2
8. Метод кинетостатики
303
Рис. 41.23.2
Решение. Расчетная схема — на рис. 41.23.2. Систему координат
Oxyz свяжем с вращающимся стержнем так, что он все время расположен
в плоскости Oyz. Действие шарнира на стержень заменим силами реакции
Хо->¥о, %о Для удобства рассмотрим две части стержня, разделенные
вертикальной осью.
К первой части стержня в центре масс Су приложена сила тяжести
mig, причем
М
mi =------а.
а + Ь
Ко второй части стержня в центре масс С) приложена сила тяжести m2g,
причем
М
т2 = ——Ь.
а + Ь
При исследовании сил инерции стержня воспользуемся результатами,
приведенными в решении задачи 41.21. В точке А (ОА = 2а/3) первой
части стержня приложена равнодействующая сила инерции
Ф1 = -m\dcx,
причем величина
М 2а
Ф, = —-a- w - sin р.
а + Ь 2
В точке В (ОВ = 26/3) второй части стержня приложена рагнодейству-
ющая сила инерции
Ф2 = —т2Ос2,
304
8. Метод кинетостатики
причем
М 2Ь
Фг =-------Ь w - cos w.
о. 4- Ъ 2
Приравняем нулю сумму моментов всех сил стержня относительно
оси Ох;
a
Ъ 1 1
m\g- sin if - m2g- sin ip - §\^асоыр - Фг-Ьсоз^ = 0.
Распишем величины:
Ma2 Mb2 Ma2 ,2
—— —gsin^-------—- — gsin^-----— — w -a sin <p cos ip-
Q t v 1 CL -|“ b 2 CL -|“ b 2 3
M b2 ,2
-------- —w -b sin ip cos w = 0.
a + b 2 3
После несложных преобразований, учитывая, что sin tp 0, получим:
3 g а2 — b2 3 g а - b
2 w2 а3 + Ь3 2 ш2 а2 — ab + Ь2
Й
ISI
вд
я
И
я
to
-)К
р
и
ПК
Ре
Г;
Ен
!8
St
'а
ч
9. Давление вращающегося твердого тела
на ось вращения (§ 42, [10])
' Задача 42.1 (42.1). Центр масс махового колеса массы 3000 кг на-
ходится на расстоянии 1 мм от горизонтальной оси вала; расстояния
подшипников от колеса равны между собой. Найти силы давления на
подшипники, когда вал делает 1200 об/мин. Маховик имеет плоскость
симметрии, перпендикулярную оси вращения.
Ответ: Сила давления на каждый из подшипников есть равнодей-
ствующая двух сил, из которых одна равна 14,7 кН и направлена по
вертикали, а другая равна 23,6 кН и направлена параллельно прямой,
соединяющей геометрический центр колеса, находящийся на оси вала,
^с центром масс колеса._______________________________________
Решение. Расчетная схема — на рис. 42.1.1. Свяжем систему коор-
динат Axyz с вращающейся системой (вал с маховым колесом). Причем
ось Ау все время направлена параллельно ОС, где С — центр масс колеса.
Внешние силы для системы: сила тяжести Mg и реакции подшипников
А и В в виде составляющих вдоль координатных осей (Ха, Ya, Хв, Yb)-
Воспользуемся принципом Даламбера для механической системы. С уче-
том сил инерции точек системы уравнения равновесия имеют вид [4,11]:
к к
5 у + 52 + Ф>/ = о,
к к
52 +52 + Фх = о,
к к /. ,
22 (^е))+52 млх(дк)+в™ = о,
к к
22 МАу (Д(е)) + 22 = 0,
к к
22 МАг (г<е)) + 22 МаА) + = 0.
. к к
Здесь RK — реакции подшипников А и В; Ф — главный вектор сил инер-
ции махового колеса, — главный момент сил инерции относительно
точки А махового колеса.
306 9. Давление вращающегося твердого тела на ось вращения
Приведем силы инерции точек махового колеса к точке О на непо-
движной оси вращения Az. Получим главный вектор сил инерции
Ф = -Мас
и главный момент сил инерции относительно точки О
f (ин) _ dK0
L° ~~~dF’
приложенные в этой точке О. Выпишем формулы для вычисления про-
екций этих векторов [4,11]:
( Ф.т = -еус - и2хс, &у = £ХС - ш2ус, Фг = 0;
< (2)
I т (ин) _ с т , ,2 т г (ин) _ р т I , .2 т г(ин) _ __ т
I J-iqx —bJxz ш jyZ, ijQy —Jxz> ^Oz ~ tJz-
Заметим, что вал системы не обладает массой по условию задачи (безы-
нерционный).
Так как вал вращается равномерно, то угловое ускорение е равно нулю.
Поэтому главный вектор сил инерции Ф определяется лишь нормальным
ускорением центра масс С. Его величина равна
Ф = Мапс = Мы2 ОС.
Направлен вектор Ф как указано на рис. 42.1.1 (параллельно оси Ау и в
ту же сторону, так как вектор Sc направлен от точки С в сторону оси вра-
щения).
_ « г(ин)
При определении проекции вектора Lo воспользуемся тем, что
е = 0. Также воспользуемся тем, что ось Оу — главная центральная
ось инерции махового колеса, так как является осью симметрии колеса.
Поэтому центробежный момент инерции Jyz = 0. Заметим что ось Oz
перпендикулярна плоскости материальной симметрии махового колеса.
9. Давление вращающегося твердого тела на ось вращения 307
Значит ось Oz — главная ось инерции колеса для точки О. Поэтому
центробежные моменты Jyz и Jxz равны нулю. Итак, получаем, что
г(нн) _ ,(ин) _ _(ин) _ „
ЬОх — LOy — LOz —
Распишем систему уравнений (1):
ХА + %в ~ Mg = 0,
YA + YB + Ф — 0,
' - YB • АВ - Ф • ^АВ = 0, (3)
Хв АВ - Mg- 1-АВ = 0.
Заметим, что уравнение для суммы проекций сил на ось Az обратилось
в тождественное равенство нулю, а уравнение для суммы моментов сил
относительно оси Az можно не выписывать, так как оно определяет
вращающий момент, обеспечивающий равномерное вращение системы, у
Решая систему (3), получим реакции подшипников:
1 1
Хв = ~Mg = - 3000 • 9,8 = 14700 (Н),
ХА = Mg — Хв = 3000 -9,8- 14 700 = 14700(H),
11, 1
YB = —Ф = —Mw2 ОС =-3000 •
2 2 2
1200 V
—— - 27Г )
60 /
0,001 » -23 687(H),
Уд = -ф - YB к, -43 374 + 23 687 = -23 687 (Н).
Силы давления на каждый из подшипников равны и складываются из двух
взаимно-ортогональных составляющих:
FAx = FBx я 14,7 (кН) и FAy = FBy я 23,7 (кН).
Ф'
рв
1ЯГ
ищи
1л,м
м®
Задача 42.2 (42.2). Однородный круглый
диск массы М равномерно вращается с уг-
ловой скоростью <д вокруг неподвижной оси,
расположенной в плоскости диска и отсто-
ящей от его центра масс С на расстояние
ОС = а (рис. 42.2.1). Определить силы ди-
намического давления оси на подпятник А
и подшипник В, если ОВ = ОА. Оси х и у
неизменно связаны с диском.
Ответ: ХА = ХВ = 0, YA = YB =
Maw2
2
308 9. Давление вращающегося твердого тела на ось вращения
Рис. 42.2.2
Решение. Расчетная схема — на рис. 42.2.2. Система координат
Oxyz связана с вращающейся системой (диск и невесомый вал). Сила
реакции подшипника В раскладывается на составляющие вдоль осей х
и у, а сила реакции подпятника А имеет составляющие вдоль всех трех
осей координат.
Чтобы воспользоваться принципом Даламбера и записать уравнения
равновесия, добавим силы инерции точек системы. Для этого приведем
силы инерции точек диска к точке О на оси вращения Oz. Получим глав-
ный вектор сил инерции
Ф = —Mac
и главный момент сил инерции относительно точки О
.(ин) _ dKo
L° ~~ dt
приложенные в точке О. Используем формулы (2) из решения задачи 42.1.
Так как w — const, то е = 0 и вектор Ф равен по величине
Ф = Мас = Мш2а
и направлен вдоль оси Оу. Так как ось Oz перпендикулярна плоскости
материальной симметрии Оху однородного круглого диска, то она явля-
ется главной осью инерции диска для точки О. Поэтому центробежные
моменты Jyz и Jxz равны нулю. В результате, вектор Lo является нуле-
вым вектором.
9. Давление вращающегося твердого тела на ось вращения 309
Уравнения равновесия удобнее записать в проекциях на оси, парал-
лельные осям системы Oxyz и проходящие через подпятник A (Axyz).
Заметим, что полные реакции в точках А и В складываются из стати-
ческих составляющих, определяемых активными силами (силой тяжести
Mg), и динамических составляющих, определяемых силами инерции си-
стемы. Поэтому для вычисления динамических реакций в уравнениях рав-
новесия (уравнения (1) задачи 42.1) не будем учитывать силу тяжести Mg.
Составим уравнения:
' ХА} + 4Д) =
Г1Л) + YB} + Ф = 0,
< 4д)=0,
- У^д) • АВ - Ф • АО = 0,
Х$ • АВ = 0,
k 0 = 0.
Решая их, получим динамические реакции подпятника А и подшипника В;
= Х(в} = 0,
(д) 40 1 1 2
YB = -Ф-----= —Ф = —Мш2а,
в ОБ 2 2
У*д) = -У^д) - ф = --Мш2а,
Z{*} = 0.
Поэтому силы динамического давления системы на подпятник и подшип-
ник следующие:
Мы2а
FAx = FBx = 0; РАу = FBy — ~ , FAz — О-
Задача 42.3 (42.3). Решить предыдущую задачу в предположении,
что при наличии сил сопротивления угловая скорость диска убывает
по закону щ = о>о - eof, где и £q — положительные постоянные.
Мас0 Mawl
Ответ: ХА = Хв =---YA = YB =
Решение. Расчетная схема — на рис. 42.3.1. Воспользуемся реше-
нием задачи 42.2. Так как по условию задачи угловая скорость системы
310 9. Давление вращающегося твердого тела на ось вращения
х
Рис. 42.3.1
не постоянная, а изменяется по закону
^z = — EqI,
то угловое ускорение
£z _ Uz — —£0.
Поэтому главный вектор сил инерции
Ф = -Мас ~ Матс = Фп + Фг.
Вектор Фп равен по величине
Фп = Мш2а
и направлен вдоль оси Оу. Вектор Фг равен по величине
Фг - Мс0 ОС
и направлен противоположно оси Ох. Заметим, что Фп и Фт приложены
в точке О.
Главный момент сил инерции диска относительно точки О имеет
ненулевую проекцию только на ось Oz:
г(ин) т / MR^ 2^
LOz — —CzJz — +£о I —~-----------\- Ma I .
9. Давление вращающегося твердого тела на ось вращения 311
Запишем уравнения равновесия системы в форме принципа Далам-
бера, в которых не будем учитывать силу тяжести Mg:
' Х{“} + Х{в} - Фг = О,
Ya} + Yb} + = О,
4"’=о,
<
- y£} • АВ - Фп • АО = О,
Х^ • АВ - Фт АО = О,
k - Мсолр - 0.
Из первых пяти уравнений системы получим динамические реакции под-
пятника А и подшипника В, действующие на систему:
у(л) ЛВ ТАО 1 = Ф АВ = 2Ме^
у(я) ЛА = Фг - Х^д) = |м£оа,
уМ „ ЛО 1 , = -Фп = —Мы2 а, АВ 2
у (А 1А = -Фп - Ид) = --Мш2а 2
4Д) = 0.
Поэтому силы динамического давления системы на подпятник А и под-
шипник В следующие:
1 1 2
Fat = Fbx = --MdEo, FAy = FBy =-Мы a, FAz = 0.
Замечание к задаче 42.3. В ответе стоит надо ы =
Задача 42.4 (42.3). К вертикальной оси АВ, вращающейся равно-
ускоренно с угловым ускорением е, прикреплены два груза С и D
посредством двух перпендикулярных оси АВ и притом взаимно пер-
пендикулярных стержней ОС = OD — г (рис. 42.4.1). Определить
силы динамического давления оси АВ на подпятник А и подшип-
ник В. Грузы С и D считать материальными точками массы М
каждый. Массами стержней пренебречь. В начальный момент система
находилась в покое. Оси х и у неизменно связаны со стержнями.
Ответ: ХА = Хв = —те(е12 + 1), YA = YB = — re(et2 - 1).
312 9. Давление вращающегося твердого тела на ось вращения
Решение. Расчетная схема — на рис. 42.4.2. Чтобы воспользоваться
принципом Даламбера для системы, включающей в себя вал с жестко
закрепленными на нем стержнями с грузами С и D на концах, к активным
силам (силам тяжести грузов) и реакциям подшипника В и подпятника А
(см. рис. 42.4.2) добавим силы инерции. Так как массой обладают лишь
точечные грузы С и D, то
Фр — —Мас — ~М(апс + ар) — ^с + Фр,
Фр = -MaD = -M(anD + ар) = Фр + ФЬ,
где
Фр = Мш2т, Фр = Мет, Фр = Мь)2т, Фр = Мет.
Так как е = const и вращение начиналось из состояния покоя, то w = et.
При определении динамических составляющих реакций подпятника
и подшипника в уравнениях равновесия не учитываем силы тяжести:
' X?’ + Х^ +Фпс + Фто = 0,
Y? + уДд) _ Фг + фП = о.
< 4д) = о, (1)
- Г^д) • 2h + Фр Л - Ф£Л = 0,
. 2h + Фр Л + ФЬЛ = 0.
Заметим, что при составлении сумм моментов сил относительно осей
координат, проходящих через точку А, третье уравнение обращается в тож-
дественное равенство нулю.
9. Давление вращающегося твердого тела на ось вращения 313
Решая систему уравнений (1), получим следующие динамические ре-
акции со стороны подпятника А и подшипника В:
Х(па) = ~|(фс + фЬ) = - l-(Me2t2r + Мег) = -^Mer(et2 + 1),
X? = "(фс + фЬ + *дД)) = ~~Mer(et2 + 1).
= |(ФЬ - Фр) = '-(Мег - Me2t2r) = ~Mer(et2 - 1),
yjfl) = Ф^ - Ф£ - Y^ = -'-Mer(et2 - 1),
4n) = 0.
Поэтому, согласно закону равенства сил действия и противодействия, силы
динамического давления системы на подпятник и подшипник следующие:
1 7 1 7
Fax = FBx = -Mer(et + 1), FAy = FBy = -Mer(et - 1), FAz = 0.
Задача 42.5 (42.4). Стержень AB длины 21, на
концах которого находятся грузы равной массы
М, вращается равномерно с угловой скоростью w
вокруг вертикальной оси Oz, проходящей через
середину О длины стержня (рис. 42.5.1). Расстоя-
ние точки О от подшипника С равно а, от под-
пятника D равно Ь. Угол между стержнем АВ
и осью Oz сохраняет постоянную величину а.
Пренебрегая массой стержня и размерами грузов,
определить проекции сил давления на подшипник
С и подпятник D в тот момент, когда стержень
находится в плоскости Oyz.
Ответ: Хс = XD = 0,
М12ш2 sin 2а
Yc = -YD =-------—----
а + b
ZD = -2Mg.
Решение. Расчетная схема — на рис. 42.5.2. Воспользуемся прин-
ципом Даламбера для механической системы. Для этого к силам тяжести
грузов А и В, к реакциям подпятника D и подшипника С добавим силы
инерции грузов А и В (материальных точек). Так как система вращается
равномерно, то силы инерции грузов направлены параллельно оси Оу
314 9. Давление вращающегося твердого тела на ось вращения
противоположно соответствующим нормальным ускорениям и равны сле-
дующим величинам:
Фл = МапА — M+2l sin а, Фв = Мапв — Mui2l sin а.
Запишем уравнения равновесия указанных сил в виде суммы проекций
их на координатные оси х, у и z, и суммы моментов сил относительно
осей, проходящих через подпятник D:
{Хс + Хр — 0, Yc + Yp — Фл + Фв = 0, Zo — Mg — Mg = О,
- Yc (а + b) 4- Mgl sin а - Mgl sin a + Фл (b -1 cos a) - Фв (b +1 cos a) — 0,
Xc(a + b) = 0.
Отсюда получаем
Xc = XD = 0, ZD = 2Mg,
> x * ,, xi -mw2l sin a • 21 cos a
Yc ~------ \ФА(Ь- I cos a) - Фд(Ь + I cos a) —----------,
a + о a + b
~ „ Mo2 2l2 sin a cos a Mw2l2 sin 2a
Yd = -Yc + *a-$b = -Yc =----------—-------=-------------.
a + b a+b
Согласно закону равенства сил действия и противодействия, проекции
сил давления на подшипник С и подпятник D следующие:
M(J2l2 sin 2а
Fcx = Fdx = 0, FCy = ~Fdv =-----’ ^Dz =
9. Давление вращающегося твердого тела на ось вращения 315
Задача 42.6 (42.5). На концы оси АВ надеты
два одинаковых кривошипа АС и BD длины
I и массы Mi каждый, заклиненные под углом
180° относительно друг друга (рис. 42.6.1). Ось
АВ длины 2а и массы М2 вращается с посто-
янной угловой скоростью (л в подшипниках Е и
F, расположенных симметрично на расстоянии
2Ь друг от друга. Определить силы давления NE
и NE на подшипники в тот момент, когда кри-
вошип АС направлен вертикально вверх. Массу
каждого кривошипа считать равномерно распре-
деленной вдоль его оси.
Рис. 42.6.1
Ответ: Сила давления
„ 1 Mialu2
Ne = -M2g 4- Mig-----——
2 2b
при NE > 0 направлена по вертикали вниз, при NE < 0 — вверх.
Сила давления
_ 1 , Mialu)2
NE = -M2g 4- Mig 4----——
2 2b
направлена по вертикали вниз.
Решение. Расчетная схема — на рис. 42.6.2. Систему координат Exyz
свяжем с вращающейся системой. На рис. 42.6.2 изображен момент време-
ни, когда кривошипы АС и BD расположены вертикально. Силы тяжести
кривошипов AC, BD и оси АВ приложены в соответствующих центрах
Рис. 42.6.2
316 9. Давление вращающегося твердого тела на ось вращения
тяжести С], С2 и Сз (серединах стержней, так как тела однородные). л
Составляющие реакций подшипников Е и F направлены вдоль коорди- ((
натных осей х и у. Е
Толщина стержней AC, BD и АВ пренебрежимо мала. Поэтому _
точки стержня АВ имеют нулевые ускорения и, следовательно, нулевые
силы инерции. Ускорения точек кривошипа АС направлены вертикально ж
вниз к оси вращения z (так как ш = const). Поэтому силы инерции точек
кривошипа АС лежат на одной прямой и направлены противоположно
ускорениям. Такая система сил имеет равнодействующую, линия действия л
которой направлена вдоль АС (см. рис. 42.6.2), равную
п Т I °
Ф] = Мас, = Мш1 2-. _
Аналогично, для кривошипа BD >
Ф2 = МапСг = мЯ.
Приравняем нулю суммы проекций всех сил на оси координат и суммы
моментов всех сил относительно осей координат, проходящих через точку Е:
1Хр + Хр — M\g — M\g + Ф] — Ф2 — Af2g = О,
Ye + Yf — 0, 1
-YF-2b = 0,
XF -2b + M\g(a -b) - Mig(b + a) - M2gb - Ф](a - b) - Ф2(Ь + a) = 0.
Решая систему уравнений, получим реакции подшипников: {
Yf = 0, Ye = 0, 1
Xf = ~^ [-M|g(a - b) + Mlg(b + а) 4- M2gb + Ф^а - Ь) + Ф2(6 4- а)] = 1
1 Мщ>2а1 Реше
— M}g + ~M2g 4----——, 1рав
. ®#l Cl
1 M}w2al
Хе — -XF 4- 2M\g + M2g - Ф| + Ф2 = M}g + -M2g-----——. X
2 2b c
Согласно закону равенства сил действия и противодействия, силы давле- W
ния на подшипники в рассматриваемом положении вращающейся систе- ®нц
мы будут следующими:
1 М]Ш2а1
Ne = Mxg + -M2g----——
2 2b
1 MiW^al
Nf = M\g + -M2g 4---——
2 2b
9. Давление вращающегося твердого тела на ось вращения 317
Причем, если Ne > 0, то вектор Ne направлен вертикально вниз, если
Ne < 0, то вектор Ne направлен вверх. Вектор NF направлен вертикально
вниз.
Задача 42.7 (42.6). К горизонтальному валу АВ, вращающемуся
с постоянной угловой скоростью ш, прикреплены два равных, перпен-
дикулярных ему стержня длины I, лежащих во взаимно перпендику-
лярных плоскостях (см. рис. 42.7.1). На концах стержней расположены
шары D и Е массы m каждый. Определить силы динамического дав-
ления вала на опоры А и В. Шары считать материальными точками;
массами стержней пренебречь.
Ответ: Na = NB =
Решение. Расчетная схема — на рис. 42.7.2. Для составления урав-
нений равновесия механической системы в форме принципа Даламбера
добавим силы инерции точечных масс D и Е:
Фо = -тао, Фо=тш21; ФЕ =-таЕ, ФЕ = ти21.
Для определения динамических составляющих реакций подшипников
в уравнениях равновесия учтем лишь силы инерции
х(£ + X + ФЕ = О,
у(А + YB} + Фр = О,
Y^} • 6а + Фр 2а = О,
k -Х{в} • 6а - ФЕ • 4а = 0.
318 9. Давление вращающегося твердого тела на ось вращения
=> Х^ = -|фд = -|таЛ,
X? =
Уд} = = -|пиЛ,
У<д) = -у^ - Фп = -^ттш21.
Силы динамического давления вала на подшипники А и В:
Na = \J (-Х^)2 + (У1Д))2 = ^-mw2l^ + = ^~-ттш21,
Nd = у/ (-^д)) + (^д^)2 = J + = ^-тпш21.
Заметим, что силы динамического давления не зависят от положения
вращающейся системы.
Задача 42.8 (42.7). К вертикальному валу АВ, вращающемуся с
постоянной угловой скоростью ш, жестко прикреплены два стержня.
Стержень ОЕ образует с валом угол <р, стержень OD перпендикуля-
рен плоскости, содержащей вал АВ и стержень ОЕ. Даны размеры:
ОЕ = OD = I, АВ = 2a. К концам стерж-
ней прикреплены два шара Е и D массы m
каждый (рис. 42.8.1). Определить силы дина-
мического давления вала на опоры А и В.
Шары D и Е считать точечными массами;
массами стержней пренебречь.
Л , mlw2
Ответ: ХА = Хв = ,
mlw2(a — I cos <р) sin <р
Yл —--------------------
2а
т1ы2(а + I cos <р) sin р
Уд = -------------------
2а
Решение. Расчетная схема — на рис. 42.8.2. Используя принцип
Даламбера, составим уравнения для определения динамических составля-
9. Давление вращающегося твердого тела на ось вращения 319
Рис. 42 8.2
ющих сил реакций опор Л и В:
' Х?* + Х{*} + Фр = О,
Г]д) + + Фр = О,
< = О,
- Урд) • АВ - ФЕ(АО + ОЕ cos <р) = О,
. xff • АВ + Фр • АО = 0.
Здесь величины сил инерции точечных масс D и Е следующие:
— manD = тпы21, ФЕ = mde — mw2l sin ip.
Решая систему уравнений, получаем:
АО 1 2,
Х{в} = -^$D = --mu I,
Л1У д
ха = ~хв - ^ = -'-mu2l,
= --^ФЕ(АО + ОЕ cos <р) = --^-тш21 sin <p(a + l cos <р),
= -КдД) - ФЕ = — mw2l sin <p(a + l cos <p) - mw2l sin tp =
2 I cos <p — a
= ты I sin <p--------,
2a
= 0.
320 9. Давление вращающегося твердого тела на ось вращения
9
Согласно закону равенства сил действия и противодействия, выпи-
шем силы динамического давления вала на опоры А и В:
1 2
Fax = FBx = -mu I,
mwH sin tp (a — I cos <p)
Fa’ =----------Ta---------
Faz = o,
ггш21 sin <p (a + I cos p)
Fny =
2a
Задача 42.9 (42.8). Использовав условие задачи 34.1, определить
силы динамического давления коленчатого вала на подшипники К
и L. Вал вращается равномерно с угловой скоростью ш. При решении
можно воспользоваться ответами к задачам 34.1 и 34.23.
3 a + b > v 3 a + b
Ответ: Хк = -XL = ш , YK = —YL = ~md— -ш2.
2 4a + 3b 2 4g + 3b
Решение. Расчетная схема — на рис. 42.9.1 и 42.9.2. Массы колен
коленчатого вала, вращающегося равномерно, сосредоточены в точках Л,
В и D. Поэтому имеем три силы инерции, приложенные в этих точках:
К[
fr
fr
vW
'I
(4<
Фд = -mAanA, Фп = -тпдав, Фу, = -mDaB;
i?
Рис. 42.9.1
9. Давление вращающегося твердого тела на ось вращения 321
Составим уравнения равновесия для определения динамических состав-
ляющих реакций подшипников К и L:
Х{£} + X? + Фл cos 60° + Фв cos СО" - Фв = 0,
+ Yi? + cos30° _ ®в cos30° = 0,
- Y?\4a + 3b) - Фл cos 30° ^а + -+ Фд cos 30° ^2а + -b) = 0,
Х^ (4а + ЗЬ) + Фл cos 60° (а + |) +
( 3 \ ( 5 \
+ Фдсо5бО° I 2а + -bi -Фр! 3a+-bl =0.
Х^ = —-— - ^л cos 60 f a + - Фв cos 60е ( 2а + -Ь j +
ь 4а + ЗЬ [ у 2 / \ 2 )
( 5,'
4-Фд I За + -Ь
3 a + Ь 2 .
-------то а,
2 4а + ЗЬ
Ад) _ 1
L
= -X?* - Фл cos 60° - Фд cos 60° + Фр =
= - |фл - + Фо = -X? =
( 3 \'
+ Фд cos30° I 2а + -Ь)
-Фл cos 30° ( а + -
4а + ЗЬ[ \ 1 2
1 2 х/З ( Ь 3 \ а + Ь 2, хЗ
-------mu) d- —- I —а — — + 2а + — Ь I — - -—-тпы d ,
4а + ЗЬ 2 \ 2 2 J 4а + ЗЬ 2
322 9. Давление вращающегося твердого тела на ось вращения
= -YP - Фл cos 30° - Фв cos 30° =
в + b
4a + 3b
2 V3 2 V3
mw d -----mw d -----2 = -
2 2
a + b
4a + 3b
2 V3
mu d----
2
Согласно аксиоме равенства сил действия и противодействия, находим
силы динамического давления коленчатого вала на подшипники К и L:
„ 3 a + b 2
Fkx = -Flx = ----
2 4a + 3b
„ „ v3 a+b ,
FK, = -Fl, = d.
Задача 42.10 (42.9). Однородный стержень KL, прикрепленный в
центре под углом а к вертикальной оси АВ, вращается равноускорен-
но вокруг этой оси с угловым ускорением е (рис. 42.10.1). Определить
силы динамического давления оси АВ на подпятник А и подшип-
ник В, если: М — масса стержня, 21 — его длина, О А — О В — h/2;
ОК = OL = I. В начальный момент система находилась в покое.
_ Ml2 Ml2 , ,
Ответ: Хв = -ХА = —— е sin 2a, YB = —YA = -—e t sin 2a.
bn bh
Решение. Расчетная схема — на рис. 42.10.2. Систему координат
Oxyz свяжем с вращающейся механической системой. Стержень KL рас-
положен в плоскости Oyz.
При определении сил инерции частиц системы разобьем стержень
KL на два одинаковых стержня КО и OL и воспользуемся рассужде-
ниями в решении задачи 41.21. В результате получим для стержня КО
9. Давление вращающегося твердого тела на ось вращения 323
равнодействующую силу инерции
М _
Ф> = -у ас,,
2 2
приложенную в точке Е (ОЕ = -ОК = -Z). Точка С\ — центр масс
стержня КО. Причем
ДТ _
Ф1 = — у (ас, + ас,) — Ф" + Ф]\
Вектор Ф" направлен параллельно оси Оу в сторону от оси вращения Oz
и равен по величине
„ М п М 21 .
Ф1 = у«с, = уш - sin а.
Вектор Ф[ направлен параллельно оси Ох в противоположном ей направ-
лении, так как касательные ускорения точек стержня КО сонаправлены
с осью Ох. Величина его равна
_ m _ m I .
Ф1 = ^-ас, = — Е- sin a.
1 2 1 2 2
324 9. Давление вращающегося твердого тела на ось вращения
Учитывая, что равноускоренное вращение системы начиналось из со-
стояния покоя, получаем величину угловой скорости w = st. Поэтому
Ф" = —ГГ- sin a.
2 2
Аналогично, для стержня OL:
- I п Г т п -М 7 М^ 7 7^
Ф2 = Ф2 + Ф2, Ф” = -or- sin a = —-£2r- sin a,
2 2 2 2
т Ml 2 2
Ф2 = — е- sin a, OF — -OL = -I;
1 2 2 3 3
вектор Ф2 направлен в сторону оси Оу параллельно ей, вектор Ф2 парал-
лелен оси Ох и направлен в ту же сторону.
Составим уравнения равновесия для определения динамических со-
ставляющих реакций в опорах А и В:
' х^’ + х^ + ф^-ф; = о, у]д)+у^д)-ф?+ф?-о, z^=o,
< ~yb 'h + ®\ ( 2 ~ ^cos«) — Фг( у + -lcosa] =0,
(h 'I. \ X 2 \
— - -I cosa j +Ф2 ( - + -Zcoso j —0.
2
-I cos a
3
-ф;
h 2
— + -I cos a
2 3
1 M I 4 M 2
= — £-sina--Icosa —-----cl sin2o,
h 2 2 3 6h
y(^) _ хг(д) г.
— Л.— Ф2 "Ь — —Ар — sin2о,
6л
YB} - ^Icosaj -Ф" ^y + |/cosa^
М 2 , 2
-—cil2 sin 2а,
6/г
<<*> = _у<") +Фп _ ф$ = _Г(Д) = M£Vz2sjn2Q)
6/z
Поэтому силы динамического давления на подпятник А и подшипник В
следующие:
М 2
FBl = ~FAx = —El sin 2a,
о/г
JVi э •> *>
Fbj, = -FAy = —e tГ
oil
sin 2a,
FAz = 0.
9. Давление вращающегося твердого тела на ось вращения 325
Задача 42.11 (42.11). Однородная прямоугольная пластинка OABD
массы М со сторонами а и Ь, прикрепленная стороной ОА к валу
ОЕ, вращается с постоянной угловой скоростью о>. Расстояние между
опорами ОЕ = 2а (рис.42.11.I). Вычислить боковые силы динамиче-
ского давления вала на опоры О и j?.
3 1
Ответ: NOx = NEx = 0, NOy = -Mbw2, NEy = -Mbw2.
О о
Решение. Расчетная схема — на рис. 42.11.2. Применим принцип
Даламбера для системы. Для этого силы инерции точек однородной пла-
стинки, вращающейся равномерно, приведем к точке О|. В результате
получим главный вектор сил инерции, приложенный к точке О\, и глав-
ный момент сил инерции относительно точки О\:
Ф = —Mac — ~М {etc 4- Gc) =
(точка С — центр масс пластинки; а^ = 0, так как a> = const), Ф = Мо?2Ь/2;
' ^й = EJ™ ~ = °’
< ЬЙ=е^+^^ = 0’
. < = - 0
(так как е = 0 и ось O\Z является главной осью инерции пластинки для
точки 01 в силу того, что она перпендикулярна плоскости материальной
симметрии пластинки О^ху).
326 9. Давление вращающегося твердого тела на ось вращения
Составим уравнения равновесия для определения динамических со-
ставляющих реакций опор О и Е вдоль осей х и у.
' х(оа) + х(/ = О,
Yoa) + + Ф = О,
- У^д) • 2а - Ф- = О,
Е 2
k Х^д) • 2а = О
(суммы моментов сил записаны относительно осей координат Ох и Оу).
Решаем уравнения:
Х^д) = 0, Х(о} = О,
ye] = -7 = Y$} = -Ф - Y™ = -|w|.
Следовательно, боковые силы динамического давления вала на опоры О
и Е имеют вид;
ЕОх = ЕЕх = 0, ЕОу = ^Мщ2Ь, FEy = | МсЛ.
о о
Задача 42.12(42.10).
Прямой однородный круглый цилиндр мас-
сы М, длины 21 и радиуса г вращается с постоянной угловой скоро-
стью ь) вокруг вертикальной оси Oz, проходящей
через центр масс О цилиндра (рис. 42.12.1); угол
между осью цилиндра О( и осью Oz сохраня-
ет при этом постоянную величину а. Расстояние
Л|Н2 между подпятником и подшипником равно
h. Определить боковые силы давления: N} на под-
пятник и Л’2 на подшипник.
Ответ: Давления Nt и Nz имеют одинаковую ве-
личину
о? sin 2а
М--------
2h
и противоположны по направлению.
Решение. Расчетная схема — на рис. 42.12.2. Приведем силы инер-
ции точек цилиндра к точке О. Получим, что главный вектор сил инерции
Ф = Мас = О,
9. Давление вращающегося твердого тела на ось вращения 327
совпадает с неподвижной
так как центр масс С однородного цилиндра
точкой О.
Распишем проекции главного момента сил инерции относительно
точки О:
Lq-c = fxz - = -^-Jyz,
L(0y} =eJyz+u2Jxz = 0,
= -eJz - 0,
так как e = w = 0 и центробежный момент инерции Jxz — 0 (ось Oz,
будучи перпендикулярной плоскости материальной симметрии цилиндра
Oyz, является главной осью инерции цилиндра для точки О}. Вычислим
центробежный момент инерции
7j/z - ^кЗ/к^к-
к
Для этого перейдем к системе координат OfrjC, (см. рис. 42.12.2), оси ко-
торой есть главные оси инерции цилиндра.
328 9. Давление вращающегося твердого тела на ось вращения
Выпишем координаты произвольной частицы цилиндра Мк массой
тк в системе Oxyz через координаты в системе О£,уС'-
Ук = ОМК sin (а + <рк) = —sin (а + <рк) =
cos <рк
= ———(sin a cos <рк + cos a sin <pK) =
cos ipK
= (K(sin a + cos a tg <pK) = sin а • (K + cos a yK, ~
Ck
zK — OMK cos (a + ^K) =-------(cos a cos <pK - sin a sin <pK) =
COS
= cos a • Ck _ sin a yK.
==> Jyz = У? ткЗ/к-гк = 5У raK(C sin a + yK cos a)«K cos a-yK sin a) =
К к
= sin a cos a — sin a cos a • У^ тпку1 —
К к
- sin2 a • mK(KJ2K + cos2 a У^ mK<Kj?K =
К к
1 1 /22
— - sin la JOfr] - - sin 2a • Jo^ + (cos a - sin a) J^Tj.
Центробежный момент инерции
J(ri — = 0,
К
так как оси ОС, и Оу — главные оси инерции.
Вычислим моменты инерции относительно координатных плоскостей
Jofr и Jop;- ПРИ определении Jo^ произведем разбиение цилиндра на
элементарные диски толщиной dC, находящиеся на расстоянии С от плос-
кости О(т]. Получим:
Г 2 f 7М Ml1
Jo(, = J С dm = J
(M) -I «JJbTi
При определении Jo^ произведем разбиение цилиндра на элементар-
ные прямоугольные пластины, находящиеся на расстоянии у = —rcosip
от плоскости ОСС, толщиной
Г1авн
dy = г sin (р dip
(см. рис. 42.12.3), высотой 21 и шириной 2r sin <р.
9. Давление вращающегося твердого тела на ось вращения 329
Рис. 42.12,3
Получим:
Jo« = j У2 dm =
(М)
7Г
= / (-г cos <р)2 —7----21 2г sin tp • г sin 92 d<p =
J irr2 21
0
f Mr2 , Г Mr2 . A x J Mr2
= / sin2 2<pd<p = I (1-cos 492)^92 =-y-.
о 0
В результате получим искомый центробежный момент
1 . /Ml2 Мт2\
Jyz — 2 s*n ?а у ”з J '
Главный момент сил инерции цилиндра относительно оси Ох:
(ин) 2 . (l2
LOx = — 2 sin 2° 3
330 9. Давление вращающегося твердого тела на ось вращения
Составим уравнения равновесия для определения боковых динамических
реакций подпятника и подшипника:
f^?+x"=o> г«+г«=о,
=> 4"> = Х« = 0, yW = -^si„2a^_^\ Г« = -Г«
Поэтому боковые силы давления на подпятник и подшипник равны по
величине:
Мы2 (I2 т2\
N\ = Ni = —— sin 2а------I.
2/i \3 4 J
Замечание к задаче 42.12. При вычислении центробежного момента Jyz можно
было воспользоваться известной формулой [4,11]:
sin2а sin2а /Ml2 Мг2\
•fyz = ~ = 2 \—3 4~ / ’
Задача 42.13(42.11). Вычислить силы дав-
ления в подшипниках А и Б при вращении
вокруг оси АВ однородного тонкого кругло-
го диска CD паровой турбины, предполагая,
что ось АВ проходит через центр О диска
(рис. 42.13.1), но вследствие неправильного
Рис. 42.13.1 рассверливания втулки составляет с перпен-
дикуляром к плоскости диска угол АОЕ =
= а = 0,02 рад. Дано: масса диска 3,27 кг, радиус его 20 см, угловая
скорость соответствует 30 000 об/мин, расстояние АО = 50 см, ОБ —
— 30 см; ось АВ считать абсолютно твердой и принять sin 2а = 2а.
Ответ: Силы давления от веса диска: 12,1 Н на подшипник А и 20,0 Н
на подшипник В', силы давления на подшипники, вызываемые враще-
нием диска, имеют одинаковую величину 8,06 кН и противоположные
^направления. ,
Решение. Расчетная схема — на рис. 42.13.2. Угловая скорость рав-
номерного вращения системы
27г • 30 000 / рад
щ =-------------- ЮООтг I -----
60 \ с
Приведем силы инерции диска к точке О. Так как центр масс С диска, сов-
падающий с точкой О, лежит на неподвижной оси вращения, то главный
вектор сил инерции Ф = mac = 0-
9. Давление вращающегося твердого тела на ось вращения 331
Ось Оу — ось симметрии диска. Поэтому эта ось является главной
осью инерции диска и центробежный момент Jyz — 0. Также, учитывая,
что угловое ускорение е — 0, получаем для главного момента сил инерции
диска относительно точки О следующие составляющие:
~ °’ LOy ~ W LOz — u-
Для вычисления центробежного момента Jxz, выразим координаты произ-
вольной точки диска массой тк в системе Oxyz через ее координаты в си-
стеме главных координатных осей Система OfpyC получается при
повороте системы Oxyz на угол а вокруг оси Оу (Оу) (см. рис. 42.13.2,
ось ОС, перпендикулярна плоскости диска, ось Оу (Оу) — вдоль диаметра
диска).
жк = Ск cos a, zK = £к sin a =>
> y mKxKzK
К
- - sin 2a • JOy
к
mr2
=-----sin 2a =
8
mru
sin 2a ~-----a,
4
mr2w2
8
так как по условию sin 2a » 2a.
Для определения статических реакций подшипников в уравнениях
равновесия, вытекающих из принципа Даламбера, учтем только силу тя-
г(ин) _
hoy -
жести диска.
' Х\ст) + х£} - mg = 0,
У*ст) + ув'} = °’
- У^ст) • АВ = 0,
xJT) • АВ - mg • АО = 0.
332 9. Давление вращающегося твердого тела на ось вращения
Отсюда
у^ст) = у}ст) = о,
/ст\ АО 0,5
4 ’ = = 3’27 •9’8^ ~ 20 <Н>’
Ab U,о
xJT) = mg - ^ст) й 12,1 (Н).
Следовательно, силы давления от веса диска на подшипники А и В равны
соответственно 12,1 Н и 20 Н.
Для определения динамических реакций подшипников в уравнениях
равновесия, вытекающих из принципа Даламбера, учтем силы инерции
X яШк
диска:
У^д) = у<д) = 0,
г(ин)
Y(n) _ Loy
в ~ АВ ~
4° + Х^ = 0,
У*д) + У^ = о,
- У^д) • АВ = 0,
Х(в} АВ + = 0.
тг2щ2а 3,27-0,04-1067г2-0,02 , ч
---777“ = —-------’ 7---------— ~ -8060 (Н),
4ДВ-----------Л п °------------' '
ГР к 8060 (Н).
4-0,8
t
я
и
ц
лз
VI
№
Следовательно, силы давления на подшипники, вызываемые вращением
диска, имеют одинаковую величину 8,06 кН и направлены противопо-
ложно.
Задача 42.14(42.14). В результате неточной сборки круглого диска
паровой турбины плоскость диска образует с осью АВ угол а, а центр
масс С диска не лежит на этой оси (рис. 42.14.1). Эксцентриситет
ОС = а. Найти боковые силы динамического давления на подшипни-
ки А и В, если масса диска равна М, радиус его R, а АО = OB = h;
угловая скорость вращения диска постоянна и равна ш.
Указание. Воспользоваться ответом к задаче 34.27
Ответ: Ул = YB = 0, ХА = -
sin 2а
--------F a cos а
2h
М Г / R2 Л sin 2а
Хв = — — + а ) -----------a cos о
2 \ 4 / 2h
9. Давление вращающегося твердого тела на ось вращения 333
Рис. 42.14.1
Рис. 42.14.2
Решение. Расчетная схема — на рис. 42.14.2 (оси Оу и Су\ направ-
лены перпендикулярно плоскости рисунка на нас). Приведем силы инер-
ции точек диска к точке О. Получим главный вектор сил инерции
Ф = -Мас,
приложенный к точке О и равный по величине
Ф = Мы2 a cos а,
а также главный момент сил инерции относительно точки О При
вычислении центробежных моментов диска воспользуемся ответом к за-
даче 34.27. Учтем, что угловое ускорение е = 0. Поэтому составляющие
главного момента сил инерции будут иметь вид:
т(ин) п г(ин) 2 М т f Г~ । 2^ г(ин) л
Ьо/=°, LOy = ш У s,n2a- ( 7+о J’ LOZ по-
выпишем уравнения равновесия для определения динамических реакций
подшипников:
' ХА} + ХВ - Ф = 0,
уЛд) + Y(/ = 0,
- Y^} -2h = Q,
_ 2h - ФЛ + = 0.
Получаем
jAa) = уМ) = 0,
X%} = -Ф - — = -Мш2а cos а - -МоД ( Г— + аЛ sin 2а,
в 2 2h у 2 4 Л \ 4 )
334 9. Давление вращающегося твердого тела на ось вращения
Х^ — Ф — = -Мш2а cos а + -Мш2 — (--h о2>) sin 2а.
А в 2 4 А \ 4 /
Поэтому боковые силы динамического давления на подшипники вдоль
оси Оу равны нулю, а вдоль оси Ох следующие:
М 2
FBx = — ш
Ha
On
IlK
/ г2 2\ sin
|----|-а I--------1- a cos а
. \ 4 J 2h
(г2 s*n 2а
----ho I---------о cos а .
4 J 2h
Задача 42.15(42.15). Однородный круглый диск массы М и ра-
диуса R насажен на ось АВ, проходящую через точку О диска и
составляющую с его осью симметрии Czi угол а (рис. 42.15.1). OL —
проекция оси z, совмещенной с осью АВ, на плоскость диска, причем
ОЕ = а, ОК — Ь. Вычислить боковые силы динамического давления
на подшипники А и В, если диск вращается с постоянной угловой
скоростью ш, а АО = О В = h.
-P
Й
aj
’.a
ш
H’
TO
T
in
m
i
Рис. 42.15.1
Указание. Воспользоваться ответом к задаче 34.27.
1 2 М
Ответ: ХА — —Маш cos а - —
2 4Л.
. -В2 + а2 ) ш2 sin 2а,
4Л \ 4 7
1 2 м (
Хв = —Маш cosa-|—-|
2
Mb / а \ 2
Ya =----I 14— sin а I ш ,
2 \ h )
1 9 9 \ 9
. -л + а ) ш sin 2а,
4Л \ 4 /
Mb
Т
С I 2
1-----sin а
h J
Решение. Приведем силы инерции точек однородного круглого
диска к точке О, лежащей на неподвижной оси вращения. Получим два
вектора, приложенные к этой точке: главный вектор сил инерции Ф
т^(ин)
и главный момент сил инерции относительно точки (J Lo .
9. Давление вращающегося твердого тела на ось вращения 335
На рис. 42.15.2 изображена плоскость диска.
Определим главный вектор сил инерции дис-
ка. Так как ш = const, то
Ф = -Мас, Ф = Mu2d
(d — расстояние от центра масс диска С до оси
вращения Oz). Ось Oz составляет с плоскостью
диска угол 7г/2 - а. Проекцией оси Oz на плос-
кость диска является прямая OL. Оси Oz и Су\
скрещиваются под прямым углом, поэтому про-
водим через прямую Су\ плоскость, перпендику-
лярную оси Oz. Тогда проекцией прямоуголь-
ного треугольника ОЕС на эту проведенную
плоскость является прямоугольный треугольник
О'ЕС, изображенный на рис. 42.15.3. Расстояние
от центра масс С до оси вращения Oz равно
d = СО' = у/(Р'ЕУ + (ЕСУ =
= yj (ОЕ cos аУ + (ЕС)2 =
= yj(a cos а)2 + Ь2.
Рис. 42.15.3
Следовательно,
Ф = Мы1 у](a cos а) + b2.
Так как вектор Ф перпендикулярен оси Oz, то
ф = Фх + Фу,
где
ЕС Ь
Ф^-Фбщ/З, Фу = - Фсоб/З, cos/3 =
СУС/ U
О'Е a cos а
sin 0 =---=-------- (см. рис. 42.15.2 и 42.15.3).
н О'С d х
Определим проекции главного момента сил инерции Lo на оси ко-
ординат системы Oxyz:
' = -i^Jyz = -w2Mabsin а,
• !.V ri,,
14"."’ = °-
sin a cos a,
Здесь воспользовались ответом к задаче 34.28.
336 9. Давление вращающегося твердого тела на ось вращения
Теперь составим уравнения равновесия, вытекающие из принципа
Даламбера. Приравняем нулю суммы проекций сил на координатные оси [
и суммы моментов сил относительно координатных эсей, проходящих
через точку А:
' х? + х$ + Фх = О,
у^ + у^ + ф^о,
< Ф<д) = о,
- у^>. дв + |ф, |-до+ 4f = о,
• ДВ-|ФХ|-ДО+ £^н) = 0.
=> 4Л)(км-ло
1 / 2 ГЪ----э--77 ucosu
— I Мм х/ a1 cos- а + о2 . А , h -
2ft \ Va2 cos2a + b2
- w2M \ -R2 + а2 | sin a cos a ) =
1 j 1 2 ( 1 2 2 A
= -Mw a cos а--mu) I -R +а I sin 2a,
2 4ft \4 J
х{*} = -ъх-х$ =
= -Macacosa4 Mw2(-R2 + a2 | sin2a,
2 4ft \4 J
Yb} = -^^-AO + Lo^ =
№
'I
III
4
и
и
И
— ( Mw2\/a2 cos2 a + b2 • . . . h — w2Mabsina
2ft \ Va2cos2a + ft2
1 2 I u i
= -Mu ft 1------sina ,
2 \ ft J
Yia} - -Mw2b| 1 + ^sina).
2 \ ft /
Динамические силы бокового давления на подшипники Д и В будут
равны реакциям связей со стороны подшипников и противоположны им
по направлению.
9. Давление вращающегося твердого тела на ось вращения 337
Задача 42.16(42.12). Однородная прямоугольная пластинка мас-
сы М равномерно вращается вокруг своей диагонали АВ с угловой
скоростью ш (рис. 42.16.1). Определить силы динамического давления
пластинки на опоры А и В, если длины сторон равны а и Ь.
—МаЬш-Чал-Ь2) МаЬш2(а2 — Ь2')
Ответ: *л = 0, ул = —А— хв = 0, YB= ЛЛЗ//
12(а2 + 62)3/2 \2(а2+Ь2у/-
Решение. Расчетная схема — на рис. 42.16.2. Пластинка все время
находится в координатной плоскости Cyz.
Приведем силы инерции точек пластинки к точке С, являющейся
центром масс пластинки и лежащей на неподвижной оси вращения z.
Поэтому главный вектор сил инерции Ф = 0.
Распишем проекции главного момента сил инерции пластинки от-
носительно точки С, учитывая, что w = const:
г(ин) _ 2т г(ин)_,,Гт г(ин) _ л
Так как ось Сх, будучи осью симметрии пластинки, является ее главной
осью инерции, то центробежный момент Jxz = 0. Поэтому = 0.
Рис. 42.16.2
338 9. Давление вращающегося твердого тела на ось вращения
Вычислим центробежный момент инерции Jyz. Для этого, повернув
a
вокруг оси Сх систему координат Cxyz на угол a = arcsin —=
Val + b2
получим систему CxyiZi, оси которой — главные оси инерции пластинки.
Далее воспользуемся известной формулой [4, 11]:
z ч . (Mb2 Ma2\ a b
zx) sin a COS a — I ~ I ....—.. ।
v v y' \ 12 12 J y/^WVa^+b2
Поэтому
r (ин) _ 2 J _ Mw2 ab(a2 - b2)
Cx ~ 12 o, + b2 •
Составим уравнения равновесия для определения динамических реакций
подшипников:
’ ХР + Х{в} = О,
Ya} + Yb} = °’
Y^-AB + L{""} = 0, =*
k -Х(в} • AB = 0.
=> X%} = X{B} = 0,
(д) _ L(c"} _ Мы2 ab(a2 -b2) 1 _ Мы2 ab(a2 - b2)
Yb ~~~aJb~ 12 a2 + b2 ' Va^+b2 ~ 12~ (a2 + b2)3/2’
Y(a) = _у(д) Мш2 ab(a2 - b2)
A B 12 (<z2 + b2)3/2'
Силы динамического давления пластинки на подшипники:
Mu2 ab(a2 - b2)
Fax = FBx = 0, FAy = -FBy = — •
Рис. 42.17.1
Задача 42.17(42.13). С какой угловой ско-
ростью должна вращаться вокруг катета АВ = a
однородная пластинка, имеющая форму рав-
нобедренного прямоугольного треугольника
ABD (рис. 42.17.1), чтобы сила бокового дав-
ления на нижнюю опору В равнялась нулю?
Расстояние между опорами считать равным
длине катета АВ.
Ответ: ш = 2лЛ/а-
9. Давление вращающегося твердого тела на ось вращения 339
Рис. 42.17.2
Решение. Расчетная схема — на рис. 42.17.2. Если привести силы
инерции пластинки к точке О, то получим:
Ф *= -Мас,
Ф = Мш ОС = Мш1-;
3
Г (ин) 2 т
L0x ~ Ш
= 0.
#=0.
так как ось Ох — главная ось инерции пластинки для точки О {Ох пер-
пендикулярна плоскости материальной симметрии пластинки), а потому
JXZ = 0.
Для определения Jyz перенесем систему координат Oxyz поступа-
тельно в точку С и повернем вокруг оси Сх на угол а — л/4. Получим
систему координат Cxiy^zi, оси которой являются главными осями инер-
ции пластинки. Поэтому [4,11]:
sin 2а
Jyz — МхсУс + {Jz\ ~ Jyi) 2
Нетрудно заметить, что
вД'2 . г- ч -.3 ,
f 1 М (ау/2 \ , Ма1
Jz'^ J 12T~;[2VT-Z7] dZ' ~ 12
о 2°
340 9. Давление вращающегося твердого тела на ось вращения
(разбиение на элементарные полоски, параллельные стороне BD и пер-
пендикулярные оси Kz\). По теореме Штейнера
Jy, = Je - М СК2,
где
(провели разбиение на элементарные полоски, перпендикулярные оси В£,
проведенной вдоль стороны BD). Поэтому
Ma2 faV2\2 Ma2
Jy>
Центробежный момент инерции
/Ma2 Ma2\ sin(тг/2) Ma2
Jyz ~ \~T2 36~J 2 = 36 ’
Следовательно,
r(»H) ,2T Ma2w2
Lox ~ Ш Jyz — 36 •
Запишем уравнения равновесия, в которых учтем условие задачи о равен-
стве нулю величин и Yff.
' = 0,
У^д) + ф = 0,
<
• АВ - Ф • OB + - Mg • ОС = 0,
ь Х(д} • АВ = 0.
Исключая из полученных уравнений получим уравнение для опре-
деления угловой скорости ш:
Ф-АВ-Ф-OB + lff-Mg-OC^O =>
а Ma2w2 а
Мы--------------Mg- = 0.
3 3 36 ^3
Отсюда ш = -
V а
9. Давление вращающегося твердого тела на ось вращения 341
Задача 42.18(42.14). Вращающаяся часть подъемного крана со-
стоит из стрелы CD длины L и массы М\, противовеса Е и груза К
массы Mi каждый. (См. рисунок к задаче 34.31.) При включении по-
стоянного тормозящего момента кран, вращаясь до этого с угловой
скоростью, соответствующей п= 1,5 об/мин, останавливается через 2 с.
Рассматривая стрелу как однородную тонкую балку, а противовес
с грузов — как точечные массы, определить динамические реакции
опор Ли В крана в конце его торможения. Расстояние между опорами
крана АВ = 3 м, М2 = 5 т, М\ = 8 т, a = 45°, L — 30 м, I — 10 м,
центр масс всей системы находится на оси вращения; отклонением
груза от плоскости крана пренебречь. Оси х, у связаны с краном.
Стрела CD находится в плоскости yz.
Указание. Воспользоваться ответом к задаче 34.31 (положив М2 = М2).
Ответ: УА = -УБ = 0, Хв = -ХА 60,8 кН.
Решение. Расчетная схема — на рис. 42.18.1. Приведем силы инер-
ции вращающейся части крана к точке А. В результате получим, что
главный вектор сил инерции Ф = 0, так как
Ф -- -Мас,
но точка С лежит на неподвижной оси вра-
щения.
Распишем проекции главного момента сил
инерции:
' r(™) 2 — eJxz
г(ин) = € Jyz “Ь Jxzi (0
г (ин) bAz = ~ejz.
Определим угловое ускорение е. Так как
тормозящий момент постоянен, то и е = const.
Поэтому щ = Шо + et. С учетом того, что через
время t* = 2 с кран остановился, имеем:
Рис. 42.18.1
(До
= -0,078 (1
60t* 60 2 \с2
Воспользуемся ответом к задаче 34.31, положив М2 — М2:
з I 1 \ п . 7
Jz = M2a + ( М2 + -Мх I 2/ sin a,
342 9. Давление вращающегося твердого тела на ось вращения
1
2
1
М2 + -Mi
2
L sin 2a — М2Ы sin a,
Jyz —
В рассматриваемый момент, т. е. в конце торможения, ш = 0. Поэтому
формулы (1) примут вид:
г(™) _ Л г(ин)_,Т г(ин) —
LAx — U’ L Ay — £jyz, ^Az — Jz-
Запишем уравнения равновесия для определения динамических ре-
акций опор А и В :
' Х\д) + Х(в} = 0,
удД) + У(в} = °>
* z^ = о,
-y£} -ab = q,
, Х^} • АВ + bf”’ = 0.
(2)
Заметим, что из ненаписанного здесь уравнения для суммы моментов сил
относительно оси Az можно определить величину тормозящего момента.
Решая уравнения (2), получим:
Y^ = -Y^ = 0, = 0,
у<Д) _ _
ЛВ — ЛА —
т (ин)
LAy
АВ
eJyz
АВ
х 1 Г 1
-(-0,78). j -
5000 + | • 8000
900 sin 90°-
- 5000 -30-10 sin 45° w 61 (кН).
10. Смешанные задачи (§ 43, [10])
Задача 43.1 (43.1). Однородная тяжелая балка АВ длины 21 при
закрепленных концах находится в горизонтальном положении. В не-
который момент конец А освобождается, и балка начинает падать,
вращаясь вокруг горизонтальной оси, проходящей через конец В
(рис. 43.1.1); в момент, когда балка становится вертикальной, осво-
бождается и конец В. Определить в последующем движении балки
траекторию ее центра масс и угловую скорость ш.
Рж. 43.1.1
2 2
Ответ: 1) Парабола у = 31х — 31 ;
момента относительно
Решение. На рис. 43.1.2 изображена балка при ее движении с за-
крепленным концом В. Балка вращается вокруг горизонтальной оси Bz.
Применим теорему об изменении кинетического
оси Bz:
M(2l)2
JBz<p = Mgl cos ip, где JBz = —j—
Проинтегрируем составленное дифференци-
альное уравнение вращения балки, переписав его
в виде:
с
Mg-
х Т
Рис. 43.1.2
Bz у
dip 3 g
-- -- COS W.
dt 41 Y
Исключим время t:
.dip 3 g
ip--- = - - COS W
r dip 41
1 dip1
2 dip
3 g
47СО^
Л-/2
- COS
3g
21
2
о
о
344
10. Смешанные задачи
Получили, что в тот момент, когда балка вертикальна и освобождается
ее конец В, угловая скорость балки равна ш = у]3g/(21). Линейная
скорость центра масс С в этот момент равна Vc — = \Z3glj2.
Составим дифференциальные уравнения плоского движения балки
после освобождения ее конца В. Для этого применим теорему о движении
центра масс балки С и теорему об изменении кинетического момента
балки в ее относительном движении по отношению к центру масс:
I Мае = £/*>,
I к
| л ) __
I ,
V о-
Распишем дифференциальные уравнения:
Мхс = Mg, Myc = 0, JCzW = b. (1)
Начальные условия получим из результатов первого этапа движения балки:
жсо = I, Усо = 0, хСо = 0, усо =
а?0 =
Интегрируя уравнения (1) с учетом начальных условий, получим:
хс = |^2 + 1, ус = t, ы = у/|^ - const.
Поэтому уравнение траектории центра масс имеет вид:
Ус = 3lxc — 312, хс > 0 (ветвь параболы).
Замечание к задаче 43.1. Угловую скорость балки в конце первого этапа ее
движения можно было найти другим способом, применяя теорему об изменении
кинетической энергии в конечной форме:
к к
Здесь
Е4-0, То = 0, T=-^- = —v2, Y,Ak=Mgl.
к к
Поэтому
Отсюда
10. Смешанные задачи
345
Задача 43.2(43.2). Тяжелый однородный стержень дли-
ны I подвешен своим верхним конном на горизонталь-
ной оси О (рис. 43.2.1). Стержню, находившемуся в вер-
тикальном положении, была сообщена угловая скорость
Wo = Совершив полоборота, он отделяется от
оси О. Определить в последующем движении стержня
траекторию его центра масс и угловую скорость враще-
ния сд.
I/f
I
С
х I 2 2
Ответ: 1) Парабола ус = - - ^хс'’
Рис. 43.2.1
Решение. На рис. 43.2.2 изображен стержень на первом этапе его
движения, когда он вращается вокруг горизонтальной оси Oz. Диффе-
ренциальное уравнение его движения:
ml2 I
—р =-mg-sin <р =>
dtp 3g . .dp 3 g .
dt 21 y dp 21 *
1 ,.2 ^g . ___ 2 2 i
=> ^dtp = ---smtpdtp => сд -сд0 = 3—(-2).
Следовательно, в конце первого этапа, когда стержень, у ь
совершив полоборота, отделяется от оси Oz, его угло- !
вая скорость равна ~
______ __________ _____
w=J^=J-6f+,f=J4. ...<--------
V I V ‘ I V I х
а скорость центра масс С равна
л Рис. 43.2.2
и направлена противоположно оси Ох.
Составим дифференциальные уравнения плоского движения стержня
на втором этапе:
тхс = 0, тус = -mg,
ml2
----сд = 0.
3
(О
Начальные условия второго этапа движения:
Хсо = о,
Усо = хсо = ~у ~gl, Усо = 0, (До = у Зу
346
10. Смешанные задачи
Интегрируя уравнения (1) с учетом начальных условий, получим:
Хс = Ус = + |> W = const = ^/з|.
Исключая время t из найденных уравнений движения центра масс, полу-
чим уравнение траектории центра масс:
I 21 2 z
Ус = 2 “ (парабола).
Задача 43.3 (43.4). Два однородных круглых цилиндра А и В, мас-
сы которых соответственно равны М\ и М2, а радиусы оснований —
Г] и Г2, обмотаны двумя гибкими нитями, завитки которых рас-
положены симметрично относительно средних
плоскостей, параллельных основаниям цилин-
дров; оси цилиндров горизонтальны, причем
образующие их перпендикулярны линиям наи-
больших скатов (рис. 43.3.1). Ось цилиндра А
неподвижна; цилиндр В падает из состояния
покоя под действием силы тяжести.
Определить в момент t после начала дви-
Рис 43 3 1 жения, предполагая, что в этот момент нити
еще остаются намотанными на оба цилиндра:
1) угловые скорости и а>2 цилиндров, 2) пройденный центром масс
цилиндра В путь s и 3) натяжение Т нитей.
Ответ: 1) ад = —-----------t, аь = —;--------
7 r,(3M, + 2М2) г2(ЗМх + 2М2)
_ g(M, + М2) 2.
’ * ~ ЗМ, + 2М2 ’
M,M2g
3) т =---- .
( ’ ЗМ| + 2М2 )
Решение. Расчленим систему и рассмотрим отдельно движение ци-
линдров А и В (рис. 43.3.2).
Применив теорему об изменении кинетического момента относи-
тельно неподвижной оси O\Z, получим дифференциальное уравнение
движения цилиндра А:
Мхг\
-^-фх=Тхтх. (1)
Чтобы получить дифференциальные уравнения движения цилиндра В,
применим теорему о движении центра масс О2 в проекции на ось х
10. Смешанные задачи
347
У>2
X
Рис. 43.3.2
O2Z
и теорему об изменении кинетического момента относительно оси
(для относительного движения цилиндра):
MiXo2 = Mig — T2,
* Mir?
= T2r2.
Так как нити невесомые, то их силы натяжения равны по величине: Т\ — Ti.
Для определения кинематических соотношений построим мгновен-
ный центр скоростей Р цилиндра В (рис. 43.3.3).
В силу нерастяжимости нити Vk —
Из геометрических соображений можно записать:
РО1
РО2 - Г2
(2)
VO2
vk
Ур2Г2
Vo2 - Vk
Поэтому
vo2
и1=РОг
vo. - Vk Vo2 - Ш1Г1 . Хо. ~ Ф1Г1
----- = , ИЛИ <j>2 = ---
Г2--------------------------------------------Г2-Г2
В результате из уравнений (1) и (2) составим следующую систему:
М'гу -п _т
Pi — -ч,
2
М}Хо2 = Mig — Т\,
М2Г2 ХОг-ф1Г1
--------=
(3)
Решая систему уравнений (3) как алгебраическую с тремя неизвестными,
получим:
2(М, + М2) .. 2М2 _ MjM2
Х°2 ~ ЗМх+2М28' " г,(ЗМ, + 2М2)8, ' ~ ЗМ, + 2М28'
Итак, силы натяжения нитей
MtM2
т' = T1 = 3Mi+2M28'
348
10. Смешанные задачи
Интегрируя дифференциальное уравнение
2M2g
г г,(ЗМ, +2М2)
к
и
с нулевыми начальными условиями, получим угловую скорость цилин-
дра А:
2M2g
~ гх(ЗМх+2М2)1
Интегрируя дифференциальное уравнение
2(МХ + M2)g I
Х°2 3 ~ 3Mi + 2М2
с нулевыми начальными условиями, получим
2(М] + M2)g (Мх + M2)g 2
хо, —-----------1 и Хп, =------------1 .
2 ЗМ2 + 2М2 2 ЗМХ+2М2
Следовательно, угловая скорость цилиндра В равна
хо, ~ Ф\гх 2Mxg
* т2 г2(ЗМ\ + 2М2)
а пройденный центром масс О2 цилиндра В путь s равен
(Мх + M2)g .
S = Хп, = ---------1 .
2 ЗМХ + 2М2
Задача 43.4(43.5). Однородный стержень АВ длины а поставлен
в вертикальной плоскости под углом 9?о к горизонту так, что концом А
он опирается на гладкую вертикальную стену, а концом В — на глад-
кий горизонтальный пол (рис. 43.4.1); затем стержню предоставлено
падать без начальной скорости. 1) Определить угловую скорость и уг-
ловое ускорение стержня. 2) Найти, какой угол
9?1 будет составлять стержень с горизонтом в тот
момент, когда он отойдет от стены.
/3g
Отзэт: 1) ф — \ —(siny?o _ sin у?);
V a
3g
2) <Р = ~—cos<p-
2a
. 2 .
3) sin 9?i = - sin 9?o-
10. Смешанные задачи
349
Решение. Расчетная схема — на рис. 43.4.2.
Составим дифференциальные уравнения плоско-
го движения стержня:
mxc = Na,
myc =NB- mg,
mar . a a
—ф = -^-со$ф + ^-$\пф,
где m — масса стержня.
Рассмотрим промежуток времени, когда стер-
жень еще не отрывается от стены. Тогда имеют
место следующие кинематические соотношения:
a a
ХС = ~СО8ф ==> Хс = --sin^-yi :
a a
Ус = -sin 9? Ус = ^со8ф-ф
Подставим их в уравнения системы (1):
(1)
О В х
Рис. 43.4.2
a . .-> .
Xc = — - (ф sin ф + ф~ cos ф);
a 2
Ус = -(фсо$ф-ф siny>).
- т^(ф sin + ф2 cos <р) = Na,
а т
т-(ф cos ф — ф sin 92) = NB - mg,
ma? a a
—ф = -NB-cos <fi 4- Na- sin <p.
(2)
Исключая в (2) нормальные реакции NA и NB, получим
э
та а
----ф = — cos ф
12 Y 2
1™. .2 • х
mg + —^-(Ф cos tp - ф sin ф) -
a . a .. . .2 ,
- - sm т-(ф sm ip + ф cos 92).
После несложных преобразований получим угловое ускорение стержня
3g
<р = -—cosy>.
2а
Для определения угловой скорости проинтегрируем полученное диффе-
ренциальное уравнение с учетом начальных условий:
^ = -~-со$ф, ^(0) = <fio, У>(0) = 0 =>
at 2а
dф 3g 1.2 3g
—> с?— =--------cos 92 => -аф =— —-cos 92 =>
dtp 2а 2 2а
350
10. Смешанные задачи
|0| = л/ — (sin 9?0 - sin^).
Для определения момента, когда стержень отойдет от стены в точке А,
выразим нормальную реакцию NA как функцию угла р из уравнений (2)
и приравняем ее к нулю:
3g । 3gr • \
— — cos <р sin Ip Н---(sin <р$ — sin <р) cos ip
2a a
а у
Na = -т-(р sin р + p со5ф) =
ma
~ T
9 3
= -mg sin 9? cos p — -mg sin фо cos p =
3
= -mg cos p I - sin p — sin фо
3
2
cos p
3
- sin p - sin фо
pi = arcsin
2 \ 7Г
- sin Ph I < -.
Поэтому стержень отойдет от стены, когда
Ф = pi = arcsin
2
т Sin Рп
Замечание к задаче 43.4. Для полноты решения следует еще определить нор-
мальную реакцию Nb в точке В как функцию угла р и показать, что Nb(p) > 0
при р € (фо, Р?]- Справедливость этого факта устанавливается несложно и предо-
ставляется читателю.
Задача 43.5(43.6). Использовав условие предыдущей задачи, опре-
делить угловую скорость р стержня и скорость нижнего его конца в
момент падения стержня на пол.
Ответ: р —
3g
a
1 , \ 1 /----------------------------------------;------
1 - 9 sin V’o I sin ф0, vB = - sin фо Vg« sin
Решение. Расчетная схема — на рис. 43.5.1. Воспользуемся ответом
к задаче 43.4. Рассмотрим движение стержня, когда он скользит концом В
по гладкому полу, а конец А — свободный. Движение начинается, когда
р\ — arcsin
2
- sin ф0
10. Смешанные зада чи
351
(sin До ~ sin ।
g .
- Sin <Pf).
a
В этот начальный момент движения угловая скорость стержня равна по
модулю
¥
a
Для определения скорости центра масс С в этот момент построим мгно-
венный центр скоростей Р стержня (точка А готова покинуть связь, но
еще находится на вертикальной стене) (см, рис. 43.5.2)
g a
vCi = W1 • CP = Л / - sin д0 • - =
Vo 2
^vl'osin <p0.
Запишем теорему о движении центра масс С стержня в проекции
на ось х: тхс = 0. Следовательно,
?ет ещ '1
П0К1Ж,
аетсяни
хс = const = vCl cos (90° - Д1) = |-y/^nsin <Ро sin Д1 =
= ^\/ga sin д0 • - sin до = - sin <po\/ga sin до (см. рис. 43.5.2).
---- Получим, что центр масс стержня движется равномерно вдоль оси х, так
шушейми как на стержень не действуют внешние горизонтальные силы.
(внеге. Определим скорость точки В в момент падения стержня на пол. Вос-
пользуемся теоремой о проекциях скоростей любых двух точек твердого
тела на прямую, проходящую через них. Считаем, что в момент падения
_ конец В остается на полу.
j
____. прсв^с = предав ^Рх^с2 = ^Рх^в => vB = - sin дол/gasin До-
определим угловую скорость стержня. Для этого воспользуемся тео-
ремой об изменении кинетической энергии в конечной форме:
ж паи-
^-^Еа^. + Е^-
о)
352
10. Смешанные задачи
Так как стержень — твердое тело, то = 0.
К
a a
mghc = mg- sin <pi = mg- sin (см. рис. 43.5.2).
к
mv2Cl Jc,u2
T' = — + —
m 1 ma2 1 g mga sin <po
— • -ga sin cv, 4---- — sin wo =-------,
2 4 y 12 2 a * 6
mv2Ci JCzu2
ll — ----4- ------
2 2
Выразим скорость центра масс С в момент падения стержня:
ga . з
= у sin Vo +
2 -2l -21
vc2 — хс\ + Ус\
\t=t2 lt=t2
2
a
—ф cos </>
d
dt
a2 2
—w2.
t=t2
ga . з
= -7- sin 9?0
₽=o v
Поэтому
ma2 2 mga 4
T2 = —-w2 + -у- sin3
O 10
Vo-
В результате уравнение (1) примет вид:
mga . з ma2 2 mga , mga
1O sin <po 4——w2-7~ sin 920 = ~~— sin </>q.
Io do 3
Отсюда
Ш2 = ф =
sin 920.
Замечание к задаче 43.5. Для полноты решения следует обосновать два следую-
щих обстоятельства:
1.
2Уд(^) > 0 при <р G [0, <р2\, <р2 = arcsin
2 \
- sm I.
2. Точка А в процессе происходящего скольжения точки В по полу, после
отхода от вертикальной стенки, уже никогда не соприкоснется с нею.
Справедливость пункта 1 следует из нетрудно получаемой формулы:
NB(V) =
3g
(1 + 3 cos2 tp)2
+ sin2 (p — 2 sin tp (e + sin <p2)
где
3 . /4 . 2 \
e = - sin <p21 т - sin ip2 I,
о \ 3 J
2
sin Vi - sin Vo-
10. Смешанные задачи
353
Непосредственной проверкои (решая квадратное относительно sm 9? уравнение)
убеждаемся, что при указанном значении параметра е NB(<p) в нуль не обращается.
Справедливость пункта 2 показывается более громоздко и поэтому здесь не
приводится.
Задача 43.6(43.7). Тонкая однородная доска ABCD прямоуголь-
ной формы прислонена к вертикальной стене и опирается на два
гвоздя Е и F без головок; расстояние AD равно FE (рис. 43.6.1).
В некоторый момент доска начинает падать с ничтожно малой на-
чальной угловой скоростью, вращаясь вокруг прямой AD. Исключая
возможность скольжения доски вдоль гвоздей,
определить угол од = АВ АВ] при котором го-
ризонтальная составляющая реакции изменяет
направление, и угол 04 в момент отрыва доски
от гвоздей.
2
Ответ: с*| = arccos - = 48° 11',
«2 = arccos - = 70° 32'.
Решение. Расчетная схема — на рис. 43.6.2.
Доска не скользит вдоль гвоздей. N — суммарная
нормальная реакция, FTp — суммарная сила трения
со стороны гвоздей Е и F. Применим теорему об из-
менении кинетического момента доски относительно
неподвижной оси z (вдоль AD);
АВ
Jz(p — mg—— sin 92, где
Отсюда получаем:
mAB2
3
Рис. 43.6.1
d(j
Y dt
,d<p 3 g
— =----------sin 92
Yd</> 2 AB Y
3 g .
-----sin 92
2 AB y
ф1 = -7^(1 - cos 92),
Ad
так как в начальный момент 920 = 0, 920 ~ 0.
Применим теперь теорему о движении центра масс доски в проекции
на ось х:
тхс = -Гтр. (2)
Нетрудно увидеть, что
АВ
хс = — s,n V-
354
10. Смешанные задачи
Поэтому
АВ 2 АВ
хс = ——ф sin 92-I——92 cos 92,
Из уравнения (2) находим величину силы трения скольжения:
т АВ 2 т АВ
Ftp = — тхс = —-—ф sin 92-
т- АВ 3g
—(1 - cos 92) sin 92 —
А 3 \
у-г,-
-—ф cos 92 =
т • АВ 3 g
—~"тг; sin 92 cos 92 =
2 2 АВ у у
2
3 i-i
= -mg sin <р I 1 — - cos 92 1.
Сила трения изменит направление тогда, когда ее величина обратится
в нуль:
3 ( 3 \
-mg sin 9211 — - cos </> 1 = 0.
Очевидно, это произойдет при <р = arccos(2/3) ~ 48°1 Iх.
Применим теперь теорему о движении центра масс доски в проекции
на ось у:
тус = -mg + N.
Выразим отсюда нормальную реакцию N, используя следующие соотно-
шения и соотношения (1):
АВ
Ус = — cos у,
АВ
Ус = —^-92 sin у?,
АВ АВ 2
Ус — sin 92------—ф cos 92.
Итак,
= mg - т^~
3 . 2 J 2
= mg I 1 — - sin‘ <p + - cos <p — - cos <p
АВ j
N = mg + тус = mg - т-^-(ф sin 92 + ф cos 92) =
АВ(3 g , . 3g \
---- 2 АВ S,n 92 sm 92 + - cos 92) cos 92 I =
? . 3 2 3 \
2 r 2 “
mg. 2 , mg, ,
— + 9cos2 92 - 6 cos 92) = —(3cos 92 - I)2.
Отрыв доски от гвоздей может произойти при N = 0, т.е. когда 3cos92 -
1 = 0. Следовательно, при 92 = arccos (1/3) яа 70°32z.
10. Смешанные задачи
355
Замечание к задаче 43.7. Отмстим, что исключение возможности скольжения
доски вдоль 1воздсй (как это предполагается в условии задачи), приводит к па-
радоксу. Действительно, пусть при ф = фг = arccos (1/3) происходит обнуление
нормальной реакции 7V(^j) = 0 и происходит отрыв точки А Тогда для послсот-
рывного движения имеем
фг = ф\фг) = const и ф — 0 при ф > фг.
Из формулы аА = ас + аАС + аАС в проекции на ось у имеем:
= /
аАи = аСу + ф1 • ОС cos фг [dAC=§ и ac=g!),
В состоянии, непосредственно предшествующем отрыву, имеем:
JV(^) =0 => aCv = -g
Кроме того, в этом состоянии было'
ар = а'с + во => о,Си = —фг1 cos — ф1 sin фг-
Следовательно:
—g = —фг1 cos фг — ф1 sin фг => — g + фг1 cos фг = —ф1 sin ф2 < 0,
так как ф < 0 для доотрывного состояния.
Объединяя полученные формулы, имеем:
аАу = —g + фг1 cos фг = — ф1 sin фг < 0.
Мы получили противоречие, так как при отрыве должно быть аАу 0!
Это указывает на неполную корректность модели абсолютно шероховатых
гвоздей (коэффициент трения / = оо). Отметим, что можно показать невозмож-
ность отрыва и при любом конечном коэффициенте трения. Стержень просто
начнет скользить и не будет отскакивать. Подробности см. в [14].
Задача 43.7 (43.8). Два диска вращаются вокруг одной и той же
оси с угловыми скоростями од и шг; моменты инерции дисков отно-
сительно этой оси равны и /2- Определить потерю кинетической
энергии в случае, когда оба диска будут внезапно соединены фрикци-
онной муфтой. Массой ее пренебречь.
1 . ,2
Ответ: Д7 = --------- (wi - ш2) .
2 J| + J2
Решение. Кинетическая энергия дисков до их соединения фрикци-
онной муфтой равна
Соединение дисков фрикционной муфтой — это мгновенное наложение
связи. Применим теорему об изменении кинетического момента системы
356
10. Смешанные задачи
относительно неподвижной оси вращения за время удара:
KZ-K^ = ^MZ^\
к
Так как внешние ударные импульсы отсутствуют, то
и kz = k<®.
к
Поэтому
(J 1 + Jljw = J\U1\ + ^2^2-
Угловая скорость соединенных дисков
+ «Ай?2
Ш = ----------------
Вычислим кинетическую энергию дисков после их соединения:
j, _ (Ji + _ (Ti^i + J2w2)2
2~ 2 ~ 2(Jt + J2)
Потеря кинетической энергии равна величине
2й?2 («Л^1 + J2b>2)2
2 2(J, + J,)
ДТ = ТХ-Т2 = —
---2 л, _ ш}2
2(Ji+J2y ' 2)
Задача 43.8 (43.8). Тело А вращается без трения относительно оси
00' с угловой скоростью ид. В теле А на оси OjOj помещен ротор В,
вращающийся в ту же сторону с относительной скоростью Оси
00' и О\О\ расположены на одной прямой
(рис. 43.8.1). Моменты инерции тела А и ро-
тора В относительно этой прямой равны
и JB. Пренебрегая потерями, определить ра-
боту, которую должен совершить мотор, уста-
новленный в теле А, для сообщения ротору В
такой угловой скорости, при которой тело А
остановится.
1
Л . 1 Г 2 ( JА \
Ответ: А — ~^^а I 1 -Ь ~— I + 2шдыв .
2 L \ Jb / j
2
Решение. Внешними силами по отношению к рассматриваемой
системе являются реакции подшипника О| и подпятника О (пересекают
ось вращения Oz) и силы тяжести тела А и ротора В (параллельны оси
и
10. Смешанные задачи 357
Рйя )Э|Ц -
л вращения Oz). Поэтому согласно теореме об изменении кинетического
' момента
^=ewd.
к
кинетический момент
Kz = const.
{l Приравняем значения кинетического момента системы до и после
остановки тела А:
Ja^a + Jb(^a + ы>в) = Ja • 0 + JbU-
Отсюда найдем величину угловой скорости ротора, при которой тело А
остановится.
т f JА ( JА \
W ш = —ША + шА + шв = 1 + — + Чв-
J;) JB \ JbJ
Применим теорему об изменении кинетической энергии:
Д'
t-to = 124)+Z4)-
к к
ipeHiw:
0|0|Щ1я
ной скр
мшв
। кнерг it.
это» лр
жряи,®
соверс-
пясооба
га. при г
Внешние силы не совершают работу, поэтому
Е4’ = о.
к
Работа мотора, установленного в теле А, это и есть работа внутренних
сил:
А = Е 4”.
к
Следовательно,
Jb^
A = T-T0 =
JAbJA Jb(.Wa+ ШвУ
~2
Jb Г (,
— — I 1 “F
2 \ Jb
2
I1 2
- I +
JB J
Jawa Jb(^a + шв)2
~2
2
гнжнДО
одами
тора Г'V
2
2
1 2 ( JА\
= -JA ыА 11 + — I + 1шАыв .
L \ jb /
358
10. Смешанные задачи
Задача 43.9 (43.9). На шкив, вращающийся без сопротивления во-
круг горизонтальной оси О с угловой скоростью wo, накинули ре-
мень с двумя грузами на концах (рис. 43.9.1). Шкив — однородный
диск массы т и радиуса г, масса каждого из грузов
М = 2т. Считая начальные скорости грузов равны-
ми нулю, определить, с какой скоростью они будут
двигаться после того, как скольжение ремня о шкив
прекратится. Найти также работу сил трения ремня
о шкив.
1
Ответ: v =
2 2
Лтр = mw(ir .
Решение. Расчетная схема представлена
на рис. 43.9.2. Применим к системе теорему об
изменении кинетического момента относитель-
но неподвижной оси Oz:
dKOz
dt
Так как массы грузов равны, то
dKOz
—— = 0,
dt
и, следовательно, кинетический момент
Kqz = const.
В начальный момент вращался лишь шкив, поэтому
тг* 2 * * * * * В 9
Koz — Joz^o =
После того как движение с грузами установилось,
тг2 2
KOz = JozV + 2Mvr — + 4тшг
9 2
= -mr w.
2
Приравняем выписанные выражения для кинетического момента:
тг2 9 2
---шо = -тг ы.
2 2
Отсюда ы = шо/9. Поэтому скорости грузов
v = wr =----
9
10. Смешанные задачи
359
Применим теперь теорему об изменении кинетической энергии:
к к
Нетрудно увидеть, что работу совершают лишь внутренние силы трения
между ремнем и шкивом. Поэтому искомая работа
, , ,М»2
Ар=Т-То = — +2---------------— =
тгл (о?о \ (ь>от \ mr 1 2 2 2
=---- — + 2ml --- )-----= —mr wn.
4 V 9 / \ 9 7 4° 9
Задача 43.10(43.10). Твердое тело массы М кача-
ется вокруг горизонтальной оси О, перпендикулярной Ч. N
плоскости рис. 43.10.1. Расстояние от оси подвеса до цен-
тра масс С равно а; радиус инерции тела относитель-
но оси, проходящей через центр масс перпендикулярно у&ХС'Х
плоскости рисунка, равен р. В начальный момент тело |
было отклонено из положения равновесия на угол <ро '
и отпущено без начальной скорости. Определить две со- Рис. 43.10.1
ставляющие реакции оси R и N, расположенные вдоль
направления, проходящего через точку подвеса и центр масс тела,
и перпендикулярно ему. Выразить их в зависимости от угла <р откло-
нения тела от вертикали.
IMga1 рг
Ответ: R = Mg cos <р + (cos <р - cos 920)> N = Mg sin V
Решение. Расчетная схема — на рис. 43.10.2. При-
меним теорему о движении центра масс С тела в проек-
ции на касательную т и нормальную п оси к траектории
точки С:
к
Manc = Y.F^-
к
Рис. 43.10.2
Получим:
MvT = N - Mg sin 92,
M — = R- Mg cos 92,
a
где vT = фа.
360
10. Смешанные задачи
Отсюда выразим силы реакции оси:
N = Mg sin p + Map,
R = Mg cos p + Map2.
Для определения угловых скорости р и ускорения р тела воспользуемся
теоремой об изменении кинетического момента относительно неподвиж-
ной оси вращения Oz:
Joz¥> = -Mga sin p,
где, согласно теореме Штейнера—Гюйгенса
Joz = Мр2 + Ma2.
Отсюда
go
V = —2—r sm p.
p2 + a2
Теперь проинтегрируем последнее выражение:
dp dp ga
3----77 ----7 sin V7 —
dp dt p2 + a2
. .. ga . ,
==> p dp = ——7 sin V dp
1 .2 ga
= 2 , 2 СО5У+ ^i-
2 p2 + a2
Так как начальные условия при to — 0 имеют вид у?(0) = р0, <р(0) = 0, то
8а
Ci = г-—г cos р0.
р2 + а2
Следовательно,
.2 э go , ,
¥> =2-v-—j (cos p- cos po).
p + a2
Выпишем искомые составляющие реакции оси как функции угла р:
N = Mg sin р + Мар = Mg sin р - Ma- &а sin р — Mg-^-—- sin р,
р1 + а2 р2 + а2
R = Mg cos р + Map2 = Mg cos p + Ma-^-—7 (cos p — cos 920) =
p 4” a
2Mga2
— Mg cos р ч—г-----7(cos р - COS 92о)-
р2 + а2
10. Смешанные задачи
361
Задача 43.11 (43.11). Тяжелый однородный цилиндр, получив ни-
чтожно малую начальную скорость, скатывается без скольжения с го-
ризонтальной площадки АВ, край которой В заострен и параллелен
образующей цилиндра (рис. 43.11.1). Радиус основания цилиндра — г.
В момент отделения цилиндра от площадки
шая через ось цилиндра и край В, отклонена
от вертикального положения на некоторый
угол СВС\ — а. Определить угловую скорость
цилиндра в момент отделения его от площад-
ки, а также угол а. Трением качения и сопро-
тивлением воздуха пренебречь.
плоскость, проходя-
Решение. Расчетная схема — на рис. 43.11.2. Применим теорему об
изменении кинетической энергии цилиндра.
Т-То^^А^ + ^А?. (1)
к к
Так как начальная скорость ничтожно мала, то 7Ь = 0- После поворота
радиуса ВС на угол кинетическая энергия равна величине
mv2c JCz^
2 2
? 2
ты г
тггшг
4
3 2 2
= -тг ш
4
так как нет скольжения и в точке касания В находится мгновенный центр
скоростей Р цилиндра.
Работу совершает лишь сила тяжести (при отсутствии скольжения сила
трения не совершает работу):
362
10. Смешанные задачи
(С) V
J mg dr с = J
(c0) о
= mgr( 1 — cos 9?).
Подставив все выражения в формулу (1), получим:
'22 i
-mr w — mgr(l — cos <р)
Для определения угла а в момент отделения цилиндра от площадки
воспользуемся теоремой о движении центра масс С в проекции на нор-
мальную ось п к траектории точки С:
vc
т— = mg cos ip - N.
г
Нормальная реакция
mti m(wr)2
N = mg cos <p-----= mg cos u>----------=
r r
= mg cos <p - -mg(l - cos <p) — cos <P ~ 4).
В момент отрыва цилиндра нормальная реакция обнуляется:
N(<p = a) = 0 ==> 7 cos a - 4 = 0.
Поэтому a = arccos (4/7) « 55,1°.
Угловая скорость цилиндра в момент отделения от площадки:
Замечание к задаче 43.11. Для полноты решения следует показать, что после
обнуления реакции N цилиндр действительно отделится от точки В, т. е. расстоя-
ние ВС будет увеличиваться с течением времени. Действительно, если отделение
произошло, то точка С движется с ускорением g по параболе, поэтому имеем:
xc(t) = г sin а + r<p(a) cos a • t,
gt2
yc(t) — r cos а — rip(a) sin a • t —
Тогда получим:
g2^
x2c(t) +Ус(1) = r2 + r2<p2(a)t2 -grt2 cos a +gr<p(a) sin a • f3 + —.
Так как
N = mg cos <p — mp2r,
10. Смешанные задачи
363
то для <f = а, когда N = 0, имеем:
g cos а = <р2(а) г.
Поэтому получим:
xc(t) + yc(t) — r2+ grip (a) sin at3 + > r2.
4
To есть процесс отделения происходит без каких-либо противоречий, и в данном
случае модель абсолютной шероховатости корректна.
Задача 43.12(43.12). Автомашина для шлифовки льда движется
прямолинейно по горизонтальной плоскости катка. Положение цен-
тра масс С указано на рисунке к задаче 35.12. В момент выключения
мотора машина имела скорость v. Найти путь, пройденный машиной
до остановки, если /к — коэффициент трения качения между коле-
сами автомашины и льдом, a f — коэффициент трения скольжения
между шлифующей кромкой А и льдом. Массой колес радиуса г,
катящихся без скольжения, пренебречь.
Ответ:
v2 Зг
Tg 2fr + fK'
v
Рис. 43.12.1
Решение. Расчетная схема — на рис. 43.12.1. Колеса катятся без
скольжения, поэтому в точках их касания с поверхностью находятся мгно-
венные центры скоростей. Применим теорему об изменении кинетической
энергии:
Л к
Так как массой колес можно пренебречь, а автомашина движется посту-
пательно, то
То =
Mv2
~Т~'
Т = 0.
364
10. Смешанные задачи
Внутренние силы не совершают работу после выключения мотора:
Е4’ = о.
к
Из внешних сил работу совершает лишь сила трения скольжения в опоре
4 и моменты трения качения колес:
52 Ак} = ~F?ps ~ ~ 2Мк29? =
к
= ~fNAs - 2(fKNt + fKN2)p = fNas - 2/к(^ + N2)-.
г
При определении нормальных реакций NA, N\ и N2 воспользуемся
решением задачи 38.12:
2 1
Na = -Mg, N\ = 0, 2N2 = -Mg.
Поэтому
Etc} 2 Is
Ak} = ~f- -Mgs- fK--Mg-.
к
Подставив все найденные выражения в теорему об изменении кинетиче-
ской энергии, получим:
Из этого уравнения находим путь s, пройденный до остановки:
ц- Зг
s =------------.
2g If г + /к
Задача 43.13(43.12). На боковой поверхности круглого цилиндра
с вертикальной осью, вокруг которой он может вращаться без трения,
вырезан гладкий винтовой желоб с углом подъема а. В начальный
момент цилиндр находится в покое; в желоб опускают тяжелый шарик;
он падает по желобу без начальной скорости и заставляет цилиндр
вращаться. Дано: масса цилиндра М, радиус его R, масса шарика т;
расстояние от шарика до оси считаем равным R и момент инерции
цилиндра равным MR?/2. Определить угловую скорость ы, которую
цилиндр будет иметь в тот момент, когда шарик опустится на высоту h.
2m cos a
Ответ: ш =---------
R
2gh
(М + 2m)(М + 2m sin2 а) ’
in
*’4,
365
'Ренику
ОД
10. Смешанные задачи
1ЙЛ00С»
Решение. Расчетная схема — на рис. 43.13.1. Применим теорему об
изменении кинетической энергии
т-т0
(0
к
(1)
raikjj
г sped
raadr
рапп
II иг,
|Л1“-
о сиро.'
опусж
Так как винтовой желоб гладкий и в опорах оси вращения нет трения, то
работу совершает лишь сила тяжести шарика: A(mg) = rrgh. Начальная
кинетическая энергия То = 0- Найдем выраж ние для кинетической
энергии Т:
Joz^2 mv2 MR2 2 m 2
T = + — = —ш + -(vr + ve)2.
Обозначим через 0 угол поворота цилиндра. Тогда ы = 0, ve = OR.
При рассмотрении относительного движения шарика (относительно
цилиндра) введем цилиндрические координаты: R = const, <р, у. Поэтому
vr = vReR + vvev + vyey = ReR + R$ev + yey = Ripev + yey,
366
10. Смешанные задачи
где единичные векторы ёц, ev и еу взаимно-ортогональны, причем
направлен по касательной к окружности радиуса R, я вляющейся сечением
цилиндрической поверхности горизонтальной плоскостью. Вектор пере-
носной скорости ve шарика также направлен по касательной к этой же
окружности, но в противоположном направлении. Следовательно,
v2 = (vr + ve)2 — (11ф - R6)2 + у2.
Окончательное выражение для кинетической энергии принимает вид:
TV/R2 ТП г 7/ *2 2т
т = —е2 + — [r2 (ф — в)2 + у2].
Расписав величины в (1), получим уравнение
^-ё1 + у [Я2(92 - ё)2 + у2} = mgh. (2)
Дифференциальное уравнение (2) — уравнение с тремя переменными в,
ip и у. Для составления второго уравнения воспользуемся теоремой об
изменении кинетического момента относительно неподвижной оси вра-
щения цилиндра Ozt
Так как все внешние силы либо пересекают (реакции R\ и Ri), либо
параллельны оси Oz (силы тяжести), то
к
и, следовательно, Kqz = const. Так как в начальный момент времени все
тела покоились, то Koz — const = 0.
Выразим величину кинетического момента Kqz-
KOz = Joz^ + npoJm0(mv)l =
MR2 • • MR2 •>
= —-—0 + m(-R<pR + RёR) = —-—ё + mR~(f) - ф).
Согласно закону сохранения кинетического момента относительно оси Oz,
имеем уравнение
ё + т1ё(ё - ф) — о. (з)
Для получения третьего уравнения, связывающего координаты в, <р
и у, воспользуемся тем, что вектор относительной скорости шарика vr
направлен по касательной к винтовому желобу, а угол подъема a — это
10. Смешанные задачи
367
угол между касательной к винтовому желобу и горизонтальным направ-
лением. Поэтому
у = Яф tg a. (4)
Исключая из уравнений (2), (3) и (4) переменные ф и у, получим соот-
ношение:
'«Цфиц
MR2-2
----02
4
т M2R2
2 4m2
mR2 f М\2 7
—— I 1 + — ) в2 tg2 a = mgh.
2 \ 2m J
Отсюда выражаем угловую скорость цилиндра:
ш — в =
mgh
М2
2М +--+ 2
т
(2т + М)2
т
2
tg a
WlBc
»Wi
МОЛИН
N
Smgh
AM, x (2m + M)2 sin2 a
R2 — (2m + M) + ±---------------y-
m m cos2 a
2m cos a
R
2gh
(M + 2m) (M 4- 2m sin2 a)'
1кцииЯ|4
1ЙВИ₽
5г
ИЙ’’
ЮМЕ
щегокос;
«сирт
IT0JIO
I
11. Удар (§ 44, [10])
Задача 44.1 (44.1). Баба Л ударного копра падает
с высоты 4,905 м и ударяет наковальню В, укреплен-
ную на пружине (рис. 44.1.1). Масса бабы 10 кг, и масса
наковальни 5 кг. Определить, с какой скоростью нач-
нется движение наковальни после удара, если баба будет
двигаться вместе с ней.
Ответ: 6,54 м/с.
Решение. Определим скорость vA, с которой тело Л ударяет нако-
вальню В. Для этого воспользуемся теоремой об изменении кинетической
энергии:
ША1)Л !--- !------------ /м \
——= mAgh => vA = x/2gh = ^/2-9,81 -4,905 = 9,81 - ).
2 \ с /
Теперь воспользуемся теоремой об изменении количества движения систе-
мы двух тел Л и В в проекции на ось у, направленную вертикально вниз:
Qy Qty
(тА + тв)и - mAvA = 0.
Отсюда скорость, с которой наковальня В будет двигаться сразу после
удара, равна следующей величине:
тА
и =-----vA =
тА +тв
10
10 + 5
•9,81 -6,54
Задача 44.2 (44.2). Груз Л массы М} падает без на-
чальной скорости с высоты h на плиту В массы М2,
укрепленную на пружине, которая имеет коэффициент
жесткости с (рис. 44.2.1). Найти величину s сжатия
пружины после удара в предположении, что коэффи-
циент восстановления равен нулю.
Ответ: s —------h
с
M* 2g2 М2
с2 + 2g/? c(Mi + М2)'
11. Удар
369
Решение. Воспользуемся теоремой об изменении кинетической
энергии груза Л для определения его скорости vA в момент падения на
плиту В:
,--------------------------------------------
—2— = Mtgh => vA = \/2gh.
Для определения скорости и, с которой груз Л вместе с плитой В
начнут двигаться сразу после удара, воспользуемся теоремой об измене-
нии количества движения системы в проекции на ось у, направленную
вертикально вниз:
М, Mt ,______
(Mi + М2)и - M\VА = 0 => и = vA = —----— y/lgh.
М\ + М2 Mt + М2
Теперь снова воспользуемся теоремой об изменении кинетической
энергии:
к к
где
г = о, £4> = 0,
к
Е4е> = (Ml+M2)gs-|(A2-A?T).
Здесь s — искомая величина сжатия пружины после удара за счет переме-
щения вниз плиты В с грузом Л; Аст = M2g/c — статическая деформация
пружины; А = ACT + s — деформация пружины в момент ее максимального
сжатия (заметим, что пружина не деформируется за малое время удара).
Итак,
2
2 2M|g
s--------s —
с
(-ЛТ1 -Т М2)и2 . С г. э ,2т
-----2----- = (Ml + M2)gs - - [(Act + s) - Аст]
(Mi+M2)u2 c 2
- = Migs --s =>
(Mt+M2)u2 Q
c
2 (Ml + M2)u2
c
Mig
с
Mig ,
=> Si,2 = ------- ±
С
Так как по условию задачи величина s > 0, то получаем единственное
решение
Mig
s =-----h
с
M^g1 Mi + М2 / Mi
с2 + с \Mi + М2
2
370
11. Удар
Mig /м& мГ
Задача 44.3 (44.3). В приборе для опытного определения коэффи-
циента восстановления шарик из испытуемого материала падает без
начальной скорости внутри вертикальной прозрачной трубки с задан-
ной высоты Л] = 50 см на неподвижно закрепленную горизонтальную
пластинку из соответствующего материала. Найти коэффициент вос-
становления, если высота, на которую подскочил шарик после удара,
оказалась равной Л2 = 45 см.
Ответ: к = J — = 0,95.
Решение. При прямом ударе коэффициент восстановления опреде-
ляется отношением скоростей шарика после и до удара:
и
V
к =
Применяя теорему об изменении кинетической энергии шарика при
его движении вниз (до удара) и при его движении вверх (после удара),
найдем скорости шарика непосредственно перед ударом о неподвижную
пластину (v) и сразу после удара (и):
mv2
— = mgh\
mir
---у- = ~mgh2
=> v = \/2ghi',
=> и = \/2gh2.
Поэтому
Задача 44.4(44.4). Упругий шарик падает по вертикали с высоты
h на горизонтальную плиту, отскакивает от нее вверх, вновь падает
на плиту и т. д., продолжая эти движения. Найти путь, пройденный
шариком до остановки, если коэффициент восстановления при ударе
равен к.
Ответ: s —
1 + к2
------тЛ
11. Удар
371
Рис. 44.4.1
Решение. Расчетная схема — на рис. 44.4.1. Рассмотрим тп-ное
соударение шарика с неподвижной поверхностью. Скорость после удара
ит = kvm. Скорость до удара vm = \/2ghm. Высота падения
где um-i = kvm-i — скорость отскока шарика при предыдущем соударе-
нии. Отсюда нетрудно получить, что
= +=+ = к2лга_, =
2g
т. е. высота падения изменяется по закону убывающей геометрической про-
грессии со знаменателем к1 < 1. Так как к 0, то это бесконечная гео-
метрическая прогрессия. Искомый путь
s
00
= 2 hm — h\ — 2
m=l
h
1 - к2
-h =
1 +k2
—----r/l
Задача 44.5 (44.5). Два тела с массами М\ и и коэффициентом
восстановления к движутся поступательно по одному и тому же
направлению. Каковы должны быть их скорости и V2, чтобы после
удара догоняющее тело М\ остановилось, а тело М2 получило бы
заданную скорость «2?
1 + к m2 mi - кт,2
Ответ: г>1 = —-------------«2, «2 = 77-----:----
к 7711 + 7712 к(7П] + 7712)
Решение. Применим теорему об изменении количества движения си-
стемы при ударе в проекции на ось х, направленную вдоль движения тел:
Qx Qox
m2ti2 - (mfii + 7712V2) = 0.
0)
372
11. Удар
При прямом соударении тел коэффициент восстановления
щ - «2 «2 г.
к =---------=--------- I4, 111.
fl - v2 v}- v2
Выражая отсюда
и2
V1 = V2 + —
к
и подставляя в (1), получим:
т2и2 - т\ I v2 Н-I - m2v2 = 0 =>
\ «/
кт2 - mi и2 1 + к т2
=> V2 = ;—\U2’ Vi = V2 + т = ---------;—“* 2-
к(тп\ + тп2) к к тп\ + m2
Замечание к задаче 44.5. В ответе, данном в задачнике, неверно указан знак в вы-
ражении для v2.
Задача 44.6 (44.5). Паровой молот массы 12 т падает со скоростью
5 м/с на наковальню, масса которой вместе с отковываемой деталью
равна 250 т. Найти работу Л], поглощаемую отковываемой деталью,
и работу А2, потерянную на сотрясение фундамента, а также вычис-
лить коэффициент т] полезного действия молота; удар неупругий.
Ответ: Л] = 143 кН • м, А2 = 6,87 кН • м, т] — 0,95.
Решение. Применяя теорему об изменении количества движения и
учитывая, что внешних ударных импульсов нет, выпишем закон сохране-
ния количества движения системы:
тп^ = (mt + m2)u2 (так как v2 — 0, к = 0) =>
ГП\
«2 =--------
ТП\ + m2
Здесь — масса молота, тп2 — масса наковальни с деталью.
Работа Л], поглощаемая отковываемой деталью и затрачиваемая на ее
пластическое деформирование, равна потере кинетической энергии Тп
системы:
л „ m m}v] (тщ+т2}и2
А\ = J-n = J-й ~ ----------2------—
mtv2 mt + TTi2 т2 2 77117712 2
2 2 (тп.] + т2)2 V1 2(t71] + m2)V'
12 000-250000-25
= —----------------- к 143 (кН • м).
2(12 000 + 250 000) V ’
11. Удар
373
Работа, потерянная на сотрясение фундамента А2, равна кинетической
энергии системы после удара:
А = (mi + m2)uj = (тп, + m2) m2 , _ mffi
2 2 (тщ + m2)2 1 2(m, + m2) ”
12 0002-25
“ 2(12 000 + 250000) ~ 6,87 ^KH '
Коэффициент полезного действия молота определяется отношением по-
терянной кинетической энергии системы к начальной кинетической
энергии:
Тп mim2tf-2 т2 250 000
То 2(mi + m2)mivf mi+m2 12000 + 250000
Задача 44.7 (44.7). Молот массы mi = 10 кг расплющивает заго-
товку до нужных размеров за 70 ударов. За сколько ударов эту опера-
цию произведет молот массы т2 = 100 кг, если приводной механизм
сообщает ему такую же скорость, что и первому молоту. Масса нако-
вальни М — 200 кг. Удар считать абсолютно неупругим.
Ответ: 10 ударов.
Решение. Воспользуемся решением задачи 44.6. За 70 ударов моло-
том массы mi деталью поглощается работа, равная
А = 704
70miM 2
2(т{ + M)V]'
Та же работа поглощается деталью за п ударов молотом массы т2. Поэтому
7Qmi М 2 пт2М 2
2(m\+M)V' = 2(т2 + М)Щ'
Следовательно,
mi т2 + М 10
п = 70— —-----= 70----
т2 mi + М 100
100 + 200
---------= 10 (ударов).
10 + 200 4
Задача 44.8 (44.6). Найти скорости после абсолютного упругого
удара двух одинаковых шаров, двигавшихся навстречу друг другу со
скоростями г>1 и v2.
Ответ: Шары после удара обмениваются скоростями.
374
11. Удар
(до удара)
(после удара)
х
Рис. 44.8.1
Решение. Расчетная схема на рис. 44.8.1. Применим теорему об из-
менении количества движения системы:
Qx ~ Qox — 'У , Skx —
к
=> mu] + ти2 — {mv] — mv2) - 0
=> Щ + U2 = V] ~ V2.
Так как удар абсолютно упругий, то коэффициент восстановления
Ui — U2
к =----------= 1 (см. рис. 44.8.1).
V1 + v2
Решим систему двух полученных уравнений относительно переменных U]
и и2:
{ut + и2 = vt - V2,
==> «2 = ^1, «I — -Д2-
-«1 + U2 — г>1 + V2
Это означает, что после удара шары обмениваются скоростями.
Задача 44.9 (44.7). Два одинаковых упругих шара А и В движут-
ся навстречу друг другу. При каком соотношении между скоростями
до удара шар А после удара остановится? Коэффициент восстановле-
ния при ударе равен к.
vA 1 + к
Ответ: — =-------
Vb 1 — к
Решение. Расчетная схема на рис.44.9.1. Согласно закону сохране-
ния количества движения, имеем:
mAvA ~ fnBvB = тпА-0 + твив.
Так как тпА = тпв, то
vA-vB=uB. (1)
11. Удар
375
до удара:
после удара:
х
Рис. 44.9.1
Воспользуемся формулой коэффициента восстановления для прямого удара:
к = -
-и в
va+vb'
Выразим отсюда величину ив и подставим ее в (1). Получим:
vA - vb = k(vA + vB).
Отсюда следует, что
vA 1 + к
Vb 1 - к
Задача 44.10(44.10). Тело А настигает тело В, имея в 3 раза
большую скорость. Каким должно быть соотношение масс этих тел,
чтобы после удара тело А остановилось? Удар считать прямым цен-
тральным. Коэффициент восстановления к = 0,8.
Ответ:
тв
тА
Решение. Запишем закон сохранения количества движения системы
двух тел:
mAvA + mBVB = тпА 0 + твив,
где
vA = 3vB.
Коэффициент восстановления
О - ив
к =----------- = 0,8.
vA - vB
Отсюда получим:
3mAvB + ttibVb = твив,
ив = 0,8(3vB - vB)
=> (Зтд + тв)гв = тв • l,6vB ==>
ЗтА = 0,6тБ
тБ
тА
376
11. Удар
Задача 44.11 (44.8). Определить отношение масс mi и 7772 двух
шаров в следующих двух случаях: 1) первый шар находится в покое;
происходит центральный удар, после которого второй шар остается
в покое; 2) шары встречаются с равными и противоположными ско-
ростями; после центрального удара второй шар остается в покое.
Коэффициент восстановления равен к.
„ , m2 m2
Ответ: 1) — = к, — = 1 + 2к.
mi mi
‘ Решение. 1. Используя закон сохранения количества движения и фор-
мулу для коэффициента восстановления, получаем:
' mi • 0 - 7712^2 — -ТЩЩ + 7712 ’ О,
т2 щ
___ — _ —
mi V2
< «1 — «2 и1
к =-----------= —
V] — V2 V2
2. Используя закон сохранения количества движения и формулу для
коэффициента восстановления, получаем:
' miVi - m2V2 = —mtUi + m2 • О,
* k -Ui-Uj Uj (1)
< г>1 +v2 Vi + V2
В формуле для коэффициента восстановления учтено, что первое
тело после удара изменяет направление движение на противоположное.
Перепишем систему уравнений (1), используя равенство = д2, и
решим ее:
(mi — m-fivi = -777]«i,
=> (7721 — 7712)V1 = — mi • IkVi =>
==> 777! (1 + 2Л) - 7712 = 0 => — — 1 + 2k.
mi
Задача 44.12(44.9). Три абсолютно упругих шара с массами 7П|,
7712 и тпз лежат в гладком желобе на некотором расстоянии друг
от друга. Первый шар, пущенный с некоторой начальной скоростью,
ударяет во второй, покоящийся шар, который, начав двигаться, в свою
очередь ударяет в третий, покоящийся шар. При какой величине массы
тпг второго шара третий шар получит наибольшую скорость?
Ответ: m2 = х/тщтщ.
11. Удар
377
Е1Ч. Иод,' Решение. Используем закон сохранения количества движения при соударении первого и второго шаров: 7П|Д| = ТЩЩ +miU2- Так как шары абсолютно упругие, то . и, - «2 к = = 1. г>1 Поэтому W| = U2 - Д1. Следовательно, 2771]
®1«1Ц ЙГ и2 - V,. ТП\ + 7772 Рассмотрим соударение второго и третьего шаров. По аналогии с преды-
} 5>? м’ душим соударением выпишем скорость третьего шара после удара: 27732 21712 27731 Щ— и,2= ш. 7732 + 773з 7772 + т3 773] + 7712
ИИ 1 Для того чтобы эта скорость была наибольшей, необходимо, чтобы выра- жение
про, 7712 (7712 + 773з)(773] + 7732) было бы наибольшим, или чтобы обратное ему выражение (7712 + 7Пз)(773] + 7772 ) 77717713
МИ Wffii иенапрт ьзиракш — 7711+ 7712 + 7713 -1- 7712 7712 было наименьшим. Приравняем нулю производную последнего выраже- ния по 771г:
7712
Следовательно, 7712 = л/771|7Пз.
=> ^Задача 44.13(44.10). Шар массы т\, движущийся поступательно^
ТП? со скоростью г>1, встречает покоящийся шар массы 7712 так, что ско-
-=14 mi рость его образует при ударе угол а с линией, соединяющей центры шаров. Определить: 1) скорость первого шара после удара, считая удар
•— абсолютно неупругим; 2) скорость каждого из шаров после удара в пред-
ж шара 11- ггором расг й иг , нашим положении, что удар упругий с коэффициентом восстановления к. 1 / \ 2 / / 7711 \ Ответ: 1) щ = v\\ sin2 a + cos2 а;
)ИйШГ-' ни ж; у \ 7711 + 7712 / ч . (ТП\ - кт2\2 , 7711(1 + к) COSO 2) и\ — V\\ sin2 a + I cos2 a, U2 — Щ У V Till + 7712 / 7711 + 771 2
378
11. Удар
Рис. 44.13.1
Решение. Расчетная схема — на рис. 44.13.1.
1. Запишем закон сохранения количества движения системы в про-
екции на общую нормаль п и общую касательную т к соударяющимся
шарам:
{m\V\ cos а = (mi 4- m2)uln,
miVi sin a = mi«ilr
(uin = «2п> так как удар абсолютно неупругий и к = 0; и2т = 0, так как
трением между шарами пренебрегаем и второй шар до удара покоился).
Отсюда скорость первого шара после удара
2
«1
= \/u2lT+u2ln = vl
sin2 a 4-
mi
mj 4- m2
cos2 a.
2. Запишем закон сохранения количества движения системы в про-
екции напит:
miV] cos a = miU\n + m2«2n,
miVj sin a — m\U\T.
В этом случае также и2т = 0, а нормальные составляющие скоростей
после удара связаны соотношением
и1п ^2п
fin
Отсюда
«2п — v\n - к + uln — kvi cos a + U\n.
Поэтому
mj - ктп2
uiT = i>i sin a, u\n =-------i»i cos a,
mi 4- m2
mi - km2 mi(l 4- k)
u2„ — kv\ cos a 4-------Д| cos a = 14 cos a-----.
mi +m2 mt 4- m2
11. Удар
379
Следовательно,
и
yJu]T + «,п = г>! Л/siп2 a +
Ш| - кт>
+ m2
cos2 a
«2 = «2п — ----------(1 + к) cos a.
mt + m2
Задача 44.14 (44.11). Абсолютно упругий шар, центр которого дви-
жется прямолинейно со скоростью v, встречает под углом а гладкую
вертикальную плоскость, Определить скорость шара после удара.
Ответ: Угол отражения равен углу падения, скорости до и после
удара по модулю равны.
Решение. При абсолютно упругом ударе о гладкую неподвижную
плоскость теорема об изменении количества движения в проекции на ось т
(рис. 44.14.1) принимает вид:
mu cos 7 — mv cos 7 = 0,
так как поверхность гладкая и ударный импульс S
перпендикулярен ей. Коэффициент восстановления
ип и sin 7
vn v sin a
Отсюда получаем
и cos 7 = v cos a,
и sin 7 = v sin a.
Возведя в квадрат и сложив левые и правые части уравнений, получаем,
что и = V. А следовательно, и 0 = 7.
Итак, скорости до и после удара по модулю равны, и угол отражения
равен углу падения.
Задача 44.15(44.12). Стальной шарик падает на горизонтальную
стальную плиту под углом 45° и отскакивает под углом 60° к вертикали.
Определить коэффициент восстановления при ударе.
Ответ: к = 0,58.
Решение. Расчетная схема — на рис. 44.15.1. Пренебрегая трением
шарика о поверхность плиты и считая, что ударный импульс S направлен
380
11. Удар
по нормали п к поверхности, запишем теоре-
му об изменении количества движения шари-
ка в проекции на ось т:
mu sin (3 — mv sin a = 0.
Отсюда
и sin (3 — v sin a
и sin a
v sin /3
Коэффициент восстановления при ударе равен:
ип и cos (3 sin a cos /3 tg a tg 45°
vn v cos a sin /3 cos a tg/3 tg 60°
1
-= 0,58.
\/3
Рис. 44.16.1
Задача 44.16(44.13). Шарик падает наклонно
со скоростью v на неподвижную горизонтальную
плоскость и отскакивает от плоскости со скоро-
стью Vi = дх/2/2 (рис. 44.16.1). Определить угол
падения а и угол отражения (3, если коэффициент
восстановления при ударе к = УЗ/З.
Ответ: а = т^1(>, (3 = тУ^.
Решение. Расчетная схема — на рис. 44.16.2. В силу отсутствия удар-
ного трения vT = V]T; коэффициент восстановления к — vln/vn.
Поэтому имеем два уравнения относи-
тельно а и 0:
У1
v sin a — —vsin/3,
2
х/2
Г- ---V COS в
УЗ _ 2 2
- 3 vcos a
11. Удар
381
г:
Задача 44.17(44.14). Два одинаковых абсолютно упругих шара,
двигаясь поступательно, соударяются с равными по модулю скоростя-
ми v. Скорость левого шара до удара направлена по линии центров
направо, а скорость правого шара до удара об-
разует с линией центров угол а (рис. 44.17.1).
Найти скорости шаров после удара.
Ответ: wtn — -rcosa, uiT = 0, и2п = v,
и2т = 27 sin а. Ось п направлена по линии
Рис. 44.17.1
центров вправо, ось т — вверх.
Etf I
8Й"7
зрж 1Щ|
Ww.
' Wilt
ЦОЦС
'^ecinij^
= ^1
Решение. Расчетная схема — на рис. 44.17.2. В силу отсутствия
ударного трения теорема об изменении количества движения, записанная
в проекции на общую касательную ось т, для первого и второго шара
(отдельно) имеет вид:
тррт - mi • 0 = О,
тп2и2т — m2v2T — 0.
ГЪ этому
U\T = 0, и2т = v2t = v sin a.
Для определения скоростей шаров после удара в проекции на ось п (вдоль
линии центров) запишем теорему об изменении количества движения для
системы двух шаров в проекции на ось п и соотношение для коэффици-
ента восстановления:
LBcfijoi
ви)=Ц
и pa
tlCOS0
COSO
=}
!
cos2/! =
' т\Щп + т2и2п - (rn,\V\ - m2v2 cos а) = 0,
* «щ ^2n П1п ^2n
V|n~®2n Ц] +122 COS а
Так как
mi — т2, V] = v2, к = I,
то уравнения принимают вид:
«in -I- и2п - v + v cos a = 0,
< =>
V +27 COS а = и2п - Ц|п
«2п = V,
22|П = — 27 COS Q.
Итак, после удара
221г = 0,
2/ щ = -27 cos a;
U2t = 27 sin a, U2n = 27.
382
11. Удар
Задача 44.18(44.15). Имеются три одинаковых шара М\, М2, Мз
радиусов R, расстояние между центрами С\Сз = о, (рис. 44.18.1).
Определить, на какой прямой АВ перпендикулярной линии С]Сз,
должен находиться центр Сз третьего шара для того, чтобы, по-
лучив некоторую скорость по направлению
АВ, этот шар после удара о шар М2 нанес
центральный удар шару М\; шары абсолютно
упруги и движутся поступательно.
Ответ: Расстояние прямой АВ от центра
равно ВС2 = 4R1 /а.
С2
Решение. Расчетная схема — на рис. 44.18.2. Рассмотрим соударе-
ние шаров М3 и М2 - Запишем теорему об изменении количества движения
шара М3 в проекции на общую касательную ось т и для системы шаров
М3 и М2 — на общую нормальную ось п (ударным трением пренебрегаем,
т. е. ударные импульсы S2 и §3 направлены вдоль п):
тпзизт — тзУзт = О,
<
m3«3n + m2«2n - m3^3n = О
х
изт = V3T = V3 sin а = V3—,
27г
I
Щп + и2п = «з COS a, cos а = у 1 — .
(1)
Так как к — 1, то
^Зп ^2п
г’зп - *>2п
И-Зп U2n
V3 cos а
и2п = u3n + V3 cos a.
Рис. 44.18.2
11. Удар
383
Лиако^
Ю С|®№1ь
'Wfih
ipuaWj|b'
ИПООущ
Поэтому из (1) получаем:
^3n — О,
Щт =
2гС
Следовательно, для того чтобы шар Му после удара о шар Му нанес цен-
тральный удар шару ЛД, необходимо, чтобы его скорость йу = йут лежала
на прямой, проходящей через центр С] шара Mt. Из геометрических
соображений выписываем соотношение:
СуСу
С\Су
мнении^
йрнымчрен
IBM и)’
Расстояние ВСу =
х
СуСу
4Д2
х =----
a
2R х
a 2R
4Д2
х =----.
a
Задача 44.19 (44.16). Для укрепления грунта под фундаментом
здания сваи массы М = 50 кг вбивались копром, боек которого массы
М[ = 450 кг падал без начальной скорости с высоты h = 2 м; при по-
следних десяти ударах свая углубилась на <5 = 5 см. Определить среднее
сопротивление грунта при вбивании свай. Удар считать неупругим.
Ответ: S = 159 кН.
Решение. Скорость копра непосредственно перед ударом о фунда-
мент определяется теоремой об изменении кинетической энергии:
«1 = y/2gh.
Скорость системы после неупругого удара определяется из уравнения
количества движения:
х Mi М\
(М.+М)и-М,»,=0 => и = -v, =
Применим теперь теорему об изменении кинетической энергии (учтем
10 ударов):
\O(T-To)=A(R) + A(P) => -10М| ^—и2 = -R-6 + (Mi+M)g-d.
Найдем
5(М. + М) , 5 М2
R = (Mi+ M)g + —------и2 = (Mi +M)g+- М'+~ 2gh =
5 4502
= (450 + 40). 9,8+ — .^^.2.9,8.2 =1292600^.
384
11. Удар
Сила Л — это сила, которая соответствует сопротивлению грунта за 10 уда-
ров. Следовательно,
Дсред — 10 ~ 159 (к^)'
Задача 44.20 (44.17). Два шара с массами т\ и т2 висят на па-
раллельных нитях длин I] и 12 так, что центры их находятся на одной
высоте. Первый шар был отклонен от вертикали на угол а, и затем
отпущен без начальной скорости. Определить угол предельного откло-
нения «2 второго шара, если коэффициент восстановления равен к.
_ . а2 mi(l+fc)
Ответ: sin — = —----------
2 гп\ + т2
Рис. 44.20.1
Решение. Расчетная схема представлена
на рис. 44.20.1. Применим теорему об измене-
нии кинетической энергии первого шара при
его движении до соударения со вторым шаром:
—— = migZi(l - cos а,).
Скорость
г>! = ^/2gZ](l -cosa,).
Рассмотрим соударение шаров:
' m\U\ + 7712^2 - TT^Tli = 0,
< Щ - 712
к =-------------
«I
71| = 712 “ kV\,
<
m\U\ + ТП2^2 - m\V\ = 0
, х m\
и2 = г>|(1 + к)--------------
7771 + 7772
777! ( 1 + к) /
712 = ------;------- COSO!).
777| + 7712 V
Для определения угла отклонения второго шара после удара применим
для него теорему об изменении кинетической энергии:
7712712 , . .
-------= -7712^121 1 - COS a2).
J-CMiJ
шар
>
fli).
ИИ,
гни:
11. Удар
Получим:
и] /mi(l+fc)\2 2gZi(l - cos си)
1 - cos a-> — '------ -2—2-------—
2gh \ m, + m2 J 2gl2
или
«2
sin —
2
m^l + fc) Ц at
-------д / — sin —.
Ш] + m2 V l2 2
Задача 44.21 (44.18). Маятник ударной машины со-
стоит из стального диска А радиуса 10 см и толщины
5 см и из стального круглого стержня В диаметром 2 см
и длины 90 см. На каком расстоянии I от горизонталь-
ной плоскости, в которой лежит ось вращения О, должен
быть помещен разбиваемый машиной брусок С, чтобы ось
не испытывала удара? Ударный импульс лежит в плоскости
рис. 44.21.1 и направлен горизонтально.
Ответ: I = 97,5 см.
Решение. Расчетная схема — на рис.44.21.2.
Если ось подвеса не испытывает удара, т.е. удар-
ные реакции подшипников оси Oz равны нулю,
то точка D, в которой приложен ударный импульс
S со стороны бруска С, является центром удара.
Найдем его положение, используя известную фор-
мулу [4, 11]:
тус
Определим момент инерции маятника Joz-
Jo, = + С - , ! m.,(L + R?.
385
О
В I
Рис. 44.21.1
Рис. 44.21.2
Введем общую для диска А и стержня В плотность 7. Получим
тд = 77гг L, тиа = yirR2h,
где h — толщина диска. Окончательно имеем:
Joz = ?7Г
г2£3
КУЬ 2 , ч2
+ — + R h(L + ву
386
11. Удар
Определим положение центра масс С маятника:
'firR2h(L + R) +утгг2Ь— R2 h(L + R) +-г2 L2
_ тАУсл + ™вуСв =_____________________£ =_____________2
тд + тпв 'ynr2L + 'yirR2h r2L + R2h
Суммарная масса
m = тна + mB = 7?г(2?2Л + r2L).
Поэтому искомое расстояние I равно следующему выражению:
,=--------------;----------
R2h(L + R) + -r2L2
<дг»+^> r4+№h
0,0^.0,9-+0,Н.0.05+0[1Д 005(0[9 + 01);
=------------------------------------------к 0,975 (м),
0,12 • 0,05(0,9 + 0,1) + - • 0,022 • 0,92
I к 97,5 (см).
Задача 44.22 (44.19). Определить положение центра удара прямо-
угольной мишени для стрельбы (рис. 44.22.1). Высота мишени равна h.
Ответ: s = 2Л/3.
Решение. Расчетная схема — на рис. 44.22.2. Воспользуемся фор-
мулой:
s = ОМ =
Jqz _ mh2/3 _ 2^
myc mh/2 3
11. Удар
387
Задача 44.23 (44.20). Определить положение центра удара к тре-
угольной мишени для стрельбы (рис. 44.23.1). Высота мишени равна h.
Ответ: s = h/2.
Рис. 44.23.1
Решение. Расчетная схема
— на рис. 44.23 2.
+ m(h/3)2 h.
2'
mh/3
s — OK — —
myc
При определении момента инерции пластины Jqz использован результат
задачи 34.12 и теорема Штейнера—Гюйгенса.
Задача 44.24 (44.21). Два шкива вращаются водной плоскости во-
круг своих осей с угловыми скоростями o7l0 и W20- Определить угловые
скорости шкивов и о>2 после того, как на них будет накинут ремень,
считая шкивы круглыми дисками одинаковой плотности с радиусами
Д| и /?2 и пренебрегая скольжением и массой ремня.
R2<jJ\Q + 7?2W20
Ответ: од = - ,—,
R^ + Rl)
_ + R2w2q
~ R2(R2+R22) '
Решение. Расчетная схема — на рис. 44.24.1. Наложение ремня на
шкивы рассмотрим как ударный процесс, при котором происходит мгно-
венное изменение угловых скоростей шкивов.
Рис. 44.24.1
388
11. Удар
Воспользуемся теоремой об изменении кинетического момента при
ударе:
кг-к^ = ^мг($Л.
К
Для первого шкива:
Joiz^l — JOiz^lO — М\,
для второго шкива:
Jo2z^2 ~ JOiZ^20 = ~М2.
Подшипники осей шкивов считаем гладкими. Ударные моменты со сто-
роны наложенного ремня равны по величине: М\ = М2.
Исключая из составленных уравнений ударные моменты, получим
уравнение:
Joiz^l - JOtZ^lO = -Jo2z<^2 + Jo2z^20- (1)
Так как ремень предполагается нерастяжимым, то W\Ri — w2R2. Масса
шкивов равномерно распределена по их ободу. Моменты инерции шкивов:
Jotz — K^Ri, Jo2z = m2R2.
Массы шкивов: mi = y-27rRi, т2 = y-27rR2, где у — плотность материала.
Из уравнения (1) с помощью последних соотношений получаем уг-
ловые скорости:
_ #1^10 + _ -RfcVio + i?2<V2o
“ RitRl+Ri) ’ “2 ~ Я2(Я2+Я22) ’
Задача 44.25 (44.22). Баллистический маятник, употребляющийся
для определения скорости снаряда, состоит из цилиндра АВ, подве-
шенного к горизонтальной оси О; цилиндр открыт с одного конца
А и наполнен песком (рис. 44.25.1); снаряд, влетающий в цилиндр,
производит вращение маятника вокруг оси О на некоторый угол.
Дано: М — масса маятника; ОС = h — рассто-
яние от его центра масс С до оси О; р — радиус
инерции относительно оси О', т — масса сна-
ряда; OD = a — расстояние от линии действия
ударного импульса до оси; а — угол отклонения
маятника. Определить скорость снаряда, предпо-
лагая, что ось маятника О не испытывает удара,
причем ah = р2.
2(Mh + ma) [g a
Ответ: v =---------«/ - sin —.
m V a 2
11. Удар
389
Решение. Расчетная схема изображена
на рис. 44.25.2. Воспользуемся теоремой об из-
менении кинетического момента системы от-
носительно оси вращения Oz при ударе:
= ^МОг(Ме)).
К
е:1Ц
Так как ось маятника не испытывает удара, то
внешних ударных импульсов нет: Kqz — K(qz.
Рис. 44.25.2
K^z — mva, Kqz = mua + Mp2w, и = wo, p2 — ah =>
mva = mwa2 + Mwah.
*,10^
An*
Выразим из полученного соотношения скорость снаряда v через угловую
скорость w маятника, приобретенную после удара:
ip! ma2 + Mah ma + Mh
!Л1 V — ------------w — ----------w.
ma m
:Mr n
'оотнж ДЛЯ послеУдаРного движения маятника воспользуемся теоремой об изме-
нении кинетической энергии:
Выразим w через угол a:
т-т0 = Е4>+£4'
К к
mw2a2 Мр2ш2
==> 0----------— = -mga(\ - cos a) - Mgh(\ — cos a).
щ, ж
си 0 hi ц
ггницОМ
жСдоосиО;,
оси 0;я-
ММ 71.
оси; о-)И
скорость^"
а 0 нем
w =
2g( 1 - cos «)(та + Mh)
ma2 + М р2
4gsin2(a/2) • (ma + Mh)
a(ma + Mh)
Искомая скорость снаряда:
ma + Mh 2(ma + Mh) [g a
v =-------w —----------4 / - sin —
m m V a 2
390
11. Удар
Задача 44.26 (44.23). Однородный стержень мас-
сы М и длины I, прикрепленный своим верхним
концом к цилиндрическому шарниру О, падает без
начальной скорости из горизонтального положения
(рис. 44.26.1). В вертикальном положении он ударяет
груз массы т, сообщая ему движение по горизон-
тальной шероховатой плоскости. Коэффициент тре-
ния скольжения — /. Определить путь, пройденный
грузом, считая удар неупругим.
Ответ: s —
3Z м2
2f(M + 3m)2'
* Решение. Расчетная схема — на рис. 44.26.2. Согласно теореме об
изменении кинетической энергии стержня при «доударном» движении
имеем:
JOz^2 „ I 2 1^8
— = м*2 =* и=- = -рГз => и = у1-
Для определения скорости и груза сразу после удара выпишем следую-
щие уравнения, используя теорему об изменении кинетического момента
относительно оси вращения Oz при ударе и условие неупругого удара:
mul + Joz^\ ~ JozU — 0 (шарнир Oz — гладкий),
и
W1 = r
Отсюда
Ml2/3 Ml [3g м ,—
и =---------=----------х — —-----------V Зя/.
Ml2 Зт + М\ I Зт + М
ml -I----
11. Удар
391
*4
й|шао>
!«Mt^
®Л1Цц>.
ИМ,
Далее рассмотрим движение груза по шероховатой поверхности, предпо-
лагая, что «почти сразу» груз и стержень после удара движутся независимо
друг от друга. Запишем теорему о движении центра масс в проекции на оси
X И у.
' mx = -Ftp,
< FtP = /N,
, 0 = mg - N
=> x = -fg =>
xdx = -fgdx
=> путь, пройденный грузом
и2
s = ^Fg
31 м2
If (Зт + М)2'
Задача 44.27 (44.24). Однородная прямая призма с квадратным
основанием стоит на горизонтальной плоскости и может вращаться
вокруг ребра АВ, лежащего в этой плоскости (рис. 44.27.1). Ребро
!6.2.Соги
«лад
основания призмы равно а, высота ее — За,
масса — Зтп. В середину С боковой грани,
противолежащей ребру АВ, ударяет шар мас-
сы т с горизонтальной скоростью v.
Предполагая, что удар неупругий и что
масса шара сосредоточена в его центре, кото-
рый после удара остается в точке С, опреде-
лить наименьшую величину скорости v, при
которой призма опрокинется.
=Э I:
ДЖ
ШВЖ
шениг
!-П«
Ответ: v =
l-y/53ga.
Решение. На рис. 44.27.2 изображено сечение призмы вертикальной
плоскостью, проходящей через центр масс С призмы.
Пусть скорость шарика, который ударяет призму, равна v. С помо-
щью теоремы об изменении кинетического момента относительно оси
вращения Oz при ударе определим угловую скорость призмы:
JozU + ти • ОС - mv-a = 0. (1)
It
цУ"1 Ударным моментом в оси вращения Oz пренебрегаем. Удар неупругий,
поэтому скорость шарика и после удара связана с угловой скоростью ш
392
11. Удар
призмы следующим образом:
Момент инерции Joz призмы вычислим, используя результат задачи 34.10
и теорему Штейнера—Гюйгенса:
Зт Г (а\2 , '>
Joz —+ (За)
= Юта2.
В результате из уравнения (1) выразим v через ш:
+ ти ОС
v —----------
, 13 2
IOmaz Ч---та
4
3
-та
2
3
-та
2
53
• w = — aw.
6
(2)
Определим центр масс Е системы «призма + шарик»:
т СЕ = Зт • ED,
или т • СЕ — Зт
3
СЕ = -а.
8
Призма опрокинется, если при ее повороте вокруг оси Oz общий
центр масс Е окажется на вертикальной прямой, проходящей через ось
Oz, т. е. если точка Е достигнет положения Е1 (см. рис. 44.27.2). Достаточ-
но, чтобы в этом положении угловая скорость призмы стала равной нулю.
11. Удар
393
Запишем теорему об изменении кинетической энергии системы при
повороте призмы на угол а:
0-
= ~(т + 3m)g • ОЕ( 1 - cos а),
где
13
—а
Из составленного уравнения выразим наименьшую угловую скорость ш,
с которой надо толкнуть призму с шариком, чтобы она опрокинулась:
13 2 2 2 2 13
-—та w - 5та w = -Утр- —а( 1 - cos а)
8 8
Теперь с помощью соотношения (2) найдем наименьшую величину ско-
рости v шарика, при которой призма опрокинется:
53
v = — аш =
6
^\/53ga.
Задача 44.28 (44.25). Платформа с поме-
щенным на ней призматическим грузом АВ
катится по горизонтальным рельсам со скоро-
стью v (рис. 44.28.1). На платформе имеется
выступ, в который упирается ребро В груза,
препятствуя последнему скользить по плат-
форме вперед, но не препятствуя вращению
его около ребра В. Дано: h — высота центра масс груза над платфор-
мой, р — радиус инерции груза относительно ребра В. Определить
угловую скорость ш вращения груза около ребра В в момент мгно-
венной остановки платформы.
А
.в ,
...
Рис. 44.28.1
Ответ: w = hv/p7.
Решение. Согласно теореме об изменении кинетического момента
груза АВ относительно оси Bz при ударе имеем соотношение:
JBza> - mvh = 0.
394
11. Удар
Отсюда
mvh mvh vh
Jbz mP2 P2
Задача 44.29 (44.26). Полагая при условиях предыдущей задачи,
что груз представляет собой однородный прямоугольный параллеле-
пипед, длина ребра которого вдоль платформы равна 4 м, а высота —
3 м, найти, при какой скорости произойдет опрокидывание груза.
Ответ: v = 30,7 км/ч.
Рис. 44.29.1
Решение. Расчетная схема изображена на
рис. 44.29.1. Воспользуемся результатами задач
44.27 и 44.28.
Угловая скорость ш груза в момент мгно-
венной остановки платформы:
ш =
mvh
Jbz
Момент инерции груза:
Jbz
Скорость v платформы, выраженная через угловую скорость w груза:
JBzV a2 + b2
V — --- = ------UJ.
mh 3h
Опрокидывание груза произойдет, если центр масс С груза хотя бы с нуле-
вой скоростью достигнет вертикального положения, т.е. если груз успеет
повернуться на угол а, такой, что
cos а —
Ъ
Va2 + Ъ2
Воспользуемся теоремой об изменении кинетической энергии:
JbzU2
2
= mg BC(l - cos а).
Отсюда
w —
2mg • ВС(1 — cos а)
Jbz
11. Удар
395
Искомая линейная скорость v платформы равна:
а2 +1»2 а2 + b2 l3g(Va2 +32 - fc) 1 la2 + b2 , / . Г”
v= —77—ш ~ —77— U---------? , .э---= тА/ —~— (V а2 + Ь2 - b)g.
3h 3h у а2 + b2 Л V 3 v 7
Если предположить, что h = то
12. Динамика точки и системы переменной массы
(переменного состава) (§ 45, [10])
Задача 45.1 (45.1). Составить уравнение движения маятника пе-
ременной массы в среде, сопротивление которой пропорционально
скорости. Масса маятника изменяется по заданному закону т = m(t)
путем отделения частиц с относительной скоростью, равной нулю.
Длина нити маятника — I. На маятник действует также сила сопро-
тивления, пропорциональная его угловой скорости: R = -/Зф.
р S
Ответ: ф + ——ф + - sin = 0.
TTlytjl I
Решение. Уравнение Мещерского в проекции на касательную к тра-
ектории (окружности) маятника имеет вид:
m(t)Gv’) = -m(t) • gsin 4- R + Fp,
где R — ~/Зф — сила сопротивления, Fp = -ve • m — реактивная сила
(ve — относительная скорость отделения частиц). Но так как (по условию
задачи) ve = 0, то имеем:
m(t)bp = -m(t)gsin - [Зф.
Отсюда получаем ответ к задаче.
Задача 45.2(45.2). Составить дифференциальное уравнение восходя-
щего движения ракеты. Эффективную скорость ve истечения газов**
считать постоянной. Масса ракеты изменяется по закону т =
(закон сгорания). Сила сопротивления воздуха является заданной
функцией скорости и положения ракеты: R(x,x).
.. /(t) R(x,x)
Ответ: х — —g--------ve-----—.
/(£) m0/(t)
Решение. Уравнение Мещерского в проекции на вертикаль х имеет
вид:
m0/(t) • х = -g- mofve - R.
Отсюда получаем ответ к задаче.
** Тяга реактивного двигателя определяется формулой Ра = —(dm/dt)ve, где v( —
эффективная скорость истечения.
12. Динамика точки
397
1е®а®ц
®Лф.
Задача 45.3(45.3). Проинтегрировать уравнение движения преды-
дущей задачи при m = mo(l — at) и В = 0. Начальная скорость ракеты
у поверхности Земли равна нулю. На какой высоте будет находиться
ракета в моменты t = 10; 30; 50 с при ve - 2000 м/с и a = 1/100 с”1?
Ответ: x(t) = [(1 - at) In (1 - at) + at]
ж(10) = 0,54 км, ге(ЗО) = 5,65 км, а: (50) = 18,4 км.
Решение. Уравнение движения из предыдущей задачи имеет вид:
х = ~g +
a
-------ve.
1 - at
Интегрируя по времени один раз, имеем:
i(t) = -gt - ve In (1 - at) (ж(0) — 0).
Интегрируя по времени второй раз, получим:
'|Ц
Ии).Йй1Е
IHBMiljS,
О[ШЦВЕ
ястсгеж"
BOOTJBEI
вд
Интеграл берем по частям:
Отсюда нетрудно получить ответ к задаче.
iprator
Задача 45.4 (45.4). Ракета начальной массы то поднимается вер-
тикально вверх в однородном поле силы тяжести с постоянным уско-
рением ng (g — ускорение земного тяготения). Пренебрегая сопротив-
лением атмосферы и считая эффективную скорость ve истечения газов
постоянной, определить: 1) закон изменения массы ракеты, 2) закон
изменения массы ракеты при отсутствии поля тяготения.
Ответ: I) m = moexp
2) m = mo exp
tl
ve J
398
12. Динамика точки
Решение. Уравнение Мещерского в проекции на вертикаль имеет
вид:
m(t) • ng = -m(t)g -ve-m.
Разделяя переменные, получим:
dm (n + l)g _________ J (n+l)g|
— =------------dt => m(t) — mo exp <------------1 >.
m ve I ve )
Если g = 0, то имеем уравнение:
/х. . __ dm ng ______________ ( ng \
m(t)ng =—vem => — =-------dt => m(t) = moexp<---------1 >.
m ve I ve )
Задача 45.5 (45.5). Масса ракеты, описанной в задаче 45.2, изме-
няется до t = to по закону m = moe~Q . Пренебрегая силой сопротив-
ления, найти движение ракеты и, считая, что к моменту времени to
весь заряд практически сгорел, определить максимальную высоту
подъема ракеты. В начальный момент ракета имела скорость, равную
нулю, и находилась на земле.
cwe . . )
Ответ: Н =-(ave-g)to, где ve — эффективная скорость истечения
2g
^газов из ракеты.J
Решение. Уравнение Мещерского в проекции на вертикаль:
тп
m(t)x — -m(t)g - vem => х = -g - ve—.
Но, так как m(t) = тпое-0*, то получим:
t2
x = -g + ve-a => x(t) = t(-g + a-ve), x(t) = -(-g + ave).
Если к моменту t — to весь заряд сгорел, то при t > t0 начинается просто
движение в поле силы тяжести. Имеем:
f2
Vo = «(to) = to(-g + ave), x(t0) = -£(-g + ave).
Максимальный подъем от координаты «(to) будет в поле тяжести с на-
чальной скоростью vq — «(to) составлять:
®0 ^0 / ч2
Лшах = Z- = y-(-g + m>e) •
2g 2g
Суммарный подъем составит:
^2 ^2 (X'U у
Н = x(to) + hmm = -у (ave - g) + - g)2 = 57 - g)«o-
12. Динамика точки
399
Задача 45.6 (45.6). При условиях предыдущей задачи определить
значение а, отвечающее максимальной возможной высоте подъема
ракеты Ятах, и вычислить Ятах (величину т] = at0 = ln(m0/mi) не-
обходимо считать постоянной; ТП| — масса ракеты в момент to).
Ответ: a = оо (мгновенное сгорание), Я,гах = ц* 1 — .
2g
Решение. Так как ц = ato = const, то имеем to = ц/a. Тогда, ис-
пользуя ответ к задаче 45.5:
ГТ ve , х Д
Н = — a(vea - g) • — = — ц I ve
2g a1 2g \
g_
a
Из последней формулы видно, что
максимум Я достигается при a — оо,
т.е.
-^Лпах
2g
Задача 45.7 (45.7). При условиях задач 45.5 и 45.6, задавшись ко-
эффициентом перегрузки к — ave/g, определить высоту подъема Я
ракеты в зависимости от Ятах.
Ответ: Я =
к
Решение. Пусть к = ave/g. Тогда из ответа к задаче 45.5 имеем:
Н = ^-t2o(ave -g) = ^-k- t20g(k - 1).
2g 2
Кроме того, так как
° a2 fc2g2 ’
то получим:
1 „ х д2г>2 n2vl к - I к - 1
я = -kg(k _ i) . — =
так как по ответу к задаче 45.6 имеем
Нтах
У2еУ2
2g
400
12. Динамика точки
Задача 45.8 (45.8). Ракета стартует с Луны вертикально к ее по-
верхности. Эффективная скорость истечения ve = 2000 м/с. Число
Циолковского z — 5*\ Определить, какое должно быть время сгорания
топлива, чтобы ракета достигла скорости v = 3000 м/с (принять, что
ускорение силы тяжести вблизи Луны постоянно и равно 1,62 м/с2).
Ответ: к 2 мин 4 с.
Решение. Уравнение Мещерского в проекции на вертикаль:
тп
mx = —mg - ve • m ==> x = -g-ve—,
m
где m — mo + m\(t), mQ — масса ракеты, mi(t) — масса топлива. По усло-
вию:
mo + mi(O)
--------— = 2 = 5.
m0
Интегрируя уравнение Мещерского, получим:
ж(0 = ~gt ~ ve In
m0 + mi(0)
В момент t = £* полного выгорания топлива имеем ТП|(£*) = 0, ж(£») =
= v = 3000 м/с. Тогда получим:
t* = -(-г> + ve In 5) а 135,1 с.
g
Отметим, что ответ задачника [10] t* к 124 с!
Задача 45.9 (45.9). Ракета движется в однородном поле силы тяже-
сти вверх с постоянным ускорением w. Пренебрегая сопротивлением
атмосферы и считая эффективную скорость ve истечения газов по-
стоянной, определить время Т, за которое масса ракеты уменьшится
в два раза.
Ответ: Т =
ve In 2
w+g’
Решение. Уравнение Мещерского в проекции на вертикаль:
mw = —mg — vem
fn
w = -g- ve—.
m
Числом Циолковского называется отношение стартовой массы ракеты к массе
ракеты без топлива.
12. Динамика точки
401
Разделяя переменные и интегрируя, получаем формулу:
, т(0)
(w+g)t = ve In——.
m(t)
При t = T имеем
™(0)
m(T) ’
тогда
w + g
Задача 45.10(45.10). Эффективная скорость истечения газов из
ракеты ve = 2,4 км/с. Какой процент должен составлять вес топлива
от стартового веса ракеты, чтобы ракета, движущаяся вне поля тяго-
тения и вне атмосферы, приобрела скорость 9 км/с?
Ответ: Примерно 98 %.
Решение. Уравнение Мещерского в проекции на вертикаль:
( т(0)\
mv — -vem => v(t) — ve In I —— =>
\m(t) J
= e_v/Ve mo + mi(Q = e_„/Ve
m(0) mo + ^i(O)
В момент полного выгорания t = tt имеем mi(t,) = 0, v — 9 км/с, тогда:
----TO> (°) ! _ е-9/(М) ~ 0)98 = 98 %
mo + mi(O) то + тЦО)
Задача 45.11 (45.11). Ракета движется поступательно при отсут-
ствии тяготения и сопротивления среды. Эффективная скорость ис-
течения газов ve — 2400 м/с. Определить число Циолковского, если
в момент полного сгорания топлива скорость ракеты будет равна
4300 м/с.
Ответ: z и 6.
Решение. Используя решение предыдущей задачи, получим:
z = m° + ml(°) = ev/vc = <,4300/2400 _ 5 999 6
т0 + 0
402
12. Динамика точки
Задача 45.12(45.12). Тело переменной массы, имея начальную j
скорость, равную нулю, движется с постоянным ускорением w по го-
ризонтальным направляющим. Эффективная скорость истечения га-
зов ve постоянна. Определить, пренебрегая сопротивлением, путь,
пройденный телом до того момента, когда его масса уменьшится
в к раз.
г>е(1п к)2
Ответ: s =----------.
_______________2w__________________________________________ J
Решение. Уравнение Мещерского в проекции на горизонталь имеет
вид:
/т(0)\ w
mw = — vem => In ( —— I = — t.
\ m(t) J ve
Но так как w = const, to
wt2
Если t — таково, что
m(°) _ k
m(t)
TO
s(0 = ^(lnA:)2.
Задача 45.13(45.13). Решить предыдущую задачу, предположив,
что на тело действует сила трения скольжения.
WV2 э
Ответ: s = -----—rr(lnfc) , где f — коэффициент трения сколь-
2(w + fg)2
жения.
Решение. Здесь уравнение Мещерского в проекции на горизонталь
и при учете силы трения принимает вид:
mw = - fmg - vem
m ve In к
w + fg = —ve • — => t —-----------------—
J m w + fg
wt2 w z>g(ln k)2
=> S 2 2 (w + fg)2'
12. Динамика точки
403
Задача 45.14(45.14). Тело переменной массы движется по специ-
альным направляющим, проложенным вдоль экватора. Касательное
ускорение wT — а постоянно. Не учитывая сопротивление движению,
определить, во сколько раз уменьшится масса тела, когда оно сделает
один оборот вокруг Земли, если эффективная скорость истечения
газов ve = const. Каково должно быть ускорение а, чтобы после од-
ного оборота тело приобрело первую космическую скорость? Радиус
Земли — R.
Ответ: В ехр
раз;
4тг
Решение. Уравнение Мещерского в проекции на касательную к эк-
ватору имеет вид:
ma — —vem ==>
a
In k — — • t
ve
Если t — таково, что пройден весь экватор, то:
at1
~Г
= 2тгЛ
(R — радиус Земли).
Тогда:
k — ехр
Первая космическая скорость находится из соотношения:
^=8
R
vj = y/gR.
Тогда, если t = y/itR/a, то
vj — at
ZVftRa — y/gR
g
a — —.
47Г
Задача 45.15 (45.15). Определить в предыдущей задаче массу топ-
лива, сгоревшую к моменту, когда давление тела на направляющие
будет равно нулю.
Ответ: mT - т0
404
12. Динамика точки
Решение. Аналогично решению предыдущей задачи имеем соотно-
шения:
(так как давление на направляющие равно нулю при достижении 1-й кос-
мической скорости!). Из уравнения Мещерского получаем:
In
m0 + "i । (0)
m0 + mi(t)
mi(0) - mi(t) = m(0)(l - e A),
где m(0) = mo + nii(0) — стартовая масса ракеты.
Задача 45.16(45.16). Тело скользит по горизонтальным рельсам.
Истечение газа происходит вертикально вниз с постоянной эффек-
тивной скоростью ve. Начальная скорость тела равна vq . Найти закон
изменения скорости тела и закон его движения, если изменение массы
происходит по закону m = mo — at. Коэффициент трения скольжения
равен f.
( т0 \
Ответ: v = г>0 - f - ve In-------- ,
\ mv - at /
fgt2 Г mo — at f , 4
s = vot - f 5 —— ve t In mo + -----(In (m0 - at) - 1 -
2
a
т0/1 п
-----(In m0 - 1)
a
Решение. Уравнения движения в проекциях на горизонталь и вер-
тикаль имеют вид:
mv = —fN; m • 0 = N — mg - ve-m
(так как относительная скорость отделяющихся частиц направлена по вер-
тикали!). Отсюда получим:
mv — -f(mg + mve)
( тп
v = -fl g + ve—
\ m
v(t) = v0- fgt + fve In
m0
mo — oct
Интегрируя это соотношение еще раз по t (интеграл берется так же по
частям, как в решении задачи 45.3), получим ответ к задаче.
12. Динамика точки
405
Задача 45.17 (45.17). Решить предыдущую задачу, если изменение
топлива будет происходить по закону m = moe-Q*. Определить, при
каком а тело будет двигаться с постоянной скоростью v0.
Ответ: v = v0 - f(g - ave)t, s = vot- f(g - ave)—, a = —
2 ve
Решение. Если m(£) = moe at, то уравнение для v из предыдущей
задачи получается таким:
v = ~f(g ~ ave)
=> v(t) = vQ- ft(g - ave) ==>
/i2
s(t) = vot- — (g — ave).
Если g - ave = 0 => a = g/ve, то v(t) — const = vq.
Задача 45.18(45.18). Какой путь пройдет ракета на прямолиней-
ном активном участке в пустоте и при отсутствии сил тяготения за
время разгона от нулевой начальной скорости до скорости, равной
эффективной скорости истечения продуктов сгорания ve, если из-
вестна начальная масса ракеты т0 и секундный расход /3?
vemQ е — 2
Ответ: s = —----------, где е — неперово число.
/3 е
Решение. Уравнение Мещерского имеет вид:
mv = -mve;
так как m = -/3, т. e. m(t) = m0 - /3t, то получим:
ve/3
v =-----------
TTIq - /3t
(4\ 1 / m° 1
v(t) = ve In I --------— I =>
\ m0 - pt /
... . m0 ,
1 I --------- I
Д \ fno J.
s(t) = ve t • In mo - t In (TOo — /3t) + t + — In
Для момента t = t*, когда v(tt) = ve, имеем
mo e — 1 m0
/3 e 1П m0 - (3t,
= 1.
И мы получим:
vemQ e-2
406
12. Динамика точки
Задача 45.19(45.19). Ракета движется прямолинейно вне поля тя-
готения и при отсутствии сопротивления. Найти работу силы тяги
к моменту, когда сгорит все топливо. Начальная масса ракеты то,
конечная — Ш]. Эффективная скорость истечения ve постоянна.
2/ Шо
Ответ: А = mive(z - 1 - In z), z = —.
Ш]
Решение. Запишем уравнение Мещерского:
77W — Vem — 2*реакт '' -^*реакт — VeTfl,
Работа реактивной силы:
й й
4[0, £i] = J\—vem)v dt = J mvvdt.
о о
Интегрируя уравнение Мещерского, имеем:
Тогда имеем следующее выражение для работы:
й
// т\ / то \
ml -ve— I • ve In —— I dt —
\ mJ \m\t) J
о
7771
2 f f Ш0 \ 2 / \
= -ve / In — dm = mive(z - 1 - In z),
J
TTIq
где z — mo/mi.
Задача 45.20 (45.20). При каком отношении z начальной то и ко-
нечной mi масс ракеты, движущейся прямолинейно в пустоте и при
отсутствии сил тяготения, ее механический КПД, определяемый как
отношение кинетической энергии ракеты после выгорания топлива
к затраченной энергии, имеет наибольшее значение?
Ответ: z — корень уравнения In z =
12. Динамика точки
407
_______m, • z>j;(ln z)2
Л[0,^| lm\V2(z- 1 - Inz)
Решение. Используя решение предыдущей задачи, имеем:
кпд = /1 = “'^/2
и=------------
2 z - 1 - In z
:ого:
ви=-
In z ( 2-------In z - In z
[ \ z z
dz 1.
(z - 1 - In z)2
= 0.
z является корнем уравнения
In z ( 1
Z
/ 1
= 2 1- -
\ z
т. е.
, 2(z - 1)
In z =-------
l+z
Задача 45.21 (45.21). Самолет, имеющий массу ttiq, приземляет-
ся со скоростью Vo на полярный аэродром. Вследствие обледенения
масса самолета при движении после посадки увеличивается соглас-
но формуле m = ttiq + at, где a = const. Сопротивление движению
самолета по аэродрому пропорционально его весу (коэффициент про-
порциональности /). Определить промежуток времени до остановки
самолета с учетом (Г) и без учета (7)) изменения его массы. Найти
закон изменения скорости с течением времени.
„ „ Шп / / 2(Wo \ Vq
Ответ: Т = — JI +-------- - I , Г, = —,
а \у ^т° fg
2то^о - /g(2m0 + at)t
v =-------------------.
2 (то + at)
-.-Г
fill ж
OClMf
ИЙ»’
Решение. Запишем уравнение Мещерского для движения самолета
по горизонтали. При этом будем учитывать, что присоединяющиеся частицы
воздуха (которые создают лед!) имеют по горизонтали относительную
скорость (-г>), где v — скорость самолета. Тогда получим:
m(t)v = -fm(t) g + (-v)m.
Учитывая, что
m(t) = mo + at,
408
12. Динамика точки
отсюда получим:
a
v = -v-----— - fg.
mo + at
Это — неоднородное линейное дифференциальное уравнение 1-го поряд-
ка. Его решение:
v(t) = Vi(t) + v2(t),
где Ц|(<) — общее решение однородного уравнения
a
= -t>,------------------------------—-
mo + at
имеющее вид:
Vi(t) = C-------, C = const;
m0 + at
v2 — частное решение неоднородного уравнения, которое найдем, ис-
пользуя вариацию С:
С'---
m0 + at
В итоге мы получим:
fg
2a
v{t) = С ’ тп 'Г^ ~ + °*)-
Шо 4- at 2a
Константу С найдем из начального условия г>(0) =
С = ^(2az>o + /gmo).
2а
Следовательно, решение:
_ т0(2аг>0 + fgm0) - /g(m0 + at)2 _ 2m(jvr - fgt(2mQ + at)
2a(mo + at) 2(mo + at)
Отсюда находим t — T — время остановки, когда v(T) = 0, т.е. ответы
из задачника.
Задача 45.22 (45.22). Эффективные скорости истечения первой
и второй ступени у двухступенчатой ракеты соответственно равны
= 2400 м/с и ц® — 2600 м/с. Определить, считая, что движение
происходит вне поля тяготения и атмосферы, числа Циолковского
для обеспечения конечной скорости г>1 = 2400 м/с первой ступени
и конечной скорости v2 — 5400 м/с второй ступени.
Ответ: Z\ = 2,72, z2 = 3,17.
12 Динамика точки
409
Решение. Уравнение Мещерского:
m
V = -Ve-
TTl
v(t2)-v(t})
-----------= In-------.
ve m(t2)
®нецц
if
Отсюда для чисел Циолковского мы получим формулы:
. , ib - г,
lnzt = —, Inz2 = ——
Ve Ve
=> Z] = e1, z2 = el2/'3
=сад,
Задача 45.23 (45.23). Считая, что у трехступенчатой ракеты числа
Циолковского и эффективные скорости ve истечения у всех трех
ступеней одинаковы, найти число Циолковского при vc = 2,4 км/с,
если после сгорания всего топлива скорость ракеты равна 9 км/с
(влиянием поля тяготения и сопротивлением атмосферы пренебречь).
Ответ: z = 3,49.
Решение. Аналогично решению предыдущей задачи запишем три
соотношения для сгорания последовательно трех ступеней:
f|
In z = —
Ve
v2 - t)| v3 - v2
In z —-------------, In z =-----------------
Ve Ve
Сложим эти равенства:
V}
3 In z = —
Ve
та#
ШИ II»
.1МГ-
Задача 45.24(45.24). Трехступенчатая ракета движется поступа-
тельно при отсутствии тяготения и сопротивления атмосферы. Эффек-
тивные скорости истечения и числа Циолковского для всех ступеней
одинаковы и соответственно равны ve = 2500 м/с, z = 4. Определить
скорости ракеты после сгорания горючего в первой ступени, во второй
и в третьей.
Ответ: г>| — 3465 м/с, v2 = 6930 м/с, = i0 395 м/с.
I, в
1Ы, в!»
(МиМ
улепи.
Решение. Используя равенства из решения предыдущей задачи, по-
лучим:
= Ve In Z, V2 = 1ve In Z, Vi = yve In z.
Подставляя числа, получаем ответы к задаче.
410
12. Динамика точки
Задача 45.25(45.25). В момент, когда приближающийся к Луне
космический корабль находится на расстоянии Н от ее поверхности
и имеет скорость г?0> направленную к центру Луны, включается тор-
мозной двигатель. Учитывая, что сила тяготения обратно пропорцио-
нальна квадрату расстояния от корабля до центра Луны и принимая,
что масса корабля изменяется по закону тп = тпов at (mo — масса
ракеты в момент включения тормозного двигателя, a — постоянное
число), найти а, при котором корабль совершит мягкую посадку
(т.е. будет иметь скорость прилунения, равную нулю). Эффективная
скорость истечения газов ve постоянна. Радиус Луны — R, ускорение
силы тяжести на Луне — gn.
Ответ: а = „ u - -I-———.
2veH ve(R + Н)
Решение. Введем ось х с началом в точке начала торможения и на-
правленную кцентруЛуны (см. рис.45.25.1).Тогда уравнение Мещерского
по оси х имеет вид:
mg„R2
mx = 7----ттгт
(х + R)2
+ vem
g.R-
(х + R)2
- vea.
луна
Рис. 45.25.1
Умножим обе части на х и проинтегрируем:
x2(t) v% gnR2 g„R2 .
—-----------=----------1-------v*o • x(t).
Полагая
получим
2 x + R R
здесь
x(t) = 0, x(t) = H,
ответ.
Задача 45.26(45.26). Найти закон изменения массы ракеты, на-
чавшей движение вертикально вверх с нулевой начальной скоростью,
если ее ускорение w постоянно, а сопротивление среды пропорцио-
нально квадрату скорости (Ь — коэффициент пропорциональности).
Поле силы тяжести считать однородным. Эффективная скорость ис-
течения газа ve постоянна.
Ответ:
m =
m0 +
2bv^w2 \
(w+g)3) еХР
ve
bw2 i 2vcbw2
----t" +-----ГТ
w+g (w+gy
2vjbw2
(w+g)3'
12. Динамика точки
411
Решение. Уравнение Мещерского по вертикали имеет вид:
гпх — -mg - bx2 4- vcm.
Используя условия задачи, имеем
х = w, х = wt.
Тогда получим уравнение для m(t):
g + w
m - m--------
ve
Ь 2 2
= — w2t2.
Ve
Это — линейное неоднородное дифференциальное уравнение 1-го поряд-
ка. Решая его по обычным правилам, имеем:
m(t) = + m2(t).
где rri](t) — общее решение однородного уравнения, имеющее вид:
\ g+w
Шць) ~~ С € , А — -
Ve
a m2(t) — частное решение неоднородного уравнения, которое следует
искать в виде:
m2(t) = a2t2 + 4- Go,
До, й|,й2 — константы.
Тогда получим:
2a2t 4- at - (a2t2 4- a\t 4- Go) • A = —w2 t2 =>
b 2 bw2
=>a2 = -—w =----------—
Xve g + w
lai — Act [ — 0
ft] — Afto — 0
2a2 2vebw2
a' A (g 4- w)2 ’
a I 2vibw2
°o = T = —v-
A (g -I- w)s
Используя начальное условие
m(0) = mo,
найдем константу С и получим ответ задачника.
412
12. Динамика точки
Задача 45.27(45.27). Ракета перемещается в однородном поле си-
лы тяжести по прямой с постоянным ускорением w. Эта прямая
образует угол а с горизонтальной плоскостью, проведенной к по-
верхности Земли в точке запуска ракеты (рис. 45.27.1). Предполагая,
что эффективная скорость истечения газов ve постоянна по величине
и направлению, определить, каково должно быть отношение началь-
ной массы ракеты к массе ракеты без топлива (число Циолковского),
если к моменту сгорания топлива ракета оказалась на расстоянии Н
от указанной выше касательной плоскости.
{cos a 2wH 1
--------\ ------>, где р — угол, образуемый ско-
тче cos fl V sin a J
го sin a 4- g
ростью ve с касательной плоскостью, равный fl = arctg-------.
w cos a
Решение. Введем систему координат Ofyj, где О£ направлена по
прямой движения ракеты, а От/ — ей перпендикулярна (рис. 45.27.2).
Уравнение Мещерского в проекциях на эти оси имеет вид:
mw — —mgsin a - vem cos (/3 - a), (1)
m • 0 = -mg cos a - vem sin (/3 — a). (2)
Умножая (1) на sin (/? - а), а уравнение (2) на cos (fl - a) и вычитая одно
из другого, получим:
mw sin (fl - a) = -mg[sin a sin (fl - a) - cos a cos (fl - a)].
Отсюда находим:
g g -I- w sin a
sin fl cos a - cos fl sin a = — cos fl => tg/3 =--------.
w w cos a
Используя полученное соотношение, имеем:
g sin a -I- w
cos (fl - a) — cos fl (cos a 4- tg fl sin a) = cos fl-.
7 w cos a
12. Динамика точки
413
Далее интегрируем уравнение (1) по времени:
(w + gsin a) • t = ve cos (Д - a) • In
m(0)\
m(f) / ’
(3)
Если ракета за время t поднялась на высоту Н, то
wt2 / 2H
£(0- . — — => t = Л
sin a 2 r w sin a
Подставляя полученное t в (3), имеем:
/ • \ / 2Н g sin a + w
(w+gsma)\ —;—=ve-cos/3-----------------Inz =>
V w sin a w cos a
z — exp
cos a
ve cos /3
2Hw
sin a
Задача 45.28(45.28). Тело переменной массы движется вверх с по-
стоянным ускорением w по шероховатым прямолинейным направля-
ющим, составляющим угол а с горизонтом. Считая, что поле силы
тяжести является однородным, а сопротивление атмосферы движению
тела пропорционально первой степени скорости (Ъ — коэффициент
сопротивления), найти закон изменения массы тела. Эффективная
скорость истечения газа ve постоянна; коэффициент трения скольже-
ния между телом и направляющими равен /.
(bwve \ ( wi 1 bv' / ve \
mo-----5- I exp <-1 >-1 t---I,
W\ ) [ Ve J Wj \ W\ J
где w\ = w + g(sin a + f cos a), mo — начальная масса тела.
Решение. Направляем ось Ох системы координат Оху вдоль на-
клонной плоскости вверх, а ось Оу — перпендикулярно к ней (рис. 45.28.1).
Уравнения движения (с учетом реактивной силы Мещерского) в проек-
циях на эти оси имеют вид:
mx = —mg sin a — fN — bx + vem, m -0 = N — mg cos a.
414
12. Динамика точки
Исключая N, получаем:
mx = -mg sin a — fmg cos a — bi + vem => (так как x = w, x — wt)
g sin a + fg cos a + w b
m - m-----------------= —wt.
ve
ve
Решая это линейное неоднородное дифференциальное уравнение 1-го по-
рядка стандартными методами, получим ответ.
Задача 45.29 (45.29). Аэростат весом Q поднимается вертикально
и увлекает за собой сложенный на земле канат. На аэростат дей-
ствует подъемная сила Р, сила тяжести и сила сопротивления, про-
порциональная квадрату скорости: R = —/Зх2. Вес единицы длины
каната — 7. Составить уравнение движения аэростата.
Ответ: х = -g +
Pg
Q 4-7Ж
fig + 7 .2
----x
Q+yx
Решение. Направим ось х вертикально вверх. Уравнение Мещер-
ского вдоль этой оси имеет вид:
2
mx = —mg + Р - /Зх + vem,
(1)
где ve — относительная скорость присоединяющихся частиц каната, которая
в данном случае равна ve = —х. Ясно, что
7 . Q , 7
m -- —х, m(t) = —I—х.
g g g
Подставляя полученные соотношения в уравнение (1), получим ответ за-
дачника:
, Pg fig + У .2
Х 8 Q + yx Q + yxX '
Задача 45.30 (45.30). При условиях предыдущей задачи опреде-
лить скорость подъема аэростата. В начальный момент аэростат непо-
движен и находится на высоте Н<,.
Ответ: х2
Pg
(fig + 7)
£+7Я»У<1+'’!’-
Q + ух )
2g
2/3g + З7
Q+7Ho\3+2^'
Q + yx J
(Q + yx).
12. Динамика точки
415
I эшение. Перейдем в уравнении, полученном в решении предыду-
щей задачи, к новой независимой переменной х:
_J/(z2)_ pS /3g
2 dx Q + ух Q 4- ух
Обозначим х — и, получим линейное дифференциальное уравнение пер-
вого порядка:
du 2(J3g + y) 2Pg
— + ------w = -2с -I---
dx Q + yx 6 Q + yx
Решая это уравнение стандартными методами, получим:
U = W| 4- U2
(и, — общее решение однородного уравнения, «2 — частное решение не-
однородного уравнения), где
U1 =C(Q + yx)~2('+M'* 1\
а частное «2 находим методом вариации постоянной С. Используя на-
чальные условия ж(0) = Hq, ±(0) = 0, получим ответ задачника.
Задача 45.31 (45.31). Шарообразная водяная капля падает вер-
тикально в атмосфере, насыщенной водяными парами. Вследствие
конденсации масса капли возрастает пропорционально площади ее
поверхности (коэффициент пропорциональности а). Начальный ра-
диус капли — г0, ее начальная скорость — г/0, начальная высота — Ло.
Определить скорость капли и закон изменения ее высоты со временем
(сопротивлением движению пренебречь).
Указание. Показать, что dr = a dt, и перейти к новой независимой перемен-
ной г.
(\2П / 4\
Го \ g ( 2 - 2 , го\
— - I г - 2г0 4- -у ,
г / J 8а2 \ г1 /
ro g ( го\ , f
v = г>0—г - — I т--, , где г = г0 4- at.
Решение. Направим ось х вертикально вниз. Тогда уравнение Ме-
щерского по этой оси имеет вид:
mx = mg 4- vem.
(1)
Ясно, что скорость ve присоединяющихся частиц есть ve — —х. Кроме
того, по условию задачи:
m — а • 4тгг2р (р — плотность воды).
416
12. Динамика точки
Но так как
4 з
m = -яг р,
3 г
то
тп = 4тгг2р • г.
Следовательно,
4тгг2рг = а4тгг2р => г — а = const.
Переходя к независимой переменной
г = at 4- го
из уравнения (1), получим:
dv а4тгг2р dv 3 g
a— = g~v-.—— =>
dr jTrr2p dr r a
где r = at + го- Решение полученного уравнения ищем стандартным спо-
собом:
v = г>1 4- Vi,
где щ — общее решение однородного уравнения:
dvt 3 С
-----1- г>1 - = 0 => г>1 = —7, С = const,
dr г г3
а «2 - частное решение неоднородного, которое ищем методом вариации
постоянной:
-3С' = ^-
rJ а
V2 =
—Г.
4а
а 4
Таким образом, получается решение:
С g
х = v = —? 4---г,
г3 4а
где г = го 4- at. Константу С находим, используя начальное условие
v(r0) = v0.
Далее:
dx dx С g
— == — СИ ~ т Ч-
dt dr г3 4а
, , / Ч С 1 V S ,2 24
=> х(г) - х(г^) =--{ -А--А I +—-2(г -г0).
у / * 0 '
12. Динамика точки
417
Таким образом,
t С ( 1 । А 5,7
х = h0 - - - - - + —- (г2 * _ г0),
а \ г4 Гр / 8а2 '
где следует подставить вместо С выражение:
После нескольких преобразований мы получаем ответы задачника.
Задача 45.32 (45.32). Решить предыдущую задачу в предположе-
нии, что на каплю кроме силы тяжести действует еще и сила сопро-
тивления, пропорциональная площади максимального поперечного
сечения и скорости капли, R = -4(3irr2v ((3 — постоянный коэффи-
циент).
Ответ: х — h0
2(4а+ЗД)
3(3 + 2а [ 4а 4- 3/3
-1(ЗД+2а)_ -2(ЗД+2а)
г г0
gr
V —-------------
4а + 3/3
5(г2 - *о)
2а(4а + 3/3)
2(4а+ЗД)
, а^+0)
4а + 3(3 '"°
. a (а+Д), где г = Го_^ а[.
X
х
Решение. Добавим в уравнение (1) предыдущей задачи силу сопро-
тивления R — -4(Зтсг2у, тогда:
mv = mg + vem - 4/Зтгг2ъ.
(О
Проводя аналогичные рассуждения, мы получим
ve = —х = —V, г — a = const => г = го + at.
Тогда
4 □ 2 2
m = -яг р, m = 4тгг рг = а4лт р.
Деля в уравнении (1) обе части на т, получим:
За
v=g-v—
г
4(3тог1
-7ГГ р
Беря за независимую переменную
г = го + at,
418
12. Динамика точки
получим:
dv g v Г 3(а + /3)
dr a г [ a
(мы положили р = 1 — плотность воды).
Интегрирование полученного уравнения выполняется совершенно
аналогично тому, как это было сделано при решении предыдущей зада-
чи. В результате нескольких, но громоздких выкладок получается ответ
задачника.
Задача 45.33 (45.33). Свернутая в клубок тяжелая однородная
цепь лежит на краю горизонтального стола, причем вначале одно
звено цепи неподвижно свешивается со стола. Направляя ось х вер-
тикально вниз и принимая, что в начальный момент х — 0, х = О,
определить движение цепи.
Ответ: х = —.
6
Решение. Пусть х направлена вертикально вниз и в момент t длина
цепи составляет x(t). Тогда ее масса px(t), где р — погонная масса цепи,
а ускорение a = х. Уравнение Мещерского:
[/?ж(«)]ж = pgx + г>е[рж]'.
Здесь для присоединяющихся частиц цепи мы должны принять ие = -х.
Тогда имеем:
• 2
XX = gx — X .
Переходя к независимой переменной х и обозначая х2 = и, получим:
1 du du 2
x-—=gx-u => — + -u = 2g => и = щ+и2,
2dx dx x
где Uy = С/х2 — общее решение однородного уравнения, и2 — частное
решение неоднородного уравнения, которое ищем методом вариации
постоянной:
С 2 з 2
= 2£ => С = -gx => и2 = -gx.
хг 3 3
Таким образом:
2 С 2
и = х = -у + -gx.
хг 3
Так как в начальный момент х = 0 и ж(0) = 0, то мы должны принять
С = 0, т.е. имеем:
.2 2
X = -gx
х
12. Динамика точки
419
Мы берем С| = 0, так как x(t — 0) = 0. Таким образом,
X ---
zg-t
1 •>
х =
о
Задача 45.34 (45.34). Цепь сложена на земле и одним концом
прикреплена к вагонетке, стоящей на наклонном участке пути, обра-
зующем угол а с горизонтом. Коэффициент трения цепи о землю — /.
Вес единицы длины цепи — 7, вес вагонетки — Р. Скорость вагонет-
ки в начальный момент — «?0. Определить скорость вагонетки в любой
момент времени и выяснить необходимое условие, при котором ваго-
нетка может остановиться.
X2 P2Vfi Pg
°твет: T = 37
1
' 3
Р2
+ — sin a 1 - —---------ry +
З7 L (P + 7®)2.
1
cos a - ^fgx cos a-
Р2
+ -gzsina + —— l-/„ x,
3 67 L (P + 7®)2J
^Остановка может иметь место при выполнении неравенства / > tg a.^j
Решение. Расчетная схема изображена
на рис. 45.34.1. Пусть х — координата ваго-
нетки, отсчитываемая вдоль наклонной плос-
кости вниз от клубка цепи. Тогда уравнение
Мещерского вдоль оси х таково:
/Р 7 \ .
— -I—х li =
g g J
- fyx cos a,
(7
= (P + yx) sin a + ve I —x
\g
где ve — относительная скорость присоединя-
ющихся частиц цепи, равная:
ve = -X.
Таким образом, получаем уравнение:
Р + ух 7 2 . .
------х Ч—х = (Р + 7®) sin a — fyx cos a.
g-----g
Вводя независимую переменную x, обозначая x2 — u и используя тожде-
ство
1 d(x2)
Х = 2 dx ’
420
12. Динамика точки
получим:
du
dx
27 Ifg^jx cos a
—-------u = 2g sin a-----------------
P 4- 'yx P + -yx
Решая это линейное дифференциальное уравнение 1-го порядка стандарт-
ным способом, получим:
и = Ut + U2,
где U] — общее решение однородного уравнения:
du 1 27
---—----------ui>
dx P + yx
равное:
_ C
Ui (P 4- 7Ж)2 ’
U2 — частное решение неоднородного уравнения, которое ищем методом
вариации постоянной:
- 1 l . 2fg'ycosa-x
С 7^------тг = 2g sin a------------- =>
(Р4-7Ж)2 Р+'уХ
С' = 2g sin а(Р + 7s)2 — 2/g7 cos a x(P 4- 7®) =>
2g sin a 3 2 2
=> C = —---------(Р + 'уХ) - fgy cos a- Px - 2/g7 cos a-—.
З7 3
Таким образом, решение
С
имеет вид:
2g sin а!
4--^-----(Р + ух)-
Зу
U = X2 — —-------ГТ
(P 4- 7®)2
, „ x2 'Ifg'Y2 cos a • x3
-,gyCKaP(P^^ 3(P + T^ ’
где константу С следует выбирать из начального условия х2 — при
х — 0, т. е.:
2
2 C 2Pg sin a
“°= p5+ 37
\ 37
В результате получаем следующее выражение:
J
X — . .
(P 4- 'yx}2
Р2
4- "7— sin a 1 - —------гт-
37 [ (Р 4- 7а:)2
Р2
Зу
2
4- -gx sin a 4-
fPg cos a [
(P4-7®)2.
3?
2
- -/geosax — Ф(ж).
2Pg .
12. Динамика точки
421
Для выяснения возможности остановки установим, когда уравнение
Ф(зт) — 0 имеет решение при х 6 [0, оо). Достаточное условие:
Ф(0) = г?о > О,
Ф(эо) < О
2
Ф(оо) ~ x-g(sin a — f cos a) -> -oo,
если f > tga. Итак, если f > tga, то уравнение Ф(х) = 0 обязательно
имеет положительный корень и будет остановка. Если же f < tga, то
2 2
-gx sin a - - fgx cos a > 0,
и, как это видно из выражения для Ф(х), будет соблюдаться неравенство
Ф(х) > 0 при х 6 [0, оо), т.е. вагонетка никогда не остановится.
Задача 45.35 (45.35). Материальная точка массы m притягивает-
ся по закону всемирного тяготения Ньютона к неподвижному центру.
Масса центра со временем меняется по закону М — Af0/(l +at). Опре-
делить движение точки.
Указание. Перейти к новым координатам с помощью соотношений
f= Х = У
1 + at ’ 77 1 + at
и к приведенному времени
1
______________ Т a(l+at)
Ответ: Уравнения движения в координатах %, т имеют вид (/ — по-
стоянная тяготения):
dr2
р-
d2V Мог}
dr2 1 p2
p=\/? + ri2,
т. e. отвечают обычным уравнениям в случае постоянных масс. Поэто-
му в зависимости от начальных условий в переменных £ и т/ имеют
место эллип* х ческие, параболические или гиперболические орбиты.
Решение. Уравнения Ньютона для плоской орбиты точки m в де-
картовых координатах (х, у) имеют вид:
х у
Делая замену
rc = (l+at)£, у = (1 + at)y,
1
a(l + at) ’
422
12. Динамика точки
имеем:
х = a£ + (1 + at) — I - —--у I = a£ - — ----- -a(- ar—,
'dr\ (\+at)2J dr \ + at dr
d( dT dT d( d2( dr
Ct------— a-------— OCT--------—
dr dt dt dr dr2 dt
df / 1 \ / 1 \ df d2f 1
Q— I--------------I 4-q I ---------- I----к cxT--------------
dr \ (1 + ad)2/ \(l + tnt)2/ dr dr2 (1 + at)2
Уравнение для координаты x примет вид:
(i+«oe _чз е
( } ат2 f 1 + at (1 + af)3(e2 + к)3/2 /Мо(аг) + ,,2)3/2 •
Отсюда получаем:
d2£ тл< £
dT2 “ ~fM°^2 + T]2)3/2'
Совершенно аналогично получается уравнение для координаты ту:
d2?/ т/
dT2 = ~fM°^2 + T]2)2/2‘
Эти уравнения уже описывают кеплеровские орбиты (эллипс, параболу
или гиперболу).
Задача 45.36 (45.36). Для быстрого сообщения ротору гироскопа
необходимого числа оборотов применяется реактивный запуск. В тело
ротора вделываются пороховые шашки общей массой то, продукты
сгорания которых выбрасываются через специальные сопла. Принять
пороховые шашки за точки, расположенные на расстоянии г от оси
вращения ротора. Касательная составляющая эффективной скорости
истечения продуктов сгорания ve постоянна.
Считая, что общий расход массы пороха в одну секунду равен д,
определить угловую скорость w ротора к моменту сгорания пороха,
если на ротор действует постоянный момент сопротивления, равный
М. Радиус ротора — R. В начальный момент ротор находится в покое.
Rqve — М Jo 2
Ответ: w =------z----In —, где Jq = Jv + mor , J„ — момент инер-
r2<z Jp
ции ротора относительно оси вращения.
12. Динамика точки
423
Решение. Можно считать все пороховые шашки за одну матери-
альную точку переменной массы, расположенную на расстоянии г от оси
ротора. Тогда уравнение моментов Мешерского относительно оси ротора
имеет вид:
[jp + m(/)r2]d> = ~vemr - М; (1)
учитывая, что
m(t) — mg - qt, тп — -q,
получим:
Г z \
I Jp + (m0 - — = veqr - М ==>
at
(veqr - M)dt
=> dw =-----------------—г =>
Jp + (тп0 - qt)r-
,,, veqr - М Г Jp + m0r2
=> w(t) =----------— In --------------.
?r2 \.Jp + (mo-qt)r\
Полное сгорание соответствует такому £*, что m0 - qt„ = 0. Подставляя,
получаем ответ задачника.
Задача 45.37 (45.37). По данным предыдущей задачи найти угло-
вую скорость ротора после сгорания пороха, если на ротор действует
момент сопротивления, пропорциональный его угловой скорости (Ь —
коэффициент пропорциональности).
Ответ: w =
Rveg Г
ь
Решение. Подставляя в уравнение (I) из решения предыдущей за-
дачи значение М — —Ьш, получим:
[Jp + (mo - qt)r2]w - veqr -bw =>
________b___________________veqr
JP + (m0 - qt)r2 Jp + (m0 - Qt)r2'
Решая это уравнение стандартным способом, получим:
W = (Д| + W1,
где CU| — общее решение однородного уравнения, равное:
Wi=C
JP + (mo-^)r2
Jp + mor2
a =
b
r2q'
424
12. Динамика точки
^2 — частное решение неоднородного уравнения, которое в данном случае
равно константе:
v€qr
Подбирая константу С из начального условия ш(0) = 0, получим ответ:
V^r 1
w(t) = — 1 -
Jp + (тп0 - qt)r2
Jp + mor2
a
В момент t = t. полного сгорания имеем m0 — qtt — 0, тогда:
а т
уедт
ь
Р
Jo = Jp + w2.
Литература
1. Булгаков Б. В. Прикладная теория гироскопов. М.: Гостехиздат, 1955.
2. Веселовский И. Н. Сборник задач по теоретической механике М.: ГИТТЛ, 1955.
500 с.
3. Граммель Р. Гироскоп, его теория и применения. М.: ИЛ, 1952. Т. I, II.
4. Дронг В. И., Дубинин В. В., Ильин И. И. и др. Курс теоретической механики. Учеб-
ник для вузов / Под обшей редакцией К. С. Колесникова. М.: Изд-во МГТУ
им. Баумана, 2000. 736 с.
5. Журавлев В.Ф. Основы теоретической механики. М.: Физматлит, 2001. 319 с.
6. Козлова 3. П., Паншина А. В., Розенблат Г. М. Теоретическая механика в реше-
ниях задач из сборника И. В. Мешерского. Динамика материальной точки /
Под ред. Г. М. Розенблата. М.: КомКнига/URSS, 2006. 312 с.
7. Космодемьянский А. А. Механика тел переменной массы. М.: Изд.-во ВВИА
им. Н. Е. Жуковского, 1947. 109 с.
8. Лурье А. И. Аналитическая механика. М.: Физматлит, 1963.
9. Меркин Д. Р. Механика нити. М.: Наука.
10. Мещерский И. В. Задачи по теоретической механике. Учебное пособие. 44-е изд.,
стереотипное / Под ред. В. А. Пальмова, Д. Р. Меркина. СПб.: Лань, 2005.448 с.
(См. также предыдущие издания задачника с 1986 по 2004 гг.)
11. Никитин Н. Н. Курс теоретической механики. М.: Высшая школа, 1990. 607 с.
12. Пэнлеве П. Лекции о трении. М.: Гостехиздат, 1954. 316 с.
13. Розенблат Г. М. Гироскопические эффекты в механике твердых тел: Методи-
ческое пособие. М.: УРСС, 2003. 96 с.
14. Розенблат Г. М. Динамические системы с сухим трением. М.; Ижевск: НИЦ
«Регулярная и хаотическая динамика», 2006. 204 с.
15. Розенблат Г. М. Механика в задачах и решениях. М.: УРСС, 2004. 160 с.
16. Neuber Н. von. Losungen zur aufgabensammlung Mestschersri. VEB Deutscher Verlag
Aer Wissenschaften. Berlin, 1961. 464 s.