Author: Никольскиий В.В. Никольская Т.И.
Tags: электромагнетизм электромагнитное поле электродинамика теория максвелла физика радиоволны
ISBN: 5-02-014033-3
Year: 1989
Text
В. В. НИКОЛЬСКИЙ, Т. И. НИКОЛЬСКАЯ
ЭЛЕКТРОДИНАМИКА
И РАСПРОСТРАНЕНИЕ
РАДИОВОЛН
ИЗДАНИЕ ТРЕТЬЕ,
ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
Допущено Государственным комитетом СССР
по народному образованию
в качестве учебного пособия для студентов
радиотехнических специальностей вузов
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1989
ББК 22.336
Н64
УДК 537.87@75.8)
Никольский В. В., Никольская Т. И. Электродинамика и распро-
распространение радиоволн: Учеб. пособие для вузов.— 3-е изд., перераб. п доп.—
М.: Наука. Гл. ред. физ.-мат. лит., 1989.— 544 с—ISBN 5-02-014033-3
Излагается теория электромагнетизма с акцентом на радиотехническую
электродинамику и анализ волновых процессов. Рассматриваются отражение
и преломление волн, излучение, дифракция, процессы в полых и диэлектри-
диэлектрических волноводах, резонаторах, периодических, квазпоптических и иных
структурах, в интегральных схемах СВЧ и пр. Обсуждаются методы матема-
математического моделирования в электродинамике, опирающиеся на применение
ЭВМ. Отличительной особенностью книги является большое число картин
электромагнитных полей, рассчитанных и построенных на ЭВМ B-е изд. в
1978 г.).
Для студентов радиотехнических специальностей, а также ппженеров-ра-
диотехников и радиофизиков.
Табл. 10. Ил. 288. Библиогр. 80 назв.
Рецензенты:
кафедра антенных устройств и распространения радиоволн МЭИ,
заведующий кафедрой доктор технических наук Е. Н. Васильев;
доктор технических наук В. М. Петров
%.¦* ~
„1604050000—085д9 8д
053@2)-89
ISBN 5-02-014033-3
©Издательство «Наука».
Главная редакция
физико-математической
литературы, 1989
ОГЛАВЛЕНИЕ
Предисловие к третьему изданию 6
Введение 7
ЧАСТЬ 1
ОСНОВЫ ТЕОРИИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
Глава 1. Исходные понятия и уравнения теории электромагнетизма 11
§ 1.0. Используемые математические понятия и символы ... 11
§ 1.1. Заряды, токи и векторы поля 22
§ 1.2. Уравнения Максвелла , 27
§ 1.3. Свойства материальных сред 35
§ 1.4. Поля на границах раздела сред 42
§ 1.5. Локализация и движение энергии поля 49
§ 1.6. Система уравнений и задачи электродинамики .... 58
Упражнения 61
Глава 2. Статические, стационарные и квазистационарные поля . . 62
§ 2.0. Используемые математические понятия и символы ... 62
§ 2.1. Стационарное поле, электростатика и магнитостатика ... 67
§ 2.2. Электростатические поля 72
§ 2.3. Стационарные магнитные поля 88
§ 2.4. Энергия стационарных полей и их общие свойства ... 99
§ 2.5. Квазистационарные поля 109
Упражнения 111
Глава 3. Основные положения электродинамики 113
§ 3.0. Используемые математические понятия и символы . . . 113
§ 3.1. Уравнения электродинамики 116
§ 3.2. Гармонические колебания. Уравнения электродинамики в комп-
комплексной форме 119
§ 3.3. Баланс энергии при гармонических колебаниях .... 123
§ 3.4. Общие свойства решений системы уравнений электродинамики
в комплексной форме 128
Упражнения 134
ЧАСТЬ 2
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ И КОЛЕБАНИЯ
Глава 4. Простейшие электромагнитные волны 135
§ 4.0. Общие сведения о волновых процессах 135
§ 4.1. Плоские однородные электромагнитные волны .... 140
§ 4.2. Поляризация и сложение волн 146
§ 4.3. Дисперсия, разные оценки скорости 149
Упражнения 153
Глава 5. Электродинамика и оптика 153
§ 5.0. Вспомогательные сведения. Вращение декартовой системы ко-
координат 153
4 ОГЛАВЛЕНИЕ
§ 5.1. Отражение п преломление 155
§ 5.2. Поля при падении волны на границу раздела сред . . . 162
§ 5.3. Полное отражение и направляемые волны 172
§ 5.4. Действие проводящих границ 185
§ 5.5. Локально плоские волны и геометрическая оптика . . . 185
Упражнения 197
Глава 6. Электромагнитные волны в структурах 198
§ 6.0. Используемые математические понятия п символы . . . 198
§ 6.1. Электромагнитные волны в продольпо-однородных структурах 201
§ 6.2. Конкретизация полей и постановка краевых задач для клас-
классов волн 206
§ 6.3. Периодические структуры 212
§ 6.4. Передача п потери энергии в структурах 216
Упражнения 222
Глава 7. Направляющие структуры 223
§ 7.0. Решение двумерного уравнения Гельмгольца методом разде-
разделения переменных 223
§ 7.1. Прямоугольный волновод 231
§ 7.2. Другие полые волноводы 243
§ 7.3. Многосвязные направляющие структуры 257
§ 7.4. Диэлектрические волноводы и родственные структуры . . 263
§ 7.5. Полосковые, щелевые и другие пленарные структуры . . 276
§ 7.6. Некоторые виды периодических структур 281
Упражнения 288
Глава 8. Резонаторы 289
§ 8.0. Трехмерное уравнение Гельмгольца п соответствующие крае-
краевые задачи 289
§ 8.1. Общая теория электромагнитных резонаторов 294
§ 8.2. Полые резонаторы 303
§ 8.3. Другие электромагнитные резонаторы 314
Упражнения 317
часть з
ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ
Глава 9. Излучение в свободном пространстве 318
§ 9.0. Предварительные математические сведения 318
§ 9.1. Излучение заданных источников 321
§ 9.2. Элементарный электрический излучатель, диполь Герца . . 324
§ 9.3. Элементарный магнитный излучатель '. 332
§ 9.4. Обобщенная задача об излучении. Принцип Гюйгенса . . 336
Упражнения 343
Глава 10. Дифракция в свободном пространстве 343
§ 10.1. Электродинамические задачи дифракции 343
§ 10.2. Отверстие в экране. Дифракция Фраупгофера .... 347
§ 10.3. Отверстие в экране. Дифракция Френеля 353
§ 10.4. Взаимно дополнительные экраны. Ограниченные тела . . 363
§ 10.5. Дифракция па цилиндре 368
§ 10.6. Дифракционная теория направляющих структур и резонато-
резонаторов с линзами и зеркалами 373
Упражнения 376
Глава И. Излучение и дифракция в изолированных структурах . 377
§ И.О. Ортогональные системы функций и ряды Фурье .... 377
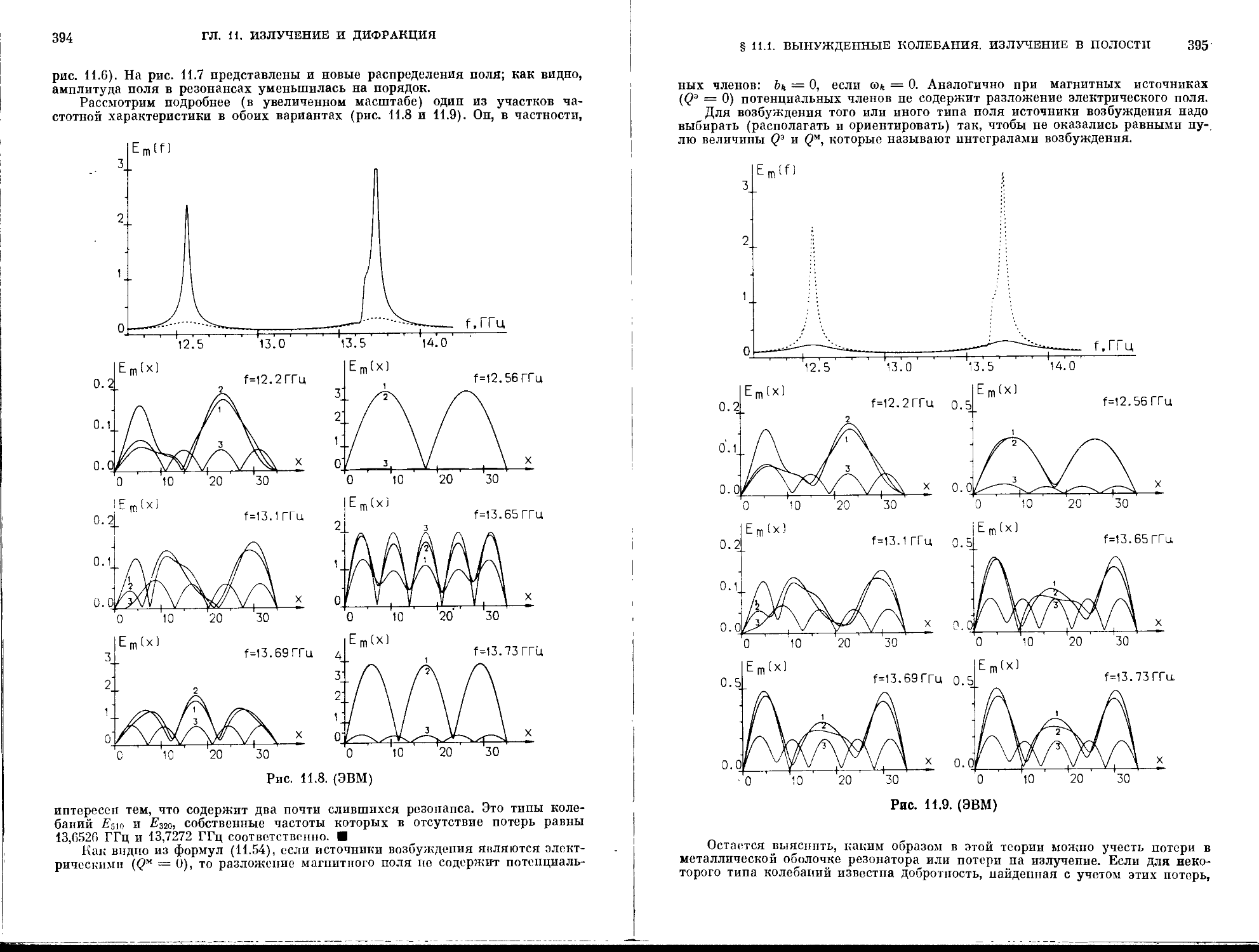
§ 11.1. Вынужденные колебании. Излучение в полости .... 384
ОГЛАВЛЕНИЕ
§ 11.2. Вынужденные волны. Излучение в волноводе .... 396
§ 11.3. Волноводпая дифракция 403
Упражнения 410
ЧАСТЬ 4
ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ В ЭЛЕКТРОДИНАМИКЕ
Глава 12. Общий подход. Проекционные методы 411
§ 12.1. Постановка задач, представление полей, алгоритмизация . 411
§ 12.2. Проекционные методы. Процесс Бубнова — Галеркина . . 416
§ 12.3. Проекционное наложение граничных условий. Сведение зада-
задачи к рассмотрению границы 427
Глава 13. Дискретизация и декомпозиция 436
§ 13.1. Дискретизационные методы 436
§ 13.2. Декомпозиционный принцип. Математическое моделирование
сложных структур 441
Упражнения 453
часть 5
ОСОБЕННОСТИ ПОЛЕЙ В РАЗЛИЧНЫХ СРЕДАХ.
РАДИОВОЛНЫ В ПРИРОДНЫХ УСЛОВИЯХ
Глава 14. Поля и заряженные частицы. Модели сред 455
§ 14.1. Стационарные поля 455
§ 14.2. Гармонические колебания 463
Упражнения 466
Глава 15. Распространение радиоволн 467
§ 15.1. Общие представления 467
§ 15.2. Геометрическая оптика и теория дифракции при анализе рас-
распространения радиоволн 472
§ 15.3. Земные радиоволны 478
§ 15.4. Влияние тропосферы 485
§ 15.5. Радиоволны в иопосфере 490
§ 15.6. Диапазонные особенности распространения радиоволн и ра-
работа радиолиний 497
Упражнения 506
Глава 16. Поля в анизотропных, активных и нелинейных средах . 506
§ 16.1. Анизотропия и гиротропия 506
§ 16.2. Поля и волны в гиротроппых средах 513
§ 16.3. Активные среды 525
§ 16.4. Нелинейные среды 528
Упражнения 537
Приложение. О графических изображепиях, полученных при помо-
помощи ЭВМ 538
Список литературы 540
ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ ИЗДАНИЮ
Книга предназначена служить учебным пособием по курсу
«Электродинамика и распространение радиоволн» и является отра-
отражением курса лекций, который читает один из авторов в Москов-
Московском институте радиотехники, электроники и автоматики
(МИРЭА). В настоящем издании курс излагается в значительной
мере по-новому.
Разумеется, традиционное содержание курса электродинамики
для радиотехнических и радиофизических специальностей подле-
подлежит постоянному обновлению по мере развития новых техниче-
технических приложений. Но, пожалуй, наиболее важной тенденцией яв-
является все возрастающее значение вычислительных методов, опи-
опирающихся на использование ЭВМ. Становятся все более мощными
машинные средства исследования сложных электродинамических
структур, которые образуют «мост» от теории к техническим рас-
расчетам. Авторы считали своей задачей отразить данную тенденцию
двояким образом. С одной стороны, книга содержит специальные
разделы (часть 4), посвященные вычислительным методам для
радиотехнических задач электродинамики с ориентацией на ЭВМ
(вплоть до автоматизированного проектирования). С другой сторо-
стороны, во всей книге демонстрируется применение ЭВМ при изучении
строения полей и волновых процессов. Авторы составили специ-
специальные программы интегрирования дифференциальных уравнений
силовых линий; они многократно применяются при изложении
учебного материала (см. Приложение, с. 538). Использованы
средства машинной графики. На наш взгляд, это должно заметно
облегчить восприятие материала при увеличении информативности
изложения.
По мнению авторов должно способствовать изучению ' курса
введение двух градаций материала. Символом А, поставленным
после названия соответствующего раздела, обозначен минимально
необходимый материал курса, а символом Б — более сложный мате-
материал, относительно громоздкие выводы, а также дополнительные
комментарии. В начале большинства глав в краткой форме приве-
приведены необходимые математические сведения. И, наконец, в тексте
специально выделены выводы формул и примеры, заканчивающие-
заканчивающиеся знаком ¦. В конце каждой главы приведены упражнения. Все
это должно облегчить самостоятельную работу студентов и, кроме
того, помочь преподавателям по-разному формировать лекцион-
лекционный курс.
ВВЕДЕНИЕ
В основе теории электромагнетизма лежит представление об
электромагнитном поле. В простейшем случае термин «поле» упот-
употребляется, когда надо сопоставить каждой точке пространства не-
некоторую физическую характеристику. В этом смысле говорят о
«поле температур» материальной среды или, например, о «поле
скоростей» частиц жидкости, газа. В сущности, при этом просто
определяются какие-то функции координат и, быть может, време-
времени: температура, скорость и т. п. Подобно этому об электрическом
поле формально можно говорить как о «поле сил»; каждый раз
имеется в виду сила, которая будет действовать на единичный по-
положительный точечный заряд, если его поместить в пространство,
где действует поле. Понятие поля в этих примерах имеет всего
лишь некоторое описательное значение.
Электромагнитное поле характеризуется некоторыми векторны-
векторными функциями координат и времени; они будут рассматриваться
в § 1.1. Какое же физическое содержание отвечает этому описа-
описательному аппарату? Рассмотрим, например, такой реализуемый в
принципе эксперимент. В вакууме расположены две антенны: пе-
передающая и приемная (рис. В.1). Передача электромагнитной
энергии производится в тече-
течение короткого интервала вре-
времени т, а остальное время пе-
передатчик бездействует. Пусть
время At, в течение которого
энергия достигает приемной
антенны, больше т (пусть да-
даже At > т). В таком случае
легко указать время, когда энергия уже излучена передающей
антенной, но еще не поступила в приемную, а следовательно, ло-
локализована в вакууме. Ее носитель, таким образом,— это не при-
привычная нам материальная среда, а иная физическая реальность.
Именно она и есть электромагнитное поле; слово «поле» мы упо-
употребили для обозначения некоторой объективной реальности.
В философском смысле электромагнитное поле следует рассматри-
рассматривать как одну из форм существования материи.
Хотя проявления электромагнитных сил в природе люди на-
наблюдали с давних времен, научные понятия в этой области сложи-
сложились сравнительно недавно; к ним, разумеется, нельзя относить
Рис. В.1
8 ВВЕДЕНИЕ
первые представления древних. В 1784—1789 гг. были опублико-
опубликованы работы Шарля Кулона об электрических и магнитных взаи-
взаимодействиях. Известный закон Кулона, который изучается в наше
время уже в средней школе, поразительно похож па открытый в
предшествующем веке Ньютоном закон тяготения. Найденный
позднее закон Ампера о взаимодействии токов и другие законо-
закономерности этого рода идейно близки закону .Кулона: действие од-
одного объекта на другой, как полагали исследователи, происходит
без всякого участия промежуточной среды, мгновенно. Это так назы-
называемый принцип дальнодействия, т. е. действия на расстоянии, во-
вошедший в науку вместе с механикой Ньютона.
С именем Майкла Фарадея A791 — 1867 гг.) связано зарожде-
зарождение иной концепции в теории электромагнетизма, принципа близ-
кодействия, согласно которому взаимодействие осуществляется че-
через посредство среды (в частности, вакуума), являющейся «вмес-
«вместилищем» электромагнитного процесса; при этом возникает вопрос
о времени передачи взаимодействия. Исключительный вклад в на-
науку было суждено внести Джемсу Клерку Максвеллу A831—
1879 гг.). В современной физике уравнения Максвелла являются
фундаментальными законами теории электромагнетизма. Максвел-
Максвеллу принадлежит теоретический вывод о существовании электро-
электромагнитных волн — вместе с гипотезой об электромагнитной природе
света. Этот вывод явился результатом анализа, отправной точ-
точкой которого были физические идеи Фарадея. Возбуждение элект-
электромагнитных волн в лаборатории и их экспериментальное иссле-
исследование было осуществлено позднее Генрихом Герцем A857—
1894 гг.), который внес также значительный вклад в теорию
электромагнетизма. Герц предвосхитил многое из того, что мы
относим теперь к радиотехнической электродинамике. В частности,
в своих опытах он использовал параболические зеркала, в которых
можно видеть прообраз современных зеркальных антенн. Тем не
менее, он не ставил вопрос о техническом применении электромаг-
электромагнитных волн. Историческая заслуга изобретения беспроводной свя-
связи — радио — принадлежит нашему соотечественнику А. С. Попо-
Попову A859—1906 гг.). Отметим еще, что для подтверждения элект-
электромагнитной природы света решающими оказались опыты другого
русского ученого П. Н. Лебедева A866—1911 гг.), измерившего
световое давление.
Можно без преувеличения сказать, что радиотехника явилась
широчайшей опытной базой теории электромагнетизма, основываю-
основывающейся на уравнениях Максвелла, а также стимулятором ее даль-
дальнейшего развития. Вместе с радиотехникой появилось понятие
радиоволн, т. е. электромагнитных волн в радиотехнических систе-
системах. Важным научным направлением стало исследование распрост-
распространения радиоволн в природных условиях — над Землей и в кос-
космосе. Проблема излучения и приема электромагнитной энергии,
переносимой радиоволнами, привела к теории антенн.
ВВЕДЕНИЕ
В первых опытах длина радиоволн измерялась метрами. В на-
начале века, когда радиосвязь приобрела уже практическое значение,
использовались главным образом длинные волны (длиной порядка
километра). Но, начиная с двадцатых годов, в радиотехнической
практике осваиваются волны все более короткие. Возникшая в
военное время радиолокация дала этому процессу мощный толчок —
в технику вошлп волны дециметровые, сантиметровые, а затем и
миллиметровые, которые теперь имеют многочисленные примене-
применения в разных областях. Эта практика изменила многое как в са-
самой радиотехнике, так и в ее теоретических основах. Дело в том,
что ранее размеры элементов радиоаппаратуры оставались намно-
намного меньше длины волны. Благодаря этому основные представле-
представления электротехники и используемая ею теория цепей были пригодны
как аппарат расчетов, а радиотехническая аппаратура во многом
напоминала электротехническую. Но такое положение не могло
сохраниться, когда понадобилось создавать радиотехнические элемен-
элементы, сравнимые по размерам с длиной волны.
Это требует пояснения. Предположим, что электромагнитная
энергия распространяется вдоль проводника, который мы хотим
считать участком цепи (рис. В.2), причем через два находящихся
на расстоянии L сечения проходят токи h(t) и
h(t) соответственно. В теории цепей считают,
что эти токи одинаковы, т. е. I\(t)= hit), но
так ли это? Пусть I\(t)= Im cos at. Поскольку
для распространения электромагнитного процес-
процесса на расстояние L нужно время At = L/v, где
v — скорость, то фазу a>t ток h будет иметь толь-
только по истечении времени At, а в данный момент
его фаза есть u>(t — At). Токи h и /2, как мы
видим, не равны, поскольку имеется фазовое
различие Аф = (oAi (может, например, оказаться,
что /г = 0, когда I\=Im). Учитывая известную
связь скорости, длины волны и частоты (v = jk, / = ю/2я), имеем
Аф = 2лЬ/К. Таким образом, фазовое запаздывание пренебрежимо
мало, когда
(В.1)
Рис. В.2
где L надо понимать как максимальный размер объекта. При этом
ток во всех сечениях цепи можно считать неизменным. Неравенст-
Неравенство (В.1) называют условием квазистационарности. Теория цепей
переменного тока, вообще говоря, пригодна, если оно выполняется.
В дальнейшем будет показано (гл. 9), что по мере ослабления
условия квазистациопарности все большая часть энергии, связан-
связанной с проводником, по которому проходит ток, излучается в прост-
пространство.
В теории аитепи существенно отклонение от условия (В.1),
а многие современные антенны, обладающие высокой иаправлен-
10
ВВЕДЕНИЕ
ностью, многократно превышают длину волны по своим размерам.
Что касается элементов радиоаппаратуры на сантиметровых и
миллиметровых волнах, то принципы их построения далеки от
старых электротехнических образцов. Примечательно, например,
использование различных волноводов в виде полых металлических
тРУб. диэлектрических стержней и т. п., а также аналогично по-
построенных резонаторов вместо так называемых колебательных кон-
контуров, включающих емкостные и индуктивные элементы. Для
понимания принципов действия, сознательного применения и кон-
конструирования подобных устройств необходимо знание теории элек-
электромагнетизма, базирующейся на уравнениях Максвелла.
Благодаря широкому применению оптических квантовых гене-
генераторов — лазеров — в радиотехническую практику вошли чрезвы-
чрезвычайно короткие волны; размеры соответствующей аппаратуры всег-
всегда очень велики в сравнении с длиной волны. В этой области
электродинамическая теория смыкается с оптикой.
Задачи теории электромагнетизма, порождаемые радиотехниче-
радиотехнической практикой, нередко настолько сложны, что только появление
современных ЭВМ делает эту теорию средством проектирования
аппаратуры, уже автоматизированного.
Главным предметом книги являются электромагнитные волно-
волновые процессы, существенно важные для радиотехники.
Изложение начинается — после краткого напоминания необхо-
необходимых математических сведений — уравнениями Максвелла, о зна-
значении которых в теории электромагнетизма уже говорилось выше.
ЧАСТЬ 1
ОСНОВЫ ТЕОРИИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
Глава i
ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ ТЕОРИИ ЭЛЕКТРОМАГНЕТИЗМА
§ 1.0. Используемые математические понятия и символы
1.0.1. Роль математического аппарата (А). В теории электро-
электромагнитного поля применяется некоторый традиционный математи-
математический аппарат, который, можно сказать, формирует язык предме-
предмета. Без него было бы невозможно построить ясное и обозримое
изложение. Надо также иметь в виду, что только математика спо-
способна сделать физическую теорию орудием расчета в технике.
В наше время, отмеченное широким распространением ЭВМ, воз-
возможности расчетов резко возросли и, соответственно, повысилась
рель теории. Едва ли не в первую очередь это относится к теории
электромагнитного поля и ее значению для радиоэлектроники.
К числу математических средств, которые понадобятся с само-
самого начала курса, относятся представления векторной алгебры и
векторного анализа. Эти разделы математики знакомы читателю,
поэтому будет дана лишь краткая сводка необходимых средств с
комментарием. Попутно вводится используемая в книге система
символов.
1.0.2. Векторы и действия над ними (А). Понятие вектора как
величины, характеризуемой — в отличие от скаляра — не только
числом, но и направлением в пространстве, соответствует многим
явлениям физической реальности. Как известно, в физике в каче-
качестве векторов рассматриваются сила, скорость и т. д. Применение
векторов позволяет отображать физические закономерности в эко-
экономной и универсальной форме, которая при необходимости кон-
конкретизируется в разных системах координат. Составление матема-
математических выражений, содержащих векторы, оказывается возмож-
возможным потому, что подобно системе арифметических действий над
числами существует исчисление векторов.
Векторы А, В можно представить как А = АоЛ и В = В05, где
Ао, Во — единичные векторы (называемые также ортами), а чис-
числа А, В — абсолютные значения векторов А, В. ¦
Орты, соответствующие направлениям осей х, у, z декартовой
системы координат, будут обозначаться Хо,, уЪ, го,. Любой вектор А
12
ГЛ, 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
можно представить в виде разложения
А = х0Ах + у0Ау + zoAz, A.1)
где Ах, Av, Аг являются его проекциями на оси декартовой систе-
системы координат; они называются также компонентами (составляю-
(составляющими) вектора А. Иногда будут использоваться векторные состав-
составляющие Ах = х0Ах и т. д.
Сложение векторов сводится к сложению их компонент:
A + B = xo(Ax + Bx) + yo(Ay + By)+zo(Az + Bz). A.2)
Скалярное произведение векторов А и В определено как
(А, В) в АВ = АВ cos а = А & + АУВУ + АгВг. A.3)
Здесь и далее знаком тождества объединяются два эквивалентных
обозначения; а — угол между направлениями векторов. Величина
(А, В) есть скаляр (число). Как видно, (А, В) может составлять
нуль и при не равных нулю А и В. Тогда эти векторы называются
ортогональными: они направлены под прямым углом.
Векторное произведение векторов А и В есть
[А, В] = А X В = v0AB sin a =
в,, в.
A.4)
Здесь vo — орт, направленный по нормали к плоскости векторов А
и В, причем так, что кратчайшее угловое расстояние между их
направлениями, обозначенное а, соответствует движению от А к В
по часовой стрелке, если смотреть вдоль vo. Раскрывая определи-
определитель, находим, например, что [А, В]х = АуВг — AZBV и т. д. Изме-
Изменение порядка сомножителей приводит к изменению знака вектор-
векторного произведения: [В, А] = —[А, В].
Для трех векторов А, В, С определено произведение
А [В, С] = [А, В] С = [С, А] В,
называемое векторно-скалярным, или смешанным: один из векто-
векторов составляет скалярное произведение с векторным произведени-
произведением двух оставшихся. Очевидно, что
А [В, С] =
вх
сх
АУ
Ву
СУ
вг
cz
A.5)
При составлении смешанного произведения должен быть сохранен
циклический порядок следования векторов: А, В, С, А, В, ...
Нам придется использовать и двойное векторное произведение
трех векторов А, В, С. Оно раскрывается по формуле
[А, [В, С]] = В (А, С)- С (А, В), A.6)
§ 1.0. ИСПОЛЬЗУЕМЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ И СИМВОЛЫ
13
где скалярные произведения, обозначенные посредством круглых
скобок, входят как числа.
1.0.3. Линейное преобразование (А). Под умножением вектора
А на скаляр (число) та понимается получение такого вектора В,
абсолютное значение которого есть В = тпА, а орт не меняется.
Запишем
В = тпА, A.7)
что равносильно трем скалярным равенствам
Вх = тпАх, Ву = тпАу, Вг = тпАг.
A.7а)
Если m — положительное число, то векторы А и В направлены
одинаково, а при отрицательном m — противоположно (параллель-
(параллельно и антипараллельно); говорят, что A pi В коллинеарны. Мы име-
имеем здесь дело с частным видом линейного преобразования набора
компонент Ах, Ау, Az в аналогичный набор Вх, Ву, Bz. Сами эти
наборы мы также можем называть векторами, отождествляя их с
векторами-столбцами линейной алгебры.
В общем случае под однородным линейным преобразованием
рассматриваемых векторов понимают сопоставление вектору А та-
такого вектора В, компоненты которого определяются по формулам
Вх =¦ тпххАх + тпхуАу + mxzAz,
Ву = тп^Ах + тПщАу + myzAz,
Вг = mzxAx + mzyAy + mzzAz,
A.8)
где
m
где тпхх, тпху, ..., mzy, m2Z — некоторые числа (однородность есть
свойство, в силу которого В = 0, если А = 0). Векторы А и В,
компоненты которых связаны соотношениями A.8), уже не колли-
коллинеарны; следовательно, записанное преобразование определяет не
только изменение абсолютного значения вектора («растяжение»
или «сжатие»), но и его поворот.
С точки зрения линейной алгебры таблица чисел
yy
A.9)
образует матрицу, а равенства A.8) определяют операцию умно-
умножения матрицы llmll на вектор-столбец (Ах, Ау, Аг), приводящую
к получению вектора-столбца (Вх, Ву, Bz) (запись в строку исполь-
использована для экономии места). В частном случае A.7) отличны от
нуля только диагональные компоненты матрицы И mil, причем
mOT = тпп = тпгг = т. Введя единичную матрицу
111 0 Oil
/= о 1 о, A.10)
Но о i|
14
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
мы определим матрицу llmll в варианте A.7а) как ml. Вместо сим-
символа матрицы llmll будем использовать т и запишем систему ра-
равенств A.8) в сокращенной форме:
В-тпА. A.11)
1.0.4. Поля и операции векторного анализа (А). Выше во Вве-
Введении при обсуждении понятия поля уже отмечалось, что формаль-
формально поля определяются заданием в каждой точке рассматриваемой
области пространства некоторой скалярной или векторной величи-
величины: скалярные и векторные поля. В векторном анализе производят-
производятся специальные операции дифференцирования и интегрирования
по отношению к соответствующим функциям пространственных
координат.
Скалярное поле, характеризуемое функцией г|з(х, у, z), можно
наглядно отобразить при помощи семейства поверхностей уровня
"Ф(х, У, z) — d, где С{ — константы; на рис. 1.1а показан пример
VA
Рис. 1.1
сечения такого семейства плоскостью чертежа. Введем вектор
grad if, называемый градиентом ty, который направлен в сторону
максимального возрастания гр и равен скорости изменения г|з в
этом направлении. Очевидно, что
grad* = vo|J-, A.12)
где v — линия, ортогональная к поверхностям уровня, a v0 есть
касательный к ней орт. Смысл формулы A.12) легко понять, рас-
рассматривая участок двух близких поверхностей уровня (рис. 1.16).
Проекция вектора grad г|з на некоторое направление I есть
lograd г|з = loV03i))/5v —«cos adty/dv; эта величина становится макси-
максимальной, когда 1о совпадает с то (соза=1). Обозначая рассматри-
рассматриваемую проекцию grad, ty, имеем также
grad, *-|*-.
A.13)
§ 1.0. ИСПОЛЬЗУЕМЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ И СИМВОЛЫ 15
Определяя по этой формуле проекции градиента ty в декартовой
системе координат (grad* if, grady ty и grad* if), получаем
grad Tf = V^ = х0 -? + Уо
Здесь употреблено также другое обозначение градиента, исполь-
использующее символ V («набла») (см. A.30)).
Мы видим, что скалярное поле ty порождает векторное поле
F = grad of. Такое векторное поле называется потенциальным,
а скалярная функция ty — потенциалом. Поверхности уровня, на
которых \f> = const, являются, как говорят, эквипотенциальными по-
поверхностями.
Для наглядного отображения векторных полей обычно строят
картины так называемых векторных, или силовых, линий. Это ли-
линии, касательные к которым в каждой точке указывают направле-
направление вектора. Густота силовых линий может соответствовать интен-
интенсивности поля. При этом количество векторных линий, проходя-
проходящих через ортогональную площадку (если она мала, то может
считаться плоской), должно быть пропорционально абсолютному
значению вектора, практически постоянному в пределах площадки.
Введем понятие векторного дифференциала длины вдоль неко-
некоторой линии I. Это вектор, направленный по касательной и по
dl=rodi
Рис. 1.2
абсолютному значению равный скалярному дифференциалу dl
(рис. 1.2а); он может быть представлен в декартовых координатах
(рис. 1.26):
dl = той = xodx + yody + zodz. A.15)
Пусть задано векторное поле у(х, у, z), которое надо описать
посредством векторных линий. Выразим v в декартовых коор-
координатах
v = xovx
16
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
и потреоуем, чтооы выполнялось условие пропорциональности
dl = kv
(к — любая константа). Приравнивая компоненты векторов v и dl,
получаем
vx vy vz K '
Это, в сущности, система двух дифференциальных уравнений, ин-
интегрирование которых приводит к уравнениям векторных линий.
На рис. 1.3 показано несколько характерных типов картин си-
силовых линий, которые могут встретиться при исследовании вектор-
векторного поля F в области V с граничной поверхностью S. Область V
Рис. 1.3
может содержать точку, из которой расходятся (исток) (а) или в
которую сходятся (сток) (б) все силовые линии. Последние могут
также проходить область насквозь (в) или совсем не пересекать ее
поверхность S (г). В векторном анализе существует простая опе-
операция, позволяющая устанавливать, имеет ли заданное поле источ-
источники и стоки, показанные на рис. 1.3а, б.
Введем сначала представление о потоке вектора F через по-
поверхность S (не обязательно замкнутую). Это интеграл
Ф = JFds,
A.17)
где векторный дифференциал ds понимается как произведение
обычного (скалярного) дифференциала поверхности ds на орт нор-
нормали vo, т. е. ds = \ods. Поэтому Fds = Fvds (рис. 1.4а). Если по-
поверхность S — замкнутая, как на рис. 1.3, то символ интеграла до-
дополняется кружком: (j). Тогда vo — орт внешней нормали; для не-
незамкнутой поверхности vo выбирается произвольно.
Поток вектора F положителен, если силовые линии выходят из
поверхности S наружу, и отрицателен, если они входят внутрь
(потому что угол между F и vo в первом случае острый, а во вто-
втором— тупой). Вообще поток вектора измеряется числом его ли-
§ 1.0. ИСПОЛЬЗУЕМЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ II СИМВОЛЫ
17
ний, выходящих из поверхности, если густота линий соответствует
интенсивности поля (см. выше). Действительно (рис. 1.46), эле-
элементарный поток АФ, проходящий через AS, равен FASX. При
зтом F = kAN/AS±, где AN — число силовых линий, проходящих
через ортогональную площадку AS±, a k — заданный коэффициент
пропорциональности. В то же время AN — это число силовых ли-
линий, проходящих через рассматриваемый элемент поверхности AS.
а
Рис. 1.4
Таким образом, оказывается, что АФ = JcAN. Поэтому и для пол-
полного потока Ф через поверхность S имеем Ф = kN, где N — число
выходящих через S силовых линий. Разумеется, выходящие нару-
наружу силовые линии рассматриваются как «положительные», а вхо-
входящие внутрь — как «отрицательные». Следует также иметь в ви-
виду, что реальные картины силовых линий не могут претендовать
на точное описание векторных полей, и равенство Ф = kN в дей-
действительности приближенное. Обращаясь в качестве примера к
рис. 1.3, видим, что там Ф>0 (а), Ф<0 (б), Ф = 0 (в) и Ф =
= 0 (г). В третьем из этих примеров число силовых линий, выхо-
выходящих из замкнутой поверхности S, равно числу входящих внутрь.
Дивергенцией (а также расхождением, расходимостью) вектора
F называется величина, определенная следующим предельным
соотношением:
div F = lim
A.18)
Дивергенция div F есть скалярная функция координат; по форму-
формуле A.18) определяется ее значение в точке, окрестностью которой
является объем AV; S — его граничная поверхность. Обозначая в
A.18) поток вектора F через поверхность S как АФ, мы можем
написать:
div F = lim АФ/AF = dO/dV.
ДУ^о
Если в некоторой точке div F > 0, то эта точка является источ-
источником силовых линий; если div F < 0, то точка является стоком:
2 В. В. Никольский, Т. II. Нш ольская
18
ГЛ. 1, ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
§ 1.0. ИСПОЛЬЗУЕМЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ И СИМВОЛЫ
19
в случае div F = 0 линии не начинаются и не кончаются в рассмат-
рассматриваемой точке. Чтобы убедиться в этом, рассмотрим внимательнее
картину силовых линий типа изображенных на рис. 1.3а.
На рис. 1.5а для такого поля показано несколько последова-
последовательных положений замкнутой поверхности 5, сжимающейся
к точке Р. Поскольку через каждую такую поверхность выходит
одно и то же число силовых линий, поток вектора все время
5
Рис. 1.5
постоянен и положителен; положительна и дивергенция, вычисляе-
вычисляемая по формуле A.18) (является ли эта величина ограниченной в
данном примере, для нас сейчас не имеет значения). Пусть теперь
поверхность S, уменьшаясь, сжимается к другой точке М
(рис. 1.5<5). Видно, что с некоторого момента число силовых липий,
выходящих из S, станет равным числу входящих линий, т. е. по-
поток вектора обратится в нуль. Поэтому величина div F, вычисляе-
вычисляемая по формуле A.18), для всех точек за исключением Р окажет-
окажется равной нулю.
На основании формулы A.18) можно убедиться, что в декарто-
декартовых координатах
№- "" • №* ' (U9)
дУ
dz
Дивергенция есть некоторая дифференциальная операция над ком-
компонентами вектора, приводящая к получению скалярной величины.
Ротацией (а также ротором, вихрем) вектора F называется век-
векторная величина, обозначаемая символом rot F. По определению
проекция rotF на некоторое направление v (в некоторой точке,
окрестностью которой является площадка AS) есть
A.20)
rotvF= lim4c$FdI-
Здесь v — направление нормали к площадке AS (орт vo), a L —
граничный контур AS, согласованный с v правовинтовои системой
(если смотреть вдоль vo, то положительное направление обхода
контура L — по часовой стрелке). Фигурирующий в A.20) интег-
интеграл называется циркуляцией вектора F по замкнутому контуру L
(смысл подынтегрального выражения ясен, если привлечь A.15)).
Пользуясь формулой A.20), нетрудно найти проекции вектора
rotF в декартовой системе координат (т. е. rot«F, rotyF и rotzF).
Тогда
rotF =
д/дх д/ду d/dz
A.21)
Ротор, как мы видим, есть некоторая дифференциальная операция
над компонентами вектора F, приводящая к получению новой век-
векторной величины rotF.
Для всякого потенциального поля F = grad ^ имеем rot F = 0,
т. е. всегда
rot grad г|э = О A.22)
(это легко проверить при помощи формул A.14) и A.21)). Поэто-
Поэтому потенциальные поля называют также безвихревыми.
Поля, для которых div F = 0, называют соленоидальными. При
помощи формул A.19) и A.21) легко убедиться, что всегда
div rot V^ 0, A.23)
т. е. соленоидальны поля F = rot V.
Если в некоторой области поле не является соленоидальным,
причем в каждой точке div F Ф 0, то все точки области — это ис-
источники или стоки; силовые линии такого поля приходится стро-
строить, начиная (заканчивая) их во внутренних точках. Если же ли-
линий не обрывать, то невозможно согласовать их густоту с интен-
интенсивностью поля.
Потенциальные поля F (для которых rotF = 0) могут быть
одновременно и соленоидальными (divF = 0), тогда они называют-
называются гармоническими.
Приведем еще несколько тождеств векторного анализа, которые
используются в математическом аппарате теории электромагнитно-
электромагнитного поля. Следующие четыре тождества имеют смысл правил диф-
дифференцирования произведения функций:
grad ф-ф = ф grad -ф + "ф grad ср, A-24)
div ifiF = г|з div F + F grad г|з, A.25)
div [F, V] = V rot F - F rot V, A.26)
rot if>F = ф rot F + [grad rf>, F]. A.27)
Мы будем также неоднократно пользоваться формулой
grad/(i) = /'(|)grad | A.28)
2*
20
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
§ 1.0. ИСПОЛЬЗУЕМЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ И СИМВОЛЫ
21
(дифференцирование сложной функции) и формулой
rot rot F = grad div F — V2F
A.29)
(ротор от ротора).
Пояснил! употребление символа V, уже использовавшегося вы-
выше в A.14) и вновь появившегося в A.29). Так называемый опе-
оператор Гамильтона V (набла) определяется как
V = xo-^ + yo^ + Zo^. A-30)
Величина v"if есть grad if согласно A.14). Действие V па вектор
приводит к дивергенции, если «улшожать» V и F по правилу сос-
составления скалярного произведения A.3): VF = div F. Если же вос-
воспользоваться правилом составления векторного произведения, то
получаем VXF = rotF. Это сразу видно из сопоставления A.4) и
A.21).
Пользуясь формулами A.14) и A.19), легко составить величи-
величину div grad if, которая истолковывается как v2ty:
^. A-31)
дх'
ay'
В декартовых координатах
V2F = XqV2Fx + y0V*F, + z0V2F,. A.32)
Символом V2, наравне с которым используется также символ А,
обозначается оператор Лапласа.
1.0.5. Интегральные формулы векторного анализа (А). Приве-
Приведем без вывода наиболее важные для теории электромагнитного
поля интегральные соотношения векторного анализа.
Теорема Остроградского — Гаусса:
f divFA;=cj>;Fd8. A.33)
Теорема Стикса:
f
rotFds= (DFdl.
в I
Теорема Грина:
f;(Vi|> Vq> + i|)V2cp) dv = & ф -Ц- ds
V S
(первая формула),
J.(i|>Va<p - cpV2i|>) dv =
(вторая формула).
A.34)
A.35)
A.36)
Аналог теоремы Остроградского — Гаусса для ротора:
JrotFcZz; = $[ds, F].
A.37)
Все выписанные соотношения имеют характер формул интегри-
интегрирования по частям. При этом объемный или поверхностный интег-
интеграл (по V или S) сводится к интегралу по замкнутой границе ис-
исходной области в виде поверхности S или, соответственно,
контура L.
1.0.6. Дельта-функция Дирака (Б). В теории электромагнитного
поля оказывается полезным особый математический объект, проис-
происхождение которого можно связывать с обобщением представления
об импульсе. Задавая площадь прямоугольного импульса равной
единице (рис. 1.6а) и устремляя его ширину к нулю, получаем
I
5(х-х')
о
а:'
ос
О
Рис. 1.6
«функцию», значение которой неограниченно в этой точке ж'
(рис. 1.66), а во всех остальных точках равно нулю. Это дельта-
функция Дирака, которая обозначается б (ж —ж'). С точки зрения
обычного математического подхода, дельта-функция везде равна
нулю за исключением одной точки, в которой она теряет смысл.
Но можно утверждать, что для всякой обычной функции /(ж) бу-
будет справедливо равенство:
{
/(ж'), *'<=?.
A.38)
Равенство A.38) является определением дельта-функции посредст-
посредством функционала. В частности, при /(ж)= 1 имеем
A.39)
Гб(ж-ж'Ыж=@- x'^L,
{ [I, x'f=L.
22
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
Определение A.38) следующим образом обобщается на трех-
трехмерные области:
"h. Z$Vv. A-40)
В этой записи точка в области V задается при помощи радиус-век-
радиус-вектора г. Как и ранее, можно в качестве частного случая взять
/(г)= 1 и получить аналог формулы A.39).
§ 1.1. Заряды, токи и векторы поля
1.1.1. Заряды и токи (А). Понятие электрического заряда бу-
будем считать не подлежащим определению. В знакомом читателю
курсе общей физики дается представление о фактах, на основании
которых формируется понятие заряда. Заряд как физическая вели-
величина обозначается символом q и измеряется в кулонах [Кл].
Положительные и отрицательные заряды присущи элементам
микромира. Строение материи таково, что они в высокой степени
уравновешены. Заряд дискретен. Наименьший по абсолютной вели-
величине отрицательный заряд |е| = 1,6021892 D6) • 10~19 Кл, ассоци-
ассоциируемый с представлением об элементарной частице, принадлежит
электрону. Мы не затрагиваем теории строения материи, ко-
которая, как известно, относится к компетенции квантовой физики.
Относящиеся сюда проблемы электромагнетизма составляют пред-
предмет микроскопической электродинамики. В ряде важных случаев
представление об элементарных частицах как о весьма малых те-
телах, перемещающихся в пространстве (подобно непосредственно
наблюдаемым объектам), сохраняет смысл. Говорят, что движение
зарядов, т. е. частиц, несущих заряды, образует электрический ток
(ток проводимости). Эта физическая величина обозначается симво-
символом /. Единица измерения тока — ампер [А]; при токе в один ам-
ампер за секунду переносится один кулон заряда.
Теория электромагнетизма, изложение которой начинается в
этой главе, является макроскопической. Это значит, что в рассмат-
рассматриваемых процессах проявляется действие огромных — «практиче-
«практически бесконечных» — количеств элементарных частиц. Структура
материи при этом обычно игнорируется. Среда представляется
сплошной, а заряды и токи — непрерывно распределенными в объ-
объеме (иногда—на поверхности).
Под плотностью заряда р понимается величина
Р =
ду->о
A.41)
где Aq — заряд, содержащийся в элементарном объеме AV. Если
не забывать о дискретности материи, то содержащийся в A.41)
предельный переход следует понимать как условный. Как бы ни
§ 1.1. ЗАРЯДЫ, ТОКИ И ВЕКТОРЫ ПОЛЯ
23
уменьшался объем AV, он все же должен содержать достаточно
большое число элементарных частиц. Но при переходе к идеализи-
идеализированной сплошной заряженной среде из A.41) можно сделать
вывод, что р = dq/dV.
Введем также представление о плотности тока проводимости j.
Это вектор
j=limio^., A.42)
где AS — элементарная площадка, ориентированная перпендику-
перпендикулярно движению зарядов, a io — орт нормали, указывающий на-
направление движения; А/ — ток, проходящий через AS (смысл пре-
предельного перехода тот же, что и в A.41)).
В современной физике остается незыблемым закон сохранения
заряда: заряд не уничтожается и не создается из ничего. Пусть
в некотором объеме F, ограниченном поверхностью S, содержится
заряд q. Если он не остается постоянным (т. е. уменьшается или
увеличивается), то объяснить это следует тем, что границу пересе-
пересекают носители заряда. Иными словами, через поверхность S про-
проходит ток, и его величина должна быть связана с зарядом соот-
соотношением
/ = -dqfdt
A.43)
(ток, выходящий через S наружу, считается положительным,
а входящий внутрь — отрицательным). Из A.43) получается также
дифференциальная формулировка закона сохранения заряда:
ВЫВОД. По смыслу определений A.41) и A.42)
pdv, I = (J) j ds,
v s
т. е. полный заряд внутри V есть объемный интеграл от плотности
заряда р, а полный ток проводимости, проходящий через S, выра-
выражается потоком вектора A.17) плотности тока /. Подставим запи-
записанные выражения для заряда и тока в A.43). Операцию диффе-
дифференцирования djdt перенесем под знак интеграла (при этом по-
появляется производная dpldt — частная производная, потому что р
также функция координат). Поток вектора j согласно теореме
Остроградского — Гаусса A.33) заменим объемным интегралом от
j. Объединив оба объемных интеграла в левой части равенства,
получаем
J(div|+ ?)*>=<>.
Поскольку этот результат справедлив для произвольного объема V,
24
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ II УРАВНЕНИЯ
из него следует, что подынтегральное выражение равно нулю. Это
прямо приводит к формуле A.44). ¦
Дифференциальную формулировку закона сохранения заряда
A.44) легко интерпретировать, пользуясь представлением о вектор-
векторных линиях. Если где-либо в рассматриваемой области плотность
заряда р убывает (др/dt <0), то при этом divj>0, а следователь-
следовательно (см. п. 1.0.4), там начинаются линии вектора j (лежат источ-
источники). Аналогично в случае возрастания плотности заряда
(др/dt > 0) мы обнаруживаем стоки, поскольку в соответствующих
точках divj<0. Если же первоначальное распределение заряда в
рассматриваемой области сохраняется (р не зависит от времени),
то согласно A.43) div j = 0, а это значит, что либо векторные ли-
линии плотности тока j пронизывают V насквозь (ср. рис. 1.3в),
либо j = 0.
1.1.2. Электромагнетизм и электромагнитное поле (А). Явления
электромагнетизма весьма многообразны, однако понятие электро-
электромагнитного поля, уже обсуждавшееся во Введении, открывает их
единую оспову. С некоторой точки зрения, сущность всех этих яв-
явлений состоит в превращениях энергии, носителем которой являет-
является поле, выступающее как особая форма материи.
Электромагнитное поле описывают при помощи следующих век-
векторных функций координат и времени:
Е = Е(г, t)—напряженность электрического поля,
Н = Н(г, t) — напряженность магнитного поля,
D = D(r, t)—электрическая индукция,
В = В(г, t) — магнитная индукция
(символ радиус-вектора г озпачает зависимость от пространствен-
пространственных координат, t — от времени).
В электромагнитном поле па заряды и токи действуют силы.
Если такого рода сила совершает работу, то у поля отбирается
некоторая энергия. В тех случаях, когда мы имеем возможность
заметить этот процесс, мы наблюдаем электромагнитное явление,
которое обнаруживает существование поля в данной области про-
пространства. В качестве «пробного тела», при помощи которого мож-
можно не только обнаружить, но и, в принципе, измерить поле, обыч-
обычно рассматривают точечный заряд, т. е. некоторое заряженное те-
тело, считающееся достаточно малым в условиях эксперимента (ни-
(ниже это будет уточнено). На точечный заряд в электромагнитном
поле действует сила
F [v, В]), A.45)
где q — величина данного заряда, a v — скорость его движения.
В случае неподвижного заряда (v = 0) сила зависит только от на-
напряженности электрического поля: F' = qE. Это равенство рассмат-
рассматривают в качестве определения вектора Е. На движущийся точеч-
точечный заряд, как видно из A.45), кроме того, действует сила
§ 1.1. ЗАРЯДЫ, ТОКИ И ВЕКТОРЫ ПОЛЯ
25
F" = q [v, В], называемая лоренцевой силой. С появлением этой си-
силы связывают определение вектора магнитной индукции В.
Итак, известны механические проявления поля, на основе ко-
которых строятся определения векторов поля Е и В (называемых
иногда силовыми). При этом используется представление о проб-
пробном заряде. Размеры тела, принимаемого за точечный заряд, долж-
должны быть весьма малы, во-первых, по сравнению с расстоянием до
Таблица 1.1
Единицы измерения электромагнитных величин в СИ *)
Название величины
Заряд
Ток
Плотность заряда
Плотность тока
Напряженность электриче-
электрического поля
Напряженность магнитного
поля
Электрическая индукция
Магнитная индукция
Электрическая постоянная
Магнитная постоянная
Обозначение
q
I
р
j
Е
Н
D
В
Единица измерения
Кулон,
Ампер,
Кулон на кубический
Ампер на квадратный
метпр,
Вольт на метр,
Ампер на метр,
Кулон на квадрат-
квадратный метр,
Тесла,
Фарад на метр,
Генри на метр,
[Кл]
[А]
[Кл/м3]
[А/м2]
[В/м]
[А/м]
[Кл/м2]
[Т]
[Ф/м]
[Г/м]
') е0 = 107/4яс а 8,854-10~12 « (l/36n)-10~9, и0 = 4Я-10-7 к 1,257-10~в; здесь с ¦
скорость света в вакууме (с = 2,99792458A,2)-Ю8 м/с).
точки наблюдения и, во-вторых, по отношению к пространственным
вариациям наблюдаемого поля. Кроме того, исчезающе малым дол-
должен быть отбор энергии поля для его индикации.
Для полноты картины необходимо подчеркнуть, что современная
экспериментальная техника располагает разнообразными средства-
средствами измерения электромагнитных полей, и практическое применение
для этой цели пробных зарядов обычно нецелесообразно. Наше
рассмотрение имеет только принципиальное значение.
Векторы D и Н в вакууме связаны с Е и В соотношениями
D = e0E, В = ц0Н, A.46)'
где to и (io — константы, зависящие только от выбора единиц из-
измерения; первая называется электрической постоянной, а вторая —
магнитной. Связь напряженностей поля и индукций для полей,
существующих в различных средах, будет предметом отдельного
обсуждения.
26
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
В табл. 1.1 приведены единицы измерения всех физических ве-
величин, уже встретившихся при изучении предмета, в используемой
нами системе СИ.
Теория электромагнитного поля сложилась в результате накоп-
накопления и обобщения экспериментальных фактов, а также развития
математического аппарата, который — при современном изложе-
изложении — опирается в первую очередь на векторный анализ. В основ-
основных уравнениях теории векторы поля Е, D, Н и В, а также р и j
связаны операциями ротора и дивергенции. Широко используется
отображение электромагнитных полей при помощи картин вектор-
векторных линий. Линии векторов Е и В называются соответственно
электрическими и магнитными силовыми линиями.
1.1.3. Идеальный точечный заряд (Б). Еще о пробных элемен-
элементах. Наряду с трактовкой точечного заряда как малого физического
тела существует и другая. Объектом теории может быть также
идеальный точечный заряд, «заряженная точка». Плотность р A.41)
такого заряда, разумеется, бесконечна в точке его локализации
М(г'), а во всех остальных точках пространства равна нулю. Не-
Нетрудно догадаться, что величину р идеального точечного заряда
можно выразить при помощи дельта-функции Дирака 6(г — г').
Точнее говоря, при наличии точечного заряда, локализованного в
М(г'), распределение заряда в пространстве описывается плот-
плотностью
= gS(r-r').
A.47)
Действительно, согласно A.40), интеграл от р A.47) по любому
объему, содержащему заряд, будет равен q.
Отметим, далее, что роль пробного тела при исследовании поля
может играть не только точечный заряд. В частности, вместо дви-
движущегося заряда для индикации маг-
магнитного поля может использоваться
неподвижный контур (замкнутый ви-
виток) тока. На плоский замкнутый кон-
контур L с током I в магнитном поле дей-
действует момент силы К, определяемый
следующим образом:
К = 75 К В].
A.48)
Здесь S — площадь, ограниченная кон-
контуром L, Vq — орт нормали к плоскости
Рис. 1.7 контура, согласованный правовинтовой
системой с направлением тока
(рис. 1.7). Происхождение момента К
объясняется действием лоренцевой силы на перемещающиеся в кон-
контуре заряды. Вывод формулы A.48) легко произвести в варианте
прямоугольного контура (см. упражнение 1).
§ 1.2. УРАВНЕНИЯ МАКСВЕЛЛА
27
§ 1.2. Уравнения Максвелла
1.2.1. Уравнения Максвелла в дифференциальной и интеграль-
интегральной формах (А). В компактной форме операций векторного анали-
анализа запишем уравнения, которые заключают в себе основания тео-
теории электромагнетизма и являются постулатами теории:
rotH = —
div D = р,
div В = 0.
A.49)
A.50)
A.51)
A.52)
С формальной точки зрения, это дифференциальные уравнения в
частных производных относительно компонент векторов поля Е,
Н, D, В, а также j и р. Каждое из первых двух уравнений явля-
является, в сущности, сокращенной записью трех скалярных уравнений:
они получаются при проецировании левых и правых векторных
частей A.49), A.50) на оси выбранной системы координат.
Формулы A.49) — A.52) выражают уравнения Максвелла в
дифференциальной форме. Если рассматриваются электромагнит-
электромагнитные процессы в пустоте, то из A.49) — A-52) при помощи соотно-
соотношений A.46) можно исключить индукции D, В или напряженности
Е, Н. Любые электромагнитные поля в пустоте описываются реше-
решениями такой системы уравнений. При рассмотрении полей в раз-
различных средах уравнения Максвелла A.49) — A-52) дополняются
некоторыми более сложными, чем A.46), соотношениями между
напряженностями и индукциями; о них будет говориться в § 1.3.
Значение уравнений Максвелла как оснований теории электро-
электромагнетизма исключительно велико. К сожалению, невозможно в
нескольких словах рассказать, как исторически появились эти
уравнения в ходе развития физических идей. Становление электро-
электродинамики с разных точек зрения обсуждается в литературе [3.1—
4], которая рекомендуется читателю. Для инженера в первую оче-
очередь важно, что уравнения Максвелла, в принципе, дают возмож-
возможность исследовать любые электромагнитные процессы. Надо лишь
уметь правильно ставить соответствующие математические задачи
и решать их, привлекая ЭВМ.
При первом знакомстве с уравнениями Максвелла кажется не-
невероятным, чтобы эти несколько строчек содержали в себе все мно-
многообразие явлений электромагнетизма. Чтобы вполне осмыслить
огромную физическую содержательность этих уравнений, надо изу-
изучить многие электромагнитные процессы. Впрочем, для уяснения
основных черт физического содержания уравнений Максвелла бу-
будут достаточны простые рассуждения.
28
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
§ 1.2. УРАВНЕНИЯ МАКСВЕЛЛА
29
С этой целью перейдем от записи A.49) —A.52) к уравнениям
Максвелла в интегральной форме:
A.53)
A.54)
A.55)
A.56)
Bds = 0.
ВЫВОД. Чтобы из A.49), A.50) получить A.53), A.54J,
рассмотрим некоторую поверхность S (рис. 1.8а), «натянутую» на
rot
Рис. 1.8
контур L. Взяв для определенности уравнение A.49), проинтегри-
проинтегрируем его левую и правую части по S, образовав поток вектора
rotH A.17) и равный ему поток вектора dD/dt + j. При этом имеем
I
rot Н ds = \ —— ds + 1 ]' ds.
s s s
Достаточно теперь к левой части применить теорему Стокса A.34),
заменив поток rotH через S циркуляцией Н по L, вынести опера-
операцию дифференцирования d/dt за знак первого интеграла справа и
учесть, что второй интеграл справа согласно определению A.42)
есть ток /, проходящий через поверхность S, чтобы получить A.53).
При этом производится замена символов d/dt -> d/dt, так как ин-
интеграл уже не является функцией координат.
Совершенно так же A.54) получается из A.50).
Чтобы вывести A.55) из A.51), левую и правую части A.51)
проинтегрируем по некоторому объему F, ограниченному поверх-
поверхностью S:
\ div D dv = \ р dv.
По смыслу определения A.41) объемный интеграл от р дает пол-
полный заряд q, содержащийся в V. Что касается левого объемного
интеграла, то он на основании теоремы Остроградского — Гаусса
A.33) преобразуется в поток D через замкнутую поверхность S
(рис. 1.86). Уравнение A.55) получено.
Уравнение A.56) получается тем же путем из A.52). ¦
1.2.2. Первое уравнение Максвелла: полный ток и магнитное
поле (А). Обсудим первое из уравнений Максвелла, привлекая и
дифференциальную форму A.49), и соответствующий интегральный
аналог A.53).
Поскольку ротор составляется из пространственных производ-
производных компонент вектора, то, как видно из A.49), изменение в про-
пространстве магнитного поля (вектор Н слева) связано с изменением
электрического поля во времени (вектор D справа).
Пусть спачала изменений во времени нет: процесс стационарен.
Тогда первое уравнение Максвелла принимает вид
rotH =
A.57)
и описывает связь магнитного поля с постоянным током. Нельзя
себе представить ток без магнитного поля, поскольку при j Ф 0
A?=0) обязательно rotH^O (или отлична от нуля циркуляция
Н), а следовательно, Н^О.
Пример 1. Рассмотрим бесконечный прямолинейный постоянный ток,
магнитное поле которого, как известно из курса общей физики, в каждой по-
поперечной плоскости описывается при помощи концентрических круговых век-
векторных линий. На рис. 1.9 показана одна из таких ли-
линий в виде окружности радиуса г. Возьмем циркуля-
циркуляцию вектора Н вдоль этой линии: /^ ^~\ <*о
Hdl = ф
L L
dl
=H(§ dl= 2nrH
(в силу симметрии системы Я имеет одно п то же зна-
значение па расстоянии г от оси тока во всех направле-
направлениях). Согласно A.57) вычисленная циркуляция рав-
равна /, отсюда // = 1/2яг, что. мы запишем в векторной
форме: рпс i 9
Н = ао//2лг, A.58)
где «о — орт касательной к окружности, указывающий поправление вектора Н.
Мы получили формулу, выражающую напряженность магнитного поля посто-
явного нитевидного тока как функцию пространственной координаты г. ш
30
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
§ 1.2. УРАВНЕНИЯ МАКСВЕЛЛА
31
Продолжим обсуждение первого уравнения Максвелла. Рассмот-
Рассмотрим случай, когда ток проводимости отсутствует G = 0), но про-
процесс уже не стационарен (происходят изменения во времени). Из
A.53) видно, что циркуляция Н, которая в случае постоянного
тока была равна /, теперь оказывается равной величине
гсм _a_
дЬ
A.59)
которая называется током смещения. Соответственно этому функ-
функция dD/dt рассматривается как плотность тока смещения.
Ток смещения — одно из важных понятий теории электромагне-
электромагнетизма. Во-первых, существенно, что по отношению к магнитному
полю ток смещения как бы копирует роль обычного тока проводи-
проводимости. Это видно из первого уравнения Максвелла, в котором ток
проводимости и ток смещения (или их плотности) выступают рав-
равноправно. Во-вторых, следует учитывать, что физическая сущность
тока смещения в вакууме никак не связана с движением зарядов.
Будем говорить, что вся правая часть первого уравнения Макс-
Максвелла в интегральной форме A.53) представляет собой обобщенный
ток Iе" + /, а величина dD/di + j в A.49) — плотность обобщенного
тока. В отсутствие магнитного поля (Н = 0) равен нулю и обоб-
обобщенный ток. Если обобщенный ток существует, то обязательно
присутствует магнитное поле.
Привлечем для дальнейшего анализа тождество A.23). Состав-
Составляя дивергенцию от левой и правой частей уравнения A.49), по-
получаем
div ^
= 0.
A.60)
Отсюда следует, что вектор плотности обобщенного тока <5D/d? + j
не имеет источников (стоков). Его векторные линии, следователь-
следовательно, замкнуты или уходят из бесконечно-
бесконечности в бесконечность (ср. рис. 13в, г). При-
Применяя к A.60) теорему Остроградского —
Гаусса A.33), т. е. интегрируя по некото-
некоторому объему V и переходя к его границе
S, записываем интегральный аналог этого
равенства:
s==/CM+/ = 0. A.61)
Рис. 1.10 Как видно, обобщенный ток через любую
замкнутую поверхность S равен нулю.
Пример 2. На рис. 1.10 схематически представлен конденсатор в цепи
переменного тока. Полагая, что вся система находится в пустоте, построим
вамкнутую поверхность так, чтобы она проходила между пластинами конден-
сатора. Применяя равенство A.61), видим, что ток проводимости / через S
(проходящий только по проводу) замыкается током смещения /см, локализо-
локализованным внутри конденсатора. ¦
Обратимся к рис. 1.11, на котором схематически в виде вектор-
векторных линий (а) показано типичное структурное соотношение между
обобщенным током и магнитным полем. Можно сказать, что неко-
некоторый пространственный максимум, «сгусток» тока охватывает се-
семейство замкнутых магпитных силовых линий. Пусть j = 0, тогда
ди/dt+j
V,E возрастают
ММ,
н,
н,в
Б
Рис. 1.11
JjB убывают
при возрастании D (dD/dt>0) этот вектор и магнитное поле связа-
связаны правовинтовой системой (б), а при убывании D (dT>/dt<0) —
левовиптовой (в).
Наконец, покажем, что первое уравнение Максвелла согласова-
согласовано с законом сохранения заряда. Действительно, переписывая
A.60) в виде -tj (divD) + div j = 0 (операции div и d/dt мы имеем
право поменять местами), а затем заменяя divD через р при по-
помощи A.51), получаем уже известное равепство A.44).
1.2.3. Второе уравнение Максвелла: обобщенный закон электро-
электромагнитной индукции (А). Обращаясь ко второму уравнению Макс-
Максвелла в форме A.50), замечаем, что оно связывает пространствен-
пространственные изменения электрического поля (Е) с изменениями во времени
магнитного поля (В). Если в качестве примера взять случай, когда
электрическое поле отсутствует (Е = 0), то равна нулю вся левая
часть A.50), откуда dB/di = O, а следовательно, магнитное поле,
существующее без электрического, может быть только неизменным
во времени, стационарным. При этом всякое изменение магнитного
поля (d~B/dt?=O) обязательно вызовет появление поля электриче-
электрического (rotE =5^0 только при Е=5^0).
Рассматривая второе уравнение Максвелла в интегральной фор-
форме A.Г>4), отметим, что поверхность S, опирающаяся на контур L,
32
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
для данного фиксированного L может быть произвольной {S = S\,
1S2, S3, ... на рис. 1.12а).
Если для потока вектора В через S, называемого магнитным
потоком, установить обозначение Ф, а для циркуляции Е по L
использовать символ Э, то уравнение A.54) примет вид
Э = —¦
dt
где
A.62)
A.63)
В этой форме второе уравнение Максвелла совпадает с законом
электромагнитной индукции Фарадея. Циркуляция Э предстает как
В
\ \
L
i
Рис. 1.12
электродвижущая сила, наводимая в контуре L изменением маг-
магнитного потока Ф. Заметим, что Э измеряется в вольтах [В], а Ф —
в веберах [В61.
Напомним, что закон Фарадея был установлен для проводя-
проводящих (например, проволочных) контуров в магнитных полях
(рис. 1.126). Закон электромагнетизма, выражаемый вторым урав-
уравнением Максвелла в интегральной форме, значительно шире ука-
указанного закона Фарадея, поскольку контур L в A.54) — это любой
мысленно очерченный в пространстве контур. Не имеет 'значения,
какие именно материальные объекты оказались в области построе-
построения: это не нарушает справедливости второго уравнения Максвелла.
Столь общая постановка вопроса далеко выходит за пределы опыт-
опытных фактов, на основе которых был сформулирован закон Фарадея.
Второе уравнение Максвелла, однако, сохраняет идейную основу
этого закона, и может рассматриваться как обобщенный закон,
электромагнитной индукции.
На рис. 1.13 показано типичное структурное соотношение между
магнитным потоком (величина В может рассматриваться как плот-
плотность магнитного потока Ф) и электрическим полем (а). Простран-
Пространственный максимум магнитного потока охватывается семейством
замкнутых электрических силовых линий. Если В возрастает
§ 1.2. УРАВНЕНИЯ МАКСВЕЛЛА
33
( > 0), то этот вектор и электрическое поле связаны левовин-
товой системой (б); если же В убывает (дВ/д?<0), то система
правовинтовая (в).
1.2.4. Третье уравнение Максвелла: электрическое поле и заря-
заряды (А). Смысл третьего уравнения Максвелла A.51), A.55) прост,
поскольку он вполне исчерпывается содержанием понятий дивер-
дивергенции и потока вектора (см. § 1.0). Линии вектора D начинаются
Ш
dt
В,Н боэрастают
В, Н убываю т
а
6
Рис. 1.13
на положительных и кончаются на отрицательных зарядах (знаки
divD и р совпадают). В случае точечных зарядов поля в их
окрестностях характеризуются картинами силовых линий типа
рис. 1.3а, б. Если в некоторой области р = 0, но электрическое поле
существует, то о его характере дают представление картины сило-
силовых линий на рис. 1.3в, г.
Третье уравнение Максвелла в интегральной форме A.55) из-
известно также под названием теоремы Гаусса. В качестве частного
момента отметим, что согласно A.55) поток ,.„
вектора D через некоторую замкнутую поверх-
поверхность S обращается в нуль не только при
отсутствии зарядов внутри S, но и при их ней-
нейтрализации, когда полный положительный за-
заряд уравновешивается отрицательным.
Пример 3. Покажем, каким образом можно ис-
использовать теорему Гаусса A.55) для нахождения по-
поля точечного заряда. Векторные линии D представляют
собой радиальные прямые, которые следует проводить
равномерно (через одинаковые угловые интервалы), Рис. 1.14
поскольку все направления- физически равноправны
(рис. 1.14). Опишем вокруг заряда сферу радиуса г и ее поверхность
примем за 5 в A.55). Тогда
1 >v
rJl\
1/ \
1/ л
ds = 4nr2D = q
S I I
(D и ds — радиальные векторы; D имеет одно и то же значение во всех точ-
3 В. В. Никольский, Т. И. Никольская
34
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
§ 1.3. СВОЙСТВА МАТЕРИАЛЬНЫХ СРЕД
35
ках сферы). Таким образом, D = q/inr2, что лучше выразить в векторной
форме:
D = r
о 4яг2
A.64)
Здесь Го — радиальный орт. Мы получили формулу, выражающую электриче-
электрическую индукцию D поля точечного заряда как функцию радиальной координа-
координаты г, т. е. расстояния от него. ¦
1.2.5. Четвертое уравнение Максвелла: непрерывность линий
вектора В (А). Четвертое уравнение Максвелла A.52), A.56) по
форме отличается от третьего нулевой правой частью. Это указы-
указывает на отсутствие фактора, который можно было бы назвать «маг-
«магнитным зарядом». Если все же формально ввести магнитный за-
заряд зм с плотностью рм, то согласно A.52), A.56)
р« = 0, 5м = 0. A.65)'
В силу четвертого уравнения Максвелла магнитные силовые линии
(линии вектора В) обязательно непрерывны, т. е. либо замкнуты,
либо идут из бесконечности в бесконечность. Общий характер кар-
картин магнитных силовых линий мы видим, таким образом, на
рис. 1.3s, г.
1.2.6. Заключительные замечания об уравнениях Максвелла
(Б). Во введении уже говорилось, что Максвелл воплотил в мате-
математической форме физические идеи Фарадея, предвосхищавшие
представление об электромагнитном поле. Фарадей рассматривал
силовые линии, как некоторую физическую реальность. Однако
Максвелл не только, употребляя современное выражение, форма-
формализовал взгляды Фарадея, но и внес в них существенно новое.
Именно Максвелл ввел ток смещения. Выше уже было показано,
что следствием первого и третьего уравнений Максвелла является
закон сохранения заряда. Если из A.49) удалить плотность тока
смещения, то вместо закона сохранения заряда A.44) мы получи-
получили бы равенство div j = 0, которое в действительности верно только
для постоянного тока. В дальнейшем мы неоднократно будем убеж-
убеждаться в особой важности представления о токе смещения. Что же
касается самих уравнений Максвелла, то в их окончательное фор-
формирование внесли решающий вклад Герц и Хевисайд.
Третье и четвертое уравнения Максвелла определенным образом
зависят от первых двух, в чем нетрудно убедиться. С этой целью
возьмем дивергенцию от левой и правой частей A.50). В силу
A.23) левая часть обращается в нуль; меняя местами в правой
части операции div и d/dt, имеем
т. е. div В = const. Эту константу остается выбрать равной нулю,
так как, несомненно, в некоторый момент поле отсутствовало, т. е.
было В = 0 и div В = 0. Следовательно, четвертое уравнение Макс-
Максвелла A.52) получается из второго A.50). При помощи аналогич-
аналогичных рассуждений можно прийти к третьему уравнению Максвелла
A.51). Для этого надо применить операцию div к первому урав-
уравнению Максвелла A.49) и привлечь закон сохранения заряда
A.44). Однако уравнения Максвелла с дивергенциями A.51),
A.52) нельзя рассматривать как простые следствия первых двух
уравнений A.49), A.50). Можно сказать, что они формализуют ту
дополнительную информацию, которая используется в процессе вы-
вывода этих уравнений.
Наконец, о соленоидальности поля В. Уравнение A.51), выра-
выражающее это свойство, и эквивалентное утверждение об отсутствии
магнитных зарядов A.65) в макроскопической электродинамике
твердо обоснованы. Однако принципиальное отсутствие магнитного
заряда в природе подвергается сомнению физиками; время от вре-
времени проводятся эксперименты с целью обнаружить объекты мик-
микромира, обладающие магнитным зарядом.
§ 1.3. Свойства материальных сред
1.3.1. Материальные уравнения (А). В макроскопической элект-
электродинамике установлено, что векторы поля D и В (электрическая
и магнитная индукции), а также плотность тока проводимости j
связаны с напряженностями поля Е и Н соотношениями, завися-
зависящими от свойств среды. Обычно существуют связи
D = D(E), B = B(H), j = 3(E). A.66)
Простейшая интерпретация этой записи состоит в том, что, напри-
например, индукция D(r, t) вполне определяется напряженностью
Е(г. t) в той же точке пространства М(т) и в тот же момент
времени t (аналогично рассматриваются В и ]). Иными словами,
процессы в среде считаются локальными и безынерционными:
в каждой точке состояние не зависит от окружающей среды и в
каждый момент времени — от «предыстории». Хотя такая трактов-
трактовка является упрощенной, она применима во многих случаях. При
этом вместо A.66) пишут:
D = eoeE, A.67)
В = цоцН, A.68)
] = аЕ. A.69)
Напомним, что входящие в первые два равенства ео и ц,о — это ко-
коэффициенты из формул A.46). Величины е и [i называются соот-
соответственно относительной диэлектрической проницаемостью и отно-
относительной магнитной проницаемостью (полные коэффициенты
вое = еа и цоц = ца — абсолютные проницаемости), а а — удельной
проводимостью.
3*
36
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
§ 1.3. СВОЙСТВА МАТЕРИАЛЬНЫХ СРЕД
37
Будем называть соотношения A.66) и все их возможные фор-
формы, включая A.67) — A.69), материальными уравнениями.
1.3.2. Поляризация и намагничивание (А). Обычно вещество
само по себе не создает макроскопически наблюдаемого поля (одно
из хорошо известных исключений — постоянные магниты). Это
объясняется уравновешенностью внутренних процессов в веществе
на микроскопическом уровне. В частности, нейтрализованы поло-
положительные и отрицательные заряды. Однако под действием внеш-
внешнего (постороннего) поля на эти заряды взаимная компенсация их
полей в той или иной степени нарушается. Можно утверждать, что
во внешнем электрическом поле происходит некоторая деформация,
а также переориентация атомов и молекул, заряды которых про-
продолжают оставаться связанными в прежней структуре вещества.
В результате отклонений зарядов, однако, появляется нескомпенси-
рованное внутреннее поле, которое, налагаясь на внешнее, заметно
изменяет его. Это называется поляризацией среды. Аналогичный
процесс, связанный с магнитным полем, называется намагничи-
намагничиванием.
Пусть некоторое электромагнитное поле в вакууме характери-
характеризуется напряженностями Е, Н. При этом согласно A.46) DBaK = eoE
и Ввак = (АоН (мы добавили нижние индексы, чтобы подчеркнуть,
что имеются в виду индукции в вакууме). Если то же поле Е, Н
существует в некоторой среде, то индукции будут иными1):
D = DBaK + P, В = Ввак + М. A.70);
Приращения Р п М будем называть поляризованностъю (электри-
(электрической поляризацией) и, соответственно, намагниченностью (маг-
(магнитной поляризацией). Процессы поляризации и намагничивания
среды выступают как независимые, т. е. первый связан только с
электрическим полем, а второй с магнитным:
Р = Р(Е), М = М(Н). A.71)
В большинстве случаев этим соотношениям можно придать простую
форму:
Р 5СэЕ М = и>ЗС"Н, A.72)
где безразмерные коэффициенты х" и Xм —это так называемые
электрическая восприимчивость и магнитная восприимчивость сре-
среды. Они выражают «меру отклика» среды на прилагаемое внешнее
поле. Восприимчивости связаны простыми соотношениями с отно-
относительными проницаемостями. Действительно, внося A.67), A.68)
и A.72) в A.70), получаем
11-1 + Х". A.73J
а
Рис. 1.15
') По традиции М имеет размерность Н. Мы отказываемся от этого ради
единообразия соотношений A.70).
1.3.3. Электропроводность (А). Обратимся к третьему матери-
материальному уравнению A.69), устанавливающему связь плотности то-
тока проводимости и напряженности электрического поля в некоторой
среде. На рис. 1.15а представлена одна из возможных картин линий
вектора j и выделена такая достаточно малая цилиндрическая об-
область V, что вектор ]' внутри нее можно считать не зависящим от
пространственных координат и
направленным по оси цилинд-
цилиндра (орт v0). Поэтому, интегри-
интегрируя левую и правую части
A.69) по выделенному объему
V = SI, имеем
jSl = oElS
(попутно мы спроецировали
векторы j и Е на vo, перейдя
к их абсолютным значениям).
Величина ]S есть не что
иное, как ток проводимости /,
проходящий по нормали через
S, a El = U можно назвать па-
падением напряжения на участ-
участке I (электротехнический термин). Таким образом, получаем
Ж = U, A.74)
где Я = 1/aS. Именно так формулируется закон Ома для участка
цепи, а полученная константа 31 есть электрическое сопротивление
выделенного цилиндрического объема среды (совершенно так же
вычисляется сопротивление отрезка проволоки). Итак, материаль-
материальное уравнение A.69) при а = const воспроизводит физическое со-
содержание известного закона Ома. В отличие от обычной формули-
формулировки этого закона оно является локальным, т. е. выражает связь
физических величин в точке. Поскольку сопротивление &L измеря-
измеряется в омах [Ом], удельная проводимость а имеет размерность
[1/@м-м)]. Она измеряется в сименсах на метр [См/м].
Подчеркнем, что перемещающиеся заряды, которые создают
ток, могут быть любого знака: положительные заряды образуют ток
в направлении своего движения, отрицательные — в противополож-
противоположном. Можно легко представить себе ток при нейтрализованном
заряде, когда в каждом макроскопическом элементе объема поло-
положительный заряд уравновешен отрицательным.
Рассмотрим некоторое распределение положительного заряда,
носители которого перемещаются со скоростью v. При этом суще-
существует ток с плотностью j, направленной, как v (то же было бы,
если бы отрицательные заряды перемещались со скоростью — v).
Если плотность заряда р, то
j = pv. A.75)
38
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
ВЫВОД. Обратимся к рис. 1.156, где показано, как смещается
элементарный цилиндрический объем V = 57, содержащий заряд
q = pV. За время At через поперечное сечение цилиндра S пройдет
заряд Aq = IAt — jSAt. В то же время Ag = pAF = pSAl, где Al —
смещение заполненного зарядом элементарного объема V за время
At (AV— смещенная часть V). Приравнивая оба выражения Ад,
имеем jAt = pAZ. Перейдем к пределу при At-* 0 и, учитывая, что
при этом AljAt = v, имеем j = pv. Этот вывод A.75) как раз и вы-
выражает j в векторной форме. ¦
1.3.4. Проводники и диэлектрики (А). В зависимости от степени
электропроводности вещества, как известно, делят на проводники
и диэлектрики (изоляторы). В теории удобно пользоваться пред-
представлениями об идеальном проводнике как среде с неограниченной
проводимостью (о -*¦ °°) и об идеальном диэлектрике—среде, ли-
лишенной проводимости (а = 0). В чем различие этих гипотетических
сред с точки зрения электродинамики?
Взяв выражение плотности обобщенного тока (см. с. 30), пре-
преобразуем его с привлечением материальных уравнений A.67),
A.69) для некоторой среды с параметрами е и а:
. , 5D т-, , 5Е /. гул,
3 + ^г = аЕ + еое^-. A.76)
Как видно, в случае идеального диэлектрика здесь исчезает первый
член j = аЕ, а при переходе к идеальному проводнику второй член
оказывается бесконечно малым в сравнении с первым (при всякой
реальной скорости процесса). Это значит, что в идеальном диэлект-
диэлектрике может существовать лишь ток смещения, а в идеальном про-
проводнике — только ток проводимости.
Теперь нетрудно найти критерий, по которому реальная среда
должна в электродинамике оцениваться как диэлектрик, проводник
либо нечто промежуточное. Естественно сравнивать плотности то-
токов проводимости и смещепия. Если первый резко преобладает, то
среда проявляет себя как проводник, а в противном случае — как
диэлектрик. Наконец, когда оба члена в A.76) одного порядка,
среду нельзя отнести ни к проводникам, ни к диэлектрикам.
Пусть для определенности рассматриваются гармонически ко-
колеблющиеся поля, т. е. временная зависимость описывается функ-
функцией cos at (напомним, что круговая частота со связана соотноше-
соотношением со = 2я/ с частотой /, измеряемой в герцах [Гц]). Произведя
дифференцирование по времени, мы получаем следующее отноше-
отношение амплитуд / и dD/dt:
-Я—. A.77)
(dDldt)m 0)808 *
Проводником будем считать среду в случае, когда это отношение
значительно превышает единицу, а диэлектриком, если оно значи-
§ 1.3. СВОЙСТВА МАТЕРИАЛЬНЫХ СРЕД
39
тельно меньше единицы:
а
> 1 — проводник,
Ш8о8 I "С 1 — диэлектрик.
A.78)
Полученные оценки показывают, что отнесение какой-то опре-
определенной среды к классу проводников или диэлектриков не имеет
абсолютного характера, а зависит от частоты процесса. Может ока-
оказаться, что среда, проявляющая себя как диэлектрик при достаточ-
достаточно высоких частотах, на низких выступает как проводник. В том
огромном диапазоне частот, которым располагает современная ра-
радиоэлектроника, свойства среды изменяются весьма значительно.
Однако вплоть до очень высоких частот, пока еще колебания ча-
частиц материи далеки от своих резонансов, параметры е и о часто
могут рассматриваться как ча-
частотно-независимые, т. е. как | б
константы в оценках A.78).
На рис. 1.16 показано, как
изменяется величина а/юеое
A.77) для некоторых распро-
распространенных сред. Видно, что
среды, расположенные на по-
поверхности земного шара, в раз-
различных вполне реальных об-
обстоятельствах могут выступать
и как диэлектрики, и как про-
проводники.
1.3.5. Типы сред в элек-
электродинамике (А). Вернемся
к материальным уравнениям
A.67) — A.69), содержащим ве-
величины ?, (I и а. Последние вы-
выступают как параметры сред.
В большинстве случаев е,
ц. и а могут рассматриваться
как скалярные коэффициенты
векторов. Это значит, что век-
векторы Е и D, Н и В, Е и j
коллинеарны (см. с. 13), а
свойства среды не зависят от направления поля. Среды, характе-
характеризуемые скалярными е, ц и о, называются изотропными.
Однако вообще материальные уравнения рассматриваются как
линейные однородные преобразования вида A.8), A.11). Таким
образом, параметры е, ц и о выступают как матрицы вида A.9).
В тех случаях, когда это надо подчеркнуть, будем писать е, ц и а
(ср. A.11)). Употребляют названия: тензор диэлектрической про-
проницаемости, тензор магнитной проницаемости, тензор удельной про-
проводимости. Среды, характеризуемые тензорными параметрами, на-
Рис. 1.16
40
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
зывают анизотропными. При анизотропии свойства среды зависят
от направления векторов поля. Векторы ? и D, Ни В, Е и j уже
не образуют (в общем случае) коллинеарные пары.
Конечно, если е и р. тензорные, то тензорами будут и соответ-
соответствующие восприимчивости %" или %*. При этом в формулах A.73)
вместо единиц следует написать единичные матрицы (тензоры) /
A.10).
Говорят, что среда однородна в области V, если параметры е,
[х и о (скаляры или тензоры) постоянны в V. Если же их следует
рассматривать как функции координат, то среда неоднородна. Ку-
Кусочно-однородными называют среды, параметры которых принима-
принимают различные постоянные значения в разных областях.
Наконец, параметры е, ц и о в большинстве случаев можно
считать не зависящими от векторов поля. Материальные уравнения
A.67) — A.69) при этом линейны. Линейными называют и соответ-
соответствующие среды. Нелинейность большинства сред проявляется
только в очень сильных полях.
1.3.6. Замечания о материальных уравнениях (Б). Материаль-
Материальные уравнения A.67) — A.69) содержат связи между векторными
функциями, недостающие в системе уравнений A.49) — A.-52). При
рассмотрении гармонических во времени процессов (гл. 3) мы смо-
сможем расширить понятия проницаемостей е и jx. При этой оговорке
можно утверждать, что материальные уравнения A.67) — A.69)
в большинстве практических случаев достаточны.
Примечательно, что очень простые материальные уравнения
оказываются удовлетворительными в макроскопической электроди-
электродинамике при огрвмной сложности микроскопических процессов в ве-
веществе, особенно в твердых телах. Хотя теория этих процессов
основательно разработана, она, вообще говоря, не в состоянии дать
средства для вычисления е, |х и о реальных веществ. Но выход
из положения очень прост: параметры е, ц и о в каждом конкрет-
конкретном случае могут быть измерены. Благодаря этому макроскопиче-
макроскопическая теория обходит трудности микроскопической.
В нашем курсе вопросы микроскопической электродинамики
будут время от времени затрагиваться, но только в тех случаях,
когда удовлетворительная трактовка оказывается возможной без
привлечения понятий квантовой физики.
Заметим, что записанные нами материальные уравнения
'A.67) —A.69) однородны: если Е = 0, Н = 0, то и D = 0, В = 0,
j = 0. Ниже в § 1.5 мы встретимся с неоднородным уравнением
типа A.69). Уравнениям A.67) и A.68) отвечают следующие не-
неоднородные:
D = eoeE + Po, В = ц0М-Н + М0. A.79)
В частности, второе из этих уравнений описывает поля в постоян-
постоянных магнитах, которые отличаются существованием самопроизволь-
самопроизвольной намагниченности Мо. В качестве сред, обладающих самопро-
самопроизвольной поляризованностью Ро, можно указать электреты.
§ 1.3. СВОЙСТВА МАТЕРИАЛЬНЫХ СРЕД
41
Наконец, поставим вопрос о том, каков может быть более общий
вид материальных уравнений. Описывая, например, электрическое
поле в некоторой изотропной среде, надо учитывать, что поляриза-
поляризация в данной точке М(г) зависит от поля в ее окрестности, а также
происходит запаздывание Р по сравнению с Е. С учетом нелокаль-
нелокальности и инерционности процесса поляризации
D (г, *) = е0 J j" Q (| г - r' |,i - О Е (»'. О dt> dv>- A-80)
V —оо
В этом обобщении материального уравнения A.67) ядро преобра-
преобразования, функция Q, определяется свойствами среды. Теперь связь
между D и Е зависит не только от характера среды, но также от
геометрических параметров тела и вида процесса в предшествую-
предшествующие моменты времени. К счастью, окрестность заметного влияния
очень мала. Поэтому все внутренние точки находятся в одинаковых
условиях и обычно геометрические параметры тела не имеют зна-
значения — за исключением случаев очень резкого изменения поля в
пространстве. Что касается инерционности поляризации (и намаг-
намагничивания), то в случае гармонических во времени процессов
(гл. 3) она может быть просто учтена, так что вид материальных
уравнений сохраняется.
1.3.7. Примеры сред (Б). Приведем некоторые справочные дан-
данные о параметрах е, jx и о распространенных веществ. Сразу под-
подчеркнем, что для большинства сред с высокой точностью ц = 1.
Строго говоря, для диамагнетиков \i < 1, а для парамагнетиков
\х > 1. В частности, медь — диамагнетик (jx = 0,99999044), алюми-
алюминий— парамагнетик (ц = 1,0000222). Ферромагнетики, к которым
в первую очередь относится железо, могут обладать весьма высо-
высокой магнитной проницаемостью. Но при частотах выше 108 Гц ц
уменьшается до единицы. Ферромагнетики относятся к нелинейным
средам. Природа ферромагнетизма имеет существенно квантовый
характер, его теория сложна и обширна. Тем не менее в гл. 16
мы обсудим некоторые свойства ферромагнетиков.
Параметры е и о распространенных сред приведены в табл. 1.2.
К первой группе отнесены вещества с низкой проводимостью, ко-
которые обычно проявляют себя как диэлектрики. Среды второй
группы выступают в зависимости от частоты и как диэлектрики,
и как проводники. К третьей группе отнесены металлы. Их прово-
проводимость настолько высока, что они — согласно оценке A.78) — вы-
выступают как проводники вплоть до границ применимости данного
критерия. К этому вопросу мы вернемся в гл. 14.
Свойства сред — предмет серьезных физических исследований,
как теоретических, так и экспериментальных. Успехи физики твер-
твердого тела обычно имеют важное значение для радиоэлектроники.
Достаточно указать на теорию полупроводников. Эта проблематика,
однако, далеко выходит за пределы нашего курса.
42
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
Таблица 1.2
Параметры г а а распространенных веществ
Вещество
Воздух
Парафин обычн.
Стекло натровое
Стеатит
Бумага из хлопка
Полистирол
Слюда
Титанат бария
Кварц плавлен.
Вода
Вода
Вода
Вода
Вода
Вода пресная (при-
(природная)
Вода морская
Земля сухая
Земля влажная
Серебро
Медь отожженная
Алюминий промыш-
промышленный
Латунь
Железо
Олово
Свинец
Ртуть
¦
1,000536
2,1
7,5
6
2,6
2,55
7
1200
3,8
81,1
80
78
64
35
80
80
3-6
10—30
_
—
—
—
—
1, Гц
0—3-101°
103
103-Ю5
10е—10е
103
10е—108
ЮЗ—106
ЮЗ—108
0
10»—10е
3-10»
10Ю
2,4-101°
—
<3-108>
—
—
—
о, См/м
ю-"
2-10-1°
10-12-Ю-13
10-ю
Ю-15
10-U—10-15
10-и
_
—
Ю-з-2,4-10-2
1-4,3
1,1-10-5-2-Ю-з
3-10-3-3-Ю-2
6,139-10'
5,8005-10'
3,54-10'
1,45-10'
1,0-10'
0,869-10'
0,48-10'
0,1044-10'
§ 1.4. Поля на границах раздела сред
1.4.1. Поля, заряды и токи на границах (А). При рассмотрении
любого реального объекта электродинамики мы встретимся с гра-
границами разнородных сред; такой границей является поверхность
всякого физического тела. С точки зрения макроскопической элект-
электродинамики, граница раздела сред — это такая поверхность, на ко-
которой параметры е, ц, о (хотя бы один из них) терпят разрыв как
функции нормали. Конечно, можно было бы полагать эти функции
непрерывными, допустив, что граница не является резкой, т. е.
имеется тонкий переходный слой, внутри которого свойства среды
продолжают изменяться плавно. Но это не дает преимуществ по
§ 1.4. ПОЛЯ НА ГРАНИЦАХ РАЗДЕЛА СРЕД
43
сравнению с использованием разрывных функций; к тому же было
бы непоследовательно рассматривать слишком тонкие слои в рам-
рамках макроскопической электродинамики.
Пусть поверхность 5 (рис. 1.17а) разделяет среды 1 я 2. Выбе-
Выберем на 5 точку М и выделим столь малую ее окрестность AS, что
этот элемент поверхности можно считать плоским. В точке М по-
построим орт нормали Vo (направление — из среды 2 в 1). Можно
Рис. 1.17
также построить на AS сколько угодно касательных ортов; выберем
из них два ортогональных: То и т0. При этом получена тройка
ортогональных векторов vo, то и т0, по которым можно разложить
любой из векторов поля Е, Н, В и D в точке М. Если орт то вы-
выбран так, что он совпадает по направлению с проекцией некото-
некоторого вектора поля F на AS, то имеем разложение F = vqFv + t<jFx.
Говорят, что вектор поля F разложен на нормальную и тангенци-
тангенциальную (касательную) компоненты.
В ряде случаев на границе раздела сред могут располагаться
микроскопические носители заряда, как неподвижные, так и обра-
образующие ток проводимости. В макроскопической электродинамике
принимается, что такого рода заряд не занимает объема, а явля-
является поверхностным. Плотностью поверхностного заряда называют
44
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
величину
A.81)
(ср. определение плотности р A.41)). Поэтому допускается также
существование поверхностного тока. Пусть такой ток проходит по
поверхности S (рис. 1.176) и ортогонально пересекает линию I,
причем в некоторой точке М на линии I его направление указыва-
указывает орт io. Плотностью поверхностного тока в М называется ве-
величина
Д?-»0
Нашей ближайшей целью является выяснение того, как ведут
себя нормальные и тангенциальные компоненты векторов поля на
различных границах раздела разнородных сред. Попутно войдут в
рассмотрение также поверхностные заряды и токи.
Поскольку s, ц и а разрывны, надо ожидать, что компоненты
векторов поля при переходе границ раздела сред тоже будут испы-
испытывать разрывы, т. е. либо обе компоненты некоторого вектора по-
поля F, либо одна из них — нормальная или тангенциальная — изме-
изменяются скачкообразно. Тогда векторная линия должна претерпевать
излом, как это показано на рис. 1.17в, г; мы предполагаем, что это
некоторая плоская кривая. На границе переход от Fi (в) к F2 (г)
происходит в общем случае с изменением как абсолютной величи-
величины, так и направления вектора.
Понятно, что в точках разрыва векторов поля мы лишены воз-
возможности применять уравнения Максвелла в дифференциальной
форме A.49) — A.52). Мы обратимся к интегральной форме этих
уравнений A.53) — A.56) и получим важные соотношения, кото-
которые называют граничными условиями.
1.4.2. Граничные условия для векторов электрического поля
(А)- Покажем, что вектор электрической индукции D подчиняется
следующему граничному условию:
(D,-D2)v0 = l,
A.83)
т. е. в граничных точках разность нормальных компонент вектора
D в обеих средах DiVo = A,i и D2V0 = А,2 равна плотности поверх-
поверхностного заряда |. Если граница не несет заряда (| = 0), то нор-
нормальная компонента D» вектора D при переходе границы остается
непрерывной.
В Ы В О Д. В основу анализа положим третье уравнение Макс-
Максвелла в интегральной форме A.55), теорему Гаусса. Построим пе-
пересекающий границу малый цилиндр высотой ДА (рис. 1.18а). Ос-
Основания его параллельны оказавшемуся внутри участку границы
AS, который рассматривается как элемент плоскости.
Пусть S в A.55) есть поверхность рассматриваемого цилиндра,
состоящая из его оснований и боковой поверхности. Ввиду малости
§ 1.4. ПОЛЯ НА ГРАНИЦАХ РАЗДЕЛА СРЕД
45
цилиндра поле на его основаниях можно считать однородным: D =¦
=• const. Внешняя нормаль к верхнему основанию направлена по
Vo, а к нижнему — противоположно. Поэтому, раскрывая интеграл
в A.55), получаем
DlVoA5 - D2v0AS + Ф|ок = Ад,
где первые два члена получены при вычислении потока вектора D
через основания цилиндра, а символом Ф1ок обозначен поток D
а
Рис. 1.18
через его боковую поверхность; в правой части — полный заряд
Ад внутри цилиндра.
Теперь будем неограниченно уменьшать высоту цилиндра Afe,
но так, чтобы его основания оставались в разных средах и в пре-
пределе при Afe -»- 0 совпали с элементом граничной поверхности AS.
При этом исчезает боковая поверхность цилиндра, а с ней Фбок-
Так как становится равным нулю его объем, то исчезает и та часть
заряда, которая могла быть распределена в объеме (если была от-
отлична от нуля плотность заряда р A.41)), т. е. в рассмотрение
входит лишь заряд Ag = 1A5, сосредоточенный на самой границе.
Итак, достаточно разделить все члены равенства на AS, чтобы по-
получить граничное условие A.83). ¦
Следующее граничное условие имеет вид
(Е!-Е2)то = О. A.84)
Оно означает, что тангенциальная компонента Ето = Ет вектора Е
при переходе границы раздела сред всегда остается непрерывной.
Вместо A.84) часто употребляется эквивалентное равенство
[vo, E,-E2] = 0, A.85)
более удобное в том смысле, что vo выбирается однозначно.
46
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
ВЫВОД. Пересечем граничную поверхность 5 плоскостью Р,
проходящей через нормаль к 5 (рис. 1.186), и построим на ней
малый прямоугольный контур ABCD, лежащий в обеих средах.
Его стороны АВ и CD параллельны пересеченному участку грани-
границы, который можно считать плоским. Обозначим АВ = CD = Al,
ВС —AD = Ah. На рис. 1.186 кроме орта нормали vo к 5 показан
также орт касательной то. Построен также орт нормали По к Р,
направленный касательно к S: то = [no, Vo].
Вывод основывается на применении второго уравнения Максвел-
Максвелла в интегральной форме A.54), причем в качестве L берется кон-
контур ABCD. Ввиду его малости поле на сторонах АВ и CD можно
считать однородным: Е = const. Направление обхода контура на
АВ будем производить по то; тогда на CD оно окажется противо-
противоположным то. Поэтому из уравнения A.54) следует
Е^дг - Е2т0дг + сэбок = - ¦? JBds.
АР
Здесь первые два члена получены при вычислении циркуляции
вектора Е на участках АВ и CD контура L, а оставшаяся часть
циркуляции обозначена Сбок (это вклад боковых участков ВС и
DA). Вычисление магнитного потока в правой части A.54) произ-
производится через площадку АР, ограниченную контуром L.
В пределе при Ah-*-0 стороны АВ и CD совпадают на грани-
границе S; при этом также АР -»- 0. В результате Cl0K и правая часть
равенства исчезают. Отбрасывая общий множитель А1, формально
приходим к граничному условию A.84).
Остается только понять, что т0 в A.84) мы имеем право рас-
рассматривать как орт совпадающих по направлению проекций Ei и
Е2 на S. В процессе вывода ориентация плоскости Р, а следова-
следовательно, и вектора то была произвольной. Поэтому равенство A.84)
справедливо для любого направления т0 на S. Направив то сначала
вдоль проекции Ei, а затем ортогонально к ней, из A.84) видим,
что во втором варианте проекция Е2 равна нулю. Это и доказывает
совпадение проекций Ei и Ег на S по направлению.
Чтобы получить граничное условие в форме A.85), заменим То
в A.84) через [no, vo], а затем учтем свойство A.5) смешанного
произведения векторов: (Ei — E2)[no, Vo] = [vo, Ei — Е2]по = О. Отсю-
Отсюда непосредственно следует A.85), поскольку орт по, задающий
ориентацию плоскости Р, является неопределенным. ¦
1.4.3. Граничные условия для векторов магнитного поля (А).
Нормальная компонента вектора магнитной индукции В всегда не-
непрерывна:
(Bi-B2)v0 = 0. A.86)
ВЫВОД. Взяв за основу уравнение Максвелла в интегральной
форме A.56), повторим все рассуждения, использовавшиеся при
§ 1.4. ПОЛЯ НА ГРАНИЦАХ РАЗДЕЛА СРЕД
47
выводе граничного условия A.83). При этом получается промежу-
промежуточное равенство
В^0Д5 - B2x0AS + Ф^ок = 0,
где Фбок — поток вектора В через боковую поверхность цилиндра,
исчезающий в пределе при Ah^-О (см. рис. 1.18а). Отсюда сле-
следует A.86). ¦
Тангенциальная компонента вектора Н непрерывна только при
отсутствии на границе поверхностного тока, а в общем случае спра-
справедливо граничное условие (см. рис. 1.186)
A.87)
A.88)
Чаще применяется эквивалентное граничное условие
ВЫВОД. Исходя из первого уравнения Максвелла в инте-
интегральной форме A.53), выполним те же операции, что и при вы-
выводе A.84). Рассмотрим промежуточный результат
н^дг - н2т0дг + с%ок = -^ J d ds + j i ds,
АР
АР
где Сбои — вклад боковых участков контура ВС и DA в циркуля-
циркуляцию Н, который исчезает при Ah -»- 0. Одновременно исчезает пер-
первый из интегралов в правой части равенства. Второй же интеграл,
выражающий полный ток проводимости, проходящий через АР,
при ц ?= 0 не уничтожится. Когда при Ah -*¦ 0 площадка АР вы-
вырождается в отрезок А1,
Ah/2
I = lim \ j ds = lim п0А1 \ j (v) dv,
где v — нормальная координата. По своему смыслу последний ин-
интеграл в пределе есть не что иное, как плотность поверхностного тока
г\. Таким образом, 1=г\п0А1, и при Ah-+0 мы получаем гранич-
граничное условие A.87).
Чтобы перейти к эквивалентному условию A.88), заменим в
A.87) то через [n0, vo] и перенесем т]п0 в левую часть. Таким обра-
образом: (Hi — Н2) [п0, vo] — т]По = {[vo, Hi — Н2] — т]}п0 = 0. Отсюда ввиду
неопределенности п0 следует A.88). ¦
1.4.4. Некоторые следствия граничных условий (А)- Рассмотрим
несколько примеров применения граничных условий.
Пример 4. Пусть на границе раздела двух изотропных сред поверхност-
поверхностные заряды и токи отсутствуют. Поведение полей — электрического или маг-
магнитного — можно охарактеризовать при помощи картин преломления силовых
линий, показанных на рис. 1.19. В одном случае (а) проницаемость e(|i) вто-
второй среды выше, чем первой, а в другом (б) — ниже. Из полученных выше
48
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
граничных условий с привлечением материальных уравнений A.67) и A.68)
следует, что Ezl — Ех2 (Hzl — Ят2) при г1Еп = e2?v2 (Hi#vi = (i2#v2). Поэтому
tg ai/tg a2 = ej/ej и tg ai/tg a2 = Ц2/Ц1. ¦ A.89)
Пример 5. Если граница раздела сред обладает свойством экранирова-
экранирования, так что поле в среде 1 может существовать, не проникая в среду 2 (Е2 =
1= 0 и В2 = 0), то из A.84) следует, что ?т1 = 0, т. е. Е| подходит к границе
E,D (H,B)
2
Рис. 1.19
I
E,U (Н,В)
У777////77777777///
Рис. 1.20
а
Рис. 1.21
по нормали (рис. 1.20а), а из A.86) получается, что 2?vi = 0 и потому вектор
В| направлен на границе касательно (рис. 1.20 6). Применяя, далее, граничные
условия A.83) и A.88) с учетом того, что D2 = 0 и Н2 = 0, получаем
= 6,
Н,] = т\.
A.90)
§ 1.5. ЛОКАЛИЗАЦИЯ И ДВИЖЕНИЕ ЭНЕРГИИ ПОЛЯ
49
Мы видим, что существование поля в среде 1 при его отсутствии в среде 2
обусловлено поверхностными зарядами и токами. ¦
Пример 6. Пусть в среде с высокой диэлектрической (магнитной) про-
проницаемостью имеется узкая щель. Если в среде вектор Е(Н) параллелен щели,
то согласно A.84) и A.87) при т| = 0 следует, что напряженность поля в ще-
щели— та же, что и в среде (рис. 1.21а). Если же вектор Е(Н) перпендикулярен
щели, то из A.83) при | = 0 и из A.86) с учетом материальных уравнений
находим, что напряженность поля в щели (при изотропии среды) в е(ц) раз
больше (рис. 1.216). ¦
1.4.5. Применение дельта-функции Дирака (Б). Поверхностный
заряд можно условно представить как объемный, который распре-
распределен с плотностью
N(-v'), A-91)
где % — плотность поверхностного заряда на поверхности 5, функция
а
Рис. 1.22
координат q\, qi, заданных на этой поверхности; v — нормаль-
нормальная координата, принимающая значение v' при пересечении 5
(рис. 1.22а).
Аналогично можно рассматривать поверхностный ток, введя
плотность (рис. 1.226)
?a)e(v-v'). A.92)
§ 1.5. Локализация и движение энергии поля
1.5.1. Закон Джоуля — Ленца и превращения энергии (А). По»
скольку электромагнитное поле физически реально, оно обладает
энергией. После ряда рассуждений и операций над уравнениями
Максвелла мы выясним, каким образом векторы поля Е, Н, D и В
определяют его энергию W. Можно подойти к этому, начав с во-
вопроса о превращениях энергии поля.
Известно, что при наличии электрического тока в реальной
среде выделяется тепло. Зная плотность тока j и напряженность
4 в. В. Никольский, Т. И. Никольская
50
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
§ 1.5. ЛОКАЛИЗАЦИЯ И ДВИЖЕНИЕ ЭНЕРГИИ ПОЛЯ
51
поля Е, нетрудно, как мы увидим, найти энергию, теряемую элект-
электромагнитным процессом за единицу времени, т. е. мощность теп-
тепловых потерь Р. Оказывается, в объеме V расходуется мощность
P = [jEdv. A.93)
v
Чтобы убедиться в справедливости записанного выражения, обра-
обратимся к простому варианту, который показан на рис. 1.15а. В этом
случае применение формулы A.93) дает:
(поле и ток внутри малого цилиндрического объема V = SI одно-
однородны, а величины / и U определяются также, как в п. 1.3.3).
Как видно, полученное равенство эквивалентно закону Джоуля —
Ленца, известному из курса общей физики. Таким образом, при-
применение формулы A.93) означает обращение к закону Джоуля —
Ленца. По смыслу равенства A.93) подынтегральное выражение
p = jE A.94)
есть не что иное, как плотность мощности, т. е. мощность, отнесен-
отнесенная к единице объема:
w- A-95)
Полученные выражения мощности и ее плотности A.93), A.94)
имеют универсальный характер. Они верны не только при расчете
джоулевых потерь, но и сохраняют смысл во всех случаях, когда
рассматриваются токи.
Пример 7. Согласно A.45) на некоторый точечный заряд в электромаг-
электромагнитном поле действует сила F= ?{E+ [v, В]}. Выделив малый элемент AV
заряженного объема, положим q = pAF. При перемещении заряда совершается
работа, которая для векторного дифференциала пути dl равна
dA = ?Edl = pdlEAF
(лоренцева сила ?[v, В], будучи поперечной, работы не производит). Связанная
с AV мощность АР может быть определена как работа, произведенная за еди-
единицу времени:
АР — dA/dt = p(dl/dt)EAV — pvEAV,
причем в силу A.75) j = pv. Определяя отсюда плотность мощности р =
= AP/AV, получаем: р = ]Е, что совпадает с A.94). ¦
Отметим, что в зависимости от направления движения зарядов
величина р может быть как положительной, так и отрицательной.
Заряды могут ускоряться полем. При этом j и Е параллельны,
р > 0, и энергия у поля отбирается. Очевидно, что р < 0, если j и Е
антипараллельны. Это будет, например, в том случае, когда дви-
движение зарядов против поля создается каким-то неэлектромагнит-
неэлектромагнитным, «сторонним» процессом, который отдает свою энергию полю,
тормозящему заряды.
где
Описание неэлектромагнитных факторов, как говорят, сторонних
сил в большинстве случаев сводится к изменению вида материаль-
материального уравнения A.69). Используется одна из следующих форма-
формализации:
i = o(E + E"), j = aE + r. A.96)
Введенные здесь функции Ест и jCT при решении электродинамиче-
электродинамических задач являются заранее заданными. Величина Ест называется
напряженностью сторонних сил (или просто сторонней напряжен-
напряженностью), а jCT — сторонним током. Теперь мы можем детализировать
выражение плотности мощности A.94). Используя A.96), имеем
p = a-'j2-jEc\ p = aE2 + jCTE A.97)
(в одном случае Е в A.94) выражено при помощи первого равен-
равенства из A.96), а в другом случае — j получено при помощи вто-
второго равенства). Таким образом, можно написать
A.98)
= -jECT = j0TE. A.99)
Первый член рп характеризует поглощение, потери энергии электро-
электромагнитного процесса, а второй — рст — действие сторонних сил. Сто-
Сторонние силы обычно локализованы. Если, например, они сосредото-
сосредоточены в некоторой области Vs, то согласно первому равенству A.96)
j = оЕ0Т в Vs и j = оЕ вне V*. Будем называть Vs областью
источника.
Позднее мы еще не раз вернемся к обсуждению понятия сто-
сторонних сил. Интерпретация пх будет несколько расширена.
1.5.2. Баланс энергии поля (А). Дальнейшее обсуждение будет
опираться на уравнения Максвелла A.49), A.50). Все члены вто-
второго из них умножим на Н, а все члены первого — на Е:
HrotE = -H4^,
at
ErotH = E-^ + Ej.
at '
Вычтем левую и правую части второй строчки из соответствующих
частей первой, тогда слева получим выражение Н rot Е — Е rot H,
которое мы свернем посредством формулы A.26). В результате
будем иметь
div [Е, Н] = - Н -f- - Е i? - jE.
A.100)
Равенству A.100) нетрудно придать интегральную форму.
С этой целью проинтегрируем все его члены по некоторому объему
V, ограниченному поверхностью 5, а затем левую часть преобра-
преобразуем на основании теоремы Остроградского — Гаусса A.33):
[E,
_JjE dv.
A.101)
52
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
§ 1.5. ЛОКАЛИЗАЦИЯ И ДВИЖЕНИЕ ЭНЕРГИИ ПОЛЯ
53
Остается проанализировать полученный результат. После неко-
некоторых рассуждений мы увидим, что равенство A.101) есть уравне-
уравнение баланса энергии поля в объеме V.
Ключевым для нас является последний член справа в A.101).
Согласно A.93) это мощность Р, причем Р будет рассматриваться
как величина, характеризующая все процессы преобразования энер-
энергии в объеме V (ниже в п. 1.5.5 будет сделано уточнение). Разу-
Разумеется, размерность мощности имеют и все остальные члены в
A.101).
Следующим важным моментом является тот факт, что для вся-
всякой энергетически изолированной системы уравнение баланса энер-
энергии имеет вид
P = -dW/dt, A.102)
где W — запас энергии. В частности, из A.102) следует, что поте-
потери энергии (Р > 0) могут происходить только в результате умень-
уменьшения этого запаса (dW/dt < 0).
Если граница 5 области V является энергетически изолирую-
изолирующей и при наличии поля внутри V оно отсутствует во внешней
среде, то поверхностный интеграл в A.101) равен нулю (это пря-
прямо следует из примера 5, с. 48 Ех — 0 на 5). Таким образом, ра-
равенство A.101) принимает вид
v, A.103)
и мы вправе истолковать его как уравнение баланса энергии для
изолированной системы. Сопоставляя A.103) и A.102), имеем
>. A.104)
В результате определена временная производная запаса энергии.
Сохраняя интерпретацию A.104) и переходя к общему случаю,
запишем A.101) в виде
Е, Н] ds + ^ + Р = 0. ' A.105)
Очевидно, что равенство A.101) предстает как уравнение баланса
энергии в области V, причем вследствие неизолированности систе-
системы появился дополнительный член в виде поверхностного интеграла
= F lids. A.106)
s
Величина Рх есть поток вектора
П = [Е, Н] (
через границу 5 области V. Он называется вектором Пойнтинга.
Поток Рг вектора Пойнтинга П показывает, насколько внутрен-
внутренние процессы не уравновешены. Если, например, Рг > 0, то это
означает потери энергии в области V из-за ее перехода во внешнее
пространство. Если же Рг < 0, то энергия поступает в V извне.
В обоих случаях абсолютная величина Рг есть не что иное, как
энергия, проходящая через граничную поверхность 5 за единицу
времени. Поэтому Ps называют потоком энергии через 5. Положи-
Положительный поток энергии равен, таким образом, мощности излучения
во внешнее пространство, а отрицательный — мощности поглощае-
поглощаемого внешнего излучения.
Поскольку вообще поток вектора можно измерять числом век-
векторных линий (см. п. 1.0.4), то, построив различные мыслимые кар-
типы линий вектора Пойнтинга П, мы получим наглядные иллю-
иллюстрации разных вариантов баланса энергии (рис. 1.23). Баланс бу-
будем называть активным, когда Рх > 0, т. е. отдача энергии во внеш-
внешнее пространство преобладает (а, б); согласно A.105) при этом
Актибный
баланс
П=О
Ней тральный
баланс
ПассиЬный
баланс
Рис. 1.23
dW/dt + Р < 0. В случае чистого излучения (а) может оказаться,
что внутренний запас энергии остается постоянным: W = const,
тогда, как видно, Рх = —Р. Поскольку Рг > 0, то Р < 0: излучение
создается сторонними силами в V (согласно A.98) Р = РП + РСТ,
и в случае отсутствия потерь Ps = — Рот). Но возможно также, что
54
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
JP = 0 (нет ни сторонних сил, ни внутренних потерь либо они вза-
взаимно уравновешены), тогда P* = —dW/dt, а поскольку Ps > 0, то
dW/dt < 0. Это значит, что излучение обусловлено убыванием за-
запаса энергии в V. Варианты (в), (г) и (д) соответствуют условию:
Ps = 0; это нейтральный баланс энергии. Поток энергии в данном
случае может проходить насквозь (в), так что число входящих
линий векторы Поинтинга равно числу выходящих; он также может
не входить в область V (г) пли вообще отсутствовать (д). Нако-
Наконец, возможен пассивный баланс, когда поглощение преобладает
над излучением (е, ж). При чистом поглощении (е) и постоянстве
внутреннего запаса энергии Ps = —Р. Если же Р = 0, то Р2 =
= —dW/dt. Поскольку Ps < 0, то dW/dt > 0: поглощение внешнего
излучения приводит к росту запаса энергии.
Пример 8. Рассмотрим поток энергии, проходящий через поверхность
бесконечного цилиндрического провода с постоянным током /. В силу аксиаль-
аксиальной симметрии системы для определения магнитного поля вплоть до поверх-
поверхности провода (г = R) можно пользоваться формулой A.58): Н = Оо//BяД).
Электрическое поле найдем из плотности тока j прп помощи A.69): Е = j/o =
= z0ll(nR2a). Поэтому на поверхности провода (рис. 1.24)
П = [Е, Н] = -г0Я/Bл2й3с). A.108)
Мы видим, что вектор Поинтинга направлен внутрь провода. Значит, из внеш-
внешнего пространства в провод входит поток энергии Р* A.106). Вычислим Рх
на участке провода длиной I. Это дает
nds=
A.109)
где Я. = //(лД2с) есть электрическое сопротивление данного участка (см.
п. 1.3.3). Входящий поток энергии равен мощности, поглощаемой согласно за-
закону Джоуля — Ленца. ¦
1.5.3. Энергия электромагнитного поля (А). Исходя из равен-
равенства A.104), можно путем интегрирования определить энергию
поля. При некоторых оговорках, которые будут сделаны в п. 1.5.5,
справедливы следующие операции:
яГ— eo8ri at ~ at
е0еЕ2
§ 1.5. ЛОКАЛИЗАЦИЯ И ДВИЖЕНИЕ ЭНЕРГИИ ПОЛЯ
55
Это значит, что операцию дифференцирования по времени можно
в A.104) вынести за знак интеграла. В результате запас энергии
в области V выражается следующим образом:
= t\ (8»eE2 + ^Ъ2) dv = i- j (ED + HB) dv. A.110)
v v
Как видно, энергия слагается из двух частей, одна из которых
связана с электрическим полем, а другая — с магнитным. Поэтому
пишут W = W* + W, различая магнитную энергию
A.111)
и электрическую энергию
^ ^ A.112)
V V
Подынтегральное выражение в A.110) есть не что иное, как
плотность энергии электромагнитного поля:
^ = \ (ED + НВ). A.113)
w = lim ^ = \-
Слагаемые имеют смысл плотностей электрической и магнитной
энергии: w==w3 + wu (wu и vf — подынтегральные выражения из
A.111) и A.112) соответственно).
Рис. 1.25
Пример 9. Допустим, что электрическое поле в объеме между пласти-
пластинами конденсатора (рис. 1.25а) однородно (Е = const). В этом приближении
W* = Ц. Г eE2dv = V E2Sd = CJL,
<6 щ) Li it
V
где U — Ed и С = eoe5/d. ¦
A.114)
56
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
§ 1.5. ЛОКАЛИЗАЦИЯ И ДВИЖЕНИЕ ЭНЕРГИИ ПОЛЯ
57
Пример 10. Найдем магнитную энергию внутри тороидальной системы
(рис. 1.25 6), совмещенной с бесконечным цилиндрическим проводом, по кото-
которому проходит постоянный ток /. Ввиду аксиальной симметрии всей системы
магнитное поле внутри кольца находится по формуле A.58). Вычисляя инте-
интеграл A.111), получаем
2я
1.5.4. Локальный баланс и движение энергии (А). Если до-
допустить, что поток вектора Пойнтинга Pz через любую, а не только
замкнутую поверхность (как в п. 1.5.2) представляет собой поток
энергии через эту поверхность, то П следует истолковать как плот-
плотность потока энергии:
П = lim л0 ~.
as-»o лл
A.116)
В этой формуле я0 — единичный вектор, указывающий направле-
направление движения энергии, Д5 — ортогонально ориентированная пло-
площадка, APZ — количество энергии, проходящей за единицу времени
через AS.
Рекомендуется сопоставить формулы A.116) и A.42). Повторе-
Повторение структуры неслучайно: существует аналогия между энергети-
энергетическими величинами, с одной стороны, и зарядами и токами —
с другой. Так, в частности, рассматривая движение энергии, мы
можем повторить все рассуждения, которые привели к формуле
A.75), и получить следующий ее энергетический аналог:
n = wv. A.117)"
Здесь v — скорость движения энергии, которая, как видно, всегда
может быть найдена, если известно поле и по формулам, A.107),
A.113) найдены П и w.
Вернемся к равенству A.100), переписав его в виде
|f+ р = 0.
A.118)
Если р = 0, то A.118) совпадает по структуре с дифференциаль-
дифференциальной формулировкой закона сохранения заряда A.44). Полной ана-
аналогии нет, потому что в отличие от заряда q энергия электромаг-
электромагнитного поля не сохраняется: она переходит в другие виды энер-
энергии, порождается ими.
Равенство A.118) есть уравнение баланса энергии в дифферен-
дифференциальной форме. Оно характеризует локальный баланс энергии.
Если в исчезающе малой окрестности некоторой точки баланс ак-
активен, то dw/dt + р<0 и в силу A.118) divII>0. При пассивном
балансе dw/dt + р>0 и divII<0, а при нейтральном dw/dt + р = 0
и div П = 0. Вспоминая смысл оператора дивергенции (см. п. 1.0.4),
мы видим, что при активном балансе рассматриваемая точка явля-
является источником линий вектора Пойнтинга, при пассивном балан-
балансе — стоком, а при нейтральном — лежит на некоторой линии век-
вектора Пойнтинга.
1.5.5. Заключительные замечания (Б). Начнем с анализа сде-
сделанных нами допущений. В п. 1.5.2 мы предположили, что все про-
процессы преобразования энергии характеризуются величиной Р, опре-
определяемой формулой A.93). Это, в частности, означает, что если
нет токов проводимости (j = 0), то не может быть ни потерь энер-
энергии, ни действия сторонних сил. На самом деле потери энергии
свойственны также процессам поляризации и намагничивания (хо-
(хотя часто этими потерями можно пренебрегать). Если отказаться
от сделанного допущения, то для изолированной системы из A.101)
и A.102) уже нельзя получить A.104).
С этим тесно связан следующий вопрос. Почему не всегда вер-
верны действия, выполненные в начале п. 1.5.3? Дело в том, что в
этих действиях были вынесены за знак оператора d/dt проницае-
проницаемости е и [х, а это допустимо только в случае безынерционной
среды. В дальнейшем — при изучении гармонических колебаний
(§ 3.2, 3.3)—мы сможем учесть инерционность процессов поляри-
поляризации и намагничивания. Соответствующие потери энергии будут
рассматриваться.
Следующее замечание затрагивает интерпретацию величин П
и w (см. пп. 1.5.2—1.5.4). Рассмотренная трактовка вектора Пой-
Пойнтинга П как плотности потока энергии A.107) и величины w
A.113)—как плотности энергии отвечает современным физическим
воззрениям (базируется на совокупности известных фактов). Но
вытекает ли она с необходимостью из уравнений электродинамики?
На этот вопрос приходится ответить отрицательно. Построим, на-
например, вектор П + F, где F — любая соленоидальная функция
(div F = 0). Поскольку величина П + F может быть подставлена
вместо П в A.101), A.105) и будет удовлетворять этим уравне-
уравнениям, на вопрос о том, какова в действительности плотность пото-
потока энергии, нет ответа. Аналогично можно говорить о подстановке
в A.118) ш + const вместо w.
Заметим еще, что действия в п. 1.5.3 были проведены в пред-
предположении, что среда изотропна. В случае анизотропии выводы
сохраняются, когда тензоры вир, симметричны: е^ = е^, е„г =
°zy ....
В заключение отметим, что вся информация об электромагнит-
электромагнитном поле получена в результате наблюдения и осмысления превра-
превращений его энергии в иные формы (табл. 1.3). Ведь непосредственно
мы «не замечаем» полей, если не говорить о световых и тепловых
воздействиях, информативность которых незначительна. Начало было
58
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
§ 1.6. СИСТЕМА УРАВНЕНИЙ И ЗАДАЧИ ЭЛЕКТРОДИНАМИКИ 59
положено наблюдением электромеханических превращений, что в
конечном счете привело к представлению о векторных функциях
Таблица 1.3
Энергетические величины в теории электромагнетизма
Название величины
Обозначение
Единица измерения в СИ
Энергия электромагнитного
поля
Электрическая энергия
Магнитная энергия
Мощность
Мощность поглощения
(мощность потерь)
Мощность сторонних сил
(мощность источника)
Плотность энергии электро-
электромагнитного поля
Плотность электрической
энергии
Плотность магнитной энер-
энергии
Плотность мощности
Плотность мощности сторон-
сторонних сил
Плотность мощности погло-
поглощения
Поток энергии
Плотность потока энергии
Джоуль
Джоуль
Джоуль
Ватт
Ватт
Ватт
Ватт
[Дж]
[Дж]
[Дж]
[Вт]
[Вт]
[Вт]
[Вт]
Джоуль на кубический метр [Дж/м31
Джоуль на кубический метр [Дж/м3]
Джоуль на кубический метр [Дж/м3]
Ватт на кубический метр [Вт/м3 ]
Ватт на кубический метр [Вт/м3 ]
Ватт на кубический метр [Вт/м3]
Ватт [Вт]
Ватт на квадратный метр [Вт/м2]
Е и В. Выше мы не обсуждали специфические особенности раз-
различных превращений энергии, например, электрохимических, фото-
и термоэлектрических, и многих других, используемых в технике.
Однако были выяснены и проанализированы закономерности, свой-
свойственные всем видам превращений энергии.
§ 1.6. Система уравнений и задачи электродинамики (А)
1.6.1. Система уравнений Максвелла. Объединяя уравнения
Максвелла A.49) — A-52) и материальные уравнения, мы получаем
полную систему уравнений электродинамики, или систему уравне-
уравнений Максвелла. Как уже отмечалось в п. 1.3.6, материальные урав-
уравнения A.67) — A.69) в большинстве случаев достаточны (впрочем,
последнее из них лучше писать в более общей форме A.96), учи-
учитывая, когда это требуется, действие сторонних сил). Запишем,
таким образом, систему уравнений Максвелла
ЯП . . „ дВ
divD = p, div В = О, A.119)
D = еоеЕ, В = \10\Л,
j = a(E+ECT) или j = aE +jCT,
которую будем рассматривать как основу анализа всевозможных
электромагнитных процессов.
Круг этих процессов весьма широк, и он может неограниченно
увеличиваться прп замене материальных уравнений, входящих в
A.119), более общими, либо иногда уравнениями специального ви-
вида, пригодными в отдельных случаях. В частности, уравнения элек-
электродинамики могут при этом объединяться с другими уравнениями
математической физики. Так, например, можно учесть зависимость
параметров е, ц и а от температуры. Но тогда в группу материаль-
материальных уравнений придется включить уравнение теплопроводности,
являющееся, в свою очередь, уравнением в частных производных
(см., например, [И.1]). Распределение тепловых источников даст
функция рп A.99), так что уравнение теплопроводности окажется
связанным с уравнениями Максвелла.
Если среда линейна, то линейны все уравнения, входящие в си-
систему уравнений Максвелла A.119). Это значит, что любые линей-
линейные комбинации решений системы A.119) также будут являться
ее решениями. Очевидно некоторое решение представляет собой
набор величин Е,-, Н,, Df, В,, ji, р„ при которых все уравнения удов-
удовлетворяются. Пусть имеется несколько решений: i = 1, 2, ..., п.
Их линейная комбинация — это набор сумм: Е = aiEi + a2E2 + ...
... + а„Е„, H = aiH[+ a2H2 +.. . + anHn и т. д., где аи, а2, ..., ап —
произвольные коэффициенты. В силу линейности системы уравне-
уравнений Максвелла (прп линейности среды) мы вновь получили ее ре-
решение, использовав, как говорят, принцип суперпозиции (наложе-
(наложения). Поскольку в линейные комбинации входят и величины, вы-
выражающие сторонние силы (Ест или jCT), то можно утверждать, что
поле, создаваемое несколькими источниками, предстает как нало-
наложение полей, существующих при раздельном действии источников.
Разумеется, принцип суперпозиции не распространяется на ве-
величины, связанные с полем нелинейно, например, на энергетиче-
энергетические характеристики. Если электрическое поле есть наложение двух
полей, так что Е = Е] + Е2, то его энергия есть
W3 = *f [ гЕЧи = \ \ zE\dv + \
V V V V
Как видно сумма первых двух членов, представляющих собой энер-
энергию первого и второго полей W\ + W\, еще не является суммар-
60
ГЛ. 1. ИСХОДНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
§ 1.6. СИСТЕМА УРАВНЕНИЙ И ЗАДАЧИ ЭЛЕКТРОДИНАМИКИ
61
ной энергией, которая включает еще взаимную энергию Wf2 (по-
(последний член). Закон сохранения энергии, конечно, не нарушается,
поскольку в баланс энергии входит работа сторонних сил.
1.6.2. Задачи электродинамики и классы электромагнитных яв-
явлений. Электромагнитные поля находятся как решения уравнений
A.119), однако не всякое решение этой системы дает электромаг-
электромагнитное поле. При постановке задач вводятся еще некоторые до-
дополнительные условия, сообщающие им физическую определен-
определенность. Таковы начальные и граничные условия, задание сторонних
сил. Под начальными условиями понимают задание поля в некото-
некоторый момент времени; в дальнейшем мы будем рассматривать, глав-
главным образом, такие переменные процессы, которые являются перио-
периодическими во времени. В этом случае вопрос о постановке началь-
начальных условий отпадает. Под граничными условиями подразумеваются
не только изученные выше в § 1.4 соотношения между нормаль-
нормальными и тангенциальными компонентами векторов поля на грани-
границах раздела сред, но и задание полей на внешних границах рас-
рассматриваемых областей.
Из системы уравнений Максвелла A.119) можно получить не-
некоторые частные системы уравнений, описывающие классы явлений
электромагнетизма. Например, устранив все члены с временными
производными, мы будем иметь систему уравнений стационарного
электромагнитного поля (она будет выписана в начале гл. 2), ко-
которая, в свою очередь, при отсутствии токов (j = 0) распадается
на две независимые системы уравнений: уравнения электростатики
и магнитостатики. Уравнения A.119) с исключением временной
зависимости оказывается возможным записать и для гармонических
во времени процессов, когда поля изменяются по закону
cos(? + p)
( p)
Переменные во времени электромагнитные поля, имеющие ха-
характер волн, составляют главный предмет этой книги. Они имеют
особое значение для радиотехники. Мы рассмотрим излучение
электромагнитных волн, различные сложные волновые процессы,
такие как, в частности, дифракция. Большое значение будет при-
придаваться общности электродинамических и оптических понятий.
Электромагнитные волновые процессы, активно используемые в
радиоэлектронике, весьма многообразны — от своеобразных по струк-
структуре направляемых волн в волноводных устройствах и интеграль-
интегральных схемах до радиоволн, распространяющихся в природных усло-
условиях. Все они будут обсуждаться в этой книге.
Почти весь материал книги относится к макроскопической элек-
электродинамике. Все же — с классических позиций — будут затронуты
и некоторые вопросы микроскопической электродинамики, посколь-
поскольку они важны для радиоэлектроники. Будут обсуждаться модели
различных сред, например, ионосферной плазмы и ферритов.
В этой книге не рассматривается электродинамика как физиче-
физическая теория, связанная с анализом пространства и времени. Элек-
Электродинамика движущихся объектов в начале XX века привела к
созданию специальной теории относительности А. Эйнштейна. Огра-
Ограничимся напоминанием некоторых фактов, известных читателю из
курса общей физики. Согласно принципу относительности законы
природы одинаковы во всех инерциальных системах (относительное
движение которых равномерно и прямолинейно). Переход от одной
инерциальной системы к другой связан с преобразованием прост-
пространственных координат и времени,— преобразованиями Лоренца.
Законы природы должны описываться уравнениями, инвариантны-
инвариантными относительно преобразований Лоренца. Этим свойством не обла-
обладают законы Ньютона, но оно присуще уравнениям Максвелла.
Сохраняется вид этих уравнений. Что касается электромагнитного
поля, то в разных системах координат оно оказывается разным.
Положим, что в некоторой инерциальной системе координат отме-
отмечено существование магнитного поля (В=?0), а электрическое поле
отсутствует (Е = 0). При этом наблюдатель в другой системе, дви-
движущейся относительно первой с постоянной скоростью и, обнаружит
электрическое поле. Действительно, на неподвижный во второй си-
системе пробный заряд q будет действовать сила F, которая равна
q [v, В], но наблюдатель припишет действие силы на заряд электри-
электрическому полю (заряд неподвижен); напряженность его будет равна
Е' = F/g. Этот простой пример, конечно, еще не дает представления
о том, как преобразуются векторы поля при переходе от одной инер-
инерциальной системы координат к другой. Но этот вопрос выходит за
пределы данного курса.
УПРАЖНЕНИЯ
1. Вывести формулу A.48) для случая прямоугольной рамки с током, по-
показанной на рис. 1.26а. С этой целью рассмотреть действие лоренцевой силы
(рис. 1.266).
2. Проверить размерность соотношений A.45) и A.48).
3. Записать уравнения Максвелла A.49) — A.52) в координатной форме,
спроецировав векторы на оси некоторой системы координат. Рассмотреть слу-
случаи декартовой системы координат, цилиндрической и сферической.
4. Пусть вектор Е некоторого гармонически колеблющегося электромаг-
электромагнитного поля везде направлен одинаково (например, по оси z). Показать, что
вектор В ему перпендикулярен.
5. Положим, что электрическое поле внутри конденсатора, представленно-
представленного на рис. 1.10, однородно (Е = const), а ток / в цепи равен /m cos <fli. Показать,
что внутри конденсатора
Е= (/m/<BeeoS)sin cat.
6. Следует ли из A.51), что всегда divE = р/еое?
7. Всегда ли соленоидальна векторная функция Н?
8. Для кристаллического кварца еет = ето = 4,55 и гг1 = 4,49, а прочив
компоненты е равны нулю. При каких направлениях векторы Е и D сохраня-
сохраняют (не сохраняют) параллельность?
9. Вывести и проанализировать уравнение р + (e0e/o)9p/9J = 0, которому
подчинена плотность заряда A.120). Объяснить его решение.
10. Почему влажная почва (см. табл. 1.2) может проявлять себя и как
проводник, и как диэлектрик? Указать соответствующие условия.
62
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
11. Для каких процессов вектор плотности тока j сохраняет непрерывность
нормальной компоненты?
12. Вектор Е ортогонален экранирующей границе (см. пример 5, с. 48). Об-
Обладает ли этим свойством вектор D?
Рис. 1.26
13. Сопоставить два типа формализации сторонних сил в A.96) и, дру-
другой стороны, употребление понятий «генератора тока» и «генератора напря-
напряжения».
14. Показать, что запас энергии изолированной системы изменяется по за-
закону W(t) = W{0)e~at, если эта величина пропорциональна мощности потерь.
Что такое а?
15. При Р = О внутри изолированной системы Н = Ит cos at. Показать, что
это возможно при Е = +Em sin at, где Ет = #тУцоц/еое.
16. Записать систему уравнений Максвелла относительно напряженностей
соля (исключив индукции).
Глава 2
СТАТИЧЕСКИЕ, СТАЦИОНАРНЫЕ И КВАЗИСТАЦИОНАРНЫЕ ПОЛЯ
§ 2.0. Используемые математические понятия и символы
2.0.1. Градиент длины направленного отрезка (А). В дальней-
дальнейшем мы не раз будем рассматривать переменное расстояние между
двумя точками Р ш Q (рис. 2.1), характеризуемыми своими радиус-
векторами г и г'. Последние представим в декартовой системе коор-
координат с началом 0: г = хох + уог/ + zoz и г' = хох' + уоу' + zoz'. Тог-
Тогда длина направленного отрезка QP = т — т' есть 1г —г'| =
= У (ж — х'J + (у — y'J + (z — z'J, и мы можем определить гради-
градиент этого скаляра, пользуясь формулой A.14),
grad!r-r'!=(r-r')/lr-r'l =ro, B.1)
(символом год обозначен орт с направлением г —г'). Расстояние
1г — г'1 фигурирует здесь как функция положения точки Р при фик-
фиксированной точке Q.
§ 2.0. ИСПОЛЬЗУЕМЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ И СИМВОЛЫ 63
Но можно также фиксировать точку Р и рассматривать |г — т'\
в качестве функции координат х', у', z . Вычисляя градиент по этим
координатам, получаем
grad' Ir —r'l (г —г')/1г —г'1 =—гОа B.2)
(штрих, отмечающий операцию векторного анализа, мы будем ис-
использовать в тех случаях, когда диф-
дифференцирование производится по
штриховым координатам).
В дальнейшем встретятся такие
скалярные функции от |r —r'l, как
!г —г'1 и |г —г'1~2. Вычисляя для
них grad или grad', следует исполь-
использовать формулу A-28) вместе с
B.1) или B.2).
2.0.2. Операции векторного ана-
анализа в криволинейных координа-
г-г
rOcf
Рис. 2.1
тах (А). Криволинейные ортогональные координаты и относя-
относящиеся к ним величины будем обозначать в соответствии с табл. 2.1.
Напомним, что метрические коэффициенты (коэффициенты Ламэ)
участвуют в соотношениях вида dlt = h(dqi, где dq( — дифференциал
координаты, a dU — дифференциал длины по данной координате.
В табл. 2.2 введенные символы конкретизированы для двух наиболее
распространенных координатных систем — сферической (рис. 2.2а)
и цилиндрической (рис. 2.26). Смысл метрических коэффициентов
Таблиц'а 2.1
Криволинейные ортогональные системы координат:
обозначения
Номер
Координата
Орт
Метрический ко-
коэффициент
1
9i
ei
К
2
?2
е2
ft,
3
Чя
ея
h.
понятен из рисунка. Отметим, что орты по угловым координатам
в этой книге обозначаются так же, как и углы (например, орт до
для координаты <&); это единичные векторы, направленные по ка-
касательной к соответствующим дугам в сторону возрастания углов.
Запишем формулы, выражающие операции векторного анализа
в криволинейных ортогональных координатах:
= e,^|5. + e2i-^ + e37i^, B.3)
64
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
2.0. ИСПОЛЬЗУЕМЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ И СИМВОЛЫ
65
div F =
rotF =
ei/*2*S e2/*S*l Vй А
Vx
V2
VS
B.4)
B.5)
Подставив в B.4) в качестве F{ компоненты градиента из B.3),
Рис. 2.2
получаем выражение divgradcp^ ^2ф (см. п. 1.0.4). Таким образом,
применение оператора Лапласа к скалярной функции дает
Формулы B.3) — B.6) легко конкретизируются в сферических
и цилиндрических координатах при помощи табл. 2.2.
Таблица 2.2
Конкретные криволинейные координаты *)
i
9i
ei
h.
Сферические
1
Г
Го
1
координаты
2
г
3
а
«0
г sin ф
Цилиндрические
1
Г
»0
1
2
а
«0
г
координаты
3
z
Zo
1
*) На рис. 2.2 обе криволинейные системы координат показаны вместе с декарто-
декартовой системой (X, У, Z); последняя указывает начало отсчета углов; как видно (о),
Нг = г есть радиус дуги О, a fti = г sin & — радиус дуги а, проходящей через точку Р;
аналогично (б) h2 = г есть радиус дуги а.
2.0.3. Уравнение Пуассона (Б). Это название употребляют для
уравнения
V2"(r) = /(r), B.7)
где функция в правой части задана.
При интегрировании уравнения Пуассона используется функция
Грина
являющаяся решением частного вида уравнения B.7), когда в пра-
правой части в качестве /(г) взята дельта-функция Дирака (см.
п. 1.0.6):
2r, г') = 6 (г-г') B.9)
Используя вторую формулу Грина A.36) и формулу A.40),
а также симметричность функции Грина B.8) относительно аргу-
аргументов г и г', из B.7) и B.9) нетрудно получить следующее важ-
важное соотношение:
и (г) = J G (г, г') / (г') dv' + (j) [и (г') JL G (г, г') - G (г, г') ± и (г')] ds'
V S
B.10)
(интегрирование производится по штрихованным переменным).
Рассматривая уравнение Пуассона в неограниченной области,
выделим класс задач, решения которых при г-»- °° убывают не мед-
медленнее, чем 1/г. Такие решения называются регулярными в беско-
бесконечности. В этом случае из B.10) следует
j'^' B.11)
и(т) = JG(r, f')f(f')dv' = -± j'^F
V
(поверхностный интеграл в B.10) при удалении S в бесконечность
исчезает). Итак, получены решения уравнения Пуассона B.7).
Для векторного уравнения Пуассона
=f(r) B.12)
B.13)
при аналогичных ограничениях
пA)= If ^
v ' 4я .) | г — г |
(уравнение B.12) можно спроецировать на оси декартовой системы
координат, в результате чего получаются три скалярных уравнения
типа B.7)).
2.0.4. Уравнение Лапласа и краевые задачи (Б). Однородное
уравнение
V2=o, B.14)
соответствующее уравнению Пуассона при /(г)= 0, называется урав-
уравнением Лапласа, а его решения — гармоническими функциями.
Обычно ставятся так называемые краевые (граничные) задачи
для уравнения Лапласа, в которых требуется найти решение B.14)
5 В, В. Никольский, Т. И. Никольская
66
ГЛ. 2. СТАТИЧЕСКИЕ II ДР. ПОЛЯ
в некоторой области V, удовлетворяющее заданным условиям на ее
граничной поверхности S. Различают внутренние и внешние задачи.
В первом случае V — некоторый внутренний объем (рис. 2.3а, б, в).
Во втором — область V бесконечна (рис. 2.3<3, е, г).
Нередко рассматриваются задачи Дирихле
V2u = 0, u = f на S B.15)
и задачи Неймана
V2u = 0, duldv = f на S. B.16)
Для того и другого типа краевых задач можно исследовать проб-
проблему единственности решения. Предположим, что внутренняя задача
а
Дирихле имеет два разных решения щ и ыг. Составим их разность
и\ — U2 = 6 и, взяв первую формулу Грина A.35), положим <р =
= i|j = б. Поскольку V26 = 0, формула Грина принимает вид
B.17)
При этом на S согласно B.15) щ = f и U2 = f (оба решения удов-
удовлетворяют одному и тому же граничному условию), так что 6 = 0
и поверхностный интеграл исчезает. Поэтому равен пулю и объем-
объемный интеграл слева, а с ним V6 = 0 в V. Это значит, что б может
быть только постоянным. Но б = 0 на поверхности S. Потому 6 = 0
§ 2.1. СТАЦИОНАРНОЕ ПОЛЕ
67
в объеме V. т. е. и\ = «2- Задача не имеет двух решений. Этот вы-
вывод распространяется и на внешнюю задачу Дирихле, если оставать-
оставаться в классе решений, регулярных в бесконечности (см. п. 2.0.3).
По этой же схеме можно исследовать и другие краевые задачи.
§ 2.1. Стационарное поле, электростатика и магнитостатика (А)
2.1.1. Система уравнений стационарного электромагнитного поля.
Если электромагнитное поле неизменно во времени, то система урав-
уравнений Максвелла A.119) принимает вид
rol Е = 0, rot Н = j,
divD = p, divB = 0, B.18)
D = eoeE, В = цо^Н,
В левом столбце собраны величины, характеризующие электриче-
электрическое поле, а в правом — магнитное. Связующим звеном является
материальное уравнение в нижней строчке. Записанная система
уравнений характеризует электромагнитное поле, связанное с по-
постоянным током. Можно было бы также записать интегральные ана-
аналоги уравнений, входящих в систему B.18), которые вытекают из
A.53)-A.56).
Если ток отсутствует (j = 0), то левый и правый столбцы урав-
уравнений в B.18) — это две независимые системы.
2.1.2. Система уравнений и общие понятия электростатики. Рас-
Рассматривая неизменное во времени электрическое поле при отсут-
отсутствии токов (j = 0), мы получаем из B.18), как уже отмечалось,
независимую систему уравнений:
rotE = 0, divD = p, D = e0eE. B.19)
Это система уравнений электростатики. Электрические поля, удов-
удовлетворяющие системе уравнений B.19), будем называть электроста-
электростатическими. Запишем также интегральные аналоги первых двух урав-
уравнений B.19), получаемые из A.54), A.55):
(f)Dds =
B.20)
Являются ли «настоящие» электростатические поля вполне ре-
реальными? Поскольку в природе все среды обладают некоторой элек-
электропроводностью (о"=И=0), иными словами, нет идеальных диэлектри-
диэлектриков, то при существовании электрического поля (Е Ф 0) условие
j = 0 в строгом смысле невыполнимо в силу материального уравне-
уравнения A.69). Так, например, заряженные предметы в воздухе посте-
постепенно теряют свой заряд из-за «утечки»; при этом существует ток,
а поле изменяется во времени.
5*
68
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
§ 2.1. СТАЦИОНАРНОЕ ПОЛЕ
69
Ясно также, что идеальное электростатическое поле вообще не
могло бы быть обнаружено. Такое поле лишено всякого энергообме-
энергообмена, поскольку Н = 0 и, следовательно, П = 0. В широко известных
опытах с заряженными предметами о существовании поля судят по
динамическим процессам, чуждым идеальной электростатике. На
самом деле притягивающиеся или отталкивающиеся заряженные те-
тела при своем движении создают ток, которому обязательно сопут-
сопутствует магнитное поле, так что П Ф 0. Только поэтому возможно
превращение энергии поля в механическую, что и наблюдается.
Несмотря на то, что идеальные электростатические поля в при-
природе отсутствуют, решения системы уравнений электростатики
B.19) дают очень хорошие приближения для широкого круга яв-
явлений, рассматриваемых на практике как электростатические. Дело
в том, что при медленных перемещениях заряженных тел или в
случае утечки токи оказываются настолько малыми, что энергия
сопутствующего магнитного поля может считаться пренебрежимой
по сравнению с электрической. Электрическое поле при этом, прак-
практически, не отличается от электростатического.
Поскольку в силу B.18) rotE = 0, электростатическое поле на-
называют безвихревым, или потенциальным (см. п. 1.0.4). Поэтому
можно написать:
E = -grad(p, B.21)
где ф — некоторая скалярная функция, называемая электростати-
электростатическим потенциалом (напоминаем тождество A.22), согласно кото-
которому поля вида B.21), действительно, безвихревые). Знак минус
в B.21) соответствует принятому определению потенциала.
Каков физический смысл функции ф? Рассмотрим перемещаемый
в электростатическом поле точечный заряд q (его движение может
быть как угодно медленным) и вычислим работу, совершаемую им
при движении на пути I от точки Mj до точки М%:
м м
A = q ) Edl=— q } gradcpdl.
B.22)
м.
м.
Раскроем подынтегральное выражение, учитывая формулы A.3),
A.14) и A.15):
grad ф dl = -^ dx + -^ dy + --=- dz = йф.
Это полный дифференциал функции ф. Таким образом, из B.22)
получаем
= — q
= q(q>1 — ф2).
B.23)
Смысл полученного результата состоит в том, что совершенная ра-
работа равна разности потенциалов в начальной и конечной точках
пути, умноженной на величину заряда. Из B.22) и B.23) непо-
непосредственно следует
1-ф2= | Edl.
B.24)
м.
m
Это своего рода обращение равенства B.21).
Как видно, первый из интегралов B.20) в силу выражения B.22)
означает, что в электростатическом поле при перемещении заряда
по замкнутому пути работа не производится.
Пусть, например, движение заряда совершается
по пути М\тМ2пМ\ (рис. 2.4). Так как полная
работа равна нулю, то, следовательно, участки
М\тМч и М2пМ\ дают противоположные вклады.
Поэтому работа на пути М\тМч будет такой же,
как на пути М\пМ2. Мы видим, что работа не зави-
зависит от пути. О том же говорит и ранее получен- м?
ный результат B.23): работа определяется только
положением начальной и конечной точек пути.
Итак, физический смысл имеет разность потенциалов. Это рабо-
работа, производимая единичным точечным зарядом (д=1) при пере-
перемещении между двумя точками, потенциалы которых рассматрива-
рассматриваются. Что касается самого потенциала ф, то это функция, которая
определена только с точностью до константы. Действительно, если
вместо ф внести в B.21) ф +const, то вычисляемая напряженность
поля Е останется прежней. Если нужно устранить эту неопределен-
неопределенность, то задаются условным значением потенциала в некоторой точ-
точке пространства (т. е. на всей поверхности ф = const, проходящей
через эту точку). Если принять равным нулю потенциал бесконечпо
удаленных точек, то из B.24) следует
Рис. 2.4
Ф
= f Edl.
м
B.25)
При таком определении потенциал ф равен работе, совершаемой в
процессе удаления единичного положительного точечного заряда из
точки М (для которой он определяется) в бесконечность.
С математической точки зрения, ф есть вспомогательная скаляр-
скалярная функция, вполне определяющая векторное поле. Вместо трех
скалярных функций, являющихся компонентами вектора Е, доста-
достаточно определить одну функцию ф, чтобы, воспользовавшись затем
соотношением B.21), найти напряженность электрического поля Е.
Поэтому задачи электростатики в большинстве случаев формулируют
относительно потенциала ф. Заменив D во втором уравнении B.19)
через Е, используя третье уравнение, а Е представив через ф при
помощи формулы B.21), получаем
ео div e grad ф = — р.
B.26)
70
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
§ 2.1. СТАЦИОНАРНОЕ ПОЛЕ
71
Это уравнение электростатики относительно неизвестного потенциа-
потенциала ф при заданной плотности заряда р. Если среда однородна, то
е = const выносится за знак оператора дивергенции, что приводит
к весьма распространенному уравнению Пуассона:
У2ф = _р/еео. B.27)
Его решение для случая неограниченной среды можно сразу выпи-
выписать на основании формулы B.11):
Ф
M - 4 Г Р(г>) rlr'
(Г) — ¦; I . ;— AЬ
1 ' 4Я8Л8 .) Г — Г I
B.28)
(ниже в п. 2.2.5 мы рассмотрим также элементарный вывод этого
результата).
Положив в B.27) р = 0, получаем уравнение Лапласа
?2Ф = 0, B.29)
которому удовлетворяет <р в областях, где отсутствует заряд.
Отметим, что из B.19) можно было бы получить векторные урав-
уравнения Пуассона и Лапласа относительно Е. Они будут вытекать из
более общих уравнений, к которым мы придем в п. 3.1.2.
Пример 1. Вычислим потенциал ф в случае точечного заряда, зная
его поле. Внося выражение A.64) для Е в B.25), получаем
B.30)
Путь интегрирования выбран для простоты радиальным: от некоторой точки
Р(г) до бесконечности (под интегралом переобозначено: г-*-1). Если перенести
заряд q из точки г = 0 в некоторую точку <?(г'), то расстоянием станет вели-
величина |г — г'| (см. рис. 2.1), так что
B.31)
как следует из B.30) при замене г-*- |г — г'|.
Сколько-нибудь сложные задачи электростатики обычно сводят
к нахождению решений уравнений Пуассона или Лапласа в виде
потенциала ф. Но в некоторых простых случаях напряженность по-
поля Е находится непосредственно. Как уже отмечалось (см. 1.64)
для точечного заряда:
D = го?/4яг2. B.32)
Для бесконечной равномерно заряженной нити с погонной плот-
плотностью заряда т:
Б = г0т/2яг. B.32а)
Действительно, если для такой нити построить коаксиальную ци-
цилиндрическую поверхность радиуса г, то поток вектора D через нее
на участке I будет DS — 2nrlD (в силу симметрии силовые линии
ортогональны S и Л = const на S), а находящийся внутри заряд
есть q = xl. Поэтому B.32) следует из A.55).
Формулы B.32) применяются в случаях, когда рассматриваемый
объект обладает того же рода симметрией, что заряженная точка
или, соответственно, нить. Поясним, как это делается.
Пример 2. Пусть дан равномерно заряженный диэлектрический щар
(рис. 2.5). Из соображений симметрии ясно, что как и в случае точечного за-
заряда, здесь линии вектора D — радиальные прямые, причем на сфере любого
П /Т
радиуса D = const. Поэтому верна формула B.32), где под q надо понимать
заряд, находящийся внутри сферы текущего радиуса. Если определяется поле
вне заряженного шара (рис. 2.5а), то внутри сферы радиуса г лежит полный
заряд шара q = pV = 4яД3р/3. Если же точка наблюдения — внутри шара
(рис. 2.56), то в качестве q в ту же формулу подставляем только часть пол-
полного заряда 4яг3р/3. В результате получаем
г,
R
rp
r -4-,
о 3 '
B.33)
График D(r) представлен па рис. 2.5в. Как видно, эта величина внутри шара
линейно возрастает, а вне его падает, как 1/г2. Поскольку диэлектрические про-
проницаемости шара и внешней среды различны (е2 ф ei), напряженность Е па
его поверхности терпит разрыв.
Изменим условие. Пусть теперь только поверхность шара S несет заряд
q = \S = 4яЯ2|(| = const). Симметрия сохраняется, и можно по-прежнему
пользоваться первой формулой B.32). Если г < R, то внутри сферы текущего
радиуса заряда пет: q = 0. Поле отсутствует. Вне шара (г > R) поле опреде-
определяется при подстановке в качестве q полного заряда. Отсюда на поверхности
шара D = го|. Полученный результат совпадает с первым из равенств A.90).
Он имеет тот же смысл. ¦
Применение B.32а) см. в упражнении 1.
2.1.3. Магнитостатика. При «расщеплении» системы уравнений
B.18) в случае j = 0 получается также система уравнений магни-
магнитостатики:
rotH = 0, divB = 0, В = {г0цН. B.34)
Сравнивая системы B.19) и B.33), можно утверждать, что при
сопоставимых средах класс решений последней более беден. Маг-
72
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
§ 2.2. ЭЛЕКТРОСТАТИЧЕСКИЕ ПОЛЯ
73
нитиые заряды отсутствуют, так что линии вектора В не могут
обрываться.
Магннтостатпческие поля подобно электростатическим лишены
энергообмеиа: П = 0.
Запишем также интегральные аналоги первых двух уравнений
из B.34), которые получаются из A.53) и A.56):
<j)Hdl = O, (j)Bds = O. B.35)
L S
Как и в электростатике, можно ввести (с точностью до аддитив-
аддитивной константы) вспомогательную функцию я|> и писать:
H = -gradi|). B.36);
Легко убедиться, что магнитостатический потенциал -ф удовлетворя-
удовлетворяет уравнению, аналогичному B.26), но однородному:
div }x grad -ф = 0, B.37)
которое для однородной среды (ц — const) переходит в уравнение
Лапласа
V2i(j = 0. B.38)
К классу магнитостатических надо отнести и поля постоянных
магнитов, но в этом случае налицо самопроизвольная намагничен-
намагниченность (см. выше п. 1.3.6) и материальное уравнение в третьей
строчке B.34) нужно писать в форме В = {хО{хН + Мо A.79), где
Мо не зависит от Н. При такой замене из B.34) и B.36) вместо
B.37) получим
{Хо div }x grad if = div Mo- B.39)
Если же }х = const, то B.39) переходит в уравнение Пуассона
= — divM0.
На основании B.11)
B.40)
B.41)
Следует, однако, иметь в виду, что металлы и керамические ма-
материалы, обладающие самопроизвольной намагниченностью, относят-
относятся к нелинейным средам, описание которых усложняется еще тем,
что требуется учитывать предысторию процесса. Поэтому получен-
полученные формулы имеют лишь очень ограничепное применение.
§ 2.2. Электростатические поля
2.2.1. Системы зарядов (А). Если задана система точечных заря-
зарядов или параллельных заряженных нитей, то полное поле легко
находится сложением полей, описываемых формулами B.32) и
B.32а). Пусть заряды (нити) локализованы в точках @(г<); в слу-
случае нитей имеются в виду их следы в поперечной плоскости. Тогда
в B.32) делается замена: г -*- |г — г(| и г0-*- Г(х = (г — г,) Ir — г4|~'.
Однако чаще удобно сначала определять потенциал системы заря-
зарядов, а поле находить потом.
В случае системы точечных зарядов на основании B.31) имеем
1 V Sr-r B-42)
Рассмотрим сначала систему двух равных по абсолютной вели-
величине, но противоположных по знаку зарядов (рис. 2.6а). Пусть
qi = — q и q2 = q. Тогда
Если такая система рассматривается на больших расстояниях
(по сравнению с ее размерами), то она называется диполем. При
этом вводится электрический момент диполя
Р = gl, B.44);
где 1 = Г2 — Г1 — направленный отрезок, соединяющий заряды. Ана-
Анализируя диполь, удобно размещать начало координат на середине
отрезка I (рис 2.66).
Обычно вводят представление об идеальном диполе, «дипольной
точке». Эта полезная абстракция есть результат перехода к пределу
4f=-9
при I -*¦ 0 с сохранением величины момента: р = const. Таким об-
образом, вычисляя ф по формуле B.43), имеем
Ф (г) = lim
г — г„
ql = const. B.45)
Из рис. 2.66 видно, что при этом Ir — riI —*- г, Ir — r2l->-г и
<? (I г — г 11 — I г — xz\)-*- ql cos •& = pro. В результате
ql COS д рг„
4яе ег
74
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
Используя сферическую систему координат, как показано па
рис. 2.бе, вычислим напряженность поля Е на основании B.21).
При этом воспользуемся формулой B.3) и табл. 2.2. Внося B.46)
в B.21), записываем:
ql f в „ 1 Л_\ COS О
T7F + v° )z
(третий член выпадает, так как <р не зависит от д3 = °0- Это дает
B.47)
Е(г) =
4ле
— (ro2 cos § + fl0 sin•
На рис. 2.7 ') представлены картины силовых линий двух точеч-
точечных зарядов, равных по абсолютной величине, в двух масштабах.
Заряды имеют одинаковые знаки (а) и противоположные (б). Та-
Таким образом, на рис. 2.76 (справа) дается представление о поле
диполя.
Аналогичные картины силовых линий в случае заряженных ни-
нитей даны на рис. 2.8.
Будем, далее, исследовать систему произвольного числа зарядов,
поставив условие, чтобы расстояние от любого заряда до точки на-
наблюдения значительно превышало наибольшее расстояние между
отдельными зарядами системы. При вычислении потенциала B.42)
разложим в ряд входящие в каждый член суммы функции рас-
расстояния:
1 1 а
7 +
(члены высшего порядка малости опущены). Поэтому из B.42)'
следует
где
B.49)
Смысл полученного результата весьма прозрачен. Первый член спра-
справа в B.48) есть не что иное, как потенциал точечного заряда, ве-
личипа которого — алгебраическая сумма всех зарядов. Если эта
сумма Q B.49) не равна нулю, то на достаточно больших расстоя-
расстояниях вторым членом в B.48) можно пренебречь. В этом случае си-
система зарядов из области наблюдения предстает как точечный заряд
Q. Если же Q = 0, или, как говорят, система зарядов нейтральна,
') Символом ЭВМ в тексте будут обозначаться рисунки, выполненные при
помощи ЭВМ (см. Приложение, с. 538).
§ 2.2. ЭЛЕКТРОСТАТИЧЕСКИЕ ПОЛЯ
75
со
00
см'
о
о
и
со
Я
76
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
то потенциал на больших расстояниях определяется вторым чле-
членом разложения B.48). Сопоставляя его с выражением B.46), ви-
видим, что это потенциал диполя с моментом Р B.49). Система про-
проявляет себя как диполь.
Заметим, что вторая из формул B.49) есть общее выражение
для электрического момента нейтральной системы. В частном слу-
случае двух зарядов отсюда следует выражение B.44).
Обратимся теперь к рис. 2.9, на котором в двух масштабах пред-
представлены картины силовых линий системы трех зарядов. В одном
варианте (а) величины зарядов (слева направо) соотносятся как
+6, —1 и —2. Видно, что с удалением от системы поле становится
радиальным. В другом варианте (б) система нейтральна при сле-
следующем соотношении величин зарядов: +6, —2, —4. В этом случав
поле на больших расстояниях явно приобретает дипольныи характер.
На рис. 2.10 аналогичные картины силовых линий построены
для системы трех заряженных нитей. Соотношения расстояний и
зарядов (в данном случае в виде погонных плотностей) прежние.
2.2.2. Проводники в электростатике (А). Электростатические по-
поля не существуют в проводящих средах. Всякому электрическому
нолю в проводнике сопутствует ток j = оЕ. Поскольку в электро-
электростатике ток отсутствует и на поверхностях проводящих тел, ока-
оказывается равной нулю тангенциальная компонента вектора Е. От-
Отсутствие любой из компонент вектора Е внутри проводящего объ-
объема V и на его поверхности S означает, в свою очередь, неизмен-
неизменность электростатического потенциала ф. Можно написать
ф = const
B.50)
в объеме V и на поверхности S, проводящие тела эквипотенциальны.
Однажды мы уже рассматривали границу раздела двух сред,
внутри одной из которых поле отсутствует (см. пример 5 в гл. 1).
Оказалось, что на такой границе
?t = 0, D, = l, B.51)
т. е. отсутствует тангенциальная компонента вектора Е, а вектор
D имеет одну нормальную компоненту, равную плотности поверхно-
стпого заряда. Теперь очевидно, что этот вывод относится к провод-
пикам в электростатике. Именно их поверхности оказываются за-
ряжепиыми.
Обсуждавшиеся свойства проводников являются следствием под-
подвижности зарядов. В процессе установления равновесия они «рас-
«расталкиваются» полем и оказываются на поверхности проводника, за-
занимая в конечном счете такие положения, что внутреннее поле
нейтрализуется.
В общем случае распределение заряда на проводнике заранее
неизвестно. Но, например, проводящий шар (в отсутствие влияю-
влияющих предметов) заряжается равномерно: | = const, что соответству-
соответствует симметрии задачи. Заметим, что выше в п. 2.1.2 (конец второго
§ 2.2. ЭЛЕКТРОСТАТИЧЕСКИЕ ПОЛЯ
77
и
со
csi
о
я
а.
78
ГЛ. 2. СТАТИЧЕСКИЕ II ДР. ПОЛЯ
примера) был рассмотрен, как это теперь ясно, именно проводя-
проводящий шар).
Полный заряд проводящего тела в электростатическом поле мо-
может, в частности, быть равным нулю, однако отсюда отнюдь не сле-
следует, что везде на поверхности проводника | = 0; последнее озна-
означало бы с учетом B.51), что поля нет. Пусть, например, незаря-
. жепный проводящий цилиндр вно-
сится в однородное электростатиче-
электростатическое поле. С учетом сохранения за-
заряда полный заряд цилиндра так и
останется равным пулю. Но поле
должно деформироваться таким об-
образом, чтобы силовые линии оказа-
оказались ортогональными проводящей
поверхности (рис. 2.11). А это и озна-
означает, что вообще | Ф 0. Как видно,
величина | меняет знак; интегриро-
интегрирование подтверждает, что «наведен-
«наведенный» поверхностный заряд действи-
действительно равен нулю в целом. Появле-
Появление заряда под действием поля назы-
называют электростатической индукцией.
Рис. 2.11
В электродинамике нередко рассматривается задача о совокуп-
совокупности проводящих тел, потенциалы которых известны. Она форму-
формулируется как следующая краевая задача для уравнения Лапласа:
V2* = °' B.52>
Ф = Ф; на Si
(Si — поверхности проводников, Ф; — заданные на них потенциа-
потенциалы). Эта задача Дирихле имеет единственное решение (см. п. 2.0.4).
Можно показать, что единственное решение будет иметь и по-дру-
по-другому сформулированная краевая задача, в которой вместо потен-
потенциалов Ф; задаются полные заряды проводников qi. После того как
потенциал <р, а затем и поле найдены, становится известным рас-
распределение заряда на каждом проводнике. Оно складывается в ре-
результате взаимного влияния — электростатической индукции — всех:
проводников.
Пример 3. Рассмотрим влияние точечного заряда на проводящую плос-
плоскость. Поле при наличии этой плоскости показано на рис. 2.12а. Оно оказывает-
оказывается таким, как если бы кроме исходного заряда q действовало также его «изо-
«изображение» — q. Действительно, поле в верхнем полупространстве удовлетво-
удовлетворяет в этом случае условию Ех = 0, и плоскость — эквипотенциальна. Желая
определить плотность наведенного заряда ?, найдем сначала Е на S
(рис. 2.126). При этом складываются поля двух точечных зарядов: действитель-
действительного и фиктивного, «отраженного». В результате получаем
E = -vo2;
cos О — — v
qh
О
B.53)
§ 2.2. ЭЛЕКТРОСТАТИЧЕСКИЕ ПОЛЯ
79
Отсюда \ = гогЕ. Вычислим полный заряд q, наведенный на плоскости. Обо-
Обозначая R = у г2 — h2, пишем:
2Л оо
П
= — q.
S-»°o
о о
О h
Если рассматриваемая плоскость — это одна из двух сторон проводящего
слоя, который был первоначально не заряжен, то на другой его стороне по-
появится противоположный поверхностный заряд q. Ш
Рис. 2.12
Примененный прием называется методом зеркальных изображе-
изображений. Он позволяет находить поля точечных зарядов и их систем
при наличии проводящих плоскостей.
2.2.3. Емкость (А). Обсудим одно из важных представлений
электростатики. Рассматривая некоторый уединенный, проводник,
будем вычислять его потенциал посредством B.25); тогда это —
вполне определенная величина. При линейности среды заряд q и
потенциал <р, определенный по формуле B.25) для конкретного про-
проводника, связаны линейной зависимостью; это следует из линейно-
линейности уравнений электростатики. Поэтому каждый проводник можно
охарактеризовать при помощи своего коэффициента пропорциональ-
пропорциональности С, связывающего потенциал и заряд:
С = д/Ф. B.54)
Можно сказать, что С есть характеристика проводника как «нако-
«накопителя» заряда. Параметр С называется емкостью уединенного про-
проводника.
Емкость измеряется в фарадах [Ф].
Пример 4. Для нахождения емкости уединенного шара определим его
потенциал по формуле B.30), взяв в качестве г радиус шара R. Дело в том,
что поле вне шара оказывается таким же, как и в случае точечного заряда
¦(см. пример 2). Далее, согласно B.54)
С = 4яе0еЯ. B.55)
При е = 1 емкостью в 1 Ф обладает шар ей» 9-Ю9 м.
80
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
На рис. 2.13 в двух вариантах показан проводник, находящийся
в полости другого проводника. Это так называемый идеальный кон-
конденсатор. Пусть внутренний проводник несет поверхностный заряд
Q. Легко убедиться, что внутренняя поверхность полого проводника
при этом имеет заряд —Q. Выберем внутри полого проводника не-
некоторую замкнутую по-
поверхность S (рис.
2.13а), охватывающую
полость. Применяя к S
второе равенство B.20),
видим, что левая часть
равна нулю, так как в
проводнике D = 0. Сле-
Следовательно равен нулго
и полный заряд q, на-
а & ходящийся внутри S.
Рис. 2.13 Отсюда видно, что за-
заряд внутреннего про-
проводника Q уравновешивается зарядом —Q, который может нахо-
находиться только на внутренней поверхности полого проводника. Ем-
Емкость конденсатора определяется как
С = д/Дф, B.56)
где Аф — разность потенциалов обоих проводников (q и Аф — од-
одного знака).
Пример 5. Определим емкость сферического конденсатора (рис. 2.136).
В силу сферической симметрии внутреннее поле оказывается таким же, как
в случае точечного заряда (пример 4). Поэтому для внутреннего и внешнего
проводников имеем соответственно: (pi = qlimozR\ и ф2 = g/4ne0ei?2. Составляя
разность этих величин и применяя формулу B.56), получаем
С = 4яе„
R
B.57)
На идеальный конденсатор внешние электростатические поля не
оказывают никакого воздействия. Действительно, внешние поля, соз-
создают такие распределения зарядов на поверхностях проводящих тел,
которые компенсируют внутренние поля. Поле будет отсутствовать
и в полости внутри проводника, если, разумеется, она не содержит
зарядов. Говорят что объекты, находящиеся в полости, электроста-
электростатически экранированы: внешние поля на них не действуют. При
этом внешнее пространство не экранировано от действия зарядов
внутри полости. Действительно, рассматривая полый проводник иде-
идеального конденсатора как нейтральный, мы должны прийти к вы-
выводу, что появление заряда —Q на его внутренней поверхности вы-
вызывает наведение заряда Q на внешней. Этот заряд, однако, на
практике можно «отвести» при помощи заземления: он распреде-
распределится па огромной поверхности и, можно сказать, исчезнет. Внеш-
Внешнее ноле практически не возникает.
§ 2.2. ЭЛЕКТРОСТАТИЧЕСКИЕ ПОЛЯ
Реальный конденсатор — это система двух проводников, электро-
электростатическое взаимодействие которых значительно превышает воздей-
воздействие внешних полей. Заряды проводников при этом, строго говоря,,
уже не одинаковы по абсолютной величине, однако не настолько,,
чтобы потеряло смысл применение формулы B.56).
Представление о емкости может быть распространено и на слу-
случай системы более чем двух проводников. Пусть имеется ./V прово-
проводящих тел. Поскольку между полным зарядом каждого из провод-
проводников и потенциалами всех существует линейная зависимость, мож-
можно, например, написать:
(Jt = Сц (ф,- — ф[) + Ci2 (ф,- — ф2) + ... + Cuffi + . ..
... + С«(ф|-Ф*), г = 1, 2, ..., N. B.58)
Коэффициенты Ctt называются частичными емкостями — собствен-
собственными (k = i) и взаимными (k?=i). Можно доказать, что Сц = См,.
т. е. матрица емкостей симметрична. Знание этой матрицы (т. е.
всех частичных емкостей системы проводников) позволяет устано-
установить однозначное соответствие между их зарядами и потенциала-
потенциалами. Равенства B.58) можно переписать в виде системы:
q = Axp, B.59)
где q и ф—векторы-столбцы, образованные всеми зарядами (q\t.
<72, ..., дч) и, соответственно, потенциалами (ф1, фг, ..., ф*г). При
этом А = 11ЛЛ!1 — матрица, элементы которой называются коэффи-
коэффициентами электростатической индукции. Связь между ними п ча-
частичными емкостями очевидна.
В заключение заметим, что собственная емкость Сн некоторого
проводника с номером i отличается от емкости этого же проводни-
проводника, рассматриваемого как уединенное тело, так как вследствие элек-
электростатической индукции в системе меняется распределение его
заряда.
2.2.4. Диэлектрики в электростатике (А). Как следует из п. 2.1.2..
истинные электростатические поля могли бы существовать только
в средах, лишенных электропроводности (о = 0), т. е. в идеальных
диэлектриках. В таких средах происходят лишь процессы поляри-
поляризации (см. п. 1.3.2). Картина внутренних процессов в диэлектрике
будет обсуждаться в конце книги (п. 14.1.1). Ограничимся пока
замечанием, что это процессы переориентации или деформации
структурных элементов вещества, проявляющих себя как диполи.
Сопоставим поведение проводников и диэлектриков в электро-
электростатическом поле на простом примере.
Пример 6. При помещении проводящего тела в электростатическое по-
поле Е,, ого внутреннее поле Е,-, как известно, оказывается равным нулю. Пусть
ноле Ee однородно (среда — вакуум: ее = 1), а проводник имеет вид ортого-
шшыго ориентированного слоя (рис. 2.14а). Отсутствие поля Е< обт.ясияется
тем, что внутри слоя па первоначальное поле Е, налагается повое поле Е' =
С В. В. Никольский, Т. И. Никольская
¦ 82
ГЛ. 2. СТАТИЧЕСКИЕ II ДР. ПОЛЯ
§ 2.2. ЭЛЕКТРОСТАТИЧЕСКИЕ ПОЛЯ
83
= —Е„ создаваемое в слое наведенным па ого поверхностях зарядом, плот-
плотность которого на основании B.51) есть % = e0Eev0 (рис. 2.146).
Пусть теперь вместо проводящего рассматривается диэлектрический слой
= — Ее = —, так что
(рис. 2.14в). Внутреннее поле в диэлектрике есть
?i < Ee: внутреннее поле ослаблено. Объясним это появлением в слое (как
V,
eL=o
¦Ф
Рис. 2.14
si в случае проводника) некоторого противоположного Ее поля Е', в резуль-
результате чего
Е; = Ее + Е'.
Каково происхождение Е'? Если диэлектрик — система диполей, то они должны
ориентироваться внешним полем, как это схематически показано на рис. 2.14г.
Внутри диэлектрика связанные заряды уравновешиваются (q = 0), но на гра-
граничных плоскостях можно отметить появление поверхностного связанного за-
заряда. Плотность последнего |Св может быть определена, как
(е = 1, так как система диполей расположена в пустоте, а поскольку Е' == 0
вне слоя, можно применить формулу B.51), взяв —v0 в качестве положитель-
положительной нормали). .,
Выражая, далее, Е' как — (Ее — Е;) (при помощи предшествующей фор-
формулы), имеем
Но е0Ее = D, и D, = D,-, так что
1св= (D; - e0E,)v0.
Привлекая, наконец, A.70), заменим разность в скобках через вектор электри-
электрической поляризации Р:
|св = Pv0 B.60)
Aсм = Р справа па рис. 2.14г и |Св = — Р слева).
Построенный пример подводит пас к пониманию физического смысла век-
вектора Р. Сделаем следующий шаг. Выделив на граничных плоскостях (рнс. 2.14г)
противоположные площадки AS, видим, что они несут заряды —q и q. где q =
= |Orn[A5. Выделенный элемент объема AV = ASI, как видно, обладает элект-
электрическим моментом P&v = qi B.44), причем
Произведя деление па IAS, мы получим электрический момент, отнесенный к
единице объема диэлектрика. Учитывая, что ввиду B.60) ||СВ|1О = Р, оконча-
окончательно получаем
р = РДУ/ДУ. B.61)
Итак, вектор Р предстает как электрический момент единицы объема данной
однородно поляризованной среды. ¦
Значение рассмотренного примера в том, что он проясняет
смысл поляризации диэлектриков при сопоставлении с электроста-
электростатической индукцией, свойственной проводникам.
Для решения задач электростатики о диэлектрических телах во
внешнем поле нет необходимости переходить к представлению
о связанных зарядах. Надо просто находить такие электроста-
электростатические поля Ее и Е; (внешнее и внутреннее), которые удов-
удовлетворяли бы на поверхности диэлектрика граничным условиям
?et = ?\Tj Dev = Diy. B.62) -
Переходя к потенциалам, ищут та- -^-
кие решения уравнения Лапласа фе
и ф,-, градиенты которых согласно
B.21) дают Ее и Е;, удовлетворяю-
удовлетворяющие условиям B.62). Для этого до-
достаточно, чтобы выполнялись следу-
следующие граничные условия относитель-
относительно потенциалов:
В качестве примера рассмотрим
поле диэлектрического цилиндра
(е = 5), помещенного в однородное
Рис. 2.15. (ЭВМ)
поле Ео (рис. 2.15). Внутреннее поле Е, при этом также оказы-
оказывается однородным, но вне цилиндра появляется дополнительное
поле Е' — такое, что полное внешнее поле Ее = Ео + Е' и внутрен-
внутреннее однородное поле Е,- удовлетворяют граничным условиям B.62).
Оказывается, поле Е' имеет характер поля дипольных нитей (см..
рис. 2.86). Решение задачи о диэлектрическом цилиндре выписано*
па с. ИЗ (см. упражнение 25).
6*
84
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
2.2.5. Дополнительные замечания (Б). Сделаем несколько заме-
замечаний, дополняющих материал по электростатическим полям.
Переход от дискретного распределения зарядов к непрерывно-
непрерывному. Отправляясь от формулы B.42), полученной для системы то-
точечных зарядов {(/Л, перейдем к случаю непрерывного распределе-
распределения заряда с плотностью р в объеме V. Разобьем V на элементар-
элементарные-объемы AV>; очевидно заряд каждого есть </; = р;ДУ(, где р,- —
некоторое усредненное значение р в AF,. Внося эти выражения q(
в B.42) и переходя к пределу при бесконечном измельчении эле-
элементарных объемов, получаем
9^ Г ')
Ф(Г)= lirn * V 9^i _ 1 Г р(г')
iV-xx) 4яеое ^ | г — г41 4яеое J | г — г'
Это — не что иное, как формула B.28), полученная теперь не на
основании B.11), а элементарным путем.
Электростатическое поле в полости проводника. Как известно,
внутри проводников электростатическое поле отсутствует (п. 2.2.2).
Нередко говорят, что по-
у>=0 этому оно будет отсутст-
отсутствовать и в полости, кото-
которая, как можно предста-
представить себе, появилась там,
где раньше был сплошной
проводник и отсутствовало
поле. На самом деле это
рассуждение (которое, ра-
разумеется, нельзя считать
строгим) приводит к пра-
а 6 вильному выводу в слу-
Рис. 2.16 чае простой полости (рис.
2.16а), но отказывает уже
при некотором усложнении ее формы (рис. 2.166).
Рассмотрим вопрос более основательно. Взяв первую формулу
Грина A.35), положим гр = ф, где <р — электростатический потен-
лиал внутри полости V. Ввиду B.29) и B.21) перепишем A.35)
в виде
Б случае простой полости (рис. 2.16а) положим <p = 0 на S (по-
(потенциал постоянен на поверхности проводника, и мы имеем право
выбрать нулевое значение). Поверхностный интеграл справа унич-
уничтожится, а следовательно, равен нулю и объемный интеграл от не-
неотрицательной величины Е2. Последнее возможно только при
? = 0.
§ 2.2. ЭЛЕКТРОСТАТИЧЕСКИЕ ПОЛЯ
85
Если же полость ограничена несколькими проводящими поверх-
поверхностями (в случае рис. 2.166 S состоит из Si и S2), то в общем
случае невозможно считать их потенциалы одинаковыми. Если же
потенциалы на Si и S2 различны, то положить равным нулю мож-
можно только один из них (сохранив разность потенциалов; пусть при
этом для второго проводника <р = Ф). В этом случае поверхност-
поверхностный интеграл в последнем равенстве не уничтожится: он распада-
распадается на интегралы по Si и 5г. Вывод об отсутствии поля в поло-
полости, показанной на рис. 2.166, таким образом, вообще неверен.
Б сущности, это следует уже из обсуждения в п. 2.2.3.
О применении теоремы Гаусса. Вернемся к приему нахождения
ноля, который был использован во втором примере п. 2.1.2. Он
Рис. 2.17
применим в более широком классе задач: рассматриваемая струк-
структура может быть как угодно сложной при условии, что она обла-
обладает требуемой симметрией. Формула A.64) остается верной при
любом числе сферических слоев (рис. 2.17а) с разными диэлектри-
диэлектрическими проницаемостями. Пусть последний слой ограничен про-
проводником (рис. 2.176). Емкость такого конденсатора определим по
формуле B.56), а входящую туда разность потенциалов — на ос-
основании B.24) и A.64):
N г N
-4яв0^ в J ^-Ш-^Т
**г—1
Поэтому
С = 4яеп У 4-
Легко убедиться, что, вычисляя поле цилиндрической структу-
структуры с поперечным сечением типа рис. 2.176 па основании второй
формулы B.32), а затем переходя к нахождению погонной
86
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
емкости цилиндрического конденсатора, вместо B.64) получим
у
B.65)
2.2.6. Простейшие граничные задачи (Б). Покажем, как нахо-
находятся некоторые электростатические поля на основе решения урав-
уравнения Лапласа с наложением граничных условий.
Однородно заряженный проводящий шар. Представим оператор
Лапласа в сферических координатах на основании B.6) ir
табл. 2.2. В данном случае ото дает
B.66)
так как решение лежит в классе функций, не зависящих от угло-
угловых координат О и а. Поскольку начало координат не входит в
рассмотрение, множитель 1/г2 в B.66) может быть опущен. Выра-
Выражение в круглых скобках следует положить равным некоторой:
константе А. Отсюда
dw A A D „ А ,„ ап,
_= ф = __ + д, Е = -го-2. B.67)
Остается определить неизвестную константу А. Используя вторую
формулу B.51), находихм: —A/R2 = %. Это дает результат, уже об-
обсуждавшийся в п. 2.1.2 (см. пример 2).
Проводящий шар в однородном поле. Напряженность первона-
первоначального поля зададим в виде Ео = z0E0. В него и помещается
шар. Очевидно, что Ео = —уфо, где
ф0 = —Eoz + А = — EQr cos О B.68)
(константа А взята равной нулю и произведен переход к сфериче-
сферическим координатам, рис. 2.18).
Чтобы найтн потенциал внешнего поля фе, который должен
быть постоянным па поверхности шара г =/?, надо найти такое
^ г решение ф' уравнения Лапласа для
внешней области r^R, которое уравно-
уравновесило бы изменение фо при г = Д. Легко
сообразить, что этим свойством обладает
потенциал поля диполя B.46), ориенти-
ориентированного по оси z и локализованного в
начале координат. Разумеется, это поле
вводится только при r^R. Итак, запи-
Z
Рис. 2.18
сываем равенство фе = фо + ф' в виде
В
фе = — Е0Г COS О -\ 2 COS О,
B.69)
где второй член справа построен на основании B.46). Потребуем,
чтобы выполнялось условие фе = 0 при r = R (вместо нуля можно
§ 2.2. ЭЛЕКТРОСТАТИЧЕСКИЕ ПОЛЯ
57
было бы взять любую константу). Отсюда определяется константа
В. В результате имеем:
B.70)
Теперь находим поле иа основании B.21):
Ее = Д0Гг0 (l +2^j cosO-
^l sin
B.71)
Итак, деформацию однородного ноля Ео = zo?o вызывает нала-
налагающееся на него поле диполя, которое, разумеется, следует при-
приписать совокупности зарядов, наведенных на поверхности шара.
На основании B.71) нетрудно найти плотность поверхностного
заряда и электрический момент эквивалентного диполя р. Очевидно,
р = 4ne0e^3E0. B.72)
Диэлектрический шар в однородном поле. Заменим проводящий
шар диэлектрическим (см. п. 2.2.3). Внешний потенциал по-преж-
по-прежнему будем выражать при помощи формулы B.69), а внутрен-
внутренний — в виде ф; = —Cr cos О. Это соответствует предположению,
что внутреннее поле Е,, как и первоначальное поле Ео, является
однородным и направлено по оси z. При г = R наложим гранич-
граничные условия B.62). Это дает два уравнения относительно В и С:
±С = Е0,
\r-w. B-73)
Определив отсюда В и С, получаем
3 Н~'
cosf).
ф{= —
ЗЕ е,г
0 е
B.74)
Наконец, при помощи B.21) определяем поле:
Ее = Ео |г0
/^ Bj - ее N>
г3 е,- + 2е„
чв1,
B.75)
Поскольку потенциал везде удовлетворяет уравнению Лапласа и
граничным условиям на поверхности шара, решение граничной
задачи найдено. Полученное поле Ес представляет собой первона-
первоначальное однородное поле Eq = zq^o, на которое наложилось поле
88
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
диполя с электрическим моментом
B.76)
В заключение заметим, что аналогичным способом нетрудно
решить задачи о внесении в однородное поле металлического или
диэлектрического цилиндра (см. упражнения 24, 25).
§ 2.3. Стационарные магнитные поля
2.3.1. Основные уравнения и закон Био — Савара (А). Вернем-
Вернемся к системе уравнений стационарного электромагнитного поля
B.18). Хотя при наличии тока (j ?= 0) все уравнения этой системы
являются взаимно связанными, существует важный класс задач,
в которых плотность тока — заданная величина. В этом случае;
магнитное поле может быть определено независимо от электриче-
электрического при решении системы уравнений
rotH = j, divB = 0, В = цоиН. B.77)
Это система уравнений стационарного магнитного поля, отличаю-
отличающаяся от системы уравнений магнитостатики B.34) наличием j в
правой части первой строчки. Выпишем также интегральные
аналоги первых двух уравнений B.77), получаемые из
A.53) и A.56):
B.78)
ф Н dl = /, (j) В ds = 0.
Решение системы уравнений B.77) можно получить разными
способами. В случае однородной среды (ц = const) определение
магнитного поля по заданному распределению тока сводится к
применению следующей интегральной формулы:
B.79)
(символ Го, пояснен выше в п. 2.0.1). Это так называемый обоб-
обобщенный закон Био — Савара. Если ток является линейным, т. е.
проходит по контуру (системе контуров) L, формула B.79) при-
принимает вид
Н(Г) '
w 4я
B.80)
На практике линейным считают ток некоторого нитевидного (про-
(проволочного) проводника, если расстояния 1г—г'| остаются в про-
процессе интегрирования значительно больше поперечного размера
§ 2.3. СТАЦИОНАРНЫЕ МАГНИТНЫЕ ПОЛЯ
89
проводника (рис. 2.19). Равенство B.80) выражает обычный закон
Био — Савара.
ВЫВОД. Чтобы получить обобщенный закон Био — Савара
B.79), допустим сначала, что распределение тока — достаточно
гладкое, а именно, компоненты вектора \ дифференцируемы. Тогда
из первого уравнения B.77) получаем
rot rot H = rot j. B.81)
Пусть, далее, среда однородна, а следова-
следовательно, из второго уравнения B.77) выте-
вытекает, что divH = 0. При этом в силу A.29),
равенство B.81) переходит в векторное
уравнение Пуассона типа B.12):
V2H = — rotj, B.82) Рис. 2.19
и мы записываем его решение на основании формулы B.13):
Н(Г)= *
w 4it
B.83)
Подынтегральное выражение преобразуем при помощи форму-
и г|) = 1г — г'|~'. Это дает
' - j [grad' p^^Tl' J (О] dv\ B-84>
др р рру
лы A.27), положив в ней F = j и т|з = 1г — г'|~'. Это дает
Нетрудно убедиться, что первый интеграл равен пулю. Для этого
используем формулу A.37), согласно которой
rot'
З(г')
[г —г'
; dV' = -
г—г'
B.85)
и отметим, что V есть область, содержащая все токи, либо более
широкая область (объемные интегралы сохранят свои значения).
Что касается поверхностного интеграла, то он явно равен нулю,
когда граница S проходит там, где нет тока. Значит, последнее
равенство есть тождество 0 = 0.
Остается вычислить grad'I г — г'|~', что делается посредством
формул A.28) и B.2) и дает гО91г —г'|. После этого B.84) пе-
переходит в B.79). ¦
Интересно, что в конечном счете снимается требование диффе-
ренцируемости j; оно только облегчало вывод.
Переход от общего выражения B.79) к случаю линейных то-
токов B.80) очевиден, однако ниже мы еще вернемся к линейным
токам для обсуждения пх формализации (п. 2.3.5).
Наконец, заметим, что закон Био — Савара нередко записывают
в форме дифференциала dH(r) = (//4n)i[dl', ro,J |г — г'|~2. При этом
90
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
dH(r) есть вклад в Н(г), создаваемый элементом контура dl'
с током /.
2.3.2. Потенциалы в теории стационарного магнитного поля (А).
Хотя обобщенный .закон Био — Савара B.79) дает полное решение
системы уравпений B.77) для заданного распределения тока в од-
однородной среде, по традиции используются также вспомогательные
функции, потенциалы, которые, как и элек-
электростатический потенциал ф, приводят к
нахождению поля после дифференциаль-
дифференциальных операций.
В п. 2.1.3 уже был введен магнитоста-
тический потенциал г|э. В принципе, пред-
представление B.36) может быть использовано
и при рассмотрении магнитного поля посто-
постоянного тока в тех областях, где j = 0. Од-
Однако оказывается, что разность потенциа-
потенциалов двух точек Mi и М2 — в отличие от
электростатики •— теперь зависит не только от положения этих то-
точек, но и от вида пути интегрирования в формуле, аналогичной
B.24). В данном случае
Рис. 2.20
f Hdl.
B.86)
м.
Пусть имеется контур тока / (рис. 2.20). Выбирая пути интегри-
интегрирования M\mMi и М\пМ2, мы явно будем получать разные резуль-
результаты, поскольку согласно первой формуле B.78)
Hdl
Hdl
B.87>
Если же при интегрировании производится /с-кратный обход тока
(путь MipM2), то
j Hdl= J Hdl + Ы,
B.88)
причем величина к положительна, когда направление обхода замк-
замкнутого контура М]тМ2рМ] и ток / образуют правовинтовую»
систему.
Таким образом, разность магнитостатических потенциалов, бу-
будучи вполне определенной величиной в магнитостатике (п. 2.1.3)г
в теории стационарного магнитного поля вообще неоднозначна.
Но если затянуть контур тока воображаемой пленкой, через кото-
которую запрещено проводить пути интегрирования, однозначность
восстанавливается. Такая «пленка», т. е. поверхность, опирающая-
опирающаяся на контур тока (причем форма ее произвольна), есть, в сущно-
сущности, поверхность разрыва if> па величину /.
§ 2.3. СТАЦИОНАРНЫЕ МАГНИТНЫЕ ПОЛЯ
91
Введем новую вспомогательную величину, называемую вектор-
лым потенциалом п обозначаемую символом А. По определению
В = rot А, B.89)
откуда следует, что векторный потенциал определен только с точ-
точностью до аддитивного градиента. Это значит, что взяв вместо А
величину A + V4/ (где W — произвольная скалярная функция),
мы получим по формуле B.89) прежнюю величину магнитной ин-
индукции В в силу A.22).
Из B.77) (первая строчка) получаем следующее уравнение,
которому удовлетворяет А:
rot ц rot A = цо], B.90)
-а для однородной среды (u, = const):
rot rot A = u-ouj- B.91)
Ввиду отмеченной выше неопределенности А можно наложить
дополнительное условие
divA = 0, B.92)
которое иногда называют «кулоповской калибровкой». Тогда B.91)
ввиду тождества A.29) переходит в следующее векторное уравне-
уравнение Пуассона:
V^A = -how- B-93)
Его решение типа B.13) есть
l^W, B.94)
а в случае линейных токов B.94) принимает вид
B.95)
Как видно, введение векторного потенциала А позволяет нахо-
находить .магнитное поле заданного тока в два приема: сначала путем
интегрирования при помощи формулы B.94) либо B.95) опреде-
определяется А, а затем согласно B.89) напряженность магнитного поля
вычисляется как (цоМ*I r°t А (дифференцирование). В ряде слу-
случаев этот путь оказывается менее трудоемким, чем непосредствен-
непосредственное применение закона Био—Савара в форме B.79) или B.80).
2.3.3. Аксиально-симметричные поля (А). Простейшее акси-
алыю-спмметрнчное магнитное поле рассматривалось еще в гл. 1
(пример 1). Имеется к виду поле прямолинейного постоянного пи-
тепидного тока. Полученная там формула A.58) справедлива для
целого класса задач, в которых магнитные силоные линии являют-
являются концентрическими окружностями. Это будет но всех случаях,
92
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
§ 2.3. СТАЦИОНАРНЫЕ МАГНИТНЫЕ ПОЛЯ
93
когда проводники обладают осевой симметрией. В данный класс
входит, например, провод круглого поперечного сечения, труба, ко-
коаксиальный кабель. Применяя формулу A.58), нужно помнить,
что / в числителе — это ток, проходящий внутри контура L, сов-
совпадающего с силовой линией радиуса г. Таким образом, вектор Н
на расстоянии г от оси системы определяется только тем током,
который проходит внутри L. На рис. 2.21 вместе с поперечными
сечениями трех систем даны графики их полей, полученные на
основании A.58); показаны также примеры контуров L, различа-
различающихся качественно. Например, L\ на рис. 2.21а охватывает ток,
величина которого пропорциональна г2, а Ьч — весь ток провода.
На рис. 2.216 контур L\ вообще не охватывает тока, и поле Н
внутри трубы отсутствует. В качестве примера запишем формулы,
соответствующие случаю коаксиального кабеля (рис. 2.21в):
ап
Ir
l° 2яг'
B.96)
О,
Интересно, что магнитное поле внутри кольцевого сердечника
с равномерной обмоткой (рис. 2.22) также может быть определено
по формуле A.58), поскольку силовые линии близки к концентри-
концентрическим окружностям. Если контур интегрирования L лежит внут-
внутри сердечника, то он охватывает ток nl, где п — число витков об-
обмотки. Ток, проходящий через всякий внешний контур, равев
Рис. 2.23. (ЭВМ)
g 2.3. СТАЦИОНАРНЫЕ МАГНИТНЫЕ ПОЛЯ
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
нулю. Поэтому
Н=а°^я7' Р<г)е5' Н = 0' р(г)
B.97)
Разумеется, запись B.97) приобретает строгий смысл, если обмот-
обмотка заменяется сплошным проводником, охватывающим сердечник
(тогда силовые линии — настоящие окружности).
На основании A.58) можно также находить ноля, создаваемые
несколькими прямолинейными токами, параллельными либо анти-
параллельпыми. Надо лишь сложить отдельные поля при соответ-
соответствующей замене координат в A.58). В качестве примеров па
рис. 2.23 показаны картины магнитных силовых линий двух токов
+7 п /, а на рис. 2.24 — токов ( + 1/2O и /.
2.3.4. Виток тока как магнитный диполь (А). В этом разделе
будет показано, что замкнутый контур тока на больших расстоя-
расстояниях действует как магнитный диполь. Конкретно будет рассмат-
рассматриваться замкнутый круглый контур, виток тока (рис. 2.25а). Эк-
Эквивалентный ему магнитный диполь (рис. 2.256) обладает магнит-
магнитным моментом
m = zqHq\iIS. B.98)
Дело в том, что создаваемое витком магнитное поле при г » а
.имеет напряженность
Н(г) =
(r02cos0
B.99)
Сопоставляя эту запись с выражением Е поля диполя в электро-
электростатике B.47), видим, что обе формулы по своей структуре иден-
идентичны. При этом роль р в B.47) в выражении B.99) играет новая
величина т. Понятие магнитного момента вводится по аналогии с
определением электрического момента B.44). Если ввести услов-
условные магнитные заряды, показанные на рис. 2.256, то m = gMl.
ВЫВОД. Рассмотрим круглый контур тока / (см. рис. 2.26а).
Для определения его поля можно было бы применить закон Био —
Савара B.80), но мы будем исходить из формулы B.95) и снача-
.ла найдем векторный потенциал.
Пусть А определяется в точке наблюдения Р(т), имеющей сфе-
сферические координаты г, О, а = 180°. При этом для текущей точки
интегрирования Q(t') оказываются фиксированными коордпиаты
г = а и "&' = 90°; изменяется лишь угловая координата а'. Рассто-
Рассто| в B.95) есть (QM2 + МР2I/2 ^рис. 2.26а) и, следова-
следова'| 2 2 + 2 ') МР2
яние |г —г () (Q )^р ) ,
тельно, |г — г'| =(г2 + а2 + 2га sind cos а') , так как МР2 =
— г2 cos2 О и QM2 = г2 sin2 О + а2 — 2ra sin О cos p. Векторный диф-
дифференциал длины dl' разложим на две компоненты (рис. 2.266):
dl' = а0 dl'a + Ro dl'R = (— а0 cos a' + Ro si n a') a da',
где оба орта ао и Ro относятся к точке наблюдения. Подчеркнем,
Рис. 2.24. (ЭВМ)
Рис. 2.25
96
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
что Ro лежит в плоскости витка (это не радиальный орт г0 сфери-
сферической системы координат). Теперь можно конкретизировать фор-
.мулу B.95) для анализируемого витка:
А(г) =
[— a0 cos a' 4- RQ sin a') a da'
4я J (r2 4- a2 4- 2ra sin fl cos a'I/2
поскольку
я
sin а
Г sing' da'
Ira sin 0 cosa')l/2 J (r2 + a2 4- 2rasintf cosa'I/2
(в этом легко убедиться, сопоставляя sin a' и cos а' в каждом
квадранте), то окончательно
AW = -a«?I(?T7
cosa' da.'
(г2 + a2 + 2m sin ^ cos a'I/2'
B.100)
Векторный потенциал оказывается направленным азимутально, как
и ток. Хотя меридиональная плоскость, в которой лежит точка
Pfr)
Q(r')
Рис. 2.26
наблюдения Р(г), была зафиксирована (а =180°), ясно что ре-
результат B.100) от а не зависит. Поэтому линии вектора А образу-
образуют концентрические окружности в плоскостях ъ = const.
Интеграл B.100) в общем случае можно свести к так называе-
называемым полным эллиптическим интегралам, которые табулированы в
математических справочниках. Что касается интересующего нас
случая, когда г > а, то здесь дальнейшие действия просты. Поло-
Положив a2/ = const, рассмотрим предельный случай а/г -*¦ 0. Разлагая
знаменатель подынтегрального выражения B.100) в ряд
<r2 +
2ra sin О cos а')-1/2 = — \\ —^-sin Ф соз а — -у (-у\* + . .. 1
и переходя в B.100) к пределу
lim an
4я
cosa' da',
Ja s=const
§ 2.3. СТАЦИОНАРНЫЕ МАГНИТНЫЕ ПОЛЯ
97
получаем
A (r) = a0 ¦
•sind.
B.101)
Теперь по формуле B.89) находим напряженность магнитного
поля:
Н (г) = — rot А (г) = tl
О
4 \ г2 «in Л <т r sirn» дг I r
(использовано выражение ротации B.5) и табл. 2.2). В результате
4г
Отсюда видно, что виток, действительно, проявляет себя в пределе
при а/г-+0 как магнитный диполь с моментом B.98), где
В заключение заметим, что плоский круглый контур тока был
выбран только для облегчения анализа. Любые распределения по-
постоянного тока, локализованные в ограни-
ограниченной области, на больших расстояниях
оказывают дипольное действие.
2.3.5. Замечания и примеры (Б). Завер-
Завершая обсуждение стационарных магнитных
полей, сделаем сначала несколько заме-
замечаний.
О линейных токах. Переходя от формул
B.79), B.94) к B.80) и B.95) соответст-
соответственно, достаточно было рассматривать весь-
весьма узкий канал тока, проволоку, с попереч-
поперечным сечением, в котором плотность тока
остается постоянной. Идеальный линейный
ток получается в пределе при исчезновении поперечного сечения
(/ = const). Можно, однако, сразу воспользоваться аппаратом
дельта-функции Дирака. Выразим линейный ток в виде
j (г) = то/б (г -г'), B.103)
где (рис. 2.27) имеется в виду двумерная дельта-функция: гиг'
описывают точки на поверхности S, к которой линия тока ортого-
ортогональна. Тогда, например, переход от B.94) к B.95) имеет вид
Рис. 2.27
4я
г —
l s L
Примеры вычисления полей линейных токов. В качестве про-
простейшего применения закона Био — Савара рассмотрим получение
7 В. В. Никольский, Т. И. Нигольская
98
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
формулы A.58). Как видно из рис. 2.28а, формула B.80) в дан-
данном случае дает
а поскольку
z, TO
= а,
¦° 2яг*
Таким образом, для бесконечного прямолинейного тока подтверж-
подтверждена формула A.58).
I
Рис. 2.28
Возвращаясь к случаю круглого витка, будем вычислять поле
на оси витка. Согласно B.80) имеем (рис. 2.286)
-г Ia f sindfta -
(учтено, что радиальная компонента подынтегрального выражения
при интегрировании уничтожается). Поэтому
H = z0
B.104)
Рассмотрим теперь соленоид (рис. 2.28в). Если допустить^ что
в этом случае ток непрерывно распределен по цилиндрической по-
поверхности, то в элементарном поясе шириной Az сосредоточен ток
д/ = n'IAz, где п — число витков, приходящееся на единицу дли-
длины соленоида, а / — ток одного витка (рис. 2.28в). Полагая z = 0
§ 2.4. ЭНЕРГИЯ СТАЦИОНАРНЫХ ПОЛЕЙ И ИХ ОБЩИЕ СВОЙСТВА
99
в точке наблюдения Р, имеем
n'T
,тт nT
сШ = zn -тг
a2dz
= _z0^d(cos0).
Интегрируя от 0j до я — 9г (рис. 2.28г), получаем выражение
напряженности поля соленоида в точке М:
п'1
= z0 — (cos 6j + cos 0,).
B.105)
При 0i -» 0 и 02-^-0 получаем выражение Н на осп бесконечного
соленоида:
H = zo«7. B.106)
§ 2.4. Энергия стационарных полей и их общие свойства (А)
2.4.1. Электрическая энергия и заряд. Вычисляя электрическую
энергию на основании A.112), мы должны произвести интегриро-
интегрирование по полной области существования поля, нередко бесконеч-
бесконечной. Ввиду первого уравнения B.18) любое стационарное электри-
электрическое поле (как, в частности, поле электростатическое) является
потенциальным. Поэтому ввиду B.21)
a7y= — i- j" D grad
B.107)
V
Учтем, далее, тождество A.25), а также используем теорему Ост-
Остроградского-— Гаусса A.33) и тпртт.п г'пяттоттпр ЛТякшолтя.
Это дает
TF3 = i-fprpfZ;,-i-i
V S
Для локального распределения заряда в неограниченном про-
пространстве, как будет показано, выражение B.108) утрачивает по-
поверхностный интеграл и принимает вид
, а также используем теорему Ост-
и третье уравнение Максвелла.
>ds. B.108)
W3 = — f рсГ dv.
B.109)
При переходе от B.107) к B.109) существенно следующее. Хотя
в процессе преобразований область интегрирования формально не
изменялась, фактически вместо непосредственного подсчета энер-
энергии в бесконечном пространстве путем интегрирования ее плотно-
плотности в V B.107) теперь энергия находится при интегрировании
только по области существования заряда: вне ее подынтегральное
выражение B.109) обращается в нуль.
ВЫВОД. Чтобы обосновать переход от B.107) к B.109) рас-
рассмотрим некоторое локальное распределение заряда (рис. 2.29) и,
7»
100
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
распространяя интегрирование по V на бесконечное пространство,
будем неограниченно увеличивать радиус шаровой области. В пре-
пределе |г—г'| -*¦ г и г0, -*- i'o; при этом все распределение проявля-
проявляет себя как точечный заряд q = ) р dv, расположенный в центре
V
шара. Вычисляя ф и D по формулам B.30) и A.64), констатируем,
что фБ па расширяющейся поверхности S
убывает, как г~3, тогда как дифференциал
поверхности ds возрастает пропорционально
г2. Таким образом, поверхностный интеграл
в B.108) убывает, как г, и в пределе
должен исчезнуть. Тогда W" выражается
только через объемный интеграл согласно
B.109). Формула обоснована.
Остается заметить, что объемный интег-
интеграл перестает изменять свое значение, как
только расширяющаяся поверхность S на-
начинает охватывать все заряды. Значит, по-
поверхностный интеграл в B.108) равен нулю уже в этом случае. ¦
Ясно, что, если распределение заряда распадается на ./V отдель-
отдельных областей F, (? = 1, 2, ..., N), несущих полные заряды qt,
выражение B.109) может быть переписано в виде
N С
w = 4-2 рф^- BЛ1°)
Рис. 2.29
В электростатике, если все F,- соответствуют проводящим телам,
N
t-l у.
(как известно B.50), потенциалы проводников постоянны). Итак,
энергия системы проводников выражается через их полные, заря-
заряды и потенциалы. Заметим, что при интегрировании в B.111) мож-
можно было бы в качестве промежуточного этапа перейти к плотности
поверхностного заряда проводников, например, при помощи форму-
формулы A.91).
Выражение энергии B.111) можно еще переписать в виде
iV N
W3 — — У •"• + —У о-ф- = W3 + W3 B112)
2 ^"^ 2 ^"
Здесь в первой сумме, обозначенной W3, фигурируют потенциалы
<р(, которыми обладают уединенные проводники с зарядами q(. Ве-
Величина W3, не зависящая от расположения и взаимного влияния
§ 2.4. ЭНЕРГИЯ СТАЦИОНАРНЫХ ПОЛЕЙ И ИХ ОБЩИЕ СВОЙСТВА Ю1
проводников, называется собственной энергией системы. Вторая
сумма W3 выражает взаимную энергию системы проводников. Из
сопоставления B.112) и B.111) видно, что цц = ф; — ф;.
Поскольку заряды и потенциалы проводников можно связать
при помощи соотношений типа B.58) и B.59), существуют еще
иные формы представления энергии системы проводников. Для
одиночного проводника (Лт = 1) из B.112) с привлечением форму-
формулы B.54) получаем
B.113)
В случае конденсатора (Лг = 2, <?i = <?, <?2 = —q), обозначая
ф1 — фг = Аф, с учетом выражения B.56) находим
W3 = '/г^Аф = 1/гС(АфJ = V29/C. B.114)
Что можно сказать об энергии точечных зарядов? При попытке
перехода к объектам исчезающе малых размеров, обладающих за-
заданными зарядами (это могут быть, например, проводящие шары),
представление о собственной энергии теряет смысл, поскольку соб-
о
ствениые потенциалы ф( ввиду B.30) расходятся при г -*¦ 0.
В этом сказывается принципиальное несовершенство физической
модели в виде «заряженной точки». Но можно говорить о взаимной
энергии системы точечных зарядов.
Рассмотрим также вопрос о взаимодействии точечных зарядов с
заданным полем Е = —grad ф при условии ф = 0 в бесконечности.
Как известно (п. 2.1.2), работа, совершаемая при удалении точеч-
точечного заряда q из поля, есть дф — энергия взаимодействия заряда с
полем. При наличии нескольких зарядов qt (? = 1, 2, ..., N) вели-
величины д,ф( складываются и получается энергия взаимодействия сис-
системы зарядов с заданным полем. Легко показать, что в случае ди-
диполя с электрическим моментом р энергия взаимодействия с полем
Е оказывается равной
WE = -pE. B.115)
Действительно, согласно сказанному, We = q14>1 + 92Фг =9(Фг—<Pi) =
= q-gf I = pgrac^, откуда и следует B.115) после привлечения
B.21).
2.4.2- Магнитная энергия. Индуктивность. Будем вычислять
магнитную энергию некоторого стационарного поля на основании
общего выражения A.111), но учтем, что магнитная индукция со-
согласно B.89) может быть выражена через векторный потенциал:
WM=~
B.116)
102
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
Далее привлечем тождество A.26), теорему Остроградского — Га-
Гаусса A.33) и первое уравнение Максвелла. В результате получаем
B.117)
-i(j)[A, Hjds.
Чтобы определить полную энергию поля, связанного с локаль-
локальными токами в однородной среде, следует распространить интегри-
интегрирование на все пространство. При этом оказывается, что поверх-
поверхностный интеграл исчезает, как только S начинает охватывать все
токи, так что
B.118)
Как п в случае электрической энергии стационарного поля, вычис-
вычисляемой по формуле B.109), здесь магнитная энергия определяется
не путем учета ее распределения в пространстве, а через источни-
источники поля.
ВЫВОД. Переход от B.117) к B.118) производится по уже
известной схеме, в которой расширяющаяся область V остается ша-
шаровой (рис. 2.29). Подынтегральное выраженпе второго члена B.117)
[А, Н] убывает, как г~5, поскольку магнитное поле токов имеет ха-
характер дипольпого (согласпо B.101) и B.102)). Поверхностный
интеграл должен в пределе исчезнуть, но поскольку объемный ин-
интеграл пе изменяется с того момента, как S начинает охватывать
все токи, то видно, что при этом поверхностный интеграл уже ста-
становится равным нулю. ¦
Формула B.118) является весьма общей. Она может быть при-
применена, если задано пекоторое распределение тока j в объеме V.
Векторный потенциал А согласпо B.91) пропорционален ]'• Поэто-
Поэтому можно сказать, что магнитная энергия TFM пропорциональна
квадрату плотности тока в любой точке объема V, а также квадра-
квадрату тока, проходящего через любую поверхность s, рассекающую V.
В большинстве случаев s выбирается однозначно. Например,' ясно,
о каком токе может идти речь в случае области, показанной на
рис. 2.30а (поперечное сечение тока s заштриховано). Итак, маг-
магнитную энергию стационарного поля можно выразить в форме
WM = -|-272, B.119)
где коэффициент пропорциональности З7 называется индуктив-
индуктивностью; эта величина измеряется в генри [Гн].
Внесем представление векторного потенциала B.94) в выраже-
выражение магнитной энергии B.118). Это дает
f f
i(r) j(r') dvdv',
T
B.120)
§ 2.4. ЭНЕРГИЯ СТАЦИОНАРНЫХ ПОЛЕЙ И ИХ ОБЩИЕ СВОЙСТВА ЮЗ
поэтому
B.121)
Очевидно, что при заданном распределении тока (той или иной
функции j(r)) результат интегрирования не будет зависеть от ве-
величины тока /.
В случае системы разделенных областей тока V{ выражение
энергии B.118) можно записать в виде
N N N
N N N
™ = Т 2 МА dv = Т 2 2 1
i-i Vi i-i *-i v{
где Ая — векторный потенциал, обязанный своим происхождением
только току области Vk (в любой точке пространства А = Ai +
+ А2 + ... + Ак). Таким образом, анергия W для iV областей тока
ч..
¦гн~П
представляется двойной суммой, слагаемые которой обозначим
Wlk. Воспользовавшись формулой B.94), можно придать этим сла-
слагаемым форму сходную с B.121):
(рис. 2.306). Подобно B.119) запишем
где (ср. B.121))
/ ,2 J .) Г—г'
v v [ h l
B.124)
B.125)
104
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
Введенные коэффициенты 2"i и М& называются соответственно
собственными и взаимными индуктивностями. Как видно из B.125),
k ki
Перепишем теперь формулу B.122) в виде
N N N
1=1
B.126)
Первая сумма выражает собственную энергию системы, а вторая —
взаимную.
Обсудим случай линейных токов. При этом (рис. 2.30в) инте-
интегрирование в B.125) по объему сводится к контурному. В частно-
частности, для взаимных индуктивностей имеем
4я
B.127)
Аналогичное представление собственных индуктивностей для иде-
идеальных линейных токов не имеет смысла: иптегралы расходятся
(ср. случай идеальных точечных зарядов в п. 2.4.1). При вычисле-
вычислении 2"i для реальных токов, принимаемых за линейные, надо поль-
пользоваться формулами B.125).
Выражая магнитную энергию, в ряде случаев используют поня-
понятие магнитного потока Ф A.63). Магнитный поток через поверх-
поверхность S с контуром L выражается в виде контурного интеграла
от А:
f В ds = cj) A dl
B.128)
(достаточно выразить В в виде rot А и применить теорему Стокса
A.34)). Поэтому, в частности, переходя в соотношении B.123)
к линейным токам, находим
f j
т. е.
И/f =JL/cp B.129)
а сопоставление B.129) и B.124) дает
Ф^/J, B.130)
В формулах B.129) и B.130) Ф№ есть магнитный поток, создавае-
создаваемый /с-м током, проходящим через i-u контур. На основании соотно-
соотношения B.130) во многих случаях удобно вычислять взаимные ин-
индуктивности.
§ 2.4. ЭНЕРГИЯ СТАЦИОНАРНЫХ ПОЛЕЙ И ИХ ОБЩИЕ СВОЙСТВА ЦM
Собственную энергию для некоторой области тока также можно
выразить при помощи формулы типа B.129):
W = !/2/Ф, Ф = 21. B.131)
пряженном с данным током / в области V, является непростым.
Однако в общем случае представление о магнитном потоке Ф, со-
Пример 7. Определим взаимную индуктивность соленоида и малого
витка, расположенного, как показано на рис. 2.31. Взяв в формуле B.130)
к = 2 (соленоид) и i = 1 (виток), при вычисле-
вычислении Ф12 будем считать магнитное поле однород-
однородным и воспользуемся формулой B.105), соглас-
согласно которой Н в средней точке соленоида есть
.г«г // J?2 . /2\ —1/2 /9 4 49^
= ЪТЫ „ I 4Л_ -4- ? I y?i.L06]
(п = п'1 — число витков соленоида). Умножая Н
скалярно на v0 и nR^ (площадь витка), полу-
получаем Ф12, а после деления па /г определяем
-Z2)~1/2cosfl. ¦ B.133)
I
ооооооооо-оо
boooooooooood
Рис. 2.31
Пример 8. Вернемся к примеру вычисления магнитной энергии внут-
внутри тороидальной системы, показанной на рис. 1.256. Было найдено, что
2 2я R
Легко убедиться, что магнитный поток Ф, проходящий через поперечное (ра-
(радиальное) сечение тороида, равен 2WM/r, роль индуктивности играет величина
2WKIP. Все это согласуется с формулами B.131). ¦
Пример 9. Вычислим магнитную энергию WM , сосредоточенную внутри
единицы длины цилиндрического провода. Выражая напряженность магнит-
магнитного поля внутри провода согласно A.58), как Н = a0Ir/2nR2 (I — полный ток
провода), находим
B.134)
16я
о о
Согласно B.131) находим величину
B.135)
не
которую называют внутренней индуктивностью провода. Как видно,
зависит от его радиуса. ¦
2.4.3. Общие свойства стационарного электромагнитного поля.
Вернемся к обсуждению системы уравнений B.18). Из первого
уравнения левого столбца следует, что стационарное электрическое
поле подобно электростатическому является потенциальным. Этот
факт уже был использован выше в п. 2.4.1. Однако нельзя утверж-
утверждать, что все свойства электростатического поля повторяются. Если
в отличие от электростатики в проводниках существуют токи, то
там имеется и электрическое поле Е = o~'j. Касательные токи на
106
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
поверхностях проводящих тел обусловливают отличную от нуля
тангенциальную компоненту вектора Е, а так как Ех = — ду/дт, то
поверхности проводников уже не эквипотенциальны. Впрочем, на
практике часто тангенциальная компонента вектора Е на поверхно-
поверхности проводника очень мала по сравнению с нормальной; иными
словами, несмотря на существование постоянного тока, электричек
ские силовые линии почти ортогональны поверхности проводника.
Пример 10. Пусть расстояние между параллельными медными шинами
с постоянным током составляет 1 см при напряжении 10 В и плотности тока
10 А/мм2. Очевидно Ех = ja~l « 0,17 В/м (ст = 5,8-107 См/м, табл. 1.2; /=.
=--•¦ 107 А/и2). Поле между шинами почтп однородно, так что Еч « 103 В/м. Та*
киы .. азом, Ex/Ev « 1,7-10-*. ¦
Рассмотрим далее баланс энергии стационарного электромагнит-
электромагнитного поля, полагая, что все токи сосредоточены в некотором объ-
объеме V. Уравнение баланса энергии A.105) в данном случае прини-
принимает вид
[Е, Н] ds + f ]Edv = 0.
B.136)
Если неограниченно увеличивать объем V, сохраняя, как это уже
делалось нами в аналогичных случаях, его шаровую форму, станет
ясно, что поверхностный интеграл равен нулю. Действительно,
в пределе он обязательно должен быть равен нулю, так как Е убы-
убывает не медленнее, чем г~2 (подобно полю точечного заряда), а Н —
как г~3 (поле диполя), тогда как дифференциал поверхности воз-
возрастает только пропорционально г2. Но объемный интеграл в этом
процессе не изменяется, поскольку с самого начала все токи лока-
локализованы внутри V. Таким образом, объемный интеграл тоже равен
нулю. Итак, из B.136) следует
(J) [E, H] ds = 0, J jEcZi; = 0, B.137)
S V
т. е. равны нулю поток энергии через поверхность S, охватываю-
охватывающую все токи в У, и полная мощность Р в объеме V.
Во-первых, отсюда можно сделать вывод, что стационарное
электромагнитное поле не создает излучения. Впрочем, из самого
факта стационарности следует, что энергия поля, связанного с дан-
данной системой токов, остается постоянной.
Во-вторых, выразив плотность мощности р = jE под знаком со-
соответствующего интеграла в B.137) как о]2 — jE" A.97), по-
получаем
j = f }ECTdv. B.138)
Если сторонние силы отсутствуют (Ест = 0), то очевидно, что j = 0.
Действительно, величина о]2 не может быть отрицательной, а сле-
следовательно, она равна нулю вместе с интегралом. Вывод заключа-
§ 2.4. ЭНЕРГИЯ СТАЦИОНАРНЫХ ПОЛЕЙ И ИХ ОБЩИЕ СВОЙСТВА 107
ется в том, что постоянные токи и сопровождающее их стационар-
стационарное поле не могут существовать без превращения энергии какого-то
вида в электромагнитную, т. е. без притока энергии.
Рассмотрим некоторый линейный ток, прохдящий по контуру
L. По этому же контуру возьмем циркуляцию вектора Е. Согласно
B.20) она оказывается равной нулю. Поэтому, представив Е как
o~'j — ECT A.96), приходим к следующему равенству:
(j) 0-1 jdl = (f E°TdI. B.139)
L L
Полагая, что речь идет о реальном линейном токе, выразим / в ви-
виде I/S, где S — поперечное сечение канала тока /, который не из-
изменяется вдоль контура. Поэтому интеграл слева в B.139) равен
a~](I/S)l (I — длина контура L). Это не что иное, как произведе-
произведение тока на сопротивление цепи M = l/aS (см. п. 1.3.3). Таким об-
образом, обозначая циркуляцию от Е" через Эст, имеем:
Ш = Эст. B.140)
Полученное равенство имеет смысл закона Ома для цепи постоян-
постоянного тока, причем Эот есть действующая в цепи э. д. с.
Переход к линейному току можно было произвести в B.138),
тогда получается РЯ = /Эст, откуда опять-таки вытекает закон Ома
B.140). В то же время соотношение B.138) дает основание для
получения более общих выражений сопротивления 31 и э. д. с. Эст:
-44v. Эст = Л- f ШСТ<Ь
B.141)
' V V
(о том, что понимается под током 7 для некоторой области V, уже
говорилось в п. 2.4.2).
2.4.4. Аналогия постоянных токов и электростатических полей.
Запишем две группы уравнений:
rotE = 0, rotE = 0,
divD = 0, divj = O, B.142)
D = eoeE; j = oE.
В левом столбце — система уравнений электростатики в отсутствие
зарядов (р = 0), а в правом — идентичные по форме уравнения от-
относительно плотности постоянного тока и напряженности электри-
электрического поля в проводящей среде. Вторая строчка справа — это
частная форма уравнения A.44). Видно, что j в правом столбце
играет такую же роль, как D — в левом, а при замене
е0е**о, D**j B.143)
одна группа уравнений переходит в другую.
Добавим, что в обоих случаях тангенциальная компонента век-
вектора Е непрерывна на границе раздела сред, а непрерывности нор-
108
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
мальной компоненты вектора D в электростатике соответствует не-
непрерывность нормальной компоненты плотности тока j (D и j соле-
ноидальны: ведут себя, как В, см. п. 1.4.3).
Хотя отмеченная аналогия имеет чисто формальный характер,
она в ряде случаев оказывается полезной на практике.
На рис. 2.32а представлено некоторое электростатическое поле
в идеальном диэлектрике при наличии двух проводящих тел А и В.
Рис. 2.32
Такую же практически структуру имеет поле токов в плохо прово-
проводящей среде, в которую помещены те же тела А и В (рис. 2.326)'
при условии их хорошей проводимости. Чтобы убедиться в этом,
надо не только учесть аналогию уравнений B.142), но и устано-
установить, что D в первом случае и j во втором одинаково ведут себя
на границах тел А и В. Как известно, в электростатике линии век-
вектора Е (а при изотропии и вектора D) ортогональны проводящим
поверхностям. Что касается вектора j, то, как уже отмечалось, его
нормальная компонента непрерывна (/vi=/v2); в то же время не-
непрерывна тангенциальная компонента вектора Е, а следовательно,
<*i hi = o^1j'x2. Если O2>Oi, то отсюда следует, что /Ti/yvi </т2//»2.
Это и дает основание считать линии вектора j почти ортогональ-
ортогональными границам с относительно высокой проводимостью областей.
Из данного рассмотрения, в частности, следует, что вместо рас-
расчета электростатического поля при наличии сложной системы про-
проводников можно поместить эти проводники (обычно металлические
элементы) в электролит, удельная проводимость которого значи-
значительно ниже, и произвести экспериментальное исследование рас-
распределения тока при заданных потенциалах. Такое моделирование
давно применяется в инженерной практике.
Как известно, в электростатике систему двух проводников с оди-
одинаковыми по величине, но разноименными зарядами можно оха-
охарактеризовать емкостью С, определяемой по формуле B.56). Запи-
Запишем выражение емкости для такой системы (рис. 2.32а), выразив
заряд q в виде потока вектора D через поверхность, охватывающую
проводник А; разность потенциалов А<р представим при помощи
§ 2.5. КВАЗИСТАЦИОНАРНЫЕ ПОЛЯ
109
формулы B.24):
/в \-i
С = ф Dds П Edl = 5/Дф.
B.144)
Сделав здесь замену D -*- j, построим аналогичный параметр для
второй задачи (рис. 2.326). При этом получается выражение про-
проводимости:
(в \-i
j Edl = //Дф. B.145)
а /
Очевидно, что поток вектора j в числителе — это полный ток 7, вы-
выходящий из поверхности тела А. Его обычно называют током
утечки.
§ 2.5. Квазистационарные поля (А)
2.5.1. Общие представления. Квазистационарными называют по-
поля, которые, будучи переменными, тем не менее сохраняют в своей
структуре основные черты стационарных. Предположим, что для
заданной системы постоянных токов найдено магнитное поле Н(г).
Можно представить себе столь медленное изменение этих токов во
времени, что оно не вызовет заметного перераспределения поля в
пространстве. Иными словами, при временном законе токов f(t) по-
поле Н(г, t) имеет вид /(i)H(r) и, следовательно, в каждый момент
t сохраняет структуру стационарного поля Н(г), изменяясь только
по величине. Аналогично описывается и поле электрическое.
Такой приближенный подход исторически появился, когда в
электротехнике приобрели практический интерес переменные токи.
Представление о цепи переменного тока позднее стало играть важ-
важную роль в радиотехнике. Во Введении уже отмечалось, что это
представление не безупречно: оно отказывает при достаточно высо-
высоких частотах. Об этом будет говориться подробнее ниже в п. 2.5.2.
Особенностью теории квазистационарных процессов является ис-
использование уравнений Максвелла в интегральной форме вместе с
такими понятиями, как индуктивность и емкость, происходящими
из теории стационарных и статических полей.
Возьмем, например, второе уравнение Максвелла в форме A.62).
Если рассматриваются контуры Lk (& = 1, 2, ..., N) с токами Ih,
то согласно B.130), B.131) можно следующим образом выразить
магнитный поток Ф„ проходящий через контур Lc
<bi = 2 ф« = 2ih + 2
fc(
Внося это в A.62), определяем э. д. с. Э„ наводимую в контуре Lt
в результате изменения магнитного потока через этот контур,
110
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
создаваемого всеми контурами:
dl.
N
k=l
ik-^. B.146)
Входящие в B.146) индуктивности определяются на основе тех
распределений поля в пространстве, которые свойственны стацио-
стационарным полям.
Такие понятия, как разность потенциалов (напряжение), ем-
емкость, применяются на том основании, что, как и при отсутствии
изменений во времени, электрическое поле полагается потенциаль-
потенциальным. На самом деле квазистационарное электрическое поле уже не
потенциально, поскольку rot E Ф 0, как,
в частности, было при получении равен-
равенства B.146).
2.5.2. Энергетический баланс и пред-
представление о цепи переменного тока. Бу-
дем рассматривать какую-либо систему,
обычно трактуемую как цепь переменно-
переменного тока, которая составлена из последова-
последовательно соединенных сопротивления 31, ин-
индуктивности 3? и емкости С, а также ге-
генератора, источника э. д. с. Эст (рис. 2.33).
Проследим, каким образом и при каких
допущениях из общих представлений электродинамики возникает
теория такой цепи.
В основу рассуждений положим уравнение баланса энергии
электромагнитного поля A.105). Пусть рассматриваемая система
находится внутри объема V, ограниченного поверхностью S. Прене-
Пренебрежем излучением, т. е. будем считать, что как и для стационар-
стационарного поля в данном случае
Рис. 2.33
(J) [E, H] ds = 0.
B.147)
Поскольку распределения электрического и магнитного полей в про-
пространстве близки к стационарным, электрическую и магнитную
энергию будем находить по формулам B.113) и B.119)
2 С
WM =
B.148)
B.149)
Здесь важно отметить следующее. Входящие в B.148) и B.149)'
параметры С и 3? только в том случае могут принять смысл емко-
емкости и индуктивности элементов обсуждаемой цепи, если один из ее
§ 2.5. КВАЗИСТАЦИОНАРНЫЕ ПОЛЯ
111
элементов действительно концентрирует в себе практически всю
электрическую энергию, а другой — всю магнитную. Тогда интегри-
интегрирование в B.148), B.149) распространяется лишь на соответству-
соответствующие реактивные элементы цепи.
Далее, ввиду A.97)
Р = \о-ЦЧи-
B.150)
и мы подобно предыдущему (п. 2.4.3) представим записанные ин-
интегралы в виде I23t и — /Эст соответственно. Таким образом, 31 и
Эст определяются формулами B.141).
Остается, учитывая B.150), внести W = W+W и Р = Р31 —
— /Э т в уравнение A.105). Это дает
dt
ЙГ' +
B.151)
Продифференцируем выражение в круглых скобках по t, учитывая,
что dq/dt = I, и разделим все члены на /. В результате
2?Цт + Ш + ^ = Эй\ B.152)
а при вторичном дифференцировании
rlt dt С
dt *
B.153)
Это известное уравнение теории цепей переменного тока.
Оно получено в препебрежении излучением, распределение по-
полей предполагалось близким: к стационарному, электрическое и маг-
магнитное поля считались сосредоточенными в различных областях.
Кроме того на стадии получения равенства B.151) был использо-
использован принцип цепи: идентичность тока I(t) в любой момент t во
всех элементах. Все эти допущения оказываются неправомерными
для достаточно быстрых процессов. К этому мы еще вернемся в
гл. 9 в теории излучения.
УПРАЖНЕНИЯ
1. Найти электростатическое поле равномерно заряженного (р = const)
бесконечного цилиндра.
Как изменится результат, если рассматривается проводящий цилиндр то-
того же диаметра при прежней погонной плотности заряда?
2. Найти емкость, приходящуюся на единицу площади системы параллель-
параллельных проводящих плоскостей.
3. Усложнить предыдущую задачу, заполнив пространство между прово-
проводящими плоскостями несколькими слоями диэлектрика с разными прони-
цаемостями.
4. Как изменится физический смысл потенциала, если изменить знак в
формуле B.21)?
5. Вывести формулу B.31), исходя из B.28).
112
ГЛ. 2. СТАТИЧЕСКИЕ И ДР. ПОЛЯ
6. Исходя из выражения напряженности поля точечного заряда, получить
формулировку закона Кулона.
7. Почему вывод формулы B.28) нельзя считать строгим?
8. Показать, что уравнение силовых линий диполя имеет вид
sin2 О/г = const. B.154)
Указание: решить обыкновенное дифференциальное уравнение, получае-
получаемое на основе аналога соотношения A.16) в сферических координатах.
9. Показать, что для системы двух параллельных нитей с погонными за-
зарядами т и —т
Ф= o^Tln^, B.155)
где п и гг — расстояния рассматриваемой точки от нитей.
10. Найти плотность поверхностного заряда на проводящей плоскости, над
которой на расстоянии h расположена бесконечная равномерно заряжен-
заряженная нить.
11. Найти поле диполя, расположенного вертикально (горизонтально) на
высоте h над проводящей плоскостью.
12. Найти потенциал в случае равномерно заряженного проводящего ци-
цилиндра, решая граничную задачу для уравнения Лапласа.
13. Показать, что из B.63) следует B.62).
14. Выписать выражения напряженности магнитного поля для случаев
провода (см. рис. 2.21а) и полого цилиндра (см. рис. 2.216) с постоянным током.
15. Найти магнитное поле при наличии плоского проводящего слоя, внут-
внутри которого равномерно распределен прямолинейный постоянный ток.
Указание: применить формулу A.53).
16. Показать, что в случае двухпроводной линии в виде параллельных ни-
нитей с противоположными постоянными токами
А =
2я
, Г2
In—,
B.156)
где ri и Т2 — расстояния рассматриваемой точки от нитей.
17. В случае равномерно заряженного проводящего шара получить фор-
формулу B.113) путем подсчета энергии интегрированием ее плотности в про-
пространстве.
18. Вычислить энергию равномерно заряженного диэлектрического шара.
19. Найти собственную и взаимную энергию двух проводящих шаров (ра-
(радиусы R\ и Яг), расположенных на расстоянии I, значительно превышающем
их размеры.
20. Найтп взаимную индуктивность двух круговых соосных контуров' тока,
лежащих в параллельных плоскостях, при условии, что площадь одного из
контуров относительно мала.
Указание: считать поле большего контура однородным в области меньшего.
21. Показать, что погонная индуктивность коаксиального кабеля равна
Здесь R1 — радиус внутреннего проводника, /?2 и из — радиусы внешнего поло-
полого проводника; уц и ц2 относятся к проводнику и внутренней среде соот-
соответственно.
22. В результате несовершенства диэлектрической изоляции в коаксиаль-
коаксиальном кабеле возникает радиальный ток. Показать, что погонная «проводимость
утечки» равна
С' 2ДЛ/Л B.158)
§ 3.0. ИСПОЛЬЗУЕМЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ И СИМВОЛЫ Ш
23. Вывести закон Кирхгофа для разветвления цепи из закона сохране-
сохранения заряда.
24. Показать, что в случае, если вместо проводящего шара в однородное
электростатическое поле вносится цилиндр, то вместо выражения внешнего
поля B.71) получается:
sina
cos«-«0 (l~
25. Показать, что при внесении в однородное электростатическое поле ди-
диэлектрического цилиндра имеем:
-^lilZIfUnal, B.160)
(ср. решение для шара B.75)).
Глава 3
ОСНОВНЫЕ ПОЛОЖЕНИЯ ЭЛЕКТРОДИНАМИКИ
§ 3.0. Используемые математические понятия и символы (А)
3.0.1. Гармонические колебания и комплексные амплитуды. Ес-
Если некоторая величина u(t) изменяется во времени по закону
и (t) = um cos (at + ц>), C.1)
то говорят, что происходят гармонические колебания этой величи-
величины. При этом ит называется амплитудой, а — круговой частотой,
а аргумент косинуса at + ф — фазой (полной фазой); ф — начальная
фаза колебаний. Гармонические колебания — периодический про-
процесс. Периодом Т называется наименьший отрезок времени, обла-
обладающий тем свойством, что u(t + T) = u(t). Очевидно,
Т = 2л/ю = 1//, C.2)'
где /— частота колебаний, число периодов в секунду.
В теории электромагнетизма встречаются скалярные и вектор-
векторные функции координат и времени, описывающие гармонические
колебания. Такова скалярная функция
и(х, у, z, t) = u(r, t)= wm(r)cos [ш? + ф(г)], C.3)
амплитуда и начальная фаза которой — функции координат.
Аналогичная векторная функция V (г, t) в общем случае распа-
распадается на три скалярных в выбранной системе координат, напри-
например:
V (г, t) = xo7mx (r) cos [at + q>, (r) ] +
+ yoVmy (r) cos [at + ф„ (г) ] + zoVmz (r) cos [at + <pz (r) ]. C.4)
8 В. В. Никольский, Т. И. Никольская
114
ГЛ. 3. ОСНОВНЫЕ ПОЛОЖЕНИЯ ЭЛЕКТРОДИНАМИКИ
Если, в частности, компоненты вектора имеют одинаковые началь-
начальные фазы, то эта запись принимает вид:
V(r, f) = Vm(r)cos[(Bt + q>(r)]f C.5);
где Vm = x0Fm* + yoFmy + zQVmz и ф = фх = ф„ = фг.
В. теории гармонических колебаний обычно применяется метод
комплексных амплитуд, суть которого состоит в том, что вместо
тригонометрических функций в выражениях типа C.1), C.3) —
C.5) употребляются экспоненциальные. При этом получаются
комплексные представления физических величин, ниже обозначае-
обозначаемые точками. Например, вместо и C.1) пишем
и = umeHai+lf) = йтеш. C.6);
Здесь введено обозначение йт = итещ; данная величина, несущая
информацию об амплитуде и начальной фазе, называется комплекс-
комплексной амплитудой. В силу известной формулы Эйлера физическая ве-
величина и есть вещественная часть ее комплексного представления:
и = Re и = Re йтеш. C.7)
Примечательно следующее. Если, как в C.3), амплитуда и фаза
являются функциями координат, то комплексное представление
C.6) есть произведение функции координат йт(г) и функции вре-
времени exp(icof).
Запишем вытекающее из формулы Эйлера соотношение:
и = Ч2(й + й*), C.8)
где звездочка означает комплексное сопряжение.
В векторном варианте C.4)
= Re Vmeiat, C.9)
где комплексная амплитуда, являющаяся функцией координат, есть
Vm = x0Vmxei(p* + y.V^v + ZoFm2e{4 C.10)
Разумеется, справедлива также формула типа C.8).
Метод комплексных амплитуд значительно упрощает технику
преобразований при получении решений дифференциальных урав-
уравнений в частных производных. Все члеры линейного дифференци-
дифференциального уравнения оказываются умноженными на exp(icot). Опу-
Опуская этот множитель, получаем уравнение относительно комплексной
амплитуды, не зависящей от времени. Если в результате ре-
решения уравнения комплексная амплитуда определена, то для полу-
получения искомой физической величины надо лишь умножить комп-
комплексную амплитуду на exp(icot) и отделить вещественную часть.
Почему такой подход правомерен? Дело в том, что если суще-
существует решение некоторого линейного уравнения (алгебраического,
дифференциального или интегрального) в виде комплексного
§ 3.0. ИСПОЛЬЗУЕМЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ И СИМВОЛЫ Ц5
представления и, то этому уравнению удовлетворяют в отдельности
его вещественная и мнимая части, а тем самым решением является
рассматриваемая физическая величина и.
3.0.2. Средние значения. Для периодической функции от t сред-
средним значением называется деленный на Т интеграл от 0 до Т. Оче-
Очевидно, что среднее значение от и C.1) равно нулю. Далее, среднее
от квадрата гармонически колеблющейся величины есть
= -у ит = -у итит. C.11)
о о
Результат усреднения дает половину квадрата, амплитуды и^ =
= итит; таким образом, результат оказалось возможным выразить
через комплексные амплитуды. Заметим, что интеграл C.11) легко
взять, преобразовав подынтегральное выражение посредством C.8).
Наряду с и C.1) введем функцию v = vmcos(at+ г|з) и найдем
среднее от их произведения:
т т
1 = -у- J uvdt = 4у
о о
(использована подстановка C.8)). Первые два члена, выражающие
гармонические колебания с частотами 2ш и — 2ш, дают при инте-
интегрировании нуль. В результате
uv = 1/2 Re um v*m = 1/2 Re um vm = M2umvm cos (ф — г|з). C.12)
Запишем, наконец, в готовом виде подобные же формулы для
векторных величин:
V2 = 1/2 VmV;, C.13)
C.14)
C.15)
uv =
um v
um v
) dt
VW = 1/2 Re Vmw; = 1/2 Re v;\Vm,
= 1/2 Re [Vm, W;] = 1/2 Re [Vm, Wm].
Здесь W —векторная функция, подобная V C.4). Формулы
C.12) — C.15) легко выводятся прежним способом — с использова-
использованием для V и W представления C.8).
3.0.3. Разложение Фурье и комплексные амплитуды. Разлагая
некоторую периодическую функцию в ряд Фурье
C.16)
C.17)
jj- + ^ ап cos пЫ + 2i bn sin recof,
n—l n=i
и (t) = -jj- +
представим его в комплексной форме:
оо
', Cn = 4- f u
Г/2
-Г/2
116
ГЛ. 3. ОСНОВНЫЕ ПОЛОЖЕНИЯ ЭЛЕКТРОДИНАМИКИ
где с_п = с*п — (ап—ibn)/2. Как видно, коэффициенты ряда
C.17) — не что иное, как комплексные амплитуды, а члены — комп-
комплексные представления гармонических колебаний с частотами то
{..., -2@, -CD, О, CD, 2CD, ...).
В случае произвольной временной зависимости запишем разло-
разложение в интеграл Фурье:
оо со
и (t) = J и (cd) ешAа, k(b) = 2y j u(t)e-
iatdt.
C.18)
Спектральная плотность и (со) также имеет смысл комплексной
амплитуды.
§ 3.1. Уравнения электродинамики (А)
3.1.1. Система уравнении Максвелла. Источники поля. В основе
электродинамики лежит полная система уравнений Максвелла
A.119), при записи которой мы ограничимся вторым вариантом
последней строки:
дЪ
rot Н = ж + j, rot Е = — -1Г,
1Г
div D = р, div В = О,
D = еоеЕ, В =
j = о-Е + Г.
C.19)
Поскольку в п. 1.6.1 уже обсуждалась общность этой системы
уравнений и ее фундаментальное значение (при некоторых оговор-
оговорках, касающихся материальных уравнений, входящих в C.19)), на
втом не будем останавливаться. Подчеркнем лишь, что вместе с си-
системой граничных условий (см. § 1.4) система уравнений Максвел-
Максвелла C.19) образует аппарат нахождения электромагнитных полей.
Интегральные аналоги уравнений Максвелла A.53) — A.56) та-
такого аппарата не представляют.
Действие сторонних сил в системе уравнений C.19) формали-
формализует плотность стороннего тока jCT. Предположим, что во всем про-
пространстве или в какой-либо энергетически изолированной области
jCT = 0, т. е. не действуют сторонние силы. Если при этом найдено
физически осмысленное решение системы уравнений C.19), то оно
выражает свободное электромагнитное поле, т. е. поле, не обязан-
обязанное своим происхождением процессу преобразования какого-то вида
энергии в электромагнитную. Свободные поля, «не имеющие при-
причины вне себя», будут рассматриваться в части 2.
При действии сторонних сил происходит возбуждение электро-
электромагнитного поля источниками. В отличие от свободного такое поле
называют вынужденным, а также полем излучения.
§ 3.1. УРАВНЕНИЯ ЭЛЕКТРОДИНАМИКИ
117
В электродинамике в качестве стороннего тока в большинстве
случаев выступает просто некоторый заданный ток. Например, при
решении задач об излучении антенн очень часто исходят из зара-
заранее известного распределения тока на антенне. Разумеется, этот
ток поддерживается питающим антенну генератором, который,
в свою очередь, получает энергию от какого-то источника питания:
аккумулятора, электроэнергетической сети и т. п. Вся цепь преоб-
преобразований энергии выходит за рамки электродинамической задачи.
Сторонний ток нередко рассматривается как поверхностный и
соответственно, характеризуется плотностью г\СТ (ср. 1.82)); эта
величина задается на границах проводников. Возбуждающим факто-
фактором может быть также проходящий через границу области поток
энергии.
3.1.2. Уравнения электродинамики второго порядка. Из системы
уравнений C.19) можно исключить все неизвестные величины кро-
кроме напряженностей поля, а затем исключить Е или Н. В конечном
счете получаются дифференциальные уравнения второго порядка
относительно одного из этих векторов.
Умножим все члены первого уравнения Максвелла на в,
а второго — на ц~' и применим операцию rot. Это дает
rot (е-1 rot Н) = е0 -^- rot E + rot e-ij,
rot (ц,-1 rot E) = — ц0 -gj- rot H.
Теперь входящие в правые части rotE и rotH заменим выражения-
выражениями, вытекающими из первых двух уравнений Максвелла. В резуль-
результате получаем
rot (e-i rot Н) + -^ д-Ц- = rot e-1 j,
с dt
rot (ц-i rot E) + -J- д-^ = -Цо |j-r
C.20)
C.21)
где обозначено еоЦо = с~2. Правые части этих уравнений в общем
случае нельзя рассматривать как известные, но при о = О (идеаль-
(идеальный диэлектрик) j = jCT. Тогда правые части определяются задан-
заданными источниками, однако они имеют смысл, если выполнимо тре-
требуемое дифференцирование.
Пусть среда однородна (е = const, ц = const)'. Вынося обратные
проницаемости за знаки операций дифференцирования и применяя
слева тождество A.29), получаем
ей о а . .
C.22)
C.23)
118
ГЛ. 3. ОСНОВНЫЕ ПОЛОЖЕНИЯ ЭЛЕКТРОДИНАМИКИ
§ 3.2, ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
119
(учтено также, что divH = 0 и divE = р/еое). Если j = jCT, то р =
= рот; эти величины связаны законом сохранения заряда A.44).
Уравнения с левыми частями такого вида называют уравнениями
Даламбера (в данном случае это векторные уравнения Даламбера).
Если токи и заряды отсутствуют, уравнения C.22), C.23) утрачи-
утрачивают правые части. Такие однородные уравнения называют волно*
выми; смысл названия выяснится в дальнейшем (см. § 4.0).
При отсутствии изменений во времени уравнения Даламбера
C.22) и C.23) переходят в уравнения Пуассона. Первое есть урав-
уравнение B.82), о втором говорилось в п. 2.1.2. Интересно, что к этим
же уравнениям Пуассона приводит пренебрежение токами смеще-
смещения (dD/dt = 0) при сохранении временной зависимости векторов
поля.
3.1.3. Потенциалы в электродинамике. Как и в теории стацио-
стационарных полей, в электродинамике традиционно используются раз-
различные вспомогательные векторные и скалярные функции. Мы об-
обсудим употребление только уже известных потенциалов Аи ф.
Зададим векторный потенциал А так, как это делалось в п. 2.3.2:
C.24)
Подстановка этого выражения Н во второе уравнение Максвелла
приводит к равенству:
0. C.25 У
Мы видим, что векторная функция в скобках является потенциаль-
потенциальной (ср. вывод о потенциальности электростатического поля в
п. 2.1.2). Приравнивая эту функцию величине — gradcp, получаем
C.26)"
Таким образом, напряженности поля Е и Н выражены при помощи
соотношений C.24) и C.26) через потенциалы А и ф, которые в
данном случае будем называть электродинамическими. Остается
найти уравнения, которым они удовлетворяют.
Внося C.24) и C.26) в первое уравнение Максвелла, 'записы-
'записываем в случае однородной среды
rotrot А
3L ?$
cot
= _ ?L grad %
При помощи A.29) введем оператор Лапласа, это дает
Налагая дополнительное условие
C.27)
C.28)
которое иногда называют лоренцевой калибровкой, получаем из ра-
равенства C.27) следующее векторное уравнение Даламбера:
72A 8(Х "А
C.29)
относительно А. Из C.26) и C.28) получается скалярное уравне-
уравнение Даламбера относительно ср:
2
Ф ц г ~ (о.оО)
(как и ранее, j = jCT и р = рст при о = 0).
При отсутствии временной зависимости уравнения Даламбера
C.29), C.30) переходят в известные уравнения Пуассона B.93),
B.27), а лоренцева калибровка C.28)—в кулоновскую B.92).
§ 3.2. Гармонические колебания. Уравнения электродинамики
в комплексной форме
3.2.1. Уравнения Максвелла относительно комплексных ампли-
амплитуд. Комплексные проницаемости (А). Как уже отмечалось в
п. 3.0.1, гармонически колеблющиеся электромагнитные поля пред-
представляют значительный интерес и, пожалуй, наиболее часто явля-
являются предметом анализа в радиоэлектронике (любые временные
зависимости можно разлагать на гармонические колебания, см.
п. 3.0.3).
Используя метод комплексных амплитуд (см. п. 3.0.1), заменим
изменяющиеся по закону гармонических колебаний C.4) векторы
Е, Н, D, В и j комплексными представлениями Е = Етехр(?<»?),
Н = Нтехр(гш?) и т. д. Внося эти комплексные представления в
первые два уравнения Максвелла из C.19) и устраняя общий мно-
множитель exp(icof), записываем:
rot Hm
C.311
Таким образом, получены уравнения относительно комплексных
амплитуд типа C.10), утратившие временную зависимость.
Легко убедиться, что уравнения Максвелла с дивергенциями яв-
являются прямыми следствиями полученной записи. Чтобы прийти
к комплексным аналогам второй строки C.19), достаточно приме-
применить операцию div слева и справа в C.31) и учесть тождество
'A.23), а также закон сохранения заряда divjm = — i<apm A.44).
Теперь мы можем оставить в уравнениях C.31) только напря-
напряженности, исключив индукции и плотность тока при помощи ма-
материальных уравпений из C.19). При этом правая часть первого
120
ГЛ. 3. ОСНОВНЫЕ ПОЛОЖЕНИЯ ЭЛЕКТРОДИНАМИКИ
уравнения Максвелла принимает следующий вид:
шЬт + jm = шг0 (г — i ~\ Em+ j" = icoeue Ет
где введено обозначение
•ст
Jm i
8=8— ? .
we.
C.32)
C.33)
Как видно, величина е по тому месту, которое она занимает в урав-
уравнении, может рассматриваться в качестве относительной диэлектри-
диэлектрической проницаемости. Это так называемая комплексная диэлектри-
диэлектрическая проницаемость.
Уравнения C.31), записанные относительно напряженностей
поля, имеют вид
rot Hm = ?сое0еЁт + fZ, rot Ёт = — ?(О|лоцНт. C.34)
Точка над е опущена; этим обозначением мы будем пользоваться
редко.
Дело в том, что в рамках метода комплексных амплитуд любой
из параметров уравнений Максвелла мы должны рассматривать уже
не в пределах вещественной оси, а на комплексной плоскости, и это
приводит к расширению физического содержания некоторых поня-
понятий. Таковы, в первую очередь, проницаемости е и |л, которые бу-
будем обозначать в виде
е = е'-?е", р = ц' - щ". C.35)
Выделение параметра вида C.33) показало, что диэлектриче-
диэлектрическая проницаемость, понимаемая как комплексная величина, может
характеризовать и процессы поляризации (напомним, что они
предполагались безынерционными), и проводимость среды. Но те-
теперь мы можем описать также инерционность поляризации диэлек-
диэлектрика. При гармонических колебаниях для этого достаточно ввести
фазовое запаздывание D по сравнению с Е, т. е. писать: Dm =»
= eoeEme~ra. Но это значит, что в данном случае роль диэлектриче-
диэлектрической проницаемости играет комплексная величина г (cos a — i sin a).
Ясно, что инерционность процессов намагничивания описывается
аналогично. Мы видим, что метод комплексных амплитуд позволил
снять одно из существенных ограничений при описании сред (см.
пп. 1.3.1, 1.3.6).
Комплексность е и |л, таким образом, может отражать разные
особенности процессов в веществе. Однако в п. 3.3.2 мы сможем
дать однозначную энергетическую трактовку величин г" и ц".
В дополнение к C.35) введем еще следующие обозначения:
tgA = e"/e', tgAM = |x'7|x', C.36)
где А называется углом электрических потерь (или просто углом
§ 3.2. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
121
потерь), а Д"- углом магнитных потерь (смысл этих названий вы-
выяснится в п. 3.3.2). Ввиду C.36) выражениям C.35) можно при-
придать новую форму:
8 = e'(l-^gA)=lele-iA, C 3?)
Заметим, что критерий классификации сред A.78) можно пере-
переписать так:
11: проводник,
Д=
(а=о)
диэлектрик
C.56)
(отмечено, что инерционность поляризации не учитывается).
В заключение необходимо подчеркнуть, что полученные выше
уравнения C.34) образуют полную систему уравнений электроди-
электродинамики для гармонических во времени процессов, которая будет
служить основанием при решении всех задач, рассматриваемых в
дальнейшем.
3.2.2. Уравнения электродинамики второго порядка в комплекс-
комплексной форме (А). Комплексные аналоги уравнений второго порядка,
выведенных в п. 3.1.2, можно было бы получить, исходя из уравнений
Максвелла в комплексной форме C.34). Еще проще учесть, что все
сводится к замене: d/dt-+ho, j -»- jCT; при этом d2/dt2 -»- — со2 и про-
проницаемости надо рассматривать как комплексные величины. Делая
указанную замену в уравнениях C.20), C.21), получаем:
C.39)
C.40)
rot (e-i rot Hm) - (со/сJ уЛп = rot g-i j?,
rot ((.i-i rot Em) — (co/cJ sEm = — icoLio j".
Выполняя такие же операции с уравнениями C.22), C.23),
привлечем также закон сохранения заряда divjm = — iwpm Для пре-
преобразования правой части второго из этих уравнений. В результате
= - rot fmT,
V2Hm + (СО/СJ ;
V2Em + («/сJ фЁт = -f- grad div ft
C.41)
C.42)
Это так называемые уравнения Гелъмголъца (неоднородные); ана-
анализируя свободные электромагнитные поля нцже в части 2, мы во
многих случаях будем исходить из однородных уравнений Гельм-
гольца, отличающихся от C.41), C.42) отсутствием правых частей
( ft = 0).
Запишем также в комплексной форме уравнения и все соотно-
соотношения, включающие электродинамические потенциалы (см. п. 3.1.3).
Во-первых, вместо C.24) имеем
C.43)
122
ГЛ. 3. ОСНОВНЫЕ ПОЛОЖЕНИЯ ЭЛЕКТРОДИНАМИКИ
а вместо C.26)
Em = — grad фт — i©Am. C.44)"
Уравнения Даламбера C.29) и C.30) переходят в следующие урав-
уравнения Гельмгольца:
V2Am + (м/сJ еиА„ = — (j.0|xjm
и
^2фт + (ю/сJеAфт = — ? («бое)-1 divj
Условие калибровки принимает вид:
?(соб|л/с2) ф™ + div Am = 0,
C.45)
C.46)
C.47)
причем теперь посредством C.47) можно исключить из C.44J
скалярный потенциал, в результате чего
т = — i(c2/coe|x)[grad div Am + (со/сJе|лАт].
C.48)
Таким образом, комплексные амплитуды напряженностей поля вы-
выражены при помощи формул C.43)
и C.48) только через векторный
потенциал.
3.2.3. Комплексная частота (Б).
Продолжая мысль (п. 3.2.1) о комп-
комплексных значениях параметров, вхо-
входящих в уравнения Максвелла C.34),
остановимся на круговой частоте ш.
Зададим ее комплексной
ю = ю' + id)" = | ю | exp ( i arctg -
C.49)
Рис. 3.1 п выясним, какой это имеет физиче-
физический смысл.
Взяв комплексные представления Е = Етехр(?со?), Н =
= Нтехр (?©?), выразим, например, напряженность электрического
поля Е при комплексной частоте ш C.49):
Е = Бе Ё = Eme-W"' cos (a't + ф) C.50)
(взято Ет = Етехр(ир)).
Как видно, при ю" >0 поле испытывает затухающие колебания
с круговой частотой ю'; при изменении знака ю" они станут воз-
возрастающими. Процесс не является периодическим, но период коси-
косинусоиды Г = ю72я условпо называют периодом затухающих коле-
колебаний. Величина Т точно определяется по нулям кривой / (t) =
= Ае~® cosifii't + ф) (рис. 3.1). В течение времени, равного 1/а>",
§ 3.3. БАЛАНС ЭНЕРГИИ ПРИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЯХ 123
амшштуда колебаний уменьшается в е раз; будем называть пара-
параметр 1/м" постоянной времени.
В большинстве случаев могут представлять интерес слабо зату-
затухающие колебания, для которых ю" "С со'; при этом на протяжении
нескольких Т процесс очень блпзок к периодическому.
Затухающими, как мы увидим, могут быть свободные поля.
В дальнейшем, если не сделано специальной оговорки, величи-
величину со будем считать вещественной.
§ 3.3. Баланс энергии при гармонических колебаниях
3.3.1. Средние величины: энергия, мощность, поток энергии (А).
Поскольку гармонические колебания электромагнитных полей, пред-
представляющие интерес для радиоэлектроники, являются весьма быст-
быстрыми, обычно имеют дело с их усредненными во времени энерге-
энергетическими характеристиками. Плотности энергии, мощности и по-
потока энергии относятся к тем величинам, которые усредняются по
формулам C.13) — C.15). Например, оба члена выражения A.113)
пропорциональны квадратам напряженностей (которые имеют вид
C.9)). Поэтому в силу C.19)
w = 1/4 (so?EmE; + VoVSmB*m). C.51)
Интегрирование этой величины по некоторому объему V даот на
основании A.110) среднюю энергию W п V. Надо, однако, пом-
помнить, что выражение энергии A.110) бы.то получено в предполо-
предположении, что среда безынерционна (см. п. 1.5.5). Поэтому проница-
проницаемости е п п и C.31) надо понимать, как в п. 1.3.1.
Среднее значение плотности мощности р A.94) находится па
осногашш (Я.1 'i):
р = Fie р, р — \ - jmEm.
C.52)
Величина р называется плотностью комплексной мощности, а сама
комплексная мощность Р есть интеграл от р по V.
Среднее значение П вектора Пойптинга П A.107) выразим, ис-
используя равенство C.15):
= Roil,
C.53)
Промежуточная воличпна П пазыиаотся комплексным вектором
Пойнтиига. Поток П чорез некоторую поверхность S называют
комплексным потоком энергии.
Как соотносятся мгновенные и сродние значения энергетических
величин, наглядно покааыпает следующий анализ плотности мощ-
мощности.
124
ГЛ. 3. ОСНОВНЫЕ ПОЛОЖЕНИЯ ЭЛЕКТРОДИНАМИКИ
Пример 1. Пусть Е = х0Ет cos at и j = xo/m cos (cof + <p), так что плот-
плотность мощности р A.94) есть
р = jmEm cos(co« + ф) cos at = lhimEm cos ф + ]l2]'mEm cos Bat + ф).
Слагаемое, пропорциональное cos ф, равно среднему значению р величины р.
Другое слагаемое — составляющая р, колеблющаяся с удвоеппой частотой.
Если <р = 0 (рис. 3.2а), т. е. Е п j синфазны, то плотность мощности p(t) не
Рис. 3.2
принимает отрицательных значений, а среднее значение р равно половине мак-
максимального. Пусть, далее, сдвиг фазы между Е и j составляет менее я/2, на-
например, ф = я/4 (рис. 3.26); среднее значение р уменьшилось, но осталось по-
положительным. Прп ф = я/2 (рис. 3.2в) оно равно нулю. С дальнейшим ростом
Ф величина р становится отрицательной (на рис. 3.2г ф = Зя/4), а при ф = я
она достигает своего максимального абсолютного значения (рис. 3.23). При
Ф = Зя/2 (ф = —л/2) также имеем р = 0 (рнс. 3.2е).
Мы видим, что колеблющаяся составляющая плотности мощности р может
как угодно превосходить по амплитуде модуль ее среднего значения \р\. Но
\р\ может достигать лишь половины этой амплитуды. ¦
3.3.2. Средний баланс энергии (А). Представление о среднем
балансе энергии электромагнитного поля в некоторой области V
можно было бы получить, отправляясь от уравнения A.105). Рас-
Рассматривая гармонически колеблющееся электромагнитное поле, мы
должны были бы внести в A.105) векторы поля, изменяющиеся
по закону гармонических колебаний, и произвести усреднение энер-
энергетических величин за период. Однако при этом были бы упущены
возможности более глубокой трактовки, которые дает введение
комплексных проницаемостей.
По этой причине основное уравнение будет получено заново.
Будем исходить из комплексной формы уравнений Максвелла C.34J,
§ 3.3. БАЛАНС ЭНЕРГИИ ПРИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЯХ
125
записывая первое пз них комплексно-сопряженным:
rotН„ = — Ё ( )\
rot Em =
* * *
Все члены первой строчки умножим на Ет, а второй — на Нт. Про-
Произведем вычитание соответственных частей и применим тождество
A.26) подобно тому, как делалось в п. 1.5.2. Отсюда
div П = i -f- (еое*Ё;Ёт - WIlmK) - рст. C.55)
Были использованы обозначения C.52) и C.53), причем р = р",
так как j = jCT. Это комплексный аналог уравнения A.100).
Внесем в C.55) представления комплексных проницаемостей
C.35). Разделение вещественной и мнимой частей дает
div Re П = - 4"
div Im П = ~ (еое'
Em-
+ цоц"НткС) - Re>,
...
raH^) - Im p«
C.56)
(учтено, что в результате комплексного сопряжения изменился знак
при е"). Полученные равенства можно было бы проанализировать,
рассуждая, как в п. 1.5.4. Но удобнее сначала произвести интегри-
интегрирование по некоторому объему V с границей S и перейти к сле-
следующим соотношениям:
Re F Шв = - -f- J (еое"Ё;Ёт + ^ом"ЯтЯ*т) dv - RePC
8 V
Im ф lids = ~ j (еое'Ё;Ёт - цо[х'НтЙ;) dv - Im PCT,
C.57)
где рст — интеграл от рст по V, выражающий комплексную мощ-
мощность источников.
Обсудим смысл первого из полученных равенств. В левой ча-
части — вещественная часть комплексного потока энергии Р2 (ис-
(используем обозначение типа A.106)). Согласно п. 3.3.1 это средний
поток энергии через S :PZ = Re^2. Последний член справа дает
среднюю мощность источников: PCT = ReiicT. Легко убедиться, что
рассматриваемое равенство, которому удобно придать вид
- -f- j (еое"Ё;Ёт + hutt) dv - Рс\
v
C.58)
есть не что иное, как уравнение среднего баланса энергии при гар-
гармонических колебаниях.
126
ГЛ. 3. ОСНОВНЫЕ ПОЛОЖЕНИЯ ЭЛЕКТРОДИНАМИКИ
Пусть источники в среднем отдают энергию полю: Рст < 0. Если
проницаемости е i ц вещественны (е" =0, ц" =0), то объемный
интеграл в C.58) исчезает. При этом_ в среднем вся мощность
источников идет на излучение: Pz = — Рст = \Р"\. Если же е">0,
ц">0, то положителен и объемный интеграл, а следовательно,
средняя мощность излучения уменьшится на его величину. В слу-
случае, когда область V энергетически изолирована, так что Pz = 0,
мощность источников полностью «гасится» объемным интегралом.
Из этих рассуждений следует, что объемный интеграл в C.58),
взятый без знака минус, выражает среднюю мощность потерь в V:
dv.
C.59)
Полученный результат проясняет смысл мнимых частей в" и
\i" комплексных проницаемостей е и |я. При в" =0 и ц" = 0, т. е.
когда е и и. веществепны, среда является непоглощающей. Потери
энергии существуют при в" >0 и (или) |.i" > 0. Эти, как говорят,
электрические и магнитные потери происходят в результате пре-
преобразования энергии поля в какие-то иные формы. В особых слу-
случаях, о которых речь пойдет в § 16.3, фигурируют отрицательные
е " и ,и ".
В простейшем варианте, когда поглощение вызвано только про-
проводимостью среды (при этом согласно C.33) в" = о/weo и |л" =
= 0), из C.59) следует:
4- \oE*mEmrh: C.60)
v
Рп =
Величины РгТ = Re Р"т и Ps = Re P2, входящие в первую строку
C.57). принято называть активными: активная мощность, актив-
активный поток энергии. Мнимые части 1тР'т и Im Pz из второй стро-
строки C.57) называют соответственно реактивной мощностью и реак-
реактивным потоком энергии. При вещественных е и ц. получаем
ImP2 = 2o(!Fa-TFM)-ImPCT C.61)
(использованы формулы C.51), A.111), A.112)). Реактивные ве-
величины связаны здесь с разностью среднпх значений электрической
и магнитной энергии в V.
Возвращаясь к примеру, рассмотренному в конце п.3.3.1, на-
помитш, что плотность мощности р была разложена на две состав-
составляющие, одна из которых — среднее значение р, которое теперь
можно назвать плотностью активной мощности. Другая составляю-
составляющая — плотность колеблющейся мощности — обращается в нуль при
усреднении. Вычисляя для того же примера плотность реактивной
мощности
Im р = Im l/2jmEme-*» = -l/2jJEm sin <p,
§ 3.3. БАЛАНС ЭНЕРГИИ ПРИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЯХ 127
видим, что она не является составляющей р. Наличие реактивной
мощности просто указывает на то, что при данных амплитудах jm
и Ет активная мощность не достигает своего максимума.
3.3.3. Дополнительные замечания (Б). Проследим, как изменя-
изменяется электрическая энергия IVя в объеме V, когда сказывается
инерционность среды. Пусть Е = Em cos (at и D = ЕоЕЕт cos (att — а).
Согласно A.104)
-г— = \ Е — dv = — ИЕ0Е \ Em cos at sin (at — a) dv. C.62)
Как происходит изменение энергии в среднем? При интегрирова-
интегрировании по времени от 0 до Т и делении на Т получаем
v. C.63)
dt
= — юеое sin a j ]
Учитывая, что Esina = E" (п. 3.2.1) и Е„ = ЁтЁт, убеждаемся,
что получено выражение мощности электрических потерь (первый
член C.58)).
Следующее замечание о роли комплексной частоты (п. 3.2.3)'.
Рассматривая в C.34) со как комплексную величину, вместо C.55)
получаем
div П = \ («*еое*ЁтЁт - шцоиНтНт) - рСТ. C.64)
Пусть среда однородна и изотропна. Взяв энергетически изолиро-
изолированную область V, не содержащую источников, будем иметь
mtfo. C.65)
ш*еое*
= muOiu
Равенство может быть выполнено только при условии
Im^ = 0 C.66)
(поскольку интегралы вещественны). Ввиду C.37) и C.49) отсюда
т. е.
C.67)
Смысл полученного вывода в том, что мыслимое поле в изоли-
изолированном объеме без источников должно быть затухающим, причем
величина со"/ю' вполне определяется углами потерь среды.
28
ГЛ. 3. ОСНОВНЫЕ ПОЛОЖЕНИЯ ЭЛЕКТРОДИНАМИКИ
§ 3.4. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЙ ЭЛЕКТРОДИНАМИКИ
129
§ 3.4. Общие свойства решений системы уравнений
электродинамики в комплексной форме (А)
3.4.1. О единственности решений. Решения уравнений Макс-
Максвелла, как и других уравнений в частных производных, принадле-
принадлежат весьма широкому классу. Нахождение того или иного решения
уравнений C.34) еще не означает, что получено электромагнитное
поле, которому можно приписать определенное физическое со-
содержание.
Поставим целью выяснить, при каких условиях система урав-
уравнений C.34) имеет некоторое единственное решение Ет, Нт. Оче-
Очевидно, что такие условия однозначно формализуют причину суще-
существования поля: единственное решение обладает физической опре-
определенностью.
В качестве первичной причины существования электромагнит-
электромагнитного поля естественно видеть превращение неэлектромагнитной
энергии в энергию поля. Поэтому будем исследовать решения при
заданных источниках, т. е. такие, которые должны представлять
вынужденные поля. Пусть требуется найти поле внутри области V,
ограниченной поверхностью S (рис. 3.3а), внутри которой задан
s
Рпс. 3.3
сторонний ток с плотностью jCT. Вместо внутренних источников или
наряду с ними может существовать поток энергии через границу S.
Какими предварительными сведениями надо располагать, чтобы
с учетом их получаемое решение оказалось единственным?
Пусть получены два решения системы уравнений C.34): Ет!,
Нт1 и Ет2, Нт2. Подставим их в C.34), так что будем иметь два
варианта записи уравнений. Произведем вычитание соответствен-
соответственных частей и в результате получим следующую систему уравнений:
roth = icoeoee, rot e = — ко|л0|лЬ C.68)
• • • ¦
относительно разностей е = Ет1 — Ет2 и h = Нт1 — Нт2. Поскольку
в обоих вариантах фигурировала одна и та же заданная величина
jmi она исчезла в C.68).
Для системы уравнений C.68) можно вывести совершенно та-
такие же энергетические соотношения, как и для C.34). Поэтому
(ср. C.58))
Re (j) [e, h*] ds = J- j (eoe"ee* + uo|/hh*) dv. C.69)
s v
Если оказывается, что поверхностный интеграл в C.69) равен
нулю, то, значит, исчезает и объемный интеграл справа. Но тогда
при положительных е" и ц" обращается в нуль подынтегральное
выражение, поэтому равны нулю \е\2 и \h\2. А это как раз и озна-
означает, что решение задачи единственно: два гипотетически различных
решения совпадают.
При каких же граничных условиях исчезает поверхностный ин-
интеграл? По крайней мере, если задано:
Ех на S,
или Нх на S, C.70)
или Ех на Si и Нх на S2 (S S)
Действительно, задание Ех, например, означает, что для любых ре-
решений эта величина — одна и та же; следовательно, ех = 0 (нор-
(нормальная компонента е не вносит вклада в смешанное произведение
векторов под знаком поверхностного интеграла). Аналогично рас-
рассматривается задание Нх.
Итак, решение уравнений C.34) при нахождении вынужденно-
вынужденного электромагнитного поля внутри области V с границей S единст-
единственно, если задано одно из граничных условий C.70), а также
е" >0 и \х," > 0. Впрочем, последнее требование может быть ослаб-
ослаблено. Можно допустить, что г" = 0 либо \i" =0. Тогда непосредст-
непосредственно доказывается единственность определения Нт либо Ет.
Остальное устанавливается с привлечением уравнении Максвелла.
Существенно, что величины е" и ц" могут быть как угодно ма-
малы. Отметим также, что сформулированные граничные условия
C.70) не исчерпывают все мыслимые условия, обеспечивающие
единственность решения задачи.
Исследованная задача о нахождении поля внутри V (см.
рис. 3.3а) называется внутренней задачей электродинамики. Все
рассуждения можно повторить и для внешней задачи (рис. 3.36),
когда вынужденное поле существует в бесконечном пространстве
вне некоторой области V.
По-прежнему исходя из энергетического соотношения C.69),
мы должны теперь распространить интегрирование в правой части
на бесконечное пространство вне V. В качестве границы S в C.69)
возьмем совокупность S' и сферической поверхности S" бесконеч-
бесконечно возрастающего радиуса. Поверхностный интеграл в C.69) ис-
исчезнет, если кроме одного из условий C.70), теперь задаваемых
9 В. В. Никольский, Т. И. Никольская
130
ГЛ. 3. ОСНОВНЫЕ ПОЛОЖЕНИЯ ЭЛЕКТРОДИНАМИКИ
на S', в пределе при г-*-°° исчезает вклад сферы S". Это будет,
если [е, h*j убывает быстрее, чем 1/г2. Для этого, в свою очередь,
достаточно, чтобы напряженности поля в рассматриваемом классе
решений убывали быстрее, чем 1/г.
Единственность решения внешней задачи (а следовательно, и
его физическая определенность) установлена при прочих равных
условиях только в классе достаточно быстро убывающих полей.
В заключение заметим, что произведенный выше анализ физи-
физической определенности решений уравнений электродинамики да-
далеко не полон. Принцип причинности в электродинамике находит
отражение в виде так называемого условия излучения; в дальней-
дальнейшем некоторые его формы будут обсуждаться и использоваться
(см., например, пп. 5.1.2, 9.0.2).
3.4.2. Принцип взаимности. Для одной и той же среды будем
рассматривать два разных решения уравнений C.34), которые по-
получаются при задании сторонних токов с плотностями jf и j".
Дважды переписывая уравнения C.34), получаем при этом
rot Hml = iu>eoeEml +
rot Eml = — ?шцоцНт1
rot Hm2 = ?ше0еЕт2 + jm2,
rotEm2= — 1шц0цНт2.
C.71)
Объединим уравнения в две пары, как показано стрелками, и про-
произведем уже знакомые действия. При этом в первой строчке лево-
левого столбца производится умножение на Ет2, а во второй строчке
правого — на Hmi, после чего вычитаются соответственные части.
Аналогичные действия производятся с оставшейся парой уравне-
уравнений. В результате имеем
div [Ёт2, Нт1 ] = — гшц0цНт2Нт1 — 1ше0еЁт1Ёт2 — jmiEms,
div [Emi, Hm2] = — 1
Для изотропных сред нет разницы между выражениями jj,Hm2Hmi
и |лНт1Нт2, еЕт1Ет2 и eEm2Emi. В этом случае из C.72) путем вы-
вычитания получаем
div {[Em2, Hml] — [Eml, Hm2]} = j J2Eml — jmiEm2, C.73)
или при интегрировании по области V с границей S:
т2, Нт1] - [Ёт1, Нт2]} ds = j ( &Т2Ёт1 - )^Ёт2) dv. C.74)
v
Полученный результат C.73), C.74) устанавливает соотношение
между полями двух различных источников в одной и той же изо-
изотропной среде. Это так называемая лемма Лоренца.
§ 3.4. СВОЙСТВА РЕШЕНИЯ УРАВНЕНИЙ ЭЛЕКТРОДИНАМИКИ
131
Если токи сосредоточены в ограниченной области, то, распро-
распространяя интегрирование на бесконечное пространство, можно прий-
прийти к выводу об уничтожении поверхностного интеграла. Тогда
О C.75)
j ( jm2Eml - j^Em2) dv
(поверхностный интеграл исчезает наверняка, если амплитуды по-
полей убывают быстрее, чем 1/г; это условие может быть ослаблено,
если использовать условие излучения п. 9.0.2).
Если первые токи сосредоточены в области Vu а вторые — в F2
(рис. 3.4), то из C.75) следует:
у 1 у2
Полученный результат выражает принцип взаимности для двух
распределений сторонних токов, двух источников. Примечательна
симметрия соотношения C.76),
совершенно не зависящая от
характера среды, которая лишь
предполагалась изотропной.
Для иллюстрации этого на'
рис. 3.4 показано несколько на-
нарушающих однородность «пас-
«пассивных» (лишенных источни-
источников) подобластей, диэлектриче-
диэлектрических и металлических.
Положим, что вся среда ли-
линейна. Это значит, что выра-
выражение C.76) справедливо при
одновременном существовании
обоих источников (не следует
забывать, что рассматриваются два независимых решения уравне-
уравнений электродинамики).
Можно ввести полные токи сервой и второй областей/" и/2Т«
определенным образом догово» .^шись, через какие сечения вычис-
вычисляются потоки векторов ji и ./. Введем величины
U
ml2
-¦=4
1ml у,-
n^dv, Um2i = -—
ml
dv, C.77)
которые можно рассматривать как комплексные амплитуды наво-
наводимых э.д.с. (Ui2 наводится в V\ током, локализованным в F2; со-
соответственный смысл имеет ?72i). Тогда C.76) можно переписать в
виде ImiUmi2 = ImzUrmi- Разделим обе части на Imjmz, это дает:
unljizt = tW/Su, CJ8>
9*
132
ГЛ. 3. ОСНОВНЫЕ ПОЛОЖЕНИЯ ЭЛЕКТРОДИНАМИКИ
т. е. Z\2 = Z2i- В этой трактовке соотношение C.76) выступает как
равенство взаимных сопротивлений Z[2 и Z2\ рассматриваемых
источников.
3.4.3. Перестановочная двойственность уравнений Максвелла.
Магнитные токи. Рассматривая уравнения Максвелла в комплекс-
комплексной форме C.34) при отсутствии источников (jm =0), легко за-
заметить, что замена1)
, Em-»-—Hm, Hm -»- Е,„
C.79)
сохраняет эту систему уравнений, причем первое уравнение пере-
переходит во второе, а второе—в первое.
Отмеченный факт имеет следующее значение. Существуют та-
такие электродинамические задачи, в которых векторы Ет и Н,„ ме-
меняются ролями. Положим, что одна из таких «парных» задач реше-
решена, так что имеются формулы, выражающие векторы Ет и Нт.
Тогда для получения решения второй задачи из той же пары до-
достаточно в готовых формулах сделать замену C.79). Говорят, что
решение в этом случае получено путем применения принципа двой-
двойственности.
Чтобы распространить принцип двойственности на уравнения
Максвелла при наличии источников, необходимо в дополнение к
уравнениям C.34) построить некоторые модифицированные. Сопо-
Сопоставим те и другие уравнения:
э .
rotHm = шеоеЕ
м
rotHm = ш
rot Em = — «ououHm, rot Em = — гюиоиНт — j™.
В левом столбце (Э) записана известная нам система уравнений
электродинамики C.34), а в правом— (М) модифицированная си-
система, физическое содержание которой мы сейчас обсудим. Но сна-
сначала надо отметить, что одна система переходит в другую (Э-*-М),
если
-]1 Em->-Hm,
C.81)
Что же представляет собой система уравнений М? Это уравне-
уравнения Максвелла с необычно заданными источниками. Появившаяся
в правой части второго уравнения функция ]„ есть магнитный ана-
аналог величины j T Это комплексная амплитуда плотности магнитно-
магнитного тока.
В природе, как полагают при формулировании основных уравне-
уравнений теории электромагнетизма, магнитные заряды отсутствуют
') Легко убедиться, что это не единственно возможная замена.
§ 3.4. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЙ ЭЛЕКТРОДИНАМИКИ
133
(см. п. 1.2.5, 1.2.6). Не может быть, следовательно, и магнитных
токов. Но это не мешает вводить такие объекты формально — с
единственной целью облегчить исследование вполне реальных полей.
Итак, посредством замены C.81) мы переводим уравнения
Максвелла с обычными, электрическими источниками в уравнения
с условными магнитными источниками (либо действуем в обратном
порядке). Существенно, что эта замена может производиться в
формулах, выражающих готовые решения задач. Такие операции
мы и будем производить.
Остается проанализировать второе уравнение Максвелла в си-
системе М C.80), поскольку по сравнению с обычным вторым урав-
уравнением Максвелла оно выражает нечто новое. Взяв в левой и пра-
правой частях уравнения дивергенцию, согласно A-23) получим:
0 = — ш div uouHm — div ]'„.
Поскольку в данном случае предполагается существование магнит-
магнитных зарядов, напишем:
div цоиНт = р?. C.82
Следовательно, предыдущее равенство — это выражение закона со-
сохранения магнитного заряда
div j? = — top*
C.83)
(ср. комплексную форму divjm = — шрт уравнения A.44)).
Наконец, следующее. Раз в рассмотрение введены магнитные
заряды и токи, оказываются полезными и представления об их
поверхностных формах. По аналогии с известными величинами |
и т] введем плотность поверхностного магнитного заряда ?м и плот-
плотность поверхностного магнитного тока г\". При этом вместо гранич-
граничных условий A.86), A.85) для В и Е возникают условия типа
A.83), A.88). Запишем их относительно комплексных амплитуд:
Bm2) v0 = ?m,
Em2, Vo] = T)m.
C.84)
C.85)
Вывод этих формул легко выполнить, взяв вместо A.56), A.54)
интегральные формы уравнения C.82) и второго уравнения Макс-
Максвелла М C.80); затем остается только повторить операции из
п. 1.4.2, 1.4.3.
Из C.84) и C.85) следует, что при ?м Ф 0 и, соответственно,
Tj" Ф 0 компоненты Вч и Ех будут иметь разрывы, которые, разуме-
разумеется, не соответствуют физической реальности. Однако введение та-
такого рода разрывов иногда оказывается полезным в теории.
134
ГЛ. 3. ОСНОВНЫЕ ПОЛОЖЕНИЯ ЭЛЕКТРОДИНАМИКИ
Пример 2. Некоторое магнитное поле (рис. 3.5а) представляет интерес
только в полупространстве у > О, причем В@)= уоВ(О). В этом случае можно
\
0
у
\
\
i
9
(//
\
3=0
а
Рис. 3.5
отбросить мысленно поле при у < 0, а при у = 0 задать распределение маг-
магнитного заряда ?м = В@) (рис. 3.56). Это делается на основании условия
C.84) заданием В2 = 0. ¦
УПРАЖНЕНИЯ
1. Задано: Ёт = х0А + у0В, где а) А = 1, В = i; б) А = i, В =—i. Найти Е.
2. Чему равно числовое значение с в C.20) и далее?
3. Между какими направлениями лежат «углы потерь» Д и Дм?
4. При каком фазовом сдвиге между Е и Н будет П = 0?
5. Вывести выражения C.51) —C.53), повторяя п. 3.0.2.
6. За какое время амплитуда свободно колеблющегося поля в изолирован-
изолированном объеме уменьшится в 100 раз (/ = 10 ГГц, полистирол)?
7. Будет ли иметь единственное решение внутренняя задача электродина-
электродинамики для системы уравнений C.34), если задано так называемое импедансное
граничное условие
= ,2-[Hmt, v0]
C.86)
(v0 — орт внешней нормали). Рассмотреть вещественные, мнимые и комплекс-
комплексные значения импеданса Z.
8. Показать, что лемма Лоренца справедлива и в случае анизотропных
сред, если тензоры виц симметричны.
9. Вывести лемму Лоренца в варианте магнитных источников, исходя из
системы уравнений М C.80).
10. Записать формулировки замены величин в уравнениях Максвелла, экви-
эквивалентные рассмотренным в п. 3.4.3.
ЧАСТЬ 2
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ И КОЛЕБАНИЯ
Глава 4
ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ (А)
§ 4.0. Общие сведения о волновых процессах
4.0.1. Исходные представления. Перед изучением электромаг-
электромагнитных волн обсудим содержание понятий волна, волновой процесс,
получивших широкое распространение в физике и технике. Про-
Прообразом здесь служат всем известные волны, возникающие на по-
поверхности воды. Существенно то, что при движении, распростране-
распространении всякой волны среда постепенно вовлекается в некоторый
физический процесс, в результате чего происходит передача энергии
в пространстве.
В основе математического описания волновых процессов лежат
простые соображения. Пусть, наблюдая некоторый физический про-
процесс, мы можем охарактеризовать его в точке М(т\) функцией
u(ih t) = <f(t) (рис. 4.1а). В другой, достаточно отдаленной, точке
о tn
t . О tn
Рис. 4.1
•P(r2) процесс не будет наблюдаться (и = 0) до тех пор, пока он
не будет передан средой, и тогда мы отметим там и (гг, t) = tf (t)
(рис. 4.16). Быть может, временной закон окажется сильно изме-
измененным, искаженным при передаче. Но в простейшем случае в
точке Р(гг) будет обнаружено лишь запаздывание того, что проис-
происходило в точке M(ti). При этом tp(f) = <p(f — т), где т — время,
требуемое для прохождения пути |гг — Г[| = ? со скоростью v.
Положим, что в пространстве какие-либо изменения происходят
только в направлении z. Тогда в соответствии со сказанным
136
ГЛ. 4. ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
процесс характеризуется функцией
u(z, t) = (f(t — z/v). D.1)
Если при z = 0 эта функция и @, t) — q>(t) имеет вид, показанный
на рис. 4.2а, то при z = I (рис. 4.26) наблюдается временная зави-
зависимость иA, ?) = ф(? — l/v), отличающаяся лишь сдвигом: u(l, t) =
-в@, t-1/v).
Рассмотренный волновой процесс — это плоская однородная вол-
волна в не деформирующей ее среде. Дело в том, что, говоря о про-
процессе в некоторой точке z = z\, мы, в сущности, можем иметь в
о *,
О to
to+l/v t
Рис. 4.2
виду любую точку плоскости, соответствующей данному постоян-
постоянному z: согласно D.1) изменение х и у в некоторой плоскости z =
= const оставляет значение и в каждый момент времени постоян-
постоянным. Обратимся теперь к рис. 4.2в, на котором для двух моментов
времени t\ и t% построена величина u(z, t) D.1), как функция z.
Зафиксируем какое-либо мгновенное значение, фазу процесса, на-
например, значение и —а (рис. 4.2а, б, е). На основании рис. 4.2в
можно сказать, что плоскость z = const, для которой и = а, за вре-
время т = t% — t\ переместилась на расстояние I = vx. Будем называть
плоскость с любой фиксированной фазой фронтом рассматривае-
рассматриваемой волны. Распространение волны можно обсуждать как движение
ее фронта. Заметим, что кривые на рис. 4.2е, построенные для мо-
моментов ti и ?2, называют «мгновенными снимками» процесса.
Как выразить волну, распространяющуюся не в направлении z,
а в противоположном? Для этого нужно изменить знак скорости v.
Считая величину v положительной, мы должны в D.1) заменить
аргумент t — z/v на t + z/v.
4.0.2. Гармонические волны. Конкретизируя выражение D.1)
для закона гармонических колебаний C.1), приходим к представлению
§ 4.0. ОБЩИЕ СВЕДЕНИЯ О ВОЛНОВЫХ ПРОЦЕССАХ
137
о гармонической волне:
u(z, t) = umcos
= umcos(cof —
D.2J
Введенный параметр k = a/v называется волновым числом, аи —
фазовой скоростью. На рис. 4.3а (ср. рис. 4.2в) построены два мгно-
мгновенных снимка гармонической волны. При каждом фиксированном
u(z,t)
Рис. 4.3
I величина u(z, t) D.2) дает косинусоидальное пространственное
распределение. Его период есть такое приращение координаты z,
при котором фаза изменяется на 2я. Этот пространственный период
называется длиной волны и обозначается символом А, таким обра-
образом, кК = 2я. Волновое число имеет, следовательно, два выражения:
к = ю/у = 2яД. D.3)
Учитывая, что со = 2я/ (см. п. 3.0.1), имеем также:
v = Я/. D.4)
Распространение гармонической волны отображается смещением
косинусоиды (рис. 4.3а) вдоль оси z со скоростью v.
Пусть навстречу друг другу распространяются две гармониче-
гармонические волны. При этом:
и (z, t) = и^ cos (cat — кг + ц>) + и~ cos (at + kz + tp). D.5)
Если, в частности, ит = u^ и ф = ty, то
и (z, t) = 2um cos kz cos (Ш + ф). D.6)
138
ГЛ. 4. ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
Такой процесс называется стоячей волной. Как видно (рис. 4.36)',
в каждый момент времени мы имеем неподвижную косинусоиду:
ее нули не смещаются вдоль оси z, а остаются фиксированными.
Применяя метод комплексных амплитуд (см. п. 3.0.1), запишем
для гармонической волны D.2) комплексное представление:
u(z, t)=umeH<"-hz-t-") = ume1at, D.7).
где йт — ит ехр (— ikz + icp) = йто ехр (— ikz); um0 = йт при z = 0.
В рамках метода волновые числа могут быть комплексными:
k = k'-ik". D.8)
Внося D.8) в D.7) и вычисляя и — Re й, получаем:
и (z, t) = ume-h"z cos (at — k'z + cp), D.9)
что при к" = 0 совпадает с D.2). Если к" > 0, это затухающая
волна (рис. 4.3б). Величина к" называется коэффициентом зату-
затухания.
Отношение u(z)/u(z + l) = ехр (/с"?) показывает, во сколько раз
уменьшилась амплитуда затухающей волны на пути I. Обычно это
отношение логарифмируют и получают величину L, называемую
затуханием, которая измеряется в неперах [Нп] либо децибелах [дБ]:
L = k"l Нп или L = 20 lg в*« 8,69 k"l дБ. D.10)
Распространение затухающей волны пояснено на рис. 4.3в: как
и ранее, показано смещение мгновенного снимка (экспоненциаль-
(экспоненциальная огибающая не смещается). Можно записать (ср. D.3)):
k' = a/v = 2n/K. D.11);
Здесь фазовую скорость можно рассматривать как скорость смеще-
смещения фронта с нулевой амплитудой; длина волны Я, уже не являю-
являющаяся периодом, также определяется по нулям. Величина к' на-
называется коэффициентом фазы.
4.0.3. Волны скалярные и векторные, неплоские и неоднород-
неоднородные. Выше рассматривались скалярные волны: процесс описывался
скалярной величиной и. Если волновой характер имеют компонен-
компоненты некоторого вектора, то говорят о векторной волне.
Рассмотрим величину
и(х, у, z, t)=um(x, у, z)cos[at-(f{x, у, z)]. D.12)
Характерно, что поверхности постоянной фазы
ф(х, у, z)= const D-13)
в общем случае не являются параллельными плоскостями, как это
было в пп. 4.0.1—4.0.2. Волна может быть неплоской. Если к то-
тому же на этих поверхностях фронта (ср. п. 4.0.1) амплитуда
ит(х, у, z) не принимает постоянного значения, то волна, как го-
говорят, неоднородна.
§ 4.0. ОБЩИЕ СВЕДЕНИЯ О ВОЛНОВЫХ ПРОЦЕССАХ
139
Неплоская и неоднородная волна может быть локально плоской
(и однородной) в некоторой достаточно малой области пространст-
пространства. Это значит, что рассматриваемый участок фронта весьма близок
к элементу плоскости (и амплитуда на нем, практически, по-
постоянна).
Уравнение поверхности фронта D.13) может принимать про-
простой вид в той или иной криволинейной системе координат. Пусть,
например, <р(х, у, z)=kr. Если г — координата цилиндрической или,
соответственно, сферической системы (табл. 2.2),
то мы имеем цилиндрическую или сферическую
волну. На рис. 4.4 показаны последовательные
положения фронта цилиндрической (сфериче-
(сферической) волны, распространяющейся от источника
Q. Такие волны называют расходящимися, по-
поскольку можно представить себе также сходя-
сходящуюся волну, направление распространения ко-
которой везде противоположно: поверхности фрон-
та сходятся к точке.
4.0.4. Простейшие решения волновых уравнений. Выражение
волновое уравнение появилось в п. 3.1.2. Рассмотрим однородное
скалярное волновое уравнение
Рис 4.4
v2 dt2
D.14)
Если рассматриваемый процесс зависит только от t и z, уравнение
принимает следующую простую форму:
„2
О U
v2 dt2
D.15)
Легко путем подстановки убедиться, что рассматривавшаяся в
п. 4.0.1 плоская однородная волна, представленная функцией D.1),
дает решение уравнения D.15). При этом ф(|) в D.1) может рас-
рассматриваться как любая дважды дифференцируемая функция. Ре-
Решением будет также обратная волна, получаемая при замене v на
~v. Общее решение волнового уравнения D.15) можно предста-
представить в виде наложения прямой и обратной волн:
u(z, t)=u*{t-z/v) + u-(t-\-z/v). D.16);
Здесь u+(?) и ц~(?)— произвольные дважды дифференцируемые
функции. Как видно, v в D.15) есть скорость волны.
Переходя к гармоническим колебаниям, введем в действие метод
комплексных амплитуд, т. е. будем рассматривать временную за-
зависимость exp(ico? + (p). Тогда в D.14) d2/dt2 -*¦ — ш2, и это уравне-
уравнение принимает вид:
V4m + k2um = 0, D.17)
где k = a/v. Мы получили однородное уравнение Гелъмголъца (см.
140
ГЛ. 4. ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
п. 3.2.2). Запишем также уравнение Гельмгольца для одномерного
процесса, зависящего от одной координаты z:
dz1
+ к2ит = 0.
D.18)
Это обыкновенное дифференциальное уравнение отвечает волново-
волновому уравнению D.15). Общее решение уравнения D.18) запишем
в виде:
ит (z) = и+ое-^ + и~ое{ъ\ D.19)
где Um0 и ы~0 — произвольные комплексные константы. Пусть ит0=
= Um exp (jcp) и Umo = «m exp (гг|)). Тогда из D.19) в результате стан-
стандартной операции (п. 3.0.1) Re [мт(г)ехр(гю^)] получаем функцию
u(z, t) D.5), которая является решением уравнения D.15).
§ 4.1. Плоские однородные электромагнитные волны
4.1.1. Волновой характер электромагнитного поля. Сопоставляя
общие сведения о волновых процессах, которые обсуждались вы-
выше в § 4.0, и уравнения электродинамики второго порядка из
§ 3.1, сделаем первый шаг к пониманию волнового характера
электромагнитного поля. Ясно, например, что при проецировании
векторных членов уравнений Даламбера C.22), C.23) и уравне-
уравнений Гельмгольца C.41), C.42) на оси декартовой системы коорди-
координат в случае j = 0 (j^T = 0) получаются скалярные уравнения типа
D.14) и D.17). Это значит, что компоненты векторов Е и Н могут
иметь вид уже известных нам волн. Более того, сравнивая волно-
волновые уравнения из п. 3.1.2 и п. 4.0.4, можно сделать вывод, что па-
параметр и, который имел смысл скорости распространения волны,
для электромагнитных процессов равен
v = с/У7й~= l/YeoeiioH- D.20)
Нетрудно догадаться, что такова должна быть скорость плоских
однородных электромагнитных волн в идеальном диэлектрике.
В случае вакуума (е = 1, ц = 1)
v = с = 1/У1^= 2,998... • 108 м/с. D.21)
Исторически величина с была известна еще до становления со-
современной теории электромагнетизма как скорость света, измерен-
измеренная в воздухе или космическом пространстве. Совпадение скорости
предсказываемых теорией Максвелла электромагнитных волн и уже
иавестной (с определенной точностью) скорости света стало аргу-
аргументом в пользу гипотезы Максвелла об электромагнитной природе
света.
Теперь мы должны подробно рассмотреть наиболее простые
влектромагнитные волны.
§ 4.1. ПЛОСКИЕ ОДНОРОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
141
4.1.2. Простейшее решение уравнений электродинамики в комп-
комплексной форме. Полагая j" = 0, запишем однородные уравнения
Гельмгольца, следующие из C.41) и C.42):
V2Em + /c2Em = 0, V2Hm + /c2Hm = 0. D.22)
Здесь введено обозначение:
D.23)
к = (ю/с)Уец. =
Уравнения, которым удовлетворяют комплекные амплитуды Ет и
Нт свободных электромагнитных полей, таким образом, одинаковы.
Будем рассматривать простейшие поля, зависящие только от
одной декартовой координаты, например, z. При этом уравнения
D.22) принимают вид следующих обыкновенных дифференциаль-
дифференциальных уравнений:
^ + /c2Em = 0, i5j2 + ft»Hm = O. D.24)
dz az
Каждое эквивалентно трем скалярным уравнениям типа D.18) от-
относительно декартовых компонент Ет или, соответственно, Нт. Ре-
Решения уравнений D.24), складывающиеся из своих проекций типа
D.19), запишем в форме:
= Е+
+
D.25)
Ёт (г) = Ё+Ое-^ + Е~
Hm (z) = H+oe-«z + Н-Ое^ = Н ,
где Ето и Нт0 — неопределенные векторные константы.
Далее необходимо учесть, что векторы Ет и Нт связаны урав-
уравнениями Максвелла C.34):
Ёт = (— i/coeoe) rot Hm, Hm = (г/соц0р,) rot Ёт- D.26)
Операцию rot выполним в декартовых координатах согласно A.21),
учитывая при этом, что дифференцирование компонент Е^ и
D25) fe
р р
D.25) по z эквивалентно умножению на Tife, а от х и у они не
зависят. Подставляя в D.26) отдельно первые и вторые слагаемые
решений D.25), имеем
Нга =
D.27)
— i
i
хо
0
Htx
хо
0
Уо
0
ktv
Уо
0
zo
+ ik
\
+ ik
142
ГЛ. 4. ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
где введен параметр
W = У цо
120яУц/е,
D.29)
называемый волновым сопротивлением, которое измеряется в
омах [Ом].
Из D.27), D.28) следуют выводы:
Векторы Е* и Н* не имеют продольных компонент:
Е$ = О, Я± = 0. D.30)
Эти векторы ортогональны (взаимно перпендикулярны):
Е^Н^О. D.31)'
Отношение скалярных величин Z?™ и Нт равно ±W D.29).
4.1.3. Волны в непоглощающей среде. Если е и ц, — веществен-
вещественные величины, то среда, как известно (п. 3.2.2), не поглощает энер-
энергии электромагнитного поля. В этом случае вещественными явля-
являются волновое число к D.23) и волновое сопротивление W D.29).
Будем рассматривать волну, распространяющуюся вдоль оси z:
Em = Em, Hm = Н„. Пусть при этом вектор Е направлен вдоль оси
х. Положив в D.25) Е„о = х0А = х0А ехр (щ) и Е„о~= 0, а также
используя D.28), находим:
Ёт = х0Ае-<к', nm = y0(A/W)e-ih' D.32)
и, далее, переходя от комплексных амплитуд Ет и Нт к самим на-
пряженностям поля Е и Н, записываем:
Е = xqA cos (at -kz + ф), R = y0(A/W)cos(at-kz + <p). D.33)
Как видно, векторы поля изменяются по закону плоской одно-
однородной гармонической волны, распространяющейся без затухания.
Вектор Пойнтинга П = [Е, Н] направлен по оси z, а следовательно,
распространяясь, волна переносит энергию. Правая тройка векто-
векторов Е, Н и П показана на рис. 4.5а. Говорят, что волна в силу
свойства D.30) является поперечной. На рис. 4.56 представлен
мгновенный снимок распределения поля, соответствующий фор-
формулам D.33).
С какой скоростью происходит перенос энергии? Обратимся к
формуле A.117). Чтобы воспользоваться ею, надо вычислить плот-
плотность энергии w волнового поля D.33) и плотность потока энер-
энергии П. На основании A.113) находим:
ш = шм+ш" = г0гА2 cos2 (at -kz + cp), D.34)
причем плотности электрической и магнитной энергии оказываются
равными: w" = w3 = w/2. Далее,
П
o (A2/W) cos2 (at - kz + q>).
D.35J
§ 4.1. ПЛОСКИЕ ОДНОРОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
143
Таким образом, из A.117), D.34) и D.35) получаем следующее
выражение скорости переноса энергии волной:
^Г D.36);
Результат показывает, что энергия переносится со свойственной
данной волне фазовой скоростью
v = а/к = с/Уец D.37)
(см. D.3)). Эта величина уже была отмечена в п. 4.1.1.
Рис. 4.5
Для волны в вакууме (е = 1, Ц = 1) v= с D.21) и W = W0 =
= 120я Ом D.29).
4.1.4. Волны в поглощающей среде. При комплексных е и ц
оказываются также комплексными к и W. Используя C.37), запи-
запишем:
к = к' - ik" = | к | е-*(л+дм)/2 = к /A - itg А) A - i tg AM), D.38)
где \к\ =((о/с)У1е|||х1=(оУео|1о1е|||х|, к = (ю/с)У7у";
W = W' + iW = \W\ ei<pw, D.39);
где цЫц Ф ()
При подстановке D.38), D.39) в D.32) мы получим комплекс-
комплексные амплитуды Ет и Нт, изменяющиеся при распространении вол-
волны и сдвинутые по фазе.
Если е' и \i' положительны (что справедливо за исключением
особых случаев), то при положительности е" и ц", соответствую-
соответствующей потерям энергии (см. п. 3.3.2), углы А и Ам лежат в пределах
0-н90°. Поскольку в этих же пределах лежит и их полусумма, то
ft'>0 и к" >0. Поэтому, переходя от Em и Нт D.32) к Е и Н,
144
ГЛ. 4. ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
теперь получаем следующую затухающую волну:
Е = x0Ae-h"z cos (со? — k'z + ф), Н =у0 ущ e~h"z cos[(at—k'z + ф—<pw),
D.40)
которая распространяется вдоль оси z с фазовой скоростью i/ =
= ю/к' D.11). Смысл коэффициента затухания к" п коэффициента
фазы к' уже обсуждался в п. 4.0.2.
Пример 1. На рис. 4.6 в двух вариантах представлен мгновенный сни-
снимок затухающей волны. В первом случае (а) волна распространяется во влаж-
влажной почве — взято: е' = 10, а = 0,03 См/м, / = 1 ГГц. При этом согласно C.33)
tgA = 0,054. Получаем: к' = 66,255 м~' и к" = 1,788 м; \W\ = 119,085 Ом и
А Н
н
a
6
Рис. 4.6
(fw = 0,054 рад. Значительно быстрее затухает волна той же частоты в мор-
морской воде (б). В этом случае е' = 80, о = 4,3 См/м, так что tgA = 0,976; к' =
= 204,841 м-1 и к" = 82,873 м; \W\ =33,124 Ом и q>w = 0,384 рад. Мгно-
Мгновенные снимки построены при <р = 0 в D.40). На рис. 4.66 заметен сдвиг ну-
нулей распределений векторов поля. ¦
Как и в этих примерах, в большинстве практических случаев
при рассмотрении электромагнитных волн не приходится учиты-
учитывать магнитные потери в среде (ц" =0). При этом согласно D.38)
к = kVl-itgA. D.41);
После разделения вещественной и мнимой частей имеем:
к' = k Vir
к" = к |/i-(_
tg2A).
D.42)
Если tg А < 1, т. е. среда — несовершенный диэлектрик, то вы-
выражение D.41) легко разложить в ряд:
!^) D.43,
§ 4.1. ПЛОСКИЕ ОДНОРОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
145
Отсюда получаются приближенные формулы:
2
D.44)
Вычисляя волновое сопротивление, в том же приближении на-
находим:
Щ1 + г ^). D.45)
Пусть теперь tgA»l: среда — проводник. Пренебрегая в D.42)
единицей по сравнению с tgA, напишем:
т. е.
к'\
Далее,
w = w0 у
к~
«к]/
е'A-
кУ-i
'tgl
2
* tR A)
tgA=(l-i)
СО -,r~!~i I
= — Кец ^
ikV(tgA)/2,
/til l/ «fl|i0(xo
2 > 2 *
^' (l + л лЛ'
tgA {l ' ^ V 2
D.46)
D.47)
i|)fl D 48)
'прободнин)
На рис. 4.7 представлены относительные величины к'Ik и к "Ik,
вычисленные по точным формулам D.42). График наглядно демон-
демонстрирует области применимости формул D.44) и D.47).
Как видно, диэлектрики и проводники резко различаются па
характеру распространения электромагнитных волн. Из D.44) сле-
следует, что затухание в случае диэлектрика очень мало, а коэффи-
коэффициент фазы к' близок к волново-
волновому числу при отсутствии потерь:
потери почти не влияют на фазо-
фазовую скорость волны v = со/А;'.
В случае проводника весьма
близкие величины к' и к" D.47)
велики, т. е. велико затухание и
мала длина волны Я, = 2я//с'
D.11). При переходе к идеально-
идеальному проводнику (а-*-00) к' и к"
неограниченно возрастают. В част-
частности, это означает, что полное затухание процесса должно проис-
происходить на любом конечном расстоянии. Волновое сопротивление
D.48) и длина волны при а -*¦ °° стремятся к нулю.
Ввиду D.47) пространственное распределение поля распростра-
распространяющейся в проводнике волны оказывается резко апериодическим.
Действительно, на расстоянии
А0 = I/ft" «= У2/юцоЦО D.49)
амплитуда колебаний уменьшается в е раз, тогда как длина волны
10 В. В. Никольский, Т. И. Никольская
10 tg/l
146
ГЛ. 4. ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
X = 2л/к' равна величине 2яА°. Таким образом, на расстоянии в одну
длину волны амплитуда уменьшается в ехрBя)« 535,5 раз. Введен-
iH ный параметр А0 будет играть важную
роль в теории поверхностного эффек-
эффекта (п. 5.4.1).
Пример 2. На рис. 4.8 представлен
мгновенный снимок волны, распространяю-
распространяющейся в меди (о = 5,8-107 См/м) при / =
= 1 ГГц. При этом к' = к" = 4,785 ¦ 105 м-',
\W\ =8,25-10-? Ом и фиг = 45°. В меди
Я = 13,12 мкм, тогда как в воздухе при / =
= 1 ГГц Я = 30 см. ¦
В заключение запишем выражение
мгновенного вектора Пойнтинга для
волны в поглощающей среде, получае-
получаемое при подстановке D.40) в A.107):
Рис. 4.8
А
П = х0 гщ e~2h"z cos (at — k'z + <p) cos (at — k'z + q> — qw) =
C0S t2 (Q* ~~ k'Z +(P) —
(cp. D.35)). При усреднении во времени получается:
z°2Wie~2fe"ZCOS4>w'
D.51)
что можно вычислить на основании C.53).
§ 4.2. Поляризация и сложение волн
4.2.1. Понятие поляризации волны. Выше в п. 4.1.3—4.1.4 мы
ограничились анализом частного вида волны, распространяющейся
вдоль оси z. При этом была зафиксирована ориентация вектора Е в
пространстве: E = xqE. Тем самым определилась и ориентация маг-
магнитного вектора: Н = у0Я. Говорят, что такая волна поляризована
в плоскости X0Z. Поляризация волны — ориентационная характери-
характеристика. Плоскость поляризации, по определению, составлена векто-
вектором Е и направлением распространения волны.
Положив в D.25) Е„о = х0А + удВ, Ешо = 0, а также опреде-
ляя Нт путем подстановки Ет в D.28), находим общее выражение
комплексных амплитуд векторов поля при распространении волны
вдоль оси z:
Е+ = (х0А + УоВ) e-
D.52)
Если в D.52) аргументы комплексных чисел А и Ё одинаковы
(.4 = Л exp(?q>) и .Й = 2?ехр(ир)), т. е. равны начальные фазы ком-
§ 4.2. ПОЛЯРИЗАЦИЯ II СЛОЖЕНИЕ ВОЛН
147
понент вектора Е, то ориентация Е при распространении волны не
меняется. Волна поляризована в плоскости, составляющей угол ¦в =
= &Tctg(B/A) с плоскостью X0Z (рис. 4.9а). Очевидно, что эту вол-
волну можно рассматривать как наложение двух волн с амплитудами
У
t = const
к"=О
СО
У1
А
z= const
/7ув°
?во°
Рис. 4.9
А и В, одна пз которых поляризована в плоскости X0Z и другая —
в плоскости Y0Z.
Итак, при синфазности декартовых компонент вектора Е рас-
распространяющейся волны ориентация поля остается неизменной. Это
называется плоской (линейной) поляризацией. Картина оказывается
иной, если компоненты поля не синфазны.
Возьмем важный случай, когда амплитуды компонент Ех и Ev
одинаковы (А=В), а начальные фазы различаются на 90е. Пусть
в D.52) А = Ае("ж В = Ле«ч>Т90о). Переходя в первой строчке
D.52) от комплексной амплитуды Е„ к напряженности Е+, имеем:
Е+ = Ae~h"z [x0 cos (at — k'z + q>) ± y0 sin (at — k'z + q>)] D.53)
(cp. D.40)). Определяя угол ¦?>, указывающий положение плоскости
поляризации волны (рис. 4.96), получаем:
tg f) = EJEx = ±tg(at-k'z + (f). D.54)
Это значит, что плоскость поляризации не остается фиксированной
148
ГЛ. 4. ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
в пространстве, а вращается. В любой плоскости z = const (напри-
(например, z = 0, рис. 4.96) вектор Е, а с ним п все электромагнитное
поле волны вращается с угловой частотой ю. Такая поляризация
называется круговой. При выборе фазового сдвига —90° (верхний
знак в D.53)) вращение вектора Е на рис. 4.96 должно происхо-
происходить против часовой стрелки. Это левая круговая поляризация. При
фазовом сдвиге 90° (нижний знак в D.53)) вращение происходит
в противоположном направлении — правая
круговая поляризация. Зафиксировав неко-
некоторый момент времени (t— const), можно
получить мгновенный снимок волны круго-
z вой поляризации. Как видно из D.53), он
должен отразить вращательное распределе-
распределение поля: конец вектора Е будет скользить
по винтовой линии (рис. 4.9е).
Волна круговой поляризации есть резуль-
результат наложения двух волн, поляризованных
в ортогональных плоскостях, если их ампли-
амплитуды равны, а фазы сдвинуты на 90°. В об-
общем случае, когда Ех и Еу могут быть не
равны по амплитуде и произвольно сдвину-
сдвинуты по фазе, волна имеет эллиптическую по-
поляризацию. При этом вектор Е, вращаясь в
плоскости z = const, изменяет свою длину,
[ так что его конец описывает эллипс. Последний оказывается впи-
вписанным в прямоугольник со сторонами 2А и 2В (рис. 4.9г).
4.2.2. Стоячие волны. Как известно (п. 4.0.2), при наложении
двух распространяющихся в противоположных направлениях гармо-
гармонических волн с одинаковыми амплитудами образуется стоя-
стоячая волна.
Рассмотрим наложение волн, одна из которых имеет комплекс-
комплексные амплитуды Ет = Е„, Нт = Н„, D.32), а другая распростра-
распространяется в противоположном направлении и характеризуется комп-
комплексными амплитудами Ет = Ей, Нт = Ни» которые получаются,
если задать в D.25) Е+о = 0 и Ё^о = хо5ехр (h|)). Мы имеем,
таким образом,
Рис. 4.10
Е+ =
Н+ = Уо (A/W) е-***,
D.55)
Пусть амплитуды обеих волн равны (А=В). Сложение их дает
Ет = Е+ + Ей = хо2Ле*«Р+ Ч»/2 cos [kz — (ф — ib)/2],
D.56)
Hm = Н+ + Ни = у0 (- i2A/W) e««P+1»/> sin [fcz - (Ф -
§ 4.3. ДИСПЕРСИЯ, РАЗНЫЕ ОЦЕНКИ СКОРОСТИ
149
В случае непоглощающей среды (к и W вещественны) из D.56)'
следует, что Е и Н сдвинуты по фазе на 90°. Согласно C.53) это
означает, что средний вектор Пойнтинга П равен нулю: стоячая
волна в среднем не передает энергии. Видно также, что простран-
пространственные распределения Е п Н сдвинуты на четверть волны
(рис. 4.10):
D.57)
Е = x02Acos[kz — -ф 'ч cos (of + ^Ц—),
Н = уо2 ? sin (te-
sin («о*
В дальнейшем (гл. 5) мы будем рассматривать существенно
более сложные наложения плоских однородных волн, направления
распространения которых могут быть и неколлинеарными, а ампли-
амплитудно-фазовые соотношения произвольны. Такие наложения обра-
образуются при наличии границ, отражающих волны. Заметим пока,
что если бы амплитуды рассмотренных нами противоположно рас-
распространяющихся волн были различны, то можно было бы выде-
выделить стоячую волну типа D.57) п бегущую волну с разностной
амплитудой.
§ 4.3. Дисперсия, разные оценки скорости
4.3.1. Общее представление о дисперсии сред и распространении
сигналов. Свойства сред, в которых распространяются реальные
электромагнитные процессы, всегда являются в той или иной сте-
степени частотно-зависимыми. Поэтому должна зависеть от частоты
и фазовая скорость электромагнитной волны
v = co/fe' = c/Re T/~eyi. D.58)
Это называется дисперсией. Заметим, что даже при не зависящих
от частоты вещественных проницаемостях е и ц дисперсия должна
существовать в силу присущей средам электропроводности (аФО).
Это видно при подстановке в D.58) комплексной диэлектрической
проницаемости вида C.33).
Природа дисперсии многообразна. В гл. 5—7 мы увидим, что
для более сложных волновых процессов, например, таких, которые
свойственны волноводам, дисперсия будет иметь место независимо
от свойств внутренней среды (даже в случае вакуума).
Существование дисперсии необходимо учитывать, оценивая рас-
распространение электромагнитных сигналов — волновых процессов,
переносящих информацию. Плоская однородная гармоническая вол-
волна не может рассматриваться как сигнал. Но такой процесс на са-
самом деле и не может существовать, поскольку, строго говоря, его
существование мыслится на бесконечном временном интервале во
всем пространстве. Если же он имеет начало и конец, то это — им-
150
ГЛ. 4. ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
§ 4.3. ДИСПЕРСИЯ, РАЗНЫЕ ОЦЕНКИ СКОРОСТИ
151
пульс, характеризуемый спектром частот. Сигналы, как известно,
всегда обладают некоторым спектром. Поэтому дисперсия влияет
на их распространение. Действительно, представляя сигнал в виде
разложения Фурье (необходим интеграл, а не ряд Фурье), мы
должны рассматривать распространение гармонических волн, соот-
соответствующих всем частотным компонентам. Скорости пх распростра-
распространения различны, так что, преодолев некоторое расстояние, эти гар-
гармонические составляющие приобретут различные фазовые запазды-
запаздывания. Но сложение с новыми фазовыми сдвигами обязательно при-
приведет к деформации, искажению сигнала. Дисперсия может быть
мала, тогда она почти не сказывается на распространении сигна-
сигналов, пока невелики расстояния. Чем они больше, тем более важно
учитывать дисперсию.
4.3.2. Анализ слабой дисперсии: групповая скорость волнового
процесса. Рассмотрим напряженность электрического поля сигнала,
взяв следующее представление:
Е = J Ё(со) eW-HOz-ida = Re j Ё (a)
D.59)
Как видно, при любом z = const компоненты вектора Е выражают-
выражаются интегралами Фурье вида C.18), а при распространении каждая
частотная составляющая приобретает фазовое запаздывание &(ю)г,
свойственное плоской однородной волне при этой частоте. Пусть
спектр заключен в полосе частот (юо — Аи, юо + Аю). Каждой ча-
частоте ю можно сопоставить к (а) п, следовательно, можно говорить,
что сигнал характеризуется спектром волновых чисел (ко — Ак,
ко + Ак), где &о = к(сао). Поэтому
E = Re
<0„—ДМ
0
E (q) e4<*-M*Wd<o = Re J Е(А;)е«а<«< hzUk, D.60)
ho-Ah
где произведена замена переменных ю -> к.
Разложим частоту как функцию волнового числа в ряд Тейлора
и ограничимся членом с первой производной:
. da
ft-fc,
(к-к0).
D.61)
Это представление можно считать оправданным, если дисперсия от-
относительно слаба, а полосы частот и соответствующих им волновых
чисел являются узкими. Такой волновой процесс называют группой
волн. Внося D.61) в D.60), получаем
ha+Ah
Е«11еегр[*(<оо*-ЗД] j Ё (к) ехр U [g I * - z\ (к - к A dk
Дй
D.62)
j
О-Д
(вне интеграла D.60) записан дополнительный множитель
ехр(—ikoz), а под интегралом — компенсирующий его множитель
exp(ifcoz)).
Пусть Ё(/с) = Е((в) может считаться постоянной величиной
(спектральные компоненты имеют одинаковые амплитуды). Тогда
этот множитель выносится за. знак интеграла, после чего интеграл
легко взять (удобно при этом сделать замену переменных к -*¦ к —
— к0). В результате получаем
Е « 2 Re Ё (к0) ехр [i (aot — koz)]
da
dk
t — z
Полагая Е(Л0) = Ете'ф, окончательно имеем
Е « 2Em5 (z, t) kk cos (at -kz
<p)
где
¦"
S (z, t) =
S—H
^t-z)Ak
dk
D.63)
D.64)
D.65)
есть огибающая гармонической волны, которая, можно сказать, ока-
оказалась модулированной.
Чтобы понять характер распространения изучаемой группы волн,
обратимся к ее мгновенному снимку (рис. 4.11). Находящаяся
внутри огибающей модулированная косинусоида перемещается
вдоль оси z с обычной фазовой скоростью v = alk. Что касается
огибающей, то условием локализации ее максимума является ра-
равенство нулю аргумента (ведь это функция sin 1/1, 1 =
= [(detfdk)t-z]bk):
Для разных моментов времени t условие выполняется при различ-
различных z, т. е. огибающая смещается. Очевидно, что скорость смеще-
смещения есть
угр = g. D.66)
Она называется групповой скоростью.
Во всех случаях, когда дисперсия еще не приводит к существен-
существенному искажению сигнала, групповая скорость рассматривается как
скорость переноса сигнала.
Внося в D.66) ю = vk, получаем
v n = v + k%. D.67)
152
ГЛ. 4. ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
Соотношение связывает групповую скорость ->гр и фазовую скорость
v. Отсюда также следует
- ,dv_ dX » dv ,, пп\
В зависимости от знака производной dv/dk (или dvjdk) групповая
Ет(ю) 2Дсо
Рис. 4.11. (ЭВМ)
скорость может быть как больше, так и меньше фазовой. Скорость
1>гр, однако, не может превышать скорости света с.
В дальнейшем мы неоднократно будем использовать понятие
групповой скорости.
§ 5.0. ВСПОМОГАТЕЛЬНЫЕ СВЕДЕНИЯ
153
УПРАЖНЕНИЯ
1. Какой смысл имеет отношение пространственного X и временного Т пе-
периодов гармонической волны?
2. Чел различается интерпретация параметров v и Я в случаях незатухаю-
незатухающей и затухающей волн? _
3. При 2 = 0 некоторый процесс описывается функцией м@, t) =sin)'«.
Какой вид будет иметь функция при z = I, если известно, что вдоль оси z рас-
распространяется плоская однородная волна типа D.1)? _
4. Рассмотреть наложение гармонических волн D.5) при итфит. Как
изменяется амплитуда функции u{z, t) в зависимости от г?
5. Записав уравнения C.34) при ]т =0 в координатной форме, показать,
что при отсутствии зависимости поля от х и у равны нулю компоненты па-
пряженностей поля Ez и ___.
6. Записать комплексные амплитуды векторов поля плоской однородной
электромагнитной волны, распространяющейся а) по оси х, б) по оси у.
7 Найти параметры к', к", v, Я и W плоской однородной волны, распрост-
распространяющейся в следующих средах (табл. 1.2): стекло (/= 105 Гц), полистирол
(/ = 107 Гц), олово (/ = 101(f Гц).
8. Представить волну, поляризованную в плоскости X0Z, в виде двух волн
круговой поляризации, правой и левой.
9. Вычислить глубину проникновения А0, а также волновое сопротивление
W при / = 1010 Гц для меди и свинца (табл. 1.2).
10. Прн выводе формулы D.53) взять В = 2А. Построить кривую, описы-
описываемую концом вектора Е в плоскости z = 0.
11. Выписать выражения векторов поля Е и Н стоячей волны в случае
поглощающей среды.
12. Рассмотреть стоячую волну круговой поляризации.
13. Фазовая скорость волны изменяется по закону v = fol'l — а/ш2 (t>o и а
не зависят от частоты). Найти групповую скорость.
14. Выразить групповую скорость в случае, когда диэлектрическая прони-
проницаемость некоторой непоглощающей среды зависит от частоты.
Глава 5
ЭЛЕКТРОДИНАМИКА И ОПТИКА
§ 5.0. Вспомогательные сведения. Вращение декартовой
системы координат (А)
На рис. 5.1а изображены две декартовы системы координат
[х, у, z) и (\, ц, ?) с общим началом 0.
Введем девять углов
Р,
указывающих ориентацию осей второй системы относительно пер-
первой. Так в первой строке мы имеем углы, составляемые осью | с
осями х, у и z (рис. 5.16). В том же порядке во второй и третьей
строках расположены углы ориентации осей ц и, соответствен-
соответственно, ?. Следовательно, между ортами обеих систем существуют
154
ГЛ. 5. ЭЛЕКТРОДИНАМИКА И ОПТИКА
§ 5.1. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ
155
соотношения:
%о = х0 cos cci + уо cos a2 + z0 cos а3,
•По = х0 cos Pi + уо cos p2 + z0 cos Рз,
So = хо cos Yi + Уо cos f 2 + z0 cos ^з
xo = locosai + iio cos Pi + Eocos Yi,
Уо = lo cos a2 + iio cos P2 + So cos ^2,
zo = %o cos a3 + tjo cos Рз + go cos ^з.
E.1);
E.2)
Аналогично преобразуются компоненты некоторого вектора
F = x0Fx + yoFv + zoFz = %oFi + 4oF, + go^:-
Таким образом,
Fi = Fx cos ai + Fy cos аг + F, cos аз,
F4 = ^ cos Pi + Fy cos p2 + Ft cos p3, E.3)
Ft = F* cos Yi + ^ cos ^2 + Ft cos 73
и
Fx = ^j cos ai + F^ cos Pi + Ft cos fi,
^и = Pt cos a2 + Fti cos P2 + Ft cos K2, E.4)
^2 = Fs cos аз + F4 cos Рз + Ft cos 73.
А поскольку в качестве F может фигурировать и радиус-вектор
г = хох + уоу + zoz = ?о| + ЛоЛ + Ъо%,
соотношения E.3), E.4) дают также преобразование координат.
Рис. 5.1
Составляя скалярные произведения строчек E.1) и E.2), на-
находим следующие соотношения:
COS2 ф] + COS2 ф2 + COS2 фз = 1,
COS ф1 COS ^1 + COS ф2 COS \|?2 + COS фз COS фз = 0, '
при ф = а, р, г, Ч = а» Р. Tf 5 Ф ^ Ч>-
cos2 aj + cos2 Pi + cos2 ^i = 1,
cos a* cos ah + cos p, cos $k + cos y» cos y* — 0
при i = 1, 2, 3; к = 1, 2, 3; i ^ Л.
§ 5.1. Отражение и преломление
5.1.1. Электромагнитные волны и оптические лучи (А). Оптика
как наука о свете в значительной степени сформировалась задолго
до установления его электромагнитной природы. В геометрической
оптике оперируют понятием луча. В случае однородной изотропной
среды луч есть прямая, указывающая направление распростране-
распространения света. Обращаясь к представлению о плоской однородной вол-
волне (гл. 4), назовем лучом нормаль к ее фронту. Анализируя раз-
различные волновые процессы, мы в ряде случаев будем сопоставлять
им лучевые схемы.
В отличие от гл. 4 нам придется рассматривать волны, распро-
распространяющиеся в разных направлениях, не совпадающих с осями
декартовой системы координат (х, у, z). Положим, что волна рас-
распространяется в некотором направлении %. Естественной для этой
волны назовем такую систему координат (|, г\, %), в которой комп-
комплексные амплитуды напряженностей поля выражаются формулами,
подобными D.32):
-*. E.7)
Пользуясь правилами преобразования ортов и координат, запишем
эти формулы в основной системе (х, у, z):
Em = (х0 cos
4- уо cos a2 + z0 cos аз) X
XA exp[—ik(x cos
+ У COSY2 + zcos
E.8)
Hm = (x0 cos Pi + уо cos p2 + zo cos Рз) X
X (A/W) exp [—ik (x cos "ii + y cos if2 + z cos 4C) ]•
Ориентация луча % и фронта волны % = const показаны на
рис. 5.2а.
Введем волновой вектор
к = ?о& = к (х0 cos y 1 + уо cos 42 + z0 cos Кз), E.9)
указывающий направление луча и по абсолютному значению рав-
равный волновому числу. Скалярное произведение kr = /c(xcosifi -Ь
+ 2/cosY2 + zcosK3) и экспоненциальный множитель в E.7), E.8)
представляется в виде:
е-йС = е-*'. E.10)
156
ГЛ. 5. ЭЛЕКТРОДИНАМИКА И ОПТИКА
Уравнение фронта волны % = const можно, таким образом, перепи-
переписать в следующих формах:
a; cos Yi + У cos ^2 + zcos ^з = const, kr = const. E.11)
Как показано на рис. 5.26, проекция г на направление ?, а с ним
и величина кг остаются постоянными в плоскости фронта волны.
--Л
Рис. 5.2
5.1.2. Падение волны на границу раздела сред. Постановка за-
задачи (А). На практике так или иначе приходится встречаться с
влиянием границ физических тел на распространяющиеся волны,
которые испытывают отражение. Это значит, что от границы рас-
распространяется новая волна, налагающаяся на первичную. Внутри
тела, играющего роль препятствия, также возникает волновой
процесс.
Будем рассматривать гармонический электромагнитный волновой
процесс в случае, когда все пространство разделено плоскостью на
два однородных полупространства с разными свойствами. Следует
найти решения уравнений Максвелла C.34) при jCT = О для каж-
каждого из полупространств, удовлетворяющие на указанной плоскости
граничным условиям. Эти решения сформируем из плоских одно-
однородных волн (гл. 4). В первой среде зададим так называемую па-
падающую волну Е°, Н°, которая распространяется из бесконечности
к границе под некоторым углом, и предположим, что суще-
существует отраженная волна Е~, Н~, распространяющаяся от гра-
границы. Во второй среде допустим существование одной прошедшей
волны Е+, Н+ (ее называют также преломленной волной), ко-
которая уходит от границы в бесконечность. Это схематически пока-
показано на рис. 5.3.
Задача состоит в том, чтобы при заданной падающей волне по-
подобрать такие комплексные амплитуды и направления распростра-
распространения двух других волн, при которых тангенциальные компоненты
векторов Е и Н остаются непрерывными на границе раздела сред.
§ 5.1. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ
157
Запишем это в форме:
— F
Ео
E.12)
Pnc. 5.3
(имеются в виду тангенциальные компоненты на плоскости z — О,
рпс. 5.3; индексы 1, 2 обозначают две разные среды).
Может возникнуть вопрос, не является ли выбор этих трех волн
произвольным. Почему, например, во второй среде ожидаемое ре-
решение задачи исчерпывается только од-
одной волной? Это требование физиче-
физической определенности задачи. При па-
падении заданной волны на границу раз-
раздела сред возникает вторичный волно-
волновой процесс, начинающийся на этой
границе, и нет оснований ожидать, что
появятся новые волны, приходящие
из бесконечности. Отказ от введения
таких волн согласуется с принципом
причинности и называется условием
излучения. В дальнейшем мы увидим,
что «трехволновое представление», дей-
действительно, приводит к единственному, а тем самым, физически
содержательному решению задачи.
5.1.3. Законы Снеллиуса (А). Лучевая схема для рассматривае-
рассматриваемой задачи дана на рис. 5.4а. Из оптики известны законы отраже-
отражения и преломления лучей:
1. Угол отражения ср' равен углу падения ср.
2. Синусы угла преломления € и угла падения ср подчинены
соотношению:
sin в/sin ф = п\]п2 = «12, E.13)
где пх п П2 — коэффициенты преломления сред, a n]2 называется
относительным коэффициентом преломления; в оптике это экспери-
экспериментально определяемый параметр.
Мы записали так называемые законы Снеллиуса.
С точки зрения электродинамики эти законы — следствия урав-
уравнений Максвелла, причем
w = V7|i E.14)
для всякой среды с данными пропицаемостями.
ВЫВОД. Падающей, отраженной и преломленной волнам сопо-
сопоставим волновые векторы к0, к~ и к+. Тогда (п. 5.1.1)
e-ik~r = ехр [— ifci(.rcos7~ + ycos^ + zcos7")]. E.15)
e-ik+r _ ехр J— j^ (x cos y+ _|_ у cos y+ _j. z cos 7+)],
158
ГЛ. 5. ЭЛЕКТРОДИНАМИКА И ОПТИКА
где к\ =(ю/с)Уе1Ц1 и к2 = (и/с)Уг2ц2 — волновые числа для первой
и второй сред, а углы fi, ^2 и ^з (с теми или иными верхними
индексами) — это ориентационные углы направлений распростране-
распространения соответствующих волн (см. рис. 5.2а).
Компоненты векторов поля в граничных условиях E.12) имеют
характер констант, умноженных на функции из E.15), взятые при
60°
60°
40°
2O°
if
4
и
1
/i
/
»*
~ i
/
/
a*
i" i
7/
2,5
10
! I
20°
60° 30°
Рис. 5.4
z = 0 (см. рис. 5.3). Эти условия могут быть удовлетворены только
при линейной зависимости1) компонент, что требует выполнения
равенств:
ехр[— i^ (ж cos 7? + У cos 72)] = exp[— ikt(x cos уГ+ ycosy^)] =
= exp [— ik2(xcosyf+ ycosyt)]• E.16)
Лишь в этом случае условия E.12), будучи удовлетворены в неко-
некоторой точке (например, в начале координат), выполняются везде
на границе.
Потребуем, чтобы луч падающей волны лежал в плоскости чер-
чертежа, т. е. составлял угол Vi = 90° с осью х (направленной по
нормали к чертежу). Тогда cos7? = 0 и из E.16) следует, что
cos7r = COS7* = 0. Следовательно, -уГ = 7i~ = 90°: все три луча ле-
лежат в одной плоскости. Смысл этого факта очень прост. Раз поле
падающей волны не зависит от координаты х, такая зависимость
отсутствует и у двух других волн.
') Функции /i, ..., /„ называются линейно зависимыми, если можно подо-
подобрать такие коэффициенты а,, ..., а„ (не все равные нулю), что линейная
комбинация ai/i + ... + а„/„ будет равной нулю при любых значениях аргу-
аргументов функций.
§ 5.1. ОТРАЖЕНИЕ II ПРЕЛОМЛЕНИЕ
159
Сосредоточим внимание на зависимости от у в E.16) и запи-
запишем, как следствие, двойное равенство:
= &2cos72~. E-17)
Во-первых, E.17) оаначает, что 7°= ъ(°^а угла—острые, рис. 5.4а).
Но 7° = 90° — ф п у~ = 90° — ф'. Поэтому
Ф' = Ф, E-18)
что составляет содержание первого закона Снеллиуса.
Во-вторых, учитывая дополнительно, что ^2 = 90° — Ф, и пере-
переходя в E.17) от косинусов к синусам, получаем
, E.19)
а это соотношение — не что иное, как выражение второго закона
Снеллиуса, вытекающее из электродинамической теории. Мы не
только пришли к оптическому закону E.13) по форме, но и можем
теперь дать электродинамическое толкование входящим в E.13)
коэффициентам преломления П\ и п2. Сопоставляя E.13) и E.19),
имеем:
E.20)
Положив «i = yei(Xi и п2 = Уг2ц2, приходим к E.14). ¦
Выполненный вывод вполне согласуется с оптической трактов-
трактовкой, пока проницаемости сред вещественны. При этом ni = c/vi и
п2 — cjv2, где v\, v2 — фазовые скорости плоской однородной волны
для обеих сред. Закону E.13), таким образом, можно придать сле-
следующий вид:
vz/vi. E.21)
При поглощении, когда проницаемости сред, а с ними и коэф-
коэффициенты преломления становятся комплексными, наглядная лу-
лучевая трактовка утрачивается. Но выполненный электродинамиче-
электродинамический вывод законов Снеллиуса остается в силе и, значит, сохраняют
справедливость их формулировки. Электродинамическая трактовка
законов Снеллиуса шире оптической; комплексным значениям три-
тригонометрических функций отвечает определенное физическое содер-
содержание (см., в частности, п. 5.1.5).
На рис. 5.46 второй закон Снеллиуса поясняется при помощи
семейства кривых^ (ф) для_случая двух идеальных диэлектриков;
при этом «1 = lei и п2 = Уг2 вещественны. Биссектриса выделяет
два класса процессов преломления. В одном из них первая среда
является, как говорят, оптически более плотной: ni2> 1. В дру-
другом — она оптически менее плотная: п\2 < 1.
5.1.4. Следствия второго аакона Снеллиуса (А). Подчеркнем,
что электродинамический вывод законов Снеллиуса — это всего
лишь промежуточный этап при решении задачи о падении электро-
160
ГЛ. 5. ЭЛЕКТРОДИНАМИКА И ОПТИКА
магнитной волны на границу раздела сред, постановка которой
обсуждалась выше в п. 5.1.2. Однако уже на этом этапе можно
сделать ряд содержательных выводов.
Полное отражение на границе непоглощающих сред. Пусть
первая среда — оптически более плотная. Из E.13) или E.19)
(см. также рис. 5.46) следует, что угол преломления -Q в данном
случае больше угла падения ф; это отражает лучевая схема на
рис. 5.5а. Следовательно, при некотором остром угле ф = ф*, кото-
который называется предельным углом внутреннего отражения, окажет-
окажется, что угол ft — прямой (рис. 5.56). Преломленный луч при этом
как бы скользит вдоль границы раздела сред. Полагая в E.13)
или E.19) ft = 90°, для ф = ф* получаем
sin ф* = к2/к1 = 1/п[2. E.22)
При дальнейшем увеличении угла падения (ф>ф*), как следует
из второго закона Снеллиуса, sinft>l. Это значит, что углам ф,
лежащим в пределах ф* < ф < 90°, не соответствуют какие-либо ве-
вещественные ft: преломленного луча нет, происходит полное отра-
отражение (рис. 5.5в). Возвращаясь к рис. 5.46, видим, что, действи-
действительно, в случае большей оптической плотности первой среды
(«12 >1) областью определения функции ft^) является о.трезок
оси абсцисс 0 < ф < ф*.
Интересное и важное явление полного отражения на границе
непоглощающих сред потребует в дальнейшем более обстоятельного
анализа (см. п. 5.3.1), основанного на изучении электромагнит-
электромагнитного поля.
Преломление в весьма оптически плотной среде. Продолжая рас-
рассматривать среды без поглощения, обратимся к случаю, когда
«2 ^ «1. Согласно второму закону Снеллиуса
sin ft = -i
1.
E.23)
Это значит, что при любом угле падения ф преломленный луч
близок по направлению к внутренней нормали (рис. 5.6).
Г
f
% 5.1. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ
161
Н
н
5.1.5. Преломление при поглощении (Б). Пусть волна, распро-
распространяясь в среде без поглощения, падает на границу раздела с
поглощающей средой {щ — величина вещественная, а «2 — комп-
комплексная). Из E.13) следует, что при любом угле
падения ф неизбежно окажется комплексным
sin в-, а следовательно, Ф уже не может рассмат-
рассматриваться как обычный пространственный угол.
Волну во второй среде характеризует функ-
функция, записанная в третьей строке E.15). Так как
cosy*=0, k2 cos Vj = k1 cos V? = А^ sin ф (см.
второй закон Снеллиуса— п. 5.1.3) и у3 ="&, то
И
= ехр {_ i [(fc1 sin ф) у + (fc2 cos ft) z]}. E.24)
В квадратных скобках первый член — веществен-
вещественный, а второй — комплексный. Действительно, вещественными яв-
являются к\ = п1а/с и эшф и, далее,
где к2 =
причем
{к2 cos ftJ = kl A - sin2 О) = *? — {К sin ФJ,
— комплексная величина. Обозначим
E.25)
E.26)
где %z и %г вещественны. Таким образом, выражение E.24) при-
принимает вид
"
[- i (%уу
E.27)
Записывая вытекающие отсюда условия постоянства амплитуды
и фазы процесса, видим, что это уравнения двух несовпадающих
плоскостей
z = const, %уу + %zz = const. E.28)
Рассматривая эквифазную плоскость как фронт волны (см. п. 4.0.3),
мы должны констатировать, что волна неоднородна: ее амплитуда
не остается постоянной в плоскости фронта, а экспоненциально
изменяется по нормали к границе сред; из физических соображе-
соображений ясно, что по мере углубления в поглощающую среду поле
должно убывать: %z > 0.
Очевидно х„ и %z в E.28) пропорциональны функциям sinf
и cos 7, где ^ — угол между нормалью к фронту волны и осью z.
Это пояснено на рис. 5.7а. На основании E.28) с учетом E.25),
E.26)
S V Xy
11 В. В. Никольский, Т. И. Никольская
sin
E.29)
162
ГЛ. 5. ЭЛЕКТРОДИНАМИКА II ОПТИКА
а поскольку вещественную величину
С A
можно заменить при
у у у p
помощи закона Снеллиуса на A^sinf), получаем:
ctg ч = Re ctg ft. E.30)
Пусть потери малы. Взяв |гег1 > П\ (вторая среда является опти-
оптически более плотной), можно убедиться, что угол "f близок к той
величине О, которая получается в пренебрежении потерями. Если
=const
Рис. 5.7
же \п2\ <п\, то различие будет заключаться в том, что полпое от-
отражение при потерях, строго говоря, уже окажется невозможным:
во всех случаях угол ¦у будет существовать.
Представляет интерес случай, когда |re2l>rei, т. е. оптическая
плотность поглощающей среды относительно весьма высока, что
может быть как при малых, так и при больших потерях. Из E.29)
видно, что угол f в этом случае становится очень малым (ctg "Y > 1):
преломленный луч уходит в глубь поглощающей среды практиче-
практически по нормали (рис. 5.76), т. е. так же, как в аналогичном случае
при отсутствии потерь (ср. рис. 5.6).
Отметим как важный факт то, что условие |re2l > П\ (Ifol ^ к{)
в сильной степени выполняется при падении волны на границу с
металлом. Мы вернемся к этому в п. 5.4.1.
§ 5.2. Поля при падении волны на границу раздела сред
5.2.1. Случай нормального падения (А). Нам нужно завершить
решение задачи о падении плоской однородной электромагнитной
волпы на плоскость раздела различных сред (п. 5.1.2). Начнем с
рассмотрения частного случая, когда падающая волна распростра-
распространяется вдоль оси z, т. е. по нормали к границе раздела. Направле-
Направления распространения отраженной и прошедшей воли коллинеарны
§ 5.2. ПОЛЯ ПРИ ПАДЕНИИ ВОЛНЫ НА ГРАНИЦУ РАЗДЕЛА СРЕД 163
(рис. 5.8). Выпишем выражения комплексных амплитуд векторов
Е и Н всех трех волн:
Ё», = xoie-iftiz, Н^уЛЛ/И^бГ^ (z<0), E.31)
Ё~ = xo5eifti2, H^-yD(B/^)eikiz (z<0), E.32)
Ё+ = х0СбГ*Ч Н+ = уо(С/^2)е-^2 (z>0). E.33)
Требуется ответить на вопрос, каковы будут комплексные амп-
амплитуды отраженной и прошедшей волн при заданной падающей
волне, которая, разумеется, может нести любой поток энергии,
г
t"+;
Рис. 5.8
так что коэффициент А является неопределенным. Определим ко-
коэффициент отражения р и коэффициент прохождения т следую-
следующими формулами:
(O). E.34)
Это отношения комплексных амплитуд вектора Е для волн на
границе раздела сред. Как видно из E.31) — E.33), р = В/А и
т = С/А.
Чтобы найти р и т, достаточно потребовать выполнения сфор-
сформулированных в п. 5.1.2 граничных условий. Векторы поля всех
волн имеют только тангенциальные компоненты на границе разде-
раздела сред. Полагая в E.31) — E.33) z = 0 и внося эти выражения в
E.12), после простых преобразований получаем систему уравнений:
1 + р = т, l-p=(HW2)T. E.35)
Отсюда
p=={W2-Wl)l(W2 + Wl), x = 2W2l(W2 + Wl). E.36)
Задача решена: теперь на основании E.34), E.36) для всякого
заданного А по формулам E.31) — E.33) можно выразить полное
электромагнитное поле в обеих средах.
И*
г
164
ГЛ. 5. ЭЛЕКТРОДИНАМИКА II ОПТИКА
Остается проанализировать полученный результат. Отметим
сначала, что отражение от границы может отсутствовать, при этом
волна полностью проходит во вторую среду. Из E.36) следует,
что эта возможность реализуется при равенстве волновых сопро-
сопротивлений:
или.
= (Wei.
E.37)
Говорят, что в этом случае среды согласованы.
Пусть Wx и W2 — вещественные. При этом удобно рассматри-
рассматривать р и т как функции отношения W2IWX (рис. 5.86). Полное от-
отражение (|р|=1) имеет место при W2/W1 = 0 и Wi/W2 = 0.
На практике отражение велико, когда W2 < Wx или Wx < W2. Да-
Далее складывая падающую и отраженную волны, на основании фор-
формул E.31), E.32), E.34) и E.36) запишем следующие выраже-
выражения комплексных амплитуд векторов поля в первой среде:
Em = xoie-V(i + peJsV)> Hm = yoAe-*V(i-_pe^) E.38)
§ 5.2. ПОЛЯ ПРИ ПАДЕНИИ ВОЛНЫ НА ГРАНИЦУ РАЗДЕЛА СРЕД 165
(z=SO). Как видно, амплитуды Ет и Нт векторов Е п Н пропор-
пропорциональны модулям комплексных чисел, заключенных в круглые
скобки. Чтобы понять характер функций Em(z) и Hm(z), рассмот-
рассмотрим диаграммы (рис. 5.9а, б, слева), представляющие 1 +
+ р exp(?2fciz) и 1 — р exp(i2fciz) в виде условных векторных сумм.
Неподвижный вертикальный отрезок изображает единицу, а слага-
слагаемое pexp(i2fciz) и, соответственно,— pexp(i2fciz) представлены
вращающимся отрезком, длина которого равна |р| (взято р < О,
что соответствует W2<-W\ в E.36)). Полный оборот вращающего-
вращающегося отрезка происходит при изменении фазы 2k\z = Anz/Ki на 2л.
Это отвечает смещению по оси z на A,i/2. Поэтому период прост-
пространственного распределения Em(z) и Hm(z) равен половине длины
волны в первой среде. Таково расстояние между соседними макси-
максимумами либо минимумами данных функций (рис. 5.9а, б, справа).
Напряженности поля принимают максимальные значения, кото-
которые в 1+lpl раз выше, и минимальные, которые в 1 — |р] раз
ниже, чем в падающей волне.
Пример 1. Рассмотрим отражение волны от проводящего полупрост-
полупространства. Взяв сначала идеальный проводник, согласно D.48) полошим Wi =
= 0, так как 02->-оо. Из E.36) следует, что р = —1 и т = 0, т. е. происходит
j-ec2k,z
Рис. 5.10
полное отражение. При подстановке р = —1 в E.38) получаем величины Ет
и Нт, соответствующие стоячей волне:
E.39)
(ср. п. 4.2.2). Распределение амплитуд поля показано на рис. 5.10. На границе
(z = 0) амплитуда магнитного поля удваивается и распределен ток с плот-
плотностью
= [- «0, Нт @)] =
E.40)
166
ГЛ. 5. ЭЛЕКТРОДИНАМИКА И ОПТИКА
Возьмем вместо идеального проводника реальный. Отношение W2/Wi =
= w — очень малая величина: согласно D.57) w =
= A + ?) 1 / ШоЕ^2. Напри-
Например, для меди @2 = 5,8 НО7 См/м), если первая среда — воздух, при / =
= 109 Гц w = A + 0Д88-10~5. Поэтому выражения р и т E.36) удобно раз-
разложить по малому параметру w. С точностью до w2 имеем:
р = — 1 + 2ш и т = 2w.
Таким образом, для меди отражение оказалось практически полпым.
E.41)
5.2.2. Наклонное падение. Формулы Френеля (А). Вернемся к
общей задаче о наклонном падении волны, на пути решения кото-
которой уже получены законы Снеллиуса (см. п. 5.1.3). Следующий
шаг — вывод формул, которые подобно E.36) позволяли бы на-
находить комплексные амплитуды полей отраженной и прошедшей
волны, когда падающая волна задана. Результат должен зависеть
от поляризации падающей волны, и мы отдельно рассмотрим две
ортогональные поляризации. В одном варианте вектор Е будет
перпендикулярен плоскости падения, а в другом — параллелен ей.
Ясно, что все иные типы поляризации можно рассматривать путем
наложения решений, полученных для этих двух вариантов, т. е.,
как говорят, для случаев перпендикулярной и параллельной
поляризации.
Рис. 5.11
На рис. 5.11а изображена лучевая схема наклонного падения
(ср. рис. 5.4а), на которой отмечены орты для представления по-
полей в случае перпендикулярной поляризации: h°, h~ и h+ — еди-
единичные векторы в выражениях Н„, Н„ и Н?. Все орты для элек-
электрических векторов направлены по оси х: е° = е~ = е+ = х0. Как и
выше в п. 5.2.1, будем пользоваться понятиями коэффициента от-
отражения и коэффициента прохождения E.34), но отметим их
индексами -L (символ перпендикулярной поляризации). Будет
§ 5.2. ПОЛЯ ПРИ ПАДЕНИИ ВОЛНЫ НА ГРАНИЦУ РАЗДЕЛА СРЕД 167
показано, что
cos cp — Wl cos &
W2 cos
+ Wi cos в '
х , =
2W cos tp
cos ф-I-Wx cos © •
E.42)
В случае параллельной поляризации (рис. 5.116) h° = h =
= h+ = —хо, а орты для представления напряженности электриче-
электрического поля е°, е~ и е+ лежат в плоскости чертежа. При этой поля-
поляризации, используя символ
Ри = —
запишем:
W2 cos ft — W cos ф
cos © -)- W cos ф '
T|| =
2W2 cos
W cos Ъ -\-W cos ф
, E.43)
Выражения E.42), E.43) называются формулами Френеля.
Прежде чем анализировать формулы Френеля, покажем, как
они получаются.
ВЫВОД. Начнем с того, что введем новое понятие. Пусть
волна перпендикулярной поляризации распространяется под углом
Рис. 5.12
а к оси z (рис. 5.12а). Проецируя Ет и Нт этой волны на некото-
некоторую плоскость z = const, получаем Ётх = Ёт и Йтх = Йт cos а. От-
Отношение Ётх/Йтх назовем импедансом при перпендикулярной по-
поляризации и обозначим Z±(a). Очевидно, что
Z±(a)=W/cosa. E.44)
Аналогично вводится импеданс при параллельной поляризации
Z,i(a) (рис. 5.126). В этом случае Ётх = Ёт cos а и Йтх = Йт,
так что
Zii (a) = W cos a. E.45)
С целью вывести формулы Френеля E.42) обратимся к
рис. 5.11а. Для падающей, отраженной и прошедшей волн импе-
импеданс Z±(a) E.44) принимает следующие значения:
_ *\
7+
cos ф
COS \j) - COS ф
COS ft
E.46)
168
ГЛ. 5. ЭЛЕКТРОДИНАМИКА II ОПТИКА
Поэтому при наложении на границе раздела сред (z = 0) гранич-
граничных условий E.12) получаем:
Ё°т @) + к~ @) = Ё+ @),
k°m@) Е-@) Е+@)
E.47)
ч
Разделив все члены на #т@) и принимая во внимание, что по-
появившиеся отношения комплексных амплитуд согласно E.34) да-
дают р = рх и т = T.J., приходим к системе уравнений:
W cos ft
Р, — tj, = — 1, P.+tjt Tj, = 1. E.48)
± _l W2 cos ф -1- v '
Выражения E.42) получаются непосредственно в качестве реше-
решения этой системы.
Аналогично в случае параллельной поляризации (рис. 5.116)
после конкретизации импеданса Zn(a) E.45)
Z^Wj^cosff, Z^ = — W1cosq>, Z| = ^F2cosft E.49)
и наложения граничных условий E.12) получим соотношения, не
отличающиеся по форме от E.47), по содержащие не полные комп-
комплексные амплитуды Е?,@), Ё~ @) и Ё+@) (вектор Ёт каждой из
волн уже не параллелен плоскости z = 0), а только Е^х@), Е„х @) и
@):
Учтем, что
Е+х@)
E.50)
Е°тх @) = Ет @) cos ф, Ё~х @) = -Ёт @) cos ф,
E.51)
Поэтому, разделив все члены E.50) на Еотх @), на основании оп-
определяющих формул E.34) получаем следующую систему
уравнений:
. cos ft ,
COS ф
E.52)
Формулы Френеля E.43)—решения этой системы.
§ 5.2. ПОЛЯ ПРИ ПАДЕНИИ ВОЛНЫ НА ГРАНИЦУ РАЗДЕЛА СРЕД 169
0,7
Итак, при наклонном падении плоской однородной волны на
плоскость раздела различных сред направления отраженной и про-
прошедшей волн подчинены законам Снеллиуса E.18), E.19), а их
комплексные амплитуды при двух характерных поляризациях на-
находятся при помощи формул Френеля E.42), E.43). Разумеется,
ранее найденные выражения коэффициентов р и т при нормаль-
нормальном падении волны E.36)—это частный случай формул Френеля
E.42) или E.43), соответству-
соответствующий ф = 0 (при этом на ос- р
новании E.19) и О = 0). Впро-
Впрочем, при переходе к E.36) от
E.43) надо учесть, что при
ф = 0 е~ = — е° (рис. 5.116),
поэтому в выражении для р 0,5
надо изменить знак.
На рис. 5.13 представлены
кривые, построенные по фор-
формулам Френеля E.42), E.43)
для случая идеального диэлек-
диэлектрика (проницаемости вещест-
вещественны, причем Hi = (Х2 = 1).
Сначала сосредоточил! внима-
внимание на семействе кривых, по-
построенных для случая, когда
оптическая плотность первой
среды выше: ei>82. Видно, Рис. 5.13
что при этом независимо от ви-
вида поляризации коэффициент отражепия (рх или р„) каждый раз
стремится к единице при ф = ф* (ср. рис. 5.46) и далее при ф > ф*
сохраняет это значение. Если же более высокой является оптиче-
оптическая плотность второй среды (е1<ег), то в области пологого па-
падения (ф ~ 90°) для обеих поляризаций и при всех значениях па-
параметра ег/ei коэффициент отражения близок к значению — 1.
При параллельной поляризации независимо от соотношения оп-
оптических плотностей сред коэффициент отражения меняет знак,
проходя через нуль. Таким образом, при некоторых углах отраже-
отражение отсутствует: происходит полное прохождение волны во вторую
среду. Угол падения ф, при котором возникает полное прохожде-
прохождение, называется углом Брюстера.
Условие обращения в нуль коэффициента отражения рп легко
получить из формулы E.43), выражающей эту величину. Для это-
этого обратим в нуль числитель указанного выражения, заменив в
Гг
нем cos t)- через V 1 — sin* xt = \ / i — | -jf- sin ф ) . Это дает
— sinaft = l/ 1 — (-± этф
- к\ sin2 Ф) =-.W\{\- sin2 Ф)
170
ГЛ. 5. ЭЛЕКТРОДИНАМИКА И ОПТИКА
откуда
E.53)
В случае jxi = цг из E.53) получаем следующее выражение угла
Брюстера:
Ф = arctg Уег/ei. E.54)
Нетрудно проверить, что нули функции при разных ег/ei на
рис. 5.13 соответствуют формуле E.54).
Обращение в нуль числителя выражения рх E.42) приводит
вместо E.53) к равенству:
sin2 ф = 2 _ 1 . E.55)
При Hi = цг не существует угла ф, удовлетворяющего этому урав-
уравнению, а следовательно, полное прохождение невозможно.
5.2.3. Полное электромагнитное поле (А). Задача о наклонном
падении решена. Остается выписать формулы, выражающие комп-
комплексные амплитуды Ет и Нт падающей, отраженной и прошедшей
волн при обеих исследованных поляризациях. Для этого надо
лишь конкретизировать запись типа E.8) и учесть формулы
Френеля.
Перпендикулярная поляризация. Чтобы записать поле падаю-
падающей волны, учтем (рис. 5.11а) что
о? = 0, а!! = 90°, а°3 = 90°,
Р° = 90°, р» = Ф, р° = 90° + ф,
Поэтому
Ёт = х0Л ехр [— ik1 (у sin ф + z cos ф)],
Нт = -jy- (у0 cos ф — z0 sin ф) ехр [— ik1 (у sin ф + z cos ф)]. .
1
Для отраженной волны (рис. 5.11а)
а7 = 0, а2 = 90°, aj = 90°,
Р7 = 90°, Р7 = 180° — ф, Р7 = 90° + ф,
у- = 90°, yl~ = 90° — ф, у7 = 180° — ф.
Внося это в E.8) и заменяя А на Ар±, пишем
Ет = хор^Л ехр [— ifcj (у sin ф — z cos ф)],
Р А
Ни = ф— (у0 cos ф + z0 sin ф) ехр [— ifc1 (у sin ф — z cos ф)].
E.56)
E.57)
§ 5.2. ПОЛЯ ПРИ ПАДЕНИИ ВОЛНЫ НА ГРАНИЦУ РАЗДЕЛА СРЕД 171
Для прошедшей волны (рис. 5.11а)
а+ = 0, at = 90°, а3+ = 90°,
р+ = 90°, pJ = ft, р^ = 90° + *,
у+ = 90°, у+ = 90° - *, yt = *•
Прежним путем с заменой А па Ах± находим
Em = xotj. Л ехр [— ik2 (у sin О + z cos ¦б1)],
Нт = -г^— (у0 cos О — z0 sin О) ехр [— ik2 (у sin О + z cos О)].
E.58)
Параллельная поляризация. Все рассуждения повторяются с
ориентацией на рис. 5.116. Для падающей волны
а? = 90°, а°2 = ф, a!J = 90° + <р,
Р» = 180°,: р^ = 90°, Рз = 90°,
7? = 90°, 72 = 90° - ф, 7з = Ф5
Ет = А (у0 cos ф — z0 sin ф) ехр [— ikx (у sin ф + z cos ф)],
E.59)
Н^= — х0— ехр[—^(г/этф
Для отраженной волпы
аГ = 90°, «7 = 180° — ф, «7 = 90° + ф,
РГ = 180°, $7 = 90°, Р7 = 90°,
уТ = 90°, у7 = 90° - ф, ^7 = 180° - ф;
й = — р и А (у0 cos ф + z0 sin ф) ехр [— ikx (у sin ф — z cos q>)],
Hm = —
E.60)
• x0 exp [— ikx (y sin ф — z cos ф)].
Для прошедшей волны
of = 90°, at = Ф, at = 90° + ¦&,
P+ = 180°, p+ = 90°, PJ = 90°,
y+ = 90°, 7+ = 90°_d, yt = f>;
Em = X|| A (y0cos § — z0sinO) exp[— ik2(y sin® + zcosO)],
«
x..A
Hm = — x0 exP [— ik2 (y sin ft + z cos ft)].
W2
E.61)
172
ГЛ. 5. ЭЛЕКТРОДИНАМИКА II ОПТИКА
5.2.4. Применение принципа двойственности (Б). Сопоставив
результаты, полученные в случаях перпендикулярной и парал-
параллельной поляризации, нетрудно заметить, что эти две задачи на-
находятся в соотношении, определяемом принципом двойственности
(см. п. 3.4.3): структуры электрического и магнитного полей при
переходе от одной задачи к другой как бы меняются ролями. Мож-
Можно было бы рассмотреть только случай перпендикулярной поляри-
поляризации, а все результаты для параллельной поляризации получить
при помощи замены C.79).
Убедимся в этом на примере формул Френеля. Делая в E.42)
замену C.79), мы должны учесть, что во-первых, таким образом
волновые сопротивления заменяются обратными величинами и, во-
вторых, вместо рх = Ёт (О)/Ё°т(Щ и тх = Ё+ @)/?* @) E.34) по-
получатся отношения Н~ @)/Я?, @) и Я+ @)/Я?, @). Таким обра-
образом, из формул Френеля E.42) получатся следующие равенства:
Ят(°) W^coscp — И" cos ft
1 cos cp -f- W1 l cos •
K@)
2W~1cos(p
coscp
cosft
E.62)
Теперь учтем, что
@)
К*
Ет(°)
H°m @)
@)
w
W
в результате чего приходим от E.62) к формулам Френеля E.43),
относящимся к другой поляризации.
Пользуясь принципом двойственности, можно было бы, в част-
частности, при исследовании полного прохождения не выводить отдель-
отдельно равенства E.53) и E.55): одно из них вытекает из другого при
замене еое ** цоЦ-
Разумеется, путем замены C.79) можно получить полные поля
E.59) — E.61) из E.56) — E.58) либо произвести обратную опера-
операцию. Общий неопределенный коэффициент при этом изменяется.
§ 5.3. Полное отражение и направляемые волны (А)
5.3.1. Волны вдоль идеально проводящей плоскости. Если плос-
плоская однородная волна при наклонном падении на границу раздела
сред полностью отражается, то отраженная волна несет такую же
энергию, как и падающая. На рис. 5.14 показана векторная диаг-
диаграмма, на которой средние значения вектора Пойнтинга падающей
и отраженной волн П° и П~ разложены па нормальные и танген-
тангенциальные границе компоненты. Поскольку нормальные компонен-
компоненты взаимно уничтожаются, а тангенциальные складываются, поток
энергии переносится вдоль границы. Мы увидим, что при этом
§ 5.3. ПОЛНОЕ ОТРАЖЕНИЕ И НАПРАВЛЯЕМЫЕ ВОЛНЫ
173
формируется особый волновой процесс, направляемый границей
раздела сред.
Сначала будет рассмотрено полное отражение от идеально про-
проводящей границы (о2 -*- °° и И7 2 = 0).
Перпендикулярная поляризация. Из формул Френеля E.42)
следует, что в этом случае
Рх = -1, тх = 0. E.64)
Учитывая это в E.57), сложим комп-
комплексные амплитуды напряженностей
падающей и отраженной волн E.56),
E.57); поскольку поле существует
только в одной среде, единицу в ин-
индексе снимем. В результате получаем:
1
у/
2
т\
\
У////.-
V/.
z
у///?'/.,,//.
У
Рис. 5.14
= хо(—НА) sin (kz cos ф)
е~шУ sln <">,
2-jp- [у0со8фсоз (kz cos (f) + zoisinq> sin (kzcos(p)]
E.65)
, z<0.
Параллельная поляризация. Аналогично из E.43) при W2 = 0
имеем:
р„ = 1, т„ = 0. E.66)
Подставим pi, = 1 в E.60). Складывая комплексные амплитуды
полей E.59) и E.60), получаем аналогичное E.65) выражение
для поля, представляющего собой наложение падающей и отра-
отраженной волн:
Ет = — НА [у0 cos ф sin (kz cos ф) — zoi sin ф cos (kz cos ф)] e~ift*/sintp,
Hm= — xa^ cos (kz cos q>)e-ihysin<<>, z < 0.
Рассмотрим внимательно выражения полей E.65) и E.67).
Каждое из них имеет характер волны, распространяющейся в на-
направлении у, а в плоскостях фронта у = const распределение поля
есть стоячая волна. В целом это плоские неоднородные волны, рас-
распространяющиеся вдоль границы. Процесс характеризуется двумя
волновыми числами Г и %, которые связаны соотношениями:
Г2 + %2 = к2.
E.68);
Величина Г называется продольным волновым числом, или посто-
постоянной распространения, ах — поперечным волновым числом. При
вещественном к (ср. D.3)) Г = со/^ф = 2я/А, где рф — фазовая ско-
скорость волны, а А — пространственный период, т. е. длина волны.
Запишем также соотношение % = 2я/Ах, вводя этим обозначение
Ах для периода стоячей волны в плоскости фронта.
Характерно, что неоднородные волны имеют не только попе-
поперечные, но и продольные компоненты векторов поля. При перпен-
174
ГЛ. 5. ЭЛЕКТРОДИНАМИКА И ОПТИКА
дикуляриой поляризации формируется неоднородная волна, имею-
имеющая продольную магнитную компоненту Ну, а при параллельной
поляризации — продольную электрическую компоненту Еу. В пер-
первом случае употребляется термин Н-волна, а во втором — Е-волна.
Фазовые скорости этих волн уф выше фазовой скорости v одно-
однородной волны в той же среде. Говорят, что это быстрые волны.
Действительно, поскольку 0 < <р < 90°, то при вещественном к =
= a/v D.37) из E.68) следует
Г < к, уф > v. E.69)
На рис. 5.15а, б представлено распределение компонент векто-
векторов поля в плоскости фронта рассматриваемых неоднородных волн.
1 -поляризация
Рис. 5.15
На расстояниях z = —иЛх/2 от границы раздела лежат плоскости,
на которых выполняется условие Ех = 0 и которые, следовательно,
могли бы быть заменены идеально проводящими плоскостями без
всякого нарушения структуры поля.
5.3.2. Плоский полый волновод. Если введена дополнительная
идеально проводящая плоскость, о которой говорилось выше, то
между ней и первоначальной границей z = 0 образуется энергети-
энергетически изолированный слой, внутри которого может существовать
прежняя Н- или ?-волна. Это простейший полый волновод.
Пусть расстояние между двумя рассматриваемыми плоскостями
фиксировано и равно d. Наложим условие
% = nn/d, n=@), 1, 2, ..., E.70)
(ге = 0 имеет смысл только в варианте параллельной поляризации).
При подстановке значений пл/d E.70) величины % = к cos ср в
E.65) и E.67) на введенной плоскости z = —d удовлетворяется
граничное условие Ех = 0. Это значит, что для плоского волновода
существует бесконечная последовательность значений %, при кото-
которых в этой структуре могут распространяться Н- и ?-волны.
§ 5.3. ПОЛНОЕ ОТРАЖЕНИЕ И НАПРАВЛЯЕМЫЕ ВОЛНЫ
175
При этом волновой процесс в обычном смысле (п. 4.0.3) возмо-
возможен лишь при достаточно высоких частотах. Действительно, исхо-
исходя из E.68), при подстановке значений % E.70) получаем:
Г = //с2 - {nn/df = к /1 - Кр/соJ, E.71)
где со„р =(с/Уец) (nn/d) называется критической (круговой) часто-
частотой. При вещественных е и ц
— Гг/), (o>c0i,p;
, со<сокр, <5'72>
поскольку с понижением частоты при прохождении точки со = сокр
постоянная распространения Г становится чисто мнимой. Фазовое
запаздывание, свойственное обычной волне (п. 4.0.3), исчезает, и
процесс экспоненциально затухает (в направлении у или —г/).
п=О
/7 = 7
)
л=2
>
X - поляризация
п=2
л=3
|- поляризация
Рис. 5.16
На рис. 5.16 показано распределение компоненты ЕХ(ЕУ) в
плоскости фронта направляемой волны при перпендикулярной (па-
(параллельной) поляризации для разных п. Это, как говорят, разные
типы волн. Чем меньше п, тем ниже критическая частота; она об-
обращается в нуль при п = 0. В этом единственном случае распрост-
распространяется плоская однородная волна, лишенная продольной компо-
компоненты поля.
176 ГЛ. 5. ЭЛЕКТРОДИНАМИКА И ОПТИКА
На основании E.68) при сопоставлении с E.71) имеем
Г = кУ 1 — cos2 ф, cos ф = соКр/со.
E.73)
На рис. 5.17 (левый столбец) показана серия лучевых картин
с постепенным уменьшением ф в интервале 90° > ф S* 0, что, как
¦///,
Hi ,'l Ни. :¦ IЧi'. IV :И'. 11liiI :li
\
; и
7VWW
Рис. 5.17. (ЭВМ)
видно из E.73), соответствует уменьшению частоты со вплоть до
критической. Там же (правый столбец) представлены картины
поля направляемой волны, отвечающие взятым углам ф; для опре-
определенности рассматривается низшая Я-волна (ге = 1), показаны
магнитные силовые линии. Несмотря на некоторую условность лу-
лучевых картин, они полезны для понимания процесса. При углах ср,
близких к 90 , однородные волны, отражающиеся от плоскостей,
§ 5.3. ПОЛНОЕ ОТРАЖЕНИЕ И НАПРАВЛЯЕМЫЕ ВОЛНЫ
177
распространяются «полого», что возможно при высоких частотах
со » со„р. G понижением со увеличивается cos ср, т. е. угол ф умень-
уменьшается, а при со = сокр обращается в нуль. При этом исходная вол-
волна распространяется по нормали к плоскостям, формируется попе-
поперечная стоячая волна и передача
энергии вдоль волновода прекра-
прекращается. Можно понижать часто- J
ту и дальше, но тогда согласно
E.73) cos ф > 1, и значения уг- 2
ла ф лежат в мнимой области.
Поле, как мы знаем, при этом 7
теряет волновой характер: стано-
становится синфазным и затухающим.
Как видно, при уменьшении ф
до нуля неограниченно возраста-
возрастает пространственный период поля Рис. 5.18
Л = 2я/Г = A,/sin ф- Вычислим
также фазовую скорость направляемой волны иф = со/Г и ее груп-
групповую скорость
1>гр =
(ср. D.66)). Получаем
ф,
v sin ф, 1;ф1;гр = v2,
E.74)
причем ввиду E.73) зтф = У1—(со„р/соJ. На рис. 5.18 представ-
представлены частотные зависимости обеих скоростей. Обращаясь к
рис. 5.17, видим, что уф во столько раз превосходит v, во сколько
лучевой путь длиннее пути направляемой волны в волноводе.
5.3.3. Волны вдоль плоской границы диэлектриков. Построен-
Построенная на рис. 5.14 диаграмма потоков энергии в равной мере отно-
относится и к случаю полного отражения плоской однородной волны
от границы с оптически менее плотной диэлектрической средой,
который уже обсуждался выше в п. 5.1.4 с позиций второго закона
Снеллиуса. Определяя граничный угол ф* по формуле E.22), мы
можем теперь убедиться, что при ф > ср*, на самом деле, незави-
независимо от поляризации волна отражается полностью. Действительно,
поскольку в этом случае sin'0>l, то cosft = У1 — sin2ft— вели-
величина мнимая. Это значит, что формулы Френеля E.42) и E.43)
для рх и ри принимают вид выражений (Р — iQ)/(P + iQ)f где Р и
Q при отсутствии поглощения вещественны. Поэтому модули р± и
Ри равны единице, и можно написать:
pJ. = e14 Р1 = е1**. E.75)
Перпендикулярная поляризация. Построим электромагнитное
поле при полном отражении от границы диэлектриков перпендику-
перпендикулярно поляризованной волны. Внесем в E.57) р± = ехр(й|зх) и
12 В. В. Никольский, Т. И. Никольская
178
ГЛ. 5. ЭЛЕКТРОДИНАМИКА И ОПТИКА
сложим обе волны в первой среде. Из E.56) и E.57) следует
Em = xo2A cos (kiz cos ф + г|зх/2)ехр [—i(k{y этф — $J2)],
Hm = — -^-[yoi cos ф sin (k\z cos ф + г|и/2) +
+ z0 sin ф cos (kj_z cos ф + i|?j_/2)] exp [— I (kxy sin <p — Hpx/2)],
z<0.
При этом во второй среде на основании E.58):
Ет = хоххАех$ [— ik2(y sin ft + г cos О)],
E.77)
= т± ттт- (Уоcos ^ — zo si
ехР [—
sin О + z cos ft)].
Параллельная поляризация. Апалогично при подстановке
Ри = exp(i\fi||) в E.60) и сложении комплексных амплитуд E.59)
и E.60) получаем:
Ёт = —2А [yoi cos ф sin (k{z cos ф + tyj2) +
+ i(kiz соэф + г|зц/2)] ехр[— i(k{y sin г|з —
E.78)
1|з,|/2)ехр[—г
На основании E.61) во второй среде:
Ет = т || 4J(y0"cos ft — z0 sin ft) expj[— ik2 (y sin ft + z cos ft)],
IA ,E-79)
Hm = — xox и -fp- exp [— ik2 (y sin ft + z cos ft)],
2
z>0.
Полученные для обеих поляризаций представления комплекс-
комплексных амплитуд векторов поля, как видпо, имеют тот же характер,
что и в случае отражения от идеально проводящей плоскости
(см. п. 5.3.1). Как показывают формулы E.76) и E.78), поле в
первой среде есть уже знакомая нам плоская неоднородная волна,
распространяющаяся в направлении у. В плоскости фронта
у = const распределение поля по-прежнему имеет вид стоячей вол-
волны, которая, однако, теперь несколько смещена по оси 2, так что
при z = 0 уже не выполняется условие Ех = 0. Как и в п. 5.3.1,
§ 5.3. ПОЛНОЕ ОТРАЖЕНИЕ И НАПРАВЛЯЕМЫЕ ВОЛНЫ
179
поле в первой среде можно охарактеризовать при помощи двух
волновых чисел, которые обозначим Г и %i- Аналогично E.68)
запишем
Г = й13тФ, Х1 = Мозф, Т2 + %1 = к1 E.80)
Что представляет собой поле во второй среде? Это продолжение
рассматриваемой неоднородной волны. Как видпо из формул E.77)
и E.79), продольные зависимости полей в обеих средах одинаковы
(достаточно учесть второй закоп Снеллиуса E.19)): в противном
случае не было бы выполнено условие непрерывности тангенци-
тангенциальных компонент на границе раздела сред. Это позволяет напи-
написать подобно E.80):
r = &2sinfl-, x2 = A-2cosd, Г2 + з? = А?, E.81)
где введено поперечное волновое число для второй среды %2-
Выясним, как распределено поле в плоскости фронта у = const
во второй среде. Согласно E.77), E.79) закон распределения
имеет вид:
/ (z) = exp [— ik2z cos ft] = е~гХ2\
где необходимо учесть, что cos ft — мнимая величина, как уже бы-
было отмечено в начале п. 5.3.3 (поскольку sinO>l). Запишем:
cos О = — i
= — i\ cos 0 |,
E.82)
т. е. выберем при извлечении корня У1 — sin2 О знак минус. Тогда
/(z)=e-pz, p = u2lcosft|. E.83)
Во второй среде (z > 0) поле экспоненциально убывает от грани-
границы раздела: говорят, что рассматриваемый процесс имеет здесь
характер поверхностной волны. Очевидно, что выбор другого знака
в E.82) не был бы физически оправдан.
На рис. 5.19а, б показано распределение компонент векторов
поля в плоскости фронта неоднородной волны в обеих средах при
двух поляризациях (Я-волна и Ё-волна): стоячая волна в первой
среде переходит в поверхностную во второй.
Легко прийти к выводу, что фазовая скорость рассматриваемой
волны 1>ф = со/Г лежит между значениями v\ и V2, т. е.
к{>Т>к2, и{<иф^и2. E.84)
Действительно, Г < ки так как Г = А;131Пф и sin ф < 1 @° < ф <
00°). В то же время Г > к2, поскольку r = A:2SinO, тогда как
sinO^l. Итак, фазовая скорость неоднородной волны, распрост-
распространяющейся вдоль границы раздела сред (при полном отражении),
выше фазовой скорости однородной волны в первой среде v\ =
12*
180
ГЛ. 5. ЭЛЕКТРОДИНАМИКА II ОПТИКА
= c/VeiHi, но ниже аналогичной величины i>2 = с/У е2|Я2 для второй
среды. В ней волна является, таким образом, медленной A>ф ^ v2),
будучи при этом поверхностной, как показано выше.
Ввиду E.82) импеданс Z% E.46) или Z\ E.49) в случае по-
поверхностной волны — чисто мнимая величина. Введем понятие
У
•z ±-поляризация
а
Рис. 5.19
У
¦z II-поляризация
б
поверхностного импеданса Zs, который определяет соотношение
Ётх и Йтх на границе раздела сред:
Етх = Zs[Bmx, v'o]. E.85)
Здесь v0 — орт внутренней нормали для первой среды: v'o = — z0.
Подставляя E.77), E.79) в E.85), получаем следующие выраже-
выражения Zs для обеих поляризаций:
— Z\ = —
Я-волны,
— Zt =¦ — W2 cos О, ?-волны.
E.86)
Принимая во впи.мание E.82), мы можем утверждать, что Zs име-
имеет емкостный характер для Я-волн и индуктивный — для Егволн.
Наличие такого поверхностного импеданса (поддерживаемого про-
процессом в первой среде), можно рассматривать как условие сущест-
существования поверхностной волны во второй среде.
Сделаем, наконец, следующее замечание. Анализируя поле, мы
существенно уточнили оптическую трактовку полного отражения
от границы непоглощающих сред (п. 5.1.4), согласно которой пре-
преломленный луч просто отсутствует. Но ведь формулы E.77) и
E.79) выражают не что иное, как волну, распространяющуюся во
второй среде под углом •&. Оказывается (как легко проверить),
этот угол преломления — комплексный, а именно, •& = 90° + ia
(а>0), т. е. при ф > ф* угол Ф получает чисто мнимое прираще-
приращение ia. Формально можно утверждать, что при полном отражении
преломленный луч ориентирован под комплексным углом.
§ 5.3. ПОЛНОЕ ОТРАЖЕНИЕ II НАПРАВЛЯЕМЫЕ ВОЛНЫ
181
5.3.4. Плоский диэлектрический волновод. Как и при полном
отражении от идеально проводящей границы (см. п. 5.3.1), в слу-
случае полностью отражающей границы диэлектриков тоже существу-
существуют плоскости (см. рис. 5.19), на которых Ех = 0. Каждую такую
плоскость можно заменить идеально проводящей границей, и в
«отсеченном» диэлектрическом слое сохранится рассматриваемое
Рис. 5.20
поле. Поэтому ясно, что слой диэлектрика фиксированной толщи-
толщины D, ограниченный с одной стороны идеально проводящей плос-
плоскостью, способен направлять различные волновые процессы.
На рис. 5.20 показано распределение компонент поля для двух та-
таких неоднородных волн а и б (ср. рис. 5.16). Необходимое условие
существования волн в этом слое, экранированном при z = —D,
имеет вид:
Ex(-D)=0,
Ey(-D) = 0,
Я-волпы,
ZJ-волны.
E.87)
Если детализировать эти соотношения при помощи формул E.76)
и E.78), подставив в них z = —D, можно было бы подойти к оп-
определению поперечпых волновых чисел (в п. 6.2.3 мы вернемся к
этому с других позиций); вопрос сложнее, чем в случае плоского
полого волновода, когда аналогично была получена формула E.70).
Не останавливаясь на этом, отметим следующее. При полном
отражении от границы диэлектриков S (рис. 5.20) тангенциальные
компоненты Ех и Нх подчинены определенному соотношению, дик-
диктуемому формулами E.85), E.86), где Zs имеет требуемый реак-
реактивный характер. Но ведь в силу симметрии поля точно такое же
соотношение тангенциальных компонент имеет место на выделен-
выделенной в диэлектрике плоскости S'. Поэтому ту часть структуры, ко-
которая лежит за этой плоскостью, можно отбросить, заменив полу-
полупространством с такими же свойствами, как и при z > 0. Тогда
смогут существовать поля, показанные на рис. 5.21. При этом
внутри диэлектрического слоя на обеих его границах выполняются
условия полного отражения для однородной волны. Каждая из этих
границ является импедапсной поверхностью, «поддерживающей»
вне слоя поверхностную волну. Плоский диэлектрический слой
182
ГЛ. 5. ЭЛЕКТРОДИНАМИКА И ОПТИКА
§ 5.3. ПОЛНОЕ ОТРАЖЕНИЕ И НАПРАВЛЯЕМЫЕ ВОЛНЫ
183
s'
\
77
¦к
ь
Рис. 5.21
Ф>Ф
\
Ф=Ф*
У\Л/\/\/\А
выступает как волновод — структура, направляющая волновой
процесс.
Как и в случае полого волновода, для пояснения процесса мож-
можно привлечь лучевые схемы (ср. рис. 5.17). Обратимся к рис. 5.22,
па котором показано несколько стадий направляемого волнового
процесса, соответствующего второй //-волне (рис. 5.216) диэлект-
диэлектрического слоя: взято d = 1 мм и е = 9. Для изображения сверху
/ = 23,497 ГГц; при этом ф = 60° > ф*; вне слоя происходит быст-
быстрое убывание поля (картина магнитных силовых линий показана
справа). Далее (во втором ряду) /=13,02 ГГц и ф = 40°>ф*;
внешнее поле убывает существенно медленнее, что заметно и по
картине силовых линий, которая свидетельствует также об увели-
увеличении длины волны Л (пространственный период направляемой
волны). Наконец, ф = ф* = 19,48°; поле вне слоя уже не имеет
поверхностного характера, оно является обыкновенной однородной
волной, распространяющейся вдоль слоя; это видно и по картине
магнитных силовых линий справа; слева на лучевой схеме показа-
показано, что преломленный луч параллелен границе раздела сред; Л = X
для внешней среды. Это имеет место при / = 7,578 ГГц, данная
частота является критической. При / г? /кр (ф ^ ф*) рассматривае-
рассматриваемая направляемая волна «разрушается» или, как еще говорят, «вы-
«высвечивается» во внешнее пространство. Снизу на рис. 5.22 показа-
показана лучевая схема для ф = 10° < ф*; видны преломленные лучи.
На рис. 5.23 аналогичные стадии показаны для случая основ-
основной //-волны того же слоя (ср. рис. 5.21а). Углы имеют те же
значения: 60°, 40° и 19,48° = ф*. Соответствующие им частоты
равны: 9,202 ГГц, 3,694 ГГц и, наконец, частота, равная нулю.
Дело в том, что критическая частота в данном случае равна нулю:
волна не имеет отсечки.
Для плоского диэлектрического волновода нетрудно вывести
следующую формулу критических частот:
<) = -Т-17==тт=-- <5'88)
ВЫВОД. Поскольку критические частоты со = со^ соответст-
соответствуют условию ф = ф*, при котором •& = 90°, то из формул Френеля
E.42) и E.43) следует: рх = р,, = 1, т. е. i|>x = г|)ц = 0. При ф = ф*
вне слоя в направлении у распространяется обычная однородная
волна, а следовательно, на границе продольная компонента (Ну
или Еу в зависимости от типа поляризации) утрачивается. Соглас-
Согласно E.76) и E.78) это будет, если
sin(/ciz cos ф*)= 0,
E.89)
Рис. 5.22. (ЭВМ)
z = 0, z = —d. При z = 0 условие заведомо выполнено, а второе
требование дает:
k\d cos у* = пп, п = 0, 1, ... E.90)
184
ГЛ. 5. ЭЛЕКТРОДИНАМИКА И ОПТИКА
Учитывая, что
coscp* = И — sin2cp* = Vl —{k2/kiJ
E.91)
и со = сокр, из E.90) получаем формулу E.88). ¦
Значение п = 0 относится к низшей Я-волне (рис. 5.23) п низшей
Е-водне. Как видно из E.88), со^ = 0, причем этот вывод следует
о о о о
р=ф*
u=ukp=0
Рис. 5.23. (ЭВМ)
и из промежуточного соотношения E.90). Действительно, если
п = 0, то это равенство удовлетворяется только при ki = 0.
Рассмотренный нами идеальный диэлектрический волновод в ви-
виде бесконечного слоя представляет собой хорошее приближение к
некоторым пленочным волноводам, используемым в интегральной
оптике. Для оптики, где частоты весьма велики, имеет важное зна-
значение тот факт, что даже в случае относительно толстой пленки
(d»A) можно не допустить существования высших волн (п>1).
Для этого, как следует из E.88), надо погрузить пленку в среду
с близкой оптической плотностью. Чем ближе показатели прелом-
преломления первой и второй сред щ = Vei^i и п2 = Уе2ц2, тем выше кри-
критические частоты. Если же удалось выполнить условие @$ > ю.
то в слое будет распространяться только низшая волна той или
иной поляризации.
§ 5.4. ДЕЙСТВИЕ ПРОВОДЯЩИХ ГРАНИЦ 185
§ 5.4. Действие проводящих границ (А)
5.4.1. Поверхностный эффект и граничный импеданс. Вернемся
к одному из следствий второго закона Снеллиуса (см. п. 5.1.5)',
согласно которому при \к2\ > к\ любые лучи в первой среде порож-
порождают во второй преломленный луч, уходящий почти по нормали.
Е,Н
Рис. 5.24
Это значит, что всевозможные поля в первой среде вызывают во
второй процесс, близкий к плоской однородной волне, фронт кото-
которой параллелен границе. Когда вторая среда — проводник, этот про-
процесс относительно быстро затухает, что называется поверхностным
Таблица 5.1
Глубина проникновения Д° [мкм] = Л///[ГГц] и поверхностное
сопротивление йпр[Ом] = В~1//[ГТц].
Металл
Серебро
Медь отожженная
Алюминий
Латунь
А
2,031
2,090
2,675
4,180
в-ю9
8,019
8,250
10,560
16,500
Металл
Железо
Олово
Свинец
Ртуть
А
5,033
5,400
7,264
15,576
В.109
19,869
21,314
28,679
61,494
эффектом, а также скин-эффектом. Выше в п. 4.1.4 уже было най-
найдено расстояние А0, на котором поле в проводнике уменьшается
в е раз:
E.92);
В данном случае расстояние Д° отсчитывается по нормали в глубь
проводника (рис. 5.24а) и называется глубиной проникновения.
Для распространенных металлов формула E.92) приведена к со-
соотношению А0 [мкм] = А/У/ [ГГц] в табл. 5.1.
186
ГЛ. 5. ЭЛЕКТРОДИНАМИКА И ОПТИКА
Пример 2. В случае меди при частоте / = 10 ГТц, как легко найти
из табл. 5.1, А0 = 0,66 мкм. На расстоянии 10 А0, т. е. в данном случае всего
лишь па глубине 6,6 мкм поле уменьшается в ехрA0) я; 22 026 раз. Это значит,
что в смысле экранирующего действия столь топкая пленка практически рав-
равноценна бесконечной толще металла. ¦
Хотя подобные рассуждения относятся — в строгом смысле — к
плоским границам, они применяются на практике к границам ре-
реальных проводящих тел, пока все радиусы кривизны поверхности
значительно больше глубины проникновения Д°. Пусть при выпол-
выполнении этого условия некоторая проводящая оболочка (рис. 5.246)
ограничивает область V, в которой рассматривается поле Е, Н. Ес-
Если оболочка — не слишком топкая (например, нигде не тоньше
10Д°), то ее поверхность S действует подобно границе сплошного
проводника: волна, уходящая вглубь, затухает, «не успевая» дойти
до внешней границы (от которой должно произойти отражение).
Значит, влияние проводника здесь определяется лишь его границей
и не зависит от занимаемого им объема.
Эти рассуждения наводят на мысль, что влияние проводника во
многих случаях можно учесть при помощи некоторого граничного
условия. Поскольку тангенциальные компоненты векторов Е и Н
па поверхности проводника непрерывно переходят в поперечные
компопенты поля уходящей в глубь волны, соотношение между
ними дается формулой D.27). Запишем
[HraT, v'o],
E.93)
где v0— орт внутренней нормали (v0 = z0) и согласно D.48),
D.49)
Wnp =A + ?) Усо[гоМ-/20 = A + г)/оД°, E.94а)
или
Wnp = RnV + iXuv, Rap = Хпр — 1/оД°. E.946)
Мы видим, что сформулировапо импедансное граничное условие
(ср. E.85)) и Wnv играет роль поверхностного импеданса. Равен-
Равенство E.93) называется приближенным граничным условием Леон-
Леонтовича.
Заметим, что поскольку при о -*¦ °° волновое сопротивление И^пр
исчезает, граничное условие Леонтовича в случае идеального про-
проводника переходит в известное условие Ех = 0.
Пример 3. Рассмотрим плоский проводящий слой (рис. 5.25а), на обеих
сторонах которого напряженность электрического поля имеет одно и то же
значение: Em(d) = Em(—d) = Emt. Поле внутри слоя представляет собой на-
наложение двух однородных волн, направленных внутрь от обеих границ:
Ёт — xo(Ae-ihz + Beihz).
Внося сюда z = d и z = —d, а затем приравнивая результаты, получаем, что
А = В. Отсюда Ет = хо2Л cos kz и Emt = xo2^4 cos kd. Поэтому окончательно
cos kz : • cos kz
Em ~ EmT mc h,l i im ~ a^mxrnahrl' E.J5)
§ 5.4. ДЕЙСТВИЕ ПРОВОДЯЩИХ ГРАНИЦ
187
где использовано материальное уравнение A.69). Входящее сюда комплексное
волновое число к согласно D.47) и D.49) есть
E.96)
к = A - ?)У(оц0Цо72 = A -
На рис. 5.25 приведены также результаты конкретных расчетов на основании
E.95). Взят слой меди (а = 5,8 • 107 См,/м) толщиной 2d = 12 мкм и для частот
от 0,05 до 8,1 ГГц вычислено распределение поля (в); для сравнения тут же
* /
' /
'///,
't.
'0
E(-d)
V//////
¦ z E(d)
jf-d)
Jfd)
l А°,мнм
б=5,в-7О7См/м
6 f,rru
4 -
Рис. 5.25
дан (б) график частотной зависимости А0. Когда d S> A°, что соответствует при-
применимости граничного условия Леонтовича, идущие от обеих границ волны
затухают, практически не взаимодействуя. При этом параметр А0, действитель-
действительно, есть глубина, на которой поле уменьшается в е раз. Когда d и А0 — одного
порядка, этот смысл утрачивается. При d <K А0, можно сказать, пропадает по-
поверхностный эффект: распределение близко к равномерному; оно становится
равномерным при постоянном токе (м->-0), поскольку при этом А°->-оо.
В случае применимости граничного условия Леонтовича обычно говорят
о сильном поверхностном эффекте. ¦
5.4.2. Поглощение при сильном поверхностном эффекте. Чтобы
найти мощность, поглощаемую проводником, или мощность потерь
Рп, падо вычислить входящий в него из внешней среды поток
энергии. Таким образом,
Рп = Re f tiv, ds = - Re f П ds E.97)
s s
(v' — направление внутренней нормали). Здесь имеется в виду
средняя величина (см. п. 3.3.1).
Ограничиваясь случаем сильного поверхностного эффекта, ис-
используем граничное условие Леонтовича E.93). При этом
IIv' = -ГГ [Emx, HmxJv/ = у [WnplHmx, Vo], HmtJv/ = о Hmt
188
ГЛ. 5. ЭЛЕКТРОДИНАМИКА И ОПТИКА
§ 5.5. ЛОКАЛЬНО ПЛОСКИЕ ВОЛНЫ И ГЕОМЕТРИЧЕСКАЯ ОПТИКА 189
и, следовательно,
Р — —— \ Н2 Ля — ^np Г
гг2
E.98)
Будем рассматривать ток в проводнике. Поскольку j = оЕ, плот-
плотность тока j, как и поле, быстро убывает в глубь проводника. На-
Напомним, что существует представление об идеальном поверхностном
токе, который не занимает объема (см. п. 1.4.1). Ток в реальном
проводнике в случае сильного поверхностного эффекта удобно от-
относить к линии, которую он пересекает на поверхности, т. е. услов-
условно рассматривать как поверхностный. На рис. 5.26а линия I орто-
ортогональна направлению тока. Ток Д/т, проходящий через всю тол-
толщу проводника на участке М, вычисляется как
оо оо
Д/га = М j }m dv' = Mo J Em dv',
где Ёт = Emxex])(—ikv'). Поэтому согласно определению A.82)
Привлекая формулы E.93) и E.96), получаем
Г\т = [Hrat, Vo] = [Vo, HmT].
E.99)
E.100)
Интересно отметить, что полученный результат формально воспро-
воспроизводит второе из равенств A.90), которое относится к случаю
идеального поверхностного тока на экранирующей границе. В рас-
рассматриваемой задаче мы переходим к такому случаю при о -*¦ °°,
когда Д° -»¦ 0 и ток, действительно, становится поверхностным, не
проникая в идеальный проводник. Это идеальный поверхностный
эффект.
Сопоставляя E.100) и E.93), видим, что
Emx = W^m. E.101)
Таким образом, поверхностный импеданс Wap получает новую ин-
интерпретацию.
Возвращаясь к выражению мощности потерь E.98) и учитывая
соотношение E.100), получаем следующую формулу:
а = ~2 #пр J Ц
E.102)
Если бы ток был равномерно распределен в слое глубиной Д°, мы
получили бы точно такой же результат. Дело в том, что /?пр E.946)
есть сопротивление единичного квадрата проводящего листа тол-
толщиной Д° (рис. 5.266). Эти соображения объясняют смысл слов
глубина проникновения.
Пример 4. Пусть ток проходит по проводнику поперечного сечения S±
с контуром 2>х (рис. 5.26в). В условиях сильного поверхностного эффекта вы-
вычислим мощность потерь, отнесенную к единице длины проводника ра =
= dPaldz. Согласно E.102) на отрезке проводника Дг поглощается мощность
АР,
1 Д f
: = ~2 Лпр J
Переходя к пределу при Дг -»- 0, находим:
E.103)
Если можно говорить о падении напряжения на единицу длпны проводни-
проводника U', то U'm = Emz = ЕтХ — величина постоянная. Тогда согласно E.101)
постоянна и плотность тока цт. В этом случае из E.103) получаем
Рп = ТЯ'7т.
1
Тт =
E.104)
где Я' — погонное сопротивление проводника, а I — длина контура Lj_ его по-
поперечного сечения (рис. 5.26в). ¦
§ 5.5. Локально плоские волны и геометрическая оптика
5.5.1. Локально плоские волны и понятие эйконала (А). Если
фронт волны, представляющий собой некоторую поверхность
ф(х, у, z) = const D.13), в малой области пространства близок к
плоскому, волну называют локально плоской (см. п. 4.0.3).
Будем рассматривать некоторое электромагнитное поле, напря-
напряженности которого характеризуются комплексными амплитудами
Нт=Э1е-1ф.
E.105)
190
ГЛ. 5. ЭЛЕКТРОДИНАМИКА И ОПТИКА
Если компоненты векторов g и 31 изменяются в зависимости от
координат значительно медленнее, чем ср, то уравнения Максвелла
C.34) при jm = 0 с высокой степенью точности сводятся к сле-
следующим:
[31, Vcp] = meoeS, [?ф,6] = шцоцЭ1. E.106)
ВЫВОД. Используя тождество A.27), запишем
rot Ет = е-" rotg + [Ve-'\ g] = е"'ф rotg - ге-'^ф, g]
и аналогично преобразуем rot .И™. Это приводит уравнения C.34)
при jm — 0 к следующей форме:
E.107)
rot g — i Рф, g] = — гсоцоцЗЬ.
Чем медленнее меняются компоненты векторов g и 31 в простран-
пространстве, тем с большим основанием можно в E.107) пренебречь чле-
членами rot g и rot 31. Это приводит к уравнениям E.106). ¦
Обсудим полученные уравнения E.106), заметив сначала, что
в случае плоской однородной волны они переходят в точные соот-
соотношения D.27), D.28). Это понятно, поскольку в этом случае g
и 31 вообще не зависят от координат, так что rotg=0 и rot3l=0.
Как видно из E.106), векторы g, 31 и Vф взаимно перпенди-
перпендикулярны и образуют правую тройку векторов: такую же тройку
образуют векторы Е, Н и ^ф. Это значит, что Е и Н касательны
поверхности ф = const. При вещественном ф напряженности Е и Н
синфазны, а рассматриваемое поле есть не что иное, как волна с
фронтом ф = const. Вектор Пойнтинга П = [Е, Н] направлен, как ^ф;
т. е. по нормали к фронту (рис. 5.27а). Очевидно, что орт нормали
v0 есть
/|| E.108)
Прежде чем дать окончательную характеристику анализируемо-
анализируемого решения, сосредоточим внимание на функции ф, которая назы-
называется эйконалом. Из E.106) непосредственно получаются урав-
§ 5.5. ЛОКАЛЬНО ПЛОСКИЕ ВОЛНЫ И ГЕОМЕТРИЧЕСКАЯ ОПТИКА 191
нения:
[[?Ф, 6], Vy]=--k2S>, [уф, [31, Уф]] = fcs0i E.109)
(среда предполагается изотропной, но может быть неоднородной).
Взяв одно из этих равенств и применяя формулу A.6), приходим
к так называемому уравнению эйконала
= /С21 E.110)
E.111)
которое в декартовых координатах имеет вид
I]2 = к*.
5ф\2 /5ф
Уравнение эйконала есть основное уравнение геометрической оп-
оптики.
Вернемся к обсуждению характера электромагнитного поля
E.105), которое — по нашему требованию — должно с высокой точ-
точностью описываться при помощи функций g, 3i и ф, удовлетворя-
удовлетворяющих уравнениям E.106) и полученному из них уравнению эйко-
эйконала E.110).
Уже было показано, что это волна с фронтом в виде поверхно-
поверхности ф = const. Учитывая E.110), видим, что согласно E.108)
vo/c = k, E.112)
где использовано представление о волновом векторе к E.9). При
этом, взяв некоторую локальную систему координат, имеем
e-i(P = exp \iq> @) + i p- v + . . .1 ж e-i4>(o)e-iftv?
L v=o J
где множитель ехр[гф(О)] можно рассматривать в качестве неопре-
неопределенного коэффициента. Это значит, что согласно предыдущему:
Ёт = g?~i
iftv
] . .
Em = W [Hn, v0], W
= у ^
У еое
E.113)
(cp. D.32), D.27)). Мы видим, что локально волновой процесс опи-
описывается как плоская однородная волна.
5.5.2. Оптическая длина луча. Принцип Ферма (А). В геомет-
геометрической оптике поверхности ф = const рассматриваются как орто-
ортогональные поверхности к семействам лучей (рис. 5.276). В силу
E.112)
E.114)
dw , со
-х = к = — п.
dv с
Поэтому, интегрируя вдоль луча от А до В, получаем следующее
выражение оптической длины данного отрезка луча:
в в
k dv =-^ § п dv = у (В) — у (А). E.115)
192
ГЛ. 5. ЭЛЕКТРОДИНАМИКА II ОПТИКА
5.5. ЛОКАЛЬНО ПЛОСКИЕ ВОЛНЫ II ГЕОМЕТРИЧЕСКАЯ ОПТИКА
193
Это разность фаз начальной и копечной точек. В случае однород-
однородной среды (п = const)
Ф (В) — ф (А) = kd = — nd,
E.116)
Рис. 5.28
где d — длина пути вдоль луча.
В п. 5.5.3 будет показано, что лучи в однородной изотропной
среде всегда — прямые линии. Пока отметим, что, например, в слу-
случае плоской волны последовательные положения фронта — парал-
параллельные плоскости, а лучи — ортого-
ортогональные прямые. Если же распростра-
распространяется сферическая волна, то лучи —
радиальные прямые.
Лучи являются векторными (сило-
(силовыми) линиями градиента эйконала
^ф, а следовательно, и вектора Пойн-
тинга П. Поэтому их естественно на-
наносить с густотой, отображающей ин-
интенсивность, а точнее, модуль плотно-
плотности потока энергии П. Эта возможность
нередко используется при построении лучевых картин.
Покажем, что из всех возможных линий, соединяющих точки А
и В, луч — это такая линия, вдоль которой оптическая длина ми-
минимальна, т. е.
в в
\ ndv = min J ndl, E.117)
A A
где слева интегрирование производится по лучу, а справа имеются
в виду всевозможные мыслимые пути (v и I соответственно на
рис. 5.28в). Сформулированное положение известно под названием
принципа Ферма.
ВЫВОД. Для доказательства принципа Ферма рассмотрим
определенный интеграл
в
J Уф dl = Ф (Я) - ф D). E.118)
А
Результат не зависит от пути интегрирования, который может сов-
совпадать или не совпадать с лучом. Это свойство было установлено
еще в п. 2.1.2, когда формально аналогичное выражение анализи-
анализировалось при обсуждении свойств электростатического потенциала.
Если путь интегрирования не совпадает с лучом (рис. 5.28в),
то
И в а
\ Уф dl = I k dl = — \п cos ос dl,
где coscc=(vo, т0) (to и Vo — касательные орты для пути интегри-
интегрирования и луча соответственно). Взяв, в частности, путь интегри-
интегрирования вдоль луча, следует положить cos a = 1. Но интеграл
E.118) от пути не зависит, поэтому
в в
| п cos a dl = 1 ndv.
А А
Отметим теперь, что существование множителя cos a =S! 1 может при-
привести только к уменьшению интеграла слева. Убрав его, имеем
в в
ndv, E.119)
что эквивалентно соотношению E.117). ¦
Пример 5. Покажем, что из принципа Ферма следует, в частности, пер-
первый закон Снеллиуса. При отражении луча от плоскости S оптическая длина
луча между точками А и В (рис. 5.28) равна геометрической длине I = U + h,
умноженной на к. Будем искать минимум этой величины, опустив несущест-
несущественный множитель к. Как видно из рис. 5.28, I = У/г2 + с2 + У^2 + (d — сJ. Вы-
Вычислив dl/dc, легко убедиться, что эта величина обращается в нуль при с = d/2,
причем получено условие минимума I. Поэтому ф = ф' при условии, что опти-
оптическая длина луча минимальна. ¦
5.5.3. Лучи в неоднородных средах (А). Распространение ло-
локально плоских волн в неоднородных средах описывается при по-
помощи криволинейных лучей. Причину искривления луча нетрудно
Рис. 5.29
понять, рассмотрев сначала многократное преломление в среде, со-
состоящей из однородных слоев, различающихся по оптической плот-
плотности (рис. 5.29а). Взято п\ > т >Щ >n4>ns < п6 < пт, характер
ломаной вполне определяется вторым законом Снеллиуса E.13). Ес-
Если «сгладить» закон изменения п в направлении нормали к грани-
13 В. В. Никольский, Т. II. Никольская
194
ГЛ. 5. ЭЛЕКТРОДИНАМИКА И ОПТИКА
цам слоев, взяв некоторую непрерывную функцию ra(z), вместо
ломаного появится искривленный луч (рис. 5.296).
Радиус кривизны луча на некоторой «высоте» z (рис. 5.296)
вычисляется следующим образом:
R = —
(dn/dz) sin О '
E.120)
ВЫВОД. Рассмотрим простейший вывод формулы E.120); с не-
необходимой строгостью вопрос будет обсуждаться в п. 5.5.4.
На рис. 5.30 показано два положения фронта локально плоской
волны ф1 и фг (штриховые линии) при ее распространении в среде,
оптическая плотность которой
изменяется в направлении z.
При данном смещении фронта
на разных уровнях будут прой-
пройдены различные пути. В част-
частности, пути AZi и AZ2 (вдоль
лучей vi и V2) равпы:
» 7 «" Т
М2=-
Рис. 5.30
dn
"dz
\z ~\-
где т — время смещения фронта волны. Дело в том, что па нижнем
уровне фазовая скорость есть v(z) = c/n, а при вычислении
v(z + Az) надо учесть приращение показателя преломления. Из
подобия треугольников на рис. 5.30 следует
2
R '
где R — радиус кривизны луча. Отсюда с учетом выражений &1\ и
А?2 получаем
Д =
Az/sin О
(dn/dz) sin О '
что совпадает с E.120). ¦
Рассмотрим некоторые следствия из формулы E.120).
При переходе к однородной среде (dn/dz -*-0) согласно E.120)
Д-»-«>: радиус кривизны неограниченно возрастает, т. е. луч ста-
становится прямым.
Учтем, что в силу записи (и выполненного вывода) формулы
E.120) радиус кривизны R считается положительным, если кри-
кривая (луч) обращена выпуклостью в сторону возрастания z. Поэтому
луч уклоняется вниз при уменьшении показателя с высотой и
вверх — при увеличении. На рис. 5.296 эти два случая соответству-
соответствуют зонам z<z' и z>z'.
§ 5.5. ЛОКАЛЬНО ПЛОСКИЕ ВОЛНЫ II ГЕОМЕТРИЧЕСКАЯ ОПТИКА 195
Искривление лучей, описывающих распространение локально
плоских электромагнитных волн в неоднородных средах, обычно на-
называют рефракцией (слово означает «преломление», но в этом
смысле употребляется редко). В дальнейшем (п. 15.5) мы встре-
встретимся с рефракцией радиоволн в
атмосфере.
5.5.4. Характеристики кривизны
лучей (Б). Малый плоский эле-
элемент Дулуча v (рис. 5.31), заключен-
заключенный между точками М и М', пред-
представим как элемент дуги радиуса R:
Av = aR. Чем меньше угол ос, тем
он ближе к величине Avo/vo = А\'о,
где А\"о — абсолютное значение при-
приращения Avo единичного вектора vo
касательной к лучу (vo=l). В пределе при а-*-0 получаем:
R^dv/dvo, К = Ro/Л = dvo/dv. E.121)
Величина К есть векторная характеристика кривизны луча.
Формальпые преобразования правой части E.121), которые мы
опускаем (см., например, [Г.2, В.6]), позволяют написать:
K = -[vo, rotvo]. E.122)
Поскольку для рассматриваемых нами лучей \оп = V<p (поле потен-
потенциально), как это следует из E.112), то в силу A.22)
rotv0rc = 0. E.123)
Поэтому, используя векторное тождество A.27), имеем
rotv0 = -4-(Vrc, v0]. E.124)
Внося E.124) в E.122), получаем следующее уравнение, характе-
характеризующее оптические лучи в неоднородной среде:
= i-[vo,[Vn,vo]].
E.125)
Если раскрыть двойное векторное произведение при помощи A.6),
то получается другая форма этого уравнения:
K=i-[Vn-vo(voVn)]. E.126)
Наконец, если учесть что
d . dvQ
dv ° ' dv
то из E.126) получаем еще одну эквивалентную форму:
Tv (V^) =
E.127)
13*
196
ГЛ. 5. ЭЛЕКТРОДИНАМИКА И ОПТИКА
Нетрудно убедиться, что ранее полученная формула E.120) вы-
вытекает из найденных общих соотношений. Пусть показатель пре-
преломления зависит от одпой координаты z. При этом Vn=zodn/dz
и Vozo = cosf3i (рис. 5.296). Делая соответствующую подстановку в.
E.126), пишем,
?r = — —^(zo— v0cos#). E.128)
it л dz
Чтобы получить отсюда формулу E.120), падо лишь возвести ле-
левую и правую часть в квадрат, а затем извлечь корни из получен-
полученных скалярпых величин (взяв справа знак минус, что отвечает
принятому нами выбору знака при определении радиуса кривизны).
Продолжая рассматривать среду, неоднородную только в направ-
направлении z и учитывая, что при этом \Уп, zo] = 0, умножим обе части
E.127) векторно на z0. В результате получаем
d[von, zo]/dv = O, n[vo, zo] = const E.129)
(zo = const) или (рис. 5.296):
n cos т> = const, E.130)
что можно рассматривать как обобщение второго закона Снеллиусаг
для любых двух касательных к лучу, составляющих углы •fl'i и ^г,
согласно E.130): «i sin •r>i = ai2 sin -r>2-
5.5.5. О пределах применимости геометрической оптики (Б).
Переход от уравнений Максвелла к уравнениям E.106) и, далее,
к уравнению эйконала E.110) был проведен в предположении, что
rotS! ,J^M-.«1,
или
|[Vcp,b
I rot S
I [31, Vcp] |
ro
t 3i I
«1.
E.131)
E.132)
Проще всего воспользоваться этими неравенствами, когда неко-
некоторое поле Е, Н уже известно и представлено в форме E.105).
Тогда можно сказать, правомерно ли трактовать поле с позиций
геометрической оптики. Обычно такая оценка переносится на род-
родственные поля, в результате чего выявляется класс электромагнит-
электромагнитных полей, допускающих геометрооптическую трактовку.
Неравенства E.131), E.132) дают информацию о допустимой
быстроте изменения векторных амплитудных коэффициентов S и
31 в представлении поля E.105). Перепишем E.132) в форме:
X 1 rot S
E.133)
, X I rot 31
.. ,_- , 2л W~-l\t
(проницаемости считаем вещественными); величины W я % = '¦
определяем обычным образом, но полагаем изменяющимися в про-
пространстве вместе с е и ц. Поскольку в числителях E.133) фигури-
§ 5.5. ЛОКАЛЬНО ПЛОСКИЕ ВОЛНЫ И ГЕОМЕТРИЧЕСКАЯ ОПТИКА 197
руют первые производные компонент S и 31 по координатам, то
неравенства E.133) будут заведомо выполнены, если
1 1
2л W\h\
«1, ^
1_
2л
dh
«1,
E.134)
где е и h — любые компоненты S и 31, а % — любая пространствен-
пространственная координата. Заметим, что (де/д%)К и (dh/d%)K это приращения
величин е и h на расстоянии К.
Требуемое слабое изменение поля мыслимо только при соответ-
соответственно слабом изменении свойств среды. Таким образом, в случав
неоднородных сред представления геометрической оптики приме-
применяют, когда относительные изменения е и и. на расстояниях поряд-
порядка длины волны малы.
УПРАЖНЕНИЯ
1. Выписать выражения комплексных амплитуд и мгновенных значений
векторов поля в случае плоской однородной волны, поляризованной в плоско-
плоскости z = const, если волновой вектор составляет угол 30° с плоскостью
х = const.
2. Волновой вектор плоской однородной волны составляет одинаковые углы
со всеми осями декартовой системы координат. Записать выражение эйконала.
3. Найти предельные углы полного отражения для ряда диэлектрических
сред (см. табл. 1.2), граничащих с воздухом (взять парафин, стеатит, плав-
плавленый кварц, тптанат бария).
4. Продолжая рассматривать границы раздела тех жо диэлектриков (см.
упражнение 3) и воздуха, определить углы Брюстера.
5. Угол падения волны на поверхность моря изменяется в пределах 0 •+¦
-г- « 90°. В каких пределах изменяется угол преломления?
6. Построить график изменения амплитуды магнитного поля внутри мед-
медного листа, на который нормально падает волна с амплитудой электрического
поля 1 В/м при частоте 20 ГГц.
7. Распространяясь внутри диэлектрика, волна падает на границу с тзозду-
хом под углом 45° к нормали. Взяв/= 10 ГГц, построить график изменения ам-
амплитуды поля в направлении нормали в воздухе для случаев сред, указан-
указанных в упражнении 3.
8. Объяснить, почему фазовая скорость неоднородной волны, распрост-
распространяющейся вдоль границы раздела диэлектриков, одна и та же в обеих
средах.
9. Исследовать отраженную п преломленную волны, возникающие при на-
наклонном падении на границу раздела сред волны круговой поляризации.
10. Выписать выражения комплексных амплитуд векторов поля и проверить
выполнение граничных условий в случае, когда волна падает на границу раз-
раздела диэлектриков под углом Брюстера.
11. Выписать выражения комплексных амплитуд векторов поля в оптиче-
оптически менее плотной среде, когда на ее границу волна надает под предельным
углом полного отражения; рассмотреть оба вида поляризации.
12. Полное отражение от границы несовершенного диэлектрика невозмож-
невозможно. Показать это математически и объяснить физическую причину.
13. Плоский полый волновод образован идеально проводящими плоскостя-
плоскостями, находящимися на расстоянии d = 3 см. Найти первые пять критических
частот для II- и столько же для ?-волн. Внутренняя среда — воздух.
14. Плоский диэлектрический волновод представляет собой расположен-
расположенный в воздухе слой диэлектрика толщиной d = 3 см с диэлектрической про-
198
ГЛ. 6. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В СТРУКТУРАХ
пнцаемостью е = 1.1. Найти критические частоты II- и ?-волн, как в преды-
предыдущем примере.
15. Можно ли применять формулу E.104) для определения погонных по-
потерь в медном проводе диаметром 0.1 мм при / = 1 Мгц, 1 Ггц. 10 Ггц?
К). Написать выражении эйконала для плоской волны, распространяющей-
распространяющейся в произвольно:.! направлении: для сферической волны.
17. Какое значение принимают левые части неравенств E.131) и E.132)
в случен плоской однородной волны?
18. Выписать выражения плотности поверхностного тока и поверхностного
заряда на идеально проводящих плоскостях, образующих полый волновод.
Глава 6
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В СТРУКТУРАХ
§ 6.0. Используемые математические понятия и символы (А)
6.0.1. Однородное уравнение Гельмгольца. Задачи для продоль-
продольно-однородных структур. В п. 4.1.2 уже приходилось решать одно-
однородное уравнение Гельмгольца. Однако анализировался процесс,
зависящий только от одной декартовой координаты, так что факти-
фактически фигурировало обыкновенное дифференциальное уравнение
D.24). В дальнейшем будут рассматриваться существенно более
сложные электромагнитные процессы. В качестве подготовки к это-
этому мы предварительно обсудим некоторый класс решений однород-
однородного скалярного уравнения Гельмгольца D.17)
v-9Mm + кЧт = 0. F.1)
Пусть пространственная структура, для которой ищется решение
йт, является однородной в направлении z, т. е. все ее сечения
плоскостями z = const тождественны. Примеры таких структур
показаны на рис. 6.1: функ-
функция и рассматривается внут-
внутри и (или) вне обобщенного
цилиндра (а) или при нали-
наличии нескольких аналогичных
подобластей (б). Параметр
к может принимать разные
постоянные значения в под-
подобластях; па их границах йт
рис сi удовлетворяет некоторым ус-
условиям. Например, могут
рассматриваться решения уравнения F.1) внутри цилиндрической
области (рис. 6.1а) при граничном условии йт = 0.
Предположим, что решение мт можно представить в виде про-
произведения двух неизвестных функций разных аргументов:
йт(х, у, z) = T(x, y)Z(z). В результате подстановки этого пред-
§ 6.0. ИСПОЛЬЗУЕМЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ II СИМВОЛЫ 199
ставления в F.1) получаем:
4
ду"
Разделим все члены на TZ и введем обозначение
Ох а у
(оно будет использоваться и в дальнейшем). Теперь имеем
F.2)
F.3)
Говорят, что в этом равенстве разделены переменные: оба сла-
слагаемых — функции разных аргументов. Поэтому, в частности, из-
изменяя z, нельзя повлиять на первый член, и он наверняка сохра-
сохраняет при этом постоянное значение. Но ввиду равенства F.3) это
означает, что остается постоянным и второй член, т. е. он равен
некоторой константе. Обозначим ее Г2, т. е. Z"/Z=r2. Мы видим,
что первый член равен противоположной константе —Г2. Рассуж-
Рассуждения приводят, таким образом, от F.3) к двум независимым урав-
уравнениям:
л7
—г + r-z = о,
dz
F.4)
- Г2. F.5)
Если решения Z ж Т найдены, то тем самым найдено и решение
первоначального уравнения Гельмгольца F.1) u = TZ. Использо-
Использованный прием называется методом разделения переменных. В гл. 7
мы будем его широко применять, доводя до конца, при решении
задач о волноводах.
В данном случае существенно, что удалось выяснить некоторые
общие черты интересующих пас решений уравнения Гельмгольца
в классе продольно-однородных структур. Действительно, вид ре-
решений обыкновенного дифференциального уравнения F.4) хорошо
известен. Как и в п. 4.1.2, предпочтем экспоненциальную форму
Z = Аехр(—iTz) + В ехр(гГг), где А и В — неопределенные кон-
константы. Поэтому
Um
x, y)eiT
F.6I
Напомним, что по форме два члена решения — не что иное, как
комплексные амплитуды волн. Это вообще неоднородные волны,
поскольку их амплитуды зависят от поперечных координат х, у.
Если Г — вещественная величина, то она играет такую же роль,
200
ГЛ. 6. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В СТРУКТУРАХ
как к в D.3). При комплексном Г имеем
Г = Г-гГ", Г' = ©К = 2я/Л
F.7)
(ср. D.11)), где А — длина волны, уф — ее фазовая скорость,
а Г"—коэффициент затухания (предполагается, что Г" >0,
Г" >0).
Величина Г называется продольным волновым числом, а также
постоянной распространения. Введенный в F.5) параметр % на-
называют поперечным волновым числом.
Постоянная распространения Г может оказаться и чисто мнимой
величиной. Такой случай нам известен из п. 5.3.2. Вообще в п. 5.3
при анализе неоднородных волн уже встречались некоторые поня-
понятия, введенные теперь с более общих позиций.
6.0.2. Краевые (граничные) задачи для двумерного уравнения
Гельмгольца. Собственные функции и собственные значения. Мож-
Можно сказать, что трехмерную задачу о распространении волн в про-
долыю-однородной структуре мы свели к рассмотрению двумерного
уравнения Гельмгольца F.5). При этом неизвестна не только функ-
функция Т(х, у), но и параметр %2. Само по себе уравнение F.5) не
имеет определенных решений. Необходимо поставить краевую (гра-
(граничную) задачу (ср. п. 2.0.4). Пусть, например, Lx — контур по-
поперечного сечения цилиндра на рис. 6.1а. Первой краевой задачей
для двумерного уравнения Гельмгольца назовем следующую:
tfT = 0, Т = 0 на L,
F.8)
Пусть это задача внутренняя (т. е. решение Т ищется внутри ци-
цилиндра). Тогда опа имеет бесконечное множество решений {Тп},
каждое из которых реализуется при определенном значении пара-
параметра "/2. Решения Тп называются собственными функциями, а со-
соответствующие пм значения %п параметра %2 — собственными зна-
значениями. Нумерация производится в порядке неубывания собствен-
собственных значений: уХ ^ У% ^ ¦ • ¦ Если разным собственным функциям
соответствуют одинаковые собственные значения, то последние на-
называются вырожденными.
Мы не можем здесь дать теорию краевых задач F.8) и анало-
аналогичных им. Однако в гл. 7 будут решаться конкретные краевые
задачи, приводящие к нахождению систем собственных функций и
собственных значений. Этот материал позволит составить представ-
представление об их свойствах, что важно для понимания электромагнит-
электромагнитных волновых процессов.
Сформулируем вторую краевую задачу для уравнения F.5):
+ х2Т = 0, dT/dv = 0 па L±.
F.9)
Эта задача также порождает систему собственных функций, кото-
которым отвечают собственные значения.
§ 6.1. ПРОДОЛЬНО-ОДНОРОДНЫЕ СТРУКТУРЫ
201
Как для первой, так и для второй краевой задачи легко полу-
получить следующее интегральное соотношение:
.1 \grad Г fds
у.2 = 8-±-
(НЛО)
Для этого обе части уравнения уравнения F.5) умножаются на Т*
и производится интегрирование по поперечному сечению S± ци-
цилиндра (см. рис. 6.1а). Далее применяется двумерный аналог тео-
теоремы Грина A.35) с заменой V-+S±, S -»- L± при ф = ф* = Т.
После этого остается только учесть граничное условие первой или
второй задачи, что приводит к уничтожению контурного интеграла.
Из F.10) следует, что собственные значения рассматриваемых
задач неотрицательны.
Если фигурирует несколько подобластей (см. рис. 6.16), и для
каждой из них к принимает свое значение kt, то соответственно
этому в F.5) возникают разные поперечные волновые числа:
Х2 = *2-Г F.11)
(имеются в виду номера подобластей). Постоянная распростране-
распространения Г является общей для всей продольно-однородной структуры:
в противном случае было бы невозможно связать решения в под-
подобластях граничными условиями на поверхностях их раздела. Со-
Соотношения F.11), фактически, уже использовались выше в п. 5.3.3.
§ 6.1. Электромагнитные волны
в продольно-однородных структурах (А)
6.1.1. Общее представление поля. Продольно-однородные струк-
структуры, понятие о которых было введено выше в п. 6.0.1, в простей-
простейших вариантах уже рассматривались в гл. 5. Продольно-однородной
структурой, направляющей неоднородную волну, может быть, как
мы видели, плоская граница раздела сред. Формирование такой
волны истолковывалось как результат наложения простейших од-
нородпых волн при полном отражении. Этот подход нагляден, но
в сложных задачах нереализуем. Гораздо более удобен другой путь,
основпые черты которого были намечены выше в § 6.0. Следуя ему,
мы с единых позиций рассмотрим в дальнейшем весьма разнообраз-
разнообразные структуры, имеющие важное практическое значение. Некото-
Некоторые из них показаны (в поперечном сечеппи) па рис. 6.2. Это раз-
различные полые волноводы (а) — металлические трубы того или иного
поперечного сечепия; диэлектрические волноводы (б); открытые и
замкнутые структуры с несколькими металлическими элементами
'(в) и ряд других, включая линии передачи, используемые п так
называемых интегральных схемах (ИС) СВЧ (г).
202
ГЛ. 6. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В СТРУКТУРАХ
Согласно п. 6.0.1, любая из компонент векторов Ет и Нт свобод-
свободного электромагнитного процесса в продольно-однородной структуре
может быть представлена в виде F.6). Рассматривая волны одного
направления, оставим первый член суммы (т. е. положим -Й = 0).
у/////////
Г
Рис. 6.2
Таким образом, векторы Ет и Нт выразим в следующем виде:
Ёт=8(х, у)е~*\ Нт=ЗЦх, у)е-"'. F.12)
Подстановка F.12) в однородные векторные уравнения Гельмголь-
ца D.22) приводит к двумерным уравнениям
Vig + х28 = 0, Vl3i + x23i = 0, F.13)
где
(если имеется несколько однородных областей i с разными свой-
свойствами, то столько же раз пишутся уравнения, причем %\ = к\ — Г2)-
Следующий шаг — использование однородных ( jm =¦- 0) уравне-
уравнений Максвелла C.34), которые будут записаны в координатной
форме. При этом учтем, что поскольку продольная зависимость всех
компонент поля описывается множителем ехр(—iTz), дифференци-
дифференцирование по z сводится к умножению на —гГ. Итак, имеем следую-
следующие шесть скалярных уравнений:
fcl lL mx
iVEmy = — i
дЕ„
mx \ / ду
-= to\io\iHmy,
t 1 ii 7Yl1t —^— tUJCrtOiJ 771V Ч
—^ = — iaeoeEmy, F.14)
dEmv дЕтх
st --jy~
§ 6.1. ПРОДОЛЬНО-ОДНОРОДНЫК СТРУКТУРЫ
203
Сосредоточим внимание па первых двух парах уравнений, которые
соединены перекрестными стрелками. Каждая из этих пар есть не
что иное, как система двух линейных алгебраических уравнений от-
относительно двух поперечных компонент векторов Ет и Нт. Решая
их, выражаем все поперечные компоненты через продольные:
Е --i-L
F.15)
Эти формулы удобно свернуть к следующей векторной форме
записи:
5
Г
¦ гмц \i
Emz 5г- rotj. Hmz
г
t^ Emz — i — V±Hmz.
X"
F.16)
Здесь, как и ранее, символ -i- употребляется в качестве знака от-
отбрасывания производных но z; Emt = Emx + Е,„ь. и Н„„ = Итх + Иту.
Выражения F.16) уже не связаны с определенным выбором по-
поперечных координат: вместо хну можно взять произвольные кри-
криволинейные ортогональные координаты в плоскости z = const.
Полученные формулы будут неоднократно применяться при
нахождении электромагнитных полей различных волноводов. Но
сначала используем их для общего анализа решений.
6.1.2. Классы волн. Волны Т. Волна, переносящая энергию
в направлении z, обязательно должна иметь как поперечную элект-
электрическую, так и поперечную магнитную компоненты: в противном
случае Пг = 0. Выражения F.15) или F.16) показывают, что та-
таким свойством может обладать электромагнитное поле с одной
только электрической или только магнитной продольной комиопеп-
той. При этом общее решение может рассматриваться как паложе-
пие двух частных, для одного из которых Ez ?= 0 и Hz = 0, а для
другого Hz Ф 0 и Ег = 0.
Поэтому, рассматривая различные волны в продолыто-одпород-
пых структурах, выделяют класс так называемых Е-волп, илтг
электрических воли, для которых Ег ?= 0 и II\ = 0, и класс 11-воли,
204
ГЛ. 6. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В СТРУКТУРАХ
или .магнитных волн, для которых Hz?=0 и Ег = 0. Вместо симво-
символов Е и Н употребляются также ТМ и, соответственно, ТЕ (говорят
поперечно-магнитные и поперечно-электрические волны).
Более сложные волновые процессы, имеющие как электриче-
электрическую, так и магнитную продольные компоненты, принято называть
гибридными волнами.
Как известно (см. гл. 4), простейшая электромагнитная волна
в свободном пространстве, которое, несомненно, является продоль-
продольно-однородной структурой, совершенно лишена продольных компо-
компонент (Ег = 0, Hz = 0). Она принадлежит классу Т-волн, или по-дру-
по-другому, ТЕМ-волн (говорят поперечно-электромагнитные волны).
Выражения F.15), F.16) допускают существование таких волн
при %2 = 0: они становятся неопределенностями типа 0/0.
Из равенства %2 = 0 вытекает, что
Г = А, F.17)
т. е. любые Г-волны в некоторой среде распространяются с той же
фазовой скоростью, что и плоская однородная волна. Внося %2 = 0
в F.13), получаем следующие двумерные уравнения Лапласа
VlS = O, V2x3i = 0, F.18)
которым удовлетворяют функции поперечных координат 8 и 31
в выражениях F.12) в случае Г-волн. Сами эти выражения при-
принимают вид:
Em = 8e-ftz, Hm=3ie-*z. F.19)
Выявлено два важных свойства Г-волн. Во-первых, они мысли-
мыслимы только в однородных средах, так как равенство F.17) не может
быть выполнено, если к (вместе с е и ц) принимает разные зна-
значения в разных подобластях продольно-однородной структуры.
Во-вторых, поперечное распределение полей в случае Г-волн долж-
должно повторять продольно-однородные (не зависящие от z) статиче-
статические распределения. Действительно, при ш = 0 и при отсутствии
продольной зависимости уравнения D.22) принимают вид F.18).
В каких из показанных на рис. 6.2 структурах могут существо-
существовать Г-волны? Возьмем, например, полые волноводы (см. рис. 6.2а),
полагая сначала их оболочки идеально проводящими. Легко убе-
убедиться, что в этих структурах Г-волн не может быть. Ведь функция
8 в точности совпадает с решением статической задачи, удовлет-
удовлетворяя уравнению F.18) и граничному условию <gx = 0, также вы-
выполняемому в электростатике. Но электростатическое поле внутри
обычной полости в проводнике тождественно равно нулю (см.
п. 2.2.5), следовательно, равна нулю и функция 8. В этих рассуж-
рассуждениях можно было бы исходить также из 31.
Обходя структуры, в которых Г-волны невозможны из-за неод-
неоднородности среды, перейдем к классу (рис. 6.2е), содержащему
6.1. ПРОДОЛЬНО-ОДНОРОДНЫЕ СТРУКТУРЫ
205
двухпроводную и коаксиальную линии, а также другие волноводы
с однородным диэлектриком и не менее, чем с двумя проводниками.
Повторяя прежние рассуждения, приходим к выводу, что в данном
случае Г-волны наверняка возможны, так как существуют стати-
статические решения. Более того, 8 и 31 должны совпадать с соответ-
соответствующими статическими (стационарными) полями, а потому легко
выясняется вопрос о количестве различных Г-волн в той или иной
структуре. Например, в коаксиальной линии возможна только одна
Г-волна, причем 8 есть поле бесконечного коаксиального конден-
конденсатора, а 31 — магнитное поле коаксиального кабеля при постоян-
постоянном токе (только в пространстве между проводниками!).
Что изменится, если ввести в рассмотрение конечную проводи-
проводимость металлических элементов? Поскольку это означает переход
к структурам с неоднородной средой, то, строго говоря, Г-волны
во всех случаях невозможны. Однако, если при а -*¦ °° Г-волна
существовала, то отвечающее ей решение при конечной проводимо-
проводимости окажется весьма близким, будучи формально ^-волной: Ег Ф О,
так как на оболочке U Ф 0. Насколько мала эта продольная элект-
электрическая компонента, можно судить на основании граничного усло-
условия Леонтовича (см. п. 5.4.1).
6.1.3. Быстрые и медленные волны. От Г-волн все остальные
волновые процессы формально отличаются невыполнением равен-
равенства F.17). Поэтому согласно F.13)
Г = 1к2-%2. F.20)
Если рассматривать только незатухающие волны, для которых по-
постоянная распространения Г — величина вещественная, то ясно,
что при %2 > 0 они будут быстрыми: Т<к и уф > v (уф — фазовая
скорость данной волны, a v — скорость Г-волны в данной среде).
При х2 < 0> т. е. при мнимых поперечных волновых числах % волны
будут медленными: Г > /с и уф < v.
Напомним, что в § 5.3 мы уже познакомились с этими катего-
категориями на примере простейших направляемых волн.
В плоском полом волноводе (см. п. 5.3.2) может распростра-
распространяться одна Г-волна (в отличие от полых волноводов, показанных
на рис. 6.2, это структура с двумя проводниками!) и существует
бесконечное множество решений в виде Е- и ff-волн. В п. 6.2.3 мы
увидим, что для Е- и Я-волн в любых экранированных структурах
с однородной средой при идеальной проводимости оболочки %2 > 0.
•Соотношение F.20) при этом удобно записать в виде:
F.21)
где / = о)/2я — частота, Я = 2л/к — длина Г-волны в данной среде,
условно называемая «рабочей» длиной волны. Введенные парамет-
206
ГЛ. 6. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В СТРУКТУРАХ
ры (ср. п. 5.3.2) выражаются следующим образом:
/кр = %с/BяУеи,), А„р = 2я/х- F.22)
Это критическая частота и, соответственно, критическая длина вол-
волны. С понижением частоты / (ростом рабочей длины волны л) по-
постоянная распространения Г, проходя через ноль при / = /1ф (К —
= Хкр), становится чисто мнимой величиной. Как было показано
в п. 5.3.2 на примере плоского волновода, поле при этом теряет
обычный волновой характер, не переносит энергии и экспонен-
экспоненциально затухает. Для быстрой волны, существующей при / > /,,Р,
на основании F.21) и F.7) имеем:
Л = ХЦ1 - (fjfJ =
v* = vlU- (fjfJ = vli I -
и, далее, вычисляя dai/dT, записываем:
р)
vTV = vii -
F.23)
F.24)
Г'/х,Г"/к
(ср. E.74)). Зависимость фазовой скорости от частоты, т. е. закон
дисперсии, пайденный при анализе плоского волновода (см.
рис. 5.18), как теперь видно, со-
сохраняется для весьма широкого
класса быстрых воли. Дополни-
Дополнительно приведем частотную зави-
зависимость относительной постояппой
распространения Т/k (рис. 6.3),
которая при / > /кР является ве-
вещественной (Г = Г'), а прп /<
< /,,-р — чисто мнимой (Г = — 1Г").
Что касается медленных волн,
то напомним медленные поверх-
поверхностные волны в среде с меньшей
оптической плотностью (пп. 5.3.3—
5.3.4), распространяющиеся при услопип, что граница раздела сред
обладает определенным импедансом E.86). Таков характер волно-
волнового процесса вне диэлектрического слоя (см. п. 5.3.4).
Реальные полые и диэлектрические волноводы будут рассматри-
рассматриваться в гл. 7.
Рис. 6.3
§ 6.2. Конкретизация полей и постанопка краевых задач
для классов волн
6.2.1. Волны Е и Н в структурах с однородной средой (А).
Комплексные амплитуды воли различных классов, имеющие вид
@.12), нетрудно выразить при помощи соотношении F.16) через
продольные компоненты.
§ 6.2. КОНКРЕТИЗАЦИЯ ПОЛЕЙ И ПОСТАНОВКА КРАЕВЫХ ЗАДАЧ
207
Рассматривая Е-аолны, положим в F.16) Hmz = 0 и, выписывая
Е,„, добавим к Е„,( величину Е„,г. В результате получаем
)[z0,
•Отсюда видно, что
Em( = WE[Rmt, z0], WE =
F.26)
т. е. поперечные компоненты векторов Е и Н ортогональны, причем
скалярные величины Emt и Йт1 различаются только постоянным
лгаожителем WE. Следовательно, распределение интенсивности
электрического и магнитного поперечных полей в сечении z=const
описывается одной и той же функцией. Величина WE называется
•волновым сопротивлением в классе ?"-волн.
Ввиду F.25) достаточно знать функцию S"z и поперечное вол-
волновое число %, чтобы определить все поле. Пусть все проводники
являются идеальными (а-»-<»); внутренняя среда — по постановке
задачи — однородна. Проецируя первое из уравнений F.13) на
ось z и учитывая условие на границе с проводником, записываем:
+
= 0, &z = 0 на Lx.
F.27)
Это не что иное, как формулировка F.8) первой краевой задачи
для скалярного уравнения Гельмгольца; под Ь± понимается идеаль-
идеально проводящий контур поперечного сечения полого волновода или
совокупность контуров в более сложных случаях (рис. 6.2а, б). Из
интегрального соотношения F.10), где теперь надо положить Т =
= &г, следует, что ^2 !Э= 0. При этом %2 = 0 соответствует предель-
предельному случаю Т-воли (<S%^0); как известно (см. п. 6.1.2), эти
волны не всегда существуют. Для Е-воли %2 > 0, т. е. это волны
быстрые (п. 6.1.3).
Итак, для определения Е-волн той или иной направляющей
структуры с однородной средой и при идеализации проводящих гра-
границ надо найти решения первой краевой задачи для скалярного
уравнения Гельмгольца F.27). При этом определяются собственные
функции ё"хп и отвечающие им собственные значения Хп (п =
= 1, 2, ...). Затем применяются формулы F.25).
Переходя к II-волнам, положим в F.16) Emz = 0 и запишем
комплексные амплитуды полных полей, добавляя Hmz к Н,„,:
Em = ~(iaiioli/x2)rot±^ze-<Tz = -{ia\io\i/x2)[v±^z, zo]e-Tz,
откуда
Em( = WH[Umt, z0], WH =
F-28)
F.29)
208
ГЛ. 6. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В СТРУКТУРАХ
Здесь WH — волновое сопротивление в классе //-волн. Как и в слу-
случае /?-волн, делаем вывод об ортогональности векторов Е, и Н,,
а также об идентичности распределений их скалярных амплитуд
в любой поперечной плоскости.
Поскольку все поле определяется через Жг, сформулируем за-
задачу, приводящую к нахождению этой продольной компоненты.
Проецируя второе из уравнений F.13) на ось z, мы получим уже
знакомое скалярное уравнение Гельмгольца. Но надо еще наложить
некоторое граничное условие на границе, принимаемой за идеально
проводящую.
Условия этого нет в готовом виде, его надо вывести. Пусть
ж = т и у = v — локальные декартовы координаты в некоторой точ-
точке контура L± (см. рис. 6.2а), тангенциальная и нормальная. Пе-
Перепишем в координатах т, v первую строку правого столбца систе-
системы уравнений F.14):
дН„
д\
+ iTHmv = ШгогЕтх.
Так как на поверхности идеального проводника Ez = 0 и В„ = 0,
а в силу однородности (и изотропии) прилегающей среды и Н, = 0,
то, как видно из сделанной записи, дЙтг/ду = 0. Поэтому для функ-
функции Жг формулируется следующая краевая задача:
+
= 0, dMjdv = 0 на Ь±.
F.30)
Это вторая краевая задача F.9) для скалярного уравнения Гельм-
Гельмгольца. Используя интегральное соотношение F.10), как и при:
анализе .Е-волн, видим, что %2>0; Я-волпы являются быстрыми^
так как случай у2 = 0 относится к предельному случаю Г-волн
(Ж^0).
Общий план определения поля в структуре остается прежним.
Только вместо F.27) решается краевая задача F.30), дающая со-
совокупность собственных функции Жг с собственными значениями
%п (п = 1, 2, ...). После этого полное поле находится из F.28).
6.2.2. Т-волны (А). Векторные уравнения, которым удовлетво-
удовлетворяют функции S и 31 в случае Г-волн, были сформулированы в
п. 6.1.2. Это уравнения Лапласа F.18). Поскольку S и 3i потен-
потенциальны, выразим их в виде
S=-VP, 3t=-v±t|). F.31)
Здесь векторные функции выражены через электростатический и
магпптостатическии потенциалы ф и г|з, как ото делалось в пп. 2.1.2
и 2.1.3. Краевые задачи для них — двумерные аналоги задач Дп-
рихле и Неймана B.15), B.16). Запишем:
Ф = Ф; па
vi* = о,
дф/dv = 0 на Ь±и
F32)
§ 6.2. КОНКРЕТИЗАЦИЯ ПОЛЕЙ И ПОСТАНОВКА КРАЕВЫХ ЗАДАЧ
209-
где граничные условия, налагаемые на ф и г|), соответствуют обра-
обращению в нуль Ех и Я, на ix; в задаче Дирнхле предполагается,
что ф принимает разные постоянные значения на отдельных (не
смыкающихся) частях Lxi границы Ь±.
Анализ показывает, что задачи F.32) не имеют ненулевых ре-
решений в случае полых волноводов (аналогичные рассуждения при-
приводились выше в п. 2.2.5).
К Г-волнам можно перейти, взяв выражения F.25) или F.28),
представляющие поля Е- и, соответственно, Я-волп. Умножив их
па —i%VF, надо перейти к пределу при Г -»- к. В результате про-
продольные компоненты исчезают, а функции <Вг и Жг приобретают
смысл потенциалов ф и -ф. Поэтому можно также воспользоваться
формулами F.26) и F.29) для нахождения волнового сопротивле-
сопротивления в классе Г-волн. Полагая в этих формулах Г = А, приходим;
к выводу, что оно совпадает с известной величиной W D.29), полу-
полученной для однородной Г-волны. Действительно, к/агоЕ /к
= W. Таким образом, для Г-волн:
Ет = \?[Ят, z0], W =
F.33)
6.2.3. Краевые задачи и их решения для плоских структур (Б)~
Для иллюстрации изложенного материала обратимся к плоским,
структурам, уже рассматривавшимся в п. 5.3.2, 5.3.4. При этом
-а/г
d/2\
Рис. 6.4
сделаем замену координат у ->- z, z->-#, x -»- у (чтобы ось % стала
продольной). Тогда для системы двух идеально проводящих пло-
плоскостей (рис. 6.4а) краевая задача F.27) принимает вид
,7 2 г^>
dx*
4- +
- 0, &г @) = 8Z (-d) = 0.
F.34)
Ее решение:
\2
] -= Вп sin Zn.r, -/?, = (^-j , (га = 1, 2, . . .) F.35)
дает собственные функции и собственные значения, отвечающие
^-волнам.
14
В. В. Никольский, Т. И. Hui ольсная
210
ГЛ. 6. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В СТРУКТУРАХ
Взяв задачу F.30)
dx-
= о,
@) -= ж[ (-d) = о,
F.36)
получаем собственные функции и собственные значения
Ш(гп) = Ап cos %„х,
= 1, 2, . . .), F.37)
отвечающие Я-волнам.
Способ получения решений F.35), F.37) очень прост: берется
общее решение уравнения в форме A cos ух + В sin ух и произво-
производится наложение граничных условий, что сразу приводит к отбра-
отбрасыванию одного члена и конкретизации %. Чтобы получить полные
поля, достаточно внести <§г в F.25) и Жг в F.28). Это даст
формулы E.65) и E.67), записанные с учетом E.68); разумеется,
надо принять во внимание преобразование координат и неопреде-
неопределенность коэффициентов Ап, Вп.
Случай, соответствующий п = 0 (параллельная поляризация)
остался вне рассмотрения: он относится к классу Т-воли. Сформу-
Сформулируем задачу F.32)
Ч (Л /-п /Г\\ /"* гг\ ( 1\ /~* (С* QQ\
где С\ и Сг — произвольные, но различающиеся константы. Общее
решение дифференциального уравнения есть ф = Ах + S, а с учетом
граничных условий:
cp=(C, -C2)x/d + Cu F.39)
Согласно F.31)
S = -V_Lcp = Xo(C2-Ci)/d = xoa'. F.40)
Чтобы найти 31, достаточно использовать соотношение F.33). Пол-
Полные комплексные амплитуды поля Г-волны даются формула-
формулами F.19).
Перейдем к случаю плоского диэлектрического волновода
(рис. 6.46). Это структура с двумя разнородными областями, в каж-
каждой из которых ищутся решения уравнений Гельмгольца F.13).
Рассматривая /?-волны, мы должны сформулировать уравнение
Гельмгольца относительно <§z дважды. Для внутренней области
(—d/2<x < d/2) запишем два типа решений (четные и нечетные):
F.41)
d/2) решение сфор-
сфорF.42)
Вне слоя (достаточно рассмотреть область х <
мулируем в виде
6.2. КОНКРЕТИЗАЦИЯ НОЛЕЙ II ПОСТАНОВКА КРАЕВЫХ ЗАДАЧ 211
т. е. Х2 = ^ IX21 • поле должно быть убывающим. Для полупростран-
полупространства х > d/2 решение четным или нечетным образом повторяет
функцию F.42)—в зависимости от выбора решения F.41).
Для согласования констант в F.41) и F.42) надо наложить
условия непрерывности тангенциальных компонент Ez — Ег и 7/т =
= Hv на границе раздела сред х = —d/2. Сначала выразим //,„„
посредством F.25): при —d/2<x<d/2
в
COS 1уХ,
F.43)
при х < — d/2
Жу= —С ((ое0е2/х2) e~i%?. F.44)
Наложение указанных граничных условий дает в двух вариантах
четности:
F.45>
_ в sinb^ =
Избавляясь от неопределенных коэффициентов, получаем трансцен-
трансцендентные уравнения относительно поперечных волновых чисел:
У.,'1 _ . Xj e2 %^d ^ •/., е2
F.46)
Поскольку «fj^ 1\\л
F.46) можно оставить
j^ — 1\\л — Г2, то /д — 7.2 =¦ 'i'i
следонателыю, в
только ¦/_, пли ул =
¦/_., |
Уранпенпн F.40) позволяют при заданных проппцасмостях обе-
обеих сред и толщине слоя паптн поперечные волновые числа, а сле-
следовательно, и постоянные распространения Г воли, направляемых
слоем. Полные поля находятся с привлечением формул F.2-~>).
Проворим характер поверхностного импеданса граничных плос-
плоскостей диэлектрического волновода. Полагая в F.42) и F.44) х =
= —d/2. получаем после очевидных операций Ё,„х и IImx. При под-
подстановке в (Г).85) это дает:
Zs = x2/o)eoe2, й'-волпы. F.47)
Поскольку y,2 = i\y^\, то, как видно, поверхностный импеданс явля-
является индуктивным.
Все выполненные операции нетрудно повторить для случая
//-воли. В этом, однако, пет необходимости, так как' вместо этого
достаточно применить принцип двойственности (и. 3.4.3). В част-
14*
212
ГЛ. 6. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В СТРУКТУРАХ
§ 6.3. ПЕРИОДИЧЕСКИЕ СТРУКТУРЫ
213
ности, сделав замену еое *± ЦоЦ C.79), мы можем сразу же записать
трансцендентные уравнения, которые получаются вместо F.46):
1 x, К
. X, И-2
i — —
Х2 Цх
F.48)
Применяя принцип двойственности C.79) к E.85) и F.47), по-
получаем
Zs = 0)ЦоЦ2/%2, Я-ВОЛПЫ. F.49)
Здесь импеданс — емкостный.
Выводы о характере импеданса, разумеется, подтверждают ранее
.сделанные в п. 5.3.3.
§ 6.3. Периодические структуры (А)
6.3.1. Постановка задачи. Общие сведения о волновых процессах.
Б технике применяются не только продольно-однородные структу-
структуры, направляющие электромагнитные волны, но и периодические,
т. е. изменяющие свои свойства по некоторому периодическому за-
закону. Примеры одномерно периодических, или продольно-периоди-
продольно-периодических структур даны на рис. 6.5. Структуры могут быть открыты-
открытыми (а, б, в, г) и экранированными (д, е); это полые периодические
у.
л
Рис. 6.5
волноводы. Гребенчатая структура (а), система поперечных р
ней (б), некоторая проволочная структура (в), система диэлектри-
диэлектрических линз (г) дают представление лишь о некоторых классах
периодических структур.
Свободные электромагнитные поля в одномерно-периодических
«структурах подчиняются так называемой теореме Флоке, выража-
выражающей следующее свойство комплексных амплитуд векторов Е и Ы:
Ет(х, у,
Йт(х, у,
, у, z)e~
x, у, z)e
F.50)
•где ф — величина вещественная, если отсутствует поглощение. Это
значит, что при сдвиге на величину пространственного периода
о
¦структуры Л обнаруживается некоторый фазовый сдвиг <р без ка-
каких-либо иных изменений поля.
В силу теоремы Флоке F.50) нетрудно построить следующие
периодические по z функции:
S (ж, у, z) = Em(x, у, z)eiT\
3i (x, у, z) = Hm(x, у, z)ei~lz,
F.51)
*Y = ф/Л, где у — специально введенный параметр. Периодичность
записанных векторных функций следует из того, что множитель
•exp(i'Yz) компенсирует «естественный» фазовый сдвиг, возникающий
о
согласно F.50) на отрезке длиной Л.
Функции 8 и 31 можно разложить в ряды Фурье типа C.17),
выразив коэффициенты Фурье через соответствующие интегралы.
Например,
8 (X, y,Z)=
n {X, у) в-«2яп/Л)г>
F.52)
где
z+Л
1
n («, У) = — 8 (X, у, Z) е*С2яп/Л)г dz =
л i
z+Л
1 Г •
— Ет (X, у, Z) е*(У+2яп
л \
/Л)г
F.53)
Точно так же можно представить 31. Введя множитель ехр(—ifz),
снова перейдем от 8иЭ1 к Ет и Нт соответственно:
Ет (х, y,z)= 2 8д (ж, у) е
71 = — с»
оо
Нт (х, у, z) = 2 3in (x, у) е-К
F.5'j)
214
ГЛ. 6. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В СТРУКТУРАХ
§ 6.3. ПЕРИОДИЧЕСКИЕ СТРУКТУРЫ
215
Полученный результат истолковывается следующим образом.
Некоторый свободный волновой процесс в периодической структуре,
создающий фазовое запаздывание ср на протяжении ее периода Л,
эквивалентен наложению бесконечного множества плоских неодно-
неоднородных волн с комплексными амплитудами Sn exp( — iFnz),
3tn ехр( — irnz) и постоянными распространения
Г„ = 7 + и =?-
Л
F.55)
(п = 0, ±1, ±2, ..., ±оо). Эти волны, называемые пространствен-
пространственными гармониками, имеют следующие фазовые скорости
F.56)
и одну общую групповую скорость
г;гр = da/dTn = da/dy. F.57)
Таким образом, фазовая скорость пространственных гармоник мо-
может как совпадать по направлению с групповой, так и быть ей про-
противоположной. Их называют прямыми и, соответственно, обратны-
обратными волнами.
Разложение процесса в периодической структуре на простран-
пространственные гармоники показывает, насколько он сложнее по сравне-
сравнению с волной продольно-однородной структуры. Не следует забы-
забывать, что процесс эквивалентен построенному наложению гармоник
в целом. Если, например, взять структуру, показанную на рис. 6..За,
то формально каждая пространственная гармоника существует на
всей линии АВ. Но внутри металла поле отсутствует. В разложе-
разложениях F.54) это совокупный эффект действия всех гармоник: ряды
сходятся к нулю.
6.3.2. Частые периодические структуры: импедансные поверхно-
поверхности. Периодические структуры, для которых Л-С А, будем условно
называть частыми: па расстоянии длины волны в однородной среде
укладывается большое число пространственных периодов.
Пусть, например, рассматривается ребристая структура, однород-
однородная в направлении у (рис. 6.6). Если она частая, то можно ожи-
ожидать, что по отношению к верхнему полупространству (х<0) гра-
граница структуры х = 0 проявляет некоторые усредненные свойства,
а волновой процесс, распространяющийся в направлении z, пред-
представляется главным образом нулевой гармоникой разложений F.54).
В пазах структуры может существовать поле, в общих чертах
показанное па рис. 6.6. Волновой процесс в целом при этом можно
считать ^-волной. В первом приближении поле внутри паза не из-
изменяется в направлении z, имея характер стояче!! У-волны по х,
так что
Em = zui2A sin k (x — A), Hm = y0 ~ cos k (x - d) F.58)
@ < x < d); выполняется условие Е,„ = 0 при х = d. Формулы
F.58) можно, например, получить из D.56), положив <р = 180°,
iji = 0 и преобразуя координаты: z->~x — d, x^z, у -»- —у. На осно-
основании F.58) нетрудно найти следующее соотношение между комп-
комплексными амплитудами Е,„ и Нт па плоскости х = 0:
хо], Zs = iWtgkd.
F.59)
Поэтому, пренебрегая площадью ребер при х = 0, можно сказать,
что эта граница структуры проявляет себя как поверхность, харак-
характеризуемая импедансом Zs. Напомним, что в п. 5.3.3 при анализе
Рис. е.б
воли, направляемых границей диэлектриков, было введено понятие
импедансной поверхности, причем соотношения F.59) и E.85)
имеют один и тот же смысл: в данном случае х0 = v0 (орт внут-
внутренней нормали), а Е,„@) и Нт@) тангенциальны границе.
В п. 5.3.3 было установлено, что поверхность «поддерживает»
медленную ?-волну, поле которой экспоненциально убывает в по-
поперечном направлении, если Zs согласно второму равенству E.86)
являясь мнимой положительной величиной, имеет индуктивный
характер. Остается распространить этот вывод на рассматриваемую
ребристую структуру. Поскольку при
igkd>0 F.60)
импеданс Zs F.59) также является индуктивным, то записанное
неравенство есть условие существования направляемой Е-вот\ы. По
мере углубления пазов или возрастания частоты это условие будет
выполняться сначала при 0 < d < А/4, т. е. пока глубина пазов не
превышает четверти длины волны в данной среде.
Хотя рассуждения с самого начала были упрощенными, они
привели к пониманию важного момента: вне частой ребристой
структуры, как и вне диэлектрического волновода могут распрост-
распространяться медленные поверхностные волны. В этом смысле ребри-
ребристая структура играет роль «искусственного диэлектрика».
Импедапсное описание границы частой периодической структуры
оказывается возможным и в других случаях.
216
ГЛ. 6. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В СТРУКТУРАХ
§ 6.4. Передача и потери энергии в структурах
6.4.1. Передаваемая мощность и погонные потери (А). Поток
энергии через поперечное сечение продольно-однородной или перио-
периодической структуры выражает передаваемую мощность. Имеет
смысл рассматривать средний поток энергии (см. п. 3.3.1). Таким
образом,
Р = j u2ds = -1 Re j" [Em, H;]2 ds = -±-Re J [Em(, H*mt]zds, F.61>
S-L S± Si-
где S± — поперечное сечение структуры, которое может быть и бес-
бесконечным. Если среда однородна и в структуре распространяется
одна Т-, Е- или Я-волна, то из F.61) следует:
Р = J_ Re W
o*=4-Re
i- Г
w* J
E2mtds,
F.62)
где W — волновое сопротивление W, WE или WH.
Пример 1. Пусть рассматривается полый волновод без потерь энер-
энергии. Если частота выше критической, то согласно F.26) или F.29) с учетом
F.21) волновое_сопротивление WE или WH вещественно. Поэтому веществен-
вещественна и величина Р, так что символ Re в F.62) опускается. Если же частота ниже-
нижекритической, то волновое сопротивление — чисто мнимое и на основании F.62)-
р = 0: передача энергии отсутствует. ¦
Потери энергии в структурах можно вычислять путем примепе-
нпя общего соотношения C.59). В случае продольно-однородных:
структур определяются погонные потери ра:
п = lim AT Т (еое"ЁтЁ; + u0u"Hmri;) dv =
= -f- J (eoe"EmE; + цои"НтН;г) ds. .F.63)
Здесь имеется в виду объем AV, заключенный между двумя попе-
поперечными сечениями z и z + Az. Отсечение поперечного слоя струк-
структуры в разных вариантах показано на рис. 6.7а, б, в. Как правило,
объем AV содержит разнородные среды, например, в случае полого
волновода (а)—металл и внутренний диэлектрик; соответственно
разделяется на подобласти поперечное сечение S±.
На практике по формуле F.63) чаще всего находятся только
потери в диэлектрике. Что касается металла, то при сильном по-
поверхностном эффекте (п. 5.4.2) простую формулу погонных потерь
можно получить, учитывая поток эпергии, уходящий внутрь метал-
металлических элементов. Таким образом, па основе граничного условия
Леоптовича была получена общая формула E.98). Обозначим че-
6.4. ПЕРЕДАЧА И ПОТЕРИ ЭНЕРГИИ В СТРУКТУРАХ
217
рез AS площадь «пояса» металлического элемента (элементов) в от-
отсеченном слое AV (рис. 6.7). Обозначая погонные потери в металле
р", имеем
Pn = lim -^-4f \n2mds = -±j f H*mdl = -i-RnV \ H*mdl, F-64)
ДО Lj i Li
где L± — контур или совокупность контуров поперечного сечения
всех металлических элементов.
б
Рис. 6.7
6.4.2. Затухание в продольно-однородных структурах: энергети-
энергетический анализ (А). В результате потерь энергии происходит зату-
затухание воли, с которым мы уже знакомы на примере однородной
Г-волиы, см. п. 4.1.3. В продольно-однородной структуре амплитуды
векторов Е и Н уменьшаются по закону ехр(—T"z), а передаваемая
мощность Р ввиду F.62)—по закону ехр(—2Г"г):
Р (Z) = Р @) е-2Г'
На отрезке пути Az в результате убывания Р(
¦отрицательное приращение передаваемой мощности:
= _ 2Г"РАг
F.65)
наблюдается
F.66)
{отброшены члены высшего порядка малости). Приращение потерь
на этом отрезке выразим через погонные потери ри:
АРа = -—- Az
. .. = PaAz
F.67)
В силу закона сохранения энергии
АР + АРп = 0. F.68)
При Az -»- 0 выражения F.66), F.67) становятся точными. Их под-
подстановка в F.68) приводит к следующему, как говорят, «энергети-
218
ГЛ. 6. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В СТРУКТУРАХ
вескому» выражению коэффициента затухания:
Г"=рп/2Р.
F.69>
Соотношение является вполне строгим.
Погонные потери можно разделить па части. Бывает удобно,.
например, разделить потерн в металле и диэлектрике, т. е. рп =
= Рп + Ра- Вообще, если рп = рп] + рп2 + ..., то согласно F.69)
Г" = ^2/";п»=^Г»' F-70)
п п
где члены Г" = рпп/2Р выражают парциальные коэффициенты за-
затухания. В большинстве случаев
Г" — Г" 4- Г"
F.71)
где Г„ = рЩР и Г„ = ра/2Р.
F.64), при ц" =0 получаем:
Используя формулы F.63) ж
Ео \ «*ЁтЁ
г
1 д =
2Re
2Re \ [Em, H;]2ds
. F.72>
В большинстве практических случаев точные значения Ет, Нта
получить гораздо труднее, чем решить идеализированную задачу,
в которой потери исключены. Но если такая задача решена, то соот-
соответствующие значения Em, Hm можно внести в F.72) в качестве
приближенных комплексных амплитуд. Это даст приближенные
значения Г„ и Гм. Так обычно и делается (см. ниже гл. 7). Та-
Таким образом, энергетический анализ дает возможность приближен-
приближенно оценивать затухание воли в различных структурах па основании
сведений о полях в тех же структурах без потерь.
Сразу же подчеркнем, что такой подход возможен не всегда.
Выше в примере было показано, что при отсутствии потерь пере-
даваемая_ мощность Р в области частот /</„р равна нулю. По-
Поскольку Р формирует знаменатели выражений F.72), то последние
при дайной подстановке теряют смысл. В действительности вели-
величина Р при наличии потерь никогда строго в нуль не обращается.
Пример 2. Вычислим коэффициент Гд для некоторой //-волны, рас-
распространяющейся в структуре с однородной средой. Поскольку в этом случай
Е„и = Е,„, то
§ 6.4. ПЕРЕДАЧА II ПОТЕРИ ЭНЕРГИИ В СТРУКТУРАХ
219
При подстановке этих выражений в формулу Гд = pfj2P интегралы сокра-
сократятся (можно было бы взять первую формулу F.72)). В результате получается:
Г'
F.73)
2Re(l/WH*) ' 2 Re Г* 2 Re Г '
где учтено, что W" = ыцоц/Г F.29), а также использовано обозначение к =
= (oi/OVe'u/ на D.38).
В произведенных действиях подразумевалось, что Е„, есть точное решение
для структуры, и которой учтены диэлектрические потери, а металл заменен
идеальным проводником. Формула F.73) является точной, однако для вычис-
вычисления Гц надо знать Re Г = Г'.
Если структура без потерь изучена и о области / > /,ф известна вещест-
вещественная постоянная распространения 3~ = |'к2 — %2, то в F.73) можно заменить
Ке Г на 9~, что даст следующую приближенную формулу:
Гд = к2 tg А/2Г. F.74)
Можно убедиться, что этот результат вереи также и в случае S-волп. На-
Наконец, переходя к 7-волпам, сделаем замену 8Г->-к. Тогда F.74) переходит
в D.44). ¦
6.4.3. Аналитическое определение коэффициента затухания (А).
Если в результате решения задачи для некоторой продольно-одно-
продольно-однородной структуры найдено поперечное волновое число %, то по
формуле F.20) можно определить и постоянную распространения
Г; для нахождения коэффициента затухания надо лишь отделить ее
мнимую часть. В частности, для Е- и Н-волп волновода с идеалыю-
проводящей оболочкой %2 > 0. Пусть внутренняя среда является
поглощающей. Внося в F.20) к в форме D.41), запишем:
F.75)
Г = Vк2A - i tg A) - х2 = IT2 - ik2 tg A.
Разделение вещественной и мнимой частей приводит к следующим
формулам:
Г = k /l/2 (
Г" = к /l/2 (
+ tg2 А +
tg2 A - ;Г2/к2).
F.76)
При 3~ ->- к отсюда получаются выражения D.42), справедливые
для Т-волн.
Пример 3. Рассмотрим некоторый полый волновод с ядеальпо-проводя-
тдей оболочкой, заполненный поглощающей средой, для которой и. = 1, е =
= е' — ia/coEo C.33), причем tg Л = сг/шеоЕ = 0,2/м,//; под /,ф понимается кри-
критическая частота рассматриваемой волны при отсутствии поглощения (tg Д =
= 0), таким образом, /,;р// = %/.к. На рис. 6.8а построены частотные зависимости
относительных величин Г'/^и Г"/к. полученные по формулам F.76). Штрихо-
Штриховые линии соответствуют случаю tg А = 0 (ср. также рис. 6.3). Как показывает
расчет, при потерях постоянная распространения в нуль не обращается и
всегда остается комплексной величиной; при / = /,,р согласно F.75)
Г= (l-
F.77)
220
ГЛ. 6. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В СТРУКТУРАХ
§ 6.4. ПЕРЕДАЧА И ПОТЕРИ ЭНЕРГИИ В СТРУКТУРАХ
221
(так как Т = 0), т. е. Г' = Г". Поскольку Г' Ф 0 при любых частотах, то в>
при / </кр существует передача энергии (действительно, Р ф 0 F.62), пото-
потому что W = WE = Г/(йеое или W = WH = м(хо|х/Г — не чисто мнимая вели-
величина). Но в этой области частот велико затухание. Па рис. 6.86 построена кри-
кривая частотной зависимости относительной фазовой скорости Уф/у, где v$ =
= ш/Г" и у = ш/ к; при отсутствии потерь (штриховая лпиия) v^jv -*- оо про
¦ Чр/я
Рис. 6.8
/->-/кр. Заметим, что взятая в этом примере поглощающая среда при /> /кр
проявляет себя как несовершенный диэлектрик (tgA<g;l), но, если / <С/крс
то она становится проводником. ¦
В большинстве случаев при нахождении Г" = Гд область / »
« /„р обходится и выполняется неравенство \&~\2 » k2 tg А. При этом
из F.75) путем разложения в ряд по малому параметру легко по-
получить следующие приближенные выражения:
\2\Г\
f<f.
F.78>
кр.
Мы видим, что при / > /нр коэффициент затухания оказывается та-
таким же, как и при вычислении по формуле F.74).
6.4.3. О скорости движения энергии (Б). Еще в п. 1.5.4 была
получено выражение, позволяющее находить скорость движения
энергии в электромагнитном поле. Рассматривая быстрые Е- и
Я-волны в некоторой продольно-однородной структуре без потерь,
установим в этом случае связь скорости движения энергии и груп-
групповой скорости. Отправляясь от формулы A.117), вместо уэ =
введем величину
о
J
wds
F.79)
По смыслу этой записи величину va надо рассматривать как ско-
скорость движения энергии v3, усредненную во времени и по попереч-
поперечному сечению структуры S±. Можно сказать, что va — скорость
переноса энергии структурой в целом.
Взяв для определенности некоторую S-водну и раскрывая
подынтегральные выражения в F.79) при помощи формул F.25).
получаем:
Vr, =
при />/Кр. Как было показано выше в п. 6.2.1, интегральное со-
соотношение F.10) справедливо при Т=^ёг. Учитывая это, в круг-
круглых скобках последнего выражения имеем %2/Т2 + 1 = к2/Т2. Даль-
Дальнейшие преобразования дают:
% = vT/k = УУ1 -(/кр//J = vTF, F.80)
где учтено выражение групповой скорости F.24). Итак, введенная
выше скорость переноса энергии va совпадает с групповой
скоростью.
Вывод оказывается справедливым и в случае Я-волн. Все вы-
выкладки нетрудно повторить, детализируя подынтегральные выраже-
выражения в F.79) при помощи формул F.28).
6.4.4. Затухание волновых процессов в периодических структу-
структурах (Б). Пусть в некотором поперечном сеченииS±(z) периодиче-
периодической структуры передается мощность
[tim,K*m]zds
F.81)
(ср. F.61)). Вычисляя передаваемую мощность на расстоянии од-
одного периода, воспользуемся теоремой Флоке F.50):
= -^Re J [E
F.82>
Сравнение результатов F.81) и F.82) показывает, что при чисто
вещественном <р (когда этот параметр выражает только фазовый
•222
ГЛ. 6. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В СТРУКТУРАХ
§ 7.0. РЕШЕНИЕ ДВУМЕРНОГО УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
22$
сдвиг), передаваемая мощность не изменяется. Затухание имеет
место при комплексном
Ф = ф'-/Ф" F.83)
(ф" >0). В этом случае ехр(—гф + «р*) = ехр( —2ф"). Поэтому убы-
убывание передаваемой мощности на рассматриваемом отрезке перио-
периодической структуры есть
Т (z) - Т (z + А) = A - е-2<Р") Р (z). F.84)
В силу закона сохранения энергии эта величина равна потерям
АРп- па том же отрезке: P(z) — P(z + Л)= АР„. Отсюда
е-2Ф» = i __ дрп/р (Z)t F.85)
а если потерн малы, так что ехр(—2ф")« 1 — 2ф", то
у" ~ SPJ2P F.86)
о
(значения Р при гиг + Л весьма близки).
Итак, в впде формул F.85), F.86) мы получили энергетическое
описание затухания волнового процесса в периодической струк-
структуре; вторая из этих формул напоминает уже известное выраже-
выражение F.69).
Параметр ф" будем называть затуханием на период, а АР„ —
потерями на период.
УПРАЖНЕНИЯ
К Привести формулы E.65) и E.67) к виду F.25), F.28), сделав нужное
"Преобразование координат и выделив продольные компоненты <&г, Збг-
Аналогично представить поля всех направляемых воли, рассматривавших-
рассматривавшихся в и. 5.3.
2. Раскрыть формулы F.25), F.28) в цилиндрических координатах г, a, z
(см. табл. 2.2). а также в обобщенно-цилиндрических координатах qu g2, z
(<7i и g2 — произвольные ортогопальные криволинейпые координаты, см.
п. 2.0.2).
3. Рассматривая существование волн различных классов, объяснить, ка-
какой принципиальной особенностью обладает плоский полый волновод при со-
сопоставлении со всеми остальными полыми волноводами.
4. Записать выражения волновых сопротивлений для всех классов собст-
собственных волн плоского полого волновода.
5. Произвести вывод формулы F.10) для первой и второй краевых задач.
6. В каком смысле волны, направляемые плоским диэлектрическим волно-
волноводом, следует рассматривать как медленные и в каком — как быстрые?
7. Проверить формулу F.24).
8. Проверить тождественность двух форм представления Нт в F.25) и
ТЁ„, в F.28).
9. Графически или при помощи ЭВМ найти несколько корней уравне-
уравнении F.46).
10. Сопоставив ребристую структуру (п. 6.3.2) и слой диэлектрика па иде-
•алыю-ироводящеи плоскости (и. 5.3.4), показать, каким образом первую струк-
структуру можно охарактеризовать некоторой эффективной диэлектрической про-
ницаедюстыо.
11. Почему формулы F.62) являются строгими лишь до тех пор, пока про-
проводник направляющей структуры (например, оболочка волновода) идеализи-
идеализируется (С—>- оо)?
12. Является ли формула F.64) всегда достаточно точной?
13. Объяснить, почему в рассмотренном примере (рис. 6.86) при со-»-О'
оказывается г> = 10г.
14. Вывести формулу F.80) в случае //-волн.
Глава 7
НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
§ 7.0. Решение двумерного уравнения Гельмгольца методом
разделения переменных (А)
7.0.1. Задачи в декартовых координатах. В этой главе при рас-
рассмотрении конкретных направляющих структур нам придется на-
находить решения двумерного уравнения Гельмгольца F.5) и решать
краевые задачи F.8), F.9). Будет использоваться метод разделения
переменных, уже обсуждавшийся в п. 6.0.1.
В декартовых координатах двумерное уравнение Гельмгольца
F.5) имеет следующий вид:
—— 4-
дх* +
д2Т
= 0.
G.1)
Применение метода разделения переменных начинается с предпо-
предположения, что неизвестное решение Т можно представить в виде-
произведения функций разных координат:.Т(х, у) = X(x)Y(y). Под-
Подстановка этого представления в G.1) дает:
dx
а после деления всех членов на XY получаем уравнение:
\ JlY \ /7" V
I (I Л. хил Y2
X dx2 Y dy2
G.2>
где слагаемые слева — функции разных аргументов. Они, таким об-
образом, независимы (см. аналогичное обсуждение в п. 6.0.1), а сле-
следовательно, каждое слагаемое равно константе; обозначив эти кон-
константы — %? и — зс?' получаем вместо G.2) следующие два обыкно-
обыкновенных дифференциальных уравнения
dX
—j- +
dx
= о, ^4
которые эквивалентны уравнению G.2) при
X* + 1у = X2-
G.3),
G.4)
224
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
§ 7.0. РЕШЕНИЕ ДВУМЕРНОГО УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
225
Общие решения уравнений G.3), как известно, можно выразить
в тригонометрической и экспоненциальной форме. Запишем:
\А cos %хх + В sin ухх, (С cos ivy + D sin yyy,
Здесь введен ряд неопределенных констант; неопределенными явля-
являются также х* и %у.
Поставим первую краевую задачу F.8) для прямоугольной об-
области, показанной па рис. 7.1. Граничное условие Т = 0 на Ьх оз-
v пачает следующие требования:
Jt А± T = Q G.6)
при х = 0, у = 0; х = а, у = Ь. Взяв триго-
тригонометрическое представление решения
—» Г (я, г/) = (A cos х*? + В sin х*я) X
Рис, 7.1 X (С cos х„# + D sin Xv#), G.7)
согласно G.6) мы должны иметь, в частности, Т @, у)—0. Подста-
Подставив в G.7) х = 0, видим, что это возможно только при А = 0. По-
Потребовав далее выполнения равенства Т(х, 0)=0, точно так же
убеждаемся, что С = 0, т. е.
Т(х, y) = N sin fox sin %yy, G.8)
где ./V — неопределенная константа, появившаяся как произведение
BD. Остается наложить на G.8) условия Т(а, у)=0 и Т(х, Ь)=0.
Они выполняются при уу7 = "и (т = 0, 1, 2, . . .) и %tJb = /ггс
Gi = 0, 1, 2, . ..), т. с.
X* = тл/а, %у = тгл/6, G.9)
тде ттг = 1, 2, ... и п = 1, 2, ... (нулевые значения тип исключа-
исключаем, так как при этом Т = 0).
Итак, мы получили систему решений первой краевой задачи для
двумерного уравнения Гельмгольца F.8) в случае прямоугольной
области. Это собственные функции Ттп, которым соответствуют
собственные значения %тп- Согласно G.8), G.9) и G.4)
Т{тп (х, у) = N^n sin (тлх/а) sin (плу/b),) ,
\m=i, 4, ..., n=i, A, ...
%mn = (тл/аJ + {пл/bf, )
G.10)
(Nmn ¦— неопределенные константы).
В случае второй краевой задачи F.9) па решение G.7) следует
наложить условие dT/dv = 0 на Ьх, что означает:
дТ
-= 0 при х = 0, х = а,
- 0 при у -0, у --- Ь.
G.11)
Дифференцируя Г(аг, у) G.7) по я, а затем по у и требуя обраще-
обращения в нуль соответствующих производных при х = 0 и у = 0, нахо-
находим, что В = 0 и D = 0, т. е.
Т(х, y) = Ncos%xxcos%yy, G.12)
где 7V — неопределенная константа. Налагая теперь условие обраще-
обращения в нуль тех же производных при х = а и у = Ъ соответственно,
приходим к прежним выражениям G.9). В результате получаем си-
систему решений второй краевой задачи F.9) в случае прямоугольной
области в виде следующих собственных функций и отвечающих им
собственных значений:
п (х, у) — N^mn cos (гплх/а) cos (nny/b)A
Xmn = (rnnlaf + (пл/ЬУ ]
771=0,1,2, ...,
п = 0,1,2,... G.13)
(как ц^ ранее, Nmn —неопределенные константы). Значения
ттг = 0 и п = 0 теперь не исключаются. При одновременном равен-
равенстве нулю тип собственная функция есть константа, а соответству-
соответствующее собственное значение — пуль.
7.0.2. Цилиндрические функции. В дальнейшем нам понадобится
решать уравнение F.5) в цилиндрических координатах. Здесь в ре-
результате разделения переменных появится обыкновенное диффе-
дифференциальное уравнение
G.14)
которое называется уравнением цилиндрических функций, а также
уравнением Бесселя п-то порядка. Общее решение уравнения G.14)
записывают в следующей форме:
Шп (х) + BNn (x),
G.15)
(оба варианта эквивалентны), где: Jn(x)—функции Бесселя п-то
порядка, Nn(x)—функции Неймана п-то порядка, #п (х)— функ-
функции Ханкеля 1-го рода п-то порядка, Я^2) (х) — функции Ханкеля
1-го рода п-то порядка. Это различные виды цилиндрических
функций.
Смысл представлений G.15) легко понять, если учесть, что при
х ~* °° уравнение G.13) переходит в хорошо известное уравнение
у" + у = 0, решение которого можно представить в двух формах:
у = cos х + sin х или у = ехр (— ix) + ехр (га:). При этом exp (± ix) =
= cos x ± i sin x. Аналогично
Н(п'2) И = Jn{x) ± iNn(x). G.16)
15 в. В. НикольскпЛ, Т. И. Никольская
226
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
Цилиндрические функции не являются периодическими, но они
«осциллируют». Функции Бесселя и Неймана с ростом х принима-
принимают значения, колеблющиеся около нуля с монотонно убывающей
амплитудой и приближающиеся к тригонометрическим при х -¦*¦ °°.
-в,5-
-7,5
Рис. 7.2
Существенно, что /о @) = 1, /„ @) = 0 при п Ф 0 и Nn @) = — °°. Ци-
Цилиндрические функции хорошо табулированы. Широко распростра-
распространены программы вычисления их на ЭВМ (рис. 7.2).
Нам понадобятся значения аргументов х, при которых функции
Бесселя и их первые производные обращаются в нуль, т. е. корни
х = Впт уравнения Jn(x) = 0 и корни х = Апт уравнения Jn (х) = О
(табл. 7.1, 7.2).
Запишем также пекоторые формулы, часто используемые при
операциях с цилиндрическими функциями; последние будем обозна-
обозначать Zn(x), подразумевая, что имеется и виду функция Бесселя, Ileii-
мана или Хапкеля целого порядка.
§ 7.0. РЕШЕНИЕ ДВУМЕРНОГО УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
227
Таблица 7.1
Корин Впт уравнения Jn(x) = 0
Таблица' 7.2
Корни Апт уравнения j'n(x)= О
п
0
1
2
3
т
1
2,405
3,832
5,136
6,380
2
5,520
7,016
8,417
9,761
О
8,654
10,173
11,620
13,015
4
11,792
13,324
14,796
16,223
в
0
1
2
3
т
1
3,832
1,841
3,054
4,201
2
7,016
5,331
6,706
8,015
3
10,173
8,536
9,969
11,346
13,324
11,706
13,170
14,586
Функциональные соотношения; дифференцирование:
7 I-г\ — / \\п7 I-г\ /7 <17\
Z/—п\А) — ^ 1) ZjnyXf, yl.lij
в частности,
Z-1(x)=-Zl(x), G.18)
d-^P- = -^Zn(x) + Zn_x (x) = ^Zn (x) - Zn+1 (x). G.19)
Далее, из G.19) следует:
в частности,
± [x-nZn{kx)\ = _ kx-nZn+1(kx),
Z'o (x) = - Z, (x), Z[ (x) = Zo (x) \
Формулы интегрирования:
G.20)
G.21)
G.22)
G.23)
G.24)
G.25)
G.26)
Я222 ( \ 1 2 )
—^— + Z; (z) I x dx = j|Zl (x) U - I-^J] + \zn (x) Z'n (x) + Z'*{x)j,,
G.27)
\ xZn (ax) Zn (p\r) dx = " x" n~' """'—""""-' '"; " '" ш G.28)
J a — В
15*
J *-"+%> (a:) dx=- x-n+1Zn_1 (a:),
J zZ^ (x) rfz = ^ [Z2 (x) - Z»-! (a:) Zn+1 (a;)] =
228
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
При неограниченно возрастающем аргумента цилиндрические
функции переходят в тригонометрические или экспоненциальные.
Используются следующие асимптотические представления:
» ю=УЪcos [* - т [п+4
Я<» И = /J ехр {- i [х-1" (и + 4")]} + О (*-3/2). G.32)
Запишем степенной ряд
При я < 1 отсюда следует:
в частности,
При малых а: имеем также:
Л'о (х) « -1 In А, Л'„ (х) « -
G.33)
G.34)
G.35)
G.36)
(T = 1,781...) (га >0).
7.0.3. Задачи в цилиндрических координатах. Двумерное уравне-
уравнение Гельмгольца F.5) в цилиндрических координатах (см. п. 2.0.2)
имеет вид:
= 0. G.37)
Решение ищем в виде произведения T(r, a) = 52(r),s#(a). После этой
подстановки, раскрыв круглые скобки, имеем:
Умножим все члены на r2\9ls4< и перегруппируем:
dr
1
Si-
G.38)
Это привело к разделению переменных: первые три члена зависят
только от г, а последний — от а. Виедем константу п2 и приравняем
§ 7.0. РЕШЕНИЕ ДВУМЕРНОГО УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
229
ей сумму членов, зависящих от г; тогда последний равен — га2. В ре-
результате получаем два обыкновенных дифференциальных уравнения:
dr*
5^ = 0
G.39)
G.40)
(при записи G.39) все члепы были умножены на 52/г2).
Обыкновенное днфференциальное уравнение G.39) — это уравне-
уравнение Бесселя G.14) при у = Я, х = уг. Его общее решение запишем
в форме G.15):
| AJn {yj) + BN» (%r),
(Г) ~~ И#^ (yr) + BH(n2) (yr). ( '
Решение уравнения G.40) нам известно:
[С cos race + D sin па,
G.42)
Итак, найден общий вид решения Т = $.$? уравнения F.5) в ци-
цилиндрических координатах, содержащий ряд неопределенных кон-
констант.
Перейдем к решению краевых задач F.8), F.9) в случаях об-
областей, показанных на рис. 7.3а, б.
Поскольку при этом Г (г, ос) =
= Т(г, а + 2яи), то п в G.41),
G.42) — целое плп нуль.
Начнем с краевой задачи F.8)
для круговой области (рис. 7.3а).
Выбирая решение в форме первой
строчки G.41), умноженной на зФ
G.42), мы должны сразу положить а
В = 0, потому что в противном слу- Рис 7.3
чае Т окажется неограниченным в
центре круга г = 0 (напомним, что Nn(x)->- — °° при х -*¦ 0). Таким
образом,
)• G.43)
Граничное условие Т = 0 на L± влечет за собой:
О. G.44)
Это значит, что %R = Bnm (см. табл. 7.1), т. е.
X = Bnm/R. G.45)
В результате мы можем записать решение краевой задачи F.8). Как
видно, систему решешш образуют собственные функции, получае-
получаемые при подстановке % G.45) в G.43). Запишем выражения этих
230
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
функций вместе с соответствующими им собственными значениями:
—ina
В
nm \COS;
" ' sin
jna
G.46)
%nm = (Bnm/RJ-
Здеаь линейные комбинации G.42) представлены в форме столбцов:
выбор одной из позиций столбца дает вариант собственной функции.
Решая для той же области (рис. 7.3а) вторую краевую задачу
F.9), опять приходим к формуле решения G.43). Граничное усло-
условие dT/dv = 0 на L± дает:
Jn(%R) = 0. G.47)
Поэтому %R = Anm (см. табл. 7.2) и
X = AnJR. G.48)
В итоге вместо G.46) получаем:
Г™ (г, а) =
) ™
г) па
ina
G.49)
%nm = (AnmfRJ-
Решение краевых задач в случае кольцевой области (рис. 7.36)
отличается тем, что теперь нет оснований отбрасывать член с функ-
функцией Неймана в G.41), так как центр круга исключен из рассмот-
рассмотрения. Вместо G.43) пишем:
Г (г, a)=[AJn(xr)+BNn(xr)]j*(a). G.50)
Решая первую краевую задачу F.8), теперь необходимо потребо-
потребовать обращения в нуль решения при г = R\ и г = R2. Отсюда
AJn(%Rl)+BNn(%Rl)=0,
0 [ -° ]
Выполняя условие совместности этой системы уравнений, обратим
в нуль ее определитель:
Это и есть уравнение относительно х- Если корни х = %пт найдены,
остается подставить их в G.50) и, далее, воспользовавшись одной
из строчек G.51), найти отношение коэффициентов В и А. По-
Получаем:
52 (г) = A \jn(%nmr)- JNn<)ynmRA Nn(%nmr)\ G.53)
Для получения полных собственных функций надо внести это
ражение (опустив А) в первую строчку G/iG) вместо /„ (-^-
§ 7.1. ПРЯМОУГОЛЬНЫЙ ВОЛНОВОД
231
Что касается %п™, то корни уравнения G.52) приводятся в равлич-
ных справочниках, например, в [К. 3].
Пусть теперь решается вторая краевая задача F.9) для кольце-
кольцевой области (рис. 7.36). Решение по-прежнему представляется в ви-
виде G.50), а вместо Т нужно обратить в нуль при г = R\ и r = R2
производную этой функции по г. Поэтому имеем следующую систему
уравнений:
= о' G>54)
Отсюда прежним путем получаем уравнение относительно %:
Jn (x^i) Nn (xRa) - fn №) N'n (xtf x) = 0. G.55)
В конечном счете вместо G.53) находим:
Jn (%nmr) - „,.*"„. Nn (%nmr) , G.56)
А/ J
где Xnm — корни G.55); они приводятся, например, в [К. 3].
Для получения полных собственных функций надо внести Я(г)
-трг) в G.49), отбросив А.
§ 7.1. Прямоугольный волновод (А)
7.1.1. Решение задачи. Среди полых волноводов (см. рис. 6.2а)
наиболее распространен прямоугольный волновод, металлическая
труба прямоугольного поперечного сечения (рис. 7.4). Мы распо-
располагаем всеми необходимыми данными, чтобы записать решение элек-
электродинамической задачи для прямоугольного
волновода, оболочка которого принимается у
за идеально проводящую, а внутренняя сре-
среда является однородной. Такая математиче-
математическая модель в большинстве случаев оказыва-
оказывается удовлетворительной. При необходимо-
необходимости она уточняется путем учета потерь в ме-
металле; это также будет сделано. >^
В прямоугольном волноводе с идеально Рис. 7.4
проводящей оболочкой могут существовать
только волны классов ? и Я (см. п. 6.1.2).
Рассматривая .Е-волны, мы должны решить краевую задачу F.27) для
прямоугольного контура, а это не что иное, как уже решенная выше
в и. 7.0.1 нерная краевая задача для уравнения G.1) с граничным
условием G.0). Итак, решение задачи (G.27) для прямоугольного
232
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
волновода (рис. 7.4) дает согласно G.10)
Pmn
' z :
0 a b
»» = (—J + (tJ '
т =1,2, ...,
га= 1, 2, ...,
G.57)
где Е™п — неопределенные коэффициенты. Зная эти собственные
функции <§™ и соответствующие им собственные значения %mm
путем подстановки G.57) в F.25) выразим полные электромагнит-
электромагнитные поля:
Е-волны
ЕТПП
m —
тпх . ппу
zn sin sin —г2—
mrcx nny \ I —iTmnz
— cos —r- e
a b
G.58)
WE У2
тп '-тп
pmn .
„mn _ . до 1тп гел . тпх ппу
"n — * ~Г~П \ Xn —Г" 5m ~~Z— СОЙ j—
тч тпх . гетп/\
— cos Т" sin ~Гj
где F.26)
- Ш G-59)
(IVT= 120яУц/е) и F.20) —F.22):
причем
/кр
V(mlaf + (nibJ '
G.61)
Анализ Я-волн требует решения краевой задачи F.30). В п. 7.0.1
это было сделано: для прямоугольного контура (рис. 7.1) было по-
поставлено граничное условие G.11) и найдена система решений урав-
уравнении G.1). Поэтому согласно G.13)
58Г = ЯГ cos^cos 2f-, 5С-п = (^J + (тJ' <7-62)
где m =@), 1, 2, . . ., n =@), 1, 2, .. ., H™n — неопределенные ко-
коэффициенты (ср. E™1 it G.57)). Нуленые .-iiiii'ionn.'i m н /t молено
брать лишь при сочетании с ненулевыми (поэтому нули взяты в скоб-
§ 7.1. ПРЯМОУГОЛЬНЫЙ ВОЛНОВОД
233
ки). Дело в том, что Ж1° есть константа, причем Хоо == 0; это ре-
решение не относится к классу Я-волн. Подставляя собственные функ-
функции Ж?п и собственные значения %тп G.62) в F.28), получаем
Н-волны
'-тп
где
. '¦тп ( тп ^-п тпх ^^ ппу
Ь '' I Хл ' S1I1 ~*"—~~~ COS j
У2 I» a a b
'-тп V
гея
sin— J \е
w
G.63)
G.64)
а постоянные распространения Гтп и критические частоты /кр" по-
прежнему выражаются формулами G.60), G.61).
7.1.2. Анализ волновых процессов. Полученные решения показы-
показывают, что прямоугольному волноводу свойственно бесконечное мно-
множество свободных электромагнитных полей классов Е и Я, которые
определяются выбором чисел т и п в G.57) или, соответственно,
G.02). Говорят, что выбранное решение дает тип поля, нлп тип вол-
волны Е„п (в классе Е) п Я„,„ (в классе Я).
При фиксированной частоте / только для некоторых достаточно
малых ш и п будет выполнено условие /> /кр G.61). Поэтому лишь
для конечного числа типов поля постоянные распространения Ттп
G.60) окажутся вещественными. Эти типы поля имеют характер
распространяющихся воли, которые переносят энергию. Все осталь-
остальные типы поля, составляющие бесконечное множество, энергии не
переносят и экспоненциально затухают (см. шг. 6.1.3, 5.3.2, 6.4.1).
Передача энергии невозможна, если / < /кр для всех тип.
Особую роль играет тип волны с наименьшей критической час-
частотой min/Up™. Если а > Ъ (см. рис. 7.4), то
4 _ / _
/кр - /кр -
G.65)
Этот минимум реализуется в классе Я (см. выбор чисел т и п в
G.62)). Волна Ню, обладающая наименьшей критической частотой,
называется основной волной прямоугольного волновода. Обычно со-
б.чюдаотст условно />/кр при /</К1, для остальных типов колн.
В этом случае и волноводе перенос энергии осуществляется только
одной основной волной.
234
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
§ 7.1. ПРЯМОУГОЛЬНЫЙ ВОЛНОВОД
235
(Z=-A/4)
в/% ^Jl_ ¦
У
—""о
—-е-
—t.
0
Л/2
(x=o/2)
Рис. 7.5. (ЭВМ)
Рассмотрим строение электромагнитных полей. В классе Е про-
простейшим является тип поля Е\\. Ему посвящена серия изображений
на рис. 7.5а (здесь п далее а = 35 мм, 6 = 15 мм). Это «мгновенный
снимок» поля, смещающегося вдоль оси z с фазовой скоростью
г;ф = ш/Гц. Он получеп при /=12 ГГц на основе формул G.58)
для момента времени t = 0. В поперечном сечении z = 0 (рис. 7.5а
внизу справа) наблюдается лишь продольное электрическое поле.
Распределение Ez, разумеется, соответствует выражению G.57) при
т = 1, п = 1, когда
1 г
= Ео sin — sin-т-. Эпюры этого распре-
распределения по осям х п у показаны вместе с поперечным сечением
z = 0. В средней точке сечения находится максимум Ех; система то-
точек — следы силовых линий вектора Е в данной плоскости. В сдви-
сдвинутом на Л/4 поперечном сечении (рис. 7.5а вверху слева) Ег = 0.
Видны системы взаимно ортогональных электрических н магнитных
силовых линий.
Подчеркнем, что характер этой картины можно предвидеть из
следующих соображений. Поскольку речь идет о волне класса Е,
вектор Н вообще не имеет продольной компоненты: все магнитные
силовые линии лежат в поперечных плоскостях. Известно, что они
обязательно должны быть замкнутыми кривыми (среда однородна,
так что линии В и Н одинаковы). Из соображений симметрии ясно,
что центром семейства замкнутых магнитных силовых линий долж-
должна быть средняя точка сечения. Заметим, что в этой же точке лежит
максимум продольного тока смещения. В панравлеппп z максимумы
Ег п dbjai сдвинуты на Л/4 (это легко проверить по формулам
G.58)). Можно сказать, что здесь реализуется одна из типичных
структур электромагнитного поля, обсуждавшаяся еще в гл. 1 (см.
рис. 1.11).
Па рис. 7.5а показаны два продольных сечения «мгновенного
снимка» волны Еп: х = а/2 и у = 6/2. Отмечен отрезок структуры
длиной Л/2. Видно, что длина волны в волноводе Л есть простран-
пространственный период поля.
При анализе любых структур в классе Е рассмотренный тпп по-
поля Ец служит «элементарной ячейкой». На рис. 7.56 в прежнем по-
порядке представлена структура поля Ею (т = 3, п = 2) при / =
= 28 ГГц. Можно сказать, что поперечное сечение разбито на 3 X 2
клеток, в каждой из которых воспроизводится поле Ец. Отметим сле-
следующее: во-первых, все плоские границы между ячейками могут
быть заменены пдеальпо проводящими плоскостями, это тте ггпрутла-
ет структуру поля; во-вторых, направления силовых лишш в сосед-
соседних ячейках согласованы таким образом, что на их границах тан-
тангенциальные компоненты Е и Н непрерывны; в-третьих, во всех
случаях, когда тип больше единицы, появляются замкнутые элек-
электрические силовые липни; сомеПстиа замкнутых электрических
и магнитных силовых липни как бы сцеплены подобно .жоньям
цени.
236
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
§ 7.1. ПРЯМОУГОЛЬНЫЙ ВОЛНОВОД
237
На рис. 7.6 дается представление об объемной картине силовых
линий волны Е\\. Показаны только электрические силовые линии,
связанные с зарядами левой и нижней стенок волновода (а); но
даже при этом картина выглядит несколько запутанной. Поэтому
отдельно (б) дана картина, на которой оставлены лишь «петли» наи-
наибольшего размера; здесь хорошо просматривается форма этих не-
неплоских кривых. Рис. 7.6 и рис. 7.5а согласованы, но число линий
в первом случае уменьшено.
Перейдем к обсуждению полей класса Н, начав с типа поля Нц\
оно не является простейшим, но более простые структуры, когда
Рис. 7.6. (ЭВМ)
т -- 0 ii.irr п ~ 0, будут рассмотрены отделы1
/=12 ГГц покапаны дпа поперечных и два
по. Па рис. 7Ло при
, ,- - --, -.-«- ,ч-« поперечных и два продольных сочегшя
структуры поля Н\\ для момента времени t = 0 согласпо G.63).
tz=-A/4)
/ Ч
• /* ,*-\ *'
I I »
х I х/ ц, V 1»
I / / ^ I
III 1 |
iii ; i i
. vw'
4 '
e о ^-e—or в в
I / \ 1
I О I «^^ !• 1 »
II,' % I I
II,' 1 I I
• • I ' ' !
* /-
'x
I
x ^-*
tf
Я.
¦"*
У
"~"~ч
i— —
. 0
Л/2
n
* ?v
(x=a)
(z=0)
1у=Ь)
B=-Л/4)
-i-f-ч—к-н—н-н-
iTji iTVi if л
\ / 4 • 4 •
^ — ч f ч /" ч
f '-ч \ / ^ч ^ / ^-\ V
i ( ) i il)! 11. )!
/' --Ч V ' '¦N » ' ,^N ^
I! I I 1A1 I! М
ic
У
0
Л/2
1
1
V
(. > I
'
1 C_) 1
i с ) i
ч — •
lx=a/3)
i О 11 C_
^-"vi= z
lz=0)
(y-t/2)
Рис. 7.7. (ЭВМ)
238
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
В сечении z = О (рис. 7.7а внизу справа) существует только про-
продольное магнитное поле. При этом распределение Hz соответствует
выражению G.62) при та = 1, п = 1, когда Ж\х = Я" cos ^ cos ^.
Эпюры этого распределения по осям х и у тут же показапы. В сред-
средней точке сечения Нг = 0; следы силовых линий вектора Н в дан-
данной плоскости показаны точками и кружками. В сдвинутом на Л/4
поперечном сечении (рис. 7.7а вверху слева) Я2 = 0; показаны си-
системы взаимно ортогональных электрических и магнитных силовых
линий. В продольных сечениях х = 0 и у = Ъ видны системы замк-
замкнутых магнитных силовых линий; отмечен полупериод структуры.
Структура поля Яц играет роль элементарной ячейки при ана-
анализе всех более сложных структур, когда т>1 ип>1. В качестве
примера на рис. 7.76 при / = 28 ГГц показана структура поля Н32-
Рис. 7.8. (ЭВМ)
| 7.1. ПРЯМОУГОЛЬНЫЙ ВОЛНОВОД
239
Замечания об особенностях структуры высших ?-полей (см. выше)
почти без изменений распространяются на высшие Я-поля.
На рис. 7.8 (ср. рис. 7.6) дана объемная картина магнитных си-
силовых линий волны Яц; построены только линии, семейства кото-
которых начинаются у левой и нижней стенок волновода, причем это сде-
сделано с большей (а) и меньшей (б) подробностью. По сравнению с
рис. 7.7а число линий уменьшено.
Все рассматривавшиеся выше Е- и Я-волны, как говорят, явля-
являются попарно вырожденными: разным собственным функциям <§™
и Ж™п при одних и тех же тип соответствуют равные собственные
значения %тп. Поэтому различные по структуре полей волны Етп
и Нтп имеют одинаковые постоянные распространения Гт„, а следо-
следовательно, равные фазовые скорости. Подчеркнем, что все сказан-
сказанное имеет строгий смысл по отношению к волноводу с идеально
проводящей оболочкой. Вырождение снимается при переходе к ре-
реальному металлическому волноводу. Более того, собственные волны
оказываются уже гибридными (п. 6.1.2): типы поля Етп и Ят,„ свя-
связываются в некоторые комбинации с преобладанием одного из них.
Отметим еще одно обстоятельство. С повышением частоты или
увеличением поперечных размеров волновода растет отношение Г/%.
В пределе отношение продольных компонент к поперечным стремит-
стремится к нулю (см. G.58) и G.63)). Волны классов Е и II переходят
в Г-волны.
7.1.3. Невырожденные волны. Основная волна в реальном волно-
поде. Волнам в классе Я с индексом т = О или п = 0 нет соответ-
соответствия в классе Е; поэтому нет указанного выше вырождения. Это
еще но значит, что не может быть вырождения иного рода. Напри-
Например, в случае волновода квадратного поперечного сечения (а=Ъ)
постоянные распространения волн Етп и Е„т, Нтп и Нпт (а в част-
частности, Нт0 п Нот) будут одинаковыми.
Рассматриваемому подклассу принадлежит основная волна Н\о.
Взяв is G.02) т = 1. п = 0, получаем: ЖУ — #o°cos —. На
рис. 7.9а при / = G ГГц тип поля Ню отображен точно так же, как
ранее отображались другие поля волновода (см. рис. 7.5 и рис. 7.7).
Отличительным свойством основной волны является однородность
ноля в направлении у. При п — О поле остается однородным по у
при любых т; структура Ню играет роль элементарной ячейки при
анализе структур Ят,о. На рис. 7.96 показано строение типа поля
Язо. Поля Яо,? отличаются от Hko поворотом структуры на 90°.
Поскольку основная волна представляет наибольший практиче-
практический интерес, рассмотрим ее подробнее. На рис. 7.10а показана объ-
объемная картина силовых линий, дополняющая рис. 7.9а. Выпишем
формулы, выражающие поле и основные параметры волны Ню-
Комплексные амплитуды Ет и Нт получаются непосредственно из
G.63). Но ниже будет удобно изменить неопределенную константу,
240
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
(z=-A/4)
(х=а/2)
S 1
\ \ 1
H 1—1-+
—X X X / X \
_,• /
»-*""x" X Xy'
-X-»" X
/ N / X X _Х_1
-x.jj^x >
-x, x xN4 »
0
Л/2
(у=Ь)
а
!=
-
-
-
-¦
-
-
z=
—
-
-
+)
[1 i Г
X
/ \ *.__'' / \
н-н—и
и ; i и > 11
ll ИИ ) I И И
vi i Г} I
И НИ ) I I с- ) I
о
Л/2
ЧЩ/
(у=Ь)
5 ,
Рис. 7.9. (ЭВМ)
(z=0)
X XX
(х=а/61
Cz=O)
ГГк хТТГк
§ 7.1. ПРЯМОУГОЛЬНЫЙ ВОЛНОВОД
чтобы упростить выражение Ёт. В результате:
* & I ТТТ 7 ТТ ТТт\ — Z
Hm = —ir — xn sin h zn -p cos — e
wh \ о a о r a aj
241"
G.66).
Я?° = t
и ввиду G.64)
f0)-J^-j. Здесь на основании G.60), G.61)
^
120яц
/
G.68)-
ец -
Здесь Я — длина Г-волны при заданной частоте / в среде с парамет-
параметрами е, ц (которой заполнен волновод), а Хо — длина Г-волны в ва-
вакууме, обычно называемая рабочей. Если е и и. — комплексные ве-
величины, удобнее пользоваться формулами G.67), G.68) во втором
варианте записи. Впрочем, для случая поглощающей внутренней
среды ранее были получены специальные формулы F.76) и F.78)^
/
/'
--%
z.
/^
~p
У
r
—
: z
¦ -^
/
Рис. 7.10. (ЭВМ)
ТТл оболочке тюлповода возникают ттппорхипстиьте токи и заряды,
KiiTnp;.ie Mij)iii.¦ rejiiiiiyii)тся ii.'idtiidctjimii tj — [vq, HJ и с = VnD A.90),
(Г). 100). где vo — орт нормали к оболочке, обращенный впутрь
1С В. В. Никольский, Т. И. Никольская
242
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
§ 7.2. ДРУГИЕ ПОЛЫЕ ВОЛНОВОДЫ
24$
волновода. На рис. 7.106 показаны линии вектора г\ на оболочке
волновода, согласованные с картиной поля (рис. 7.10а).
Отметим, что невырожденные волны прямоугольного волновода
имеют такую же структуру, как //-волны плоского волновода, рас-
рассмотренного выше в п. 5.3.2. Роль отражающих плоскостей играют
стенки, вдоль которых поле однородно: х = 0 и х = а для волн Нт0
(см. рис. 7.4). Наличие двух других стенок не влияет на структуру
поля.
Неидеальность оболочки волновода в формулах G.66), разумеет-
разумеется, не учтена. Но этот фактор практически не влияет на структуру
волны Н\о. Что касается затухания, вносимого металлом реального
волновода, то его можно учесть при помощи второй формулы F.72).
Сначала выразим мощность, передаваемую волной Ню при иде-
идеальной проводимости оболочки. Пусть также внутренняя среда —
идеальный диэлектрик; />/кР, так что W^o— величина вещест-
вещественная. Внося Ет G.66) в F.62), получаем
а Ь
up-
G.69)
о о
Подчеркнем, что используя эту формулу при наличии потерь, когда
она становится приближенной, надо учитывать резкую потерю точ-
точности при / « /кр (см. п. 6.4.2).
Для подстановки в формулу типа F.69) вычислим погонные по-
потери в проводнике рк (G.G4):
п = 4 йпр J Hlul =
= /?
+
] (Hmz + НтХ) \y=odx =
о J
;)'b + ll G.70)
что легко провеять, используя вторую строчку G.66). На о'спова-
пии F.69), G.69) и G.70) окончательно получаем:
26 I К у
¦ 1 ( 2а )
1 —
ЯЛ2
2а
/кр-
G.71)
Это частный вид формулы F.72).
Приближенная формула G.71) теряет смысл при / =/кр (X =
— 2а). Несмотря па ото, она вполне пригодпа для расчета затуха-
затухания волны /710 при частотах, не слишком близких к критической.
ТГа рис. 7.11 нрлг.едепы результаты вычисления Гм при изменении
материала волновода (а) и размеров поперечного сечения (б). Как
видно, Гм имеет минимум. Относительно слабый рост затухания
с повышением частоты вызывается увеличением поверхностного со-
сопротивления /?пр E.94), которое пропорционально величине У/.
Если уменьшать размер Ъ поперечного сечения волновода, то оп-
определяемая по формуле G.67) постоянная распространения Гюг
0,06
0,02
0,06 -
Латунь
i i i i i
О
О,О2 -
4 f/fKp=2ct//L
Рис. 7.11
а вместе с ней — фазовая скорость основной волны и соответствую-
соответствующая длина волны Л, групповая скорость F.24) и волновое сопро-
сопротивление Wlo G.68) останутся неизменными. Но, как видно из
G.71), это существенно затронет коэффициент затухания, который
при Ъ < а почти обратно пропорционален Ъ.
§ 7.2. Другие полые волноводы
7.2.1. Круглый волновод. Решение задачи (А). Рассматривая по-
полый волновод кругового поперечного сечения, называемый круглым
волноводом (рис. 7.12), мы, как и ранее, можем 7
сразу же записать решение электродинамической
задачи, полагая внутреннюю среду однородной,
а оболочку — идеально проводящей.
В случае ?-волн надо получить собственные
функции и отвечающие им собственные значе-
значения, порождаемые краевой задачей F.27) при
контуре L± в виде окружности. Опи были пай-
дены выше в п. 7.0.3. На основании G.46) ~
пишем: рис. 7.12
я
COS
па =
sin
fe
(а-)'= 13=
G.72)
16»
244
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
где Впт — корни уравнения G.44), сведенные в табл. 7.1. Внося
G.72) в F.25), получаем комплексные амплитуды полных полей:
Е-волны
ЁГ = ВТ fzo/n (xnmr) & (па) -
Н'
УУ-пт) L
' (па)]
7пт
'О
G.73)
/
¦Здесь
(па)]е iTam
cos
e
(па) = . па = ,
V ' Sin inct
G.74)
где подразумевается любая линейная комбинация функций, распо-
расположенных в столбце. Штрихом в G.73) обозначены производные
функций указанного в скобках аргумента (если, например, s4-(na) =
= cos па, то S&'(па)= — sin па). Далее, согласно F.26), F.20) —
F.22)
f \лкр /
где
rim с n
/КР ~ 2яЛ/^Г ~
nm « пш
Впт'
G.76)
G.77)
Рассматривая Я-волны, выпишем собственные функции и соб-
собственные значения, порождаемые краевой задачей F.30); они для
кругового контура L± были получены в п. 7.0.3. Используя G.49),
получим:
/А„„
Я \2
)
G.78)
где Апт — корпи уравнения G.47), сведенные в табл. 7.2. Комп-
§ 7.2. ДРУГИЕ ПОЛЫЕ ВОЛНОВОДЫ
245
лексные амплитуды полных полей получаем, подставляя G.78) в
F.28):
Н-волны
Гн г
Епт . гтпттттН nm П т ( н \ ^л i , \ ,
m =ш0 Wnm H \—T0~Jn(xnmr)s? (па) +
ТТ
r
ЙГ = НГ jzo/n (xLr) si (na) -
(та) + а0 у /„ (хпг,
Здесь (см. 6.29)
тт/Н
н
'nm
G.79)
-&птг
G.80)
Постоянная распространения Тпт выражается формулой G.76),
в которой
Аг
пт л пт ^"
G.81)
7.2.2. Анализ волновых процессов (А). Как и в случае прямо-
Згголыюго волновода, мы отмечаем, что круглому волноводу свой-
свойственно бесконечное множество свободных электромагнитных полей
классов Е и Я. Чтобы выбрать решение, соответствующее классу
Е, надо задать порядок п функции Бесселя и номер т корня Впт
уравнения G.44). Выбирая решение из класса Я, задают порядок п
функции Бесселя и номер т корпя Апт уравнения G.47). Эти ре-
шенпя (ср. п. 7.1.2) дают типы полей (типы волн) Епт или, соот-
ьегствепно, Нпт. Наименьшим оказывается корень An = 1,841... Та-
Таким образом, волна Яц обладает низшей критической частотой
,пт с 11 с 1.811 ,П оо\
2я 1/ец
Это основная волна круглого волновода.
Прежде чем обсуждать строение полей, обратим внимание на
"характер их азимутальной зависимости. Неопределенность в s?(na)
G.74) отражает свободу азимутальной ориентации собственных воли.
Если для некоторого типа поля при п Ф 0 в одном случае взять
s?(na)= cos па, а в другом М- (па) = sin па, то получатся две струк-
структуры, различающиеся только поворотом па угол 90°/и. Вообще при
вещественных Л и В пмеем: s4- (па) = A cos па. + В sin па =
= С cos (па — i|i), где С = У Л2 + В2 и \р = arcig(B/A). Это значит, что
но сравнению со случаем В = 0 отмечается поворот структуры на
246
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
§ 7.2. ДРУГИЕ ПОЛЫЕ ВОЛНОВОДЫ
247
(z=-A/4)
(z=-A/4)
; i
1
i
! i
11! ; ' i
(а=90
°)
Л/2
(z=0)
Рис. 7.13. (ЭВМ)
угол i])/rc. Если же взять 5 = ±L4, то получится структура, вращаю-
вращающаяся относительно оси z, аналог круговой поляризации однород-
однородной Г-волны (см. п. 4.2.1); при этом s?(na) = exp(±mcc).
При построении картин силовых линий положим М- (па) = cos па.
Возьмем R = 8,7335 мм. На рис. 7.13а построен «мгновенный сни-
снимок» волны Ео\. Общий тип построения картин силовых линий, на-
например, выбор поперечных и продольных сечений в случае круглого
волновода производится подобно предыдущему (см. § 7.1). Отме-
Отметим, что при п = 0 множитель s4>(na) превращается в константу
и поле оказывается азимутально-однородным (не зависящим от а).
В данном случае согласно G.72) имеем: ё^г = El°J0 (Boir/R), где
i?oi = 2,405 (см. табл. 7.1). Магнитные силовые линии при этом —
окружности в плоскости поперечного сечения, поперечное электриче-
электрическое поле радиально. Построение на рис. 7.13а выполнено при / =
= 39 ГГц. Для этой же частоты на рис. 7.136 представлена струк-
структура волны Ец. Из G.72) при т = 1, и = 1 следует: cf" =
= E1Jj1 {BlxrlR) cos а, где /?ц = 3,832 (см. табл. 7.1). Поэтому ноле
при изменении ее от 0 до 360° образует период.
Сопоставляя рис. 7.13а и рис. 7.5а, убеждаемся, что волпа Eoi
круглого волновода и волна Еп волновода прямоугольного име-
имеют однотипную структуру; что касается волны Ец круглого волно-
волновода, то она в такой же мере сопоставима с волной ?21 прямоуголь-
прямоугольного (достаточно взять две соседние ячейки на рис. 7.56). Но такое
соответствие существует только для некоторых видов волн. Легко,
например, убедиться, что среди собственных волп прямоуг ;.ч,ного
волновода нет соответствия волнам Еот круглого при т ?= 1.
На рис. 7.14 показаны еще две структуры, относящиеся к классу
Е круглого волновода; по-прежнему, / = 39 ГГц. Для волны ?",2 (а)
<g>f = Eo2J,(Bl2r/R)cosa, где Bi2 = 7,016. Поскольку т = 2. (бе-
(берется второй корень уравнения Ji(x)=0), в интервале 0<r<J?
имеется значение г = R', соответствующее корню х = В и = -J.832.
Поэтому па окружности радиуса R' = {Bn/Bi2)R = 0,5462й уттглет-
воряется такое же граничное условие, как и на оболочке волновода.
Для волны Е31 (б) ё\1= E301J3 (B3lr/R) cos За, где #3i = 6,380. В дан-
данном случае при изменении а поле образует три периода. На ради-
радиальных линиях, ограничивающих каждый полупериод F0° — сек-
сектор в поперечном сечении) удовлетворяется условие Ех = 0; для
первого сектора это радиусы а = ±30°.
Анализируя волны круглого волновода Епт при различных ??? и
п, можно, как и в случае прямоугольпого волновода, выделить ячей-
ячейки, ограниченные координатными липиями, но уже не ортогональ-
ортогональными прямыми, а окружностями и радиальными прямыми. Ячейки
будут иметь равные угловые размеры, но окажутся все одинаковы-
одинаковыми только при т = 1.
Перейдем к обсул{деиию //-волн. Рис. 7.15 построен аналогично
рис. 7.1.'!; иока.чапы структуры ноля типа #oi (а) п ноля типа
248
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
Cz=-A/4)
ta=90°
Г\
U\J
П\
Г\
шщит
1
1
+-
1
1
1
1
1
1
1
—
0
-
-
- .
—(-
Л/2
(a=0
(z=01
[г=-Л/4)
6
ta=90°
)
z
а
fz-01
ta=O°
Рис. 7.14 (ЭВМ)
§ 7.2. ДРУГИЕ ПОЛЫЕ ВОЛНОВОДЫ
(z=-A/4) (a=90°)
249
С !П||М]|П|!Г1]|М1|м||Г
Л/2
' / ^ i
I I. у 1
v —— — **
i( ) i
." -.
1 ^ —' )
(':
( ;
>._
l4
lv
s~
1
(
4_
(_
Г
z
~)^
:2)
^
f \ 1
•-— /
(z=0)
[2=-Л/4)
(a=90°
¦
t
Л/2
*
1
1 I TCU ' t
,4 «^f-к *,
(a=0°)
(z=0!
Рис. 7.15. (ЭВМ)
250
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
§ 7.2. ДРУГИЕ ПОЛЫЕ ВОЛНОВОДЫ
251
#п (б), в первом случае / = 39 ГГц, во втором /=12 ГГц. Рас-
Рассматривая поле Н01, заметим, что согласно G.78) Ж11=Н°0110 (rAQ1/R)r
где Л01 = 3,832. Наиболее интересным свойством этого типа поля
(а также и всех типов Нот) является то, что на оболочке волновода
(г = R) сохраняется только продольная магнитная компонента /72,
которой соответствует азимутальный ток r\ = o.qHz. С ростом часто-
частоты или радиуса R отношение Hz/IIr уменьшается, в пределе обра-
обращаясь в нуль; это видно из формул G.79). Таким образом,, могут
быть созданы условия, при которых токи в оболочке очень малы.
К обсуждению этого вопроса мы вернемся ниже в п. 7.2.3. Для Нц
из G.78) имеем: Ж? = #JVn (rA11/R)cosa, где Ап = 1,841. Уже
отмечалось, что волна Нц — основная. Интересно, что структура
ее поля и поля основной волны Ню прямоугольного волновода
(рис. 7.9а) аналогичны.
На рис. 7.16 показаны структуры полей Н^ (а) и Н31 (б).
В этих случаях из G.78): Ж? = Hfj1 (rA12/R) cos a (Ап = 5,331) и
Ж? = Hl1J3 (rA3l/R) cos За (Ац =4,201). При построении взято / =
= 39 ГГц. Замечание о ячейках, ограниченных координатными ли-
линиями, сделанное при обсуждении Е-полей, разумеется, сохраняет
смысл и для //-полей.
Чтобы дать представление о более сложных полях, на рис. 7.17
в поперечном сечении показаны структуры ?32 и Н%2-
Волновые процессы в прямоугольном и круглом волноводах име-
имеют ряд общих черт. Это было видно, например, при рассмотрении
основной волны. Однако волна Нц круглого волновода в отличие от
волны Ню прямоугольного, как говоря!, пиллризационно неустойчи-
неустойчива: небольшие деформации оболочки могут вызывать заметные по-
повороты структуры поля. Это связано с поляризационным вырожде-
вырождением, которое свойственно всем волнам круглого волновода за иск-
исключением азимутально-однородных (и = 0). Действительно, как уже
отмечалось, могут существовать две азимутальные ориентации
{s?(na)~ cos па и s?(na)— sin na); соответствующие поля ор-
ортогональны и при наложенип порождают любые другие
ориентации.
Вернемся к вопросу о волнах, поля которых вращаются относи-
относительно оси z. Можно взять, например, две ортогонально ориентиро-
ориентированные основные волны Нц с одинаковымп амплитудами и фазовым
сдвигом ±90°. Результирующее поле представляет собой уже изве-
известную структуру (рис. 7.156), которая вращается относительно про-
продольной оси, причем в цептре (г = 0) поло оказывается таким же,
как при круговой поляризации Г-волны: вектор Е вращается без
изменения величины. Не следует, однако, думать, что вращающиеся
структуры возможны только в круглом волноводе. Взяв волновод
квадратного поперечного сечения и рассматривая одновременное су-
существование волн Ню и Hoi при том жо амнлитудпо-фа.чоном соот-
соотношении, легко убедиться, что результирующая структура вращается
z=-A/4)
t
— ¦
.
. _ .
(а=90°
¦ — ¦
. _..
z
А/21
( Н
( I
(z=0)
(a=0°
a
AK
(z=-A/4)
(а=90°
0
z
А/2
( С'-':
Г?с
( Сс
(Cs'J
' -1
?J)
-}->)
:-:--0
z
(z=0)
(а=0°)
Рис. 7.16. (ЭВМ)
252
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
32
Рис. 7.17. (ЭВМ)
§ 7.2. ДРУГИЕ ПОЛЫЕ ВОЛНОВОДЫ
253;
(правда, деформируясь), а в средней точке сохраняется обычная
круговая поляризация.
Наконец, отметим, что, как видно из табл. 7.1 и 7.2, Айт = В\т
(т = 1, 2, ...). Это означает, что каждая пара волн Е\т и Нот яв-
является вырожденной. Например, вырождены волны Ец и Hoi.
7.2.3. Передача энергии. Учет проводимости металла (А). Волны
реального металлического круглого волновода, строго говоря, остают-
остаются волнами Е и Н только при п = 0. Прочие волны являются гиб-
гибридными, хотя фактически отличаются от рассматривавшихся выше
Е- и ./7-волн незначительно.
Мощность Р, передаваемая основной волной Ни фиксированной
поляризации, выражается следующим образом:
711 I2 11 V 11/
?2 A2 —
-. G.83).
ЗдесьЯ"—амплитудный коэффициент из G.79), а Ео— амплитуда:
электрического поля на оси волновода (г = 0). Запись имеет смысл
при / > /,<р.
Запишем также коэффициент затухания, обусловленного потеря-
потерями в металле:
1
Гм =
1 Zli
WH
Xй/
2 А* ~ 1
'п
R
W^R
прИЗ,413Д
3,4181
WR
г кр-
G.84)
ВЫВОД. Будем исходить из выражения F.62) и положим
G.79) xnm = Ац/R, Ж (па) = cos a:
„ „ 2Я В
_ W С W С С
р = ^\ H2mtds= -f J J {Hlr + Hla) r dr da =--
__ | o-i
о о
: H
_ rr
ll12
I
— (x«)* .
*
254
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
7.2. ДРУГИЕ ПОЛЫЕ ВОЛНОВОДЫ
255
Чтобы получить формулу G.83) в первом варианте, надо взять по-
последний интеграл при помощи G.27), учитывая при этом, что
Ji (^u) = 0.
Далее, найдем амплитуду вектора Е волны Ни при г = 0 и а —
= 90° (при s?(na) = cos а). Согласно G.79)
Sm @,90°) = r0
Н
rii
г->0
^11
G.85)
(из G.33) видно, что Ji(x)/x-^- 1/2 при х^О).
Обозначая 8m@, 9Ос) = го2?о, приходим к второму варианту за-
записи G.83). Числовой коэффициент получен с учетом того, что
J\ (Ац) = 0,58137...
Для получения формулы G.84) вычислим погонные потери р™
F.64):
Ра
_ .1 в Г Я2 A1 —
J\
sin2 a + j\ (Atl) cos2 a R da=
. G.86)
¦Формула G.84) получается при подстановке G.86) и G.83) в
F.69). ¦
Запишем без вывода коэффициент затухания Гм для азимуталь-
-но-однородных волн.
В случае волны EOi
R
пр
WR V 1 - (X/2,612R)
В случае волны Hoi
р" = "пр _Ло1 = "пр
н
G.87)
G.88)
Сопоставление формул G.71), G.84) и G.87) показывает, что
общий характер частотной зависимости Г^ во всех этих случаях
одинаков: резкое возрастание затухания вблизи критической частоты
(напомним, что при / = /кр формулы теряют смысл) и медленный
рост (как У/) при высоких частотах. Иной характер имеет частотная
.зависимость Гм для волцы//о1 (рис. 7.18). С ростом частоты затухание
О,О4
0,О2
Я=1Омм
О, Of
J I L
0,02
лагунь
А\
— Си
Al
Н„
— Я-1ОМН
I ' ' I
.20
¦\ЭО
О 1
0 12
О, О2
Ft=10 MM
?O1 0,04
^Латунь
0,02
_L... I I L
Ft=10MM
0 12 3 f/-fKp=2t6M/A 0 12
0,04 -
0,02 -
i
0,04
0,02
Г",м-!
-\
-к
Al
НО1
R=10mm
/ 20
0 12 3 ffap=1,64R/A 0 12
Рис. 7.18
:256
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
§ 7.3. МНОГОСВЯЗНЫЕ НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
257
исчезает. Причина этого — в монотонном уменьшении токов в обо-
оболочке, о котором уже говорилось выше.
7.2.4. Волноводы некругового поперечного сечения (Б). На
рис. 7.19 в поперечных сечениях показано несколько полых волно-
волноводов, которые встречаются значительно реже, чем прямоугольный
(см. § 7.1) и круглый, рассматривавшийся выше. Для волноводов
(а, б, в, г) краевые задачи F.8), F.9) могут быть решены методом
разделения переменных, причем в случаях, когда области (а, б)
образуют элементарные ячейки поперечного сечения круглого вол-
волновода, эти задачи уже решены выше. Если угол секториальной об-
области (а) не подчинен условию а0 = л/п, то порядок функций Бес-
-селя, описывающих собственные функции, уже не будет целым;
Рис. 7.19
в более сложном случае (в) при произвольном соотношении радиу-
радиусов приходится строить решение с включением функции Неймана
(см. п. 7.0.3).
Эллиптический волновод (г) отличается от круглого поляриза-
поляризационной устойчивостью; в ряде случаев такие волноводы применя-
применяются на практике.
Для эллиптического цилиндра существует особая система коор-
координат и построены специальные функции, благодаря чему решения
краевых задач F.8), F.9) могут быть получены методом разделе-
разделения переменных в замкнутой форме.
Волноводы с поперечным сечением невыпуклого профиля, назы-
называемые П-образным C) и //-образным (е), по ряду причин находят
применение в технике СВЧ. Сужение поперечного сечения приводит
к весьма существенному понижению критической частоты (по срав-
сравнению с прямоугольным волноводом, получаемым при d = a). Это
значит, что для заданной частоты такие волноводы оказываются от-
относительно малогабаритными. Следует, однако, иметь в виду, что
миниатюризация аппаратуры СВЧ развивается значительно более
радикально: широкое распространение получили пе П- и Я-образпые
полионоды, а полосконые и щелевые структуры, о которых будет
говориться ниже в § 7.5.
Заметим, что хотя границы контура поперечного сечепия П- и
Я-образного волноводов описываются как координатные линии де-
декартовой системы, решения задач F.8), F.9) в замкнутой форме
получить не удается. Хотя для каждой прямоугольной подобласти
поперечного сечения можно найти частные решения, пользуясь пред-
представлениями G.5), однако наложение условий на границах подоб-
подобластей возможно лишь при формировании рядов таких решений.
В результате возникают бесконечные системы алгебраических урав-
уравнений относительно коэффициентов этих рядов. Подобные задачи
решаются при помощи ЭВМ (см. гл. 12—13).
Наконец, отметим следующее: основной волпой любого полого
волновода должна Оыть обязательно Я-волна. Средствами вариацион-
вариационного исчисления (см., например, [И. 3]) удается сопоставить соб-
собственные значения, отвечающие задачам F.8) и F.9). При этом
оказывается, что
min xH sS min хЕ, G.89)
откуда и следует такой вывод.
§ 7.3. Многосвязные направляющие структуры
7.3.1. Коаксиальная линия (А). В п. 6.1.2 уже отмечалось, что
эта линия относится к классу продольно однородных структур, спо-
способных направлять Г-волны (см. рис. 6.2в); строго говоря, имелись
в виду структуры с идеальными проводниками. Поперечные сечения
всех таких структур являются многосвязными. Поясним термин на
примере коаксиальной линии (рис. 7.20а); одновременно рассмотрим
также однопроводную линию (рпс. 7.206). Дело в том, что имеются
6
Рис. 7.20
два класса контуров в поперечном сечении — таких, что в одном слу-
случае контур может быть стянут к точке (?i), а в другом это невоз-
невозможно (?2)- По этому признаку область поперечного сечения на-
называется двусвязной. Очевидно, что в случае любого полого волно-
иода любой контур стягивается к точке, т. е. существует лишь одни
класс контуров, а например, и поперечном сечении двухпроводной
17 В. В. Никольский, Т. II. Никольская
258
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
линии (см. рис. 6.2е) можно выделить три принципиально различ-
различных класса контуров. Поперечные сечения являются соответственно
односвязным и трехсвязным. Итак, лишь многосвязные структуры
могут направлять Г-волны, что обусловлено существованием ненуле-
ненулевых решений краевых задач F.32). Можно показать, что число
решений этих задач, а следовательно, число Г-волн в той или иной
структуре на единицу меньше порядка связности. В двусвязной ко-
коаксиальной линии возможна одна Г-волна.
Рассматривая Г-волну коаксиальной линии, можно идти от задач
F.32) и, определив потенциалы ф i if, найти векторные функции
8 и Э1 по формулам F.31), а затем выписать выражения комплекс-
комплексных амплитуд полного поля при помощи формул F.19). Но в дан-
данном случае мы уже знаем S и 3i (в п. 2.2.5 рассматривался коак-
коаксиальный конденсатор, а в п. 2.3.3 — аксиально-симметричные маг-
магнитные поля при постояпном токе). Будем исхо-
исходить из выражения A.58) (см. п. 2.3.3), так
что первоначально запишем:
Далее определим Нт как Hm = JH,e-!ftr F.19) и
Em = W[Hm, z0] F.33). В результате получаем:
Ё -
„-ihz
-ihz
Рис. 7.21
G.90)
На рис. 7.2 показана картина силовых линий
этой У-волпы в поперечном сечеипц.
Поскольку в каждом поперечпом сеченпи z = const, вектор Em
есть градиент некоторого потенциала F.31), можно говорить о раз-
разности потенциалов между проводниками коаксиальной лиши, кото-
которая определяется по формуле типа B.24). Комплексную амплитуду
разности потенциалов при некотором z обозначим Cm(z). Тогда, ис-
используя G.90), пишем:
л»
„—ihz
Um (z) = Ет (z) dr =
«1
w
2я
Обозначая Um(z) = °Ume lh\ введем понятие волнового сопротивления
линии, определяемого по напряжению и току:
G.91)
Это величина, используемая в так называемой теории длинных ли-
линии. Г> случае вакуума (практически, и во.чдуха) IF = 120л (см.
и. 4.1.3), так что \УЛ = 60In{R2IR\) ¦
§ 7.3. МНОГОСВЯЗНЫЕ НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
259
Вычисляя мощность Р, передаваемую основной волной коакси-
коаксиальной линии, т. е. рассматриваемой нами Т-волной, имеем
i& G.92)
2 .
S.i.
4я
0 R,
или, с учетом G.91),
р 1/ т2ш
" — I2'm'' л-
Чтобы определить обычным путем Гм, надо также найти
G.93)
R,
2) da =
4л
поэтому согласно F.69)
¦р" пр
G.94)
0,003 -
0,002 -
0,001
Частотная зависимость коэффициента затухания (рис. 7.22) обуслов-
обусловлена поверхностным сопротивлением У?пр, которое, как известно, про-
пропорционально У/, однако при достаточно низких частотах (см. § 5.4)
становится неприменимой теория
сильного поверхностного эффекта,
приводящая к представлению о по-
поверхностном сопротивлении йпр.
Как и в круглом волноводе,
в коаксиальной линии может су-
существовать бесконечное множест-
множество полей классов Е и //. Как и в
прочих случаях (см. § 7.1, 7.2),
для исследования этих волн надо
определить собственные функции
и собственные значения,, порож-
порождаемые задачами F.27), F.30)
при данном поперечном сечении.
Решения этих задач были найдены выше в п. 7.0.3. Собственные
значения получаются как решения уравнений G.52), G.55). Полные
поля можно представить по той же схеме, что и в случае круглого
волновода.
Среди Е- и /7-волп наименьшей критической частотой обладает
волна П[\. При относительно малом радиусе внутреннего провод-
проводника она по структуре ноли напоминает волну У7ц круглого вол-
волновода.
17*
2 f/Ги,
Рис. 7.22
260
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
Как правило, для передачи энергии коаксиальной линией ис-
используется основная волна Т. При этом рабочая частота обычно зна-
значительно ниже наименьшей критической частоты множества высших
волн, т. е. критической частоты волны Ни.
Наконец, заметим, что формулы G.90) формально справедливы
также в случае однопроводной линии. Попробуем вычислить мощ-
мощность р, передаваемую такой волной. По сравнению с действия-
действиями G.92) различие состоит в том, что теперь нужно интегрировать
не от R\ до i?2, а от R\ до °°. Полагая i?2 -*¦ °°, видим, что интеграл
G.92) расходится: при конечном токе мощность оказывается беско-
бесконечной. Это значит, что конечная мощность соответствует исчезаю-
ще малому току провода, а следовательно, и нулевому локальному
полю. В этом смысле Т-волна провода не отличается от однородной
Т-волны свободного пространства, это также некоторый идеализиро-
идеализированный образ: волна физически иереализуема. Рассуждение, однако,
сохраняет силу только для идеального проводника. Ниже в п. 7.4.4
будет учтена проводимость реального провода, направляющего
Г-волну.
7.3.2. Обоснование теории длинных линий (Б). При рассмотрении
коаксиальной линии уже отмечалось, что, так как поле потенциаль-
потенциальное, то правомерно понятие разности потенциалов между проводни-
проводниками в любой плоскости поперечного сеченпя z = const. Пусть А и
В — точки на разных проводниках некоторой многосвязной структу-
структуры, a L — замкнутый контур, охватывающий один из проводников,
причем и точки, и контур лежат в некотором поперечном сеченгш z.
Функции
U(z,t)= \ EdI, I(z, t) = (pBdl
A L
G.95)
это разность потенциалов (напряжение) н ток. Если векторы поля
Е и Н подчинены волновому закону, то то же самое можно сказать
о напряжении и токе. Второй интеграл справедлив потому, что Ег —
= 0, а следовательно, через поперечное сечение не проходит ток
смещения.
Будем рассматривать систему двух проводников, т. е., например,
открытую двухпроводную либо коаксиальную линию, пренебрегая
потерями. Для этого случая существуют уравнения теории длинных
линий, или телеграфные уравнения:
dU_
dz
dl
dU
dl '
G.96)
где 2" и С — погонные индуктивность и емкость, которые опреде-
определяются при отсутствии временной зависимости (электростатика, ио-
иоле постоянного тока).
g 7.3. МНОГОСВЯЗНЫЕ НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
261
Покажем, что уравнения G.96) непосредственно следуют из
уравнений Максвелла.
ВЫВОД. На рис. 7.23 показана продольно-однородная струк-
структура иэ двух проводников в вариантах открытой и экранированной
Sfz+Az)
-Lfz+Az)
5
Рис. 7.23
линий. Будем вычислять V G.95) в двух поперечных плоскостях
z и z +Az (рис. 7.23а):
N Р
U (z, 0 = f E dl, U (z + Az, t) = 1 Е dl. G.97)
м Q
При этом
N Р
ф Edl = - JEdl+ f EdI
NMQP M Q
(на участках NP и QM, лежащих на проводниках, Ех = 0). Это зна-
значит, что
ф EdI = C/(z + AZ)-C/(Z) = ^-Az+ ... G.98)
NMQP
Полученное равенство выражает циркуляцию вектора Е слева во
втором уравнении Максвелла в интегральной форме A.54).
262 ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
Рассмотрим теперь правую часть уравнения A.54), которая дает:
где АФ — магнитный поток через поверхность S, ограниченную в
данном случае контуром NMQP. Поскольку АФ = /2"Az + ..., где
SB' = dSfdz — погонная индуктивность, то
= —2"-§f Az+ ... G.99)
Приравнивая левую G.98) и правую G.99) части второго уравнения
Максвелла и переходя к пределу при Az -*- 0, приходим к первому
из телеграфных уравнений G.96). Чтобы вывести второе из урав-
уравнений G.96), рассмотрим построение на рис. 7.236 (в двух вари-
вариантах). Имеется в виду цилиндр, основания которого лежат на по-
поперечных сечениях z и z + Az. В силу первого уравнения Максвелла
A.53) для этих оснований:
j Hdl = /(z + Az, t) G.100)
L(z) L(z+Az)
(поток вектора D равен нулю, так как Dz = 0); здесь L(z) есть кон-
контур области основания цилиндра S(z), аналогичный смысл имеет
Z(z + Az). Поскольку
(j) Hdl— ф Hdl= (j) Hdl,
L() L(z'+Az) L0oK
L(z)
где Z60K — контур боковой поверхности цилиндра
^бок
Это левая часть первого уравнения Максвелла A.53).
Рассматривая правую часть этого уравнения, запишем
G.101)
at J
5бок
где Ад — заряд проводника на участке Az; ток проводимости в дан-
данном случае отсутствует. Очевидно, что Ag = UC'Az + ..., где С'=
= dC/dz — погонная емкость. Поэтому
D ds = С Щ- Az + ... G.102)
s6ok
Остается приравнять выражения G.101) и G.102) в соответствии
с первым уравнением Максвелла. Переходя при этом к пределу при
Az -*¦ 0, получаем второе из уравнений G.96).
§ 7.4. ДИЭЛЕКТРИЧЕСКИЕ ВОЛНОВОДЫ
263
В случае гармонического во времени процесса производится пере-
переход к комплексным представлениям напряжения и тока и телеграф-
телеграфные уравнения записываются в комплексных амплитудах. Пусть в
линии вдоль оси z распространяется Т-волна. При этом С =
= С/техр(?(о? — ikz) и / =/техр(«о? —i&z). Внося это в G.96)',
получаем:
Wm = (n2"L, kL = «aC'ff». G.103J
Отсюда нетрудно найти А; и \УЯ
v = ¦
W, =
= IS'1С,
G.104)
G.105)
причем волновое сопротивление \?л можно определить, зная поле,
при помощи интегральных представлений G.95) напряжения и то-
тока. На основании G.104), G.105) легко выразить погонные реак-
реактивности:
Z' = WJv, C' = ll(Wav). G.106)
В заключение заметим, что при выводе телеграфных уравнений
фигурирует Т-волна, называемая противофазной: токи проводников,
как и их заряды, сдвинуты по фазе на 180°. В случае двухпровод-
двухпроводной линии, которая является трехсвязной (см. выше п. 7.3.1), сле-
следует также учитывать существование решения в виде синфазпой
Г-волны, которая подобна волне однопроводной линии.
§ 7.4. Диэлектрические волноводы и родственные структуры
7.4.1. Типы структур с диэлектрическими элементами (А). На
рис. 7.24 показаны поперечные сечения ряда продольпо-однородных
структур с неоднородными средами, начиная с плоского слоя диэлек-
диэлектрика (а), который рассматривался еще в п. 5.3.4 (см. также
п. 6.2.3) в качестве идеализированного диэлектрического волновода.
Реальны прямоугольный (б) и круглый (в) диэлектрические волно-
волноводы. Однопроводная линия (г) показана здесь потому, что при
конечной проводимости она анализируется по той же схеме, что и
круглый диэлектрический волновод. Круглый диэлектрический вол-
волновод может быть двухслойным (д); применяются и другие волно-
волноводы из нескольких диэлектрических элементов (е). Используется
однопроводная линия с диэлектрической оболочкой (ж). Следующие
структуры (з, и, к) являются экранированными; это круглый и пря-
прямоугольный волновод с диэлектрическими включениями.
Некоторые диэлектрические волноводы находят широкое приме-
применение в оптическом диапазоне частот. Уже отмечалось (см. п. 5.3.4),
что диэлектрический слой (а) есть модель используемых в интег-
интегральной оптике пленочных волноводов; в оптике применяются так-
также круглые волноводы (в, д), прямоугольный волновод па диэлек-
264
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
§ 7.4. ДИЭЛЕКТРИЧЕСКИЕ ВОЛНОВОДЫ
265
трическом слое (е), называемый в этом случае полосковым оптиче-
оптическим волноводом, и ряд других.
Если граница раздела сред рассматриваемой структуры описы-
описывается как цилиндрическая координатная поверхность г = const
(в, г, д, ж, з), то, как и в случае полого круглого волновода (см.
§ 7.2), в основе анализа лежит использование решений скалярного
2R
IWWJ
7.4.2. Круглый диэлектрический волновод (А). Этой структуре
свойственны гибридные волны, а также волны классов Е и Н. Та-
Таким образом, в общем случае для представления поля надо выра-
выразить продольную электрическую и магнитную компоненты. В обла-
области диэлектрического стержня 0<r<R (рис. 7.24е) функции <§г
и Жг представим в виде:
<§г = AJn(%ir)cosna,
Жг = BJn (xiO cos (па —
G.107)
Аналогичные выражения <gz и Жг были получены для круглого по-
полого волновода (см. § 7.2) в классах полей Е и Н. В гибридной
волне такие поля связаны, причем до решения задачи неизвестен
ориентационный угол г|з. В G.107) индексом 1 обозначены величи-
ны, относящиеся к области стержня; при этом к\ =((о/с)Уе1Ц1.
Вне стержня при r>R (рис. 7.23е):
G.108)
= DH™ (Хаг) cos (па -
2R-;
/777777777777//.
Рис. 7.24
уравнения Гельмгольца в цилиндрических координатах (см.
и. 7.0.3), получаемых методом разделения переменных. Решение
электродинамической задачи выражается в замкнутой форме; неко-
некоторые трудности могут быть связаны лишь с нахождением попереч-
поперечных волновых чисел как корней трансцендентных уравнений. Лег-
Легко выписывается решение задачи о прямоугольном волноводе со
слоистым диэлектрическим заполнением (и). Что касается структур
с прямоугольными подобластями (б, е, к), то здесь замкнутые вы-
ражепия решепий отсутствуют; необходимо применение методов ал-
алгоритмизации, ориентированных на ЭВМ (гл. 12—13).
Вместо функций Бесселя здесь фигурируют функции Ханкеля вто-
второго рода (см. п. 7.0.2). Это означает выбор решения уравнения
G.39) в форме второй строчки G.15) с сохранением того члена,
который с ростом г убывает быстрее, чем 1/Уг, если %2 = —115C21J что-
чтобы убедиться в этом, достаточно привлечь асимптотическое пред-
представление G.32). В G.108) индексом 2 обозначены величины, от-
относящиеся к внешнему пространству r>R; в частности, &2 =
= (со/с)Уе2Ц.2 (если внешняя среда — воздух, то практически, ег = 1,
1*2 = 1).
При решении электродинамической задачи о диэлектрическом
волноводе сначала надо выразить полное электромагнитное поле в
комплексных амплитудах: Ет = Етг + Ет(, Нт = Нт2 + Нт4 во внут-
внутренней и внешней областях. Для получения поперечного поля Em(t
Hm, продольные компоненты Emz = z^ze~iTz и Hmz = 2оЖге~'Тг, сле-
следующие из G.107), G.108), вносятся в F.16). При наложении ус-
условий непрерывности тангенциальных компонент векторов напря-
женностей поля на поверхности стержня r = R устраняются неопре-
неопределенности в представлениях полей и формулируется уравнение
относительно поперечных волповых чисел. Все эти операции при-
приведены ниже в п. 7.4.3, а здесь опускаются.
266
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
§ 7.4. ДИЭЛЕКТРИЧЕСКИЕ ВОЛНОВОДЫ
267
В общем случае указанное уравнение имеет вид
гибридные волны
, G.109)
причем связь между поперечными числами в обеих средах
уХ-Ъ-hl-kl G.110)
которая следует из G.107), G.108), позволяет исключить из G.109)
Xt или Х2.
Если п = 0, т. е. поле является азимутально-однородным, то ле-
левая часть в G.109) исчезает и уравнение распадается на два более
простых: поочередно приравниваются нулю выражения в квадрат-
квадратных скобках. Как показано ниже в п. 7.4.3, азимутально-однород-
ные волны не являются гибридными, а относятся к классам Е и Н,
так что уравнения, получаемые из G.109) при п = 0, соответствуют
этим классам. Ниже они записаны после небольших преобразований:
Е-волны
Н-волны
К2)
G.111)
G.112)
(в частности, учтено первое из соотношений G.23)).
Анализ полученных уравнений приводит к выводу, что общий
характер волн, направляемых диэлектрическим стержнем, близок к
тому, что уже известно о волнах плоского диэлектрического волно-
волновода (см. п. 5.3.4). Рассмотрим ?"-волны. Выше отмечалось, что для
направляемых волн %2 = —ф (Р^О); при достаточно большом [}
волна имеет резко поверхностный характер. Так как yj < 0 и Xi > 0,
то (см. G.107), G.108))
Т2>к1 Г2</с?. G.113)
Волны, таким образом, являются быстрыми по отношению к внут-
внутренней и медленными — по отношению к внешней среде, ср. E.84).
Характер распределения корней уравнения G.111) или G.112)
легко понять, проанализировав левую и правую части, как функции
от х = %\R. Левая часть F%'H (x) (индексы соответствуют случаям
волн Е и Н) в обоих вариантах построена на рис. 7.25; взято ei =
= 9,6 и |i,i = 1 при ё2 = 1 и |Я2 = 1 (диэлектрический стержень в
воздухе). Правая часть F%'Н (^) при %2 = —ф (jl > 0) отрицатель-
отрицательна, а значит, в рассмотрение входят только отрицательные участки
ветвей Ff'H(x). Правая часть Fn'H (х) имеет одно и то же значе-
значение в вариантах Е и Н. Поскольку ввиду G.110)
= Ух2 — (со/сJi?2(eiHi — егцг), то
рис. 7.25 эта функция построена для
R = 7 мм при нескольких частотах.
На самой низкой из них корней нет,
но с повышением частоты сначала
появляется один корень, затем два
и три. Как видно, все они лежат
между нулями и полюсами функ-
функции F%'H (х), т. е. между нулями ее
числителя и знаменателя, а это кор-
корни Вот и В\т уравнений J0(x)=0 и
J\(x)~ 0 соответственно.
При критической частоте / = /кр,
для которой %2 = 0, вне стержня по-
поле утрачивает продольную электри-
электрическую (магнитную) компоненту и
становится Т-волной; при этом Г = ~
= &2- Как и в случае плоского ди-
диэлектрического волновода (см. п. -
5.3.4), это «разрушение» направляе-
направляемой волны: энергия распространяет-
распространяется во внешнем пространстве. Из
G.111) и G.112) следует, что при
Х2 = 0 обращается в нуль и J0(%\R), т. е. Xi^ =
G.110), получаем:
(тп) от С
/l Л/ р || р II
зависит от частоты. На
Рис. 7.25
Привлекая
G.114)
(ср. E.101)).
Разумеется, корни трансцендентных уравнений G.111), G.112)
и G.109) находят не графически, а путем численного решения на
ЭВМ. Для прежнего диэлектрического стержня (ei = 9,6; Д = 7мм)
в воздухе таким путем найдены частотные зависимости, представ-
представленные на рис. 7.26 и рис. 7.27. По оси ординат отложена величи-
величина fo/r = ЛДг = рф/р2 (V2 = c). Отношение фазовой скорости уф на-
направляемой волны к скорости v2 = с волны Т во внешней среде
стремится к единице при отсечке. На рис. 7.26 отмечены
критические частоты типов волн ЕОт и НОт, отвечающие фор-
формуле G.114).
Кривые на рис. 7.27 относятся к гибридным волнам, анализируе-
анализируемым при помощи уравнения G.109). Существенно, что основпая
волна рассматриваемого волновода является гибридной. Она обозна-
268
ГЛ. 7, НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
чается символом НЕ и и имеет критическую частоту, равную нулю.
Минимальная критическая частота в классе всех остальных волн
(Е, Н и гибридных) определяется по формуле G.114) при т = 1:
1
о, в
0,6 -
0,2
кр
20
Рис. 7.26
f,rru,
Рис. 7.27
это критическая частота типов волн Eoi и Нои Таким образом, в по-
полосе частот
0</<
GЛ15)
может существовать лишь осттовпая волна НЕ\\. При фиксирован-
§ 7.4. ДИЭЛЕКТРИЧЕСКИЕ ВОЛНОВОДЫ
2С9
ном R полоса такого одноволнового (говорят еще одыомодового) ре-
режима тем шире, чем ближе коэффициенты преломления обеих сред
п\ = Уеця1 и п2 = Уе2|Я2 (ср. п. 5.3.4).
В оптических системах нередко используют двухслойные диэлек-
диэлектрические волноводы (см. рис. 7.243). Достаточно толстая внешняя
диэлектрическая оболочка оказывает па внутренний стержень почти
такое же действие, как безграничная среда с теми же проницаемо-
стями е и ц. Полосу одномодового режима при этом можно оце-
оценивать по формуле G.115).
7.4.3. Вывод основных соотношений (Б). Приведем вывод выраже-
выражений комплексных амплитуд полного поля круглого диэлектрического
волновода и уравнения G.109).
Отправляясь от формул G.107) и G.108), потребуем непрерыв-
непрерывности продольных компонент векторов Е и Н на поверхности стерж-
стержня г = Н. Это дает:
С _ D fo
А д
Чтобы получить поперечные компоненты векторов поля внутри и
вне стержня, внесем в F.16) Emz = z^zqxv(-iTz) и Нтг =
= zo<5^exp(—iTz). Таким образом,
= —j- {^rVj./n (xjO cos na +
—— {Ат^ [z0, Vj_/n (улг) cos na] +
Тп (улг) cos (па — г|5), z0]} e-iVz,
G.117)
±Jn (улг) cos (па — г|5)} e~irz,
и затем с учетом G.116):
7.±Я^2) (-/or) cos тгос +
7±#12> (у_2г) cos (?га^— ijj), z0]} e~lTz,
Ucoeoe2[zo,
G.118)
' (%2r) cos (na —
Здесь согласно B.3) и табл. 2.2
Vi^n (yr) cos (na + P) = royZ'n (//) cos (та + p) —
— «о ^n ^/-r) sin
где Zn есть /„ пли Я^2); р = 0, i[i; у. = xi.2-
270
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
Выделяя из G.117) и G.118) азимутальные компоненты и при-
приравнивая их при r = R, получаем два равенства:
cos (па -
юе0Л cos па | — —
-^ X (Х1Д)
#} (х.Д)
G.119)
7.120)
Если ?г v^= 0, равенства G.119) и G.120) могут быть удовлетворены
только при if = ±90°, тогда тригонометрические множители сокра-
сокращаются. Исключая константы А и В, получаем из G.119), G.120)
непосредственно уравнение G.109).
Остается показать, что уравнения G.111) и G.112), действи-
действительно отвечают классам полей Е и Н соответственно. Это следует
из G.119) и G.120). Пусть удовлетворяется уравнение G.111),
тогда не выполнено равенство G.112), а потому при /г = 0 выра-
выражение в квадратных скобках справа в G.119) не равно нулю. Но
ввиду п = 0 левая часть в G.119) уничтожается. Отсюда 5 = 0,
т. е. согласно G.107), G.108), G.116) Нг = 0: мы имеем ZJ-волны.
Аналогично показывается, что G.112) отвечает Я-волнам.
7.4.4. Цилиндрические проводники (Б). Все полученные выше
основные соотношения, начиная с формул G.107) и G.108) сохра-
сохраняют справедливость при комплексных проиицаемостях стержня и
окружающей среды; при этом, разумеется, анализ корней уравнений
G.109), G.111) и G.112) оказывается в общем случае более слож-
сложным. Таким путем можно учесть потери в диэлектрическом волно-
волноводе и решить другие задачи. В частности, можно рассмотреть ме-
металлический стержень в диэлектрической среде и цилиндрический
канал в металле, заполненный диэлектриком.
Однопроводная линия и полый волновод. Из сказанного следует,
что можно учесть действие реального проводника в случаях одно-
проводпой линии (см. конец п. 7.3.1) и круглого волновода (см.
§ 7.2), взяв ei = — ia/coeo в первом случае и е2 = — га/соео — во вто-
втором. Как известно (см. п. 6.1.2), при наличии реального провод-
проводника чистых Г-волн быть не может и основную волну однопровод-
ной линии следует искать в классе ?-волн; это низшая волна, обо-
обозначаемая ?"оо- Поэтому обратимся к уравнению G.111).
Постоянная распространения Г волны Еоо должна быть близка
к величине к2, которая является постоянной распространения
§ 7.4. ДИЭЛЕКТРИЧЕСКИЕ ВОЛНОВОДЫ
271
Г-волны линии при идеализации проводника. Поскольку Г=з|/ к\ — %%,
то при Г ~ к2 поперечное волновое число %2 оказывается весьма ма-
малым: 1хг1 "^ 1. Учитывая также неравенство Ifcil > \к2\, на основа-
основании G.110) приходим к выводу, что xi ~ ^и причем его значение
очень велико fti =A — i)/A° E.96). Следовательно, в левой части
G.111) можно использовать асимптотическое представление функ-
функций Бесселя G.29). В результате
и уравнение G.111) принимает вид:
G.121)
где Wnp=(l + i)/oA° E.94).
Для представления функций Ханкеля малого аргумента можно
привлечь формулы G.35), G.36) с учетом G.16). Полагая /i(z) = 0
и /0(х)= 1, имеем:
Н[2) (х) = 121лх
и
#<2) (х) = 1 + i B/п) In B/yx) = i[-i + B/я) In B/y*)].
А поскольку — i =B/n)ln(—i), то
Уравнение G.121) принимает вид:
iaeoe2WupR =(x2RJlnB/iU2R). G.122)
Это уравнение, полученное Зоммерфельдом, традиционно обсужда-
обсуждается в литературе ([А.2], [А.З], [В.2] и др.). В одном из примеров
его решения для медного провода диаметром 2 мм в воздухе при
/=1 ГГц было получено: Г/к2 = 1,00006—i ¦ 0,000064. Как видно,
замедление и затухание волны довольно малы.
Поскольку волна Еоо является, в принципе, поверхностной, ра-
радиальное убывание поля происходит быстрее, чем 1/Уг. Поэтому при
вычислении передаваемой мощности Р интеграл уже не расходится,
как было в случае идеального проводника в п. 7.3.1.
Перейдем к задаче о полом волноводе, который будем рассмат-
рассматривать как канал в толще металла. Выше в п. 7.2.3 было отмечено,
что только азимутально-однородные волны (п = 0) принадлежат
классам Е и Н, а остальные волны круглого волновода при конеч-
конечной проводимости оболочки являются гибридными. Теперь можно
сказать, что этот факт — следствие уравпепия G.109), обсуждав-
обсуждавшееся в п. 7.4.2.
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
Азнмуталыю-однородные Е- и Я-волны анализируются при по-
помощи уравнений G.111), G.112). Поскольку в данном случае к% —
= A —i)/A° очень большая величина, также велико и число %.2 =>
= у к\— Г2. Поэтому в правой части уравпепий G.111) и G.112)
можно использовать асимптотическое представление функций Хан-
келя .{7.32). В результате Я(п2) (%2R)/H{2) (%2R) ж — i. Заменяя в
G.111) и G.112) %2 на весьма близкую величину к%, получаем:
Xi
R-
для Е-ъолп и
Xl /, (Х.Я)
G.123)
G.124)
для Я-волп.
Гибридные волны обозначают символами ЕН и НЕ; первые близ-
близки к ?"-волнам, а вторые — к Я-волнам идеализированного полого
волновода. Решения в классах ЕН и НЕ при а -»- °° переходят в из-
известные из § 7.2 решения в виде Е- и Я-волн.
Поверхностный эффект в случае провода. Рассмотренный подход
позволяет без упрощений исследовать поверхностный эффект для
металлического цилиндра; напомним, что выше в п. 5.4.2 мы смогли
рассмотреть только сильный поверхностный эффект в проводе.
Переменный ток цилиндрического провода будем считать распре-
распределенным равномерно по азимуту (д/да = 0) п в продольном на-
направлении (djdz = O). Сопутствующее ему поле есть не что иное,
как волна Еоо при Г = 0. Поэтому yj = ki и электрическое поле ли-
лишено поперечной составляющей (это видно из G.117), G.118)).
Значит, полное электрическое поле внутри провода .можно выразить
прп помощи первого равенства G.107);
Em = w9Aj0(k1r)^,9En(BLSPw (r<Rh G-125)
где Em(R)= Ётх — поле на поверхности проводника и к\ = к =
= A —г')/А°; напомним, что параметр Д° = У2/со|л0ца имеет смысл
глубины проникновения в случае плоской границы (см. п. 4.1.4,
п. 5.4.1).
Формула G.125) имеет такой же смысл, как и первое из ра-
вепств E.95) в случае проводящего слоя. Поскольку j = о\Е, закон
распределения плотности тока в проводнике повторяет зависимость
G.125) (ср. второе равенство E.95)). На рис. 7.28 (ср. рис. 5.25)
при разных значениях параметра i?/A° представлена плотность тока
как функция радиальной координаты.
Путем интегрирования илотпости тока по поперечному соче-
тпо проводника находим полный ток; при г»том используется
§ 7.4. ДИЭЛЕКТРИЧЕСКИЕ ВОЛНОВОДЫ
273
формула G.24):
2Л В
2^W**>. G.126)
kJ (kR)
0 0
Следующий шаг — определение погонного импеданса провода SL' =
CVI
i (kR) '
G.127)
На рис. 7.29 приведены зависимости Ж', S6' и погонной индуктив-
индуктивности S' = 86'/со от параметра i?/A°. Эти величины отнесены к их
г
Рпс. 7.28
значениям при постоянном токе 5?0, <^0 и &oi соответственно, при-
причем 3?0 определяется по формуле B.135).
Простая проверка показывает, что в пределе прп A°/R -»- 0 полу-
получается погонное сопротивление 31' = l/aA°Z (? = 2лД), соответству-
соответствующее сильному поверхностному эффекту E.104); надо лишь учесть,
что Jo(kR)/J\(kR)->- i. При i?/A° -»- 0 приходил! к случаю постоян-
постоянного тока.
7.4.5. Заключительные замечания (Б). В § 7.2—7.4 было проде-
продемонстрировано, насколько физически разнообразны могут быть струк-
структуры, рассматриваемые в цилиндрической системе коордипат. Схе-
Схема операций, производившихся в пп. 7.4.2—7.4.3, является доволь-
довольно общей. Покажем, как она применяется в несколько более слож-
сложных случаях.
Другие типы структур. Рассмотрим, например, провод с диэлек-
диэлектрической оболочкой (см. рис. 7.24ж), пазываемый также липиой
Губо. Для представления поля внутри диэлектрика в данном случае
18 П. В, IIin-o.iLCinift, Т. II. Никольская
274
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
§ 7.4. ДИЭЛЕКТРИЧЕСКИЕ ВОЛНОВОДЫ
275
вместо функций Бесселя G.107) надо использовать более общую
форму решения в виде первой строки G.41). Соотношение между
функциями Бесселя и Неймана выбирается таким, чтобы на границе
провода выполнялись условия ёг = 0 и дЖт1дг = 0 (ср. п. 7.2).
В результате вместо G.107) пишется (ср. G.53), G.56)):
= В Г/„ (Xlr) - У*1*1* Nn(XiOl cos {па - i,),
| л ('") J
Г
G.128)
для R\<r <i?2- Представление поля G.108) остается справедливым
для области r>i?2 и все операции, произведенные выше в п. 7.4.3,
повторяются. Таким путем вместо G.109) получается следующее
уравнение:
X
X
Xl 3
G.129)
Как и уравнение G.109), полученное тоже распадается при /г = 0
на два более простых, которые отвечают классам полей Е и Н.
Низшая азимутально-одпородная ?-волна имеет тот же харак-
характер, что и основная волна однопроводной линии, рассматриваемая
без идеализации проводника (п. 7.4.4); она называется также Z?oo-
Круглый полый волновод с коаксиальным диэлектрическим стер-
стержнем (см. рис. 7.24з) можно считать диэлектрическим волноводом
в экране. В данном случае также справедлива известная нам схема
рассуждений (п. 7.4.2, 7.4.3). Представление G.107) остается при-
пригодным для области 0<r<i?i, а при /?i<r<i?2 вместо G.108)
нужно взять
cos
= О Г/„ (х2г) - ^"(Хх2дг) ^n (X-2r)\ cos (na - ^),
G.130)
Следуя прежней схеме (п. 7.4.3), нетрудно получить уравнение:
у2у2 Д.2
п(Хз
X
х
n
i l
G.131)
Это уравнение, как и аналогичные уравнения G.109), G.129), опи-
описывает гибридные волны, а при п = 0 распадается на два уравнения,
которые уже отвечают классам волн Е и Н.
Если экран достаточно широк, волны, направляемые диэлектри-
диэлектрическим стержнем, мало отличаются от тех, которые были бы в от-
отсутствие экрана, т. е. от волн диэлектрического волновода, рассмот-
рассмотренного выше в п. 7.4.2. Подчеркнем, что при любой частоте стер-
стержень направляет лишь конечное число волн.
Но существует еще бесконечное множество типов поля, которые
свойственны полому волноводу (см. § 7.2). Несколько упрощая,
можно сказать, что эти же поля, возмущенные и при п ?= 0 попарно
связанные, также фигурируют в виде собственных волн рассматри-
рассматриваемой структуры. Чем шире экран, тем ближе постоянные распро-
распространения этих типов волн (это легко проверить на примере круг-
круглого волновода, взяв формулы G.76), G.77) и G.81)). В пределе
при i?2 -*¦ °° влияние экрана на волны, направляемые стержнем, ис-
исчезает, а обсуждаемые «экранные» волны образуют непрерывный
спектр. Волны непрерывного спектра не являются поверхностными;
при анализе диэлектрического волновода они были исключены ил
рассмотрения.
13*
276
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
Импедансная трактовка поверхностных волн. Еще в п. 5.3.3 при
анализе полного отражения от границы диэлектриков было выясне-
выяснено, что для направляемых волн — поверхностных вне слоя — гра-
граница раздела сред выступает как импедансная поверхность. Цилинд-
Цилиндрическая граница диэлектрического стержня или провода (без идеа-
идеализации проводника) линии Губо также может быть охарактеризо-
охарактеризована поверхностным импедансом. Так в случае диэлектрического
волновода, применяя определение E.95) при v'o = — го,из G.107) и
G.117) нетрудно получить:
X, /0 (x.R)
— ZJ-волны,
s =
rr
- #-волны
(в первом случае E* = EZ, Нх = На, а во втором Е* = Еа, Hr = Hz).
Поскольку функции J0(x) и Ji(x) при fiOm < х < Bim (см. п. 7.4.2)
имеют разные знаки (ср. п. 5.3.3), из записанных формул следует,
что ZB имеет индуктивный характер для Е-вопп и емкостный — для
Я-волн.
§ 7.5. Полосковые, щелевые и другие пленарные структуры (А)
7.5.1. Типы пленарных структур. О развитии линий передачи.
На рис. 7.30 в поперечном сечении показаны некоторые продольно-
однородные структуры, называемые планарными. Полосковая (мик-
рополосковая) линия (а) представляет собой металлическую полос-
полоску, нанесенную на диэлектрический слон, подложку; последняя,
в свою очередь, располагается на плоском металлическом экране.
Можно рассматривать полосковую линию нли иную пленарную
структуру в варианте полного экранирования. Экран при этом по-
подобен прямоугольному волноводу; его контур показан штриховой
линией. Полосковых проводников может быть несколько (б);
в этом случае говорят о связанных полосковых линиях. Подложка
иногда не лежит на экране (в) н называется подвешенной. Сле-
Следующая структура (г)—это щелевая линия, называемая при на-
наличии экрана волноводно-щелевой. Две связанные щелевые линии
(д) можно трактовать как особого вида полосковую линию — так
называемая комплапарная линия. Пленарные структуры могут
быть многослойными и многоуровневыми. Имеется в виду много-
слойность диэлектрика и размещение металлических элементов на
различных границах раздела слоев. В качестве примера показаны
двухуровневые структуры: полосково-щелевая (е), двухнолосковая
'(ж) и двущелевая (з).
Распространение плапарных структур связано в первую очередь
с происходящей уже в точонпе ряда лот миниатюризацией СВЧ
аппаратуры. Так называемые интегральные схемы (ИС) СВЧ
§ 7.5. ПОЛОСКОВЫЕ, ЩЕЛЕВЫЕ, ПЛАНАРНЫЕ СТРУКТУРЫ
277
обычно формируются из полосковых элементов, располагаемых на
единой подложке. Как известно, поперечные размеры полых волно-
волноводов (см. § 7.1, 7.2) не могут быть меньше некоторых критиче-
критических. Например, в случае прямоугольного волновода передача энер-
энергии возможна лишь при а > Х/2. Что касается полосковой линии,
В
5
i 1
\
1
1
|\*
1
I
A
В
i
I
1
Xl
1
г
L
j
е ж э
Рис. 7.30
то ее поперечные размеры могут быть, практически, как угодно
малыми.
Интересно, что шаг от устройств на полых волноводах к ИС
СВЧ, использующим полосковые линии, есть, в сущности, возврат
к многосвязным структурам (к которым относится двухпроводная
линия), в свое время уступившим место полым волноводам. Как
здесь не вспомнить знаменитое диалектическое «отрицание отрица-
отрицания»! Полые волноводы широко распространились, начиная с 40-х
годов прн освоении сантиметровых волн. Обладая допустимыми
поперечными размерами, волноводные линии в отличие от провод-
проводных обеспечивали отсутствие взаимного влияния элементов аппа-
аппаратуры п других нежелательных эффектов. Следует иметь в виду,
что уже на дециметровых волнах полые волноводы оказываются
слишком громоздкими.
Полосковые линии, вытесняющие в ряде случаев полые волно-
волноводы, во многих отношениях выгодно отличаются от проводных
линии. Решающим фактором является концентрация поля осповпой
волпы в области подложки под полосковым проводником и, вслед-
278
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
ствие этого, малость паразитных влияний; иначе было бы невоз-
невозможно построить ИС СВЧ. Но как бы ни развивалось в дальней-
дальнейшем это направление, полые волноводы сохранят весьма значитель-
значительную область применения, в частности, при передаче большой мощ-
мощности.
7.5.2. Волновые процессы в планарных структурах. Электроди-
Электродинамическая теория направляющих структур, показанных на
рис. 7.30, оказывается довольно сложной. Общий подход к подоб-
подобным структурам будет обсуждаться ниже в п. 12.3.3, он ведет к
построению алгоритмов, реализуемых на ЭВМ.
Волны, направляемые полосковыми и щелевыми линиями, яв-
являются гибридными. Это касается и низшей (основной) волны по-
лосковой линии, которая аналогична Г-волне двухпроводной линии.
/п0
f
O,5
J
7
WMWCW
f,rru,
±ЯеГ/ка
60 f,rm,
Она также не имеет отсечки (/кр = 0). В типичных условиях — при
относительно малых поперечных размерах — поперечные компонен-
компоненты резко преобладают над продольными.
Рассмотрим дисперсионные кривые для основной и нескольких
высших волн экранированной полосковой линии (рис. 7.31)'). Это
') Никольский В. В., Никольская Т. И. // Машинное проектирование уст-
устройств и систем СВЧ.—М.: МИРЭА, 1979.—С. 17.
§ 7.5. ПОЛОСКОВЫЕ, ЩЕЛЕВЫЕ, ПЛАНАРНЫЕ СТРУКТУРЫ
279
частотные зависимости относительной постоянной распространения
). На рисунке линия представлена в двух
Т/ko (ко = сйУео|Хо =
вариантах, различающихся шириной полоскового проводника; все
размеры указаны в миллиметрах; кривые, относящиеся к линии с
более широким проводником, отмечены штрихом (иногда кривые
для обеих линий сливаются).
Если бы речь шла о настоящей Г-волне, распространяющейся в
среде подложки (в данном случае |х = 1, е = 9), то относительная
постоянная распространения была бы равна к/ко = Уец, т. е. Т/ко =
= Уе = 3 (см. рис. 7.31, штриховая прямая). Основная волна по-
полосковой линии характеризуется дисперсионной кривой 1, лежащей
несколько ниже. Дисперсия невелика. Заметим, что величину
(ГУ&оJ для основной волны называют эквивалентной диэлектриче-
диэлектрической проницаемостью еэ полосковой линии.
Все остальные кривые относятся к волнам той же симметрии,
что и основная волна полосковой линии (антисимметричные вол-
волны пропущены). Кривые 2 и 3, как показывает проверка, почти не
изменяются, если вообще удалить полосковый проводник, оставив
прямоугольный экран с диэлектрическим слоем. Соответствующие
волны можно назвать экранными. Видно, что экранные волны вы-
выходят из области отсечки (постоянные распространения из мнимых
становятся вещественными) при частотах около 35 ГГц и выше
57 ГГц. Следующие две волны (кривые 4, 5) необычны. Сначала
дисперсионные кривые оказываются такими же, как в случае эк-
экранных волн, но затем кривые смыкаются, образуя петлю, а на
частотах выше 56 ГГц ей отвечает другая петля. На участке меж-
между петлями постоянные распространения рассматриваемых волн
оказываются комплексными. Нить, соединяющая петли,— участок
семейства дисперсионных кривых, который дает одинаковые мнимые
части постоянных распространения этих волн. Их вещественные
части, различающиеся знаком, отображает отдельный фрагмент
графика (справа внизу). Волны такого рода называют комплексны-
комплексными. По-видимому, впервые такого рода волны были обнаружены
при анализе круглого волновода с коаксиальным диэлектрическим
стержнем1) (рис. 7.24з). Не привлекая теорию комплексных волн,
отметим, что они, как и другие волны в состоянии отсечки
(рис. 7.31), не переносят энергии: поток энергии внутри подложки
компенсируется противоположным потоком вне ее. Необходимо под-
подчеркнуть, что потери энергии не учитывались. Практического зна-
значения рассмотренные комплексные волны не имеют, однако они
интересны с принципиальной точки зрения. Можно сказать, что
они образуются в результате связи экранных волн, обусловленной
внесенным полосковым проводником.
При дальнейшем повышении частоты все большее число волн
выходит из области отсечки. Среди них оказываются и такие вол-
') Clarrlcoats Р. 1. В., Stnn К. R. Ц Electron. Letters, 1965.— V. 1.— P. 145.
280
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
ны, поля которых подооно полю основной волны сконцентрированы
в области подложки под полосковым проводником. Эти волны мож-
можно назвать подполосочными. Основная и высшие подполосочные
волны будут направляться полосковой линией и без замкнутого
экрана; достаточно широкий экран на них почти не оказывает
влияния.
На рис. 7.32 показано строение поля пленарной структуры на
примере двух связанных полосковых линий. Такой структуре свой-
свойственны две основные волны; одна существует при параллельных
Рис. 7.32. (ЭВМ)
токах полосковых проводников, а другая — при антипараллельных
(размеры экрана 2,3X1,5 мм2, толщина подложки 0,5 мм, е = 2,32,
ширина полоски 0,5 мм, зазор между полосками 0,3 мм, / = 20 ГГц).
В инженерной практике нередко используются интегральные вол-
волновые сопротивления, характеризующие осповпые волны плапар-
§ 7.6. НЕКОТОРЫЕ ВИДЫ ПЕРИОДИЧЕСКИХ СТРУКТУР
281
ных структур (ср. Wn в п. 7.3.1). В случае полосковой линии (см.
рис. 7.30а) можно определить волновое сопротивление как
в
dl,
G.132)
где имеется в виду полный ток полоскового проводника. Существу-
Существует также «энергетическое» определение, согласно которому
m,H;]ds. G.133)
Обе формулы дают весьма близкие значения в типичных случаях,
когда толщина подложки значительно меньше длины волны в ее
диэлектрике (поле в подложке квазистационарно).
В случае щелевой линии (рис. 7.30г)
3z
G.134)
а Р вычисляется, как и ранее, обычным образом.
§ 7.6. Некоторые виды периодических структур (Б)
7.6.1. Цилиндрические замедляющие системы. В п. 6.3.2 было
установлено, что частые периодические структуры могут — при
определенных условиях - направлять медленные волны (фактиче-
(фактически речь идет о нулевой пространственной гармонике структуры).
При этом фазовая скорость волнового процесса ниже скорости
Г-волны в прилежащей однородной среде, где волна проявляет сеоя
как поверхностная.
На рис. 7.33 показаны три периодические структуры: ребристый
стержень (а) диафрагмированный волновод (б) и спиральный вол-
волновод (в). Первые две из них родственны рассматривавшейся в
п 6 3 2 плоской ребристой структуре, однако ввиду их цилиндриче-
цилиндрической симметрии анализ естественно производить в цилиндрических
координатах. При рассмотрении нулевой пространственной гармо-
гармоники имеющей характер азимутально-однородной (ге = 0) ?-волны,
поле в пазах между ребрами, как и ранее, отождествляют с по-
поперечной стоячей Г-волной; но теперь это — радиальная волна с
векторами Е = г0Е и Н = а0Н. Ранее было установлено, что граница
системы ребер выступает как импедансная поверхность. В данном
случае подобно F.59) запишем:
+г0],
G.135)
где верхний знак берется в случае ребристого стержня (рис. 7.33а),
а пижпий —в случае диафрагмированного волновода (рис. 1.666).
282
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
Поверхностная Е-волна поддерживается структурой, когда Z8 име-
имеет индуктивный характер.
Рис. 7.33
Запишем уравнения, которым подчинены поперечные волновые
числа % азимутально-однородных Е-волн ребристого стержня и диа-
диафрагмированного волновода (рис. 7.33а, б):
ребристый стержень
диафрагмированный волновод
= i
. У.
шео8
причем
o (kRu) No (fcfl)
G.136)
G.137)
G.138)
где верхний знак берется при RM<R (первый случай), а нижний
при ДМ>Д (второй случай). Если |ДМ — R\ < R, т. е. пазы неглу-
неглубоки, то
Zs~iWtgkd, G.139)
где d= \RM-R\ (ср. F.59)).
ВЫВОД. Начнем с вывода формулы G.138). Поскольку струк-
структура является частой (Л«А,), будем считать, что поле внутри
пала по меняется в naiipau.ieiimi z (такое прии.итжепие ислоличо-
валось и в и. 6.3.2). Тогда для области паза Г = 0 и к = %. Выра-
§ 7.6. НЕКОТОРЫЕ ВИДЫ ПЕРИОДИЧЕСКИХ СТРУКТУР
283
жая это поле, для представления продольной электрической компо-
компоненты используем формулу G.53), положив га = 0, 1 = к и R\=Ra
(так как Ez = 0 при г = Дм); при этом на основании F.25)
Ёт = г0А Г /0 (кг) -
No (кг)
G.140)
Выражение поверхностного импеданса G.138) получается при под-
подстановке комплексных амплитуд G.140) в G.135) при r — R.
Чтобы прийти к приближенной формуле G.139), надо лишь
внести в G.138) асимптотические представления цилиндрических
функций G.29), G.30).
При выводе уравнения G.136) учтем, что формулы G.140) вы-
выражают поле ребристого стержня (для некоторого паза) в области
/?м < г < R. Для внешней области г > R положим <SZ = ВН? (уг)
и из F.25) получим:
= В
r)
г0 -^ Я<2> (Xr)j ,
,-irz
G.141)
Компоненты Emz и Йта внутреннего G.140) и внешнего G.141)
полей приравняем при г = Д (множитель ехр(—iTz) в G.141)
опускается). Это дает два равенства, содержащих неизвестные ко-
коэффициенты А и В. Исключеппе А и В приводит к G.136).
В случае диафрагмированного волновода представление поля
G.140) относится к области Д<г<Дм. При 0<г<Д положим
Si = BJ0(xr), так что на основании F.25):
Ет = В |zo/o (Хг) + г0 Я- J, (Хг)] е-*
Е
-гГг
G.142)
Дальнейшие операции производятся по прежней схеме. При r = R
приравниваются тангенциальные компоненты электрического и маг-
магнитного полей (Emz и Йта), получаемые из G.140) и G.142);
экспоненциальный множитель в G.142) здесь отбрасывается. Из
двух формулируемых равенств исключаются коэффициенты А и В,
что дает уравнение G.137). ¦
Ребристый стержень, направляющий Е-волну, естественно сопо-
сопоставить с однопроводной линией, которая имеет диэлектрическую
оболочку (см. п. 7.4.5): система ребер действует подобно слою
диэлектрика. Впрочем, структура поля а.чимуталыю-одпородпой
Е-волпы вне ребристого или имеющего диэлектрическую оболочку
284
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
стержня оказывается такой же, как и в случае круглого диэлектри-
диэлектрического волновода (см. п. 7.4.2). Что касается диафрагмированного
волновода, то его можно сравнить с круглым волноводом, на внут-
внутренней поверхности которого лежит коаксиальный диэлектрический
слой.
Обратимся, наконец, к рассмотрению третьей периодической
структуры, спирального волновода (рис. 7.33в). Можно представить
себе некоторый волновой процесс, распространяющийся вдоль про-
провода с фазовой скоростью v, свойственной У-волне. Полное поле
есть волна, распространяющаяся в направлении оси спирали. Ее
фазовая скорость уф настолько меньше v, насколько шаг спирали d
меньше длины витка 2nR. Поэтому иф = v sin у, где i — угол на-
намотки (рис. 7.32е), а следовательно,
Г = Л/8ш^ G.143)
Полученная приближенная формула оказывается удовлетворитель-
удовлетворительной для относительно высоких частот.
Нередко используется более сложная модель спирального волно-
волновода, в которой он рассматривается как цилиндрическая поверх-
поверхность с анизотропной проводимостью: допускаются лишь токи в
направлении намотки. Пусть So —• орт этого направления. Тогда на
поверхности г = Д, моделирующей спиральный волновод, задается:
Es = 0, Н, {В — 0) = Hs (R + 0). Непрерывность компоненты вектора
Н вдоль намотки означает отсутствие тока в ортогональном направ-
леппп. Кроме того па всей поверхности г = R налагается требова-
требование непрерывности полной тангенциальной компоненты вектора Е.
Поле внутри и вне цилиндра представляется точно так же. как при
анализе круглого диэлектрического волновода (см. п. 7.4.2, 7.4.3).
Желая исследовать основную волну, задаются в G.107), G.108)
нулевым порядком цилиндрических функций, получают поперечные
компоненты и связывают поля указанными выше граничными усло-
условиями при г = Д. Это приводит к следующему уравнению относи-
относительно поперечных волновых чисел %:
1 =
J
у.
Y
G.144)
Поскольку основная волна является медленной, то х — величина
мнимая (см. п. 6.1.3). Чем больше % по модулю, тем сильнее вы-
выражен поверхностный характер волны. При помощи асимптотиче-
асимптотических формул G.29) и G.32) легко убедиться, что Jt (х) Н[2) (х) х
x[jo(x)H^)(x)]~1-*-l, если х -*¦ -г°°. Тогда из G.144) %2 =
= —/с2 ctg2 Y, а поскольку Г2 = /с2 — %2, то получается выражение
G.143).
В заключепие отметим, что основная волна спирального волпо-
вода, будучи азимутально-однородпой (тг = О), тем не менее, яв-
§ 7.6. НЕКОТОРЫЕ ВИДЫ ПЕРИОДИЧЕСКИХ СТРУКТУР
285
ляется гибридной, т. е. ее поле имеет электрическую и магнитную
продольные компоненты.
7.6.2. Оптические и квазиоптические структуры. Если размеры
технических объектов многократно превышают длину волны, что
характерно для оптики, то, как известно (см. гл. 5), широко ис-
используется лучевая трактовка. В оптике давно применяются зер-
зеркала н линзы, на основе которых можно, в частности, строить пе-
периодические структуры, направляющие потоки энергии. Примеры
Рис. 7.34
зеркальных и линзовых линий передачи представлены на рис. 7.34;
направление передачи энергии указывает выделенный центральный
луч. Подобные линии передачи с характерными размерами, значи-
значительно превышающими длину волны, мыслимы не только в оптике;
онп паходят применение на субмиллиметровых, миллиметровых и
даже на сантиметровых волнах. При этом употребляется выраже-
выражение квазиоптические структуры.
При передаче энергии в зеркальной или линзовой линии фор-
формируется волновой процесс, при котором практически вся энергия
поля локализована в некоторой осевой зоне. Ее границы на
рис. 7.346 несколько условно показаны штриховой линией. С точки
зрения оптики, это некоторый параксиальный пучок лучей (лучи
близки к параллельным); граница пучка строится как огибающая
этих лучей и называется каустикой. Электродинамический анализ
показывает, что на границе пучка поле быстро убывает в попереч-
поперечном направлении, причем возможны процессы с различными по-
поперечными распределениями поля, по аналогии с различными соб-
собственными волнами волновода. Мы еще вернемся к этому вопросу
(см. § 10.6) после рассмотрения теории дифракции.
Остановимся пока на простейшей оптической трактовке линзовой
линии. На рис. 7.35а показана отдельная линза, на которую пада-
падает параллельный пучок лучей, сходящийся после ее прохождения
в фокусе. Суть в том, что оптическая длина всех лучей (см.
п. 5.5.2) — одна и та же. Этого добиваются выбором формы линзы
(для параксиальных пучков обе поверхности линзы можно считать
сферическими); средпий, самый короткий луч проходит наибольший
путь внутри линзы, где п > 1 (волна замедляется); зато крайние
лучи проходят большие пути в воздухе. Необходимость того, что
лучи сходятся в фокусе, можно понять, если исходить из принципа
286
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
§ 7.6. НЕКОТОРЫЕ ВИДЫ ПЕРИОДИЧЕСКИХ СТРУКТУР
287
Ферма^ Действительно, траектория среднего луча не вызывает со-
сомнений, но, исходя из этого принципа, мы должны считать его
оптически кратчайшим. При должном выборе профиля линзы край-
крайний луч на рис. 7.35а будет иметь ту же оптическую длину, т. е.
<0
а
осп >0
он тоже будет кратчайшим, а следовательно, должен физически
реализоваться. Этим же свойством обладают все лучи падающего
на линзу параллельного пучка.
Процесс фокусировки в известном смысле устойчив: при не-
небольших отклонениях падающего параллельного пучка от осевого
направления (рис. 7.356) он также фокусируется.
Лучи, принадлежащие параксиальным пучкам, будем характе-
характеризовать параметрами г и dr/dz = tg a « а. Так на рис. 7.35а для
крайнего случая на входе линзы имеем г = г{, а. = 0, а на выходе
г = г2 « п и а = а.2 < 0. При этом аг = —г2// (в дальнейшем при
замене тангенсов углами будем ставить знак строгого равенства).
Если же перейти к отклоненному пучку лучей (рис. 7.356), то, как
легко видеть, а2 — а.\ = —г2//.
На этом основании для периодической линзовой структуры
(рпс. 7.35е) запишем соотношение:
an-an_i = -/•„//, G.145)
где имеются в виду условные помера линз. Пусть Л — период струк-
структуры. Считая линзы топкими, будем иметь: гп — /-„_, = ап-\к и
г„+1 — г„ = а„Л. Вычтем первое равенство из второго; учитывая
G.145), получаем следующее рекуррентное соотношение:
г„+,+(Л//-2)гп + гп-, = 0. G.146)
Путем непосредственной проверки устанавливается, что
rn = Ae-ine + Beine, G.147)
где в удовлетворяет требованию:
cosG = 1-Л/2/. "G.148)
Неопределенные константы А и В можно выразить через п и г2.
Для этого надо решить систему двух уравнений, получающихся при
подстановке в G.147) п = 1 и п = 2. После подстановки получен-
полученных выражений А и В в G.147) представление г„ принимает вид:
sin (га—1) в
iin~e
sin (га — 2) в
sine
G.149)
Линзовая линия называется конфокальной, если Л = 2/, т. е.
фокусы лежат на середине расстояний между соседними линзами.
Тогда согласно G.148) cosG = 0; внося в G.149) G = 90°, получа-
получаем в этом случае:
rn = rlainn-^—ricoan^. G.150)
Важен следующий вывод. Величина 6 в G.147) — G.149) долж-
должна быть вещественной. В противном случае из-за появления в вы-
выражении г„ комплексного аргумента лучи могут с ростом п неогра-
неограниченно отклоняться от оси. Если же в — величина вещественная,
то в G.148) -1 «S cos в «S 1. Поэтому
0 s? Л *? 4/,
G.151)
т. е. — с позиций геометрической оптики — получено условие пере-
передачи процесса в линзовой линии, согласно которому расстояние
A=2f
Рис. 7.36
между липзами ле должно превышать четырех фокусных рас-
расстояний.
II ]) и м о р. Построим несколько лучей Для конфокальной .Tniii;iouoii линии.
Пусть Г] = а, 12= —а (а > 0), т. е. между линиями 1 ж 2 луч проходит через
288
ГЛ. 7. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
§ 8.0. ТРЕХМЕРНОЕ УРАВНЕНИЕ ГЕЛЬМГОЛЬЦА
289
фокус. Тогда на основании G.150)
( . п я
rn = a sin n -п- + cos n ~2
и луч идет так, как это показано на рис. 7.36 (линия 1). Можно взять г, = — а
и гг = а; при этом получится симметричный луч Г. Ту же картипу двух сим-
симметричных лучен, но сдвинутую по оси на расстояние Л, получаем, взяв г( =
= г2 = —а п Г| = г2 = а. Возьмем, далее, г( = а и гг = 0. При этом
Я
rn = a sin n-тр.
Лучи 2 ж 2' на рис. 7.36 соответствуют случаям п = + a z г2 = 0. Сдвинутую
о
на А картину лучей получим, внося в G.148) г, = 0 и r2 = qr a. ¦
УПРАЖНЕНИЯ
1. Размеры поперечного сечения прямоугольного волновода составляют:
а = 2 см, 6=1 см. Перечислить типы волн волновода, способных переносить
энергию, если / = 10 ГГц, 20 ГГц, 30 ГГц (внутренняя среда воздух, оболочка
считается идеально проводящей).
2. Сопоставив формулы G.66) и E.65) при надлежащей замене координат,
показать, что поле Ню прямоугольного волновода имеет ту же структуру, что
и в случае отражения наклонно падающей однородной Г-волны от идеально
проводящей плоскости при перпендикулярной поляразиции.
3. В прямоугольном волноводе при а = 2 см, 6 = 1 см, / = 10 ГГц (внут-
(внутренняя среда — воздух) мощность, передаваемая волновым процессом, состав-
составляет 1 Вт. Вычислить продольный ток, проходящий в оболочке волновода в
направлении передачи энергии. Чему равен полный продольный ток оболочки?
4. Вывести выражение типа G.71) при т ф 1, п = 0 (т = 0. п ф 1).
5. Показать, что в центре системы замкнутых магнитных силовых линий
ноля Ню лежит максимум ортогонального тока смещения, хотя максимум элект-
электрического поля сдвинут по осп z на Л/4.
С. Охарактеризовать сходство и различие строения свободных полей пря-
прямоугольного и круглого волноводов.
7. Почему в случае круглого волновода основной является волна Яц, оба
индекса которой не являются наименьшими (что можно сказать о волнах
Яо1 и Eoi)?
8. Перечислить типы волн круглого волновода радиусом 1 см (внутренняя
среда — воздух), способные переносить энергию при / = 10 ГГц, 20 ГГц. 30 ГГц.
9. Как известно, в случае однородной Г-волны круговой поляризации (см.
п. 4.2.1) вектор Е(Н) вращается в плоскости фронта, сохраняя постоянную
амплитуду. Можно ли это сказать в отношении волны Яц круглого волновода
при si-{а) = ехр( + гсс)?
10. Показать, что как в прямоугольном, так и в круглом волноводе при
/->- оо все волны становятся волнами Г.
11. Вывести формулу, выражающую полный ток в оболочке круглого вол-
волновода при наличии волны Ео] через максимальную амплитуду продольного
электрического поля.
12. Рассмотреть волновод, поперечное сечение которого есть полукруг. Со-
Сопоставить его с круглым волноводом того же радиуса. Что можно сказать об
основной волне в обоих случаях, имеет ли она одну и ту же фазовую скорость?
13. Пользуясь формулами G.106) с учетом G.91), вывести выражения по-
погонной емкости и индуктивности для коаксиальной линии.
14. Вывести формулу, выражающую коэффициент затухания основной пол-
полны коаксиальной линии, стержень и оболочка которой выполнены из разных
металлов.
15. Произвести подробную запись формул G.117) и G.118), раскрыв опе-
операцию Vj_ и разделяя компоненты векторов, азимутальные и радиальные.
16. В п. 7.4.3 произвести все действия, положив с самого начала п = 0, т. е.
рассматривая азимутально-однородные поля.
17. Сравнить изменение характера волнового процесса при /->/кр в полом
и диэлектрическом волноводах.
18. Сравнить низшие ?-волны круглого диэлектрического волновода, одпо-
проводной линии с диэлектрической оболочкой (или рассматриваемой с уче-
учетом конечной проводимости металла) и ребристого стержня. Однотиппы ли их
внешние поля? Чем отличаются критические частоты? Каким образом приме-
применяется в этих случаях представление об импедансноп поверхности?
19. Почему основная волна полосковой линии не является в строгом смыс-
смысле Г-волной?
20. Почему ребристые структуры называют замедляющими?
21. Как найти погонное сопротивление круглого провода при различпых
частотах?
22. При выводе формулы G.143) использовалось представление о Г-волно,
фактический путь которой вдоль провода зпачительпо превышает смещение
процесса вдоль оси спирали, так что фазовый сдвиг в этом направлении оказы-
оказывается соответственно большим: волповой процесс является медленным. Поче-
Почему такого рода рассуждение совершенно неприменимо по отношению к луче-
лучевой картине для полого волновода (см. рис. 5.17)?
Глава 8
РЕЗОНАТОРЫ
§ 8.0. Трехмерное уравнение Гельмгольца и соответствующие
краевые задачи
8.0.1. Декартовы координаты (А). Перед изучением основного
материала этой главы, посвященного полям в ограниченных объ-
объемах, снова вернемся к скалярному уравнению Гельмгольца F.1),
которое в декартовых координатах имеет вид
д2и
дх
'т
Т
д"иг
dz*
= 0.
(8.1)
Желая найти его общее решение, мы можем сразу же применить
метод разделения переменных, как это было сделано для аналогич-
аналогичного двумерного уравнения G.1). При этом положим: йт(х, у, z) =
= X(x)Y(y)Z(z). После подстановки этого представления в (8.1)
и деления всех членов на XYZ получаем:
1 d2X
1 d2Y
I dH _ ,2
Рассуждая так же, как в п. 7.0.1, записываем три обыкновенных
дифференциальных уравнения
—j + У.ХХ = 0, -p + y_yY = 0, —2+ y_2Z = 0, (8.3)
19 В. В. Никольский, Т. И. Пиколг.сьни
290
ГЛ. 8. РЕЗОНАТОРЫ
§ 8.0. ТРЕХМЕРНОЕ УРАВНЕНИЕ ГЕЛЬЛГОЛЬЦА
291
которые эквивалентны уравнению (8.3) при
'&+ '? + -& = **• (8-4)
Решения первых двух уже были выписаны в п. 7.0.1 в тригономет-
тригонометрической п экспоненциальной формах G.5). Совершенно такой же
впд имеет решение третьего уравнения (8.3):
1 cos
sin
(8'5)
Заметим теперь, что это третье уравнение есть не что иное, как
уравнение F.4), которое «отщепляется» и в более общем случае
разделения переменных (см. п. 6.0.1). Общее решение уравнения
F.1), когда анализируемая структура однородна вдоль оси z, мож-
можно искать в виде TZ, что ведет к уравнениям F.4) и F.5); разу-
разумеется, это верно, когда все три координаты — декартовы.
Для области в виде параллелепипеда (рис. 8.1а) можно ставить
различные краевые задачи. Например, потребовав, чтобы на всей
x\
Гч*
0
7
L z
Рис. 8.1
его поверхности выполнялось условие йт = 0, мы пришли бы к
первой краевой задаче типа G.6). Можно было бы также поставить
вторую краевую задачу, налагая вместо этого условие дйт/д\> = 0
(ср. G.11)). Однако для дальнейшего более интересны так назы-
называемые смешанные задачи, когда одно из данных граничных усло-
условий ставится на торцах 2 = 0, L, а другое — на остальной части по-
верхпостп.
Первая смешанная задача:
иi.i — 0 rip»
= 0. у = 0,
~- а, у ----- Ь;
B = 0,
" "I \-> — L
<-S.I-j>
Чтобы найти некоторое решение йт = XYZ, подчиненное этим гра-
граничным условиям, надо взять Т = XY G.8) и построить нужную
функцию Z, положив в (8.5) G = 0, %г = рп1Ь. Легко видеть, что
решения первой смешанной задачи образуют систему собственных
A) 7 2
функций Umnp при собственных значениях Kmnv:
(8-7)
'^
pnz
i\mnpsin -^sm-^cos-^
m = l, 2...; n = l, 2...; p = 0, 1, 2...
— неопределенные коэффициенты). Здесь использованы вы-
р
ражения Tmn G.10).
Вторая смешанная задача:
ди.
—— = 0 при х = 0, х = а;
—— = 0 при у = 0, у = Ь;
йт = О при z = 0, z = L.
(8.8)
В данном случае решения um = XYZ строятся как призведения
T = XY G.12) и Z = sin(paz/L) (в (8.5) F = 0). Задача порождает
следующие собственные функции:
= Л ml COS -^ COS
Sin
7 2 / '«¦' , I "" \ , '_11
Ьртр ~ — "Г Л — г
(8.9)
. = 0, 1, 2...; 72 = 0. 1. 2...; р = 1, 2. ...
8.0.2. Цилиндрические координаты (А). Уравнение F.1) в ци-
липдрпческих координатах (см. п. 2.0.2)
от
_1_ _^ ^.' i
г" 5а2
= 0
тоже приводится к уравнениям F.4) и F.5), причем
(8.10)
(8.11)
(вместо Г в F.4), F.5) пишем %z). Уравнение F.5), имеющее в
данном случае вид G.37), подробно рассматривалось в п. 7.0.3. Та-
Таким образом, um = TZ, где Т = Я(г)яФ(я), и эти сомножители вы-
выражаются фор.муглмп G.41), G.42). Формула (Я.5) по-прежнему
дает Z(z).
292
ГЛ. 8. РЕЗОНАТОРЫ
Получив общее представление решения йт, сформулируем, как
и выше в п. 8.0.1, решения смешанных краевых задач, рассматри-
рассматривая теперь цилиндрическую область (рис. 8.16).
Первая смешанная задача:
ди„
= 0 при r =
dz
= 0 при z =
= L. (8.12)
Отправляясь от формул G.46) и получая Z так же, как в случав
параллелепипеда, запишем порождаемые задачей (8.12) собствен-
собственные функции и соответствующие им собственные значения:
Jnпа cos
(8.13)
B™Y
И
m = l, 2,...; гс = 0, 1, 2 ..., p = 0, 1, 2 ...
(собственные значения подчинены равенству (8.11)). Для крат-
краткости записи использована только одна форма множителя s4-(na.).
Вторая смешанная задача:
^ = 0 при r = R, ыт = 0 при z = 0, z = L. (8.14)
Прежним способом, но используя в данном случае формулы G.49),
выпишем собственные функции и собственные значения:
"ti
mp — ''nmpt/nl"^—"/ . «a Sill —
(8.15)
= l, 2, ...; n = 0, 1, 2, ...; p = i, 2, ...
На основе выражений (8.13), (8.15) легко получить выражения
собственных функций, порождаемых краевыми задачами для ци-
цилиндрической области с кольцевым поперечным сечением
(рис. 8.1в). Надо лишь заменить бесселевы функции Jn(%r) ком-
комбинациями цилиндрических функций G.53) и, соответственно,
G.56).
8.0.3. Сферические координаты (Б). В сферических координа-
координатах (см. п. 2.0.2) уравнение F.1) имеет вид:
±±
г*дг
дг
J 9_f . o^O 1 02И„
sinftM 3ft / + r2sin2ft da2
= 0.
(8.16)
§ 8.0. ТРЕХМЕРНОЕ УРАВНЕНИЕ ГЕЛЬЫГОЛЬЦА
293
Для разделения переменных делается подстановка и (г, ¦&, а) =
= &l(r)®(%)s4-(a). Внося это в (8.16), а затем умножая все члены
2 2 $l$®4 имеем:
2 ^> /o a n
(817
на г2 sin
sin2-0 d
sin-ft d
1 d2
Третий члеп зависит только от а. Приравняем его некоторой кон-
константе —т2. Тогда сумма остальных членов будет равна т2, а урав-
непие распадется па два. Члены второго разделим на sin2 Ф, после
чего выражение, зависящее только от г, приравнивается константе
/г. Оставшаяся часть будет равна — р2, и возникают два обыкновен-
обыкновенных дифференциальных уравнения. В конечном счете получаются
следующие три обыкновенных дифференциальных уравнения:
da2
; _ о -- — г2—
-и' Я dr Г dr
1
6 sin ft
+ P2 = 0.
(8.18)
Решение йт, а следовательно, и з4- для шаровой области
(рис. 8.1г) должно переходить в себя при замене а на а + 2я.
Поэтому т = 0, 1, 2, ... Функцию s4-{a) нетрудно выразить в три-
тригонометрической или экспоненциальной форме.
Далее, если сделать замену cos b = t, то уравнение относительно
9 в (8.18) принимает следующий вид:
N| в = 0 (8.19)
jL
1 — г
(—1<?<1). Его решения ®(t) — это собственные функции, реали-
реализующиеся при собственных значениях р2 = п(п + 1). Они равны
так называемым присоединенным функциям Лежандра Pnm) (О
(п = 0, 1,2,...).
Наконец, второе из уравнений в (8.18) преобразуется путем
замены S2(r) = p(r)/V/cr и с учетом того, что р2 = п(п+1), к виду:
dr2
2-^4- к2-
г дг
р = 0.
Это не что иное, как уравнение Бесселя G.14) порядка п+1/2 от-
относительно р как функции аргумента кг. Таким образом, общее
решение уравнения (8.20) представляется формулами G.15), в ко-
которых надо заменить п иа п+1/2 и положить х = кг. Для области
0<г<Д сохраняется лишь функция Бесселя, так что 52(г) =
„+1/2()№
Итак, для внутреппей области шара (см. рис. 8.1в) получаем:
ит
А
у /,:г
Г*ОЧ
\ мЛкг)Р{п1) (cost1)) . та.
(8.21)
294
ГЛ. 8. РЕЗОНАТОРЫ
Представляют интерес две краевые задачи:
первая задача вторая задача
ит = 0 при г = R,
дгиг
= 0 при г = R.
(8.22)
Выражение (8.21) в том п другом случае представляет собственные
функции. Что касается собственных значений к2, то они согласно
(S.22) получаются при решении уравнения
0 (8.23)
(8.24)
или, соответственно,
Jn+i/2 (Щ + 2kRj'n^1/2 (kR) = 0.
В заключение приведем справочные сведения о специальных
функциях, входящих в (8.21). Присоединенные функции Лежандра
вычисляются следующим образом:
<т) (f\ _ (А _
df
_
п =
.. ., т,
(8.25)
где Pn(t) — полиномы Лежандра:
(8.26)
(п + 1) Pn...! (t) - f Bн + 1) Pn (i) + пР„_, (f) = 0.
Для функций Бесселя полуцелого порядка существует пред-
представление:
dn sin x
1! частности,
(8.27)
= l/ 4 sin *' ^/2 (a:) = ]Л| (~ - cos г). " (8.28)
§ 8.1. Общая теорпя электромагнитных резонаторов
8.1.1. Накопление энергии в объеме. Резонатор и направляющая
структура (А). Рассматривая в предыдущих главах различные вол-
uoiibie процессы, мы отмечали, что распространяющиеся, бегущие
подлы переносят энергию. Между тем, еще в пп. 4.0.2, 4.2.2 было
введено представление о стоячей волне, наложении двух противо-
ноложно направленных воли с одинаковыми амплитудами; в этом
с [учае (при отсутствии тютерь) энергия п среднем пе переносится.
^¦' |!t в y.i.'i.i.v :j.[OJv;|iii'jucivci о no.ui u,i,:ioi<ur{uoii стоячей У-волны
§ 8.1. ОБЩАЯ ТЕОРИЯ ЭЛЕКТРОМАГНИТНЫХ РЕЗОНАТОРОВ
295
П
Рис. 8.2
(n. 4.2.2) установить идеально проводящие плоскости z = const,
прежнее поле сохранится в отсеченном энергетически изолирован-
изолированном объеме. Можно сказать, что противоположно направленные
бегущие волны полностью отражаются этими плоскостями, на ко-
которые они падают по нормали. Движение энергии прп этом имеет
колебательный характер, как схематически показано на рпс 8.2а.
Направление вектора Пойптннга меня-
меняется через четверть периода колебаний
поля: он колеблется с удвоенной ча-
частотой (см. п. 3.3.1). Расстояние между
соседними плоскостями составляет по-
половину волны. Таким образом, условие
существования поля между ними вы-
выполняется прп вполне определенной
частоте. Изолированный объем, в котором происходит колебатель-
колебательное движение энергии, в сущности, выступает как ее накопитель.
Условие накопления энергии можно реализовать не только при
колебательном, но и прп циклическом движении энергии (рпс. 8.26)
внутри некоторого объема. Поскольку во всех случаях свободные
электромагнитные поля в энергетически изолированных объемах
могут существовать только прп определенных частотах, такие объ-
объемы являются резонаторами.
Легко показать, что резонатором будет любой отрезок некото-
некоторой продольно-однородной структуры, отсеченный двумя поперечны-
поперечными идеально проводящими плоскостями (рис. 8.3). Если исходной
структурой является прямоугольный (а) или. например, круглы it
(и) во. 11ш1;<>д. то образуется по.;ып ]>e,ion(iTi>]i', то же можно сказан,
о резонаторе, образованном коаксиальной линией (в). По все даль-
дальнейшие рассуждения будут справедливы и в отношении отсеченного
отрезка диэлектрического волновода (г) пли какой-нибудь иной
открытой структуры, например, двухпроводной лптпит (д).
В отсеченной области (рпс. 8.3) возможно существование лишь
таких полей, которые в дополнение к граничным условиям, свой-
свойственным исходной направляющей структуре, удовлетворяют также
условию Е,=0 на введенных перегородках. Таким свойством мо-
может обладать наложение прямой и обратной волн одного типа.
Сосредоточив внимание на поперечной электрической компоненте
поля, запишем:
л j qp> iY z I DSP iY z /С ОО\
где &t—поперечная проекппя вектора S F.12). а .4 п В — неко-
некоторые комплексные коэффициенты. Потребуем обращения Emi и
нуль па плоскости 2 = 0, что реализуется при В ——Л, причем вы-
выражение (8.29) принимает вид:
Emi=En&iSmTz, (8.30)
где Ео = —Г2Л; :>то стоячая полна. Налагая такое же условие при
296
ГЛ. 8. РЕЗОНАТОРЫ
z = L, мы должны положить в (8.30) sin YL = 0. Отсюда
T = pn/L, р = 0, 1, 2, .... (8.31)
т. е. постоянная распространения Г не может быть произвольной
величиной, а принимает одно значение из этой последовательности.
Поскольку Г = 2я/Л F.7), то из (8.31) следует
L = PAJ2, p = 0, 1, 2, ... (8.32)
При jd = 0, как видно из (8.30), Ent = 0: поперечная электрическая
компонента вообще отсутствует; эту возможность мы обсудим от-
отдельно. Во всех остальных случаях равенство (8.32) означает, что
L z
L \
к—
L
Рис. 8.3
длина отсеченного отрезка направляющей структуры должна быть
кратна половине длины волны (того или иного типа).
Ввиду F.13) Г2 = к2 — %2. Приравнивая этому выражению вели-
величину Г2, следующую из (8.31), получаем:
k* = %2 + (pnfL)». (8.33)
Поскольку к2 = (co/cJeji, то отсюда
со ----- ——¦
(8.34)
§ 8.1. ОБЩАЯ ТЕОРИЯ ЭЛЕКТРОМАГНИТНЫХ РЕЗОНАТОРОВ
297
Полагая пока е и ц вещественными константами, будем считать
также не зависящим от частоты поперечное волновое число % (как
в случае полых волноводов, см. § 7.1, 7.2). Тогда (8.34) выражает
в явной форме частоты, при которых поле может существовать в
рассматриваемом объеме. Они называются собственными частотами.
Объем выступает, таким образом, как резонатор.
Для каждого типа волны в направляющей структуре, которому
отвечает определенное %, существует бесконечное множество соб-
собственных частот, получаемых при переборе р. Собственные частоты,
соответствующие всем типам волн при всех значениях р, образуют
последовательность
О < coi «? юг «? ... «? со„ «? ... < оо.
Заметим, что в случае Г-волн % = 0, так что согласно (8.34)
собственные частоты зависят только от продольного размера L и
являются кратными низшей частоты:
(8.35)
Значение р = 0 в данном случае невозможно. Это означало бы пол-
полное отсутствие электрического поля: для Г-волн оно чисто по-
поперечное.
Что касается случая р~0, то поскольку при этом Г = 0, со-
соответствующая собственная частота резонатора, определяемая по
формуле (8.34)
',, (8.36)
равна критической (круговой) частоте сокр для данной волны на-
направляющей структуры (ср. /кр = сокр/2я F.22)). Так как при р — 0
поперечное электрическое поле отсутствует, то должно существо-
существовать продольное, а следовательно, речь может идти только о Е-вол-
нах. Как известно, при критической частоте поле не изменяется
по z и Л->-<». Согласно (8.32) длина резонатора при этом оказы-
оказывается неопределенной: L = 0 ¦ °°. Две поперечные плоскости могут
располагаться на любом расстоянии друг от друга (рис. 8.3е).
Заметим, что Я-волны при критической частоте имеют подобное же
продольное магнитное поле (и поперечное электрическое), так что
граничные условия на поперечных идеально проводящих перего-
перегородках не могут быть удовлетворены.
8.1.2. Свойства полей резонаторов (А). Мы рассмотрели только
определенный класс резонаторов, каждый из которых можно трак-
трактовать как энергетически изолированный участок направляющей
структуры. Их поля обладают свойствами стоячей волны. В про-
простейшем случае (см. п. 4.2.2) векторы Е и Н стоячей волны при
отсутствии потерь сдвинуты по фазе па 90 °, причем электрическое
я магнитное поля синфазны на участке между соседними узлами.
298
ГЛ. 8. РЕЗОНАТОРЫ
§ 8.1. ОБЩАЯ ТЕОРИЯ ЭЛЕКТРОМАГНИТНЫХ РЕЗОНАТОРОВ
299
Этим свойством отличаются многие поля резонаторов. Из (8.30)
видно, что при вещественных Г и <%\ поле Е, сннфазно в области
постоянного знака синуса. Пусть Ет = Ете!ф?, где фаза <гЕ не зави-
зависит от координат. Определяя комплексную амплитуду Н. имеем:
где
rot Ет =
rot Е„
— величина вещественная. Это значит, что фаза срн вектора Н от-
отличается от ф? на л/2. При таком фазовом соотношении наступают
моменты, когда существует только электрическое поле или только
магнитное. Поток вектора Пойнтинга, проходящий через любое
сечение резонатора, в среднем равен нулю. Движение энергии име-
имеет колебательный характер (рис. 8.2а).
Можно убедиться, что в ряде случаев возникают и циклические
движения энергии (рис. 8.26). Если, например, рассматривать ре-
резонатор, показанный на рис. 8.36, при круговой поляризации (см.
п. 7.2.2), то в этом случае
существует азимутальный
циклический поток энергии
(рис. 8.4а); через заштрихо-
заштрихованное сечение проходит по-
поток вектора Пойнтппга.
? * в среднем не уничтожаю-
Рис. 8.4 Щ1ШСЯ. Между основаниями
цилиндра z = 0 и z = L уста-
устанавливается уже рассматривавшаяся стоячая волна, однако функ-
функция <St в (8.30) при этом не является вещественной величиной и
сделанный ранее вывод о фазовом соотношении Е и Н оказывается
неприменимым. Как отмечалось в п. 7.2.2, волны круговой поляри-
поляризации возможны не только в круглом волноводе. То же можно
сказать п о циклических потоках энергии в резонаторах; мы могли
бы рассматривать, в частности, прямоугольный резонатор.
Существуют резонаторы, образованные замкнутой направляю-
направляющей структурой того или иного вида. На рис. 8.46 показан такой
резонатор, который можно рассматривать как изогнутый в кольцо
прямоугольный волновод. Если в волноводе распространяется пере-
переносящая энергию волна, то также образуется циклический поток
вектора Пойптинга. Это возможно, если вдоль замкнутого волново-
волновода укладывается целое число волн (чем больше радиус кольца, тем
с большим основанием можно определять длину волны, как в
п. 7.1). Впрочем, этот кольцевой резонатор можно трактовать как
отсеченным двумя параллельными плоскостями отрезок коаксиаль-
коаксиальной линии, п это представление является точным.
Кроме резонаторов, примеры которых представлены на рис. 8.3,
нередко применяются и такие, которые уже нельзя рассматривать,
как это делалось выше в п. 8.1.1. Резонатором, например, может
быть любая металлическая полость, какое-либо диэлектрическое
тело, система зеркал, планарная структура и пр.
В общем случае в теории электромагнитных резонаторов ищутся
решения уравнений Максвелла или производных уравнений второго
порядка при требуемых граничных условиях. В частности, для
произвольного полого резонатора с однородной изотропной средой
формулируется одна из следующих двух задач:
= 0 в V,
г = 0 на S
или
= 0 в V,
(rotHm)t = 0 на S
(8.37)
(8.376)
(V — объем резонатора, S — граничная поверхность). Соленоидаль-
ные решения этих задач (divEm = 0, divHm = 0) дают систему по-
полей, называемых собственными колебаниями. Каждое такое реше-
решение Е„) или Ни' (ге = 1, 2, ...) реализуется при некотором
собственном значении k~n параметра к2 = со2ец/с2. Соответствующие
значения со = соп — это собственные круговые частоты резонатора,
а к„ — собственные волновые числа.
Трехмерные векторные задачп (8.37) аналогичны двумерным
скалярным задачам F.8), F.9).
Если полый резонатор относится к уже рассматривавшемуся
классу (см. рис. 8.3), то векторы Ет и Нт в (8.37) удобно спроеци-
спроецировать на ось z. Это приводит к скалярным задачам относительно
Ётг и Йтг. Легко убедиться, что первая смешанная задача в
пп. 8.0.1—8.0.2 — это задача относительно йт = Ётг, а вторая —
относительно йт = Йтг. Полное поле можно определить через Emt
(ZJ-поля) или через Йт1 (Я-поля), подобно тому как это делалось
в п. 6.1.1 для направляющих структур.
Аналогично первая и вторая задачи из п. 8.0.3 интерпретируют-
интерпретируются как задачи относительно йт = Йтг и, соответственно йт = Ётт
шарового резонатора. Они также приводят к двум классам соб-
собственных колебаний, а полное поле восстанавливается по радиаль-
радиальной компоненте Ётт или Йтг.
8.1.3. Учет потерь. Добротность резонаторов (А). Потери энер-
энергии в реальных резонаторах обусловлены поглощением в диэлект-
диэлектрических и металлических элементах, а также в ряде случаев из-
излучением во внешнее пространство (папрпмер, полый резонатор
излучает при наличии отверстия).
300
ГЛ. 8. РЕЗОНАТОРЫ
§ 8.1. ОБЩАЯ ТЕОРИЯ ЭЛЕКТРОМАГНИТНЫХ РЕЗОНАТОРОВ
301
Пусть W — запас энергии резонатора при собственных колеба-
колебаниях некоторого типа с частотой со, а Ра — мощность потерь. Вве-
Введем величину
Q W/P (8.38)
которая, как мы убедимся, для каждого типа колебаний является
константой и называется добротностью резонатора. Поскольку рас-
рассматривается полная энергия некоторого свободного электромагнит-
электромагнитного поля, W и Ра связаны соотношением A.102); объединяя его
с (8.38), получаем следующее обыкновенное дифференциальное
уравнение:
dW CO ТТт г\ /О QO\
_ ] \у = 0. (о.оУ)
Его решение
(8.40)
показывает, что запас энергии собственных колебаний экспоненци-
экспоненциально падает. Поскольку энергия квадратично связана с полем, то
оно также экспоненциально затухает, причем амплитуды компонент
Е и Н изменяются по закону ехр I — ^ t\. Это значит, что поле
испытывает затухающие колебания (п. 3.2.3), причем в методе
комплексных амплитуд комплексной величиной оказывается соб-
собственная частота C.49):
со = со' + гсо", (8.41)
где в данном случае
со' = со, со"=со/2<?. (8.42)
Комплексность собственных частот резонаторов при наличии
потерь может быть установлена и непосредственно из полученных
ранее формул. Пусть, например, рассматривается полый резонатор
с идеально проводящей оболочкой, заполненный поглощающей сре-
средой. При этом согласно (8.33) к2 > 0 — величина вещественная, но
в силу комплексности е и ц собственная частота, определяемая по
формуле (8.34), комплексна:
м = ,/г^-:У Xя + "Г ехр —-^— (8.43)
Vh
(использованы обозначения C.37)).
И.ч комплексности собственной частоты вытекает экспоненциаль-
экспоненциальный ил кон убывания запаса энергии, а следовательно, и постоянство
параметра Q, определяемого по формуле (8.38): надо лишь при-
привлечь A.102).
15 большинстве случаев рассматриваются слабо затухающие ко-
лебппмл. дли которых со" «со'. Так как при этом локально про-
процесс близок к периодическому, под Ра в (К.38} можпо понимат1.
среднюю мощность Р„ (см. § 3.3).
При вычислении добротности резонаторов различные факторы,
определяющие потери, можно учитывать отдельно. Пусть ^п =
= ^п + ^п + Рш где имеются в виду потери в диэлектрических
элементах, в металлических элементах и на излучение, соответ-
соответственно. Введем парциальные добротности
каждая из которых вычисляется с учетом одного из этих факторов.
Из (8.38) следует, что
b = $~K + ?u + h (8-45)
т. е. обратные добротности складываются. Правда, этот вывод нель-
нельзя считать строгим (ср. аналогичный случай в п. 6.4.1): действие
разных факторов приводит к некоторому перераспределению поля,
а следовательно, величина W не будет одной и той же при вычис-
вычислении разных парциальных добротностей и полной добротности. На
практике запас энергии W обычно вычисляют, исходя из распре-
распределения поля в резонаторе без потерь. В этом приближении и при-
применяются формулы (8.44), (8.45).
Обратимся теперь к п. 3.3.3, в котором, в частности, рассмат-
рассматривался энергетически изолированный объем с поглощающей сре-
средой и было установлено, что свободное электромагнитное поле
внутри него должно иметь характер затухающих гармонических
колебаний. Воспользуемся выведенной там формулой C.67). Выра-
Выражая со' и со" при помощи (8.42), находим:
Получено выражение добротности резонатора, все потери которого
обусловлены поглощением в некоторой однородной изотроппой сре-
среде (диэлектрике); в большинстве случаев магнитные потери отсут-
отсутствуют: Д51 = 0.
При вычислении парциальной добротности Q = (9Д можно вместо
формулы (8.46) исходить из соответствующего выражения в (8.44).
В знаменателе_положим: WR — Wmax = 21УЭ (очевидно, что также
W = Wmax = WM), a P2 найдем, как Р%; магнитные потери бу-
будем считать отсутствующими. Таким образом, согласно C.51),
A.110) и C.59)
И' = Ц- \ EmK'dv, Ра = ^f. J ЁтЁ; dv. (8.47)
Отсюда
С>ж == 1/tg Д. (8.48
Замена величнпы Рп сродпой мощностью Fn закономерна в обыч-
обычных услшших. когда о>"«. о>' (('»!): югда l.L'A^A и формул г..
302
ГЛ. 8. РЕЗОНАТОРЫ
(8.46), (8.48) дают одни п тот же результат. Заметим, что, строго
говоря, применение выражения C.51) справедливо только для
безынерционных сред (потери не связаны с процессами поляриза-
поляризации: tg A = о/соеое).
Для определения парциальной добротности Qyl будем вычислять
запас энергии W через магнитную энергию, как VFmax = 2И' , а по-
потерн— из теории сильного поверхностного эффекта, а именно при
помощи формулы E.98):
w
= ф* f н;н; dv,
2стА
Внося это в (8.42), получаем
Qx = 2 ? -1 f НтЙ; dv I f Н
нтн;
ds,
(8.49)
(8.50)
где цм — относительная магнитная проницаемость металла (А0 =
= У2/со}ХоЦмО). Обычно им = ц = 1.
Отношение интегралов в (8.50) при сохранении формы резона-
резонатора и типа колебаний пропорционально линейному размеру и, сле-
следовательно, обратно пропорционально собственной частоте со. Учи-
Учитывая частотную зависимость А0, видим, что добротность (?м изме-
изменяется, как 1/Усо.
Вычисление парциальной добротности Qx не сводится к приме-
применению некоторой общей формулы. Резонатор нужно рассматривать
одновременно со связанной через отверстие электродинамической
структурой.
8.1.4. О собственных значениях идеальных полых резонаторов
(Б). Для полых резонаторов с идеально проводящей оболочкой
справедливы соотношения:
I rot Em |2
rot Hm |2 dv
Отсюда следует, что
P>0
(8.51)
(8.52)
независимо от того, является ли внутренняя однородная изотроп-
изотропная среда поглощающей. Выше это было установлено в частном
случае, когда резонатор является отрезком полого волновода. Что
касается соотношения (8.51), то оно не зависит от формы резо-
резонатора.
Заметим, что два равенства, содержащиеся в (8.51), аналогичны
интегральному соотношению F.10), выражающему собственные
значения двумерных задач F.8), @.9).
§ 3.2. ПОЛЫЕ РЕЗОНАТОРЫ
303
ВЫВОД. Чтобы получить выражение А через электрическое
поле, обратимся к формулировке первой краевой задачи (8.37).
Умножив оба члена уравнения Гельмгольца на Е,„ и применяя
тождество A.29), получим:
Em (rot rot Em — grad divEm) = А2ЕтЕ„.
Второй член в круглых скобках в дальнейшем отбрасывается, так
как поле соленопдально (divEm = 0). Учитывая, что на основании
A.26)
Ё„ rot rot Em = rot Em rot Е„ Jr div [rot Em, E^],
проинтегрируем все члены по объему резонатора V и применим
теорему Остроградского — Гаусса A.33). Это дает:
\ rot Em rot Ё; dv +ф [rot Ёт. Ё;;] ds = /с2 f EmE*m dv, (8.53)
V S V
где S — идеально проводящая оболочка объема V. Поскольку Ёт^ =
= 0 па iS", поверхностный интеграл исчезает и из (8.53) следует
первое из равенств (8.51). Чтобы получить второе, заменим в
(8.53) Е„ на Нт. Поверхностный интеграл п здесь исчезает, так
как (rotHm)T = 0 на S. ш
§ 8.2. Полые резонаторы (А)
8.2.1. Прямоугольный резонатор. Рассмотрим подробно полый
резонатор, показанный выше на рис. 8.3а. В приближении идеаль-
идеальной проводимости оболочки собственные частоты определяются по
формуле (8.34). в которую надо подставить выражение поперечных
волновых чисел % = у.тп G.57), G.62). В результате имеем:
со — <атпр —
3.54)
(символ (omnp отражает тот факт, что собственная частота опреде-
определяется тремя индексами т, п и р). Заметим, что выражение соб-
собственных волновых чисел (8.33) в данном случае переходит в (8.4).
Собственные колебания будем классифицировать, опираясь на
представление о Е- и Я-волнах волновода. Поскольку каждой из
собственных волн Етп или Нтп соответствует бесконечный ряд соб-
собственных колебаний, различающихся числами р, будем говорить о
типах собственных колебаний Ewnp ri IImnV. Выпишем выражения
соотиетствукпцпх полей:
304
ГЛ. 8. РЕЗОНАТОРЫ
Е-колебания
утпр _ ртпрГ . тлх . плу рлг
1
2
тл тлх . геЛ1/ , гел . тлх плу\
COS Sin -г- + у„ — Sin COS-гЧ Sin ,
'а а Ъ J0 b a b L
тлх гел //
. — cos—r^ —
(I Q
^PI (8.55)
Amu
где Eo — неопределенные коэффициенты. Индексы т, п, р могут
принимать следующие значения: т, п = 1, 2, ... и р — О, 1, 2, ...
(см. пп. 7.1.1, 8.1.1).
Н-колебания
тГППр
1»2
¦v гел тлх . пли
— хо-г cos sin -г^
у\ • рлг
-JSin—'
Нт = Я
тпр I тлх плу ¦ рлг
' Zn COS COS —г2- Sin —.
а Ъ L
1 рл [ тл . тлх плу , гея тлх . nni/\ рлг~] /о _„.
— 4- хп — sin -cos-H- + Уп-г cos sin -г^ cos V- . (8.56)
'¦т« ¦ / ¦- J
В отличие от Е-колебаний в данном случае т, ге = @), 1, 2. ...
и р= 1, 2, ...; нуль в скобках означает, что то и ге не могут вме-
вместе быть равны нулю.
Вывод формул (8.55), (8.56) несложен. Надо либо сложить две
распространяющиеся навстречу волны, взяв выражения их полей
из п. 7.1.1, либо исходить из продольных компопент Ётг и Йтг, ко-
которые, как отмечалось в п. 8.1.1, даются формулами (8.7), (8.9).
В этом случае поперечные компонепты Ет, и Нт, можно получить
из уравнений Максвелла, которые приводят к формулам, почти не
отличающимся от F.16): вместо — ?Г в F.16) надо записать опера-
операцию d/dz.
Прежде чем анализировать собственные колебания прямоуголь-
прямоугольного резонатора, отметим, что записанное представление полей не
является единственно возможным. Можно тремя различными спо-
способами выбирать продольную ось z, т. е. получать резонатор, мыс-
мысленно перегораживая три разных ортогонально ориентированных
прямоугольных волновода, как показано на рис. 8.5а. Мы получим
гри различных классификации собственных колебаний.
Возвращаясь к выбору индексов то, п, р в формулах (8.55)
и (8.56), видим, что любая комбинация трех целых чисел, одно и;*
§ 8.2. ПОЛЫЕ РЕЗОНАТОРЫ
305
которых может быть заменено нулем, определяет один или несколь-
несколько типов колебаний резонатора. Разные собственные колебания
(в частности, Етпр и Нт„р), имеющие одинаковые собственные ча-
частоты, называются вырожденными (в п. 7.1.2 было введено пред-
представление о вырожденных волнах). Очевидно, что различные ли-
линейные комбинации полей такого рода также представляют собой
собственные колебания.
Какова низшая собственная частота резонатора без потерь?
Чтобы найти ее значение при заданных размерах а, Ъ и L, надо
/
/
/
/
/ ,
\ /
/——
/
/
/
/
/
к
/ У
/ х
/ /
А у
/ ! /
/ 1/
V
ff
У-
||
У
/
У
Рис. 8.5
минимизировать выражение wmnP (8.54) соответствующим выбором
чисел то, п и р. Одно из них, которое отвечает наименьшему раз-
мору, берется равным пулю, а каждое из оставшихся — единице.
(Соответствующий тип колебаний резонатора называется основным.
20 li. в. Никольский, Т. И Никольская
306
ГЛ. 8. РЕЗОНАТОРЫ
§ 8.2. ПОЛЫЕ РЕЗОНАТОРЫ
Структура его поля показана на рис. 8.56 при трех вариантах вы-
выбора системы координат. Одна и та же структура получает разные
обозначения: Ецо, #mi, Нои- Нулевой индекс соответствует той оси
,(х, у или z), вдоль которой поле однородно.
Заметим, что в случае, когда ни один из индексов не равен ну-
нулю, тип колебаний Е и Н при повороте оси z на 90° воспринима-
воспринимаете» как гибридный ЕН (НЕ), т. е. как наложение вырожденных
колебаний типов Е и Н.
Рассмотрим несколько картин силовых линий собственных ко-
колебаний прямоугольного резонатора. На рис. 8.6 показаны типы
колебаний Н\о\ (а) и #3о4 (б); на рис. 8.7 — типы Ещ (а) и Езп
(б); на рис. 8.8 — типы Нщ (а) и #324 (б). Эти изображения по-
полезно сравнить с соответствующими мгновенными снимками волн
в прямоугольном волноводе: рис. 7.9а, б; рис. 7.5а, б; рис. 7.7а, б.
Таким образом, сопоставляются стоячие и бегущие волны. Разли-
Различие картин силовых линий состоит в том, что системы электриче-
электрических и магнитных линий в одном случае сдвинуты на Л/4 по отно-
отношению к другому. При этом в волноводе вектор Пойнтинга вдоль
оси z не меняет знака. В резонаторе полные поля Е и Н сдвинуты
по фазе на 90°, а среднее значение вектора Пойнтинга равно нулю.
В заключение приведем формулу, выражающую добротность (?„
для типа колебаний H\q\'.
аЫ(г- - (Г)
V-n Д° aL {L- 4- a") - 26 (l3 — a3)
\0'
(8.57)
Имеющий размерность длины параметр D в случае кубического
резопатора (a = b=L) равен а/3, а для плоского резонатора
(b < a, b < L) D « Ъ. Так как обычно fi = fiM=l, можно сказать,
что добротность QK плоского резонатора есть отношение его наи-
наименьшего размера Ъ к глубине проникновения А0.
ВЫВОД. Из (8.56) следует, что при то = 1, ге = 0, р = 1
2
тт2 / rrlol \2 / 9 И
Нт = (#о .Г | cos2 — sin
Поэтому
-у- Н—5 sin- — cos2 -y
L I- a L
Ь L
V 0 0 0
L a
а Ъ
Ъ L
oo
[ El ds = 2 j j" П1 \y^dz dx + 2 j |н=г |г_0 d,x dy+2$ \ H^ \x=odydz=
s oo
И + Та + 72 + »L •
Подставляя результаты интегрирования is (8.50), получаем (8.57).
(z=0)
a 0
x
t о о « в 4
V • • • • f
\в в^в-Л-Л-Л.Л^в'
(у=Ь)
i' (' ^i \ \ С ") 11 (' ;¦ i
ч ^ ^ ' "^
,-*. \ I , . V I , — - <
I > I I ( ЧМ Ч
s v ^ -v _-'
I ('""") 11' t' "> 11' Г ; i
\ Г "i in' 1 1'
У
е о в
ее с
о е с
(х=а/2)
L
Z
'101
(z=L/2)
—
:
о
в
ft
.
о
о
о
к
X
X
X
К
У
е' >
о >
¦
<
о о
в в
>
L
(х=а/6)
¦
X X
¦
(
<
с
•
m
z
(z=L/8)
4JJ
(у=Ь)
д
Рис. 8.6. (ЭВМ)
20*
308
ГЛ. 8. РЕЗОНАТОРЫ
(z=L/2)
а О
У
х^'
ft
L
(х=а/2)
z
-111
(у=Ь/2)
¦^ti-тТП
(z=0)
(х=а/6)
DO О О С
Рис. 8.7. (ЭВМ)
§ 8.2. ПОЛЫЕ РЕЗОНАТОРЫ
309
(х=а)
(z=0)
У
1С ) II С ) 11
ч__ __• v-^~"^-/ ч
i4O,i '4Oj i4
L
(x=a/3)
С~Л ('О i
^ — - *" v -~— - y
О 11 О I
2
I! II 11I UK
II !l If )l К ij
I! )l till
4 | \ V^ |
KM KM K)i
(у=Ь/2)
Рис. 8.8. (ЭВМ)
(z=L/8)
7
L
310
ГЛ. 8. РЕЗОНАТОРЫ
8.2.2. Цилиндрический резонатор. Конкретизируем % в (8.34)
при помощи G.72), G.78) и представим полные поля собственных
колебаний, как это делалось в п. 8.2.1. В результате получаются
следующие выражения:
Е-колебания
СО =
КГ - К"»
(%Lr) M (na) cos SI _
Li
~
ттптр
/
Н-колебания
= 0,1,2, ...);
(па)]8тЩ
J L I
(8.59)
4- (па)] COS ^
со =
(8.60)
/
jnmp туПт
' (па) -
n(Xnmr)st(na)]sin^,
(8.61)
(na) + «0 i
«0 i Jn (хнтг) ^- (na)| cos^*
В формулах (8.58) — (8.61) использованы обозначения G.72),
G.74), G.78).
Как и волны круглого волновода, собственные колебания рас-
рассматриваемого резонатора поляризационно вырождены; другой тип
вырождения связан с равенством корней ^40m = 5im (см. п. 7.2.2).
При определенных соотношениях размеров могут наблюдаться и
другие случаи вырождения. Так, например, при выполнении ра-
равенства (B0i/RJ = (Aii/RJ + (n/LJ (при этом L/R « 2,03) типы ко-
колебаний /7ц1 и Eqiq имеют одинаковые собственные частоты, как
ото ьндио из (8.58) и (8.60). Поскольку речь идет о наименьшей
8.2. ПОЛЫЕ РЕЗОНАТОРЫ
311
собственной частоте резонатора без потерь, то оба тина колебаний
оказываются основными. Можно говорить о трехкратном вырожде-
вырождении основного типа колебаний, поскольку тип 7/ш уже двукратно
вырожден (поляризационно). Как видно, для резонаторов более
плоской формы (L/R < 2,03) основным будет тип ?oio, а для более
удлиненных (L/R > 2,03) — тип Н\\\.
Строение полей цилиндрического резонатора легко представить
себе по рис. 7.13—7.16. По сравнению со случаем волновода
электрическое и магнитное поля оказываются сдвинутыми на Л/4,
Как это уже было показано на примере прямоугольного резонатора.
Добротность (9М для произвольного типа колебаний Нптр выра-
выражается следующим образом:
^*'lLA ' (8'62)
А*пп-п*
ВЫВОД. Взяв $Ф(па) = cos па, на основании (8.61) пишем:
К 2Л L
Г2 1 *
dr da dz =
0 0 0
= 5 -4 jiL f "-H
¦/ i I x
jrdx = б —, (А2пт - /г2) Л (Апт) лЬ
2'/.4
(псшпьзована формула G.27)); здесь 6=1 прп п=0 и 5 = 1/2
при п =f- 0;
R -2 Л 2 Л L
) E*mds = 2 j j H;n I1Z=O rdr da + R j j Нгш |r=R da dz =
0 0
= 64л^УЛ
;2(,r) ,rc/.r +
Подстановка найденных интегралов в (8.50) приводит к (8.62). ¦
Без вывода приведем простую формулу, выражающую доброт-
добротность Qyi для типа колебаний EoW-
(8.63)
-1."
312
ГЛ. 8. РЕЗОНАТОРЫ
8.2.3. Другие полые резонаторы. Рассмотрим в краткой форме
некоторые другие полные резонаторы.
Рассекая идеально проводящими поперечными плоскостями ко-
коаксиальную линию (см. п. 7.3.1), получаем коаксиальный резона-
резонатор. Если ограничиться рассмотрением собственных колебаний ти-
типа Т, собственные частоты со = сор будут определяться формулой
(8.35). Соответствующие типы колебаний будем обозначать Тр. По-
Поле в этом классе представляется формулами, получаемыми из G.90).
Em = -T0iHv0W±sin^, Hm = a0tfPi-cos^. (8.64)
Здесь #о = -^т/2л, где I°m — комплексная амплитуда тока внут-
внутреннего проводника в пучности.
На рис. 8.9а показано строение поля типа Т\.
На основании (8.50) и (8.64) нетрудно получить следующее
выражение добротности QM коаксиального резонатора для типа ко-
колебаний Тр:
2L\n(RjR \
1
1/Ла) '
Чтобы рассмотреть типы колебаний коаксиального резонатора,
принадлежащие классам Е и Н, надо действовать так же, как в
<: * с
^ с ^ ф & fх
г; . v
Рис. 8.9
случае резонатора цилиндрического (см. п. 8.2.2), но заменить бес-
селевы функции Jn{yj) комбинациями цилиндрических функций
G.53), G.54); см. также п. 8.0.2.
Идеально проводящая шаровая полость дает пример резонатора,
который не сводится к отрезку регулярной направляющей струк-
структуры, но строго анализируется на основе метода разделения пере-
переменных. Типы колебаний этого полого сферического резонатора де-
делятся на классы Е и Н относительно радиального направления
(для Е-колебаний Ётт=?0, Йтг — 0; для Я-колебаний — наоборот).
Чтобы найти соответствующие электромагнитные поля, надо решитг.
краевые задачи (8.37). При построении решений векторных уран
пений Гельмгольца, входящих в (8.37), используется решение ска
§ 8.2. ПОЛЫЕ РЕЗОНАТОРЫ
313
лярного уравнения (8.21) йт = йт(к; г, 0, а). Радиальные компо-
компоненты Ётт и Йтт, исходя из которых можно восстановить полное
электромагнитное поле в классах Е и Н соответственно, отличают-
отличаются от мт (8.21) множителем 1/г:
COS
Enr, Hnr = A -±^ Jn+1/2 (kr) PT} (cos Q) s.n ma. (8.66)
При этом k есть корень уравнения (8.23) в классе # и (8.24) —
в классе Е. Как видно, собственные частоты со = &/Уеоеи.0и. не за-
зависят от индекса т. Низшим является первый из корней уравне-
уравнения (8.24) при га = 1: kR = 2,75. Взяв т = 0, ге=1 и р = 1 (р —
номер корня), получаем, таким образом, основной тип колебаний
Eon', структура поля показана на рис. 8.96. Тип колебаний трех-
трехкратно вырожден, поскольку при га=1 кроме т = 0 возможно
также значение т = 1 (как следует из (8.25) и (8.26), при т > 1
все Р™** равны нулю). Ту же, что и Е0\\, собственную частоту
имеют типы колебаний Ещ с азимутальными зависимостями cos a
и sin а (поляризационное вырождение). Разумеется, все три типа
колебаний различаются только ориентацией поля. Они аналогичны
типам Е\\о, #ioi и #оц кубического резонатора.
Как известно, при относительно низких частотах используются
квазистационарные резонаторы (колебательные контуры), составляе-
составляемые из индуктивных и емкостных элементов. Поскольку электри-
электрическое и магнитное поля при этом можно считать пространственно
разделенными (см. п. 2.5.2), применяется теория цепей. Близкими
свойствами обладают некоторые полые резонаторы, используемые,
в частности, в электронике СВЧ. Таков, например, тороидальный
резонатор, показанный на рис. 8.10. Его электрическое поле при
/
*
2R2
Рис. 8.10
основном типе колебаний можно рассматривать как сосредоточен-
сосредоточенное между центральными плоскими элементами в узком зазоре.
Принимая эту часть за плоский конденсатор, имеем: С = zzoS/d
[(рис. 8.106). Магнитное поле описывается концентрическими сило-
силовыми линиями и подобно полю тороидального солепоида (см.
п. 2.3.3), так что Н = 1/2лг, где / — полный ток резонатора, линии
314
ГЛ. 8. РЕЗОНАТОРЫ
§ 8.3. ДРУГИЕ ЭЛЕКТРОМАГНИТНЫЕ РЕЗОНАТОРЫ
315
которого расходятся в радиальных сечениях (рис. 8.10а). Поэтому
2л .1 г •
Собственную частоту основного типа колебаний определим по фор-
формуле со =B'С)~и2. Внося сюда выражения 9? и С, имеем
(О =
(8.67)
§ 8.3. Другие электромагнитные резонаторы (А)
8.3.1. Различные резонаторы в технике СВЧ. Рассматривавшие-
Рассматривавшиеся выше полые резонаторы типичны для техники СВЧ, главным
образом для диапазона сантиметровых волн. Их отличительным
признаком является весьма высокая добротность, которая в отдель-
отдельных случаях может превышать 10s. В силу ряда причин (в част-
частности, технологических) наиболее распространены цилиндрические
полые резонаторы. Интересно, что цилиндрический резонатор легко
сделать перестраиваемым, снабдив передвижным дном — «порш-
«поршнем». Для типов колебаний Нотр так называемый бесконтактный
поршень, т. е. дно, не касающееся цилиндрической поверхности,
почти не нарушает условий существования поля, не разрывая пу-
путей токов в оболочке (они азимутальны, как уже отмечалось в
п. 7.2.2). Различные полые резонаторы сложпой формы незамени-
незаменимы в СВЧ электронике.
Развитие линий передачи (см. п. 7.5.1) затронуло и принципы
конструирования резонаторов. Миниатюризация полых резонаторов
возможна лишь па пути применения все более оптически плотных
заполняющих сред. Поскольку собственные частоты изменяются
как е'2, можно изготовить электромагнитпый резонатор малых
размеров, металлизировав поверхность диэлектрического шарика
Рис. 8.11
или, например, диска с высокой проницаемостью. Однако в метал-
металлизации нет необходимости (к тому же появятся потери в метал-
металле): диэлектрическое тело в оптически менее плотной среде (па-
пример, воздухе) само способно быть резонатором. Диэлектрические
резонаторы, действительно, находят применение на практике. >Га
рис. 8.11а показаны диэлектрические резонаторы, помещенны" в
полый волповод. Фпзическая причина, обусловливающая накопле-
накопление энергии внутри диэлектрического тела, в определенном смысле
та же, что при полном отражении волн от границы с менее опти-
оптически плотным диэлектриком (см. п. 5.1.4, 5.3.3). Задача о собст-
собственных колебаниях диэлектрического шара строго решается методом
разделения переменных. При этом внутреннее поле представляется
так же, как в случае полого резонатора, а внешнее — через функ-
функции Ханкеля. Удовлетворение условиям непрерывности Ех ц Нх на
поверхности шара приводит к дву.м уравнениям относительно соб-
собственных волновых чисел — для классов колебаний Е п Н.
Поскольку миниатюризация линий передачи привела к появле-
появлению различных планарпых структур (см. § 7.5), были созданы и
соответствующие планарные резонаторы. Таковы различные поло-
сковые резонаторы, например, прямоугольный и дисковый
(рис. 8.116), а также аналогичные щелевые резонаторы (рис. 8.Не).
8.3.2. Оптические и квазноптпческие резонаторы. В п. 7.6.2 уже
обсуждались системы зеркал и линз, направляющих потоки элек-
электромагнитной энергии. Если в такого рода структуре созданы усло-
условия существования стоячих волн, мы получим резонатор. Ясно, что
простейшим будет резонатор, образованный двумя зеркалами.
Па первый взгляд, такая открытая структура кажется менее вы-
выгодной, чем полый резонатор, поскольку можно ожидать значитель-
значительных потерь на излучение. Но необходимо учитывать, что зеркаль-
зеркальные резонаторы применяются в условиях, когда пх размеры на
несколько порядков превышают длину волны. При подобных относи-
относительных размерах полого резонатора, т. е. при использовании соо-
стылшых колебаний весьма высокого порядка, мы попадаем в сгу-
шеппую область его спектра: на некоторый фиксированный интервал
час; от приходится относительно много типов собственных колеба-
колебаний. Это нежелательно по ряду причин; учитывая потери, можно
установить, что, начиная с некоторой частоты, полый резонатор
должен утратить резонансные свойства (см. п. 11.1.4). Существова-
Существование эффекта сгущения спектра легко проверить на примере пря-
прямоугольного резонатора. Взяв формулу (8.54), видим, что с ростом
m, n и р, соседние собственные частоты действительно сближаются.
Между тем сгущение спектра отсутствует в классе Г-колебанпй:
согласно (8.35) частотные интервалы между соседними типами ко-
колебаний везде одинаковы. Заметим, что в лучевой трактовке раз-
различным типам колебаний полого резонатора сопоставляются разные
типы допустимых многократных отражений (рис. 8.12а). Если же
рассматривать Г-колебаиия для системы двух параллельных иде-
идеально проводящих плоскостей, то они описываются простейшей лу-
лучевой схемой (рис. 8.126), содержащей прямой и обратной нор-
нормальные лучи.
Оптический резонатор пз двух плоских параллельных зеркал
характеризуется тем, что при достаточно больших углах ос
(рис. У.12б') многократные отражения невозможны. Не слишком
316
ГЛ. 8. РЕЗОНАТОРЫ
§ 8.3. ДРУГИЕ ЭЛЕКТРОМАГНИТНЫЕ РЕЗОНАТОРЫ
317
большие потери на излучение будут только при малых а. Поэтому
спектр собственных колебаний оказывается в значительной степени
«прореженным». Если иметь в виду лучевые схемы, то возможны
лишь параксиальные системы лучей. Поля собственных колебаний,
практически, являются Г-полями.
Плоские резонаторы, однако, не обладают удовлетворительной
устойчивостью по отношению к деформациям, например, перекосам
УПРАЖНЕНИЯ
1. Показать, что запас энергии полого резонатора без потерь W равен
максимальной электрической энергии ^a]! или максимальной магнитной энер-
2. Собственная частота резонатора / = 10 ГГц, а добротность Q = 105. За
какое время запас энергии собственных колебаний уменьшится в е раз?
3. Кроме запаса энергии резонатора W введем в рассмотрение величину
AWT, выражающую изменение запаса энергии за период Т' = 2я/со'. Как вы-
выразить добротность через W и AVFr?
4. Для прямоугольного резонатора с размерами а = 1 см, Ь = 2 см и L =
= 3 см (внутренняя среда — вакуум) вычислить первые пять собственных ча-
частот и идентифицировать соответствующие типы колебаний.
5. Выписать выражения компонент поля основного типа для резонатора
из предыдущего примера.
6. Построить наложение вырожденных типов колебаний Яш и Нои для пря-
прямоугольного резонатора при а = Ь, взяв амплитуды полей равными, а фазы —
отличающимися на -j- 90°. Показать, что при этом
i>>
Рис. 8.12. (ЭВМ)
зеркал, которые приводят к резкому возрастанию потерь на излу-
излучение. Чаще применяются резонаторы с вогнутыми зеркалами, зна-
значительно более устойчивые по отношению к деформациям, но отли-
отличающиеся несколько меньшим разрежением спектра. При лучевой
трактовке типов колебаний таких резонаторов приходят к некото-
некоторым замкнутым конфигурациям, не выходящим за пределы каусти-
каустики: линия, ограничивающая систему лучей нарис. 8.12г (ср. п. 7.6.2).
Имеется сходство между процессами в линзовой линии и резо-
резонаторе с вогнутыми зеркалами. В обоих случаях существуют типы
волн (бегущих и, соответственно, стоячих), которые имеют разные
поперечные распределения; вне некоторой осевой зоны поля быстро
убывают. К обсуждению подобных структур мы вернемся в п. 10.6.2.
п=±
¦ (— xQ sin %x cos %y + yQ cos %x sin Щ sin2 —
(8.68)
и, следовательно, существует циклический поток энергии, направленный ор-
ортогонально оси z. Поглощение не учитывается.
7. Вывести формулы (8.55) и (8.56) двумя способами: а) составляя нало-
наложение прямой и обратной волн прямоугольного волновода и б) на основе ска-
скалярных решений, полученных в п. 8.0.1.
8. Показать, что в случае собственных колебаний цилиндрического резо-
резонатора с вращающейся структурой (при азимутальной зависимости
ехр(+г'геа)) существует циклический поток энергии, так что, в частности, для
типа колебаний Яш
•^i (X'-) sin -?-.
(8.69)
9. Показать, что для резонатора на рис. 8.106 формула (8.67) принимает
следующий вид:
»=l/s
(8.70)
10. Вычислить добротность <?м цилиндрического резонатора для типа коле-
колебаний ЯОц при следующих данных: материал — медь; R = 2,5 см; внутрен-
внутренняя среда — воздух.
ЧАСТЬ 3
ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ
§ Э.О. ПРЕДВАРИТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СВЕДЕНИЯ 319
Внося выражение функции Грина (9.3) в (9.4), получаем
(г'\ -,— iftlr—г'|
Глава 9
ИЗЛУЧЕНИЕ В СВОБОДНОМ ПРОСТРАНСТВЕ
§ 9.0. Предварительные математические сведения (А)
9.0.1. Интегрирование неоднородного уравнения Гельмгольца.
Различные векторные уравнения Гельмгольца с правой частью, ха-
характеризующей источники электромагнитного поля, обсуждались
выше в н. 3.2.2. Начнем с рассмотрения неоднородного скалярного
уравнения Гельмгольца
V2um(r) + &2Mm(r) = /m(r), (9.1)
которое отличается от уравнения Пуассона B.7) наличием второго
члена в левой части равенства.
Как и при интегрировании уравнения Пуассона (см. п. 2.0.3),
в данном случае вводится функция Грина G(x, г'), являющаяся
решением исходного уравнения (9.1) при правой части в виде
дельта-функции Дирака
(9.2)
, г')=б(г-г').
Теперь в отличие от B.8) функция Грина имеет вид
G(r, г') = — -г-г-1—г-ге-^-т'К
(9.3)
Используя, как и в п. 2.0.3, вторую формулу Грина A.36) и
соотношение A.40), получаем па основе (9.1) п (9.2) интеграль-
интегральное соотношение
V
+ § \ип (г') ^ G (г, г') - G (г, г') ± um (r')l ds' (9.4)
(в процессе выкладок использована симметрия функции Грнна от-
нпситс'гмгп аргумента г н г', т. е. возможность замены г ^ г' в
(!>.'))). Как видно, (9.1; пи ферме совпадает с (_!.10j.
Для нас важен случай, когда решение йт(г) ищем во всем безгра-
безграничном пространстве, так что граница 5 области V относится в
бесконечность, тогда как функция /m(r) отлична от нуля только
в некоторой ограниченной области.
Выделим класс решений, обладающих таким свойством, что при
отнесении в бесконечность границы 5 поверхностный интеграл в
(9.5) исчезает. Напомним, что в п. 2.0.3 рассматривались обладаю-
обладающие аналогичным свойством решения уравнения Пуассона, регу-
регулярные в бесконечности. В данном случае выделенный класс по-
потребует отдельного исследования, которое будет произведено ниже
в п. 9.0.2. Пока же констатируем, что в рассматриваемом случае
из (9.5) следует:
Интегрирование здесь фактически распространяется только на об-
область, в которой fm(r)?=O. Мы получили выражение решения неод-
неоднородного скалярного уравнения Гельмгольца (9.1).
Возьмем векторное уравнение
Рассматривая его проекции на оси декартовой системы координат
(ср. п. 2.0.3), получим три скалярных уравнения типа (9.1), реше-
решения которых при оговоренных условиях выражаются формулой
(9.6). Складывая их, запишем справедливое при тех же условиях
представление решения неоднородного векторного уравнения Гельм-
Гельмгольца (9.7):
= —Lf-
4я J
¦dv'.
(9.8)
9.0.2. Условие излучения. Остается выяснить характер реше-
решений, для которых получены представления (9.6), (9.8), и уточнить
требования, которым они должны удовлетворять.
Схема, поясняющая роль радиус-векторов г и г' при интегриро-
интегрировании (ср. рис. 2.1). л.ша па рис. 9.1. Пустг, точка Р(г), в которой
рассматривается решение, фиксирована. Jljiir пнтегрирошимш л
320
ГЛ. 9. ИЗЛУЧЕНИЕ В СВОБОДНОМ ПРОСТРАНСТВЕ
(9.6), (9.8) конец Q радиус-вектора г' пробегает область, внутри
которой /т^О (рис. 9.1а), т. е., иными словами, локализованы ис-
источники.
При вычислении поверхностного интеграла в (9.5) Q находится
на поверхности S (рис. 9.16). Будем относить S в бесконечность,
Рис. 9.1
считая эту поверхность сферой радиуса г'. Тогда v' = r , а посколь-
поскольку при г'-*¦ оо исчезает различие между [г —г'[ и г', то подынте-
подынтегральное выражение в пределе принимает вид:
ikl-
e-ihr>
e-ihr>
Поскольку поверхность сферы пропорциональна (г'J, то, как вид-
видно, поверхностный интеграл в (9.5) при отнесении границы S в
бесконечность исчезнет, если
lira r'e-w \d'u™{Tl) + ikum{v') + ^1 = 0.
' L дг> Г> J
дг
Отбрасывая несущественный общий множитель и бесконечно малый
член в скобках, а также изменяя обозначение аргумепта (г -*-г),
получаем следующее условие:
(9.9)
+ ikum (г) = О,
которому должны удовлетворять решения йт(т), определяемые по
формуле (9.6). Это так называемое условие излучения Зом-
мерфелъда.
Легко убедиться, что условию излучения (9.9) удовлетворяют
только решения, имеющие при г -»- °° вид расходящихся сфериче-
сферических волн (см. п. 4.0.4):
Km (г)
¦е~г
(9.10)
§ 9.1. ИЗЛУЧЕНИЕ ЗАДАННЫХ ИСТОЧНИКОВ
321
Это значит, что из рассмотрения исключаются все те решения, ко-
которые нельзя пптерпретпровать как волны, создаваемые заданными
источниками.
Чтобы записать условие, определяющее класс решений вектор-
векторного уравнения Гельмгольца (9.7), представляемых формулой
(9.8), надо лишь заменить в (9.9) и,п на um- Это векторное условие
излучения.
Как видно, решения (9.6), (9.8) ио своему характеру, действи-
действительно, выражают расходящиеся волны, т. е. волновой процесс,
возбуждаемый в области источника (где /^0), который, запазды-
запаздывая, распространяется в пространстве. Такой характер имеет уже
функция Грппа (9.3). Надо иметь в виду, что ири замене
ехр(—ikr) на exp(iAr) формула (9.3) определяет другую функцию
Грина (решение уравнения (9.2)), которая сама имеет смысл схо-
сходящейся волны и порождает такого же рода решения уравнения
(9.1). Этот класс решений лишен физической содержательности.
§ 9.1. Излучение заданных источников (А)
9.1.1. Постановка и обсуждение задачи. Понятие излучения так
или иначе уже затрагивалось в этой книге. Так в п. 3.1.1 говори-
говорилось об электромагнитных полях, существующих в результате дей-
действия сторонних сил, т. е. в результате преобразования некоторого
вида энергии в электромагнитную. В свою очередь, сторонние силы
в электродинамике удобно формализовать при помощи задания сто-
сторонних токов. Как уже отмечалось в п. 3.1.1. н качестве стороннего
может рассматриваться любой заданный ток. Таков, например, ток
антенны, поддерживаемый действием генератора. Область суще-
существования стороннего тока выступает как источник излучения. Поле
излучения находится как решение уравнений Максвелла пли выте-
вытекающих из них уравнении второго порядка (см. ни. 3.1.2, 3.1.3,
3.2.2) ири заданной плотности стороннего тока jCT. Напомним, что
до спх пор, решая различные задачи электродинамики в гл. 4—8,
мы полагали j" = 0 и определяли некоторые свободные электро-
электромагнитные иоля, существование которых не связано с источниками.
При решении задачи об излучении заданного распределения то-
тока в однородной изотропной среде предпочтем два подхода. В одном
из них исходным является неоднородное уравнение Гельмгольца
относительно вектора Н,„:
V2Hm + кЩт = - rot fm\ (9.11)
а в другом — относительно векторного потенциала:
V2Am + /AVm = - цо.и}?. (9.12)
Оба уравнения были сформулированы в и. 3.2.2 (k2 =(w/cJe|i).
Если найдено решение IIm уравнения (9.11), то Ет определяется
21 В. В. Пш.ольсмш, Т. И. Пш ольская
322
ГЛ. 9. ИЗЛУЧЕНИЕ В СВОБОДНОМ ПРОСТРАНСТВЕ
из первого уравнения Максвелла. Если же в результате решения
уравнения (9.12) определен вектор Ат, то согласно C.43) нахо-
находится Нт, а затем Ет.
Используем тот факт, что записанные неоднородные уравнения
Гельмгольца (9.11) и (9.12) при со -*¦ О переходят в уравнения
Пуассона. Это значит, что мыслимы столь низкие частоты, при ко-
которых Нт и Ат можно определять как решеиия уравнений Пуассо-
Пуассона, полученных для постоянного тока; в частности, Ат находится
на основании B.93). Прежде чем воспользоваться этой формулой,
перейдем в (9.12) от комплексных амплитуд к полным комплекс-
комплексным представлениям А и jCT путем умножения всех членов на
()t). В силу B.94)
4л J |г-г'| йь •
(9.13)
Этот результат относится к теории квазистационарных полей, об-
обсуждавшихся выше в п. 2.5.1.
Как легко сообразить, недостаток формулы (9.13) заключается
в том, что не учитывается время, необходимое для передачи элек-
электромагнитного взаимодействия от элементов тока, локализованных
в точках Q(r'), в точку наблюдения Р(г) (см. рис. 2.1). Попро-
Попробуем устранить дефект, полагая, что для определения А(т, t) надо
заменить jCT(r', t) под интегралом на j(r', t — т), где т=1г —г'1/w
есть время, требуемое для преодоления пути QP=\r — r'\ со ско-
скоростью у = с/Уе1и. Тогда получается:
(9.14)
а так как
jCT (г'; t — | Г — Г' \/V) = j" (r') e*«(f-|r-r'l/e) = j? (г') ei(@i-fe|r-r'|))
где k = a/v, n A (r, t) = Am (r) ei(Oi, то из (9.14) следует
!|Г-Г'|
-. dv'. (9.15)
Лт КХ) ~ 4л ,
I г
Интересно, что эвристический подход привел в данном случае к
строгому решению уравнения (9.12), которое соответствует форму-
формуле @.8). Действительно, (9.8) переходит в (9.15), если в соответ-
соответствии с (9.12) переобозпачить в (9.7) ит как Ат и i'm как —Hoiijm»
5 !' 1. ИЗЛУЧЕНИЕ ЗАДАННЫХ ПСТОЧНПКОГ
323
9.1.2. Анализ решений. Итак, мы получплп представление век-
векторного потенциала поля излучения заданных источников в одно-
однородной среде с щюницаемостямп е п и.
Чтобы получить такое же представление решения уравнении
@ 11), снова кос пользуемся формулой (9.8), полон.'пр и, = II.,. п
t - ¦ — rot j". ,1то дает
(штрих у rot о.шачает, что дифференцирование производится но
штриховапным координатам). Формула (9.16), однако, пеудоПпа
из-за необходимости дифференцировать функцию }т- При помощи
ряда преобразований, похожих на вывод обобщенного закона Бпо —
• авара в п. 2.Я 1. полученный результат приводится к виду
™{T'hToq]e~Mr~r']dr ¦ (<tU7)
ВЫВОД. Подынтегральное выражение в (9.16) преобразуем
при помощи A.26). положив F= j" <: ф = e-iftlr-r'i/j г — г'|; Как
видно, под интегралом мы имеем выражение г|" rot F. Поэтому
dv
'ттзттт-, im(V)\du . (9.18)
-1 (С
НГ. (Т} = ±\\ rot'
' 4л 1J
Взяв любую замкнутую поверхность 5, охватывающую все источ-
источники, преобразуем первый интеграл прп помощп формулы A.37):
VT (г') е—ift-lг—ж-'|
rot' —^—:—__ , dv' -
v T s
Поверхностный интеграл явно равен нулю, так как S проходпт там,
где нет тока. Следовательно, равен нулю рассматриваемый объем-
объемный интеграл, а в (9.18) остается только второй член.
Используя формулы B.2) и A.28), произведем следующее пре-
преобразование
grad •
э—iftlr—г'
I г - г' I
= Гп
+ ik
где i\i,— едпипчпыи вектор, введепныИ в п. 2.0.1. В результате из
(9.18) следует (9.17). ¦
21*
324
ГЛ. 9. ИЗЛУЧЕНИЕ В СВОБОДНОМ ПРОСТРАНСТВЕ
§ 9.2. ЭЛЕМЕНТАРНЫЙ ЭЛЕКТРИЧЕСКИЙ ИЗЛУЧАТЕЛЬ
325
Теперь мы можем произвести некоторый анализ поля излуче-
излучения на основании представления Нт; сначала отметим, что для
пользования формулой (9.17) нет необходимости требовать, чтобы
функция jra была дифференцируемой.
Подынтегральное выражение в (9.17) представляет собой сумму
двух членов; второй из них исчезает при со -*¦ О, а выражение в це-
целом при этом переходит в закон Био — Савара B.79).
Отношение подынтегральных слагаемых равно ik\r — г'|; пусть
среда является непоглощающей, так что к = 2лД — велпчппа ве-
вещественная; как видно, в зависимости от соотношения величин
1г —г'| и К может преобладать первый пли второй член. Во всех
случаях при удалении точки наблюдения Р(т) расстояние 1г — г'|
неограниченно возрастает. Когда отношение |г — т'\/Х достаточно
велико, первым членом подынтегрального выражения можно пре-
пренебречь. Если при этом величина 1г —г'| также достаточно велика
по сравнению с размерами области источников, то компоненты век-
вектора Нт(г) все более приобретают пространственное распределение
типа сферической волны (9.10). Это так называемое дальнее поле.
Очевидно, что магнитное поле в целом удовлетворяет условию
излучения
lim г
(r)J = 0
(9.19)
(ср. (9.9)).
Еслп область источников мала по сравнению с длиной волны,
то можно указать такую область расстояний |г—г'| < К, когда пре-
преобладает первый член подынтегрального выражения, так что при
оценке пространственного распределения поля вторым членом мож-
можно пренебречь. Это ближнее поле фактически подчинено закону
Био — Савара.
Вернемся, паконец, к условию излучения. С одной его формой
мы уже встретились в п. 5.1.2 при обсуждении задачи о палении
волны на границу раздела сред; было отмечено, что условие излу-
излучения есть отражение принципа причинности в электродинамике.
Пусть условие излучения Зоммерфельда (9.9) наложено на век-
векторы Ет и Нт (т. е. записано также равенство (9.19) с заменой
Нт на Ет). Можно показать, что в этом случае решение внешней
задачи электродинамики является единственным без дополнитель-
дополнительных требований, рассматривавшихся выше в п. 3.4.1.
§ 9.2. Элементарный электрический излучатель, диполь Герца (А)
9.2.1. Элемент переменного тока и колеблющийся диполь. Поль-
Пользуясь полученными выше формулами, можно находить поля излу-
излучения, создппаемыо различными распределениями тока. Естестиеп-
по начать с простейших из них. Обычно рассматривается малый
прямолинейный элемент тока, называемын элементарным электри-
электрическим излучателем, а также диполем Герца: Генриху Герцу при-
принадлежит как практическая реализация, так п теория этого объек-
объекта. Представление о диполе Герца имеет отнюдь не только исто-
историческое значение, оно играет существенную роль в теории антенн.
Поле излучения, создаваемое эле-
элементарным электрическим излучателем,
проще всего найти, отправляясь от
формулы (9.17), и это будет сделано
ниже в п. 9.2.2. Но сначала мы долж-
ны обсудить физическое содержание
«открытого» элемента переменного то-
тока, не принадлежащего какой-то замк-
замкнутой цепи.
Элемент тока с постоянной комп-
¦J7*
[I
I
гСТ
•• 71
Рис. 9.2
лексной амплитудой 1т~, занимающий
участок длиной I на оси z, показан на рис. 9.2а. Будем рас-
рассматривать его как весьма тонкий цилиндр с поперечным сече-
сечением S и постоянной плотностью тока. Таким образом, 1т = j'mS
и Зга = z0/m. Привлекая закон сохранения заряда A.44), имеем:
d'fjjdz = — гсар". (9.20)
Умножив левую и правую части равенства на SAz, слева получим
(cWJJdz) Az — Aim. а справа (>т5Лг = р"ЛУ = Aq"
дящийся па элемент Az:
Л/Сгат = -
заряд прихо-
прихо(9.21)
Перемещая элемент Az по оси z, видим, что как на отрезке I, так
и вне его Л/„ = 0. Изменение тока от нуля до максимального
зпачепия и от максимального значения до нуля происходит только
на концах отрезка I. Из (9.21) следует, что на этих концах сосре-
сосредоточены колеблющиеся заряды (рис. 9.26) с комплексными ампли-
амплитудами:
дга = ±г/Сга7с0. (9.22)
Таким образом, с элементом тока Im совмещен диполь, момент
которого р B.4) имеет комплексную амплитуду
zn.
(9.23)
Отсюда и происходит название диполь Герца.
Физический смысл полученного вывода состоит и том, что от-
открытый элемент переменного тока и силу закона сохранения заря-
заряда поддерживается колеблющимися зарядами на ci'o концах, пмно-
щими разные знаки, колеблющимся диполем. Фазовый сдвиг па
82G
ГЛ. 9. ИЗЛУЧЕНИЕ В СВОБОДНОМ ПРОСТРАНСТВ!
§ 9.2. ЭЛЕМЕНТАРНЫЙ ЭЛЕКТРИЧЕСКИЙ ИЗЛУЧАТЕЛЬ
327
п^90° между зарядами и током означает, что в момент, когда оОа
наряда максимальны по абсолютной величине, ток равен нулю.
Синхронное изменение зарядов вызывает ток, который с уменьше-
уменьшением \q\ растет и при отсутствии зарядов становится максима.и
ным, а затем, уменьшаясь, перезаряжает диполь: заряды оказыва-
оказываются противоположными предшествующим. Это половина периом»
процесса.
И.2.2. Поле излучения диполя Герца. Продолжая рассматривай,
элемент тока, как равномерно обтекаемый током тонкий цилиндр,
Рис. 9.3
ориентированный вдоль осп z, расположим начало координат в
средней точке. При этом формула (9.17) принимает вид:
т
f
= ^ f
-г/2
(9.24)
В дальнейшем будем пользоваться сферической системой коор-
координат (рис. 9.3а) и потребуем выполнения двух неравенств:
г «г, г«а (9.25);
(пусть потери отсутствуют). Элемент должен быть мал по сравне-
сравнению с расстоянием наблюдения (ср. п. 2.2.1) и мал в волновом
масштабе. При этих условиях из (9.24) получается:
Um = ao^(jr + ^ e-«r ana, (9.26)
(9.27)
Эти формулы представляют собой строгое решение задачи при
pm = const (9.23), Z ->- 0, когда излучающий элемент становится то-
точечным (ср. п. 2.2.1).
ВЫВОД. В силу первого из требований (9.25) векторы г —г'
и г оказываются близкими по величине и направлению (рис. 9.36).
Поэтому заменим |г — г'| на г п вынесем за знак интеграла (9.24)
все выражение в круглых скобках. Поскольку при этом Го3 можно
заменить па го, то выносится также [z0, го] = ао sin #. Вынесем и
постоянную величину /"• Что касается оставшейся пока под ин-
интегралом функции ехр(—1к\т — г'|), то следует иметь в виду, что
в процессе интегрирования величина |г —г'|, изменяясь, может от-
отличаться от г не более, чем на Z/2. Как бы ни было это изменение
мало в сравнении с г, экспонента под интегралом будет испыты-
испытывать сильное влияние, если длина Z не мала в сравнении с К. Но
при выполнении второго требования (9.25) можно положить
ехр(—ik\r — r'l) равным ехр(—ikr) и также вынести за знак инте-
интеграла. В результате интегрирование дает множитель Z, и из (9.24)
получается равенство (9.26).
Чтобы выразить Ет (вне элемента тока), возьмем первое урав-
уравнение Максвелла. Используя B.5) и табл. 2.2, имеем:
ro//-2sinft »0/rsind «0/r
д/дг д/д& dlda
О 0 (± +
Выполняя эти действия, приходим к равенству (9.27). ¦
Поле излучения, представляемое формулами (9.26) и (9.27),
есть не что иное, как сферическая волна. При переходе от комп-
комплексных амплитуд Е,„ и Нт к самим векторам поля Е и Н члены
cos
полученных выражений приобретут множители . (со? — кг + <р).
Видно, что на каждой сферической поверхности г = const любая из
компонент поля Ег, Е$ и НгХ спнфазна, по амплитудное распреде-
распределение зависит от 0; оно ие остается постоянным при изменении г.
Поле обладает осевой симметрией: отсутствует зависимость от ази-
азимутальной координаты а. Магнитные силовые линии — концентри-
концентрические окружности в плоскостях, ортогональных элементу тока.
Электрические силовые линии лежат в меридиональных плоскостях
а = const.
Рассмотрим поле в ближней зоне, т. е. на расстояниях г<Я,
(&г« 1). Отбросив в формулах (9.26) и ('.'.27) пренебрежимо ма-
малые члены и полагая ехр( —гАт)« 1, получаем
~з (го2 cos ft + #0 sin 0), Н,„ :
а0
, sin и = а„
4лг2
! sin f>
(9.2S)
328
ГЛ. 9. ИЗЛУЧЕНИЕ В СВОБОДНОМ ПРОСТРАНСТВЕ
§ 9.2. ЭЛЕМЕНТАРНЫЙ ЭЛЕКТРИЧЕСКИЙ ИЗЛУЧАТЕЛЬ
329
(использовано обозначение (9.23)). Это, так называемое, ближнее
поле элементарного электрического излучателя (см. п. 9.1.2) имеет
знакомую нам структуру. Распределение электрического поля ока-
оказывается таким, как в случае электростатического диполя, ср. B.47);
однако оно испытывает гармонические колебания синфазно с мо-
моментом р = pm cos((d? + ф). Что касается магнитного поля, то при
сопоставлении (9.28) и B.80) видно соответствие результата зако-
закону Био — Савара. Поскольку в (9.28) Е и Н сдвинуты по фазе
на 90°, П — мнимая величина, а следовательно (см. п. 3.3.1), П = 0.
Получаемый отсюда вывод об отсутствии (в среднем) переноса
энергии, относится, конечно, к приближенному представлению поля.
В дальней зоне, т. е. на расстояниях г>Я, (&г>1) поле оказы-
оказывается совершенно иным. Действительно, теперь в выражениях
(9.26) и (9.27) становятся пренебрежимо малыми как раз те чле-
члены, которые при г«?, преобладали, в результате
4л
Н
(9.29)
AnW
Это дальнее поле есть сферическая волна, электрическая и магнит-
магнитная компоненты которой синфазны и имеют характер, отвечающий
условию излучения (ср. (9.10)). Поле не имеет компонент, нор-
нормальных поверхности фронта г = const, т. е. может быть отнесено
к классу Т.
Волна неоднородна: амплитуды векторов Е и Н не постоянны
па поверхности фронта, но угловое распределение поля уже не за-
зависит от г, оно окончательно сформировалось. Формулы (9.29) со-
соответствуют представлению E.113) и, в частности,
Em = W[Hm,r0], (9.30)
где W — волновое сопротивление в классе Г-волн. Это значит, что
волна является локально-плоской (п. 5.5.1) и в достаточно малой
области пространства практически не отличается от плоской одно-
однородной Г-волны (см. § 4.1).
Синфазность векторов Е и Н рассматриваемой сферической вол-
волны означает вещественность вектора П, который, таким образом,
равен средней величине П:
Итак, та составляющая поля, которая пренебрежимо мала в
ближней зоне, в дальней становится преобладающей из-за относи-
относительно медленного убывания с расстоянием и образует сферическую
волну, переносящую энергию, создающую излучение.
Рассмотрим развитие поля излучения диполя Герца во времени.
Сначала отметим, что согласно (9.22) временные зависимости за-
заряда и тока диполя выглядят, как это показано на рис. 9.4. Для
нескольких моментов времени, которым соответствуют фазы ш? = О,
л/8, л/4, Зл/8, я/2, 5я/8, на рис. 9.5 построены картнны
электрических силовых линий (в первом квадранте меридиональ-
меридиональной плоскости). При t = 0 заряды диполя максимальны по абсо-
абсолютной величине, а ток отсутствует; на малых расстояниях от на-
начала координат г < К поле имеет такую же структуру, как в случае
идеального электростатического диполя (см. п. 2.2.1). В момент ti
(фаза л/2) заряд равен нулю (рис. 9.4). Поэтому (рис. 9.5) не
может быть электрических силовых линий, начинающихся на за-
зарядах: все они замкнуты. В предшествующие моменты про-
происходит характерная деформация ближнего поля. Силовые линии
вытягиваются и отрываются от диполя. При t = t2 уже сформиро-
сформировался вихрь, система замкнутых электрических силовых лпипй,
в дальнейшем расширяющаяся и уходящая на периферию. А в сле-
следующий момент (фаза 5я/8) при появлении зарядов противопо-
противоположных знаков (рис. 9.4) вблизи начала координат возникло повое
квазпетационарное поле. При at= я, когда заряды вновь станут
максимальными по абсолютной величине, структура поля окажется
такой же, как при t = 0, только изменится направление Е. Мы
обсудили, таким образом, развитие поля в течение половины пе-
периода процесса.
Для более полного представления о поле излучения на рпс. 9.6
показаны еще две картины силовых лпнпй для некоторого про-
промежуточного момента. Сверху показано поле во всех четырех квад-
квадрантах, снизу изменен масштаб, так что видна почти сформировав-
сформировавшаяся периодическая зависимость поля по радиальной координате.
Штриховыми лилиями на рис. 9.5 и рис. 9.6 показаны следы по-
поверхностей, па которых Ег = 0. На достаточно большом расстоянии
каждая такая поверхность есть фронт сферической волны с макси-
максимальным значением П.
Заметим, что первые картины силовых линий поля излучения
диполя Герца — в несколько схематической форме — были построе-
построены еще самим Герцем [3.2].
9.2.3. Элементарный электрический излучатель как антенна.
Из формул (9.29) и (9.31) видно, что элемент тока вообще не из-
излучает в направлении своей оси (д = 0), а в экваториальной пло-
плоскости @ = 90°) излучение максимально. Распределение излучения
в пространстве удобно охарактеризовать при помощи функции
F (д, а) = /П (д, а)/ VП^ = | sin О |. (9.32)
Это так называемая нормированная характеристика направлен-
направленности, которая используется в теории антептт. График этой функции
показывает распределение излучения п некоторой меридиональной
плоскости (рис. 9.7а) и называется диаграммой направленности.
330
ГЛ, 9. ИЗЛУЧЕНИЕ В СВОБОДНОМ ПРОСТРАНСТВЕ
9crJCT
Рис. 9.4
шт=я/4 > 0 tOT=3it '8 X
} ( ^ч\\ }
I ,—OV\N
1- — .
Рис. 9.5. (ЭВМ*
uT=rt/4+rt/i6
Рис. 9.6. (ЭВМ)
r=F(&,cc)
Piic. 9.7
332
ГЛ. 9. ИЗЛУЧЕНИЕ В СВОБОДНОМ ПРОСТРАНСТВЕ
Пространственная диаграмма направленности — тело вращения
этой кривой, тор, показанный на рис. 9.76. Употребляется еще
характеристика, называемая коэффициентом направленности дей-
действия. Это отношение П к некоторой величине По, полученной в
предположении, что при той же мощности излучение распределено
равнемерно: _
, а) = П(д, а)/По. (9.33)
Какова мощность излучения элементарного электрического из-
излучателя? Эту величину можно найти как поток вектора П (9.31)
через некоторую координатную сферу:
-и*
16л W
sin3 ОйО (9.34)
о о
(разумеется, можно было бы взять любую замкнутую поверхность,
охватывающую излучатель). В результате интегрирования находим
(9.35)
Нередко пишут, используя форму закона Джоуля — Ленца,
= x(x) w
(9.36)
и называют параметр 52Г сопротивлением излучения. Очевидно S?z
ecib сопротивление, которое при токе 7'т рассеивает мощность, рав-
равную мощности излучения диполя Герца в свободное пространство,
характеризуя его как «поглотитель энергии».
Теперь мы можем вернуться к формуле (9.33). Учитывая, что
при равномерном излучении через сферу радиуса R средняя плот-
плотность потока энергии По есть Р2/4лй2, а Птах= ЗР2/8лЛ2, нахо-
находим, что
Anas = 3/2. (9.37)
На примере элементарного электрического излучателя было по-
показано применение некоторых представлений теории антенн.
В антенной практике подобно диполю Герца ведут себя метал-
металлические стержни, отрезки провода и даже целые сооружения в
виде башен п мачт при выполнении условий (9.25).
§ 9.3. Элементарный магнитный излучатель
9.3.1. Постановка задачи (А). Контур постоянного тока на боль-
больших расстояниях проявляет себя как магнитный диполь (см.
п. 2.'ЛА). Поэтому следует ожидать, что замкнутый переменный
ток при выполнении некоторых условий будет подобен колеблю-
колеблющемуся магнитному диполю.
§ 9.3. ЭЛЕМЕНТАРНЫЙ; МАГНИТНЫЙ ИЗЛУЧАТЕЛЬ
333
Поле излучения, создаваемое контуром стороннего тока, можно
найти при помощи интегрирования но формуле (9.17), выполнив
действия, несколько более громоздкие, чем выше в § 9.2. Мы бы
установили, что достаточно малый контур тока излучает как ди-
диполь Герца, векторы поля которого Е и Н поменялись ролями. По-
Поэтому употребляется название элементарный магнитный излуча-
излучатель, или магнитный диполь Герца.
Поскольку задача об элементарном электрическом излучателе
выше уже решена, поле аналогичного магнитного излучателя про-
проще всего найти, воспользовавшись принципом двойственности (см.
п. 3.4.3). Если в готовом решении задачи (9.26), (9.27) сделать
замену величин в соответствии с C.81), то мы получим решение
уравнений Максвелла М C.80) при заданном элементе магнитного
тока 7м, который расположен так же, как ранее сторонниц ток 7"
(рис. 9.3, а).
Остается уяснить, как в (9.26), (9.27) выполнить замену
jm-*— jm- Соответствующий заданному элементу магнитного тока
магнитный момент имеет следующую комплексную амплитуда:
mm = —
(9.38)
Эта формула — магнитный аналог ранее полученного выражения
(9.23). Она выводится совершенно так же (см. п. 9.2.1), но вместо
(9.33) надо взять закон сохранения магнитного заряда C.82). Те-
Теперь мы можем сформулировать окончательное правило замены
величин. Так как замена ]",!-» h', ведет к 7"->-— 7щ, то па
основании (9.38): 7„т->—штт/1.
Окончательно вместо C.81) имеем:
(9.39)
9.3.2. Поле излучения магнитного диполя Герца (А). Замена
величин в соответствии с (9.39) приводит формулы (9.26), (9.27)
к следующему виду:
тг + -f )*"'*'sinfl.
(9.40)
(9.41)
Это представление ноля излучения, создаваемого колеблющимся
магнитным моментом ш. Формулы ииляются точпымп в случае
334
ГЛ. 9. ИЗЛУЧЕНИЕ В СВОБОДНОМ ПРОСТРАНСТВЕ
идеального магнитного диполя (тт = const, Z->-0); в остальных
случаях должны быть выполнены условия (9.25).
Совершенно так же, как это делалось в случае элементарного
электрического излучателя, выпишем на основании (9.40), (9.41)
представления ближнего п дальнего полей. В первом случае г <S A
(кг -С 1) и формулы принимают вид
1@111
a0 21 sin 0,
• (го2 cos О + О0 sin О).
(9.42)
Во втором случае г>Х (Ат>1) и получается следующее пред-
представление поля:
Нт л? —
Sin О
(9.43)
з— iftr
Основные свойства ближнего п дальнего полей и, в частности,
их энергетические характеристики остаются такими же, как для
элементарного электрического излучателя. Ближнее поле квазпста-
ционарно; сопоставление формул (9.42) и B.102) показывает, что
в ближней зоне воспропзводптся структура поля магнитостатпче-
ского диполя. Электрическое и магнитное поля сдвпнуты по фазе
на 90°. В дальней зоне поля синфазны. Установившаяся сфериче-
сферическая волна является локально плоской и удовлетворяет соотноше-
соотношению (9.30). Развитие поля во времени происходит так же, как в
случае электрического диполя Герца, только взяв изображения на
рис. 9.5, рис. 9.6, надо трактовать электрические силовые линии как
магнитные.
Если магнитный диполь Герца реализован в виде контура- сто-
стороннего тока /ст с площадью 5, то в формулах (9.40) —(9.43) надо
взять тт как абсолютное значение вектора
Эта запись — прямое следствие соотношения B.98).
Из полученного представления поля следует, что
n" О
(9.44)
(9.45)
Излучение распределено в пространство совершенно так же, как
в случае элементарного электрического излучателя. По-прежнему
§ 9.3. ЭЛЕМЕНТАРНЫЙ МАГНИТНЫЙ ИЗЛУЧАТЕЛЬ
335
F@, a)= I sin 01 и сохраняют свое значение диаграммы на рис. 9.7,
а также формула (9.37). _
Вычислив поток вектора П (9.44) через некоторую координат-
координатную сферу подобно тому, как это делалось в п. 9.2.3, получаем
р2 _ i^l „2 С2 J_ ,g щ
Имея в виду контур тока /ст, можно ввести представление о сопро-
сопротивлении излучения 52Z. Тогда
L _ 1 f r
" — "о" \1
rcna
1т)
,4 •
(9.47)
Очевидно 5?2 можно истолковать как дополнительное сопротивле-
сопротивление в цепи вследствие излучения. Таким путем можно оценивать
потери на излучение в цепях переменного тока.
В антенной технике элементарный магнитный излучатель реа-
реализуется в виде ряда конструкций.
9.3.3. Другой способ определения поля излучения (Б). Рассмат-
Рассматривая замкнутый контур стороннего тока, вместо определения поля
излучения на основании (9.17) будем исходить из выражения век-
векторного потенциала (9.15). При этом окажутся полезными проме-
промежуточные результаты, полученные выше в п. 2.3.4 в случае конту-
контура постоянного тока.
Пусть круглый контур стороннего тока 1" радиусом а располо-
расположен, как было показано на рис. 2.26я. Формулу (9.15) перепишем
в виде:
(9.48)
она отличается от использовавшегося в п. 2.3.4 выражения B.95)
только экспоненциальным множителем под интегралом. Поэтому
вместо B.100) в данном случае будем иметь
А„, (г, --=
га
= - «0-V- J
(9.49)
где
г — г' | = (г2 т й" t 2ra sin со? а )' :
Как и в п. 2.3.4, рассмотрим предельный случай, взяв а';— 0
при аа/„ = const. Поскольку
( !'.-Г Г'| _ g-ikr(\ _ Цгп si|| ,'t C05; r, I
336
ГЛ. 9. ИЗЛУЧЕНИЕ В СВОБОДНОМ ПРОСТРАНСТВЕ
теперь надо вычислить:
2Л
' СТ 2
]т a =const
что дает:
X e~ihr (I — ika sin d cos ее' + . ..) cos a' da',
-*r sin d (9.50)
(cp. B.101)). Вычисляя Hm = (u^-i)-1 rot Am, т. е.
2
Hm =
ijr sin * #0/r sin ft
«V
д/да
0 (T
приходим к выражению (9.40), где тт — \io\ina4m (9.44).
§ 9.4. Обобщенная задача об излучении. Принцип Гюйгенса (А)
9.4.1. Обобщенная задача об излучении и ее решение. Как мож-
но было убедиться на примере задачи об элементарном магнитном
излучателе, введенное в п. 3.4.3 представление о магнитных токах,
на первый взгляд довольно абстрактное, выступает как полезный
инструмент анализа. Поэтому можно ожидать пользы и от дальней-
дальнейшего обобщения, когда электрические и магнитные источники вво-
вводятся в рассмотрение в рамках одной задачи. Эта обобщенная за-
задача об излучении, которая формулируется в виде следующей си-
системы уравнений Максвелла:
rot Hm = шеоеЁга + j",
rot Em =
(9.51)
Действительно, в силу линейности уравнений (при линейности сре-
среды) решение Ет, Нт есть наложение двух решений
Ега = Ега + Em, Hra = Hm + Hm, (9.52)
решения уравнений Максвелла Э и М
где Ет, Нга и Ет, Нр р
C.80), которые представляют поля, создаваемые только электри-
электрическими и, соответственно, только магнитными источниками.
§ 9.4. ОБОБЩЕННАЯ ЗАДАЧА ОБ ИЗЛУЧЕНИИ
337
Согласно п. 9.1.2,
1
Нт =
4л
г — г
Ё™ = — rot Н™ — вне источников.
(9.33)
Чтобы найти поле Ёт, Нт, применим принцип двойственности в
форме C.81) к представлению (9.17). В конечном счете имеем:
(9.54)
нм
rot
— вне источников.
Решение обобщенной задачи об излучении можно выразить и в
другой форме. Используя понятие векторного потенциала, согласно
(9.15) и C.43) имеем:
~1СТ (г') е—ift.|r—г'|
d' <955>
а Ет находится из первого уравнения Максвелла, как в (9.53).
Применение принципа двойственности в форме C.81) приводит от
(9.55) к следующему равенству:
¦ dv .
(9.56)
Далее НЦ, находим как в (9.54).
9.4.2. Эквивалентные источники. Принцип Гюйгенса. При опре-
определении поля излучения иногда бывает удобно вместо действитель-
действительных источников рассматривать их эквиваленты. Именно так де-
делалось в § 9.3, когда анализировался элемент фиктивного магнит-
магнитного тока для определения поля излучения, создаваемого кольце-
кольцевым сторонним током.
Важную роль играет представление об эквивалентных поверх-
поверхностных источниках. Рассмотрим некоторое электромагнитное поле
Е, Н; характеризующие его электрические и магнитные силовые
линии изображены на рис. 9.8а. Пусть это же поле существует
только в области 1 и отсутствует в области 2 (рис. 9.86). Какие
условия надо поставить на разделяющей границе S (штриховая ли-
линия), чтобы их действие оказалось эквивалентным отброшенному
полю?
Ясно, что при переходе через поверхность S все компоненты
векторов поля теперь будут обрываться. Остается лишь выяснить,
22 в. В. Никольский, Т. И. Никольская
338
ГЛ. 9. ИЗЛУЧЕНИЕ В СВОБОДНОМ ПРОСТРАНСТВЕ
§ 9.4. ОБОБЩЕННАЯ ЗАДАЧА ОБ ИЗЛУЧЕНИИ
339
как согласовать это с общими положениями электродинамики. Раз-
Разрывы компонент Z?v и Их, как известно (см. § 1.4), соответствуют
существованию поверхностного заряда и поверхностного тока. По-
Поскольку поле отсутствует в области 2, на поверхности S выполня-
выполняются условия A.90). Запишем их в комплексных амплитудах:
t]
= [
v0,
(9.57)
(среду полагаем изотропной); индексом S обозначены поля на 5.
Но в рассматриваемом случае имеются также разрывы компо-
компонент Bv и Ех, что противоречит граничным условиям, выведенным
Рис. 9.8
в § 1.4 из обычных уравнений Максвелла. Здесь на помощь при-
приходят условия C.84) и C.85), полученные при введении магнит-
магнитных зарядов и токов. В отсутствие поля в области 2 из них следует:
Ёт = 1«оА>, T]m=[ELv0]. (9.58)
Мы приходим к выводу: первоначальное поле Е, Н будет су-
существовать в области 1 вплоть до границы S (без продолжения в
область 2), если на поверхности S распределены электрические и
нагнптные заряды и токи, связанные с полем соотношениями
(9.57) и (9.58).
Сделанный вывод означает, что поле в объеме можно рассмат-
рассматривать как результат излучения источников, распределенных на
некоторой поверхности, причем для определения источников до-
достаточно знать поле на поверхности. Полное поле восстанавлива-
восстанавливается на основании информации о его состоянии на поверхности,
Здесь уместно вспомнить идеи Христиана Гюйгенса о волновых
процессах. Согласно известному принципу Гюйгенса, каждую точ-
точку фронта некоторой скалярной волны можно принять за источник
локальной сферической волны; новое положение фронта может быть
найдено при учете действия всех локальных волн, т. е. при помо
щи условных поверхностных источников. В широком смысле под
принципом Гюйгенса можно попимать введение такого рода нсточ
пиков.
Е,Н
Как же применяется принцип Гюйгенса в электродинамике?
Пусть требуется найти поле Е, Н в некоторой области V при усло-
условии, что источники поля, лежащие вне F, неизвестны, но зато из-
известно поле Es, Hs на ограничивающей V поверхности 5. Постанов-
Постановка задачи поясняется в двух вариантах на рис. 9.9: задача может
быть внутренней (а) и внешней (б), т. е. поле Е, Н ищем внутри
ограниченного объема или, со-
соответственно, в бесконечном
пространстве. Как следует из
п. 3.4.1, знания Es и Hs — при
некоторых оговорках — вполне
достаточно, чтобы поле в V оп-
определялось единственным обра-
образом; эта информация даже из-
избыточна.
Мысленно отбросим поле за
границей S вне V и в соответ-
соответствии с (9.57), (9.58) введем
эквивалентные поверхностные Рпс. 9.9
источники if* и if. Ограничим-
Ограничимся внешней задачей (рис. 9.96). Это не что иное, как обсуждавшая-
обсуждавшаяся в п. 9.4.1 обобщенная задача об излучении. Ее решение выра-
выражается при помощи формул (9.52) — (9.54) или (9.52), (9.55),
(9.56). Разумеется, вместо объемных записываются поверхностные
интегралы (V -*¦ S, dv -+¦ ds); при этом
&T-*4m = [v0,H*] и J?-*4m = [E?,v0]. (9.59)
Поле Е, Н находится, таким образом, по его тангенциальным ком-
компонентам на поверхности 5, входящим в (9.59). Это п есть реали-
реализация принципа Гюйгенса в электродинамике.
Надо иметь в виду, что Е и Нт в (9.59)—это векторные
функции, связанные уравнениями Максвелла. Рассматривать элект-
электрические и магнитные эквивалентные поверхностные источники как
независимые было бы ошибкой. Это приводит к противоречию с
выводами, сделанными в п. 3.4.1, согласно которым поле единст-
единственным образом определяется заданием только электрической или
только магнитной продольной компоненты.
9.4.3. Элементы Гюйгенса. Согласно предыдущему, элементы по-
поверхности S с заданным распределением поля могут фигурировать
как элементарные излучатели. Это так называемые элементы Гюй-
Гюйгенса, которые можно выделять на самых различных поверхностях
в разных полях.
Рассмотрим простейший элемент Гюйгенса в виде элементарной
площадки AS на плоскости z = 0, параллельной фронту плоской
однородной волны (рис. 9.10). Распространение волны вдоль оси
z можно истолковать как результат излучения всей совокупности
340
ГЛ. 9. ИЗЛУЧЕНИЕ В СВОБОДНОМ ПРОСТРАНСТВЕ
таких элементов при 2 = 0. Поле излучения рассматриваемого эле-
элемента Гюйгенса в дальней зоне (г > к) имеет следующий вид:
Ет
A + cos ft) (ft0 cos oc — a0 sin oc)
1 m - A + cosi'*) (ft0 sin oc + a0 cos oc) -
г
— ihr
(9.60)
г
(излучатель расположен в сферической системе координат,
рис. 9.11).
Рпс. 9.10
Рпс. 9.11
ВЫВОД. При заданной поляризации плоской однородной вол-
волны плотности эквивалентных поверхностных токов элемента Гюй-
Гюйгенса выражаются следующим образом:
Ч? = К Н?1 = -х0Я* , чт = [Ё?, z0] = - уо?«, (9.61)
где имеется в виду, что взятая плоская волна при z = 0 характе-
характеризуется векторами Е„ = х0Ет и Нт = у0Нт. Пусть размеры эле-
элемента малы в сравнении с расстоянием наблюдения (аналогичное
условие ставилось при рассмотрении электрического и магнитного
элементарных излучателей).
Начнем с определения поля Ет, Нт, создаваемого электриче-
электрическим током элемента Гюйгенса. Поскольку нас интересует только
дальнее ноле, отбросим в выражении Н^ (9.53) первый член в
круглых скобках. Переходя к поверхностному интегралу и учиты-
учитывая первое равенство (9.61), имеем
Йэ
«* Г
4T.J
¦ [х0, го1
(9.62)
§ 9.4. ОБОБЩЕННАЯ ЗАДАЧА ОБ ИЗЛУЧЕНИИ
341
Поскольку х0 = Ro cos а — ао sin а = (r0 sin ft + #о cos ft) cos a — a0 sin a
(рис. 9.11), это дает
П„
}0 sin а + а0 cos ft cos а) ¦
-—ihr
(9.63)
Из первого уравнения Максвелла в сферических координатах вы-
вычисляем:
,—ikr
о cos ft cos a — «0 sin a) -—
(9.64)
(члены, убывающие быстрее, чем 1/г, отброшены).
Аналогично определяем создаваемое магнитным током элемента
Гюйгенса поле Е™, Нт- Исходя из (9.54), пишем:
^м — ik
,»„_„
,
4л
,
AS
а поскольку у0 = Ro sin a + ceo cos a = (r0 sin ft + #o cos ft) sin a +
+ aocosa (рис. 9.11), выражение принимает вид:
„-ihr
0 cos a — a0 cos ft sin a) ^~y~-
(9.66)
Наконец, используется второе уравнение Максвелла, которое дает:
„—ihr
-Т-. (9.67)
ikEs\S
Чтобы получить полное поле излучения элемента Гюйгенса в
дальней зоне, сложим согласно (9.52) поля (9.64) и (9.66), (9.63)
и (9.67). Учитывая также, что Е„ = WHfn, приходим к (9.60). ¦
Как излучает элемент Гюйгенса? Вычисляя среднее значение
вектора Пойнтинга, находим
П = Re П = rn
(9.68)
и, следовательно, нормированная характеристика направленности
(см. определение в п. 9.2.3) имеет вид
F(ft. cc) =
cosft).
(9.69)
Диаграмма направленности в произвольной меридиональной пло-
плоскости а = const есть кардиоида (рис. 9.12а); объемная диаграмма
направленности — ее тело вращения (рис. 9.126). Таким образом,
элемеп-i Гюйгенса максимально и.члучает и направлении осп z (ft =
= 0), в обратном направлении @=180°) излучение отсутствует.
342
ГЛ. 9. ИЗЛУЧЕНИЕ В СВОБОДНОМ ПРОСТРАНСТВЕ
Пусть элемент Гюйгенса выбран в впде прямоугольника со сто-
сторонами Ах и Ау (рис. 9.13а). Согласно (9.61), он является носи-
носите лем токов:
/т = ЛтДг/ = - Hi Ay, 'H='nlAx=-EsmAx. (9.70)
Это значит, что элемент Гюйгенса должен действовать подобно
270
Рис. 9.12
системе двух ортогонально ориентированных диполей Герца — элек-
электрического и магнитного (рис. 9.136) с моментами
О)
*о>
mn
О)
' Уо-
(9.71)
Лас
п
1
7"
Формулы (9.60) можно было бы получить путем наложения полей
этих двух элементарных излучателей в дальней зоне. Но, отправ-
отправляясь от формул (9.29) и (9.43), мы были бы вынуждены преобра-
преобразовать их к единой сферической системе координат, что требует
применения элементов сфериче-
сферической тригонометрии.
Отметим, наконец, следующее.
_^ При выводе формул (9.60) было
Р rS
использовано соотношение Ьт =
= WHm. Именно оно отражает тот
факт, что элемент Гюйгенса по-
построен в плоскости фронта одно-
однородной Г-волны. Заменив W на
некоторый импеданс Z, легко получить представление поля излуче-
излучения некоторого обобщенного элемента Гюйгенса. В зависимости от
выбора Z можно придавать различный смысл такому элементарному
излучателю. В частности, взяв Z=WE или Z = WH F.26), F.29),
мы располагаем элемепт Гюйгепса в плоскости фронта некоторой
Е- и, соответственно, //-волны.
Рис. 9.13
§ 10.1. ЭЛЕКТРОДИНАМИЧЕСКИЕ ЗАДАЧИ ДИФРАКЦИИ
343
УПРАЖНЕНИЯ
1. Записать формулы (9.15) и (9.17) для случая линейных токов (ср.
п. 2.3.1).
2. Какой вид должны принять формулы (9.15) и (9.17), если сторопшш
ток является поверхностным и распределен с плотностью т|ст на S.
3. Найти комплексную амплитуду векторного потенциала А поля излуче-
излучения диполя Герца.
4. Продолжая действия, начатые в упражнении 3, найти вектор Н поля из-
излучення диполя Герца.
5. Почему только в дальней зоне поле излучения диполя Герца может рас-
рассматриваться как локально плоская волна?
15. Взяв выражения комплексных амплитуд (9.26), (9.27), выписать напря-
напряженности Е и Н как функции координат и времени: а) при отсутствии погло-
поглощения в среде, б) при наличии поглощения.
7. Площадь некоторой плоской цепи переменного тока составляет 0,2А.2. Най-
Найти ее сопротивление излучения.
8. Показать, что поле излучения обобщенного элемента Гюйгенса (с. 342)
выражается следующим образом:
Е™ * —ЙГ" К [Т cos в + 1 j cos ос - аД-g- т- cos &] sin оj —^,
1 e~ihr
¦\~y~-
(9.72)
(W \ ( W
ufl 1 ~2~-f cos 01 sin а + аД ~^~ cos 0 -f- II cos а
Глава 10
ДИФРАКЦИЯ В СВОБОДНОМ ПРОСТРАНСТВЕ
§ 10.1. Электродинамические задачи дифракции (А)
10.1.1. Общие представления. Постановка задач. Термин ди-
дифракция, относящийся к теории волновых процессов, имеет доволь-
по широкое значение. Первоначально явлениями дифракции назы-
называли отклонения свойств света от тех идеализированных норм, ко-
которые диктуются геометрической оптикой. Свет в определенной
степени огибает препятствия, границы света и тени не бывают
идеально резкими. Однако, пока размеры рассматриваемых объек-
объектов весьма велики по сравнению с длиной волны (d>K), что ха-
характерно для света, геометрическая оптика остается полезным и
часто вполне достаточным инструментом теории. Объекты относи-
относительно больших размеров нередки, например, и в антенной техни-
технике, но здесь неравенство d > Я уже но выполняется в столь силь-
сильной степени; поэтому отклонения от представлений геометрической
оптики существенно сильнее. Накоиец, когда размеры объекта срав-
сравнимы с длиной волны (а это типично для многих важных задач),
геометрическая оптика теряет силу: волновой процесс в целом остг
Ш'ч'ю, in1 укладимающесся и се рамкп.
Обсудмм содержание и постановку лаОач Ьифрикции и злектро-
дмпамикр. Kin.- 11 нише и и. 5.1.2, будет рассматриваться надоит
344
ГЛ. 10. ДИФРАКЦИЯ В СВОБОДНОМ ПРОСТРАНСТВЕ
некоторой волны Е°, Н° на заданный объект (рис. 10.1), которым
может быть какое-либо диэлектрическое (а) или металлическое (б)
тело; нас будет интересовать, в частности, металлический экран с
отверстием (е). Внутри диэлектрического тела возникает поле Е*,
IE°,H°J.
^ //<*•"¦
Н+, называемое внутренним полем дифракции (металлические объ-
объекты принимаем за идеально проводящие). Вне объектов появляет-
появляется внешнее поле дифракции Е~, Н~. Оно называется также полем
рассеяния.
Для нахождения внутреннего и внешнего полей дифракции при
заданной падающей волне (которая не обязательно должна быть
плоской) поставим граничную задачу. А именно, потребуем, чтобы
решения уравпеннй Максвелла Е°, Н°; Е4", Н+; Е~, Н~ на поверх-
поверхности S объекта дифракции V удовлетворяли условиям непрерыв-
непрерывности тангенциальных компонент:
[Ё°, + Е„, v0] = [Ё+, v0],
[1С + Н-, v0] = [Н+, v0].
A0.1)
Поле Em, Hm должно также удовлетворять условию излучения
(см. пи. 5.1.2, 9.0.2, 9.1.2).
Если тело V — идеально проводящее, то внутреннее поле дифрак-
дифракции отсутствует и в постановку задачи входит только первая стро-
строка из A0.1), принимающая вид:
[Ё°т + Ё~, vj = 0,
вторая же согласно A.90) приводит к соотношению
[Н„ + Н„, v0] = цт,
A0.2)
A0.3)
которое может быть использовано для нахождения поверхностного
тока после определения внешнего поля дифракции.
Итак, в задаче дифракции, как и в рассматривавшейся ранее
(см. п. 5.1.2) задаче о падении плоской однородной волны на гра-
§ 10.1. ЭЛЕКТРОДИНАМИЧЕСКИЕ ЗАДАЧИ ДИФРАКЦИИ
345
ницу раздела сред, фигурируют в общем случае три поля, которые
мы обозначили при помощи одних и тех же индексов @, +, —).
Одинаковыми по смыслу являются и налагаемые на эти поля усло-
условия A0.1) и E.12); для обеих задач существенно условие излуче-
излучения. Различие состоит в том, что в задаче дифракции рассматрива-
рассматривается уже не бесконечная плоская граница, а некоторый ограничен-
ограниченный объект. Плоская волна в первом случае порождает две другие
плоские волны, тогда как во втором — возникают сложные поля
дифракции. В немногих задачах удается представить эти поля в
виде рядов, коэффициенты которых находятся непосредственно при
наложении условий A0.1); таковы, например, задачи дифракции
на цилиндре и шаре. Однако к настоящему времени развиты ме-
методы и построены различные алгоритмы, предназначенные для ре-
решения задач дифракции на ЭВМ (см. п. 12.3.3).
При оценке дифракционных процессов используются некоторые
интегральные характеристики. Таков параметр S±, называемый по-
поперечным сечением рассеяния. Он определяется как отношение
<? - — = —
- П0 n°
ds,
A0.4)
где П° — абсолютное значение средней плотности П° потока энер-
энергии падающей_ волны (плоской и однородной), а Р~ — полный по-
поток вектора П~ через поверхность 2, охватывающую объект диф-
дифракции (рис. 10. 1й); он называется потоком рассеяния.
Пример 1. Пусть илоская однородная волна падает па металлический
лист (рис. 10.2). размеры которого велики в сравнении с длиной волны. В прп-
блшкешт геометрической оптики вычислим поток энергии волны, отраженной
от листа:
РОтр = П cos ср = П°5 cos ф,
где S — площадь листа и ф — угол падения (лист
принимается за идеально-проводящий). Однако
¦^отр —эт0 еЩе пс полныи поток рассеяния. Су-
Существование области тени следует рассматривать
как наложение на падающую волну Е°, Н° локалп-
зованпого в этой области поля —Е°, —Н°, в резуль-
результате чего полное поле уничтожается. Полный поток
рассеяния оказывается поэтому вдвое больше Ротр.
Итак, согласно A0.4) для рассматриваемой задачи
в приближении геометрической оптики
S± = 2/~отр/П° = 25 cos ф. ¦ A0.5)
Рис. 10.2
В случае дифракции на отверстии (рис. 10.1е) вводится поня-
понятие поперечного сечения прохождения
rr _T 1
A0.6)
346
ГЛ. 10. ДИФРАКЦИЯ В СВОБОДНОМ ПРОСТРАНСТВЕ
где 2 — некоторая поверхность, построенная так, что через нее
проходит весь поток рассеяния в полупространство за отверстием.
В приближении геометрической оптики параметр Т± равен пло-
площади отверстия 5.
10.1.2. Приближенные подходы; метод Гюйгенса — Кирхгофа.
Поскольку решение электродинамических задач дифракции — за
исключением простейших — было практически недоступным в те-
течение ряда десятилетий, получили распространение различные
идеализации. Заметим, что, хотя геометрическая оптика обычно
применяется при больших относительных размерах объектов (d ^
>?i), одного этого условия в действительности еще мало. Требу-
Требуется также, чтобы поверхность рассматриваемого тела была гладкой
и минимальный радиус кривизны оставался значительно больше
длины волны (.ffmin^X). Тогда каждый элемент поверхности мож-
можно принимать за участок плоской границы раздела сред, для кото-
которой справедливы законы Снеллиуса, выведенные в п. 5.1.3. Можно
строить картины отраженных и преломленных лучей; уравнение
эйконала E.110) описывает поверхности волновых фронтов, кото-
которые ортогональны лучам. Эта идеализация есть приближение гео-
геометрической оптики. Ясно, что при со -*¦ эо (^ -> 0) мы имеем так-
также: RmiJ'k -*¦ °°, т. е. в этом случае мы переходим к пределу геомет-
геометрической оптики в теории дифракции. Впрочем, необходима важ-
важная оговорка. Тело не должно иметь идеальных ребер, на которых
i?min = 0. В противном случае останутся краевые эффекты. Пло-
Плоский лист, рассмотренный выше в примере 1, строго говоря, не под-
подлежит анализу геометрической оптики. Заметим, что в теории диф-
дифракции существует целое направление, называемое геометрической
теорией дифракции, выработавшее методы учета влияния ребер в
рамках концепции лучей.
В ряде случаев размеры тел малы по сравнению с длиной вол-
волны (d<^K). При этих условиях можно получить информацию о
структуре полей дифракции, рассматривая предельный случай, со-
соответствующий и -*¦ 0 (h ~+°°), т. е. переходя к квазистационарно-
квазистационарному пределу. В этом пределе А;2 = 0, так что, в частности, однород-
однородные уравнения Гельмгольца переходят в уравнения Лапласа.
Большое значение имеет так называемый метод Гюйгенса —•
Кирхгофа, применяемый при решении задач дифракции на метал-
металлических (и любых непрозрачных) телах. С точки зрения геомет-
геометрической оптики, такое тело просто создает область тени, как это
показано на рис. 10.3 в случаях некоторого ограниченного тела (а)
и экрана с отверстием (б), если падающая волна — сферическая.
Построим поверхность 5 (штриховая линия на рис. 10.3), по одну
сторону которой остается источник падающей волны. Эта поверх-
поверхность состоит из частей S' и S" E = 5" + S"); S" лежит в обла-
области тени. Если бы распределение поля на 5 было известно, то поле
но всей бесконечной области V можно было бы найти без всякого
упрощения, используя принцип Гюйгенса (см. п. 9.4.2). Но при
§ 10 1 ОТВЕРСТИЕ В ЭКРАНЕ. ДИФРАКЦИЯ ФРАУНГОФЕРА
347
постановке задачи дифракции известно только поле падающей вол-
волны Е°, IIе'. Поэтому делается следующее допущение, которое на-
называется приближением Кирхгофа:
I Е° на 5 ,
0 на 5':
Hs =
(Н° на 5'.
1 0 на 5".
A0.7,
Смысл ею очевиден: распределение ноля на поверхности 5 соответ-
соответствует продет а нлениям геометрической оптики, ноле отсутствует is
зато лонной части 5 п не отличается от падающей волны в осве-
освещенной. Однако ;>то не геометрическая оптика (ведь допущение не
Рис. 10.3
распространяется на всю область Г), а только лишь геометрооп-
тичесшш способ задания эквивалентных источников.
Па следующей стадии вступает в действие весь аппарат опре-
определения полей Еэ, Нэ и Ем, Нм (см. п. 9.4.2) и согласно (9.52) на-
находится поле Е. Н в бесконечной области V. Надо иметь^в виду,
что в случае дифракции на отверстии (рис. 10.36) Е = Е- и Н =
= Н~, тогда как при дифракции на теле ограниченных размеров
(рис'10.3а) поле в объеме Г включает и падающую волну: Е =
Весь изложенный подход и есть метод Гюйгенса — Кирхгофа,
первоначально развитый в волновой оптике (в скалярной форме).
В сущности он является эвристическим приемом широко исполь-
использующимся в теории антенн.
§ 10.2. Отверстие в экране. Дифракция Фраунгофера
10.2.1. Постановка задачи. Применение метода Гюйгенса — Кирх-
Кирхгофа (А). Будем рассматривать нормальное падение плоской одно-
однородной волны Е°, Н° на идеально проводящий экран с отверстием 5.
Введем декартоиу и совмещенную с пей сферическую системы коор-
координат (рис. \0Ла). Падающую из левого полупространства (z < 0)
348
ГЛ. 10. ДИФРАКЦИЯ В СВОБОДНОМ ПРОСТРАНСТВЕ
волну зададим при помощи комплексных амплитуд
ЕЛ, = х0Ае
— ikz
A0.8)
и для определения поля дифракции Е~, Н~ в правом полупростран-
полупространстве (z < 0) применим метод Гюйгенса — Кирхгофа.
Итак, в соответствии с A0.7) на теневой стороне экрана поло-
положим Ё® = 0, Н® = 0, а на отверстии Ё„ = Ё^ @) = xoi, Н^ =
= Hj, @) = y0A/W согласно A0.8). В этом приближении достаточ-
достаточно малые элементы отверстия являются элементами Гюйгенса, рас-
рассмотренными в п. 9.4.3. Поэтому нет необходимости приводить
в действие весь аппарат эквивалентных поверхностных источников,
Рпс. 10.4
описанный в п. 9.4.2. Гораздо проще воспользоваться уже получен-
полученными выражениями поля излучения элемента Гюйгенса (9.60) и ох-
охватить все элементы Гюйгенса, выполнив соответствующее интегри-
интегрирование по S. Определяя таким путем поле дифракции, выразим
комплексную амплитуду напряженности электрического поля:
Ей = JdEm = lk\l@) J A + cos 0g) X
,—ih\t—r'|
X (ftog cos aq — aoq sin aq) e. _ ,. ds'. A0.9)
Здесь использована первая строка из (9.60) и символом q отмечены
угловые сферические координаты (а также орты) локальной систе-
системы координат с началом в Q; радиальная координата этой системы
есть |г —г'|. Дело в том, что формулы (9.60) записаны в системе
координат с началом на элементе Гюйгенса, и это надо было учесть
при интегрировании. Отметим, что текущая точка интегрирования
Q(r') в декартовых координатах есть Q(x', у', 0), а фиксированная
§ 10.2. ОТВЕРСТИЕ В ЭКРАНЕ. ДИФРАКЦИЯ ФРАУНГОФЕРА
349
точка наблюдения Р(г), в которой определяется Ет, это —
P(x,y,z).
Возьмем прямоугольное отверстие (рпс. 10.46), а точку паблю-
денпя Р отнесем так далеко, чтобы векторы г — г' и г можпо было
считать параллельными. Отверстие 5 при этом видно из Р под ну-
нулевым углом, т. е. представляется точкой. Говорят, что в этом слу-
случае наблюдается дифракция в дальней зоне; употребляется также
термин дифракция Фраунгофера, происходящий из волновой оптики.
Интегрирование по формуле A0.9) приводит к следующему резуль-
результату:
Em = е
4я
X
cos а — а0 sin а) A + cos 0) X
sin A/2A:a sin ft cos a) sin J^ljkb sin 0 sin a) ,, „ , q.
1/2ka sin ft cos a xl^b sin ft sin a
Эта сферическая волна является локально плоской, так что
H" = --L[r0, Ё-]. A0.11)
ВЫВОД. Поскольку в дальней зоне все точки отверстия имеют
одинаковые угловые координаты •О, = 0, aq = а и множитель
Ir —r'l можно поменять на г, под интегралом в A0.9) остается
только экспоненциальный множитель. Интегрирование производим
по прямоугольнику — а/2 < z < а/2, —Ы2<у^Ъ/2. Таким обра-
образом, имеем:
ikEt @)
Е~ = —^-г— A + cos 0) (tt0 cos a — a0 sin a) x
a/2 b/2
X \ ( e-ift|r-"ldx'dyr. A0.12)
—a/2 —b/2
Несмотря па близость значений |r — r'l и г, экспоненту под интегра-
интегралом нельзя принять за ехр(— ikr), так как размеры отверстия а и b
не малы по сравнению с длиной волны (ср. п. 9.2.2, где условие
малости выполнялось).
Разлагая Ir —r'l в биномиальный ряд, пишем:
I г - г' | = [(х - x'f + (у - у'J + z2]i/2 =
= [Г2 _ 2 (хх' + уу') + х'2 + y'2Y'2 = r -^±JUL + ..., A0.13)
где отброшены члены второго порядка малости. Внося это в показа-
показатель экспоненты под интегралом A0.12), производим интегрирова-
интегрирование; так как
а/2 Ь/2 . . sin
о/2-Ь,2
^7
-ТГ^ У
35')
ГЛ К. ДИФРАКЦИЯ В СВОБОДНОМ ПРОСТРАНСТВЬ
¦ю из A0.12) следует результат A0.10). Надо лшць заменить ?„. @)
ни Л и перептп от декартовых координат к сферическим, используя
i («отношения: х = г sin ft cos а и г/ = ?¦ sin 0 sin а (рис. 10.46).
Выражение A0.11) получается при сопоставлении первой и вто-
второй строчек формул (9.60). Действительно
[t'r,. $о cos а — tto sin а] = $о sin а + «0 cos о.
о поэтому представление Н^ A0.11) Судет получено н,ч BTOpoii
п'рочкп (9.00) при помощи точно тех же операции, которые прнио-
мп к A0.10) от первой строчки (9.E0). щ
10.2.2. Анализ дифракции Фраунгофера. Сначала уточним, при
i.aii'iix условиях можно пользоваться формулами A0.10), A0.111.
Г. представлении A0.13) не сохранены члены, квадратичные отно-
относительно х' и у . которые принимают максимальное значение при
г' = а и у' = Ь. Так, отбрасывая член (х'2 + г/'2)/2, мы пренебре-
пренебрегаем приращением фазы А:|г — r'i = Л:(а2 + &2)/2г. Это допустимо,
если
dVr/.<i. A0.1 Г;)
1де d = а, Ь — размер отверстия. Мы получили критерий дифрак-
дифракции Фраушофорн.
Излучение из отверстия в правое полупространство удобно оха-
охарактеризовать при помощи функции /'(ft, а) = у П (¦О1, а)/ У Птах,
которая унге неоднократно использовалась нами в гл. 9 в качестве
нормированной характеристики излучения. Определяя П = Re П при
помощи выражений Е„ A0.10) и Н^г A0.11), отмечаем, что Umd^ =
= 11@, а), т. е. излучение максимально в направлении осп z, и
F (#, а) =
~Г COS 1
sin и
и
sm v
A0.16)
где и —(ka/2)sin ¦& cos а и v =(kb/2)sin u sin и. Первый множитель
в A0.16), зависящий только от {). есть не что иное, как характери-
характеристика направленности элемента Гюйгенса (9.69). Множители вида
F(l)= [sin |/|I (| = и, v) отображают эффект наложения лбкаль-
ных волн, создаваемых всеми элементами Гюйгенса на отверстии 5;
они пазываются интерференционными множителями. При а^> К
(Ь > X) соответствующий интерференционный множитель изменяет-
изменяется в зависимости от ¦& гораздо быстрее, чем cos ¦&, и фактически оп-
определяет характеристику направленности в области малых ¦&.
Будем рассматривать излучение из отверстия в зависимости от
Ф при а = 0, пли, как говорят, в Е-плоскости, и при а = 90° —
в Н-плоскости. Характеристика /?(#, а) A0.16) в этих случаях при-
принимает вид:
cos
hft{ (ft) =
1 -f COS fl1
sin
¦-H
til
A0.17)
r;irj
t,E=(ka/2)sin
и %" =(kb/'l)sin 0.
10
.2. ОТВЕРСТИЕ В ЭКРАНЕ. ДИФРАКЦИЯ ФРАУНГОФЕРА
351
На рис 10.5 (сверху) показан график функции F(|)-lsin|/|l.
Как видно при | = 0 функция имеет главный максимум, соответст-
вКуюЩиГмаксимуму излучения при 0 = 0, т. е. в направлении z.
90°
Рпс. 10.5. (ЭВМ)
Поскольку в A0.17) при малых ft можно пренебречь влиянием мно-
множителяA + cos ft) /2 то об угловой ширине зоны наибольшего из-
л"еппя можно судить по характеру интерференционного множите-
множителя На рис 10.5 отмечена угловая ширина «луча» как зопы: ограпи
352
ГЛ. 10. ДИФРАКЦИЯ В СВОБОДНОМ ПРОСТРАНСТВЕ
§ 10.3. ОТВЕРСТИЕ В ЭКРАНЕ. ДИФРАКЦИЯ ФРЕНЕЛЯ
353
ченной ближайшими к главному максимуму нулями, которые полу-
получаются при выполнении условий
— зтДФЕ = л, — siaA'&H = n, A0.18)
где АФ0 и АФ0 — угловые расстояния от главного максимума до
ближайшего направления нулевого излучения в Е- и /^-плоскости
соответственно. Ширина луча есть при этом 2АФ0 п 2АФ0. Ввиду
малости этой величины можно заменить синусы в A0.18) их аргу-
аргументами, поэтому
2АФ^ да 2К,'а, 2AG? да 2К/Ъ. A0.19)
Весьма примечательно, что угловая ширина луча обратно пропор-
пропорциональна размеру отверстия. В пределе при а/К -»- °°, Ь/К -*¦ °° уг-
угловая ширина зоны прямого (Ф = 0) излучения стремится к нулю:
зона становится нерасширяющейся, что п ожидается в пределе гео-
геометрической оптпки.
На рис. 10.5 в трех вариантах построена диаграмма направлен-
направленности отверстия, получаемая по формулам A0.17); при этом 2АФ0 =
= 30°, 12° и 4°. Такие диаграммы называют игольчатыми. Отметим,
что в первом варианте отверстие еще недостаточно велико в срав-
сравнении с длиной волны для вполне уверенного применения прибли-
приближения Кирхгофа, которым мы пользовались.
10.2.3. Идеальная поверхностная антенна (Б). Существует поня-
понятие поверхностной антенны; имеется в виду, что излучение такой
антенны может быть истолковано как действие источников, распре-
распределенных на некоторой поверхности. В теорпн антенн к поверхност-
поверхностным относят, в частности, зеркальные и рупорные антенны. В боль-
большинстве случаев поверхностные антенны анализируют с позиций
принципа Гюйгенса.
Рассмотренное нами отверстие, излучающее в полупространство
в режиме дифракции, анализировалось выше как объект с равно-
равномерным по амплитуде синфазным распределением поверхностных
источников. Это так называемая идеальная поверхностная антенна.
Вычислим коэффициент направленности действия Dmax (см.
п. 9.2.3) в направлении максимального излучения Ф = 0. Для этого
определим мощность излучения Р2:
A0.20)
Плотность среднего потока энергии П° при равномерном излучении
такой мощности во всех направлениях есть
11° =
А*аЬ
4лг2
A0.21)
а для направления максимального излучения Ф = 0 рассматривае-
рассматриваемого отверстия имеем:
(на основании A0.10), A0.11)). Поэтому
Ртах = Йт„/П° = 4л5Д2, (Ю.23)
где 5 = аЪ. Эта формула имеет важное значение в теории антенн.
Она применяется и для оценки реальных антенн; тогда под S пони-
понимается некоторая эффективная поверхность антенны.
§ 10.3. Отверстие в экране. Дифракция Френеля (А)
10.3.1. Изменение условий наблюдения. Рассматривая прежнюю
задачу дифракции плоской однородной волны на прямоугольном
отверстии в экране, поставим целью приблизить точку наблюдения.
Условие A0.15) при этом уже не будет выполняться: будут учтены
квадратичные члены в разложении величины |г — г'1, формирую-
формирующей показатель экспоненты под интегралом A0.12). Исследуемый
X
%-
Рис. 10.6
волновой процесс, который предстанет теперь в ином виде, называ-
называется дифракцией Френеля.
Будем использовать интегралы Френеля — специальные функ-
функции, представляемые как следующие определенные интегралы:
с {и) = / A j cos f- dt,
(и) = /4 _f si
sin i2 dt. (Ю.24)
Эти функции табулированы (см., например, [К. 1]) и ниже в
п. 10.3.2 будут рассмотрены подробнее.
Пусть точка наблюдении Р{г) лежит в некоторой плоскости
z — const (рис. 10.0а). Поле дифракции Е", И", которое мы получим
23 в. Е. Шпгольс.nit, Т. II. Пш.олг.сгия
354
ГЛ. 10. ДИФРАКЦИЯ В СВОБОДНОМ ПРОСТРАНСТВЕ
при невыполнении условия A0.15), выражается через интегралы
Френеля:
Ё- (х, у, z) = -1 Ё°т (z) [С (и) - iS (и)] I2 [С (v) - i
б 1
(.г, y,z) = ± Н™ (z) [С (и) - i
? [С (v) - iS (v)]
где
A0.25)
<10-26>
(верхний знак соответствует индексу 1, нижний — индексу 2).
ВЫВОД. Возвращаясь к выражению Е„ A0.12), представим
расстояние |г — г'| под интегралом в виде
I г - г' | = [(х - x'f + (у- y'f + z2]^ = z + (*-*'? +(»-У'? + . ..
A0.27)
(удержаны квадраты координат х' и у' точки Q). Кроме того, огра-
ограничиваясь областью относительно малых 0, не будем различать г
и z, примем cos 0 за единицу и учтем, что do cos а — «о sin а = х0.
(рис. 10.66). Таким образом, вместо A0.12) получаем:
а/2 Ы-1
—а/2 — Ь/2
A0.28)
Записанный двукратный интеграл есть произведение Двух оди-
одинаковых по форме однократных. Рассмотрим первый из них. При
подстановке к(х — x'J/2z = t2 имеем:
а/2 Yh/2z(,x—a/2)
j [fj j e~ir-dt. A0.29)
YhJTz(x+al2)
Представляя exp(—it2) как cos t2 — i sin t2, используем символы ин-
интегралов Френеля A0.24) и обозначения пределов интегрирования
A0.26); в результате:
а/2
j ехр[- гА
-а/2
Аналогично
Ь/2
j
dx' - - УЦ-[С (и) - iS (и)] |"х2. A0.30)
/
j exp[- i
к/
-к/а
A0.31)
§ 10.3. ОТВЕРСТИЕ В ЭКРАНЕ. ДИФРАКЦИЯ ФРЕНЕЛЯ
355
Подставляя в A0.28) произведение результатов A0.30) и
A0.31), а также принимая во внимание, что х0Л ехр (—ikz) =
= Em(z), приходим к выражению Е„ в первой строке A0.25).
Совершенно так же можно вывести выражение Нт. ¦
10.3.2. Анализ дифракции Френеля. Введем в рассмотрение ве-
величину
A0.32)
где d — a, b — один пз размеров отверстия. Будем называть 3, диф-
дифракционным параметром. Порядок d существенным образом опреде-
определяет характер наблюдаемого процесса. Напомним, что в случае диф-
дифракции Фраунгофера в силу A0.15) S < 1; при этом а > К, b > X.
Исследуя дифракцию Френеля, рассмотрим сначала поле Е~, Н~
в некоторой точке наблюдения Р@, 0, z), лежащей против средней
точки отверстия ()@, 0, 0). Пусть d » 1. Тогда, как видно из
A0.26), весьма велики по абсолютному значению
«1.2@) = ±-^Г7=,
УБ'
A0.33)
Обратимся к графику интегралов Френеля на рис. 10.7. При боль-
больших значениях аргумента они близки к 1/2; учтем также, что это
1.0
I—I—I—.—I—I—I—.—I—.—I—<—I—I—I
0.
0 '10 20 '30 'АО 50 '60 '70 'ВО '90 '100
Рис. 10.7. (ЭВМ)
нечетные функции. Полагая СA12)= — С(и\) = S(V2)— — S(v\) =
= — 1/2, имеем:
[С (и) - iS (и)] р; [С (v) - iS (v)] \1[ = 4 (- \ + Щ = - И.
Г! лтом приближении
Е- @, 0, z) = El (z), II" @, 0, г) - IIS, (z), A0.34)
356
ГЛ. 10. ДИФРАКЦИЯ В СВОБОДНОМ ПРОСТРАНСТВЕ
т. е. поле дифракции Е~, Н~ в средней точке наблюдения не отлича-
отличается от поля падающей волны Е°, Н°. Последняя как бы не испы-
испытывает влияния экрана. При этом П~@, 0, z) = z0A2/2W.
Сохраняя условие d > 1, исследуем изменение поля дифракция
в плоскости z = const. Точнее говоря, будем рассматривать функцию
F(r,y) =
Согласно A0.25)
где
(ж' У)
*' У)
F{x,y)=l/2O(x)O(y),
A0.35)
A0.36)
Ф(х)= !C(B2)-i5(M2)-[C(Bi)-i5(Bi)]|,
Ф(У)= \C(v2)- iS(V2)-[C(Vl)- iS(Vl)]l A0.37)
Чтобы найти Ф(х) или Ф(г/), надо вычислить модуль разности
двух значений комплексной функции C(u)—iS(u). Наглядность
этим действиям придает диаграмма, на которой нужные комплекс-
комплексные числа представляются в виде радиус-векторов. Это так называе-
называемая спираль Корню (рис. 10.8): по осям декартовой системы коор-
координат отложены С (и) и — S(u), а кривая соединяет точки, отвечаю-
отвечающие равным аргументам и этих функций; значения и нанесены
на самой кривой. Поэтому надо лишь выбрать па кривой требуемое
значение аргумента; отрезок, соединяющий начало координат с этой
точкой, изображает соответствующее значение функции С(и) —
— iS(u). Чтобы вычислить Ф(х), выбираем точки и\ и и%. Их ра-
радиус-векторы изображают комплексные числа, которые вычитаются
в A0.37). Нужная нам разность изображается отрезком, соединяю-
соединяющим точки щ п й2- Длина этого отрезка дает Ф(х).
Преяаде чем двигаться дальше, отметим, что связь функций С(иO
S(u) и спирали Корню наглядно отображается пространственной
кривой на рис. 10.9. Кривые всех трех функций получаются как ее
проекции на ортогональные плоскости.
Будем рассматривать функцию F(x, у) A0.35), положив у = 0,
т. е. исследуя поле в iJ-плоскости. Согласно A0.36), A0.37)
F(x, 0)=Ф(ж)Ф@)/2 = Ф(ж)/У2. При х = 0 точка наблюдения за-
занимает то самое центральное положение, для которого получено
представление поля A0.34). Поскольку дифракционный параметр 3
A0.32) весьма велик, то, как уже отмечалось при выводе формул
A0.34), И]@)« 1/2 и М2@)« — 1/2, а это значит, что точкп щ@)
п мг@) находятся, практически, в фокусах спирали Корню. Иными
словами, соединяющий фокусы отрезок изображает F@, 0), что со-
соответствует полю A0.34). Он показан на рис. 10.10 (начало).
Перемещая далее точку наблюдения Р в плоскости z = const из
среднего положения х = 0 в сторону возрастания х, заметим, что
Mi (х) = }k/2z(x + а/2) уиеличинастся, т. с. с еще большим основа-
основанием можно считать точку щ (х) лежащей в фокусе спирали Корню.
§ 10.3. ОТВЕРСТИЕ В ЭКРАНЕ. ДИФРАКЦИЯ ФРЕНЕЛЯ
357
-0.5
[C(u)-LS(u)]|^
-0.5
-S(u)
0.5
0.5
Рис. 10.S. (ЭВМ)
Рис. 10.9. (ЭВМ)
358
ГЛ. 10. ДИФРАКЦИЯ В СВОБОДНОМ ПРОСТРАНСТВЕ
Что касается величины и2(ж) = 1kl2z(x — а/2), то она с ростом х
в интервале @, а/2) уменьшается до нуля. При этом один конец
изображающего отрезка на диаграмме остается неподвижным, а дру-
roii скользит по спирали Корню, как показано на рис. 10.10, обходя
ее витки. Длина отрезка, а следовательно, величина F(x, 0) сначала
Рис. 10.10. (ЭВМ)
колеблется с ростом амплитуды, а затем монотонно убывает. Когда
точка наблюдения Р находится точно против края отверстия
(х = а/2), длина изображающего отрезка оказывается вдвое мень-
меньше его значения при х = 0:
F(a/2, 0)=V2F@, 0).
A0.38)
При дальнейшем увеличении х значение ii2(x) становится положи-
положительным и возрастает, приближаясь к и\(х). Длина отрезка на
рис. 10.10 (конец) при х> lka монотонно падает, что соответствует
убыванию поля дифракции в области геометрической тени. Подчерк-
Подчеркнем, что согласно A0.38) амплитуды Е„, Н~ поля дифракции на
границе тени оказываются вдвое меньше, чем в центре освещенной
области.
Па рис. 10.11 построена кривая F(х, 0) для d ~ I03. Ход кршюй
при х > 0 соответствует произведенным рассуждениям (ср.
рис. 10.10), а при х<0 все повторяется. Заметим, что колебания
интенсивности происходят относительно постоянного значения, пред-
предсказываемого геометрической оптикой (штриховая линия). Вблизи
границы геометрической тени лежит ник наибольшем"! лптопсиипости.
Чем больше величина d A0.32), тем уже краевая зона, в которой
8 10.3. ОТВЕРСТИЕ В ЭКРАНЕ. ДИФРАКЦИЯ ФРЕНЕЛЯ
f (x.O)
359
-d/2
d/2
Рис. 10.11. (ЭВМ)
d=13.5M
d=1.23
d=27M
d=2.46
d=54M
d=4.93
-d/2 0 d/2
d=94.5M
d=8.63
-d/2
О d/2
d=135M
d=12.3
-d/2 0 d/2
Рис. 10.12. (ЭВМ)
360
ГЛ. 10. ДИФРАКЦИЯ В СВОБОДНОМ ПРОСТРАНСТВ»
заметно проявляется дифракционный эффект. Общий тип картины
сохраняется, пока d > 1.
Рассмотрим ряд кривых F(x, 0) (рнс. 10.12), полученных для
расстояния z = 4 км при К = 3 см, когда размер отверстия меняется
от 135 м (что соответствует очень большому радиотелескопу) до
z=1km
1
-d/2
d/2
z=10km
-d/2
d/2
d=24.6
d=7.8
z=400km
-d/2
d/2
z=10000km
d=i.23
d=0.25
-d/2 0 d/2
Рис. 10.13. (ЭВМ)
13,5 м. Дифракционный параметр 3, в данном случае значительно
меньше, чем в предшествующем случае (рис. 10.11). Пока 3 > 1,
кривая /'(ж, 0) остается похожей, но заметны .мелкомасштабные ос-
осцилляции; их происхождение связано с тем, что в данном случае
§ 10.3. ОТВЕРСТИЕ В ЭКРАНЕ. ДИФРАКЦИЯ ФРЕНЕЛЯ
361
уже нельзя рассматривать один конец изображающего отрезка
(рис. 10.10) как фиксированный в фокусе спирали Корню. Ои не-
несколько смещен, но приближается к фокусу с ростом \х\.
На рис. 10.13 представлена еще одна серия кривых F(x, 0) для
d = 135 м при л = 3 см. Изменяется расстояние z, так что параметр
с7, будучи при z = 1 км большим, при z = 104 км становится малым.
Здесь уже наблюдается дифракция Фраупгофера, и, в сущности, мы
видим центральный участок кривой |sin|/|l. Ширина центрального
максимума составляет согласно A0.19) 2ЛФ0 = 2,B) • 10~4 рад, т. е.
2,B) км, поэтому видимый на чертеже малый участок кривой вы-
выглядит, как постоянный уровень.
На рпс. 10.13 видно, как с увеличением расстояния постепен-
постепенно разрушается картина дифракции Френеля, свойственная области
больших значений дифракционного параметра 3.
10.3.3. О спирали Корню. Зоны Френеля. Простое графическое
построение (рис. 10.14) поясняет происхождение спирали Корню.
В качестве некоторого приближения представим себе, что число
элементов Гюйгенса па отверстии является конечным. Желая найти
поле дифракции, например, в средней точке Р@, 0, z), мы должны
Рис, 10.14
сложить ряд комплексных величин АЕт(гп), выражающих комп-
комплексные амплитуды полей излучения отдельных элементов Гюйген-
Гюйгенса (мы берем скалярные величины). Модули АЕт(гп) приблизи-
приблизительно одинаковы, а соответствующие фазы изменяются тем быст-
быстрее, чем дальше от средней части отверстия расположены элементы.
Используя для сложения комплексных амплитуд АЁт(гп) век-
векторную диаграмму (рис. 10.14), видим, что ломаная линия «закру-
«закручивается ¦>. При достаточно мелком разбиении можно, в принципе,
получить ломаную, приближающуюся к спирали Корню. Нахожде-
Нахождение результирующего поля производится при помощи соединения
концов ломаной, это дискретный аналог построения на рис. 10.10
(начало).
Обсудим также широко распространенное про.четавлеппо о попах
Фрспал. Рассматривая поле дифракции в средней точке Р@, 0, z)
362 ГЛ. 10. ДИФРАКЦИЯ В СВОБОДНОМ ПРОСТРАНСТВ
^(рис. 10.15), выделим в плоскости отверстия круг радиуса
П = У (z + V2J-z2« III
A0.39)
Все расстояния от элементов Гюйгенса, лежащих в пределах этого
круга, до Р различаются не более, чем на полволпы. Так строится
Рис. 10.15
первая зона Френеля. Аналогичными свойствами обладают кольце-
кольцевые области с внешними радиусами
г„ = У (z + nl/2J - z2 « inTz A0.40)
(п> 1); внутренние радиусы колец равны rn-t. Это зоны Френеля
номеров н. = 2. 3. .. . .
Чем выше номер зоны Френеля, тем ближе площади соседних
зон. Можно полагать, что элементы Гюйгенса двух соседних зон
Френеля достаточно высоких номеров создают в точке Р@, 0, z)
одинаковые по амплитуде поля. Но эти поля противофазиы и, сле-
следовательно, взаимно компенсируются.
Пусть размеры отверстия весьма велики в сравнении с первой
зоной Френеля
d»n, A0.41)
т. е. d » Viz" A0.39), или — что то же: 3 >1 A0.32). Это значит,
что в отверстии (относительно произвольной формы) укладывается
много зон Френеля. Действие зон высших номеров при этом в доста-
достаточной мере скомпенсировано, и, если отверстие увеличивать, то это
уже практически не изменит ноле дифракции в Р@, 0, z). Влияние
экрана перестает сказываться. Действительно, именно к такому за-
заключению мы пришли, получив в случае 3 > 1 формулы A0.34).
Теперь этот результат осмыслен при помощи представления о зонах
Френеля. Можно сказать, что ноле дифракции создается, главным
обра.чом, элементами Гюйгенса нескольких центральных зон.
10.4. ВЗАИМНО ДОПОЛНИТЕЛЬНЫЕ ЭКРАНЫ
363
§ 10.4. Взаимно дополнительные экраны. Ограниченные тела (А)
10.4.1. Принцип Бабине в приближении Кирхгофа. Оказывается,
полученное выше решение задачи дифракции па отверстии в беско-
бесконечном экране (будем называть ее задачей А) дает также поле диф-
дифракции для некоторой задачи В, отличающейся тем, что теперь рас-
рассматривается падение прежней волны Е°, Н° на ограниченный эк-
экран, имеющий форму и ориентацию прежнего отверстия, т. е., как
говорят, конгруэнтный отверстию. Точнее говоря,
Ев = - Е2, Щ = - HI, A0.42)
где индексами А и В отмечены поля дифракции для обеих задач.
Запись выражает так называемый принцип Бабиие.
Покажем сначала, что принцип Бабине справедлив в приближе-
приближении Кирхгофа.
ВЫВОД. Постановка задач А и В поясняется на рис. 10.16.
В первой из них (а) поле в правом полупространстве (z > 0) есть
{Е=О,Н=О)
Z>O
Z<:O
r>O
z>O
a 6 6
Рис. 10.16
поле дифракции: ЕА = Ед, НА = Нд. Именно это поле рассматри-
рассматривалось выше в § 10.2, 10.3. Во второй задаче (б) поле в нравом
полупространстве представляет собой наложение падающей волны
и поля дифракции: Ев = Е° + Ев, Нв = Н° + Нд. Рассмотрим су-
суперпозицию обоих полей:
Нд + Н°в + Нв. A0.43)
Ед + Е
в =
E
Е° + Е
в,
Нд + Н
Мы имеем право говорить, что поле ЕА + Ев, НА + Нв имеет источ-
источниками наложение элементов Гюйгенса задач А и S, т. е. оно соз-
создается всем фронтом падающей волны Е°, Н° в плоскости z = 0. Яс-
Ясно, что это поле не отличается от Е°, Н° во всем полупространстве
z>0:
ЕА + ЕВ = Е°, НА + НВ = №. A0.44)
Из сопоставления A0.43) и A0.14) вытекает принцип Бабине в
форме A0.42). ¦
364
ГЛ. 10. ДИФРАКЦИЯ В СВОБОДНОМ ПРОСТРАНСТВЕ
Итак, в приближении Кирхгофа поля дифракции в задачах А и
В о взаимно дополнительных экранах связаны соотношением
A0.42). Можно пойти и дальше: вместо экрана в задаче В
(рис. 10.166) введем в рассмотрение некоторое тело (рис. 16.16в),
обладающее тем свойством, что его сечение плоскостью z = 0 имеет
форму прежнего экрана. Казалось бы, в произведенном выводе ни-
ничего пе меняется: источники остаются прежними. В действительно-
действительности ;ке правое полупространство частично занято введенным телом,
оно уже не однородно. Однако, оставаясь в рамках приближения
Кирхгофа, этим до определенных пределов пренебрегают (в частно-
частности, тело пе должно выходить за пределы тени экрана). Тогда фор-
формулы A0.42) позволяют судить и о дифракции на телах конечных
размеров.
В частности, выводы о характере поля дифракции Фраунгофера
и Френеля, сделанные выше в пп. 10.2 и 10.3, с некоторыми оговор-
оговорками можно перенести и на задачи о непрозрачных телах конечных
размеров.
11 е следует, однако, забывать, что эвристический по своей сути
метод Гюйгенса — Кирхгофа не приводит к точным решениям за-
задач дифракции.
10.4.2. Симметрия полей и принцип двойственности. Продолжая
рассматривать две задачи дифракции на взаимно дополнительных
экранах (рис. 10.16а, 6), введем еще одпо различие, связанное с по-
поляризацией падающей волны. Пусть падающие волны Ед, Но
Рис. 10.17
(рис. 10.17а) и Ев, Нв (рис. 10.176) ориентированы так, что век-
векторы Ед и Ид иараллельпы, а На и Ев> соответственно этому,
гштииараллельпы.
§ 10.4. ВЗАИМНО ДОПОЛНИТЕЛЬНЫЕ ЭКРАНЫ
365
Полное поле во всем пространстве в обоих случаях можно пред-
представить в виде:
Ед,в = Е°д,в + Е1,в, Нд,в = Н°д,в + Щ,в, A0.45)
д,в
где Е^в, Н2,в — поля, связанные с токами и зарядами, наведен-
наведенными падающей волной в экране. При такой трактовке поля диф-
дифракции в правом полупространстве z > 0 выражаются следующим
образом:
д = ЬА + ЬА, Нд = Нд + Нд; t,B — Ев, НВ=НВ. AU.40)
Поскольку токи и заряды лежат в плоскости z = 0, введенные поля
обладают вполне определенной симметрией относительно этой плос-
плоскости. Так, в частности, магнитное поле Нв (рис. 10.176) возбуж-
возбуждается токами, направленными вдоль оси у; линии вектора Нв
лежат поэтому в плоскости .rOz и симметрично охватывают экран.
Рассмотрим распределение тангенциальных компонент полей ди-
дифракции Ед, Нд и Ев, Нв при z = + 0. В задаче А на всем бес-
бесконечном экране SA равна нулю тангенциальная компонента векто-
вектора Ед (полного поля); поэтому Едт = 0 (при z^0 полное поле есть
поле дифракции). В задаче В на такой же части Sb плоскости z =
= 0 (S'B = S"A) Квх = 0, что следует из симметрии поля Нв = Нв
(рис. 10.176). Возвращаясь к задаче А (рис. 10.17а), видим, что на
отверстии S'A поле Нд, наведенное токами в экране, имеет только
нормальную компоненту: НАт = 0. Поэтому в силу A0.46) НАт = Нд.
В задаче В па конгруэнтной части SB должно быть равно пулю
полное электрическое тангенциальное поле: Евг = 0. Следовательно,
ИЗ (IV.ЦП). Xjbx — *-^Вх — — '-'В-
В итоге оказывается, что в задачах А ж В тангенциальные ком-
компоненты напряжеппостей полей дифракции на границе правого по-
лупрострапстна поменялись ролями. Поставив электродинамические
задачи в форме
А В
гоШ„д = icoe0eE~A,
Етдт = 0 на SA,
Н — Н° ття <?'
А1тДт — llmA ud " А
rot Етв = — ioj^
rot Н~в = шгоеЕтв,
НтВт = 0 на S'B,
Етвг = — Е^в на SB,
мы видим, что они паходятся в соотношении, которое отвечает прин-
принципу двойственности (см. л. 3.4.3). Это значит, что, имея решение
электродинамической задачи А в щтдо поля Ё„л, Н~А, мы можем
получить решение Е„в, Нтв задачи В (при измененной поляри-
366
ГЛ. 10. ДИФРАКЦИЯ В СВОБОДНОМ ПРОСТРАНСТВЕ
зацни падающей волны), сделав в готовом решении замену C.79).
Точно так же получается решение задачи А, если имеется решение
задачи В. Это утверждение называется принципом Бабине.
10.4.3. Щелевые излучатели. На основании предыдущего мы
можем сравнивать задачи дифракции на щели в идеально проводя-
проводящем экране (рис. 10.18а) и дополнительной полосе (рис. 10.186).
Рис. 10.18
При указанной поляризации падающей волны в полосе возникает
продольный ток /. Поэтому каждый элемент полосы Д/ < К (усло-
(условие d < К подразумевается) будет вести себя как элементарный
электрический излучатель (см. § 9.2). Зная ток, можно по формулам
из п. 9.2.2 выразить поле излучения, которое в данном случае есть
не что иное, как поле дифракцииЕд, Нд. Для дальней зоны на
основании (9.29) имеем:
Е
тВ ¦
н;
е '
A0.48)
причем нетрудно связать ток / с магнитным полем на поверхности
полоски:
в
Hbmdl = 2\Rmdl; A0.49)
L A
здесь имеется в виду, что замкнутый контур интегрирования L
«прижат» к самой полоске: L есть АВВА (рис. 10.186).
Теперь мы можем выразить поле дифракции в случае щели
(рис. 10.18а), применив принцип двойственности, т. е. сделав заме-
замену величин в соответствии с C.79): е =** \i, Етв—>—Н„А, Н~в->
-*-Е„А, IIm —>-Ет. При этом, как видно из A0.49),
в
EiUl = 2f/m, A0.50)
§ 10.4. ВЗАИМНО ДОПОЛНИТЕЛЬНЫЕ ЭКРАНЫ
387
где Cm истолковывается как напряжение между краями щели. Пред-
Представляемое формулами A0.48) поле Е^в, НтВ переходит в поле
.дифракции задачи А:
е;
е '
Н
тА
= _ # мты
о—хкт
При сопоставлении A0.51) и (9.43) становится ясно, что элемент
хцели проявляет себя как элементарный магнитный излучатель,
причем
тт = i2
m = — 2U
A0.52)
я
Рис. 10.19
Второе из этих равенств отвечает соотношению (9.38).
Анализ излучения щели на основе принципа взаимности ведет
начало от работ А. А. Пистолькорса ').
Короткая щель (рис. 10.19а), как и короткий металлический эле-
элемент (рис. 10.196), близки по своему действию к элементарным из-
излучателям, магнитному и электрическому;
надо, однако, иметь в виду, что распределе-
распределение Em и, соответственно, Нт на излучате-
излучателях не является равномерным: существенны
краевые эффекты.
Проведенное рассмотрение нельзя считать
решением дифракционных задач, так как
не получена связь Ет и Нт (Um и Im) с по-
полем падающей волны. Были лишь исследованы общие свойства
полей дифракции. Отметим следующее важное обстоятельство. При
той поляризации падающей волны, которая показана на рис. 10.18а,
вектор Н° параллелен щели. Это значит, что при отсутствии щели
.а акране будет распределен ток с плотностью ц = 2 [v0, H°] = xq2H°,
что соответствует стоячей волне, образующейся в результате полно-
полного отражения падающей. Щель «перерезает» ток проводимости в эк-
экране под прямым углом. Это обусловливает сильное возмущение по-
поля с излучением из щели. Прерванный ток экрана замещается то-
током смещения в щели.
Если изменить поляризацию падающей волны, сделав Н° пер-
перпендикулярным щели, то она окажется параллельной току в экране.
Вносимое возмущение при этом невелико, так что излучение — пока
узка щель — незначительно. При конструировании антенн и в тех-
технике СВЧ важно попимать, какие щели (разрезы) в металлических
элементах будут существенно излучать, а какие — нет. Так, напри-
') Пистолькорс А. Л. / ЖТФ.—1944.—Т. 14.— С. 081, 093.
368
ГЛ. 10. ДИФРАКЦИЯ В СВОБОДНОМ ПРОСТРАНСТВЕ
мер, «неизлучающпм» будет разрез прямоугольного волновода плос-
плоскостью х = а/2, если распространяется основная волпа. Действи-
Действительно, этот разрез, проходя по средним линиям широких стенок»
почти не повлияет на их токп.
§ 10.5. Дифракция на цилиндре (Б)
10.5.1. Постановка задачи. Рассматриваемый ниже пример позво-
позволит нам поставить и решить задачу дифракции как электродинами-
электродинамическую краевую задачу (см. и. 10.1.1), не прибегая к эвристиче-
эвристическим приемам. Постановка за-
задачи поясняется на рис. 10.20.
Бесконечный круговой цилттидр,
однородное тело с проипцаемо-
стями ег, р-2 расположен в среде
с прошщаемостями еь ui и орп-
ептироваи по оси z. Иидекса-
мп 1 и 2 будем обозначать и
другие параметры, относящееся
к соответствующим средам. Па-
Падающая полна Е°, II0 распрост-
распространяется по нормали к оси
цилиндра; возьмем два вари-
вариРпс. 10.20
параллельная поляризация
анта:
пш = - Уо уГ
о уГ
перпендикулярная поляризация (J-)
A0.53)
A0.54)
Требуется паптп внутреннее п внешнее поля дифракции: Е+, Н+ и
Е-, Н-.
Уравнепия Максвелла для обеих однородных сред приводят
к уравнениям Гельмгольца; источники отсутствуют, так что эти
уравнения пмеют вид D.22). Учтем также, что ожидаемое реше-
решение не зависит от z. Таким образом,
V/2 тЦ , 7,2 "р А МП 'лпЪ
V i l!i*M "Г Ai r>?jm =\J AU.OOI
И X m i t._ \ /
VlHm + fr?i2Hra = 0. A0.56)
( :,\;:; , ' с::;,i'i.ioi'. ч го фигурируют координат ы г. плоскости попе-
ре'и:г-:':< cc'ici:::;! цилиндра, т. о. х, у пли г, а.
% 10.5. ДИФРАКЦИЯ НА ЦИЛИНДРЕ
3G0-
Учтем, что х = г cos а и запишем следующее разложение, кото-
которое при решзпип задачи будет ключевым:
e-Ve<*«= ^ (-i)n/n(V)e'"a- A0-57)
Это не что иное, как ряд Фурье функции ехр(— iAvcosoc) no систе-
системе (ехр(шсс)}; здесь фигурируют коэффициенты Фурье, которые
представляются в виде:
я
J_
2л
A0.58)
Формула A0.58)—одно из основных соотношении теории цилинд-
цилиндрических функций.
Для решения задачи дифракции нужно получить представления
полей Е+, Н+ и Е~, Н~ как суперпозиции подходящих решении урав-
уравнений Гельмгольца A0.55), A0.56) в цилиндрических координатах
и наложить условия A0.1) па поверхности цилиндра г — R.
10.5.2. Параллельная поляризация. Согласно A0.53) и A0.57)
имеем:
¦Ana
R
A0.59)
-.4'
11
A0.60)
(учтено, что уо = Го sin a + ao cos a). Но магнитное поле удобнее
представить в иной форме. Поскольку при Е,„ = zo?',,1
сор, (.1
дг
A0.61)
а каждый член ряда A0.59) есть решение уравнений Максвелла,
применяя к A0.59) почленно операцию A0.61), получаем следую-
следующее разложение HJ}, по решениям уравнений Максвелла:
(~ «Г
in
г
R.
A0.62)
?J:)-.i.iio убе .и i i.csi. ч |Ч) ряды A0.00) и A0.П2) iii.iMiiia.ieii nn.i (при
iipeou[)a.ioi!:ii!ii;[v используются формулы G.1'J), G.2U)).
2i В. В. ITuro.ii.crnii, Т. И. iiir ол;,с: ;-п
ГЛ. 10. ДИФРАКЦИЯ В СВОБОДНОМ ПРОСТРАНСТВЕ
Внутреннее поле дифракции представим при помощи рядов, по-
подобных A0.59), A0.62), но с неизвестными коэффициентами bl:
2 n = -oo L
r<R, A0.63)
R.
A0.64)
Заметим, что каждый член в A0.63) есть решение Т = @l{r)s4-(a),
построенное из первой строчки G.41) при В = 0 и второй строчки
G.42), где сохранен один член (% = &г).
Аналогичным образом выражается внешнее поле дифракции, од-
однако теперь вместо бесселевых надо использовать функции Ханкеля,
так что. берется вторая строчка G.41) при Л = 0. Только в этом
случае внешнее поле дифракции будет удовлетворять условию из-
излучения, которое мы обсудим после получения решения. Итак,
пишем:
(Ю.65)
¦ 11
^aTi n=—oo L J
A0.66)
Условия A0.1) в данном случае принимают вид:
El + k-^kz, H°ma + H-a = Hna, r = R. A0.67)
Входящие сюда величины выразим при помощи разложений A0.59),
A0.62), A0.63) — A0.66). Равенства A0.67) удовлетворяются по-
почленно, что приводит к уравнениям:
bl /„ (KR) - cl H{? (k^R) = /n (KR),
л" Л2 г' С7- /?\ ^'i Л1 л@-У п- п\ - fei г' и- п\ (Ю-68)
"•2 ' 1 ^1
решения которых дает следующие выражения коэффициентов в раз-
разложениях A0.63) —A0.66):
^(M)-/;(^^(^) A0.69)
^
W
пГУп (k2R) Jn (\
cl =
(Ю.70)
/„
Таким образом, решение задачи получено.
§ 10.5. ДИФРАКЦИЯ НА ЦИЛИНДРЕ
371
10.5.3. Перпендикулярная поляризация. Задачу дифракции в дан-
данном случае можно было бы решать прежним путем, отправляясь
от разложения Н™ A0.54), повторяющего A0.59), и затем воспро-
воспроизводя выкладки уже известного вида. Но в этом нет необходимо-
необходимости, поскольку принцип двойственности позволяет воспользоваться
готовой формой решения, полученного выше в случае параллель-
параллельной поляризации. Надо лишь произвести замену неличин в соот-
соответствии с правилом C.79). Как видно из A0.53), A0.54), при
е =*=*= jj,, переход от параллельной поляризации к перпендикулярной
происходит по схеме: Ет -»- Нт, Нт -»- — Ет. Выполняя требуемые
операции, включая замену символов II -»- -L, из A0.63) — A0.66) по-
получаем:
Ё™ = 7о7Т- 2 (-*)nb^[ro^-/n(fr2r)-«oM»(V)leine, r<R,
О 2 п= —оо L J
A0.71)
сю
iti^z^ S (-0nbn/n(fr2r)ein«, r<R; A0.72)
,
0 1 )l = — o
ff'
где коэффициенты выражаются следующим образом:
х Jn (k!R) Я(п2)' (к R) — /', (к Л) Н\?) (к R
A0.73)
I, A0.74).
A0.75)
п (А\Л)
- К (hR) J'n {\
^(^)
A0.76)^
Эти последние формулы получены из A0.69), A0.70) при замене
проницаемостей е ==* \i.
10.5.4. Обсуждение результатов. Путем непосредственной про-
проверки легко убедиться, что полученные поля рассеяния A0.65),
A0.66) и A0.73), A0.74) удовлетворяют условию излучения
в форме
A0.77)
Urn V? [д1^ + ikFm) = 0
372
ГЛ. 10. ДИФРАКЦИЯ В СВОБОДНОМ ПРОСТРАНСТВЕ
(для этого надо перейти к асимптотическим представлепиям G.32)).
Поскольку задача дифракции была двумерной, в A0.77) в отличие
от соотношений (9.9), (9.19), фигурирует Vr вместо г (при выводе
A0.77) вместо сферы, как в и. 9.0.2, должна рассматриваться ци-
цилиндрическая поверхность).
Рассмотрим некоторые численные результаты исследования ди-
дифракции иа цилиндре. Пусть поляризация — параллельная, а ци-
цилиндр является идеально проводящим; для получения решения до-
достаточно в A0.69), A0.70) перейти к пределу при ег -»- — ?°°. В ре-
результате имеем:
ъ* - о,
сп = —
A0.78)
Внутреннее поле дифракции Е+, Н+, как и следовало ожидать, от-
отсутствует. При этом иа поверхности цилиндра распределен ток, плот-
плотность которого в силу A0.3) есть
п. = -z0 (#? + #«). A0.79)
Чтобы выразить внешнее поле дифракции (поле рассеяния) Е~,
Н~ в дальней зоне, используем асимптотическое представление
120"
40 270° 301
JJO°
Рис. 10.21
G.32); формулы A0.65), A0.66) при этом дают:
A0.80)
(радиальная компонента Нг становится исчезающе малой), где
(a)= 2 c*eina- A0-81)
На рис. 10.21 приведены результаты в виде диаграмм направ-
направленности ноля рассеяния цилиндра [Г.4] (величппа У W как
§ 10.6. ДИФРАКЦИОННАЯ ТЕОРИЯ НАПРАВЛЯЮЩИХ СТРУКТУР
373
функция угловой координаты ее) при относительно малых диамет-
диаметрах 2R; следует иметь в виду, что с увеличением радиуса цилинд-
цилиндра сходимость ряда Q(a) A0.81) быстро падает; обычно таким
нутом производятся расчеты при k\R < 10. Интересно, что при рас-
рассматриваемых размерах вместо тени наблюдается максимум излу-
излучения.
§ 10.6. Дифракционная теория направляющих структур
и резонаторов с линзами и зеркалами (Б)
10.6.1. Теория линзовой линии. Линзовая линия уже рассмат-
рассматривалась выше в п. 7.6.2, по лишь с позиций геометрической опти-
оптики. Между тем, процесс передачи энергии здесь является типично
дифракционным. Обычно для линзовой линии (см. рис. 7.346) од-
одновременно выполняются условия
Я» А, Я «Л, A0.82)
где 7? — радиус линзы, так что заранее не определено соотношение
величин R2 и АЛ, получаемых перемножением соответствующих
частей обоих неравенств. Между тем, принимая одну из липз за
излучающую апертуру, мы видим, что согласно A0.39) величина
V АЛ есть не что иное, как радиус первой зоны Френеля в обла-
области соседней линзы. Это значит, что при невыполнении требова-
ния^1> У "/.А (ср. A0.41)) лппза может не «перехватывать» в до-
^татичной степени направленный иа пес поток энергии. Тогда пе-
передача энергии будет сопровождаться существенным затуханием в
Q
1 О"
Рис. 10.22
результате излучения за пределы линзовой линии; будут велики,
как говорят, радиационные потери.
Рассмотрим одну из. теорий линзовой линии, трактующую про-
процесс передачи энергии как дифракцию Френеля в периодической
структуре.
Пусть па отдельную линзу падает параллельный пучок лучей
(рис. 10.22A); лл лпп.чой он собирается г> фокусе, что о.шачаст су-
существование сходящейся сферической волны. Как видно, выполни-
374
ГЛ. 10. ДИФРАКЦИЯ В СВОБОДНОМ ПРОСТРАНСТВЕ
ется равенство (А + /J = /2 + г2, где Л — расстояние вдоль луча
от плоскости Q" до фронта Q'" сходящейся сферической волны.
Пренебрегая малой величиной Л2 в сравнении с 2/Д, будем иметь:
ЛД =
-?-.
A0.83>
Это не что иное, как фазовый сдвиг в плоскости Q" (функция ра-
радиальной координаты) по отношению к сфере Q'". Поля на Q л
Q" (вход и выход линзы) связаны соотношением:
Ёт{х, y,z + l) = Ет(х, у, z)exp — i[% — k~)l A0.84)
где фо — постоянный сдвиг фазы между плоским и сферическим^
фронтами. Такое же соотношение можно было бы записать и в от-
отношении Нт. Результат верен для параксиальных пучков (см.
п. 7.6.2); продольные компоненты векторов поля пренебрежимо
малы, и процесс представляет собой некоторую Г-волну.
Перейдем к анализу периодической линзовой структуры. Исхо-
Исходя из заданной на Q' (рис. 10.225) величины Ет(х', у', z'), опре-
определим Ет(х, у, z) на Q на основании принципа Гюйгенса. Посколь-
Поскольку имеется в виду дифракция Френеля, исходным будет соотноше-
соотношение тппа A0.28). Различие состоит в том, что в данном случае
нельзя выносить за знак интеграла величину Ет@) (она зависит
от поперечных координат) я, разумеется, интегрирование выпол-
выполняется не по прямоугольнику. Таким образом:
Em (x, у, z)=-
ik e
2л~
-ihL
i
Em(x', (/', z') X
x exp | -
dx'dy', (tO.85>
z — z'
L.
Так как структура — периодическая, свободные электромагнит-
электромагнитные поля должны удовлетворять требованию F.50):
Ет(х, у, z' + A) = Em(x, у, z')e~\
A0.86)
При этом Ёт(х, у, z' + А) = Ёт(х, у, z + I). Учитывая A0.84),
пишем:
[/ 2 \Т
— i [ц>0—Л-^-jJ = кЕт(х, у, z'), х = е-**, A0.87)
§ 10.6. ДИФРАКЦИОННАЯ ТЕОРИЯ НАПРАВЛЯЮЩИХ СТРУКТУР
375
X
я, следовательно, па основаиии A0.85)
хЁт (х, у, z') = ^ ехр {- i [к (Ь - J) + ср0]} f Ёт (х', у', г')
~X'f+L{y~V'f]dx'dy'. A0.88)
X exp — ik
Мы получили не что иное, как интегральное уравнение относитель-
относительно Ет. В краткой записи имеем:
^Ёт = хЁт, A0.89)
где S — интегральный оператор в A0.88), а х — неизвестный па-
параметр. Сформулирована задача на собственные значения (ср.
п. 6.0.2). Совокупность ее решений — система собственных функ-
функций Ет = Ет , которым отвечают собственные значения х = х„,
описывает различные волновые процессы в линзовой линии. Дока-
Доказывается, что основной волне соответствует паиболее узкий пучок
лучей (в геометрооптической трактовке), а радиационные потери
при этом минимальны.
10.6.2. Линзовая линия и зеркальный резонатор. Будем счи-
считать, что на плоскости Q' (см. рис. 10.226) вне апертуры линзы
поле можно считать равным нулю. Тогда каждую линзу периоди-
периодической структуры можно мысленно поместить в отверстие пепро-
зрачного экрана, пусть это будет идеально проводящая перегород-
перегородка. Линия, состоящая из таких экранов с отверстиями (рис. 10.23я),
S
ЕГ=О
О
Л
S
о
Л
Рис. 10.23
может рассматриваться как предельный случай линзовой линии
(A — L, 1// = 0). Это так называемая диафрагменная линия.
На рис. 10.236 показана периодическая структура, состоящая
из экранов, дополнительных к диафрагменной линии. Очевидно,
что два соседних экрана (пара экранов отдельно изображена па
рис. 10.23е) можпо рассматривать как зеркальный резонатор. Не-
Несомненно, режим резонанса возможен и и днафрагмеииой лпинп,
.причем векторы Е и Н в обоих случаях меняются ролями. Исходя
370
ГЛ. 10. ДИФРАКЦИЯ В СВОБОДНОМ ПРОСТРАНСТВЕ
11.0. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ II РЯДЫ ФУРЬЕ
377
из того, что диафрагменпая линия может быть описана посредст-
посредством интегрального уравнения A0.88) при Л = L, ]// = 0, (?0 = 0,
тем„.
ТЕМп.
ТЕМ„
¦
ф
\
i
ф
Т?Мго
\
t
А 1 1
111а
ТЕМ
t
г?
Т
ТЕМ -
Квадратные зеркала
Круглые зеркала
Рис. 10.24
мы можем сразу же получить аналогичное интегральное уравне-
уравнение для зеркального резонатора, применив принцип днойстленпо-
сти. Оно имеет вид:
xHm (x, у. z') = —
С ¦ Г
\Um(x\ у', z')exp — ikK—
s i
2л\ •« | -л j
A0.90)
Собственные функции Hm = Н„, , которым от^^рмт собствен-
собственные значения х = у.п, дают поперечные расп1:еделенпя различных
типов полей собственных ко.лебапи».
На рис. 10.24 показана классификация структур! собственных
колебаний по Фоксу ц Ли ') для случаев квадратных и кругльгл
зеркал.
УПРА/КНЕНИЯ
1. Плоская однородная волна (/ = 10 ГГц) нормально падает па металли-
металлический экран с отверстием а X Ь = 1X2 и2. Найти поле дифракции за экра-
экраном па расстоянии г = 5 м п 1 км.
2. Чему равно поперечноо сечение прохождения A0.6) в прпближопик
Гюйгенса — Кирхгофа?
3. Какой вид примет интеграл A0.9), если рассматривать дифракцию вол-
волны при наклонном падении?
') Fox Л. С, Li Т. II Bell System Teclm. J.— lOGI.— V. 40, X 2.—Г. 453.
См. также [Д.7].
Указание: воспользоваться представлением об обобщенном элементе Гюй-
i-enca в п. 9.4.3 и (9.72).
4. Можно ли найти диаметр отверстия, если сказано, что при длипе волны
А = 1 м он равен размеру первой зоны Френеля?
5. Плоская однородная волна (/ = 10 ГГц) нормально падает на металли-
металлический экран в виде прямоугольника с размерами оХ Ь = 1X2 м2. Выразить
полное электромагнитное поло за экраном па расстоянии г = 5 м и 1 км.
6. Щель в экране длиной 1 см при напряжении между краями 1 В (его
можно считать неизменным по длине щели) надо заменить круглой рамкой
с током, идентично излучающей в полупространство. Найти диаметр и ток
рамки; / = 1 ГГц.
7. При помощи спирали Корню проанализировать дифракцию Фраунгофе-
ра. Объяснить происхождение главного пространственного максимума
излучения.
Глава 11
ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ В ИЗОЛИРОВАННЫХ СТРУКТУРАХ (Б)
§ 11.0. Ортогональные системы функций и ряды Фурье
11.0.1. Некоторые свойства оператора Лапласа. Выше в § 6.0,
7.0, 8.0 уже рассматривались краевые (граничные) задачи для
уравнения Гельмгольца, являющиеся задачами на собственные
зпачения. Формулируя одну из таких задач, напишем:
xii, A1.1)
тде под 3? понимается операция — ^2. Задавая то пли иные гра-
граничные условия, налагаемые па и, .мы определяем класс функции,
на которые распространяется операция SS, задаем область опреде-
определения оператора Лапласа данной задачи Фд> (разумеется, фупк-
ции u= 0g?) должны допускать заданные операции дифференци-
дифференцирования). Входящий в A1.1) параметр у, в обсуждавшихся ранее
краевых задачах — двумерных и трехмерных — обозначался %2 и к2.
Рассматривая и, ге%, введем интеграл
(u, v) = ( u\*dv, A1.2)
v
где V — пространственная область задачи, некоторый объем (при
переходе к двумерным и одномерным задачам V заменяется па S
п L). Символ (u, v) (ср. A.3)) употреблен потому, что введенный
интеграл называется скалярным произведением функций и и v.
Заметим, что (v, u) = (u, v)*.
Оператор 3? называется симметрическим, если
BЧц v) = (u, 24). A1.3)
Для скалярных и, v па основании первой формулы Грипа A.35)
B'и, V) -—
v*\'2udv =
v v
OV
1
(Is.
A1.'
378
ГЛ. 11. ИЗЛУЧЕНИЕ II ДИФРАКЦИЯ
§ 11.0. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ II РЯДЫ ФУРЬЕ
379
Поэтому, если и, v = 0 на S либо ди/дх, dv/dv = 0 на S (или на
одной части S выполняется первое условие, а на другой — второе:
смешанная задача), то поверхностный интеграл в A1.4) равен ну-
нулю. Рассматривая аналогично (гг, 2v) (достаточно в A1.4) сде-
сделать замену и =* v*), убеждаемся, что при данных граничных
условиях
Bи, i») = (Vtt, vy)? (и, 2'i;) = (v«, vy), (Ц.5)
т. е. равенство A1.3) выполняется. Таким образом, возвращаясь к
задачам, обсуждавшимся в § 6.0, 7.0, 8.0, легко убедиться, что опе-
оператор Лапласа был симметрическим.
Возьмем векторные u, v. Используя соотношения A.29), A.25),.
A.26) и A.33), получаем
Bп, у) — — ) \*S/2udv = \ (rot rot u — grad div u) \*dv =
v v
= \ (rot u rot v* -j- div u div v*) dv + Ф {[rot u, v*] — v* div u} ds..
V S
A1.6)'
Если принадлежащие ?>2> функции таковы, что их, vx = 0 и
div u, div v = 0 на S; либо гг„, vv = 0 и (rotu)t, (rotv)t = 0 на S
(можно рассматривать и смешанную задачу), то поверхностный
интеграл в A1.6) исчезает. Тогда
Bм, v) = (rotu, rot v) + (divu, divv),
(u, i?v) = (rotu, rolv) + (divu, div v)
A1.7)
(вторая строка получается при замене u^v* в A1.6)). Оператор
2 является, таким образом, симметрическим и в рассмотренном
случае, т. е., в частности, в задачах (8.37).
Собственные значения к задачи A1.1) в случае симметриче-
симметрического 2 вещественны и неотрицательны. Действительно, образуя
в A1.1) справа и слева скалярные произведения с и, получаем
(и, и) v г
Знаменатель (и, и) в силу A1.2) положителен. Ввиду A1.3)'
Bм, u) = (u, 2м), но в то же время (и, 2м) = Bм, и)*. Отсюда
следует, что числитель в A1.8)—веществен. Таким образом, соб-
собственные значения х. вещественны.
Рассматривая отдельно скалярные и векторные задачи, преоб-
преобразуем Bм, и) при помощи A1.5) и A1.7). Это дает
(и, и) -" \ г
(rot и, го!, и) ! (div и, divu) ^ п t\\ \t\\
Отсюда видно, что собственные значения задачи A1.1) при сим-
симметрическом 2 = —V2 неотрицательны. Они могут быть располо-
расположены в следующем порядке:
О«?Х, s? Х2< ...??Х.;??... A1.11)
11.0.2. Ортогональные системы функций. Две функции и и v
называют ортогональными, если
(u, v)=0. A1.12)
Будем рассматривать собственные функции и = и, (i = l, 2,...)
задачи A1.1) при симметрическом 2. Для двух разных номеров
г, к имеем
2Ч = и,и,, 2щ = хкщ. A1.13)
Образуя скалярпые произведения Bии щ) и (и,-, 2щ) и прини-
принимая во внимание вещественность собственных значений, получаем
Bи{, u,)-(uf, 2щ) = (Хг-кк)(и{, щ), A1.14)
или
(х,-х.,)(и„ и*), A1.15)
поскольку оператор симметричен. Отсюда следует, что (u,, uft)= 0,
т. е. собственные функции ортогональны, если им отвечают нерав-
неравные собственные значения. Если встречаются вырожденные собст-
собственные функции (которым отвечают одинаковые собственные зна-
значения), то, как доказывается, их всегда можно выбрать ортого-
ортогональными.
Буде.л[ говорить, что задача A1.1) порождает ортогональные
системы функций {и,}.
Ортогональная система всегда может быть нормирована, т. е.
можно так подобрать постоянные коэффициенты в выражениях и„
что (u,, Ui)=7Vi, где Nt — любые положительные константы.
В большинстве случаев берут Nt = 1 для всех i. Тогда получается
ортонормированная система, для которой
(и„ 11*)= о,*, A1.16)
:где б,-* = 0 при 1Фк и 6,„ = 1 при i = к (символ Кронепера).
Пример 1. Убедимся, что ортогональны собственные функции (8.7)
тплх . ппу pnz
T" Sin T" cos ~T~ ¦
A) _ дгA) ,
итпр " тпр ¦
'Скалярное произведение функций
а Ъ L
/„(I) „A) \ Г Г Г Л/^1^ 7V(I)* gin mJTrciTi '"'ЛХ У
\итир' ит'п'р')— ) 1 | " тпр т'п'р' bu ~~^~ —^—
A1.17)
т'п'р'
имеет впд
pnz
]> TiZ
ппц п яу , ..- , .._
У sm -у- sin —^— cos —j— cos —-.— d.c dy dz A1.IS)
^совокупность чисел m, и и /) определяет номер l функции).
380
ГЛ. ii. ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ
Интеграл A1.18) есть произведение трех одиотиппых табличных интегра-
интегралов, которые дают пуль при т ф т', п ф п' п р ф р' соответственно. Система
("
"тпрЬтаким образом, ортогональна. Для нормировки в соответствии с A1.16)
надо взять
если р ф 0 (т и п в A1.17) не могут быть пулями). Если же р = 0, то правая
часть в A1.19) делится па )'2. ¦
11.0.3. Ортогональные ряды. Взяв ортоиормнропапную систему
iuj и некоторую функцию /, определенную в той же области, по-
построим ряд
= 2 апип,
ап =
ип)
A1.20)
Он называется ортогональным рядом, пли рядом Фурье функции /•
ап называются коэффициентами Фурье.
Отличительным свойством ряда Фурье (/) является выполне-
выполнение равенства:
((/), ц») = (/, и») A1.21)
для всех к. Действительно, при составлении скалярного произве-
произведения с и справа в A1.20) в силу ортопормпровки A1.16) полу-
получаем нуль во всех членах за исключе-
исключением к-то, который дает ап.
Если система {ип} обладает, как го-
говорят, свойством полноты, то ряд
Фурье (/) A1.20) сходится в сред-
среднем к /, т. е.
Л" N \
/ — 2 anUn, / — 2 anUn -*- 0 Iipil
\ п=1 п=1 /
.V->oo. A1.22)
Рассматриваемые нами системы собст-
собственных функций оператора Лапласа
обладают этим свойством.
Сущность разложения Фурье пояс-
Рис. 11.1 няется следующим примером из век-
векторной алгебры. Выберем в трехмер-
трехмерном пространстве декартову систему координат. Осям х, у и з соот-
соответствуют орты Хо, уо, zo. Переобозначим эти единичные взаимно
перпендикулярные векторы следующим образом: xo = Ui, уо = иг,
zo = U3. Мы имеем, таким образом, ортонормпрованную систему
элементов {un}n=i: ведь скалярное произведение (и,-, и„) удовлетво-
удовлетворяет условию A1.16). Эта система полна в том смысле, что по ней
может быть разложен любой вектор F (рис. 11.1):
F = ¦-- 2
== (F, и,,),
A1.23)
§ 11.0. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ II РЯДЫ ФУРЬЕ
38Г
причем an=(F, и„)—это не что иное, как проекции вектора F на
оси х, у и z. Но именно так выражаются и коэффициенты Фурье
ап A1.20). Аналогия между разложениями A1.20) и A1.23) не
является чисто формальной. Дело в том, что разлагаемая функция
/ трактуется как вектор в бесконечномерном пространстве, а ее
ряд Фурье A1.20) есть разложение, подобное A1.23). При этом
коэффициенты Фурье ап выступают как проекции / на и„.
Пример 2. Ряд Фурье C.17) мы можем рассматривать как ряд вида
A1.20) функции u{t), заданной па интервале —Т/2 < t < Г/2, по системе {и„},
ортонормировашюй согласно A1.1G), где
Г/2
ип = r~l/2 exp (inZntIT), \ uiU*kdt = bih A1.24)
—г/а
(при определении скалярного произведения A1.2) вместо V фигурирует дан-
данный отрезок). Коэффициенты Фурье равны:
Г/2 Г/2
j uu*dt = -L^ J ue-inxa'Tdt. A1.25),
-Г/2 * -Г/2
Мы видим, что формула ряда C.17) эквивалентна A1.20).
Функции A1.24) получаются как собственные функции оператора Лапла-
Лапласа, т. е. из A1.1) при периодических граничных условиях: и(—Г/2) = и(Т/2).
Равенство A1.1) есть при этом обыкновенное дифференциальное уравнение-
— ^ = х«, A1.26>
dt
а собственные значения хп оказываются равными Bпл;ТJ. Щ
11.0.4. Собственные векторные функции оператора Лапласа.
Конкретизируем задачу A1.1), взяв объем V в виде параллелепи-
параллелепипеда 0<х<а, 0<y<b, 0<-z<L и сформулировав определен-
определенные граничные условия на его поверхности. Пусть
V2u+xu = 0bF; ггт = О, div u = 0 на S. A1.27)
Нас интересуют собственные функции этой задачи и = Е,-, которым
отвечают собственные значения к = к,-.
При проектировании векторов на оси координат задача A1.27)
сводится к трем скалярным задачам, которые решаются методом
разделения переменных, как было показано в п. 8.0.1. Выпишем
результаты, которые понадобятся в дальнейшем.
Получаемая в конечном счете система {Е;} распадается на две
подсистемы {Е*| и {Е?}> объединяющие соленоидиальные функции
Ei(divEf = 0) и потенциальные функции Ei(rotEi=0). Те и
другие выражаются в форме:
Ef = хоЛх cos %xX sin Xyy sin y_zz + yo4v sin -fax cos y_yy sin y_zz +
+ z0Azsin%xxs'iuxyy cosjCzZ, A1.28)
382
ГЛ. 11. ИЗЛУЧЕНИЕ II ДИФРАКЦИЯ
где
Хх = тл/а, y_y = rmlb, %z = pn/L A1.29)
(т, », р =@), 1, 2, . ..). При этом
х>=(тл/аJ + (пл/ЬJ+(рл/ЬJ A1.30)
(индекс i понимается как номер набора чисел т, п, р внутри
каждой подсистемы).
Ниже будут записаны выражения коэффициентов в A1.28) при
следующей ортонормировке:
iE*hdv = 8ik/e0\e\. A1.31)
v
Внутри соленоидалыюй подсистемы {Ejl выделим подсистемы
Е-фуикций и Н-функций: {Ег } и {Е* ] соответственно. Введем
обозначение:
Q = 2 /2/ /eo|e|abL(xS+Xy)x.
Для /J-фупкций:
A1.32)
х5) (Н-33)
(если тФО, пФО, рФО); р может быть нулем, тогда все коэф-
коэффициенты в A1.34) делятся на V2. Для Я-функций:
Ах = <Ш'*, Ay=-QXxU, Аг = 0 A1.34)
(если т Ф 0, и Ф 0, рФО). Числа т и п могут порознь быть ну-
нулями, тогда все коэффициенты делятся на V2.
Для потенциальной подсистемы (Ef}:
5С„, Аи ^ Qlv
.(нулевые т, п и р исключаются).
Поставим теперь задачу
Аг =
A1.35)
u = 0bF; uv = 0, (rotu)t = 0 на S. A1.36)
Собственным функциям и = Н, отвечают собственные значения
% = y.i, которые но-нрежиему выражаются формулой A1.30). Сис-
Система Ш,} распадается на солепоидальную п потенциальную под-
•систсмы {Н|| и (Hf). В свою очередь, (Н|) есть совокупность
подсистем ^-функций (Hf) и Я-функций {Hf). Все собственные
функции представляются в форме:
II, = \1)/1х sin /vr cos yvy cos y_zz + Уо/?„ cos yxx sin ¦/„;/ cos y_zz +
+ ZqB, ens y_Aj: cos ^„/y sin y;z, A1.37)
§ 11.0. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ И РЯДЫ ФУРЬЕ 383--
где употреблены обозначения A1.29). Соотношение ортонормиров-
ки возьмем в форме:
, B2 = 0. A1.39)
Тогда для подсистемы {Hj ):
Bx = iQxvVx
Для подсистемы {Hf):
Формулы записаны для т Ф 0, п Ф0, рФО. Могут быть равны;
нулю р в A1.39) и т или п в A1.40), тогда соответствующие вы-
выражения делятся на У2.
Для потенциальной подсистемы {Hf}:
Bv=- iQxy Уу% +
Вх=- i
+
Вг = - iQXv У-й + Xl/W (И.41)
(тФО, п Ф 0, рФО). Одно или два из этих чисел могут быть
нулями, тогда выражения A1.41) делятся на У2 или, соответст-
соответственно, на 2.
Постановка краевых задач типа A1.27), A1.36) уже обсужда-
обсуждалась в п. 8.1.2. Соленопдалытые подсистемы {Е*( п {Н*( представ-
представляют комплексные амплитуды векторов Е и Н собственных коле-
колебаний прямоугольного резонатора. Нормировка A1.31), A1.38)
произведена так, что Ef и Hf, Ef и Hf связаны уравнениями
Максвелла; поэтому также в A1.39), A1.40) введены мнимые
единицы. Потенциальные функции Е? и Hf можно рассматривать,
как решения уравнений Максвелла при со = 0.
Нас будут также интересовать двумерные аналоги задач
A1.27), A1.36), когда вместо параллелепипеда рассматривается
прямоугольник 0<z<a, 0<y<b. При этом V2-*Vl, V -> S и
S -> L (L — контур прямоугольника S). Соответствующие собствен-
собственные функции будем обозначать символами е,- и h,-. Выражения
е{ и h; получаются, если в A1.28), A1.37) отбросить множители
sin %zz, cos xzz и положить А г = 0, Bz = 0.
Оказывается, собственные функции ег, h( представляют попе-
поперечные компоненты собственных волн прямоугольного волновода
(без множителя ехр(—iTz)), причем имеется следующее со-
соответствие:
{е?, Ь-)-»-?-волны, {е-, hf)-*¦ #-волны, A1.42)
т. е. поперечное электрическое поле АЧюлны является иотепциа.чь-
ным, а магнитное — солопопдальиым (по координатам х, у); для
384
ГЛ. 11. ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ
§ 11.1. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ИЗЛУЧЕНИЕ В ПОЛОСТИ
385
//-воли имеет место обратное соотношение. Заметим, что это свой-
свойство любых волн данных классов, что вытекает из представлений
F.25). F.28).
Нормировку е,-, h, произведем так, чтобы учитывалась их связь
при формировании воли волновода (обусловленная уравнениями
Максвелла). Возьмем:
iCftds = Sift \wf'H |, \ h^ds = 6ift/| Wf'H |, A1.43)
s s
при этом справедливо также:
f [еь h*k]z Js = bikWlH/
A1.44)
где
'
— волновые сопротивления F.26), F.29). При данной ор-
тонормировке функции е*, h, можно получить при помощи формул
G.58), G.63), а именно (при отбрасывании ехр( — iTz)):
is
A1.45)
если взять в G.58) ?™п - i2Xmn
Аналогично
| Гт„ | У Ж
е| = ЁГ, Ь? = Н™Г, (Н-46)
если в G.63) полошить H^n = — i2imn/Tnn Vab\W" | (m#0, пфО);
если 7/7 = 0 или /г = 0, производится деление на 1 2.
Везде в двумерном варианте i — номер набора чисел т, п;
меняются и петлевые элементы (в), подобные элементарному
магиитному излучателю. Полые резонаторы возбуждаются также
через отверстия в оболочке без всяких дополнительных элементов;
в частности, при формировании резонаторов используются волно-
водные диафрагмы (г).
Подлежащее возбуждению электрохмагнитпое поле должно
иметь проекцию вектора Е па ось штыревого элемента или проек-
проекцию вектора Н на нормаль к плоскости петлевого. Как будет по-
показано ниже в п. 11.1.3, возбуждаемое поле мало отличается по
§ 11.1. Вынужденные колебания. Излучение в полости
11.1.1. Постановка задачи. Рассматривая в гл. 8 различные
электромагнитные резонаторы, мы исследовали только свободные
электромагнитные ноля. Между тем, на практике в большинстве
случаев имеют дело с вынужденными колебаниями. Резонатор при
этом связан с источником энергии, и внутреннее электромагнитное
иоле находим в результате решения задачи об излучении некото-
некоторого внесенного элемента. Обычно она называется задачей о воз-
возбуждении резонатора. Собственные колебания г, большинстве слу-
случаев предполагаются известными.
На рис. 11.2 схематически представлены некоторые устройства
возбуждения резонаторов. Полые резонаторы нередко соединяются
с коаксиальными кабелями. Конец внутреннего проводника кабеля,
прохоляп'пй внутрь полости, подобен элементарному электрическо-
электрическому и.).]\'чатслн». Талоны шгыровые элементы, показанные в случа-
случаях прямоугольного (а) и цилиндрического (б) резонаторов. При-
Присвоему строению от того или иного типа собственных колеоании,
если частота источника близка к соответствующей собственной
частоте.
Полосковые резонаторы, применяемые в интегральных схемах
СВЧ, возбуждаются близко расположенными полосковыми линия-
линиями; это показано в двух вариантах A и 2) на рис. 11.29. Диэлек-
Диэлектрический резонатор может возбуждаться полем любой направляю-
направляющей структуры, например, полого волновода, внутри которого он
помещается (рис. 11.2е).
11.1.2. Собственные колебания резонатора и базис полей. Ниже
в п. 11.1.3 будут подробно рассматриваться вынужденные колеба-
колебания полого резонатора. Но чтобы выработать способ представления
электромагнитного поля, мы должны предварительно вернуться к
обсуждению некоторых свойств собственных колебаний.
Как известно, в случае свободных полей из уравнений Максвел-
Максвелла следуют однородные уравнения Гельмгольца относительно ком-
комплексных амплитуд Ег„ и Н,„. В п. 11.0.4 па примере области в ви-
виде параллелепипеда мы рассмотрели характерные краевые задачи
25 в. В. Никольский. Т. И. Иигольскаи
386
ГЛ. 11. ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ
для такого уравнения, взяв граничные условия, свойственные век-
вектору Ет A1.27), а затем вектору Нт A1.36) при идеально прово-
проводящей поверхности. Были получены решения этих задач в виде
ортонормированных систем собственных функций {Е(} и ШД. Как
и следовало ожидать, при этом были найдены поля, отвечающие
собственным колебаниям полого резонатора и соответствующие
собственные частоты. Эти поля, являющиеся соленоидальными,
образуют подсистемы {Е*) и {Н*} систем {EJ и (HJ; последние
содержат также подсистемы потенциальных векторных функций
{Е?! и (Н|), которые полями резонатора не являются. Однако,
если исключить из {Е,} и {HJ потенциальные функции, то эти сис-
системы уже не будут обладать свойством полноты (см. п. 11.0.3).
Будем говорить, что системы {EJ и {HJ образуют базис полей
полого резонатора. Хотя в п. 11.0.4 рассматривался только парал-
параллелепипед, обладающий аналогичными свойствами базис полей су-
существует во всех случаях. В тех случаях, когда задачи A1.27),
A1.36) решаются методом разделения переменных (например, в
цилиндрических и сферических координатах), базис полей можно
легко построить.
ПодчеркнехМ, что векторные функции Е\, H| и соответствую-
соответствующие собственные значения к{ дают электромагнитное поле и соот-
соответствующую собственную частоту ш( некоторого г-го типа колеба-
колебаний данного резонатора: ki = к\ = ((Oi/cJ ец. Но функции Е?, Н?
такое поле не образуют, причем их собственные значения х(
нельзя рассматривать как квадраты волновых чисел. Формально
можно трактовать пару Ef, H? в качестве решения уравнений
Максвелла при собственной частоте сог = 0. Это сразу выясняется
при прямой подстановке, если учесть, что потенциальные функции
Ef и Hf — градиенты некоторых скалярных функций, тогда как
rotgradcp^O A.22).
В дальнейшем будем пользоваться ортонормировкой вида
A1.31), A1.38), согласно которой
= \i01 ц | J
A1.47)
Но надо убедиться, что это соотношение во всех случаях соответ-
соответствует уравнениям Максвелла.
ВЫВОД. Рассматривая собственные колебания номеров i и к
некоторого полого резонатора с идеально проводящей оболочкой
запишем соответствующие уравнения Максвелла:
rot Ej = — 1С0г|Л0|лНг,
rot Hi = ic
^ rotE* = гсо*ио|л*Н*,
4 rot H* = — ico*e0e*Eft.
A1.48)
§ 11.1. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ИЗЛУЧЕНИЕ В ПОЛОСТИ
387
Здесь опущены точки и индексы т, отмечающие комплексные ам-
амплитуды, причем для номера к применено комплексное со-
сопряжение.
Уравнения Максвелла объединим попарно, как это указано
стрелками. В первой строке левого столбца составим скалярное
произведение с Н^, а в другом уравнении этой пары — с Ег; анало-
аналогичные действия производятся и с другой парой уравнений. Надо
выполнить такие же операции, как при выводе равенства C.55).
Затем производится интегрирование по У и учитывается, что
Ef = 0 на S. В результате получаем:
4иоц \ KiR*kdv — со*е
V
¦ cofteoE* J EiEhdv = 0,
V V
<o*h\x0\i* ) RJltdv — со4Е0е j EiE*hdv = 0.
v v
A1.49)
Отсюда можно исключить первый, а затем второй интегралы. Это
дает следующие равенства:
? - &2) J HjHjdy = 0,
&tdv = 0, A1.50)
справедливые при Ej = Ef, Hj = R\. При их получении учтено, что
в силу вещественности волновых чисел (см. п. 8.1. 4)(со*/сJе*^* =
= (coj/cJ e^. Напомним, что при Ej = Ef, Hj = Hf все собственные
частоты ©i равны нулю.
Из A1.50) следует, что при к\ Ф к\ интегралы равны нулю, т.е.
системы собственных функций ортогональны, если все собственные
колебания являются невырожденными. В случае вырождения (ког-
(когда разным полям отвечают одинаковые собственные частоты) всег-
всегда можно составить такие линейные комбинации полей, которые
дадут ортогональные собственные функции.
Положим теперь в A1.49) i = к. Рассматривая соленоидальные
поля, с учетом вещественности собственных значений к\ =
= (coi/cJ ец. получаем:
J HjH'cfo.
A1.51)
Если же Е,- и Н( — потенциальные функции, то они не связаны
между собой, при этом равенство A1.51) можно выполнить как
наложенное условие. Теперь, чтобы прийти к ортонормировке
A1.47), достаточно положить интегралы в A1.51) равными едини-
единице для всех i. ш
11.1.3. Вынужденные колебания полого резонатора. Решение
•адачи. Рассматривая некоторый полый резонатор, зададим внутри
25*
388
ГЛ. 11. ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ
— j
A1.52)
его объема V электрические и магнитные источники, характеризуе-
характеризуемые плотностями токов jCT и зм; допустим также существование
отверстия Sz в оболочке S, на котором задано поле Ест (рис. 11.3).
ст ФоРмУлиРОвка задачи имеет следующий вид:
л^ sB
rot Hm == ШЕ0Е Е„ ' 'СТ
rot Em = — Ш
в объеме V
mi — U lid О О 2, &ГПХ = '-'m
на поверхности Sx. Здесь использованы урав-
уравнения Максвелла в форме (9.51).
Решение задачи Ет, Нт при помощи разложений по системам
{EJ и ШЛ, обсуждавшимся в п. 11.1.2 имеет вид
Рис. 11.3
71 = 1
Hm =
6nHn,
где
Ьп =
Здесь обозначено:
QI = П '
1^1
+ со
m).
A1.53)
A1.54)
Q% = f j?H> + J [Ё?, Hn*] ds. A1.55)
Напомним, что ш„ — собственные частоты резонатора, когда соот-
соответствующие собственные функции ЕП) Н„ соленоидальны; при
потенциальных Е„, Н„ они равны нулю.
ВЫВОД. Любые решения Ет, Нт уравнений Максвелла в
A1.52), рассматриваемые в V, удовлетворяют следующей беско-
бесконечной системе интегральных соотношений:
J (
rot Hm — шеоеЁт — j
v
f (rot E
E*kdv = О,
tttdv = 0,
A1.56)
fc = l, 2, ..., oo.
Действительно, поскольку заключенные в скобки функции соглас-
согласно A1.52) равны нулю, обращаются в нуль и все эти интегралы.
В сущности, они — не что иное, как коэффициенты Фурье а„
A1.20) при/ = 0.
§ 11.1. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ИЗЛУЧЕНИЕ В ПОЛОСТИ
389
К первым членам подынтегральных выражений применихМ фор-
формулу A.26) и образовавшиеся интегралы от дивергенций преобра-
преобразуем в поверхностные при помощи теоремы Остроградского — Га-
Гаусса A.33). Эти действия, которые можно назвать интегрировани-
интегрированием по частям, приводят к соотношениям:
j Hm rot E*hdv - f (шеоеЁт + j?) E*kdv = 0,
V V
f EmvotR*hdv + f (йоцоц
V V
f [Ё?, Я*к] ds=O,
A1.57)
k=i, 2, ...,
Поверхностный интеграл сохранился только во второй строке, так
как на S обращаются в нуль тангенциальные компоненты всех ЕА.
Перепишем этот результат с учетом уравнений Максвелла A1.48),
которым подчинены собственные функции:
w*heoe
f H
V
j E
- сое0е ( EmE*kdv =-i
V V
f H
A1.58)
Л = 1, 2, ...,».
Неизвестное поле вынужденных колебаний Ет, Нт представим
в виде сумм:
Л' N
EN = S a E ilN = 5 Ь Н A1 59)
П=1 П=1
которые можно рассматривать как частичные суммы разложений
Е,„ и Нт по полным системам {Е,} и {Нг}. Заменяя Ет п Нт в
A1.58) суммами Ет и Нт A1.59), видим, что в силу ортогональ-
ортогональности использованных систем остаются только члены с п = к.
Учитывая A1.47), получаем
„ е „ * Iх* '- -^э
Oft = l(
A1.60)
где применены обозначения A1.53). Задача приведена, таким об-
образом, к совокупности п&р линейных уравнений типа A1.60).
Каждая такая система имеет решение A1.54). Так как результат
390
ГЛ. ii. ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ
не зависит от числа членов N в суммах A1.62), номер к в A1.60)
может быть любым и, следовательно, определены члены бесконеч-
бесконечных рядов A1.53). Решение A1.53) —A1.55) обосновано. ¦
Прежде чем перейти к обсуждению найденного решения задачи
о возбуждении полого резонатора, отметим ряд элементов идеали-
идеализации в ее постановке. Во-первых, подчеркнем, что это была зада-
задача об. излучении заданных источников, тогда как устройствам, по-
показанным на рис. 11.2, адекватны задачи дифракции. Например, в
случаях, когда к полому резонатору присоединяется коаксиальный
кабель (рис. 11.2а, б, в), происходит дифракция Г-волны, падаю-
падающей из кабеля. Волна наводит ток на штыревом или петле-
петлевом элементе и отражается от резонатора. Распределение тока
можно считать заданным лишь в известном приближении, его
необходимо найти. Представляет интерес и амялитуда отраженной
волны.
^Во-вторых, непосредственно учтены лишь потери во внутрен-
внутренней среде, поскольку проницаемости рассматриваются как комп-
комплексные величины. Оболочка считалась идеально проводящей,
а потери на излучение можно строго учесть, только определив
внешнее (по отношению к резонатору) поле дифракции. Правда,
мы увидим, что в некотором приближении все потери можно ввес-
ввести в расчет и в рамках данной теории.
11.1.4. Обсуждение решения. Анализ вынужденных колебаний.
Ряды A1.53) сходятся в среднем (см. A1.22)) в объеме резонато-
резонатора; в этом смысле и надо понимать знаки равенства. Но, например,
па отверстии 5Е ряд для Ет будет давать значение Етх = 0 (так
как это свойство каждого члена ряда), что, разумеется, не соответ-
соответствует походному условию A1.52).
Возьмем сначала случай отсутствия потерь. При этом все собст-
собственные частоты резонатора со„ вещественны. Это значит, что час-
частота источника возбуждения резонатора со может оказаться как
угодно близкой к одной из собственных частот шк. Как видно из
A1.54), соответствующие коэффициенты рядов A1.53) при этом
неограниченно возрастают: ah -*- °°, bh -*- °°. Поскольку значения
всех остальных членов (если данный тип не вырожден) ограниче-
ограничены, то поле вынужденных колебаний в своей структуре, можно
сказать, не отличается от собственных колебаний Е„, Kh. Это иде-
идеальный резонанс типа к.
Если учесть потери, что мы можем сделать вполне строго в
случае поглощения во внутренней среде, то собственные частоты
со„ окажутся комплексными величинами. Это значит, что не су-
существует таких значений частоты возбуждения ш, при которых
знаменатели выражений ап и Ьп A1.54) могут обратиться в нуль.
Выражая собственные частоты согласно (8.41), (8.42) в виде
' N A1.61)
§ 11.1. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ИЗЛУЧЕНИЕ В ПОЛОСТИ
391
запишем:
1
Эта функция имеет максимум
max -г
при частоте
M(ft) =
- 1/4$,
A1.62)
A1.63)
A1.64)
которая и является, таким образом, резонансной частотой. Она от-
отличается от соответствующей собственной частоты со^, понимаемой
как вещественная часть ык.
Очевидно, что
о. (ш)
1
A1.65)
Эта зависимость (рис. 11.4) есть типичная резонансная кривая.
Если учесть, что(со/сойJ— 1 « 2 (со — сой)/сой, и отбросить в A1.62)
малый член l/iQ2k, то оказывается, что
(О* ~ tD(t) > fAoifc, Vfc ~ tt>(ft)/ZAcOft, A1.bo)
где 2Aoit — так называемая полоса пропускания, на краях кото-
которой отношение A1.65) умень-
уменьшается в У2 раз.
Зависимость A1.65), одна-
однако, является достаточно точной
частотной характеристикой вы-
вынужденных колебаний в ок-
окрестности со(к) только в том
случае, если все прочие члены
рядов A1.53) кроме k-х не
оказывают заметного влияния ~5 ~3 -1 о 1 3 5
хотя бы в пределах полосы (ш~ш/,>/^м/(
пропускания. Это возможно на Рис. 11.4
достаточно «разреженном»
участке спектра при высокой добротности. Во всех случаях частот-
частотная зависимость поля возбуждения в широкой полосе частот ока-
оказывается довольно сложной.
Пример 3. Рассмотрим возбуждение прямоугольного резонатора
(рис. 11.5) нитью тока Q, параллельной оси z; в этом направлении поле одно-
однородно, так что возбуждаются только типы колебаний ЕтП(). На рис. 11.6 (свер-
(сверху) сплошной линией показана частотная зависимость амплитуды Ет векто-
вектора Е в точке Р, получепная по первой формуле A1.53); было учтено 100 чле-
членов суммы. Стенки резонатора — идеально проводящие, по внутренняя среда —
реальный диэлектрик с комплексной проницаемостью е = 3A — I- Ю-3). Ниже
392
0.05"
0.0"
0.05"
0.0"
ГЛ. 11. ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ
к У, мм
15
10
5
•Р
OS 20 30 х,мм
Рис. 11.5
т=5.9ГГц
0 10 20 30
Em(x)
Em(x)
3
1
.
-.—1—
f=6.
28 ГГц
Ч Х
О 10 20 30
Ет(х)
f=7.6Tru
О 10 20 30
Ет(х)
О 10 20 30
Ет(х)
f=9.4Tru
О 10 20 30
О 10 20 30
§ 11.1. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ИЗЛУЧЕНИЕ В ПОЛОСТИ
393
на рнс, 11.6 показано, как изменяется поло в резопаторе в зависимости от х
при разных у (уровни 1, 2 и 3 на рис. 1,1.5) на нескольких частотах. В правом
столбце изображений взяты резонансные частоты. Видно, что в резонансах по-
поле значительно сильнее (ср. левый столбец) и меняется в пространстве почти
по закону соответствующих собственных колебаний.
1
f.rru
0.05'
0.0"
0.05"
0.О
О 10 20 ЗС
'О 10 20 30
Ет(х)
0.05-
0.0"
0.4
х 0.0
10
20 30
20 30
Рис. 11.7. (ЭВМ)
На рис. 11.7 аналогичные результаты представлены при ухудшении до-
добротности: теперь взят диэлектрик с е = 3A — МО-2), Сплошной линией по-
ка.чапа изменившаяся частотная характеристика, пунктиром для сравнения
повторопа прежняя кривая (новая кривая также нанесена пунктиром на
394
ГЛ. ii. ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ
рис. 11.6). На рис. 11.7 представлены и новые распределения поля; как видно,
амплитуда поля в резонансах уменьшилась на порядок.
Рассмотрим подробнее (в увеличенном масштабе) один из участков ча-
частотной характеристики в обоих вариантах (рис. 11.8 и 11.9). Он, в частности,
20
30
Рис. 11.8. (ЭВМ)
ипторесеи тем, что содержит два почти слившихся розоиапса. Это типы коле-
колебаний ?510 и Е32о, собственные частоты которых в отсутствие потерь равны
13,652В ГГц и 13,7272 ГГц соответственно. ¦
Как видно из формул A1.54), если источники возбуждения являются элект-
электрическими (QM = 0), то разложение магнитного поля но содержит потепциаль-
§ ii.i. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ИЗЛУЧЕНИЕ В ПОЛОСТИ
395
ных членов: bk = 0, если он = 0. Аналогично при магнитных источниках
(Q0 = 0) потенциальных членов не содержит разложение электрического поля.
Для возбуждения того или иного типа поля источники возбуждения надо
выбирать (располагать и ориентировать) так, чтобы не оказались равными ну-,
лю величины Q3 и Q™, которые называют интегралами возбуждения.
Emm
-¦—'—h
12.5
Ет(х)
13.0
г=12.2ГГц 0.5
х 0.0
f.ITu,
г=12.56ГГц
f=!3.1 ГГи 0.S[_
0.0
X о
0 10 20 30
Ет(х)
f=13.65[Tu
f=13.691Гц 0.5
0 10 20 30
Ет(х)
г=13.73ГГи
0.0
i х_ о. о]
'0 ¦ '10 '20 '30 0 Ю 20 30
Рис. 11.9. (ЭВМ)
Остается выяснить, каким образом в этой теории можно учесть потери в
металлической ооолочке резонатора или потери на излучение. Если для неко-
некоторого типа колебаний известна добротность, найденная с учетом этих потерь
396
ГЛ. 11. ИЗЛУЧЕНИЕ II ДИФРАКЦИЯ
то обычно допустимо приближение, заключающееся в том, что даппая доброт-
добротность вносится в A1.65).
Пример 4. Рассмотрим возбуждение прямоугольного резонатора
(рис. 11.10) элементарным электрическим излучателем в виде отрезка то-
тока, плотность которого задана следующим
образом:
0<z<h.
A1.67)
Вычислим член разложения Ет A1.53),
соответствующий основному типу колебаний
Епо (вместо номера п будем писать 110). Со-
Согласно A1.28), A1.33)
F z 2
biio^zoT
, 0 I e | аЪЬ
На основании A1.54)
^ sin 1Z_ sin _
a b
<в
| е | аЪЬ шг —
A1.69)
,,,„,, ,,' i\ _i_ inn \ При резонансе можно
где в соответствии с A1.61) ш110 = шцо ( ' ' vnor F H
определить вектор Ет полного поля вынужденных колебаний:
^««„oKJ^^-o^^V-^Bin^ A1-70)
(в знаменателе выражения A1.69) вещественная часть обращается в нуль)И
§ 11.2. Вынужденные волны. Излучение в волноводе
11.2.1. Постановка задачи. Рассматривая в гл. 6 и 7 различные
свободные электромагнитные поля направляющих структур, мы,
фактически, исследовали возможные волновые процессы, которые
им свойственны: собственные волны. На практике всегда имеют
дело с вынужденными волнами; при этом электромагнитный про-
процесс вполне определен его источником.
Устройства возбуждения обычно являются сочленениями на-
направляющих структур. Если в одной из структур к месту соедине-
соединения распространяется некоторая волна, вынужденные волны вто-
второй структуры составляют ее внешнее поле дифракции. Как и в
случае возбуждения полого резонатора (см. п. 11.1.1), в аналогич-
аналогичных волноводных задачах (рис. 11.11) мы можем различать эле-
элементы, выступающие как штыревые (а), петлевые (б) и иные из-
излучатели, близкие к элементарным (например, в виде отверстия
{в)). В утих случаях можно ставить задачу об излучении задан-
заданных источников, что является лишь некоторым приближением к
реальности. Имеется, впрочем, множество задач, когда такой под-
§ Н.2. ВЫНУЖДЕННЫЕ ВОЛНЫ. ИЗЛУЧЕНИЕ В ВОЛНОВОДЕ
397
ход нецелесообразен. На рис. 11.11 представлены соответствующие
примеры: возбуждение полосковой линии путем ее сочленения с
коаксиальной (г), несколько более сложный переход от коаксиаль-
коаксиальной линии (д) к линии Губо (см. п. 7.4.5), одно из типичных со-
соединений прямоугольного волновода с коаксиальной линией (е). На
рис. 11.12 (слева) поясняется постановка задачи о возбуждении
полого волновода заданными электрическими и магнитными источ-
источниками. Последние заданы при помощи функций jCT и jM, а также
"Г Г
д
Рис. 11.11
в виде поля Е'т на отверстии в оболочке. Все источники локализо-
локализованы между поперечными сечениями S\ и Si на отрезке волновода
0 < z < L. Ставится условие излучения, состоящее в том, что в по-
полубесконечных волноводах — °°<z<0 и Z < z < оо поле может
представлять собой лишь наложение собственных волн, уходящих
tj"
s,
Высшие поля
Рис. 11.12
от области локализации источников. Среди них — при отсутст-
отсутствии поглощения — только некоторые переносят энергию, распростра-
распространяясь без затухания; этим свойством может обладать лишь одна
основная волна (при соответствующем выборе частоты или попе-
поперечного сечения волновода). Для всех остальных типов волн час-
частота оказывается ниже критической, т. е. они не переносят энер-
энергии и экспоненциально затухают, оставаясь синфазными. Слово
«волна» употребляется в данном случае условно, так же, как и
398
ГЛ. ii. ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ
«направление распространения» (имеется в виду направление за-
затухания поля). Характер процесса поясняется на рис. 11.12 справа.
В задаче о возбуждении волновода заданными источниками на-
надо, по крайней мере, определить комплексные амплитуды векторов
Е и Н всех типов волн, существующих вне области локализации
источников.
11.2.2. Собственные волны волновода. Поскольку в отличие от
гл. 6 и 7 мы должны одновременно рассматривать собственные
волны обоих направлений, произведем необходимую детализацию.
Сняв точки и амплитудные индексы т, будем обозначать комп-
комплексные амплитуды векторов Е и Н волны типа i следующим
образом:
= 6iV
iV"'r**
+
H+ =
iri* — направление z,
ЕГ = 8~е;1Ч НГ = 3ireiTiZ — направление — z.
При этом Г* > 0, если со > сокР, и jFj > 0, если со < сокР; здесь сокР —
критическая частота для типа волны i; потери отсутствуют.
Выделим поперечные компоненты
6Й = et, Э1Й = ± h; = ± [z0, еЦ/Wf'", A1.72)
где Wf'H — волновые сопротивления F.26), F.29). При со>сокр они
положительны: Wf'H>0. Если же со < сокР, то
iWf>0, iWf<0. A1.73)
Напомним, что на примере прямоугольного волновода функции
ег и Ь; уже обсуждались в п. 11.0.4. Было отмечено, что опп обра-
образуют полные ортогональные системы {ej и {hj двумерного опера-
оператора Лапласа (при соответствующих граничных условиях), причем
каждая из этих систем распадается на соленоидальную и потен-
потенциальную подсистемы, связанные правилом соответствия A1.42).
Сказанное справедливо для любых полых волноводов. Сохраняется
и ортонормировка A1.43), A1.44), так что, в частности,
1
I П'н I
A1.74)
где S^ — поперечное сечение волновода (рис. 11.12). Последнее
соотношение нуждается в обосновании.
ВЫВОД. Отметим сначала, что на основании A.27)
rot Fe-Tz = e-lTz rotF + [grad e-Tz, F] = e~irz {rot F
iT [4, F]l
A1.75)
и, если F не зависит от z, то rot F = rotx F. Поэтому при подста-
подстановке Ej , Hj- A1.71) в однородные уравнения Максвелла полу-
получаем следующие уравнепия относительно функций поперечных
§ Н.2. ВЫНУЖДЕННЫЕ ВОЛНЫ. ИЗЛУЧЕНИЕ В ВОЛНОВОДЕ
399
координат Si , 31, :
± гТ
[
, z0] =
z0, Sf] = —
A1.76)
Заменив i на к, запишем эти же уравнения в комплексно сопря-
сопряженной форме:
0] = —
± iV*h[zQ,
A1.77)
Взяв первое из уравнений A1.76) и второе из A1.77), образу-
образуем скалярные произведения с Ss * и 31* соответственно. Анало-
Аналогичные действия выполним по отношению к оставшейся паре урав-
уравнений. В каждой из пар произведем вычитание соответственных
частей равенств, после чего используем тождество A.26), произве-
произведем интегрирование по Sx и применим теорему Гаусса в двумер-
двумерном варианте (F -» S±, S -*¦ Lx). Так как на контуре L± попереч-
поперечного сечения S± волновода Ех = 0, то контурный интеграл уничто-
уничтожится, и будем иметь:
(Г, - ГЮ f [ БГ, 31*] zQds = соео8 J
S S
A1.78)
(Г; - Г*) f [%$,
ods=-
В смешанных произведениях под знаком поверхностных интег-
интегралов участвуют только поперечные компоненты векторов, которые
можно выразить при помощи формул A1.72). После вычитания
соответственных частей A1.78) сделаем замену SiTfe—>- ei,ft и ЗЦь ->-
-»-± hi,ft. Это дает:
Как и в предшествующих выражениях, здесь подразумеваются
волны обоих направлений, т. е. наряду с тройкой величины е,-, h,-,
Г( рассматривается также тройка е(, —h(, —Г, (а следовательно,
допускается обращение знака Г).
Из A1.79) видно, что для таких волн, которым отвечают не-
неравные Г( и Г*, должен обратиться в нуль весь интеграл. Если же
заменить в A1.79) ei]k через hih (или наоборот) при помощи
A1.72), то выясняется, что равен нулю интеграл от каждого сла-
слагаемого' в отдельности. Этим обосновывается ортогональность не-
400
ГЛ. 11. ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ
вырожденных собственных волн в смысле соотношений A1.43) и
A1.44); в случае вырождения, как обычно, можно построить орто-
ортогональные собственные функции.
Остается рассмотреть нормировку. Пусть волны типов i и к
имеют вещественные постоянные распространения (<»кр< со).Тогда
Гй = 1\, так что при i = к множитель перед интегралом в A1.79)
обращается в нуль. При этом оба подынтегральных слагаемых
равны: [еь h*]z = [е*, Ь{]г = [еь Ь{]г = el/Wf 'н = h\Wf'H. Таким об-
образом,
J [eit hf]
A1.80)
Положим теперь, что Г; и Тк — мнимые (сокр > со). При этом
Г* = —Гй. Поэтому разность Г{ — Г* в A1.79) обращается в нуль,
если Гй = —Г„ т. е. к-я волна есть волна типа i, распространяю-
распространяющаяся в противоположном направлении: eh = е„ hh = —h,. Оба
члена подынтегрального выражения при этом равны. Действитель-
Действительно, [еь h*] = — [е{, h*] и [е*, hj = [e*, h,] = — [еь h*j, так как
это чисто мнимые величины. Как видно, и в этом случае выпол-
выполняется неравенство A1.80).
Подводя итог, убеждаемся, что ортонормировка A1.74) воз-
возможна. ¦
11.2.3. Вынужденные волны полого волновода. Решение задачи.
Вернемся к задаче о возбуждении полого волновода заданными ис-
источниками, поставленной выше в п. 11.2.1 (см. рис. 11.12). Поле
в полубесконечных каналах слева и справа от области локализа-
локализации источников представляется в виде:
71 = 1 71 = 1
оо ос
¦t'm = 2ii C-n &n i 4m ~ ^j C/i xiji , Z jjs i/
n = i тг=1
A1.81)
(как отмечалось, такое представление согласуется с условием из-
излучения). Коэффициенты рядов выражаются следующим образом:
tf = -j-{OF+ <%*), corK(p<co,
Cn = -о- ТпГТ (<?«" + (?n+), СОкр > CO,
где
V
A1.82)
f [ECJ, Uf] da. A1.83)
§ 11.2. ВЫНУЖДЕННЫЕ ВОЛНЫ. ИЗЛУЧЕНИЕ В ВОЛНОВОДЕ
401
ВЫВОД. Запишем следующие две пары уравнений Максвелла:
rot Em = — г
rot EJ* = io>\iQ\)R?*,
A1.84)
rotHm = jtoeoeEm + jL / rotHjf* = — гсое^Е^*.
В левом столбце — уравнения в форме (9.51), которым подчине-
подчинены комплексные амплитуды Ет и Нт поля, возбуждаемого в вол-
волноводе заданными источниками. В правом столбце в комплексно
сопряженпой форме записаны однородные уравнения Максвелла
относительно комплексных амплитуд собственных волн A1.71).
Подобно многим аналогичным случаям (см., например,
пп. 11.1.2, 11.1.3) уравнения объединены в пары, как показано
стрелками. Уравнепия первой пары умножаются скалярно на Hg-*
и Ет соответственно, а уравнения второй пары — на Ef* и Нт. Все
операции в дальнейшем аналогичны предыдущим. При этом в ка-
качестве V берется объем, ограниченный поперечными сечениями
Si и »?2 (см. рис. 11.12), а также боковой поверхностью соответст-
соответствующего отрезка волновода; пусть S — полная граница V. Резуль-
Результат имеет вид
- UR:t*)dv, A1.85)
а поскольку па боковой поверхности за исключением области от-
отверстия Ех = 0 (для собственных волн — и па Sz), то
ds = — <?Г" — ()"=, A1.86)
где использованы обозначения A1.83).
Левую часть этого равенства обозначим l?. При подстановке
представлений поля A1.81) получаем
1к = - 2 сп f I[E,7, Н^*] + [Е/;;*, Н"]1 zods +
+ 2 с+ \ |[Е+, НП + [Е{*, Н+]) zods A1.87)
(учтено, что внешняя нормаль направлена по z на S2 и против z
на Si). Принимая во внимание соотношения A1.71), A1.72) и ор-
тонормировку A1.74), видим, что в рядах остаются только к-е чле-
члены, причем равенство A1.87) дает
= сТЛ =F-
WE,H
+ ct
\wk-"\+ Кя
s-i(rftT-rt)i_
A1.88)
20 в. В. 11ш.ольс;,ий, Т. И. Ни o.ii.(.i,.i;i
402
ГЛ. И. ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ
§ 11.3. ВОЛНОВОДНАЯ ДИФРАКЦИЯ
403
Далее учтем свойства волновых сопротивлении W^ , которые оста-
остаются вещественными, пока соКр < со, а затем становятся мнимыми
согласно A1.73). В результате получаем
2c~t, (сокР<со), A189)
\-2{Whl\Wh\)cf, (со^р>со).
Представляя левую часть в A1.86) при помощи A1.89), прихо-
приходим к формулам A1.82). ¦
11.2.4. Излучение диполя Герца в прямоугольном волноводе.
Покажем применение полученных результатов A1.81) — A1.83) на
1
{
/
/
\
У
л
/
О
"г/ '
у. ^>
/
/
Zi
а
)
Л
ь V
z L
Рпс.
11
13
0
1
Zf
Z
6
1
1
1
i_
L
примере прямоугольного волновода, возбуждаемого малым элемен-
элементом тока (рпс. 11.13а), плотность которого задается в виде
fmT = yo>m6(z-z1N(z-z1), 0<y<h A1.90)
(ср. A1.67)).
Определим коэффициенты си A1.82) разложений A1.81), где
номер к соответствует основной волне Ню; вместо с* будем писать
с^0. Поскольку
то и при вещественном, и при мнимом Гю справедливо равенство
4=-^~|-J &fodv. A1.92)
10 I у
Действительно, (Е*о)* = Е^, при сокр < со и (Е^о)* = E^j при
>>со. Внося в A1.92) представление тока A1.90), получаем
о
>•
с,,, — —
KK10
A1.93)
Напомним, что Г10 = BяД) У1 - (А/2аJ и W"o = W/ /l - (к/2аJ
(см. п. 7.1.3).
Если при заданной частоте со размеры волновода таковы, что
только тип поля Н\о имеет характер распространяющейся волны
Bа > к), то на достаточном расстоянии от элемента тока полное
поле будет выражаться одним членом ряда:
v
— Jo
vv Id1 ma
гsin —- sin — e
ab a a
A1.94)
(верхний знак соответствует области z > Z\, нижний — области
z<z\). Ток в A1.94) можно заменить моментом диполя Герца;
очевидно рт=—УцНтЫ® (9.23). Полный поток энергии создается
только волной Н\о. Интегрируя средний вектор Пойнтинга по S\ и
Е2 1
5г, дважды получим ob-^ Re—^-. Сумма (т. е. удвоенная величи-
W
ю
на) и дает полный поток энергии; с учетом A1.94)
Т2, 2
lab
A1.95)
При к > 2a, когда W?l становится мнимой величиной, Pz = 0: ди-
диполь Герца не излучает в волновод при частоте ниже критической.
На рис. 11.136 при z = 0 в волноводе введена идеально прово-
проводящая перегородка (обычно возбуждающий элемент располагается
вблизи закрытого конца волновода). Волна Ню, излучаемая влево,
отразится от плоскости z = 0 (с пзменение.м фазы на 180°) и сло-
сложится с волной, излучаемой вправо. Легко убедиться, что полное
поле справа будет представлять собой следующую волну:
sin
sin И
A1.96)
§ 11.3. Волноводная дифракция
11.3.1. Постановка задачи. Матрица рассеяния. В § 11.1 и 11.2
отмечалось на примерах устройств возбуждения резонаторов и вол-
волноводов, что при рассмотрении волновых процессов в изолирован-
изолированных структурах обычно должна быть задана падающая волна. Про-
Процесс в целом есть дифракция, поскольку эта волна возбуждает
некоторое поле в структуре и отражается назад. Если все входящие
в рассмотрение волны являются направляемыми, будем употреб-
употреблять выражение волноводная дифракция.
Простейший пример волноводной дифракции — реакция некото-
некоторого тела А (рис. 11.14а), помещенного в полый волновод. Если,
например, в волноводе слева из бесконечности распространяется
волна типа к, то она частично отразится и пройдет в правый по-
26*
404
ГЛ. 11. ИЗЛУЧЕНИЕ II ДИФРАКЦИЯ
лубесконечный волновод. Но, кроме того, возникнет множество всех
мыслимых волн волновода (т. е. его собственных волн), уходящих
в оба полубесконечных волновода и удовлетворяющих, таким обра-
образом, условию излучения. Слово «волна» здесь употребляется в том
же смысле, что и выше в п. 11.2.1. Появление этих волн можно
трактовать по-разному. Например, если тело А — металлическое,
s.
3 i
о7 z7
сс=1,2,...,Р
Рис. 11.14
говорят, что падающая волна наводит на нем токи проводимости,
которые, в свою очередь, излучают (переизлучают) все появляю-
появляющиеся волны. Как во всех дифракционных процессах, формируется
такое поле, которое удовлетворяет граничным условиям (ср.
п. 10.1.1).
Наиболее естественным средством описания волноводной ди-
дифракции является аппарат так называемой матрицы рассеяния.
Рассмотрим его достаточно подробно.
При помощи поперечных сечений Si и S2 (рис. 11.14а) отделим
участок, на котором, как говорят, нарушается регулярность волно-
волновода. Каково бы ни было поле внутри отсеченного объема V, на
Si и 52— это наложение полей собственных волн. То же самое бу-
будет и в более сложном случае (рис. 11.146), когда к некоторой изо-
изолированной структуре присоединяется Р различных волноводов.
Если, например, на вход с номером а падает волна типа к волно-
волновода а, то, как в этом, так и во всех остальных волноводах появят-
появятся всевозможные собственные волны, уходящие от области V.
Опишем дифракцию при наиболее общих предположениях: пусть
имеются падающие волны всех типов, так что в каждом присоеди-
присоединенном волноводе (рис. 11.146) задается первичное поле
A1.97)
(а = 1, 2, ..., Р). Здесь Е^а), Н?(а) определяются согласно A1.71),
но, поскольку для каждого волновода система координат и перечис-
перечисление полей свои, вводится индекс а (например, za вместо z).
§ 11.3. ВОЛНОВОДНАЯ ДИФРАКЦИЯ
405
В результате процесса внутри V во всех присоединенных волново-
волноводах появляется вторичное поле в виде наложений собственных волн,
распространяющихся в обратном направлении:
— Zj С
"(а) Н-
A1.98)
а = 1, 2, ..., Р.
Если рассматриваемая электродинамическая структура линейна,
то существует некоторый линейный оператор, сопоставляющий
каждому первичному полю — сигналу вполне определенное вторич-
вторичное поле — отклик. Поскольку эти поля характеризуются наборами
коэффициентов с\а) и Сп(сф которые можно трактовать как векто-
векторы с+ и с~ соответственно, то интересующий нас оператор пред-
представляется матрицей S в соотношении
c~ = Sc+. A1.99)
Это и есть матрица рассеяния. Заметим, что подразумевается пас-
пассивность структуры, т. е. отсутствие внутренних источников, в ре-
результате чего при с+ = 0 должно быть с = 0.
Равенство A1.99) удобно детализировать следующим образом:
(cZ
(S-1 15
,12
(СР
S'~
сРР
Л
A1.100)
где
A1.101)
(а, р = 1, 2, ...,). Здесь векторы с+ и с разделены на подвекторы
Са по числу присоединенных волноводов. В свою очередь, каждый
подвектор имеет компонентами коэффициенты
с^{
рядов A1.97),
St Н
др ффц {) рд ()
A1.98). Соответственно этому выделяются подматрицы Sat. На
практике матрица рассеяния всегда имеет конечный порядок, по-
скольку в волноводах учитывается лишь ограниченное число волн:
ряды A1.97), A1.98) заменяются конечными суммами. Чем дальше
(в сторону убывания za) отнесены сечения Sa, тем в большей сте-
степени затухают все волны, не переносящие энергии. Если же эта
переда-ia может осуществляться только одной основной волной каж-
каждого волновода, то путем достаточного смещения всех Sa мы полу-
406
ГЛ. 11. ИЗЛУЧЕНИЕ II ДИФРАКЦИЯ
чаем возможность оставить в каждом из рядов только по одному
члену. Тогда матрица S A1.100) будет иметь порядок Р: в подмат-
подматрицах Sa^ остается по одному элемепту, векторы с? —однокомпонент-
ные.
Какой смысл имеют элементы матрицы рассеяния S^n? Зададим
в волноводе В одну падающую волну типа п и единичной ампли-
амплитуды. При этом компоненты вектора с+ равны нулю, кроме един-
единственной ненулевой компоненты с^р) = 1, так что согласно A1.100),
A1.101) ck(a) = S%n. При а = В получаем амплитуды обратных
волн того же волновода В. Очевидно Snn есть коэффициент отра-
отражения волны типа п волновода Р (это диагональный элемент мат-
матрицы S), а все iSfcn можно назвать коэффициентами преобразова-
преобразования при отражении; имеется в виду преобразование волны типа п
в волны типов к. Что касается элементов S%n при а Ф В, то это
коэффициенты преобразования при прохождении (или просто коэф-
коэффициенты прохождения) из волновода В в волноводы а.
Матрица рассеяния, как видно, определяет все мыслимые про-
процессы дифракции для данной структуры, все ее режимы. Тем са-
самым она дает полное математическое описание соответствующей
электродинамической структуры.
Как будет показано в гл. 12, для определения матриц рассеяния
реальных устройств необходимо применение методов, существенным
образом опирающихся на применение ЭВМ.
11.3.2. Матрицы сопротивления и проводимости. Тангенциальные
(поперечные) поля на всех сечениях Sa можно разложить в ортого-
ортогональные ряды по полным системам {е„(а)} и {hn(a)} (см. п. 11.2.2):
— Z
A1.102)
Ясно, что задание всех Е(сс определяет тангепциальпое электриче-
электрическое поле на замкнутой поверхности, ограничивающей объем V
(см. рис. 11.14), поскольку на дополнительной части этой границы
Ех = 0. Поэтому задание всех Е(а однозначно определяет процесс
в объеме V (см. п. 3.4.1), а тем самым, и все H(tt. Справедливо и
обратное утверждение, потому что и задание всех Н(а однозначно
определяет процесс в объеме V. Иными словами, некоторый задан-
заданный набор коэффициентов an(a) (a = l, 2, ..., Р) в A1.102) одно-
однозначно определяет набор всех bn(a) п обратное тоже верно. Образу-
Образуем векторы а и Ь, компонентами которых являются эти коэффици-
коэффициенты. Указанную зависимость выразим при помощи соотношений:
a = Zb, b = Ya, A1.103);
где Z называется матрицей сопротивления, а Y—матрицей прово-
проводимости.
§ Н.З. ВОЛНОВОДНАЯ ДИФРАКЦИЯ
407
Связь между матрицами Z, Y и матрицей рассеяния S оказыва-
оказывается очень простой. Полные поперечные поля на всех Sa можно
также выразить, складывая все падающие и отраженные волны.
Взяв представления A1.97), A1.98) и учитывая соотношения
A1.71) и A1.72), пишем:
= Zi \сп(а) + сп(а)) e,i
l
A1.104)
n=i
Отсюда при сопоставлении с A1.102) следует, что cn(a) + сП(«) =
= ап(а) и ct(a) — Сп(а) = bnW\ таким образом, полные векторы
удовлетворяют равенствам
с+ + с- = а) с+^с- = ъ. A1.105)
Подставляя их в A1.103), получаем
(Z-/)c+ = (Z + /)c-, (I-Y)c+ = (I+Y)c- A1.106)
(/—единичная матрица). При сравнении с равенством A1.99)
приходим к следующим соотношениям:
A1.107)
Из A1.99), A1.103) и A1.105) получаются также формулы')
Z = (I — S)-1(I + S), Y = (I + S)-1(I-S). A1.108)
На основании соотношений A1.107), A1.108) описания некоторой
электродинамической структуры через матрицы Z, Y и S следует
рассматривать как эквивалентные. При этом надо заметить, что
равенства
2=y-i, y = Z~1 A1.109)
справедливы не всегда, так как матрицы Z и Y могут не иметь
обратных.
11.3.3. Некоторые свойства матриц Z, Y и S. Подробный анализ
введенных матриц не входит в нашу задачу. Но даже на простых
примерах можно показать, как их свойства отражают особенности
электродинамических структур.
Пусть все отсчетные сечения 5Т (у = 1, 2, ..., Р) рассматривае-
рассматриваемого объекта (см. рис. 11.146) отнесены в дальнюю зону, где поле
с удовлетворительной точностью представляется волной одного ос-
основного типа. При этом каждому сечению S-, сопоставляется пара
векторов ет, hT (вместо бесконечных систем {en(T)}, {hn(T)}).
') Множители п A1.107), A1.108) коммукгппшы.
408 ГЛ. 11. ИЗЛУЧЕНИЕ II ДИФРАКЦИЯ
В соответствии с A1.74)
[ev, hv] zoyds = 1
A1.110)
(ет и hT вещественны).
Если внутренняя среда удовлетворяет требованиям, при соблю-
соблюдений которых справедлива лемма Лоренца, то согласно C.74)
р
2 1 {[Ёт2, Нт1] - [Ёт1, Нт2]} zoyds = 0, A1.111)
так как внутренние источники отсутствуют, а все сечения ?т обра-
образуют замкнутую поверхность, если их дополнить металлической
границей, принимаемой за идеально проводящую (на ней подын-
подынтегральное выражение исчезает).
Пусть Hmi = бтеЬе (т. е. Hmi=hp на 5Р и Hmi=0 на остальных
сечениях). Тогда Emi=Z7fieT ("f = 1, 2, ..., Р). Зададим аналогично
Hm2 = STaha, так что Em2 = Z7aeT ("f = 1, 2, ..., Р). Подставляя эти
выражения в A1.111), получаем
f [Zp%, hp] zopds - J [Л«, ha] zoads = 0,
откуда с учетом A1.110):
A1.112)
Матрица сопротивления Z оказывается симметрической, что выра-
выражает принцип взаимности (п. 3.4.2).
Совершенно аналогично устанавливается, что
yp« = y«P- A1.113)
Надо лишь поменять ролями электрическое и магнитное поля в
предыдущих рассуждениях.
Несколько более громоздко выводится соотношение взаимности
?Ра=?ар A1.114);
ВЫВОД. Пусть в режиме 1 основная волна падает на вход ?р,
а в режиме 2 — на Sa. Зададим соответственно
Ёт1=ет(бте + ^тР), kmi = hTFTP —
Т = 1, 2, ..., Р.
§ 11.3. ВОЛНОВОДНАЯ ДИФРАКЦИЯ
409
Подставляя это в A1.111), пишем:
f j[(l + S™) ea, - Ла] -[Ла, A - Saa) ha]l zoads
.f
+
7=1
] j zoyds = 0.
Все члены последней суммы, как видно, равны нулю, а интегралы
по Sa и S$ с учетом нормировки A1.110) приводят к A1.114). ¦
Потребуем, далее, чтобы в рассматриваемой структуре отсут-
отсутствовали потери энергии. Тогда
р
\ [ayey,b*hv]zoyds = O, A1.115)
v=is,
a
что следует из C.57). Отсюда
р р р
Re 2 oyb* = Re 2 (Zb)yb* = Re 2 ay(Ya)*v = 0. A1.116)
7=1 V=l 7=1
Равенство выполняется при любых а и Ъ, что возможно только при
чисто мнимых Z и У. Итак, при отсутствии потерь матрицы сопро-
сопротивления и проводимости — мнимые.
Подставим в A1.115) ау — с^ + су и Ьу = с^ — с.у. Это дает:
7 = 1
ИЛИ
r+\2 -
7=1
7=1
A1.118)
Свойство матрицы рассеяния S, в силу которого при любых с+ вы-
выполняется равенство A1.118), называется унитарностью. Для уни-
унитарной матрицы S
SS = I, A1.119)
где S—сопряженная матрица (т. е. транспонированная с комплекс-
комплексно-сопряженными элементами).
Представление о волноводной дифракции имеет широкое значе-
значение и используется не только при описании изолированных струк-
структур. Матрица S, а также матрицы Z и Y могут быть применены и
при рассмотрении дифракции в свободном пространстве.
Пусть на некоторое тело А (рис. 11.15) падает плоская или
сферическая волна Е°, Н°. Вокруг А можно построить сферу, игра-
410
ГЛ. 11. ИЗЛУЧЕНИЕ II ДИФРАКЦИЯ
ющую такую же роль, как отсчетное поперечное сечение волновода
Sa. Дело в том, что свободное пространство вне этой сферы может
трактоваться как шаровой волновод, собственными волнами кото-
которого являются сходящиеся и расходящиеся сферические волны.
Можно показать, что эти волны образуют
i(e°,h°) подсистемы Е- и //-волн (первые имеют
, радиальную электрическую, а вторые —
v ^-'--. 4(е~н~) радиальную магнитную компоненты).
/ х\,^ Тангенциальные к сфере компоненты
\ s этих волн образуют полные ортогональ-
'""* ные системы {еЛ и {hj. Весь аппарат мат-
{' ^ риц S, Y и Z оказывается похожим на
* "~--Г'Т л рассматривавшийся, однако имеются и от-
к v лпчия, связанные с двумя фактами: во-
Рпс. 11.15 первых, волновые сопротивления сходя-
сходящихся и расходящихся волн не равны
ДРУГ другу, во-вторых, падающую волну Е°, Н° (рис. 11.15) нельзя
представить в виде наложения одних сходящихся сферических волн,
концентрических выделенной сфере.
УПРАЖНЕНИЯ
1. Прямоугольный резонатор возбуждается диполем Герца, расположенным,
как в примере 4, п. ИЛА. Из перечисленных ниже тппов колебаний EUi, Ёпи,
Яш, ?2!о, Еш, ?|зо, #101, #011, #111, #221 некоторые будут иметь нулевые коэф-
коэффициенты а„, Ъп A1.57). Какие именно? Как изменить положение и (или) ори-
ориентацию диполя Горца, чтобы возбуждались все эти типы колебаний?
2. Пусть рассматриваемый резонатор — идеально проводящий (см. упраж-
упражнение 1); а = b = 2 см. L = \ см; внутренняя среда характеризуется пара-
параметрами: е = 9 — i • 0,001, A = 1. Построить резонансную кривую для типа ко-
колебании ?ц0.
3. Построить резонансную кривую для типа колебаний, ближайшего к ос-
основному (данные из упражнения 2).
4. Какие типы колебаний можно возбудить в резонаторе (см. рис. 11.5),
если вместо штыревого возбуждающего элемента взять петлевой, расположив
его в том же месте и ориентировав в плоскости z0#? Перечислить пять низших
типов колебаний.
5. Выписать несколько функций, принадлежащих системам {е„} и {Ь„},
для прямоугольного и круглого волноводов.
6. Пусть в случае прямоугольного волновода, возбуждаемого элементом то-
тока (см. рис. 11.8а) а/Х = 0,7; а = 26 = 2 см; среда — вакуум; длина элемента
тока h = 0,1 см, xi = а/4. Найти амплитуду тока (полагая, что она постоянна
вдоль элемента), если средняя мощность, излучаемая в направлении оси г,
составляет 10 мВт.
7. В том же примере найти амплитуду Ет типа колебаний #го как функ-
функцию z. На каком расстоянии по г от элемента тока эта величина при х = а/4
в 100 раз меньше амплитуды Ет основной волны?
ЧАСТЬ 4
ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ В ЭЛЕКТРОДИНАМИКЕ (Б)
Глава 12
ОБЩИЙ ПОДХОД. ПРОЕКЦИОННЫЕ МЕТОДЫ
§ 12.1. Постановка задач, представление полей, алгоритмизация
12.1.1. Математические модели электродинамики в радиоэлектро-
радиоэлектронике. Базирующаяся на уравнениях Максвелла теория электромаг-
электромагнитных явлений представляет собой естественную основу матема-
математического моделирования в технике, использующей эти явления.
В особенности это относится к радиоэлектронике.
Согласно существующим воззрениям, которые вряд ли будут
пересмотрены в обозримом будущем, система уравнений Максвелла
вполне определяет закономерности электромагнитных процессов
(см. п. 1.6.1). Имея в виду макроскопические объекты, можно ска-
сказать, что надо лишь правильно формулировать входящие в эту си-
систему материальные уравнения. Очень часто последние имеют про-
простой вид, а среды характеризуются параметрами е, ц и а. Решение
электродинамической задачи, т. е. некоторая совокупность матема-
математических операций (над уравнениями Максвелла при наложении
тех или иных условий), даст исчерпывающие сведения о конкрет-
конкретном физическом процессе. Иными словами, математические модели
электродинамики адекватны физической реальности (разумеется,
уточнение этого высказывания потребовало бы ряда оговорок). От-
Отмеченное очень важно. Казалось бы, в области электромагнитных
явлений нет необходимости экспериментировать или заниматься
трудоемкой отработкой технических конструкций при помощи изме-
измерений, если все подлежит точному расчету с единых позиций.
В действительности до появления современных ЭВМ подобная
постановка вопроса была бы бессмысленной, а в настоящее время
наука и техника лишь приближаются к построению удовлетвори-
удовлетворительных математических моделей электродинамики для таких слож-
сложных объектов радиоэлектроники, какими являются, например, не-
некоторые реальные волноводные тракты, интегральные схемы СВЧ
и антенные устройства. Дело в том, что неупрощенная постановка
задач электродинамики, отвечающих реальным объектам техники,
приводит к серьезным трудностям. Если под решениями понимать
некоторые формулы (позволяющие вычислять требуемые величи-
величины), то можно утверждать, что для иеидеалп.чпровапных электро-
412
ГЛ. 12. ОБЩИЙ ПОДХОД. ПРОЕКЦИОННЫЕ МЕТОДЫ
динамических задач они получаются крайне редко. Зато к настоя-
настоящему времени разработаны методы, позволяющие получать решения
весьма сложных задач при помощи вычислительных процессов, по-
потенциально бесконечных, но редуцируемых таким образом, что за
конечное число операций требуемые величины могут быть вычис-
вычислены с желательной точностью. В большинстве случаев электроди-
электродинамическая задача сводится к системе алгебраических уравнений,
порядок которой в принципе не ограничен, а для реализации доста-
достаточной точности модели должен быть сделан настолько большим,
что принципиально важно применение ЭВМ. Математические моде-
модели электродинамики, отвечающие сложным объектам техники, реа-
реализуются в виде комплексов программ для больших ЭВМ.
В настоящее время в радиоэлектронике еще играют значитель-
значительную роль эвристические средства расчета электродинамических
структур, основанные на различных догадках и упрощающих пред-
предположениях. Такой подход сложился еще в «домашинный» период.
Эвристические средства полезны, поскольку концентрируют инже-
инженерный опыт, но полезность их ограниченна. Тот или иной упро-
упрощенный подход оправдан в какой-то области изменения параметров,
которая известна весьма приблизительно. Поэтому он оказывается
непригодным для применения в новых, нетрадиционных условиях.
В упрощенную модель уже заложено нечто ожидаемое — образ,
подсказанный предшествующим опытом. Нужно много времени,
а порой и счастливое стечение обстоятельств, чтобы найти новый
подходящий образ, который должен быть еще опробован. Между
тем, применение неупрощенных моделей электродинамики не нуж-
нуждается в предварительных догадках, так как источник их в фунда-
фундаментальных положениях теории. Поэтому также практика машин-
машинных расчетов становится источником информации. «Мысленный
эксперимент», реализуемый на ЭВМ, во многом выгодно отличается
от натурного: он может производиться гораздо быстрее, в несрав-
несравненно более широких масштабах и без посторонних влияний.
Важно следующее: математические модели электродинамики со-
создаются для целых классов объектов, к которым относятся и
еще не изобретенные технические устройства. Заранее разра-
разработанный программный комплекс может оказаться готовым к тех-
техническим идеям завтрашнего дня или даже способствовать их ста-
становлению.
Если учесть быстрый прогресс средств вычислительной техники,
не остается сомнений, что в будущем техническое проектирование
в высокой степени должно базироваться на строгой теории. К ра-
радиоэлектронике это относится в первую очередь, потому что здесь
имеется надежная основа в виде системы уравнений Максвелла.
12.1.2. Электродинамические задачи радиоэлектроники. Начнем
с обсуждения некоторых моментов радиоэлектронной проблемати-
проблематики, обнаруживающих прямую связь с электродинамической те-
теорией.
§ 12.1. ПОСТАНОВКА ЗАДАЧ, ПРЕДСТАВЛЕНИЕ ПОЛЕЙ
413
Целую эпоху составило развитие теории цепей, которая и сей-
сейчас является важнейшим инструментом электротехники и радио-
радиоэлектроники, хотя само понятие цепи переменного тока, как отме-
отмечалось (см. п. 2.5.2), строится на допущениях, теряющих смысл с
повышением частоты. Образы теории цепей оказались удобными
для восприятия и в ряде случаев послужили началом дальнейших
обобщений. Например, понятие импеданса употребляется уже без
всякой связи с исходным представлением о цепи. Однако с разви-
развитием радиоэлектроники появляется все больше проблем, подход к
которым должен быть строго электродинамическим. Отвлечься от
существования электромагнитного поля невозможно при проектиро-
проектировании антенн и анализе распространения радиоволн как в природ-
природных условиях, так и в аппаратуре. По мере того, как в практику
входили дециметровые, сантиметровые и еще более короткие волны,
принципы построения радиоаппаратуры заметно менялись. Элемен-
Элементы аппаратуры СВЧ существенно неквазистационарны и могут на-
напоминать акустические или оптические устройства в большей сте-
степени, чем электротехнические. Особого подхода требуют современ-
современные интегральные схемы СВЧ или, например, устройства опто-
электроники. Но дело не только в принципах построения, а также
и в проектировании, которое либо остается в значительной мере
эмпирическим, либо должно опираться на неупрощенные математи-
математические модели электродинамики.
Подчеркнем, что неидеализированные задачи электродинамики,
отвечающие объектам радиоэлектроники, почти всегда являются за-
задачами дифракции. На приемную антенну падает некоторая волна,
и нужно знать ее реакцию. В случае передающей антенны только
при упрощении рассматривается излучение заданных источников,
а в действительности распределение токов надо еще найти, и это —
локальная задача дифракции. В частности, к антенне может под-
подходить волновод или другая направляющая структура, и должна
рассматриваться дифракция соответствующей падающей волны. Лю-
Любое устройство СВЧ, волноводное или построенное в виде инте-
интегральной схемы, соединяется с другими посредством каких-либо
направляющих структур (например, полых волноводов или коакси-
коаксиальных кабелей). Опять-таки речь должна идти о дифракции соот-
соответствующих направляемых волн.
Разумеется, при построении математических моделей электроди-
электродинамики приходится решать различные промежуточные задачи.
К ним относятся задачи о собственных волнах направляющих
структур и о собственных колебаниях резонаторов.
Реальным объектам отвечают граничные задачи электродинамики:
решения уравнений Максвелла должны удовлетворять известным
условиям на границах раздела сред или некоторых подобла-
подобластей. Простейшие граничные задачи в этой книге не раз рассмат-
рассматривались (см. гл. 7, гл. 8 и пр.). При этом каждый раз использо-
использовался метод разделения переменных, а система координат соответ-
414
ГЛ. 12. ОБЩИЙ ПОДХОД. ПРОЕКЦИОННЫЕ МЕТОДЫ
ствовала конфигураций области пространства, в которой ищем
решение. Так, например, было получено решение задачи о собствен-
собственных волнах прямоугольного волновода; система координат в этом
случае — декартова, граница области описывается как совокупность
нескольких координатных поверхностей (линий). Казалось бы,
в задаче о полом волноводе Я-образного поперечного сечения вы-
выполняются подобные условия, но здесь уже не удается получить
решение задачи в явном виде. Метод разделения переменных, не
имеющий альтернативы как средство нахождения таких решений,
отказывает. Следует также иметь в виду, что существует немного
систем координат, в которых этот метод может быть применен.
Важнейшие из них: декартова, цилиндрическая, сферическая, эл-
эллиптическая и эллипсоидальная. При этом переход к новой системе
требует введения аппарата специальных функций. Построение, ис-
исследование и, наконец, табулирование различных специальных
функций составило целую эпоху в развитии математической физи-
физики. Достигнутые при этом успехи важны и сейчас. Однако этот
путь не давал надежды приблизиться при постановке граничных
задач к условиям практики, если не говорить о редких исклю-
исключениях.
12.1.3. Вычислительная электродинамика. Перейдем к краткому
обсуждению методов, которые стали мощным орудием благодаря
современной вычислительной технике и в настоящее время позво-
позволяют строить математические модели электродинамики, все более
отвечающие нуждам практики. Методы эти различны и зародились
давно, однако их значение связано именно с такими возможностя-
возможностями реализации, которые дают современные ЭВМ. В последние годы
все чаще употребляется словосочетание «вычислительная физика»
для обозначения того направления в физике, которое опирается на
вычислительные методы, реализуемые на ЭВМ. Не менее правомер-
правомерно говорить о «вычислительной электродинамике». Ведь в электро-
электродинамике такое направление стало традиционным.
Вычислительные методы в электродинамике — тема этой и сле-
следующей глав. Разумеется, вопрос не удастся рассмотреть во всей
полноте, но мы обсудим ряд ключевых положений и результатив-
результативных подходов.
Центральным является способ представления решения задачи,
т. е. электромагнитного поля.
Применяя метод разделения переменных (например, в упоми-
упоминавшейся уже задаче о прямоугольном волноводе), мы получаем
некоторые формульные выражения векторных функций, которые
точно удовлетворяют уравнениям Максвелла и граничным услови*
ям. В таких случаях иногда говорят, что решение получено в замк-
замкнутой форме. Хотя в большинстве технически интересных задач
это недостижимо, метод разделения переменных оказывается полез-
полезным как средство построения систем функций, служащих для пред-
представления полей п различных случаях.
§ 12.1. ПОСТАНОВКА ЗАДАЧ, ПРЕДСТАВЛЕНИЕ ПОЛЕЙ
415
Пусть, например, методом разделения переменных получена си-
система решений уравнений Максвелла {Е„, Н„} (га = 1, 2, ...); каж-
каждая пара удовлетворяет граничным условиям на некоторой простой
границе. В ряде случаев, пользуясь этой системой, можно по-
построить представление решения вида:
EJV=|]CnEn, Н"=|]С?1НП A2.1)
71=1 71=1
(с„ — пока неизвестные коэффициенты). Взяв область со сложной
границей, можно тем или иным способом (например, в системе то-
точек) подчинить EN и HN требуемым граничным условиям, что при
правильном подходе приведет к системе N линейных алгебраиче-
алгебраических уравнений относительно N коэффициентов с„. Чем выше N,
тем лучше удается удовлетворить граничным условиям, если систе-
система {Е„, Н„} обладает нужными свойствами.
Иногда в распоряжении имеются системы функций {Е„} и Ш„},
не связанных уравнениями Максвелла, но удовлетворяющих требуе-
требуемым граничным условиям. Решение представляется в виде:
EN = 2 впЕ„, Пи = 2 ЬпЯп. A2.2)
71=1 71=1
Если системы {Е„} и Ш„} обладают некоторыми свойствами (час-
(частично обсуждавшимися в п. 11.0.3), удается приблизить пару Ew,
HN к решению уравнений Максвелла. Это опять-таки сводит задачу
к системе линейных алгебраических уравнений относительно неиз-
неизвестных коэффициентов а„ и Ь„ в суммах A2.2). С ростом N ка-
качество получаемого решения граничной задачи оказывается выше.
Сущность того или иного метода состоит в том, каким путем
граничная задача сводится к системе алгебраических уравнений.
Ниже в этой главе будут рассмотрены так называемые проекцион-
проекционные методы. Представления полей подчиняются в этом случае си-
системам интегральных соотношений. Производимые операции можно
назвать проецированием в том смысле, который обсуждался в
п. 11.0.3.
Другой важный класс составляют дискретизационные методы.
Область, в которой ищут решение, при этом подвергается дискре-
дискретизации, разбиению. Можно, например, рассматривать решение
только на некотором множестве точек, выделенных в области. Об-
Образуя разности соседних значений, формируют аналоги производ-
производных, так что дифференциальный оператор задачи (например, опе-
оператор Лапласа) приближенно заменяется разностным оператором.
Такой подход, называемый разностным методом, также сводит за-
задачу к системе линейных алгебраических уравнений. Существуют
другие дискретизационные методы, базирующиеся на выделении
системы подобластей, а по точек; обычно они имеют черты проек-
проекционных. В гл. 13 мы обратимся к этой теме.
41
ГЛ. 12. ОБЩИЙ ПОДХОД. ПРОЕКЦИОННЫЕ МЕТОДЫ
§ 12.2. ПРОЕКЦИОННЫЕ МЕТОДЫ
417
При построении математических моделей электродинамики те
или иные вычислительные методы нередко применяются не к гра-
граничным задачам для уравнений Максвелла, а к эквивалентным ин-
интегральным уравнениям.
И, наконец, следующее. Налицо быстрый прогресс вычислитель-
вычислительной техники; так в настоящее время большие надежды связаны с
предстоящим появлением следующего поколения ЭВМ. Однако ре-
реальные технические объекты очень сложны. Поэтому не только
сейчас, но и в будущем для большого количества реальных задач
прямая алгоритмизация окажется невозможной (или будет требо-
требовать неправомерно большого расхода машинного времени), как бы
ни был эффективен применяемый проекционный или дискретиза-
ционный методы. Выход из положения дает принцип декомпозиции
(см. гл. 13): сложный (протяженный) объект можно расчленить
на относительно простые (малые) части. Математические модели
строятся для этих частей, причем предусматриваются все мыслимые
режимы их взаимодействия. Затем математическая модель исходно-
исходного сложного объекта получается посредством рекомпозиции, т. е.
восстановления из частей при наложении конкретных связей.
§ 12.2. Проекционные методы. Процесс Бубнова — Галеркина
12.2.1. Основная проекционная схема: процесс Бубнова—Га-
Бубнова—Галеркина. Выше в п. 11.0.3 при обсуждении рядов Фурье уже было
введено представление о проецировании в функциональном про-
пространстве. 13 сущности, была лишь намечена главная мысль, по-
поскольку последовательное изложение всех сопутствующих понятий
составило бы обширный математический материал. Однако уже на
этой основе можно понять сущность проекционных методов.
Большой общностью обладает подход, называемый методом, или
процессом Бубнова — Галеркина по именам двух выдающихся ин-
инженеров и ученых, наших соотечественников, пришедших к цент-
центральной идее в 1913—15 г. [И.2]. Непосредственным предметом бы-
были задачи технической механики.
Рассмотрим процесс Бубнова — Галеркина, т. е. построение ос-
основной проекционной схемы. Поставленную задачу сжато сформу-
сформулируем в виде равенства:
Su = l A2.3)
Здесь & — какой-либо оператор задачи, например, дифференциала
ный (с заданием граничных условий), интегральный или иной; бу-
будем полагать его линейным. В правой части — заданная функция
/, выражающая обычно то или иное внешнее воздействие на объект.
Символом и обозначено неизвестное решение задачи.
Рассмотрим тождественно равную нулю функцию 9?и — / = 0.
Разлагая се в ряд Фурье типа A1.20) но полной ортогональной
системе {и,,}, мы должны положить все коэффициенты Фурье рав-
равными нулю:
(J?o-/, в,) = 0, 4 = 1, 2, .... во. A2.4)'
Приближенное решение задачи будем искать в виде ортого-
ортогонального представления:
N
% A2.5)
N
uN = 2 а%ип,
где ап — неизвестные коэффициенты; систему N функций {wn}n«=i
будем называть базисом процесса Бубнова — Галеркина. Для каж-
каждой базисной функции «„ должно иметь смысл выражение 3?ип,
т. е. ип е 2bg> (обозначение употреблялось в п. 11.0.1). Тогда пред-
представление uN A2.5) можно подставить в A2.4) вместо и. Сохра-
Сохраняя ./V таких соотношений, имеем:
BV-/, «А) = 0, k = i,2,...,N. A2.6);
Это и есть требование, налагаемое на приближенное решение.
В сущности, совокупность равенств A2.6)—это условия ортого-
ортогональности невязки S'u" — f функциям ик, принадлежащим базису
{wn}n=1. Выполнение требования A2.6) должно привести к опреде-
1 ленному выбору коэффициентов ап и, следовательно, формирова-
формированию приближенного решения uN A2.5).
Как видно иэ A2.6), при подстановке A2.5) возникает следу-
следующая система линейных алгебраических уравнений:
и,)
щ)
и2, их) af + ... + (SuN, щ) а% = (/, щ),
иг, и2) а* + .. . + BuN, u2) а% = (/, и2),
A2.7)
uN)
, un) a& = (/, uN),
или в краткой записи:
LaN = /, A2.8)
где aN — вектор коэффициентов ап (столбец чисел а^, af, ..., a$),
вектор правой части / имеет компоненты (/, «„), а матрица L —
элементы Lhn — (&ип, uh).
Назовем систему уравнений A2.7) (или A2.8)) проекционной
моделью физической системы, которую отображает задача A2.3).
Нахождение коэффициентов ап (и последующее построение при-
приближенного решения A2.5)) сведено, таким образом, к решению
алгебраической задачи.
Можно представить себе серию проекционных моделей A2.8),
построенных при неограниченном возрастании N. В этом смысле
можно говорить о переходе к пределу при N ->- °°. в пределе невяз-
невязка S'u" — / оказывается ортогональной системе Ып}, как и точный
27 В. В. Никольский, Т. И. Никольская
418
ГЛ. 12. ОБЩИЙ ПОДХОД. ПРОЕКЦИОННЫЕ МЕТОДЫ
N
нуль Su — /. Можно ожидать, что представление lim и" в опреде-
ленном смысле не отличается от точного решения. Если это ожида-
ожидание оправдывается, то говорят, что процесс Бубнова — Галеркина
(или проекционная модель) сходится к решению задачи A2.3).
Обычно при этом
а,п-+ап при N-+oo, п = 1, 2, ..., A2.9)
где ап = (и, и„)—коэффициенты Фурье решения и задачи A2.3).
Следует подчеркнуть, что вообще апфап' при NФ N'. Строгое до-
доказательство сходимости процесса Бубнова — Галеркина для того
или иного класса задач может оказаться трудной проблемой.
Рассмотрим процесс Бубнова — Галеркина в случае задачи на
собственные значения
= 0. A2.10)
Можно сказать, что A2.10) получается из A2.3) при / = 0 и 3? =
= s4- — %&, где х— параметр; в частности, &и = и (т. е. 3& — еди-
единичный оператор). Задача на собственные значения имеет серию
решений u = «(i), «B)( ..., которые реализуются при соответствую-
соответствующих значениях параметра х: Xi, хг, ... По определению, «(П) — соб-
собственные функции, а х„ — отвечающие им собственные значения
задачи A2.10). И те, и другие необходимо найти.
Применяя метод Бубнова — Галеркина, вместо A2.6) имеем:
{s4-uN-y.N$uN, ик) = 0, fc = l, 2, ..., N, A2.11)
где к" означает приближенное значение х, которое будет получено
при реализации метода. Далее вместо A2.8) будем иметь
AaN -
а* = 0, A2.12)
где матрицы А и В имеют элементы Акп = C?ип, ик) и Вк„ =
= (&ип, ик), соответственно. Из условия совместности системы урав-
уравнений A2.12)
DetU-x*5l=0 A2.13)
следует характеристическое уравнение относительно х", являющее-
являющееся алгебраическим уравнением степени N. Его корни хх, х2, ... —
это приближенные значения искомых величин xi, хг, При ре-
решении системы уравнений A2.12) находятся отвечающие этим
приближенным собственным значениям векторы а". Внося соответ-
соответствующие наборы коэффициентов в представление A2.5), получа-
получают собственные функции иц), ИB>,
В заключение сделаем несколько замечаний.
1. Нетрудно заметить, что все операции процесса Бубнова —
Галеркина, а также вид окончательной алгебраической формы
S 12.2. ПРОЕКЦИОННЫЕ МЕТОДЫ
419
A2.8) или A2.10) не изменятся, если система {и„} будет неорто-
неортогональной. Действительно, ортогональность базиса Бубнова — Га-
Галеркина не является необходимой.
2. Применяются и такие базисные функции и„, которые не вхо-
входят в область определения оператора i?, но в этом случае исполь-
используется специальный прием, который будет продемонстрирован на
примере электродинамических задач ниже в п. 12.2.2.
3. Проекционная модель A2.8) или A2.10) может быть полу-
получена и совершенно иным путем. Главная альтернатива — примене-
применение вариационного исчисления. Не останавливаясь на этом, отметим
только, что приводящий к A2.8) или A2.10) вариационный под-
подход называется методом Ритца. Иногда проекционные методы на-
называют вариационными.
Для детального ознакомления с проекционными методами как
инструментом математической физики рекомендуется монография
[И.2]; применение проекционных методов в электродинамике изло-
изложено в [И.З].
12.2.2. Основная проекционная схема для уравнений Максвелла.
Электродинамическую задачу того или иного типа, сформулирован-
сформулированную для некоторой области V, нетрудно выразить в форме A2.3).
Для этого достаточно применить так называемый оператор Мак-
Максвелла Ж, ввести обобщенную проницаемость я и вместо Е и Н
рассматривать столбцы F; применение такого аппарата наряду с
другими возможностями подробно обсуждалось в [И.З]. Вводится
символика:
0 — rot
* о
„е 0
5
При этом уравнения Максвелла C.34) принимают вид:
A2.15)
где J — столбец с компонентами —ijm и 0.
Но в последующих действиях мы не воспользуемся аппаратом
оператора Максвелла. Чтобы сохранить легко обозримую преем-
преемственность с предшествующим материалом этой книги, будем стро-
строить основную проекционную схему, отправляясь непосредственно
от уравнений Максвелла в форме C.34).
Итак, пусть некоторое электромагнитное поле в виде комплексных
амплитуд Ет и Нт надо найти в области V с границей S; внутрен-
внутренняя среда неоднородна: е и ц — функции координат. Постановку
задачи пока уточнять не будем. В объеме V зададим системы функ-
функций {Е„} и Ш„}, которые не являются решениями исходных урав-
уравнений Максвелла C.34) при заданных со, е и ц.
27*
420
ГЛ. 12. ОБЩИЙ ПОДХОД. ПРОЕКЦИОННЫЕ МЕТОДЫ
Применительно к уравнениям Максвелла C.34) проекционная
форма A2.4) записывается следующим образом:
f (rot Hm — ШгогЕт — jm) E*hdv = О,
V A2.16)
[ (rot Em + i©fiofiHm) H*hdv = 0,
V
ft = 1, 2, . . ., oo.
Действительно, если системы {Е„} и Ш„} ортогональны, то запи-
записанные соотношения имеют очевидное истолкование: равны нулю
все коэффиценты Фурье функций rotHm—ШгогЕт — jm = 0 и
rot Em + шцоцНт = 0.
В качестве Ш„} и Ш„} удобно взять системы векторных функ-
функций, рассматривавшиеся в п. 11.1.2, для некоторого объема Fo, ко-
который в общем случае охватывает V: V <= Fo, т. е. используется ба-
базис полей полого резонатора с объемом Fo; в частности, Fo = V.
В методе Бубнова — Галеркина известное решение задачи пред-
представляется в форме:
N W
FN — У /7N,F HN — У bNE. A2 17)
или — при переходе к индукциям:
A2.18)
Но прямая подстановка этих представлений в A2.16) допустима
далеко не всегда; это может привести к неверным результатам.
Действительно, рассчитывая на сходимость процесса, надо требо-
требовать, чтобы подстановка сохраняла смысл при N -> °°. А это озна-
означает, что должно быть оправдано почленное дифференцирование
(точнее, применение операции rot) по отношению к ортогональным
рядам, в которые переходят представления A2.17). Возникшую
трудность легко обойти, выполнив в A2.16) интегрирование по ча-
частям, т. е. надо использовать формулы A.26) и A.33). В последу-
последующих преобразованиях учтем также уравнения Максвелла A1.48),
которым подчинены функции базиса (в них положим е = 1, ц = 1;
при этом со„ вещественны). В результате соотношения A2.16) при-
принимают вид
\ &*kdv]= 0,
A2.19)
сое0
[ eEmE*hdv - ш*щ> f HmH*di; - i f [E*h, Hm] da-
V v s
— cofceo ) EmE*hdv +
v
j yjlmU*hdv — i J [Ёт, II*] ds = 0.
§ 12.2. ПРОЕКЦИОННЫЕ МЕТОДЫ
421
При подстановке в A2.19) представлений A2.17) или A2.18)
(в последнем случае предварительно делается замена Ёт =
= (eoe)-1Dm и Нт =((ioM-)~1Bm) получается некоторая алгебраическая
форма. Однако такая подстановка должна делаться осмысленно; ее
правомерность для той или иной граничной задачи должна быть
обоснована.
12.2.3. Применение метода Бубнова — Галеркина к некоторым
классам электродинамических задач. Рассмотрим построение проек-
проекционной модели полого резонатора, содержащего некоторое тело,
характеризуемое заданными проницаемостями; в объеме V прони-
проницаемости е и ц — функции координат (если требуется, тензоры).
Структура показана на рис. 12.1; колебания могут быть вынужден-
вынужденными и собственными, в последнем случае отверстие отсутствует.
0
A
Рис. 12.1
Будем считать, что собственные колебания при отсутствии вносимо-
вносимого тела, нарушающего однородность среды, заранее изучены. При
этом известны системы функций {Е„} и Ш„} при Vo = V. Это усло-
условие, в частности, выполнено в случае прямоугольного резонатора
(рис. 12.16); функции Е„, Н„ выписаны в п. 11.0.4.
В варианте вынужденных колебаний на отверстии Sz в оболоч-
оболочке резонатора задано Ет = Е", а внутри — сторонний ток с плот-
плотностью j". Внося в A2.19) представления EN, H* A2.17) получа-
получаем следующую систему алгебраических уравнений:
соЭа" - Qb" = i
A2 20)
где матрицы Э и М имеют элементы
Эк„ = е0 J eEnE*<fo, Mhn = цо§ цН„Н*^. A2.21)
V У
Матрица fi — диагональная и составлена из собственных частот:
^ап = б4псоп (напомним, что для потенциальных функций эти
422
ГЛ. 12. ОБЩИЙ ПОДХОД. ПРОЕКЦИОННЫЕ МЕТОДЫ
§ 12.2. ПРОЕКЦИОННЫЕ МЕТОДЫ
423
величины равны нулю); векторы Q3 и Q" имеют компоненты
т, Н:] ds A2.22)
= J
(при получении A2.20) учитывались соотношения ортонормировки
A1.47), в которых е = 1 и ц = 1).
В варианте собственных колебаний полагаем jm = 0 и Ет = 0,:
так что правая часть в A2.20) обращается в нуль. Частота со
оказывается неизвестной величиной. Поскольку получаемые мето-
методом Бубнова — Галеркина собственные частоты зависят от N, обо-
обозначим частоту со*. Система уравнений A2.20) принимает вид
а"Эа* - QbN = 0, - Qa" + со"М> = 0. A2.23)
Собственные частоты находим при обращении в нуль определителя
этой системы.
При анализе собственных колебаний может иметь преимущест-
преимущество использование представлений индукций A2.18). Дело в том,
что при отсутствии источников в разложениях индукций A2.18) ос-
остаются лишь соленоидальные функции Е„, Нп и, соответственно это-
этому, нет нулевых а„. Все соп — собственные частоты рассматриваемого
резонатора без заполнения. Алгебраическая форма при этом такова:
a'a» - QMb" = 0, Qda" - а"Ь" = 0, A2.24)
где элементы новых матриц выражаются следующим образом:
дкп = ггЛг-1ЕпЕ1сЬ, МЛ„ = ца0 J ц^НЖЛ;. A2.25)
Л v Л у
Диагональная матрица Q в данном случае имеет обратную (это мат-
матрица Q, составленная из диагональных элементов сой1).
Заметим, что как из A2.23), так и из A2.24) можно получать
иные формулировки, исключая какой-то один вектор; тогда полу-
получаются системы N уравнений.
Возвращаясь к началу наших рассуждений, отметим, что дей-
действия, которые производились еще в п. 11.1.3 при анализе возбуж-
возбуждения полого резонатора, в сущности, также базировались на проек-
проекционной схеме. Действительно, соотношения A1.56) — это не что
иное, как проекционная форма A2.16). Однако в п. 11.1.3 не было
необходимости решать системы алгебраических уравнений высокого
порядка, чтобы точно выразить коэффициенты представлений поля
A1.53). Можно сказать, что в п. 11.1.3 бесконечная система рас-
распалась на независимые пары уравнений A1.60). Сопоставляя зада-
задачи о возбуждении резонатора, одна из которых решалась в п. 11.1.3,
а другая рассматривалась сейчас, можно дать полученным резуль-
результатам определенную физическую интерпретацию. Соотношение ор-
ортонормировки A1.47) означает, в частности, что собственные коле-
колебания резонатора не взаимодействуют, а величины Экп и Мкп A2.21)
при к Ф п истолковываются как взаимные энергии, электрическая и
магнитная, появляющиеся при внесении в полость тела, которое
нарушает однородность среды. При е = const и ц = const, как следу-
следует из A1.47), интегралы Экп и, соответственно, Мк„ для к Ф п равны
нулю. Это возвращает нас к задаче из п. 11.1.3.
Среди различных полых резонаторов, которые можно анализи-
анализировать на основании полученных результатов, выделим волновод-
ные, т. е. образованные отрезками регулярных волноводов
(рис. 12.2а, 6) с продольно-однородным заполнением (на расстоя-
расстоянии L располагаются идеально проводящие перегородки, рис. 12.26).
u.
1-6
Рис. 12.2
Определив собственную частоту такого резонатора, мы заранее зна-
знаем, какой постоянной распространения (одной из собственных волн
волновода) она соответствует. Пусть, например, рассматривается
тип колебаний, для которого р = 1 (п. 8.1.1), что учитывается при
формировании базисов {Е„} и Ш„} (для компонент всех векторных
функций продольная зависимость берется в виде cos(nz/L) и
sin(nz/L)). Тогда согласно (8.32) L = Л/2 и Г = n/L. Поэтому, за-
задаваясь некоторой длиной резонатора L и определяя а", мы получа-
получаем точку кривой Г (а). Можно поступать и по-другому, а именно
фиксировать требуемую частоту а в A2.23) или A2.24) (вместо
неизвестной со*). Определению подлежит при этом длина L
(рис. 12.26), один из пределов интегрирования при вычислении мат-
матричных элементов A2.21) и A2.25). Последние сводятся к интег-
интегралам по поперечному сечению S± волновода, например,
= e0 f гЕп (X) Et О.) ds^-,
где символ (-L) означает, что векторная функция уже не зависит
от z. Величина L = я/Г (можно писать L" = л/Т" ввиду зависимости
результата от N) определяется из характеристического уравнения,
получаемого при обращении в нуль определителя системы A2.23)
или A2.24).
424
ГЛ. 12. ОБЩИЙ ПОДХОД. ПРОЕКЦИОННЫЕ МЕТОДЫ
Итак, рассмотрен способ построения проекционной модели по-
полого волновода с продольно-однородным заполнением. При анизо-
анизотропии среды постоянная распространения волны может зависеть
от направления (по z или против z), и вся схема нуждается в неко-
некоторой модификации. Не входя в подробности, отметим, что при этом
достаточно использовать базисные функции Е„, Н„, удовлетворяю-
удовлетворяющие условиям повторяемости на концах выделенного отрезка вол-
волновода [И.З].
Обратимся теперь к задачам дифракции, обсуждавшимся выше
в п. 11.3.1. Оказывается, и в этом случае можно воспользоваться
полученными результатами применения метода Бубнова — Галер-
кина. Покажем это на примере волновода, содержащего некоторое
тело А, характеризуемое заданными проницаемостями е и ц (см.
рис. 11.14а).
Вместо исходной задачи (рис. 12.3а) достаточно решить две се-
серии вадач о возбуждении полого резонатора через отверстие. Они
'~еп{1)\
•V
О О
i S-,
Рис. 12.3
получаются, когда одно из отсчетных поперечных сечений волново-
волновода 5] или 5г заменяется идеально проводящей перегородкой, а па
другом (которое играет роль отверстия) задается некоторое сторон-
стороннее электрическое поле. Эти ключевые задачи (рис. 12.36, в) ста-
ставятся путем наложения следующих условий:
md) , (О на S,,
Ех= п с Ет= с A2-26)
10 на S; [e( на S
emB) на S2
на 5.,
с Е
на S2;
(то = 1, 2, ...), где имеются в виду функции еп(а), использовавшие-
использовавшиеся в п. 11.3.2. Постановка задач поясняется на рис. 12.36,'в. Оба
поперечных сечения одинаковы, но направления осей z\ и Z2 проти-
противоположны. Поэтому берется: етA) =етB) = ет и hm(i) = — hmB) =
= hm, где ет, hm — собственные функции волновода (см. п. 11.2.2).
Чтобы найти поле вынужденных колебаний резонатора, надо ре-
решить систему уравнений A2.20), взяв т — 0 и Em= em
в A2.22); Ss = S\ или Ss = &. При этом внутреннее поле опреде-
определяется при помощи формул A2.17). Можно сказать, что таким пу-
путем находятся поля в различных режимах короткого замыкания
исходной структуры (рис. 12.3а), которые задаются условиями
A2.26).
Знание поля в каждом из режимов A2.26) позволяет вычис-
вычислить один из элементов матрицы проводимости У для поставленной
§ 12.2. ПРОЕКЦИОННЫЕ МЕТОДЫ
425
вадачи дифракции (см. рис. 11.14а; рис. 12.3а). Далее посредством
A1.107) матрица проводимости У пересчитывается в матрицу рас-
рассеяния S.
Действительно, пусть, например, задан какой-то режим коротко-
короткого замыкания согласно первому столбцу A2.26). В соответствии
с A1.102) это означает, что E,i = em(i) и Е,2 = 0, т. е. для всех п
8а исключением п = т равны нулю все коэффициенты ап1\) и
аПB), а птЦ) — 1. Поэтому, как следует из A1.103),
= Y
A2.27)
(вектор а имеет единственную ненулевую компоненту am(i) = 1). Ес-
Если же задать один из режимов согласно второму столбцу A2.26), то,
аналогичным образом, легко убедиться, что
°пA) =
A2.28)
Таким образом, для нахождения любого из элементов матрицы про-
проводимости У надо уметь вычислять коэффициенты Ь„(о, из A1.102).
В качестве Н,о (а = 1, 2) берется поле Н." (на Si и 5г), представ-
представляемое суммой A2.17), где коэффициенты Ь% вычисляются в ре-
результате решения системы уравнений A2.20) с правой частью, ко-
которая соответствует требуемому режиму A2.26).
Первые проекционные модели полых резонаторов и волноводов
с включениями, нарушающими однородность, а также изотропию
внутренней среды, были построены более четверти века назад; они
были реализованы на ЭВМ первого поколения «Стрела» [И.З, гл. 7].
В частности, рассматривался полый резонатор с диэлектрическим
включением (рис. 12.4а), постепенно заполняющим объем (взято
е = 10 — ? • 10~3). Анализировался низший тип собственных коле-
колебаний, для которого вектор Е параллелен границе диэлектрика
(ось z); структура однородна по z. В качестве базиса разложений
A2.17) использовалось девятнадцать собственных функций, которые
отвечают полям пустого резонатора Ецо, ¦ • ., #15о; #210, • • •, ?250;
?310, • • •, ?340; ?410, ..., Ецо', Еыо (потенциальные собственные функ-
функции отсутствуют, так как поле не имеет нормальной компоненты на
границе раздела сред). По оси ординат на рис. 12.4а отложено низ-
низшее собственное число к^ = СОA)К ео[хо = 2л/ХA), вычисленное в ус-
условных единицах обратной длины (для пустого резонатора kli) со-
составляет 0,7721429...); по оси абсцисс — относительное заполне-
заполнение р. График показывает изменение вещественной и мнимой частей
&A) в зависимости от степени заполнения объема диэлектриком. На
рис. 12.46 показаны зависимости изменения коэффициентов Ъп 9
в A2.17) от р (взяты только первые пять величин). Видно, что при
малом (/><0,1), а также при большом заполнении (р > 0,9) замет-
заметное значение имеет только одна низшая гармоника Еио- Резкое воз-
возрастание вклада высших гармоник при р > 0,15 (б) соответствует бы-
426
ГЛ. 12. ОБЩИЙ ПОДХОД. ПРОЕКЦИОННЫЕ МЕТОДЫ
строму уменьшению Re k^ (а). Какова же точность метода на этом
сложном участке? На рис. 12.4в для р = 0,3 приведены значения отно-
относительной (условной) ошибки величины &A) (co^j) с изменением N.
Это величина Sco = (coji) — <B(i))/<B(i>: за точное принимается значение
со"). Как видно, при N > 13 решение быстро стабилизируется (в ал-
алгоритме уменьшалось N так, что гармоники отбрасывались в поряд-
порядке: 250, 150, 510, 440, 340, 430, 420, 410, 240, 140, 330, 320, 310,
230, 130, 220, 210, 120, НО).
Прежде чем двигаться дальше, подчеркнем, что во всех случаях
использовалось представление поля типа A2.2), где Е„, Н„ не удов-
удовлетворяют уравнениям Максвелла для рассматриваемой задачи ни в
Ъ=71
0,2 0,4 0,6 0,8 1 р
а
0,2 0,4 ' '0,6 1 р
В
Рис. 12.4
N-11
N-12M5
'N-17
4 В 12 16 20 N
одной точке. Тот факт, что взятые нами Е„, Н„ (если говорить о со-
леноидальных функциях) описывают собственные колебания неко-
некоторого полого резонатора, ничего не меняет: Е„, Н„ — решения дру-
других уравнений Максвелла, в которые вместо со входят со-
соответствующие собственные частоты со„, a s и ц — констан-
константы. Что же было существенно при выборе именно этих систем функ-
функций? В первую очередь то, что по этим системам могут быть разло-
разложены любые векторные функции в V и в том числе неизвестное ре-
решение задачи Е, Н. Несколько упрощая, припишем это свойство,
т. е. полноту систем, тому факту, что принадлежащие им функции
образуют бесконечные наборы кратных гармоник вдоль каждой из
осей декартовой системы координат. Другое существенное обстоя-
обстоятельство заключается в том, что на внешней оболочке функции Е„,
Н„ удовлетворяют тем же граничным условиям, что и неизвестное
решение Е, Н.
§ 12.3. ПРОЕКЦИОННОЕ НАЛОЖЕНИЕ ГРАНИЧНЫХ УСЛОВИЙ
427
§ 12.3. Проекционное наложение граничных условий.
Сведение задачи к рассмотрению границы
12.3.1. Проекционное наложение граничных условий: процесс
Трефтца. Метод Бубнова — Галеркина весьма универсален. Пред-
Представление поля типа A2.2) можно строить, не располагая какими-
либо решениями уравнений задачи. Выбор систем {Е„} и Ш„}, та-
таким образом, не определяется свойствами среды в той области, где
ищем поле. За эту универсальность, как говорится, «надо платить»;
ниже мы вернемся к этому вопросу.
Если же среда обладает относительно простыми свойствами, на-
например, однородна, то обычно можно построить такую систему
{Е„, Н„}, где каждая пара функций связана уравнениями Максвел-
Максвелла решаемой задачи. При этом неизвестное решение задачи ищем
в форме A2.1); коэффициенты разложений Ей Н во {Е„} и Ш„},
соответственно, здесь принципиально одинаковы. Такая сумма удов-
удовлетворяет уравнениям задачи при любых коэффициентах с„. Чтобы
получить решение некоторой рассматриваемой электродинамической
задачи, остается наложить на представление A2.1) необходимые
граничные условия, что приведет к определению коэффициентов с„.
При конечном N это, вообще говоря, можно сделать лишь с некото-
некоторой точностью.
Процесс наложения граничных условий можно произвести в про-
проекционной форме, т. е. аналогично тому, как в методе Бубнова —
Галеркпна удовлетворяются уравнения. Такой подход называют ме-
методом, пли процессом Трефтца. Введенную выше систему решений
уравнений Максвелла {Е„, Нп} будем называть базисом Трефтца,
если {Е„} и {Н„} пригодны для разложения произвольного танген-
тангенциального поля на той поверхности, где требуется удовлетворить
граничным условиям.
Пример 1. Поясним применение метода Трефтца на простом примере.
В случае возбуждепия волноводного резонатора через отверстие S% в его торце
(осповаппп цилиндра, рис. 12.5а) нетрудно построить базис Трефтца из
стоячих волн волновода с узлом поперечного электрического поля Е,
при z = L. Каждое из базисных полей получается при наложении двух про-
противоположных волн A1.71). Оказывается, что такое поле Е„, Нп удовлетворяет
пе только уравнениям Максвелла, но и граничным условиям везде за исклю-
исключением торца z = 0. При этом Eni = en sin Tn(z — L); положив z = 0, полу-
получаем полную ортогональную систему (о полноте {е„} говорилось в п. 11.2.2),
пригодную для разложения любого поля Е(, заданного на этом торце резо-
резонатора. Характеризуя это поле, запишем:
на
на
Sy,
A2.29)
Надо стремиться к выполнению равенства Е^ @) =Е(@), где EN — представ-
представление поля в базисе Трефтца A2.1). Наложить это условие в проекционном
смысле — значит, обратить в нуль коэффициенты Фурье функции Е j @) —
— Ej @) в каком-нибудь базисе на Sx- Ввиду A1.74). запишем следующую
428
ГЛ. 12. ОБЩИЙ ПОДХОД. ПРОЕКЦИОННЫЕ МЕТОДЫ
проекционную форму:
J [EN@)-E@), h*k]zds =
= 1,2,...
A2.30)
(здесь остаются только поперечные компоненты полей, поэтому индекс * опу-
опущен). Внося представление EN A2.1) в A2.30) и учитывая A2.29), получаем:
2 сп [Е„ @), b*h]zds = J [ECT, hft*]r<fc, A2.31)
n=1 s
I
n=1
причем слева в качестве Еп @) подставляются функции Е„( @) = —en sin TnL.
D
4
\>
t>
z 1 2 3
В
Рис. 12.5
1,2,3
Привлекая A1.74), видим, что в сумме сохраняется только один к-й член.
В результате находим:
\Wh\
ch ~ Wb sin Гь
A2.32)
В данном случае найденные коэффициенты сп представления A2.1) не зави-
зависят от N. Для рассмотренной нами простой задачи применение метода Трефтца
свелось к разложению функции Е< @) A2.29) в ряд Фурье по {е„}. ¦
Напомним (см. п. 12.2.3), что в п. 11.1.3 при решении задачи
о возбуждении резонатора, в сущности, использовался метод Буб-
Бубнова — Галеркина. Чтобы наглядно продемонстрировать различия
процессов Трефтца и Бубнова — Галеркина, построены некоторые
схематические изображения. На рис. 12.56 для первых трех функ-
функций базиса Трефтца показаны возможные продольные распределе-
распределения компонент Е„,, соответствующие закону sinrn(z — L); третья
волна (а значит, и все следующие) имеет уже мнимую постоянную
распространения Г„, и синус становится гиперболическим. Это стоя-
стоячие волны в волноводе, «закороченном» при z = L; их поперечные
распределения е„ несколько условно представлены па рис. 12.5в.
§ 12.3. ПРОЕКЦИОННОЕ НАЛОЖЕНИЕ ГРАНИЧНЫХ УСЛОВИЙ 429
По этим кратным гармоникам можно разложить произвольную функ-
функцию на ?х при z = 0 (где задано стороннее поле). Что касается про-
продольных распределений (рис. 12.56), то они отнюдь не образуют
полной системы функций, по которой может быть разложена про-
произвольная зависимость f(z). Но базис Трефтца и не должен обла-
обладать свойством полноты для объема резонатора. Требуется лишь
полнота по отношению к той части границы, на которой должны
быть удовлетворены граничные условия; это S± при z = 0. Если бы
задача решалась методом Бубнова—Галеркина, проекционная фор-
форма записывалась бы для объема: базисы {Е„} и Ш„} должны содер-
содержать наборы гармоник по всем направлениям и, в частности, по z.
Для каждого из поперечных распределений (рис. 12.5в) надо было
бы предусмотреть ряд гармоник по z, как это показано на рис. 12.5г.
При той же степени аппроксимации поля количество базисных
функций в процессе Бубнова — Галеркина окажется значительно
больше. Представление поля A2.2) при N -> °° способно сойтись к
решению задачи Е, Н в среднем по объему V. Но, например, при
z = 0 для любых N будет получаться Et = 0, и поле воспроизвести
не удастся. Этим свойством обладают разложения A1.53), которые
не воспроизводят Ет на отверстиях и медленно сходятся вдали от
резонансных частот а„.
12.3.2. Процесс Трефтца как метод частичных областей. На
рис. 12.6 схематически представлено несколько электродинамических
задач, для которых естественно применение метода Трефтца. Все
7
2
Рис. 12.6
они характерны тем, что область существования поля разделяется
на несколько подобластей, в каждой из которых базис Трефтца мо-
может быть найден методом разделения переменных. Базисы Трефтца
430
ГЛ. 12. ОБЩИЙ ПОДХОД. ПРОЕКЦИОННЫЕ МЕТОДЫ
должны обладать свойством полноты на смешных границах подобла-
подобластей, где производится проекционное наложение граничных условий
непрерывности тангенциальных компонент Ew и Hw, или, как иногда
говорят «проекционное сшивание» представлений поля типа A2.1).
Такой подход называют методом частичных областей; он был впер-
впервые применен к задачам электродинамики около полувека назад1),
но, разумеется, в сколько-нибудь сложных случаях может быть реа-
реализован только с применением ЭВМ.
На рис. 12.6 показаны: /Т-образный волновод (в поперечном се-
сечении) (а); волновод (резонатор) с диэлектрическим включением
(б); сферический резонатор, излучающий через отверстие в свобод-
свободное пространство (в); сферическое зеркало, на которое падает вол-
волна (г); два варианта сочленения направляющих структур (д, е).
Число таких примеров легко увеличить. Отметим, что в случаях (в)
и (г) подобласти одинаковы — шаровая и дополнительная к ней.
Для определенности рассмотрим задачу о скачкообразном сочле-
сочленении волноводов (д, е). Пусть решается задача дифракции некото-
некоторой волны ЕтA), НтA) первого волновода (падающей слева) на
стыке со вторым (z = 0). Построим представление поля в обеих по-
полубесконечных подобластях:
A2.33)
A2.34)
где в каждом пз волноводов поле дифракции представляет собой на-
наложение собственных воли A1.71), расходящихся от плоскости сты-
стыка. Запишем проекционные аналоги условий непрерывности Ех и Нх
на стыке:
f [Ef - Е?, h*h{2)]zds = 0, к - 1,2,..., .V, A2.35)
S2
f [e*A), Hf - B?]tds = О, к = 1, 2, ..., М. A2.36)
Подчеркнем, что непрерывность Ех имеет место на большем сече-
сечении 5г; при этом вне отверстия S\ на перегораживающей части сты-
стыка Ех{—0) = Ех{+ 0) = 0. Компонента Нх непрерывна лишь в облас-
области меньшего сечения S\.
Внося A2.33), A2.34) в A2.35) и A2.36), учтем соотношение
ортонормировки A1.74), в котором надо брать Sx = Si>2 дляе„A,2),
') Hahn W. С. A new method for the calculation of cavity resonators. II J.
Appl. Phys.— 1941.— V. 12, N 1,— P. 62—68.
§ 12.3. ПРОЕКЦИОННОЕ НАЛОЖЕНИЕ ГРАНИЧНЫХ УСЛОВИЙ
431
hn(i,2) (направление оси z остается неизменным). Это приводит к си-
системе линейных алгебраических уравнений относительно коэффи-
коэффициентов представлений A2.33), A2.34); запишем ее в форме:
A2.37)
где с^ и cf — векторы коэффициентов сумм A2.33) и A2.34);
П — матрица с элементами
A2.38)
П — сопряженная матрица (элементы которой являются транспони-
транспонированными и комплексно-сопряженными по отношению к A2.38));
Wl 2 — диагональные матрицы с элементами:
.2I. A2.39)
Наконец, в правой части A2.37) фигурируют векторы со следую-
следующими компонентами:
Flh = и>Гы*8к», F2h = Ukm. A2.40)
Смысл решения системы уравнений A2.37) ясен. Поскольку
с™A) и СпB) — эт0 комплексные амплитуды расходящихся от сты-
стыка волн при падающей волпе единичной амплитуды заданного ти-
типа, то это — элементы матрицы рассеяния стыка (п. 11.3.1), а имен-
именно: спA) = S"m й спB) = S2nm. Разумеется, точность этих ра-
равенств зависит от М и N. При правильном выборе соотношения М
и N (отметим только, что М < N) увеличение этих чисел с удовлет-
удовлетворительной быстротой приводит к довольно точным результатам.
Чтобы находить любые элементы матрицы рассеяния, надо еще
рассмотреть дифракцию волны, падающей справа, со стороны вто-
второго волновода. При этом меняется только вид правой части систе-
системы A2.37), так что вместо A2.40) имеем:
Flk=п:
A2.41)
Решая систему уравнений A2.37) с правой частью A2.41), полу-
М с12 тх /.N — С22
чаем: cn(j) = оПт и сПB) — оПт-
Путь, который мы обсудили, типичен для алгоритмизации задач,
показанных на рис. 12.6, и многих аналогичных.
Отметим, что построенные выше представления поля A2.33),
A2.34) удовлетворяют условию излучения: кроме заданной падаю-
падающей волны они содержат лишь расходящиеся волны. Аналогично
этому в задачах, соответствующих рис. 12.бе, г, в области 2 решение
ищется в виде системы расходящихся сферических волн.
432
ГЛ. 12. ОБЩИЙ ПОДХОД. ПРОЕКЦИОННЫЕ МЕТОДЫ
12.3.3. Об интегральных уравнениях электродинамики. Выше
было показано, что, располагая базисами Трефтца, уже не дума-
думают об удовлетворении уравнениям во внутренних точках рассмат-
рассматриваемых областей: какие бы то ни было операции производятся на
их границах. Поэтому задачу электродинамики можно с самого на-
начала привести к такой форме, в которой фигурирует только эта
граница.
Для определенности будем рассматривать задачу дифракции для
волновода с диафрагмой (рис. 12.7а). Подобно предыдущему зто за-
задача дифракции некоторой волны ЕтA), НтA), падающей слева.
1
7
г iZ -
щ
Поэтому сохраним представление поля в базисах Трефтца A2.33),
A2.34).Однако в данном случае нет оснований брать неодинаковое
число учитываемых в подобластях волн, так что М = N. Поскольку
слева и справа волноводы одинаковы, то en(i) = е„B) = е„ и hn(i, =
= hnB) = Ь„. Будет также удобно изменить ортопормировку A1.74)
(которой соответствует A1.43)) наследующую:
e*hends = 8hn.
A2.42)
Электромагнитное поле в плоскости диафрагмы {%, = 0) должно
удовлетворять следующим граничным условиям:
Et(-0)=Et(+0) на S± = SM +
Е,@)=0 на S*,
Ht(-0)=HI(+0) на Sx.
Первое из них наложим в проекционной форме:
(E,(+0)-Et(-0))e* = 0
A2.43)
A2.44)
A2.45)
A2.46)
(к = 1, 2, ...). Отсюда при подстановке Е^ @) и Е%х @) получаем:
C
A2.47)
§ 12.3. ПРОЕКЦИОННОЕ НАЛОЖЕНИЕ ГРАНИЧНЫХ УСЛОВИЙ
433
Выражая, далее, chB) как коэффициенты Фурье функции Et@) =
= & в базисе {е„}, имеем:
cfe<2)= ) Seftds=J
A2.48)
При переходе к последнему интегралу учтено условие A2.44)
& = 0 на 5„. Остается лишь наложить граничное условие A2.45).
Для этого просто приравняем выражения Н1т@) и Н2Т @), сле-
следующие из A2.33), A2.34). При этом входящие в них коэффици-
коэффициенты Сщ1), Сщ2) представим, пользуясь формулами A2.48) и
A2.47). Это дает:
на Ss.
2 f SoUdsK = S - | f Se*nds- 8nm) К + h
"=1ss "=1 \sS J
Полученное равенство легко упростить. При этом также умножим
векторно все члены на zo и учтем, что согласно A1.72) [hn, z0] =
= •*?-• В результате получаем
W.
N
A2.49)
Это интегральное уравнение относительно неизвестной функции
па отверстии Ss в плоскости диафрагмы (см. рис. 12.7).
Перепишем интегральное уравнение в форме
Г YN (r, r') g (r')ds'= w-en(i),
A2.50)
где г, г' — координаты в плоскости z = 0, причем штрихованные
меняются в процессе интегрирования. Ядро интегрального уравне-
уравнения YN(r, г') есть сумма
N
N (г, г') = ^ W-
е"
п=1
где кружок ° — символ так называемого диадного произведения
векторов1). Ядро имеет размерность проводимости, и интегральное
уравнение будем называть адмитансным. При некотором фиксиро-
фиксированном N оно формулирует электродинамическую задачу, как мы
будем говорить, в TV-приближении. Если решение 8 найдено, то по
') Здесь о падо попимать как своего рода разделительный символ: пусть
V—любой вектор, тогда vei ° е2 = (v, ei)e2 и ei о e2v = ei(e2, v), где скобки —
скалярное произведение.
28 В. В. Никольский, Т. И. Никольская
434
ГЛ. 12. ОБЩИЙ ПОДХОД. ПРОЕКЦИОННЫЕ МЕТОДЫ
формулам A2.48) и A2.47) сразу определяются коэффициенты
представлений A2.33) и A2.34), которые, как и выше в п. 12.3.2,
имеют смысл элементов матрицы рассеяния.
Прежде чем решать адмитансное интегральное уравнение
A2.50), отметим следующее. Если изменить порядок и способ нало-
наложения граничных условий A2.44) и A2.45) так, что сначала ис-
используется условие A2.45) в проекционной форме, то вместо A2.50)
получается интегральное уравнение относительно плотности тока
т] = [z0, Н(+0)—Н(—0)] на диафрагме
A2.52)
где
A2.53)
Ядро Z"(г, г') имеет размерность сопротивления, и уравнение
A2.52) называется импедансным. Нахождение решения х\, как ра-
ранее поля S, легко приводит к определению элементов матрицы рас-
рассеяния.
Как адмитансное, так и импедансное интегральные уравнения
могут быть решены методом Бубнова — Галеркина. Запишем A2.50)
и A2.52) в форме A2.3):
2". V'z = F-z, A2.54)
6
= ур-л fz = 2em, а интегральные операторы
имеют вид
(...) = j YN(...)ds\ Sz {...) = f ZN(...)ds'. A2.55)
S
Выбрав какой-то базис на Ss или, соответственно, Sa, запишем про-
проекционное соотношение типа A2.4):
zuY<z-iY-z)u*hds = 0, A2.56)
и представим решение в том же базисе:
м
U I = Za amUm.
A2.57)
Подстановка A2.57) в A2.56) приводит к системе линейных алгеб-
алгебраических уравнений в двух вариантах:
рт, zDy. zPy, zau = Fr, Z) A2.58)
§ 12.3. ПРОЕКЦИОННОЕ НАЛОЖЕНИЕ ГРАНИЧНЫХ УСЛОВИЙ 435
где ам — вектор коэффициентов A2.57); матрица Pr-Z имеет эле-
элементы
Щ= J n*mends( A2.59)
Pr'z — сопряженная матрица, так что Ртп =\Рпт) ; матрица
DT-z — диагональная, причем
DYm'z = JF-\ Wm. A2.60)
Наконец, вектор правой части имеет компоненты
A2.61)
Оказывается, полученные интегральные уравнения почти не ус-
усложняются при переходе от диафрагмы (см. рис. 12.7а) к серии
родственных задач (см. рис. 12.76, в, г, и т. п.) Все сводится к то-
тому, что в ядрах уравнений A2.51) и A2.53) происходит следую-
следующее изменение: 2WU1 -*-Zu(i) + %п(г) (см., например, [И. 11],
п. 1.3.4, п. 2.1.2). Импедансы Zn(i) и ZnB) находятся непосредственно
из базисов Трефтца для подобластей. Например, в случае полого ре-
резонатора (рис. 12.Те) с плоским проводником на границе раздела
сред Zn(i) = iWnii) tg rn(i)Zi и Zn{2) = iWnl2)tg TnB)h (Г„A,2) и
Wn(i,2> — постоянные распространения и волновые сопротивления
собственных волн для левого и правого волноводов). В данной за-
задаче правая часть в A2.50) или A2.52), а следовательно, и в
A2.58) равна нулю. При решении однородной системы A2.58) ее
определитель приравнивается нулю, что дает уравнение относитель-
относительно собственных частот анализируемой структуры. Аналогично ис-
исследуются полосковые, щелевые и другие линии передачи [И. 11,
п. 2.2.2] планарного типа. Приведенные выше в § 7.5 результаты
получены этим методом. Интегральные уравнения пмпедансного
и адмитансного типов можно получить и для многих других задач,
например, в случае ряда внешних задач (см. рис. 12.6г и т. п.).
Мы рассмотрели только один путь получения интегральных урав-
уравнений, связанный с существованием базисов Трефтца. Интеграль-
Интегральные уравнения электродинамики весьма разнообразны и существу-
существуют разные способы их вывода. Наиболее типично использование
различных функций Грина, которые в случае внешних задач элек-
электродинамики известны в замкнутой форме. Вообще при решении
внешних задач получение интегральных уравнений наиболее рас-
распространено [Г.5, И.4, 5]. Запишем одно известное *) интегральное
') В. Л. Фок. Распределение токов, возбуждаемых плоской волной на по-
поверхности проводника II ЖЭТФ.—1945.—Т. 15, № 12.—С. 693 (см. [Г. 7]).
28*
436
ГЛ. 13. ДИСКРЕТИЗАЦИЯ И ДЕКОМПОЗИЦИЯ
уравнение:
= [vo,H»] A2.62)
(ср. подынтегральное выражение в (9.17)). Оно относится к задаче
дифракции волны Е°, Н° на идеально прово-
проводящем теле V с поверхностью S (рис. 12.8).
Если в результате решения этого уравнения
найдена плотность поверхностного тока г\
на S, то поле дифракции определяется при
помощи формулы (9.17) с заменой объем-
объемных величин на поверхностные (как в (9.59)).
Рис. 12.8 Уравнение A2.62) широко используется
в численных исследованиях (см., например, [И.5]).
Глава 13
ДИСКРЕТИЗАЦИЯ И ДЕКОМПОЗИЦИЯ
§ 13.1. Дискретизационные методы
13.1.1. Коллокации. Рассматривая некоторую задачу, сформули-
сформулированную в виде A2.3), выделим в области существования решения
систему^ точек, как это схематически показано на рис. 13.1а. Сохра-
1 Ч
t
1—'—
Рис. 13.1
няя представление решения A2.5), вместо проекционной формы
A2.6) просто потребуем выполнения равенства
2V(rj) = /(r;) A3.1)
(i = 1, 2, ..., N), что приводит к системе N алгебраических уравне-
уравнений относительно N неизвестных коэффициентов представления
A2.5):
г() = /(г,). A3.2)
§ 13.1. ДИСКРЕТИЗАЦИОННЫЕ МЕТОДЫ
437
7
Это коллокационный метод нахождения приближенного решения за-
задачи A2.3), сводящий ее к алгебраической задаче A3.2).
Рассмотрим, например, задачу о собственных колебаниях полого
резонатора, содержащего некоторое тело с проницаемостями 8 и ц
(см. п. 12.2.3). Представление решения берется в форме A2.17),
где {Е„} и Ш„} — прежние базисы; граничные условия на оболочке
резонатора ими удовлетворяются. Внося A2.17) в уравнения Мак-
Максвелла, потребуем, как и в A3.2), выполнения равенств на множе-
множестве точек:
N
2 bn rot Н„ (Г1) - ш\е (г4) а*Е„ (г4) = О,
V A3-3)
2 an rot En (г4) + icoNu0u. (г4) СН„ (г4) = О
(неизвестная собственная частота, которая может быть найдена
только приближенно, обозначена a>N, как и в п. 12.2.3). С учетом
A1.48) пишем:
N
ю„е0Нп (rj а„ — со цоц (г4) Нп (г4) Ъп = О,
A3.4)
со еое (Fj) tin (Fj) an — cunu.0?in (Tj) on = и.
п=\
Если взять М точек (i = 1, 2, ..., М) и каждое из равенств спрое-
спроецировать на оси декартовой системы координат, то количество
уравнений будет QM. В принципе можно взять N = ЗМ и получить
в A3.4) квадратную матрицу. Если оказывается желательным при
фиксированном N в A2.17) усилить дискретизацию (увеличить М),
то система уравнений A3.4) окажется переопределенной, однако и
в этом случае может быть получено решение (см., например, [И.6]).
Коллокационный подход применим и к интегральным уравне-
уравнениям. Базис, как и выше, может строиться в виде набора гармоник
(см. схематическое изображение на рис. 13.1а), но в данном слу-
случае его можно взять как набор констант, каждая из которых задана
только на своем носителе At (рис. 13.16). Применение такого бази-
базиса есть, по существу, реализация простейшего способа приближен-
приближенного интегрирования.
Вместо проекционного наложения граничных условий (метод
Трефтца) возможно коллокационное; система точек при этом выби-
выбирается на нужной границе. В результате получается система урав-
уравнений относительно граничных значений компонент поля.
Коллокационные методы, будучи очень простыми по замыслу,
применяются относительно редко: во-первых, оптимальный выбор
коллокационных точек в каждом отдельном случае требует исследо-
исследования; во-вторых, они, вообще говоря, менее выгодны по сравнению
438
ГЛ. 13. ДИСКРЕТИЗАЦИЯ И ДЕКОМПОЗИЦИЯ
с проекционными, которые в ряде случаев приводят к удовлетвори-
удовлетворительным решениям при малых порядках системы алгебраических
уравнений.
13.1.2. Разностные схемы. Как видно из предыдущего, для дис-
кретизационного подхода характерно выделение в области задачи
множества точек (рис. 13.1а), или, как говорят, сетки. Заметим, что
поэтому дискретизационные методы в ряде случаев называют сеточ-
сеточными. На рис. 13.2а показана равномерная координатная сетка в
h
i
1
^•Ун
Рис. 13.2
плоскости хОу с шагом h. Приближенный метод решения краевой
задачи можно построить так, чтобы решение рассматривалось толь-
только в узлах сетки, т. е. в точках с координатами хт, уп. Для этого все
производные в формулировке задачи надо заменить пх конечно-
разностными аналогами. Исходная задача сводится такпм путем
к системе линейных алгебраических уравнений посредством так на-
называемой разностной схемы. К настоящему времени теория разност-
разностных схем основательно разработана (см., например [И.7]).
Рассмотрим кратко суть вопроса. Пусть нужно построить раз-
разностный аналог частной производной по х функции и(х, у) в точке
xh, yk (рис. 13.26); значения и(хт, уп) будем кратко обозначать
Mm, п. Возможны, например, правый аналог 1пр и левый 1Л:
7
«¦пр =
h
ди_
дх
"k,h
"fe-l.ft
h
Если теперь требуется построить вторую частную производную, то
пишут:
дх*
1
xh>Vh
¦д- ('пр 'л) —
_ uh+l,h
-2м
¦h,h'
¦ и
h—l,h
hf
A3.6)
Совершенно аналогично строится производная д2и/ду2. Поэтому
имеем следующий разностный аналог двумерного лапласиана v*,p:
uh+i,h + uh-i,k + uh,h+i
Поэтому, если, например, решается граничная задача
V|>vw=/ в S, м = 0 на L,
A3.7)
A3.8>
§ 13.1. ДИСКРЕТИЗАЦИОННЫЕ МЕТОДЫ
439
где фигурирует уравнение Пуассона, то для некоторого узла сетки
с номером (к, к) согласно A3.7) имеем:
— и*+1,» — »к, k+i + 4»к. к — Ик-i, к — «к, k-i = — h2fK к, A3.9)
что дает систему линейных алгебраических уравнений, матрица ко-
которой будет очень разреженной: для всех внутренних точек — неза-
независимо от числа узлов — количество отличных от нуля элементов
матрицы в строке равно пяти.
Разностные схемы — распространенный метод алгоритмизации
краевых задач. Поскольку аппроксимации подвергается дифферен-
дифференциальный оператор задачи, число узлов оказывается большим. По-
Порядки систем линейных уравнений весьма высоки, по сравнению,
например, с проекционными методами.
Но разреженность матриц помогает в ряде
случаев преодолевать эту трудность.
Для электродинамических задач разно-
разностные схемы применялись относительно
мало, что связано с рядом специфических
трудностей. Заметим, что в электродинами-
электродинамике разностные схемы иногда получают ')
на основе уравнений Максвелла в инте-
интегральной форме. Поясним это на приме-
примере объемной равномерной координатной
сетки (рис. 13.3). Точка М(х, у, z), для
которой составляются разностные соотно-
соотношения, лежит в средней точке куба с
ребром 2h. Применяя уравнение A.54) в рамках метода комплек-
комплексных амплитуд (d/dt-*-ш) и заменяя В на Н, возьмем в качестве
S заштрихованное сечение куба плоскостью х = const; направление
обхода его контура L показано стрелкой. При достаточно малом h
из A.54) приближенно следует
тх(х, у, z)= —2hJEmy(xJ у, z + h) +
Рис. 13.3
, у,
или
2hEmz(x, y+ h, z)+ 2hJEmy(x, у, z — h)— 2hJEmz(x, y — h,z),
A3.10)
= — JEmy(z + h) + Emz(y + h) +
+ Emy{z-h)-Emz{y-h).
Аналогично из A.53) получаем
= - Hmv (z+h) + Нт
Hmy (z — h) — Hmx (y - h). A3.11)
') См., папримср, M. Albani, P. Bernardi. A numerical method based on the
discretization of Maxwell equations in integral form II IEEE Trans.— 1974.—
V. MTT — 22, N 4.— P. 446—449.
440
ГЛ. 13. ДИСКРЕТИЗАЦИЯ И ДЕКОМПОЗИЦИЯ
Чтобы достроить систему разностных соотношений, нужно еще вы-
выполнить подобные же операции в плоскостях у = const и z = const,
проходящих через точку М(х, у, z).
В этом кратком изложении мы совершенно не затрагиваем хоро-
хорошо разработанные вопросы устойчивости и сходимости разностных
схем.
1В. 1.3. Конечные элементы. В процессе дискретизации можно
строить представление решения в некоторых малых областях, назы-
называемых конечными элементами. В п. 13.1.1 уже рассматривался при-
пример (рис. 13.16), позволяющий говорить о применении простейших
конечных элементов в виде носителей констант Д4; речь шла об ал-
алгоритмизации интегрального уравнения. Обычно под методом конеч-
конечных элементов, который называется также проекционно-сеточным,
понимают процесс Бубнова — Галеркина для некоторой краевой за-
задачи, в котором базис формируется из функций, определенных не во
всей области задачи, а на специально построенной системе носите-
носителей в ней. В сравнении с разностными схемами метод можно счи-
считать новым: его детальная разработка была произведена 10—15 лет
назад; наиболее удачно, на наш взгляд, метод изложен в моногра-
монографиях [И.8-9].
Обсудим сущность метода конечных элементов. На рис. 13.4а
показаны функции в виде констант на своих носителях (ср.
рпс. 13.16). По таким функциям ип можно было бы построить пред-
представление решения задачи uN A2.5), если оператор 3? — интеграль-
интегральный; выражение &ип при этом имеет смысл. Если же выполняет-
выполняется1) операция однократного дифференцирования, то нужно, чтобы
[L.Q.
a
L + 6
ДУЛ
Рис. 13.4
базисные функции ип были непрерывными. При этом конечно-эле-
конечно-элементное представление uN A2.5) строится из функций-крышек
(рис. 13.46), носители которых пересекаются. Что дает метод конеч-
конечных элементов в сравнении с обычным процессом Бубнова — Галер-
кина, когда базисные функции ип определены во всей области зада-
задачи? Главное — это разреженность матрицы L в A2.8). Действитель-
Действительно, будут отличны от нуля только те из элементов Lkn = {3?ип, uk),
которые образованы функциями-крышками ип соседних (пересекаю-
(пересекающихся) носителей.
') Обычно после преобразовапия (Sun, Uk) интегрированием по частям.
§ 13.2. ДЕКОМПОЗИЦИОННЫЙ ПРИНЦИП
441
Существуют разные способы построения конечных элементов на
поверхности и в объеме. Часто используется треугольная сетка, удоб-
удобная, в частности, в случае криволинейной границы (рис. 13.4s). При
этом базисные функции можно строить в виде
и» = ап + Ъпх + спу, A3.12)
где константы а„, Ъп и с„ однозначно связаны со значениями ип
в узлах (вершинах треугольника). Совокупность всех узловых зна-
значений образует неизвестный вектор решения. Весьма существенно,
что представление uN A2.5) в этом случае непрерывно. Представле-
Представления типа A3.12) образуют линейные конечные элементы; можно
построить квадратичные элементы и элементы более высокой
степени.
При алгоритмизации электродинамической задачи Е„ и Н„ в
A2.17) или A2.18) строятся так, что их координатные составляю-
составляющие (Епх, Епу и т. д.) имеют конечно-элементное представление.
В отличие от базисов (EJ и Ш„}, использовавшихся в п. 12.2.3,
в данном случае существует возможность получить Е„ и Н„, удов-
удовлетворяющие требуемым условиям на внутренних границах разде-
раздела сред.
Дальнейшее развитие дрискретизационных методов связано с де-
декомпозиционным принципом, который обсуждается ниже.
§ 13.2. Декомпозиционный принцип. Математическое
моделирование сложных структур
13.2.1. Декомпозиция сложной структуры и рекомпозиция ее ма-
математической модели. Всякой электродинамической структуре мож-
можно сопоставить некоторую краевую задачу для уравнений Максвел-
Максвелла, затем в результате алгоритмизации (посредством применения
одного из обсуждавшихся выше методов) мыслимо получить матема-
математическую модель, реализуемую на ЭВМ. Однако конфигурационная
сложность, а также протяженность реальных технических объектов
очень быстро ставят предел такому прямому подходу: не только
существующие ЭВМ, но и те, которые ожидаются в обозримом бу-
будущем, оказываются недостаточно мощными. Но и относительно
простым объектам часто невыгодно сопоставлять краевую задачу,
формулируемую для структуры как единого целого. Это ведет к
слишком большому расходу машинного времени. Выходом из поло-
положения является расчленение структуры на независимо моделируе-
моделируемые части, автономные блоки. Такой подход называется декомпози-
декомпозиционным [И. 10].
Начнем с рассмотрения простого для понимания примера. Чтобы
построить математическую модель сложной волноводной структуры,
было бы нерационально формулировать краевую задачу для всей
области существования поля (рис. 13.5). Рассечем соединительные
442
ГЛ. 13. ДИСКРЕТИЗАЦИЯ И ДЕКОМПОЗИЦИЯ
волноводы поперечными плоскостями (они показаны штриховыми
линиями), в результате чего оказываются выделенными частичные
объекты А, В, С, ... Алгоритмизировать краевую задачу для каж-
каждого такого отдельного объекта гораздо легче. Сосредоточим внима-
внимание на объектах А и В. Рассматривая каждый из них с присоеди-
присоединением полу бесконечных волноводов, мы можем в результате реше-
а в
ния краевых задач определить их матрицы рассеяния S и S (см.
п. 11.3.1). Таким образом, имеем соотношения:
АА А ВВ В
Sc+ = с-, Sc+ = с-, A3.13)
в которые входят векторы падающих и отраженных волн для объ-
объектов А и В.
А В
Порядки матриц S и S вообще различны (пА Ф пв); они равны
количествам учтенных типов волн. Отмечая, что объекты А и В
Рис. 13.5
соединены волноводом (*), в котором учтено к волн, перепишем
равенства A3.13) следующим образом:
A3.14)
где порядок столбцов и строк выбран так, что последние к компо-
компонент каждого вектора относятся к волнам общего волновода.
Ясно, что волны общего волновода, которые являются падающп-
ми для объекта В, будут отраженными для объекта А (и обратно).
§ 13.2. ДЕКОМПОЗИЦИОННЫЙ ПРИНЦИП
443
Поэтому подвекторы
условиям связи:
cf и cf в A3.14) подчинены следующим
А+
-
= с2
с» = с2
A3.15)
Рассматривая последние клеточные строки равенств A3.14),
с учетом условий связи A3.15) получаем:
А А,
В , А А,
с+ = S21c+,
А В В ВВ.
С 2 О Cg :=z О С\ .
A3.16)
Решая эту систему уравнений относительно подвекторов общего ка-
канала, находим:
А , В I В А \-1 (В А А. В В,
t (/ S2iS22) [S22S21ct
\-1 (В А А.
) [S22S21ct
В,( А В \
¦- = 4 = [I — s22s22)
В \-1 (А А
А В В
A3 171
Посредством этих соотношений нетрудно исключить
A3.14). Результат запишем в следующей форме:
где
А± в±
ct и cf
из
A3.18)
АВ А
Sn = 51
АВ А
В А \-1 В А
— 1 В
АВ
АВ
?22 =
А В \-1 А
) S21,
А В \ — 1 А В
_ ?22?22j ?22?21_
A3.19)
Смысл состоит в том, что найдено соотношение между векторами
падающих и отраженных волн для того фрагмента волноводной
структуры АВ, который на рис. 13.5 заключен в штриховую рамку.
А, В
Действительно, подвекторы cf, cy охватывают падающие и отра-
отраженные волны именно для тех волноводов, которые пересекают рам-
рамку. Мы получили матрицу рассеяния для фрагмента, представляю-
представляющего собой объединение объектов А и В и названного АВ. Краткая
форма записи соотношения A3.18) имеет вид:
АВ АВ АВ
S с+= с~. A3.20)
Теперь ясно, как получить матрицу рассеяния всей структуры,
которую можно обозначить символом АВ... Е. Надо принять фраг-
444
ГЛ. 13. ДИСКРЕТИЗАЦИЯ И ДЕКОМПОЗИЦИЯ
мент АВ за новый объект А, а С за новый объект В и по формулам
A3.19) найти матрицу рассеяния расширенного фрагмента ABC.
Затем аналогично присоединяются объекты D и Е.
Итак, на первом этапе производится декомпозиция сложной
структуры и находятся матрицы рассеяния полученных ее частей,
автономных блоков (они анализируются независимо от того, куда
присоединены). На втором этапе выполняется декомпозиция мате-
математической модели полной структуры, т. е. получение ее матрицы
рассеяния по матрицам рассеяния автономных блоков. Формулы
A3.18) — A3.20) будем называть рекомпозиционными.
Почему расчленение структуры на автономные блоки и после-
последующая рекомпозиция вообще возможны, ведь казалось бы, при от-
отсечении связей должна теряться какая-то информация? Дело в том,
что описание автономных блоков при помощи матриц рассеяния ох-
охватывает все мыслимые режимы этих блоков, а объединение этих
матриц на втором этапе восстанавливает именно те связи, которые
реализуются в полной структуре.
Отметим, что вместо матриц рассеяния можно было бы также
использовать матрицы проводимости или матрицы сопротивления
[И. 10].
13.2.2. Декомпозиционные методы. Расчленение волноводной
структуры, показанной на рис. 13.5, на отдельно анализируемые
части довольно очевидно потому, что реально существуют соедини-
соединительные волноводы. Рассмотрим другую структуру (рис. 13.6а), ко-
которую можно алгоритмизировать, используя метод частичных обла-
областей (см. п. 12.3.2), поскольку в каждой из подобластей А, В, С
л
Рис. 13.6
и D легко построить базисы Трефтца. Так как внутренних границ
«сшивания» полей довольно много, процесс Трефтца приведет к си-
системе линейных алгебраических уравнений весьма высокого порядка.
Но эта трудность легко преодолевается путем применения декомпо-
декомпозиционного подхода.
Дело в том, что все подобласти можно рассматривать как авто-
автономные многомодовые блоки (АМБ), как это пояснено на рис. 13.66.
Для того чтобы сделать очевидным принципиальное сходство с преж-
прежней структурой (рис. 13.5), введем в рассмотрение виртуальные
каналы — бесконечно короткие волноводы, которыми якобы соеди-
§ 13.2. ДЕКОМПОЗИЦИОННЫЙ ПРИНЦИП
445
нены подобласти. По отношению к соответствующим входам
(рис. 13.66) каждая подобласть может быть охарактеризована по-
посредством матрицы S, У или Z; она может анализироваться отдель-
отдельно и фигурировать как автономный блок. Математическая модель
всего объекта (рис. 13.6а) получается путем рекомпозиционных опе-
операций, которые можно производить по формулам A3.19). Но более
удобным оказывается применение матриц проводимости. Такой под-
подход называется методом автономных многомодовых блоков (методом
АМБ); он был предложен недавно (см. [И.Ю]) .
Отметим, что к рассмотренной структуре можно применить и
другой декомпозиционный подход. Рассекая ее системой поперечных
плоскостей Si, ?2, S3 и &4, имеем между ними (рис. 13.7а) участки
1
2
Э
Рис. 13.7
регулярных волноводов (между плоскостями S% и Бъ заключен от-
отрезок волновода, частично заполненного диэлектриком). Каждый
стык регулярных волноводов можно охарактеризовать посредством
матрицы рассеяния, получение которой обсуждалось выше в
п. 12.3.2. Декомпозиционная схема имеет каскадный вид, рис. 13.76;
каждый нумерованный элемент отображает стык двух полубесконеч-
полубесконечных волноводов (первому и третьему элементам сопоставлены соот-
соответствующие стыки). Матрица расссеяния всей структуры находится
по формулам A3.19). Надо иметь в виду, что объединяемыми эле-
элементами являются не только стыки, как таковые, но и промежуточ-
промежуточные регулярные отрезки, также описываемые своими матрицами
рассеяния.
Далее, рассмотрим применение декомпозиционного подхода в слу-
случае так называемых интегральных схем (ИС) СВЧ [И.10—11]. На
рис. 13.8а схематически представлена некоторая микрополосковая
структура (см. § 7.5), которую можно разбить на ряд регулярных
отрезков при помощи системы поперечных сечений Si, ..., Si0 (слева
и справа показаны поперечные сечения микрополосковых линий на
входе и выходе). Это точно такая же линейная декомпозиция, как
и в случае, рассмотренном выше на рис. 13.7а. Декомпозиционная
схема на рис. 13.76 подходит и в данном случае: надо только уве-
увеличить число звеньев. В общем случае декомпозиция ИС СВЧ по-
446
ГЛ. 13. ДИСКРЕТИЗАЦИЯ И ДЕКОМПОЗИЦИЯ
яснена на рис. 13.86. Структура рассекается двумя системами вза-
взаимно перпендикулярных плоскостей (их следы показаны штриховой
линией). При этом она распадается на элементы, один из которых
отмечен звездочкой и показан отдельно справа. Выделенные эле-
элементы — автономные блоки, которые могут быть охарактеризованы
Рис. 13.8
своими матрицами рассеяния; поперечные сечения виртуальных вол-
волноводов, по отношению к которым вводится матрица рассеяния для
элемента *, показаны. Общий подход здесь тот же, что и в методе
АМБ. Однако построить математические модели отдельных автоном-
автономных блоков гораздо сложнее; здесь можно, например, сформулиро-
сформулировать и алгоритмизировать интегральные уравнения адмитансного и
импедансного типа (см. п. 12.3.3).
Из многочисленных примеров математического моделирования не-
нерегулярных элементов пленарных структур на основе линейной де-
декомпозиции ') рассмотрим два. На рис. 13.9 показаны результаты,
относящиеся к возбуждению полоскового резонатора щелевой ли-
линией (отрезок структуры представляет собой полосково-щелевую ли-
линию, рис. 7.29е). Размеры указаны в миллиметрах; для подложкэ
е = 9. Показано, как модуль коэффициента отражения основной
волны щелевой линии | S\[ | меняется с длиной полоскового элемен-
элемента. Данные получены для частоты /=10 ГГц. Отмечена длина I,
') В. В. Никольский, Т. И. Никольская // Изв. вузов. Радиофизика.— 1981.—
№ 12.—С. 1423—1458; препринт/ИРЭ АН СССР.—М., 1984.—№ 19 C91).— 71 с.
§ 13.2. ДЕКОМПОЗИЦИОННЫЙ ПРИНЦИП
447
равная кратному числу половины длины основной волны полоско-
полоскового типа полосково-щелевой линии (Л/2). Как видно, резонансы
имеют место при близких значениях I. Отметим, что при моделиро-
моделировании регулярной щелевой и полосково-щелевой линий в представ-
представлениях типа A2.51), A2.53) было около НО членов; в суммах типа
0,5
I I I 1 U 1 L*.
5 Л/2
10 Л 15
Рис. 13.9
ЗЛ/2 20 I
Рис. 13.10
A2.57) — одиннадцать (для щели) и семь (для полоски). При ре-
решении задачи дифракции учитывалось по семь собственных волн
каждой структуры.
448
ГЛ. 13. ДИСКРЕТИЗАЦИЯ И ДЕКОМПОЗИЦИЯ
§ 13.2. ДЕКОМПОЗИЦИОННЫЙ ПРИНЦИП
449
В качестве второго примера рассмотрим математическое модели-
моделирование так называемого согласующего трансформатора для волно-
водно-щелевых линий (рис. 13.10). Дан график изменения модуля
коэффициента отражения основной волны узкой линии в зависимо-
зависимости от длины промежуточного отрезка I при разных значениях ши-
ширины его щели d; размеры в миллиметрах, / = 11 ГГц, для подлож-
подложки е = 9. В представлениях типа A2.53) было взято около 100 чле-
членов, а в суммах типа A2.57)— от 10 до 20. В трех щелевых линиях
учитывалось от 6 до 15 собственных волн, однако результаты ока-
оказались очень близкими к одномодовым (учет только одной волны
в каждой линии). Как видно из рис. 13.10, согласование ( | S\{ \ = 0)
достигается при d = 4 мм и I = 5,08 мм.
Интересно следующее. Если пользоваться упрощенным подходом,
базирующимся на теории длинных линий, то согласование ожидает-
ожидается, когда длина среднего отрезка — четверть волны, а его волновое
сопротивление Wa есть среднее геометрическое волновых сопротив-
сопротивлений согласуемых линий. Расчеты показали, что четверть волны
в средней линии составляет 5,0806 м. При этом волновые сопротив-
сопротивления трех линий, получаемые по формуле G.134), равны: Wai =
= 206,4675 Ом, Wn2 = 384,2857 Ом и Р^л3 = 711,2656 Ом, так что
(Р^Л1^лзI/2 = 383,2143 Ом « Wn2- Таким образом, в данном случае,
элементарная теория оказывается удовлетворительной.
13.2.3. Метод минимальных автономных блоков- На основе де-
декомпозиционного подхода был разработан новый дискретизационный
метод [И.10]. Он был построен специально для задач электродина-
электродинамики (что, разумеется, не несет каких-то специфических ограниче-
ограничений). Как в методе конечных элементов (см. п. 13.1.3), в данном
случае строится система элементарных подобластей. Однако в отли-
отличие от него поле внутри этих подобластей, называемых минималь-
минимальными автономными блоками (МАБ), точно удовлетворяет уравнени-
уравнениям Максвелла, так что требуется только сшить представления реше-
решения на границах соседних подобластей. В этом смысле метод конеч-
конечных элементов и метод МАБ соотносятся как процессы Бубнова —
Галеркина и Трефтца. Но этим вопрос не исчерпывается. В. методе
МАБ каждая элементарная подобласть выступает как независимая
электродинамическая система; она описывается своей матрицей рас-
рассеяния, известной заранее, независимо от того, в какой конкретной
структуре эта подобласть выделена. Это автономный блок. Мини-
Минимальным он называется потому, что минимизирован базис, в кото-
котором представляется граничное поле.
Поясним сказанное. Однородную область некоторой электродина-
электродинамической структуры можно разбить на малые кубические объемы
(или параллелепипеды), как показано на рис. 13.11а. Отдельный
куб мы вправе рассматривать как среднюю часть соединения шести
условных (виртуальных) волноводов (рис. 13.116), по отношению
к которым он характеризуется многомодовой матрицей рассеяния.
Чем меньше кубические объемы, тем с большим основанием можно
считать электромагнитное поле однородным на каждой грани (но,
конечно, его направление произвольно). При соединении всех куби-
кубических объемов виртуальные волноводы имеют бесконечно малую
длину, поэтому их природа условна. Если все такие волноводы взять
с периодическими граничными условиями па оболочке, то, как не-
нетрудно убедиться, в спектре собственных волн будут присутствовать
\
I ,
I
!
Z.-A
Рис. 13.11
две однородные Г-волны ортогональных поляризаций. Этих двух
ьолн достаточно для представления любого однородного тангенциаль-
тангенциального поля, а следовательно, малый однородный куб описывается все-
всего лишь двухмодовон шестиканальной матрицей рассеяния (две
волны в каждом канале, соответствующем грани). Чем меньше раз-
размеры куба, тем данное описание будет все более точным при дпск-
ретнзапии любой электромагнитной структуры.
Матрицы рассеяния различных МАБ (не только кубических и
не только для случая изотропной среды) известны [И.10]. Примене-
Применение метола МАБ сводится к использованию рекомпозициопиых фор-
формул A3.19) и еще нескольких стандартных действий. В отличие
от других дпекретнзацпонпых методов (см. § 13.1)—в силу деком-
декомпозиционного характера — метод МАБ не требует формулирования
системы алгебраических уравнений, отвечающей структуре в целом.
Выпишем без вывода матрицу рассеяния кубического МАБ в случае
изотропной среды:
<:¦
( 0
а
Р
Р
Р
-Р
0
0
0
0
0
( 0
а
0
Р
Р
-Р
Р
0
0
0
0
0
0
р
р
0
а
0
0
и
0
0
0
-Р
Р
Р
Р
а
0
0
0
0
0
0
0
Р
-Р
Р
-Р
0
0
0
а
0
0
Р
Р
0
0
-р
р
0
0
а
0
0
0
Р
р:
0
0
0
0
0
0
0
0
0
а
-Р
Р
Р
Р
0
0
0
0
0
0
а
0
Р
-Р
Р
Р
0
0
0
0
р
р
-р
р
0
а
0
0
0
0
0
0
Р
Р
Р
-Р
а
0
0
и
0
0
-р
р -
0
0
р
р
0
A
0
а
0)
0
Р
-Р
0
0
р
р
0
0
а
0)
A3.21)
29 В. В. Пш ольский, Т. II. Никольская
450
ГЛ. 13. ДИСКРЕТИЗАЦИЯ И ДЕКОМПОЗИЦИЯ
ё 13.2. ДЕКОМПОЗИЦИОННЫЙ ПРИНЦИП
451
где
а =
т-г
J,
р = i
T-I2
__2_ginM T
А — длина ребра куба, к = -^ l/eu. Нумерация позиций в A3.21)
соответствует нумерации граней кубического МАБ (рис. 13.11s),
0,6 Л.
1,0
\ i\\!f
1 Z
причем сначала перечисляются волиы первой, а затем — второй по-
поляризации: сплошные и штриховые линии векторов еР(,-, (р = I, 2;
г = 1, 2 6).
Для двумерных задач вместо A3.21) получается матрица рас-
рассеяния только четвертого порядка.
Приведем лишь один пример применения метода МАБ [И. 10] (из
первой публикации по реализации метода, 1977 г.). Рассматривается
дифракция основной волны Ню прямоугольного волновода на ди-
диэлектрическом параллелепипеде полной высоты (рис. 13.12), прони-
проницаемость которого варьировалась. Количество МАБ менялось в зна-
значительных пределах. Иптереспо, что даже всего при четырех МАБ
в поперечном сечении волновода (Nx = 4) получаемые результаты
сохраняют смысл, что было бы невозможно, например, в случае при-
применения конечно-разностного метода. При Nx > 16 МАБ-модель и
высокого порядка проекционная модель дают практически одинако-
одинаковые результаты.
13.2.4. Системы автоматизированного проектирования устройств
СВЧ. В современной практике математические модели электродина-
электродинамических объектов, например, устройств техники СВЧ, объединяют-
объединяются в специально организованные системы взаимодействующих ЭВМ-
программ. Так строятся системы автоматизированного проектирова-
проектирования (САПР) устройств СВЧ [И.11].
Существующие САПР устройств СВЧ в значительной степени ис-
используют различные упрощенные эвристические средства моделиро-
моделирования, но по мере развития ЭВМ все большее практическое значение
приобретают строгие электродинамические методы моделирования.
В САПР неизбежно применение принципа декомпозиции сложно-
сложного объекта на относительно простые автономные блоки. Блоки эти
унифицируются п называются базовыми, элементами (БЭ). Ядро
САПР составляет библиотека базовых элементов (ББ), т. е. совокуп-
совокупность программ, реализующих их математические модели (а также
выполняющих некоторые иные функции). Модель сложного устрой-
устройства в целом формируется компилятором рекомпозиции (КР). Ос-
Основная роль этой программы — нахождение матрицы рассеяния
устройства в целом по матрицам рассеяния базовых элементов, по-
потенциально содержащихся в ББ.
Схема, поясняющая функционирование САПР устройств СВЧ,
показана на рис. 13.13. Ввод исходной информации осуществляется
при помощи формализованного задания (ФЗ), которое составляется
на специальном проблемно-ориентированном языке, т. е. посредством
системы символов, разработанной для данной САПР. Обычно при
этом считаются известными общая структура и состав БЭ проекти-
проектируемого объекта. Не определены только их параметры, т. е. геомет-
геометрические размеры, параметры сред и т. п. Исходная разработка
структуры проектируемого устройства, называемая структурным син-
синтезом, как правило, еще не может быть автоматизирована. В ФЗ
содержится также ряд директив, определяющих режим проектиро-
проектирования, включая выбор параметров программ БЭ (например, объемы
Пазпсон для проекционных моделей и типы разбиения облаете», по-
построение сеток и т. п.— для дискретизационпых).
29*
452
ГЛ. 13. ДИСКРЕТИЗАЦИЯ II ДЕКОМПОЗИЦИЯ
§ 13.2. ДЕКОМПОЗИЦИОННЫЙ ПРИНЦИП
453
САПР предусматривает и отказ от моделирования, когда пара-
параметры структуры пзвестны заранее и введены посредством ФЗ. Тог-
Тогда входная информация отсылается в систему проектирования кон-
конструкции (ПК); последняя производит автоматизированный выпуск
Исходная
структура
директивы
алгоритмизации
<
Состав па-
раметробБЭ
ФЗ
\
у^Нужно ч
^^вание 1^^
]да
^ нет
Целевые
характеристики
Лирептивы
проектирования
-з»-л ПК
НужнсГ _
'ли оптимиза-q> >| ftp
библио тека
Компилятор
оптимизации
•к ПК
стПК
я ФЗ
Нужно л
редактиро —
вание?
да
Рис. 13.13
чертежей или, например, такой технологически ориентированной ин-
информации, которая непосредственно используется для управления
производственным процессом; изготовляются, например, фотошабло-
фотошаблоны для ИС СВЧ.
В режиме анализа данные ФЗ поступают в КР. Эта программа
при информационном обмене с ББ формирует математическую мо-
модель исходного объекта. Вычисляются и выводятся для контроля
необходимые технические характеристики, например, частотные за-
висимосш элементов матрицы рассеяния. Если они оказываются не-
неудовлетворительными, то производится редактирование ФЗ, после
чего анализ повторяется. Такой процесс называют режимом диалога
с системой, а также эвристическим синтезом объекта. Проектирова-
Проектирование завершается обращением к ПК.
В ряде случаев возможен полностью автоматизированный синтез
на основе использования включенных в САПР алгоритмов оптимиза-
оптимизации. Тогда исходными данными являются целевые характеристики,
содержащиеся в ФЗ. При помощи направленного поиска на множе-
множестве решений задачи анализа объекта синтезируется оптимальная
конструкция: выработанная информация отсылается в ПК для вос-
воспроизведения.
На современном уровне режим автоматизированного синтеза реа-
реализуется только при весьма упрощенном моделировании; при этом
может оказаться приемлемым требуемое машинное время. Что ка-
касается режима диалога, то его привлекательность состоит в возмож-
возможности использовать неформализуемый опыт инженера.
УПРАЖНЕНИЯ
1. Объяснить, почему в представлении поля типа A2.1) коэффициенты при
Е„ и Н„ обязательно одинаковы, а в A2.2) —различны?
2. Объяснить различие проекционных и дискретизационных методов. По-
Почему метод МАБ является и дискретизационным, и проекционным?
3. Внутрь прямоугольного резонатора помещен диэлектрический паралле-
параллелепипед (рис. 13.14а). Выписать элементы матриц Э, М и Q в A2.24) и тем
Ь
\
L
\
\ 1 а
\
Ъ
\
i\
\ъ\\
а
\\_
г л
У
Ъ
У1
О з:7 а
а
Рис. 13.14
самым подготовить для программирования задачу о собственных колебаниях
резонатора с диэлектрическим телом.
4. Выполнить аналогичные действия в случае задачи о регулярпом волно-
волноводе с диэлектрическим стержнем (рис. 13.146) с целью алгоритмизации за-
задачи о собственных волнах такого волновода.
5. Подготовить для программирования задачу о нахождении матрицы Y
(и затем S) в случае волновода с диэлектрическим включением, показанного
на рис. 13.14в.
454
ГЛ. 13. ДИСКРЕТИЗАЦИЯ И ДЕКОМПОЗИЦИЯ
6. Подготовить для программирования одну из задач о волноводных диаф-
диафрагмах, показанных на рис. 13.15а, б.
7. При помощи рекомпозиционных формул найти матрицу рассеяния в сле-
следующих случаях: а) прямоугольный волновод на некотором участке заполнен
Рис. 13.15
диэлектриком (между плоскостями г = 0иг = 1); б) тот же волновод перего-
перегорожен идеально проводящей плоскостью, матрица рассеяния находится на рас-
расстоянии I от перегородки.
ЧАСТЬ 5
ОСОБЕННОСТИ ПОЛЕЙ В РАЗЛИЧНЫХ СРЕДАХ.
РАДИОВОЛНЫ В ПРИРОДНЫХ УСЛОВИЯХ
Глава 14
ПОЛЯ И ЗАРЯЖЕННЫЕ ЧАСТИЦЫ. МОДЕЛИ СРЕД
§ 14.1. Стационарные поля
14.1.1. Электростатическая модель диэлектрика (А). В п. 1.3.2
было дано общее представление о процессах поляризации и намаг-
намагничивания. Напомним, что взаимодействие электромагнитного поля
с веществом в макроскопической электродинамике определяет раз-
различие векторов D и Е, В и Н. Оно характеризуется существованием
векторов поляризованности и намагниченности Р и М, входящих в
соотношения A.70).
Микроскопические процессы в веществе сложны и разнообразны.
Разумеется, они требуют трактовки с позиций квантовой физики.
Но и классические представления сохраняют ценность для понима-
понимания основных черт этих процессов.
С точки зрения электростатики, поляризация диэлектрика есть
изменение состояния некоторой системы диполей; в п. 2.2.4 такая
концепция уже обсуждалась на простом примере. Вернемся к элек-
электростатической модели диэлектрика.
Заряды внутри атомов (ионов) и молекул, которые не могут пе-
перемещаться на макроскопически заметные расстояния, называются
связанными. Поскольку в электростатике входят в рассмотрение
только идеальные (лишенные электропроводности) диэлектрики, то
можно сказать, что они представляют собой электрически нейтраль-
нейтральные (см. п. 2.2.1) системы связанных зарядов. Молекулы некоторых
типов в силу симметрии распределения заряда не обладают диполь-
ным моментом в отсутствие внешнего электрического поля, но под
влиянием поля приобретают его; это схематически пояснено на
рис. 14.1а. Диэлектрик в таком случае называют неполярным. В от-
отличие от этого каждая молекула полярного диэлектрика с самого
начала обладает некоторым моментом ро. При этом во внешнем
электростатическом поле — гораздо легче, чем деформация — проис-
происходит переориентация молекул (рис. 14.16). В обоих случаях ре-
результирующий момент молекулы есть
р = ро + Ар, A4.1)
где ДрИЕ, но ро Ф 0 только в случае полярного диэлектрика. В прак-
практически широких пределах дополнительный дипольный момент Ар
456
ГЛ. 14. ПОЛЯ И ЗАРЯЖЕННЫЕ ЧАСТИЦЫ. МОДЕЛИ СРЕД
пропорционален напряженности внешнего поля, т. е. Ар = аЕ. По-
Поэтому говорят, что деформирующая или ориентирующая сила поля
уравновешивается как бы силой упругости. Таким образом, содержа-
содержащиеся в макроскопической области AF молекулы будем рассматри-
рассматривать как систему диполей, которая обладает моментом
N N
Рду = 2 Pi = 2 Poi + Л'ссЕ = ЛгаЕ, A4.2)
i=l г=1
где N — число молекул. Здесь предполагается, что в случае поляр-
полярного диэлектрика сумма начальных моментов ро« обращается в нуль
в силу хаотичности ориентации молекул.
Относя момент рду к объему AF и переходя к пределу (при из-
известных допущениях, см. п. 1.1.1), получим плотность электрическо-
электрического момента поляризованного диэлектрика в некоторой точке:
A4.3)
Р = lim ^ = аЛг'Е,
где N' = dN/dV есть количество молекул в единице объема.
Какой смысл имеет вектор Р A4.3)? Обратимся к п. 2.2.4. Там
на простом примере было показано, что плотность электрического
е=о
О
Рис. 14.1
момента есть вектор электрической поляризации Р B.61). Таким
образом, Р = Р. Сопоставляя A4.3) и A.72), видим, что %3 = ccN'/eq-
Можно также получить
divP = -pCB, A4.4)
где рсв — плотность связанных зарядов диэлектрика.
Дополним рассуждения из п. 2.2.4 следующим более общим ана-
анализом.
ВЫВОД. Пусть в однородный диэлектрик, относительная про-
проницаемость которого есть е, внесено некоторое распределение заряда
с плотностью р. Воспользовавшись формулой B.28), мы можем вы-
вычислить электростатический потенциал в произвольной точке М(т):
A4.5)
§ 14.1. СТАЦИОНАРНЫЕ ПОЛЯ
457
Но ф(г) можно найти и другим путем. Рассматривая диэлектрик
как систему связанных зарядов в вакууме, запишем:
ср (г) = Фо (г) + Ф„ (г) =
0
^гтТ dv' + фд (Г>' A4-6)
где фо(г)—потенциал, создаваемый заданным распределением заря-
заряда в вакууме, а фд(г)— потенциал системы диполей.
При вычислении фд(г) учтем, что согласно A4.3) каждый эле-
элемент среды AF' обладает моментом p' = P(r')AF' и создает потен-
потенциал Афд(г), который легко определить, отправляясь от формулы
B.46). В последней надо лишь учесть перенос начала координат
в точку <?(г')- Запишем: ^
Аф„ (г) = ? <Г ) Го". » AF'
4лео| г — г' j
и, далее,
A4.7)
Здесь, как и в A4.5) и A4.6), интегрирование распространяется
на всю среду.
Подынтегральное выражение в A4.7) преобразуем при помощи
формулы A.25), учитывая, что
г — г'
(равенство следует из A.28) и B.2)). Затем применяется теорема
Остроградского — Гаусса A.33). Таким образом, имеем
А поскольку поверхность S здесь надо рассматривать как отнесен-
отнесенную в бесконечность границу (которую удобно считать сфериче-
сферической), то поверхностный интеграл обращается в нуль (см. § 2.4).
В результате из A4.6) и A4.8) получаем
Ф (г) = 1—
* х I 4ле
4ле0.
Р(г')—div'P(r')
A4.9)
Теперь можно сопоставить два различных представления одного
и того.же потенциала A4.5) и A4.9). Мы видим, что
р/е = р — div P.
Привлекая A.51), A.67) и A.70), получаем
div P = div P. A4.10)
458
ГЛ. 14. ПОЛЯ И ЗАРЯЖЕННЫЕ ЧАСТИЦЫ. МОДЕЛИ СРЕД
Это значит, что плотность электрического момента поляризованного
диэлектрика Р и поляризованность (электрическая поляризация) Р,
введенная в п. 1.3.2, совпадают с точностью до аддитивной соленои-
дальной величины, которая несущественна. Мы отождествляем Р и Р.
Наконец, отметим, что по смыслу выражения потенциала B.28)
величину р — div P, стоящую в числителе подынтегрального выра-
выражения A4.9), надо истолковать как плотность полного заряда в ва-
вакууме. Кроме заданного заряда, распределенного с плотностью р,
там имеются еще связанные заряды дипольной модели диэлектрика,
которым припишем плотность рсв. Как видно, эта величина равна
—div P, что приводит к формуле A4.4). ¦
В заключение отметим, что для A4.4) интегральным аналогом
является равенство
Р ds = - qc
A4.11)
(см. вывод A.55) из A.51) в п. 1.2.1). Пусть S в A4.11)—поверх-
A4.11)—поверхность некоторого диэлектрического тела V, расположенного в ваку-
вакууме, так что вне этого объема Р = 0 и рсв = 0. Тогда из A4.11)
следует
Pvo = -6». A4.12)
Действительно, надо лишь повторить вывод граничного условия
A.83) из A.55). Напомним, что соотношение A4.12) ранее уже
было получено в частном варианте в виде формулы B.60).
14.1.2. Движение частиц в стационарных полях (А). Согласно
законам классической механики ускорение d2r/dt2 материальной точ-
точки с массой т под действием силы F есть F/m. Таким образом, для
частицы с зарядом q согласно A.45) можпо написать следующее
уравнение движения в электромагнитном поле:
*
A4.13)
Уравнение сохраняет смысл при относительно малых, нерелятиви-
нерелятивистских скоростях (\di/dt\ <. с). Вообще говоря, уравнение движе-
движения A4.13) следует рассматривать вместе с уравнениями Максвелла,
так как поле, действующее на частицу, само зависит от ее движе-
движения: соответствующий сторонний ток возбуждает поле.
Пользуясь уравнением A4.13), легко анализировать движение
частиц в приближении заданного стационарного поля, что является
допустимым при нерелятивистских скоростях. Можно, например,
рассматривать движение в электрическом поле (В = 0) или магнит-
магнитном (Е = 0).
Пример 1. Пусть Е = 0 и В = zu\x.qH, а пачальпоо положение и скорость
частицы характеризуются векторами г@) и г'@).
§ 14.1. СТАЦИОНАРНЫЕ ПОЛЯ
459
Учитывая заданные условия в правой части A4.13), перепишем это урав-
уравнение в координатной форме:
"Га — М^ ~~гН-тг = 0, —ъ + Н-„"Г- Н-тг = 0, —г = 0. A4.14)
.*
Из первых двух уравнений A4.14) исключаем компоненты скорости rx = dx/dt
ТЯГ
¦ н
У
Рис. 14.2
и (в другом варианте) r'y = dy/dt. При этом получаются следующие два урав-
уравнения второго порядка относительно гх и г :
df
Здесь введено обозначение:
dtL
A4.15)
A4.16)
Как известно, общие решения уравнений A4.15) имеют вид
г'х =А cos fif + В sin Qt, r'y= С cos Qt+DsinQt. A4.17)
При подстановке A4.17) в A4.14) выясняется, что С = В и D = —А, а из
A4.17): А = г'х @) и С = гу @). Поэтому придадим решениям A4.17) следую-
следующую форму:
dx dy
dJ=v± cos (Qt - Ф((), -Jt = -v± sin (Qt - Фо),
A4.18)
где Р^ = К frx@)]2 "l" [Гн^]2 — абсолютное значение скорости в плоскости
хОу и q>e=arctg[r^(O)/r;(O)].
В результате интегрирования A4.18), а также третьего уравнения из
A4.14) получаем
v ,
~ фо) +7Гsin фо + х
A4.19)
= ^ cos (Qt - Ф())- ИЛ cos ф0 + у @) 2 = ^
где r'z = dz\dt.
460
ГЛ. 14. ПОЛЯ II ЗАРЯЖЕННЫЕ ЧАСТИЦЫ. МОДЕЛИ СРЕД
Из первых двух уравнений A4.19) легко получить
= Ы)- A4-20)
Это уравнение окружности радиуса R = v±/Q. Если rz @) = 0, то частица
движется в плоскости z = z@) по данной окружности с круговой частотой ?2
A4.115), как показано на рнс. 14.2а. Если же rz @) Ф 0, то это будет дви-
движение по винтовой линии (рис. 14.26). ¦
Итак, под влиянием лоренцевой силы заряженные частицы «за-
«закручиваются» постоянным магнитным полем в перпендикулярной
ему плоскости. Далее, наряду с магнитным полем введем в рассмот-
рассмотрение постоянное электрическое поле.
Пример 2. Пусть Е = уо-Е1 и В = zo\ioH; как и раньше, начальные ус-
условия заданы векторами г@) и г'@).
Теперь вместо A4.14) имеем
dfx
dfi~
dx
'~dl~
dt
Я
m
A4.21)
где использовано обозначение A4.16). Исключая ry = dyfdt, получаем относи-
тельно rx = dx/dt
Отсюда
,2 '
d г„
d?
= Q
r'x = A cos Ш + В sin Ш + -j=j- -^-
A4.22)
A4.23)
(правая часть построена как сумма общего решеппя однородного уравнения и
частного решения неоднородного). Привлекая первое и третье уравнения из
A4.21), находим
г'у = - A sin Qt + В cos Qt, r'z e= dz/dt = r'z @). A4.24)
Интегрирование уравнений A4.23) и A4.24) дает ')
* = Ж sin (Qt ~ Фо) + it sin ^o + ПГН f + x <°) -
= ^_ cos (Q* -
^. cos Ф|) + у @),
A4.25)
') Здесь v± и фо связаны с Л и В, как в предыдущем примере (начальная
скорость в плоскости .гОу есть \± -\Е/П)
§ 11.1. СТАЦИОНАРНЫЕ ПОЛЯ
461
Вдоль оси ;, как п в предыдущем примере, происходит лишь равномерное дви-
движение. Пусть г2 @) = 0. Рассматривая первые два уравнения A4.25), отме-
отметим, что это параметрические уравнения циклоиды. Движение в плоскости
ХТХ1Г
H=z0H
Рис. 14.3
я0у совершается по циклоиде (рис. 14.3). Из 14.25) нетрудно получить:
cos ф» ~ у
if
.Можно представить сеие, что частица движется но окружности радиуса R =
= v±/Q с круговой скоростью Q, по центр этой окружности смещается вдоль
иен х с постоянной скоростью Е1\\с,Н. Ш
14.1.3. Уравнение движения намагниченности (Б)- Подобно то-
тому как поляризовапность Р есть плотность электрического момента
среды (см. п. 2.2.4 и п. 14.1.1), намагниченность М — плотность
магнитного момента. Происхождение магнитного момента материаль-
материальных частиц имеет простое классическое объяснение: орбитальные
движения электронов в атомах и их спины можно истолковать как
круговые токи, которые проявляют себя как магнитные диполи.
Напомним, что замкнутому току соответствует магнитный момент,
определяемый формулой B.98). Отождествляя в B.98) и A.48)
орты Vo и zo, получаем следующее выражение момента силы К, дей-
действующего на магнитный диполь в поле Н:
К = [ш, Н]. A4.27)
Для частицы, обладающей магнитным моментом т, можно записать
следующее соотношение
т = чЬ, A4.28)
где L — момспт количества движения, а ] — постоянная. В частно-
частности, для спина электрона f = —2,21 • 105 (А/м)'1 с. На основании
462
ГЛ. 14. ПОЛЯ II ЗАРЯЖЕННЫЕ ЧАСТИЦЫ. ПОДЕЛИ СРЕД
известного закона классической механики
m(t+At)
Рис. 14.4
н
A4.29)
с учетом A4.27), A4.28), получаем уравнение движения магнитного
момента рассматриваемой частицы в поле Н (рис. 14.4а)
? = V[m,H]. A4.30)
По своему смыслу вектор dm/dt должен быть направлен, как
приращение Am = m{t + At)- m{t) при At-+O. Из A4.30) видно,
что производная dm/dt перпенди-
перпендикулярна плоскости, в которой ле-
лежат векторы m и Н. Поэтому каж-
каждое бесконечно малое приращение
вектора m оказывается касатель-
касательным к окружности, показанной на
рис. 14.4а. Это значит, что при
фиксированном начале конец маг-
магнитной стрелки m движется по
данной окружности; подобным об-
образом смещается ось волчка в гра-
гравитационном поле. Рассмотренное
движение называется прецессией.
Легко установить, что в этом движении длина вектора m не ме-
меняется. Действительно, из A4.30) имеем:
dm
mdF =
> HI =
т. е.
d{m2)/dt = 0. A4.31)
Постоянным остается угол ¦& (рис. 14.46) и линейпая скорость кон-
конца стрелки v=\dm/dt\ = \1[m, H] I = lymHsini}]. При этом абсо-
абсолютное значение угловой скорости Q есть Q = v/R, где R = m sin ft.
Поэтому
fl = —][Н. A4.32)
При ^ < 0 направление вращения составляет правовинтовую систе-
систему с вектором Н. i
От уравнения движения магнитного момента частицы A4.25)
непосредственно переходим к уравнению движения намагниченности
среды:
-g- =у[М, Н].
A4.33)
При этом (ср. п. 14.1.1) вектор М отождествляется с М = iV'm.
На практике вместо A4.33) приходится использовать несколько
более сложные уравнения, учитывающие также потери энергии в
§ 14.2. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
463
среде. Широко известно уравнение Ландау — Лифшица
A4.34)
содержащее по сравнению с A4.33) так называмый диссипативный
член. Легко убедиться, что этот член влияет на амплитуду прецес-
прецессии, не изменяя величины М. Параметр г| > 0 можно рассматри-
рассматривать, как экспериментально определяемый параметр среды.
§ 14.2. Гармонические колебания (А)
14.2.1. Простейшая модель плазмы. Плазма, т. е. ионизован-
ионизованный электрически нейтральный газ, в дальнейшем (гл. 15) будет
иптересовать нас как среда, в которой распространяются радиовол-
радиоволны. Пусть задано некоторое гармонически колеблющееся электромаг-
электромагнитное поле Е, Н. Предстоит описать плазму, введя в рассмотрение
ее диэлектрическую проницаемость.
Плазма предстает как система электронов, ионов и нейтральных
молекул; в первом приближении их соударения не учитываются.
Под влиянием поля Е, Н все заряженные частицы совершают гар-
гармонические колебания. Поэтому наряду с комплексными амплиту-
амплитудами векторов поля Ет, Нт будет также фигурировать комплексная
амплитуда гт смещения частицы. Движение частицы можно описать
посредством уравнения A4.13), где лорепцевой силой пренебрегают,
поскольку отношение \[dr/dt, B]| к Е равно г/с. В комплексных амп-
амплитудах это уравнение принимает вид:
m
A4.35)
Отсюда находится rm.
Далее выразим комплексную амплитуду электрического момента
pmAv системы N различных частиц плазмы, находящихся в объеме
AV. Воспользовавшись второй формулой B.49) и следующим из
[A4.35) выражением rm, пишем:
N
РтдУ =
Е
N
V
A4.36)
1=1
1=1
При этом допустимо сохранить только те члены суммы, которые
соответствуют электронам: вклад отброшенных членов невелик из-за
большой массы ионов. Все суммируемые члены оказываются одина-
одинаковыми, и мы получаем:
РтдУ = —
5
(от
A4.37)
464
ГЛ. 14. ПОЛЯ II ЗАРЯЖЕННЫЕ ЧАСТИЦЫ. МОДЕЛИ СРЕД
где т и е — масса п заряд электрона, a Na — чпсло электронов в
объеме AV.
Переходя к пределу, как в A4.3), найдем комплексную ампли-
амплитуду вектора поляризованности среды:
р __
am
A4.38)
где N' — чпсло электронов в единице объема. Теперь иа основании
A.72) и A.73) сразу находим электрическую восприимчивость %'
и относительную диэлектрическую проницаемость е плазмы:
х» = -eW/eoco2™, е = 1 - e2N'/&0&2m. A4.39)
Нередко пишут также:
е = 1-(й)р/соJ, A4.40)
где о)р = \e\YN /гот называется плазменной частотой, или
е = 1 - 80,67V'//2. A4.41)
В последней формуле частота / выражена в герцах, если N' — ко-
количество электронов, приходящихся на 1 м3 (либо / измеряется в
кГц, а чпсло электронов берется в 1 см3).
Мы видим, что в построенной модели плазмы диэлектрическая
проницаемость вещественна. Следовательно, рассмотренная система
колеблющихся частиц в среднем не отбирает энергии поля. Приме-
Примечательно, что е может быть отрицательной величиной.
14.2.2. Поглощающая плазма. Произведем уточнение построенной
модели плазмы. При столкновении электронов с нейтральными мо-
молекулами и ионами происходит, можно сказать, потеря импульса
электронами. Это вызывает поглощение энергии электромагнитного
поля. Будем считать, что электрон, движущийся со скоростью dr/dt,
полностью передает при столкновении свой импульс mdr/dt неко-
некоторой массивной частице. Если среднее число соударений электро-
электронов с тяжелыми частицами за единицу времени есть v, то в урав-
уравнение A4.13) надо ввести дополнительный член xm dr/dt, посред-
посредством которого учитывается соответствующее изменение импульса
в единицу времени. Поэтому в комплексных амплитудах вместо
A4.35) теперь будем иметь:
— co2r
= — Em.
A4.42)
Определяя прежним способом поляризованпость среды, выразим
г,„ не из A4.35), а из A4.42). Это дает:
1 ,4
р __?1
m
am о) — jv
A4.43)
§ 14.2. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
465
Таким образом, вместо A4.39) теперь:
А\"
8о(от о) — ;
8=1 —
е~ У
е to hi о) — ;v
A4.44)
Из A4.44) следует, что комплексная диэлектрическая проницае-
проницаемость плазмы е = е' — i&" имеет следующие действительную и мни-
мнимую части:
е" AT'v
е' = 1 —
¦ i
-r v
ЕЛМ ((О" -f- V")
A4.45)
Поскольку е " > 0, то среда, действительно, является поглощающей.
Можно положить г" = а/шео (ср. C.33)) и выразить проводимость
плазмы:
/m(a2 + v2). A4.46)
14.2.3. Модель диэлектрика. Напоминаем, что при обсуждении ста-
статической модели диэлектрика (см. п. 14.1.1) связанные заряды рас-
рассматривались как частицы, на которые действует не только поле,
по и пропорциональная смещению «восстанавливающая» сила, по-
подобная силе упругости. Действие ее на частицу можно учесть, вве-
введя в правую часть уравнения A4.13) член — $г/т, где р > 0. Пере-
Переходя к уравнению A4.42), перенесем соответствующую комплекс-
комплексную амплитуду — $гт/т в левую часть равенства:
- orrm + fcovr,» + ¦?- rm = -О- tm. A4.47)
m m m m in '
Полученное уравнение лежит в основе модели неполярного ди-
диэлектрика. Параметр v в данном случае, разумеется, уже не имеет
смысла частоты соударений электрона с тяжелыми частицами. Од-
Однако п при рассмотрении поляризации диэлектрика введение чле-
члена, пропорционального скорости, необходимо: он описывает некото-
некоторое условное «трение», ведущее к потере энергии.
Из A4.47) получим комплексную амплитуду смещения г,„ п,
как в пп. 14.2.1, 14.2.2, перейдем к выражению поляризовапности:
- e"N' { " A4.48)
—JG)V
Отсюда согласно A.72), A.73):
„,э _ Av 1
em о)" — а>0—;o)v
е= 1
-, A4.49)
где введено обозначение о)д = $jm.
Существенной особенностью построенной динамической модели
диэлектрика является ее резонансный характер. Очевидно, (оо есть
собственная частота среды. Резонанс наблюдается при совпадении
30 п. I!. IIin:oii.ri:ii(l, Т. И. Никольская
466
ГЛ. 14. ПОЛЯ II ЗАРЯЖЕННЫЕ ЧАСТИЦЫ. МОДЕЛИ СРЕД
§ 15.1. ОБЩИЕ ПРЕДСТАВЛЕНИЯ (А)
467
Рис. 14.5
частоты электромагнитного процесса со с соо. На рпс. 14.5 показаны
кривые, построенные на основании A4.49). Это кривая дисперсии,
отображающая частотную зависимость е'(со)— 1, и кривая абсорбции
(поглощения), которая отображает функцию е"(со). Под нормаль-
нормальной дисперсией понимают возрастание е' с частотой. В области ре-
резонанса — между максимумом и
минимумом функции е'(со) — ле-
лежит участок аномальной диспер-
дисперсии.
Рассмотренная модель являет-
является весьма упрощенной. Однако в
случае газов (при малой плотности
12 ш/а> частиц), когда взаимодействие ди-
диполей еще существенно не меняет
среднюю действующую силу, она
более удовлетворительна; заме-
заметим, что е в A4.49) это, вообще
говоря, не заряд электрона. Ввиду
ограниченности классических представлений модель выявляет толь-
только одну резонансную частоту среды. В действительности каждая
молекула среды — система с бесконечным спектром собственных ча-
частот; с позиций квантовой физики модель диэлектрика может быть
уточнена.
В заключение заметим, что выражение %э A4.49) по своей сути
сходно с формулами типа A1.54), представляющими члены рядов
A1.53) (см. также A1.62)). Уточнение модели диэлектрика озна-
означает переход к аналогичному ряду.
УПРАЖНЕНИЯ
1. Решить уравнение A4.15) для случая частицы в заданном электростати-
электростатическом поло Е = х0Е при начальных условиях г@) = 0, г'@) = Xoi'o.
2. Получить траекторию частицы согласно A4.21), если г@) = 0 и г'@) =
3. Как влияет соотношение электрического и магнитного полей ца дви-
движение частицы во втором примере п. 14.1.2?
4. Как изменится характер прецессии вектора М в результате введения
диссипативного члена согласно уравнению Ландау — Лифшица?
5. Сравнить распространение Г-волиы в нспоглощающей плазме и одной
из волн полого волновода. С каким параметром теории волноводов можно со-
сопоставить плазменную частоту?
6. Написать приближенные выражения комплексной диэлектрической про-
проницаемости плазмы в случаях в > v и и < v.
7. Как затухает распространяющаяся в плазме Г-волна? Написать выра-
выражение коэффициента затухания.
8. Рассмотреть изменение фазовой и групповой скоростей Г-волны, рас-
распространяющейся в диэлектрике, с частотой / = 1 Lpn нормальной и апомаль-
диспорсии (см. рис. 14.5).
9. Пользуясь справочными данными, проверить числопой коэффициент в
формуле A4.41).
Глава 15
РАСПРОСТРАНЕНИЕ РАДИОВОЛН
§ 15.1. Общие представления (А)
15.1.1. Радиоволны. Говоря об электромагнитных волнах, исполь-
используемых в радиотехнике, употребляют термин радиоволны. В широ-
широком смысле радиоволнами являются всевозможные волновые про-
процессы в аппаратуре (например, в волноводных устройствах, интег-
интегральных схемах СВЧ и пр.), в линиях передачи и, наконец, в при-
природных условиях, в среде, разделяющей приемную и передающую
антенны. Прпемник и передатчик, можно сказать, соединены вне-
аппаратурной линией передачи, радиолинией. В узком смысле слова
под радиоволнами понимают электромагнитные волновые процессы
на таких радиолиниях, которые называют также естественными ра-
радиотрассами, радиотрактами и пр. В то же время радиолинией
иногда называют и всю совокупность средств передачи информации
в радиосистеме.
Различают следующие основные диапазоны радиоволн:
сверхдлинные волны (СДВ): X = 10 н- 100 км (/ = 3-н 3 • 10 кГц);
длинные волны (ДВ): X = 1-^ 10 км (/ = 3 • 10 + 3 • 102 кГц);
средние волны (СВ): X = 100 м ^ 1 км (/ = 3 • 102 -^ 3 • Ю3 кГц);
короткие волны (KB): X =10^- 100 м (/ = 3-^3-10 МГц);
ультракороткие волны (УКВ): А, = 0,1 мм -МО м (/ =
= 3 10 МГц-^-3-103 ГГц).
Разумеется, .мыслимы как более длинные, так и более короткие
радиоволны. Освоение все более коротких воли происходило по мере
развития средств генерации соответствующих электромагнитных ко-
колебаний. Уже более четверти века назад в результате изобретения
оптических квантовых генераторов, лазеров, стали доступны коге-
когерентные электромагнитные колебания, соответствующие оптическо-
оптическому спектру. Техника располагает, таким образом, радиоволнами
оптического диапазона, в котором различают следующие поддиа-
поддиапазоны:
инфракрасная область: X = 7,5 • 10~4-^-10 мм (/ = 3 103-н
-^4-105 ГГц);
видимый свет: X = 4 • 10 -^ 7,5 • 10 мм (/ = 4 • 105 -н
-*¦ 7,5 • 105 ГГц);
ультрафиолетовая область: X = 10~4 •*- 4 • 10~4 мм (/ = 75- 105 -г-
-3 106ГГц).
В дополнение к этому приведем также сведения о классифика-
классификации радиоволн в соответствии с международным Регламентом радио-
радиосвязи, установленным МККР (Международный консультативный ко-
комитет по радио). Ниже в табл. 15.1 приведены соответствующие по-
полосы частот (см., например, [Е.4]). Таким образом, полосам 4 5,
6, 7 отвечают СДВ, ДВ, СВ и KB, а полосам 8 -н 12 — УКВ.
30*
408
ГЛ. 15. РАСПРОСТРАНЕНИЕ РАДИОВОЛН
15.1. ОБЩИЕ ПРЕДСТАВЛЕНИЯ (А)
469
Таблица 15.1
Полосы частот по номенклатуре МККР
4-
5
6
7
8
9
10
11
12
Обозначение частот
ОНЧ (очень низкие)
НЧ (низкие)
СЧ (средние)
ВЧ (высокие)
ОВЧ (очень высокие)
УВЧ (ультравысокие)
СВЧ (сверхвысокие)
КВЧ (крайне высокие)
Границы частот
3
30
300
3
30
300
3
30
300
30 кГц
300 кГц
3000 кГц
30 МГц
300 Мгц
-г-3000 Мгц
30 ГГц
300 ГГц
3000 ГГц
;оответствующее наименова-
Мпрпаметровые
Километровые
Гектометровые
Декаметровые
Метровые
Дециметровые
Сантиметровые
Миллиметровые
Дещшиллиметровые
Каждому диапазону радиоволн свойственны характерные особен-
особенности распространения в природных условиях, о чем будет говорить-
говориться ниже.
15.1.2. Роль антенн. При рассмотрении радиолиний необходимо
учитывать свойства антенн. В простейшем идеализированном случае
приемную и передающую антенны можно считать точечными объек-
объектами, которые расположены в свободном пространстве. Если бы пе-
передающая антенна излучала равномерно во всех направлениях, то
создаваемый ею на расстоянии г поток энергии должен был бы
иметь плотность
По(г) = РА/4лг2, A5.1)
так как в этом случае Ра = По?, где S — сферическая поверхность,
из центра которой происходит излучение. Реальные антенны излу-
излучают неравномерно, что можно учесть, введя так называемый ко-
коэффициент направленности действия D(i}, а) в соответствии с опре-
определением (9.33). Поэтому вместо A5.1) имеем:
П(г,
, a)PA/Anr2,
A5.2)
где имеется в виду плотность потока энергии в некоторой точке с
координатами г, ¦&, а. Локально поле излучения можно рассматри-
рассматривать как плоскую волну и, следовательно (см. п. 5.5.1),
П (г, 0, а) = Е2т (г, О, a)/2W. A5.3)
Из A5.2) и A5.3) получаем формулу, выражающую напряжен-
напряженность электрического поля в рассматриваемой точке:
Ет (г, 6, а.) = -1
(для свободного пространства W = 120л ,0м, D.29)). Нередко фор-
мулу A5.4) записывают относительно эффективного значения на-
напряженности, которое меньше амплитудного в У2 раз.
Теперь мы можем говорить о радиолинии в целом, полагая, что
А я В — точки локализации передающей и, соответственно, прием-
приемной антенн (рис. 15.1). Напряженность электрического поля в точ-
точке приема В определяется по формуле A5.4). Но можно перейти
и к мощности, отбираемой
приемной антенной, которую
обозначим Рв.
Локально плоская волна
падает на приемную антен-
антенну в направлении, которое в
ее системе координат харак-
характеризуется углами тЭ1', ее
(рис. 15.1). Плотность пото-
потока энергии есть П (г, ¦&, а)
A5.2). Запишем:
Рв = П(г, 0, «)&,(*', ее')
A5.5) Рис. 15.1
(линия, соединяющая точки А и В, имеет угловые координаты ¦&, а
в одной системе и ¦&', а' — в другой). Коэффициент^ Sb(®', a'),
зависящий только от типа антенны (при данных ¦&', а' п заданной
поляризации волны), называется эффективной поверхностью прием-
приемной антенны. В курсах антенн доказывается (см., например, [В.5]),
что эффективная поверхность антенны S и ее коэффициент направ-
направленности действия D связаны соотношением:
A5.6)
(аналогичная формула A0.23) была получена в связи с представ-
представлением об идеальной поверхностной антенне). Подставляя ^A5.2) в
A5.5) и заменяя 5в@', а') в соответствии с A5.6) на X2D{-&', a')/4л,
получаем следующую формулу
которая характеризует передачу энергии для радиолинии в свобод-
свободном пространстве; такую радиолинию условно будем называть иде-
идеальной.
Формула A5.7) имеет весьма ограниченное применение; опа, на-
например, пригодна в случае не слишком протяженных радиолиний
космос — космос. Но нередко используют формулу:
(.5.8)
470
ГЛ. 15. РАСПРОСТРАНЕНИЕ РАДИОВОЛН
Функция F(r), квадрат которой фигурирует в A5.8), называется
множителем ослабления.
Таким путем формально учитываются потерн энергии в различ-
различных реальных радиолиниях.
В инженерной практике формулу A5.8) обычно логарифмируют,
выражая все величины в дБ.
15.1.3. Основные факторы распространения радиоволн. Ввиду разно-
разнообразия, сложности и изменчивости природных условий анализ рас-
распространения радиоволн порождает трудные задачи. Радиоволны
излучаются и принимаются антеннами в относительной близости
Земли, реже одна или обе антенны радиолинии находятся в космо-
космосе. Околоземное пространство неоднородно. Поверхность Земли и
атмосфера оказывают решающее влияние на формирование электро-
электромагнитных волновых процессов. Представим себе сначала, что в си-
силу направленности действия передающей антенны А (рис. 15.2а)
Ионосфера
излучение происходит под малыми углами к горизонту. В этом слу-
случае характер волнового процесса существенно определяется свойства-
свойствами почвы (или морской поверхности). В результате поглощения,
вызываемого действием материальной среды, поле убывает с рас-
расстоянием гораздо быстрее, чем в свободном пространстве. Но осо-
особенности строения атмосферы в данном случае могут и не сказы-
сказываться, и передача энергии происходит так, как если бы атмосфера
вообще отсутствовала. Такого рода волновой процесс называют зем-
земной волной.
Но радиопередача из А в В при определенных условиях может
быть с выгодой осуществлена иным путем, посредством так называе-
называемой ионосферной волны. Ионосферой называют область атмосферы,
нижняя граница которой лежит на высоте около 60 км. Разрежен-
Разреженный газ этой области ионизован, причем степень ионизации ионо-
ионосферной плазмы сначала возрастает с высотой (в так называемой
внутренней ионосфере) и затем убывает, а как известно (см.
п. 14.2.1), с ростом концентрации свободных электронов N' умень-
уменьшается диэлектрическая проницаемость среды; о существовании по-
потерь пока можно не говорить. Таким образом, внутренняя
ионосфера — среда с вертикально падающим коэффициентом
преломления.
§ 15.1. ОБЩИЕ ПРЕДСТАВЛЕНИЯ (А)
471
Излучение антенны А, представляющее собой вблизи нижней
границы ионосферы локально плоскую волну, можно охарактеризо-
охарактеризовать при помощи луча, приходящего под некоторым углом 0О
(рис. 15.2). Луч этот претерпевает рефракцию (см. п. 5.5.3) и мо-
может вернуться к Земле, как показано на рис. 15.26, причем рефрак-
рефракция в ионосфере может несколько раз чередоваться с отражением
от земной поверхности. Характер искривления луча нетрудно по-
понять, исходя из формулы E.120), учитывая, что во внутренней ио-
ионосфере dn/dz < 0. При многократном переотражении от ионосферы
и Земли радиоволны распространяются на огромные расстояния при
сравнительно малом поглощении. Роль ионосферы весьма значитель-
значительна: она образует нечто вроде природного зеркала. Но для достаточ-
достаточно коротких волн (именно для диапазона УКВ) ионосфера уже не
играет роли отражателя. Из формул A4.39) видно, что при данной
концентрации N' с ростом частоты диэлектрическая проницаемость
плазмы все ближе к единице. Если луч «не успевает» искривиться
во внутренней ионосфере настолько, чтобы повернуть к Земле, то
он уходит во внешнюю ионосферу (рис. 1Ь.2в), где концентрация
N' постепенно падает. Это обстоятельство также играет положи-
положительную роль, поскольку именно облагодаря отмеченной «прозрач-
«прозрачности» ионосферы оказывается возможной радиосвязь с космически-
космическими объектами, а также радиоастрономия.
Нижние слои атмосферы, в свою очередь, оказывают некоторое
влияние на распространение радиоволн. В так называемой тропо-
тропосфере, верхняя граница которой лежит на высоте порядка 15 км,
сосредоточено около 80 % всей массы воздуха. В тропосфере проис-
происходит сравнительно слабая рефракция, заметная на больших рас-
расстояниях. Существенную роль, как мы увидим, играют случайные
неоднородности тропосферы.
Мы обсудили лишь общие и главные особенности природных ус-
условий, определяющих характер распространения радиоволн. Просле-
Проследим, как они проявляются в разных диапазонах радиоволн.
Для таких диапазонов как СДВ л ДВ все виды почв (и, тем бо-
более, водные среды) выступают как проводники. Земная поверх-
поверхность отражает эти волны без значительного поглощения. Сверх-
Сверхдлинные и длинные волны неглубоко проникают в ионосферу. При
малых частотах изменение диэлектрической проницаемости плазмы
в зависимости от концентрации электронов является резким (см.
п. 14.2.1), так что нижняя граница ионосферы выражена более чет-
четко. Говорят, что длинные волны распространяются между двумя
хорошо отражающими поверхностями, как в волноводе.
Средние волны сильнее поглощаются почвой и глубже прони-
проникают в ионосферу. Для объяснения особенностей их распростране-
распространения надо рассматривать суточный режим ионосферы.
В диапазоне KB земная волна при распространении быстро по-
поглощается: почва проявляет себя как несовершенный (поглощаю-
(поглощающий) диэлектрик. В ионосферу волны проникают глубоко. Путем
472
ГЛ. 15. РАСПРОСТРАНЕНИЕ РАДИОВОЛН
многократных возвращении из ионосферы и отражений от земной
поверхности короткие волны покрывают практически любые рас-
расстояния, относительно мало затухая.
Сопоставляя связь на длинных и коротких волнах, надо учиты-
учитывать, что в первом случае передающие аптенны, представляющие
собой огромные сооружения, все же остаются малыми по сравнению
с длиной волны. Они имеют небольшой к. п. д. п обладают слабой
направленностью действия. В этом смысле на коротких волнах по-
положение резко улучшается. Дальняя связь осуществляется при по-
помощи направленных антенн; мощности передатчиков относительно
малы. Однако изменчивость ионосферы приводит к неустойчивости
коротковолновой радиосвязи.
Характеризуя диапазон УКВ, следует в первую очередь принять
во внимание, что здесь ионосфера уже не обладает способностью
возвращать рефрагирующий луч к Земле. Типично использование
распространения УКВ лишь в пределах прямой видимости (трасса
АВ', рис. 15.2а) и для связи с космическими объектами.
Систематические и случайные изменения свойств природных сред
оказывают сильное влияние на работу радиолиний. Свойства ионо-
ионосферы зависят от солнечной активности, испытывая суточные, се-
сезонные и более медленные изменения. Тепловые режимы воздуш-
воздушной массы определяют свойства тропосферы. Случайные изменения,
флуктуации свойственны в той или иной мере всем радиолиниям.
Одно из проявлений этого — «замирания» передаваемых сигналов,
случайные амплитудные вариацпп. При измерениях сигналов произ-
производят усреднение результатов. Случайные изменения, разумеется,
ведут к искажениям сигналов. Следует, однако, иметь в виду и по-
полезную роль флуктуации в виде пространственных образований в
тропосфере и ионосфере. Рассеяние на этих иеоднородностях обус-
обусловливает распространение УКВ за пределы прямой видимости.
§ 15.2. Геометрическая оптика и теория дифракции
при анализе распространения радиоволн
15.2.1. О возможностях постановки электродинамической задачи
(А). В принципе, задача о распространении радиоволн в природных
условиях есть задача электродинамики, которая ставится для урав-
уравнений Максвелла. Но даже, если отвлечься от изменчивости при-
природных условий, остается исключительное разнообразие материаль-
материальных сред и границ отдельных образований; соответствующую ин-
информацию просто невозможно учесть при постановке электродина-
электродинамической задачи в полной мере. Возникает вопрос, какого рода идеа-
идеализации при постановке задачи являются допустимыми. Можно по-
поставить и другой вопрос: какие упрощения придется ввести, чтобы
задача могла быть решена строго?
В строгой постановке задачи Земля заменяется однородным ша-
шаром в однородной или даже радиалыю-неодпородкон среде; при этом
§ 15.2. АНАЛИЗ РАСПРОСТРАНЕНИЯ РАДИОВОЛН
473
находят электромагнитное поле заданных источников, формализую-
формализующих антенну. Представляет интерес и плоская модель, в которой
рассматриваются заданные источники вблизи границы разнородных
полупространств. Задачи эти не просты; возникающие математиче-
математические трудности преодолевались поколениями специалистов; доста-
достаточно сказать, что этими вопросами занимались такие выдающиеся
физики-теоретики, как А. Зоммерфельд и наш соотечественник
В. А. Фок [Г.6, 7]. Изложение этого круга идей в данном курсе
потребовало бы неправомерно большого объема.
Расстояния между передающими и приемными антепнамп обыч-
обычно во много раз превышают длину волны. Поэтому при рассмотре-
рассмотрении радиолиний стараются применять представления оптики. На
Рпс. 15.3
рис. 15.3а схематически показана радиолиния над земной поверх-
поверхностью. Лучевая схема означает, что поле в точке приема В рас-
рассматривается как наложение, вообще говоря, трех волновых процес-
процессов: прямой волны — луч АВ, отраженной от Земли — луч АВ'В и
пришедшей из ионосферы — луч АВ" В. Насколько удовлетворитель-
удовлетворительна такая схема?
Пусть существует только земная волна (луч АВ"В отсутствует).
Ясно, что окрестность точки В' должна представлять собой доста-
достаточно гладкую площадку. Если, например, в этом районе располо-
расположены горы, здания, деревья и т. п., размеры которых не малы в
сравнении с длиной волны, то каждый такой предмет порождает
сложное поле дифракции. Понятно также, что приемная антенна В
может лежать в области тени (рис. 15.36). С точки зрения геомет-
геометрической оптики поле в В должно быть равно нулю. Но правиль-
правильную информацию может дать только решение задачи дифракции.
Электромагнитные волны в известной мере огибают выпуклость Зем-
Земли — тем больше, чем длиннее волна. Поэтому в начале века — до
выяснения роли ионосферы — считалось, например, что короткие
волны непригодны для дальней связи.
Заметим, что действие предмета, затеняющего радиотрассу, на-
например, горного хребта (рис. 15.4а), можно уподобить влиянию края
экрана в задаче дифракции на отверстии (см. п. 10.3.2). В этом при-
приближении распределение поля за препятствием показано на
рис. 15.46. Интересно, что вблизи края геометрической тени имеет-
имеется область усиления ноля: первый дифракционный максимум. Об-
Обсуждавшаяся схема анализа препятствия была упрощенной; кроме
474
ГЛ. 15. РАСПРОСТРАНЕНИЕ РАДИОВОЛН
§ 15.2. АНАЛИЗ РАСПРОСТРАНЕНИЯ РАДИОВОЛН
475
прямых волн в общем случае рассматриваются также волны, пере-
переотраженные земной поверхностью.
В заключение надо сказать, что подход геометрической оптики
на рис. 15.3а, нуждается в дополнительном обосновании, которое бу-
будет проведено в п. 15.2.3. Оказывается, для прямого луча АВ можно
(о)
i
v'/T
Рис. 15.4
построить эллипсоидальную зону (рис. 15.5а), вне которой простран-
пространство, практически, не влияет на формирование соответствующего
поля в точке В. Ее называют областью, существенной для формиро-
формирования поля, или — кратко — доминантной областью. Чем короче вол-
волна, тем доминантная область уже. Построение доминантной области
отвечает на вопрос о размерах достаточно гладкой площадки в ок-
окрестности точки отражения В', при
которых подход геометрической оп-
оптики применим (рис. 15.56), а также
о необходимой высоте поднятия ан-
антенн. Если она недостаточна, так
что доминантная область пересекает
земную поверхность (рис. 15.5в),
такой подход оказывается, строго
говоря, неприменимым.
15.2.2. Оценка неровностей зем-
земной поверхности (А). Пусть пло-
плоская волна падает на поверхность
раздела сред сложной формы, от-
отклоняющуюся от плоскости не более, чем па высоту (глубину) h
(рис. 15.6). Это — задача дифракции. Не решая ее, можно попы-
попытаться оцепить, насколько поле рассеяния отличается от плоской
Рис. 15.6
волны, которая отражалась бы плоской границей (при отсутствии
неровностей).
Можно ожидать, что малые элементы неровной поверхности дей-
действуют подобно элементам Гюйгенса, фаза которых определяется
падающей волной. Рассмотрим разность фаз двух лучей, как бы от-
отраженных от верхнего и нижнего уровней неровной поверхности.
Эта величина Дер равна различию оптических путей A'Q'B' и AQB.
Как видно из рис. 15.6,
Дф = 2Ш=^со8«. A5.9)
к
Если Аф « 0, что будет при h < X, то точки В ж В' можно счи-
считать синфазными, а это значит, что поле рассеяния можно рассмат-
рассматривать как плоскую волну: неровности границы не влияют на про-
процесс. Считают, что пренебрежение неровностями в какой-то мере
оправдано вплоть до фазовых отклонений Аф порядка л/2. Согласно
A5.9) этому соответствует высота неровностей
А < Я/8 cos 0. A5.10)
Чем ближе направление падающей волны к «скользящему» (О -»-
-*-90°), тем большая высота неровностей допустима в соответствии
с неравенством A5.10), которое называют критерием Рэлея.
В диапазонах длинных и средних волн лесистую местность или
даже населенный пункт можно рассматривать как ровную поверх-
поверхность, характеризуемую некоторым коэффициентом отражения, кото-
который может быть определен экспериментально. Но, например, для
сантиметровых волн отдельный камень или растение есть самостоя-
самостоятельный объект дифракции.
Измерение свойств различных почв, морской воды в масштабах
географических регионов и исследование эквивалентных электроди-
электродинамических параметров (например, коэффициентов отражения) раз-
различных видов местности проводится в широких масштабах во всем
мире. Эти данные публикуются в специальной литературе и исполь-
используются при проектировании радиолиний.
15.2.3. Доминантная область радиолинии (Б). Чтобы выяснить,
какая область пространства существенна при формировании поля
излучения источника А в точке В, используем задачу о дифракции
волны па отверстии в экране (см. § 10.3). На трассе можно мыс-
мысленно разместить экран с отверстием и увеличивать отверстие до
тех пор, пока влияние экрана на поле в точке В перестанет ска-
сказываться. Тогда экранируется только несущественная часть поля.
Перемещая экран с отверстием вдоль трассы, мы убедимся в том,
что размер отверстия (при одной и той же степени малости влия-
влияния экрана) оказывается наибольшим па середине трассы, а по ме-
мере приближения экрана к точкам А и В уменьшается.
СоПстнеппо говоря, о певлияющем экране уже говорилось в
§ 10.3, по там исследовалась дифракция плоской волны, а пас бу-
476
ГЛ. 15. РАСПРОСТРАНЕНИЕ РАДИОВОЛН
15.2. АНАЛИЗ РАСПРОСТРАНЕНИЯ РАДИОВОЛН
477
дет интересовать волна сферическая (рпс. 15.7а). Можно сказать,
что задачу дифракции не придется решать заново, достаточно будет
внести в полученные ранее результаты некоторые коррективы.
Итак, сферическая волна, распространяющаяся из точки А (пере-
(передающая антенна), индицируется в точке В (приемная антенна).
Рис. 15.7
Если точка А достаточно далека от экрана, амплитуду сферической
волны в плоскости отверстия можно считать постоянной, но необ-
необходимо учесть непостоянство фазы. Обозначая АР2 = г и АР] = z
(кратчайшее расстояние), имеем: г= V(.г'J + (г/'J + z2, где х' и
у' — поперечные координаты точки Р2. Очевидно (ср. A0.27)),
г = z + 27 + • • • 1 еперь для нахождения поля дифрак-
дифракции сферпческой волны на отверстии достаточно ввести лишь очень
небольшие изменения в формулы из § 10.3. Действительно, под
интегралом A0.12) должен дополнительно присутствовать мно-
множитель
e-ihf __ e-ik7 ovn I il- Iх )
отражающий изменение фазы падающей волны в отверстии. Таким
образом, теперь вместо A0.28):
1кЁт@) e-i
2л
а/2 Б/2
X j j exp{-tt[<
-a/2 -5/2 l L
22
dz'dy'. A5.11)
Поскольку точка наблюдения В имеет координаты х = 0, у = 0,
показатель экспоненты под знаком интеграла принимает вид
I——Ь -т^\. Интеграл, как и в 10.3, распадается на
¦ik{-
два идентичных по форме (по х' и у'); один из них:
В сравнении со случаем дифракции плоской волны, когда член 1/z
в показателе экспоненты отсутствует, различие свелось к тому, что
вместо 2 теперь фигурирует величина zz/(z + z). Таким образом, для
нахождения поля дифракции Em в точке В надо лишь внести оче-
очевидные изменения в результаты § 10.3.
Для наших целей достаточно получить повое выражение ди-
дифракционного параметра, а для этого в формуле A0.32) надо за-
заменить z на zz/(z + z), что дает
),zz /(z-\-z)
A5.12)
Из п. 10.3.2 известно, что при d > 1 поле в средней точке за экра-
экраном оказывается таким, как если бы экрана не было. Поэтому, по-
положив в A5.11) сГ = Сз>1, мы получаем условие, что на поле в
точке В (см. рис. 15.7а) не повлияло экранирование. Взяв некото-
некоторое допустимое значение С, получаем
d = Cl/ji4:. A5.13)
Это выражение размера отверстия в экране, при котором экраниро-
экранирование можно считать несущественным. Как видно, этот размер
зависит от положения экрана па трассе.
Чтобы осмыслить результат, отметим, что z + z — это расстоя-
расстояние АВ = А между передающей н приемной антеннами. Введем де-
картову систему координат ?, ц (рпс. 15.76) с началом па середнпе
этого расстояния. Пусть Р(Ё,, ц) — точка на краю отверстия. Учи-
Учитывая, что z = A/2 + 1, z = A/2 — ? и d — 2r\, сделаем соответствую-
соответствующие подстановки в A5.13) и после преобразований получим урав-
уравнение
il + J]!=l, а==*_, 6 = ?/ХА. A5.14)
Это уравнение эллипса, представляющего собой геометрическое
место краевых точек отверстия в невлияющем экране, который пе-
перемещается вдоль трассы. Это означает, что продольное сечение
доминантной области радиолинии ограничено эллипсом (рис. 15.76).
Ввиду осевой симметрии всей системы доминантная область есть
эллипсоид вращения. Его малая полуось Ъ уменьшается с длпной
волны /.; при h -*• 0 эллипсоид вырождается в отрезок прямой.
Обсудим вопрос с иных позиции. В п. 10.3.3 было введено пред-
представление о зонах Френеля. Эти зоны можно выделить и на сфе-
сферическом фронте волны с центром в точке А (рис. 15.8). Их гра-
границами являются окружности, описываемые па сфере радиальным
отрезком r = z + n}./2 (га=1, 2, ...) с началом в точке В. Пусть
гиг — расстояния от А и, соответственно, от В до края отверстия
478
ГЛ. 15. РАСПРОСТРАНЕНИЕ РАДИОВОЛН
в экране, которое вырезает п зон Френеля. Тогда
~ + r = z + z + пК/2. A5.15)
Поскольку величина справа постоянна, при продольном перемеще-
перемещении экрана краевая точка его отверстия скользит по эллипсу, фо-
фокусы которого лежат в точках А и В.
Для сопоставления с предыдущим используем следующие при-
приближенные равенства:
Подставляя это в A5.15), получаем:
и, следовательно,
!Z + —
27 2 •
= 2/nl/>
A5.16)
jz>=const
Рпс. 15.8
При обозначении С = 2}'п это соотношение повторяет A5.13). На-
Напомним (см. п. 10.3.3), что экран с отверстием можно считать не-
влияющим, когда число зон Френеля,
укладывающихся в нем, велико.
Иногда определяют доминантную
область, исходя из п = 1 (С = 2). По
смыслу проведенных рассуждений это
неверно. В заключение заметим, что
в двух вариантах построения доми-
доминантной области расстояние между ан-
антеннами А совпадает то с большой
осью эллипса, то с расстоянием между
его фокусами (рассуждения не были
вполне эквивалентными). Это разли-
различие, однако, не имеет никакого зна-
значения, так как, во-первых, экран не может быть очень близок к
точкам А ж В, а. во-вторых, имеются в виду весьма вытянутые эл-
эллипсы: а » Ъ.
§ 15.3. Земные радиоволны (А)
15.3.1. Лучевая модель радиолинии. Рассматривая некоторую
радиолинию, функционирующую при отсутствии влияния ионосфе-
ионосферы, будем исходить из лучевого представления на рис. 15.3а, со-
согласно которому поле в точке В находится как наложение двух
волн, одна из которых соответствует лучу АВ, а другая — лу-
лучу АВ'В. Такая лучевая модель (другое название — отражательная
трактовка) может быть применена, если антенны расположены на
линии прямой видимости и достаточно высоко подняты. При стро-
§ 15.3. ЗЕМНЫЕ РАДИОВОЛНЫ
479
гом выполнении второго условия доминантная область должна ле-
лежать над земной поверхностью (см. рис. 15.5а). В большинстве
случаев практики это недостижимо. Действительно, при едва допу-
допустимом С = 6 (т. е. п = iI в A5.16)) для малой оси (поперечника)
эллипса доминантной области получаем: 26 = ЗУ^А. Таким обра-
образом, например, при А =104Л, находим: 6 = 150А.. Такова должна
быть приблизительно высота антенн, что трудно достижимо уже на
метровых волнах. На практике лучевую модель применяют и в слу-
случае невыполнения рассматривавшегося условия. Считается, что для
ориентировочных расчетов лучевая модель пригодна, когда высота
расположения антенн превышает длину волны. Разумеется, вычис-
вычисляемая в точке приема напряженность поля может оказаться су-
существенно завышенной.
Детализируем лучевую модель радиолинии, полагая соответ-
соответствующий участок земной поверхности плоским (рис. 15.9). Надо
сложить в точке В поля прямой и отраженной волн. При этом
= е
01
е02р
2, а)
A5.17)
Действительно, первый член соответствует выражению A5.4). При
этом введен орт eOi (на рис. 15.9 он показан в варианте параллель-
параллельной поляризации) и фазовый множитель; начальная фаза ф в даль-
дальнейшем несущественна. Второй
член требует дополнительного по-
пояснения. Отраженную волну мож-
можно трактовать как излученную
отраженным источником А', при-
причем амплитуда волны получается
при умножении на коэффициент
р, определяемый по формулам
Френеля E.42), E.43); очевидно,
что при этом г.2 = г2 + г2. Форму-
Формула A5.17) реализует лучевую мо-
модель радиолинии.
Поскольку обычно hi <s n и
^2 < П, ОТреЗКИ 7*1, Г2 И Г2 ПОЧТИ
параллельны. Поэтому орты eOi и еог будем считать идентичными
(при перпендикулярной поляризации это верно в строгом смысле).
Полагая ft-2 ~ fti = ft, не будем различать величины 0(fti, cc) и
D (ft2, ее). При этом также r2 « r\ + 2h\ cos fti = г + 2h\ cos ft (индекс 1
при г и ft опущен). В знаменателе второго члена A5.17) отожде-
отождествим г2 и и = г. Теперь выражение A5.17) дает:
A5.18)
Рпс. 15.9
= е0
—i2hh1cos& \
_&, a)Pe'4liT~w'-jr{l + ре
Далее, учтем, что при пологом падении (ft» 90°) независимо
от характера почвы и вида поляризации р«—1. В этом легко убе-
убедиться, взяв формулы Френеля для рх и рп и положив в них
480 ГЛ- 15- РАСПРОСТРАНЕНИЕ РАДИОВОЛН
Ф = 90°. Таким образом, полагая р = — 1, имеем
1 + pe~i2h
и из A5.18) получаем
in (kh1 cos Ь)
а так как cosO«l, то можно написать:
A5.19)
Ет = ео2
, a) Pi- Мх Cos#.
A5.20)
- - У1"ем, что в предшествующих действиях вместо cos#
более правильно брать среднее арифметическое cos в, и cos О' где
О -угол АА В на рис. 15.9. Это значит, в A5.20) делается замена:
" , -г cos О'
2 -Т
В результате находим так называемую
Введенского:
ео2
согласно которой напряженность поля в месте приема пропошгао
пальпа произведению высот передающей и приемпо антенн Ин-
Интересно, что формула Введенского в явном виде показывает рост
в рхпГсГпои "по С РаССТ0Я"ием " Результате действия зеГо/но-
верхпости при пологом падении. Поле убывает, как 1/г2 вместо 1/г
геТв°оСМ Пр°Стра11СТве- Д*"> в том, что складываемы в точ-
/пгтГ почтп противофазпы, поскольку взято р = -1 п Г2«Г1
(при г2 = гх поле оы полностью уничтожалось)
Сделаем несколько замечаний о формулах A5 17) — A5 с>\) т
торые называют интерференционными,^ как они они шш пи-
терферонцто двух волновых процессов. При переходе от 15 17)
к Aо.18) ооычно предполагается, что передающая антенна - сля-
нравленнй6^3^/ ПР0ТИВП0М СЛуЧае ЗНаЧе1 m»D ^ близких н-
жепие п - 1 2 УТ значительпо Различаться. Далее, прибли-
приближение р--1 ирп перпендикулярной поляризации лучше чем
щ среды. Однако при этом формулы A5 19) —Aci 21? для
параллельной поляризации оказываются" Достоверными, когда паде-
падение волны на отражающую поверхность является существенно бо
еП)ОЛи75М43^пшГГ ПР°В^РИТЬ' сопо—« ФорУ^ЛыВфрНенел°я
) и (b.4d) при малых W2, когда также мал угол падения m
хода ™й ВгЬШп°Лг1Ш10ТСЯ ^отношения hl«ri и hj<ru то ра пос^ь
хода лучей г2 и г, уже нельзя определять, как это делалось при
§ 15.3. ЗЕМНЫЕ РАДИОВОЛНЫ
481
переходе к формуле A5.18). На относительно малых расстояниях
П фазовый сдвиг может оставаться большим, в результате чего за-
зависимость поля в точке В от расстояния между антеннами имеет
100
150 г
Рис. 15.10
ряд интерференционных «провалов» (рис. 15.10). С ростом рас-
расстояния оптические пути прямого и отраженного лучей сближают-
сближаются, так что, начиная с какого-то момента, фазовый сдвиг мало от-
отличается от значения 180° (обусловленного коэффициентом отра-
отражения р = — 1) и все более приближается к нему. Мы определили
области применимости формулы
Введенского: поле убывает, как
1/г2. Заметим, что огибающая кри-
кривой (рис. 15.10) в соответствии
с A5.17) изменяется, как 1/г.
Остается обсудить, как в луче-
лучевой модели учитывается сферич-
сферичность Земли. Это поясняется на
рис. 15.11, из которого видно, что
роль высот антенн теперь играют
приведенные высоты \ и Ъ2. Если
углы АОВ' и В'ОВ невелики
(ЭТО ТИПИЧНО), ТО %!«/»! —6i И
Й2«Й2-б2, где б! и б2 —высоты точек, находящихся на расстоянии
прямой видимости А1В1 = г0. Как видно из рис. 15.11,
• О
Рис. 15.11
где До = 6370 км — радиус Земли.
31 В. В. Никольский, Т. И. Никольская
A5 22^
482
ГЛ. 15. РАСПРОСТРАНЕНИЕ РАДИОВОЛН
15.3.2. Применение неэлементарных моделей. Лучевая модель
радиолинии становится, в строгом смысле, неприменимой, если до-
доминантная область не лежит целиком над земной поверхностью.
В относительно простом случае антенны А и В находятся в пре-
пределах прямой видимости, причем участок земной поверхности на
трассе близок к плоскому. Когда антенны расположены непосред-
непосредственно у Земли (их высоты значительно меньше длины волны),
лучевая модель теряет всякий смысл и применяется строгий элек-
электродинамический подход (см. п. 15.2.1), при котором, однако, вме-
вместо земной поверхности вводят бесконечную плоскую границу, раз-
разделяющую два разнородных полупространства. Этот подход, разра-
разрабатывавшийся еще А. Зоммерфельдом [Г.6], потребовал усилий
многих специалистов для преодоления вычислительных трудностей.
Приведем лишь окончательные результаты в форме, используемой
в инженерной практике.
Пусть некоторая передающая антенна А находится в непосред-
непосредственной близости Земли. Для определения напряженности поля в
точке В применяется формула
?m = yi20DP-^rF, A5.23)
которая отличается от A5.4) лишь множителем 12F, где F — мно-
множитель ослабления (см. п. 15.1.2), а коэффициент Y2 означает
удвоение потока энергии при той же мощности в сравнении со слу-
случаем излучения в свободное пространство. Нетрудно сообразить,
что такое удвоение будет иметь место, если, например, диполь
Герца вместо свободного пространства расположить вблизи идеаль-
идеально проводящей плоскости и ориентировать ортогонально.
Равенство A5.23) вместе с системой правил определения F на-
называют формулой Шулейкипа — Ван-дер-Поля. На практике F на-
находится посредством кривых Берроуза1) (рис. 15.12), где по осп
абсцисс откладывается значение параметра ?. зависящего от
расстояния г между антеннами, находящимися вблизи Земли,
и комплексной диэлектрической проницаемости е среды, соответ-
соответствующей участку Земли на трассе. В типичном случае, когда пе-
передающая антенна может рассматриваться, как наложение верти-
вертикальных диполей Герца (вертикальная поляризация),
1 { A5.24)
айв A5.23) есть коэффициент направленности антенны в свобод-
свободном пространстве. Определив ?, находят F при помощи указанного
графика (рис. 15.12) или — приближенно — по формуле
A5.25)
4 -)- ? + 0,3?2
') Burrows С. R., Gray М. С. Ц Ргос. IRE.— 1941.— V. 29,— Р. 10.
§ 15.3. ЗЕМНЫЕ РАДИОВОЛНЫ
483
31 *
484
ГЛ. 15. РАСПРОСТРАНЕНИЕ РАДИОВОЛН
S 15.4. ВЛИЯНИЕ ТРОПОСФЕРЫ
Формулу Шулейкина — Вап-дер-Поля A5.23) применяют и приг
горизонтальной ориентации токов антенны (горизонтальная поля-
поляризация). В этом случае
1 ' A5.26)
Трактовка величины D в этом случае оказывается непростой, и мы
на этом не останавливаемся; интерес представляет уже вычис-
вычисление F.
Для применения рассмотренного подхода должна быть обеспе-
обеспечена возможность охарактеризовать всю среду на трассе при по-
помощи достоверного значения е. При уменьшении длины волны это..
14 8 12 16 20 24 2в
> Ыу)
t/з
0,01 0,02 Орч 0,031 2 4 в в 10 20 40 50 100
5 у=-
Рис. 15.13
как известно (см. п. 15.2.2), становится затруднительным уже из-за
неровности земной поверхности.
Радиолинии, на которых приемная антенна лежит в области
тени (см. рис. 15.36), оцениваются при помощи математических
моделей, базирующихся на решении сложной дифракционной зада-
задачи; в эту проблематику важный вклад внес В. А. Фок [Г.7]. Огра-
485
ничимся записью множителя ослабления для подстановки в A5.23)
которая, пе претендуя на высокую достоверность (параметры сое-
ды в (Ю.2/) вообще не фигурируют), пригодна для ориентировоч-
ориентировочных оценок поля в области тени. Сомножители находятся при по-
помощи графиков, приведенных на рис. 15.13 [Е.5].
В заключение рассмотрим несложный вопрос о характере ти-
типичного электромагнитного поля вблизи земной поверхности по-
полагая, что оптическая плотность почвы (водной среды) достаточна
, ,.т
Рис. 15.14
для применения граничного условия Леонтовича. Волна имеет вер-
вертикальную поляризацию: вектор Е перпендикулярен земной по-
видаТис' 15а14а)еМЛеЙ (лОкально) пОле близК0 к плоской волне
)-i6z. A5.28)
Рассматривая эти формулы в качестве начального приближения
поля над Землей (х>0), будем считать, что Нт „е нуждается в
уточнении. Пользуясь граничным условием Леонтовича E ПЗ) ви-
видим, что на земной поверхности существует тангенциальная элек-
электрическая компонента:
W
Emt = Wnp [x0, Hm] = z0 -ip Ae-«". A5.29)
Она является продольной (рис. 15.146). Эта компонента относи-
относительно мала, поскольку |ТУпр| «W и сдвинута по фазе относитель-
относительно Ех. Результирующий вектор близок к х0Ех. Точнее говоря он
описывает сильно вытянутый эллипс в продольной плоскости.'
§ 15.4. Влияние тропосферы (А)
о т!™4Л °бЩИе свойства тропосферы. В п. 15.1.3 уже говорилось
° тропосфере, как о нижней области атмосферы, вмещающей около
80 /0 всей массы воздуха. Температура воздуха, который нагрева-
нагревается земной поверхностью, падает с высотой и стабилизируется там
486
ГЛ. 15. РАСПРОСТРАНЕНИЕ РАДИОВОЛН
§ 15.4. ВЛИЯНИЕ ТРОПОСФЕРЫ
487
Ь,км
где принято различать верхнюю границу тропосферы. Это высота
10-^-12 км в умеренных широтах; в полярных шпротах она надает,
а в экваториальных—увеличивается. Диэлектрическая проницае-
проницаемость увлажненного воздуха тропосферы песьма близка к единице.
У земной поверхности в среднем п¦ — Те = 1,000325, а с высотой
коэффициент преломления п в пор-
\ мальных условиях все более приближа-
приближается к единице, уменьшаясь вместе с
плотностью воздуха. Это показано па
рис. 15.15, где представлена зависи-
зависимость так называемого индекса прелом-
преломления N=(n— 1) - 106 от высоты. Это
идеализированный закон изменения N
[Е.1]. В результате конвекции воз-
воздушная масса тропосферы находится
в движении; изменения влажности,
а также температурного режима обусловливают в первую очередь
плавные изменения показанного па рис. 15.15 профиля индек-
индекса преломления. При специфических распределениях темпера-
температуры и влажности возможно и нарастание Лт с высотой. Суще-
Существенны локальные — мелкомасштабные — изменения плотности воз-
воздуха, а следовательно, и параметра Лг, которые имеют флук-
туациоппый характер. Роль этих неоднородпостей, а также осадков
и свойств газовой среды тропосферы мы обсудим в и. 15.4.3. Сна-
Сначала же рассмотрим тропосферу как среду с плавно меняющимися
свойствами.
15.4.2. Тропосферная рефракция. В условиях применимости лу-
лучевой модели радиолинии (в первую очередь, па УКВ) распростра-
распространение радиоволн в тропосфе-
ре как слабо неоднородной ^
среде естественно истолковы-
истолковывать, используя понятие ре-
фрикции, искривления лучей
(см. п. 5.5.3). При этом ' \ \
обычно применяется форму- но ]„ я^<*>
ла E.120). \ . яо \
Обратимся к рис. 15.16а, \ < \
на котором штриховой ли- \
ниен показано направление ° , \
луча в среде, принимаемой j , \
за однородную. Поскольку „ $
для нормального состояния p,ICj 15.10
тропосферы dn/dz < 0, то
R > 0: искривление луча происходит в сторону Земли (сплошная
линия па рис. 15.1Ь'а). В результате увеличивается расстояние пря-
прямом видимости, что можно истолковать как кажущееся возрастание
радиуса Земли. Воображаемая картина представлена па рис. 15.166;
кажущийся радиус земного шара Яо больше действительного его
радиуса /?0, а среда вблизи Земли однородна (п = 1), так что луч —
прямой. Условием эквивалентности лучевых картин па рис. 15.16а
и рис. 15.106 будем считать равенство
Разности слева п справа выражают относительную кривизну луча
и контура земной поверхности. Поскольку lt-+°°, то из A5.30)
следует:
^о = Г=%777- A5.31)
Получив таким путем выражение эквивалентного радиуса земного
шара при рефракции, мы можем исключить радиус кривизны лу-
луча И посредством формулы E.120). Взяв до = 90°, получаем:
1 — — я
' п dz Я0
A5.32)
Отсюда при /?о = 0370 км п dn/dz = — 4 • 10~5 км~' (это соответству-
соответствует линейному участку кривой на рис. 15.15) получаем, что Ло «
~ 8о00 км. Подставляя Ло вместо /?о в различные формулы, учиты-
учитывающие кривизну земной поверхности, можно оценивать влияние
тропосферы на распространение радиоволи. Так. например, на осно-
основе A5.22) легко прийти к выводу, что при нормальном состоянии
тропосферы расстояние прялгоп видимости увеличивается приблизи-
приблизительно па 15 %.
Обсудим различные типы тропосферной рефракции — реальные
и гипотетические, (,'твечакпцпе мыслимым состояниям тропосферы.
При dn/dz>0 рефракция называется отрицательной; луч уклоня-
уклоняется от зомной поверхности, а расстояние прямей"! видимости умень-
уменьшается (рис. 15.17а). Если dn/dz = 0, рефракция отсутствует, луч
остается прямым (рис. 15.176). Уже обсуждавшаяся рефракция,
наблюдаемая при dn/dz < 0, называется положительной (рис. 15.17а).
Можно представить себе и так называемую критическую рефракцию,
при которой луч совпадает с дугой окружности, конце!прической
земному шару (рис. 15.17г); трудно ожидать, что условие реализа-
реализации критической рефракции может быть выполнено па трассах боль-
большой протяженности, а тем более — привести к кругосветному рас-
распространению радиоволны. Упомянутое условие выводится при по-
помощи формулы E.120): требуется, чтобы производная dn/dz была
равна величине dn/dz\Kp « —1,57 • 10~4 км. В случае, если dn/dz <
< dn/dz\Kp, будет иметь место сверхрефракция (рис. 15.173), когда
луч возвращается к Земле; отразившись от земной поверхности, он
может вновь испытать сверхрефракцию в тропосфере. Если это про-
ГЛ. 15. РАСПРОСТРАНЕНИЕ РАДИОВОЛН
§ 15.4. ВЛИЯНИЕ ТРОПОСФЕРЫ
исходит многократно, говорят об образовании тропосферного волно-
волновода (рис. 15.17е).
Хотя различные отклонения от нормального распределения плот-
плотности тропосферы имеют местный и нерегулярный характер, их
нельзя не принимать во впимапие. Давно производятся исследования
dz
dz
\ 9,
dz
3050 100 200 300 400 г,нм
Рис. 15.18
ИнтенсиЬность
'осадноЬ,мм/ч
0,01
0,5 1
Рис. 15.19
Рис. 15.17
метеорологических условий, способствующих образованию тропо-
тропосферных волноводов. Последние, в принципе, могут быть использо-
использованы для передачи УКВ па дальние расстояния, однако по этому
поводу существуют разные точки зрения.
15.4.3. Рассеяние и поглощение радиоволн в тропосфере. Тропо-
Тропосфера подвержена разным изменениям случайного характера, при-
причем турбулентные движения воздуха вызывают многочисленные ло-
локальные изменения его плотности, а следовательно, и оптической
плотности среды. Каждое такое образование есть, в сущности, объект
дифракции волн, переизлучатель. Разумеется, колебания диэлектри-
диэлектрической проницаемости среды настолько малы, что только наложе-
наложение огромного количества полей, рассеянных отдельными образова-
образованиями, может привести к заметному эффекту. Полагают, что значи-
значительную роль играет рассеяние радиоволн на неодпородностях
слоистого типа. Теория тропосфернего рассеяния базируется на
статистических принципах. Она еще не может считаться вполне
разработанной. В существовании процессов рассеяния радиоволн в
тропосфере, которыми нельзя пренебречь, убеждают в первую оче-
очередь паблюдопия. Давно уже отмечено, что в диапазоне УКВ
10 15 20 30
(Л -Jcm)
до wo ко zoo .wo fjru,
(Л - 1мм)
Рис. 15.20
490
ГЛ. 15. РАСПРОСТРАНЕНИЕ РАДИОВОЛН
измерения средней напряженности поля в области тени системати-
систематически дают значительно более высокие значения, чем можно ожи-
ожидать па основании дифракционной теории для стабильной среды.
Это демонстрируется на рис. 15.18 [Е.7], где экспериментально
найденные значения множителя ослабления F показаны сплошны-
сплошными линиями, а результаты указанных расчетом — штриховыми.
Хоти- поле тропосферного рассеяния испытывает резкие случайные
колебания — аамирапия,— наличие этого поля дает основание гово-
говорить о дальнем распространении УКВ. Специальные системы свя-
связи, использующие тропосферное рассеяние, обеспечивают радиопе-
радиопередачу на расстоянии и многие сотни километров.
Ло мере уменьшения длины волны, уже начиная с X ~ 10 см,
все более заметно проявляется действие осадков. В сантиметровом
диапазоне волн капли дождя — весьма существенные объекты ди-
дифракции. В системе капель рассеяние многократно: поле рассеяния
каждого объекта дифрагирует на других. Появляется дополнитель-
дополнительное поглощение, по и непоглощенное поле рассеяния отпимает
энергию у распространяющейся волны, вызывая излучение в сто-
стороны. Па рис. 15.19 представлены кривые, характеризующие зату-
затухание радиоволн в зависимости от интенсивности осадков [Е.5]; они
получены путем измерений. Как и следовало ожидать, затухание
возрастает с уменьшением длины волны.
В п. ] 1.2.3 кратко обсуждалась сущность резонансного погло-
поглощения в диэлектрической среде. Частотная характеристика коэф-
коэффициента затухания радиоволн и тропосфере, обусловленного мо-
молекулярным поглощением в воздухе с примесью водяных паров
A0 г/м3). представлена на рис. J5.20 [Е.5].
Проблема прозрачности тропосферы весьма важна при исполь-
использовании оптических волн. В частности, ивпду молекулярного по-
поглощения здесь можно выделить лишь ряд окон прозрачности, к ко-
которым относится п участок спектра 0,1 -г 0.8 мкм, содержащий
область видимого спета.
§ 1.1.5. Радиоволны в ионосфере (А)
15-5.1. Общие свойства ионосферы. Начиная с высоты около
50 -г G0 км, существенно проявляется ионизация атмосферной сре-
среды. Это нижняя граница так называемой ионосферы. Степень иони-
ионизации характеризуют числом свободных электронов Л' в единице
объема среды (см. и. 14.2.1). Величина N' достигает максимума на
высоте 250 -н 400 км. Ионосферу, лежащую ниже этого уровня, на-
называют внутренней, а лежащую выше — внешней. Последняя
вплоть до высоты порядка радиуса земного шара может оказывать
заметное влияние на распространение радиоволн.
Основной причиной ионизации атмосферы является ультрафио-
ультрафиолетовое и рентгеновское излучение Солнца (в диапазоне воли ко-
короче 0,1 мкм); известно, что на эту часть спектра приходится до-
§ 15.5. РАДИОВОЛНЫ В ИОНОСФЕРЕ (А)
491
День
волыю малая доля солнечного излучения. Более длинноволновое
излучение (с меньшей энергией квантов), можно сказать, не в со-
состоянии произвести требуемую работу ионизации. Вторым по зна-
значению фактором ионизации являются корпускулярные потоки,
также в основном солнечного происхождения. Плотность энергии
ионизирующего потока, приходящего к Земле, по мере проникно-
проникновения в атмосферу падает в результате поглощения. Плотность же
газа по мере приближения к Земле возрастает. Поэтому-то элек-
электронная концентрация N' как функция высоты имеет максимум:
на некоторой высоте ионизация наиболее интенсивна.
Ввиду многообразия и сложности физических процессов в око-
околоземном пространстве действительная структура ионосферы от-
отнюдь не исчерпывается этим простым описанием. В ионосфере раз-
различают три основные области, обозначаемые буквами D, Е и F;
их называют также слоями,
а при детальном рассмотрении
фигурирует и более топкая
структура ионосферы, в част-
частности, выделяют области F\ и
Fz. На рис. 15.21 представле-
представлено несколько идеализированное 400
распределение электронной
концентрации N' (в см) в
ионосфере с высотой [Е.О] (см.
также [Е.1]). Днем степень
ионизации значительно выше;
в ночное время слои I"\ a Fi не
имеют резкой границы, а ниж-
нижняя граница ионосферы подин- 7™
мается до высоты около 100 км,
причем исчезает область 1).
Б з;ипнр111[(н i п |>т степени сол-
солнечной активности (П-.тетппп
цикл), сезона и времени суток
это распределение варьирует-
варьируется. Пределы изменения высо-
высоты максимума электронной
концентрации и максимально-
максимального значения Л"' на рпс. 15.21
показаны крестом стрелок.
Указаны также основные фак-
факторы ионизации для областей D, E n F (вертикальные стрелки);
символы La. и Lf, — обозначения линий серии Лаймана спектра
водорода. В табл. 15.2 приведены некоторые подробности струк-
структуры ионосферы [Е.8]. (lnoii ?], согласно существующим дан-
данным, и дневное время имеется во все сезоны па всем земном
шаре, а слой Ь'г -- только и некоторых местах. Так называемые
492
ГЛ. 15. РАСПРОСТРАНЕНИЕ РАДИОВОЛН
спорадические слои Е, состоят из образований небольшой горизон-
горизонтальной протяженности (десятки километров); появление этих об-
образований подчинено сложным закономерностям. В области F часто
нет четкого выделения слоев Fx и F2. Вообще слой F наиболее
нерегулярен и подвержен влиянию магнитного поля Земли. Неко-
Некоторые исследователи считают необходимым выделять так называе-
называемый слой F]i/2. Следует также иметь в виду, что ионосфера обладает
нерегулярной тонкой структурой; речь идет о локальных вариа-
вариациях электронной концентрации случайного характера.
Для характеристики ионосферы в целом весьма существенно,
что имеют место крупномасштабные нерегулярные явления. При
Таблица 15.2
Строение ионосферы
Область
ионосферы
D
Е
F
Высота, км
504-90
904-120—140
120-=-140 и выше
Слой
С
D
Ei
Е%
Es
F2,F i
1
2 '
F2
Приблизительная
высота, км
65
75ч- 80
110
100
200
250
Л", м-1 *)
~108
~109
~10и
?
—2.1011
~1012
*) Примечание: Л" соответствует дневному времени.
магнитных бурях, возникающих в результате вторжения в ионосфе-
ионосферу корпускулярных потоков, вызываемых вспышками на Солнце,
происходит резкое изменение режима области F. По меньшей мере
можно говорить о сильном уменьшении электронной концентрации
и увеличении высоты ее максимума. Влияние магнитных бурь силь-
сильнее в полярных зонах. Другого рода вспышки на Солнце — хромо-
сферпые — характерны весьма значительным усилением ультрафио-
ультрафиолетового и рентгеновского излучения. В результате глубокого про-
проникновения излучения происходит резкое повышение ионизации
в области D.
15.5.2. Ионосферная рефракция. Об особой роли ионосферы, вы-
выступающей как «природное зеркало», уже говорилось выше в
п. 15.1.3. Рассматривая рефракцию в ионосфере, будем исходить из
общих результатов, обсуждавшихся в пп. 5.5.3—5.5.4 и 14.2.1.
Обратимся к рис. 15.22а. на котором показано, как падающий
под углом 0о па нижнюю границу ионосферы луч искривляется
в пей. Пусть на некотором уровне мгновенное направление луча
характеризуется углом О, а среда — коэффициентом преломления п.
Тогда
no sin Go = n sin О, A5.33)
§ 15.5. РАДИОВОЛНЫ В ИОНОСФЕРЕ (А)
493
где щ = 1 — коэффициент преломления воздушной среды, которую
можно считать однородной (соответственно этому падающий луч —
прямой). Равенство A5.33) прямо следует из E.130); еще проще
прийти к нему, рассматривая дискретную модель среды (см.
рис. 5.29а). Действительно, записывая второй закон Снеллиуса для
х Граница
ионассреры
У////////////////Л У/////////////////////////}//;
Земля
а 6 6
Рис. 15.22
жаждой из границ, убеждаемся, что все величины п<зшФ< равны
между собой.
Итак, мы рассматриваем плоскую модель ионосферы. На пер-
первых порах не будем также учитывать потери в ионосферной плаз-
плазме и действие магнитного поля Земли. Подставляя в A5.33) в ка-
качестве п согласно A4.40), A4.41) величину Ye = Y1 — (соР/соJ =
= У1 — 80,67V'//2, получаем:
sin eo = Vl-80,67V'//2 sin tf.
A5.34)
Равенство A5.34) может быть выполнено, только если подко-
подкоренное выражение положительно. Последнее с ростом высоты долж-
должно уменьшаться во внутренней ионосфере (пока N' растет) п уве-
увеличиваться во внешней (где Л' падает). Таким образом, iso внут-
внутренней ионосфере угол Ь будет возрастать. Общий характер лу-
лучевой траектории зависит от того, «успеет» ли он увеличиться до
30°, т. е. существует ли (для данных 0о и /) достаточно высокая
концентрация Л'=ЛГ*, при которой будет выполнено равенство
sin90 = VI -80,67V*//2,
A5.35)
получаемое при О = 90° из A5.34). Если N*<CNmax, то условие
A5.35) будет выполнено (на какой-то высоте) и луч достигнет
точки поворота (рис. 15.226); дальнейшая — нисходящая — часть
траектории симметрична первоначальной. Заметим, что в точке по-
поворота реализуется предельный случай полного отражения. Если
же N* > /Vmax, то в ионосфере не найдется уровня, на котором
N'=N*. Равенство A5.36) уже не может быть выполпепо (при
данных 0о и /). Луч будет уклоняться к Земле вплоть до уровня
494
ГЛ. 15. РАСПРОСТРАНЕНИЕ РАДИОВОЛН
N' = Nmax, а при переходе во внешнюю ионосферу начнет укло-
уклоняться от Земли (рис. 15.22в) и в конечном счете уйдет за
атмосферу.
Условие поворота луча к Земле A5.35) легко привести к форме:
Пусть угол 0о задан, а частота / варьируется. Как из A5.35), так
и из A5.36) ясно видно, что всегда найдется достаточно низкая
частота, при которой луч повернет к Земле (соответ-
(соответствующая величина N* выбирается из интервала
@, Nynnx)). Легко попять, что существует предель-
предельный угол падения луча па границу ионосферы
0о пР, определяемый с учетом сферичности Земли
(рис. 15.23):
cos0onp = VBNo + h) h/(R0 + К). A5.37)
Это минимальное значение функции cos 0О для зем-
земной радиолинии. Таким образом, из A5.36) и A5.37)
следует, что существует наибольшая возможная частота в условиях
земной радиолинии, использующей ионосферные волны:
Рис. 15.23
9 /л-;,ах (Яо + Щ/ УЩТЩ,
A5.38)
где h — высота нижней границы ионосферы (рис. 15.23). Эта ча-
частота лежит приблизительно па границе KB и УКВ диапазонов:.
Рис. 15.21
и годы наибольшей солнечной активности она сдвигается в область
ОВЧ (метровые волны).
Поскольку для поворота луча к Земле па более длинных вол-
волнах нужны меньшие электронные концентрации, то чем длинпео-
полна, тем менее глубоко луч (и поле) проникает в ионосферу. При
фиксированной частоте глубина проникновения луча тем Польше,
чем .меньше* угол Оо- На рис. 15.24 показана серия лучевых траек-
траектории [К.8], соответствующих различным углам 00 при фикеяровап-
15.5. РАДИОВОЛНЫ В ИОНОСФЕРЕ (А)
495
¦ной частоте /: величина 0о убывает в порядке возрастания номера
траектории. Интересно, что расстояние между начальной и конеч-
конечной точками луча (длина радиолинии) сначала падает, но при
дальнейшем убывании 0О снова возрастает. Существует некоторая
минимально возможная длина. Поэтому вводят понятие зоны
молчания (мертвой зоны). Для радиолиний, использующих толь-
только ионосферные волны, это круг, в центре которого — передаю-
передающая антенна, а радиус равен указанной минимально возмож-
возможной длине.
Наш анализ, как уже отмечалось, является упрощенным. От пло-
плоской модели ионосферы можно перейти к сферической, по мы этого
делать не будем. Потери энергии при распространении радиоволн
в ионосфере будут рассмотрены ниже в п. 15.5.3. Что касается
влияния магнитного поля Земли, то о нем будет говориться в гл. 16:
Д1ы увидим, что плазма в магнитном поле обладает анизотропией,
которую в той или иной мере надо принимать во внимание и при
рассмотрении ионосферных волн.
Заметим также, что применение лучевой трактовки требует ряда
оговорок. Во-первых, мы не имеем права говорить о сколь угодно
низких частотах: геометрические размеры (например, высота ионо-
ионосферы) должны во много раз превосходить длину волны. Во-вто-
Во-вторых, лучевой подход теряет смысл, если свойства среды значитель-
значительно изменяются на расстояниях порядка длины волны. Когда ди-
диэлектрическая проницаемость приближается к пулю, длина волны
в среде сильно увеличивается. В этом случае строгий электродина-
электродинамический анализ необходим. Тем не менее, изложенная выше про-
простая теория правильно передает основные черты процесса при
распространении радиоволи в ионосфере.
15.о.Л. Дисперсия и поглощение радиоволи. Интересно, что в
пренебрежении потерями дисперсия электромагнитной Г-волны,
распространяющейся в плазме, имеет характер полноводной дис-
дисперсии. Внпду (M/iO) но.тпоппе чисто Г-волны есть
к = fe0M-(/p//)-, U = Шр/2я, A5.39)
где А'о = со/1'еоио = со/с. Такой же вид согласно F.21) имеет выра-
выражение постоянной распространения Е- или //-волны полого волно-
волновода: плазменная частота в A5.39) играет роль критической часто-
частоты, входящей в F.21). Поэтому выражения фазовой и групповой
скоростей Г-волпы в плазме получаются из F.23), F.24) при за-
замене /1ф — /Р, v-*¦ с. При /</р рассматриваемая идеализированная
Г-волпа в плазме испытывает такое же превращение, как полно-
полноводная волна при /</кр: иоле экспоненциально затухает без пе-
переноса энергии.
Чтобы выразить волновое число jT-волпы в плазме без препебре-
жения потерями, используем формулы D.42) и внесем в них к =
= (ю/с) Ге'ц/ D.38) и tgA = e"/e', где и/= 1, а г' и е" даются их
496
ГЛ. 15. РАСПРОСТРАНЕНИЕ РАДИОВОЛН
выражениями A4.45). Это дает
к' = —
1
1-
@2 + v2y
1 + 1/ 1 +
1 +
V-CO2)
1
где со2, = W'e2/e0m, как в A4.40).
Если tgA<Kl, т. е. плазма может рассматриваться как несовер-
несовершенный диэлектрик, то
J
VW'
ш2
-. A5.41)
Эти выражения можно получить, отправляясь от формул A5.40).
Пусть также со > v. Тогда из A5.41) следует
-*- , к" ж 4 ,VMp A5.42)
'Й / Zc "I/ 2 2
' Р
и если, кроме того, со > соР) то получается следующая формула для
коэффициента затухания:
= А-
A5.43)
где А = е2/8я2ео»гс. Эта формула обычно применяется для оценок
затухания в диапазоне КВ. Согласно A5.43) коэффициент затуха-
затухания к" обратно пропорциопалеп квадрату частоты и прямо про-
пропорционален произведению vN'. Из рпс. 15.25 [Е.8] видно, что хотя
электронная концентрация N' быстро растет с высотой во внут-
внутренней ионосфере, частота соударений v с еще большей скоростью
падает, что связано с уменьшением плотности среды. В результате
произведение vN', а с ним и к", значительно уменьшается с вы-
высотой. Наиболее поглощающей является область D.
Возвращаясь к формулам A5.41), замечаем, что при достаточпо
больших v величина к" с ростом v уменьшается. Если v2 > со2, то
из A5.41) следует:
к" ж 4- — со2 = 4я2Л —, A5.44)
где А то же, что и в A5.43).
При небольших электронных концентрациях и низких частотах
(roP<Sv, co<v) из A4.45)
tg A ?t; co^/cov.
A5.45)
§ 15.6. ОСОБЕННОСТИ РАСПРОСТРАНЕНИЯ РАДИОВОЛН
497
Если в то же время о)р ^> cov, плазма проявляет себя как провод-
пик. Тогда ввиду D.47)
1 W A5.46).
к"
у
с
В заключение подчеркнем, что все обсуждавшиеся результаты
основываются на элементарной теории столкновений электронов
10
зоо'1
10'
Рис. 15.25
плазмы с тяжелыми частицами (см. п. 14.2.2). Преодолепие допу-
допущенных упрощений требует уже значительного усложнения тео-
теории (см., например, [Д.12]).
§ 15.6. Диапазонные особенности распространения радиоволн
и работа радиолиний (А)
15.6.1. Вводные замечания. Сверхдлшшые и длинные волны.
Общие черты распространения радиоволи в природных условиях
уже обсуждались в п. 15.1.3. Теперь — после изучения роли земной
поверхности, тропосферы и ионосферы в § 15.2—15.5 — можно со-
сосредоточить внимание на диапазонных особенностях распростране-
распространения радиоволн и связанных с этим вопросах работы радиолиний.
Для электромагнитных полей, соответствующих диапазонам СДВ
и ДВ, различные виды почв, а тем более все водные среды высту-
выступают как проводники. Справедливость сделанного утверждения мо-
может нарушаться лишь вблизи границы диапазона СВ для сухих
почв (см. табл. 1.2). Но, например, для сухой почвы с е=4 и
о = 10~3 См/м при / = 10 кГц находим: tg А « 45, что ужо вполпе
отвечает критерию проводника.
Добавим, что на СДВ и СВ земная поверхность оценивается как
наиболее гладкая. Поскольку это граница проводника, магнитное
32 В. В. Никольский, Т. И. Никольская
498
ГЛ. 15. РАСПРОСТРАНЕНИЕ РАДИОВОЛН
§ 15.6. ОСОБЕННОСТИ РАСПРОСТРАНЕНИЯ РАДИОВОЛН
499
поле вблизи нее близко к тангенциальному, а электрическое —•
к нормальному. Волновое сопротивление проводящей среды мало
по модулю, так что невелико поглощение при отражении. Поэтому
так называемая земная волна слабо затухает и может использо-
использоваться для связи па расстояниях даже порядка 3000 км. Посколь-
Поскольку передающая и приемная антенны находятся непосредственно
вблизи земной поверхности, естественной оказывается вертикаль-
пая поляризация волны (параллельная поляризация, п. 5.2.2). По-
Поэтому одной из типичных антенн является вертикальная металли-
металлическая башня, близкая по своему действию к элементарному элек-
электрическому излучателю (§ 9.2), так как размеры антенны, разуме-
разумеется, малы но сравнению с длиной волны.
Ионосферные волны тоже поглощаются слабо, потому что в
ионосфере проходит относительно небольшая часть трассы. Ведь,
как было показано в п. 15.5.2, чем ниже частота, тем (при прочих
равных условиях) меньше электронная концентрация N' = N*, не-
необходимая для поворота луча к Земле. Высота поворота с умень-
уменьшением частоты падает и на СДВ — СВ оказывается близкой к вы-
высоте нижней границы ионосферы. Днем отражение происходит от
границы области D, а ночью (когда последняя отсутствует)—от
границы области Е.
Можно сказать, что область пространства, в которой распростра-
распространяются рассматриваемые волны, есть сферический слой, лежащий
между земной поверхностью и нижней границей ионосферы; обе
.границы в значительной степени осуществляют энергетическую
, ,9 / изоляцию. Передающая антен-
на в точке А (рис. 15.26а), в
сущности, возбуждает электро-
Динамическую структуру, по-
\ добную полому резонатору, раз-
\ меры которого даже на СДВ
' весьма велики но сравнению с
длиной волны, а добротность
низка, поскольку «через обо-
оболочку» все же уходит заметный
поток энергии (потери в Земле
и ионосфере). Движение энер-
энергии происходит, как в сферическом аналоге плоского полого вол-
волновода (см. и. 5.3.2). Если задаться некоторыми постоянными па-
параметрами обеих сферических границ атмосферного слоя (внутрен-
(внутреннюю среду можно при этом считать однородной и даже принять
за вакуум), то можно получить строгое электродинамическое ре-
решение задачи тина A1.53). На этой основе анализируют распро-
распространение СДВ и СВ, используя представление о возбуждении
различных типов воли сферического слоя. Наглядны лучевые схе-
схемы. Анализ показывает, что лучи, выходящие из точки А, сходятся
в точке антипода В (рис. 15.26а), где должна возрасти напряжен-
напряженность иоля.
Рис. 15.20
Обсудим этот эффект антипода в предположении, что обе сфе-
сферические границы являются идеально изолирующими. Тогда вся
энергия, излучаемая антенной А, проходит через конический пояс
(рис. 15.26G, E), площадь которого S может быть достаточно точно
вычислена, как произведение высоты h границы ионосферы па
среднюю длину пояса 2ji/?i = 2ji(/?o + А/2) sin О ~ 2nRah sin #
(рис. 15.266). Если поток энергии в слое равномерен по высоте, то,
исходя из заданной мощности антенны^, имеем 1'а — US — EmS/2W.
Отсюда находим напряженность ноля в точке приема, характери-
характеризуемой углом О:
Ет ~ 1i2QPAIR0hsm% A5.47)
(на близких расстояниях от антенны А выражепие теряет смысл).
Согласно A5.47) напряженность поля в точке антипода В (v) =
= 180°) должна быть бесконечной. В действительности в точке В
можно ожидать возрастания поля несколько менее, чем на поря-
порядок, по сравнению с величиной, наблюдаемой в близкой зоне.
В практике расчета радиолиний СДВ и СВ используется эмпи-
эмпирического происхождения формула Остина
sin О
• exp —
0,0014
A5.48)
Здесь угол О отечнтывается, как показано на рис^ 15.26о; г п X
выражены в км; мощность, излучаемая антенной, РА — в кВт. на-
напряженность поля в месте приема Ет — и мВ/.м. Формулой Остнпа
пользуются до расстояний 16 000-^18 000 км при расчете радио-
радиолиний, функционирующих в дневные часы и проходящих над мо-
морем п сушен (в последнем случае, начиная с расстояний 2000-^-
н- 3000 км). При расчетах напряженности поля земной волны до
расстояний порядка 500 км применяется формула ИТулепкипа—
Ван-дер-Поля (ipmjjniK Перроуза. см. рис. i-j.i2); начинай с такпч:
расстоянии, земная полна существенно слабее ионосферном. Lpono-
ефера практически не оказывает влияния на распространение
СДВ п ДВ.
Впервые и истории рассматриваемые полны использовались для
трансатлантической связи (частоты 15 н-50 кГц).
Радиолинии па СДВ и ДВ характеризуются высоким уровнем
грозовых помех. Антенные сооружения имеют громадные размеры,
оставаясь малыми по сравнению с длиной волны, они весьма до-
дороги, направленность излучения невелика, узка полоса частот. В то
же время снизь устойчива по отношению к ионосферным возмуще-
возмущениям; зона действия передатчика плавно — без резких колебаний
поля — охватывает огромные пространства. Международными согла-
соглашениями предусматривается применение СДВ и ДВ, главным об-
образом, для радионавигации и радиовещания. Отметим: также, что
с понижением частоты увеличивается глубина проникновения поля
32*
500
ГЛ. 15. РАСПРОСТРАНЕНИЕ РАДИОВОЛН
в проводящие среды. Поэтому СДВ имеют преимущество при реа-
реализации радиолиний под водой (связь с подводными лодками
и пр.). Некоторые особенности распространения СДВ, связанные с
действием земного магнетизма, будут затронуты в гл. 16.
15.6.2. Средние волны. По мере увеличения частоты условия
распространения радиоволн изменяются настолько, что для диапа-
диапазоне СВ характерными оказываются уже иные особенности. Из-за
большего поглощения в почве радиолинии СВ, использующие зем-
земную волну, могут пметь протяженность лишь порядка 1000 км. Что
касается ионосферной волны, то она способна отразиться лишь при
электронной концентрации, свойственной слою Е. Поэтому днем,
когда существует более низкий слой D, волна проходит через него
и практически полностью поглощается. Ночью же поглощение со-
соответственно гораздо меньше, и радиолиния может работать на
ионосферной волне; ее протяженность при этом весьма значительно
возрастает. Существенно, что ночью в точку приема В могут прийти
одновременно земная и ионосферная волны (рис. 15.27а) или, на-
например, две ионосферные волны (рис. 15.276). Поскольку состоя-
шие ионосферы подвержено постоянным изменениям (а участок
а
Рис. 15.27
грассы в ионосфере по сравнению с ДВ может быть значителен),
фаза проходящей волны будет заметно изменяться со временем.
По этой причине в обоих отмеченных случаях интерференция волн
приводит то ic ослаблению, то к усилению поля в месте приема.
С этими замираниями (другое их название — фединг) борются, ста-
стараясь уменьшить излучение передающей антенны под большими
углами к горизонту (малые 6о), чтобы подавить возбуждение ионо-
ионосферной волны. Тогда увеличивается так называемая зона увереп-
ного приема (земной волны).
Средние волны используются, главным образом, в радиовеща-
радиовещании; имеются и радионавигационные системы на СВ. Типичная
дальность радиолиний соответствует применению земной волны.
Приведем эмпирическую формулу [Е.1] для напряженности поля
в месте приема средневолновой радиолинии, полученную в резуль-
результате длительпых наблюдений в условиях европейского радиове-
радиовещания: __
Ет =A0 233г/2) 12FADA exp(-8,94 • КИАг0-26) A5.49)
(обозначения те же, что и в A5.48)).
§ 15.6. ОСОБЕННОСТИ РАСПРОСТРАНЕНИЯ РАДИОВОЛН
501
15.6.3. Короткие волны. Для коротких волн почва ведет себя
иак несовершенный диэлектрик, и они глубоко проникают в ионо-
ионосферу. Первое приводит к сильному поглощению земной волны,
которая оказывается пригодной для радиосвязи лишь на десятки
километров. Основной практический интерес представляют ионо-
ионосферные волны, причем типичные электронные концентрации, со-
соответствующие повороту луча к Земле, лежат в области F; области
D и Е в основном обусловливают поглощение волны. В п. 15.5.2
говорилось о зоне молчания, круговой области, внутри которой не-
невозможен прием ионосферных радиоволн. В более точном смысле
зоной молчания называют кольцевую область, внутренний радиус
которой соответствует дальности приема земной волны в диапазо-
диапазоне КВ. Таким образом, это зона, в которой уже не принимается
земная волна, но еще не может быть использована волна ионосфер-
ионосферная. Другим характерным эффектом, свойственным диапазону KB,
является кругосветное эхо — наложение на принимаемый сигнал
другого, который создается волной, обошедшей земной шар путем
многократных отражений от ионосферы и Земли (в прямом или
•обратном направлении). Время запаздывания при однократном об-
обходе земного шара составляет около 0,13 с.
На коротких волнах впервые в практике радиосвязи были реа-
реализованы остронаправленные антенны, позволяющие экономно рас-
расходовать энергию при двусторонней связи. Наличие таких антенн
и относительная малость поглощения KB при рефракции в ионо-
ионосфере и отражении от Земли (в типичных условиях) делают корот-
короткие волны весьма подходящими для дальней радиосвязи. Интерес-
Интересно, что значение коротких волп было понято под влиянием радио-
радиолюбительской практики.
Основу понимания главных закономерностей распространения
KB, определяющих выбор рабочих частот, составляют простые со-
соображения, рассматривавшиеся в п. 15.5.2. Со стороны высоких
частот ограничение этого диапазона приблизительно соответствует
прекращению поворота ионосферной волны к Земле в дневное вре-
время. Наиболее короткая волна, для которой такой поворот еще про-
происходит, оценивается по формуле
/п
A5.50)
следующей из A5.36). В практике радиосвязи соответствующая ча-
частота называется максимально применимой частотой (МПЧ). Так
называемая оптимальная рабочая частота (ОРЧ) лежит ниже МПЧ
на 15-^- 30 %. Некоторое спижение частоты вызвано необходимостью
стабилизировать условие поворота луча. Поскольку затухапие вол-
волны растет обратно пропорционально квадрату частоты (см.
п. 15.5.3), снижение частоты нежелательно. Существует понятие
наименьшей применимой частоты (НПЧ), т. е. частоты, при кото-
которой для данной мощности передатчика напряженность поля в ме-
месте приема оказывается на грани требуемой нормы. При расчете
502
ГЛ. 15. РАСПРОСТРАНЕНИИ РАДИОВОЛН
МПЧ
2 6 10 14 18
Местное бремя
Рис. 15.28
радиолиний диапазона KB используются графики суточного изме-
изменения МПЧ и НПЧ, составляемые при помощи различных полу-
полуэмпирических правил на основании данных измерений, осуществля-
осуществляемых так называемыми ионосферными станциями. Пример такого
графика приведен па рис. 15.28 [Е.2]. Что касается ионосферных
станций, то производимой на них стан-
стандартной операцией является вертикаль-
вертикальное зондирование. Присылая в зенит
(80 = 0) волну той или иной частоты,
устанавливают, на какой высоте проис-
происходит отражение.
Напомним, что электронная концен-
концентрация в области F, где при типичных
условиях происходит поворот луча на
KB, существенно меняется от дня к
ночи и сезонно, не говоря уже о раз-
разного рода несистематических возмущепиях. Днем — при более вы-
высокой электронной концентрации — МПЧ повышается, ночью — сни-
снижается. Поэтому существуют так называемые дневные и ночные
волны. Это поддиапазоны 10-^25 м и 35-^100 м соответственно.,
рекомендуемые для связи в зависимости от времени суток.
Относительно стабильный режим ионосферы, как уже отмеча-
отмечалось в п. 15.5.1, нарушается время от времени под влиянием про-
цессои па Солнце. Действие интенсивных корпускулярных потоков,,
приходящих от Солнца, приводит к сильному изменению структу-
структуры и падению электронной концентрации области F, к ее «разру-
«разрушению», в результате чего рефракция коротких воли к Земле ста-
становится невозможной и радиолиния перестает действовать. Такие
возмущения ионосферы, сопровождаемые магнитными бурями, наи-
наиболее сильны в полярных областях, куда преимущественно попада-
попадают корпускулярные потоки, направляемые магнитным полем Зем-
Земли. Другой вид нарушения коротковолновой связи — вис житное
поглощение из-за возникновения повышенной ионизации и обла-
области D под влиянием хромосферных вспышек на Солнце.
Для диапазона KB типичны интерференционные замирания, вы-
вызываемые наложением нескольких относительно независимо рас-
распространяющихся волн, несущих принимаемый сигнал. Одна из
причин — приход в AiecTo приема волн, претерпевших разное число
отражении от атмосферы (см. выше п. 15.6.2). Можно также гово-
говорить об изменяющейся во времени фокусировке (дефокусировке)
параксиального пучка лучей в ионосфере в результате неравномер-
неравномерного изменения ее свойств. Другие причины мы обсудим после вы-
выяснения роли магнитного поля Земли в гл. 16. Отметим, что при
высокой солнечной активности лучевые траектории могут быть зна-
значительно сложнее обсуждавшихся. В частности, область Е (и даже
D) может вызвать поворот пли преломление луча (изменение тра-
траектории при прохождении слоя насквозь). Некоторые типы траек-
§ 15.6. ОСОБЕННОСТИ РАСПРОСТРАНЕНИЯ РАДИОВОЛН
503
торий, возникающих при участии слоев F и Е {Е,), показаны на
рис. 15.29 [Е.8]; надо иметь в виду, что это не действительные тра-
траектории, а качественные схемы.
Нестабильность ионосферы, необходимость учета потерь и дис-
дисперсии волн, проходящих через нее, а также иные факторы обуслов-
обусловливают ряд трудностей на пути расчета KB радиолиний. В инже-
инженерной практике обычно используются но-
луэмпирпческие методы.
15.6.4. Ультракороткие волны. В годы
максимума солнечной активности рефракция
в ионосфере приводит к отражению воли,
выходящих за пределы диапазона KB (на-
лример, около 6 м). Можно также отметить
отражение метровых волн от спорадического
слоя Еа, обладающего высокой концентра-
концентрацией, но образующегося нерегулярно. За
этим исключением всему диапазону УКВ
лрисуще то качество, что рефракция в ионо-
ионосфере не приводит к возвращению луча.
В силу сказанного обычные радиолинии
:на УКВ действуют в пределах прямой види-
видимости; для увеличения дальности радиосвя-
радиосвязи антенны поднимают над земной поверх-
поверхностью. Если последняя является достаточно
гладкой, то радиолиния часто принадлежит
к типу, рассматривавшемуся в п. 15.3.1 па
основе лучевой трактовки. При этом часто
применяется формула Введенского A5.21).
В случае остроиаправленных антенн, как
уже отмечалось в п. 15.3.1, нужно исполь-
использовать более общую формулу A5.17). Впро-
Впрочем, если такие антенны подняты достаточ-
достаточно высоко, отражение от земной поверхно-
поверхности окажется пренебрежимо малым. Тогда
напряженность поля в месте приема может быть найдена при по-
31 о щи A5.4). При необходимости учитывается сферичность Земли
(см. п. 15.3.1, 15.3.2) и тропосферная рефракция (см. п. 15.4.2).
Чем короче волна, тем менее относительно гладкой оказывается
земная поверхность. Но даже в тех случаях, когда критерий глад-
гладкости A5.10) нарушается, нередко пользуются представлением об
эффективном коэффициенте отражения от поверхности. Однако ти-
типичны случаи, когда этот подход непригоден даже для очень грубых
оценок. Таковы условия распространения УКВ в пределах города.
Иногда в подобных условиях учитывают действие отдельных «пре-
«препятствий», оказывающихся в доминантной области (см. п. 15.2.1).
Типично применение УКВ па радиорелейных линиях, протяжен-
протяженность которых многократно превышает расстояние прямой види-
Рис. 15.29
504
ГЛ. 15. РАСПРОСТРАНЕНИЕ РАДИОВОЛН
мости; в пределах этого расстояния находится каждая пара приемо-
приемопередающих радиорелейных станций.
Практический интерес представляют также различные типы
дальнего распространения УКВ. Именно в этом диапазоне реали-
реализуются возможности существенного влияния нерегулярных тропо-
тропосферных явлений (п. 15.4.3). Весьма значительное превышение-
расстояния прямой видимости возможно в результате сверхрефрак-
сверхрефракции, в особенности как следствие процессов рассеяния. В тропо-
тропосферных радиорелейных линиях связи приемопередающие станции;
находятся на расстояниях сотен километров. Дальнее распростра-
распространение УКВ может быть обусловлено рассеянием на случайных не-
однородностях ионосферы, а также на ионизированных областях,,
образующихся при вхождении в атмосферу метеоров («следы» ме-
метеоров) и при полярных сияниях. Существуют весьма протяжен-
протяженные линии, использующие эти явления (свыше 1000 км).
15.6.5. О космической радиосвязи. Диапазон УКВ ввиду про-
прозрачности для этих волп ионосферы используется в системах кос-
космической связи. Нужно сделать оговорку, что связь с космически-
космическими объектами, находящимися в пределах внутренней ионосферы,
возможна и в диапазоне КВ. Не перечисляя многочисленные функ-
функции космических радиолиний, отметим, что, по крайней мере, сле-
следует различать радиолинии, связывающие Землю и космический:
объект (искусственный спутник Земли или Луны, космический ко-
корабль, направляющийся к планетам и пр.), космические объекты
между собой и, наконец, используемые для связи между земными
объектами. Существует также проблематика местной связи при
освоении Луны и планет.
Космические радиолипии могут быть беспрецедентно протяжен-
протяженными, простираясь на многие миллионы километров. Поэтому, хотя
поглощение в межпланетной среде весьма невелико в расчете на
единицу длины, оно, в принципе, подлежит оценке.
Действие атмосферы Земли приводит к искривлению -выходя-
-выходящего через нее луча. Теория рефракции позволяет оценивать на-
направление выходящего луча.
Отдельную проблему составляет исследование влияния плазмен-
плазменного окружения космического объекта, входящего в плотные слои
атмосферы, или плазменной области, появляющейся при наличии
факела ракеты. Эти явления приводят к нарушепию связи.
Связь в неземных условиях может иметь различные особенности.
Так, например, отсутствие у Луны атмосферы затрудняет проблему
связи между лунными объектами, лежащими за пределами прямой
видимости. Известно предложение использовать в этом случае ре-
ретранслятор на Земле.
Проблематика распространения радиоволн в космосе (см., на-
например, [Е.12, Е.13]) важна не только в рамках проектирования
радиосистем, по и для паучпых исследований: радиоастропомин,
радиолокации плапет и пр.
§ 15.6. ОСОБЕННОСТИ РАСПРОСТРАНЕНИЯ РАДИОВОЛН
505
Все большее значение приобретают спутниковая связь и веща-
вещание. Радиолинии, использующие ретрансляцию через ИСЗ, имеют
ряд особенностей. В частности, в результате движения ИСЗ относи-
относительно наземной станции сказывается эффект Доплера — смещение
частоты, меняющееся па трассе; это приводит к искажепию спект-
спектра сигнала. Вопросы проектирования спутниковых радиолиний рас-
рассмотрены в специальных руководствах [Е.14].
15.6.6. О помехах при работе радиолиний и электромагнитной
совместимости. Через приемную антенну на вход радиоаппаратуры
вместе с полезным сигналом неизбежпо поступают посторонние
электромагнитные воздействия. Это помехи радиолинии, вносящие
вклад в полную мощность шумов Рт. Отношение мощности полез-
полезного сигнала Рс к Рш для разных радиолиний должно удовлетво-
удовлетворять соответствующим нормативным требованиям.
Существуют индустриальные помехи — радиоизлучение различ-
различных электроустановок, включая бытовые; атмосферные — грозо-
грозовые — помехи; шумы космического происхождения; шумы, обуслов-
обусловленные атмосферой и земной поверхностью. Наконец, важна про-
проблематика взаимных помех при работе радиолиний.
Борьба с индустриальными помехами производится путем раз-
размещения приемных пунктов вне больших городов; принимаются
также разные меры с целью уменьшить уровень этих помех. При
наличии остронаправленных антенн (главным образом, на СВЧ)
индустриальные помехи несущественны.
Атмосферпые помехи тем слабее, чем выше частота. Они осо-
особенно заметпы в диапазопах СДВ и ДВ — также еще потому, что
в этих диапазонах могут применяться лишь аитенпы, обладающие
•слабой направленностью. Грозы особенно часты в тропических об-
областях; однако надо иметь в виду, что мешающее влияние грозо-
грозового излучения в указанпых диапазонах может сказываться на рас-
расстояниях сотеп и тысяч километров.
Рассматривая шумы космического происхождения, различают
фон радиоизлучения Галактики и излучепие дискретных источни-
источников, которыми являются Солнце, планеты и звезды. Отмечается
также излучение содержащегося в космическом пространстве водо-
водорода па волне К = 21 см.
Земная поверхность создает тепловое излучение, влияние кото-
которого уменьшает применение остронаправлеипых аптепн. Излучение
атмосферы имеет резонапепый характер; его частотное распределе-
распределение характеризует график поглощения на рис. 15.20. На СВЧ
атмосферные шумы резко преобладают пад остальными помехами
радиолиний.
Роль взаимных помех радиолиний возрастает вместе с разви-
развитием радиоэлектронных средств в мире. Использование тех или
иных полос частот различными службами регламентируется между-
международными соглашениями. При проектировании радиосистем пер-
востепепное значение приобретает обеспечение их электромагнит-
506
ГЛ. 16. АНИЗОТРОПНЫЕ, АКТИВНЫЕ И НЕЛИНЕЙНЫЕ СРЕДЫ
ной совместимости (ЭМС) с другими существующими и планируе-
планируемыми системами. Современные транспортные и другие объекты на-
насыщены радиоэлектронной аппаратурой, размещенной в ограничен-
ограниченном объеме. Это остро ставит вопросы ЭМС. Проблематика ЭМС
разрабатывается экспериментальными и теоретическими средствами,
УПРАЖНЕНИЯ
_ 1. Найти требуемую мощность передатчика РА при следующих условиях:
1'в = Ю-12 Вт, ВА = 50 дБ, D,, = 50 дБ. F = —20 дВ, г = Ш км, А = 3 см.
2. Пользуясь таблицей 1.2, сделать оценки: а) пределов изменения tgA для:
разных природных сред на границах диапазонов волн; б) значений глубины
проникновения Д° для морской воды при тех и;о частотах.
3. Для каких диапазонов волн поверхность современного города согласно
критерию Рэлея может считаться ровной? Пусть угол лежит в пределах 0 -f- 80°.
4. Пользуясь спиралью Корню, исследовать влияние экрана на прямую пе-
передачу энергии, когда сторона квадратного отверстия равна диаметру десятой:
зоны Френеля.
5. Взяв значение параметра С в формуле A5.13), соответствующее десяти
зонам Френеля, найти наибольший поперечный размер доминантной области
при протяженности радиолинии А = 100 км и длине волны X = 3 м.
fi. Два вертикально ориентированных диполя Герца расположены на высо-
высоте h\ = >/2 = И) м; Л = 3 см. При какой протяженности радиолинии допусти-
допустимо применение лучевой модели, если задано С = 6 в A5,13)?
7. В условиях предыдущего примера выяснить, пользуясь спиралью Кор-
Корню, до каких расстояний можно использовать лучевую модель, если ошибка
по напряженности поля в месте приема может иметь порядок 50 %•
8. Передающая антенна имеет вид вертикальной мачты высотой h = 50 м,.
Я = 500 м. Принимая ее за_диполь Герца, вычислить напряженность поля па
расстоянии г = 150 км при Ра = МО Вт. Использовать формулу Шулейкнпа —
Вап-дер-Поля (график Берроуза).
9. На основе формулы A5.27) и соответствующих графиков выяснить, как
изменяется поле излучения в области тени в зависимости от длины волны.
10. Вывести условие критической рефракции.
11. Пусть 0° = 45°. Пользуясь графиком па рис. 15.21, определить высоту
поворота луча в дневное и ночное время па границах диапазонов волн.
12. Какова кратчайшая волна, пригодная для связи между земными объ-
объектами ночью и дном согласно графику на рпс. J5.21?
13. Найти коэффициент затухания волны в плазме при параметрах, соот-
соответствующих высоте 300 кн согласно графику па рис. 15.25, и "к = 20 м.
14. Насколько уменьшается расстояние прямой видимости на Лупе по>
сравнению с земным? Учесть рефракцию в земной атмосфере.
Глава 16
ПОЛЯ В АНИЗОТРОПНЫХ, АКТИВНЫХ И НЕЛИНЕЙНЫХ СРЕДАХ
§ 16.1. Анизотропия и гиротропия (А)
16.1.1. О природе анизотропии. Об анизотропных средах гово-
говорилось в п. 1.3.5. Было отмечено, что свойства среды — электриче-
электрические или магнитные — могут зависеть от направления. При этом
параметры материальных уравнений A.67) — A.69) следует рас-
рассматривать как матрицы вида A.9). Так, анизотропный диэлектрик
§ 16.1. АНИЗОТРОПИЯ И ГИРОТРОПИЯ
507
описывается при помощи тензора диэлектрической проницаемости
г, и материальное уравнение A.67) в координатной записи прини-
принимает вид
/Г> \ /р р.... е..,\ / с,. \
A6.1)
Анизотропию могут проявлять кристаллические среды, характер-
характерным свойством которых является упорядоченность строения. Рас-
Рассмотрим, подобно тому, как это делалось в п. 14.1.1, систему поля-
поляризуемых частиц. Пусть выделен макроскопически малый объем
AV, содержащий достаточно большое количество частиц (рис. 16.1).
Если допустить, что при заданном внешнем поле среднее значение
Б в любой точке зависит только от плотности частиц, то при всех
направлениях поля объем А У приобретает один и тот же по абсо-
абсолютному значению момент piF, который каждый раз параллелен Е
(ср. (а), (б), (в)). Среда проявляет себя как изотропная.
Но при определенных типах упорядочения частиц их поляриза-
поляризация зависит от направления внешнего поля. Пусть (рис. 16.2) в
Рис. 16.2
двух случаях (а) и (б) под влиянием внешнего поля возникают
параллельные ему, по разные по абсолютной величине электриче-
электрические моменты pAF (они обозначены стрелками разной длины). Оче-
Очевидно, что в третьем случае (в) векторы рдт- и Е уже не парал-
параллельны. Это анизотропия. В качестве простейшей причины ее про-
происхождения можно представить себе, что в одном направлении
(рис. 16.2а) частицы следуют чаще, чем в другом (рис. 16.26). При
508
ГЛ. 16. АНИЗОТРОПНЫЕ, АКТИВНЫЕ И НЕЛИНЕЙНЫЕ СРЕДЫ
должном расположении координатных осей х, у, z тензор диэлект-
диэлектрической проницаемости будет диагональным:
е=
Если структура характеризуется только одним выделенным направ-
направлением, с которым совмещена ось z, то в A6.2) гх = гуФгг. Среда=
называется в таком случае одноосной.
В § 6.3 рассматривались периодические структуры, свойства ко-
которых изменяются в одном направлении. Простое обобщение при-
приводит к представлению о структурах трехмерно-периодических; та-
такова, например, система шаров, дисков и т. п., распределенных в-
пространстве через равные промежутки в трех ортогональных на-
направлениях. Если в электродинамической задаче все три период»
подобной структуры значительно меньше длины волны, то ее мож-
можно рассматривать подобно сплошной среде; внутреннее поле усред-
усредняется. Каждая макроскопическая частица под влиянием прило-
приложенного поля может действовать подобно диполю; в п. 2.2.6 отме-
отмечалось дипольное действие шара. Мы приходим к представлению-
об искусственном диэлектрике. Последний будет анизотропным да-
даже в случае шаровых элементов, если пространственные периоды
различны.
16.1.2. Гиротропия намагниченной плазмы. Если в задаче о»
плазме в переменном электромагнитном поле (см. пп. 14.2.1, 14.2.2)
ввести еще постоянное магнитное поле Но = z0#o, то на заряжен-
заряженные частицы будет также действовать лоренцева сила. Это приведет
к характерной анизотропии среды, которая будет описываться уже-
не скалярной диэлектрической проницаемостью вида A4.44), а тен-
тензором
где
гт = 1 —
ег О
o о
со [(со - ivf ~ Q2J
причем
со [(со— ivJ — Q2]
, eL=l-
со (со— iv) '
A6.3)
A6.4)
A6.5)
Анизотропия, при которой тензор е имеет вид A6.3), называет-
называется гирогропией. Смысл термина будет понятен, после того как в
16.2 мы рассмотрим волповые процессы в гиротропных средах.
§ 16.1. АНИЗОТРОПИЯ И ГИРОТРОПИЯ
50»
ВЫВОД. Возвращаясь к уравнению движения A4.42), введем
в дополнение к силе qEm действующую в данном случае на частицу
лоренцеву силу q [v, Bo] = q [i©rm, zO[Xo#o]- Это дает:
и (со — iv) rm + i© -|- ц0Я0 [ rm, z0] = ~ Em. A6.6>
Поляризованность Р определим, как это делалось в п. 14.2.1
при получении формулы A4.38), учитывая только электроны. Тог-
Тогда Pm = N'erm (q = e). Поэтому из A6.6) следует:
ш (ю — iv) Pm — iojQ [Pm, z0] = — e0copEm, A6.7>
где использованы обозначения A6.5). В координатной форме
имеем:
ю (ю — iv) Pmx — шпРту = — eo(alEmx,
+ ш (ю — iv) Рту = — е0а2рЕту, A6.8>
© (и — iv) Pmz = — e0(o2pEmz.
Решая эту систему, выражаем компоненты вектора Рт:
Ртх =
—^ гГ Kffl - iv) Emx + iQEmy],
р
ту
? ai
A6.9)
р о р
mz~ со (со — iv)
Мы получили развернутую запись соотношения Рт = еоХэЕт A.72) р
где %э — тензор электрической восприимчивости (см. также
п. 14.1.1). Как видно, среда анизотропна. Выписав из A6.9) коэф-
коэффициенты при компонентах вектора Ет, мы получим элементы тен-
тензора %э, а поскольку е = / + %" (I — единичный тензор), можно
сразу получить и тензор диэлектрической проницаемости. Это при-
приводит к формулам A6.3), A6.4). ¦
Нетрудно понять, почему плазма в постоянном магнитном поле-
оказывается гиротропной. Если напряженность переменного элект-
электрического поля Е, а с ней и скорость электрона v, имеет проекцию
на плоскость, перпендикулярную вектору Во постоянного поля, то
электрон «закручивается» в этой плоскости (см. п. 14.1.2). Поэто-
Поэтому кроме параллельных Е компонент PhD появляются и перпен-
перпендикулярные компоненты, лежащие в квадратуре.
Возвращаясь к формулам A6.3) и A6.4), отметим, во-первых,,
что вдоль направления постоянного «подмагничивания» (ось zf
510
ГЛ. 16. АНИЗОТРОПНЫЕ, АКТИВНЫЕ И НЕЛИНЕЙНЫЕ СРЕДЫ
плазма сохраняет прежние свойства: гь в A6.4) совпадает с е из
A4.44). Во-вторых, формулы A6.4) свидетельствуют о резонанс-
резонансном характере процесса в намагниченной плазме. В идеализиро-
идеализированном случае отсутствия поглощения (v = 0) при со -*- Q компо-
компоненты тензора ел и i$ A6.4) неограниченно возрастают; взяв v Ф 0,
легко заметить, что этот гиромагнитный резонанс несколько сдви-
сдвигается и компоненты тензора диэлектрической проницаемости оста-
остаются ограниченными. Величина Q есть не что иное, как круговая
частота вращения электронов в постоянном магнитном поле (см.
п. 14.J.2); она называется гироскопической частотой.
В заключение заметим, что ввиду пренебрежения влиянием
гтонон при выводе тензора е полученные формулы A6.4) в той или
иной мере утрачивают достоверность вблизи гироскопических ча-
частот Q' = цо\е\Но/пг', где пг'— масса иона (предполагается одно-
одновалентность) ; Q' < Q, поскольку пг' > пг.
16.1.3. Гиротропия намагниченного феррита. Магнетикам свой-
свойственна гиротропия, обусловленная прецессией вектора М в посто-
постоянном магнитном поле (см. п. 14.1.3). Так называемые ферриты,
обладая ферромагнитными свойствами, по характеру диэлектриче-
диэлектрических потерь могут быть отнесены к диэлектрикам: tg А «С 1. Они,
таким образом, в отличие от ферромагнитных металлов «прозрач-
«прозрачны» для электромагнитного поля. Поэтому гиротропия ферритов,
проявляющаяся в диапазоне СВЧ, нашла многочисленные техниче-
технические применения.
Пусть феррит намагничен, так что внутреннее постоянное поле
характеризуется векторами Ho = zo#o и Mo = zoMo. При этом по
отношению к переменному полю среда будет выступать как анизо-
анизотропный магнетик с комплексной проницаемостью в виде тензора
^l =
где
причем
, —1
__ л
2
CO — I
а =
A6.10)
= 1, A6.11)
A6.12)
есть собственная частота прецессии (см. п. 14.1.3), если потерями
можно пренебречь; об учете потерь будет сказано ниже.
ВЫВОД. Взяв уравнение движения намагниченности A4.33),
отметим сначала, что в случае постоянного поля его левая часть
обращается в нуль, а следовательно [М, Н] = 0, т. е. векторы М и
II параллельны — среда изотропна. Пусть теперь М = М0 + М(?)
и Н = Н0 + Н(?), где нулевыми индексами отмечены постоянные
S-
§ 16.1. АНИЗОТРОПИЯ II ГИРОТРОПИЯ 51f
составляющие. Внося это в A4.33), получаем:
^ = 7{[М0, Н(*)] + [М@, Но] + [Мо, Но] + [M(f), H (*)]}. A6.13)
Если, как это часто бывает, |М(?)| < |М0| и ]H(t)\ < |Н01. то квад-
квадратичным членом [М(?), Н(^)] можно пренебречь, и уравпение
A6.13) оказывается линеаризованным относительно переменной;
Нп Нп
}нп+нт
-Нп^А^Нт
Рис. 16.3
составляющей. Рассматривая гармонические колебания, применим
метод комплексных амплитуд, что означает замену: М(?)-»- Mme'mt
и H(t)->- Hme""f. Тогда из A6.13) следует:
[Мо, Н0] = 0, icoMm = v{[M0, Hm] + [Mm, Но]}. A6.14)
Взяв Мо = zojI/o, Но = zo#o и представляя второе равенство в ко-
координатной форме, записываем:
mSlmx — чНойту = —чМ0Йту,
vH0Mmx + taA'lmy = чМоЙтх, AG. 15)
тЙтх = 0,
(Y < 0, компоненты вектора Мт перенесены влево). Решая эту си-
систему уравнении, получаем:
г (- антх - шнту),
'"Л co'"-fi"
| y| М
Мщу = — \ {шНтх — пНту),
Mmz = 0,
AG.16)-
где применено обозначение A4.32); вместо вектора Q использован
его модуль Q.
512
ГЛ. 16. АНИЗОТРОПНЫЕ, АКТИВНЫЕ И НЕЛИНЕЙНЫЕ СРЕДЫ
\у\но-*и>
Получена координатная запись соотношения Мт = |ло%мНт
A.72), в котором магнитная восприимчивость %м есть тензор. Из
A6.16) нетрудно выписать элементы %м и получить тензор магнит-
магнитной проницаемости ц = / + %м. Это приводит к формулам A6.10),
A6.11). ¦
Итак, тензор магнитной проницаемости феррита |л A6.10), как
оказалось, имеет такую же структуру, как тензор диэлектрической
проницаемости плазмы е A6.3). Обе
среды гиротронны; в 16.2 будет пока-
показано, что волновые процессы в обоих
случаях аналогичны.
Осмысливая причину гиротропии
намагниченного феррита, надо иметь в
виду, что постоянное магнитное поле
создает выделенное направление, около
которого происходит прецессия вектора
М. Приближение со к собственной ча-
частоте прецессии Q обусловливает фер-
ферромагнитный резонанс среды. Посколь-
Поскольку в выражениях A6.11) не учтены
потери, цх и а при резонансе обраща-
обращаются в бесконечность. В упрощенном
представлении совпадение частот со и
Q означает, что прецессионное движе-
движение М совершает один цикл синхронно
с «качанием» результирующего векто-
вектора Н из положения Но — Нт в положе-
положение Н0 + Нт (рис. 16.3). Поскольку Н
задает мгновенную ось прецессии, ее
радиус возрастает.
Изложенная теория является идеа-
идеализированной уже в силу допущенной
липеаризации уравнения A6.13). Учет
потерь можно было бы произвести,
взяв вместо A4.33) уравнение Ландау — Лифшица A4.34); соот-
соответствующие формулы можно найти в специальной литературе
[Д.5 — Д-7]. Но н этого для практических целей недостаточно. Для
определения компонент тензора |я реального феррита используются
специальные измерения. Величины |лт, а и ць в силу существования
потерь комплексны: \1т = Цт— Щт> а = а — га , ц^ = Ць — фь-
На рис. 16.4 показан характер зависимостей этих величин от
напряженности постоянного поля Но, получаемых путем изме-
измерений.
Заметим, что для учета поглощения можно ввести понятие соб-
собственной комплексной частоты прецессии Q = Q' + iQ" (ср. п. 3.2.3
и п. 11.1.4). При этом в формулах A6.11) делается подстановка
Ml
Ml
Рис. 16.4
§ 16.2. ПОЛЯ И ВОЛНЫ В ГИРОТРОПНЫХ СРЕДАХ
513
Q -*¦ Q. В случае достаточно узкой резонансной кривой (зависи-
(зависимость цт или а" на рис. 16.4) полагают Q'= Q и Q"*=AQ =
= Д#оЫ, где АН о полуширина резонансной кривой, понимаемая
так же, как в п. 11.1.4.
§ 16.2. Поля и волны в гиротропных средах
16.2.1. Запись уравнений Максвелла (А). Для исследования раз-
различных свободных электромагнитных полей в гиротропных средах,
являющихся решениями однородных уравнений Максвелла
rot Hm = гсое0еЕт, rot Em = —г"
Нт A6.17)
произведем подробную запись этих уравнений в декартовых коор-
координатах.
Сначала возьмем случай магнетика (феррита), который з по-
постоянном магнитном поле Но = 2,qHq для поля переменного проявля-
проявляет себя как гиротропная среда, характеризуемая тензором \i вида
A6.10). Таким образом, в A6.17) магнитная проницаемость ц есть
указанный тензор, а диэлектрическая проницаемость е — скаляр.
Поэтому уравнения A6.17) принимают следующую форму:
дН.
дНт
dz
дх
дН
mv = шеогЕтх,
= ШгогЕту,
™mz дЕпу . ¦ •
—-; з - = — г*й[Хд ([Хт-Птх— l(Xttmy),
ТПХ ТПХ • / • ТТ | ТТ \
—д 7 = — г(О^10 AСШ mXi + Цт-П my)i
A6.18)
дЕту дЕтх
дх
дх
В случае подобным же образом намагниченной плазмы (Но =
= zqHq) |л — скаляр, а е — тензор вида A6.3), так что теперь
получаем:
дНтг дНту . , i -ah \
= 1ме0 (гТЕтх — фЕту),
8E
ду
dz
ду
9Hmx dHmt . ,.0?,
дх
A6.19)
дН.
ту тх
дх бУ —o-b-mz,
33 В. В. Никольский, Т. И, Никольская
дЕт
дх
514
ГЛ. 16. АНИЗОТРОПНЫЕ, АКТИВНЫЕ И НЕЛИНЕЙНЫЕ СРЕДЫ
Системы уравнений A6.18) и A6.19) переходят друг в друга;
при следующей замене величин:
еое *=*= [д-оМ- (скаляры),
,**BOeLl A6.20)
Em ~^ —Hm, Hm -»- Em.
Записанные соотношения обобщают принцип двойственности для1
однородных уравнений Максвелла C.79) па гиротропные среды.
Существование правил замены A6.20) означает, что нет необ-
необходимости отдельно находить решения систем уравнений A6.18) тт
A6.19). Можно, например, производить все операции только с си-
системой A6.18), т. е. искать поля в гиротропном магнетике. Приме-
Применяя к готовым решениям системы A6.18) соотношения A6.20), мы
получим решения системы A6.19), т. е. найдем поля в гиротропной
плазме.
16.2.2. Продольные волны. Эффект Фарадея (А). Начнем с рас-
рассмотрения воли в гиротропном магнетике, распространяющихся
вдоль направления постоянного намагничивапия — по оси z.
Как и в изотропных средах (см. п. 4.1.2), будем рассматривать
поля, зависящие только от координаты ъ. Из последних строчек
уравнений A6.18) видно, что в этом случае Emz = 0 и Йтх = 0, т. е.
однородные волпы оказываются Г-волнами. Будем искать решение-
уравнений A6.18) в форме
г)
A6.21)
где <эх, <эу, Жх, <Ж, — константы и Г — неизвестная пока постоянная
распространения. При подстановке A6.21) в A6.18) получаем
ГЖ = -
A6.22)
Исключим отсюда &х и <У„. Это дает два равенства:
Г2 И_
1 9
С"
A6.23)
= — i-n- гаЖу
с
Если теперь перемножить левые и соответственно правые части
обеих строчек, то получается следующее уравнение относительно Г:
] ^ A6.24)
с- ¦ I с-
При извлечении корня слева и справа нужно учесть, что знаки
§ 16.2. ПОЛЯ И ВОЛНЫ В ГИРОТРОПНЫХ СРЕДАХ
515
могут быть как одинаковы, так и различны. Поэтому
A6.25)
Это значит, что возможны значения Г = ±Г+ и Г = ±Г~, где
г+ = _ш_
A6.2G)
а следовательно, существуют два типа продольных волн, которые
могут распространяться в прямом и обратном направлениях.
Если подставить A6.25) в A6.23), то выясняется, что при
Г2 = (Г+J и Г2 = (Г~J соответственно
Жи=:1Жх, *%>у — —1ЖХ- A6.27)
Мы видим, таким образом, что каждая из волн имеет круговую
поляризацию. Для волн, распространяющихся вдоль оси z, индекс
плюс в A6.26) отвечает правой круговой поляризации, а индекс
минус — левой (ср. п. 4.2.1).
Выпишем комплексные амплитуды векторов Е и Н рассматри-
рассматриваемых воли; па основании A6.21), A6.26) и A6.22) имеем:
правой
волна ; круговой поляризации в направлении z
левой
= А (хи ± ?у0)
= AW± (± гх0 - у0) e-*r
A6.29)
правой
волна—1—z—круговой поляризации в направлении — z
левой
Ш=А (х0 =F iyo)e-Hrx*, Ё^ЛТУХ (± ix0 + у0) е^'Г
(Л—неопределенный коэффициент); при этом
W* = Vlk7e0V(nr±a)/e. A6.30)
Особый интерес представляет случай, когда волны обеих круго-
круговых поляризаций существуют одновременно. Рассматривая нало-
наложение двух таких волн с одинаковыми амплитудными коэффици-
коэффициентами А, распространяющихся вдоль оси z, на основании A6.28)
получаем:
Нт (z) = И" (z) + Ни (z) = Л [х0 (e'ir~z + e-*r-z) +
_.г++г~
+ iy0 (е-т+r - в-т-z)] = - ¦ -"
Уо sin
2
г+~г-
A6.31)
Обсудим ото выражение. Взяв плоскость z = 0, имеем: Нт@) =
¦=хо2А (рис. 16.5а), а па расстоянии z=l вектор Hm = "H.m(l), как
33*
516
ГЛ. 16. АНИЗОТРОПНЫЕ, АКТИВНЫЕ И НЕЛИНЕЙНЫЕ СРЕДЫ
видно из A6.31), повернут (при вещественных Г+ и Г ) на угол5
Г+ Г"
I
A6.32)
(рис. 16.56). Направление вектора Н, оставаясь фиксированным в
каждой плоскости z = const, изменяется по мере распространения
рассматриваемой совокупности волн. Век-
Вектор Н поворачивается.
Причина этого поворота пояспяется на
рис. 16.6. Как при z = 0, так и при
Мт@
Рис. 16.5
z = I складываются вращающиеся навстречу векторы Н+ и Н~„
Они принадлежат волнам, распространяющимся с разными фа-
фазовыми скоростями со/Г+ и со/Г~ (если нет потерь). Поэтому нри
прохождении пути I векторы Н+ и Н~ приобретут разные фазы
(повернутся на неодинаковые углы). Окажется повернутым и ре-
результирующий вектор Н.
Несколько упрощая, можно сказать, что в обсуждаемом случае-
распространяется волна, плоскость поляризации которой поворачи-
поворачивается при распространении (это тем верпее, чем ближе волновые
сопротивления W+ и W~). Вращение плоскости поляризации назы-
называется эффектом Фарадея. Сам термин гиротропные среды (т. е.
вращающие) связан с существованием этого эффекта.
Как видно из A6.33), при эффекте Фарадея определенный
смысл имеют полусумма и полуразность постоянных распростра-
распространения A6.26)
Гф = (Г+ + Г-)/2, # = (Г+-Г-)/2. A6.33.).
При отсутствии потерь величина R выражает угол поворота плос-
плоскости поляризации на единицу расстояния и называется постоянной
Фарадея. Величина Гф играет роль постоянной распространения.
Эффект Фарадея необратим. Величина а A6.11) меняет знак
при изменении направления постоянного намагничивания. Поэтому
изменит зпак и постоянная Фарадея. Это значит, что поворот плос-
плоскости поляризации при распространении волны в направлении г
§ 16.2. ПОЛЯ И ВОЛНЫ В ГИРОТРОПНЫХ СРЕДАХ
517
не может быть компенсирован при обратном распространении (на-
(например, при отражении волны). Поворот увеличится.
Наконец, перейдем к рассмотрению продольных волн в намаг-
намагниченной плазме — среде, характеризуемой тензором диэлектриче-
диэлектрической проницаемости A6.3). Как уже указывалось в п. 16.2.1, нет
необходимости заново производить аналогичные выкладки. Доста-
Достаточно применить принцип двойственности в форме A6.20).
Отправляясь от формул A6.26), A6.28) — A6.30), мы можем
утверждать, что в памагниченной плазме могут распространяться
следующие волны круговой поляризации:
правой
волна -— круговой поляризации в направлении
? = А (х0 ± fy0) е-«г
w± \± «о Jo)
A6.34)
правой
волна z— круговой поляризации в направлении
левой
= А (х0 + гу0).
где
-^(±*xo + yo)e+irTZ) A6.35)
A6.36)
A6.37)
% /|i/(er±P).
В гиротропной плазме также наблюдается эффект Фарадея.
Сохраняют справедливость формулы A6.33), в которые теперь под-
подставляем постоянные распространения A6.36).
16.2.3. Поперечные волны. Двойное преломление (А). Будем
рассматривать плоские однородные волны, распространяющиеся в
гиротропном магнетике перпендикулярно к направлению постоян-
постоянного намагничивания z. Все поперечные направления равноправны,
и мы можем в качестве направления распространения выбрать
ось х. Тогда все комплексные амплитуды будут фупкциями коор-
координаты х вида ехр(—iTx), где Г — не известная пока постоянная
распространения; от координат уиг поле не зависит.
Учитывая сказанное, конкретизируем систему уравнений A6.18).
При этом будем использовать обозначения: Em = Snu?~iTx, Нтз:=^
ir* и т. д. В результате получаем:
A6.38)
Нетрудно заметить, что эти шесть уравнений образуют две незави-
независимые системы. Одна из них включает вторую строку первого
?
518
ГЛ. 16. АНИЗОТРОПНЫЕ, АКТИВНЫЕ И НЕЛИНЕЙНЫЕ СРЕДЫ
столбца и последнюю —¦ второго. Действительно, только эти два
уравнения содержат неизвестные <%у и 2f6z. Перемножая их левые
и соответственно правые части, получаем следующее уравнепие
относительно постоянной распространения:
r2 = -^-euL. A6.39)
с
Нетрудно выписать следующее решение рассматриваемой систе-
системы уравнений:
V ._ „ Л -{Тобх Л _ „ А -гТобх
W
об
где
AG.40)
^1/^. A6.41)
Это так называемая обыкновенная волна, распространяющаяся
вдоль оси х. Действительно, речь идет о Г-волне простейшего вида.
Оставшиеся в A6.38) четыре уравнения составляют вторую не-
независимую систему. Из них находим
и выражаем поле:
'нб
A6.42)
о~)е-{Г^, A6.43)
где
1 нб — ¦
цТ
\i-r — a
. A6.44)
Эта распространяющаяся вдоль осп х волна называется необыкно-
необыкновенной. Как видно, она является //-волной, так как имеет продоль-
продольную магнитную компоненту Нх.
Отмстим, что в случае обыкновенной волны в гиротропном маг-
магнетике вектор Н коллинеарен направлению постоянного намагни-
намагничивания, а в случае необыкновенной волны — вектор Е.
В качестве примера, показывающего роль этих волн, рассмотрим
так называемое двойное преломление на границе с гиротропным
магнетиком. Пусть он занимает полупространство заштрихованное
на рис. 16.7, а постоянное магнитное поле Но, обусловливающее
гиротропню, направлено перпендикулярно плоскости чертежа. По-
Поляризация падающей волны (луч 1), которая распространяется в
изотропном полупространстве, произвольна. Разлагая ее на волны пер-
перпендикулярной и параллельной поляризации (см. п. 5.2.2), видим,
что в одном случае вектор Е, а в другом —¦ вектор Н коллинеарпы
16.2. ПОЛЯ II ВОЛНЫ В ГИРОТРОПНЫХ СРЕДАХ
519
Но. Это значит, что одна из выделенных падающих волн способна
возбудить в гиротропной среде только необыкновенную, а другая —
обыкновенную волну. Так как фазовые скорости последних различ-
различны, то соответствующие преломленные лучи не совпадают. Их на-
направления нетрудно найти, используя второй
закон Спеллиуса E.14):
sinft
но
sin (
"об
S1I1 ф
A6.45)
(предполагается, что потери отсутствуют). По-
Показателями преломления п(Л и п11б, разумеется,
будут величины Го5/(со/с) п Гн5/(со/с). В слу-
случае гиротропного магнетика /г„б = Уець и пи6 =
= у е (\jlt — a")/\iT.
Переходя к случаю гиротропной плазмы,
ограничимся, как в п. 16.2.2, применением
принципа двойственности A6.20) к уже полученным результатам
A6.40) —A6.44). Таким образом,
-;гобж
Рис. 16.7
Em = x.tAWOue
где
Гоп - - V eLu,
W
т = — [у0Ае
Ш 1 / ''о 1 / ^
o6 =Ty — у —
(обыкновенная волна) и
где
! Н
= — z0Ae
Г ш
Гнб z т
»*-V*\
A6.46)
A6.47)
A6.48)
A6.4U)
(необыкновенная волна).
В случае гиротропной плазмы при уже обсуждавшихся обстоя-
обстоятельствах также будет наблюдаться двойное преломлепие. Вектор
Но, как и ранее, должен быть перпендикулярен плоскости падения
волны. Формулы A6.45) сохраняют силу; теперь по6 = Vetfx и
пнб = V V- (ег — Р //Ет- Надо только иметь в виду, что в данном
случае обыкновенная волна имеет электрическую компоненту, кол-
линеарную Но, а необыкновенная волна — магнитную. Соответст-
Соответствующими компонентами падающей волны порождаются две пре-
преломленные.
16.2.4. Гиротропия ионосферы (А). Вследствие влияния магпит-
пого поля Земли плазма ионосферы представляет собой гиротроп-
ную среду, диэлектрическая пропицаемость которой описывается
520
ГЛ. 16. АНИЗОТРОПНЫЕ, АКТИВНЫЕ И НЕЛИНЕЙНЫЕ СРЕДЫ
2л
2itm
формулами A6.3), A6.4J. Величина #о в среднем имеет значение
около 40 А/м, так что частота гиромагнитного резонанса A6.5)
оказывается около 1,4 Мгц. Гироскопиче-
Гироскопические частоты ионов весьма низки. Например, для ионов атомарного
кислорода F' = й'/2я « 54 Гц. Поэтому
пренебрежение влиянием ионов при вы-
выводе формул A6.3), A6.4) для большин-
большинства случаев допустимо.
Учет гиротропии ведет к существенно
более сложной картине процессов распро-
распространения радиоволн в ионосфере. При
сколько-нибудь полном рассмотрении на-
надо было бы учитывать изменение вели-
величины и направления поля Земли на радиотрассе, а также ряд иных
факторов. Ограничимся обсуждением упрощенной задачи.
Пусть радиоволна приходит к границе ионосферы, распростра-
распространяясь перпендикулярно Но; вектор Е ориентирован относительно
Но произвольным образом. Тогда падающая волна порождает в ги-
ротроппой плазме обыкновенную и необыкновенную волны (см.
п. 16.2.3): рефрагирующий луч «расщепляется», как показано на
рис. 16.8. Ясно, что условия поворота обыкновенного и необыкно-
необыкновенного лучей различны, поскольку неодинаковы соответствующие
показатели преломления. Подставляя в A5.33) в качестве п соот-
соответствующие величины, для щ = 1 и Ф = 90° получаем:
Рис. 16.8
sin 90 —
поб =
"но = /(е2г - Р2)/ет,
A6.50)
где. как п в п. 15.5.2, пренебрегаем потерями.
Поскольку согласно A6.4) еь не отличается от е изотропной
плазмы, детализация первой строчки A6.50) приведет к уже из-
известной формуле A5.35). Что касается необыкновенной волны, то
детализация второй строчки A6.50) при помощи A6.4) при v = 0
дает
Задаваясь тем или иным значением угла падения 0о, отсюда при
подстановке выражения юР через N' A6.5) можно найти значение
электронной концентрации (N'~N*), которое соответствует пово-
повороту необыкновенного луча.
Рассмотрим, далее, условия распространения радиоволи вдоль
направления магнитпого поля Земли. Согласно A6.36) с учетом
§ 16.2. ПОЛЯ И ВОЛНЫ В ГИРОТРОПНЫХ СРЕДАХ
521
'A6.4) при v = 0 получаем:
о)((о± Q) *
A6.52)
Как видно из A6.52), при достаточно низких частотах постоянная
распространения левополяризованной волны Г~ будет оставаться
вещественной. Поэтому, если при падении радиоволны на границу
ионосферы порождаются продольные волны, то одна из них, рас-
распространяясь вдоль магнитного поля Земли, может пройти через
ионосферу.
Одно из явлений, к объяснению которого можно подойти, от-
отправляясь от этого факта,— это так называемые свистящие атмо-
сферики. В диапазоне СДВ (главным образом, на частотах 1 -з-
н-10 кГц) наблюдаются сигналы, порождаемые грозовыми разря-
разрядами, которые в звуковом канале приемника вызывают свист с ощу-
ощутимо возрастающей частотой. Такие сигналы распространяются из
одного полушария Земли в другое вдоль силовых линий магнитно-
магнитного поля Земли.
В заключение заметим, что упрощенный анализ распростране-
распространения радиоволн в ионосфере, в котором влияние земного магнетиз-
магнетизма не учитывается (см. § 15.5), дает — в основных чертах — доста-
достаточно достоверную картину. В то же время из-за сложности исход-
исходных условий точный учет влияния гиротропии ионосферы при рас-
расчете радиолиний невозможен. На практике это влияние выступает
как источник дополнительных замираний. Если, например, в диа-
диапазоне KB волна, распространяясь в слое F, проходит значитель-
значительный участок трассы вдоль магнитного поля Земли, то в силу эф-
эффекта Фарадея плоскость ее поляризации поворачивается. А так
как из-за нестабильностп иопосферы угол поворота не остается
постоянным, мепяется уровень принимаемого сигнала, поскольку
приемная атттеппа (например, типа дпполя Герца) чувствительна
к поляризации падающей волны.
16.2.5. О применении ферритов в радиотехнике СВЧ. Намагни-
Намагниченные ферриты, являющиеся гиротропными магнетиками, весьма
широко применяются в волноводных и иных устройствах СВЧ.
Принципы их построения многообразны, они подробпо рассмотрены
в ряде монографий [Д.5 — Д.7]. Электродинамические задачи, к ко-
которым приводит анализ этих устройств, сложны и требуют приме-
применения методов, рассматривавшихся в гл. 12.
Интересно отметить, что существует волноводный аналог эффек-
эффекта Фарадея, открытием которого, по-видимому, и было положено
начало применению намагниченных ферритов в технике СВЧ1).
Если в круглый волновод поместить аксиально-симметричный фер-
ритовый элемент (рис. 16.9) и приложить продольное постоянное
магнитное поле Но, то приходящая слева основная волна #ц, струк-
') Hogan С. L. II Bell System Techn. Journ.—1952.—V. 31, № 1.—P. 1.
522
ГЛ. 16. АНИЗОТРОПНЫЕ, АКТИВНЫЕ И НЕЛИНЕЙНЫЕ СРЕДЫ
тура которой в сечении Si (рис. 16.96) показана на рис. 16.9а,
окажется повернутой на некоторый угол ¦&; структура в сечении
$2 показана на рис. 16.9е. Сущность явления заключается в том,
что гиротропный элемент по-разному действует на поля, вращаю-
вращающиеся в противоположных направлениях. Падающую волну Нц с
азимутально фиксированной структурой, как известно (см. п. 7.2.2),
можно разложить на две такие вращающиеся по азимуту волны.
s,
Рис. 16.9
При прохождении участка волновода с гиротропным элементом эти
волны приобретут разные фазовые сдвпги, так что их наложение
образует повернутую структуру.
Разумеется, это упрощенное объяснение. Задача дифракции вол-
волны Н\\ на гиротропном элементе может быть решена лишь метода-
методами, опирающимися на ЭВМ (см. гл. 12). Поле на участке волно-
волновода с ферритом не исчерпывается структурой Нц. Но существенно,
что каждая вращающаяся составляющая падающей волны Н\\
возбуждает на участке с ферритом также вращающееся поле, при-
причем на оси волновода поляризация будет круговой. Между тем, из
п. 16.2.2 можно сделать вывод, что при круговой поляризации в
плоскости, перпендикулярной направлению намагничивания, гиро-
гиротропный магнетик проявляет себя как среда с магнитной прони-
проницаемостью \хт ± ос. где знак зависит от направлеппя вращения. Это
п определяет различие фазовых сдвигов, о котором говорилось
выше.
Фарадеевская ячейка па круглом волноводе (см. рис. 16.9) ис-
используется на практике, хотя и значительно реже, чем различные
элементы, построенные на основе прямоугольного волновода. Отли-
Отличительным свойством волповодпых элементов с применением фер-
ферритов является их управляемость: меняя намагничивающее поле,
можно влиять на волновой процесс. Весьма существенна необрати-
необратимость волновых процессов при наличии гиротроппых сред. Можно,
например, строить волповодные элементы, осуществляющие пере-
передачу энергии, главным образом, в одном направлении, это так на-
называемые вентили.
Возвращаясь к рис. 16.9, отметим, что в силу необратимости
эффекта Фарадея волна 7/ц, отразившаяся от какого-нибудь пре-
препятствия справа от сечепия Sz, при обратном прохождении ячейки
испытает поворот на угол •0 в прежнем направлении, так что по
§ 16.2. ПОЛЯ И ВОЛНЫ В ГИРОТРОПНЫХ СРЕДАХ
523
отношению к ориентации падающей волны (рис. 16.9а) поворот
составит 2Ф. Если •& = 45°, то отраженная волна придет к Si с
ортогональной ориентацией. Она «развязана» по отношению к вол-
волне падающей. Можно, например внести в волновод вблизи сечепия
Si продольную поглощающую пластинку, которая будет действо-
действовать только па отраженную волну (будучи параллельной ее век-
вектору Е); тогда фарадеевская ячейка превратится в вентиль.
Обсудим также проявление эффекта Фарадея в резонаторе, по-
построенном на основе круглого волновода и содержащего коаксиаль-
коаксиальный продольно намагниченный ферритовый стержень (рис. 16.10а).
Пусть сначала феррит размагничен. Будем рассматривать тип
колебаний Я) и с фиксированной азимутальной ориентацией, который
к
A
,1
/
J
\
\
V
>-
ч"
г
. ^
Рис. 16.10
лишь незначительно возмущен присутствием тонкого феррптового
цилиндра. На обе вращающиеся составляющие этого типа колеба-
колебаний (с азимутальными зависимостями ехр(—tec) и exp tec) стержень
действует одинаково. Эти колебания остаются вырожденными; мож-
можно сказать, что соответствующие резонансные кривые «нераздели-
«неразделимы» (рис. 16.106). С приложением постоянного поля Но феррит
по-разному возмущает противоположно вращающиеся типы коле-
колебаний. В случае достаточно тонкого стержня можно считать, что
в одном случае его эквивалентная магнитная проницаемость есть
|лт + ее, а в другом \iT — ее. Собственная частота одного вращающего-
вращающегося типа колебаний увеличивается, а другого — уменьшается. Наблю-
Наблюдаемая резонансная кривая сначала становится двугорбой
(рис. 16.10е), а при дальнейшем увеличении поля Но собственные
частоты могут быть разнесены значительно (рис. 16.Юг). При этом
кривая, соответствующая типу колебаний с правой круговой поля-
поляризацией на оси, не только сдвигается в сторону низких частот
524
ГЛ. 16. АНИЗОТРОПНЫЕ, АКТИВНЫЕ И НЕЛИНЕЙНЫЕ СРЕДЫ
(сс'>0), но и сужается в результате повышения добротности
(а" <0). Другая же кривая смещается в сторону высоких частот
и расширяется.
16.2.6. Некоторые свойства полей в гиротропных средах (Б).
Обсуждая в п. 3.4.2 принцип взаимности, мы ограничились изотроп-
изотропными- средами. В случае среды анизотропной все выводы останутся
в силе, если выполняются соотношения:
цНт2Нт1 - ^Нт1Нт2 = 0, еЁт2Ёт1 - еЁт1Ёт2 = 0. A6.53)
Легко убедиться в том, что для этого тензоры ц и е должны быть
симметрическими, т. е. такими, что ц^, — \iyx, \iVz = и*» и т. д. (рав-
(равны элементы, симметрично расположенные относительно главной
диагонали). Гиротропные среды этому условию не удовлетворяют.
В частности, для гиротропного магнетика цху = — jv = —ia. Поэтому
[xH,n2Hmi — (j,HmlHm2 =
= i2a (Hm2xHmly — Hm2yHmlx) = i2a [Hm2, Hml]z. A6.54)
Правая часть обращается в нуль только в том случае, если в рас-
рассматриваемом классе полей компоненты вектора Нт в плоскости,
перпендикулярной направлению постоянного намагничивания па-
параллельны (либо отсутствуют).
Общие энергетические соотношения, полученные в п. 3.3.2,
в стучае гиротропных сред нуждаются лишь в очевидном обобще-
обобщении. Основное уравпение баланса C.55) сохраняет силу. Далее
нужно так же, как и в п. 3.3.2, произвести разделение веществен-
вещественных и мнимых частей. При этом, например, получим
Рп = |- 1ш
dv,
A6.55)
что при изотропии переходит в C.59).
Говорят, что тензоры и. и е некоторой анизотропной среды яв-
являются эрмитовыми, если \хху = \i*x, Цуг = ^*у V-zx = Kz' а Диаго-
Диагональные компоненты (д,**, (хга, jxrz веществепны (для эрмитовых мат-
матриц выполняется соотношение типа A1.3)). Для эрмитовых ц и е
подынтегральное выражение в A6.55) обращается в нуль, что
означает отсутствие потерь.
Действительно,
И
zH mx.
% 16.3. АКТИВНЫЕ СРЕДЫ
525
Лри эрмитовости |л первые три члена суммы вещественны, а осталь-
остальные образуют вещественные пары, например,
lixyHmxHmy + liyxHmyHmx = 2 Re (\\,^НтхНту).
Апалогично раскрывается e*EmEm.
Возвращаясь к формулам A6.3) и A6.10), видим, что тензоры
проницаемостей гиротропных сред, на самом деле, являются эр-
эрмитовыми при отсутствии потерь. В случае намагниченного ферри-
феррита потери с самого начала не учитывались; согласно A6.11) \\1ХХ==
= |лге = цТ и \1гг = Цх. вещественны, а цжу = \i*K = — ia. Что касается
намагниченной плазмы, то аналогичные соотношения получаются
. при v = 0.
§ 16.3. Активные среды (А)
16.3.1. Общие представления. Активной, или регенеративной,
будем называть среду, которая в противоположность поглощающей
среде отдает энергию электромагнитному полю. Такого рода ба-
баланс эпергии неизбежно связан с действием сторонних факторов.
Однако в данном случае нельзя говорить о заданных ECI или j0T,
поскольку признаком активной среды является отклик на некото-
некоторое электромагнитное поле: сторонние процессы не являются не-
независимыми, они совершаются под действием поля, которому от-
отдают свою энергию. В п. 3.3.2 уже отмечалось, что при гармони-
гармонических колебаниях (или для гармонических составляющих более
сложной временной зависимости) активные среды описываются, как
и поглощающие, посредством комплексных проницаемостей е и (X,
но с мнимыми частями другого знака: е" <0 и ц" < 0.
Понятие активной среды удобно тем, что дает единое средство
формализации всевозможных регеперативных факторов, выступаю-
выступающих в задач? х прикладной электродипамики. Их многообразие ве-
велико. Для построения усилителей и генераторов используются
макроскопические движения частиц в полях (электроника) и мик-
микроскопические эффекты (квантовая электроника). Большое значе-
значение приобрело параметрическое усиление и возбуждение колеба-
колебаний в радиотехнике СВЧ. Интересно, что значение этого круга про-
процессов было понято еще в начале 30-х годов [Г.1, с. 189].
Для построения теории активных сред, применяемых в разно-
разнообразных полупроводниковых приборах, а также в квантовых уси-
усилителях и генераторах (мазерах), оптических квантовых генерато-
генераторах (лазерах) и др. необходимо рассматривать внутренние про-
процессы в веществе (см., например, [Д.8, Д.13, Д.14]). Но коль скоро
микроскопическая теория построена и на ее основании найдены
комплексные проницаемости г и ц, среда становится объектом
макроскопической электродинамики.
526
ГЛ. 16. АНИЗОТРОПНЫЕ, АКТИВНЫЕ И НЕЛИНЕЙНЫЕ СРЕДЫ
16.3.2. Об электромагнитных полях. Для исследования полей в
активных средах не требуется специальных методов. Более того,
на основании уже полученных решений ряда электродинамических
задач можно ввести в рассмотрение активные среды и выяснить,
какие новые свойства приобретают электромагнитные поля. В ка-
качестве простейшего примера возьмем случаи плоской однородной
электромагнитной волны.
Формально оказываются справедливыми все соотношения, полу-
полученные в п. 4.1.4 при рассмотрении волн в поглощающей среде, но
поскольку теперь е"<0 и (или) |д,"<0, то ввиду C.38) tgA<0
и (или) tg Ди < 0 (при е'> 0 и |/>0). Поэтому в D.38) может
оказаться отрицательной величина к". Если же к" <0 при к'>0,
вместо D.40) получаем:
E = x0Ae\h"\z cos (at — k'z + ц
H = y0 , elft"i2 cos (at — k'z
A6.56)
Рис. 16.11
Это уже не затухающая волна, как в п. АЛЛ, а возрастающая, уси-
усиливаемая средой (рис. 16.11). Величину \к" \ при к" <0 можно
называть коэффициентом усиления (в
отличие от к">0, называемого коэф-
коэффициентом затухания, см. п. 4.0.2). От-
Отношение Ет (z + l)jEm (z) = elft"l( пока-
показывает, во сколько раз увеличивается
амплитуда волны на расстоянии I. Уси-
Усилением волны называют величину
G=\k"\l, измеряемую в неперах
или — после умножения на 20 lg e — в
децибелах (ср. п. 4.0.2).
Безграничная активная среда, ра-
разумеется, физически нереализуема.
Но в технике используются различные усилители бегущей вол-
волны, построенные на основе отрезка той или иной направляющей
структуры с активной средой. В случае полого волновода, пол-
полностью заполненного активной средой, для вычисления постоянной
распространения можно было бы воспользоваться способом, рас-
рассмотренным в п. 6.4.3. Разумеется, реальная структура кроме ак-
активной среды содержит и поглощающую (в случае полого волново-
волновода поглощает металлическая оболочка). Поэтому, оценивая отноше-
отношение амплитуд волны на выходе и входе отрезка структуры, за-
запишем:
Ет (z + 1I Ет (z) = ехр (- Г;' + | Г;' | ) I, A6.57)
где 1\>0— коэффициент затухания, обусловленный поглощени-
поглощением, а IГ2 | — коэффициент усиления волны активной средой.
§ 16.3. АКТИВНЫЕ СРЕДЫ
527
Активность среды всегда обусловлена действием какого-то внеш-
внешнего источника, генератора накачки. Соответственно этому | Г21 в
A6.57) есть монотонно возрастающая от нуля функция | Г2 (Рн) |,
где Рн— мощность накачки. Как видно из A6.57), при Рн = 0 бу-
будет происходить затухание волны. Только при некотором значении
Рн = 13н — поглощение окажется скомпенсированным: — 1\ +
+ | Г', — 0; волна пройдет без затухания. Усиление же имеет ме-
место При Рн> Рн-
Рассмотрим, далее, включенный в волноводный тракт полый ре-
резонатор с активной средой (рис. 16.12а). При резонансе амплитуда
внутреннего поля Ет пропорциональна
добротности резонатора Q и, разумеет-
разумеется, амплитуде падающей (слева) вол-
волны Ет1, возбуждающей резонатор (см.
л. 11.1.3), т. е. Em = KlQEmU где К, -
некоторый коэффициент пропорцио-
пропорциональности. Амплитуда волны па выхо-
де Е„,о. возбуждаемой в волноводе по-
полем резонатора через отверстие, в свою
очередь, пропорциональна этой вели- Q
чипе: Ет2 = KiK2QEmi (введен еще
один коэффициент пропорциональности
К2). Пусть записанное соотношение
относится к пассивному режиму, когда
Р„ = 0 (генератор накачки отключен).
Если же Рн ^ 0, добротность и выход-
выходной сигнал изменятся, что можно обо-
обозначить Ет2 = K\K-2QEm\. Поскольку коэффициенты К\, А'г можно
считать неизменными, получаем
Ет21Еп2 = QIQ.
Рпс. 1С.12
A6.58)
'Мы получили выражение относительного коэффициента усиления
в тракте.
Пусть Ро — мощность потерь внутри резонатора, Р2 — мощность
излучения из резонатора в присоединенные волноводы, и Рст < 0 —
мощность, отдаваемая полю резонатора активной средой. Тогда со-
согласно п. 8.1.3
~!рС
и, следовательно,
Е„
A6.59)
A6.60)
Величину |РСТ| выразим через мощность накачки Р„, введя
к. п. д. этого процесса: |РСТ| = г\(Рк)Ра. С ростом Р„ добротность
528
ГЛ. 16. АНИЗОТРОПНЫЕ, АКТИВНЫЕ И НЕЛИНЕЙНЫЕ СРЕДЫ
резонатора Q A6.59) неограниченно возрастает, пока |РСТ| прибли-
приближается к величине Ро + Рх (рис. 16.126). Коэффициент усиления-
при этом становится бесконечным, т. е. выходной сигнал сущест-
существует при исчезающе малом входном. Это порог возбуждения систе-
системы, начинающей работать как генератор. График относительного'
коэффициента усиления представлен на рис. 16.12е. В качестве
усилителя резонатор функционирует, начиная с момента компенса-
компенсации внутренних потерь: |РСТ| = Pq.
§ 16.4. Нелинейные среды (А)
16.4.1. О ферромагнетиках и сегнетоэлектриках. Нелинейность,
большинства распространенных сред проявляется только в сравни-
сравнительно сильных полях (см. п. 1.3.5), редко встречающихся в тех-
технике. Однако давно известны и нелинейные явления, наблюдаемые-
при значениях Е и Н, которые типичны для практики. Таковы в
первую очередь явления ферромагнетизма; нелинейность ферромаг-
. нетиков учитывалась еще в XIX веке при проектировании электри-
электрических машин. Ферромагнетикам формально аналогичны сегнето-
электрики: существует сходство зависимостей В(Н) в первом слу-
случае и D(E)— во втором. Существенно нелинейной является зависи-
зависимость j(E) для частиц в вакууме и в случае плазмы. Нелинейные
элементы, как известно, необходимы при построении радиоаппара-
радиоаппаратуры. Наконец, отметим, что в результате появления мощных ла-
лазеров стали доступными беспрецедентно сильные электромагнитные
поля в оптическом диапазоне и расширился круг наблюдаемых
нелинейных электромагнитных явлений, имеющих волновой харак-
характер. Возникла нелинейная оптика.
Возвращаясь к ферромагнетикам, отметим, что для них харак-
характерна самопроизвольная намагниченность (см. п. 1.3.6). При по-
построении модели среды в виде совокупности магнитных диполей
(см. пп. 14.1.1, 14.1.3) в данном случае приходится вводить силь-
сильные внутренние ориентирующие факторы, сущность которых полу-
получает объяснение лишь с позиций квантовой физики. Под действием
этих факторов диполи должны ориентироваться параллельно, и' это
действительно происходит внутри очень малых, но макроскопиче-
макроскопических областей, называемых доменами. Последние — если иметь в
виду поликристаллическое вещество — образуют хаотическую струк-
структуру. Является ли при этом вещество в среднем намагниченным,
зависит от его «предыстории».
Если в исходном состоянии ферромагнетик размагничен (равна
нулю средняя самопроизвольная намагниченность Мо), то с прило-
приложением магнитного поля средняя индукция В в зависимости от Н
будет меняться, как показано на рис. 16.13а. Домены деформиру-
деформируются с тенденцией превратиться в один-единственный домен, в ко-
котором вектор намагниченности параллелен напряженности поля —
насыщение. Интересно, что скачкообразность этого процесса может
§ 16.4. НЕЛИНЕЙНЫЕ СРЕДЫ
529>
быть замечена экспериментально (скачки Варкгаузена); на
рис. 16.13а схематически представлен участок кривой В (Я) в уве-
увеличенном масштабе.
Кривая намагничивания В(Н) (рис. 16.13а) демонстрирует су-
существенную нелинейность процесса, но еще не говорит о зависимо-
зависимости наблюдаемого состояния от предшествующих. Пусть, намагни-
намагничивая ферромагнетик (кривая 1 на рис. 16.136), мы полу-
получаем индукцию В\ при напряженности #ь точка Р{Н\, В\). Если
а
Рис. 16.13
теперь уменьшать Н, то зто не приведет к возвращению в прежнее
состояние (начало координат). Ход изменения В будет соответство-
соответствовать движению по кривой 2, так что при Я = 0 будет В = ВГ —
остаточная индукция.
Дальнейшее движение по кривой 2 отвечает изменению
знака (направления) напряженности поля при прохождении через
нуль. При Н=—Н{ мы придем в точку Р'(—Я,, —5,), которая
симметрична Р(Ни В{) относительно начала координат, а из-
мепив здесь направление Я, будем уже двигаться по кривой 3
п, снова пройдя через нуль, вернемся в Р(Ни Я,). При этом ока-
оказывается описанной замкнутая кривая, называемая петлей гисте-
гистерезиса.
Если, прилагая поле к размагниченному ферромагнетику, оста-
остановиться не в точке Р(Ни Я,), а «раньше» — при меньшем'значе-
меньшем'значении Я, то можно пройти другую петлю гистерезиса, которая будет
лежать внутри первой. Ряд таких частных петель показан на
рис. 16.13е. При очень малых полях петли гистерезиса вырожда-
вырождаются в отрезки прямой начального участка на кривой намагничи-
намагничивания (и ее продолжения в область отрицательных Я); в этой обла-
области процесс обратим.
Рассмотрим изменение состояния ферромагнетика с энергетиче-
энергетических позиций. Согласно п. 1.5.3 бесконечно малое приращение
34 В. В. Никольский, Т. И, Никольская
.530
ГЛ. 16. АНИЗОТРОПНЫЕ, АКТИВНЫЕ И НЕЛИНЕЙНЫЕ СРЕДЫ
§ 16 4. НЕЛИНЕЙНЫЕ СРЕДЫ
энергии магнитного поля в объеме V можно выразить в виде
dWu = ) Н dB dv.
Поэтому следующее равенство
2
W? - W? = f \ BdBdv
A6.61)
A6.62)
v в.
выражает изменение энергии при переходе от состояния Hi, Bi к
Нг, Вг. При циклическом перемагничивании ферромагнетика, совер-
совершив один обход петли гистерезиса, получим:
AWM = f j> H dB dv,
A6.63)
где контурный интеграл есть не что иное, как площадь петли ги-
гистерезиса на графике зависимости В{Н). Таким образом, возвраще-
возвращение в первоначальное состояние достигается ценой потери энергии
АИ-™. Эти потери энергии на перемагничивание связаны с дефор-
деформацией доменной структуры.
Если поле гармонически колеблется, петля гистерезиса обходит-
обходится за каждый период колебаний. Потери оказываются пропорцио-
пропорциональными площади петли и частоте процесса. Надо отметить, что
сам характер петли гистерезиса зависит от быстроты перемагничи-
ваппя, т. е. от частоты колебаний.
Подчеркнем, что хотя рассмотренный выше процесс намагни-
намагничивания ферромагнетика имеет резко нелинейный характер, гисте-
гистерезис — явление, которое может заключаться всего лишь в запаз-
запаздывании линейного процесса. В рамках метода комплексных амп-
амплитуд при этом имеем: Вт = ЦоиНт, где и. = |ц| ехр(—гДм) (ср.
п. о.-.1). Это значит, что при H = Hmcosco? магяптная индукция
есть В = lio',u!H,,, cos(at — А"). Легко убедиться, что график В(Н)
цпклнчеп (кривая имеет вид эллипса), т. е. имеется гистерезис.
Вычисляя интеграл A6.63), учтем, что dB = — \io\\i\coHmsm'(cu? —
— AN)dt. Поэтому
cos at sin (at — AM) dt dv =
A6.64)
Получено выражение мощности магнитных потерь, дающее то же
значение, что и формула C.59) (см. также аналогичный вывод
в п. 3.3.3).
В заключение сделаем замечание о сегнетоэлектриках. Это ди-
диэлектрические среды, процессы поляризации которых довольна-
сложны [Д.4] и, в сущности, несопоставимы с намагничиванием
ферромагнетиков. Тем не менее, можно говорить о сходстве макро-
макроскопических характеристик: зависимость D(E) для сегнетоэлектри-
ков близка к типу зависимости В(Н), показанному на рис. 16.13.
16.4.2. Формализация нелинейных процессов при слабых полях.
Общего вида нелинейные зависимости D(E), В(Н) и j(E) допу-
допускают простое представление в случае слабых
полей или переменных составляющих этих по-
полей. Рассмотрим в качестве примера изотроп-
изотропный диэлектрик, характеризуемый зависи-
зависимостью D(E). Разлагая эту функцию в ряд
Тэйлора в окрестности точки Е = ?0, ограни-
ограничимся начальными членами:
dD
dE
Е = Е
(Е-Ео)+ ...,
A6.65)
Рис 1б
что допустимо при достаточно малых прира- О
щениях Е — Ео. Как видно, в этом приближе-
приближении приращения АЕ = Е — Ео и AD=D(E) —
— D(Eo) связаны линейной зависимостью. Произведена локальная:
линеаризация зависимости D(E) (рис. 16.14).
Пусть при данной постоянной составляющей Ео = const прира-
приращение Е меняется гармонически: АЕ = Ет cos at. Тогда также AD =
= Dmcosat (в этом приближении процесс безынерционен) и из
A6.65) следует:
Dm = eoez(E0)Em, e;i(?0)=—4? ¦ A6.66)
eQ аь е=еп
Играющая роль относительной диэлектрической проницаемости ве-
величина ел, постоянная при выбранном Ео, называется дифференци-
дифференциальной. Подобным же образом производится линеаризация зависи-
зависимостей В(Н) и /(?); при этом вводятся дифференциальные пара-
параметры (Хл И О"л.
Линеаризация отнюдь не всегда допустима, поскольку даже в
случае слабых полей основной интерес может представлять откло-
отклонение от линейной зависимости. Продолжая рассматривать изо-
изотропный диэлектрик, примем во внимание, что согласно A.70)
D(E) = e0E + P(E). Исходя из разложения Р(Е) в ряд Тэйлора в
окрестности Ео, запишем:
A6.67)
где АР = Р(Е)— Р(Е0), а слагаемые справа имеют вид:
Рл = е0%ааАЕ и Рнл = г0(%°АЕ + 11АЕ*+ ...J^zalAE, A6.68)
3-1*
532
ГЛ. 16. АНИЗОТРОПНЫЕ, АКТИВНЫЕ И НЕЛИНЕЙНЫЕ СРЕДЫ
§ 16.4. НЕЛИНЕЙНЫЕ СРЕДЫ
533
причем
dP
dEn+1
Е=Е
A6.69)
о
{отметим, что 1 + Хл = ел).
Далее положим АЕ = Emcos(cot +q>), или согласно C.8) АЕ =
= (Ете™* + Ё*пе~ш)/2. Внося это в A6.68), легко убедиться, что
Рал предстает как ряд, члены которого изменяются по закону
ехр(±ши?)
= Р™ (± гс
(п = 0, 1, 2, ...).
ехр (± incut). Тогда
Обозначим их Рнп(±ли?) =
со) = е0 [хя (со + со - со) Я»,Я' + A6.70)
+ Хэ (» + со + и — и — и) EzmEm + . .. ],
со + со - со)?^ + ...]
и т. д., где постоянные коэффициенты у/(со...) просто связаны с
различпыми Хп из A6-68).
Вследствие нелинейности закона Р(Е) гармонические колебания
Е с частотой со порождают (в общем случае) постоянную составля-
составляющую и колебания со всевозможными кратными частотами вектора
поляризованности Р. Чтобы найти составляющую частоты ли, надо
сложить Рш (па) и Р™ (- па).
Можно было взять АЕ в виде наложения нескольких частотных
составляющих: АЕ = Етр cos(copi
АЕ 1
cos(co,
Как
( ) ( j)
видно, при подстановке АЕ в A6.68) получится разложение Рнл,
содержащее компоненты Рил(±Аир ± тгсо, ± .. .). Соответствующпе
комплексные амплитуды Рт (± кар ± пад ± . . .) можно выразить
как в A6.70). Говорят, что поляризовапность содержит составляю-
составляющие различных комбинационных частот.
Наконец, перейдем к записи уравнений электродинамики и
представлению их решений в случае изотропного нелинейного ди-
диэлектрика. Пусть в данном случае Еа = 0. Материальные уравнения
имеют вид:
= jxO(.iH,
A6.71)
где использованы соотношения A6.67) — A6.69). Уравнения Мак-
Максвелла, таким образом, можно записать в виде:
iotH = еоеп —
где j = аЕ + jCI.
арн'
dt
rot E = — liou, —г-,
A6.72)
В случае, если источник совершает гармонические колебания с
частотой со, поле содержит все кратные гармоники. Поэтому, взяв
Г = fmT cos (at + Ф) == ( )™e«»t + \Те-™*)/2, разложим Е = E(t),
H = H(i) иРнл = Рнл(?) в ряды Фурье типа C.17):
Е=
Рнл=
(га©)
H=
(то) e
ine>t
A6.73)
Подставляя A6.73) в A6.72), получаем следующую бесконечную
систему уравнений:
rot Hm (ли) = ши [еоел (па) Ет (па) + Р*л (ли)] + j" (ли),
rot Em (па) = — ши[до[хНт (ли), A6.74)
га = 0, ±1, ±2, ...
где ел (ли) = ел — га/еоли и j" (ли) = 0 для всех л кроме л = ± 1
лричем ],С„Т (а) = )™/2 и ]% (- и) = )Т/2.
Если бы среда была линейной, то все пары уравнений Максвел-
Максвелла в A6.74), соответствующие отдельным гармоникам, были неза-
независимы. Но присутствие функций Рт (па) делает их связанными,
так как каждая из этих гармоник зависит от серии гармоник
Ет(гссо). Действительно, подобпо A6.70)
-К* И = е0 [%э B<а - и) Ет Bи) Ет (- а) +
+ /»(За - 2со) Ёт (За) Ет (- 2а) + ...
...+Хэ(со + со-и)?^(и) Ёт(-а)+ ...], A6.75)
Р%" Bи) = е0 [Хэ (со + и) Ёгт (и) + »/э (Зсо - и) Ет (Зи) Ет (- а) + ...
... + хэ (<в + и + и — и) Ёп (а) Ет (— и) + ... ]
и т. д.
При оцепке отдельных нелинейных эффектов оказывается воз-
возможным оставлять лишь несколько уравнений в системе A6.74).
Такие «укороченные» системы используются, например, в нелиней-
нелинейной оптике.
В частности, если компонента Р™ (и) относительно мала, ею
можно пренебречь, анализируя первую гармонику векторов поля;
тогда соответствующая пара уравнений из A6.74) (при л = 1)
534
ГЛ. 16. АНИЗОТРОПНЫЕ, АКТИВНЫЕ II НЕЛИНЕЙНЫЕ СРЕДЫ
оказывается независимой:
rot Hm (со) = шеоел (со) Ёт (со) + j" (со),
rot Em (со) = — icoiiouHm (со).
A6.76)
При исследовании второй гармоники в определенных условиях мож-
можно не учитывать влияния высших. Тогда во второй строке A6.75)
остается лишь первый член, так что из A6.74) при п = 2 полу-
получаем
= г2юе0елBю)ЕтBю) +
co)Em(co)?m(co), A6.77)
rot Ет
где Ет(со)—решение уравнений A6.76).
Таким образом, мы получаем приближенный подход для нахож-
нахождения второй гармоники, порождаемой в нелинейной среде задан-
заданным полем первой гармоники. Аналогично рассматривается и воз-
возбуждение комбинационных частот.
16.4.3. О нелинейных явлениях в плазме. Будем рассматривать
поле в плазме, которое при ее разрежении (N' ->- 0) все более при-
приближается к плоской однородной волне в вакууме вида
E = x0A cos (at — kz), H = y0 -ту- cos (coi — kz)
A6.78)
(к = к0 = соУеоЦо, W = Wo = У(хо/ео). Формулы A6.78) будут играть-
роль начального приближения к решению.
В отличие от обсуждения свойств плазмы в § 14.2 и п. 16.1.2'
учтем теперь влияние лорепцевой силы, обусловленной переменным
магнитным полем. Выражая лоронцеву силу F == g(E + \.io[dr/dt. H]),
подставляем сюда Е и Н ил A6.78). В отличие от A4.17) имеем
dr
dt'
с1т ,-,
^ У0Е
,.а ,-п,
A6./9)
Здесь Е = A cos (at — kz) и с = 1/Уцоео; мы не имеем права, как в
§ 14.2, переходить к методу комплексных амплитуд, исключая вре-
временную зависимость, поскольку уравнение нелинейно.
Действительно, переходя к координатной форме при v = 0, на-
находим
m с dt
dt'
dt"
Нелинейность заключена в произведениях компонент скорости vz —
= dz/dt и vx = dx/dt на Е. Так как v < с (иначе нельзя использо-
использовать законы классической механики), то соответствующие члены
§ 16.4. НЕЛИНЕЙНЫЕ СРЕДЫ
535
в A6.80) весьма невелики и в первом — линейном — приближении
могут быть отброшены. Тогда A6.80) становится (при переходе к
комплексной форме записи) просто частной формой A4.35). При
этом
у = 0, z = 0, х = — A cos ((at — kz)
и, следовательно,
e2N' . . . . . eN' -^
T- A cos (mt — kz) — 5-Е
A6.81)
A6.82)
(^ = g); это же следует нз A4.38). Далее можно было бы, как и в
II. 14.2.1, найти диэлектрическую проницаемость плазмы (теперь
.мы бы назвали ее ел) н от начального приближения A6.78) перей-
перейти к первому приближению, заменив ео на еоел.
Но наша задача состоит в том, чтобы получить следующее при-
приближение, найдя нелинейную поправку. С этой целью подставим
A6.81) в третье из уравнений A6.80). Учитывая также A6.78),
получаем
Lf^Ji!^ A6.83)
'Откуда
z = —
Safe
dt
— sin (Ztiit — 2kz).
A6.84)
'Таким образом, вследствие нелинейности плазмы, обусловленной
действием лорепцевой силы, возникает продольпое колебательное
движение частиц с удвоепной частотой. Соответствующая составля-
составляющая вектора полярнзованности находится умножением z A6.84)
.на
= — z,,
2o>^ — 2kz).
A6.85)
Найделпая компонента вектора полярнзованности ортогопальна
напряженности электрического поля. Поэтому для перехода к пред-
представлению типа A6.70) понадобилось бы некоторое обобщение:
восприимчивость имеет тензорный характер — нелинейность влечет
за собой анизотропию.
Существует еще целый ряд факторов, обусловливающих нели-
нелинейность плазмы. В частности, значение v зависит от средней
энергии электронов. Если, например, мощность радиоволны, рас-
распространяющейся в ионосфере, настолько велика, что скорости
электронов, находящихся под ее воздействием, не малы в сравне-
сравнении со средней тепловой скоростью, то, можно сказать, что волна
вызывает разогрев ионосферной плазмы, которым нельзя прене-
пренебречь. Комплексная диэлектрическая проницаемость плазмы, зави-
зависящая от v, оказывается функцией амплитуды поля. При прочих
равных условиях эта нелинейность должна возрастать с уменыпе-
536
ГЛ. 16. АНИЗОТРОПНЫЕ, АКТИВНЫЕ И НЕЛИНЕЙНЫЕ СРЕДЫ
иием частоты (согласно A4.38) vm = — ieEm//rea>), но на СДВ и ДЕГ>
поле лишь незначительно проникает в ионосферу, и отмеченныйг
тип нелинейности проявляется, главным образом, в диапазоне СВ.
Если мощная волна несет некоторый сигнал, то соответственно это-
этому сигналу оказывается промодулированной частота столкновений
v. Это может повлиять на распространяющуюся здесь же слабую
волну таким образом, что она воспримет указанную модуляцию.
Такая кросс-модуляция называется люксембург-горъковским эф-
эффектом.
Возможно и самовоздействие мощной волны; волна, так сказать,-
изменяет свойства среды на своей трассе, а среда, в свою очередь,
влияет на структуру волны (интерпретация несколько упрощен-
упрощенная) . В результате самовоздействия может, в частности, порождать-
порождаться вторая гармоника несущей.
16.4.4. О нелинейной оптике. Уже отмечалось (см. п. 16.4.1),
что в сильных волновых полях, создаваемых мощными лазерами,,
начинает проявляться нелинейность сред. Этой проблематикой за-
занимается нелинейная оптика (см., например, [Д.10, Д.11]).
Один из эффектов нелинейной оптики — порождение средой выс-
высших гармоник. Соответствующие электродинамические задачи обыч-
обычно решаются в приближении заданного»
поля (см. п. 16.4.2). Можно, например,
рассмотреть задачу о наклонном падения
плоской однородной волны из линейного
полупространства на границу с нелиней-
нелинейным. Исследуя при этом порождение вто-
второй гармоники, приходят к выводу (см.,
например, [Д.И]), что процесс характери-
характеризуется лучевой схемой (рпс. 16.15), на
которой кроме обычных трех лучей, соот-
соответствующих падающей, отраженной и
прошедшей волнам, имеются еще два лу-
луча, которые обозначены символами ( —)гш,
(+J<«. Они отвечают порождаемым в обеих средах волнам на вто-
второй гармонике. Чтобы охарактеризовать направления этих лучей;
запишем соотношения:
ел И вШФ -, / ел Bю)
(O)w
sine
sind
Bco)
(магнитные проницаемости сред одинаковы). Формулы A6.86) до-
дополняют обычные законы Снеллиуса. Вместе с соответствующими
аналогами формул Френеля они были получены в начале 60-х
годов').
Важное значение имеет представление о самовоздействии неко-
некоторого волнового процесса, распространяющегося в нелинейной сре-
§ 16.4. НЕЛИНЕЙНЫЕ СРЕДЫ
537
;де (этот термин уже использовался в п. 16.4.3). При распростране-
распространении через жидкость или газ волны, создаваемой мощным лазером,
учитывают нелинейность поляризации среды, вызываемую целым
рядом факторов. Помимо поведения электронов в сильном электро-
электромагнитном поле существенно механическое воздействие поля на
вещество: возникает давление, пропорциональное средней мощно-
мощности волны, в результате чего в областях сгущения увеличивается
диэлектрическая проницаемость. Часто приближенно полагают с
учетом всех факторов, что
e = l + aF2, cc>0. A6.87J
При распространении резко неоднородной волны — луча лазе-
лазера,— можно сказать, увеличивается оптическая плотность среды в
области сильного поля. Иными словами, в определенных условиях
волновому процессу сопутствует образование канала, направляю-
направляющего его энергию — нечто вроде диэлектрического волновода. Это
называется самоканализацией. Если этот канал сужается, проис-
происходит так называемая самофокусировка.
УПРАЖНЕНИЯ
1. Воспользовавшись результатами из п. 2.2.6, показать, что для искусст-
искусственного диэлектрика в виде системы металлических шаров радиуса R, равно-
равномерно распределенных в пространстве с плотностью N' (число шаров на еди-
единицу объема), справедлива следующая квазистатпческая оценка диэлектриче-
диэлектрической проницаемости
е = 1 + AnN'R3. A6.88)
2. Как изменится формула A6.88) при замене металлических шаров ди-
диэлектрическими?
3. Найти гироскопическую частоту электропов в магнитном поле Земли,
полагая Па = 40 А/м.
4. Найти частоту ферроиагпптпого резонапса при условии, что для фер-
феррита Л„ = 3-104 А/м.
5. Исходя из формул AС.Ю) и A6.11), детализировать выражение постоян-
постоянной Фарадея для плазмы, взяв v = 0.
6. Как соотносятся направления и скорости вращепия векторов поля волн
правой и левой круговой поляризации в гиротропном магнетике с одной сто-
стороны и прецессирующего вектора М — с другой?
7. Какой смысл имеет отрицательная добротность резонатора?
8. Найти соответствие между коэффициентами %э(со...) и %п из A6.70)
а A6.68), соответственно.
') Bloembergen N.. Pershan P. S. // Phys. Rev.—1962.—V. 128.—P. 606..
ПРИЛОЖЕНИЕ
О ГРАФИЧЕСКИХ ИЗОБРАЖЕНИЯХ,
ПОЛУЧЕННЫХ ПРИ ПОМОЩИ ЭВМ
В книге имоотся целая серия изображений, полностью воспроизведенных
при помощи ЭВМ с управляемым графопостроителем. Ото, в первую очередь-
картины силовых линий разных полей (при заданных зарядах или токах, в
полых и диэлектрических волноводах, при излучении диполя Герца и пр.),
а также графические характеристики дифракционных процессов (в частности,
дифракции Френеля), процессов возбуждения полых структур и различные
иные изображения. Все машинные рисунки отмечены символом ЭВМ.
Программы расчета функциональных зависимостей, решения систем диф-
дифференциальных уравнений силовых линий и пр. были составлены на языке
ФОРТРАН. Программы графического воспроизведения зависимостей и сим-
символов написаны с использованием ГРАФОРа.
Благодаря разнообразию, подробности и точности машинных изображений,
по-видимому, рождается новое качество подачи материала по курсу электро-
электродинамики. Па наш взгляд, дело по только в том, что графические образы легко
лоенршшмаются и запоминаются. Важна еще большая информативность ма-
машинных изображении в отлично от широко распространенных схематических,
рисунков, не только неподробных и неточных, но часто также неверных в не-
некоторых деталях. Ото можно сказать о большинстве ранее публиковавшихся
картин силовых линий.
Немаловажен также эстетический элемент: машинные изображения и»
только «просто красивы», по позволяют в разнообразии форм ощутить общ-
общность, гармонию полей, волновых процессов.
Наконец, следующее замечание. Все картины силовых линий построены
для солеиоидальпых или гармонических (за исключением нескольких точек)
полей. Таким образом. divF = 0. Но па плоском чертеже показывается разрез
ноля, и в этой плоскости уже divj_ F ф 0 (оператор двумерный). Поэтому, во-
обше говоря, п плоскости чертежа густота силовых линий не может быть со-
согласована с интенсивностью поля (см. п. 1.0.4); это выполнимо в пространстве.
Разумеется, для двумерных полей (не зависящих от одной координаты) ука-
уашгая трудность снимается. В качестве примера можно сопоставить рис. 2.7а:
и рис. 2.8а. Во втором случае (заряженные нити) все силовые линии'лежат
параллельно плоскости чертежа. Поэтому их густота на плоскости чертежа от-
отражает распределение интенсивности поля в пространстве. В первом же слу-
случае (когда заряды — точечные) правильное распределение интенсивности отра-
отражается лишь пространственной картиной силовых линий, а на рис. 2.8а наблю-
наблюдается кажущееся увеличение поля в направлении, перпендикулярном оси
зарядов. Желая выяснить величину поля, надо каждый раз подсчитывать
число силовых линий, выходящих через элемент ортогональной поверхности
в пространстве, а не через отрезок линии в плоскости чертежа.
Заметим, что иа рис. 7.9 магнитные силовые линии в плоскости xOz своей
густотой правильно отражают интенсивность поля, поскольку оно не зависит
от у. В других случаях (например, на рис. 7.7) это качество не сохраняется,
однако линии построепы так, что по оси z интенсивность передана правильно.
Для численного интегрирования уравнений силовых линий, следующих из
A.16), использовался метод Рунге — Кутта второго порядка. Выбор шага про-
производился в зависимости от предшествующей стадии процесса. Для устране-
устранения бесконечностей применилась выполняемая программой замена координат.
Г
ПРИЛОЖЕНИЕ
539
Заметим, что применение равномерного (достаточно малого) шага пеэффектив-
но из-за резкого возрастания времени.
Построение силовых линий в разных случаях имеет свои особенности.
Например, для заряженных нитей линии равномерно выводятся из окруж-
окружности, охватывающей малую окрестность одного заряда, и приходят к другим
зарядам практически равномерно (в малых окрестностях). В случае точечных
зарядов этого не происходит из-за трехмерности поля.
В варианте цилипдра, возмущающего параллельное поле, линии равномер-
равномерно выводятся из отдаленной эквииотенциали.
В случае двух нитей тока густоту линий определяло значение Д. которое
задавало величину потока вектора Н через элемент прямой, соединяющей ни-
нити, через который выходит одна линия. Аналогичные приемы использовались
и в других задачах.
Для диполя Герца учитывалось, что элементарная площадка, к которой
надо относить число электрических линий растет пропорционально г. Поэтому
при в =90° через отрезок Аг вычислялся поток вектора гЕ#.
В случае прямоугольного волновода для согласования картин линий в
двух продольных сечениях было необходимо выводить липии по единому за-
закону вдоль z. Отметим, что интегрирование уравпепий силовых линий здесь
может быть произведем в явном виде.
Особо следует отметить случай полосковой структуры (см. рис. 7.32).
Здесь решению уравнений силовых линий предшествовало решение гораздо
¦более сложной задачи численного нахождения электромагнитного поля (во
всех остальных случаях поле задавалось известными формулами).
'Ж
СПИСОК ЛИТЕРАТУРЫ ')
А. ЭЛЕКТРОДИНАМИКА
1. Тамм И. Е. Осповы теории электричества.— М.: Наука, 1989.
2. Стрэттон Дж. А. Теория электромагнетизма: Пер. с англ./Под ред. С. М. Ры-
това.— М.: Гостехиздат, 1948.
3. Зоммерфелъд А. Электродинамика: Пер. с нем./Под ред. С. А. Элькинда.—
М.: ИЛ, 1958.
Б. ЭЛЕКТРОДИНАМИКА ДЛЯ ФИЗИКОВ
1. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Элект-
Электричество и магнетизм: Пер. с англ./Под ред. Я. А. Смородинского.—М.: Мир,
1966.— Т. 5.
2. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Элект-
Электродинамика: Пер. с англ./Под ред. Я. А. Смородинского.—М.: Мир, 1966.—
Т. 6.
3. Джексон Дж. Классическая электродипамика: Пер. с апгл./Под ред. Э. Л. Бур-
штейна.— М.: Мир, 1965.
4. Пановский В., Филипс М. Классическая электродинамика: Пер. с англ./Под
ред. С. П. Капицы.— М.: Физматгиз, 1963.
В. ЭЛЕКТРОДИНАМИКА ДЛЯ РАДИОТЕХНИКОВ И РАДИОФИЗИКОВ
1. Рамо С, Уиннери Дж. Поля и волны в современной радиотехнике: Пер. с
апгл./Под ред. Ю. Б. Кобзарева.— М.: Гостехиздат, 1950.
2. Вайнштейн Л. А. Электромагнитные волны.— М.: Радио и связь, 1988.
3. Никольский В. В. Теория электромагпитпого поля.— М.: Высшая школа, 1964.
4. Каиенеленбаум Б. 3. Высокочастотная электродинамика.— М.: Наука, 1966.
5. Никольский В. В. Антеппы.— М.: Связь. 1966.
6. Никольский В. В. Электродипамика и распространение радиоволн.— М.: На-
Наука, 1978.
7. Вольман В. И., Пименов Ю. В. Техническая электродинамика.— М.: Связь,
1971.
8. Марков Г. Т., Петров Б. М., Грудинская Г. П. Электродинамика и распрост-
распространение радиоволн.— М.: Сов. радио, 1979.
Г. ТЕОРИЯ КОЛЕБАНИЙ И ВОЛНОВЫХ ПРОЦЕССОВ
1. Мандельштам Л. И. Полное собрание трудов.— М.: Изд-во АН СССР, 1955.—
Т. 4.
2. Зоммерфельд А. Оптика: Пер. с нем./Под ред. М. Л. Ельяшевича.—М.: ИЛ,
1953.
3. Горелик Г. С. Колебания и волны.—М.: Гостехиздат, 1950.
4. Потехин А. И. Некоторые задачи дифракции электромагнитных волн.—М.:
Сов. радио, 1948.
') Не ставилось целью дать полный список литературы последних лег»
Указываются только некоторые рекомендуемые и цитируемые книги.
СПИСОК ЛИТЕРАТУРЫ
54*
5. Хенл X., Maya А., Вестпфалъ К. Теория дифракции: Пер. с нем./ Под ред-
Г. Д. Малюжинца.— М.: Мир, 1964.
6. Зоммерфелъд А. Дифференциальные уравнения в частных производных фи-
физики: Пер. с нем./Под ред. А. Н. Тихопова.— М.: ИЛ, 1950.
7. Фок В. А. Проблемы дифракции и распространения электромагнитных:
волн.— М.: Сов. радио, 1970.
8. Борн М., Вольф Э. Основы оптики: Пер. с англ./Под ред. Г. П. Мотуяевич.—
М.: Наука, 1970.
Д. ЭЛЕКТРОДИНАМИКА СРЕД И СМЕЖНЫЕ ВОПРОСЫ
1. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановскио лекции по физике. Физи-
Физика сплошных сред: Пер. с англ./Под ред. Я. А. Смородипского.— М.: Мир,
1966,— Т. 7.
2. Ландау Л. Д., Лифшиц Е. М. Электродинамика сплошных сред.— 2-е изд.—
М.: Гостехиздат, 1982.
3. Хиппелъ А. Р. Диэлектрики и волны: Пер. с апгл./Под ред. Н. Г. Дроздова.—
М.: ИЛ, 1960.
4. Киттелъ Ч. Введение в физику твердого тела: Пер. с англ.— М.: Наука, 1978.
5. Гуревич А. Г. Магнитный резонанс в ферритах и антиферромагнетиках.—
М.: Наука, 1973.
6. Лаке Б.. Баттон К. Сверхвысокочастотные ферриты в ферромагнетики: Пер.
с англ./Под ред. А. Г. Гуревича.— М.: Мир, 1965.
7. Микаэлян А. Л. Теория и применение ферритов на сверхвысоких часто-
частотах.— М.: Госэнергоиздат. 1963.
8. Файн В. М., Ханин Я. И. Квантовая радиофизика.— М.: Сов. радио, 1965.
9. Лоудон Р. Кваптовая теория света: Пер. с англ./Под ред. Г. В. Скроцко-
го.—М.: Мир, 1976.
10. Ахманов С. А., Хохлов В. В. Проблемы нелинейной оптики.—М.: Изд-во
ВИНИТИ, 1964.
11. Вломберген Н. Нелинейная оптика: Пер. с англ./Под ред. С. А. Ахмапова
и Р. В. Хохлова.— М.: Мир, 1966.
12. Гинзбург В. Л. Распространение электромагнитных волп в плазме.— М.:
Наука, 1967.
13. СВЧ полупроводниковые приборы и их применение: Пер. с апгл./Под ред.
В. С. Эткипа.— М.: Мир, 1972.
14. Ярив А. Введепие в оптическую электронику: Пер. с англ./Под ред.
О. В. Богданкевича.— М.: Высшая школа, 1983.
15. Туров Е. А. Материальные уравпения электродинамики.— М.: Наука, 1983.
Е. РАДИОВОЛНЫ В ПРИРОДНЫХ УСЛОВИЯХ
1. Долуханов М. П. Распространение радиоволн.— М.: Связь, 1972.
2. Грудинская Г. П. Распространение радиоволн.— М.: Высшая школа, 1975.
3. Введенский Б. А., Аренберг А. Г. Вопросы распространепия ультракорот-
ультракоротких волн.— М.: Сов. радио, 1948.
4. Использование радиоспектра: Пер. с англ./Под ред. М. С. Гуревича.— М.:
Связь, 1971.
5. Распространение ультракоротких волн: Пер. с англ./Под ред. Б. А. Шилле-
рова.— М.: Сов. радио, 1954.
6. Калинин А. И., Черепкова Е. Л. Распространение радиоволн и работа ра-
радиолиний.— М.: Связь, 1971.
7. Долуханов М. П. Дальнее распространение ультракоротких волн.— М.:
Связьиздат, 1962.
8. Дэвис К. Радиоволны в ионосфере: Пер. с англ./Под ред. А. А. Корчака.—-
М.: Мир, 1973.
542
СПИСОК ЛИТЕРАТУРЫ
9. Николе М. Аэрономия: Пор. с англ./Под ред. М. Подоснова.— М.: Мир, 1973.
10. Алыгерт Я. Л., Гинзбург В. Л., Фейнберг Е. Л. Распространение радиоволн.—
М.: Гостехиздат, 1953.
11. Черепкова Е. Л., Чернышев О. В. Распространение радиоволн.— М.: Радио
и связь, 1984.
12. Гершман Б. //., Ерухи.мов Л. М., Яшин Ю. Я. Волновые явления в ионосфе-
ионосфере и космической плазме.— М.: Наука, 1984.
13. Яковлев О. И. Распространение радиоволн в космосе. М.: Наука, 1985.
14. Справочник по спутниковой связи и вещаниго./Под ред. Л. Я. Кантора.— М.:
Радио и связь, 1983.
Ж. НАПРАВЛЯЮЩИЕ СТРУКТУРЫ И РЕЗОНАТОРЫ
1. Кисунько Г. В. Электродинамика полых систем.— Ленинград: Изд-во ВКАС,
1949.
2. Гуревич А. Г. Полые резонаторы и волноводы.—М.: Сов. радио, 1952.
0. Силин Р. А., Сазонов В. П. Замедляющие системы.— М.: Сов. радио, 1966.
4. Вийнштейн Л. А. Открытые резонаторы и открытые волноводы.— М.: Сов.
радио. 1966.
5. Маркузе Д. Оптические волноводы.— М.: Мир, 1974.
6. Михалевский В. С. Элементы теории сверхвысокочастотных замедляющих
систем.— Ростов-па-Дону: Изд-во Ростовского ун-та, 1964.
7. Умер Х.-Г. Пленарные и волоконные оптические волноводы: Пер. с англ./
Под ред. В. В. Шевченко.— М.: Мир, 1980.
U. Григорьев А. Д., Янкевич В. Б. Резонаторы и резонаторные замедляющие
системы СВЧ.— М.: Радио и связь, 1984.
3. ИСТОРИЯ НАУКИ
1. Кузнецов Б. Г. Развитие физических идей от Галилея до Эйнштейна в све-
свете современной науки.— М.: Наука, 1966.
2. Григорьян А. Т., Вяльцев А. И. Генрих Герц.—М.: Наука, 1968.
3. Дуков В. М. Электродинамика.— М.: Высшая школа, 1975.
И. МАТЕМАТИЧЕСКАЯ ФИЗИКА II ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
1. Тихонов А. П., Самарский А. А. Уравнения математической физики.— М.:
Наука. 1977.
2. Михлин С. Г. Вариационные методы в математической физпке.— М.: Нау-
Наука. 1970.
3. Никольский II. В. Вариационные методы для внутренних задач электро-
электродинамики.— М.: Паука. 19(i7.
А. Васильев Е. Н. Возбуждение тел вращения — М.: Радио и связь, 1987.—•
272 с.
5. Вычислительные, методы в электродпна.мике/Под ред. Р. Митры: Пер. с
англ./Под ред. Э. Л. Бурштейпа.— М.: Мир. 1977.
6. Стренг Г. Линейная алгебра и ее применения: Пер. с аигл./Под ред.
Г. II. Марчука.— М.: Мир, 1980.
7. Самарский Л. А. Теория разностных схем.— М.: Наука, 1977.
8. Стренг Г., Фикс Дж. Теория методов конечных элементов: Пер. с англ./
Под ред. Г. И. Марчука.— М.: Мир, 1977.
9. Мирчук Г. И., Лгошков В. И. Введение в проекционно-сеточные методы.^
М.: Наука, 1981.
10. Никольский В. В., Никольская Т. И. Декомпозиционный подход к задачам
электродинамики.— М.: Наука, 1983.
11. Автоматизированное проектирование устройств СВЧ/Под ред. В. В. Николь-
Никольского.— М.: Радио и связь, 1982.
12 Кочии II. Е. Векторное исчисление и начала тензорного вечислепия.— М.:
Изд-во АН СССР, 1961.
СПИСОК ЛИТЕРАТУРЫ
543
13. Тарасов И. Е. Векторный анализ и начала тензорного исчисления.—М.:
Высшая школа, 1966.
14. Никольский В. В. Математический аппарат электродинамики.—М.: Изд-во
МИРЭА, 1973.
К. СПРАВОЧНИКИ
1. Янке Е., Эмдэ Ф., Леш Ф. Специальные функции: Пер. с ием./Под ред.
Л. И. Седова.—М.: Наука. 1977.
2. Кой Дж., Лэби Т. Таблицы физических и химических констант: Пер. с-
англ./Под ред. К. П. Яковлева.— М.: Физматгиз, 1962.
3. Справочник по волноводам: Пер. с англ./Под ред. Я. Н. Фсльда.—М.: Сов.
радио, 1952.
Учебное пособие
НИКОЛЬСКИЙ Вячеслав Владимирович
НИКОЛЬСКАЯ Татьяна Ивановна
ЭЛЕКТРОДИНАМИКА
И РАСПРОСТРАНЕНИЕ РАДИОВОЛН
Заведующий редакцией Я. А. Носова
Редактор Г. Г. Борисова
Художественный редактор Г. М. Коровина
Технический редактор С. Я. Шкляр
Корректоры Г. С. Вайсберг, Л. С. Сомова
ИВ М 12847
Сдано в набор 10.07.88. Подписано к печати 26.04.89. Фор-
Формат 60X90/16. Бумага книжно-журнальная. Гарнитура
обыкновенная новая. Печать выоокая. Усл. печ. л. 34.
Усл. кр.-отт. 34. Уч.-изд. л. 35,62. Тираж 23 850 экз.
Заказ М 265. Цена 1 р. 50 к.
Ордена Трудового Красного Знамени
издательство «Наука»
Главная редакция физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
Четвертая типография издательства «Наука»
630077 г. Новосибирск 77, Станиславского, 25