Биоэнергетика и линейная термодинамика необратимых процессов (стационарное состояние) - Кеплен С.Р., Эссиг Э.

Author: Кеплен С.Р. Эссиг Э.
Tags: термодинамика энергетика общая биофизика биохимия биофизика биоэнергетика
Year: 1986
Similar
Термодинамика реальных процессов
Термодинамика химических процессов
Анализ неравновесных процессов сжатия неидеального газа
Исследование в области термодинамики процессов информации и мышления
Text
                    Bioenergetics
and linear nonequilibrium
thermodynamics
the steady state
S. Roy Caplan and Alvin Essig
Harvard University Press
Cambridge, Massachusetts, and London,
England 1983
С. Р. Кеплен, Э. Эссиг
БИОЭНЕРГЕТИКА
И ЛИНЕЙНАЯ
ТЕРМОДИНАМИКА
НЕОБРАТИМЫХ
ПРОЦЕССОВ
(стационарное состояние)
Перевод с английского
д-ра хим. наук М. Г. Гольдфельда
МОСКВА „МИР“ 1986
ББК 28.071
К35
УДК 536.7 + 577.3
Кеплен С. Р., Эссиг Э.
К35 Биоэнергетика и линейная термодинамика необратимых
процессов (стационарное состояние): Пер. с англ. — М.:
Мир, 1986. — 384 с., ил.
В книге содержится глубокое и последовательное изложение основ термодина-
мики необратимых процессов и дана практически исчерпывающая характеристи-
ка всех важнейших биохимических и транспортных процессов в организме. Авто-
ры представили оригинальный труд монографического характера, основанный
на собственных исследованиях и тщательно отобранной библиографии, включаю-
щей основополагающие работы в данной области.
Для исследователей в области биохимии, физико-химической биологии, термо-
динамики и кинетики; для преподавателей и студентов вузов, специализирую-
щихся в области биохимии, биофизики.
К«—2	ББК 28.071
Редакция литературы по химии
© 1983 by the President and Fellows of Harvard
College
© перевод на русский язык, «Мир», 1986
Предисловие к русскому изданию
Как известно, в основе метаболизма лежат биохимические пре-
вращения веществ, сопровождающиеся превращением одной
формы энергии в другую. Естественно, что применение методов
термодинамики для анализа этих процессов давно стало пред-
метом серьезных исследований. Уже на первых этапах мето-
дами классической термодинамики были получены важные ре-
зультаты по изменению свободной энергии в отдельных биохи-
мических процессах. В биохимических работах этот подход и
сейчас с успехом применяется для того, чтобы выявить прин-
ципиальную возможность энергетического сопряжения различ-
ных метаболических реакций (например, гидролиз АТФ и по-
требляющие энергию реакции).
Однако в классической термодинамике расчеты энергетиче-
ских эффектов основаны на сравнении значений характеристи-
ческих функций в начальном (неравновесном) и конечном
(равновесном) состояниях системы. При этом из рассмотрения
выпадают фактор времени и характер переходных процессов,
что делает невозможным непосредственный термодинамический
анализ кинетических особенностей переходных процессов в от-
крытых биологических системах. Классическая термодинамика
не могла объяснить и свойства биологических систем, в кото-
рых самопроизвольно протекающие процессы ведут к уменьше-
нию их энтропии, что, как казалось, противоречит второму за-
кону термодинамики.
С позиций основного постулата термодинамики необратимых
процессов о разделении приращения энтропии открытой си-
стемы на две независимые части удалось объяснить общие за-
кономерности изменения энтропии в биологических системах.
Было показано, что в стационарном состоянии скорость произ-
водства энтропии в ходе внутренних необратимых процессов
в открытых системах достигает минимального положительного
значения (теорема Пригожина). Эти результаты, однако, спра-
ведливы только вблизи равновесия в области «линейной термо-
динамики». Именно здесь выполняются линейные соотношения
между скоростями и движущими силами процессов, а также со-
отношения взаимности Онзагера.
6
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
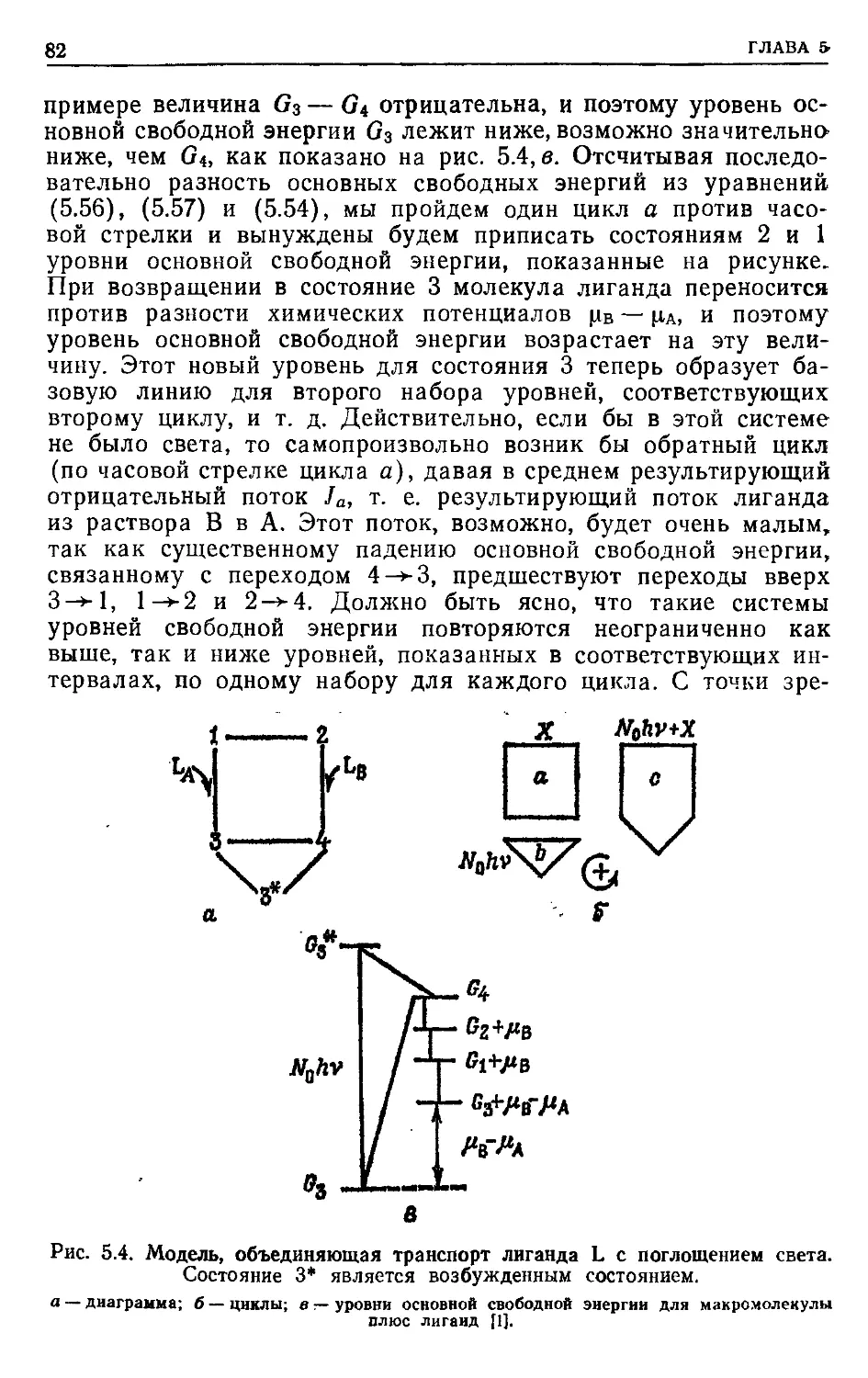
Применение методов термодинамики в области, далекой от
равновесия, показало, что здесь уже не удается найти общих
термодинамических критериев, характеризующих стремление
системы к стационарному состоянию. Вдали от равновесия
основную роль играют кинетические закономерности, которые
и определяют общие свойства системы.
В настоящее время в нелинейной термодинамике главным
образом проводятся теоретические исследования, касающиеся
процессов самоорганизации в биологических системах. В то же
время применение термодинамического подхода для нахожде-
ния условий и способов регуляции энергетического сопряжения
конкретных биологических процессов ограничено линейной тер-
модинамикой. Однако в последние годы был получен ряд важ-
ных результатов, позволивших распространить область приме-
нимости линейных соотношений на биохимические процессы,
далекие от равновесия. Это дало возможность провести термо-
динамический анализ свойств ряда молекулярно-биологических
преобразователей энергии и выявить свойства внутренних ре-
гуляторных связей, механизм которых остается пока неясным.
В этом проявилась сила термодинамического подхода, для при-
менения которого не требуется знания молекулярных механиз-
мов рассматриваемых процессов.
Систематическое изложение основ линейной и нелинейной
термодинамики необратимых биологических процессов можно
найти в современной отечественной литературе *.
Ценность настоящей книги состоит в том, что в ней прово-
дится конкретный анализ важнейших биохимических и транс-
портных процессов в организме. Это оригинальный труд, авто-
рами которого являются крупные специалисты, принадлежащие
к школе А. Качальского. Несмотря на относительную простоту
математического аппарата, понимание основного материала
потребует от читателя известного напряжения. Книга будет не-
сомненно полезна биологам различных специальностей и помо-
жет им в проведении сравнительного анализа молекулярных
преобразователей энергии в биологических системах.
А. Рубин
* Волькенштейн М. В. Биофизика. — М.: Наука, 1981; Рубин А. Б. Тер-
модинамика биологических процессов. — М.: Изд. МГУ, 1984.
Предисловие
При ознакомлении с новым, не совсем обычным подходом к био-
логическим явлениям у читателя неизбежно возникает ряд воп-
росов. Есть ли на самом деле необходимость привлекать не-
равновесную термодинамику при изучении биологических про-
цессов? Можно ли рассчитывать, что биолог будет тратить
время и усилия на освоение этого подхода? Нельзя ли при рас-
смотрении имеющихся проблем ограничиться более привычны-
ми физическими и математическими методами? Даже если нам
удастся доказать применимость неравновесной термодинамики
к некоторым задачам и этот подход окажется привлекатель-
ным для ряда исследователей, не будет ли это просто означать,
что экспериментальные результаты втиснуты в некую новую
форму? Не имеем ли мы в данном случае дело с логическими
построениями, которые адекватны лишь особенностям нашего
мышления и существующим предрассудкам? И наконец, мо-
жет ли термодинамика что-нибудь сказать нам о механизме
биологических явлений? По словам одного критика, «это один
из законных подходов, но, пока объект рассматривается как
черный ящик, по-настоящему интересные вопросы нельзя даже
поставить».
Мы утверждаем, что неравновесная термодинамика кон-
структивна, поскольку образует самосогласованную, логичную
и компактную форму организации и систематизации информа-
ции. Построение систематических корреляций по разнородным
данным позволяет выявить единообразие между разными на
первый взгляд системами. Часто оказывается, что формализм,
развитый при анализе одной системы, непосредственно приме-
ним к совершенно другой системе. Так, например, обстоит дело,
когда мы рассматриваем случай поддержания градиента элек-
трохимического потенциала на эпителиальной мембране и изо-
метрического напряжения в мышце. Кроме того, в пределах
данной системы термодинамический подход позволяет выявить
связи между различными явлениями, которые с других точек
зрения отнюдь не очевидны. Например, расхождения между
коэффициентом проницаемости для изотопной -метки и для сум-
марного потока дают количественную меру «аномальности» от-
ношения потоков. При других способах рассмотрения связь
8
ПРЕДИСЛОВИЕ
между этими характеристиками остается непонятной, но она
непосредственно следует из термодинамической теории.
Утверждение, что термодинамика ничего не говорит о ме-
ханизме, является общеизвестной истиной. Необходимо, однако,
уточнить, что, собственно, подразумевается под «механизмом».
Если, например, речь идет о молекулярных механизмах функ-
ционирования натриевого насоса, то понятно, что термодина-
мика сама по себе не может дать никаких конечных ответов,
но и здесь она часто устанавливает некоторые пределы, кото-
рым должны удовлетворять предлагаемые кинетические мо-
дели. Если же механизм понимать в более широком смысле
этого слова, включая подвод энергии к насосу и его регуля-
цию, то термодинамические соображения оказываются исклю-
чительно ценными.
Сказанное выше дает нам возможность утверждать, что не-
равновесно-термодинамический подход представляет важную
часть арсенала методов современной биофизики. Чтобы дока-
зать справедливость этого утверждения, в данной книге мы до-
вольно подробно проанализируем небольшое число систем, с
которыми авторы сами работали и которые хорошо иллюстри-
руют общие принципы. Ограниченность во времени и в объеме
книги не позволила нам в полной мере использовать результаты
других авторов, которые заслуживают более пристального вни-
мания. Ясно, что многие системы можно рассмотреть с ана-
логичных позиций, и мы надеемся, что читатели воспользуются
развитыми здесь представлениями при анализе интересующих
их проблем.
Эта книга — результат плодотворного сотрудничества с уче-
ными различных институтов. Поэтому мы хотели бы выразить
благодарность за гостеприимство д-ру Рюи Де Суза (медицин-
ский факультет Женевского университета), д-рам Барбаре
Бэнкс и Чарлзу Вернону (колледж Лондонского университета),
д-рам Францу Грюну и Дитеру Вальцу (биоцентр Базельского
университета), д-рам Рейнхарду Шлёглю и Фридриху Зауеру
(Институт биофизики Макса Планка, Франкфурт-на-Майне),
д-ру Террелу Хиллу (Национальный институт здравоохране-
ния, Бетесда, шт. Мэриленд). Многие из изложенных в книге
основополагающих идей возникли в ходе дискуссий с д-ром
Орой Кедем. Мы признательны также д-ру Дональду Мику-
леску за тщательное прочтение и критику первоначального ва-
рианта рукописи.
Мы глубоко благодарны своим женам, Теолее и Каролине,
поддерживавших нас во время написания книги и проведших
немало часов за чтением рукописей и корректур.
С. Р. Кеплен
Э. Эссиг
I
Общие соображения
Несмотря на очевидность того, что большинство биологических
процессов протекает вдали от состояния равновесия, многие
считают, что известные методы классической равновесной тер-
модинамики в сочетании с соответствующим кинетическим
анализом достаточны для рассмотрения этих явлений. Приме-
рами, такой позиции изобилует биофизическая литература. По-
этому, вероятно, полезно сказать несколько слов о том, почему
эта точка зрения неверна. Как отметил много лет назад При-
гожин, классическая термодинамика как метод макроскопиче-
ского описания энергетики биологических процессов имеет серь-
езные ограничения. Этот метод основан на рассмотрении рав-
новесных состояний и на концепции «обратимых процессов»
(гипотетические идеальные процессы, которые протекают без
нарушения равновесия и, следовательно, без прироста энтро-
пии). Вопрос о длительности перехода из одного состояния
в другое находится вне компетенции классического метода.
В противоположность этому неравновесная термодинамика, яв-
ляющаяся дальнейшим развитием термодинамического метода,
основана на рассмотрении состояний, удаленных от равнове-
сия, и сопутствующих необратимых процессов (реальных про-
цессов, в которых производится энтропия). Необходимое усло-
вие рассмотрения таких процессов — учет временного фактора
в явном виде.
Даже классическая равновесная термодинамика имеет дело
не только с полностью равновесными состояниями, но и с со-
стояниями частичного или ограниченного равновесия, такого,
как доннановское..равновесие, в котором достижению полного
равновесия препятствует барьер проницаемости для определен-
ных компонентов системы. Другой пример частичного равнове-
сия— смесь химических реагентов при неравновесных концен-
трациях, взаимодействие между которыми затруднено из-за от-
сутствия катализатора. Наоборот, стационарное состояние
в неравновесной термодинамике поддерживается исключитель-
но за счет прироста энтропии. Расчет скорости прироста эн-
тропии— основа метода, обеспечивающего фактически есте-
ственную базу для выбора соответствующих комбинаций пото-
ков и сил при феноменологическом описании системы. Это опи-
10
ГЛАВА 1
сание вводит кинетические параметры в форме феноменологи-
ческих коэффициентов. Для данной комбинации коэффициен-
тов функционирование системы и ее эффективность полностью
определяются в широком диапазоне действующих условий, и
легко рассчитать ее максимальный к. п. д. Чтобы получить ана-
логичную информацию с помощью классической термодина-
мики в сочетании с кинетическими моделями, потребовался бы
очень трудоемкий процесс, применимый только в простейших
случаях.
Главное достоинство термодинамического метода заключа-
ется в его способности предсказывать взаимосвязь между на-
блюдениями в отсутствие детальных сведений о структуре си-
стемы: он устанавливает рамки, в пределах которых могут
быть построены и испытаны на самосогласованность модели
поведения систем. В этом отношении неравновесная термоди-
намика расширяет и дополняет классический метод. Хотя ее
кинетические параметры не вытекают из специфических моде-
лей, на них накладываются определенные ограничения, из ко-
торых следуют их наиболее вероятные величины. Мы увидим,
что лучше всего прогнозируются те процессы, которые проте-
кают в «стационарном состоянии». Однако в стационарных
условиях параметры состояния системы не дают информации
о протекающих в ней процессах. Для изучения этих процессов
необходимо рассматривать их влияние на окружение, и это
действительно оказывается весьма эффективным подходом. Ре-
зультирующий анализ непосредственно дает очень ценную ин-
формацию: число и природу степеней свободы системы. Экспе-
риментатору это показывает, сколько (и каких) ограничений
потребуется для определения стационарного состояния системы,
и позволяет предсказать взаимосвязь между такими состояния-
ми. Зачастую эта информация будет побуждать к новым экс-
периментам. Теоретики получают информацию для выбора тех
моделей, которые удовлетворяют соответствующим термодина-
мическим ограничениям.
В большинстве рассматриваемых случаев мы будем пред-
полагать, что силы и потоки, характеризующие данное стацио-
нарное состояние системы, связаны друг с другом линейной мат-
рицей откликов. Хотя это не может быть справедливо всегда,
мы полагаем, что во многих системах, которые будут обсуж-
даться, отклонения от линейности часто будут слишком малы,
чтобы их следовало учитывать. Это может быть обусловлено
регуляторными механизмами, возможно включающими обратную
связь, что в настоящее время не полностью выяснено. В других
случаях мы можем изучать системы в линейном диапазоне
вблизи равновесия. Даже системы, которые на первый взгляд
кажутся сильно нелинейными, могут в действительности ока-
заться линейными, когда рассматриваются соответствующие
Общие соображения У
степени свободы. Дальнейшее упрощающее обстоятельство со-
стоит в том, что, согласно соотношению взаимности Онзагера,
матрица откликов должна быть симметричной. Это уменьшает
число феноменологических коэффициентов, характеризующих
систему.
Если мы примем этот подход, полностью зная его ограниче-
ния, то увидим бросающуюся в глаза особенность, вытекаю-
щую из множества исследований, — замечательную способность
неравновесной термодинамики унифицировать различные яв-
ления. Поэтому не так существенно, являются ли системы
истинно линейными во всем диапазоне, представляющем ин-
терес для биологии; гораздо важнее выбрать единую четкую
логическую структуру системы. Подобно этому, не обязательно,
чтобы наблюдаемая линейность отражала простое линейное
поведение фундаментальных кинетических параметров. Если
учесть возможность сложной регуляции, то линейность вполне
может быть следствием сложного взаимодействия нелинейных
параметров. В противоположность громоздкому конгломерату
кинетических параметров, которые часто вытекают из построе-
ния модели, феноменологические уравнения впечатляюще про-
сты. Хотя эти уравнения не могут описывать молекулярные
механизмы (если только они не интерпретируются через моле-
кулярные параметры), они дают ограничивающие условия, ко-
торые должны выполняться в любой рассматриваемой модели,
и это всегда вносит ясность в вопросы энергетики.
В следующих главах мы рассмотрим ряд общепринятых то-
чек зрения на биологические системы. Некоторые из них осно-
ваны на моделях, другие — на классических термодинамических
представлениях, которые мы считаем либо ограниченно приме-
нимыми, либо просто ошибочными. Представляя неравновесный
термодинамический метод, мы сосредоточим внимание на рас-
смотрении вопросов, относящихся к широкому разнообразию
транспортных и других энергопреобразующих систем. Для
удобства мы будем неоднократно обращаться к наиболее изу-
ченным системам, которые могут быть охарактеризованы с точ-
ки зрения неравновесной термодинамики. Так, из эпителиаль-
ных тканей мы рассмотрим кожу лягушки и мочевой пузырь
жабы; в качестве' симметричных систем будут обсуждаться
главным образом митохондрии, хлоропласты и мышцы. Мыш-
це, по праву, будет уделено большое внимание как механохи-
мическому преобразователю.
Часто придется возвращаться к вопросу о стехиометрии.
Например, считается, что транспорт определенного числа ионов
натрия связан с потреблением соответствующего числа молей
кислорода. Аналогичная ситуация возникает при изучении окис-
лительного фосфорилирования. По-видимому, это мнение явля-
ется следствием рассмотрения указанных процессов по анало-
12
ГЛАВА 1
гии со стехиометрическими реакциями в пробирке. Однако сте-
хиометрия не является обязательной в том случае, когда про-
цесс рассматривается с позиций неравновесной термодинамики.
Другой круг проблем, который нас будет интересовать,—
это энергетика и эффективность утилизации энергии. Здесь
также существует тенденция проводить обсуждение этих вопро-
сов в рамках кинетических моделей. А это приводит к допу-
щению, что молекула в ходе транспорта должна преодолевать
трение, откуда и возникает понятие «внутренней работы». Так
же обстоит дело при рассмотрении мышечного сокращения.
При оценке к. п.д. сумма «внутренней работы» и всей осталь-
ной работы связывается с затратами энергии. Этот расчет
обычно включает как стехиометрические соотношения, так и
энтальпию реакции — энергетический параметр, получаемый в
опытах с калориметрической бомбой. И в этом случае анализ
становится значительно яснее с позиций неравновесной термо-
динамики.
2
Основы равновесной
и неравновесной термодинамики
В этой главе мы рассмотрим основные понятия равновесной
термодинамики, а затем дадим в общих чертах основы анализа
стационарного состояния систем с позиций неравновесной тер-
модинамики. Сущность этого анализа заключается в оценке
скорости производства энтропии в зависимости от потоков и
сил, действующих в системе. Будет показано, что, хотя произ-
водство энтропии является следствием необратимого процесса
или процессов, происходящих внутри системы, параметры си-
стемы, находящейся в стационарном состоянии, не изменяются
со временем, и, следовательно, скорость производства энтропии
должна оцениваться путем рассмотрения изменений, вызван-
ных этой системой в окружающей среде.
2.	1. Некоторые основные принципы и функции
равновесной термодинамики
Первый закон термодинамики — это закон сохранения энергии,
согласно которому общая энергия изолированной системы не
изменяется. Общая энергия системы состоит из кинетической
энергии (определяемой движением системы), потенциальной
энергии (определяемой положением системы) и внутренней
энергии (определяемой свойствами компонентов системы).
В большинстве процессов, представляющих интерес для био-
физиков, кинетическая и потенциальная энергии системы оста-
ются постоянными, и, следовательно, нас будет интересовать
только внутренняя энергия U. Внутренняя энергия является
примером функции состояния, т. е. она полностью определяется
величинами ряда термодинамических параметров, достаточных
для однозначного определения системы, таких, как температура,
давление и концентрация. Для закрытой системы, допускаю-
щей обмен энергией, но не веществом с окружающей средой,
первый закон термодинамики устанавливает зависимость внут-
ренней энергии от тепла Q, поглощенного системой из окружаю-
щей среды, и работы W, совершенной системой над своим
окружением. В дифференциальной форме такая зависимость
имеет вид
dU = dQ — dW
(2.1)
14
ГЛАВА 2
Этот закон легко проверяется для любого перехода между
двумя данными состояниями. Необходимо отметить, что рабо-
та— это способ передачи энергии, принимающей различные
формы, любая из которых в принципе может быть полностью
использована для поднятия груза. Внутренняя энергия, или по
терминологии Бриджмена функция внутренней энергии, явля-
ется логической конструкцией, оправдываемой тем фактом, что
разность между dQ и dU7, каковы бы ни были их индивидуаль-
ные величины, полностью определена для любого заданного
изменения состояния.
Во втором законе термодинамики речь идет о том, что, хотя
определенные изменения состояния внутри системы (например,
Л->В) могут происходить спонтанно, обратные превращения
(такие, как В-*Л) невозможны. Как писал Денбиг [2], воз-
можность или невозможность протекания процессов Л-*В и
В->Л полностью зависит от природы состояний Л и В и опре-
деляется величинами таких переменных, как температура и дав-
ление в начале и в конце процесса; поэтому можно надеяться
найти функцию этих переменных, характеристики которой
должны показать, какой из процессов (Л->В или обратный
процесс В-э-Л) будет единственно возможным. Такой функ-
цией является функция энтропии 5, определяемая выражением
dS = (dQ/Т) Обр, относящимся к гипотетическому предельному
случаю обратимого процесса, в котором термодинамические па-
раметры окружающей среды бесконечно мало отличаются от
параметров самой системы; Т — абсолютная температура си-
стемы. Второй закон в дифференциальной форме утверждает,
что в закрытых системах для любых процессов, которые в прин-
ципе возможны,
dS^dQiT	(2.2)
Так же как и первый закон, уравнение (2.2) легко проверяется
для любого перехода между двумя данными состояниями.
Эти два закона легко объединяются. Для обратимых про-
цессов dQ — TdS и, ограничиваясь только работой расширения,
dW = pdV, vjpe. р — давление внутри системы (в данном случае
также и вне), а V — объем системы, получим
dU = TdS — pdV	(2.3)
Хотя уравнение (2.3) было выведено для обратимого перехода,
оно применимо и в общем случае, так как все Параметры явля-
ются функциями состояния. Однако для необратимого процесса
величины TdS и pdV не могут уже определяться как тепло и
работа соответственно. Для таких процессов dQ <Z TdS и dW <
< pdV. Например, при необратимом расширении внутреннее
давление р должно быть больше, чем внешнее, против которого
совершается работа.
Основы равновесной н неравновесной термодинамики
15
Можно сказать, что введенные до сих пор величины U, S,
Т, р и V олицетворяют всю классическую термодинамику. Все
они являются функциями состояния в отличие от величин Q
и W, зависящих не только от начального и конечного состоя-
ний системы, поглощающей тепло и совершающей работу, но
также и от конкретного пути или способа, которым система пе-
реходит из начального состояния в конечное. Исключительно
для удобства принято вводить три аддитивные функции состоя-
ния, которые являются просто комбинацией рассмотренных
выше величин. Это энтальпия Н, свободная энергия Гельм-
гольца F и свободная энергия Гиббса G. Эти аддитивные вели-
чины определяются соотношениями
H = U + pV, F — U — TS, G = H — TS (2.4-2.6)
Основное уравнение для закрытых систем [уравнение (2.3)]
можно выразить через эти новые величины следующим об-
разом:
dH — TdS-]- Vdp	(2.7)
dF = -SdT — pdV	(2.8)
dG = -SdT+ Vdp	(2.9)
Диаграмма на рис. 2.1, которая, согласно Тицу [7], была впер-
вые предложена Борном, является прекрасным мнемоническим
Рис. 2.1. Мнемоническое средство
для запоминания термодинамических
функций состояния (см. текст).
средством, дающим возможность сразу записать уравнения
(2.3), (2.7) — (2.9) (Зависимые параметры в этих уравнениях
показаны на сторонах квадрата; каждый из них расположен
между соответствующей парой независимых параметров, нахо-
дящихся в углах квадрата, с приписанным им знаком. Коэффи-
циент, связанный с данным дифференциалом, располагается на
противоположном конце соответствующей диагонали.)
Смысл энтальпии для системы при постоянном давлении мо-
жет быть пояснен следующим образом. Рассмотрим закрытые
системы, которые, кроме расширения, могут совершать любой
вид работы. Комбинируя первый закон [уравнение (2.1)] с
* Примечания к этой и последующим главам приведены в конце книги
после списка обозначений. — Прим, перев.
16
ГЛАВА 2
определением энтальпии [уравнение (2.4)], получим
dH = dQ - dW + pdV = dQ - (dW — pdV) =
= dQ — dW' (p — постоянная) (2.10)
где W представляет собой работу, отличающуюся от работы
расширения, совершаемой системой, и обычно называется «по-
лезной работой». Это, например, поднятие груза или растя-
жение пружины2. В случае когда нет полезной работы, совер-
шенной при постоянном давлении,
dH = dQ (dW' = 0)	(2.11)
По этой причине энтальпию иногда называют «теплосодержа-
нием» системы.
Понятие полезной работы делает ясным и смысл термина
«свободная энергия». Так, из уравнений (2.6) и (2.10) для
дифференциала свободной энергии Гиббса при постоянных
температуре и давлении получим
dG = dQ — dW' — TdS (р и Т — постоянные)	(2.12)
Следовательно,
dQ = TdS + (dG + dW')	(2.13)
Таким образом, в обратимом процессе при постоянных р и Т
dW' = — dG (обратимый процесс)	(2.14)
В необратимом процессе dQ<ZTdS. Поэтому dG + dW'<Z0,
так что
dW'< — dG (необратимый процесс) (2.15)
На основании этого можно сделать вывод, что максимальная
полезная работа, которая может быть получена в процессе при
постоянных давлении и температуре, равна изменению отрица-
тельной свободной энергии Гиббса, причем это становится воз-
можным лишь в предельном случае гипотетического обратимого
процесса. Путем совершенно аналогичных рассуждений можно
показать, что изменение отрицательной свободной энергии
Гельмгольца в системе соответствует максимальной полезной
работе, которая может быть получена при постоянных объеме
и температуре. Обычно в биологических системах различие
между свободными энергиями Гиббса и Гельмгольца несуще-
ственно, В любом случае их применение ограничивается изо-
термическими системами.
В неравновесной термодинамике мы будем иметь дело с от-
крытыми системами, и поэтому очень важно ясно представлять
себе трактовку таких систем с позиций классической термоди-
намики. Для открытых систем, в которых происходит обмен
веществом с окружающей средой, элементарные уравнения
Основы равновесной н неравновесной термодннамнкн 17
(2.3), (2.7) — (2.9) в том виде, как они даны, недостаточны.
Так как состав таких систем может изменяться, то для описа-
ния их состояния необходимы дополнительные переменные,
(Это справедливо также для закрытых систем, в которых про-
текает химическая реакция.) Например, выражая U по-преж-
нему как функцию независимых переменных S и V, мы долж-
ны, кроме того, учесть и ее зависимость от независимой пере-
менной — числа молей п,. Следуя трактовке Пригожина и Ди-
фэй [6], имеем
dU = (dU/dS)v, П{ dS + (dUfiV)s. nfiV+X (dUfinds. v, n/ . dnt
(2.16)
Когда открытая система подвергается изменению, при котором
все т остаются постоянными, ее состояние изменяется точно
так же, как это было бы в закрытой системе постоянного со-
става. Поэтому, сравнивая с уравнением (2.3), получим
(dUfiS)v,n. = T и (dU/dV)s,n. = -p (2.17)
По терминологии Гиббса величина
(dU finds, г. п,- ф П1 = Pi	(2.18)
называется химическим потенциалом t-ro компонента. Комби-
нируя уравнения (2.16) — (2.18), получим уравнение Гиббюа
dU = TdS-pdV+ £ Pidtit	(2.19)
i
Аналогично для адекватного описания изменения состава не-
обходимо добавить член У*, рг dtii в оставшиеся три элементар-
i
ные уравнения (2.7) — (2.9). Видно, что
Pi = (dUfinds. v, nj = (ОНfinds, р, П{ =
= fiFfindr, v, nj = (dGfindr. P. nj (2.20)
Следует отметить, что в открытых системах величина TdS не
может быть однозначно интерпретирована как тепло, даже
в случае обратимого процесса. Дело в том, что само понятие
переноса тепла в открытых системах не вполне определено, так
как вместе с веществом переносится и энергия.
Если проинтегрировать уравнение Гиббса между двумя со-
стояниями, так чтобы во втором состоянии система увеличи-
лась в размере без изменения ее интенсивных переменных
(температуры, давления и концентраций), то химический по-
тенциал остается постоянным. Тогда получаем
&U = Т АЗ — р АГ + ]£ p.i Ап( (Г, р, ц, постоянны)
2 Кеплен, Эссиг
18
ГЛАВА г
Такие изменения могли бы быть вызваны простым добавлением
вещества к системе. При увеличении размера системы в k раз,
(k- l)U = T(k- l)S-p(k-l)V+ ЕМ*~ 1)«/
i
тогда
U = TS-pV+ E ИЛ	(2.21>
i
Этот вывод уравнения (2.21), который предложил Денбиг [2] г
основан на том физическом факте, что интенсивные параметры
не зависят от размера системы, в то время как экстенсивные
параметры пропорциональны размеру. Таким образом, с учетом
определений Н и G, данных в уравнениях (2.4) и (2.6), из
уравнения (2.21) следует, что
G=E^Hi	(2.22)
i
Рассмотренное интегрирование приводит также к взаимоза-
висимости между одновременными изменениями интенсивных
переменных. Если записать полный дифференциал уравнения
(2.21) и сравнить его с уравнением Гиббса (2.19), то найдем,
что
S dT — V dp Е nt dpi — 0	(2.23)
i
Это соотношение известно как уравнение Гиббса — Дюгема.
На этом заканчивается краткий обзор наиболее существен-
ных элементов классической термодинамики. Литература к этой
и другим главам приведена в конце книги.
2.	2. Некоторые основные понятия
неравновесной термодинамики
Чтобы проиллюстрировать метод, используемый для вычисле-
ния скорости производства энтропии, рассмотрим систему, по-
казанную на рис. 2.2. Необратимый процесс происходит в об-
ласти, обозначенной (0). Хотя процесс ограничен этой обла-
стью, его влияние ощущается в окружающей области (1). Об-
ласть (0) может представлять собой, например, бактерию, ми-
тохондрию или фрагмент эндоплазматического ретикулума
(или даже синтетическую мембрану, обладающую фермента-
тивной активностью). Во всех этих случаях субстраты, присут-
ствующие в (1), входят в (0), подвергаются реакции и возвра-
щаются в (1) в виде продуктов. Область (1) можно предста-
вить себе как часть локального окружения области (0), доста-
точно большую для полного обеспечения всех возможных про-
цессов в (0). Для удобства мы можем считать, что область (1)
Основы равновесной и неравновесной термодинамики
19
Рис. 2.2. Система: необратимый процесс протекает в области (0), имеющей
малый объем по сравнению с окружающей областью (1). Область (1) огра-
ничена жесткими адиабатическими стенками.
Т — температура, р —давление,	—химический потенциал i-то компонента.
ограничена жесткими адиабатическими стенками, т. е. изоли-
рована или полностью отделена от внешнего окружения — си-
туация, которая часто реализуется в эксперименте. Следова-
тельно, область (1) можно рассматривать как полное окруже-
ние области (0), другими словами, как всю оставшуюся часть
Вселенной, игнорируя все явления, не относящиеся к интере-
сующему нас процессу. По аналогии с обычными методами
классической равновесной термодинамики предполагается, что
область (1) хорошо перемешана, так что всюду достигается
равновесие, т. е. температура Т, давление р и химический по-
тенциал ц/ везде постоянны. Эта ситуация также часто реали-
зуется в эксперименте.
В таком случае возникают две возможности. Первая со-
стоит в том, что область (0) является закрытой системой, ко-
торая может обмениваться с областью (1) только теплом. Ни
один из примеров, рассмотренных ранее, не принадлежит к этой
категории, и, по-видимому, трудно найти соответствующий при-
мер в биологии. Однако для начала полезно рассмотреть такую
умозрительную возможность. Записывая первый закон для об-
ласти (0), получим
dU™ = dQM-dW™	(2.24)
где, как обычно, dU^ — изменение внутренней энергии обла-
сти (0) в результате поглощения некоторого количества тепла
dQW из области (1) и совершения определенного количества
работы dWm над окружающей средой (1) в процессе беско-
нечно малого изменения состояния. Согласно второму закону,
область (0) подчиняется общему неравенству
d5 = dQo6p/r>dQ/F	(2.25)
где dS — производство энтропии, определяемое теплом dQoep,
которое могло бы поглотиться при обратимом изменении. (Тож-
дество существует по определению.) Так как мы рассматри-
2*
20
ГЛАВА 2
ваем реальные (необратимые) процессы, то TdS всегда больше,
чем dQ— действительно поглощенное тепло. Из этого следует,
что на практике область (0) не в состоянии извлечь из своего
окружения максимальное количество тепла, которое теоретиче-
ски могло бы превратиться в работу. Вместо неравенства для
реальных процессов можно записать
dS = dQ/Т + dQ'/T	(2.26)
где dQ, как и ранее, — действительное потребление тепла и
dQ' — положительная величина. По существу основой неравно-
весной термодинамики является вычисление величины dQ' как
функции соответствующих переменных. Ясно, что dQ' есть до-
полнительное тепло, которое должно было бы поглотиться из
среды (1), если бы изменение происходило обратимо3. При
действительном изменении состояния прирост энтропии dS
определяется также производством некоторого количества эн-
тропии dQ'/T. Эта величина может представлять собой, напри-
мер, энтропию смешения или реакции в области (0).
В неравновесной термодинамике уравнение (2.26) обычно
принято записывать в форме
dS = deS + dtS	(2.27)
Правая часть уравнения (2.27) аналогична правой части урав-
нения (2.26). Таким образом, deS является «обменным» вкла-
дом изменения энтропии в области (0), a diS — «внутренним»
вкладом, создаваемым благодаря необратимости процессов и
поэтому неизбежно положительным.
Вторая возможность состоит в том, что область (0) явля-
ется открытой системой, которая может обмениваться с обла-
стью (1) как веществом, так и теплом. Это гораздо более ин-
тересный случай. Однако уравнения (2.24) — (2.26) в этом слу-
чае неоднозначны, так как вещество переносит связанную с ним
энергию и количество переданного тепла становится не вполне
определенным. Необходимо переписать уравнение (2.24) в
форме, которая сделает явными количественные изменения в
составе. Такой формой является уравнение Гиббса (2.19), ко-
торое будет играть основную роль в дальнейшем изложении.
Уравнение (2.27) все же можно написать для области (0),
но члены в правой части больше не будут отождествляться
с соответствующими членами уравнения (2.26). Это не создает
дополнительных трудностей. Чтобы лучше понять смысл вели-
чины diS, центральной во всем дальнейшем изложении, полезно
рассмотреть изменения энтропии в обеих областях системы,
имея при этом в виду, что необратимый процесс возникает
только в области (0). Общее изменение энтропии в такой си-
стеме, очевидно, равно
= dS<n + dS^
(2.28)
Основы равновесной и неравновесной термодинамики 21
Однако, согласно уравнению (2.27),
dS<°) = deS<°) + dtSm, dS^ = deS(1> = - deS^ (2.29, 2.30>
так как изменение энтропии в области (1) обусловлено исклю-
чительно обменом с областью (0). Из уравнений (2.28) — (2.30)
следует, что
dS°^ = diS^	(2.31>
Таким образом, diSm представляет собой общее увеличение
энтропии в окружающей среде благодаря процессам, прохо-
дящим в области (0).
2.	3. Диссипация энергии в скалярных
необратимых процессах
Интуитивно мы лучше разбираемся в понятии работы, чем эн-
тропии. Легко показать, что необратимое производство энтро-
пии связано с потерями свободной энергии или способности
совершить работу. При постоянных температуре и давлении
максимальная способность совершить работу измеряется сво-
бодной энергией Гиббса G. В этих условиях изменение G в каж-
дой области определяется выражениями
dG<°> = dt/<0> + р dV® — Т dS<°>	(2.32}
dG^ = dU^ +pdV^ — TdS^f	(2.33}
Суммируя эти два уравнения и учитывая, что dVw = — dVm
и dltt1'1 — — dU^ (в силу сохранения внутренней энергии в изо-
лированной системе), получим
dGo6m = rfG‘°> + dG<‘> = - Т dS06^	(2.34)
Так как для любых реальных процессов dS06'11 — величина по-
ложительная, то свободная энергия всей системы уменьшается.
Рассмотрим скорость этой потери или диссипации свободной
энергии, которая задается диссипативной функцией Ф:
Ф = 7\$обш'= — Ообщ^О (Тир постоянны) (2.35)
(Равенство нулю относится лишь к равновесию или гипотети-
ческим обратимым процессам.) Диссипативная функция имеет
размерность мощности и может быть измерена в ваттах.
Для системы в стационарном состоянии диссипативную
функцию легко вычислить с помощью уравнения Гиббса, выра-
жающего связь между различными термодинамическими пара-
метрами окружающей среды. Предположим, например, что
процесс, проходящий в области (0), представляет собой фер-
22
ГЛАВА 2
ментативное расщепление субстрата X на v идентичных фраг-
ментов Y:
X vY	(2.36)
После достижения стационарного состояния свойства области
(0) не изменяются во времени. Скорость, с которой расходу-
ется X, равна скорости его образования из Y, и последняя ско-
рость как раз компенсирует потери X в окружающей среде.
Следовательно, внутренняя энергия, энтропия, объем и концен-
трация, связанные с областью (0) или с любой малой «локаль-
ной» частью области (0), если ее свойства неоднородны, по-
стоянны во времени4. Поэтому уравнение Гиббса необходимо
записать лишь для области (1):
d[7(1) = ТdS(1) — рdV(I) + Е И*’’dn(i} (2.37)
i
Сумма в правой части уравнения отражает изменения в со-
ставе области (1) в результате реакции, происходящей в об-
ласти (0); [xV> и nV1— химический потенциал и число молей
i-ro компонента в области (1) соответственно. Так как dV(1) =
= — dIA0) = 0 и dU^ = — dUl0'> — 0, то сразу получаем, что
Г</3(1) = - EpV’rf	(2.38)
i
Кроме того, поскольку dSw — 0, из уравнения (2.28) следует,
что
Т </30бщ = - Е ц?1 dnf-1	(2.39)
i
Нужно также отметить, что в стационарном состоянии, со-
гласно уравнению (2.30),
jSoem = _ deS(o)	(2.40)
т. е. производство энтропии в области (0) как раз компенси-
рует ее потери в окружающей среде. Диссипативная функция
получается дифференцированием уравнения (2.39) по времени:
ф = Г3общ = - Е nV’nV’	(2.41)
i
Таким образом, скорость, с которой область (0) расходует
свободную энергию, может быть определена путем исследова-
ния области (1). Для конкретной ферментативной системы,
рассмотренной выше,
ф = -и^>-№>	(2.42)
За скорость реакции v можно принять скорость исчезновения X
(в моль/с):
v =	=(l/v)z?V’	(2.43)
Основы равновесной и неравновесной термодинамики 25
Подставляя уравнение (2.43) в (2.42), получим
Ф = и(цх) — vpr*)	(2.44}
В этом уравнении величина цх — vpy, впервые введенная
Де Дондером, является примером функции состояния, назван-
ной сродством реакции. В более общем случае сродство опре-
деляется выражением
A = -Ev^	(2.45}
i
где vi — стехиометрический коэффициент i-ro компонента в ре-
акции, который берется с положительным знаком, если i-й ком-
понент является продуктом реакции, и с отрицательным знаком,,
если он расходуется как реагент. Поэтому уравнение (2.44)
удобно переписать в виде
Ф = vA	(2.46}
где А — сродство реакции (2.36) в области (1) (измеренное,,
например, в ккал/моль). Из уравнения (2.41) ясно, что если
одновременно протекает г различных независимых реакций, то
мы получим
Ф = и1А1 v2A2 + V3A3 + ... + vrAr (2.47}
Уравнение (2.47)—это характеристическая форма диссипатив-
ной функции для системы, в которой происходят только хими-
ческие реакции.
Мы определяли скорость данной реакции как v = hilvi для
случая, когда несущественно, что имеется в виду: реагент или
продукт. В неравновесной термодинамике принято следовать
системе обозначений Де Дондера (d£ — dn^/vi — dn2/v2 = ...),.
который называл £ мерой реакции, степенью полноты реакции
или координатой реакции. Ясно, что g увеличивается на единицу
всякий раз, когда прореагирует один эквивалент, и можно за-
писать u=j. Однако обычно в эксперименте скорость реакции,
определяется по скорости расходования или образования неко-
торого легко измеряемого, скажем /-го, компонента. Если мы
обозначим эту измеренную скорость реакции через ц(;), то, оче-
видно, и(/) = |V/1V. Так как скорость расходования свободной
энергии не зависит от выбора компонента реакции, то в этом
случае сродство должно выражаться в ккал/моль /-го компо-
нента. Таким образом, A(/) = А/1v, | и О(/)А(/) = vA независимо
от того, какой компонент / выбран.
Сродство связано с изменением свободной энергии Гиббса,
происходящим в системе в результате реакции. Из уравнений
(2.22) и (2.45) видно, что если в реакции, протекающей при
постоянных Т, р и ц, (т. е. в достаточно большом объеме, так
что химические потенциалы всех компонентов существенно не
24
ГЛАВА 2
изменяются), прореагировал один эквивалент, то изменение
свободной энергии Гиббса AG равно
— AG = А (Т, р, ц, — постоянные)	(2.48)
Эта зависимоость может быть выведена и в дифференциальной
форме. Из уравнений (2.20) и (2.45), используя данное выше
определение получим
-(dG/dl)T,p = A	(2.49)
2.	4. Диссипация энергии в векторных
необратимых процессах
Уравнение (2.47) учитывает только скорости и сродство хими-
ческих реакций, которые представляют собой скалярные про-
цессы, не связанные с каким-либо направлением в простран-
стве. Чаще мы будем иметь дело с векторными процессами,
так как окружающая среда не обязательно гомогенна и в си-
стеме могут возникать потоки. В этом случае система, как пра-
вило, представляет собой мембрану, разделяющую различные
области.
Мембранные процессы особенно благоприятны для приме-
нения неравновесной термодинамики, но, поскольку об этом
имеется несколько обширных публикаций [1, 3—5], мы огра-
ничимся кратким обзором. Для получения диссипативной функ-
ции рассмотрим устройство, показанное на рис. 2.3. Мембра-
на (0) встроена в соответствующую камеру и разделяет ее на
два отсека (1) и (2). Отсеки заполнены разбавленными вод-
ными растворами, содержащими единственное проникающее
растворенное вещество, которое может быть или не быть элек-
тролитом (концентрации его в двух отсеках могут различать-
ся). Кроме того, растворы могут содержать одно или более
Рис. 2.3. Система транспорта: необратимый процесс протекает в мембране (0),
которая установлена между отсеками (1) и (2). Область (3) ограничена
жесткими адиабатическими стенками.
Т — температура, р — давление, Др — разность гидростатических давлений по обе сто-
роны мембраны, Е— разность электрических потенциалов между обратимыми электро-
дами (см. текст), —поток i-ro компонента в указанном направлении.
Основы равновесной и неравновесной термодинамики 25
непроникающих веществ. Предполагается также эффективное
перемешивание. В отсеках установлены вертикальные трубки
с отверстием достаточно широким, чтобы поддерживать раз-
ность давлений Ар фактически постоянной в течение продол-
жительного периода времени. В отсеках также имеются элек-
троды, обратимые по одному из присутствующих ионов, напри-
мер электроды Ag/AgCl5. Так как ионы хлора в растворах на-
ходятся в равновесии с ионами на электродах, то эти электро-
ды рассматриваются как неотъемлемая часть отсеков.
Камера погружена в большую ванну с постоянной темпера-
турой воздуха (3), ограниченную адиабатическими стенками.
Ясно, что области (1) — (3) на рис. 2.3 соответствуют области
(1) на рис. 2.2, а мембрана — области (0). Проникающие ве-
щества могут двигаться между областью (1) и областью (2)
под влиянием градиентов концентрации и/или электродвижу-
щих сил; разность потенциалов между электродами по жела-
нию может быть установлена на любом заданном уровне. По
сравнению с обоими отсеками камеры мембрана является об-
ластью с малой вместимостью и быстро достигает стационар-
ного состояния при данных условиях. Далее можно рассуждать
так же, как при рассмотрении реакции (2.36). Но поскольку
в этом случае i-й компонент может иметь заряд, в уравнении
Гиббса необходимо учесть его электрохимический потенциал
Й/ = Ц/ + ztFlp	(2.50)
где Zt — заряд иона i-ro компонента, F — число Фарадея, ф—
электрический потенциал; а,Гф представляет собой электриче-
ский вклад в парциальную молярную свободную энергию. Од-
нако необходимо отметить, что приведенный ниже вывод явля-
ется общим и применим и к незаряженным компонентам, т. е.
при zt = 0. Имеем
dU(l) = Т dS(l) - р dV{x} + 2 й’1’ dn(i}
i
du(2}=т ds(2) - р dv{2) + z Й'2)^2)
dU™ = Т dS® — pd И3’	(2.51)
Здесь под dr№_, например, подразумевается общее изменение
концентрации ионов хлора в отсеке (2) как в растворе, так и
на электроде. Таким образом, видно, что изменения в составе
в областях (1) и (2), dn^ и dn®\ полностью отражают необ-
ратимый поток i-го компонента через мембрану. Складывая
уравнения (2.51) и учитывая, что сумма всех dU' и dV' равна
нулю, получим
TdSo6ax = — 2 й«- Z Й^>	(2.52)
i	i
26
ГЛАВА 2
Поток i-ro компонента (J<) через мембрану со стороны (1)
к (2) равен
=	=	(2.53)
и, следовательно,
ф = TS06^ = X h	(2-54)
i
где	— й^2> — разность электрохимических потенциалов
t-го компонента с двух сторон мембраны6. Отметим, что так же,
как в уравнении (2.47), диссипативная функция имеет форму
суммы произведений сил и потоков. В нашем случае проникаю-
щим компонентом является вода, и единственным растворен-
ным веществом может быть соль. Обозначая катион и анион
индексами 1 и 2 соответственно, а воду — w, получим
Ф = /даДцда + ЛДрч-1- /2АЙ2	(2.55)
2.	5. Диссипация свободной энергии в сопряженных
скалярных и векторных процессах
Выше мы рассмотрели скорость диссипации свободной энергии
отдельно в скалярных и векторных процессах. Однако в био-
логических системах скалярные и векторные процессы часто
сочетаются. Например, метаболизм субстратов влечет за собой
активный транспорт; с другой стороны, можно ожидать, что
транспорт влияет на скорость сопряженной метаболической
реакции. В таких сопряженных процессах свободная энергия,
которая в других случаях должна была бы рассеиваться, будет
в некоторой степени сохраняться. Таким образом, при актив-
ном транспорте химическая реакция, для которой vA больше
нуля, может совершать электроосмотическую работу путем
«переноса» i-ro компонента против его электрохимического гра-
диента. В этом случае /(Дщ- меньше нуля. Тогда скорость про-
изводства энтропии равна
Ф = ЛДц; + иД	(2.56)
Хотя, согласно второму закону, Ф > 0, мы видим, что Ф<иЛ.
Другими словами, часть химической свободной энергии, которая
могла бы рассеиваться в несопряженных реакциях, будет со-
храняться. В более общем случае для транспортного процесса,
рассмотренного в разд. 2.4, диссипативная функция принимает
вид
Ф == Jw АЦа, “Ь11ДЦ1 ~Ь J2 ДЙ2 И- ®А	(2.57)
Основы равновесной и неравновесной термодинамики 27
2.	6. Выводы
1.	Используя понятие обратимости и вводя определения функ-
ций внутренней энергии и энтропии, мы рассмотрели первый
и второй законы термодинамики для закрытых систем.
2.	На основе первого и второго законов внутренняя энергия
представлена как функция температуры, объема, давления и
энтропии. Полученное выражение интерпретировано как для
обратимых, так и для необратимых процессов, что привело
к определению энтальпии, свободной энергии Гельмгольца и
свободной энергии Гиббса, являющихся функциями тех же че-
тырех параметров. Приведено простое мнемоническое правило,
с помощью которого легко запомнить эти функции.
3.	Показано, что максимум полезной работы, которая мо-
жет быть получена в процессе при постоянных давлении и тем-
пературе, равен отрицательному изменению свободной энергии
Гиббса, причем это становится возможным только в предель-
ном случае гипотетического обратимого процесса.
4.	Рассмотренный термодинамический подход распростра-
нен на открытые системы, которые обмениваются веществом
с окружающей средой. Это требует введения понятия химиче-
ского потенциала компонентов и приводит к уравнению Гибб-
са— обобщенной форме первого и второго законов. Выведено
также уравнение Гиббса — Дюгема, т. е. соотношение между
одновременными изменениями интенсивных переменных.
5.	Показано, что изменение энтропии в системе, которая
не находится в равновесии со своим окружением, содержит два
вклада: «обменный» и «внутренний»; последний создается не-
обратимыми процессами и потому неизбежно положительный.
Предложен общий метод оценки скорости производства эн-
тропии.
6.	При рассмотрении систем, находящихся в стационарном
состоянии, основной функцией является диссипативная, соот-
ветствующая скорости рассеяния свободной энергии. Диссипа-
тивная функция выведена из уравнения Гиббса как для ска-
лярных, так и для векторных процессов. Эти процессы могут
быть объединены в одну систему. Во всех случаях диссипатив-
ная функция принимает форму суммы произведений термоди-
намических сил и потоков.
7.	Сродство, или движущая сила, химической реакции яв-
ляется функцией состояния, и эта функция представляет собой
логическое следствие всего рассмотренного ранее. Дано опре-
деление сродства химической реакции и четко установлена его
связь с изменением свободной энергии Гиббса.
Связь между потоками и силами:
уравнения Кедем —Канальского
В предыдущей главе было показано, что диссипативная функ-
ция для различных систем может быть выражена в виде сум-
мы произведений сопряженных потоков и сил (эти термины
использованы в общепринятом смысле). Таким образом, в об-
щем случае можно записать
ф = /1Х1 + /2Х2 + /3Хз+...	(3.1)
Здесь J — термодинамические потоки, такие, как скорости ре-
акций, скорости транспорта или мышечного сокращения и элек-
трический ток; X — термодинамические силы, такие, как срод-
ство реакций, разность электрохимических потенциалов и мы-
шечное напряжение, а также разность электрических потенциа-
лов, гидростатическое и осмотическое давление.
Диссипативная функция, выведенная из уравнения Гиббса
в предыдущей главе, дает очень важную информацию: число
степеней свободы системы. Каждый член соответствует одной
степени свободы.
Для экспериментальной работы данный набор сил и потоков
не всегда удобен. В таких случаях исходную диссипативную
•функцию можно преобразовать так, что она становится функ-
цией сил и потоков, которые легко фиксируются или измеря-
ются. Например, форма диссипативной функции, данная в урав-
нении (2.55), с экспериментальной точки зрения является бес-
полезной:
Ф = Jw Дцш + /, АЙ! + /2 Др2
Ни один из потоков или сил в этом уравнении нельзя измерить
непосредственно. Преобразования, приводящие к рабочим фор-
мам диссипативной функции для мембранных процессов, были
рассмотрены в классической серии статей Кедем и Качальского
[10, 13—17], а также Михаэли и Кедем [20] .
3.1.	Феноменологические уравнения
Хорошо известны несколько простых линейных зависимостей
между соответствующими потоками и силами, например закон
Ома для электрического тока, закон Фика для диффузии, за-
Связь между потоками и силами 29
кон Фурье для теплового потока и законы Пуазейля и Дарси
для потока жидкости. В каждом из этих случаев поток зада-
ется произведением коэффициента проводимости и силы. Од-
нако во многих других случаях приходится рассматривать мно-
жество взаимодействующих потоков. Например, транспорт иона
через биологическую мембрану может зависеть не только от
градиента его электрохимического потенциала, но также и от
потоков любых других присутствующих ионов и от потока рас-
творителя. Несмотря на сложность возможных взаимодействий,
зависимость между силами и потоками часто остается линей-
ной. Неравновесная термодинамика с успехом применяется для
таких линейных процессов в различных живых и неживых
системах. В этом приближении простая линейная зависимость
распространяется на все возможные взаимодействия.
Чтобы проиллюстрировать это, предположим, что имеется
система, которая приводит к трехчленной диссипативной функ-
ции, указывающей на наличие трех независимых процессов.
Удобным способом связи потоков и сил будут следующие фе-
номенологические уравнения, где потоки записываются как ли-
нейные функции сил:
Ji = LuXi + A12A"2 + Дз^з
J2 = Wi + L22X2 + L23X3
/3 = W. + ^-32-^2 + ^33-^3	(3-2)
Видно, что каждый поток Л связан со своей «сопряженной»
силой X, через «прямой» коэффициент Lu. Этот поток может
также зависеть от любой другой силы X; через коэффициент
взаимодействия или «перекрестный» коэффициент Ьц. Априори
можно ожидать, что линейная связь справедлива только для
относительно медленных процессов, близких к равновесию, в то
время как более быстрые процессы потребуют добавления чле-
нов более высокого порядка, создавая неудобные нелинейные
связи.
Можно было бы думать, что полезная на практике область
линейности будет слишком узкой. Однако критерий близости
к равновесию является эмпирическим, и для векторных про-
цессов линейность часто наблюдается в удивительно широком
диапазоне изменения величины силы. Для химических реакций
этот критерий обычно значительно жестче. Эта проблема будет
подробно обсуждаться в гл. 6.
Явные преимущества термодинамического метода говорят
сами за себя. На феноменологические коэффициенты любой си-
стемы независимо от числа степеней свободы накладываются
существенные ограничения, не позволяющие оперировать пол-
ностью произвольными величинами. Во-первых, согласно за-
кону Онзагера для системы потоков и сил, основанной на
30
ГЛАВА 3
соответствующей диссипативной функции, матрица коэффициен-
тов является симметричной, так что
Lti< = LJ{	(3.3)
Это позволяет значительно уменьшить число измеряемых ко-
эффициентов. Во-вторых, поскольку диссипативная функция не
может быть отрицательной, можно показать, что прямые ко-
эффициенты должны удовлетворять условию
Lu > 0	(3.4)
а перекрестные коэффициенты — условию
L2{i^LtiLn	(3.5)
В пределах этих ограничений коэффициенты изменяются в очень
широком диапазоне величин в соответствии со степенью связи
между процессами.
Часто бывает полезен альтернативный способ записи фено-
менологических уравнений с использованием коэффициентов
сопротивления вместо коэффициентов проводимости. Вслед-
ствие линейности уравнений (3.2) можно с равным успехом
записать
Х\ — Ruh +
%2= R21J 1 "Ь R22J2 4~ R23J3
Х3 = R31J1 + R3J2 4" ^зз/з	(3-6)
Термодинамические ограничения, которые накладываются на
этот набор коэффициентов, полностью аналогичны рассмотрен-
ным выше *, т. е.
Ru = Rii’ Ru>0, Ru^RuRii (3.7, 3.8,3.9)
Здесь следует проявить особую осторожность. К сожалению,
феноменологические коэффициенты нельзя рассматривать как
абсолютно постоянные величины при любых эксперименталь-
ных условиях независимо от способа, с помощью которого вы-
зываются потоки. Коэффициенты являются функциями пара-
метров состояния и могут быть более или менее чувствитель-
ными к изменению состояния системы. Однако они не являются
функциями сил или потоков, за исключением таких изменений
сил или потоков, которые косвенно могут вызвать изменение
в состоянии системы. Поэтому необходимо удостовериться, что
эксперименты проводились в диапазоне условий, при которых
коэффициенты остаются в достаточной мере постоянными. На-
пример, уравнения (3.2) и (3.6) оказываются не в состоянии
охарактеризовать ионный транспорт через синтетические мем-
Связь между потоками и силами 31
браны при больших градиентах концентрации, но могут очень
хорошо описывать потоки, вызванные эквивалентными электри-
ческими силами.
3.2.	Сопряжение между реакциями и потоками
Уравнения (3.2) и (3.6) носят общий характер. Подобные
уравнения можно записать для любого числа степеней свободы.
В зависимости от природы мембраны эти уравнения могут свя-
зывать потоки и силы векторного или скалярного характера
при условии, что J и X выводятся из соответствующей дисси-
пативной функции. Этот метод особенно результативен в при-
ложении к явлениям активного транспорта. Кедем [11] впервые
предложила способ, которым скалярную химическую реак-
цию можно связать с векторным потоком. Ее вывод основы-
вался в неявном виде на диссипативной функции уравнения
(2-57):
Ф — Jw Ан,,, + /1 Ag! + /г Айг -f- vA
где индексы w, 1 и 2 относятся к воде, катиону и аниону. Со-
ответствующие феноменологические уравнения, записанные че-
рез сопротивления, имеют вид
АЦд, Rww^w Н- Rwl^l Н“ Rw2^2
Api — R\WJW + /?ц/1 + RvJi + Rlrv
Арг = RiwJw Ч- W1 Ч- /?22^2 Ч- Rzrv
A^Rnh + R^ + RrrV	(3.10)
Причина выбора /^-описания вместо /.-описания состоит в том,
что, как будет показано в гл. 4, в системе, где взаимодействуют
несколько потоков, именно перекрестные /^-коэффициенты не-
посредственно отражают степень взаимодействия. Неравенство
нулю коэффициентов Rir и Rir в уравнениях (3.10) указывает
на сопряжение между ионными потоками и реакцией. При этом
предполагается, что прямая связь между потоками воды и ре-
акцией отсутствует. Кедем полагала, что транспорт i-го иона
является активным, если коэффициент Rir отличается от нуля.
Например, в определенных случаях электрический ток через
короткозамкнутую кожу лягушки, разделяющую идентичные
растворы, состоит почти полностью из потока ионов натрия.
Это наблюдение согласуется с тем фактом, что Rir = Rn = 0,
в то время как Rir не равен нулю. (Для выяснения этого во-
проса необходимо было бы определить величины Riw и Riw-)
Между коэффициентами Rir и другими коэффициентами в
уравнениях (3.10), включая Rrr, имеется существенное разли-
чие. Последние являются скалярными величинами. С другой
32
ГЛАВА 3
стороны, поскольку и v и А являются скалярами, в то время
как Др» и J, — векторы, коэффициенты Rtr и Rn должны иметь
векторный характер.
3.3.	Принцип Кюри — Пригожина
Каков смысл коэффициентов векторного сопряжения? Чтобы
понять это, мы должны задуматься над природой сопряжения
между потоками и силами, имеющими существенно различный
характер. Если реакция внутри мембраны сопряжена с пото-
ком, как в короткозамкнутой коже лягушки, упомянутой выше,
интуитивно кажется очевидным, что направление потока долж-
но определяться свойствами мембраны. Если бы мембрана
была полностью изотропна и гомогенна, т. е. если бы ее равно-
весные свойства были одинаковы во всех направлениях, тогда
нельзя было бы ожидать возникновения такого взаимодей-
ствия. Не ясна причина, по которой в такой мембране потреб-
ление метаболической энергии могло бы вызвать транспорт
ионов предпочтительно в каком-либо одном направлении. Эта
идея заключена в первоначально сформулированном принципе
Кюри, который на основе неравновесной термодинамики При-
гожина [22] и более поздних работ (см., например, [5, 7])
указывал, что сопряжение между скалярным и векторным по-
токами невозможно в изотропной среде в линейном режиме.
Однако в анизотропной среде такое сопряжение не запрещено.
Коэффициент сопряжения неизбежно должен отражать анизо-
тропию среды и, следовательно, сам должен быть векторным.
Принцип Кюри — Пригожина был первоначально предложен
при рассмотрении симметрии причинно-следственных связей в
кристаллографических системах [4]. Интерпретация этого
принципа на основе неравновесной термодинамики сопровож-
далась некоторыми осложнениями, поскольку, как отмечали
Финлайсон и Скривен, не всегда полностью учитывались те ра-
дикальные ограничения изотропии и линейности, которые ста-
вили под сомнение возможность скалярно-векторного взаимо-
действия. В этой книге исследование транспортных и других
процессов будет ограничено главным образом линейным режи-
мом, и, следовательно, необходимо рассмотреть только понятия
изотропии и анизотропии среды. Использованное здесь понятие
изотропии относится к локальным свойствам, другими словами,
к свойствам микроскопических элементов среды, достаточно
больших, чтобы быть связанными с термодинамическими пара-
метрами. Если элементы системы анизотропны, то в принципе
возможно локальное скалярно-векторное сопряжение. Так, дав-
ление может вызывать электрическую поляризацию в пьезо-
электрических кристаллах, а гидролиз АТФ — транспорт натрия
Связь между потоками и силами____________________________??
в клеточной мембране. Известно, что анизотропия —характер-
ная черта обеих систем. Однако важно также рассмотреть сре-
ду, которая является локально-изотропной, но пространственно
неоднородной [6]. Например, в мембране может быть несим-
метричное распределение связанного фермента. Разумно ожи-
дать, что такое неоднородное распределение транспортных
и/или реакционных параметров — непрерывное или прерыви-
стое— может влиять на общее поведение мембраны, и можно
показать, что «асимметрия» такого рода приводит к специфи-
ческим проявлениям скалярно-векторного сопряжения даже в
локально-изотропных системах. Коэффициенты сопряжения в
этом случае всегда скорее связаны с системой в целом, чем
с ее локальными элементами. Такая связь возникает в усло-
виях, приводящих к сопряжению в «стационарном состоянии»,
и будет обсуждаться в разд. 3.5.
3.4.	Стационарные состояния с минимальным
производством энтропии
Теперь рассмотрим некоторые важные и типичные свойства
стационарного состояния. Что произойдет, если изменится число
ограничений, накладываемых на систему в стационарном со-
стоянии? Например, возьмем систему, описываемую уравне-
ниями (3.10). Если накладывается максимальное число огра-
ничений, скажем все четыре силы фиксированы, то стационар-
ное состояние полностью определено, так как больше не оста-
лось степеней свободы. Если ограничения вовсе отсутствуют,
то все силы будут стремиться к уменьшению до тех пор, пока
система в конце концов не достигнет равновесия. Однако чаще
всего мы налагаем промежуточное число ограничений. В таких
случаях, как было показано Пригожиным, производство энтро-
пии в линейных системах с симметрией Онзагера постепенно
достигает минимума, совместимого с наложенными ограниче-
ниями (см., например, [23]). Таким образом, если несколько
сил фиксировано, то оставшиеся силы в стационарном состоя-
нии будут достигать таких величин, чтобы связанные с ними
потоки обращались в нуль.
3.5.	Стационарное сопряжение
в определенных обстоятельствах стационарные состояния мо-
гут приводить к особому типу взаимодействия между процес-
сами, протекающими в системе в целом. Это взаимодействие
названо Пригожиным стационарным сопряжением. Характерно,
что такое взаимодействие проявляет себя как сопряжение
3 Кеплен, Эссвг
34
ГЛАВА 3
между химической реакцией и диффузионным потоком. Оно
является прямым следствием условия стационарности, которое
создает взаимные линейные зависимости для некоторых из по-
токов, что приводит к сокращению числа членов в выражении
диссипативной функции. Ряд впечатляющих примеров подоб-
ного рода описан Хироном [8] для биологических процессов.
Для одного простого случая, который может интерпретиро-
ваться как модель живой клетки, Пригожин [23] проанализи-
ровал зависимости между феноменологическими уравнениями
о.
\ Рис. 3.1. Система, иллюстрирующая
м I M-*N ) возникновение стационарного нерав-
\ s 1 новесного распределения вещества.
и показал, что в этом случае возможно возникновение стацио-
нарного неравновесного распределения вещества, определяе-
мого скоростью метаболической реакции в клетке. Это воз-
можно в открытой системе, такой, как область (0) на рис. 2.2.
Предположим, что незаряженные компоненты М и О до-
бавляются во внеклеточную среду. М движется в клетку, где
превращается в N; некоторая часть последнего вытекает из
клетки, как показано на рис. 3.1. Превращение осуществляется
благодаря активности внутриклеточного фермента. Компо-
нент О не участвует ни в какой химической реакции, однако
его поток за счет вязкости взаимодействует с потоком М. Ни
поток М, ни поток О не взаимодействуют с потоком N. Через
некоторое время определенное количество М войдет в клетку,
перенося с собой О, и некоторое количество N появится во
внешнем растворе. Общее феноменологическое описание этой
системы в линейном приближении имеет вид
Дцм = RmJm.	+ RmoJo
Ацы =
Ацо = /?мо/м	-}-RoJo
Ata =	Rrv	(3.11)
Здесь J — потоки, направленные внутрь клетки, Ац( =	—
—р1” и Ain — сродство реакции внутри клетки. Приведенные
выше уравнения даны, чтобы проиллюстрировать сопряжение
между определенными потоками и отсутствие его между дру-
гими. В частности, метаболическая реакция в клетке не свя-
зана ни с одним из потоков. Через некоторое время система
достигает состояния, в котором концентрации Ми N, но не
Связь между потоками и силами 35
обязательно О становятся постоянными. В этом стационарном
состоянии
u = JM = -jN	(3.12)
В таких условиях поток О оказывается эффективно сопряжен-
ным с метаболической реакцией, оцениваемой во внешней сре-
де. Это видно из следующего. Если мы обозначим через Лех
сродство реакции, измеренное извне (где, конечно, отсутствует
необходимый фермент), то получим
лех _ АШ = (цех _ цвх) _ (цт _ ц”) = Дцм _ A|Xn (3.13)
Подстановка уравнения (3.12) в (3.11) дает
Ацм = Rmv + /?мо/о> Ацы = — /?№
Ацо = Rmov + /?о/о, Л1П = Rrv	(3.14)
Комбинируя уравнения (3.13) и (3.14), в конечном счете по-
лучим
Apo = Rmo® + RoJo
Лех = (Rr + /?м Rn) v -|- /?мо/о	(3.15)
Уравнения (3.15) можно записать проще:
Apo — RoJo + RmoU, Аех = RmoJo + RrV (3.16)
где Rn = Rr + Rm + Так как накладывается единственное
ограничение — фиксирование величины Дех, то в конце концов
система достигнет состояния, в котором Jo — 0. В этом состоя-
нии происходит накопление О внутри клетки:
Ацо — Rmo® — (Rmo/Rr) Аех	(3.17)
Уменьшение числа феноменологических уравнений, необхо-
димых для функционального описания системы, рассмотренной
выше, сопровождается сокращением диссипативной функции.
Уравнения (3.11) получены стандартным методом с учетом того,
что клеточная мембрана находится в стационарном состоянии,
так как она имеет гораздо меньший объем, чем внутренняя и
внешняя среда .Эти уравнения соответствуют следующей дис-
сипативной функции:
Ф = /м Ацм + /n Ajin + Jo Apo + vA1П (3.18
Состояние стационарности для клетки в целом, описываемое
уравнением (3.12), непосредственно ведет к сокращению дис-
сипативной функции, соответствующей уравнениям (3.16):
Ф = Jo Ацо + и А**	(3.19)
^3°12)ВИДН(3 3) ком^инации УРавнения (3.18) с уравнениями
3*
36
ГЛАВА 3
В упомянутом выше примере стационарное сопряжение воз-
никает между потоком компонента О и реакцией. В сущности,
это система, состоящая из двух камер, одна из которых недо-
ступна (иначе, чем через мембрану) и содержит фермент. В све-
те того, что обсуждалось в разд. 3.3, эта система фактически
является несимметричной. Из этого следует, что для возникно-
вения стационарного сопряжения между реакцией и потоком
не обязательно существование анизотропии, пока сохраняется
несимметричное распределение изотропных элементов.
Активный транспорт в таких клетках, как мышцы или эри-
троциты, в действительности не связан с механизмом, рассмот-
ренным выше в рамках модели Хирона — Пригожина. Обычно
считается, что сопряжение является свойством самой мембра-
ны, связанным с ферментами, которые составляют ее неотъем-
лемую часть. В случае такой мембраны, как кожа лягушки,
где обе стороны эпителия легко доступны, метаболическая ре-
акция протекает, несомненно, внутри мембраны. Простая мо-
дель такой системы, основанная на стационарном сопряжении,
исследовалась экспериментально и теоретически Блюмента-
лем, Кепленом и Кедем [1]. Эта модель состоит из последова-
тельной комбинации двух мембран, одна из которых обладает
катионообменными, а другая — анионообменными свойствами,
с заключенным между ними тонким слоем водного раствора
фермента. Эта система при наличии снаружи соответствую-
щего субстрата способна создавать электрический ток между
двумя идентичными растворами. В стационарном состоянии ее
диссипативная функция имеет сокращенную форму
Ф = IE +	(3.20)
где / и Е — электрический ток и разность потенциалов соответ-
ственно. Подробно эта модель будет обсуждаться в разд. 3.9.
3.6.	Преобразования диссипативной функции
Важное преобразование, которое оказалось особенно полезным
в случае разбавленных растворов, выражает Ф через объем-
ный поток, потоки соли и электрического тока, а также через
соответствующие силы. Эта форма диссипативной функции по-
лучена следующим образом. Если молекула рассматриваемой
соли диссоциирует на vi катионов с зарядом z\ и v2 анионов
с зарядом Z2, то условие электронейтральности дает
ViZi + v2z2 = 0	(3.21)
Термодинамические свойства соли связаны со свойствами со-
ставляющих ее ионов соотношением
Hs = 'viHi + v2p.2 или = v( Aftj + v2 Дц2 (3.22)
Связь между потоками я силами 37
Электродвижущая сила, действующая в системе, определяется
путем измерения разности электрических потенциалов Е между
двумя электродами, помещенными соответственно в два рас-
твора. Если эти электроды обратимы по аниону, как в случае
электродов Ag/AgCl, то
Е —	(3.23)
Необходимо отметить, что электродвижущая сила Е, измерен-
ная с помощью таких обратимых электродов, отличается от
разности потенциалов Дф, которая могла бы быть измерена
с помощью стандартных электродов, таких, как каломельный
электрод с солевым мостиком. Учитывая основное определение
[уравнение (2.50)], получим
Д-ф = f — Ap“/z2F	(3.24)
где Дц^—зависящая от концентрации часть ДЦг (зависящей
от давления частью Др2, которая обычно мала, пренебрегаем).
Зависимость между плотностью электрического тока и пото-
ками ионов через единицу площади определяется выражением
I = (zYh + z^F	(3.25)
[Нужно отметить, что при наличии тока правильное примене-
ние уравнения (3.23) требует измерения Е с помощью отдель-
ной пары обратимых измерительных электродов.] В рассматри-
ваемом случае перенос соли из раствора (1) в раствор (2)
(см. рис. 2.3) можно определить по потоку катионов через
мембрану (/]):
Л = уЛ	(3.26)
В общем случае поток соли не может быть связан с Jz (по-
током анионов через мембрану), так как при 1=^=0 часть
анионов, входящих в раствор, извлекается из токовых электро-
дов. Отсюда следует, что, в то время как /i, Jz, Jw и / пред-
ставляют собой действительные потоки через мембрану, Js
должен рассматриваться как кажущийся перенос соли, кото-
рый может включать компонент, обусловленный приэлектрод-
ными процессами [12,26]. Путем комбинации уравнений (3.21),
(3.25) и (3.26) для потока анионов получим
Jz^VzJs + 1/ZzF	(3.27)
Подставляя в уравнение (2.55) величины /1 из уравнения (3.26),
А из (3.27) и Ар2 из уравнения (3.23), с учетом уравнения
(3.22) получаем
Ф = Jw Ара, + Js Дцз + IE	(3.28)
Достоинством этого выражения, впервые выведенного Михаэли
и Кедем [20], является тот факт, что в него входят легко
38
ГЛАВА 3
измеряемые электрические величины, однако первые два члена
все еще остаются неудобными для использования. Более удобное
выражение диссипативной функции получается при подстановке
соответствующих выражений для Дцш и Др5:
Дрш = Vw Др — Дл) = Vw Др — Дл, — Дл,5)	(3.29)
Др,8 = Др.«+ VsNp	(3.30)
где и Vs — парциальные молярные объемы воды и соли
соответственно; Др = р(1) — р<2> — разность гидростатических
давлений с двух сторон мембраны; Дл,— разность осмотиче-
ских давлений, обусловленная проницаемостью растворенного
вещества (здесь соли); Дл,— разность осмотических давлений
за счет любых присутствующих непроникающих растворенных
веществ; Дц£ — часть разности химических потенциалов соли,
зависящая от концентрации. Удобно выразить Дц£ через Аля
и «среднюю» концентрацию соли, определяемую как2
cs = Дл5/Др* = kxs/RT Д In as	(3.31)
где а—активность. Подставляя уравнения (3.29)—(3.31) в
(3.28), получим
Ф = JWVW Др - Дл) + JSVS Др + Js (Aas/cs) + IE (3.32)
Необходимость экспериментально трудоемкого измерения Jw
исключается благодаря введению выражения для объема, свя-
занного с переносом воды и соли между двумя растворами:
Jv = JwVw + JsVs	(3.33)
Заслуживает внимания то обстоятельство, что в общем случае
/0, подобно Js, не является скоростью потока вещества через
мембрану. Скорее это тоже кажущийся поток, так как в усло-
виях прохождения тока Jv содержит вклад, обусловленный
электродными процессами, такой же, как в случае Js [12,26].
Экспериментально J-j оценивается путем измерения изменения
объема одного или обоих отсеков камеры, разделенных мем-
браной. Хотя это измерение не отражает приэлектродного про-
цесса, на практике возникающая ошибка обычно незначитель-
на. Особый случай, требующий коррекции этого «наблюдаемого
объемного потока», будет рассмотрен в разд. 3.8. Обозначая
объем растворенного вещества через <j>s = csVs и комбинируя
уравнения (3.32) и (3.33), получим
Ф = J, Др - Дл) + Is Ля*(1	+ {Е (3.34)
Cs
Наконец, растворы, используемые в экспериментальных иссле-
дованиях, обычно являются достаточно разбавленными, так что
Связь между потоками и силами 39
^sAn/Ans С 1, поэтому
Ф = (Др — Дл) + Js^s/cs + IE =Jv(kp — Дл) + Js Ац‘ + IE
(3.35)
Диссипативная функция уравнения (3.35) положена в осно-
ву обширных исследований составных мембран, проведенных
Кедем и Канальским [16,17]. Эта диссипативная функция,
естественно, приводит к удобному набору феноменологических
уравнений. В линейном приближении для потоков можно запи-
сать следующие уравнения (в L-форме):
70 = Ан (Др — Дл) + Л12 (kns/cs) + Ll3E
Is=== -^21 (Др	Д’») “1“ 7.22 №s/cs) -J- L23E
I = L3X (kp — Дл) + 7.32 (Дл^/Cs) + L33E (3.36)
Так как уравнение (3.35) является соответствующим образом
выведенной диссипативной функцией, состоящей из суммы про-
изведений сопряженных потоков и сил, то, по закону Онзагера,
матрица феноменологических уравнений (3.36) симметрична,
т. е.
=	(3.37)
Если требуется выразить силы как функции потоков, то мы
получим
Др — Дл = 7?ц70 + /?1гЛ + Rl3I
kns/cs = /?217 о + RilE + Т?23/
E = RuJv + R32Js + R33I	(3.38)
где матрица /^-коэффициентов является обратной /.-матрице,
и снова
Ril = Rii	(3.39)
Уравнения (3.36) — (3.39) применимы к целому ряду клас-
сических исследований электрокинетических явлений, так как
они обеспечивают последовательный формализм для описания
сопряженных процессов и, естественно, приводят к целому ряду
симметричных зависимостей, которые уже давно наблюдались
экспериментально. Сами по себе эти уравнения дают убеди-
тельное доказательство эффективности методов неравновесной
термодинамики. Легче всего это оценить при исследовании си-
стем с одинаковыми растворами по обе стороны мембраны,
когда Дл = Ans = 0. Такая система имеет только две степени
свободы. В этом случае
Ф = 1окр + 1Е	(3.40)
и соответствующие феноменологические уравнения (в 7,-фор-
ме) приобретают вид
Л — Lu кр + Ll2E, I = L12kp + LnE (3.41)
40
ГЛАВА 3
В эти уравнения включено соотношение симметрии Онзагера
L12 = L21> поскольку Lis = L3i в уравнении (3.36). Феноменоло-
гические уравнения (3.41) охватывают всю классическую элек-
трокинетику. Например, ясно, что величина электроосмотиче-
ского объемного потока на единицу потенциала при нулевой
разности давлений (/0/£’)др=о и величина тока на единицу раз-
ности давлений при коротком замыкании (//Ар)в=о должны
быть тождественны. Подобным же образом можно легко выве-
сти хорошо известные уравнения Саксена, связывающие отно-
шения сил и отношения потоков [9,21]:
(/o//)ap-0=-(W)/=0	(3.42)
(/0//)£=o=-(W)/0=o	(3.43)
Различные классические модели электрокинетики, развитые
Гельмгольцем, Смолуховским и другими, предсказывают все
эти соотношения, но они не приложимы ко всем типам рас-
смотренных систем [13, 14]. Мазур и Овербек [19] впервые
показали, что независимо от специфических особенностей ка-
кой-либо данной модели наблюдаемые разнообразные симмет-
ричные зависимости в самой общей форме вытекают из линей-
ных феноменологических уравнений неравновесной термодина-
мики. Таким образом, любые линейные модели, которые не
предсказывают этих связей, вероятно, не могут быть правиль-
ными.
Часто полезно рассмотреть системы без электродов. В та-
ких случаях, конечно, не может течь ток, и диссипативная
функция уравнения (3.35) сокращается до
Ф = Jo (Ьр ~ Ал) + Js bns/cs	(3.44)
Это выражение указывает на зависимость между объемным
потоком и потоком соли. Иногда нас интересуют процессы,
в которых объемный поток связан со значительным выделением
соли из воды. В этом случае полезно переписать диссипативную
функцию в форме, которая учитывает это выделение в явном
виде. При рассмотрении растворов, в которых Ал, <С Ал, так
что /0Ал =: 70Ans, подстановка уравнения (3.33) дает
Ф == 7р Ар Гц, Ал5 (/sis) (1 c*Vs) Ал5
Для достаточно разбавленных растворов (csTs <С ~ 1)
приближенно получим
Ф = 70 Ар + (Js/cs — JJcw) \as = Jv\p + JD Ал	(3.45)
Выражение в скобках, которое представляет собой скорость
диффузии соли относительно воды, названо диффузионным по-
током. Ясно, что диссипативная функция, выраженная уравне-
Связь между потоками и силами 41
нием (3.45), дает естественную основу для анализа систем,
в которых механическая энергия, полученная из объемного
потока по градиенту гидростатического давления, используется
для выделения соли из воды, несмотря на отрицательный гра-
диент концентраций [2].
3.7.	Преобразование феноменологических уравнений:
практические феноменологические коэффициенты
Возвращаясь теперь к более общему обсуждению уравнений
(3.36) — (3.39), мы видим, что каждое описание системы с тре-
мя степенями свободы характеризуется шестью независимыми
феноменологическими коэффициентами. Для их эксперименталь-
ного нахождения надо наложить такие ограничения, чтобы
данный поток или сила стали функцией соответствующей не-
зависимой переменной. В случае L-описания легче всего было
бы оценить коэффициенты, если бы оказалось возможным кон-
тролировать две силы, например
L = Г 1
12 L ДЛз/Сз ]дР-Дл = 0, Е=0
ИЛИ
L,2 = r_ a/°  1	(3.46)
12	L<? (kns/cs) Лдр-дл, е	v '
в то время как для /^-коэффициентов было бы желательно
контролировать два потока. Часто, однако, в эксперименте до-
статочно сложно контролировать одновременно две силы или
два потока, ибо для теоретического расчета необходим другой
подход. В таком случае полезно рассмотреть другие выраже-
ния, которые могут быть получены путем преобразования ос-
новных феноменологических уравнений без изменения дисси-
пативной функции. Коэффициенты этих модифицированных
уравнений будут комбинацией исходных Ьц (или /?,/)-коэффи-
циентов. В качестве примера таких «практических транспорт-
ных коэффициентов» мы подробно рассмотрим систему I Кедем
и Качальского.
Начнем с диссипативной функции по уравнению (3.35) и
рассмотрим соответствующий набор феноменологических урав-
нений (3.38), выражающих силы как функции потоков. Ясно,
что для практических целей желательно использовать соотно-
шения, в которых независимые переменные легко контролиру-
ются в эксперименте. Одним из удобных наборов независимых
переменных являются /0, &ns/cs и I. Поэтому мы преобразуем
уравнения (3.38) таким образом, чтобы Sns/cs стало неза-
висимой переменной, a Js — зависимой. Соответствующие
42
ГЛАВА 3
алгебраические преобразования приводят к уравнениям
*_ a™ RiiRm— Л12^?21 г г Riz Ал$ . RiiR13— R12R23 Г
—д,+——+———/
г    Rii т ।	1	_ R23 j
Js~	R22 °‘r/?22 CS R22‘
r? R22R3I — R21R32 r I R32 Alts . R22R33 — R32R23 r (1 Л1\
Ez=z--------J- + -R^~ +-----------1 (3-47)
Поскольку независимые переменные включают теперь как
силы, так и потоки, набор полученных феноменологических ко-
эффициентов не является более симметричным. Однако в этом
случае потеря симметрии затрагивает только знаки.
Ясно, что сложные коэффициенты уравнений (3.47) слиш-
ком громоздки для обычного использования. Поэтому полезно
заменить их выражениями, включающими так называемые
практические транспортные коэффициенты, которые могут-быть
измерены экспериментально при условии, что две из трех не-
зависимых переменных Jv, hns/cs или I устанавливаются рав-
ными нулю. (Другая возможность состоит в определении транс-
портных коэффициентов дифференциальным методом [20], при
этом параметры, подвергающиеся ограничению, поддержива-
ются на постоянном уровне, а не на нуле.) Набор коэффициен-
тов, представленных в табл. 3.1, может быть непосредственно
отождествлен с шестью коэффициентами уравнений (3.47)3.
Оставшиеся три коэффициента могут быть просто рассчитаны,
учитывая, что исходные коэффициенты подчиняются закону
симметрии Онзагера, так что
/ЛХ =_р£.-А?_Х	=сД1_(г)
I \ &ns/cs Jjv,I s v 7
— ( —-—)	= — (A')	= _
\^ns/cs;jv, I k I Jiv,^s V1Z1F
(A)	( Ар - Ал \	- p
\/o/Ans, 7 \ I J/O,±ns	Lp
(3.48)
(3.49)
(3.50)
Используя эти выражения, уравнения (3.47) можно переписать
в виде
Др - Д„ _ (,, _ с, (1 _ а) - (А.) !
£4AA)v<)'	<3.51)
Такой выбор коэффициентов определяется, в частности, тем
эмпирическим фактом, что некоторые величины весьма слабо
Связь между потоками и силами
43
Таблица 3.1. Два набора практических транспортных коэффициентов3
Транспортные коэффициенты	Набор I	или / пренебрежимо малы)^	Набор II (Др—Дл, Для или I пренебрежимо малы)^
Прямые		
коэффициент		L ( Iv \
фильтрации	р у Др-Дл^д^у	Р \^P-^nKns,I
проницаемость	<0 = (7$/ДЛ$)у у	= s/&ns)bp-fat, I
растворенного вещества		
электрическая проводимость	X —	Ans	x ~ (J/Е)bp-fat, bns
Перекрестные		cs (1 — o) = (1 si1 v)fats, I
коэффициент отражения	cs (1 — <т) = 		( Кр — Дл \ \ Ajts/c5 / г г нлн /Др — Дл. \ \ Дл$	) j у J V* 1	
элекгроосмо-	/Др—Дл\	= Е V Е ),.	Электроосмотическая проиицае-
тнческое дав-		мость
ление	— — (Д^о)длг Е (ток течения)	P = (Jv/I)bp—дл, Дл5 = = -(—E— ) k Др-ДлУд^у (потенциал течения)
число переио-	д^ =	< = v121F(Zs//)Ap_AjtAjts =
са		
	= - viZiF (д-4-) \&Jts/CsJ j j JV* 1 (мембранный потенциал)	= - viZiF (	£	) k Kns/cs J fa>-fat, i (мембранный потенциал)
а По Кедем и Качальскому [15]. б Нижние индексы показывают потоки или силы,
поддерживаемые равными нулю.
зависят от концентрации. Для некоторых целей удобно пере-
писать уравнения (3.51) как уравнения потоков в форме, пред-
ложенной Кедем и Канальским:
/0 = Lp (\р —	— oLp \ns + р/
Js = cs (1 — <r) Jv + to Ans +	I
/ = x (P/Z.p) /„ + x	Др* + кЕ (Ар.3 = Ans/cs) (3.52)
44
ГЛАВА 3
Показано, что уравнения (3.51) и (3.52) полезны при рассмот-
рении составных мембран, состоящих из последовательного
ряда элементов [17].
Преобразования, полностью аналогичные рассмотренным
выше, приводят к альтернативным выражениям, которые мож-
но легко применить в случае, когда переменные, подвергаю-
щиеся ограничению, выбираются из набора Др — Дл, Дл$ или I
(набор II Кедем и Качальского, табл. 3.1):
Jo = Lp (\р — Дл) + cs (1 — a) Lp (bns/cs) +
Js = cs (1 — о) lp (ДР — Ал) + cs®' (Ms/Cs) + (t'/viZiF) 1
E = — ₽ (Др — Дл) —	(bnjcj + (1/x') I (3.53)
Снова переписывая их в форме уравнений потоков, получим
/0 — Ер (\р Ал;) tsLp Дл5 -]-
Js = csLp (1 — о) (Др — Дл) + со' Дл5 + (t'/vjZjF) I
I = х'р (Др — Дл) + х' (т'/v^F) ДрС + х'Е (3.54)
В отличие от практических коэффициентов набора I коэффи-
циенты набора II удобны при рассмотрении составных мем-
бран с параллельным расположением элементов [16,27].
Как уже отмечалось, практические феноменологические ко-
эффициенты в уравнениях (3.51) и (3.52) были выбраны на
основании наблюдений, хорошо известных задолго до появле-
ния неравновесной термодинамики. Однако применение их в
комплексе и самосогласованное рассмотрение обеспечивают
надежную основу для анализа и сопоставления бесчисленных
экспериментальных данных и приводят к важным предсказа-
ниям для самых различных систем. Ясно, что точная характе-
ристика системы требует знания числа ее степеней свободы и
применения соответствующих ограничений, так чтобы поток
или сила, представляющие интерес, стали функцией единствен-
ной независимой переменной. В принципе в таком случае ока-
зывается возможным оценить все феноменологические коэф-
фициенты. Хотя иногда это может оказаться невыполнимым,
но даже в таких случаях можно установить, какие коэффици-
енты уже известны и какие еще осталось определить. К сожа-
лению, во многих исследованиях в биологической литературе
пытаются описывать поведение системы на основе неполных
уравнений, не учитывающих всех степеней свободы. В таких
случаях экспериментальные наблюдения не могут точно опре-
делить внутренние характеристики системы, поскольку они не-
избежно будут зависеть также от конкретных условий прове-
дения эксперимента, в частности от величины неконтролируемой
независимой переменной. Следовательно, наблюдения, сделан-
ные при различных условиях, могут приводить к кажущимся
Связь между потоками и силами 45
противоречиям. Например, если мы рассмотрим способ опре-
деления коэффициента проницаемости путем измерения потока
растворенного вещества, вызванного различием в его концен-
трации по обе стороны мембраны, уравнения (3.52) и (3.54)
покажут, что в общем случае нельзя ожидать равенства и =
= (Js/\ns)jvi и со' = (Js/Ans)Др_Дя>;. Более того, легко видеть, что
o/ = co + es(l-<т)2Ар	(3.55)
Таким образом, эти формулы служат не только для установле-
ния подходящих условий с целью точного определения основ-
ных параметров, но также для демонстрации разумной связи
между ними. Это можно оценить на примере коэффициента
отражения о, впервые введенного Ставерманом [24] для объ-
яснения расхождения между теоретическими и эксперименталь-
но измеренными величинами осмотического давления. Общее
представление о смысле коэффициента отражения можно по-
лучить при использовании какого-либо из уравнений (3.52) —
(3.54) для различных условий эксперимента. Простой пример,
когда проникающее растворенное вещество — неэлектролит,
рассмотрен Ставерманом. В этом случае отсутствует электри-
ческий ток или электродвижущая сила, и уравнения (3.52)
сводятся к виду
J0 = Lp(\p-\ni)-cLp^s	(3.56)
Л = М1 ~ о)/0 + соДл5	(3.57)
Эти уравнения аналогичны соответственно уравнениям (39) и
(41) Кедем — Качальского [13] для разбавленных растворов.
Ясно, что величина о должна зависеть как от растворенного
вещества, так и от изучаемой мембраны. Рассматривая урав-
нения (3.57) для объемного потока без градиента концентра-
ции проникающего вещества (Ans = 0), мы видим, что вели-
чина 1—о представляет собой прямой критерий степени со-
пряжения между потоком растворенного вещества и объем-
ным потоком: 1 — а = (l/cs) (Js/Ja)bas, ;=о- Если мембрана пол-
ностью неселективна (Js/Jv = cs), то о = 0; если же мембрана
обладает идеальной избирательностью, т. е. проницаема только
для растворителя, то а=1. В большинстве случаев а нахо-
дится между 0 и 1, но может лежать и вне этого интервала
(см., например, [25]).
Уравнение (3.56) показывает, что растворенное вещество
может влиять на объемный поток лишь в той степени, в кото-
рой его коэффициент отражения отличается от нуля. Это урав-
нение позволяет также исключить ошибки в оценке осмотиче-
ского давления при использовании мембранных методов. Если
раствор уравновешен с чистой водой через идеальную полупро-
водящую мембрану, то разность гидростатических давлений,
46
ГЛАВА 3
возникающая при равновесии, точно равна осмотическому дав-
лению. Поскольку мембраны, которые полностью непроницае-
мы для малых молекул растворенного вещества, требуют не-
осуществимо длительных периодов времени для установления
равновесия, растворы таких веществ часто исследовались с по-
мощью слабопроницаемых «быстрых» мембран. При таком
подходе осмотическое давление оценивалось методом экстрапо-
ляции экспериментальных величин Др к нулевому моменту вре-
мени в предположении, что это устраняет влияние утечки рас-
творенного вещества. Ставерман ясно показал, что на самом
деле это не так. Утечка растворенного вещества влияет на гра-
диенты давления в стационарном состоянии сильнее, чем эф-
фекты, приписываемые изменению концентрации соли: «в пер-
вый момент мембрана ведет себя, как если бы в растворе при-
сутствовало не tit молекул, а только о,пг» [24]. Это хорошо
видно из уравнения (3.56). При отсутствии проникающего ве-
щества (Дл5 = 0) (Др)/о=о = Длг. Другими словами, разность
гидростатических давлений при равновесии равна разности
осмотических давлений, тогда как в присутствии проникающего
вещества (Дл, = 0) (Др)/о=0 = <тДл3.
3.8.	Определение объемного потока в трактовке
Кедем — Канальского
Как уже отмечалось, в то время как величины Jw, J\ и /2 пред-
ставляют собой истинные потоки вещества через мембрану, ве-
личины Js и /0, согласно уравнениям (3.26) и (3.33), представ-
ляют собой кажущиеся потоки, так как в присутствии тока они
будут включать вклад электродных процессов [12,26]. Точное
вычисление практических коэффициентов набора I Кедем —
Качальского требует правильного измерения или контроля Jv,
но на практике эта величина обычно аппроксимируется наблю-
даемой скоростью изменения объема в любом из отсеков
(“7”абл“)_ Если пренебречь эффектами второго порядка, обус-
ловленными изменениями парциальных молярных объемов
анионов, когда они входят или выходят из электродов, то оче-
видно, что /»абл представляет собой действительную скорость
переноса объема через мембрану и поэтому равно
/”абл = j.Vj + j2V2 + JWVW	(3.58)
Если парциальные молярные объемы ионов рассматриваются
как аддитивные:
ys = V1yl + v2y2	(3.59)
Связь между потоками и силами
47
то, учитывая уравнения (3.21), (3.25), (3.26), (3.33) и (3.58),
получим связь между Jo и 7“абл;
у0 = у«абл-У2//г2Г	(3.60)
В случае токовых электродов Ag/AgCl
у0 = у“абл+1,61 • 10“4Z	(3.61)
где Jv выражается в см/с и I — в А/см2. Хотя часто этот по-
правочный член не будет иметь практического значения, в прин-
ципе он может быть значимым. Одно из возможных следствий
использования У“абл вместо 70— расхождение между величи-
нами практических феноменологических коэффициентов, полу-
ченных различными экспериментальными методами. Например,
величины электроосмотической проницаемости р, полученные
из измерения — [£/(Ар — Ал)] , могут заметно отличаться
I
от величин, найденных при измерениях потока, так как
/ j ч	/ >набл ч
Р = 1-г)	=(-v-j— )	+ 1,61 • 10-4 (3.62)
' 1 ' Ар-Дл, Ац£	V 1 /Ар-Ал, Дц®
Для ионообменных мембран рыхлой структуры, которые обыч-
но имеют высокие значения р, поправка может оказаться
весьма незначительной, но в плотных мембранах она может
быть существенной.
Коррекция практически важна при исследовании зарядово-
мозаичных мембран, содержащих анионо- и катионообменные
области. Для таких мембран значение р может быть очень
мало, так как электроосмотические потоки через соседние об-
ласти имеют противоположные направления и стремятся ком-
пенсировать друг друга. В табл. 3.2 сравниваются рассчитанные
Таблица 3.2. Различие между рассчитанными и истинными величинами
электроосмотической проницаемости в аииоиообменных, катиоиообмениых
и зарядово-мозаичных мембранах [26]
Мембрана	Концентрация раствора, М	рвыч_. унабл/д смЭ/(А-с) (х 1(H)	М/. см3/(Ас)(х 104)
Анионообменная	0,1	—9,2	-7,6
	0,01	-11,1	-9,5
	0,001	-11,7	-10,1
Катионообменная	0,1	10,3	11,9
	0,01	13,0	14,7
	0,001	14,0	15,5
Мозаичная	0,1	1,2	2,8
	0,01	1,4	3,1
	0,001	2,6	4,3
48
ГЛАВА 3
величины (Рвыч) и исправленные величины (Р) в таких
мозаичных мембранах, а также в мембранах, образованных
мозаикой из элементарных анионо- и катионообменных компо-
нентов.
3.9.	Модель активного транспорта
Модель Блюменталя, Кеплена и Кедем [1], которая рассматри-
валась в конце разд. 3.5, состоит из двух последовательных
ионообменных мембран: одной, несущей положительный фик-
сированный заряд, и другой с отрицательным фиксированным
зарядом. Слой водного раствора, содержащий протеолитиче-
ский фермент (папаин), изолирован между ними. Эта состав-
ная мембрана расположена между идентичными растворами,
содержащими низкомолекулярный субстрат фермента. Давле-
ние с обеих сторон мембраны одинаково. В присутствии фер-
мента реакция, по существу, представляет собой гидролиз суб-
страта с образованием соли:
XF ++ X+ + Y~	(3.63)
При известных концентрациях продукта и субстрата в обоих
резервуарах сродство реакции Аех может быть рассчитано че-
рез известную величину константы равновесия. В этой системе
не происходит транспорта вещества через мембрану, но возни-
кает «активный транспорт» электрического тока. При коротком
замыкании реакция вызывает ток между идентичными рас-
творами, в то время как при разомкнутой цепи между идентич-
ными растворами возникает разность потенциалов при усло-
вии, что Аех =/= 0.
Блюменталь, Кеплен и Кедем рассмотрели потоки всех про-
никающих веществ через обе мембраны и показали, что в ста-
ционарном состоянии диссипативная функция для составных
мембран сводится к двучлену, как в уравнении (3.20):
Ф = IE + иАех
В этом случае наблюдается такая же ситуация, как в уравне-
нии (3.19), а именно модификация локальных химических по-
тенциалов при реакции. Можно записать соответствующие фе-
номенологические уравнения:
E = RJ + R{iv, A^R^I + R^v	(3.64)
Феноменологические коэффициенты в уравнениях (3.64) выво-
дятся через кинетические параметры реакции и практические
феноменологические коэффициенты составных мембран. В част-
Связь между потоками и силами
49
ности, перекрестный коэффициент имеет следующий вид:
Т<Х_
^12 ~ ^21 ~	/ а . р	(3.65)
cs (®“ + ®Р) F
где а и р относятся к двум ионообменным мембранам, а про-
ницаемости <о“ и ю₽ — к соли; cs — средняя концентрация соли
в ионообменных мембранах. Направленность составной мем-
браны появляется вследствие различия чисел переноса.
Важным аспектом рассмотренной физической модели явля-
ется тот факт, что в ней проявились как довольно широкий
диапазон линейности, так и симметрия Онзагера. Это можно
Г, мкА
Рис. 3.2. Поведение модели системы активного транспорта (см. текст).
а — зависимость стационарной электродвижущей силы от сродства внешней реакции
для двух мембранных систем. Эксперименты проводились при нулевом токе; б —за-
висимость стационарного потока реакции от тока для двух мембранных систем. Экс-
перименты проводились при сродстве Дех=2,6 ккал/моль Ц].
50
ГЛАВА 3
видеть из рис. 3.2, а и б, на которых изображена зависимость
разности потенциалов при разомкнутой цепи (э. д. с.) от срод-
ства и зависимость скорости реакции от тока. На каждом гра-
фике показаны две группы результатов, соответствующих раз-
личным ионообменным мембранам. Единицы выбраны таким
образом, чтобы наклоны кривых стали безразмерными и было
видно, что соответствующие кривые на рис. 3.2, а и б фактиче-
ски параллельны. В этом выражается соотношение Онзагера
(dv/дГ)^----(Е/А^,_о	(3.66)
Линейную зависимость между v и I можно рассматривать как
кажущуюся стехиометрию системы, но фактически она не отра-
жает ни устойчивого сопряжения между транспортом и реак-
цией, ни линейной кинетики. Действительно, прямые линии на
рис. 3.2, б не проходят через начало координат как раз из-за
того, что сопряжение является неполным. Было бы явным аб-
сурдом рассматривать пересечение оси ординат как меру основ-
ного метаболизма, который, конечно, следует учитывать в ре-
альных эпителиальных мембранах (см. гл. 8).
Важно понять, что возможность описания такой составной
мембраны на основе стационарного сопряжения зависит от
предварительного знания ее структуры. Мы должны детально
рассмотреть явления, происходящие между ионообменными
мембранами в области локализации фермента. Если же струк-
тура и внутренняя функция мембраны неизвестны из-за недо-
ступности ее внутренней части, то мы были бы вынуждены
прийти к заключению, что представляет собой механизм
прямого сопряжения. Таким образом, вполне возможно, что
активный транспорт, по крайней мере в некоторых случаях,
может оказаться в конечном счете стационарным сопряжением
на молекулярном уровне.
3.10.	Выводы
1.	Диссипативная функция, выведенная из уравнения Гиббса,
показывает число степеней свободы системы. Соответствующие
феноменологические уравнения описывают потоки как линейные
функции сил (путем использования коэффициентов проводимо-
сти) или силы как линейные функции потоков (путем исполь-
зования коэффициентов сопротивления). Эти уравнения явля-
ются обобщениями хорошо известных линейных соотношений,
таких, как закон Ома и закон Фика. Для векторных потоков
диапазон линейности обычно гораздо больше, чем для химиче-
ских реакций (детальнее этот вопрос обсуждается в гл. 6).
2.	Матрицы коэффициентов проводимости или сопротивле-
ния должны удовлетворять двум условиям: первое обеспечивает
Связь между потоками и силами 51
положительность диссипативной функции, второе является усло-
вием симметрии между всеми парами соответствующих пере-
крестных коэффициентов, т. е. Ьц = Ьц и Rij = R^ (взаимность
по Онзагеру).
3.	Сопряжение между химической реакцией и трансмем-
бранным потоком, такое, как в активном транспорте, требует
применения векторного коэффициента сопряжения. Согласно
определению Кедем, активный транспорт возникает, если пере-
крестные коэффициенты сопротивления между реакцией и по-
током не равны нулю.
4.	Согласно принципу Кюри — Пригожина, сопряжение
между скалярными и векторными потоками в линейном режиме
возможно только в анизотропной среде. Векторный характер
коэффициентов сопряжения отражает анизотропию среды.
5.	В линейных системах с симметрией Онзагера производ-
ство энтропии принимает минимальное значение, совместимое
с налагаемыми ограничениями. Такие «стационарные состояния
с минимальным производством энтропии» могут приводить
к взаимодействию между процессами с общим потоком, назван-
ному стационарным сопряжением. Обсуждается ряд примеров.
6.	Рассмотрено несколько важных преобразований диссипа-
тивной функции для процессов мембранного транспорта. Эти
преобразования приводят к такому набору потоков и сил, ко-
торые более удобны для экспериментатора, так как легко мо-
гут быть зафиксированы или измерены.
7.	Преобразованные формы диссипативной функции могут
использоваться для соответствующих преобразований феноме-
нологических уравнений, что приводит к практическим феноме-
нологическим коэффициентам. Примеры таких преобразований
дают уравнения потоков Кедем — Качальского.
8.	Детально рассмотрены коэффициенты в уравнениях Ке-
дем — Качальского, причем особое внимание уделено опреде-
лению объемных потоков, с тем чтобы учесть возможные ошиб-
ки, обусловленные электродными процессами. Подчеркнуто, что
хорошо известный коэффициент отражения, первоначально
предложенный Ставерманом, является показателем степени
связи между потоком растворенного вещества и объемным по-
током.
9.	Обсуждается простая экспериментальная модель актив-
ного транспорта, основанная на стационарном сопряжении.
В этой модели составная мембрана, включающая фермент, при
обеспечении извне подходящим субстратом способна вызвать
электрический ток между двумя идентичными растворами. Эта
модель проявляет как линейность, так и симметрию.
4
Эффективность превращения энергии
Ясно, что общность трактовки сопряженных процессов, изло-
женной в гл. 2 и 3, позволяет применять ее для анализа раз-
нообразных биологических систем. В частности, она позволяет
провести последовательный анализ эффективности использова-
ния метаболической энергии в жизненно важных процессах
активного транспорта и мышечного сокращения. В гл. 3 мы
обсуждали определение активного транспорта и связанные
с этим вопросы. В данной главе мы сначала рассмотрим клас-
сический подход к активному транспорту, ограничиваясь глав-
ным образом транспортом натрия как в силу его важного зна-
чения, так и потому, что он лучше Изучен; отметим существен-
ные, на наш взгляд, недостатки классического метода и затем
рассмотрим превращение энергии с точки зрения неравновесной
термодинамики.
4.1.	Активный транспорт: основы
Давно уже известны важность процессов активного транспорта
в биологических системах, их общий характер и разнообразие.
При поверхностном изучении нормального метаболизма обна-
руживаются многочисленные продукты, которые непрерывно
образуются и должны специфично и быстро выводиться, зача-
стую несмотря на отрицательный градиент концентраций. По-
добным же образом необходимость активного транспорта сле-
дует из постоянства состава и динамической функции клетки
в норме.
В связи с процессами активного транспорта естественно
возникают следующие вопросы: Как однозначно проявляется
активный транспорт? Что является источником энергии? Каков
механизм, посредством которого (скалярная) химическая сво-
бодная' энергия производит (векторный) транспорт и электро-
осмотическую работу? Какова природа энергетики системы ак-
тивного транспорта? Этот последний вопрос представляет ин-
терес как сам по себе, так и в связи с предыдущими вопросами.
Активную природу транспорта, а также источники энергии
и механизмы этих процессов пытались исследовать с помощью
Эффективность превращения энергии 55
эффектов ингибирования аэробного и анаэробного метаболиз-
ма. Такие исследования были полезны, но вызывают суще-
ственные возражения. Прежде всего метаболизм может влиять
не только на функцию транспортной системы, но и на другие
функции, так же как и на структуру системы. К тому же эф-
фекты ингибиторов метаболизма могут быть либо первичными^
либо вторичными. Например, первичное воздействие на актив-
ный натриевый транспорт может приводить к вторичному влия-
нию на пассивный транспорт хлора. Таким образом, ингибиро-
вание метаболизма само по себе не всегда может свидетель-
ствовать об активной природе процесса. Более того, даже когда
изменение метаболизма позволяет отличить пассивный транс-
порт от активного, нельзя оценить эффективность использова-
ния метаболической энергии в различных состояниях, представ-
ляющих интерес. Это является одной из проблем термодина-
мики. Термодинамическое определение было сформулирована
Розенбергом [14], который полагал, что «наличие транспорта
от более низкого к более высокому потенциалу... единственный
несомненный критерий активного транспорта», но этот критерий
не включает очевидные случаи активного транспорта, в кото-
рых разность электрохимических потенциалов может быть ну-
левой или отрицательной и, естественно, не может служить
последовательной и исчерпывающей формулировкой.
4.2.	Классический анализ энергетики: модель
эквивалентных схем
Большинство исследований энергетики ионного транспорта
основывалось на работах Уссинга, который рассматривал ак-
тивный транспорт натрия на языке эквивалентных электриче-
ских схем и оценивал работу, необходимую для транспорта
одного эквивалента натрия [18,19]. Считалось, что эта работа
включает три компонента: «(а) работу, требуемую для преодо-
ления градиента концентрации... (б) работу, требуемую для
преодоления градиента потенциала... (в) работу, требуемую
для преодоления сопротивления движению натрия в коже». Эта
последняя величина вычислялась из «отношения потоков» или
отношения «однонаправленных» потоков натрия. Таким обра-
зом, общая работа (на моль натрия) вычислялась из уравнения
W = RT In (Сг/Со) + FE + RT In (Afm/Mout) (4.1}
где Min/A40Ut — отношение потоков. Так как кожа рассматрива-
лась на языке электрических аналогий, то Уссинг ввел поня-
тие «электродвижущая сила активного транспорта натрия»
ENa. Эта величина получалась путем деления работы W на чи-
сло Фарадея F.
54
ГЛАВА 4
Для оценки W и ENa использовались два общих метода.
Первый состоял в определении электрохимической разности
потенциалов, требуемой для уменьшения результирующего
транспорта натрия [и, следовательно, In (Afin/Afout) ] до нуля.
Это достигалось путем измерения разности концентраций или
разности электрических потенциалов на мембране либо путем
замены непроникающих анионов на проникающие. Во втором
методе кожа помещалась между двумя идентичными раство-
рами, устанавливалась нулевая разность электрических потен-
циалов на коже и измерялось отношение потоков в условиях
«короткого замыкания».
Как отмечал Уссинг, эти методы позволяли оценивать толь-
ко кажущуюся величину ENa, поскольку они не учитывали
влияние утечек. Кроме того, на основании работы Ходжкина и
Кейнса на отравленных аксонах кальмара, а также если учесть
возможность обменной диффузии, становится ясным, что суще-
ствуют серьезные трудности в попытках использовать отноше-
ние потоков для оценки энергетических параметров. Действи-
тельно, для того чтобы оба вышеупомянутых метода давали
одинаковые величины ENa, необходимо выполнение^трех усло-
вий: 1) отсутствие утечки, 2) отсутствие изотопного взаимодей-
ствия и 3) равенство метаболизма в состояниях статического
напора и установившегося потока [10]. (Состояние статиче-
ского напора, или состояние с фиксированной силой, и состоя-
ние установившегося потока — два важных стационарных со-
стояния, характеризующихся нулевым трансмембранным пото-
ком и нулевой трансмембранной силой соответственно; точные
определения будут даны в разд. 4.6.) Такое сочетание обстоя-
тельств, по-видимому, совершенно невероятно. Даже если пер-
вые два требования выполняются, то третье почти наверняка
нет, так как было показано, что скорость окислительного мета-
болизма в коже лягушки, коже жабы и мочевом пузыре жабы
зависит от разности электрохимических потенциалов натрия в
ткани (см. гл. 8).
Другое возражение против вышеупомянутой формулировки
связано с существенно различным характером трех компонен-
тов «работы». Первые два члена правой части уравнения (4.1),
взятые вместе, представляют собой разность электрохимических
потенциалов натрия и поэтому соответствуют скорости выпол-
нения электроосмотической работы, очевидно требующей рас-
хода метаболической энергии с равной или большей скоростью.
С другой стороны, третий член представляет собой не полезное
превращение энергии, а ее диссипацию, которая к тому же не
может быть точно определена с помощью измерений, проводи-
мых извне системы. Величину RT ln(Afin/Afout) можно считать
«внутренней работой», так же как при обсуждении энергетики
мышц, где предполагалось, что она представляет собой затра-
Эффективность превращения энергии
55
ты энергии на преодоление сопротивления, обусловленного тре-
нием и вязкостью (см. [11]). Возникает вопрос, уместно ли
включение диссипативного члена в выражение для работы, со-
вершаемой процессом. Это не принято при термодинамическом
анализе тепловых машин или других энергопреобразующих си-
стем. Основным правилом при анализе таких систем является
недвусмысленное разделение скорости, с которой энергия рас-
ходуется, и скорости, с которой она выделяется.
Еще одна трудность, связанная с классическим описанием,,
состоит в том, что при рассмотрении кожи лягушки на языке
электрических аналогий имеется опасность предположения о су-
ществовании постоянной или стехиометрической зависимости
между скоростями транспорта и метаболизма при всех усло-
виях эксперимента [18,20]. Отсюда иногда возникало убежде-
ние, что линейная зависимость между скоростями транспорта
и метаболизма доказывает существование стехиометрии и по-
зволяет рассчитать стехиометрические соотношения, несмотря
на то что линейность не эквивалентна пропорциональности.
К тому же, когда экспериментально обнаруживается перемен-
ная стехиометрия, как часто случается, например, при иссле-
довании окислительного фосфорилирования, это приписывают
обычно техническим недостаткам, вместо того чтобы исследо-
вать ее внутренний смысл. Полное сопряжение (стехиометрия)
транспорта и метаболизма фактически найдено в идеальных
электрохимических ячейках. Однако в биологических системах
следовало бы ожидать частичного десопряжения вследствие
либо разложения метаболических интермедиатов, либо дисси-
пации градиента электрохимического потенциала из-за утечки
[16]. В таких случаях поддержание разности электрохимиче-
ских потенциалов в ткани, даже в отсутствие результирующего
потока, потребовало бы затраты метаболической энергии. Это
находится в очевидном противоречии с трактовкой, лежащей
в основе уравнения (4.1), которая подразумевает, что в отсут-
ствие результирующего потока скорость совершения работы
(1FX скорость натриевого транспорта) будет равна нулю. Счи-
тается, что уравнение (4.1) дает только минимальную величину
необходимой скорости расходования метаболической энергии,,
но если это так, то данная трактовка несколько утрачивает
свою ценность как средство точного анализа энергетики транс-
портной системы.
Другой важный аспект классического анализа энергетики
транспорта натрия — способ оценки эффективности процесса.
Обычно эффективность определяется как отношение скорости
совершения работы, измеренной как описано выше, к скорости
расходования метаболической энергии. Считается, что эта по-
следняя величина является произведением скорости потребле-
ния кислорода сверх основного обмена и «теплотворной спо-
56
ГЛАВА 4
собности» 1 г-экв. кислорода при окислении глюкозы, опреде-
ляемой с помощью калориметрической бомбы. Таким образом,
где скорость потребления (сверх основного обмена) кислорода
Qo, выражается через стехиометрическое отношение (число
молей Ог на эквивалент перенесенного натрия) и (—ДЯ) — теп-
лотворная способность глюкозы. При таком определении функ-
ции эффективности возникают дополнительные сомнения в
уместности включения диссипативного члена в выражение для
работы. Увеличение диссипации неизбежно должно уменьшать
эффективность процесса, однако, согласно уравнениям (4.1) и
(4.2), рост диссипации энергии будет увеличивать эффектив-
ность. В дополнение к этому возражению можно подвергнуть
сомнению определение количества доступной энергии методом
калориметрии. Такими измерениями можно определить только
энтальпию в условиях, существующих внутри калориметра,
в то время как желаемой величиной является свободная энер-
гия Гиббса в условиях, существующих in vivo. Нгйконец, как
упоминалось выше, существует широко распространенная тен-
денция считать, что отношения скоростей транспорта натрия и
потребления кислорода постоянны при всех условиях, хотя
в принципе для неполностью сопряженных систем это отноше-
ние будет изменяться в зависимости от термодинамических
сил; более того, возможно, что при любой степени сопряжения
и силе это отношение может изменяться от одного животного
к другому.
4.3.	Энергетика с позиций неравновесной
термодинамики
Учитывая недостаточность классического подхода к энергетике,
необходимо разработать соответствующую термодинамическую
трактовку, которая, можно надеяться, даст исчерпывающее са-
мосогласованное описание активного транспорта при широком
разнообразии условий. Проблема энергетики интересна сама
по себе, но такое описание могло бы привести также к понима-
нию механизма действия факторов, влияющих на транспорт.
Поскольку исследуемые нами системы большей частью да-
леки от равновесия, наше изложение должно основываться на
неравновесной термодинамике. Некоторые авторы подходили
к проблемам превращения энергии в биологических системах
с этой точки зрения (например, [7]). Хошико и Линдлей [6]
дали исчерпывающую формальную линейную математическую
трактовку активного транспорта, которая облегчает анализ ак-
Эффективность превращения энергии 67
тивного солевого и водного транспорта в односолевых и би-
ионных системах. Для облегчения планирования эксперимента
и анализа мы ограничимся системами с активным транспортом
только одного иона (натрия), несопряженного с потоком дру-
гих веществ. В этом отношении наша работа является расши-
рением подхода с позиций линейной неравновесной термодина-
мики, данного первоначально Кедем [8]. Однако до начала
анализа специфических характеристик процесса активного
транспорта натрия с этой точки зрения мы дадим более общее
изложение процессов с двумя потоками, чтобы показать умест-
ность основных термодинамических соображений, рассмотрен-
ных выше, и их широкую применимость. Общее описание про-
цессов с двумя потоками приводит к определению двух полез-
ных параметров, которые позволяют легко сравнивать системы
с различной природой потоков и сил [9]. Степень сопряжения
q — безразмерный параметр, абсолютная величина которого из-
меняется от нуля для полностью несвязанных систем до еди-
ницы для систем, в которых потоки связаны стехиометрически.
Для данной степени связывания и данного отношения сил па-
раметр Z определяет отношение потоков. Для полностью сопря-
женных систем Z представляет собой стехиометрическое отно-
шение.
4.4.	Степень сопряжения и взаимосвязь
сил и потоков
Система, которую мы хотели бы рассмотреть, схематически
представлена на рис. 4.1. Сопряжение, механизм которого, во-
обще говоря, может быть неизвестен, происходит внутри «чер-
ного ящика». Этот черный ящик обычно содержит рабочий
элемент преобразователя энергии, например мембрану в про-
цессе активного транспорта. Так как происходят два процесса,
то диссипативная функция будет содержать два члена. В об-
щем случае мы можем выбрать один процесс, который всегда
приводит к положительному члену и, следовательно, может
рассматриваться как источник энергии или вход. Второй про-
цесс обычно приводит к отрицательному члену и представляет
собой выход. Поскольку в биологических системах выход, в из-
вестном смысле, ближе к наблюдателю и обычно более досту-
пен, чем вход, обозначим его индексом 1, а вход — индексом 2.
Тогда диссипативная функция принимает вид
Ф= + J2X2	(4.3)
выходная входная
энергия энергия
Отметим, что входной поток J2 всегда течет в самопроизволь-
ном направлении, другими словами, его направление находится
58
ГЛАВА 4
ВыхоЗ

ВхоЭ	у
Рнс. 4.1. Схематическое представление преобразования энергии.
Направление Л по часовой стрелке указывает на то, что входной поток является са-
мопроизвольным в соответствии со связанной с ннм силой, тогда как направление J\
против часовой стрелки показывает, что выходной поток протекает против соответ-
ствующей ему силы вследствие его сопряжения с А.
в соответствии с парной ему силой Х2. Однако выходной по-
ток Ji может протекать против соответствующей силы Xi вслед-
ствие его сопряжения с J2. В этих случаях выходной член имеет
отрицательный- знак, показывая, что свободная энергия пере-
дается от рабочего элемента в окружающую среду. Таким об-
разом, часть свободной энергии, израсходованная процессом 2,
преобразуется в форму, характерную для процесса 1. Так как
диссипативная функция всегда отрицательна, то поток на вы-
ходе никогда не может превышать поток на входе. Интуитивно
ясно, что эффективное преобразование энергии требует тесного
сопряжения между двумя процессами.
Феноменологические уравнения потоков в этой системе опре-
деляются выражениями
~ L\\X\ + L\2X2, J2 = L2lXiL22X2	(4.4, 4.5)
Их анализ значительно упрощается благодаря учету соотно-
шения взаимности Онзагера между феноменологическими пе-
рекрестными коэффициентами:
Л12 = /.21	(4-6)
Хотя эта зависимость до сих пор не проверена для случая ак-
тивного транспорта, она успешно применялась для описания
Эффективность превращения энергии 59
огромного разнообразия физико-химических процессов при
условии, что потоки и силы получены из соответствующей дис-
сипативной функции [12]. Эта зависимость была применена
также в случае искусственных «активно-транспортирующих»
систем, рассмотренных в гл. 3 [2], и окислительного фосфори-
лирования в митохондриях [15]. Предполагая общую приме-
нимость этой зависимости, можно написать
/1 = L^Xi + Li2X2, J2 = Li2X[ -f- L22X2	(4.7, 4.8)
Иногда удобнее исследовать систему путем ее описания через
сопротивления, в котором силы выражаются как функции по-
токов:
X{ = RJx + R.2J2, X2 = Rx2Jx + R^J2 (4.9,4.10)
Уравнения (4.7) и (4.8) определяют отношение потоков
J\/Ji (которое мы обозначим /), связанное с данным отноше-
нием сил Ai/X2 (которое мы обозначим х). Деление уравне-
ния (4.7) на уравнение (4.8) и затем деление числителя и зна-
менателя на (V ^н/^-22) -^2 дают
• _ (V^n/^22) х + 7-12/V^-iД22	(411)
Д22) х + V La/Lit
Видно, что в общем случае отношение потоков не постоянно и
изменяется в зависимости от отношения сил. Анализ отноше-
ния потоков становится яснее при рассмотрении параметра
Когда Л12/д/стремится кнулю,j-+(Lu/L22)x,
т. е. каждый поток становится пропорционален связанной с ним
силе, так что оба потока оказываются независимыми. С дру-
гой стороны, когда Ai2/V^u^22 стремится к ±1, / —>±
±х/Ьц/Ь22’ т. е. оба потока связаны фиксированным стехио-
метрическим отношением при любой величине обеих сил. Та-
ким образом, удобно ввести определение
9 =	(4.12)
и использовать q как меру степени сопряжения при сравнении
различных типов систем с двумя сопряженными потоками. Лег-
ко показать, что q определяется также выражением
9 =	(413)
Значение знака q наиболее наглядно в том случае, если оба
потока — векторные величины. Например, поток растворенного
вещества через мембрану может увлекать за собой другое рас-
творенное вещество в том же направлении (q > 0) или при
обменном процессе может выталкивать его назад (д<0).
Если q положительно, то Li2 также положительно, а /?12 отри-
цательно и наоборот *.
«о
ГЛАВА 4
Точное определение характера диссипативной функции на-
кладывает ограничения на q. Для процесса с двумя потоками
уравнения (4.7) и (4.8) дают
Ф = 71X1 + 12Х2 = LnXi + 2Z,i2XiX2 + Л22Х2 > 0	(4.14)
Так как это неравенство справедливо в общем случае, то
можно рассмотреть состояние, в котором Xj = —l/V^Z-n и
Х2= l/-\/2L22; тогда получим 1 —	7-1 Д22^= 0, в то время как
при рассмотрении состояния, в котором = 1/V2Z-H и Х2 =
= 1/д/2£22, мы видим, что 1 + 712/д/7-цТ22	0. Следовательно,

(4-15)
Зависимость между отношением потоков и отношением сил
-становится ясней, если ввести определение
z=vwu2	(4.16)
и переписать уравнение (4.11) в форме
. Zx + g
! qx+1/Z
v(4.17)
Как видно, для данных q и х величина / полностью определя-
ется Z, которое в современной литературе принято называть
«феноменологической стехиометрией» [17]. В случае полного
сопряжения (<? = ±1) отношение потоков оказывается фикси-
рованным и равно Z. В более общем случае Z служит для при-
ведения обоих отношений потоков и сил к безразмерным вели-
чинам. Зависимость между приведенным отношением потоков
i/Z и приведенным отношением сил Zx при различных величи-
нах q показана на рис. 4.2; Нужно учесть, что, хотя истинная
стехиометрия наблюдается только при полном сопряжении, учи-
тывая неизбежные экспериментальные ошибки, кажущаяся сте-
хиометрическая зависимость между 7j и /2 может наблюдаться
в широком диапазоне даже при умеренной степени нарушения
сопряжения. Таким образом, чтобы осуществить соответствую-
щий экспериментальный тест на степень несопряженности, мо-
жет оказаться необходимым установить Z(Xj/X2) на уровне,
при котором Zj становится близким к нулю.
Термодинамические следствия полного сопряжения очень
важны. Поскольку в этом случае потоки не являются линейно
независимыми, диссипативная функция может быть сокращена
до одного члена:
Ф = 72(Х2±гХ!)	(? = ±1)	(4.18)
Если Xi и Х2 могут изменяться независимо, то суммарная сила
X2±ZX] может стать как угодно малой. Следовательно, ве-
личина Ф может становиться пренебрежимо малой по сравне-
Эффективность превращения энергии
61
Рис. 4.2. Зависимость приведенного отношения потоков от приведенного от-
ношения сил для различных степеней сопряжения [9].
нию с входным и выходным потоками энергии. Это означает,
что процесс приближается к обратимости, когда скорость стре-
мится к нулю. Например, электрохимическая ячейка может
быть полностью сопряженной при условии, что имеется один
гомогенный электролит и нет побочных реакций. Тогда дисси-
пативная функция может быть записана как
Ф = /Е+»Л	(4.19)
где I и Е— электрический ток и потенциал, a v и А — скорость
и сродство протекающей химической реакции. В современной
системе обозначений Z — nF, где п — число электронов, пере-
несенных на моль реагента, и F — число Фарадея. Поэтому,
если сопряжение является действительно полным, имеем
ф = v (Д + nFE)	(4.20)
При обратимом равновесии Ф = о = 0 и A — nF (— Е}1=(). Вели-
чина (— £)/=о является электродвижущей силой ячейки.
62
ГЛАВА 4
4.5.	Эффективность превращения энергии
В биоэнергетике уделяется большое внимание понятию эффек-
тивности. Однако, к сожалению, определение этой величины
разными исследователями существенно отличается, так что ча-
сто трудно сравнивать результаты, полученные в различных
лабораториях. Более того, как отмечалось выше, интуитивное
представление о том, что биологические системы должны быть
эффективными во всех физиологических состояниях, часто при-
водило к неестественным определениям, которые непродуктив-
ны и внутренне противоречивы.
Согласно концепции классической термодинамики, однознач-
ное и удобное определение эффективности следует из диссипа-
тивной функции [уравнение (4.3)]:
„__ Выход _ — ZiXi	,, п 1 \
"I Вход J2Xt	' ‘ '
(Отметим, что т] и q не являются однозначными характери-
стиками системы, так как может существовать ряд различных
способов выбора потоков и сил, согласующихся с данной ско-
ростью производства энтропии. Однако обычно выбор входа и
выхода диктуется практическими соображениями. В случае
полного сопряжения q= 1 при любом выборе.)
Наибольший биологический интерес представляют те со-
стояния, в которых процесс 2 самопроизволен, а процесс 1 нет.
В этих случаях /2Х2 > 0, a JiXi 0. Условием таких состоя-
ний, выраженным через силы, является
— ! Z (Х./Хг)	0	(4 22)
Всякий раз, когда эго условие выполняется, процесс 2 «приво-
дит в движение» процесс 1 и
0 < n < 1	(4.23)
Величину т] можно легко получить как функцию отношения
сил и степени сопряжения:
л =	(4.24)
д + Z (Xt/X2)
Так как эффективность обращается в нуль, когда Ji или
равны нулю, то очевидно, что она должна проходить через
максимум при промежуточных величинах. Эта максимальная
величина эффективности т]тах зависит только от степени сопря-
жения:
Птах=07ТГ=^	(4,25)
Эффективность превращения энергии
63
Рис. 4.3. Зависимость эффективности т] от приведенного отношения сил для
различных степеней сопряжения.
Рассмотрение ограничивается областью, в которой —1< Z(X,/X2)/4< 0. Для каждой ве-
личины q левый предел представляет собой стационарное состояние с фиксированной
силой, а правый — стационарное состояние с фиксированным потоком [9].
(Следствием этого результата является то, что если т)тах из-
вестно, то q может быть найдено из q2= 1 — [(1 — т)тах)/(1 +
+ т)тах)]2- Другой метод определения q будет обсуждаться
в гл. 7.) Для полностью сопряженных систем значение т)тах
может приближаться к 1 как пределу при обратимом равнове-
сии. Однако, как отмечалось ранее, скорость процесса при этих
условиях стремится к нулю2.
На рис. 4.3 изображена эффективность как функция отно-
шения сил для разных величин q. Отметим очень быстрое па-
дение iimax с уменьшением q. Заслуживает внимания также тот
факт, что, хотя эффективности придают особое значение, т)
часто слишком мала в тех областях, которые представляют
интерес для физиологии. В самом деле, очевидно, что значе-
ния q, скорости совершения работы и, следовательно, эффек-
тивности становятся равными нулю всякий раз, когда либо У],
либо Xi равны нулю. Несмотря на то что при таких обстоя-
64
ГЛАВА 4
тельствах не совершается работа, эти два состояния имеют
большое физиологическое и общее значение и заслуживают
особого внимания [9].
4.6.	Затрата энергии без совершения работы
4.6.1.	Состояние статического напора
Если Х2, входная или движущая сила, поддерживается посто-
янной, а на ограничений не накладывается, то поток Ji бу-
дет продолжаться до тех пор, пока не достигнет величины,
достаточной для его прекращения. После этого /1 будет оста-
ваться равным нулю и, таким образом, Xi будет постоянной
до тех пор, пока Х2 и феноменологические коэффициенты со-
храняют свои исходные значения. Мы будем называть такой
режим состоянием с фиксированной силой, или состоянием
статического напора (static head). Примерами систем в состоя-
нии статического напора являются топливный элемент при
разомкнутой цепи, мембраны растительных или животных кле-
ток, поддерживающие постоянные градиенты концентраций
с помощью активного транспорта, и мышцы при изотермиче-
ском сокращении. В неполностью сопряженных системах для
поддержания состояния статического напора должна затрачи-
ваться энергия, даже если выходной поток равен нулю.
4.6.2.	Состояние установившегося потока
В случае внешних резервуаров конечной емкости Х\ может
поддерживаться постоянной, только если J\ стремится к нулю
или компенсируется равным потоком с внешней .стороны. Пу-
тем соответствующей регулировки этого внешнего потока мож-
но поддерживать Х\ на любом заданном уровне, как, например,
в случае измерения тока короткого замыкания в биологических
системах. Вместо электрического тока при нулевой разности
потенциалов на нулевом уровне может поддерживаться любая
другая сила (например, высота гидростатического напора).
Хотя часто X] поддерживается на нулевом уровне с помощью
компенсирующего устройства, это в общем случае не обяза-
тельно. Стационарные состояния, в которых Хх — 0, мы будем
называть состоянием с фиксированным потоком, или состоянием
установившегося потока (level flow).
Примерами систем в этом состоянии являются топливный
элемент при коротком замыкании, проксимальные извитые ка-
нальцы почки, транспортирующие соль и воду между изотони-
ческими физиологическими растворами, мышца при ненагру-
женном сокращении. Ясно, что для поддержания состояния
установившегося потока должна затрачиваться энергия, даже
если выходная сила равна нулю.
Эффективность превращения энергии	65
4.6.3.	Продуктивность использования энергии
При анализе как живых, так и неживых систем основное вни-
мание уделяется продуктивности использования энергии. При-
меры, рассмотренные выше, наглядно показывают, что энергия
может полезно расходоваться и в случаях, когда скорость со-
вершения работы и эффективность равны нулю. Поэтому оче-
видно, что функция эффективности не может рассматриваться
как универсальный критерий продуктивности использования
энергии. Действительно, по-видимому, не существует единого
критерия, подходящего для этой цели; вернее, условия функ-
ционирования системы определяют соответствующий критерий.
Ясно, 4го эффективность представляет интерес, когда си-
стема превращает одну форму энергии в другую, например
когда мышца поднимает груз. Другой важный пример — петля
Хенле, где хлор переносится против большой разности электро-
химических потенциалов со скоростью, которая позволяет воде
вытекать из собирательной трубочки для концентрирования
мочи. Однако вблизи состояний с фиксированной силой или
потоком, где степень превращения энергии становится малой,
преобразование энергии не является функцией системы и по-
этому эффективность не имеет значения. Тем не менее необхо-
димо оценить продуктивность использования энергии и в таких
случаях. При исследованиях мышечного сокращения, напри-
мер, предполагалось, что сравнение различных тканей или раз-
личных состояний может успешно проводиться с помощью по-
нятия «изометрической эффективности», определяемой как на-
пряжение, развитое на единицу скорости потребления макро-
эргического фосфата [1]. Однако изменение свободной энергии
на единицу скорости реакции может значительно отличаться
в различных тканях. Поэтому мы предположили, что правиль-
нее относить выходную силу (или поток) к скорости затраты
энергии [4].
4.6.4.	Эффективность силы и потока
Очевидно, что вблизи состояния статического напора функция
системы состоит в том, чтобы поддерживать разность электри-
ческих потенциалов, напряжение или какую-нибудь другую
подходящую силу. В этом случае параметром, представляющим
интерес, является сила, развиваемая при данной скорости за-
траты метаболической энергии. Эта величина — эффективность
силы — обозначается ех,:
ex, = -XjJ2X2	(4.26)
При фиксированной Х2 эффективность силы увеличивается мо-
нотонно, по мере того как — Х\ возрастает, и достигает своей
максимальной величины в состоянии статического напора.
5 Кеплен, Эссиг
66
ГЛАВА 4
Вблизи состояния установившегося потока функцией систе-
мы, очевидно, является быстрый транспорт вещества. Здесь
следует рассмотреть скорость транспорта при данной скорости
затраты метаболической энергии. Эта величина — эффектив-
ность потока — обозначается е/,:
8л = Л//2^2	(4.27)
При фиксированной Х2 эффективность потока возрастает моно-
тонно, по мере того как уменьшается (за исключением слу-
чая </2 = 1), и достигает своей максимальной величины в со-
стоянии установившегося потока.
Эти соображения показывают, что в системе с фиксирован-
ной входной силой, функция которой заключается не в преоб-
разовании энергии, а в поддержании внешней силы или по-
тока, наиболее эффективно энергия используется в состояниях
с фиксированной силой или потоком соответственно.
4.7.	Степень сопряжения в неизотермических
системах: тепловые машины и цикл Карно
В заключение для полноты изложения следовало бы связать
энтропийную эффективность с тепловой эффективностью ма-
шины. В термодинамике тепловых машин обратимая машина
Карно является стандартом для сравиеиия. Если проследить
за состоянием рабочего вещества, проходящего через ряд ступе-
ней, каждая из которых в идеальном случае достигает обрати-
мости, то затрату свободной энергии можно приписать отсут-
ствию обратимости на какой-то ступени. Однако в таком
термоэлектрическом элементе, как термопара, в которой необра-
тимый тепловой поток связан с потоком электричества, подоб-
ное разделение невозможно. В этом смысле термопара явля-
ется более близким аналогом энергопреобразующих биологи-
ческих систем.
Рассмотрим теперь тепловую машину, работающую циклич-
но между Г] и То. Предположим, что мы выбрали масштаб
времени достаточно большой, чтобы время одного,цикла в усло-
виях стационарной работы было пренебрежимо мало. Мы мо-
жем теперь рассмотреть поток тепла входящий в машину
при Ть который фактически является стационарным. Предпо-
ложим, далее, что машина связана с некоторым процессом, про-
текающим при То, который допускает стационарный или почти
стационарный отвод энергии; например поршень может быть
связан с генератором постоянного тока. Производство энтропии
в этой системе определяется выражением
diS/dt = IE/Tq + Jq АТ/Т^о	(4.28)
Эффективность превращения энергии 67
где I — электрический ток, Е—разность электрических потен-
циалов и Д7’ = 7’1 — То. То же самое выражение можно приме-
нить в случае термопары [9]. Выражение для энтропийной
эффективности получается точно так же, как ранее:
11 = — Jq (дт/т^	<4,29)
Тепловая эффективность тр определяется как отношение (вы-
ход)/(тепло, поступающее в систему):
•п* = (ДГ/ГО П	(4.30)
где коэффициент пропорциональности представляет собой эф-
фективность цикла Карно, действующего между теми же тем-
пературными пределами. Следовательно, тепловая эффектив-
ность этой машины не может превышать эффективность цикла
Карно. Она может приближаться к эффективности цикла Кар-
но, только если степень сопряжения равна единице и при этом
скорость работы цикла стремится к пулю.
Определение эффективности, которое выводится из произ-
водства энтропии, является общим и включает циклические
процессы как частный случай. Действительно, для неизотерми-
ческих систем она представляет собой нормировку тепловой
эффективности. Это становится яснее из зависимости т] от q.
В рассмотренном выше примере, даже в случае, когда тепло-
вая машина действует бесконечно медленно, эффективность
цикла Карно может достигаться только при полном сопряже-
нии входного и выходного процессов. Между машиной и клем-
мами генератора не должно быть потерь. Если потери возни-
кают, то степень сопряжения будет неполной, но можно рас-
считать максимальную эффективность и скорость работы, при
которой она будет достигаться. Часть входной энергии, затра-
чиваемой на трение, будет уменьшаться с уменьшением скоро-
сти. С другой стороны, энергия, рассеиваемая из-за таких
потерь, как утечка тепла между резервуарами, является основ-
ной частью общей энергии, затрачиваемой при низких скоро-
стях. Максимальная эффективность представляет собой опти-
мальный компромисс между этими двумя видами потерь.
4.8.	Выводы
1.	Критически рассмотрена классическая трактовка активного
транспорта в рамках эквивалентной электрической схемы. По-
казано, что имеются теоретические и практические трудности,
связанные с использованными в этой трактовке понятиями ра-
боты, эффективности, электродвижущей силы активного транс-
порта и стехиометрии.
5*
68
ГЛАВА 4
2.	Изложение энергетики с позиций неравновесной термо-
динамики проведено на примере системы с двумя потоками.
Даются определения степени сопряжения (q) и феноменологи-
ческой стехиометрии (Z); эти величины используются для уста-
новления связи между отношением сил и отношением потоков.
Обсуждаются последствия полного сопряжения (</—1).
3.	Показано, что однозначное и удобное определение эффек-
тивности вытекает из диссипативной функции (или в более об-
щем случае для неизотермических систем — из функции произ-
водства энтропии). Обсуждаются два важных физиологических
состояния, в которых затрата энергии происходит без совер-
шения работы и, следовательно, эффективность равна нулю.
Это — состояние с фиксированной силой (нулевой выходной
поток) и состояние с фиксированным потоком (нулевая выход-
ная сила).
4.	Множество стационарных состояний между состояниями
с фиксированной силой и фиксированным потоком характери-
зуются значениями эффективности, большими нуля и меньшими
единицы. В пределах этой области действия эффективность
должна проходить через максимум. Максимальная величина
эффективности зависит только от степени сопряжения.
5.	Лишь полностью сопряженные системы могут в пределе
достигать эффективности, равной единице. Этот предел соот-
ветствует обратимому равновесию, причем скорость процесса
при этих условиях стремится к нулю.
6.	Вблизи состояний с фиксированной силой или потоком
эффективность системы может быть очень низкой; функция
системы в состоянии статического напора состоит в поддержа-
нии разности электрохимических потенциалов, напряжения или
какой-либо другой подходящей силы, в то время как в состоя-
нии установившегося потока ее функция состоит в быстром
транспорте вещества. Параметрами, представляющими интерес
в этих состояниях, являются эффективность силы, т. е. сила,
развитая при данной скорости расходования метаболической
энергии, и эффективность потока или скорость транспорта при
данной скорости расходования метаболической энергии.
7.	Показано, что определение эффективности, которое вы-
водится из производства энтропии, является общим и включает
циклические процессы как частный случай. В неизотермических
системах эффективность представляет собой нормировку тепло-
вой эффективности относительно эффективности цикла Карно,
действующего в том же самом температурном интервале. Эф-
фективность цикла Карно может быть достигнута только при
бесконечно малой скорости действия и полном сопряжении
с выходным процессом.
5
Метод диаграмм
В этой главе мы кратко рассмотрим еще один важный метод,
который дополняет и расширяет изложенное в предыдущих
главах. Это — «метод диаграмм» для анализа кинетики ста-
ционарного состояния макромолекулярных энергопреобразую-
щих систем, введенный Т. Л. Хиллом и широко разработанный
им и сотрудниками в течение прошедшего десятилетия. Так
как этот метод очень подробно описан в превосходной моногра-
фии [1], то мы не будем останавливаться на строгой количе-
ственной методологии, а попытаемся дать читателю качествен-
ное описание, чтобы показать возможности и универсальность
этого метода и как с его помощью можно получить представ-
ление о природе сопряжения.
5.1. Состояния и циклы
Для начала рассмотрим применение метода диаграмм на про-
стом примере. На рис. 5.1, а показана гипотетическая модель
сопряженного транспорта (симпорт), детально описанная Хил-
лом [1]. Фактически здесь рассматривается ансамбль, который
содержит большое число (JV) эквивалентных и независимых
элементов, где одна молекула транспортного белка составляет
один элемент. Каждый элемент может находиться в одном из
пронумерованных дискретных состояний. Омывающие растворы
А и В содержат оба лиганда Ц и L2 в указанных концентра-
циях, однако центр связывания L2 на белке Е активируется
только тогда, когда Li уже связан. В этом состоянии Е может
подвергаться конформационному изменению (2ч=^3 или 4*±5),
фактически переключаясь на тот из омывающих растворов,
в котором центры связывания оказываются доступными. Диа-
грамма для этой системы показана на рис. 5.1,6. Стрелки на
диаграмме означают связывание; например, 1А указывает на
связывание Ц из А; стрелки десорбции не изображены. Кон-
формационные изменения Е обозначаются горизонтальными
стрелками. На рис. 5.1, в показаны полные циклы трех возмож-
ных типов для указанных на диаграмме переходов системы,
причем результирующий эффект состоит в транспорте Li и L2
70
ГЛАВА 5
из одного омывающего раствора в другой. При равновесии ре-
зультирующий транспорт какого-либо лиганда отсутствует,
так как йа = с1В и с2а = с2в- Однако в стационарном состоя-
нии при неодинаковых концентрациях лигандов в омывающем
растворе достаточная разность концентраций одного из лиган-
дов может вызвать результирующий поток другого лиганда
против его собственного градиента, концентрации (заметим, что
в более общем случае заряженных лигандов, по существу,
можно пользоваться теми же понятиями). Подробный вывод
выражений для сил, действующих в каждом цикле, будет дан
позже.
Очевидно, что кинетику системы можно описать с помощью
констант скоростей первого (или псевдопервого) порядка для
каждого перехода, причем каждая линия диаграммы соответ-
ствует двум константам скорости: одна для прямого, а вторая
для обратного перехода. Несомненным достоинством этого ме-
тода является возможность вычисления стационарных потоков
перехода (между любой парой состояний) и вероятностей со-
Сосшояние 1	2	3	4	5
Раствор В(с1в,сгв)
а
Рис. 5.1. а — иллюстративная модель мембранного транспорта двух лиган-
дов Li и L2 между двумя омывающими растворами А и В: • место связы-
вания Li, X место свизывания L2, Е — белок; б — диаграмма, соответствую-
щая рис. а; в — циклы (указаны силы, действующие в каждом цикле) [1].
Метод диаграмм
71
Рис. 5.2. Направленные диаграммы для состояния 2 модели показанной на
рис. 5.1. Даны алгебраические величины первой и третьей направленных
диаграмм [1].
стояний (относительная степень заполненности). Показано, что
число независимых неравных нулю стационарных потоков пере-
хода, определяемое числом линий на диаграмме минус едини-
ца, меньше, чем число состояний. Для того чтобы получить
потоки и вероятности как явные функции всех констант скоро-
стей, необходимо в принципе решить большое число линейных
алгебраических уравнений (в сложных моделях это может по-
влечь за собой необходимость весьма трудоемких вычислений).
Вместо этого можно найти и записать решения с помощью гра-
фического алгоритма, первоначально разработанного Кингом и
Альтманом [3]. Для этой цели необходимо построить полный
набор парциальных диаграмм, каждая из которых содержит
максимальное число линий, не образующих какого-либо цикла
или замкнутого пути. В данном случае имеется 11 таких пар-
циальных диаграмм. Следующий. этап состоит в получении на-
бора направленных диаграмм из парциальных диаграмм. Один
набор для каждого состояния в рассматриваемом примере дает
всего 55 направленных диаграмм. Это делается путем расста-
новки стрелок в парциальных диаграммах так, чтобы получить
все возможные пути перехода к данному состоянию. Направ-
ленные диаграммы, соответствующие состоянию 2 рассматри-
ваемой модельной системы, показаны на рис. 5.2. Обозначая
константы скорости первого порядка для перехода i->j через
<*ц, каждой направленной диаграмме можно приписать неко-
торую алгебраическую величину, как показано на рисунке.
Тогда вероятность стационарного t-ro состояния (р“) равна
РТ~ (сумма направленных диаграмм в состоянии i)/2 (5.1)
где
2 = сумма направленных диаграмм всех состояний (5.2)
72
ГЛАВА 5
Таким образом, для состояния 2 получим
„ _ (я45«5зДз1а12 + ai3«35«54«42 + 9 других членов)	gv
^2	(a46a53a3iai2 + а13аз5а54а42 + 53 других члена)	' ’ '
Результирующий средний стационарный поток перехода между
состояниями i и j в направлении, г-*/ обозначается Теперь
сразу можно записать
= N ~ ацР?)	(5-4>
Из приведенного выше критерия очевидно, что если диа-
грамма содержит лишь один цикл, то имеется только один
независимый поток перехода; другими словами, для таких си-
стем стационарные потоки переходов между последовательными
парами состояний цикла оказываются равными. Это приводит
к понятию «циклического потока», которое может быть обоб-
щено для диаграмм со многими циклами. Действительно, цик-
лические потоки более информативны, чем потоки переходов и,
как будет видно, являются основными в неравновесной термо-
динамике. Более того, многоцикличные диаграммы делают яс-
ными понятия нецелочисленной и переменной стехиометрии.
Если снова обратиться к рис. 5.1, то станет очевидно, что цикл а
переносит L] и L2 между растворами А и В, цикл b переносит
Li и цикл с переносит Ё2. Циклическая диаграмма получается
из направленной диаграммы путем добавления одной стрелки
для завершения цикла стрелок. Такие диаграммы возникают
парами, которые отличаются лишь направлением прохождения
цикла, причем алгебраическая разность между парой цикличе-
ских диаграмм названа диаграммой потока. Диаграммы по-
токов содержат только один цикл (стрелки не показаны, так
как учитываются оба направления) и обычно включают один
или более направленных потоков, текущих в цикле. Рис. 5.3
иллюстрирует все возможные диаграммы потоков для рассмот-
ренной модели. Например, если какая-либо линия I—j вклю-
чена в цикл диаграммы потока, то мы считаем, что диаграмма
Рис. 5.3. Шесть диаграмм потоков для модели на рис. 5.1, классифицирован-
ные по циклам [1].
Метод диаграмм
73
потока j-*-i определяется следующим образом (через алгебраи-
ческие величины):
(диаграмма потока /->/) = (циклическая диаграмма —
— (циклическая диаграмма	(5.5)
Например, для диаграммы потока II на рис. 5.3 получим
П12 = (а12а23а31 — а21а32а1з) а45а53
Условно считается, что направление цикла против часовой
стрелки образует положительную диаграмму потока, как по-
казано на рис. 5.1. Можно показать, что потоки переходов
равны
Z^ = (jV X сумма диаграмм потоков /->г)/2	(5.6)
Различные диаграммы потоков, содержащие один и тот же
цикл, могут быть суммированы. Эта сумма также называется
циклом. Таким образом, согласно рис. 5.3,
цикл а = 1, цикл & = 11 +III + IV, цикле —V +VI
(5-7)
Циклические потоки JK, где % = а, Ь, с, равны
Ja = N (цикл a)/S, Д = ЛДцикл &)/S, /е = М(цикл c)/S
(5-8)
Эти потоки определены только для стационарного состояния.
Из уравнения (5.6), обобщая (5.7) и (5.8), получаем
= сумма циклических потоков / -> i	(5.9)
Для примера на рис. 5.1 имеем
7“ = /а + Д> 72°°3 = Д-Л> J^ = Ja + Jc (5.10)
Кроме того,
/з“ = /П- J2~4 = /4~ = /5°°3	(5.11)
Отметим, что имеются три цикла и, следовательно, три незави-
симых циклических потока.
Для дальнейшего изложения введем специальные алгебраи-
ческие обозначения. Если Па+= а12а24а45а53а31, Пй_ —
и т. д., то из уравнений (5.7) и (5.8) получим, что в общем
случае
4 = ^(Пи+-Пи_)2и/2	(5.12)
где сумма всех диаграмм потоков, принадлежащих к к,
т. е. «придатков», питающих цикл. Из рис. 5.3 видно, что
2a — 1 , S* — «15а53 + a54a42 “Ь a42a53> Sc = <Х12 + <Х13	(5.13)
74
ГЛАВА 5
Можно показать, что всегда возможно расщепление цикличе-
ских потоков на отдельные однонаправленные циклические по-
токи, например:
7и+==ЛШи+2и/2, V = Mnz_Sz/S	(5.14)
Перед тем как рассмотреть силы, действующие в системе, не-
обходимо отметить одно общее допущение, что константы ско-
рости связывания лигандов являются константами псевдопер-
вого порядка, т. е. зависят от концентрации (или активности)
лиганда в омывающем растворе, из которого он связывается.
Таким образом, а12 = а*с1А и а13 = а*с1В, где а* — константа
скорости связывания Li второго порядка. Аналогично а24 =
= а'с.,, а,, = а*соп Таким образом, разность химических по-
тенциалов равна
= ДЦ1 = RT In (ci a/cib) = RT In (а12/а13)
Х2 == Дц2 = RT In (с2а/с2в) = RT In (а24/а35)	(5.15)
Необходимо отметить, что упрощающие предположения, вве-
денные выше (а*2 = а’3 = а^ и а24=а35 = а2), оказываются не-
нужными по следующей причине. При равновесии для цикла b
(рис. 5.1, в)
П6+ = П6_ или а12а23а31 = а21а32а13	(5.16)
Но так как Cia = Cib и, следовательно, ai2 = ai3, получаем со-
вершенно общую зависимость между константами скоростей
при равновесии:
®23®31 == ^21^32	(б>17)
Таким образом, в стационарном состоянии
Теперь, используя уравнения (5.14) и (5.15), находим
=	=	=	(5.19)
V 1ь- с1в
Аналогично для цикла с имеем
Пс+ - Пс_ =	- 1) Пс_	(5.20)
П .	J . с
=	=	(5.21)
П	J с „	'	'
С~ с~ 2В
Метод диаграмм
75
Для цикла а найдем
(5.22)
(5.23)
Л ,	! .	с с,
а+ __ а+ - 1А 2А — Р(Х,> XiHRT
П«-	Ja-	С1ВС2В
Трансмембранные стационарные потоки лигандов 1 и 2 обозна-
чим 7“ и 7“ соответственно. Очевидно, что /” = /” и 7“ = 7^.
Из уравнений (5.10) и (5.12), используя (5.18), (5.20) и (5.22)
и вводя обозначение
х = М1и_2и/2 = 4- (к = а, Ь, с)	(5.24)
[ср. с уравнением (5.14)], а также учитывая тождество
e(X, + X,)/Z?r _ 1 —.	_ 1) (еВДГ _ 1) _[_ (gXi/RT _ 1) (eX2/RT _ J)
получим
J“ = (а + b) (ex,lRT - 1) + а (е™т -- 1) + а (ех^т - 1) (ех^т - 1)
(5.25)
7“ = a(ex,IRT — 1) + (а + с) (eX2/RT — 1) + a (eXllRT — 1) (eXilRT — 1)
(5.26)
Часто удобно выбрать один раствор, скажем В, в качестве
стандартного раствора, ограничивая все изменения и Х2
изменениями в растворе А. В этом случае мы будем считать,
что коэффициенты х не зависят от изменений состава рас-
твора А. Действительно, это уже учтено выше, за исключением
того, что S содержит ai2 и «24, которые пропорциональны Cia
и с2а соответственно, и Sc содержит ai2 [см. уравнение (5.13)].
Предполагая, что S будет относительно нечувствительна к из-
менениям в растворе А, мы используем подстановку для с,
которая легко выводится из уравнений (5.13), (5.15) и (5.24):
с = [(ex,!RT - 1) + 2] с' (с' = Мх13Пс_/2)	(5.27)
Тогда уравнение (5.26) приобретает вид
7” = a (ex'lRT - 1) + (a + 2с') (e™RT - 1) +
+ (a + c') (ex,!RT - 1) (ex’!RT - 1) (5.28)
Интересно, что этот тип преобразования возможен также, ко-
гда а*2	а*3. В этом случае подстановка дает
С = [(еадГ_ 1) _[_ (1 _[_ у)] с'
(У = <зК- ^' = ^2c1Bnc_/S)
76
ГЛАВА 5
и второй член в правой части уравнения (5.28) принимает вид
[а+ с' + V)] (eXitRT — 1). Уравнения (5.25) и (5.28) описывают
потоки лигандов как функции сил в произвольном стационар-
ном состоянии не обязательно вблизи равновесия. Если изме-
нения ограничены раствором А, то коэффициенты должны быть
постоянны в той степени, в которой постоянна S (в противном
случае уравнения могут быть умножены на S, приводя к по-
стоянным коэффициентам, связывающим силы с «потоками»,
содержащими переменный коэффициент). Нужно отметить, что
перекрестные коэффициенты при членах «индивидуальных сил»
удовлетворяют соотношению взаимности. (Заметим, что эти ко-
эффициенты относятся к свойствам данного стационарного со-
стояния, но не к равновесному состоянию.) Поэтому ясно, что
для условий, близких к равновесию (Xj и Х2 малы), разлагая
экспоненциальные члены в ряд, в пределе получим обычные
феноменологические уравнения; например, из уравнений (5.25)
и (5.26) находим
7“ = (а + b) XJRT + aX^RT	(5.29)
/» = aX1/7?f + (a + c)X2/7?7’	(5.30)
[При удалении от равновесия получается другой тип уравне-
ний, который будет обсуждаться в гл. 13: ср. уравнения
(13.33) и (13.34).] В стационарном состоянии результирующая
скорость диссипации свободной энергии в ансамбле плюс рас-
твор А плюс раствор В, как обычно, равна
Ф = /“Х1 + /“Х2	(5.31)
Сравнивая уравнения (5.29) и (5.30) с уравнениями (5.24)
и (5.14), мы видим, что коэффициенты оказываются просто
комбинациями однонаправленных циклических потоков. Вооб-
ще можно сказать, что всякий раз, когда пару циклов в диа-
грамме разделяет общая линия, эти,циклы представляют со-
бой сопряженные процессы. Если общая линия не принимается
во внимание, то образуется больший цикл, охватывающий оба
малых цикла; в таком случае этот больший цикл представляет
собой гипотетический «полностью сопряженный» цикл. (Ко-
нечно, если две силы действительно действуют в одном цикле,
то соответствующий процесс должен быть полностью сопря-
женным.) Больший цикл может быть сам сопряжен с допол-
нительным циклом и т. д. Феноменологические коэффициенты
для тайих уравнений, как (5.29) и (5.30), могут быть записаны
следующим образом: для «прямых» коэффициентов какого-либо
процесса однонаправленные циклические потоки суммируются,
охватывая цикл, относящийся к данному процессу и ко всем
возможным большим циклам, включающим его; для «перекрест-
ных» коэффициентов между двумя процессами однонаправлен-
Метод диаграмм 77
ные циклические потоки суммируются для всех больших циклов,
которые включают оба элементарных цикла, относящихся
к данным процессам (в случае отрицательного сопряжения
сумма имеет отрицательный знак).
Вместо записи диссипативной функции^через произведения
действующих потоков и сил, как в уравнении (5.31), ее можно
записать как сумму произведений циклических потоков и сил.
Подставляя уравнения (5.10) в (5.31), получим
Ф = 4^а + 7Л + /Х	(5.32)
где
Xa = Xl + X2, Xb = Xt, ХС = Х2	(5.33)
Здесь величина Хх, связанная с каждым циклическим пото-
ком /и, является суммой всех термодинамических сил, дей-
ствующих в цикле %. Заметим, что результирующая сила
в цикле может быть равна нулю. Как мы видели [уравнения
(5.19), (5.21) и (5.23)], Хх определяется уравнением
= Пх+/Пи-	(5.34)
а — уравнением (5.12). Отсюда следует, что /и и всегда
имеют одинаковый знак и в уравнении (5.32) каждый член
будет положительным или равным нулю.
5.2. Уровни свободной энергии
Для описания состояний макромолекулярных агрегатов или
систем Хилл и сотр. [1] использовали понятие свободной энер-
гии, которое существенно облегчает понимание природы сил,
действующих в системе. Здесь важно иметь в виду, что, хотя
в общем случае разные состояния не находятся в равновесии
друг с другом, каждое состояние является внутренне равно-
весным. Если же между «внутренними» подсостояниями воз-
никают относительно медленные переходы, что приводит к вну-
тренней неравновесности некоторого состояния, то необходимо
разделить его на подсостояния, для которых внутреннее равно-
весие сохраняется. Для любого данного перехода ij опреде-
лены три вида изменения свободной энергии: стандартное, ос-
новное и общее. Эти изменения рассматриваются как разность
между уровнями свободной энергии между состояниями i и /;
для удобства уровни свободной энергии связываются с инди-
видуальными состояниями, хотя реальное значение имеют
только разности уровней энергии.
В статистической механике показано, что для ансамбля
конденсированных систем рассматриваемого вида химический
78
ГЛАВА 5
потенциал произвольного компонента в состоянии / равен
p — Gj + RTinpi	(5.35)
где pj — вероятность или степень заполнения /-го состояния.
Если все системы находятся в состоянии /', то р/ = 1 и р,/ = G/.
Таким образом, G; может быть представлена либо как моляр-
ная свободная энергия Гиббса одиночной изолированной си-
стемы в состоянии /, либо как молярная свободная энергия
Гиббса всей системы, если весь ансамбль находится в состоя-
нии /. Уравнение (5.35) показывает, что G/ является стандарт-
ной свободной энергией Гиббса состояния / (стандартное со-
стояние с р/=1). Стандартная свободная энергия G/ — это
внутреннее равновесное свойство только состояния /, в то время
как химический потенциал цу—очевидно, свойство всего ан-
самбля (так как он включает р,). Как обычно, стандартные
свободные энергии можно связать с константами равновесия.
Чтобы сделать это, рассмотрим вначале взаимные переходы
между такими состояниями i и /, в которых не происходит
связывание или освобождение лиганда. Если представить себе
гипотетическое равновесие системы (или даже только двух со-
стояний, когда другие переходы блокированы), то, исходя из
принципа детального равновесия,
aijPei =anPei	(5-36)
где е обозначает равновесную величину. Кроме того,
= Gt + 7?Пп р? = Ц, = Gj + RT In р' (5.37)
и, следовательно, константа равновесия К,-у равна
К И =	= exp [- (G, - GJ/RT]	(5.38)
Уравнение (5.38) всегда справедливо, так как G и а являются
внутренними свойствами состояний i и / каждой системы. Рас-
смотрим затем вероятность связывания лиганда L при переходе
i-+j. Равновесие между этими состояниями снова приводит
к уравнению (5.36), но теперь мы имеем дело с константой
скорости псевдопервого порядка af/. = a!ycL, где ^—концен-
трация L в растворе. Условием равновесия является
Pz + pL = Gz + RT In pf + pL = Ц, = Gj + RT In p° (5.39)
и поэтому
= az//ct/z = exp {— [G; — (Gz + к)]Ж}	(5.40)
или иначе
4^ =	= ехР 1°' “ (G‘ + Иь)]М} (5.41)
L	/1
Метод диаграмм 79
Здесь константа равновесия «второго порядка» оказыва-
ется инвариантной, т. е. не зависит от Cl, и введена стандарт-
ная свободная энергия (химический потенциал) лиганда L
с помощью соотношения
= Р?, + ЛТ In cL	(5.42)
Термин изменение основной свободной энергии будет исполь-
зован в дальнейшем для обозначения вида изменения свобод-
ной энергии, непосредственно связанного с константами скоро-
сти первого порядка, которые возникли в уравнениях (5.38) и
(5.40). Если же лиганд участвует в процессе при концентрации
cL, тогда необходимо учитывать щ,- Важно отметить, что изме-
нения основной свободной энергии являются не зависящими от
времени внутренними свойствами каждой индивидуальной си-
стемы ансамбля. Изменения стандартной свободной энергии,
которые соответствуют этим изменениям основной свободной
энергии, видны из уравнений (5.38) и (5.41). Если процесс яв-
ляется чисто изомерическим [уравнение (5.38)], то изменения
стандартной и основной свободной энергии оказываются оди-
наковыми.
В то время как изменения основной и стандартной свобод-
ной энергии являются характеристическими свойствами инди-
видуальных макромолекулярных систем вместе с окружающим
их раствором или растворами (и, следовательно, не зависящими
от граничных условий и времени), изменения общей свободной
энергии относятся к ансамблю в целом в произвольный момент
времени t. Если ансамбль имеет структуру, обозначенную
рг, р2, • • •, Рп, то изменения свободной энергии во всем ансам-
бле, вместе с окружающими его растворами [связанные с про-
цессами/—>- /в уравнениях (5.38) и (5.40)] равны
Р/ — Р» = О/ — Gi + RT In (pj/pi)	(5.43)
И/ — (Pi + Pl) = Gj — (Gt + pL) + RT In (ру/р<)	(5.44)
Эти величины будут называться изменениями общей свободной
энергии. Они являются, по существу, изменениями обычной
свободной энергии Гиббса, которая определяет равновесие в
ансамбле вместе с омывающими растворами. Вслед за Хиллом
введем следующую систему обозначений и выбора знака для
изменений основной и общей свободной энергии. Для процесса
будь то изомерическое изменение или изменение, вклю-
чающее связывание и освобождение лиганда, изменения основ-
ной и общей свободной энергии соответственно описываются
выражениями
/\Gij = G'i — G'j> Ap'ij = Pi — n'j (5.45)
80
ГЛАВА 5
(величины в правой части уравнений могут рассматриваться
как уровни основной и общей свободной энергии этих состоя-
ний). Штрихи означают, что, где это необходимо, учтены хи-
мические потенциалы лиганда или субстрата. В таком случае
ао/ап = ехР (ДО////??’) = К ц	(5.46)
Др'/(/) = Аб;/ + /?Пп[^-]	(5.47)
Произведение уравнений, подобных (5.46), в произвольном
цикле % с состояниями, пронумерованными, например, против
часовой стрелки 1,2, ..., т, равно [ср. с уравнением (5.34)]
Пн+/Пн_ = ех^Т = К12К23.. .Кт1 •	(5.48)
Поэтому общая термодинамическая сила цикла Хя равна сумме
последовательных изменений основной свободной энергии в
цикле:
Хк = AGi2 Н- AG23 Ч~ • • • Ч~ XG т\	(5.49)
Так как при суммировании уравнения (5.47) по циклу в произ-
вольный момент времени t члены, содержащие вероятность,
сокращаются, то получим
=аи;2 (0 + АИ;3 (/)+...+ А/т1 (/)	(5.50)
Таким образом, AGC является «движущей силой» перехода
ij цикла. Члены правой части уравнения (5.49) являются инва-
риантными и характеризуют каждую индивидуальную систему
в ансамбле, тогда как соответствующие величины уравнения
(5.50) являются зависящими от времени характеристиками
всего ансамбля.
Сказанное выше позволяет определить направление само-
произвольного перехода. Например, рассмотрим ансамбль из
N систем с произвольной кинетической диаграммой и пусть pi
является вероятностью состояния I в какой-либо момент вре-
мени t. Для любого перехода ij результирующий средний поток
перехода l-+j равен [ср. с уравнением (5.4)]
Л/ (0 = N [<*nPi (0 — аир/ (0]	(5.51)
Из уравнений (5.46) и (5.47) получаем
^£1 =	(5.52)
aiipt (О
При сравнении двух вышеприведенных уравнений видно, что
поток перехода Лу для любого перехода ij всегда имеет тот же
знак, что и разность уровней общей свободной энергии Ац]у
(для любого момента времени t). Если I имеет более высокий
Метод диаграим 81
уровень общей свободной энергии, то результирующий средний
поток будет идти в направлении j (случайные отклонения
возможны в одиночных системах или в малых группах систем).
Следовательно, результирующий положительный поток (или
реакция) всегда направлен от более высокого к более низкому
уровню общей свободной энергии. Для уровней основной сво-
бодной энергии это не так. Из этого также следует, что дисси-
пативная функция для всего ансамбля вместе с омывающими
растворами может быть записана в виде
Ф=ЕЛ/(0А^/(0	(5-53)
а
где суммирование осуществляется по всем линиям диаграммы,
причем каждый член берется положительным.
Сказанное выше приводит к заключению, что при исследо-
вании ионных насосов и аналогичных энергопреобразующих
механизмов во многих случаях бесполезно искать критическую
ступень или ступени ферментативного цикла, в котором действи-
тельно возникает перенос свободной энергии между лигандами.
Как убедительно отмечалось Хиллом и Эйзенбергом [2], пере-
нос свободной энергии между малыми молекулами является
неотделимым свойством полного цикла.
Мы проиллюстрируем возможность использования этих
идей на примере простой модели фототранслокации в хорошо
известной пурпурной мембране галобактерии, рассмотренной
Хиллом [1]. (Более подробно протонный насос в пурпурной
мембране, возбуждаемый светом, будет рассмотрен в гл. 13.)
Эта модель изображена на рис. 5.4. Термодинамическая сила,
соответствующая транспорту лиганда, является отрицательной:
Св > сА, цв > ца, X = р,д — цв < 0. Для начала рассмотрим
только цикл а. Запишем уравнения типа (5.38) или (5.40):
О1з/«31 = exp {[(G, + |1А) — G3]/RT} = К13	(5.54)
a34/a43 = exp [(G3 - GJ/RT] = Кз4	(5-55)
а42/а24 = exp {[G4 — (G2 + рв)]//??’} = К42	(5.56)
а21/а12 = exp [(G2 - GJ/RT] = К21	(5.57)
Перемножая их, получим
_5±. = е(м.А-Ив)//?г = ex/RT =	(5.58)
Как видно из уравнения (5.55), разность основных свободных
энергий состояний 3 и 4 равна G3—G4. Следовательно, состоя-
нию 3 можно приписать энергетический уровень основной сво-
бодной энергии G3, а состоянию 4 — уровень G4. Так как пе-
реход 3->4 можно рассматривать как трансмембранный пере-
нос связанного лиганда, то предположим, что в данном
6 Кенлеи, Эссиг
82
ГЛАВА &
примере величина G3 — G4 отрицательна, и поэтому уровень ос-
новной свободной энергии G3 лежит ниже, возможно значительно-
ниже, чем Gt, как показано на рис. 5.4, в. Отсчитывая последо-
вательно разность основных свободных энергий из уравнений
(5.56), (5.57) и (5.54), мы пройдем один цикл а против часо-
вой стрелки и вынуждены будем приписать состояниям 2 и 1
уровни основной свободной энергии, показанные на рисунке.
При возвращении в состояние 3 молекула лиганда переносится
против разности химических потенциалов цв — Ца, и поэтому
уровень основной свободной энергии возрастает на эту вели-
чину. Этот новый уровень для состояния 3 теперь образует ба-
зовую линию для второго набора уровней, соответствующих
второму циклу, и т. д. Действительно, если бы в этой системе
не было света, то самопроизвольно возник бы обратный цикл
(по часовой стрелке цикла а), давая в среднем результирующий
отрицательный поток Ja, т. е. результирующий поток лиганда
из раствора В в А. Этот поток, возможно, будет очень малым,
так как существенному падению основной свободной энергии,
связанному с переходом 4-»-3, предшествуют переходы вверх
3—>-1, 1-»-2 и 2->4. Должно быть ясно, что такие системы
уровней свободной энергии повторяются неограниченно как
выше, так и ниже уровней, показанных в соответствующих ин-
тервалах, по одному набору для каждого цикла. С точки зре-


а
Рис. 5.4. Модель, объединяющая транспорт лиганда L с поглощением света.
Состояние 3* является возбужденным состоянием.
а — диаграмма; б — циклы; в — уровни основной свободной энергии для макромолекулы
плюс лигаид [1].

Метод диаграмм	83
ния теории вероятности можно сказать, что в такой системе
возникает смещенное одномерное блуждание по уровням сво-
бодной энергии. Вероятности перехода являются константами
скорости первого порядка, и предпочтительным оказывается
смещение в сторону более низких уровней основной свободной
энергии.
Предположим теперь, что существует возбужденное состоя-
ние 3*, возникающее из состояния 3 при поглощении фотона
с энергией hv, при этом оказывается возможным переход из 3*
в 4. Это расширяет кинетическую диаграмму вследствие вклю-
чения циклов b и с, как показано на рис. 5.4, б. Предположим,
далее, что уровень энергии Оз* выше О4, как показано на
рис. 5.4, в. Действительно, согласно схеме энергетических уров-
ней, Оз* — Оз = Nohv (рассматривается поглощение энергии на
один поглощенный эйнштейн2). При облучении ансамбля не-
прерывным излучением с частотой v и достаточной интенсив-
ностью цикл с будет действовать в положительном направле-
нии. Таким образом, при каждом прохождении цикла с моле-
кула L будет переноситься из раствора А в раствор В против
градиента ее химического потенциала за счет части энергии
фотона hv. Использование энергии фотона в цикле b не сопро-
вождается транспортом и поэтому является бесполезным. Цик-
лические потоки 1ь и Jc положительны, a Ja отрицателен.
Так как энергия света расходуется со скоростью Nohv(jb-\-Jc),
то эффективность преобразования энергии света в свободную
энергию равна
т) = 	(5.59)
1 WoAv (Д + Jc)	v '
Ясно, что циклы а и b стремятся уменьшить т].
Когда условия оказываются такими, что т] > О, одномерное
блуждание по уровням свободной энергии (обсуждавшееся
выше только для цикла а) для основного цикла с становится
блужданием, направленным вверх. Однако в условиях экспери-
мента исследуемое стационарное состояние часто оказывается
состоянием с фиксированной силой. В этом случае, если не
учитываются другие пути утечки, Ja + Л = 0, т. е. направлен-
ный по часовой стрелке цикл а действует с той же скоростью,
что и направленный против часовой стрелки цикл с. В этом
случае свободная энергия цв — ца, приобретенная при прохож-
дении цикла с, теряется (одновременно) при прохождении
цикла а.
Для расчета вероятностей стационарных состояний, цикли-
ческих и направленных потоков так же, как и раньше, могут
быть использованы 12 констант скоростей первого порядка, со-
ответствующих рис. 5.4, а. Однако этот метод и вообще нерав-
новесную термодинамику нельзя применять для изучения
6*
84
ГЛАВА 5
зависимости Nohv от уровней основной свободной энергии и кон-
стант скоростей. Сугубо формально поглощение фотонов до
некоторой степени можно рассматривать как связывание ли-
ганда, чтобы продемонстрировать поглощение одного эйнштей-
на в цикле по мере того, как «основная свободная энергия» па-
дает относительно величины Nohv. Но эта аналогия не точна
из-за существенно «нетермодинамического» характера пучка
фотонов с частотой v при некоторой произвольной интенсивно-
сти. Точнее, для переходов 33* в циклах b и с нарушается
принцип детального равновесия, а значит, для отношения
азз*/«з*з не выполняется основное соотношение (5.46). Следо-
вательно, хотя кинетический результат
Пи+/Пи- = 4+/4- (х = &,с)	(5.60)
как обычно, справедлив, Пб+/П6_ не равно eN<,h'llRT и
не равно	Действительно, оба этих отношения зави-
сят от интенсивности пучка, в то время как величины Nohv и X
не зависят от нее. Более того, использование неравновесной
термодинамики, которая подразумевает справедливость соотно-
шения взаимности, в этом случае невозможно, так как для мо-
нохроматического пучка фотонов «термодинамическая сила»
Nohv постоянна, и бессмысленно рассматривать постепенное
приближение к равновесию как к предельному стационарному
состоянию. К тому же, хотя уровни общей свободной энергии
могут определяться, как и раньше, ни уравнение (5.52), ни
уравнение (5.53) нельзя использовать в случае фотонных пе-
реходов. Для этих переходов /ц не обязательно имеет тот же
знак, что и и, таким образом, бессмысленно рассматривать
уровни общей свободной энергии.
5.3.	Стехиометрия и сопряжение
Метод диаграмм позволяет нам лучше понять сущность фено-
менологической стехиометрии Z и степени сопряжения q.
В гл. 4 было показано, что эти величины весьма полезны при
описании работы линейных преобразователей энергии. Теперь
можно объяснить их на примере однонаправленных цикличе-
ских потоков а, Ъ и с для систем, аналогичных описанным
на рис. 5.1. Для этого перепишем уравнения (5.25) и (5.26)
следующим образом:
z; = (а-+ 6)(/> _ 1) + а (еХ^Т - 1) + a (еХ'!*Т - \\еХ^Т-1)
,	(5-61)
/2 = а	- 1) + (а + с) (eXJRT - 1) +
+ а (еХ'11*Т - 1) (еХ^Т - 1) (5.62)
Метод диаграмм 85>
Здесь отброшены верхние индексы оо, имея в виду, что речь
идет только о стационарных состояниях. Величины и Х\
использованы потому, что в общем случае, когда п молей ли-
ганда Li может связываться с белком Е на каждый моль свя-
занного L2, описание потоков должно соответствовать сумми-
рованию сил, действующих в цикле а. Это требование может
привести к неудобному выбору единиц, чего легко избежать,
используя следующие преобразования для перехода к «есте-
ственным» величинам /1 и
Ji = nj\, Xi=~	(5.63,5.64}
Целое число (или отношение целых чисел) п будем называть
«механической стехиометрией» («mechanistic stoichiometry»)*.
Подставляя уравнения (5.63) и (5.64) в (5.61) и (5.62), по-
лучим
J1 = п (а + Ь) (епХ^т - 1) + па (ех^т — 1) +
+ па (епХ^т - 1) (ех^т - 1) (5.65)
/2 = а (enX,IRT - 1) + (а + с) (ех^т - 1) +
+ а (епХ^т - 1) {ex^RT - 1) (5.66)
Заметим, что теперь сила, действующая в цикле а [ср. с урав-
нением (5.23)], равна пХ\ + Х2 и будет обращаться в нуль
либо при Xi=X2 = 0, либо при Х\ = —Х2/п. Здесь также мо-
жет быть использована подстановка, аналогичная уравнению
(5.28). В линейном диапазоне, соответствующем области приме-
нимости уравнений (5.29) и (5.30), уравнения (5.65) и (5.66)
принимают вид
= п2(а + b) Xt/RT + naX^RT	(5.67)
/2 = naXiIRT + (а + с) X^RT	(5.68)
Следовательно, для таких моделей можно записать
Z = п	а =	1	----- (5.69, 5.70)
V а-г с	д/(1 + bl а) (1 + с/а)
Отсюда видно, что степень сопряжения в явном виде зависит
от отношения величин циклических потоков b и с к величине
потока а. Когда b и с равны нулю, мы имеем полное сопряже-
ние, и феноменологическая стехиометрия идентична стехиомет-
рии п. В общем случае 7.=f=n, исключая маловероятное обстоя-
тельство, когда b = с. Но на практике это случается очень
редко. Действительно, из уравнений (5.69) и (5.70) видно, что
* Правильнее было бы назвать это число приведенным стехиометриче-
ским коэффициентом. — Прим, перев.
86
ГЛАВА 5
для модели этого типа при любой данной степени сопряжения q
величина Z/n может принимать значения в диапазоне от \/q
до q. Поэтому при довольно высокой степени сопряжения при-
ближение п будет достаточно точным.
5.4.	Применимость диаграммных методов
Хотя метод диаграмм можно использовать как метод вычисле-
ния, однако главное его достоинство заключается в том, что
с его помощью можно выяснить основные взаимосвязи в поли-
циклической кинетической системе, а также сущность понятий
степени сопряжения и феноменологической стехиометрии. В этом
отношении метод диаграмм аналогичен методу термодинамиче-
ских цепей [4—6]. В обоих методах используется линейная не-
равновесная термодинамика для состояний вблизи равновесия,
причем предполагается, что контурные диаграммы термодина-
мических цепей изоморфны кинетическим диаграммам, обсуж-
давшимся выше. Однако в очень важном отношении контурные
диаграммы находятся по крайней мере на одну ступень дальше
от реального микроскопического мира, чем кинетические диа-
граммы. Поэтому метод термодинамических цепей, возможно,
менее удобен для работы в области молекулярной биологии,
хотя в области электрофизиологии, где проблемы обычно ста-
вятся на более высоком уровне организации, он весьма поле-
зен. Эти два метода служат аналогичным целям и, по-види-
мому, дополняют друг друга.
5.5.	Выводы
1.	Рассмотрен метод диаграмм, разработанный Хиллом и со-
трудниками, — важный альтернативный подход к проблеме пре-
образования свободной энергии, особенно результативный при
обсуждении сложных и/или нелинейных систем. Хорошим при-
мером является фотоцикл бактериородопсина благодаря его
полициклическому характеру.
2.	Для иллюстрации взаимосвязи между диаграммами и
циклами в методе диаграмм используется простой пример (ко-
транспорт двух лигандов мембранным белком). Дается краткое
описание использования парциальных диаграмм, направленных
диаграмм и диаграмм потоков при расчете вероятностей ста-
ционарных состояний, потоков перехода и циклических потоков.
3.	Рассматриваются причины взаимности как свойства
стационарного состояния, особенно при выводе феноменологиче-
ских уравнений неравновесной термодинамики в околоравно-
весной области.
Метод диаграмм 87
4.	Обсуждается использование уровней свободной энергии.
Для интерпретации упрощенной модели бактериородопсина
привлекаются диаграммы уровней свободной энергии. Показа-
но, что существенно «нетермодинамический» характер этой
особой системы исключает возможность использования неравно-
весной термодинамики, в частности соотношений взаимности.
5.	Ошибочно утверждать, что малые молекулы системы об-
мениваются свободной энергией в особой части цикла преоб-
разования. Изменения свободной энергии малых молекул и
фермента неразделимы в индивидуальных переходах. Они мо-
гут быть идентифицированы только при рассмотрении полного
цикла.
6.	Выведена зависимость феноменологической стехиометрии
Z и степени сопряжения q от однонаправленных циклических
потоков для простой модели котранспорта. Показано, что сте-
хиометрия п равна Z, только если q = 1 (за исключением од-
ного маловероятного случая неполного сопряжения). Однако,
когда q близко к единице, Z почти не отличается от п.
7.	Кратко обсуждается взаимосвязь метода диаграмм с ме-
тодом термодинамических цепей.
6
Возможные условия линейности
и симметрии сопряженных процессов
вдали от равновесия
Из сказанного в предыдущих главах видно, что, возможно,
наиболее важной проблемой при теоретическом и эксперимен-
тальном анализе биологических реакций и транспортных про-
цессов является установление взаимозависимости между си-
лами и потоками. Необходимы такие соотношения, с помощью
которых стал бы возможным самосогласованный анализ дан-
ных при разнообразных условиях. Для несопряженных потоков
такими соотношениями являются закон Фика и закон Ома,
а также описание кинетики ферментативных реакций Михаэли-
са — Ментен. Главное их достоинство состоит в легкости, с ко-
торой эти соотношения поддаются обработке. Попытка учесть
влияние сопряженных потоков привела к созданию аппарата
линейной неравновесной термодинамики.
Однако многие исследователи продолжают считать, что для
биологии соотношения Онзагера имеют скорее теоретическую,
чем практическую ценность, так как биологические процессы
обычно протекают вдали от равновесия. В частности, выража-
ются сомнения относительно сложных процессов, включающих
химические реакции. Считается, что даже скорость простой
несопряженной реакции является существенно нелинейной
функцией соответствующей силы, если только термодинамиче-
ское сродство реакции А не удовлетворяет условию А-С RT
[7,19]. Было высказано предположение, что, поскольку для
биологических систем характерны многостадийные процессы и
каждая стадия практически обратима, применение линейных
феноменологических соотношений между скоростью и срод-
ством для каждой стадии возможно даже при условии, что об-
щее сродство А RT [19]. Эта точка зрения не учитывает тот
факт, что в общем случае феноменологические коэффициенты
элементарных реакций зависят от концентраций интермедиатов,
которые могут изменяться с изменением А и, следовательно,
исключать линейность в широком диапазоне.
Тем не менее существует достаточное количество экспери-
ментальных данных в пользу линейной зависимости между по-
токами и силами в широком диапазоне условий при трансэпи-
телиальном активном транспорте Na+ и Н+, а также при окис-
лительном фосфорилировании в митохондриях. Конкретные
Сопряженные процессы вдали от равновесия 89
примеры будут рассмотрены в гл. 8 и 13. Были предприняты
попытки проанализировать также эти процессы с позиций не-
равновесной термодинамики [4]. Эти попытки основаны на
предположении, что наблюдаемая линейность представляет со-
бой термодинамическую линейность, т. е. линейную зависи-
мость потоков от термодинамических сил при плавном прибли-
жении к равновесию. Термодинамическая линейность отличается
от того, что можно назвать кинетической линейностью, т. е.
областью приблизительной линейности, узкой или широкой,
проявляющейся благодаря некоторой, обычно нелинейной, ки-
нетической схеме (примеры рассматриваются в гл. 13). При
наблюдении кинетической линейности для системы вдали от
равновесия может возникнуть мысль о наличии также и термо-
динамической линейности (или квазитермодинамической линей-
ности, которая обсуждается ниже). Априори нельзя с уверен-
ностью утверждать или отрицать такую возможность, но для
некоторых систем это можно экспериментально проверить. Если
термодинамическая линейность действительно присутствует, то
измерения в удаленных от равновесия состояниях отражают
свойства соответствующих околоравновесных состояний, к ко-
торым они могут быть проэкстраполированы, даже когда такие
состояния не реализуются на практике.
Термодинамическая линейность вдали от равновесия может
возникать по различным причинам, не имеющим никакого от-
ношения к внутренней линейности, присущей самой системе.
В настоящей главе мы предлагаем два возможных объяснения
наблюдаемых линейных зависимостей, основанных на рассмот-
рении кинетических моделей, которые умышленно значительно
упрощены. Это рассмотрение приводит к выводу, что возможны
и действительно существуют условия, в которых можно приме-
нять неравновесную термодинамику для анализа линейного по-
ведения в сопряженной системе. Например, исследование эпи-
телиев амфибий позволяет оценить с помощью неповреждаю-
щих методов сродство окислительной реакции, приводящей в
действие активный транспорт, тем самым обходя неопределен-
ности, связанные с компартментацией ткани, стандартными
свободными энергиями и коэффициентами активности.
6.1. Правильные траектории: несопряженные
процессы
Первое объяснение состоит в том, что, вообще говоря, набор
феноменологических уравнений дает неполное описание изу-
чаемых процессов, так как данная термодинамическая сила
может быть введена конечным числом способов. Следовательно,
как подчеркивал Зауер [23], скорость процесса нельзя
90
ГЛАВА 6
предсказать только на основании величины силы, не зная «стан-
дартного состояния». Например, поток растворенного вещества
через мембрану зависит не только от разности его электрохи-
мических потенциалов, но также и от его термодинамического
состояния с обеих сторон мембраны. Таким образом, нельзя
ожидать, что поток незаряженного вещества из области I в об-
ласть II при концентрации с1 = 2 и с11 = 1 будет таким же, как
при с1 =4 и с" = 2, несмотря на то что в обоих случаях без
учета коэффициентов активности разность химических потен-
циалов Др. = RT 1п(с'/с") одинакова. Это относится и к хими-
ческим реакциям, где, например, для реакции первого порядка
S-+P с единственным субстратом и продуктом удвоение кон-
центраций субстрата и продукта будет удваивать скорость ре-
акции, несмотря на одинаковые величины сродства. Это объяс-
нение станет более наглядным, если рассмотреть специальные
примеры, которые показывают, как путем соответствующего
ограничения способа, применяемого для варьирования силы,
можно обеспечить постоянство феноменологических коэффици-
ентов. Рассмотрим сначала несопряженный поток вещества че-
рез мембрану, который может быть проанализирован с по-
мощью уравнения Нернста — Планка (опять пренебрегаем ко-
эффициентами активности)
J = -uC (^^+zF^-)==-uC(^-\	(6.1)
\ С dx 1 dx /	\ dx J	'	’
где u — подвижность, C — концентрация, x — положение внутри
мембраны, z — заряд, ф— электрический потенциал и р— элек-
трохимический потенциал; R, Т и F имеют свои обычные зна-
чения. Для стационарного состояния, когда J всюду постоянно,
.имеем
Дх
I =	<6-2)
о
Следовательно,
JR = X или / = LX	(6.3)
Так как X = —Др является сопряженной силой для /, то полу-
чаем решение в форме уравнений неравновесной термодинамики.
Однако без знания природы феноменологического коэффици-
ента L (или R) это решение особой ценности не представляет.
Оно будет, конечно, отражать природу мембраны, но, кроме
того, будет зависеть и от способа, применяемого для изменения
силы X. Например, если с обеих сторон тонкой гомогенной мем-
браны устанавливается одна и та же концентрация с опреде-
ленного вещества, а поток вызван исключительно разностью
Сопряженные процессы вдали от равновесия
91
электрических потенциалов, то видно, что L остается постоян-
ным при изменении X и равен
L = puc/Дх (Ас = 0)	(6.4)
где р — коэффициент распределения. Если, с другой стороны,
X представляет собой разность химических потенциалов, опре-
деляемую только концентрациями растворенного вещества в
омывающих растворах, то
L — fiuc/'&x (Дф = 0)	(6.5)
где с — логарифмическое среднее концентраций в омывающих
растворах (Дс/Д1пс). В этом случае L, вообще говоря, изме-
няется с изменением Ас, но если выбрана некоторая величина с
и тем самым выбор концентраций ограничен геометрическим
местом точек, удовлетворяющих соотношению Ас = (с)А1пс, то
L снова будет инвариантным к изменению X (рис. 6.1, а). Мы
уже встречались со средней логарифмической концентрацией
в гл. 3, где она играет существенную роль в линеаризации, вве-
денной Кедем и Качальским. Если X изменяется при варьиро-
вании как концентраций во внешнем растворе, так и Дф, то
выражение для L усложняется. Для мембраны с постоянным
электрическим полем принято использовать формулу Гольдма-
на — Ходжкина — Катца:
_ р«сп (- zF Mp/RT) {eXIRT - 1)
Дх (e~*F™*T-\)(XIRT)	1	'
Эта формула необходима просто для поддержания постоянной
величины Z,, так как в принципе для каждой величины X суще-
ствуют два неопределенных параметра, которые при решении
дадут два совместных уравнения. Например, предположим, что
значения L вычисляются для некоторого стационарного состоя-
ния, согласно уравнению (6.3), путем измерения / и X. В этом
случае полезно переписать уравнение (6.6) в виде
Р«сп f — zFk^/RT \	X/RT \	zc
дх	'
Тогда для любой величины X правая часть уравнения (6.6а)
полностью определена. Если выбрана величина Дф, то уравне-
ние (6.6а) дает соответствующую величину с11, в то время как
выражение для Др — необходимое отношение концентраций
с11/с1 и, следовательно, абсолютное значение обеих концентра-
ций. В общем случае априори часто невозможно предсказать
соответствующие ограничения для X, но в таком случае можно
экспериментально определить траекторию изменения X, кото-
рая обеспечит однозначную постоянную величину L, характе-
ризующую изучаемую систему.
•92
ГЛАВА 5
Аналогично для химических реакций, при условии что кине-
тика системы хорошо известна, можно определить условия по-
стоянства L. Например, для упомянутой выше реакции пер-
вого порядка скорость равна
J — k{cs — k-[Cp — k_{cP (eAlRT — 1)
(6-7)
Предположим теперь, что в данном стационарном состоянии
вдали от равновесия для описания реакции мы выбрали соот-
к?
5
а: с1/?, S: fyCf-juiT
Рис. 6.1. Траектории постоянного L (правильные траектории).
а — концентрации растворенного вещества, обеспечивающие линейную зависимость по-
тока от разности химических потенциалов на однородной мембране. Для любой данной
средней логарифмической концентрации вещества в омывающих растворах (с) поддер-
жание концентраций и в растворах с обеих сторон мембраны иа указанной
траектории гарантирует выполнение соотношения J — LX, где L определяется уравне-
нием (6.5); б — концентрации реагента и продукта, обеспечивающие линейность скоро-
сти для реакции первого порядка, описываемой уравнением (6.7). Для любых данных
величии ftp и L —RTL поддержание и ср на указанной траектории гарантирует
выполнение соотношения J — LA. (Легко обобщается на более сложные случая.)
Сопряженные процессы вдали от равновесия
93
ношение
J = LA = L'A/RT	(6.8)
где L' = RTL, и приступили к вычислению L' (путем измере-
ния J и Л). Тогда
к,с,-г(^,-)	(М)
[ср. с уравнением (6.6а); заметим, что если и заменяется коэф-
фициентом диффузии RTu = D, то L становится равным L'\.
Видно, что в других стационарных состояниях, соответствую-
щих различным величинам А, та же самая величина L', со-
гласно уравнению (6.8), будет продолжать описывать скорость
реакции при условии соответствующего выбора концентраций.
При решении двух совместных уравнений снова получаются
два неопределенных параметра. В этом случае уравнение (6.9)
определяет при любой данной величине А, а выражение
для А определяет отношение концентраций cP/cs- Таким обра-
зом, этот способ обеспечивает постоянство L путем ограничения
изменений сР и cs соответствующей траекторией. (Согласно
рис. 6.1,6, вдоль этой траектории величина Cs + сР не остается
постоянной.) Очевидно, что, когда при этих ограничениях ре-
акция достигает равновесия, т. е. А стремится к нулю, k-iCP
стремится к величине L'. Легко показать, что этот способ с рав-
ным успехом может быть использован для более сложных реак-
ций. За исключением двух концентраций (субстрата и продук-
та), все остальные концентрации могут быть установлены про-
извольно, а концентрации субстрата и продукта, которые при
любой данной величине А должны удовлетворять уравнению
(6.8), обеспечивая постоянное значение L', определяются также,
как и раньше. Например, рассмотрим реакцию, включающую
много субстратов и продуктов:
+ v2S2 + • • • + V/S/ -> V/+iP/+i + ... +
где v — стехиометрические коэффициенты. Тогда J = kYn —
s
— k_la — LA, где л — произведение концентраций субстратов
р	s
... и л — соответствующее произведение концентраций
1 2	р
продуктов, т. е. наблюдается полная аналогия с уравнениями
(6.7)—(6.9). Траектории в пространстве состояний (как, на-
пример, траектории на рис. 6.1), которые по какой-либо при-
чине приводят к термодинамической линейности, в дальнейшем
мы будем называть «правильными траекториями».
94
ГЛАВА &
6.2. Правильные траектории: сопряженные
процессы
Хотя, как может показаться, искусственность средств, приме-
ненных выше для варьирования сил, делает некоторые приме-
ры непригодными для практических экспериментов, их рас-
смотрение облегчает понимание трактовки сопряженных про-
цессов, представленной ниже. Важно понять, что мы не ищем
алгоритм, обеспечивающий линейность, а скорее показываем»
что линейность возможна и что, когда она возникает по какой-
либо причине, это может существенно помочь эксперимента-
тору. Например, как будет показано ниже, даже кинетическая
линейность может сопровождаться приближенным выполне-
нием соотношения взаимности.
Априори зависимость между потоками и силами для двух
сопряженных процессов может быть записана как
/[ = Лц.¥1 + L12X2’ У2 “ ^21-^1 “Ь ^22-^2	(6.10)
где требуется только, чтобы 1) при равновесии оба потока были
равны нулю и 2) каждый поток зависел от обеих сил. До тех
пор пока у нас нет ограничений для варьирования Х} и Х2г
нельзя ожидать ни того, что потоки будут однозначно опреде-
лены для любых данных величин сил, ни того, что любой коэф-
фициент L будет постоянным. Мы можем расширить примене-
ние понятий, обсуждавшихся выше для несопряженных потоков,
используя метод, описанный в гл. 5. Рассмотренные в ней ки-
нетические модели обладают значительной общностью. Они
дают описание системы где-то на уровне между молекулярным
и феноменологическим и фактически заключают в себе оба
этих описания. Рис. 6.2 представляет собой гипотетическую мо-
дель, в которой метаболизм АТФ может приводить к транс-
порту ионов натрия через мембрану против градиентов элек-
трохимического потенциала. (Эта простая модель приведена
только для того, чтобы облегчить понимание рассматриваемых
общих принципов.) В отличие от случая полных наблюдаемых
потоков скорость результирующего потока вдоль какого-либо
компонента цикла будет определяться единым составным коэф-
фициентом скорости. Из уравнений (5.12) и (5.18) — (5.24) сле-
дует, что стационарные циклические потоки можно записать
в виде 1
.	J0 = a(e^«+*’)/«r—1), Jb = b(eXilKT ~ 1)	(6.11,6.12)
Jc = c(ex^T- 1)	(6.13)
где Xi и Х2 представляют собой —Ациа и А соответственно.
Величины а, b и с являются функциями индивидуальных кон-
стант скоростей и внешних концентраций и, следовательно, из-
Сопряженные процессы вдали от равновесия
95
I (внутренний ойъем клвткй)
П (внешняя среЭа)
а
Рис. 6.2. Иллюстративная модель активного транспорта натрия.
а— гипотетическая схема сопряженного транспорта натрия и метаболизма АТФ; Е—
фермент, подобный Na, К-АТФазе, осуществляющий транспорт. Для простоты не рас-
сматривается связанный циклический поток калия, хотя это необходимо в более реали-
стической модели. Показано шесть состояний фермента. При соединении с Na фермент
может взаимодействовать с внутриклеточным АТФ и переносить Na против градиента
электрохимического потенциала из внутриклеточной среды наружу, одновременно пре-
вращая АТФ в АДФ и Фн. Предполагается, что Фи внутри клетки постоянно и не
учитывается в явном виде. В этой модели рассматриваются две причины нарушения
сопряжения, а именно обратимый поток натрия без образования АТФ и расщепление
АТФ в отсутствие транспорта. В мочевом пузыре жабы, хотя было показано наличие
активного обратного транспорта [5, 6, 29], обратной утечки внутрь клетки, не зависящей
от метаболизма, не обнаружено [2]. Таким образом, постоянная скорости перехода из
состояния 3 в состояние 2 может быть очень низкой; б — диаграммы, соответствующие
рис. а, показывают возможные переходы между состояниями. Из-за быстрых переходов
между конформациями свободного фермента состояния 1 н Г объединяются, приводя к
сокращенной диаграмме справа. Стрелки показывают направление перехода, соответ-
ствующего связыванию; в — циклы соответствуют сокращенной диаграмме на рис. б.
Цикл а представляет собой полное сопряжение между транспортом и метаболизмом,
в то время как циклы b и с являются источниками нарушения сопряжения. Все три
цикла протекают конкурентно.
96
ГЛАВА в
меняются при изменении сил. Будет показано, что эти уравне-
ния аналогичны уравнению (6.7). (В общем случае электро-
статические эффекты влияют не только на термодинамические
силы, но и на константы скоростей. Усложнение этой модели
путем включения электростатических эффектов в явном виде
будет рассмотрено ниже.)
Далекие от равновесия стационарные потоки, связанные
с Xi и Х2, в этом случае равны2
71 — h + Ja ~ b (eXllRT — 1) + а(е(Х1+Хг)/ет — 1)	(6.14)
/2 = Ja + J с — а (e^Xt+X1}IRT — 1) 4- с (eX2<RT — 1)	(6.15)
Как обычно, приведенные выше соотношения могут быть пре-
образованы:
Jj = (Ь + a) (eXllRT — 1) + a (eX1!RT — 1) + a (ex'IRr — 1) (eX2lRT — 1)
(6.16)
/2 = a (ex'/RT - 1) + (а + с) (ex>iRT - 1) + a (ex'IRT - 1) (ex'<RT - 1)
(6.17)
Рассмотрим стандартное стационарное состояние, далекое
от равновесия и характеризуемое данными величинами Х\ и Х2.
Мы будем исследовать существование вблизи этого состояния
правильных траекторий, вдоль которых и Х2 изменяются
таким образом, что приводят к линейной зависимости потоков
от сил3. По аналогии с проведенным выше обсуждением несо-
пряженного транспорта вещества и химической реакции запи-
шем циклические потоки в форме уравнений неравновесной тер-
модинамики путем введения соответствующих феноменологиче-
ских коэффициентов La, Lb и Lc. Вначале для потока натрия
запишем уравнение, используемое для вычисления Lb-
Jb^LbX^LbXilRT	(6.18)
Потребуем теперь, чтобы все значения Х) находились на пра-
вильной траектории, определяемой согласно методу, описанному
выше, так, чтобы коэффициент Lb оставался постоянным. Воз-
вращаясь затем к циклическому потоку Ja, запишем уравнение,
используемое для вычисления La’
Ja = La (Х1 + X2) = La (Xj + X2)!RT	(6.19)
Потребуем снова, чтобы все значения находились на пра-
вильной траектории, уже заданной так, чтобы коэффициент Lb
поддерживался постоянным [уравнение (6.18)]. Теперь оста-
ются два неопределенных параметра в Х2, которые подбира-
ются таким образом, чтобы обеспечить постоянство коэффи-
циента La- Изменения Х\ и Х2 должны ограничиваться доста-
точно малым диапазоном, чтобы значения La и Lb существенно
Сопряженные процессы вдали от равновесия
97
не отклонялись от значений в стандартном стационарном со-
стоянии.
Наконец, рассмотрим уравнение, используемое для вычисле-
ния Lc\
Jc = LcX2 = L'cX2IRT	(6.20)
Априори, конечно, нельзя предполагать, что правильная траек-
тория для изменения Х2, обеспечивающая постоянство Lc в
уравнении (6.20), всегда будет соответствовать правильной
траектории, обеспечивающей постоянство La в уравнении (6.19).
Однако, если это произойдет, получим
/1 = {ь'ь + Ад) X\/RT + LaX^RT (правильные траектории) (6.21)
I2 = LaX\lRT + {b'a + Lc) X2/RT (правильные траектории) (6.22)
Линейная зависимость Л и J2 от Xi, наблюдаемая в экспери-
ментальных исследованиях активного транспорта в эпителии,
наводит на мысль о возможном соответствии правильных
траекторий, которое не является автоматическим, так как
транспорт и метаболизм в этих тканях, по-видимому, не пол-
ностью сопряжены [4]. Во всяком случае, эти уравнения будут
хорошо аппроксимировать высокосопряженные системы, не-
смотря на то что правильная траектория для Х2 только одна,
поскольку при возрастании степени сопряжения циклические
потоки h и Jc будут играть все более и более второстепенную
роль. Необходимо отметить, что уравнения (6.21) и (6.22) со-
ответствуют околоравновесному диапазону уравнений (6.14) и
(6.15), где a~L', b ~ L'b и с ~ L'c. По аналогии с уравне-
нием (6.10) уравнения (6.21) и (6.22) можно переписать более
компактно, используя черточку для обозначения того, что рас-
сматриваются изменения только вдоль правильных траекторий:
Л == LjjX] + L12X2, J2 — ^21X1 + L2aX2 (6.23, 6.24)
Здесь L означают постоянные коэффициенты, причем каждый
поток является теперь однозначной функцией сил. Как можно
видеть из уравнений (6.21) и (6.22), L12 = L2t.
Возможности этого метода можно оценить путем более де-
тального анализа модели на рис. 6.2. Как показано в гл. 5, яв-
ная форма кинетических коэффициентов в уравнениях (6.11) —
(6.13) имеет вид х == jVIIx_Sx/S (к=а, Ь, с), где N — (большое)
число молекул, осуществляющих транспорт в мембране, Пх_ —
произведение констант скоростей в цикле % в отрицательном
(по часовой стрелке) направлении, Sx — сумма произведений
констант скоростей процессов, входящих в цикл х, и S — сумма
всех возможных произведений констант скоростей процессов,
входящих в данное состояние. В рассматриваемой модели все
7 Кенлеи, Эссиг
98
ГЛАВА 6
константы скорости ац (где а,-, относятся к переходу j)
являются истинными константами скорости первого порядка,
за исключением а12 = сiaa;2, а13 = с»Х3, а24 = сктФа24 и “35 =
“скдфаз5’ где аи—константы скорости второго порядка. В этих
обозначениях коэффициент с равен
С =	(а42а54а3эа2з) “12 Стп- + * ^САДФС”а =
4 cNa “12 '
= (^г)(ех‘ж +у)скдфСиа	(6.25)
\ 2 /	\	а12 7
Подставляя уравнения (6.13) и (6.20) в уравнение (6.25), по-
лучим ограничивающие условия для правильной траектории:
С1 сп=_____________Ь___________(6 26)
АДФ Na (С/2){ех'1*т + У) ех^т-\	{	’
Аналогично для циклов а и b находим
а ~ "2" (а21а42а54а35а1з) САДФСЫа =	) САДФсЫа (6.27)
~ “2“ (а21а32а1з) (а45а53 "Ь а54а42 "Ь а42а5з) CNa =	) CNa (6.28)
Следовательно, используя уравнения (6.11) и (6.19), а также
(6.12) и (6.18), соответственно получим
С1 СИ __£L_E1±£2&
сАДФсНа	е(Х,+Хг)/ДГ_ j
с„____£L _Ж_
Na~ (В/2) Ида-1
(6.29)
(6.30)
Для любого данного стандартного стационарного состояния
L'a, L'b и L' полностью определены и описываются уравне-
ниями (6.18) — (6.20). В принципе, зная все константы скоро-
сти, можно рассчитать величины А, В, С, у и S и, следователь-
но, как показано выше, можно вычислить концентрации с”а и
садф> связанные с отклонениями от стандартного стационар-
ного состояния вдоль правильных траекторий. В таком случае
возникает вопрос, согласуются ли концентрации, вычисленные
из уравнений (6.26), (6.29) и (6.30), с теми, которые необхо-
димы дл’я циклов а, b и с, чтобы одновременно следовать вдоль
правильных траекторий. В частности, величины произведения
САДФс”а, вычисленные из уравнений (6.26) и (6.29), т. е. из
циклов с и а, должны совпадать при изменении сил. Область
совпадения была проверена вблизи стандартного стационарного
XjRT
Рис. 6.3. Зависимости поток —сила для модели на рис. 6.2.
Величины кинетических коэффициентов выбраны в относительных пропорциях А « 102,
В в 0,12, С « 52 с тем, чтобы величина Q равнялась приблизительно 0,8 (точнее, q ~
— 0,82). Использованные величины других параметров следующие: —20R.T,	—0,1М,
сддфв1мМ» V = 0,005. Пунктирные линии построены на основании расчетов по фе-
номенологическим уравнениям [уравнения (6.21) н (6.22)] с использованием величии фе-
номенологических коэффициентов для стандартного стационарного состояния, получен-
ных нз уравнений (6.26), (6.29) и (6.30). Сплошные линии построены на основании
кинетических уравнений [уравнения (6.14) н (6.15)] с использованием величин а, b и с,
рассчитанных из уравнений (6.27), (6.28) и (6.25) соответственно. При расчете а, b и с
для стационарных состояний, возмущенных относительно стандартного стационарного
состояния, вычислялась нз уравнения (6.30), а величина сддфс^а выбиралась
между величинами, полученными из уравнений (6.26) и (6.29). Не было сделано по-
пытки оптимизировать такой выбор в отношении линейности, хотя в принципе это
можно было бы сделать. В этом расчете мы считали 2 постоянной при изменении Х|,
так как изменения тех из 55 членов 2, которые обладают концентрационной зависи-
мостью, имеют тенденцию к компенсации в пределах достаточно малого диапазона.
В более широком диапазоне необходимо рассмотрение изменений в 2 в явном виде.
В той степени, в которой 2 не постоянна, это не влияет на отношение между величи-
нами сддфс^а, рассчитанными из уравнений (6.26) и (6.29). и поэтому не влияет на
отклонение этого отношения от единицы, которое приводит к отклонению сплошной
линии от пунктирной. Здесь не учтено в явном виде влияние электрических полей иа
константы скорости (см. текст). Однако общий диапазон исследованных возмущений Xi
соответствует ±125 мВ и сокращенный диапазон (между пунктирными вертикальными
линиями) составляет ±40 мВ. Сокращенный диапазон ближе соответствует современной
экспериментальной практике, чем полный диапазон.
100
ГЛАВА 6
состояния с фиксированным потоком (Xi=0), когда значение
Х2 было выбрано так, чтобы получить величину 20RT (около
12—13 ккал/моль АТФ) [8]. В стандартном стационарном
состоянии были выбраны следующие концентрации: cJ/a=O,l М,
Сддф=1 мМ. Значение у было определено равным 0,005 на
том основании, что кажущееся сродство натриевого насоса для
внешнего натрия приблизительно в 160 раз меньше, чем для
внутреннего [9]. Вычисления были сделаны для нескольких
степеней сопряжения q системы. Действительно, если величины
произведения с^Дфс”а, рассчитанные из уравнений (6.26) и
(6.29), полностью совпадают, то вычисленные из феноменоло-
гических уравнений [уравнения (6.21) и (6.22)] потоки будут
равны потокам, вычисленным из кинетических уравнений
[уравнения (6.14) и (6.15)]. Если этого совпадения нет, то
потоки будут различаться. Рис. 6.3 показывает, что результат,
полученный для q = 0,82, близок к результату, найденному экс-
периментально [4]. Пунктирные и сплошные линии получаются
соответственно из феноменологических и кинетических уравне-
ний. Отклонения от линейности увеличиваются при q = 0,7 и
несколько уменьшаются при q = 0,9. Диапазон линейности для
всех испытанных величин q был существенно уже вблизи ста-
ционарного состояния с фиксированной силой (Д = 0).
Для высокосопряженных систем рассмотренный выше слу-
чай по существу сводится к случаю единственного несопряжен-
ного потока. Очевидно, для полностью сопряженных процессов
линейные зависимости от парных сил неизбежно связаны с ли-
нейными зависимостями от непарных сил, как это можно уви-
деть, если рассмотреть только цикл а, предполагая, что циклы
b и с не играют существенной роли. Можно ожидать, что при
уменьшении степени сопряжения отклонения от линейности не
будут слишком сильными. Для анализа степени, до которой
полнота сопряжения может быть понижена без возникновения
заметной нелинейности, необходимы дальнейшие исследования.
Однако ясно, что вблизи состояния с фиксированной силой
(Xi ~— Хъ) можно ожидать возникновения линейности при q,
очень близком к единице.
6.3.	Точка перегиба в многомерном пространстве
Ротшильд и сотр. [20] показали существование в определенных
условиях точки перегиба (ТП) в многомерном пространстве
сил и потоков для системы ферментативных реакций, другими
словами, существование стационарного состояния, вблизи кото-
рого в значительном диапазоне возникают линейные зависимо-
сти между стационарными потоками и связанными с ними си-
лами. Этот диапазон кинетической линейности может быть
Сопряженные процессы вдали от равновесия 101
очень далеко от равновесия. Для проверки любого данного со-
стояния с кинетикой первого или псевдопервого порядка на
возможность наличия ТП может быть использован набор до-
статочных условий. Как отмечали Ротшильд и сотрудники, эти
условия не являются слишком жесткими. Было обнаружено
также, что хотя, вообще говоря, в ТП взаимность отсутствует,
она может существовать в особых случаях, наиболее очевид-
ным из которых является случай совпадения ТП с равновесием.
Примером более интересной возможности существования взаим-
ности вдали от равновесия служит модель четырех состояний
двух сопряженных процессов, как, например, облегченный об-
мен двух подобных ионов через мембрану: при особом (сим-
метричном) распределении констант скоростей, которое допол-
нительно накладывает жесткие ограничения на концентрации
реагентов, два потока в ТП становятся равными. Было пока-
зано, что в этом случае выполняется соотношение взаимности.
Ниже мы обсудим это наблюдение. А сейчас необходимо отме-
тить, что с точки зрения диаграммы Хилла для такой системы
равенство потоков в данном стационарном состоянии в неко-
тором смысле моделирует полное сопряжение, так как резуль-
тирующая «утечка» потока перехода должна быть равной нулю.
Доказательство существования ТП лежит вне рамок настоя-
щего обсуждения. Цель этого раздела — показать, что в ТП,
как бы она ни была удалена от равновесия, все полностью со-
пряженные системы проявляют взаимность, причем в высоко-
сопряженных системах, которые часто встречаются в биологии,
приближение к взаимности оказывается довольно точным [3].
Это уникальное свойство ТП, поскольку хорошо установлено,
что как линейность, так и взаимность химических реакций даже
для полностью сопряженных систем неизменно ограничены об-
ластью, близкой к состоянию равновесия. Таким образом, мат-
рица Якоби, характеризующая отклонения от стационарного
состояния вдали от равновесия, не симметрична [1, 15, 17, 18],
и соответственно добавочное производство энтропии [10, 16, 24]
не является обязательно положительным. Однако, как уже от-
мечалось выше, в некоторых системах можно наблюдать от-
клонения от этого правила или специально создать условия,
вызывающие их. Это оказывается возможным благодаря неод-
нозначной зависимости данной термодинамической силы от за-
данного произвольного набора параметров состояния. В этих
случаях отклонения ограничены правильными траекториями,
полученными путем соответствующего подбора сил.
Как и раньше, рассмотрим ансамбль из N одинаковых мо-
лекул фермента или молекулярных комплексов, не обладающий
кооперативностью (в большинстве систем, представляющих ин-
терес, эти молекулы являются мембранными белками). Этот
макромолекулярный ансамбль связывает вместе М процессов
102
ГЛАВА 6
(реакций, векторных потоков). Диаграмма Хилла для таких
систем может принимать различные формы, но в общем случае
она состоит из набора циклов и субциклов, соответствующих
циклическим потокам, которые связывают различные индиви-
дуальные процессы во всех возможных комбинациях. Например,
диаграмма, изображенная на рис. 6.4, где А1 = 3, служит при-
мером, демонстрирующим основные свойства таких диаграмм.
Обозначая циклический поток в цикле х через 7И (х = а,Ь, с),
запишем стационарные термодинамические потоки в следующем
виде (см. гл. 5):
Il — Ia~\~ Ib~\~ If’
12 — Ia~t~Ib~l~Ic~l~Ig>
1з — la + Ic + Ih (6.31)
Если приведенные стехиометрические отношения в каждом
цикле (механизм реакции известен), в котором возникает со-
пряжение, одинаковы, что является простейшим случаем, то из
уравнений (6.31) получаем
Д = а (е<-х'+^+х^т — 1) + b (е<х‘+х^т — 1) + f (ех^т — 1)	(6.32)
а также соответствующие выражения для J2 и J3, где Xi —
термодинамическая сила, связанная с А и т. д. Здесь кинети-
ческий коэффициент х перед экспоненциальным членом, свя-
занный с циклом х, включает множитель 2V/S (обычно запи-
санный в явном виде), где X — сумма направленных диаграмм
всех состояний. Каждый х (т. е. а,Ь, , h) является, конечно,
функцией концентраций, а также констант скоростей. Деталь-
ная структура этих коэффициентов для данной модели будет
рассмотрена ниже.
Пренебрегая электрическими эффектами, для начала пред-
положим, что система удовлетворяет критериям существования
Рис. 6.4. Диаграмма Хилла и компоненты циклов для характерной сопряжен-
ной мембранной системы с тремя потоками.
Фермент, осуществляющий транспорт, имеет восемь состояний с переходами между
ними, показанными на рисунке. Стационарные термодинамические потоки (Л, А, Л)
относятся к указанным процессам. J\ и h представляют собой транспорт, Li и L2-
лигаиды, связывающиеся или освобождающиеся на внутренней (if или наружной (о)
поверхности мембраны. Показаны только направления переходов, сопровождающихся
связыванием лигандов. А представляет собой реакцию, включающую присоединение
субстрата (S) и освобождение продукта (Р) на одной поверхности (обычно внутренней).
Термодинамические силы (Х\, Х2, Х3) показаны под циклами, в которых оии действуют.
Считается, что циклы положительны при прохождении против часовой стрелки.
Сопряженные процессы вдали от равновесия ЮЗ
ТП Ротшильда и сотр. [20], а именно: 1) каждый реагент, кон-
центрация (активность) которого может быть изменена, влияет
на скорости перехода только одного оставшегося состояния;
2) кинетика перехода, включающая данный реагент, имеет
фиксированный порядок по отношению к этому реагенту; 3) для
каждой возможной комбинации реагентов, чьи концентрации
изменяются, имеется по крайней мере одна направленная диа-
грамма, содержащая только эту комбинацию и не содержащая
других. Первый критерий сразу же исключает из рассмотрения
автокаталитические системы, подобные хорошо известному
брюсселятору [10,16], но для многих биологических преобра-
зователей энергии эти критерии вполне могут выполняться. Обоб-
щая уравнения (6.31), мы для удобства сконцентрируем свое
внимание на i-м и j-м сопряженных процессах, которые будем
считать связанными стехиометрией п (для простоты эти про-
цессы считаются мономолекулярными). Разложим эти два
потока как функции сопряженных им сил в ряд Тейлора относи-
тельно некоторого стандартного стационарного состояния, пред-
полагая, что все другие силы фиксированны. Для членов пер-
вого порядка это дает конечные разности:
ы‘ = \4<7п Е + Е 4W,+ -
L ие(и); J	L «е{и)| J
(6.33)
«/-[•Я7 Е ЧМ, + [^7 £ Ч“'+"'
хе={и}у J	L и <= {и} j J
где {х}, и {х}/ — наборы циклов, связанных с Ji и соответ-
ственно, а коэффициенты [ ] вычислены для стандартного со-
стояния. Ротшильд и сотрудники показали, что разложение
потоков в ряд Тейлора относительно ТП дает выражения, ли-
нейные относительно In (с,) и 1п(с/) вплоть до третьего порядка,
если с, и с/ — концентрации реагентов. Таким образом, если
уравнения (6.33) представляют собой разложение относительно
ТП с Xi(Ci) и Xj(cj), зависящими от с,- и С/, тогда как все
остальные концентрации сохраняют величины, определяемые
точкой перегиба, то они соответствуют разложению потоков по
Ротшильду и линейны в той же самой степени приближения4.
С нашей точки зрения, замечательной особенностью уравнений,
подобных уравнениям (6.33), является то, что соответствующие
сопряженные силы входят в эти уравнения в явном виде. От-
метим, что стандартное стационарное состояние должно быть
точкой перегиба только по отношению к с, и с/.
Рассмотрим два перекрестных коэффициента в уравнениях
(6.33). Изучение рис. 6.4 и уравнений (6.31) и (6.32) показы-
вает, что Xi действует во всех циклах множества {х},- и,
104
ГЛАВА 6
следовательно, X/ непосредственно влияет на /г- (как часть одной
или более сил, термодинамически сопряженных с циклическими
потоками) через подмножество циклов {х},/, в которых дей-
ствуют как Xi, так и X/. Аналогично Х,: непосредственно влияет
на /, (в упомянутом выше смысле) через подмножество циклов
{х}/< <= {х};-, где, очевидно, {х}/, = {х}//. Последствия этого
типа симметрии в произвольном стационарном состоянии уже
обсуждались [11]. Покажем теперь, что в ТП для любого
цикла х в подмножестве {х},/ справедливо следующее выра-
жение:
^-n[x(e№+x/+2X^r- 1]) =
dXj L х	л/
=	1)]	(6.34)
где Xk (k =И= i, /) обозначает любую (постоянную) силу, которая
может действовать в цикле. Чтобы доказать это, необходимо
только показать, что в ТП
п (ди/dXj) = дк/dXi	(6.35)
Как обсуждалось ранее, х определяется выражением х =
==УПи_2и/2, где Пи_ — отрицательное (по часовой стрелке) про-
изведение констант скоростей в цикле х и — сумма «придат-
ков», питающих данный цикл, аналогичная сумме направленных
диаграмм, питающих данное состояние. Так как X, и X/ дей-
ствуют в цикле х, согласно критерию 1 существования ТП, то
должна быть постоянной. Что касается Пи_, то рассмотрим
три случая.
Случай 1. Обе переменные с, и с,- являются концентрациями
субстрата, т. е. они определяют стадии связывания (в положи-
тельном направлении прохождения цикла) в некоторой точке
цикла. Тогда Пи_ — константа. Так как система удовлетворяет
критериям 2 и 3, то 2 имеет вид [20]
^ = f + flcf+f2cl + fl2c'}cj	(6.36)
где f—константы. Уравнение (6.36) можно переписать в виде
S = f + f'ieaXi!RT + f2exilRT + f'{2enXilRTexilRT (6.37)
Отсюда
n (дк/dXj) = - (ум/RT) [(f2Cj + MM = - (n%/RT) (a;/S) (6.38)
(ди/дХ.) = - (пн/RT) [(frf + /12c?C/)/S] = —(пн/RT) (<r./S)	(6.39)
где Oi и ст/ представляют собой вклады в S членов, включающих
Ct и Cj соответственно. Но в ТП с> и с/ связаны соотношениями
<7 =	и =	и> следовательно, ficnl=f2c} и
Сопряженные процессы вдали от равновесия 105
f = fi2cfcj [20]. Отсюда легко видеть, что в ТП
ст. = сту = S/2	(6.40)
и из уравнения (6.35) следует, что
п (ди/дХ,) = (дк/dXi) = - п-л^Т	(6.41)
Случай 2. Обе переменные с/ и с;- являются концентрациями
продуктов, т. е. внешними концентрациями в несвязывакицих
стадиях (в положительном направлении прохождения цикла)
в некоторой точке цикла. Тогда Пи- = П‘_с?Су, где П*_ — кон-
станта. Поделив числитель и знаменатель выражения для %
на cfCj и действуя далее так же, как и выше, снова находим,
что уравнение (6.41) справедливо в ТП.
Случай 3. Только одна из переменных с,- и с;- является кон-
центрацией продукта в упомянутом выше смысле. Если это
концентрация с>, то мы имеем Пя- = П* _с", где снова П* _ —
константа. Поделив числитель и знаменатель выражения для %
на с?, действуя как и раньше и применяя ограничения для ТП,
получаем уравнение (6.41).
Если J; и Jj являются полностью сопряженными, то {и}у
оказывается единственным набором циклов, который включает
члены с перекрестными коэффициентами уравнений (6.33).
В этом случае матрица Якоби для системы симметрична с точ-
ностью, соответствующей степени приближения к линейности.
Если Ji и J/ являются неполностью, но тем не менее высоко-
сопряженными, то члены, входящие в {х}(/, доминируют, и
симметричность матрицы Якоби остается полезным приближе-
нием, точность которого зависит от степени сопряжения. Это
иллюстрируется в следующем разделе с помощью простой мо-
дели, которая включает заряженный лиганд и, следовательно,
требует рассмотрения электрических сил. Ограничения для лю-
бой подобной модели заключаются в том, что электрические
коэффициенты должны входить таким образом, чтобы удовлет-
ворять трем критериям существования ТП.
6.4.	Линейность и симметрия в модели
электрогенного ионного насоса
На рис. 6.5 показана простая модель активного ионного тран-
спорта, свойства которой совместимы с существованием ТП.
Очевидно, что это расширенный вариант моделей, данных на
рис. 5.1 или 6.2, который может представлять собой, например,
протонный насос, приводимый в действие АТФ, с п = 3 или 4
(в зависимости от системы) при постоянном уровне Фн. Так
как аналогичные модели подробно обсуждались, то мы опишем
106
ГЛАВА В
только соответствующие электрохимические характеристики..
Рассмотрим сначала полную диаграмму в левой части рис. 6.5.
Мы принимаем, что для переходов, включающих заряженный
лиганд, скорость освобождения лиганда зависит главным об-
разом от разности потенциалов на границе раздела фаз ф£—
— Фг и Фо— Фо» в т0 вРемя как связывание является в основ-
ном диффузионно-контролируемым процессом. Это удобное и
логичное упрощающее приближение, поскольку константа ско-
рости освобождения зависит главным образом от глубины по-
тенциальной ямы свободной энергии связывания, которую L+
должен преодолеть, чтобы вернуться в раствор [11]. Более того,
мы предполагаем, что связывание и освобождение происходят
на поверхности или очень близко к поверхности мембраны, так
что потенциалы на границе раздела фаз, определяющиеся свой-
ствами поверхностей, по существу, можно считать постоянными.
Величины потенциалов на границе раздела фаз не играют роли
в последующем обсуждении; для простоты будем считать их
Внутренняя фаза
1	1'	2	5	4	5
Рис. 6.5. Детальная модель электрогенного катионного насоса.
Одновалентный катион L+ связывается на внутренней или наружной стороне фермен-
та, осуществляющего транспорт и несущего заряд —п. Предполагается, что связывание
происходит через последовательные стадии с образованием короткоживущих промежу-
точных продуктов, которые нет необходимости уточнять [11]. Показаны шесть состояний
фермента: каждое состояние может представлять собой «объединение» нескольких со-
стояний, между которыми достаточно быстро устанавливается равновесие [И]. Связыва-
ние субстрата S и освобождение продукта Р происходят на внутренней поверхности.
н %- электрические потенциалы во внутренней и наружной объемных фазах соот-
ветственно, а и Фо~ потенциалы в плоскостях, близких к внутренней и наружной
поверхностям мембраны, которые, как показано, отвечают положениям центров связы-
вания. 7, н 7S —потоки, соответствующие транспорту и реакциям для рассматриваемого
процесса, a Xi н Х2 — соответствующие нм силы.
Сопряженные процессы вдали от равновесия
107
равными и противоположными, так что ф'— ф' = ф£—	=
Тогда получаем следующие соотношения для констант скоро-
стей а:
а12 = а12С"+’	<6-42)
где а*9 и а*,3— константы скоростей (п + 1)-порядка, и
<х21 = а21(0)гд^/ЛГ, азг = а3г(0)гд^ВДГ (6.43)
где F — постоянная Фарадея, Дфь = ф£ — ф£ = ф' — ф0, а а21 (0) и
а31,(0) — константы скорости в отсутствие соответствующей раз-
ности потенциалов. Если диаграмма сокращена, как показано
на рис. 6.5, исходя из предположения, что между состояниями 1
и Г быстро устанавливается равновесие, можно опустить ин-
декс со штрихом в уравнениях (6.42) и (6.43), но теперь нельзя
считать а*2 и а*3 независимыми от электростатических эффек-
тов, так как они оказываются функциями ащ и ап:
„о „
» __ и12аП
12 ajjz + aj/j
» __ а?зап'
13 ап, + аи
(6.44)
где а^2 и а^3—исходные величины а*2 и а*,3 до сокращения
диаграммы. Рассматривая равновесие перехода 11', мы имеем
а1И(А^ = Г аЧ'(°> 1 е-п WRT
«1'1 (дф) L аг1 (°) J
Следовательно,
а;2 = а»2аи (0) е* WW/D, aj3 = <x»3an, (□)/£»	(6.46)
где	О = а11/(0) + ап(0)е'1Д’1’^7’	(6.47)
Легко показать, что эти константы скорости совместимы с де-
тальным равновесием циклов а и Ь в условиях общего равно-
весия.
Если рассчитать кинетические коэффициенты и (и = а, Ь, с)
для этой модели, то получим
а = (A/D'S) срс^+> b — (B/D'S) с"+
с = (C/D2) срсп+ (enXllRT 4- у) = с' (епХ^т + у) (6.48)
Lo
где А, В, С и у — постоянные. Величина у, как мы видели ра-
нее, представляет особый интерес; она равна
108
ГЛАВА 6
и, таким образом, зависит от отношения внешней и внутренней
констант связывания лиганда L+. Из уравнений (6.42) и (6.46)
видно, что выражение для ai2 включает множитель
cn+ en&*FlRr/D, а выражение для оцз— множитель с"+/^- Такие
Ч	Lo
множители в направленных диаграммах никогда не встреча-
ются в каких-либо других комбинациях. Легко также показать,
что направленные диаграммы не содержат произведения ai2«i3,
и, следовательно, произведение этих двух множителей не мо-
жет появиться в S. Если в качестве переменных параметров мы
выберем сп+ и либо с8, либо с₽, то критерий 3 существования
Li
точек перегиба окажется выполненным, и мы сможем написать,
например,
2 = f + f^+ en^v/D + f2cs + fl2cscn+en^FIRTID (6.50)
4
где f = f' + f"cn+ID и f2 = f2 + f2cn+/D. Это наводит на мысль,
^0	Lo
что, до тех пор пока выполняется критерий 3, вероятность из-
менения en^F/RT больше, чем сп+. Чтобы проверить это, рас-
Ч
смотрим знаменатель Z)S в уравнениях (6.48). Для удобства
обозначим его через S' и после перегруппировки получим тре-
буемую билинейную форму:
S'5=Z)S = </>+ $ienWlRT + ф2с8 + ф12с8еп^р^т (6.51)
Легко видеть, что знаменатели в уравнениях циклических
потоков (6.48) должны быть линейными функциями en^F,Rr. Та-
ким образом, мы показали, что для этой модели точка пере-
гиба существует, когда одним из переменных параметров явля-
ется Аф и когда учитываются соображения симметрии, приве-
денные выше. Фактически величина	играет роль
концентрации, но необходимо отметить, что S' не содержит более
комбинацию cn,en^FlRT
Ч
Уравнения потоков для этой модели имеют следующий вид:
J\ — na(e( nx.+xiiiRT j) _|_	(епх,/«г_ 1)
J2 = а (е(«х.ч-хо/лг - 1) + с' (enXiiRT + у) (ex^RT - 1)	(6.52)
Эти уравнения удобнее снова преобразовать к виду
= п (а + b) (enXllRT — 1) + па (eX2lRT — 1) +
+ па (enX,lRT — 1) {eXilRT — 1)
J2 = a (enXilRT —l) + [a+c'(l +у)] (ex^RT - 1) +
+ (a + c') (enXi!RT - l)(eXilRT - 1) (6.53)
Сопряженные процессы вдали от равновесия
109
Приводя уравнения (6.53), полученные вблизи равновесия,
к линейной форме, найдем для степени сопряжения выражение
’ = л/ЖШ" - л/(' + -Ж + Ж)
и для феноменологической стехиометрии:
/№,/№),, л/ (‘+^)	,655)
Z— V (5/2/5Л)%2 —П \	! С(1+у) )	1
где ср можно заменить на Кс$, причем К является константой
равновесия реакции, если cs поддерживать постоянной. При
нарушении линейности равновесные величины q и Z не имеют
более своего обычного значения, но в некотором смысле они
продолжают характеризовать систему. Например, мы уже ви-
дели, что в линейной области вблизи равновесия состояние
с фиксированной силой (стационарное состояние с /1=0) удов-
летворяет соотношению —X\IX2 = qlZ. Если мы обозначим
приведенную феноменологическую стехиометрию как £ = Z/n
[из уравнений (6.54) и (6.55) следует, что q 1 /q], то
для состояния с фиксированной силой это соотношение при-
нимает вид — пХ\/Х2 — q/t,. Для сравнения, в нелинейном диа-
пазоне то же соотношение для состояния с фиксированной си-
лой, согласно уравнениям (6.52), (6.54) и (6.55), имеет вид
(6.56)
(6.57)
для высо-
значение
е-«х,/«г_1 q
еХ2/ЛГ_] — £
Отсюда следует, что если Х2 не слишком мало, то
-nXjX2=l+(RT/X2)ln(q®
Таким образом, в состоянии с фиксированной силой
косопряженных систем и больших величин Х2
— пХ\/Х2~ 1. Этот результат будет использован ниже. В со-
стоянии с фиксированным потоком (Л) = 0) соотношение
/1//2 = qZ остается справедливым при любой величине Х2.
Вдали от равновесия q все еще может определяться левой
частью уравнения (6.54). Для вычисления q в ТП уравнения
(6.33) проще всего записать в следующей форме, впервые вве-
денной Реттенбергом [21] и с тех пор широко используемой
другими авторами [28]:
/1 = ЕцХ]Л12Х2 +/Сь J2 = /-21Х1 + /-22Х2 + К2 (6.58)
Здесь /G и /С2“ константы, т. е. K\—j\ —Ц\Хй\ —Ь\2Х2 и
/С2	/2— /-21%? — /-22Х?, где А7?, Х2 и /?, /2 обозначают величины
но
ГЛАВА 6
сил и потоков в исходной точке перегиба. (Дальнейшее об-
суждение смысла Ki и К2 дается в приложении к этой главе.)
Тогда мы имеем q-m — Li2L2JLuL22. Вычисляя коэффициен-
ты, как обсуждалось выше, получим
= (n2aj'2RT)	+ 1) + (n2bj2RT) (e^lRT + 1)
Ll2 = (na/2RT)(.e^X°l+X^RT + 1) + (nbl2RT)(enX°^T - 1)
T21 = (na/2RT) (e("xi+x2)/«r + 1) +
+ (пс'/2КТ)(епХ°^г - Y)(eX“//?r - 1)
L& = (a/2RT) (e(nX°+x2)/RT _|_ 1) 4.
+ (c'/2RT) (enX^Rr + у) (еХУКГ +1) (6.59)
Ясно, что g?rn не может превышать 1. Уравнение (6.59) по-
зволяет найти приближенную зависимость между отношениями
перекрестных коэффициентов L2\/Li2 и q. Для высокосопряжен-
ного насоса, действующего при физиологических условиях,
Х2 RT и — nX°i RT. Заметим, что ограничения на b/а и
с'/а могут быть установлены, используя уравнение (6.54). На-
пример, если вблизи равновесия q — 0,95, то эти величины мо-
гут изменяться (в противоположных направлениях) между 0,1
и нулем. Для большой величины </тп значение с'/а должно
достигать более низкого предела, если только у не слишком
мало. Оказывается, что если аз2 <С а.31 и а23	«21 (а это во-
обще должно быть в случае высокосопряженных систем), то
для изменения Дф и с$ в ТП получим приближенное выра-
жение
- В^С <6-60)
[ср. с уравнением (6.51)]. Аналогичное выражение с несколько
меньшей степенью приближения будет справедливым, если вме-
сто Дф изменяется сп
Из этого следует, что в данной модели
вклады «несопряженности» в Li2 и L2i [уравнения (6.59], по
существу, равны. Было показано, что для параметров, приве-
денных в табл. 6.1, это справедливо в широком диапазоне кон-
центраций. Даже когда а23 и а32 увеличивались в 107 раз, так
что равновесная величина q при Ср = 10~3 М (которая обычно
гораздо ниже, чем дтп) падала до ~10~3, отношение L2i/Ll2
отличалось от единицы только на 0,6%. При более высокой
степени сопряжения, даже если </тп может падать значительно
ниже единицы, отношение L2i/Li2 незначительно отличается от
Сопряженные процессы вдали от равновесия
111
Таблица 6.1. Произвольный самосогласованный набор параметров,
используемых при моделировании ионного насоса. Константы скорости
первого порядка ai;- даны в с-1. Объяснение см. в тексте
Параметр	Значение	Параметр	Значение
«щ (0)	ю12	* а24	20
аи/(0)	5- 109	И42	0,2
«21 (0)	5- 102	а35	2
«з1 (0)	5- 102	«53	20
а?2	102	“45	50
“13	102	«54	0,1
«23	ю~и	К	10s
«32	2-10“9	V	5- 10“3
			— 130 мВ
Вблизи равновесия q = 0,816 при ср = 10 4 М и ^ = 0,976 при ср = 10 3 М.
единицы. (ТП практически нечувствительна к изменению кон-
центраций лиганда или реагента.) Необходимо отметить, что
могут возникнуть обстоятельства, когда qm ~ 1, даже если
цикл а играет незначительную роль. В этом случае для состоя-
ний с фиксированной силой и фиксированным потоком могут
быть получены результаты, несовместимые с полным сопря-
жением.
6.5.	Правильные траектории в окрестности точки
перегиба в многомерном пространстве
Выше было показано, что, по крайней мере в случае одной
простой модели, ионный насос может содержать ТП, когда од-
ним из переменных параметров является разность электриче-
ских потенциалов на мембране. Было также показано, что в
окрестности ТП высокосопряженная система будет характери-
зоваться приближением к взаимности, так что для рассматри-
ваемой модели «отношение взаимности» Л21Д-12, по существу,
равно единице, даже если равновесная величина q равна всего
лишь IO-3. Нет оснований полагать, что эти результаты не
имеют общего характера, и, действительно, исследования на
митохондриях [21, 22, 27, 28] подтверждают это.
Стаки [27] показал на митохондриях, что изменение потен-
циала фосфата (Лфосф) при поддержании потенциала
112
ГЛАВА 6
кислорода (Акисл) постоянным дает линейную зависимость по-
ток— сила, так что деление отрезка, отсекаемого на оси ординат
прямой (зависимость /ф0Сф от Хфосф), на наклон прямой (зависи-
мость /кисл ОТ Хфосф) приводит К ПрЭВИЛЬНОЙ Оценке Хкисл с точ-
ностью несколько процентов. Уравнения (6.58) можно приме-
нять и в этом случае, поэтому необходимо, чтобы не только
<7тп было достаточно велико (что, очевидно, выполняется), но
и должна быть пренебрежимо мала. Последнее условие
выполняется автоматически, когда ТП оказывается достаточно
близкой к стационарному состоянию с фиксированной силой.
Если это состояние находится в линейном диапазоне, то из
уравнений (6.58) получим следующее соотношение:
-пХ^Х^пЬ^ + пКЛЦ (Х2	(6.61)
Так как этот результат справедлив для величин Х2, близких
к Х2> то можно сделать вывод, что для высокосопряженных
систем по аналогии с уравнением (6.59) nLl2/Ln ~1 и по ана-
логии с уравнением (6.57) nKi/LnX2(=^ Ki/Ll2X2) должно
быть пренебрежимо мало. Эти соотношения являются кинети-
ческой основой описанного выше экспериментального метода;
он широко используется для определения сродства реакции,
обеспечивающей энергией активный транспорт натрия в эпи-
телиальных мембранах, в которых обнаружен широкий диапа-
зон линейности (см. гл. 8). Хотя в настоящее время невозмож-
на независимая оценка движущей силы транспорта в эпителии,
известно, что натриевый насос действует вблизи стационарного
состояния с фиксированной силой. Вполне возможно, что мак-
симальная эффективность достигается в пределах линейного
диапазона, хотя вдали от равновесия q-m не приводит к про-
стому соотношению для максимальной эффективности (если
только К2 по какой-либо причине не оказывается пренебре-
жимо малой). Однако в ограниченных пределах вблизи ста-
ционарного состояния с фиксированной силой кинетическая ли-
нейность, по существу, моделирует термодинамическую линей-
ность в ТП. При определении сродства реакции система ведет
себя так, как если бы она находилась на правильной траек-
тории.
6.6.	Заключительные замечания
Ранее мы обсуждали особый случай, рассмотренный Ротшиль-
дом и сотр. [20], в связи с моделью четырех состояний — ста-
ционарное состояние, в котором в ТП оба потока равны. В при-
нятых нами обозначениях это описывается условием Ji = nj2,
которое, если его применить к уравнениям (6.53), приводит
Сопряженные процессы вдали от равновесия 113
к следующему соотношению между силами:
1,(^1 _ 1) =	+ v)(e^Rr _ ,)	(6.62)
Отбрасывая тривиальные решения, легко видеть, что для вы-
полнения этого соотношения X°i и Х2 должны иметь один и
тот же знак; это будет означать, что система находится в не-
физиологических условиях. Для Х2 Jg> RT, пХ°RT и у по-
рядка 1 или меньше из уравнений (6.59) и (6.62) следует, что
7-12 = Агь
Важно понять, что данная ТП не является единственной:
могут существовать другие условия, когда Ji и Л одновременно
проходят через точку перегиба при изменении Xi и неизмен-
ном Х2 и наоборот. В этом случае взаимность отсутствует. Сле-
довательно, хотя линейное поведение обнаружено при сугубо
физиологических условиях в эксперименте in vitro и поэтому,
как предполагается, может проявляться также и in vivo, воз-
никает вопрос: имеется ли основание предполагать, что такое
поведение отражает наличие ТП? Ответ можно получить из
анализа устойчивости. Исследование уравнений (6.46) и (6.47)
показывает, что даже в этой простой модели константа скоро-
сти отличается от константы первого порядка на множитель
еп^р/цт_ Анализ устойчивости выходит за рамки этой главы,
но возможно, что именно в приближенной линейности и взаим-
ности, присущей высокосопряженному преобразователю энер-
гии в ТП, заключен определенный физиологический смысл, так
как в этом случае выполняются условия локальной асимптоти-
ческой устойчивости [16,24]. Хотя крайне маловероятно, что
все, что можно извлечь из точной линейности и взаимности,
например минимум диссипации энергии и критерий эволюции
[10], можно применить к описанной здесь системе, тем не ме-
нее существование приблизительной линейности и взаимности
может автоматически обеспечить правильную траекторию и,
следовательно, даст возможность получить из эксперимента та-
кую информацию, которую в настоящее время, по крайней мере
для эпителиальных тканей, невозможно получить каким-либо
другим способом.
В принципе рассмотренные выше методы в тех случаях, ко-
гда их можно применять, позволяют охарактеризовать систему
в широком диапазоне разнообразных условий. Если система
является достаточно изученной, так что известно, как изменя-
ются Х[ и Х2 вдоль правильных траекторий, то из количествен-
ного определения феноменологических коэффициентов без
оценки эффективной степени сопряжения в стандартном состоя-
нии можно извлечь дополнительную пользу. С другой стороны,
часто невозможно желаемым способом изменять обе силы не-
зависимо, особенно в биологических системах, где некоторые
8 Кеплен, Эсснг
114
ГЛАВА 5
из сил нельзя изменить экспериментально с помощью непо-
вреждающих методов. По этой причине важно отметить, что
если одна из сил, скажем Xi, может быть изменена экспери-
ментально вдоль правильной траектории [в соответствии с
уравнениями (6.23) и (6.24)], тогда как Х2 остается постоян-
ной, то зависимость потоков от Х\ обеспечивает полное термо-
динамическое описание системы. Это можно увидеть, учиты-
вая, что вдоль правильной траектории наклоны равны:
тдхх)х2=гп и	= L2i- Принимая во внимание прин-
цип взаимности Онзагера, получим Li2 — L2i, так что (71[Х| =
= 0])x2/(5/2/^i)x2= Х2, и наконец (/2	= 0])уД2 =~Ь22. Напри-
мер, на рис. 6.3 точки, в которых кривые, вычисленные из кине-
тических уравнений (сплошные линии), пересекают ординаты при
X\/RT =— 5, 0 и 5, близки к точкам, полученным эксперимен-
тально. Построение прямых линий через эти точки для Ц и J2
методом наименьших квадратов позволяет оценить Х2, которая
превышает истинную величину только на 4 %. На практике
этот вид анализа применялся в экспериментах на коже живота
лягушки и мочевого пузыря жабы, т. е. на тканях, которые
осуществляют интенсивный трансэпителиальный активный
транспорт натрия за счет окислительного метаболизма. Деталь-
ное обсуждение этих данных будет дано в гл. 8.
В .заключение остановимся на интересном замечании, ко-
ротко затронутом во введении, что правильные траектории мо-
гут быть обусловлены высокой линейностью, присущей системе
(в термодинамическом смысле) в пределах некоторого физио-
логического диапазона. Вероятно, это может достигаться бла-
годаря очень общей форме «термодинамического демпфирова-
ния», обусловленного ферментами [25], которые не включены
в данную здесь кинетическую схему. Однако из анализа мо-
дели типа приведенной на рис. 6.2 можно показать, что вообще,
если только степень сопряжения не является предельно малой,
максимальная эффективность системы резко уменьшается, ко-
гда условия ее функционирования выходят за пределы линей-
ной области [27]. Это наводит на мысль, что механизмы, про-
являющие внутреннюю, или «встроенную», линейность, имеют
энергетическое преимущество и вполне могли бы возникать
в процессе эволюции.
6.7.	Выводы
1.	Стандартные феноменологические уравнения неравновесной
термодинамики дают неполное описание исследуемых процес-
сов, поскольку данная термодинамическая сила может быть
введена конечным числом способов. Поэтому в общем случае
как несопряженные, так и сопряженные потоки являются ли-
Сопряженные процессы вдали от равновесия 115
нейными функциями сил и подчиняются соотношениям взаим-
ности Онзагера только в непосредственной близости к состоя-
нию равновесия.
2.	Показано, что в случае несопряженного транспорта и
химических реакций силы могут быть ограничены «правиль-
ными траекториями», обеспечивающими линейное поведение.
С этой целью проводится различие между «термодинамической»
линейностью, которая подразумевает линейную зависимость
потоков ст термодинамических сил, плавно приближающих
к равновесию, и «кинетической» линейностью, которая не обя-
зательно характеризуется этим свойством. Правильные траек-
тории связаны с термодинамической линейностью.
3.	Если силы двух сопряженных процессов могут быть од-
новременно ограничены правильными траекториями, так что
каждый поток будет линейной функцией каждой силы, то пе-
рекрестные феноменологические коэффициенты вдали от рав-
новесия будут равны. Природа таких правильных траекторий
исследуется на примере простой модели активного транспорта
натрия.
4.	Показано, что при специальном выборе параметров со-
стояния сопряженные ферментативные процессы могут содер-
жать точку перегиба (ТП) в многомерном пространстве термо-
динамических сил и потоков. Исследованы условия существо-
вания взаимности в области кинетической линейности вблизи
такого стандартного состояния, которое может находиться вдали
от равновесия. Путем исследования связанных диаграмм Хилла
показано, что все циклы, в которых действует данная пара сил,
дают соответствующую пару симметричных членов в матрице
Якоби, характеризующей возмущения около этого стационар-
ного состояния. Соотношение взаимности или приближенная
взаимность будет выполняться в той степени, в которой эти
циклы доминируют, т. е. в той степени, в которой эта система
оказывается высокосопряженной.
5.	Так как асимптотическая устойчивость выполняется при
локальной симметрии, то линейное поведение во многих высо-
косопряженных биологических энергопреобразующих системах
может быть следствием функционирования системы в точках
перегиба в многомерном пространстве или вблизи него. В этом
случае можно использовать некоторые приложения линейной
неравновесной термодинамики, т. е. кинетическая линейность
до некоторой степени может имитировать термодинамическую
линейность и приводить к правильной траектории.
6.	Свойства ТП иллюстрируются с помощью простой кине-
тической модели активного транспорта ионов, в которой в яв-
ном виде учитываются электрические силы. Для этой модели
показано, что даже несопряженные циклы дают симметричные
члены в матрице Якоби в предельно широком диапазоне.
8*
116
ГЛАВА 6
7.	В тех случаях, когда это возможно, использование пра-
вильных траекторий позволяет дать полное термодинамическое
описание системы, даже если экспериментально может контро-
лироваться только одна из двух сил, в то время как другая
остается постоянной.
8.	Было высказано предположение, что «встроенная» ли-
нейность может быть даже энергетически выгодной и возникать
в процессе эволюции.
Приложение: линейные феноменологические
коэффициенты и равновесные однонаправленные
циклические потоки; поведение биохимических
систем вблизи состояния с фиксированной силой
Как было отмечено Хиллом [12, 13], феноменологические
коэффициенты в линейных уравнениях поток — сила для про-
извольной диаграммы, описывающей систему в стационарном
состоянии вблизи равновесия, физически интерпретируются про-
сто: коэффициенты Ьц, по существу, являются суммами равно-
весных однонаправленных циклических потоков. Те циклы, ко-
торые включают процесс I, дают вклад в La, в то время как
циклы, которые включают оба процесса i и /, дают вклад в Ьц.
Например, в общем случае из уравнений (5.12), (5.14) и (5.34)
получаем (как было показано ранее)
4=4+ - 4-=Л- (ЛЖ- -1) = 4- (e^/RT - 0 (6-п1)
Вблизи равновесия это дает
(б-п2>
Так как два равновесных однонаправленных циклических по-
тока для цикла х равны, т. е.
=	=	(6.ПЗ)
то 7£± обозначает любой из двух однонаправленных потоков.
Таким образом, учитывая уравнение (5.24), уравнения (5.67)
и (5.68) можно записать в виде
А =	+ 'У Х№Т +	(6.П4)
72 = <±Х1//?7’ + (Га± + /:±)Х2//?Т	(6.П5)
Следовательно,
£и = п2 «± + fb±)!RT, £12 = nfa±/RT
=	+	(6.П6)
Сопряженные процессы вдали от равновесия
117
Для нас гораздо интересней ситуация вблизи состояния
с фиксированной силой. Так как биохимические системы явля-
ются обычно высокосопряженными, то будет существовать один
доминирующий цикл, который действует вблизи равновесия
в стационарном состоянии с фиксированной силой, в то время
как оставшиеся циклы «утечки» действуют очень далеко от
равновесия. Чтобы рассмотреть стационарное состояние в этой
области с той же самой точки зрения, мы начнем с уравнений
(6.14) и (6.15), причем будем учитывать наличие стехиометрии
путем замены Л на JJn и X! на пХх [ср. с уравнениями (5.63)
и (5.64)]. Эти уравнения непосредственно преобразуются в
уравнения (6.52). Мы имеем
J1 — tljь -р tlJа, J2==Ja~\~^c	(6.П7, 6.П8}
Вводя однонаправленные циклические потоки и учитывая, что
цикл а протекает вблизи равновесия, получим
/, = П (4+ - /ь-) + nfa±Xa/RT	(6.П9)
h =	+ (Jc+ - Jc~)	(6.ПЮ)
В этом случае, несмотря на то что значение Ха(= пХ\ + Х2)
очень мало, значение Хь(=^пХ<:) становится большим и отри-
цательным, в то время как ХС(=Х2) велико и положительно.
Из сравнения с уравнением (6.П1) видно, что в данном случае
Jb+ и могут быть незначительными, и уравнения (6.П9)
и (6.П10) принимают вид
J, = - njb- + nJ^XjRT, J2 = Jea±XalRr + Jc+ (6.П11, 6.П12)
Так как циклы b и с действуют фактически однонаправленно,
то силы, соответствующие этим циклам, больше не появляются
в уравнениях потоков. Уравнения (6.ПИ) и (6.П12) можно
переписать в следующем виде:
J, = nfa±XjRT + nJea±X2/RT + п (- J6_)	(6.П13)
J2=nJea±XJRT + Jea±X2lRT + Jc+	(6.П14)
Уравнения (6.П13) и (6.П14) описывают стационарное пове-
дение системы вблизи состояния, удаленного от равновесия,
в котором Ха = 0: для высокосопряженных систем это состоя-
ние будет близким к состоянию с фиксированной силой. Необ-
ходимо отметить, что эти уравнения имеют форму уравнений
потоков Роттенберга [уравнения (6.58)] и, следовательно, дают
физическую интерпретацию констант К, введенных Роттенбер-
гом. Очевидно, что диапазон применимости уравнений (6.П13)
и (6.П14) должен быть наиболее широким для случая совпа-
дения единственной ТП с состоянием, в котором Ха = 0.
118
ГЛАВА 6
Несмотря на высокую степень сопряжения, третий член правой
части уравнения (6.П13) может быть незначительным, как это
обсуждалось ранее в отношении уравнений (6.57) и (6.61). По-
этому для всех экспериментов, в которых Х2 поддерживается
постоянной, уравнения (6.П13) и (6.П14) полезно записать
в виде
J, = nzJea±XJRT + nl^X^RT	(6.П15)
/ RTJ j. \
J2=nJea±X1/RT+Jea± h+ x2!RT (6.П16)
\	2a- /
причем кажущаяся степень сопряжения в этих условиях равна
<7каж = —7= , 1 ,	/ PG — константа) (6.П17)
V1 + («П+/V.±)
В заключение отметим, что при исследовании Na, К-АТФазы,
по-видимому, получены данньие о том, что вблизи так называе-
мого потенциала реверсии, т. е. разности электрических потен-
циалов, при которой прекращается гидролиз АТФ, потоки ионов
более или менее не зависят от напряжения (см., например,
[14]). С точки зрения настоящего рассмотрения, если система
является высокосопряженной ш вблизи состояния с фиксирован-
ной силой /2 ~ О, то из уравнений (6.П11) и (6.П12) получим
Ji = _ra(J6_+Jc+)	(6.П18)
Тогда, действительно, в пераом приближении Ji оказывается
не зависящим от напряжения однонаправленным потоком. Этот
вывод может быть распространен на модели типа показанных
на рис. 6.4.
7
Энергетика активного транспорта:
теория
Вследствие неадекватности стандартных методов, используемых
для анализа энергетики процессов активного транспорта, в этой
главе будет рассмотрен еще один подход, основанный на об-
щих принципах, обсуждавшихся ранее. Для удобства мы ис-
пользуем простую модель транспортной системы, которая под-
дается математическому описанию; возможность применения
этих принципов к более реальным моделям станет очевидной.
Наш подход будет основываться на концепции правильных
траекторий, изложенной в гл. 6, так как во многих случаях
могут быть подобраны условия эксперимента, соответствующие
таким траекториям. Экспериментальные доказательства, под-
тверждающие эту точку зрения, будут представлены в следую-
щей главе.
7.1.	Предпосылки
Многие исследователи применяли методы неравновесной термо-
динамики для анализа активного транспорта. Жардецки и
Снелл [10] сделали общий теоретический анализ транспорта и
различных метаболических процессов, используя понятия не-
равновесной термодинамики, без привлечения требований ли-
нейности и выполнения соотношений взаимности Онзагера. Ке-
дем [12] дала формальное описание активного транспорта,
основанное на неравновесной термодинамике, предполагая спра-
ведливость соотношений Онзагера, и показала, как этот фор-
мальный подход позволяет связать различные типы измерений
в системе двух потоков. Хошико и Линдлей [9] подчеркнули
важность ясного функционального определения активного
транспорта и распространили методы Кедем и Качальского
[14] на активный транспорт односолевой и биионной систем.
Эти методы базировались на оценке необходимых феноменоло-
гических коэффициентов (10 или 15 коэффициентов в зависи-
мости от условий). Гейнц [6], основываясь на работе Рапо-
порта [19], проанализировал с позиций неравновесной термо-
динамики сопряженный с натрием транспорт аминокислот. Для
того чтобы провести различие между сопряженными и
120
ГЛАВА 7
несопряженными процессами, была введена квазихимическая си-
стема обозначений, которая трактовала все несопряженные
процессы как стехиометрическую химическую реакцию, ослож-
ненную утечками. Эта точка зрения была недавно подробно
изложена в монографии Гейнца [7].
Мы предпочли ограничиться системами активного транспор-
та только одного иона, не сопряженного с потоками других
веществ [4]. Теоретической основой нашей работы является
развитие идей, предложенных Кедем. В противоположность Ра-
попорту и Гейнцу мы трактуем сопряжение между транспортом
и метаболизмом в самой общей форме, допуская возможность
того, что сопряжение может быть внутренним свойством про-
цесса.
7.2.	Модель активного транспорта одного иона
Анализ энергетики активного транспорта необходимо начать
с простой модели. В коже лягушки и мочевом пузыре жабы,
по-видимому, имеется только один значимый процесс активного
транспорта, а именно транспорт натрия и,следовательно, только
один значимый выходной процесс термодинамической системы.
Несмотря на значительную сложность биохимических тканей,
мы предположим, что можно выделить один метаболический
процесс, который «приводит в движение» активный транспорт.
Такая модель представлена на рис. 7.1. Здесь единственный
процесс — метаболизм субстрата — связан с единственным вы-
ходным процессом — транспортом натрия. В этой модели, очень
похожей на общую схему, изображенную на рис. 4.1, реак-
ция превращения М и N в Р и Q создает свободную энер-
гию, которая обеспечивает активный транспорт через мемб-
рану.
Рассмотрим упрощенную структуру системы (рис. 7.2). Про-
цесс активного транспорта происходит в прямоугольной камере.
В соответствии с многочисленными экспериментальными дан-
ными (хотя это не обязательно для нашего анализа) мы пред-
ставим наружную или апикальную мембрану как простой пас-
сивный барьер, через который натрий движется по градиенту
своего электрохимического потенциала. (В данном случае мы
не рассматриваем системы с котранспортом Na и Cl в апикаль-
ной мембране.) На внутренней или базолатеральной поверхно-
сти имеется механизм, ответственный за активный транспорт
натрия, так называемый натриевый насос. Поскольку система
активного транспорта переносит только ионы натрия, в то вре-
мя как ткань в целом реадсорбирует хлористый натрий, должен
существовать путь, по которому может двигаться хлор. Этот
путь представлен в виде простого пассивного канала, парад-
Энергетика активного транспорта: теория	121
лельного пути активного транспорта, который, по-видимому,
доступен для всех ионов в омывающих растворах.
Так как мы считаем активный транспорт процессом с двумя
потоками, то необходимо рассмотреть два соответствующих
уравнения потоков: одно для транспорта катиона и другое для
метаболизма. (Хотя мы имеем в виду в первую очередь транс-
порт натрия, в принципе это описание применимо для любого
катиона и в связи с этим легко модифицируется для случая
активного транспорта любого растворенного вещества.) Мы
могли бы непосредственно приступить к написанию феномено-
логических уравнений для системы на рис. 7.2, рассматривая
ткань как черный ящик. Однако в некоторых целях полезно
связать свойства этой ткани со свойствами ее элементов.
ВыхоЗ
mM+riN pP+qQ
ВхоЗ
Рис. 7.1. Схематическое представление биологического преобразователя энер-
гии, который может использовать метаболическую энергию для совершения
электроосмотической работы.
Направление реакции внизу по часовой стрелке показывает, что превращение М и
в Р н Q происходит спонтанно, в то время как направленная в противоположную сто-
рону верхняя стрелка показывает, что транспорт натрия протекает против градиента
У его электрохимического потенциала за счет его сопряжения с метаболизмом.
Рис. 7.2. Модель изучаемой составной транспортной системы, включающей
пассивный барьер для входа натрия на апикальной поверхности, натриевый
насос для базолатеральиой поверхности и параллельный пассивный канал,
доступный для всех ионов в омывающих растворах.
122
ГЛАВА 7
7.2.1.	Насос
Рассмотрим сначала работу простого «насоса», который осуще-
ствляет активный транспорт единственного катиона, не сопря-
женный с потоками других веществ (рис. 7.3). Предположим,
что имеется единственная реакция, обеспечивающая активный
транспорт метаболической энергией. Обозначая скорость актив-
ного транспорта через 7“ и скорость метаболизма через Jr,
получим следующие уравнения для активного транспорта:
Ja+ = La+X+ + La+rA, Jr = La+rX+ + LarA (7.1, 7.2)
где Л+ — отрицательная разность электрохимических потенциа-
лов катиона и А — сродство метаболической реакции, обеспе-
чивающей транспорт. В этих условиях сродство эквивалентно
_-+______________._____Рис. 7.3. Схема натриевого (катион-
Jfa-I	—-—		—tZ*	ного) насоса.
изменению отрицательной свободной энергии Гиббса для реак-
ции, обеспечивающей энергией транспорт и пока еще не опре-
деленной биохимически. Феноменологические коэффициенты La
предполагаются постоянными во всем диапазоне применяемых
сил. J+ является, конечно, функцией отрицательной разности
электрохимических потенциалов Х+, и, кроме того, она должна
быть также функцией сродства А в той степени, в которой
активный транспорт сопряжен с метаболизмом. Jr является,
очевидно, функцией А, и, кроме того, она должна быть также
функцией Х+ в той степени, в которой реакция связана с транс-
портом. По аналогии с изменением транспортных процессов
в неживых системах [1, 16] предполагается справедливость со-
отношения взаимности Онзагера, т. е. перекрестные коэффи-
циенты в обоих уравнениях принимаются равными. (Это пред-
положение подразумевает, что Х+ и А ограничиваются правиль-
ными траекториями.)
Часто уравнения (7.1) и (7.2) удобно переписать через ко-
эффициенты сопротивления:
X+ = 7?V+ + ^+r/r, A = Ra+rJa+ + RarJr (7.3, 7.4)
где феноменологические /^-коэффициенты связаны с L-коэффи-
циентами простой матрицей преобразования.
Энергетика активного транспорта: теория 123
Поскольку имеется только одна реакция, обеспечивающая
энергией транспорт, скорости потребления и производства ме-
таболитов связаны стехиометрически. Поэтому для описания
скорости метаболизма можно взять любой из этих процессов,
если только сродство выражено соответствующим образом (см.
приложение к этой главе). Таким образом, мы можем считать,
например, что Jr является скоростью потребления О2. В этом
случае, так как JrA представляет собой скорость производства
свободной энергии, сродство А может быть выражено как от-
рицательное изменение свободной энергии метаболической ре-
акции на моль потребляемого О2. В случае активного транс-
порта вход JrA должен быть положительным, в то время как
выход —J+X+ может быть любого знака. В определении по-
лярности реакции имеется некоторая степень произвола. Мы
примем, что Jr и А больше нуля для Х+ = 0. Тогда
£“г > 0, a R+r < 0, и в этом случае сопряжение будет положи-
тельным. Из положительности диссипативной функции следует,
что прямые феноменологические коэффициенты (£“ и L? или
R+ и R“) должны быть больше нуля.
Отметим некоторые основные моменты, касающиеся урав-
нений (7.1) — (7.4).
1.	Ясно, что априори здесь не предполагается стехиометрия;
факт наличия двух уравнений подразумевает, что в общем слу-
чае можно не предполагать стехиометрии. Как мы видели, сте-
хиометрия имеет место только в случае специальной зависимо-
сти между феноменологическими коэффициентами.
2.	Эти уравнения относятся только к стационарным состоя-
ниям.
3.	Чтобы эти уравнения могли быть использованы для ана-
лиза экспериментальных данных, феноменологические коэффи-
циенты должны быть постоянными в достаточно большом диа-
пазоне изменения сил и потоков, допускающем их точное из-
мерение. Это возможно только тогда, когда силы ограничены
правильными траекториями. В случае кинетической, а не тер-
модинамической линейности (гл. 6) необходим другой подход,
который детально обсуждается в гл. 13 для окислительного
фосфорилирования.
В определенных экспериментальных ситуациях и для тео-
ретического анализа оказываются полезными две комбинации
феноменологических коэффициентов, обсуждавшиеся в гл. 4.
В случае простого насоса такими комбинациями являются
Za = л/La+[L“ = '\Ir“IR+	(7.5)
<7a = £“r/VW = -₽+r/V₽^	(7.6)
124
ГЛАВА 7
где, как и в общем случае, рассмотренном в гл. 4,
- 1< qa < 1
(7.7)
Преобразование уравнений (7.3) и (7.4) приводит к урав-
нениям, выражающим потоки как функции сил и коэффициентов
сопротивления
а_ RarX+-Ra+rA
+
или при другом выборе коэффициентов:
а _ Х+ + (<Za/Z“) А
+ ^[1-(/)2]
Аналогично
__ (qa/Za)X+ + (1/Za)24
Г~ Ra+[l~(qa)2]
(7.8)
(7.9)
(7.Ю)
Хотя приведенная выше модель полезна для ориентировки,
биологические мембраны, которые осуществляют транспорт раз-
нообразных веществ, должны быть, конечно, сложнее. Поэтому
мы рассмотрим две более реальные модели.
7.2.2.	Последовательная составная мембрана
Первая модифицированная модель, показанная на рис. 7.4,
отличается от основной модели введением пассивного барьера
последовательно с насосом. Для этой составной мембраны
в формальном описании изменяются только прямые феномено-
Рис. 7.4. Схема натриевого (катион-
ного) насоса и последовательного
пассивного барьера.
логические коэффициенты. Следовательно, уравнения (7.3) и
(7.4) продолжают выполняться, если теперь 7?+ представляет
собой 'общее последовательное сопротивление активному транс-
_	^барьера пбарьера rfl
порту. Это очевидно, если учесть, что у барьера л +	—л +	J +
и у насоса Х+ - Х+рьера = я™соса7“ _|_ #а rjr, где вместо R+ записа-
но /^асоса. Тогда
Х+ =	+ £“+acoca) + Ra+rJr	(7.11)
Энергетика активного транспорта: теория 125
Уравнение (7.4) остается неизменным. В этом случае степень
сопряжения равна
ря
qa =------. +f	(7.12)
V(/?+₽ьера + /?+соса)
и, таким образом, оказывается меньше, чем в простом насосе
(если только система не является полностью сопряженной)2.
7.2.3.	Составная мембрана с последовательными
и параллельными элементами
Так как мы полагаем, что активному транспорту подвергается
только один ион, тогда как ткань в целом переносит соль, то,
следовательно, должен существовать пассивный канал, прони-
цаемый для ионов. В противном случае накопление заряда при-
водило бы к установлению стационарного состояния с фикси-
рованной силой, вызывающего остановку транспорта. Сочета-
ние параллельного пути утечки с составной последовательной
мембраной представляет собой модель изучаемой составной
транспортной системы, показанную на рис. 7.2. При анализе
такой системы мы будем использовать параметры обобщенного
метода неравновесной термодинамики, изложенного в гл. 4,
ограничиваясь верхними индексами аир для обозначения ак-
тивных и пассивных элементов соответственно.
Комбинирование соответствующих феноменологических урав-
нений для этих элементов легко приводит к уравнениям для
составной системы. Формально оказывается несущественным,
является ли утечка внутриклеточной или межклеточной. Если
пассивный поток /(J. не сопряжен с потоком другого вида, то
X+=RP+J+	(7.13)
Так как /+ = /“+/+> то мембрана в этом случае также опи-
сывается линейными уравнениями3.
Полезно выразить феноменологические коэффициенты со-
ставной мембраны через коэффициенты ее элементов. Комбини-
руя уравнения (7.9) и (7.13), получим
/+=([1 - (/п+	+G* [1 - (/п)А (7,14)
Для данных сил наличие утечки не оказывает влияния на /г,
и уравнение (7.10) остается справедливым.
Хотя мы не в состоянии описать все барьеры проницаемости,
вышеизложенный метод предполагает, что при соответствую-
щих предосторожностях даже сложные системы могут быть
126
ГЛАВА 7
описаны с помощью общих линейных соотношений. Предпола-
гая, что это справедливо и для рассматриваемой здесь системы,
мы можем применить обобщенные параметры и записать
Х+ + (9/2) А
Я+(1 -92)
(9/Z)X+ + (l/Z2)4
Я+0 -92)
(7.15, 7.16)
В общей теории сопряженных процессов важное значение
имеют два стандартных стационарных состояния: «состояние
с фиксированным потоком» (Хг = 0) и «состояние с фиксиро-
ванной силой» (/j=0) [13]. Транспорт через эпителиальные
ткани часто приближается к состоянию с фиксированным по-
током. Это, по-видимому, имеет место, например, в случае про-
ксимальных извитых канальцев почки млекопитающих, где
почти 70 % фильтруемого натрия повторно адсорбируется, оче-
видно, благодаря активному процессу. Связанное движение
воды является достаточно быстрым, чтобы поддерживать при-
близительную изотоничность жидкости канальцев, и разность
электрических потенциалов оказывается небольшой. Наоборот,
симметричные клетки, такие, как эритроциты и клетки мышц,
находятся в состоянии с фиксированной силой для целого ряда
растворенных веществ, и в некоторых случаях полярные ткани
также могут приближаться к этому состоянию.
Обобщая уравнения, которые описывают эти два стацио-
нарных состояния для катионов, получим
(J+)X+=sQ—	(фиксированный поток) (7.17)
Х+ = (Х+)/+=о = —(фиксированная сила) (7.18)
Важно подчеркнуть, что, учитывая характер нашей модели,
уравнения (7.15) и (7.16) можно было бы записать сразу, не
рассматривая раздельно влияние на транспорт насоса, после-
довательных барьеров и утечки. Действительно, уравнения
(7.15) и (7.16) применимы для любой линейной системы двух
потоков, в которой активный транспорт одного вещества явля-
ется следствием одного метаболического процесса. Для описа-
ния и сравнения таких систем можно провести анализ, исполь-
зуя обобщенные параметры. Однако, учитывая, что модель,
изображенная на рис. 7.2, широко используется для описания
ряда важных систем (например, транспорта натрия в мочевом
пузыре жабы), целесообразно также рассмотреть зависимость
поведения таких систем от параметров элементов, составляю-
щих систему. Особенно важно тщательно исследовать влияние
утечки, поскольку существует тенденция рассматривать утечку
как отклонение от идеального поведения, объясняющее нару-
шение стехиометрии и уменьшение эффективности.
Энергетика активного транспорта: теория 127
Степень сопряжения при активном транспорте действитель-
но уменьшается из-за утечки и равна
«2 =__________------------ (7 19)
Как и следовало ожидать, при уменьшении утечки (/?+-> оо)
q—+qa. При наличии утечки q становится меньше, чем qa. Для
эффективной работы qa должно быть как можно больше, и,
по-видимому, аналогично общая степень сопряжения должна
быть как можно больше. Однако мы видели, что при неселек-
тивных утечках эффективное получение большого потока тре-
бует, чтобы /?+ было достаточно малым, и поэтому q2 будет
существенно меньше, чем (qa)2. Таким образом, для системы,
функцией которой является транспорт соли, оптимальная сте-
пень сопряжения общего механизма транспорта катионов не
может быть слишком большой. Ясно, что оптимальная степень
сопряжения определяется функцией системы. Поэтому, прежде
чем предполагать наличие полного сопряжения, мы должны
попытаться оценить степень сопряжения и понять смысл этой
величины.
Интуитивно ясно, что величина утечки не оказывает влия-
ния на состояние с фиксированным потоком, и это видно при
подстановке Х+ = 0 в уравнение (7.14). Если Х+ установлено
на определенном уровне, меньшем нуля, то /+ уменьшится
из-за обратного потока через канал утечки. Если, однако, в экс-
перименте, так же как в условиях in vivo, Х+ не фиксировано,
то ситуация может быть совершенно другой. В этом случае
утечка будет допускать не только обратный поток, но и частич-
ную потерю отрицательной разности электрических потенциа-
лов, обусловленную активным транспортом. Рассмотрим для
простоты мембрану, разделяющую одинаковые растворы NaCl,
и предположим, что кроме активного транспорта натрия име-
ется пассивный транспорт Na+ и СН Если проницаемость для
воды очень велика, так что транспорт NaCl сопровождается
транспортом достаточного количества воды для поддержания
приблизительной изотоничности, то Xw = 0, тогда
Х+ ~ - ЕДф ~ - X-	(7.20)
где F — число Фарадея и Дф— разность электрических потен-
циалов на мембране. Если обозначить феноменологический
коэффициент сопротивления для хлора через /?₽, то селектив-
ность пассивной проницаемости характеризуется величиной
которую мы обозначим через (При отсутствии
сопряженного потока воды равно отношению чисел пере-
носа т+/т_.)
128
ГЛАВА 7
Поток хлора равен
Jp_ = X-lR-	(7.21)
В стационарном состоянии, когда результирующий ток равен
нулю, из уравнений (7.14), (7.20) и (7.21) следует, что
(Дс=0) (7-22>
Видно, что, когда Х+ экспериментально не установлено, при
данной селективности пассивной проницаемости изотоническая
реадсорбция соли непосредственно связана с величиной утечки.
(Можно показать, что это имеет место даже тогда, когда по-
токи ионов и растворителя сопряжены.) Необходимо учесть, что
это заключение справедливо только в том случае, если факто-
ры, изменяющие степень утечки, не оказывают влияния на се-
лективность проницаемости или на феноменологические коэф-
фициенты системы активного транспорта. Как отмечал Боул-
пап, понижение реадсорбции Na с увеличением параклеточной
проводимости, приводящее к накоплению соли в Necturus, ве-
роятно, связано с изменением селективности проницаемости
[2].
Величина силы в стационарном состоянии с фиксированной
силой зависит от величины утечки и, как можно показать с по-
мощью уравнения (7.14), равна
______________(<Za/Za) А
1 + (^М)Ь -(4е)2]
(7.23)
Как отмечалось выше, поток катиона обратно пропорционален
^?а. С другой стороны, уравнение (7.23) показывает, что если
R+ велико по сравнению с /?“, то А’’+ становится нечувстви-
тельным к R+ и оказывается равным (R+r/R“)A. Нечувстви-
тельность Л+ к антидиуретическому гормону — агенту, кото-
рый стимулирует транспорт натрия в мочевом пузыре жабы,
приводилась для подтверждения точки зрения, что это вещество
может действовать путем уменьшения последовательного барье-
ра проницаемости, не оказывая существенного прямого влияния
на натриевый насос [3].
7.3.	Экспериментальное описание транспортной
системы
С нашей точки зрения, было бы идеальным охарактеризовать
транспортную систему путем определения ее феноменологиче-
ских коэффициентов и сил при всех соответствующих видах
работы. Практически, однако, в большинстве случаев, представ-
Энергетика активного транспорта: теория
129
ляющих интерес, такое полное описание отсутствует. В первую
очередь мы рассмотрим те данные, которые можно легко полу-
чить с помощью обычных электрических методов и интерпрети-
ровать с точек зрения классической и неравновесной термоди-
намики, а затем обсудим способы, которые могут быть исполь-
зованы для более адекватного описания транспортной системы.
Чтобы сделать анализ системы транспорта поддающимся обра-
ботке, необходимо принять определенную рабочую гипотезу.
Система транспорта характеризуется феноменологическими
коэффициентами, которые определяют ее поведение при всех
значениях двух независимых переменных. Поскольку можно
контролировать только величину Х+, практически, однако, от-
вет системы оказывается непредсказуемым без знания вели-
чины второй независимой переменной. Если Jr поддерживается
постоянным, как в электрической системе с фиксированным то-
ком, то такую систему можно легко охарактеризовать [9].
Другая возможность, которая априори кажется нам более ве-
роятной, состоит в том, что сродство некоторого участка мета-
болической цепи может быть постоянным. Это могло бы про-
изойти, например, в случае полной (глобальной) метаболиче-
ской реакции, если бы концентрации субстрата и продукта
были бы велики. Или же сродство в некоторой более локальной
области метаболической цепи может поддерживаться постоян-
ным благодаря действию регулятора. В этом разделе мы бу-
дем считать, что сродство некоторого участка метаболической
цепи является фактически постоянным, и будем рассматривать
эту область в качестве реакции, приводящей в действие транс-
портную систему (см. приложение к этой главе). Эксперимен-
тальные результаты, на которых основаны эти рассуждения,
представлены в гл. 8.
7.3.1.	Ток короткого замыкания и потенциал разомкнутой
цепи
Стало уже обычным исследование эпителиальных мембран,
таких, как кожа лягушки и мочевой пузырь жабы, путем уста-
новления с обеих сторон мембраны одинаковых физиологиче-
ских растворов и измерения тока короткого замыкания /д^о,
потенциала разомкнутой цепи Аф/=о и электрического сопро-
тивления — с///с/(Дф). Для систем, в которых активный транс-
+
порт ограничен единственным ионом (в данном случае Na),
эти величины легко интерпретируются в свете изложенного
выше. Из уравнений (7.14) и (7.15) видно, что ток короткого
замыкания равен
=	____F(q°/Z°)A
°	я+ (1 _	_ (<7а)2] (Де - 0)	(7.24)
9 Келлен, Эссиг
130
ГЛАВА 7
Когда Ас — 0, ln/F оказывается просто величиной потока в ста-
ционарном состоянии с фиксированным потоком. Из уравнений
(7.14), (7.20) и (7.21) следует, что потенциал разомкнутой
цепи равен
(Аф), ,> = —?-/	----5ТГ (Ас = 0)	(7.25)
Таким образом, в то время как ток короткого замыкания яв-
ляется характеристикой только системы активного транспорта
натрия, потенциал разомкнутой цепи отражает также величину
тока ионной утечки. Комбинируя уравнения (7.18) и (7.25),
получим зависимость между потенциалом разомкнутой цепи и
величиной силы в состоянии с фиксированной силой:
= - F[! + («+/«.)О-Л]	(7'26>
Из уравнений (7.17) и (7.18) находим зависимость между то-
ком короткого замыкания и величиной силы в состоянии с фик-
сированной силой:
=	= - ,+ (1^г)	(7.27)
Дс=0	+
7.3.2.	Вычисление электрического сопротивления
Электрическое сопротивление легко вычисляется с помощью
простого метода, описанного выше. Однако его интерпретация
через основные параметры дает наглядный пример зависимости
реакции системы от способа ее описания. При условии посто-
янства Jr можно измерить феноменологический коэффициент
сопротивления. Если пренебречь коэффициентами активности
и предположить, что растворы содержат только одну соль с од-
новалентными катионом и анионом, то Х± определяется выра-
жением4 — Х+ — RT& In с + ЕДф. Из уравнений (7.15) и (7.16)
получим
Если, однако, Jr не постоянно, что априори нам кажется го-
раздо более вероятным, то изменение /+ при изменении Аф
зависит не только от R+, но и от степени сопряжения. Напри-
мер, если сродство остается постоянным, то из уравнения (7.15)
находим
- Т ( д (Дф) )д 1Пс. А =	(7’29)
Энергетика активного транспорта: теория
131
Для анионов, которые не подвергаются активному транспорту,
1 ( д/_
Л1пс
1
Rp_
(7.39)
При условии что изменения Дф достаточно продолжительны,
чтобы переходные потоки К и С1 через клеточную мембрану
прекратились и установился чистый поток натрия, из уравне-
ний (7.29) и (7.30) получим электрическое сопротивление, ко-
торое обозначим через 5?:
/ 1 \	/ д! \	__/.____1_______।	1 \ /у 311
Л 1п с, А “	(Лф) Л !пС, А “ I * + (1 - 92)	'
Таким образом, в этом случае электрическое сопротивление
зависит как от «пассивных» параметров, так и от степени со-
пряжения. Если ни Jr, ни А не остаются постоянными при из-
менении Дф, то зависимость становится еще более сложной.
Если между I и Дф имеется линейная зависимость, то
«w= mfr ил" (ад'-=<'>.»-»« <7-32> 7-33>
Уравнение (7.32) является экспериментальным тестом для про-
верки линейности. Если производная и отношение не равны,
то, следовательно, отношение определяется не только электри-
ческим сопротивлением. Если они равны, это означает, что
либо А, либо Jr постоянны или что они линейно зависят от Дф.
7.3.3.	Сродство А и его вычисление
В общем случае экспериментально невозможно направленно
изменять сродство реакции, обеспечивающей транспорт. Однако
на сродство реакции можно оказывать влияние путем введения
гормона или лекарственного препарата. Из уравнений (7.15),
(7.16) и (7.18) видно, что J+, Jr п — Х°+ возрастают при уве-
личении Д5. Между тем влияние А на параметры эффективно-
сти оказывается более сложным, что будет обсуждаться ниже.
Если сродство некоторого участка метаболической цепи по-
стоянно, то его можно вычислить. Например, в случае одина-
ковых растворов с обеих сторон мембраны из уравнений (7.15),
(7.16) и (7.18) получаем
А = - (Z/q) Х°+ = (4т^)л F т+.о (7.34)
Когда величины (dJ+/dJr)A определяются вблизи состояния
с фиксированной силой, правильная величина А может быть
9*
132
ГЛАВА 7
получена даже в том случае, если феноменологические коэф-
фициенты существенно зависят от состояния.
Если же предположить, что с изменением Аф при постоян-
ной концентрации Х+ находится на правильной траектории, то
уравнения (7.15) и
измерения сродства:
(7.16) дают другой независимый способ
.__________
[й/г/5(Дф)]л
(7.35)
Совпадение величии А, определенных с помощью этих двух не-
зависимых способов, может подтвердить постоянство сродства
и совместимость использованных методов. (Однако нельзя по-
казать справедливость соотношений Онзагера.) Необходимо
отметить, что оба метода применимы даже при наличии сопря-
жения между пассивными потоками ионов и воды [4].
Значения сродства, полученные упомянутыми выше мето-
дами, являются в общем абстрактной термодинамической вели-
чиной, смысл которой не вполне ясен. Тем не менее сродство
имеет некоторый физиологический смысл, так как оно должно
отражать отношение концентраций субстрата и продукта в не-
которой критической реакции метаболической цепи, обеспечи-
вающей активный транспорт, и должно зависеть от плохо кон-
тролируемых параметров, таких, как локальный pH, стандарт-
ные свободные энергии и коэффициенты активности. Величина
сродства не коррелирует с отношениями средних концентраций
различных субстратов и продуктов в клетке, включая нуклео-
тиды, такие, как АТФ и АДФ, а также креатинфосфат и креа-
тин [5]. Хотя были предприняты попытки исследования движу-
щих сил транспорта с помощью таких измерений, оказалось,
что отношения средних концентраций зависят главным образом
не от трансэпителиального транспорта, а от других функций
ткани. Попытки вычислить цитоплазматическое отношение
АТФ/(АДФ X Фи) [23] также сопряжены с теоретическими и
экспериментальными трудностями. Необходимо, однако, учиты-
вать, что величины А, вычисленные из измерений потребления
О2, могут быть интерпретированы через свободную энергию
гидролиза АТФ только при условии знания отношения Ф/О,
которое в принципе может значительно изменяться при различ-
ных условиях работы.
7.3.4.	Вычисление феноменологических коэффициентов
Если в линейной системе сродство оказывается постоянным при
изменении Х+ вдоль правильной траектории, то вполне целесо-
образно вычисление феноменологических коэффициентов про-
водимости. Так же как и ранее, проще всего это сделать, по-
мещая с обеих сторон ткани одинаковые растворы и изменяя
Энергетика активного транспорта: теория
133
Дф. Тогда из уравнений (7.1) и (7.2) находим
L+ = ~дхТ = д (Г АфТ = А (?А)~ <Ас = °> а - константа) (7.36)
L+r =	d(Fd^T = А?Лф)- = О, А - константа)
(7.37)
Определяя А и La+r так же, как и раньше, для Lr в этом слу-
чае получим
L? = Jsrb0/A (Ас == 0)	(7.38)
где JrS — скорость метаболизма сверх основного обмена ве-
ществ при Ac, Аф = 0. (Возможные экспериментальные методы
определения 7°, Jr и Jsb будут обсуждаться ниже.)
Для системы с постоянным А феноменологические коэффи-
циенты сопротивления нельзя определить так же легко, как
/.-коэффициенты, поскольку это потребовало бы независимого
определения двух потоков. Однако, если величины 7.“, L+r и
Lar известны, соответствующие /^-коэффициенты можно рассчи-
тать с помощью матрицы преобразования.
7.3.5.	Вычисление степени сопряжения
Если известны величины феноменологических коэффициентов
проводимости или сопротивления, то с помощью уравнения
(7.6) можно также рассчитать степень сопряжения активного
транспорта. Иногда удобнее определять q без предваритель-
ного нахождения феноменологических коэффициентов и А. Учи-
тывая постоянство А, это возможно сделать любым из двух
методов [13]:
(7.39)
где 7^ =0 обозначает состояние, в котором активный транс-
порт катиона равен нулю вследствие использования соответ-
ствующей разности электрохимических потенциалов этого ка-
тиона. Или же:
(dJ“+/dJ°rb)A
(7.40)
134
ГЛАВА 7
7.4.	Стехиометрия и степень сопряжения
Неявным допущением классического описания биоэнергетики
является (по аналогии с жестко сопряженными химическими
реакциями) существование фиксированного стехиометрического
отношения скоростей транспорта и метаболизма. Считается, что
такое отношение должно существовать как в различных тканях,
так и в данной ткани, исследуемой при различных условиях.
Ясно, что в первом случае, когда ткани исследуются в состоя-
нии короткого замыкания с одинаковыми растворами у каждой
поверхности, отсутствует термодинамическое ограничение для
отношения потоков, так как в этих условиях не совершается
электроосмотическая работа. В общем случае величина
Л-о/Ло может довольно сильно различаться для различных
тканей.
Когда транспорт и метаболизм изменяются вследствие из-
менения сил, необходимо учесть следующее соображение. Если
система активного транспорта является полностью сопряжен-
ной, т. е. если (<?а)2= 1, то, как это следует из уравнений (7.9)
и (7.10), отношение Ja+IJr должно быть тождественно равно Za.
В этих случаях уместно говорить о стехиометрическом отноше-
нии. Однако Ja+/Jr имеет однозначную величину, только если
система активного транспорта полностью сопряжена. Априори
нет оснований полагать, что это действительно так, и вполне
возможно, что определенные преимущества связаны с отсут-
ствием стехиометрии [20]. Тем не менее вычисление «стехио-
метрического отношения» обычно проводится на основе наблю-
даемой линейной зависимости между потоками. Между тем из
уравнений (7.9) и (7.10) видно, что, если А постоянно, линей-
ность следует непосредственно из линейности феноменологиче-
ских уравнений независимо от степени сопряжения. Таким об-
разом, хотя {dJ+fdJ^A тождественно равно' Zafqa, величина
Ja+/Jr постоянна, только если <?“ равно единице. Поведение
J+lJг в более общем случае описывается уравнением (4.17).
Хотя для эффективного функционирования сопряжение в ак-
тивном транспорте должно быть достаточно большим и, воз-
можно, в некоторых случаях даже полным, ясно, что изучаемая
система является не полностью сопряженной из-за наличия
утечки. Этот вопрос вызывает интерес в связи с общими пред-
ставлениями, касающимися стехиометрии. По-видимому, нали-
чие стехиометрии часто предполагается из-за естественной ана-
логии с химическими реакциями in vitro, где для повышения
эффективности стремятся исключить побочные реакции. По-
этому кажется, что в случае транспортных процессов было бы
желательно исключить эквивалент побочных реакций, а именно
утечки. Однако видно, что, хотя исключение утечек могло бы
Энергетика активного транспорта: теория 135
обеспечить наличие стехиометрии в системе (если бы сам ме-
ханизм активного транспорта был полностью сопряженным),
в то же время это привело бы к прекращению результирующего
транспорта соли. Поэтому ясно, что нельзя рассматривать на-
личие стехиометрии в качестве единственного и основного кри-
терия идеальной системы транспорта. Вернее, необходимо учи-
тывать конкретное назначение и характер работы каждой си-
стемы. Если системе «предназначено» поддерживать состояние
с фиксированной силой, как в случае симметричных клеток, то
утечка нежелательна. Если функцией системы является обес-
печение большого потока соли против малого градиента хими-
ческого потенциала, как в эпителиальных тканях (например,
проксимальные извитые канальцы почки), то некоторая степень
утечки необходима в том смысле, что это требуется по другим
причинам. Если же функцией системы не является ни поддер-
жание состояния с фиксированной силой, ни поддержание
большого почти фиксированного потока, а что-то промежуточ-
ное, т. е. заметный поток против заметных градиентов, то будет
желательным некоторый другой характер утечек, причем опти-
мальная ситуация должна изменяться с изменением характера
деятельности системы, скажем в присутствии гормонов, лекар-
ственных веществ или нервного стимула, активирующих транс-
порт. Этой стороне механизма активного транспорта не уделя-
лось того внимания, которого он, по-видимому, заслуживает.
7.5.	Эффективность превращения энергии
Изложенная выше теория позволяет сделать самосогласован-
ную оценку эффективности преобразования энергии для любого
состояния системы активного транспорта, но единого критерия,
пригодного для этой цели, не существует. Вернее, условия
функционирования системы диктуют соответствующий критерий.
Если скорость совершения электроосмотической работы зна-
чительна, то в этом случае эффективность равна
У+Х+ __ (ZX+ + qA)X+
JrA	[<7Х+ + (1/Z) Д] А
(7-41)
Изменения коэффициентов сопротивления, которые приводят
к возрастанию /+, будут также увеличивать ц (для фиксиро-
ванной Х+ < 0 и фиксированного Л). Эффективность возра-
стает с увеличением q2, но для любого конечного J+ она всегда
меньше единицы. Характер зависимости ц от Z(X+/A) при раз-
личных значениях q можно оценить с помощью рис. 4.3.
Симметричные клетки в стационарном состоянии должны
находиться в состоянии с фиксированной силой (Х+ = Х+)>
в котором, очевидно, функция системы транспорта состоит
136
ГЛАВА 7
в поддержании разности электрохимических потенциалов.
В этом случае полезно рассмотреть силу, развивающуюся при
данной скорости расходования метаболической энергии, т. е.
эффективность силы
е%+ = - x+/JrA	(7.42)
Эффективность силы — монотонно возрастающая функция — Х+,
достигающая своего максимума (—R+r/A) в состоянии с фик-
сированной силой. Интересно, что е 0 не зависит от значений
% +
двух прямых коэффициентов изучаемой системы. Так же как
и Х+, еуо уменьшается при увеличении утечки (рис. 7.5).
х+
Необходимо отметить, что, хотя анализ транспорта ионов
часто проводится на примере электрохимической ячейки без
побочных реакций, где не требуется расхода энергии для под-
держания состояния с фиксированной силой, эта аналогия не-
действительна для неполностью сопряженных систем, поскольку
метаболическая энергия расходуется даже при отсутствии
транспорта, как это следует из уравнений (7.15) и (7.16), если
подставить (Л)/+=о = A/Rr.
Усиление утечки—*•
Рис. 7.5. Пример влияния утечки на величину и эффективность силы в ста-
ционарном состоянии с фиксированной силой для произвольно выбранных
значений параметров: qa — 0,9, Za= 1,0,	= 1,0 ккал • см2 - с/моль2, А =
— 1,0_ккал/моль, R.p+lRv_ = 1.
Энергетика активного транспорта: теории	137
Эпителиальные ткани часто функционируют вблизи состоя-
ния с фиксированным потоком, где, по-видимому, функцией си-
стемы является транспорт большого количества вещества.
В этом случае параметром, представляющим интерес, служит
скорость транспорта при данной скорости расходования мета-
болической энергии:
/ ।	ZX । 4- qA
£j+=	=	+ (1/Z) Л] А	<7-43)
Так же как и г), при данной величине сил е/+ возрастает при
изменении коэффициентов сопротивления, соответствующем
увеличению скорости транспорта. В отличие от т] (при фикси-
рованном Л) sj+ является монотонно возрастающей функ-
цией X... (если только q2 =/= 1), достигающей величины «yZ/Л
в состоянии с фиксированным потоком.
Выше было показано, что, если Х+ в эксперименте не под-
держивается постоянным, изотоническая реадсорбция соли не-
посредственно связана с величиной утечки при условии неиз-
менности ее селективной проницаемости и постоянства Xw.
В этих условиях то же самое справедливо для эффективности
Рис. 7.6. Пример влияния утечки на изотоническую реадсорбцию соли и эф-
фективность потока при разомкнутом контуре. Величины параметров те же,
что и на рис. 7.5. Объяснение см. в тексте.
138
ГЛАВА 7
потока (рис. 7.6):
(е, )	=-;-----------------i— (Дс=0)	(7.44)
7+^=о	[Я“ (1 + Zq_ _) + Кр_ ] А
Аналогичный результат получается и тогда, когда потоки иона
и растворителя сопряжены.
С помощью этих двух функций эффективности можно оце-
нить эффективность превращения энергии даже в том случае,
если система не совершает электроосмотической работы. Однако
в отличие от т] величины ех и е/ не нормированы и не являются
безразмерными. Тем не менее они могут быть полезны при
сравнении эффективности использования энергии в различных
системах и особенно при сравнении функций данной системы
в различных состояниях. Подобно функции Ех и ej— фун-
даментальные параметры, которые могут быть полезны незави-
симо от механизма линейности или чувствительности свободной
энергии метаболизма к изменению условий функционирования
системы.
7.6.	Модель эквивалентного контура
Многие исследователи считают логичным и плодотворным ана-
лиз активного трансэпителиального транспорта натрия на осно-
ве аналогии с эквивалентной линейной электрической схемой
(рис. 7.7). Важно рассмотреть, как параметры этой модели
связаны с параметрами неравновесного термодинамического
описания, и сравнить их возможности в интерпретации энерге-
тики. Для этого необходимо, чтобы оба набора параметров оце-
нивались в стационарных состояниях.
В модели эквивалентного контура путь активного транс-
порта представлен элементом проводимости (которому в ста-
хр
Рис. 7.7. Простая модель эквивалентного контура для активного транспорта
натрия.
В соответствии с моделью на рис. 7.2 предполагается, что вход натрия через апикаль-
ный барьер является пассивным и что электродвижущая сила транспорта натрия
связана с работой натриевого иасоса в базолатеральиой мембране. Любая разность
электрохимических потенциалов, которая может возникать на апикальной мембране,
ие дает независимого вкл-ада в Bj^a, так как появляется в результате работы
насоса.
Энергетика активного транспорта: теория 139
ционарном состоянии может быть приписана величина х^а),
включенным последовательно с «электродвижущей силой на-
триевого транспорта» Е^а. Транспорт соли требует наличия па-
раллельного пассивного элемента проводимости хр. В этом слу-
чае электрический ток равен
1 = «Na£Na ~ « А^ = «Na (ЕNa “ А^) ~ %₽ A^'	(7‘45)
а ток короткого замыкания
= (7-46)
Таким образом, вычисление /0 и x\asx — х₽ дает величину
Подставляя 1 — 0 в уравнение (7.45), получим зависимость
между потенциалом разомкнутой цепи и £'ма:
(^о = ВД£Иа	(7.47)
Считается, что величина Е^а представляет собой движущую
силу активного транспорта натрия, и предполагается, что для
характеристики влияния данного агента нужно различать его
влияние на fNa и %Na [21,22]. Таким образом, модель экви-
валентного контура демонстрирует важность как кинетического,
так и энергетического факторов и приводит к попыткам разли-
чить их в эксперименте. Однако анализ рис. 7.7 показывает,
что описание механизма активного транспорта с помощью этих
средств не может одновременно учесть существование двух по-
токов: метаболического потока и потока натрия. В общем слу-
чае выходной параметр ENa не дает точной величины энергети-
ческого параметра, представляющего главный интерес, — сво-
бодной энергии входного процесса метаболизма, обеспечиваю-
щего транспорт. Это видно из комбинации уравнений (7.1),
(7.36) и (7.46):
/о = F (7+).м=0 = FLa+rA = F2La+ENa
или	E^a = (l/F)(La+r/La:)A	(7.48)
Таким образом, в противоположность сродству А электродвижу-
щая сила £Na отражает как кинетический, так и энергетический
факторы. Это справедливо даже для полностью сопряженных
систем. В этом случае La+r/La+ = l/Za+ = JT/J?ia является обрат-
ной величиной стехиометрического отношения. Для более слож-
ных моделей эквивалентного контура зависимость Е^а от ки-
нетических факторов, конечно, усложнится. Такие модели удобно
анализировать с помощью метода термодинамических цепей
140
ГЛАВА 7
7.7.	Зависимость и Jr от А
При рассмотрении методов, основанных на неравновесной тер-
модинамике и анализе эквивалентного контура, исходят из
предположения, что изменения Дф соответствующей продолжи-
тельности и амплитуды не изменят феноменологических коэф-
фициентов при А или £ма. В гл. 8 мы рассмотрим эксперимен-
тальные результаты, показывающие, что во многих случаях
это предположение справедливо6. В таком случае при условии
существования правильных траекторий, как обсуждалось в гл. 6,
уравнения (7.1) и (7.2) позволяют дать соответствующее опи-
сание системы и вычислить А независимо от влияния, которое
произвольное изменение А могло бы оказывать на Л\а и Jr
С этой точки зрения интересно исследовать зависимость
между потоками и сродством по мере того, как сродство изме-
няется либо физиологически, либо в результате изменения
условий эксперимента, например вследствие введения субстра-
тов или ингибиторов метаболизма, лекарственных препаратов
или гормонов. Хотя эти воздействия могут оказывать влияние
и на величину феноменологических коэффициентов, в первую
очередь это необходимо для исследования возможных эффек-
тов изменения только величины А.
В общем случае нельзя ожидать, что потоки будут линейно
зависеть от А, исключая условия вблизи равновесия, так как
для линейности изолированной химической реакции требуется,
чтобы А RT, где R— газовая постоянная и Т — абсолютная
температура. Однако биологическая ситуация оказывается го-
раздо сложнее, и, как отмечал Пригожин [18], биохимические
реакции с большим значением А часто представляют собой
целый ряд последовательных реакций. В таких случаях вели-
чины А промежуточных реакций могут быть достаточно малы,
и поэтому эти реакции оказываются линейными. Так как в ста-
ционарном состоянии все последовательные реакции протекают
с одинаковой скоростью, то считается, что Jr линейно зависит
от общего сродства, являющегося суммой величин сродства
промежуточных реакций. Эта точка зрения не учитывает тот
факт, что феноменологические /.-коэффициенты промежуточных
реакций суть параметры состояния и, таким образом, могут
весьма существенно изменяться, когда изменение общего срод-
ства вызывает изменение концентраций промежуточных про-
дуктов 'метаболизма.
Хотя это означает, что сами по себе последовательные
реакции необязательно приводят к линейности общего срод-
ства, тем не менее не исключено, что в некоторых случаях ли-
нейность все же будет иметь место. В качестве примера усло-
вий, в которых это могло бы произойти, рассмотрим простую
Энергетика активного транспорта: теория
141
реакцию
А :?=> 2В	(7.49)
предполагая возможность применения кинетики Михаэлиса —
Ментен. В этом случае кинетический анализ приводит к сле-
дующему результату (см., например, [1]):
_ H'-BWI	„ 50)
1 + (л-шМ + (и/И(4/^)
где v — скорость результирующей реакции, V и V' — макси-
мальные скорости прямой и обратной реакций соответственно,
Кт и К— константа Михаэлиса — Ментен и константа равно-
весия, сА и св — концентрации А и В. [При сл ~ О уравнение
(7.50) сводится к уравнению Михаэлиса — Ментен.] В доста-
точно разбавленных растворах сродство равно
МТ1п(ЗД	(7.51)
Подстановка уравнения (7.51) в (7.50) дает
v = V (1 — е~А^Т)	52
^+^m/cA}+(V/W)e-A^
Из этого результата видно, что промежуточная реакция будет
действительно линейной, если А <С RT, так как при разложе-
нии в ряд экспоненты в уравнении (7.52) получим
v = LrA	(7.53)
где
Lr = ^T[l + (KmlcA) + (V/V')]	(7'54)
Чтобы общая реакция была линейной, коэффициенты Lr про-
межуточных реакций должны быть нечувствительны к измене-
нию общего сродства, приводящего к изменению концентраций
субстратов. Для рассматриваемой реакции это условие в слу-
чае правильной траектории удовлетворяется, если
К!П <сл[1 + (У/И]	(7.55)
Поскольку биологические реакции часто состоят из большого
числа последовательных ферментативных реакций, многие из
которых лишь незначительно отклоняются от равновесия [8],
разумно ожидать, что некоторые реакции и процессы активного
транспорта могут оставаться приблизительно линейными при
изменении А в диапазоне, представляющем биологический ин-
терес. Конечно, не предполагается, что это должно происходить
всегда. Соответствующее исследование данного вопроса потре-
бует более детальной информации о системах реакций, чем
имеющаяся в настоящее время. Одной из интересных систем
142
ГЛАВА 7
является окислительное фосфорилирование в митохондриях;
для этой системы зависимости сила — поток изучены рядом ав-
торов, результаты исследований которых будут обсуждаться
в гл. 13.
7.8.	Сопряжение потока растворенного вещества
и объемного потока
Важной стороной активного транспорта является его тесная
связь с объемным потоком в отсутствие благоприятных транс-
эпителиальных градиентов осмотического или гидростатиче-
ского давления. Пытаясь объяснить эту зависимость, Каррен
с сотрудниками предложил простую модель, состоящую из двух
последовательных мембран, разделенных узким пространством
(рис. 7.8). Мембрана I осуществляет активный транспорт рас-
творенного вещества з из отсека 1 в отсек 2, тем самым уста-
навливая разность осмотических давлений, вызывающую объ-
емный поток. Вообще можно ожидать, что процесс активного
транспорта должен быть связан с объемным потоком в цен-
тральной части отсека 2. Главной особенностью модели, изо-
браженной на рис. 7.8, является то, что она предсказывает
наличие объемного потока через составную мембрану из от-
сека 1 в отсек 3. Основой такого поведения является различие
в «эффективном осмотическом давлении» Дпэфф = aRT&c, со-
здаваемом растворенным веществом з на двух последователь-
ных мембранах. Таким образом, в мембране I (представляю-
щей собой клеточные барьеры и плотные контакты между клет-
ками) сп » 1, так как транспорт з из отсека 1 в отсек 2 связан
с потоком воды между этими двумя областями (из раствора,
омывающего внешнюю, слизистую, поверхность мембраны, в ла-
теральное межклеточное и/или субэпителиальное пространства;
Рис. 7.8. Система последовательных мембран. Центральный отсек замкнут,
и растворенное вещество активно транспортируется через мембрану I из от-
сека 1 в отсек 2 (ссылка [9] из гл. 3).
Энергетика активного транспорта: теория 143
см. рис. 7.9). Этот водный поток приводит к возникновению
гидростатического давления в отсеке 2. В мембране II, находя-
щейся в области межклеточных базальных щелей, стенок ка-
пилляров и/или серозных оболочек, 0 < ац «с 1, так что эф-
фективная разность осмотических давлений, стремящаяся вы-
звать поток воды из отсека 3 в отсек 2, оказывается меньше
разности гидростатических давлений в противоположном на-
правлении. Таким образом, возникает объемный поток из от-
сека 2 в отсек 3.
Игнорируя влияние непроникающих веществ и малый гра-
диент трансэпителиального гидростатического давления, путем
формального применения уравнения (3.51) для каждой мем-
браны с учетом скорости активного транспорта Js можно прий-
ти к уравнению Качальского — Каррена
3? (а. — ап) J*
,7'5S)
где = LpiLpn/(LpiLpU). Таким образом, как было обнару-
жено в эксперименте с различными эпителиальными тканями,
скорость объемного потока пропорциональна скорости актив-
ного транспорта. Коэффициенты пропорциональности определя-
ются свойствами обеих мембран, в частности различием их ко-
эффициентов отражения.
щк
Рнс. 7.9. Схема морфологических структур слизистой оболочки кишечника,
иллюстрирующая механизм транспорта воды.
ЩК щеточная каемка слизистой поверхности клетки, ПК — плотный контакт и К —
капилляр. I и П соответствуют последовательным мембранам, изображенным на
рис. 7.8.
144
ГЛАВА 7
7.9.	Влияние более/ложных механизмов насоса
Для простоты в разд. 7.2.1 рассматривался насос, который осу-
ществляет активный транспорт одного катиона, несопряженный
с потоками других веществ. Так как механизм функционирова-
ния насоса в действительности гораздо сложнее, то может по-
казаться, что данная выше трактовка активного транспорта
совершенно нереальна. Однако легко показать, что независимо
от специфики механизма можно применять простое линейное
+	Рис. 7-10- Сопряженный механизм
Na	активного транспорта Na+ — К+-на-
к coca и утечки на базолатеральной по-
верхности клетки.
описание при условии, что каждый элементарный процесс сам
является линейным. В качестве примера рассмотрим обычную
модель базолатерального Na+-Hacoca, в котором выход Na+
сопряжен с входом К+, причем активный приток К+ компенси-
руется его утечкой (рис. 7.10). В этом случае работа насоса
описывается следующими фундаментальными соотношениями:
7Na = ^Na*Na + ^Na. КХК + L^.	(7’57)
= ^йа, Ла +	+ Lt гА	(7-58)
/г = LSa. r*Na + Lt rXK + LarA	(7.59)
а утечка в базолатеральной мембране равна
J'=LUK	(7.60)
Рассматривая теперь стационарное состояние, в котором/к =
=sJk + 7k = 0, так как в трансэпителиальном активном транс-
порте /“=7Йа> и комбинируя уравнения (7.57) — (7.60), полу-
чим уравнения (7.1) и (7.2), в которых =Лйа — (^Na, к)7(^к+
-|-Лк)> Ltr = Ltla, г— Lua, xLt г/(,Lt Lr) и Lr = L“— (.Lt г}2/
I (Lt -f- Z-к)-
7.10.	Выводы
1.	Энергетика процессов активного транспорта успешно анали-
зируется на основе модели системы двух потоков, в которой
поток одного катиона приводится в действие одной метаболи-
ческой реакцией.
Энергетика активного транспорта: теория	 145
2.	Постулируется, что разность электрохимических потен-
циалов Х+ и сродство движущей метаболической реакции А
можно ограничить «правильными» траекториями, так что по-
токи /+ и Л оказываются линейными функциями Х+ и А.
3.	Это описание применимо как к катионному насосу, так
и к составной системе, включающей последовательные и парал-
лельные элементы.
4.	Рассмотренная модель не предполагает полноты сопря-
жения (стехиометрии). Сопряжение оценивается безразмерным
параметром q\ — 1 < q < 1.
5.	Важными стандартными стационарными состояниями яв-
ляются состояния с фиксированным потоком (Х+ = 0) и с фик-
сированной силой (7+ = 0).
6.	Критерий эффективности системы транспорта зависит от
ее функции. Совершение электроосмотической работы оцени-
вается с помощью эффективности ri = — J+X+/]rA. Вблизи со-
стояний с фиксированным потоком и с фиксированной силой
величина ц мала; в этом случае подходящими критериями яв-
ляются эффективность потока е, == J+/JГА и эффективность
силы er, = — X, /JrA соответственно.
7.	Изменение Х+ вдоль правильной траектории, в то время
как А остается постоянным, позволяет экспериментально оце-
нить феноменологические коэффициенты L (проводимости) и
R (сопротивления), степень сопряжения q и сродство А. В про-
тивоположность оценкам свободной энергии, основанным на
средних отношениях концентраций в тканях, величина А, по-
лученная этим (неповреждающим) методом, отражает отноше-
ние активностей субстрата и продукта метаболической реакции,
обеспечивающей транспорт, и зависит от влияния локального
pH, стандартных свободных энергий и коэффициентов актив-
ности.
Приложение
Пример системы, с которой мы имеем дело, показан на
рис. 7.11. Это схема использования энергии метаболизма для
транспорта Na+ с левой стороны мембраны на правую. В не-
которой точке основной цепи реакций имеется дополнительная
цепь последовательных стадий, непосредственно сопряженных
с некоторой частью механизма насоса (неважно, какая именно
стадия вовлечена). В этом случае наш метод может быть при-
ложим либо к системе в целом, либо к этой локальной обла-
сти. Локальным процессом, обеспечивающим транспорт Na+,
является реакция mM-\-nN pP-\-qQ, для которой сродство7 А
равно (гпр.м-ф пцл/) — (рцР -ф qpQ); М и N могут представлять
собой АТФ и Н2О, в то время как Р и Q — это АДФ и Фн.
10 Коплен. Эссиг
146
ГЛАВА 7
С точки зрения локальной систе-
мы несущественно, каким обра-
зом поддерживается концентра-
ция реагентов и продуктов. (На-
пример, имеется отсек, в котором
реагенты и продукты находятся
практически в равновесии с рас-
творами в больших резервуа-
рах.) Стехиометрическое превра-
щение М и N в Р и Q требует,
чтобы в этой области не было
«ответвлений» цепи; это является
нашим основным предположе-
нием. Однако, как показано на
рисунке, может существовать ряд
других замкнутых цепей (пе-
тель). В стационарном состоянии
потребление М и N все же долж-
но быть связано стехиометрически
с производством Р и Q. Некото-
рые из этих петель могут быть не
сопряжены с насосом, и ясно, что,
хотя они не оказывают влияния
на обоснованность применения
общего подхода, они могут умень-
шать степень сопряжения между
метаболизмом и транспортом. Не-
обходимо понимать, что даже ло-
кальная скорость диссипации
свободной энергии должна выра-
жаться как разность потоков на
входе и выходе. Входным чле-
ном является JrA, где сродство
А, определенное выше, представ-
ляет собой движущую силу про-
цесса. С этой точки зрения си-
стема может рассматриваться как
черный ящик с тМ -j- nN-+рР +
4- qQ в качестве входа и тран-
спорта Na+ слева направо в ка-
честве выхода (рис. 7.1).
Может показаться, что было
бы полезно считать взаимное пре-
вращение веществ насосом/., на-
cocomr, Na+-HacocoML и Ыа+-на-
cocomr как составляющие входа.
Но этого не стоит делать по еле-
Энергетика активного транспорта: теория	 147
дующей причине. Диссипативная функция для черного ящика
на рис. 7.1 имеет вид
ф = АЛа + М	(7.П1)
или же мы можем рассматривать реакции, происходящие вну-
три черного ящика:
(a)	Na/-+ насосЛ-> Ыа+-насосЛ
(Р)	Na+-HacocL —> №+-насося
(у)	Ыа+-насосЛ-> насосЛ+Na+
(6)	насосR -> насос^
(e)	mM + nN -> pP 4- qQ
Каждая из этих реакций, конечно, может быть суммой несколь-
ких промежуточных реакций. Комбинация (е) с одной из
остальных реакций, возможно, представляет собой действитель-
ный механизм сопряжения. В любом случае диссипативная
функция имеет вид
Ф = 7аЛа + /рЛр -ф /V4V +	+ JГА	(7.П2)
где величины сродства, выраженные через электрохимические
потенциалы, равны
Н~Ь Ннасоса^ l^Na + -Hacoca^
KNa+-Hacoca£	^Na + -Hacoca^
Йха+-насоса^ ^насоса^ ^Na^
Z^6 l^Hacoca l^Hacoca^
В стационарном состоянии
/а=:/р=/у —/б = Д\а	(7.ПЗ)
и поэтому
Ф = Л\а (Ла 4~ 71g 4-	4-	+ J	(7-П4)
Легко видеть, что уравнения (7.Ш) и (7.П4) идентичны.
Мы считали JrA ВХОДОМ, а —/Na^Na выходом. Поскольку
члены Ja/la, JyAy и J&A& могут быть положительными, т. е.
представлять спонтанный процесс, их можно рассматривать
так же, как и JrA, т. е. как входы. Тогда выходом будет
— Этот способ нам кажется неестественным и непродук-
тивным, ибо насос оказывается включенным в циклический
процесс. Как отмечали Качальский и Спанглер [11], циркуля-
ция веществ формально не дает вклада в диссипативную функ-
цию, хотя она влияет на феноменологические коэффициенты.
10*
148
ГЛАВА 7
/
Иногда удобнее принять более общую точку зрения, чем та,
которая рассматривалась выше, и анализировать систему с по-
мощью сродства некоторой большей области цепи при усло-
вии, что эта область включает реакцию тМ 4- nN рР 4- qQ
и не включает незамкнутых ветвей. Это было бы справедливым
и для всей последовательности реакций, если бы Y' было иден-
тично У и 2' идентично Z и они оба находились бы в одном
отсеке (например, СО2 и Н2О). Тогда имелась бы единственная
метаболическая реакция и сродство ее было бы равно (ард +
+ бцв) — (уцг + zpz) • Другая возможность, когда вся последо-
вательность реакций представляет собой единственный метабо-
лический вход, реализуется, если Е полностью образуется
только за счет распада С, а Е'— только за счет распада D.
В этом случае общей реакцией является аА 4- ЬВ yY 4- zZ +
4- y'Y' 4- z'Z' и сродство равно (ацл 4- 6цв) — (yp,Y + zu.zA~y'PY'A-
4- z'Pz')- общем случае рассмотренные выше возможно-
сти не реализуются, и каждая ветвь может представлять раз-
личные реакции, одна из которых характеризуется сродством
(ацд4- бцв) — (уру + zpz), а другая — сродством (арл 4-6цв) —
— (t/'цу'4-z'pz')- Априори не имеется причин, по которым эти
две реакции были бы связаны стехиометрически, и, таким об-
разом, при рассмотрении всей последовательности реакций мы
получаем два входных процесса. Здесь мы не будем проводить
такой анализ. Однако в некоторых системах расход свободной
энергии одним или несколькими дополнительными потоками
может оказаться настолько незначительным, что его можно не
учитывать. Таким примером является почка млекопитающих,
в которой потребление О2 в отсутствие реадсорбции Na+ может
уменьшаться всего лишь на 20 % по сравнению с потреблением
при высоких скоростях реадсорбции Na+.
Хотя в принципе мы можем рассматривать как полную по-
следовательность метаболических реакций, так и любую ее
часть, величина степени сопряжения будет зависеть от нашего
выбора. Рассмотрим участок цепи реакции сС 4- dD yY 4- zZ.
Он включает следующие промежуточные реакции:
(X)
(а)
сС + dD тМ + nN
тМ + nN рР + qQ
СО
рР+ qQ +=± yY + zZ
При рассмотрении локального участка цепи реакций мы можем
применить уравнения (7.3) и (7.4), где реакция (о) является
метаболическим входом, т. е.
%Na = /?Na/Na 4~ /?Na, rlг	(7.П5)
А(а) = /?Na. Ла + Я?(а/,	(7.П6)
Энергетика активного транспорта: теория
149
Для полной цепи реакций мы должны рассмотреть дополни-
тельные феноменологические соотношения
Ащ = Ыг, A(v = tf(X)Jr (7.П7, 7.П8)
Складывая уравнения (7.П6) — (7.П8), получим
Аобщ = Aft) + Л(О) 4- А(Т) = /?Na, Дна 4~
+ (/?г(1) +/?г(о) +Л (7.П9)
Уравнения (7.П5) и (7.П9) являются феноменологическими
уравнениями полной цепи реакций. Ясно, что в этом случае сте-
пень сопряжения
__________~*Na.r_________
V^a + *f(a) + *?(T>)
меньше, чем степень сопряжения для локального участка цепи
реакций, исключая случай полного сопряжения (см. примеча-
ние 1 к этой главе). Хотя оба этих подхода приводят к различ-
ным значениям q, Z и А, противоречий не возникает.
При попытке применить такой подход в эксперименте ка-
жется естественным рассмотреть полную цепь реакций и учиты-
вать концентрации экзогенных субстратов и суммарных конеч-
ных продуктов. Однако это не всегда возможно. Например,
если имеется ветвление метаболической цепи, то вообще нельзя
допустить, что в системе есть лишь один выход. Другая воз-
можность состоит в том, что сродство дополнительной части
цепи поддерживается постоянным благодаря саморегулирую-
щемуся процессу (который, вообще говоря, может вносить не-
линейность в оставшуюся цепь). Если это так, то сродство яв-
ляется характеристическим свойством системы и может быть
параметром, определяемым линейными уравнениями (7.34) и
(7.35). Даже в системах, в которых рассмотрение полной цепи
реакций экспериментально возможно, полезно проанализиро-
вать также подсистемы. Этот подход был успешно применен
в случае экстрагированных глицерином мышечных волокон, ко-
торые не имели эндогенных источников АТФ. В таких волокнах
в принципе возможно экспериментально регулировать сродство
реакции гидролиза АТФ. Аналогичный метод можно было бы
использовать в случае эпителиальных тканей, но это потребо-
вало бы существенных методических разработок.
8
Энергетика активного транспорта:
экспериментальные данные
В предыдущей главе мы попытались дать исчерпывающее са-
мосогласованное описание энергетики активных транспортных
процессов, учитывающее неадекватность классических подходов
в этой области. Было показано, что во многих случаях можно
получить существенные кинетические и энергетические пара-
метры, если только активный транспорт и сопряженный с ним
обмен веществ удается описать в рамках простого линейного
формализма. Помимо того что это создает основу для содер-
жательного анализа энергетических соотношений как таковых,
появляются предпосылки для выяснения механизмов влияния
различных факторов, действующих на активный транспорт. В на-
стоящей главе мы рассмотрим экспериментальные данные, по-
зволяющие судить об обоснованности и возможностях приме-
нений линейных соотношений термодинамики необратимых про-
цессов при анализе активного транспорта, особенно в случае
транспорта ионов натрия в эпителии земноводных, и обсудим
различные другие задачи с целью проверки и установления
возможности применения теоретических формул. Хотя по при-
чинам, которые мы отметим далее, такого рода проверка пока
еще не является исчерпывающей, имеющиеся результаты обна-
деживают и создают стимул для дальнейших усилий по исполь-
зованию линейных соотношений термодинамики необратимых
процессов в анализе множества систем.
8.1.	Обоснование линейных феноменологических
уравнений
8.1.1.	Выбор объектов эксперимента
В принципе любая биологическая ткань может служить объек-
том для проверки границ применимости линейных соотношений
термодинамики необратимых процессов, но на самом деле весьма
важно рассмотреть ряд практических деталей, которые могут
существенно влиять на реализацию программы такого рода экс-
периментов.
Для начала лучше всего взять эпителиальную ткань, омы-
ваемую с обеих сторон физиологическими растворами. Посколь-
Энергетика активного транспорта: эксперимент
151
ку оба раствора легко доступны, можно непрерывно следить и
регулировать термодинамические силы и трансэпителиальные
разности электрохимических потенциалов любых интересующих
нас веществ, переносимых через ткань. Выбрав подходящие
объемы растворов и методы измерения, можно поддерживать
состав растворов в течение длительного времени примерно по-
стоянным и одновременно проводить измерения скоростей
транспорта и метаболизма. К сожалению, в таких препаратах
не удается фиксировать сродство метаболических реакций на
произвольном уровне. При существующих биохимических мето-
дах обычно оказывается невозможным оценить сродство рас-
сматриваемых реакций из-за сложности структуры тканей и
клеток. В противоположность асимметричным эпителиальным
тканям такие симметричные клетки, как эритроциты или клетки
мышечной ткани, создают большие трудности для измерений
трансмембранной разности электрохимических потенциалов.
Кроме того, в долгоживущих стационарных состояниях суммар-
ные потоки должны быть равны нулю, а при этом измерения
противоположно направленных активной и пассивной компонент
затруднительны и неточны. Установление же условий, приводя-
щих к ненулевому суммарному потоку, должно вскоре изменить
внутриклеточные параметры.
с
мешалки.
Рис. 8.1. Прибор для одновременного измерения электрических параметров
н поглощения кислорода кожей лягушки или мочевым пузырем жабы.
Когда какая-нибудь из этих тканей находится в контакте с одинаковыми растворами
Рингера по обе стороны, возникает разность электрических потенциалов, отражающая
активный транспорт натрия от внешней поверхности кожи лягушки (или от слизистой
поверхности мочевого пузыря жабы) к внутренней, или серозной, поверхности. КЭ —
кислородный электрод, ПЦ — полярографическая цепь, С — самописец [41].
152
ГЛАВА 8
Важное практическое соображение, касающееся выбора
объекта эксперимента, состоит в том, что соотношения, подле-
жащие проверке, должны быть самыми простыми, например
они могут включать всего лишь один транспортный процесс,
сопряженный с одной метаболической реакцией. Для наших це-
лей важны результаты, полученные Уссингом с сотрудниками
в опытах на коже лягушки и Лифом с сотрудниками на моче-
вом пузыре доминиканской жабы, которые показали, что при
подходящем выборе условий трансэпителиальный активный
транспорт ограничивается почти исключительно натрием и опре-
деляется в основном окислительным обменом [27, 39, 46]. Ис-
следования таких простых систем, интересные и сами по себе,
должны, кроме того, создать основу для анализа более слож-
ных систем, включающих несколько транспортных процессов,
в том числе сопряженных.
По всем этим причинам для проверки применимости линей-
ных соотношений термодинамики необратимых процессов при
анализе активного транспорта мы избрали транспорт натрия
и сопряженное поглощение кислорода кожей лягушки и моче-
вым пузырем жабы. Схема установки, используемой в этих це-
лях, показана на рис. 8.1. Поскольку независимым образом
можно менять только разность электрохимических потенциалов
Хыа, полностью проверить справедливость формул не удается.
Однако, как мы увидим далее, при некоторых обстоятельствах
можно ожидать, что сродство реакции будет примерно постоян-
ным, и в этом случае используемый формализм обоснован.
8.1.2.	Выбор уравнений для анализа эксперимента
Линейные феноменологические уравнения можно записать с лю-
быми силами и потоками, рассматриваемыми как независимые
переменные, взяв за основу формулы с проводимостью L или
сопротивлением R. С теоретической точки зрения оба способа
записи эквивалентны. С точки зрения эксперимента этот вы-
бор — вопрос удобства. Ввиду легкости, с которой можно варьи-
ровать разность электрохимических потенциалов натрия Хиа,
и предполагаемого постоянства сродства А при кратковремен-
ных изменениях XNa удобно ввести формулы, в которых за осно-
ву принимается L, и определить влияние изменений XNa на по-
токи натрия и метаболизм. Таким образом, наши фундамен-
тальные уравнения для системы активного транспорта натрия
имеют'вид
7.\а = 7.NaANa "Т ^Ха, г А	(8.1)
Jsrb = Аыа, г%№ + LrA	(8.2)
Поскольку в этой главе мы в основном имеем дело с потоками
ионов, создаваемыми активным транспортом, опустим верхний
Энергетика активного транспорта: эксперимент	153
индекс а при феноменологических коэффициентах. Величина
/йа принимается положительной, когда поток направлен от
наружной (слизистой) к внутренней (серозной) поверхности ’
ткани. Величина Jsrb представляет собой скорость супрабазаль-
ного поглощения кислорода и предполагается независимой от
поглощения, связанного с метаболическими процессами, отлич-
ными от транспорта ионов. В основе предположения о равенстве
перекрестных коэффициентов лежит требование, чтобы XNa
было ограничено только правильно выбранными траекториями.
8.1.3.	Влияние условий опыта на параметры уравнений
термодинамики необратимых процессов
При попытках охарактеризовать транспорт и метаболизм на
основе линейного приближения, введенного выше, очевидно, су-
щественно, чтобы феноменологические параметры рассматри-
ваемой системы, которые мы хотим оценить, были примерно
постоянны при изменении внешних переменных. Только в этом
случае можно ожидать, что 7£а и Jr будут линейными функ-
циями Хиа- Однако в общем случае величины L(R) и А будут
функциями состояния, и вполне возможно, что на них будут
влиять различные манипуляции, заметно изменяющие конфигу-
рацию и/или состав ткани. Важность такого рода связей сле-
дует из ранних наблюдений «эффекта памяти» после продол-
жительных изменений Дф. Так, если потенциал изменить таким
образом, чтобы резко усилить транспорт натрия и сопряжен-
ный метаболизм на достаточно длительное время, то после воз-
врата к короткозамкнутому состоянию обе величины /0 и Ло
оказываются меньше, чем их исходные значения. Эти резуль-
таты представлены светлыми кружочками на рис. 8.2. Темные
кружочки отражают эффект противоположного знака, отмечен-
ный после сдвига Дф в сторону замедления транспорта и мета-
болизма. Эти отличия значений /0 и Jra от контрольных уровней
ясно указывают на изменения Lnb, r, Lr и/или А. Очевидно, что
экспериментальные приемы, применяемые для варьирования
%Na, а вместе с тем /fta и Л> весьма важны при описании ак-
тивного транспорта.
Априори представляется, что изменения трансмембранного
электрического потенциала в меньшей степени должны нару-
шать параметры системы, чем изменения концентрации натрия
в омывающей жидкости, которые вполне могут влиять также
на внутриклеточный состав, а также на размеры и организацию
внутриклеточных и внеклеточных компартментов системы. В со-
ответствии с этим в наших опытах значения Лыа варьировали
только путем изменения Дф. При этом уравнения (8.1) и (8.2)
154
ГЛАВА 8
принимают вид
Jk = LNa(-F^) + LKa,rA	(8.3)
J? = ANa> r (- F At) + LrA	(8.4)
где Alp = tin — tout-
Даже когда состав омывающей жидкости поддерживается
постоянным, существование эффекта памяти затрудняет интер-
претацию. С одной стороны, чтобы охарактеризовать с высокой
точностью параметры в уравнениях термодинамики необрати-
мых процессов, система должна находиться в квазистационар-
ном состоянии в процессе наблюдений, в том числе и в период
до и после изменения Дф, и, следовательно, эти изменения не
Препарат кожа!
Д Jr0, пмоль/(смг.-.(г)
--20
-» О °
о
20 AJ0,MKa/cm*
О
--20
• после' +160 мВ
о после -160 мВ
Препарат кожа2 дуг0
-20 О
О 0
20
Рис. 8.2. Влияние изменений электрического потенциала на последующие зна-
чения тока короткого замыкания 1а и скорость поглощения кислорода Ло
кожей лягушки [42].
Энергетика активного транспорта: эксперимент 155
могут быть очень кратковременными. С другой стороны, чтобы
параметры уравнений были примерно постоянными, длитель-
ность изменения Дф не должна быть слишком велика. Допол-
нительные осложнения возникают из-за нестабильности эпите-
лия в процессе измерений. В результате весь цикл измерений
надо провести достаточно оперативно, чтобы избежать суще-
ственных изменений фона.
Ниже мы подробнее обсудим условия, выбранные для ана-
лиза на основе линейных соотношений.
8.1.4.	Зависимость от Дф
Если растворы, контактирующие с обеими поверхностями,
идентичны и если скорость активного транспорта натрия на са-
мом деле линейно зависит от сил, стимулирующих перенос
ионов, то можно ожидать, что в стационарном режиме будет
выполняться линейное соотношение между током и напряже-
нием. На практике, как и следует ожидать, вид взаимосвязи
между I и Дф существенно зависит от условий опыта. Так, если
монотонно варьировать Дф с интервалами менее секунды, то
кривая I — Дф разбивается на линейные участки, соединенные
«точками излома» [10,19]. Если Дф варьировать симметрично
относительно 0 мВ с интервалами 5—10 с, то кривая I—V
примерно линейна в области потенциалов —75->+ 100 мВ
[35, 45]. Эти наблюдения указывают на линейность активного
транспорта натрия, но не вполне убедительны, поскольку при
кратковременных изменениях Дф неясно, в какой мере / отра-
жает короткоживущие потоки К и С1, а не поток Na на базаль-
ной латеральной поверхности. Если же потенциал меняют на
более длительное время, то кривая I — Дф становится явно не-
линейной. При 15-минутных интервалах наблюдается насыще-
ние в области отрицательных Дф, что указывает на изменения
клеточных параметров [45].
По-видимому, наиболее убедительные примеры линейности
/ыа при варьировании Дф получены в исследованиях мочевого
пузыря жабы и кожи лягушки, в которых Дф изменяли сим-
метрично с 6-минутными интервалами в области 0—>- + 80 мВ
[23]. Поскольку в условиях опытов на мочевом пузыре жабы
идет активный транспорт через эпителий только ионов натрия,
зависимость от Дф можно определить в явном виде из ста-
ционарных соотношений тока и напряжения, что позволяет
оценить вклад пассивных ионных потоков. Таким образом,
I = Ia+r = FJ^-^^, /йа^Т(1^---рАф)	(8.5)
Поскольку воздействие 10~5 М амилоридом на слизистую по-
верхность мочевого пузыря жабы сводит активный транспорт
-Ki’
пмолъ Na /(смг-с)
Дер,мВ
Энергетика активного транспорта: эксперимент[57
натрия почти к нулю и при этом заметным образом не влияет
на vP (20,21], этот агент можно использовать для оценки /ыа-
Полученное в пределах 4—6 мин после симметричного измене-
ния Aip линейное соотношение между током и напряжением
в присутствии и в отсутствие амилорида показывает, что /£а
действительно линейно зависит от Дф в данных условиях опыта
(рис. 8.3). Это становится особенно очевидным при сопоставле-
нии с исследованиями скорости поглощения кислорода, которые
мы обсудим ниже [23].
Демонстрация линейности активного транспорта указывает
на то, что феноменологические коэффициенты и сродство не из-
менялись под влиянием изменений Дф в использованных здесь
интервалах величины и длительности. Это позволяет предпо-
ложить, что варьирование Дф при постоянной Дсиа обеспечивает
ожидаемые значения XNa. Альтернативное предположение, со-
стоящее в том, что феноменологические коэффициенты ANa, г
или сродство — линейные функции Дф, представляется малове-
роятным.
8.1.5.	Зависимость Jfb от Дф
Представив экспериментальные данные, подтверждающие спра-
ведливость уравнения (8.3) при анализе активного транспорта
в условиях, близких к физиологическим, мы обратимся теперь
к аналогичным соотношениям для метаболизма, сопряженного
с активным транспортом [уравнение (8.4)]. В исследуемых тка-
нях активный транспорт натрия в значительной мере обуслов-
лен окислительным обменом. Как показано на рис. 8.1, в этих
опытах величину Jr определяли с применением кислородных
электродов. Наклон графика временной зависимости концен-
трации кислорода, полученного за время в пределах 2 мин, дает
меру скорости потребления кислорода. При оценке этим спо-
собом величин Jr исключительно важно, как и при исследова-
нии транспорта, чтобы ткань находилась в квазистационарном
состоянии в течение всего эксперимента, включая период до
начала и после окончания изменений Дф. Чтобы облегчить до-
стижение стационарных состояний, измерения снова проводи-
лись в течение 4—6 мин после изменения Дф. Возможные мед-
ленные изменения функциональных свойств тканей оценивались
путем повторных измерений тока короткого замыкания /0 и со-
пряженного поглощения кислорода Jro-
Первые исследования были проведены на коже лягушки.
Типичный результат состоял в том, что при симметричных воз-
Рис. 8.3. а — соотношение между и Дф; б — соотношение между Jsb и
Дф в мочевом пузыре жабы [24].
158
ГЛАВА 8
мущениях потенциала соотношение между Jr и А-ф было линей-
ным в интервале, охватывающем по крайней мере ±70 мВ, а
иногда и ±100 мВ. Чтобы подробнее рассмотреть связь между
Jr и Дф, придется определять Jr несколько раз, охватывая более
длительные интервалы времени, при которых может наблю-
даться заметное спонтанное затухание транспорта натрия и
метаболизма. Поскольку такого рода нестабильность мешает
выявлению соотношений между Jr и Аф, было важно найти бо-
лее стабильный препарат. По этой причине мы использовали
продолжительные экспозиции в присутствии 10~6 М альдосте-
рона в среде Рингера с глюкозой. При этом стабильность воз-
растает с одновременным увеличением /0 по сравнению с необ-
работанной кожей того же животного. Более того, Jro остается
близким к его значению в свежих препаратах и также оказы-
вается сравнительно стабильным.
При использовании более стабильных препаратов была про-
демонстрирована линейность в широких пределах изменений
Дф. На рис. 8.4 приведены результаты одного из таких экспе-
риментов. Как можно видеть из этого рисунка, линейность со-
блюдается в интервале ±160 мВ (во всех опытах такого рода
мы избегали давать подряд несколько положительных или от-
рицательных периодов, например 0, —40, —80, —120, —160,
Рис. 8.4. Зависимость скорости поглощения кислорода от разности электриче-
ских потенциалов Дф в присутствии альдостерона [42].
Энергетика активного транспорта: эксперимент
159
—200, с последующей сменой на положительные значения,
чтобы устранить возможные систематические эффекты поляр-
ности). Дальнейшие наблюдения подтвердили линейность соот-
ношения между скоростью поглощения кислорода и Дф, если
значение Дф варьировали симметрично и принимали необходи-
мые меры предосторожности для обеспечения стабильности пре-
паратов кожи лягушки [22, 34] и мочевого пузыря жабы [23]'.
При установлении связи между метаболизмом и силами,
действующими на мембране, разумеется, важно, чтобы наблю-
даемые результаты изменения Дф были специфичными, отра-
жающими собственно изменения функции активного транспорта.
Специфичность подтверждается тем, что Jr становится нечув-
ствительным к Дф после подавления транспорта натрия уабаи-
ном [33,41] или амилоридом [21,22]. Это показано на рис. 8.5.
Получен ряд данных, показывающих, что скорость поглоще-
ния кислорода после подавления активного транспорта натрия
уабаином или амилоридом дает хорошую оценку скорости ба-
зального поглощения кислорода, не связанного с трансэпите-
лиальным переносом натрия [25]. Поэтому данные, полученные
после введения уабаина, свидетельствуют о том, что скорость
Рис. 8.5. Зависимость скорости поглощения кислорода Jr от разности элек-
трических потенциалов Дф на коже лягушки, обработанной альдостероном.
Влияние уабаина (10-3 М), добавленного за 30 мин перед изменением Дф
[34].
160
ГЛАВА 8
базального поглощения кислорода не зависит от разности элек-
трических потенциалов на коже. Взятые вместе с результатами
такого типа, как на рис. 8.4, эти данные подтверждают линей-
ную взаимосвязь между скоростью супрабазального поглоще-
ния кислорода и Aip. Как и для случая линейного соотношения
между скоростью активного транспорта натрия и Атр, они ука-
зывают на постоянство феноменологических коэффициентов и
сродства при изменении Аф в пределах величины и длительно-
сти, использованных в данных экспериментах, откуда снова
следует, что значения Хыа меняются ожидаемым способом.
8.1.6.	Зависимость и Jfb ОТ Хыа
Приведенные выше данные, подтверждающие линейную зави-
симость /йа и Jsrb от Аф, очень важны, поскольку они указывают
на возможность обоснованного описания параметров активного
транспорта с помощью уравнений (8.3) и (8.4). Хотя примене-
ние этих уравнений само по себе создает основу для система-
тического изучения транспортной системы в различных усло-
виях, часто нас интересует ситуация в тканях, контактирующих
с растворами различного состава, который может меняться со
временем. В связи с этим надо разобраться, в какой мере воз-
Рис. 8.6. Зависимость скорости активного транспорта натрия (тока короткого
замыкания) от разности химических потенциалов натрия Др.№ на коже жабы.
Варьировали наружную концентрацию натрия, сохраняя постоянной внутрен-
нюю концентрацию. Разность электрических потенциалов была нулевой [13].
Энергетика активного транспорта: эксперимент 161
можно описание с помощью уравнений (8,1) и (8.2), выражаю-
щих зависимость транспорта и метаболизма от полной разности
электрохимических потенциалов, в более общем случае. Эта
разность включает и разность химических потенциалов натрия
Лцна, и разность электрических потенциалов Аф, Как отмечалось
выше, поскольку феноменологические коэффициенты в принципе
являются функциями состояния, нет оснований предполагать,
что скорости транспорта и метаболизма будут давать одина-
ковый отклик на данное значение термодинамической силы Хиа
независимо от относительного вклада Арща и ГАф. Этот вопрос
можно решить только экспериментальным путем. Он был изу-
чен Виейра и сотрудниками, работавшими с препаратами кожи
жабы. Из соображений удобства опыты проводили при нулевой
разности электрических потенциалов. Было показано, что в ши-
роком интервале внешних концентраций (5—ПО мэкв./л по
сравнению с ПО мэкв./л во внутренней среде) скорость пассив-
ного истечения примерно постоянна, а скорость активного транс-
порта натрия удовлетворительно согласуется с значениями, рас-
считанными для тока короткого замыкания. Была изучена зави-
симость скорости активного транспорта натрия (ток короткого
замыкания) от наружной концентрации натрия в условиях по-
стоянства его внутренней концентрации. Как показывает рис. 8.6,
Рис. 8.7. Зависимость средней скорости супрабазальиого поглощения кисло-
рода от разности химических потенциалов натрия Д|Хца на коже жабы.
Варьировали наружную концентрацию натрия при постоянной внутренней
концентрации. Разность электрических потенциалов была нулевой [13].
1 1 Крпттам Лгсмг
162
ГЛАВА 8
ток короткого замыкания — линейная функция логарифма отно-
шения концентраций 1п(сиа/сиа)> т. е. скорость активного транс-
порта натрия линейно зависит от разности химических потен-
циалов натрия Ацыа на мембране, в согласии с уравнением
(8.1). В параллельной серии экспериментов показано, что ско-
рость супрабазального поглощения кислорода также линейно
зависит от Дцма (рис. 8.7) [13].
На основе этих наблюдений и с учетом более ранних резуль-
татов разумно заключить, что в эпителии земноводных, который
в данном случае был объектом исследований, скорости актив-
ного транспорта натрия и скорости сопряженного поглощения
кислорода — линейные функции разности электрохимических
потенциалов натрия независимо от того, изменяем ли мы Хиа
путем варьирования Дф или наружной концентрации натрия.
Осторожности ради отметим: пока не было показано, что в дан-
ной ткани отклик на изменение электрического потенциала ко-
личественно совпадает с откликом на термодинамически экви-
валетное изменение разности химических потенциалов. Для
этого надо провести комбинированное исследование 7&а и Jsrb
в условиях варьирования Дф и Дцма в одном и том же образце.
Если Хиа изменять путем варьирования внутренней концен-
трации натрия, то линейность уже не соблюдается [40]. Следо-
вательно, уравнения (8.1) и (8.2) неприменимы. Нелинейность
вполне может определяться изменениями микроструктуры и
состава ткани.
8.2.	Оценка параметров в уравнениях
неравновесной термодинамики
8.2.1.	Оценка сродства
Приведенные ранее результаты согласуются с тем, что линей-
ные уравнения неравновесной термодинамики применимы к ак-
тивному транспорту при условии, что выбрана правильная тра-
ектория для варьирования XNa (траектория термодинамической
линейности), тогда как А остается постоянным. В случае кине-
тической линейности следует видоизменить подход, как пока-
зано в гл. 13.
Полагая, что варьирование Дф соответствует правильной
траектории, можно определить сродство, используя одно из двух
уравнений (7.34) или (7.35), выведенных в гл. 7. Для тканей,
в которых варьирование наружной концентрации натрия также
дает правильную траекторию, эти уравнения можно дополнить
соответствующими выражениями, включающими Дриа- С точки
зрения эксперимента обычно удобнее всего выражение, вклю-
чающее ток короткого замыкания и зависимость скорости по-
Энергетика активного транспорта: эксперимент 163
глощения кислорода от напряжения2:
А= (Л постояни°)
Следует напомнить, что А представляет собой изменение
свободной энергии для специфического участка метаболической
цепи, в котором А остается постоянным при варьировании Аф.
В ряде случаев мы будем пользоваться обозначением До»
имея в виду, что в наших исследованиях А выражается через
изменения свободной энергии в расчете на моль Ог. Значения
Ло2 в необработанных образцах кожи лягушки и мочевого пу-
зыря жабы находятся в интервале 20—80 ккал/моль О2. По-
скольку предполагается, что активный транспорт в этих тканях
осуществляется за счет гидролиза АТФ, представляется целе-
сообразным выразить сродство на основе поглощения АТФ, од-
нако осуществление этого намерения затрудняется отсутствием
сведений о стехиометрии окислительного фосфорилирования в
интактном эпителии. Если же считать отношение P/О равным
3, как это наблюдается в нормальных митохондриях в присут-
ствии подходящих субстратов, то поглощение каждого моля О2
будет приводить к синтезу (а в стационарном режиме — и
к дальнейшей утилизации) 6 молей АТФ, что даст значения Ар
в интервале 3—13 ккал/моль АТФ. Эти значения близки к оцен-
кам, полученным при экспериментальном исследовании тканей,
например около 7,6 ккал/моль АТФ в стандартных условиях
или 11,4 ккал/моль АТФ для изолированных клеток печени
крыс [44]. Теоретические преимущества, которые дает анализ
энергетики, основанный на оценке А, по сравнению с измере-
ниями средних концентраций метаболитов в тканях, были рас-
смотрены в разд. 7.3.3. Ясно, однако, что полное понимание
энергетики активного транспорта натрия требует знания не
только Ао2, но и отношения P/О, полученного в условиях тех
же экспериментов. В этом случае можно найти и Ар. Такого
рода сведения пока недоступны.
8.2.2.	Влияние модельных соединений иа А
Окончательное выяснение смысла сродства, рассчитанного опи-
санным выше термодинамическим методом, требует дополни-
тельных экспериментов по термодинамическому изучению био-
химических процессов. Тем не менее интересно рассмотреть
влияние на сродство различных факторов, воздействующих на
транспорт и метаболизм в уже изученных случаях. В двух та-
ких работах были использованы соединения, которые подав-
ляли транспорт, но при этом непосредственно не влияли на ме-
таболизм. Одним из этих соединений является гликозид уаба-
ин— ингибитор натрий-калиевой АТФазы, которую обычно
11*
164
ГЛАВА 8
Рис. 8.8. Влияние 10-7М уабаина на зависимость скорости поглощения кис-
лорода Jr от разности электрических потенциалов Дтр.
Исходно наклоны прямых dlr/d (Атр) Для парных препаратов кожи (контроль I и опыт I)
различаются несущественно. После введения уабаина | dJrfd (Атр) | резко уменьшается
(опыт II) по сравнению с необработанной тканью (контроль II) [30}.
Энергетика активного транспорта: эксперимент
165
идентифицируют как натриевый насос. Если ввести в систему
уабаин в концентрации, достаточной для подавления активного
транспорта, то поглощение кислорода становится независимым
от разности электрических потенциалов. Чтобы использовать
приведенные выше формулы для оценки сродства, надо суще-
ственно, но не полностью подавить активный транспорт натрия
с целью определения А в уравнении (8.6). Эта задача была вы-
полнена путем использования низких концентраций уабаина
(10~7 М). В течение 2,5-часовой экспозиции при такой концен-
трации уабаина ток короткого замыкания в обработанном
образце кожи постепенно снижался примерно на половину по
сравнению с контрольным образцом. Это привело к существен-
ному понижению чувствительности поглощения кислорода к из-
менениям Аф, как показано на рис. 8.8, где представлены ти-
пичные результаты девяти опытов. Неполное подавление транс-
порта натрия на сравнительно короткое время не было связано
с заметным влиянием на сродство (рис. 8.9).
Время ,ч
Рис. 8.9. Влияние 10~7 М уабаииа иа сродство в препарате кожи лягушки
[30].
166
ГЛАВА 8
Другой ингибитор транспорта — амилорид (мочегонное сред-
ство) — мешает пассивному проникновению натрия через внеш-
нюю поверхность. В исследованиях кожи лягушки амилорид
вводили со стороны внешней поверхности в концентрации, до-
статочной для снижения /0 примерно на 2/3 по сравнению
с исходным уровнем в течение 4 ч (рис. 8.10). Сначала кажу-
щееся сродство было одинаковым в опыте и контрольном об-
разце. Час спустя после введения амилорида А заметно не из-
менилось (рис. 8.11). Однако через 4 ч после введения амило-
рида А существенно возросло по сравнению с контрольными
препаратами и по сравнению с исходным значением в том же
самом препарате. Возрастание А может объяснить тот факт,
что после удаления амилорида примерно через 4 ч обработки
значение 10 в обработанных тканях увеличилось и достигло
Рис. 8.10. Влияние 10-7—10-5 М амилорида на ток короткого замыкаиия
в препарате кожи лягушки [34].
Энергетика активного транспорта: эксперимент 167
уровня, существенно превышающего исходный и более высокий
чем в контрольных образцах (рис. 8.10). Разумеется, перехлест
вполне может быть объяснен и кинетическими факторами.
Представляют интерес также те вещества, которые непосред-
ственно подавляют метаболизм. К ним относится, например,
2-дезокси-О-глюкоза. Это вещество дезорганизует энергетиче-
ский обмен клетки тремя основными путями: конкурируя с глю-
козой при поглощении клетками, конкурируя с глюкозой в про-
цессе ее фосфорилирования гексокиназой, а также путем
подавления 2-дезокси-0-глюкозо-6-фосфатом изомеризации глю-
козо-6-фосфата в фруктозо-6-фосфат. Поскольку 2-дезокси-О-
глюкозо-6-фосфат далее не подвергается метаболическим изме-
нениям, эти эффекты стимулируют распад АТФ и подавляют
активный транспорт. В исследованиях кожи лягушки, находя-
щейся в контакте с 1 мМ раствором глюкозы, при концентра-
ции 16 мМ 2-дезокси-П-глюкозы активный транспорт подав-
лялся, по данным измерений тока короткого замыкания, в сред-
нем на 58 % от контрольного уровня. Это было связано со
значительным понижением сродства, в данном случае на 53 % от
контрольного значения (рис. 8.12). Такое понижение А легко
объяснить исходя из известных типов влияния 2-дезокси-П-глю-
козы на метаболизм.
контроль
амилори.3
(среднее значение,п=11)
Ами.лори.3
01____I____1____I I_______I____I_______
-10	1	2	3	4
Время, ч
Рис. 8.11. Влияние амилорида на сродство в препарате кожи лягушки [34].
168
ГЛАВА 8
Время,ч
Рис. 8.12. Влияние 16 мМ 2-дезокси-В-глюкозы на сродство в препарате кожи
лягушки [30].
Рис. 8.13. Модель активного транспорта. Возможные механизмы регуляции
транспорта [16].
Энергетика активного транспорта: эксперимент
169
Поучительно сравнить описанный выше отклик системы с ее
поведением в присутствии другого ингибитора метаболизма —
ротенона. Это вещество подавляет окислительный обмен на
уровне переноса электрона между НАД и цитохромом Ь. Влия-
ние ротенона было изучено путем выдерживания препаратов
кожи лягушки в контакте с 5—10 мкМ растворами его, в при-
сутствии или в отсутствие альдостерона. В противоположность
2-дезокси-О-глюкозе подавление транспорта и супрабазального
поглощения кислорода на половину и менее от контрольного
уровня было сопряжено лишь с незначительными (статистиче-
ски недостоверными) изменениями А, рассчитанного по уравне-
нию (8.6) (Лау, Ланг, Эссиг, неопубликованные данные). Хотя
окончательное объяснение этих расхождений требует дополни-
тельных исследований, следует отметить, что различные эф-
фекты этих двух ингибиторов согласуются с существующими
в настоящее время представлениями о взаимодействии между
окислительным и гликолитическим путями образования АТФ.
Так, частичное подавление ротеноном окислительного обмена и,
следовательно, сродства АР, как можно ожидать, будет суще-
ственно стимулировать гликолиз [28]. В результате повыше-
ние АР будет частично восстанавливать натриевый транспорт
(и тем самым /0), но слабо влиять на dJr/d(Aty), как это и на-
блюдается из зависимости поглощения кислорода от разности
электрических потенциалов. В соответствии с этим необосно-
ванное применение уравнения (8.6) в тех случаях, когда глико-
литический обмен дает существенный вклад в величину /0, при-
ведет к переоценке А. В отличие от этого 2-дезокси-О-глюкоза,
снижающая концентрацию АТФ другими способами, действует
таким образом, что не активируются никакие механизмы, ком-
пенсирующие Ар (как будет показано в разд. 8.2.4, завышенная
оценка А приведет к заниженной оценке феноменологического
коэффициента Lr).
8.2.3.	Влияние гормонов на А
Оценки сродства были также использованы при попытках уста-
новить природу эффектов альдостерона и антидиуретического
гормона (АДГ) — физиологических веществ, которые стимули-
руют активный транспорт натрия по механизмам, пока еще не
вполне понятным. Три общие возможности указаны на рис. 8.13.
Механизм (1) состоит в том, что облегчается проникновение
натрия через внешний барьер для пассивной проницаемости;
механизм (2) —это стимулирование фосфорилирования АДФ
с возрастанием сродства АР; механизм (3)—непосредственная
активация натриевого насоса.
Как показано на рис. 8.14, после выдерживания кожи ля-
гушки 14—18 ч в присутствии 5-10-7 М альдостерона стимуля-
170
ГЛАВА 8
140
5 контроль
| альЗостерон
(среЗнее значение,п=8)
1Z0
100
80
60
АльЗостерон
40
20
1-е сутки
।______
2-е сутки
Рис. 8.14. Влияние 5 10-7 М альдостерона на сродство в препарате кожи
лягушки [34].
Рис. 8.15? Влияние 100 мЕд./мл АДГ на Лио, Ло и параметры уравнений
неравновесной термодинамики в коже лягушки спустя 30, 60 и 90 мин после
введения препарата.
Расчет коэффициентов L описан в разд. 8.2.4. В этих исследованиях парных препаратов
тканей предпрннята попытка ввести поправку иа спонтанные изменения параметров во
времени путем сравнения результатоа наблюдений в опыте (е) и в контроле (с) с по-
мощью дважды нормированной величины R’=(xt/xt=o)e/(xt/xt=o)c- Цифры над столб-
цами указывают на значимость отклонений йот 1,00; 3:р(Д)< 0,01; 4: р(Д)< 0,001. От-
сутствие цифры означает, что различия незначимы [25].
Энергетика активного транспорта: эксперимент 171
ция /ns о и /го была сопряжена с возрастанием сродства А. На
рис. 8.15 показан аналогичный отклик на обработку АДГ в кон-
центрации 100 мЕд./мл. (Возможность возрастания А в ответ
на первичное влияние на проницаемость для натрия и транс-
порт натрия, по-видимому, можно исключить, по крайней мере
в случае АДГ, поскольку этот агент индуцирует возрастание А
даже в присутствии амилорида при скоростях транспорта ниже
контрольного уровня.)
При описании влияния первичных воздействий на энергети-
ческий обмен весьма важно убедиться, что в присутствии иссле-
дуемого вещества уравнение (8.6) все еще сохраняет силу для
оценки А. В частности, как отмечено для случая ротенона, надо
выяснить, в какой мере гликолиз может сделать /0 непримени-
мым для оценки скорости активного транспорта натрия, свя-
занной с окислительным обменом. Есть веские основания пола-
гать, что в контрольном состоянии аэробный гликолиз столь
незначителен, что не может привести к заметной ошибке при
определении А [41]. Кроме того, если интенсивность гликоли-
тического обмена постоянна, то он может дать только некоторое
занижение эффекта усиления А добавляемыми веществами при
стимуляции транспорта. Однако при использовании альдосте-
рона и АДГ возникает особая проблема, так как имеются дан-
ные, полученные в опытах с мочевым пузырем жабы, свидетель-
ствующие о том, что оба гормона стимулируют гликолиз [17,
18]. Поскольку гликолиз сам по себе дает АТФ, может пока-
заться, что оба реагента могут существенно стимулировать ак-
тивный транспорт натрия даже без воздействия на окислитель-
ный обмен. При этом результирующее усиление /0 без всякого
воздействия на потенциалзависимое поглощение кислорода,
d/,/d(Ai|>), приведет к обманчивому впечатлению, что А воз-
росло [см. уравнение (8.6)]. Такая ошибка должна быть весьма
незначительной, так как обмен молекулы глюкозы по гликоли-
тическому пути дает только 2 молекулы АТФ, в то время как
при полном окислении образуются 32 молекулы АТФ. Поскольку
оба гормона существенно стимулируют супрабазальное погло-
щение кислорода (рис. 8.14 и 8.15),вклад АТФ,образовавшегося
в результате гликолиза, должен быть пренебрежимо малым.
Другое молчаливо принимаемое предположение при оценке
сродства по гидролизу АТФ из данных рассматриваемого типа
состоит в том, что альдостерон и АДГ не влияют на отношение
P/О. Так как имеются данные, свидетельствующие о неполноте
сопряжения окислительного фосфорилирования (см. гл. 13), то
нельзя исключить изменения 7Р//о при варьировании физиоло-
гических условий. Этот важный вопрос требует дальнейших ис-
следований.
Наконец, мы еще раз хотим подчеркнуть, что изменения
сродства и феноменологических коэффициентов в различных
172
ГЛАВА 8
условиях нельзя рассматривать как данные, позволяющие од-
нозначно интерпретировать механизм процессов в отсутствие
гораздо более детальной физиологической и биохимической ин-
формации, чем та, которой мы располагаем в настоящее время.
8.2.4.	Оценка феноменологических коэффициентов L
Если уравнения (8.3) и (8.4) применимы при постоянном зна-
чении А, то коэффициенты L можно определить непосредствен-
но, как это показано в разд. 7.3.4.
(Де = О, А постоянно)	(8.7)
(Дс = О, А постоянно)	(8.8)
(Дс = 0)	(8.9)
Легко видеть, что величина (F2)LNa представляет собой про-
водимость, а £иа, г отражает связь между транспортом и мета-
болизмом; Lr можно рассматривать как обобщенную константу
Таблица 8.1. Неравновесно-термодинамические параметры активного
транспорта натрия в мочевом пузыре жабы (средние значения
параметров по 11 препаратам) [24]
Параметр	Значение
/о rsb Jr0 =о Na ^Na ^Na, г Lr AI A3 qi qt (jsb\ { r •^Na oArO	25,6 ± 2,2 мкА/см2 24,3 ± 2,9 пмоль/(см2 • c) 18,1 ± 2,3 пмоль/(см2  c) 117 ± 8 мВ 103,9 ± 12,5 мкмоль2/(см2 • c • ккал) 5,41 ± 0,83 мкмоль2/(см2 • c • ккал) 0,369 ± 0,073 мкмоль2/(см2 • c • ккал) 56,0 ± 5,8 ккал/моль O2 58,2 ± 6,5 ккал/моль O2 0,87 ± 0,05 0,85 ± 0,05 4,4 ±1,9 пмоль/(см2 • c) 21,5 ±2,0 моль Ма+/моль O2 14,8 ±0,9 моль №+/моль O2
Энергетика активного транспорта: эксперимент
173
скорости для метаболической реакции, служащей движущей
силой. Хотя для исчерпывающего понимания природы феноме-
нологических коэффициентов необходимо развить детальную
модель системы активного транспорта, может оказаться, что
количественное определение коэффициентов L или У?, а также
величины А позволит различать факторы, влияющие на кинети-
ческие и энергетические параметры. В табл. 8.1 приведены ти-
пичные значения коэффициентов L для мочевого пузыря жабы.
В табл. 8.2 дана сводка качественных эффектов различных
реагентов в опытах на коже лягушки. Как видно из этих дан-
ных, в ряде случаев и ингибиторы, и стимуляторы транспорта
влияют на феноменологические коэффициенты и А. Возможно,
в некоторых случаях такие комбинированные эффекты отра-
жают механизмы, модифицирующие трансэпителиальный пере-
нос, в условиях примерного постоянства внутриклеточной кон-
центрации электролитов. Например, после введения альдосте-
рона возрастание А и £ма, г, которое должно было бы снизить
концентрацию натрия в клетках, может компенсироваться уси-
лением апикальной проводимости (что проявляется как возра-
стание Z.Na) с повышением внутриклеточного уровня натрия.
Чтобы выяснить, в каких условиях параллельные эффекты, за-
трагивающие А и коэффициенты L, представляют собой дискрет-
ные процессы, в противоположность взаимодействиям между
кинетическими и энергетическими факторами, модулирующими
транспорт, необходимы дальнейшие исследования. При этом
формализм неравновесной термодинамики позволяет дать си-
стематическое описание функций системы активного транспорта
в разнообразных условиях.
8.2.5.	Оценка степени сопряжения: стехиометрия
Из разд. 7.3.5 можно видеть, что если известны феноменологи-
ческие коэффициенты, то можно рассчитать степень сопряже-
ния q непосредственно по уравнению (7.6). В других ситуациях
удобнее оценить q, не определяя заранее все феноменологиче-
ские коэффициенты, по методу, основанному на использовании
уравнений (7.39) или (7.40), которые мы здесь представим
в виде
В табл. 8.1 сопоставлены значения q\ и q2, измеренные в
опытах с мочевым пузырем жабы [23]. Как и следует ожидать
для линейной системы, получено хорошее согласие между ре-
зультатами двух методов. Среднее значение 0,86 весьма суще-
ственно отличается от 1,00, что указывает на неполноту сопря-
Таблица 8.2. Влияние различных реагентов на параметры в уравнениях неравновесной термодинамики для кожи
лягушки
Реагент	Концентрация	Время	7Na 0	/sb го	LNa	LNa. r	L r	A	n	Литература
Уабаин	10“7 м	2,5 ч	Ф	1	—	1	—	0	9	30
Амилорид	(1-5)  10“s М	30 мнн	> f			> f		'I	9	Лау и др.,
		60 мин	v	J		v	;	0	9	неопублико-
		90 мин					;	0	4	ванные дан-
										ные
	10~7 — 10~s Ма	1 ч			—		i	0	11	34
		4 ч	ф	ф	—		ф	t	11	
2-Дезоксиглюкоза	16 • 10“3 Мб	1 ч		0	—	0	—	'I	10	29, 30
Альдостерон	5-10“7 М	14—18 ч	t	t	—	0	—	t	8	34
Антидиуретический гор-	100 мЕд./мл	30 мнн					0		9	26
МОН		60 мин					0		9	
		90 мин		t			0		9	
	10 мЕд./мл	30—120 мин		tB	r	r	0	t	6	26
Антидиуретический гор-	10 мЕд./мл	30—90 мин	0	0			Ф	t	4-9	26
мон (амилорнд)г										
Цикло-АМФ	10-2 М	60—90 мнн	t	t		t	0		6	26
Стрелками | и О обозначено усиление, ослабление или отсутствие эффекта по сравнению с контролем. а В присутствии 5-10 7 М
d-альдостерона. ® В присутствии 1 мМ глюкозы. в Эффекты слабее, чем в тканях, контактирующих со 100 мЕд./мл АДГ. г Чтобы исследо-
вать влияние АДГ на А в отсутствие повышенных скоростей транспорта и метаболизма, ткани выдерживали в присутствии 1—5 мкМ амило-
рида до введении АДГ.
Энергетика активного транспорта: эксперимент
175
жения. Примерно такая же степень сопряжения получена для
кожи лягушки [22].
В системе, где нет полного сопряжения, метаболическая
энергия должна тратиться на поддержание разности электро-
химических потенциалов натрия даже в отсутствие активного
транспорта, т. е. (/rb)za =0 =#=0
(табл. 8.1). Если это действи-
тельно так, то, хотя /йа и Jsrb линейно зависят от Аф, жесткого
стехиометрического соотношения не существует. Рис. 8.16 пока-
зывает, как меняется отношение Jsb при варьировании 7\-а
путем изменения3 Аф. Кроме того, при анализе графиков зави-
симости /йа от Jsrb следует избегать ошибок, связанных с сопо-
ставлением стехиометрических соотношений, определяемых из
наклонов (d/Na/rf/rb = ^-Na/^-Na, г), с оценками, полученными в
УСЛОВИЯХ короткого замыкания (/^а оАгО = L^a, rfL?)’ поскольку
они должны различаться между собой при q=/= 1 (см. табл. 8.1).
Эффективность конверсии энергии — чувствительная функ-
ция степени сопряжения. При q = 0,86 максимальная эффек-
тивность не превышает 35 %. Тем не менее следует помнить,
что малая степень сопряжения имеет свои биологические пре-
имущества [38]. Существующий уровень знаний механизмов
обмена веществ недостаточен для окончательных суждений по
Рис. 8.16. Примеры взаимосвязи между отношением Na+/O2 и активным
транспортом натрия.
Отношение Na"*"/®г(^ЙаАг^) показано при различных скоростях транспорта (^Na)"
При Дтр = 0 отношение Na+/O2 постоянно (линия Л). Если Дтр варьируют, то Na+/O2
увеличивается с ростом скорости активного транспорта (линия Б) [23].
176
ГЛАВА 8
этому вопросу. В наших исследованиях величина q не обнару-
живала четких корреляций с /Nao. /го или А.
В принципе неполнота сопряжения может возникать различ-
ными путями. Одна из возможностей — это повторная циркуля-
ция перенесенного натрия (рис. 8.17). В той мере, в какой пас-
сивная утечка через серозную поверхность допускает повторное
попадание перенесенного натрия в пул активного транспорта,
установление значения Aip, соответствующее /ца = 0, не приве-
дет к инактивации насоса, а обеспечит лишь полную компенса-
цию активного транспорта утечкой. В соответствии с этим ско-
рость супрабазального поглощения кислорода (Jfb) а не бу-
дет равна нулю. Эту возможность, по-видимому, удалось
исключить в опытах с мочевым пузырем жабы, где измеряли ско-
рость образования СО2 в тканях в условиях, когда активный
транспорт натрия через эпителий был подавлен амилоридом.
Поскольку удаление серозного натрия в этих опытах слабо
влияло на /со2> можно предположить, что повторное включение
натрия в цикл было минимальным [9]. Ранние данные о по-
Рис. 8.17. Модель системы трансэпителиального транспорта натрия.
Натрий может пересекать мембрану в результате активного или пассивного транспорта
с проводимостями ха и х? соответственно. При обычных условиях опыта натрий по-
падает в активный канал через барьер пассивной проницаемости с проводимостью хт
на слизистой поверхности и покидает активный канал с проводимостью на сероз-
ной поверхности. Возможна также некоторая утечка в обратном направлении через
серозную поверхность с проводимостью [23].
§
без обработки
без обработки + АДГ
без обработки + АДГ + уабаин
Рис. 8.18. Значения dNa/dO2 для препарата кожи лягушки в условиях короткого замыкания, рассчитанные
исходя из i/F(d/r0/d/0). Указаны доверительные интервалы с вероятностью 95 % [41].
178
ГЛАВА 8
вторном переносе натрия через базолатеральную мембрану
кожи лягушки [6] позже также были оспорены [11]. Остается
еще возможность, что частичное разобщение окислительного
метаболизма и транспорта отражает или неполноту сопряже-
ния окислительного фосфорилирования, или неполноту сопря-
жения механизма, связывающего утилизацию АТФ с трансло-
кацией натрия.
Помимо изменений /ма//гЬ, которые можно объяснить варьи-
рованием Аф в разобщенных тканях, было найдено, что отноше-
ние скоростей транспорта и метаболизма различно в разных
тканях даже в условиях короткого замыкания (рис. 8.18). Так,
в опытах на коже лягушки, когда значения 7ыао и Jr0 менялись
самопроизвольно или при введении антидиуретического гормона
или уабаина, значение d/Na о/dJп для каждой ткани было фик-
сированным, но значения для разных тканей варьировали в ин-
тервале 7,1—30,9 [41]. Точно так же значение /йао//го для це-
лого мочевого пузыря жабы при обработке амилоридом было
характерным для каждой ткани, но значения для разных тка-
ней варьировали в интервале 9,3—20,4 [23]. Эти различия тре-
буют объяснений. Поскольку Jr оценивали по скорости поглоще-
ния кислорода, изменения отношений нельзя объяснить разли-
чиями дыхательного коэффициента. Такое объяснение было
предложено для переменных значений /йа//со2 [2,8]. Одна из
возможностей состоит в том, что различаются субстраты, ис-
пользуемые в каждой ткани; это приводит к разным значениям
отношения P/О и, следовательно, Na/O2. Однако, как и в опы-
тах с кожей лягушки, нельзя полностью исключить повторное
использование натрия4.
8.2.6.	Сопоставление величин Еиа и А
При анализе активного трансэпителиального транспорта натрия
часто использовались модельные эквивалентные контуры [39].
В такой модели активная стадия отображается как проводящий
элемент х\-а> последовательно соединенный с источником элек-
тродвижущей силы для транспорта натрия Еыа и параллельно
с пассивным элементом проводимости хр (рис. 7.7). При этом
ток короткого замыкания дается выражением
/0 = XNa^Na	(8.12)
Как отмечено ранее, попытки использовать параметры эк-
вивалентного контура с целью различить кинетические и энер-
гетические факторы, влияющие на транспорт, не были вполне
удовлетворительными, поскольку ENa не является чисто энер-
гетической величиной [см. уравнение (7.48)]. В принципе дан-
ное вещество может изменять влияя или на феноменологи-
Энергетика активного транспорта: эксперимент 179
ческие коэффициенты, или на А. В связи с этим интересно
сравнить влияние ряда веществ на Е^а и А [20].
При использовании уравнения (8.12) для расчета ENa нужно
различать токи, определяемые активным транспортом натрия,
и токи, обусловленные другими ионными потоками. С этой
целью в работе [20] использовали амилорид. Была выбрана
концентрация, почти полностью подавляющая включение нат-
рия в активный транспорт. В этом случае остаточная проводи-
мость характеризует «пассивную» проводимость хр, что позво-
ляет, учитывая исходное значение полной проводимости х, опре-
делить «активную» составляющую ха, чувствительную к амило-
риду:
х“ = х —хр	(8.13)
Чтобы оценивать параметры многократно и с достаточно высо-
кой частотой, было удобно определять х из —Д//Д(Дф), фик-
сируя значения Дф последовательно при +20, 0, —20, 0 мВ на
5 с с интервалами длительностью 1 мин. Считая, что значение
х“, полученное таким способом, дает х^а, можно рассчитать £Na.
Этот метод был использован для изучения влияния антиди-
уретического гормона, уабаина, амилорида и 2-дезоксиглюкозы
на транспорт в мочевом пузыре жабы. Результаты представ-
лены в табл. 8.3. В табл. 8.4 сопоставлены влияния трех из
этих агентов на кажущиеся значения и А, а также влияние
альдостерона, изученное ранее. Результаты показывают, что
Таблица 8.3. Влияние различных реагентов на параметры эквивалентного
контура мочевого пузыря жабы [20]а
Реагент	Концентрация	Время, мня	7о,	0		£Ыа, t / £Na. 0	п
Антидиуре- тнческнй гормон	100 мЕд./мл	7	2,25±0,114	2,53±0,194	0,89±0,032	17
Контроль	—	7	1,04±0,01	1,08±0,02	0,97 ±0,02	17
Уабаин	10-4 м	30	0,41 ±0,06*	0,54±0,074	0,76±0,072	8
Контроль		30	0,99±0,02	1,04±0,03	0,95±0,03	8
Амилорид	5-10~7 М	5	0,41±0,044	0,21 ±0,05	1,92±0,333	6
Контроль	—	5	1,00±0,01	1,02±0,02	0,98 ±0,02	6
2-Дезоксн- глюкоза	7,5-Ю-3 М	60	0,33±0,034	0,38±0,034	0,89±0,05	7
Контроль	—	60	1,05±0,05	1,11 ±0,08	0,94±0,05	7
а
Данные выражены как средние	± среднеквадратичная ошибка. Надстроч-
ные индексы характеризуют значимость различий между опытом н контролем: 2:р(А)<
<0,025; 3:р(Д)<0,01; 4:р(Д)<0,001.
12*
180
ГЛАВА 8
Таблица 8.4. Сопоставление влияния ряда реагентов ва ,,£Na“ н
Реагент	“^Ыа*				А			
	Концен- трация, М	Время	"*Na“	Лите- ратура	Концентра- ция, м	Время, ч	А	’Лите- ратура
Уабаин	1(Г4	5—30 мии	1	20	10~7	2,5	0	30
Амилорид	5-10“7	1—60 мни		20	10“7- 10~5	1	0	34
Амилорид	—	—	—	—	ю-7 - ю-5	4	А	34
2-Дезокси-	7,5- 10“3	5—60 мни	0	20	1,6-10~2	1	V	30
глюкоза Альдостерон	5.10“7	1—6 ч	0	34	5-10“7	14-18		34
“2?Na“ определяли для мочевого пузыря жабы, А - для кожи лягушки. Стрелками
I, | и 0 обозначены существенное снижение, существенное возрастание и отсутствие
эффекта по сравнению с контролем.
Е^а нельзя рассматривать как надежную характеристику сво-
бодной энергии метаболической реакции, обеспечивающей дви-
жущую силу для активного транспорта. Однако этот анализ
не вполне убедителен, поскольку в нем используется чувстви-
160
140
120
60
40
Рнс. 8.19. Связь между (Дф) а
(статический напор) и А. Коэффи-
циент корреляции г = 0,63 [24].
ol-----1----1-----1_____L
20	40 60	80
А, ккал/моль Ог
тельная к амилориду проводимость иа, полученная в режиме
5-секундного изменения Дф. При этом требуется, чтобы до-
статочно точно аппроксимировала значение натриевой проводи-
мости к^а, правильное для стационарных условий, когда транс-
мембранный поток натрия консервативен и задается, чувстви-
Энергетика активного транспорта: эксперимент 181
тельным к амилориду током 1а. Если такая аппроксимация не-
верна, то полученное значение э. д. с. не может рассматриваться
как точная мера ENa (т. е. как значение Аф, обеспечивающее
нулевой стационарный активный транспорт натрия) [45]. Этот
вопрос находится в стадии исследований.
В связи с этим более важное значение имеет соотношение
между А и Еыа, полученное исходя из точки пересечения с осью
ординат на графике 6-минутного эксперимента в координатах
1а — Аф, (Аф)7а =0 в режиме статического напора (рис. 8.19).
Как видно из рисунка, эти две величины коррелируют, но кор-
реляция не точна.
8.3.	Анализ активного транспорта в других
видах эпителия
Линейность соотношений между током и напряжением в ряде
эпителиальных тканей показывает, что формализм, использо-
ванный ранее для анализа активного транспорта натрия в коже
лягушки, жабы, мочевом пузыре жабы, вероятно, применим и
к другим транспортным процессам. В большинстве таких слу-
чаев анализ ограничивался рассмотрением эквивалентных элек-
трических контуров. Шульц и др. [36] продемонстрировали
линейность зависимости между скоростью активного транспорта
натрия и Аф в толстой кишке кролика и на этой основе пред-
ложили эквивалентный контур, для анализа которого были вве-
дены феноменологические коэффициенты сопротивления и срод-
ство в рамках уравнений линейной неравновесной термодина-
мики. Однако параметры этих уравнений экспериментально не
определялись.
8.3.1.	Активный транспорт протонов в мочевом пузыре черепахи
Одна из систем активного транспорта, которая была система-
тически изучена как с точки зрения неравновесной термодина-
мики, так и методом эквивалентных электрических контуров,—
это система транспорта протонов в мочевом пузыре черепахи
[1, 3—5, 37]. В этой ткани осуществляется активный транспорт
как натрия (от слизистой оболочки к серозной), так и протонов
(в обратном направлении). В присутствии СОг в надлежащей
концентрации, а также в условиях регуляции трансэпителиаль-
ной разности электрических потенциалов оба транспортных про-
цесса происходят независимо друг от друга. Для нашего ана-
лиза несущественно, в чем именно состоит молекулярный ме-
ханизм транспорта — в переносе ионов Н+ изнутри наружу, как
указано здесь, либо в переносе ионов ОН- или НСОГ в обратном
направлении, как это предполагается в некоторых работах.
182
ГЛАВА S
Поскольку протонная проводимость параллельного пассив-
ного пути в мочевом пузыре черепахи очень мала, можно при-
мерно приравнять скорости суммарного транспорта протонов /н
н их активного транспорта /н- Соответственно скорость актив-
ного транспорта можно оценить или используя pH-стат, или
(в отсутствие активного транспорта натрия) из тока короткого
замыкания, т. е. тока, измеряемого при нулевой разности по-
тенциалов Дф = 0, когда обе поверхности мембраны омываются
растворами идентичного состава, за исключением, может быть,
значения pH. При низкой пассивной проницаемости для про-
тонов пассивный трансэпителиальный поток протонов пренебре-
жимо мал. Активный транспорт натрия легко устранить, под-
бирая соответствующую концентрацию уабаина.
Если использовать омывающие растворы, не содержащие
СО2, то скорость окислительного обмена можно оценить из
Jco2 — полной скорости образования СО2, измеренной кондукто-
метрическим методом, как и ранее в случае активного транс-
порта натрия. Транспорт протонов, однако, осуществляется
сильнее в присутствии СО2. В этом случае скорость окислитель-
ного обмена оценивалась путем измерения скорости образова-
ния 14СО2 из меченной 14С глюкозы (/со2)-
Транспорт и метаболизм легко нарушить, изменяя окружаю-
щую концентрацию СО2, т. е. рСО2 (и для удобства поддержи-
вая разность электрохимических потенциалов Хн на нулевом
уровне), или изменяя Хн путем изменений Дф и значения pH
на внутренней поверхности тканиs. При изменении Хн вели-
чина /н достигает нового стационарного состояния в пределах
минуты. Кажущаяся скорость образования СО2 изменяется мед-
леннее, достигая нового стационарного уровня за 10—15 мин6.
В стационарном состоянии строго линейное соотношение
было получено между /н, с одной стороны, и /со2 и /со2 —
с другой. Значения dJaldJco! или с/7н/^7со, примерно совпа-
дали для двух половинок мочевого пузыря, взятого у одного
и того же животного. Поскольку была доказана полнота сопря-
жения транспорта протонов и окислительного метаболизма в
этой ткани (см. ниже), было сделано заключение, что эти на-
клоны дают оценку стехиометрического соотношения независимо
от того, каким способом варьировали транспорт и метаболизм.
У различных особей данного вида эти значения варьировали
в широких пределах: в присутствии 1 % СО2 значения dJnldJco,
варьировали в пределах от 4,4+ 1,2 до 38,2 + 3,5 (п = 40);
в отсутствие СО2 значения dj^/dj^ варьировали в пределах
от 1,41+0,26 до 11,23+1,17 (« = 6). Такой разброс превы-
шает величину, которую можно ожидать исходя из различий
в дыхательных коэффициентах. Таким образом, как и в случае
Энергетика активного транспорта: эксперимент 18$
активного транспорта натрия через эпителий земноводных,
между скоростями транспорта и окислительного обмена, по-ви-
димому, нет единой стехиометрии.
8.3.2.	Неравновесио-термодииамический анализ активного
транспорта протонов
В других исследованиях показано, что транспорт протонов и
сопряженный метаболизм в мочевом пузыре черепахи подда-
ются анализу методами линейной термодинамики неравновес-
ных процессов, поскольку /н> /со, и /со, линейно зависят от
значения pH во внешнем пространстве (рис. 8.20). Кроме того,
при сопоставлении зависимости /н от pH на внешней стороне
и от Aip значения d/H/d(ApH) и d/H/d(Aip) в пределах стати-
стического разброса совпадали, так же как и точки пересече-
ния с осью pH, в которых скорость активного транспорта про-
тонов обращается в нуль. В результате по аналогии с актив-
ным транспортом натрия можно написать
J?[ = Mh+Z.hM, Ггь = ЬНгХн + ЬгА (8.14,8.15}
Чтобы согласовать эти выражения с условным выбором поляр-
ностей в работе [4], которые противоположны таковым, при-
нятым ранее для активного транспорта натрия, будем считать,
что Ун положителен, когда протоны движутся изнутри наружу,
и Хц = — Арн = — (RTA In ан + ЕАф) берется в виде
Хн = (In 10) RT АрН — F Aip = 2,3RT (pHm — pHs) — F (фт — ips)
(8.16)
Таким образом, снова, при правильном выборе траектории,
можно принять, что соотношения взаимности Онзагера справед-
ливы, и для метаболизма, как и для транспорта, несуществен-
но, меняем ли мы Хн путем варьирования значения pH на внеш-
ней стороне или Агр. По аналогии с транспортом натрия в коже
жабы эти уравнения неприменимы в условиях варьирования
концентрации протонов снаружи.
8.3.3.	Степень сопряжения системы транспорта протонов
Описанный выше формализм был первоначально использован
для оценки степени сопряжения транспортной системы. Если
сопряжение полное, то скорости транспорта и метаболизма
должны быть во всех случаях связаны жестким стехиометриче-
ским соотношением. Если же сопряжение неполное, то dJii/dJ сот
будет зависеть от способа, использованного для нарушения
транспорта. В работе [5] для этой цели использовали два спо-
соба: 1) варьировали pH на внешней стороне (переменное Хн);
184
ГЛАВА 8
pH ни Внешней стороне
;£02?нмоль/(мин > мг сухого Веса)
Рис. 8.20. Связь скорости выделения протонов 1ц и скорости образования
14СО2 (/co j с величиной pH на внешней стороне и друг с другом в мочевом
пузыре черепахи [5].
Энергетика активного транспорта: эксперимент 185
2) изменяли рСОг, поддерживая значения pH на внутренней н
внешней сторонах постоянными и равными (Хн = 0). В пред-
положении, что Хн не влияет на А, как это следует из наблю-
даемых линейных соотношений, авторы работы [5] заключили,
что первый способ дает оценку величины
(д7н/д7со2)д — £н/£нг	(8.17)
а второй —
HMo2k=o = Lnr/Lr	(8.18)
н
Обращаясь к уравнению (4.12), видим, что
(5/h/3/CO2)x н = 0	LHr
’	-TT = q2	(8Л9)
(д/н/д/со2)л
В серии из 14 опытов значения Й7н/^7со2 с переменной Хн
и постоянной Хн существенно не различались. Применение урав-
нения (8.19) дало среднее значение <7 — 0,97 + 0,05 (нижний
предел с вероятностью 95 % равен 0,90). На этой основе за-
ключили, что сопряжение в основном полное. Ингибитор про-
тонного насоса (дициклогексилкарбодиимид) дал значения
^/н/^/сол неотличимые от значений, полученных путем варьи-
рования pH на внешней стороне (Аль-Авкати, частное сообще-
ние). Если бы сопряжение было неполным, то в состоянии ста-
тического напора величина 7СОз должна была бы включать
вклад от супрабазального метаболизма, который, как можно
ожидать, подавляется агентом, инактивирующим протонный на-
сос. Точно так же тот факт, что в состоянии статического на-
пора концентрация 1 мМ ацетазоламида (ингибитора карбо-
ангидразы), подавляющего /н в обычных условиях эксперимен-
та, не влияла на метаболизм, расценивается как еще одно
подтверждение полноты сопряжения (</~ I)7.
8.3.4.	Сродство системы транспорта протонов
Справедливость уравнений (8.14) и (8.15) позволяет также
оценить сродство, как и для системы активного транспорта нат-
рия [1]. Полагая, что А постоянно в условиях варьирования Хн,
напишем
(/н)хн=о
“ (dJr/dXH)
(8.20)
В этом случае удобно варьировать Хн путем изменения зна-
чения pH на внешней стороне и следить за метаболизмом пу-
186
ГЛАВА 8
-гем измерения скорости образования СОг из радиоактивной
глюкозы Усо2- Чтобы такой подход был справедливым в усло-
виях данного эксперимента, необходимо, чтобы окисление глю-
козы было единственным источником энергии обмена веществ.
В таком предположении рассчитано, что значения А в контроль-
ных препаратах мочевого пузыря черепахи (без обработки аль-
достероном) варьируют в пределах от 28 до 99 ккал/моль СО2
или в пределах от 5 до 17 ккал/моль АТФ, если дыхательный
коэффициент принять равным 1, а отношение P/О равным 3.
Эти значения находятся в том же интервале, что и приведен-
ные выше для кожи лягушки и мочевого пузыря жабы, т. е.
20—80 ккал/моль О2 или 3—13 ккал/моль АТФ. Хотя это при-
близительное соответствие само по себе интересно, нужно по-
мнить, что для обеих систем точное количественное описание
энергетики на основе обмена АТФ требует столь же точного
определения отношения P/О в условиях данного эксперимента.
Кроме того, когда мы следим за обменом веществ путем изме-
рения образования СО2, надо точно знать дыхательный коэф-
фициент. Можно ожидать, что обе эти величины в действитель-
ности меняются в зависимости от условий опыта. То, что такие
изменения вполне могут оказаться существенными, следует из
широкого диапазона значений б/Ун/б/Усо_> приведенных ра-
нее.
Анализ мочевых пузырей, в которых транспорт протонов
стимулировался альдостероном, можно использовать для выяс-
нения механизма действия этого гормона. При выдерживании
•с альдостероном 1—6 ч сродство А оказалось ниже в стимули-
рованных, чем в нестимулированных тканях, и одновременно
возрастало значение б/Уц/бЦАрН). Однако после 20-часового
выдерживания, как и для транспорта натрия в коже лягушки,
А оказалось существенно выше в стимулированных тканях, чем
в контрольных препаратах. Интересно, что альдостерон посте-
пенно влияет на кажущееся стехиометрическое соотношение
между транспортом протонов и метаболизмом таким образом,
что когда оба этих процесса модифицировали путем изменения
значения pH на внешней стороне, то спустя 20 ч экспозиции
с гормоном (но не 1—6 ч) значение бУУн/бУУсо2 оказалось суще-
ственно выше в стимулированных тканях. Эти наблюдения
в совокупности позволили предположить, что альдостерон сна-
чала влияет на транспортную систему с соответствующим сни-
жением А, после чего наступает адаптация, сопровождаемая
ростом А. Оценить справедливость этого предположения до-
вольно трудно, поскольку нет данных о величине А до введения
альдостерона. Кроме того, нужны дополнительные сведения,
чтобы связать значения А, рассчитанные из обмена *СО2 и
лолученные на основе метаболизма АТФ.
Энергетика активного транспорта: эксперимент 187
8.3.5.	Анализ активного транспорта протонов методом
эквивалентных контуров
По аналогии с транспортом натрия функцию транспорта про-
тонов можно проанализировать на основе эквивалентного кон-
тура, состоящего из протонного насоса с последовательно со-
единенными проводящими элементами в активном пути и
параллельно соединенным проводящим элементом, соответствую-
щим пассивной утечке. Если задана эквивалентная зависи-
мость /н от Дф и значения pH на внешней стороне, то анализ
эквивалентного контура удобно провести двумя альтернатив-
ными способами. Рассмотрим ткани, в которых активный транс-
порт натрия подавлен. Тогда в отсутствие разности pH на мем-
бране активный поток протонов можно выразить в виде элек-
трического тока Ih^FJh, а его зависимость от Дф в стацио-
нарном состоянии — в виде
=	(8.21)
При интегрировании это дает
/н = %н (Ен - Дф) (ДрН = 0)	(8.22)
С другой стороны, в отсутствие разности электрических потен-
циалов на мембране
а (	1	\ ( dlf, \
Хн = k 2,3RT/F J к d (ДрН) J	(8.23)
или
7н = %н [Ен + 2,3 (ЕГ/Е) ДрН] (Дф = 0)	(8.24)
(Здесь, как и ранее, мы приняли условие полярности, данное
в работе [4], т. е. 1н считается положительным, когда он на-
правлен снаружи внутрь, Дф = фт — фэ и ДрН = рНт — pHs.)
Аль-Авкати и сотрудники оценили параметры такого мо-
дельного эквивалентного контура. Они ввели «силу насоса, или
кажущуюся протонодвижущую силу». Пренебрегая снова ма-
лым вкладом пассивного трансэпителиального потока протонов,
выразим протонодвижущую силу (ПДС) уравнением
ПДС = (- Хн)/н_о = FEh	(8.25)
Мы игнорируем здесь различие между кажущейся и истинной
ПДС, которое возникает, если значение pH в цитоплазме слегка
отличается от pH раствора, омывающего внутреннюю поверх-
ность. Значения, полученные из величин градиентов электри-
ческого потенциала и pH, неразличимы: 144 + 9 и 161 ±8 мВ
соответственно в единицах потенциала или 2,44 + 0,16 и
2,73 + 0,13 в единицах pH.
188
ГЛАВА 8
Выражая ПДС на основе линейного формализма неравно-
весной термодинамики по уравнению (8.14), имеем
ПДС = (£нг/£н) А	(8.26)
в точном соответствии с уравнением (8.13). Очевидно, как и
для ZiNa, ПДС (или Ен) не является чисто энергетическим па-
раметром, а зависит и от кинетических факторов.
Это заключение было проверено в модельных опытах, в ко-
торых транспорт модифицировали, влияя на метаболизм. Как
видно из табл. 8.5, подавление метаболизма путем дезоксигена-
ции, введения 2-дезоксиглюкозы или удаления субстратов во
всех случаях приводило к существенному подавлению актив-
ного транспорта протонов и снижению %н со сравнительно сла-
бым влиянием на ПДС. Только при введении в омывающий
раствор 2,4-динитрофенола влияние на %н и ПДС было сопо-
ставимым. Влияние этого вещества на ПДС, по-видимому, обус-
ловлено усилением проницаемости мембран для протонов, что
приводит к усилению пассивной утечки протонов в клетки через
плазматические мембраны по пути, параллельному активному
насосу. Такое объяснение подтверждается тем фактом, что
2,4-динитрофенол существенно снижает ПДС (на 12%) даже
при введении его со стороны внешней поверхности в низкой
концентрации (2-10-6 М), не влияющей на /но- В соответствии
Таблица 8.5. Влияние различных обработок на параметры эквивалентного
контура для мочевого пузыря черепахи3
Обработка	Концен- трация, М	(7но)е/(;но)с	(ха)е/(х°)с	(ПДС)е/(ПДС)е	п	Лите- ратура
Дезоксиге- нация	—	0,39	0,44	0,90	6	3
2,4-Диии- трофеиол	10 4	0,55	0,73	0,77	15	3
2-Дезокси- глюкоза	10 2	0,56	0,67	0,87	9	3
После уда- ления	—	0,26	0,29	0,88	6	3
Глюкоза	5-10“3	1,70	1,84	0,94	6	3
Альдосте- рон6	5- 10-7	1,58	1,68	0,96	—	4
Данные взяты нз указанных источников н выражены в виде отношения среднего
значения в опытном образце (е) к одновременно полученному среднему значению в пар-
ном контрольном образце (с). & Эти измерения проведены после 20 ч выдерживания с
.альдостероном. Показано, что в этот период времени сродство А возрастает [1].
Энергетика активного транспорта: эксперимент 189
с этим введение в систему глюкозы дает отчетливо выражен-
ную стимуляцию транспорта протонов, сопряженную с сопо-
ставимым возрастанием хн, но без увеличения ПДС.
Все эти наблюдения подтверждают интерпретацию, основан-
ную на уравнении (8.26), а именно: ПДС, как и ENa, пред-
ставляет собой сложный параметр, включающий кинетические
и энергетические факторы. Эти результаты особенно интересны,
поскольку они позволяют избежать неоднозначности, возникшей
при изучении «Еыа», где для определения х£а пришлось исполь-
зовать данные 5-секундных измерений проводимости, чувстви-
тельной к амилориду. В противоположность этому при изуче-
нии транспорта протонов измерялись стационарные токи; сле-
довательно, можно считать, что по уравнениям (8.23) и (8.24)
в данном случае оцениваются Хн и Ен (или ПДС) в пределах
ошибки эксперимента.
Интересно также, что активация транспорта протонов после
продолжительного выдерживания с альдостероном сопряжена
с возрастанием хн при отсутствии влияния на ПДС. Хотя мы
пока недостаточно ясно понимаем механизм действия альдосте-
рона, чтобы объяснить природу этого эффекта, напомним, что
для системы транспорта протонов, как и для транспорта натрия,
продолжительное выдерживание с альдостероном приводит
к повышению сродства А. Вероятно, это отражает возрастание
свободной энергии метаболической реакции, которая служит
движущей силой для транспорта. Следует ожидать, что удале-
ние субстрата, его обратное введение и действие 2-дезоксиглю-
козой также должны влиять на свободную энергию. Тот факт,
что различные изменения обменных процессов влияют на хн,
но при этом существенно не влияют на ПДС, снова приводит
к выводу о динамическом взаимодействии между проницае-
мостью и энергетическими факторами, как и в случае транспор-
та натрия.
8.3.6.	Корреляции биохимических процессов и активного
транспорта протонов
Диксон и Аль-Авкати [15] показали, что если подавить инги-
биторами нормальный синтез АТФ в мочевом пузыре черепахи,
то при наложении обращенного градиента электрохимического
потенциала протонов, превышающего 180 мВ (эта величина как
раз обеспечивает подавление сопряженного транспорта прото-
нов и метаболизма), происходит синтез АТФ. Отсюда был сде-
лан вывод, что насос представляет собой обратимую протон-
транслоказу. Чтобы изучить соотношение между транспортом
я свободной энергией — АСдтф гидролиза АТФ, были прове-
дены одновременные измерения /но и отношения концентраций
]АТФ]/[АДФ] [Ф„], соответствующего закону действующих
190
ГЛАВА а
масс, в широком интервале условий [14]. В контрольном пре-
парате — АСатф было в интервале 40—50 кДж/моль (около
11 — 12 ккаль/моль). Эти значения можно сравнить с величи-
нами 20—70 кДж/моль, рассчитанными из контрольных экспе-
риментов для Лдтф в исследованиях по влиянию альдостерона,,
описанных ранее. Эффекты активаторов и ингибиторов транс-
порта дали согласующиеся результаты: 5 % СО2 понижали
—АСатф» а ацетазоламид и закисление внешней среды повы-
шали его. Однако в каждом случае изменение —Д6атф было
порядка 10 % и меньше. Напомним, что при обработке альдо-
стероном Латф возрастало примерно на 50 %.
Хотя эти результаты не поддаются однозначной интерпрета-
ции, они указывают на существование фундаментальных труд-
ностей, с которыми сталкиваются имеющиеся в настоящее вре-
мя подходы к анализу энергетики процессов активного транс-
порта. С одной стороны, биохимические методы дают прямые1
доказательства участия АТФ. Однако эти методы сопряжены
с разрушением биологического материала и, возможно, с суще-
ственным изменением уровней адениннуклеотидов и фосфата
в процессе анализа. Кроме того, в тканях, образующих множе-
ство компартментов, отношение концентраций, следующее из
закона действующих масс, будет сложной функцией распреде-
ления АТФ, АДФ и Фн в клетках различных типов и субклеточ-
ных органеллах, что также может маскировать изменения в ин-
тересующей нас области. Наконец, расчет —ДСатф, основан-
ный на значениях стандартной свободной энергии —ДСдтф-
из справочников, не учитывает изменения этой величины, опре-
деляемые распределением Н+, Mg2+ и Са2+. С другой стороны,
сродство ЛОг, рассчитанное по уравнениям неравновесной тер-
модинамики,— это абстрактная величина, основанная на пред-
положении о справедливости двухпотокового линейного форма-
лизма. Ее нельзя непосредственно связать с —Д6атф> не зная
отношения P/О в данных условиях. Однако там, где этот фор-
мализм применим, он дает значение —ДСатф, относящееся
к функционирующей транспортной системе, а не к ткани в це-
лом и отражающее влияние факторов, модифицирующих ло-
кальное значение — Дб°, так же как и отношение концентра-
ции реагентов.
Учитывая нынешнее положение, далекое от полного пони-
мания энергетики активного транспорта, оба подхода представ-
ляются заслуживающими дальнейших исследований.
8.4.	Выводы
1.	Экспериментальные исследования показывают, что активный
транспорт натрия в коже лягушки и мочевом пузыре жабы и
активный транспорт протонов в мочевом пузыре черепахи
Энергетика активного транспорта: эксперимент 191
можно успешно анализировать с применением двухпотокового
формализма линейной неравновесной термодинамики, исполь-
зуя при этом определенные способы для варьирования транс-
эпителиальных сил.
2.	В рамках такого подхода модуляция XNa (или Хн) по
правильно выбранной траектории позволяет оценить феномено-
логические коэффициенты L или R и сродство А метаболиче-
ской реакции, создающей движущую силу для активного транс-
порта. При этом удается различить кинетические и энергетиче-
ские факторы, влияющие на транспорт. Линейность, обуслов-
ленная кинетическими, а не чисто термодинамическими факто-
рами, требует модификации этого подхода.
3.	Величины сродства АОг (в расчете на моль супрабазаль-
ного поглощения кислорода) совместимы с биохимическими
оценками. Расчет А? (сродство на моль использованного АТФ)
требует знания величины отношения P/О в данной ткани.
4.	Влияние модельных соединений на коэффициенты L и
АОг согласуется с данными о механизмах их действия. Альдо-
стерон и антидиуретический гормон, по-видимому, стимулируют
транспорт, влияя и на кинетические, и на энергетические пара-
метры.
5.	Не существует единого стехиометрического соотношения,
связывающего скорости транспорта натрия и супрабазального
поглощения кислорода. Сопряжение этих процессов, по-види-
мому, неполное.
6.	Проведено сопоставление методов линейной неравновес-
ной термодинамики и эквивалентных электрических контуров.
Теоретические соображения и результаты экспериментов ука-
зывают на то, что в отличие от сродства А электродвижущая
сила для транспорта натрия ENs (или Ен) явно зависит от ки-
нетических параметров.
7.	С учетом нынешнего явно недостаточного понимания
энергетики процессов активного транспорта требуется дальней-
шее исследование возможностей и биохимического, и формально
термодинамического подхода к этой проблеме.
9
Кинетика изотопных потоков:
основные факты и теории
В исследованиях транспортных процессов анализ кинетики по-
токов изотопов использовался двояко: во-первых, для изучения
проницаемости мембран и, во-вторых, для изучения сил, дви-
жущих транспорт. Разумеется, потоки изотопов можно изучать
и без неравновесной термодинамики, и в дальнейших разделах
мы рассмотрим несколько таких примеров. Однако неравновес-
ная термодинамика помогает внести ясность в интерпретацию
результатов, поскольку она дает критерии для проверки закон-
ности некоторых наших предположений и строгий формализм
для оценки следствий, вытекающих из этих предположений.
Сначала рассмотрим, как до сих пор использовались изо-
топы, какие при этом были обнаружены аномалии и какие были
предложены объяснения для этих аномалий, основанные на
классическом подходе. Затем перейдем к применению неравно-
весной термодинамики к общей проблеме анализа изотопных
потоков. В гл. 10 мы обсудим некоторые частные модели, а
в гл. 11 рассмотрим экспериментальные данные, позволяющие
оценить правомерность использованных термодинамических со-
отношений. По ходу дела мы будем отмечать несоответствия и
промахи, характерные для классического рассмотрения.
9.1.	Исторический очерк
Вскоре после того, как стали доступными изотопы (особенно
радиоактивные), их стали широко использовать для оценки
проницаемости биологических мембран. Причины этого оче-
видны. Даже в простом случае вещества, поток которого обус-
ловлен только его собственным градиентом концентраций,
оценка проницаемости требует измерения концентраций по обе
стороны мембраны, а также скорости потока.
Часто такие измерения приводят к существенным ошибкам,
если, например, концентрации малы или имеющиеся химические
методы неточны. Кроме того, в физиологических условиях гра-
диенты концентраций могут быть очень малыми, а потоки или
очень малы, или вообще равны нулю. Всякая попытка улучшить
качество измерений путем повышения градиента концентраций
Кинетика изотопных потоков: основные факты и теории 193
или ускорения потока может вывести систему далеко от ее фи-
зиологического состояния. В противоположность этому радио-
активные изотопы действительно можно ввести в мизерных ко-
личествах, в концентрации, которая часто на несколько поряд-
ков меньше, чем концентрация исходного вещества. Хотя при
этом суммарная концентрация вещества почти не изменится,
градиент концентрации изотопно-меченного аналога, равно как
и скорость его потока, может быть легко измерен. Отсюда мож-
но рассчитать коэффициент проницаемости ’.
Величина, которую мы хотим определить, — это проницае-
мость; в принципе ее можно получить путем измерения суммар-
ного потока, индуцированного разностью концентраций исход-
ного вещества:
a = -J/RT\c	(9.1)
где 1— поток из камеры I в камеру II и Дс = сп — с1. (Для
простоты мы будем опускать индексы там, где это не может
привести к путанице.) Это определение часто применяют, не
рассматривая возможное влияние сопряжения J с потоками
других веществ. Это, однако, приводит к несопоставимости ре-
зультатов измерений <о в различных условиях эксперимента.
В частном случае, когда отсутствуют объемный поток и элек-
трический ток, уравнение (9.1) становится эквивалентным урав-
нению (3.51) для Js, которое теперь можно переписать в виде
<о = -(Л/ДО/а /=0	(9.2)
(В гл. 9—11 в соответствии с нашими ранними публикациями
мы примем правило знаков, которое в ряде случаев отличается
от правил, используемых в предыдущих главах этой книги.)
При использовании изотопных меток, чтобы избежать труд-
ностей, связанных с определением проникающей способности
химическими методами, проникающую способность изотопа при-
мем равной
и‘ = —Д/^ГАс*	(9.3)
или, точнее, учитывая возможность сопряженных потоков:
«•* = -(/;/A<)7b,Zs,z=0	(9.4)
Если мы имеем дело с изотопами, которые не дают изотоп-
ного эффекта, т. е. с такими, атомные массы которых различа-
ются столь незначительно, что их кинетические и термодинами-
ческие свойства практически совпадают, то может показаться,
что величина со* в уравнении (9.3) или (9.4) всегда совпадает
с со, поскольку изотопно-меченные молекулы ведут себя точно
так же, как основное вещество. Однако это заключение неверно.
Действительно, если пренебречь мизерным изотопным эффек-
13 Кеплеи, Эссиг
194
ГЛАВА 9
том и считать, что ион 24Na ведет себя подобно иону 23Na, то
отсюда еще не следует, что 24Na как диффундирующее веще-
ство в данной системе будет вести себя точно так же, как ве-
щество 23Na: эти два вещества различны, имеют совершенно
разные концентрации и концентрационные градиенты, поэтому
нет никаких оснований ожидать, что со* обязательно будет
равна со. Почему это так, станет яснее позже.
В ранних работах не всегда обращали внимание на это раз-
личие. Однако очень скоро после начала измерений изотопных
потоков было обращено внимание на кажущееся расхождение
между данными изотопных и обычных экспериментов. Прони-
цаемость кожи лягушки для воды, как может показаться, имеет
два совершенно разных значения в зависимости от того, изме-
ряем ли мы суммарный поток под действием осмотического гра-
диента или поток меченой воды в отсутствие суммарного по-
тока. Эта кажущаяся аномалия была разъяснена Кэфед-
Джонсеном и Уссингом [8], которые отметили, что диффунди-
рующая молекула (в данном случае изотопно-меченная моле-
кула воды) «может иметь собственную скорость диффузии, на
которую накладывается скорость потока растворителя». Дру-
гими словами, для случая потока воды через кожу лягушки
различие между двумя типами коэффициентов проницаемости
было связано с явлением сопряжения потоков. Здесь проницае-
мость для изотопного потока со* меньше, чем проницаемость
для суммарного потока со. Отмечены и расхождения обратного
знака, когда со* больше, чем для суммарного потока со, напри-
мер в случае пассивного транспорта сахара через мембрану
эритроцита. Как будет показано, оба этих кажущихся расхож-
дения— естественное следствие сопряжения потоков, рассмат-
риваемого в рамках формализма неравновесной термодина-
мики.
Другая обширная область, которую нам предстоит рассмот-
реть,— это попытки использовать изотопные потоки для оценки
сил, которые индуцируют потоки через мембраны. Уссинг и Те-
релл [16, 18—20] отметили в этой связи, что, хотя мы во мно-
гих случаях очень слабо представляем себе структурные харак-
теристики и проницаемость биологических мембран, можно
установить, движется то или иное вещество под действием
только своего собственного градиента электрохимического по-
тенциала или нет. Такое определение включает измерение «от-
ношения потоков», т. е. отношения противоположных «однона-
правленных» потоков через мембрану. Для этого случая было
предложено простое соотношение, которые мы запишем в виде
In / = — Др = Л'	(9.5)
где In f — натуральный логарифм отношения потоков, а другие
величины обозначены как обычно. В отсутствие электрических
Кинетика изотопных потоков: основные факты и теории
195
эффектов уравнение (9.5) приобретает особенно простую форму:
f = ci/сП	(9.6)
где с1 и с11 — концентрации исследуемых веществ по обе сто-
роны (снаружи и внутри) мембраны. Принятое здесь правило
знаков иллюстрируется на рис. 9.1. Рассматриваемое нами от-
ношение потоков — это отношение потока внутрь к потоку на-
ружу.
Если применить уравнение (9.5) или (9.6) к данной экспе-
риментальной ситуации, то кажется разумным заключить, что
исследуемое вещество движется только под действием своего
собственного электрохимического градиента. Если же эти урав-
нения неприменимы, то такое заключение считалось неверным,
Рис. 9.1. Потоки внутрь, наружу и
суммарный поток между наружным
и внутренним растворами, омываю-
щими мембрану.
Поток внутрь
Поток наружу!
Суммарный поток!
и для таких случаев рассматривалась возможность влияния
каких-то других сил па суммарный поток. Кроме того, предпо-
лагалось, что степень «аномальности» потоков, т. е. в какой
мере они отклоняются от приведенных простых соотношений,
может дать представление о величине этих внешних сил, ка-
кова бы ни была их природа. Измерения отношения потоков
при попытке выяснить природу потока воды привели к пред-
ставлению об «объемном потоке», согласно которому молекулы
воды движутся через мембрану не по отдельности, а в виде
кластеров. В ряде близких по существу исследований были из-
мерены аномальные потоки ацетамида и тиомочевины при на-
личии осмотического потока воды, и из этих опытов был сделан
вывод, что данные субстраты — аналоги мочевины, — проникая
через эпителиальные мембраны, пользуются водными каналами,
причем растворитель «несет» субстраты, усиливая их поток.
Дальнейшее использование отношения потоков при изучении
сил, активирующих транспорт, было предпринято Уссингом и
сотрудниками, чтобы охарактеризовать механизмы, ответствен-
ные за активный транспорт солей через эпителиальные мем-
браны. Кожа лягушки переносит соли против исключительно
высокого градиента концентрации — 104— 105).Поскольку
натрий в этой ситуации движется и против градиента концен-
трации, и против электрических сил, его перенос следует счи-
тать активным. Тем не менее, поскольку NaCl, возможно, дви-
жется в виде ионных пар, считалось важным показать, что по-
токи натрия и хлорида независимы друг от друга. Для этого
измеряли отношения потоков натрия и хлорида, связанные
13*
196
ГЛАВА 9
с вполне определенными разностями электрохимических потен-
циалов Ар№ и Ajlci [8, 18, 20]. Как оказалось, отношение пото-
ков натрия больше, чем ожидается исходя из разности элек-
трохимических потенциалов (т. е. RT In fNa > XNa), что как
будто бы согласуется с активным транспортом. С другой сто-
роны, отношение потоков С1~ соответствовало ожидаемому на
основе разности электрохимических потенциалов этого иона
(/?Г1п fci = Xci) (рис. 9.2). Это согласуется с пассивным пе-
Рис. 9.2. Сравнение теоретических и
наблюдаемых отношений потоков для
хлорида в коже лягушки. Теорети-
ческие отношения потоков рассчита-
ны с помощью уравнения Уссинга
(9.5) [9].
реносом ионов вдоль градиента электрохимического потенциа-
ла, возникающего за счет транспорта натрия. На основании
этого предположили, что, исходя из отношения потоков, можно
различить активный и пассивный транспорт и что это возмож-
но и тогда, когда транспорт осуществляется вдоль или против
градиента электрохимического потенциала. Кроме того, сте-
пень отклонения отношения потоков от ожидаемого значения
для пассивного транспорта рассматривалась как мера метабо-
лической силы, движущей суммарный поток («£Na»).
Эти подходы в историческом аспекте имели большое значе-
ние в исследованиях процессов биологического транспорта. Тем
не менее уже давно было осознано, что столь уверенное исполь-
зование отношения потоков как меры энергетических факторов
может в принципе привести к грубым ошибкам. По-видимому,
первыми дали пример ограниченности возможностей использо-
вания отношения потоков для указанных целей Ходжкин и
Кейнс [6] в своих исследованиях потоков калия в аксонах
кальмара, в которых было показано, что отношение потоков
существенно аномально, причем RTlnf резко отличается от
разности электрохимических потенциалов калия (рис. 9.3), не-
смотря на отсутствие несущего эффекта растворителя и актив-
ного транспорта. В этом случае, который часто называют «од-
норядной диффузией», отношение потоков дает завышенную
Кинетика изотопных потоков: основные факты н теории
197
оценку силы, влияющей на транспорт. С другой стороны, в ме-
ханизмах, связанных с «обменной диффузией», отношение по-
токов приводит к заниженным оценкам [10]. Поскольку ясно,
что при таких обстоятельствах измерение отношения потоков
не позволяет оценивать силы, индуцирующие суммарный поток,
приходится с недоверием отнестись и к общему случаю исполь-
зования отношения потоков для этих целей, если нам детально
неизвестны механизмы проницаемости.
Непригодность отношения потоков для надежной оценки
сил, движущих транспорт, а также трудности при оценке про-
ницаемости мембран приводят к необходимости систематиче-
ского анализа кинетики изотопных потоков. Такой анализ дол-
жен дать основу для исследования проницаемости и энергети-
ческих факторов, влияющих на транспорт, как в теоретическом,
так и в экспериментальном аспекте.
Рнс. 9.3. Влияние разности электрических потенциалов на отношение потоков
калня в волокнах гигантского аксона Sepia, обработанного диинтрофенолом.
п—	/ потенциален на мембране (внешний потенциал минус внутренний),
"СД="(«т/г) In (сК1 ext). так что Е—Ед равно отрицательной разности электро-
химических потенциалов калия [6].
198
ГЛАВА 9
9.2.	Термодинамический анализ
9.2.1.	Основные уравнения
Термодинамический анализ, к которому мы приступаем, бази-
руется на работе Кедем и Эссига [7]. В соответствии с нашими
основными целями он будет развит на основе линейных урав-
нений неравновесной термодинамики. Читателей, интересую-
щихся более фундаментальным подходом к проблеме, мы от-
сылаем к работе Зауера [13]. Как отмечено выше, наша цель
состоит в том, чтобы объяснить две аномалии: расхождения
между коэффициентами проницаемости, полученными изотоп-
ными и неизотопными методами, и «аномалию» отношения по-
токов в отсутствие несущего эффекта растворителя и активного
транспорта. Формальные соотношения показывают, что эти так
называемые аномалии можно объяснить исходя из сопряжения
между потоками различных изотопных форм исследуемого веще-
ства. Это явление было названо «изотопным взаимодействием».
Поскольку процессы, к рассмотрению которых мы присту-
паем, зависят большей частью от сопряжения консервативных
потоков, естественно использовать уравнения с коэффициен-
тами сопротивления. Позже мы дадим их соотношение с коэф-
фициентами проницаемости. Рассмотрим сначала транспорт,
который осуществляется только по одному способу, игнорируя
пока влияние утечек2. Для достаточно медленных процессов
обычно предполагается, что электрохимический потенциал опре-
делен в любой точке, а силы и потоки линейно связаны также
в любой точке мембраны. (Предположение о локальной линей-
ности— это мягкое предположение. При этом не обязательно,
чтобы потоки были линейно связаны с интегральной силой Др
на мембране.) При выводе соотношений с коэффициентами со-
противления мы начинаем с соотношений, выражающих дви-
жущие силы как функции стационарных потоков в мембране.
Пусть ось х перпендикулярна плоскости мембраны. Тогда урав-
нения для локальных потоков запишем в форме
п
--Й- = гоо/ + £М/	(9-7)
7=4
п
—=	+ Г12Л +''[зЛ +	^i///	(9.8)
/=4
п
—^2i7i ~t~ r22J2-f- r2373 + У, ?*2/7/	(9-9)
/=4
п
— ^3i7i -\-r32J2 + r3373 -f- У r3/Jj	(9.10)
7=4
Кинетика изотопных потоков: основные факты и теории 199
Здесь индекс 0, опущенный удобства ради в обозначениях сум-
марного потока J, указывает на то, что соответствующая вели-
чина относится ко всему рассматриваемому веществу, которое
может быть ионным или незаряженным. Индекс 1 относится
к преобладающему изотопу, а индексы 2 и 3 — к изотопным
меткам исследуемого вещества. Множители гц — локальные ко-
эффициенты сопротивления. Потоки J, (принятые положитель-
ными, если они направлены вдоль оси х) включают не только
потоки всех веществ, проходящих через мембрану, например
воды, но и движения подвижных компонент мембраны. Сумма
может также содержать члены г-rJr, представляющие прямой
вклад метаболической реакции в ориентированный поток рас-
творенного вещества.
Уравнения (9.7) — (9.10) взаимосвязаны, поскольку изотопы
предполагаются неразличимыми по всем своим термодинами-
ческим и кинетическим свойствам. Следовательно, для рассмат-
риваемого вещества в целом
=	+	dp (э.Ц)
dx	dx 1 dx	dx ' dx '	’
а для одной из изотопных меток
dx	dx	dx	dx '	1 dx '	’
Поскольку мы приняли идентичность термодинамических
свойств различных изотопов, можно утверждать, что 7 = 72,
z=z2 и v = v2. Таким образом, обозначая удельную актив-
ность с2/с как р2, имеем
dgz   dg  d In рг
dx	dx	К fix
(9.13)
Такое же соотношение можно написать для веществ 1 и 3. По-
скольку и кинетические свойства изотопов считаются идентич-
ными, мы вправе утверждать, что сопряженные процессы не
могут привести к разделению изотопов. Если удельные актив-
ности постоянны по всей мембране, то отношения потоков изо-
топов должны совпадать с отношениями их концентраций, ка-
ковы бы ни были другие потоки.
=	=	=	(9.14)
dx dx dx dx \ dx }	'	’
Уравнение показывает, что в этих условиях движущие силы
равны.
Отвлекаясь на некоторое время от изотопов, получим соот-
ношение между полным потоком и разностью электрохимиче-
200
ГЛАВА 9
ских потенциалов на мембране. Для этого проинтегрируем
уравнение (9.7):
Ах п
- (р - й1) = X = JR + J £ Го/Л dx (9.15)
О 4
Здесь интегральное сопротивление, которое дает сопротивление
суммарному потоку, определяется как
Дх
r^dx	(9.16)
о
(х = 0 на внешней поверхности мембраны, х = Ах на внутрен-
ней). Интегрируя таким образом уравнение (9.7), мы прини-
маем, что / постоянно по всей мембране в стационарном со-
стоянии. Однако не обязательно, чтобы У/ были консервативны.
Обе поверхности мембраны находятся в равновесии с омы-
вающими растворами, и предполагается, что р непрерывны по
всей мембране. Допускается, однако, что производная d^/dx
имеет конечное число точек разрыва. Именно такова, несо-
мненно, ситуация в биологических мембранах, где можно ожи-
дать нарушений непрерывности локальных сопротивлений и на-
личия метаболических потоков. Мы ограничимся рассмотрением
таких систем, в которых исследуемое вещество находится по
обе стороны мембраны, так что Ац всегда конечно. По уравне-
нию (9.15),
Полезно на этой стадии ввести естественное обобщение
определения коэффициента проницаемости, которое мы дали
в гл. 3. Для разбавленных растворов электролитов, которые
обычно встречаются в биологических системах, нередки случаи,
когда Уо ~ Ушцш. Поэтому можно написать
(9.18)
где с — средняя концентрация, в соответствии с тем, что ска-
зано в гл. З3.
К сожалению, условия, для которых получено уравнение
(9.18),-часто не достигаются в биологических системах. Кроме
того, не всегда удается оценить величины R и со в уравнении
(9.15). Их определение требует знания движущей силы и
вклада сопряженных потоков в силы, активирующие транспорт,
а в биологических исследованиях такие данные часто получить
не удается. Поэтому надеялись, что недостающие данные удаст-
Кинетика изотопных потоков: основные факты н теории
201
ся получить с помощью изотопных методов. Полезно начать
рассмотрение этой ситуации с анализа того случая, когда ника-
ких изотопных взаимодействий нет.
9.2.2. Случай, когда изотопные взаимодействия
отсутствуют
В этом случае поток вещества индуцируется его собственным
градиентом концентрации, электрическими силами и, возмож-
но, за счет сопряжения с потоками растворителя, других рас-
творенных веществ или за счет метаболизма, однако поток дан-
ной изотопной разновидности вещества не зависит от потока
любой другой его изотопной разновидности. Поэтому уравнения
(9.8) — (9.10) можно упростить, так как
rtk = 0	i, k=l, 2, 3)	(9.19)
Поскольку для суммарного потока J мы имеем, как и ранее,
уравнение (9.7), получим
Потоки преобладающего изотопа и изотопной метки Ji и
даются выражениями
<9-2»
X	/ = 4	/
+£'«'/') <9-22)
X	j=4	/
и аналогичным выражением для метки 3. Отметим, что прямые
коэффициенты rOo, Гц и т. д. должны быть положительны по
второму закону термодинамики, тогда как перекрестные коэф-
фициенты могут быть любого знака.
Выше было отмечено, что в отсутствие градиента удельной
активности потоки изотопов всегда должны быть пропорцио-
нальны их концентрациям. Таким образом, из уравнений (9.20)
и (9.22) с учетом (9.14) получаем
4г + Z г*'7'
=	------=Р2 (^=0)	(9.23)
+ S г°'7/
4
и аналогичное соотношение для У3/7.
202
ГЛАВА 9
Поскольку уравнения типа (9.23) должны выполняться для
любых значений У,- в соответствии с предположением о кинети-
ческой неразличимости изотопов, получаем
rii = r2i = r3l =rOj	(9.24)
П1Р1 = Г22Р2 = ^эРз = Гоо	(9.25)
Обратимся теперь к фундаментальной концепции неравновес-
ной термодинамики, состоящей в том, что хотя малые измене-
ния локальных сил влияют на потоки, они не меняют локаль-
ных параметров состояния. Иными словами, хотя локальные
коэффициенты сопротивления при х зависят от локальных кон-
центраций и потому могут меняться при изменении удельной
активности, они не зависят от изменений градиента удельной
активности. Следовательно, уравнения (9.24) и (9.25) остаются
справедливыми независимо от того, существует ли градиент рг
или нет.
Если теперь подставить уравнения (9.13), (9.24) и (9.25)
в уравнение (9.22), то уравнение потока меченого вещества
приобретает вид
A = -S-(# + S''»A + w^)	<9 26>
Это выражение надо сравнить с выражением для суммарного
потока [уравнение (9.20)]. Тогда становится ясно, что, когда
р изменяется в зависимости от х, поток меченого субстрата не
будет равным рУ, а будет отличаться от этой величины из-за
изотопного обмена. Комбинируя уравнения (9.20) и (9.26), по-
лучаем
Это уравнение показывает, что, хотя поток метки и суммарный
поток зависят от всех величин Го/У/, поток метки, отнесенный
к р2У, зависит только от градиента р2 и сопротивления гоо- В от-
сутствие градиента удельной активности отношение между У2
и У равно р2, как это и следовало из наших предыдущих рас-
суждений. При наличии градиента удельной активности это
соотношение уже неприменимо. Поток метки теперь «обгоняет»
суммарный поток. При этом интуитивно ясно, что степень, в ко-
торой пбток метки обгоняет суммарный поток, пропорциональна
градиенту удельной активности. Следует отметить, что коэф-
фициент пропорциональности, связывающий градиент удельной
активности с обменным потоком, определяется здесь величиной
/ос — локальным коэффициентом для суммарного потока. Зна-
чение этого факта будет яснее из дальнейшего рассмотрения.
Кинетика изотопных потоков: основные факты и теории
203
Для использования уравнения (9.27) в экспериментах необ-
ходимо провести его интегрирование по мембране или ткани,
чтобы можно было сопоставить наблюдаемые потоки с другими
экспериментально измеряемыми параметрами. Отметим, что это
интегрирование допустимо до тех пор, пока мы рассматриваем
консервативные потоки и непрерывные функции удельной ак-
тивности вдоль параллельных и идентичных путей. Нарушения
непрерывности локальных коэффициентов сопротивления или
градиента удельной активности вполне возможны при движе-
нии вдоль координаты х в различных интересующих нас мем-
бранах, но это в данном случае несущественно.
Уравнение (9.27) имеет столь простой вид, что легко под-
дается интегрированию. Полезно рассмотреть отдельно два со-
стояния. В одном из них нет суммарного потока. При этом мы
имеем просто эксперимент по изотопному обмену. Тогда инте-
грирование уравнения (9.27) при введении сопротивления сум-
марному потоку по уравнению (9.16) дает
72Я = -Я7’(р'1-р') = -Я7’Ар2 (7 = 0)	(9.28)
При этом предполагается, что удельная активность на каждой
поверхности равна таковой в омывающем растворе. Тогда Ар
относится к разности удельных активностей в омывающих рас-
творах. Уравнение (9.28) показывает, что в рассматриваемых
условиях для системы с идентичными каналами движения в от-
сутствие сопряжения между изотопными потоками эксперимент
по простому изотопному обмену позволяет определить сопро-
тивление суммарному потоку [и, следовательно, проницаемость
для суммарного потока по уравнению (9.18)] даже без всяких
данных о движущей силе, действующей на рассматриваемое
вещество, и при наличии сопряжения с потоками других ве-
ществ или даже при активном транспорте. Так, например, если
Ас — 0, то
J2cR = — RTNc2 (7 = 0)	(9.29)
и
® =	(9.30)
cR V RT \сг Jj„0	v ’
При условии что суммарный поток рассматриваемого вещества
равен нулю, не существенно, какие другие потоки имеются в
системе. Однако нет даже необходимости устанавливать это
условие. При наличии суммарного потока интегрирование урав-
нения (9.29) дает по аналогии с уравнением для метки 3 и
уравнением (9.16)
J2 р2 J 73 р3 I
—— = *п-------;— = <П-------Г-
7	72 р27	73 р37
(9.31)
204
ГЛАВА 9
где удельную активность мы обозначили р1 при х = 0 (снару-
жи) и р11 при х = Дх (внутри). Если в одном из компартмен-
тов, скажем наружном, добавляется одна изотопная метка 2,
а внутренний объем достаточно велик, то можно написать
р”~0
(9.32)
При этом уравнение (9.31) сразу же упрощается и принимает
вид
ZR	У2/Рг
-----= 1п --------------
RT J2/pl2 - J
(9.33)
Таким образом, в отсутствие изотопных взаимодействий опре-
деление потока одной из меток и суммарного потока дает со-
противление суммарному потоку R. Поэтому R можно опреде-
лить, не зная ни движущей силы, ни природы сопряженных
потоков. Проницаемость для суммарного потока снова можно
оценить как 1/cR.
Если мы измеряем два однонаправленных потока и каждая
метка добавляется только в один из компартментов системы,
так что
р>’~р’~О	(9.34)
то уравнение (9.31) сводится к виду
^/Рз   з/рГ J
Аг/ Р2	W Рз'
(9.35)
или, в более простой форме,
/ = /2/р1 + /з/рз’^/-/	(9.36)
где в принятой нами терминологии, введенной Уссингом и Те-
реллом, J = J2Ip\ — поток внутрь, а/3//р”—поток наружу
или истечение. Поэтому уравнение (9.36) представляет собой
широко используемое соотношение: суммарный поток равен по-
току внутрь минус поток наружу. Подставляя уравнение (9.36)
в (9.33), с учетом уравнения (9.30) имеем
JR = J/c® = RTlnf = RTln(jiT)	(9.37)
Приведенные выше уравнения показывают, что для систем рас-
сматриваемого типа измерение двух однонаправленных потоков
(или, наоборот, одного однонаправленного потока и суммарного
потока) позволяет оценить сопротивление (а следовательно, и
проницаемость) для суммарного потока, несмотря на отсут-
ствие сведений о силах, индуцирующих транспорт, какова бы
ни была их природа. Кроме того, те же измерения позволяют
Кинетика изотопных потоков: основные факты и теории
205
количественно охарактеризовать суммарную силу, индуцирую-
щую транспорт, как это можно видеть, комбинируя уравнения
(9.15) и (9.37):
Дх п
RT In f = X - J £ r0/Jz dx	(9.38)
О 4
Это соотношение аналогично уравнению для отношения потоков
Уссинга и Терелла.
9.2.3.	Случай, когда имеется изотопное взаимодействие
До сих пор мы полагали, что на поток метки влияет ее соб-
ственный градиент электрохимических потенциалов и, возможно,
сопряженные потоки других веществ, а также метаболизм, ио
нет прямого взаимодействия между изменениями суммарного
потока данного вещества и рассматриваемой его изотопной раз-
новидности. Однако мы уже отметили ранее, что Уссингу и
сотрудникам удалось объяснить аномалии проницаемости кожи
лягушки для воды тем, что в действительности на движение
изотопно-меченной воды влияет поток воды, рассматриваемой
как растворитель. Теперь мы рассмотрим возможность сопря-
жения не только потоков разных изотопных разновидностей
воды, но и изотопных разновидностей любого растворенного ве-
щества. Хотя для разбавленных водных растворов это может
показаться не очень актуальным, такой случай вполне может
реализоваться в высокоспециализированных мембранах и си-
стемах переносчиков, так что следствия такого рода изотопного
взаимодействия мы рассмотрим в самой общей форме.
Как и ранее, уравнение (9.7) применимо к полному потоку
рассматриваемого вещества. Однако для изотопных форм ве-
щества в уравнениях (9.8) — (9.10) уже не выполняются усло-
вия г,* = 0, как утверждалось в уравнении (9.19). Важно отме-
тить, что, когда мы говорим: вид уравнения для полного по-
тока не изменился при наличии изотопного взаимодействия, мы
не утверждаем, что изотопные взаимодействия не влияют на
величину коэффициентов сопротивления гОо и го/- Для такого
утверждения нам понадобилась бы весьма детальная физиче-
ская картина системы.
Рассматривая уравнение (9.8), мы видим, что кинетическая
неразличимость изотопных форм требует, чтобы для данных
значений dp^/dx и поток Jj зависел не от отдельных значе-
ний J2 и /3, а от их суммы J2 + /з- Следовательно, г12 — г13, и
эта величина не должна зависеть от отношения концентраций
с2/сз- Аналогично г2> = г2з и г31 = г32. Мы знаем также, что,
поскольку уравнения (9.8) — (9.10) связывают сопряженные
силы и потоки, появляющиеся в диссипативной функции про-
206
ГЛАВА 9
цесса, выполняются соотношения взаимности Онзагера: г,*=ги.
Взятые совместно, эти уравнения приводят к заключению, что
все rik идентичны (i^=6; z, 6=1,2, 3). Если вспомнить, что
J = Ji + h + h, то отсюда следует, что г21Д + ггзЛ—пИ7— -М
и уравнение (9.9) можно переписать в виде
п
—	= (Г22~ г1к)^2~\- rikJ + X !	(9.39)
/ = 4
Как и ранее, для постоянной удельной активности р, по всей
мембране dp,/jx = Jpz/Jx, и, поскольку появляется изотопное
взаимодействие, h — pj. Из уравнений (9.7) и (9.39) имеем
W + Го/Л = (r22 Г ik) 72 + rij + 52 Г2/7/
(dpjdx = 0)
и, таким образом,
п
г	г — г	52	~	Т,
4 =	+	-----—4 = р2 (9.40)
1	Г22 ~ rik	(Г22 - rik)	7
[Легко видеть, что если метка 2 присутствует только в следо-
вых количествах, то знаменатели в уравнении (9.40) никогда
не обращаются в нуль.] Поскольку эти уравнения должны вы-
полняться при любых значениях независимых переменных,
уравнение (9.24) должно, как и ранее, выполняться и
(Too — rik)/(r22 — rik) = р2	(9.41)
То же самое относится и к другим изотопным разновидностям.
Как уже указывалось, эти соотношения не зависят от того, по-
стоянна ли удельная активность.
Знаки Пк могут создавать путаницу. Если имеется эффект
взаимного увлечения изотопных потоков (положительное со-
пряжение), то rik отрицателен. Если поток изотопа z снижает
поток изотопа k (отрицательное сопряжение), то г(* положите-
лен. Как и ранее, если р меняется с изменением х, то поток
изотопа р/ будет превышать значение изотопного обмена. Од-
нако в данном случае сопротивление обменному потоку будет
изменяться за счет изотопного взаимодействия. Вычитая урав-
нение (9.7) из уравнений (9.39), получаем
__ dpi , dji _
dx ' dx
п
— (Г22 rik) 72	(r00 “ rik) 7 +	(r2j — Г01) Jj
!=i
Кинетика изотопных потоков: основные факты и теории
207
но, поскольку уравнения (9.13) и (9.24) дают соответственно
с/цг . dp. _______d In рг
dx ' dx К dx
и r2j = r0!
можно написать
Разделив на r22— rtk и подставляя уравнение (9.41), приходим
к соотношению
Это уравнение аналогично уравнению (9.27). Между ними, од-
нако, есть существенная разница: степень влияния градиента
удельной активности на обгоняющее движение изотопа зависит
теперь не только от гоо — локального сопоставления суммарному
потоку, но и от г,к — сопротивления, выражающего взаимодей-
ствие между различными изотопными формами одного и того
же вещества.
Отметив это различие, можно завершить наше формальное
рассмотрение точно так же, как и в отсутствие изотопного
взаимодействия. Снова полезно оценить сопротивление с по-
мощью изотопных измерений в отсутствие суммарного потока.
Интегрируя уравнения (9.42), в данном случае получаем
Дх
4 5 (rw-riti)dx^J2R^-RT^-^^-RT\p2 (7 = 0)
о
(9.43)
Это выражение можно сравнить с уравнением (9.28). Ясно, что
коэффициент сопротивления здесь уже не является интеграль-
ным коэффициентом сопротивления суммарному потоку R: при
наличии изотопного взаимодействия эксперимент по простому
изотопному обмену уже не позволяет оценить сопротивление
(или проницаемость) для суммарного потока. Полученный здесь
коэффициент мы назвали обменным коэффициентом сопротив-
ления R*. По аналогии с уравнением (9.16)
Дх
(Лю — rik)dx	(9.44)
о
Отметим, что если г,> < 0, т. е. имеется положительное сопря-
жение, то R* > R. Если же сопряжение отрицательно, то
rik >0 и R* < R. Из уравнения (9.43) можно сразу же вы-
вести уравнение типа (9.30):
®* = (1/cR*) = (- J./RT Дс2)/=0	(9.45)
Здесь со* — обменная проницаемость.
208
ГЛАВА 9
Снова можно рассмотреть локальное уравнение (9.42) при
наличии суммарного потока и, интегрируя, как и ранее, полу-
чить для метки 2
JR* , /2 ~
----= In-------,—
RT Z2 —p’z
(9.46)
и в конечном счете
/Я* = 7/«о* = ЯГ In /
(9-47)
в полном соответствии с уравнением (9.37). Отметим, что, как
и в отсутствие суммарного потока, изотопный эксперимент при
наличии суммарного потока не позволяет оценить коэффициент
сопротивления суммарному потоку Я, но дает обменный коэф-
фициент сопротивления Я*. Последний может быть больше или
меньше Я.
Если объединить уравнения (9.47) и (9.15), то получим4
ЯГ In f =
(9.48)
Следует отметить, что это уравнение, как и соответствующее
выражение (9.38), выполняющееся при отсутствии изотопных
взаимодействий, справедливо независимо от того, зависят ли
коэффициенты проницаемости от концентраций омывающих
растворов или от разности электрических потенциалов, со и <о*,
будучи функциями локальных феноменологических коэффици-
ентов, являются, конечно, параметрами состояния, и ничто в
наших соотношениях не наводит на мысль, что они не должны
быть весьма чувствительными функциями состояния. Тем не
менее если только со и со* применимы к данной системе, то эти
уравнения также должны выполняться5.
Как мы видим, при наличии изотопного взаимодействия из
отношения потоков нельзя определить силы, активирующие
транспорт. Однако уравнение (9.48) полезно в том плане, что
факторы, способствующие отклонению от «нормального» отно-
шения потоков, ехр(Х/ЯГ), становятся очевидными: 1) сопря-
жение с потоками других веществ, 2) сопряжение с метаболиз-
мом (активный транспорт) и 3) изотопное взаимодействие. До-
полнительный практический аспект — влияние параллельных
каналов утечки. Значение этого фактора будет рассмотрено
в разд. 9.3.
Кинетика изотопных потоков: основные факты и теории 209
9.2.4.	Отношение потоков и энергетика активного
транспорта
Ввиду большого значения, которое придается анализу энерге-
тики активного транспорта, часто предполагается, что влияние
изотопного взаимодействия и утечек минимально, а это позво-
ляет широко пользоваться отношением потоков. Так, при клас-
сическом подходе Уссинга и Церана [21] систему активного
транспорта анализируют с помощью эквивалентного электро-
химического контура, в котором в отсутствие сопряженных
трансэпителиальных потоков сила, участвующая в работе нат-
риевого насоса, дается величиной FE^a, где £ыа— э. д. с. транс-
порта натрия. В предположении что Е^а будет влиять на
отношение потоков натрия так же, как приложенная электродви-
жущая сила влияет на отношение потоков пассивно диффунди-
рующего иона, принимают, что
RT In f = X 4- ££Na	(9.49)
а при коротком замыкании (при идентичных омывающих рас-
творах и Дф = 0)
RT\nfQ = FENa	(9.50)
Уравнение (9.49) интуитивно кажется правдоподобным и
приводит к удобному заключению, что FENa эквивалентно ста-
тическому напору (—Х°), т. е. силе, при которой 7 и Inf равны
нулю. Тем не менее легко видеть, что это, по-видимому, не со-
вместимо с уравнением (9.48), даже в отсутствие изотопных
взаимодействий. Так, при отсутствии сопряженных трансэпите-
лиальных потоков уравнение (9.48) можно переписать в виде
/?Tlnf = (<o/<o*)(A'-/?or/r)	(9.51)
SAX
ГО г (IX. Поэтому FEtia = — Х° ==
= — Ro Г (Jr)j=a, тогда как RT In f0 = — (<о/ю*) Ro r (Е)х=0- Соот-
ветственно даже без всяких изотопных взаимодействий
(ю/и* = 1) уравнения (9.48) и (9.50) дают одинаковое значе-
ние £ыа только при (7Г)/=О = (Л)х=0. Поскольку это маловероятно,
в общем случае уравнение (9.50) неверно. Действительно, для
рассматриваемых здесь линейных систем, учитывая, что, по
уравнению (7.39), (7r)/=0 = (1 — <?2) (7Г)Х=О, имеем
££ыа = (®7<о) (1 - <72) RT In fo	(9.52)
Для значений £Na, которые обычно находятся в интервале
100—120 мВ, уравнение (9.52) дает для высокосопряженных
систем весьма значительные отношения потоков активного
транспорта. Некоторые экспериментальные примеры будут рас-
смотрены в гл. 11.
[4 Кеплен, Эссиг
210
ГЛАВА 9
На этой стадии читатель может спросить, до какой степени
наши заключения, касающиеся изотопных взаимодействий, от-
ражают реальную ситуацию. Можно видеть, что, поскольку
неравновесная термодинамика в явной форме включает все воз-
можные сопряжения потоков, изотопные взаимодействия учи-
тываются в ней автоматически. Но это не значит, что они обя-
зательно должны быть существенными. Некоторые теоретиче-
ские основы изотопных взаимодействий будут рассмотрены
в разд. 9.3 и гл. 10, а экспериментальные примеры мы обсудим
в гл. 11. Однако сначала целесообразно обсудить следствия из
того факта, что мембраны, представляющие интерес с точки
зрения биологии, часто не являются гомогенными.
9.3.	Функции составных мембран
9.3.1.	Параллельные области
Рассмотренный выше подход был применим к области парал-
лельных идентичных каналов и к составному ряду мембран при
условии, что соблюдается непрерывность электрохимического
потенциала транспортируемого вещества. Однако для гетеро-
генных мембран, образующих параллельные каналы, в которых
на потоки влияют различные факторы, этот подход надо видо-
изменить. При попытках анализа природы транспортных про-
цессов по данным изотопных измерений это соображение не
всегда учитывается. Распространенный пример, который мы
только что приводили, — использование отношения потоков для
оценки ENa. Если принять такой подход, то по крайней мере
для «плотного» эпителия сопротивление канала неспецифиче-
ской утечки столь велико, что в отсутствие любой разности
электрохимических потенциалов рассматриваемого вещества его
однонаправленный поток достаточно хорошо отражает харак-
тер преобладающего транспортного процесса. При этом упу-
скают из виду тот факт, что отношение потоков может суще-
ственно меняться в присутствии малых каналов утечки, даже
если суммарный поток утечки равен нулю (рис. 9.4).
Другой пример основан на применении однонаправленных
изотопных потоков для оценки энергетических ограничений, на-
кладываемых на предполагаемую систему насос — утечка в
симметричных клетках. Здесь обычно считают, что скорость
поглощения изотопа определяет суммарную скорость утечки
в клетку, которая в отсутствие специальных механизмов транс-
порта должна быть равна суммарной скорости обратного транс-
порта при участии насоса. В таком предположении, зная раз-
ность электрохимических потенциалов рассматриваемого веще-
ства, можно рассчитать скорость совершения электрохимической
работы. При таком подходе упускают из виду, что значитель-
ная часть потока изотопа в клетку может осуществляться по
Кинетика изотопных потоков: основные факты и теории
211
Накачка
J«=7S-JS>O
Утечка
J?
JP
t JP=JP-JP = 0
Рис. 9.4. Модель системы эпителиального транспорта натрия, учитывающая
параллельные каналы активного транспорта и утечки.
В отсутствие разности электрических потенциалов для натрия (режим установивше-
гося потока) суммарный транспорт осуществляется только по активному пути, ио
пассивные потоки и JP влияют на отношение потоков.
Утечка.
J₽=j’r-jP<0
Рис. 9.5. Модель системы транспорта натрия в симметричных клетках, учи-
тывающая параллельные каналы активного транспорта и утечки.
Предполагается, что поток по активному каналу двоякоиаправлениый [1, 3, 22]. В отсут-
ствие суммарного потока натрия (режим статического напора) результирующая ско-
рость утечки в клетку JP компенсируется результирующей скоростью активного транс-
fl	~	->р
порта J из клетки. Однако измерения /=/=’/ +J могут давать результат, суще-
ственно превышающий J —J —Jat и поэтому приводить к завышенной оценке скорости
совершения электроосмотической работы [4].
14*
212
ГЛАВА 9
механизму активного транспорта, и в той мере, в какой это
имеет место, измерения поглощения изотопа будут завышать
вклад активного транспорта и электрохимической работы
(рис. 9.5). (Экспериментальные данные, относящиеся к этому
вопросу, будут представлены в гл. 11.) Все эти разнообразные
примеры можно подвергнуть строгому анализу, используя вве-
денный нами общий формализм. Прежде чем перейти к отдель-
ным случаям, целесообразно, однако, вывести некоторые общие
соотношения.
Комбинируя уравнение (9.36) и определение отношения по-
токов f = J/J, получим (для элементарного канала транспорта
или для составной системы)
/ =	! =	(9-53, 9-54)
Вводя уравнение (9.47), находим
'-(rh-)-^ ЧтМ™ <9-55’ 9-5в>
Для составной области, содержащей независимые пассив-
ные каналы, каждый из которых подвергается одной и той же
силе, с учетом J*= ^Ji уравнение (9.45) дает	и
Таким образом, каждый элемент вносит в общее значение со*/о
вклад, пропорциональный его доле в мембранной проницае-
мости.
В более общем случае, даже когда силы, действующие в каж-
дой отдельной области, различаются, как, например, в случае
активного транспорта или сопряжения потоков между химиче-
ски различными веществами, получается простое соотношение
между отношениями потоков: поскольку 7=^7/, уравнение
(9.47) показывает, что
f-nf!*’’	(9-58>
(Здесь мы считаем, что с примерно одинаковы по всем элемен-
тарным каналам.) В отсутствие изотопного взаимодействия для
каждого канала <о*/<о = 1 [см. уравнение (9.57)], так что
f =	[((О-/®). S1]	(9.59)
Полезно также выразить отношение потоков исходя из эле-
ментарных однонаправленных потоков. Для системы из двух
Кинетика изотопных потоков: основные факты и теории
213
дискретных параллельных областей аир
faJa .
Za + z*3 _ fa - 1	- 1
т~Т- + Р !а	।	/р
/“ - 1 '	-1
(9.60}
Очевидно, даже при отсутствии активного транспорта, если в
какой-нибудь области имеется изотопное взаимодействие, на-
блюдаемое отношение потоков может заметно отличаться от
такового для элементарного канала проводимости. Действи-
тельно, при наличии циркулирующего объемного потока в со-
ставной системе могут проявляться изотопные взаимодействия,
несмотря на отсутствие изотопных взаимодействий в любом из
элементарных каналов. Это явление обсуждается в гл. 10.
Для рассматриваемого эпителия отношение потоков в си-
стеме с активным транспортом равно
ta + JP  l/fl-l Д Ra J \fp—lJ\RpJ
lr-1 Д Ra J up-l Д Rp J
где верхние индексы аир относятся к параллельным актив-
ным и пассивным каналам. Отношение потоков часто измеря-
ется в режиме с фиксированным потоком (Jf = O). Если пола-
гать для простоты, что между пассивными потоками нет сопря-
жения, когда X—^0, то >-1 [уравнение (9.48)] и lnfp->
—1), поэтому из уравнений (9.55) и (9.56) имеем
Jp->JP-+RT[RP* = RTIRP. Обозначив отношение обменных со-
противлений активного и пассивного каналов через
= Ra*/Rp* = Ra*/Rp) и вводя уравнение (9.61), получим
/ \
п + | ---- I In f“
I f<2 _ 1 I '°
= =-------7 , <-----	(9.62}
I + I -1--1 In fn
Uo-d 0
Это уравнение дает соотношение между наблюдаемым отноше-
нием потоков и отношением потоков в активных каналах, когда
мембрана омывается двумя одинаковыми растворами и в усло-
виях короткого замыкания (Дф = 0). На рис. 9.6 представлены
типичные результаты для различных п. Только в отсутствие
утечки (/г = 0,00) наблюдаемое отношение потоков / совпадает
с fa для активного пути. Будет показано, что даже для плотных
мембран, в которых Rp^>Ra*, отношение потоков того порядка,
какое обычно встречается в литературе (~50—100), может
214
ГЛАВА 9
существенно отличаться от fa. Так как оценить величину такого
рода ошибок невозможно без параллельных измерений Ra* и
Rp*, а такие данные часто недоступны, то следует быть весьма
осторожным при интерпретации смысла полученных в опытах
значений f.
Для симметричной ячейки в стационарном состоянии сум-
марный поток находится в режиме статического напора, так
что / = Ja 4- Jp = 0. Тогда уравнение (9.54) дает
^=/ = 752^т + -Н^Г = ^('Нл--7^=т) (/ = о) (9’63)
Вводя уравнения (9.15) и (9.47) и снова полагая, что пассив-
ные потоки не сопряжены, получаем
fa
Рис. 9.6. Влияние канала утечки на соотношение между наблюдаемым отно-
шением потоков f н отношением потоков в активном канале fa в отсутствие
разности электрохимических потенциалов (режим короткого замыкания, уста-
новившийся поток). Только в отсутствие утечки (п = 0,00) наблюдаемое от-
ношение потоков совпадает с таковым в активном канале [7].
Кинетика изотопных потоков: основные факты н теории
215
Рис. 9.7 дает соотношение между J J) и Ja. Как можно ви-
деть, при малых значениях Ra*/Rp или —X однонаправленный
поток может очень сильно превосходить скорость суммарного
активного транспорта. Это нетрудно понять. Когда Ra*/Rp мало,
большая доля потока в клетку происходит по активному пути,
так что поток внутрь превосходит суммарную скорость пассив-
ной утечки, которая в стационарном состоянии должна быть
равной скорости суммарного активного транспорта. С другой
стороны, при малом значении —X отношение потоков в пас-
сивных каналах приближается к единице, и поэтому снова по-
ток внутрь может превосходить суммарные скорости утечки и
активного транспорта.
Как было отмечено, при анализе допустимости механизмов
мембранных насосов и утечек измерения однонаправленного
потока часто использовались для оценки скорости активного
транспорта. Это приводило к расчетным оценкам /а, которые
в сочетании с обычно принятыми значениями X давали очень
высокие энергетические затраты, иногда превышающие
Рис. 9.7. Зависимость отношения однонаправленных потоков к стационарной
скорости активного транспорта в симметричной клетке от отношений Ra*IRp
н -XIF [4].

216
ГЛАВА 9
имеющиеся источники энергии. Линг [11] объяснил это противо-
речие тем, что были завышены значения —X. Согласно его гипо-
тезе ассоциации — индукции, натрий в протоплазме находится
в состоянии, которое резко отличается от его состояния в вод-
ном растворе. Поэтому, несмотря на его низкую концентрацию
и электроотрицательность внутри клетки, он находится в рав-
новесии с внешним натрием, так что через плазматическую мем-
брану нет активного транспорта. Однако Уссинг уже давно от-
метил, что «скорость, с которой Na+, как показывает опыт
с применением радиоактивной метки, покидает мышечные во-
локна, не обязательно равна скорости (суммарного) активного
выброса», и что «часть кажущегося транспорта может пред-
ставлять собой просто-напросто обмен» [10,17]. Один из воз-
можных и часто предполагаемых механизмов обмена —это дви-
жение подвижных переносчиков, облегчающих установление
изотопного равновесия на мембране без всяких затрат энергии.
Для примера обратимся к работе Минкоффа и Дамадяна [12],
которые анализировали высокие скорости потоков шести раз-
личных изотопно-меченных растворенных веществ в клетках
Е. coli. Эти авторы заключили, что такая обменная диффузия
по фиксированным заряженным центрам представляет собой
механизм, с помощью которого клетки обменивают метку на
стабильный изотоп. На этой основе они исключили мембранные
насосы, зависящие от АТФ, тем самым избежав, по их мнению,
«тепловой катастрофы» [12]. Тем не менее приведенный выше
анализ показывает, что в принципе высокие скорости однона-
правленного потока не являются несовместимыми с мембран-
ными насосами при условии, что эти насосы допускают поток
метки в любом направлении. Оценить энергетические ограни-
чения такого механизма можно только путем точных измерений
Ra'/RP и X.
9.3.2.	Последовательные области
Применяя уравнения (9.46) и (9.47) к каждому элементу по-
следовательных областей, получим для каждого элемента i
j — р11 j
JR\ = RT\n 2 I — RT\nfi	(9.65)
^2	Р2,
где р”у и Р2 i — удельные активности меченого вещества 2 со-
ответственно на внутренней и внешней границах данного эле-
мента I. Поскольку р”/ — Р2 i+i’ суммируя по всем элементам,
получим
/ —о11/
£//?; = ЯПп 2	= JR‘ = RT\nf (9.66)
Кинетика изотопных потоков: основные факты н теории 217
Таким образом,
/?•=!>;	(9.67)
4-хй)т-Е(4),о)	<«•«»
так	что	каждый элемент дает вклад в общее	значение R*/R,
пропорциональный доле своего вклада в мембранное сопротив-
ление. Этот результат следует сопоставить с уравнением
(9.57) — соответствующим уравнением для со*/со при параллель-
ной организации областей (помня, однако, что при оценке
со*/со мы считали силы, действующие на каждый канал, одина-
ковыми). Кроме того, поскольку У in Л = in Л
/ =	(9.69)
Это сотношение имеет силу независимо от наличия или отсут-
ствия изотопных взаимодействий. [Ср. с уравнениями (9.58) и
(9.59).]
При анализе суммарного потока или потока метки некото-
рого иона через последовательно соединенные барьеры на сли-
зистой (т) и серозной (s) поверхностях эпителия Шульц и
Фриццел [14] обратили внимание на то, что общий трансэпи-
телиальный коэффициент проницаемости, полученный из ана-
лиза составной мембраны (со в наших обозначениях), не явля-
ется точной мерой проницаемости двух предельных мембран,,
соединенных последовательно, поскольку на него влияют усло-
вия, которые не влияют на со™ или со$ (т. е., скажем, концен-
трация в клетке и профили электрического потенциала). Та-
ким образом, они считают, что эти коэффициенты проницаемо-
сти имеют физический смысл, только когда потоки ограничены
параллельными путями. Соглашаясь с тем, что при попытках
выяснить детали механизма на основании измерений коэффи-
циентов проницаемости требуется осмотрительность, мы придер-
живаемся несколько иной точки зрения. Она состоит в том, что
коэффициенты проницаемости (и сопротивления) являются па-
раметрами, имеющими вполне определенный физический смысл,
и характеризуют состояние составных мембран. Надо, однако,
помнить, как и всегда при манипуляциях с феноменологиче-
скими коэффициентами, что нет никаких оснований заранее
считать, что со и R не являются функциями состояния исследуе-
мой системы. В соответствии с этим, хотя уравнение (9.67)
является аналогом для формулы, выражающей аддитивность
последовательно соединенных сопротивлений, хорошо знакомой
в электрических контурах, R* будет зависеть от концентрацион-
ного профиля на мембране, несмотря на формальную простоту
218
ГЛАВА 9
этого соотношения. Эти соображения подразумеваются в ис-
ходном подходе Кедем — Качальского и развиты в их анализе
составных мембран.
9.4.	Выводы
1.	В весьма общих предположениях может быть получено со-
отношение между суммарным потоком, отношением потоков и
силами, индуцирующими транспорт. Если проницаемость обус-
ловлена одинаковыми каналами, то в отсутствие изотопных
взаимодействий измерение отношения потоков позволяет коли-
чественно оценить силы. Измерение одного из однонаправленных
потоков (в отсутствие суммарного потока) или обоих одно-
направленных потоков (при наличии суммарного потока) опре-
деляет (сопротивление суммарному потоку) или ш (прони-
цаемость) без привлечения каких-либо сведений или предполо-
жений о движущих силах или сопряженных потоках.
2.	Для однородных каналов отклонения отношения потоков
от нормальной величины объясняются сопряжением с потоками
других веществ, активным транспортом или изотопным взаимо-
действием. При наличии изотопного взаимодействия измерение
обменного сопротивления /?* или обменной проницаемости со*
не позволяет количественно оценить 7? или со, а отношение по-
токов не позволяет оценить силы.
3.	Измерение отношения потоков в условиях короткого за-
мыкания— классический способ оценки электродвижущей силы
транспорта натрия — ненадежно, поскольку [0 зависит не только
от £Na, но и от эффективности утечки, изотопного взаимодей-
ствия и сопряжения транспорта с обменом веществ.
4.	Неоднородность параллельных областей и элементов, со-
единенных последовательно, модифицирует изотопное взаимо-
действие и отношение потоков предсказуемым образом. Наблю-
даемое отношение потоков в системе с активным транспортом
очень чувствительно к параллельной утечке. Энергетические
ограничения в системе насос — утечка нельзя оценить из изме-
рений однонаправленного потока без детальных данных об
обоих каналах транспорта.
10
Кинетика изотопных потоков:
механизмы изотопного взаимодействия
Хотя формальное рассмотрение имеет преимущества в точности
и общности, оно не дает физической картины транспортных
процессов. Его следует дополнить рассмотрением некоторых
частных моделей. Для анализа кинетики изотопных пото-
ков и аномалий отношения потоков было предложено множе-
ство разнообразных моделей. Мы рассмотрим некоторые из них,
которые удобно сопоставить с приведенными ранее соотноше-
ниями.
10.1.	Модели, основанные на трении
Модели, основанные на трении, успешно использовались при
изучении транспортных процессов в синтетических мембранах
[9, 14, 18] и для анализа отношения потоков [4, 8, 19]. Мы
рассмотрим ранние результаты [4], следуя подходу, развитому
Кедем и Качальским.
В этом подходе предполагается, что в стационарном состоя-
нии термодинамическая сила Xi, действующая на t-е вещество,
точно уравновешена фракционным взаимодействием с частицами
других транспортируемых веществ и с мембраной. Сила трения
Fij = — fij(Vi—Vj), где ft, — коэффициент трения, отнесенный
к молю t-го вещества, a v — средние скорости движения веще-
ства относительно мембраны, которые задаются отношениями
потока к концентрации (J/c). Рассмотрим сначала поток через
гомогенную мембрану т. Сопротивление суммарному потоку
дается выражением
Rw == f wm Ax/cw	(10.1)
где Ах— толщина мембраны. С другой стороны, обменное со-
противление потоку воды определяется формулой
оо-2>
где f2w — коэффициент трения воды с водой, так что
(R*/RK = 1 + (f2w/fwm)	(10.3)
220
ГЛАВА 10
Уравнение (10.3) показывает, что при наличии фрикционного
взаимодействия между молекулами воды обменное сопротивле-
ние превосходит сопротивление суммарному потоку, а отноше-
ние потоков будет аномальным. Однако в противоположность
тому, что можно было бы интуитивно ожидать, степень ано-
мальности отношения потоков будет зависеть не только от эф-
фективности взаимодействия между молекулами воды, но и
от взаимодействий между молекулами воды и мембраной. Сле-
довательно, уже такая простая фрикционная модель позволяет
объяснить наблюдаемые существенные изотопные взаимодей-
ствия в каналах большого диаметра, в которых fwm будет мало,
тогда как изотопное взаимодействие оказывается слабым в тон-
ких каналах, там, где /wm велико.
Точно так же можно рассмотреть взаимодействие между
частицами растворенного вещества. Хотя и предполагается, что
такие эффекты очень малы в разбавленных водных растворах,
они могут оказаться весьма значительными в гидрофобном
окружении, например в плазматических мембранах. Если выра-
зить взаимодействие между частицами растворенного вещества
с помощью коэффициента трения ^s, то получим
(/?7/?)s = 1 + Mfsm + fsw)	(10.4)
Снова 7?* > 7?. Очевидно, что простая фрикционная модель не
позволяет объяснить отрицательное изотопное взаимодействие.
Действительно, изложенные соображения слишком грубы и не
учитывают детали молекулярных взаимодействий. Они могут
дать лишь чисто качественную картину явления.
10.2.	Решеточная модель и модель переносчиков:
пассивный транспорт
Во многих системах, представляющих интерес для биологии,
электрохимический потенциал транспортируемых частиц не обя-
зательно меняется непрерывно в каждой точке. Так, в некото-
рых случаях факторами, лимитирующими скорость транспорта
через очень тонкие мембраны, могут быть адсорбция или де-
сорбция на поверхностях. В этих случаях поверхности мембра-
ны не будут находиться в равновесии с омывающими раство-
рами. В других случаях транспорт может включать движение
между центрами решетки с дискретными изменениями химиче-
ского потенциала. Обе эти возможности нетрудно описать с по-
мощью кинетического формализма, введенного Хиллом (гл. 5),
поскольку это облегчает количественный анализ множества хо-
рошо известных моделей транспорта. Рассмотрим сначала не-
сколько простых примеров пассивного транспорта в отсутствие
электрических сил, когда интересующие нас растворенные ве-
Кинетика изотопных потоков: изотопное взаимодействие 221
щества движутся вдоль градиента без взаимодействия с пото-
ками других веществ [5]. Для таких систем удобнее исполь-
зовать коэффициенты проницаемости, а не коэффициенты со-
противления. Для наших целей полезно обратиться к состоя-
ниям вблизи равновесия, так как в этом случае относительная
простота анализа позволяет в явном виде оценить коэффициен-
ты проницаемости исходя из кинетических параметров, выявив
при этом ограничения, связанные с изотопными взаимодей-
ствиями. Таким путем можно показать, что нарушения непре-
рывности у. сами по себе не приводят к противоречиям между
со и со*. Это является, как было показано ранее для непрерыв-
ных систем, следствием сопряжения (изотопного взаимодей-
ствия) .
Как и ранее, рассмотрим «мембраны», представляющие со-
бой ансамбли из большого числа эквивалентных единиц, каж-
дая из которых содержит один или более центров, либо фикси-
рованных, либо подвижных. Каждая мембрана находится в
контакте, по двум своим поверхностям, с двумя большими изо-
термическими объемами (А и В), содержащими разбавленные
идеальные растворы единственного неэлектролита при концен-
трациях Сд и св соответственно. Концентрации изотопно-мечен-
ного вещества обозначим и с^. Каждый элемент мембраны
может находиться в одном из множества дискретных состояний,
соответствующих различным возможным комбинациям вакант-
ных центров или центров, занятых преобладающей или мечен-
ной изотопом формой растворенного вещества. Как и ранее, ки-
нетическое описание системы можно дать на основе констант
скорости первого и псевдопервого порядка для каждого из пе-
реходов между состояниями.
В принципе даже сложный механизм транспорта можно про-
анализировать с помощью диаграммных методов, использован-
ных в гл. 5 для описания сопряжения транспорта и обмена ве-
ществ. Однако для рассматриваемых здесь базовых моделей
лучше подходит более простой и прямой подход. Суть метода
удобно объяснить, исходя из нашей первой модели, состоящей
из одного ряда, который включает N одинаковых центров на
единицу площади мембраны. На рис. 10.1 показаны три воз-
можных состояния такой системы. Рассмотрим сначала ско-
рость суммарного потока в отсутствие метки. Пусть константа
скорости адсорбции из z-ro объема выражается как а,- — a°ci,
где а0 включает стандартный химический потенциал растворен-
ного вещества и специфическую кинетическую константу для
адсорбции в данной системе растворенное вещество — мембра-
на, которую мы считаем симметричной. Константа скорости де-
сорбции в каждом омывающем объеме обозначена через 0,
а доля занятых центров — через х. Тогда адсорбция на единице
площади мембраны из t-го объема идет со скоростью Мхг(1—- х),
222
ГЛАВА 19
а десорбция в тот же объем — со скоростью Nfix, так что в ста-
ционарном состоянии
dx/dt = [аА(1 — х) — ₽х] 4- [ав(1 — х) — ₽х] = О
и	х = а/(а-}-Р)	(10.5)
где а = (аА + ав)/2. Тогда поток через мембрану дается выра-
жением
,	, 7VB ("а.— aR) NRa° (сх—cR)
/ = N [аа (1 — X) — рлг] = 2(а+ Р) = 2 (а°с + 0)	(10-6>
где с — среднеарифметическая концентрация, а проницаемость
для суммарного потока равна
Wa°0	Wa»P
2RT (a + Р) 2RT (a°c + 0)
(10-7)
Таким образом, изменение проницаемости с ростом средней
концентрации растворенного вещества описывается функцией
с насыщением и не зависит от величины Дс.
Для наблюдения изотопных потоков можно добавить радио-
активную форму исследуемого вещества, которое в следовых
количествах, как предполагается, не влияет на распределение
основного вещества и на суммарный поток. Кинетические и
термодинамические свойства меченого и основного вещества
одинаковы: а0* = а0 и р* — р. Рассуждая как и ранее, можно
показать, что в стационарном состоянии
dx*jdt = [ад (1 — х) — рх‘] + [aR(l — х) — рх*] = 0
Это выражение в сочетании с уравнением (10.5) дает
_ «а+«в
Х~ 2(а+р)
(10.8)
Раствор Д
раствор В
Рис. 10.1. Решеточная модель транспортной системы, состоящей из одного
ряда идентичных центров.
Большим кружком обозначена преобладающая изотопная форма, а звездочкой — изо-
топная метка транспортируемого вещества [sj..
Кинетика изотопных потоков: изотопное взаимодействие
223
так что
j* = N[aA(l — х) — рх*] =
=	(«А ~ «в) _ №а° (СА ~ св)
2 (а + Р)	2 (а°с + 0)
(10.9)
Поскольку на поток метки суммарный поток не влияет (он не
зависит от Дс), из сравнения уравнений (10.6) и (10.9) мы ви-
дим, что (о = ю*. Таким образом, в этом случае проницаемость
для метки, определяемая в опытах по самодиффузии (при
Дс==0), равна проницаемости для суммарного потока, индуци-
рованного малой разностью концентраций по обе стороны мем-
браны. (Равенство со и со* требует, чтобы при варьировании
разности концентраций Дс средняя концентрация с поддержи-
валась постоянной.)
Следующая наша модель будет ближе к действительности
и включает связывающие центры на каждой поверхности, а
также, возможно, и внутри мембраны. На рис. 10.2 представ-
лена схема и-рядной модели, в которой транспорт может осу-
ществляться от любого центра в одном ряду к любому свобод-
ному центру в соседнем ряду. Здесь потоки зависят не только
от констант скорости аир для адсорбции и десорбции, но
также от константы k для транспорта между центрами. Рассмот-
рение этой системы очень похоже на рассмотрение однорядной
Рис. 10.2. Общая л-рядная
модель со свободным движением лигандов, за-
полняющих центры в соседних рядах.
224
ГЛАВА 10
модели и приводит вблизи равновесия к следующему резуль-
тату:

(10.10)
®	® ЯГ (а+ ₽)[(«- 1)(а+0)+2й]
Равенство <о и <о* здесь является следствием предоставленной
молекулам свободы движения между различными субъедини-
цами мембраны. Это можно показать, рассматривая случай,
когда молекулярное движение затруднено.
Простоты ради мы ограничимся в нашем анализе двухряд-
ной решеткой, в которой каждая пара центров образует неза-
висимую субъединицу. В этом случае молекулы в своем дви-
жении из одного ряда в другой ограничены пределами одной
и той же субъединицы. На рис. 10.3 изображены девять воз-
можных состояний этой системы. Ниже мы покажем, что эта
система представляет собой один из возможных типов класси-
ческой однорядной модели диффузии 17]. Снова проведя
рассмотрение, аналогичное предыдущему, мы придем к выводу,
что теперь to не
весия)
равно to*. В этом случае (также вблизи равно-
NaPfik
® tfr(a+fJ)(a + fJ + 2fe)
(10.11)
тогда как
Так что, вообще
.	Wa°pfe(a + 2p)
КТ(а + № (a + 2p + 4fe)
говоря, to превосходит to*, и
<о* __.____________2afe______
to ~ 1 (а + 0) (а + 20 + 4k)
когда k становится большой по
Интересно, что
с а и р, т. е. когда скорость транспорта ограничена
О
*1
(10.12)
(10.13)
сравнению
скоростями
*	*
О	*
Раствор В
Состояние
1	2	3	4	5 I 7	*	•
Рис. 10.3. Двухрядная модель с лигандами, которые могут находиться только
в пределах отдельных единиц.
Кинетика изотопных потоков: изотопное взаимодействие
225
адсорбции и десорбции, уравнение (10.11) сводится к (10.7).
Таким образом, пока мы рассматриваем суммарный поток, два
ряда с быстрым взаимным обменом эквивалентны одному ряду.
Это, однако, неверно для потока метки, поскольку to* =# to даже
при k > а и р. С другой стороны, однорядное движение
само по себе не означает, что id и to* должны различаться, так
как, когда поверхности находятся вблизи равновесия с омы-
вающими их растворами (А<^а, 0), to* ~ to. Это равенство вы-
полняется и тогда, когда средняя концентрация (и, следова-
тельно, а) становится очень малой. В этих условиях перескоку
молекулы в соседний ряд лишь очень редко будет препятство-
вать занятость соседнего центра.
Совершенно другой тип поведения обнаруживается у дру-
гой модели, часто привлекаемой в биологических исследова-
ниях. Простейший пример такого рода показан на рис. 10.4.
Здесь растворенное вещество может входить в мембрану,
только соединяясь с молекулой переносчика, доступного с од-
ной или с другой стороны мембраны, и пересекать мембрану
лишь в комплексе с переносчиком. (При этом неважно, дей-
ствительно ли сам переносчик пересекает мембрану или он
только изменяет свою конфигурацию так, что влияет па движе-
ние растворенного вещества.) В этом случае, если мы припи-
шем пенагруженному и нагруженному переносчикам различные
константы скорости kc и k соответственно, проницаемость для
суммарного потока дается выражением
NaQfikkc
2RT (а + 0) (ak +	+ 2kkc)
Раствор А
Состояние	Раствор В
1	2	3	4	5 В
Рис. 10.4. Модель, в которой вещество пересекает мембрану только в виде
комплекса с переносчиком.
15 Кеплен, Эссиг
226
ГЛАВА 10
тогда как для проницаемости метки имеем
,	Na°$k
® ~ 2RT(a + fi)(P+2k)
(10.15)
так что to* превосходит со, и
Снова видно, что степень отличия со* от со зависит от условий
эксперимента: если средняя концентрация растворенного веще-
ства с и, следовательно, а становятся малыми, то со*/со—>-1.
Отметим также, что со* ~ со, когда константа скорости ненагру-
женного переносчика много больше константы скорости нагру-
женного (kc k). С другой стороны, если kc становится суще-
ственно меньше k, то со* может стать очень большой. При
йс->-0 ненагруженный переносчик неподвижен, а значит, сум-
марного потока вообще не будет, и со*/со-»-оо, как при чисто
обменной диффузии [11].
Хотя рассмотренные здесь модели привлекательны тем, что
позволяют просто объяснить противоречия между коэффициен-
тами проницаемости для суммарного потока и для потока мет-
ки, мы еще. раз подчеркиваем, что в основе этих противоречий
могут быть и другие механизмы, отличные от однорядной
диффузии и образования комплексов с переносчиками. Для
двухрядной решетки, показанной на рис. 10.3, при наличии воз-
можности обмена между молекулами, находящимися в сосед-
них занятых центрах, отрицательное изотопное взаимодействие
может смениться положительным [5]. В более общем случае
для решеточных моделей имеется возможность того, что связы-
вающие центры будут изменять свою конформацию после того,
как они становятся занятыми, и что между различными цен-
трами существует взаимодействие. Такая аллостерическая ко-
оперативность может индуцировать положительное или отрица-
тельное изотопное взаимодействие [10]. В разд. 10.4 мы рас-
смотрим, как циркуляция потока может приводить к положи-
тельному или отрицательному изотопному взаимодействию.
В гл. 11 обсуждается экспериментальный пример еще одного
механизма изотопного взаимодействия, связанного с неодно-
родностью мембраны.
10.3.	Модель переносчиков: активный транспорт
Блюменталь и Кедем [2] представили многое проясняющий
анализ соотношений между однонаправленными потоками и об-
меном веществ для системы с переносчиком, осуществляющим
активный транспорт. Их рассмотрение, как и представленное
в предыдущем разделе, непосредственно восходит к Хиллу. Для
Кинетика изотопных потоков: изотопное взаимодействие
227
простоты они рассматривают транспорт неэлектролита. В ка-
честве примера переносчика берется расширяющийся и сокра-
щающийся белок внутри мембраны (рис. 10.5). Предполагается,
что белок имеет один связывающий центр, который, как чел-
нок, снует через мембрану туда и обратно. Этот белок взаимо-
действует с переносимым веществом. Имеется, кроме того, дру-
гой связывающий центр, всегда локализованный на внутренней
стороне мембраны, который является каталитическим центром
превращения субстрата в продукт и обратно. На рис. 10.5, а
показаны возможные состояния этой модели, а на рис. 10.5,6 —
возможные переходы между состояниями. (Мы следуем здесь
Блюменталю и Кедем, обозначая расширенное состояние чет-
ными, а сокращенное нечетными цифрами.) Белок может про-
ходить через три циклические последовательности состояний.
В цикле а (12431) одна молекула F переносится внутрь через
мембрану. В цикле b (156821) одна молекула субстрата S пре-
вращается в одну молекулу продукта Р. В цикле с (15682431)
происходят оба процесса. С помощью последнего цикла можно
объяснить сопряжение между транспортом и метаболизмом.
Рис. 10.5. а — возможные состояния в активном транспорте при участии
белка-переносчика (четырехугольник — субстрат, перевернутый треугольник —
продукт, кружок — транспортируемая форма); б — переходы между состоя-
ниями и их частоты [2].
15*
228
ГЛАВА 10
Если белок не может расширяться и сокращаться иначе как
в состоянии, нагруженном переносимым веществом или суб-
стратом, т. е. если переходы 1—2 невозможны, сопряжение
между транспортом и метаболизмом полное. В той мере, в ка-
кой этот переход имеет место, степень сопряжения понижена.
Чтобы проанализировать кинетику изотопных потоков, мы
можем теперь рассмотреть две изотопные формы переносимого
вещества, причем будем считать, что исходно весь изотоп 1
находится с наружной, а весь изотоп 2 — с внутренней стороны
мембраны. Это позволит оценить потоки внутрь и наружу J
и J, суммарный поток внутрь J—J и отношение потоков
f = При наличии двух изотопов вместо семи состояний
появляется уже девять (рис. 10.6, а). Предполагается, что бе-
лок, нагруженный переносимым веществом, может быть в че-
тырех состояниях: 31 и 41 для сокращенного и расширенного
комплексов с изотопом 1; 32 и 42 для сокращенного и расши-
ренного комплексов с изотопом 2. Соответственно оба цикла а
и с распадаются на два цикла каждый, протекающие парал-
лельно (рис. 10.6,6). Поскольку изотопы 1 и 2 предполагаются
кинетически и термодинамически неразличимыми (кроме своей
радиоактивности), все константы скорости в flj и flj и в С[ и Сг
одинаковы. Частоты циклов зависят от концентраций изотопов
1 и 2. Можно отметить, что помимо расщепления цикла а
in
Состояние 1
Рис. 10.6. а — возможные состояния белка-переносчика в присутствии двух
изотопных форм вещества 1 и 2 (четырехугольник — субстрат, перевернутый
треугольник — продукт); б — переходы между состояниями. Указаны только
вероитиости переходов, зависящие от концентрации.
Кинетика изотопных потоков: изотопное взаимодействие
229
на два цикла ai и а2, по одному для каждого изотопа, наличие
двух изотопов создает новый цикл ai2 (24i3il32422). Цикл ai2
осуществляет обменную диффузию-—обмен изотопа 1 на изо-
топ 2 — без всякого суммарного транспорта или метаболиче-
ской реакции. Если переходы между состояниями 1 и 2 проис-
ходят медленно по сравнению с переходами между другими
состояниями цикла а, то цикл Oi2 будет превалировать над
циклами щ и а2, и сопряжение между J и J окажется жест-
ким. Так как низкая скорость переходов между состояниями 1
и 2 также оказывается условием полноты сопряжения, то ясно,
что изотопное взаимодействие и эффективный активный транс-
порт осуществляются одновременно.
Очевидно, подбирая надлежащие комбинации циклов и при-
меняя диаграммные методы, описанные в гл. 5 и 6, можно ко-
личественно охарактеризовать все интересующие нас потоки.
Для этой цели достаточно суммировать некоторые существен-
ные результаты. Поскольку нас интересуют прежде всего отно-
шения потоков, мы будем, следуя Блюменталю и Кедем, рас-
сматривать только приведенные потоки / и коэффициенты про-
ницаемости to. Тогда для транспорта имеем
/=(1+^)07~ О+О-Д-) (10Л7)
а для обмена веществ:
<1018)
Здесь со и с; — концентрации переносимого вещества снаружи
и внутри соответственно; cs и ср — концентрации субстрата и
продукта метаболической реакции, создающей движущую силу
для транспорта; К — константа равновесия реакции; 7?s про-
порционально kn — константе скорости перехода 1->-2, общего
для циклов а и Ь, и константе диссоциации комплекса пере-
носчик— субстрат и является функцией других констант ско-
рости цикла b; R?— аналогичное выражение для цикла а. Если
CoZ^Ci И Ср/с$~К, ТО (Co/Ct— 1)~ \n(Co/Ci) = X/RT и (1 —
— cp/Rcs)^ ln(Kes/Cp) = А/RT. Поэтому вблизи равновесия
(или когда для X и А выбраны правильные траектории) урав-
нения (10.17) и (10.18) приводятся к виду, обычному для со-
отношения сил и потоков в линейной неравновесной термодина-
мике с онзагеровской взаимностью. Обращаясь к уравнению
(4.12), видим, что степень сопряжения выражается соотноше-
нием
0++	(10Л9)
230
ГЛАВА Iff
где с ~ с0 ~ d. Поскольку /?5 и пропорциональны А12, па
мере того как скорость перехода ненагруженного переносчика
(1->-2) возрастает от очень малых до больших значений, q2
падает от ~1 до 0.
Для коэффициентов проницаемости получаем
cs + Ks + (^s/^f) с	Л О 901
—	(10-2ь>
w* = cs + 7?s + (7?s/7?f)c	(10.21)
так что
со*/со = 1 + c/Rp	(10.22}
Таким образом, при не слишком малых с и не слишком боль-
ших Rf имеет место отрицательное изотопное взаимодействие.
Такие условия возникают, когда константа диссоциации ком-
плекса F-переносчика велика или скорость движения ненагру-
женного переносчика значительна.
Как уже отмечалось в разд. 9.2.4, часто предполагается, что
FE^3 = (X)J=0 дается выражением RT\nf0. Для такой модели
при коротком замыкании (со~ ci — с)
RTlnfa = RT^^^^c	(10.23)
<10-24>
тогда как
(ю.25)
так что если транспорт осуществляется за счет метаболизма
(cs > Ср/К), то RT\nf0< (Х)/=о. Это неравенство теряет смысл,
когда устранено изотопное взаимодействие, а также разобща-
ются транспорт и метаболизм [см. уравнение (10.19)]. Вблизи
равновесия (es->-Cp//() уравнение (10.23) становится эквива-
лентным соответствующему выражению для потока электро-
лита [уравнение (9.52)].
10.4.	Изотопное взаимодействие, определяемое
неоднородностью
Описанные выше фрикционные и решеточные модели приводят
к хорошо известным механизмам изотопного взаимодействия,
которые представляются вполне правдоподобными исходя из
физических взаимодействий между проникающими молекула-
ми— или непосредственных, или как косвенное следствие влия-
ния проникающих молекул на транспортную систему (такое, на-
Кинетика изотопных потоков: изотопное взаимодействие 231
пример, как блокирование канала или нагружение переносчика).
Важно, однако помнить, что изотопное взаимодействие, как и
другие типы сопряжения потоков, определяется феноменологи-
ческими членами, поэтому в принципе нет необходимости в
прямом физическом взаимодействии между основным веществом
и его изотопно-меченной формой. Действительно, можно пока-
зать, что в отсутствие такого взаимодействия и кажущаяся од-
норядная диффузия, и обменная диффузия могут возникать
просто в результате неоднородности мембран. Кроме того, в
этом случае результаты измерений коэффициентов проницае-
мости могут существенно зависеть от условий эксперимента,
например от того, проводятся ли измерения в отсутствие гра-
диента гидростатического давления, как это обычно имеет
место в исследованиях эпителия в камерах Уссинга, или в отсут-
ствие объемного потока, как это чаще всего бывает при изуче-
нии симметричных клеток (эритроцитов, мышц, нервных тка-
ней). К этому выводу нетрудно прийти, рассматривая некото-
рые примеры экспериментального изучения сопряженных
потоков электролитов. Например, в коже лягушки и жабы
обнаружено положительное взаимодействие между потоками
мочевины и маннита [1,6]. Точно так же Уссинг и Йохансен
[20] обнаружили, что суммарный поток внутрь мочевины уси-
ливает поглощение сахарозы и задерживает ее выброс из кожи
лягушки. Лиф и Эссиг [13] нашли такое же взаимодействие
между потоками мочевины и ее меченого аналога в мочевом
пузыре жабы. Во всех этих случаях для системы растворенное
вещество—мембрана с положительными коэффициентами от-
ражения осмотический поток воды должен быть направлен в
сторону, противоположную потоку растворенного вещества
внутрь. Это мешало бы выявлению основного эффекта, по-
скольку подавляло бы поток метки внутрь и усиливало бы
выброс по всем каналам. Поэтому отмеченные выше данные
о влиянии макроскопического потока растворенного вещества
на поток метки рассматривались в качестве доказательства
прямого молекулярного взаимодействия как причины аномаль-
ного значения отношения потоков.
Хотя демонстрация положительного взаимодействия потоков
основного вещества и его меченой формы дает много полезных
сведений, интерпретация результатов измерения при Др = О
существенно неоднозначна, поскольку осмотический поток воды
мешает правильному определению эффективности взаимодей-
ствия между потоками растворенного вещества. Если его ско-
рость достаточно велика, то поток растворителя может поме-
шать обнаружению положительного взаимодействия или даже
привести к ошибочному впечатлению о наличии отрицательного
взаимодействия между потоками растворенных веществ. Так,
при исследовании синтетических мембран было показано обра-
232
ГЛАВА 10
щение направления суммарного потока метки при изменении
экспериментальных условий от нулевого градиента гидростати-
ческого давления (Ар=О) до нулевого объемного потока
(/v=0) [6]. Эти результаты заставили обратить внимание на
значение указанного фактора при строгой оценке природы
взаимодействий между потоками растворенных веществ. Пат-
лак и Рапопорт [15] показали, что неоднозначность может по-
являться даже при отсутствии суммарного объемного потока
из-за возможности циркуляции объемных потоков в неоднород-
ных мембранах с дискретными параллельными каналами, имею-
щими различные транспортные параметры.
Мы рассмотрим здесь влияние такой циркуляции на фено-
менологическое изотопное взаимодействие [12]. Чтобы выявить
эффекты циркуляции в чистом виде, предположим, что ни в ка-
ком отдельном канале нет никакого прямого взаимодействия
между потоками растворенных веществ. Пусть wj й — со-
ответственно коэффициенты проницаемости для метки и для
суммарного потока рассматриваемого вещества в г-м канале,
<т,-— соответствующий коэффициент отражения, а £рг-—гидрав-
лическая проводимость. Параметры различных каналов могут
быть разными вследствие неоднородной пористости или других
факторов. Простоты ради нормируем все потоки на единицу
полной площади мембраны. Тогда 7=2^7, Для всех потоков.
Рассмотрим сначала состояния, в которых нет суммарного
объемного потока через мембрану, и начнем с анализа коэф-
фициента проницаемости для метки со*, определяемого из опы-
тов по самообмену метки. В отсутствие макроскопической раз-
ности концентраций или разности гидростатических давлений на
мембране ни по какому каналу не возникает макроскопического
потока, так что
® “ (шД о = ~ (л>ГДс* ) Е СО,. _0 =
=-(s7t)E(-“>^r4c‘)=Z“; <ю-2в>
Если нет изотопного взаимодействия, то для любого канала
cojssscik, и мы имеем
(10.27)
Таким образом, коэффициент проницаемости для метки опреде-
ляетсй просто суммой коэффициентов проницаемости отдель-
ных каналов.
Коэффициент проницаемости для суммарного потока может
быть совершенно иным. Чтобы определить эту величину, при-
ведем обе поверхности мембраны в контакт с растворами, ко-
торые одинаковы во всем, кроме концентраций интересующего
Кинетика изотопных потоков: изотопное взаимодействие 233
нас растворенного вещества. Тенденция к возникновению сум-
марного объемного потока за счет разности осмотических дав-
лений компенсируется разностью гидростатических давлений,
которая в точности обеспечивает нулевой объемный поток
(/о = 0). Тогда, по уравнению (9.2), имеем
Потоки в каждом отдельном канале равны
Д=-®;/?ТАс + с(1-а,)/рг	(10.28)
где с — средняя логарифмическая концентрация (с = Ас/А1пс).
В общем случае объемный поток в каждом канале отлича-
ется от нуля и равен
701 = £р/(о^ТАс-Лр)	(10.29)
Суммируя по всем каналам и принимая 7„ У 7oi = 0, полу-
чаем значение Ар, которое полностью подавит суммарный
поток:
У a.LniRT Ьс
_0 =	----- (ю.зо)
Поэтому имеем
/ = Z Л = Z [ - Ас + с (1 - <rf) 70/] =
= Е (— \с — c<JiJvi) =
- atRT Ac - с<т; ГLpi (а^Т Ас - £
(Д> = 0)
и
Сопоставление с уравнением (10.27) показывает, что
® = со* + су	(10.31)
или	со/со* = 1 -|- cy/to*
где	=	(Ю.32)
Видно, что коэффициенты © и со* различаются при всех у #= 0.
А это в свою очередь имеет место, когда не все а, равны между
234
ГЛАВА 1»
собой. С другой стороны, если значения а,- для каждого канала
одинаковы, то изменение Lpt не приведет к отличию у от нуля.
Поскольку все LPi положительны, у должно быть больше или
равно нулю независимо от значений о,. Следовательно, а» ©*,
т. е. коэффициент проницаемости, полученный путем измерения
суммарного потока, должен быть равен или превосходить ко-
эффициент, измеренный из обмена меткой. В отсутствие сум-
марного объемного потока через мембрану это расхождение
между а и о* проявилось бы феноменологически как положи-
тельное изотопное взаимодействие, несмотря на отсутствие
взаимодействия между изотопами в каждом отдельном канале.
Естественно, что величину такого изотопного взаимодей-
ствия невозможно прогнозировать без детальных сведений о па-
раметрах мембраны, которые, к сожалению, для биологических
мембран, как правило, отсутствуют. Полезно, однако, рассмот-
реть общую природу соотношения между © и <в* для системы
с двумя типами параллельных каналов, которые могут соответ-
ствовать, например, пути через клетку и внеклеточному пути
(1 и 2 соответственно). Для такой системы уравнение (10.32)
дает
Y	Р2)2^р1^р2
£pi + LP2
(10.33)
так что с учетом уравнения (10.31)
® _ 1 I с (а1 — al)2Lp\Lp2	МП
“ 1 + " а*(Ар. + Ар2)	(1 °-34>
Максимальное значение этого выражения достигается при
LPi = Lp2, ой — 1 и 02 = 0. Тогда у = Lp/2 и
©/©* = 1 -|- cLpj2&*
Подставляя теперь Lp — ^cow/^w» где (Ow, Pw и c-w— ко-
эффициенты проницаемости, парциальный молярный объем и
концентрация воды соответственно, и учитывая, что мольная
доля растворенного вещества xs = c/cw, имеем
со/®* = 1 + xs<ow/2(o*
так что для 10 мМ раствора вещества (для которого xs =
= 1,8-10-4) ©/©* ~ 1	10~4©w/(o*. Исходя из этого, нет основа-
ний ожидать сильного изотопного взаимодействия для неэлек-
тролитов в плотном эпителии такого типа, как мочевой пузырь
жабы. -В этой ткани в присутствии антидиуретического гормона
Пиетрас и Райт [16] нашли, что ©w « И)-3 см/с, причем сла-
бопроникающий неэлектролит никотинамид имеет значение
— 2,3-Ю-6 см/с. Таким образом, даже если концентрация
раствора равна 10 мМ, то 10~4®w/<o‘ic~0,04< 1. Эффект, од-
нако, может быть гораздо отчетливее выражен в рыхлом эпи-
Кинетика изотопных потоков: изотопное взаимодействие
235
телии, таком, например, как в желчном пузыре кролика. В этой
ткани, по данным [21], осмотический коэффициент проницае-
мости воды (OwOiS-lO-3 см/с. В то же время для сахарозы
в той же системе получено со*~4-10-6 см/с [17]. Поскольку
было интуитивно ясно, что из-за наличия неперемешиваемых
слоев величина cow получилась заниженной, по меньшей мере
на порядок, тогда как на величине ®*ис этот эффект не сказы-
вается, вполне вероятно, что 10-4<ow/o>* ~ 1. Это, конечно, надо
рассматривать только как грубую оценку. Между тем приня-
тые нами упрощающие приближения могут быть недалеки от
реальности. Как отмечено Даймондом [3], неясно, проходит ли
через плотное соединение 5 или 95 % воды. Поэтому разумно
считать Lp\ ~ Lp2. Точно так же, несмотря на низкое значение
<о*ис по сравнению с a»w, величина <jsuc, 2 может оказаться ближе
к нулю, чем к единице, тогда как osuc. i^l. Кроме того, хотя
часто определяется с использованием лишь изотопных кон-
центраций исследуемого вещества, не является необычным и
использование концентраций более 10 мМ.
Нередко отношения потоков и коэффициенты проницаемости
определяют путем измерения потока метки, не обращая при
этом внимания на возможное влияние объемного потока или
разностей гидростатических давлений или концентраций на
мембране. Однако при со =^= отношение потоков f и кажу-
щийся коэффициент проницаемости «со*» будут меняться в за-
висимости от условий измерения. Это нетрудно показать, рас-
сматривая однонаправленные потоки через мембрану.
Однонаправленные потоки нельзя рассчитать непосред-
ственно по уравнению (10.28), поскольку оно описывает сум-
марный поток. Кроме того, в случае однонаправленного потока
вещества не вполне определен подходящий интервал средних
концентраций. Однако можно провести мысленный эксперимент,
в котором мы добавим следовые количества двух различных
изотопов (веществ а и Ь) в омывающие растворы I и II соот-
ветственно. При достаточно больших стоках метки будут сильно
разбавляться, проникая через мембрану, и можно считать, что
в таком опыте полная концентрация метки в растворе I равна
с*1 ~ са сь — а в растворе II равна с,п = с” + с” ~ ctf.
Если концентрации метки в двух растворах примерно одина-
ковы, то Дс* = с*11 — с*1 мала и
с* = Дс‘/Д 1п с* ~ (с*1 + с*п)/2
Для малой Дс* и точно известной с* в отсутствие изотопных
взаимодействий в каждом отдельном канале можно обратиться
к уравнению (10.28), что дает

(10.35)
236
ГЛАВА 1»
Таким образом, в отсутствие изотопного взаимодействия в каж-
дом отдельном канале величины Л в явном виде не зависят
от разности концентраций или потока основного вещества че-
рез мембрану. Для данной средней концентрации с при изме-
нении Дс без нарушения Jvi будут меняться и Jt, но не I*.
[см. уравнение (10.28)]. (Однако со*, о. и 7и£ могут, конечно,,
зависеть от с.)
Рассматривая сначала ситуацию в отсутствие суммарного
объемного потока, добавляя 7/ и вводя уравнения (10.26) и
(10.32), получим
J* = - <о* ЯТ Ьс* — c\RT\c (4 = 0)	(10.36)
Видно, что в противоположность потокам метки в каждом от-
дельном канале при постоянном 70(- полный поток метки меня-
ется при варьировании Дс, что опять-таки согласуется с фено-
менологическим взаимодействием потоков метки и основного
вещества.
Поток изотопа J* должен быть связан с однонаправленными
потоками метки соотношениями
Г = ®*/?7’с‘1-(с*1/2)у7?7’Дс + а	(10.37)
Т* = в>’ЯТсп + (с’11/2)у7?7’Дс + а	(10.38)
которые необходимы, чтобы 7* = 7* — J*. Поскольку мы имеем
дело с потоками метки, 7* должно быть пропорционально с*1
и не зависеть от с*11, а Г должно быть пропорционально с*11
и не зависеть от с*1. Следовательно, а = 0. Разделив выражения
для каждого из потоков метки на удельную активность в соот-
ветствующем растворе, для однонаправленных потоков получим
(10-40>
Ясно, что эти соотношения справедливы независимо от истин-
ных концентраций метки и основной изотопной формы, исполь-
зованной в эксперименте, при условии, что он проводится в пре-
делах применимости уравнения (10.28).
Рассматривая далее ситуацию в отсутствие разности гидро-
статических давлений на мембране и комбинируя уравнения
(10.29) и (10.35), находим
Г = - a'RT Ьс* - c'QRT Ьс (Др = 0)	(10.41)
где	0 = Е °iLPi(9i — 1)	(10.42)
Кинетика изотопных потоков: изотопное взаимодействие
237
Те же соображения, что и ранее, приводят к соотношениям
=	-0Дс/2)	(10.43)
<-	(Др = 0)
7 = /?7’сп(®*4-0Лс/2)	(10.44)
Отметим, что, поскольку у Js О, для 0 <Ti 1 значение 0^0.
Имея эти выражения для расчета однонаправленных пото-
ков, можно проанализировать величину отношения потоков.
В случае нулевого объемного потока
f4 (со У Дс/2)   4 (1 у Дс/2со )	(j __ Q) (1Q
Т с11 (ш* + у Дс/2)	с11 (1 + У Лс/2®*)
Ясно, что для у =4= 0 отношение потоков аномально, так как
f =#= с’/с” Ч
Интересно также рассмотреть величину логарифма отноше-
ния потоков. При достаточно малых Дс значение |уДс/2®*|<^1
и
In f In —~In —------vAc/2m2
с11	(1+уЛс/2е>’)
Поскольку Дс = с (Д 1п с),
In f сы (1 4- ус/®*) In (cVc11)
С jyAc (104б)
Сп (й*
и, по уравнению (10.31),
In f ~ (©/©’) 1п (ci/с») = (a/®*) (X/RT)
Таким образом, для достаточно малых Дс все еще выполняется
общее уравнение отношения потоков, выведенное для случая
однородных мембран [уравнение (9.48)]. Так как a Js и*, то
In f | |Х|. Рис. 10.7 показывает, каким образом в отсут-
ствие объемного потока в простых системах с двумя дискрет-
ными параллельными каналами с разными значениями о мо-
жет получаться аномальное значение отношения потоков, как
и в случае однорядной диффузии.
Для систем, где нет разности гидростатических давлений,
аналогичный подход приводит к выражению
f = = gI (1 ~ 6 Ас(2и>1 (др = о) (10.47)
/	с11 (1+0Дс/2®‘)
Следовательно, и в отсутствие разности гидростатических дав-
лений отношение может оказаться аномальным (т. е. f=£cl/c11)
из-за того, что не учитывается влияние сопряженного объем-
ного потока.
Сравнение уравнений (10.45) и (10.47) показывает, что
в принципе (при О^ст^ 1) fy =0 > fдР-о и, конечно, 7/о=о >
238
ГЛАВА 10
>/ар=о- Величины этих разностей, очевидно, могут варьиро-
вать в широких пределах в зависимости от типа мембраны и
исследуемой системы. В табл. 10.1 даны оценки у и 0 для си-
стемы с двумя дискретными каналами в различных возможных
условиях, накладываемых на значения у и Lp.
Как отмечено выше, проницаемости для метки часто опре-
деляют путем измерения величины	не принимая во
внимание возможные эффекты объемных потоков. Рассматри-
вая уравнение (10.39), можно видеть, что если поток метки
Рис. 10.7. Влияние циркулирующего объемного потока на однонаправленные
потоки (результирующий объемный поток устраняется благодаря разности
гидростатических давлений).
Каналы 1 и 2 взяты как типичные каналы в неоднородной мембране, причем сп > а2.
(Хотя мембрана изображена как система с неоднородной пористостью, причины раз-
личий между величинами а могут быть и другими. Для простоты считается, что
одинаковы для всех каналов.) Предполагается, что eJ > р^ > р^. Объемный поток
обусловлен Ас и направлен из II в I. Он больше по абсолютной величине в ка-
нале 1 (где выше а), чем в канале 2. Поток Jvp обусловлен Др, направлен из I в II
и одинаков в обоих каналах. При правильно выбранной величине Др /01 < О,
и суммарный объемный поток !v~Zoi + /oo=0. Влияние циркулирующего объемного по-
тока на поток метки состоит в существенном усилении J* нз I в 11 через канал 2 (с низким
значением а) и в слабом усилении /* нз II в I через канал I (с более высоким
значением а). При равных исходных концентрациях метки в каждом из омывающих
растворов результирующий поток метки /* > 0, а отношение потоков равно
гДс^/с1) с1
J*/(c*”/c”)
как в случае однорядной диффузии [12].
Кинетика изотопных потоков: изотопное взаимодействие
239
Таблица 10.1. Свойства неоднородной мембраны с параллельными
каналами3
Условия, накл	адываемые на	V	0
а	Lp	(gl~g2)2 LplLp2 Lpl + Lp2	al (al~1)Lpl + + °2 (a2~i)LP2
(Т1 = Ог — Р	Lp\ Z,p2== Lp	0	2a (a — 1) Lp
(У 1 = (у2 = Q	Lp\ Lp2	0	a (a — 1) Lp2
<Т1= 1; а2 = 0	Lp\ = Lp^= Lp	Lp/2	0
од = 1; а2 = 0	Lp\ Lp2	Lp\	0
Каждая мембрана представляет собой совокупность параллельных каналов двух
типов, обозначенных 1 и 2. Для каждой совокупности условий, ограничивающих возмож-
ные значения а и L , рассчитаны у и 6 из приведенных теоретических уравнений.
определяется в направлении снаружи внутрь в отсутствие объ-
емного потока, то
«со*» = 1 - == ——- = а* —	(J =0)	(10.48)
RTc1 RTc1	2	°	’
если же соответствующие измерения проводятся в отсутствие
разности гидростатических давлений, то
«(о‘» = (о‘ — (Др = 0)	(10.49)
Естественно, что и в этом случае значение того факта, что
мы игнорируем величины у и 0, существенно зависит от кон-
кретных особенностей условий опыта.
Часто изотопные потоки исследуют в системах, где проти-
воположные стороны мембраны омываются различными рас-
творами. Именно такова ситуация при изучении симметричных
клеток, например эритроцитов, мышц, нервных клеток. Оче-
видно, в той мере, в какой различные вещества могут прони-
кать через мембрану, в этом случае проявляются дополнитель-
ные эффекты. Полный анализ, охватывающий влияние множе-
ства потоков и сил, активный транспорт и т. д., практически
трудно осуществим. Однако можно рассмотреть некоторые упро-
щенные модели транспортных систем, и такой анализ приводит
к полезным результатам. Рассмотрим случай, когда омываю-
щие растворы отличаются не только концентрацией тестового
вещества, но и концентрацией другого проникающего вещества,
которое мы обозначим верхним штрихом. Пусть разность гидро-
статических давлений отсутствует и разность концентраций
второго («осмотически активного») вещества такова, что Jv=0.
240
ГЛАВА 10
Рассуждая как и ранее, можно показать, что теперь
со = со* + се	(10.50)
где	8 = У &L . -	(Ю.51)
1 pl ZaiLPi
При этом мы полагаем, что в каждом отдельном канале изо-
топного взаимодействия нет и что нет также взаимодействия
между химически различными веществами. Очевидно, чтобы
осмотически активное вещество проявляло себя как-то иначе,
чем непроникающее вещество, надо, чтобы о'. не были одина-
ковыми во всех каналах. Другими словами, ст' = о' и е = у.
В более общем случае характер соотношения между со и со*
будет зависеть от того, существенна ли неоднородность мем-
браны для тестового или для осмотически активного вещества.
Это отчетливо видно, если простоты ради принять, что все Lpt
одинаковы для всех каналов. Тогда Ьр, = Lp и
[ £ £ (°< - °/) (°Х/ - *Х) j (1 °-52)
Ясно, что при коэффициентах отражения, больших или равных
нулю,	и, следовательно, 8 > 0, когда конечные
разности а( — ст;- и — ofa' имеют одинаковый знак (для
всех г, /), и 6 < 0, когда знаки этих разностей различаются.
Значение этих соотношений становится понятнее при рассмотре-
нии величины
О.. = (gi~g/) (g//~g/gc) =
2 г
<г,а,
(10.53)
для некоторой пары каналов {/,/}. Если неоднородность кана-
лов сильнее выражена для тестового вещества, чем для осмо-
тически активного компонента (т. е. значения ст различаются
сильнее, чем значения а'), то для о./оf > l(0'z/°/)/(Of/°/) > 1, а
для ст,/ст,<1 (с^/О/)/^/0/) < так что 6<,С другой
стороны, если неоднородность сильнее выражена относительно
осмотически активного компонента, то 0(, / < 0. При всех 0«,/>О
имеем 8 > 0, а при 0,-. / < 0 в < 0. Таким образом, если меха-
низм не является однорядным или основанным на действии
переносчика, то возможно соотношение со > со* (положитель-
Кинетика изотопных потоков: изотопное взаимодействие
241
ное изотопное взаимодействие) или ш < и* (отрицательное изо-
топное взаимодействие) в соответствии с тем, что неоднород-
ность мембраны выражена сильнее для тестового или для осмо-
тически активного вещества (рис. 10.8). При более случайном
характере неоднородности каналов изотопное взаимодействие
может быть положительным, отрицательным или вообще отсут-
ствовать. И конечно, характер взаимодействия может изме-
Рис. 10.8. Влияние циркулирующего объемного потока на однонаправленные
потоки (результирующий объемный поток компенсируется разностью концен-
траций «осмотического» вещества).
Каналы 1 и 2 представляют неоднородность мембраны, причем для рассматриваемого
вещества (Ji > (Ъ, а для осмотически активного вещества > (Jg* Для изображенного
здесь примера предполагается, что неоднородность мембраны сильнее выражена при-
меиительно к осмотически активному веществу, чем к веществу, транспорт которого
мы изучаем, т. е. ai/a2>al/a2* Рассмотрим случай с^>с^,	Объемный
поток обусловленный Дс транспортируемого вещества, направлен из II в I и не-
сколько больше в канале 1. Объемный поток обусловленный Дс' осмотически
активного вещества, направлен из I в И и больше в канале 1. При правильном
выборе Дс'> 0, /С2 < 0 и результирующий объемный поток ^—^{+^2^’
Влияние циркуляции по часовой стрелке объемного потока на поток метки состоит
в небольшом усилении /* нз I в II через канал I (с более высоким о) и в суще-
ственном усилении Т* из II в I через канал 2 (с пониженным о). При равных ис-
ходных концентрациях метки в омывающих растворах результирующий поток метки
/♦ < 0. Отношение потоков равно
^/(с*т/с9 с1
- Г/(с*П/е11) с”
как в случае обменной
сильнее выражена по
активному.
диффузии. В противном случае, если неоднородность мембраны
отношению к транспортируемому веществу, чем к осмотически
f>d/cH как в случае однорядной диффузии [12].
16 Кеплен, Эесиг
242
ГЛАВА 10
няться в широких пределах при изменении тестового раство-
ренного вещества или осмотически активного компонента. Во
всех случаях при достаточно малых потоках общее отношение
потоков определяется уравнением (9.48).
10.5. Выводы
1. Как положительное, так и отрицательное изотопное взаимо-
действие можно объяснить самыми разнообразными механиз-
мами. В случае пассивного транспорта фрикционное взаимодей-
ствие может привести к положительному взаимодействию рас-
творителя и растворенных веществ при условии непрерывности
электрохимического потенциала. Для растворенных веществ
с разрывной функцией электрохимического потенциала проник-
новение через решетку по однорядному механизму способствует
положительному взаимодействию, а транспорт при участии пе-
реносчика сопряжен с отрицательным взаимодействием. Цирку-
лирующий объемный поток может индуцировать как положи-
тельное, так и отрицательное взаимодействие.
2. Анализ модели активного транспорта с переносчиком по-
казывает, что для такой системы изотопное взаимодействие
определяется полнотой сопряжения транспорта с обменом ве-
ществ. Отношение потоков в условиях короткого замыкания
дает заниженные результаты по сравнению с режимом статиче-
ского напора.
11
Кинетика изотопных потоков:
проверка и применение
термодинамических соотношений
В гл. 9 и 10 мы рассмотрели общие теоретическое основы при-
менения и интерпретации изотопных кинетических методов при
изучении транспортных процессов. Были получены основопола-
гающие соотношения, которые, как можно рассчитывать, ока-
жутся полезными в широком диапазоне условий эксперимента.
Комбинируя уравнения (9.47) и (9.48), находим
«•-7у-ет1п/ = 4-(х-Х«»Л)--у(^-Х'?»л)
(111)
(Здесь мы написали RQlJj вместо '£ii'ojJjdx—вклада со-
пряженных потоков в силы, стимулирующие транспорт. Как и
ранее, мы обычно будем пользоваться коэффициентами прони-
цаемости, а не коэффициентами сопротивления.)
В данной главе будут рассмотрены более практические ас-
пекты. Мы обсудим способы экспериментальной проверки тео-
ретических соотношений и рассмотрим, каким образом можно
использовать изотопные методы для изучения мембранной про-
ницаемости и сил, определяющих транспорт. Хотя имеется боль-
шое число экспериментальных работ, в которых однонаправлен-
ные потоки и отношения потоков связывают с различными ме-
ханизмами транспорта, мы ограничимся лишь исследованиями,
наиболее тесно связанными с теоретическими соотношениями,
выведенными ранее. Следует подчеркнуть, что при интерпрета-
ции данных по потокам изотопов на основе какого-либо опре-
деленного механизма необходимо соблюдать большую осто-
рожность.
11.1. Обоснование теоретических соотношений
на примере синтетических мембран
11.1.1. Мембраны с неполной селективностью проницаемости
и заметной проницаемостью для воды
Мирс и Уссинг [15] сначала провели проверку уравнения Ус-
синга для отношения потоков путем измерения отношений по-
токов Na+ и С1", индуцированных градиентами концентраций
16*
244
ГЛАВА 11
NaCl и диффузионными потенциалами на хорошо охарактери-
зованных синтетических мембранах на основе катионообмен-
ной смолы. Содержание воды в использованной фенолсульфо-
кислотной мембране (Зео-Карб 315) составляло около 75 %
по весу, и имел место существенный поток растворителя. От-
ношение потоков определялось как отношение потоков веществ
а и Ь, различающихся только как изотопные разновидности хи-
мически идентичного вещества, помещенного по разные стороны
мембраны. Проверке подлежало уравнение, связывающее отно-
шение потоков с силами, индуцирующими суммарный транс-
порт. Это уравнение помимо четырех членов, зависящих от раз-
ности электрохимических потенциалов тестового вещества, по
Бену и Тереллу, содержало пятый член, представляющий «по-
токи а и Ь, индуцированные градиентами химического потен-
циала всех остальных присутствующих компонентов». Возмож-
ное значение изотопного взаимодействия (взаимодействия по-
токов а и 6) не рассматривалось. Между теоретическими и
экспериментальными значениями отношений потоков получено
хорошее согласие как для натрия, так и для хлорида. Перенос
с растворителем имел существенное значение, тогда как учет
коэффициентов активности не дал заметных поправок. Был
сделан вывод, что в использованных условиях эксперимента
в качестве исходного теста для дифференциации активного и
пассивного транспорта можно применять уравнение для отно-
шения потоков.
В совместном исследовании Мирс и Уссинг [16] проверили
различные уравнения для отношения потоков при наличии элек-
трического тока с заметным электроосмосом. Теоретические от-
ношения потоков, рассчитанные исходя из сил, включая элек-
троосмотические, дали результаты, удовлетворительно согла-
сующиеся с экспериментальными отношениями потоков для про-
тивоиона натрия, но не для хлорида. Был сделан вывод, что при
наличии электрического тока введение поправки на поток
массы для электроосмотического потока приводит к неопреде-
ленности при использовании в общем случае уравнения, связы-
вающего отношение потоков с силами. Однако было обнару-
жено, что экспериментальные отношения потоков как для нат-
рия, так и для хлорида согласуются с теоретическими значе-
ниями, рассчитанными исходя из разности электрических по-
тенциалов, эквивалентной проводимости и коэффициента само-
диффузии иона (см. уравнение 18 в работе [16]).
Поз>йе было проведено более обширное исследование на
тех же мембранах Зео-Карб 315 [13]. Измерены отношения
потоков Na+, Вг~ и Sr2+ в ряде смесей NaBr и SrBr2 при полной
концентрации 0,1 н. Отношение потоков анализировали на
основе уравнений типа (9.47) и (9.48), ранее выведенных Мир-
сом и сотрудниками. При использовании уравнений для сопря-
Кинетика изотопных потоков: термодинамические соотношении
245
женных потоков, учитывающих электропроводность при посто-
янном составе, было получено, что отношение потоков (в нашей
терминологии) выражается формулой
In f = bxIrlzFcD'	(11.2>
где Ах — толщина мембраны, I — плотность электрического
тока, Т7 —число Фарадея, т — электрическое число переноса для
тестируемого вещества, с— концентрация омывающих раство-
ров, D* — коэффициент диффузии метки. Это уравнение будет
выведено позже. Экспериментальное отношение потоков Вг~
и Sr2+ при умеренных эквивалентных долях Л^а натрия в мем-
бране хорошо согласуется с величинами, рассчитанными из
уравнения (11.2). При более высоких значениях Мыа были от-
мечены расхождения, которые объяснить не удалось.
При анализе этих результатов Мирс и др. [13] заключили,,
что, поскольку отношение /?*//? в уравнении (11.2) не встреча-
ется, «нельзя получить сведений об изотопном взаимодействии
из отношения потоков при постоянном составе». Однако далее
мы покажем, что при данном значении Аф величина Ix/cD*
пропорциональна R*/R. Кроме того, можно в принципе рас-
смотреть отношение потоков с применением уравнения (11.1).
По всей вероятности, далеко не всегда можно оценить вклад
сопряженных потоков в силы, влияющие на транспорт, но если
величина ^RojJj известна, то с помощью уравнения (11.1)'
можно определить R*/R (см. разд. 11.1.2).
Мирс и Саттон [14] позже представили вывод уравнений
для потока метки на основе коэффициентов L вместо коэффи-
циентов R. Это удобнее, когда пользуются электропроводностью
и числами переноса. При этом также получены уравнение (11.2)
и соответствующие выражения для прямого и обратного пото-
ков тестового вещества на основе электрического тока и коэф-
фициента диффузии метки. Утверждалось, что, хотя уравнение
(11.2) было получено с учетом изотопного взаимодействия, та-
кие же соотношения можно получить из уравнений потока, при-
веденных в более ранней работе [16], «в которой возможными
эффектами изотопных взаимодействий молчаливо пренебрегали.
В частном случае нулевого суммарного градиента концентрации
изотопное взаимодействие в результате компенсации членов
выпадает из уравнений для потоков метки». По нашему мне-
нию, правильнее было бы сказать, что уравнение (11.2) может
быть справедливым независимо от наличия или отсутствия изо-
топных взаимодействий.
Впоследствии Мирс и Саттон провели обширные и весьма
точные измерения потоков противотоков и коионов вдоль и про-
тив электрического тока в растворах NaBr, CsBr и SrBr2 по-
стоянного состава в интервале концентраций 0,01—1,00 экв./л.
246
ГЛАВА 11
Теоретическое отношение потоков рассчитывали по уравнению
(11.2). Как правило, наблюдаемые и теоретические отношения
потоков удовлетворительно совпадали, кроме самых разбавлен-
ных растворов, для которых расхождения были объяснены кон-
центрационной поляризацией.
Очень подробные исследования транспорта через мембраны
на основе смолы Зео-Карб 315 дали много полезных сведений
о факторах, влияющих на потоки метки и отношения потоков
как противоионов, так и коионов. Однако применение мембран,
допускающих существенные потоки ионных соединений и рас-
творителя, наряду с потоком тестового вещества осложняет ис-
следование возможного вклада изотопных взаимодействий.
Мембраны из Зео-Карба 315 в контакте с 0,1 М NaBr харак-
теризуются числом переноса коиона 0,045 и числом переноса
воды около 40 моль/экв. В связи с этим оценка степени изо-
топного взаимодействия по уравнению (11.1) требовала бы мно-
гочисленных измерений для определения величины всех сил,
влияющих на суммарный транспорт. Даже для самых простых
систем такие исследования очень трудоемки.
11.1.2. Мембраны с высокой селективностью проницаемости
и низкой проницаемостью для воды
По этим причинам было интересно исследовать анионообмен-
ные мембраны, описанные Готлибом и Солнером [6], для ко-
торых скорости обмена меткой больше, чем можно ожидать на
основании их электрического сопротивления. Если такие мем-
браны должным образом подготовлены путем адсорбции хло-
ристого поливинилбензилтриметиламмония на коллодии (Доу)
с последующим медленным высушиванием, то они обнаружи-
вают почти идеальную селективность проницаемости с числами
переноса для катионов менее 0,01. Кроме того, в этих мембра-
нах осмотический поток и электроосмос минимальны. В связи
с этим представляется вероятным, что в таких мембранах
должно иметь место слабое взаимодействие потока анионов
с потоками катионов или растворителя, и, следовательно, рас-
хождение между скоростями обмена метки и электрическим со-
противлением будет проявлением изотопного взаимодействия.
Чтобы рассмотреть влияние изотопного взаимодействия, им-
прегнированные детергентом мембраны исследовали в широком
наборе солевых растворов. В предварительных опытах прони-
цаемость*для метки и обменное сопротивление оценивали в от-
сутствие суммарного потока по уравнению (9.45):
й)*=1/с7?’ = -(Г//?ГАс*)/=о (Ас = 0)	(11.3)
где — поток метки, а Ас* — разность концентраций изотопной
метки, добавленной в один из омывающих растворов. Поскольку
Кинетика изотопных потоков: термодинамические соотношения
247
мембрана имеет почти идеальную проницаемость, феноменоло-
гическая проницаемость и коэффициенты сопротивления иссле-
дуемого анионного вещества удобно определять непосредственно
из электрического сопротивления в отсутствие разности концен-
траций. Полагая, что электроосмоса также нет, имеем
— = 7? = ^- = -^ = —=	(11.4)
сш	J J	I	'	'
В согласии с данными Готлиба и Солнера для некоторых мем-
бран получены существенные расхождения между потоком
метки и результатами электрических измерений, причем <в ока-
залось меньше, чем со*. Эти мембраны использовали для про-
верки справедливости формулы отношения потоков [3, 11].
Ожидается, что в отсутствие изотопного взаимодействия
f = exp(///?7’cfi>)	(Н.5)
Для электрических движущих сил и в отсутствие электроосмоса
также из уравнения (9.38) имеем
f = exp (— zF	(11-6)
В более общем случае при наличии или в отсутствие изотоп-
ного взаимодействия
f = exp(J/RTc&)	(11.7)
и для электрических сил
f = exp К®/®*) (- zF W/RT)]	(11.8)
Для концентрационных движущих сил в отсутствие изотопного
взаимодействия, поскольку осмотическая проницаемость мем-
бран рассматриваемого типа, как было показано, несуществен-
на, из уравнения (9.6) получаем
f = с’/сВ * * 11
тогда как при наличии изотопного взаимодействия уравнение
(9.48) дает
f = (ci/с11)	(11.9)
В принципе уравнения, составленные на основе потоков и сил,
эквивалентны, и можно использовать любую систему. Однако
в опытах с низкими концентрациями омывающих растворов
(0,01 М) показано, что даже низкие скорости потока анионов,
достаточны для изменения концентрации раствора заметным
образом, так что в ходе опыта изменяются как электрические,
так и концентрационные движущие силы. В связи с этим, по-
скольку в эксперименте непрерывно измеряются электрический
ток и 7, было удобно проводить анализ данных с помощью
уравнений (11.5) и (11.7). В табл. 11.1 собраны результаты
248
ГЛАВА 11
Таблица 11.1. Теоретические и наблюдаемые отношения потоков
в мембранах из коллодия с хлористым поливинилбензнлтриметил-
аммоннем [11]
Раствор		(0/(0*	мВ	f	f
				exp (J iRIciu)	exp (J/RTcto*)
Электрическая движущая сила 0,10 М КС1	8/4	0,42—0,71	10,0—75,0	0,24—0,91	0,99±0,03
0,03 М КС1	6/3	0,40—0,71	32,0-41,8	0,41—0,72	l,05±0,03
0,01 М КС1	11/5	0,17—0,76	10,0—25,0	0,47—0,88	l,00±0,01
0,10 М KI	2/2	0,74—1,19	25,0—50,0	0,72—1,34	0,94±0,02
0,01 М KI	2/1	0,38—0,44	50,0—75,0	0,17—0,38	l,02±0,05
0,10 М КАс	3/2	0,47—0,72	10,0—25,0	0,60—0,89	0,99±0,01
0,01 М КАс	4/3	0,26—0,56	15,0—50,0	0,26—0,73	0,98 ±0,00
0,01 М K2SO4	6/2	0,29-0,52	25,0—50,0	0,12—0,31	0,87+0,02
Концентрацион- ная движущая сила 0,10/0,05 М КС1	1/1	0,36	0	0,61	0,95
0,05/0,02 М КС1	6/3	0,40-0,71	0	0,31—0,66	0,88±0,04
п — число опытов,
п~— число использованных образцов мембран.
исследований с использованием различных анионов (одно- и
двухвалентных) при наличии электрических и концентрацион-
ных сил. Как видно, значение f заметно отличается от величины
exp (J/RTca), однако в большинстве случаев получено удовлет-
ворительное согласие между опытом и теоретическим значе-
нием, учитывающим, по уравнению (11.7), влияние изотопного
взаимодействия.
Легко показать, что уравнение (11.7) эквивалентно уравне-
нию (11.2), поскольку
J — (Ix/zF)	(11.10)
и по уравнению (11.3)
®* = -(ГЖДс*)/=о
где J* можно выразить как
(Л/=о = -^*(Ас7Дх)	(11.11)
Подставляя эти выражения в уравнение (11.7), получаем урав-
нение (11.2):
Inf = /\.x!x[zFcD*
Кинетика изотопных потоков: термодинамические соотношения 249
Теперь, вводя уравнение (11.1), находим
<о _ R* _ RT (hxIx/zFcD*)	,ц
” R X-XRoA	’ '
Следовательно, невозможность оценки изотопного взаимодей-
ствия в опытах, в которых используются электрические силы
при постоянном составе, обусловлена не компенсацией вклада
изотопного взаимодействия, а тем, что не учитывается возмож-
ное влияние сопряженных потоков J, различных растворенных
веществ и растворителя. В опытах с мембранами, пропитанными
хлористым поливинилбензилтриметиламмонием, вклад сопряже-
ния потоков различных химических веществ был незначитель-
ным (числа переноса катионов и осмотическая проницаемость
были малы, а число переноса воды не превышало 2 моль/экв.
против ~40 моль/экв. в мембранах Зео-Карб 315 в 0,1 М
NaBr). При таких обстоятельствах действительно можно оце-
нить степень изотопного взаимодействия.
11.1.3. Сопряжение изотопных потоков
В соответствии с термодинамическими соотношениями, которые
мы хотим проверить, расхождение между со* и со и аномальное
значение отношения потоков — это проявления сопряжения изо-
топных потоков. Удовлетворительное согласие между теорети-
ческими и экспериментальными отношениями потоков дает убе-
дительное подтверждение этой точке зрения, однако более пря-
мое доказательство можно получить путем рассмотрения влия-
ния суммарного потока на два однонаправленных потока метки.
Наблюдения влияния разности электрических потенциалов на
потоки метки не вполне удовлетворительны, поскольку измене-
ние Аф меняет не только суммарный поток (и тем самым влияет
на поток метки), но и движущую силу (гГАф), действующую
на меченые частицы. Более веские аргументы в пользу сопря-
жения можно получить, устанавливая разность концентраций
преобладающей изотопной формы в отсутствие разности элек-
трических потенциалов. При этом возникнет суммарный поток,
но при условии, что состояние мембраны не изменилось; в от-
сутствие электроосмоса и изотопного взаимодействия потоки
метки также не изменяются. Однако при наличии изотопного
взаимодействия ситуация будет совершенно иная. При отрица-
тельном сопряжении, соответствующем случаю ®/со* < 1, поло-
жительный суммарный поток (/ > 0) должен уменьшать ско-
рость потока внутрь J* и увеличивать скорость потока наружу
J*. В табл. 11.2 показано, что оба этих эффекта проявляются
в мембранах, пропитанных упомянутым выше детергентом, и
это дает прямое доказательство существования изотопного
взаимодействия или сопряжения между потоками изотопов.
250
ГЛАВА 11
Таблица 11.2. Влияние суммарного потока на поток метки [11]
Мембрана	п	<!)/<!)*	5* £ V	А ° vi. i
F	4	0,71	0,84	1,27
F	4	0,64	0,77	1,66
Н	4	0,51	0,77	1,99
Н	3	0,49	0,73	1,90
К	4	0,40	0,72	2,21
к	4	0,41	0,70	2,26
п. — число опытов; J* н /* - потоки метки внутрь и наружу соответственно;
V*)/=0 «	измерены в системе, где обе поверхности омывались 0,03 М КС1; />0 —
суммарный поток при использовании 0,05 М КС1 во внешнем отсеке и 0,91 М КС1 во
внутреннем; Аар = О.
При интерпретации описанных выше наблюдений следует
постоянно помнить, что доказательство наличия сопряжения
представляет собой феноменологический способ описания си-
стемы без всяких конкретных требований к механизму. Это
взаимодействие не обязано отражать взаимодействие между
частицами на молекулярном уровне. В биологических исследо-
ваниях сплошь и рядом отрицательное сопряжение приписыва-
ется транспорту противоионов («обменная диффузия») при
участии переносчика, совершающего челночные движения через
мембрану. Неприменимость модели подвижных переносчиков
в случае мембран с хлористым поливинилбензилтриметиламмо-
нием показывает, что эта общепринятая интерпретация часто
неверна. Такая возможность подтверждается также наблюде-
ниями параметров транспорта гетерогенной системы, включаю-
щей параллельные каналы различного сопротивления [12]. Хотя
для каждого элемента R* = R, составная область дает отрица-
тельное изотопное взаимодействие. Как и в исследованиях, ре-
зультаты которых представлены в табл. 11.1, отношение потоков
хорошо согласуется с величинами, рассчитанными по уравне-
нию (Н.7). Не зная ни геометрических, пи электрических
свойств мембраны, нельзя точно прогнозировать ее транспорт-
ные параметры. Однако влияние неоднородности мембраны на
R*, R и отношение потоков можно объяснить по крайней мере
качественно. При определении R* из обменной диффузии в от-
сутствие электрических сил разные каналы будут давать вклад
в поток метки, обратно пропорциональный их собственному
сопротивлению, так что будут преобладать каналы с низким
сопротивлением. Между тем при определении R в условиях
Кинетика изотопных потоков: термодинамические соотношения
251
действия электрических сил мы наталкиваемся на затруднение,
состоящее в том, что, хотя при феноменологическом подходе
предполагается единая разность электрических потенциалов,
в действительности мы не имеем дела с эквипотенциальными
поверхностями. А именно, трансмембранная разность потенциа-
лов будет ниже в области каналов с низким сопротивлением,
чем в области каналов с высоким сопротивлением. Таким обра-
зом, относительный вклад в суммарный поток каналов с низ-
ким сопротивлением может быть меньше, чем при обменной
диффузии, и, следовательно, можно ожидать, что потоки в ка-
налах с низким сопротивлением будут играть большую роль, чем
потоки в каналах с высоким сопротивлением. В этих условиях
величина f отражает в большей степени значение разности элек-
трических потенциалов в области каналов с низким сопротив-
лением.
Хотя представленные в таблице эффекты можно качественно
объяснить, количественное согласие с формулами, выведенными
для однородных мембран, оказывается несколько неожиданным.
Возможно, это приписывается существенным различиям в со-
противлениях двух типов каналов в мембранах, таких, что
в пределах точности измерений все величины J, R*, J и f опре-
деляются преимущественно каналами с низким сопротивлением.
Будет ли выполняться уравнение (11.1) для мембран с менее
выраженной неоднородностью — предстоит еще выяснить.
11.2. Обоснование теоретических соотношений
в биологических мембранах: пассивный
транспорт
11.2.1. Общие соотношения
Чен и Уолсер [1] исследовали применимость выведенных выше
формул в опытах с мочевыми пузырями жаб, обработанными
уабаином, с целью устранения активного транспорта натрия.
Использование интактного замкнутого препарата позволяло
устранять краевые повреждения, возникающие при закреплении
лоскутов ткани в камере. Поэтому остаточный трансэпителиаль-
ный перенос ионов в присутствии уабаина, по всей видимости,
отражает истинный физиологический пассивный транспорт. Ре-
зультаты опытов анализировали, пользуясь различными выра-
жениями, полученными путем модификации соотношений в ра-
ботах Мирса и Саттона, а также Кремера и Мирса.
Первое соотношение утверждает, что однонаправленный по-
ток пассивно переносимого иона при нулевой разности потен-
циалов представляет собой логарифмическое среднее двояко-
•252
ГЛАВА 11
направленных потоков при любом значении потенциала. Это
соотношение легко выводится с помощью переменных, приме-
няемых в нашем подходе. В отсутствие суммарных активного
или пассивного потоков путем введения уравнений (9.36) в
уравнение (11.3) получаем
RTca = -(—)	=4 = ^о	(ИЛЗ)
\ Ар	Р2
RTca = -(-4 =4 = ^0	(Н.14)
\ Ар Zj=0 Рз
где /0 и /0 относятся к потоку внутрь и наружу соответственно
в состоянии короткого замыкания. Теперь введение уравнения
(11.1) дает
J = X In f =/0 In f	(11.15)
-> <- -><
Подставляя J = J — J и / =///, получаем желаемое выра-
жение
70=7o=J-4-	(11.16)
In (Z/J)
Чен и Уолсер [1] сопоставили среднее из двух однонаправлен-
ных потоков при нулевом потенциале (/о + Д)/2 с величиной,
ожидаемой из потоков при 100 мВ для случая Na+, С1~ и
SOT- В пределах ошибки эксперимента получено согласие
•с уравнением (11.16).
В другом способе проверки определялось выражение, кото-
рое связывало отношение потоков, электрический ток и число
переноса рассматриваемого вещества. Комбинируя уравнения
(9.36) и (11.10), имеем
=	1	(11.17)
J J	J	zFJ
или, в другой форме,
4-=1--4	(П-18)
'	zFJ
Комбинируя получаем 1	уравнения (11.10), (11.15) и (11.17) или (11.18), т=-42-1п(—4+ 1")	(И-19) '	\ zFJ	)
или	T=Z5pinfl-44	(Н.20) \	zFJ /
Числа переноса, рассчитанные таким путем, хорошо согласу-
Кинетика изотопных потоков: термодинамические соотиошеиия
253
ются с данными, полученными непосредственно измерением
•суммарного потока и электрического тока при 100 мВ.
Для пассивно переносимого вещества оказалось целесооб-
разным ввести парциальную проводимость g, которая опреде-
ляется уравнением
j = Ft/zF = - g&ty/zF	(11.21)
Комбинируя уравнения (11.15) и (11.21), имеем
In f = - g bty/zFJQ	(11.22)
Вводя в наших обозначениях определение Чена и Уолсера
Q^RTg/(zF)2F>	(11.23)
получаем
\п f = — Q(zFhty/RT)	(11.24)
где отклонение величины Q от 1 отражает факторы, определяю-
щие отклонение поведения системы от уравнения Уссинга для
отношения потоков. В этом исследовании отклонения были зна-
чительными: Q для Na+, Cl-, SOl- варьировали от 0,40 до
0,76.
Величину Q можно также выразить как функцию коэффи-
циента интегральной «объемной» диффузии и коэффициента
диффузии метки. Эти величины, обозначаемые D и D* соответ-
ственно, даются выражениями
<4; = °>	<»-25>
°’=--Ч^),.о=^г	О'-26»
Объединяя уравнения (11.25), (11.26) и (11.23), получаем
Q = £)/£>*	(11.27)
Таким образом, было показано, что отношение потоков, полу-
ченное путем наложения разности электрических потенциалов,
имеет аномальные величины только в том случае, когда коэф-
фициент «объемной» диффузии отличается от коэффициента
диффузии метки.
Значение величины Q, введенной Ченом и Уолсером, можно
далее уяснить, выражая ее через параметры нашего уравнения
(П-1):
RT In f = - QzF Дф = - (zF Дф + £
так что
Q = — 1 + У-Л-г	(11.28)
Видно, что Q — произведение двух сомножителей, каждый из
которых отражает определенный фактор, дающий вклад в ано-
254
ГЛАВА 11
мальное значение отношения потоков: изотопное взаимодействие
и сопряжение с потоками других веществ. Поскольку никаких
данных о возможности сопряжения потоков различных веществ
в их системе не было, Чен и Уолсер не сделали заключений
о степени изотопного взаимодействия (или, по их терминоло-
гии, «самовзаимодействия»). Независимо от этих эффектов их
подход позволил оценить числа переноса и парциальные про-
водимости.
Сайто, Лиф и Эссиг [17], исследуя мочевые пузыри жаб,
закрепленные в камере, также рассмотрели проблемы приме-
нения изотопной метки при оценке пассивной проводимости.
В общем случае такие попытки осложняются необходимостью
учитывать вклад потоков нескольких веществ. Если, однако,
показать, что пассивные потоки ионов в основном осуществля-
ются по общим каналам, то задача упрощается в том плане,
что измерения потока одного иона могут дать сведения о пото-
ках и всех остальных веществ. Именно так, по-видимому, об-
стоит дело применительно к мочевому пузырю жабы, как это
видно из пропорциональности потока 42К от серозной к слизи-
стой поверхности мембраны (S-э-А!) потоку 22Na в том же на-
правлении, а также потокам 36С1 и 1311 в обратном направлении
(А!->-£). Учитывая эти данные, свидетельствующие о том, что
пассивный перенос различных ионов идет по общим каналам
и меняется пропорционально изменениям пассивной проницае-
мости, можно использовать измерения потока одного вещества
как меру потоков других веществ. Потоки метки могут ока-
заться очень полезными в этом плане, но, используя их, нужно
обращать внимание на изложенные выше соображения. В част-
ности, нельзя считать заранее, что в биологической системе по-
ток одного вещества не будет зависеть от потоков других ве-
ществ. Это надо каждый раз проверять экспериментально. Как
это можно сделать, уже говорилось: в отсутствие изотопного
взаимодействия и сопряжения потоков различных веществ от-
ношение потоков будет «нормальным», т. е. выражается урав-
нением (9.5) или, когда поток определяется электрическими
силами, уравнением (11.6). Однако на практике не всегда
удобно находить отношение потоков, особенно когда имеется
всего одна изотопно-меченная форма данного химического ве-
щества. При этом определение двух противоположно направ-
ленных потоков затруднительно или невозможно.
11.2.2. Зависимость однонаправленного потока
от потенциала: пассивные каналы
В этом случае практически целесообразнее получить желаемые
сведения путем измерения только одного однонаправленного
потока при двух значениях электрического потенциала. Снова
Кинетика изотопных потоков: термодинамические соотношения
255
обозначая поток внутрь через J, а поток наружу через / и ком-
бинируя выражения для суммарного потока и отношения по-
токов (9.36) и (9.37), имеем
J = (f-1)A, j = (f-l)j (11.29,11.30)
Уравнения (11.15) и (11.29) дают
* _ f inf
Г
J о
(11.31)
Таким образом, с учетом уравнения (9.5), применяемого в от-
сутствие изотопного взаимодействия и других сопряженных
потоков, получаем
или
7 дм,
К
Тх (X/RT) exp (X/RT)
exp (X/RT) - 1
zF &ty/RT
exp (zF Aty/RT) — 1	0)
(11.32)
(11.33)
Точно так же уравнения (11.15) и (11.30) дают
t = T=T	(11.34)
а в сочетании с уравнением (11.6):
7дм,	-zFbtyRT
exp (— zF Д1р//?Г) — I
(Ac = 0)
(11.35)
В опытах Сайто и др., где измеряли поток натрия от серозной
к слизистой поверхности препаратов мочевого пузыря жабы,
.закрепленных в виде плоских мембран в камере типа Уссинга—
Церана, отношение потоков при Aip = 50 мВ и Aip = 0 не отли-
чалось от 2,27 — теоретического значения, полученного по урав-
нению (11.35). Отсюда следует, что поток был почти полностью
пассивным, и на него не влияли изотопное взаимодействие,
электроосмос или сопряжение с потоками других ионов. Однако
для потока С1_ со слизистой на серозную поверхность ситуация
оказалась совершенно иной. Здесь отношения потоков при
Aip = 50 мВ и Aip = 0 существенно отличались от 2,27, причем
средняя величина составила 1,84. Поскольку при измерениях
потока натрия не было обнаружено электроосмоса и сопряже-
ния с потоком хлорида и поскольку в данном типе препарата
.нет активного транспорта хлорида, это расхождение было при-
256
ГЛАВА II
писано эффекту изотопного взаимодействия. Между тем одно-
значно этот вывод проверен не был. При изучении мочевых пу-
зырей, взятых в виде замкнутого мешка, Чен и Уолсер обнару-
жили, что пассивные потоки как натрия, так и хлорида реаги-
руют на изменение Дф, хотя и в меньшей степени, чем это ожи-
дается по уравнениям (11.32) —(11.35).
Если отклонение от уравнений (11.32) и (11.33) в действи-
тельности не определяется взаимодействием потока хлорида с
потоками воды и других ионов, то рассмотрение, аналогичное
проведенному ранее, позволяет оценить степень изотопного
взаимодействия. Так, при наличии изотопного взаимодействия,
но без сопряжения с потоками других ионов, вводя уравнение
(11.1) в (11.31), получим
Тх [(®/®‘) (Х/RT)} ехр [(®/®‘) (X/RT)]
exp [(®/®‘) (Х/RT)] - 1
Jo
ИЛИ
(®/®*)(гРАф//?Т)
Т ехр [(®/м*) (zF kty/RT)] — 1 С '
> о
Точно так же из уравнений (11.8) и (11.34) имеем
Кф	-(&/^)(zF^IRT)
ехр [— (ш/®*) (zF kty/RT)] — 1	' С '
JQ
Для пассивного потока как в присутствии, так и в отсутствие
изотопного взаимодействия J0 = J0 и /дм>//о^/-дчДо. Это, од-
нако, неверно для полного потока натрия в мочевом пузыре
жабы, поскольку поток от серозной к слизистой поверхности
в значительной мере пассивен, а обратный поток преимуще-
ственно представляет собой активный транспорт.
Уравнения (11.36) — (11.38) нельзя в явном виде решить
относительно ю/ю*, но последнее можно оценить графически
(5]. Это облегчается введением следующего определения:
/ = |(-ЖП	(11.39)
= (zF Mp/RT) (Ac = 0)	(11.40)
Теоретическое соотношение между величиной Jx/Jx=o=Jx/Jo
( = J-x/Jo) и —(RT/F) % дается сплошной линией на рис. 11.1.
Таким образом, в случае, когда действует электрическая сила,
экспериментально определяемое значение /д^/То (^/-дщ//о) гра-
фически связано с единственным значением %. Зная z и Аф,
(11.36)
(11.37)
(11.38)
Кинетика изотопных потоков: термодинамические соотношения
257
можно теперь рассчитать и/и*: если Aip выражено в милли-
вольтах, то
СО* V г Дтр 7 \ F 7 А \ z Дтр ) А
(Н.41)
Справедливость этих соотношений была проверена в упомяну-
том выше исследовании потоков анионной метки в мембранах,
пропитанных хлористым поливинилбензилтриметиламмонием,
в которых слабо выражены электроосмос и сопряжение с по-
токами различных химических веществ [11]. На этом рисунке
точки соответствуют экспериментальным значениям однонаправ-
ленных потоков, полученным при различных значениях X.
В большинстве случаев Ас = О, так что Х = — zF&ty и х =
Каждое значение однонаправленного потока представляет собой среднее нз трех или
четырех измерений. Сплошная линия соответствует теоретическому соотношению (11.36).
Для удобства по абсциссе отложены электрические единицы. Теоретически ордината
17 Кеплен, Эссиг
258
ГЛАВА 11
= (<<)/(<)*) (zFAip/RT). В некоторых случаях Д-ф = 0, поэтому
X = RT In^'/c11) и х = (й)/й)*) In (си/с‘). Как видно из рисунка,
согласие между теорией и экспериментом вполне удовлетвори-
тельное.
Применяя эти формулы к экспериментальным данным, по-
лученным при измерениях на мочевом пузыре жабы, из
рис. 11.1 можно видеть, что значение /so//o = 1»84, найденное
для СР, связано со значением % = —1,4. Тогда уравнение
(11.42) дает (<d/oP)ci = [25,3/(—1) (50)] (—1,4)~0,71. Значение
/5о//о = 2,27 было получено для потока натрия с соответ-
ствующим значением х = — 2Д чт0 дает (<о/ю*)ка =
= 125,3/(1) (—50)] (—2,0)» 1,0. Эти результаты несколько от-
личаются от приведенных выше данных Чена и Уолсера для
мочевых пузырей в виде замкнутых мешков.
Расчет (<о/<о*)ма и (<o/<o*)ci указанным способом требует,
конечно, чтобы на потоки натрия и хлорида не влияли потоки
растворителя и других ионов. Ранее мы изложили некоторые
соображения, делающие это допущение правдоподобным. Од-
нако надо отметить, что в противоположность оценкам степени
изотопного взаимодействия парциальную проводимость иона
можно оценить однозначно из двух значений однонаправленного
потока независимо от природы факторов, влияющих на поток
метки. Действительно, в самом общем случае уравнения (9.30),
(9.45) и (9.48) дают
f = j = exp [(J ) ( - zF Аф - R.^/RT] (11.42)
где мы снова написали ROjJj вместо £r0/A-— вклада
потоков, сопряженных с силами, создающими суммарный транс-
порт. При пассивных сопряженных потоках, пропорциональных
Дф, можно ввести коэффициент пропорциональности а, опреде-
ляемый соотношением
Еад^агГАф	(11.43)
Тогда удобно ввести и величину, которая включает все фак-
торы, создающие аномальные значения отношения потоков [5].
Как видно из уравнения (11.28), эта величина эквивалентна Q
в обозначениях Чена и Уолсера:
Q = (fi>/w)(l+а)	(11.44)
Подставляя уравнения (11.42) — (11.44) в (11.31), получим
.	? exp<QzFAt/ffr)-l	'",”1
Кинетика изотопных потоков: термодинамические соотношения
259
и снова /дм>,//о = /-лч>/7о- Так же как и уравнения (11.36) —
(11.38), это уравнение нельзя решить в явном виде. Однако
его опять можно проанализировать графически, вводя общее
определение
X^QzF^/RT	(11.46)
которое соответствует определению, данному уравнением
(11.40), при а = 0. Соотношение между и /, построенное
графически на рис. 11.1, позволяет теперь использовать экспе-
риментально измеренное значение /дф//о (или Лдф//о) для оцен-
ки Q. Вообще интерпретация величины Q остается не вполне
однозначной, поскольку, как видно из уравнения (11.44), слу-
чай, когда Q=#l, может возникнуть или из-за изотопного вза-
имодействия (и/и*У=1), или из-за сопряжения потоков раз-
личных веществ (а=#0). Однако определение Q этим способом
позволяет оценить парциальную проводимость g, приписывае-
мую данному иону. Из уравнений (9.15) и (9.18) имеем
] = — са (zF Дф + £ /?о//у) =
= — си* [(и/и*) (zF Дф + У, W/)] = — ctiFQzF Дф (11.47)
В то же время для пассивных потоков уравнение (11.21) дает
J = — g Дф/zF
По уравнению (9.45), Jq = RTc<&, так что
g = [(zF)2/FF] q70 (zF/Дф) 4	(Н -48)
Если Дф выражено в милливольтах, /0— в ммоль/(см2-с) и
g — в обратных мегаомах на кв. сантиметр, то
g — 9,65 • 1О'(г/Дф)/о%	(11.49)
(В отсутствие сопряженных потоков других веществ Q = &/&*,
что позволяет оценить степень изотопного взаимодействия, как
и ранее. В отсутствие изотопного взаимодействия оценка /
дает возможность определить влияние сопряженных потоков
других веществ.)
11.3. Обоснование теоретических соотношений
в биологических мембранах: активный транспорт
11.3.1. Общие соотношения
Ввиду большой общности предположений, используемых для
вывода уравнения (11.1), можно ожидать, что полученные на
его основе соотношения будут применимы в самом широком
17*
260
ГЛАВА 11
диапазоне условий экспериментов. В частности, следует ожи-
дать, что их можно использовать для анализа кинетики и ме-
ханизма активного транспорта. Пытаясь применить уравнение
для отношения потоков с этой целью, необходимо, однако, учи-
тывать, что при выводе уравнения (11.1) вклад обменных реак-
ций в создание сил, определяющих транспорт, был отражен
только путем формальных аналогий с силами, обусловленными
сопряженными потоками растворенных веществ и растворителя,
тогда как по своей природе эти два фактора в корне различны:
потоки массы 7/ представляют собой векторную величину, а со-
ответствующие локальные феноменологические коэффициенты
сопротивления — скалярную, в то же время метаболический по-
ток Jr (такой, например, как поглощение кислорода) —скаляр-
ная величина, и, следовательно, коэффициент сопротивления г1Г
должен быть вектором. Поэтому, хотя включение силы nrJr
кажется интуитивно оправданным, важно экспериментально
проверить уравнение для отношения потоков при наличии ак-
тивного транспорта, как это было сделано ранее для пассив-
ного транспорта.
Одна из таких проверок была проведена Ченом и Уолсером
[2] при исследовании активного транспорта натрия в мочевом
пузыре жабы. Чтобы определить зависимость активных ком-
понент натриевого потока от трансэпителиальной разности элек-
трических потенциалов, были измерены однонаправленные по-
токи до и после добавления уабаина для подавления активного
транспорта. Поскольку, как было показано, уабаин не влияет
на пассивный поток натрия от серозной к слизистой поверхно-
сти в мочевом пузыре жабы, предполагалось, что подавляемая
уабаином компонента и есть активный транспорт. Этим спосо-
бом было найдено, что при Дф = 100 мВ подавляемый уабаином
поток натрия S-^M не обнаруживается, а при Дф = 150 мВ
его среднее значение в электрических единицах равно 0,073±
±0,001 мкА/мг (л = 15). Таким образом, транспорт натрия по
активным каналам является двояконаправленным. Хотя это
обстоятельство неявно предполагается в самой концепции ко-
личественного определения отношения потоков по активному
пути, насколько нам известно, ранее никаких эксперименталь-
ных обоснований двояконаправленности активного транспорта
не существовало.
Если действительно применить уравнение (11.1) при наличии
активного транспорта, то уравнение (11.13) остается справед-
ливым, что дает
ja=j“a
j —(j	•	Л	С *
->а	1а_ [а
JE = JE =	+ 1
Е Е in (ja/7a)
(11.50)
(11.51)
Кинетика изотопных потоков: термодинамические соотношения
261
где верхний индекс а означает активный транспорт. Поскольку
мы рассматриваем здесь только поток натрия, соответствующий
индекс опущен. В случае активного транспорта равенство
^“a=o = ^“a=o не определяется/“~=0, а, скорее, дается Ja^=zFE^
== JE, где Е — электродвижущая сила транспорта натрия —
представляет собой значение Аф, необходимое для снижения
скорости суммарного активного транспорта натрия Ja до нуля.
Практически удобный способ проверки уравнения (11.1) можно
предложить теперь, вводя фундаментальное соотношение, осно-
ванное на методе эквивалентных контуров [18]. В наших обо-
значениях имеем
/a = F7a = F(/a-7a)==XNa(5-A^)	(11.52)
Комбинируя уравнения (11.50) и (11.52), получаем
=------------------- (И.53)
exp(/a//E) —1 exp (E — \^)/FJE — 1] — 1
F7a =____=(Ц.54)
1 — exp (— JaIJE} 1 — exp [—	(£ — Mp)/FJ
В табл. 11.3 представлены экспериментальные данные Чена и
Уолсера [2], позволяющие сравнить стационарные активные
потоки натрия при Ai|- = 0, 100 и 150 мВ с величинами, полу-
ченными из приведенных выше соотношений. Как мы видим,
теория очень хорошо согласуется с экспериментом. При среднем
Таблица 11.3. Теоретическая и наблюдаемая зависимости активных
потоков натрия в мочевом пузыре жабы от электрического потенциала [2]
мВ	мкА/мг		Т	а, мкА/мг
	теор.	набл.	теор.	набл.
0	2 • 10~6	0	1,50	1,56±0,19
100	3- 1(Г3	0	0,55	0,54±0,06
150	0,076	0,073±0,001	0,15	0,14±0,03
ya ya
' и J — компоненты активного потока натрия, направленные соответственно от
слизистой к серозной поверхности и обратно. В описызаемой системе активный транспорт
дает около 8ЭЯз наблюдаемого электрического тока. Теоретические значения и J а рас-
считаны по уравнениям (11.53) и (11.54).
262
ГЛАВА 11
значении £=154 мВ в их мембранах величины потока натрия
от серозной к слизистой поверхности при Дф = 0 и 100 мВ ока-
зались пренебрежимо малыми в соответствии с теоретическими
предсказаниями.
Справедливость общего уравнения для отношения потоков
при наличии активного транспорта была также проверена на
примере плоских мембран мочевого пузыря жабы, укрепленных
в камерах [19]. При использовании бикарбонатного раствора
Рингера в активном транспорте участвует в основном натрий,
а пассивный поток натрия не зависит от изотопного взаимодей-
ствия и не сопряжен с потоками других веществ. Поэтому из-
мерения электропроводности ткани и потока натрия внутрь при
наличии и в отсутствие активного транспорта дают удобный
способ определения зависимости от потенциала потоков натрия
внутрь и наружу по активному пути. В согласии с результатами
Чена и Уолсера [2] было показано, что по мере приближения
Дф к £ становится заметным активный выброс Ja. Когда Дф
превосходит £, 1а становится больше Ja, так что суммарный
поток Ja оказывается отрицательным. И в этом случае экспери-
ментальные значения 1а хорошо согласуются с величинами, рас-
считанными теоретически.
11.3.2. Зависимость отношения потоков от потенциала:
активный транспорт
Чена и Уолсера интересовал также вопрос о том, в какой
мере однонаправленные потоки и отношение потоков активного
транспорта натрия зависят от «аномальных» значений пара-
метра Q° («отношения коэффициента объемной диффузии к ко-
эффициенту диффузии метки по данному пути»), т. е. при
Q°#=l. Чтобы оценить эту величину, модифицировали уравне-
ние для отношения потоков, использованное ранее при анализе
пассивного транспорта [уравнение (11.24)], путем включения
в него электродвижущей силы натриевого насоса, что дает
In fa = - QazF (Дф - E)/RT	(11.55)
Применяя это уравнение и введенные ранее соотношения к их
данным, эти авторы получили Qa = 2,54 ± 0,34, что характерно
для однорядной диффузии.
Использование уравнения (11.55) для анализа активных по-
токов представляется интуитивно оправданным, учитывая экспе-
риментально наблюдаемые линейные соотношения между Inf
и Дф в разнообразных системах и выполнение условия fw=E= 1-
Полезно, однако, рассмотреть природу и значение параметра Qa
на основе подходящих термодинамических переменных [4]. Это
Кинетика изотопных потоков: термодинамические соотношения
.263
можно сделать, приравнивая выражения для отношения пото-
ков [уравнения (11.1) и (11.55)]. Удобно рассмотреть случай,
когда нет разности концентраций на мембране, так что в отсут-
ствие сопряженных потоков веществ, кроме натрия, как это
имеет место в мочевых пузырях доминиканских жаб, взятых
в виде плоского препарата в камере Уссинга,
QazF (Дф - Е) = (®/®*)а (zF ДЧ> + ЛоЛ) (11 -56)
Установив Дф = Е, получим
ROr = — zFEUrE	(11.57)
так что Q°(A^ — Е) = (а/а*)а [Дф— (Е/Ле)Л-]. Приняв далее
Дф = о, находим
(11.58)
Параметр Q° можно также выразить через степень сопряже-
ния q. Так как для линейных систем с постоянным сродством
qa — единственная в своем роде величина и дается JrElJr<y—\—q2
[см. уравнение (7.39)], то
Qa = (®/®*)a[l/(l-92)]	(11.59)
Эти выкладки показывают, что Qa отражает не только сте-
пень изотопного взаимодействия, но и сопряжение транспорта
с метаболизмом. Если поток натрия сопряжен с потоком како-
го-нибудь вещества — такая возможность допускается для пре-
паратов, изученных Ченом и Уолсером, — то Qa будет отражать
и это сопряжение. В отсутствие сопряженных потоков массы,
поскольку Jro > JrE(q2 > 0), Qa должна давать завышенную
оценку значения (ю/ш*)а. Ясно, что величину Qa нельзя рассмат-
ривать как надежную меру изотопного взаимодействия. Решаю-
щее значение имеет тот факт, что в отсутствие изотопного
взаимодействия, т. е. при w/w*= 1, Qa не была бы равна 1. По-
этому, как отмечено в разд. 9.2.4, даже в этой ситуации не сле-
дует ожидать, что отношение потоков будет подчиняться клас-
сическому соотношению RT In f = F(E — Дф), если бы даже
было возможно полностью исключить поток через параллельные
пассивные каналы. Эти соображения имеют прямое отношение
к интерпретации того факта, что в условиях короткого замыка-
ния на коже лягушки при минимальных краевых повреждениях
RT In f согласуется со значениями Е, полученными другими спо-
собами [7]. Такое соответствие кажется случайным, отражаю-
щим совместное влияние значения Q > 1 в активных каналах,
что способствует росту f, и остаточных малых потоков через
пассивные каналы, что снижает /. Такое объяснение бьую бы
полезно проверить путем определения Qa в опытах на коже
лягушки.
264
ГЛАВА 11
11.3.3. Изотопное взаимодействие в каналах
с активным транспортом
Как уже отмечалось ранее, в опытах с закрепленными в ка-
мерах фрагментами мочевого пузыря доминиканской жабы, по-
видимому, не были обнаружены сопряженные потоки, отличные
от метаболизма и активного транспорта натрия. Следовательно,
применение уравнения (11.58) позволило бы оценить степень
изотопного взаимодействия в активных каналах. Мы пока не
можем с высокой точностью определить эту величину, посколь-
ку необходимые для этого переменные еще не были измерены
одновременно в условиях одного и того же опыта. Однако
удалось грубо оценить значение <о/(о*. Путем комбинирования
значения Qa для мочевых пузырей в виде замкнутых мешков
из опытов Чена и Уолсера с величинами JrE/Jro = 1—<?2, изме-
ренными в опытах с камерами Ланга, получено среднее значе-
ние (<о/ы*)а = 0,82 [4]. Приняв, вероятно, более точное значе-
ние q = 0,86 [10] и значение Qa = 2,07 для мочевого пузыря
жабы в опытах с камерами [19] получаем значение (ы/<о*)а=
— 0,54. Лабарка, Канесса и Лиф [9] предположили, что сопря-
жение транспорта и окислительного обмена в мочевом пузыре
очень жесткое. Если это верно, то значения (ы/<о*)я должны
были бы быть значительно ниже, чем приведенные выше. Оче-
видно, ни одно из них нельзя принять на веру безоговорочно.
Однако из них следует наличие отрицательного изотопного
взаимодействия в активных каналах. Хотя без дополнительных
данных это еще не доказывает наличия какого-либо специфиче-
ского механизма транспорта, имеющиеся результаты свидетель-
ствуют в пользу общепринятого механизма, основанного на при-
нятии транспортной функции Ка,К-АТФазы для активного
транспорта натрия, но не согласуются с однорядной диффузией.
Важно подчеркнуть, что для исключения последней возмож-
ности, допускаемой с учетом условия Qa > 1, надо в неявной
форме принять во внимание все сопряженные потоки, включая
обмен веществ.
Комментируя эти выводы, Чен и Уолсер отметили, что по-
токи К и Na могут взаимодействовать в совокупности с работой
Ка,К-АТФазы и что такое взаимодействие может влиять на
величину (со/со*)а. И это действительно верно. Однако мы ранее
уже отмечали, что надо не упускать из виду природу ю и о*
как феноменологических коэффициентов, и термин «изотопное
взаимодействие» также относится к феноменологической харак-
теристике, которая не может заменить описания на моле-
кулярном уровне. Таким образом, отношение (a>/w*)a описы-
вает «поведение системы независимо от того, чем оно вы-
звано.
Кинетика изотопных потоков: термодинамические соотношения
265
11.4. Выводы
1.	Применение синтетических мембран с высокой селективно-
стью проницаемости и низкой проницаемостью для воды позво-
ляет изучить транспорт в условиях, когда хорошо определены
действующие здесь силы. При этом теоретические уравнения
позволяют прогнозировать однонаправленные потоки и отно-
шение потоков с учетом также влияния изотопного взаимодей-
ствия.
2.	Аргументы в пользу изотопного взаимодействия не дают
прямых сведений о механизме транспорта: в искусственных си-
стемах без переносчиков можно доказать наличие отрицатель-
ного сопряжения потоков изотопов (транспорт противоионов,
обменная диффузия). Отрицательное изотопное взаимодействие
может быть индуцировано сочетанием однородных мембранных
элементов, образующих неоднородные параллельные области.
3.	Теоретические уравнения для однонаправленных потоков
и отношений потоков выполняются также в эпителии как для
пассивного, так и для активного транспорта.
4.	Зависимость однонаправленного потока иона от напря-
жения позволяет определить его парциальную проводимость.
5.	Сведения о взаимодействии различных потоков и/или ме-
таболизма позволяют также оценить степень изотопного взаи-
модействия. Значение R*/R или со/со* можно затем определить
из зависимости отношения потоков или однонаправленного по-
тока от напряжения, используя тот способ, который в данном
случае удобнее.
6.	Приведенные уравнения были использованы в экспери-
ментах на мочевом пузыре жабы. Измерения потоков метки от
серозной к слизистой поверхности позволяют оценить пассив-
ную, вероятнее всего межклеточную, проницаемость.
7.	Даже с поправками на пассивные потоки, как это и ожи-
дается исходя из теоретических уравнений, измерение отноше-
ния потоков в условиях короткого замыкания не позволяет ко-
личественно определить электродвижущую силу транспорта
натрия ENa.
8.	Комбинированные измерения зависимости потока меченого
натрия и окислительного обмена от напряжения дают возмож-
ность оценить величину изотопного взаимодействия в активном
транспорте. Наиболее надежные оценки, полученные в опытах
с мочевым пузырем жабы, показывают, что (со/со*)а < 1 в со-
гласии с общепринятым механизмом действия АТФазы как пе-
реносчика в активном транспорте натрия.
12
Мышечное сокращение
Механохимическое превращение энергии в мышцах — вероятно,
самый впечатляющий пример биологической конверсии энергии,
поскольку он нам ближе всего по непосредственному опыту.
Мы не только повседневно используем энергию на выходе этого
устройства, но и живо ощущаем затраты на входе. Уилки [71]
отметил, что «эффективность наших мышц — вопрос величай-
шей важности для животных и человека». Может быть, это
и верно, хотя еще важнее, несомненно, регуляция, согласован-
ность работы мышц. При изометрическом и преимущественно
ненагруженном сокращении эффективность в действительности
равна нулю, хотя такие сокращения случаются очень часто:
изометрические — когда надо поддержать существующее поло-
жение, противодействуя изменениям, ненагруженное —для
обеспечения быстрых движений. Рассмотрение сопряжения при
конверсии энергии в этом случае определенно требует привле-
чения подходов неравновесной термодинамики. Это не означает,
что не нужны измерения эффективности в хорошо охарактери-
зованных состояниях. Такого рода измерения сыграли централь-
ную роль в физиологии мышечного сокращения (см., например,
[35, 38]), но до последнего времени все они были основаны
исключительно на одновременных измерениях работы и теп-
лоты ’.
Из предыдущего ясно, что эффективность можно предста-
вить как отношение полученной работы к работе плюс диссипи-
рованная энергия. Диссипация ни в коей мере не совпадает по
смыслу с теплотой, выделяемой в процессе диссипации. Такое
совпадение возможно лишь в некоторых частных случаях, ко-
торые мы обсудим в дальнейшем. Поэтому следует осторожно
подходить к широко используемой величине отношения эффек-
тивности (работа)/(теплота + работа), иногда называемой ме-
ханической эффективностью. Уилки [70] предположил, что это
отношение можно превратить в истинную меру эффективности,
умножив знаменатель на У = Дб/Д/7, где ДЯ— изменение эн-
тальпии на моль. Исходя из соотношения между сродством и
свободной энергией Гиббса (см. гл. 2) и учитывая сказанное
выше, получим У =—А/АН. К сожалению, множитель У — не
обязательно постоянная величина. Он может быть постоянным,
Мышечное сокращение	267
если постоянно А. Однако А может изменяться, да и А// не
является независимым от изменений активностей реагентов и
продуктов, за исключением идеальных растворов.
Хотя применение неравновесной термодинамики к мышеч-
ному сокращению не продвинулось так далеко, как в области
мембранного транспорта, в последующих разделах мы наметим
возможности этого подхода и сравним с результатами, полу-
ченными при обычном рассмотрении. Как и в других случаях,
неравновесная термодинамика, по-видивому, дает незамени-
мый метод построения логически самосогласованного описания
энергетики системы и позволяет систематизировать множество
дотоле разнородных фактов. Кроме того, зависимости между
силой и скоростью сокращения мыщцы позволяют рассмотреть
важные проблемы регуляции и контроля. Для этого можно ис-
пользовать линейную неравновесную термодинамику, и резуль-
таты независимо от того, насколько они существенны примени-
тельно к мышцам, несомненно, представляют большой интерес
с общей точки зрения.
В этой главе мы не будем использовать в явном виде диа-
граммный метод, хотя мышечное сокращение можно рассмат-
ривать как частный случай активного транспорта: согласно ги-
потезе скольжения филаментов, энергия метаболизма расходу-
ется на транспорт актиновых филаментов относительно миози-
новых, преодолевая при этом механическое напряжение. Однако
два осложняющих фактора существенно ограничивают наши
возможности использовать этот метод обычным путем. Во-пер-
вых, актин нельзя считать «малой молекулой» лиганда, сопо-
ставимого с ионами водорода или натрия. Он является частью
макромолекулярной машины. Во-вторых, стационарность в
строгом смысле слова выполняется в мышцах только при изо-
метрическом сокращении. Несмотря на эти трудности, представ-
ление об основных уровнях свободной энергии (гл. 5) можно
использовать весьма эффективно для определения количествен-
ных параметров некоторых специфических молекулярных моде-
лей. Рассмотрение такого рода моделей мышцы выходит за
рамки данной книги. Заинтересованного читателя мы отсылаем
к важной серии исследований Хилла и сотр. [24, 28, 41—43].
12.1. Неравновесно-термодинамический анализ мышц
12.1.1. Диссипативная функция
К функции диссипации мышцы можно подойти так же, как
п в случае «разрывных систем» при исследовании транспорт-
ных задач (гл. 2). На рис. 12.1 представлена диаграмма попе-
речной мышцы, на которой показана отдельная фибрилла, не-
сущая нагрузку. Эрнст [27] рассмотрел в деталях предположе-
268
ГЛАВА 12
ние, что миофибрилла — наименьшая функциональная единица
мышцы. Принимая это предположение, мы рассмотрим фибрил-
лу или полный ансамбль филаментов в пределах фибриллы
как существенный рабочий элемент или «черный ящик» систе-
мы и для малого стационарного тетанического сокращения
будем считать, что фибрилла находится в стационарном состоя-
нии (экспериментальные данные, подтверждающие эти пред-
положения, будут приведены позже). Ограничимся рассмотре-
нием только стационарной фазы тетанического сокращения, т. е.
начальной фазой с постоянной скоростью и постоянным напря-
жением (включая нулевую скорость, или изометрическое со-
кращение, как один предельный случай, а нулевое напряжение,
или ненагруженное сокращение, — как другой). Эти ограниче-
ния в неявном виде исключают всякие рывки.
К фибрилле (0) присоединен резервуар реагентов в ком-
партменте (1), от которых она получает энергию. Область, обо-
значенная (2), является внешним пространством, которое вклю-
чает массу т. При бесконечно малом сокращении фибриллы
при температуре Т в стационарном состоянии уравнение Гиббса
для компартмента (1) имеет вид
dU^ = TdS^-pdV^+ £ V^dnl" (12.1)
i
где р и V — давление и объем, a U и S — внутренняя энергия
и энтропия, как обычно. Соответствующее уравнение для ком-
Рис. 12.1. Мышца как преобразователь энергии. Отдельная фибрилла пред-
ставлена как «черный ящик» или рабочий элемент. Она поднимает массу :п
на высоту х.
Мышечное сокращение 269
партмента (2), представляющее изменение полной энергии во
внешнем пространстве за счет сокращения мышцы, таково:
dl№ = Т dS™ - Р dV<2> + Е l^dnW + mg dx (12.2)
где х — расстояние, на которое поднимается масса m, a g—
ускорение силы тяжести. Член, содержащий сумму, учитывает
перенос вещества между компартментами (2) и (1), например
поглощение кислорода. Поскольку рассматриваются только ста-
ционарные сокращения, уравнение не содержит инерциальных
членов. Изменение потенциальной энергии, сообщаемой ком-
партменту (2), включено в dUf2^, соответствующее изменение
в компартменте (1) рассматривается как пренебрежимо малое,
т. е. мышца считается невесомой. Суммируя эти две величины
и применяя первый закон термодинамики, получаем
TdStot = TdiS = -mgdx - £ iiWdnW - Е н)2)<Ц2> (12.3)
где, как и ранее, diS — «внутренний прирост энтропии», или
полное возрастание энтропии за счет необратимых процессов.
По определению диссипация дается выражением
Ф ев {TdiS/dt) = - mgx + Е	(12.4)
i
и, как мы видели ранее, эта величина положительна, хотя каж-
дый отдельный член в ней может быть отрицательным (х =
= dx/dt). При написании уравнения (12.4) мы ввели пара-
метры реакции, описанные в гл. 2. Суммирование по двум сум-
мам в уравнении (12.3) с введением сродства и скоростей
реакции относится к системе независимых химических реакций
[диффузионные процессы в компартменте (1) нетрудно вклю-
чить в этот же формализм]. Предположим теперь, что между
химическими реакциями j можно выбрать одну k-ю, которая
непосредственно сопряжена с любой из оставшихся реакций.
Это эквивалентно разделению Ф на две положительно-опреде-
ленные части:
Ф ==: ФшесЬ Н- ФсЬет	(12.5)
где в стационарном состоянии
ФтесЬ = — mgx + Akvk	(12.6)
(механохимическая часть диссипации), а также
ФсЬет=Е-^/у/ (У #= £)	(12.7)
/
(чисто химическая часть диссипации, не включающая k-ю реак-
цию). Отсутствие прямого сопряжения между Л-й реакцией и
остальными j реакциями означает, что реакция k не получит
270
ГЛАВА 12
никаких преимуществ, если ее собственное сродство равно нулю
и не приложено механических сил, даже в том случае, когда
другие реакции имеют конечное сродство и скорость. Однако
нельзя исключить косвенное влияние некоторых или всех этих
процессов, заключенных в Фсьет, на fe-ю реакцию и, таким об-
разом, на Фтесь- Например, j-e реакции могут идти так, чтобы
А/i поддерживалось на постоянном уровне.
Теперь становится ясно, что фибрилла не может быть в ис-
тинно стационарном состоянии в ходе укорочения. Тем не менее
подход, описанный выше, может быть хорошим приближением,
если фибрилла «квазистационарна», другими словами, если па-
раметры ее состояния изменяются очень медленно по сравнению
с параметрами компартмента (1). Это напоминает ситуацию
в эпителиальных тканях, рассмотренную в гл. 7. Имеется целый
ряд данных в пользу допущения о квазистационарности. Дей-
ствительно, такое предположение весьма широко применяется
при обсуждении тетанического сокращения. Мы рассмотрим
здесь эти данные очень коротко по следующим основным на-
правлениям.
Механические доказательства стационарности. При изомет-
рическом тетаническом сокращении напряжение развивается до
максимального значения, которое затем остается постоянным
в течение интервалов времени порядка секунд в случае икро-
ножной мышцы лягушки и жабы при 0°С [31, 36]. При изо-
тонических сокращениях после начального короткого периода
согласования с нагрузкой скорость сокращения становится уди-
вительно постоянной и может сохраняться при 60—70 % пол-
ного сокращения мышцы [64]. Это весьма примечательно, если
учесть, что изометрическое напряжение зависит от длины, очень
быстро снижаясь, когда длина становится меньше или больше,
чем в состоянии «покоя».
Тепловые доказательства стационарности. Поскольку на-
чальная скорость сокращения в изотонических условиях посто-
янна, хорошо известный факт, состоящий в том, что «теплота
сокращения» прямо пропорциональна расстоянию, на которое
укоротилась мышца [1,34], отражает постоянную скорость,
с которой выделяется тепло в процессе сокращения. Это выде-
ление тепла, обеспечивающее поддержание изометрического со-
кращения, теперь называют «стабильной теплотой» [16]. Как
и при изометрическом напряжении, эта величина зависит от
длины, достигая максимума при длине в состоянии покоя [1].
Химические доказательства стационарности. Показано, что
между расщеплением АТФ и временем имеется линейное соот-
ношение при изометрическом сокращении икроножной мышцы
лягушки [47, 54]. Здесь снова существует зависимость от дли-
ны, причем расщепление АТФ достигает максимума при длине
покоя. Это было установлено (в присутствии иодацетата) пу-
Мышечное сокращение 271
тем измерения скорости образования неорганического фосфата,
а также при измерениях скорости поглощения АТФ непосред-
ственно в икроножной мышце с помощью фтординитробензола.
Такой же результат получен для утилизации фосфокреатина
прн изометрических сокращениях прямой кишки [46]. Другое
красноречивое доказательство стационарности — прямая про-
порциональность между расщеплением фосфокреатина и меха-
нической работой, совершенной при постоянной нагрузке, в опы-
тах с мышцами прямой кишки лягушки, которые сокращались
при О °C однократно или дважды до различной степени и при
различных временах [11]. Этот результат подробнее мы обсу-
дим позже.
Структурные доказательства стационарности. Предположе-
ние, что параметры состояния миофибриллы изменяются срав-
нительно медленно в процессе стационарного сокращения, по-
видимому, вполне совместно с тем, что известно о ее структуре.
Например, можно было бы ожидать, что конфигурационная
энтропия фибриллы будет существенно изменяться при ее уко-
рочении. Однако одно из следствий механизма скольжения
филаментов состоит в том, что такие изменения в действитель-
ности минимальны. Филаменты сами по себе представляются
жесткими [26, 45], и «энтропия смешения» актина и миозина
при сокращении саркомера не может быть велика. Для малых
сокращений объемные элементы сечения взаимодействующих
областей в зоне А не имеют характеристик, сильно зависящих
от времени, хотя и были отмечены изменения параметра перио-
дичности [26].
12.1.2. Феноменологические уравнения для мышц:
линейность и неполнота сопряжения
Теоретические соображения. При описании мышечного сокра-
щения с той точки зрения, которая нас сейчас интересует, важ-
но вывести линейные феноменологические соотношения с посто-
янными коэффициентами. Поскольку химические реакции ли-
нейны лишь при некоторых особых обстоятельствах, надо по-
дробнее рассмотреть требования, обеспечивающие линейность.
В гл. 6 и 7 было отмечено, что если сродство химической реак-
ции велико, то часто реакцию можно разбить на значительное
число элементарных реакций. В стационарном состоянии ско-
рости всех элементарных реакций становятся одинаковыми.
Если система открытая, но с окружающей средой обмениваются
только исходные реагенты и конечные продукты реакции, при-
чем стационарность распространяется и на транспортные про-
цессы, т. е. имеется только поток реагентов в систему и поток
продуктов из системы, то такая ситуация соответствует мини-
мальному приросту энтропии для данного значения внешнего
272
ГЛАВА 12
сродства [60]. Транспортные процессы могут быть линейными
в очень широком интервале сил (разностей электрохимических
потенциалов) по сравнению с реакциями. Кинетические схемы
ферментативных реакций всегда состоят из ряда последователь-
ных стадий. Механохимический гидролиз АТФ в мышце явно
включает достаточно сложный ряд промежуточных состояний,
начиная со стадии связывания АТФ с поперечными мостиками
Н-меромиозина с последующими трансформациями и конформа-
ционными переходами, прежде чем окончательно отщепляются
АДФ и Фн [16]. Поэтому в общем случае реакционный член
Фтесь [уравнение (12.6)] состоит из ряда членов, соответствую-
щих элементарным стадиям:
Г
ФтееЬ = — mgx + Aava + £	(12.8)
Р=1
где полное сродство Ак дается суммой
4 = 4+ЕЛр + Лв	(12.9)
Здесь процесс а может относиться к переносу реагента из цито-
плазмы или локального компартмента к миозиновому фила-
менту, со — к транспорту продуктов из филамента; р указывает
на ряд промежуточных стадий г. В стационарном состоянии
уа = у1 = у2== ...	=	(12.10)
и Фтесъ сводится к исходному виду. Требование линейности
было бы удовлетворено, если бы отдельные величины сродства
Ар были достаточно малы или располагались в определенный
ряд, при условии что факторы, которые изменяют Ар, суще-
ственно не влияют на соответствующие кинетические парамет-
ры. Это, разумеется, априорное требование, которое едва ли
будет выполняться для систем, сильно удаленных от равновесия.
Тем не менее, чтобы продвинуться дальше, нам придется вве-
сти здесь представление о правильных траекториях (гл. 6) при-
менительно к механохимическому процессу [т. е. траекториях,
удовлетворяющих уравнению (12.6)]. Хорошо известная нели-
нейность соотношения между силой и скоростью реакции будет
полностью определяться химическим процессом [соответствую-
щим уравнению (12.7)].
Эти соображения, конечно, не означают, что х однозначно
связана' с vk, т. е. что отношение x/vk постоянно при любых
условиях. Если бы это было так, то сопряжение в мышце
было бы полным (9=1). В этом и только в этом случае реак-
ция осуществлялась бы до полной остановки при изометриче-
ском сокращении и обращалась бы при любых напряжениях
в состоянии тетануса. Если же мышца сопряжена не полностью.
Мышечное сокращение
273
то реакция в принципе может происходить до остановки и об-
ращаться, но лишь при достижении напряжения, превышаю-
щего изометрическое. Чем меньше значение q, тем больше воз-
растание напряжения сверх изометрического, необходимое для
этой цели. Напряжения, недостаточно превышающие изометри-
ческое, лишь замедляли бы реакцию. Аббот, Обер и Хилл [2]
показали, что вся работа, совершенная мышцей при ее сокра-
щении в результате стимуляции, может быть поглощена, т. е.
не приводить к выделению тепла. Инфанте и др. [48] показали,
что растяжение активированной икроножной мышцы лягушки,
предварительно обработанной фтординитробензолом, более чем
на 90 % подавляет расщепление АТФ, хотя развиваемые при
этом напряжения на 70 % превышают изометрическое при дли-
не покоя (ресинтез АТФ в конечном счете не наблюдается).
Эти авторы показали также, что в процессе изометрического
сокращения имеет место стационарный гидролиз АТФ при 0°С.
К обсуждению этих явлений мы вернемся несколько позже. На
данном этапе достаточно, что можно сделать вывод о неполноте
сопряжения трансформации энергии в мышцах.
Прежде чем выписать феноменологические уравнения для
мышцы как преобразователя энергии, целесообразно переписать
уравнение (12.6) для механохимической функции диссипации
в более удобной форме с помощью привычных обозначений
силы и потока, введенных Хиллом:
ФтесЬ = V (- Р) + JrA	(12.11)
где Р — напряжение, V — начальная постоянная скорость при
сокращении в условиях тетануса, Л — скорость сопряженной
метаболической реакции, А — как обычно, сродство. Удобно
рассматривать — Р как эквивалент обычной силы па выходе
системы Х}, приняв в качестве положительного направление
сокращения, поскольку самопроизвольный эффект Р состоит
в растяжении мышцы. Тогда Ро — «изометрическое напряже-
ние», или напряжение, развиваемое, когда мышца лишена воз-
можности сокращаться, — является прямым аналогом э. д. с.
электрохимической ячейки, Vm — скорость сокращения при ну-
левой нагрузке — аналогична току короткого замыкания. Если
V выражена в м/с, то Р надо выразить в ньютонах, чтобы со-
блюсти размерность. Нагрузочное, или механическое, сопротив-
ление Rl = P/V можно варьировать от нуля до бесконечности.
Уравнение (12.11) представляет собой двучленную функцию
диссипации, смысл которой состоит в том, что система имеет
две степени свободы. Таким образом, уравнению (12.11) соот-
ветствуют следующие феноменологические уравнения:
V =LC(-P) + LCrA, Jr = Lcr(-P) + LrA (12.12,12.13)
18 Коплен, Зесиг
274
ГЛАВА 12
где предполагается онзагеровская симметрия (индексы сиг
указывают на сокращение и реакцию соответственно). Уравне-
ния (12.12) и (12.13) содержат векторные перекрестные коэф-
фициенты. Поэтому подразумевается, что сопряжение осуще-
ствляется в анизотропной среде. В этом плане трактовка не
отличается от теории Кедем для активного транспорта (гл.З).
Приведенные выше феноменологические соотношения можно,
конечно, записать и другим способом:
-P = RcV + RcrJr, A = RcrV + RrJr (12.14, 12.15)
Сопоставление с экспериментом. Уравнение (12.14) можно
представить так:
Jr = (-l/Rcr)P + (-Rc/Rcr)V	(12.16)
Если ввести подстрочные индексы о и m для обозначения изо-
метрического и пена груженного сокращения или соответственно
состояний статического напора и установившегося потока2, то
легко видеть, что уравнение (12.16) эквивалентно
Л = (Jro/Po) Р + UrmlVm) V	(12.17)
Борнхорст и Минарди |8] обратили внимание на постоянство
Jro/Po при достаточно больших изменениях длины при сокра-
щении мышц прямой кишки и икроножной мышцы лягушки
[46,47]. Они считали, что это согласуется с предположением
о постоянстве феноменологических коэффициентов при измене-
ниях длины мышц. Для мышцы прямой кишки лягушки полу-
чены достаточно надежные экспериментальные доказательства
постоянства Jrm/Vm и стационарности сокращения: показана
прямая пропорциональность между расщеплением фосфокреа-
тина и совершенной механической работой при постоянной на-
грузке [11]. Постоянная нагрузка подразумевает постоянную
скорость при стационарном сокращении. Таким образом, для
сокращений различной продолжительности при постоянной на-
грузке уравнение (12.17) можно переписать в виде
]r = (.UPoV + JrmIVmP)PV
Умножая обе его части на продолжительность сокращения, по-
лучим результат из работы [11]. Дополнительные аргументы
в пользу постоянства Irm/Vm были получены в работе [56]. Они
также согласуются с линейными уравнениями, в которые вхо-
дят постоянные феноменологические коэффициенты. Борнхорст
и Минарди проанализировали некоторые дополнительные дан-
ные опытов Кейна и сотр. [11]. Интегрируя (12.17) в условиях
изотонического сокращения, они получили
- АРС = (7r0/P0) Pt + (7rm/V,n) А/	(12.18)
Мышечное сокращение
275
где ДРС — изменение содержания фосфокреатина, А/— измене-
ние длины мышцы, t — продолжительность сокращения. На
рис. 12.2 сопоставлены механохимические данные из работы
[11] с результатами расчета по уравнению (12.18). Данные
относятся к сокращениям, соответствующим одному и тому же
укорочению мышцы (мышца прямой кишки лягушки) при раз-
ных нагрузках. При этом нагрузку Р в уравнении (12.18) за-
менили на IV/А/, где W— внешняя работа, совершенная мыш-
цей. Как видно из этого рисунка, линейность выглядит вполне
убедительно. Значения Rcr и Rc легко получить из наклона и
точки пересечения с осью ординат графика, приведенного на
рис. 12.2. Следует помнить, что перекрестный коэффициент со-
противления Rcr в системе с положительным сопряжением дол-
жен быть отрицательным.
Для изометрического сокращения уравнение (12.16) упро-
щается и принимает вид
]ro = <-VRcr)Po	(12.19)
Паул, Петерсон и Кеплен [57,58] рассмотрели это соотношение
применительно к гладким сосудистым мышцам с использова-
нием методов, развитых в аналогичных исследованиях на эпи-
телиях [67]. С экспериментальной точки зрения гладкие сосу-
дистые мышцы дают значительные преимущества в механохи-
мических исследованиях, поскольку эта система относится к
числу самых медленно действующих [7, 63] и в отличие от ске-
летных мышц в них не содержится избыточного пула высоко-
энергетических фосфатов [22,51]. Дэмерс-Ламберт и Роланд
Рис. 12.2. Изменения содержания фосфокреатнна АРС в прямой кншке ля-
гушки в условиях сокращения при «постоянном укорочении» с варьирова-
нием нагрузки. IF— внешняя работа. AZ— расстояние сокращения [8, 11].
18*
276
ГЛАВА 12
[23] показали, что в процессе сокращения за счет гликолиза и
окислительного фосфорилирования синтезируется АТФ, причем
достигается стационарное состояние. В стационарном режиме,
когда суммарная концентрация АТФ постоянна, скорость его
гидролиза в мышце равна скорости синтеза за счет метаболиз-
ма. Вклад аэробного гликолиза в суммарное производство АТФ
мал [57,58]. Таким образом, наблюдая за поглощением кисло-
рода в этих тканях, можно получить меру скорости движущей
химической реакции. Для этой цели был использован метод
полярографии с кислородным электродом Кларка. На рис. 12.3
показаны результаты одновременных измерений Jro и Ро в
брыжеечной бычьей вене в условиях постепенно меняющейся
стимуляции различными стимуляторами. Многократно получено
линейное соотношение. Ясно, что уравнение (12.19) относится
только к супрабазальным значениям Jr0. Отметим, что различие
Рис. 12.3. График зависимости Jro от Ра для брыжеечной бычьей вены, полу-
ченный путем применения различной концентрации адренэргического стиму-
лятора адреналина (Epi)—норадреналина. Аналогично влияет неадренэрги-
ческий стимулятор гистамин (Hist). Показано также влияние адреиэргиче-
ского a-блокирующего реагента дигидроэрготамина (Dhe).
Линия регрессии относится ко всем точкам. Линии регрессии, построенные для каждой
подсистемы точек, статистически не различаются. А стимуляция максимальными кон-
центрациями Hist и Epi с последующим разбавлением; ф максимальная стимуляция
гистамином ткани, блокированной Dhe, с последующим разбавлением J58].
Мышечное сокращение	277
между базальным Jro, измеренным непосредственно (до начала
стимуляции), и полученным путем экстраполяции линии регрес-
сии Jro — Ро составляет всего 4 % от значения базального по-
тока Jro и не зависит от природы используемых средств стиму-
ляции. Это пренебрежимо малое отличие означает, что всякий
вклад супрабазального Jro от несократителъного, равно как и
сократительного процесса должен быть пропорциональным ге-
нерируемой силе. Если такой вклад имеется, то он должен
определяться регуляторными функциями промежуточных реак-
ций обмена веществ.
Инвариантность отношения Jro — Ро при изменении природы
фармакологического стимулянта дает убедительное подтвержде-
ние тому, что наклон графика действительно является мерой
собственного коэффициента механохимического сопряжения.
Эти опыты можно объяснить и таким образом, что значение А
меняется при разных уровнях стимуляции. Однако, как мы уви-
дим ниже, можно предложить и другие интерпретации.
12.2.	Регуляция превращения энергии
12.2.1.	Уравнение Хилла
Основная модель. Характеристическое соотношение между си-
лой и скоростью для мышцы, которое точно описывает поведе-
ние мышц всех типов, взятых у различных видов животных,
было экспериментально получено Хиллом [34]. Обычно его за-
писывают в виде
(Р + а) (V + b) = (Ро + «)b = (Vm + b)a (12.20)
Величины а и b — чисто механические постоянные [37], хотя
исходно а определялась как «теплота укорочения» на единицу
длины сокращения мышцы. Отсюда следует, что отношения
afP0 и b/Vm равны. Мы обозначим их 0. Наиболее примеча-
тельное свойство указанного соотношения — свойство, которое
выделяет его из ряда всех остальных соотношений между силой
и скоростью, — это его симметрия [13,14]. В этом плане оно
резко отличается от соотношения, предложенного ранее Фен-
ном и Маршем [30]:
P = Poexp(-aV)-fcV	(12.21)
где а и k — постоянные, а также от других сходных соотноше-
ний, предложенных Полисаром [59] и Обером [6]. Симметрия
уравнения (12.20) становится очевидной, если нормировать ве-
личины напряжения и скорости. Тогда получим
(m + 0)(V/Vm + 0)-(1+0)0	(12.22)
278
ГЛАВА 12
Ясно, что вид функциональной зависимости P(V) совпадает
с V(P) — ситуация, напоминающая феноменологические урав-
нения неравновесной термодинамики. Значение этого факта ста-
нет понятнее в дальнейшем. Нормированное уравнение дает
семейство гипербол, пересекающих обе оси при единичных зна-
чениях переменных. Кривизна каждой данной гиперболы зави-
сит от величины 9, которая была названа Хиллом [34] пока-
зателем эффективности мышцы. Типичные значения 9 уклады-
ваются в интервал 0,2—0,3, а кривизна довольно большая. Хотя
уравнение (12.20) резко отличается от других своей симмет-
рией и алгебраической простотой, все они были предложены
в значительной мере эмпирически. Кратко Хилл так объяснил
свой выбор [39]: «Реальный вопрос при выборе между четырь-
мя уравнениями состоит в том, какое из них полезнее всего.
Полезно для чего? Чтобы сложную смесь наблюдаемых фактов
сделать более обозримой, наметить, в каком направлении ис-
кать новые факты, и обеспечить плацдарм для нового прорыва
в неведомое». Действительно, широкое применение уравнения
(12.20) в литературе показывает, что выбор в пользу этого
уравнения уже давно сделан большинством исследователей,
работающих в данной области. Поэтому у нас есть основания
серьезно отнестись к замечанию Прингля [61]: «Можно пред-
положить, что всякая концептуальная модель всегда связана
с уравнением».
Нелинейность соотношения между силой и скоростью ука-
зывает на возможность того, что при работе мышцы действует
регуляторный процесс и что мышца сама способна приспосаб-
ливать свою работу к нагрузке. В этом отношении важным
свойством уравнения Хилла является то, что при достаточно
малых значениях 9 выходная мощность остается в основном
постоянной в широком интервале нагрузок, демпфируя таким
образом скорость совершения работы в условиях резких и не-
ожиданных изменений, которые могут произойти в величине на-
грузки. Представление о саморегуляции мышц — отнюдь не
ново. В принципе эта идея была известна уже в 1864 г. [39]
и, как обычно считается, в явном виде была высказана Фенном
[29]. В сущности, ту же идею использовал Прингль [61], ко-
гда он постулировал свойство сократительной компоненты, на-
званное им «активацией», которое возрастает при наличии на-
пряжения и контролирует скорость сокращения при данном на-
пряжении. Феноменологически регуляция может осуществляться
по двум механизмам, действующим порознь или согласованно.
С одной стороны, феноменологические коэффициенты могут
сильно зависеть от напряжения или скорости. Это означает
фундаментальную нелинейность системы. С другой стороны,
в ответ на изменения напряжения может меняться мощность
на входе, особенно сродство движущей реакции.
Мышечное сокращение	279
Был проведен анализ системы последнего типа путем рас-
смотрения последовательно соединенных преобразователя энер-
гии (с линейными свойствами) и регулятора, модифицирую-
щего работу первичного источника энергии [12]. Выход регу-
лятора соединен с входом преобразователя. Нелинейность
заключена в регуляторе. Диаграмма такой системы представлена
на рис. 12.4. Можно отметить, что характеристики стабильности
системы неоднократно рассматривались и подробно изучены
(см., например, [66,68]). В приведенной схеме петля обратной
связи возвращается к регулятору от преобразователя энергии,
а не от какой-либо произвольной точки за пределами выходных
«терминалов». Это важное свойство системы. Регулятор не
пользуется никакими источниками информации о нагрузке, кро-
ме тех, которые основаны на работе самого преобразователя.
Было показано (см. приложение к этой главе), что если пре-
образователь энергии не полностью сопряжен, действует в пре-
делах между состояниями статического напора и установивше-
гося потока и характеризуется однозначным адаптационным
откликом па любую нагрузку, то его поведение всегда можно
описать одним и тем же общим уравнением, которое можно
рассматривать как каноническое уравнение регулятора. В своей
простейшей форме это выражение сводится к соотношению
Хилла между силой и скоростью. Такая интерпретация приводит
к весьма примечательному заключению: степень сопряжения
преобразователя дается выражением
7=.(i/vT+e)	(12.23>
При этом уравнение (12.22) имеет только один параметр, под-
лежащий уточнению: это степень сопряжения, которую можно
определить из кривизны графика сила — скорость. Хилл [34]
показал, что 0 обычно равно около 0,25 для икроножной мышцы
лягушки. Отсюда степень сопряжения составляет приблизитель-
но 90 %, что соответствует максимальной эффективности около
40%- Определение механической (а лучше сказать механохи-
мической) эффективности сразу же вытекает из уравнения
(12.11):
= (12-24>
Как уже говорилось ранее, эффективность данного сократи-
тельного процесса в стационарном режиме можно определить
Пвтля обратной связи
Рис. 12.4. Диаграмма саморегулируемого преобразователя энергии [12].
280
ГЛАВА 12
экспериментально, не прибегая к тепловым измерениям, с при-
сущими таким измерениям допущениями и приближениями.
В гладких мышцах, как показано в работах Паула и сотрудни-
ков, можно непосредственно определить три из четырех пара-
метров. Для нахождения четвертого — сродства — требуется
специальное рассмотрение. Однако в дальнейшем мы покажем,
что и его можно оценить экспериментально, не прибегая к де-
структивным методам исследования.
Экспериментальная оценка сродства в мышце. В отличие от
систем активного транспорта, рассмотренных ранее, проблема
в данном случае состоит в том, что мы допускаем возможность
изменения сродства в ответ на действие регулятора. Тем не
менее и в данном случае можно рассмотреть два подхода по
аналогии с методами, описанными в гл. 7 для определения
сродства в эпителии. Кратко эти подходы можно суммировать
с помощью следующих двух
легко вывести из
(12.15) :
уравнении
операционных уравнений, которые
(12.12) и (12.13) или " '
(12.14) и
Ат =
Ао
Ро
(dJr/dV)A
ЯО
(небольшие нагрузки,
V близко к Vm)
максимальной нагрузки,
Р близко к Ро)
ут
{д/г/дР)А
Лт
(вблизи
(12.25а)
(12.256)
Для применения уравнения (12.25а) потребовалось бы оценить
изменения, скажем, потребления кислорода по мере изменения
напряжения в области очень малых нагрузок, при которых
сродство соответствует работе мышцы в ненагруженном со-
стоянии и, как можно ожидать, существенно не меняется. Точно
так же по (12.256) можно оценить сродство в ряде опытов, про-
веденных в режиме, близком к изометрическому сокращению.
Опыты такого типа пока не проведены и были бы крайне инте-
ресны в том плане, что они. могли бы ответить на вопрос, дей-
ствительно ли величины сродства существенно различаются в
условиях установившегося потока и статического напора. Од-
нако эти значения сродства (Ат и До) относятся только к двум
крайним случаям. В любом стационарном состоянии, отличном
от тех, для которых справедливы уравнения (12.25а) и (12.256),
сродство можно в принципе определить с помощью более об-
щих формул, которые также выводятся из феноменологических
уравнений:
Р___________У	(малые изменения нагрузки /| 2 or)
(dJr/dV)A	(д/г/дР)А	вблизи данного состояния)	'
Здесь требуется, чтобы скорость потребления кислорода и ско-
рость сокращения определялись одновременно в сравнительно
малом интервале изменений нагрузки вокруг данного состоя-
Мышечное сокращение
281
ния, характеризуемого соответствующим набором значений Р
и V. Если А остается примерно постоянным при таких малых
возмущениях, то можно попытаться оценить А.
12.2.2.	Мышцы с автономным преобразователем энергии
«Аффинная регуляция» (регуляция по сродству), основанная
на энергетических факторах. В соответствии с принятой выше
точкой зрения (рис. 12.4) соотношение между скоростью и
силой [уравнение (12.20)] содержит только один параметр,
подлежащий уточнению, если это уравнение взято в нормиро-
ванной форме: этот параметр — степень сопряжения рабочего
элемента мышцы. Чем полнее сопряжение, тем больше кри-
визна хилловских гипербол. Это легко видеть из нормирован-
ных графиков, приведенных на рис. 12.5. Как отмечалось ранее,
свойство уравнения Хилла состоит в том, что при высокой сте-
пени сопряжения выходная мощность остается в основном по-
стоянной в широком интервале нагрузочного сопротивления.
Грубо говоря, именно так обстоит дело в мышце, как отмечено
в работе Фенна и Марша [30]. Уже говорилось также, что для
икроножной мышцы лягушки среднее значение 0 составляет
около 0,25; это соответствует q = 0,89 и i-|max ~ 38%. Основы-
ваясь на измерениях работы и теплоты и используя эргометр
Левина — Ваймана для поддержания постоянной скорости со-
кращения, Хилл получил максимальную механическую эффект
тивность икроножной мышцы лягушки (39,4%) [35, 40]. Позже
он получил максимальное значение около 45 % для изотониче-
ского сокращения [38]. Это соответствует q = 0,92 и 0 = 0,17.
Обычно в мышцах этого типа 0 варьирует от 0,2 до 0,3.
Рис. 12.5. Нормированные графики Хилла при разной степени сопряжения q
[12].
282
ГЛАВА 12
Следует, однако, осторожно относиться к интерпретации
этих измерений, так как они дают отношение PV/(Q + PV),
где Q—наблюдаемая скорость выделения тепла в мышцах.
С другой стороны, вспомнив уравнения (12.6) и (12.11), выра-
зим эффективность как РУ/(Фтесь + PV). Поскольку Фтесь и
Q не идентичны, эти два отношения не должны совпадать.
Первое из них можно рассматривать как разумное приближе-
ние к величине второго при условии, что 1) выделение тепла,
сопряженное с Фсьет, пренебрежимо мало или для этого разли-
чия вводится поправка, 2) мышцы представляют собой практи-
чески закрытую систему во время опыта и 3) абсолютное зна-
чение dSw/dt пренебрежимо мало по сравнению с dSm/dt,
поскольку diS/dt есть сумма этих двух величин [см. уравнения
(12.1)-(12.4)].
Обратное уравнение Хилла, связывающее сродство и ско-
рость движущей реакции, вытекает из феноменологических урав-
нений и уравнений (12.22) и (11.23) [13]:
J-r-7/r°](-r—А1 ---) = 1	О2-27)
\ Am J гт / \ J го Aq /
Как и ранее, подстрочные индексы о и т означают изометри-
ческое и ненагруженное сокращение соответственно. Степень
сопряжения входит в это уравнение в неявном виде, так как
константы связаны друг с другом через д2:
42L4IP-=l-<72	(12.28)
Aq J rm
Для использования уравнения (12.27) может оказаться необ-
ходимым варьировать сродство в широких пределах, особенно
если степень сопряжения высока. Как следствие этого наличие
регулятора приводит к большим изменениям активностей ре-
агентов или продуктов (или и тех и других) в движущей реак-
ции. Ясно, что такие эффекты могут носить только локальный
характер. Возможность того, что локальные концентрации или
активности адениннуклеотидов существенно изменяются, т. е.
что они участвуют в мышечном сокращении в «связанной фор-
ме» или внутри малых компартментов, отмечена рядом иссле-
дователей [55, 65, 74, 75]. В некоторых публикациях предпо-
лагается, что важное функциональное значение имеет метабо-
лический контроль путем комиартментации АТФ, АДФ и фос-
фата [53].
Рассмотренный здесь тип механизма регуляции лучше всего
оценить на основе схемы, введенной нами при обсуждении ак-
тивного транспорта натрия (см. приложение к гл. 7). Те стадии
в последовательности реакций, которые ранее считались непо-
средственно сопряженными с натриевым насосом, теперь сопря-
жены с сократительным механизмом: он представляет собой ли-
Мышечное сокращение 283
нейный преобразователь энергии. Остальные стадии образуют
нелинейный регулятор. Предполагается, что активности проме-
жуточных форм в этих стадиях чувствительны к напряжению
или скорости. Гидролиз основного пула фосфокреатина соот-
ветствует всем последовательностям (или большой их части),
а промежуточные стадии могут соответствовать локальной ком-
партментации. В стационарных условиях стационарное сопря-
жение относится ко всей цепи реакций, т. е. и к регулятору, и
к преобразователю энергии. Полное сродство для процесса
аА -j- ЬВ -+yY + zZ рассматривается как постоянная величина
(фиксированное значение которой определяется, например,
фосфокреатиновым пулом), однако доля сродства, относящая-
ся к промежуточной движущей реакции тМ + nNрР + qQ,
определяется регулятором в соответствии с механической на-
грузкой. Когда нагрузка меняется, происходят изменения неко-
торых или всех химических потенциалов интермедиатов в по-
следовательности реакций от С к X. Если сродство для после-
довательности реакций в преобразователе должно возрасти, то
сродство реакций регулятора уменьшается (и наоборот).
Оплатка [56] предложил один из возможных механизмов, бла-
годаря которому изменение силы, создаваемой нагрузкой, мо-
жет влиять на сродство реакции, создающей движущую силу.
В этом механизме предполагается обратимое связывание ионов
кальция тропомиозином.
Следует подчеркнуть, что способ регуляции, обсуждаемый
здесь, в корне отличается от рассмотренного нами (иногда не-
явно) при обсуждении активного транспорта в эпителии (гл. 7).
В эпителиальных системах функция регулятора состоит в под-
держании сродства некоторого промежуточного пула реагентов,
например АТФ, АДФ и Фн, постоянным. Именно к такому за-
ключению приводят имеющиеся экспериментальные данные.
В мышцах ситуация иная, и весьма вероятно, что сродство пе-
ременно, так что именно эти изменения следуют за изменением
нагрузки.
Уилки и Уоледж [72] подвергли эту точку зрения подроб-
ному критическому рассмотрению. Они установили, что такой
подход дает не только правильное соотношение между силой
и скоростью, но и что экспериментально наблюдаемые соотно-
шения между максимальной эффективностью и максимальной
нормированной выходной мощностью (для мышц различных
животных), по-видимому, соответствуют ожидаемым на этой
основе. Однако они заключили, что соотношение между скоро-
стью движущей реакции и нагрузкой не соответствует ожидае-
мому и что ожидаемые изменения величины свободной энергии
движущей реакции столь велики, что реально они недостижимы.
Кеплен [14] отметил, что эти возражения основаны па множе-
стве сомнительных предположений, в частности: 1) скорость
284
ГЛАВА 12
движущей реакции при стационарном сокращении можно опре-
делить исходя из экспериментальных измерений скорости вы-
деления тепла и скорости совершения работы и оценок энталь-
пии гидролиза фосфокреатина; 2) сродство движущей реакции
зависит от концентраций реагентов и продуктов, определяемых
путем химического анализа целой мышцы. Борнхорст и Ми-
нарди [8] определили сродство движущей реакции по данным
работы [11] на мышце прямой кишки лягушки и получили сле-
дующие результаты: Ао=10,6 ккал/моль АТФ,АОТ=7,5 ккал/моль
АТФ. Максимальное значение находится в пределах, ожидае-
мых по Уилки и Уоледжу [72]. (Уилсон и сотр. [73] получили
сродство 11,4 ккал/моль АТФ для использования АТФ в усло-
виях изолированных клеток печени крыс.) Позже Уилки и сотр.
[21,32] заключили, что при тетаническом сокращении икро-
ножной мышцы лягушки скорость гидролиза фосфокреатина
в любой момент, как правило, не пропорциональна скорости
выделения тепла и совершения работы (в сумме). Следова-
тельно, первую величину нельзя получить непосредственно из
второй. С другой стороны, эти исследователи показали, что
расщепление фосфокреатина специфически связано с соверше-
нием работы и что его распределение как раз соответствует
совершенной работе. Ошибочные оценки, не учитывающие этого
обстоятельства, содержатся не только в критическом обсужде-
нии Уилки и Уоледжа [72], но и во многих других теоретиче-
ских работах, включая исследования Хаксли [44], Борнхорста
и Минарди [9], Чэплейна и Фромелта [17].
Схема химических реакций, очерченная выше в качестве
механизма регуляции, означает, что если через Atot обозначить
полное фиксированное сродство всей реакции, то
Atot —A —Areg	(12.29)
где А — сродство реакций в преобразователе энергии, т. е. на
входе в линейный преобразователь, a Areg — комбинированное
сродство для нелинейного регулятора. Если написать
Areg = RtegJr	(12.30)
где нелинейность выражена в том, что Rreg в явной или неяв-
ной форме зависит от Jr, то уравнение (12.15) можно заменить
на уравнение
Atot = RcrV + (Rr +/? reg) Jr	(12.31)
Степень сопряжения всей системы (регулятор плюс преобразо-
ватель энергии) при некоторых условиях равна
’“ = Т7ГЙТТ	|12'32)
У Кс (Kr + Kres)
Мышечное сокращение
285
И, очевидно, <7tot < q, а степень сопряжения преобразователя
выражается как
’=уйг	<12-33>
Таким образом, для системы в целом с этой точки зрения по-
ниженная степень сопряжения — это та цена, которую прихо-
дится платить за наличие регуляции. Использование энергии
на чисто регуляторные нужды в биоэнергетических механизмах
в настоящее время признается как явление весьма общего зна-
чения [33]. Вероятно, всю систему можно рассматривать как
преобразователь энергии с переменной степенью сопряжения
и под ^tot понимать величину, которая сама подстраивается под
нагрузку. Величина q тоже не обязана быть постоянной, но ее
постоянство является существенным свойством рассматривае-
мого здесь класса преобразователей. Полезно отметить, что
если бы /?reg были постоянными, причем система в целом
вела бы себя как линейная, то регуляция описанного типа все
еще была бы возможна и А возрастало бы с ростом нагрузки.
Поскольку Jr неизбежно снижается с ростом нагрузки, когда
система переходит из режима установившегося потока в режим
статического напора, Ares должно падать в соответствии с урав-
нением (12.30). Это привело бы к возрастанию А по уравне-
нию (12.29) в условиях постоянства Д(Оь Однако такая система
была бы неоправданно неэффективной, так как потребова-
лись бы очень низкие значения gtot, чтобы обеспечить мало-
мальски равномерную мощность на выходе в широком интер-
вале нагрузок.
«Регуляция по стехиометрии-», основанная на кинетических
факторах. Регуляторная схема, описанная выше, имеет тот не-
достаток, что регулятор является диссипативным устройством.
В результате эффективность всей системы, рассчитанная на
основе полного сродства, всегда будет ниже, чем эффективность
самого преобразователя энергии. Как уже отмечалось, такова
может быть цена, уплачиваемая за регуляцию. Однако Борн-
хорст и Минарди [9] попытались решить проблему, исключив
потери, и выдвинули феноменологическую модель, действую-
щую при постоянном сродстве. При этом регуляция осуществля-
ется путем изменения стехиометрических коэффициентов. Из-
менение коэффициентов в этой модели связывается с моделью
скольжения филаментов в сокращающейся мышце. Предпола-
гается, среди прочего, что 1) поперечные мостики, которые
рассматриваются как фундаментальные субъединицы, представ-
ляют собой линейные преобразователи энергии с постоянными
стехиометрическими коэффициентами (такое же предположение
лежит в основе модели регуляции путем изменения сродства),
2) число активных поперечных мостиков меняется в зависи-
286
ГЛАВА 12
мости от скорости и нагрузки и 3) выполняется соотношение
Хилла между скоростями и силами.
Борнхорст и Минарди отметили, что коэффициенты системы
в целом находятся в простом соотношении с коэффициентами
отдельных поперечных мостиков, в то время как число мости-
ков меняется. Обозначим через п число «активированных
мостиков» в данном стационарном состоянии. В соответствии
с уравнениями (12.12) и (12.13) Llc, Llcr и Llr—коэффициенты
отдельного мостика. Тогда, поскольку V = V‘, P = npl, Jr = tiJlr
и А = А', получим
=	=	=	(12.34)
При условии что п надлежащим образом зависит от силы или
скорости, такая система будет следовать уравнению Хилла.
Если исходить из скорости, то эта зависимость будет иметь вид
п	а/Рр
по V/Vm + a/Pp
Уравнение (12.35) не имеет априорного основания. Легко ви-
деть, что выполняются следующие соотношения:
q = ql, Z=Vln	(12.36, 12.37)
(12.35)
где, как обычно, Z = -\jLcjLt (см. гл. 4). Таким образом, степень
сопряжения системы в целом постоянна, но Z меняется. По-
скольку qZ — мера кажущейся стехиометрии системы Vm/Jrm,
«регуляция по стехометрии», по-видимому, представляет собой
вполне адекватный способ описания процесса. В противополож-
ность этому описанный ранее тип регуляции по сродству экви-
валентен введению переменной степени сопряжения для системы
в целом (регулятор плюс преобразователь энергии). Интересно,
что для любого преобразователя энергии с постоянным q, но
переменным Z, зависящим от силы или отношения потоков,
максимальная эффективность все еще выражается формулой
92/(1 + V 1 - <?2)2.
В модели регуляции по стехиометрии степень сопряжения
уже не связана простым соотношением с 0 и вместо этого да-
ется выражением
д= . . 1	-11	(12.38)
4 Vl + (AJroIPoVm)
Ожидаемое изменение скорости реакции в зависимости от на-
пряжения также существенно отличается от прогноза, который
дает модель регуляции по сродству. В случае изометрического
сокращения, изученного Паулом и сотр. (рис. 12.3), модель ре-
гуляции по стехиометрии приводит к выводу, что стимулятор
Мышечное сокращение
287
влияет на по, а не на А, поскольку из уравнений (12.12),
(12.34) и (12.35) следует, что
Ро-^Сг!^поА	(12.39)
Чтобы выяснить, насколько верна каждая из моделей, требу-
ется анализ химических данных в широком интервале условий
опыта. В качестве первого шага в этом направлении Борнхорст
и Минарди [10] модифицировали обе модели таким образом,
чтобы они в явном виде учитывали влияние изменения длины
мышцы.
Эти же авторы [9] показали, что оба типа регуляции можно
представить на основе простой электрической аналогии. Регу-
ляция по сродству соответствует цепи, в которой батарея пи-
тает мотор, соединенный последовательно с сопротивлением
переменной величины, а регуляция по стехиометрии — цепи,
в которой батарея питает ряд моторов, соединенных парал-
лельно, причем все моторы работают на одну и ту же механи-
ческую нагрузку. Каждый из моторов может быть включен в
цепь или выключен произвольно, и контроль состоит в отключе-
нии и включении различного числа двигателей. Подключение
двигателей, которое эквивалентно активации поперечных мости-
ков, на первый взгляд кажется недиссипативным процессом,
однако это не более чем иллюзия, поскольку никакой реальный
процесс не может идти без соответствующей диссипации. Ко-
нечно, вполне возможно, что диссипация, сопряженная с регу-
ляцией по стехиометрии, окажется меньше, чем при регуляции
по сродству.
12.2.3.	Связь между феноменологическими коэффициентами
и молекулярными параметрами
Уже давно известно, что мышца способна поддерживать посто-
янную выходную мощность в широком интервале нагрузок.
Однако для очень малых и очень больших нагрузок выходная
мощность не имеет никакого значения. В этих важных предель-
ных случаях, при изометрическом и ненагруженном сокращении,
тот факт, что не совершается работа и эффективность равна
нулю, не существен. ЛАы уже обсуждали это обстоятельство
в связи с рассмотрением состояний статического напора и уста-
новившегося потока. Для мышц существенна способность и в
этих предельных ситуациях поддерживать напряжение и обес-
печивать высокую скорость сокращения. Действительно, можно
показать, что если уравнение Хилла, связывающее силу и ско-
рость, отражает регуляцию по сродству, то эффективности по
напряжению и по скорости [ср. с уравнениями (6.23) и (6.24)]
остаются высокими в широком интервале условий [28].
288
ГЛАВА 12
Эти соображения имеют прямое отношение к результатам
исследований механохимии скелетных мышц позвоночных, ко-
торые провел Оплатка [56]. Он обнаружил, что уравнения со-
стояния этих мышц можно записать на основе трех универсаль-
ных молекулярных постоянных: 1) средней молекулярной со-
кратительной силы ф0, развиваемой за время жизни активного
комплекса при изометрическом сокращении, 2) относительного
смещения на полутолщину Д/т филамента (молекулярный «ска-
чок» или длина шага) при расщеплении каждым из его суО-
фрагментов-1 одной молекулы АТФ при ненагруженном сокра-
щении и 3) отношения скоростей при ненагруженном и изомет-
рическом сокращении (важная роль этого отношения была
отмечена также в работах [13, 81]). Записав феноменологиче-
ские уравнения для одной активной единицы через коэффи-
циенты сопротивления [ср. с уравнениями (12.14) и (12.15)],
Оплатка получил
Rcr = - MmRc = - &0/а0) Rr	(12.40)
где a0 — сродство в расчете на молекулу гидролизуемого АТФ
при изометрическом сокращении. Для различных поперечных
мышц величина ао оказывается почти одинаковой, поэтому сте-
пень сопряжения можно также рассматривать как универсаль-
ную молекулярную постоянную:
q==^,Mao	(12.41)
Подставляя значения молекулярных параметров, полученные
путем обработки литературного материала, Оплатка рассчитал,
что степень сопряжения q примерно равна 0,9 в согласии с
оценками, полученными Кепленом [12] на основе уравнения
(12.23).
Уравнение (12.40) можно также использовать для определе-
ния феноменологической стехиометрии Z, которая является еще
одной универсальной молекулярной постоянной:
Z = V«oA/m/?o	(12.42)
Как и ожидалось, кажущаяся стехиометрия для ненагружен-
ного сокращения qZ = /\lm.
12.3.	Некоторые общие замечания
12.3.1.	Целесообразность применения уравнений
неравновесной термодинамики
Классический подход к энергетике мышечного сокращения
всегда выражался на основе классической (равновесной) тер-
модинамики. Карлсон и Уилки [16] особо отметили, что ни
один из законов классической термодинамики не ограничен в
Мышечное сокращение 289
своих применениях только системами, находящимися в равно-
весии. Они указывают далее, что оба закона термодинамики
применимы ко всем системам независимо от того, близки ли
они к состоянию равновесия. Именно это составляет основу
прменимости термодинамики в биологии, поскольку в живых
системах мы почти всегда имеем дело с превращениями хими-
ческой энергии в процессах, не являющихся равновесными, и
в условиях, которые далеки от равновесия.
Эти замечания абсолютно верны, но в действительности
они естественным образом подводят к необходимости рассмот-
рения энергетики сократительных систем в рамках термодина-
мики необратимых процессов, которая восходит к первому и
второму законам термодинамики и является модификацией
основных термодинамических соотношений специально для не-
равновесных систем. Вместо того чтобы рассматривать только
начальное и конечное состояния при различных переходах в
системе, неравновесная термодинамика учитывает в явной
форме сам процесс перехода. В отличие от классической тер-
модинамики, в которой неявно предполагается, что мышца
действует как закрытая система, это предположение не подразу-
мевается и не является необходимым в неравновесной термоди-
намике, которая превосходно приспособлена к исследованию
открытых систем.
Однако, вероятно, наиболее важная черта неравновесной
термодинамики состоит в ее способности представлять мышцу
как систему с двумя потоками. Этот факт невозможно выразить
в терминах классической термодинамики, поскольку она имеет
дело в основном не с процессами, а с состояниями. Например,
при классическом рассмотрении электрохимического элемента
обязательно предполагается полное сопряжение между элек-
трическим током и химической реакцией. Другими словами, этот
подход рассматривает систему как однопотоковую [ср. с урав-
нением (6.20)]. Феноменологические уравнения (12.12) и (12.13)
или (12.14) и (12.15) дают, по нашему мнению, простейший
возможный способ описания системы, имеющей две степени
свободы.
Ниже мы перечислим четыре механохимические характери-
стики, которые время от времени создавали трудности концеп-
туального характера, легко преодолеваемые на основе нерав-
новесной термодинамики.
1.	Изменения эффективности в зависимости от скорости.
Было установлено, что с операционной точки зрения изменение
эффективности в зависимости от скорости означает, что степень
сопряжения между работой и гидролизом АТФ в механическом
генераторе переменна [50]. Как было показано в гл. 4, такое
изменение в действительности не кажется неожиданным, оно
является отчетливо предсказуемым результатом для рассмот-
19 Кенлен, Эссиг
290
ГЛАВА 12
ренных ранее систем с фиксированной степенью сопря-
жения.
2.	Затраты энергии при изометрическом сокращении. В ра-
боте [50] утверждалось, что при кратковременном изометри-
ческом сокращении может быть совершена значительная внут-
ренняя работа. Основанием послужили данные [47] о том, что
использование АТФ связано главным образом с внешней ра-
ботой, совершаемой при изотонических сокращениях, а также
экстраполяция этого наблюдения на изометрические сокраще-
ния. При этом принималась «унитарная концепция» механизма
механохимического сопряжения. Однако с термодинамической
точки зрения понятие внутренней работы лишено смысла, по-
скольку работа есть способ передачи энергии между системами
и ее всегда можно уподобить подъему груза. В неполностью
сопряженной системе состояние статического напора связано
с диссипацией энергии в чистом виде, так что работа не со-
вершается. Система тратит энергию просто для того, чтобы
поддерживать это состояние.
3.	Замедление гидролиза АТФ: активное растяжение. Кор-
тин и Дэвис [19,20] показали, что при низких скоростях рас-
тяжения скорость гидролиза АТФ значительно ниже, чем при
изометрическом сокращении. Кроме того, они заключили, что
в процессе растяжения поперечные мостики могут образовы-
ваться и сохранять силу в пределах смещения без расщепле-
ния АТФ. В связи с этим они отмечают, что «любая теория
мышечного сокращения должна объяснить способность мышцы
развивать напряжение, даже превышающее Ро, и поддерживать
его на больших расстояниях при растяжении в условиях крайне
слабого гидролиза АТФ» [47]. Однако уравнения (12.12) и
(12.13) ясно показывают, что если мышца растянута в условиях
тетанической стимуляции, т. е. если V становится отрицатель-
ной, то Р>РО (можно считать, что в этих условиях А ~АО,
поскольку, как показано в приложении к этой главе, регуляция
по сродству означает, что Ао — предельное значение) и
В принципе, если бы феноменологические коэффициенты и срод-
ство оставались в основном постоянными в таких экстремальных
условиях, то Jr должен был бы обратиться в нуль при доста-
точно высоком значении Р, а при еще больших значениях —
стать отрицательным. Другими словами, мог бы начаться син-
тез АТФ. Такое экстремальное поведение никогда не наблю-
далось.
4.	Механизм «захвата». Мышцы моллюсков могут нахо-
диться в фиксированном положении (см., например, [16]), под-
держивая напряжение примерно так же, как напряженное упру-
гое тело, и могут продолжать стягивать фиксированные точки
при очень малом расходе энергии. Энергетические соотношения
таковы, что в данном типе мышц сократительная система
Мышечное сокращение 291
должна быть полностью или по крайней мере очень сильно
сопряженной [14]. В рамках рассматриваемых моделей ника-
кого особого механизма захвата не требуется: полностью со-
пряженная мышца не должна расходовать метаболическую
энергию (сверх базального процесса) при стационарном изо-
метрическом сокращении.
12.3.2.	Следствия саморегуляции
Регулятор, существование которого мы здесь предположили
в мышце, no-видимому, точно соответствует идее, которую имел
в виду Фенн, когда много лет назад писал: «В пределах каж-
дого отдельного волокна имеется другой регуляторный меха-
низм, который может в известных пределах приспосабливать
выходную энергию к совершаемой работе... Этот механизм не
зависит от нервной системы и действует благодаря некоторым
фундаментальным свойствам мышечной машины безотноси-
тельно к его природе... Освобождаемая энергия... может ме-
няться за счет груза, который мышца должна поднять» [29].
Процессы, участвующие в регуляции, заключены в величине
Фсьет [уравнение (12.7)]. Малые изменения сродства соответ-
ствуют весьма значительным изменениям активности, которые
можно объяснить только на основе представления о локальных
активностях в области реакционных центров. Олберти [3]
отметил сильное влияние магния и кальция на стандартное
сродство реакции гидролиза АТФ. Нельзя также исключить
влияние pH среды. Ввиду важной роли кальция в возбуждении
вполне возможно, что локальное сродство регулируется ка-
ким-то образом уровнем кальция в согласии с предположением
Оплатки [56]. Такой механизм не совместим с теорией Прингла
[62]. Кон и Лонгли [18] предположили, что обратимое связы-
вание двухвалентных катионов тропомиозином может выпол-
нять регуляторную функцию при мышечном сокращении. Ат-
кинсон [5] и Гесс [33] обсудили регуляцию по типу обратной
связи на молекулярном уровне и взаимодействие между фер-
ментами, которые модулируются метаболитами.
Если соображения, которые приводят к уравнению (12.23),
действительно правильно отражают основы наблюдаемых меха-
нохимических свойств мышцы, то ее можно рассматривать как
регулируемый линейный преобразователь энергии с постоян-
ными коэффициентами. Однако можно, как обсуждалось ранее,
рассматривать мышцу и как преобразователь энергии с пере-
менными коэффициентами. Разница между этими двумя спо-
собами описания может оказаться лишь результатом выбора
модели «черного ящика» или рабочего элемента. Было бы стран-
но, если бы систему, описываемую вторым способом и подчи-
няющуюся уравнению Хилла, невозможно было охарактеризо-
19*
292
ГЛАВА 12
вать и первым способом. Дилемма между двумя возможными
способами описания может быть разрешена путем определения
А по уравнениям (12.25) — (12.27).
Представление о саморегуляции требует, чтобы скорость
сокращения зависела только от напряжения. Это предположе-
ние хорошо согласуется с механическими измерениями, как,
например, в изящных опытах Макферсона [52] по определению
соотношений между силой и скоростью на начальных стадиях
двух изометрических сокращений. Другой способ определения
соотношений между силой и скоростью, который, насколько
нам известно, пока никем не был использован, может состоять
в том, чтобы предоставить мышце возможность сокращаться и
преодолевать ряд чисто диссипативных механических сопротив-
лений (амортизаторов). При этом регулятор должен реагиро-
вать непосредственно на механическое нагрузочное сопротив-
ление R.l = P/V, а не на Р, как при изотоническом сокращении,
или на V, как в эргометре Левина — Ваймана. Способность от-
кликаться таким образом, чтобы получалась хилловская кри-
вая соответствующего вида, — необходимое следствие модели,
показанной на рис. 12.4 (см. приложение к этой главе). Среди
соотношений, которые описывают химические свойства системы,
линейная зависимость напряжения от скорости сокращения и
скорости реакции [уравнение (12.14)] легко проверяется экспе-
риментально. Частично такая проверка уже была выполнена
в работах [57,58]. Остается проверить то же самое для изото-
нических сокращений. Если линейность подтвердится, то в
принципе можно определить все параметры в уравнениях (12.14)
и (12.15), поскольку величина q известна из кривых, связываю-
щих силу и скорость.
12.4.	Заключительные замечания
Мышечную фибриллу можно рассматривать как рабочий эле-
мент, характеризуемый двучленной функцией диссипации: вы-
ходной механической мощностью и химической работой на
входе. Получено множество данных в пользу того, что в про-
цессе изометрического или изотонического тетанического сокра-
щения, по крайней мере на начальной его стадии, фибрилла
достигает стационарного состояния. Такая стационарность, по-
видимому, часто имеет место in vivo, как это показано Уилки
[69] на' примере хилловского соотношения в мышцах чело-
века.
Механохимический гидролиз АТФ в мышце вполне может
представлять собой длинный ряд промежуточных стадий, каж-
дая из которых характеризуется низким сродством. Некоторые
из этих стадий могут сводиться к транспорту реагентов и про-
Мышечное сокращение 293
дуктов внутрь или из локальных компартментов. В связи с
этим применение линейных феноменологических соотношений
к начальной фазе тетанического сокращения может оказаться
необоснованным. В любом случае, чтобы продвинуться вперед,
нам пришлось ввести представление о «правильных траекто-
риях» механохимического процесса. Это позволило рассматри-
вать фибриллу как линейный преобразователь энергии.
Степень его сопряжения (гл. 4) может быть меньше единицы,
как это показано, например, для продолжительного гидро-
лиза АТФ в процессе изометрического тетанического сокра-
щения.
Мышца в принципе может относиться к классу простых
саморегулируемых преобразователей энергии [12], поскольку
механохимический процесс может быть линейным и, по-види-
мому, удовлетворяет требованиям стационарности и неполного
сопряжения. Если это так, то соотношение Хилла между силой
и скоростью содержит лишь один параметр, подлежащий уточ-
нению, — степень сопряжения.
Тип регуляции, который характеризует этот класс преобра-
зователей энергии, можно описать как регуляцию по сродству,
основываясь на энергетических факторах. Другой, в некотором
смысле противоположный тип рёгуляции — по стехиометрии —
основан на кинетических факторах.
Как степень сопряжения q, так и феноменологическая сте-
хиометрия Z механохимического процесса могут быть выра-
жены на основе трех молекулярных параметров этой системы:
средней молекулярной сократительной силы, развиваемой за
время жизни активного комплекса при изометрическом сокра-
щении, относительного смещения на полутолщину филамента
при расщеплении каждым из его субфрагментов-1 одной мо-
лекулы АТФ при ненагруженном сокращении и сродства в рас-
чете на одну молекулу АТФ, гидролизованную при изометриче-
ском сокращении.
Можно ожидать, что расход химической энергии мышцей
будет подчиняться уравнению Хилла (12.27). Последнее тре-
бует значительного изменения сродства реакции при высо-
кой степени сопряжения. Соответствующие изменения актив-
ности могут осуществляться локально под действием регуля-
тора.
Значения сродства при любом заданном напряжении в прин-
ципе можно определить в гладких мышцах из одновременных
измерений напряжения, скорости потребления кислорода и ско-
рости сокращения. Эти значения целесообразно сопоставить
с результатами химических оценок на целых мышцах (см., на-
пример, работы [21,50]), основанных на ряде предположений,
весьма удаленных от собственно эксперимента.
294
ГЛАВА 12
12.5.	Выводы
1.	Путем рассмотрения фибрилл как рабочего элемента мышцы
получена функция диссипации сокращающейся мышцы. По-ви-
димому, она разделяется на две положительно-определенные
части, одна из которых связана с механохимическим процессом,
а другая — с чисто химическим. Представлены данные в пользу
того, что фибриллы можно рассматривать таким образом, как
если бы они находились в процессе сокращения в стационарном
состоянии.
2.	Если представить «механохимическую» диссипацию в виде
Omech==V(—p)_\-jrA, Где в привычных обозначениях, введен-
ных Хиллом, Р — напряжение, V — начальная постоянная ско-
рость при тетаническом сокращении (остальные обозначения
имеют обычный смысл), то легко записать феноменологические
соотношения через коэффициенты L или R. Представлены экс-
периментальные данные, подтверждающие предполагаемую ли-
нейность этих уравнений. Кратко обсуждено соотношение между
феноменологическими коэффициентами и молекулярными пара-
метрами.
3.	Показано, что характеристическое гиперболическое со-
отношение между силой и скоростью для мышц (уравнение
Хилла) приводит к концептуальной модели, основанной на по-
нятии саморегуляции. Теоретический анализ саморегулируемых
линейных преобразователей энергии проведен в приложении.
Анализ показывает, что уравнение Хилла содержит всего один
параметр, подлежащий уточнению, — степень сопряжения; этот
параметр можно определить из кривизны графика зависимости
между силой и скоростью. В частности, для икроножной мыш-
цы лягушки получена степень сопряжения около 90 %, соответ-
ствующая максимальной эффективности 40 %.
4.	В отличие от систем активного транспорта, рассмотрен-
ных ранее, следует ожидать, что сродство в мышцах меняется
в зависимости от нагрузки под действием регулятора. Рассмот-
рены способы экспериментальной оценки сродства в данном
состоянии.
5.	Рассмотрена природа регуляторного процесса. Отмечен
ряд существенных следствий саморегуляции. Регуляция на ос-
нове энергетических факторов (по сродству) сопоставлена с
регуляцией на основе кинетических факторов (по стехиомет-
рии). В настоящее время сделать обоснованный выбор между
этими двумя моделями не представляется возможным.
6.	Рассмотрены преимущества подхода, основанного на не-
равновесной термодинамике, при выяснении природы мышеч-
ного сокращения. Этот подход включает использование следую-
щих механохимических характеристик: изменения эффективно-
сти в зависимости от скорости, затрат энергии при изометриче-
Мышечное сокращение
295
ском сокращении, замедления гидролиза АТФ при активном рас-
тяжении, экономичного использования энергии при механизме
«захвата».
7.	На основе молекулярных параметров рассмотрены сте-
пень сопряжения и феноменологическая стехиометрия механо-
химического процесса.
Приложение: вывод уравнения Хилла для
саморегулируемых линейных преобразователей
энергии
Оптимальная нагрузка
Превращение энергии в линейных системах, т. е. в системах,
которые можно описать с помощью линейных феноменологи-
ческих соотношений неравновесной термодинамики, обсужда-
лось в гл. 4, где было показано, что степень сопряжения —
очень полезная величина при описании таких систем. В боль-
шинстве случаев ее в принципе можно измерить, что позволяет
рассчитать максимальную эффективность системы, а также эф-
фективность при максимальной выходной мощности без каких-
либо дополнительных сведений. Эффективность при максималь-
ной выходной мощности часто представляет наибольший интерес
и имеет одинаковое значение независимо от того, дей-
ствует ли в системе постоянная движущая сила (режим «источ-
ника постоянного напряжения») или поддерживается постоян-
ный поток («постоянное значение электрического тока» в экви-
валентном контуре). Выходная мощность в системах с разумно
высокой степенью сопряжения преобразователя энергии при
этих двух способах работы достигает максимума при весьма
различных величинах нагрузки: режим фиксированной силы
благоприятен при низких нагрузках, а режим фиксированного
потока — при высоких.
Если линейный преобразователь энергии должен дать вы-
сокую выходную мощность в широком интервале нагрузок, то
работа только в одном из указанных режимов смысла не имеет.
Целесообразнее снабдить преобразователь специальным устрой-
ством, которое регулирует подводимую энергию в зависимости
от нагрузки и тем самым оптимизирует режим работы. В тех-
нике хорошо известны сервомеханизмы такого типа. Например,
в тепловой машине всегда имеется автоматический регулятор.
Известно, что регуляторные механизмы весьма важны и в био-
логии. Преобразователь энергии с таким регулятором мы на-
зовем саморегулируемым. Задача состоит в рассмотрении ха-
рактеристических соотношений между подводимой и выходной
мощностями в системах этого типа.
296
ГЛАВА 12
Линейные преобразователи энергии рассматриваемого нами
типа, очевидно, имеют две степени свободы, т. е. стационарное
состояние определятся двумя контролируемыми извне парамет-
рами. Один из них — обычное нагрузочное сопротивление, ко-
торое само по себе достаточно, чтобы фиксировать эффектив-
ность работы. Обобщенное нагрузочное сопротивление выража-
ется как
RL = -XJJi	(12.П1)
где используются те же обозначения, что и в гл. 4. (Это выра-
жение положительно в области совершения внешней работы
рассматриваемой системой.) Чтобы достигнуть максимальной
эффективности или максимальной выходной мощности, нагрузка
должна соответствовать свойствам преобразователя энергии.
Например, оптимальная нагрузка по эффективности дается вы-
ражением	______
Rl = Rl = 1/Лца/1 - 91 2	(12.П2)
Величина 1/£ц представляет собой обобщенное «внутреннее со-
противление» системы при постоянном значении Х2, т. е. когда
преобразователь энергии действует как источник постоянного
напряжения. Показано [49], что, если тк— отношение между
нагрузочным и внутренним сопротивлениями, т. е.
mR = Rl^h
эффективность выражается как
дг
Объединяя уравнения (12.П2) — (12.П4), можно
через отношение Rl/ROl:
(12.ПЗ)
(12.П4)
выразить я
1 +----1 +-------------....
\	/?ЁУ1-<72Д
Уравнение (12.П5) можно также переписать через квадратич-
ную функцию Rl, следовательно, каждое значение ц соответ-
ствует двум значениям RL. При т]тах они совпадают.
Диаграммы входа—выхода
Во многих случаях ситуация существенно проясняется при гра-
фическом представлении свойств преобразователя энергии. Про-
стейший способ такого представления — диаграмма выходной
мощности, приведенная на рис. 12.6, где множество возможных
траекторий через область, соответствующую совершению внеш-
ней работы, образуют траектории в двумерном «выходном про-
Мышечное сокращение 297
странстве». (Чтобы избежать отрицательных значений, дана
зависимость величины —от Л.) Диаграмма этого типа отли-
чается от обычных индикаторных диаграмм, применяемых для
описания работы машины, действующей циклически. Каждая
точка здесь отвечает стационарному состоянию, а соответствую-
щая выходная мощность определяется площадью прямоуголь-
ника, ограниченного осями координат и имеющего вершины
в начале координат и в данной фигуративной точке. Каждая
траектория представляет ряд соседних стационарных состояний,
через которые система может пройти в результате последова-
тельных изменений некоторого внешнего параметра, например
Rl. Траектория ограничена линией, соответствующей выходу
из области совершения внешней работы, где Rl достигает нуля
или бесконечности.
На данном этапе у нас нет оснований заранее ограничивать
работу системы какой-либо определенной траекторией. В прин-
ципе доступны все точки «выходного пространства», и описа-
ние определенной траектории требует знания способа, которым
система регулируется. Поэтому выходная диаграмма дает све-
дения о способах работы каждой частной системы. Сама по
себе эта диаграмма не позволяет различить системы с разными
значениями q. Наоборот, все возможные траектории для дан-
ной системы совпадают, если построить график зависимости
эффективности от отношения сил (или потоков) или график
зависимости отношения сил от отношения потоков, поскольку,
как показано в гл. 4, такие диаграммы различают только си-
стемы с разными значениями q.
Ось устаноОивш-егося потока
Рис, 12.6. Диаграмма выхода, показывающая некоторые нз возможных тра-
екторий в выходном пространстве.
Такая же диаграмма получена для входного пространства путем построения графика
зависимости Х2 от Л. Линии постоянства (линии нагрузки) исходят нз начала коор-
динат [12].
298
ГЛАВА 12
Более сложный способ графического представления (диа-
грамма входа — выхода) показан на рис. 12.7. В основе этой
диаграммы лежит тот факт, что феноменологические уравнения,
будучи линейными, описывают аффинное преобразование. Вы-
ходное пространство можно отобразить на входном пространстве
и обратно. При таком преобразовании прямые линии переходят
в прямые, а параллельные — в параллельные. Такая операция
просто переводит каждую точку одного пространства в точку
другого пространства. Следовательно, любая кривая на диа-
грамме представляет траекторию в обоих пространствах одно-
временно (в сущности, это двумерная проекция четырехмерюго
графика). Диаграмма входа — выхода дает сведения как о са-
мой системе, так и о способе ее работы. Действительно, ири
подходящем выборе осей координат диаграмму можно исполь-
зовать на практике при управлении такими преобразователями
энергии или получить с ее помощью сжатое графическое опи-
сание их поведения. Когда степень сопряжения приближается
к нулю, выходное пространство вырождается в одну прямую
линию, т. е. оси статического напора и установившегося потока
сливаются'. Когда сопряжение приближается к полному, наклон
j >
АЛ
Махс.ВыхоЭ, Хгфико.
О,
МаксЛыхо8л Х2Хг фикёх}
о»,0"*
Макй;8ыхоЭ, 7г фикс.




Рис. 12.7. Диаграмма входа — выхода, показывающая две траектории (а
и Ь), которые видны на рис. 12.6.
Выходное пространство теперь отображается на входном (указаны доли трансфор-
мированной координатной системы выхода). Три линии нагрузки уточняют оптимальные
режимы при фиксированном значении различных величии [12].
Мышечное сокращение 299
оси статического напора стремится к бесконечности. Величина
q2 имеет прямой геометрический смысл: любая горизонтальная
или вертикальная линия на диаграмме делится осями в отно-
шении <?2/(1 —92)- Таким образом, доля q2 полной длины любой
из линий а и Ь на рис. 12.7 находится между осями выходного
пространства. Площадь за пределами выходного пространства
(т. е. за пределами области совершения внешней работы) пред-
ставляет области, в которых оба члена функции диссипации
положительны, и, следовательно, в любом направлении не мо-
жет быть преобразования энергии.
Мы отметили, что установление любых двух параметров,
иными словами, использование двух ограничений полностью
определяет стационарное состояние. Обычно одно ограничение
накладывается со стороны выхода, т. е. нагрузкой, а другое —
на входе, т. е. природой питающего процесса. Два обычных
класса машин — это такие, в которых вход ограничен путем
фиксирования или постоянного значения движущей силы Х2
(«источник постоянного напряжения»), или постоянного значе-
ния движущего потока /2 («источник постоянного тока»). Ти-
пичные траектории, соответствующие таким машинам, даются
линиями а к b соответственно на рис. 12.6 и 12.7. Любое ста-
ционарное состояние в траектории, обозначенной этим спосо-
бом, определяется единственным ограничением на выходе. Это
ограничение можно наложить, фиксируя значения Xit или
Rl- Каждую из этих возможностей можно представить прямой
линией на диаграмме входа — выхода, которая пересекает тра-
екторию, определенную ограничением на входе, в точке, соот-
ветствующей стационарному состоянию. Видно, что ни одно из
ограничений на выходе, отмеченных выше, не может определить
траекторию через область внешней работы.
На рис. 12.7 имеются три линии нагрузки, представляющие
три различные оптимально подобранные нагрузки. Нагрузка,
при которой эффективность максимальна, не зависит от огра-
ничений на входе. Но если необходима максимальная выходная
мощность, то ограничения на входе становятся существенными.
Если фиксировано значение Х2, то нагрузочное сопротивление
должно соответствовать внутреннему сопротивлению; если же
фиксировано значение J2, то нагрузочная проводимость долж-
на соответствовать внутренней проводимости [49]. Эти значе-
ния показаны на диаграмме. Отношение двух нагрузок, обес-
печивающих максимальную выходную мощность, равно 1—q2
и далеко от единицы, если степень сопряжения велика. Дей-
ствительно, преобразователи энергии типа источника постоян-
ного напряжения должны иметь низкое внутреннее сопротив-
ление, а источники, поддерживающие постоянный ток, — низкую
внутреннюю проводимость. Первые плохо приспособлены для
работы с высокими нагрузочными сопротивлениями Rl, когда
300
ГЛАВА 12
требуется высокая выходная мощность. Точно так же вторые
плохо приспособлены для низких нагрузочных сопротивле-
ний Rl.
Саморегуляция преобразователей энергии
Чтобы получить высокую или более однородную выходную
мощность при сравнительно больших изменениях нагрузки,
вместо способов работы, отражаемых траекториями а и Ь,
можно ввести другие способы. Ясно, что, обсуждая работу при
фиксированном значении Х2 или /2, мы уже постулировали су-
ществование регулятора того или иного типа, контролирующего
режим на входе. Рассмотрим теперь свойства систем с обратной
связью, в которых регулятор контролирует вход в ответ на на-
грузку, как показано на рис. 12.4. Задача состоит в том, чтобы
выяснить, ограничен ли каким-либо образом выбор траектории,
которой система должна следовать, и если такие ограничения
существуют, то какова их природа.
Из физических соображений ясно, что пространство входа —
выхода, в пределах которого должен действовать регулятор,
ограничено со всех сторон. Таким образом, для любого преобра-
зователя энергии, очевидно, существует максимальная входная
мощность для каждого значения нагрузки, которое нельзя пре-
высить без разрушения системы. Следует ожидать, что регуля-
тор будет подстраивать выходную силу к максимуму, когда
Rl = оо, так что система будет развивать наибольшее усилие,
встречаясь с максимальным сопротивлением. В то же время
при Rl — О по тем же причинам будет устанавливаться макси-
мальный выходной поток. На рис. 12.8 показана соответствую-
щая ограниченная диаграмма входа — выхода, на которой пре-
дельные значения потоков и сил, достигаемые в состоянии ста-
тического напора, обозначены надстрочным индексом s, а пре-
дельные значения при установившемся потоке — индексом I.
Область совершения внешней работы может быть ограничена
линиями —Xi = — Xi и Ji = j{ или линиями X2 = X® и /2=ЛГ
Однако точная природа двух границ менее существенна, чем
две точки, в которых они пересекают оси статического напора
и установившегося потока. В этих двух точках —X! или Ц
могут превосходить все другие значения, определяемые регуля-
тором, чтобы не нарушить требование стабильности, описанное
ниже. Это верно также для любой данной траектории незави-
симо от того, находятся ли состояния статического напора и
установившегося потока в действительных рабочих пределах,
определяемых физической природой преобразователя энергии.
Поэтому мы рассматриваем — Xi = —Х* и /i = j{ как пределы,
установленные регулятором, чтобы предохранить преобразова-
Мышечное сокращение 301
тель энергии от разрушения. Важно понять, что — Xi и не
обязательно точно соответствуют статическому напору и уста-
новившемуся потоку для некоторого семейства траекторий. Они
представляют прежде всего максимальные значения —Х} и J],
допустимые для данной системы, а их связь с состояниями
статического напора и установившегося потока, хотя и может
быть установлена из общих соображений, определяется также
требованиями стабильности. Ничто в последующем анализе не
исключает Xl < Х1ч или /2 < Л, хотя такие ситуации, по-види-
моу, маловероятны. Отметим, что знание величин всех потоков
и сил в обоих граничных состояниях или в любых двух стацио-
нарных состояниях той же области дает более чем достаточную
информацию для оценки всех феноменологических коэффициен-
тов, если эти коэффициенты постоянны.
Как только установлены пределы, в которых должен рабо-
тать регулятор, задача сводится к исследованию класса допу-
стимых траекторий между этими пределами. Начнем с рассмот-
рения природы данных о нагрузке, которые передаются обратно
к регулятору. Это зависит от природы ограничений, наклады-
ваемых на выходном конце системы. В инженерной практике
преобразователя энергии обычно работают с диссипативной на-
грузкой, т. е. Rl фиксировано и регулятор должен выбрать
Рис. 12.8. Ограниченное пространство входа — выхода, на котором показана
траектория саморегуляции (d).
л	/
Пиковые значения выходной силы и потока —и достигаются только в режиме
статического напора и установившегося потока	соответственно. Границы можно
точно так же задать при помощи X® и [12].
302
ГЛАВА 12
точку на линии Rl- В биологии более вероятно, что фиксиро-
вана величина —или, возможно, Л (в мышцах возможны
все три варианта). Общее требование состоит в том, что си-
стема должна осуществлять устойчивую регуляцию независимо
от ограничений, накладываемых на выходе. Очевидно, все,
к чему сводится действие регулятора, — это обеспечить режим
на входе таким образом, чтобы поддерживать стационарное
состояние. Это можно выразить множеством способов, однако
целесообразно сделать это через поток и силу на выходе в яв-
ном виде. Например, можно просто написать 
71 = ф(—XJ	(12.П6)
и затем рассмотреть класс функций ф, которые удовлетворяют
требованию, чтобы Ji было однозначной функцией —Xj с пра-
вильно выбранными пределами. Дальнейшее требование, кото-
рое резко сужает круг возможностей, состоит в том, что обрат-
ная функция
-Х^ф-'СЛ)	(12.П7)
также должна иметь единственное значение, откуда, кроме
того, следует, что —X, и Ji будут однозначными функциями Rl-
Всеобщее условие однозначности функций необходимо для
устойчивой регуляции, поскольку любое ограничение на выходе
приводит при этом только к одному определенному стационар-
ному состоянию. Далее мы увидим, что функции ф и ф-1 не мо-
гут быть однозначными, если значения или — X? достига-
ются или превышаются где-либо еще за пределами области
создания движущей силы.
Очевидно, функции ф и ф-1 характеризуют эффективность
регулятора и могут рассматриваться как функции регулятора.
Однако, как функции режима на входе, они могут также вклю-
чать свойства преобразователя энергии. Поскольку восприни-
мается ограничение на выходе, функции регулятора, записан-
ные через параметры входа, не рассматриваются как более
фундаментальные. В любом случае один тип легко переходит
в другой. В биологии границу между двумя черными ящиками
едва ли можно различить, даже если она существует, и может
оказаться невозможным изолировать вход от преобразователя
энергии. (При этом комбинированные свойства регулятора и
преобразователя означают наличие одного нелинейного чер-
ного ящика.) Поэтому предпочтительно представить регулятор
на основе выходных функций. Мы допускаем возможность от-
деления «программирующей» функции, которую можно произ-
вольно варьировать смотря по обстоятельствам, набирая ее из
некоторых элементов, существенных для выполнения основных
функций регулятора. Точнее, предположение состоит в том, что
Мышечное сокращение 303
можно найти каноническое выражение для функции регуля-
тора, принимающее две формы:
71 = ’ф[—-Xf, J‘, q\ h(RLy] (12.П8)
= -Xf, jL q\ h(RL)] (12.П9)
где — одно из возможных представлений произвольной
функции. Здесь —Xt и рассматриваются как однозначные
функции друг друга в пределах области, где создается движу-
щая сила; H(Rl) является функцией обеих этих величин. Важно
иметь в виду, что уравнение в форме (12.П8) и (12.П9) пред-
ставляет траекторию между двумя граничными точками, кото-
рая характеризуется программирующей функцией h(Ri).
Среди важных элементов, содержащихся в уравнениях
(12.П8) и (12.П9), имеется степень сопряжения. Функция ре-
гулятора не обязательно должна содержать в явном виде фе-
номенологические коэффициенты преобразователя энергии. Но
если эффективность преобразователя энергии должна оцени-
ваться регулятором в соответствии с некоторым энергетическим
критерием, то степень сопряжения едва ли может быть остав-
лена без внимания. Важным является то, что регулятор пере-
водит преобразователь энергии в ответ на ограничение, скажем
величины —Хг, через ряд стационарных состояний в соответ-
ствующее конечное состояние. Информация, которая направля-
ется обратно, может состоять из таких величин, как {dJJdX2)_Xi
и (dJ^/dX^)-^. В дальнейшем из них можно получить все
феноменологические коэффициенты, если дано q2. Регулятор
может также в любом стационарном состоянии воспринимать
абсолютные отношения тех же величин. Однако в полностью
сопряженных системах меньше потенциальных источников ин-
формации такого типа. Различия между частично и полностью
сопряженными преобразователями энергии глубоки, как это
отмечено в гл. 4, и последние мы исключим из дальнейшего
рассмотрения.
Следует подчеркнуть, что однозначность Ji как функции
—Xt не обязательно подразумевает обратное, она также не
означает однозначности каждой из этих величин как функ-
ции Rl. Это ясно видно при рассмотрении траектории с на
рис. 12.6. Один из подходов к проблеме охвата всех условий
однозначности одновременно состоит в том, чтобы выразить
выходную мощность как однозначную функцию нагрузки, т. е.
как функцию вида
- JiXi = ф	q2, h (/?L)]	(12.П10)
Действительно, основная задача при описании регулятора со-
стоит в установлении природы ф. Класс траекторий, описывае-
мых уравнением (12.П10), включает все траектории, для кото-
304
ГЛАВА 12
рых и гр и г)?-1 — однозначные функции. Этот класс можно
также описать с помощью следующих параметрических уравне-
ний, где f и g— снова однозначные функции, если ф однозначна:
Ji = f[RL, -Xsit J[, q\ h(RL)]
~Xi = g[Ri, -Xf, 4 q2, h(RL)] (12.П11)
Эти две функции связаны простым соотношением
RL = g(RL)/f(Ri)	(12.П12)
Однако мы рассмотрим их отдельно, поскольку нас интересуют
их пределы. Они таковы:
/?£->оо: f—>Q, g^-Xb Rl^O:	g^Q
Отсюда ясно, что функции fag можно заменить нормирован-
ными функциями fug:
Ji=j\f[RL, -Xf, /{, q2, h(RL)]
-X^-XtglRb, -Xf, q\ h(RL)] (12.П13)
Видно, что ф — произведение двух однозначных функций и что
уравнение (12.П10) можно переписать в форме
- /,Х, = - /{xTf [т?£, - XL /!, q2, h (/?£)] X
Xik. XL J{, q\ h(RL)] (12.П14)
Задача свелась к нахождению канонического выражения
в явном виде, соответствующего уравнению (12.П14). В этом
нам поможет следующее обстоятельство. Величина— /{XL ко-
торая появляется в уравнении (12.П14), однозначно связана
с режимом на входе в некотором ряду стационарных состояний,
находящихся в пределах создания движущей силы. Это соот-
ношение таково:
-/‘Х1 = Г2Х‘2Т^-	(12.П15)
Оно применимо ко всем состояниям, в которых входная мощ-
ность равна J2X2. Эти состояния лежат на гиперболах во вход-
ном пространстве ар, показанном на рис. 12.9. Для данной
системы стационарных состояний, учитывая уравнения (12.П5)
и (12.П15) и вспомнив определение т], можно написать
-zfxf
-ЛХ, = -------------------------------- (12.П16)
(1+—4=Д f1+—Л
\	R°L^l-q2)\ RLX\~q2J
Мышечное сокращение
305
Из уравнения (12.П16) сразу же становится ясно, как можно
построить требуемую функцию. Правая часть — не что иное,
как произведение входной мощности и эффективности. Теперь
уравнение (12.П14) охватывает все возможные траектории
между заданными пределами и, следовательно, те траектории,
которые включают стационарные состояния из совокупности,
описываемой уравнением (12.П16). Другими словами, среди
траекторий, описываемых уравнением (12.П14), имеются и та-
кие, которые встречаются или пересекают кривую ар. Во всех
таких точках правая часть уравнения (12.П14) должна со-
впасть с правой частью уравнения (12.П16). Это означает, что
всякий выбор пределов для выходного потока и силы связан
с единственной совокупностью стационарных состояний, в кото-
рых уравнение (12.П14) в основном выражает взаимосвязь
между мощностью на входе, выходе и нагрузочным сопротив-
лением. В этих состояниях каноническая форма уравнения
(12.П14) сводится к характеристической форме, включающей
простую функцию переноса — эффективность, и потому следует
ожидать, что во всех других состояниях она должна содержать
существенные черты математической структуры этой функции.
Каждое стационарное состояние на кривой ар соответствует
различным значениям Rl. Поэтому любую гиперболу в выход-
Рнс. 12.9. Соотношение между пиковыми значениями выходной мощности и
потоком и ряд стационарных состояний оф, описываемых уравнением (12.П16)
(см. текст).
*
Две линии нагрузки, отмеченные характеризуют единственную кривую постоянного
выхода (гипербола в выходном пространстве), которая проходит через их точки пере-
сечения с ар. Они связаны с линией нагрузки Яд, которая пересекает траекторию
саморегуляции на той же кривой постоянного выхода [12].
20 Кенлен, Эссиг
306
ГЛАВА 12
ном пространстве можно охарактеризовать парой сопряженных
значений Rl[RlRl = (Rl)2], связанных с точками пересечения
выходных гипербол с ар. Даже гиперболы, которые не пересе-
кают кривую ар, т. е. те, что соответствуют сравнительно боль-
шим постоянным выходным мощностям, связаны с комплекс-
ными или отрицательно сопряженными значениями RL благо-
даря квадратичной форме уравнения (12.П16). Любое значение
Rl, характеризующее таким способом уровень выходной мощ-
ности, обозначим как Rl- Рассмотрим типичную траекторию,
пересекающую область создания движущей силы между фик-
сированными пределами на рис. 12.9. Видно, что в любой точке
траектория пересекается выходной гиперболой, так что дей-
ствительное значение Rl в любой точке связано с двумя значе-
*
ниями /?£> каждое из которых задает определенное значение
выходной мощности. Когда Rl меняется от нуля до бесконеч-
ности, одно значение Rl варьирует также от нуля до бесконеч-
ности в том же направлении, а другое значение Rl — от беско-
нечности до нуля в обратном направлении. Может встретиться
область комплексных или отрицательных значений Rl или
даже область разрыва, так что будет иметь место скачок Rl
между двумя сопряженными значениями при одном и том же
значении Rl- В последнем случае данная траектория пересекает
кривую ар, идет ниже ее и касается какой-то гиперболы (кото-
рая отвечает максимальному выходу для данной траектории),
причем точка касания соответствует рассматриваемому значе-
нию Rl- Таким образом, Rl можно выразить как функцию Rl
для любой траектории. Функция может быть однозначной или
может иметь «сопряженные» нарушения непрерывности. Соот-
ветственно для любой траектории с учетом уравнения (12.П16)
можно написать
— yfjtf
-М. = 7----------?---------------о-----Г- (12.П17)
(1 +--------- | (1 н---7^-—I
\ Rl^-Q2 J\ Rl^i-v2)
где в силу уравнения (12.П14) Rl представляет собой функцию
вида
Rl [fli, - Xi, A, q2, h (/?ь)]
которая сводится к Rl или (RlAIRl, когда траектория пере-
секается или касается кривой ар. Пределы RL, хотя и иден-
тичны пределам RL, не обязательно с ними совпадают. Оказы-
вается, что, каким бы способом ни задавались пределы, урав-
нение (12.П17) приводит непосредственно к функциям fag
из уравнения (12.П13), имеющим точно такие свойства, кото-
Мышечное сокращение
307
рые требуются. Например, если пределы R*L совпадают с преде-
лами RL, то получаем
—4’ _х,=—-%—h (12-ш8)
! +---1 + -.
R°l 1 - q2	RL^J\-q2
где для общности надо ввести величину h, которая является
функцией RL. В противном случае функция /?£ была бы пол-
ностью определена уравнениями (12.П1) и (12.П18), и послед-
нее было бы параметрическим уравнением единственной траек-
тории. Таким образом, h представляет произвольную часть
и мы ее идентифицируем как введенную ранее программирую-
щую функцию. Она безразмерна и имеет пределом единицу,
когда Rl достигает нуля или бесконечности. Если h постоянна,
то она должна быть равна единице и никогда не может достиг-
нуть нуля или бесконечности, поскольку это означало бы ну-
левую мощность на выходе при конечной нагрузке и, кроме
того, что функции ip и ip-1 неоднозначны. При другом выборе
пределов R*L просто меняются местами знаменатели в уравне-
ниях (12.П18).
Поскольку правая часть уравнения (12.П17) является функ-
цией ф из уравнения (12.П10), можно теперь обратиться к функ-
циям ip и гр-1 из уравнений (12.П8) и (12.П9). Если сложить
уравнения (12.П18) и подставить уравнения (12.П15) и
(12.П17), то параметрическая функция R*L исключается и полу-
чаем соотношение
М = 1 +	(12.П19)
Введем для удобства две постоянные:
J2X2	s ( 1 “ Я2 А ,
a=-^r- = -Xi[—~ ,	Ь=-^-
U	1 \	’	y-s
—2-	(12.П20)
я /
так что
2
(12.П21)
Из уравнений (12.П19) и (12.П20) находим
т l(~Xi + X^
J 1 — V
— X, ah
-*> = Чтг+ж) <12-п22)
Уравнения (12.П22) прямо соответствуют уравнениям (12.П8)
н (12.П9).
20*
308
ГЛАВА 12
Программа регулятора
Полезно рассмотреть кибернетическую интерпретацию выведен-
ных ранее уравнений. Чтобы заставить преобразователь энер-
гии следовать произвольно выбранной траектории, очевидно,
надо построить соответствующую «программу», заложенную в
его регулятор. Наша концепция состоит в том, что функция
h(RL) наилучшим образом подходит для составления такой
программы. Например, ее можно использовать для обеспечения
максимальной выходной мощности при выбранном значении
нагрузочного сопротивления. Эшби [4] отметил, что введение
регулятора и есть акт взаимодействия (коммуникации) между
управляющим объектом (таковым может быть, например, ген)
и самим регулятором. Между ними должна передаваться ин-
формация, описывающая регуляторную функцию. Ограничение,
накладываемое в рассматриваемой нами задаче, состоит в том,
что если	постоянна, то она может быть равна только
единице, а ее информационное содержание для программы
равно нулю. Мы назовем ее немодулированной й-функцией.
Путем модуляции /г-функции можно выбрать и видоизменить
характеристики регулятора, хотя и в известных пределах. По-
ступая таким образом, мы вводим в программу информацию
сверх того минимума, который необходим, чтобы регулятор во-
обще мог действовать.
Наиболее интересная особенность этого анализа состоит
в том, что траектория немодулированной /г-функции точно со-
ответствует соотношению между силой и скоростью для мыш-
цы, экспериментально установленному Хиллом [34]. Уравнение
Хилла (12.20) можно записать в любой из следующих двух
форм:
Г =	г = “(-ттг)	(12.П23)
Установив h равной единице, видим, что уравнения (12.П22)
можно сразу же совместить с уравнениями (12.П23). Перепи-
сав уравнения (12.П21) в этих обозначениях, получаем
q = л/Р0/(Ро + а) = ^Vml(Vm + b) (12.П24)
[ср. с уравнением (12.23)].
13
Энергетическое сопряжение
в митохондриях, хлоропластах
и галофильных бактериях
В настоящее время общепринято, что в митохондриях и хлоро-
пластах имеется сопряжение между тремя главными процесса-
ми, каждый из которых в принципе обратим: это электронный
транспорт, фосфорилирование АДФ и транслокация протонов
через сопрягающую мембрану. Как отметил Роттенберг [29],
между этими органеллами можно наметить структурную ана-
логию, хотя полярности сопрягающих мембран в них противо-
положны. Поэтому многие различия в процессах транспорта
ионов и фосфорилирования определяются просто тем обстоя-
тельством, что протонный насос качает протоны из митохон-
дрий наружу, тогда как в хлоропластах протоны накачиваются
внутрь тилакоидов. Природа сопряжения в обоих случаях до
конца не выяснена, но существует твердое убеждение, что оба
механизма определяются циркуляцией протонов и в основном
эти механизмы одинаковы. Ключевая роль циркуляции прото-
нов в механизме сопряжения получила дальнейшее подтвержде-
ние благодаря открытию фотоиндуцированного протонного на-
соса, который создает движущую силу для фосфорилирования
у некоторых галофильных бактерий в анаэробных условиях.
13.1.	Окислительное фосфорилирование
и фотофосфорилирование
Окислительное фосфорилирование в митохондриях (и бакте-
риях)— это процесс, в котором интермедиаты цикла Кребса
(или другие восстановители) окисляются при каталитическом
участии дыхательной- цепи, в результате чего синтезируется
АТФ (рис. 13.1). В большинстве случаев термодинамическое
рассмотрение этого процесса основано на определении «стехио-
метрического отношения», т. е. отношения между скоростями
фосфорилирования и окисления (отношение P/О). Как прави-
ло, экспериментально найденное максимальное отношение,
округленное до ближайшего целого числа, рассматривается как
стехиометрический коэффициент, который должен получаться
в идеальных условиях (например, 3 для окисления НАД и
родственных субстратов или 2 для окисления янтарной кисло-
310
ГЛАВА 13
ты). В совокупности с некоторыми другими данными эта вели-
чина, как полагают, указывает на число сопрягающих центров
[34]. Сопоставляются свободные энергии реакций и рассчиты-
вается эффективность процесса. Далее, второй закон термоди-
намики дает критерий самосогласованности данных. Так, если
п — предполагаемый стехиометрический коэффициент, то необ-
ходимо, чтобы
— AGOX n AGphos	(13.1)
или, другими словами, эффективность подчиняется соотношению
— п AGphos/AGox 1	(13.2)
Это соображение можно использовать также при рассмотрении
возможности сопряжения в различных участках дыхательной
фосфорилирование
Н++АДФ+Фн	АТФ + Н20
И Рис. 13.1. Общая схема окислитель-
ного фосфорилирования.
AH2+fO2	А+Н20
Окисление cyScmpama.
цепи. Так, полагая п=1 в данном центре сопряжения, можно
сравнить окислительно-восстановительные потенциалы (свобод-
ные энергии) с фосфатным потенциалом [22, 34]. Однако тер-
модинамика вовсе не требует, чтобы п было равно 1 в данном
центре. Вполне возможно, что окислительное фосфорилирова-
ние может происходить в центрах, которые обычно не рассмат-
риваются и в которых п<1. Подробная термодинамическая
трактовка окислительно-восстановительных реакций (равновес-
ных и неравновесных) содержится в превосходном обзоре [41].
Как было отмечено в работе [31], изложенные выше сооб-
ражения однозначно верны только в том случае, когда имеется
полное сопряжение. Поскольку это явно не так1, нельзя об-
суждать стехиометрическое соотношение безотносительно к со-
стоянию системы, или, вернее, такие расчеты лишь случайно
могут отражать ее физические параметры. Следует отметить,
что величины п, &GOx и AGphos редко определяются одновремен-
но, а расчеты часто основаны на экстраполяции полученных оце-
нок, которые не обязательно относятся к тому же состоянию.
Сопряжение в митохондриях, хлоропластах и галобактериях 311
Точно так же не приведены в соответствие различные под-
ходы к энергетическому анализу данных, полученных в состоя-
нии 4 (окисление в отсутствие фосфорилирования из-за огра-
ниченного количества АДФ [10]) и в состоянии 3 (стационар-
ное фосфорилирование после добавления АДФ). При класси-
ческом рассмотрении рассчитывают «коэффициент дыхатель-
ного контроля», т. е. отношение скорости окисления в состоя-
нии 3 к скорости окисления в состоянии 4 [10]; однако, хотя
этот коэффициент принимают за меру полноты сопряжения, его
нельзя рассматривать как надежный источник информации.
Ясно, что система в состоянии 4, когда Р/О = 0, находится
в состоянии статического напора и, следовательно, отражает ра-
боту механизма преобразования энергии так же, как и система
в состоянии 3.
Фотофосфорилирование в хлоропластах (и хроматофорах
бактерий) во многом похоже на окислительное фосфорилирова-
ние. Так, если суспензия хлоропластов класса II (с разрушен-
ной внешней оболочкой), в которых имеется свободный доступ
метаболитов и реагентов к преимущественно интактным гра-
нальным мембранам, освещается в среде, содержащей АДФ
и Фн, то происходит синтез АТФ (2]. Как и в митохондриях,
этот синтез сопряжен с транспортом электронов, который здесь
идет от воды к НАДФ. Движущую силу для транспорта создает
энергия излучения, поглощенного двумя различными фотоси-
стемами. Электроны текут спонтанно вдоль цепи окислительно-
восстановительных ферментов, как и при окислительном фосфо-
рилировании, при этом образуется АТФ. Однако в данном слу-
чае отношение Р/2е~ редко превосходит 1 [3].
Более прямая форма фотофосфорилирования имеет место
в крайних галофильных бактериях Halobacterium halobium —
облигатном аэробе, который может существовать при низкой
концентрации кислорода (а иногда и совсем без кислорода)
при условии, что на них действует свет. При этом галобактерии
синтезируют бляшки, содержащие пурпурный пигмент, распре-
деляемый по клеточным мембранам. Пигмент заменяет элек-
трон-транспортную систему, действуя как протонный насос,
приводимый светом в рабочее состояние.
Роттенберг [29] отметил, что примерное совпадение разоб-
щителей окислительного фосфорилирования в митохондриях и
фотофосфорилирования в хлоропластах указывает на сходные
механизмы сопряжения обоих процессов. Мы пока еще не об-
суждали механизм сопряжения при окислительном фосфорили-
ровании. Хотя нельзя полностью исключить тот факт, что меха-
низмы сопряжения в митохондриях и хлоропластах могут ока-
заться совершенно различными, такая возможность представ-
ляется маловероятной. Поэтому нет смысла ограничивать об-
суждение только какой-нибудь одной из этих двух систем. Од-
312
ГЛАВА 13
нако для удобства и ясности мы сосредоточим свое внимание
в основном на митохондриях. Хотя термодинамические соотно-
шения как таковые не зависят от механизма, частные молеку-
лярные модели нередко имеют термодинамические следствия,
которые можно проверить экспериментально. Большинство тео-
рий и моделей, выдвинутых для окислительного фосфорилиро-
вания, распадается на две категории: химическую гипотезу и
хемиосмотическую гипотезу.
Химическая гипотеза постулирует прямое химическое сопря-
жение: окисление приводит к образованию высокоэнергетиче-
ского интермедиата, который является движущей силой фос-
форилирования [34]. Поскольку известно, что в митохондриях
могут поддерживаться градиенты концентрации ионов (в том
числе протонов) [23], в эту гипотезу обычно включают и со-
пряжение с транспортом ионов за счет расщепления высоко-
энергетического интермедиата. В отличие от этого хемиосмоти-
ческая гипотеза постулирует, что окисление сопряжено с вы-
бросом протонов из митохондрий [24,25]. Образующийся при
этом градиент электрохимического потенциала протонов дви-
жет фосфорилирование в мембранах путем обращения работы
АТФазного протонного насоса. Градиенты концентрации катио-
нов рассматриваются как прямой результат электрического
мембранного потенциала, возникающего благодаря переносу
протонов.
оит
Рис. 13.2. Модель сопряжения окисления, фосфорилирования и транслокации
протонов с параллельным сопряжением окисления и фосфорилирования по
двум механизмам ['31).
Сопряжение в митохондриях, хлоропластах и галобактериях 313
Обе теории связывают ионный транспорт с окислительным
фосфорилированием. Однако в химической теории сопряжение
является следствием расходования высокоэнергетического ин-
термедиата, тогда как в хемиосмотической потоки ионов отно-
сятся собственно к механизму окислительного фосфорилирова-
ния. Термодинамические следствия этих двух концепций весьма
различны. Между тем, как отмечено в работе [31], эти два ме-
ханизма не обязательно исключают друг друга. Возможно, что
оба они имеют место, как это показано на рис. 13.2, где дана
схема параллельного сопряжения. Чтобы рассмотреть проблему
в целом, надо подробнее обсудить каждую из моделей.
13.2.	Модели энергетического сопряжения
при окислительном фосфорилировании
13.2.1.	Возможные способы сопряжения
На рис. 13.3 дана схема всех возможных способов сопряжения.
7р и Jo — скорости фосфорилирования и окисления соответствен-
но, 7н — поток протонов наружу через сопрягающую мембрану.
X — гипотетический интермедиат, который, возможно, сопрягает
все три процесса, X— так называемое высокоэнергетическое
состояние этого интермедиата. X и X могут также представлять
собой различные конформационные состояния одного или боль-
шего числа ферментов системы. Предполагается, что все шесть
«потоков» или процессов обратимы в соответствующих усло-
виях. Шесть возможных способов сопряжения, отмеченных
Рис. 13.3. Возможные способы сопряжения окислительного фосфорилирования
(см. текст).
В процессах Jq, Jp н /де стрелки указывают принятые нами знаки положительного
направления потока. Антипараллельный характер потоков в случае Б означает отри-
цательное сопряжение в соответствии с принятым правилом знаков.
314
ГЛАВА 13
кольцами, охватывающими соответствующие потоки, пронуме-
рованы в следующем порядке:
А.	Положительное сопряжение между окислением и фосфо-
рилированием.
Б. Отрицательное сопряжение между фосфорилированием
и потоком протонов наружу.
В.	Положительное сопряжение между окислением и пото-
ком протонов наружу.
Г. Положительное сопряжение между окислением и синте-
зом высокоэнергетического интермедиата.
Д. Положительное сопряжение между фосфорилированием
и расщеплением высокоэнергетического интермедиата.
Е. Положительное сопряжение между транслокацией прото-
нов наружу и расщеплением высокоэнергетического интерме-
диата.
Обратимость потоков означает, например, что при сопряже-
нии типа Б, которое мы назвали отрицательным в соответствии
с принятой полярностью, гидролиз АТФ будет способствовать
выбросу протонов наружу, как это показывает стрелка, тогда
как поглощение протонов способствует фосфорилированию. При
сопряжении типа Е поток протонов внутрь приведет к накопле-
нию X за счет X. Сопряжения Б, В и Е отражают работу обра-
тимого протонного насоса, т. е. они означают наличие актив-
ного транспорта протонов.
Мы покажем далее, что с чисто феноменологической точки
зрения, пока не удается экспериментально идентифицировать
высокоэнергетический интермедиат, сопряжение типа А экви-
валентно комбинации сопряжений ГД, сопряжение Б эквива-
лентно ДЕ, а В эквивалентно ГЕ.
13.2.2.	Химическая гипотеза
В своей наиболее общей форме химическая гипотеза включает
обратимое сопряжение транспорта протонов с реакцией высо-
коэнергетического интермедиата [35]. Таким образом, в этой
гипотезе учитываются сопряжения типа Г, Д и Е. С этой точки
зрения путь расщепления X, сопряженный с транспортом про-
тонов, является, в сущности, побочной реакцией. В той мере,
в какой сопряжение типа Е неполное, что обусловлено либо
утечкой протонов через сопрягающую мембрану, либо потерей
X из центра фосфорилирования за счет побочных реакций или
диффузии, общее сопряжение ГД будет частично или даже
весьма значительно разобщено. С другой стороны, разность
электрохимических потенциалов протонов на сопрягающей мем-
бране (Арн) могла бы служить важным способом запасания
энергии, поскольку емкость мембраны может оказаться гораздо
больше, чем емкость активного интермедиата. Той же цели
Сопряжение в митохондриях, хлоропластах и галобактериях
315
мог бы служить, конечно, и активный транспорт других ионов
при условии, что скорости их утечки через мембрану доста-
точно низки.
13.2.3.	Хемиосмотическая гипотеза
В соответствии с хемиосмотической гипотезой, выдвинутой Мит-
челлом [24,25], существуют только способы сопряжения типа
Б и В. Они связаны с физически разделенными центрами со-
прягающей мембраны: сопряжение В в центре I, а сопряже-
ние Б в центре II, как показано на рис. 13.4. Центры I и II
эквивалентны соответственно митчелловской окислительно-вос-
становительной цепи, имеющей свойства протон-транслоказы, и
Центр II
АТФ	АДФ
АТФазной системе, также переносящей протоны. Таким обра-
зом, /Р и /о сопряжены только через циркуляцию Н+, а не через
высокоэнергетический интермедиат (хотя, конечно, формализм
не исключает наличия высокоэнергетического интермедиата в
каждом из этих центров).
Хотя сущность хемиосмотической гипотезы исчерпывается
схемой, приведенной на рис. 13.4, Митчелл включает в свою
модель весьма детализированные представления о структурной
организации электрон-транспортной цепи: три «петли» на пути
от НАДН к О2 или две петли на пути от янтарной кислоты
к Ог. Петли образуют центры сопряжения, в которых связаны
транспорт протонов и транспорт электронов. При этом пред-
полагается стехиометрия 2Н+/2е~ в каждой петле: два протона
захватываются из внутреннего пространства мембраны и вы-
талкиваются наружу. Это приводит к отношениям Н+/О, рав-
316
ГЛАВА 13
ным 6 для окисления НАДН и 4 для сукцината. Далее вводится
еще одно предположение, что стехиометрия протон-транслоказ-
ной АТФазы соответствует 2Н+/АТФ, и поэтому общее отно-
шение P/О становится равным 3 для НАДН и 2 для сукцината
при условии, что в системе нет утечек и независимых процес-
сов, сопряженных с транспортом протонов. Последние исследо-
вания, однако, показывают, что отношения Н+/О, и Н+/АТФ
следовало бы примерно удвоить, причем общее отношение Р/О
остается без изменений (подробно этот вопрос обсуждается
в статье Роттенберга [30]).
Механизм разобщения такими классическими разобщителя-
ми, как 2,4-динитрофенол (ДНФ), карбонилцианид-и-трифтор-
метоксифенилгидразон и т. д., которые рассматриваются как
мембранорастворимые переносчики протонов [4, 24, 25], оче-
видно, сводится просто к диссипации «протонодвижущей силы»
(Дцн/-Р)- Разобщающий эффект различных ионофоров опреде-
ляется или диссипацией Дф, или диссипацией ДрН в результате
облегченной или обменной диффузии [9]. Можно добиться пол-
ного или почти полного разобщения окислительного фосфори-
лирования, что представляется несовместимым с химической
гипотезой. Хотя эти явления разобщения рассматриваются как
аргументы в пользу хемиосмотической гипотезы, Роттенберг
[29] придерживается точки зрения, согласно которой хемиосмо-
тическую и химическую (в том виде, как мы ее здесь изложили)
теории нельзя различить на такой основе, поскольку диссипа-
ция протонодвижущей силы приведет к установлению равнове-
сия между высокоэнергетическим интермедиатом и продуктом
его гидролиза. По-видимому, это крайняя позиция, которую
трудно обосновать. Сопряжение типа Е образует протонный
насос, приводимый в действие интермедиатом Я, и хотя он,
очевидно, будет работать быстрее в состоянии установившегося
потока, чем в других условиях, нет оснований предполагать,
что он будет работать настолько быстро, что исчерпает воз-
можности источника энергии.
13.2.4.	Гипотеза параллельного сопряжения
Чтобы подчеркнуть, что названные выше гипотезы не исклю-
чают друг друга, Роттенберг и др. [31] выдвинули модель па-
раллельного сопряжения, в которой оба механизма объедине-
ны. Это означает наличие сопряжения типа А (или ГД), как
в химической гипотезе, а также сопряжений типа Б и В в двух
различных центрах, как в хемиосмотической гипотезе (рис. 13.2).
Экспериментальные данные в пользу такой модели будут об-
суждены ниже.
Сопряжение в митохондриях, хлоропластах и галобактериях 317
13.3.	Анализ окислительного фосфорилирования
и ионных потоков с точки зрения
термодинамики необратимых процессов
13.3.1.	Функция диссипации
Значительные усилия, направленные на то, чтобы сделать вы-
бор между моделями окислительного фосфорилирования, были
сконцентрированы на попытках выделить высокоэнергетические
интермедиаты. Однако неравновесная термодинамика дает кри-
терии, которые не зависят от выделения интермедиата. Нет
также надобности наблюдать ту компоненту потока протонов,
которая используется для фосфорилирования [8]. Хотя необ-
ходимо определить Арн (и, может быть, Арк), другие пара-
метры оцениваются из внешних условий. В принципе можно
ввести условия, при которых /н будет поддерживаться отлич-
ным от нуля и постоянным в течение коротких периодов вре-
мени путем установления подходящего значения АДН- Для та-
кой системы в изотермических условиях, по-видимому, разумно
написать
Ф = JpAp + 7Н Ацн + J0Ao	(13.3)
Как и ранее, подстрочные индексы Р, Н и О относятся соот-
ветственно к фосфорилированию, суммарному потоку протонов
и окислению субстрата. Несмотря на сложность системы, урав-
нение (13.3) вполне адекватно. Мы рассматриваем только
стационарные состояния, в которых потоки таких частиц, как
Са2+, Mg2+ и Н2О, останавливаются, поскольку сопряженные
силы, т. е. градиенты электрохимического потенциала, экспери-
ментально не контролируются2 Генерация и расщепление вы-
сокоэнергетического интермедиата, если они имеют место, бу-
дут, вероятно, осуществляться за время, которое на несколько
порядков меньше, чем время, необходимое для установления
или релаксации стационарной протонодвижущей силы. В любом
случае эта реакция образует в принципе типичный циклический
процесс сопряжения, который ранее обсуждался Качальским и
Шпенглером [20]. В стационарном состоянии такие процессы
выражаются лишь в неявном виде через феноменологические
коэффициенты, а не в явном виде через функции диссипации.
В обзоре Роттенберга [29] показано, что в данном случае цик-
лический сопрягающий процесс (при участии высокоэнергети-
ческого интермедиата) действительно в неявном виде выража-
ется через феноменологические коэффициенты.
Записанная выше функция диссипации неоднозначна в том
смысле, что величины сродства могут быть измерены изнутри
системы или снаружи. Кроме того, поскольку потоки могут быть
неконсервативными, т. е. вещество может метаболизировать
318
ГЛАВА 13
внутри составной мембраны, скорости, с которыми субстраты
входят через одну поверхность мембраны, могут быть не равны
скоростям, с которыми они покидают другую поверхность мем-
браны. Следовательно, имеется также неоднозначность в опре-
делении потоков. Очевидно, было бы удобно определить вели-
чины сродства и скорости реакций извне, так как внутренние
активности определить трудно. Это оказывается возможным,
как показано ниже, если 7Н принимается равным скорости
уменьшения концентрации протонов внутри митохондрий, а
Дцн определяется как jig — (1^х. (В отсутствие реакций, про-
текающих при участии протонов внутри митохондрий, 7н про-
сто равен суммарному потоку протонов через внутреннюю по-
верхность мембраны.)
Рассмотрим окисление субстрата в митохондрии с образо-
ванием продукта. Скорость диссипации свободной энергии в
изотермическом стационарном состоянии равна
Ф = — £ (n‘nji‘n + й^х)	(13.4)
где р/ и n.j — электрохимический потенциал и число молей час-
тиц f-го типа (ftj = dtij/dt). Эти частицы включают субстрат,
продукт, О2, СО2, Н2О, АТФ, АДФ, Фн, Н+ и, возможно, такие
дополнительные компоненты, как К+, Са2+ и Mg2+. Введем
Aji/ = ji’n — jijx, тогда уравнение (13.4) можно переписать в
виде
Ф = - £ [п‘РДй/ + (п‘п + п«х)й'х]	(13.5)
Обозначив теперь г-ю метаболическую реакцию как А, а соот-
ветствующий стехиометрический коэффициент через v/г, получим
(п'п + П-) = Z («£ + П-) = Z v!rJr
и, следовательно, уравнение (13.5) приобретает вид
Ф = — (й)пДй/+ Е\ДГЙ/Х) (13.6)
Неважно, происходят ли реакции полностью внутри мембраны
митохондрий или до некоторой степени во внутреннем простран-
стве митохондрий. Однако мы исключаем возможность проте-
кания реакций снаружи органеллы. Сродство Аг в любой обла-
сти системы определяется как
Ar= S	(13.7)
i
Объединяя уравнения (13.6) и (13.7), получим
Ф = -КДЙ/+1Л<	(13.8)
i	г
Сопряжение в митохондриях, хлоропластах и галобактериях 319
Уравнение (13.8) можно использовать, чтобы развить феноме-
нологическое описание системы, если учесть в явном виде все
происходящие в ней транспортные процессы. Исчерпывающая
разработка этого подхода содержится в работе Хилла [19],
и мы не будем подробно останавливаться на этом.
Если рассмотреть стационарное состояние, в котором и Дцн,
и 7Н (— п’ц) отличаются от нуля, то п)п = 0 для всех /V Н и
уравнение (13.8) дает
Ф = 7рДрХ + 7нДцн + J0Ae*	(13.9)
С другой стороны, когда внутреннее пространство митохондрии
находится в стационарном состоянии по всем компонентам,
л)п = 0 для всех j, и, следовательно, в нашем примере
Ф = Z JrA™ = JPA? + J0A%	(13.10)
Г
Таким образом, в стационарном состоянии достаточно измерить
изменение состава во внешнем растворе, хотя обычно 7? и Jo
даются суммой скоростей изменения по обе стороны мембраны.
Уравнение (13.10) выражает тот общий принцип, что, если
хотя бы некоторые силы в системе не регулируются, она до-
стигает стационарного состояния, в котором сопряженные по-
токи равны нулю. Потоки J? и Jo не исчезают, поскольку пред-
полагается, что Лрх и Лох фиксированы экспериментально.
При приближении к упомянутым выше стационарным со-
стояниям применимо уравнение (13.8), т. е. каждый поток за-
висит от нескольких сил. Однако в стационарном состоянии,
которому соответствует уравнение (13.9), каждый поток зави-
сит только от трех сил. Если ДЦН непосредственно регулируется,
то 7н становится равным нулю, что приводит к стационарному
состоянию, выраженному уравнением (13.10), в котором каждый
поток зависит только от двух сил. Хотя ни один из потоков
теперь в явном виде не зависит от Дцн, существование меха-
низма транспорта протонов влияет на феноменологические ко-
эффициенты [20].
Как указано ранее, применение функции диссипации, кото-
рой соответствует уравнение (13.3), требует, чтобы предвари-
тельно было установлено, будут ли определяться потоки и ве-
личины сродства внутренне или внешне. Уравнение (13.9) по-
казывает, что реакционные потоки и величины сродства следует
определять во внешней системе. Поскольку митохондрия в дан-'
ном случае рассматривается в стационарном состоянии, это мо-
жет показаться самоочевидным. Тем не менее ситуация может
осложниться в том отношении, что в системе появится некон-
сервативный поток протонов, так что интуитивно неочевидно,
следует ли измерять поток по изменению концентрации во
320
ГЛАВА 13
внутреннем или внешнем пространстве. Этот вопрос решается
с помощью уравнения (13.8): если величины сродства опреде-
ляются во внешней среде, то поток протонов должен опреде-
ляться по изменению внутренней концентрации. Хотя может
оказаться, что эту величину трудно измерить, для большинства
приложений такие измерения не являются необходимыми.
Аналогичные рассуждения показывают, что мы могли бы
выразить функцию диссипации исходя из внешних потоков и
внутренних значений сродства. Хотя такая постановка вопроса
вполне обоснована, по ряду причин она практически не прием-
лема. При оценке внутреннего сродства встречаются очевидные
затруднения. Митохондрия — это высокоорганизованная струк-
тура, разделенная на компартменты, поэтому сведения об ак-
тивностях во внутреннем пространстве неточны3. Кроме того,
даже когда внутренние концентрации постоянны, надо рассмат-
ривать множество потоков и силы, поскольку внешние потоки
в отличие от внутренних не обязаны быть нулевыми для некон-
сервативных частиц, когда митохондрия находится в стационар-
ном состоянии.
13.3.2.	Феноменологические соотношения
Уравнения (13.9) и (13.10) задают функции диссипации, кото-
рые приводят к феноменологическим описаниям системы, вклю-
чающим соответственно три уравнения с шестью независимыми
коэффициентами или два уравнения с тремя независимыми
коэффициентами. Эти описания применимы к различным си-
туациям, возникающим в эксперименте, как будет показано
ниже. Наиболее общее описание основано на уравнении (13.9).
Соответствующие феноменологические уравнения таковы:
/р = £рАерх + £рнАйн + £РХх	(13.11)
7Н = W“ + Lh АЙн + Wo (13-12)
/o==Lpo^p +^онАЙн + ^о^о	(13.13)
Какая бы из гипотез ни была верна, этот формализм приме-
ним, по крайней мере вблизи равновесия. Мы здесь сделали
обычные предположения Онзагера о симметрии и линейности.
Рассмотрим теперь каждую из гипотез в свете этих уравнений.
Химическая гипотеза. В рамках этой гипотезы, так как
окисление субстрата приводит к образованию высокоэнергети-
ческого интермедиата, который создает движущую силу для
фосфорилирования или выброса протонов, Jo положительно
сопряжен с Jp и /н, как показано на рис. 13.3. Однако, по-
скольку выброс протонов может также происходить за счет
гидролиза АТФ, /Р и JH сопряжены отрицательно. Ясно, что
Сопряжение в митохондриях, хлоропластах и галобактериях 321
для этой системы на каждый поток будет действовать любая
из сил. Другими словами, феноменологически все коэффици-
енты в уравнениях (13.11) —(13.13) отличаются от нуля.
Хемиосмотическая гипотеза. Уравнения (13.11) — (13.13)
снова применимы. Однако в этом случае результирующие коэф-
фициенты можно охарактеризовать исходя из коэффициентов,
соответствующих центрам, показанным на рис. 13.4.
Центр I
4 = 4ЛЦН + 4Х	(13.14)
4 = ^онАЙн + ^Х	(13-15)
Центр II
7р = 41Л“+£’1нДйн	(13.16)
В центре I окисление приводит к транспорту протонов против
Арн, тогда как в центре II спонтанный поток протонов приво-
дит к фосфорилированию.
Суммарный поток протонов выражается как
Аг = 4 + А1	(13.18)
так что сложение уравнений (13.14) и (13.17) дает
/н=4нд“+(4+L") Д йн + О о	(13
Уравнения (13.16), (13.19) и (13.15) соответствуют уравнениям
(13.11) — (13.13). Таким образом, коэффициенты Lo. L? и пере-
крестные коэффициенты Дон и LpH просто совпадают с коэффи-
циентами для соответствующих элементарных центров, тогда
как LH =	+ />н- Весьма важно также, что в хемиосмотиче-
ской гипотезе	/ton™
Lpo = 0	(13.20)
„ . .... поддерживается постоянным, то фосфорилирова-
ние не зависит от окисления и наоборот. Как можно было ожи-
дать исходя из модели, если ДЦН = 0, то сопряжение неполное,
и /р = 0 при Лрх = 0 независимо от Jo, тогда как /о = 0 при
До =0 независимо от J?.
Гипотеза параллельного сопряжения. Как видно из рис. 13.2,
эта гипотеза охватывает химическую гипотезу для центра I и
хемиосмотическую для центра II. Формально химическая ги-
потеза и гипотеза параллельного сопряжения неразличимы: все
коэффициенты в уравнениях (13.11) — (13.13) снова отличаются
от нуля. В данном случае коэффициент LPO в уравнениях
(13.11) — (13.13) специфично связан с центром I. Однако
21 Кеплен, Эссиг
322
ГЛАВА 13
исследования Гриффитса [14] показали, что высокоэнергетиче-
ский интермедиат, образуемый в центре I, возможно, диффунди-
рует к центру II, прежде чем обеспечить фосфорилирование. Если
это так, то Аро включает кинетические параметры обоих цент-
ров, а также диффузионную стадию.
Следует иметь в виду, что, хотя Lpo отличается от нуля
в химической гипотезе и гипотезе параллельного сопряжения,
в последней он может быть очень мал. Это означает, что если
Арн поддерживать равным или близким к нулю, то фосфат-
ный потенциал в состоянии 4 будет соответственно небольшим.
Слабое сопряжение между окислением и фосфорилированием
в этих условиях отражало бы диссипацию энергии, запасенной
в высокоэнергетическом интермедиате с помощью реакций, дви-
гающих протоны в режиме установившегося потока (как это
уже обсуждалось ранее). Однако, если окисление продолжа-
ется, сродство постулированной реакции высокоэнергетического
интермедиата не может в действительности уменьшиться до
нуля за счет этого процесса и должно увеличиться за счет воз-
растания окислительно-восстановительного потенциала 4.
Очевидно, применение феноменологических уравнений со-
пряжено со значительными экспериментальными трудностями.
Между тем можно варьировать и измерять величины сродства
Лох и ЛеРх в широких пределах [28]. Кроме того, разность pH
и разность электрических потенциалов можно оценивать и ре-
гулировать в функционирующих митохондриях [27]. Хотя фик-
сировать значение Арн точно на нуле трудно, можно, по-види-
М0МУ> сделать его очень небольшим.
13.3.3.	Степень сопряжения и эффективность
использования энергии
см>^трп11ИТелЬН0 К окислительномУ фосфорилированию мы рас-
чено в "гл. 6?пэт!?Тп?®.ни сопРяжения: z/рн, дон и qPO. Как отме-
менологических уравнений, пос1й!^1о9лУчить из обратных фено-
„	п / /~п—п~.	-"'тамн с п пото-
ками (Jij Rijl RiiRjj•
Лр = /?р/р + /?рн/н + RpcJo	(13.21)
ДРн = Wp + V + Vo	(13.22)
Лох =/?ро.7р + ^?он/н +	(13.23)
Если выполняется хемиосмотическая гипотеза, то имеет место
специальное соотношение5
Яро = ЧрнЧон	(13.24)
Так как /Р и /н отрицательно сопряжены, то дРН отрицательно.
Сопряжение в митохондриях, хлоропластах и галобактериях 323
Любые факторы, уменьшающие qOH или — qPH, будут снижать
qpo и, следовательно, эффективность, с которой энергия окис-
ления используется для фосфорилирования.
13.4.	Применение неравновесно-термодинамического
анализа
13.4.1.	Стационарные состояния
Подход, описанный ранее, можно использовать при анализе как
окислительного фосфорилирования, так и в основном фотофос-
форилирования независимо от деталей механизма. Можно рас-
смотреть систему в различных условиях опыта, описываемых
уравнениями неравновесной термодинамики. Проще всего рас-
смотреть ситуацию, в которой функция диссипации сводится
к двум членам, так что каждый поток зависит только от двух
сил. Степень сопряжения q, которая характеризует результи-
рующую двухпотоковую систему, определяется частными усло-
виями опыта [6]. Поскольку обычно нас интересует превраще-
ние свободной энергии окисления в свободную энергию фосфо-
рилирования, мы особо рассмотрим только те случаи, когда
член 7нАрн равен нулю, т. е. режимы статического напора и
установившегося потока.
Если Лох поддерживать постоянным или путем соответ-
ствующих экспериментальных манипуляций, или путем под-
бора характеристик системы in vivo, а Арн не регулировать,
то 7н станет равным нулю в стационарном состоянии. В этом
случае q = qPo (случай 1 ниже). С другой стороны, было бы
полезно, если это возможно, провести эксперименты, в которых
Арн поддерживается равным нулю6. В этом случае q — (<7р0+
+ <7рн<7он)/д/(1 ~ ?рн) (1 - <7он) (случай 2 ниже). Эти два
случая можно охарактеризовать так:
1.	7н = 0 (режим статического напора). При этом уравне-
ния (13.21) и (13.23) сводятся к виду
Лрх = RpJp -(- RpoJo	(13.25)
Лох = RpqJp + RoJo	(13.26)
Следовательно, эффективная степень сопряжения равна
<? = ( ^ро/л/^р^о) = ^ро (Ai = 0)	(13.27)
2.	Арн = 0 (режим установившегося потока). Тогда уравне-
ния (13.21) — (13.23) дают
^р =^р0 #рн)Л> V^p^o(4po”^ ^рн9он)^о (13-28)
^о = л/^р^о (<7ро Н" <7рн?он) -^р Н" *о О ?он)^о (13.29)
21*
324
ГЛАВА 13
Следовательно,
(д-н=0)
V(* ~ 9рн) (1 — <7он)
(13.30)
К этим двум случаям применимы графики на рис. 13.5 и 13.6,
которые соответствуют рис. 4.2 и 4.3. Путем введения уравне-
ния (13.24) можно показать, что в рамках хемиосмотической
гипотезы при Дцн = 0 окисление и фосфорилирование эффек-
тивно разобщаются, так что в области линейности феноменоло-
гических уравнений Jp/Jo прямо пропорционально Арх/Лох, как
показано на рис. 13.5. При ненулевом, но постоянном значении
Дцн/Ао* пропорциональность утрачивается, но линейность оста-
Рис. 13.5. Зависимость отношения P/О от отношения величин сродства.
В митохондриях соответствующие величины сродства относятся к внешнему раствору.
При полном сопряжении отношение P/О дается величиной Z при всех условиях. Не-
давние исследования показали, что при q — 1 значение Z — 3 для некоторых субстра-
тов. При 4^=1 значение Z может измениться. В диаграмме учтены два случая:
1) /н-0: <7-<7р0; 2) АДН—0: <?=(<?ро+<7рн<?он)/'\/(1~'7Рн) (1-<7Он)-
Сопряжение в митохондриях, хлоропластах и галобактериях
325
zWF'Z’Sf)
Рис. 13.6. Зависимость эффективности от отношения величин сродства.
В митохондриях соответствующие величины сродства относятся к внешнему раствору.
При q по последним данным» Z = 3 для некоторых субстратов. При q 1 зна-
чение Z может измениться.
ется. В той мере, в какой соотношение между JP/Jo и Арх/Аох
становится нелинейным, когда ДЦн = 0 или Дрн/А®х поддержи-
вается постоянным (д' отличается от нуля), система отклоня-
ется от хемиосмотической гипотезы, которую можно рассматри-
вать как крайний случай. Если бы система не была хемиосмо-
тической, то окисление могло бы обеспечить фосфорилирование
даже при Дцн = 0. В этом случае верна или химическая гипо-
теза, или гипотеза параллельного сопряжения.
Роттенберг [28,33] провел серию экспериментов для про-
верки линейных соотношений типа (13.25) и (13.26) в мито-
хондриях как в условиях нормального окислительного фосфо-
рилирования, так и в режиме «обратного электронного транс-
порта», когда движущей силой является гидролиз АТФ. Как
показано на рис. 13.7, который иллюстрирует режим нормаль-
ного фосфорилирования, линейность выполняется в широких
пределах изменения сродства. Более того, в этих пределах вы-
держивается с достаточно высокой точностью и свойство взаим-
ности. Отмечено, однако, что линейность не выполняется при
326
ГЛАВА 13
высоких или низких величинах сродства. Следовательно, линей-
ный режим нельзя экстраполировать к равновесию, и Роттен-
берг выразил эти результаты в форме
/р — LpAp + Lpo^o “Ь /Ср	(13.31)
Jo — £роЛр “Ь LqAo “Ь Ко	(13.32)
где /Ср и Ко — постоянные. Интерпретация этих постоянных не
вполне ясна. Один из возможных подходов к задаче обсуж-
дался в приложении к гл. 6. Другой, который не исключает
предыдущего, состоит в следующем. Линейность считается
лишь кажущейся. Иными словами, то, что наблюдается, — по
всей вероятности, некоторая окрестность многомерной точки пе-
региба, которую можно с хорошим приближением описывать
линейными уравнениями. В гл. 6 эту ситуацию мы назвали
кинетической линейностью.
В самом общем случае нелинейную систему вдали от рав-
новесия можно описать следующим образом:
/р = £рЛр + £роЛо + Гр(Л2р, АРА0, Л20, ...)	(13.33)
JO = LOPAP + LOAO + FO(A2P, ЛрЛ0, Л^, ...)	(13.34)
где Fp и Fo — функции, состоящие из членов второго и более
Рис. 13.7. Скорости окисления и фосфорилирования в митохондриях печеии
крыс.
/р(—О-) и /о (---------)как функции ДрХ при постоянном значении ^4^=36,7 ккал/моль.
Jp (---• ) и Jq(—А—) как функции	при постоянном значении ДрХ= 9,7 ккал/моль.
Совпадение пунктирных линий указывает на симметрию перекрестных эффектов [28].
Сопряжение в митохондриях, хлоропластах и галобактериях 327
высоких порядков по сродству, содержащих также соответ-
ствующие феноменологические коэффициенты [ср. с уравне-
ниями (5.25) и (5.26)]. Вполне вероятно, что в некоторой об-
ласти значений сродства функции FP и Fo становятся в основ-
ном, если не полностью, постоянными. Если это верно, то
появляется возможность определить экспериментальные коэффи-
циенты в членах первого порядка из наклона прямых. Воз-
можно также, что путем некоторых манипуляций систему удаст-
ся перевести в гипотетическое (или даже реальное) состояние
вблизи равновесия, так что функции FP и Fo выпадут, а коэф-
фициенты в членах первого порядка не изменятся. Это состоя-
ние можно теперь охарактеризовать степенью сопряжения.
Взаимность, экспериментально наблюдаемая для рассматривае-
мой системы, дает убедительный аргумент (хотя, конечно, и не
доказывает этого однозначно) в пользу того, что коэффициенты
в членах первого порядка действительно постоянны в широких
пределах условий опыта. Из наклонов графиков на рис. 13.7
Роттенберг рассчитал, что qPo = 0,92. Следует подчеркнуть, что
в принципе это значение относится только к данному состоя-
нию, которое может экспериментально достигаться, а может
оказаться и не достижимым. Но если коэффициенты L действи-
тельно постоянны, то расчеты Роттенберга дают правильное
описание системы в этом гипотетическом равновесном состоя-
нии, а линии, проведенные на рис. 13.7, параллельны линиям,
представляющим правильные траектории.
13.4.2.	Оценка степени сопряжения и кажущейся
стехиометрии с использованием стандартного
состояния
В гл. 7 было показано, что степень сопряжения для системы
с термодинамической линейностью можно получить из отноше-
ния входного потока в состояниях статического напора и уста-
новившегося потока [уравнение (7.47)]. К сожалению, в ми-
тохондриях и хлоропластах трудно поддерживать установив-
шийся поток по фосфорилированию или транспорту протонов.
В первом случае аденилаткиназная реакция не позволяет до-
статочно сильно снизить отношение АТФ/АДФ, а во втором —
быстрое нарастание электрического потенциала обычно подав-
ляется даже в сильно забуференных системах. Однако состоя-
ние статического напора можно получить за несколько секунд.
Роттенберг [29] предложил метод определения степени сопря-
жения, который снимает проблему установившегося потока без
слишком сложных измерений. Этот подход основан на класси-
ческом определении коэффициента дыхательного контроля. Он
включает сопоставление статического напора (состояние 4 для
окислительного фосфорилирования) и подходящего стандарт-
328
ГЛАВА 13
ного состояния, отличного от установившегося потока (очевид-
но, состояние 3 для окислительного фосфорилирования). В прин-
ципе допустимо, чтобы стандартное состояние менялось в очень
узких пределах или не менялось вовсе в экспериментах, необ-
ходимых для определения его свойств. Однако на практике это
требование обеспечивается с трудом.
Для удобства дальнейшее обсуждение будет дано на основе
коэффициентов сопротивления в предположении, что 7Н = О
в обоих рассматриваемых состояниях. Предполагается также,
что систему можно изучать достаточно близко от равновесия,
так что наблюдаемые свойства отражают линейность в термо-
динамическом смысле. Если же, как показано на рис. 13.7,
линейность преимущественно кинетическая, т. е. режим опытов
требует введения дополнительных постоянных по типу уравне-
ний (13.31) и (13.32), то рассмотрение усложняется в отличие
от предложенного Роттенбергом. Таким образом, альтернатив-
ный, чисто эмпирический подход к уравнениям (13.31) и (13.32)
сводится к введению аддитивных постоянных в величины срод-
ства:
/₽ = MV Л'р) + LPO Ио + Л'о)	(13.35)
/0 = Аро (Лр + Л'р) + Lo (Ло + Л'о)	(13.36)
где
АРЛ'Р + ЛРОЛ'=КР, LPOA'P + LOA'O = KO (13.37, 13.38)
И Лр и Ло, а также коэффициенты L можно, в принципе, опре-
делить из опытов такого типа, как показано на рис. 13.7. По
следующим причинам мы примем, что если величины ЛР и Ло
не равны нулю, то они включаются в соответствующие вели-
чины Л, относящиеся к любому данному состоянию, и что фе-
номенологические коэффициенты постоянны. Следует отметить,
что в этом подходе мы рассматриваем величины, обозначенные
А', чисто формально, как если бы это были дополнительные
члены, добавляемые к стандартному сродству. Таким образом,
до этого момента неявно принималось следующее соотношение
в нашем обсуждении величин сродства:
Л = Л8‘ап + Лсопс	(13.39)
где Л3*ап означает стандартное значение сродства, удобное для
избранных условий опыта, а Лсопс— часть, зависящую от кон-
центрации. В оставшейся части этой главы мы будем считать,
что сродство выражается суммой:
Л = А' + Л3‘ап + Лсопс	(13.40)
Определенное таким способом сродство целесообразно рассмат-
ривать как «эффективное» сродство, помня при этом, что оно
Сопряжение в митохондриях, хлоропластах и галобактериях
329
всего лишь вспомогательная величина, введенная в расчетных
целях, которая не имеет реального термодинамического смысла
и не фигурирует в функции диссипации.
Имея в виду все эти соображения, можно дать наиболее
общее описание системы с помощью уравнений (13.25) и
(13.26). Опуская ради простоты индекс «ех» и вспомнив, что
Ло поддерживается постоянным, можно охарактеризовать два
состояния следующим образом:
Состояние статического напора (состояние 4)
AsP = RPOji, Ao = RoJo (13.41, 13.42)
Стандартное состояние (состояние 3)
Л* = /?Р7* + /?РО7§, Ло = /?р0/«+/?0/§ (13.43, 13.44)
где надстрочные индексы S и /? относятся к состоянию стати-
ческого напора и стандартному состоянию соответственно. Из
уравнений (13.41), (13.42) и (13.44) имеем
Л£ = Rpo_ = 1 ~ (/g/zS)
40	(Ж) Go/^o)
(13.45)
На этом этапе полезно обозначить отношение дыхательного
контроля /о//о символом Rc и отношение потоков (или кажу-
щееся стехиометрическое отношение) Jp/Jo символом R;. Тогда
уравнение (13.45) дает
Л|	1-/?е
ло	RfRc
(13.46)
Таким образом, отношение Лр/Ло и, следовательно, Rpo/Ro
можно определить путем измерения Rc и Rf. Это отношение
относится к величинам эффективного сродства. Независимые
измерения истинных величин Лр и Л о покажут, надо ли в дей-
ствительности вводить аддитивные постоянные (за исключе-
нием маловероятного случая, когда А'р/А'о = RPO/RO)- Если та-
ковые имеются, то простейший подход состоит в проведении
ряда измерений в состоянии статического напора путем варьи-
рования Ло и измерения Л| и 7g. Линейная экстраполяция
данных к 7g = 0 по уравнениям (13.41) и (13.42) даст Лр и А'о
соответственно. Располагая такими данными, можно уже опре-
делить qPO. (Конечно, qPO можно получить из экспериментов
такого типа, как на рис. 13.7, но поскольку состояние статиче-
ского напора так легко достигается, опыты рассматриваемого
типа кажутся проще.) Используя определение Rc, легко
330
ГЛАВА 13
показать из уравнений (13.41) —(13.44), что
Яро~ RPR0~ (A«/A^-Rc	( • У
Аналогичные соотношения можно вывести для <?Рн и <?он. Таким
образом, степень сопряжения можно получить, измеряя отно-
шение дыхательного контроля при условии, что были также
определены величины соответствующего эффективного сродства.
Если система полностью сопряжена, то Rc должно стре-
миться к бесконечности, тогда как R; дает истинную стехиомет-
рию процесса. Снова встает вопрос, как оценить максимальную
кажущуюся стехиометрию реакции, создающей движущую силу,
в системах, которые сопряжены неполностью. Как отмечалось
в гл. 4, эта величина представляет собой просто отношение по-
токов в состоянии установившегося потока (это состояние
с трудом достигается в рассматриваемых системах) и равно
<?poZ (как видно из рис. 13.5). В данном случае А = VRo/Rp-
Учитывая, что Z дает стехиометрию полностью сопряженной
системы, Роттенберг [29] заключил, что даже в отсутствие
полного сопряжения Z все-таки соответствует приведенному сте-
хиометрическому коэффициенту п, т. е. выражает стехиометрию,
которая была бы получена, если бы система была полностью
сопряжена, причем максимальная кажущаяся стехиометрия как
раз отвечает стехиометрии п, модифицированной неполнотой
сопряжения. Такая точка зрения привлекательна, особенно в
том случае, когда мы заранее считаем, что стехиометрия п
нам известна. Как отмечено в разд. 5.3, совпадение фено-
менологического коэффициента Z и стехиометрии п при
q < 1 маловероятно, но не является невозможным. Однако
при больших q ошибка, возникающая в результате при-
равнивания Z к п, не будет велика (например, при q = 0,9 зна-
чение Z будет в пределах 10 % от п). В этом случае степень
сопряжения можно было бы определить очень просто, из одного
измерения отношения величин сродства в состоянии статиче-
ского напора А$/Ао (или, если это удобнее, из отношения ве-
личин эффективного сродства), которое есть не что иное, как
—</po/Z. Мысль о том, что Z может представлять собой сте-
хиометрию п даже когда qPo < 1, неявно предполагалась и
при построении графика зависимости отношения потоков
от отношения величин сродства при окислительном фосфо-
рилировании, который приведен в работе Реттенберга и др.
[32] (см. рис. 6 в этой работе). Однако необходимо под-
черкнуть, что нет никаких термодинамических оснований пред-
полагать следующее: 1) факторы, стремящиеся разобщить си-
стему, не будут влиять на Ro, Rp или их отношение; 2) гипо-
тетическое полностью сопряженное состояние системы должно
Сопряжение в митохондриях, хлоропластах и галобактериях 331
существовать даже в тех случаях, когда оно нигде не было
найдено, и отношение -y/Ro/Rp относится к этому состоянию
и является целочисленным. Таким образом, на рис. 5.1 и 6.2
циклы бис точно так же относятся к системам, описываемым
циклом а.
Оказывается, что эту проблему легко разрешить уже рас-
смотренными экспериментальными приемами, т. е. путем ис-
пользования стандартного состояния. Если этим способом опре-
делена qp0, то разумно использовать отношение величин срод-
ства в состоянии статического напора, написав для этого случая
г = ~др0(Ао/А$	(13.48)
С другой стороны, имеем
Z =-	RcRf -	(13.49)
л/(1-Дй)(л£/л£-яй)
Максимальная кажущаяся стехиометрия выражается как
<7POZ = - <7*0((13-5°)
Следовательно, не надо делать никаких предположений о вели-
чине Z, но и в этом случае снова приходится принимать во вни-
мание вопрос об аддитивных постоянных. Необходимо отметить,
что при высоких значениях qpo, как можно видеть из рис. 13.5,
Rf равно q?oZ с хорошим приближением даже в стандартных
состояниях, в которых отношение величин сродства Ар/А$ су-
щественно выше их нулевого значения в состоянии установив-
шегося потока. Другими словами, при достаточно высоких зна-
чениях qP0 Rf становится нечувствительным к изменениям стан-
дартного состояния в широких пределах условий, когда имеет
место состояние 3. Однако, когда состояние 3 переходит в со-
стояние 4, Rf быстро падает (но без нарушений непрерывности,
как видно из рис. 13.5). Роттенберг [29] отметил, что при обыч-
ной постановке экспериментов, когда состояние 3 оценивается
путем усреднения континуума состояний, эволюционирующих
к состоянию 4, результаты неадекватны анализу рассматривае-
мого типа. Средние значения и полученные такими ме-
тодами, могут оказаться строго несопоставимыми. Это и может
быть причиной противоречий, отмеченных Слейтером и сотр.
[36] в оценках значений в митохондриях печени крыс, из-
меренных непосредственно и рассчитанных по уравнению
(13.36). Другая возможная причина противоречий — неучет
величин Ар и А'о.
Хотя описанные выше методы в принципе могут дать много
ценной информации, эти возможности были осознаны лишь
332
ГЛАВА 13
недавно. Главная проблема состоит в том, что не всегда ясно,
проводились ли описанные в литературе опыты в области тер-
модинамической или кинетической линейности, поэтому следует
уделить внимание вопросу об аддитивных постоянных. Пример
того, что можно сделать в данном направлении, дает исследо-
вание Реттенберга [29], в котором измерялись (в митохондриях
печени крыс) в сопоставимых условиях величины qPo, <?рн и дон
методами, основанными на уравнении (13.47). К сожалению,
справедливость приведенных выше формул была принята без
всякого учета возможности того, что надо вводить аддитивные
постоянные. Полученные значения были равны: qP0 = 0,96,
qPH — — 0,92 и <7он = 0,94. Отсюда следует, что уравнение
(13.24) не выполняется, поскольку —<?рн<7он = 0,87. Таким об-
разом, если принять это значение безоговорочно, то получается,
что хемиосмотическая теория приводит к заниженной оценке
степени сопряжения. Это могло бы быть весьма важным резуль-
татом, если бы он был однозначным. Например, продолжая
расчеты на той же основе и заложив в них модель параллель-
ного сопряжения, из уравнения (13.30) можно получить степень
сопряжения «химической» компоненты при Ацн = 0, равную
0,71. Отметим, что даже если бы эти результаты были вполне
однозначными, то на основе данных такого типа все-таки
нельзя сделать выбор между химической моделью и моделью
параллельного сопряжения.
Необходимо еще раз подчеркнуть, что во всех случаях, ко-
гда наблюдаемая линейность имеет кинетический, а не термо-
динамический характер, т. е. в уравнениях (13.31) и (13.32)
содержатся аддитивные постоянные, все соотношения (13.41) —
(13.50) также должны включать величины эффективного срод-
ства, определенные по уравнению (13.40).
13.4.3.	Экспериментальные примеры
В разд. 13.3.2 мы обсудили в примечаниях влияние добавок
разобщителя на митохондриальную систему. Эксперименталь-
ное исследование, основанное на анализе такого типа, когда
вводили различные концентрации разобщителя, проведено Ван
Дамом и др. [40]. Результаты представлены на рис. 13.8. Об-
наружена четкая линейность зависимости JP от Jo, причем на-
клон графиков возрастает с ростом концентрации разобщителя.
Ван Дам и др. [40] полагают, что единственная причина раз-
общения — канал утечки протонов, создаваемый разобщителем.
Другими словами, они считают, что справедлива хемиосмоти-
ческая модель с полным сопряжением в центрах I и II. В этом
случае с помощью уравнений (13.14) — (13.17) легко показать,
учитывая значение £[|ак (и помня, что в центрах II сопряжение
Сопряжение в митохондриях, хлоропластах и галобактериях
333
отрицательно), что
/ 1еакЛ
ьн о
(13.51)
Следовательно, ожидается, что все прямые пересекутся в одной
точке (независимо от величины А]|ак), пРичем в этих условиях
отношение потоков дается выражением
7p//o = ZIZ11
а соответствующее отношение сил равно
Ар___ ^-нАн
Ао — ZlZn
(13.52)
(13.53)
Эти результаты в какой-то мере напоминают ситуацию в пра-
вом верхнем квадрате на рис. 4.2. И фосфорилирование, и окис-
ление происходят одновременно, а Арн = 0 [т. е. протоны нака-
чиваются в центре II с точно такой же скоростью, с какой они
потребляются (переносятся в обратном направлении) в цен-
тре I]. Однако если в центрах I и II сопряжение неполное, то
единая точка пересечения графиков на рис. 13.8 будет утра-
чена, хотя линейность и сохранится. Поскольку Ван Дам и др.
[40] принимали полное сопряжение в каждом типе центров,
/р//о в точке пересечения должно дать произведение стехиомет-
Jo, нм.оль/(мг - мин)
Рис. 13.8. Соотношение между скоростью фосфорилирования и скоростью
поглощения кислорода в митохондриях печени крыс при различных степенях
разобщения.
Митохондрии печени крыс (1 мг белка/мл) инкубировали в среде, содержащей 10 мМ
сукцината, 10 мМ малата, 1 мкг ротенона/мл, 15 мМ КС1, 50 мМ трис —НО. 20 мМ
фосфатного буфера, Ю мМ глюкозы, 5 мМ MgCi2, 2 мМ ЭДТА; конечное значение
pH 7,4» температура 25 сС. За поглощением кислорода следили с помощью электрода
Кларка. Образование глюкозо-б-фосфата определяли ферментативным путем, Скорость
поглощения кислорода варьировали добавками гексокиназы. В среде содержался 2.4-дн-
ннтрофенол в концентрации 0, 2, б и 10 мкМ слева направо [40].
334
ГЛАВА 13
рий по уравнению (13.52), и действительно было получено
значение 1,45. К сожалению, в момент написания этой работы
не была выполнена строгая статистическая проверка единствен-
ности точки пересечения, так что неясно, можно ли из этих
опытов сделать заключение о полноте сопряжения.
Отчетливая линейность связи между окислительным обме-
ном и транспортом натрия в эпителии, описанная в гл. 8, пока-
зывает, что линейные свойства вполне могут быть общей ха-
рактеристикой митохондрий. Как мы видели, последние иссле-
дования, проведенные в лабораториях Роттенберга и Ван Дама,
в значительной мере подтверждают это положение, хотя и оста-
ется решить ряд вопросов, касающихся интерпретации экспери-
ментов. Поэтому целесообразно обсудить здесь некоторые ре-
Рис. 13.9. Эффективность окислительного фосфорилирования при наличии и
в отсутствие аденилаткиназы.
Митохондрии печени крыс инкубировали при 37 °C. Из измеренных значений
/р, /о и н экспериментально установленного значения Aq рассчитывали эффек-
Сопряжение в митохондриях, хлоропластах и галобактериях
335
зультаты, более понятные с рассматриваемой точки зрения. На
рис. 13.9 и 13.10 представлены результаты исследований мито-
хондрий печени крыс, выполненных Стаки [39] при наличии
и в отсутствие диаденозинпентафосфата — ингибитора аденил-
аткиназной реакции. Фосфатный потенциал ЛР варьировали, до-
бавляя глюкозу и различные количества гексокиназы в инку-
бационную среду. Видно, что в отсутствие аденилаткиназной
активности отношение сил может быть снижено почти вдвое
по сравнению с его значением в состоянии статического на-
пора. Превосходное согласие с теоретическими кривыми типа
приведенных на рис. 13.5 и 13.6 показывает, что, по-видимому,
имеет место термодинамическая линейность зависимости между
силами и потоками, из которой методом линейного регрессион-
ного анализа можно определить феноменологические коэффи-
тивность н нормированное отношение сил. Показано, что феноменологический стехиомет-
рический коэффициент Z — 2.38. а — объединенные данные трех опытов без диадено-
зинпентафосфата; б—объединенные данные трех опытов с диаденозинпеитафосфатом.
Сплошная лнння — теоретическая кривая прн q — 0,94; -^Opt_отношение сил, обеспечиваю-
щее оптимальную эффективность [39].
336
ГЛАВА 13
циенты. Для этого можно воспользоваться уравнениями (13.31)
и (13.32). Показано, что £Р0, оцениваемый из точки пересече-
ния при ДР = 0 по уравнению (13.31) в предположении, что
КР = О, в основном согласуется с Аро, полученным из наклона
графика по уравнению (13.32). Поскольку в этих опытах Ло
не варьировали, нельзя исключить возможность ненулевого зна-
чения Ко, хотя высокая степень сопряжения, обнаруженная
этим способом, показывает, что Ко должно быть небольшим.
С другой стороны, возможность ненулевого значения Кр явно
исключается в предположении симметрии. [В условиях опытов
Реттенберга (рис. 13.7) этого не наблюдалось.] При таком
предположении получено значение До = 45,27 ккаль/моль со
стандартным отклонением ±3,09 ккал/моль, которое превос-
ходно согласуется с независимой оценкой 45 ккал/моль, осно-
Рис. 13.10. Зависимость отношения потоков от отношения сил для окисли-
тельного фосфорилирования.
Нормированный график по данным рис. 13.9, б. Сплошная линия — теоретическая кри-
вая с параметрами, указанными на рис. 13.9 (Дж. Стаки, частное сообщение).
Сопряжение в митохондриях, хлоропластах и галобактериях 337
ванной на известном, составе инкубационной среды (Дж. Стаки,
частное сообщение). Читатель наверняка отметит, что этот спо-
соб оценки движущей силы полностью совпадает с таковым при
исследовании эпителиальных тканей [ср. с уравнением (8.6)].
Очень сходные результаты получены в недавних исследова-
ниях протонных насосов, приводимых в действие в митохон-
дриях окислительно-восстановительными реакциями и гидролизом
АТФ(Г. Аццоне, частное сообщение). Что особенно суще-
ственно в этих исследованиях — это то, что неполнота сопря-
жения почти целиком определяется протонным насосом, при-
водимым в действие окислительно-восстановительными реак-
циями, и что значения </(<1) почти не зависят от усиления
ингибирования дыхательной цепи. Отсюда следует, что разоб-
щение, связанное с утечкой протонов, пренебрежимо мало.
13.5.	Фотоиндуцированный протонный насос
Hatobacterium halobium
В гл. 5 уже упоминались пурпурные мембраны галофильных
бактерий Н. halobium, которые позволяют этим бактериям вы-
живать в анаэробных условиях. Пурпурный пигмент представ-
ляет собой один белок, бактериородопсин, в какой-то мере род-
ственный зрительному пигменту, обнаруженному в дисках
палочки сетчатки глаза млекопитающих. Этот белок имеет широ-
кий максимум поглощения при 570 нм [5,26]. Поглощение
света приводит к превращению формы, поглощающей при
570 нм, через ряд короткоживущих промежуточных форм в про-
дукт, который поглощает максимально при 412 нм и возвра-
щается путем обычной термической реакции к исходной форме
с максимумом при 570 нм в течение нескольких миллисекунд.
Все это явно сопровождается изменением конформации моле-
кулы, причем частота конформационных переходов составляет
около 100 Гц. При этом происходит выброс протонов во внеш-
нюю среду и их захват из внутреннего пространства. Таким
образом, в интактных клетках бактериородопсин действует как
фотоиндуцированный протонный насос. В результате его ра-
боты бактерия может поддерживать необходимые ионные гра-
диенты и фосфорилировать АДФ [11,38]. В силу относительной
простоты системы есть все основания полагать, что этот про-
тонный насос может оказаться первым примером механизма
активного транспорта, который удастся расшифровать на мо-
лекулярном уровне.
Однако при попытке описать бактериородопсиновую систему
на основе используемого нами формализма встречаются боль-
шие затруднения. Они касаются и выбора соответствующей
функции диссипации, и составления феноменологических урав-
22 Кеплен, Эссиг
338
ГЛАВА IS
нений. Но и после их преодоления оказывается, что у нас нет
прямого способа охарактеризовать свободную энергию, которую
несет и расходует падающий луч света. Роттенберг [29] попы-
тался рассмотреть источник света как абсолютно черное тело,
т. е. как источник излучения, имеющий непрерывный спектр
с распределением по длинам волн, соответствующим черному
телу при определенной температуре. В этом случае может быть-
оценена энтропия излучения. Ценность такого подхода сомни-
тельна, и расчеты эффективности на этой основе не представ-
ляются достаточно осмысленными, особенно в связи с тем (как
это отмечал Роттенберг), что эффективная температура черного
тела, служащего источником излучения, очень чувствительна
к рассеянию. Кроме того, хотя хорошо известно (по крайней
мере в фотосинтезе), что при интенсивностях, далеких от на-
сыщения, такие процессы, как транспорт электронов и прото-
нов, фосфорилирование и связывание углекислоты, линейно за-
висят от интенсивности света (см., например, [21]), следует
учитывать, что фотоны не сохраняются в этих реакциях, так
что соотношения взаимности Онзагера применять нельзя, даже
вблизи равновесия. Этот вопрос подробно обсуждался в
разд. 5.3. Как отмечено Хиллом [18], системы, поглощающие
и испускающие излучение, во многих важных аспектах состав-
ляют исключение и не вполне удовлетворяют формализму диа-
граммного метода, как, впрочем, и простым соотношениям не-
равновесной термодинамики. Тем не менее диаграммный метод
может хорошо работать применительно к кинетическим свой-
ствам таких систем. Мы ограничимся этим подходом, а заинте-
ресованным читателям рекомендуем более исчерпывающие по-
пытки рассмотрения липосом, содержащих бактериородопсин,
на основе линейных уравнений неравновесной термодинамики
[15, 17, 42]. В этой серии исследований проведено как теорети-
ческое рассмотрение, так и экспериментальное изучение систем
такого типа. К сожалению, как и в случае митохондрий, описан-
ном в разд. 13.4.3, неполноту сопряжения приписывали исклю-
чительно утечкам, так что рассмотренные выше фундаменталь-
ные затруднения и здесь не были удовлетворительно разрешены.
На рис. 13.11 представлена принятая в настоящее время
«классическая» модель фотоцикла адаптированного к свету
бактериородопсина [37,38]. Диаграмма связывает последова-
тельность спектроскопически идентифицированных состояний.
Простейшая кинетическая информация введена в схему в виде
времен жизни состояний. Природа состояний в смысле соответ-
ствующей каждому из них конформации молекулы пока выяс-
нена весьма неполно, и существование некоторых переходов
(отмеченных пунктирными линиями) надежно не установлено.
Кроме того, в ряде случаев предполагается существование до-
полнительных состояний и переходов, не указанных на диа-
Сопряжение в митохондриях, хлоропластах и галобактернях
339
грамме рис. 13.11 [11], так что картина, которая при этом вы-
рисовывается, довольно сложна. Становится все более вероят-
ным, что некоторые из известных на данном этапе состояний
в действительности соответствуют не одному, а нескольким со-
стояниям, и почти нет сомнений, что в системе имеются раз-
ветвления. Можно, конечно, усложнить диаграмму, но предпоч-
тительнее, как видно из дальнейшего, слегка модифицировать
ее форму таким образом, чтобы она соответствовала подходу,
описанному в гл. 5.
На рис. 13.12 представлена диаграмма, включающая наи-
более важные из обсуждаемых в настоящее время переходов
бактериородопсина (ее уместно сравнить с рис. 5.4). Отдельно
показаны содержащиеся в ней основные циклы. Между состоя-
нием наименьшей энергии bRsro и первым короткоживущим
продуктом фототрансформации Ksso введено возбужденное со-
стояние bR*. Оно может представлять собой общее возбужден-
ное состояние bRs?o и Ksso, участвующее как в прямом, так и
в обратном фотопревращениях, указанных на рис. 13.11, однако
по этому вопросу в литературе согласия нет [1,12]. Впрочем,
при малых интенсивностях света (именно таких, которые встре-
чаются в естественных условиях) фотостационарное состояние
Рнс. 13.11. «Классический» фотоцикл бактериородопсина.
Указаны стадии, на которых происходит связывание протонов из внутреннего объема
и их выброс во внешнюю среду. Использованы обычные обозначения, принятые в ли-
тературе. Приведены также длины волн в максимумах поглощения отдельных продук-
тов (в нм), а также времена жизни прн комнатной температуре, при нейтральном
значении pH и низкой ионной силе среды. Собственно фотопревращення в данной схе-
ме— это только прямой и обратный переходы между bRszo н Кззо; все остальные реак-
ции — термические [38].
22*
340
ГЛАВА 1?
характеризуется незначительной потерей bRsvo, так что и обратной
реакцией можно пренебречь [11]. Состояние bR*, по-види-
мому, релаксирует термически по двум конкурентным безызлу-
чательным каналам: вперед к Кьэо И назад к bRszo [12]. Мы
будем считать, что система освещается монохроматическим све-
том, который значительно слабее насыщающего, и не будем
учитывать циклы, включающие состояние Lf50 (и все другие
состояния, не имеющие значения при освещении слабым све-
том частоты v, т. е. при 570 нм). Будем также пренебрегать
переходом М|12—>О660, который, вероятно, ничего существен-
ного не добавляет к нашему рассмотрению. Тогда у нас
Рис. 13.12. Диаграмма, соответствующая фотоциклу бактериородопсина.
Подстрочные индексы «in» н «out» относятся к стороне мембраны, где происходит
связывание или выброс протонов. Стрелки указывают направление преобладающего
движения протонов при нормальном функционировании системы. Двадцать основных
циклов с соответствующими силами представлены отдельно (см. текст; указано поло-
жительное направление, приписываемое циклам h, i, j н	>— ц .	[7].
н+ <п
Сопряжение в митохондриях, хлоропластах и галобактериях 341
получится диаграмма из 13 штрихов и 8 состояний, так что
число независимых ненулевых стационарных переходных по-
токов равно 6. Как было показано в гл. 5, число независимых
циклов может быть больше, и, действительно, мы могли бы
пронумеровать 20 циклов, как показано на рис. 13.12. Отметим,
что циклы f, h, i, j, о и р требуют освобождения протона сна-
ружи с последующим связыванием протона с той же стороны
мембраны в следующем переходе. Из 20 циклов 4 характери-
зуются нулевой суммарной силой (b, d, f и /). Следовательно^
можно полагать, что функция диссипации будет содержать
16 членов, будучи записана в форме, заданной уравнением
(5.32). Однако на этом этапе формализм начинает «трещать»
по причинам, отмеченным ранее. Предполагаемая 16-членная
функция не является «термодинамической» величиной, посколь-
ку, как отметил Хилл [18], пучок фотонов нельзя рассматри-
вать как термодинамическую систему. Тем не менее эта псевдо-
функция диссипации должна быть положительной, так как
представляет суммарную скорость потери энергии фотонов плюс
свободная энергия ансамбля бактериородопсина вместе с рас-
творами, омывающими мембрану. Соответственно эффектив-
ность превращения энергии фотонов в электрохимическую сво-
бодную энергию равна
__ (~X)(Ja + Je + Je + Jg + J/1 + Jf + Jfe + /z + Jf? + Jr + ^ + /f) _
Nohv (Jm + п + /о + Ip + Iq + ?r + Js + Л)
=	(13.54)
Ntfivlr '
где ЛГ = АЦн+ = Цн+ — Цн+ , 7Н+— суммарный поток протонов-
in	out
изнутри наружу, Jr — суммарная скорость поглощающей свет
реакции bR570 ->-bR*. Очевидно, все циклы, отличные от q, г,
s и t, являются источниками разобщения.
Для таких систем часто измеряют квантовый выход, иногда
ошибочно называемый «квантовой эффективностью». Приведен-
ные ниже соображения показывают важное значение правиль-
ного описания условий измерения для получения необходимой
воспроизводимости результатов. При достаточно низких значе-
ниях X и интенсивности света было бы возможно найти об-
ласть линейности, для которой можно написать
ZH+ = L+X + L+r2V>, Jr = Lr+X + LrNohv (13.55)
где L+r Lr+ и Lr+, конечно, может быть равен нулю. Тем не
менее максимальный квантовый выход, очевидно, дается выра-
жением (JH+/Jr)x_ — L+r[Lr. Следовательно, квантовый выход
надо определять в состоянии установившегося потока. Это тре-
бование удовлетворяется в суспензии фрагментов пурпурных
342
ГЛАВА 13
мембран, для которой Голдшмидт и др. [12, 13] эксперимен-
тально установили, что значение квантового выхода одной
только прямой фотореакции равно 0,3 моля Кзэо в расчете на
один моль возбужденного bRszo- Таким образом, цикл т должен
в значительной мере определять долю рассеиваемой энергии.
Схема основных уровней свободной энергии, соответствую-
щих кинетической диаграмме для бактериородопсина (рис. 13.12),
показана на рис. 13.13. Помимо того, что на ней указаны раз-
личные источники разобщения, которые уже обсуждались ранее,
схема хорошо иллюстрирует одно из важных и характерных
свойств системы. Циклы т, п, о и р (рис. 13.12) приводят
к полной потере энергии, тем не менее они играют важную
роль в системе. Вполне возможно, что, когда пурпурные мем-
браны переходят из состояния установившегося потока в со-
стояние статического напора, снижение Jq + Jr + Js + Jt точно
или приблизительно компенсируется возрастанием 7m + /n +
+ /о + /р- Этим можно объяснить тот факт, что суммарная
скорость потребления энергии света в данном процессе оказы-
Рис. 13.13. Схема основных уровней свободной энергии бактериородопсина,
соответствующих кинетической диаграмме на рис. 13.12.
Предполагается, что транспорт протонов осуществляется в режиме статического напора.
Стрелками указано преобладающее направление цикла. Относительное положение уров-
ня Lc-n пока неизвестно [7].
Сопряжение в митохондриях, хлоропластах и галобактериях 343
вается практически постоянной (Гарти и Кеплен, неопублико-
ванные данные). Неоднократные сообщения о том, что удается
различить замедление реакции, вызванное «обратным давле-
нием» протонов [16], основаны на крайне слабых эффектах.
Поскольку существенное снижение скорости фотореакции
bRs7o^bR* в условиях монохроматического освещения при по-
стоянной интенсивности следует исключить, циклы т, п, о и р
могут действовать как своеобразные «клапаны безопасности».
Как правило, наличие множества циклов связано с регулятор-
ными свойствами и является необходимым условием эффектив-
ной накачки.
13.6.	Заключительные замечания
Термодинамические соображения, изложенные в этой главе, мо-
гут быть использованы для проверки и построения ряда моде-
лей. На практике это оказывается не простой задачей. Даже
когда число независимых переменных сведено к минимуму,
встречаются затруднения при определении величин сродства
различных реакций и разностей электрохимических потенциалов
на мембране. Показано, что применительно к стационарному
состоянию митохондрий для измерения сил (отличных от АЦн)
можно пользоваться концентрациями компонентов во внешней
среде. Такие измерения представляются вполне реальными, по
крайней мере для некоторых экспериментальных условий. Мы
подчеркиваем важное значение одновременных измерений сил
и потоков в одной и той же системе везде, где это возможно.
Все термодинамические параметры, относящиеся к эффек-
тивности трансформации энергии в митохондриях, можно оце-
нить из опытов, проведенных в двух режимах: в состоянии ста-
тического напора (состояние 4) и в стандартном состоянии
(состояние 3). Всегда, когда это возможно, следует в качестве
стандартного состояния выбирать стационарное или почти ста-
ционарное состояние, а не континуум состояний, через которые
система эволюционирует, переходя в состояние 4. Все измере-
ния в стандартном состоянии должны выполняться в сопоста-
вимых, а лучше — в идентичных условиях. Для установления
того, действительно ли феноменологические уравнения линейны
в термодинамическом смысле или же необходимо допустить
наличие в них аддитивных постоянных, требуются измерения
в нескольких состояниях статического напора.
Между хемиосмотической моделью, с одной стороны, и хи-
мической моделью или моделью параллельного сопряжения —
с другой имеются фундаментальные термодинамические разли-
чия. В то же время последние две модели с термодинамической
точки зрения неразличимы.
344
ГЛАВА 13
13.7.	Выводы
1.	Рассмотрены три модели сопряжения окислительного фос-
форилирования и фотофосфорилирования: химическая гипотеза
(образование высокоэнергетического интермедиата), хемиосмо-
тическая гипотеза (сопряжение через циркулирующий поток
протонов) и гипотеза параллельного сопряжения (представляю-
щая собой комбинацию двух первых). Показано, что эти три
модели включают различные комбинации шести возможных
способов сопряжения.
2.	Сконцентрировав свое внимание на окислительном фос-
форилировании в митохондриях, мы показываем, что функцию
диссипации для этой системы можно записать в виде Ф =
= /р4|>х +7нЛцн + 70Лох, где Арх и А^х — величины сродства
реакций фосфорилирования и окисления соответственно, изме-
ренные вне митохондрий; Дцн— разность электрохимических
потенциалов протонов на митохондриальной мембране, т. е.
ji1” — Йн > Л> и — скорости фосфорилирования и окисления;
Jh — поток протонов наружу, принятый равным скорости потери
протонов из внутреннего пространства митохондрий.
3.	На основе трех моделей сопряжения обсуждаются фено-
менологические уравнения, соответствующие охарактеризован-
ной выше функции диссипации. Химическая гипотеза и гипотеза
параллельного сопряжения не могут быть дифференцированы
по формальным признакам, поскольку все феноменологические
коэффициенты в обоих случаях отличаются от нуля, тогда как
хемиосмотическая гипотеза представляется как крайний случай,
когда коэффициент Lpo равен нулю.
4.	Приведены данные в пользу того, что митохондрия явля-
ется линейной и симметричной системой. Возможно, это свой-
ство определяется тем, что наблюдения обычно проводятся
вблизи многомерной точки перегиба, как рассмотрено в гл. 6.
Степень сопряжения можно определить путем измерений в со-
стоянии статического напора при подходящем выборе стандарт-
ного состояния, поскольку состояние установившегося потока
в митохондриях и хлоропластах поддерживать не удается. Этот
способ основан на классическом определении коэффициента ды-
хательного контроля. Осложнение здесь связано с тем, что си-
стема может вести себя как линейная, хотя и находится недо-
статочно близко к равновесию, если в феноменологические
уравнения ввести аддитивные постоянные. В этом случае необ-
ходима осторожность при интерпретации результатов.
5.	Условием, подтверждающим справедливость хемиосмоти-
ческой гипотезы, является специальное соотношение между сте-
пенями сопряжения: qPo = — <7рн<?он. То, что это соотношение
имеет силу, пока не доказано экспериментально.
Сопряжение в митохондриях, хлоропластах и галобактериях 345
6.	Представлен ряд примеров линейных свойств митохон-
дрий. Показано, что при правильном выборе условий сродство
реакций окисления можно корректно определить эксперимен-
тальными методами, аналогичными тем, что были использо-
ваны при изучении эпителиальных тканей.
7.	Дан вводный очерк по бактериородопсину. Показано, что
проблема описания фотоиндуцированного протонного насоса на
основе общепринятых уравнений неравновесной термодинамики
неразрешима.
8.	Фотоцикл бактериородопсина представлен в виде кинети-
ческой диаграммы, перечислены составляющие его циклы, ко-
торые связаны с эффективностью трансформации энергии. Рас-
смотрены вопросы измерения квантового выхода в этом случае.
9.	С помощью кинетической диаграммы и диаграммы
уровней свободной энергии удается без труда перечислить
возможные источники разобщения фотоцикла. Более того, мы
приходим к предположению о важной функциональной роли
многочисленных циклов дл регуляции бактериородопсиновой
системы.
Послесловие
Развитый в этой книге формализм не является вполне устано-
вившимся, и можно ожидать, что по мере накопления экспери-
ментальных данных, которые в настоящее время появляются
очень быстро, на первый план будут выходить другие аспекты
и потребуются изменения в интерпретации. Неравновесная
термодинамика возникла из попыток устранить ошибки, обус-
ловленные тем, что влияние взаимодействия между потоками
не учитывается в явном виде. По причинам практического ха-
рактера первые разработки в этой области были по необходи-
мости линейными (как и обычный анализ эквивалентных элек-
трических цепей), хотя известно, что истинная линейность мо-
жет выполняться только вблизи равновесия. Как показывает
эксперимент, во многих системах линейность выполняется го-
раздо дальше от равновесия, чем ожидалось, что позволяет
охарактеризовать ряд систем в широком интервале условий.
Параметры, оцениваемые таким путем, естественно, относятся
к чисто феноменологическим и требуют дальнейшей детальной
интерпретации на молекулярном уровне. Ясно, что следует
принять во внимание локальную нелинейность, т. е. нелиней-
ность элементов, образующих систему. Механизмы, по которым
локальные нелинейности в совокупности образуют общую ли-
нейную систему, представляют значительный интерес [2], од-
нако они находятся за рамками данной книги. К этой проблеме
можно подойти с помощью весьма эффективных методов тер-
модинамики сетей. Какова бы ни была природа регуляторных
механизмов, представляется, что линейность может обеспечить
ряд преимуществ, связанных с устойчивостью системы [1], ко-
эффициентом полезного действия и эффективностью сил [3].
Список обозначений
А — сродство химической реакции;
yjconc— компонента сродства, зависящая от концентрации;
— аддитивная постоянная сродства;
Areg — сродство для нелинейного регулятора;
Atot — полное сродство для последовательности реакций;
Astand ~ стандартное сродство;
а — механическая постоянная в уравнении Хилла;
ai — активность i-ro компонента;
Ь — механическая постоянная в уравнении Хилла;
С — концентрация внутри мембраны;
с — средняя логарифмическая концентрация омывающего раство-
ра;
ci — средняя концентрация i-ro компонента;
С/А (с/в) ~ концентрация i-ro компонента в растворе А (В);
D — коэффициент «объемной» диффузии;
D* — коэффициент диффузии метки;
Е — разность электрических потенциалов между двумя обратимы-
ми электродами;
Е, ENa— электродвижущая сила транспорта Na+;
— электродвижущая сила транспорта Н+;
»£ыа“ — кажущаяся электродвижущая сила транспорта Na+;
F — число (постоянная) Фарадея;
F — свободная энергия Гельмгольца;
Ft — нелинейная компонента в уравнении потока;
Fif— сила взаимодействия за счет трения между компонентами i
с и /;
f — отношение потоков;
f — функция регулятора, связывающая поток и нагрузку;
f — нормированная функция регулятора;
G— свободная энергия Гиббса;
Gj — стандартная свободная энергия /-го состояния макромолеку-
лярной системы;
ДО^ — изменение свободной энергии для перехода изомерного
или связанного с присоединением лигандов;
g — парциальная проводимость;
g — ускорение силы тяжести;
g — функция регулятора, связывающая силу и нагрузку;
g — нормированная функция регулятора;
Н — энтальпия;
h — постоянная Планка;
h — программирующая функция мышечного регулятора;
I — электрический ток;
348
СПИСОК ОБОЗНАЧЕНИИ
J — поток внутрь;
4г
J — поток наружу, утечка;
D — диффузионный поток;
Л поток i-го компонента;
Л — Ji/n-,
—суммарный средний стационарный поток между состояниями
I и /;
L/.— циклический поток;
Сх_) — однонаправленный положительный (отрицательный) цикличе-
ский поток;
J — отношение потоков наружу н внутрь;
ii — приведенные потоки в модели активного транспорта с пере-
носчиком;
Ki — постоянная составляющая в уравнении потока;
Кт— константа Михаэлиса;
Ktj — константа равновесия для перехода между состояниями i и /;
К И ~ константа равновесия второго порядка для перехода между
состояниями i и /;
k — константа скорости для транспорта между центрами;
kc, k — коистаиты скорости для иеиагружеииого и нагруженного пере-
носчиков соответственно;
Аг, A_t- — константы скорости для (-стадии реакции;
L' - RTL;
L — лиганд;
Lp — коэффициент фильтрации;
Lij — феноменологический коэффициент проводимости, связывающий
_ i-й поток с /-й силой;
Lij — феноменологический коэффициент вдоль правильно выбранной
траектории;
I — длина;
Min — поток внутрь;
Afout — ноток наружу;
т — масса;
mR — отношение между нагрузочным и виутревиим сопротивле-
ниями;
N — число единиц в ансамбле;
N — число центров на единицу площади;
Na — число Авогадро;
п — число рядов в решетке;
п — число электронов иа моль реакции;
п — число активированных мостиков в мышце;
nt — число молей;
Р — натяжение;
РБ — электроосмотическое давление;
Ро — изометрическое напряжение;
,РС — содержание фосфокреатииа;
Р/О — отношение скоростей фосфорилирования и окисления;
ПДС — протонодвижущая сила;
р	— давление;
р	™ — вероятность стационарного i-ro состояния;
Q	— тепло;
Q	— отношение коэффициентов диффузии всего вещества и метки;
Q' — нескомпенсированное тепло;
исок обозначений
349
Q — скорость выделения тепла;
QOj ~ скорость поглощения кислорода;
q — степень сопряжения;
qtj— степень сопряжения между i-м и /-м потоками;
R — универсальная газовая постоянная;
R — сопротивление суммарному потоку;
R* — обменное сопротивление;
Я — электрическое сопротивление;
Rc — коэффициент (отношение) дыхательного контроля;
Rf — отношение потоков при окислительном фосфорилировании в
стандартном состоянии;
Rl — механическое сопротивление; нагрузка;
Ry — феноменологический коэффициент сопротивления;
гц— локальный феноменологический коэффициент сопротивления,
связывающий i-ю силу с /-м потоком;
S — энтропия;
deS — энтропия обмена со средой;
diS — энтропия, произведенная внутри системы;
Т — абсолютная температура;
t — время;
U — внутренняя энергия;
и — подвижность;
V — объем;
V — скорость сокращения;
V,	V' — максимальные скорости прямой и обратной реакций;
Vi,	vi — парциальные молярные объемы i-ro компонента;
Vm — скорость сокращения при нулевой нагрузке;
о — скорость реакции;
1Г — работа;
W' — полезная работа;
X — термодинамическая сила;
X — гипотетический промежуточный продукт в метаболизме;
X — гипотетический интермедиат в метаболизме; состояние с вы-
сокой энергией;
X — термодинамическая сила вдоль правильно выбранной траек-
тории;
X't - пХ{;
Хк — сумма термодинамических сил, действующих в цикле х;
х — линейная координата;
х — доля занятых центров;
х — отношение сил, направленных наружу и внутрь;
Y — &G/&.H;
Z — феноменологический стехиометрический коэффициент;
— заряд i-ro компонента;
а — определяется по уравнению (11.43);
а° — константа скорости второго порядка для адсорбции;
а/ — константа скорости первого порядка для адсорбции из i-ro
раствора;
ац — константа скорости n-го порядка для связывания i-ro лигаида;
а;/— константа скорости первого или псевдопервого порядка для
перехода i -> /;
ац— коистаита скорости n-го порядка для перехода i-+j;
fl — коистаита скорости десорбции лигаида;
350
СПИСОК ОБОЗНАЧЕНИИ
0 — коэффициент распределения;
₽ — проницаемость;
у — коэффициент активности;
Y — отношение внешней и внутренней констант связывания лиган-
да;
Y—определяется по уравнению (10.32);
Y± — средний коэффициент активности ионов;
е} — эффективность потока;
ех — эффективность силы;
t, — приведенная феноменологическая стехиометрия;
Г] — эффективность;
Timax — максимальная эффективность;
Tlmech — механохимическая эффективность;
0 —. определяется по уравнению (10.42);
0— параметр уравнения Хилла: а/Ро, b/Vm;
©^—показатель неоднородности мембраны [уравнение (10.53)];
х, V.' — электропроводность;
—	однонаправленный отрицательный циклический поток;
ха — чувствительная к амилориду «активная» проводимость;
—	проводимость активных каналов для транспорта Н+;
xNa — проводимость активных каналов для транспорта Na+;
{%}/ — система циклов, связанных с потоком /,;
{*}//— подсистема циклов, в которых действуют X,- и X,;
14 — химический потенциал t-ro компонента;
ц/ — электрохимический потенциал t-ro компонента;
Hl — стандартный химический потенциал i-го компонента;
ц.; — зависящая от концентрации часть ц<;
[ij — химический потенциал /-го компонента в ансамбле;
Дц^-у — суммарное изменение свободной энергии при переходе
v — частота излучения;
V, — стехиометрический коэффициент для i-ro компонента;
Vjr — стехиометрический коэффициент для j-го компонента в реак-
ции г;
£ — глубина превращения в реакции; координата реакции;
л — осмотическое давление;
Пх+ (П_) ~ произведение констант скорости первого или псевдопервого
порядка в цикле положительного (отрицательного) направ-
ления;
Pi — удельная активность i-ro компонента;
S — сумма направленных диаграмм всех состояний;
Sx — сумма «придатков», питающих данный цикл;
а — коэффициент отражения;
а, — вклад в сумму членов, содержащих с,-;
т;,	— числа переноса i-го компонента;
Ф — функция диссипации;
ФсЬет — химическая компонента функции диссипации;
ФтесЬ — механохимическая компонента функции диссипации;
Ф — функция регулятора, связывающая выходную мощность и на-
грузку;
Ф1 — мольная доля i-ro компонента;
X— определяется по уравнениям (11.39) и (11.46);
тисок обозначений
351
Ф — электрический потенциал;
ф. ф-1 — функция регулятора, связывающая выходную силу и поток;
ш, ш' — проницаемости для суммарного потока;
а* — обменная проницаемость.
Подстрочные индексы
с — контроль; сокращение;
е — экспериментальный;
i—i-й компонент; непроникающее вещество; i-й путь (канал);
внутренний;
т — слизистый; максимальный (при ненагруженном сокращении);
о — наружный; изометрический;
р — продукт;
г — реакция;
з — растворенное вещество; проникающее вещество; субстрат; се-
розный;
t — время;
v — объем;
w — вода;
Ч--- катион;
----анион.
Надстрочные индексы
а — активный;
е — равновесный; внешний;
i — внутренний; отдельный поперечный мостик в мышце;
I — базолатеральная утечка; состояние установившегося потока;
о — оптимальный;
р — пассивный;
г — стандартное состояние;
S — состояние статического напора;
ех — внешний;
in — внутренний;
<х> — стационарное состояние;
sb — супрабазальный;
О — состояние статического напора; точка перегиба в многомерном
пространстве;
* — радиоактивная метка;
' — преобладающий изотоп; выделенное вещество.
Примечания
Глава 2
1.	Она позволяет также сразу же записать хорошо известные соотноше-
ния Максвелла. Например,
(dp/dS)v = - (dT/dV)s
2.	По-видимому, электрическая работа, совершаемая электрохимической
ячейкой или батареей, которая часто рассматривается в связи с этим, больше
соответствует открытым системам.
3.	Эта величина названа Клаузиусом «нескомпенсированным теплом».
4.	Необходимо иметь в виду, что область (0) будет достигать стацио-
нарного состояния только в том случае, если она обладает очень малой
емкостью по сравнению с окружающей областью (1). За период наблюдения
интенсивные параметры области (1) должны изменяться лишь минимально,
хотя некоторые небольшие изменения, конечно, неизбежны. Эти изменения
точно соответствуют тому, что измеряется в исследуемой системе.
5.	Электрод обратим по отношению к данному иону, если равновесие с
раствором этого иона устанавливается предельно быстро. Поскольку мы
хотим, чтобы необратимые процессы ограничивались мембраной, мы не вво-
дим солевых мостиков. По той же причине электроды помещаются как мож-
но ближе к мембране.
6.	В прерывистом режиме часто используется такой же выбор знака, ка-
кой приведен здесь, для того чтобы избежать повторения знака минус. Одна-
ко непрерывные режимы позволяют, естественно, рассмотреть отрицательные
градиенты — dp/dx в качестве локальных сил. Интегрирование приводит к
полярности общих сил, противоположной той, которая используется здесь.
Мы не будем пытаться применять единый способ выбора знака во всей книге,
чтобы избежать путаницы при сравнении с литературными данными, а в
каждой главе будем придерживаться способа, который использовался в ори-
гинальных статьях. То же самое относится к таким параметрам, как давле-
ние, концентрация и электрический потенциал.
Глава 3
1	В предположении симметрии Онзагера в матричной записи R,, =
= \Ц |/|Л|, IL//I является алгебраическим дополнением элемента Ьц в мат-
рице коэффициентов L, а | L | — детерминантом этой матрицы.
2	Как можно видеть из обсуждения, данного в работе [3], величина cs
часто аппроксимируется логарифмическим средним. Введем понятие «соответ-
ствующего» раствора, концентрация которого cs соответствует химическому
потеницалу растворенного вещества в точке х внутри мембраны [3, 15—17].
Тогда для разбавленных растворов, омывающих мембрану при постоянной
температуре, используя уравнение (2.23), получим

Примечания
353
Так как по определению dp^,= -''’аЛ и cwvw— *» т0
dit = с* dp*	(а)
Для соли, диссоциирующей на Vj катионов и v2 анионов,
Hs = viHi + v2g2
И
dpj= V\RTd In aL + v2RTd In a2= vtRTd In (v^y^.) + v2RTd In (v2csy±) =
= v/?7’dln(ciy±) (6)
где мы ввели средние коэффициенты активности ионов у± и величину
v = vi-f-V2. Соответствующее выражение справедливо для Др°. Таким об-
разом, из уравнениия (3.31) получим
(2)	(2)	(2)
$ Csdln(csY±) (dcs + c?d ln Y±)
(1)= (1)_________________________ (1)__________________
ДРз	Д In (csY±)	Д In cs + Д In y±
(в)
В большинстве случаев, представляющих практический интерес, правые члены
в квадратных скобках малы по сравнению с единицей и часто близки друг
другу по величине, хотя и возможны значительные отклонения от идеально-
сти [18]. В этом случае уравнение (3.31) приводит к выражению
cs = &cs/k In cs	(г)
Например, для двух растворов, содержащих 0,1 и 0,01 М NaCl, величины cs,
согласно уравнениям (3.31) и (г), различаются менее чем на 2 %. Однако,
когда меньшая концентрация стремится к нулю, величины, вычисляемые по
этим двум уравнениям, становятся несовместимыми. При с^/с^-> 1 арифме-
тическое среднее становится гораздо ближе к логарифмическому среднему.
Уравнения (б) и (в) применяют также для растворов неэлектролитов,
если v устанавливается равным 1 и у± заменяется на у. Поскольку растворы
неэлектролитов часто близки к идеальным, для определения cs в неэлектро-
литах используется главным образом уравнение (г).
3. В своих работах Кедем н Качальский использовали коэффициент
PeIk, где электроосмотическое давление Р Е = [(Др — Дл)/£]у^ Дп^. Мы при-
меняли эквивалентную величину —filLp, так как в эксперименте чаще изме-
ряется электроосмотическая проницаемость (или потенциал течения) р, чем
электроосмотическое давление.
Глава 4
1. Степень сопряжения между двумя потоками может также использо-
ваться для системы, в которой взаимодействуют более двух потоков [3].
В этом случае выражение для величины сопряжения аналогично уравнению
(4.13), т. е. ?t/ = — Rijl->/RiiRij. Эта величина отражает степень увлечения
23 Кеплен, Эссиг
354
Примечания
t-ro потока j-м потоком, когда другие потоки отсутствуют, и сила, связанная
с t-м потоком, равна нулю.
2. Эти соображения были распространены на системы многих потоков
(3, 13] и на системы двух потоков, которые не обязательно постоянны во
времени или симметричны [13]. Стаки [17] показал невозможность получения
благоприятного выхода с максимальной эффективностью, если q < 1. Он
вывел четыре «характерные» степени сопряжения (оптимальные величины q)
путем оптимизации четырех различных физически значимых выходных
функций.
Глава 5
1. Для удобства и единообразия термодинамические силы определяются
здесь на молярной основе, т. е. газовая постоянная R используется вместо
постоянной Больцмана k (последняя величина применяется в оригинальных
статьях Хилла и сотр.).
2. Число Авогадро (Ао) для фотонов.
Глава 6
1.	Во многих системах общие стационарные потоки, например транспорт
или потребление кислорода, легко наблюдаются, в то время как наблюдение
и измерение циклических потоков может быть сопряжено с эксперименталь-
ными трудностями. Однако в некоторых случаях оказывается возможным с
помощью оптических или других соответствующих методов различить от-
дельные состояния системы и измерить их кинетику.
2.	В уравнении (6.14) для простоты потоки нормированы, так что для
цикла а (полное сопряжение) их отношение равно 1. Методы анализа пото-
ков со стехиометрическим отношением, отличающимся от единицы, рассма-
тривается в разд. 5.3
3.	Необходимо отметить, что содержание применяемого нами термина
«стандартное стационарное состояние» отличается от содержания термина
«стандартное состояние», использованного Зауером [23]. В его употреблении
«стандартное состояние» означает определение минимального набора пара-
метров, которые вместе с соответствующими величинами сил достаточны для
определения всех потоков. Выбор стандартного состояния из бесконечного
числа возможностей произволен. В этих условиях правильная траектория яв-
ляется следствием такого изменения выбранного стандартного состояния,
которое обеспечивает линейное описание системы. В нашей трактовке «стан-
дартное стационарное состояние» имеет отношение к специфическому стацио-
нарному состоянию системы, относительно которого осуществляются изме-
нения.
4.	Разложение Ротшильда и др. в рассматриваемом случае включает
только один член второго порядка, а именно а 1п (cf/c®) In (су/с*-), где а —
константа (для данного потока), а с° и с° — концентрации в стандартном
состоянии. В нашем изложении это соответствует члену	который
может быть незначительным в случае таких изменений, когда по крайней
мере одна сила остается очень близкой к своей исходной величине.
Глава 7
1.	В случае полностью сопряженных систем все коэффициенты R стано-
вятся бесконечными, приводя к неопределенности. Эти системы можно рас-
сматривать с помощью коэффициентов L.
2.	Последние данные показывают, что в коже лягушки как пассивный
транспорт на апикальной поверхности клетки, так и активный транспорт на
внутренней базальной поверхности являются нелинейными процессами [17],
в то время как траисэпителиальный активный транспорт и окислительный
Примечания
355
метаболизм линейны. Для феноменологического анализа не нужны механизмы
взаимодействия нелинейных элементов, обеспечивающих общую линейность.
Как указывалось выше, при условии линейности феноменологические уравне-
ния для сложной транспортной системы могут быть записаны прямо без рас-
смотрения содержимого черного ящика. Остается важный вопрос о природе
феноменологических коэффициентов и А. Для его решения необходимы не-
которые модели. Поиск решения можно упростить с помощью термодинами-
ческих цепей.
3.	Хотя феноменологические уравнения, выведенные этим способом, об-
наруживают линейность, следует помнить, что коэффициенты сопротивления
являются функциями состояния. Влияние Х+ на внутриклеточные концентра-
ции не известно. Концентрационный профиль канала утечки в общем случае
должен нарушаться сильнее из-за изменений разности концентраций на мем-
бране, чем из-за термодинамически эквивалентных изменений разности элек-
трических потенциалов, особенно в случае сопряжения потоков ионов и воды.
Поэтому можно ожидать, что уравнение (7.14) полезнее при описании влия-
ния Дф, чем влияния разности концентраций Дс+. В отсутствие электриче-
ского поля и сопряженных потоков/^. — X+/r^_ = — RT Д In c+lRp+, а также
]р+ ~ — <£>р_ RT\c+, где для идеальных разбавленных растворов <о^_
приблизительно постоянно. Таким образом, ~ Л 1п с+/<о^_ Дс+.
4.	Разность электрических потенциалов между двумя растворами (Дф)
обычно измеряется с помощью каломельных электродов с солевыми мости-
ками. Для измерения разности электрохимических потенциалов используются
обратимые электроды. Если два раствора одинаковы, то —Хг//?=Дф; если
они различаются, этого не наблюдается. В этих случаях Дф определяется
неточно в силу того, что вклад диффузионного потенциала на концах мости-
ка неизвестен. Однако Х+ всегда определяется точно, даже в присутствии
сильно заряженных коллоидных частиц или макромолекул во внутриклеточной
среде, где оценки Дф могут содержать значительную ошибку. Обратимые
электроды пригодны для нескольких ионов; коммерчески доступны высоко-
специфичные электроды для Na+, К+, Н+, Са2+ и С1~, и предполагается их
дальнейшее развитие.
5.	В различных публикациях сродство обозначалось символами А, «Л» и
Лкаж (кажущееся сродство).
6.	См. выше примечание 2.
7.	Сродство реакции определяется как А — — ууц, (Де Дондер; см.
гл. 2), где стехиометрические коэффициенты v, считаются положительными
для продуктов и отрицательными для реагентов. Здесь скорость реакции
определяется как Jr= (1/vz) (dn,-/dt), где dni'dt — скорость возникиовеиия
i-ro компонента (очевидно, несущественно, что рассматривать — реагент или
продукт). Скорость затраты свободной энергии в реакции равна
— (dtii/df) = 22/ v/Pf (1/Vi) (driildt) = AJr. Однако для определения
экспериментатор обычно выбирает скорость потребления или производства
любого легко измеримого вещества, например dnj/dt. Если обозначить эту
измеренную скорость реакции через то получим 7, = | V/ |7Г. Поскольку
скорость расходования свободной энергии не зависит от нашего выбора,
сродство должно выражаться в ккал/моль вещества j. Таким образом,
А! = А!\ vj и A‘Jjr=AJr независимо от того, какое вещество / выбрано.
Более того, справедливость соотношения Онзагера не зависит от выбора
вещества, так как уравнения (7.3) и (7.4) приобретают следующий вид:
*№ = «а + («йа, r/\ I ) 4 =	+ «й4, Л
Al = А!\ \ I = («йа, г!\	| ) /йа + П = <, /йа + Ф'Н
23*
356
Примечания
Заметим, что степень сопряжения также не изменяется, поскольку
= яа
Очевидно, если метаболизм кислорода полностью сопряжен с метаболизмом
глюкозы (/г= Z°2/| Vq2 I = У®/] vG |), то несущественно, что из них обозна-
чить j. Кроме того, так как набор стехиометрических коэффициентов может
быть умножен на произвольное число без изменения величины JrA, то можно
установить |v/| = 1 для любого желаемого вещества ], например кислорода,
тогда Z' = Z°2 = Zr KAi=AQ‘=A.
Глава 8
1.	Мы подчеркиваем необходимость симметрии н 6-минутной длительно-
сти изменений потенциала в описанных выше исследованиях в связи с наблю-
дениями Виейра и др., упоминавшимися ранее, что продолжительное выдер-
живание системы при каком-нибудь определенном значении Дф изменяет
скорость обмена веществ с последующим возвратом к исходному коротко-
замкнутому состоянию. В других работах показано, что даже при соблюде-
нии этих мер предосторожности выдерживание при отрицательных значениях
Дф вносит неоднозначность в соотношения 1а — Дф из-за эффектов, разви-
вающихся как в клеточном, так и во внеклеточном каналах проводимости
[7, 43, 45]. Поэтому в дальнейших исследованиях желательно ограничиться
положительными значениями Дф, симметричными относительно равновесного
потенциала.
2.	Применение уравнения (8.6) требует, чтобы А оставалось постоянным
при изменении Дф. Тем не менее в этой главе, где рассматриваются экспери-
ментальные методы, мы будем использовать полные, а не частные производ-
ные, поскольку значение А непосредственно не контролируется в экспери-
менте.
3.	Лабарка и др. [21] не согласны с этим анализом. Они показали, что
^Na/-fCO2 статистически одинаково при -f-50 и —50 мВ. Такое расхождение
во взглядах, по-видимому, обусловлено тем, что мы несколько иначе опреде-
ляем смысл стационарного состояния. Поскольку эти авторы считали, что
изменения Дф вызывают зависящие от времени изменения Z^a и 7^0,> Для‘
щиеся 20—40 мин, в их работе сопоставлялись результаты измерений, прове-
денных спустя 20 мин после возврата к исходному значению потенциала,
когда отношение уже стало постоянным. Мы же рассматриваем «квазиста-
ционарное состояние», в котором 7^а консервативен и соответствующим
образом связан с Jsrb. Это состояние достигается значительно быстрее. Вна-
чале мы рассчитывали на это в связи с отмеченным выше наблюдением, что
при симметричных изменениях Дф на 6 мин 1а и ZOj линейно зависят от ДФ
в широком интервале. Позже было проведено исследование мочевого пузыря
жабы в камере для непрерывной перфузии, в которой хорошо известные ха-
рактеристики смешивания позволяли постоянно поддерживать определенное
соотношение между концентрацией СО2 в омывающем растворе и скоростью
выброса СО2 из тканей (7со2)13!’ 32Ь Как бь1л0 показано, хотя постепенное
изменение Дф приводит к длительным изменениям концентрации СО2 в омы-
вающем растворе, расчеты, учитывающие емкость системы, позволяют сде-
лать вывод, что /СОг сохраняет постоянство (в пределах шума системы)
в течение 3 мин и остается на том же уровне до 7 мин после изменения Дф.
Это дает возможность проверить стехиометрию путем варьирования ДФ в
подходящих пределах (см. рве. 8.16). Принимая, например, средние пара-
метры, полученные Лангом и др. [23] для 11 половинок мочевого пузыря,
q = 0,86, Z = ^L^ijLr = 16,8 и А = 57,1 ккал/моль О2, при Дф = —50 и
Примечания
357
+50 мВ должны получиться значения	равные 15,6 и 12,4 соответ-
ственно, т. е. снижение иа 21 % в интервале 100 мВ. С другой стороны, уста-
новив Дф = 0 и +100 мВ, можно получить /^а/Jq.= 12,3 и 7,2, т. е. сни-
жение иа 41 %. При исследовании 11 других половинок мочевого пузыря
в начале плато в течение примерно 4—7 мии после установления Дф при
+ 100 мВ средний декремент/a/.f7cbo2 составил 46,9 ±6,1 %. Полагая, что
в начале плато Ia[F = /^-а, можно заключить, что эти данные согласуются
с неполным сопряжением, обнаруживаемым еще до изменений параметров
ткани, обусловленных длительным изменением Дф.
4.	Очевидно, для оценки q и	необходимо, чтобы в условиях
наших опытов процессы базального и супрабазальиого обмена были дискрет-
но различимы н чтобы скорость базального обмена существенно не менялась
при изменении скорости активного транспорта Na. Многие авторы [2, 11, 23,
24] представили аргументы в пользу того, что такие условия имеют место
в мочевом пузыре жабы. В ряде других исследований показано, что в при-
сутствии адекватных концентраций амилорида скорость обмена в коже ля-
гушки н в мочевом пузыре жабы постоянна и не зависит от активного
транспорта натрия в эпителиальных клетках: отношение ^мао/^гО’ рассчитан-
ное на основе этого предположения, остается постоянным при варьировании
/као в различных условиях. Введение амилорида снижает Jro до такого же
уровня, который наблюдается при замещении Mg иа внешний Na. В отсут-
ствие внешнего Na амилорид ие влияет иа Jro [25] и в мочевом пузыре жабы
циркуляция Na ие возобновляется [9].
5.	В системе, свободной от СО2, хотя высокочувствителен к измене-
ниям значения pH на внешней стороне, эта величина в то же время суще-
ственно не зависит от больших изменений pH на внутренней стороне.
6.	Исследования метаболизма в мочевом пузыре жабы в камере с точно
определенными величинами потока и параметрами смешивания показывают,
что величина J со, примерно постоянна в пределах 3—7 мин после измене-
ния Дф, тогда как концентрация СО2 в омывающем растворе становится
постоянной только спустя 15 мии [31, 32]. Данные, опубликованные Аль-Ав-
кати и другими, не позволяют рассчитать J со, за время, когда меняется
концентрация СО2 в омывающем растворе.
7.	Хотя эти наблюдения говорят в пользу высокой степени сопряжения
транспорта протонов с окислительным обменом, могут оказаться необходи-
мыми дальнейшие исследования при определении того, является ли сопряже-
ние в действительности полным. Одни из факторов, который может иметь
существенное значение, — это время 10—15 мии, требуемое для того, чтобы
установились постоянные концентрации ,4СО2 и СО2 в омывающем растворе
после изменения pH; последнее, вероятно, отчасти обусловлено емкостью ка-
меры, которая может создать ошибочное впечатление о длительности интер-
вала времени, необходимого для того, чтобы скорость выброса СО2 из тканей
стала постоянной [31, 32]. Как и для системы транспорта натрия, было бы
важно рассмотреть сопряжение на основе измерений за возможно более ко-
роткие интервалы времени, тем самым сведя к минимуму вероятность изме-
нений параметров ткани. Точно так же интересно было бы пересмотреть этот
вопрос, когда окажутся доступными дополнительные сведения, касающиеся
механизмов, по которым СО2 и ингибиторы влияют иа функцию насоса.
Глава 9
1.	Одним из раииих примеров полезного применения радиоизотопных ме-
тодов было исследование проницаемости мембран для натрия. В течение
ряда лет считали, что заметная разница в ионном составе внутри и вие
типичных животных клеток, в которых концентрация натрия существенно
358
Примечания
ниже, чем во внеклеточной среде, может быть связана с непроницаемостью
клеточных мембран для этого иона. Однако демонстрация высокой прони-
цаемости клеточных мембран для 24Na потребовала серьезного пересмотра
представлений, касающихся регуляции ионного состава клеток.
2.	Шварц [15] отметил, что однородность вдоль плоскости мембран не
является необходимой в отсутствие переносчиков и сопряжения потоков.
3.	Для трехпотоковой системы величина I/B22, появляющаяся в уравне-
нии (3.46), совпадает с csco в уравнении (3.50). Хотя уравнение (9.18) фор-
мально аналогично соотношению для случая п потоков, следует подчеркнуть,
что природа сопряженных сил и потоков в этих двух случаях различна.
В последнем случае мы имеем дело только с потоками вещества.
4.	Хотя, как отмечено выше, было вполне естественно использовать коэф-
фициенты сопротивления при выводе общих уравнений, при использовании
этого формализма часто удобнее рассматривать коэффициенты проницаемости.
Эквивалентность обеих форм очевидна. В дальнейшем мы обычно будем
пользоваться коэффициентами проницаемости, за исключением тех случаев,
когда целесообразно также, а может быть, и предпочтительно, рассматривать
коэффициенты сопротивления.
5.	Доусон [2] представил остроумную комбинацию термодинамического
н кинетического выводов, которая приводит к уравнению, связывающему
отношение потоков с силами, индуцирующими транспорт, аналогично урав-
нению (9.38). Поскольку сопряжение потоков включает сопряжение между
потоками преобладающего вещества и его изотопно-мечеиной формы, урав-
нения должны учитывать влияние изотопного взаимодействия, однако без
явного определения отношения R*/R. Поучительно, что эквивалентность со-
пряжения (изотопного взаимодействия) н расхождение между коэффициен-
тами проницаемости для метки и суммарного вещества можно продемонстри-
ровать просто для систем вблизи равновесия, где линейность по X ( и Дс) и
оизагеровская взаимность заведомо могут выполняться [5]. Для потока изо-
топной метки запишем
J* = A6c* + B6c	(1)
где В 0 означает изотопное взаимодействие. Для суммарного потока
J = Обе. Чтобы рассмотреть подходящие сопряженные потоки и силы, под-
ставим У* +1' вместо Ун с* + с' вместо с, где надстрочный индекс «штрих»
относится к преобладающей изотопной форме. Тогда
У* = (Д + В) бс* + В 6с'	(2)
J' = (С - А - В) 6с* + (С -В) 6с'	(3)
Для систем вблизи равновесия в отсутствие градиента гидростатического
давления X* ~ RT6 In с* ~ RT6c*/c* и Х' у RT6c'jc', так что
,* (Д И" В) «у* । В , ,
1 - RT СХ + RTCX
(С-А-В) (С-В)
J ~-------ВТ-----сХ + RT СХ
Оизагеровская взаимность дает затем Вс'= (С — А— В)с*. Заменяя с' на
с — с*, после некоторых преобразований получаем
А _ ._____
С ~ 1 с* С
Однако Д/С = <£>*/<£>, с/с* = 1/р и В/С = (У*/У)вс»=0, поэтому
<о*/<о=1-(У*/У)вс.=о	(4)
Таким образом, мы видим, что здесь со* отличается от со в том и только в
том случае, когда имеется сопряжение между суммарным потоком и потоком
Примечания	359
изотопной метки, и что величина этого расхождения определяется степенью
Изотопного взаимодействия. Отметим также, что, хотя приведенное доказа-
тельство требует, чтобы и суммарное вещество и его изотоп были вблизи
равновесия, иа самом деле неважно, будет ли 6с* С с*, так как проницае-
мость для метки J*/RT8c* нечувствительна к величине с*.
Глава 10
1.	Строго говоря, нормальное отношение потоков равно
f = exp (X]RT) = exp [in (c’/c11) — 7S Др/7?т] = (c’/c11) exp (— Vs &p/RT)
'Однако, вводя уравнение (10.30), можно показать, что
exp (- Vs Лр/RT) 1 - Vs Acs (£ a.Lpf/£p)
Поскольку 0<or> < 1,	и VsAcs<l, величина exp(X/RT) су-
щественно не отличается от сЧс”.
Глава 11
1.	Уравнения (11.19) и (11.20) эквивалентны соотношениям, выведенным
впервые Ченом н Уолсером [1] [см. уравнения (12) — (15) в этой работе].
Уравнения (11.16), (11.24) и (11.27) соответствуют их уравнениям (7), (22)
и (30), а уравнения (11.53) и (11.54) эквивалентны (19) и (18). Следует
отметить, что нх выбор правила полярностей состоит в том, что ток I и
суммарный поток J имеют знаки, противоположные нашим, тогда как отно-
шение потоков такое же, как у нас.
Глава 12
1.	Наиболее важной энергодоиорной реакцией в поперечных мышцах in
vivo является расщепление фосфокреатнна. Концентрация АТФ остается по-
стоянной в результате его быстрого ресинтеза [11, 15]. Одиако АТФ — един-
ственный источник энергии в мышцах, предварительно обработанных 2,4-ди-
нитрофторбеизолом, который подавляет активность креатннфосфотрансфера-
зы. Эффективность, основанная на использовании АТФ в таких мышцах, не-
посредственно измерена в работе [50].
2.	Отметим, что символ Jro, используемый для обозначения скорости ме-
таболической реакции в условиях статического напора, согласуется с обще-
принятым в литературе по мышечному сокращению. Однако его не следует
путать с обозначениями, принятыми в наших исследованиях транспорта, где
/го — величина установившегося потока.
Глава 13
1.	Во многих случаях дыхание имеет место с разумными скоростями без
результирующего фосфорилирования. Разобщение может быть следствием
побочных реакции или утечек, как будет показано далее.
2.	Ясно, что электронейтральность требует, чтобы суммарный поток про-
тонов сопровождался эквивалентным потоком анионов и/или катионов. Если
эти потоки осуществляются по каналам утечки, то они не сопряжены с мета-
болическими реакциями и их нет надобности включать в функцию диссипа-
ции, т. е. каждый поток в уравнении (13.3) зависит только от трех сил. Если
случится, одиако, что какой-то компенсирующий поток сопряжен с метабо-
лизмом, то его вклад можно полностью иключить из функции диссипации,
поддерживая сопряженную ему силу на нулевом уровне. По-вндимому, в ми-
360
Примечания
тохондриях важное значение для компенсации такого рода имеет ион калия,
поток которого не связан с метаболизмом [32].
3.	За исключением случая равновесия, величины внутреннего и внешнего
сродства не будут равны. Рассмотрим ограниченную область, в которой
реагент а диффундирует и образует продукт р, диффундирующий из системы.
Тогда |х®х > и njjn > Складывая, получаем р.®х — р.|х >
т. е. Дех > Такие же соображения можно высказать и об окислитель-
ном фосфорилировании.
4.	Отметим, что добавление разобщителя, приводящего к утечке прото-
нов через сопрягающую мембрану, можно рассматривать так же, как метод
фиксированного потенциала, описанный в гл. 8. Тогда суммарный поток /н
в уравнениях не включает поток через центр, занятый разобщителем, но Дцн
снижается. Можно продолжать использовать исходные феноменологические
коэффициенты, помня, что они характеризуют исходную мембрану (к кото-
рой добавлен параллельный канал). С другой стороны, если надо измерить
полный поток протонов включающий поток утечки, то предпочтительно
охарактеризовать мембрану в целом. В этом случае единственный эффект,
связанный с введением параллельного канала утечки, состоит в том, что
уравнение (13.12) принимает форму
= /н +	= Й’н^р' + (^Н + ^-нак) дРн + ^'он^о'
и уравнение (13.19) меняется аналогичным образом. Здесь /-нак — коэффи-
циент проводимости для утечки — может быть велик (что приведет к соот-
ветственно малым значениям Дцн в состоянии статического напора по срав-
нению с такими же условиями без разобщителя. Другие способы разобщения,
например, применение валиномицина при наличии высоких концентраций
калия для понижения Дф практически до нуля, могут в принципе привести
к изменениям всех шести коэффициентов проводимости, поскольку состояние
системы в стационарных условиях может теперь оказаться существенно иным.
Феноменологические коэффициенты, соответствующие уравнению (13.9), за-
висят от коэффициентов в уравнении (13.8), н изменения последних могут
вызвать изменения первых, даже в том случае, когда основные потоки,
имеющие к ним отношение, находятся в условиях статического напора или
в равновесии.
5.	Llj = RiijD, гд,е Rn — алгебраическое дополнение Rij, a D — детер-
минант матрицы сопротивления. Поскольку Lpo = 0 в хемиосмотической ги-
потезе, /?рО = Крн^он ~ Яро^н — °- Разделив на /?н -у/RPRO, получим
уравнение (13.24).
6.	Здесь имеются в виду способы, которые, как можно полагать, влияют
на силу, но не на элементарные феноменологические коэффициенты.
Литература
Глава 2
1.	Caplan S. R., Mikulecky D. C., In: Ion exchange, vol. 1, ed. J. A. Marinsky,
New York, Dekker, 1966.
2.	Denbich K, The principles of chemical equilibrium, London, Cambridge Uni-
versity Press, 1966.
3.	Katchalsky A., Curran P. F., Nonequilibrium thermodynamics in biophysics,
Cambridge, Mass, Harvard University Press, 1965.
4.	Lakshminarayanaiah N., Transport phenomena in membranes, New York,
Academic Press, 1969.
5.	Mikulecky D. C., In: Transport phenomena in fluids, ed. H. J. M. Hanley,
New York, Dekker, 1969.
6.	Пригожин И., Дефэй P. Химическая термодинамика. Пер. с англ. — Ново-
сибирск: Наука, 1966.
7.	Tisza L., Generalized thermodynamics, Cambridge Mass, M. I. T. Press, 1966.
Глава 3
1.	Blumenthal R., Caplan S. R.t Kedem O., Biophys. J., 7, 735 (1967).
2.	Caplan S. R., Quaderni dell’ Istituto di Recerca Sulla Acque, 10, 7 (1973).
3.	Caplan S. R., Mikulecky D. C., In: Ion exchange, vol. 1, ed. J. A. Marinsky,
New York, Dekker, 1966.
4.	Curie P., Journal de Physique ser, 3, 3, 393 (1894).
5.	Де Г poor С., Мазур П. Неравновесная термодинамика. Пер. с англ. — М.:
Мир, 1964.
6.	DeSimone J., Caplan S. R., J. Theoret, Biol., 39, 523 (1973).
7.	Finlayson B. A. Scriven L. E., Proc. Roy. Soc. London. Ser. A, 310 183
(1969).
8.	Hearon J. Z., Bull. Math. Biophys. 12, 57, 135 (1950).
9.	Katchalsky A, Curran P. F., Nonequilibrium thermodynamics in biophysics,
Cambridge, Mass, Harvard University Press, 1965.
10.	Katchalsky A., Kedem O., Biophys., J., 2, 53 (1962).
11.	Kedem O., In: Membrane transport and metabolism, ed. A. Kleinzeller and
A. Kotyk, New York, Academic Press, 1961.
12.	Kedem O., Phys. Chem., 77, 2711 (1973).
13.	Kedem O., Katchalsky A., Biochim. Biophys. Acta, 27, 229 (1958).
14.	Kedem	O.,	Katchalsky	A.,	J. Gen. Physiol, 45, 143	(1961).
15.	Kedem	O.,	Katchalsky	A.,	Trans.	Faraday Soc., 59,	1918	(1963).
16.	Kedem	O.,	Katchalsky	A.,	Trans,	Faraday Soc. 59,	1931	(1963).
17.	Kedem	O.,	Katchalsky	A.,	Trans.	Faraday Soc., 59,	1941	(1963).
18.	Kedem O., Leaf A., J. Gen Physiol., 49, 655 (1966).
19.	Mazur P„ Overbeek J. T., Rec. Trav. chim., 70, 83 (1951).
20.	Michaeli I., Kedem O., Trans. Faraday Soc., 57, 1185 (1961).
21.	Miller D., Chem. Rev., 60, 15 (1960).
22.	Prigogine I., Etude thermodynamique des phenomenes irreversibles, Liege,
Belgium, Desoer, 1947.
362
Литература
23.	Prigogine J., Thermodynamics of irreversible processes, New York, Wiley,
1961.
24.	Staverman A. J., Recueil trav. chim., 70, 344 (1951).
25.	Weinstein J. N„ Caplan S. R., Science, 161, 70 (1968).
26.	Weinstein J. N. Phys. Chem., 77, 2710 (1973).
27.	Weinstein J. N., Bunov B. J., Caplan S. R., Desalination, 11, 341 (1972).
Глава 4
1.	Awan M. Z., Goldspink G., J. Mechanochem. Cell Motility, 1, 97 (1972).
2.	Blumenthal R., Caplan S. R., Kedem O., Biophys. J., 7, 735 (1967).
3.	Caplan S. R., J. Theor. Biol., 10, 209 (1966); 11, 346 (1966).
4.	Essig A., Caplan S. R., Biophys. J., 8, 1434 (1968).
5.	Hodgkin A. L., Keynes R. D., J. Physiol., 128, 61 (1955).
6.	Hoshiko T., Lindley B. D., J. Gen. Physiol., 50, 729 (1967).
7.	Jardetzky O., Snell F. M., Proc. Nat. Acad. Sci. USA, 46, 616 (1960).
8.	Kedem 6., In: Proc. Symp. Transport and Metabolism, New York, Academic
Press, 1961.
9.	Kedem O., Caplan S. R., Trans. Faraday Soc., 61, 1897 (1965).
10.	Kedem O., Essig A., J. Gen. Physiol., 48, 1047 (1965).
11.	Kushmerick M. J., Larsen R. E., Davies R. E., Proc. Roy. Soc. B174, 293
(1969).
12.	Miller D. G., Chem. Rev. 60, 15 (1960).
13.	Peusner L., Ph. D. thesis, Harvard University, 1970.
14.	Rosenberg T., In: Active transport and secretion, ed. R. Brown and J. F. Da-
nlelli, New York, Academic Press, 1954.
15.	Rettenberg H., Biophys., J., 13, 503 (1973).
16.	Rettenberg H., Caplan S. R., Essig A., Nature, 216, 610 (1967).
17.	Stucki J. W„ Eur. J. Biochem., 109, 269 (1980).
18.	Ussing H. H., In: The alkali metal ions in biology, ed. H. H. Ussing at al.,
Berlin, Springer, Verlag, 1960.
19.	Ussing H. H., Zerahn K., Acta Physiol. Scand., 23, 110 (1951).
20.	Zerahn K, Ph. D. thesis, Copenhagen University, Aarhus, Denmark, 1958.
Глава 5
1.	Hill T. L., Free energy transduction in biology — The steady-state kinetic
and thermodynamic formalism, New York, Academic Press, 1977.
2	Hill T. L., Eisenberg E., Quart. Rev. Biophys., 14, 463 (1981).
3.	King E. L., Altman C., J. Phys, chem., 60, 1375 (1956).
4.	Mikulecky D. S., J. Theor. Biol., 69, 511 (1977).
5.	Mikulecky D. S., Thomas S. R.t J. Theor. Biol., 73, 697 (1978).
6.	Oster G. E., Perelson A. S., Katchalsky A., Quart. Rev. Biophys., 6, 1 (1973).
Глава 6
1.	Bunow B„ J. Theor. Biol., 78, 51 (1978).
2.	Canessa M., Labarca P., Leaf A., J. Membrane Biol., 30, 65 (1976).
3.	Caplan S. R., Proc. Nat. Acad. Sci. USA, 78, 4314 (1981).
4.	Caplan S. R., Essig A„ In: Current topics in membranes and transport,
vol. 9, ed. F. Bronner and A. Kleinzeller, New York, Academic Press, 1977.
5.	Chen J. S., Walser M., J. Membrane Biol., 21, 87 (1975).
6.	Dawson D. C., Al-Awqati Q., Biochim. Biophys. Acta, 508, 413 (1978).
7.	Де Гроот С., Мазур П. Неравновесная термодинамика. Пер. с англ. М.:
Мир, 1964.
8.	Essig A., Caplan S. R., Proc. Nat. Acad. Sci. USA, 78 1647 (1981).
9.	Garay R. P., Garrahan P J., J. Physiol., 231, 297 (1973).
Литература	363
10.	Гленсдорф П., Пригожин И. Термодинамическая теория структуры, устой-
чивости и флуктуаций. Пер. с аигл. — М.: Мир, 1973.
И. НШ^Т. L., Free energy transduction in biology, New York, Academic Press,
12.	Hill T. L., J. Chem. Phys., 76, 1122 (1982).
13.	Hill T, L., Unpublished studies, 1982.
14.	Marmor M. F., J. Physiol., 218, 599 (1971).
15.	Mikulecky D. C., J. Theor. Biol., 69, 511 (1977).
16.	Николае Г., Пригожин И. Самоорганизация в неравновесных системах.
Пер. с англ. — М.: Мир, 1979.
17.	Oster G. F., Perelson A. S., IEEE Trans. Circuits and Systems, CAS, 21,
709 (1974).
18.	Oster G. F., Perelson A. S., Katchalsky A., Quart. Rev. Biophys., 6, 1
(1973).
19.	Пригожин И. Введение в термодинамику необратимых процессов. Пер. с
англ. — М.: ИЛ. 1960.
20.	Rothschild К J., Ellias S. A., Essig A., Stanley Н. Е., Biophys. J., 30, 209
(1980).
21.	Rottenberg H., Biophys. J., 13, 503 (1973).
22.	Rottenberg H., Gutman M., Biochemistry, 16, 3220 (1977).
23.	Sauer F., In: American Physiological Society (Washington), Handbook of
physiology; renal physiology, ed. J. Orloff and R. W. Berliner, Baltimore,
Williams and Wilkins, 1973.
24.	Stucki J. W., Prog. Biophys. Molec. Biol., 33, 99 (1978).
25.	Stucki J. W„ Eur. J. Biochem., 109, 257 (1980).
26.	Stucki J. W., Eur J. Biochem., 109, 269 (1980).
27.	Stucki J. W., Compiani M., Caplan S. R., Unpublished studies, 1982.
28.	Westerhoff H. V., van Dam K-, In: Current topics in bioenergetics, vol. 9,
ed. D. R. Sanadi, New York, Academic Press, 1979.
29.	Wolff D., Essig A., Biochem. Biophys. Acta, 468, 271 (1977).
Глава 7
1.	Blumenthal R., Caplan S. R., Kedem 0., Biophys. J., 7, 735 (1967).
2.	Boulpaep E., Am. J. Physiol., 222, 517 (1972).
3.	Civan M. M., Kedein O., Leaf A., Am. J. Physiol., 211, 569 (1966).
4.	Handler J. S., Preston A. S„ Orloff J., J. Biol. Chem., 244, 3194 (1969).
5.	Handler J. S., Preston A. S., Orloff J., J. Biol. Chem., 244, 3194 (1969).
6.	Heinz E., In: Current topics in membranes and transport, vol. 5, ed. F. Bron-
ner and A. Kleinzeller, New York, Academic Press, 1975.
7.	Heinz E., Mechanics and energetics of biological transpot, Berlin, Springer-
Verlag, 1979.
8.	Hess B., Brand K, In: Control of energy metabolism, ed. B. Chance,
R. W. Esterbook, and J. R. Williamson New York, Academic Press, 1965.
9.	Hoshiko T., Lindley B. D., J. Gen. Physiol., 50, 729 (1967).
10.	Jardetzky 0., Snell F. M, Proc. Nat. Acad. Sci. USA, 46, 616 (1960).
11.	Katchalsy A., Spangler R., Quart. Rev. Biophys., 1, (1968), 127.
12.	Kedem O., In: Membrane transport and metabolism, ed. A. Kleinzeller and
.4. Kotyk, New York, Academic Press, 1961.
13.	Kedem O., Caplan S. R., Trans. Faraday Soc., 61, 1897 (1967).
14.	Kedem O., Katchalsky A., Biochim. Biophys. Acta, 27, 229 (1958).
15.	Mikulecky D. C., Huf E. G., Thomas S. R„ Biophys. J. 25, 87 (1979).
16.	Miller D. G., Chem. Rev., 60, 15 (1960).
17.	Nagel W., Essig A., J. Membrane Biol., 69, 125 (1982).
18.	Prigogine I., Thermodynamics of irreversible processes, New York, Hohn
Wiley and Sons, 1961.
19.	Rapoport S. L, Biophys. J., 10, 246 (1970).
20.	Stucki J. W., Eur. J. Biochem., 109, 269 (1980).
364	Литература
21.	Ussing Н. Н., Windhager Е. Е., Acta Physiol. Scand., 61, 484 (1964).
22.	Ussing H. H., Zerahn К, Acta Physiol. Scand., 23, 110 (1951).
23.	Veech R. L., Raijam L., Krebs H. A., Biochem. J., 117, 499 (1970).
Глава 8
1.	Al-Awqati Q., J. Chin. Invest. 60, 1240 (1977).
2.	Al-Awqati Q., Beauwens R., Leaf A.. J. Membrane biol., 22, 91 (1975).
3.	Al-Awqati Q., Mueller A., Steinmetz P. R., Am. J. Physiol., 233, 1502
(1977).
4.	Al-Awqati Q., Norby L. H., Mueller A., Steinmetz P. R., J. Clin. Invest., 58,
351 (1976).
5.	Beauwens R., Al-Awqati Q., J. Gen. physiol., 69, 421 (1976).
6.	Biber T. U., Muellen T. L., Ann. J. Physiol. 232, C67 (1977).
7.	Bobrycki V. A,, Mills J. W., Macknignt A. D. C., DiBona D. R., J. Mem-
brane Biol., 60, 21 (1981).
8.	Canessa M., Labarca P., DiBona D. R., Leaf A., Proc. Nat. Acad. Sci. USA.
75, 4591 (1978).
9.	Canessa M., Labarca P., Leaf A., Membrane Biol., 30, 65 (1976).
10.	Civan M. M., Am. J. Physiol., 219, 234 (1970).
11.	Copion N. S„ Steele R. E„ Maffly R. H„ J. Membrane Biol., 34, 289 (1977).
12.	Corcia A., Lahav J., Caplan S. R., Biochim. Biophys. Acta, 596, 264 (1980).
13.	Danisi G., Vieira F. L., J. Gen. Physiol., 64, 372 (1974).
14.	Dixon T. E., Al-Awqati Q., Kidney Int., 16, 41A (1979).
15.	Dixon T. E„ Proc. Nat. Acad. Sci., USA, 76, 3135 (1979).
16.	Fanestil D. D., Herman T. S., Fimognari G. M., Edelman L S., In: Regula-
tory functions in biological membranes, ed. J. Jarnefelt, Amsterdam, Else-
vier, 1968.
17.	Handler J. S., Preston A. S., Orloff J., Biol. Chem., 244, 3194 (1969).
18.	Handler J. S., Preston A. S., Rogulski J., Biol. Chem., 243, 1376 (1968).
19.	Helman S. L, Milter D. A., Science, 173, 146 (1971).
20.	Hong C. D., Essig A., J. Membrane Biol., 28, 121 (1976).
21.	Labarca P., Canessa M., Leaf A„ ibid, 32, 383 (1977).
22.	Lahav J., Essing A., Caplan S. R., Biochim. Biophys. Acta, 448, 389 (1976).
23.	Lang M. A., Caplan S. R., Essig A., ibid, 464, 571 (1977).
24.	Lang M. A., Caplan S. R., Essig A., J. Membrane Biol., 31, 19 (1977).
25.	Lau У. T., Lang M. A., Essig A., Biochim. Biophys. Acta, 545, 215 (1979).
26.	Lau У. T., Lang M. A., Essig A., ibid, 647, 177 (1981).
27.	Leaf A., Anderson J., Page L. B., Gen. Physiol., 41, 657 (1958).
28.	Nishiki K-, Erichinska M., Wilson D. F., Am. J. Physiol., 237 C221 (1979).
29.	Owen A., Caplan R. S., Essig A., Biochim. Biophys. Acta, 389, 407 (1975).
30.	Owen A., Caplan S. R., Essig A., ibid, 394, 438 (1975).
31.	Rosenthal S. J., King J. G., Essig A., Am. J. Physiol., 236, F413 (1979).
32.	Rosenthal S. J.. King J. G., Essig A., J Membrane Biol., 63, 157 (1981).
33.	Saito T., Essig A., J. Membrane Biol., 13, 1 (1973).
34.	Saito T., Essig A.. Captan S. R., Biochim. Biophys. Acta, 318, 371 (1973).
35.	Saito T., Leaf P. D., Essig A., Am. J. Physiol., 226, 1265 (1974).
36.	Schultz S. G., Frizzell R. A., Nellans H. N.. J. Theor. Biol., 65, 215 (1977).
37.	Steinmentz P. R., Physiol., Rev., 54, 890 (1974).
38.	Stucki J. W., Eur. J. Biochem., 109, 269 (1980).
39.	Ussung H. FL, Zerahn K-, Acta Physiol. Scand., 23, 110 (1951).
40.	Vararlda W. A., Vieira E. L., J. Membrane Biol., 39, 369 (1978).
41.	Vieira F. L„ Caplan S. R., Essig A., J. Gen. Physiol., 59, 60 (1972).
42.	Vieira F. L., Caplan S. R., Essig A., ibid, 59, 77 (1972).
43.	Voute C. L., Ussing H. H., J. Cell. Biol., 36, 625 (1968).
44.	Wilson D. F„ Stubbs M., Veech P. L., Erecihska M., Krebs H„ Biochem. J.,
140, 57 (1974).
45.	Wolff D., Essig A., Membrane Biol., 55, 53 (1980).
46.	Zerahn K-, Acta Physiol. Scand., 36, 300 (1956).
Литература	365
Глава 9
1.	Chen Т. S., Walser М., Membrane Biol., 21, 87 (1975)
2.	Dawson D. C., ibid., 31, 351 (1977).
3.	Dawson D. C.. Al-Awqati Q., Biochim. Biophys. Acta 508, 413 (1978)
4.	Essig A., Biophys. J., 8, 53 (1968).
5.	Essig A., Kedem O., Hill T. L., J. Theor. Biol., 13, 72 (1966).
6.	Hodgkin A. L., Keynes R. D., J. Physiol., 128, 61 (1955).
7.	Kedem O., Essig A., J. Gen. Physiol., 48, 1047 (1965).
8.	Koefoed-Johnsen K, Levi H., Ussing H. H., Acta Physiol Scand, 25 150
(1952).
9.	Koefoed-Johnsen V., Ussing H. H., Acta Physiol. Scand 28, 60
(1953).
10.	Levi H., Ussing H. H., Acta Physiol. Scand., 16, 232 (1948).
11.	Ling G. N., A physical theory of the living state: The association induction
hypothesis, New York, Blaisdell, 1962.
12.	Minkoff L., Damadian R., Biophys. J., 13, 167 (1973).
13.	Sauer F. A., In: Membrane transport in biology, ed. G. Giebisch, D. C. To-
steson and H. H. Ussing, Berlin, Springer-Verlag, 1978.
14.	Schultz S. G., Frissell R. A., Biochim. Biophys. Acta, 443, 181
(1976).
15.	Schwartz T. L., Biophvs. J., 11, 596 (1971).
16.	Teorell T„ Arch. Sci. Physiol., 3, 205 (1949).
17.	Ussing H. H„ Nature, 160, 262 (1947).
18.	Ussing H. H., Physiol. Rev., 29, 127 (1949).
19.	Ussing H. H., Adv. in Enzymol., 13, 21 (1952).
20.	Ussing H. H., The alkali metal ions in biology, Berlin, Springer-Verlag,
1960.
21.	Ussing H. H., Zerahn K., Acta Physiol. Scand., 23, 110 (1951).
22.	Wolff D., Essig A., Biochim. Biophys. Acta, 468, 271 (1977).
Глава 10
1.	Biber T. U. L„ Curran P. F„ J. Gen. Physiol., 51, 606 (1968).
2.	Blumenthal R., Kedem O., Biophys. J. 9, 432 (1969).
3.	Diamond J. M., J. Membrane Biol., 51, 195 (1979).
4.	Essig A., J. Theor. Biol., 13, 63 (1966).
5.	Essig A., Kedem О., T. L., ibid, 13, 72 (1966).
6.	Franz T. J., Galey W. R. Van Bruggen J. T., J. Gen. Physiol., 51, 1
(1968).
7.	Hodgkin A. L., Keynes R. D.. J. Gen. Physiol., 128, 61 (1955).
8.	Hoshiko T„ Lindley B. D., Biochim. Biophys. Acta, 79, 301 (1964).
9.	Kedem O., Katchalsky A., J. Gen. Physiol., 45, 143 (1961).
10.	Lee M. H., Berker A. N., Stanley H. E., Essig A., J. Membrane Biol. 50,
205 (1979).
11.	Levi H., Ussing H. H.. Acta Physiol. Scand., 16, 232 (1948).
12.	Li J. H., Essig A., J. Membrane Biol., 29, 255 (1976).
13.	Lief P. D„ Essig A., ibid, 12, 159 (1973).
14.	Mackay D., Meares P., Trans. Faraday Soc., 55, 1221 (1959).
15.	Patlak C. S., Rapoport S. I. J. Gen. Physiol., 57, 113 (1971).
16.	Pietras R. J., Wright E. M„ Nature, 247, 222 (1974).
17.	Smulders H. P., Tormey J. McD., Wright E. M, J. Membrane Biol., 7, 164
(1972).
’.8. Spiegler K. S., Trans. Faraday Soc., 54, 1408 (1958).
19.	Ussing H. H., Adv. in Enzymol., 13, 21 (1952).
20.	Ussing H. H., Johansen B., Nephron, 6, 317 (1969).
21.	Wright E. M., Smulders A. P„ Tormey J. McD., J. Membrane Biol., 7, 198
(1972).
366
Литература
Глава 11
i.	Chen J. S., Walser M., Membrane Biol. 18, 365 (1974).
2.	Chen J. S.. Walser M., ibid. 21, 87 (1975).
3.	DeSousa R. C., Li J. H,. Essig A.y Nature, 231, 44 (1971).
4.	Essig A., Lang M., J. Membrane Biol., 24, 401 (1975).
5.	Essig A., Li J. H.y ibid, 20, 341 (1974).
6.	Gottlieb M. H.y Sollner K., Biophys. J., 8, 515 (1968).
7.	Helman S. I., O’Neil R. G., Fischer R. S., J. Physiol., 229, 947 (1975).
8.	Kramer //., Meares P.y Biophys. J., 9, 1006 (1969).
9.	Labarca P.y Canessa AL, Leaf A., J. Membrane Biol., 32, 383 (1977).
10.	Lang M. A., Caplan S. R., Essig A., ibid, 31, 19 (1974).
11.	Li J. H.y DeSousa R. C.y Essig A, ibid, 19, 93 (1974).
12.	Li J. H., Essig A., Biochim. Biophys. Acta, 465, 421 (1977).
13.	Meares P.y Dawson D. G., Sutton A. H., Thain J. F., Berichte Bunsenges.
Physik. Chemie, 71, 765 (1967).
14.	Meares P., Sutton A. H.y J. Colloid Interface Sci., 28, 118 (1968).
15.	Meares P., Ussing H. H., Trans. Faraday Soc., 55, 142 (1959).
16.	Meares P.y Ussing H. H.y ibid, 55, 244 (1959).
17.	Saito Г., Lief P. D., Essig A., Am. J. Physiol., 226, 1265 (1974).
18.	Ussing H. H.y The Alkali metal ions in biology Berlin, Springer-Verlag,
1960.
19.	Wolff D.y Essig A., Biochim. Biophys. Acta, 468, 271 (1977).
Глава 12
1.	Abbott В. C.y J. Physiol. (London), 112, 438 (1951).
2.	Abbott В. C. Aubert X. M. Hill A. V., J. Physiol. (London), 111, 41 (1950).
3.	Alberty R. A„ J. Biol. Chem., 243, 1337 (1968).
4.	Эшби У. P. Введение в кибернетику. Пер. с англ. — М.: ИЛ, 1959.
5.	Atkinson D. Е., Science, 150, 851 (1965).
6.	Aubert D. Е., Le couplage energetique de la contraction musculaire, Brus-
sels, Editions/Arsia, 1956.
7.	Bdrany AL, J.	Gen. Physiol., 50, 197 (1967).
8.	Bornhorst	W.	J.,	Minardy J. E.y Biophvs. J.,	9, 654 (1969).
9.	Bornhorst	W.	J.,	Minardi J. E., ibid, 10, 137	(1970).
10.	Bornhorst	W.	J.,	Minardi J. E., ibid, 10, 155	(1970).
11.	Cain D. F.y Infante A. A., Davies R. E., Nature, 196, 214 (1962).
12.	Caplan S. R., J. Theor. Biol. 11, 63 (1966).
13.	Caplan S. R.y Biophys. J., 8, 1146 (1968).
14.	Caplan S. R.y ibid, 8, 1167 (1968).
15.	Carlson D. E.y Siger A., J. Gen. Physiol., 44, 33 (1960).
16.	Carlson F. D., Wilkie D. R., Muscle Physiology, Englewood Cliffs, N. J.
Prentice-Hall, 1974.
17.	Chaplain R. A., Frommelt B.y J. iMechanochem. Cell motility, 1, 41 (1971).
18.	Cohen	N.	A.y	Longley	W.y Science, 152, 794 (1966).
19.	Curtin	N.	A.,	Davies	R.	E.y Cold Spring Harbor Symp., 37,	619 (1973).
20.	Curtin	N.	A.,	Davies	R.	E.y J. Mechanochem. Cell Motility,	3, 147 (1975).
21.	Curtin	N.	A.	Gilbert	C.,	Kretzschmar K- AL, Wilkie D. R.y J. Physiol., 238,
455 (1974). ’
22.	Daemers-Lambert C.y Angiol., 1, 249 (1964).
23.	Daemezs-Lambert C.y Roland J., ibid, 4, 69 (1967).
24.	Eisenberg E. Hill T. L. Progr. Biophys. Mol. BioL, 33, 55 (1978).
25.	Eisenberg E. Hill T. L„ Chen У., Biophvs J., 29, 195 (1980).
26.	Elliott G. F.y Lowy J., Millman B. AL, Nature, 206, 1357 (1965).
27.	Ernst E.y Biophysics of the striated muscle, Budapest, Akademia Kiado,
1963.
28.	Essig A.y Caplan S. R.y Federation Proc., 29, 655 (abstract) (1970).
29.	Fenn W. O., J. Physiol. (London), 58, 175 (1923).
Литература
367
30.	Fenn W. О., Marsch В. О., ibid, 85, 277 (1935).
31.	Gasser H. S„ Hill A. V., Proc. Roy. Soc., B96, 398 (1924).
32.	Gilbert C.t Rretzschmar R. M., Wilkie D. R. Cold Spring Harbor Svmp.,
37,613 (1973).
33.	Hess B., Ciba Foundation Symp., 31, 369 (1975).
34.	Hill	A.	V.,	Proc. Roy.	Soc., B126, 136 (1938).
35.	Hill	A.	V.,	ibid,	B127,	434	(1939).
36.	Hill	A.	V.,	ibid,	B136,	399	(1949).
37.	Hill	A.	V.,	ibid,	B159,	297	(1964).
38.	Hill	A.	V.,	ibid,	B159,	319	(1964).
39.	Hill A. V., Trails and trials in physiology, London, E. Arnold 1965.
40.	Hill A. K, Woledge R. C., J. Physiol. (London), 162, 311 (1962).
41.	Hill T. L., Progr. Biophys. Mol. Biol., 28, 267 (1974).
42.	Hill T. L., ibid, 29, 105 (1975).
43.	Hill T. L., Free energy transduction in biology New York, Academic Press,
1977.
44.	Huxley A. F„ Progr. Biophys. Chem., 7, 255 (1957).
45.	Huxley H. E.t Brown W., Holmes R. C., Nature, 206, 1358 (1965).
46.	Infante A. A., Rlaupiks D., Davies R. E., ibid, 201, 620 (1964).
47.	Infante A. A., Rlaupiks D., Davies R. E., Biochim. Biophys. Acta, 88, 215
(1964).
48.	Infante A. A., Rlaupiks D., Davies R. E., Science, 144, 1577 (1964); see
also Davies R. E., Proc. Roy. Soc., B160, 480 (1964).
49.	Redem O., Caplan S. R., Trans. Faraday Soc., 61, 1897 (1965).
50.	Rushmerick M. J., Davies R. E., Proc. Roy. Soc. B174, 315 (1969).
51.	Lundholm L., Mohme-Lundholm E., Acta Physiol. Scand., 55, 45 (1862).
52.	Macpherson L., J. Physiol. (London), 122, 172 (1953).
53.	Maitra P. R., Chance B.t In: Control of energy metabolism, ed. B. Chance
et al., New York, Academics Press, 1965.
54.	Marechai G„ Le metabolisme de la phosphorycreatine et de 1’adenosine
triphosphate durant la contraction rmisculaire, Brussels, Editions Arsicia,
1964.
55.	Mommaerts W. F. H. M., Brady A. J., Abbott В. C., Ann. Rev. Physiol., 23,
529 (1961).
56.	Oplatka A., J. Theor. Biol., 34, 379 (1972).
57.	Paul R. J., Peterson J. W., Caplan S. R., Biochim. Biophys. Acta, 305, 474
(1973).
58.	Paul R. J., Peterson J. W., Caplan S. R., J. Mechanochem. Cell Motility.
3, 19 (1974).
59.	Polissar M. J., Am. J. Physiol., 168, 766 (1952).
60.	Prigogine I., Thermodynamics of irreversible processes. New York, John
Wiley and Sons, 1961.
61.	Pringle J. W. S., Symp. Soc. Exptl. Biol., 14, 41 (1961).
62.	Pringle J. W. S., Progr. Biophys. Mol. Biol., 17, 1 (1967).
63.	Riiegg J. C., Physiol. Rev. 51, 201 (1971).
64.	Sandow A., In: Biophysics of physiological and pharmacological actions,
ed A. M. Shanes, Washington, Americana Association for the Advancement
of Science, 1961.
65.	Seraydarian R. Mommaerts W. F. H. M. Wallner A., Biochim. Biophys.
Acta, 65, 443 (1962).
66.	Stucki J. W„ Progr. Biophys. Mol. BioL, 33, 99 (1978).
67.	Viera F. L., Caplan S. R.t Essig A., J. Gen. Physiol., 59, 60 (1972).
68.	Walter C., In: Biochemical regulatory mechanisms in eukaryotic cells
ed. F. Kun and S. Grisolia, New York, Wiley, 1972.
69.	Wilkie D. R., J. Physiol. (London), 110, 249 (1950).
70.	Wilkie D. R., Progress in biophysics, 10, 259 (1960).
71.	Wilkie D. R., Symp. Biol. Hung, 8, 207 (1967).
72.	Wilkie D. R.t Woledge R. C., Proc. Roy. Soc., B169, 17 (1967).
________________________________________________________________Литература
73.	Wilson D. F., Stubbs M., Veech R. L., Erecinska M., Krebs H., Biochem J
140, 57 (1974).
74.	Yagi K„ Mase R., J. Biol. Chem., 237, 397 (1962).
75.	Yagi K, Mase R., In: Molecular biology of muscular contraction ed. S. Eba-
shi et al., New York, Elsevier, 1965.
Глава 13
1.	Applebury M. L., Peters K. S., Renzepis P. M„ Biophys. J., 23, 375 (1978).
2.	Arnon D„ Allen M. Whatley F. R„ Nature, 174, 394 (1954).
3.	Avron M., In: Structure and function of chloroplasts, ed. M. Gibbs Berlin.
Springer, Verlag, 1971.
4.	Bakker A. E., van den Hauvel E. J., van Dam К Biochim. Biophys Acta,
333, 12 (1974).
5.	Blaurock A: E., Stoeckenius W„ Nature New Biol. 233, 152 (1971).
6.	Caplan S. R., J. Theoret. Biol., 10, 209, errata, 11, 346 (1966).
7.	Caplan S. R., In: Dynamic aspects of biopolyelectroytes and biomembranes,
ed. F. Oosawa N. Imai, I. R. Miller, S. Sugai and Y. Kobatake, Amsterdam,
Elsevier, 1982.
8.	Caplan S. R„ Essig A„ Proc. Nat. Acad. Sci. USA, 64, 211 (1969).
9.	Chance B., Montal M., In: Current topics in membranes and transport
vol. 2, ed. F. Broner and A. Kleinzeller, New York, Academic Press, 1971.
10.	Chance B., Williams G. R., In: Advances in enzymology, vol. 17,
ed. F. F. Nord, New York, Interscience, 1956.
11.	Eissenbach AL, Caplan S. R., In: Current topics in membranes and trans-
port vol. 12, ed. F. Bronner and A. Kleinzeller, New York, Academic Press,
1979.
12.	Goldschmidt C. R., Ottolenghi O., Rosenfeld T., Ottolenghi M., Biophys. J.,
16, 839 (1976).
13.	Goldschmidt C. R., Kolinsky O., Rosenfeld T., Ottolenghi M., ibid, 17, 179
(1977).
14.	Griffiths D. E., Biochem. J., 160, 809 (1976).
15.	Hellingwerf K- Arents J. C., Scholte B. J., Westerhoff H. V., Biochim.
Biophys. Acta, 547, 561 (1979)
16.	Hellingwerf K- J., Schuurmans J. J., Westerhoff H. V., FEBS Lett., 92, 181
(1978).
17.	Hellingwerf K. J. J., Tegelaers F. P. W., Westerhoff H. V., Arents J. C.,
van Dam K., In: Energetics and structure of halophilic microorganisms,
ed. S. R. Caplan and M. Ginzburg Amsterdam, Elsevier/North-Holland, 1978.
18.	Hill T. L„ Free energy transduction in biology, New York, Academic Press,
1977.
19.	Hill T. £., Proc. Nat. Acad. Sci. USA, 77, 2681 (1980).
20.	Katchalsky A., Spangler R., Quart. Rev. Biophys., 1, 127 (1968).
21.	Kok B., In: Horizons of bioenergetics, ed. A. San Pietro and H. Guest,
Vew York, Academic Press, 1972.
22.	Ленинджер А. Митохондрия. Молекулярные основы структуры и функции.
Пер. с англ. — М.: Мир, 1966.
23.	Lehninger A. L., Carafoli Е., Rossi С. S„ In: Advances in enzymology,
vol. 29, ed. F. F. Nord, New York, Interscience, 1967.
24.	Mitchell P., Nature, 191, 144 (1961).
25.	Mitchell P., Biol. Rev., 41, 445 (1966).
26.	Oesterhelt D., Stoekenius W., Nature New Biol., 233, 149 (1971).
27.	Rottenberg H., Eur. J. Biochem., 15, 22 (1970).
28.	Rottenberg H., Biophys. J., 13, 503 (1973).
29.	Rottenberg H., In: Progress in surface and membrane science vol. 12,
ed. J. F. Danielli et al. New York, Academic Press, 1978, p. 245—325.
30.	Rottenberg H., Biochim. Biophys. Acta, 549, 225 (1979).
31.	Rottenberg H., Caplan S. R., Essig A., Nature, 216, 610 (1967).
Литература	 369
32.	Rottenberg Н., Caplan S. R., Essig A., In: Membranes and ion transport
vol. 1, ed. E. E. Bittar, New York, Wiley-Interscience, 1970.
33.	Rottenberg H., Gutman M., Biochemistry, 16, 3220 (1977).
34.	Slater E. C., In: Comprehensive biochemistry, vol. 14, ed. M. Florkin and
E. H. Stotz, New York, Elsevier, 1966.
35.	Slater E. C., Quart. Rev. Biphys., 4, 35 (1971).
36.	Slater E. C., Rosing J., Mol. A., Biochim. Biophys. Acta, 292, 534 (1973).
37.	Stoeckenius IF., Soc, Gen. Physiol. Ser., 33, 39 (1979).
38.	Stoeckenius M., Lozier R. H., Bogomolni R. A., Biochim. Biophys. Acta,
505, 215 (1979).
39.	Stucki J. W., Eur. J. Biochem., 109, 257 (1980).
40.	van Dai.: K., Casey R. P., van der Meer R„ Groen A. K., Westerhoff H. V.,
In: Frontiers of biological energetics vol. 1. ed. P. L. Dutton J. Leigh and
A. Scarpa, New York, Academic Press, 1978.
41.	Walz D., Biochim. Biophys. Acta, 505, 279 (1979).
42.	Westerhoff H. V., Scholte B. J., Hellingwerf K. J., ibid, 547, 544 (1979).
Послесловие
1.	Caplan S. R„ Proc. Nat. Acad. Sci., USA, 78, 4314 (1981),
2.	Nagel W., Essig A., Membrane Biol., 69, 125 (1982).
3.	Stucki J. W., Compiani M., Caplan S. R., Unpublished studies 1982.
24 Кеплен, Эссиг
Предметный указатель
Автокаталитические системы 102
Аденилаткиназа 327, 334—336
Аксон, гигантский 197
Активное растяжение 290
Активный транспорт 31, 36, 119—
191. См. также Степень сопряже-
ния; Электродвижущая сила транс-
порта натрия; Модель эквивалент-
ных схем; Потребление кислорода
— — влияние модельных соединений
163—169, 180, 185, 188
----- зависимость от химического по-
тенциала 160—162, 183
----- — от электрического потен-
циала 155—160, 183
------и метаболизм 145—150
— — и отношение потоков 209—210
----- кинетика изотопных потоков
259—264
-----линейность 153, 155, 182
----- механизм активации 169
-----модель 48—50, 105, 120—128
----- — переносчиков 226
-----натрия 95—96, 126—127, 147,
150—162
-----однонаправленные потоки, за-
висимость от потенциала 261
----основы 52
------ протонов 181—190, 312, 315,
337—343
----- экспериментальное описание
128—133
Альдостерон 158, 159, 169—170, 179,
186, 188
Амилорид в эпителии 155, 166, 167,
179
Амортизатор 292
Анализ изотопных потоков (Чен —
Уолсер} 253—254 , 258, 261—262
Анизотропия 32, 33
Антидиуретический гормон (АДГ)
169, 170, 178, 234
Апикальная поверхность 121
Асимметрия 33
АТФ, гликолитический и окислитель-
ный путь образования 169
Ацетазоламид, мочевой пузырь чере-
пахи 185, 186
Базолатеральная поверхность 121
Бактерии, галофильные 311
Бактериородопсин 337—343
— фотоцикл 339—343
Безызлучательные переходы 120
Брюсселятор 103
Брыжеечная бычья вена 276
Векторные процессы 23—27
Векторный коэффициент сопряжения
32
Вероятности переходов 82
—	состояний 70
Взаимность см. Соотношение взаим-
ности Онзагера
Вход 57, 120, 122, 147
Входная мощность, максимальная 300
Входное пространство 296—300
Входной поток 195, 205
Высокоэнергетический интермедиат
312, 314—315, 317
Выход 57, 120, 122, 287
Выходная мощность 295
Выходное пространство 297—298, 300
Выходной поток 205
Галофильные бактерии 311
------ фотоиндуцнруемый протонный
насос 337—343
Гетерогенность 47, 125—128, 210—
217, 230—242, 251
Гиббса — Дюгема уравнение 18
Гиббса уравнение 17, 18, 22, 268
Гипотеза параллельного сопряжения
316, 322
—	ассоциации — индукции 216
Гистамин 276
Гликолиз 168, 170
Гольдмана — Ходжкина — Катца
уравнение постоянного поля 91
Гормоны 170—172
Предметный указатель
Давление
— осмотическое 37, 142—143
—	электроосмотическое 42
Де Дондера обозначения 23
2-Дезокси-В-глюкоза, в эпителии
167—169, 179, 188
Диаграммы
— входа — выхода 296—300
— индикаторные 297
—	направленные 70—72
—	парциальные 70
—	потока 72—74
—	• Хилла 101 —103
—	циклические 72
Дигидроэрготамин, в мышцах 276
2,4-Динитрофенол 188, 197
Диоксид углерода, образование 181 —
184
Диссипативная функция 21, 28, 76,
81, 123, 147, 316—320
—• — входные и выходные члены 57
—	— для мышцы 267—271
----для окислительного фосфорили-
рования 317, 319
---- преобразования 36—41
Диффузия
—	облегченная 316
— обменная 197, 216, 226, 228, 231,
241, 316
— однорядная 196, 224, 231, 237, 240,
262, 264
Дыхательный коэффициент 182, 186
Дыхательная цепь 310
Зависимость сила — скорость 267,
272, 277, 278, 283, 293
Закрытые системы 15—16, 19—20
Затрата энергии без совершения ра-
боты 64—66
Захват, механизмы 290—291
Зрительный пигмент 337
Излучение черного тела 338
Изменение свободной энергии
-------общей 79—80
------- основной 79—80
------- стандартной 79
Изотопное взаимодействие 55, 198,
210, 212, 216, 254
----в активном транспорте 263—
264
— — в неоднородной мембране 251
---- в отсутствие градиента кон-
центрации 245—246, 249
---- в пассивном транспорте 256—
257
----и сопряжение 228, 230
________________________________371
Изотопное взаимодействие
---- кооперативность 227
— — модели 220—230, 250
— — — основанные на трении 219—
220
----прямое доказательство 250
----решеточные модели 220—227
----связанное с аллостерической
кооперативностью 226
------ — с неоднородностью 230—242
Изотопные эффекты 193
Изотопный обмен 202, 203, 206, 207
Изотропность 32—33
Икроножная мышца 270
Ионные потоки и окислительное фос-
форилирование, анализ с позиций
неравновесной термодинамики 316—
322
Ионный транспорт и окислительное
фосфорилирование 312, 316—322
Ионофоры 316
Источник постоянного напряжения
295, 299
---- тока 299
Калориметрическая бомба 56
Кальций, ионы 283, 291
Квазистационарное состояние 154,
156, 270
Квантовый выход 341
Кедем — Канальского уравнения 28—
51
Кибернетическая интерпретация про-
граммы регулятора 308
Кинетика
— изотопных потоков 219—265
----анализ с позиций неравновес-
ной термодинамики 198—210
----в синтетических мембранах
244—251
----метки 193, 224—225, 232, 238
----механизмы 220—242
----основы 192—198
---- проверка и применение термо-
динамических соотношений 243—
264
----сопряжение 249—251
---- теория 198—217
—	Михаэлиса — Ментен 140—141
Кинетическая линейность 89, 123, 163,
326
Кислородный электрод 156
Классическая термодинамика см.
Равновесная термодинамика
Клетки
—	кровь 126
—	мышцы 126
—	симметричные 126, 136
ол*
372
Предметный указатель
Кожа жабы 160—162, 231
— лягушки 54, 129, 150, 157, 159,
168—172, 174, 177, 231
Компартментация 282
Константы равновесия 78
— скорости второго поряда 74
---первого порядка 70, 79, 82
Конформационное изменение 69—70,
338
Концентрация
— локальная 282
— средняя логарифмическая 37—38,
90—92, 352
Координата реакции 23
Котранспорт Na—Cl 120
Коэффициенты '
— диффузии метки 252
---интегральной, объемной 252
— дыхательного контроля 311, 328,
329
— дыхательный 182, 186
— отражения 42, 44—45, 143, 240
—	перекрестные 29
— проницаемости 44, 193, 194, 198,
217, 225, 231—233, 238, 246
—	прямые 29
— сопротивления 199, 200, 355
— стехиометрии см. Стехиометрия
— фильтрации 43
Кюри — Пригожина принцип 32—34
Линейность 88—118, 125—126, 134,
140, 144, 158, 321, 355
— активного транспорта 154—155,
157, 184
—	внутренняя 114
—	и мышцы 271—277
— кинетическая 89, 123, 163, 326
—	локальная 198
— окислительного фосфорилирования
325
— термодинамическая 89, 123, 163,
327
Линейные зависимости 28
Линейные феноменологические урав-
нения см. Феноменологические
уравнения
Линии нагрузки 297, 298, 305
Липосомы, содержащие бактериоро-
допсин 338
Локальная - асимптотическая устойчи-
вость 113
Максвелла соотношения 352
Матрица преобразования 133
— Якоби 102
Мембраны
— гетерогенные 47, 125—128, 210—
217, 230—242, 251
— зарядово-мозаичные 47
— мозаичные 47
— неоднородные 47, 125—128, 210—
217, 230—242, 251
— последовательные 124—128, 142—
144, 216—218
— пурпурные 81, 337, 341
— селективность 45, 127, 138, 246
— синтетические 244—251
— составные 38—39
Мембранные процессы 24
Мембранный потенциал 42
Мера реакции 23
Метаболизм
— влияние 2-дезокси-О-глюкозы 166
— зависимость от химического потен-
циала 160—162
— — от электрического потенциала
156—161
— и отношение потоков 195—196,
208—210, 213—214, 260—263
— окислительный 156, 335, 357
— основной 159, 356
— промежуточный 276
— сопряжение с транспортом 145—-
149
— специфичность 159
Метаболическая реакция
----- локальная 129
-----общая 129
Метод диаграмм 69—86, 229
Миозиновые филаменты 272
Миофибрилла 267
Митохондрии 111, 318—320, 326, 327,
332____336
— печени крыс 326, 333—335
Модели решеточные 220—227
----- активного транспорта 226—230
-----изотопного взаимодействия
220—230, 250
----- пассивного транспорта 220—
227
Модель изотопного взаимодействия,
основанная на трении 219—220.
См. также Электродвижущая сила
транспорта натрия; Протонодви-
жущая сила
— эквивалентных схем 53—56, 137—
139, 178—179
-------транспорта натрия 137—139,
178—179
----------протонов 181 —190
Молекулярные параметры мышцы
287—288
Мочевой пузырь жабы 96, 126, 128,
129, 150, 155—156, 172-174, 179,
234, 251, 254. 257, 260—264, 357
Предметный указатель
373
Мочевой пузырь
— — черепахи 181—190
Мышечное сокращение 266—308
-----изометрическое 266, 270, 274,
290
----- изотоническое 270
----- контроль 266
-----ненагруженное 266, 274
-----регуляция 266, 278—279, 308
----- тетаническое 268, 270
Мышца
— анализ с позиций неравновесной
термодинамики 267—277
— гладкая 293
— сосудистая 275—276
— икроножная лягушки 270
— линейность 271—277
— молекулярные параметры 287—288
-----постоянные 287
— моллюска 290—291
— поперечная 297
— преобразование энергии 277—283
— прямая кишка лягушки 271, 275
— саморегуляция 278, 291—292
— скелетная 275, 287
— сродство 280—281
— феноменологические уравнения
271—277
— функция диссипации 268—271
— цитоплазма 272
Нагрузка, оптимальная 295—297
Напряжение, изометрическое 273
Н асос
— ионный 80, 106—ПО, 120—125
— натриевый 120—125, 283. См. так-
же Активный транспорт натрия
— протонный 185, 186, 189, 311, 337,
343
— сложный 143—144
— электроген ный 106—НО
Неизотермические системы 66—67
Нелинейность 157, 162, 183, 284,327,
346
Необратимые процессы 9, 16
-----векторные 23—26
— — скалярные 21—23, 26—27
Неравновесная термодинамика
-----общие соображения 9—12
-----основные положения 19—21
Нернста— Планка уравнение 90—91
Норадреналин, в мышце 276
Обратимые процессы 9, 14, 16
Объемный поток 38, 45, 232—239
— — наблюдаемый 38, 46
— — определение 46—47
Объемный поток
-----сопряжение с потоком раство-
ренного вещества 142—143, 232—
239, 241
— — электроосмотический 40
Окислительно-восстановительные ре-
акции 311
Окислительное фосфорилирование 11.
309—313. См. также Химическая
гипотеза окислительного фосфори-
лирования; Хемносмотическая гипо-
теза
----- анализ с позиций неравновес-
ной термодинамики 316—337
— — вычисление степени сопряжения
327—332
----- диссипативная функция 317.
319
— — и степень сопряжения 322
----линейность 325
— — модели энергетического сопря-
жения 312—316
-----отношение потоков и отноше-
ние сил 336
----- скорость 326
----- сукцинат 315
----- транспорт протонов 313—323
-----эффективность 334—336
Оптимизация 295, 298
Основной метаболизм 159, 356
Открытые системы 16—17, 20—21,
289 352
Отношение Р/О 133, 163, 171, 186,
190, 310, 324
-----и метаболизм 195—196, 208—
210, 213—214, 260—263
-----и утечка 53, 213, 214
-----и электродвижущая сила транс-
порта натрия 53, 195—196, 209—
210, 260—261
— — приведенное 60, 61
— потоков 53, 59, 134, 194—198,
208—209, 212—214, 229, 235—239,
244—245, 257, 260—263, 329, 336
— сил 59, 336
Параллельные области 210—216
Параметры состояния 140, 202
Пассивный транспорт
----- вычисление в эпителии 157
— — изотопные потоки в биологи-
ческих мембранах 252—259
----- модели переносчиков 220—227
-----решеточные модели 220—227
-----уравнения Кедем — Качальско-
го 28—51
Переходы 70
—	безызлучательные 80
—	спонтанные 120
374
Предметный указатель
Поверхность апикальная 121
—	базолатеральная 121
—	серозная 176
—	слизистая 176
Показатель эффективности 278
Последовательные мембраны 124—
128, 142—144, 216—217
—• области 216—218
— реакции 140—142
Постоянные, аддитивные 328, 331
Потенциал
— границы раздела фаз 107—108
—	мембранный 42
—• окислительно-восстановительный
310
— разомкнутой цепи 42, 129—130,
138
—	реверсии 118
—	течения 42
—	фосфатный 310
—	химический 17
—	электрический 25, 355
— электрохимический 25, 220
Поток
— воды 28. См. также Объемный
поток
— входной 195, 205
— выходной 195, 205
—	действительный 37
—	действующий 77
— зависимость от сродства 140
— диффузионный 40
— ионов в окислительном фосфори-
лировании 316—322
— кажущийся 37, 38, 46
— метки 235—236, 254
— натрия см. Активный транспорт
— объемный 38, 40, 45—47
— однонаправленный 194, 204, 210,
215, 235—238, 241, 252—253, 255—
261
—• перехода 71, 72
— протонов 181—189. См. также
Транспорт протонов
---консервативный 188
---иеконсервативный 320
— растворенного вещества, сопряже-
ние с объемным потоком 142—143,
232—239, 241
—	стационарный 75
—	тепла 67
—	термодинамический 28—29
— фиксированный 55, 63—65, 126,
134, 138, 274, 287, 300, 323,
327
—	циклический 72—77
---однонаправленный 74, 76, 84,
116—118
Потребление кислорода 122, 152, 153,
158, 159, 164—165. См. также Ме-
таболизм
Правильные траектории 119, 122, 132,
133, 152, 156, 160, 163, 229, 293,
327
----в точке перегиба в многомер-
ном пространстве 111—112
----несопряженных процессов 90—
93
----сопряженных процессов 94—
102
----транспорта натрия 153, 156,
160, 163
------- протонов 185
Практические транспортные коэффи-
циенты 41, 42, 353
Превращение энергии
—	— механохимическое 265
---- регуляция 277—288
---- эффективность 52—67, 135—
138
Преобразователи энергии
---- линейные 296
----саморегулируемые 278, 279,
295—307
Проводимость
— активная 138, 179, 181, 186
—	внутренняя 300
—	парциальная 252, 258
— пассивная 138, 157, 179, 186, 254
—	• электрическая 42
Программа регулятора 308
Программирующая функция 302
Производство энтропии ,
----внутреннее 20, 268
---- добавочное 101
— — минимальное 271
Проксимальные канальцы в почке
126, 134
Проницаемость
— для воды, аномальная природа
194
— вычисление изотопным методом 193
— коэффициент 44, 193, 198, 217,225,
229, 231—233, 238, 246
— метки 193, 224—225, 232, 238
—	модель переносчика 225
—	обменная 207
—	пассивный барьер 176
—	растворенного вещества 42
—	решеточная модель 222, 224
—	электроосмотическая 42
Протонодвижущая сила 187—188,316
Протонный насос см. Протонный
транспорт
Протонный транспорт 181—190, 309,
311, 314, 342
— — анализ с позиций неравновес-
ной термодинамики 184—185
Предметный указатель
375
Протонный транспорт
--------эквивалентной цепи 186—
189
---- биохимическая корреляция
189—190
---- влияние модельных соединений
185, 188
----в мочевом пузыре черепахи
181—183
----в окислительном фосфорилиро-
вании 314—322
----протонодвижущая сила 187—
188
----сродство 185—186
— — степень сопряжения 183—184
Прямые коэффициенты 29
Пурпурная мембрана 81, 337, 341
Работа 14, 19, 283
— внутренняя 54, 290
— полезная 15—16
— электроосмотическая 135, 210—211
Рабочий элемент 57, 267
Равновесие, обратимое 63
Равновесная термодинамика
----и неравновесная термодинами-
ка 9—10
----принципы и функции 13—18
Разобщители 311, 315—316, 332
Разрывные системы 267
Растяжение, активное 290
Регулятор 129, См. также Мышечное
сокращение
Регуляция по стехиометрии 285—287,
293
Решеточные модели 220—227
Ротенон в коже лягушки 169
Саксена уравнения 40
Саморегуляция 278, 279
— преобразования энергии 295—308
— следствия 291—292
Саркомер 271
Свободная энергия
— Гельмгольца 14, 16
— Гиббса 14, 16—18, 21—23, 78, 79,
120, 122
— гидролиза АТФ 132, 163, 168, 171,
189
— общая 77
— основная 77, 81—82, 342
—	стандартная 77
—	уровни 77—84
Селективность 45, 127, 128, 138, 246
Сервомеханизмы 295—296
Серозная поверхность 176
Сила
—	движущая 64
— оценка с помощью изотопного ме-
тода 194, 205, 263
— протонодвижущая 187—188
—	сопряженная 29
—	термодинамическая 28, 80
— транспорта натрия 138—139, 178—
181, 209, 210, 262—263
— электродвижущая 37, 53, 61
—	эффективность 66
Симметрия 32. См. также Соотноше-
ние взаимности Онзагера
Снмпорт 69
Системы 18
—	закрытые 15—16, 19—20
— насос —утечка 144, 210, 211
— неизотермические 66—67
— открытые 16—18, 20—21, 289,352
— разрывные 267
Скалярные процессы 21—24, 26—27
Скорость и эффективность в мышце
289—290. См. также Зависимость
сила—скорость
Слизистая оболочка желудка 143
---кишечника 143
Сокращение см. Мышечное сокраще-
ние
Соотношение взаимности Онзагера
--------- доказательство обоснован-
ности 40, 49, 59, 75, 111, 325, 327,
337
------- и правильная траектория
122, 152, 183, 229
--------и точка перегиба в много-
мерном пространстве 101, 102, 111
--------- кинетическая основа 75, 88—
118
------- непригодность 338
-------применение 11, 29, 39, 58,
120, 122, 123, 152, 183, 206, 229,
274, 321
Сопротивление
—	внутреннее 296, 299
—	механическое 292
—	нагрузки 296
—	обменное 208
— феноменологическое 122—124, 130,
133, 199, 200
— электрическое 130—131
Сопряжение 31—32, 42, 45, 84—86,
120, 126, 254, 309—343. См. также
Активный транспорт; Степень со-
пряжения
— водных потоков 194
— изотопных потоков 249—251
— модели 312—316
— неполное 174—179, 271—276, 279
— параллельное 312, 316, 321
376
Предметный указатель
Сопряжение
—	полное 183
—	положительное 123
— при изотопном взаимодействии
229
— растворенного вещества и объем-
ного потока 142—144
— скалярно-векторное 33
— стационарное 33—36, 49, 51, 283
— степень 56, 60, 95, 120, 134, 135,
184, 227
— транспорта и метаболизма 145—
149
—	циклическое 317
Состояние установившегося потока
63, 64, 126, 128, 134, 138, 274, 287,
300, 323, 327
Состояния 310, 328, 331. См. также
Стационарное состояние
—	вероятность 70
—	возбужденные 339
—	объединение 106
Специфичность метаболизма 159
Спонтанный процесс 62
Средняя логарифмическая концентра-
ция 37—38, 90—92, 352
Сродство 23, 122, 129—130, 318,
355—356
— влияние модельных соединений
163—169, 180
— в мышце 280—281
— вычисление 131—132,	162—163,
170, 335
— гидролиза АТФ 132, 163, 169, 171,
189—190
— зависимость от потенциала 155—
157
— и потоки 140
— общее 140, 148
— последовательных реакций 140
— регуляция 149, 281, 292
— стандартное значение 328
— транспорта натрия 163—171
— — протонов 185—186
— эффективное 328
Стандартный раствор 75
Статический напор 54, 64, 83, 101,
109, 112, 116—118, 126—128, 130,
136, 274, 287, 300, 310, 323, 327,
342
Стационарное сокращение 283
---в митохондриях 318, 322—327
---в мышце 270, 283, 292
— — в эпителии 154, 184
— сопряжение 33—36, 49—51
— состояние 22, 296
Степень полноты реакции 23
— свободы 28, 33, 289, 296
Степень сопряжения 57—63, 66—68,
108, 130, 133—134, 145, 206, 215,
327, 353—355. См. также Активный
транспорт; Сопряжение
-----в мышце 271—277, 279, 281—
282, 284, 288
-----в неизотермических системах
66—68
-----вычисление 133—134, 173—178,
327—332
-----кажущаяся 117
----- локальная 148
-----общая 127, 148
-----при окислительном фосфорили-
ровании 322
—	— оптимальная 126
—	— преобразователя 279
-----системы транспорта натрия 173
-----— — протонов 184—185
Стехиометрический коэффициент см.
Стехиометрия
Стехиометрическое отношение 57, 59,
133, 183, 310. См. также Стехио-
метрия
Стехиометрия 11, 23, 54—55, 84—86,
133—134, 173—178, 356
— в митохондриях 329—331, 334—
335
— в эпителии 120, 122, 123, 126,
133—134, 173—178, 186, 356
— кажущаяся 329—331
— механическая (приведенная) 85,
101, 103
— нецелочисленная 72
— регуляция 285—287, 293
— феноменологическая 60, 84, 86,
108, 334
Сукцинат и окислительное фосфори-
лирование 315
Тепловая катастрофа 216
Тепловые машины 66—67
Теплосодержание 16. См. также Эн-
тальпия
Теплота 14, 18, 19
— сокращения 270, 277
— стабильная 270
Термодинамика, законы 13—18.
См. также Равновесная термоди-
намика; Неравновесная термодина-
мика
— второй закон и окислительное фос-
форилирование ЗЮ
Термодинамическая линейность 88,
123, 163, 327
Термодинамические потоки 28—29
— силы 28—29, 80
— цепи 86, 139
Термопара 65—66
Предметный указатель
377
Тилакоиды 309
Ток короткого замыкании 129—130,
161, 166
— течения 40, 42
Толстая кишка кролика 181
Точка перегиба в многомерном про-
странстве (ТП) 101, 105, 111—112,
326
—---------п соотношение взаимно-
сти Онзагера 101, 102, 111
Траектория 298, 306
— саморегуляция 301, 305
Транспорт см. Активный транспорт;
Пассивный транспорт; Протонный
транспорт
Транспорт аминокислот, сопряженный
с натрием 119
—	механизмы 265
—	модели
---- активного транспорта 226—230
---- изотопного взаимодействия
220—230, 250
---- пассивного транспорта 220—
226
•	— противоионов 250
— электронов 309
Транспортные коэффициенты, прак-
тические 41, 42, 353
Тропомиозин 283, 291
Уабаин в эпителии 163—165, 179,
252, 260
Уравнения
— Гиббса 17, 18, 22, 268
— Гиббса—Дюгема 18
— Кедем—Канальского 28—51
— Нернста —Планка 90—91
— постоянного поля Гольдмана —
Ходжкина — Катца 91
— регулятора, каноническое 279
— Саксена 40
— Хилла 277—281
----вывод 295—308
---- обратное 282
— феноменологические 28—31. См.
также Феноменологические урав-
нения
Уровни свободной энергии 77—84
Утечка 54, 56, 125—128, 134, 210—
215
— влияние утечки 56, 127—129, 134—
136, 138, 157
— вычисление 157, 181, 255—259
— и отношение потоков 53, 213, 214
— как источник неполного сопряже-
ния 55, 120, 127
— протонов при окислительном фос-
форилировании 314, 332, 337
Феноменологическая стехиометрия 60,
84, 86, 108—109, 334—335
Феноменологические коэффициенты
29, 32, 120, 122—124, 319
----векторные 260
---- вычисление в эпителии 133
---- зависимость от потенциала
157—158
----и молекулярные параметры в
мышце 287—288
---- линейные 116—118
----как функции состояния 140,
160, 202
---- практические 40—46
---- преобразователя энергии 302
----проводимость 122, 133, 172—
173
----скалярные 260
----сопротивления 122—124, 130,
133, 199, 200, 355
---- составная мембрана 125—126
Феноменологические уравнения 28—
31
----вычисление 151 —162
----для мышц 271—277
-------окислительного фосфорили-
рования 320—322
-------эпителия 124, 126
---- преобразования 40—47
Фибриллы 268, 270, 292
Филаменты 268—269
—	механизмы скольжения 271
—	миозин 272
Фосфокреатин, расщепление 274, 275,
283
Фосфорилирование см. Окислитель-
ное фосфорилирование
Фотофосфорилирование	311 —312,
337—343
Фотоцикл 339—344
Функция состояния 14, 140, 160, 202
—	регулятора 302
Хемиосмотическая гипотеза 312—313,
315—316, 320—322, 324
Хилла уравнение 277—281
— — вывод 295—308
---- обратное 282
Химическая гипотеза окислительного
фосфорилировании 311—314, 316,
321
Химические реакции 17, 101—102
Хлоропласты 311, 327
Хроматофоры 311
Центры связывания 69
—	сопряжения 319
378
Предметный указатель
Циклический поток 72—77, 340
----однонаправленный 74, 76, 84,
116—118
— процесс сопряжения 317
Циклы 69—77, 102, 147, 227—229
— доминирующие 117
— Карно 67—68
— утечки 117
Циркуляция повторная 176
Черный ящик 57, 267—269
Числа переноса 43, 127, 252
Электрическая разность потенциалов
122, 184, 355
Электрогенный ионный насос 106—
110
Электродвижущая сила транспорта
натрия 138—139, 178—181, 209,
210, 261—263
----------и отношение потоков 54,
195—196, 178—181, 209—210, 260—
264
Электроды
- Ag/AgCl 37
— измерительные 37
— кислородные 156
— обратимые 24, 37, 352—353
— токовые 38
Электрокинетические явления 39—40
Электронейтральность 36
Электронный транспорт 309
Электрохимическая разность потен-
циалов 122, 184, 355
Энергетика и активный транспорт
-------и отношение	потоков 208—
210
-------классический	анализ 53—57
— ----- с позиций	неравновесной
термодинамики 56—57
Энергетика и активный транспорт
------- теория 119—149
-------экспериментальные резуль-
таты 150—191
Энергетическое сопряжение в орга-
неллах и галофильных
бактериях 309—344
Энергия
— внутренняя 14
— диссипация 21—27
— кинетическая 13—14
— потенциальная 14
— свободная 14, 16—18, 21—24, 77—
84, 120, 127, 267, 309, 341
—	сохранение 13—14
Энтальпия 14—16
Энтропия 19—21
— производство
-----внутреннее 20, 268
----- добавочное 101
----- минимальное 271
Эпинефрин в мышце 276
Эпителиальная ткань 112, 126, 137,
151, 180—181, 211, 231, 234, 283,
337. См. также Кожа лягушки;
Кожа жабы; Мочевой пузырь чере-
пахи
Эргометр Левина — Ваймана 281,292
Эффективность 62—66, 127, 135—138,
287, 309, 325
— и скорость в мышцах 289—290
— использования энергии 135—138
— максимум 63, 284
— механическая 279
— механохимическая 279
— окислительного фосфорилирования
334—336
—	тепловая 66
—	энтропийная 66
Эффект памяти 153
Содержание
Предисловие к русскому изданию 5
Предисловие 7
1.	Общие соображения 9
2.	Основы равновесной н неравновесной термодинамики 13
2.1.	Некоторые основные принципы и функции равновесной термоди-
намики 13
2.2.	Некоторые основные понятия неравновесной термодинамики 18
2.3.	Диссипация энергии в скалярных необратимых процессах 21
2.4.	Диссипация энергии в векторных необратимых процессах 24
2.5.	Диссипация свободной энергии в сопряженных скалярных и век-
торных процессах 26
2.6.	Выводы 27
3.	Связь между потоками и силами: уравнения Кедем — Качальского 28
3.1.	Феноменологические уравнения 28
3.2.	Сопряжение между реакциями н потоками 31
3.3.	Принцип Кюри — Пригожина 32
3.4.	Стационарные состояния с минимальным производством энтро-
пии 33
3.5.	Стационарное сопряжение 33
3.6.	Преобразования диссипативной функции 36
3.7.	Преобразование феноменологических уравнений: практические
феноменологические коэффициенты 41
3.8.	Определение объемного потока в трактовке Кедем — Качаль-
ского 46
3.9.	Модель активного транспорта 48
3.10.	Выводы 50
4.	Эффективность превращения энергии 52
4.1.	Активный транспорт: основы 52
4.2.	Классический анализ энергетики: модель эквивалентных схем 53
4.3.	Энергетика с позиций неравновесной термодинамики 56
4.4.	Степень сопряжения и взаимосвязь сил и потоков 57
4.5.	Эффективность превращения энергии 62
4.6.	Затрата энергии без совершения работы 64
4.6.1.	Состояние статического напора 64
4.6.2.	Состояние установившегося потока 64
4.6.3.	Продуктивность использования энергии 65
4.6.4.	Эффективность силы и потока 65
4.7	Степень сопряжения в неизотермических системах: тепловые ма-
шины и цикл Карно 66
4.8.	Выводы 67
380
Содержание
5.	Метод диаграмм 69
5.1.	Состояния и циклы 69
5.2.	Уровни свободной энергии 77
5.3.	Стехиометрия и сопряжение 84
5.4.	Применимость диаграммных методов 86
5.5.	Выводы 86
'6. Возможные условия линейности и симметрии сопряженных процессов
вдали от равновесии 88
6.1.	Правильные траектории: несопряжеиные процессы 89
6.2.	Правильные траектории: сопряженные процессы 94
6.3.	Точка перегиба в многомерном пространстве 100
6.4.	Линейность и симметрия в модели электрогенного ионного насоса 105
6.5.	Правильные траектории в окрестности точки перегиба в много-
мерном пространстве 111
6.6.	Заключительные замечания 112
6.7.	Выводы 114
Приложение: линейные феноменологические коэффициенты и равновесные
однонаправленные циклические потоки; поведение биохимических систем
вблизи состояния с фиксированной силой 116
7.	Энергетика активного транспорта: теория 119
7.1.	Предпосылки 119
7.2.	Модель активного транспорта одного иона 120
7.2.1.	Насос 122
7.2.2.	Последовательная составная мембрана 124
7.2.3.	Составная мембрана с последовательными и параллельны-
ми элементами 125
7.3.	Экспериментальное описание транспортной системы 128
7.3.1.	Ток короткого замыкания и потенциал разомкнутой цепи 129
7.3.2.	Вычисление электрического сопротивления 130
7.3.3.	Сродство А и его вычисление 131
7.3.4.	Вычисление феноменологических коэффициентов 132
7.3.5.	Вычисление степени сопряжения 133
7.4.	Стехиометрия и степень сопряжения 134
7.5.	Эффективность превращения энергии 135
7.6.	Модель эквивалентного контура 138
7.7.	Зависимость и 1Г от А 140
7.8.	Сопряжение потока растворенного вещества и объемного потока 142
7.9.	Влияние более сложных механизмов насоса 144
7.10.	Выводы 144
Приложение 145
8.	Энергетика активного транспорта: экспериментальные данные 150
8.1.	Обоснование линейных феноменологических уравнений 150
8.1.1.	Выбор объектов эксперимента 150
8.1.2.	Выбор уравнений для анализа эксперимента 152
8.1.3.	Влияние условий опыта на параметры уравнений термоди-
намики необратимых процессов 153
8.1.4.	Зависимость ]^а от Дф 155
8.1.5.	Зависимость Jsb от Дф 157
8.1.6.	Зависимость 7^а и Jsb от XNa 160
8.2.	Оценка параметров в уравнениях неравновесной термодинамики 162
8.2.1.	Оценка сродства 162
Содержание
381
8.2.2.	Влияние модельных соединений на А 163
8.2.3.	Влияние гормонов на А 169
8.2.4.	Оценка феноменологических коэффициентов L 172
8.2.5.	Оценка степени сопряжения: стехиометрия 173
8.2.6.	Сопоставление величии Екл и А 178
8.3.	Анализ активного транспорта в других видах эпителия 181
8.3.1.	Активный транспорт протонов в мочевом пузыре черепахи 181
8.3.2.	Неравновесно-термодинамический анализ активного транс-
порта протонов 183
8.3.3.	Степень сопряжения системы транспорта протонов 183
8.3.4.	Сродство системы транспорта протонов 185
8.3.5.	Анализ активного транспорта протонов методом эквива-
лентных контуров 187
8.3.6.	Корреляции биохимических процессов и активного транс-
порта протонов 189
8.4.	Выводы 190
9.	Кинетика изотопных потоков: основные факты и теории 192
9.1.	Исторический очерк 192
9.2.	Термодинамический анализ 198
9.2.1.	Основные уравнения 198
9.2.2.	Случай, когда изотопные взаимодействия отсутствуют 201
9.2.3.	Случай, когда имеется изотопное взаимодействие 205
9.2.4.	Отношение потоков и энергетика активного транспорта 209
9.3.	Функции составных мембран 210
9.3.1.	Параллельные области 210
9.3.2.	Последовательные области 216
9.4.	Выводы 218
10.	Кинетика изотопных потоков: механизмы изотопного взаимодействия 219
10.1.	Модели, основанные на трении 219
10.2.	Решеточная модель и модель переносчиков: пассивный транспорт 220
10.3.	Модель переносчиков; активный транспорт 226
10.4.	Изотопное взаимодействие, определяемое неоднородностью 230
10.5.	Выводы 242
11.	Кинетика изотопных потоков: проверка и применение термодинамиче-
ских соотношений 243
11.1.	Обоснование теоретических соотношений на примере синтетиче-
ских мембран 243
11.1.1.	Мембраны с неполной селективностью проницаемости и
заметной проницаемостью для воды 243
11.1.2.	Мембраны с высокой селективностью проницаемости и
низкой проницаемостью для воды 246
11.1.3.	Сопряжение изотопных потоков 249
11.2.	Обоснование теоретических соотношений в биологических мем-
бранах: пассивный транспорт 251
11.2.1.	Общие соотношения 251
11.2.2.	Зависимость однонаправленного потока от потенциала:
пассивные каналы 254
11.3.	Обоснование теоретических соотношений в биологических мем-
бранах: активный транспорт 259
11.3.1.	Общие соотношения 259
11.3.2.	Зависимость отношения потоков от потенциала: активный
транспорт 262
11.3.3.	Изотопное взаимодействие в каналах с активным транс-
портом 264
11.4.	Выводы 265
382
Содержание
12.	Мышечное сокращение 266
12.1.	Неравновесно-термодинамический анализ мышц 267
12.1.1.	Диссипативная функция 267
12.1.2.	Феноменологические уравнения для мышц: линейность и
неполнота сопряжения 271
12.2.	Регуляция превращения энергии 277
12.2.1.	Уравнение Хилла 277
12.2.2.	Мышцы с автономным преобразователем энергии 281
12.2.3.	Связь между феноменологическими коэффициентами и
молекулярными параметрами 287
12.3.	Некоторые общие замечания 288
12.3.1.	Целесообразность применения уравнений неравновесной
термодинамики 288
12.3.2.	Следствия саморегуляции 291
12.4.	Заключительные замечания 292
12.5.	Выводы 294
Приложение: вывод уравнения Хилла для саморегулируемых линей-
ных преобразователей энергии 295
Оптимальная нагрузка 295
Диаграммы входа—выхода 296
Саморегуляция преобразователей энергии 300
Программа регулятора 308
13.	Энергетическое сопряжение в митохондриях, хлоропластах и гало-
фильных бактериях 309
13.1.	Окислительное фосфорилирование и фотофосфорилирование 309
13.2.	Модели энергетического сопряжения при окислительном фосфо-
рилировании 313
13.2.1.	Возможные способы сопряжения 313
13.2.2.	Химическая гипотеза 314
13.2.3.	Хемиосмотическая гипотеза 315
13.2.4.	Гипотеза параллельного сопряжения 316
13.3.	Анализ окислительного фосфорилирования и ионных потоков с
точки зрения термодинамики необратимых процессов 317
13.3.1.	Функция диссипации 317
13.3.2.	Феноменологические соотношения 320
13.3.3.	Степень сопряжения и эффективность использования
энергии 322
13.4.	Применение неравновесно-термодинамического анализа 323
13.4.1.	Стационарные состояния 323
13.4.2.	Оценка степени сопряжения и кажущейся стехиометрии с
использованием стандартного состояния 327
13.4.3.	Экспериментальные примеры 332
13.5.	Фотоиндуцированный протонный насос Halobacterium halobium 337
13.6.	Заключительные замечания 343
13.7.	Выводы 344
Послесловие 346
Список обозначений 347
Примечания 352
Литература 361
Предметный указатель 370
Монография
С. Рой Кеплен, Элвин Эссиг
биоэнергетика
И ЛИНЕЙНАЯ ТЕРМОДИНАМИКА
НЕОБРАТИМЫХ ПРОЦЕССОВ
(стационарное состояние)
Старший научный редактор С. К. Оганесян
Младший редактор Н. П. Власова
Художник В. И. Шаповалов
Художественный редактор М. Н. Кузьмина
Технический редактор И. И. Володина
Корректор Т. П. Пашковская
ИБ № 5615
Сдано в набор 03.12.85. Подписано к печати 18.08.86
Формат 60Х90’/1б- Бумага типографская № 1.
Печать высокая. Гарнитура литературная. Объем
12,0 бум. л. Усл. печ. л. 24,0. Усл. кр.-отт. 24,0.
Уч.-изд. л. 24,03. Изд. № 3/4521. Тираж 2700 экз.
Зак. 48. Цена 3 р. 90 к.
ИЗДАТЕЛЬСТВО «МИР»
129820, ГСП, Москва, И-110, 1-й Рижский пер., 2
Ленинградская типография № 2 головное пред-
приятие ордена Трудового Красного Знамени Ле-
нинградского объединения «Техническая книга»
им. Евгении Соколовой Союзполиграфпрома при
Государственном комитете СССР по делам изда-
тельств, полиграфии и книжной торговли. 198052,
г. Ленинград, Л-52, Измайловский проспект, 29.
Отпечатано в Леикиградской типографии № 8
ордена Трудового Красного Знамени Ленинград-
ского объединения «Техническая книга» им. Евге-
нии Соколовой Союзполиграфпрома при Государ-
ственном комитете СССР по делам издательств,
полиграфии к книжкой торговли. 190000, Ленин-
град, Прачечный переулок, 6. Зак. 662.
С.РКеплен, Э.Эссиг
Биоэнергетика
и линейная
термодинамика
необратимых
процессов