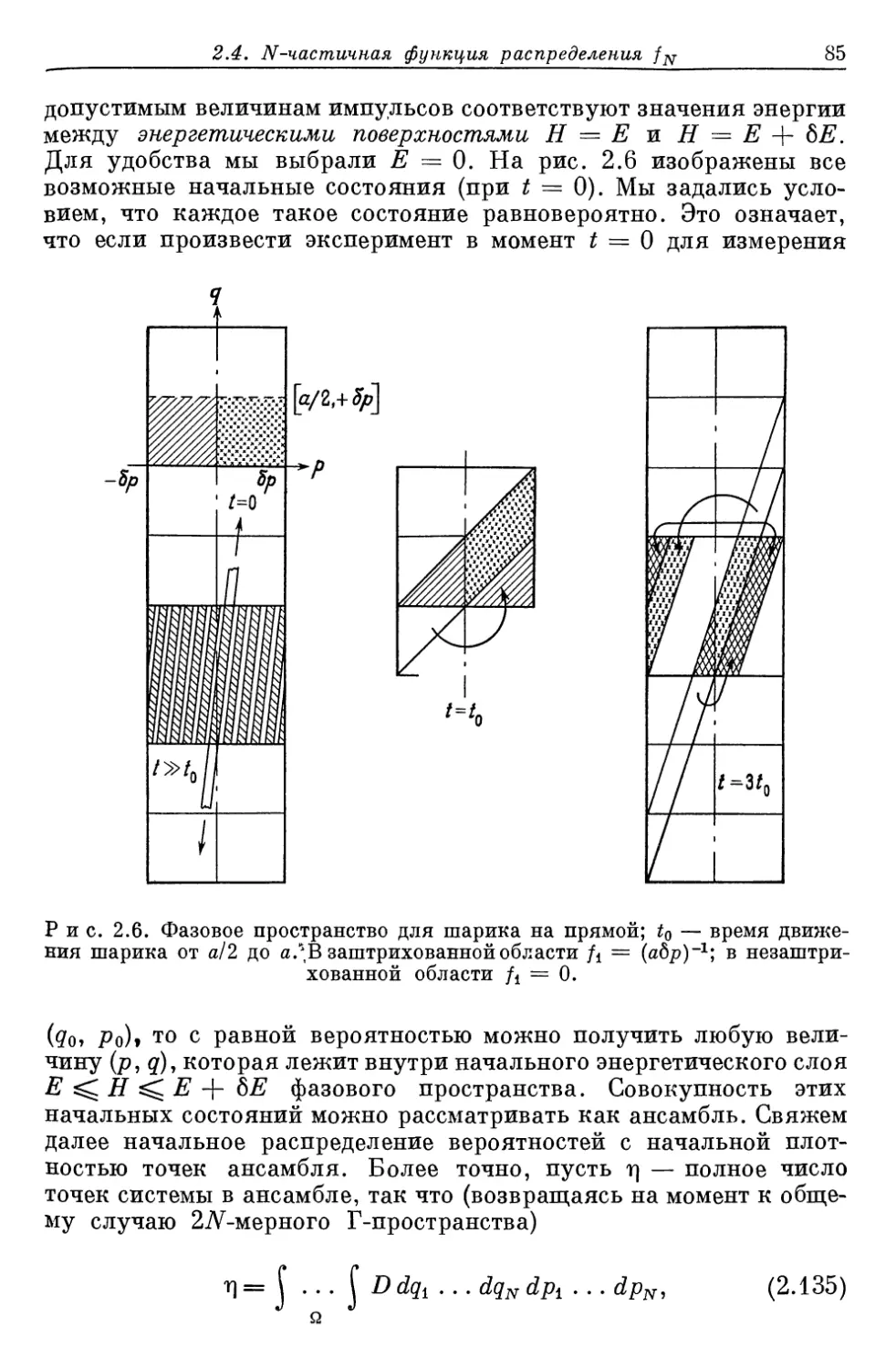
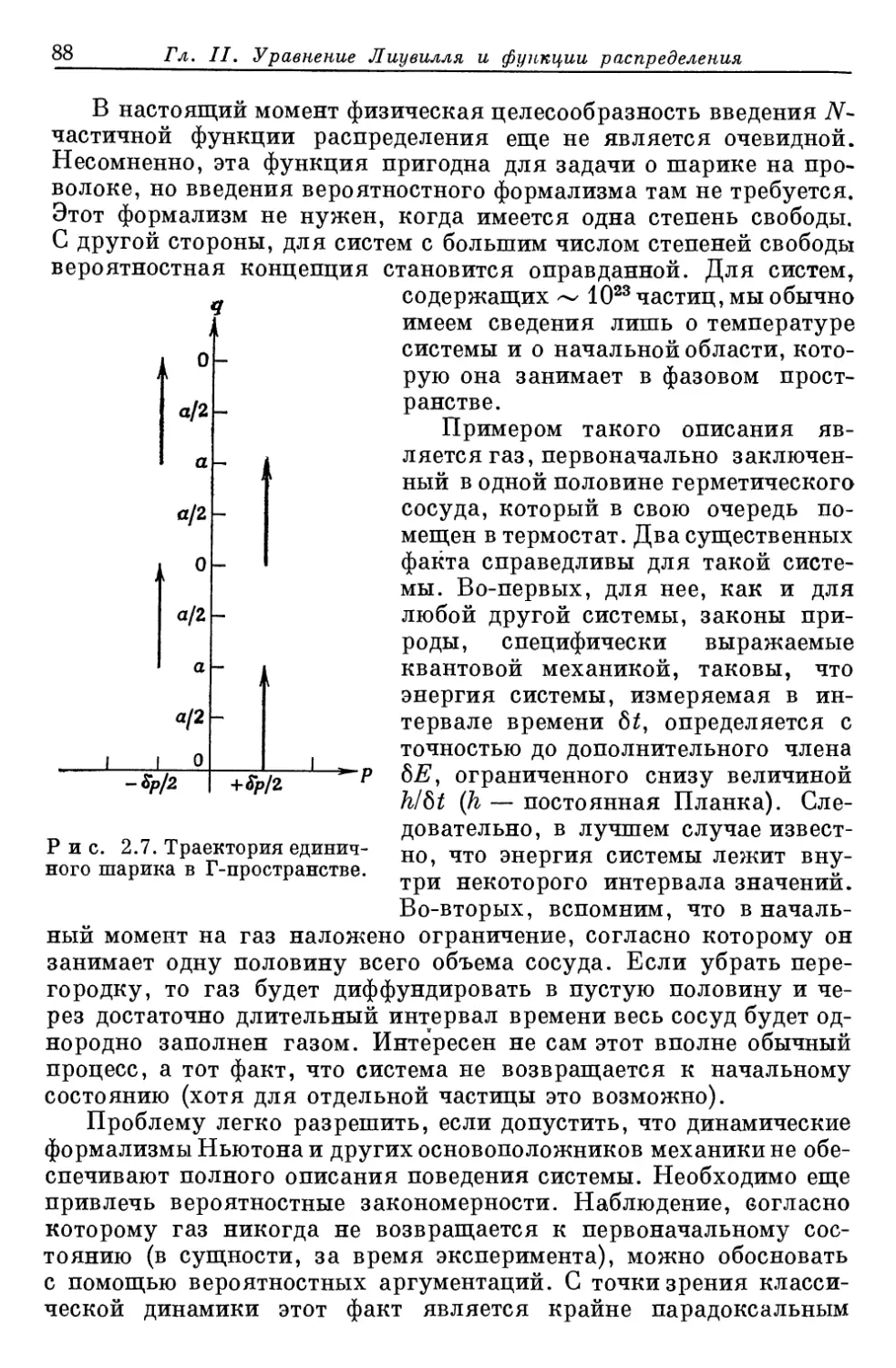
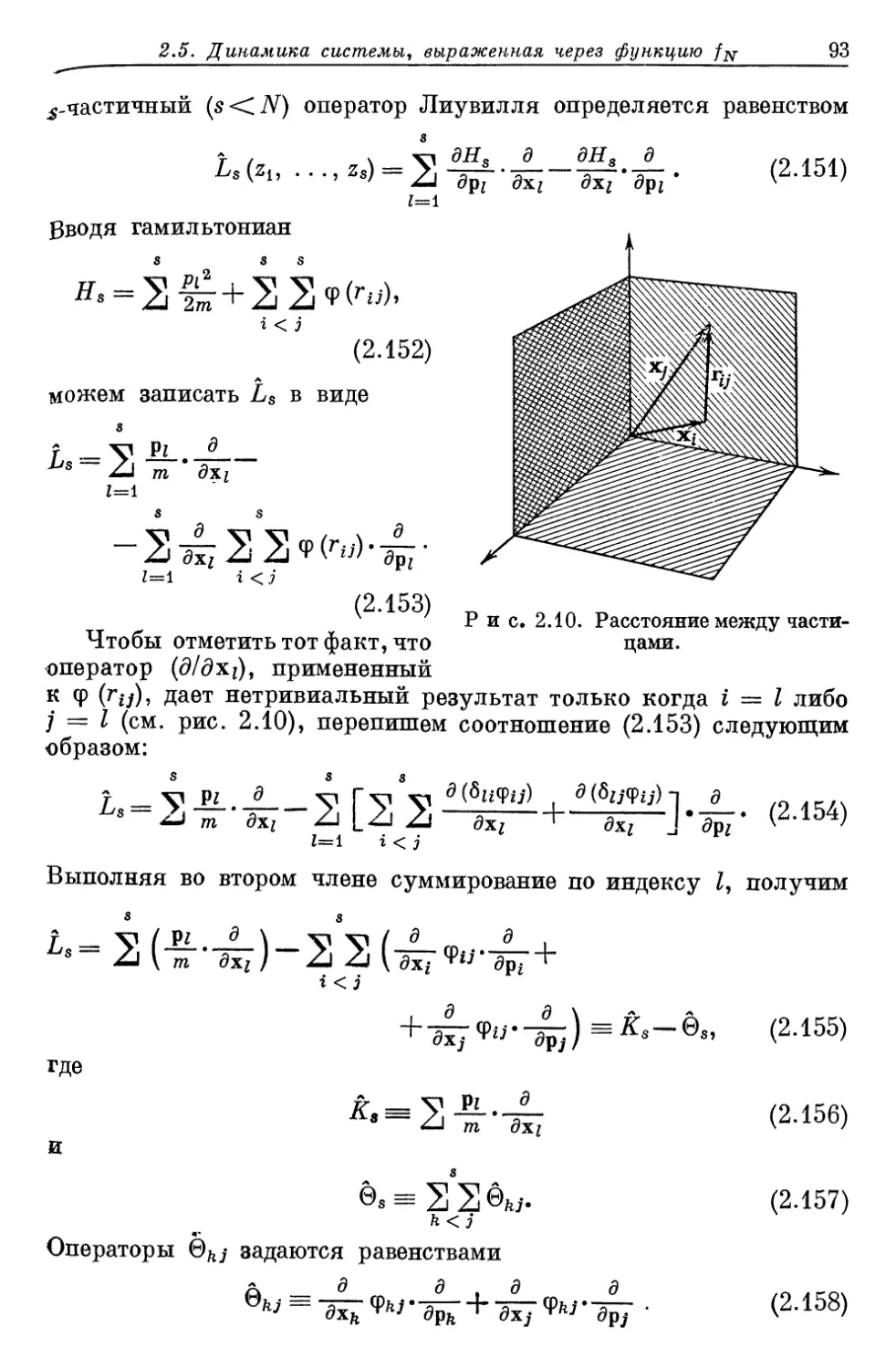
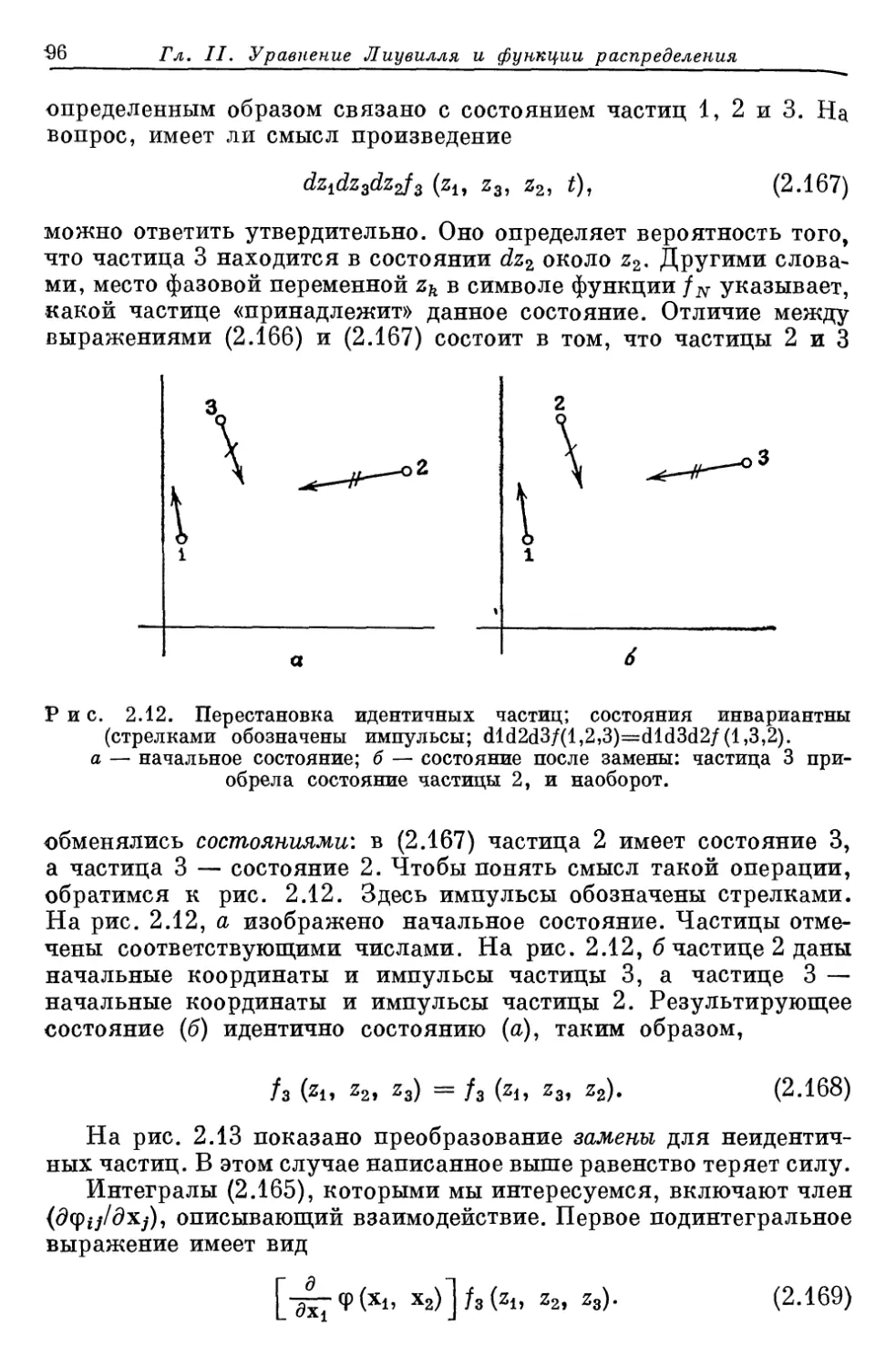
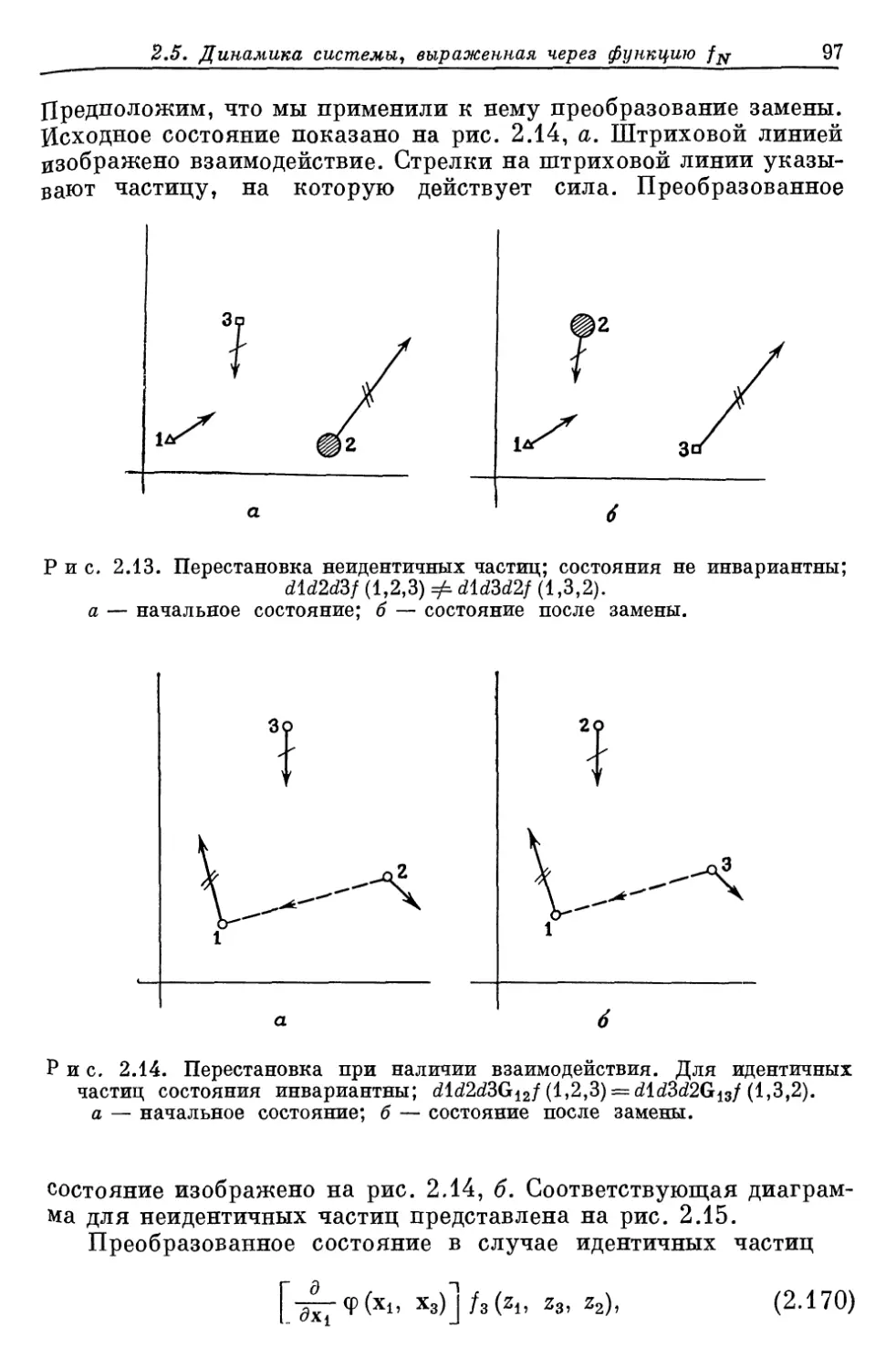
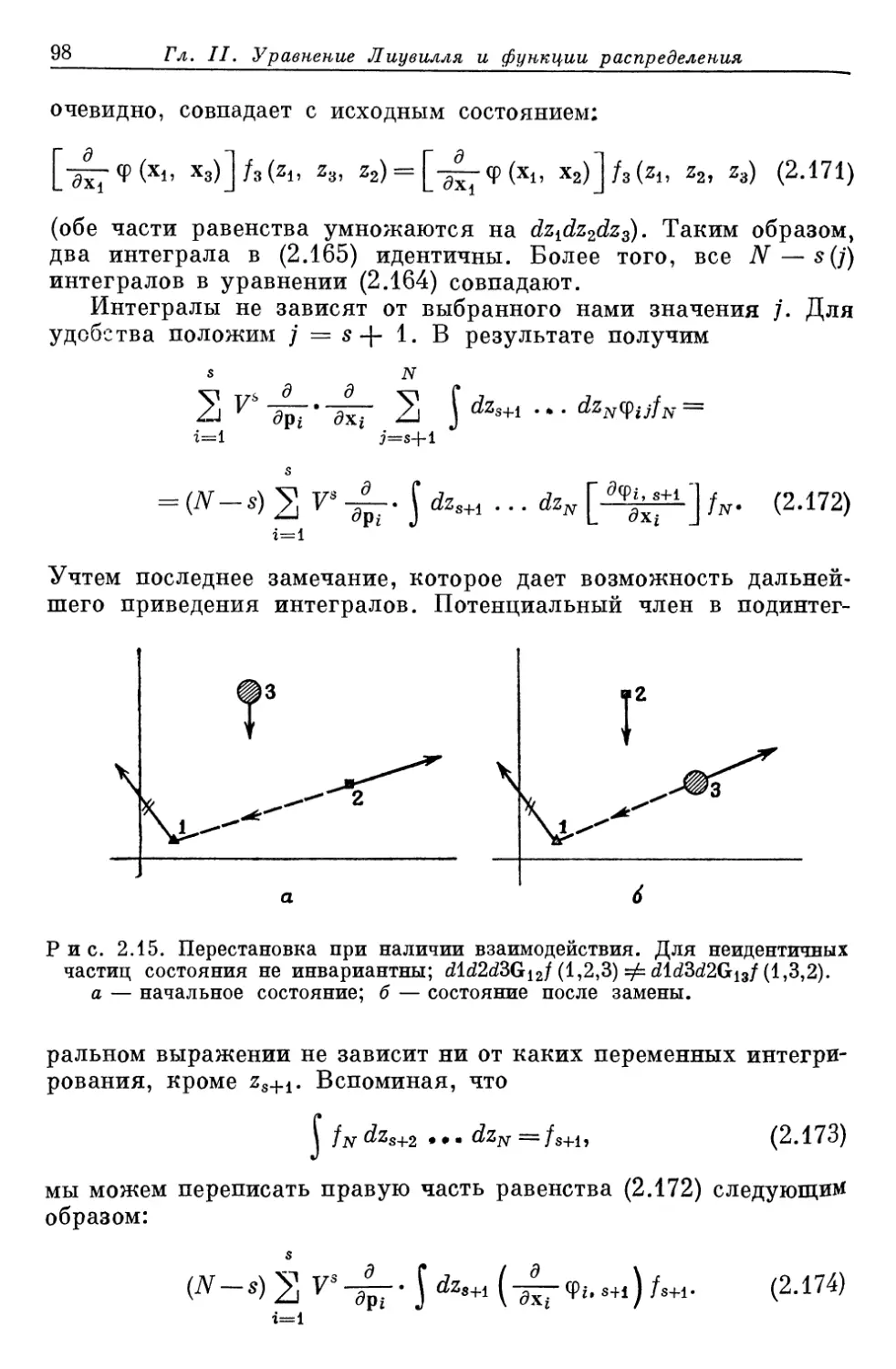
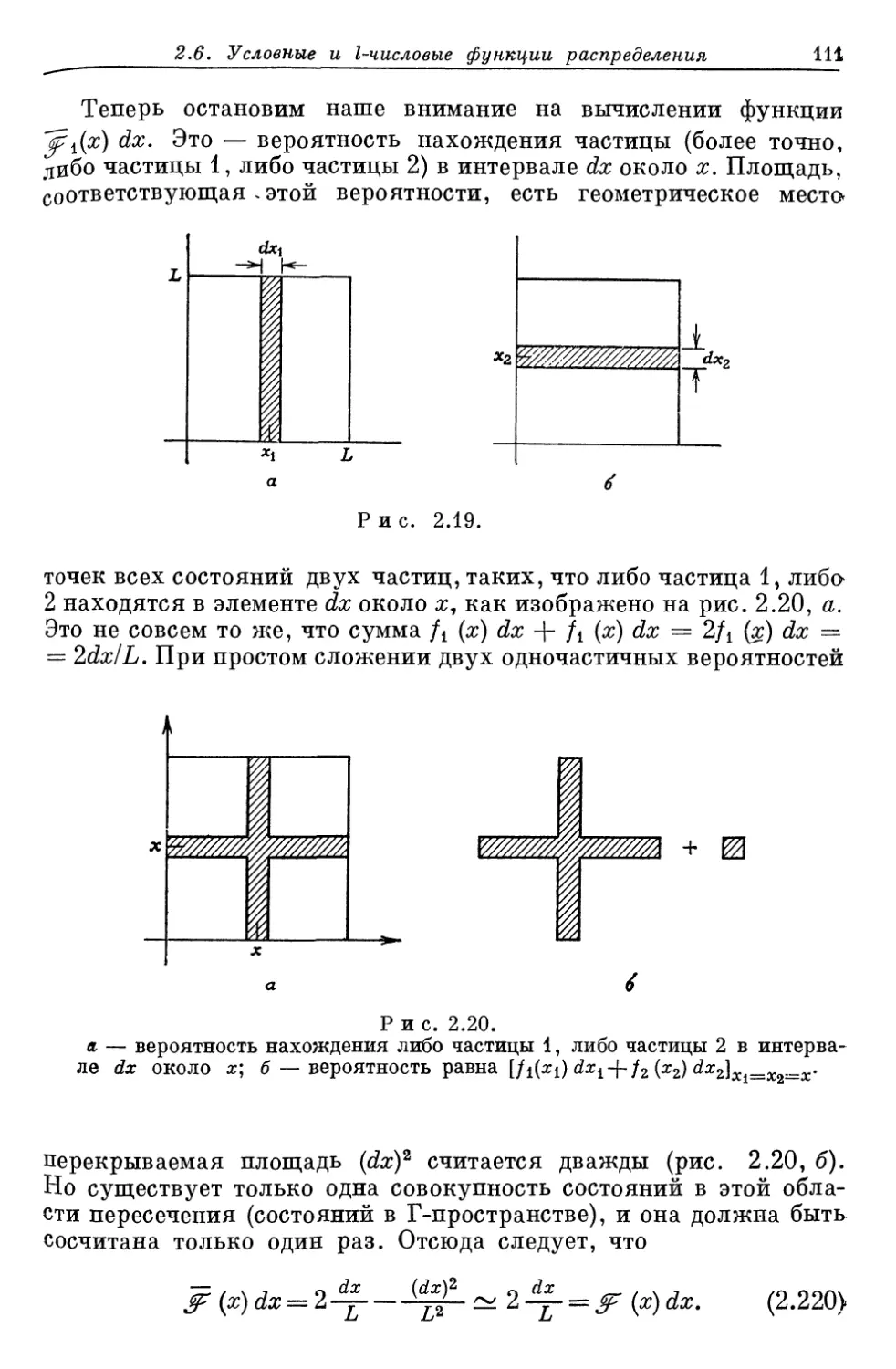
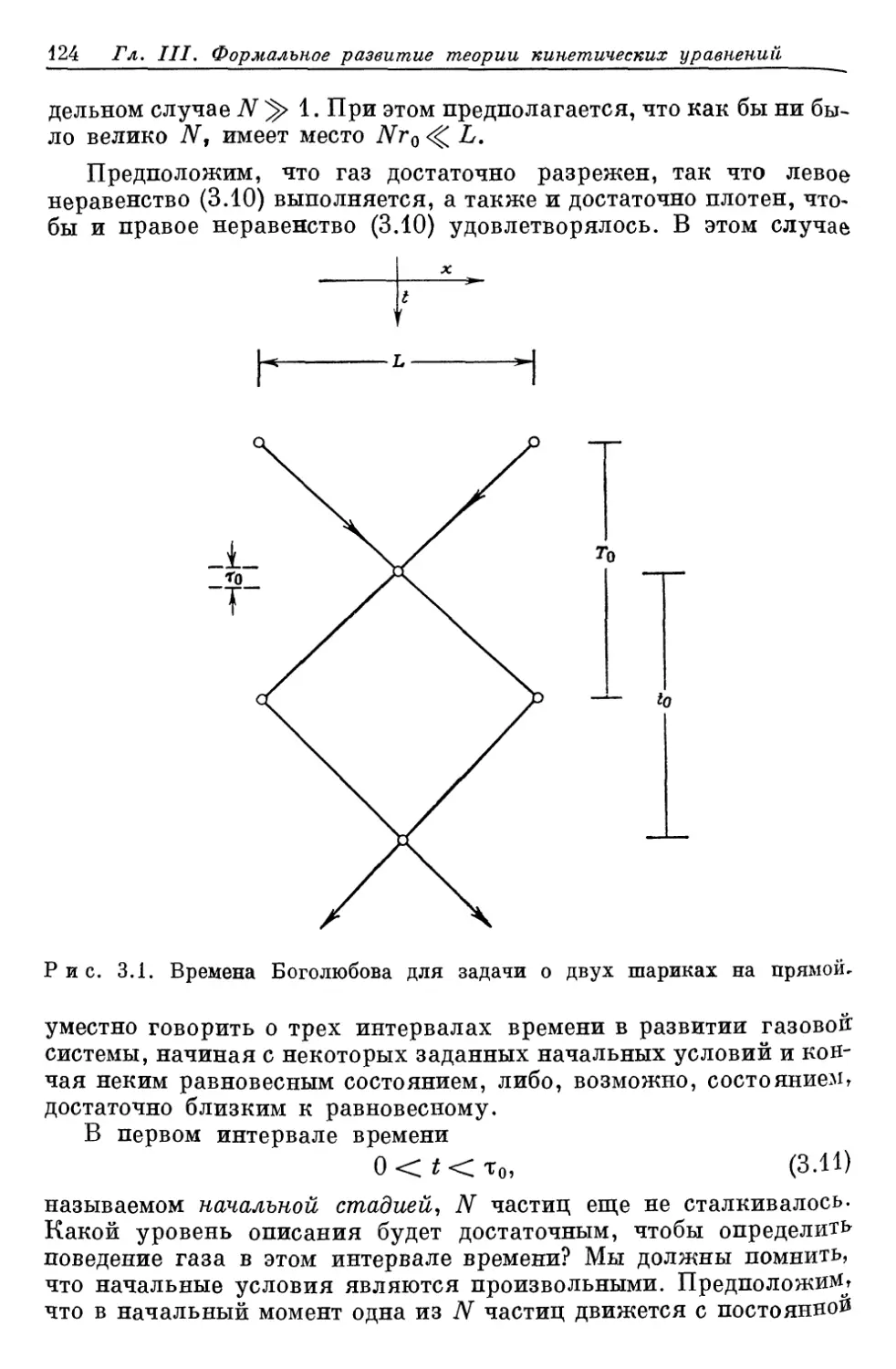
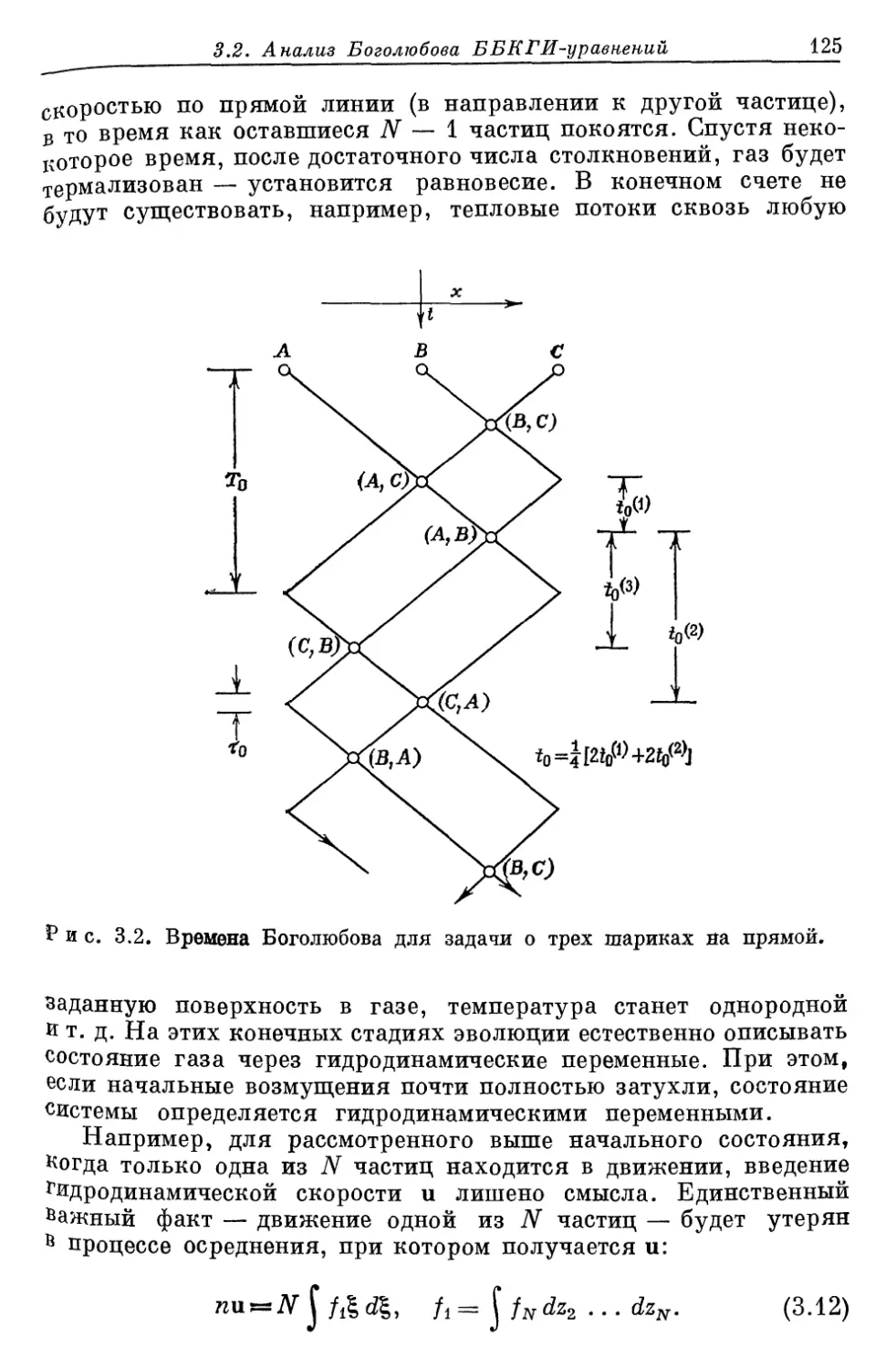
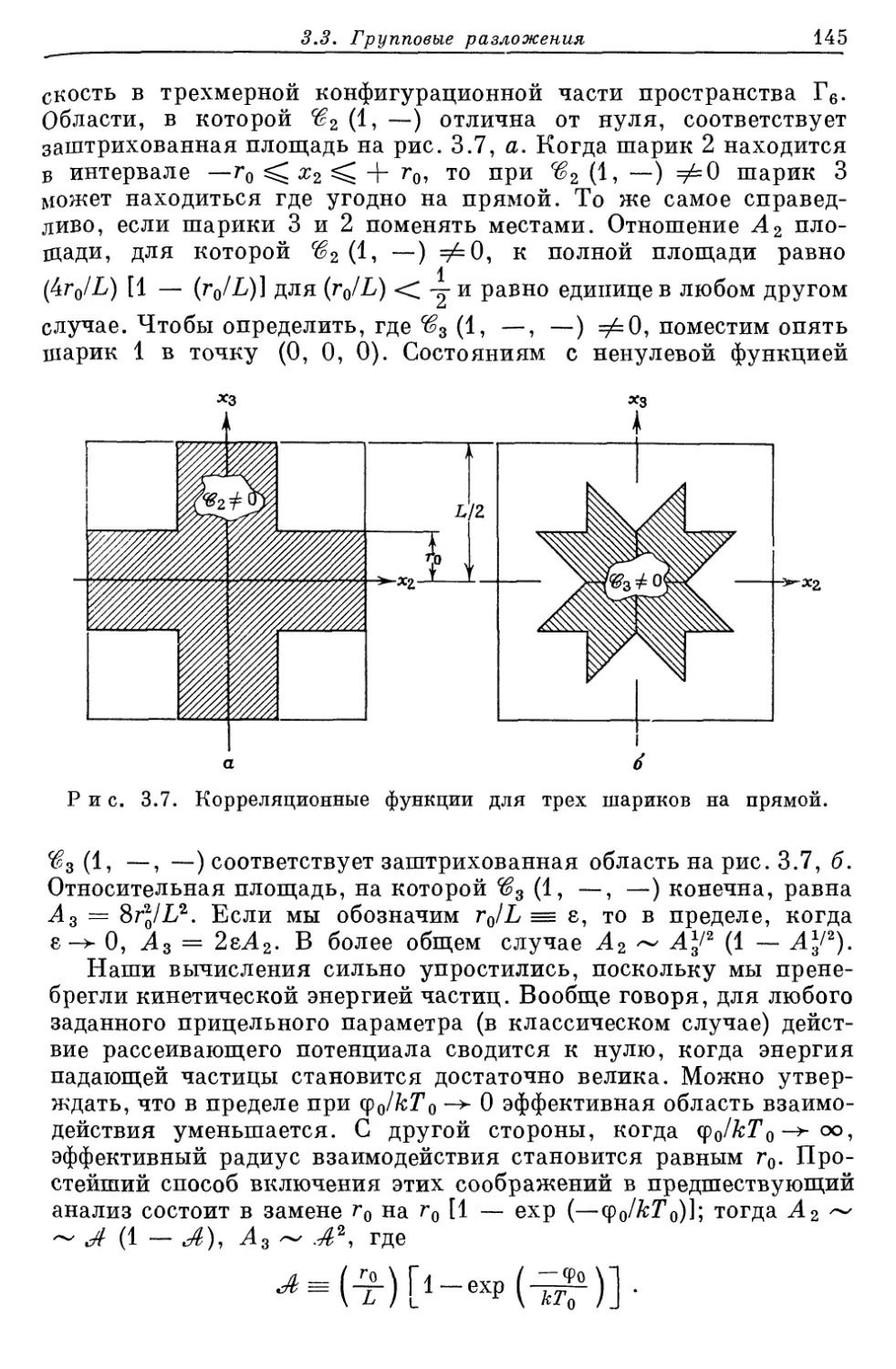
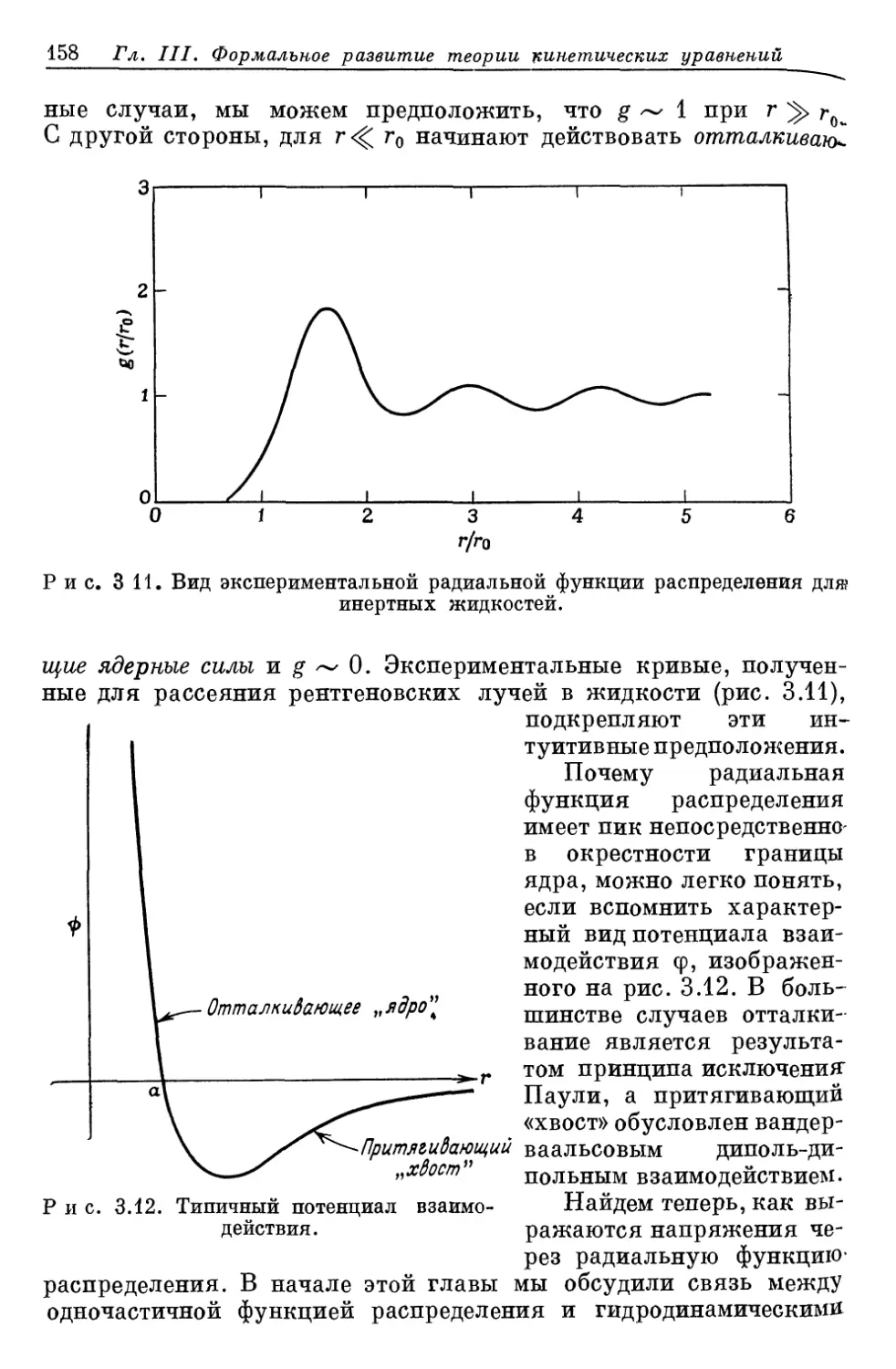
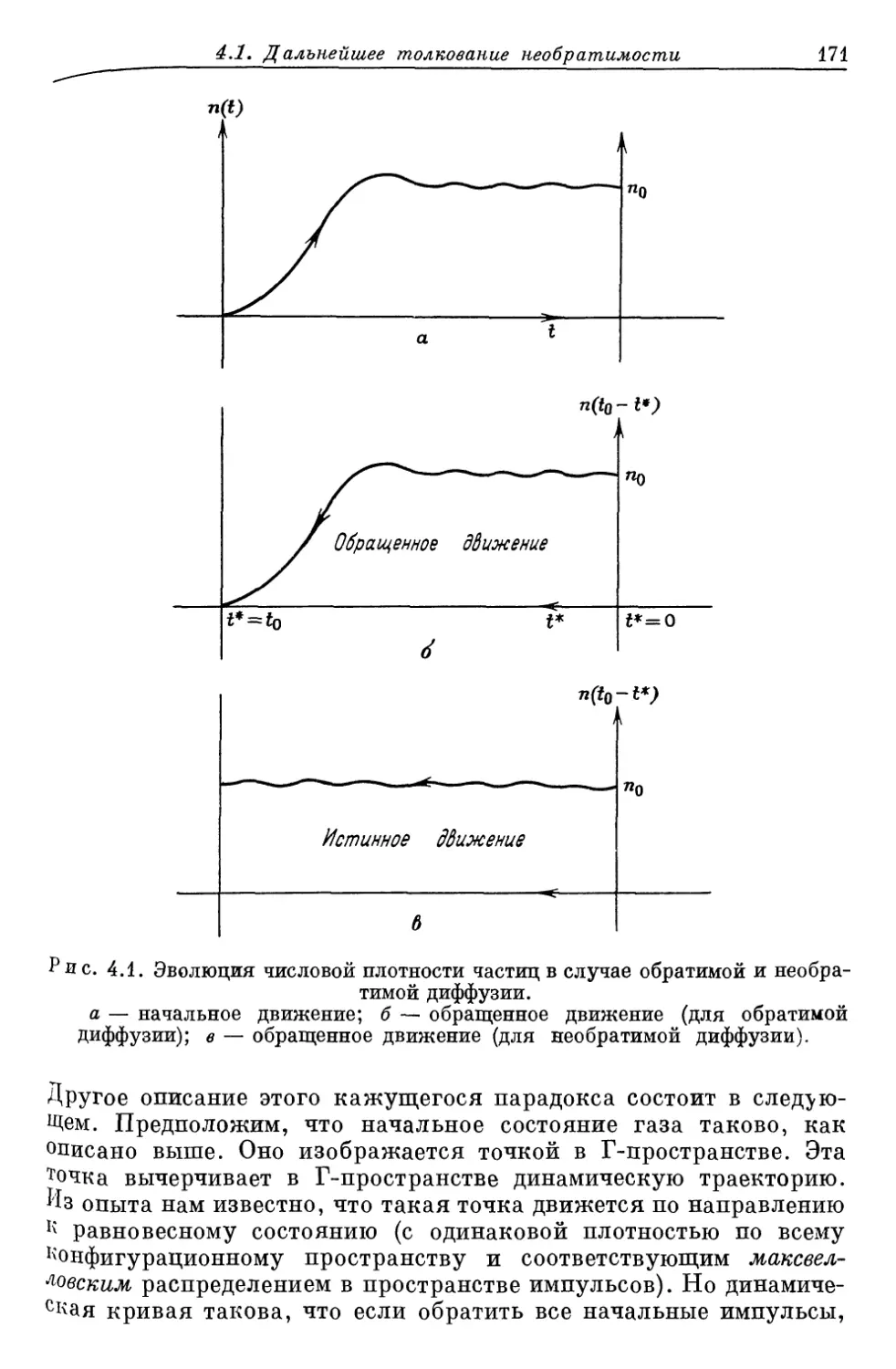
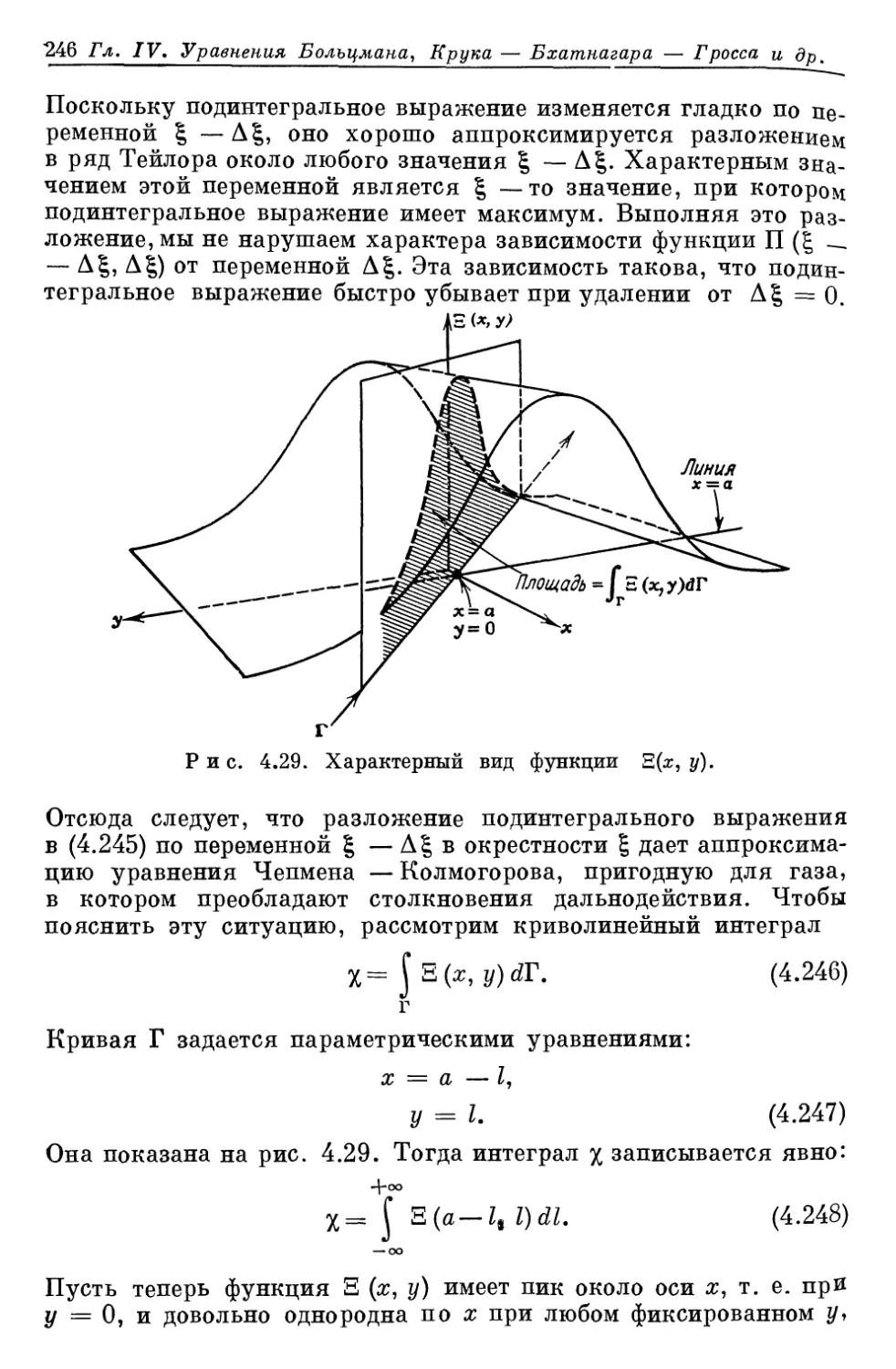
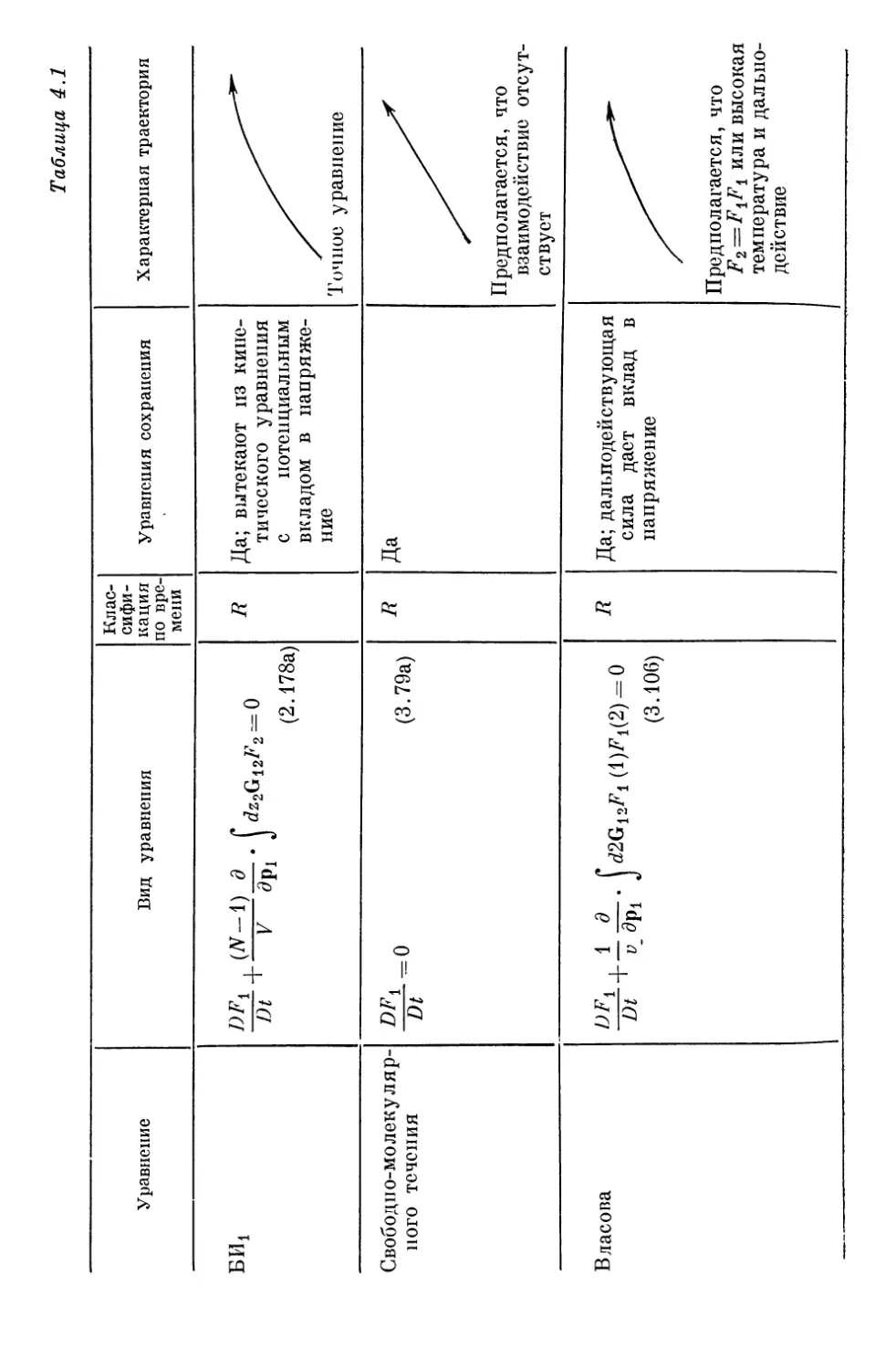
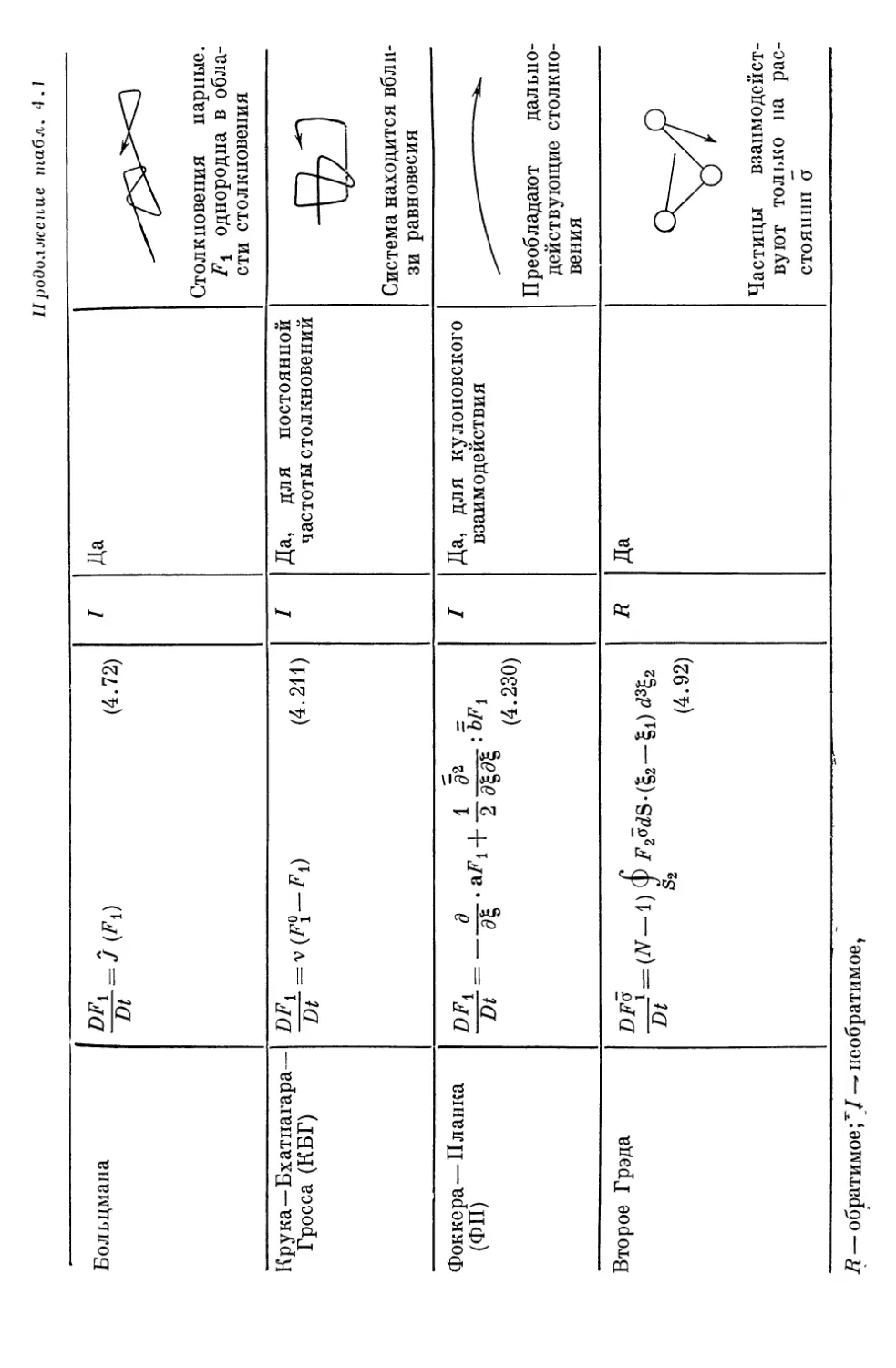
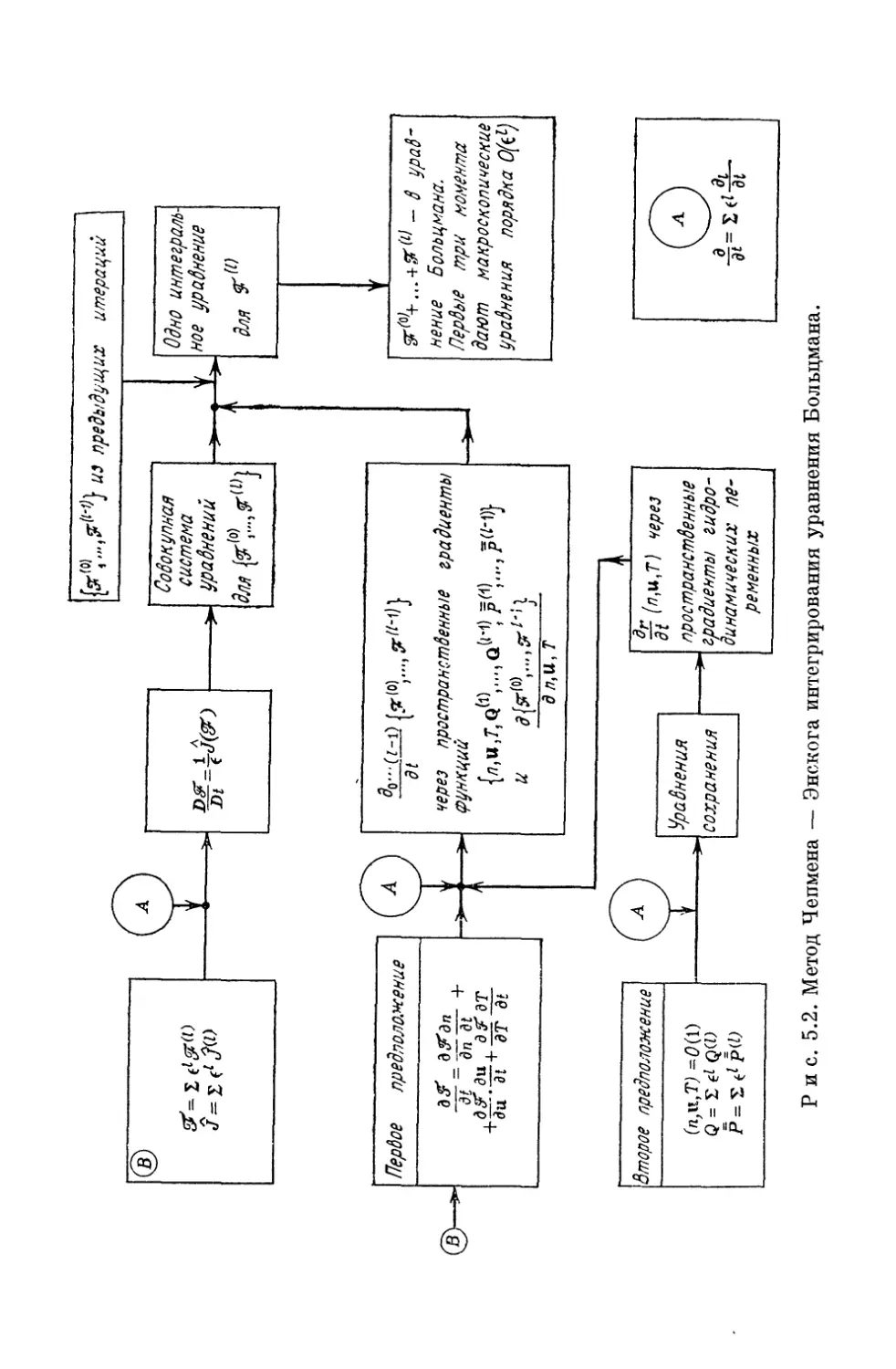
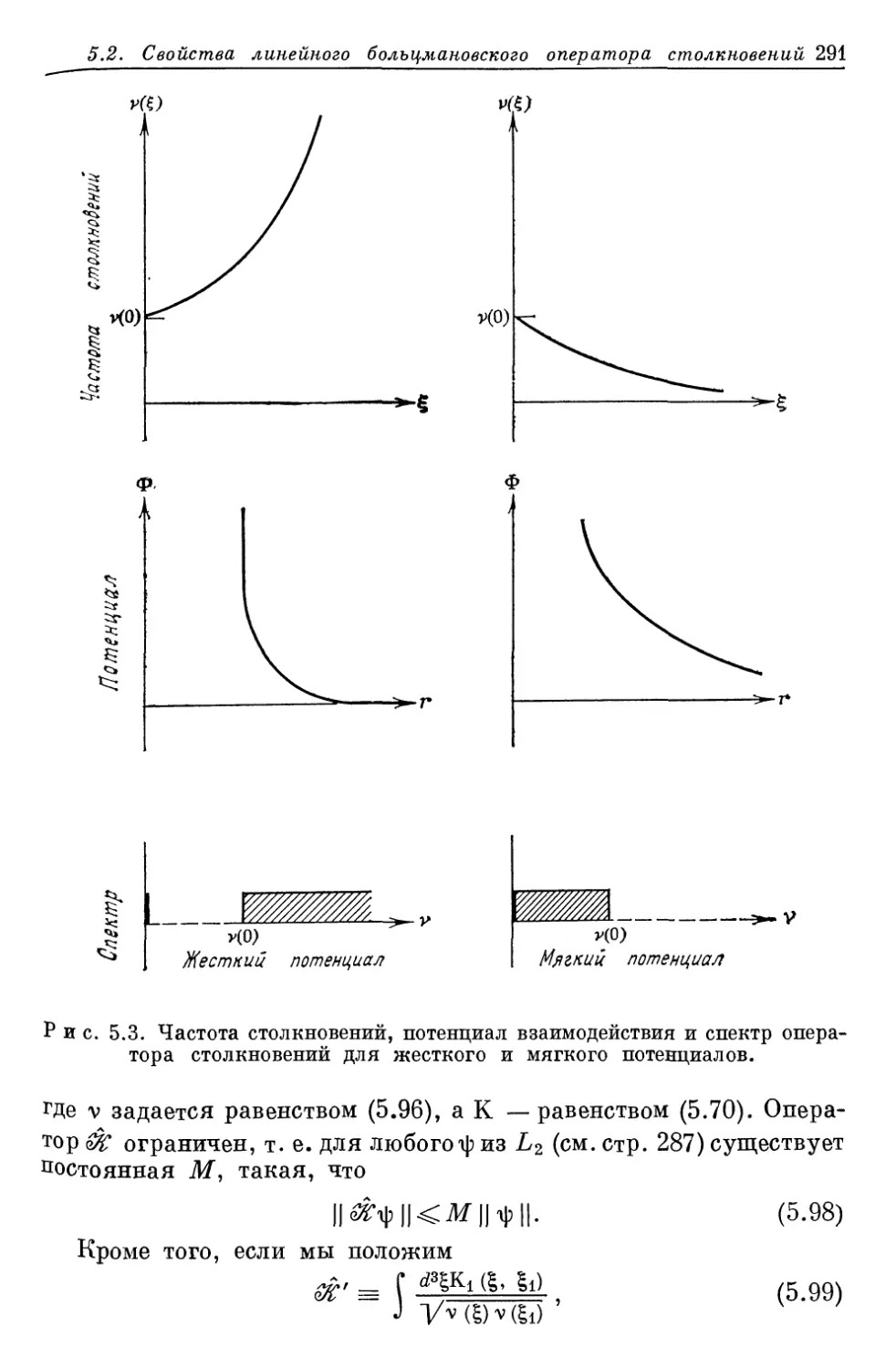
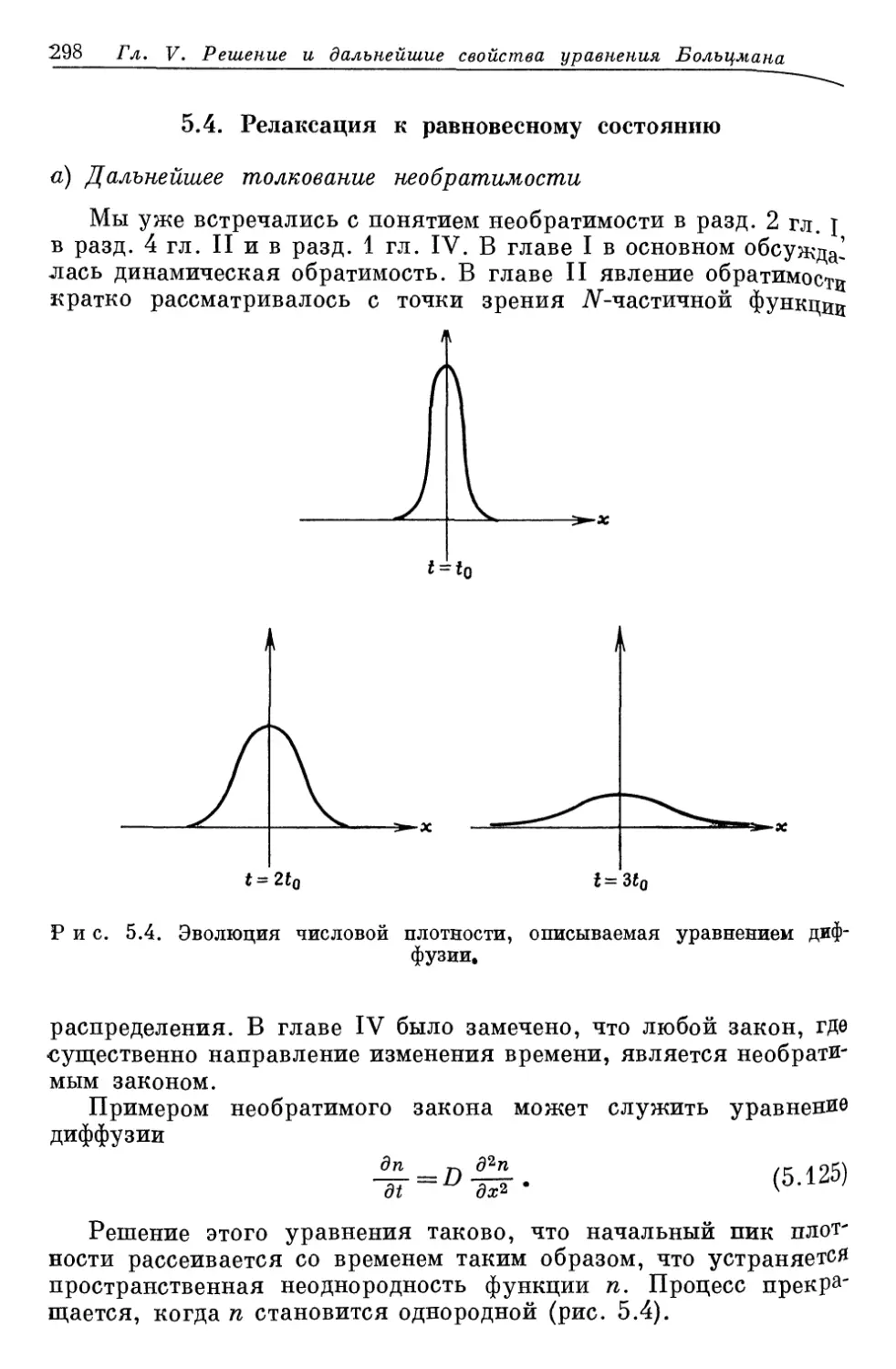
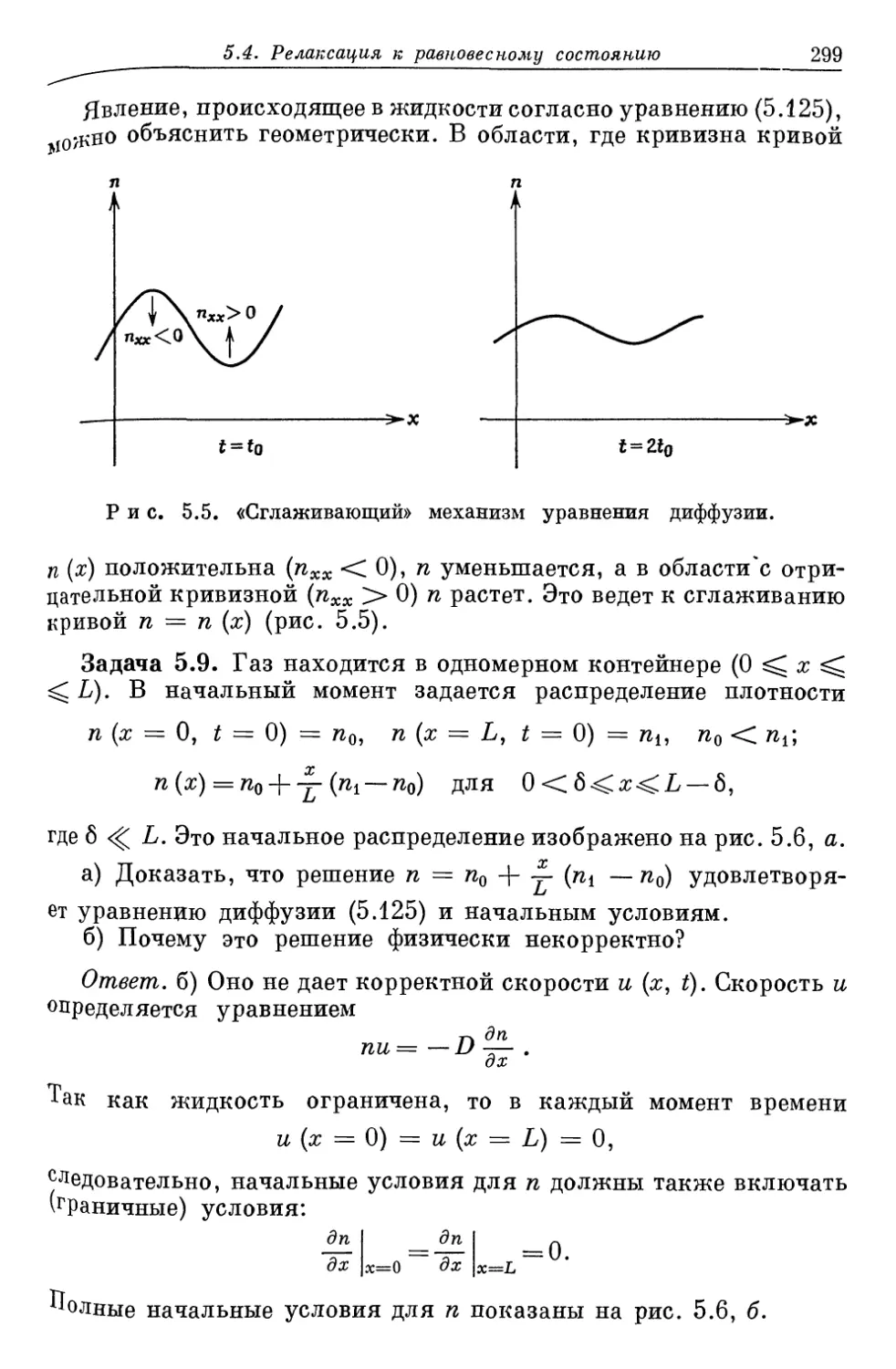
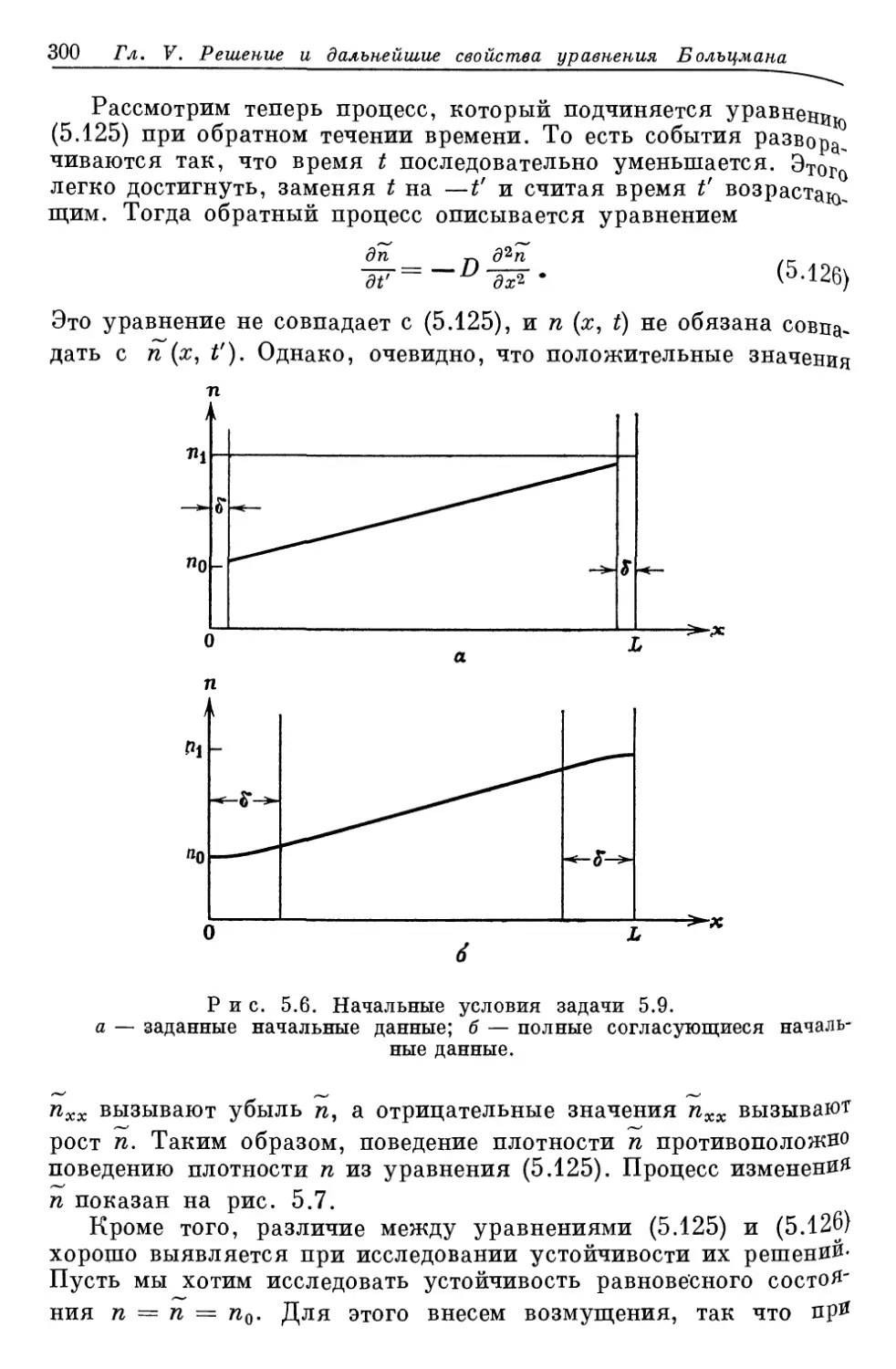
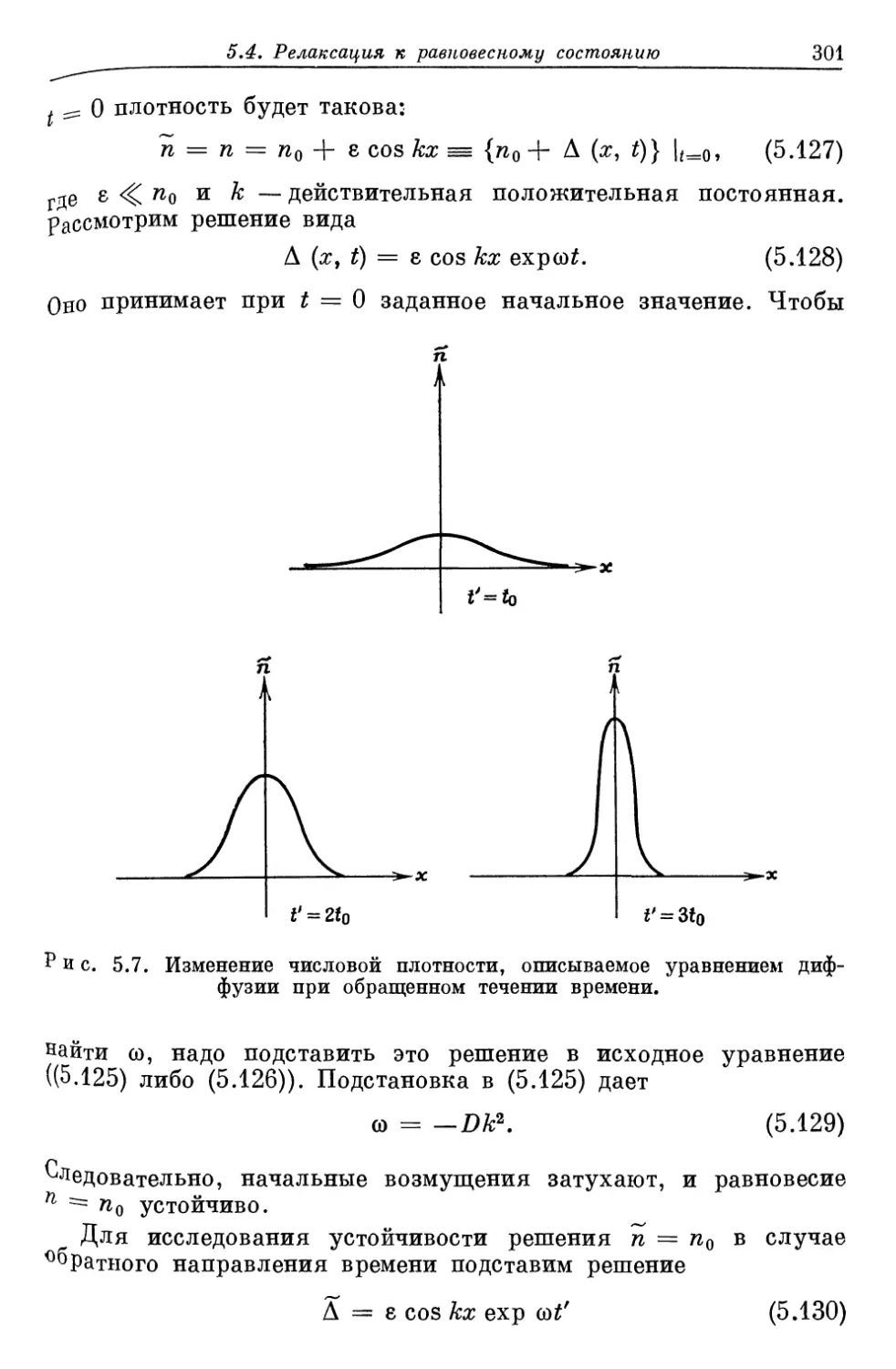
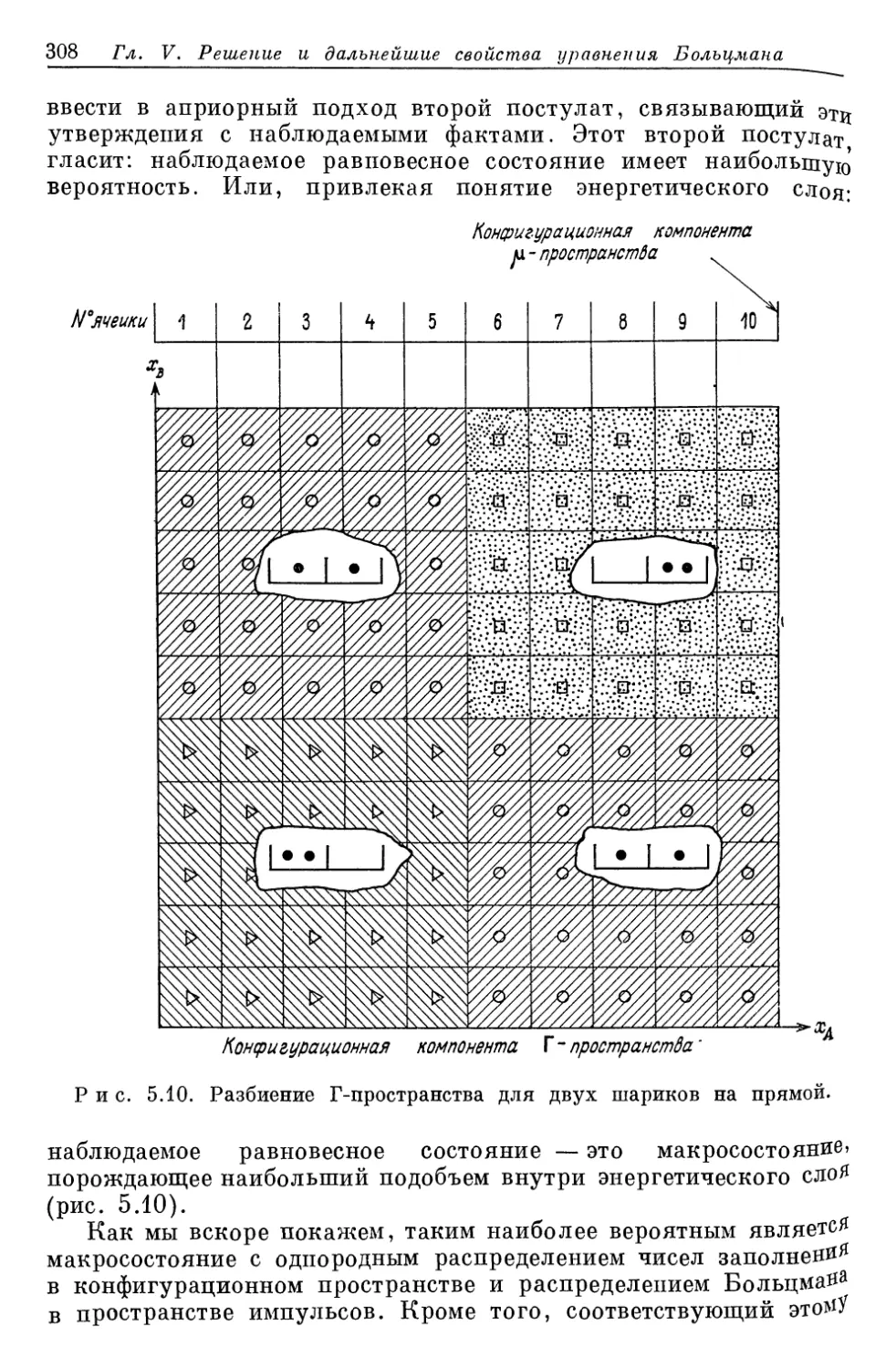
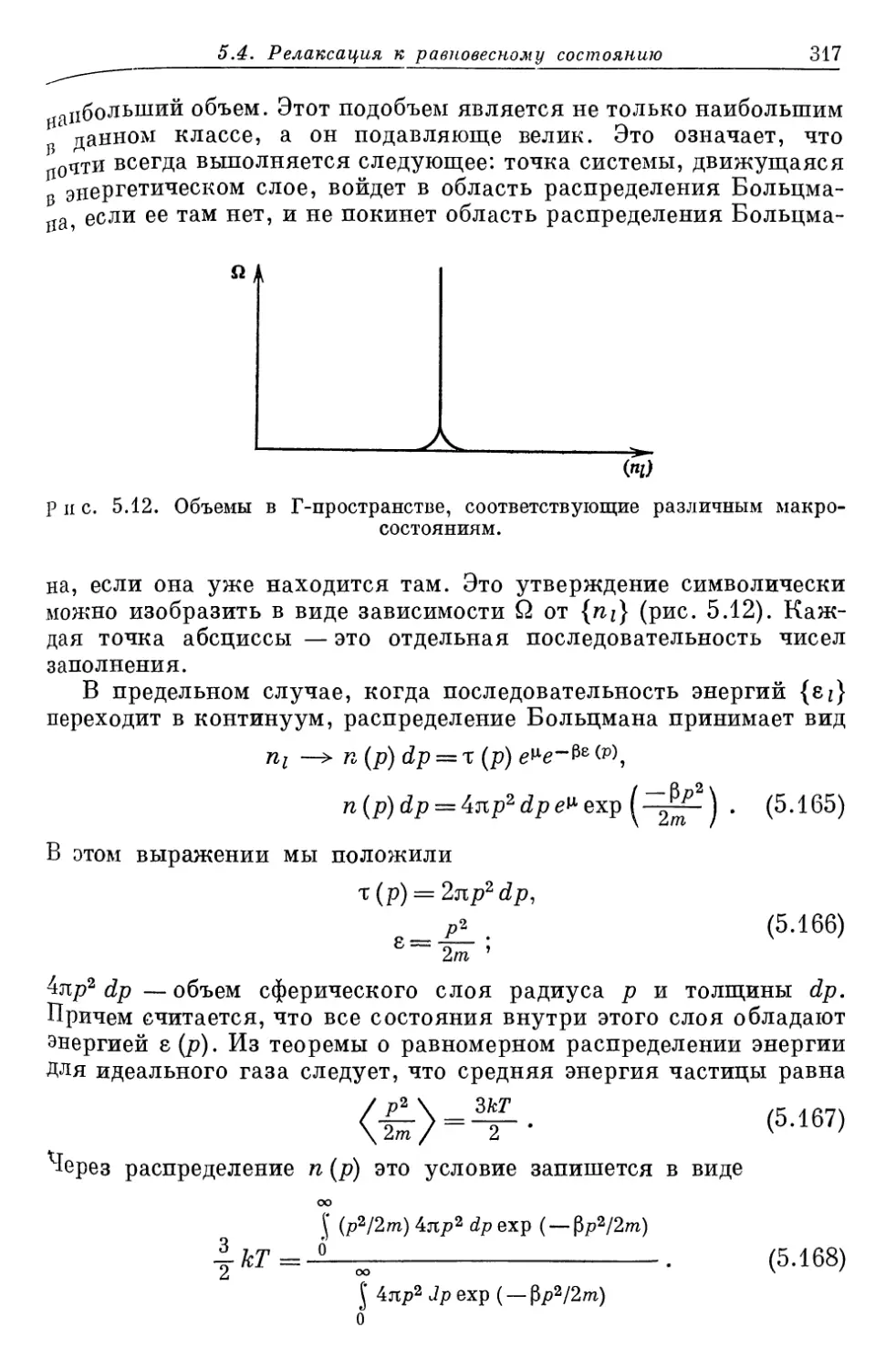
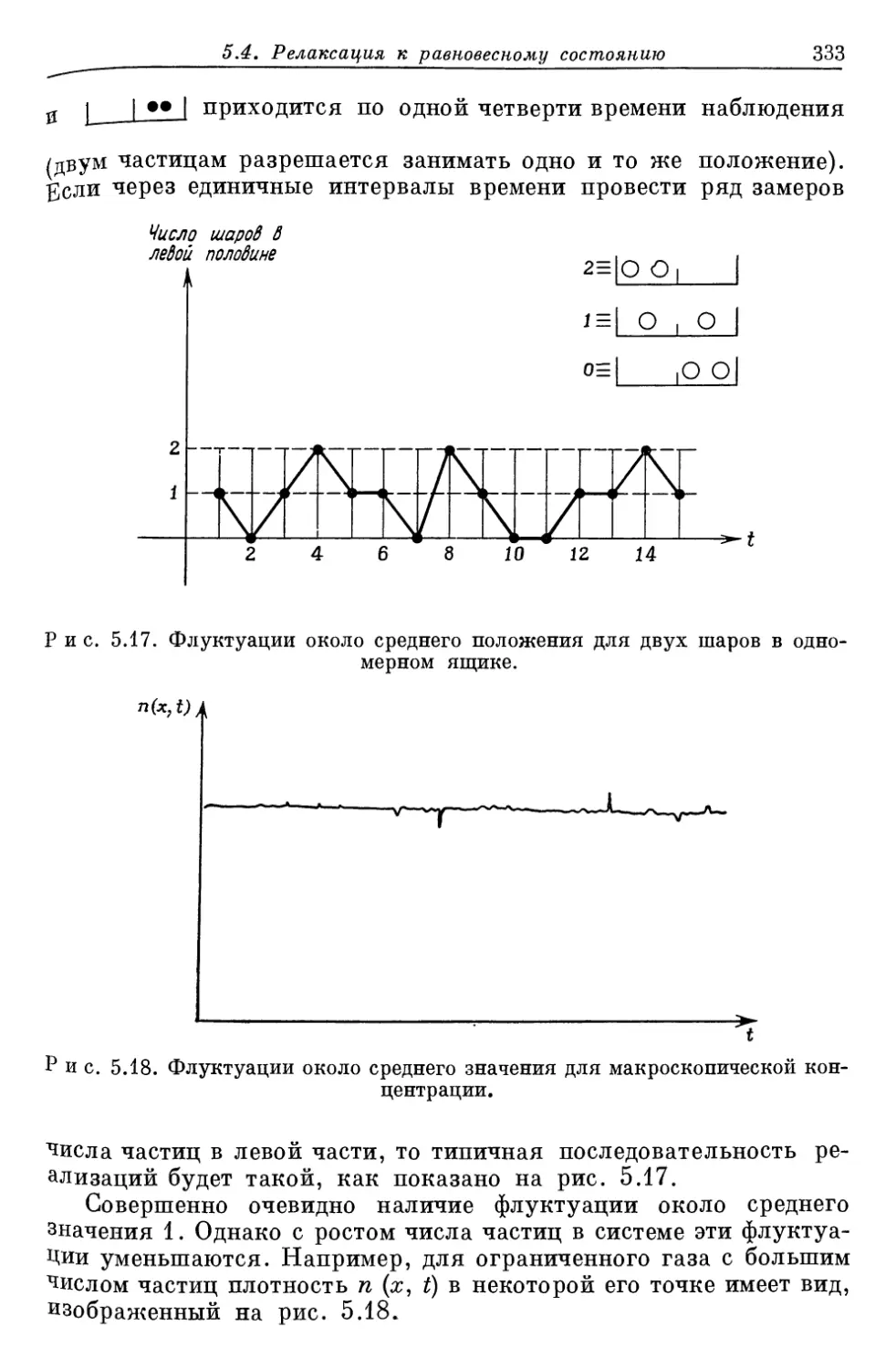
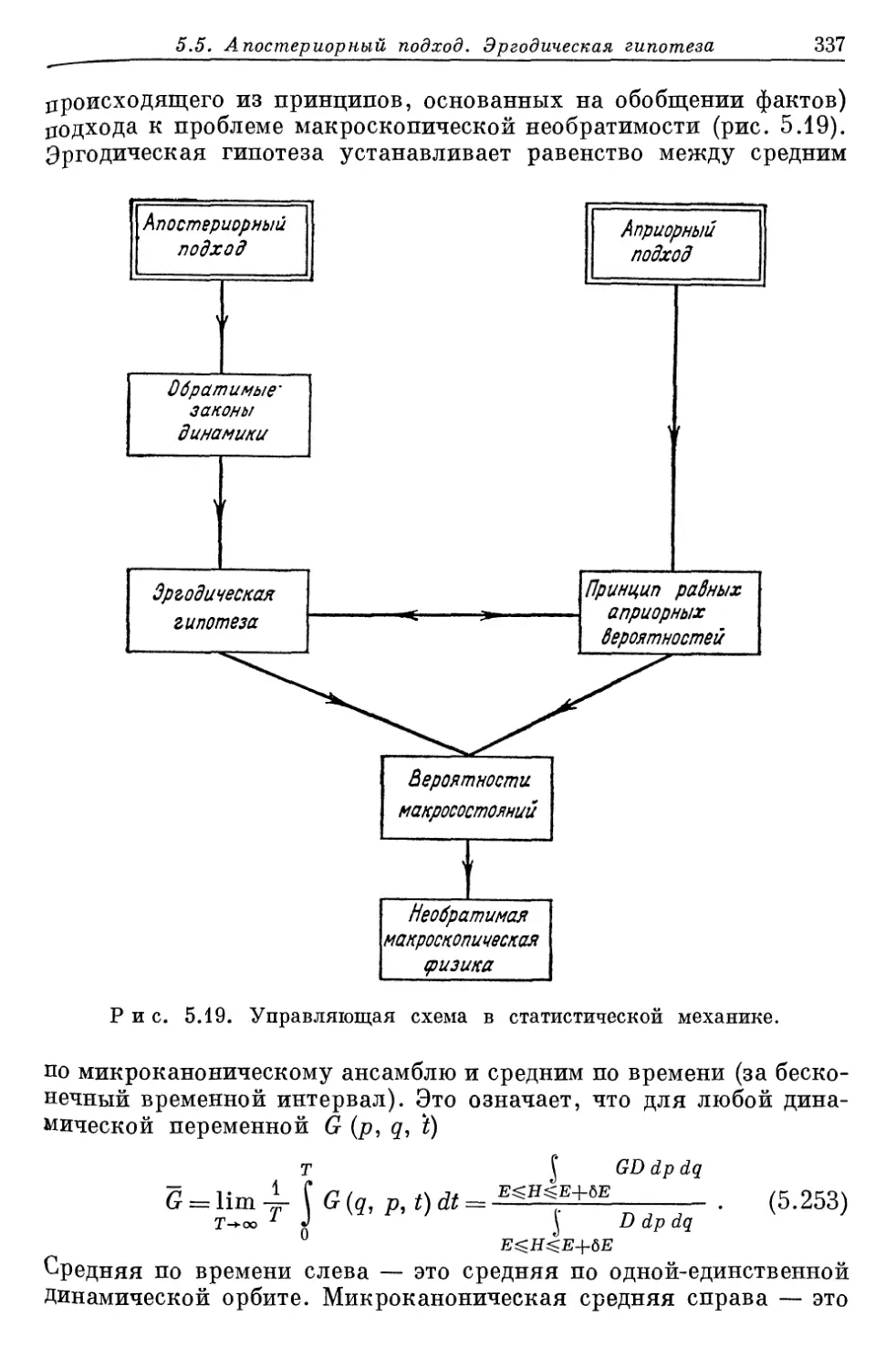
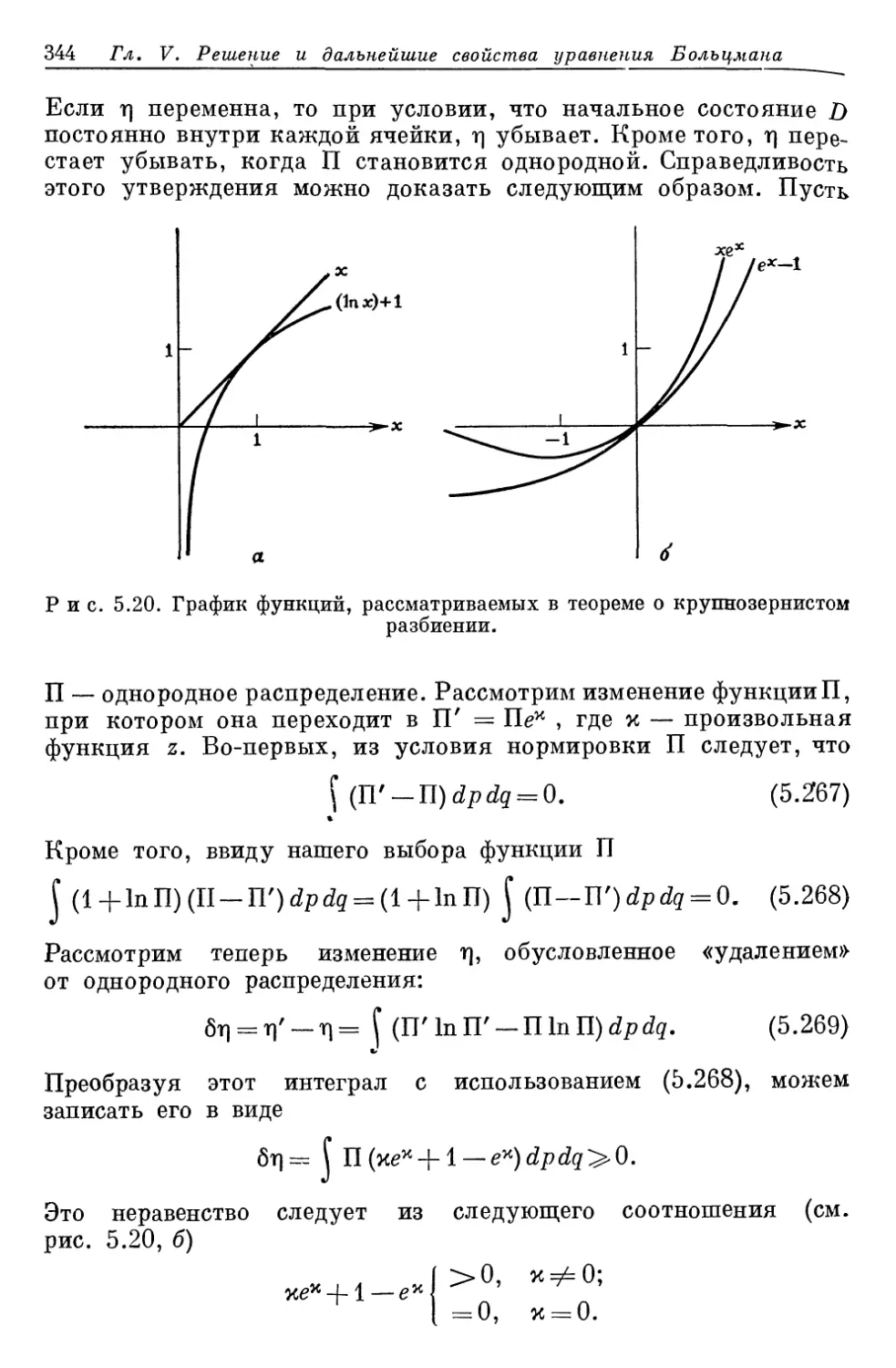
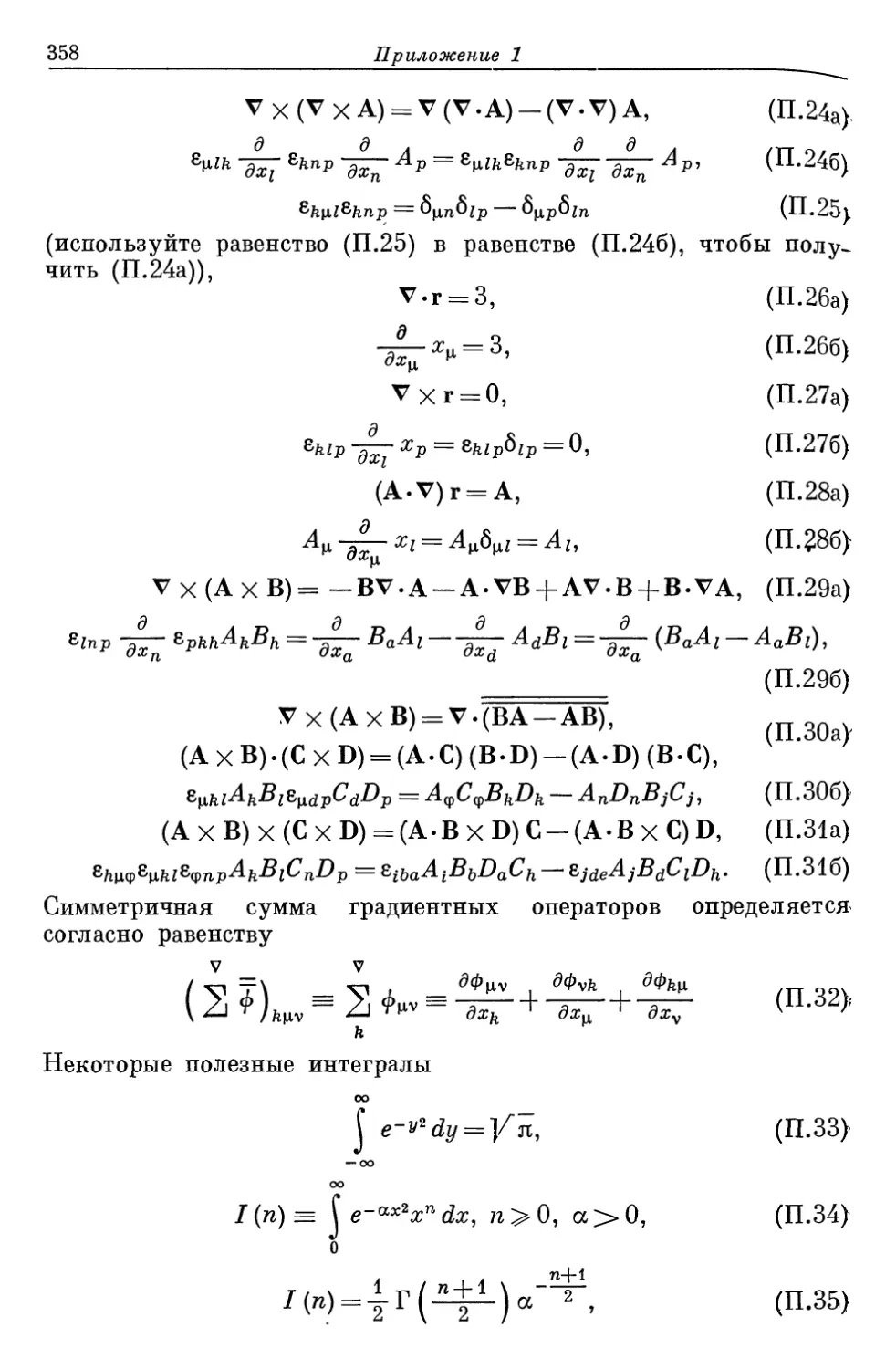Author: Либов Р.
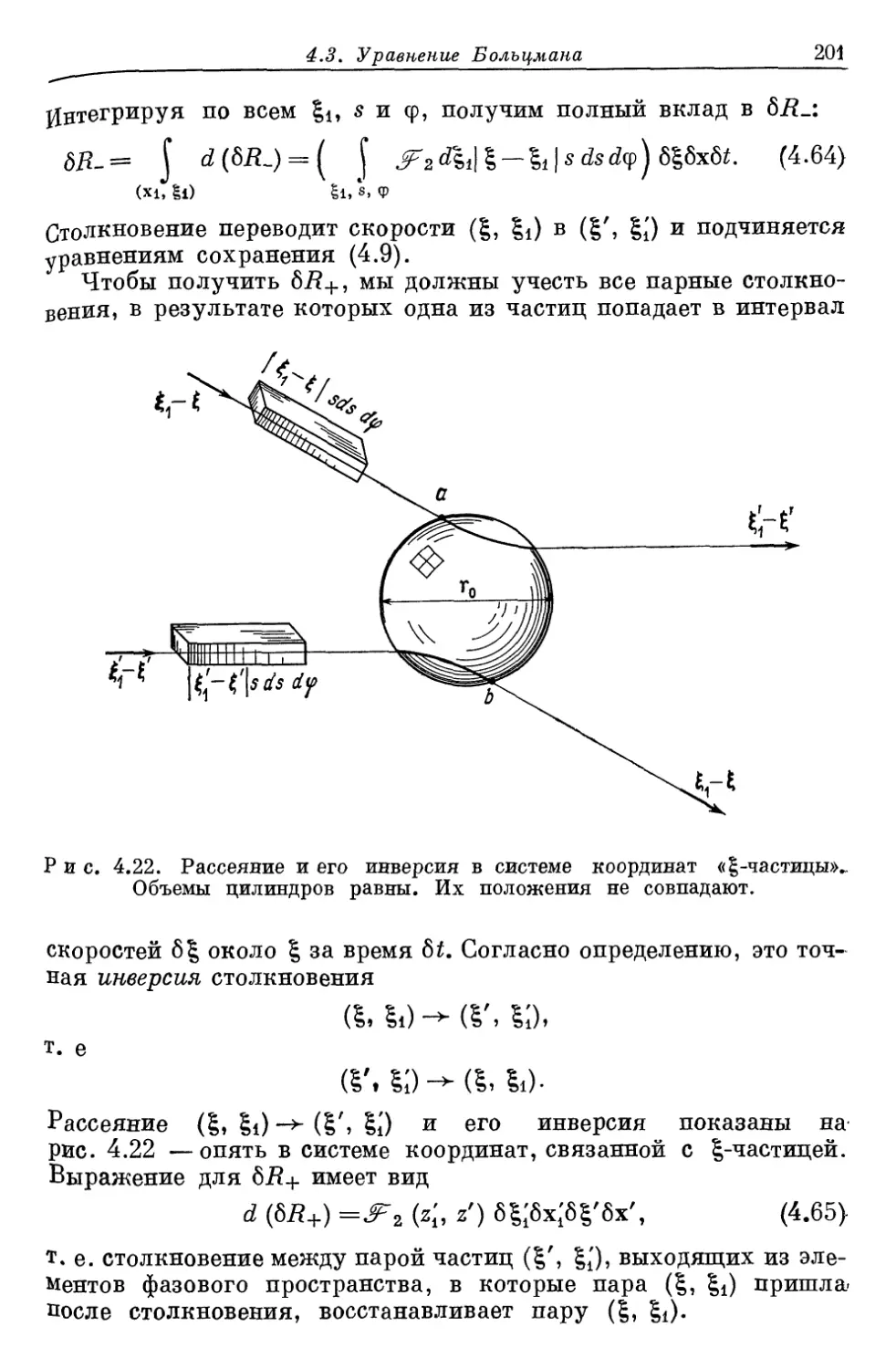
Tags: кинетическая теория газов непрерывность агрегатных состояний физика математика кинетика
Year: 1974
Text
РЛИБОВ
ВВЕДЕНИЕ
В ТЕОРИЮ
КИНЕТИЧЕСКИХ
УРАВНЕНИЙ
INTRODUCTION TO THE THEORY
OF KINETIC EQUATIONS
RICHARD L. LIBOFF
CORNELL UNIVERSITY
JOHN WILLEY and SONS, INC.
NEW YORK • LONDON • SYDNEY • TORONTO
1969
Р. ЛИБОВ
ВВЕДЕНИЕ В ТЕОРИЮ
КИНЕТИЧЕСКИХ УРАВНЕНИЙ
Перевод с английского
О. И. ТКАЧЕНКО
Под редакцией
Л. П. СМИРНОВА
Издательство «Мир»
Москва 1974
У ДК 533.7
Интерес к кинетическим уравнениям связан с возмож-
возможностью их применения в различных областях механики и физи-
физики — в кинетической теории газа, механике взвешенных
частиц, плазме, астрофизике, теории реакторов. Книга Р. Ли-
бова написана как учебник повышенного типа. В ней дано
ясное изложение основ теории кинетических уравнений, обсуж-
обсуждаются методы анализа уравнения Больцмана, рассмотрены
вопросы о приближении к равновеспому состоянию, о соотно-
соотношении между микро- и макросостояниями. Устанавливается
связь между известными теориями и обсуждаются области
их применимости.
Богатство содержания и методические достоинства книги
делают ее весьма ценной для различных специалистов по при-
прикладной математике, механике, физике. Она может служить
учебником повышенного типа для студентов и аспирантов
физико-технических специальностей.
Редакция литературы по математическим наукам
20302—044
Л Q4i/Qn_74 44-74 © Перевод на русский язык, «Мир», 1974
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Вниманию читателя предлагается весьма своеобразная по содер-
содержанию и построению книга Р. Либова, посвященная кинетическим
уравнениям, их обоснованиям, выводу при различных условиях
и получающимся из них следствиям.
В настоящее время метод кинетических уравнений получил
широкое развитие и применение в механике жидких и газообраз-
газообразных сред, при исследованиях плазмы, в задачах о движения
газовых смесей при наличии протекающих в них релаксационных
или химических процессов. Делаются более или менее удачные
попытки использовать кинетические методы также в механике
аэрозолей, при изучении дисперсных и многофазных сред. Вопро-
Вопросы обоснования применяемых макроскопических уравнений наи-
наиболее удобно и просто разрешаются путем обращения к методам,
истоки которых лежат в основополагающих работах Больцмана
по кинетической теории газа. Вычисление коэффициентов пере-
переноса (коэффициентов вязкости, теплопроводности, диффузии)
для простых и сложных систем также является прерогативой
кинетических подходов.
Несомненно, что значение и место кинетических методов в со-
современной механике газоподобных и жидких сред требует при
обращении к ним хорошей ориентировки в вопросах о пределах
их применимости, их обоснованиях, связях между различными
модификациями кинетических уравнений и возможностями исполь-
использования при встречающихся условиях. Задачу освещения этих
вопросов поставил перед собой автор настоящей книги и довольно
успешно решил ее. В этой книге собраны воедино сведения о раз-
различных кинетических уравнениях и подходах и дано их сопостав-
сопоставление.
В первой главе автор дает краткий обзор основных положений
аналитической динамики, включая лагранжевы и гамильтоновы
уравнения, скобки Пуассона, канонические преобразования, тео-
теорию Гамильтона — Якоби и интегральных инвариантов Пуан-
Пуанкаре. Эта вводная глава позволит читателю, не обращаясь к спе-
специальной литературе, освежить в памяти имеющиеся у него сведе-
сведения по аналитической мехахрьй^л-шшентирует внимание читателя
Предисловие редактора перевода
на тех положениях динамики, которые лежат в основе вывода
кинетических уравнений.
Во второй главе рассматривается концепция ансамбля, уравне-
уравнение Лиувилля и его решение, а также различные виды функций
распределения. Здесь же дается представление о цепочке ББКГИ-
уравнений и об уравнении Чепмена — Колмогорова. Большое
внимание уделено анализу уравнения Лиувилля, проведенному
Пригожиным.
В третьей главе рассматриваются взаимоотношения между
кинетическими уравнениями и гидродинамикой, в первую очередь
на основе одночастичной функции распределения. Читатель зна-
знакомится с анализом Боголюбова цепочки ББКГИ-уравнений,
а также с другим подходом, связанным с введением корреляцион-
корреляционных функций и групповых разложений. В зависимости от зна-
значений определяющих параметров, связанных с близко- или даль-
дальнодействием наложенных силовых полей, степенью разреженно-
разреженности газа, его температурой и интенсивностью взаимодействий
молекул, изучаются различные случаи получения соответствую-
соответствующей цепочки уравнений и их решения. Здесь же в качестве при-
примера кинетического уравнения рассматривается уравнение Вла-
Власова. Особо обсуждается радиальная функция распределения
и получающееся при ее использовании уравнение состояния.
В самой обширной четвертой главе приводятся различные
выводы уравнения Больцмана, начиная с выводов самого Больц-
мана, причем подчеркиваются все допущения, лежащие в основе
вывода. Далее рассматриваются выводы уравнения Больцмана,
которые даны Трэдом и Кирквудом. Еще раньше, в гл. III, ко-
коротко был намечен вывод уравнения Больцмана, вытекающий
из анализа Боголюбова. Сопоставление и анализ всех этих выво-
выводов основного кинетического уравнения интересны и поучительны.
В качестве следствий, вытекающих из уравнения Больцмана, рас-
рассматриваются гидродинамические уравнения сохранения, а затем
<0-теорема Больцмана и условия равновесия, приводящие к рас-
распределению Максвелла. Далее приводятся некоторые обоснова-
обоснования релаксационного уравнения Крука — Бхатнагара — Гросса
и подчеркивается его нелинейный характер. Рассматриваются
столкновения при дальнодействующих потенциалах взаимодейст-
взаимодействия и дается вывод уравнения Фоккера — Планка из уравнения
Больцмана и из уравнения Чепмена — Колмогорова. Показы-
Показывается справедливость <$?-теоремы для уравнения Фоккера —
Планка и дается представление о родственных кинетических урав-
уравнениях — уравнениях Ландау и Балеску — Ленарда.
Наконец последняя пятая глава содержит различные методы
решения у равнения, Больцмана и подробную трактовку вопроса
о релаксации макроскопической системы к положению равнове-
равновесия. Обосновывается и подробно разъясняется метод решения
Предисловие редактора перевода
Чепмена — Энскога и выводятся гидродинамические уравнения,
вытекающие из приближений различного порядка. Получаются
выражения для, коэффициентов вязкости и теплопроводности.
Далее подробно рассматриваются свойства линеаризованного
оператора Больцмана, а затем автор переходит к изложению мето-
метода моментов Грэда, дающего возможность получить одно из наи-
наиболее общих решений уравнения Больцмана путем использова-
использования разложений по полиномам Эрмита и вывести при определен-
определенных предположениях замкнутую систему гидродинамических
уравнений.
В последней части пятой главы обсуждается с различных то-
точек зрения приближение системы к положению равновесия и свя-
связанная с этим процессом проблема необратимости макроскопиче-
макроскопических явлений. Этого вопроса автор касался уже в предыдущих
главах. Вводятся понятия о микро- и макросостояниях и о «круп-
«крупнозернистом» разбиении фазового пространства. Используется
принцип равных априорных вероятностей и другие положения
статистической механики и термодинамики, в частности различ-
различные аспекты понятия энтропии. Выводится знаменитая формула
Больцмана для энтропии, распределение Больцмана для наибо-
наиболее вероятного макросостояния. Дается представление о трех
видах канонических ансамблей в статистической механике, о ста-
статистических суммах и связях этих понятий с энтропией и другими
термодинамическими функциями системы. Наконец, применяются
понятия о флуктуациях и среднеквадратичном отклонении.
Кроме априорного, рассматривается также и апостериорный
подход к проблеме необратимости макроскопических явлений, свя-
связанный с эргодической гипотезой, с помощью которой вопросы
пеобратимости могут быть наиболее чистым образом сопоставлены
с обратимыми динамическими законами. Проблема связи необра-
необратимых макроскопических процессов с обратимыми динамическими
законами имеет исключительно важное принципиальное значение
в физике, и настоящая книга, привлекающая внимание читателя
к этим вопросам и дающая достаточно подробную их трактовку,
приобретает тем самым дополнительную ценность.
По манере изложения материала книга имеет характер учеб-
учебника и вполне может рассматриваться как таковой, имеющий
впрочем повышенный уровень и требующий для усвоения мате-
материала определенных усилий и проработки. Этому способствуют,
однако, предлагаемые читателю многочисленные задачи, вкрап-
вкрапленные в основное содержание книги, и обширные списки литера-
литературы, сопровождающие каждую главу книги. К спискам, пред-
предложенным автором, добавлены некоторые не упомянутые им
работы советских исследователей.
Проведенный здесь обзор содержания книги показывает широ-
гаий охват ею многочисленных вопросов теории и приложений
Предисловие редактора перевода
кинетических методов. Она может служить хорошим путеводите-
путеводителем, освещающим основы применяемых подходов и связи между
ними. Несомненно, что книга будет полезна студентам, аспиран-
аспирантам и научным работникам, интересующимся возможностями,
которые открывает перед исследователем метод кинетических
уравнений, и желающим более отчетливо представить себе место,
занимаемое этим методом в общем плане построения науки, вклю-
включающем динамические и статистические закономерности.
Перевод книги сделан О. И. Ткаченко, которая хорошо спра-
справилась с не всегда легким, живым языком автора книги.
Л. П. Смирнов
ПРЕДИСЛОВИЕ
Настоящая книга возникла из курса лекций по статистиче-
статистической механике, который был мною прочитан в Нью-Йоркском
университете в 1964 г. В наши дни среди физиков вновь пробу-
пробудился интерес к уравнению Больцмана, хотя полвека о нем почти
не вспоминали. Выражение «кинетическое уравнение» стало частью
словаря таких разделов физики, как физика плазмы, теория реакто-
реакторов, астрофизика. В аэродинамике кинетическая теория давно'
уже привлекается для исследования сложной проблемы, касаю-
касающейся структуры ударной волны. Кроме того, становится все оче-
очевиднее увеличивающийся разрыв между материалом, излагае-
излагаемым в стандартных курсах по статистической механике, и новыми
оригинальными работами по кинетическим уравнениям, которые
начали появляться в литературе. Это побудило меня включить
в курс несколько лекций на данную тему.
Когда в 1965 г. я приехал в Корнелл, было целесообразно
предложить вниманию аудитории двухгодичный курс по физике
плазмы, охватывающий дисциплины, которые примыкают к тео-
теории кинетических уравнений. Этот курс лекций предназначался
для студентов, специализирующихся в области аэромеханикит
механики, электротехники, космических исследований и некото-
некоторых других областях физики.
Недавно мне довелось прочесть курс, основанный на материале
данной книги, и я нахожу, что при трех часах лекций в неделю
легко можно изложить за год почти три четверти всего материала.
Необходимо отметить, что предлагаемую вниманию читателя
книгу можно было назвать «Введение в теорию классической
неравновесной статистической механики», поскольку теория кине-
кинетических уравнений является частью более широкой области
неравновесной статистической механики.
Я пытался, насколько это возможно, представить материал
в замкнутой форме, не требующей чтения дополнительной литер.а-
туры. Введение в динамику в гл. I служит этой цели и, кроме
того, является хорошим обзором для студентов инженерных спе-
специальностей. Концепция Г-пространства, также встречающаяся
в гл. I, подводит нас к уравнению Лиувилля, которое детально
исследуется во второй главе. В этой же главе обсуждается цепочка
'10 Предисловие
уравнений ББКГИ. Первое из них, называемое в тексте
дает общий вид кинетических уравнений.
В главе IV проведен детальный анализ уравнений Больцмана,
Крука — Бхатнагара — Гросса, Фоккера — Планка. Эта глава
является центральной для всего материала книги.
Основным предметом изучения в книге служат кинетические
уравнения как часть более общей дисциплины — неравновесной
статистической механики. В связи с этим показано, как ББКГИ-
цепочка ведет к кинетическим уравнениям и как из последних
следуют законы сохранения. Меньшая часть материала посвящена
необратимости макроскопических систем и приближению к равно-
равновесию. Другая часть касается концепции напряжений и природы
привносимых сюда вкладов кинетического и потенциального
характера. Выясняется также различие между «абсолютными»
и «относительными» гидродинамическими переменными. Вклю-
Включено обсуждение неадекватности конечных систем уравнений пол-
полному описанию явлений, происходящих в газе. Это отражается
в ББКГИ-цепочке, любая подсистема уравнений которой содер-
содержит больше неизвестных, чем уравнений. На данном уровне описа-
описания этот недостаток преодолеть нельзя, и он вновь возникает
в уравнениях гидродинамики. Именно в связи с этой ситуацией
и вводятся коэффициенты переноса. Обсуждается также роль
уравнений Чепмена — Колмогорова в теории кинетических урав-
уравнений, описывающих марковские процессы.
Я пытался в своих рассуждениях ориентироваться на студен-
студентов, а не на более искушенных в предмете лиц. Эта книга — учеб-
учебник, и я надеюсь, что она будет использована как таковой.
Мне хочется выразить благодарность профессору О. Бунеману,
любезно пригласившему меня прочесть курс лекций в летнем
семестре 1966 г. в Стэнфорде. Это пришлось как раз на то время,
когда черновая рукопись книги была приведена к более «отшли-
«отшлифованному» виду. Я также благодарен сотрудникам Принстон-
ской лаборатории физики плазмы, чья критика оказалась очень
полезной на последней стадии написания книги.
Я особо обязан не только за эту, но и за все мои предыдущие
работы моему учителю и другу Гарольду Трэду — приношу ему
самую глубокую благодарность. Его поощрение и творческая
критика постоянно сопутствуют моей деятельности. В подготовке
книги к изданию участвовало также много моих студентов. Про-
Профессор Нью-Йоркского университета Г. Вейцнер и профессора
Корнеллского университета Т. Файн и Р. Садэн вели со мной пло-
плодотворные дискуссии по многим вопросам. Я благодарен всем
им и многим другим, любезно принявшим участие в создании
.этой книги.
Р. Ливов
ГЛАВА I
ЭЛЕМЕНТЫ КЛАССИЧЕСКОЙ МЕХАНИКИ
1.1. Вводные замечания
Одна из главных целей данного курса состоит в том, чтобы
определить, какое место в неравновесной статистической меха-
механике занимает теория кинетических уравнений. Грубо говоря,
кинетическая теория находится между «микроскопическими»
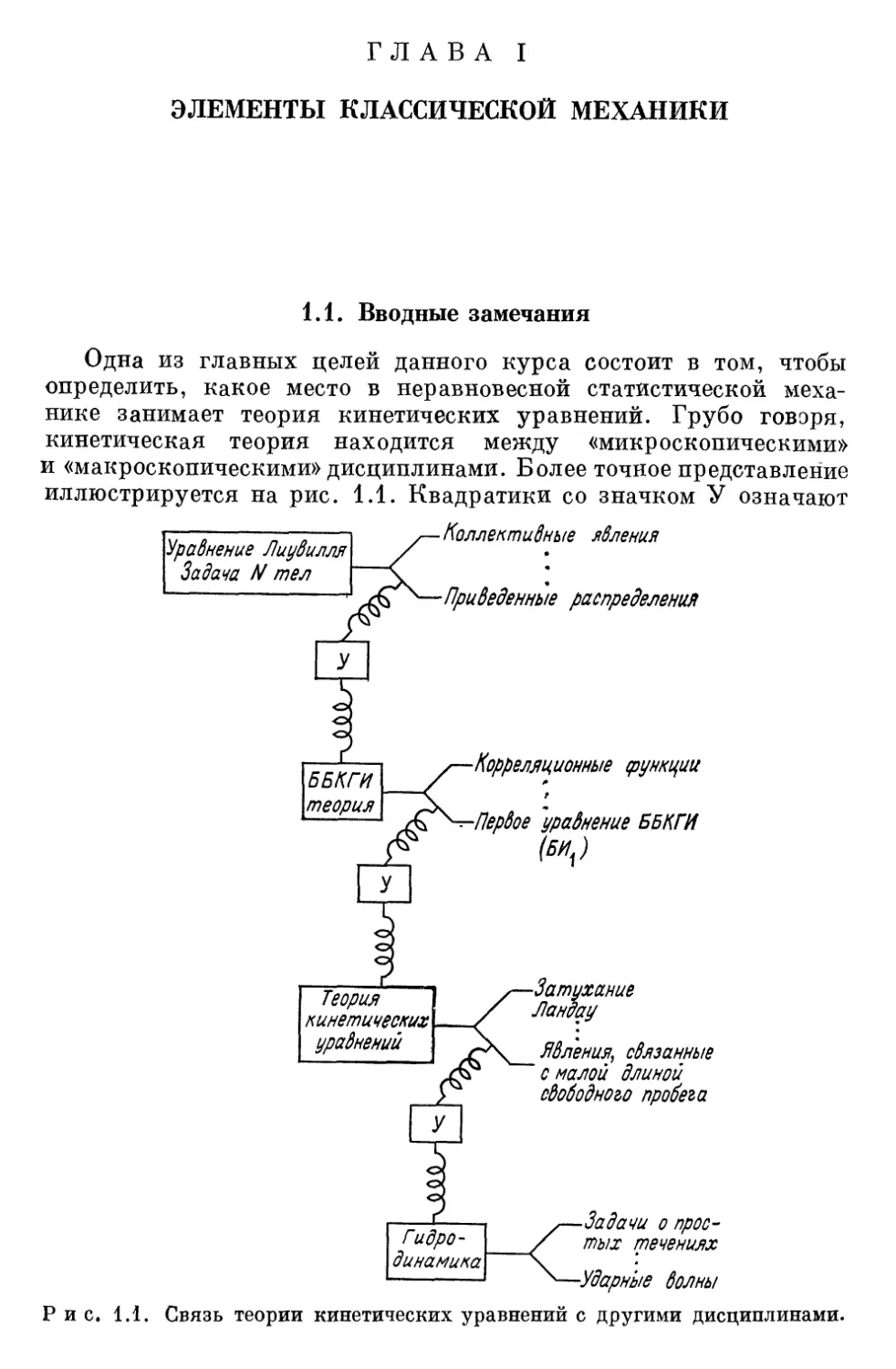
и «макроскопическими» дисциплинами. Более точное представление
иллюстрируется на рис. 1.1. Квадратики со значком У означают
-Коллективные явления
уравнение Лиувилля
Задача N тел
Приведенные распределения
Теория
кинетических
уравнений !
•Корреляционные функции
уравнение ББКГИ
I у—Затухание
' / Ландау
Ядления, связанные
с малой длиной
сШодном пробега
Гидро-
Гидродинамика
¦Задачи о прос-
простых течениях
-Ударные долны
Рис. 1.1. Связь теории кинетических уравнений с другими дисциплинами
12 Гл. I. Элементы классической механики
«усилители». Они служат для разработки подобластей теории,,
вытекающих из ее более широких разделов, отмечаемых в рамоч-
рамочках, расположенных левее. Например, теория ББКГИ уравнений
(обсуждаемая в гл. II) является малой частью темы «Уравнение
Лиувилля...», помещенной в верхней рамочке. Двигаясь внизг
мы переходим ко все менее детальному описанию физических
явлений.
На этой диаграмме теория кинетических уравнений находится
между двумя крайними областями — задачей iV-тел и гидро-
гидродинамикой. Так оно и есть на самом деле. Для того чтобы понять
этот факт, необходимо достичь некоторой ясности по всему кругу
вопросов, относящихся к «соседним» областям. В соответствии
с этим наша книга состоит из трех главных разделов: 1) уравнение
Лиувилля, 2) кинетические уравнения и 3) уравнения сохране-
сохранения. В качестве подготовки к исследованию уравнения Лиувилля
совершим экскурс в классическую механику.
1.2. Формализм Лагранжа
Говорят, что система имеет N степеней свободы, если не менее
чем N переменных единственным образом определяют положение
и ориентацию системы в физическом пространстве. Эквивалентное
утверждение состоит в том, что данная система имеет N и только
N обобщенных координат.
При выборе надлежащей последовательности обобщенных
координат необходимо удостовериться, что они независимы.
Наличие функционального соотношения между переменными
(либо фиксирование одной из переменных, например х = 3 см)
делает их зависимыми. Такое соотношение является математиче-
математическим выражением связи. Если, например, движение шарика огра-
ограничено жесткой проволокой, имеющей форму окружности радиуса
а, то декартовы координаты этого шарика будут связаны соот-
соотношением х2 -\- у2 = а2. Шарик имеет только одну степень сво-
свободы, и «система» имеет только одну обобщенную координату.
Задача 1.1. Определить число степеней свободы каждой из
следующих систем и найти совокупность переменных, которые
можно принять за обобщенные координаты.
а) Шарик, движущийся по круговому обручу, положение ко-
которого фиксировано.
б) Шарик, перемещающийся по неподвижной винтовой пру-
пружине постоянного шага и радиуса.
в) Прямолинейный стержень конечной длины, движущийся
в плоскости.
г) Прямолинейный стержень, движущийся в трехмерном про-
пространстве.
1.2. Формализм Лагранжа
13
д) Растяжимая одномерная пружина, движущаяся в плоско-
плоскости.
е) «Ножницы», движущиеся в плоскости.
ж) «Точечная» частица, движущаяся в трехмерном простран-
пространстве.
з) Две частицы, движущиеся в трехмерном пространстве,
и) N частиц, движущихся в трехмерном пространстве.
к) Твердое тело произвольной формы, движущееся в трех-
трехмерном пр остр анств е.
л) Твердое тело произвольной формы с одной неподвижной
точкой, движущееся в трехмерном пространстве.
Рассмотрим систему с N обобщенными координатами. Пусть
(#!, q2, . . ., qN) = q, так что символом q обозначается iV-мерный
вектор. Отсюда следует, что кинетическая энергия системы, вооб-
вообще говоря, будет функцией дид, где q == (g4, q2, . . ., qN) также
является -/^-мерным вектором. Если
потенциальная энергия V зависит
только от д, т. е. V = V (д), то вы-
выражение
L=T(q, q)-V (q) A.1) ^ Ч*
называется лагранжианом системы.
(Точкой обозначено дифференцирова-
дифференцирование по времени.)
Законы классической механики
можно выразить через функцию L,
не опираясь на второй закон Ньюто-
Ньютона. Основным постулатом этого но-
нового формализма является принцип
Гамильтона, согласно которому движение динамической системы
между двумя точками, 1 = [gt1), *J и 2 == [q&\ t2], таково, что
Рис. 1.2. Вариация относи-
относительно экстремали.
б j L(q, q, t)dt=O.
A.2)
Пусть q (t) — движение, сообщающее интегралу S = f Ldt
экстремальное значение. Положим, что q заменено на
q(t) + 6q(t), A.3)
где 8q — произвольная функция, бесконечно малая в интервале
от t = ti до t = t2 (рис. 1.2) и такая, что
(tt) = 8q (t2) = 0.
A.4)
14 Гл. I. Элементы классической механики
Изменение «действия» S, обусловленное такими вариациями,
должно равняться нулю, поскольку q (t) сообщает S экстремум:
2
, q + 8q, t) dt- j L (g, g, О Й,
1 1
2
«5= |(-^-.б?+у-в?)л, A-5)
Здесь мы проинтегрировали последний член второй строки
по частям х). Проинтегрированная часть равна нулю согласно
условию A.4). Так как оставшийся интеграл должен обращаться
в нуль при любой произвольной (бесконечно малой) вариации
8q, то необходимо, чтобы
{JL)*L = o. A.6)
Здесь мы вернулись к записи через компоненты (qi). В A.5)
каждое произведение скалярное, так что производится суммиро-
суммирование по компонентам вектора q. Дифференциальное уравнение
A.6) представляет необходимое и достаточное условие того, что
8S = О2).
В вариационном исчислении уравнения A.6) известны как
уравнения Эйлера и могут быть применены при решении всевоз-
всевозможных вариационных задач. Ниже дано несколько соответст-
соответствующих примеров.
*) В момент t точка, изображающая систему, имеет положение q (t),
а точка на смещенной кривой: q (t) + 6# (t). Здесь 6# (t) — «виртуальное»
перемещение относительно точки q (t), т. е. перемещение, происходящее
за нулевой интервал времени и допускаемое наложенными на систему свя-
связями.
2) Принцип Гамильтона налагает ограничение только на начальное
и конечное положения точки, изображающей систему. Начальные и конеч-
конечные обобщенные скорости могут быть произвольными. Из элементарной
механики известно, что движение частицы определяется ее начальными
положением и скоростью. Однако фактически принцип Гамильтона позво-
позволяет однозначно определить динамическую траекторию системы. Поскольку
уравнения движения (уравнения Лагранжа) имеют второй порядок по вре-
времени, то для их решения надо задать два условия. Эти условия не обязатель-
обязательно должны быть начальными данными. В задаче о наикратчайшем расстоя-
расстоянии между двумя точками на плоскости (х, у) соответствующие уравнения
Эйлера — Лагранжа дают у = ах + Ъ (q = at + Р). Решение можно сде-
сделать единственным, задавая либо у @) ж у @), либо у @) и у (х^.
1.2. Формализм Лагранжа 15'
Задача 1.2. Показать, что наикратчайшее расстояние между
двумя точками на плоскости есть прямая линия.
Задача 1.3. Пусть поверхность образована вращением вокруг
оси, у кривой, проходящей через точки {хи z/i) и (х2, У2>- Показать,,
что кривая у = a Arch (x/a) + b порождает поверхность с мини-
минимальной площадью.
В динамике уравнения A.6) называются уравнениями
Лагранжа. Ими удобно пользоваться для получения соответст-
соответствующих уравнений движения, выражающих закон F = та. При
этом задача полностью формализуется, и вся трудность сводится
к тому, чтобы получить правильное выражение для кинетической
энергии системы.
Задача 1.4. Найти уравнение движения шарика по прямой
жесткой проволоке, конец которой фиксирован, а сама она вра-
вращается в плоскости с угловой скоростью со.
Ответ. Поскольку потенциальная энергия в задачу не входит,
то L = Т. Кинетическая энергия определяется равенством
T = ±-m(r2 + rW), со = 0. A.7)
Здесь г — расстояние от закрепленного конца, 0 — угол между
положением проволоки в момент i и ее начальным положением
и т — масса шарика.
Уравнение Лагранжа имеет вид
V— г со2 = 0. A.8)
Его общее решение
г = Ае*>*+ Ве~<*\ 0 = со*, A.9)
где А и В — произвольные постоянные, определяемые из началь-
начальных условий.
Отметим, что выражение для кинетической энергии также мо-
может быть получено формальным путем. Для каждой из частиц,
составляющих систему, Т =-7r m (х2 + У2 + z2)-
Чтобы найти Т в новых переменных E, т|, С)» необходимо
задать преобразование
I = I (х, у, z, *),
т| =т| (х, г/, z, *), A.10)
? = ?(*, I/, z, t).
Самым важным вопросом при построении лагранжиана является
выбор такой совокупности переменных, которая наиболее тесно
связана с геометрией задачи.
16
Гл. I. Элементы классической механики
Задача 1.5. Найти уравнение движения шарика по жесткой
винтовой линии
х = a cos 0t
у = a sin 9f A.11)
z = fee.
Ось винтовой линии расположена вертикально и параллельна
гравитационному полю. Вследствие ограничений z = &6 и г = а
имеется только одна степень свободы 6.
Задача 1,6. Шарик движется по проволочной окружности
радиуса а. Окружность вращается с угловой скоростью со вокруг
Рис. 1.3,
фиксированной оси, совпадающей с диаметром. Найти движение
шарика, начальный радиус-вектор которого определяется углом 6
относительно диаметра (сила тяжести отсутствует).
Задача 1.7. Шарик движется по жесткой проволочной окруж-
окружности радиуса Ь. Плоскость окружности вертикальна и ее цешр
связан жестким стержнем длины а с фиксированным началом
координат. Этот стержень вращается в горизонтальной плоскости
с частотой со/2я (рис. 1.3). Силой тяжести пренебрегаем. Найти
движение.
Ответ. Основная трудность состоит в определении кинетиче-
кинетической энергии
± ^). A.12)
1.3. Формализм Гамильтона 17
Уравнения преобразования имеют вид
% = Ъ sin 0,
х = a cos гр -^- Л sin г|), г|э = со?, A.13)
у = a sin if) — A cos г|), А = Ъ cos G.
Существует только одна обобщенная координата, 9. Остальные
переменные удовлетворяют записанным выше уравнениям связи.
Кривая, изображающая путь частицы в трехмерном простран-
пространстве, задается параметрическими уравнениями:
z = Ъ sin 0,
х = a cos Ы + Ь cos 8 sin со?, A.14)
г/ = a sin со* — Ъ cos 0 cos co?,
где решение 0 = 0 (t) завершает параметризацию. Уравнения]A.14)
являются уравнениями преобразования особого вида — неста-
нестационарного преобразования. С важными свойствами таких пре-
преобразований мы вскоре встретимся.
Используя уравнения A.14) и проводя ряд длинных вычисле-
вычислений, получаем выражение для Г, а следовательно, и для L (= Т).
Теперь можем записать уравнения Лагранжа. Остается, однако,
неисследованной интересная проблема устойчивости. Мы рассмот-
рассмотрим ее в задаче 1.8.
Задача 1.8, Из рис. 1.3 видно, что существуют четыре «равно-
«равновесных» решения. Исследуя уравнения движения, убедимся
в этом. Затем подставим решения в форме 0A) = 0i + zeh* в урав-
уравнения движения и пренебрежем членами порядка е2. Получим
условие для X (в виде алгебраического уравнения), которое долж-
должно удовлетворяться, чтобы записанные выше выражения для 0
действительно были решениями. Исследуя корни характеристиче-
характеристического уравнения Ях, . . ., Я4, можно судить об устойчивости равно-
равновесных решений. Например, если %i > 0, то любое бесконечно
малое возмущение равновесного решения 0 экспоненциально
растет со временем, т. е. равновесие 0i не является устойчивым.
Задача 1.9. Пренебрегая силой тяжести, решить задачу 1.5,
когда ось винтовой линии расположена в горизонтальной пло-
плоскости и вращается относительно фиксированной оси с угловой
скоростью со.
1.3. Формализм Гамильтона
Уравнения Лагранжа являются лучшим средством для иссле-
исследования многих задач, возникающих в классической механике.
При подробном рассмотрении уравнений обнаруживается инте-
•
ресный факт. Если L не зависит от qi, то величина dL/dqt постоян-
18 Гл. I. Элементы классической механики
на по времени. Такие координаты qi называются циклическими.
В механике существует метод, который не только использует
этот факт, но и позволяет представить обширное поле механики
как науку с принципами симметрии. Этот метод воплощен в фор-
формализме Гамильтона.
Первой задачей нашего нового подхода является переход
от переменных (g, q) к (q, dL/dq). Такой переход достигается при
использовании преобразования Лежандра, которое переводит
L — функцию q, q и t — в гамильтониан Н, являющийся функ-
функцией g, dL/dq, t. Преобразование имеет вид
Образуя дифференциал от Н, легко проверить, что Н действитель-
но является функцией g, dLldqi и t.
Если мы введем
^г^Рг A.16)
— канонические импульсы, или импульсы, сопряженные координа-
координатам qu то Я = Н (д, р, t).
Чтобы найти уравнения движения системы через эту новую ди-
динамическую функцию, мы сначала запишем дифференциал Н
как функцию g, p (г t, если Н явная функция времени). Это дает
N N
d# = 2gzd^-2 Pidqi-^r<tt, A.17)
где при построении дифференциала мы воспользовались уравне-
уравнениями Лагранжа. Отсюда следует, что
*< = Ж' <1Л8а>
л--Ж' AЛ8б>
и dH/dt = —dL/dt. Если L не зависит явно от времени, то имеют
смысл только уравнения A.18). Они называются уравнениями
Гамильтона и, как мы видим, представляют собой 2N уравнений
первого порядка в противоположность уравнениям Лагранжа,
которые являются N уравнениями второго порядка.
Из уравнения A.186) видно, что если гамильтониан не зависит
от координаты q\ (т. е. q\ циклическая), то импульс ри сопряжен-
сопряженный этой координате, сохраняется. Этот факт, связанный с неотъ-
1.3. Формализм Гамильтона 19
емлемыми свойствами симметрии пространства и времени, приво-
приводит к основным теоремам сохранения в механике. Сначала мы
исследуем свойство однородности пространства.
Рассмотрим изолированную систему из N частиц, координаты
которых относительно некоторой фиксированной системы коорди-
координат равны Г;. Пусть система может иметь поступательное виртуаль-
виртуальное перемещение А, так что координаты г^ -> г* = г^ + Д. Урав-
Уравнения движения системы после такого перемещения не отличают-
отличаются от уравнений, которые описывали систему в первоначальной
ориентации. Простой эксперимент покажет, что принцип одно-
однородности пространства будет нарушен, если эти уравнения ока-
окажутся различными. Если уравнения движения инвариантны при
указанных перемещениях, то этим же свойством должен обладать
и гамильтониан, т. е.
Согласно определению виртуальных перемещений, ни импульсы,
ни время не варьируются. Так как приращение А — произвольно,
то наш эксперимент означает, что гамильтониан изолированной
системы подчиняется условию
N
V дН о
Объединяя это свойство с уравнениями Гамильтона, получаем
желаемый результат:
Что представляют собой rt и pf? Ясно, чтотг являются радиус-век-
радиус-векторами частиц, составляющих систему, так что кинетическая
энергия Т равна
N
l^ A.21)
Поскольку потенциал взаимодействия частиц от скорости не зави-
зависит, импульс
Р«—^- = |*Л, A.22)
т. е. это обычный линейный импульс.
Таким путем устанавливается, что однородность пространства
означает постоянство по времени полного линейного импульса
изолированной системы.
20
Гл. I. Элементы классической механики
Другим исследуемым свойством пространства является его
изотропность. Это свойство означает, что уравнения движения
изолированной системы инвариантны относительно виртуального
бесконечно малого поворот системы
вокруг некоторой фиксированной
оси. Такой поворот показан на
рис. 1.4. Каждая частица испытывает
перемещение, при котором гг- ->¦ т\ =
= rt + бгь где 8rt = 69 X г^.
Снова гамильтониан должен быть
инвариантным; таким образом,
N N
A.23)
Поскольку 60 произвольна, мы полу-
получаем второе важное свойство гамиль-
гамильтониана изолированной системы:
]Lxif- = O. A.24)
Рис. 1.4. Виртуальный по-
поворот на угол 66.
Это соотношение совместно с уравнением A.22) и кинематиче-
кинематическим равенством d (rt X Tt)/dt = rt X (dri/di) дает желаемый
результат:
iV
0 О' A-25а)
N
2г*ХР|==#. A.256)
Полный] угловой момент X (относительно произвольного фикси-
фиксированного начала координат) постоянен во времени.
Задача 1.10. Как изменяется полный угловой момент систе-
системы при преобразовании координат г^ —>- х\ + а, где а — постоян-
постоянный вектор?
Задача 1.11. Построить в декартовых координатах (исходя
из лагранжиана) гамильтониан для свободной частицы, движу-
движущейся в трехмерном пространстве. Какие величины сохраняются
при таком движении?
Задача 1.12. Решить задачу 1.11, выражая Н в сферических
координатах (г, 0, -ф). Построить уравнения движения (т. е.
уравнения Гамильтона) для координат, не являющихся цикли-
циклическими.
1.3, Формализм Гамильтона
21
Задача 1.13. Построить гамильтониан для частицы, движу-
движущейся по поверхности цилиндра радиуса а, если ось цилиндра
горизонтальна. Сила тяжести направлена вниз. Найти движение
при следующих начальных условиях (рис. 1.5):
z @) - 0, Э @) = к/2, z @) = 17, 6 @) = 0.
Мы подошли теперь к важной теореме о гамильтониане: для
консервативных систем, связи которых не зависят от времени,
гамильтониан равен полной энергии Т + V и постоянен по вре-
времени. Точнее, условие независимости связей от времени означает,
Рис. 1.5.
что уравнения преобразования (ср. с A.10)), общий вид которых
есть rt = тг (qt, . . ., qN, t) (индекс i связан с полным числом
частиц в системе), явно от времени не зависят (заметим, что урав-
уравнения A.14) являются хорошим примером связи, зависящей
от времени).
Так как силовое поле консервативно и связи не зависят от вре-
времени, то лагранжан L не содержит время явно. Следовательно,
N ,
dL _ x^ dL dqi . dL dqt
~~dt"~ 2j I dqi ЧГ~^ д* ~df
При получении этого результата мы использовали уравнения
Лагранжа. Результат можно переписать в виде
N
Таким образом,
Н = const. A.28)
Кроме того, если потенциал V не является функцией скорости,
то pi = dLldqi — dT/dqi и сумма в уравнении A.27) имеет вид
2jqi (dT/dqi). Если уравнения преобразования не содержат время
22 Гл. I. Элементы классической механики
явно, то Т будет однородной квадратичной формой скоростей:
2 A.29)
Коэффициенты aik не содержат обобщенных скоростей.
Задача 1.14. Исходя из
(N — число частиц в системе) и уравнений преобразования в фор-
форме тг = тг (qu . . ., qN), доказать, что коэффициенты агк не содер-
содержат обобщенных скоростей.
Из -теоремы Эйлера, которая утверждает, что если g является
однородной функцией порядка vот переменных хи то 4yixi{dgldxi) =
= vg (для нашего случая v = 2), следует, что
2<7;^- = 2Г A.30)
d
A.31)
— полная энергия системы. Для консервативной системы с неза-
независящими от времени связями гамильтониан равен полной энергии
и постоянен во времени. Отметим, что изолированная система
не может описываться уравнениями преобразований, явно содер-
содержащими время. В таком случае гамильтониан также не будет
явной функцией времени, и Н сохраняется. Тот факт, что гамиль-
гамильтониан изолированной системы не может содержать явно время,
выражает однородность времени. В данном случае, как мы уже
видели, Н представляет собой константу движения, а именно
энергию.
Время, также как и пространство, обладает еще одним фунда-
фундаментальным свойством — свойством изотропности. Этого рода
симметрия ведет к принципу динамической обратимости. Если
одномерный объект, такой, как время, является изотропным, то
не существует различия между временем прогрессирующим и вре-
временем регрессирующим. При обращении времени законы движе-
движения остаются инвариантными, так что Н (t) = Н (—t). В свете
уравнений Гамильтона это означает, что если [q (t), p (t)] являет-
является динамическим решением, то [q (—?),— р(—t)] также будет
решением.
Чтобы сделать доказательство более убедительным, рассмот-
рассмотрим сначала начальные и конечные условия:
р @) = ро, q @) = q0; P (h) = Pu Q (*i) = Qi-
1.3. Формализм Гамильтона
23
Далее найдем динамический путь, соответствующий новым началь-
начальным условиям р* @) = —pi, q* @) = qle Имеем решение
Р* = -Р (-** +''*!), <?* = q (-*¦ + *0,
где t* есть время в задаче с переменными, отмеченными звездочкой
(заметим, что р ж q — те же самые функции, что ив первом слу-
случае). Таким образом, мы нахо-
находим, что
р* (*¦ = 0) = -р (ь) = -Ри
<7* @) = qu
так что начальные условия вы-
выполняются.
При ?* = ti имеем р* (?4) =
= — ро и g* {ti) = q0. Следова-
Следовательно, полученное решение яв-
является точным обращением ре-
решения [q (t), p (t)]. Уравнения,
которые порождают решения с
такими свойствами, называются
динамически обратимыми. На
рис. 1.6 изображены цва таких
движения. Каждому решению
динамических уравнений соот-
соответствует другое обращенное
решение.
Задача 1.15. Как в задаче 1.6
Pi
PG
~Ро
-pi
Рис. 1.6. Движение а и динами-
динамически обращенное движение б.
изменяется по времени энергия
шарика? Если эта энергия возрастает (убывает), то откуда (куда)
идет прирост (убыль) энергии?
Утверждение, что некая динамическая переменная постоянна
по времени, означает, что существует функция координат и им-
импульсов, которая не изменяется при изменении q\ и р\ по времени.
Такая функция
h (qu . . ., qNj pu . . ., pN, t),
постоянная вдоль «динамического пути системы», называется
константой движения. Эта концепция, в сущности, является
одной из наиболее важных во всей классической динамике. Сколь-
Сколько независимых констант движения существует для системы с N
обобщенными координатами? Из второго закона Ньютона либо
из уравнений Лагранжа или Гамильтона мы видим, что решение
включает 2N постоянных интегрирования. Обращая эти решения
так, что постоянные интегрирования становятся функциями дина-
динамических переменных, получаем совокупность 2N независимых
констант движения. Разрешенные относительно индивидуальных
24
Гл. I. Элементы классической механики
координат и импульсов, эти 2N первых интеграла уравнений
движения, как мы видим, будут эквивалентны решению задачи.
Существование 2N независимых констант движения можно также
усмотреть из геометрического построения.
2iV-MepHoe декартово пространство с координатами (qu . . ., qN;
Pi, . . ., р^) называется фазовым пространством (а также Г-про-
странством). В этом пространстве вся система изображается одной
точкой. Состояние системы в любой
момент есть точка Г-пространства.
Так как система изменяется по
времени, то точка системы прочер-
прочерчивает путь (динамическую траек-
траекторию системы) в Г-пространстве.
Однако в этом пространстве вре-
временной параметр отсутствует. Та-
Таким образом, кривая в Г-про-
странстве не показывает временную
эволюцию точки системы. Она дает
соотношение, которому должны
удовлетворять координаты и им-
импульсы системы.
Решение задачи для одномер-
.ного гармонического осциллятора
можно записать в виде p = acos(otj
х = &sinco?. В соответствующем
двумерном Г-пространстве дан-
данные уравнения будут парамет-
параметрическим представлением эллипса (р/аJ + (х/ЬJ = 1. Хотя
уравнение этой динамической кривой является важным соот-
соотношением, которому должны удовлетворять р и х, она не дает
информации о развитии системы во времени. С другой стороны,
в BN + 1)-мерном расширенном фазовом пространстве (Г-про-
(Г-пространстве), которое включает ось времени, кривая, прочерчивае-
прочерчиваемая точкой системы, дает полное динамическое решение задачи.
Для рассмотренной задачи с гармоническим осциллятором эта
кривая является пересечением двух поверхностей а = p/cos ®t9
Ъ = xlsmat. Динамический путь изображен на рис. 1.7.
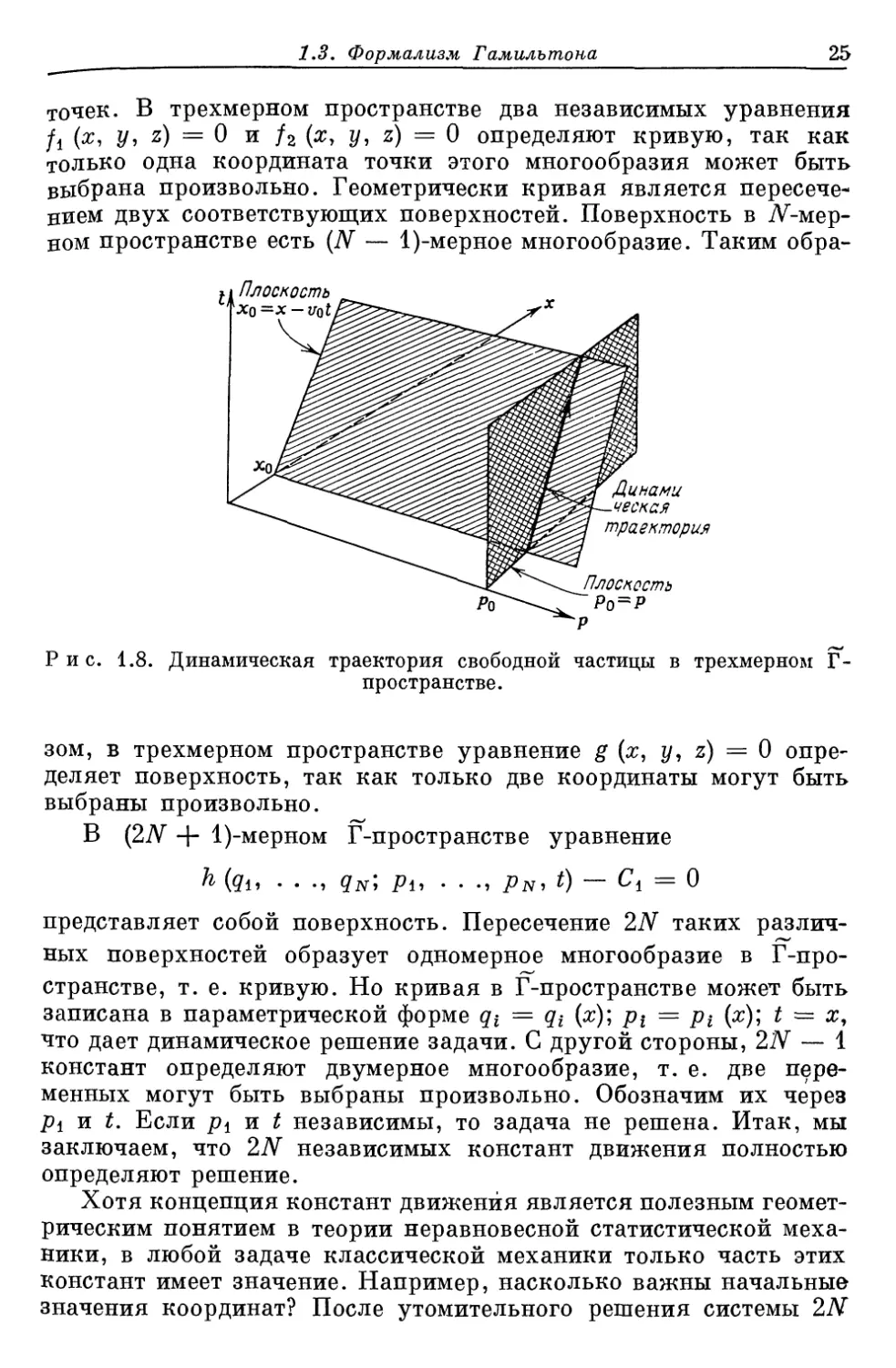
Для одномерного движения свободной частицы кривая системы
в трехмерном Г-пространстве представляет собой пересечение
двух плоскостей р = роя х0 = х — vot, как показано на рис. 1 8.
Обычно решением для системы с N обобщенными координатами
служит кривая в BN + 1)-мерном f-пространстве. «Кривая»
в таком пространстве соответствует пересечению 2N «поверхно-
«поверхностей» в этом же пространстве. Кривая в пространстве с любым
числом измерений является одномерным геометрическим местом
Рис. 1.7. Динамическая траек-
траектория точки системы для просто-
простого гармонического осциллятора в
трехмерном Г-пространстве.
1.3. Формализм Гамильтона
25
точек. В трехмерном пространстве два независимых уравнения
/i (х, У, z) = 0 и /2 {х, у, z) = О определяют кривую, так как
только одна координата точки этого многообразия может быть
выбрана произвольно. Геометрически кривая является пересече-
пересечением двух соответствующих поверхностей. Поверхность в Л^-мер-
ном пространстве есть (N — 1)-мерное многообразие. Таким обра-
i Плоскость
Динами
м е екая
траектория
Плоскость
Рис. 1.8. Динамическая траектория свободной частицы в трехмерном Т-
пространстве.
зом, в трехмерном пространстве уравнение g (х, у, z) = 0 опре-
определяет поверхность, так как только две координаты могут быть
выбраны произвольно.
В BN + 1)-мерном Г-пространстве уравнение
Pu
> t) — С± =
представляет собой поверхность. Пересечение 2N таких различ-
различных поверхностей образует одномерное многообразие в Г-про-
Г-пространстве, т. е. кривую. Но кривая в Г-пространстве может быть
записана в параметрической форме qt = qt (x); pt = pt (x); t = х,
что дает динамическое решение задачи. С другой стороны, 2N — 1
констант определяют двумерное многообразие, т. е. две пере-
переменных могут быть выбраны произвольно. Обозначим их через
Pi и t. Если р{ и t независимы, то задача не решена. Итак, мы
заключаем, что 2N независимых констант движения полностью
определяют решение.
Хотя концепция констант движения является полезным геомет-
геометрическим понятием в теории неравновесной статистической меха-
механики, в любой задаче классической механики только часть этих
констант имеет значение. Например, насколько важны начальные
значения координат? После утомительного решения системы 2N
26 Гл. I. Элементы классической механики
дифференциальных уравнений такие константы, конечно, необхо-
необходимы, чтобы единственным образом определить движение. Но до
этого они, несомненно, были не нужны. С другой стороны, как
мы видели, существуют константы, которые следуют из неотъем-
неотъемлемых свойств симметрии системы. Эти функции координат
и импульсов, постоянные вдоль динамической траектории систе-
системы, являются крайне важными. Во многих случаях с помощью
этих констант решение можно представить в виде квадратур
(мы вернемся к этой теме в нашем последнем обсуждении эргоди-
ческой теоремы в гл. V).
Задача 1.16. а) Рассмотреть две частицы в трехмерном про-
пространстве с потенциалом взаимодействия V (| г4 — г2 |). Выбрать
обобщенные координаты таким образом, чтобы они включали
координаты центра масс системы. Построить гамильтониан и пока-
показать, что задачу можно описать через движение относительно
центра масс. Доказать также, что это движение происходит в пло-
плоскости, вектор нормали которой постоянен по времени.
б) Построить гамильтониан для плоского движения, выбирая
за обобщенные координаты скаляр г = | г4 — г2 | и угол 0 между
векторами г4 @) — г2 @) и r4 (t) — r2 (t). Получить константы
движения и свести задачу к квадратурам.
1.4. Скобки Пуассона и канонические преобразования
Рассмотрим некоторую динамическую характеристику систе-
системы, т.е. функцию и от координат, импульсов и времени. Скорость
изменения этой функции со временем задается равенством
N
du ^ / ди - ди ' \ ди , ~9ч
1=1
Подставляя уравнения Гамильтона A.18) в это выражение, полу-
получим:
N
du sr\ / ди дН ди дП \ ди .. «т
~df=2j \1^Т^~1^~д^')+~дГ ' ^ 6б)
1=1
или, что эквивалентно,
Скобки Пуассона для любых двух динамических переменных
А и В определяются как
[А,В]^уA±™эв1А) A.35)
1 ' -I л-1 \ dqi dpi dqt дрг ) v
1=1
1.4. Скобки Пуассона и канонические преобразования 27
и сами являются динамической функцией. Образование скобок
Пуассона представляет математическую операцию, обладающую
рядом простых алгебраических свойств, часть которых дается
соотношениями A.36). (Постоянная к не зависит от q я р.)
U, В] = -[Я, А], A.36а)
U, к] = О, A.366)
[А + В, F] = U, F] + [В, Л, A.36в)
[АВ, F] = А Ш, Я + BW, Л, A.36г)
U, IB, F]] + Ш, [F, А]] + [F, U, Б]] = 0. A.36д)
Соотношение A.36д) известно как тождество Якоби. Произ-
Производная по времени от скобки Пуассона удовлетворяет соотношению
A.36е)
Задача 1.17. Показать, что динамическая переменная и, не
содержащая время явно и имеющая нулевую скобку Пуассона
с гамильтонианом, является константой движения.
Задача 1.18- Показать, что если и и v — константы движения,
то [и, v] также является константой движения. Исследовать
общий случай, когда и и v — явные функции времени
Если совокупность координат и импульсов выведена формаль-
формально из лагранжиана, то они, конечно, удовлетворяют уравнениям
Гамильтона, которые через скобки Пуассона запишутся в виде
%Г=[Я1,Н], 2A.37а)
g]- A-376)
Данная совокупность координат и импульсов системы не обя-
обязательно представляет действительные динамические координаты.
Это можно полностью уяснить на следующем примере. Рассмотрим
свободную частицу в двумерном пространстве. Переходя от декар-
декартовой системы координат (х, у) к полярной (г, 0), мы не можем
произвольно вводить новые импульсы (рг, ро). Формальное
построение этих переменных из лагранжиана дает
Преобразуя гамильтониан, имеем в результате
^) A.386)
28 Гл. I. Элементы классической механики
Уравнения Гамильтона для г и 0 дают истинную динамическую
траекторию. Полагая, например, рх = 2pr cos0 — (pe/r) sin в
вместо предшествующих уравнений преобразования, мы полу-
получили бы в результате
Такой гамильтониан не дает верных уравнений движения. Сово-
Совокупность координат и импульсов, которые являются динамически
согласованными и приводят к физически реализуемым выводам
из уравнений Гамильтона, называются каноническими координа-
координатами и импульсами. Преобразование qi-^qi = qi(qu • • •» Q.N,
Ри • • •» Pn> t); pi-*~ pi = pi (?i, . . ., Qn, Pu • . ., Pn, *)» УД0В~
летворяющее этим условиям, называется каноническим. Или, что
эквивалентно, преобразование является каноническим, если суще-
существует функция Hf (qf, р', t), посредством которой движение
между двумя точками q'{t^) и q'(t2) задается уравнением
2 N
б J [2 q'lPi -Н' (qf, p\ *)] dt = O, A.39)
т. е. является истинным динамическим движением. Это не что
иное, как принцип Гамильтона, записанный в новых координатах.
Старые координаты (q\, pi) также удовлетворяют принципу
Гамильтона, так что
[y'qp-H(q,p,t)]dt = 0. A.40)
Для того чтобы уравнения A.39) и A.40) были одновременно
справедливы, подинтегральные выражения этих двух интегралов
должны отличаться самое большее на полную производную по вре-
времени от произвольной функции G. Интеграл от dG/dt задается
через значения G в конечных точках, где, по определению, вариа-
вариации равны нулю.
Функция G называется производящей функцией и имеет большое
значение в теории преобразований классической механики. Любое
каноническое преобразование q->- q' = q' (g, p), p ->¦ p' = p'{q, p)
полностью определяется производящей функцией. Поскольку
имеется 2N уравнений преобразования, то G может быть функ-
функцией самое большее от 2N независимых переменных и времени.
В противоположность этому полное число «старых» и «новых»
переменных равно AN. Четырьмя возможными формами функции
G являются:
G± = Gi (g, q\ t),
G2 = G2 (g, p\ t),
*G3=sG3(p, q', t), A.41)
G4 ^ G4 (p, p\ t).
1.4. Скобки Пуассона и канонические преобразования 29
Чтобы понять, каким образом G определяет каноническое
преобразование, рассмотрим функцию G±. Разность подинте-
гральных выражений в уравнениях A.39) и A.40) является пол-
полной производной по времени от G±:
Полную производную по времени от Gi можно также записать
в виде
Приравнивая коэффициенты при независимых параметрах q ж q',
придем к желаемому результату
* = (
Р'ь=-Щ A.446)
Ж
Я' = Я + -^. A.45)
Число уравнений A.44) равно 2N, что позволяет нам решить
их и выразить (qf, р') через (q, р). Таким образом, G «производит»
каноническое преобразование.
Задача 1.19. а) Построить G2 из G±, используя преобразова-
преобразование Лежандра. Далее, повторяя проведенную выше процедуру,
найти неявные уравнения преобразования через производные
от G2.
б) Проделать то же самое для G3 (из G±).
в) Проделать то же самое для G4 (из Gi).
Во всех трех случаях установить соотношение между Я и Я'.
Ответ, a) G2 (#, р', t) задается равенством
G2{q9 P', t)=G±(q, q\ t)+^q'pr. A.46)
Подстановка в уравнение A.42) дает
4 [ ] 3 2 Н), A.47)
так что
^=2и+Е«У+(я'-^)- с1-48)
Сравнивая это выражение с
30 Гл. I. Элементы классической механики
получим
ft = -ff' A'50a>
# = -7Г7- • A.506)
Ответ, б)
i = 2j PQ* ^з (^ » Р? ч<> (l.ola)
Ответ, в)
G4 = ^i+2/)/^/ — 2 Р?> A.52а)
9=-^-. A-526)
?'=#• A.52в)
Рассмотрим преобразование, производимое функцией
(*2~Zj PifiiQi t)> A.53)
так что
q'k z=fk (g, ?), A.54a)-
Преобразование, в котором новые координаты суть функции
одних только старых координат, называется точечным. Частым*
заблуждением является отождествление всех точечных преобра-
преобразований с каноническими. После задания преобразования коорди-
координат только специальный выбор новых импульсов согласно урав-
уравнению A.546) делает преобразование каноническим. Если, напри-
например, преобразование координат A.38а) подставить в A.546),.
то это дает
Рх = Рг 1? + Ре Ж = Pr cos G ~"Т sin 9#
Однако уравнение точечного преобразования A.38а) совместно'
с рх = Рг не является каноническим преобразованием.
Два других важных примера канонических преобразований
в рамках производящих функций составляют тождественное
преобразование и преобразование обмена. Первое получается из
G2 = S?P'. A.55а),
1.4. Скобки Пуассона и канонические преобразования 34
Вместе с A.50) это дает:
Р' = Р,
Я' - Ъ i
Н' = Н A.556)
— тождественное преобразование. С другой стороны,
G1 = 2g?' A.56а)
вместе с A.44) определяет
р' = — q A.56б>
— преобразование обмена. Новые координаты равны старым
импульсам, а новые импульсы равны старым координатам со зна-
знаком минус. В новом представлении координаты и импульсы поме-
поменялись ролями.
Остается обсудить два важных вопроса, касающихся канони-
канонических преобразований. Первый относится к преобразованию
координат и импульсов, дающему действительное перемещение,
которое точка, изображающая систему, совершает в фазовом про-
пространстве за интервал времени от t до t + Т. Мы увидим, чта
таким — самым важным из всех преобразований — является
каноническое. Второй вопрос связан с концепцией канонических
инвариантов. Канонические инварианты суть динамические вели-
величины, инвариантные по отношению к каноническим преобразова-
преобразованиям. Примером канонического инварианта служит функция
[А, В], где А ж В — две любые динамические функции. Это можно
расписать в явном виде. Если (q, p) ->- (qf, p')y то
А (<?, р) -+ А' (<?', Я =Alq (<?', р'); р (<?', р')]
и
2(_дА_^дВ_ d#_J^_\ Vi / дА' дВ' дВ' дА'
\ dqi dpi 6qi dpi) — 2j\ dq{ др{ dq[ др[
Другим примером являются фундаментальные скобки Пуас-
Пуассона:
ku Qk\ =0, A.58а)
Ipu Pk] = 0, A.586)
Iqu Pk\ = SZft. A.58в)
Инвариантность этих соотношений относительно любой кано-
канонической системы независимых переменных дает другой критерий,
которому должны удовлетворять канонические переменные.
Для того чтобы рассмотреть действительное перемещение
системы как каноническое преобразование, введем понятие бес-
бесконечно малого преобразования. Бесконечно малым каноническим
32 Гл. I. Элементы классической механики
является такое преобразование, при котором новые координаты
и импульсы отличаются от старых на бесконечно малые величины.
Если 8 — бесконечно малый параметр, то преобразование
Яг = Я.г + бдь
A.59)
pi = Pi + йри
где Sq и Sp имеют порядок О (е), представляет собой бесконечно
малое каноническое преобразование. Это можно просто показать,
построив функцию, которая производит преобразование A.59).
Поскольку это преобразование отличается от тождественного
членом О (е), попытаемся взять в качестве производящей функ-
функцию G2, которая отличается от функции, задаваемой уравне-
уравнением A.55а) (дающий тождественное преобразование), членом О (г):
G* = 2 fctf + вф (?,/)• A-60)
Тогда уравнения A.50) дают
Или, что то же,
Последнее выражение показывает, что замена d/dpi на д/дрг будет
взаимно согласованной, если первоначальный оператор включает
множитель 8.
Из полученных уравнений следует, что бесконечно малое пре-
преобразование определяется только возмущенной производящей
функцией ф, поэтому достаточно сказать, что ср производит пре-
преобразование.
Ясно, что ввиду отсутствия каких-либо ограничений на функ-
функцию ф (q, p') вид вариаций 8р и Sq совершенно произволен. Среди
всех этих преобразований наиболее существенно бесконечно
малое преобразование координат и импульсов, происходящее
при действительном движении системы за время dt. Такое пре-
1.4. Скобни Пуассона и канонические преобразования 33
образование задается соотношениями
ОН t1'63)
8pi = dpi = Pidt= —g—• dt.
Отсюда следуют два важных вывода: 1) гамильтониан производит
действительное движение системы; 2) это движение, совершаемое
системой за время dt, является бесконечно малым каноническим
преобразованием. «Произведение» двух канонических преобразо-
преобразований будет также каноническим преобразованием. Отсюда сле-
следует, что динамическая траектория точки, изображающей систему,
представляет собой каноническое преобразование, поскольку она
является не чем иным, как последовательностью бесконечно
малых канонических преобразований, уводящих систему от
начальных величин q0 и р0. Гамильтониан производит движение
системы во времени.
Существует более прямой путь, показывающий, чтЪ перемеще-
перемещение, которое система совершает из одного динамического состоя-
состояния [q (t), p (t)] в другое lq' (t + Г), р' (t + Т)] за время Т,
является каноническим преобразованием. Рассмотрим преобра-
преобразование q' = q' [q (*), р (*), Т]; р = р' [q (t), p (t), T]. В любой
момент t это преобразование дает новую совокупность перемен-
переменных д\ р\ Частный вид преобразования зависит от одномерного
параметра Т. В качестве специального случая преобразования
такого типа рассмотрим интеграл действия
t+T
j 2)z. A.64)
Переменная интегрирования х под знаком интеграла — это время.
Интеграл всегда распространяется на фиксированный интервал
времени Г. Нижний предел интегрирования — переменная t.
Эквивалентной записью для A.64) будет
t+т t
S(t,T)= j - f , A.65)
о о
так что
A.666)
34 Гл. /. Элементы классической механики
где р' = р (t + Г), qr = q (t + Т). Параметризованное действие
S (t, Т) производит каноническое преобразование (д, р) -> (q\ р'),
которое само является действительным движением системы (ср*
с A.42)).
1.5. Переменные «действие — угол» и теория
Гамильтона — Якоби
Тот факт, что движение системы само является каноническим
преобразованием, очень важен для нашего дальнейшего исследо-
исследования уравнения Лиувилля. Остается еще другой класс канониче-
канонических преобразований, представляющий для нас особый интерес.
Это преобразования, которые приводят к переменным «действие—
угол». Они используются в анализе Пригожина уравнения Лиу-
Лиувилля, который будет рассматриваться в гл. П.
Теория переменных «действие — угол» основана на более
общих представлениях, называемых теорией Гамильтона —
Якоби, В этой теории стремятся найти каноническое преобразова-
преобразование, которое приводит к гамильтониану, циклическому по всем
новым координатам. Преимущество такого преобразования огром-
огромно. Если все новые координаты циклические, то все новые импуль-
импульсы — константы движения. С другой стороны, новый гамильто-
гамильтониан Нг (р') является функцией только новых постоянных импуль-
импульсов. Поэтому, продифференцировав его по этим импульсам, полу-
получим функцию от новых постоянных импульсов, дН'Idp' = q'*
которая сама будет константой. Уравнения Гамильтона в новых
координатах просто интегрируются и дают q\ = vtt + (Зг. Следо-
Следовательно, проблема сводится к алгебраической задаче обращения
преобразования, т. е. переходу к первоначальным координатам
и импульсам.
Таким образом, решение данной динамической задачи заклю-
заключается в нахождении такого канонического преобразования
(т. е. производящей функции), чтобы новые импульсы были кон-
константами движения. А эта последняя задача тесно связана с непо-
непосредственной проблемой интегрирования уравнений движения,
что является в свою очередь не более чем формальной операцией
отображения начальных координат и импульсов на их величины
в момент времени t. Действительно, для всех динамических задач,
кроме особого класса, теория Гамильтона — Якоби более важна
своей близкой причастностью к нейтральной области между клас-
классической динамикой и квантовой механикой, чем своими прило-
приложениями.
Как было отмечено ранее, теория Гамильтона — Якоби опи-
опирается на нахождение производящей функции, которая все новые
импульсы делает константами движения. Из четырех фундамен-
фундаментальных форм производящей функции наиболее подходящей будет
функция G2 = G2 (g, p').
1.5. Переменные «действие — угол» 35
Напомним уравнения A.50):
A.50а)
9i =-щ{Яи ---,9*; Ри ...,PW- A-506)
Предположим, что задача такая, в которой движение разде-
разделимо. Если это так, то функция G имеет вид
G = Gi{<lu Ри • ••» Pn) + G2(<12> Ри • • •> Pn)+ •. .,
* A.67)
G= 2j g*(?*; Pi. •••> Рл)-
г=1
Обозначим через (аь ..., aN) новые постоянные импульсы,
которые образуются при надлежащем выборе G, так что
N
Тогда уравнения A.50а) примут вид
или, что эквивалентно,
рг = pz (gj; а4, . . ., aN). A.70)
Каждое из этих соотношений есть проекция1) орбиты в 2Л^-мерном
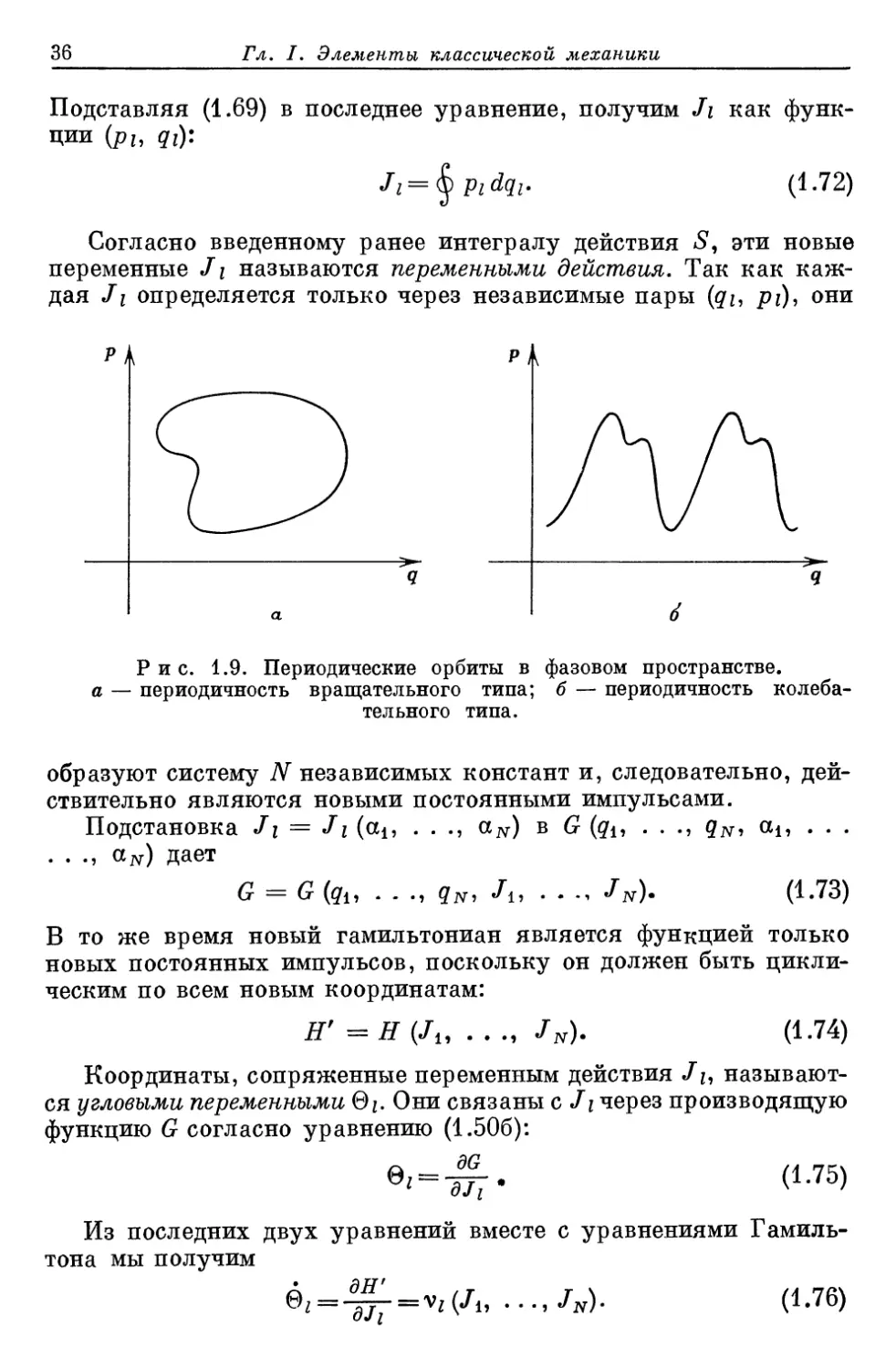
Г-пространстве на плоскость (qu Pi)- Говорят, что движение будет
периодическим, если pi является периодической функцией qi или
если орбита в плоскости (qu pi) замкнута. Эти два случая изобра-
изображены на рис. 1.9, а и 1.9, б.
Формализм «действие — угол» использует эту периодичность
в спроектированном на (qi, pi) движении для определения новых
постоянных импульсов в виде
где интегрирование производится по полному периоду колебания
либо вращения в соответствии со спецификой задачи.
Из A.71) совершенно ясно, что переменные J\ — функции
одних только констант а$ и, следовательно, так же постоянны.
х) Эти кривые расположены в гиперпдоскостях (qi,Pi). Они могут и не
быть проекцией одной-единственной кривой системы. Это имеет место, когда
гиперповерхности в Г-пространстве, порождаемые кривыми (qiiPi), не пере-
пересекаются. С другой стороны, очевидно, что кривая системы {qt = qt (t);
Pi ^ Pi 0)} (* = 1» • • •» Ю имеет проекции на гиперплоскостях (qi,Pi).
36
Гл. I. Элементы классической механики
Подставляя A.69) в последнее уравнение, получим Ji как функ-
функции (ри qi):
Ji=
A.72)
Согласно введенному ранее интегралу действия S, эти новые
переменные J \ называются переменными действия. Так как каж-
каждая Ji определяется только через независимые пары (qi, pi), они
р i
Рис. 1.9. Периодические орбиты в фазовом пространстве.
а — периодичность вращательного типа; б — периодичность колеба-
колебательного типа.
образуют систему N независимых констант и, следовательно, дей-
действительно являются новыми постоянными импульсами.
Подстановка J\ = J\ (а1? . . ., aN) в G fa, . . ., qN, а1? . . .
. . ., aN) дает
G = G (qu . . ., qN, Ju JN). A.73)
В то же время новый гамильтониан является функцией только
новых постоянных импульсов, поскольку он должен быть цикли-
циклическим по всем новым координатам:
Н' = Н
A.74)
Координаты, сопряженные переменным действия /ь называют-
называются угловыми переменными в*. Они связаны с J\ через производящую
функцию G согласно уравнению A.506):
©* = -#-• A.75)
Из последних двух уравнений вместе с уравнениями Гамиль-
Гамильтона мы получим
Л дН'
t, ..., JN).
A.76)
1.5. Переменные «действие — угол» 37
Переменные vu как функции N констант Jи также будут
постоянными. Проинтегрировав уравнение A.76), получим
@i = vit+ $?i. A.77)
Каков физический смысл переменных (в г, /*)? Чтобы полу-
получить ответ, вычислим 8i@j — полное изменение ву, когда qi совер-
совершает целый цикл:
§^ §^, A.78)
и мы окончательно получим, что
С1-79)
где 8ji — дельта Кронекера, 8ji = 1, если / = Z, и 67ч =0,
если j ф1. Отсюда следует, что Э; изменится на единицу, если
qj пройдет полный цикл, и останется неизменной в любом другом
случае. Когда qi совершает полный цикл, из уравнений A*77)
и A.79) вытекает, что
вг(тг)-вг@) =vin= 1. A.80)
Очевидно, что %i есть период колебания для движения, связан-
связанного с изменением qi. Но vi определяется через %i предшествую-
предшествующим уравнением,
v* = -^, A.81)
и, следовательно, является частотой периодического движения,
соответствующего изменениям qi. Если мы положим G* = 0г/2я,
уравнение A.77) примет вид
0, = 2nvit+ Ш'и
Qt = alt+ SCu A-82)
так что переменная 2n@i играет роль углового перемещения,
связанного с периодическим изменением qi.
Для системы, координаты которой осуществляют периодиче-
периодические движения, настоящая техника дает метод получения частот
движения без детального решения динамической задачи.
Теперь совершенно очевидно, что имеется значительный пробел
в нашей теории. Весь анализ опирается на производящую функ-
функцию G. Рассмотрим вкратце метод ее вычисления. Тогда мы полу-
получим замкнутую теорию в переменных «действие — угол».
Напомним прежде всего, что для всех четырех ранее рассмот-
рассмотренных типов производящих функций старый гамильтониан Н
и новый гамильтониан Я' всегда связаны равенством И' = Н +
+ dG/dt.
38 Гл. I. Элементы классической механики ^
Для систем, у которых Н постоянна и не содержит времени
явно, мы можем принять, что dGldt = 0. Полагая Н' = а4 в равен-
равенстве Н' = Н, получим (используя A.50а))
fa, A-83)
Это уравнение называется пространственно неоднородным урав-
уравнением Гамильтона — Якоби. Чтобы показать, что все новые
импульсы р' постоянны, мы положим
G = G (дь . . ., qN, аь . . ., aN).
Новый гамильтониан зависит только от р\ = аь так как он цикли-
чен по всем новым координатам. Следовательно, все новые импуль-
импульсы суть константы аи . . ., а^. Чтобы удостовериться в том, что
новые переменные (qf, а) являются «хорошими» координатами,
вспомним, что они получаются с помощью производящей функ-
функции, которая делает их «хорошими» согласно определению. Функ-
Функция G называется характеристической функцией Гамильтона.
В новых координатах движение становится тривиальным:
так что
<?;=Ц = Рь l?=l. A-856)
Функция G, определенная из дифференциального уравне-
уравнения A.83). совместно с уравнениями A.85) дает решение qi = q\ (t).
Для разъяснения метода обратимся к задаче об одномерном
гармоническом осцилляторе:
где к — коэффициент упругости, а т — масса. Уравнение Гамиль-
Гамильтона — Якоби A.83) имеет вид
\2 kq* ,л й7ч
) +—=«! = « A.87)
(только одна степень свободы)» Оно легко интегрируется и при-
приводит к следующему результату:
G =
j dq У^-q^G (a, q). A.88)
1.6. Интегральные инварианты Пуанкаре 39
Подстановка в уравнение A.85а) дает
^\ =-]/^arccosg]/^. A.89)
k J УBа//с) —д2 V к ^ 2а
Полагая к/т == со2 и обращая последнее уравнение, получим
A.90а)
«2 = А. A.906)
Если в начальный момент осциллятор находится в положении
q @) = q0 и р0 = 0, то «новый импульс» а = AgJ/2 является функ-
функцией только начальных условий.
В формализме переменных «действие — угол» действие /
задается согласно уравнениям:
f^f, A.91)
f ^ A.92)
где v = со/2п, и а = Я, так что
а = Я = v/. A.93)
Угловая переменная G определяется из уравнения A.75):
©dG dG dec dG , A ^, ч
A.95)
Задача 1.20. Построить формально преобразование (q, p) ->-
->¦ (G, /) и показать (в случае гармонического осциллятора),
что оно имеет вид
g=B/v//cI/2sin2ne
A.96)
1.6. Интегральные инварианты Пуанкаре
Прежде чем закончить этот краткий обзор классической меха-
механики, вернемся ненадолго к одному очень важному классу кано-
канонических инвариантов — к каноническим инвариантам Пуанкаре.
Чтобы понять значение этих инвариантов, полезно сначала
рассмотреть некоторые простые примеры преобразований пере-
переменных под знаком интеграла.
40
Гл. I. Элементы классической механики
У;
Рис. 10. Геометрическая интерпретация интегралов, определяющих пло-
площадь.
В настоящем обсуждении мы ограничимся двумерными
интегралами. Если С — замкнутая кривая в декартовом про-
пространстве (х, у), то площадь, ограничиваемая этой кривой,
равна А = \ \ dxdy, как показано на рис. 1.10, а. При пре-
D
образовании переменных (#, у)-+¦ {х', у') интеграл А-+А' =
y/z'i У*) dx' dyr = А. Площадь, конечно, остается
р
\ \
d
неизменной. Она не зависит от того, в каких координатах ее вы-
вычислять. Символ / обозначает якобиан преобразования. Кривая
С представляет собой тот же геометрический объект, что и кри-
кривая С. Это есть кривая С, выраженная через новые координаты.
1.6. Интегральные инварианты Пуанкаре
41
Кривые, на которых х' и у' являются соответственно постоян-
постоянными, образуют координатную сетку в плоскости (х, у). Они:
также изображены на рис. 1.10, а. Площадь поверхности Ау
естественно, не зависит от того, какой координатной сеткой
она покрыта. Это обеспечивается наличием якобиана, который
дает правильное значение элемента площади в новой системе
координат.
Существует другое важное геометрическое представление коор-
координат (хг, у') — в их собственном декартовом пространстве.
Оно иллюстрируется рисунком 1.10, б. Что представляет собой
кривая С, являющаяся кривой С в этом новом декартовом про-
пространстве? В общем случае, это, конечно, не тот же самый гео-
геометрический объект, что кривая С в начальном декартовом про-
пространстве (х, у). Вычислим площадь А, ограниченную кривой Сг
т. е.
'= ( j dx'dy'.
D
Согласно предшествующему обсуждению,
А= j j Jdxf dy',
A.97)
A.98)
так что А = А, если / = 1. Хотя кривые С" и С представляют
собой один и тот же аналитический объект, в большинстве случаев
они являются различными геометрическими объектами. В случае^
когда якобиан / {хг, у'/х, у) равен единице, площадь, ограни-
ограниченная кривой С в декартовом пространстве (ее, г/), будет той же-
самой, что и площадь, ограниченная искаженной кривой С в декар-
декартовом пространстве (хг, у').
Следующий тривиальный пример разъясняет сказанное выше.
Пусть преобразование (х, у)->(х', у') задается уравнениями
г' — х •
дх'
дх
~~дх
дх'
~д~п~
ду'
ду
А
1
а
0
0
а
= 1.
A.99)
A.100)
Рассмотрим площадь
ь ъ
А = \ dx \ dy = Ь2 = \ \ dx dy.
0 0 D
A.101)
42
Гл. I. Элементы классической механики
Через новые координаты она выразится следующим образом:
Ь/а Ъа Ъ/а ab
А-+А'=\ dx' \dy'J=\dx' \dy'=\ \dx'dy' = A. A.102)
о
о
о
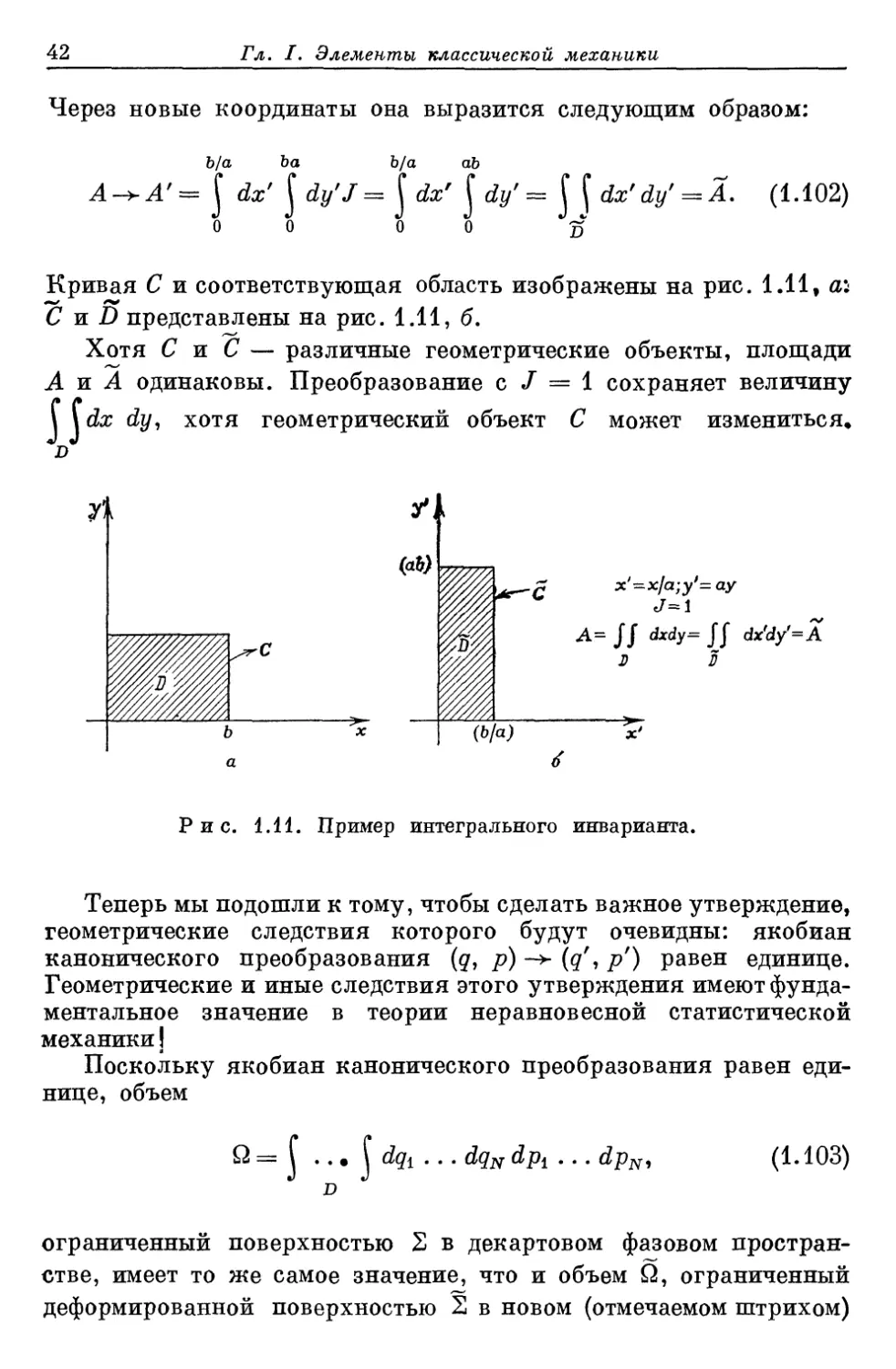
Кривая С и соответствующая область изображены на рис. 1.11, а:
С и D представлены на рис. 1.11, б.
Хотя С ж С — различные геометрические объекты, площади
А и А одинаковы. Преобразование с / = 1 сохраняет величину
\ \ dx dy, хотя геометрический объект С может измениться*
х'-х/а;у'= ау
JJ dxdy= JJ
d д
х'
Рже. 1.11. Пример интегрального инварианта.
Теперь мы подошли к тому, чтобы сделать важное утверждение,
геометрические следствия которого будут очевидны: якобиан
канонического преобразования (q7 р) ->¦ (д', рг) равен единице.
Геометрические и иные следствия этого утверждения имеют фунда-
фундаментальное значение в теории неравновесной статистической
механики!
Поскольку якобиан канонического преобразования равен еди-
единице, объем
D
dqi . . . dqN dpt . . . dpN,
A.103)
ограниченный поверхностью 2 в декартовом фазовом простран-
пространстве, имеет то же самое значение, что и объем Q, ограниченный
деформированной поверхностью 2 в новом (отмечаемом штрихом)
1.6. Интегральные инварианты Пуанкаре 43
декартовом фазовом пространстве г):
Q = U = \ ... \dq[...dqNdp[... dp'N. A.104)
D
Тогда, согласно предыдущему определению, объем Q является
каноническим инвариантом.
Существует подкласс в классе всех канонических преобразо-
преобразований, для которого эти интегральные инварианты имеют особое
динамическое значение. Этот подкласс представляет собой множе-
множество преобразований, соответствующих действительному динами-
динамическому перемещению системы. Мы вернемся к этой теме при
одном из наиболее простых выводов уравнения Лиувилля.
В конце девятнадцатого столетия теория динамических преоб-
преобразований находилась в своем зените. Основы этой теории были
заложены Лагранжем A788) и Гамильтоном A833), а ее дальней-
дальнейшее развитие связано с работами Максвелла A859) и Пуанкаре
A890). Почти на рубеже двух столетий эта фундаментальная основа
познания дала начало новой науке — неравновесной статистиче-
статистической механике. Новый формализм опирался на явления необра-
необратимости и концепцию ансамбля (Больцман A871), Максвелл A879),
Гиббс A902), Эйнштейн A902)).
В главе II вводится понятие ансамбля, которое естественным
образом приводит к определению новой динамической перемен-
переменной — N-частичной функции распределения. Уравнение, кото-
которому удовлетворяет эта функция,— уравнение Лиувилля — являет-
является одним из наиболее важных во всей классической неравновес-
неравновесной статистической механике. Из теории этого уравнения исходит
теория кинетических уравнений, а из последней — количественное
описание явлений необратимости.
Некоторые темы, развитые в этой главе, найдут применение
в последующих главах. Переменные «действие — угол» будут
использованы в анализе Пригожина уравнения Лиувилля, пред-
представленном в гл. II. Концепция констант движения применяется
при нахождении самого общего решения уравнения Лиувилля
и в заключительной дискуссии этой книги, касающейся эргодиче-
ской теории. К динамической обратимости орбит мы будем часто
возвращаться в связи с парадоксом видимой необратимости
г) Интегральные инварианты Пуанкаре определяются с большей общ-
общностью и включают такие формы, как \ \ HNdqidpi, где интегрирование
ведется по двумерным поверхностям в фазовом пространстве. Соответствую-
Соответствующие интегралы для четырех-, шести-, . . . TV-мерных поверхностей в фазовом
пространстве также будут каноническими инвариантами. Для дальнейшего
ознакомления с этими вопросами можно обратиться к литературе, указан-
указанной в конце главы.
44 Гл. I. Элементы классической механики
макроскопических систем. Уравнения Гамильтона являются наи-
наиболее широко используемым аппаратом на протяжении всей книги.
Основой теории кинетических уравнений служит динамика.
Теория только тогда будет незыблемой, когда этот фундамент
прочен.
Задача 1.21. Показать, что произведение двух канонических
преобразований само будет каноническим преобразованием.
Задача 1.22. Показать, что скобки Пуассона для любых двух
динамических переменных являются каноническим инвариантом.
Задача 1.23. Показать, что если преобразование (д, р) ->•
¦*" (?'» Р') (Для N обобщенных координат) каноническое, то яко-
якобиан / (g, plq', p') равен единице.
Задача 1.24. Вычислить якобиан преобразования, задаваемого^
уравнениями A.38а). Каково будет значение этого определителя,
если вместо рх = pr cos 8 — (pq/г) sin 8 положить рх — 2рг?
Задача 1.25. Показать, что скобки Пуассона для двух декар-
декартовых компонент углового момента X частицы удовлетворяют
соотношению \Х\, Xf] = Хъ, где (i, /, k) представляют собой
круговую перестановку переменных (х, у, z).
Задача 1.26. Рассмотреть одномерную задачу о рассеянииг-
т v V М
ДО О—> <—О,
•о' т MY'
после <^-о о—>.
Указание. Соотношение между у, V и i/, V можно записать
в матричной форме:
v'\ _ 1ац ai2\ lv\
V'j-[a2iaJ \V) "
а) Предположим, что эксперимент производится много раз,
так что начальные скорости располагаются в малой непрерывной
области 2 около (у, V). Показать тогда, что
Г \dvdV= \ ^dv'dV'.
б) Для случая т — М показать, что углы, изображенные
на рис. 1.12, сохраняются, т. е. я|э = i(/.
1.6. Интегральные инварианты Пуанкаре
45
v
Рис. 1.12. Каноническое отображение процесса бинарного столкновения.
Задача 1.27. Для свободной частицы, движущейся в одном
измерении, имеются две константы движения:
pt
Показать, что [hu H] = 0 и [Л2, Н] + dh2/dt = 0.
Задача 1.28. а) Если в данной задаче переменные q я р кано-
канонические, показать, пользуясь уравнениями Гамильтона, что они
удовлетворяют уравнению
дд
~dq
dp
б) Решение данной динамической задачи приводит к уравне-
уравнениям
р = sin q.
Будут ли переменные (q, p) каноническими?
Задача 1.29. Показать, что [u, g (и)] = 0.
Задача 1.30. Доказать равенства A.57) и A.58).
Задача 1.31. Формализмы Лагранжа и Гамильтона можно
сохранить для случая сил, зависящих от скоростей, если выпол-
выполнены некоторые условия. Требуется, чтобы сила Fi в направлении
обобщенной координаты qi выражалась в форме
F dV d i dV
F+(
46 Гл. I. Элементы классической механики
В противоположность этому для консервативных сил выполняется
условие
При таких ограничениях динамика системы по-прежнему может
быть задана через уравнения Лагранжа или Гамильтона, где
dL
Pl = —
Рассмотрим частицу с массой т и зарядом е, движущуюся
со скоростью v в электрическом поле Е и магнитном поле В.
Сила, действующая на эту частицу, равна (в гауссовых единицах)
Пытаясь использовать формализм канонического электромагнит-
электромагнитного поля, удобнее работать с потенциалами АиФ, чем с Е и В.
Потенциалы и поля связаны уравнениями:
= VxA,
Последнее уравнение служит для того, чтобы сделать соотноше-
соотношение определенным (Ф -> Ф' = Ф — dtyldt и A->A'=A + V<i|?
оставляет первые два уравнения неизменными), и называется
преобразователем Лоренца.
а) Показать, что обобщенный потенциал для заряженной
частицы в электромагнитном поле равен
б) Показать, что канонический импульс
__ тх I — А
с
в) Показать, что гамильтониан для такой частицы
2т
г) Какие уравнения вытекают из уравнений Максвелла для Ф
и А, связанных преобразователем Лоренца?
1.6. Интегральные инварианты Пуанкаре 47
Задача 1.32. Если гамильтониан не зависит от времени,
то всегда ли перестановочны операции d/dt и д/др? То есть спра-
справедливо ли, что
dt \ др ) — др \ dt ) #
Ответ. Если dH/dt = 0, то Н = const и dHldt = О, что обра-
обращает в нуль правую часть предшествующего уравнения. Однако
левая часть равна дине обязательно равна нулю.
Задача 1.33. а) Показать, что движение, соответствующее
гамильтониану
инвариантно относительно преобразования
я (Ф) -+ н' = я (Ф +чд> @),
где я|) — произвольная функция времени.
б) Исследовать инвариантность движения, соответствующего
гамильтониану
при преобразованиях:
1) Я(А,Ф)->Я' =
2) H-+B' = H(A + W{t), Ф),
3) Я + Я^
Задача 1.34. а) Если # — перемещение, то какая форма вто-
второго закона Ньютона следует из гамильтониана
б) Пытаясь устранить явную зависимость этого гамильтониана
от времени, вызывающую затруднения, можно перейти к новому
каноническому представлению, где Н' постоянна. Используя
метод Гамильтона — Якоби, это можно сделать следующим обра-
образом. Записать уравнение Гамильтона — Якоби для G (#, t)\
построить решение, при котором / и g будут линейными функциями,
т.е. f = at ж g = §х. Какой вид имеет «новый» гамильтониан?
Ответ.
а) тх= —f(t)gx,
б) ^-G
Гл. I. Элементы классической механики
СПИСОК ЛИТЕРАТУРЫ
А. Ранние работы, по аналитической механике
Гамильтон (Hamilton W. R.)
A833) Problem of Three Bodies by My Characteristic Function.
A834) On a General Method in Dynamics, by which the Study of the Motions
of all Free Systems of Attracting or Repelling Points is Reduced to
the Search and Differentiation of One Central Relation, or Characte-
Characteristic Function. Phil. Trans, Roy, Soc, Part II, 247—308.
A835) Second Essay on a General Method in Dynamics, Phil, Trans, Roy.
Soc, Part I, 95—144.
Лагранж (Lagrange J.L.)
A773) Mecanique Analytique A788); Oeuvres, v. 6, p. 335 A773). Русский
перевод: Лагранж Ж. Л., Аналитическая механика, М.— Л.9 ГИТТЛ,
1950.
A808) Mem. de L'Institute de France.
Лиувилль (Liouville J.)
A838) Note sur la theorie de la variation des constants arbitraries, /• de
Math,, 3, 342.
Пуанкаре (Poincare H.)
A951—54) Oeuvres, Paris, Gauthier — Villars.
A892) Methodes Nouvelles de la Mechanique Celeste, 1892. Reprinted by
Dover, New York, 1957. Русский перевод в сб. Пуанкаре А.,
Избранные труды, М., «Наука», т. 1, 1971, т. 2, 1972.
A890) Sur le probleme des trois corps et les equations de la dynamique,
Ada Math., 13, 1; Oeuvres, v. 7, p. 272*
Пуассон (Poisson S. D.)
A823) Sur la chaleur des gaz et des vapeurs, Ann, Chim,, 23, 337 A823),
Ann, Physik, 76, 269 A824). Английский перевод с примечаниями
Хиапаса (J. Herapath), Phil, Mag., 62, 328 A823).
A807) Memoire sur la theorie du son, Nouv, Bull, Sci. Soc. Philomat (Paris),
1, 19 A807), /. Ecole Polyt (Paris), 7, 14e Cah., 319 A808).
A831) Nouvelle theorie de Faction capillaire, Paris, Bachelier#
A835) Theorie mathematique de la chaleur, Paris, Bachelier.
Якоби (Jacobi K. G. J.)
{1866) Vorlesungen uber Dynamik, Berlin, G. Reimer, 1866; second edition,
1884. Русский перевод: Якоби К. Г. Я., Лекции по динамике,
Л.— М., ОНТИ, 1936.
В* Ранние работы по кинетической теории и статистической механике
Больцман (Boltzmann L.)
A872) Vorlesungen uber Gastheorie, Leipzig, A896—1898); Wien, Ber,, 66,
275 A872). Имеется английский перевод (S. G. Brush):
A964) Lectures on Gas Theory, University of California Press, Berkeley,
California. Эта книга содержит исчерпывающую историю развития
Список литературы 49
теории и обширную библиографию. Русский перевод: Больцман Л.,
Лекции по теории газов, М., Гостехиздат, 1956.
Гиббс (Gibbs J. W.)
A906) The Scientific Papers of J. Willard Gibbs, London and New York,
Longmans, Green, 1906. Second edition. The Collected Works of J. Wil-
Willard Gibbs, 1928. Reprinted by Yale University Press, 1948, and by
Dover, New York, 1960.
A875) On the equilibrium of heterogeneous substances, Trans. Conn. A cad.,
3, 108, 343 A875); Arner. J. Sci., 16, 441 A878); Works, v. 1, p. 55.
Немецкий перевод (W. Ostwald): Thermodynamische Studien, Leipzig,
Engelmann, 1892. Французский перевод (G. Matisse): L'equilibre
des substances heterogenes, Paris, Gauthier — Villars, 1919. Русский
перевод в сб. Гиббс Дж. В., Термодинамические работы, М.—Л.,
ГИТТЛ, 1950.
A902) Elementary principles in statistical mechanics, developed with espe-
especial reference to the rational foundation of thermodynamics, New
York, Scribner, Works, v. 2, p. 1. Русский перевод: Гиббс Дж. В.,
Основные принципы статистической механики, излагаемые со спе-
специальным применением к рациональному обоснованию термодина-
термодинамики, М.— Л., Гостехиздат, 1946.
Максвелл (Maxwell J. С.)
A890) The Scientific Papers of James Clerk Maxwell, Cambridge Uni-
University Press, 1890; reprinted by Hermann, Paris, 1927, and by
Dover, New York. 1952.
A859—1860) Illustrations of the dynamical theory of gases. I. On the motions
and collisions of perfectly elastic spheres. II. On the process
of diffusion of two or more kinds of moving particles among one
another. III. On the collision of perfectly elastic bodies of any
form, Phil. Mag. [4], 19,19; 20, 21, 33 A860); Brit. Assoc. Rept.,
29 B), 9 A859); Athenaeum, p. 468 (Oct. 8, 1859); L'lnstitut
364 A859).
A866) Viscosity or internal friction of air and other gases, Phil. Trans,,
156, 249 A866); Proc. Roy. Soc. (London), 15, 14 A867).
A867) On the dynamical theory of gases, Phil. Trans., 157, 49; Proc.
Roy. Soc. (London), 15, 146.
A873) A discourse on molecules, Nature, 8, 437 A873); Phil. Mag. [4],
46, 453 A873); Les Mondes, 32, 311, 409 A873); Pharmaceut. /.,
4, 404, 492, 511 A874).
A875) On the dynamical evidence of molecular constitution of bodies
(lecture). Nature, 11, 357, 374; /. Chem'. Soc, 13, 493; Gazz.
Chim. ItaL, 5, 190.
A878) On stresses in rarified gases arising from inequalities of tempe-
temperature, Phil. Trans., 170, 231 A880); Proc. Roy. Soc. (London),
27, 304 A878).
A879) On Boltzmann's theorem on the average distribution of energy
in a system of material points, Trans. Cambridge Phil. Soc,
12, 547 A879); Phil. Mag. [5], 14, 299 A882); Ann. Physik
BeibL, 5, 403 A881).
Эйнштейн (Einstein A.)
A902—03) Ann. Physik, 9, 417 A902); 11, 170 A903). Русский перевод в сб.
Эйнштейн А., Собрание научных трудов, М., «Наука», т. 3,
1966, статьи 3, 4.
50 Гл. I. Элементы классической механики
В. Классическая механика
Аппель (Appell P.)
A902—37) Traite de Mechanique Rationelle E vols), 2nd ed., Paris, Gau-
thier — Villars, Русский перевод (с 5-го франц. изд.): Аппель П.,
Теоретическая механика (в 2-х томах), М., Физматгиз, 1960.
Вебстер (Webster A. G.)
A904) The Dynamics of Particles and оГ Rigid, Elastic and Fluid Bodies,
Leipzig, B. G. Teubner, 1904 (New York, Stechert—Hafner, 1920),
Chapters 5, 7, 10. Русский перевод: Вебстер А. Г., Механика мате-
материальных точек, твердых, упругих и жидких тел, Л.— М., ГТТИ,
1933.
Голдстейн (Goldstein H.)
A959) Classical Mechanics, Reading, Mass., Addison — Wesley. Русский
перевод: Голдстейн Г., Классическая механика, М., Гостехиздат,
1957.
Детуш (Destouche J. L.)
A948) Principes de la Mechanique Classique, Paris, Centre National de la-
Recherche Scientifique.
Зоммерфельд (Sommerfield A.)
A949) Vorlesungen tiber Theoretische Physik. Vol. 1: Mechanik, 4th ed.,
Wiesbaden: Dieterich'sche Verlagsbuchhandlung, Chapters 2, 3, 5.
Русский перевод с 3-го издания: Зоммерфельд А., Механика, М.г
ИЛ, 1947.
Коэ (Сое С. J.)
A938) Theoretical Mechanics, New York, MacMillan Co., Chapter I.
Ландау Л. Д., Лифшиц Е. М.
A973) Теоретическая физика; т. 1, Механика, М., «Наука», изд. 3-е.
Лэмб (Lamb H.)
A929) Higher Mechanics, 2nd ed., Cambridge, Cambridge University Press.
Русский перевод: Лэмб Г., Теоретическая механика (в 3-х томах)г
М.4— Л., ГТТИ, 1935.
Мак-Миллан (MacMillan W. D.)
A927) Theoretical Mechanics, New York, McGraw-Hill. Vol. 1: Statics and
the Dynamics of a Particle, 1937, Chapter 3. Vol. 3: Dynamics of Rigid
Bodies, 1936, Chapter 5. Русский перевод: Мак-Миллан В. Д., Дина-
Динамика твердого тела, М., ИЛ, 1951.
Милн (Milne E. А.)
A948) Vectorial Mechanics, New York, Interscience, Chapters 1, 5.
Осгуд (Osgood W. F.)
A937) Mechanics, New York, MacMillan, Chapters 1, 2, 4.
Синг, Гриффис (Synge J. L., Griffith B. A.)
A949) Principles of Mechanics, 2nd ed., New York, McGraw-Hill, Chapters 1, 5.
Слейтер, Фрэнк (Slater J.C., Frank N.H.)
A947) Mechanics, New York, McGraw-Hill, Chapters 3, 11.
Тимошенко, Юнг (Timoshenko S., Young D.H.)
A948) Advanced Dynamics, New York, McGraw-Hill, Chapters 5, 10.
Список обозначений к гл. I 51
Уиттекер (Whittaker E.T.)
A901—35) Encyklopadie der Mathematischen Wissenschaften. Vols. IVi and
IV2: Mechanik, A: Grundlagen der Mechanik; B: Mechanik der
Punkte und Starrer Systeme. Leipzig, B. G. Theubner.
A927) Handbuch der Physik, Vol. V: Grundlagen der Mechanik der
Punkte und Starrer Korper, Berlin, Julius Springer, Chapters 1, 5,
7, 8, 9.
A944) A Treatise on Analytical Dynamics of Particles and Rigid Bodies,
New York, Dover. Русский перевод: Уиттекер Э., Аналитиче-
Аналитическая динамика, М.— Л., ОНТИ, 1937.
Шефер (Schaefer С.)
A929) Eifiihrung in die Theoretische Physik. Vol. 1: Mechanik materieller
Punkte; Mechanik starrer Korper und Mechanik der Kontinua (Elasti-
zitat and Hydrodynamik), 3rd ed. Berlin, Walter de Gruyter, 1929
(Ann. Arbor: J. W. Edwards, 1948). Русский перевод: Шефер К.,
Теоретическая физика, т. 1—3, М.— Л., ГТТИ, 1934—1938.
Эймс, Мурнаган (Ames J. S., Murnaghan F. D.)
A929) Theoretical Mechanics, Boston, Ginn and Company.
Г. Дифференциальная геометрия
Эйзенхарт (Eisenhart L. P.)
A947) An Introduction to Differential Geometry, Princeton N. J., Princeton
University Press.
Список обозначений к гл. I
А — векторный потенциал,
А — динамическая переменная,
В — магнитное поле,
В — динамическая переменная,
с — скорость света,
Е — электрическое поле,
F — сила,
Gi — производящая функция,
Н — гамильтониан,
/ — переменная действия,
/ — якобиан,
L — лагранжиан,
X — угловой момент,
N - - число степеней свободы.
52 Гл. I. Элемент классической механики
р — канонический импульс,
q — каноническая координата,
S — действие,
Т — кинетическая энергия,
и — динамическая переменная,
v — скорость,
V — потенциальная энергия,
Д — перемещение,
8in — дельта Кронекера,
8 — бесконечно малая,
Ф — потенциал,
[,] — скобки Пуассона,
v — частота,
Q — объем в Г-пространстве,
0 — угловая переменная,
х — период.
ГЛАВА II
УРАВНЕНИЕ ЛИУВИЛЛЯ И ФУНКЦИИ
РАСПРЕДЕЛЕНИЯ
2.1. Концепция ансамбля и уравнение Лиувилля
Представим себе стеклянный сосуд, заполненный газом. В сосу-
сосуде имеется огромное количество частиц (молекул). Если частицы
являются точечными и всего их N, то имеется 3iV обобщенных
координат и размерность Г-пространства равна 6iV. Состояние
газа в любой момент времени изображается единственной точкой
в Г-пространстве. Представим себе другой сосуд, идентичный
первому во всем, кроме одного: в любой данный момент состояние
во втором сосуде отлично от состояния в первом сосуде. Состояния
двух одинаковых сосудов — с идентичными молекулами —изобра-
—изображаются двумя различными точками Г-пространства. В ходе изме-
изменения времени два идентичных множества молекул в двух сосудах
перемещаются и одновременно две точки, описывающие эти мно-
множества, прочерчивают две различные динамические траектории
в Г-пространстве. Эти траектории не пересекаются. Если бы они
коснулись одна другой, то состояние первого газа, определяемое
6N числами (д, р), совпало бы с состоянием второго газа. Эти два
множества из 6N чисел можно было бы принять за начальные
условия, которые в свою очередь единственным образом опреде-
определили бы движение, и данные две траектории слились бы в одну.
Следовательно, одна и только одна динамическая траектория
проходит через каждую точку Г-пространства.
Задача 2.1. а) Обращаясь к рис. 1.6 и предшествующей аргу-
аргументации, доказать, что двумерное движение (с исключенным
временем, так что g = q (p)) всегда удовлетворяет условию dq/dp =
= 0 при р = 0. Показать также, что замкнутая орбита, пересе-
пересекающая ось /?, должна иметь симметричное отражение относитель-
относительно оси д. (Эти теоремы теряют силу на границах фазового про-
пространства.)
Указание. Предположить, что кривая р = р (д) не пересекает
ось д по нормали, и затем построить обратную динамическую траек-
траекторию. (Заметим, что доказательство должно включать соображе-
соображения о гладкости dp/dq.)
Утверждение можно доказать без применения геометрии путем
рассмотрения гамильтониана изолированной системы в виде
Я = Т {р2) + V (д). Поскольку Я = 0 = 2ррТР2 + qVq, то
dq/dp = -2pTp2/Vq.
54 Гл. II. Уравнение Лиувилля и функции распределения
б) Доказать (аналитически) пункт а) в случае N измерений
для движения в плоскости (qu pi).
Пусть теперь мы имеем две динамические траектории в Г-про-
странстве, и они не пересекаются. Каждая из этих двух кривых
представляет один из двух идентичных газов. Различие между
двумя плавно изменяющимися последовательностями состояний
объясняется только несовпадением начальных условий. Мы пред-
представили себе второй сосуд, чтобы легче усмотреть различие между
двумя динамическими траекториями, проистекающее из несов-
несовпадения начальных условий.
Вместо только двух (одинаковых) сосудов, наполненных газом,
рассмотрим 30 миллионов таких сосудов, или, что эквивалентно,
рассмотрим один и тот же газ при 30 миллионах различных
начальных условиях. Чтобы физически реализовать последнюю
ситуацию, необходимо провести 30 миллионов экспериментов.
В любом случае представляющие точки каждой из этих мно-
многочисленных газовых систем образуют скопление (не пересекаю-
пересекающихся) динамических траекторий в Г-пространстве. Пусть число
таких тождественных систем достаточно велико, так что можно
ввести функцию плотности!) (р, q, t) точек системы в Г-простран-
Г-пространстве х). Эта плотность такова, что
D (g, р, t) dqdp = D (g, р, t) dQ B.1)
есть число точек системы в объеме dq dp около точки (р, q) в
в момент t.
Число точек в конечном объеме Q фазового пространства
в момент t равно \ DdQ. Поскольку эти точки не создаются и не
уничтожаются (каждая из них представляет мыслимое воспроиз-
воспроизведение одной-единственной системы), скорость изменения со вре-
временем величины \ DdQ должна равняться со знаком минус
h
потоку частиц через поверхность 2, ограничивающую Q. Если
и — скорость точек системы в окрестности элемента поверхности
dS, то суммарный поток через поверхность 2 равен i xiD-dl*.
Отсюда следует, что
j =— [ V.uDdQ, B.2a)
0. B.26)
Напомним, что в силу наших обозначений q = (qt, . . ., </злг)» р =
) (для N точечных частиц).
2.1. Концепция ансамбля и уравнение Лиувилля 55
В пределе, когда Q —>- 0 (используя теорему о среднем значении),
получим хорошо известное в гидродинамике уравнение неразрыв-
неразрывности:
•^¦D + V.uD = 0. B.3)
Это уравнение выражает закон сохранения точек системы. Оно
никак не связано с динамикой индивидуальных систем. Информа-
Информация о последней заключена в переменной и —«скорости». Что
представляет собой этот вектор в точке (q, p) в момент t? Если
движение точки системы задано уравнениями qt = qt (t), pi =
= Pi(t) (для N частиц индекс I пробегает значения от 1 до 3iV), то
«скорость» точки системы (q, р) равна (qi, . . ., q3N; pu . . ., p3N).
«Скорости» бесконечно близких динамических траекторий будут
отличаться от (д^, ...,/?!, . . .) на бесконечно малые (поскольку
соответствующие начальные условия отличаются на бесконечно
малые). Отсюда следует, что скорость и точек в элементе
(dqu . . ., dq3N; dpu . . ., dp3N) около (g, p) задается производ-
производными координат и импульсов частиц, образующих систему, кото-
которая проходит через точку (#, р) в момент t:
u = @i» • • -7 Qsn, Pi» • • -7 Psn)-
Оператор градиента V —это вектор (д/dqi, . . ., d/dq3N; д/dpi, ...
. . ., d/dp3N). Выражение дивергенции V-uZ) через компоненты
(для N точечных частиц) имеет следующий вид:
3N 3N
B.4в)
B.4т)
При выводе равенства B.4в) были использованы уравнения
Гамильтона для скорости (q, p) точек траектории системы, так что
в соотношении B.4г) учитываются динамические законы движе-
движения. Теперь уравнение B.3) принимает вид
-^-D + u-VD^O. B.5)
Здесь функция D — это плотность точек динамической систе-
системы, в то время как в уравнении B.3) эта функция представляла
просто плотность точек, которые не возникают и не уничтожаются.
56 Гл. II. Уравнение Лиувилля и функции распределения
Из уравнения B.5) следует, что «жидкость», для которой D
является плотностью, несжимаема. Рассмотрим для простоты
одномерное движение жидкости с массовой плотностью р =
= р (х, t). Если жидкий элемент находится в положении х в момент
t, то он будет находиться в точке х + и At в момент t + At, где
и — скорость жидкого элемента. Если жидкость несжимаема,
то при движении жидкого элемента количество жидкости рАх
в объеме Ах остается неизменным. Отсюда следует, что р (х, t) Ax=
= р (х + uAt, t + At) Ахг. Объем Ах' — это новый объем, кото-
который занимает в момент t -\- At количество жидкости р (х, t) Ax.
Если жидкость несжимаема, то Ах = Ах'. Разлагая правую
часть написанного выше равенства по степеням At, получим
... B.6)
В пределе, когда At-*- О, будем иметь уравнение для плотности
несжимаемой жидкости:
Согласно этому уравнению, плотность в окрестности точки являет-
является инвариантным свойством точки, когда последняя совершает
свое динамическое движение.
То, что уравнение B.5) отражает свойство несжимаемости
динамической переменной Z?, можно увидеть более наглядным
путем. Сначала перепишем это уравнение в виде
0. B-7в>
где мы опять использовали уравнения Гамильтона. Вспоминая
обозначение скобок Пуассона, можно записать последнее уравне-
уравнение иначе:
¦|+[Д,Я] = 0. B.8)
Но в гл. I мы установили, что полная производная по времени
от любой динамической переменной задается как раз таким выра-
выражением. Отсюда следует, что полная скорость изменения D по вре-
времени равна нулю:
ТГ-°- B'9>
В производную dDldt входят производные решений q (t) и р (t).
В любой момент t дифференцируемые функции q и р определяют
положение точки системы в этот же самый момент времени. Опера-
2.1. Концепция ансамбля и уравнение Лиувилля
57
дия dDldt представляет производную по времени от D (g, р)у
вычисленную в системе отсчета, которая движется вместе с точкой
динамической системы.
Уравнение B.8) называется уравнением Лиувилля. Выведем
его снова, используя теорему об интегральных инвариантах
Пуанкаре. Теорема утверждает, что при каноническом преобразо-
преобразовании (g, p)-+ (q', pf)
f ... \,dqi...dqNdpi... dpN = j ... j dq[ . . . dq'N dp[ . . . dp'N,
B.10)
где Й — образ области й, ограниченной поверхностью 2 в новом
Г'-пространстве при данном (но произвольном) каноническом
преобразовании.
Применим эту теорему к каноническому преобразованию
(?i i9) ^ \Я •> Р )•> которое представляет собой деиствительное-
перемещение системы за время Т. Координаты и импульсы со
90 + Тр0
Рис. 2.1. Каноническое преобразование в различных фазовых пространст-
пространствах.
Штрихом равны значениям, которые принимают q (t)iip (t) в момент
t + Г. При изображении изменения формы, которое претерпевает
поверхность 2 в силу канонического преобразования ? (Т),
имеются две возможности. Либо мы можем рассматривать Г'-про-
странство отдельно от начального пространства Г, либо мы можем
эти два пространства наложить одно на другое.
Для свободной частицы с единичной массой движение задается
Уравнением q = Pot-\-qo (если q — линейное перемещение, ар —
Линейный импульс). Пусть начальные условия для этой частицы
«размазаны». Область в Г-пространстве, занимаемая этими началь-
начальными точками, изображена на рис. 2.1, а. Спустя время Т пре~
58
Гл. II. Уравнение Лиувилля и функции распределения
•образование ? (T) переведет эту область Q и ограничивающую
ее кривую 2 в область Q' (Т) с границей 2' (Г), как показано
на рис. 2.1, б.
Задача 2.2. а) Описать аналитически кривую 2' и доказать,
что Q' = Q для случая, изображенного на рис. 2.1.
б) Повторить предшествующее геометрическое построение
..
и доказательство для движения q = g, где g — постоянная. Масса
предполагается равной единице.
С другой стороны, если пространства Г' и Г наложены одно
на другое, то динамическое преобразование будет таким, как
Рис. 2.2. Каноническое преобразование в одном и том же фазовом прост-
пространстве.
показано на рис. 2.2. Поскольку преобразование ? (Т) порож-
порождает само динамическое движение, область Q' представляет собой
•совокупность таких точек системы в момент времени 7\ которые
в момент t = 0 находились в Q.
Физически более естественно рассматривать теорему Пуанкаре
с точки зрения представлений о геометрическом наложении, как
изображено на рис. 2.2. Хотя для только что рассмотренного
простого одномерного случая равенство Q = Q' почти тривиально,
теорема Пуанкаре говорит нам, что даже для более общего случая
iV-мерной задачи Q >Q' остается инвариантом, так что Q = Q'-
Каково число точек системы в Q? Может ли внутренняя точка
стать внешней точкой при преобразовании ? (Г)? Обозначим через
2 геометрическое место граничных точек области Q. Если точка,
внутренняя по' отношению к 2, станет внешней к 2 после пре-
преобразования ? (Г), то она должна пересечь граничную точку.
Пусть она пересечет ее в момент t'', удовлетворяющий условию
2.1. Концепция ансамбля и уравнение Лиувилля
59
О < t' < Т. В момент t' значения g и р для граничной точки
и рассматриваемой внутренней точки имеют соответственно оди-
одинаковые значения. Но движение точек единственным образом
определяется «начальными данными». Таким образом, в последую-
последующие моменты времени, включая время f, положение этих точек
Г- пространство
Рис. 2.3. Теорема Лиувилля в интерпретации Пуанкаре.
Число точек системы: N ->¦ N' = N.
Объем: Q ->¦ Q' = Q.
Поверхность 2 искажается: 2 Ф 2'.
системы должно совпадать. Следовательно, внутренняя точка
не может пересечь границу. Число точек N (Q) в Q сохраняется;
N (Q) Л% N' (Q') = N (Q) (рис. 2.3).
Задача 2.3. а) Доказать, что для данной системы (т. е. для
заданного гамильтониана) из точки (р @), q @)) выходит только
одна динамическая траектория.
Указание. Разложить q (t) около t = 0 и использовать уравне-
уравнения Гамильтона.
б) Доказать, что две траектории системы, выходящие из двух
различных начальных точек в Г-пространстве, не могут пересечься.
В пределе, когда Q становится очень малой, предшествующие
Доказательства остаются в силе. Число точек AiV в малом объеме
AQ (называемое согласно Гиббсу протяженностью по фазе) про-
пропорционально AQ с коэффициентом Z), так что
AN = DAQ. B.11а)
Если мы подвергнем это соотношение преобразованию ? (Г),
то получим (разумеется, AiV' по-прежнему пропорционально
AQ')> что
&N' D'AQ' B.116)
60 Гл. II. У равнение Лиувилля и функции распределения
ИЛИ
AN = D'AQ. B.11в>
Сравнение этого последнего равенства с B.11а) показывает, что
Отсюда следует, что величина D является постоянной для рассмат-
рассматриваемого малого объема, так что
тг=°- <2Л2>
Таким образом, мы снова приходим к уравнению Лиувилля.
Вернемся к одномерной задаче, изображенной на рис. 2.2.
Каков физический смысл множества точек, которые содержатся
в объеме Q? Если мы примем момент времени t за начальный,
то эти точки представят непрерывную область начальных условий
для одной и той же единственной одномерной системы. Динамиче-
Динамические траектории точек системы являются траекториями множест-
множества систем, воспроизводящих одну-единственную систему. Разли-
Различие между ними заключается только в начальных условиях. Сово-
Совокупность этих точек представляет образец ансамбля. Существенног
что понятие ансамбля связано с описанием единственной системы.
В только что рассмотренном простом случае системой является
единичная частица, движущаяся в одном измерении. Для газа,
заключенного в сосуд, система имеет 3N обобщенных координат
и 3N сопряженных импульсов. Тем не менее в обоих случаях
системы изображаются единственной точкой Г-пространства. Если
начальные условия изменить на бесконечно малую величину,
то начальная точка получит бесконечно малое смещение. Если
начальные условия изменяются непрерывно, так что представляю-
представляющая точка описывает непрерывную область Q в Г-пространстве,.
то эта область представит тогда начальную конфигурацию ансамбля
системы.
2.2. Решение уравнения Лиувилля
Обратимся теперь к построению наиболее общего решения урав-
уравнения Лиувилля. Если система, которую представляет ее ансамбль,
имеет N степеней свободы, то существует 2N констант движения.
Рассмотрим одну из них вида
h (ft, . . ., qN, pi, . . ., pN, t) = Ct. B.13)
Это поверхность^ в Г-пространстве. Если t входит явно, то она
будет перемещаться и деформироваться, в противном случае эта
поверхность будет неизменной, С течением времени точка системы
движется в Г-пространстве по поверхности hx = С\. Движение
2.2. Решение уравнения Лиувилля 61
таково, что hv не изменяется за время б?, так что
8fei = hi(p + put, q + q8t, t + 8t)— hi (p, g, t) = 0,
л r^/^ ' , db * \ , дкл~\ ~, B.14)
г
Откуда для ЫфО следует:
^ Щ = 0. B.15)
Таким образом, любая константа движения является решением
уравнения Лиувилля и обратно, любое решение уравнения Лиу-
Лиувилля является константой движения. Но существует 2N таких
независимых констант х). Следовательно, самым общим решением
уравнения Лиувилля будет произвольная функция 2N констант
движения:
D =D (hu fe2, . . ., h2N). B.16)
Самым общим называется такое решение уравнения, которое
включает в себя все решения как частные случаи. Какая-либо
определенная функция всех констант движения не будет являться
самым общим решением уравнения Лиувилля. Например, решение
D = h{h2 . . . h2N не включает решения D = h{ + fe4- Следова-
Следовательно, самое общее решение может быть только вида D =
= D (hx, h2, . . ., hoN). Чтобы построить это решение, надо запи-
записать 2N уравнений:
К = К (?i, . . ., $n, Pi, - • .» pni 0»
B.17)
h2N == ^2N (Gi, • • •» Qn, Pi, • • •» PK, 0«
Обращение этих уравнений дает соотношения:
?i = Si (fei. • • •» ^2iV» ^)»
5 B.18)
P.v = Pn (^i, . . ., u2iv> ^),
которые являются решениями динамических уравнений движения.
Отсюда мы заключаем, что самое общее решение уравнения Лиу-
Лиувилля эквивалентно знанию всех N динамических орбит. Одно-
единственное уравнение Лиувилля описывает поведение всей
системы.
1) Когда полное число степеней свободы равно N, Г-пространство явля-
ется 2ЛГ-мэрным. Когда N—полное число частиц системы и каждая частица
й у степеней свободы, Г-пространство является 2у^-мерным. С обоими
толкованиями мы встречаемся в тексте.
62 Гл. II. Уравнение Лиувилля и функции распределения
К этому заключению можно прийти и другим путем. Напомним
уравнение Лиувилля:
dt ' Zl \ dqt dpi dpi dqi
В BN + 1)-мерном Г-прострапстве градиент D имеет компоненты
dt ' dqi ' '••' dPN
так что уравнение B.19) можно записать в виде
\.VfD = 0. B.21)
Компоненты1) вектора V (в Г-пространстве) равны A, HPl, . . .
. . ., —HqN). Согласно уравнению B.21), решение D таково, что
его градиент нормален вектору V. Для того чтобы это обеспечить,
поверхности, описываемые уравнением D = С, где С — перемен-
переменный параметр, должны быть образованы кривыми, которые в каж-
каждой своей точке касаются векторного поля V. Такие кривые
задаются уравнениями:
_^ йд^ __ dq2 __ _ dpN (*> 22\
" дН/др2 ' ' ' dH/dqN ' ^ ]
Это будут уравнения движения в форме Гамильтона (если проста
приравнять каждый член первому). И опять мы нашли, что самое
общее решение уравнения Лиувилля является произвольной
функцией всех динамических орбит.
Из предшествующих рассуждений следует, что, зная самое
общее решение уравнения Лиувилля, мы тем самым знаем движе-
движение всех частиц, составляющих систему. Такова вторая интерпре-
интерпретация функции D. В первой интерпретации D определялась как
плотность ансамбля точек системы в фазовом пространстве. Разу-
Разумеется, эти две интерпретации взаимно согласуются. Так как
самое общее решение уравнения Лиувилля является произволь-
произвольной функцией всех^ констант движения, то оно само будет кон-
константой движения. Как мы знаем, константа движения — это
динамическая функция, которая остается неизменной при эво-
эволюции системы во времени. Она постоянна вдоль динамической
траектории точки системы в Г-пространстве. Примечательно,
что плотность точек ансамбля около любой точки, изображающей
систему, остается постоянной. Плотность изображающих точек
в бесконечно малой окрестности произвольной точки -системы
остается связанной с этой точкой, когда последняя движется
по своей динамической траектории. Плотность точек системы
х) В наших обозначениях HPi =
2.2. Решение уравнения Лиувилля 63-
ведет себя подобно плотности несжимаемой жидкости. Она остает-
остается постоянной, если следовать за элементом жидкости, но может
изменяться поперек динамических траекторий.
Получение самого общего решения уравнения Лиувилля хотя
и поучительно, связь его с классом решений, относящихся к «про-
«проблеме ансамбля», является не больше чем академической. Более
целесообразно рассматривать задачу с начальными данными.
Пусть задана функция Do = D (p, q, 0). Каково будет значение D
через бесконечно малое время Дг? Разложение D в ряд Тейлора
около t = О имеет вид
dD
D(p> q, M)=D(p, q, 0)+ —
B.23)
Согласно теореме Лиувилля,
-!?- = [#, D]. B.24)
Таким образом,
w t-* г тт г тт 7~I1 I г 17" г ZT Г) 11
'=0 ' ' B.25)
= [Я, [Я, [Н, D]]]t=0 = [H, [H, [H,D0]]].
Решение (равенство 2.23) можно теперь записать только череа
начальные данные DQ:
D(p, q, M) = D0 + At [H, D0]+-^f-[H, [H, Do]] +
.... B.26)
Задача 2.4. Распространить решение B.23) на случай, когда
Я явно зависит от времени (используя равенство A.36е)).
Разложение решения по степеням Дг определяется единствен-
единственным образом через одно начальное условие. Это, конечно, не являет-
является неожиданностью, поскольку уравнение Лиувилля — дифферен-
дифференциальное уравнение первого порядка по времени.
Решению, полученному таким путем, можно дать геометриче-
геометрическую интерпретацию. Значение!) при t = 0 соответствует заданию
D на «плоскости» t = 0 в BN + 1)-мериом Г-простраистве. Ряды
Тейлора B.23) определяют значение D (p0, q0, Дг) через значение
^of(po7 #о) в непосредственно «нижней» точке, лежащей в плоско-
плоскости t ~ 0, в которой задано одно из начальных значений (рис. 2.4).
Значение D в точке (pQ, q0, Дг) совпадает со значением D в точ-
Ке (Ро> ?о> 0), которая является пересечением с плоскостью 2 = 0
Динамической траектории, проходящей через точку (р0, q0, Дг).
64 Гл. II. Уравнение Лиувилля и функции распределения
При построении D через Do (p0, q0, 0) с помощью ряда Тейлора
переменные (q, p, t) должны рассматриваться как независимые.
Это требование особенно легко выполнить при нашем прежнем
подходе, если просто предусмотреть специальную форму реше-
решения. Если, например, для одиночной свободной частицы началь-
начальное условие выражается равенством Do = lip sin q, то в после-
последующее время t решением будет D = Ир sin [q — (pirn) t], т.е.
Динамическая траектория
Рис. 2.4. Геометрия построения рядов Тейлора при решении уравнения
Лиувилля.
функция р, q, t. Она оказывается постоянной вдоль динамиче-
динамического пути Ci = q — (pi™) t; р — p0. Но это не мешает нам вычис-
вычислить величину D (p, q, t) (для любых трех чисел (р, g, t)) из
начальных данных, используя разложение в ряд Тейлора.
Задача 2.5. Для начального ансамбля свободных частиц Do =
= 1/\р | sin | q \. Найти D (At), используя разложение в ряд
Тейлора.
В общем случае мы можем применять разложения типа рядов
Тейлора, чтобы найти изменение функции N переменных вдоль
заданного направления. Рассмотрим функцию / (хи . . ., xN).
Мы хотим найти / в точках х + 6, т. е. в окрестности точки х =
= (хи . . ., xN). Разложение в ряд Тейлора можно записать
следующим образом:
/(x + 6) = e6-V/(x)=/(xR6.v/ + -LF.VJ/+... B.27)
Предположим, что б имеет направление базисного вектора Xi
(в декартовом пространстве). Тогда 6-V = bdldxi. Именно такой
тип разложения имеет место в равенстве B.26).
2.3. Анализ Пригожипа уравнения Лиувилля 65
Хотя данное решение уравнения Лиувилля можно получить,
зная действительные динамические орбиты, в своем конечном
виде оно является функцией q, р и t. Для любого фиксированного
значения t мы можем рассматривать D как функцию (q, p). Это,
разумеется, соответствует переходу с одних динамических орбит
на другие при заданном значении t. Для каждой динамической
траектории D принимает определенное значение, которое остается
постоянным вдоль траектории.
Последнее утверждение указывает наиболее элегантный метод
решения задачи с начальными значениями для уравнения Лиувил-
Лиувилля. Он напоминает метод характеристик в теории гиперболиче-
гиперболических уравнений с частными производными. Сходство состоит в том,
что решения обоих типов уравнений остаются постоянными вдоль
некоторых характеристических линий.
Мы знаем, что D не меняется вдоль динамических траекторий
в Г-пространстве. Пусть движение системы задается уравнениями
q = 2o + g (t); p = Po+J> (t), так что q @) = р @) = 0. Пусть
начальное значение D равно Do (q, р). Тогда D (q, p, t) будет
определяться соотношением
D =D0[q-q(t), p —p(t)].
В такой форме D является функцией констант движения, и ее
нахождение сводится к заданию начального значения D при
t = 0. Однако задача о решении уравнения Лиувилля ничуть
не упростилась. Если в предыдущем методе необходимо было
знать D в окрестности (q0, p0), то настоящий формализм требует
знания решений динамических уравнений движения.
Задача 2.6. На сферической поверхности (в Г-пространстве)
2р| + 2д? = о? задается начальное значение D : Do = 2g| X
X exp [—Spf]. Функция D — это плотность ансамбля одномер-
одномерных гармонических осцилляторов с потенциалом V — q2/2. Найти
решение D (q, p, t) уравнения Лиувилля.
2.3. Анализ Пригожина уравнения Лиувилля
Недавно Пригожий отметил, что уравнение Лиувилля удиви-
удивительно похоже на уравнение Шредингера, и воспользовался
этим, чтобы дать новый метод его решения. Здесь уместно дать
обзор сделанных им выводов.
Определим линейный оператор Лиувилля А, исходя из рас-
расширенного уравнения Лиувилля:
г^-^ + г-^^H. B.28)
66 Гл. II. Уравнение Лиувилля и функции распределения
Для N обобщенных координат оператор Л будет таким:
N
А= у, i( дН д ~[ дН д ) . B.29)
z=i i 9i
Уравнение Лиувилля, записанное через оператор А,
illL^XD B.30)
очень похоже на уравнение Шредингера в квантовой механике:
В этом уравнении Н — оператор Гамильтона с импульсом, заме-
замененным на градиентный оператор —idldq. В уравнении Лиувилля
оператор Лиувилля представляет собой просто оператор скобки
Пуассона, умноженный на i (i2 = —1), т. е. Л = i [Я,].
Перечислим теперь несколько свойств оператора Л, которыми
также обладает и оператор Гамильтона Н.
а) Суперпозиция
Если Di и ZJ — решения уравнения Лиувилля B.28), то ввиду
присущих ему свойств линейности и однородности сумма
D = aiDi + a2D2 B.32)
также будет являться его решением.
б) Л — эрмитов оператор
Пусть б — произвольный оператор, определенный на полном
множестве функций {Фп}- Тогда матричное представление О
имеет вид
°M = H<btO<bidpdq, B.33)
где звездочкой обозначена комплексно-сопряженная величина.
Пусть функции {Фп} таковы, что они обращаются в нуль на гра-
границах фазового пространства. Оператор б называется эрмитовым,
если элементы матрицы удовлетворяют соотношению
Okl = Ofk. B.34)
Каждый матричный элемент должен равняться 'своему эрмитову
сопряженному. Записанное через соответствующие интегралы,
это условие имеет вид
j j OtOOidpdq^ j j OtdOkdpdqY^ j |[FФЛ)* ®idpdq. B.35)
2.3. Анализ Пригожина уравнения Лиувилля 67
Эрмитовость оператора Л можно показать прямой подстановкой,
используя интегрирование по частям:
Задача 2.7. а) Показать, что оператор Л' = ih. не является
эрмитовым.
б) Каким свойством должен обладать гамильтониан Я, чтобы
равенства B.36) были справедливы?
в) Собственные значения А — действительные числа
Собственные значения coz и собственные функции *фг (q, р)
оператора Л определяются уравнением
Aifo=G>ii|)j. B.37)
Отсюда следует, что на базисе этих функций
Ahh = j j фЦЛ^ dpdg = юл j j | я|>л |2dpdj. B.38)
Так как Ahk = A*fe вследствие того, что оператор Л — эрмитов,
и I I l^ft \2 dp dq— действительное число, cofe также должно быть
действительным. То обстоятельство, что собственные значения
эрмитова оператора действительны, является, конечно, хорошо
известной теоремой.
г) Ортогональность собственных функций
Пусть две различные собственные функции % и i|?fe удовлетво-
удовлетворяют соответственно уравнениям
B.39а)
B.396)
Умножая уравнение B.39а) на of»*, a B.396) на i|)j, получим
A B.40а)
B.406)
68 Гл. II. Уравнение Лиувилля и функции распределения
Вычитая одно равенство из другого и интегрируя по всему фазо-
фазовому пространству, получим следующий результат:
Akl—Afk = (со,—со,,) J j y^tdpdq. B.41)
Так как Л — эрмитов оператор, то левая часть предшествующего
уравнения обращается в нуль; следовательно, если со? Ф coft, то
O (кф1). B.42)
Это равенство выражает свойство ортогональности системы функ-
функций {x|)n}, что снова представляет собой хорошо известную теорему
относительно собственных функций эрмитовых операторов.
Собственные функции можно нормировать. Это следует из того
факта, что если a|)ft является решением уравнения B.37), то Atyk
также будет его решением. Постоянная А — произвольна. Следо-
Следовательно, функции фь всегда можно выбрать так, чтобы
J j
B.43)
Эти функции {tyn} образуют ортонормированную последователь-
последовательность собственных функций оператора Лиувилля Л.
д) Собственные функции оператора Л — комплексные
Образуя уравнение, комплексно-сопряженное уравнению B.37),
получим
A*^f = co^f. B.44)
Из B.29) следует, что
Л*=-Л, B.45)
так что уравнение B.44) примет вид
А-фГ = —cozipf, B.46)
и мы можем заключить, что ij)* — собственная функция операто-
оператора Л, соответствующая—соь ai|)j — собственная функция, соот-
соответствующая со г. Если г|)г действительна, то iff равна г|)г и им долж-
должны соответствовать одинаковые собственные значения. Из соот-
соотношения B.46) следует, что либо со г равно нулю, либо г^ является
комплексной.
Так как г^ комплексная (для нетривиального со г), ее можно
представить в виде
u B.47)
2.3. Анализ Пригожипа уравнения Лиувилля 69
где функции Ли/ являются действительными. Подействовав
на это равенство оператором Л2, получим
АЦг = A*Ri + iA4h B.48)
или, что эквивалентно,
= Л (Л%) = @ Дя|); = СО?Я|); = CO?i?; + KD?/j. B.49)
Так как оператор Л2 действительный, то единственный мнимый
член в правой части равенств B.48) и B.49) — это слагаемое,
содержащее число i. Следовательно, действительные и мнимые
части этих двух тождественных комплексных функций выделены
явно и соответственно равны.
Таким образом,
(Л2 —со?) Ri = О, (Л2— со?) 1Х = 0. B.50)
Мы видим, что действительная и мнимая части собственных функ-
функций я|)г удовлетворяют одному и тому же уравнению второго
порядка по р и q.
Тот факт, что собственные функции комплексны, можно уста-
установить другим путем, записав их в виде
где
Ы = (М?I/2. B.52)
Отсюда следует, что
Ai|>, = A|%|eiK', B.53)
или
А|ф,| + *|Ф/|Лх, = ©,|я|>,|. B.54)
Из соотношений B.37) и B.46) вытекает:
A|iM = 0, B.55)
поэтому
Ак1= — гсо;. B.56)
Напомним, что полная производная по времени от динамической
функции F задается равенством
*~%—W + l*'*n-%- + tAF. B.57)
Если F является константой движения, то F = 0, и обратно,
если F = 0, то F — константа движения. Произвольная констан-
70 Гл. II. Уравнение Лиувилля и функции распределения
та движения удовлетворяет уравнению
^- + iAF = 0, B.58)
или, что то же,
ilL^XF. B.59)
Уравнение B.55) говорит о том, что модули собственных
функций % оператора Л являются константами движения, если
они не зависят от времени явно.
Опираясь на эти свойства оператора Лиувилля, перейдем
к более общему исследованию. А именно, построим формальное
решение уравнения Лиувилля в рамках формализма Пригожина.
Более точно, займемся опять решением задачи с начальными
данными. Пусть D0 = D (q, р, 0). Решение уравнения Лиувилля,
записанного через оператор Л (т. е. B.30)), которое удовлетворяет
начальным данным Do, имеет вид
t
D{q, р, *) = exp(— i j&A)i)(g, р, 0). B.60)
о
Экспоненциальный оператор определяется через свое разложение:
t
— i \ dtA ) DQ =
{ '
t t
= \i + (-i [ dtA)+4r(—i [ dtAY+... }dq. B.61)
и о
В случае, когда гамильтониан не является явной функцией вре-
времени, оператор Л также от времени не зависит и
t
[dtk = At. B.62)
о
При таких условиях разложим D по собственным функциям
оператора Л:
оо
D (q, p, 0) = 2a7i'llOi- B.63)
о
Подставляя это выражение в B.60), получим
В(Яч Р» t)=e~lAt 2 #71^71 = 2 ane~i(*nt}\>n {Q, p)- B.64)
2.3. Анализ Пригожипа уравнения Лиувилля 71
Задача 2.8. Доказать второе равенство в B.64).
Задача 2.9. Показать, что
an = j tfkD (q, p, 0) dq dp.
Построим теперь решение уравнения Лиувилля для системы,
состоящей из N невзаимодействующих частиц. Гамильтониан такой
системы задается равенством
Я=3^. B-65)
Соответствующий оператор Лиувилля имеет вид
А=-iy^.J-. B.66)
1=1
Если куб, содержащий газ, настолько велик, что специальный
выбор граничных условий становится несущественным, то мы
тогда свободны в выборе условий, которые лучше всего подходят
для иллюстрации метода. С этой целью наложим периодические
граничные условия на собственные функции i|v.
(х) = Ц{к} (х + L). B.67)
Здесь L — вектор, направленный по ребру кубического контей-
контейнера и равный его длине. Последовательность {к} представляет
систему векторов (кь . . ., kN), которые входят в собственные
функции оператора Л:
^{k}==L-3N/2 ехр(* S krxj) . B.68)
Собственные значения co{t} определяются равенством
Sk»-?-- B-69>
i=i
Каждый вектор
кг = ^пг B.70)
выбирается таким образом, чтобы удовлетворялось граничное
условие B.67). Компоненты вектора иг являются целыми числами.
Мы теперь можем выразить начальное значение
DQ = D (xf, . . ., xN; plf . . ., p^, 0)
для N невзаимодействующих частиц через собственные функции
B.68) и собственные значения B.69).
72 Гл. II. Уравнение Лиувилля и функции распределения
Поскольку собственные функции Л не зависят от р, коэффи-
коэффициенты ап в уравнении B.63) являются теперь функциями импуль-
импульсов р. Кроме того, индекс п заменен на переменную {к}, характе-
характеризующую последовательность. В соответствии с этим обозначим
коэффициенты апчерез!){k> (pi, . . ., рЛт). Они таковы, что началь-
начальное распределение Do задается выражением
D0(xi7 ...,xN, p1? ..., р*) == 2 Ak> (Pii ...,Рл-)Ф{к>, B.71а)
{к}
или, что эквивалентно,
N
DQ = L-SN/2^1Dmexv(iT1 krxi). B.716)
{k} Z=l
Каждому набору переменных {к} соответствуют различные экспо-
экспоненциальные члены в слагаемых выражения B.71а). Используя
ортогональность функций i|){kb получим значения коэффициентов
D{k}- Учитывая B.70), находим
D{k) (Pi, • • •, Pn) = { • •. J Atf>?k> dx±... dxN. B.72)
Зная эти коэффициенты, а также собственные значения, опреде-
определяемые равенством B.69), получим нестационарное решение урав-
уравнения Лиувилля (ср. с B.64)). Оно имеет вид
D(xl7 ...,xN, p<? ..., р^, t) =
D{k} (pi? #. -f Vn) |-exp | ^ kr (x,|-^)] • B.73)
Суммирование указывает на то, что D является функцией пере-
переменных
(Pi, P2, . . ., Pn; txi — (Pi/^i) t], [x2 — (Р2/АП2) t], . . .).
Кроме того, если каждую из этих 2N независимых переменных
положить равной константе, то D будет постоянна. Таким образом,
D постоянна вдоль траекторий
п _ no Y Plr _
Pi-Pi, Xi — —-
Vn* о
— — xN.
B.74)
Эти уравнения описывают динамическую траекторию точки систе-
системы, состоящей из N свободных частиц. Элемент упрощения, введен-
введенный в данную задачу о свободных частицах, обусловлен главным
образом следующим фактом. Оператор Лиувилля А действует только
на конфигурационные переменные х^. В более реальных случаях А
2.3. Анализ Пригожина уравнения Лиусилля 73-
будет включать в себя также и оператор д/др г. Разумеется, было бы
весьма полезно рассмотреть эти более сложные задачи в новых
координатах, которые все отсутствовали бы в преобразованном
гамильтониане. В нашем обзоре классической механики мы
встречались с формализмом «действие — угол», который именно
это и осуществляет. Напомним, что через переменные действия /
(«новые» импульсы) гамильтониан записывается в виде
Н = Н (/4, . . ., /jv)«
Сначала ограничимся задачей с одной степенью свободы, Н =
= Н (/). Тогда получим следующий оператор Лиувилля А (ср.
с A.76); (o = 2nv):
^-^^--ъ-т- <2-75>
Мы достигли желаемого результата: свели Л к оператору; дейст-
действующему только на пространственную переменную. Как и в-
обычном формализме «действие — угол», трудность заключена
в том, чтобы найти производящую функцию, с помощью которой
и выполняется требуемое преобразование. Предположим, однако,
что такая функция найдена, и обратимся к формальному анализу.
Нормированными собственными функциями (периодическими
с периодом 2я) оператора Л являются
**' B-76)
где п — целое число. Собственные значения соп (см. уравне-
уравнение B.37)) имеют вид
©п = тгсо. B.77)
Они равны произведению целого числа на фундаментальную часто-
частоту со, связанную с рассматриваемым периодическим движением
одномерной системы. Когда число степеней свободы больше еди-
единицы, задачу все еще можно хорошо формализовать, при условии
разделимости гамильтониана; это означает, что
Я = Jj #,(/,) B.78)
(каждая из N степеней свободы отделима). В этом случае собствен-
собственные функции имеют вид
N
*/2 2 nfa. B.79)
Компоненты вектора п — целые числа:
п = (Пи . . ., nN). B.80>
74 Гл. II. Уравнение Лиувилля и функции распределения
Собственные значения, соответствующие собственным функциям
B.79), равны
о)п = ^tCOi + лг2со2 + . . . + nNcx)N. B.81)
Аналогично тому, что было выполнено в случае задачи о свобод-
свободном движении N тел, мы можем построить решение задачи с на-
начальными значениями, гамильтониан которой задается равен-
равенством B.78), а начальное распределение — соотношением Do =
= DQ (/, Э, 0). Решение имеет вид
D (/i, .. ., JN, 6i, ..., QN, t) =
= Bn)-W2SZ>n(/b ...,/ff)exp[iS»,(ej-©iO]. B-82)
П
Суммирование распространяется на все векторы п. Коэффициенты
Dn равны
2я 2я
d(ju ...,jn, еь ...,eN, 0)x
о о
X ехр ( —i 2 nfit) d6i ... de^, B.83)
Из решения B.82) следует, что D остается постоянной вдоль
траекторий:
;
оо. B.84)
Тот факт, что это решение похоже на решение задачи о свободном
движении N тел, не является неожиданностью. В новой системе
координат — системе Гамильтона — Якоби — все новые импуль-
импульсы постоянны. А это эквивалентно ситуации свободно-молекуляр-
свободно-молекулярного течения.
Рассмотрим теперь, каким образом можно обобщить теорию,
чтобы учесть взаимодействие частиц, образующих систему. Огра-
Ограничимся случаем слабых взаимодействий, т. е. взаимодействий,
вызывающих малые возмущения описанной выше ситуации сво-
свободно-молекулярного течения. В соответствии с этим полный
гамильтониан имеет вид
H = HO(JU . . ., JN)+ *V(JU . . ., JN, e1? . . ., QN), B.85)
где e — малый параметр, а V — взаимодействие. Соответствующее
уравнение Лиувилля записывается в форме
^ A ]>. B.86)
Вспоминая решение, определяемое равенством B.60), видим, что
удобно перейти от D к новой переменной D:
D -> Ъ = ехр (itАо) D. B.87)
2.3. Анализ Пригожина уравнения Лиувилля 75
f) удовлетворяет следующему уравнению:
*^ = е(в«АобЛ*-«Ао) Ъ. B.88)
В координатах «действие—угол» невозмущенный оператор Лиу-
вилля Ао = — ш (д/дд) (см. 2.75), так что
еи ло / @) = е<оцд/дв) д0) = / @ + со*). B.89)
Таким образом, оператор ехр НА0 производит сдвиг начальной
функции плотности для задачи о свободной частице в момент
времени t.
Уравнение B.88) записывается в форме
^ = еК(х, t)D(x,t), B.90)
где К — оператор, явно зависящий от параметров х и t. Если
D (х, 0) = Dq, to интегральная форма уравнения B.90) имеет вид
t
D(x, t) = D0 + s \к(х, t')D(x, t')dt'. B.91)
Поскольку е — бесконечно малый параметр, удобно искать
решение в виде
D (ж, t) = D0 + sDi + e2D2 + тт. . B.92)
Подставляя этот ряд в уравнение B.91) и приравнивая коэф-
коэффициенты при одинаковых степенях е, получим:
B.93)
Это есть бесконечная последовательность зацепляющихся урав-
уравнений, которую формально можно решить до любого желаемого
порядка по е. Подставляя уравнения B.93) в ряд B.92), получим
t
K(x, t')DQ{x)dt' +
+ ... . B.94)
t V
+ e2 J К (x, t') j К (x, t") Do (x) dt' dt"
76 Гл. II. Уравнение Лиувилля и функции распределения
Отсюда следует, что решение уравнения B.88) представляете»
в форме
t
D (/, Э, t) = Do (/. Э) — is j ^'ЛобЛе-^АоД, dt' + ... . B.95)
Другой эквивалентный метод решения уравнения B.86) вытекает
из так называемой нестационарной теории возмущений, хорошо
известной в квантовой механике. Первый шаг состоит в разложе-
разложении решения D (/, Э, t) по собственным функциям невозмущен-
невозмущенного оператора Лиувилля Ло, а именно по функциям, задаваемым
выражением B.79). Разложение имеет вид
D (/, Э, t) = 2 Ai (/, t) г|)п (Э) ехр ( -1 2 "*»*)• <2'96)
п
Подставляя его в уравнение B.86), получим
n
= ебЛ 2 Ai^n exp ( — i 2 ni®it) • B.97)
n
Умножая обе части этого равенства на оператор
2я 2я
[ dQi ... [ dQN№> @i, *.., QN), B.98)
J J
о о
получим
X ехр ( -i 2 л«ю^) ^n(/i, ..., /N, 0 B.99>
(хотя оператор 6Л может зависеть от времени, он не содержит
операторов производной по времени). В последнем выражении
введено обозначение
2я 2я
<п' | 6Л | п) = [ dQ± ... j dQN№>8A%. B.100)
Уравнение B.99) — это не что иное, как уравнение B.88),
записанное в особой форме — в так называемом представлении
взаимодействия. Метод возмущений, введенный для решения
2.3. Анализ Пригожина уравнения Лиувилля 11
уравнения B.90), можно снова использовать, что дает
t
j
n'
X
exp[— i 2
J
n' 0
X <n' | 6Л | n"> exp Г - i 2 ®vh К - M] D* (°) + • • • • B-101)
После исследования математических аспектов] уместно теперь
указать некоторые физические интерпретации теории Пригожина.
До сих пор мы дали две интерпретации решения уравнения Лиу-
вилля. Мы дадим еще третью интерпретацию — самую важную.
Она связана с тем фактом, что средняя величина любой динамиче-
динамической переменной G в любой момент времени t равна
G= [ DGdpdql f Ddpdq,
(Более подробно это будет обсуждаться в разд. 2.4.) Такая фор-
формулировка средних величин поразительно схожа с формализмом
квантовой механики, задаваемым через функцию состояния W.
Более того, как мы видели, уравнения, которым удовлетворяют
Т иВ, имеют одинаковую математическую структуру.
Аналогия простирается и далее. Ранее мы нашли, что решение
уравнения Лиувилля можно выразить через ряды по собствен-
собственным состояниям оператора Л, т. е. по функциям ехр (—icont) X
X *Фп (р, о) (см. уравнение B.64)). Каждая такая функция, будучи
решением уравнения Лиувилля, представляет возможное незави-
независимое состояние системы. Для многомерных периодических систем
расширенные собственные состояния ехр (i^Z со init)^n @Ь . . ., 0N)
становятся связанными с собственными колебаниями такой систе-
системы. Задача с начальными данными, решение которой дается выра-
выражением B.101), иллюстрирует значение элементов матрицы
(п | 6Л | п'). Коэффициент Dn — это распределение собственных
состояний, характеризуемых вектором п. Элементы (п | 6Л | п')
пропорциональны вероятности того, что взаимодействие 6Л инду-
индуцирует переход от множества п' к множеству п. Для очень слабых
взаимодействий, когда е2 <^ е, имеют место только переходы пер-
первого порядка; тогда как если е2 значительно, то и переходы второго
порядка будут вносить вклад в скорость изменения Dn @). В пере-
переходах второго порядка 6Л сначала индуцирует изменение от п" до
п', а затем от п' до п.
78 Гл. II. Уравнение Лиувилля и функции распределения
Важным коэффициентом является Do. Он задается следующим
равенством (см. B.96)):
2я 2я
Do =—^щ \ dQi . . . \ dQND(Ju . .., JN, Qu . .., QN, t). B.102)
Bя) J J
Поскольку движение периодическое, энергия Е связана с пере-
переменными действия посредством соотношения Е = 2vz/;. Как мы
вскоре увидим, D пропорциональна вероятности того, что состоя-
состояние системы в момент времени t соответствует конфигурации
(/i, . . ., JN, 6i, . . ., Одг). Если D проинтегрировать по всем
значениям 6, то в результате получим функцию распределения
энергии. Она связана с энергией системы, находящейся в данном
частном состоянии в момент t.
Задача 2.10. Показать, что
Задача 2.11. Рассмотрим частицу с зарядом е, находящуюся
в нестационарном электрическом поле гЕ (t). Невозмущенное
движение является одномерным и гармоническим, так что полный
гамильтониан имеет вид
а) Показать, что в переменных «действие — угол»
Я = о/ + 8 sin G/V2 g(t),
где g (t) включает все величины, не зависящие от / и 0.
б) Вывести выражение для возмущенного оператора Лиувилля
6Л и потом показать, что
(п | 6Л | ri) = 0 для п' фп + 1 или п — 1.
в) Используя решение раздела б), получить уравнение для
dDjdt.
Возвращаясь к анализу задач, где используемыми переменны-
переменными являются (х, р), можно разложить функцию D (х, р, f) no соб-
собственным функциям я|){к} свободной частицы:
D (Pj, .. ., xi, .. ., t) = 2 Dw (рь ..., pN, t) я|){к} (Xi, ..., xN).
{k> B.103)
2.3. Анализ Пригожина уравнения Лиувилля
Тогда аналогом уравнения B.99) будет такое уравнение:
=e% exp (*2
{к'}
Х
ехр(-* 2kz'.vz*)l>{k>}, B.104)
Выясним теперь, какой вид имеют элементы матрицы б Л для
системы частиц, которые попарно взаимодействуют по законам
притяжения или отталкивания центров тяготения с потенциалами
у1п. В этом случае гамильтониан имеет вид
2
Если потенциалы взаимодействия <pin разложить в ряды Фурье,
B.106)
к
то возмущенный оператор Лиувилля будет иметь вид
) ^4)
1<п К
= 2б^'п- B-ю7)
1<п
Элементы субматриц оператора 6Л определяются равенством
({к} 16Л*'п | {к'}) = (±)N J dxt ... dxN x
Хехр(— i 2 ks*xsNA*'nexp (t У k;«xs) =
2 Jdxi ••• ^exp(—t 2 ks-xs) X
к
.[^-^-]ехрA2 k;«xs) . B.108)
Отсюда следует, что
x6(k;-kz+KN(k;-kn-K) Д б (к;-к.). B.Ю9)
•ФИ, п)
80 Гл. II. Уравнение Лиувилля и функции распределения
В последнем равенстве использовалось соотношение
f dxe^'x = L4 (p) B.110)
{для больших L). б-Функция обращается в нуль для всех р,
кроме Р = 0, где она равна единице. Отсюда мы заключаем, что
единственными отличными от нуля элементами субматрицы будут
следующие:
<кь к2, ..., кь ..., кп, ..., к^ 16Л*'п | к{, к?, ..., к?,..., к«, ...
v3 .Т7. / д д
Мы проделали эти выкладки, чтобы показать сохраняемость вол-
волновых векторов:
кг + кп = (к* - К) + (К + К) = к,' + к;. B.112)
Все волновые векторы с другими индексами сохраняют свои зна-
значения (ks = kg, s ф1, п). Этот принцип сохранения следует
из инвариантности ц)щ относительно поступательного смещения:
Ф (I х, - хп |) = <р (I (х, + Ь) - (хп + Ь) | ). B.113)
Подставив в уравнение B.104) матричные элементы, задаваемые
равенствами B.111), получим
dt
1<п К
хАк1)...|кгк к^+к,...,^}. B.114)
Это явный вид уравнений, которые определяют коэффициенты
разложения функции D. Данные'уравнения по форме совпадают
с уравнениями B.90), и, следовательно, к ним применимы те же
методы решения.
В другом способе разложения по возмущениям используется
метод резольвентного оператора. Для этого надо сначала перейти
к преобразованию Лапласа D (s) для функции плотности D (i):
оо
D(s)= [ dte~stD(t). B.115)
о
Уравнение для D получается, если произвести операцию
B.116)
2.3. Анализ Пригожииа уравнения Лиувилля
81
Это приводит к следующему результату:
— ID @) + isD (s) = Л D (s), B.117)
из которого вытекает операционное соотношение
/)(*)= —i (Л—ад)/) @). B.118)
Если Z) (^) известна, то D (t) получается из формулы обращения:
Y+гоо
B.119)
V—i
Путь интегрирования параллелен мнимой оси 7/тг E), и все особен-
особенности D (s) лежат слева от него, (Замыкание контура полукругом
слева обеспечивает сходимость для t > 0.) Последнюю формулу
удобнее записать через переменную z = is:
z. плоскость
~2^ \ w*f vxx — *) ^ \^j- B.120)
Интегрирование проводится теперь параллельно действительной
оси Re (z), выше особенностей оператора
Д(з) eee(A-z)-1. B.121)
Этот оператор называется резольвентным оператором, соответ-
соответствующим оператору Лиувилля А. Так как А — эрмитов оператор,
то, как было показано, он име-
имеет только действительные соб-
собственные значения. Отсюда
следует, что R ограничен г)
для всех комплексных z, так
что особенности Я лежат на
действительной оси. Вслед-
Вследствие этого факта и наличия
экспоненциального множите-
множителя, ехр (— izt), (?^0), гори-
горизонтальный путь интегриро-
интегрирования в рассмотренном выше
интеграле можно замкнуть
полукругом, лежащим в нижней половине плоскости, как по-
показано на рис. 2.5. Отсюда следует, что
D{t) = -±:tidze-bW{z)D{0).
Рис. 2.5. Точками обозначены возмож-
возможные особенности R (z).
JL
B.122)
г) Если R действует на пространстве функций S с нормой || г|э ||, то R
ограничен, если для любой -ф ? S существует такая постоянная М > 0, что
l| -fli|) || ^ М || г|) ||, К этой теме мы вернемся в гл. V.
82 Гл. II. Уравнение Лиувилля и функции распределения
В методе возмущений будем исходить из невозмущенной резоль-
резольвенты
R0 = (A0-z)-1 B.123)
и соотношения
= -&R8AR0. B.124)
Подставляя разложение для R,
R = %snRn, B.125)
в уравнение B.124) и приравнивая коэффициенты при одинако-
одинаковых степенях е, получим
Л = 2 (-e)nR0[8AR0]n. B.126)
Мы подставим теперь этот результат вместе с разложением
B.103) в интеграл равенства B.122). Прежде всего мы получим
(z) 2 Ак'> @) ф^,. B.127)
{к'} С {к'}
Подействовав на это равенство оператором I dxt .. ¦ dx
будем иметь
=-as§ dze~izt
Ь {к'}
Теперь подставим сюда выражение для Л из равенства B.126)
и получим, что
е-&'3 S (-е)
{к'} п=0
B.129)
Эта формула является наиболее важным результатом анализа
Пригожина. Так как мы еще не подошли к наиболее подходящей
интерпретации функции D, то нам пока трудно выяснить физиче-
физический смысл коэффициентов D{k}. В данный момент это просто
коэффициенты, определяющие плотность D. В следующем разделе
будет установлена их связь с приведенными s-частичными функ-
функциями распределения, смысл которых также будет выяснен
позднее. Здесь же мы рассмотрели лишь основы метода Приго-
Пригожина, который важен сам по себе как метод решения полного урав-
уравнения Лиувилля..
2.4. N-частичпая функция распределения /jy 83
2.4. Третья интерпретация JD\ ^-частичная функция
распределения /у
Теперь вполне очевидно, что уравнение Лиувилля является
важным инструментом исследований в классической механике.
Мы убедились в этом дважды. Во-первых, с точки зрения аналити-
аналитической динамики одно скалярное уравнение Лиувилля полностью
эквивалентно 2N (N — число степеней свободы) динамическим
уравнениям движения — уравнениям Гамильтона. Физическая
уместность такой интерпретации заключается лишь в том, что
появляется возможность исследовать задачи совершенно иным
образом, минуя формализм Ньютона, Лагранжа или Гамильтона.
Вторая интерпретация состоит в том, что решение уравнения
Лиувилля является плотностью точек ансамбля в фазовом про-
пространстве. Эти две интерпретации представляются не имеющими
ничего общего. Понятие ансамбля и его отношение к уравнению
Лиувилля введены абстрактно. Однако эта концепция приводит
к новому подходу, который позволяет нам получить более глубокое
понимание уравнения Лиувилля. В свете новой интерпретации
уравнение Лиувилля приобретает наибольшую ценность и приво-
приводит к важным физическим следствиям. Это проявляется через связь
функцииD с iV-частичной функцией распределения/^ (#i, q2, • • •
• • •» Qn, Pu • • •» Pn, t). Функция fN такова, что произведение
fir (Qu • • •» Qn, Pi, • • .» Pn, t) dqi . . . dpN B.130)
представляет вероятность нахождения системы [с каноническими
координатами (дь . . ., qN, pu . . ., pN)\ в состоянии dqi ...
... dpN около фазовой точки (qu . . ., pN) в момент t* Из
вероятностного характера функции fN следует, что
B.131)
где интегрирование распространяется на все фазовое пространство.
Какова связь между fN и D? iV-частичная функция распреде-
распределения относится к одной-единственной системе, в то время как
плотность распределения D — к множеству идентичных систем,
различающихся по фазе.
Предположим, что в начальный момент функция fN отлична
от нуля только в фазовой точке (gj, . . ., р%). Отсюда следует, что
fN @) = 6 fo - q\) ...&{pN- p°N) B.132)
есть TV-мерная б-функция Дирака. В более поздние моменты вре-
времени значение fN определяется соотношением
42-133)
84 Гл. II. Уравнение Лиувилля и функции распределения
где
?i=<rt+?z(O BЛ34)
— уравнения динамических траекторий.
Из предшествующего анализа следуют два очевидных вывода.
Во-первых, представляется нелепым вводить в этом случае понятие
вероятности. Точность результатов и начальных данных делает
применение вероятностных представлений ненужным. Во-вторых,
мы имеем дело с одной представляющей точкой, блуждающей в Г-
пространстве. Предшествующий анализ при выводе уравнения
движения для плотности D показал, что ансамбль должен быть
настолько плотным, чтобы к нему можно было применить форма-
формализм механики континуума. Одноточечная система далека от удо-
удовлетворения этому требованию.
При каких условиях в сферу классической механики вводится
вероятностный формализм? Рассмотрим шарик, ограниченный
в своем движении прямой проволокой длины а. Классическая
динамика такой системы может быть точно сформулирована и точно
решена. Но предположим, что начальные условия для системы
(шарика) точно не известны. Мы можем только сказать, что перво-
первоначально шарик находится где-то в области 0 ^ х ^ а/2. В рав-
равной степени вероятно, что шарик находится в любой точке этого
интервала в момент t = 0. Предположим далее, что начальные
импульсы лежат в некоторой малой области, так что все значения
р из интервала р' — 8р' ^ р ^ р' + Ьр' равновероятны.
Эти начальные условия определяют характер любых вопросов,
касающихся последующей динамики такой системы. Можем ли мы
спросить, где будет частица в момент времени ?? Предположим, что
кто-то, проведя длинные вычисления, заключил, что в момент t
частица будет находиться в точке (р, q),. Если это так, то такая
частица должна была находиться в точке (р0, q0) при t = 0, по-
поскольку существует одна и только одна динамическая траектория,
проходящая через точку (р, q). Но если при t = 0 частица нахо-
находится в точке (ро, qo), то утверждение, согласно которому она
может с равной вероятностью находиться в начальный момент
времени в любой точке области (р' — бр', 0) ^ (р, q) ^ (р' +
+ бр', а/2), становится неверным. Следовательно, поставленный
вопрос несовместим с описанием начального состояния системы.
Мы можем лишь спросить: каково вероятное состояние системы
в момент времени ?? Такой вопрос не только корректен, но на него
и не слишком трудно дать ответ. Сначала изобразим область в соот-
соответствующем двумерном фазовом пространстве, которая содержит
все допустимые точки рассматриваемой системы. Эта область (пря-
(прямоугольник (—8р, бр, 0, а)) показана на рис. 2.6. Отметим, что
2.4. N-частичная функция распределения
85
допустимым величинам импульсов соответствуют значения энергии
между энергетическими поверхностями Н = Е и Н = Е + 8Е.
Для удобства мы выбрали Е = 0. На рис. 2.6 изображены все
возможные начальные состояния (при t = 0). Мы задались усло-
условием, что каждое такое состояние равновероятно. Это означает,
что если произвести эксперимент в момент t = 0 для измерения
i=lo
Р и с. 2.6. Фазовое пространство для шарика на прямой; t0 — время движе-
движения шарика от а/2 до а.\В заштрихованной области /4 = (адр)'1; в незаштри-
хованной области fi = 0.
(#о» Ро)у то с равной вероятностью можно получить любую вели-
величину (p,q), которая лежит внутри начального энергетического слоя
Е ^ Н ^ Е + 8Е фазового пространства. Совокупность этих
начальных состояний можно рассматривать как ансамбль. Свяжем
далее начальное распределение вероятностей с начальной плот-
плотностью точек ансамбля. Более точно, пусть г\ — полное число
точек системы в ансамбле, так что (возвращаясь на момент к обще-
общему случаю 2#-мерного Г-пространства)
= J
Ddqt ...dqNdpi . . . dpN,
B.135)
86 Гл. II. Уравнение Лиувилля и функции распределения
где интегрирование проводится по всему объему Q. Тогда величина
-М ... \ D dqt .. . dqN dpt .. . dpN = j . . . ^ fNdq± . . .dpN B.136)
выражает «отношение числа систем, находящихся в пределах обла-
области Q', к полному числу систем. А это не что иное, как вероятность
того, что некоторая система ансамбля находится внутри данной
области» г). В предельном случае континуума т) обращается в бес-
бесконечность, но отношение B.136) остаетсЯ(Конечным, причем таким,
что
( [Ndqi...dpN = i. B.137)
Это уравнение выражает тот факт, что вероятность нахождения
системы в некоторой точке внутри всего допустимого объема в Г~
пространстве равна единице. Функция fN является iV-частичной
функцией распределения и такова, что произведение fNdqx . . ,dpN
есть вероятность нахождения системы в состоянии dqi ... dpN
около состояния (#!, . . ., pN) в момент t. Поскольку функция fN
отличается от D на постоянный множитель
<2Л38)
она также удовлетворяет iV-частичному уравнению Лиувилля.
Другой путь, иллюстрирующий связь между fN ж D, состоит
в использовании понятия средней по ансамблю. Пусть G — неко-
некоторая динамическая характеристика системы, такая, например,
как полная кинетическая энергия Ир\12т, полная потенциальная
энергия 22 ф^7- (ф^- — потенциал взаимодействия двух частиц),
полный линейный импульс 2 pj. Если D — плотность ансамбля
данной системы, то средняя по ансамблю от G определяется равен-
равенством
- jG(q,Pt)D(q,P>t)dpdq_
W \Ddpdq V J
Равенство предполагает, что D (q, р, 0) dp dq пропорциональ-
пропорциональна вероятности нахождения системы в начальный момент времени
в состоянии dpdq около (р, q).
Экспериментально G определяется следующим образом. Про-
Произведем N экспериментов. Начальное макроскопическое состояние
системы во всех экспериментах одинаково. Спустя t секунд изме-
*) Гиббс [1928]. Отметим также, что равенство B.136) можно записать
в дифференциальной форме: D dp dq/ J Ddp dq = /jv^p dq.
2.4. N-частичпая функция распределения fN 87
ряем G(t). Тогда в пределе, когда iV> 1 (более точно, когда
ф — GJ <^ G2), средняя величина G определяется равенством
в<*) = 2пг-. BЛ4°)
z=i
где G\ — значение (?, измеренное в процессе Z-ro эксперимента.
Если мы введем вероятностную функцию, в соответствии с ко-
которой fN dpdq является вероятностью нахождения системы в состо-
состоянии dpdq около (р, q) в момент t, то получим другое выражение
для среднего значения G:
G=[ fNG°dpdq. B.141)
Сравнение этого соотношения с B.139) снова дает нам равенство
B.138).
Вернемся к рассмотренной ранее задаче о шарике на прямой
проволоке. А^-частичное распределение станет одночастичным
распределением /1# Начальными условиями для Д будут Д =
= (абр)-1 = К, 0 < q < а/2, — 8р < р < 8р и f± = 0 вне
этой области. Кроме того, Д удовлетворяет одночастичному
уравнению Лиувилля
Ц^ #] = 0 B.142)
при
Я = -^+У, B.143)
F = 0, 0<g<a;
Г—. 3<0,»>„. <
Решением уравнения B.142) является функция /i (q, p, t) = К
для величин (р, q) и ^, которые связаны с начальными значения-
значениями (т.е. вдоль динамических орбит), а для всех других (g, p,t) —
функция, равная нулю: f± (g, p, t) = 0. Графически это реше-
решение изображено последовательностью фигур на рис. 2.6. Почти
очевидно, что с течением времени начальный ансамбль станет
однородно заполнять весь допустимый объем Г-пространства. Это
составляет сущность эргодической теоремы, которая будет более
полно обсуждаться в гл. V. Чтобы лучше понять временную после-
последовательность графиков на рис. 2.6, проследим за траекторией
одного шарика в Г-пространстве, как показано на рис. 2.7. Учтем,
что за равные промежутки времени частицы с меньшим импульсом
покрывают меньшие расстояния, чем частицы с большим импуль-
импульсом. Этим объясняется скос начальной области на рис. 2.6.
Гл. II. Уравнение Лиувилля и функции распределения
В настоящий момент физическая целесообразность введения N-
частичной функции распределения еще не является очевидной.
Несомненно, эта функция пригодна для задачи о шарике на про-
проволоке, но введения вероятностного формализма там не требуется.
Этот формализм не нужен, когда имеется одна степень свободы.
С другой стороны, для систем с большим числом степеней свободы
вероятностная концепция становится оправданной. Для систем,
содержащих ~ 1023 частиц, мы обычно
имеем сведения лишь о температуре
системы и о начальной области, кото-
которую она занимает в фазовом прост-
пространстве.
Примером такого описания яв-
является газ, первоначально заключен-
заключенный в одной половине герметического
сосуда, который в свою очередь по-
помещен в термостат. Два существенных
факта справедливы для такой систе-
системы. Во-первых, для нее, как и для
любой другой системы, законы при-
природы, специфически выражаемые
квантовой механикой, таковы, что
энергия системы, измеряемая в ин-
интервале времени б?, определяется с
точностью до дополнительного члена
Р &Е, ограниченного снизу величиной
h/8t (h — постоянная Планка). Сле-
Следовательно, в лучшем случае извест-
известно, что энергия системы лежит вну-
внутри некоторого интервала значений.
Во-вторых, вспомним, что в началь-
начальный момент на газ наложено ограничение, согласно которому он
занимает одну половину всего объема сосуда. Если убрать пере-
перегородку, то газ будет диффундировать в пустую половину и че-
через достаточно длительный интервал времени весь сосуд будет од-
однородно заполнен газом. Интересен не сам этот вполне обычный
процесс, а тот факт, что система не возвращается к начальному
состоянию (хотя для отдельной частицы это возможно).
Проблему легко разрешить, если допустить, что динамические
формализмы Ньютона и других основоположников механики не обе-
обеспечивают полного описания поведения системы. Необходимо еще
привлечь вероятностные закономерности. Наблюдение, согласно
которому газ никогда не возвращается к первоначальному сос-
состоянию (в сущности, за время эксперимента), можно обосновать
с помощью вероятностных аргументаций. С точки зрения класси-
классической динамики этот факт является крайне парадоксальным
i
0
а/2
а
а/г
i 0
а/2
а
а/2
1 0
-SplZ
Ч
-
-
-
-
-
-
1 _
+fo/2
Рис. 2.7. Траектория единич-
единичного шарика в Г-пространстве.
2.4. N-частичная функция распределения fN
и называется парадоксом обращения времени (или, более вну-
внушительно, Umkehreinwand по Лошмидту и Wiederkehreinwand
оо Цермело). Мы займемся этими парадоксами позднее. В данный
момент наше основное внимание будет обращено на тот факт, что
естественная эволюция системы (со многими степенями свободы)
может быть истолкована вероятностными методами. Можно пока^
зать (используя iV-частичную функцию распределения), что описа-
описание такой эволюции частично опирается на основные понятия тео-
теории вероятностей.
Обратимся к определению функции fN для системы многих
тел. Относящийся к этой {первичной) системе ансамбль состоит
из совокупности идентичных копий данной системы. Когда пер-
первичная система изолирована, ее классическая константа энергии
не является точной, а скорее «размазана» с неопределенностью 6Z?,
о которой уже упоминалось. В соответствующем Г-пространстве
уравнение Н (р, q) = Е представляет поверхность. Так как пара-
параметр Е принимает значения от Е до Е + 6Z?, то энергетическая
поверхность «выметает» энергетический слой в Г-пространстве.
Важность энергетических поверхностей в противоположность
другим константам движения была отмечена Пуанкаре A892)
и Ферми A923). Пуанкаре доказал, что единственной поверхностью,
которую точка системы не покидает при своем движении, является
энергетическая поверхность. Он показал, что если динамическая
траектория системы не сходит с поверхности, то такая поверхность
может быть только энергетической. Ферми обобщил эти результа-
результаты и доказал, что для систем, которые он назвал Kanonische Nor-
malsysteme, не существует никаких других однозначно определен-
определенных стационарных аналитических интегралов, кроме интеграла
энергии.
Задача 2.12. В ящике, имеющем форму куба с длиной ребра L,
движутся две частицы. Потенциал взаимодействия частиц равен
V (\ Xi — х2 | ), так что гамильтониан задается соотношением
= —2ж
Г-пространство является 12-мерным. Выяснить (геометрически
и физически) пригодность трех констант движения: 1) энергии,
2) линейного момента (импульса), 3) углового момента. В каком
смысле энергия является единственной «пригодной» константой
движения?
Ответ. Столкновения со стенками изменяют угловой и линей-
линейный моменты, но не энергию.
Задача 2.13. Показать, что угловой момент системы частиц,
движущихся внутри полой сферы с идеально гладкими стенками,
сохраняется.
90
Гл. II. Уравнение Лиувилля и функции распределения
Начальное энергетическое состояние исходной системы неопре-
неопределенно и может отклоняться от значения Е на величину, не пре-
превышающую ЬЕ. Это определяет энергетический слой. Кроме'того,
если начальное состояние стеснено условием, что оно лежит в под-
подпространстве допустимой области конфигурационного простран-
пространства, то заполняется только некоторый подобъем энергетического
слоя. Такая начальная конфигурация схематически изображена
на рис. 2.8.
Свойства симметрии энергетической поверхности следуют из об-
обратимости (относительно времени) орбит, порождающих поверх-
поверхность х) (см. гл. I). Хотя энергетическая поверхность несомненно
Рис. 2.8. Энергетический слой в Г-пространстве. Область из допустимых
точек, \ \ dpdq = Q.
является важнейшей классической константой движения, в ста-
статистической механике более уместно рассматривать энергетический
слой. Ранее было показано, что уравнение Лиувилля следует из
объемных интегральных инвариантов Пуанкаре и единственности
траекторий системы. Уравнение Лиувилля является утверждени-
утверждением, относящимся к объемным, а не к поверхностным элементам.
Именно из этого уравнения для объемной плотности D получаются
все динамические орбиты. Геометрический объект в Г-простран-
Г-пространстве, которому динамика не уделяет внимания, представляет со-
собой объемный, а не поверхностный элемент.
| J1) Гамильтониан Н не обязан быть четной функцией pi. Для случая
простого гармонического осциллятора в координатах «действие — угол»
Н -> Н' — со/, т. е. является нечетной функцией /.
2.5. Динамика системы, выраженная через функцию
91
Первоначально fN @) = 1/QO в предписанной выше области
N = 0 вне ее. В последующие моменты времени решение таково,
/дг остается постоянной вдоль динамических траекторий.
Когда начальная область заполнения деформируется, то это проис-
происходит таким образом, что объем деформированной области остается
постоянной величиной Qq.
Если точка (р0, q0) перехо-
переходит в точку (р (t), q (*)), то
fN М*)(*)]Ы)
Рис. 2.9. Начальное распределение
Г-пространстве.
o
Совсем не обязательно,
чтобы начальный ансамбль
однородно заполнял под-
подобласть объема Q. Напри-
Например, для газа, заключен-
заключенного внутри цилиндра,
можно сделать начальное
состояние таким, чтобы на-
начальная плотность моно-
монотонно убывала от одного
конца оси цилиндра к другому. Положим, что первоначально более
вероятным является состояние, когда большая часть молекул нахо-
находится в левом конце, а не в правом. Плотность начального ансамбля
такова, что она меньше для координат, лежащих справа от центра,
и больше для координат, лежащих слева от центра. Схематически
этот случай изображен на рис. 2.9.
А^-частичная функция распределения подчинена ограничению:
\ /iv = 1 в любой момент времени, и изменяется со временем в соот-
соответствии с уравнением Лиувилля. В любом случае правильно опре-
определенная функция распределения fN удовлетворяет уравнению
Лиувилля и содержит в себе всю классическую информацию,
относящуюся к изучаемой системе.
Задача 2.14. Дать интерпретацию задаче 2.6, используя iV-час-
тичную функцию распределения.
2.5. Динамика системы, выраженная через функцию fN:
приведенные распределения. ББКГИ-уравнения
Как описать динамическую эволюцию системы, если для нее
задано начальное распределение вероятности fN @)? Динамика
системы задается через физические наблюдаемые величины (или
свойства), связанные с системой. Аналитически эти наблюдаемые
величины являются некоторыми определенными функциями коор-
координат и импульсов системы. Они представляют собой функции
состояния системы.
92 Гл. II. Уравнение Лиувилля и функции распределения
Пусть динамическое свойство (например, полная кинетиче-
екая энергия ^j р\12тг, N — число частиц) записывается как
& (?» Р-> *)• Снова, вследствие формализма Лг-частичной функ-
функции распределения, единственным уместным вопросом, который
мы можем поставить относительно эволюции во времени наблю-
наблюдаемой величины G, будет вопрос: каково среднее значение G в мо-
момент t? Вспоминая, что fN — функция распределения вероятности,
получим ответ (см. уравнение 2.141):
G (t) = j J G (p, q, t) fN (p, q, t) dpdq. B.145)
Среднее значение, или математическое ожидание G в момент вре-
времени t, равно взвешенному интегралу от fN по всему допустимому
фазовому пространству.
Здесь удобно ввести новые обозначения. Пусть z^ = (gi, pi)t
так что dzi = dqidpi. Другие важные свойства системы, помимо Gy
можно сформулировать через приведенные распределения f г\ I <C N»
Эти функции таковы, что
fidzidz2 . . . dzi B.146)
есть вероятность того, что система находится в состоянии dzit . .dzx
около (zi, . . ., Z\) в момент t. В определении молчаливо подразу-
подразумевается фраза: «независимо от того, какие значения принимают
( zN)>>. Функции fN и fi связаны соотношением
NdzM.>.dzN. B.147)
Обратимся теперь к выводу уравнений, которым удовлетворяют
эти Z-частичные функции распределения. Введем прежде всего
ренормированную функцию распределения FN, связанную с fN
простым соотношением:
Fs = VS J fNdzs+i .. . dzN =Vsf8, B.148)
так что
Fi = V \fNdz2...dzN = Vfu
, B.149)
F2 = V2 J fNdzs...dzN = V2f2.
Кроме того, вероятность нахождения частицы в состоянии dzi
около Zi в момент времени t равна (FJV) dzt = F^dpi (dxJV)
и т. д.
Введем снова оператор Лиувилля L, через который уравнение-
Лиувилля запишется в виде
)N = O; B.150)
2.5. Динамика системы, выраженная через функцию fN
93
^частичный (s<.N) оператор Лиувилля определяется равенством
s
1=1
]3водя гамильтониан
B.151)
г < д
B.152)
можем записать Ls в виде
1=1
B 153)
^ Р и с. 2.10. Расстояние между части-
Чтобы отметить тот факт, что цами.
оператор (д/dxi), примененный
к ф (ги), дает нетривиальный результат только когда i = I либо
j = I (см. рис. 2.10), перепишем соотношение B.153) следующим
образом:
J
B.154)
1=1 г < ,
Выполняя во втором члене суммирование по индексу Z, получим
-2 (?-кг)-
где
Операторы eft7- задаются равенствами
B.155)
B.156)
B.157)
B.158)
94
Гл. II. Уравнение Лиувилля и функции распределения
Оператор Лиувилля Ls выражается через эти операторы
явной записи оператора Ks) в виде
B.159}
г <}
Так как LN включает Ls, мы можем записать
i Ж.^.)_^.«]. B.160)
Оператор 6N'S, который является «остатком» от суммы по 0^-.
таков, что
J dz8+i ... dzNSN* sfN = 0 B.161)
(как будет показано). Более того, весь член в квадратных скобках
обладает тем же свойством. Этот способ выражения LN в виде
Рис. 2.11. Упорядочение членов 0fJ- в Ljy.
линейной комбинации операторов Ls, ©^ и QN>S, определяемой
равенством B.160), изображен схематически на рис. 2.11.
Все члены 6f7-, входящие в LN, заполняют целый треугольник.
Члены этого же вида, входящие в Ls, занимают область, отмечен-
2.5, Динамика системы, выраженная через функцию /jy 95
яу как Ls. Оставшиеся члены 0^- занимают области, обозначен-
обозначенные буквами А и Б. Ясно, что оператор 22 ®и в равенстве B.160)
занимает только область А, тогда как оператор ®N>S занимает
область Б.
Используя теорему о дивергенции, можно записать интеграл
B.161) как поверхностный интеграл, распространенный по грани-
дам (импульсным) фазового пространства, где функция fN обра-
обращается в нуль. Аналогичные рассуждения остаются в силе для
N
оператора 2 (j>i/m)'(d/dxi).
s + l
Имея удобное разбиение LN согласно равенству B.160), мы
можем теперь вывести уравнение, которому удовлетворяют Fs.
Для этого подействуем на уравнение Лиувилля B.150) (где tN
имеет вид B.160)) оператором
Vs J dzM ... dzN. B.162)
Мы получим
JLfs + LsFs-Vs j dzs+i ...dzN% 2 &ufN = 0 B.163)
Интегральный член можно еще более упростить. Запишем его
в развернутой форме:
s N
v )dzs+i...dzNy} 2
JV
( ()fN ^ • • - ^). B.164)
Остальные члены {d/dj>j) сводятся к поверхностным интегралам.
Чтобы упростить ряды из интегралов в выражении B.164), рассмот-
рассмотрим случай трехчастичного газа при 5 = 1. Соответствующие
интегралы принимают вид
dz2dz3
B.165)
Поскольку мы имеем дело с идентичными частицами (массы частиц
не снабжены индексами), то должна существовать симметрия отно-
относительно нумерации частиц. Напомним, что произведение
dzidz2dz3f3 (zu z2, z3, t) B.166)
Гл. II. Уравнение Лиувилля и функции распределения
определенным образом связано с состоянием частиц 1, 2 и 3. На
вопрос, имеет ли смысл произведение
dz1dz3dz2fs
2, t),
B.167)
можно ответить утвердительно. Оно определяет вероятность того,
что частица 3 находится в состоянии dz2 около z2. Другими слова-
словами, место фазовой переменной zk в символе функции fN указывает,
какой частице «принадлежит» данное состояние. Отличие между
выражениями B.166) и B.167) состоит в том, что частицы 2 и 3
\
\
\
2
\
Рис. 2.12. Перестановка идентичных частиц; состояния инвариантны
(стрелками обозначены импульсы; dld2d3/(l,2,3)=dld3d2/A,3,2).
а — начальное состояние; б — состояние после замены: частица 3 при-
приобрела состояние частицы 2, и наоборот.
обменялись состояниями*, в B.167) частица 2 имеет состояние 3,
а частица 3 — состояние 2. Чтобы понять смысл такой операции,
обратимся к рис. 2.12. Здесь импульсы обозначены стрелками.
На рис. 2.12, а изображено начальное состояние. Частицы отме-
отмечены соответствующими числами. На рис. 2.12, б частице 2 даны
начальные координаты и импульсы частицы 3, а частице 3 —
начальные координаты и импульсы частицы 2. Результирующее
состояние (б) идентично состоянию (а), таким образом,
/з
= /з
B.168)
На рис. 2.13 показано преобразование замены для неидентич-
неидентичных частиц. В этом случае написанное выше равенство теряет силу.
Интегралы B.165), которыми мы интересуемся, включают член
(dcpij/dXj), описывающий взаимодействие. Первое подинтегральное
выражение имеет вид
Г-^-ф(Х!, X2)]/3(Z1, Z2, Z3).
B.169)
2.5. Динамика системы, выраженная через функцию fN
97
Предположим, что мы применили к нему преобразование замены.
Исходное состояние показано на рис. 2.14, а. Штриховой линией
изображено взаимодействие. Стрелки на штриховой линии указы-
указывают частицу, на которую действует сила. Преобразованное
Рис. 2.13. Перестановка неидентичных частиц; состояния не инвариантны;
dld2d3f A,2,3) =?dld3d2f A,3,2).
а — начальное состояние; б — состояние после замены.
Рис. 2.14. Перестановка при наличии взаимодействия. Для идентичных
частиц состояния инвариантны; dld2d3Gl2/ A,2,3) = dld3d2G13/ A,3,2).
а — начальное состояние; б — состояние после замены.
состояние изображено на рис. 2.14, б. Соответствующая диаграм-
диаграмма для неидентичных частиц представлена на рис. 2.15.
Преобразованное состояние в случае идентичных частиц
3)]
B.170)
98
Гл. II. Уравнение Лиувилля и функции распределения
очевидно, совпадает с исходным состоянием;
B.171)
(обе части равенства умножаются на dzidz2dz3). Таким образом,
два интеграла в B.165) идентичны. Более того, все N — s(j)
интегралов в уравнении B.164) совпадают.
Интегралы не зависят от выбранного нами значения /. Для
удобства положим j = s -f- 1. В результате получим
s N
г=1
:(N-8)
^. J
/я- B-172)
Учтем последнее замечание, которое дает возможность дальней-
дальнейшего приведения интегралов. Потенциальный член в подинтег-
V
ч
V
Рис. 2.15. Перестановка при наличии взаимодействия. Для неидентичных
частиц состояния не инвариантны; dld2d3Gi2f A,2,3) =^=dld3d2Gi3/ A,3,2).
а — начальное состояние; б — состояние после замены.
ральном выражении не зависит ни от каких переменных интегри-
интегрирования, кроме zs+1. Вспоминая, что
I fN dzs+2
• ¦ - dzN =
B.173)
мы можем переписать правую часть равенства B.172) следующим
образом:
- *) 2
dZ
s+i
2.174)
2.5. Динамика системы, выраженная через функцию fN 99
Выражая интегралы в последней сумме через функцию распреде-
распределения Fs, получим
s
г=1
где G^, s+i — сила, действующая на частицу с номером i со стороны
частицы с номером 5+ 1:
G.,s+1= —JLcpbs+1. B.176)
Мы можем теперь записать уравнение B.163) в окончательной
форме:
s
4r'[dzs+iGi>s+iFs+i = 0. B.177)
Совокупность этих уравнений называется ББКГИ-уравнениями
(Борн, Боголюбов, Кирквуд, Грин, Ивон). Запишем в явном виде
первые два уравнения. Первое уравнение
далее всюду будет называться БИ^ Уравнение
dF2 , /Pi д , р2 д \ J? ! Г д
B.1786)
мы назовем БИ2 и т, д.
Задача 2.15, Показать, что из уравнения B.1786) следует урав-
уравнение B.178а).
Вся совокупность уравнений образует систему N зацепляющих-
зацепляющихся интегро-дифференциальньпг уравнений для последовательности
приведенных распределений i^, F2i . . ., FN. Единственным авто-
автономным уравнением является последнее, которое представляет
само уравнение Лиувилля. (N — 1)-е уравнение содержит FN-t
и FN. Если уравнение Лиувилля решено для FN, то в принципе
(N — 1)-е уравнение можно решить для .Fjv-i. После того как Fjv-i
найдена, (N — 2)-е уравнение является тогда уравнением для един-
единственной неизвестной FN_2 и в принципе также может быть реше-
решено. Таким образом, после того как мы найдем FNi оставшуюся сис-
систему ББКГИ-уравнений можно последовательно решить для рас-
распределений более низкого порядка. Однако существует, разумеет-
разумеется, более простая процедура: если FN известна, то Fs получается
100 Гл. II. Уравнение Лиувилля и функции распределения
из соотношения
FS = VS"N j FNdzs+i ... dzN B.179)
по определению. При таком формальном подходе ББКГИ-уравне-
ния являются бесполезными. С другой стороны, кажущийся логи-
логически несостоятельным метод решения, когда сначала находится
F±, имеет важное значение в теории неравновесной статистической
механики.
Сейчас мы ненадолго вернемся к анализу Пригожина, для того
чтобы установить связь между коэффициентами разложения Фурье
в равенстве B.103) и приведенными распределениями /s. Для этого
сначала запишем разложение функции /N, аналогичное разложе-
разложению функции D:
n (P tf ) 2
{k}
X%k}(x1, ..., xN). B.180)
Эти ряды чрезвычайно сложны. Чтобы выписать явно характерный
член ряда, потребуется около 1014 лет (если считать, что для систе-
системы из 1022 частиц за секунду можно выписать 3 k-векторов). Но
положение не является столь плохим. Дело в том, что для макро-
макроскопической физики наиболее важными коэффициентами /{к}
будут те, у которых почти все k-векторы нулевые. Имея в виду
именно этот случай, упорядочим члены записанных выше рядов.
Пусть /0 @) — коэффициент Фурье, у которого все к-векторы
нулевые, /i (кг) — коэффициент Фурье с единственным ненулевым
k-вектором, относящимся к 1-й частице, /2 (кг, кт) — коэффициент
Фурье только с двумя ненулевыми k-векторами для частиц I и т
соответственно. Подробно это можно записать так:
%(kh km) = /{0, о, ...,кг, о,.,., о,kmt о, ..., о}- B.181)
Эти коэффициенты зависят от импульсов. Ряды B.180) в таких
^обозначениях примут вид:
N
N
i 2 2 2
у2, *
N
1 vi VI ^1 V —
где V = V/Bnf.
2.5. Динамика системы, выраженная через функцию fN 101
В таком представлении функция /s при s фО обращается в нуль,
если любой ее k-векторный аргумент равен нулю. Например,
U (kif 0, кто) = 0.
Согласно определению, такой элемент уже включен в суммирова-
суммирование в членах /2.
Разделение слагаемых на члены, включающие в себя коэффи-
коэффициенты Фурье с нулевой суммой к-векторов Bк* = 0), и на члены,
не обладающие этим свойством, обусловлено следующими сообра-
соображениями. Когда fN описывает пространственно-однородную систе-
систему, то
/iv (Рь • • м Pjv> xi + a, х2 + а, . . ., х^ + а) =
fN (Pi, • . ., Vn, хь х2, . . ., xN). B.183)
Тогда из разложения B.180) следует, что
{к} {к}
Это равенство справедливо, если
/{к} = 0, когда 2 ^i Ф0.
Отсюда вытекает, что дополнительные коэффициенты имеют осо-
особое значение в однородном случае.
Возвращаясь к нашему анализу, перейдем теперь к термоди-
термодинамическому пределу
N
JV—>-оо, У-э-оо, -pr = const.
В этом случае суммирование по к переходит в интегрирование
согласно правилу
к , B.185)
У. бк -*• Ыкб (к),
к J
и разложение B.182) примет вид
N
fN (x, P, t) = -ju- { То @) + 2 J dkjh (k,) ехр (I
3
N
N
2 jdk/2(k,, -к;)ехр[Лг(х;-хг)]+...} . B.186)
102 Гл. II. Уравнение Лиувилля и функции распределения
Рассмотрим теперь обращение этого уравнения. С этой целью сна-
сначала подействуем на него оператором
pi ... dpxdxi . .. dxN.
Уцелеет только первый член, поскольку fs обращаются в нуль
вместе с любым из своих k-векторов (s ФО). В результате имеем
fN dp,. .. dpN dx[...dxN = l = j f0 @) dp, ... dpN. B.187)
Чтобы получить выражение для fi (kz), подействуем на уравнение
B.186) оператором
J dpi . . . dpN dxi ... dx^ dxl+i . .. dxN.
Придем к следующему результату:
J /iv dpt ... dpN dxi ... dxj.i dxM . . . dxN = щ (xh t) =
...dpN] . B.188)
Функция Nrii = n — это числовая плотность частиц (или плот-
ностъ числа частиц) в динамике жидкости; о ней мы будем гово-
говорить в начале гл. III.
Чтобы получить выражение для /2 (km, k^), подействуем
на B.186) оператором
\ dpt . .. d$N ... dxm-idxm+i .. . dx/^idx/t+i .. . dxN.
В результате получим
... dpN dxi ... dxm-i dxm+i ... dxh^ dxh+1 . . . dx^ =
-^2 { J Йк^ dk/J2 (km, кЛ) exp [i (km-xm + k/t• хЛ)
(km, — km) exp [ ikm.(xm — xh)] dp{ ... d$N } . B.189)
Функция У2^ = g — это радиальная функция распределения,
хорошо известная в кинетической теории жидкостей. С этой функ-
функцией мы ознакомимся более подробно в гл. III.
В пределе, при однородном распределении, уравнения примут
вид
N
n = Nni(xi, t) =-тГ = const,
g = V2n2{xm, хЛ, t) =
jL ...dpN. B.190)
2.6. Условные и l-числовые функции распределения 103
Задача 2.16. Получить соответствующее выражение для
Пг (хь Хь, хЛ, t) в однородном пределе.
Функции пв связаны с приведенными s-частичными функциями
распределения через интегралы:
щ (хь *) = j /i (Рь
П2(ХЬ Х2, *) = j ЫРь Р2, Х1? Х2, 0dPidP2, B.191)
tzs (хь „.., xe, t)= \ fsd^ ч«. dp8.
Задача 2.17. Вывести формулы, аналогичные равенствам
B.187), B.188) и B.189) для пространственно-приведенных функ-
функций распределения импульсов:
Фо (Pi • • •, Pjv, t)
Ф! (рь .. ., pN, xb t) = J d
= j
i-! dxM ... dxh_i dx
h+1
Задача 2.18. а) Какой вид имеют «зацепляющиеся» уравнения,
описывающие эволюцию во времени функций /s (kt, k7-, . . .)?
б) Каков характер этих уравнений для однородного газа?
2.6. Условные и ^-числовые функции распределения
а) Условные вероятности
Мы увидим, что при некоторых исследованиях удобно обозна-
обозначить точки фазового пространства числами. В этих обозначениях
число 2 есть фазовая точка z2 s= (p2, q2), a d 2 — элемент фазового
объема dp2dq2. Двухчастичная функция распределения записы-
записывается как /2 A,2). Произведение /2 A,2) dld2 определяет вероят-
вероятность того, что частица 1 находится в фазовом элементе dl около 1,
а частица 2 — в фазовом элементе d2 около 2. Функция /2 —
это совместная вероятность. Аналогично fN A, 2, . . ., N) X
X dld2. . . dN есть совместная вероятность того, что частица 1 на-
находится в dl около 1, частица 2 — в d2 около 2, ... и частица N
в dN около N.
Кроме совместной функции распределения можно определить
Условную функцию распределения, которая записывается как
W) A 1 2, 3, . . ., I).
104 Гл. II. Уравнение Лиувилля и функции распределения
Эта функция такова, что
Щ) A | 2, 3, . . ., I) dl B.192)
представляет собой вероятность нахождения частицы 1 в состоянии
dl около 1 при условии, что частица 2 находится в состоянии 2,
3 — в состоянии 3, . . . и I — в состоянии I. В случае, когда все
частицы не зависят одна от другой, Ыр A | 2, . . ., I) dl становит-
становится просто вероятностью того, что частица 1 находится в состоянии
dl около 1, т. е. она равна Д A) dl. Таким образом, для незави-
независимых вероятностей
Л«A |2, 3, . . ., l)dl = Д A)<И, B.193)
или, что то же,
Щ){1 12 г) = ДA). B.194)
Этому равенству противопоставляется форма произведения сомно-
сомножителей
/,A, 2, ..., I) = h A) U B) ...ЛA), B-195)
на которые расщепляется fi в случае, когда все частицы незави-
независимы.
В общем случае fi и h® связаны соотношением
(Отметим, что у функции /^_i B, . . ., I) первая цифра 2 обозна-
обозначает состояние частицы 2 и т. д.)
Для I частиц можно ввести также другие условные распределе-
распределения вероятности. Например, h^ A, 2 | 3, . . ., I) такова, что
&(*>A, 2 |3, . . ., I)dld2 B.197)
есть вероятность того, что частица 1 находится в состоянии dl
около 1 и 2 в состоянии d2 около 2 при условии, что 3 находится
в состоянии 3, 4 — в состоянии 4 и т. д. Соотношение между fi
и hW имеет вид
,21з,..., i) = /г)^з3'::;'0г) • (
Для случая независимых вероятностей
Л(ОA, 2 13,..., *)=ДA)ДB). B.199)
Задача 2 19. а) Как связаны между собой htf и fi (N > I > п)?
б) К какой функции сводится Ы?> в случае независимых веро-
вероятностей?
б) Уравнение Чепмена — Колмогорова
5-частичное совместное распределение fs A, . . ., s, t), отне-
отнесенное к начальному состоянию A0, . . ., s0, t0), принимает форму
условного распределения.
2.6. Условные и l-числовые функции распределения 105
Соответствующая функция распределения такова, что
Jsdl . . . as I c начальными """*"
условиями
П8 A, 2, . . ., s, t\ lo, 20, . . ., so, t0) ей. . .& B.200)
является вероятностью нахождения системы из s частиц в состоя-
состоянии d\ . . .ds около A, . . ., s) в момент t при условии, что в момент
t0 система находилась в состоянии A0, . . ., s0) г). Такая функ-
функция удовлетворяет хорошо известному в теории вероятностей
уравнению Чепмена — Колмогорова 2) (или Смолуховского). Это
уравнение получается следующим образом. Сначала мы запишем
B.200) в таком виде:
П («, t\ в0, *0) dz. B.201)
Поскольку в момент t система, очевидно, находится в некотором
состоянии, то П подчинена условию нормировки:
l(sf t\zo, to)dz = l. B.202a)
Точно так же очевидно, что за нулевой интервал времени состоя-
состояние системы не изменится, следовательно,
П («, ?0 I «о, to) = в (z - «о), B.2026)
где б — дельта-функция Дирака.
Пусть t' — любой промежуточный момент времени, t0 < tr < t.
Достигнув состояния z в момент t, система должна была пройти
через некоторое состояние z' в момент f. Отсюда следует, что
П(*, t\zo, to)= \ll(z, t\zf, tf)U(z\ tr\zs, to)dz'. B.203)
Мы получили непрерывную форму уравнения Чепмена — Кол-
Колмогорова. Его также называют допущением Маркова. Смысл послед-
последнего уравнения становится совершенно ясным, если рассмотреть
более общее уравнение, из которого следует B.203) (переменная
t в записи опущена):
П (z | *0) = { П (z | z\ z0) П (z* | zQ) dz'. B.204)
Функция П (z I zr, zQ) определяет вероятность того, что система
в момент t находится в состоянии z при условии, что она была
bz'b момент t' и в z0 в момент tQ. При сведении уравнения B.204)
к вырожденной форме B.203), мы вводим предположение, что сис-
х) П8 также называется «двухвременной функцией распределения».
2) Kolmogorov A. N., Foundations of the Theory of Probability, Chelsea,
New York, 1950; Б. Parsen, Stochastic Processes, Holden-Day, San Francisco,
1962; and Smoluchowski M. V., Physik., Z., 17, 557 A916).
106 Гл. II. Уравнение Лиувилля и функции распределения
тема «потеряла память». В уравнении B.203) вероятность П (z \ z',
z0) не зависит от того, где была система в момент t0. Описываемый
таким уравнением процесс называется марковским.
Чаще встречается запись уравнения Чепмена — Колмогорова
через интервалы т = tf — t0 и а = t — t''. Изменения в обозна-
обозначениях таковы, что
П (z, t\ z0, *0) = П (z | z0; a+ т). B.205)
В силу этого равенства П не зависит от t0. Тогда уравнение Чеп-
Чепмена — Колмогорова примет вид
U(z\zo\ x + a)=\u(z\z'; о)П(z' |z0; т)dz , B.206а)
или, что эквивалентно,
П (z | z0; X) = f П (z | z', Я— т) П (zf \ z0; т) dz'. B.2066)
В квантовой механике состояния z могут образовывать дискрет-
дискретное (счетное) множество. Для учета этого изменения запишем:
z+Z; Z = 0, 1,2, . . .
П (z \z'; т) ^П (Z|Z'; т). B.207)
При таких условиях интегральное уравнение B.2066) примет вид
Щ1\1оЛ) = ^Щ1\]\ Х-т)ПG|г0; т). B.208)
Условие B.202) запишется в виде
Sn(Z|Z0; Я) = 1, B.209)
n(Z|Z0; O)=6ZZo. B.210)
Рассмотрим теперь как получается так называемое основное
уравнение, или уравнение Паули1), которое, как часто говорят,
представляет собой квантовомеханический аналог уравнения
Лиувилля. Чтобы вывести это уравнение, рассмотрим вероятность
того, что за малый интервал времени Д? система переместится
из состояния / в состояние Z. Для I -ф] эта «переходная вероят-
вероятность» стремится к нулю вместе с Д?, и мы получим, что
U(l\j; М) = а„Ы+... AФ)). B.211)
Коэффициент аи — это скорость переходной вероятности. Когда
/ = /, вероятность П (Z | Z; At) стремится к единице при Д?->- 0.
Кроме того, она должна всегда оставаться положительной. Отсюда
г) Pauli W., Festschrift zum 60. Geburtstage A. Sommerfelds, Leipzig,
1928, L. Van Hove, in Ergodic Theories, Course 14, Academic Press, New York,
1960, and B. R. A. Nijboer, in Fundamental Problems in Statistical Mechanics,
ed. E. G. D. Cohen, Interscience, New York, 1962.
2.6. Условные и l-числовые функции распределения 107
следует, что
fl(l\l; Д?) = 1 — вероятность того, что I не стремится к I за Д?=*
= 1 - S П (Г | Z; Д*) = 1 - Д* 2 **-?. B.212)
Уравнения B.211) и B.212) можно объединить в одно:
II(Z|jf; М) = аиМ + диA~М 2 *rz). B.213)
по всем V
Если это уравнение подставить в уравнение Чепмена — Колмого-
Колмогорова (т = t, о = At)
U(l\l0; t + M)=^U(l\j; Д*)П(/|/0; 0.
3
то мы получим
В пределе при Дг^ ->¦ 0 приходим к основному уравнению
W{l\Wt)^ j\l0; t)-ann(l\l0; t)}. B.214)
3
Оно описывает скорость изменения переходной вероятности
, е - ©
no\i0)
Р и с. 2.16. Члены, дающие вклад в скорость изменения П (I \10). Суммиро-
Суммирование производится по всем промежуточным состояниям /.
для систем, которые эволюционируют, следуя марковскому про-
процессу. На рис. 2.16 изображена модель, удовлетворяющая этому
уравнению.
б) l-числовые распределения
Другой важной функцией распределения является ер\ —
^-числовая функция распределения.
Произведение
JTZA, 2, . . ., I)dld2 . . . dl B.215)
есть вероятное число таких совокупностей из I частиц, для которых
одна из частиц находится в состоянии dl около 1, другая — в 62
около 2 и т. д. до Z-ro состояния включительно. Например, 3^\d\
есть вероятное число частиц в фазовом элементе dl около 1 в мо-
108 Гл, II. Уравнение Лиувилля и функции распределения
мент t х). Произведение ^2did2 есть вероятное число пар частиц^
«аких, что в каждой паре одна из частиц находится в состоянии d\
около 1, а другая — в состоянии 62 около 2.
Как связаны между собой ер i и f{> Функция fi относится к кон-
конкретному множеству из Z частиц, которые в определенном порядке
распределены по всем / состояниям. С другой стороны, $f x хотя
и относится к тому же самому множеству Z состояний, является
невосприимчивой 1) к особому порядку, в котором Z частиц зани-
занимают эти состояния, и 2) к тому, какие Z частиц выбираются из
всего множества N частиц. Аргументы A, 2, . . ., Z) функции
Jf i A, 2, . . ., Z) определяют только состояния, но не указывают,
что какая-то определенная частица находится в состоянии 1 либо
в состоянии 2 и т. д., в то время как fi A, 2, . . ., Z) связывает
именно частицу 1 с состоянием 1 и т. д.
Чтобы получить Jf i из fu вычислим сначала число способов
выбора Z частиц из множества N частиц. Этим числом будет
(N\ n\
Каждая такая совокупность из I частиц, упорядоченных определен-
определенным образом путем нумерации от 1 до Z, с определенной вероятно-
вероятностью находится в состоянии A, . . ., Z). Эта вероятность равна
fi A, 2, . . ., 1) dld2 . . . dl. Отсюда следует, что величина
dl ... dl^f=iljfl(l, ..., l)di ... dl B.216)
есть вероятное число совокупностей, каждая из которых состоит
из I частиц, занимающих состояния A,2, . . ., Z), причем в каж-
каждой совокупности частицы занумерованы и определенным образом
распределены по состояниям A, . . ., Z). Другими словами, при
вычислении jF* мы каждой совокупности частиц приписываем
только один из возможных способов распределения по состояниям
A, . . ., Z). Однако остается много других способов распределения
каждой совокупности из Z частиц по состояниям A, 2, . . ., Z).
Действительно, полное число таких возможных способов равно 1\.
Соответствующее вероятное число совокупностей из Z частиц
в состоянии dl . . . dl около A, . . ., Z) равно
dl ...dZjF,= (^)[/z(l, 2, ...,Z) + /ZB, 1, ...
+ ...+/,(Z, Z-l, ..., l)]dl ...dl, B.217)
где содержится Z! одинаковых функций. Следовательно,
х) Оговорка «в момент и подразумевается и во всех предшествующи*
определениях.
2.6. Условные и l-числовые функции распределения 109
Приведем несколько соответствующих примеров:
B 219а)
i)/ B-219a)
Если частицы независимы одна от другой, то
, 2) = N(N- l)h{l)h B),
A) .F, B) « jFi A) ^, B). Bl2196)
Последняя аппроксимация справедлива в предельном случае,
когда Ny 1.
Сейчас мы попытаемся разрешить дилемму относительно функ-
функции j^z. При выводе соотношения B.218) казалось бы более умест-
1
1
1
1
1
i
A
A
A
A
A
A
2
1 в |
1 в |
1 в |
1 -в 1
1 в |
1 в |
3
с 1
с I
1
1
D |
D |
4
Л 1
|
с 1
Л 1
С 1
ь
D
D
С
с
1
1
1
1
1
1
1
• 1 •
I • I • I I ¦ I •
Рис. 2.17. Модель, иллюстрирующая смысл функции ?F'2.
а — число конфигураций, дающих вклад в /2 (А, В), равно (i) 2!;
полное число конфигураций равно f |j 4!; следовательно, /2 (А, В) = (?) 2! /
/(!") 4!5 из B.218) для ^2 находим ^2 A, 2) = №\ 2! /2 = 3/5.
б — число конфигураций, дающих пару частиц в первых двух ящиках,
равно 3; полное число конфигураций равно f ^J; следовательно, вероятность
нахождения пары частиц в первых двух ящиках равна 3/5; среднее число пар,
находящихся в первых двух ящиках, равно 3/5.
Из B.218) функция ^2 A? 2) равна среднему числу пар в ящиках 1 и 2
и равна вероятности нахождения пары частиц в ящиках 1 и 2.
ньтм определить $р tdl ... dl как вероятность (а не вероятное
число) того, что совокупность из I частиц находится в элементе
d\ . . . dl фазового пространства. В данном случае обе интерпре-
интерпретации одинаково справедливы. Для примера рассмотрим задачу
о четырех идентичных частицах, распределенных в пяти ящиках
(в каждом ящике может быть только по одной частице). Присвоим
ящикам номера 1, . . ., 5. Тогда вероятность нахождения пары
частиц в ящиках 1 и 2 равна3/5. Это есть также среднее число пар,
таких, что одна частица находится в ящике 1 и одна — в ящике 2
(рис. 2.17).
110
Гл. II. Уравнение Лиувилля и функции распределения
Определяя jpjKaK Z-числовое распределение вероятности, мы
встречаемся с противоречием: I ер xdl . . . dl Ф 1. С другой сто-
стороны, достоверно, что совокупность Z-частиц занимает какое-то
состояние из \ dl . . . dl. Разрешение этого парадокса заключает-
заключается в следующем: интерпретация ер г как
функции распределения вероятности
является ошибочной.
Для элемента фазового объема
dl . . . dl произведение epxdl . . . dl бу-
будет отличаться от истинной вероятно-
вероятности на член порядка объема, к которо-
которому имеет отношение вероятность. Таким
образом, вероятностная интерпретация
<f i по отношению к элементарным
*1 объемам является почти точной. Для
всего пространства такая интерпрета-
интерпретация ерi абсолютно не пригодна. Более
правильно трактовать ер \ как Z-число-
вую плотность. Для элемента фазового
объема dl . . . dl соотношение ер\dl .. .dl
определяет среднее число совокупностей из I (незанумерован-
ных) частиц, находящихся в объеме dl . . . dl. Для всей области
\ dl . . . dl функция ер i нормируется на
Рис. 2.18. Конфигурацион-
Конфигурационная часть Г-пространства
для двух шариков на пря-
прямой длины L.
т. е. на число различно упорядоченных последовательностей из
частиц, которые можно получить из N занумерованных частиц.
Чтобы сделать все наши рассуждения более ясными, исследуем
соотношение ^ = Nfo для очень простого случая двух (N = 2)
невзаимодействующих идентичных свободных частиц (шариков),
движущихся по прямой жесткой проволоке длины L. Проволока
натянута между двумя абсолютно отражающими стенками. Кроме
того, ограничимся лишь конфигурационной частью задачи (счи-
(считая импульсы обеих частиц определенными и известными). Фазовое
пространство этой системы из двух частиц есть квадрат с длиной
стороны L, как показано на рис. 2.18. Вероятность того, что части-
частица 1 находится в «объеме» &х\ около #i, равна площади Ldxi, раз-
разделенной на полную площадь L2, т. е. /i (#i) dx^ = dxJL, как
показано на рис. 2.19, а. Отметим, что заштрихованная площадь
есть геометрическое место точек всех состояний в Г-пространстве,
для которых частица 1 находится в dx± около х±. Вероятность того,
что частица 2 находится в dx^ около хл аналогичным образом равна
Д (х2) dx2 = dx2/L, как показано на рис. 2.19, б.
2.6. Условные и l-числовые функции распределения
111
Теперь остановим наше внимание на вычислении функции
Ifiix) dx. Это — вероятность нахождения частицы (более точно,
либо частицы 1, либо частицы 2) в интервале dx около х. Площадь,
соответствующая . этой вероятности, есть геометрическое место
1
Рис. 2.19.
точек всех состояний двух частиц, таких, что либо частица 1, либо
2 находятся в элементе dx около ху как изображено на рис. 2.20, а.
Это не совсем то же, что сумма Д (х) dx + /i (x) dx = 2Д (х) dx =
= 2dx/L. При простом сложении двух одночастичных вероятностей
Рис. 2.20.
а — вероятность нахождения либо частицы 1, либо частицы 2 в интерва-
интервале dx около х\ б — вероятность равна [/i(#i) ^ + / () d]
перекрываемая площадь (dxJ считается дважды (рис. 2.20, б).
Но существует только одна совокупность состояний в этой обла-
области пересечения (состояний в Г-пространстве), и она должна быть
сосчитана только один раз. Отсюда следует, что
dx
о dx
~ 2—т~ =
(х) dx. B.220)
112 Гл. II. Уравнение Лиувилля и функции распределения
Отметим, что это выражение представляет собой как вероятность
нахождения частицы в интервале dx около х, JFdx, так и среднее
число частиц в интервале dx около х, <fdx B1L есть числовая плот-
плотность) .
Ясно, что вероятность нахождения частицы в интервале (а, Ь)
можно опять вычислить путем простого построения (заштрихо-
(заштрихованных) пересекающихся прямоугольников на рис. 2.20, а. Выра-
Выражение для вероятности будет отличаться от приближенного резуль-
результата (который получается, если $р\ принять за распределение
вероятности)
ь ь
f =\ 2Д dx=2 ^- (/4 = const) B.221)
на величину (Ъ — aJ/L2, пропорциональную площади перекрытия
(Ъ— аJ. В пределе для всего интервала (а = 0, b = L) площадь
перекрытия занимает целый квадрат. Вследствие этого некорректное
выражение для $р^, т. е. 2dxlL, приводит к неверной нормировке:
dx
L
= j 2 ^- = 2. B.222)
о
Правильное выражение для функции распределения $р± приводит
к надлежащей нормировке:
L L L L
[ JF±dx= [2f±dx— [^- [^- = 2—1 = 1. B.223)
J J J L J L
О 0 0 0
Задача 2.20. Обозначим цифрой 1 только конфигурационную
часть состояния, так что dl = d3x^. Для однородного газа, заклю-
заключенного в объем V и находящегося в равновесии,
где n = N/V — числовая плотность частиц. Если частицы независи-
независимы, то какова функция ^2 A> 2)? Решить задачу двумя способами,
используя сначала формулу B.219), а затем подсчитав число пар
частиц в элементах объема d3xu и d3x2.
Ответ. Используя B.219), получим
&2<Pxx(Fx2 = Jfi A)^3^1^1 B) d3x2 =
так что
2.6. Условные и l-числовые функции распределения 113
Кроме того, jF2 можно вычислить, если заметить, что пд?х^ частиц
находится в (Рх^ и ndsx2 частиц — в d?x2, так что общее число пар
будет равно п2.
Задача 2.21. Найти связь между F\ = Vlfi и 1) ер г\ 2) hp;
3) hW. Здесь V — объем сосуда, заполненного газом.
В начале этой главы мы впервые встретились с концепцией
ансамбля и уравнением Лиувилля. Там они использовались глав-
главным образом для изучения геометрических свойств Г-пространства.
Глубокий смысл уравнения Лиувилля становится очевидным в све-
свете вероятностной интерпретации его решения, что немедленно при-
приводит к методу получения средних значений динамических пере-
переменных. К теории ансамбля мы вернемся в гл. V в связи с при-
принадлежащей Гиббсу и Эйнштейну формулировкой равновесной
статистической механики.
Если обратиться к рис. 1.1, то в настоящий момент мы находим-
находимся в области, схематически обозначенной вторым усилителем.
Он ведет от БИ4 к теории кинетических уравнений. Само уравнение
BHi важно для нас тем, что оно является «предшественником» всех
кинетических уравнений — уравнений для одной неизвестной
функции Fi (более полное определение будет дано ниже). Исключи-
Исключительное значение функции F\ заключается в том, что из нее следует
большая часть гидродинамики. Связь F^ с гидродинамикой мы
подробно обсудим в начале гл. III, а в конце ее выясним, какое
значение для гидродинамики имеет функция Fz. Вопрос о соотноше-
соотношении между гидродинамикой и кинетической теорией снова встре-
встретится в гл. IV в связи с интегралом столкновений в уравнении
Больцмана и, наконец, в гл. V при рассмотрении анализа Чеп-
мена — Энскога уравнения Больцмана.
ББКГИ-уравнения исследуются в гл. III двумя способами.
Вначале мы ознакомимся с анализом Боголюбова цепочки ББКГИ-
уравнений. По существу, эта теория вскрывает физический смысл
одночастичной функции распределения. После этого ББКГИ-по-
следовательность будет разложена около «нулевых корреляций»
и будет получено формальное упорядочение простых кинетических
уравнений. Одно из них, уравнение Власова, приведет к понятию
самосогласованных решений.
Уравнение Чепмена — Колмогорова, рассмотренное в этой
главе, опять встретится нам в гл. IV в одном из выводов дру-
другого важного кинетического уравнения — уравнения Фоккера —
Планка.
Задача 2.22. Если через БИ8 обозначено 5-е уравнение в ББКГИ-
последовательности, то покажите, что
114 Гл. II. Уравнение Лиувилля и функции распределения
Задача 2.23. Доказать, что s-частичная (s ^ N) функция рас-
распределения удовлетворяет уравнению
где
... dN
... dN
UN = (ЧЬ • • •> Члг, Pi,
И
д д д д
V, =
Задача 2.24. Используя уравнение Лиувилля, доказать, что
для произвольного гамильтониана \ /ivdl . . . dN = const.
В частности, доказательство должно иметь силу как для потенци-
потенциалов, зависящих от импульсов, так и для нестационарных гамиль-
гамильтонианов.
Указание. Проинтегрировать \ dl ... dN [fN, H] по частям.
Задача 2.25. Доказать, что
/i (х4, Pi) = g (Pi)
и
h (xi, РГ, x2, p2) = h (| x2 — Xi |, pt, p2),
если fN инвариантна по отношению к поступательному сдвигу,
т. е. если
fN (х4 + a, Pi", х2 + а, Ра'» • • •'> xn + a, pN) =
= /w (xi, РГ» х2, р2; • • -5 xn? Pjv)»
Функции g ж h — произвольны.
Задача 2.26. Доказать, что движение проекции ансамбля на ги-
гиперплоскость (qu . . ., gs; p4, . . ., ps) (s < iV — число степеней
свободы системы) является несжимаемым.
Ответ. Это движение задается уравнениями:
qi = Qi (t),
Pi = Pi (t),
Оно будет несжимаемым, если
Список литературы 115
Задача 2.27. Показать, что ББКГИ-уравнения B.177) можно
записать следующим образом:
dt
г=1
Задача 2.28. Проинтегрировать разложение B.186), чтобы
найти соотношение между функциями
{Ъ(ки ..., kz)}
и
а) /i (x, р, t);
б) /2 (х, р; х', р', t).
Ответ.
а)
1 f
/i (хь Рь Ч =1-^у~ \ d\>i • • • ^Vi-i^Vi+i • • • d\*N X
X
СПИСОК ЛИТЕРАТУРЫ
Л. Ансамбли; N-частичные функции распределения и ББКГИ-уравнения
Боголюбов Н. Н.
A946) Проблемы динамической теории в статистической физике, М.— Л.,
Гостехиздат.
Де Боер (de Boer J.)
A948-49) Repts. Progr. Phys., 12, 305 A948-1949).
Больцман (Boltzmann L.)
A872) Vorlesungen tiber Gastheorie, Leipzig, 1896—1898; Wien. Ber., 66,
275 A872). Русский перевод: Больцман Л., Лекции по теории газов,
М., Гостехиздат, 1956.
Борн, Грин (Born M., Green H. S.)
A946—47) Proc. Roy. Soc. (London), A188, 10 A946); А189 103 A947); А190,
455 A947); А191, 168 A947).
Гиббс (Gibbs J.W.)
A928) The Collected Works, London, Longmans, Green and Co.
грин (Green M. S.)
A958) Proceedings of the International Symposium on Transport Processes
in Statistical Mechanics (Brussels, 1956), New York, Interscience.
ГРэд (Grad H.)
A958) Handbuch der Physik, v. XII, Berlin, Springerverlag.
116 Гл. II. Уравнение Лиувилля и функции распределения
Ивон (Yvon J.)
A935) La Theorie Statistique des Fluides et l'Equation d'Etat, Paris, Her-
Hermann.
Кац (Кае М.)
A959) Probability and Related Topics in] Physical Sciences, New York,
Interscience. Русский перевод: Кац М., Вероятность и смежные
вопросы в физике, М., «Мир», 1965.
Кирквуд (Kirkwood J. G.)
A946-47) /. Chem. Phys., 14, 180 A946); 15, 72 A947).
Кирквуд, Росс (Kirkwood J. G., Ross J.)
A958) Proceedings of the International Symposium on Transport Processes
in Statistical Mechanics (Brussels, 1956), I. Prigogine (ed.), New York,
Interscience, 1958.
Ландау Л. Д., Лифшиц Е. М.
A964) Теоретическая физика. Т. 5. Статистическая физика, изд. 2-е, М.,
Физматгиз.
Майер Дж., Майер М. (Mayer J. E., Mayer M. G.)
A940) Statistical Mechanics, New York, Wiley. Русский перевод: Майер Дж.,
Гепперт-Майер М., Статистическая механика, ИЛ, М., 1952.
Пригожий (Prigogine I.)
A958) Proceedings of the International Symposium on Transport Processes
in Statistical Mechanics (Brussels, 1956), New York, Interscience.
Толмен (Tolman R. C.)
1938) The Principles of Statistical Mechanics, Oxford, Clarendon Press.
(Фаулер, Гуггенгейм (Fowler R., Guggenheim E.A.)
A939) Statistical Thermodynamics, Cambridge, Cambridge University Press.
Русский перевод: Фаулер Р., Гуггенгейм Э. А., Статистическая тер-
термодинамика, М., ИЛ, 1949.
Хаар (ter Haar D.)
A954) Elements of Statistical Mechanics, New York, Rinehart.
Хилл (Hill T. L.)
A956) Statistical Mechanics, New York, McGraw-Hill. Русский перевод:
Хилл Т. Л. Статистическая механика, М., ИЛ, 1960.
Гиршфельдер, Кертисс, Берд (Hirschfelder J. О., Curtiss С. F., Bird R. В.)
A954) The Molecular Theory of Gases and Liquids, New York, Wiley. Русский
перевод: Гиршфельдер Дж., Кертисс Ч., Берд Р., Молекулярная
теория газов и жидкостей, М., ИЛ, 1961.
Эренфест Р., Эренфест Т. (Ehrenfest P., Ehrenfest Т.)
A911) Begriffliche Grundlagen der Statistischen Auffassung der Mechanik,
Encyclopedie der Mathematischen Wissenschaften, v. 4, p. 4, 1911'»
reprinted by Cornell University Press, Ithaca, N. Y., 1959,
В. Метод Пригожина
Балеску (Balescu R.)
A962) Statistical Mechanics of Charged Particles, New York, Interscience»
Русский перевод: Балеску Р., Статистическая механика заряженный
частиц, М., «Мир», 1967.
Список литературы 117
Пригожий (Prigogine I.)
A962) Non-Equilibrium Statistical Mechanics, New York, Wiley. Русский
перевод: Пригожий И., Неравновесная статистическая механика,
М., «Мир», 1964.
В. Парадоксы обращения времени и константы движения
Лошмидт (Loschmidt J.)
A876) Wien. Ber., 73, 139.
Пуанкаре (Poincare H.)
A892) Methodes Nouvelles de la Mechanique Celeste, Paris, Gauthier — Vil-
lars, 1892; reprinted by Dover, New York, 1957. Русский перевод
в сб. Пуанкаре А., Избранные труды, М., «Наука», т. 1, 1971, т. 2,
1972.
Ферми (Fermi E.)
A923) Physik. Z., 24, 261.
Цермело (Zermelo E.)
A896) Ann, Physik., 57, 485; 59, 793.
Г. Квантсвая механика
Бом (Bohm D.)
A951) Quantum Theory, Englewood, Cliffs N.J., Prentice-Hall. Русский
перевод: Бом Д., Квантовая теория, М., Физматгиз, 1961.
Дирак (Dirac P. A. M.)
A947) The Principles of Quantum Mechanics (third edition), Oxford, Cla-
Clarendon Press. Русский перевод (с 4-го англ. изд.): Дирак П. А. М.,
Принципы квантовой механики, М., Физматгиз, 1960.
Д. Корреляционные функции
Делькруа (Delcroix J. L.)
A965) Plasma Physics, New York, Wiley.
Крамер (Cramer H.)
A946) Mathematical Methods of Statistics, Princeton, N. J., Princeton Univer-
University Press. Русский перевод: Крамер Г., Математические методы ста-
статистики, М., ИЛ, 1965.
Либов (Liboff R. L.)
A965-66) Phys. Fluids, 8, 1236 A965); 9, 419 A966).
Майер Джм Майер М. (Mayer J. E., Mayer M. G.)
A940) Statistical Mechanics, New York, Wiley. Русский перевод: Майер Дж.,
Гепперт — Майер М., Статистическая механика, М., ИЛ, 1952.
^рселл (Ursell H. D.)
A927) Proc. Cambridge Phil. Soc, 23, 685.
118 Гл. II. У равнение Лиувилля и функции распределения
Список обозначений к гл. II
ain — скорость переходной вероятности,
D — плотность системы точек в Г-пространстве,
/s — s-частичная функция распределения, нормированная на еди-
__ ницу,
Is )—коэффициенты Фурье,
F — динамическая функция,
Fs — s-частичная функция распределения, нормированная на Vs,
(N\
) ^'
G — динамическая функция,
Gkn— сила взаимодействия между частицами,
Н — гамильтониан,
h — константа движения,
few — функция распределения условной вероятности,
/ — мнимая часть -ф,
/ — переменная «действие»,
К — волновое число для потенциала взаимодействия частиц,
Ks — s-частичный оператор кинетической энергии,
Ls — s-частичный оператор Лиувилля,
т — масса частицы,
ns — пространственное s-частичное распределение,
N — число частиц,
N — число степеней свободы,
б — произвольный оператор,
р — канонический импульс,
q — каноническая координата,
Д — действительная часть -ф,
Т — кинетическая энергия,
Т — интервал времени,
и — скорость точек системы в Г-пространстве,
V — потенциал,
V — объем системы в физическом пространстве,
V — ренормированный объем,
х — координата,
zn — координаты и импульсы п-ш частицы,
&in — дельта Кронекера,
Список обозначений к гл. II
ф — решение уравнения Шредингера,
фп — произвольная собственная функция,
Ф — потенциал взаимодействия частиц,
х — фаза -ф,
Л — оператор Лиувилля,
со — собственные значения оператора А,
фп — собственные функции оператора Л,
П — функция распределения условной вероятности,
р — плотность жидкости,
2 — поверхность в Г-пространстве,
9 — угловая переменная,
@tj— оператор потенциальной энергии,
0 ' — оператор потенциальной энергии,
?(Т)— динамическое преобразование.
ГЛАВА III
ФОРМАЛЬНОЕ РАЗВИТИЕ ТЕОРИИ КИНЕТИЧЕСКИХ
УРАВНЕНИЙ И ИХ СВЯЗЬ С ГИДРОДИНАМИКОЙ
3.1. Одночастичная функция распределения и ее
связь с гидродинамикой
При исследовании свойств газа мы чаще всего имеем дело
с измерением некоторых макроскопических, или гидродинамических,
переменных. Эти переменные определяют макроскопическое состоя-
состояние системы. Таких переменных бесконечно много, но все они
могут быть определены, если известна одночастичная функция
распределения Д.
Большинству из нас эти макроскопические переменные хорошо
известны. Первыми из них являются плотность числа частиц п7
макроскопическая скорость и и температура Т. Если нам известна
только плотность числа частиц п (х, t), то мы знаем о данном газе
значительно меньше, чем знали бы, имея п (х, t) и u (x, t) и т д.
Другими менее стандартными макроскопическими переменными
являются напряжение Р^ и тепловой поток q. Последовательность
гидродинамических переменных неограниченна, >и хотя, кроме
перечисленных, они не имеют наименований, но тем не менее мно-
многие из этих переменных обладают физическим смыслом.
Чтобы установить связь между макроскопическими перемен-
переменными и /ь необходимо ввести одночастичную функцию распреде-
распределения с новой нормой. Если N есть полное число частиц в газе, то
положим JFi = Nfi. Плотность числа частиц п (х, t) определяется
через ^i следующим образом:
тг(х, *)= jdRFifx, P, t). C.1)
Произведение ndx дает число частиц в элементе объема dx. Оче-
Очевидно, что это определение совместимо с введенным ранее опреде-
определением для /ь согласно которому произведение /А dx dp представ-
представляет собой вероятность того, что частица находится в состоянии
dxdp около (х, р) в момент t.
В настоящем исследовании, оказывается, намного удобнее
иметь дело со скоростями §, чем с импульсами р. (В гидродинами-
гидродинамике чаще используется макроскопическая скорость жидкости, а не
макроскопический импульс.) В связи с этим введем функцию
/ (х, |, t). Произведение / (х, §, t) dx d\ есть вероятность того,
что частица находится в состоянии dxd | около (х, |) в момент t.
Функция ер (х, |, t) — это функция распределения, нормирован-
3.1. Одночастичная функция распределения 121
лая на N (^ — Nf). Макроскопическая скорость u (x, t) опреде-
определяется из следующего равенства:
t)u(x, t) = jdllJT (x, ?, *), C.2)
л (х, t)^dl&(x, §, 0- C.1')
Другие макроскопические параметры, дающие более детальное
описание системы, приобретают смысл только тогда, когда они
измеряются в системе координат, движущейся со (средней) макро-
макроскопической скоростью u (x, t). Например, газ, у которого все части-
частицы движутся с одинаковыми скоростями, обладает большой полной
кинетической энергией, но его температура равна нулю. Гидроди-
Гидродинамическая внутренняя энергия такого газа (без потенциала взаи-
взаимодействий) также равна нулю.
Введем относительную скорость с, так что
с = I - и. C.3>
Переменная с удовлетворяет уравнению
C.4)
Напряжения Ptj определяются согласно равенству
C.5)
в то время как (кинетическая) внутренняя энергия п % равна
половине суммы нормальных напряжений или половине следа
матрицы напряжений TrPtj. (Согласно обозначению Эйнштейна,.
по повторяющимся индексам производится суммирование.)
гДе р — скалярное давление, an — внутренняя энергия единицы
°бъема. Это равенство служит также для определения темпе-
температуры Т через одночастичную функцию распределения ??;
k — постоянная Больцмана.
Хотя тензор третьего ранга
Sijk ===m^ с^ск^ d\ C.7)
имеет названия, его свертка
fts{ SUJ = \ m J Cic*& d\ C.8)
122 Гл. III. Формальное развитие теории кинетических уравнений
является хорошо известным вектором теплового потока, который
определяет среднюю скорость переноса энергии через поверхность
в направлении i в системе координат, движущейся со скоростью и.
Аналогичным образом Ptj определяет среднюю скорость потока
i-ж компоненты импульса через единичную площадку с нормалью
в направлении /.
Во всех этих определениях предполагается, что взаимодействие
между молекулами через заданную поверхность мало по сравнению
с кинетическим вкладом. Такое предположение наиболее справед-
справедливо, когда газ является идеальным газом, где взаимодействие
между частицами отсутствует.
Экспериментальные наблюдения подтверждают тот факт, что
для жидкости вблизи равновесия определяющими переменными
являются га, и и Т. Вблизи равновесия моменты от Jf более высо-
высокого порядка становятся малыми, и состояние системы целиком
определяется тремя отмеченными переменными.
Предположим, что начальное состояние газа отличается силь-
сильной нерегулярностью, т. е. в газе имеются большие градиенты
температуры, напряжения, тепловые потоки и т. д. С течением
времени состояние «сглаживается», нерегулярности стремятся
к нулю и единственными нетривиальными переменными остаются
моменты низшего порядка — п, и, Т.
Данное состояние газа с любым конечным числом макроскопи-
макроскопических переменных, как бы велико это число ни было, является
сильным упрощением микроскопического описания. При микро-
микроскопическом описании требуется знать функцию ^, которая
в свою очередь определяет бесконечную последовательность мак-
макроскопических переменных:
j tjk ... (с) d% C.9)
где Л — полиномиальный тензор по компонентам с, т. е. Ло = 1>
Л* = сг + щ.
Пусть газ приближается к равновесию. Существует ли интер-
интервал времени, для которого состояние системы определяется по
меньшей мере функцией Д? Из этого вопроса вытекает и более общий
вопрос: существует ли интервал времени, для которого состояние
системы можно определить, только зная функцию fNl
Формализм, который применил Боголюбов для решения цепоч-
цепочки ББКГИ-уравнений, основывается на выяснении этих двух воп-
вопросов.
3.2. Анализ Боголюбова ББКГИ-уравнений
Для любого реального газа существуют три характерных интер*
вала времени.
1. т0 — среднее время, в течение которого две частицы нахо-
находятся каждая в области влияния другой. Это время называется
3.2. Анализ Боголюбова Б Б К Г И-у равнений
123
временем столкновения. Для газа этот интервал времени обычно
много меньше, чем следующий, рассматриваемый нами.
2. t0 — среднее время, в течение которого столкновения
отсутствуют, называемое также средним временем между столкно-
столкновениями.
3. То — интервал времени, много больший первых двух, пред-
представляет собой среднее время, которое требуется частице, чтобы
пересечь сосуд, заполненный газом.
С этими тремя интервалами времени связаны три характерные
длины.
1- го — радиус потенциала взаимодействия.
2. I — средняя длина свободного пробега.
3. L — характерный размер сосуда, заполненного газом.
При средней скорости 300 м/сек (и давлении = 1 атм) порядок
величины этих характерных времен и расстояний дан в табл. 3.1.
Таблица 3.1
Фундаментальные времена и расстояния в анализе Боголюбова
см
сек
го
ЗхЮ-8
то
Ю-12
l
зхю-5
*0
Ю-9
L
3
Го
Ю-4
Характерные времена т0, t0 и То удовлетворяют соотношению
то< *o<?V C.10)
Предположим, что на прямой проволоке длины L имеется толь-
только два шарика. Диаметр каждого шарика равен г0. Шарики
могут проникать один через другой. Если оба они движутся
со скоростью V, то т0 = rJV, То = L/V = t0 (рис. 3.1) и неравен-
неравенство грубо нарушается. Очевидно, что, чем больше будет шариков
н& прямой, тем лучше будет удовлетворяться правая часть соот-
соотношения C.10) (см. рис. 3.2). Точно так же ясно, что если N (пол-
(полное число частиц) становится слишком велико, то нарушается
Девая часть неравенства C.10): если условие Nro^L перестает
ВьШолняться, то т0 не будет много меньше чем t0.
Задача 3.1. Поместить на прямую проволоку три шарика и най-
тя соотношение между ^оиГо. Произвести оценку для t0 и То в пре-
124 Гл. III. Формальное развитие теории кинетических уравнений
дельном случае N ^> 1. При этом предполагается, что как бы ни бы-
было велико N, имеет место NrQ <^ L.
Предположим, что газ достаточно разрежен, так что левое
неравенство C.10) выполняется, а также и достаточно плотен, что-
чтобы и правое неравенство C.10) удовлетворялось. В этом случае
Рис. 3.1. Времена Боголюбова для задачи о двух шариках на прямой.
уместно говорить о трех интервалах времени в развитии газовой
системы, начиная с некоторых заданных начальных условий и кон-
кончая неким равновесным состоянием, либо, возможно, состояниемг
достаточно близким к равновесному.
В первом интервале времени
0<*<T0, (З.И)
называемом начальной стадией, N частиц еще не сталкивалось.
Какой уровень описания будет достаточным, чтобы определить
поведение газа в этом интервале времени? Мы должны помнить,
что начальные условия являются произвольными. Предположи^
что в начальный момент одна из N частиц движется с постоянной
3.2. Анализ Боголюбова ББКГИ-уравнений
125
скоростью по прямой линии (в направлении к другой частице),
в то время как оставшиеся N — 1 частиц покоятся. Спустя неко-
которое время, после достаточного числа столкновений, газ будет
термализован — установится равновесие. В конечном счете не
будут существовать, например, тепловые потоки сквозь любую
to
Рис. 3.2. Времена Боголюбова для задачи о трех шариках на прямой.
заданную поверхность в газе, температура станет однородной
й т. д. На этих конечных стадиях эволюции естественно описывать
состояние газа через гидродинамические переменные. При этом,
если начальные возмущения почти полностью затухли, состояние
системы определяется гидродинамическими переменными.
Например, для рассмотренного выше начального состояния,
Когда только одна из N частиц находится в движении, введение
Гидродинамической скорости и лишено смысла. Единственный
важный факт — движение одной из N частиц — будет утерян
в процессе осреднения, при котором получается и:
.. . dzM.
C.12)
126 Гл. III. Формальное развитие теории кинетических уравнений
Если с помощью функции и нельзя описать состояние системы,
то обратимся к более детальному описанию, которое дает функция
/i. До первого столкновения iV-частичная функция распределения
имеет вид
fN = б (х, - Ы) б (х2 - х°2) б (х3 - х°3) . . .
... 6 (х* - х&) 6 (|, _ ?}) б (?2) б (У ... б (lN). C.13>
Интегрируя по z2, . . ., zN, получим:
Какую полезную информацию несет в себе полученное соотноше-
соотношение? Оно определяет только то, что вероятность, с которой частица
1 находится в положении х и имеет скорость § в момент t (в интерва-
интервале dx d|), отлична от нуля лишь для тех значений х и |, которые
принадлежат кривой х = |°?. Но что мы можем сказать относитель-
относительно остальных частиц? Тот факт, что они остаются в покое в опре-
определенных начальных положениях был совершенно утерян при
вычислении /4. В самом деле, предположим, что в выражении
C.13) для функции fN множитель б (х2 — х°) б (|2) заменен на
б (х2 — |2 0 б A2 — !!!). Теперь частица 2 также движется па
прямой линии со скоростью |g. Вычисляя /i, мы должны выпол-
выполнить интегрирование
j dx2 J dl2 б (х2 - ht) б A2 -12°) = j dx28 (x2 - Ut) = 1,C.15)
в результате которого будет полностью утеряна информация отно-
относительно частицы 2. Допустим тогда, что достаточно знать функ-
функцию /2, чтобы описать начальное состояние до столкновения любых
двух частиц. Опять очевидно, что в процессе осреднения при вычис-
вычислении /2 исчезает информация относительно N — 2 оставшихся
частиц. Продолжая далее такие же рассуждения для /3, /4, . • «»
придем к заключению, что в интервале времени 0 < t < т0 состоя-
состояние газа определяется функцией fN и никакой другой.
Следующий интервал времени т0 < t < t0 — это кинетиче-
кинетическая стадия, когда после ряда столкновений частицы приобрета-
приобретают некоторый элемент сходства. При таких условиях среднее сос-
состояние любой из частиц дает нам информацию относительно всех
частиц, так что динамика газа определяется функцией /i. Фор-
Формально эти идеи можно выразить так: предполагается, что на ки-
кинетической стадии все функции распределения fa являются функци-
функционалами от fu так что
/. = /, A, 2, . . ., s, t; h). C.16)
3.2. Анализ Боголюбова ББ К ГИ-у равнений
127
{{роме того,/8 зависит от времени неявно,
через функцию Д. Примером такой зависи-
зависимости может служить функция /s для s ста-
статистически независимых частиц:
C.17)
Наконец, на гидродинамической стадии
to^t ^ ^о все функции распределения /s
зависят только от п, и и Г, т. е. первых
пяти моментов функции Д.
На рис. 3.3 схематически изображена
последовательность только что рассмотрен-
рассмотренных случаев (когда при t = 0 только одна
частица из всего стационарного газа при-
приходит в движение).
При изменении состояния системы от
начального хаотического до конечного хо-
хорошо организованного равновесного со-
состояния нам требуются резко различаю-
различающиеся уровни описания системы. Вначале
необходимо знать не меньше чем TV-ча-
TV-частичную функцию распределения. В конеч-
конечной, равновесной, стадии достаточно знать
термодинамические переменные, дающие
несравненно менее подробное описание си-
системы.
Анализ Боголюбова иерархии ББКГИ-
уравнений касается кинетической стадии
и включает следующее ограничение:
_Ш.(^)-±. C.18,
У->оо
где 1/v является конечным малым пара-
параметром. (Соответствующим безразмерным
малым параметром будет rjj/y, где г0—ра-
Диус взаимодействия.) В этом предель-
предельном случае (см. задачу 2.27) уравнение И
имеет вид
о о о
о
о о
Рис. 3.3. а — началь-
начальная стадия: 0<? < т0, fN
определяет состояние га-
газа; б — кинетическая ста-
стадия: т0 <С t<t0. Части-
Частицы приобретают некото-
некоторый элемент сходства,.
fs = fs [/il; в ~ гидроди-
гидродинамическая стадия: t0 <
< t < То. Состояние га-
л /• за близко к равновесно-
LiFi -Y^ ^d(Z-flNi, 1+1^+1 = 0- му и задается через функ-
г=1 " C.19) ЦИИ П' U?
Напомним, что Ft == Vlfi и i = ( хг, р^). Функциональная зави-
зависимость мел^ду Fs и F\ имеет следующий вид:
Fa = Fs (I, . . ., s; Ft). C.20)
128 Гл. III. Формальное развитие теории кинетических уравнений
Уравнения C.19) для 1 = 1, . . ., s запишутся так:
dF± __ Pl dF± 1 г ,9А ^
"й ~^+v J d2@^ (
i)S+1JFe+1. C.22)
Используя C.20), производную по времени от Fs можно предста-
представить следующим образом:
dFs_/6Fs dF±\
где скобками обозначено внутреннее произведение по всем функ-
функциям, a 8Fs/8Fi — функциональная производная от Fs no Fit
В простейшем случае, когда Fs является алгебраической функ-
функцией от jP1? эта производная запишется в виде
dFs
dt Л OFi (I) dt '
1=1
Исходными уравнениями анализа Боголюбова являются послед-
последние три уравнения C.21) — C.23). Формальное разложение, кото-
которое будет использовано для получения замкнутой системы уравне-
уравнений, задается равенством
s V »•••>> l) s'~ s -Г • • • » Ч • )
Ft = Fi (Fi не разлагается, поскольку она является «независимой
переменной»).
Подставляя C.24) в C.21), получим
-Aa> + ±-A™+... . C.25)
Это соотношение служит для определения коэффициентов A{l)t-
C.26)
3.2. Анализ Боголюбова ББКГИ-уравнений 129
Если мы подставим разложение C.25) для dFJdt в функциональ-
функциональное внутреннее произведение C.23), то в результате будем иметь
lA4...). C.27)
Путем перемножения членов, получим
C.28)
Это разложение можно записать в следующем виде:
i^A = ?"»^<°> + -i- [Д"»^1' + ДA)^о>] + • • •, C.29)
где операторы /У0' и Da> определяются равенствами:
Вернемся теперь к оставшимся уравнениям ББКГИ C.22) и ис-
используем в них разложение C.24). В результате получим
-b.= -L[ ]
[±] C.31)
г=1
Приравнивая коэффициенты при одинаковых степенях V1 в раз-
разложениях C.29) и C.31), придем к замкнутой системе функци-
функциональных уравнений для переменных F® [1, . . ., s; F^:
Ь C.32а)
. C.326)
Последовательный ход решения этих уравнений представлен
на рис. 3.4.
Резюмируя изложенное, отметим три этапа анализа Боголю-
Боголюбова: 1) предполагается, что FS = FS [Fj; 2) находится уравнение
Для Fs [F±]; 3) построение завершается выводом двух разложений
Для dFJdt. Ими являются уравнения C.29) и C.31).
130 Гл. III. Формальное развитие теории кинетических уравнений
В данном формализме мы вывели замкнутую систему уравне-
уравнений для функций F8, но две задачи остались нерешенными. Это,
во-первых, получение конкретных выражений для операторов
Ь{1) и, во-вторых, метод вычисления Fle
Именно на этих двух проблемах мы сосредоточим сейчас наше
внимание. В частности, дадим стандартный метод, с помощью
C.32) -*{F5w,FJl>i}
C.26)—Л^
C.28H3.30) — ?>Ы
C.326) -^{FsA)}
C.26)—^1B>
1
C.28И3.30)—^2>
1
C.32)-
- (Ff2^
Рис. 3.4. Метод решения системы уравнений C.32).
которого получается уравнение для Fiy справедливое до членов
порядка Z7. Для этого используем замкнутую систему уравнений,
получаемую из C.25) и C.32а),
dFl i Pi dFl 1 Г
6@)Fi0)=-L2Fi0). C.32a')
Первый шаг состоит в том, чтобы решить второе из этих уравне-
уравнений для
Fio)=JF;o)(l, 2; F4)
при некоторых определенных «граничных условиях». Это дает
явную функциональную зависимость F{20) от F± при соответствую-
соответствующим образом выбранном начале отсчета времени. Последнее озна-
означает, что система частиц (со взаимодействиями, препятствующими
существованию связанных состояний) становится некоррелиро-
некоррелированной, когда протечет достаточно длительный интервал времени
в обратном направлении. Уравнение C.32а) решается именно
при этом условии. Такое условие поставлено в связи с его дальней-
дальнейшим приложением к процессам столкновения и означает, что до
столкновения частицы не коррелированы.
На втором шаге полученное таким образом решение для FBQ}
подставляется в уравнение C.25') и выводится соответствующее
выражение для ®12Р{20\ что приводит к характерной форме
боголюбовского обобщения уравнения Больцмана.
3.2. Анализ Боголюбова ББКГИ-уравнений 131
Для решения этих задач вводится оператор сдвига
A(t° = exp[*Lz], C.33)
где Li — Z-частичный оператор Лиувилля (ср. с Аи который
задается уравнением B.30)). Определение Ъх вытекает из уравне-
уравнения Лиувилля для изолированной системы из I частиц:
Ц*- = [Ни FA^-UF:. C.34)
Решение этого уравнения имеет вид
Ft(l9 ...,Z; 0 = A(Vz(l, -.../; 0)., C.35)
Оператор Д^т действует на фазовые переменные Fi. Он «сдвигает»
их обратно по времени на интервал т по отношению к значениям,
определяемым Z-частичным гамильтонианом Hi. Для единичной
свободной частицы мы получим
bPji (х, р, *) =Ft (х —?• т, р, t) . C.36)
В более общем случае (возвращаясь к обозначению фазовой
переменной через z) для произвольной фазовой функции if) мы имеем
..,А?>^; О- C.37)
Из C.35) следует, что Ft постоянна вдоль траекторий системы в Г-
пространстве I частиц. Ниже приведено несколько других свойств
оператора А:
Ао=1, C.38)
C.39)
= - LA_t = - A_tL. C.40)
Последнее соотношение справедливо для операторов, не завися-
зависящих от времени. Решением неоднородного уравнения Лиувилля
^ t) = P(z,t) C.41)
является функция
F{z, t) = LtF (z, 0) + A_, J dt'hvP(z, t') C.42)
_, J dt'hv
(здесь использовалось свойство C.40)).
Упомянутое выше граничное условие для s-частичной функции
Распределения как функционала от F± легко задать через опера-
132 Гл. III. Формальное развитие теории кинетических уравнений
торы А. Как мы помним, это условие состоит в том, что система
s взаимодействующих частиц в далеком прошлом была некор-
релированной, т. е.
I ( )] f[Fi(l,t). C.43)
Т->оо Т->оо 1=1
Поскольку данное условие справедливо для произвольной функ-
функции F±, оно будет справедливо и для F[ = lim A^^i A, t).
Т->оо
Подставляя эту функцию в предшествующее равенство, получим
lim A<V. [I, ...,*; №Ft A, 01 =Hm A% Д ^Ft (Z, t). C.44)
T->oo T->oo 1=1
Такая форма граничных условий используется при решении функ-
функционального уравнения C.32а). Явный вид правой части (ПЧ)
равенства C.44) легко получить, используя C.36). Это дает
ПЧ
= ПЛ[х!!), pis)]. C.45)
1=1
Переменная рР} — это постоянный импульс, который имеет 1-я
частица, взаимодействующая с совокупностью s частиц, если про-
проследить за этой частицей из состояния р^ в далекое прошлое.
Переменная x\S) — это координата, которую имела бы 1-я частица,
если бы она двигалась с импульсом pjs) при начальной координате
A^ooXj. Такая интерпретация обусловлена той операцией, которая
определена последним равенством:
Как мы увидим, эта интерпретация весьма полезна при нахож-
нахождении явного выражения для 012^О) в уравнении C.25').
Перейдем теперь к интегрированию уравнения C.32а):
Согласно C.26) и C.30), операция D{C)Ff} определяется следую-
следующим образом:
^ Щ-Ш. C.46)
3.2. Анализ Боголюбова ББКГИ-уравнений 133
Эту функциональную операцию можно привести к виду, удобному
для дальнейшего исследования и в то же время позволяющему
включить предшествующее граничное условие, если воспользо-
воспользоваться следующим приемом. Поскольку C.46) справедливо для
любой функции F±, оно будет справедливо также и для Ai^i-
Таким образом,
Z><°>F<°> [1, ..., s; АЭД = .,я%°' f-lM'xFi] . C.47)
Вспоминая свойство C.40), мы можем записать это уравнение так:
тую pte, &ПЮ dA'-Vt
D Fs =тт^)^^' C-48)
что дает нам желаемый вид функциональной операции:
b™F?>[l,...,s;texF1] = -lLF2»[l, ...,s; АЗД]. C.49)
Подставляя это выражение в C.32а), получим
± FT [1, • • •, s; A'i'^J = -If™ [1, ..., s; А%Р,]. C.50)
Рассмотрим пробное решение
/Г [1, ..., *; A(^i] = №XFT A, ... .s; Ft). C.51)
Подстановка его в C.50) дает
-^ AA\F^ A, . . ., s; Ft) = ~Ls№xFl°> A, ..., s; F,). C.51a)
Если мы вспомним C.40) и заметим, что ^0) в таком виде, как она
записана в уравнении C.51а), не зависит от т, то увидим, что это
уравнение является тождеством. Отсюда следует, что решением
уравнения C.50), а следовательно, и уравнения C.32а) будет про-
произвольный функционал от функционала, заданного соотношением
C.51).
Другой формой решения может быть следующая:
/Г A, ...,*; F1) = A(l\F^(li ...,*; A^F,). C.52)
Это решение пригодно для всех интервалов т, так что
^°> A, . .., s; Fx) = lim k{i\Fr A, • • •, s; A^F,) C.53)
T->oo
также является решением. Используя предшествующее граничное
условие, а также C.44) и C.45), получим
F<s°> A, ..., s; Fx) = Д Fi (xiS), iff). C.54)
134 Гл. III. Формальное развитие теории кинетических уравнений
Это решение удовлетворяет уравнению C.32а) и граничному усло-
условию C.44). Таким образом, первая часть задачи о получении одно-
одного уравнения для Fi из уравнений C.25') и C.32а') завершена.
Из C.54) видно, что решение низшего порядка F(s0) в анализе Бого-
Боголюбова обнаруживает s-частичную корреляцию между частицами
(через переменные x(S), p(S))-
Следующий шаг состоит в том, чтобы получить в уравнении
C.25') соответствующее выражение для Q^F^ • С этой целью
напомним сначала соотношение B.155) и последующие:
L2 = К2— в12,
fr =_Pl д_ | JP2_ _д__
Л2— т #dXl~T m дх2 •
Отсюда вытекает, что
Чтобы получить надлежащее выражение для L2FB°\ вернемся
опять к уравнениям C.32а') и C.26):
C.56)
/1@) Р^ dFl /Y n \
Выполняя функциональное суммирование, соответствующее внут-
внутреннему произведению ( , ), и вспоминая решение F™, которое
задается посредством C.54), получим явный вид для L2F^:
C-57)
Наконец, чтобы получить нормальную форму обобщенного
уравнения Больцмана, произведем в операторе К2 замену перемен-
переменных Xi и х2 на Xi и г = х2 — хь что дает
Используя выражение C.57) для L2F™ и C.58) для K2FB°\ под-
подставим C.55) в C.25') и придем к обобщенному уравнению Больц-
Больцмана в форме Боголюбова:
Ж + lt-Wr ld2KF^ + ±^d2(K'L)F-\ C.59)
В случае, когда ^0) однородна по всей области взаимодействия,
второй интеграл обращается в нуль (К'2 и L2 оба содержат про-
3.2. Анализ Боголюбова ББКГИ-уравнений
135
странственные производные), в то время как К2, в переходит
в обычный больцмановский оператор столкновений.
Чтобы это показать, в соотношении
J d2K2, Б*Г = J
C.60)
(где аргумент х в F± выпадает, поскольку Fi однородна по всей
области столкновения) выполним интегрирование по х2 в цилин-
цилиндрических координатах с осью цилиндра т], параллельной отно-
относительной скорости
_ Р2-Р1 . „ V-Г
у =
V
C.61)
Радиус цилиндра Ъ и азимут ф лежат в плоскости, нормальной к V.
Отсюда следует, что
7Эо
До столкно-
деиия *
V- — = V— . C.62)
or дх\ v
Интегрируя сначала по т], получим
+0О
ОУ\ ' — оо
— ОО
Области после столкновения соответствует т] = + °° (рис. 3.5).
Если из этой области (т] = +оо) проследить в бесконечно далекое
прошлое, то каковы будут зна-
значения Pi и р2 в случае парного х2
взаимодействия частиц? Ими
должны быть те значения им-
импульсов, которые перейдут в р!
и р2 после столкновения, т. е.
импульсы pi и Ра инверсивного
столкновения. (Эти понятия бу-
будут подробно обсуждаться в
гл. IV.)
Области до столкновения со-
соответствует т] = —оо (рис. 3.5).
Каковы будут значения р4 и р2
при парном взаимодействии ча-
частиц, если из этой области (т| =
= —оо) проследить в бесконеч-
бесконечное прошлое, которое представ- р и с. 3.5. Связь между знаком х\ и
ляет собой состояние «до до областью столкновения,
столкновения», т. е. область,
Находящуюся далеко за пределами зоны взаимодействия двух ча-
частиц? В этой области две частицы движутся независимо одна от
136 Гл. III. Формальное развитие теории кинетических уравнений
другой как свободные, поэтому их импульсы равны Pi и р2. Сле-
Следовательно,
Fi [Pi2'] Fi [РЛ Г? = Fi (РО Ft (pj) -Fx (Pl) Fi (pa)- C.64)
Подставляя это соотношение в C.63), а затем в C.59) (и удержи-
удерживая только однородный вклад K2i б)> получим обычное уравнение
Больцмана:
C.65)
Уравнение Больцмана подробно рассматривается в гл. IV,
где представлены три других его вывода. Более прямой из них
не опирается на последовательность ББКГИ-уравнений. Но весь-
весьма примечательно, что анализ Боголюбова дает независимый
(т. е. опирающийся только на уравнение Лиувилля) метод, кото-
который позволяет получить больцмановский интеграл столкновений
в явном виде. В данный момент важно, что такой метод существует.
В главе IV будет дана всесторонняя трактовка уравнения Больц-
Больцмана, которая обеспечит более глубокое его понимание.
3.3. Групповые разложения
Совсем недавно были предложены другие методы разложения
для исследования ББКГИ-уравнений. Сюда относятся работы
Ростокера и Розенблюта A960), Гернсея A960), Ленарда A960),
Балеску A960), Сэндри A963) и Дюпри A961). Однако эти работы
в противоположность предыдущим больше связаны с выводом
определенного кинетического уравнения, чем с получением реше-
решения для TV-частичной функции распределения. (Кинетическим
называется любое уравнение в переменных (t, |, х) для неизвест-
неизвестной функции Д.) Тем не менее все эти методы объединяет то, что
в каждом из них решение ищется в виде некоторого разложения.
В частности, метод Боголюбова связан с разложением по обратным
степеням параметра v — удельного объема.
Существуют другие способы разложения, непосредственно
опирающиеся на свойства F2i F3, - - ., FN в предельном случае,
когда у~1~^0. Что это за свойства? Очевидно, что, когда объем,
приходящийся на одну частицу, становится большим, а следова-
следовательно, и расстояние между частицами также возрастает, тогда
фаза какой-либо частицы становится менее связанной с фазой
любой другой частицы. Это утверждение о независимости состоя-
состояний, записанное через функцию распределения Fs, выглядит так:
Fa = ^Fi(l). C.66)
3.3. Групповые разложения 137
Для случая s = 2
F2(l9 2)=Fi(i)FiB). C.67)
Если состояния двух частиц не зависят одно от другого, то гово-
говорят, что эти частицы не коррелированы. Мера влияния состояния
одной частицы на состояние другой частицы (отличной от первой)
определяется корреляцией между частицами. Равенство C.67)
справедливо в предельном случае, когда корреляция отсутствует.
Отклонение функции F2 A, 2) от факторизованной формы
Fi (I) Pi B) называется корреляционной функцией %г- Таким
образом,
F2(i, 2) = Fi{l)FiB) + %i(l, 2).
Если ^2 мала по сравнению с Fi A) F2 B), состояния частиц 1 и 2
являются независимыми. Ясно, что это будет иметь место в случае
«большого» удельного объема v при условии, что газ однородно
заполняет конфигурационное пространство. Этот результат можно
сформулировать более точно с помощью г0 — радиуса потенциала
межмолекулярного взаимодействия ср и средней тепловой скоро-
скорости У^кТ/т (к — постоянная Больцмана, Т — температура, m —
масса частицы). Если v — средний объем, приходящийся на одну
частицу, то при у, большом по сравнению с г*, каждая из частиц
«не подозревает» о существовании другой. В этом случае соответ-
соответствующим малым параметром будет Si = (rjj/i;).
Классический механизм взаимодействия между частицами осу-
осуществляется через потенциал ср. Если температура такова, что
кинетическая энергия значительно превышает потенциальную,
то последняя не будет играть роли в изменении фаз рассеиваю-
рассеивающихся частиц. В этом случае малым параметром является е2 =
= фо/ЛГо? где ср0 — «напряженность» потенциала.
Существование в различных предельных случаях малых корре-
корреляций между частицами было использовано Сэндри для приведе-
приведения ББКГИ-уравнений к безразмерному виду. Получающаяся
в результате теория одновременно и формальна и иллюстративна.
Введем сначала обозначение, в котором последовательность
ВБКГИ-уравнений C.19) примет следующий вид:
^ |в+1. C.68>
Здесь Uq^v'1 и оператор As определяется равенством
г=1
138 Гл. III. Формальное развитие теории кинетических уравнений
Кроме того, напомним, что
Ls = Ks — @s»
s s
p' _Y1 Pi д & — V V Й
^«^Zj l^'lhT^ ^* = ZjZu*./>
do о /л I*--' • • U)
о о о '
Запишем систему ББКГИ-уравнений C.68) через эти новые опе-
операторы:
ut
При такой записи уравнений выявляется только действие
параметра п0. Однако рассматривать предельный случай большого
размерного удельного объема физически бессмысленно. Корректно
только лишь сравнение v с некоторым известным постоянным
объемом.
Для того чтобы устранить все размерные параметры в урав-
уравнении C.71), мы должны привести к безразмерному виду все
переменные, входящие в это уравнение. С этой целью введем без-
безразмерные (отмечаемые значком ~) переменные:
4>и = ФоФ*j (либо Gu = 51 Gu
C.72)
где
p0 = mC, mC2 = kT0. C.73)
Расстояние r0 — это радиус потенциала взаимодействия. Определе-
Определение безразмерной силы G и потенциала ф обеспечивает согласован-
согласованность введенных переменных.
Подставляя эти новые переменные в уравнение C.71), получим
1 1^- <3-74)
-Опуская значки «тильда» (все переменные и операторы являются
¦безразмерными), придем к ББКГИ-уравнениям в форме Сэндрв:
Fs = ctpAsFs+1,
C.75)
3.3. Групповые разложения
139
(«"SO
A,0
(«
A
«
-1
,0
.«
1)
(,-
A,
«,
Сильное Взаимодействие;
низкая температура c-i
Слабое Взаимодействие;
Высокая температура
€ 1 с J3 = г^го3
КороткодейстВу- ДальнодеистВу
ющие силы; ющие силы;
разреженная плотная среда
среда
Рис. 3.6. Упорядочение параметров (а, Р) в групповых разложениях.
Эти уравнения имеют два характерных физических параметра:
Фо/fcjTo и пог*. Область, представляющая физический интерес,
полностью исчерпывается, если позволить этим параметрам при-
принимать значения, равные по порядку величинам 8, 1 и 8 (е —
бесконечно малая). Возникающие в результате девять возможных
случаев представлены на рис. 3.6.
Задача 3.2. Что можно сказать относительно %ъ, если ^2 — О»
и относительно ^2» если %ъ — 0? Описать словами «физику»
каждой ситуации.
Корреляции более высокого порядка определяются по следую-
следующей схеме:
F2(l, 2) = Fi(i)FiB) + V2(l, 2),
F3 A, 2, 3) = Ft A) F, B) Fx C) + Ft A) %г B, 3) +Ft B) <ё2 C,1) +
+ ^C)«2A, 2) + «зA, 2,3),
(l, 2, 3, 4)=Fi{l)F1B)FiC)F1D)+Fi(i)FiB)<e2@, 4) +
D)^A)^B,3) + ^ A)^C)^D, 2)+C.76)
«,C,4,1L-^1C) «.D, 1,2)
«,(lf 2, 3) + «a(l, 2)«8C, 4)
140 Гл. III. Формальное развитие теории кинетических уравнений
Эти формулы обладают следующим свойством:
Fs -> П Fi (Z), при <ё% -> 0, 2 < i < 5.
Кроме того, если из данной группы частиц выделяется некото-
некоторая подгруппа, то функция распределения этой группы частиц
соответствующим образом разлагается на множители. Предполо-
Предположим, например, что в группе из четырех частиц A, 2, 3, 4)
частицы 1 и 2 находятся каждая в области влияния другой,
но далеки от частиц 3 и 4. Каждая из последних двух частиц,
подобно первым двум, находится в области влияния другой.
Такое состояние характеризуется следующими соотношениями:
^4A, 2, 3, 4) = F2A, 2)iM3, 4),
#4 = о, «8 = 0,
«2 A, 4) = Ъ2 B, 3) = <ё2 A, 3) = «2 B, 4) = 0.
Подставляя эти выражения в последнее из равенств C.76), полу-
получим
ЛA, 2, 3, 4) = ^A)^B)^C)^D) + ^A)ЛB)«2C, 4) +
+ F± C)^D)«2A, 2) + «2A, 2)«2C, 4) =
+ «2A, 2I1^C)^D) + «2C, 4)] =
3, 4). C.77;
Рассмотрим также другое часто встречающееся представление
корреляционных функций. Оно соответствует так называемому
разложению Кирквуда, хорошо известному химикам-теоретикам.
Корреляционные функции в этой схеме обозначаются через
f A, 2), К A, 2, 3), А A, 2, 3, 4) и т. д. Они определяются сле-
следующим образом:
F2(l,2) = Fi(l)FiB) [I + у A,2I,
Fs(l. 2, 3)=Fi(l)FiB)FiC) [1 + »A, 2) + *B,3)+*C,4)+АA, 2,3I.
Предположим, что рассматриваемая система бесконечно близка
к состоянию с нулевыми корреляциями. В таком случае все I-
частичные корреляционные функции имеют порядок 8 и выше,
так что
Fs = Д F, (I) + 0 (е) = Fie> + eF?> +..., C.78)
где ^0) записывается в форме произведения C.66).
Поскольку F(s0) описывает равновесное состояние (разрежен-
(разреженного газа), то представленное выше разложение справедливо я
3.3. Групповые разложения 141
достояний, близких к равновесию. Рассмотрим теперь некоторые
из предельных случаев, изображенных на рис. 3.6.
Случай а: р = О (е), а = О A).
Если положить р = пог1 = е, то система уравнений C.75)
сведется к следующей (удержим только члены наинизшего порядка
до е):
^ = 0, C.79а)
(i+K2) (F^)-ссв2ЗД = 0, C.796)
Д Fi(Q=O. C.79b)
Имеем N уравнений для одной неизвестной функции F^. В этом
случае нетривиальное решение возможно, только если уравне-
уравнения совместны. То же самое справедливо относительно всех раз-
разложений ББКГИ-системы около нулевых корреляций. Данное
условие существования нетривиального решения следует из пред-
предположения о форме ведущего члена в разложениях C.78), соглас-
S
но которому Fl0) = [J F± (I). Совместность уравнений нулевого
порядка является необходимым условием факторизации Fs0).
Задача 3.3. Установить, являются ли совместными уравне-
уравнения C.79).
Случай б: а = О (е), р < О A).
Полагая а = О (е) в разложении C.78) и удерживая в C.75)
только члены наинизшего порядка по 8, придем к следующим
уравнениям:
(l )Fi(l)^0. C.80)
Эта согласованная система уравнений имеет решение в виде
свободно-молекулярного течения:
C.81)
где ty — любая функция от х — (р/ттг) t и р. Таким образом, реше-
решения уравнений C.80) постоянны вдоль траекторий свободных
частиц р = ро и х — (р/ттг) t = х0.
Полученный результат имеет силу, когда р ^ О A), так что
решение пригодно для областей (е, г) и (8, 1) (рис. 3.6). Следова-
142 Гл. III, Формальное развитие теории кинетических уравнений
тельно, г0 может быть порядка по/3 при условии, что напряжен-
напряженность потенциала много меньше кинетической энергии кТ0. Пер^
вые два уравнения системы C.75) до членов О (е) включительно
имеют вид:
(^ ) = eccpA^, A)FxB), C.82а)
е^2]-еав2ЛA)ЛB) =
1)^B)^C). C.826)
Для s — З будем иметь
= &a$A3F\F\F\F\. C.82b)
Получающуюся в результате систему уравнений в принципе
очень легко решить. Во-первых, F4 получается из C.82а). Когда Ft
найдена, оставшиеся уравнения все являются неоднородными
уравнениями следующего вида:
s= Ps(Fu «..). C.83)
При таком методе решения функции распределения находятся
в соответствии со следующей схемой (до членов О (г)включительно):
Полезно, между прочим, отметить одно важное свойство корреля-
корреляционных функций %х A, 2, . . ., Z). Рассмотрим уравнение, опре-
определяющее %ч\
F2 A, 2) = Ft A) Ft B) + %г A, 2). C.84)
Но функция Fi в, свою очередь определяется через F2'-
B)й2 = У. C.85)
Сравнивая последние два уравнения, заключаем, что
J ^2 A, 2) d2 = J %г A, 2) dl - 0. C.86)
3.3. Групповые разложения
Для
мы находим
i
C.87>
, 1) + «8A,2,3)] = 0
йли, используя соотношение C.86),
= ( dld2#8 = 0. C.88)
Аналогичные утверждения справедливы для сё8Л s > 3. Эти усло-
условия могут служить дополнительными уравнениями в любом
данном методе разложения. Они определяют ограничения, нало-
наложенные на корреляционные функции. Так, например, из усло-
условия C.86) следует, что ^2 не может быть четной функцией по всем
из своих аргументов.
Задача 3.4. Доказать, что I ^sd& = 0, к== 1, 2, ..., s.
Случай в: а = О (&), 0 = О (е).
Этот предельный случай впервые был введен Розенблютом
и Ростокером A960) при исследовании соответствующих урав-
уравнений для высокотемпературной плазмы. Плазмой называется
состояние вещества за пределами атомарной газообразной фазы.
Когда атомарный газ нагревается выше некоторого пределат
появляется механизм, который непрерывно поглощает кинетиче-
кинетическую энергию хаотического движения. Это подобно энергии
диссоциации в жидкости с полукристаллической структурой, кото-
которая является как бы каналом для непрерывного поглощения
энергии при переходе из жидкого состояния в газообразное. При
переходе в плазменную фазу поглощающим каналом является
механизм ионизации, и в новой фазе частицами будут положи-
положительные ионы и отрицательные электроны. Законы, управляющие
поведением плазмы, так же сильно отличаются от законов газо-
газообразной фазы, как законы газообразной фазы отличаются от зако-
законов жидкой фазы. Силы взаимодействия в плазме — кулоновские.
Они отличаются от всех других сил взаимодействия между части-
частицами очень большим радиусом действия. Эти две характеристики —
Дальнодействие и высокая температура — дают возможность пред-
предположить, что (ро/кТо ~ 8 и rln0 ~ 8, так что цог1по/кТо ~ 1.
Для кулоновского закона взаимодействия
Ф*У = -7 г- г (мкс)> C-89)
Yiy 4я80|Хг —Xj| N " V /
где е — заряд каждой частицы, а 80 — диэлектрическая прони-
проницаемость вакуума. Радиус г0 и напряженность ср0 взаимодействия
144 Гл. III. Формальное развитие теории кинетических уравнений
связаны соотношением
г0
В силу того что cporlno/kTo ~ 1, мы можем оценить соответствую,
щий радиус взаимодействия гр:
Характерная частота сор определяется равенством
Расстояние гр — это эффективный радиус действия кулоновского
потенциала в плазме. Более точные вычисления (впервые прове-
проведенные для электролитов Дебаем и Гюкелем A923)) показали, что
заряженная частица, помещенная в нейтральную плазму, вызы-
вызывает перераспределение заряда, стремящееся экранировать проб-
пробную частицу, так что вне гр (радиус Дебая) кулоновский потенциал
в е (In e = 1) раз меньше своего значения в вакууме.
Частота сор связана также с основным коллективным колеба-
колебанием, которое будет совершать возмущенная плазма, выведенная
из состояния локальной зарядовой нейтральности. Установлено,
что время образования около пробного заряда дебаевского экра-
экранирующего облака имеет порядок со^1.
Ознакомившись с самыми элементарными понятиями физики
плазмы, вернемся теперь к разложению ББКГИ-уравнений, когда
а ~ 8 и р ~ 8, и к концепции предельного случая нулевых
корреляций между частицами. До настоящего момента мы просто
считали, что надо положить %\ ~ г%\ ^&\ = О A)), чтобы формаль-
формально описать этот предел. Однако мы получим более последователь-
последовательный формализм, если положим %ъ ~ &к~1(&и- В этом случае $4
имеет порядок е3, %2 имеет порядок вит. д. Но обосновано ли физи-
физически такое упорядочение? Иными словами, если ^2 мала, то будет
ли $з еЩб меньше?
Хотя точное доказательство этого факта получить трудно,
некоторые простые оценки, по-видимому, подтверждают правиль-
правильность сделанного нами предположения. Их можно получить,
вычисляя объем допустимых областей фазового пространства,
где с&8 отлична от нулях). Рассмотрим элементарную задачу
о трех шариках на прямой проволоке длины L. Областью взаимо-
взаимодействия между любыми двумя из них является г0 (в данном слу-
случае это диаметр шариков). Чтобы вычислить %г A, —), зафикси-
зафиксируем шарик 1 в начале координат, тем самым мы определим пло-
1) Можно рассматривать <gft как ^-частичное распределение. В этом
случае мера ^ равна отношению объема в Г-пространстве, который включает
состояния с ^-частичными корреляциями, ко всему объему Г-пространства.
3.3. Групповые разложения
145
скость в трехмерной конфигурационной части пространства Г6.
Области, в которой ^2 A> —) отлична от нуля, соответствует
заштрихованная площадь на рис. 3.7, а. Когда шарик 2 находится
в интервале —г0 ^ х2 ^ + г0, то при %2 A> —) Ф® шарик 3
может находиться где угодно на прямой. То же самое справед-
справедливо, если шарики 3 и 2 поменять местами. Отношение А2 пло-
площади, для которой c&2(i, —) ?=0, к полной площади равно
(iro/L) [1 — (rJL)] для (ro/L) <-тИ равно единице в любом другом
случае. Чтобы определить, где *ё3 A> —» —) Ф0, поместим опять
шарик 1 в точку @, 0, 0). Состояниям с ненулевой функцией
Рис. 3.7. Корреляционные функции для трех шариков на прямой.
%3 A> —* —) соответствует заштрихованная область на рис. 3.7, б.
Относительная площадь, на которой %ъ A, —, —) конечна, равна
А3 = SryL2. Если мы обозначим rJL = 8, то в пределе, когда
е-> О, А3 = 2гА2. В более общем случае А2 ~ АЦ2 A — А\/2).
Наши вычисления сильно упростились, поскольку мы прене-
пренебрегли кинетической энергией частиц. Вообще говоря, для любого
заданного прицельного параметра (в классическом случае) дейст-
действие рассеивающего потенциала сводится к нулю, когда энергия
падающей частицы становится достаточно велика. Можно утвер-
утверждать, что в пределе при цH/кТ0 -> 0 эффективная область взаимо-
взаимодействия уменьшается. С другой стороны, когда сро/кТо-*- сю,
эффективный радиус взаимодействия становится равным г0. Про-
Простейший способ включения этих соображений в предшествующий
анализ состоит в замене г0 на г0 [1 — ехр (—цH/кТ0)]; тогда А2 ~
~ <А A — Л), А3 — Л%, где
146 Гл. III. Формальное развитие теории кинетических уравнений
Если ^2 и ^з сравнительно однородны в областях, где они отличны*
от нуля, то приведенные выше доводы дают возможность пред-
предположить, что
C.93>
(где Р ~ ro/L и а ~ (ро/кТо). В области высоких температур
(а = О (г)) эта зависимость сводится к следующей:
^з-^^ C.94)
в то время как в области низких температур
и корреляции более высокого порядка могут быть значительными.
Это простое эвристическое рассуждение показывает, что в неко-
некоторых предельных случаях корреляционные функции можно упо-
упорядочить по величине в соответствии со степенью рассматриваемой
корреляции. Пределы задаются посредством введенных ранеа
коэффициентов аир. Интересно отметить, что даже в таком очень
простом представлении мы встречаемся с трудностью, которая
появляется в сингулярном пределе а ~ г, р ~ е (высокая
температура, дальнодействие), когда упорядочение согласно сте-
степени корреляции становится сомнительным.
Мы пытались показать, что упорядочение по относительным
величинам корреляционных функций в соответствии со степенью
корреляции подсказывается некоторыми простыми физическими
соображениями. Соглашаясь с этим, мы формально приходим
к следующей последовательности корреляционных функций:
%3 = г [е^1} + е2<^2> +...], C.95>
Полагая а ->- еа, Р -> е^Р и используя C.95) и C.76) в урав-
уравнениях C.75), получим следующую систему уравнений (до чле-
членов О (г)):
(U2)], C.96а)
± + К2 - гав2 ) [F± A) Fi B) + etf ?>] =
= арА2 [F± A) Ft B) F± C) + eFs A) %? B, 3) +
+ BFt B) «i11 C, 1) + eF± C) «J» A, 2)]. C.9Go>
3.3. Групповые разложения 147
Сохраняя в них только члены низшего порядка, получим;
(l) = afAiFi(l)FiB), C.97а)
B) = a$A2Ft (l)Ft B) Ft C), C.976)
@- C.97в)
Легко показать, что система C.97) взаимно согласована. Для
этого рассмотрим два простых равенства:
D l)i(l) C.98)
1=1
И
s+1
П
C'99)
А^
Задача 3.5« Доказать справедливость формул C.98) и C.99).
Подставляя эти соотношения в C.97в), получим:
(з.юо)
или, что эквивалентно,
Член в квадратных скобках обращается в нуль согласно C.97а).
Отсюда следует, что уравнению C.97в) удовлетворяет та же
самая функция Fb которая удовлетворяет уравнению C.97а).
Таким образом, система C.97) совместна. При данном апостериор-
148 Гл. III. Формальное развитие теории кинетических уравнений
ном подходе мы убедились, что в предельном случае а ~ 8 и р —
—'б предположение о факторизации Fm в разложении C.78)
не приводит к противоречиям.
Отметим следующее различие между случаями (б) и (в). Для
случая (б), когда а ~ 8, Р ~ 1, сила взаимодействия между
частицами не входит в уравнение нулевого порядка C.80) и мы
получаем решение в виде свободно-молекулярного течения. Только
лишь когда учитываются члены О (е), начинают действовать опе-
операторы 6S и As и частицы «видят» одна другую. Это противополож-
противоположно случаю (в), когда интенсивность взаимодействия все еще зна-
значительно меньше тепловой энергии (а ~ е), но радиус взаимодей-
взаимодействия очень велик (Р ~ е)- Вследствие этого уравнения наиниз-
наинизшего порядка C.97а) характеризуют непосредственно влияние
соседних частиц. Однако из развитой нами теории как раз следует,
что уравнения первого порядка для F{ C.82а) в случае (б) (Р ~ 1;
умеренный радиус взаимодействия) имеют тот же вид, что и урав-
уравнения наииизшего порядка для F\ C.97а), в случае (в) (Р ~ е,
очень большой радиус взаимодействия).
В последнее время этому уравнению уделяется много внима-
внимания, а для нас оно представляет особую важность, поскольку
является кинетическим уравнением, которое, как было пока-
показано, формально следует из ББКГИ-системы. По причинам,
которые для нас уже вполне очевидны, уравнение C.97а) часто
называют бескорреляционным уравнением.
3.4. Определение кинетического уравнения.
Самосогласованные решения
Используя метод разложения около нулевых корреляций
между частицами, мы впервые сталкиваемся с кинетическим урав-
уравнением. Кинетическим является любое уравнение вида
^ C-102)
где М — известный функционал, отображающий F± на функции
от (р, х, t\ Fi). Исходной формой любого кинетического урав-
уравнения является BHi:
4A'2) <3-103)
(в размерном виде).
Чтобы получить из него кинетическое уравнение, необходимо
ввести некоторую аппроксимацию для F2, т. е. мы должны вычис-
вычислить
F2 - F2 (I, 2; F±) C.104)
3.4. Определение кинетического уравнения 149
я получить F2 как некоторый известный функционал от F^. Внося
C.104) в C.103), получим кинетическое уравнение:
ifL + —-4^-=—--/-• f d2G12F2(l, 2;F0. C.105)
Мы нашли, что в пределе, когда а —>- 8, р -> 1, 8, е, уравне-
уравнение, которое получается для /^ при разложении около нулевых
корреляций (ср. C.82а) и C.97а)), имеет такой вид:
F^)Fii2)=0 (ЗЛ06)
(переменные размерные).
Это уравнение известно как уравнение Власова и широко исполь-
используется в теории высокотемпературной плазмы. Оно также приме-
применяется в теории кристаллических структур (Власов A961)),
теории конденсации (Либов A963)) и в кинетическом описании
теории Ньютона — Джинса образования звезд (Линден-Белл
A962)). Объединяющее общее свойство всех таких приложений
связано с коллективными взаимодействиями и дальнодействую-
щей природой доминирующих сил.
Уравнение Власова C.106) можно привести к более традицион-
традиционной форме записи, если вспомнить, что числовая плотность п (х, t)
задается через F\ соотношением (ср. с C.1))
тг(х, *)=7" 1 Fldp' C.107)
Кроме того, если мы определим среднюю силу G (х) в точке х как
G Ы = j n2 (x2) G12 (Xl, x2) dx2, C.108)
то интеграл в уравнении C.106) можно выразить через G и F^
i2 (Xt, Х2) F± A)^- =
^-F1(l)-G(x1). C.109)
Теперь уравнение C.106) можно записать так:
OF p dF .dF
G (Xl) = j G12 (Xl, x2) n (x2) d**2, C.111)
vn(x2)= \jFlB)d3p2. C.112)
Интересно сравнить уравнение Власова с уравнением Лиувил-
ля для одной частицы в силовом поле, потенциал которого равен
150 Гл. III. Формальное развитие теории кинетических уравнений
Ф (х), т. е.
G(x)=—Аф(х).
В этом случае гамильтониан системы имеет вид
^ (ЗЛ13>
и соответствующее «одночастичное уравнение Лиувилля» будет
таким:
— 4- — . — — — — — О C НА)
dt ' dp * dx dx * dp * * '
Очевидно, что оно совпадает с уравнением C.110). Следовательно,
уравнение Власова описывает динамику одиночной частицы в поле
средней силы. Это поле является результатом осреднения двух-
двухчастичного взаимодействия по плотности оставшихся частиц.
Сила G в уравнении Власова C.110) является функционалом
от F, что видно из соотношений C.111) и C.112). Силовое поле G,
которое присутствует в одночастичном уравнении Лиувилля,
приложено извне и от F не зависит. В так называемой «теории
орбит первого порядка» мы считаем силовое поле в уравнении
Власова известным и постоянным, и в этом случае уравнение
Власова вырождается в одночастичное уравнение Лиувилля.
А решением уравнения Лиувилля является плотность точек
системы в Г-пространстве. В данном случае каждая система —
это одиночная частица, поэтому в таком простом случае и Г-
и [х-пространства являются шестимерными. К тому же динамика
ансамбля будет идентична динамике множества невзаимодействую-
невзаимодействующих частиц, эволюционирующих под влиянием внешнего потен-
потенциального поля. Решением являются «орбиты первого порядка»,
которые дает уравнение Власова в случае силы G, не завися-
зависящей от F.
Так как уравнение Власова описывает движение частицы под
влиянием силы, осредненной по всем оставшимся частицам,
то можно предполагать, что траектория частицы будет гладкой.
Это можно показать, найдя решение уравнения C.110). Из преды-
предыдущих рассмотрений в гл. II нам известно, что самое общее реше-
решение этого уравнения будет являться функцией решений характе-
характеристических уравнений х)
j+ dx dp /о л л с\
которые представляют собой уравнения орбит одной частицы,
C.116)
1) Обозначения
Р
таковы,
= т
что
а
b ^
dx
ьх
G =
ЬУ
dp
dt
az
bz'
3.4. Определение кинетического уравнения
151
Исключая р, получим:
Это уравнение дает интеграл
т I dx
C.117)
C.118)
Полученные формулы показывают, что для Ф, гладкой по х и t,
производная dx/dt будет гладкой. То же справедливо и для х (t)
(в определенных пределах). Помимо этого, мы заключаем, что
любая функция вида
= F{E) C.119)
является решением уравнения Власова, если потенциал Ф удов-
удовлетворяет уравнению
дх4
= ~ { F (x2, p2) G12 (Xl, x2)
C.120)
Это пример самосогласованных уравнений. Задавая Ф, мы можем
затем получить F согласно C.119). Эти функции определят Ф
Ф
Одночастичное
уравнение Лиубилля
Рис. 3.8. Стационарные самосогласованные решения уравнения Власова.
через уравнение C.120). Будет ли это тот самый потенциал Ф,
который мы задали вначале? Если это так, то мы нашли самосогла-
самосогласованные поле и распределение (рис. 3.8).
Более часто уравнение Власова встречается в форме C.110)—
C.112). В эти уравнения входят три переменные — F, G и п.
Самосогласованность здесь проявляется в следующем. Функция F
определяет Gun через уравнения C.111) и C.112). Поле G опре-
определяет затем F из C.110). Полученное значение F должно сов-
совпасть с первоначальным (рис. 3.9).
Другие интерпретации уравнения Власова можно получить,
сравнивая его с BHt. Интегралы в уравнении Власова и в урав-
152 Гл. III. Формальное развитие теории кинетических уравнений
нении
соответственно равны
J F2 A, 2) G12 (Xl, x2) <Р*2 d*p2.
C.121)
C.122)
Оба интеграла определяют средние силы в точке х4. В первом
интеграле интенсивность источника для силы взаимодействия
двух частиц около состояния z2 равна F± B) d2 и не коррелиро-
вана с частицами около Z\. В /bhi интенсивность источника около
= \F
G -
Ураднение Власода
F = F(G)
Рис. 3.9. Самосогласованная схема для уравнения Власова.
состояния z2 характеризуется величиной F2 A, 2) d2 и зависит
не только от частиц в состоянии z2, но также и от частиц в z^.
В описании Власова типовая частица в каждый момент времени
«ощущает» силовое поле, создаваемое остальными, мгновенно
зафиксированными частицами системы, которые в этот же самый
момент не коррелируют с типовой частицей. В уравнении BHj
частицы системы, напротив, коррелируют с типовой частицей.
Напомним, что для вывода уравнения Власова из BHi мы просто
полагаем F2 = F^F^, или, что эквивалентно, сё2 = 0.
Если имеется внешняя сила К (х), которая действует на рас-
рассмотренную выше систему частиц, уравнение C.110) заменяется
следующим:
dF p dF_ , 6F
dt ' т ' дх ~*~ дщ
C.123)
Сила К не является самосогласованной. Это известная заданная
сила. В таком случае C.119) примет следующий вид:
где
= — \ F (x2, p2) G12 (x1? x2) d?x2
C.124)
C.125)
5--К W.
C.126)
3.5. Формальное выражение для ^2 в однородном пределе 153
Задача 3.6. Пусть сила взаимодействия] G12 = к (г2 — *i)r~N,
где I ri — r2 I = г и к — постоянная. Внешний потенциал —
дняейный гравитационный, W = mgz. Он одномерный и возрастает
с высотой. «Барометрическая формула» получается, если задать F
следующим образом:
[J) C.127)
Оценить погрешность между этим значением Fo и самосогласован-
самосогласованным решением F. Отметим, что постоянная нормировки А такова,
что интеграл от Fo по всем импульсам и по цилиндру бесконечной
высоты с единичной площадью поперечного сечения равен единице.
Задача 3.7. Вывести ББКГИ-уравнения, учитывая потенциал
Y (х), так что гамильтониан системы имеет следующий вид:
1=1 гфз г=1
Задача 3.8. Показать, что уравнения Власова динамически
обратимы. То есть если F (p, x, t) — решение, то F (—р, х, —t}
также будет являться решением.
3.5. Формальное выражение для %ъ
в однородном пределе
В любом из предшествующих разложений около нулевых
корреляций мы сталкивались с проблемой, как найти ^2^ если
известна F^. В данном разделе мы исследуем метод, позволяющий
это сделать. В частности, будет рассмотрен предел Розенблюта —
Ростокера. Большая часть анализа проводится согласно работе
Дюпри A961). Получаемые результаты служат также индуктив-
индуктивным обоснованием гипотез Боголюбова.
Уравнения, которые в указанном предельном случае (слу-
(случай (в), уравнения C.96); безразмерный вид; верхние индексы
опущены) связывают ^2 с Fu имеют вид
1 = apA1[F1(l)F1B) + e«2(l,2)], C.128)
], C.129)
Р[г, i, ft]
ГДе Р [ц /, к] — перестановка из чисел 1,2,3, такая, что ^2 Сь &)
11 ^2 (к, j) подсчитываются только один раз. Предположим, что
154 Г л, III* Формальное развитие теории кинетических уравнений
мы решили уравнение низшего порядка, т. е. уравнение Власова
для F±. Если мы теперь подставим это решение в последние два
уравнения, то в результате получим:
, 2)= ~сф^-. j d2G12«2(l, 2), C.130)
3)«2(l,2)]. C.131)
Переписывая уравнение C.130) в виде
-A-.jdAGfft«2(i,*)=0 C.132)
и подставляя в C.131), получим
B, 3) + Л C) <ё2 A, 2)] -)-
Задача 3.9. Третье уравнение (т. е. БИ3) в системе C.128)
опять является уравнением для Ft и ^2« Установить, будет ли это
уравнение излишним.
Обычно в данном месте исследования вводится ограничение,
а именно предполагается пространственная однородность функции
Fu так что dFJdXi = 0. Функция F^ зависит только от импуль-
импульсов. При таком ограничении два интеграла в уравнении C.133)
обращаются в нуль:
(р3) ^2 A, 2) = j d3G23^i (р3) ^2 (I, 2) = 0. C.134)
Чтобы получить эти равенства, достаточно рассмотреть в них
интегрирование только по пространству конфигураций. Сила
<J^ имеет вид
°" - * <Г)- C.135)
Г = Хг — Xj.
Рассмотрим первый интеграл. Конфигурационная часть этого
интеграла в сферических координатах с началом в частице 1 запи-
запишется так:
136)
, 2) J j j n|)(r)dcosedcpr2dr==0. C.
Интеграл равен нулю, поскольку подинтегральное выражен^
представляет собой изотропное векторное поле. Аналогичный
3.5. Формальное выражение для ^2 в однородном пределе 155
результат получается для второго интеграла, если начало коорди-
координат выбрать в частице 2. Подставляя оба результата в уравнение
C.133), получим:
h A> 2) + оф -gz- Fi (Pi) • \ d?>G^ce2 B,3) +
j ], C.137)
или, что то же,
?i.^r + aP^-F1(p1) J d3Gl3]<e2( , 2) +
J
i2-^ + G-2i~] Л (Pi) Л (Pa). C.138)
Обозначения таковы, что
ё2C,2) = Л>2. C.139)
Опущенные аргументы таковы, что при их подстановке соответст-
соответствующие операторы становятся некоммутирующими с ^2. Среднее
равенство в C.139) служит для определения оператора Ait Полагая
далее [(р2/яг).(д/<Эх2) + «Р {dld^2)-Fi (p2) j d3G23] «2 ( , 1)= i2«2,
введем оператор
A = Ai + A2. C.140)
Гогда уравнение C.138) примет вид
= S, C.141)
i Де через S обозначен неоднородный член в правой части уравне-
уравнения C.138). Такая форма уравнения была получена Дюпри.
Задача 3.10. Установить, является ли обратимым уравне-
уравнение C.141).
Задача 3.11. Показать, что А1А2 = А2А1.
Уравнение C.141) легко разрешить относительно (ё2, если
мьт заметим, что Л не зависит явно от времени, а ехр At является
Интегрирующим множителем. Интегрируя от 0 до t, получим
156 Гл. III. Формальное развитие теории кинетических уравнений
решение
t
%2(t) = [ e^-t)S(i)dx + e-lt(e2@), C.142х
о
t
C.143)
Последнее равенство справедливо, поскольку операторы А^ и Л2
коммутируют. Уравнение C.142) представляет собой формальное
обращение уравнения C.138) через
операторы Ах и А2. Это решение при-
принимает более простой вид, когда в
начальном состоянии газа можно пре-
пренебречь корреляцией между части-
частицами, так что F2 (O)=jFijFi и %2 @)=0.
Кроме того, мы можем ввести пред-
предположение адиабатичности, которое
Рис. 3.10. Предположение состоит в том, что Fi (t) пренебре-
адиабатичности. жимо мало меняется за время, необ-
необходимое для изменения *ё2 (рис. ЗЛО).
Это аналогично боголюбовскому описанию кинетической стадии,
когда все распределения высшего порядка сводятся к функцио-
функционалам от одночастичной функции распределения /\. При таких
ограничениях C.142) примет следующий вид:
t
= j
C.144)
Поскольку член типа источника S — известный функционал
от Fu уравнения C.142), C.143) или C.144) определяют %2 как
функционал от F4 и, следовательно, F2 также будет являться
функционалом от F±. Таким образом, мы пришли к уравнению
в форме C.20) для s = 2, что некоторым образом подтверждает
гипотезу Боголюбова. Тот материал, который мы здесь рассмот-
рассмотрели, конечно, не исчерпывает анализа Дюпри. Так, в случае
кулоновского потенциала из анализа Дюпри получается явное
выражение для св2, что приводит к уравнению Балеску — Ленар-
да, которое будет рассмотрено в гл. IV.
3.6. Радиальная функция распределения и уравнения состояния
Для достаточно разреженного газа обычно полагают, что
аппроксимация F2 = F^^ справедлива большую часть времени-
Это означает, что большую часть времени всякая наугад выбрав
3.6. Радиальная функция распределения 157
гая частица не будет находиться в области влияния любой другой
частицы. С возрастанием плотности среды это интуитивное пред-
предположение становится все менее справедливым. В предельном
сЛучае жидкости оно абсолютно не верно. Дело обстоит так, что
^яассическая теория жидкости в своем развитии за прошедшие
50 лет была сосредоточена главным образом на вычислении объек-
объектов, тесно связанных с парной функцией распределения jF2-
Таким объектом является функция g:
= g(xi, x2). C.145)
Отсюда следует, что
g(x1,x2)d*x1d*x2 C.146)
определяет вероятное число таких пар частиц, что одна из частиц
находится в конфигурационном объеме dx^ около хь а другая —
в объеме dx2 около х2. Для жидкости в состоянии равновесия,
когда g изотропна, мы полагаем
?(х4,х2) = ?(г), C.147)
г = |х2 —х±|.
В пределе, когда положения любых двух молекул жидкости
некоррелированы, мы получим
g<Px± <Px2 = N{NvZi] <Рхх d*x2. C.148)
Если мы теперь определим
то будем иметь, что в предельном случае отсутствия корреляций
между двумя частицами
g~l. C.150)
Функция g называется радиальным распределением.
Представим теперь себе следующий воображаемый экспери-
эксперимент. Выберем в жидкости наугад две молекулы. Окрасим одну
молекулу в красный цвет, а другую — в синий, оставив без
изменения все другие свойства молекул. Теперь мы хотим выяс-
выяснить вид функции g (г), когда, скажем, красная молекула при-
приближается к синей из положения, находящегося далеко вне обла-
области влияния красной молекулы (г ^> г0). Можем ли мы сразу
сказать, что g (г) = 1? Да, при условии, что влияние синей моле-
молекулы на красную достаточно мало. Это будет тот случай, когда
(фо//сГо) <С 1 (если сила взаимодействия между частицами не отно-
относится к классу далънодействующих). Исключая такие сингуляр-
158 Гл. III. Формальное развитие теории кинетических уравнений
ные случаи, мы можем предположить, что g ~ 1 при г ^> г^
С другой стороны, для г<<^ г0 начинают действовать отталкиваю!
Рис. 3 11. Вид экспериментальной радиальной функции распределения для?
инертных жидкостей.
щие ядерные силы и g ~ 0. Экспериментальные кривые, получен-
полученные для рассеяния рентгеновских лучей в жидкости (рис. 3.11),
подкрепляют эти ин-
интуитивные предположения.
Почему радиальная
функция распределения
имеет пик непосредственно-
в окрестности границы
ядра, можно легко понять,
если вспомнить характер-
характерный вид потенциала взаи-
взаимодействия ф, изображен-
изображенного на рис. 3.12. В боль-
большинстве случаев отталки-
отталкивание является результа-
результатом принципа исключения:
Паули, а притягивающий
«хвост» обусловлен вандер-
-Притлгидающии ваальсовым диполь-ди-
„хдост" польным взаимодействием.
Р и с. 3.12. Типичный потенциал взаимо- Найдем теперь, как вы-
действия. ражаются напряжения че-
через радиальную функцию*
распределения. В начале этой главы мы обсудили связь между
одночастичной функцией распределения и гидродинамическими
3.6. Радиальная функция распределения 159*
еременными. Мы отметили, что при определении напряже-
напряжений Рц был учтен только кинетический вклад. Однако в бо-
1ее общих случаях потенциал взаимодействия частиц также
злосит вклад в напряжения. Определение этих напряжений более
общего вида приводит нас в конце концов к уравнению состоя-
я, записанному через радиальную функцию распределения.
Перепишем уравнение БИЬ заменяя импульс р на скорость |:
Напомним, что гидродинамическая скорость и задается соотно-
соотношением
тш =
п что
При переходе к системе координат, движущейся с локальной
скоростью и, уравнение C.151) примет вид (с = § — и):
= 0. C.152>
Необходимо отметить, что с не коммутирует с д/дх либо с dldt..
Запишем следующие соотношения:
Действуя на уравнение C.152) оператором \ тсРс, получил*
(р == т \ jFd3^ — массовая плотность):
-l + ^-pu^O. C.153).
(Интегральный член обратился в нуль, поскольку он преобразо-
преобразовывается в интеграл по поверхности.) Уравнение C.153) представ-
160 Гл. III. Формальное развитие теории кинетических уравнений
ляет собой хорошо известное уравнение неразрывности. Оно
жает тот факт, что масса данного объемного элемента
меняться только при наличии потока массы через ограничивав
щую этот элемент поверхность. Такая форма уравнений характер,
на для всех законов сохранения1). Эти законы, будучи записаны
в указанной выше форме, вскрывают механизмы, посредством
которых происходит изменение во времени рассматриваемых
величин. Все уравнения гидродинамики могут быть записаны
в такой форме, для чего надо образовать соответствующие момент-
ные уравнения (по скоростям) от уравнения C.152).
В заключительном разделе данной главы мы рассмотрим момент -
ное уравнение, которое описывает изменение во времени импульса
жидкого элемента. Это просто второй закон Ньютона, записанный
в несколько ином виде.
Применяя к уравнению C.152) оператор \ д?стси получим
C.154)
где тензор Pfj определяется соотношением C.5) (индекс К озна-
означает «кинетический»). Интегральный член имеет вид
^=- \ d?cAt. C.155)
Интеграл \ д?с (д/dci) CiA\ обращается в нуль, так как он преоб-
преобразуется в поверхностный. Подставляя этот результат в уравне-
уравнение C.154), получим
J Px!G\t&2 = 0. C.156)
Произведя интегрирование по скоростям и вспоминая соотноше-
соотношение C.145) и следующие за ним, придем к уравнению
N(N —
C.157)
Чтобы привести это уравнение к нормальной форме, положим
-ijPt - -^f± \ dbftgfr, x2), C.158)
х) Эти вопросы значительно подробнее будут обсуждаться в разд.
3.6. Радиальная функция распределения 161
где индекс Ф означает «потенциальный». В этих новых перемен-
переменных уравнение C.157) примет следующий вид:
=7Р'' = 0' C.159)
Из этого уравнения видно, что скорость изменения импульса
жидкого элемента (измеренная в системе координат, движущейся
с локальной скоростью жидкости и) обусловлена напряжениями,
передаваемыми через ограничивающую этот элемент поверхность.
На такой элемент жидкого объема т (достаточно малый, так что
в пределах т локальная скорость считается постоянной), огра-
ограниченный поверхностью 2, действует сила
N^i) j j х&д (хи x2). C.160)
Первый интеграл есть сила, обусловленная скоростью переноса
импульса через ограничивающую поверхность 2, а второй инте-
интеграл — это сила, обусловленная взаимодействием между моле-
молекулами объема т и внешними к нему. Первый интеграл дает кине-
кинетический вклад и зависит только от одночастичной функции рас-
распределения, в то время как второй интеграл определяется потен-
потенциальной энергией взаимодействия между частицами и является
функционалом от радиальной функции распределения g и двух-
двухчастичной силы G12. Этот потенциальный член ответствен за любое
отклонение от идеального уравнения состояния.
В первом разделе настоящей главы мы ввели скалярное давле-
давление
р = ±-ТтРк = пкТ. C.161)
Теперь мы нашли, что в более общем случае
Рф C.162)
^ТтР.
О
Чтобы записать потенциальную часть тензора Р в обычном виде^
положим, во-первых,
3, = ^, C.163)
где гг является ?-й компонентой единичного вектора
Г== /2~Г11 =:±. C.164)
I Г2 — Г1 1 Г V
162 Гл. Ill, Формальное развитие теории кинетических уравнений
Подставляя это соотношение в C.158), получим
д оф N(N — 1
dxj """ гз — Щ 1 ** ^ l ~~дг~ б ^ЛЬ Л2'Ф C.165)
Чтобы завершить преобразование переменных, введем (см. Грин
A952)) переменную R (рис. 3.13) (xt заме-
заменены на rt):
r = T2-ru r1 = R — у г; C.166а)
2К = г2 + Г!, r2 = R + yr' C.1666)
!* d3r2 = d3r; C.166в)
Рис. 3.13. Векторы г
и R- C.166г)
Вектор R определяет положение середины отрезка между двумя
молекулами, а г — радиус-вектор, направленный от молекулы 1
к молекуле 2. Так как обычно g изменяется медленно вместе с R
в пределах молекулярных размеров, то разложение (штрихи
опущены)
g(t, R) = *(r, rO + dl-ri) — g(t, R)|R=ri+ .-. =
= g(*, r1) + |-^-g(r,r1)+...C.167)
должно быстро сходиться. Подставляя последнее выражение
в C.165), получим
д бф_ N(N-1) ^з^д^'^._д_гГ^ *.\ C.168)
(первый член обратился в нуль, как интеграл от изотропного
векторного поля). Вынося dldvi за знак интеграла, будем иметь
1-^-, C.169)
так что
*^. C.170)
В однородном изотропном пределе g не зависит от положения
молекулы 1; она зависит только от расстояния между молекулами,
так что g = g (г). Для N ^> 1 (что для жидкости всегда выполняет-
выполняется) комбинируя последнее равенство с C.162) и вводя условие
3.6, Радиальная функция распределения 163
однородности и изотропности, придем к соотношению
NkT ~"х 6VkT „
о
Это есть хорошо известное уравнение состояния жидкости, запи-
записанное через радиальную функцию распределения g.
Задача 3.12. Выяснить, как влияют на давление, передавае-
передаваемое через поверхность в жидкости, межмолекулярные силы оттал-
отталкивания и притяжения.
Задача 3.13. Чему будут равны V-P° n РФ в однородном
[g (rt, r2) = g (r)] изотропном [g = g (r)] пределе? Используйте
точное выражение C.158). Обсудите полученный результат, исходя
из принципов симметрии. Следует ли из равновесия однород-
однородность g?
Частичный ответ. Дивергенция обращается в нуль, и, следо-
следовательно, сила взаимодействия в любом малом элементе объема
также равна нулю. Чтобы ответить на последний вопрос, надо
просто построить пример равновесия с неоднородной плотностью.
В этой главе мы показали, что одночастичное распределение
единственным образом определяет макроскопические переменные.
Эти макроскопические переменные являются компонентами тер-
термодинамического состояния. Из одной функции получаются все
данные, которые необходимо знать в гидродинамике. Если плот-
плотность становится слишком большой, так что межмолекулярные
силы вносят вклад в напряжение, как это имеет место в жидкости,
то в гидродинамические переменные начинает давать вклад
двухчастичная функция распределения.
Двухчастичная функция распределения, неся в себе больше
информации, чем одночастичная функция распределения, обла-
обладает и большим числом свойств. Из функции F2 получается Fu
для F2 существует счетное множество моментов по скоростям
(импульсам). Мы встретились только с первым из них, \ F2 dp* dp2,
который называется радиальным распределением и имеет крайне
важное значение в теории жидкостей. Когда мы имеем дело
с жидкостью, то для любого полного гидродинамического описа-
описания мы должны вводить функции распределения более высокого
порядка именно потому, что межмолекулярные взаимодействия
становятся существенными. Когда это имеет место, то одночастич-
ной функции распределения недостаточно, чтобы описать гидро-
гидродинамическое состояние. То, что жидкость может находиться
в равновесии, не умаляет роли межмолекулярных взаимодей-
11*
164 Гл. III. Формальное развитие теории кинетических уравнений
ствий, и чтобы дать полное описание, все еще необходимо знать
радиальную функцию распределения.
Это можно представить себе как более подробное описание
гидродинамического состояния в анализе Боголюбова. Напом-
Напомним, что в анализе Боголюбова «история» газа подразделяется
на три этапа. Чтобы описать газ в начальной стадии, необходимо
знать не меньше чем iV-частичную функцию распределения.
На кинетической стадии, которая наступает после нескольких
столкновений, состояние газа определяется одночастичным рас-
распределением. На конечной, гидродинамической, стадии существен-
существенными являются только первые пять моментов (по скоростям)
функции Ft, т. е. р, и, Т. Для более плотного газа вклад межмоле-
межмолекулярных сил в функцию распределения, а следовательно, и в гид-
гидродинамические переменные становится существенным. В этом
случае идеальная боголюбовская последовательность описатель-
описательных интервалов увеличивается, так что конечные стадии иссле-
исследуются более подробно, и для полного описания необходимо
знать некоторые свойства функции F2.
Теория двухчастичного распределения, так же как и распре-
распределений более высокого порядка, может быть рассмотрена в рам-
рамках корреляционных функций. Эти функции определяются как
разность между Fs и некоррелированным факторизованным рас-
s
пределением П^1@- Корреляционная функция характеризует
свойства функции распределения. Например, зная двухчастичную
корреляционную функцию, мы не можем определить двухчастич-
двухчастичную функцию распределения. Наиболее просто в этом можно
убедиться, полагая %2 — 0; в этом случае мы знаем только, что
F2 = FiFf. Разумеется, две функции Fi и сё2 определяют F2,
так что разложения, из которых сначала находится Ft, а затем
^ дают нам много информации. Другим свойством F2 является
радиальная функция распределения g (гь г2), которая связана
только с совместной вероятностью в пространстве конфигураций.
Когда и потенциальное взаимодействие вносит вклад в напряже-
напряжения (дополнительно к кинетической компоненте), единственной
частью F2, через которую выражаются напряжения, является
радиальное распределение.
Выяснив, какую роль в макроскопической физике играют
функции распределения низшего порядка, мы приступим теперь
к получению других уравнений для одночастичной функции рас-
распределения. Пока мы познакомились со следующими кинетиче-
кинетическими уравнениями: с уравнением свободно-молекулярного течения
(совпадающим по форме с одночастичным уравнением Лиувилля);
с уравнением Власова и очень кратко (как упражнение в анализе
Боголюбова) с уравнением Больцмана. Последнее уравнение,
Список литературы 165
а также уравнения Крупа — Бхатнагара — Гросса и Фоккера —
Планка детально исследуются в гл. IV, где рассматриваются
и другие, тесно связанные с ними кинетические уравнения.
СПИСОК ЛИТЕРАТУРЫ
А. Радиус Дебая
Дебай, Гукель (Debye P., Htickle E.)
A923) Physik. Z., 24, 185, 305.
Либов (Liboff R. L.)
A959) Phys. Fluids, 2, 40.
Лэндшофф (Landshoff R.)
A949) Phys. Rev., 76, 904.
Маршак (Marshak R. E.)
A941) Ann. N. Y. Acad. Sri., 41, Art. 1, 49.
Спитцер, Коэн, Роутли (Spitzer L., Jr., Cohen R.S., Routly P.
A950) Phys. Rev., 80, 230.
Б. Анализ Боголюбова
Боголюбов Н. Н.
A946) Проблемы динамической теории в статистической физике, М.— Л.,
Гостехиздат.
Коэн (Cohen E. G. D.)
A962) Fundamental Problems in Statistical Mechanics, ed. by E. G. D. Co-
Cohen, New York, Wiley
Уленбек (Uhlenbeck G. E.)
A959) Probability and Related Topics in Physical Sciences, compiled by
M. Kac, New York, Wiley. Русский перевод: Кац М., Вероятность
и смежные вопросы в физике, М., «Мир», 1965.
В. Кинетические уравнения и групповые разложения
Балеску (Balescu R.)
A960) Phys. Fluids, 3, 52.
Гернсей (Guernsey R. L.)
A960) Ph. D. dissertation, University of Michigan.
Грэд (Grad H.)
A958) Handbuch der Physik, vol. XII, Berlin, Springerverlag.
166 Гл. III. Формальное развитие теории кинетических уравнений
Делькруа (Delcroix J. L.)
A965) Plasma Physics, Wiley, New York.
Дюпри (Dupree Т. Н.)
A961) Phys. Fluids, 4, 696.
Ленард (Lenard A.)
A960) Ann. Phys. (N.Y.), 3, 390.
Либов (Liboff R. L.)
A965—66) Phys. Fluids, 8, 1236 A965); 9, 419 A966).
Либов, Пирона (Liboff R. L., Perona G.)
A967) /. Math. Phys., 8, 2001.
Майер Дж., Майер M. (Mayer J. E., Mayer M.G.)
A940) Statistical Mechanics, New York, Wiley. Русский перевод: Майер Дж.,
Гепперт-Майер М., Статистическая механика, М., ИЛ, 1952.
Монтгомери, Тидмен (Montgomery D., Tidman D.)
A964) Plasma Kinetic Theory, New York, McGraw-Hill.
Ростокер, Розенблют (Rostoker N., Rosenbluth M. N.)
A960) Phys. Fluids, 3, 1.
Стелл (Stell G.)
A964) The Equilibrium Theory of Classical Fluids, ed. by H. Frisch and
J. Lebowitz, New York, Benjamin.
Сэндри (Sandri G.)
A963) Ann. Phys. (N. Y.), 24, 332.
Урселл (Ursell H.)
A927) Proc. Camb. Phil. Soc, 23, 685.
Фримап (Frieman E. A.)
A963) /. Math. Phys., 4, 410.
Чен (Tchen С. М.) ,
A959) Phys. Rev., 114, 394.
Г. Теория жидкостей и радиальная функция распределения
Де Боер (de Boer J.)
A949) Repts. Prog. Phys., 12, 369.
Борн, Грин (Born M., Green H. S.)
A949) A General Kinetic Theory of Liquids, Cambridge.
Грин (Green H. S.)
A952) The Molecular Theory of Fluids, Amsterdam, North Holland.
Зумипо (Zumino B.)
A959) Phys. Fluids, 2, 20.
Орнстейн, Зернике (Ornstein L. S., Zernike F.)
A941) Proc. Amst. Acad. Sci., 17, 793.
Список обозначений к гл. III 167
райе, Грэй (Rice S. A., Gray D!)
A965) The Statistical Mechanics of Simple Liquids, New York, Interscience,
уленбек, Бэч (Uhlenbeck G. E., Beth E.)
A936-37) Physica, 3, 729 A936); 4, 915 A937).
фишер И. З.
A961) Статистическая теория жидкостей, М., Физматгиз.
Френкель Я. И.
A945) Кинетическая теория жидкостей, М.— Л., изд. АН СССР.
Фриш, Либовиц, (Frisch Н., Lebowitz J. (eds))
A964) The Equilibrium Theory of Classical Liquids, New York, Benjamin.
Хилл (Hill T. S.)
A956) Statistical Mechanics, New York, McGraw-Hill. Русский перевод:
Хилл Т. С, Статистическая механика, М., ИЛ, 1960,
Д. Приложения уравнения Власова к изучению явлений
в неплазменных средах
Власов А. А.
A950) Теория многих частиц, М.— Л., ГИТТЛ,
Либов (Liboff R. L.)
A963) Phys. Rev., 131, 2318; Physics Letters, 3, 322.
Линден-Белл (Lynden-Bell D.)
A962) Month. Not. Roy. Soc, 124, 279.
Список обозначений к гл. III
A2i A3 — относительные площади, связанные с корреляционными
функциями ^2 и ^з соответственно,
А{1) —коэффициент в разложении Боголюбова,
А — оператор в БИ2,
As —интегральный оператор в ББКГИ-уравнениях,
Jk — корреляционная площадь,
БИ8 —5-е уравнение ББКГИ-системы,
С — тепловая скорость,
%s —s-частичная корреляционная функция,
168 Гл. III. Формальное развитие теории кинетических уравнений
с — относительная микроскопическая скорость,
D{h) —оператор в разложении Боголюбова,
Е — энергия,
Fs —5-частичная функция распределения, нормированная
на Vs,
fs —5-частичная функция распределения, нормированная
на единицу,
JF4 — одночастичная функция распределения, нормирован-
нормированная на Лг,
Gjm — сила взаимодействия между частицами,
g — радиальная функция распределения,
f,h,l —'2,3,4-частичные корреляционные функции,
Ks —s-частичный оператор кинетической энергии,
К —внешняя сила,
к — постоянная Больцмана,
L — длина ребра контейнера,
I — средний свободный пробег,
т —масса,
N —полное число частиц,
п —числовая плотность частиц (плотность числа частиц) 7
п0 — равновесная концентрация,
Ps —s-перестановочный оператор,
Р —тензор давлений,
Рф -— потенциальная часть тензора давлений,
РК — кинетическая часть тензора давлений,
Ро — тепловой импульс,
Q —тепловой поток,
R — вектор перемещения,
г — вектор, соединяющий две частицы,
гр —плазменная длина (дебаевский радиус),
г0 — радиус взаимодействия,
Т —температура,
То — характерное макроскопическое время,
?0 — среднее время между столкновениями,
и — гидродинамическая скорость,
V — объем сосуда,
v —удельный объем,
а — коэффициент в безразмерном уравнении Лиувилляг
Список обозначений к гл. III 169>
Р — коэффициент в безразмерном уравнении Лиувилля,
б0 —диэлектрическая проницаемость вакуума,
А — динамический проектирующий оператор (оператор
сдвига),
Ф — потенциал,
ф —потенциал взаимодействия частиц,
ф0 —напряженность потенциала,
о)р — плазменная частота,
Y — потенциал,
65 —s-частичный оператор потенциальной энергииг
т0 —время столкновения.
ГЛАВА IV
УРАВНЕНИЯ БОЛЬЦМАНА,
КРУКА - БХАТНАГАРА — ГРОССА, ФОККЕРА — ПЛАНКА
И РОДСТВЕННЫЕ ИМ.
ВЫВОД УРАВНЕНИЙ И ИХ СВОЙСТВА
4.1. Дальнейшее толкование необратимости
До настоящего момента мы познакомились с двумя кинетиче-
кинетическими уравнениями: уравнением свободно-молекулярного течения,
или одночастичным уравнением Лиувилля C.79а), и уравнением
Власова C.106) х). Оба они естественным образом следуют из
iV-частичного уравнения Лиувилля или, что эквивалентно, из 3JV
совместных дифференциальных уравнений второго порядка (вто-
(второй закон Ньютона для N частиц). Поэтому не является неожи-
неожиданностью тот факт, что решения этих двух кинетических урав-
уравнений удовлетворяют принципу динамической обратимости. Это
означает, что одновременно с решением / (х, |, t) существует
и решение / (х, —§, —t). Уравнения в такой форме сами по себе
не могут выражать необратимый макроскопический закон. Макро-
Макроскопический закон A VS (t)] для макроскопической переменной
д (t) является обратимым, если A V§ (—t)] также представляет
собой закон. В этом случае никакой эксперимент для & не может
указать, возрастает или убывает время t. Если A V§ (—t)] не имеет
смысла, то закон А является необратимым. Функция W характе-
характеризует некоторое свойство данной макроскопической системы.
Пусть W —числовая плотность частиц газа п (х, t), занимающего
в начальный момент одну половину замкнутого прямоугольного
контейнера, разделенного перегородкой. В момент t = 0 пере-
перегородка убирается и п (х, t) асимптотически приближается к зна-
значению, постоянному для всего сосуда. Проследим за изменением
плотности в точке х, где первоначально плотность была нулевой.
Вид этой функции изображен на рис. 4.1, а. Динамически обра-
обращенное решение показано на рис. 4.1, б.
Разумеется, это динамически обращенное решение в природе
не встречается. Предположим, что в некоторый момент времени
мы можем внезапно обратить импульсы всех частиц. Тогда изме-
изменение во времени фактической плотности будет происходить так,
как показано на рис. 4.1, в. Равновесное состояние не восприим-
восприимчиво к описанному выше изменению микроскопического состояния.
Казалось бы, что законы динамики, составляющие основу
науки, не допускают такого свойства равновесного состояния»
И очень кратко с уравнением Больцмана,
4.1. Дальнейшее толкование необратимости
171
7l(f)
Рис. 4.1. Эволюция числовой плотности частиц в случае обратимой и необра-
необратимой диффузии.
а — начальное движение; б — обращенное движение (для обратимой
диффузии); в — обращенное движение (для необратимой диффузии).
Другое описание этого кажущегося парадокса состоит в следую-
следующем. Предположим, что начальное состояние газа таково, как
описано выше. Оно изображается точкой в Г-пространстве. Эта
точка вычерчивает в Г-пространстве динамическую траекторию.
Из опыта нам известно, что такая точка движется по направлению
к равновесному состоянию (с одинаковой плотностью по всему
конфигурационному пространству и соответствующим максвел-
ловским распределением в пространстве импульсов). Но динамиче-
С1<ая кривая такова, что если обратить все начальные импульсы,
172 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара — Гросса и др
то рассматриваемая точка будет двигаться к состоянию с более.
«испорченным» распределением плотности, чем заданное началу
ное распределение. (Это состояние должно предшествовать да1ь
ному начальному состоянию.)
Пусть известно, что начальное состояние
ftf (х1э . . ., xN; р4, . . ., pN; 0)
естественным образом эволюционирует к равновесному состояние
U (Рь . . ., Vn)- Состояние же ftf (хи . . ., х^; —рь . . ., —р^;0)
будет удаляться от равновесия. .Законы динамики сами по себе
не отдают предпочтения одному из этих состояний. Тем не менее
эксперимент говорит нам, что в природе происходит иначе.
Это противоречие явилось источником парадокса обратимости,
выдвинутого первоначально в 1876 году Лошмидтом в связи
с работой Больцмана. Больцману удалось получить кинетиче-
кинетическое описание, которое согласовывалось с наблюдаемыми необра-
необратимыми явлениями в природе, но противоречило основным зако-
законам механики. Парадокс равным образом вытекает из обоих
фактов: утверждающей необратимость макроскопических состоя-
состояний $6-теоремы Болъцмана (которая вскоре будет обсуждаться)
и наблюдаемых необратимых явлений в природе. Парадокс
заключается в следующем: каким образом обратимые законы
микроскопической механики (законы Ньютона, уравнение Лиу-
вилля) могут приводить к наблюдаемым (релаксация к равнове-
равновесию) либо формулируемым (с^-теорема Больцмана) необратимым
макроскопическим законам?
Другое возражение по поводу результатов, полученных Вольц-
маном, которое к тому же придает парадоксальную окраску
наблюдаемым необратимым свойствам естественных макроско-
макроскопических явлений, заключено в парадоксе возвратимости Цер-
мело. Этот парадокс основан на возвратной теореме (Wie-
derkehrsatz) Пуанкаре и называется парадоксом возвратимости.
Теорема Пуанкаре утверждает, что изолированная динамическая
система с ограниченной энергией и конечными размерами вернется
за достаточно большой промежуток времени (называемый време-
временем возврата Пуанкаре) к состоянию, сколь угодно близкому
к первоначальному. Однако этот промежуток времени неестествен-
неестественно велик. Для газа, заключенного в сосуд умеренных размеров,
время возврата превышает оцениваемый возраст вселенной-
В этом смысле данная теорема не противоречит наблюдаемым
явлениям — она не имеет к ним отношения. Но очевидно, можно
было бы думать, что макроскопический закон будет совмести^
с теоремой Пуанкаре; однако второй закон термодинамики, урав'
нение диффузии, ^-теорема Больцмана и другие закономерности
с ней не согласуются. (Рассказывают, что столкнувшись с воз--
4.2. Концепция столкновений 173
>Кением Цермело, Больцман ответил: «Вам придется долго
)
!ьдать)
Итак, в чем же состоит учение Больцмана, которое, несомненно,
возбудило негодование пуристов того времени и явилось единст-
единственным наиболее важным связующим звеном между полностью
обратимым микромиром и несовершенным необратимым макро-
макромиром? Оно объединяет уравнение Больцмана и его непосредст-
13еР1Иое следствие — больцмановскую с2%?-теорему, которая, образ-
образно выражаясь, возвышается как монумент новаторскому гению
Людвига Больцмана (род. в 1844, ум. в 1906).
Оставшаяся часть данной главы посвящена классическим
методам вывода и изучению свойств уравнения Больцмана, которое
было первым кинетическим уравнением, появившимся в литерату-
литературе, и до сих пор является наиболее важным из всех существующих
кинетических уравнений.
До настоящего момента мы познакомились с тремя кинетиче-
кинетическими уравнениями. В этой главе мы рассмотрим еще три других:
уравнения Крука — Бхатнагара — Гросса, Фоккера — Планка
и Ландау. Все они получены сравнительно недавно, большей
частью в последние десятилетия. Каждое уравнение определяет
по существу один и тот же объект — одночастичную функцию
распределения. Поскольку уравнения различны, очевидно, что
они применимы в разных областях. Тем не менер мы увидим, что
уравнение Больцмана, как ни одно из других,' связано со всей
совокупностью кинетических уравнений.
Кроме того и помимо возражений, выдвинутых Цермело и Лош-
мидтом, уравнение Больцмана благодаря работам Чепмена,
Энскога и позднее Грэда явилось основой для последовательного
получения коэффициентов переноса (см. классическую моногра-
монографию Чепмена и Каулинга A939)). Побочный продукт теории —
разложение Чепмена — Энскога и моментный метод Грэда —
позволит нам получить замкнутые системы гидродинамических
Уравнений (например, уравнений Эйлера, Навье —Стокса, Бар-
нетта) и выделить области, где эти уравнения справедливы. Неко-
Некоторые из этих методов будут подробно обсуждаться в гл. V.
Непосредственная цель настоящей главы — ознакомить чита-
читателя с теорией уравнения Больцмана. Что касается упомянутых
Ранее противоречий, связанных с необратимостью, то относя-
относящиеся к ним рассуждения Гиббса и Больцмана будут рассмотре-
рассмотрели в гл. V.
4.2. Концепция столкновений
Чтобы получить уравнение Больцмана, необходимо более
Детально ознакомиться с теорией парных столкновений. Столкно-
Столкновения двух частиц можно исследовать в одной из трех систем
к°ординат. Ими являются а) лабораторная система координат,
174 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара — Гросса и др.
б) система координат, связанная с центром масс, и в) система
координат, связанная с одной из частиц.
Гамильтониан двух частиц, взаимодействующих посредство^
центрального потенциального поля У (г), в лабораторной системе
координат имеет вид
где /tti и пг2 — индивидуальные массы частиц, г — модуль вектора
относительного смещения г = г2 —r1? a (pl7 т±) и (р2, г2) ^
сопряженные импульсы и координаты. Рассмотрим теперь преобра-
преобразование системы переменных (р1? р2, г1? г2) в систему (Р, R, р, г),
определяемое следующими соотношениями:
D.26)
D.2в)
В новой системе координат, гамильтониан, заданный уравне-
уравнением D.1), примет вид
++г(г)' D-3)
где
P = MR = (m1 + m2)R D.4)
— импульс центра масс, а
— приведенная масса. Р2/2М есть кинетическая энергия тела мас-
массы М, имеющего скорость R, т. е. это кинетическая энергия центра
масс. Обозначим ее Нцм. Оставшаяся часть гамильтониана,
(р2/2|ы) + У, — это энергия частицы с массой fx и импульсом р»
находящейся в центральном потенциальном поле У (г). Эта
часть гамильтониана, обозначаемая Лоты, представляет собой
энергию рассматриваемых тел относительно системы координат,
движущейся со скоростью центра масс. В таких обозначениях D.3)
примет вид
Н = НЦШ + Яотн. D.6)
Поскольку Н является циклическим по R, то Р сохраняется,
а следовательно, Р2/2М также сохраняется и Яцм будет констан-
константой движения. Как только заданы начальные условия R @) и Р @)т
4.2. Концепция столкновений
175
движение центра масс тотчас же может быть определено. Затем
определяется и все движение, если известен радиус-вектор г (t).
Поскольку НцМ постоянна, ее можно включить в °]Г (г), и при
этом уравнения движения останутся теми же. (Законы движения
пНвариантны относительно смещения
лотенциала.) Следовательно, мы можем
записать, что
# = #отн, D.7)
Рис. 4.2. Радиус-вектор
г (t) «выметает» плоскость.
п все еще получим корректную динами-
динамику. Из уравнений Гамильтона находятся
г и р, которые вместе с сохранением
движения центра масс определяют пол-
полное движение системы.
Таким образом, задача двух тел с
центральным потенциалом взаимодей-
взаимодействия свелась к задаче одного тела.
Массой такой частицы является при-
приведенная масса |х, а координатой—отно-
координатой—относительный вектор г = г2 —г1в Сила, действующая на эту квазича-
квазичастицу (или (i-частицу), положение которой совпадает с положе-
положением частицы 2, направлена вдоль радиуса-вектора (задачу можпо
сформулировать и для частицы 1, результат будет тот же).
На (i-частицу действует момент —г X (дТ*/дг) (относительна
начала координат г = 0). Он обращается в нуль, так что угловой
момент (i-частицы относительно центра силы сохраняется. Пусть
угловой момент направлен по вектору I. Через заданный интервал
времени dt вектор г перейдет в г + dr. Угловой момент, соответ-
соответствующий этому интервалу времени, будет пропорционален
у (г X dr) = К I — вектору-площади треугольника (г, dr). В сле-
следующий интервал времени радиус-вектор г + dr перейдет в г +
+ dr + dr', и угловой момент будет пропорционален у (г + dr) X
X dr' = K\ —вектору-площади треугольника (г + dr, dr').
Отсюда следует, что эти два треугольника с общей стороной
r + dr имеют параллельные векторы-площади и поэтому лежат
в одной плоскости (рис. 4.2). Продолжая рассуждение для после-
последующих моментов времени, придем к заключению, что траекто-
траектория г (t) будет плоской.
Начальные данные [^ @), г2 @)] и [pi @), р2 @)] определяют
значения R @) и Р @) = Р (t). Решение для двумерного вектора
r {t) завершает задачу. Соответствующее движение изображено
на рис. 4.3.
Задача 4.1. Как построить на рис. 4.3 плоскость относитель-
относительного движения масс?
176 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара — Гросса и др.
Процесс рассеяния подразделяется на три этапа: до взаимодей.
ствия, в течение и после него. Как до, так и после столкновения
частицы являются свободными и не взаимодействуют одна с дру.
@)
Траектория центра
масс .
+ К@)
Р?и с. 4.3. Траектория двух частиц.
Рис. 4.4. Движение в лабораторной системе координат.
гой. Типичное рассеяние в лабораторной системе координат
изображено на рис. 4.4. Мы видим, что в лабораторной системе
координат 7тг2 отклоняется на угол Э2. Ситуация в системе коор'
4.2. Концепция столкновений
ill
динат, связанной с центром масс (т. е. когда мы ведем наблюде-
наблюдение, будучи «привязанными» к центру масс), показана на рис. 4.5.
Смысл понятий до и после столкновения определяется через
потенциал взаимодействия f" {r) либо через радиус взаимодейст-
взаимодействия г0. До столкновения — это любой момент времени, когда
частицы приближаются одна к другой и г > г0, или, что эквива-
эквивалентно, Т* (г) =0. После столкновения —это любой момент
времени, когда частицы уда-
удаляются одна от другой и f* (г) =
- 0 (г>г0).
Относительная скорость г до
и после столкновения обладает
очень важным свойством. Обо-
Обозначим относительную скорость
до и после столкновения через
V. Так как относительный им-
пульс р равен (j,r, то из D.3) с
учетом того, что Н является кон-
константой движения, следует ра-
равенство
jliV2 = ±iiV'\ D.8а)
так что
V = V, D.86)
где V —величина относитель-
относительной скорости до столкновения,
aF' — после столкновения. Таким образом, величина относитель-
относительной скорости после завершения столкновения сохраняется. Она
не является константой движения, а, вернее, принимает свое
первоначальное значение после столкновения.
Задача 4.2. Доказать следующую теорему. Угол рассеяния
в системе координат, связанной с центром масс, равен углу рас-
рассеяния в системе координат, связанной с какой-либо из двух рас-
рассеивающихся частиц. В системе координат, связанной с данной
частицей, последняя находится в состоянии покоя.
Omeqm. В системе координат, связанной с частицей, угол
рассеяния 6Р есть угол поворота вектора относительной скоро-
скорости V при рассеянии, т.е.
Р и с. 4.5. Ориентация относитель-
относительного радиуса-вектора г до и после
столкновения в системе координат
центра масс.
cos UD = -
у.у
Здесь мы использовали полученный ранее результат: V = V.
В системе координат, связанной с центром масс, угол рассеяния
178 Гл. IV. Уравнения Болъцмана, К рука — Бхатнагара — Гросса и др.
Эс — это угол поворота скорости ^ — R при столкновении, т. е.
COS 6с = . )*^~ т ' .
(Отметим изменение в обозначениях: §1 = ^.) Но
Аналогично
так что
172"-
Сравнивая последнюю формулу с предшествующим выражением
для 6Р, получим желаемый результат:
Соответствующие углы и векторы, использованные в данном
доказательстве, показаны на рис. 4.5 и 4.6.
Рис. 4.6.
а — рассеяние в системе координат частицы ттг2; б — рассеяние в систе-
системе координат ЦМ.
В лабораторной системе координат уравнения сохранения
импульса и энергии имеют вид
D-9а)
D.96)
Pi + Р2 = Pi + P2>
Pi . Pi = Pi2 I P22
2mi ' 2т2 2т± *~ 2т2
4.2. Концепция столкновений 179
Эти уравнения связывают р^, j)'2 с рь р2. Однако для заданной
совокупности начальных импульсов рь р2 существует континуум
значений pi, Pg, удовлетворяющих уравнениям сохранения. Это
по является неожиданностью, поскольку уравнения сохранения
но содержат информации относительно потенциала взаимодейст-
взаимодействия f (r). Какую начальную информацию достаточно иметь, чтобы
определить конечные импульсы р,', Pg? Мы нашли, что за^ач
Рис. 4.7. Рассеяние в системе координат, связанной с относительным век-
вектором г.
двух тел эквивалентна задаче одного тела с фиктивной массой \х
и радиусом г. Случай рассеяния в системе координат, где начало
этого вектора фиксировано, изображен на рис. 4.7.. Единичный
апсидальный вектор а делит пополам угол между V и V. При-
Прицельный параметр s таков, что угловой момент рассматриваемой
совокупности частиц в данной системе координат (эквивалентный
моменту в системе координат, связанной с центром масс) равен
\xVs. Прицельный параметр s, а также векторы относительной
скорости V и V характеризуют свойства асимптотических состоя-
состояний при столкновениях. Модуль скорости V и прицельный пара-
параметр s сохраняются при данном столкновении, так что эти две*
скалярные величины могут характеризовать данное столкновение
Задача 4.3. Пусть в данный момент времени положение
и импульс центра масс системы двух тел определяются векторами
(R, Р). Показать, что угловой момент системы равен
L = R х Р +
где е — единичный вектор нормали к плоскости, в которой лежит
вектор г (t).
Как будет показано, pj и р'2 определяются через V и постоян-
постоянный вектор Р. Вектор V имеет величину F, а его ориентация
J80 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара — Гросса и др.
задается углом рассеяния Э (или углом г|э = \ (я — Э)). Угол
рассеяния определяется как функционал от потенциала взаимо-
взаимодействия ТГ (f), относительной скорости V и прицельного пара-
параметра s, т. е.
в = е (s, г, V). D.Ю)
(Это также будет установлено позднее.) Теперь мы можем заклю-
заключить, что для заданного взаимодействия Т(г) и импульса центра
Исходное столкновение
ИндерсиВное столкновение
Рис. 4.8. Столкновение и его инверсия.
масс Р конечные импульсы pj[, P2 определяются через s и рь р2.
Поэтому изменение импульсов при парном столкновении можно
представить следующим образом:
Upi, P2)-*(Pi', рЭ!.. D.11)
Индекс s указывает, что прицельный параметр есть свойство
столкновения.
Существуют два типа столкновений, которым в теории кинети-
кинетических уравнений уделяется особое внимание. Это инверсив-
инверсивные и реверсивные столкновения. Инверсивным по отношению
к [(pi, P2) ->¦ (Pi, Рг)Ь является столкновение, которое имеет конеч-
конечным состоянием (pl7 р2). Мы видим, что если [(pl7 р2) —>¦ (р[, p^ls
удовлетворяет уравнениям сохранения, то [(р[, р'2) —>¦ (р4, p2)ls
также им удовлетворяет (следует только прочитать уравнения
сохранения справа налево). Прицельный параметр s гарантирует,
что (Pi, Pa) правильно ориентированы, чтобы дать (рь р2). Отсюда
следует, что начальными импульсами инверсивного столкновения
являются (pj[, \)'2)s, T- e. конечные импульсы первоначального
столкновения (рис. 4.8). Можно применить следующую символи-
4.2, Концепция столкновений 181
ческую запись:
Инверсия [(рь р2) -> (р;, p;)]s = [(pi, р;) -> (р4, p2)]s. D.i2>
Второй важный тип столкновения —реверсивное столкновение.
Реверсивным по отношению к [(рь р2) -> (pi, Pa)]s является
столкновение, которое имеет конечным состоянием (—р1? —р2).
Обращаясь опять к уравнениям сохранения, приходим к выводу,
Исходное столкновение
Реверсивное столкновение
\
Время —*~
-*— Время
Рис. 4.9. Столкновение и его реверсия.
что начальными импульсами будут (—pi, —Рз)8 (рис. 4.9). То естьу
если частицы с импульсами (—pi, —pg) взаимодействуют с при-
прицельным параметром 5, то в результате взаимодействия получают-
получаются (—рА, —РгЬ» Снова можно использовать символическую запись:
Реверсия [(рь p2)->(pi, рЭЬ = [(— Pi> — Pi)-*(— Рь —P2)ls. D-13)
Хотя эти утверждения выведены для общего случая, когда
щ1 =^= т2, при изучении уравнения Больцмана для газа из одина-
одинаковых частиц достаточно рассмотреть только частный случай
т± = т2. Тогда уравнения сохранения импульса и энергии D.9)
будут зависеть только от скоростей |А и |2 (р = т%). Они примут
вид:
Эти уравнения имеют решения:
D.15)
182 Гл. IV. Уравнения Болъцмана, Крука — Бхатпагара — Гросса и др.
(См. рис. 4.7.) Из последних формул явно видно, что существует
целый континуум скоростей рассеяния (l^, l^ совместимых
в силу уравнений сохранения с начальными скоростями (|1? |2).
Этот континуум порождается при варьировании единичного апси-
дального вектора а. Однако, если заданы s, V и взаимодействие
f" (г), то динамическое решение для орбит определяет значение а,
(т. е. либо 8, либо я|э), которое в свою очередь фиксирует "(|[, %'2).
Здесь остаются нерешенными две задачи. Во-первых, угол
рассеяния 0 должен быть записан как функционал от 5, V и потен-
'-'////*Пучок nadaviubz частиц
Рис. 4.10. Координаты в эксперименте по рассеянию.
циала взаимодействия °Г.. Во-вторых, мы должны определить,
какая часть пучка (невзаимодействующих) частиц рассеивается
на данном рассеивателе. Мы найдем, что, сформулировав решение
второй задачи, мы естественным образом придем к решению
первой.
Рассмотрим однородный пучок падающих частиц с энергией Е
и интенсивностью / (число частиц/сек см2). (См. рис. 4.10.) Число
частиц, рассеянных в элементе телесного угла dQ около Q, пропор-
пропорционально интенсивности падающего пучка / и элементу телес-
телесного угла dQ. Множитель пропорциональности о — это диффе-
дифференциальное сечение рассеяния.
Io (Q) dQ равно числу частиц, отклонившихся в пределах dQ
около Q за секунду. D.16)
Но такое же число частиц прошло через элемент кольца s ds dcp,
так что
IadQ = I йФ5 ds. D.17)
Азимутальный угол ср, который определяет сечение падающего
пучка частиц,— это тот же угол, что и в сферической системе
4.2. Концепция столкновений 183
координат с началом, фиксированным в рассеивателе. Таким
образом, dQ = d cos 0 dy. Подставляя это равенство в D.17),
получим
|Й?г. D.18)
Как находится s = s (Е, 9), будет описано ниже. В то время как о
связано с числом частиц, рассеянных в определенном направле-
направлении, величина
\ nrl D.19)
— полное сечение рассеяния, связана с полным числом частиц,
рассеянных из падающего пучка. Радиус взаимодействия равен г0,
так что частицы с прицельным параметром s > г0 не рассеиваются
из пучка. Полное поперечное сечение 2 — это заградительная
площадь, которую представляет рассеиватель для падающего
пучка частиц. Для однородного пучка с площадью поперечного
сечения 4^2 величина 2Л4 является долей частиц, рассеян-
рассеянных из пучка (по всем направлениям).
В дальнейшем мы вернемся к более детальному описанию того,
как вычисляется дифференциальное сечение рассеяния от (Э, Z?),
что, в свою очередь, связано с более точной оценкой угла рас-
рассеяния Э. Этот угол просто вычисляется при исследовании приве-
приведенного движения фиктивной частицы массы [г, управляемого
относительным гамильтонианом. Хотя сама частица фиктивная,
ее радиус-вектор г — нет. Действительно, г является относитель-
относительным вектором между т^ и т2. Угол между векторами гдо и гПОсле
(прежнее обозначение соответственно г и г') равен углу рассея-
рассеяния Э.
Поскольку относительное движение, описываемое вектором г,
лежит в плоскости, состояние системы определяется двумя обоб-
обобщенными координатами, углом ф и модулем г. Относительный
гамильтониан частицы с массой \х и импульсом р, движущейся
в поле центральной силы с потенциалом Т\)
? , D.20)
запишется через эти переменные в виде
Так как Ацикличен по ф, то р$ является константой движения,
обозначаемой через L. Относительный гамильтониан сам по себе
также постоянен, поскольку энергия совокупности частиц, изме-
измеренная в системе координат, связанной с центром масс, будет
184 Гл. IV. Уравнения Болъцмана, Ирука — Бхатнагара — Гросса и др.
равна
Уравнения Гамильтона дают:
d<j> L
Ldt
D.22)
D.23)
D.24)
D.25)
Типичный случай рассеивания вследствие отталкивания в системе
координат, где начало вектора г фиксировано, показан на рис. 4.7.
Выражая в первом уравнении dt через d§, получим
L dr/r2
1 + const.
Исходное столкнове-
столкновение
Редерсыбное столкнове-
столкновение
-V'
-V
ИнВерсиВное столкновение
Рис. 4.11. (Сеченне рассеяния одинаково для всех трех столкновений.)
Это не есть система координат, связанная с центром масс. В послед-
последней г вращается относительно фиксированного центра масс
(рис. 4.5). Однако, как мы видели, угол рассеяния 0 в этой системе
координат тот же самый, что и в системе координат центра масс.
В каждом случае 0 — это угол между гд0 и гПОсле1 который не
зависит от выбора начала координат.
4.2. Концепция столкновений 185
Диаграмма рассеивания (рис. 4.7) симметрична относительно
апсиды rmin, так что г = О для rmjn. Эта симметрия являет-
является следствием сохранения углового момента L = \iVs = \iV'sr
и относительной скорости V = V, так что s = s'. Поскольку г
обращается в нуль на апсиде, из уравнения D.23) следует, что
в этой точке знаменатель в интеграле D.25) равен нулю. Однако
сам интеграл остается ограниченным.
Угол i|), изображенный на рис. 4.11, получается при интегри-
интегрировании D.25) от rmin до оо. В результате будем иметь
со
Ц= [ , (L/r2) dr D.26)
rmin
Угол рассеяния 0 связан с i|), как показано на рис. 4.7:
0 + 2я1> = п. D.27)
Лучше выражать угол i|) через величину, обратную радиусу,
и = г. Кроме того, угловой момент L = \xVs связан с энергией
Е = y \iV2 соотношением
? = !&• D-28)
Если этим воспользоваться, то D.26) примет вид
w' <4-29>
Так какг|) определяет вектор а, то D.29) представляет собой явное
решение для «, выражаемое через ТГ^ Ens. Для потенциала
в форме
Т (г) = Кг-я = Яи* D.30)
D.29) примет вид
t Ы D.31)
Вводя безразмерный обратный радиус
Р == su D.32)
186 Гл. IV. Уравнения Волъцмапа, Крупа — Бхатпагара — Гросса и др
и безразмерный прицельный параметр
Е
в D.31), получим
¦ = | _JL=:, D.34
Задача 4.4. Для притягивающих потенциалов из D.34) полу-
получаем:
Показать, что это уравнение не имеет положительных решений
для N > 2 и Ь < 1.
Ответ. Перепишите уравнение в форме
Как мы далее увидим, Vo d cos 9 является важным множите-
множителем, входящим в уравнение Больцмана. Вспоминая D.17), полу-
получим, что
Fad cos 9 = Vsds. D.35)
Через безразмерный параметр Ъ это сечение выражается следую-
следующим образом:
D.36)
Полученный результат явным образом демонстрирует зависимость
сечения рассеяния от скорости F, которая целиком заключена
в мультипликативном коэффициенте у(Л—4)/n#
Очевидно, что случай N = 4 заслуживает особого внимания.
Молекулы, взаимодействие которых описывается таким потен-
потенциалом, называются максвелловскими молекулами. Для таких
молекул вес рассеяния Vo d cos 9 не зависит от V. Этот факт
значительно упрощает вычисления, относящиеся к линеаризован-
линеаризованному уравнению Болъцмана. С этими вопросами мы столкнемся
в гл. V, где линеаризованное уравнение Больцмана будет подробно
обсуждаться.
Сейчас обратимся к вычислению а для кулоновского взаимо-
взаимодействия, когда °1Г = К/г. Интегрируя D.34) при N = I, получим
b2> = -r-tg2"\p. D.37)
4.2. Концепция столкновений
187
tjepe3 Э (8 + 2я|) = я) это равенство выразится так:
D.38)
Подставляя полученный результат в D.36), которое можно пере-
переписать в виде
К \2 bdb .. Qm
Ы D39)
D.40)
Это хорошо известное сечение Резерфорда для кулоновского рас-
рассеяния. Расходимость при 0 = 0 обусловлена далънодействующей
природой кулоновской силы.
Другим очень важным законом взаимодействия в природе
является взаимодействие жестких сфер. В этом случае при вычис-
учитывая, что 2 sin2 @/2) = 1 — cos 0) получим:
\ 4? / sin4 @/2) '
7 Л d cos гЬ К2
od COS 0 = ^
Рис. 4Л2, Рассеяние жестких сфер в относительной системе координат.
лении а исходят прямо из геометрии. Опять рассмотрим рассеяние
в системе координат, где начало относительного вектора фикси-
фиксировано. Если сферы имеют радиусы аиЬ соответственно, то взаимо-
взаимодействие определено ограничением г ^ а + b и симметрией рас-
рассеяния в относительной системе координат. Схема рассеяния
в этой системе координат представлена на рис. 4.12. Отметим
еще раз, что данная система координат не является системой
координат центра масс. В системе координат, связанной с центром
масс, сферы а и Ъ «привязаны» к концам относительного вектора г,
188 Гл. IV. Уравнения Болъцмана, Крупа — Бхатнагара — Гросса и др
который проходит через фиксированный центр масс и вращает^
относительно него. На рис. 4.12 фиксирована сфера Ъ. Тем йе
менее а @) имеет одно и то же значение в обеих системах коордй^
нат. Сечение а получается прямо из треугольника, изображенного
на рис. 4.12, для которого
D = а+ Ь,
s = D sin i|), D.41)
D-
sds = D2 sin i|) cos i|) di|) = j- sin 9 dQ.
Отсюда следует, что
а @)=—^-, D.42)
так что в системе координат, связанной с центром масс, рассеяние
изотропно. Полное сечение 2 равно
1
2 = 2п [ ud cos 9 = jcD2, D.43)
т. е. площади диска радиуса D.
В следующих разделах, где будет получено выражение для
интеграла столкновений уравнения Больцмана, мы придем к тако-
такому заключению: система координат, в которой будет рассматри-
рассматриваться рассеяние при вычислении интеграла столкновений, — это
относительная, связанная с любой из рассеиваемых частиц систе-
система координат, в которой, как было показано выше, значение а
то же самое, что и в системе координат центра масс. При форму-
формулировке уравнения Больцмана и его приложений к частным
видам сил взаимодействия предшествующий формализм для вычис-
вычисления а (в системе координат центра масс) является достаточным.
Однако любое описание рассеяния не может рассматриваться как
полное, пока оно каким-либо путем не будет связано с типом рас-
рассеяния, который мы наблюдаем в «реальной жизни», т. е. рассея-
рассеяние в лабораторной системе координат. В заключение мы дадим
метод вычисления aL (сечения рассеяния в лабораторной системе
координат) через ос (сечение рассеяния в системе координат
центра масс, обозначавшееся прежде через а).
Вычисления проводятся следующим образом. Запишем вновь
уравнения сохранения D.9) (в лабораторной системе координат):
D.44
Pi , Р\ = РГ , /У
2mi ' 2т2 2т1 "^ 2т2
4.2. Концепция столкновений
189
рведя черту над переменными в системе координат центра масс,
запишем, что до столкновения
D.45)
2
После столкновения имеем опять 2 Р* = 0 и
i
D.46)
Относительные скорости до и после столкновения равны соответ-
соответственно V и V\ Послед-
Последние два уравнения можно
записать для скоростей:
D.47)
ттг2
Соответствующие соотно-
соотношения в лабораторной си- ^Р -?^р
стеме координат получают- р и с 4 13. Геометрия связи индивидуаль-
ся, если к правой части ного импульса с импульсом ЦМ.
этих уравнений для ско-
скоростей прибавить скорость центра масс:
D.48)
эцм*
Отсюда следует, что в лабораторной системе координат импульсы
частиц после столкновения равны:
D.49)
Уравнения D.49) представляют нужное нам обращение уравне-
уравнений D.44). Векторные уравнения D.49) дают векторную диаграм-
диаграмму, как показано на рис. 4.13. Если мы примем, что частица 2
До столкновения покоится, то рА = т{\[, р2 = 0 и Р = т^У.
Отсюда следует, что
-?-P = |iV. D.50)
190
Гл. IV. Уравнения Болъцмана, К рука — Бхатнагара — Гросса и др.
Соотношение V = V указывает, что на рис. 4.13 векторы |д,у>
и (li/rrii) P являются радиусами одного и того же круга. Случаи (а)
ич < т2 и (б) mi > w-2 представлены на рис. 4.14. На этом рисун-
Р и с. 4.14. Геометрия связи между углами рассеяния в различных системах
координат. Здесь 6i F2) — угол рассеяния частицы mi (m2) в лабораторной
системе координат; 0 — угол рассеяния в системе координат ЦМ,
Р и с. 4.15. Углы 0,, 62 и 0.
а — лабораторная система координат, б — система координат ЦМ.
ке 01 —угол между Pi и р^ (следовательно, это угол рассеяния
частицы rrii в лабораторной системе координат), 02 —угол между
Р2 и Pi (т. е. угол рассеяния частицы т2 в лабораторной системе
4.2. Концепция столкновений
191
ординат). Наконец, 9 —угол между V и V —угол рассеяния
1 системе координат центра масс. Резюмируя сказанное, запишем:
г> 01 —угол рассеяния т± в лабораторной системе координат,
02 — угол рассеяния т2 в лабораторной системе координат,
9^ — угол рассеяния т± (или т2) в системе координат центра
масс.
,}ти углы рассеяния показаны на рис. 4.14 и рис. 4.15. Связь
меЖДУ углами рассеяния в лабораторной системе координат
п в системе координат центра масс наглядно представлена на
4.16:
a jliV sin G .. гл\
g 1= (/ni//n DDIj
гпс
Подставляя соотношение V = V, получим
. Л m2sin G
Таким образом, мы пришли к нужной нам формуле, которая свя-
связывает угол рассеяния в системе координат центра масс с углом
рассеяния в лабораторной систе-
системе координат.
Итак, мы получили ос (9) и
выражение, связывающее 9 с 9^
Теперь из самого определения а
(см. D.16)) получим окончатель-
окончательное соотношение между ос и oL.
Выражение Io (Q) dQ пред-
представляет число частиц, рас-
рассеянных из пучка (интенсивно-
стн /) внутрь телесного угла dQ
(около Q) за секунду. Очевид-
но, это число не зависит от то-
го,^в какой системе координат
наблюдать рассеяние. Все эти
системы координат относятся к
°Дному и тому же случаю рассеяния и используются просто для
Различных способов его наблюдения. Следовательно,
IaL (QL) dQL = Iac (Qc) dQc, D.53)
11 мы получаем искомое соотношение:
gl (9A) d cos 9i = oc (9) d cos 9. D.54)
Задача 4.5. Как связаны 2С и 2Ь?
Задача 4.6. Каково значение ос для максвелловских молекул?
Задача 4.7. Каково значение aL для кулоновского рассеяния?
р и с> 4Л6 ГеОметрия связи углов
рассеяния в системе координат ЦМ
и в лабораторной системе координат.
192 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара — Гросса и
Задача 4.8. Каково сгь для рассеяния жестких сфер?
Задача 4.9. Какова связь между 0! и Э при рассеянии
одинаковой массы?
Задача 4.10. Показать, что полное сечение рассеяния 2 обра„
щается в бесконечность, если | Т (г) | > 0 для всех г.
Задача 4. 11. Каково значение 2, если потенциал ТГ (г) является
усеченным при г = г0 (т. е. Т (г) = 0 для г> г0)?
Задача 4.12. Какой максимальный угол рассеяния может иметь
налетающая частица тпх при столкновении с покоящейся части-
частицей тп2, если a) mjm2 = а, а < 1; б) а > 1?
Рис. 4.17. Геометрическое построение 6 для случая рассеяния жестких
сфер.
Указание. Решить эту задачу геометрически, используя диаг-
диаграммы рассеяния (рис. 4.13).
Задача 4.13. Показать (геометрически), что в предельном слу-
случае, когда тп\ = 77i2, две частицы всегда рассеиваются под прямым
углом одна к другой, т. е. pj*Pa = 0.
Задача 4.14. Доказать, что для неразличимых частицы-мишенп
и налетающей частицы с энергией Ег сечение рассеяния в лабо-
лабораторной системе координат (для кулоновского взаимодействия)
определяется соотношением:
Задача 4.15. В плоскости рассеяния лежат два жестких д
Рассеяние в системе координат центра масс имеет вид, изображен
ный на рис. 4.17.
4.2. Концепция столкновений
193
а) Поясните геометрическое построение, которое определяет 0.
б) Будет ли 0 определяться однозначно в пределе, когда
Ь < D -+ О?
Ответ. Начертить вектор к' параллельно вектору к на рас-
расстоянии Ъ от последнего. Далее повернуть вектор к (к' закреплен),
пока он не пересечет точку О,
Сечение рассеяния а является инвариантной величиной при
инверсии, обращении времени, при вращении координат относи-
относительно некоторой оси и при отражении координат относительно
плоскости.
Инвариантность а при некотором процессе означает следующее.
В данном эксперименте по рассеянию измеряемой величиной
'/
Рис. 4.18. Схема каналов рассеяния.
является IodQ (см. D.16)). Инвариантность о относительно опера-
операции S (S IodQ] = o'dQ') означает, что величина Io'dQ', измеряе-
измеряемая в новом эксперименте, совпадает со своим значением в перво-
первоначальном эксперименте, т. е. IodQ = Io'dQ'.
Этим свойствам инвариантности легко придать наглядность,
введя понятие о каналах рассеяния. Обычно физический процесс
протекает по множеству каналов (подобно тому, как вход корабля
в порт может осуществляться различными путями). В классиче-
классическом эксперименте по рассеянию каналы рассеяния образуют кон-
континуум, непрерывную область Q. Соответствующая диаграмма рас-
рассеяния имеет вид, изображенный на рис. 4.18.
194 Гл. IV. Уравнения Болъцмана, Крупа — Бхатнагара — Гросса и др.
В эксперименте по рассеянию измеряется, скажем, отноше-
отношение {С : /] исходов, идущих по каналу С, к числу случаев / нале-
тания частиц. В эксперименте с обращенным временем отрицатель-
отрицательные по импульсу события С становятся числом случаев налетания
частиц, а канал / —каналом рассеяния. Инвариантность а
по отношению к обращению времени означает, что мы получаем
то же самое отношение для двух совокупностей событий:
[__/: __с] и [С : Л.
При инверсии совокупность событий +С становится исходной,
а события +/ будут финальными событиями.
Инвариантность сг относительно вращения координат означает
постоянство этих отношений при вращении системы координат,
в которой ставится эксперимент по рассеянию. Однако сам экспе-
эксперимент остается фиксированным в пространстве х).
Инвариантность относительно отражения означает, что при
наблюдении за отражением эксперимента в плоском зеркале
«отраженные отношения» будут те же самые, что и первоначаль-
первоначальные отношения (т. е. измеренные в реальном эксперименте).
Задача 4.16. Доказать четыре свойства инвариантности а для
случая двух частиц (частицы двумерные), которые имеют следую-
следующую форму:
4.3. Уравнение Больцмана
а) Вывод Болъцмана — Stosszahlansatz (вероятностная гипотеза
о столкновениях)
Рассмотрим изолированный газ, подверженный действию одно-
однородного силового поля К. Пусть газ состоит из невзаимодействую-
невзаимодействующих частиц, т.е. частицы никогда не сталкиваются. Это означает,
что газ идеальный. Каким кинетическим уравнением будет описы-
описываться такой газ? Чтобы ответить на этот вопрос, сначала ясно
представим себе, что в случае невзаимодействующих частиц зако-
закономерно рассматривать только одну частицу без оставшейся сово-
совокупности других. Уравнение Лиувилля для этой системы (т. е.
*) Если указанное выше отношение [остается постоянным, |когда сам
эксперимент вращается в пространстве (а система координат, |в которой
проводится измерение, фиксирована), то будет иметь место менее тривиальный
физический закон. Эти два случая инвариантности эквивалентны, если про-
пространство изотропно.
4.3. Уравнение Болъцмана 195
одной частицы во внешнем силовом поле) имеет вид
Это не уравнение Власова, а одночастичное уравнение Лиувилля,
поскольку сила К в D.55) — это известная внешняя сила, а в урав-
уравнении Власова — это самосогласованная сила, являющаяся функ-
функционалом от /. Но использовать уравнение D.55) для описания
динамики изолированной частицы бессмысленно, поскольку намно-
намного проще пользоваться непосредственно вторым законом Ньютона.
В чем же заключается польза одночастичного уравнения Лиу-
билля?
Рассмотрим ансамбль одночастичных систем. Пусть общее
число идентичных систем ансамбля равно N., Г-пространство
является шестимерным. Каждая система представляется точкой
в Г-пространстве (определяющей состояние одной частицы во внеш-
внешнем силовом поле). Предположим, что в любой данный момент
времени мы рассматриваем ансамбль в трехмерной конфигура-
конфигурационной части шестимерного Г-пространства. Мы будем наблю-
наблюдать iV-частичный газ. .Следить за движением ансамбля одно-
частичных систем в Г-пространстве (рис. 4.19, а) —это все равно,
что следить за динамикой системы из N невзаимодействующих
частиц (рис. 4.19, б). В этом состоит отличие одночастичного
уравнения Лиувилля от TV-частичного уравнения Лиувилля
(N = 2, 3, . . .). Определяемый им ансамбль является динами-
динамической системой, имеющей физический смысл.
То, что уравнение D.55) относится к системе невзаимодейст-
невзаимодействующих частиц в силовом поле К, можно показать путем простых
вычислений. Число частиц в элементе фазового пространства
6x61 в момент времени t равно
6N = б!бх & (х, 1, *). D.56)
(Напомним, что JF нормирована на TV, в то время как / нормирова-
нормирована на единицу.) Во время t + St эти 8N частиц будут находиться
в другом месте фазового пространства. Так как единственное
возмущающее влияние на частицы обусловлено силой К, то очень
просто определить, куда перешли частицы. Частица, находящаяся
в момент t в точке (х, |), в момент t + St будет находиться в точке
IX -f- |б?, | + (К/т) 62], так что (вспоминая инварианты Пуан-
Пуанкаре)
6iV==6x61tF(x, 1, 0 =
(l + 8) ( l8 1 ^ ). D.57)
196 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара — Гросса и др.
Разлагая правую часть около 8t = 0, получим в пределе при
60
—
= 0. D.58)
Это есть суммарное число частиц, которые входят в движущийся
фазовый элемент 61бх за время 8t. Так как уравнение справедливо
Линии постоян-
постоянного бремени
Траектория 1
Траектория 2
Траектория /
- Траектория 2
Рис. 4.19. Схематическое изображение а двух траекторий в Г-пространст-
ве и б соответствующих кривых в конфигурационном пространстве.
для малых, но в остальном произвольных бх, 61, б?, то из него
следует уравнение D.55).
Это мысленное построение проделано нами не только для того,
чтобы формально показать связь уравнения D.55) с системой
невзаимодействующих частиц, но оно служит отправной точкой
рассматриваемого вывода уравнения Больцмана. Соотношв"
4.3. Уравнение Болъцмана 197
ян D.58) отличается по смыслу от D.55), поскольку в нем при-
присутствует элемент объема. Левая часть D.58) представляет пол-
рое число частиц, входящих в элемент фазового объема бхб|
(примыкающий к траектории | (?), х (t)) за время 8t. Согласно
правой части D.58), это число равно нулю. Отсутствие потока
внутрь данного элемента фазового объема объясняется тем, что
движение фазового элемента точно совпадает с движением уско-
ускоряющихся частиц (т. е. с движением, описываемым соотноше-
соотношением D.55)).
Далее, хотя частицы, описываемые уравнением D.55), могут
иметь пересекающиеся орбиты в конфигурационном пространстве
(см. рис. 4.19), они не взаимодействуют одна с другой.
В результате чего возникает взаимодействие (точнее столкно-
столкновение) частиц в нашей первоначальной системе без взаимодействий?
Рассмотрим две частицы, которые не коррелируют и расположены
каждая вне области взаимодействия с другой, но находятся на
пути к столкновению (т.е. прицельный параметр s меньше радиу-
радиуса взаимодействия). В процессе столкновения (войдя каждая
в область взаимодействия другой) они становятся коррелирован-
коррелированными. Столкновения порождают корреляции. С другой стороны,
пусть две частицы а и Ь, каждая из которых находится вне обла-
области взаимодействия другой, будут коррелированы. После того
как частица Ъ столкнется с тремя последующими частицами с, d
и е, любая начальная зависимость (например, в виде начальных
условий) между состояниями Ъ и а будет ослаблена. Столкновения
разрушили корреляцию. В более общем случае столкновения
разрушают и создают корреляции.
Вернемся к нашей задаче. Мы хотим учесть взаимодействия,
или столкновения, в первоначальном газе из невзаимодействую-
невзаимодействующих частиц. В теории уравнения Больцмана рассматриваются
только такие столкновения, которые подчиняются неравенствам
-Ь<1; ^<1, D.59)
где о — это среднее время между столкновениями ж I — средний
свободный пробег. Если произвольная частица сталкивается N раз
за время Т, то в предельном случае, когда N ^> 1, имеем t0 = TIN.
Если С —тепловая скорость, то I = Ct0 и г0 — Ст. Время т —
это среднее время, в течение которого одна частица находится
в области взаимодействия другой. Область взаимодействия имеет
размер г0. Величина | G | силы взаимодействия равна §drQ, где
<Ь0 — напряженность взаимодействия.
Согласно неравенствам D.59), частица должна большую часть
времени проводить между столкновениями, и расстояние, про-
проходимое частицей между столкновениями, значительно превышает
радиус взаимодействия. Если на газ не действует внешняя сила,
198 Гл. IV. Уравнения Болъцмана, Крука — Бхатпагара —Гросса и др.
то вместе с D.59) это обеспечивает прямолинейность движения
частиц между столкновениями. С другой стороны, если К =^=0,
мы должны наложить ограничение, согласно которому частицьг
входят в области взаимодействия по прямолинейным траекто-
траекториям. Это будет так, если отклонение от прямолинейности, созда-
создаваемое силой К за время t0, мало по сравнению с отклонением,
вызываемым силой G за время т, что выполняется, если
К < G. D.60)
Условие D.59) эквивалентно требованию, чтобы газ был разре-
разреженным. Условие D.60) обеспечивает прямолинейность движения
частиц непосредственно перед столкновением. Второе условие
заключено в первом, если К = 0, но для К =^0 оно должно быть
оговорено особо. На рис. 4.20 показано несколько типичных
траекторий, для которых выполняются эти условия.
Теперь мы лучше подготовлены, чтобы рассмотреть влияние
столкновений на первоначальную систему невзаимодействующих
частиц. Существуют два подхода к получению кинетического
уравнения. Во-первых, мы можем обратиться к TV-частичному
уравнению Лиувилля и исследовать соответствующее БИ* урав-
уравнение для описанного выше случая разреженного газа с взаимодей-
взаимодействующими частицами. Этот метод имеет преимущество, будучи
автономным и формальным. Но его недостаток состоит в том, что
кинетическое уравнение по своему характеру противоположно
уравнению Лиувилля в том смысле, что первое необратимо, а вто-
второе обратимо, следовательно, придется вводить целый ряд пред-
предположений, чтобы учесть необратимость. В этом состоит слабость
метода, исходящего из уравнения Лиувилля, поскольку он в зна-
значительной мере формален по своей природе. Заметим, что при
разложениях около нулевых корреляций, выполненных в гл. III,
необратимость никак не вводилась в теорию. Все полученные
кинетические уравнения были обратимыми.
Второй подход осуществляется совершенно иначе. Рассматри-
Рассматривают только одночастичное распределение, для которого надо
найти уравнение. Вместо того чтобы исходить из уравнения Лиу-
Лиувилля для iV-частичного распределения и продвигаться вплоть
до одночастичного распределения, берут за основу уравнение
свободно-молекулярного течения (одночастичное уравнение Лиу-
Лиувилля) и получают кинетическое уравнение, включающее эффек-
эффекты столкновений. Такова точка зрения Больцмана.
Исходным является соотношение D.58), которое, как мы пом-
помним, дает полное число частиц, входящих в элемент фазового
объема бхб? за время 8t. Если частицы не взаимодействуют, это
число равно нулю. Если они взаимодействуют (в описанном
выше случае разреженного газа), то, прослеживая за группой
частиц внутри их собственного фазового элемента 6x61, нельзя
4.3. Уравнение Болъцмана
199
быть уверенным, что ни одна из частиц не покинет этот объем
ляи что в него не войдет «посторонняя» частица.
Пусть число частиц, которые входят в элемент фазового объема
6x61 за время б?, вследствие столкновений равно 8R+, a 6i?_ —
б
Рис. 4.20. Траектории Больцмана.
а — К = 0; б — К однородна и направлена вниз; в — пробная частица
несет заряд, К = е\ х Во. Магнитное поле Во направлено перпендикулярно
чертежу.
число частиц, покидающих за время б? объем 6x61. Тогда вместо
D.58) имеем:
(^ ^ |*:)бЯ+-6Я_. D.61)
Поскольку естественной системой координат для уравнения D.61)
является система, фиксированная относительно частицы, движу-
движущейся со скоростью 1, то уместно и рассеяние рассматривать
200 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара —Гросса и др.
,> 51 - частица имеет
спорость V ё системе
координат ,?-шстиць/!!.
в этой же системе координат. Сначала рассмотрим 6i?_. Скорость
всех частиц газа можно разделить на две группы. В первую вхо-
входит небольшой диапазон скоростей, заключенных в интервале б?
около |, а во вторую —все остальные скорости, которые обозна-
обозначим через переменную ^. Число частиц, которые выходят из эле-
элемента фазового объема 6x61 за время б?, — это просто полное число
столкновений «1-частиц» со всеми другими частицами (т. е. «|г
частицами») за время 8t. Следовательно, чтобы вычислить 8R^
мы должны учесть все столкновения между парами частиц, пра
которых одна из частиц «вы-
«выбрасывается» из интервала 6|
около |. Другими словами,
это должны быть пары, обла-
обладающие следующими свойст-
свойствами.
1. Одна частица находится
в фазовом элементе 6§6х око-
около (|, х), а другая —в фа-
фазовом элементе б^бх* около
2. li-частицыв бх! претер-
претерпевают столкновения с §-ча-
стицами в бх за время б?.
Согласно определению
JF2, число таких пар частиц
задается следующим соотно-
соотношением:
sdsdw
d FЛ_) =
= ^2 (z, z±)
. D.62)
Рис. 4.21. Рассеяние в системе коор-
координат «|-частицы».
Чтобы построить элемент
объема бх! так, чтобы он об-
обладал свойством 2, рассмо-
рассмотрим рассеяние в системе ко-
координат, связанной с частицей 1 (рис. 4.21). В этой системе коор-
координат все li-частицы, расположенные в цилиндре с высотой
I Si — I I б? и площадью основания sdsdq>, претерпевают столкно-
столкновение с S-частицей за время 8t. (Частицы, находящиеся немного
выше цилиндра, не достигнут его основания за время б?.) Сле-
Следовательно, элемент объема бх! равен
бх! = btsdsdtp I I -Si I,
и выражение D.62) примет вид
d (вД_) = ^ав§1 I S — Si I btsdsdqblbx. D.63)
4.3. Уравнение Болъцмана
201
Интегрируя по всем g4, s и ср, получим полный вклад в 6i?_:
D.64)
(xi, li)
,s> Ф
Столкновение переводит скорости (g, It) в (g', g{) и подчиняется
уравнениям сохранения D.9).
Чтобы получить 8R+, мы должны учесть все парные столкно-
столкновения, в результате которых одна из частиц попадает в интервал
Рис. 4.22. Рассеяние и его инверсия в системе координат «|-частицы»^
Объемы цилиндров равны. Их положения не совпадают.
скоростей б| около g за время б?. Согласно определению, это точ-
точная инверсия столкновения
A, у -+ (im;),
т. е
Рассеяние (g» gi)-> (g', gi) и его инверсия показаны на
рис. 4.22 —опять в системе координат, связанной с g-частицей.
Выражение для 6jR+ имеет вид
d (бд+) =^2 (*;, Z') б1;бх;б|'бх', D.65>
т. е. столкновение между парой частиц (!', |А'), выходящих из эле-
элементов фазового пространства, в которые пара (g, gj) пришла»
после столкновения, восстанавливает пару (|, gi).
202 Гл. IV. Уравнения Болъцмана, Крупа — Бхатнагара — Гросса и др.
В выражении D.65) объем 8х^ = V'bts' ds'dy'. Вследствие налц-
чия симметрии между столкновением и его инверсией s' ds'dy' ^
= sdsdy (или, что эквивалентно, o'dQ' = odQ). Кроме того
V = V, что справедливо для любого столкновения. Отсюда
следует, что
6х4 = бх;. D.66)
Сейчас мы покажем, что дифференциалы в D.65) совпадают с диф-
дифференциалами в D.62). Обычный метод таков: уравнение D.66)
используется для подстановки бх^ в D.65) и далее проводится
доказательство для остальных членов.
Однако существует более простой метод. В интегральные
инварианты Пуанкаре входит форма 6x6|6xi6|i для двух частиц
в системе из N частиц. Следовательно, бхб^бх^^ = бх'б|'бх^б|^
и, таким образом, наша цель достигнута.
Отметим, между прочим, что выражение «J^* 2бхб^бх±б ^± выглядит
как величина, сохраняющаяся в силу теоремы Лиувилля. Это
справедливо, если система состоит только из двух частиц. Тогда
&2 — функция распределения для ансамбля двухчастичных сис-
систем, и из соответствующего уравнения Лиувилля следует, что
^гбхб^бх^^ —инвариант действительного движения системы.
Но, конечно, в данном случае это не имеет места, поскольку в на-
нашем доказательстве распределение JF2 относится к двум частицам
в системе из N частиц.
Окончательно уравнение D.65) примет следующий вид:
d FД+) = JF2 (zl, z') 6Si | Si - I | 6*dq*ds6Sex, D.67)
так что суммарное число частиц, рассеянных внутрь фазового
интервала б|бх около (|, х) за время б?, равно
6Д+ = [ J ^2 ft, z') 11- Si I 6Si* ds йф] 616x6*. D.68)
E1, s, ф)
Хотя это утверждение является точным относительно скоростей
рассеянных частиц, оно не точно относительно их пространствен-
пространственного положения. Приращение 8R+ пополняет число частиц в про-
пространстве скоростей (около значения 1), но не число частиц в кон-
конфигурационном пространстве (около значения х). При инверсив-
инверсивном столкновении частица не обязана появиться около значения х.
Куда же она попадет? Инверсивное столкновение, как видно из
рис. 4.22, инжектирует частицу в систему в положение Ь, которое
смещено относительно положения вновь введенных частиц Fi?+)
на расстояние порядка величины радиуса взаимодействия г0.
Предположим теперь, что $Fi (x, 1) не изменяется при смещений
4.3. Уравнение Болъцмаиа 203
произвольного х на г0, т. е.
&i (х) = ^ (х + vr0), D.69)
где У — величина порядка единицы. Это означает, что число частиц
в интервале бх около точки а (рис. 4.22) то же самое, что и в ин-
интервале бх около точки Ъ. Следовательно, хотя частицы из числа
б/?+ D-68) инжектируются в элемент объема бх около &, число
0Х такое же, что и в элементе бх около а (при условии, что выпол-
дяется соотношение D.69)). В этом случае 6i?+ — это в точпости
число частиц, входящих за время 8t в фазовый элемент бхб|
около х, | вследствие столкновений.
Объединяя уравнение D.61) с соотношениями D.64) и D.68),
получим
ОЕ-л. s i!?-4-iL д^ —
dt "~^# дх "i~ т " д% ~~
ь l)]|li-l|. D.70)
Уравнение D.70), подобно ББКГИ-системе, представляет собой
одно уравнение для двух неизвестных. Чтобы прийти от него
к уравнению Больцмана, необходимо только наложить ограниче-
ограничение, подобное тому, которое мы ранее называли ограничением
нулевых корреляций:
I, li) - -^ ^i (I) &i (Si), D.71а)
JF2 (l\ Id = -^ ^i (!') ^i (К). D.716)
В первом равенстве скорости (|, |i) независимы. Однако скоро-
скорости (|\ |i) не являются независимыми. Если заданы скорости
налетающих частиц (|, |i), то скорости (|', |{) связаны с ними
уравнениями сохранения D.9) г). Этим дается формальное пояс-
пояснение того утверждения, что столкновения создают корреляции.
Чтобы наш анализ был последовательным, необходимо показать,
что столкновения также и разрушают корреляции. За достаточно
длительный интервал времени после данного столкновения каждая
частица испытывает множество столкновений и поэтому обязана
вновь вернуться к общему столкновительному состоянию, для
которого снова должны быть справедливы уравнения D.71),
и частицы опять будут некоррелированными. Таким образом,
в результате столкновений корреляции разрушились.
Свойство, описываемое уравнением D.71), называется молеку-
молекулярным хаосом. Внося это ограничение в уравнение D.70) и прене-
пренебрегая единицей по сравнению с N, получим уравнение Больц-
Уравнение D.716) несколько менее корректно, чем уравнение D»71а).
204 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара — Гросса и дрч
мана1) (ср. с C.65)):
где
^; = jr(i;), ^-' = ^A'), ^ = ^-F0. D.73)
(Теперь ^ означает одночастичную функцию распределения.
Индекс «1» указывает на то, что аргументом функции является |ьу
Конечные скорости являются известными функциями начальных
скоростей, что получается из уравнений сохранения при силе
взаимодействия G, которая также определяет сечение рассеяния
о = о (V, 6, параметры G). D.74)
Заметим, что система координат, в которой рассматривается рас-
рассеяние и вычисляется а, связана с «|-частицей». Однако, как было
замечено выше, то же самое а будет описывать рассеяние и в сис-
системе координат центра масс (см. задачу 4.2). Уравнения D.72)
и D.73) составляют уравнение Больцмана. Оно является автоном-
автономным, только когда известен явный вид уравнений D.74) и D.15).
Уравнение D.72) часто записывают в сокращенной форме:
где D/Dt —индивидуальная производная:
а /—нелинейный оператор столкновений:
D.77)
Задача 4.17. Получить явный вид оператора столкновений
/ (JF) для газа, состоящего из жестких сфер диаметра D*
Ответ. В данной задаче удобно пользоваться сферическими
системами координат, изображенными на рис. 4.23. Угол я|) тот
же самый, что и на рис. 4.7. Отметим, что вектор «можно изменять,
оставляя V фиксированным, а вектор %х можно изменять, остав-
оставляя | фиксированным. Различные элементы / (JF) в этом пред-
г) Отметим сходство между уравнением (Больцмана и следующим уп-
управляющим уравпением, предложенным Клаузиусом (около 1862 года):
- 2
i, k, i
где коэффициенты а — скорости перехода.
4.3. Уравнение Болъцмана
205
давлении будут иметь вид:
? ds dtp (P^i = D2 cosij? d cos\|) dpJ-Jdx d cos Я
V2 = l]+I2 -26^ cos b,
a = (cos я|э, sin i|) sin ф, sin of) cos ф),
a- V = У соэ-ф.
Рис. 4.23.
Подставляя эти выражения в дифференциал оператора
и в аргументы функций
ffi* =^[|+ a(a.V)l,
получим решение.
Задача 4,18. Определить, являются ли обратимыми следующие
уравнения (т. е. показать, что если у (t) —решение, то у (— t) —
также решение; штрихами обозначены производные по времени):
а)
б)
в)
г)
'-i
= j у (
у' = j у ix) Ax->
a
У' = J y(x — t)dx.
206 Гл. IV. Уравнения Болъцмана, Крупа — Бхатнагара — Гросса и др.
Ответ. Для уравнения а) исследуем, является ли также реше-
решением у (—t). Подставляя у (—t) вместо у (t), получим:
dy(-t)
dt
или, что эквивалентно,
dy{%)
dx
-а
= \ у (z) dz.
Это уравнение не совпадает с а), так что у (—t) не является реше-
решением и уравнение а) необратимое. С другой стороны, мы могли
бы показать, что данное уравнение не инвариантно при преобра-
преобразовании обращения времени, t ->¦ t' = —t. Здесь уместно отме-
отметить, что правая часть данного уравнения постоянна и не зависит
от времени. Способом, аналогичным первому, мы найдем, что
б) необратимое, в) обратимое и г) необратимое. Отметим, что при
дифференцировании а) получается обратимое уравнение. Решения
уравнения у" = 0 являются обратимыми относительно этого
уравнения. Подмножество этих решений, которое является реше-
решением а), состоит из решений, необратимых относительно а).
Задача 4.19. Показать, что уравнение Больцмана необратимое*
т. е. если / (|, t) — решение, то / (•—|, —t) не обязано быть тако-
таковым.
При получении уравнения Больцмана были сделаны следую-
следующие предположения.
1. Тройными столкновениями можно пренебречь.
2. Непосредственно перед столкновением орбиты прямолинейны
в противоположность столкновительной части траектории.
3. Функция распределения частиц не меняется на расстояниях
порядка размера области столкновения.
4. Справедлива гипотеза молекулярного хаоса.
б) Вывод Грэда
Описанный только что метод получения уравнения Больцмана
концентрируется в основном на вычислении членов 8R±. Одно-
частичная функция распределения изменяется (вдоль траектории
частицы) только благодаря беспорядочным столкновениям, вслеД"
ствие которых частицы выходят из элемента фазового объема
и входят в него. Но это не единственная причина изменения функ-
функции JF4. Полный механизм изменения определяется интегралом
в уравнении BHi [см. уравнение B.178а)].
Было бы очень поучительно вывести уравнение Больцмана
непосредственно из ЕИ^. Можно вполне надеяться, что при такол*
4.3. Уравнение Больцмана 207
подходе различные предположения, которые необходимы для полу-
получения уравнения Больцмана, выявятся яснее. За последнее время
бьТл проведен ряд таких попыток. Это работы Кирквуда A947),
Боголюбова A946) и совсем недавняя работа Грэда A958). В настоя-
настоящем разделе мы рассмотрим вывод Грэда, после чего в общих
чертах ознакомимся с выводом Кирквуда. Анализ Боголюбова
был рассмотрен в гл. III.
Прежде всего запишем уравнение Лиувилля в следующем виде:
'V N
dfN , ^ d /% * \ \ _iw V Г d/jv __ ^ ,, rjQ\
~~дГ~г 2л dxl'\biiN)-\- т 2л ^1'~щг —и" ^•'°;
Полная сила, действующая на частицу I со стороны всех других
частиц, равна Gj. Она связана с введенной ранее двухчастичной
силой G ij соотношением
N
ЗФ1
Выпишем формулы, необходимые нам в дальнейшем.
t, y)dy= [ divAdy=— § A-dS, D.80)
|У-х|>а |y_x|>a |y-x|=a|
-j^ \ A (x, y)dy— \ ~7Г~*А ^У— Ф A-dS. f(
ly-x|>a |y-x|>a jy-x|r=a
Для того чтобы получить уравнение, похожее по форме на
уравнение Больцмана, оказывается полезным ввести усеченное
распределение f°(zi). Эта функция определяет вероятность того,
что в пределах расстояния а от частицы 1 нет ни одной молекулы,
а частица 1 находится в состоянии z4. Чтобы получить уравнение
для /J7, проинтегрируем уравнение Лиувилля по области D.
Область D содержит все такие состояния частиц B, . . ., N),
в которых ни одна частица не находится ближе чем на расстоя-
расстоянии о от частицы 1 (рис. 4.24). |В результате будем иметь:
N N
* =0, D.82)
ff=\ fNd2 ... dN, D.83)
= {\xi — x2|>a; |xt—x3|>a; ... |Xl —
208 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара — Гросса и др
Рис. 4.24. Области в конфигурационном пространстве при выводе уравнения
Больцмана методом Грэда.
а — область D; б — область D2', в — область DT.
Dr: |Xl-xr|>;a,
, fi=>\fNd3...dN.
Если через DT обозначить область |xf — хг|>а, то
D=D2 x D3x . . X DN.
Из этих уравнений мы получим
-#+2 Н-яг^+^
D
D.84)
1.85)
4.3. Уравнение Болъцмана 209
Пусть Sl — сфера \xL — xi\ = o. Рассмотрим первый член суммы
N
1=1
интеграл от которого есть
D 1=2 t
D.87)
Здесь мы использовали соотношение D.81), отождествляя интег-
интеграл в левой части D.87) с первым интегралом в правой части D.81).
Аналогичным образом можно разложить оставшиеся члены сум-
суммы D.86):
N N
2 \^'(hfN)d2 ... dN=- 2 j§/?(!, l)lrdSdh. D.88)
1=2 Ь 1=2 St
В этом случае использовано соотношение D.80).
В силовом члене уравнения D.85) все слагаемые, кроме члена
с d/d§i, приводятся к поверхностным интегралам, которые обра-
обращаются в нуль. Соответствующий множитель при д1д\^ после
интегрирования дает
N
{ GJNd2 ... dN= ^ J Gu (xlf xt)fNd2 ...dN =
D h=2 D
= (iV-l) j G12(Xl, x2)/?(l, 2)d2. D.89)
Область D2 содержит все состояния частиц 1 и 2, в которых рас-
расстояние между частицами не будет более близким чем а (т. е.
| х2 —х± | > а). Усеченное двухчастичное распределение /? опре-
определяется через интеграл
/f(l, 2)= j/w(l, ..., N)d3 ...dN, D.90)
D'
Df = D3 X Dk X ... X DN.
Область D' содерлшт все состояния молекул C, . . ., N), в кото-
которых ни одна из этих частиц не подходит к частице 1 ближе чем на а.
210 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара — Гросса и др.
Объединяя уравнения D.82) и D.89), получим требуемый
результат:
Это уравнение называется первым уравнением Трэда,
При выводе данного уравнения было учтено, что поверхност-
поверхностные интегралы в правой части соотношений D.87) и D.88) пред-
представляют собой (N — 1) одинаковых членов. Это отождествление
было сделано почти по той же причине, что и в ББКГИ-последо-
вательности, где мы также получили (N — s) одинаковых членов
[ср. с уравнением B.150) и последующими, а также с относя-
относящимися к ним рассуждениями]. Область D2 в уравнении D.91)
включает | х2 — х4 | > а, тогда как поверхностный интеграл
в этом же уравнении вычисляется по поверхности | х2— х4 | = а.
Чтобы раскрыть смысл первого уравнения Грэда, предполо-
предположим, что G12 = 0 для | х2 — xi | > сг (что выполняется для жест-
жестких сфер диаметра а). Тогда мы придем ко второму уравнению
Грэда:
-1) J J/fdS-di-la)^. D.92)
s
Левая часть этого уравнения представляет полную производную
по времени от функции /f. Из вида поверхностного интеграла
в правой части мы заключаем, что скорость изменения числа частиц
в данном элементе фазового объема обусловлена только убылью
пары частиц, когда они входят каждая в область влияния другой,
либо приростом пары частиц, когда они покидают каждая область
влияния другой.
Эта ситуация резко противоречит тому, что имеет место в слу-
случае уравнения BHi*.
которое описывает изменение /i, обусловленное действием непре-
непрерывной коллективной силы со стороны всех оставшихся частип.
Второе уравнение Грэда D.92) дает точное описание газа из
твердых сфер, для которого единственным имеющим смысл рас-
распределением является /?. В следующих разделах мы покажем,
что это уравнение, кроме того, является естественным предшест-
предшественником уравнения Больцмана.
4.3. Уравнение Болъцмана
211
Эти замечания наводят на мысль, что между любым газом,
хорошо описываемым уравнением Больцмана, и фундаментальным
газом (т. е. газом из жестких сфер) существует формальное сход-
стВо. Оно состоит в следующем. Для обоих классов газа (мы имеем
в виду систему из жестких сфер) траектория характерной частицы
(до столкновения)
\sdsdy\
Каждый такой элемент
площади имеет проекцию
на S? и S7
V- d S> 0 (после столкновения)
Рис. 4.25. ?2-сфера в выводе уравнения Больцмана методом Грэда.
является свободной, за исключением стохастических дискретных
отклонений, которые испытывает частица, когда она входит в сфе-
сферу влияния другой.
Для того чтобы представить второе уравнение Грэда D.92)
в форме уравнения Больцмана, рассмотрим сначала сферу 52,
которая изображена на рис. 4.25.
Точки #2 отображаются на меридиональный диск простым
проектированием. Точки диска имеют радиальную координату s
(прицельный параметр) и азимут ср. Чтобы сделать отображение
взаимнооднозначным, две полусферы различают согласно усло-
условиям:
S\\ V«dS > 0 (после столкновения),
S~ : V»dS < 0. (до столкновения).
Относительная скорость V задается соотношением
V = h - S,. D.94)
Для фиксированной скорости V,
Точка на S*, которая проектируется на E, ср), обозначается х? (s, ф),
а точка на 5", которая проектируется в эту же точку, обозначает-
212 Гл. IV. Уравнения Болъцмана, Крупа — Бхатнагара — Гросса и др.
с я х~ (s, ф). В результате получим:
(Si- h)-dS = -Vsdsdy на S2\ D.95)
(h—h)'dS = +Vsdsdq> на S~.
Если через 2+ обозначить точку (§2, х*), а через 2~ —точку
(|2, х~), то в наших координатах уравнение D.92) примет вид
= (N-1) J [/|A, 2+)-/f (lf2U7*&d9d8E2. D.96)
Пока это то же самое уравнение, что и D.92), просто записанное
в другой форме. Однако сходство его с уравнением Больцмана D.72)
вполне .очевидно. Введем сейчас ряд ограничений, почти таких
же, как в выводе Больцмана.
1. Заменим аргументы в /? A, 2+, t) на значения, которые они
должны иметь в начале бинарного столкновения (скажем, 1, 2, 1),
для того чтобы в момент t они приняли значения A, 2+). Начало
столкновения определяется условием | х2 — х4 | = ст. Эта опера-
операция аналогична использованию инверсивных столкновений (f[, /')
в представленном ранее выводе Больцмана. Оба приема вводятся
для того, чтобы член с положительным коэффициентом в интег-
интеграле столкновений вносил вклад в Dfi A)/Dt в момент t.
2. Положим
/|A, 2) = /?(!)/? B),
т. е. введем предположение о молекулярном хаосе.
3. В четырех функциях^/f (I, f), /f(r, t), /f (T, 7), /?B, J)
заменим х2, xl7 xj на х4 и t на ?.
Произведя соответствующие изменения в уравнении D.96)
и пренебрегая единицей по сравнению с N, получим (вспоминая,
что JFi = Nfi) уравнение Больцмана:
*l2 D.97)
(a dQ = s ds йф).
Это завершает вывод уравнения Больцмана методом Грэда. Обра-
Обратимся теперь к выводу Кирквуда уравнения Больцмана.
4.3. Уравнение Больцмана 213
Задача 4.20. Показать, что второе уравнение Грэда обратимо,
т е. показать, что его решением является также
[/?(-li, -t); /?(-&, -h, -t)].
Задача 4.21. Установить справедливость соотношений D.95).
Ответ.
V.dS = VG2dcosQdq>cose
вместе с
sz = a2 sin2 0
дает желаемый результат.
в) Вывод Кирквуда уравнения Больцмана
Вывод уравнения Больцмана Кирквудом A947) г) также осно-
основывается на уравнении Лиувилля. Он использовал последнее,
чтобы вывести уравнение для расширенной функции распределе-
распределения. В этом смысле вывод Кирквуда подобен выводу Грэда,
который получил уравнение для усеченной функции распределения,
обладающей характерным свойством в пространстве конфигураций
(ни одна из частиц не приближается к данной ближе чем на рас-
расстояние а). С другой стороны, отличительной чертой распределе-
распределения Кирквуда является его временное свойство, s-частичное
усредненное по времени распределение Кирквуда /s задается
уравнением
ДA, ..., s, *) = ± jMl, 2> •••> *; * + Л)*1. D.98)
о
Эта операция обладает эффектом «сглаживания» функции по вре-
времени. Чтобы это увидеть, рассмотрим производную
* D.99)
dfs =fs^+t)-fs(t)
dt x
Тангенс угла наклона /s в точке t зависит от значения /s в двух
точках (t и t + т) и не чувствителен к виду функции fs между
этими двумя точками. Чем больше т, тем более гладкой получает-
получается функция /s. Ступенчатая функция 5 и ее сглаженный по вре-
времени «дубликат» S показаны на рис. 4.26.
Вывод, приводимый в тексте, отличается от кирквудовского.
214 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара — Гросса и др.
Предположим опять, что мы проинтегрировали уравнение
Лиувилля (N—1) раз, чтобы получить BHi B.178а):
¦1Н-•?-?'» Ю + <*-1> ^Г- J <*2G12/2@ = 0. D.100)
Заменяя t на t-{-v\ и затем действуя на это выражение операто-
X
ром х I dx\, получим
J! ^ ^\j0. D.101)
Заметим, что интеграл содержит оператор Gi2*d/3pi. Чтобы пре-
преобразовать этот оператор, введем первое предположение: за интер-
Рис. 4.26. Ступенчатая функция S и сглаженная по времени функция
Рис. 4.27.
а — парное взаимодействие; б — тройное взаимодействие.
вал времени (t, t + т) частица 1 взаимодействует только с части-
частицей 2 (т. е. в любое время не более чем две частицы сталкиваются
одна с другой). Такая ситуация изображена на рис. 4.27, а. Есл#
4.3. Уравнение Болъцмана
215
эТо так, то
сводится к
N
1=2
t = G12
D.102)
D.102a)
G
12 * Яп J
D.103)
Предположим далее, что справедлива следующая цепочка нера-
неравенств:
7//( т|чЧ ' д J ' Ю Т I . * "^ Т . ^ Г
I ^P2 C/X4 I "A-2 ^"
D.104)
Тогда полная производная по времени
1, 2, *) / Л д , • 5 , • 5
примет вид
dt
-h*
D.106)
Из D.103) и D.106) следует, что в пределах радиуса взаимодей-
взаимодействия | х± — х2 | ^ г0 (т. е. для ненулевой области взаимодей-
взаимодействия) интеграл в усредненном по времени уравнении BHi D.101)
будет равен
d2G12 .-L-U = j d2^J2 = \ ^L[f2{t + x)-f2(t)]. D.107)
При получении этого равенства мы использовали D.99). Подстав-
Подставляя в уравнение D.101) полученное выражение для интеграла
и пренебрегая единицей по сравнению с ЛГ, придем к следующему
уравнению:
4г + ^--^Г^+Ж1т-^(« + т)-/2(*)]=0. D.108)
Для дальнейшего преобразования интегрального члена этого
уравнения перейдем к системе координат, связанной с частицей 1,
и построим Stosszahlansatz-jijidLTipdLMMy (рис. 4.21). Однако вер-
вертикальный рассеивающий цилиндр имеет теперь высоту | |4—12 I T
вместо | |i —12 I Si. Элемент объема d3x2 равен sdsdy | |4 — |2 | т.
Переходя теперь в D.108) от р к |, получим следующее уравнение:
dt
дх<
= ЛГ j
i - Sa | [/2 (i) - U (t + x) J. D.109)
216 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара — Гросса и др.
Из условий D.104) следует, что функция /2 однородна на разме-
размерах области столкновений. Кроме того, эти условия означают
что /2 не зависит явно от времени, хотя может от него зависеть
через g4 и g2. Если в момент t + т скорости равны (g4, g2), To
в момент t они равны (gj, %>'2)- Напомним, что в результате инвер.
сивного столкновения начальные скорости восстанавливаются.
Внося соответствующие изменения в D.109), используя гипо-
тезу молекулярного хаоса (/2 = fji) и проведя ренормализацию,
так что 3F \ = Nfu придем к уравнению Больцмана.
Необходимые для предшествующего вывода неравенства D.104)
и уравнения D.101) и D.102а) интересны сами по себе. Они, в сущ-
сущности, определяют область применимости уравнения Больцмана.
Их можно сравнить с теми предположениями, которые понадо-
понадобились при выводе методом Больцмана и перечислены непосред-
непосредственно после уравнения D.77) (условия 1—4).
Таким образом, мы показали, что области применимости урав-
уравнения Больцмана, подразумеваемые каждым из трех приведенных
методов его получения, очень схожи между собой, как это и долж-
должно быть, поскольку они относятся к одному и тому же уравне-
уравнению — уравнению Больцмана. (Их также необходимо сравнить
с предположениями, которые делаются при выводе Боголюбова,
представленном в гл. III.)
4.4. Свойства больцмановского оператора столкновений
а) Сумматорные инварианты
В разделе 3.1 мы показали, что все гидродинамические пере-
переменные можно получить, зная функцию J^i. Отсюда следует, что
из верного кинетического уравнения должны получаться уравне-
уравнения движения для гидродинамических переменных (уравнения
гидродинамики). Таким образом, первое «испытание», которое
должно пройти предлагаемое кинетическое уравнение, состоит
в том, что оно должно привести к уравнениям гидродинамики.
Их также называют макроскопическими уравнениями, гидродина-
гидродинамическими уравнениями и уравнениями сохранения. Для того
чтобы получить их из уравнения Больцмана, необходимо сначала
ввести понятие сумматорных инвариантов.
Напомним вид оператора столкновений /.
/(.Я see \\од&дЪР[&\&'-&х&\. D.110)
Отсюда следует, что
= j J J
4.4. Свойства болъцмановского оператора столкновений 217
?сли переменные интегрирования § и §! поменять местами, то мы
найдем, что
1(ф) = 1(ф1)- D.112)
рассмотрим теперь интеграл
d%<i>(l')V {&[&'-^ир). D.113)
Вводя (Z>[,V) B качестве переменных интегрирования (они связаны
с (?ь 1) уравнениями динамики столкновений), получим1)
Цф')=\ \ j odQd%d%'j, {l')V{&[&'-&&). D.114)
Поскольку о dQ и У —инварианты столкновений, последнее
выражение можно переписать так:
/ w)= - j И °'dQ' ^ ^'ф (I') v (jf^f - ^;^') = -^ ю-
D.115>
Наконец, если в D.114) поменять местами переменные интегри-
интегрирования (%, %'), мы получим
- D-116)
Объединяя эти результаты, будем иметь
41 (ф)*=1(ф) + 1 (фд-1(ф')-1(фд, D.117)
ИЛИ
Задача 4.22. Показать, что
а) /(ф)=4
4
б) /(<?)=
Задача 4.23. При получении уравнений D.112) и D.116) под-
подразумевалось, что a dQ является инвариантной величиной. Какие-
конкретные свойства инвариантности здесь участвуют?
Функция я)) (|) является сумматорным инвариантом (или
инвариантом столкновений) тогда и только тогда, когда
ь + •ф = •ф; + v, D.H8)
т. е. когда \|) представляет собой свойство молекулы, сохраняю-
сохраняющееся при столкновении. Объединяя последнее определение-
1) Произведение d3^3^ является инвариантом Пуанкаре.
218 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара — Гросса и др.
с уравнением D.117), получим, что
Ш = 0, D.119)
если г[) —инвариант столкновения. Существуют три фундамен-
фундаментальных сумматорных инварианта: 1, §, ?2. Эти функции свя-
связаны с тремя законами сохранения (вещества, импульса и энер-
энергии):
7(^) = о. D.120)
Задача 4.24. Доказать, что оператор / линейный, т. е. что
Задача. 4.25. а) Определить достаточное условие существова-
существования равенства
Ъ d d' Ъ'
j j Y(z, y)Z(y)dxdy = J j У(гл x)Z(x)dydx.
а с с' а'
б) Каков будет вид интеграла
ь
1= ]z[x(ij)\W{y)dy,
а
если произвести преобразование переменных
у-+у* = х (у).
В следующем разделе мы покажем, как от этих сумматорных
инвариантов можно легко прийти к уравнениям сохранения.
Другие свойства оператора столкновений будут обсуждены в гл. V.
б) Уравнения сохранения
При рассмотрении уравнений сохранения используются два
различных способа представления гидродинамических переменных.
Во-первых, их можно вычислять в фиксированной системе коор-
координат, где скорость равна |. Такая формулировка приводит к так
называемой нормальной консервативной форме уравнений сохра-
сохранения. Переменные р, u, e, p, q —это абсолютные макроскопиче-
макроскопические переменные. Их определения через функцию $р и уравнения,
которым они удовлетворяют, представлены следующими равенст-
равенствами:
JL u = 0, D.121а)
dt
n= \&д?\; D.1216)
4.4. Свойства болъцмановского оператора столкновений 219
^ F D.122а)
D.1226)
~ne + V.q = pK'U, D.123a)
\ j D.1236)
D.124)
D.125)
K=^-. D.126)
Чтобы получить три уравнения сохранения D.121—4.123),
мы просто подействовали на уравнение Больцмана
тремя операторами I &ъ\\ I ?d3?; \ ?2d3?. Используя D.120),
мы получим
D.128)
Хотя при такой записи уравнений сохранения (в абсолютных
переменных) физический смысл их ясен, этого мы не можем
утверждать относительно самих переменных (особенно е, р, q).
Например, внутреннюю энергию более уместно вычислять в ло-
локальной системе координат, движущейся с жидкостью, где ско-
скорость частицы будет равна с (например, температура воды в ста-
стакане не зависит от движения стакана как целого). Эти относи-
относительные макроскопические переменные определяются следующим
образом (см. C.6) и C.8)):
п%^\т j ^c*d% D.129)
F=m jycccPg, D.130)
jn j^cc2d3g D.131)
220 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара — Гросса и др.
Если в эти соотношения подставить с = § — и, то в результате
получим:
Р пп^ D.132)
D.133)
u-^. D.134)
Внося эти выражения в нормальную форму уравнений сохране-
сохранения D.121) — D.123), получим обычный вид уравнений сохране-
сохранения для относительных переменных (Р, Q, %\.
=
Zl_l_V.us + P: Vu + V.Q-0. D.136)
В этом уравнении e является энергией единицы объема. Она
связана с % (энергией, отнесенной к одной частице) и р соотно-
соотношением
е = п% =\т j с*?д?\--=\ р = ±пкТ, D.137)
которое служит также для определения температуры Т. Констан-
Константа пропорциональности к —это постоянная Больцмана. Часто
встречается другая форма записи уравнения D.136). Введем сим-
симметричный тензор скоростей деформаций Л:
Тогда уравнение D.136) примет вид
Jl+V.ue + V.Q + F: Х = 0. D.139)
Задача 4.26, а) Доказать, что Р : Vu = Р : Л.
б) Для Ptj = 8tjp доказать, что Р : Л = pV-u.
в) Вычислить Тг Л.
Дифференциальный оператор
! = JL + «-V D.140)
иногда называют индивидуальной производной. Действуя на функ-
функцию от х и t, он дает скорость изменения функции в системе коор-
координат, движущейся с локальной скоростью и (или, как говорят
в гидродинамике, вдоль линий тока). Поскольку относительные
гидродинамические переменные определяются через относитель-
4.4. Свойства болъцмановского оператора столкновений 221
иую скорость с = | — и, то, естественно, что многие из предше-
предшествующих уравнений определяют скорость изменения этих пере-
переменных не в фиксированной системе координат (d/dt), а в системе
координат, движущейся с локальной скоростью (д/dt + u-V).
Именно в этой системе координат, если ограничиться адиабатиче-
адиабатическими невязкими течениями, уравнение энергии приводится к хо-
хорошо известному виду. Количественно эти ограничения выгля-
выглядят так:
V.Q = 0.
p = ±TrP. D.141)
При этом уравнение энергии D.136) примет вид
Объединяя его с уравнением неразрывности и исключая
получим
<4-143>
Из этого фундаментального уравнения следует, что величина
-^- = const D.144)
вдоль линий тока. Уравнение D.143) называется адиабатическим
законом.
Интересное различие между уравнениями сохранения для
относительных и для абсолютных переменных заключается в том,
что в уравнении относительной энергии не проявляется какое-либо
непосредственное действие силового поля К (см. уравнение D.136)).
В уравнение Больцмана макроскопическая сила К входит в виде
члена
As-.4- = K-4* D.145)
Уравнение для относительной энергии % получается, если на
уравнение Больцмана подействовать оператором
0= j d3g-J-mc2. D.146)
Когда оператор б действует на AjF, то в результате получается
= —pK.(u — u) = 0. D.147)
222 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара — Гросса и др.
С другой стороны, внешнее силовое поле К непосредственно влияет
на абсолютную энергию е. Это легко показать, действуя на Д^г
оператором абсолютной энергии
*l\ml\ D.148)
В результате получим правую часть уравнения D.123а), так что
внешнее силовое поле оказывает непосредственное влияние на из-
изменение во времени абсолютной энергии е.
Из абсолютных уравнений сохранения явно видно, что физиче-
физические переменные (например, п, ри, пе) изменяются во времени
вследствие дивергенции соответствующих переменных типа век-
векторов потока (например, mi, р, q). Если вычислить интеграл
по конечному объему от любого из уравнений D.121) — D.123),
то мы придем к заключению, что изменение любого конечного эле-
элемента плотности, импульса или энергии обусловлено только
полным несбалансированным потоком этих величин через замкну-
замкнутую поверхность, ограничивающую рассматриваемый элемент
объема. Это точно выполняется для плотности числа частиц, неза-
независимо от того, действует или нет внешняя сила К. Независимо
от присутствия внешнего поля частицы сохраняются. Однако
законы сохранения импульса и энергии справедливы только для
изолированных систем, или, что эквивалентно, для сцстем, на
которые не влияет внешнее силовое поле. Если на систему дейст-
действует поле К, то оно влияет на изменение во времени импульса ри
и энергии пе согласно D.122а) и D.123а).
Однако для некоторых частных силовых полей возможно
записать эти потоковые члены в виде
D.149)
D.150)
Здесь Г — это плотность импульса, связанного с силовым полем К,
Q — напряженность поля, U — плотность внутренней энергии
поля и S — вектор проводимости энергии поля. Подставляя эти
соотношения в абсолютное уравнение импульсов D.122а) и абсо-
абсолютное уравнение энергии D.123а), вновь придем к нормальной
консервативной форме этих уравнений:
L D.151)
D.152)
Очень хороший пример формализма, связанного с гидродина-
гидродинамическими полями, дает плазма. Плазма состоит из частиц трех
4.4. Свойства болъцмановского оператора столкновений 223
сортов —нейтральных молекул, ионов и электронов. В гидро-
гидродинамическом пределе плотность частиц достаточно велика, так
ЧТО пла&ма хорошо описывается уравнениями гидродинамики.
Соответствующими переменными будут плотность (полная) час-
тйЦ п (частица — это ион, электрон или молекула), напряжение р,
макроскопическая скорость и и тепловой поток q. Все эти четыре
переменные связаны с гидродинамическим описанием плазмы
з целом в противоположность переменным, относящимся к инди-
индивидуальным компонентам (например, плотность электронов). Гид-
Гидродинамическое описание завершают следующие переменные:
плотность заряда д, ток J, электрическое Е и магнитное В поля.
Уравнения сохранения имеют вид:
4гП + Х?.пи = 0, D.153)
eft
д
?fi <-—, D.154)
:В, D.155)
D.156)
' DЛ57>
V.B = 0, D.158)
VxE=-f, D.159)
V.E = ^- . D.160)
Последние четыре уравнения этой системы {уравнения Макс-
Максвелла) связывают поля с током и плотностью электрического
заряда системы. Здесь с —скорость света, [i0, 80—соответствен-
80—соответственно магнитная и диэлектрическая проницаемость вакуума (в МКС).
Уравнения импульса D.155) и энергии D.156) не соответствуют
нормальной консервативной форме записи уравнений сохранения.
Однако, используя уравнения Максвелла, легко показать, что
мы можем записать силовой член в уравнении импульсов в виде
xB=—^-Г —V-Й D.161)
11 член типа источника в уравнении энергии как
J.E=—^-ff-V.S. D.162)
Подставляя эти выражения в уравнения D.155) и D.156) соот-
ветственно, получим нормальную форму уравнений сохранения.
224 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара — Гросса и др.
Новыми переменными, характеризующими электромагнитное поле
являются: '
Г = 80ЕхВ —плотность импульса поля, D.163)
— ( е0ЕаЕ$ Н j — тензор напряжений Максвелла, D.164)
S = — Е X В = с2Г — вектор Пойнтинга, D.165)
И-о '
1 / 1 \
U = -тр ( е0Е2-| В2\ —плотность энергии поля. D.166)
Задача 4.27. Получить приведенные выше выражения для
Г, Q, S, U из уравнений Максвелла.
Задача 4.28. Пусть макроскопическая переменная (Л*) опре-
определяется согласно равенству
Используя уравнение Больцмана, доказать, что (Л*) удовлетво-
удовлетворяет следующему уравнению:
JL {п (Л*)) + п (Л*) -А. u + -А. (п (Л*с>) -
Это уравнение часто называют максвелловским уравнением переноса.
Задача 4.29. Каково различие между уравнениями импульсов,
полученными из уравнения Больцмана и из BHi уравнения
(см. разд. 3.6)?
в) $6-теорема Болъцмана
Рассмотренные выше свойства больцмановского оператора
столкновений приводят нас к выводу, что из уравнения Болыгмаяа
вытекают макроскопические уравнения сохранения. Все кинети-
кинетические уравнения должны удовлетворять этому требованию*
Однако то свойство оператора /, которое мы хотим сейчас обсу-
обсудить, не обязательно должно выполняться для всех кинетически*
уравнений. Это свойство подразумевает существование динами-
динамической функции, убывающей со временем. Из трех свойств опера-
оператора столкновений Больцмана это свойство исключительно #о
4.4. Свойства болъцмановского оператора столкновений 225
с точки зрения физики. Из него следует, что особая динамическая
величина — (^-функция Больцмана рассматриваемой системы —
ведет себя необратимым образом, давая предпочтение одному
направлению течения времени перед другим. Она убывает при
прямом течении времени и возрастает при обратном.
с^-функция Больцмана (так называемая энтропия Болъцмана)
определяется уравнением
^j\i\jd%dzx. D.167)
Аналогичная функция для fN
S?N = { fN In fNdld2 ... dN D.168)
называется энтропией Гиббса. Напомним, что fx удовлетворяет
уравнению Лиувилля:
-^=-^+[/w, Я] = 0, D.169)
где Н — гамильтониан для N частиц. Из этого уравнения следует,
что
45 ^г<И ...dN = 0. D.170)
Таким образом, 3?N подчиняется обратимому уравнению и явля-
является константой.
Функция St, jv связана с неравновесной термодинамической
энтропией S соотношением
S = -kSEN, D.171)
где к —постоянная Больцмана. Это уравнение дает чисто кине-
кинетическое описание энтропии для изолированной системы из N
частиц. То, что из уравнения Лиувилля следует постоянство
питропии S, согласуется со вторым законом термодинамики,
который утверждает: если в изолированной системе происходит
какой-либо процесс, то A«S ^ 0, причем равенство имеет место для
обратимого процесса. Поскольку уравнение Лиувплля относится
к изолированной системе и включает только обратимые процессы,
то вытекающее из него постоянство S, как мы видели, согла-
согласуется с термодинамикой.
Вблизи равновесия (для нулевых взаимодействий)
226 Гл. IV. Уравнения Болъцмана, Крупа — Бхатнагара — Гросса и др.
И
N N
>=1 z=1 D.172)
n ^(]
3 = 1
Отсюда получается хорошо известное выражение для энтропии,
данное Больцманом:
S= —Nkffl. D.173)
Свойство обратимости уравнения означает, что если уравнение
имеет решение для возрастающего времени, то оно также должна
содержать решение для убывающего времени. Уравнение (выте-
(вытекающее из больцмановского), которому удовлетворяет энтропия
Больцмана, не обладает этим свойством. Из него следует, что Ж
убывает со временем (Ж <СО). Кроме того, Ж становится постоян-
постоянной для некоторого частного вида функции / — для распределения
Максвелла, которое описывает равновесное состояние газа. Этот
важный факт впервые был экспериментально установлен Цартма-
ном в 1931 году.
То, что функция Ж всегда убывает со временем, есть необра-
необратимый закон, ибо если мы «наблюдаем» возрастание Ж, то мы
должны прийти к заключению, что на этом интервале время течет
в обратном направлении. С другой стороны, если перемещение
свободной частицы происходит согласно неравенству х > 0, то это
не является необратимым законом. Существует другое, также
верное решение, которое удовлетворяет условию я<0 (а именно
отраженное движение рассматриваемой частицы). «Закон», управ-
управляющий движением свободной частицы, — это х = 0. Он допускает
как возрастающие (х > 0), так и убывающие (х < 0) со временем
решения. «Закон», которому подчиняется Ж {Ж < 0), допускает
только убывающие решения (для времени, текущего в прямом
направлении).
Формулировка о&'-теоремы Больцмана начинается с уравне-
уравнения Больцмана:
где У —оператор столкновений Больцмана. Напомним также, что
все символы Fi, F, /i, /, jFi и ер изображают одыочастичную функ-
функцию распределения. Они отличаются тем, что соответствуют раз-
различным нормировкам функции.
4.4. Свойства болъцмановского оператора столкновений 227
Действуя на D.174) оператором \ d3xd3^(l + ln/), получим
= \ d%d3xJ(f) A + In /)= j /(l + ln/)#;r. D.175)
Оператор / определяется выражением D.111). Свойство /, зада-
задаваемое соотношением D.117), позволяет нам записать:
D.176)
Среднее равенство справедливо ввиду линейности оператора /.
Явный вид этого уравнения следующий:
47= - j d% j d^odQViff-hftln (M.) . D.177)
Если мы обозначим f[f ^ X и fJ==Y, то уравнению D.177)
можно придать более компактную форму:
4/= — f d3^ (P^adQF (X—У) In (у-) =
X, У). D.178)
Функция L (X, Y) определяется как
) D.179)
Все значения X и Y таковы, что X и Y положительны и либо
X = У, либо X > У, либо X < У. Для X = У имеем L = 0.
Для X > У и X < У имеем L > 0. Следовательно,
L > 0, D.180)
п равенство справедливо тогда и только тогда, когда X = У.
Остальные множители в интеграле D.178) все либо больше нуля,
либо равны нулю: д?\д?\^ — элемент объема в пространстве ско-
скоростей, odQ — площадь поперечного сечения, V — модуль ско-
скорости. Итак, мы заключаем, что
/ A + In/) <0. D.181)
^бперь докажем, что равенство имеет место тогда и только тогда,
fj' = fju Достаточность непосредственно следует из того
, что L = 0, когда ff = Д/. Для доказательства необходи-
228 Гл. IV. Уравнения Болъцмана, К рука — Бхатнагара — Гросса и др.
мости заметим, что оставшиеся множители в интегралу все поло-
положительны либо равны нулю, так что для всех значений |4, таких,
что V фО и odQ фО, L должпа равняться нулю, чтобы опера-
оператор J обратился в нуль. Но VodQ = 0 тогда и только тогда, когда
нет столкновений. Следовательно, для всего спектра (|ь |)ч
который включает конечные столкновения, условие f[f = frf
является необходимым для обращения в нуль оператора /.
Обратимся к формулировке <$f-теоремы. Если неравенство
D.181) подставить в D.175) и использовать определение Ж соглас-
согласно D.167), то мы получим
-d3ldsx-?C0. D.182)
Используя теорему Гаусса, объемный интеграл можно преобразо-
преобразовать в поверхностный. Если 2Х —поверхность в конфигурацион-
конфигурационной части фазового пространства, a S^ —поверхность в простран-
пространстве скоростей, то уравнение D.182) примет вид
^/1п/<0. D.183)
Если система ограничена, то / -> 0 при х-+- оо и / -> 0 при ?• -> оо,
поскольку не существует частиц с бесконечными скоростями.
Опуская поверхностные члены, окончательно будем иметь
——<.О. D.184)
Для произвольной начальной функции / функция Ж монотонно
убывает до момента, когда начинает выполняться равенство f[f =
= /]/, после чего Ж все время остается постоянной.
Важное следствие функционального уравнения для /, f[f =
= /j/, заключено в следующей теореме: если газ находится в рав-
равновесии, то f[f = /i/. (Это условие часто называют условием
детального, или статистического баланса.) Эта теорема была
впервые установлена Максвеллом A867), а затем Больцманом
в связи с его c$f-теоремой A872). Справедливость ее можно пока-
показать следующим образом. Если газ находится в равновесии, то
Следовательно,
D.186)
Первая цепочка равенств следует из определения Ш, согласно
которому
¦?A + 1п/). D-187)
dt
4.4. Свойства болъцмановского оператора столкновений 229
Если К = 0, и / — функция только §, то прямо из уравнения
Больцмана D.72) следует, что равенство f'J' = fj является также
достаточным условием равновесия.
Задача 4.30. Показать, что уравнение для \flnfdl, которое
следует из БИ^ обратимое.
Задача 4.31. Рассмотреть случай, когда К = 0. Показать, что
произвольная функция / = / (|) не может быть равновесным
решением.
Указание. Используйте уравнение Больцмана для получения
противоречия. Отметим тот факт, что если даже dfldt — 0, то
данная функция / не обязана быть (совместимым с налагаемыми
условиями) равновесным распределением.
Подведем итог.
1. Условие f'J' = /i/ является необходимым для равновесия.
Если внешнее силовое поле отсутствует и / зависит только от §,
то это условие также является и достаточным условием равнове-
равновесия.
2. Равенство f'J' = fj является необходимым и достаточным
условием стационарности SB.
3. Для того чтобы / была постоянна во времени, необходимо,
чтобы SB обладала этим же свойством.
г) Распределение Максвелла
Физический смысл функционального уравнения fj' = fj впол-
вполне очевиден. Теперь возникает вопрос относительно метода реше-
решения такого уравнения. Решив его, мы получим функцию распре-
распределения, которая является как необходимой, так и достаточной
для равновесия, при условии что внешние силы отсутствуют и / за-
зависит только от |. Обозначив решение этого уравнения индексом
нуль, паходим
Гн /,' = /о/о, D.188)
гДе /о — равновесная одночастичная функция распределения.
Прологарифмировав это равенство, получим
In f4 + In /; = In /Oi + In /0, D.189)
или, в более явном виде,
In /о (Ю + In /о (Г) = In /о (It) + In /о A). D.190)
Далее, любое свойство У молекулы, удовлетворяющее уравнению
= ^1 + ^, D.191)
является инвариантом столкновения, т. е. оно сохраняется при
столкновении. Обратно, если свойство *§ сохраняется при столк-
23С Гл. IV. Уравнения Болъцмаиа, Крука — Бхатнагара — Гросса и др.
новении, то оно удовлетворяет уравнению D.191). Отсюда следует,
что самое общее решение уравнения D.190) является линейной
комбинацией всех величин, которые сохраняются при столкнове-
столкновении. Это — три компоненты скорости, энергия и числовая постоян-
постоянная; таким образом
In /о = -А (I - loJ + In Я, D.192а)
или, что эквивалентно,
/о = В exV[-A (? - 1оJ]. D.1926)
Постоянные А, В и |0 определяются через плотность числа час-
частиц п, макроскопическую скорость и и температуру Т, которые
выражаются с помощью функции распределения. Чтобы отметить,
что эти макроскопические переменные вычисляются для равно-
равновесного состояния, им также приписывается индекс нуль. Возвра-
Возвращаясь к функции jFo = NfQ, напомним, что
Щ = j J^o d3l, nouo =
3n0RT0= j ^o(l-noJ^, D.193)
Отметим, что R не является «газовой постоянной», последняя
равна 31 = кА0, где Ао —число Авогадро.
Соотношения D.193) служат для определения постоянных |о»
А и В. В результате получим
Рассмотрим, например, как определяется |0- В декартовом
пространстве, где вектор |0 направлен вдоль оси z (|0 = кЫ*
будем иметь
= В j j j (itx + ilu + k?2) exp { - 4 [й + Й + (Hz - g0J]} X
X d%x dlv d\z = kS J j { L exp { - Л [(H2 - |oJ +
+ U + ll]}dlxdl!/dlz. D.195)
Остальные интегралы обращаются в нуль ввиду нечетности подин-
тегральных функций. Переходя от переменной |г к г) = |г — |о>
4.4. Свойства болъцмановского оператора столкновений 231
получим
«оио = kB j j j (г] +10) exp [ - Л (Ц + ?J + П2)] dg* <*?„ *1 =
D-196)
Следовательно, ?0 = ио- Отметим, что при интегрировании по г\
член с т] обратился в нуль, поскольку он является нечетным
вкладом в подинтегральную функцию.
В однородном случае (9/9х = 0) при отсутствии силового поля
(К = 0) JFo становится абсолютным распределением Максвелла.
Входящие в него функции п0, и0 и То не зависят от пространствен-
пространственных координат и времени.
Хотя абсолютное распределение Максвелла подразумевает
равновесное состояние и само вытекает из равновесия, оно
не является распределением самого общего вида, для которого SB
стационарна. $6 будет стационарной и в том случае, если п0, и0
и То (в выражении D.194)) являются функциями х и t. Очевидно,
что функция такого вида удовлетворяет уравнению D.188). Если
в равенстве D.194) п0, и0 и То выбрать так, чтобы они представля-
представляли собой фактическую числовую плотность, макроскопическую
скорость и температуру газа (в точке х в момент ?), то Jf0 перейдет в
Эта функция называется локальным распределением Максвелла.
Она обладает двумя очень важными свойствами: а) первые пять
моментов функций Jf° и Jf совпадают:
D.198a)
D.1986)
uJd3g; D.198b)
б) если спустя некоторое время jF = jF°, то SB становится посто-
постоянной г).
Обычно считают, что при подходе к равновесию сначала уста-
устанавливается локальное максвелловское распределение. Отметим,
что на этой конечной стадии описания системы функция рас-
распределения определяется через п, и и Т. Таким образом, мы полу-
получаем грубое представление о переходе от (боголюбовской) кине-
кинетической стадии к гидродинамической стадии. На первой из них
*) Проблемы, возникающие при таком локальном равновесии в сравнении
абсолютным равновесием, рассматривались Трэдом A965).
232 Гл. IV. Уравнения Болъцмана, Крупа — Бхатнагара — Гросса и др.
состояние газа определяется одночастичной функцией распределе-
распределения, которая в свою очередь подчиняется уравнению Больцмана.
Эволюция системы характеризуется функцией SB, которая моно-
монотонно убывает. Когда SB приближается к своему минимальному
значению, устанавливается локальное распределение Максвелла.
Здесь / определяется через п, и и Г, и система находится в гид-
гидродинамической стадии. Затем система релаксирует к абсолютно-
абсолютному равновесию, когда динамические функции не зависят от про-
пространственных координат и времени. Механика этого последнего
этапа релаксации описывается гидродинамическими уравнениями.
Задача 4.32. Как изменяется 3? при переходе / от локального
к абсолютному максвелловскому распределению?
То, что с помощью уравнения Больцмана нельзя описать
релаксацию к абсолютному равновесию, объясняется приближе-
приближениями, присущими интегралу столкновений. Дело в том, что-
он не чувствителен к изменениям в пространстве и времени.
На конечной же стадии релаксации к абсолютному равновесию
изменяются именно эти два параметра, и только они.
д) Неоднородный газ во внешнем силовом поле
Рассмотрим опять уравнение Больцмана D.174), когда К =^0
и д/дх фО. Мы хотим получить равновесное распределение
и в этом случае.
Сила К консервативная, так что она может быть выведена
из потенциала Ф:
К=—g-. D.199)
Если sp такова, что
?.i?l_ M>.ifo.J_ /4 200>
и
/(#„)= 0, D.201)
то распределение JF0 является равновесным, и при этом из урав-
уравнения Больцмана следует, что d^ro/dt = O.M.1 обратно, чтобы быть
равновесным, распределение jFo H© может явно зависеть от вре-
времени.
Далее, jF будет удовлетворять уравнению D.201), если jFi'jF'^
= 3*'iJF'• Поскольку последнее уравнение налагает ограничение
только на скорости, его решение самого общего вида задается
не соотношением D.192а), а выражением, содержащим дополни-
дополнительное слагаемое:
. D.202)
4.5 Уравнение Крука — Бхатнагара — Гросса 233
0одставляя его в D.200), получим, что % —это потенциал Ф,
при условии что go* ^Ф = 0- Обращением уравнения D.202)
является
D-203)
Параметры п0, и0 и Го являются константами, и вектор и0 норма-
нормален к VO. Равновесная плотность числа частиц задается выра-
выражением
j [^] D.204)
так что п0 — это значение п при ф = 0. Равновесная температура
определяется следующим образом:
3n(x)RT= J #оA-ИоJ^=--3/2оЙГоехр [-^-], D.205)
следовательно, постоянная Го равна значению Т при ф = 0.
Задача 4.33. Вычислить равновесную скорость газа при нали-
наличии внешнего потенциала.
4.5. Уравнение Крука — Бхатнагара — Гросса х)
В предыдущем разделе мы пришли к заключению, что из кине-
кинетического уравнения должны получаться уравнения сохранения.
Более «ценное» кинетическое уравнение будет также давать
релаксацию к равновесному состоянию. Однако если оно описыва-
описывает этот процесс, то получаемое равновесное состояпие должно быть
максвелловским. Больцман A877) впервые показал, опираясь
на равновесную статистическую механику, что физически кор-
корректное равновесное состояние является максвелловским состоя-
состоянием. В статистической механике максвелловское состояние
называется каноническим. Этот подход будет подробно обсуждать-
обсуждаться в гл. V.
Уравнение, обладающее всеми желаемыми свойствами, и в то
же самое время вполне простое по форме, — это уравнение Крука —
Бхатнагара —Гросса. С целью обоснования этого уравнения рас-
рассмотрим опять оператор столкновений Больцмана J (jf), который
можно записать в виде
J . D.206)
г) Гросс, Бхатнагар, Крук A954). Это уравнение часто называют КБГ-
Уравнением.
234 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара — Гросса и др
Во втором члене мы вынесли функцию JF за знак интеграла
поскольку она не зависит от |1# Напомним теперь, что штрихам^
обозначены переменные, соответствующие состоянию после столк-
столкновения. Скорости (!, Ю до столкновения переходят в скорости
{%', Ъ?) после столкновения. Предположим, что система прибли-
приближается к равновесию, т. е. к максвелловскому состоянию. Восполь-
Воспользовавшись результатами ^-теоремы, придем к заключению, что
будет существовать такое время, когда функция ^ станет локаль-
локальным максвелловским распределением. В интервале времени
представляющем близкую окрестность этого критического значе-
значения, система характеризуется тем свойством, что распределение
более близко к максвелловскому после столкновения, чем д0
столкновения. Следовательно, можно считать, что в некоторый
момент времени, близкий к равновесному, Jfr =?pQr. Вводя это
предположение в D.206), получим:
~ J jF*'&1TVodQ(Pti-& j ^.Vadud^. D.207)
Но так как jF0' —максвелловское распределение, то JF0'jFi°' =
— JF°jFj- Следовательно, выражение D.207) сводится к следую-
следующему:
J(&) = &* J ^VodQd^-^ j jf.VodQd^. D.208)
Вспомним теперь, что jF° обладает некоторыми общими свой-
свойствами с распределением ер\ их первые пять моментов (по скоро-
скоростям) совпадают (см. D.198)). Если мы предположим, что осталь-
остальная часть подинтегрального выражения в D.208) разложена по сте-
степеням \и то эти интегралы станут не чем иным, как суммой момен-
моментов функций $р\ и jFi- Первые пять из этих членов будут равны
согласно определению jF°- Оставшиеся члены уменьшаются с при-
приближением к равновесию.
Задача 4.34. Вычислить Q и Р, если $F = jF°.
Если все это учесть, то мы получим окончательную форму J
для КБГ-уравнения:
D.209)
v (!) = j &\Ve dQ d%. D.210)
Функция v называется частотой столкновений. Произведение
v (|) d3? представляет собой число столкновений, испытываемых
в единицу времени частицами, имеющими скорости в интервале dz?
около !, причем состояние частиц описывается функцией распре-
распределения Максвелла. Хотя соотношение D.210) дает точную меру
частоты столкновений при равновесии, более общее выражение
4.5. Уравнение Крупа — Бхатнагара — Гросса 235
Бключает $F± вместо JF?. Однако, как мы показали, в области при-
применимости КБГ-уравнения в выражении для v можно исполь-
использовать ^"J.
Полный вид КБГ-уравнения следующий:
??! D-2и»
Если это действительно кинетическое уравнение, то оно должно
обладать уже отмеченным свойством —необходимо, чтобы из него
получались уравнения сохранения. Если, к тому же, оно приводит
газ к равновесному состоянию, то оно является еще более полез-
полезным уравнением.
Чтобы упростить исследование этих свойств, рассмотрим част-
частный случай, когда частота столкновений v постоянна, т.е. когда v
не зависит от |. Подействуем на уравнение D.211) операторами
¦3?, т
Получим три уравнения сохранения, D.121) —D.123). Это еле
дует непосредственно из свойств jF°, заданных соотношениями
D.198). Возвращаясь к абсолютным переменным, будем иметь
-j
d3
2
Задача 4.35. При каких значениях а, Р, у, С функция
удовлетворять отношениям D.198)?
Рассмотрим теперь релаксационные свойства КБГ-уравнения.
Так как проблема установления равновесия прежде всего связана
с исследованием временной зависимости, то ограничимся рас-
рассмотрением однородного (д/дх = 0) случая без внешнего силового
поля (К = 0). При этих условиях уравнение D.211) примет вид
dffr v&°. D.212)
dt
236 Гл. IV. Уравнения Болъцмана, Крука — Бхатпагара — Гросса и д-р
Предполагается, что частота столкновений не является явной
функцией времени. С другой стороны, локальное распределен^
Максвелла зависит от времени через гидродинамические перемен-
ные /г, и и Т.
Проинтегрировав уравнение D.212), получим
g: (t) = ve-vt J e+vt>^o ^ dt* + ^ @) e-vtm (А.2Щ
о
Если jF° изменяется медленно по сравнению с e~vt, т. е.
99:0
дг
D.214)
то, вынося ^° из под знака интеграла, можно получить для него
хорошую аппроксимацию. В результате будем иметь
^ = ^о A __e-vt) + ^ @) e-vti D.215а)
так что
^^#° D.2156)
после нескольких столкновений.
Из КБГ-уравнения вытекает надлежащая релаксация к макс-
велловскому состоянию. Может показаться, что КБГ-уравнение
приводит к тем же выводам,что и уравнение Больцмана,и в то же
время обходит очень трудный анализ, навязываемый больцманов-
ским интегралом столкновений. В действительности кажущаяся
простота структуры КБГ-уравнения обманчива.
Рассмотрим прежде всего параметр v. Любые следствия, кото-
которые получаются из анализа КБГ-уравнения, существенно зависят
от параметра v. В приведенном выше «выводе» предполагалось, что
частота столкновений v есть взвешенный интеграл определенного
вида от локального максвелловского распределения jF°. Однако
этот «вывод» является не более чем обоснованием «типа наведения».
Мы могли бы просто постулировать это кинетическое уравнение
и показать, что из него следуют законы сохранения (при постоян-
постоянной v).
Задача 4.36. Как должны изменяться во времени п, и и Т,
чтобы не нарушалось условие D.214)?
Задача 4.37. Является ли условие постоянства v необходимым,
для того чтобы КБГ-уравнение давало законы сохранения?
Задача 4.38. Вычислить v, заданную выражением D.210), для
газа, состоящего из жестких сфер диаметра D. Получаются ли
уравнения сохранения из КБГ-уравнения с такой частотой v?
Задача 4.39. Для какого значения N в потенциале взаимодей-
взаимодействия f = K/rN частота v является постоянной?
4.6. Уравнение Фоккера — Планка 237
КБГ-уравнение, в которое входит внешний параметр v, явля-
являйся феноменологическим уравнением, поскольку оно не следует
логическим путем из некоторых исходных принципов, а, вернее
говоря, оправдано своей явно пригодной формой. Наличие такого
внешнего параметра, как v, — очевидная слабость КБГ-уравне-
ния. Получающиеся из него результаты зависят от v, и мы долж-
должны искать другие средства (отличные от КБГ-уравнения), чтобы
найти выражение для v. С этим феноменологическим свойством
КБГ-уравнения тесно связана и узкая область его применимости.
Приведенное выше обоснование типа наведения дает возможность
предположить, что КБГ-уравнение лучше всего подходит для
описания газообразных состояний, близких к равновесному,
т. е. находящихся в интервале, отделенном от максвелловского
состояния только несколькими временами столкновений. Это очень
узкая область.
В чем заключается кажущаяся простота КБГ-уравнения?
В том, что оно похоже па линейное неоднородное уравнение. Это
«сходство» можно увидеть, если записать КБГ-уравнение в сле-
следующей форме:
(^ + v)^ = v^«, • D.216)
которая наводит на мысль, что если gn h являются его решения-
решениями, то существует и решение (g + h)/2. Однако ошибочно рас-
рассматривать правую часть данного уравнения как неоднородный
член, не зависящий от JF. Это, скорее, (сильно) нелинейный
оператор от $р. Чтобы показать это, напомним, что JF0 содержит
фактические значения п, и и Т для газа, которые в каждый момент
времени и в каждой точке определяются функцией j^\ Таким обра-
образом jF определяет ??,ии 7\ которые в свою очередь определяют jF°.
Чтобы обнаружить, что КБГ-уравнение сильно нелинейно, надо
просто записать jF° как явную функцию от Jf. Тогда мы увидим,
что КБГ-уравнение намного более громоздкое, чем уравнение
Больцмана.
Задача 4.40. Записать КБГ-уравнение, заменяя jF° на jFV Бу-
Будут ли в этом случае следовать из него уравнения сохранения?
Задача 4.41. Следуют ли уравнения сохранения из уравнения
Власова (см. разд. 3.4)?
4.6. Уравнение Фоккера — Планка *)
а) Столкновения при дальнодействии
В главе III мы встречались с понятием радиуса взаимодей-
взаимодействия г0. Что характеризует процесс столкновения между двумя
частицами, потенциал взаимодействия которых является далъно-
*) Фоккер A914), Планк A917).
238 Гл. IV. Уравнения Болъцмана, Крупа — Бхатнагара — Гросса и др.
действующим} При дальнодействии, как бы велик ни был прицел^
ный параметр, частицы все же обмениваются конечными импуль^
сами. Концепция дальнодействия первоначально была введена
Истинный путь
частицы
Аппроксимирующая
траектория
Рис. 4.28. Вычисление &рх для дальних столкновений.
в кинетическую теорию газов при вычислении некоторых интегра-
интегралов. Эти интегралы связаны с различными макроскопическими
свойствами системы, как, например, вязкость, теплопроводность.
Такие параметры называются коэффициентами переноса. Они
будут подробно исследованы в гл. V.
Чтобы выяснить смысл столкновений при дальнодействии,
обратимся к вычислению полного импульса, сообщенного в задан-
заданном направлении пробной частице в результате столкновений
за единицу времени с остальными частицами газа. Разобьем все
4.6. Уравнение Фоккера — Планка 239
столкновения на два вида в зависимости от того, является
прицельный параметр s меньше либо больше некоторой харак-
характерной величины s0. Столкновения, прицельный параметр которых
больше 50, называются дальними столкновениями. Для достаточна
больших s можно ввести некоторые упрощающие предположения,
которые значительно облегчат вычисления. Например, чтобы
получить грубую оценку приращения импульса при дальних
столкновениях, считаем, что скорость рассеиваемой частицы
постоянна.
Пусть 8рх —импульс, сообщенный пробной частице в случае
единичного (дальнего) столкновения, вычисленный в системе
координат ЦМ, как изображено на рис. 4.28.
Пусть движение газа двумерное (в плоскости рис. 4.28). Кроме
того, нас интересует только тот вклад в 8рх, который обусловлен
частицами, движущимися в направлении +у со скоростью v.
Пусть плотность п (число частиц на единицу площади) таких
частиц однородна. Двумерный газ простирается до х = —оо.
Полное приращение импульса Арх, сообщенное пробной частице
со стороны всех частиц, движущихся в направлении -\-у (за еди-
единицу времени), дается интегралом
оо
Дрх = f 8px (dsvAt) тг, D.217)
где Д? = 1. Если сила взаимодействия G такова, что прираще-
приращение &рх бесконечно, то G — далънодействующая сила. Если интег-
интеграл конечен, то сила G — короткодействующая. В такой схеме
легко классифицировать все силы взаимодействия, определяе-
определяемые законом степенной зависимости от обратных расстояний
между частицами
G = w~N, N = 1, 2, . . . . D.218)
Кулоновская (или гравитационная) сила получается, если поло-
полошить N = 2. Приращение импульса за столкновение, 8рх, связа-
связано с силой Gx соотношением
8рх= \ Gxdt. D.219)
— оо
Обращаясь к рис. 4.28, получим:
240 Гл. IV. Уравнения Болъцмана, К рука — Бхатнагара — Гросса и дп
Подставляя эти значения в D.219), получим
я
ус С у,
(&Рх)х = —кгт- \ sinN-1QdQ = —^—t^n- D ^^n
vs" г J vsIS~i •-•-ij
Задача 4.42. Доказать, что
где Г (х) —гамма-функция (см. Приложение 2).
Для N — 1 интеграл 1х = п. Для кулоновского случая /2=2.
Для JV = 3 интеграл /3= я/2. (Отметим, что всюду здесь мы вычис-
ляли абсолютные значения интегралов.) Для N ^ 1 импульс
/v —конечен. Подставляя выражение D.221) в D.217), получим
{Apx)N =xn/-v J в1-"*. D.222)
Для iV > 2 Дрх —конечно. Для /V<12 интеграл расходится.
Для кулоновского случая
) D.223)
S S0 I
расходимость логарифмическая.
Итак, мы пришли к выводу, что две силы взаимодействия при
N = 1 и N = 2 являются да л ьно действующими.
Задача 4.43. Вычислить (Ap)zv для трехмерного случая.
Расходимость обусловленной дальними столкновениями ком-
компоненты (Дрх) означает, что в кулоновском газе на движение
частицы оказывают значительно большее влияние дальние кол-
коллективные взаимодействия по сравнению со столкновениями
в ближней зоне. При-выводе уравнения Больцмана методом Трэда
(см. разд. 4.36)) для N = 2 мы должны были бы сохранить интеграл
столкновений дальней зоны, а столкновительный член ближней
зоны опустить. Интеграл столкновений ближней зоны дает урав-
уравнение Больцмана.
При другом подходе к выводу кинетического уравнения для
кулоновского газа исходят из того факта, что в этом случае доми-
доминирующую роль играют дальние столкновения. Но для боль-
большинства дальних столкновений углы столкновения малы. Этот
факт положен в основу двух наиболее известных выводов уравне-
уравнения Фоккера —Планка.
б) Вывод из уравнения Болъцмана
Уравнение Больцмана, которое получено в разд. 4.3а), учи"
тывает столкновения при всех значениях прицельного параметра-
4.6. Уравнение Фоккера — Планка 241
Хотя интеграл столкновения в уравнении Больцмана записан
через угол рассеяния dQ = dcp d cos Э, это эквивалентно интегри-
интегрированию по прицельному параметру, что следует из соотношения
sds = od cos 0. Область, где справедливо уравнение Фоккера —
Цланка, можно определить либо большими величинами прицель-
soro параметра, либо малыми углами столкновения. Важно
отметить, что это есть подобласть той области, где применимо
уравнение Больцмана. Это лучше всего проиллюстрировать сле-
следующим образом. Мы покажем, что для частного случая кулонов-
ского газа уравнение Фоккера — Планка следует из разложения
уравнения Больцмана в ряд Тейлора около нулевого угла столк-
столкновения.
Для кулоновского газа с силой взаимодействия
'«-''> D-224)
уравнение Больцмана имеет вид
В2__/
D.225)
Напомним, что V — это относительная скорость |t — |2, a (|t, |)
связаны с (|i, |') соотношениями:
?' = l+ a(a.V),
I г / VX D-226)
Если полярную ось направить по V, то яр — это угол между a
и V, а ф — азимутальный угол (см. рис. 4.23). Если преобладают
столкновения с малыми углами рассеяния, то |' — | и |j — |4
малы. Это позволяет разложить разность (jFiJF' — JFiJF) в ряд
Тейлора около |' = | и Ц = ?i. Соответствующие разложения
имеют вид:
D.227)
(Вспомните B.27) —экспоненциальное представление рядов Тей-
лора.) Оператор V —это оператор градиента в пространстве
скоростей. Выполняя в уравнении D.225) сначала интегрирова-
242 Гл. IV. Уравнения Болъцмана, Крупа — Бхатнагара — Гросса и др.
ние по ф и затем подставляя туда соотношения D.227), получим
= я cos2 г|> 12V- (V — Vi) pgr^ + L [sjn2 ^ (/F2 — Щ) +
L
+ 2cos2i|)VV] : [VT^i —2W4+fv] J^Tj} + ... . D.228)
Задача 4.44. а) Вычислить интеграл
б) Показать, что уравнение D.228) следует из уравнений
D.225) -D.227).
Расходимость последующих интегралов по i|) демонстрирует
дальнодействующую природу кулоновской силы. Угол (я— 2i|)) —
это угол отклонения вектора V (V = |4 — |), тогда как i|) есть
угол между а и V (рис. 4.7). Отметим, что i|) изменяется от нуля
до я/2. Следовательно, малые углы столкновения соответствуют
•ф я^ у, где оба интеграла по i|) расходятся. Чтобы интеграл по ф
был конечным, его «обрезают», т. е. проводят интегрирование
не от нуля до я/2, а от нуля до я/2 — 8. Тогда получаются два
сходящихся интеграла:
Я/2-8
\ cos2ib Vr1- = -In sineL
я/2-е
J y -y^-ln|sin8|. D.229)
Пренебрежение 1/2 по сравнению с логарифмом, согласуется с от-
отбрасыванием в рядах Тейлора членов с большим углом рассеяния.
Подставляя интегралы D.229) в уравнение D.225), выполняя
интегрирование по i|) и вычисляя интеграл по частям, получаем
нормальную форму уравнения Фоккера — Планка:
К
где
D.231)
4,6, Уравнение Фоккера — Планка 243
Задача 4.45. Показать, что V.6 = а, где V = д/д|.
Из уравнения Фоккера —Планка в форме D.230) можно
получить интерпретацию коэффициентов а и Ь. Коэффициент Ъ
управляет изменением во времени функции ?р следующим обра-
образом:
-^.=4&V\F. D.232)
(Предполагается, что тензор Ъ изотропен и не зависит от §.)
Оператор V2 представляет диффузию в пространстве скоростей.
Как возникает это упрощенное линейное уравнение диффузии?
Рассмотрим газ (с дальнодействующей силой взаимодействия),
находящийся в равновесии (максвелловском состоянии) с тепловой
скоростью С = УRT и плотностью п0. Пусть в момент t = О
в эту систему вводится небольшое число «холодных» частиц
(^г — п8 (!)). Эти холодные частицы взаимодействуют с максвел-
ловским фоном посредством коэффициента &, который вычисляется
для распределения Максвелла. Дальнейшее поведение холодных
частиц описывается (приближенно) уравнением D.232), согласно
которому возникает диффузия скоростей этих частиц от нуля до
нормального распределения
w (*) <4-233>
За время
г-!%—%- D.234)
холодные частицы «разогреваются» до равновесия с температу-
температурой Т,
Спустя время т начинает «действовать» коэффициент силы тре-
трения а, который стабилизирует распределение Максвелла. Вычис-
Вычисляя коэффициент Ъ для этого максвелловского распределения,
получим
Ь = -^-8 1пе-\ D.235)
где символом © обозначен безразмерный интеграл. Исключая Ъ
из выражений D.235) и D.234), получим
244 Гл. IV. Уравнения Болъцмана, Крука — Бхатпнагара — Гросса и др.
Это время релаксации часто выступает в вычислениях как время
которое необходимо для возвращения в равновесное состояние
газа, выведенного из равновесия.
Другой коэффициент в уравнении Фоккера —Планка, а,
называется коэффициентом трения. Влияние а на эволюцию
во времени функции в? определяется следующими членами урав-
уравнения Фоккера —Планка:
4т JF + b'-irJF = 0- D.237)
01 Oil I
(Предполагается, что а не зависит от |.) Общее решение этого
уравнения имеет вид
& = -Г A -а*). " D.238)
Вид этого решения говорит о том, что частицы «ощущают» силу
та. В зависимости от знака коэффициента а эта «самосила»
будет либо ускорять (а > 0), либо замедлять (а < 0) частицы.
Однако в более общем случае вектор а зависит от | и его знаку
нельзя придать такого явного смысла.
Предшествующий вывод уравнения Фоккера — Планка опи-
опирается на особенности кулоновского взаимодействия, а именно
на его дальнодействие. Теперь мы дадим другой вывод, который
следует непосредственно из того факта, что в системе преоб-
преобладают «скользящие» столкновения.
Задача 4.46. Предполагая, что частица движется только в од-
одном направлении, доказать, что для диссипации Рэлея
а = —ао1 (и Ъ = Ьо)
уравнение Фоккера —Планка дает равновесное решение jlFo-
Как а0 и Ьо выражаются через п0 и Го? Получаются ли при этих
значениях а и Ь уравнения сохранения?
в) Вывод из уравнения Чепмена — Колмогорова
Предположим, что частицы газа испытывают случайные пере-
перемещения в результате большого числа малых отклонений. Такой
стохастический процесс хорошо описывается условным вероят-
вероятностным распределением
П (S + AS I S; АО, D.239)
введенным в гл. II (уравнение B.200) и следующие за ним). Для
фиксированной скорости \ произведение
П (S + AS I S; АО d (I + А|) = ПЙА1 D.240)
представляет вероятность того, что скорость частицы | перей-
перейдет в | + AS за время Д?. Функция П удовлетворяет уело-
4.6. Уравнение Фоккера — Планка 245
вию нормировки:
j П (S + Д1 | 1; A*) dAl = 1 D.241)
й уравнению Чепмена —Колмогорова B.203):
П A, t\ So, t0) =
ASn(S, * I 1-A1, *-A*)II(S-AS, *-A* I So, *o). D.242)
Напомним обозначение: П (x \ у; t —10) = U (x, t \ y, t0). Чтобы
записать уравнение D.242) через jF, вспомним, что П — это одно-
частичная функция распределения / (|, t), которая содержит
начальные данные (см. B.200)). Отсюда следует, что если мы умно-
умножим уравнение D.242) на N (N —полное число частиц), то в ре-
результате будем иметь
^(lAl, t — Д*)ПA IS-AS; A*)<*AS. D-243>
j
При получении последнего уравнения мы считали, что П
не зависит явно от времени. Это предположение требует, чтобы
эволюция системы происходила таким образом, что изменение
состояния системы в момент t зависело бы только от ее состояния
в интервале времени Д? около t, но совершенно не зависело от
более ранней предыстории системы. Стохастический процесс,
который обладает этим свойством (т. е. процесс, происходящий
в момент t и зависящий явно только от состояния системы в этот
же момент ?), называется марковским процессом.
Задача 4.47. Какому уравнению будет удовлетворять ^, если
процесс ее развития не является марковским?
Абсолютно ясно, что в той области, где применимо уравнение
Фоккера —Планка (т. е. где доминируют столкновения при
дальнодействии), П обладает особым свойством. В обозначении
П (S + AS I 1; ДО = П A, AS) D.244)
это свойство запишется следующим образом: П (|, Д|) имеет пик
около AS = 0 (и гладко изменяется по |). В таком обозначении
интеграл в уравнении Чепмена — Колмогорова D.243) имеет
следующий вид:
Интеграл D.243) = j & A — AS, * - Д*) П (S - AS, A1) <*ДS.
D.245)
Подинтегральное выражениб является функцией трех переменных
1 — AS, t — Д?, Д|. Причем по первым двум оно изменяется глад-
гладко, но имеет пик по AS вблизи Д| = 0. Отсюда следует, что наи-
наибольший вклад в интеграл дает именно эта область около Д| = 0.
246 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара — Гросса и др.
Поскольку подинтегральное выражение изменяется гладко по пе-
переменной | —Д|, оно хорошо аппроксимируется разложением
в ряд Тейлора около любого значения | — Д|. Характерным зна-
значением этой переменной является | —то значение, при котором
подинтегральное выражение имеет максимум. Выполняя это раз-
разложение, мы не нарушаем характера зависимости функции П (? -,
— Д|, Д|) от переменной Д|. Эта зависимость такова, что подин-
подинтегральное выражение быстро убывает при удалении от Д| = 0.
is (*, у)
Линия
Рис. 4.29. Характерный вид функции 2(я, у).
Отсюда следует, что разложение подинтегрального выражения
в D.245) по переменной § — Д| в окрестности ? дает аппроксима-
аппроксимацию уравнения Чепмена — Колмогорова, пригодную для газа,
в котором преобладают столкновения дальнодействия. Чтобы
пояснить эту ситуацию, рассмотрим криволинейный интеграл
l(z,y)dT. D.246)
Кривая Г задается параметрическими уравнениями:
х = а — Z,
у = 1. D.247)
Она показана на рис. 4.29. Тогда интеграл % записывается явно:
= J E(a-Zs
D.248)
Пусть теперь функция S (#, у) имеет пик около оси х, т. е. при
у = 0, и довольно однородна по ж при любом фиксированном у.
4.6. Уравнение Фоккера — Планка 247
что производные дпЕ/дхп малы. Для такой функции разло-
разложение
является хорошей аппроксимацией и быстро сходится. Полагая
Хо = а, х = а — Z, у = I и внося это разложение в выраже-
выражение D.248), получим
D.250)
Записанное таким образом подинтегральное выражение дает зна-
значение В в точке кривой Г через ряд Тейлора около линии х = а.
Это разложение является хорошей аппроксимацией особенно для
функций типа В, рассмотренной выше и представленной на
рис. 4.29. Наибольший вклад в интеграл % получается в точке
х = а, у = 0, где функция В имеет максимум. Это такая точка,
где Г-линия пересекается с линией х = а, так что именно это
значение подинтегрального выражения входит в аппроксима-
аппроксимацию D.250). Для больших у значения функции S при х = а
и на кривой Г становятся различны, и, чтобы это учесть, необхо-
необходимо в разложении для S удержать большее число членов. Одна-
Однако, поскольку S быстро уменьшается при удалении от оси х,
то вклад в интеграл % в этой области мал, и достаточно ограничить-
ограничиться несколькими первыми членами разложения D.250), чтобы полу-
получить хорошую аппроксимацию для %. Эта .качественная оценка
тем точнее, чем быстрее спадает функция S с удалением от оси г/.
Для уравнения D.243) имеет место именно такой тип разло-
разложения:
J Al. D.251)
Разлагая подинтегральное выражение около | — А| = | опи-
описанным выше способом и удерживая члены до О [(А|J] включи-
включительно, получим
, t)=
щ
1
J- D.252)
248 Гл. IV. У равнения Болъцмана, Крупа — Вхатнагара — Гросса и др.
Интегрируя полученное выражение по всем Д| и вспоминая
условие нормировки D.241), придем к соотношению
У (S, *) = .F(S, t) -Д* Щ—^-.р j Д|П A,
- D.253)
При выводе уравнения D.253) из D.252) было учтено, что функ-
функция J^, которая фигурирует в рядах Тейлора в D.252), не зависит
от Д|, так что ее можно вынести за знак интегралов по Д|.
Введем определения:
D.254)
D.255)
. D.256)
Тогда уравнение D.253) сведется к следующему:
dt
столки
Величина д^ / dtcrj:omm представляет скорость изменения $р
вследствие столкновений, при условии что доминирующий вклад
в такое изменение дают «скользящие» столкновения. Опять пола-
полагая D^plDt равной этому изменению вследствие столкновений,
получим
dZF ? dgF К d$F __
. D.257)
Это есть уравнение Фоккера — Планка. Необходимо отметить, что
предположения, перечисленные в том разделе, где было выведено
уравнение Больцмана, опять имеют силу, а также учитывается
сделанное выше предположение о «скользящих» столкновениях.
При вычислении djfldt |столки предположения Больцмана опи-
опираются на ограничения о пространственной однородности, нало-
наложенные на &.
Последний вывод уравнения Фоккера — Планка имеет преи-
преимущество по сравнению с предыдущим (когда рассматривался
кулоновский газ). А именно, коэффициенты (Д|/Д?) и (Д|Д|/Д^>,
возникшие в процессе получения уравнения, имеют ясный физи-
физический смысл.
4.6. Уравнение Фоккера — Планка 249
Сравнивая уравнения D.257) и D.230), мы увидим, что коэф-
коэффициент трения а надо отождествлять с (Д|/Д?), тогда как коэф-
коэффициент диффузии Ъ = (Д|Д|/Дг). Такая интерпретация прямо
следует из определения интегралов D.254) и D.255). Рассмотрим
сначала
Это есть среднее приращение скорости частицы за интервал вре-
времени At. С другой стороны, в пределе, когда At ->¦ 0, это будет
среднее ускорение частиц, обусловленное столкновениями. А эта
совпадает с нашей прежней интерпретацией коэффициента тре-
трения а.
Оставшийся коэффициент
K*) D-259>
при At ->¦ 0 дает среднее значение произведения ?-й компоненты
ускорения на /-ю компоненту отклонения скорости вследствие
столкновений.
При таком толковании коэффициентов (Д|/Д?) и (Д|Д|/Д?)
возможно получить выражения для этих коэффициентов через
функцию распределения $р. Рассмотрим, например, коэффициент
трения (Д|/Д?). При столкновении ? с |4
Вероятная частота таких столкновений с «gi-частицами» в интер-
интервале скоростей d%i около |А (вспомните формулу D.210) для
частоты столкновений) определяется соотношением
dA8v = 1 It - % | ^(It) dl&du D.260)
При каждом таком столкновении | изменяется на Д|. Следователь-
Следовательно, вероятная скорость изменения | вследствие таких столкно-
столкновений равна
AgdAftv = Д1 I h - I I JF(h) d^edQ. D.261)
Средняя скорость изменения | в результате столкновений со все-
всеми частицами (напомним, что V = |i — |) равна
= J
D.262>
Поучительно показать, что для случая кулоновского рассея-
аия это выражение для (Д|/Д^) сводится к D.231). Для таких
столкновений
s*, D.263)
250 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара — Гросса и др,
где Р2 определяется соотношением D.225). Отклонение скорости
равно (см. D.226))
М = а(а-\). D.264)
Подставляя эти величины в D.262), получим:
Df) = j «(а• V) V& (li) о d% dQ, D.265a)
2я
о о
Если за полярную ось выбрать вектор V, то декартовы коорди-
координаты единичного вектора а будут иметь вид
а = (cos i|), sin i|) cos <p, sin ty sin ф). D.266)
Одна только V-компонента (т. е. cos \|э) уцелеет при интегриро-
интегрировании по ф. В результате получим
"?**>. D-267)
Чтобы обойти особенность при интегрировании по cosij), нижний
предел принимаем равным 8. (Отметим еще раз, что особенность
возникает из-за столкновений с нулевым углом рассеяния:
я|) = ох/2, 6=0.) В результате получим
= 2яР* In e-i j Щ^ . D.268)
А это не что иное, как соотношение D.231).
Задача 4.48. Проделав аналогичные вычисления, получить
(Д|Д|/Д?) в зависимости от <р (аналогично соотношению D.262)
для (Д|/Д?)). Для частного случая кулоновских взаимодействий
установить, удовлетворяет ли полученная формула для Ъ соотно-
соотношению V.& = а, и показать, что она сводится к D.231).
Ответ.
= j j {a-VfaaVo dU^^d^.
Используя D.263) для кулоновского взаимодействия, можно это
выражение представить в виде
Полагая
а = (cos i|), sin of) cos ф, sin i|) sin ф)
4.6. Уравнение Фоккера — Планка 251
(вектор V опять направлен вдоль полярной оси) и интегрируя
п0 <ф и ф, увидим, что все недиагональные элементы обращаются
в яуль. Два диагональных элемента вдоль осей, нормальных к V,
расходятся, а компонента в направлении V остается конечной.
Соответствующие интегралы имеют вид
так что
1
/ш = /B)==я j ^ A _ ^) = jx [in e-i_± + ^] ^ jr In е,
То есть две компоненты (Д?Д?/Д?), которые не обратились в нуль,
равны между собой и являются диагональными компонентами,
нормальными к V. Теперь система координат, в которой проводи-
проводились эти вычисления, содержит одну ось в направлении V. В дан-
данной системе координат тензор (T^26?j- — ViVj)/Vs имеет только две
ненулевых компоненты. Они равны (с точностью до V'1) и лежат
вдоль двух направлений, нормальных к V. Поскольку тензор
является объектом, не зависящим от системы координат, то ниже-
нижеследующая запись (F26jy — ViVj)IVz, приводящая к правильным
значениям в частных осях, справедлива в любой системе коорди-
координат. Приходим к соотношению
что совпадает с ранее полученным нами результатом D.231).
^) 3?-теорема
После того как мы двумя способами вывели уравнение Фок-
Фоккера — Планка, остается показать, следует или нет из уравнения
Фоккера — Планка ^-теорема и является ли она совместимым
с уравнениями сохранения.
Напомним х), что ^-функция Больцмана задается равенством
х) Предлагаемое ниже доказательство впервые было проведено Либови-
ем A961) для случая кулоновского газа; см. также работу Либова и Фиде-
я A967). Хочется отметить весьма полезные дискуссии по этим вопросам
А. Оппенгеймом.
252 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара—Гросса и др.
Из уравнения Фоккера — Планка следует, что
= i J d'x j #i(l + luУ)-щ (br,^-a,?) , D.269)
где мы учли, что а = V-Ь (см. задачу 4.45). Интегрируя послед-
нее уравнение по частям, получим
о д In & I, _. д
Or
-A). D.270)
Это уравнение служит также для определения А и В. Чтобы
завершить доказательство, предположим, что коэффициент диф-
диффузии имеет следующий характерный вид:
bTS = j (V*8rs - VTVS) Л (У) f (ч) d4|. D.271)
Функция Л зависит от частного вида (дальнодействующей) силы
взаимодействия и положительна для всех V. Подставляя D.271)
в D.270), получим для первого члена:
В = j d3td?r\A& (DjF(ti)[F2 (Viln jFJ -(V- Vgln #-J], D.272)
или, что эквивалентно,
В = i j d*t d^A^ (|) ^ (r,) [F2 (V| in>FJ_
-(V.VeIn^J + V2(V4ln^)»-(V.V4Iii^J]. D.273)
Определим далее:
Y^VglnjFd); Я = Vn In jr (n). D.274)
Тогда выражение D.273) можно записать в следующем виде:
В = \ J (РЕ d3riAjF A) .Г(Л) {F2 (Т2 + А,« - 2Y • Л, + 2Y • Я) -
_[(V.yJ+(V.^_2(V.y)(V.?,) + 2(V.y)(V.X)]}. D.275)
Задача 4.49. Используя соотношение
доказать, что для любых двух векторов Р и F справедливо сле-
следующее равенство:
— (P-FJ = (Р X FJ.
4.6. Уравнение Фоккера — Планка 253
Учитывая результаты последней задачи, соотношение D.275)
записать в следующем виде:
х (Y - К)? +
+ 2[F2y^-(V.Y)(V^)]}. D.276)
Рассмотрим теперь последний член в этом выражении:
С & { d*tJ? (I) V { *ЧГ (П) Л [F2b- V (V.X)] =
уг { й3г]Л [F26rs-VrVs] Щ-8. D.277)
Интегрируя по частям, получим
т|[-.Г (т,)] A[A(F26rs-FrFs]. D.278)
Так как F — это величина относительной скорости V = ч\ — |,
то 3/9g8 = —d/dr\s. Внося это соотношение в D.278), будем иметь
С = { d*l&yr (-J^brs) = { dbTv-a, D.279)
где мы учли, что dbrs/dls = аг.
Сравнивая этот результат с членом А в уравнении D.270),
получим А = С. Следовательно, в выражении для В уцелеет
только член с векторным произведением (см. D.276)). В резуль-
результате получим
= —i j j д?х&*1&*х\&& [Vx (v-b)]2<0. D.280)
Кроме того, d$?ldt = 0, когда V параллелен y — ^ либо когда
Л — | параллелен вектору {[д In ff? (|)/dg] — [д In g? (ц)/дг\]}. Это
будет так, если
^^Zr + 2Sgr, D.281)
где 1 —постоянный вектор, a S —постоянный скаляр. Выра-
Выражение D.281), в свою очередь, означает, что
ln#r = U+hl+ St\ D.282)
где U —другой постоянный скаляр. Используя последнее урав-
нение, можно сделать следующий вывод.
Из кинетического уравнения Фоккера — Планка следует, что
$? — монотонно убывающая функция. Она перестает уменыпать-
Ся, когда ^становится распределением Максвелла. Все это верно
пРи условии, что коэффициент диффузии имеет вид D.271).
254 Гл. IV. Уравнения Болъцмана, К рука — Бхатнагара — Гросса и др
В последние годы уравнение Фоккера — Планка нашло шир0.
кое применение в плазме -— двухкомпонентном кулоновском газ
из электронов и ионов. В этом случае имеются два кинетических
уравнения: одно для jFV и другое для jF_. Вид этих уравнений:
следующий:
Dt
Аналогичное уравнение можно записать для ^_.
Задача 4.50. Исследовать однокомпонентное уравнение Фок-
Фоккера — Планка, чтобы показать, совместимо ли оно с тремя урав-
уравнениями сохранения. С этой целью вычислить сначала три момен-
момента A, |, ?2) для столкновительного члена Фоккера — Планка.
Сейчас уместно сделать одно замечание относительно кинети-
кинетических уравнений и столкновений при дальнодействии. В гл. III
мы пришли к заключению, что уравнение Власова пригодно для
газа, частицы которого испытывают дальнодействующие столкно-
столкновения, которые* в свою очередь, были определены через радиус
взаимодействия. Соответствующим параметром для кулоновского
газа является плазменный параметр nd3, где d — радиус Дебая.
Для nd3 > 1 (в дебаевской сфере много частиц) мы получили
уравнение Власова. В настоящей главе (исходя из импульса, сооб-
сообщаемого при столкновении пробной частице) была введена концеп-
концепция дальнодействующих столкновений и получено уравнение
Фоккера — Планка.
Различие между этими двумя уравнениями связано с природой
входящих в них сил, действующих на частицу. В уравнении Вла-
Власова — это «моментальное» «размазанное» силовое поле. Оно
не восприимчиво к индивидуальным парным столкновениям.
В каждый момент времени на типовую частицу действует сила
со стороны всей совокупности частиц газа. Эта частица «не ощущает^
действия отдельных частиц. С другой стороны, столкновительпый
член Фоккера — Планка, хотя он также соответствует случаю
дальнодействия, содержит двухчастичные столкновения. Пр#
таком взаимодействии частицы «видят» одна другую. Чтобы отли-
отличить столкновения Фоккера — Планка от власовских столкнове-
столкновений в плазме, мы введем понятие «дальних» и «самых дальних»
столкновений.
Для самых дальних столкновений прицельный параметр больше
дебаевского радиуса и они хорошо описываются моделью Власова-
Дальние столкновения — это столкновения между данной част^
цей и другими, находящимися в периферийной зоне дебаевской
4.6. Уравнение Фоккера — Планка 255
Такие взаимодействия вызывают суперпозицию большого-
злсл малых сил и хорошо описываются столкновительным членом
фоккера — Планка. Такое истолкование мотивировано предшест-
предшествующим выводом уравнения Фоккера — Планка из уравнения
рольцмана, если учесть, что последнее получается из уравнения
Дяувилля методом Грэда. Там, как мы помним, область столкно-
столкновения была разделена на две зоны: ближнюю и дальнюю. Первая
йз них приводит к уравнению Больцмана, вторая (самые дальние-
столкновения) дает уравнение Власова. Радиус сферы, которая
разделяет две зоны — это радиус Дебая, так что для столкнове-
столкновений внутри этой сферы применимо уравнение Больцмана. Для
дальних столкновений в пределах этой сферы мы получаем урав-
уравнение Фоккера — Планка.
Таким образом, мы показали, что плазма хорошо описывается
уравнением Власова со столкновительным членом Фоккера —
Планка. Именно, столкновительный член Фоккера —Планка
вводит необратимость в модель Власова.
д) Родственные уравнения
В последнем разделе этой главы мы вкратце остановимся
на некоторых совсем недавно полученных кинетических уравне-
уравнениях, которые находят широкое применение в кинетической тео-
теории плазмы. Это уравнение Ландау A937) и уравнение Балеску —
Ленарда A960). Они тесно связаны с уравнением Фоккера —
Планка. Первое непосредственно следует из уравнения Фоккера —
Планка для кулоновского газа, что видно из предлагаемой ниже
задачи.
Задача 4.51. Показать, что столкновительный член уравнения
Фоккера — Планка в случае кулоновского газа может быть
представлен в форме Ландау:
) ~w~ \f (Si)
Второе кинетическое уравнение, тесно связанное с изучепием
Плазмы, уравнение Балеску — Ленарда, является самым новым
йз всех имеющихся в настоящее время кинетических уравнений.
" нашем вводном курсе достаточно просто записать это уравнение
11 Указать на его сходство с уравнением Ландау.
Уравнение Балеску — Ленарда получается с помощью метода
Преобразования Фурье и записывается в форме квадратуры с яв-
Н интегралом по преобразованной переменной к. Уравнение
256 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара — Гросса и др.
имеет следующий вид:
D& BjtKjt д С к d*k 1 Ф (k) p
Dt ~~ т* д% J \D( — к, ik-|)|2 X
D.285)
*Ф (к) BяK
/с ' ди ~ к ' д% '
где б —дельта-функция Дирака.
Функция Ф (к) является фурье-образом потенциала взаимо-
взаимодействия Ф (х)у который для кулоновского газа имеет вид Ф =
= е2/х (Ф ~ &~2) (в системе СГС). Плотность числа частиц рав-
равна п, и масса частицы — т.
Уравнение D.285) можно привести к виду, очень схожему
с уравнением Ландау (см. задачу 4.50):
D& BяK я д [j+'fift' *\ Г *г,г>\ д^ E) бг: (Г\дЖЖ1\ (A
-Ж=—^Г-Щ; J ^ 0A , g).|^r(g )_ ^r(|)__j. D.
При сравнении этого уравнения с D.285) увидим, что
б- [ dk Й б Г к'&-Ъ') 1 1Ф(*I2 /
Задача 4.52. Показать, что уравнения D.286) и D.287) совпа-
совпадают с уравнением D.285).
Хотя уравнения Ландау и Балеску — Ленарда похожи по
форме, необходимо ввести ряд аппроксимаций и предположений,
прежде чем О приведется к виду [б^« —VtVj/V2].
Задача 4.53. Показать, что для кулоновского газа уравнение
Балеску — Ленарда с D = 1 дает уравнение Ландау.
При вычислении коэффициентов в столкновительном члене
Фоккера — Планка необходимо было «обрезать» интеграл при
интегрировании по углу рассеяния, чтобы получить конечный
результат. В этом смысле уравнение Балеску —Ленарда не тре-
требует такой вольной процедуры. Однако надо быть аккурат-
аккуратным при вычислении сингулярного интеграла по %, который
содержится в выражении для диэлектрической функции "
в D.285). Другим характерным свойством данного уравнений
является то, что в нем учитывается эффект экранирования межДУ
частицами. Это свойство уравнения Балеску —-Ленарда заклю-
4.6. Уравнение Фоккера—Планка 257
в диэлектрической функции D. Фурье-образ Ф (к) —это
образ неэкранированного парного взаимодействия, который появ-
появляется в уравнении Балеску—- Ленарда в форме Ф/D. Наличие
«фона» частиц вызывает экранирование *), которое в свою очередь
усиливает неэкранированное парное взаимодействие Ф.
Этот краткий вводный обзор наиболее известных из недавно
полученных кинетических уравнений завершает раздел, посвящен-
посвященный уравнению Фоккера — Планка. Некоторые из наиболее важ-
важных свойств рассмотренных кинетических уравнений собраны
в табл. 4.1.
Итак, мы ознакомились со свойствами наиболее широко при-
применяемых кинетических уравнений. В главе V дано решение
уравнения Больцмана методом Чепмена — Энскога и методом
Грэда. В заключение вновь исследуется проблема релаксации
к равновесию макроскопических систем как в духе классической
статистической механики, где мы опять сталкиваемся с ансамбля-
ансамблями в Г-пространстве, так и методом эргодической гипотезы. Пер-
Первый, априорный подход, опирается на постулат равных априорных
вероятностей, тогда как при втором (апостериорном) подходе
делаются попытки доказать эргодическую гипотезу. Оба метода
исследуют необратимое приближение к равновесию макроскопи-
макроскопических систем. Они представляют собой статистическо-механиче-
ский эквивалент метода теории кинетических уравнений, в кото-
котором с помощью (^-теоремы изучается та же самая проблема.
Задача 4.54. Напомним, что фурье-образ Ф (к) функции Ф (х)
имеет вид
Ф (к) = -gL J f j gik-жф (Х) сРх.
Найти фурье-образ кулоновского взаимодействия Ф = е2/х.
Ответ.
Ф (к) = еУ2л2к2.
Задача 4.55. Уравнение Больцмана для двухкомпонентного
газа имеет вид
Dt
где jr — одночастичная функция распределения, / — интеграл
столкновений следующего вида:
*) Для более детального ознакомления с этими вопросами, можно обра-
обратиться к монографии Монтгомери и Тидмена A964), гл. 7.
a § a
IV ¦: CO "
Д Й g (j
3 о л
Я V Ч О
'<S н о я Я
щ
с: g *
о Ч сб
ь
с
лек
о
-01
0Д1
VO
о
ю
и
1ИЯ
401
о
н
2
О
PQ
о а
о
§1
43 Ч?,
I
s«
н
ев
Ph
*8
ев
О
I
Ph
a.
g
PQ
I.
о
260 Гл. IV. Уравнения Болъцмана, Крука — Бхатнагара — Гросса и др.
Рассмотрим предельный случай:
Это означает, что плотность па и масса Ма частиц а-газа много
меньше соответствующих величин ft-газа. В этом случае «пере-
«перекрестные столкновения» / (jfa \ $ръ) определяют изменение функ-
функции д?а, тогда как «самостолкновения» / (jFb I ЗРъ) определяют
ЭВОЛЮЦИЮ JTb.
а) Предполагая, что $ръ известна и равна постоянной и что
= СаЬ2аЬ/4я = const, вывести уравнение
1
Dt
б) Выяснить структуру двух членов, которые входят в JFan.
В предшествующем выражении индекс «ан» означает «анизотроп-
«анизотропный». Изотропная компонента Jfmo удовлетворяет соотношению
Ответ, а)
аЪ
б) Если легкая частица сталкивается с тяжелой (в системе
координат, связанной с тяжелой частицей), то энергия легкой
частицы сохраняется. Следовательно, a-частицы, которые после
столкновения приходят в интервал скоростей dz\ около |, должны
до столкновения быть в интервале dz\' около |' с 1 |' 1 = | 1 I-
Чтобы учесть все вклады для данной скорости §, мы должны
просто проинтегрировать J^a (|) по всем направлениям, т. е. по
телесному углу 4я. С другой стороны, если a-частица испытывает
столкновение, то вектор % изменяется и частица «выбрасывается»
из элемента объема d?% около |.
Список литературы
А. Вопросы, связанные с обращением времени
Голд (Gold Т.)
A962) The Arrow of Time, Am. J. Physics, 30, 403.
Ли (Lee T. D.)
<1966) Space Inversion, Time Reversal, and Particle-Antiparticle Conjugation,
-' s. Today, 19, 23.
Список литературы 261
дошмидт (Loschmidt J.)
A876—1877) Wien. Ber., 73, 139 A876); 75, 67 A877).
рейхенбах (Reichenbach H.)
/1956) The Direction of Time. Berkeley, University of California Press. Рус-
Русский перевод: Рейхенбах Г., Направление времени, М., ИЛ, 1962.
цермело (Zermelo E.)
A896) Ann. Phys., 57, 485.
Б. Ранние работы по кинетической теории
Больцман (Boltzmann L.)
/1872) Further Studies on the Thermal Equilibrium among Gas-Mole-
Gas-Molecules, Wien. Ber., 66, 275.
A875)- On the Thermal Equilibrium of Gases Subject to External For-
Forces, Wien. Ber., 72, 427.
A876) On the Formulation and Integration of Equations which Deter-
Determine the Molecular Motion in Gases, Wien. Ber., 74, 503.
A880-1883) Wien. Ber., 81, 117 A880); 84, 40, 1230 A881); 86, 63 A882);
88, 835 A883).
A889) Jahresb, d. D. Math. Verein, 6, 130.
Максвелл (Maxwell J. C.)
A867) On the Dynamical Theory of Gases, Phil. Trans. Roy. Soc, 157, 49.
A873) Nature, 8, 537.
A877) Nature, 16, 244.
A879) On Stresses in Rarefied Gases Arising from Inequalities of Temperature,
Phil. Trans. Roy. Soc, 170, 231.
В. Кинетические уравнения (см. также литературу к гл. III)
Балеску (Balescu R.)
A960) Phys. Fluids, 3, 52.
Гросс, Бхатнагар, Крук (Gross E., Bhatnager D., Krook M.)
A954) Phys. Rev., 94, 511.
Трэд (Grad Н.)
A958) Thermonuclear Reaction Rates in an Electrical Discharge, NYO-7977,
New York, University (Jan.).
A958) Principles of the Kinetic Theory of Gases, Hand. d. Physik, vol XII,
Berlin, Springer.
A960) Theory of Rarefied Gases, in Rarefied Gas Dynamics, ed. by F. Devien-
ne, New York, Pergamon Press.
A961) The Many Faces of Entropy, Comm. Pure and Ap. Math., 14, 323.
Кейлсон, Сторер (Keilson J., Storer J.)
A952) Quart. Ap. Math., 10, 243.
(Kirkwood J. G.)
/. Chem. Phys., 15, 72.
рвуд, Росс (Kirkwood J. G., Ross J.)
A958) Proceedings of the International Symposium on Transport Processes
in Statistical Mechanics, I. Prigogine (ed.), New York, Interscience.
262 Гл. IV. Уравнения Болъцмана, Крупа — Бхатнагара—Гросса и др.
Ландау Л. Д.
A937)* ЖЭТФ, 1, 203.
Ленард (Lenard A.)
A960) Ann. Phys., 3, 390.
Монтгомери, Тидмен (Montgomery D., Tidman D.)
A964) Plasma Kinetic Theory, New York, McGraw-Hill.
Планк (Planck M.)
A917) Sitz. der Preuss. Acad., 324.
Розенблют, Мак-Дональд, Джудд (Rosenbluth M., McDonald W., Judd D.
A951) Phys. Rev., 107.
Уленбек, Вонг (Uhelenbeck G., Wang M. C.)
A945) Revs. Mod. Phys., 17, 323.
Фоккер (Fokker A.)
A914) Ann. d. Physik, 43, 312.
Чандрасекхар (Chandrasekhar S.)
A943) Rev. Mod. Phys., 15, 1.
Г. Гидродинамика и кинетическая теория
Ватсон, Бонд, Уэлч (Watson К. М., Bond J. W., Welch J. A.)
A965) Atomic Theory of Gas Dynamics, Reading, Mass., Addison-Wesley.
Гиршфельдер, Кертисс, Берд (Hirschfelder J. О., Curtiss С. F., Bird R. B.)
A954) The Molecular Theory of Gases and Liquids, New York, Wiley. Русский
перевод: Гиршфельдер Дж., Кертисс Чм Берд Р., Молекулярная
теория газов и жидкостей, Мм ИЛ, 1961.
Грэд (Grad H.)
A949) Сотт. Pure and Ар. Math., 2, 331.
Гуггенгейм (Guggenheim E. А.)
A960) Elements of the Kinetic Theory of Gases, New York, Pergamon Press.
Джине (Jeans J.)
A952) An Introduction to the Kinetic Theory of Gases, Cambridge, Cambridge
University Press.
A946) Kinetic Theory of Gases, Cambridge, Cambridge University Press.
Зоммерфельд (Sommerfeld A.)
A956) Thermodynamics and Statistical Mechanics, New «Jfork, Academic
Press. Русский перевод нем. изд.: Зоммерфельд А., Термодинамика
и статистическая физика, М., ИЛ, 1955.
Кеннард (Kennard Е. Н.)
A938) Kinetic Theory of Gases, New York, McGraw-Hill.
Лоэб (Loeb L. B.)
A934) The Kinetic Theory of Gases, 2d ed., New York, McGraw-Hill.
Паттерсон (Patterson G. N.)
A956) Molecular Flow of Gases, New York, Wiley. Русский перевод: Паттер'
сон Г. Н., Молекулярное течение газов, М., Физматгиз, I960.
Список обозначений к гл. IV 263
Презент (Present R. D.)
A958) Introduction to the Kinetic Theory of Gases, New York, McGraw-Hill.
Уолдмен (Waldman L.)
A958) Transporterschemungen in Gasen von mittlerem Druck, Hand. d. Phy-
sik, vol. XII, p. 295—514, Berlin, Springer.
Чепмен, Каулинг (Chapman S., Cowling T. G.)
cA952) The Mathematical Theory of Non-Uniform Gases, Cambridge, Cam-
Cambridge University Press. Русский перевод: Чепмен С, Каулинг Т.,
Математическая теория неоднородных газов, М., ИЛ, 1960.
Д. с7?-теорема (см. также литературу к гл. V)
Больцман (Boltzmann L.)
.A964) Lecture on Gas Theory, translated by G. Brush, Berkeley, University
of California Press. Русский перевод нем. изд.: Больцман Л., Лекции
по теории газов, М., Гостехиздат, 1956.
Трэд (Grad H.)
A965) On Boltzmann's (^-Theorem, /. Soc. Indust. Appl. Math., 13, 259»
Либов, Фидель (Liboff R., Fedele J.)
A967) Phys. Fluids, 10, 1391.
Либовиц (Lebowitz J.)
A961) Bull. Am. Phys. Soc, Ser. II, 6, 289.
Толмен (Tolman R. C.)
A938) The Principles of Statistical Mechanics, Oxford.
Эренфест П., Эренфест Т. (Eherenfest P., Eherenfest Т.)
A911) Encykl. d. Math. Wiss., vol IV, part 32, Leipzig»
E. Экспериментальный максвеллиаи
Миллер, Куш (Miller R., Kusch P.)
A956) /. Chem. Phys., 25, 860.
Цартман (Zartman I. F.)
A931) Phys. Rev., 37, 383.
Список обозначений к гл. IV
а — радиус твердой сферы,
а —коэффициент Фоккера — Планка,
Ъ —радиус твердой сферы,
Ъ — безразмерный прицельный параметр,
264 Гл. ТУ. Уравнения Болъцмана, Крука — Бхатнагара — Гросса и др.
Ъ — коэффициент Фоккера — Планка,
с — скорость света,
ЦМ —центр масс,
D —диаметр твердой сферы,
D —диэлектрическая функция,
D —область в конфигурационном пространстве,
DIDt —индивидуальная производная по времени,
Е — энергия,
е — абсолютная внутренняя энергия,
% —относительная внутренняя энергия на частицу у
е —плотность относительной внутренней энергии,
/? —одночастичное усеченное распределение,
/о — абсолютное распределение Максвелла, нормиро-
нормированное на единицу,
jFo —абсолютное распределение Максвелла, нормиро-
нормированное на JV,
/° — локальное распределение Максвелла, нормиро-
нормированное на единицу,
/з —усредненное по времени s-частичное распределе-
распределение, нормированное на единицу,
ер — одночастичная функция распределения, нормиро-
нормированная на N,
$Ръ —парная функция распределения,
G —сила взаимодействия между частицами,
&' = & (?') — значение динамической переменной *§ после столк-
столкновения,
3 —макроскопическая переменная,
—kS€ — энтропия Больцмана,
—k$gN — энтропия Гиббса,
Н —гамильтониан,
/ —интегральный оператор,
/ —интегральный оператор Больцмана,
К —внешнее силовое поле,
К —константа в выражении для силы,
к —постоянная Больцмана,
I —средний свободный пробег,
L —угловой момент ^-частицы,
Список обозначений к гл. IV 265
т — масса частицы,
М —масса системы двух тел,
п — плотность числа частиц,
О — оператор относительной энергии,
о — оператор абсолютной энергии,
р — относительный тензор давлений,
Р —импульс центра масс
р — канонический импульс
р —импульс (х-частицы,
р' — импульс после столкновения,
р —импульс в системе координат ЦМ,
р — абсолютный тензор давлений,
Q — относительный вектор теплового потока,
q — абсолютный вектор теплового потока,
q —плотность заряда,
R — радиус-вектор центра масс
bR± —число частиц, которые (входят/покидают) фазовый
элемент бхб| за время 8t,
г — радиус-вектор между двумя частицами,
г0 — радиус взаимодействия,
S — вектор элемента площади поверхности,
S — вектор Пойнтинга,
5 — прицельный параметр, параметр столкновения,
t0 — среднее время между столкновениями,
U — плотность энергии поля,
и — величина, обратная радиусу,
и — гидродинамическая скорость,
и — скалярная скорость в уравнении Балеску — Ле-
нарда,
V —относительная скорость системы двух тел,
°JT — потенциал взаимодействия частиц,
xs — каноническая координата 5-й частицы,
а — единичный апсидальный вектор,
Р — безразмерный обратный радиус-вектор,
р — безразмерная константа в выражении для силы*
Ф — потенциал взаимодействия частиц,
Ф — азимутальный угол рассеяния,
Гл. IV. Уравнение Болъцмана, Крука — Бхатнагара — Гросса и др.
ф —динамическая функция,
ф —полярный азимут,
Г —плотность импульса поля,
Г —кривая в пространстве (#, у),
ус — силовая постоянная,
Л —тензор скоростей деформаций,
Л* — полином от микроскопической скорости,
\х —приведенная масса,
v —частота столкновений,
й —телесный угол,
Q —тензор максвелловских напряжений,
П — функция распределения условной вероятности,
хр —динамическая функция,
я|э — угол рассеяния,
2 —полное сечение рассеяния,
а —дифференциальное сечение рассеяния,
т — время столкновения,
0 —угол рассеяния,
S —произвольная функция,
| — скорость частицы,
^ —скорость частицы в системе координат ЦМ.
ГЛАВА V
РЕШЕНИЕ И ДАЛЬНЕЙШИЕ СВОЙСТВА
УРАВНЕНИЯ БОЛЬЦМАНА.
РЕЛАКСАЦИЯ К РАВНОВЕСИЮ
5.J. Анализ Чепмена — Энскога уравнения Больцмана.
Приближение малого среднего свободного пробега
а) Коэффициенты переноса
До сих пор мы мало касались вопроса о решении произволь-
произвольного кинетического уравнения и о возможностях его каких-нибудь
других практических приложений. Одно из наиболее важных
применений кинетического уравнения связано с вычислением
коэффициентов переноса. Эта задача особенно поучительна,
поскольку она сосредоточена на построении одночастичной функ-
функции распределения, т. е. на получении решения данного кинети-
кинетического уравнения.
Коэффициенты переноса играют большую роль в кинетической
теории газов. Неотъемлемая слабость теории макроскопических
уравнений состоит в том, что системы этих уравнений всегда
незамкнуты: число неизвестных всегда больше числа уравнений.
Уравнение неразрывности является одним уравнением для четы-
четырех скалярных величин (п, и). Если мы попытаемся исправить
положение, вводя уравнение импульсов, то в действительности
ситуация только ухудшается. В уравнения импульсов, которые
состоят из трех скалярных уравнений, входит шесть независимых
компонент тензора напряжений Р. Следовательно, первые два
закона сохранения дают четыре уравнения для десяти неизвест-
неизвестных. Очевидно, что добавление к системе третьего уравнения
сохранения, уравнения энергии, не улучшит дела, точно так же
как добавление любого уравнения из оставшегося счетного мно-
множества моментных уравнений. Мы всегда будем иметь больше
неизвестных, чем уравнений.
Выход из этой «безнадежной» ситуации — на феноменологичес-
феноменологическом пути. Феноменологическими называются утверждения физики,
основанные на эксперименте (и интуиции) и не вытекающие
из фундаментальных законов. Например, если ограниченный
(но свободный от внешних воздействий) газ первоначально обла-
обладает градиентом плотности, то с течением времени система будет
релаксировать к однородному состоянию с нулевым градиентом.
Другими словами, макроскопическая скорость и «сдвигает» жид-
жидкие элементы из плотных областей в разреженные. Этот феноме-
феноменологический закон описывается уравнением
mi = — D V п, E.1)
268 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
где D называется коэффициентом диффузии. Если это уран,
нение подставить в уравнение неразрывности (одно уравнение ддя
четырех скалярных величин п и и)
то мы получим (считая, что D не зависит от х)
1г = ^2/г E.2)
— так называемое уравнение диффузии, где D —коэффициент
переноса. Этот простой пример показывает, каким образом коэф-
коэффициенты переноса помогают получить замкнутую систему гидро-
гидродинамических уравнений. Но так как D все еще неизвестная вели-
чина, то мы попросту только изменили задачу, а не решили ее.
Тем не менее существует формальный подход к вычислению коэф-
коэффициентов переноса1). Он основан на построении самой функции JF *
Например, пусть решение уравнения Больцмана имеет вид
jF(x, I, t) = -jLg&).Vn(x, t), E.3)
где g — известная функция | и п — числовая плотность:
п=
Образуя моментное (по скорости) соотношение от равенства
E.3), будем иметь:
пи = j &U4 = - Vn j gd% E.4)
Из последнего равенства заключаем следующее. Во-первых, если
мы положим D = \ gd3^, то E.4) примет вид
пи = —D V п.
Это означает, что феноменологическое утверждение, заключенное
в E.1), в действительности является точным аналитическим
утверждением. Во-вторых, коэффициент D должен определяться
тождеством D = \ gd3l.
Вообще для газовой динамики важны следующие три коэф-
коэффициента переноса.
1. Коэффициент диффузии D, который связывает и с градиен-
градиентом п согласно E.1).
2) Менее формальный подход состоит в вычислении средней длины
свободного пробега. Иллюстрацию этого метода можно найти в работе Ли*
Сирса, Таркотта A963).
5.1. Анализ Чепмена — Энскога уравнения Болъцмана 269
2. Коэффициент вязкости ji, связывающий Р с градиентом
функции и следующим образом:
f(X|7) E.5)
Ответим, что такая форма записи требует, чтобы р = у
Здесь / — единичная матрица, р —скалярное давление и Л — (сим-
(симметричный) тензор скоростей деформаций, определенный равенст-
D.138); хх и ^-компоненты тензора Р имеют вид
(
Задача 5.1. Показать, что тензор давлений, задаваемый в фор-
ме E.5),
обладает следующими тремя свойствами:
1) Р не содержит пространственных производных порядка
выше первого, т. е. Р = О (Vu);
2) S равен нулю, если жидкость вращается как твердое тело,
т. е. если и = Й X г, где ?2 —вектор постоянной угловой скоро-
скорости;
3) Тг Р = Зр.
В этой формулировке, связанной с разреженным газом, толь-
только перенос импульса, обусловленный потоком частиц, вносит
вклад в напряжение. Вкладом от межмолекулярных взаимодей-
взаимодействий можно пренебречь (см. разд. 3.6). Феноменологический смысл
равенства E.5) очевиден. Оно утверждает, что силы, которые стре-
стремятся вызвать диссипацию любых градиентов скорости, могущих
возникнуть в жидкости, линейно пропорциональны этим гра-
градиентам.
3. Коэффициент теплопроводности х, который связывает век-
вектор теплового потока Q с градиентом температуры:
Q = -KVT. E.7)
Феноменологическое обоснование этого соотношения также ясно.
Если в газе существуют две области с разными температурами,
то тепло будет переходить из области более теплой в область
более холодную, чтобы произошла диссипация градиента темпе-
температуры. (Тепло никогда не течет в противоположном направле-
направлении — это второй закон термодинамики.)
270 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
Все феноменологические законы, в которые входят коэффи
циенты переноса, стремятся сохранить пространственную одн0^
родность (равновесие) в системе. Они служат для замыкания
системы уравнений сохранения, но при этом система становится
необратимой. Обратимые уравнения, несомненно, не могут оцц-
сывать релаксацию системы к равновесию. В противном случае
существовало бы нечто, дающее нам возможность определить гьря^
мое направление времени, а именно направление, которое ведет
к равновесию 1).
Казалось бы, что решить уравнение Больцмана для функции ер
а потом вычислить коэффициенты переноса и получить замкнутую
систему гидродинамических уравнений —все равно, что «стрелять
из пушки по воробьям». Если функция $р известна, то может по-
показаться, что и все макроскопические переменные известны.
И какой тогда смысл решать уравнения сохранения, чтобы опре-
определить эти макроскопические переменные, коль скоро одночастич-
ная функция распределения $р известна? Однако, зная jF, мы
не можем определить гидродинамические переменные, так как
они могут входить в $р в виде параметров. Прекрасным примером
этого является локальный максвеллиан
^ - {2nRTf* XPL 2RT
Если мы проинтегрируем jF°, чтобы найти, скажем, плотность
числа частиц п, то получим
Ч^ = п9 E.8)
Это равенство ничего не говорит о структуре п. Оно представляет
собой просто часть определения локального максвеллиана J^°.
Назначение коэффициентов переноса состоит в том, чтобы сде-
сделать систему уравнений сохранения замкнутой:
rc + V.rcu = 0, E.9а)
р (-^- + u.v)u + V.P = pK, E.96)
X = 0. E.9в)
Два из этих уравнений являются скалярными, а одно — вектор-
векторное. Они включают две скалярные величины пи Т, две векторные
и и Q и одну тензорную Р. Выражая последние две (не скалярные)
х) Более точно: если решение обратимого уравнения описывает при'
ближение к равновесию, то существует другое, также верное решение, соглас-
согласно которому происходит отклонение от равновесия.
5.1. Анализ Чепмена — Энекого, уравнения Болъцмана 271
ременные через и,ииГ, получим в результате замкнутую систе-
систему гидродинамических уравнений1). Отметим, что знание коэф-
коэффициента вязкости \i (уравнение E.5)) и коэффициента теплопро-
оДности % (уравнение E.7)) как раз обеспечивает такое замы-
В-аяие системы уравнений. Если \л и х известны, то коэффициент
Эффузии становится излишним.
Задача 5.2. Подставить E.5) и E.7) в уравнения E.9) и получить
замкнутую систему гидродинамических уравнений с \i и х в явном
виде-
(j\ формальное разложение и решение
Анализ Чепмена — Энскога начинается с того, что уравнение
Больцмана записывается в виде
где в — бесконечно малый параметр. Такую запись уравнения
Больцмана можно обосновать следующим образом. Оператор /
задается равенством
= J j
Если сечение рассеяния сг положить равным
o = rl5, E.12)
то а будет безразмерным параметром, который, как мы ожидаем,
должен быть порядка единицы; г0 —радиус взаимодействия. Для
жестких сфер (см. D.42)), где г0 = 2а,
Введем безразмерное распределение JF согласно уравнению
& = ^&i E.14)
где С — тепловая скорость и п —плотность числа частиц. Нако-
НеЦ, все скорости запишем в виде
1 = С%. E.15)
J) Вспомните определения
i
= 1
272 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
В этих безразмерных переменных уравнение Больцмана прщ1е
вид * т
7") *2Р /~> "-'
Dt -nbroJ<T' @.16)
Размерность произведения пСт\ равна величине, обратной
ни. Это согласуется с тем фактом, что время t в левой части
Площадь сечения рассеяния=л'г} = 1
Радиус бзаимо-
действия
4 Начальная тбердая саоера
Рис. 5.1.
нения является размерным. Полностью безразмерное уравнение
Больцмана получается, если положить
E.17)
t = nCr20t.
Ио физически более целесообразно иметь дело с уравнением
в форме E.16). Переменные п и г0 связаны простым соотношением
E.18)
nlr\ ^ 1.
Величина, обратная числовой плотности — это удельный объем
у, а I —средняя длина свободного пробега. На рис. 5.1 приведено
построение, поясняющее соотношение E.18).
Идея такова, что в среднем частицы проходят без столкнове-
столкновений (после любого данного столкновения) расстояние Z, так что
в объеме jtZr^ имеется только одна частица. Используя E.l8)i
чтобы выразить г0 через Z, получим уравнение E.16) в виде
E.19)
С у ~
Тепловая скорость С и средняя длина свободного пробега / свя-
связаны с частотой столкновений v приближенным равенством
lv ^ С. E.20)
В среднем частица проходит расстояние I за время v. Поскольку
параметры Z, v и С связаны соотношением E.20), только Дра
5.1. Анализ Чепмена — Энскога уравнения Больцмана 273
й3 них могут быть выбраны произвольно. Как только такой
выбор сделан, третий параметр определяется из E.20). Другими
словами, мы вправе рассмотреть предельный случай, когда в урав-
уравнении E.19) I ->- 0 и С = const. Это будет предельный случай
малой средней длины свободного пробега или, что то же (из E.20)),
высокой частоты столкновений. Он также называется гидродина-
гидродинамическим пределом. (Противоположный экстремальный случай
описывается газом Кнудсена, в котором частицы сталкиваются
с0 стенками значительно чаще, чем друг с другом.)
Вид уравнения E.19) дает возможность предположить, что
мы получим хорошую отправную точку для исследования решений
уравнения Больцмана в предельном случае малой средней длины
свободного пробега, если запишем его в виде
Введение параметра е представляет собой математический прием.
Этот параметр именуется «бухгалтерским» параметром и служит
дели учета членов одинакового порядка величины.
Первый шаг анализа Чепмена — Энскога состоит в том, чтобы
записать уравнение Больцмана в виде
(&) т E-22)
где
& = 1-4- + — -ж E-23)
И
J (/1 g) s j j й%,оdQV {f'g[-fSl). E.24)
Такая более явная запись оператора столкновений будет полезна
для дальнейшего анализа.
В качестве второго шага надо ввести разложение
Это в свою очередь порождает разложения в виде рядов для трех
операторов, dldt, 3) и /.
Прежде чем получить эти разложения, полезно обсудить вопрос
о нормализации ^г. Константы, содержащиеся в j^, задаются со-
согласно определениям:
274 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
Подставляя ряд E.25) в эти равенства, получим разложения мак-
макроскопических переменных п, и, Т. Если мы предположим, что все
эти переменные являются величинами О A), то
W E.26a)
п х
пи . E.266)
ЗпкТ/т/
Однако, переменные Q и Р все еще содержат полные ряды по
{jF(i)}i так что
Q = 2 e'Q(Z) = 1 2 ег j ^(Z)mc2cd3g, E.27)
^= 2 e^(Z) = S 8^ J i^^cc^- E.28)
Метод Чепмена — Энскога содержит два сильных предположения.
Первое из них, о котором мы уже говорили, состоит в том, что
гидродинамические переменные п, u, T все являются величинами
порядка единицы. Второе предположение, с которым мы вскоре
столкнемся, заключается в том, что jF зависит от времени только
через 7г, и и Т.
Из бесчисленного множества гидродинамических переменных
только эти три определяют равновесное состояние системы. Напом-
Напомним, что в боголюбовском описании релаксации к равновесию
на гидродинамической стадии одночастичное распределение являет-
является функцией п, и и Т. Следовательно, мы можем считать, что реше-
решение Чепмена— Энскога описывает эволюцию $р на этой конечной
гидродинамической стадии.
На каждой ступени анализа Чепмена — Энскога получается
соответствующая система уравнений законов сохранения. Напри-
Например, как будет показано, решение низшего порядка jF<°) не содер-
содержит тепловых потоков и напряжений. Если эту функцию подста-
подставить в уравнение Больцмана и образовать три первых момента,
то вследствие структуры ^г@) получаемые в результате макроско-
макроскопические уравнения будут содержать только п, и и Т. Это уравне-
уравнения Эйлера. Они описывают газ, который не содержит ни тепловых
потоков, ни напряжений (идеальная жидкость). Такое свойство
присуще состоянию жидкости, близкому к равновесию. Чтобы
описать состояния, более удаленные от равновесного, где суще-
существуют напряжения и тепловые потоки, необходимо использовать
следующие члены разложения^. Например, J^A) уже содержит Q
и S. Соответствующие макроскопические уравнения называются
5.1, Анализ Чепмена — Энскога уравнения Болъцмана 275
уравнениями Навъе — Стокса. Их также можно получить, под-
подставляя выражение E.5) для Р и E.7) для Q в уравнения сохране-
сохранения E.9). Такое феноменологическое задание Р и Q заключает
в себе предположение, согласно которому Р и Q вполне определя-
определяются пространственными производными (только) первого порядка
от гидродинамических переменных низшего порядка (например,
u, T). Это предположение вполне пригодно вблизи равновесия, где
полагается, что пространственные вариации более высокого поряд-
порядка стремятся к нулю.
Макроскопические уравнения, получающиеся при учете членов
более высокого порядка в разложении jF, содержат и простран-
пространственные производные высшего порядка в соответствующих аппро-
аппроксимациях Р и Q. Смысл введения членов высшего порядка в раз-
разложении Чепмена — Энскога для $F состоит в том, что получающие-
получающиеся в результате макроскопические уравнения лучше описывают
состояния, отклоненные от равновесного.
Возвращаясь к получению разложений для операторов 35
и /, отметим, что они вытекают из E.25) для j^, так что
i^ = i^@) + ei^A)+ ... . E.29)
Для /мы получим
1=0
= 2! St|) ()
Z=0 n=0
С использованием соотношения
JW{JFW, <Fa\ .... ,Fw>) = 22./(.rI>l.riw), l + n = s, E.31)
n I
E.30) запишется в виде
^A), jFB)) + ... . E.32)
Равенства E.29) и E.32) определяют разложения <2^ и /(jFljF)
по степеням 8.
Разложение dtfldt нельзя получить непосредственно, так как
его обоснование связано со вторым предположением метода Чеп-
Чепмена— Энскога, согласно которому jF зависит от времени не'явно,
через тг, и и Г, так что
д& д& дп 8F дп д^ дТ _ qQ
276 Гл. V. Решение и дальнейшие свойства уравнения Волъцмана
Из этого уравнения следует, что d$pldt задается через шесть вели-
величин: д^/дп, д^/ди, d^ldT, dnldt, du/dt, dT/dt. В разложении
операторы d\ldt определяются через производные по времени
от макроскопических переменных п, и и Г. Мы получим эти соот-
соотношения таким способом, который обеспечит, чтобы макроскопи-
макроскопические переменные, получаемые из j^, удовлетворяли уравнениям
сохранения E.9). Подставляя ряд E.34) вместе с разложениями
E.27) и E.28) в уравнения сохранения E.9) и учитывая, что п,
и и Т все являются членами порядка единицы, получим
^-V.no,
E.35)
Вводя тензор скоростей деформаций Л, последние два выраже-
выражения можно записать в виде
Подставляя ряды для ^, д/dt, 3)JF и / в уравнение Больцмана
E.21), получим
где
^т) {г) {г) дщ . д&кт) дхт
•^r +
dt дп dt ' ди dt ~ ОТ dt '
Приравнивая коэффициенты при одинаковых степенях е, придем
к искомой бесконечной системе зацепляющихся интегральных
5.1. Анализ Чепмена — Энскога уравнения Болъцмана 211
уравнений для
/), E.37а)
a)+^^rm = Jl24ff:?)^a\ ^B)), E.37в)
Решение нулевого порядка получается из E.37а):
Из предыдущего обсуждения <$?-теоремы (разд. 4.4 (в)) следует,
что решением этого уравнения является локальное распределение
Максвелла jF°'«
(^) E-38)
Напомним, что относительная скорость с равна
с = 1 —и.
Согласно предыдущим ограничениям (равенства E.26)), тг, и
и Г в JF0 представляют собой фактическую концентрацию, макро-
макроскопическую скорость и температуру газа. Все они являются
функциями х и t.
Решение нулевого порядка в приближении малого свободного
пробега дается локальным максвеллианом jF°. Это решение в свою
очередь можно использовать для получения системы гидродина-
гидродинамических уравнений нулевого порядка. Чтобы их построить,
вычислим сначала тепловой поток Q и напряжение Р. Из определе-
определений, данных в гл. III,
Р = т \
Подстановка Jf° в эти две формулы дает
Q@) = 0, E.39а)
]*о> =Jp = TnkT. E.396)
В записи по компонентам последнее равенство имеет вид
278 Гл. V. Решение и дальнейшие свойства уравнения Больцмана
Подставляя эти величины в уравнения .сохранения E.9), получим
аппроксимацию нулевого порядка, т. е. уравнения Эйлера:
g u = O, E.40а)
Напомним, что размерность К равна силе, деленной на массу.
Условие адиабатичности течения (даваемое уравнением E.40в))
согласуется с тем, что в максвелловском состоянии тепловые
потоки отсутствуют.
Построив аппроксимацию нулевого порядка для jF и соответ-
соответствующие ей макроскопические уравнения, мы можем теперь
найти, какой вклад в jp дают члены первого порядка, а именно
найти jFA). Метод решения, которому надо следовать, схемати-
схематически изображен на рис. 5.2. Функция jFA} определяется уравне-
уравнением E.376):
При исследовании этого, а также доследующих уравнений систе-
системы E.37) удобно ввести функции {Ф(Г)}, определяемые соотно-
соотношением
^(Г> ЕЕЕ^°Ф(Г>. E.42)
Решение нулевого порядка ^@) = ^° дает
Ф<0) = 1. E.43)
Кроме того, если мы определим линейный оператор
-ФA)], E.44)
то уравнение E.41) примет вид
) E.45)
Первую производную по времени вычислим с помощью определен-
определенной ранее последовательности равенств E.33) и E.35):
д0 0 д&° доп д&о дои д&° дот
dt ^ "" дп dt ' ^u ' dt ' дТ dt
!
3
\
If *
It 4
1
t
§!
1
w !*
S S § S "«
'i
i
•
G)
к it
®
c5
предпол
i
§ti|
LQ ^ ^ §
V
Jr
S* Г
§¦ s ^
! г-
<
+ fe
-
a
ч? ^ *§• ^
aT ^$ ^
^? g 5s ^
i
KIT
1
1
I
^»
I
1 ^_^ ^
к II II
v5olic^
280 Гл. V. Решение и дальнейшие свойства уравнения Больцмана
Подставляя значения (см. E.35))
E.47)
в уравнение E.46), получаем dojf°/dt как функцию только про-
пространственных градиентов от п, и и Т. Если затем подставить
выражения E.46) и E.47) в уравнение E.45), то после некоторой
перегруппировки и сокращения членов мы получим
- !¦) s.VlnT + 2 (ss—g"s2f y. fS=DOa», E.48)
где s — безразмерная относительная скорость,
52 = -2^. E.49)
Если Ф(Х) найдена, то jF известна до членов первого порядка:
), E.50)
Чтобы найти Ф(Х), мы должны решить линейное неоднородное
интегральное уравнение E.48), при условии что
E.51)
Общее решение уравнения E.48) получается путем сложения
некоторого частного решения Ф|1} этого уравнения с общим реше-
решением ФI1) однородного уравнения
ПФ^ = 0. E.52)
Решением этого уравнения будет являться линейная комбинация
трех сумматорных инвариантов:
* E.53)
где а, р, у —произвольные постоянные. Форма среднего чле#з
продиктована тем фактом, что Ф скаляр. Чтобы получить частное
5.1. Анализ Чепмена — Энскога уравнения Болъцмана 281
уравнения E.48), отметим сначала, что его левая часть
имеет вид
X(s).BRT)i/2VlnT + f (s): V^. E.54)
Поскольку оператор Q линейный, а ФA) —скаляр, из E.54)
следует, что частное решение уравнения E.48) имеет вид
ф\» = A(s)-BRT)i/2V ЫТ + Ё(з): ^. E.55)
Таким образом, получение неоднородного решения Ф|Х) свелось
к задаче отыскания вектор-функции А и тензор-функции В. Под-
Подставляя эту форму решения в уравнение E.48) и приравнивая
коэффициенты при различных компонентах V In Г и Vu, получим
следующие уравнения, которым должны удовлетворять А и В:
E.56а)
E.566)
Теперь А зависит только от s, n и Т. Из этих трех величин
можно образовать только одну векторную величину —сам век-
вектор s. Таким образом, мы запишем, что
А = -~%(s*)s,
где % —некоторая скалярная функция. (Вектор ? А должен
иметь направление вектора s.)
Помимо этого, из линейности уравнения E.566) и вида входя-
входящего в него неоднородного члена следует, что В — симметричный
тензор с нулевым следом. И опять В зависит только от s, n и Т.
Из этих переменных можно образовать единственный симметрич-
симметричный тензор с нулевым следом (ss —"q2j4 > так Чт0
Ъ = -®(s2){Ts-js2T у E.57)
[^Тензор ?# должен иметь «направление» тензора f ss —-^ s2l\ . 1
Скалярные функции g и @ удовлетворяют интегральным урав-
уравнениям:
D(sg)=-s(s2-4), E.58а)
П [(ss—5" 52П @] = -2 р-1Г52П • E'58б)
Если эти уравнения разрешить относительно % и @, то ФA) будет
°нределена. Однако однородная часть решения Ф}^ все еще
282 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
«одержит неизвестные постоянные (а, р, у). Они определяются
из условий E.51). Подставляя
^ = ^°[1+Фг)+Ф?)] E.59)
в эти ограничительные уравнения получим три интегральных
условия:
J &°(а + у±™2)*с = 0, E.60а)
J ?~° 1% (s2)V inT -m$]mc2 dc =0, E.606)
:0- E-60в)
Из первого и третьего уравнений следует, что
а = 7 = 0. E.61)
Из второго уравнения вытекает, что р имеет направление
вектора V In Г, следовательно, его можно объединить с членом
V In Г в Ф\г\
Полное решение уравнения Больцмана до членов первого
порядка включительно имеет вид
-ys2f): Vu
], E.62)
где скалярные функции ^, @ являются частными решениями
интегральных уравнений E.58).
Определив <р до членов О (в), можно теперь построить QA)
и Р{1). Они получаются путем подстановки последнего выражения
для $р в определяющие уравнения:
= m2RT \^dc = Tp + Pa\ E.63a)
. E.636)
Здесь мы выделили члены низшего порядка в выражениях для Р
и Q. Для Р{1) мы будем иметь
j*i>= _2-^-^ui [ss(ss — ys2f)@(s)j^°dc. E.64)
Чтобы получить отсюда коэффициент вязкости \i, надо представить
результат в виде E.5). Проще всего это сделать с помощью сле-
следующей теоремы, доказательство которой предлагается читателю
в качестве задачи.
5.1. Анализ Чепмена — Энскога уравнения Болъцмана 283
Задача 5.3. Доказать следующую теорему. Пусть W —любой
е#зор1 не зависящий от с, a F —любая скалярная функция от с
]р = F (с2)]. Тогда следующие пять интегралов представляют
дпн и тот же тензор (F такова, что интегралы являются сходя-
сходящимися):
A) j Fee (w0: W) dc,
B) \
C) ^
D) f .Fccq (cc<>: W) dc,
E) 4"^soj ^(^°: ™o)dc.
В этих выражениях тензор
аБ0 =
имеет нулевой след и
является симметричным тензором с нулевым следом. Напомним,
что транспозиция тензора ab определяется так:
аЬ = Ьа, (аЬ)^ = atbh = Ьгак,
и что
Тг ее = схсх + су су + czcz = с2,
TrV^ = Vxux+ . . .= V -u.
Использование равенств A) и C) предшествующей теоремы
позволяет записать E.64) в виде (W — V и; кроме того, V us = Л)
I \ ^~tv#u^)- E-65)
^Равнение этого выражения с равенством E.5) дает следующую
Формулу для коэффициента вязкости (х:
E.66)
284 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
Равенство E.65) (также как и E.62)) указывает, что @ Им
размерность времени, так что более правильно записать щ ет
= е (s, т, п).
Коэффициент теплопроводности % определяется из E.7). Цо
ставляя E.62) в E.636), получим
Q= ~[^~- J Л—g (s)ds] VT. E.67)
Следовательно, коэффициент теплопроводности равен
E.68)
Опять мы видим, что §, как и @, имеет размерность времени,
так что более правильно писать g = g (s, Г, га).
Таким образом, данный формализм позволил нам получить
выражения для коэффициентов теплопроводности, и вязкости.
Метод Чепмена — Энскога схематически представлен на рис. 5.2.
При всех условиях мы не должны забывать, какой важный вклад
в теорию дает уравнение E.62). Оно представляет собой формаль-
формальное разложение функции распределения до членов О (е). Однако
задача определения функций % и @ остается нерешенной. Эти
функции удовлетворяют линейным интегральным уравнениям
E.58). Кроме того, линейный оператор ? можно преобразовать
к виду
D*KS)=-v(S)iKS)+JKF, liH(li№, E.69)
где К —симметричная функция % и |1# Тогда уравнения E.58)
станут известными линейными симметричными неоднородными
интегральными уравнениями второго рода (в уравнения первого
рода однородный член не входит). Решения таких уравнений в виде
рядов подробно исследованы многими авторами х). Так как эти
решения в лучшем случае можно получить в виде ряда, то оконча-
окончательная структура решения Чепмена — Энскога представляет
собой аппроксимацию внутри аппроксимации. Решение уравнения
Больцмана до данного порядка по е является первой ступенью
аппроксимации. Вторая ступень аппроксимации связана со сте-
степенью точности решения соответствующих интегральных уравне-
уравнений (например, уравнения E.69)).
См., например, Курант, Гильберт A953) и Гильдербранд A952)-
? 2. Свойства линейного болъцмановского оператора столкновений 285
функция v A) называется частотой столкновений. Такая тер-
#ология обусловлена следующей записью оператора Па|г.
= - ф A) J
), E.70)
§ (| — Ю — дельта-функция Дирака. Последняя форма запи-
записи оператора ? иллюстрирует его сингулярную природу. Сле-
Следующее отсюда определение функции v A) тождественно определе-
определению D.209) для частоты столкновений в кинетическом уравнении
КБГ.
Задача 5.4. Показать, что для жестких сфер диаметра D
частота столкновений v E) имеет вид
с2 ^о ., /"
2пкТ
и что в пределе, когда s> 1,
v E) ^ /^v = n>nD2c.
Функция К (|, li) в уравнении E.69) является симметричным
ядром. Это будет показано в разд. 5.2, где исследуются свойства
линейного оператора столкновений ?•
5.2. Свойства линейного больцмановского оператора
столкновений
Если состояние газа близко к равновесному, то $р близка к ^0-
*Ри таких условиях мы положим
,F=^o[l + <Hl)], E.71)
Де Ф A) мала по сравнению с единицей. Если эту форму функции
^ подставить в уравнение Больцмана (без внешней силы)
286 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
—,
и пренебречь квадратичными членами по ф, то мы получим
E.72)
Оператор X равен со знаком минус оператору ? , определенно-
му равенством E.44). Отметим также, что максвеллиан в пред.
шествующем уравнении является абсолютным максвеллианом
в то время как в анализе Чепмена — Энскога мы имели дело
с локальным распределением Максвелла. Однако, что касается
свойств 1-зависимости операторов X и— ?, они идентичны.
Операюр X имеет следующие важные свойства.
а) Симметрия ядра
Ядро оператора X определяется соотношением
Хф == J ^OidsliK A, Ю ф A0 = J dpik A, Ю Ф (Si), E.73}
где d\i — весовая функция,
d[i = Jfod3ln E.74)
Чтобы доказать симметрию ядра К, т. е. что
K(l, Si)=*(Si, I), E.75)
мы введем следующее матричное представление для X:
Хф$ = (ф | X | я|р) = \ dja^^il? = \ а|я а^^ A) л. (§, Ю ^ (Ю =
J J
Сначала мы покажем, что
т.е. что Хфуи — симметричная матрица. Тем же самым путем, что
и при выводе инвариантов столкновений (см. гл. IV), мы получим
dddav(ф + фф'Фl)№+Ъl-V--Vl)^ E-77)
Это в свою очередь можно переписать как
Х^ = J dp dw dQVy (ф + ф±-ф
что и доказывает справедливость равенства E.76).
Следствием из E.77) является положительность всех диагональ'
ных элементов Хфф, кроме случаев, когда ф —любая линейна
5.2. Свойства линейного больцмановского оператора столкновений 287
к0>1бинацид сумматорных инвариантов A, §, ?2):
%фф > 0, E.79)
%фФ = О, только если ф = а + P-l + vl2- E-80)
рассмотрим разность
0 = ^фф —^ф= J ^цф (фК^ — ^КфО- E-81)
Меняя местами 1 и |t во втором интеграле, получим
0= [ ^фЛ-Ж!, ?j)^i-^Ai, 1)ф],
t . . E-82)
0=
В последнем выражении подразумевается, что ядро К(х, у) дей-
действует только на функции от у. Если мы определим ядро
f A, 10 = К A, Ю - К AЬ 1), E.83)
то E.82) можно записать в виде
для всех допустимых ф и г|). Функции ^ и г|) называются допусти-
допустимыми, если
|| ф ||2 = /фф < оо и || ф ||2 - /^ < со,
где / = I d[x, а || ф || называется нормой функции ф. (|| ^ || также
называют ?2-нормой функции (^>). Множество всех функций
с конечной 1/2-нормой образует Ь2-пространство.)
Предположим, что ядро Т не равно тождественно нулю. Это
означает, что существует ^акая функция G, что TG отлична от нуля
в некоторой области пространства |, |1# Тогда существует под-
?бласть D этой области, в которой TG не меняет знак. Определим
^=6 в D и 6 = 0 вне D. Для такой функции G интеграл
] TG =ф0. Это противоречит равенству E.84). Следовательноt
еДинственный способ удовлетворить условию I Гф-ф = 0 для всех
Ф й \|) —это тождественное обращение в нуль ядра Г. Итак,
^ -—симметричное ядро.
288 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
б) Положительность собственных значений и сумматору
инвариантность собственных векторов х)
Собственные значения vn и собственные функции tyn оператора ?
определяются обычным образом:
= ЧпЦ>п E.85)
(при условии, что X имеет дискретный спектр). Матричные эле-
элементы, соответствующие этим собственным векторам, являются
диагональными элементами, что обусловлено симметрией X (см
разд. 2.3):
Хпт = J dli^nX^m = Vm j dlltyntym = Vm8nm. E.86)
Диагональные элементы удовлетворяют неравенству E.79) и ра-
равенству E.80), так что
j = vn || Цп ||2. E.87)
Следовательно,
vn > 0. E.88)
Равенство нулю будет только в том случае, если г|)п — любой из
пяти скалярных сумматорных инвариантов. Если начать нумеро-
нумеровать собственные значения и собственные векторы оператора X
с этих нулевых величин, то для произвольной силы взаимодействия (!)
первыми пятью собственными функциями всегда будут
= v2 = v3 = v4 = v5 = О
где а," р, б, 7? ^ —произвольные постоянные. Кроме этого пяти-
пятикратного вырожденного нуля, все остальные vn положительны
(опять для произвольной силы взаимодействия), т. е.
vn>0, тг>5. E.89)
Эти свойства vn и г|)п для п ^ 5 являются следствием трех законов
сохранения, а сами законы, конечно, не зависят от частного вида
силового поля. Положительность остальных собственных значения
вытекает из (^-теоремы Больцмана.
Чтобы убедиться в этом, рассмотрим задачу с начальный
данными для пространственно-однородного (д/дх = 0) случая»
*) Метод собственных функций в анализе линеаризованного оператору
столкновений первоначально был введен Вэнь-Ченем и Уленбеком A95^)-
5.2. Свойства линейного болъцмановского оператора столкновений 289
когда уравнение E.72) принимает вид
E.90)
Будем искать решение этого уравнения, обращающееся в ф0 (|)
при t = 0:
ф (?, 0) » ф0 (Ю- E.91)
Если ф = ап (t) ij)n подставить в предыдущее уравнение, то мы
получим ап = ехр (—vnt). Любая суперпозиция этих решений
также является решением уравнения E.90). Чтобы построить
решение, обращающееся в ф0 при t = 0, полагаем
vn*)*MS). E.92)
так что
ФоA) = 2М>*(|). E.93)
Вследствие ортогональности последовательности {/фп} из равен-
равенства E.93) имеем
**= {фофФЛЮФ, E.94)
что вместе с E.92) дает искомое решение.
Параметры Vn1 являются временами релаксации для собствен-
собственных состояний ilv Будем считать, что начальное значение функции
распределения ф (|, t) задается (невырожденной) собственной
функцией я|)п. Тогда соответствующим решением уравнения E.90)
будет
ф A, t) = tyn (I) exp (-vn*). E.95)
Система остается в состоянии г|)п и затухает экспоненциально
во времени. Время релаксации этого собственного состояния —
время, за которое ф0 уменьшится в е раз по сравнению со своей
первоначальной величиной, — равно v^1. Так как все собственные
значения больше либо равны нулю, то ни одно из собственных
состояний системы не растет со временем.
Собственные частоты {v^} интересны с формальной точки зре-
зрения. Эти параметры связаны с микроскопическим описанием систе-
системы. В частности, они описывают эволюцию во времени функции
распределения <р (до членов О (ф)). Если какие-либо собственные
частоты отрицательны, то в системе может развиться микронеустой-
чивостъ. Эта неустойчивость связана с функцией распределения.
Простым примером такого явления служит непрерывный рост
числа частиц в некотором интервале скоростей. Понятно, что
такой процесс может не вызвать никакого заметного изменения
в любой из макроскопических переменных.
290 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
в) Дальнейшие свойства X и vn
До сих пор мы лишь отметили тот факт, что последователь-
последовательность {vn} содержит пятикратное вырожденное собственное зна-
значение (v4 = 0), соответствующее пяти сумматорным инвариантам.
Остальные собственные значения оператора X все лежат на поло-
положительной части действительной оси.
Недавно Грэд A963) доказал четыре других свойства спектра
(т. е. последовательности собственных значений) оператора х.
Для уяснения этих свойств необходимо сначала ввести концепцию
жесткого потенциала, который определяется через частоту столк-
столкновений (ср. с E.70))а
j E.96)
Потенциал является жестким, если v (?) изменяется от минималь-
минимального значения до бесконечности, и мягким, если v (?) изменяется
от максимума до нуля. Отметим, что потенциал жесткого ядра,
рассмотренный в задаче 5.4, включается в класс жестких потенциа-
потенциалов, так как для него v (?) возрастает как ? для больших ?. Для
взаимодействий по закону обратной степенной зависимости (см.
задачу 4.39) G ~ r~N и при N > 5 функция v (?) является моно-
монотонно возрастающей функцией ?, изменяющейся с ростом ? от
своего минимального значения v @) до бесконечности. Следова-
Следовательно, взаимодействия такого рода относятся к классу жестких
потенциалов. Для N <С 5 частота v (?) монотонно убывает от своей
максимальной величины v @) до нуля, когда ? неограниченно
растет (рис. 5.3). Для особого случая максвелловских молекул
TV" = 5 и v = v0 не зависит от ?.
Для широкого класса пороговых потенциалов Грэд A963)
установил следующие свойства оператора X.
1. Для жестких потенциалов частота vi = 0 изолирована от
остального спектра частот оператора X. Кроме Vi = 0, спектр &
содержит континуум значений, принимаемых частотой столкнове-
столкновений v (|), т. е. все значения от минимума v @) до бесконечности.
Для мягких потенциалов континуум собственных значений про-
простирается от максимума v @) до нуля.
2. Запишем X в виде
E.97)
5.2. Свойства линейного больцмановского оператора столкновений 291
v@)
ф
s
t
2
Жесткий потенциал
Мягкий потенциал
Рис. 5.З. Частота столкновений, потенциал взаимодействия и спектр опера-
оператора столкновений для жесткого и мягкого потенциалов.
гДе v задается равенством E.96), а К —равенством E.70). Опера-
Оператор $с ограничен, т. е. для любого if) из L2 (см. стр. 287) существует
постоянная М, такая, что
<М ||t|, ||. E.98)
E.99)
Кроме того, если мы положим
= г
J
292 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
то легко установить следующее. Если (г|/, V) —соответственно
собственная функция и собственное значение оператора (/ — Фс'\
т. е. если
(/-0Г'I/ = ЯЧ>', E.Ю0)
то
Х^ = Щ, E.101)
где
И
Я = vV. E.103)
Это преобразование лучше всего годится для случая усеченного
максвелловского закона взаимодействия (см. разд. 4 нише), при
котором v не зависит от ?.
3. Оператор &С является вполне непрерывным. Ограниченный
линейный оператор &С называется вполне непрерывным, если он
обладает следующим свойством. Для любой ограниченной после-
последовательности {§п) функций пространства L2 (это означает, что
|| i|)n || ^ R для некоторого R и любого п) последовательность
{<2^Фп} содержит по крайней мере одну сходящуюся подпоследова-
подпоследовательность. Из этого факта и спектральной теоремы х) следует,
что оК имеет дискретный точечный спектр с единственной предель-
предельной точкой в начале.
Физический смысл непрерывной части спектра X заключается
в следующем. Предварительно отметим, что собственные значения
V; входят в решение задачи с начальными значениями в виде чле-
членов ехр (—vit). Для жестких потенциалов, где v отделена от нуля
@< v< v), все вклады экспоненциальной формы убывают по
крайней мере так же быстро, как ехр (~ v@) t). С другой стороны,
для мягких потенциалов v может быть как угодно близка к нулю
и вполне вероятно, что некоторые свойства функции ер не будут
убывать со временем по экспоненциальному закону.
4. Для усеченного максвелловского взаимодействия G ~ г~ъ
для г ^ r0; G = 0 для г > г0; спектр оператора X является чисто
дискретным с единственной точкой накопления v = const. Кроме
того, для максвелловских молекул собственные функции операто-
оператора X будут полиномами Эрмита ЩпУ с соответствующими собствен-
собственными значениями:
х\п) = (Н{п)\Х\Н[п)). E.104)
х) Краткое изложение этих вопросов можно найти у Лорча A962).
Более полное представление см. в книге Стоуна A932).
5.2. Свойства линейного болъцмановского оператора столкновений 293
Двойной индекс у полинома Эрмита Н[п) указывает на то, что это
полиномиальный тензор ранга п в трехмерном пространстве.
Символом i обозначена последовательность из п индексов
(&i, *2> • • ч *п)« Полиномы порождаются весовой функцией
Полином Я(п) = Я^г2 in задается равенством
Я(п)- • -( —Лп 1 / ^ * * U- (~~1)п у?пш
E.106)
или через порождающую функцию
exp| -T(o ~x)J- ^Uii,...,in{x)yiiyi2...yin, Eл07)
Несколько первых полиномов имеют вид
Я@) = 1,
ЯA) - а:
(ж Аь + гДь + xk8,j).
Нормировка Я<п) задается равенством
|я^...,^?>...,/лсол=п1 a};; :::;t E.Ю9)
где
если {^} является перестановкой {/J, и
аЛ> • .., Зп — и
в противном случае. Таким образом, Н™ образуют ортогональ-
ортогональную с весом d\i систему функций (см. E.74)).
В следующем разделе мы коснемся в общих чертах метода иссле-
исследования нелинейного уравнения Больцмана, который в значи-
значительной мере опирается на только что рассмотренные свойства
Полиномов Эрмита.
Задача 5.5. Установить, является ли вполне непрерывным
** интервале @,1) при нулевых граничных условиях оператор
2
294 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
5.3. Моментный метод Грэда
В 1949 году Грэд в своей докторской диссертации A949) раз-
разработал более общий метод решения уравнения Больцмана. Он
известен сейчас как моментный метод Грэда. Причина такого
названия вскоре станет ясна. Моментный метод отличается от
метода Чепмена — Энскога, поскольку построенные решения не
имеют функциональной формы tf (x, | | p, u, T).
Исследование начинается с определения безразмерной ско-
скорости v:
E.110)
и безразмерного распределения g для функции jF> нормированной
на полную массу системы М = \ Jf dg dx:
Отсюда сразу следуют три свойства функции g:
dv = 0, E.112)
Функция распределения g, разложенная по полиномам Эрмита
с весовой функцией ю, определенной равенством E.105), имеет вид
оо
g (х, v, t)=(о (V) 2 2 in-аГ> (х'г) я'п) w <5-113>
п=0 г
или, что то же, можно выразить $р через локальное распределе-
распределение Максвелла
^ = &°21^аГНГ(у). E.114)
Функция Щп) является тензором порядка п и полиномом сте-
степени п. Нижним индексом i обозначена совокупность из п индек-
индексов Некоторые примеры таких функций даны в E.108).
В развернутом виде E.113) будет выглядеть так:
E.115)
Разложение справедливо (в смысле средней квадратичной схо-
сходимости), если функция О)-1^ квадратично интегрируема, т. е.
5.3. Момептный метод Грэда 295
если существует интеграл
^) E.116)
Обращая ряды E.114), получим
а[Л}= \ gHid\=— \ врН™ а\. E.117)
J P J
Так как функции #-п) —полиномы по скорости |, то коэффи-
коэффициенты а[п) являются моментами функции распределения jF-
Каждый из этих моментов будет некоторой гидродинамической
переменной. Коэффициенты a(in) разложения функции распределе-
распределения по полиномам Эрмита являются гидродинамическими пере-
переменными. Например,
„@) Л
и — 1,
ТгаB) = 0, ('
^'~ pVrt
(повторяющиеся индексы означают свертку).
Чтобы построить решение ^, мы должны получить выражения
для коэффициентов а|п). С этой целью мы сначала подставим раз-
разложение E.114) для j^ в уравнение Больцмана и над полученным
выражением произведем операцию \ H[n*dv. Полагая
получим
+ Са\п+и ~ In (pCn+1) + С S a'"»
-^(S С2) 6a'"'3> = /<">. E.119)
Для простоты записи нижние индексы у а(П) и /(П) опущены;
D/Dt —индивидуальная производная, а символом 2 обозначена
296 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
симметричная сумма градиентов. Например,
Символом 6 обозначен дельта-тензор Кронекера1). Столкнови-
тельный член /(П) имеет вид
/<n> = JL^g{y)g (Vl) /<»> (v, vO dw dvi, E.121)
где
~ ' n ' n E.122>
Уравнение E.119) тензорное порядка п. Полезно самим убедить-
убедиться, что каждый член этого уравнения является тензором п-то
порядка. Примером может служить член
если его записать более подробно:
0^ o. .. = tlklmro.. . •
Задача 5.6. Доказать следующие тождества:
A) ^Я<«> =
B)
C)
D) vt 4- Я<"> = пН^ + 26Я<П'.
OV i
Выражение с Ьг представляет сумму по всем членам, в кото-
которых индекс i привязан к 6. Например, iУс-компонента 6^ЯA) равна
Метод решения состоит в аппроксимации рядов E.113) конеч-
конечным числом членов. Так как старший член разложения пред-
представляет собой локальное распределение Максвелла (см. E.115)),
то, чем ближе состояние газа к равновесному, тем меньше членов
ряда требуется для описания состояния газа.
В предыдущих обозначениях 5 = 6; компоненты 6 (или 6) равны
5.3. Моментный метод Грэда 297
Самой простой является аппроксимация первого порядка
E.123)
Опуская в E.119) все члены с аC), получим
Если при вычислении /B) пренебречь всеми членами выше аB\
т0 в последнее уравнение будут входить {р, и, Г, а($) или, что
то же, {р, и, Т, Рц). Поскольку а?2) —симметричный тензор
с нулевым следом, то он (аB)) имеет только шесть компонент-
В сумме с переменными р, u, T это составит одиннадцать скаляр-
скалярных величин, которые определяют состояние системы в прибли-
приближении первого порядка.
Тензорное уравнение E.124) содержит шесть скалярных
величин. Эти уравнения,, вместе с уравнением неразрывности
уравнением импульсов
и условием
Тг а<2> = О
составят одиннадцать скалярных уравнений. Система замкнута.
Задача 5.7. Вычислить вектор теплового потока Q, используя
аппроксимацию первого порядка (уравнение E.123)).
Задача 5.8. Используя приближение E.123), получить явное
выражение для /B) в частном случае взаимодействия максвеллов-
Ских молекул. Другими словами, показать, что
где
я
Vo sin2 0 cos2
298 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
5.4. Релаксация к равновесному состоянию
а) Дальнейшее толкование необратимости
Мы уже встречались с понятием необратимости в разд. 2 гл. I
в разд. 4 гл. II и в разд. 1 гл. IV. В главе I в основном обсужда^
лась динамическая обратимость. В главе II явление обратимое^
кратко рассматривалось с точки зрения TV-частичной функции
Рис. 5.4. Эволюция числовой плотности, описываемая уравнением диф-
диффузии.
распределения. В главе IV было замечено, что любой закон, где
существенно направление изменения времени, является необрати-
необратимым законом.
Примером необратимого закона может служить уравнение
диффузии
E.125)
дп — П
"dt~~~u
Решение этого уравнения таково, что начальный пик плот-
плотности рассеивается со временем таким образом, что устраняется
пространственная неоднородность функции п. Процесс прекра~
щается, когда п становится однородной (рис. 5.4).
5.4. Релаксация к равновесному состоянию
299
Явление, происходящее в жидкости согласно уравнению E.125),
о объяснить геометрически. В области, где кривизна кривой
пхх<0
t=Zt0
Рис. 5.5. «Сглаживающий» механизм уравнения диффузии.
п (х) положительна (пхх < 0), п уменьшается, а в области^ отри-
отрицательной кривизной (пхх > 0) п растет. Это ведет к сглаживанию
кривой п = п (х) (рис. 5.5).
Задача 5.9. Газ находится в одномерном контейнере @ ^ х ^
^ L). В начальный момент задается распределение плотности
п (х = 0, t = 0) = п0, п (х = L, t = 0) = пи п0 <С щ\
n(x) = no + -^-(ni — no) для 0<6<o:<L — б,
где б <^ L. Это начальное распределение изображено на рис. 5.6, а.
а) Доказать, что решение п = щ + ^- (rii —п0) удовлетворя-
удовлетворяет уравнению диффузии E.125) и начальным условиям.
б) Почему это решение физически некорректно?
Ответ, б) Оно не дает корректной скорости и (х, t). Скорость и
определяется уравнением
пи= —и -5— .
дх
Так как жидкость ограничена, то в каждый момент времени
и (х = 0) = и {х = L) = 0,
следовательно, начальные условия для п должны также включать
(граничные) условия:
дп
дх
х=0
дп
дх
x=L
= 0.
начальные условия для п показаны на рис. 5.6, б.
300 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
Рассмотрим теперь процесс, который подчиняется уравнению
E.125) при обратном течении времени. То есть события развора
чиваются так, что время t последовательно уменьшается. Этого
легко достигнуть, заменяя t на —t' и считая время t' возрастаю,
щим. Тогда обратный процесс описывается уравнением
§=-°Ш' E-126)
Это уравнение не совпадает с E.125), и п (х, t) не обязана совца~
дать с n(x,t'). Однако, очевидно, что положительные значения
Рис. 5.6. Начальные условия задачи 5.9.
а — заданные начальные данные; б — полные согласующиеся началь-
начальные данные.
пхх вызывают убыль тг, а отрицательные значения пхх вызывают
рост п. Таким образом, поведение плотности п противоположи0
поведению плотности п из уравнения E.125). Процесс изменения
п показан на рис. 5.7.
Кроме того, различие между уравнениями E.125) и E.126)
хорошо выявляется при исследовании устойчивости их решений-
Пусть мы хотим исследовать устойчивость равновесного состо#~
ния п = п = п0. Для этого внесем возмущения, так что
5.4. Релаксация к равновесному состоянию
301
0 плотность будет такова:
п = п = п0 + г cos kx = {п0 + Д (ж,
E.127)
где ? <С ^о и ^ — действительная положительная постоянная,
рассмотрим решение вида
Д (х9 t) = г cos kx expco*. E Л28)
Оно принимает при t = 0 заданное начальное значение. Чтобы
5.7. Изменение числовой плотности, описываемое уравнением диф-
диффузии при обращенном течении времени.
найти со, надо подставить это решение в исходное уравнение
(E.125) либо E.126)). Подстановка в E.125) дает
со = — Dk2. E.129)
Следовательно, начальные возмущения затухают, и равновесие
п ^ по устойчиво.
Для исследования устойчивости решения п = п0 в случае
00ратного направления времени подставим решение
Д = 8 cos kx exp (otf
E.130)
302 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
в уравнение E.126). Получим
jo = +Dk*. E.131)
Начальные возмущения А @) = 8 cos кх растут со временем
и равновесие п = п0 является неустойчивым.
Если уравнение E.125) выражает истинный закон природы
то в мире с обратным течением времени состояние однородной
плотности должно быть неустойчивым. Из этого факта следуем
простой эксперимент по определению направления течения вре-
времени. Пусть газ однородно заполняет некоторую колбу х). Встрях-
Встряхнем ее. Если будут образовываться капельки, то время течет
назад. Поскольку существует эксперимент, определяющий направ-
ление течения времени, то уравнение E.125) описывает необрати-
необратимый закон.
Для обратимого закона нельзя указать эксперимента, опре-
определяющего направление течения времени. Если бы все фундамен-
фундаментальные законы природы были обратимы, то невозможно было бы
определить, куда течет время, назад или вперед. Точно так же, как
законы природы не зависят от того, в какой момент времени их
начали применять, они также не будут зависеть и от направления
течения времени. Время будет однородным и изотропным.
Рассмотрим опять эксперимент со свободным расширением.
Предположим, что в начальный момент газ заполняет весь сосуд.
Ио потом (что совершенно неправдоподобно) он внезапно сжимает-
сжимается. Или, что более впечатляюще, пусть все, что мы наблюдаем,
внезапно обратит свое направление движения, подобно обратному
движению киноленты. Люди будут молодеть, земля станет вра-
вращаться в противоположную сторону. Тогда, конечно, время поте-
потечет в обратном направлении. Но этого нет!
Хотя справедливо, что такое движение будет иметь место,
когда время изменит свое направление, неверно считать, что
при обратном течении времени возможно только такое движение.
Существуют процессы, вполне согласующиеся с законами природы
и при обратном течении времени.
Динамические законы обратимы. Если бы из только что рас-
рассмотренного движения (при включении его в число фундаменталь-
фундаментальных законов) следовало, что время течет в определенном направле-
направлении, то это давало бы эксперимент, опирающийся на закон,
который указывал бы направление течения времени. А это в свою
очередь означало бы, что законы необратимы, а это не так. ОтсюДа
следует, что такое движение ничего не говорит относительно
направления течения времени.
Мы показали, что необратимое уравнение диффузии дает
дисперсионное соотношение со = —Dk2 для прямого направления
х) При температуре и давлении, когда газовая фаза термодинамически
устойчива.
5.4. Релаксация к равновесному состоянию 303
яем и со = +Dk2 —для обратного. В более общем случае
^цеаризация обратимого закона около равновесного состояния
юЛ/Кна включать как возрастающие, так и затухающие решения,
ак что оба движения возможны для прямого течения времени.
Если существуют только возрастающие решения, то, несомненно,
быть возможен эксперимент, устанавливающий различие
ДВУМЯ направлениями течения времени.
Задача 5.10. а) Рассмотреть дисперсионное соотношение для
уравнений Максвелла в вакууме и доказать обратимость этих
уравнений.
б) Подобным же образом исследовать обратимость уравнений
dt + дх
дЕ _q_
дх е0
В чем заключается основное различие между этими уравнениями
и электромагнитным уравнением в вакууме?
6) Равновесные распределения. Микросостояния и макросостояния.
Априорный подход
Уравнение диффузии
ж=°& <5-125>
и ему подобные необратимы и, следовательно, находятся в про-
противоречии с фундаментальными законами механики, которые
являются обратимыми. Однако эксперимент подтверждает спра-
справедливость уравнения E.125). А раз оно всегда удовлетворяется
(при условии, что имеется достаточное число частиц, чтобы можно
было ввести плотность п), то, по-видимому, закон диффузии (на-
(называемый иногда законом Фика) является верным. Но если этот-
закон справедлив, то существует различие между временем, теку-
Щпм в прямом и обратном направлениях {стрелка времени).
Экспериментальное подтверждение уравнения E.125), каза-
казалось бы, ставит под сомнение справедливость законов механики
(которые, по-видимому, также всегда верны). Как согласовать
эти два факта?
Хорошего «примирения» можно достичь, если ввести в тео-
Ри*о вероятностные законы. Это так называемый априорный под-
Х°Д — вывод следствий из определений или принципов, рассматри-
аемых как самоочевидные. Введем прежде всего постулат равных
^риорных вероятностей, согласно которому все состояния на
Иергетической поверхности равновероятны.
304 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
Данный принцип применим к системам, находящимся в
весии. В этом отношении данный формализм весьма ^зо
к равновесной термодинамике, которая хотя и всегда способн
-описать равновесные состояния, однако не может указать нацрав^
ление изменения системы.
Ясно, что подобную методику можно ввести в равновесную
«статистическую механику. Рассмотрим простой пример. Пусть
известно, что вероятность одного состояния системы (газ занимает
половину сосуда) много меньше вероятности другого состояния
(газ однородно заполняет сосуд). Все «шансы» за то, что более
вероятным является то состояние системы, которое мы наблюдаем.
С другой стороны, предположим, что система приведена в наименее
вероятное состояние (газ сжат в одном конце сосуда). Если суще-
существует механизм, изменяющий состояние системы, то при после-
последующем наблюдении мы должны увидеть систему в более вероят-
вероятном состоянии (т. е. в однородном состоянии).
Этим идеям можно дать количественную основу, формулируя
их через микросостояния и макросостояния. Микросостояние изо-
изображается вектором в Г-пространстве. Макросостояние опреде-
определяется через [Х-пространство. Это фазовое пространство для одной
частицы (\i —для молекулы; Г —для газа). Хотя координаты
и импульсы для N частиц системы изображаются одной точкой
в бУУ-мерном Г-пространстве, в 6-мерном [г-пространстве они
будут представлены множеством из N точек (отдельной точкой
изображаются координаты и импульсы каждой частицы).
Разделим теперь (i-пространство на маленькие «ячейки». После-
Последовательность чисел заполнения, задающая количество частиц
в каждой ячейке, определяет макросостояние. В этом состоит
процедура крупнозернистого разбиения (а-пространства.
Когда определено микросостояние, то известны координаты
и импульсы всех частиц. Каждой частице присваивается индекс.
То есть мы должны считать, что частица 1 находится в (q1? pi)»
частица 2 —в (q2, р2) и т. д. для того, чтобы определить микро-
достояние.
С другой стороны, чтобы определить макросостояние системы,
мы просто говорим, что щ частиц находятся в ячейке 1, иг """*
в ячейке 2 и т. д. Какие частицы из всей совокупности N частяД
находятся в ячейке 1, не существенно. Макросостояние несет
в себе много меньше информации об объекте, чем микросостояние.
Чтобы задать микросостояние системы, нужно знать всю ее струк-
структуру. Чтобы знать макросостояние, необходимо знать лишь сово-
совокупность чисел заполнения.
Можно проиллюстрировать различие между этими двумя уроГ
нями описания на примере системы из двух частиц. Система так0'
ва, что каждая частица может быть только в одном из четыре
возможных состояний. Обозначая частицы через а и Ь, ^°
5.4. Релаксация к равновесному состоянию 305
представить микросостояние в виде диаграммы 1^1 1^1 I
Так как таблица L.J—I—I—I представляет состояния одной
частицы, то она изображает \i-пространство. Одним из возможных
делений (^-пространства является | t | j [ , т. е. разбиение его
на две ячейки. Тогда типичные макросостояния задаются парами
чисел заполнения, например A, 1); B, 0); @, 2).
Макросостояние A,1) представлено графически на рис. 5.8.
Как много микросостояний соответствует этому одному макро-
I • 1 • 1
Рис. 5.8. Макросостояние, соответствующее последовательности чисел
заполнения A,1).
состоянию? Мы изобразили эти микросостояния на рис. 5.9. Вось-
Восьми микросостояниям соответствует одно и то же макросостояние.
Таким образом, имеется восемь путей реализации одного макро-
макросостояния.
С точки зрения этих понятий постулат равных априорных
вероятностей означает, что все микросостояния изолированной
системы, находящейся в равновесии, равновероятны х).
hi I ъ , 1
1
1
1
1
1 а 1 Ь
, а |
i Ь |
1 |
1 b |
1 ь i
1 ь i
1 ,
1 ,
b
b
1 a
\
1 о
1
1
1
1
1
1
" 1
1
« 1
Pic. 5 9. Микросостояния, соответствующие макросостоянию ] • | • |
Каким бы, однако, всеобъемлющим ни было знание микро-
микросостояния системы, оно гораздо детальнее того, которое тре-
*) Результирующая сила для изолированной системы равна нулю.
Следовательно, все состояния изолированной системы равновесные. Сила,
вЫзывающая свободное расширение, не относится к типу F = та.
306 Гл. V. Решение и дальнейшие свойства уравнения Больцмана
буется в макроскопической физике, где мы чаще имеем дело
с макросостояниями. Например, распределение энергии п (Е) dE
задающее число частиц с энергией dE около Е, характеризуем
макросостояние. Одночастичное распределение по скоростям
JFt d3!, задающее число частиц со скоростями в элементе сР% около
|, также определяет макросостояние.
В рассмотренной элементарной задаче с двумя частицами
каждая из которых может находиться в одном из четырех упомя-
упомянутых состояний, мы нашли, что существует восемь микросостоя-
микросостояний, соответствующих макросостоянию 1 ¦ • 1 • 1 . Анало-
Аналогично можно установить, что существуют два микросостояния,
дающие одно макросостояние 1**1 I , и два микросостоя-
микросостояния, реализующие одно макросостояние I 1 •• 1 .Длярас-
.Длярассмотренной системы эти три макросостояния являются единст-
единственно возможными.
Итак, в целом имеется двенадцать микросостояний, и все они
равновероятны. Это означает, что в любой заданной (достаточно
многочисленной) совокупности производимых измерений систе-
системы все микросостояния встречаются одинаково часто. При доста-
достаточно большом числе экспериментов 4/6 измерений дадут макро-
макросостояние ] • 1 • 1 , 1/6 измерений придется на макросостоя-
макросостояние 1 •• 1 I и 1/6 —на 1 | ¦§ |, . Этот простой пример
иллюстрирует два момента. Во-впервых, как видно из рис. 5.9Г
одному макросостоянию соответствует много микросостояний.
Во-вторых, вероятность макросостояния (называемая иногда тер-
термодинамической вероятностью) пропорциональна полному числу
различных микросостояний, реализующих данное макросостояние.
Так как концепция макросостояния основана на разбиении
^-пространства на ячейки с некоторыми шестимерными объемами,
то уместно вывести правило для получения вероятностей макро-
макросостояний через объемы Г-пространства, которое является есте-
естественной системой координат для микросостояния.
Поскольку любое заданное макросостояние определяется через
объем в [^-пространстве, относящиеся к нему микросостоянйЯ
5.4. Релаксация к равновесному состоянию 307
та находятся внутри соответствующего объема в Г-простран-
стве. Пусть, например, шестимерные ячейки в ^-пространстве
(числа заполнения которых образуют макросостояние) имеют
каждая одинаковый объем т. Тогда для совокупности N частиц
любое соответствующее микросостояние лежит в области с объемом
xn в Г-пространстве. Это можно легко понять из следующего рас-
рассуждения. Пусть объем в Г-пространстве равен со, так что
й)=1 • • • \ dqi . . . dq3N dp± . . . dp3N =
= I dxidpi \ dx2dpz . . . I dxNdpN = TN. E.132)
XX X
В последнем интеграле dxt dpi является элементом фазового
объема 1-я частицы.
Теперь предположим, что макросостояние (задаваемое после-
последовательностью чисел заполнения {пг}) эквивалентно любому
из W микросостояний. Тогда объем, занимаемый в Г-пространстве
этим множеством микросостояний, равен
Q = T*W. E.133)
Число микросостояний W является функцией последователь-
последовательности чисел заполнения {rii}, которая определяет макросостояние.
Вероятность макросостояния пропорциональна Q.
Рассмотрим изолированную систему из N частиц, полная
энергия которой изменяется в пределах Е и Е + 6Z?, 62? <^ Е.
Полагая гамильтониан Н равным Е, получим поверхность
II = Е в Г-пространстве. Когда Е изменяется от Е до Е + 8Е,
то поверхность «выметает» энергетический слой. Точка системы
движется внутри энергетического слоя.
Разделим теперь ^-пространство на ячейки с шестимерным
объемом т. Любое макросостояние {rii} порождает объем в энерге-
энергетическом слое:
Q (Ы) = *NW (W). E.134)
Когда точка системы движется в энергетическом слое, она входит
и выходит из областей различных макросостояний. Предположим,
что существует макросостояние, которое порождает объем Q,
занимающий подавляющую часть энергетического слоя. Тогда,
если точка системы находится в этом объеме, то почти несомнепно,
что она никогда его не покинет, а если она находится вне его,
то столь же вероятно, что точка войдет в этот объем.
Для реального газа это утверждение означает, что газ будет
Сходиться наибольшую часть времени в том состоянии, которое
«вырезает» подавляющую часть энергетического слоя.
Хотя из постулата равных априорных вероятностей вытекает,
^то вероятность макросостояния пропорциональна Q, мы должны
308 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
ввести в априорный подход второй постулат, связывающий этц
утверждения с наблюдаемыми фактами. Этот второй постулат
гласит: наблюдаемое равновесное состояние имеет наибольшую
вероятность. Или, привлекая понятие энергетического слоя:
Конфигурационная компонента
ja - пространстба
№ячеики
Конфигурационная компонента Г- пространстба'
Рис. 5.10. Разбиение Г-пространства для двух шариков на прямой.
наблюдаемое равновесное состояние — это макросостояние»
порождающее наибольший подобъем внутри энергетического слоя
(рис. 5.10).
Как мы вскоре покажем, таким наиболее вероятным является
макросостояние с однородным распределением чисел заполнений
в конфигурационном пространстве и распределением Больцма#а
в пространстве импульсов. Кроме того, соответствующий это>*У
5.4. Релаксация к равновесному состоянию 309
макросостоянию объем в Г-пространстве почти целиком заполняет
энергетический слой.
Задача 5.11. Рассмотрим газ из N атомов, заполняющий кон-
контейнер. Предположим, что каждый атом может занимать ячейку
такого размера, что 2v ячеек заполняет весь контейнер.
Пусть 1 <^ N4i v ( газ разрежен). Найти относительную вероят-
вероятность R того, что газ заполнит только половину сосуда по сравне-
сравнению с вероятностью того, что заполнится весь сосуд. Каково
значение R для N = 1020?
Ответ.
Я — л N ' — v!Bv~7V)! _ v(v —1) ... [у — (N — 1)]
m ( 2у \ ~~ {v — N)\ By) ! ~~ 2у By —1) ... [2у —(iY —1)J
Для v>iV
Для ЛГ = -
Таким образом, в среднем «сжатое» состояние будет встречаться
(менее чем) один раз на Ю1019 случаев однородного состояния.
Если однородное состояние наблюдается каждую секунду,
то в среднем необходимо ждать Ю1019 секунд (~10A°19-7) ~
~ 101(I9 лет), прежде чем мы заметим сжатое состояние. Но воз-
возраст вселенной равен только ~1010 лет!
Перечислим два постулата, являющиеся частью априорного
подхода в равновесной статистической механике: 1) принцип
равных априорных вероятностей и 2) наблкЗдаемые равновесные
состояния являются наиболее вероятными. Последний постулат
служит для установления связи теории с термодинамикой.
В термодинамике говорят о термодинамических состояниях.
Термодинамическое состояние задается последовательностью тер-
термодинамических переменных. Термодинамическими переменными
являются макроскопические свойства системы, например темпе-
температура 7\ объем F, полная внутренняя энергия Е, полное число
частиц N. Термодинамические переменные обладают тем свойством,
что их значения в любой заданный момент времени не зависят
От предистории системы. Очевидно, что упомянутые переменные
обладают этим свойством. Термодинамические переменные под-
подразделяются на два класса: экстенсивные и интенсивные перемен-
переменные. Рассмотрим термодинамическую переменную X однородной
310 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
системы. Перегородкой разделим систему па две части, 1 и 2
Значение X для подсистемы 1 равно Хи а для подсистемы 2 — X?
Если
Х± = Х2 = X, E.135)
то переменная X —интенсивная. Если
X = Xi + X2, E.136)
то переменная X — экстенсивная. Такие переменные, как N, V
и Е, являются экстенсивными. Температура Т —интенсивная
переменная.
Другой очень важной экстенсивной переменной является
энтропия S. Она определяется согласно дифференциальному
соотношению
E.137)
где индекс R указывает, что тепло dQ передается в результате
обратимого процесса при температуре Т. Обратимый процесс —
это геометрическое место точек равновесных состояний.
Второй закон термодинамики утверждает, что если термодина-
термодинамическое состояние изолированной системы изменяется, то свя-
связанное с этим изменение энтропии подчиняется неравенству
AS >0, E.138)
причем равенство справедливо только для обратимых процессов.
Истоки этого закона лежат в теории коэффициента полезного
действия (к. п. д.) тепловых машин. Тепловой машиной назы-
называется циклический процесс, при котором тепло забирается от
горячего резервуара, часть его поглощается холодным резервуа-
резервуаром, а часть превращается в работу. Неравенство E.138) вытекает
из того факта, что к. п. д. т] (полученная работа/отобранное от
горячего резервуара тепло) для любой такой тепловой машины
ограничен сверху согласно неравенству
г]<1--|А , E.139)
где 2*1 и Т2 —температуры холодного и горячего резервуаров
соответственно. Равенство справедливо для обратимого режима
(цикл Карно). Второму закону термодинамики можно придать
другую формулировку: не существует полностью совершенных
машин (с г] = 1).
Этой последней формулировкой второй закон термодинамики
обязан работам Румфорда A798), Карно A824), Клапейрона
A834), Клаузиуса A850) и Кельвина A851). Термодинамика была
полностью сформировавшейся наукой уже в середине девятнадца-
5.4. Релаксация к равновесному состоянию 311
того столетия. Однако корректная микроскопическая интерпрета-
интерпретация энтропии оставалась загадкой для этой науки.
Только на рубеже двух столетий, благодаря главным образом
работе Больцмана, была дана микроскопическая интерпретация
энтропии, которая легла в основу третьего постулата априорного
подхода в равновесной статистической механике. Этот постулат
гласит: энтропия системы, находящейся в данном термодинами-
термодинамическом состоянии, пропорциональна объему Q в Г-пространстве,
который занимают микросостояния, совместимые с данным термо-
термодинамическим состоянием:
S ~ Q. E.140)
Объем Q иногда называют объемом, допустимым для системы.
Система может иметь любое микросостояние в Q, а заданное термо-
термодинамическое состояние останется одним и тем же. Термодинами-
Термодинамическое состояние — это форма макросостояния, которая может
быть реализована посредством большого числа микросостояний.
Опять, как уже было обсуждено, чем больший объем в Г-про-
Г-пространстве занимают эти микросостояния, тем больше вероятность
соответствующего макросостояния.
Вполне очевидно, что естественная тенденция развития систе-
системы состоит в движении к макросостояниям, которым соответствуют
большие по объему области в Г-пространстве. Система эволюциони-
эволюционирует к более вероятным макросостояниям. Эти идеи можно сфор-
сформулировать в виде следующего утверждения. При изменении
макроскопического состояния изолированной системы соответ-
соответствующий объем в Г-пространстве увеличивается:
AQ >0. E.141)
Равенство достигается при макросостоянии с максимальным объе-
объемом.
Постулат E.140) основан на уравнениях E.138) и E.139).
Согласно этому постулату энтропия интерпретируется как мера
термодинамической вероятности состояния системы.
Итак, мы выяснили смысл пропорциональности между 5иЙ,
но вопрос о функциональном соотношении между ними пока еще
остается открытым. Чтобы получить это соотношение, вспомним,
что S —экстенсивный параметр и Q —объем в Г-пространстве.
Рассмотрим некоторую систему, разделенную на две части. Пусть
^i — объем в Г-пространстве, допустимый для первой подсистемы,
a Q2 —объем, допустимый для второй подсистемы:
dp dq,
E.142)
Й2= j... ^
312 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
Объем, допустимый для всей системы, равен
Q==\ ' " J 1 "•" 1 dpdf dqdqr =0,^. E.143)
С другой стороны, если *5± и S2 суть энтропии первой и второй
подсистемы соответственно, то вследствие свойства экстенсивности
энтропия S всей системы будет равна
S = S± + S2. E.144)
Объединяя E.143) и E.144), получим функциональное соотноше-
соотношение между 5ий:
S (О) = S (Q4) + 5 (Q2) = S (Q4Q2). E.145)
Его решением будет
S = ft'lnQ, E.146)
где к' не что иное, как постоянная Больцмана! Это можно пока-
показать следующим образом.
Рассмотрим свободное расширение идеального газа, при кото-
котором объем его удваивается, т. е. идеальный газ переходит из
состояния G1, V) в состояние (Г, 2V). Происходящее при этом
изменение энтропии можно вычислить двумя путями: термодина-
термодинамически и статистически.
Термодинамический метод опирается на тот факт, что энтропия
является «хорошей» термодинамической переменной, т. е. ее вели-
величина зависит только от состояния системы, но не зависит от того,
как данное состояние было достигнуто. Вследствие этого мы
можем вычислить AS вдоль любого удобного термодинамического
пути, соединяющего точки (Г, V) и (Г, 2V). Выберем изотерми-
изотермический процесс. Так как внутренняя энергия Е идеального газа
является функцией только Г, то первый закон термодинамики
примет вид
E.147а)
E.1476)
2 У2
Д5= J dS = Nk J y- = Nkln2. E.147b)
1 Vi
Чтобы найти AS методом статистической механики, надо вычислить
допустимый объем в Г-пространстве, которым обладает система
в каждом состоянии. Начальный и конечный объемы соответствен-
соответственно равны
j J dSl . . . dqm = AVN, E.148a)
dqi...dq3N = ABVf. E.1486)
5.4. Релаксация к равновесному состоянию 313'
tjepe3 А обозначен результат интегрирования по импульсной
^сти Г-пространства. При свободном расширении идеального
а а не изменяется. Согласно E.146), энтропии этих двух состоя-
состояли имеют вид
Sin = Nk' In V + k' In A, E.149a)
Snn = Nk' In 27 + kf In A. E.1496)
Следовательно,
AS = Nk'In 2. E.150)
Сравнивая это равенство с термодинамическим результатом
AS = Nk\n2,
видим, что
к' = к — постоянная Больцмана. E.151)
Отметим, между прочим, что объем О. является функцией объе-
объема V, занимаемого системой, и энергии Е этой системы. Тогда
соотношение E.146) дает: S = S (Е, V), где Е и V— это так назы-
называемые «естественные» независимые переменные для энтропии
(см. E.147а)).
в) Наиболее вероятное макроскопическое состояние
Для идеального газа, т.е. газа, состоящего из невзаимодей-
невзаимодействующих частиц, (^-пространство приобретает особое значение:
энергия частицы является функцией только ее положения
(Pxi Py, Pz, х, У, z) в (^-пространстве. Если, например, к системе
не приложен извне никакой потенциал, то энергия частицы е
равна
в = ?. E.152).
При наличии внешнего потенциала
г = -?г + Ф(х, у, z) E.153)
и s все еще является функцией только (х, р). В этом частном слу-
случае имеет смысл разбить (^-пространство на ячейки таким образом,,
чтобы внутри заданной ячейки все частицы обладали одинаковой
энергией. Если этим ячейкам присвоить номера, 1, 2, . . ., Z, ...
• • ., то в Z-й ячейке будет п\ частиц, каждая из которых имеет
энергию &i. Такое разбиение (^-пространства изображено на
Рис. 5.11, где %i — шестимерный объем 1-й ячейки.
Последовательность чисел заполнения пи п2, . . . ={ni} обра-
3Ует (энергетическое) макросостояние. Мы хотим найти наиболее
вероятное макросостояние или, что то же, макросостояние
с наибольшим допустимым объемом в Г-пространстве. При этом
314 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
должны выполняться два условия:
= N — полное число частиц системы,
i = E — полная энергия системы. Ф
Объем Q допустимой области Г-пространства, соответствующе
макросостоянию {ni}, равен
^Ь&^ E.1Ц
Это выражение получается следующим образом. При макросостоя-
макросостоянии {rii} имеется п1 частиц в первой ячейке. Если любая из них
заменена, скажем, частицей из 20-й ячейки, то макросостояние
I П 1 т2 1 Т3 1 т4 | •••
(«1, Ci) fe,^)"'
Рис 5.11. Энергетические ячейки в ^-пространстве.
¦остается тем же самым. Однако вектор состояния в Г-пространстве
изображает теперь новое состояние. Следовательно, полное число
микросостояний Wy реализующих одно и то же макросостояние
{ni}, равно числу способов распределения N объектов по ячейкам
так, что щ из них находятся в первой ячейке, п2 —во второй, ....
Это число равно
(N\ (N — nA /iV — /г± — лг2\ m лм
W = ... =—i—j— = тт—i • E.156
\Щ/ \ П2 I \ Щ ) гц\п2\... Uni\ v
Каждое такое микросостояние лежит в области Г-пространства
с объемом (т?1 Т22 . . .) (ср. с E.132)). Таким образом, объеи
в Г-пространстве, соответствующий макросостоянию {пг}, опре-
определяется равенством E.155).
Теперь мы хотим найти макросостояние {тгг}, сообщающее
максимум объему Q при выполнении условий E.154). Вместо Q
удобнее иметь дело с энтропией
S = felnQ. E.157)
Ясно, что макросостояние {ni}, сообщающее максимум In ?2, также
максимизирует и й.
Запишем выражение для In й, используя E.155).
"--1)- E-158)
5.4. Релаксация к равновесному состоянию 315
\Ы использовали аппроксимацию Стирлинга, заменив In n\ на ь
: (In п — 1)- Это справедливо для п, достаточно больших до срав-
сравнению с единицей.
Если {ni} — макросостояние, которое сообщает максимум объе-
объему ?2, то при вариации {ni} около этого состояния значение Q
Iie изменяется. То есть для максимального Q
8{ni} In Q =0. E.159)
Символом 8{ril} обозначена вариация последовательности чисел
заполнения {ni}. Из E.159) имеем
E.160)
Когда варьируются соотношения E.154), мы получаем два допол-
дополнительных условия:
ti^ix^Snt, E.161а)
0=— P2sz6^. E.1616)
Постоянные [х и р называются неопределенными множителями
Лагранжа. Назначение этих множителей и знака минус в E.1616)
вскоре станет ясно. Суммируя последние три уравнения, получим
E.162)
Теперь все перемещения 8ni, кроме двух, могут быть выбраны
произвольно. Как только такой выбор сделан, оставшиеся два
перемещения определяются из E.154). Обозначим эти два пере-
перемещения через 8nv и бя^- Предположим, что [х и р выбраны так,
что
E.163а)
E.1636)
Тогда все оставшиеся вариации {8ni} в сумме E.162) могут быть
выбраны произвольно. Чтобы обеспечить равенство нулю всей
сУммы, необходимо потребовать
Г. E.163в)
Из E.163) следует, что написанцый выше трехчлен равен нулю
Цля всех I. Мы можем сделать заключение: если объем Q максима-
максимален, то макросостояние {ni} задается распределением Больцмана
316 Гл. V. Решение и дальнейшие свойства уравнения Болъцмаиа
Задача 5.12. Предшествующий анализ показывает, что,
объем Q экстремален, {ni} —распределение Больцмана.
зать, что экстремум является максимумом.
Ответ.
б2 In Q |БольцМал = - 2 "^ < О-
Задача 5.13. Показать, что для изолированного газа однород.
ное распределение является наиболее вероятным пространстве^
ным распределением.
Задача 5.14. Величина й, задаваемая равенством E.155),
это объем в Г-пространстве, занимаемый макросостоянием {^д
Если весь объем ^-пространства равен соо, то полным допустимым
объемом Г-пространства будет со^. Показать, что вероятность
макросостояния {rti} равна
Показать также, что
где p{rti) —множество перестановок из
Ответ. Переписывая coj7 в виде
rN П1+П2+... ГП1 n2
°°о = °°о = С00 С00 . . .,
получим, что
^N \ о)о / \ 0H /
Так как оH — полный объем ^-пространства и последнее разбито
на ячейки с объемами Т/, то
где
6 соо
Тогда
Здесь мы использовали теорему о разложении многочлена N-&
степени вида (gi + g2 + . . .)N-
Макросостояние, задаваемое распределением Больцмана, являет-
является наиболее вероятным. Из полного достижимого объема в энер'
гетическом слое в Г-пространстве данное макросостояние вырезав
5.4. Релаксация к равновесному состоянию 317
япболыний объем. Этот подобъем является не только наибольшим
**' данном классе, а он подавляюще велик. Это означает, что
Цо^ти всегда выполняется следующее: точка системы, движущаяся
энергетическом слое, войдет в область распределения Больцма-
ja? если ее там нет, и не покинет область распределения Больцма-
рис. 5.12. Объемы в Г-пространстве, соответствующие различным макро-
макросостояниям.
на, если она уже находится там. Это утверждение символически
можно изобразить в виде зависимости Q от {ni} (рис. 5.12). Каж-
Каждая точка абсциссы — это отдельная последовательность чисел
заполнения.
В предельном случае, когда последовательность энергий {&i}
переходит в континуум, распределение Больцмана принимает вид
щ —> п (р) dp = x (p) е»е-
K^j E.165)
В этом выражении мы положили
__^2_ E.166)
8~ 2т '
4яр2 dp —объем сферического слоя радиуса р и толщины dp.
Причем считается, что все состояния внутри этого слоя обладают
энергией 8 (р). Из теоремы о равномерном распределении энергии
для идеального газа следует, что средняя энергия частицы равна
1ерез распределение п (р) это условие запишется в виде
сю
SJ (p2/2?n) 4jxjo2 dp exp (— P/?2/2?n)
2 '"x ~
! Jp exp (—
E.168)
318 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
Кроме того, интегрируя п(р) по всем р, получим
оо
N = e» J
О
Последние два условия служат для определения постоянных
и р. В результате получим
Мы видим, что JFо —распределение Максвелла. Это равновес-
равновесное распределение, к которому, согласно <$?-теореме' Больцмана,
будет приближаться система. Хотя сЖ1-теорема имеет сугубо необ-
необратимый вид, наш анализ иллюстрирует, как этот вывод совме-
совмещается с обратимой динамикой. Даже при обратном течении вре-
времени «судьба» точки системы в энергетическом слое останется той
же — она фактически ничего не будет «видеть», кроме максвеллов-
ских макросостояний (по импульсам) и пространственно-однород-
пространственно-однородных макросостояний.
Рассмотренный вероятностный анализ, который приводит
к тем же результатам, что и <$?-теорема, первоначально был осу-
осуществлен Больцманомкак возражение против критики результатов
©^-теоремы, считавшихся неверными ввиду их свойства необра-
необратимости.
г) Г-пространственное описание несовершенных систем. Ансамбли
Изложенный выше метод вычисления наиболее вероятного
макросостояния хотя и является вполне общим, тем не менее уяз-
уязвим в одном отношении. А именно, он основан на разбиении \i-
пространства. Энергии sj связаны с ячейками [х-пространства —
фазового пространства одной частицы. Это вполне пригодно для
систем, состоящих из невзаимодействующих частиц (идеальный
газ), где энергия частицы является функцией только ее положе-
положения в [х-пространстве. Такое описание также годится и для систе-
системы невзаимодействующих частиц при наличии внешнего потен-
потенциала. В этом случае состояние частицы все еще определяется
ее положением в (^-пространстве. Например, для вертикального
столбика газа энергия частицы в 1-й ячейке равна
где z — вертикальное перемещение, a g — ускорение силы тя-
тяжести .
Для неидеального газа энергия молекулы зависит от взаимо-
взаимодействий этой молекулы со всеми остальными молекулами систв'-
мы. При таких условиях положение частицы в [i-пространстве
5.4. Релаксация к равновесному состоянию 319"
ле определяет ее энергию. Теперь правильнее принять за систему
je одну молекулу, а целый газ. Состояние всего газа определяется
,гочкой в Г-пространстве. Энергия системы является функцией
тОчки г) (ffi, ?2» • • •» Qsn'i Ри Рг, . . ., Psn) и выражается череа
гамильтониан
?». E-170>
где ф№ —потенциал взаимодействия частиц:
4>ik = ф/ft A гг — rfe |) E.171)
(ср. с B.152)). Вектор rt задает положение 1-й частицы, а г^ —
/с-й, так что двойное суммирование по yih ведется до N.
Для несовершенного газа уместно использовать Г-пространство,
поскольку состояние такой системы характеризуется точкой
в Г-пространстве. Формализм ансамбля наилучшим образом объе-
объединяет все эти свойства. Он был введен в самом начале XX века
независимо Дж. У. Гиббсом A902) и А. Эйнштейном A902).
Концепция ансамбля уже обсуждалась на многих страницах
гл. II. Там мы определили ансамбль как совокупность идентичных
систем. Каждая система имеет представляющую точку в Г-про-
Г-пространстве. Число таких тождественных систем достаточно велико,
так что можно ввести плотность D (p, q, t) точек систем в Г-про-
Г-пространстве. В гл. II было доказано, что функция D удовлетворяет
уравнению Лиувилля:
| + [ДЯ] = 0, E.172)
где Н — гамильтониан системы. Функция плотности D и функция
совместной вероятности fN отличаются только постоянной норми-
нормировки, fN = D \ D dp dq, так что fN также удовлетворяет урав-
уравнению Лиувилля.
В равновесной статистической механике нас интересуют только
Установившиеся решения уравнения E.172), т. е. решения урав-
уравнения
LD, Я] = 0. E.173)
Самое общее решение уравнения E.172) является произвольной
Функцией 2N (N —число степеней свободы) констант движения
С11стемы. Эта же функция будет решением уравнения E.173) при
Условии, что константы явно от времени не зависят. Решения
Уравнения E.173) называются стационарными решениями.
^ 1) Частицы предполагаются точечными. Для частиц с / степенями сво-
°Дны Г-пространство является 2/ЛГ-мерным.
320 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
Задача 5.15. Гамильтониан изолированной свободной частиц
равен *
а) Доказать, что
2т
решение уравнения Лиувилля E.172).
б) Доказать, что
Ф = Ф (Р)
— (стационарное) решение.
Заметим, что шестью константами движения для гамильтониана
свободной частицы будут
Функция плотности D определяет среднее (по ансамблю) от
любой динамической переменной G (см. гл. II, разд. 2.5) согласно
равенству
1о(р g,t)D{p,q,t)apdq ^
W \D (p, q, t) dpdq
Эквивалентное утверждение состоит в том, что вероятность
нахождения системы в состоянии dp dq около (р, q) равна
fNdpdq= °Ь'Р)*Р** . E.175)
\D(q,p)dpdq
Чтобы использовать это соотношение для случаев, когда D
зависит от времени, надо ввести в теорию формализм, связываю-
связывающий начальное значение D с начальным состоянием рассматривае-
рассматриваемой системы. Это уже обсуждалось в гл. П.
С другой стороны, в стационарном случае D постоянна, а сле-
следовательно, и G. Именно для этого случая концепция ансамбля
наиболее применима. Число типов ансамблей, необходимых для
описания (равновесных) систем, обычно встречающихся в природе,
исчерпывается тремя: а) микроканонический ансамбль, б) канони-
канонический ансамбль, в) большой канонический ансамбль. Во все*
трех случаях принцип равных априорных вероятностей определяет
плотность D посредством такого соотношения, что вероятность
макросостояния равна бй/ЙП0Лн- Допустимый объем точек систе-
системы, соответствующий упомянутому выше макросостоянию, раве#
SQ (см. задачу 5.19).
5.4. Релаксация к равновесному состоянию 321
Микроканонический ансамбль
Рассмотрим изолированную систему с разбросом энергии
Е ^ Н ^ Е + 8Е. Полагая гамильтониан равным этому интер-
интервалу энергий, получим энергетический слой —полную допусти-
допустимую область системы в Г-пространстве. Ввиду того что система
изолирована, ее состояния подчинены постулату равных априор-
априорных вероятностей. Так как все состояния имеют одинаковую
вероятность, то fN в E.175) равна константе. Это в свою очередь
означает, что плотность D постоянна по всему энергетическому
слою и равна нулю вне его. Соответствующий (однородный)
ансамбль называется микроканоническим. Таким образом, мы
получили формулировку постулата равных априорных вероят-
вероятностей через формализм ансамбля:
D = const, Е < Я ^Е + 8Е; E.176)
D = 0 вне этой области.
Макросостояние (или тегрмодинамическое состояние) обладает
соответствующими микросостояниями, которые занимают объем
Ш в Г-пространстве. Вероятность макросостояния с допустимым
объемом 8Q равна
I Ddpdq
б^макро^-^-^ У ПЙ А • EЛ77)
«полн \ и dp dq
Е-слой.
И вновь вероятность макросостояния пропорциональна его
допустимому объему в Г-пространстве. Наконец, связь с термоди-
термодинамикой выражается уравнением
S = Л In 6Q, E.178)
где Ш —объем в Г-пространстве, соответствующий термодина-
термодинамическому состоянию с энтропией S. Микроканоническое распре-
распределение, определяемое равенствами E.176) и E.177), применяется
далее к изолированной системе, находящейся во вполне определен-
определенном термодинамическом равновесном состоянии вместе с любой
своей малой частью. В одном случае (канонический ансамбль)
две компоненты системы могут обмениваться энергией, тогда
как в другом случае (большой канонический ансамбль) они могут
обмениваться как частицами, так и энергией.
Канонический ансамбль
Обратимся теперь к рассмотрению ансамбля, который наилуч-
наилучшим образом описывает систему, находящуюся в контакте с тепло-
вым резервуаром. С этой целью рассмотрим сначала изолирован-
322 Гл. V. Решение и дальнейшие свойства уравнения Больцмана
ную систему из iV частиц, предварительно приведенную к равнове-
равновесию при температуре Т. Пусть, далее, система разделена на две
подсистемы (рис. 5.13), подсистему 1 с гамильтонианом Н^ и под-
подсистему 2 с гамильтонианом Н2. Частицы в каждой подсистеме
фиксированы. Имеется iV4 частиц в подсистеме 1 и N2 —в под-
подсистеме 2. Объемы подсистем V\ и V2 фиксированы и таковы, что
Vt < V2. E.179a)
Кроме того,
Nt < N2. E.1796)
Энергии подсистем могут изменяться таким образом, чтобы выпол-
выполнялись ограничения
Е = Е± + Е2, E.179в>
Ei < Е2. E.179г)
Подсистемы не могут обмениваться частицами. Однако они обме-
обмениваются энергией. Это завершает описание нашей модели, пред-
представляющей систему A) в контакте с тепловым резервуаром B).
Теперь возникает вопрос, какова вероятность того, что вся
система находится в только что описанном состоянии, или, что
= COnst
и фиксированы
и фиксированы
Рис. 5.13. Система A), описываемая каноническим распределением.
эквивалентно, каков достижимый объем этих состояний в Г-про-
странстве? Какую часть энергетического слоя занимают эти
состояния? Ограничение, согласно которому искомые состояния
включают разделение энергии, несколько осложняет задачу. Что-
Чтобы учесть это, применим соотношение, следующее из первого
закона термодинамики:
dS = Т-1 dE + pT-1 dV. E.147)
А именно
7- = -§|у. E.180)
Сначала нам надо будет получить вероятность бРмакро, соответ-
соответствующую термодинамическому состоянию (Ni4 У4, Ей N2, V2i Ег)
5.4. Релаксация к равновесному состоянию 323
ри предположениях E.179). Это мы сделаем, вычисляя объем
з Г-пространстве, совместимый с данным состоянием. После того
как мы найдем бРмакр0, соответствующая плотность точек ансамбля
яолучается, если использовать E.177).
Обозначим фазовые координаты iVi-частиц через zu а фазовые
координаты ]У2-частиц —через z2. При упомянутых ограничениях
допустимый объем z2 равен Q2. Пусть теперь состояние А^-частиц
фиксировано, в то время как А^-частицы могут находиться в лю-
любом состоянии, совместимом с указанными выше ограничениями.
дггчастицы находятся в состоянии dz^ около z^. Состояния N%-
частиц находятся где угодно в допустимом объеме Q2. При этих
условиях допустимый объем 8Q всей системы станет равным
6Q = \
\ = dziQ2(E2), E.181)
6Q = dziQ2(E — E^. E.182)
Энтропия системы 2 равна
S2 (Е - Еи V2) = k In Q2 (E - Еи V2). E.183)
При этом предполагается, что система 2 является изолированной
(как член микроканонического ансамбля). Справедливость такого
предположения оправдана жесткостью неравенств E.179).
Так как Е^ <^ Е2, то E.183) можно разложить около Е^ = 0.
В результате, используя термодинамическое соотношение E.180),
получим
S2(E-Eit V2) = S2(E, V2)-
Е2=Е
= S2{E, V2)—A + E.184)
Отсюда с ледует, что при упомянутом выше ограничении {Е^ <^ Е2)
E.185)
Мы получили объем Q2 в виде явной функции параметров, описы-
описывающих термодинамическое состояние (Ei4 T) подсистемы 1. Под-
Подставляя это выражение в E.181), получим
, E.186)
гДе i? = const = exp [S2 (E, V2)/k]. Вероятность бРмакро и плот-
плотность Dc получаются из E.177):
RD Dc dzt 6Q _ dZjKexip( — Ei/kT) .-
О^макро— f. n j_— o — p7~ . (O.
'ПОЛИ
324 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
Отсюда плотность канонического ансамбля равна
E.188)
где мы положили Е± = Hi —гамильтониан подсистемы 1. Функ-
Функция DK является плотностью точек системы, которая удовлетворя-
удовлетворяет ограничениям E.179), и поэтому она также является мерой
вероятности того, что iVi-подсистема находится в описанном
выше состоянии.
Как непосредственное приложение полученного результата,
запишем выражение для средней энергии Е системы, находящейся
в контакте с тепловым резервуаром при температуре Т. Вспоми-
Вспоминая соотношение E.174) (и опуская индекс 1), получим
Задача 5.16. Какова средняя внутренняя энергия идеального
газа, который заполняет сосуд объема V и находится в тепловом
равновесии с резервуаром при температуре Г?
Ответ. Для упрощения вычислений заметим, что равенство
E.189) можно переписать в виде
Е= — 1
что служит определением функции Z —статистической суммы.
Для идеального газа гамильтониан чисто кинетический,
и не зависит от д, так что
N jtN I 2кт \ЗЛГ/2
О
В результате получим
Задача 5.17. Решить задачу 5.16 для идеального газа, состоя"
щего из твердых гантелеобразных молекул.
5.4. Релаксация к равновесному состоянию
325
Задача 5.18. Как с помощью одного гамильтониана можно
ввести в теорию ограничительную длину L (L3 = У)?
Ответ. Положим
где ф имеет вид, изображенный на рис. 5.14, а аргументами яв-
являются координаты центра масс каждой частицы.
(L,L)
Рис. 5.14. Потенциал
твердой стенки.
=A/L2
Рис. 5.15.
Свободный гамильтониан Но задается равенством E.170).
Следовательно,
L L
. . . J dq± . . . dq3Ne-*H= \ . . . j dq, . . . dq3Ne^H°.
о о
Задача 5.19. а) Рассмотреть одномерную систему из двух
частиц. Система разделена так, что 0 ^ х^ ^ а, а ^ х2 ^ L.
Изобразить допустимую часть Г-пространства (только его х-часть)
до и после разбиения.
б) Какова вероятность того, что система из двух частиц нахо-
находится в описанном выше состоянии?
Ответ. См. рис. 5.15.
В настоящем исследовании канонического распределения
остается найти выражение для энтропии. Постулат S = k In Q
относится к микроканоническому ансамблю. Однако меньшая из
Двух подсистем, описанных выше (подсистема A)), несомненно,
не является изолированной. Существуют два подхода к решению
этой проблемы. В первом случае мы определим энтропию канони-
канонического ансамбля со средней энергией Е как равную энтропии
^йкроканонического ансамбля с энергией Е. С точки зрения термо-
326 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
динамики такой путь возможен, поскольку в термодинамике
энтропия фиксируется заданием энергии (и объема) независимо
от того, находится ли система в равновесии с тепловым резервуа-
ром или она изолирована.
Другой метод связан с введением понятия внешних параметров,
Внешними являются параметры, которые входят в гамильтониан
системы иначе, чем канонические координаты и импульсы. Приме-
Примером может служить объем V (либо длина L ребра грани) интен-
интенсивности приложенных извне полей. В общем случае мы можем
написать
Н = Н (?, р; хи х2, . . ., хп) = Н (д, р; х), E.190)
X = (#!, Х2, • . ., Хп),
где хг —внешние параметры. Отсюда следует, что среднее значе-
значение любой динамической переменной А является функцией внеш-
внешних параметров:
Т lAD(H)dpdq -
Когда система «перемещается» таким образом, что изменяется
только внешний параметр xk, вариация энергии системы опре-
определяется равенством
8kE=dH{q'p'x) 8xk. E.192)
При этом изменении энергии система находится в микросостоя-
микросостоянии (q, p). Работа, совершаемая системой при таком перемеще-
перемещении, равна
6*^=—Ц**- E-193)
(Если &Е > 0, то 8W <0, и работа совершается над системой.)
Средняя работа при таком перемещении равна
&kW = FkAxk. E.1946)
Это уравнение служит для определения обобщенной силы Fh
и обобщенного перемещения kxh.
Рассмотрим пример, где xh —объем. Тогда
Ш = FA7 = pbV, E.195)
так что
5.4. Релаксация к равновесному состоянию 327
Для канонического ансамбля
JfL __ \ (дН/дУ) е~№ dpdq _ 1 I (де^Н/дУ) dp dq
dV I e-VHdpdq " P I e'^dpdq { }
или, что эквивалентно,
E.198)
Функция Z называется статистической суммой. Как макроскопи-
макроскопический параметр, она является функцией внешних параметров х
и р:
Z = Z{x, P). E.199)
В данном примере
Z = Z(V, p). E.200)
Средняя внутренняя энергия системы равна
_ •„, *. E.201)
Образуя дифференциал от In Z (V, C), получим
dlnZdV]<Ф
d In Z = pp dV — E dp, E.202)
dlnZ = $pdV — d (P#) + p dE,
d(lnZ+ p?) = p (p dF + d?). E.203)
Согласно первому закону термодинамики, правая часть последнего
соотношения равна р?1 dS, так что (вспоминая, что р s= 1//сГ)
d [/с (In Z + Р^I = dS. E.204)
С точностью до аддитивной постоянной
TS = kTlnZ + Е. E.205)
Вводя свободную энергию
F = Е - TS = —kT In Z E.206)
и используя первый закон термодинамики, получим
dF =—pdV— S dT, E.207)
так что
7 ГП &
W^Z E.208)
И
д
у- дТ V" --,' С509)
328 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
Уравнение E.208) тождественно уравнению E.198). Оно является
одним из наиболее важных соотношений в равновесной стати-
статистической механике, поскольку дает способ получения уравнения
состояния, если известен гамильтониан. Равенство E.209) задает
энтропию как функционал канонического распределения.
Задача 5.20. Вычислить Z и затем р для идеального газа,
заполняющего ящик с длиной ребра L.
Задача 5.21. а) Показать, что
б) Продифференцировать обе части этого равенства по
чтобы прийти опять к уравнению E.209).
Ответ.
1 дТ v
Следовательно,
s дЕ_
дТ у'
Отметим мимоходом, что более универсальной корректной фор-
формой статистической суммы является выражение
N\h3N J
Множитель (iV! fe3^) остался от общей квантовомеханической
формы записи. В частности, член N\ происходит от неразличи-
неразличимости идентичных частиц. (В классической физике идентичные
частицы смогут быть различимыми, однако в квантовой механике
они неразличимы.) Здесь h — постоянная Планка. Ее включение
дает размер минимального объема h3N в Г-пространстве, для кото-
которого можно определить микросостояние. Поскольку термодина-
термодинамические переменные являются производными от In Z, то наличие
множителя (Nlh31*)-1 для классического уравнения состояния
не существенно.
Большой канонический ансамбль
Вновь рассмотрим изолированную систему, разделенную на две
подсистемы. Однако теперь системы могут обмениваться не только
энергией, но и частицами. Остается постоянным только объем
каждой подсистемы (рис. 5.16). На систему наложены следующие
5.4, Релаксация к равновесному состоянию
329
оГраничения:
Е2 = Е,
< Е2,
N2 = N,
< No.
E.210а)
E.2106)
E.211а)
B.2116)
Макроскопическую вероятность 6Рмакро, соответствующую тер-
термодинамическому состоянию (Nu Vu Ei, N2, V2, E2), теперь не-
необходимо связать с возможностью изменения JV± и N2 согласно
E = Et+E2 = const
N-Nt+N2 = COnst
ho Щ и Nz могут изме-
и фиксиробаны
Рис. 5.16. Система A), описываемая большим каноническим распределением.
E.211). Эта вероятность опять получается при вычислении объема
в Г-пространстве, совместимого с этим макроскопическим состоя-
состоянием. Используя те же обозначения, что и выше, положим, что-
Z] — фазовые координаты А^-частиц, а Z2 — фазовые координаты
Лг2-частиц. Пусть известно, что Л^-частицы находятся в элементе
фазового объема dzt около zb в то время как Л^-тастицы — в любом
состоянии из допустимого объема Q2- При таких ограничениях
допустимый объем 8Q для всей системы равен
6Q = dziu2 {E2, N2) = dZiQ2 (E - Еи N - ЛГ±). E.212>
Энтропия большей системы задается приближенно как
S2 (E - Еи N - Ni) = k In Q2 (E — Et, N — NJ. E.213)
Разложение в ряд Тейлора левой части этого равенства имеет вид
dSo
дЕ2
-^
dS9
No=N
... E.214)
E.215>
330 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
Термодинамический параметр \i называется химическим
циалом. Подставляя E.215) в E.213), получим
E.216а)
E.2166)
где К — постоянная. Из E.177) вместе с E.2166) находим следую.
щий результат:
с т\ БК 1 ОЙ
о
''П
Плотность ансамбля, описывающая систему, находящуюся в рав-
равновесии с большей системой, с которой она может обмениваться
частицами, задается равенством
DBK = К' ехр [-(Я^Г^] = K'e^Ne^HN. E.218)
Здесь индекс 1 опущен, HN — гамильтониан системы из N частиц.
Ансамбль, описываемый такой плотностью распределения, назы-
называется большим каноническим ансамблем. Выраженная через актив-
активность % плотность имеет вид
Dm = K* е , 2ig
% = #\
Поскольку число частиц N не постоянно, средняя от динамической
переменной равна
e~mNdpdq
220)
N
Особенно важными являются средняя энергия Е и среднее число
частиц N:
Ё = Л -_ , E.221)
y\N\* N*P
N
E.222)
5.4. Релаксация к равновесному состоянию 331
л _— большая статистическая сумма. Она связана с ZN — стати-
сТической суммой для системы из iV-частиц, соотношением
JjN E.223)
N
Смысл активности S или ее логарифмического эквивалента, хими-
химического потенциала, становится очевидным, если рассмотреть
выражение для среднего числа частиц N в системе. Вновь обра*
щаясь к E.220), получим
E.224)
Tv" N
Кг sr д \r\O (^ 99^\
Большая статистическая сумма так же просто связана с функцией
Гиббса G, как каноническая статистическая сумма со свободной
энергией F. Мы имеем:
" = G = F + pV. E.226)
Из левого равенства (которое, как можно показать, следует из
правого; см., например, Райф A965)) видно, что химический
потенциал \х — это удельная функция Гиббса (рассчитанная на
молекулу). Функции G и Q связаны соотношением
ewc-|) = S2%-9 E.227)
N
или, что эквивалентно»
f>pV = In Q. E.228)
К индуктивному обоснованию соотношения E.227) можно прийти
путем следующих логических рассуждений. Сначала перепишем
это уравнение в виде
2 J
N
J = 1. E.229)
N
Дифференцирование обеих частей по [3 дает
^E-G + F + liN-^ + ^ + 0^ = O. E.230)
Используя тождество
вместе с соотношением
HJV = G, E.232)
332 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
последнее уравнение можно переписать так:
-E + F-T^O. (
Это уравнение служит для определения функции F (ср. с E.206)).
Задача 5.22. Вычислить N для идеального газа.
Ответ.
Для идеального газа
VN I 2пт \ЗЛГ/2
так что
7 _ V" ( 2пт \ЗЛГ/2
JN~ N\h3N \ P /
[XVBnm/h^f^__ Xv/X*
— е ч
^-1 ЛГ!
N
где X — длина тепловой волны де Бройля:
2кт
Итак, приходим к следующим равенствам:
которые дают желаемый результат:
N = PpF.
д) Флуктуации
Одним из наиболее важных понятий в равновесной статисти-
статистической механике является понятие флуктуации. Нами были рас-
рассмотрены свойства системы, находящейся в наиболее вероятном
состоянии. Эти свойства будут иметь смысл только в том случае,
если система проводит в этом предпочтительном состоянии наиболь-
наибольшую часть времени. Для двух частиц в одномерном ящике
при достаточно долгом интервале наблюдения макросостояние
) • | • ( занимает половину времени, а на состояния | •• [ _J
5.4. Релаксация к равновесному состоянию
333
приходится по одной четверти времени наблюдения
/двум частицам разрешается занимать одно и то же положение).
Если через единичные интервалы времени провести ряд замеров
Число шаров в
лебой половине
12 14
Рис. 5.17. Флуктуации около среднего положения для двух шаров в одно-
одномерном ящике.
n(x,t)l
t
Рис. 5.18. Флуктуации около среднего значения для макроскопической кон-
концентрации.
числа частиц в левой части, то типичная последовательность ре-
реализаций будет такой, как показано на рис. 5.17.
Совершенно очевидно наличие флуктуации около среднего
значения 1. Однако с ростом числа частиц в системе эти флуктуа-
флуктуации уменьшаются. Например, для ограниченного газа с большим
числом частиц плотность п (х, t) в некоторой его точке имеет вид,
изображенный на рис. 5.18.
334 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
Мера интенсивности флуктуации наблюдаемой величины д
задается средним квадратичным отклонением (бАJ:
(б!р=(Л-1J. E.234)
Из этого равенства следует, что
(8А2) = А2 + (АJ- 2АА = А2- (АJ. E.235)
Особенно важным является относительное среднее квадратичное
отклонение <пь (А):
{). E.236>
А
Если эта величина мала, то равновесное значение величины А
хорошо представляется величиной А. Если относительное среднее
квадратичное отклонение не является малым (по сравнение
с единицей), то А теряет свой физический смысл.
Рассмотрим следующие две важные переменные. Для системы,
которая может обмениваться энергией и частицами с резервуаром,
мы получим выражение для относительного среднего квадратично-
квадратичного отклонения плотности (или «концентрации») N/V.
Используя представление большого канонического ансамбля,
получим
Возводя первое уравнение в квадрат и вычитая его из второго,
имеем
E.239>
Но выражение в скобках равно N. Следовательно,
t J^ E.240)
Для относительного отклонения получим
mily) = ¦
E.241)
N 1
В случае идеального газа
N = M-, E.24Г)
5.4. Релаксация к равновесному состоянию 335
так
_L-.
У N
E.243)
E.244)
Для ^V" ~ 1023 величина <пь ~ 10~12 <^ 1. Выражая <пг через п =
^ iV/F, будем иметь
^ E.245)
ш(п) = ^г .
Рассмотрим теперь другую интересующую нас переменную —
энергию системы, когда последняя может обмениваться с резер-
резервуаром только энергией. Для этого случая используется пред-
представление канонического ансамбля. Сначала мы вычислим Е2:
ipg 1 а» z_ 1 а
_ ^ <l_g JL_i?_2= !L? I /?\2 /5 246\
c?p 2 ^p ^B
Отсюда мы заключаем, что
ZT^ /77\2 ^ Г^ /сг O/7V
= ? —(^) = — Tr"^' (о.^4/>
Но (вспоминая определение |3)
^) E-248>
где Су — удельная теплоемкость при постоянном объеме. Для
идеального газа, состоящего из точечных частиц,
^ E.249)
так что
W T E-250>
относительное среднее отклонение принимает вид
х =^ , E.251)
^±=. E.252)
336 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
Задача 5.23. Показать, что для идеального газа
д7-2/3
(ivK / ~~J
Для типичных газов N имеет порядок ч:исла Авогадро, так цТо
относительное среднее квадратичное отклонение является беско-
бесконечно малой величиной. Иногда этот результат рассматривают:
как доказательство эквивалентности канонического и микрокано-
микроканонического ансамблей, поскольку E.252) указывает на то, что
в каноническом ансамбле почти все системы обладают энергией Е.
В более общем случае каноническое распределение пригодно
когда т (Е) .<^ 1, тогда как большое каноническое распределение
имеет место при ш(Е) <^ 1 и m(iV) <^ 1. Эти предположения были
использованы в приведенных выше выводах.
5.5. Апостериорный подход. Эргодичеекая гипотеза
Выше мы видели, что кажущаяся необратимость макроскопи-
макроскопических систем естественным образом вытекает из постулата равных
априорных вероятностей и формализма для вычисления вероят-
вероятностей макросостояний. Однако, интуитивно являясь удовлетво-
удовлетворительным, этот априорный подход специфичен в одном своем
аспекте: он не является чисто динамической теорией. Это, скорее,
объединение вероятностных и динамических закономерностей.
Существует ли какой-нибудь способ получить необратимость макро-
макроскопических явлений чисто динамическим путем? Мы уже'сталки-
вались с такой попыткой в ©^-теореме Больцмана, Однако эта
теорема опирается на справедливость уравнения Больцмана,
вывод которого, если мы вспомним, включает множество пред-
предположений. Одним из них является гипотеза молекулярного
хаоса. Этот Ansatz полагает двухчастичную функцию распределе-
распределения /2 равной произведению одночастичных функций распределе-
распределения Д/i, что в представлении фазовых чисел записывается так:
/2 A,2)= Ml)/, B).
Это, разумеется, представляет собой утверждение о независимости
вероятностей. Фазовые состояния частиц 1 и 2 независимы.
В таком простом толковании ^-теорема Больцмана не является
прямым следствием одной только динамики.
Другой путь к раскрытию необратимости макроскопически*
законов с использованием одной только динамики лежит через
эргодическую гипотезу, также впервые выдвинутую БольцманоМ-
Эргодическую гипотезу можно рассматривать как динамическое
обоснование принципа равных априорных вероятностей. Эта
гипотеза является краеугольным камнем апостериорного (т. е>
5.5. Апостериорный подход. Эргодическая гипотеза
337
происходящего из принципов, основанных на обобщении фактов)
подхода к проблеме макроскопической необратимости (рис. 5.19).
Эргодическая гипотеза устанавливает равенство между средним
Апостериорный
подход
f
Обратимые'
законы
динамики
)
Зргодическая
гипотеза
Априорный
подход
Принцип равных
апоиооных
вероятностей
Вероятности
макросостояний
Необратимая
макроскопическая
физика
Рис. 5.19. Управляющая схема в статистической механике.
по микроканоническому ансамблю и средним по времени (за беско-
бесконечный временной интервал). Это означает, что для любой дина-
динамической переменной G (p, q, i)
= lim-Jr \G(q, p,t)dt =
T-oo 1 J
GD dp dq
Ddpdq
E.253)
+
Средняя по времени слева — это средняя по одной-единственной
Динамической орбите. Микроканоническая средняя справа — это
338 Гл. V. Решение и дальнейшие свойства уравнения Больцмана
средняя по ансамблю систем. Равенство легко установить, если^Т
одна и та же для всех систем ансамбля, что в свою очередь может
быть доказано, если система эргодическая. Система называется
эргодической, если ее динамическая орбита за бесконечный интер-
вал времени проходит через все точки энергетической поверхности
или, что эквивалентно, если энергетическая поверхность состоит
из единственной динамической траектории (это было исходньщ
предположением Больцмана). Напомним, что орбита, проходящая
через некоторую точку, единственным образом этой точкой опре-
определяется. Следовательно, все орбиты эргодической системы оди-
одинаковы. Единственное различие заключается во времени про-
прохождения через заданную точку. Так как все орбиты совпадают,
то G для всех них одна и та же, и равенство E.253) установлено.
Однако можно показать, что это достаточное условие справед-
справедливости предшествующего равенства никогда не реализуется
в природе. Одна из возможных аргументаций осуществляется
через 2N (N — число степеней свободы) констант движения {hi}.
Так как все орбиты на энергетической поверхности обладают оди-
одинаковой энергией, то остается 2N — 1 произвольных постоянных.
Но одну из них можно использовать, чтобы фиксировать начальное
время (см. следующую задачу).
Задача 5.24. Рассмотрим систему с N степенями свободы. Два
члена представляющего ансамбля таковы, что все 2N констант
движения, кроме одной пары, попарно одинаковы для обоих
членов, т. е.
Доказать, что орбиты точек двух систем совпадают, если не
учитывать время запаздывания. Рассмотреть частный случай
двух свободных частиц, движущихся в одном измерении, чтобы
установить связь времени запаздывания с А.
Из задачи 5.24 следует, что две точки на одной и той же траек-
траектории могут иметь только одну пару констант (из 2N констант),
различных для каждой из этих точек. Теперь выберем две точки,,
у которых только одна постоянная движения общая, а все остав-
оставшиеся 2N— 1 постоянных различны. Это означает, что вторая
точка никогда не может быть настигнута первой. Мы получили
простую аргументацию в пользу того, что большая часть систем
не являются эргодическими. Полностью убедительное доказатель-
доказательство этого факта было дано Розенталем и независимо Планчерелем
в 1913 г. Они показали, что геометрическое место точек любой
динамической траектории образует множество меры нуль на энер-
энергетической поверхности, мера которой отлична от нуля. Выра-
5.5. Апостериорный подход, Эргодическая гипотеза 339
жаясь нестрогим языком, единственная динамическая траектория
не может «заполнить» энергетическую поверхность.
Сейчас уместно указать на некоторые существующие различия
между константами движения. Например, константы, опреде-
определяющие фиксированную поверхность в фазовом пространстве,
называются изолирующими интегралами. Значение этих постоян-
постоянных hi таково, что траектория С системы лежит на гиперповерх-
гиперповерхности, являющейся пересечением энергетической поверхности
и изолирующих интегралов:
с ={z \zeh n h2 n ...}.
Изолирующий интеграл уменьшает размерность многообразия
фазового пространства, на котором лежит траектория системы.
Другой класс постоянных составляют аддитивные константы.
Их значения для системы, состоящей из нескольких частей
(взаимодействием которых можно пренебречь), равны суммам соот-
соответствующих значений для каждой отдельной части системы.
Динамические постоянные, связанные со свойствами симметрии
пространства и времени, являются аддитивными константами.
К ним относятся энергия, импульс и угловой момент.
С более общей точки зрения динамические константы разде-
разделяются на два класса: глобальные и локальные. Глобальными назы-
называются интегралы, постоянные для всего времени и по всей энер-
энергетической поверхности. Локальные константы постоянны на
ограниченной области энергетической поверхности и (или) в огра-
ограниченном интервале времени.
Возвращаясь к основному направлению нашей дискуссии,
вспомним, что вскоре после первого десятилетия нашего века
было установлено, что эргодических систем не существует. Тогда
были сделаны попытки доказать существование квазиэргодических
систем. Система является (слабо) квазиэргодической, если точка
системы на энергетической поверхности доходит как угодно близко
до всех точек этой поверхности.
Ферми A923), обобщая теорему Пуанкаре A892) (не существует
никакого иного класса поверхностей, кроме энергетическихг
обладающих тем свойством, что орбита целиком лежит на поверх-
поверхности), доказал существование большого класса систем, являющих-
являющихся (слабо) квазиэргодическими.
Тем не менее одной этой теоремы недостаточно, чтобы устано-
установить равенство E.253). Необходимо сделать дополнительное пред-
предположение. Его нестрогая формулировка состоит в следующем:
время, проводимое точкой системы в некоторой области энерге-
энергетической поверхности, пропорционально площади этой областд.
Для более строгого обсуждения этой полной эргодической гипоте-
гипотезы необходимо обратиться к языку теории меры.
340 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
Как было указано в гл. II, концепция энергетического слоя
была введена, во-первых, чтобы лучше использовать следствия
уравнения Лиувилля. С другой стороны, именно к энергетической
поверхности относится любое из предыдущих утверждений эрго-
дической теории.
Существует простой путь, чтобы ввести в формализм энерге-
энергетической поверхности свойства инвариантности, связанные
с уравнением Лиувилля. Рассмотрим энергетический слой, по-
порождаемый двумя поверхностями Н = ЕиН = Е + 8Е.В любой
точке внутренней поверхности нормальное перемещение 6z между
двумя поверхностями удовлетворяет соотношению. 8Е =
= | Sz | | VH |. Таким образом, если 62 — элемент поверхности
в той же самой точке, то соответствующий элемент объема в энер-
энергетическом слое равен | 6z | | 62 |. Но вектор VH нормален
к поверхности постоянной энергии, откуда заключаем, что данный
объем пропорционален 62/1 ViJ |. Следствием теоремы Лиувилля
является сохранение этого фазового объема (говоря более точно,
это интегральный инвариант Пуанкаре).
Введем теперь меру fx (^4) множества точек z ? А на энерге-
энергетической поверхности согласно равенству
- E>254)
Мерой множества точек (z ? E) на всей энергетической поверх-
поверхности будет
J- E-25<5)
При естественном движении системы (порождаемом оператором ?*)
множество точек А за время t перейдет в множество А', тогда
Л->Л' = ЬЛ. E.256)
Теорема Лиувилля утверждает, что
V l?t (A)] = \i (А). E.257)
Теперь мы можем сформулировать полную эргодическую гипотезу.
Почти все (за исключением множества меры нуль г)) орбиты на
энергетической поверхности Е проходят через каждую область
поверхности Е с положительной мерой и остаются в данной обла-
*) Если для любого сколь угодно малого е существует открытое мно-
множество В, которое покрывает множество А и \х (В) <С 8, то А — множество
меры нуль. Любое счетное множество на действительной прямой (множество,
которому можно поставить во взаимно однозначное соответствие натураль-
натуральный ряд чисел) является множеством меры нуль. Его покрытие составляют
открытые интервалы, каждый длиной е/2п.
5.5. Апостериорный подход. Эргодическая гипотеза 341
сти в течение среднего времени, равного отношению ее меры
к мере Е.
В 1931 г. фон Нейман доказал так называемую среднюю эрго-
дическую теорему, которая состоит в следующем. Пусть кривая CZq
содержит начальную точку ?0, и ?a {zq, t) — часть времени из
интервала t, проводимая кривой CZq в области А. Тогда теорема
фон Неймана утверждает: если последовательность преобразований
{?,} является метрически транзитивной (определение этого
понятия будет дано позднее), то ТА сходится в среднем к ТА=^^
То есть
'"*" __ E.258)
A= \i(E) '
Биркгоф A931) уточнил эту теорему, доказав, что для z0
почти всюду в Е сходимость является точечной:
lim TA(z0, t) = TA. E.259)
Группа преобразований {?*} множества точек Е называется метри-
метрически транзитивной, если единственными множествами, инва-
инвариантными по отношению к этим преобразованиям, является вся
совокупность множеств меры нуль. Более наглядное определение
таково: множество Е не может быть разложено (при преобразова-
преобразованиях {^} множество Е является метрически неразложимым)
на два инвариантных множества х) At и Л2, имеющих положитель-
положительную меру. Можно считать, что \t полностью «перемешивает» мно-
множество Е. Именно в этом механизме «перемешивания» (или «рас-
«рассеяния») заключена сущность эргодической теоремы. Он объясняет
необратимость макроскопических законов.
Мы видим, что эргодическая гипотеза заключается в следую-
следующем. Ансамбль, первоначально занимающий только часть энерге-
энергетической поверхности, со временем самораспределяется однород-
однородным образом по всей энергетической поверхности, чтобы принять
микроканоническое распределение. На первый взгляд это кажется
не совместимым с уравнением Лиувилля, которое требует, чтобы
плотность ансамбля оставалась постоянной вдоль динамических
траекторий. Наглядное разрешение этого кажущегося парадокса
впервые было предложено Гиббсом с помощью следующей модели.
г) При данном преобразовании ^ точки системы изменяют свои началь-
начальные координаты [z @) 6 Л] и спустя время t достигают конечных координат
U{t)?A']. Если эти конечные координаты занимают область начальных
координат А' = А, то преобразование ^ отображает начальное множество А
на само себя, и А является инвариантом преобразования \f.
342 Гл, V. Решение и дальнейшие свойства уравнения Болъцмана
Рассмотрим закрытую мензурку, наполовину заполненную водой,
а наполовину маслом (обе жидкости предполагаются несжимаемы-
несжимаемыми). Вначале вода занимает нижнюю половину мензурки, а масло—
верхнюю. После сильного встряхивания масло разбивается на
множество мельчайших капелек, которые однородным образом
заполняют всю мензурку. Если смотреть на расстоянии, плотность
суспензии кажется однородной. Однако при близком осмотре
обнаружится, что плотность осталась постоянной вдоль путей
частиц, а суспензия в действительности является однородной
самое большее в смысле крупнозернистости. Другое толкование
«участия» динамических законов в необратимости может быть
дано посредством так называемой «крупнозернистой» плотности
ансамбля. Прежде чем коснуться этого формализма, нам хотелось
бы рассмотреть вопрос о строгости предположения о метрической
транзитивности операторов ?*.
Например, предположим, что энергетическая поверхность
является метрически неразложимой. Пусть начальное распределе-
распределение ансамбля отлично от нуля в области А а /?, [Л (Е — А) >> 0.
Тогда в любой последующий интервал времени этот начальный
ансамбль должен исказиться, иначе Е была бы разложимой.
Начальное множество z @) 6 А переходит в z (t) ? А' Ф А. Те же
рассуждения можно вновь применить к А' и т. д. Таким образом,
мы видим, что предположение, согласно которому гамильтониан
порождает метрически транзитивные преобразования, влечет за
собой очень схожие эргодические условия. Разумеется, если это
свойство преобразований Гамильтона будет доказано, то аналцз
Биркгофа станет, несомненно, уместным. В этом направлении было
выдвинуто предположение (Окстоби, Улем A941)), согласно кото-
которому почти каждая группа непрерывных преобразований является
метрически транзитивной. С другой стороны, Кац A959) доказал,
что фактически невозможно установить, порождает ли гамильто-
гамильтониан метрически транзитивные преобразования. В качестве послед-
последнего замечания укажем, что если любая из оставшихся 2N — 2
(N — число степеней свободы) констант движения является изоли-
изолирующим интегралом, то Е разложима.
Задача 5.25. Доказать справедливость последнего утвержде-
утверждения.
5.6. «Крупнозернистое» разбиение
Описываемый ниже метод был введен Гиббсом, чтобы согласо-
согласовать возможное сглаживание и приближение к микроканони-
микроканоническому распределению с любым начальным распределением
ансамбля, каким бы «искаженным» оно ни являлось. Анализ
начинается с разбиения энергетического слоя на такие подобласти,
что 1-я подобласть имеет объем Q*. Если D (z, t) — плотность
5.6. «Крупнозернистое» разбиение 343
ансамбля во время t, то «крупнозернистая» плотность Ui(t) опре-
определяется согласно равенству
П, (*) = -i- j D (*', t) dp' dq' = П (z, t) E.260)
для z?Qi. Отсюда следует, что П постоянна в каждой ячейке
и что D и П имеют одинаковую нормализацию. Покажем это:
i=^1Ql-^-\ Ddpdq =
Н=Е
=r 2 ^Ddpdq= ^ Ddpdq. E.261)
Введем энтропию Гиббса1):
г] (t) = 2 Q* П, In П{ = \ П (z, 0 ln П (z, Q dp dg. E.262)
Подставляя введенное ранее интегральное выражение для П,
получим энтропию Гиббса в виде
г] (t) = \ D (z, t) In П (z, t) dp dq. E.263)
Имея в нашем распоряжении эти определения и свойства, рас-
рассмотрим частный случай, когда в начальный момент функция D
постоянна в пределах каждой ячейки. Тогда D @) = П @) и
— т)(О)= j П (*) In П(*) dp dg— ^ D{0)lnD{0)dpdq =
—/)(*) In Z)@] dpdg. E.264)
Здесь мы использовали теорему Лиувилля и равенство E.263).
Прибавляя и вычитая выражение
[ Ddpdq= f Udpdq,
получим
j[(^) (^)] E.265)
Так как In г/ + 1 ^ у (рис. 5.20, а) и функция J9 положительна,
то отсюда следует, что
т) (*) - т) @) < 0. E.266)
-1) Она не совпадает с ранее введенной энтропией Гиббса <&&н =
= J/w In
344 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
Если г) переменна, то при условии, что начальное состояние D
постоянно внутри каждой ячейки, г\ убывает. Кроме того, к] пере-
перестает убывать, когда П становится однородной. Справедливость
этого утверждения можно доказать следующим образом. Пусть
Рис. 5.20. График функций, рассматриваемых в теореме о крупнозернистом
разбиении.
П — однородное распределение. Рассмотрим изменение функцииП,
при котором она переходит в П' = Не* , где х — произвольная
функция z. Во-первых, из условия нормировки П следует, что
\ (u'-Tl)dpdq = O. E.267)
Кроме того, ввиду нашего выбора функции П
(l+lnn)(II-n')dpdg = (l + lnII) j {H—W)dpdq = 0. E.268)
Рассмотрим теперь изменение г], обусловленное «удалением»
от однородного распределения:
E.269)
6т) = т)'—Ti= ( (ГТ'1п1Г — UlnU)dpdq.
Преобразуя этот интеграл с использованием E.268), можем
записать его в виде
=, [ nfaK + l—e^
Это неравенство следует из следующего соотношения (см.
рис. 5.20, б)
= 0, х = 0.
Список литературы 845
Таким образом, когда П однородна, г\ — минимальна (поскольку
любое изменение распределения П от однородного состояния вызы-
вызывает увеличение энтропии г\).
На первый взгляд может показаться, что мы получили необра-
необратимый закон E.266) из одной только динамики (уравнение Лиувил-
ля). Но это не так. Слабым местом теоремы является предположе-
предположение о том, что D изменяется, удаляясь от своего начального зна-
значения D @), постоянного в подобластях энергетического слоя.
Это очень сильное предположение. Оно эквивалентно предполо-
предположению о метрической неразложимости. Во-вторых, теорема свя-
связана с введением «крупнозернистой» функции распределения П.
При переходе к П-представлению часть информации теряется.
Знать П — это много меньше, чем знать чисто динамическую»
функцию распределения D. Знание П не дает никакой информации
о структуре каждой ячейки. Именно на этом «рафинированном»
детализованном уровне динамики законы природы являются
обратимыми. При получении «крупнозернистых» макроскопиче-
макроскопических средних переменных приносится в жертву это детальное
описание и тогда выступает необратимость макроскопической
физики.
Задача 5.26. Используя теорему Биркгофа, доказать, что-
частица, ограниченная в своем движении замкнутой сферической
идеально отражающей стенкой, не является эргодической систе-
системой.
Указание. Сохранение углового момента означает, что прицель-
прицельный параметр частицы (относительно центра сферы) постоянен.
Используя этот факт, найти континуум траекторий, которые*
отображают фиксированную подобласть на саму себя.
СПИСОК ЛИТЕРАТУРЫ
А. Работы, связанные с теорией газов, решением уравнения Больцмана
и коэффициентами переноса
Барнетт (Burnett D.)
A935) The Distribution of Velocities in a Slightly Non-Uniform Gas, Proc.
bond. Math. Soc, 39, 385.
(^935) The Distribution of Molecular Velocities and the Mean Motion in?
a Non-Uniform Gas, Proc. bond. Math. Soc, 40, 382.
Альберт (Hilbert D.)
(!912) Math. Ann., 72, 562.
ГРэд (Grad H.)
(*949) Comm. Pure and Applied Math., 2, 331.
А>комс (James C.G.F.) '
(l92l) Proc. Camb. Phil. Soc, 20, 477.
346 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
Джине (Jeans J. Н.)
<1901) Phil. Trans. Roy. Soc. A, 196, 399.
<1904) Quart. J. Math., 25, 224.
Джонс (Леннард) (Jones J. E. (Lennard))
<1924) Proc. Roy. Soc. A., 106, 441.
Лоренц (Lorentz H. A.)
A887) On the Equilibrium of Kinetic Energy among Gas-Molecules,
Ber., 95, 115.
A905) The Motions of Electrons in Metallic Bodies, Proc. Amsterdam Acad
7, 438, 585, 684.
A905) Arch. Neerland, 10, 343.
Массей, Mop (Massey H. S. W., Mohr С. В. О.)
A933) On the Rigid Sphere Model, Proc. Roy. Soc, A, 141, 434.
41934) On the Determination of the Laws of Force between Atoms and Mole-
Molecules, Proc. Poy. Soc, 144, 188.
Лиддак (Pidduck F. B.)
A916) The Kinetic Theory of the Motions of Ions in Gases, Proc. bond. Math.
Soc, 15, 89.
A922) The Kinetic Theory of a Special Type of Rigid Molecule, Proc. Roy,
Soc A, 101, 101.
Хэсс (Hasse H. R.)
<1926) Phil. Mag., 1, 139.
Хэсс, Кук (Hasse H. R., Cook W. R.)
A927) Phil. Mag., 3, 977.
41929) Proc. Roy. Soc, 196.
A931) Phil. Mag., 12, 554.
Чепмен (Chapman S.)
A912) Phil. Trans. Roy. Soc. A., 211, 433.
A916) On the Law of Distribution of Velocities, and on the Theory of Visco-
Viscosity and Thermal Conduction, in a Non-Uniform Simple Monatomic
Gas, Phil. Trans. Roy. Soc. A, 216, 279.
A917) Phil. Trans. Roy. Soc. A, 217, 115.
A917) Phil. Mag., 34, 146.
A919) Phil. Mag., 38, 182.
A922) On Certain Integrals Occuring in the Kinetic Theory of Gases, Manches-
Manchester Mem., 66, 1.
A929) Manchester Mem., 7, 1.
<1928) On Approximate Theories of Diffusion, Phil. Mag., 5, 630.
A933) On the Convergence of the Infinite Determinants in the Lorentz Case,
/. bond. Math. Soc, 8, 266.
Чепмен, Хейнсуорс (Chapman S., Hainsworth W.)
{1924) Some Notes on the Kinetic Theory of Viscosity, Conduction and Dif-
Diffusion, Phil. Mag., 48, 593.
Энског (Enskog D.)
A911) Phys. Zeit., 12, 56, 633.
<1912) Ann. der Phys., 38, 731.
A917) The Kinetic Theory of Phenomena in Fairly Rare Gases, Dissertation.
Uppsala.
<1921) The Numerical Cumulation of Phenomena in Fairly Rare Gases, Svensk-
Vet. Akad. (Arkiv. f. Mat. Ast. och Fys.), 16, 1.
Список литературы 347
Л922) Kinetic Theory of Thermal Conduction, Viscosity, and Self-Diffusion in
* Certain Dense Gases and Liquids, Svensk. Akad. HandL, 63, № 4.
/A928) Svensk. Akad. (Arkiv. f. Mat. Ast. och Fys.)» 21A, № 13.
Б. О линейном операторе столкновений
Вэнь-Чень, Уленбек (Wang-Chang С. S., Uhlenbeck G. Е.)
A952) On the Propagation of Sound in Monatomic Gases, University of Michi-
Michigan Engineering Research Inst. Rept.
Грэд (Grad H.)
A963) Phys. Fluids, 6, 147 and in Rarefied Gas Dynamics, ed. by J.Laur-
mann, New York, Academic Press.
Карлеман (Carleman T.)
A957) Problemes Mathematiques dans la Theorie Cinetique des Gas, Almqvist
and Wiksells, Uppsala. Русский перевод: Карлеман Т., Математиче-
Математические задачи кинетической теории газов, М., ИЛ, 1960.
Мак-Леннан (McLennan J. А.)
A965) Phys. Fluids, 8, 1580.
Мотт-Смит (Mott-Smith Н. М.)
A954) A New Approach in the Kinetic Theory of Gases, M. J. Т., Lincoln
Lab. Rept.
€ирович (Sirovich L.)
A963) Phys. Fluids, 6, 10.
Финкельстейн (Finkelstein L.)
A965) Phys. Fluids, 8, 431.
В. Прикладная математика и анализ
Гильдербранд (Hilderbrand F.)
A952) Methods of Applied Mathematics, Englewood Cliffs N. J., Prentice-
Hall.
Курант, Гильберт (Courant R., Hilbert D.)
<1953) Methods of Mathematical Physics, vols. I and II, New York, Interscien-
ce, 1953 and 1965. Русский перевод нем. изд.: Курант Р., Гильберт Д.,
Методы математической физики, т. 1, 2, М.— Л., ГИТТЛ, 1951.
Лорч (Lorch E. R.)
A962) Studies in Modern Analysis, vol. I, ed. by R. С Buck, Englewood
Cliffs N. J., Prentice-Hall.
Стоун (Stone M. H.)
A932) Linear Transformations in Hilbert Space and Their Application to
Analysis, New York, American Math. Soc.
Г. Ранние работы по термодинамике
Д*оуль (Joule J. P.)
(l857) Phil. Mag., 14, 211.
Карно (Carnot S.)
"824) Reflections sur la Puissance Motrice du Feu.
348 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
Клапейрон (Clapeyron E.)
A834) /. d'Ecole Polytech., 14, 153.
Клаузиус (Clausius R.)
A864) Abhandlung iiber die Mechanische Warmetheorie, Braunschweig
Vieweg, 1864, 1867; second ed., 1879; third ed., 1887. **
Кельвин (Kelvin W.)
A852) On a Universal Tendency in Nature to the Dissipation of Mechanical
Energy, Phil. Mag., 4, 304A852); Proc. R. С Edinburgh, 3, 139 A857).
Румфорд (Rumford В. Т.)
A798) Inquiry Concerning the Source of Heat which is Excited by Friction
Phil. Trans.
Хороший обзор этих работ можно найти в книге Тейта:
Тейт (Tait P. G.)
A877) Sketch of Thermodynamics, Edinburgh, Douglas.
Д. Основные работы по статистической механике, термодинамике
и кинетической теории
Андрюс (Andrews F. С.)
A963) Equilibrium Statistical Mechanics, New York, Wiley.
Беккер (Becker R.)
A955) Theorie der Warme," Berlin, Springerverlag.
Бриллюен (Brillouin L.)
A962) Science and Information Theory, 2nd ed , New York, Academic Press.
Русский перевод 1-го изд.: Бриллюен Л., Наука и теория информа-
информации, М., Физматгиз, 1960.
Броут (Brout R.)
A965) Phase Transitions, New York, W. A. Benjamin.
Вильсон (Wilson A. H.)
A957) Thermodynamics and Statistical Mechanics, Cambridge, Cambridge
University Press.
Гуггенгейм (Guggenheim E. A.)
A960) Thermodynamics, 4th ed., New York, Interscience Publishers. Русский
перевод 1-го изд.: Гуггенгейм Э. А., Современная термодинамика,
изложенная по методу У. Гиббса, Л.— М., Госхимиздат, 1941.
Дэвидсон (Davidson N.)
A962) Statistical Mechanics, New York, McGraw-Hill.
Земанский (Zemansky M. W.)
A957) Heat and Thermodynamics, 4th ed., New York, McGraw-Hill.
Кал лен (Callen H. В.)
A960) Thermodynamics, New York, Wiley.
Кирквуд, Оппенгейм (Kirkwood J. G., Oppenheim I.)
A961) Chemical Thermodynamics, New York, McGraw-Hill.
Киттель (Kittel C.)
A958) Elementary Statistical Physics, New York, Wiley. Русский перевод^
Киттель Ч., Элементарная статистическая физика, М., ИЛ, I960.
Список литературы 349
Кяудсен (Kmidsen M.)
A934) Kinetic Theory of Gases, London, Methuen.
Ландау Л. Д., Лифшиц Е. М.
A964) Теоретическая физика., т. 5, Статистическая физика, М., Физматгиз.
Ля, Сире, Таркотт (Lee J. F., Sears F. W., Turcotte D. L.)
A963) Statistical Thermodynamics, Reading, Mass., Addison-Wesley.
Линдсей (Lindsay R. B.)
A941) Introduction to Physical Statistics, New York, Wiley.
Майер Дж., Майер M. (Mayer J. E., Mayer M. G,)
A940) Statistical Mechanics, New York, Wiley. Русский перевод: Майер Дж.,
Гедперт-Майер М., Статистическая Механика, М., ИЛ, 1952.
Мак-Дональд (MacDonald D. К. С.)
A963) Introductory Statistical Mechanics for Physicists, New York, Wiley.
Мато, Такаги (Muto Т., Takagi Y.)
A955) Order — Disorder in Alloys, in Advances in Solid-State Physics, vol. 1,
pp. 194—282, New York, Academic Press.
Мюнстер (Minister A.)
A956) Statistische Thermodynamik, Berlin, Springerverlag.
A959) Prinzipien der Statistischen Mechanik, in Handbuch der Physik, vol.
III/2, pp. 176—412, Berlin, Springerverlag.
Пиппард (Pippard A. B.)
{1957) The Elements of Classical Thermodynamics, Cambridge, Cambridge
University Press.
Рашбрук (Rushbrooke G. S )
A949) Introduction to Statistical Mechanics, Oxford, Oxford University Press.
Райф (Reif F.)
A965) Fundamentals of Statistical and Thermal Physics, New York, McGraw-
Hill.
Толмен (Tolman R. C.)
A938) The Principles of Statistical Mechanics, Oxford, Oxford University
Press.
Tpan6yc(TribusM.)
{1961) Thermostatics and Thermodynamics, Princeton N. J., D. Van Nostrand.
Русский перевод: Трайбус M., Термостатика и термодинамика, М.,
«Энергия», 1970.
Уилкс (Wilks J.)
A961) The Third Law of Thermodynamics, Oxford, Oxford University Press.
Фаулер (Fowler R. H.)
A955) Statistical Mechanics, 2nd ed., Cambridge, Cambridge University
Press.
р, Гугтенгейм (Fowler R. H., Guggenheim E. A.)
A949) Statistical Thermodynamics, rev. ed., Cambridge, Cambridge Univer-
University Press. Русский перевод 1-го изд.: Фаулер Р., Гуггенгейм Э.,
Статистическая термодинамика, М., 1949.
350 Гл. V. Решение и дальнейшие свойства уравнения Больцмана
Ферми (Fermi E.)
A957) Thermodynamics, New York, Dover Publications. Русский перевод-
Ферми Э., Термодинамика, изд. Харьк. ун-та, 1969. д*
Френкель Я. И.
A948) Статистическая физика, М.— Л., Изд-во АН СССР.
Хаар (ter Haar D.)
A955) Foundations of Statistical Mechanics, Rev. Mod. Phys., 27, 289.
A954) Elements of Statistical Mechanics, New York, Holt, Rinehart and
Winston.
Хилл (Hill T. L.)
A960) An Introduction to Statistical Thermodynamics, Reading, Mass. Ad-
dison-Wesley.
A956) Statistical Mechanics, New York, McGraw-Hill. Русский перевод;
Хилл Т. Л., Статистическая механика, М., ИЛ, 1960.
Хинчин А. Я.
A943) Математические основания статистической механики, М.— Л., Гос-
техиздат, 1943.
Хуанг (Huang К.)
A963) Statistical Mechanics, New York, Wiley. Русский перевод: Хуант К.,
Статистическая механика, М., «Мир», 1966.
Чайшолм. Борд (Chisholm J. S. R., Borde A. H.)
A958) An Introduction to Statistical Mechanics, New York, Pergamon Press,
Шредингер (Schrodinger E.)
A952) Statistical Thermodynamics, 2nd ed., Cambridge, Cambridge Univer-
University Press.
Эйринг Г., Хендерсон, Стовер, Эйринг Е. (Eyring H., Henderson I}., Sto-
Stover В. J., Eyring Е. М.)
A963) Statistical Mechanics and Dynamics, New York, Wiley.
E. 38-теорема и эргодическая теорема
Биркгоф (Birkhoff G. D.)
A931) Proe. Nat. Acad., 17, 650, 656.
Биркгоф, Купмен (Birkhoff G. D», Koopman В О )
A932) Proc. Nat. Acad., 18, 279.
.Больцман (Boltzmann L.)
A895) Nature, 51, 413.
A877) Wien. Ber., 76, 373.
A887) Wien. Ber., 95, 153.
Борн, Грин (Born M., Green H. S.)
A948) Proc. Roy. Soc. (London), A192, 166.
Гиббс (Gibbs J. W.)
A948) Elementary Principles in Statistical Mechanics (Vol. II of his Collected
Works), Chap. XII, New Haven. Русский перевод 1-го изд.: Гиббс
Дж. В., Основные принципы статистической механики, излагаемы6
со специальным применением к рапиональному обоснованию термо-
термодинамики, М.~- Л., Гостехиздат, 1946.
Список" литературы 351
джине (Jeans J. H.)
A921) The Dynamical Theory of Gases, Chap. IV, Cambridge.
Джордан (Jordan P.)
A933) Statistische Mechanik auf Quantentheoretischer Grundlage, Braun-
Braunschweig.
Кац (Кае М.)
A959) Probability and Related Topics in Physical Theory, Interscience,.
New York. Русский перевод: Кац М., Вероятность и смежные*
вопросы в физике, М., «Мир», 1965.
Кембл (Kemble E. С.)
A939) Phys. Rev., 56, 1013, 1146.
Клайн М. (Klein M. J.)
A952) Phys. Rev., 87, 111.
Клайн О. (Klein О.)
A931) Z. Physik, 72, 767.
Кольрауш, Шредингер (Kohlrausch К. W. F., Schrodinger E.)
A926) Physik. Z.f 27, 306.
Лоренц (Lorentz H. А.)
A887) Wien. Ber., 95, 115.
Лошмидт (Loschmidt J.)
A876) Wien. Ber., 73, 139.
A877) Wien. Ber., 75, 67.
Мизес (von Mises R.)
A931) Wahrscheinlichkeitsrechnung, Leipzig — Vienna.
Нейман (von Neumann J.)
A932) Proc. Nat. Acad., 18, 70, 263.
A929) Z. Physik, 57, 30.
Окстоби, Улем (Oxjoby I., Ulam S.)
A941) Ann. of Maths., 42, 874.
Паули (Pauli W.)
A928) Probleme der Modernen Physik (Sommerfeld Festschrift, ed. by
P. Debye), Leipzig.
Паули, Фирц (Pauli W., Fierz M.)
A937) Z. Physik, 106, 572.
Планчерель (Plancherel M.)
A913) Ann. Physik, 42, 1061.
Пуанкаре (Poincare H )
A892) Les Methodes Nouvellerde la Mechanique Celleste, vol. I, Paris. Русский
перевод в сб. Пуанкаре А., Избранные труды, М., «Наука», т. I,.
1971; т. 2, 1972.
Розенталь (Rosenthal A.)
W913) Ann. Physik, 42, 796.
352 Гл. V. Решение и дальнейшие свойства уравнения Болъцмана
Смекаль (Smekal A.)
{1926) Encyklopadie der mathematischen Wissenschaften, V, Pt. 28,
zig — Berlin.
Смолуховский (Smoluchowski M.)
A912) Physik. Z., 13, 1069. Русский перевод в сб. Эйнштейн А., в
ский М., Броуновское движение, М.— Л., ОНТИ, 1936, стр. igg
Толмен (Tolman R. С.)
{1938) The Principles of Statistical Mechanics, Oxford, Oxford University
Press.
Уленбек (Uhlenbeck G. E.)
A927) Over statistische methoden in de theorie der quanta, Dissertation,
Leiden.
Фаулер (Fowler R. H.)
A936) Statistical Mechanics, Cambridge.
•Ферми (Fermi E.)
{1923) Physik. Z., 24, 261.
Хаар, Грин (ter Haar D., Green G. D.)
{1953) Proc. Phys. Soc. (London), A66, 153.
Халмош (Halmos P. R.)
{1956) Lectures on Ergodic Theory, Math. Soc. Japan, Tokyo. Русский пере-
перевод: Халмош П. Р., Лекции по эргодической теории, М., ИЛ, 1959.
Хинчин А. Я.
A943) Математические основания статистической механики, М.— Л., Гос-
техиздат.
Хопф (Hopf E.)
A937) Ergodentheorie (Ergeb. Math., 5, № 2), Berlin*
Цермело (Zermelo E.)
A896) Ann. Physik, 57, 485.
Чандрасекхар (Ghandrasekhar S.)
A943) Revs. Mod. Phys., 15, 1.
Эренфест П., Эренфест Т. (Ehrenfest P., Ehrenfest Т.)
A911) Encyklopadie der mathematischen Wissenschaften IV, Pt. 32, Leipzig —
Berlin.
A907) Physik. Z., 8, 311.
Список обозначений к гл. V
А —множество точек,
А —вектор-функция, являющаяся множителем в ФA)»
В —тензор-функция, являющаяся множителем в Ф( }»
С —тепловая скорость,
Список обозначений к гл. V. 353
CZQ — кривая системы в Г-пространстве, включающая на-
начальную точку z0,
D —коэффициент диффузии,
Е — энергия,
F — свободная энергия,
% — скалярная функция, являющаяся множителем в А,
j^o — абсолютный максвеллиан,
$Р — одночастичная функция распределения,
@ — скалярная функция, являющаяся множителем в В9
g — безразмерная функция распределения,
jfiTin) — полиномы Эрмита,
/ — оператор столкновений Больцмана,
К —ядро оператора X,
К — внешнее силовое поле,
Ж —оператор (v — X),
к — постоянная Больцмана,
X —оператор (— П),
I — средняя длина свободного пробега,
ш — среднее относительное отклонение,
т — масса частицы,
п — плотность числа частиц,
Р — относительный тензор давлений,
р — скалярное давление,
р — импульс частицы,
Q — большая статистическая сумма,
Q —вектор относительного теплового потока,
Д — постоянная к/т,
г0 — радиус взаимодействия,
S — энтропия,
S — относительный тензор напряжений,
s — безразмерная скорость,
Т —температура,
^(ь t) — доля времени из интервала t, проводимого кривой
CZo в области А,
и — гидродинамическая скорость,
V — объем,
v —удельный объем,
W — число микросостояний, реализующих данное макро-
макросостояние,
W — работа,
Z — каноническая статистическая сумма,
% — активность,
Р — неопределенный множитель Лагранжа,
Р —переменная (кТ)'1,
354 Гл. V. Решение и дальнейшие свойства уравнения Больцмана
8 — бесконечно малая величина,
г] — термодинамический коэффициент полезного дей-
действия,
т] — «крупнозернистая» энтропия Гиббса,
^го фA> — аппроксимация первого порядка для $f
К —ядро оператора еЖ\
Ф — потенциал взаимодействия частиц,
к — коэффициент теплопроводности,
Л —тензор скоростей деформаций,
\i —химический потенциал,
(Л — коэффициент вязкости,
\1 — неопределенный множитель Лагранжа,
|л (А) —мера множества А,
v — частота столкновений,
vn —собственное значение оператора X,
Q — объем в Г-пространстве,
со — безразмерный максвеллиан,
П — «крупнозернистое» распределение,
я|)п —собственные функции оператора X,
р —массовая плотность,
v
2 — симметричная сумма градиентных операторов,,
т — объем в (^-пространстве,
?f — оператор динамического преобразования,
? —линейный оператор Больцмана.
ПРИЛОЖЕНИЕ 1
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ, ТЕНЗОРНЫЕ
ОБОЗНАЧЕНИЯ И НЕКОТОРЫЕ ПОЛЕЗНЫЕ
ИНТЕГРАЛЫ
Векторная функция положения А (г) представляет собой систе-
систему трех функций А^; \i = 1, 2, 3. Они являются проекциями
вектора А на декартовы оси координат, так что А± = Ах, А2 =
= Ау, А3 = Az. A^ — это тензорное обозначение вектора А.
В более общем случае система Зп функций,
'Фи, г2... „nW»
где каждый из п индексов {ip} изменяется от нуля до трех, назы-
называется тензором ранга п в трехмерном пространстве. Скаляр не
содержит индексов и, таким образом, является тензором нулевого
ранга. Вектор есть тензор первого ранга.
В тексте употребляется векторное обозначение тензора второго
ранга фрд,, а именно
Часто встречающийся тензор второго ранга в качестве своих
девяти компонент имеет произведения компонент двух векторов А
и В. Например,
D = АВ, (П.1)
iV = A^BV. (П.2)
Тензор второго ранга o|^v является симметричным если
ilVv^vn, (П-3)
и антисимметричным (или косым), если
Симметричный или антисимметричный тензор всегда можно
образовать из произвольного тензора следующим образом:
(п.6)
356 Приложение 1
Следом тензора называется сумма его диагональных компонент:
з
Tr^v= 2 %*• (П.7)
Тензор с нулевым следом также можно образовать из я|?:
^-1(Тг^)б^. (П.8)
(По повторяющимся индексам производится суммирование.)
Дельта-символ Кронекера второго ранга 6^ определяется соглас-
согласно равенствам
буд, = 1 при ii = v;
8^v = 0 при \л фч. (П.9)
Симметричный тензор с нулевым следом задается равенством
*С = 4$ - Т (Тг *N^- (П'10)
В векторных обозначениях равенства (П.8) и (П.10) запишутся так:
(ТгфO. (П.10)
О
Символ Леви-Чивита третьего ранга &jVM, определяется так:
?jv[i = +1? если lv\i —четная перестановка из 1, 2, 3,
== —1, если Zvjli —нечетная перестановка из 1, 2, 3,
= 0, '4 если любые два индекса совпадают.
Векторное, или перекрестное, произведение двух векторов опре -
деляется равенством
i J
АЛЛ
**-х **-у **-г
Вх By Bz
(П.И)
Триада единичных векторов (i, j, k) лежит вдоль декартовых осей
координат, причем i — по направлению х, j —по направлению у
и к —по направлению z. Тензорное обозначение векторного про-
произведения имеет вид
2)
Внутреннее, или скалярное, произведение двух векторов опреде-
определяется следующим образом:
v + AzBz, (П.13а)
Вц. (П.136)
Приложение 1 357
Оператор V записывается так:
V^i^ + j^ + k-^-, (П.14а)
^-4Г- (П.146)
Градиент скалярной функции ф определяется так:
V<?, (П.15а)
-J-J. (П.156)
Ротор вектора определяется так:
rotA = VxA, (П.16а)
(rot А)^ — 4ivj^ Av (П. 166)
Дивергенция вектора определяется так:
V.A, (П.17а)
-g^V (П.176)
Ниже даются некоторые полезные векторные формулы вместе
с их эквивалентными тензорными обозначениями:
(П.18а)
J-tA^tAt + A^tf,, (П.186)
(П.19а)
-^-ф, (П.196)
, (П.20а)
^ Av, A1.2U6)
(VxA), (П.21а)
Л-А^ = А^В» + В^А„ (П.216)
(П.22а)
47^ (П.226)
V.(VxA) = 0, (П.23а)
ЫА0 (П.236)
358 Приложение 1
—(V.V)A, (П.24а>.
д д . ^|
(используйте равенство (П.25) в равенстве (П.246), чтобы полу-
получить (П.24а)),
V.r = 3, (П.26а)
(П.27а)
^ 0, (П.276)
(A-V)r = A, (П. 28а)
(П.286)
4^, A, 4
V х (А х В)= — BV.A — A-VB + AV.B + B.VA, (П.29а)
(П.296)
(П.30а>
(AxB).(CxD) = (A.C)(B.D)-(A.D)(B.C),
SiikiAkBiS^dpC dDp = AyCyBkDh — AnDnBjCj, (П.306)
(A x B) x (C x D) = (A-B x D) C-(A-B x C) D, (П.31а)
jBaCiDh. (П.316)
Симметричная сумма градиентных операторов определяется
согласно равенству
v v
ft
Некоторые полезные интегралы
, (П.ЗЗ)
— оо
оо
/ (и) = j е-аж2жп da:, /г > 0, а > О, (П.34)
тг+1
" 2 , (п.35)
Приложение 1 359
где
оо
Г (п) = J е'Хх71-1 dx. (П.36)
о
Запишем два значения Г-функции:
/я, (П.37)
ГA) = 1. (П.38)
Для целых п, больших единицы, Г-функция принимает значения
Г(гс) = (п-1)!. (П.39)
Это следует из рекуррентной формулы
Г(гс) = (>г-1)ГGг-1>. (П.40)
Некоторыми характерными значениями / являются:
7E) = а.
Интеграл вероятности ошибок определяется так:
2 Г
iy = —^ \ e~xidx.
Для у<1
(Подинтегральное выражение разложено в ряд Тейлора.) Для
(Повторное интегрирование по частям.)
ПРИЛОЖЕНИЕ 2
ФИЗИЧЕСКИЕ КОНСТАНТЫ
Скорость света в ва-
вакууме
Постоянная Планка
Число Авогадро
Постоянная Больцма-
на
Газовая постоянная
Объем одной грамм-мо-
грамм-молекулы совершенно-
совершенного газа при нор-
нормальных температу-
температуре и давлении
Заряд электрона
Масса покоя электро-
электрона
Масса покоя протона
Магнетон Бора
Масса покоя нейтрона
Отношение массы про-
протона к массе элект-
электрона
Отношение заряда
электрона к его мас-
массе
Постоянная Стефана—
Больцмана
с 2,9973-108 м/с
2,9973-1010 см/с
h 6,625-Ю-34 Дж-с
6,625-Ю-27 эрг-с
Ао 6,0247-1023 атом/г-атом
к 1,3804-Ю-23 Дж/°С
1,3804-Ю-16 эрг/°С
ъ = М 8,3166 Дж/(г-моль.°С)
8,3166-107 эрг/(г-моль.°С)
1,9870 кал/(г-моль-°С)
22,421 л
е 1,6021-Ю-19 Кл
4,8029-Ю-10 ед. СГСЭ
т 9,1085-Ю1 кг
9,1085-Ю-28 г
МР 1,6724-Ю-27 кг
1,6724-Ю-24 г
1,00759 а. е. м.
= ehllmc 2,2732-Ю-21 эрг-Гс
Мп 1,00898 а. е. м.
Мр/т 1836,1
elm 1,7589-1011 Кл/кг
5,2730.1017ед. СГСЭ/г
О 5,6697 • 10 эрг • см-2 • сек • град
Постоянная Ридберга
Радиус первой водо-
водородной орбиты
Тройная точка воды
Атомная единица мас-
массы
Приложение
Roo
а
1 а. е. м
2 361
109 737,31 см
0,52916 А
273,16 °К
. 1,6598-Ю-24 г
Полезные переводные константы и единицы
Масса электрона, ev
Атомная единица мас-
массы, ev
Константы в системе
единиц МКС
Электрон-вольт
т
а. е. м.
во
[АО
1 эВ
1 МэВ
1 ГэВ
0,51098 МэВ
931,16 МэВ
8,8542- Ю-12 Ф/м
4я.10Г/м
1,6021. Ю-12 эрг
1,6021-Ю-19 Дж
106 эВ
109 эВ
1 кулон 0,1 ед. СГСМ 3-109 фран-
клин (ед. СГСЭ)
1 вебер на квадрат- 104 Гс
ный метр
Основание натураль- е 2,718
ных логарифмов
СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ
Власов А. А.
A966) Статистические функции распределения, М., «Наука».
Гуров К. П.
A966) Основания кинетической теории, М., «Наука».
Зубарев Д. Н.
A971) Неравновесная статистическая термодинамика, М., «Наука».
Коган М. Н„
A967) Динамика разрежепного газа, М., «Наука».
Румер Ю. Б., Рыбкин М. С.
A972) Термодинамика, статистическая физика и кинетика, М., «Наука».
Силин В. П.
A971) Введение в кинетическую теорию газов, М., «Наука».
Терлецкий Я. П.
A973) Статистическая физика, изд. 2-е, М., «Высшая школа».
Толмачев В. В.
A968) Основные уравнения кинетической теории газов, М.
ИМЕННОЙ УКАЗАТЕЛЬ
Андрюс (Andrews F. С.) 348
Аппель (Appell P.) 49
Балеску (Balescu R.) 116, 136, 165,
255, 261
Барнетт (Burnett D.) 345
Беккер (Becker R.) 348
Берд (Bird R. В.) 116, 262
Биркгоф (Birkhoff G. D.) 341, 350
Боголюбов Н. Н. 99, 115, 165, 207
Де Боер (de Boer J.) 115, 166
Больцман (Boltzmann L.) 43, 48, 115,
172, 228, 233, 261, 263, 338, 350
Бом (Bohm D.) 117
Бонд (Bond J. W.) 262
Борд (Borde A. H.) 350
Борн (Born M.) 99, 115, 166, 350
Бриллюеп (Brillouin L.) 348
Броут (Brout R.) 348
Бхатнагар (Bhatnager D.) 233, 261
Бэч (Beth E.) 166
Ватсон (Watson К. М.) 262
Вебстер (Webster A. G.) 50
Вильсон (Wilson A. H.) 348
Власов A. A. 149, 167
Вонг (Wang M. C.) 262
Вэнь-Чень (Wang-Chang С S.) 347
Гриффис (Gruffith B. A.) 50
Гросс (Gross E.) 233, 261
Грэд (Grad H.) 115, 165, 207, 231,
261, 262, 263, 290, 294, 345, 347
Грэй (Gray D.) 166
Гуггенгейм (Guggenheim E. A.) 116,
262, 348, 349
Гюкель (Huckel E.) 144, 165
Дебай (Debye P.) 144, 165
Делькруа (Delcroix J. L.) 117, 165
Детуш (Destouche J. L.) 50
Джемс (James С G. F.) 345
Джине (Jeans J.) 262, 346, 351
Джонс (Леннард) (Jones J. E. (Len-
nard)) 346
Джордан (Jordan P.) 351
Джоуль (Joule J. P.) 347
Джудд (Judd D.) 262
Дирак (Dirac P. A. M.) 117
Дэвидсон (Davidson N.) 348
Дюпри (Dupree Т. Н.) 136, 153, 155,
156, 165
Земанский (Zemansky M. W.) 348
Зернике (Zernike F.) 166
Зоммерфельд (Sommerfeld A.) 50, 262,
Зумино (Zumino B.) 166
Гамильтон (Hamilton W. R.) 43, 48
Гернсей (Guernsey R. L.) 136, 165
Гиббс (Gibbs J. W.) 43, 48, 86, 113,
115, 319, 341, 342
Гильберт (Hilbert D.) 284, 345, 347
Гильдербранд (Hilderbrand F.) 284,
347
Гиршфельдер (Hirschf elder J. O.)
116, 262
Голд (Gold T.) 260
Голдстейн (Goldstein H.) 50
Грин (Green M. S.) 99, 115, 166,
350, 352
Ивон (Ivon J.) 99, 116
Каллен (Callen H. В.} 34&
Карлеман (Carleman T.) 347
Карно (Carnot S.) 310, 347
Каулинг (Cowling T. G.) 173, 263
Кац (Нас М.) 116, 342, 351
Кейлсон (Keilson J.) 261
Кельвин (Kelvin W.) 310, 348
Кембл (Kemble E. С.) 351
Кеннард (Kennard E. H.) 262
Кертисс (Curtiss C. F.) 116, 262
364
Именной указатель
Кирквуд (Kirkwood J. G.) 99, 116,
207, 261, 348
Киттель (Kittel С.) 348
Клайн М. (Klein M. J.) 351
Клайн О. (Klein О.) 351
Клапейрон (Clapeyron E.) 310, 348
Клаузиус (Glausius R.) 204, 310, 348
Кнудсен (Knudsen M.) 349
Колмогоров А. Н. 105
Кольрауш (Kohlrausch К. W. F.)
351
Коэ (Сое С. J.) 50
Коэн Е. Г. Д. (Cohen E. G. D.) 106,
165
Коэн Р. С. (Cohen R. S.) 165
Крамер (Cramer H.) 117
Крук (Krook M.) 233, 261
Кук (Cook W. R.) 346
Купмен (Koopmen В. О.) 350
Курант (Courant R.) 284, 347
Куш (Kusch P.) 263
Лагранж (Lagrange J. L.) 43, 48
Ландау Л. Д. 50, 116, 255, 262, 349
Ленард (Lenard A.) 136, 165, 255,
262
Ли Т. Д. (Lee T. D.) 260
Ли Дж. Ф. (Lee J. F.) 349
Либов (Liboff R. L.) 117, 149, 165,
166, 167, 251, 263
Либовиц (Lebowitz J.) 167, 251, 263
Линден-Белл (Lynden-Bell D.) 149,
167
Линдсей (Lindsay lR. B.) 349
Лиувилль (Liouville J.) 48
Лифшиц Е. M. 50, 116, 349
Лоренц (Lorentz H. A.) 346, 351
Лорч (Lorch E. R.) 292, 347
Лошмидт (Loschmidt J.) 117, 261,
351
Лоэб (Loeb L. B.) 262
Лэмб (Lamb H.) 50
Лэндшофф (Landshoff R.) 165
Майер Дж. (Mayer J. E.) 116, 166,
349
Майер M. (Mayer M. G.) 116, 166,
349
Мак-Дональд (McDonald W.) 262, 349
Мак-Леннан (McLennan J.) 347
Мак-Миллан (MacMillan W. D.) 50
Максвелл (Maxwell J. C.) 43, 49,
228, 261
Маршак (Marshak R. E.) 165
Массей (Massey H. S. W.) 346
Мато (Muto T.) 349
Мизес (von Mises R.) 351
Миллер (Miller R.) 263
Милн (Miln E. A.) 50
Монтгомери (Montgomery D.) 166
257, 262
Mop (Mohr С. В. О.) 346
Мотт-Смит (Mott-Smith H. M.) 347
Мурнаган (Murnaghan F. D.) 51
Мюнстер (Munster A.) 349
Нейман (von Neumann J.) 341, 351
Окстоби (Oxtoby I.) 342, 351
Оппенгейм (Oppenheim I.) 251, 348
Орнстейн (Ornstein L. S.) 166
Осгуд (Osgood W. F.) 50
Парсен (Parsen E.) 105
Паттерсон (Patterson G. N.) 262
Паули (Pauli W.) 106, 351
Пиддак (Piddack F. B.) 346
Пиппард (Pippard A. B.) 349
Пирона (Perona G.) 166
Планк (Planck M.) 237, 262
Планчерель (Plancherel M.) 338, 351
Презент (Present R. D.) 262
Пригожий (Prigogine I.) 65, 116, 117
Пуанкаре (Poincare H.) 43, 48, 89,
117, 339, 351
Пуассон (Poisson S. D.) 48
Райе (Rice S. A.) 166
Райф (Reif F.) 349
Рашбрук (Rushbrooke G. S.) 349
Рейхенбах (Reichenbach H.) 261
Розенблют (Rosenbluth M. N.) 136,
143, 166, 262
Розенталь (Rosenthal A.) 338, 351
Росс (Ross J.) 116
Ростокер (Rostoker N.) 136, 143, 166
Роутли (Routly P.) 165
Румфорд (Rumford В. Т.) 310, 348
Синг (Synge J. L.) 50
Сирович (Sirovich L.) 347
Сире (Sears F. W.) 349
Слейтер (Slater J. C.) 50
Смекаль (Smekal A.) 352
Смолуховский (Smoluchowski M.)
105, 352
Спитцер (Spitzer L. Jr.) 165
Именной указатель
365
Стелл (Stell G.) 166
Стовер (Stover В. J.) 350
Сторер (Storer J.) 261
Стоун (Stone M. Н.) 292, 347
Сэндри (Sandri G.) 136, 166
Такаги (Takagi Y.) 349
Таркотт (Turcotte D. L.) 349
Тейт (Tait P. G.) 348
Тидмен (Tidmen D.) 166, 257, 262
Тимошенко (Timoshenko S.) 50
Толмен (Tolman R. С.) 116, 263,
349 352
Трайбус (Tribus M.) 349
Уилкс (Wilks J.) 349
Уиттекер (Whittaker E. Т.) 50
Улем (Ulam S.) 342, 351
Уленбек (Uhlenbeck G. Е.) 165, 166,
262, 347, 352
Уолдмен (Waldman L.) 263
Урселл (Ursell H. D.) 117, 166
Уэлч (Welch J. A.) 262
Фаулер (Fowler R.) 116, 349, 352
Ферми (Fermi E.) 89, 117, 339, 350,
352
Фидель (Fedele J.) 251, 263
Финкельстейн (Finkelstein L.) 347
Фирц (Fierz M.) 351
Фишер И. 3. 166
Фоккер (Fokker A.) 237, 262
Френкель Я. И. 166, 350
Фриман (Frieman E. А.) 166
Фриш (Frisch H.) 167
Фрэнк (Frank N. Н.) 50
Хаар (ter Haar D.) 116, 350, 352
Халмош (Halmos P. R.) 352
Хейнсуорс (Hainsworth W.) 346
Хендерсон (Henderson D.) 350
Хилл (Hill Т. L.) 116, 167, 350
Хинчин А. Я. 350, 352
Хопф (Hopf E.) 352
Хуанг (Huang К.) 350
Хэсс (Hasse H. R.) 346
Ван Хов (L. Van Hove) 106
Цартман (Zartman I. F.) 263
Цермело (Zermelo E.) 117, 261, 352
Чайшолм (Chisholm J. S. R.) 350
Чандрасекхар (Chandrasekhar S.) 262,
Q CO
Чен (Tchen С. М.) 166
Чепмен С. (Chapman S.) 173, 263,
346
Шефер (Schaefer C.) 51
Шредингер (Schrodinger E.) 350, 351
Эйзенхарт (Eisenhart L. P.) 51
Эймс (Ames F. D.) 51
Эйнштейн (Einstein A.) 43, 49, 113,
319
Эйринг Г. (Eyring H.) 350
Эйринг E. M. (Eyring E. M.) 350
Энског (Enskog D.) 346
Эренфест П. (Ehrenfest P.) 116, 263,
352
Эренфест Т. (Ehrenfest Т.) 116, 263,
352
Юнг (Joung D. H.) 50
Якоби (Jacobi K. G. J.) 48
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Активность 330
Ансамбль 319
-— канонический 321, 324
большой 328, 330
— микроканонический 321, 341
Вектор апсидальный 182
— Пойнтинга 224
— теплового потока 121
Вероятность переходная 106
— термодинамическая 307
связь с энтропией 312, 329
Взаимодействие жестких сфер 187,
271
— кулоновское 186, 239, 241, 257
Взаимодействия напряженность 197
— радиус 138, 202, 271
Вращение виртуальное 20
Времени изотропность 22
— однородность 22
Время возврата Пуанкаре 172
— релаксации 244, 289
— среднее между столкновениями
123, 197
— столкновения 122
Газ идеальный 122, 194, 324
— Кнудсена 273
— кулоновский см. Плазма
— несовершенный (неидеальный) 318
— фундаментальный 211
Гамильтониан 18, 79, 93, 322
— включающий внешний потенциал
153
— для свободных частиц 71
— относительный 174
— как производящая функция 33
Гипотеза Боголюбова 122, 156, 164
— эргодическая см. Теорема эрго-
дическая
Градиент 357
Давление (скалярное) 121, 163, 269
Дальнодействие 187, 237, 252
Движение периодическое 35
— разделимое 35
Действие 14, 33
Дивергенция 357
Длина волны де Б рой л я 332
— свободного пробега средняя 123,
197, 272
Допущение Маркова 105
Закон адиабатический 221
— феноменологический 267
— Фика 303
Инварианты канонические 31, 43
— Пуанкаре интегральные 43, 57,
202
— сумматорные (столкновений) 217,
229
Интеграл вероятности ошибок 359
Интегралы изолирующие 339
Каналы рассеяния 193
Константы движения 23, 43, 61, 89,
174
— — аддитивные 339
— — глобальные 339
— — локальные 339
— физические 360
Координаты и импульсы канониче-
канонические 18, 28
— обобщенные 13, 53
— циклические 18
Коэффициент вязкости 269, 283
— диффузии в уравнении Фоккера —
Планка 243, 249, 252
— самодиффузии 268
— силы трения в уравнении Фокке-
Фоккера — Планка 244, 249
— теплопроводности 269, 284
Коэффициенты переноса 268, 270
Предметный указатель
367
Лагранжиан 13
Линии тока 220
Масса приведенная 174
Метод Грэда моментный 294
— характеристик 65
Механика квантовая 65, 77, 106
Микронеустойчивость 289
Множества мера 340
Множество метрически неразложи-
неразложимое 341
Множители Лагранжа неопределен-
неопределенные 315
Молекулы максвелловские 186, 297
Молекулярный хаос 203
Момент угловой 20, 185
Напряжения 121, 159, 269
— кинетическая составляющая 160,
164
— потенциальная составляющая 161,
164
Необратимость динамическая 298,
345
Обратимость динамическая 22, 153,
170
Оператор вполне непрерывный 292
— кинетической энергии 93, 134, 138
— Лиувилля LN 92
— — линейный Л 65, 66
возмущенный 74, 79
для невзаимодействую-
невзаимодействующих частиц 71
свойства 66
собственные функции 73
приведенный Ls 92, 131
— набла 357
— ограниченный 291
— потенциальной энергии 93, 138
— резольвентный 81
— сдвига 131
— столкновений Больцмана линей-
линейный 278, 284, 286
— — — — свойства 285
нелинейный 204, 233, 273
— — — свойства 216
— — спектр 288
Описание микроскопическое 122
Орбита динамическая см. Траекто-
Траектория динамическая
Отклонение среднее квадратичное
334
— — — относительное 334
Отклонение среднее
плотности 360
— — — энергии 335
квадратичное
Парадокс возвратимости Цермело 89,
172
Параметр прицельный 179, 180
— — безразмерный 186
Параметры внешние 326
Переменные гидродинамические (мак-
(макроскопические) 120, 163, 274
— — — абсолютные 218
— — — относительные 219
— «действие — угол» 34, 36, 39, 73,
78, 90
— термодинамические интенсивные
309
— — экстенсивные 309
Перемещение виртуальное 14, 19
— обобщенное 326
Переходы первого и второго порядка
Плазма 143, 222, 254
Плотность импульса электромагнит-
электромагнитного поля 224
— числа частиц 120
— энергии электромагнитного поля
224
Поверхность энергетическая 85, 90,
340
Подход в статистической механике
апостериорный 336
— —- — — априорный 303
постулаты 309
Последовательность преобразований
метрически транзитивная 341
Постоянная газовая 230
— Планка 88
Потенциал жесткий 290, 292
— пороговый 290
Предел гидродинамический 273
— Розенблюта — Ростокера 143, 153
— термодинамический 101
Предположение адиабатичности 156
Преобразование каноническое 28
— — бесконечно малое 31
— — точечное 30
— — обмена 31
— — тождественное 31
— Лежандра 18, 29
Принцип Гамильтона 13
— динамической обратимости 23, 43
— исключения Паули 158
— равных априорных вероятностей
303
Произведение векторное 356
— скалярное 356
368
Предметный указатель
Производная индивидуальная 220
Пространства изотропность 20
— однородность 19
Пространство Г 24, 53, 304, 309,
311, 319
— Т 24
— L2 287, 291
— jli 304, 313, 318
Процесс марковский 106, 245
Радиус дебаевский 144
Разложение Кирквуда 140
Разложения групповые 136
Распределение Больцмана см. Рас-
Распределение МаксвелЛа
— «крупнозернистое» 343, 345
— Максвелла 226, 229, 233, 243, 278,
290, 292, 315, 317
— — абсолютное 230, 231
локальное 231, 270, 277, 294
— нормальное 243
Расширение газа свободное 312
Ротор 357
Сечение рассеяния дифференциаль-
дифференциальное 182, 183
для кулоновского взаимо-
взаимодействия 187
— — полное 183
Сила дальнодействующая 239
— короткодействующая 239
— обобщенная 326
Символ Леви-Чивита 356
Система квазиэргодическая 339
— координат центра масс 174, 177,
178, 184, 187, 190, 238
— — лабораторная 174, 176, 188,
190
— эргодическая 338, 345
Скобки Пуассона 26, 44
— — фундаментальные 31
Скорости обобщенные 22
Скорость макроскопическая 120, 121
— относительная 121, 219, 277
— тепловая 243
Соотношение дисперсионное 302
Состояние макроскопическое 120, 304
наиболее вероятное 313, 316
— микроскопическое 304, 326
— равновесное 172, 229, 231, 270,
305; см. также Распределение Мак-
Максвелла
— — неустойчивое 302
— термодинамическое 309; см. также
Состояние макроскопическое
Сохраняемость волновых векторов 80
— импульса 19, 178
Среднее по ансамблю 86, 320, 326, 330
Стадия гидродинамическая 127, Ifi/
231, 274
— кинетическая 126, 164, 231
— начальная 124, 164
Степени свободы системы 12
Столкновения дальние 239, 240, 254
— инверсивные 135, 180, 201
— реверсивные 181
— самые дальние 254
Стрелка времени 303
Сумма градиентных операторов сим-
симметричная 358
— статистическая 327, 328, 331
— — большая 331
Сфера дебаевская 254
Тензор напряжений Максвелла 224
— скоростей • деформаций 220, 269,
276
Тензора след 356
(^-теорема Больцмана 172, 224, 277,
288, 318, 336
для уравнения Фоккера —
Планка 251, 253
Теорема Биркгофа 341, 345
— о гамильтониане 21
— Пуанкаре возвратная 172
— спектральная 292
— (гипотеза) эргодическая 87, 337
— — — полная 340
— — — средняя 341
Теория возмущений нестационарная
76
— — — метод 76
— Гамильтона — Якоби 34
— Ньютона — Джинса 149
— орбит первого порядка 150
Теплоемкость удельная 335
Термодинамика 309
— закон первый 312
— — второй 310
Тождество Якоби 27
Точка представляющая (изображаю-
(изображающая) 319
Траектория динамическая 53, 61 89,
170, 341
Угол рассеяния 177, 180, 183, 185
Уравнение Балеску — Ленарда 156»
256
— Барнетта 173
— бескорреляционное 148
— Больцмана 136, 188, 204, 232Г
241, 259
анализ Чепмена — Энскога 271,
274, 277, 282
Предметный указатель
369
Уравнение Больцмана безразмерное
272
в обобщении Боголюбова 134
— — вывод Боголюбова 122
— — — Больцмана 194
Трэда 206, 212
Кирквуда 213
для двухкомпонентного газа 257
линеаризованное 186, 278
— БИ1 91, ИЗ, 148, 152, 159, 214,
258
— БИз 91, ИЗ, 127, 153
— Власова 149, 237, 254, 258
— — обратимость 153
— Гамильтона — Якоби 38
— Грэда первое 210
второе 210, 213, 259
— диффузии 268, 298
— Крука — Бхатнагара — Гросса
235, 237, 259
— Ландау 256
— Лиувилля 56, 60, 66, 74, 90
одночастичное 87, 141, 195, 258
— — в представлении взаимодейст-
взаимодействия 76
— — решение 61, 64, 77
— анализ Пригожина 65, 100
— неразрывности 55, 159, 218, 297
— обратимое 205
— Паули 106
— переноса максвелловское 224
— состояния 163
— управляющее 106, 204
— Фоккера — Планка 239, 242, 244,
248, 251, 259
вывод из уравнения Больц-
Больцмана 240, 242
— Чепмена — Колмогорова 105, 106,
245
— Шредингера 66
Уравнения ББКГИ 12, 91, 99, ИЗ,
115, 137
— — анализ Боголюбова 122
— — в форме Сэндри 138
— Гамильтона 18, 44, 56
— кинетические 148, 164, 233, 258,
259
— Лагранжа 14
— Максвелла 223
— моментные 160, 164
— Навье — Стокса 276
— решение самое общее 61
— решения самосогласованные 151
— самосогласованные 151
— сохранения 160, 216, 270
— — в относительных переменных
220
Уравнения ББКГИ для плазмы в од-
ножидкостном приближении 223
— — и КБГ-уравнение 235
— — нормальная форма 218
— — и ФП-уравнение 254
— Эйлера 275, 278
Условие детального (статистического)
баланса 228
Флуктуации 332
Функции корреляционные 137, 139,
143, 146, 164
в однородном пределе 156
представлении Кирквуда 140
Функция весовая 286
— Гамильтона см. Гамильтониан
характеристическая 38
— Лагранжа см. Лагранжиан
— плотности 54, 55, 83
— производящая 28, 34, 38
— распределения, анизотропные и
изотропные компоненты 260
Кирквуда ^-частичная усред-
усредненная по времени 213
— — Z-числовая 107
N- и 5-частичная (s < N) 83, 114
одночастичная, связь с гидро-
гидродинамикой 120
приведенная 92, 114
радиальная 102, 157
скорости нормальная 243
совместная 103
усеченная 207
условная 103, 105
Формализм Гамильтона 17
— Лагранжа 12
Цикл Карно 310
Частицы идентичные 95
— неидентичные 96
Частота плазменная 144
— столкновений 234, 237, 285, 290
. для двухкомпонентного газа
260
Числа заполнения 304, 314
Энергетический слой 85, 89, 90, 307,
321, 340
Энтропия Больцмана 225
— Гиббса 225, 343
— термодинамическая 226, 310—312,
321
Kanonische Normalsysteme 89
Stosszahlansatz 194, 215
Umkehreinwand 891
Wiederkehreinwand 89
Wiederkehrsatz 172
ОГЛАВЛЕНИЕ
Предисловие редактора перевода 5
Предисловие 9
Глава I. Элементы классической механики 11
1.1. Вводные замечания 11
1.2. Формализм Лагранжа 12
1.3. Формализм Гамильтона 17
1.4. Скобки Пуассона и канонические преобразования .... 26
1.5. Переменные «действие — угол» и теория Гамильтона — Якоби 34
1.6. Интегральные инварианты Пуанкаре 39
Список литературы 48
Список обозначений 51
Глава II. Уравнение Лиувилля и функции распределения 53
2.1. Концепция ансамбля и уравнение Лиувилля 53
2.2. Решение уравнения Лиувилля 60
2.3. Анализ Пригожина уравнения Лиувилля 65
2.4. Третья интерпретация D: iV-частичная функция распределе-
распределения fN 83
2.5. Динамика системы, выраженная через функцию fN: приве-
приведенные распределения. ББКГИ-уравнения 91
2.6. Условные и Z-числовые функции распределения 103
Список литературы 115
Список обозначений 117
Глава III. Формальное развитие теории кинетических уравнений
и их связь с гидродинамикой 120
3.1. Одночастичная функция распределения и ее связь с гидро-
гидродинамикой 120
3.2. Анализ Боголюбова ББКГИ-уравнений 122
3.3. Групповые разложения 136
3.4. Определение кинетического уравнения. Самосогласованные
решения 148
3.5. Формальное выражение для %% в однородном пределе ... 153
3.6. Радиальная функция распределения и уравнение состояния 156
Список литературы 165
Список обозначений 167
Глава IV. Уравнения Болъцмана, Крука — Бхатнагара — Гросса,
Фоккера — Планка и родственные им. Вывод уравнений
и их свойства 170
4.1. Дальнейшее толкование необратимости 170
Оглавление 371
4.2. Концепция столкновений 173
4.3. Уравнение Больцмана 194
4.4. Свойства больцмановского оператора столкновений .... 216
4.5. Уравнение Крука — Бхатнагара — Гросса 233
4.6. Уравнение Фоккера — Планка 237
Список литературы 260
Список обозначений 263
Глава V. Решение и дальнейшие свойства уравнения Болъцмана. Релак-
Релаксация к равновесию 267
5.1. Анализ Чепмена — Энскога уравнения Больцмана. Прибли-
Приближение малого среднего свободного пробега 267
5.2. Свойства линейного больцмановского оператора столкнове-
столкновений 285
5.3. Моментный метод Грэда 294
5.4. Релаксация к равновесному состоянию 298
5.5. Апостериорный подход. Эргодическая гипотеза 336
5.6. «Крупнозернистое* разбиение 342
Список литературы 345
Список обозначений 322
Приложение 1 355
Приложение 2 360
Список дополнительной литературы 362
Именной указатель 8 363
Предметный указатель . 366
Либов Р.
ВВЕДЕНИЕ В ТЕОРИЮ КИНЕТИЧЕСКИХ
УРАВНЕНИЙ
Редактор Л. Н. Бабынина
Художник Е. К. Самойлов
Художественный редактор В. И. Шаповалов
Технический редактор Л. П. Бирюкова
Сдано в набор 25/IX 1973 г.
Подписано к печати 6/II 1974 г.
Бумага тип. № 2 60x901/ie=H,75 бум. л.
23,50 усл. печ. л., Уч.-изд. л. 20,60
Изд. № 1/6963
Цена 2 р. 09 к. Зак. 01243
ИЗДАТЕЛЬСТВО «МИР»
Москва, 1-й Рижский пер., 2
Ордена Трудового Красного знамени
Московская типография № 7
«Искра революции» Союзполиграфпрома
при Государственном комитете
Совета Министров СССР по делам
издательств, полиграфии и книжной торговли
Москва К-1, Трехпрудный пер., 9