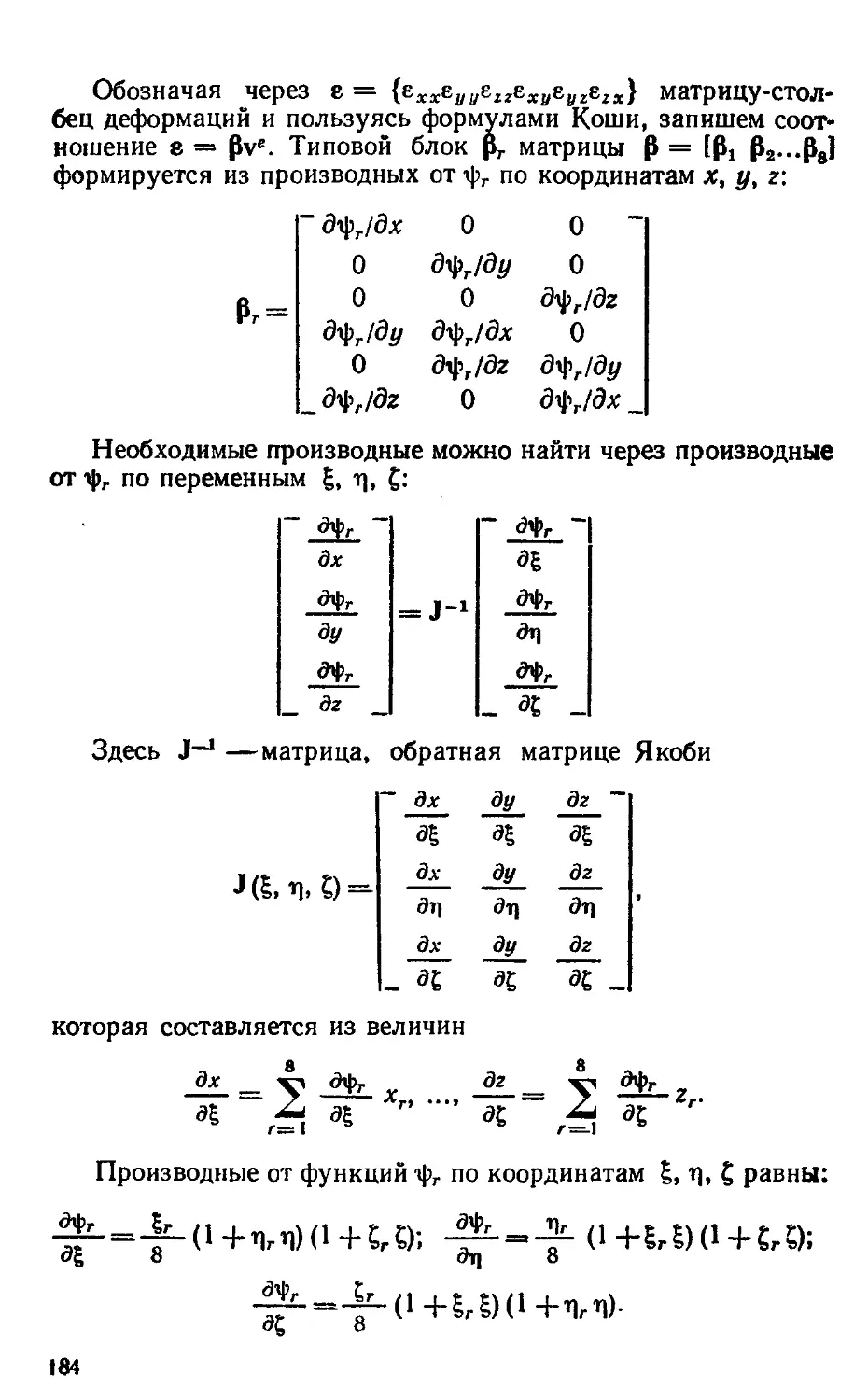
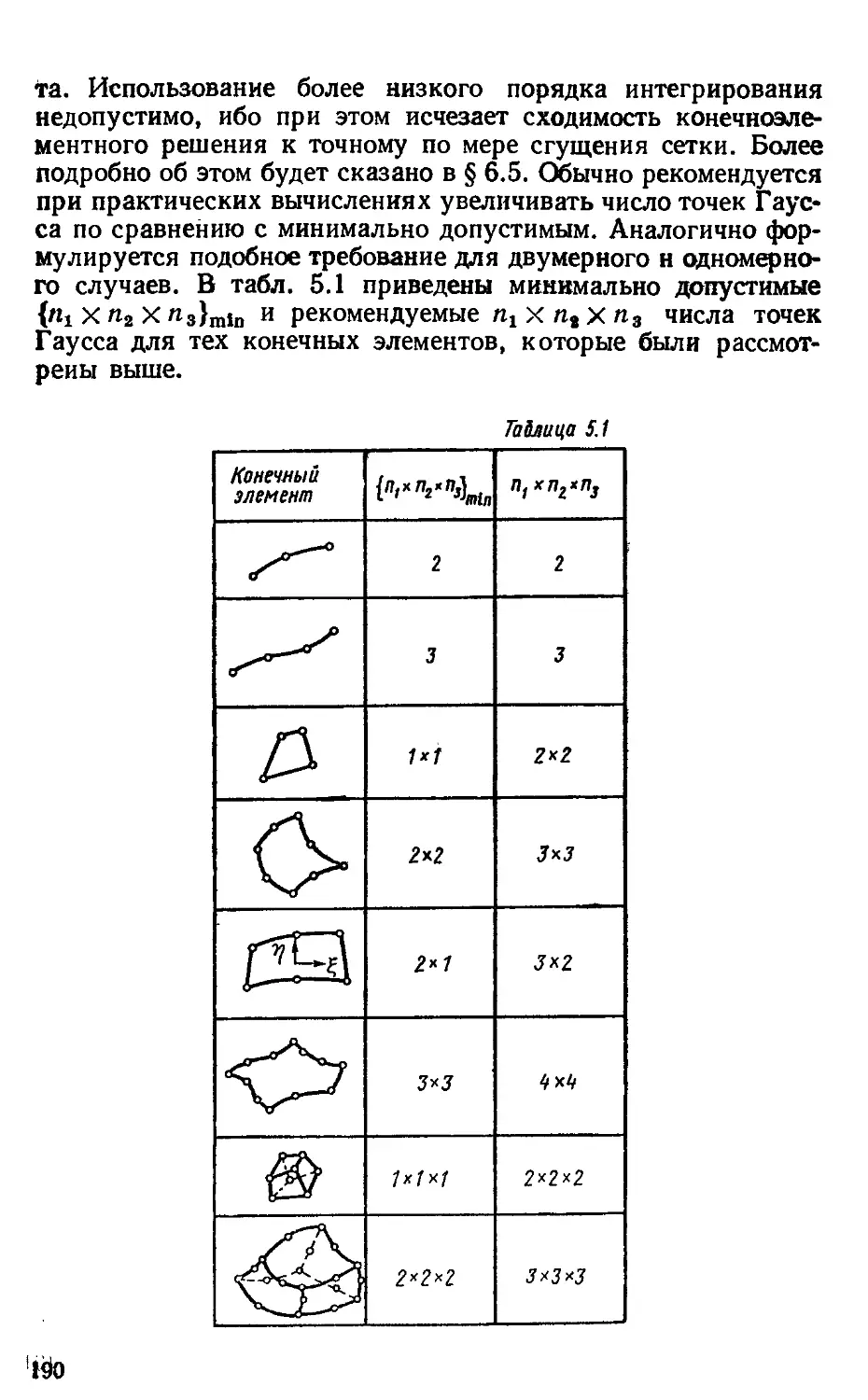
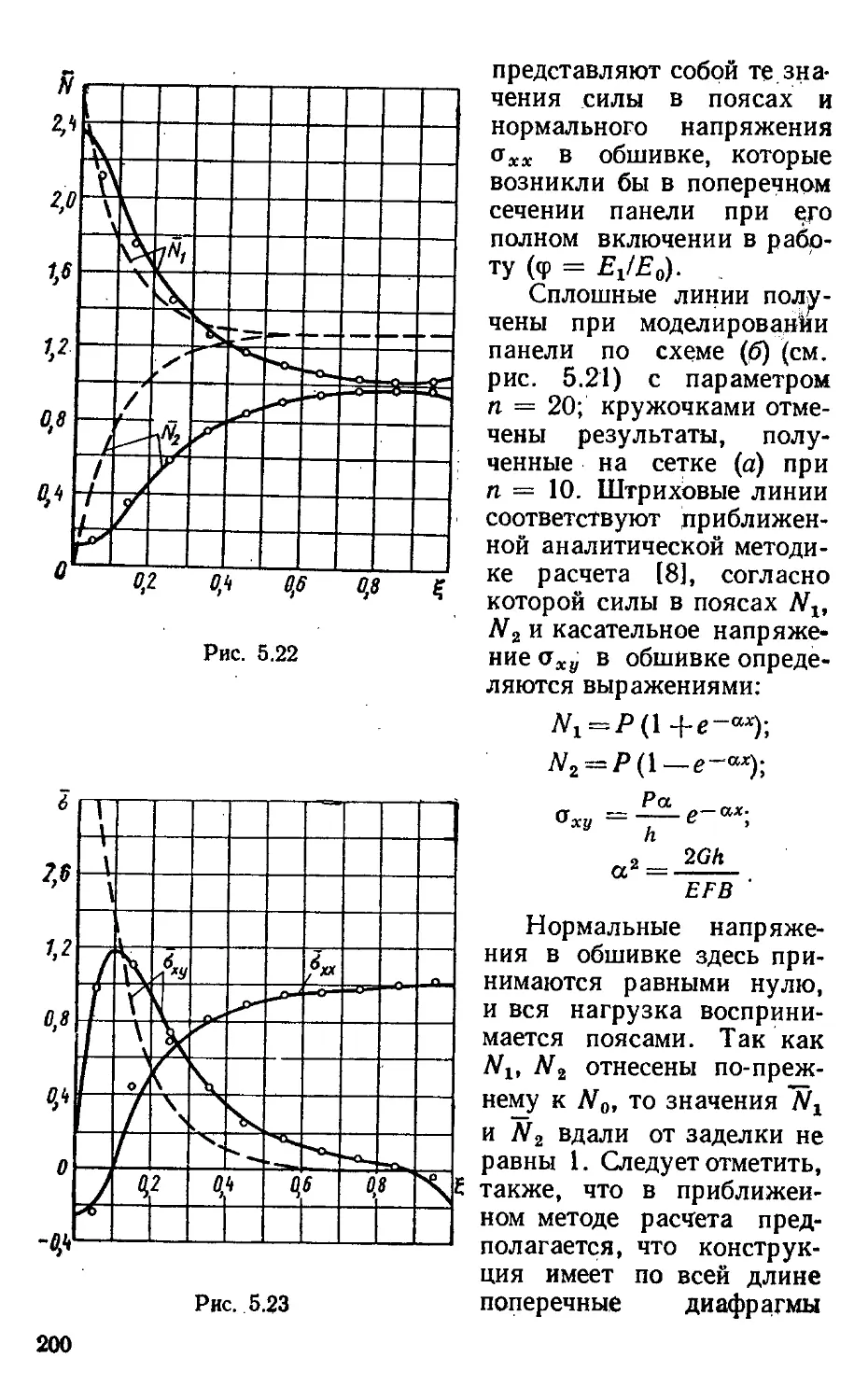
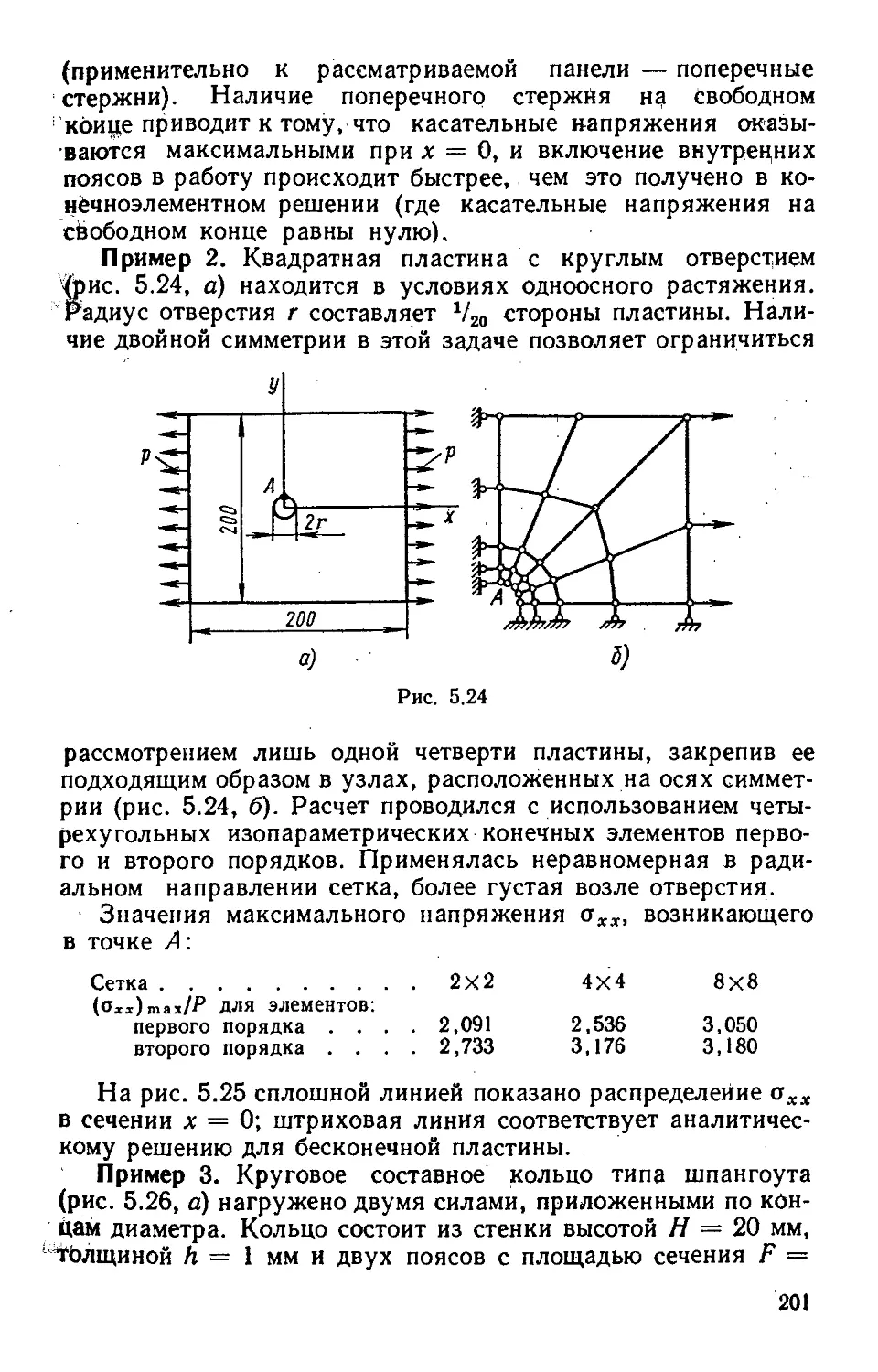
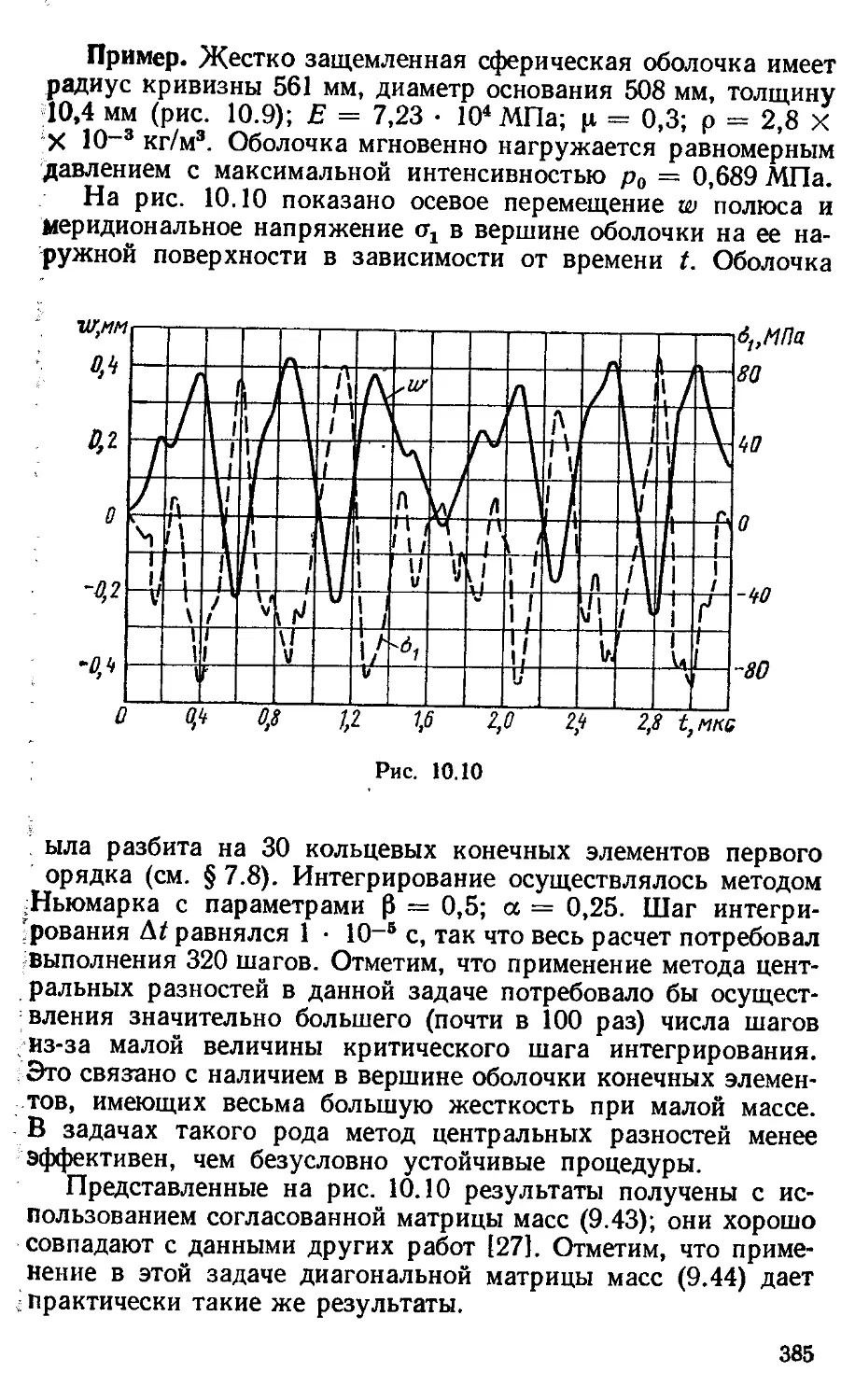
Author: Образцов И.Ф. Савельев Л.М. Хазанов Х.С.
Tags: механика машиностроение летательные аппараты
Year: 1985
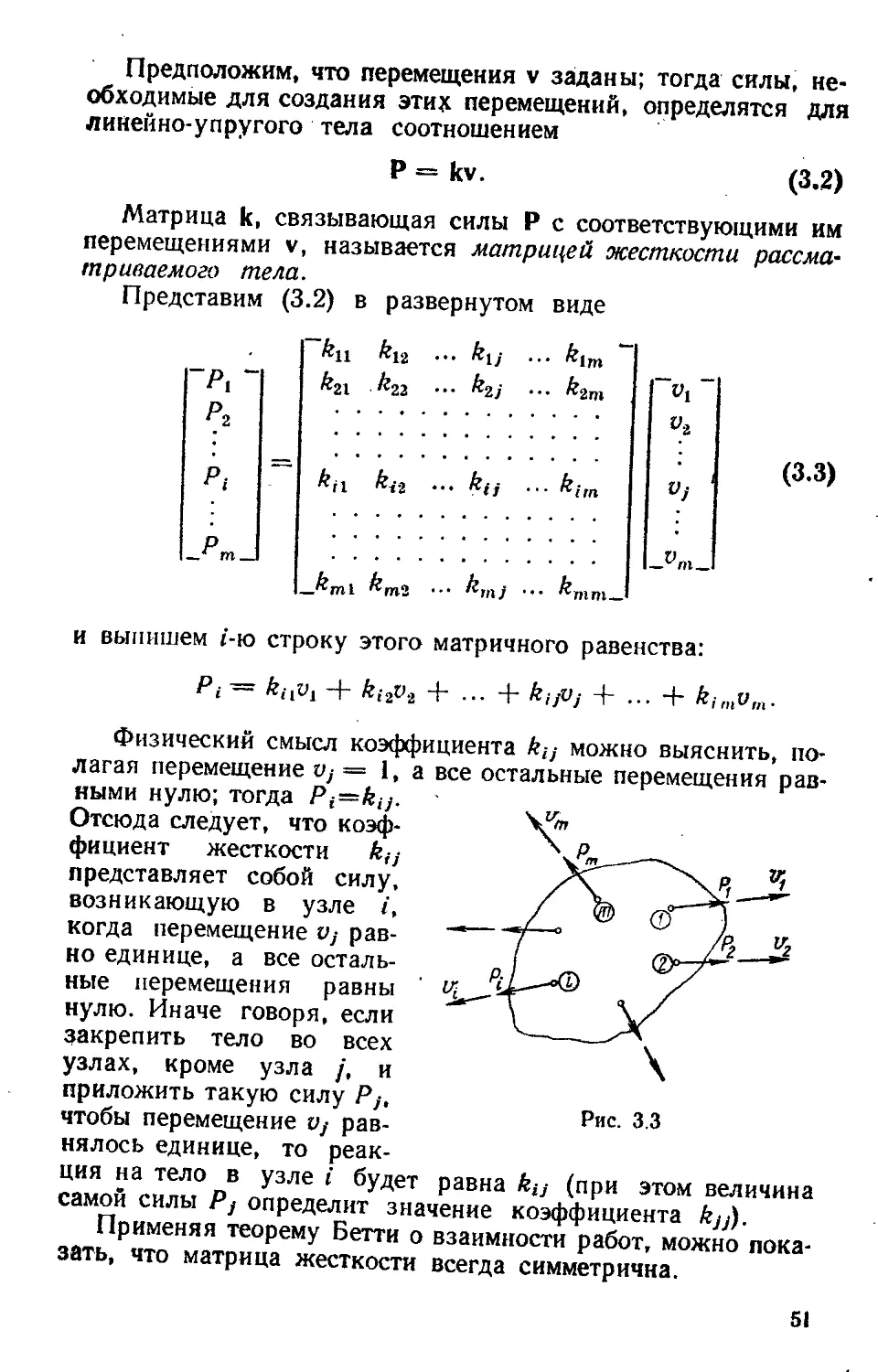
Text
И Ф. ОБРАЗЦОВ, Л. М. САВЕЛЬЕВ,
X. С. ХАЗАНОВ
МЕТОД
КОНЕЧНЫХ
ЭЛЕМЕНТОВ
в задачах
строительной механики
летательных
аппаратов
Д опушено
Министерством высшего и среднего
специального образования СССР
в качестве учебного пособия для студентов
авиационных специальностей вузов
МОСКВА «ВЫСШАЯ ШКОЛА» 1985
J
БВК 22.25"
О-23
УДК-5^534
Рецензенты: кафедра строительной механики летатель-
летательных аппаратов Казанского авиационного института им. А. Н. Ту-
Туполева (зав. кафедрой — д-р техн. наук, проф.. Ю. Г. Одинокрэ};;
д-р техн. наук, проф. Л. А. Колесников (Харьковский авиацион-
авиационный институт им. Н. Е. Жуковского).
Образцов И. Ф., Савельев Л. М., Хазанов X. С.
О-23 Метод конечных элементов в задачах строитель-
строительной механики летательных аппаратов: Учеб. пособие
для студентов авиац. спец. вузов. — М.: Высш. шк:,
1985. — 392 с, ил.
В пер.: 1 р. 10 к.
В книге изложены общие принципы метода конечных элементов в пе-
перемещениях, его связь с вариационными принципами механики. Рассмотре-
Рассмотрены вопросы сходимости конечиоэлементного решения, способы построения
матриц жесткости и матриц масс типовых конечных элементов, схемы ко-
иечпоэлементной идеализации авиационных конструкций, их расчет на
прочность и колебания. Приведены примеры расчетов.
л 3606030000—335 ББК 22.25
О 172—85
001@1)—85 531
Иван Филиппович Образцов
Леонид Макарович Савельев
Хацчель Соломонович Хазанов
МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ В ЗАДАЧАХ
СТРОИТЕЛЬНОЙ МЕХАНИКИ ЛЕТАТЕЛЬНЫХ АППАРАТОВ
Зав. редакцией К. И. Аношииа. Редактор Л. Н. Шатунова. Художник
Н. Ю. Бабнкова. Худ. редактор Т. А. Дурасова. Техи. редактор И. А.
Балелина. Корректор В. В. Кожуткииа
ИБ № 4904
Изд. № ОТ-483. Сдано в набор 11.01.85. Подп. в печать 18.06.85. Т-04444.
Формат 84XI08'/i2. Бум. кн.-жури. Гарнитура литературная. Печать высокая.
Объем 20,58. усл. печ. л. 20,58. усл. кр.-отт. 19,16 уч. изд. л. Тираж 6000 экз.
Зак. № 651. Цена 1 р. 10 к.
Издательство «Высшая школа», 101430. Москва. ГСП-4. Неглиниая ул., д. 29/14
Московская типография № 4 Союзполиграфпрома
при Государственном комитете СССР
но делам Издательств, полиграфии и книжной торговли
129041, Москва, Б. Переяславская, 46
© Издательство «Высшая школа», 1985
ОГЛАВЛЕНИЕ
Предисловие . . 6
Введение ...... . . ......'.... 9
Основные обозначения 11
Часть [. Матричная формулировка соотношений теории
упругости и задач строительной механики стержневых
систем
Глава 1. Основные соотношения теории упругости
§ 1.1. Определения и уравнения 13
§ 1.2. Плоская задача ¦ 20
§ 1.3. Подкрепленная панель как конструктнвно-орто-
тропная пластнна 23
Г л я в а 2. Вариационные методы теории упругости
§ 2.1. Работа внешних сил. Дополнительная работа ... 27
§ 2.2. Энергия деформации. Дополнительная энергия де-
деформации 32
§ 2.3. Вариационное уравнение Лаграижа . . ... 35
§ 2.4. Вариационное уравнение Кастнльяно .... 39
§ 2.5. Метод Ритца . . . 43
§ 2.6. Метод Канторовича—Власова .... .46
Глава 3. Матричный метод перемещений для стержневых
систем
§ 3.1. Понятие о матрице жесткости 49
§ 3.2. Преобразование координат .54
§ 3.3. Ферменный элемент 58
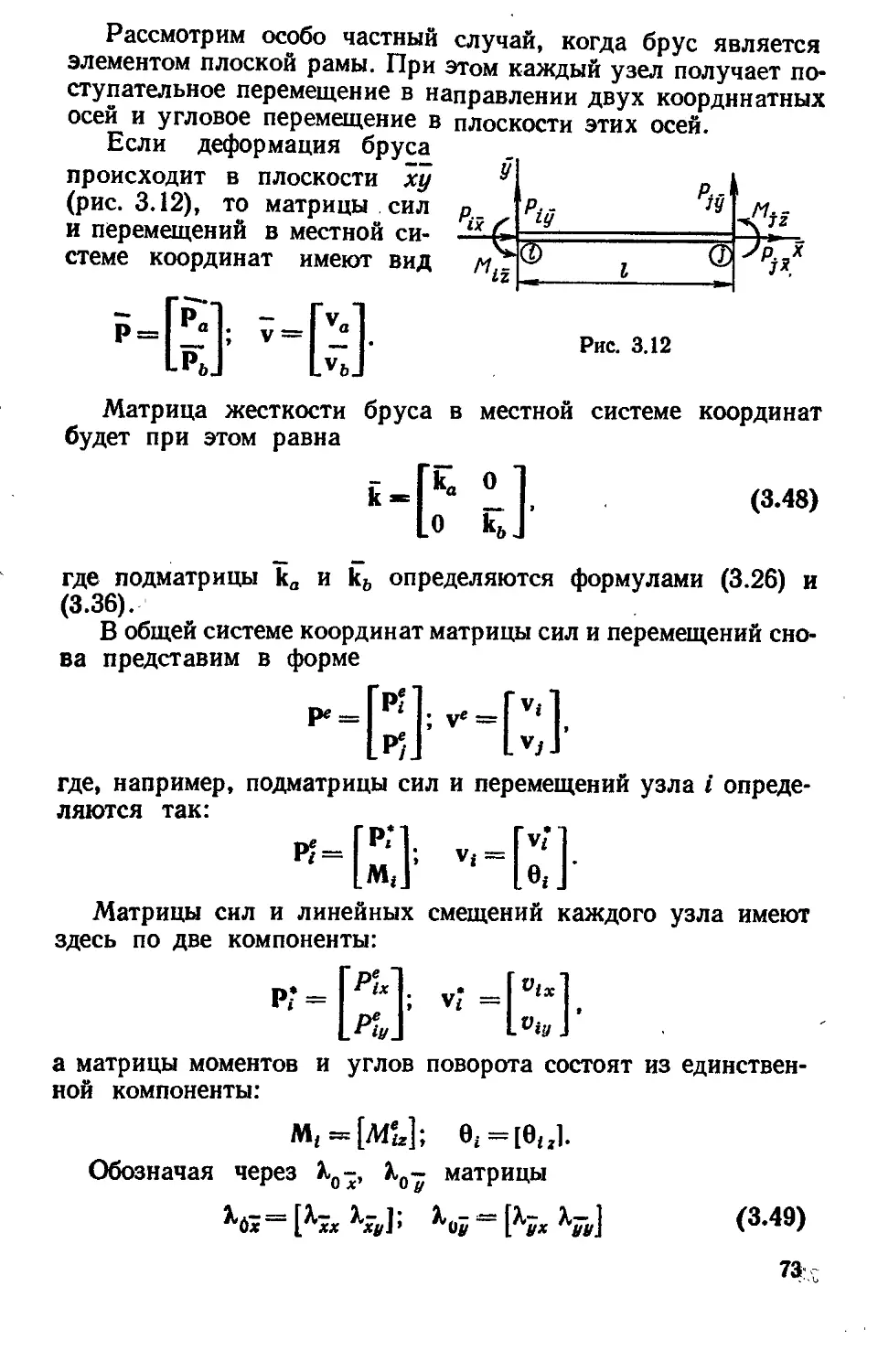
§ 3.4. Прямой брус в местной системе координат . . 61
§ 3.5. Прямой брус в общей системе координат .... 69
§ 3.6. Учет внеузловой нагрузки . . 74
§ 3.7. Плоский круговой брус . . 78
§ 3.8. Стержневая система .... 84
§ 3.9. Определение узловых перемещений . . . 91
§ 3.10. Примеры расчета . . . .93
Часть II. Метод конечных элементов
Глава 4. Теоретические основы метода
§ 4.1. Дискретизация тела .... 106
§ 4.2. Перемещения, деформации и напряжения в конеч-
конечном элементе 108
§ 4.3. Матрица жесткости конечного элемента 111
§ 4.4. Учет внеузловой нагрузки 113
§ 4.5. Определение узловых перемещений 114
§ 4.6. Связь метода конечных элементов с методом Ритца 117
§ 4.7. Конечноэлементнан форма метода Канторовича—
Власова .... 124
Глава 5. Конечные элементы сплошной среды
§ 5.1. Плоский треугольный элемент 133
§ 5.2. Совместный прямоугольный элемент 139
§ 5.3. Несовместный прямоугольный элемент 145
§ 5.4. Внутренние узлы и подконструкцин 150
§ 5.5. Неузловые степени свободы 156
§ 5.6. Четырехузловой изопараметрический элемент .... 160
§ 5.7. Несовместный четырехугольный элемент 166
§ 5.8. Плоские изопараметрические элементы высших
порядков 169
§ 5.9. Деформация пространственного криволинейного
стержня 175
§ 5.10. Одномерные конечные элементы 179
§ 5.11. Трехмерные конечные элементы 182
§ 5.12. Численное интегрирование в методе конечных
элементов ¦. . 186
§ 5.13. О вычислении напряжений 193
§ 5.14. Примеры расчета 198
Глава 6. Критерии сходимости
§ 6.!. Предварительные замечания 204
§ 6.2. Применение рядов Тейлора к исследованию схо-
сходимости 205
§ 6.3. Критерии сходимости совместных элементов .... 210
§ 6.4. Сходимость несовместных элементов 214
§ 6.5. Влияние на сходимость численного интегрирования 220
§ 6.6. Исключение ложных деформаций сдвига с помощью
численного интегрирования 222
Часть III. Приложение метода конечных элементов к рас-
расчету авиационных конструкций
Глава 7. Конструкции в виде пластин и оболочек
§ 7.1. Предварительные замечания 227
§ 7.2. Основные соотношения теории изгиба пластин . . . 228
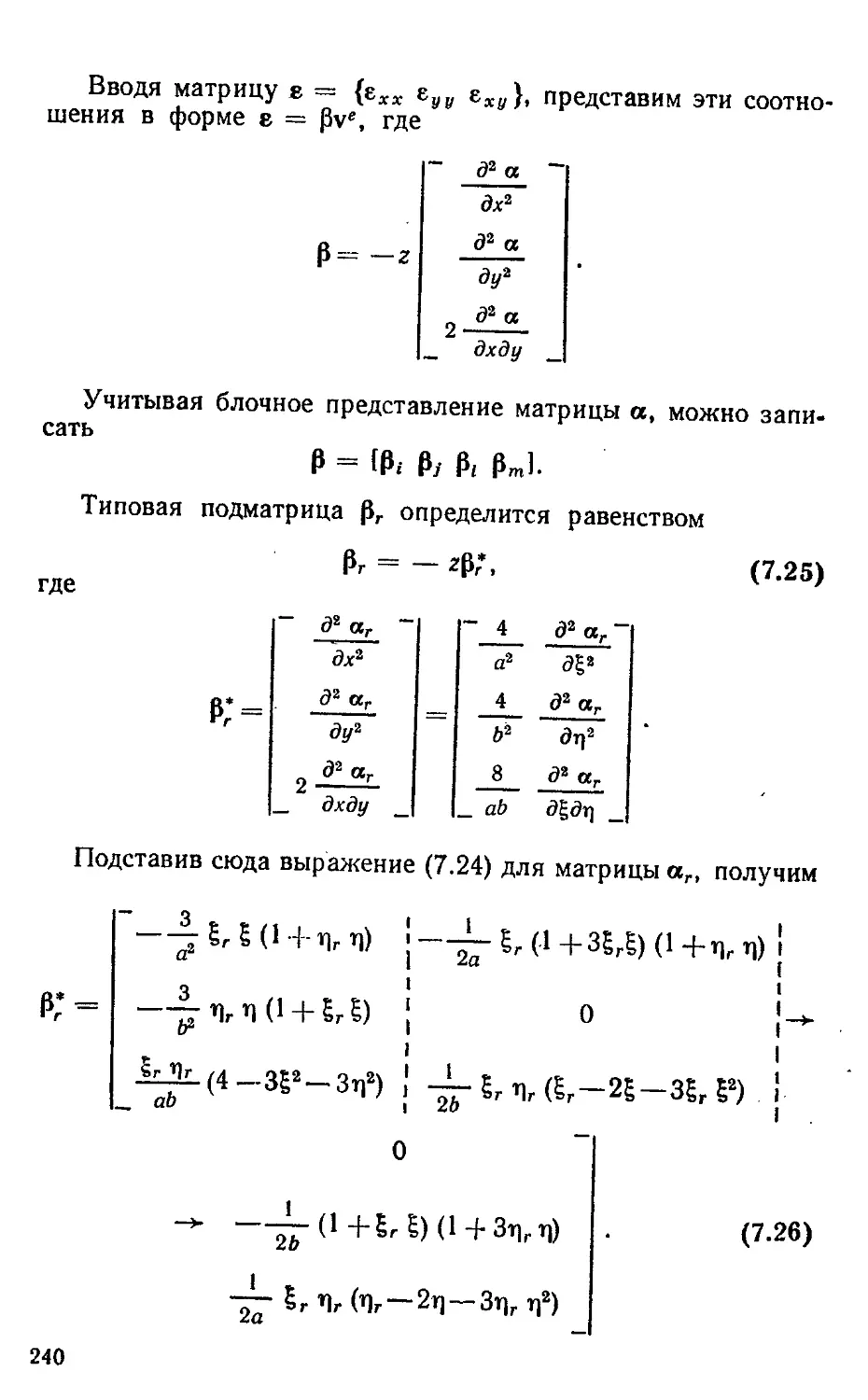
§ 7.3. Изопараметрическне конечные элементы пластины 231
§ 7.4. Несовместный прямоугольный элемент пластины 236
§ 7.5. Несовместный четырехугольный элемент пластины 241
§ 7.6. Учет внеузловой нагрузки. Определение узловых
перемещений 244
§ 7.7. Основные соотношения для оболочек вращения при
осесимметричном нагружении 247
§ 7.8. Изопараметрические конечные элементы оболочки
вращения 251
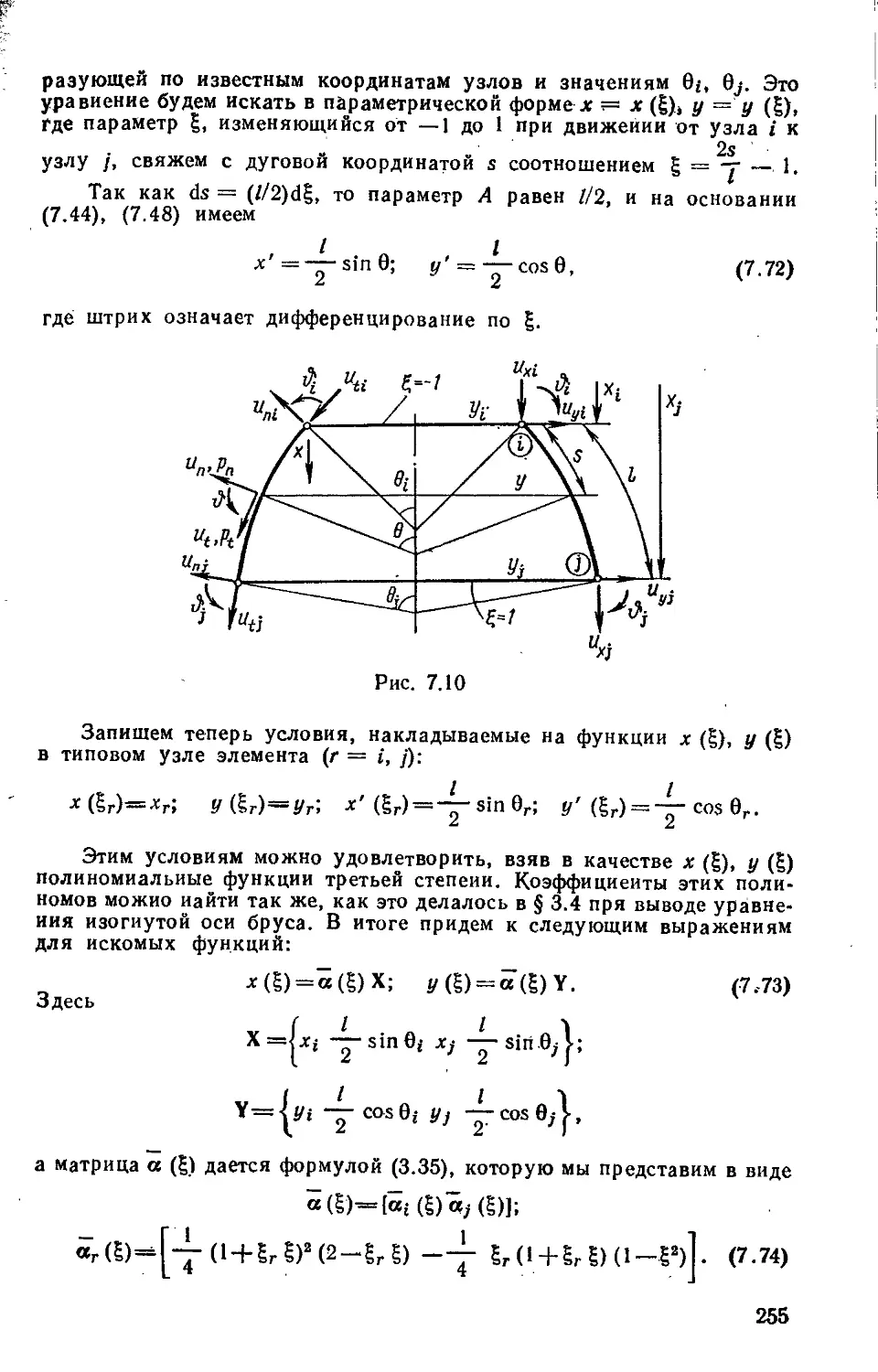
§ 7.9. Двухузловой криволинейный конечный элемент
оболочки вращения 254
§ 7.10. Матрица жесткости шпангоута 262
§ 7.11. Объединение конечных элементов. Определение
перемещений и напряжений 263
§ 7.12. Деформации произвольной поверхности 267
§ 7.13. Конечные элементы произвольной оболочки. . . . 272
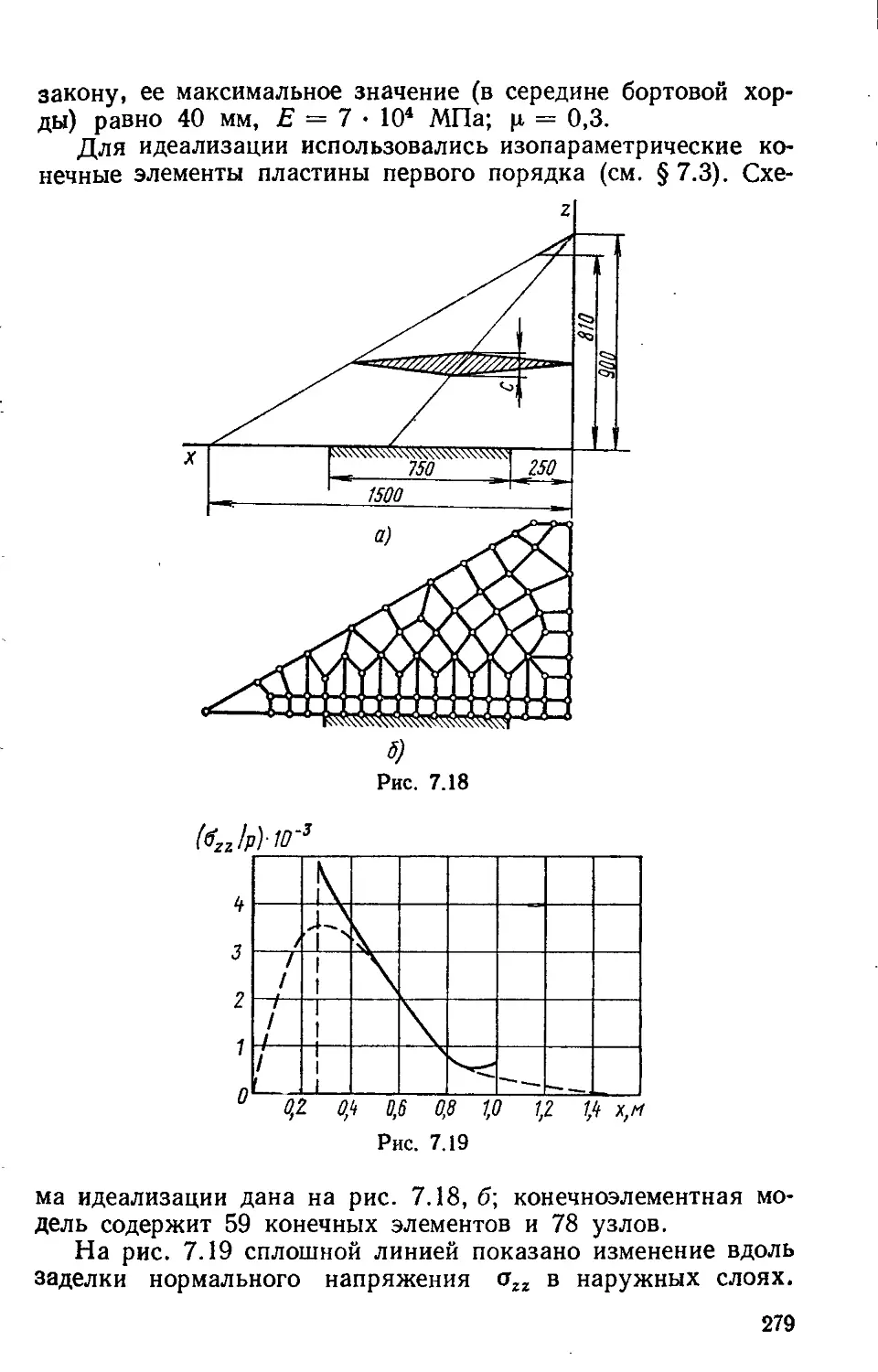
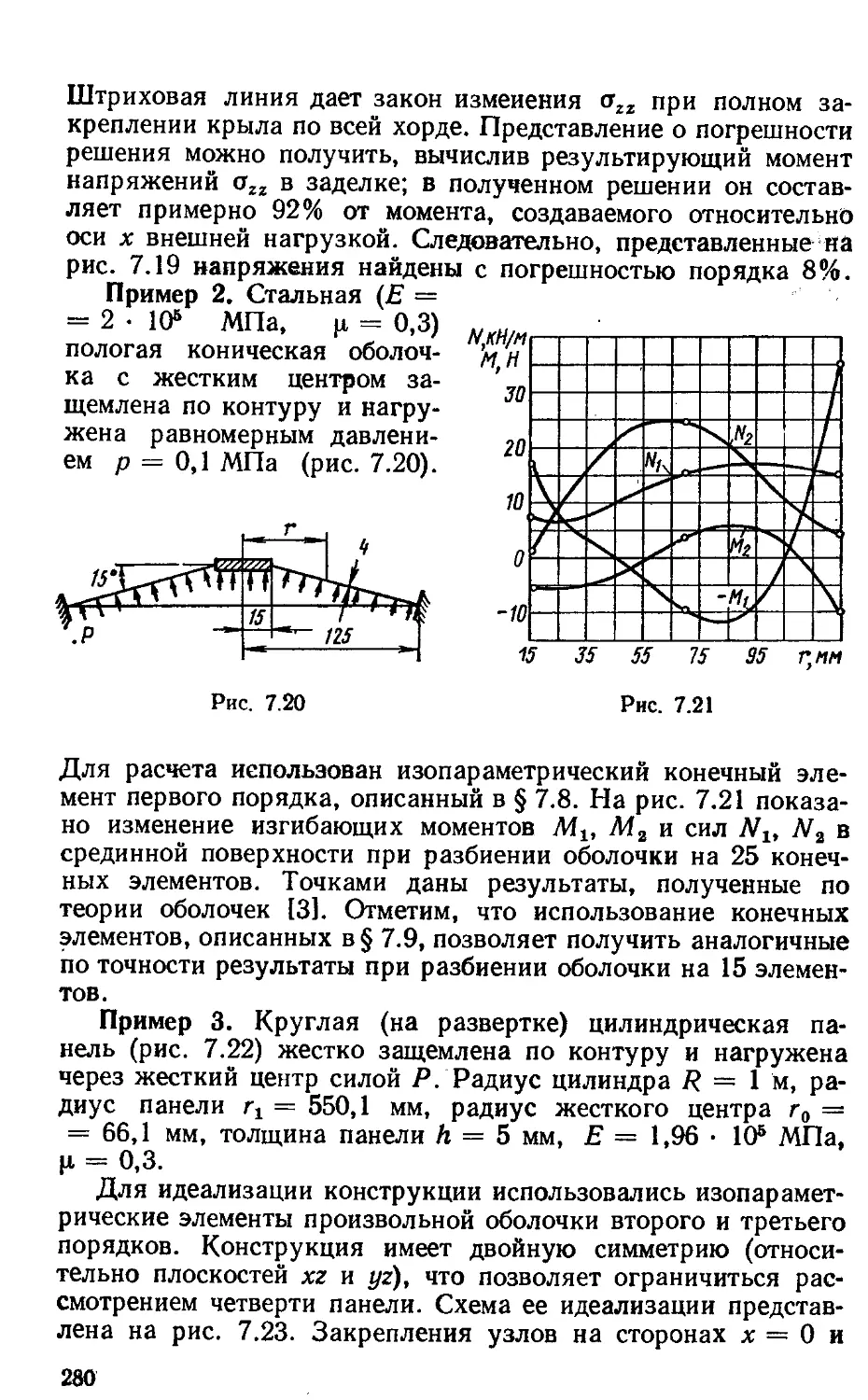
§ 7.14. Примеры расчета . 278
4
Глава 8. Каркасированные тонкостенные конструкции
§ 8.1. Конечиоэлементная идеализация конструкции . . . 283
§ 8.2. Конечные элементы безмоментной обшивки .... 85
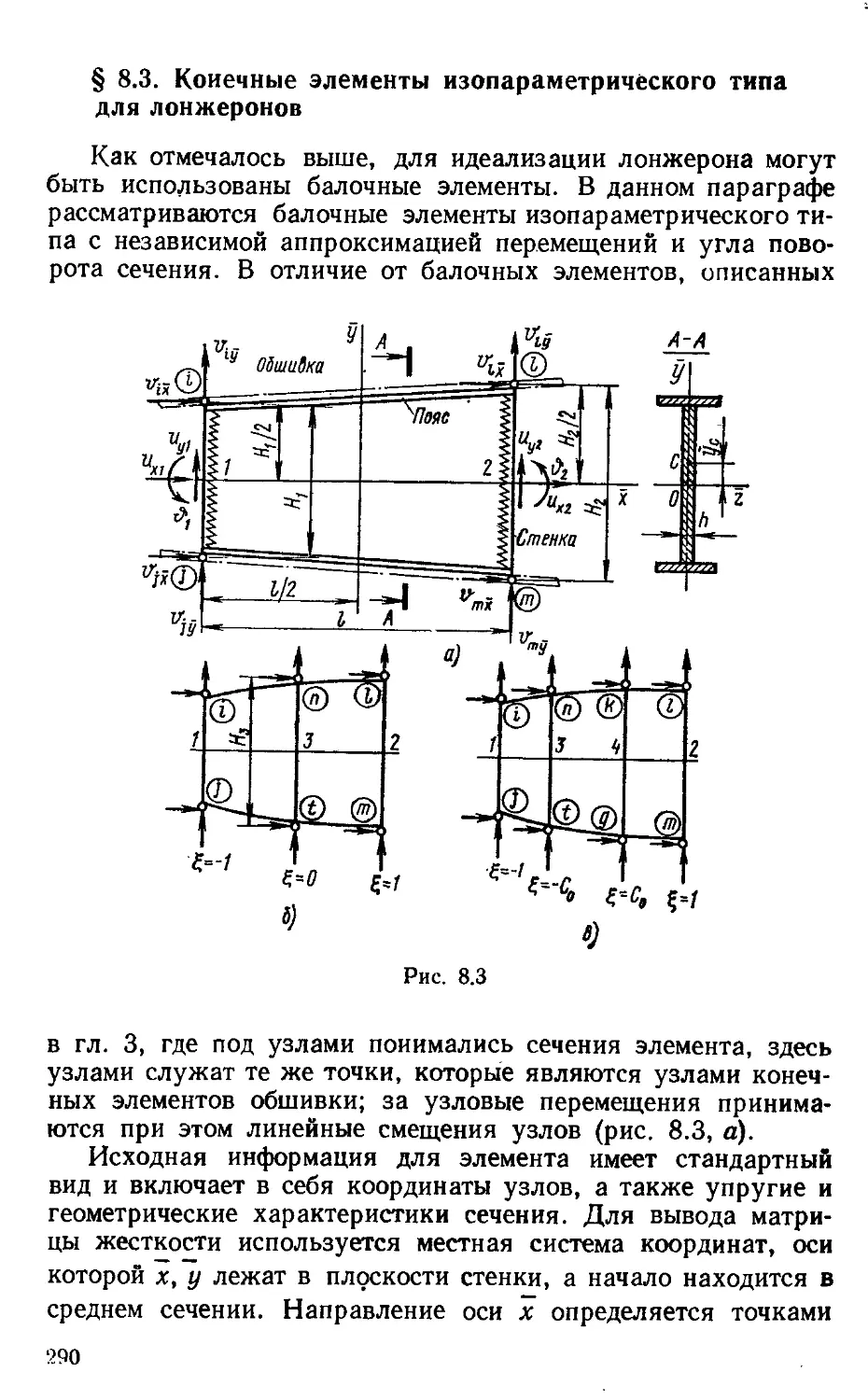
§ 8.3. Конечные элементы изопараметрического типа для ¦
лонжеронов . . 290
§ 8.4. Составные конечные элементы лонжеронов .... 300
§ 8.5. Двухузловой конечный элемент шпангоута ..... 310
§ 8.6. Криволинейные конечные элементы шпангоута . . 320
§ 8.7. Заключительные замечания 324
§ 8.8. Примеры расчета 325
Часть IV. Динамические задачи
Глава 9. Соотношения метода конечных элементов в задачах
динамики
§ 9.1. Предварительные замечания -329
§ 9.2. Матричное уравнение движения конструкции . . . 330
§ 9.3. Согласованная и диагональная формулировки ма-
матрицы масс 338
§ 9.4. Матрицы масс конечных элементов с линейными
смещениями узлов 342
§ 9.5. Матрицы масс конечных элементов изгибаемых пла-
пластин .- . . 344
§ 9.6. Матрицы масс конечных элементов оболочек .... 348
§ 9.7. Матрицы масс конечных элементов бруса ..... 351
Глава 10. Расчет динамического поведения конструкции
§ 10.1. Собственные колебания 357
§ 10.2. Ортогональность собственных форм колебаний . . . 360
§ 10.3. Примеры расчета 362
§ 10.4. Разложение двнжения по формам собственных ко-
колебаний 369
§ 10.5. О прямом интегрировании уравнений движения 373
§ 10.6. Метод центральных разностей 375
§ 10.7. Метод Ньюмарка 379
Заключение 386
Список литературы 389
Предметный указатель 391
ПРЕДИСЛОВИЕ
Создание прочных и надежных в эксплуатации машин <р
высоким ресурсом работы, обладающих высокой экономичною
стью и минимальным весом, — это вопрос большой важности*
на который постоянно обращается внимание в директивных^
документах Коммунистической партии и Советского прави-
правительства. Его решение затрагивает множество проблем, сре-
среди которых важное место занимает проблема совершенствова-
совершенствования методов расчета конструкций на прочность. Особенно это
относится к конструкциям летательных аппаратов, где про-
противоречие между требованиями прочности и минимального
веса проявляется наиболее остро.
Бурное развитие вычислительной техники приводит к опре-
[деленной переоценке традиционных взглядов на исследование
'прочности летательных аппаратов, вызывая к жизни новые
численные методы расчета. Среди методов, ориентированных
'на эффективное использование ЭВМ, наибольшее признание
у нас в стране и за рубежом получил метод конечных элемен-
элементов, обладающий целым рядом достоинств в сравнении с дру-
другими, методами.
Целью авторов данной книги было создание учебного по-
пособия, содержащего достулное для студентов и в то же вре-
время достаточно строгое изложение метода конечных элементов
в перемещениях с акцентом на его приложения к задачам строи-
строительной механики летательных аппаратов. При написании
книги особое внимание было уделено методической отработ-
отработке материала; учтен многолетний опыт преподавания метода
конечных элементов на кафедрах строительной механики и
прочности летательных аппаратов Московского и Куйбышев-
Куйбышевского авиационных институтов.
Пособие состоит из четырех частей. Первая часть имеет
вводный характер. Здесь (главы 1, 2) дана краткая сводка
уравнений теории упругости в матричной записи и изложены
вариационные методы, составляющие теоретическую базу ме-
метода конечных элементов. В гл. 3 подробно описан матричный
метод расчета стержневых систем в перемещениях. Исполь-
Используемые здесь принципы, алгоритмы, терминология во многом
характерны и для метода конечных элементов. По этой причи-
причине расчет стержневых систем излагается иногда в рамках
метода конечных элементов. Но между матричным методом
перемещений стержневых систем и методом конечных эле*
ментов имеются и принципиальные различия. Например,При
статическом расчете стержневых систем решение в рамках
технической теории бруса получается точным. Поэтому рас-
расчет стержневых систем выделен в отдельную главу. Вообще
говоря, изучение метода конечных элементов можно начинать
сразу с чтения второй части книги, лишь по мере надобности
обращаясь за справками к соответствующим главам первой
части. Но усвоение метода существенно облегчится, если про-
проработать сначала материал гл. 3 и приведенные здесь приме-
примеры расчета.
Во второй части, являющейся центральной, излагается соб-
собственно метод конечных элементов. Показана его связь.с ме-
методом Ритца (гл. 4), описаны некоторые конечные элементы
сплошной среды (гл. 5), рассмотрены вопросы сходимости при-
приближенного решения к точному (гл. 6). Для более глубокого
понимания существа метода конечных элементов необходимо
иметь хотя бы общую ориентировку в вопросах его сходимо-
сходимости. Именно такую ориентировку дает гл.6, не претендующая
на математическую строгость, но содержащая зато доступное
для инженера изложение этой темы.
В третьей части (главы 7, 8) рассматривается приложение
метода конечных элементов к расчету характерных для лета-
летательных аппаратов конструктивных элементов — пластин,
оболочек и тонкостенных подкрепленных систем типа фюзе-
фюзеляжа или крыла самолета. Основное внимание уделено здесь
описанию подходящих конечных элементов для расчета тех
или иных конструкций: их применение иллюстрируется при-
примерами расчета.
Наконец, в четвертой части затрагиваются вопросы дина-
динамических расчетов конструкций летательных аппаратов. Зна-
Значительное место отведено обоснованию эффективных способов
представления массовых характеристик конструкции, обеспе-
обеспечивающих сокращение времени счета (гл. 9). В гл. 10 рассмо-
рассмотрен расчет собственных колебаний конструкции, а также рас-
расчет динамического поведения путем прямого интегрирования
уравнений движения.
Учитывая, что книга предназначена для первоначального
ознакомления с методом конечных элементов, авторы избра-
избрали способ изложения от простого к сложному. При этом неиз-
неизбежны некоторые повторы, но, как показывает опыт препода-
преподавания, это оправдывается более быстрым и прочным усвоением
метода. Чтобы облегчить читателю отбор наиболее важного
материала, те места в книге, которые без ущерба для понима-
понимания существа дела можно пропустить прн первом чтении, на-
напечатаны мелким шрифтом.
От читателя не требуется какой-либо дополнительной под-
подготовки сверх обычной вузовской программы в объеме первых
трех курсов. Необходимым условием усвоения материала
является уверенное владение простейшим аппаратом матрич-
матричной алгебры, язык которой используется на протяжении всей
книги. Хотя пособие адресовано в первую очередь студентам
авиационных институтов, оно может быть использовано для
учебных целей и в других технических вузах, а также для са-
самостоятельного изучения основ метода конечных элементов.
Общий замысел книги принадлежит И. Ф. Образцову. Им
написаны введение, заключение, §2.6, 4.6, 4.7, 6.2, 6.3, 7.1,
7.2, 7.4, 7.5, а также осуществлено общее редактирование
книги; §5.10—5.13, 7.7—7.9, 7.12, 7.13, 9.3 и 9.6 написаны
Л. М. Савельевым, 9.5 и 10.3 — И. Ф. Образцовым и Л. М.
Савельевым, §3.1—3.5, 3.8, 3.9, 5.1, 5.2, 5.6, 5.8 — X. С.
Хазановым. Остальные параграфы написаны Л. М. Савелье-
Савельевым и X. С. Хазановым.
Авторы выражают свою признательность профессорам
М. Б. Вахитову и Л. А.Колесникову, доценту Н. А. Шеломо-
ву и старшему научному сотруднику В. Ф. Снегиреву, вни-
внимательно ознакомившимся с рукописью и высказавшим мно-
много ценных замечаний, которые были учтены авторами и спо-
способствовали улучшению книги. Авторы благодарят инжене-
инженеров Г. В. Канову и Л. К. Мещерякову за помощь в выполнении
числовых расчетов, а также Т. Н. Верещагину, проделавшую
большую работу по оформлению рукописи.
Авторы будут благодарны всем читателям, которые при-
пришлют свои пожелания и замечания. Их следует направлять в
издательство «Высшая школа» по адресу: 101430, Москва,
ГСП-4, ул. Неглинная, 29/14.
Авторы
НВПДЕНИЕ
Основные уравнения теории упругости известны уже более
полутора веков. Несмотря на это, количество задач, имеющих
1 очное решение, относительно невелико. Для решения прак-
шчееких проблем разработаны хорошо зарекомендовавшие
i Kin методы сопротивления материалов и строительной меха-
механики. Однако эти методы применимы, как правило, лишь к те*
ллм простой конфигурации. Они зачастую оказываются бес-
бессильными, если требуется найти распределение напряжений
и сложной реальной конструкции.
В этих условиях приходится либо упрощать до крайно-
• in расчетную схему, сводя такой ценой всю проблему к ре-
решению одной из классических задач, либо обращаться к како-
какому либо подходящему численному методу. Последний путь
и настоящее время становится наиболее предпочтительным,
поскольку успехи в развитии численных методов и в создании
>НМ делают его вполне осуществимым даже для таких слож-
сложных и нерегулярных систем, какими являются конструкции
лп-лтельных аппаратов.
Существует много различных численных методов, пригод-
пригодных для эффективного решения тех или иных частных задач.
Начиная с конца 60-х годов предпочтение все больше отдается
методу конечных элементов как наиболее гибкому и универ-
универсальному. По оценке специалистов этот метод будет в течение
плпжайших десятилетий служить основным расчетным ин-
i Фументом при исследовании прочности конструкций летатель-
летательных аппаратов. Отметим, что область применения метода ко-
конечных элементов не ограничивается задачами прочности;
oii.i охватывает широкий круг разнообразных технических
проблем, включая, например, задачи теплопередачи, расчета
HOI |),1НИЧНОГО СЛОЯ И Т. Д.
11рименение метода конечных элементов способствует по-
т.ппепию точности и надежности расчетов,а также автомати-
иппн инженерного труда. Это дает большой экономический
-»||н|и-кт, поскольку влечет за собой сокращение сроков довод-
Mi н (делий, а в отдельных случаях позволяет даже отказать-
г проведения некоторых видов дорогостоящих прочност-
ш.1\ испытаний.
1'ождение метода конечных элементов относится ко второй
in lomine 50-х годов нашего столетия. Базой для его появле-
появлении послужили предшествующие работы, среди которых осо-
бое значение имели три направления: развитие методов рас-
расчета стержневых систем, применение метода конечных разно-
разностей и разработка вариационных методов решения задач тео-
теории упругости и строительной механики. Неоценимый вклад
в эти исследования внесли советские ученые И. Г. Бубнов,
Б. Г. Галеркин, Л. В. Канторович, В. 3. Власов, А. Р. Ржа-
ницин, С. Г. Михлин и многие другие. Развитию и популяри:
зации в СССР метода конечных элементов способствовали ра-
работы А. Ф. Смирнова, А. П. Филина, В. А. Постнова, В. Г.
Корнеева, 3. И. Бурмана, Л. А. Розина, А. В. Александрова,
Б. Я. Лащеникова, Н. И. Шапошникова и целого ряда других
ученых.
Имеется несколько разновидностей метода конечных эле-
элементов: решение в перемещениях, в силах, смешанная форму-
формулировка, гибридный подход. Наибольшее распространение у
нас в стране и за рубежом получил метод перемещений, по-
поскольку он обладает целым рядом достоинств, среди которых
можно отметить простоту, удобство реализации на ЭВМ, ес-
естественную приспособленность к анализу динамических проб-
проблем. Применительно к расчету пластин и оболочек, где созда-
создание эффективных конечных элементов в перемещениях дли-
длительное время наталкивалось на серьезные трудности, были
разработаны и успешно использовались конечные элементы
так называемого гибридного типа. Однако в конце 70-х годов
эти трудности удалось в значительной степени преодолеть,
что позволяет избежать применения сложных гибридных эле-
элементов.
В данном пособии рассматривается метод конечных эле-
элементов в перемещениях применительно к линейным задачам
строительной механики летательных аппаратов. Не затраги-
затрагиваются такие важные темы, как расчет на устойчивость или
учет пластических деформаций. Можно, однако, надеяться,
что материал пособия послужит достаточной базой для по-
последующего самостоятельного изучения этих вопросов.
10
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
Для обозначения матриц используется полужирный шрифт. Эле-
Элементы матриц заключаются в квадратные скобки. Для экономяи места
иногда применяется запись матрицы-столбца в строку; в этом случае
используются фигурные скобки. Операция транспонирования матри-
матрицы отмечается верхним индексом «Г».
Наиболее часто встречающиеся обозначения:
В s=s Eh/(\ — fi2) —г жесткость пластины или оболочки на растяжение
D = ?Л3/[12 A — fi2)] — изгибная жесткость пластины, оболочки
е — единичный вектор
Е — модуль продольной упругости
G = ?/[2 A + цН — модуль сдвига
Л — толщина пластины, оболочки
J; |J| — матрица Якоби н ее определитель
k, krs, kij — матрица жесткости конечного элемента, ее блоки I/,
s — номера узлов) и скалярные компоненты (i, / — номера узло-
узловых перемещений) в местной системе координат
ke, k*s, k\j — то же, в общей системе координат
К, Krs, kfj — матрица жесткости конечноэлементной модели, ее
блоки и скалярные компоненты
L — матричный дифференциальный оператор в соотношении е =
== Lu
m, mrs, iriij — матрица масс конечного элемента, ее блоки н скалярные
компоненты в местной системе координат
те, mers, m'lj — то же, в общей системе координат
М, mrs, тц—матрица масс конечноэлементной модели, ее блоки и
скалярные компоненты
р, рх, Ру, Рг — матрица-столбец распределенных поверхностных на-
нагрузок н ее компоненты
Р, Pr, Pt — матрица-столбец узловых сил конечного элемента, ее бло-
блоки (г — номера узлов) и скалярные компоненты (i — номера пе-
перемещений) в местной системе координат
Vе, Рег, Р\ —то же, в общей системе координат
Р, Рг, Pi — матрица-столбец узловых сил конечноэлементной модели,
ее блоки н скалярные компоненты
Ре, РеГ — матрица-столбец узловых снл конечного элемента, эквива-
эквивалентных внеузловой нагрузке, и ее блоки
Р, Рг — матрица-столбец эквивалентных узловых сил конечноэлемент-
конечноэлементной модели и ее блоки
Ро> Рог —матрица-столбец узловых сил, уравновешивающих внеузло-
вую нагрузку, и ее блоки для элемента стержневой системы
в местной системе координат
11
P^,, PeOr — то же, в общей системе координат
Ро. Рог—то же, для стержневой системы
Ч. Чх> Яу, <7* — матрица-столбец погонных нагрузок и се компоненты
R. Rx, Ry, Rz — матрица-столбец объемных сил и ее компоненты
/ — время
Те, Т — кинетическая энергия конечного элемента и всего тела
u, ux, uy, uz — матрица-столбец перемещений произвольной точки те-
тела и ее компоненты
Ue, U — потенциальная энергия деформации конечного элемента
и всего тела
vr, vi — матрица-столбец перемещений узла г и ее скалярные компоие-
ты (i — номер перемещения) в местной системе координат
vr, vi — то же, в общей системе координат
v, Vе — матрицы-столбцы узловых перемещений конечного элемента
соответственно в местной и общей системах координат
v — матрица-столбец узловых перемещений конечиоэлементной мо-
модели
Vе, V — полная потенциальная энергия конечного элемента н всего
тела
а» — прогиб пластины
Wj—формы собственных колебаний конечноэлементной модели
х, у, г — декартовы координаты
«— матрица аппроксимирующих функций (функций формы)
Р—матрица связи между деформациями и узловыми перемещениями
б — знак вариации
Е—матрица-столбец деформаций
?, т), ?—безразмерные координаты
X — матрица упругих постоянных
к — матрица преобразования координат
ц — коэффициент Пуассона
W, П — потенциал внешних сил для конечного элемента и для всего
тела
р — плотность материала
а — матрица-столбец напряжений
хе, т—объем конечного элемента и всего тела
i|)i — аппроксимирующие функции (функции формы)
о>е, w—поверхиость конечного элемента и всего тела
12
ЧАСТЬ I
МАТРИЧНАЯ ФОРМУЛИРОВКА СООТНОШЕНИЙ
ТЕОРИИ УПРУГОСТИ И ЗАДАЧ
СТРОИТЕЛЬНОЙ МЕХАНИКИ СТЕРЖНЕВЫХ
СИСТЕМ
ГЛАВА 1
ОСНОВНЫЕ СООТНОШЕНИЯ ТЕОРИИ УПРУГОСТИ
Уравнения теории упругости лежат в основе любого метода рас-
расчета на прочность, в том числе метода конечных элементов. Так как
при изложении последнего систематически применяются матричные
обозначения, соотношения теории упругости представлены здесь в ма-
матричной форме. Особое внимание уделено записи физических соотно-
соотношений для конструктивно-ортотропной панели, поскольку подобная рас-
расчетная схема часто используется для моделирования подкрепленной
ребрами обшивки".
§ 1.1. Определения и уравнения
Отнесем исследуемое упругое тело к декартовым коорди-
координатам х, у, z и обозначим через Rx, Ru, Rz — проекции на
координатные оси объемных сил, приходящихся на единицу
объема тела, рх, ру, pz—проекции поверхностных сил, при-
приходящихся на единицу граничной поверхности тела.
Выделим из тела элементарный параллелепипед сечения-
сечениями, параллельными координатным плоскостям (рис. 1.1). Обо-
Обозначим компоненты напряжения в площадке, перпендикуляр-
перпендикулярной оси х, через охх, оху, ах1, в площадке, перпендикулярной
оси у, — через оух, ауу, ayz, а в площадке, перпендикулярной
оси z, — через azx, azy, czz. Первый индекс в этих обозначе-
обозначениях характеризует ориентацию площадки, а второй — на-
направление действия соответствующей составляющей напря-
напряжения. Нормальные напряжения охх, ауу, ozz считаются по-
положительными, если оии направлены по внешней нормали к
площадке. Положительные направления касательных напря--
жений на грани принимаются совпадающими с положитель-
положительными направлениями координатных осей, если внешняя нор-
нормаль к этой грани совпадает с положительным направлением
соответствующей оси. Если же внешняя нормаль направлена
противоположно соответствующей оси, то и положительные
касательные напряжения в этой грани действуют в отрица-
отрицательных направлениях двух других осей. Как известно, имеет
13
место следующее свойство парности касательных напряже-
напряжений:
а-*У = аУх> ауг = <*гу. <*гх = Охг.
Рассмотрим произвольную точку М (х, у, г) упругого те-
тела. Под действием внешних сил она переместится в положение
Мх. Вектор полного перемещения ММХ можно разложить
по координатным осям на три составляющие их, ии, uz, назы-
называемые компонентами перемещения. Так как деформация те-
тела совершается при сохранении непрерывности материала, то
перемещения являются не-
непрерывными функциями ко-
координат.
Деформация тела в каж-
каждой точке характеризуется
величинами ехх, eU!/, e,zl, вхи,
ej/г. ezx- Первые три из них
представляют собой относи-
относительные изменения длин бес-
бесконечно малых отрезков,
первоначально (до дефор-
деформации) параллельных осям
z соответственно; они считаются положительными, если
происходят удлинения отрезков, и отрицательными — в слу-
случае их укорочения. Последние три величины суть деформа-
деформации сдвига, представляющие собой изменения углов между
элементарными отрезками, первоначально параллельными тем
координатным осям, которые указаны в нижних индексах. Де-
Деформации сдвига считаются положительными, если углы меж-
между отрезками, ориентированными в положительных направле-
направлениях координатных осей, становятся острыми.
Объемная деформация 0 представляет собой отношение
изменения объема элементарного параллелепипеда к его пер.
воначальному объему и может быть выражена как. сумма.
Рис. 1.1
х, у,
8 =
Исходными уравнениями для решения задач теории упру-
упругости являются статические, геометрические и физические со-
соотношения.
Статические соотношения. Сюда относятся дифференциаль-
дифференциальные уравнения равновесия:
14
&°хх i
дх
д°ху i
дх
дохг ,
дх '
да уХ
ду
ду
doyz
ди
• +
dazx
дг
dazy
дг
дагг
дг
A.1)
и формулы для напряжений в наклонных площадках:
=°зсх пх
Qnу
Охи
=o»z «* -t- oyz tty + агг пг.
A.2)
Здесь пх, пу, пг — косинусы углов между внешней нор-
нормалью к наклонной площадке и координатными осями х, у, г;
о„», ovy, апг — проекции полного напряжения в наклонной
площадке на координатные оси.
Если наклонная площадка совпадает с граничной поверх-
поверхностью о упругого тела, то апх, апу, anz можно рассматривать
как составляющие вектора поверхностной нагрузки, т. е.
опх = рХ1 впу — Ру* anz — Pz- Поэтому для точек поверх-
поверхности тела имеем
Рх=
Ру =
Pz =
оуу пу
zy пг;
т Пу + Огг Пг.
A.3)
Равенства A.3) устанавливают связь между поверхностны-
поверхностными силами и компонентами напряжения вблизи поверхности
тела и выражают так называемые статические граничные
условия.
Введем следующие матрицы-столбцы:
°ху
*„==
°ух
; Р'
15
дг
= 0;
A.4)
Тогда равенства A 1), A.2) и A.3) могут быть представле-
представлены матричными соотношениями
до\ до и
дх ду
Р - <*х пх + ауп,.-\~агпг A.6)
Геометрические соотношения устанавливают связь между
компонентами деформации и компонентами перемещения. Если
деформации и перемещения малы, то между ними имеет место
линейная зависимость, выражаемая уравнениями Коши:
дх
дчу
~дУ~
диг
дг
_ дпу
дх
диг
e,v=-
дп л
"+
4-
-V-
дих
~ду~
дг
дп.
A.7)
дг дх
Эти соотношения можно представить одним матричным ра-
равенством
е = Lu, A.8)
связывающим матрицы-столбцы деформаций
и перемещений и =¦ {мк. ии и2).
Здесь и далее матрица, записанная в строку и заключен-
заключенная в фигурные скобки, означает матрицу-столбец. Через L
в A.8) обозначен матричный дифференциальный оператор вида
L =
д
дх
0
д
д
дг
0
д
ду
д
дх
д
дг
0
д
дг
д
ду
д
дх
A.9)
16
Если из уравнений A.7) исключить перемещения их иу и
иг, то между компонентами деформации получим шесть
дифференциальных соотношений, именуемых условиями сов-
совместности (или неразрывности) деформаций Сен-Венана:
д' е-хх ,д* е.!П1 __ д- е.х„ . д /дех,, _?е«г , дегх\ __
ду* дх- дхду ' дх \ дг дх ду )
дудг
дг-
ду- дудг ' ду \ дх
,
A.10)
дхду
Физические соотношения. Сюда относятся соотношения,
устанавливающие связь между напряжениями и деформация-"
ми. В пределах упругости эта связь выражается законом Гу-
ка, согласно которому компоненты деформации являются ли-
линейными функциями компонент напряжения. Для изотроп-
изотропного тела, т. е. тела, обладающего во всех направлениях оди-
одинаковыми упругими свойствами, закон Гука имеет вид:
*<-¦
_1
Е
I
IF
_ i
i — ОТ
*e. ew —
I
\ A.11)
где Е — модуль упругости; G — модуль сдвига; (х — коэффи-
коэффициент Пуассона; упругие постоянные материала Е, G и ц
связаны между собой равенством ? — 2A 4- ц) G.
Введя матрицу-столбец напряжений
HOlYj A JmP-.'Arf'
17
запишем •A.11) в форме одного матричного равенства
е= Ф0, A.J2)
где
. A.13)
1
E
1
—ft
-ft
— ft
1
-ft
0
—ft
— ft
1
|2(l + fi)
0
0
0
0
2 A + ft]
0
0
0
2A+ft)
Разрешив уравнения A.11) относительно напряжений, мож-
можно представить закон Гука в так называемой форме Ляме:
ахх = 2Gexx + Я.6; ауу =
A.14)
где
ме.
1—2ц
Константы G а К называются упругими постоянными Ля-
В матричной записи соотношения A.14) имеют вид
а — хе, A.15)
ft I—ft
X IX
О
ft
ft
i-ft
1 —2ц
2
1
О
О
О
1-2,х
2
О
О
О
1 —2ц
A.16)
Очевидно, что матрица а является обратной матрице Ф.
Совокупность дифференциальных уравнений равновесия
A.1), геометрических A.7) и физических 1A.11) или A.14)]
18
соотношений образует систему из 15 уравнений, в которые
входят 6 компонент напряжения, 6 компонент деформации и 3
компоненты перемещения. Таким образом, получается замкну-
замкнутая система уравнений.
Решение этой системы можно искать либо «в перемещениях»,
либо «в напряжениях». В первом случае за основные неизвест-
неизвестные функции принимают перемещения иг (х, у, г), иу (х, у, г),
<W2 (x, у, г), а систему уравнений теории упругости сводят к
трем уравнениям относительно этих функций. Для этого на-
напряжения в дифференциальных уравнениях равновесия A.1)
выражают по закону Гука A.14) через деформации, а послед-
последние по формулам Коши A.7) — через перемещения. В резуль-
результате получают уравнения Ляме:
GV*«.V + (G+ *)-—-+ Rx = 0;
дх
где
, ди„ , днг «_,, дг
О =
дх ду дг дх" ду'1 дг-
К этим уравнениям необходимо присоединить граничные
условия. Если на поверхности тела заданы перемещения, то
граничные условия сводятся к требованию, чтобы в точках
поверхности отыскиваемые функции их, ии, иг приняли задан-
заданные значения и'х, и*и, и*г. Такие условия называются гео-
геометрическими (или кинематическими). Однако чаще геоме-
геометрические условия задаются лишь на части поверхности, а на
остальной части задаются поверхностные нагрузки. Обозна-
Обозначим через сои и <о/( соответствующие части поверхности тела
(о. Тогда на <ор должны удовлетворяться статические гранич-
граничные условия A.3). Их следует также записать через перемеще-
перемещения, в результате чего они примут вид:
дх ду
дг )
19
Другой подход заключается в том, что за основные неиз-
неизвестные функции принимают напряжения. Для их отыскания
следует в первую очередь использовать дифференциальные
уравнения равновесия A.1). К ним присоединяют условия сов-
совместности деформаций A.10). Чтобы можно было ими восполь-
воспользоваться, нужно выразить в них по закону Гука деформации
через напряжения. Подобная замена после ряда преобразова-
преобразований с использованием уравнений равновесия A.1) приводит
к так называемым уравнениям Бельтрами-Мичелла 1281.
§ 1.2. Плоская задача
Существует широкий класс важных в практическом отно-
отношении задач, в которых перемещения, деформации и напря-
напряжения зависят лишь от двух координат — скажем, х и у.
Этот класс задач под общим названием «плоская задача тео-
теории упругости» подразделяется на плоскую деформацию и
обобщенное плоское напряженное состояние.
Если в процессе нагружения все точки тела перемещают-
перемещаются только параллельно одной плоскости (плоскости ху, на-
например), то соответствующее деформированное состояние на-
называется плоской деформацией. Таким образом, для плоской
деформации имеем их = их (х, у), и„ = и,, (х, у), uz — 0.
В соответствии с уравнениями Коши A.7), деформации егг,
?*z и гуг оказываются равными нулю, а из закона Гука A.14)
вытекает, что касательные напряжения oxz и оуг также рав-
равны нулю. Остальные компоненты деформации и напряжения
являются функциями только координат х и у.
Если, далее, тонкая пластина, параллельная плоскости
ху, нагружена объемными и по контуру—поверхностными си-
силами, параллельными ее плоскости и равномерно распределен-
распределенными по толщине, то имеем дело с обобщенным плоским напря-
напряженным состоянием. В этом случае можно пренебречь компо-
20
нентами напряжения агг, ахг и ауг, а ахх, ауу и ахи считать
постоянными по толщине:
°zz — °xz — <*yz
= 0;
= oxx (x, y)\ ayy = ayy (x, y)\ axy
'УУ ~ "УУ VA> Vh "xy —' axy (X, У).
Из закона Гука A.11) следует, что при обобщенном пло-
плоском напряженном состоянии деформации сдвига ехг — е.иг я»
— 0, а остальные компоненты деформации представляются как
функции только координат х и у.
Выпишем основные уравнения теории упругости примени-
применительно к плоской задаче. Из трех дифференциальных уравне-
уравнений равновесия A.1) остается два; в матричной записи они
имеют вид
дах . дау
дх ду
где ах ~ {ахх аху); оу = {аух ауу}\ R = {Rx Ry).
Для напряжений в наклонных площадках имеем
Опх— ОххПх + оухпу; аиу — ахупх + ауупу. A.18)
Матричная форма статических граничных условий будет
Qxnx + Oytiy — р, A.19)
где р = {рх ру).
Из уравнений Кошн A.7) остаются только три соотношения
дих л" 3" л"
A.17)
дх
еш/ — ¦
дх
A.20)
Понимая под е и и матрицы е = {ехх еуу^ еху}; и ==¦
— {ихиу}, этим соотношениям снова можно придать форму
е = Lu, где матрица L имеет вид
--L о
дх
о
д
дх
A.21)
Наибольшие упрощеиия получаются в условиях совместно-
совместности деформаций A.10), из которых остается только одно:
ду%
¦+¦
-ху
дхду
21
Закон Гука по-прежнему можно записать в форме а —
~ не или в форме в = Фст, где а = {ахх ауу аху). При этом
для плоской деформации имеем
<l+|i)(l-2|i)
Ф = ±±Е
?
о
—**
о
1.-1*
о
о
о
1-2ц
A.22)
— ц
1-ц
О
°1
о .
2J
A.23)
а для обобщенного плоского напряженного состояния
и—¦
1
ц
1
1
О
О О
1
О
О
о
1-ц
О
О
2A
A.24)
A.25)
Отметим, что в случае плоской деформации нормальное
напряжение ozl отлично от нуля, но оно не имеет самостоя-
самостоятельного значения, поскольку выражается через ахх и аи!/ по
формуле alz = ц (ахх + ауц).
Точно так же в обобщенном плоском напряженном состоя-
состоянии деформация ггг ф 0 и может быть найдена через ехх и
Решение плоской задачи теории упругости удобно выпол-
выполнять в напряжениях. При постоянных объемных силах Rx,
JRy оно сводится к отысканию некоторой функции ф (х, у),
удовлетворяющей бигармоническому уравнению
+ 2-
дх* дхг ду2
ду*
A.26)
22
Напряжения вычисляются через функцию <р посредством
формул
хх дуг иу дх* у дхду *
Помимо равенства A.26) должны быть удовлетворены еще
граничные условия A.19) на боковой поверхности.
§ 1.3. Подкрепленная панель как конструктивно-
ортотропная пластина
В летательных аппаратах часто встречаются подкреплен-
подкрепленные ребрами пластины, воспринимающие нагрузки в своей
плоскости. Ребра увеличивают жесткость пластины в соот-
соответствующем направлении. Если -
они расположены регулярно и '
достаточно часто, то их жест-
жесткость можно осреднить и заме-
заменить реальную панель гладкой
пластиной, работающей в усло-
условиях обобщенного плоского на-
напряженного состояния и имею-
имеющей различные упругие харак-
характеристики в продольном и по- *
перечном направлениях. Такая Рис. 1.2
пластина называется конструк-
тивно-ортотропной. Статические и геометрические соотно-
соотношения остаются для нее такими же, как и для изотропной
пластины. Отличие будет в записи закона Гука.
Отнесем пластину к системе координат |, i], направив ось
I параллельно ребрам (рис. 1.2). Будем полагать, что все
ребра имеют одинаковую площадь F и расположены равно-
равномерно с шагом t. Рассмотрим однородное (т. е. не зависящее
от координат ?, т|) деформированное состояние панели с ком-
компонентами г1Ь е„„ и еЕч. При этом в ребрах возникает одноос-
одноосное напряженное состояние, а пластина будет находиться в
условиях обобщенного плоского напряженного состояния.
Обозначив через ар напряжение в поперечном сечении
ребра, а через а^г, <х^„, оч„ — компоненты напряжения в пла-
пластине, свяжем эти напряжения с деформациями. Для ребра
такая связь дается законом Гука для одноосного напряжен-
напряженного состояния
<»„=¦?> 5*. С-28)
где ?", — модуль упругости материала ребер.
23
Для пластины же матрица напряжений а выражается через
матрицу деформаций е посредством зависимости а = не,
где матрица и имеет вид A.24). Это соответствует трем скаляр-
скалярным равенствам:
A.29)
Чп,
где Е2 и ц — модуль упругости и коэффициент Пуассона ма-
материала пластины.
Пусть, далее, эквивалентная гладкая пластина имеет та-
такую же толщину Л, что и действительная пластина, и в ней со-
созданы такие же деформации е66, ецп и е$ц, как и в реальной
Н й
фр 66 цп $ц р
панели. Напряжения, возникающие в эквивалентной пласти-
пластине, обозначим через <jg|, ацц и airi и определим их из условия
равенства сил, воспринимаемых подкрепленной панелью и этой
пластиной. В частности, для нормальных сил в сечении
5 = const имеем o^th + opF = a^th; отсюда
F
Остальные компоненты напряжения в эквивалентной пла-
пластине будут совпадать с соответствующими напряжениями в
панели:
Из последних трех равенств с учетом A.28) и A.29) получа-
получаем:
ап
где
[A
kP=
E.th
A.30)
24
В матричной записи эти соотношения примут вид
где сг0
е0 =
i-и2
1 +kF
и-
0
1
0
0
0
A.3!)
A.32)
Зависимости A.31), A.32), определяющие упругое пове-
поведение конструктивно-ортотропной пластины, выведены в пред-
предположении об однородности деформированного состояния, но
ими можно приближенно пользоваться и в случае переменно-
переменного поля деформации.
Рис. 1.3
Найдем еще связь между напряжениями а — {аххаууаху}
и деформациями е= {?xx&yy&xii} в произвольных осях х, у
(рис. 1.3, а). Пусть ось | составляет с осью л; угол 9, который
будем считать положительным, если поворот оси х до совмеще-
совмещения с положительным направлением | необходимо выполнить
против часовой стрелки.
В соответствии с A.18) проекции напряжений в произволь-
—*-
ной площадке с внешней нормалью п на оси I, г\ вычисляются
по формулам
где П| и пп — косинусы углов между нормалью п и коорди-
координатными осями ?, г].
25
Если нормаль к площадке совпадает с направлением оси
х, то пг — cos (х,%) — cos В; /гп ¦= cos (х,ц) = — sin В. За-
Заменив в обозначениях ст„ 6 и а„п индекс /г на л;, имеем для та-
такой площадки
(Тд. Е =
cos В
sin 6; <Tvn
cos В — о,,,, sin В.
Проектируя эти компоненты на направления осей х ну
(рис. 1.3, б), найдем нормальное и касательное напряжения
в площадке, нормальной к оси х:
Охх = o*s cos 9 — аЛЧ sir 6 == oJ? cos- В +• <тпп sin'- В —
—г 0tt| sin 20;
— a*i sin
*ч cos 9 —§ '
4- aJn cos 29.
sin
Аналогично определяются компоненты напряжения в пло-
площадке с нормалью, параллельной оси у, у которой п -.=¦ sin О,
н„ г* cos 0. Нормальное напряжение в этой площадке
ани ** <7%8 sin2 0 -j- о,,,, cos- B-f au sin 29.
Полученные формулы можно записать в виде одного матрич-
матричного равенства
-a
a
a
XX
uu
w -
=
cos29 sin2В —sin 20
sin* 0 cos2 В sin 29
— sin 20 !-sin2fl
2 2
cos 20
41
которое устанавливает связь между напряжениями в двух ко-
координатных системах
а = Т о„.
где
cosJ0
sin2 В
sin 20
I
sina6
cos20
- — sin 20
2
— sin 20
sin 20
cos 20
A.33)
A.34)
Матрицу деформаций е в системе координат х, у свяжем с
из условия равенства удельной энергии деформации в рас>
26
сматриваемых двух координатных системах*:
— а е— 2 <тоей,
где индекс «Г» обозначает транспонирование матрицы.
Внося сюда A.33), получаем о* Тт е = а\ в0. Это равен-
равенство должно соблюдаться для любых компонент матрицы <т0,
откуда следует, что
е„= Тте. A.35)
Подставляя теперь A.31) и A.35) в A.33), получим закон
Гука для произвольной ориентации ребер:
а — Ти01Т г.
Это соотношение можно представить в стандартной форме
а— хе, где
х= Тх0Тг. A.36)
ГЛАВА 2
ВАРИАЦИОННЫЕ МЕТОДЫ ТЕОРИИ УПРУГОСТИ
Вариационные принципы теории упругости позволяют свести
проблему определения напряженно-деформированного состояния тела
к задаче отыскания минимума того или иного функционала. На этом
основаны различные прикладные методы расчета, в которых удается
получить приближенное решение задачи, не прибегая к интегрированию
системы дифференциальных уравнений теории упругости. Вариацион-
Вариационные принципы составляют теоретический фундамент н метода конечных
элементов, позволяя, в частности, обосновать его сходимость к точ-
точному решению.
§ 2.1. Работа внешних сил. Дополнительная работа
Рассмотрим упругое тело (рис. 2.1), находящееся в равно-
равновесии под действием п сил. Представим эти силы матрицей-
столбцом
— /р р р р \
и введем матрицу перемещений
v = {у, у2 ... V-, ... у,,}.
Здесь у, есть проекция полного перемещения А,- (рис. 2.1)
точки приложения силы Pt на направление этой силы.
* Необходимые формулы для вычисления удельной энергии дефор-
деформаций будут даны в следующей главе.
27
Вычислим работу, которую совершают силы Р в процессе
деформирования тела. Будем полагать, что имеет место ста-
статическое погружение, т. е. внешняя нагрузка возрастает на-
настолько медленно, что можно не учитывать инерционные силы.
Для линейно-упругого тела процесс деформирования являет-
является обратимым, а работа сил Р на перемещениях v не зависит
от способа нагружения, а зависит лишь от окончательного
значения этих сил. Поэтому при вычислении работы можно
принять, что все силы возрастают одновременно от нуля до
своего конечного значения, причем в процессе нагружения
Рис. 2.1
Рис. 2.2
между ними сохраняется постоянное соотношение. Тогда для
линейно-упругого тела зависимость между силами Pt и соот-
соответствующими перемещениями у,- будет линейной (рис. 2.2).
Подчеркнем, что перемещение у,- вызвано действием всех
сил.
Площадь под диаграммой, заштрихованная на рис. 2.2
вертикально, представляет собой работу Л,- = Р&{/2, кото-
которую совершает сила Pt в процессе нагружения тела. Совершен-
Совершенно аналогично можно подсчитать работу, производимую дру-
другими силами. Суммарная работа, затраченная на деформиро-
деформирование тела,
п
~^, l~T(PlVl + PiV2 + - + PnVn)-
Это выражение можно записать более кратко с использо-
использованием матричных обозначений:
B.1)
28
Полученный результат выражает теорему Клапейрона,
согласно которой работа, произведенная внешними силами
при статическом деформировании линейно-упругого тела,
равна полусумме произведений окончательных значений сил
на окончательные значения соответствующих им перемеще-
перемещений.
Обобщим теорему Клапейрона на случай действия объем-
объемных R = {Rx Ry Rz) и поверхностных р = {pxpypz} сил.
Сначала рассмотрим бесконечно малые силы Rdx и pda», где
dx и dco — элементы объема и поверхности тела соответствен-
соответственно. Если перемещения точек тела представить матрицей и =
= {их uv uz), то работа элементарных объемных сил будет
равна u7'RdT/2, а поверхностных ur pdco/2. Последующее ин-
интегрирование дает полную работу, затраченную на деформи-
деформирование тела:
А =— /(VRdx+ jVpdcoV • B.2)
Здесь первый интеграл берется по всему объему, а вто-
второй — по поверхности рассматриваемого тела.
В дальнейшем нам потребуется выражение для прираще-
приращения, которое получает работа А при возрастании сил от Р до
Р + SP. где через SP = {8Р1 8Р2 ... 8Рп} обозначена матри-
матрица произвольных бесконечно малых приращений внешних
сил. Соответствующие приращения перемещений определяют-
определяются матрицей Sv = {6у, 8v2 ... 8vn}.
Приращение AAi работы At численно равно площади тра-
трапеции, заштрихованной на рис. 2.2 наклонными линиями:
/±A,=Pi8v,+ — 6P,8vl.
Для всей системы сил получаем отсюда
Первое слагаемое в правой части этого равенства являет-
является главной частью приращения АА и называется первой
вариацией (или просто вариацией) работы внешних сил 8А,
ЬА =» 6vrP. B.3)
29
Если на тело действуют объемные и поверхностные силы,
то
6Л =. f 6ur Rdr -f Г 6u' pcko,
где 6u = {f>ux f)utl bu:) — матрица бесконечно малых при:
ращений перемещений точек тела.
Формула для 6Л выведена в предположении, что R и р
получили приращения 6R и бр, а матрица би определяет дей-
действительные приращения перемещений, которые соответст-
соответствуют такому возрастанию внешни* нагрузок. Однако вариа-
вариации сил 6R и бр в эту формулу не вошли, поэтому при вычисле-
вычислении ЪА внешние нагрузки можно считать вообще неизменны-
неизменными, понимая при этом под элементами матрицы би некоторую
произвольную систему бесконечно малых перемещений.
До сих пор речь шла о свободном теле. Если же на тело
наложены связи, то его поверхность w можно разбить на две
части — to,, и ыи, на которых заданы соответственно поверх-
поверхностные нагрузки р и перемещения и. Для практических
приложений полезно ограничиться такими функциями би,
которые на tou обращаются в нуль. Тогда выражение для 6/4
примет вид
6Л =.|urRdT 4- J6u^pdo>, B.4)
где поверхностный интеграл берется лишь по со,,.
Такие бесконечно малые перемещения би, которые удовлет-
удовлетворяют лишь требованию непрерывности внутри тела и со-
согласуются с наложенными на него связями, называются воз-
возможными (иногда их называют также виртуальными). Любые
возможные перемещения можно было бы действительно создать,
прикладывая к телу, закрепленному заданным образом, не-
некоторую систему бесконечно малых нагрузок, но связывать
их с действительными приращениями внешних сил нет необ-
необходимости.
Из сказанного следует, что величину 6Л можно трактовать
не только как вариацию действительной работы Л, но и как
работу внешних сил на возможных перемещениях. Поэтому
иногда 6Л называют возможной (или виртуальной) работой
внешних сил.
Введем далее в рассмотрение так называемый потенциал
внешних сил П. В случае действия сосредоточенных сил
П = -vrp B.5)
30
и представляет собой работу, необходимую для перемещения
точек приложения сил Р в исходное положение, которое они
занимали до деформации тела; значения сил при этом сохра-
сохраняются неизменными.
Рассматривая величину П как функцию перемещений v,
для вариации 6П запишем
6П = —б (vrP) = —6vrP.
Сопоставляя этот результат с выражением B.3) для 6Л,
видим, что
6П = -6Л, B.6)
т, е. формально вариация потенциала внешних сил 6П отлича-
отличается от вариации работы 6Л лишь знаком. В действительности
различие между ними является более глубоким; оно вытекает
лз определения величин Л и П как функций от v согласно
B,1) и B.5). Первое из указанных соотношений получено в
предположении, что силы возрастают от нуля до своего ко-
конечного значения и прэтому в процессе нагружения сами яв-
являются функциями перемещений v. При записи же второго
принято, что силы сохраняют свое окончательное значение
и не зависят от перемещений.
Равенство B.6) положим в основу определения функции
11 для случая произвольного нагружения тела. В соответст-
соответствии с B.6) под потенциалом внешних сил П будем понимать
такую функцию от перемещений v, вариация которой совпада-
совпадает по величине с виртуальной работой 6Л, отличаясь от нее
знаком; внешние силы при варьировании П считаются неизмен-
неизменными. Тогда при действии объемных и поверхностных сил их
потенциал с точностью до произвольной постоянной опреде-
определится в соответствии с B.4) выражением
П=—/ fu7Rdx+ fu^pdoA B.7)
\ * «р )
Рассмотрим теперь площадь слева от диаграммы /»,- — щ; эта
площадь на рис. 2.2 заштрихована горизонтально. Обозначим ее че-
через At и назовем дополнительной работой силы Pi на перемещении
VI. Хотя эта величина и не имеет физического смысла, она окажется
в дальнейшем весьма полезной для формулирования некоторых важ-
важных теорем. В рассматриваемом случае линейно-упругого тела допол-
дополнительная работа Ai численно совпадает с действительной работой.
At, но между ними все же остается принципиальное различие, выте-
вытекающее нз самого определения этих величин.
Запишем выражение для приращения AAi, которое получает до-
дополнительная работа Ai при возрастании нагрузки на величину
31
¦5Pj АЛ/ = 1,6Р, +• 6vi6Pj/2 Главная часть приращения &Ai —
= i.'jbPi Вариация дополнительной работы для всей системы сил
Сопоставляя это равенство с B 3). видим существенное отличие а
определениях ЬА и ЬА *
При действии объемных и поверхностных сил вариация дополни-
дополнительной работы
6.4*=Jur6RdT-j-Jur6pdo), B.8)
Т (О
где 6R=rFA\. &R,,6RZ}, бр= {6/)л. Ьри Ьрг\
По аналогии с функцией П можно ввести дополнительный потен-
потенциал внешних сил П* Определим его как такую функцию внешних
нагрузок, вариация которой равна по- величине и обратна по знаку
6А* т е
6П*=—6Л*. B 9)
перемещения при варьировании П* считаются постоянными
и сохраняющими свое окончательное значение. Таким образом,
urpdo,). B.10)
/
§ 2.2. Энергия деформации. Дополнительная энергия
деформации
Если к упругому телу приложить внешние силы, то, как
было ранее сказано, они совершат некоторую работу, которая
затрачивается исключительно на деформацию; других затрат
энергии здесь нет При этом изменится потенциальная энергия
положения внешних сил. При разгрузке за счет накопленной
потенциальной энергии может быть совершена такая же ра-
работа, какая была затрачена на деформацию тела. Процесс здесь
обратимый.
Вычислим потенциальную энергию, накопленную дефор-
деформированным телом. Выделим для этого элементарный парал-
параллелепипед со сторонами dx, dy, dz и определим работу сил,
действующих по граням этого элемента.
Примем сначала, что на элемент действуют лишь нормаль-
нормальные напряжения aXJC (рис. 2.3). Поскольку длина элемента
при деформации возрастает на vxxdx, силы axxdydz в соот-
соответствии с теоремой Клапейрона произведут работу, равную
oxyexxdxdydz/2 = axxzxxAil2.
В общем случае объемного напряженного состояния ра-
работу напряжения ахх можно подсчитать по этой же формуле,
32
понимая поде^д. окончательное значение деформации, вызван-
вызванное действием всех компонент напряжения.
Рассмотрим далее действие касательного напряжеиия oxt).
Как видно из рис. 2.4, сила oxydxdz производит работу иа
перемещении txydy. Эта работа равна
ax,,e,xudxdydz/2 = axye-X!ldr/2.
Рассматривая аналогично все остальные компоненты на-
напряженного состояния, найдем накопленную в элементе энер-
ЬЙ,
. i
Рис. 2.3
Рис. 2Л
гию, равную суммарной работе внутренних сил:
(Ш = - (vxxexx + Оц^ии 4- о/ге„ -f- oXIJExy +- oy2Eyz +
-f- o.xe,!X) dx.
Вводя, как и прежде, матрицы напряжений и деформаций
о ~ {оххаииаггаХ11аигагх);
перепишем это выражение в кратком виде
d U = — ar edx
2
eT adx.
Величина
All
<1т
г =г
B.11)
представляет собой энергию деформации единицы объема уп-
упругого тела и называется удельной, энергией деформации.
Потенциальная энергия деформации, накопленная всем телом,
U <= f W(h
2 Знк. 651
Пользуясь законом Гука в форме A.12), можно выразить
величину W только через компоненты напряжения: •¦
W =— ат Фв = -!-
2 ?
а|г —
хх ауу
yyozz+ozzoxx)+ 2A
B.12)
С другой стороны, запись закона Гука в форме A.15) по-
позволяет выразить удельную энергию деформации W только
через компоненты деформации:
W =—
2
Рис. 2.5
J. B.13)
Из последней формулы, в
частности, видно, что энергия
деформации является величи-
величиной неотрицательной.
Предположим теперь, что
напряжения о и перемеще-
перемещения и получили бесконечно
малые приращения
zz 8axy 6oyz 6azx};
8о = {8ахх ЬОуУ 8a
6u = {8их Ьиу 8uz}.
В соответствии с формулами Коши A.7) деформации
также получают некоторые приращения
6ё — {Se,xxteyyfezz8eXy8vyZ8zzx}.
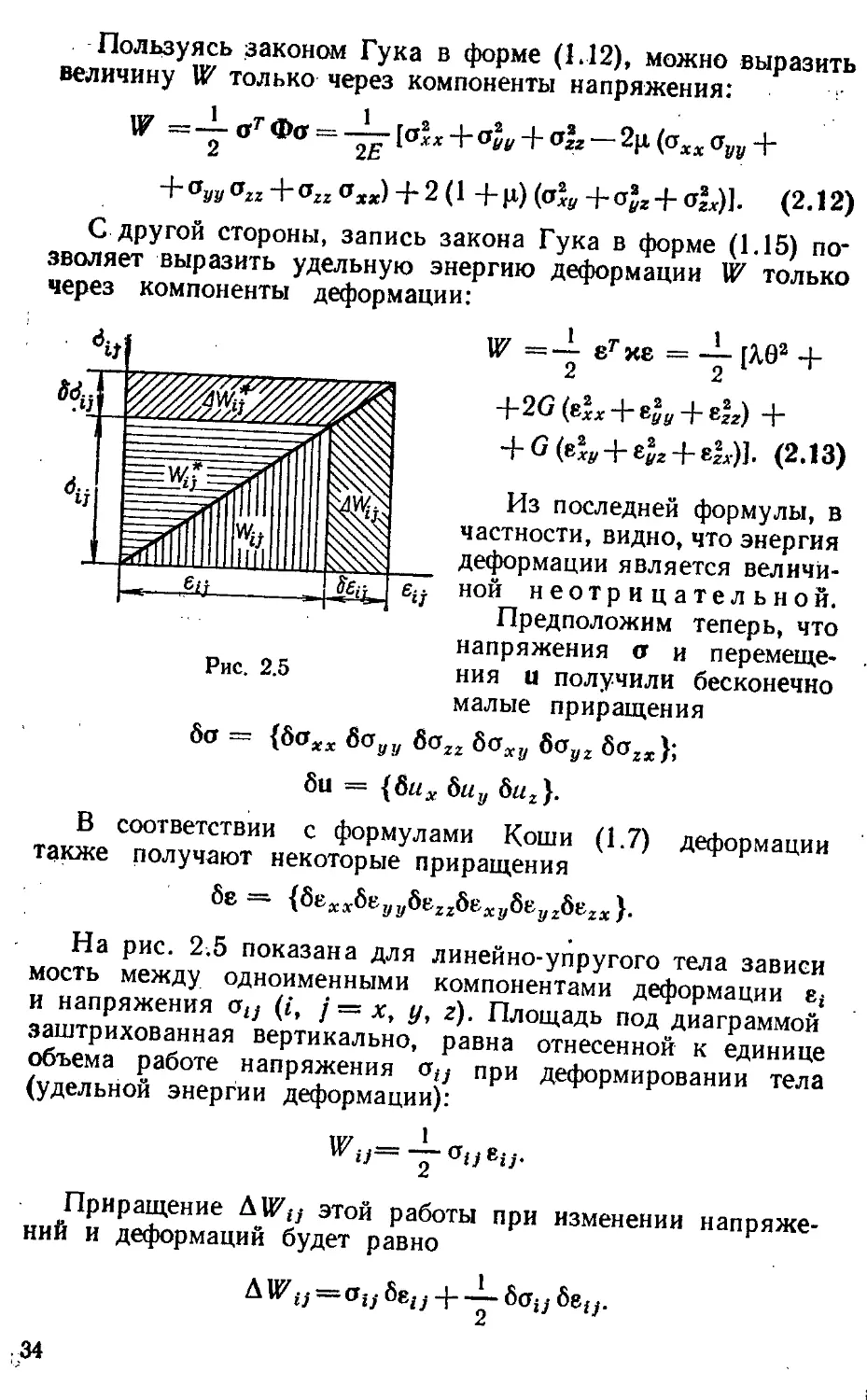
На рис. 2.5 показана для линейно-упругого тела зависи
мость между одноименными компонентами деформации е,-
и напряжения atj (i, j — х, у, г). Площадь под диаграммой
заштрихованная вертикально, равна отнесенной к единице
объема работе напряжения otj при деформировании тела
(удельной энергии деформации):
Приращение AWtj этой работы при изменении напряже-
напряжений и деформаций будет равно
AWi}=ov 8ги + у бог;,- 8еи.
34
Суммарное изменение удельной энергии деформации, обус:
ловленное действием всех компонент напряжения, определит-
определится как сумма
Л W =• Z Д Wit = бег в + — бег б<г.
Главная часть этого приращения дает вариацию удельной
энергии деформации bW «=. бего. Если под би понимать воз-
возможные перемещения, то матрица бе будет определять возмож-
возможные деформации, которые выражаются через компоненты би
по формулам Коши. Тогда 8W следует трактовать как удель-
удельную работу действительных напряжений на возможных пере-
перемещениях.
Горизонтально заштрихованная площадь на рис. 2.5 определяет
удельную дополнительную работу И/// напряжения а,/. Если учесть
осе компоненты напряжения, то в сумме получим величину W*. кото-
которая называется удельной дополнительной энергией деформации. В
случае линейно-упругого тела W* совпадает по величине с W. Вариа-
Вариация, же б W* определяется соотношением 6U^* = e7 60, так как
6 Wtj — ец bo(j в соответствии с рнс. 2.5.
Интегрируя 6№ и 6W* по всему объему тела найдем вариации,
энергии деформации и дополнительной энергии деформации:
B.14)
B.15)
§ 2.3. Вариационное уравнение Лагранжа
Рассмотрим тело, находящееся в равновесии под действием
внешних нагрузок R и р. Дадим точкам тела дополнитель-
дополнительные возможные перемещения бц = {6их Ьиу but}. Этим воз-
возможным перемещениям соответствуют возможные деформации
бе = {бе** бе,,„ 6ezz ЬеХ1/ &еуг бегж}.
Вариация энергии деформации, согласно B.14),
би-\бвта6т= Г (аххбгхх + аиу беиу + агг бе„ +
Преобразуем подынтегральное выражение следующим об-
образом. Воспользовавшись сначала формулами Коши A.7),
запишем
2* 35
Тогда Выражение для 6U можно представить в виде
* -?- Фих) 4- оЛ, -^- Fи„) + о„ -?- Fu
Группируя члены, перепишем:
Fия) + ода -|- (бы,) + о„г -±- (Ьиг)
?- (в«в) + а„ -?- (8н2)
Вводя матрицы
дг
{двих д6иу д&иг
~Тх Тх дх~У
I дбих д&ии d6uz |
1 ду ду ду у
I д6их д&иу д6иг ]
\дг д~г дГ~]'
ду
дби I дби
а также учитывая введенные в § 1.1 матричные обозначения
ох = {ахх axv axzy, оу = {<УуХ оуу ayz); az = {aZK aZIJ azz}f
будем иметь
.) \ дх ду дг J
Используя преобразование тина
36
где / и <р —две любые дифференцируемые функции аргумента
t, приведем это выражение к виду ; ;
дх ду дг
х
Первый интеграл заменим поверхностным, применяя фор-
формулу Остроградского—Гаусса, согласно которой
где Q*, Q» и Qz — произвольные дифференцируемые функции»
заданные в области т, а «х, п„ и «г — направляющие,косину-
направляющие,косинусы внешней нормали к поверхности со, ограничивающей эту
область.
В результате получаем
6U = \ 6ur(orxпх+ вуity + azпг)d(o —
Так как на (ои имеет место равенство би = 0, то интегри-
интегрирование в первом члене достаточно выполнить лишь по сор.
Тогда
= Г
дх
Поскольку предполагалось, что в исходном состоянии тело
находится в равновесии, то напряжения должны удовлетво-
удовлетворять уравнениям статики A.4) и A.6):
дах * до» , даг _ D.
— (_ г. -}- — к.,
дх ду дг
ахпх + о„п„ -f <Гг«г = Р на wp.
37
Отсюда имеем
8i/=
Согласно B.4), в правой части полученного выражения на-
находится вариация работы внешних сил &А, и мы приходим
окончательно к равенству
6U =* 6А. B.17)
Уравнение B.17) выражает собой принцип возможных пе-
перемещений (принцип виртуальных работ) применительно к
упругому телу, согласно которому работа внешних сил на
возможных перемещениях равна вариации потенциальной
энергии деформации.
Полагая в соответствии с B.6) 6П = —8А, приведем ра-
равенство B.17) к виду б (U + П) = 0. Величина
V-= U + П B.18)
называется полной потенциальной энергией системы, а равен-
равенство
6V=0 B.19)
называется вариационным уравнением Лагранжа.
Поскольку U и П вычисляются для равновесного состоя-
состояния тела, уравнение B.19) утверждает, что в состоянии равно-
равновесия полная энергия системы имеет стационарное значение.
Исследуя знак второй вариации 82V, можно строго показать,
что это стационарное значение является минимумом;
мы для пояснения данного утверждения ограничимся просты-
простыми рассуждениями.
В самом деле, если тело, находящееся в состоянии устой-
устойчивого равновесия, под действием какого-либо внешнего
воздействия несколько изменит свою форму, то после устра-
устранения этого воздействия оно снова займет первоначальное по-
положение. При возвращении в исходное положение будет со-
совершена работа, т. е. высвободится некоторое количество-по-
количество-потенциальной энергии. Значит, в соседнем положении тело рб-
ладает большей потенциальной энергией, чем в положении'
устойчивого равновесия.
Уравнение B.19) получено в предположении, что тело на-
находится в равновесии, так что это уравнение представляет
собой необходимое условие равновесия тела. Пока-
Покажем, что оно является также достаточным. Предполо-
жнм'для этого, что равенство 8V = 0 выполняется; тогда име-
3R
ет место и равенство 8U — 6Л = 0. Записав выражение для
6С/ в виде B.16) и вспомнив, что
придем к уравнению
Г биг (ах пх +випи-\- ог пг —р) dw —
дх ду дг
B.20)
Равенство нулю в B.20) должно выполняться для любых
функции бид., Ьии, 8uz, образующих матрицу би. Это воз-
возможно лишь в том случае, если равны нулю выражения, за-
заключенные в B.20) в круглые скобки. Отсюда вытекают диф»
ференцнальные уравнения равновесия A.4) и статические гра-
граничные условия A.6). Таким образом, если удастся найти пе-
перемещения, удовлетворяющие вариационному уравнению Ла-
гранжа B.19), то при этом автоматически будут удовлетворены
уравнения равновесия, а также статические граничные усло-
условия .
Изложенные выше соображения позволяют сформулировать
вариационный принцип Лагранжа: из
всех перемещений, допускаемых наложенными на тело связя-
связями, в действительности имеют место такие, при которых
полная энергия системы V минимальна.
§ 2.4. Вариационное уравнение Кастильяно
В предыдущем параграфе был установлен вариационный принцип
для перемещений. Аналогичный принцип можно установить, рассма-
рассматривай вариации компонент напряжения.
Пусть для упругого тела известны напряжения а, деформации
е и перемещения и, возникающие при действии внешних нагрузок
R и р. Напряжения а удовлетворяют дифференциальным уравнениям
равновесия A.4) и условиям на поверхности A.6). Отметим, что на ча-
части (Op поверхности тела равенство A.6) дает статические граничные
условия, а на <ои оно выражает связь между напряжениями и реакция-
реакциями на тело со стороны наложенных связей.
Предположим далее, что напряжения получили бесконечно малые
приращения
8ауу dalz f>axll бо„г 6агк)
39
Вариации напряжения во подчиним единственному требованию,
чтобы новое напряженное состояние было также равновесным,
т. е. чтобы удовлетворялись уравнения
-тр (ах + 6ох)+— (а, + 6оу) -f —- (az + Ьаг) -f R=0;
». B.2 !)
Здесь через &ах, &ау, &az обозначены матрицы
оахх I I оОух I I oozx I
&?ху г ^а»==| UOyy v &Oz — l Sazy I»
v°xz J Loopz J L u°zz J
При записи условий равновесия B.21) принято для общности, что
изменение напряжений сопровождается изменением поверхностных на-
нагрузок на величину .
объемные же силы предполагаются при варьировании напряжений не-
неизменными.
Вычитая из B.21) соотношения A.4) и A.6), найдем, что вариации
напряжений удовлетворяют уравнениям
д6ах dbay d6az
дх + ду + дг '
B.22)
8ая пх -f 6av nv+ 8аг пг — 6р.
В результате изменения поверхностных сил дополнительная ра-
работа получит приращение
Далее, варьирование напряжений приведет к изменению допол-
дополнительной энергии деформации U* на величину
J ег 6а dt=J (exx 6asx + egy 8ауу+ехг &azz+
X X
+6xy8axy+eyz8ayz+ezx&aZx)dx.
Преобразуем выражение для &U* аналогично тому, как это дела-
делалось при выводе вариационного уравнения Лагранжа. Подставляя
формулы Коши A.7) в подынтегральное выражение и группируя соот-
соответствующие члены, имеем
J \ дх ду * дг )
40
где
ди ( дих ди„ диг ] да ( дих duv диг )
дх =\ дх дх дх Г ду *( ду ду ду }'
дц ( дих диу диг )
дг \ дг дг дг )
Применив далее формулу дифференцирования произведения, за-
запишем
¦ В силу первого равенства B.22) второй интеграл здесь равен нулю.
Заменяя первый интеграл поверхностным по формуле Остроградско-
Остроградского—Гаусса, приходим к соотношению
Ы/*•= J и' (&ах пх + 6ав пи + &oz nz) dm
(О
Ha основании второго соотношения B.22) приведем этот резуль-
результат к виду
В правой частн этого равенства стоит вариация дополнительной
работы 6А*, поэтому можно записать
6U* = 6A*. B.23)
Полученное соотношение выражает собой так называемый прин-
принцип дополнительных виртуальных работ. При выводе формулы B.23)
использовались формулы Коши A.7), следствием которых являются
уравнения совместности деформаций A.10). Таким образом, исход-
исходное напряженное состояние неявно предполагалось не только статиче-
статически возможным, ио и удовлетворяющим уравнениям совместности.
Напряженное состояние, для которого удовлетворяются уравнения
совместности деформаций, будем называть совместным. Из урав-
уравнения B.23) следует, что для совместного напряженного состояния
вариация дополнительной энергии деформации равна вариации допол-
дополнительной работы внешних сил.
Заменяя согласно B.9) 6А* на —6П*, придадим равенству B.23)
вид
S (U* 4- П*) =. 0.
Так как мы приняли, что 6R = 0, то в выражении B.10) для П*
останется лишь поверхностный интеграл:
П*= — furpd(u.
(О
Величину
V* = U* + П* B.24)
будем называть полной дополнительной энергией системы.
41
Таким образом, мы приходим окончательно к уравнению
6V* = 0. B.25)
Вариационное уравнение B.25) устанавливает, что в действи-
действительном (т. е. совместном) напряженном состоянии полная дополни-
дополнительная энергия системы имеет стационарное значение. Можно показать,
что это стационарное значение есть минимум. Таким образом, мини-
минимальность V* является необходимым условием совместности
напряженного состояния. Уравнение B.25) является также и доста-
достаточным условием совместности, т. е. при выполнении равенства
6V* »= 0 уравнения совместности деформаций будут также удовлетво-
удовлетворены. Строгое доказательство этого положения оказывается несколь-
несколько громоздким, вследствие чего здесь не приводится.
На основании сказанного выше сформулируем вариацион-
вариационный принцип К а с т и л ь я н о: из всех статически возмож-
возможных напряженных состояний в действительности имеет место та-
такое, для которого полная дополнительная энергия системы минималь-
минимальна.
При практическом использовании вариационного уравнения Ка-
стильяно во многих задачах оказывается возможным варьировать на-
напряженное состояние таким образом, что поверхностные нагрузки на
шр остаются неизменными. В этом случае бр ¦= 0 на ш,, и выражение
для П* принимает вид
П*=— Jurpdo>.
где матрица р содержит реакции на тело со стороны наложенных на
него связей.
Если при этом на всей поверхности тела ы заданы статически* гра-
граничные условия (ш„ = 0) илн если перемещения на ш„ равны нулю,
та П* = 0, и мы приходим к уравнению 61/* = 0. Для линейно-уп-
линейно-упругого тела, для которого U* = U, получаем известное начало наи-
наименьшей работы, илн начало Кастильяно
Таким образом, в этом частном случае из всех статически возмож-
возможных напряженных состояний в действительности имеет место такое,
для которого потенциальная энергия деформации имеет минимальное
значение.
Исходя из общей формулировки B.25), можно вывести важную те-
теорему. Пусть на тело действуют сосредоточенные силы
Р = '{/>, Р2 ... Р„)
н пусть этим силам соответствуют перемещения
v — {vt v2 ... vn).
Тогда 6А* — 6РГ v, и из B.23) имеем &U* = 6PTv.
Если известно напряженное состояние, вызванное силами Р,
то напряжения, а следовательно, и дополнительная энергия деформа-
деформации U* будут известными функциями Р. Тогда можно записать
dU* dU* dU* ,. (Ш*
«/•-— *+-?».+ ¦ +— ^6Р'— •
42
Сопоставляя два полученных выражения для SU*, находим
dU* dU*
vs=__ MHPje_(/eIi2 я).
Для лииейно-упругого тела V = U*, так что в этом случае
AU dU
«.„.
«,.
Эти равенства, выражающие так называемую первую тео-
теорему Кастильяио, устанавливают, что перемещение точки
приложения некоторой силы Pi в направлении этой силы равно для ли-
линейно-упругого тела частной производной от потенциальной энергии
деформации по этой силе.
Располагая вариационными уравнениями Лагранжа и
Кастильяно, можем теперь дать вариационную постановку
задачи теории упругости: если задача решается впереме-
щ е н и я х, то требуется найти такие перемещения и, которые
непрерывны внутри тела, удовлетворяют геометрическим гра-
граничным условиям и минимизируют полную потенциальную
энергию системы V; если задача решается внапряже-
н и я х, то требуется найти такие напряжения о, которые удов-
удовлетворяют уравнениям равновесия и статическим граничным
условиям и минимизируют полную дополнительную энергию
системы V*,
§ 2.5. Метод Ритца
Метод Ритца приближенного решения задач теории упру-
упругости заключается в прямой минимизации полной энергии си-
системы V. Следуя этому методу, перемещения будем искать в
следующем виде:
их(х, у, z)^ux0(x, у, г) -f-2 a*h"*k(x, у, z);
т
uv (х, у, z) = иу0 (х, y,z)+ 2 avh uyh (*. У> z)> B-26)
*,
иг(х, у, г)=^иг0(х, у, zL- 2 azhUzh(x, у, г).
k=\
Здесь axh ayh и azh есть некоторые постоянные, подлежа-
подлежащие отысканию, остальные же величины представляют со-
собой выбранные заранее подходящие функции координат. При
этом функции их0, ul/0, uz0 должны принимать заданные зна-
значения на части ыи поверхности тела м; все остальные функции
должны на wu обращаться в нуль. Тогда при любых значениях
43
постоянных а будут удовлетворяться геометрические гранич-
граничные условия. Постоянные а подбирают таким образом, чтобы
при выбранных функциях B.26) полная энергия системы бы-
была минимальна.
Воспользуемся выражением для W в форме B.13) и заме-
заменим в нем деформации через перемещения по формулам Ко-
ши:
Если теперь в это равенство подставить приближенные вы-
выражения для перемещений B.26), то удельная энергия дефор-
деформации IF будет представлена как известная функция коорди-
координат х, у, z и постоянных a: W = W (х, у, г, с). Как следует
из B.27), W будет квадратичной формой относительно постоян-
постоянных а.
После подстановки W в формулу U — J Wdr и интегри-
X
рования по всему объему тела потенциальная энергия дефор-
деформации окажется некоторой функцией относительно искомых
постоянных U — U (а).
Для удобства дальнейших рассуждений представим за-
зависимости B.26) в следующей матричной форме:
и = и0 + и*а, B.28)
где
[«Л Г«*о1 1X0 0 1 ГаЛ
и I; uo=lu I; и* —10 и* 0 1;а = |а Г
"zj UoJ L0 0 u;J LaJ
Через u?, u^, uj здесь обозначены матрицы-строки вида
u* = \uKl ux2 ... uxm], а через аж, ay, az — матрицы-столбцы
вида ax = {axxari ... axm).
Подставим далее заданные функции R = (Rx Ry Rz\ и
P = {Px Pu Pzh a также перемещения в форме B.28) в выраже-
выражение для П и выполним интегрирование:
W_(B0+arB). B.29)
44
Здесь
jJr, B
Складывая (/иП, найдем полную энергию системы V как
функцию неизвестных параметров а:
V = (/ (с) - (Во + а7* В). B.30)
В соответствии с уравнением Лагранжа B.19) запишем не-
необходимое условие минимума V:
6V = б{/ (а) — баг В = 0.
Вариацию потенциальной энергии деформации можно вы-
вычислить по формуле
Вводя матрицу
AU _( dU dU dU dU
da \ даХ1 дахг дат даг1
представим выражение для 8U в форме
da '
Таким образом, условие bV — О приводит к равенству
В силу независимости элементов матрицы ба получаем от-
отсюда уравнение
^-В. B.31)
da
Это матричное равенство заключает в себе систему алге-
алгебраических уравнений относительно искомых постоянных а.
Общее число уравнений равно Зт, поэтому система являет-
является замкнутой. Как отмечалось выше, энергия деформации U
является квадратичной функцией относительно параметров а,
поэтому элементы матрицы (Ш/da содержат эти параметры в
первой степени. Таким образом, система уравнений B.31)
будет линейной, и ее решение не представляет принципиаль-
принципиальных трудностей.
Коль скоро постоянные а найдены, выражения B.26) или
эквивалентное им B.28) дают приближенное решение задачи.
45
По формулам Коши можно найти деформации, а затем по за-
закону Гука — напряжения.
В заключение отметим, что в B.26) для их, ии, uz совсем
не обязательно брать одинаковое количество функций uxk,
uyh, игк. В любом случае минимизация полной энергии си-
системы по всем параметрам а дает столько уравнений, сколько
имеется этих параметров.
§ 2.6. Метод Канторовича—Власова
Как говорилось выше, в методе Ритца задаются приближенным
характером распределения перемещений внутри тела. Входящие в ап-
аппроксимирующие функции постоянные подбираются из условия ми-
минимума полной энергии системы.
Подобная схема используется и в
методе Канторовича—Власова, ио
здесь вместо постоянных а вводят-
вводятся неизвестные функции, зависящие
от одной из координат. Минимиза-
Минимизация полной энергии относительно
этих функций приводит к системе
обыкновенных дифференциальных
уравнений, последующее интегриро-
интегрирование которых позволяет получить
приближенное поле перемещений.
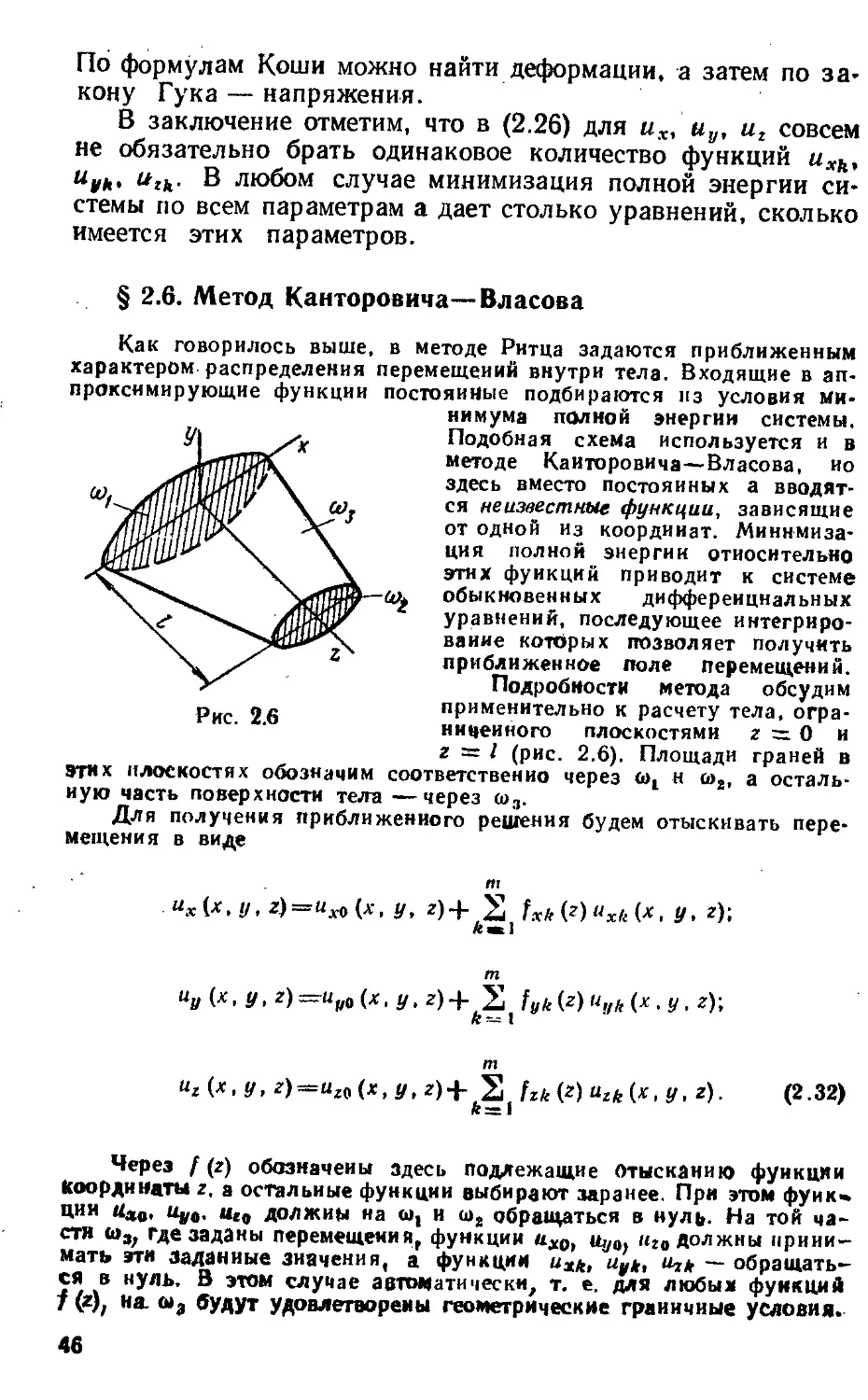
Подробности метода обсудим
применительно к расчету тела, огра-
ограниченного ПЛОСКОСТЯМИ 2=0 И
г = / (рис. 2.6). Площади граней в
этих плоскостях обозначим соответственно через <at н юг, а осталь-
остальную часть поверхности тела —через <а3.
Для получения приближенного решения будем отыскивать пере-
перемещения в виде
со,
Рис. 2.6
у,
, у, г);
uu{x,y,z) — иу0 (х, y.z)+ S fyk (г) «,/* (х • У • гУ>
иг(х.у,г)=игО(х,у,г) + S /z* (*)«**(*, jr. г). B-32)
Через f (г) обозначены здесь подлежащие Отысканию функции
координаты г, а остальные функции выбирают заранее. При этом функ-
функции аяо, Uyt, Uc0 должны на Ш| и шг обращаться в нуль. На той ча-
части си3; Где заданы перемещения, функции иХ0) щ/0> «гоЯолжмы прини-
принимать эти ладанные значения, а функции ихц, и^/,, иц, — обращать-
обращаться в нуль. В этом случае автоматически, т. е. для любых функций
/ (z), на. (из будут удовлетворены геометрические граничные условия.
46
Подобно тому, как это делалось в методе Ритца, перемещения
B.32) можно представить С матричной форме
и (*, у, г) == и0 (х, у, г) + и* (*, у, г) \ (г).
B.33)
Здесь матрицы и0 и и* имеют такой же вид, как и в B.2$), а че-
через f (г) обозначена матрица-столбец неизвестных функций
где
fxi (*) ~
»(*) =
1 ** (г)
7»i (г) '
/j/2 (г)
7я (г) ¦
/га (г)
/г (^
»»<«)¦
Подставим теперь приближенные выражения B.32) в формулу
B.27) для удельной энергии деформации VC. Это позволяет получить
W как функцию координат *, у, г с известным характером зависимости
от х и у. Потенциальная энергия деформации V определяется как ин-
интеграл U — I W&X, взятый по всему объему тела. Обозначим через
т
F (г) площадь сечения тела плоскостью, перпендикулярной оси г. Тогда
/=J / f f
><z>
/
Поскольку зависимость W от переменных х, у известна, то можно
выполнить по этим координатам интегрирование и получить выра-
выражение для U в виде функционала типа
, fxk, fyk, ftk, fxk, fyk,
B.34)
Штрихами обозначены здесь производные по г.
Найдем далее потенциал внешних сил
П
—| ит Rdr— J u^pdw.
Для простоты дальнейших рассуждений считаем, что работа по-
поверхностных сил иа гранях coj и со2 равна нулю. Это возможно, если на
<аг и oi2 отсутствует поверхностная нагрузка, либо если эти грани за-
закреплены. Тогда
П=-—
— J urpdco,
где через <азр обозначена та часть а>3, на которую не наложены связи.
Подставим в правую часть этого равенства функции B.33). После ин-
47
тегрирования по координатам хну выражение для П может быть при-
приведено к виду
П= -f Ф,(г.Л.*,^*.Ы««г. B.35)
о
где Ф-.— некоторая функция, известным образом зависящая от г.
fxh (г), fyh (г), fzh (г).
Объединив B.34) и B.35), для полной энергии системы V = U +
•f- П получим
K=f Ф(г,
о
йг
B.36)
где Ф = Ф, — Фг.
Таким образом, полная энергия представлена как функционал, за-
зависящий от неизвестных функций f (г). Необходимое условие миниму-
минимума этого функционала заключается в требовании, чтобы функции
f (г) удовлетворяли следующим . уравнениям Эйлера:
дФ
— I —————— ¦ —у
^ { С* /
_d_ /_дФ_ V
д(ик ~ ^ [ дГик }~°'
dfxk
дФ
дФ
<>tzk
Такие уравнения записываются для к = 1.2 т; в результате
получается система 3/я обыкновенных линейных дифференциальных
уравнений второго порядка относительно 3/й функций. Решение этой
системы содержит 6/л неопределенных постоянных, которые должны
быть определены из граничных условий при г— 0 н г = /, т. е. на o)t
и ш2. Если в каком-либо из этих сечений перемещения равны нулю, то
все функции f (г) должны здесь обращаться в нуль. Если же на пере-
перемещения не наложено никаких ограничений, то следует воспользовать-
воспользоваться естественными граничными условиями вариационной задачи, кото-
которые для г-=-I, например, записываются так.
= 0;
r=/
= 0;
дФ
= 0
Таким образом, в рассмотренном методе совокупность уравнений
теории упругости в частных производных приводится к системе обык-
обыкновенных дифференциальных уравнений,' интегрирование которых
осуществляется значительно проще. Приведение к обыкновенным диф-
дифференциальным уравнениям выполняется путем приближенной мини-
минимизации полной энергии.
Для практического использования метода Канторовича—Власо-
па удобнее отыскивать перемещения и (х, у, г) в виде
и (*, у, г) ¦= и„ (*. у, г) + и* (х, у) f (г),
где функции и* зависят только от координат х, у.
48
Чаще всего метод Канторовича —Власова применяется 8 двумер-
двумерны* задачах. В этом случае приближенное распределение неремещеннй
можно искать в форме
и (х, у) = и0 (*, у) + и* {у) t (х).
Отметим в заключение, что если функции и* удовлетворяют оп-
определенным условиям ортогональности, то система уравнений отно-
относительно функций f (г) получится несвязанной И ее интегрирование
будет выполняться наиболее просто 19].
ГЛАВА 3
МАТРИЧНЫЙ МЕТОД ПЕРЕМЕЩЕНИЙ
ДЛЯ СТЕРЖНЕВЫХ СИСТЕМ
Стержневые системы широко применяются в конструкциях лета-
летательных аппаратов. Эффективным средством их расчета иа ЭВМ яв-
является метод перемещений в матричной формулировке. В терминологии
и основных процедурах он имеет много общего с методом конечных
элементов. Жесткости ые характеристики стержней вычисляются
здесь на основе соотношений технической теории бруса, и в рамках
этой теории решение получается точным.
§ 3.!. Понятие о матрице жесткости
Рассмотрим консольную балку, нагруженную силой на
свободном конце (рис. 3.1). Вертикальное перемещение точки
приложения силы, как известно, равно v = P13/CEJ), где
Е— модуль упругости; J—момент инерции поперечного
сечения балки. Если перемещение v задано, то из этой форму-
формулы можно найти силу, необходимую для создания такого пере-
перемещения: Р = 3EJvlP или
Р — ко, где к = 3EJ/13.
Величина k называется коэффициентом жесткости кон-
консольной балки. Если положить v — 1, то сила Р будет равна
k. Отсюда вытекает физический смысл коэффициента жест-
жесткости: k есть сила, которую необходимо приложить на конце
балки, чтобы его прогиб равнялся единице.
Пусть, далее, к балке приложены две силы, как показа-
показано на рис. 3.2. Используя известные методы сопротивления
материалов, можно найти перемещения и, и v.t в направлении
этил сил.
где ftfj (i, i = I, 2) суть перемещение в направлении vt под
дейстоием единичной силы, направленной по Pj Величины
6)j, называемые коэффициентами влияния, зависят от геоме-
49
трических параметров балки и от модуля упругости материа-
материала.
Запишем Связь между перемещениями и силами в матрич-
матричной форме:
v = ДР. C.1)
Здесь введены матрицы-столбцы сил и перемещений
а через А обозначена так называемая матрица податливости
К fi
v
IP,
*f '
Рис. 3.1
Рис. 3.2
Если принять, что перемещения v известны, то из C.1)
можно найти силы Р, вызывающие эти перемещения: Р =
= A-Xv. Полагая к = А-1, придадим последнему равенству
вид Р = kv. Введенная здесь матрица к имеет размер 2x2
и называется матрицей жесткости рассматриваемой системы.
Согласно теореме Максвелла о взаимности перемещений,
справедливо равенство б1а = ба1, т. е. матрица податливости
А является симметричной. Обратная к ней матрица к будет
поэтому также симметричной.
Теперь рассмотрим общий случай, когда на произвольное
упругое тело действует система т сил (рис. 3.3), которую пред-
представим матрицей
Р= {РгР2 ... Рт).
Пусть перемещения точек приложения сил Р (в дальней-
дальнейшем эти точки будем называть узлами) в направление этих
сил образуют матрицу .!.," ; ,
vn).
v =
v2
Здесь принято, что все перемещения v отличны от нуля. Ес-
Если в некоторых из рассмотренных точек тело закреплено, то
соответствующие элементы матрицы v будут равны нулю.
50
Предположим, что перемещения v заданы; тогда силы, не-
необходимые для создания этих перемещений, определятся для
линейно-упругого тела соотношением
Р = kv. C.2)
Матрица к, связывающая силы Р с соответствующими им
перемещениями v, называется матрицей жесткости рассма-
рассматриваемого тела.
Представим C.2) в развернутом виде
"Pi
Pi
Pm
~kn
&21
... k
m
kn kn ... k,
C.3)
и выпишем i-ю строку этого матричного равенства:
Pi — biiVi -f ki2o2 + ... + ki/Vj + ... + kimvm.
Физический смысл коэффициента кц можно выяснить, по-
полагая перемещение Vj = 1, а все остальные перемещения рав-
равными нулю; тогда Р,=?,7.
Отсюда следует, что коэф-
коэффициент жесткости kfj
представляет собой силу,
возникающую в узле I,
когда перемещение Vj рав-
равно единице, а все осталь-
остальные перемещения равны
нулю. Иначе говоря, если
закрепить тело во всех
узлах, кроме узла /, и
приложить такую силу Pjt
чтобы перемещение V/ рав-
равнялось единице, то реак-
реакция на тело в узле i будет
самой силы
Рис. 3.3
равна ku (при этом величина
j определит значение коэффициента kjj).
Применяя теорему Бетти о взаимности работ, можно пока-
показать, что матрица жесткости всегда симметрична.
51
Если силы Pt имеют произвольные направления, то удоб-
удобно разложить эти силы по. координатным осям х, у, г и вве-
ввести для каждого узла / матрицу сил Pj =* {PtxPiy Pit}-
Тогда V| будет также матрицей-столбцом, элементы которой
суть перемещения узла i по координатным осям: Vj =
= {vtx viy viz}- Связь между силами и перемещениями
можно по-прежнему определить соотношением вида C.3),
только элементами кц матрицы к, представляющей уже блоч-
блочную матрицу, будут квадратные подматрицы размера 3, X 3,
Для практических вычислений удобнее иногда пользовать-
пользоваться сквозной нумерацией компонент узловых сил и перемеще-
перемещений. В этом случае силы Plx, Plv и Р1г, действующие в узле /,
обозначаются соответственно через Р„ Р2 и Р3; силы Paxt
Ргу и Р2г, действующие в узле 2, — через Pt, Ръ и Рв и т. д.
При такой индексации элементы матрицы сил для узла г
будут иметь номера 3/ — 2, 3/ — 1 и 3/, т. е.
Аналогично для перемещений имеем
Наконец, в самом общем случае, в каждом узле могут по-
помимо сил действовать моменты относительно координатных
осей. Тогда подматрицы Р| и vt будут состоять из шести ком-
компонент, которые мы условимся перечислять в следующем по-
порядке:
Р. = {Pix Piy Piz Mix Mty Miz};
v; = {vlx viy viz 0ix Qiy Qiz), C.4)
где Miq и Qiq — момент и угол поворота относительно оси q
(q = х, у, z).
Если использовать сквозную нумерацию сил и перемеще-
перемещений, то вместо C.4) следует писать
П3К Ог-5 P(li-i Pei-3 °вг-2 °6<-1 °в/}>
Положительные направления сил и моментов даны на
рис. 3.4, а, линейных и угловых перемещений — на рис. 3.4, б;
52
моменты и угловые перемещения лредставляются векторами
в соответствии с правилом правого винта.
Подматрица ktJ будет иметь размер 6 X 6: Смысл отдель-
отдельных элементов этой подматрицы можно выяснить, полагая,
Как и ранее, всё перемещения (линейные и угловые) равными
нулю, за исключением одного, которое берется равным еди-
единице. Так, коэффициент 6вг_2. w_3 равен обобщенной силе
Ры-г (т- е- моменту Mix), которая возникнет в узле /, если
р#-з — "I (T- e- vJz — I), а остальные пять перемещений уз-
узла / и всё перемещения остальных узлов равны нулю.
V
Рис. 3.4
Вычисление матриц жесткости отдельных конструктивных
элементов, из которых состоит стержневая система, составля-
составляет важный этап ее расчета матричным методом перемещений.
Узлами для элементов служат точки соединения их друг с
другом. Для расчета матриц жесткости элементов могут при-
применяться различные способы; мы остановимся на трех из них
как наиболее простых и употребительных.
В простейших случаях можно исходить непосредственно
из физического смысла коэффициентов жесткости; этот под-
подход иллюстрируется ниже на примере прямолинейного стерж-
стержня, работающего на растяжение-сжатие (ферменного элемен-
элемента).
Другой способ получения связи между узловыми силами
и узловыми перемещениями заключается в применении ана-
аналитического или численного интегрирования дифференциаль-
дифференциального уравнения, описывающего деформацию элемента; этот
подход будет подробно рассмотрен в § 3.4 применительно к
изгибу бруса.
Можно, наконец, с помощью известных методов сопротив-
сопротивления материалов найти сначала зависимость узловых пере-
53
мещений от узловых сил, а затем обратить ее, разрешив отно-
относительно узловых сил. Детали этого варианта описаны в § 3.7
при вычислении матрицы жесткости криволинейного бруса.
§ 3.2. Преобразование координат
Если, как говорилось выше, в качестве компонент матриц
Pit vt принять проекции сил и перемещений на координатные
оси, то элементы матрицы жесткости будут зависеть от приня-
принятой системы координат, выбор которой произволен. Для рас-
расчета конструкции применяют некоторую общую координат-
координатную систему. Однако для вычисления матриц жесткости от-
отдельных конструктивных элементов может оказаться выгод-
выгоднее воспользоваться местными системами координат. Для
каждого конструктивного элемента местная система выбира-
выбирается так, чтобы свести к минимуму вычислительную работу.
В таких случаях после отыскания матрицы жесткости в ме-
местных координатах необходимо выполнить переход к общей
системе координат.
Пусть х, у, z и х, у, z — соответственно местная и общая
системы координатных осей. Обозначим через
Р={Р1Р,...РМЛ v = {viv2...v"M}
матрицу сил и матрицу узловых перемещений в местных, а
через
Р= {Рх Р2... Pm}; v= {vlV2...vm}-
в общих координатах. Количество элементов в подматрицах
"Pi, v,- или Р,, v,- определяется числом степеней свободы от-
отдельного узла.
Выразим прежде всего v через v. Чтобы получить связь
между перемещениями в двух системах координат, необходимо
разложить перемещения v по направлениям перемещений v.
Если перемещения (линейные и угловые) типового узла •/
в общей системе координат спроектировать на местные коор-(
динатные оси, то придем к соотношениям, которые в матрич-
матричной форме имеют вид
v, = Vb C.5)
где Хо — матрица,_ составленная из косинусов углов между
осями х, у, г и х, у, г.
54
Подобные соотношения могут быть записаны для всех
узлов рассматриваемого тела. Сведем их в одно матричное ра-
равенство:
Л> о
о л«
о
о
О 0...
v*
Введя обозначение
Я,-
о
представим последнее соотношение в форме
v =» i.v.
C.6)
C.7)
Матрица Х, представляет собой матрицу преобразования ко-
координат. Отметим, что число диагональных блоков в C.6)
равно числу узлов тела (или рассматриваемого конструктив-
конструктивного элемента).
Придадим далее точкам тела возможные перемещения и обо-
обозначим через 6v матрицу-столбец возможных перемещений
узлов, отнесенных к местной системе, а через 6v — к общей
системе координат. На основании C.7) эти матрицы связаны
соотношением
&7=Ш. C.8)
Если узловые силы отнесены к местной системе координат
то на возможных перемещениях они произведут работу
(см. §2.1) 8vr P; если же они отнесены к общей системе, то
работа будет равна fivr P. Поскольку работа не зависит от
того, в какой системе координат производятся вычисления,
то
Р = dvT Р.
Подставляя сюда C.8), получим
Р -
55
откуда в силу независимости элементов матрицы 6V прихо-
приходим к равенству _
Р = W Р, C.9)
которое устанавливает связь между матрицами сил Рк Р.
Пусть, далее, к — матрица жесткости в местных коорди-
координатах; тбгда согласно C.2) имеем Р =jcv. Учитывая C.7),
получим Р — kX,v. Наконец, под-
подстановка последнего равенства в
C.9) дает
Рис. 3.5
Эта формула связывает силы и
перемещения в общей системе ко-
координат в стандартной форме
Р = kv, где _
к = Яг кХ. C.10)
Таким образом, если матрица
жесткости к" в местной системе
координат известна, то для вы-
вычисления матрицы жесткости в
общей системе достаточно построить матрицу к и вос-
воспользоваться формулой C.10). Матрица Я имеет вид C.6),
и задача сводится к составлению матрицы к0, конкретный вид
которой зависит от того, какие перемещения (степени свобо-
свободы) узлов учитываются при расчете.
В качестве примера покажем составление матрицы Л,о для
случая, когда в каждом узле рассматривается по три линей-
линейных перемещения в направлении координатных осей. На
рис. 3.5 показаны проекции перемещения узла i на координат-
координатные оси двух систем — местной и общей.
Обе матрицы v{ и v{ будут состоять здесь из трех элемен-
элементов:
Щх
Обозначим косинус угла между осью р (р =~"х, у, z) мест-
местной системы и осью q (q — х, у, z) общей системы координат
через ХРд. Проектируя перемещения vtx, vty, vtz на ось х,
получим
m
Аналогично выразим v{~ и vt- через v{
В этих формулах обозначено:
Отсюда находим
—
V
А'-
Сопоставляя эту запись с
,-
Лй.
C.5), по
"ч?"
•
C.12)
Заметим, что матрица Я имеет блочно-диагональный вид
C.6) лишь в том случае, когда в матрицах v и v узловые пе-
перемещения перечисляются в одном и том же порядке:
... vm}; v = {v1v2... vm}.
При выводе матрицы жесткости в местных координатах
иногда оказывается удобнее принять иной порядок располо-
расположения элементов матрицы v. В таких случаях X уже не будет
иметь вид блочно-диагональной матрицы. Более подробно
этот вопрос будет рассмотрен в § 3.5 при вычислении матрицы
преобразования для пространственного бруса.
Отметим также, что в некоторых случаях удобно пользо-
пользоваться криволинейной местной системой координат (см., на-
например, § 3.7), для которой матрицы преобразования отдель-
отдельных узлов будут отличаться друг от друга. Пусть тело имеет
узлы ./, 2, ..., т; через klt A,2, .... %т обозначим матрицы пре-
преобразования в соответствующих узлах. Если в обеих матри-
матрицах v и v последовательно перечисляются перемещения уз-
57
дов 1,2, ..., т, то матрица X будет иметь вид, подобный C.6)
но диагональные блоки здесь будут различными:
>., О
О 1т
Подобным же образом строится матрица Ьв случае, ког
да в разных узлах тела учитывается различное число степене!
свободы, т. е. когда матрицы v,- имеют неодинаковый размер
Отметим в заключение, что, как вытекает из сути вывода
преобразование к =* №кк справедливо не только при поворо
те координатных осей, но и вообще при любой замене узловьп
перемещений, представленной в форме v <*= kv.
§ 3.3. Ферменный элемент
Ферменным элементом будем называть прямолинейный
стержень, который присоединяется к другим конструктивны!*,
элементам посредством идеальных шарниров. Если к нему ш
приложены поперечньк
нагрузки, то он буде1
испытывать лишь растя
жение или сжатие. Вы-
Выведем матрицу жестко-
жесткости этого элемента, вы-
выбрав местные координа-
координаты таким образом, что-
чтобы ось х совпадала с
продольной осью стерж-
стержня (рис. 3.6, а).
В рассматриваемом
случае узлами являют-
являются концы стержня i, /,
в которых действуют силы Рц и Pfx, направленные
вдоль оси 1с. Перемещения этих узлов вдоль оси стержня
обозначим через v.- и v.~. Узловые силы и перемещения в ме-
местной системе координат образуют матрицы
р..
вг
Нг
Ф
hi
Ф
1,
®
,1
б) vr*
pii
ft».
X
%Pj* =kn
w
irig-ff
Рис. 3.6
р =
58
которые связаны зависимостью Р — kv или
Для вычисления элементов матрицы жесткости к стерж-
стержня предположим сначала, что узел / получил единичное пере-
перемещение в положительном направлении оси к, в то время как
узел / остался неподвижным (рис 3.6, б). В соответствии
с физическим смыслом сила Р.-, создающая такую деформа-
деформацию, совпадает численно с величиной Ъц, а реакция Р.- в
закрепленном узле / — с величиной кцш.
Лгв*«: р1х-^Ьи- C.13)
Воспользуемся далее известной из сопротивления материа-
материалов формулой А/ = Pll(EF) для изменения длины стержня,
нагруженного осевой силой Р (F — площадь поперечного
сечения). Подставив сюда А/= vt~ = 1, Р = Р.- = kit, на-
находим ka = EFII.
Из условия равновесия стержня следует равенство Р.- =
¦=*—Р,-, так что с учетом C.13) имеем &,-,-=—kit =
= — EFII.
Совершенно аналогично рассмотрим деформирование стерж-
стержня по схеме рис. 3.6, в; это дает значения kjj = — кц — EFII.
Таким образом, матрица'жесткости ферменного элемента
в местной системе координат оказывается равной
г EFT 1 —
Здесь для определенности указаны номера /, / строк и
столбцов в соответствии с порядком расположения элементов
в , матрицах Р и v.
Отнесем теперь ферменный элемент к общей системе коор-
координат (рис. 3.7). Пусть ось стержня составляет с осями х, у,
г углы, косинусы которых равны
- V(xj - хгГ + (yj -уif + (zj -ztf. C.15)
59
Перемещение каждого узла имеет составляющие по всем
трем осям общей системы координат, поэтому матрица: щ
перемещений узла / будет иметь три элемента: . , ¦ ,
v; = {v,x vtu vit).
Силы, действующие в узле i, образуют матрицу*
Проектируя перемещения узла / на направление местной
оси х, получим
У
Матрица v,- перемеще-
перемещений узла I в местной си-
системе координат состоит
из единственного элемента
и_, поэтому последнее
Рис. 3.7 равенство устанавливает
требуемую связь между
перемещениями узла i в местных и общих координа-
координатах. Если обозначить через Хо матрицу
*Ч> — "'Ох
C.16)
то оно примет стандартную форму v( = A,ov,-. Для стержня
в целом получаем
Обозначая через
* Здесь и далее верхним индексом «г» будем отмечать в общей си-
системе координат те величины, которые относятся к отдельному кон-
конструктивному элементу (от англ. «element»). Так, Р^ будет означать
матрицу сил, действующих в узле / на рассматриваемый конструктив-
конструктивный элемент, в отличие от матрицы Pj внешних сил приложенных к
узлу I конструкции. Ясно, что v' = v/.
60
матрицу узловых перемещений стержня в общей системе ко-
координат, представим это равенство в виде v*— far*, где
[о *
C.17)
Пользуясь, далее, формулой C.10), вычислим матрицу
жесткости к' ферменного элемента в общей системе коорди-
координат:
—F
l L
l ULov
Выполнив перемножение матрицы, можно получить сле-
следующее блочное представление матрицы жесткости к':
^[к-'к''!1 (зл8)
где все подматрицы
к;/==к;у = — к-/ = — k'a^^j-XlXo C.19)
имеют размер 3x3.
Если рассматриваемый стержень является элементом пло-
плоской фермы, то в общей системе координат каждый узел име-
имеет перемещения лишь в направлении двух осей (например,
х н у). В этом случае матрицы vf и Р| состоят из двух элемен-
элементов:
а матрица А,,, равна
Ло •= \XJx K-J. C.20)
Матрица жесткости ке по-прежнему вычисляется по C.18),
но ее подматрицы C.19) будут иметь размер 2X2.
§ 3.4. Прямой брус в местной системе координат
Рассмотрим прямолинейный брус, воспринимающий в об-
общем случае все виды нагрузок (растяжение, изгиб в двух пло-
плоскостях и крученне). В качестве узлов i, / элемента возьмем
его концы. Местные оси выберем так, чтобы ось х совпадала с
продольной осью стержня, а оси у и ~г совпадали с главными
центральными осями его поперечного сечения
61
В каждом узле будем рассматривать б перемещений C ли
нейных и 3 угловых) и соответствующие им силовые факторы
(рис. 3.8).
Матрицы сил и перемещений для всего бруса можно соста-
составить, как и раньше, перечислив сначала силы (перемещения)
узла (, а затем узла /. Однако здесь удобнее расположить пере-
перемещения и силы в матрицах v и Р в ином порядке. При вы-
выбранной системе местных осей узловые силы распадаются на
четыре группы, которые можно рассматривать независимо друг
от друга. Силы Р(- иР^ вызывают только осевую деформацию
бруса и определяются перемещениями v.- и v.-. Образуем из
них соответствующие подматрицы, которые обозначим через
Р„
И V,
ча
Эти подматрицы связаны между собой равенством
Pe = kov0, C.21)
где ка — некоторая квадратная матрица размером 2x2
Силы Р.-, Р.-, а также моменты М(~, М.- вызывают из-
изгиб бруса только в плоскости ху и определяются только пере-
перемещениями v(~, v.- и углами поворота 9^-, 9. -. Составив из
этих компонент подматрицы
Р -
V
G2
связь между ними снова представим в форме
C.22)
где кь — квадратная 4x4 матрица.
Аналогично образуем подматрицы сил и перемещений
; v~ =
е.-
- У J
определяющих изгиб бруса в плоскости хг; соответствующую
матрицу жесткости обозначим через кс:
Рс=кс vc. C.23)
Наконец, кручение стержня вокруг оси х характеризуют
подматрицы
которые связаны соотношением
Pd = kdvd. C.24)
Через kd здесь обозначена еще одна подлежащая отыска-
отысканию матрица размером 2x2.
В совокупности формулы C.21)—C.24) дают связь между
узловыми силами Р = {Ра Рь Рс Pd} и перемещениями v =
= {vo \ь vc vd} рассматриваемого конструктивного эле-
элемента. Объединим эти формулы общим равенством
Ра
Рй
Рс
К
0
0
0
К
0
0
0
К
0
0
0
О 0 0 к,
Оно имеет стандартную форму Р = kv, где
"к„ О
C.25)
63
_ Таким образом, при выбранном расположении компонент
Р н v матрица жесткости к оказывается блочно-диагональной.
Переходя к вычислению отдельных блоков матрицы жест-
жесткости, начнем с матрицы ка. Эта подматрица связывает силы
Ро и перемещения va равенством C.21). Перемещения и силы
в матрицах \аи Ро расположены в том же порядке, что и в
матрицах v и Р для ферменного элемента, и определяют они
о.
Рис. 3.9
деформацию бруса вдоль оси. Поэтому подматрица ka совпа-
совпадает с матрицей жесткости C.14) ферменного элемента в мест-
местной системе координат:
k-
EF
_,
C.26)
Для вычисления подматрицы к6 необходимо рассмотреть
изгиб бруса в плоскости ху (рис. 3.9,а). Пусть и—прогиб
бруса на расстоянии х от левого конца. Полагая ? =
= 2x11— 1, введем безразмерную координату ?, которая
изменяется от —I в узле i до +1 в узле /.
Если на концах бруса заданы поперечные смещения и углы
поворота, то изогнутая форма бруса будет однозначно опреде-
определена. Другими словами, в соответствии с технической теори-
теорией изгиба балки прогиб и- однозначно определяется узловы-
узловыми перемещениями vft. В матричных обозначениях это озна-
означает существование равенства
u-(S) = a(g)v6, C.27)
где а. (?) — матрица-строка, четыре элемента которой являют-
являются функциями координаты \. Эта матрица будет в явной фор-
форме получена ниже, а сейчас перейдем к вычислению подмат-
подматрицы к,„ считая, что матрица a {&) известна.
Выпишем известные из курса сопротивления материалов
дифференциальные соотношения для изгиба балки постоян-
постоянной жесткости в плоскости ху:
d2u- АЛЛ d3ti.
йхг dx dx3
q
dx г d'x*
где J- — момент инерции поперечного сечения относительно
оси г; М — изгибающий момент в сечении балки; Q — пе-
перерезывающая сила; q — погонная поперечная нагрузка. По-
Положительные направления Q и М показаны на рис. 3.9, б,
а положительная нагрузка q действует по оси у. Такое прави-
правило знаков для М, Q и q при выбранной системе координат оп-
определяет положительные знаки в записанных выше формулах.
Переходя к дифференцированию по ?, перепишем данные со-
соотношения в виде
^- C>28)
Здесь и далее производные по ? отмечены штрихами.
На концах балки (при 5 = =П и ? = 1) изгибающий
момент и перерезывающая сила должны совпадать с их узло-
узловыми значениями. Учитывая направления сил и моментов,
приведенные на рис. 3.9, запишем Р{-= Q (—1); М{- =
= —М (—1); Pf- = —Q A); ЛГ~ = М A). Подстановка в
эти равенства соотношений C.28) дает
8?У- „ 4?7-
C.29)
SEJ- 4?У_
:
С учетом C.27) получаем отсюда следующую связь между
узловыми силами и узловыми перемещениями:
8EJ- _ 4EJ-
аA)^ Mtto(),>:
'' C.30)
8EJ- AEJ-
Зак. 651
В матричной записи эти формулы имеют стандартный вид
- Мь, где
EJ-
г
13
8а'" (—1)
C.31)
Таким образом, для формирования матрицы кь необхо-
необходимо определить матрицу-строку а (?) и воспользоваться фор-
формулой C.31).
Для отыскания матрицы а (?) обратимся к последнему со-
соотношению C.28). Здесь рассматривается изгиб бруса под
действием одних лишь узловых сил и моментов. Полагая в со-
IV
ответствии с этим q = 0, запишем и- (?) = 0. Решение это-
этого однородного дифференциального уравнения имеет вид
U- E) — C1 + C25 + С з§ + С4§Л, (о.о^)
где Clt .... С4 — произвольные постоянные, подлежащие оп-
определению из граничных условий. Последние заключаются в
том, что на левом конце балки прогиб и- должен равняться
vil}>
du- „ &и-
а угол поворота -— = - -т— должен
их ' ds
равняться
аналогичные соотношения имеют место на правом конце.
Таким образом, решение C.32) необходимо подчинить следую-
следующим условиям:
C.33)
Дифференцируя C.32) по |, находим
На основании C.33) приходим к уравнениям
C"i — Q-f C3 — С4 = у,-; Cj + С2 + С3 + С4 = v.-;
С2 -2С3
4= X 0 .г; С2 + 2С3 + ЗС4 = -~ в,- .
C.34)
66
Решая эту систему, находим
1
3
После подстановки постоянных в C.32) получим уравнение
изогнутой оси бруса
^ = J-B-36 + 6») V + -?-(l-?-
В матричной форме это выражение имеет требуемый вид
и- = а F) vb, где
C.35)
( + 3SS) 4A
4 8
Дифференцирование последнего равенства дает
«*G) = [-f-& -f (-1+36) -\\ -f
V ' [2 4 2 4 J
По формуле C.31) получаем искомую матрицу:
EJ-
г_
I3
12 6/ —12 6/'
6/ 4/2 —6/ 2/2
-12 —6/ 12 —6/
6/ 2/2 —6/ 4/2
C.36)
Отметим, что в некоторых случаях (например, для тонко-
тонкостенных балок) существенное влияние на перемещения может
3* 67
оказать деформация поперечного сдвига, которая не учитыва-
учитывалась при выводе формулы C.36). Значение матрицы жесткости
бруса при изгибе, учитывающее деформацию сдвига, можно
найтн в книге [20].
Далее рассмотрим изгиб бруса в плоскости xz (рис. 3.10).
В этой плоскости положительные узловые моменты (а также
углы поворота) направлены по сравнению с предыдущим слу-
случаем (см. рис. 3.9) в противоположную сторону. В остальном
У
tpr «Ч
Рис. 3.10
Рис. 3.11
обе схемы идентичны. Повторяя предыдущие выкладки, най-
найдем подматрицу
?/_
у
12
6/
12
6/
—б/
4Z2
6/
2/2
— 12
6/
12
6/
—б/
2/2
6/
4/2
C.37)
где J- — момент инерции сечення бруса относительно оси у.
i Рассмотрим, наконец, кручение бруса (рис. 3.11). Сече-
Сечение /относительно сечения i закручивается на угол df- — 8{.-,
Из курса сопротивления материалов известно, что крутящий
момент в сечении бруса М.~, необходимый для создания тако-
такого угла закручивания, равен
%¦*
GJ
кр
где GJKP — жесткость стержня на кручение.
Из уравнения равновесия имеем также
68
получаем Pd = kdvd
Объединяя эти соотношения в одно матричное равенство)
где
г- a i
C.38)
Формулами C.25), C.26), C.36), C.37) и C.38) определя-
определяется матрица жесткости бруса постоянной жесткости в мест-
местной системе координат.
§ 3.5. Прямой брус в общей системе координат
В общей системе координат матрицу Vе образуем, пере-
перечисляя, как обычно, сначала перемещения узла i, а затем —
узла /. В свою очередь, в каждом узле условимся перечислять
сначала линейные смещения, а затем угловые. Обозначим че-
через v* и 8, матрицы линейных и угловых перемещений узла i:
V, —
Vty
Тогда матрица Vj перемещений узла i будет
аналогичные обозначения введем для перемещений узла /.
Матрица узловых перемещений всего бруса в общей систе-
системе координат будет иметь следующую блочную форму:
-[:;]¦
V?
в,
-А.
Подобным же образом составим матрицу узловых сил Ре,
перечисляя сначала силы и моменты в узле i, а затем в узле /.
Полагая
~Р'и
р%
-Pi,-
Ml
Miy
-Ме»_
I.M,J
69
и пользуясь подобными обозначениями для узла /, запишем
Р.8
р;
Выразим, далее, v через v«, используя введенные в § 3.2
обозначения:
Проекция линейных перемещений узла i в общих коорди-
координатах на местную ось х равна vt- = ^-^г* + ^7 viy + Х^г х
X viz = Я,о-У; ; аналогичное соотношение запишем для узла
j:v.~ = ^o-v/ . Эти равенства устанавливают связь между пе-
перемещениями va и перемещениями vc:
в.
или в краткой записи
vo=a,ove, C.39)
где через Ка обозначена прямоугольная 2 х 12 матрица
*» = \ °Х - C-40)
Выразим, далее, перемещения \ь = {v{~ д.- v.- 0д} через
Vе. Проектируя перемещения vj, vy* на направление оси у,
находим
Если угловые перемещения, входящие в Qit Qj, предста-
представить векторами и спроектировать их на направление оси г,
то получим также
70
Объединяя все эти соотношения общим равенством
vfy
~%0- 0 0 0
о xE о о
о о к0- о
о о о х„
приходим к выражению
в котором
~к0- 0 0 0
о ьо~ о о
о о х0- о
0 0 0 кп
C.41)
C.42)
Подобные рассуждения позволяют выразить также матри-
матрицы vc и vd через Vе посредством соотношений
! = *Ч Vе,
где
0
0
0
[°
L0
0
к0-
0
0
0°"
0
0
0
0
0
0
0
к
0
Отметим, что все подматрицы, в том числе нулевые,
мулах для Я,а1 Л,ь, Я-,, и kd имеют размер I X 3.
C.43)
C.44)
C.45)
C.46)
в фор-
71
Связь между v и ve можно записать в виде одного равен-
равенства:
Введя обозначение
Vе.
_vL
К
J-d.
придадим этому равенству стандартную форму v = kve. Ма-
Матрица жесткости бруса в общей системе координат может
быть вычислена далее по формуле ke = №kk.
Удобнее, однако, преобразовать эту формулу таким обра-
образом, чтобы избежать формирования полных матриц к и К
Для этого нужно в правой части равенства
JtJ]
К о
О к.
К
выполнить перемножения блочных матриц; тогда
а V C47)
Отметим, что если общая система координат совпадает с
местной, то матрицы v" и \е (или Р и Ре) отличаются лишь
порядком перечисления компонент. В этом случае
Я,о- = [1 0 0]; *<0р = [0 1 0]; *,0- = [0 0 1]
и преобразование ке — Vkh будет заключаться в простой пере-
перестановке строк и столбцов матрицы к. В результате такой пере-
перестановки расположение элементов матрицы жесткости будет
согласовано с порядком следования сил и перемещений в ма-
матрицах Vе и Vе.
74
Рассмотрим особо частный случай, когда брус является
элементом плоской рамы. При этом каждый узел получает по-
поступательное перемещение в направлении двух коордннатных
осей и угловое перемещение в плоскости этих осей.
Если деформация бруса
происходит в плоскости ху
(рис. 3.12), то матрицы сил р
и перемещений в местной си- -
стеме координат имеют вид
¦й из
Рис. 3.12
Матрица жесткости бруса в местной системе координат
будет при этом равна
C.48)
где подматрицы ка и кь определяются формулами C.26) и
C.36).
В общей системе координат матрицы сил и перемещений сно-
снова представим в форме
-кна
где, например, подматрицы сил и перемещений узла / опреде-
определяются так:
"[» -К1-
Матрицы сил и линейных смещений каждого узла имеют
здесь по две компоненты:
а матрицы моментов и углов поворота состоят из единствен-
единственной компоненты:
Обозначая через \~, к0- матрицы
C.49)
73л
и проектируя компоненты матрицы Vе на направления местных
осей, получим
где
*..=
к
0
0
0
0
1
0
0
0
0
К
0
0
0
0
1
C.50)
Угловые перемещения Biz и Qjz при повороте координат в
плоскости изгиба не изменяются, поэтому на соответствующих
местах матрицы, связывающей v и ve, стоят единицы. Матри-
Матрицу к' можно вычислить по формуле
кв = *?квЬв +kTbkbkb. C.51)
В частном случае, когда общая система координат для пло-
плоского бруса совпадает с местной, имеем
V«=H 0];X0i=[0 1].
§ 3.6. Учет внеузловой нагрузки
Выше получена связь между узловыми силами и узловыми
перемещениями для бруса при отсутствии какой-либо внеузло-
внеузловой нагрузки. Рассмотрим случай, когда помимо узловых сил
на брус действуют также внеузловые нагрузки (распределен-
(распределенные или сосредоточенные).
Отнесем сначала рассматриваемый конструктивный эле-
элемент к местной системе координат. Если узловые перемещения
элемента равны нулю (концы стержня защемлены), то внеузло-
вая нагрузка вызовет появление реакций в виде сил и момен-
моментов. Образуем из них подматрицы Р0о, Роь, Рос и Pod, со-
соблюдая тот же порядок перечисления сил, что и в матрицах
Ра, Рь, Рс, Pd. Таким образом, в подматрицу РОа войдут реак-
реакции, действующие на стержень вдоль его оси; Роь и РОс бу-
будут состоять из поперечных сил и моментов, действующих на
концах стержня соответственно в плоскостях ху и xz; наконец,
в POd войдут моменты относительно оси х. Объединив эти под-
подматрицы, получим матрицу узловых сил, уравновешивающих
при неподвижных узлах внеузловую нагрузку:
•*0 —
ОЬ
'и\
74
Положительные направления реакций примем совпадаю-
совпадающими с положительными направлениями сил и моментов, ука-
указанными на рис. 3.8.
При вычислении матрицы Ро предполагалось, что узловые
перемещения отсутствуют. Если же узлы бруса получают пере-
перемещения, определяемые матрицей v, то дополнительные узло-
узловые силы, необходимые для их создания, определятся, как и
ранее, произведением kv. Таким образом, при наличии вне-
узловой нагрузки матрицу узловых сил Р можно иайти по
формуле
C.52)
Перейдем к общей системе координат х, у, z. Для вычис-
вычисления матрицы узловых снл Ре рассматриваемого бруса в об-
общих координатах воспользуемся формулой C.9), в которую
подставим выражение C.52). Это дает
Учитывая, что перемещения v и Vе связаны соотношением
v = Ъ/е, получаем
Произведение WkX дает матрицу жесткости ке бруса в об-
общей системе координат. Введя также обозначение
P*o=brPo, C.53)
имеем
pe = keve-f Р$. C.54)
Равенство C.54) определяет связь между узловыми сила-
силами и перемещениями в общей системе координат при наличии
внеузловой нагрузки. Матрица Ре0 содержит компоненты узло-
узловых сил и моментов, уравновешивающих внешнюю нагрузку
при Vе = 0 и отнесенных к общей системе координат. Учитывая
блочное представление матриц Ро и к, формулу C.53) можно
привести к более удобному для практических вычислений виду:
Р + *J" Рос + *-* Pod• C.55)
Компоненты матрицы Ре0 располагаются в том же поряд-
порядке, что и компоненты Ре. Поэтому равенство C.54) может быть
представлено в следующей блочной форме:
75
Здесь Р^ и Ро/ — подматрицы сил, уравновешивающих
внеузловую нагрузку, для узлов / и / соответственно. Так же
как и в Р?, первые три элемента матрицы Ре01 — проекции си-
силы, действующей в узле /, на координатные оси х, у, z, а по-
последние три — моменты относительно этих осей. Аналогич-
Аналогичным образом располагаются компоненты сил и моментов в под-
подматрице Ро/.
Таким образом, при действии внеузловой нагрузки необ-
необходимо сформировать матрицу реакций Ро и по C.55) найти
матрицу Ре0. Значения реакций, составляющие матрицу Ро,
для многих встречающихся на практике видов нагружения
имеются в справочной литературе. При отсутствии справочных
данных можно вычислить их, пользуясь известными методами
сопротивления материалов. Для наиболее часто встречающе-
встречающегося случая действия на брус поперечной нагрузки можно вы-
вывести простую формулу для расчета матрицы реакций.
Рассмотрим нагрузку, действующую в плоскости ху. Задача сво-
сводится к вычислению матрицы
Для решения этой задачи обратимся к дифференциальному урав-
уравнению изгиба бруса в плоскости ху C.28):
16EJ-
г
Общее решение этого уравнения имеет вид
где «о (?) — какое-либо частное решение неоднородного уравнения.
Постоянные Cj ... С4 должны быть найдены нз условия полного за-
закрепления бруса на концах: и- (—1) = 0; и- A) = 0; и'_ (—1) = 0;
ui A) = 0.
у
Получаемая отсюда система уравнений относительно произволь-
произвольных постоянных полностью совпадает с C.34), если в правых частях
заменить у;-, v - на —«„ (—1), —«0A), а '^-/2. /9.-/2 — на —«о (—1).
—«о (О соответственно. Решив эту систему, представим выражение
для и- (|) в виде
где матрица а (|) дается равенством C.35), а через v0 обозначена ма-
матрица-столбец
B 2 )
vo = |M-l) — «„(-О «оA) -y-«;(l)j.
Для вычисления узловых сил, входящих в Роь. воспользуемся
равенствами C.29). Учитывая C.31), для искомой матрицы получаем
выражение
D * — D^ \г \1 /о сс\
¦о& — " —*¦»& »о» («*5о/
где
4?7_
г
Итак, для вычисления Ро& необходимо построить частное решеиие
ио (?) Уравнения изгиба бруса, сформировать матрицы Р* и v0 и вос-
воспользоваться затем формулой C.56). Проиллюстрируем эту процедуру
на двух примерах.
Рис. 3.13
Пример I. По всей длине бруса действует распределенная попе-
поперечиая иагрузка q = const (рис. 3.13, а). Частным решением урав-
уравнения изгиба будет функция
ql*
Матрицы Р* и v0 оказываются равными
р*_
3L
— 4
ql*
384EJ-
г
-8/1
I
811
Согласно C.56), находим искомую' матрицу
<//. _.
2
Роб
I 2 12 2 12 f
C.57)
Пример 2. Сосредоточенная сила S приложена на расстоянии дг0
от левого конца балки (рис. 3.13, б). Величине *„ соответствует безраз-
безразмерная координата So = 2ij//— 1.
Здесь мы имеем два участка, для одного из которых —1 < ? < U»
а для другого So < | ^ 1; на каждом из иих поперечиая иагрузка от-
отсутствует. На первом участке принимаем щ (S) = 0; тогда на втором
частное решение должно при | = So обеспечивать непрерывность пере-
77
мещеиий и угла поворота, а также непрерывность изгибающего момен-
момента; при этом перерезывающая сила должна претерпевать скачок иа
величину 5. Для выполнения этих условий возьмем и0 (|) для второго
участка в форме общего решения однородного уравнения, а именно:
- |„K.
«о (I) = С, + С2 а - |„) + С, (I - 1оJ +
Постоянные С; определяются условиями
последние два равенства вытекают из соотношения C.28).
Отсюда находки Сг — С2 = С3 = 0; С4 = S/s/D8?7-) и оконча-
окончательно выражение для и„ (i) получаем в виде
0 при — 1 < | < |0;
г
Пользуясь далее описанной выше процедурой, приходим к матрице
—2A—goJB + io)
2-6t)
Если, в частности, сила приложена в середине пролета, то |0 = 0,
в этом случае
РоЬ= {—S/2 —S//8 —S/2 S//8}. C.58)
§ 3.7. Плоский круговой брус
Рассмотрим плоский круговой стержень радиусом г, нагруженный
силами в своей плоскости (рис. 3.14). Предполагаем, что одна из глав-
главных осей инерции поперечного сечеиия стержня также лежит в его пло-
плоскости. В качестве узловых возьмем перемещения и силы, показанные
на рис. 3.14. На стержень может действовать также внеузловая нагруз-
нагрузка (на рис. 3.14 показано для примера действие распределенной ради-
радиальной нагрузки q). _
Матрица Vj перемещений узла i включает в себя касательное уц
и радиальное и,-2 перемещения, а также угол поворота и,-3:
Vi — {vn vi2 vi3);
матрица перемещений узла /:
V]={Vh Vjj Vji).
Аналогично образуются матрицы узловых сил
78
Для всего элемента имеем,
¦-№ Ч
Связь между матрицами Рву при наличии внеузловой нагрузки
дается соотношением C.52). Для вычисления матриц к и Ро можно вос-
воспользоваться решением дифференциального уравнения изгиба кру-
гового бруса. Мы, однако, продемонстрируем здесь другой подход,
пригодный для случая бруса переменной жесткости. Запишем соотно-
соотношение C.52) в блочной форме:
Puj
отсюда следуют два равенства
C.59)
Здесь через krs (r, s =
= i, j) обозначены подмат- л /л, >'
рицы жесткости_ размером <г' И'
3 X 3, а Р„г и "p0J- со дер- ( \
жат силы, вызываемые вне- >^С—
узловой нагрузкой соответ- р г- /р /^ \
ственно в узлах j н / при ivvul i3 i3'
полном закреплении этих
узлов.
Если положить v; = О
(узел / защемлен), то из
первого _равенства CJ59)
получим Р,- = кц\1 + Ро,-. _
Умножая это соотношение слева на 1Ш1, имеем
ic,7 ' Pj = ^i + k,7 ' Pot-
Последний результат можно представить в виде
где введены обозначения:
Рис. 3.14
C.60)
C.61)
Полагая
8ц б12 б13
б2
цб31б32
21
б31б3
запишем C.60) в скалярной форме:
Via= б21 7>ц
2+ «3
«30 •
Мы получили соотношения, которые устанавливают связь между
перемещениями узла i и силами, действующими в этом узле, при за-
защемленном узле /. Элементами Ьтп матрицы Д;$ являются перемеще-
перемещения узла_( от действия единичных сил, совпадающих по направлению
с силами Pjj матрица же voj определяет перемещения узла i от дейст-
действия иеузловых нагрузок. Поскольку перемещения можно легко найти,
пользуясь, например, известным методом Мора, то отсюда вытекает
следующий способ отыскания матриц ки и Pai.
Защемив _узел_ / и прикладывая единичные силы по направлению
перемещений vilt i>,-2, vt3 узла i, а также внеузловую нагрузку, вычис-
вычислим по методу Мора элементы матриц А;,- н vO(. Интересующие нас
матрицы кц и Poi найдем затем, пользуясь соотношениями C.61),
из которых следует, что
• k"ii = A/71; Poj-= —"k/i v"oi- C.62)
Для отыскания остальных подматриц жесткости, а также матрицы
Ро;- можно воспользоваться условиями равновесия всего стержня в
целом. Запишем, например, условие равенства нулю суммы проекций
всех сил на направление перемещения v;1 (см. рис. 3.14):
Р~и cos ф — P~i2 sin ty + Pji +P}j = 0,
где через Pjx обозначена проекция результирующей внеузловой внеш-
внешней нагрузки на направление vj1. Отсюда
Pji— — ~Р~ц cos г|) + Pi2 sin г|) — Я/'i.
Проектируя силы на направление Vj.it находим аналогично
Наконец, вычисляя сумму моментов относительно узла /, получим
Яуз="Ра г A —cos У)-\-РцГ sin гр — Pi3 — Р/л.
В последних формулах через Р/г обозначена проекция внеузловой
нагрузки на направление перемещения vj2, а через Р'-3 — ее момент от-
относительно узла / (Pfi, P'j2 H Р)г считаются положительными, если
они совпадают по направлению с i';1, и/2 и vj3).
Получеиные соотношения дают связь между силами в узлах < и /.
В матричной форме их можно записать так:
pJ = ftPj—P', C.63)
где
—cos г|) sin г|) 0
— sin tp —costp 0
г A—cosip) r sin -ф —Ij
80
Если в C.63) внести формулы C.59), то получим равенство
к л ^i+kjj vj+ Ро/= п (k"ii vH- k~ij \r\- P0!) — P'0J.
Это равенство должно выполняться при любых значениях узловых
Перемещений, поэтому из него вытекают соотношения
О!/-.* 1г . .— OL .* Р з ОР Р' /Ч fid^
it —*u"li* JJ— "•!/» Oj— r0i 0/' \ ¦ /
Совместно с равенством k,7= kj{, которое является следствием
симметрии матрицы жесткости к, эти формулы позволяют вычислить
все подматрицы жесткости по известной матрице к,-,-, а также матрицу
Рис. 3.15
Ро; по известной матрице POj. Вычисления по формулам C.62) н C.64)
удобно выполнять численно с помощью ЭВМ, сформировав предвари-
предварительно матрицы A;,-, vOi, Q и Р'о-.
Перейдем к вычислению элементов матриц А,-,- и v0,-. В соответствии
со сказанным выше рассмотрим действие на стержень единичных
сил и внеузловой нагрузки. На рис. 3.15 даны эпюры изгибающих мо-
моментов в каждой единичной системе^ и от внеузловой нагрузки.
Перемещение 6т„ в направлении силы Pim от действия единичной силы,
совпадающей по направлению с Рц, (т, я— 1, 2, 3), определяется ин-
интегралом Мора.
C.65)
где F, J — площадь поперечного сечения и его момент инерции относи-
относительно центральной оси, перпендикулярной плоскости кольца; М
N и Q — изгибающий момент, осевая и перерезывающая силы в сече-
пин стержня; kg—- коэффициент, зависящий от формы поперечного се-
сечения.
81
Первое слагаемое в подынтегральном выражении учитывает изгиб,
а два других — растяжение и поперечный сдвиг. Если пренебречь вли-
влиянием деформаций растяжения и сдвига, то вычисление перемещений
несколько упрощается. Полагая, кроме того, момент инерции бруса
постоянным н переходя к нитегрированию по углу а посредством заме
ны d/ = rda, имеем
^ [тМ„ da. C,66)
Зависимости изгибающих моментов в единичных системах от угла
а даны иа рис. 3.15. Подставляя их в формулу C.66), находим:
г3 Г 3 1)> "|
6п ="?у — (ф — sin ij>) —sin i|) sin2 — ;
2/* ф
S12 = 621= — Мп«т;
613 = 63i = — -gj- (ф —sin ф);
«« = ¦¦
Если угол i() мал, то во избежание потери точности коэффициенты
^13 и <522 лучше вычислять по формулам:
e 11=^-v у (_d* * — фа*.
~ BA+3)! * "
22 ?7 * ^ * ; BЛ+3)!
полученным из предыдущих формул разложением функций в степен-
степенные ряды, либо вести счет с двойной точностью.
Перемещения узла i в направлении Pilt Pt3 и Рг3от виеузловой на-
нагрузки определяются формулой
?
82
Пренебрегая деформациями растяжения й сдвига, в случае посто-
постоянной жесткости получим отсюда
fi —
Мо Мт da (т = 1, 2, 3).
Для каждого конкретного типа виеузловой нагрузки можно найти
зависимость изгибающего момента Мо от угла i)> и вычислить переме-
перемещения бт0.
Значения коэффициентов бтП и
5т0 при необходимости нетрудно
уточнить, используя полные выра-
выражения для интеграла Мора C.65)
и C.67). Если брус имеет перемен-
переменное сечение, то интегрирование луч-
лучше выполнять непосредственно иа
ЭВМ каким-либо численным мето-
методом (например, методом Симпсона).
Выше получена связь между
узловыми силами и перемещениями
рассматриваемого бруса в местных
координатах. Отнесем теперь брус
к общей системе координат х, у.
Пусть радиус-вектор /•*, соеди- ис' '
няющий центр кольца О с узлом j,
составляет угол г|>; с осью х, а радиус-вектор rj — угол tyj (рис. 3.16).
Введем матрнцы проекций узловых сил на координатиые оси
Vе —
Р1:.
а также матрицы узловых перемещений
IV
Vjx
Проектируя перемещения v; на направления перемещений
vi2* vi3- устанавливаем связь v,- = A.(V,-, где
Sin 1));
COS I));
0
— COS 1));
sin ij);
0
0
0
!
83'
Аналогично, Vj = kjVj, где
sinijty
COSIjty
0
—COS ypj
sin ypj
0
0
0
1
Связь между узловыми перемещениями v = {vtvj} и Vе =
= {V[ vj} определится тогда равенством v = Xv*, в котором
По формуле к* = Х,гкХ, вычисляем матрицу жесткости в общей сис-
системе координат. Учитывая, что матрица жесткости в местной системе
координат получена в блочной форме
к =
удобно н матрицу к* представить в виде
Выражение для типовой подматрицы к", получим из соотношения
к* = Хг кЛ,, представив входящие в него матрицы в блочной форме:
k^ = ^krsbs (r, s=«, /).
Изложенный в этом параграфе способ построения матрицы жестко-
жесткости можно применить и при изгибе бруса нз своей плоскости, а также в
общем случае пространственного изгиба бруса (в том числе с пронз.
вольным расположением главных осей инерции поперечного сечеиия).
Отличне будет лншь при вычислении коэффициентов податливости бтП;
в случае пространственного изгиба матрица жесткости к будет иметь
размер 12X12.
§ 3.8. Стержневая система
Рассмотрим стержневую систему, отнесенную к некоторой
системе координат х, у, г. Обозначим через v,- матрицу пере-
перемещений типового узла i. Число элементов этой матрицы
(число степеней свободы узла) зависит от типа конструкции.
Так, для пространственной фермы матрица v,- будет содержать
три перемещения узла в направлении координатных осей
v,- = {vix vly vlz),
а для плоской фермы — два перемещения
v,- = {vix viy).
84
В случае пространственной рамы матрица
V; = {Uix Viy Viz 0ix Qiy Э,г}
состоит из трех линейных смещений и трех углов поворота.
Если же плоская рама нагружена силами в своей плоскости,
то матрица
V; = {Vix Vty Э;}
включает в себя два линейных смещения и угол поворота.
Матрицу внешних сил, действующих в узле i в направле-
направлении перемещений vb обозначим через Р,. Число элементов
этой матрицы совпадает с числом степеней свободы узла; пе-
перечислять силы в матрице Р, всегда будем в том же порядке,
в каком перемещения располагаются в матрице v;. Так, на-
например, для пространственной рамы
Pi = {PtxPtv PizMixMiuMiz).
Матрицы узловых сил и перемещений для всей конструк-
конструкции обозначим буквами Р и v и составим их следующим об-
образом:
p _
где т — число узлов стержневой системы.
При отсутствии внеузловои нагрузки связь между матри-
матрицами Р и v может быть представлена в виде Р = Kv, где К —
матрица жесткости системы.
Если же помимо узловых сил действуют внеузловые на-
нагрузки, то можно рассуждать так же, как и в случае отдель-
отдельного стержня. Предположим, что все узлы защемлены; тогда,
в результате действия внеузловои нагрузки, со стороны нало-
наложенных связей возникнут силы реакции. Перечисляя реакции,
действующие в узле i, в том же порядке, что и для матрицы
Р,, образуем матрицу Ро/; число элементов этой матрицы сов-
совпадает, конечно, с числом степеней свободы узла. Для всей
конструкции можно составить матрицу
"Рог
Ро2
p2
pm
; v =--
_vm_
_r0m_
85
Если, далее, узлы имеют некоторые смещения v, то для их
создания необходимо дополнительно приложить силы, вели-
величина которых зависит от жесткостных характеристик систе-
системы; матрица этих сил может быть вычислена как произведение
Kv. Таким образом, связь между узловыми силами и узло-
узловыми перемещениями можно в общем случае записать jтак:
Р = Kv + Ро. C.68)
Покажем теперь, как можно найти матрицы К и Ро, зная
матрицы ке и Р* для отдельных конструктивных элементов,
образующих систему. Запишем прежде всего уравнение C.68)
в блочной форме:
Kii ... Ki f ... Ki^.
и
kir
01
U U U
лт1 ••¦ лпи ••• лтт
и выпишем его i-ю строку:
Рг = kuVx + ... + ktjVj + ... + kimvm + Po{. C.69)
Для вычисления подматриц ktl, ..., kim, а также подма-
подматрицы Ро; рассмотрим равновесие узла L В качестве примера
на рис. 3.17 показан узел плоской рамы со всеми сходящими-
сходящимися в нем стержнями. Выделим один из конструктивных эле-
элементов, соединяющихся в узле i (например, стержень /).
Рассматриваемый элемент соединяет узел i с некоторым дру-
другим узлом г. Пусть матрица жесткости этого типового элемен-
элемента в общей системе координат равна ке. Силы Р = {Pet Рег),
действующие в узлах данного стержня, связаны с перемеще-
перемещениями ve = {v,- vr} его узлов соотношением Ре — keve ¦+• PS.
где Р% = {Р'о,- Рог} — матрица реакций, возникающих в уз-
узлах элемента от внеузловой нагрузки при Vе = 0.
Перепишем это соотношение в блочной форме:
Гг\ IX Кг.
Отсюда получим выражение для матрицы сил, действую-
действующих в узле t на рассматриваемый элемент:
Pj=k«Vj + k'rVr + Po«. C.70)
86
Соединим теперь все стержни; тогда из условия равновесия
узла имеем Р* — 2 Р?, где суммирование ведется по всем стерж-
стержням, сходящимся в узле i. Подставляя сюда C.70), получаем
Р, = 2 к% vt + '2к?, vr + 2 Р5*. C.71)
Для представленного на рис. 3.17 примера равенство
(ИЛ) примет вид
Р.=(|# >+М1Г + КГ + W1) vt+(к#» + k/p") vp+
+ к<|> vq + k//> v. + Pi}> +РЙ> + РЦ> + Рй>, C.72)
где верхний индекс в скобках относится к номеру стержня.
Рис. 3.17
Сопоставим полученный результат с равенством C.69).
Прежде всего замечаем, что в C.72) или для общего случая
в C.71) отсутствуют члены, содержащие перемещения тех уз-
узлов /, которые не связаны стержнем непосредственно с узлом i.
Это означает, что соответствующие подматрицы кц являются
нулевыми. Если узел /связан с узлом / одним стержнем (в рас-
рассматриваемом примере таковыми являются узлы q и s), то мно-
множителем при vy оказывается подматрица к'/ этого элемента,
поэтому для таких узлов к,-; = к?/. Если же узел / связан с
узлом i несколькими элементами (узел р на рис. 3.17), то мно-
множителем при Vj будет сумма подматриц kj/ элементов, соеди-
соединяющих узлы i и /, т. е. в этом случае кц — 2kf/. Наконец,
множитель при у{, являющийся диагональной подматрицей
матрицы К, равен кц = 2к«, где суммирование выполняет-
выполняется по всем элементам, сходящимся в узле /.
87
Из сказанного следует, что матрицу жесткости стержневой
системы можно образовать из матриц жесткости разрознен-
разрозненных конструктивных элементов по следующему правилу:
ktj = 0, если узлы * и / не связаны непосредственно никаким
элементом; к^ = 2к*,-, если узлы i и / связаны несколькими
элементами (суммирование выполняется по этим элементам);
кц = 2к«, где суммирование ведется по всем элементам,
сходящимся в узле *. Все эти случаи можно объединить общей
формулой
к„ = Щ (i, /=1,2, .... т), C.73)
где суммирование выполняется по всем конструктивным эле-
элементам, входящим в стержневую систему. При этом следует
принимать для элемента кец = 0, если этот элемент не соеди-
соединяет узлы i, /.
Таким образом, для получения матрицы жесткости стержне-
стержневой системы можно все элементы матрицы жесткости каждого
стержня
поместить в соответствующие ячейки общей матрицы жестко-
жесткости (положение ячеек определяется нижними индексами) и
произвести затем суммирование всех накладывающихся эле-
элементов.
Аналогичное правило суммирования получается и для вы-
вычисления матрицы Р„. Сравнивая последние слагаемые в
C.69) и C.71), заключаем, что подматрицу Рог можно найти по
формуле
Po«=2Po» (З-74)
где суммирование ведется по всем конструктивным элемен-
элементам, сходящимся в узле L
Поясним схему формирования общей матрицы жесткости
на примере плоской рамы (рис. 3.18).
Эта рама имеет четыре узла и включает в себя пять стерж-
стержней. Матрицы жесткости стержней в общей системе координат
представим в блочной форме:
t B) __ Ml М
k»> ¦ • ¦' ~
kiV kiV
12 I. fcC)
I*
'. .,„ rktt» kiV
1 « ' " "I ,t« - tm\
"kJV kia34
.k^i' k^}J:
Напомним, что нижние индексы », / означают номера уз-
узлов данного стержня, а верхний индекс — номер стержня.
В соответствии с числом узлов рамы матрица жесткости
системы К будет иметь 4x4 блоков. Подматрицы ki7- (», / =
-= 1, 2, 3, 4) образуются путем суммирования всех подматриц
К-
0
?
t
Рис. 3.19
жесткости отдельных элементов с одинаковыми нижними ин-
индексами. Так, подматрица k12 = kiV + k[%\ В итоге получим
-kJV+kH4kiV
кй'+кй»
kiV
0
|K2
[0
11
0
kiV
k|V
IkJV+kiVj
Некоторые подматрицы (например, k14) оказались нуле-
нулевыми, так как соответствующие узлы непосредственно не
связаны между собой стержнем.
Расположение нулевых подматриц в матрице жесткости К
определяется порядком нумерации узлов. Нумеруя узлы опре-
определенным образом, можно иногда добиться того, чтобы все
ненулевые подматрицы были сгруппированы вблизи главной
диагонали, т. е. добиться ленточной структуры матрицы
жесткости (рис. 3.19). Примеры такой нумерации узлов пока-
8b
заны на рис. 3.20 для случая плоской рамы. Рассмотрим, на-
например, узел 10 в схеме 3.20, а. Максимальный номер узла,
с которым он связан непосредственно стержнем, — 16, мини-
минимальный — 4. Поэтому в десятой строке матрицы жесткости
К (записанной в блочной форме) первая ненулевая подматри*-
ца появится в четвертом, а последняя — в шестнадцатом
столбцах. Выполняя подобные рассуждения для других узлов,
можно убедиться, что все ненулевые подматрицы образуют
ленту коэффициентов, ширина которой в данном примере по-
постоянна и равна 13 подматрицам. Учитывая симметрию ма-
матрицы жесткости, можно говорить о полуленте, ширина ко-
19 be
13
14
21
К
22
16
23~<
17
7 W \9 \10 \11
24
18
12
7
6
12
11
W
16
15
п
2& 2к
19
23
№} 22
1 г з ь s 6
а)
9 13 11
5)
21
Рис. 3.20
торой (включая диагональную подматрицу) равна 7. Посколь-
Поскольку в случае плоской рамы каждая подматрица имеет размер
3-х 3, фактическая ширина полуленты будет равна 21.
Ленточная структура матрицы жесткости обладает боль-
большими вычислительными достоинствами по сравнению со слу-
случаем полного заполнения. Во-первых, в памяти ЭВМ нет на-
надобности хранить всю матрицу: достаточно иметь лишь те
коэффициенты, которые заключены внутри полуленты. По-
Поскольку ее ширина Af0 часто значительно меньше размера мат-
матрицы N, то это позволяет достичь существенной экономии па-
памяти, что весьма важно в задачах с большим числом степеней
свободы. Во-вторых, все операции, в которых участвует ма-
матрица жесткости, можно выполнять только с теми элементами,
которые ограничены шириной ленты; это значительно эконо-
экономит время вычислений. Чем меньше ширина ленты, тем эф-
эффективнее будет решение задачи. Поэтому всегда следует
тщательно продумывать порядок нумерации узлов. Так, в
рассмотренном выше примере более удачной является схема
нумерации узлов, показанная на схеме 3.20, б. Она приводит
к ленточной матрице с шириной полуленты, равной 15.
90:
§ 3.9. Определение узловых перемещений
До сих пор мы полагали, что зависимость C.68) служит для
определения сил Р, необходимых для создания известных пе-
перемещений v. Если же, наоборот, известны силы, действующие
внузлах конструкции, то C.68) можно рассматривать как си-
систему алгебраических уравнений относительно перемещений v.
-•- Если конструкция закреплена, то перемещения соответст-
соответствующих узлов в направлении опорных связей равны нулю,
остальные же перемещения подлежат отысканию. Все компо-
компоненты перемещений можно расположить таким образом, что-
чтобы в матрице v сначала перечислялись все неизвестные, а
затем — известные (нулевые) перемещения. Тогда матрица v
будет представлена в блочной форме
v =
где матрица va содержит только неизвестные перемещения,
а подматрица vp нулевая. Порядок перечисления сил в мат-
матрицах Р и Ро всегда должен строго соответствовать порядку
следования перемещений в матрице v:
В Pa входят известные внешние силы, действующие в на-
направлении перемещений \а. Подматрица Рр содержит силы,
действующие по направлению наложенных связей и представ-
представляющие собой реакции опор.
Строки и столбцы матрицы жесткости К мы должны рас-
расположить в том же порядке, в котором силы и перемещения
перечисляются в матрицах Р и v, т. е. матрица жесткости бу-
будет иметь следующую блочную структуру:
__ F
.Kpa
Представляя уравнение C.68) в развернутом виде и учи-
учитывая, что vB = 0, получим
ГКаа KapUVal ГР.1 ГРо.1
[КР« KppJ (.0 j [PpJ [PopJ-
Отсюда следуют два матричных равенства:
KaaVa = Р« - Рос! C.75)
Kpa va = Рв - Роэ. C.76)
91
Решая уравнение C.75), находим неизвестные перемещения
va, a C.76) позволяет найти реакции опор:
Рр — КрсЛа + РоE-
Заметим, что практически нет необходимости производить
перестановку элементов матриц Р, Ро и К. Матрицы Ра и Р0<х
можно получить, вычеркнув в исходных матрицах Р и Ро
элементы, соответствующие опорным связям; при этом вы-
чернутые члены составят матрицы Р6 и РоK. Матрица Каа
получится также вычеркиванием соответствующих строк и
столбцов из полной матрицы К- Матрица К/зе будет образова-
образована элементами, находящимися на пересечении вычеркнутых
строк и столбцов, а матрица Кра — элементами на пересече-
пересечении вычеркнутых строк и оставшихся столбцов.
Пользуясь аналогичными рассуждениями, можно рассмо-
рассмотреть и более общий случай, когда заданные перемещения vp
не равны нулю. Тогда вместо C.75) и C.76) имеем
Ka<xVa = Р<х — Роа — Ko8vpl
Р/3 = Kpav<x + KppVp + Р
ое-
Если перемещения узлов найдены, то для любого конструк-
конструктивного элемента будет известна матрица Vе перемещений
в общей системе координат. Применяя формулу C.7), можно
найти узловые перемещения элемента в местных координатах
v = К\е, а по формуле Р = kv + Ро —¦ вычислить узловые
силы, действующие на элемент.
Мы рассмотрели случай, когда конструкция закреплена на
опорах. Если система свободна, то непосредственно из урав-
уравнения C.68) перемещеиия найти нельзя, так как матрица жест-
жесткости К для всей конструкции является вырожденной. Дей-
Действительно, силы, действующие на свободную конструкцию,
не могут быть произвольными; они должны удовлетворять
уравнениям равновесия всей системы в целом. Таких уравне-
уравнений будет 6 для пространственной и 3 для плоской стержне-
стержневой системы. Таким образом, в случае пространственной кон-
конструкции 6 элементов матрицы Р — Ро в уравнении C.68)
определяются через остальные элементы, являясь некоторыми
линейными комбинациями последних. Но тогда и соответст-
соответствующие 6 элементов матрицы-столбца Kv будут также линей-
линейными комбинациями остальных. Это говорит о том, что строки
матрицы жесткости связаны между собой линейными зависи-
зависимостями. Определитель подобной матрицы равен нулю, т. е.
матрица жесткости для свободного тела является вырожден-
вырожденной.
Это обстоятельство математически отражает тот факт, что
перемещения свободного тела не определяются однозначно
действующими на него силами, поскольку оно может получить
произвольное перемещение в пространстве как жесткое тело
(т. е. без деформации). Перемещение системы как жесткого це-
целого можно устранить, закрепив ее статически определимым
образом. В случае пространственной конструкции мы должны
наложить 6 соответствующим образом ориентированных свя-
связей, а в случае плоской — 3. Дальнейший расчет выполняет-
выполняется так же, как и в случае закрепленной конструкции.
Изложенный метод расчета стержневых систем носит назва-
название матричного метода перемещений. В нем в качестве основ-
основных неизвестных принимаются перемещения узлов. Процедура
матричного метода перемещений не зависит от того, является
ли система статически определимой или неопределимой. При-
Причем чем больше внешних связей наложено на систему, тем ни-
ниже порядок разрешающей системы уравнений C.75), так как
количество неизвестных в ней равно числу элементов матри-
матрицы va.
В заключение отметим, что для решения системы линейных
алгебраических уравнений C.75) могут быть использованы
различные методы — как точные, так и итерационные. Чаще
всего применяется одна из разновидностей метода последова-
последовательного исключения неизвестных (метода Гаусса). Для до-
достижения необходимой эффективности решения должны учи-
учитываться такие специфические свойства матрицы жесткости,
как симметрия и ленточная структура. Подробное описание
соответствующих процедур можно найти в книгах [1, 15, 20,
25].
§ 3.10. Примеры расчета
Пример 1. Ферменная конструкция (рис. 3.21, а) состоит
из трех стержней, каждый из которых одним концом закреп-
закреплен неподвижно, а другим связан шарнирно с остальными
стержнями. К свободному узлу приложена горизонтальная
сила 5, направление которой указано на рисунке. Компоненты
узловых сил и перемещений перенумеруем последовательно,
как показано на рис. 3.21, б. Площади сечений F и модули уп-
упругости Е всех трех стержней примем одинаковыми. Пос-
Поскольку узлы 1, 3 а 4 неподвижны, матрица неизвестных пе-
перемещений будет содержать всего две компоненты:
[::]¦
Матрица сил
Матрица Каа, связывающая va и Ра, имеет вид
Г «38 ^34 1
U k \
L К43 К44 J
Для отыскания элементов этой матрицы рассмотрим преж-
прежде всего жесткостные характеристики стержней в местных
У
S
-л
la A
\
Ь а ^
а
X
Рис. 3,21
координатах. Для определенности будем принимать, что мест-
местная ось х направлена от узла с меньшим к узлу с большим но-
номером.
Длины всех стержней, а также косинусы углов между
местными н общими осями находим по формулам C.15), по-
получаем следующие значения:
Стержень
X] — Xi
I .
X-
XX
X-
xy
I
2a
a
2/VT
1/V
2
0
—a
a
0
1
3
a
—a
1/V
-1/V1
По C.14) находим матрицы жесткости стержней в мест-
местных осях:
EF
aV 5
1 —1
-1 1
EF
¦ к<2> =
1 —1
-1 1
?L[ 1-1].
" l-i ij
Используя полученные значения Х^х, Х- , выпишем матрицы
Яо для каждого стержня в соответствии с C.20):
-[0 -1];
Применяя формулы C.18) и C.19) к каждому стержню,
получаем матрицы жесткости отдельных элементов в общей си-
системе координат:
L1/K5
EF
l/]/5 ] =
2/5
1/5
1
4
2
— 4
9
2
1
2
. j
4
. _2
4
2
— 2
— 1
2
1
~0
0
0
0
3
0
1
0
— 1
4
0
0 ¦
0
0
5
or
-1
0
1
6
T 1C) —
-1/K2
1/2 —1/2
— 1/2 1/2
3 4 7 8
Цифры внизу и сбоку матриц означают номера сил и пере-
перемещений.
Наконец, сформируем матрицу Ка<х- Для этого просумми-
просуммируем соответствующие элементы матриц жесткости отдельных
1
— 1
— 1
1
J
1
1
J
— 1
1
1
— 1
1
J
J
1
95
стержней, стоящие на пересечении строк и столбцов с индек-
индексами 3 и 4. В результате получим
Коса =
EF
а
/5
?f Г 0,711 —0,174 1
= а [—0,174 1,442 \
1
2/2
1
Согласно C.75), система уравнений относительно неизвест-
неизвестных перемещений принимает вид
EF
Г?_Г 0,711 —0,1741 Г^зТ^Г — -S1
а [-0,174 1,442J [oj [ 0 J
Решая эту систему, находим
V,-— 1,450-^Ц; и4 = — 0,175 Sa
EF
EF
Отрицательные знаки в этих формулах указывают на то,
что узел 2 перемещается в отрицательных направлениях осей
х, у.
Матрицы перемещений \е в общей системе координат рав-
равны:
Sa
EF
- о -
0
— 1,450
_ — 0,175_
1
2
3
4
C) Sa
V "~ E~F
. ,.,21 S«
EF
"—1,450 ~
—0,175
0
0
3
4
7
8
~—1,450"
— 1,175
0
0
3
4
5
6
По формуле v=A<ve , где
96
находим перемещения в местных координатах:
-л, Г2/КГ i/j/T о о 1A)==_^Г о 1
[ 0 0 2/]/5 l/j/TJ EF L-1.373J'
fo -1 0 О1(8)в_5вГО.175].
[О 0 0 — 1 J EF [ о J '
_(8)
-C) Г1/К2 -l/J/2 О О 1C) =
[о О \fV~2 — 1/J/2J
— 0,900 1
о ]'
Наконец, по формуле Р = kv вычисляем узловые силы,
действующие на каждый стержень вдоль его оси:
1 _1 l_So_r 0 1 =5Г 0.615"
[EF
Г 0,6151.
[-0,615]'
,175 | 5Г 0,175 1
о J 1-0,175 J
r 1 -1 ] Sa г - 0,9001 Г -0,6331
[—1 1 J ?f [ 0 J [ 0.633J
Как видно из рис. 3.6, а, для растянутого стержня первый
элемент матрицы Р является отрицательным, а второй —
положительным и наоборот. Таким образом, стержни 1 и 2
сжаты, а стержень 3 растянут; осевые силы в этих стержнях
равны соответственно — 0,6155, —0,1755 и 0,6335.
Пример 2. Многоопорная балка постоянной жесткости
(рис. 3.22, а) нагружена сосредоточенным моментом Мо. Мо-
Момент инерции сечения балки относительно оси z равен Jг;
ось у совпадает с одной из главных осей инерции поперечного
сечения.
В данном случае имеет место изгиб балки в плоскости ху,
и в каждом узле достаточно рассмотреть два перемещения —
вертикальное и угол поворота. Узловые перемещения перену-
перенумеруем последовательно в соответствии с рис. 3.22, б. Неиз-
Неизвестными являются углы поворота vit ve, u8; все остальные
4 Зак. 651 97
перемещения равны нулю. Таким образом, матрица неизвест-
неизвестных узловых перемещений имеет вид
Матрица сил, действующих в направлении перемещений va,
j J,
Рис. 3.22
С
ф
Рис. 3.23
Поскольку внеузло-
вые силы отсутствуют,
матрицы Ра и va свя-
заны соотношением
где
Кок» —=
[I
«84 "86 «88 J
Для вычисления коэффициеитов матрицы Каа рассмотрим
сначала отдельные элементы балки в местных осях координат
(рис. 3.23, а). Поскольку рассматриваются лишь перемещения
изгиба в плоскости ху, матрицы узловых сил и перемещений
каждого элемента совпадают с Рь и v"b:
= Р6= \РГу
п РГу
= v6 = [v,- вй v,- 6,-}
а матрица жесткости к = кь определяется по C.36).
Далее, общая система координат ху совпадает с местной
системой ху для каждого элемента (рис. 3.23, б). Матрицы
98
сил и перемещений элемента в общей системе координат в рас"
сматриваемом случае имеют по четыре элемента:
ре — I ре ре I _ I ре ре ре ре \ ¦
V — (»f »// — V2i-\ r2t r2i-\ r2j\>
Vе ={v,- \]) = {V2t-\ V2l V2/~l V2j}.
Матрицы v и ve содержат одни и те же компоненты и при-
притом в одинаковом порядке, поэтому матрицы жесткости в об-
общей и местной системах координат совпадают. Учитывая это,
имеем
к<2> =•
к<3> =
EJ
/з
EJ
/з
EJ
I3
~ 12
6/
— 12
6/
1
~ 12
6/
— 12
6/
3
~ 12
6/
— 12
6/
6/
4/2
—6/
2/2
2
6/
4/2
—6/
2/2
4*
6/
4/2
—6/
2/2
— 12
— 6/
12
—6/
3
— 12
—6/
12
— 6/
5
— 12
—6/
12
—6/
6Г
2/2
— 6/
4Я
4*
6/ ~
2/2
—6/
4/2
6*
6/ '-
2/2
—6/
4/2
1
2 .
? '
4*
3
4*
5
6*
5
6*
7
8*
Звездочкой'помечены те строки и столбцы, на пересечении
которых находятся элементы, требуемые для формирования
матрицы Каа- Суммируя эти элементы, находим
?7
I3
8/2 2/2
2/2 8/2
0 2/2
О
6 = •
2EJ
4 1 О
1 4 1
О 1 2
Теперь система уравнений относительно vo примет вид
2?7
Щ
Л.
—
0
0
99
Решая систему, находим
Матрицы узловых перемещений отдельных элементов равны:
~vt
Щ
v3
Л-
М01
26EJ
~C)
у -—
0
0
0
J _
• 7А2> .,<2>
> V = V =
C)
V =
Щ
щ
1
з~
v6
_ Мв 1
26EJ
_ лу
26EJ
" 0"
4
0
2
*
' 0
1
0
.—4
Силы, действующие в концевых сечениях элементов, най-
найдем по формуле Р= kv:
- p(i)~
i У
Д/гС)
р(О
i у
_ ^1о_
13/
¦ з"
2
.21 _
- р(_2)~
iy
рB)
/I'
_ ма
13/
-_g-
— 2/
9
— 71
~ р(?)~
iff
д,C)
рC)
^ Гу
__Мо_
13/
-—6"
— 6/
6
.. 0_
Так как внеузловая нагрузка отсутствует, то в пределах
каждого участка перерезывающие силы Q будут постоянны,
а изгибающие моменты М изменяются по линейному закону.
Эпюры Q и М представлены на рис. 3.24.
Пример 3. Рассмотрим плоскую раму (рис. 3.25, а). Го-
Горизонтальный стержень нагружен равномерной нагрузкой q,
а в середине вертикального действует сосредоточенная сила
ql. Оба стержня имеют одинаковые площадь F и момент инер-
инерции J поперечного сечения относительно оси, перпендикуляр-
100
ной плоскости рамы. Схема нумерации и положительные на-
направления узловых сил и перемещений показаны на
рис. 3.25, б.
До сих пор при построении матрицы жесткости рамы учи-
учитывались осевые деформации стержней. Однако, как из-
известно, влиянием осевых деформаций на перемещения в рамах
можно пренебречь, если
размеры поперечных сече-
ний стержней достаточно
малы по сравнению с их
длинами. Полагая удли-
удлинения стержней равными
нулю, можно упростить
расчет, так как это позво-
позволяет снизить число неиз-
вестных. В самом деле,
если считать стержни не-
не3/13
9/13
6J13
?/i3
6/13
м/м0
Рис. 3.24
растяжимыми, то гори-
зонтальное перемещение
узла 2 следует приравнять к горизонтальному перемеще-
перемещению узла 3, а вертикальное — к вертикальному перемеще-
перемещению узла /. Так как узлы 1 и 3 неподвижны, то это равносиль-
равносильно требованию равенства нулю также и линейных перемещений
узла 2. Таким образом, при использовании указанного упро-
ql
1/2
****** tet
TB
#
ф
-с»
'fcL
©>7
Рис. 3.25
щения неизвестным остается единственное перемещение ve —
угол поворота узла 2. Следовательно, матрица неизвестных пе-
перемещений состоит из одного элемента: va = lva].
Поскольку внешний сосредоточенный момент в узле 2 от-
отсутствует, то Ра = [Рв] = [0] и равенство KaaVa = Pa — Poa
принимает вид kmvt — — Р06.
101
Вычислим, далее, матрицы жесткости элементов 1 и 2
в местных координатах, направив местную ось х в первом слу-
случае от узла / к узлу 2, а во втором — от узла 2 к узлу 3. По
C.26) и C.36) находим
EF
Г 1
- i L-i
12
6/
— 12
6/
6/
4/2
—6/
2/2
.]
— 12
—6/
12
—6/
*
6/
2/2
—6/
EJ
Матрицы Р„ содержат уравновешивающие внеузловую на-
нагрузку силы в направлении перемещений v: Ро = {Рва Роь}.
Подматрица Р0о включает в себя силы, действующие вдоль
оси стержня. Так как внеузловые нагрузки вдоль осей х от-
отсутствуют, то эти подматрицы для обоих стержней будут ну-
нулевыми. Подматрицы Роь для рассматриваемых нагрузок да-
даются выражениями C.57) и C.58), где, учитывая направление
нагрузок, следует сменить знаки на обратные и положить
5 = ql. В итоге имеем:
ql/2
ql/2—ql2/l2}.
Координаты узлов /, 2 и 3 в общей системе координат рав-
равны соответственно @, 0), @, /) и (/, /). Пользуясь формулами
C.15), находим матрицы:
==[о П; СЧ^
В соответствии с C.50) составляем матрицы преобразова-
преобразования для каждого стержня:
г0 1
о о
о
о о
0 1
о о
1 о
Ю2
1
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
1
0
0
0
1
0
0
о
о
о
1
По формуле ке = Xakjka + Я,(,кьХь вычисляем матрицы
жесткости элементов в общей системе координат, что дает
о о
о о
— 1 О
1 О
о о
о о
О 1
о о
EJ
Р
¦12 0 —6/
Т О
4/2
Симм.
-12
О
6/
12
О б/'
_Y О
О 2/2
О
Y
6/
О
4/а
в '
к<2>;=
EJ
Р
12 3 4 i
-у о 0 —у 0 0 '
12 6/ 0 —12 6/
4/2 0 —6/ 2/2
у О О
Симм. 12 —6/
4 5 6 7
где у = FIVJ.
Наконец, согласно C.55), находим
8
АР
2 8
12 3
о
4 5
Р<2) = %т Т р<2а> J U2) Т рB) = Г0 JL J1L О 3L
О а & 0& 1 2 12 2
7 8
12
9
Теперь имеем
403
+ *l * *l *
— • — 8 ~12 24~'
Подставляя k6e и POe в уравнение &6et>6 = — POe, находим
v, = qP/(\92EJ).
Матрицы перемещений элементов 1 и 2 в общей системе
координат оказываются равными
v<»={0 0 0 0 0 qPl(\92EJ)}\ v<2> = {0 0 qP/(\92EJ) 0 0 0}.
12 3 4 5 6 4 5 6 7 8 9
В местных координатах перемещения элементов равны:
vJ/^C vA) = {0 0}; vi"-^1* vA) = {0 0 0 qP/(l92EJ);
vi2) =kla2) vB) = {0 0}; Ti2) =U2) v<2> {qP/A92EJ) 0 0 0}.
Узловые силы в местных координатах могут быть найдены
по формуле C.52), из которой следуют соотношения
Р^= If V I Р " Р г= |г V | Р
а "а va 1* 0а> Ь Ь ?Ь 1^ 06*
Отсюда имеем
р^>=р^2) = {0 0};
— {6/ 2/а —6/
tjli j^ji _^1_^{51 13/ 45 -10/};
4 2 8 2 8 J 96 Х '
^-^-{6/ АР -6/ 2Р} +
I3
192?У I3
<Л1 j?_ «I —2?L1—2? {51 10/ 45 -71).
I 2 12 2 12 J 96 Х '
Напомним, что расположение элементов в матрицах Рь
определяется соотношением Рь = {Р,- Mt- P.- М.~}.
Далее вычисляем распределение изгибающих моментов и
перерезывающих сил по длине каждого стержня и строим
соответствующие эпюры (рис. 3.26).
Матрицы P(a> и РB* оказались нулевыми, т. е. в получен-
полученном решении осевые силы в стержнях равны нулю вследствие
принятого нами предположения о равенстве нулю вертикаль-
вертикального, и горизонтального смещений узла 2. Такое предположе-
предположение равносильно наложению связей на узел 2 (рис. 3.27, а).
104
Реакции наложенных опорных связей Р4 и Ръ (рис. 3.27, б)
разгружают стержни, обеспечивая равенство нулю их осевой
деформации. Эти реакции можно найти из условий равнове-
равновесия узла 2 (рис. 3.27, в):
45
S -0
: = —o,46V;
ql = 0,53lql.
Рис. 3.26
Поскольку в действительности силы Р4 и Ръ отсутствуют,
в узле 2 следует приложить равные им и противоположно на-
направленные силы, которые вызовут появление осевых сил в
стержнях рамы. Горизонтальная сила будет равна 0,469^/
t1>
(О-
Рис. 3.27
и вызовет сжатие стержня 2, вертикальная сила составит
0,53 Iql и вызовет сжатие стержня /.
Данные примеры рассмотрены с иллюстративной целью.
Преимущества матричного метода перемещений выявляются
при расчете сложных многократно статически неопределимых
систем; эти преимущества обусловлены однообразием вычисле-
вычислений, которые могут быть эффективно выполнены на ЭВМ.
105
ЧАСТЬ II
МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
ГЛАВА 4
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ МЕТОДА
Метод конечных элементов является мощным современным сред-
средством приближенного решения разнообразных задач математической
физики, ориентированным на эффективное использование ЭВМ. В за-
задачах теории упругости и строительной механики он позволяет распро-
распространить принципы расчета стержневых систем иа случай непрерывных
тел н сложных конструкций. С другой стороны, его можно трактовать
как специфическую форму метода Рнтца, что дает ключ к теоретичес-
теоретическому обоснованию метода конечных элементов.
§ 4.1. Дискретизация тела
Рассмотрим тело, нагруженное произвольным образом. С по-
помощью сетки секущих плоскостей (или криволинейных по-
поверхностей) разобьем его на отдельные части (рис. 4.1). Полу-
Получаемые подобласти имеют хотя и малые, но все же конечные
размеры, откуда и происходит их название «конечные элемен-
элементы».
Таким образом, непрерывное тело представляется в виде
совокупности конечных элементов, жесткостные свойства каж-
каждого из которых рассматриваются затем независимо от осталь-
остальных. На границах между конечными элементами выбирают-
выбираются некоторые точки — узлы; перемещения узлов в направле-
направлении координатных осей (а иногда и производные от перемеще-
перемещений) принимаются в качестве основных неизвестных*.
Здесь можно сразу усмотреть аналогию с матричным мето-
методом перемещений для стержневых систем, в котором за основ-
основные неизвестные также принимают узловые перемещения.
Однако в случае непрерывных тел возникает целый ряд за-
затруднений, которые можно преодолеть лишь с помощью вве-
введения дополнительных гипотез.
Прежде всего встает вопрос о том, как найти перемещения
(а следовательно, деформации и напряжения) внутри каждо-
* Здесь рассматривается решение в перемещениях. Существует
разновидность метода конечных элементов, в которой в качестве ос-
основных неизвестных принимают силы взаимодействия между элемен-
элементами [4; 5]; возможна также смешанная формулировка.
106
го конечного элемента, зная перемещения принадлежащих ему
узлов. Напомним, что в случае стержневых систем расчет ба-
базируется на использовании технической теории растяжения,
изгиба и кручения бруса, которая и позволяет выразить пере-
перемещения и напряжения в любом сечении бруса через узловые
перемещения. Для сплошного тела эта задача может быть реше-
решена приближенно, если сделать те или иные предположения о
характере поля перемещений в элементе. Точнее, необходимо
выбрать некоторую совокупность функций, которые позволя-
позволяют аппроксимировать поле перемещений внутри конечного
элемента по известным уз-
узловым перемещениям. Вы- у
бор аппроксимирующих
функций является одним
из наиболее ответственных
и важных этапов в методе
конечных элементов. Если
такой выбор сделан, то де-
деформированное и напря-
напряженное состояние элемен-
элемента будет однозначно опре-
определяться узловыми пере-
перемещениями. Поэтому под
конечным элементом сле-
следует понимать не просто некоторую малую область тела, а
область тела в совокупности с заданными в ней аппроксими-
рающими функциями.
Вторая трудность возникает при объединении конечных эле-
элементов в единую систему. В расчете стержневых систем такое
объединение производилось путем составления уравнений рав-
равновесия для узловых точек, в которых конструктивные эле-
элементы соединяются друг с другом. В сплошном теле число то-
точек соединения между элементами бесконечно. Задаваясь рас-
распределением перемещений внутри каждого элемента, тем
самым задаем и распределение напряжений во всех его точках,
в том числе и в граничных. На границах раздела смежных эле-
элементов напряжения, найденные для каждого из них независи-
независимо, совпадать не будут. Следовательно, обеспечить выполне-
выполнение условий равновесия на всей поверхности раздела не пред-
представляется возможным.
Чтобы обойти возникшее затруднение, можно напряжения,
действующие по границе каждого элемента, условно заменить
эквивалентными сосредоточенными узловыми силами; тогда
уравнения равновесия узлов в направлении узловых перемеще-
перемещений могут быть составлены обычным образом. При этом эк-
Рис. 4.1
107
бивалентные узловые силы определяются из условия^ чтобы
производимая ими на узловых перемещениях работа равнялась
работе действительных напряжений на перемещениях точек
граничной поверхности элемента.
Еще одна трудность связана с нагружением упругого тела
распределенными поверхностными и объемными силами. Эти
силы могут быть учтены также заменой их на эквивалентные
в энергертическом смысле внешние узловые силы.
После введения указанных упрощений тело можно рассма-
рассматривать как дискретную систему, т. е. как совокупность эле-
элементов, соединенных между собой в узловых точках. Разбие-
Разбиение конструкции на подобласти и выбор аппроксимирующих
функций для каждой из них можно осуществить различными
способами. При этом должны быть учтены особенности гео-
геометрии тела и обеспечена хорошая аппроксимация перемеще-
перемещений, деформаций и напряжений для всего тела в целом. В этом
случае решение, полученное по методу конечных элементов,
будет в пределе (при уменьшении размеров элементов) стре-
стремиться к точному. Более подробно вопрос о сходимости при-
приближенного решения к точному будет рассмотрен в гл. 6.
§ 4.2. Перемещения, деформации и напряжения
в конечном элементе
Рассмотрим типовой конечный элемент упругого тела, имею-
имеющий узлы i, j,... .Обозначим через xlt Vj, ... матрицы переме-
перемещений соответствующих узлов. Количество элементов в этих
матрицах зависит от характера задачи. Так, в случае простран-
пространственной задачи матрица vr обычно включает в себя три компо-
компоненты:
Vr=
где vrx, vTy, vTZ — проекции перемещений узла г на коор-
координатные оси х, у, z (рис. 4.2). В плоской задаче компонентами
матрицы vr будут vTX, vTy. В некоторых конечных элементах
матрицы vr содержат помимо линейных также и угловые пере-
перемещения или производные от перемещений. Все узловые пере-
перемещения элемента образуют матрицу
Vе = {V, Vj ...}.
Рассмотрим теперь произвольную точку внутри элемента.
Перемещения этой точки в направлении координатных
108
осей образуют
рез и:
матрицу-столбец, которую обозначим че-
где их, иу, uz — смещения рассматриваемой точки в направле-
направлении осей х, у, z (см. рис. 4.2). В плоской задаче матрица и
содержит два элемента. Подчеркнем, что компоненты матрицы
и представляют собой
функции координат.
Как говорилось выше,
в методе конечных элемен-
элементов принимается допуще-
допущение, согласно которому
перемещения всех точек
элемента однозначно опре-
определяются его узловыми
перемещениями. В матрич-
матричных обозначениях это оз-
означает существование ра-
равенства
iz
(XVе.
D.1)
Рис. 4.2
Здесь а — прямоугольная матрица, в которой количество
строк равно числу компонент матрицы и, а количество столб-
столбцов — числу компонент матрицы Vе. Элементами матрицы а
являются некоторые функции координат (аппроксимирующие
функции). Выбор подходящих функций, как отмечалось ра-
ранее, представляет собой важный этап в методе конечных эле-
элементов. Для некоторых элементов этот вопрос будет рассмот-
рассмотрен ниже. Здесь же мы будем предполагать, что аппроксими-
аппроксимирующие функции уже известны.
Воспользовавшись формулами Коши, можно выразить де-
деформации в каждой точке конечного элемента через его узло-
узловые перемещения. По формуле A.8) имеем г — Lu, что с уче-
учетом D.1) дает г = Lave. Эту связь между е и v' будем записы-
записывать в виде
8 = PV, D.2)
где через р обозначена прямоугольная матрица
Р = La;
D.3)
число строк матрицы р равно числу компонент матрицы г.
109
В общем случае пространственного тела, когда матрица U
содержит три компоненты их, иу, иг, из зависимости D.1)
следует, что матрицу а можно представить в виде
а =
а„
D.4)
В этой записи ах, av, az — матрицы-строки, элемента-
элементами которых являются известные аппроксимирующие функции.
Матричный оператор L дается в этом случае выражением A.9),
так что согласно D.3) имеем
дах/дх
д ау/ду
даг/дг
дау/дх-\-дах/ду
даг/ду-\- дау1дг
_д az/dx + дах/дг _
D.5)
В плоской задаче компонентами и являются перемещения
их, иу,~ а матрица а имеет соответственно две строки
D.6)
д/дх.
0
0
д/ду
0
д/дг
0
д/ду
0
д/дх
д/дг
0
0
0
д/дг
0
д/ду
д/дх
а-.
а,
Матрица L в этом случае определяется выражением A.21):
д/дх О
О д/ду
д/ду д/дх
д ах/дх
дау/ду
дау/дх+дах/ду
D.7)
Воспользуемся далее законом Гука в форме A.15) а ¦=
= Х?, где а — матрица-столбец напряжений; к — матрица
упругих постоянных. Подставляя сюда соотношение е = (V,
имеем
a = xflv". D.8)
Формулы D.1), D.2), D.8) показывают, что при известной
матрице аппроксимирующих функций а напряженное и дефор-
деформированное состояние конечного элемента однозначно опреде-
определяется узловыми перемещениями Vе.
110
§ 4.3. Матрица жесткости конечного элемента
Рассмотрим упругое равновесие деформированного конеч-
конечного элемента. Внешними нагрузками для него являются на-
напряжения, возникающие на его границе в результате взаимо-
взаимодействия со смежными элементами, объемные силы R и, воз-
возможно, поверхностные нагрузки р (если часть его поверхно-
поверхности совпадает с поверхностью, ограничивающей тело). Пред-
Предположим, что узловые перемещения \е получили произвольные
бесконечно малые приращения, определяемые матрицей
Поскольку перемещения и точек элемента связаны с узло-
узловыми перемещениями равенством и = а\е, то они получат
приращения би = аЬ\е. Работу внешних нагрузок на пере-
перемещениях би обозначим через 8Ае, а изменение потенциальной
энергии деформации конечного элемента — через 8Ue. Со-
Согласно принципу возможных перемещений (см. § 2.3) должно
выполняться равенство 8Ue = б/К
В соответствии со сказанным в §4.1 заменим напряжения
D.8) на поверхности элемента эквивалентными им сосредо-
сосредоточенными узловыми силами, действующими в направлении
узловых перемещений:
P' = {Pf Р; . . . },
где Р;, Р/, ... —матрицы сил для узлов i, /, .... Объемные
R и поверхностные р силы также заменим эквивалентными уз-
узловыми силами^ Ре — {Р" Р/...}.
Силы Ре + Ре будем считать эквивалентными действитель-
действительным нагрузкам, если нх работа на перемещениях 6v" равна
6Л', т. е. если выполняется равенство (см. §2.1)
D.9)
Подсчитаем теперь вариацию потенциальной энергии де-
деформации 8Ue. Так как деформации связаны с Vе соотношением
е = pv", то изменение узловых перемещений вызовет прираще-
приращение деформаций
бв = рбу. D.10)
По формуле B.14) имеем
= Г 6ererdT,
где хе — объем занимаемы^ конечным элементом
111
Подставив в подынтегральное выражение D.8) и D.10),
получим
В силу постоянства элементов матриц 6ve и Vе их можно
вынести за знак интеграла:
Tl ve.
Выражение, заключенное здесь в квадратные скобки,
представляет собой квадратную матрицу. Ее элементы полу-
получаются интегрированием элементов симметричной матрицы
J3r xp. Введя обозначение
ке= Г prxpdt, D.11)
представим выражение для 8Ue в виде
№ = Fve)r k'V.
D.12)
Приравнивая D.9) к D.12) и учитывая независимость эле-
элементов матрицы 6ve, получаем
k've = Pc + Pe. D.13)
Это соотношение связывает узловые силы с узловыми пере-
перемещениями в стандартной форме C.2), поэтому матрицу ке,
определяемую по D.11), можно назвать матрицей жесткости
конечного элемента. Из D.11) видно, что при известной гео-
геометрии конечного элемента и заданных упругих характери-
характеристиках материала матрица жесткости вполне определяется
выбором аппроксимирующих функций.
Матрица узловых перемещений имеет блочную структуру
Vе = {уг vj ...}. В соответствии с выражением е = pve ма-
матрицу р можно также разбить на блоки:
Р = IP/ P, -.].
Тогда на основании D.11) получим
х[р,Р; .. ]<1т.
112
Из этой записи вытекает следующее блочное представление
матрицы жесткости конечного элемента:
~ке
где
к'..
(г, s=i,
D.14)
D.15)
§ 4.4. Учет внеузловой нагрузки
Выведем теперь формулу для вычисления матрицы Ре.
Рассмотрим такой конечный элемент, часть поверхности кото-
которого совпадает с внешней поверхностью, ограничивающей тело.
Придадим узловым перемещениям бесконечно малые при-
приращения 6v*; приращения перемещений би определятся при
этом формулой би =. абуг Вычислим работу fiAe объемных
R и поверхностных р сил на перемещениях би. В соответст-
соответствии с B.4) имеем
е=,Г fiu^Rdt-f-f 6urpdo>
Первый интеграл в правой части этого выражения берет-
берется по объему элемента, а второй — по его поверхности. Под-
Подчеркнем еще раз, что нагрузка р действует лишь по той части
поверхности элемента, которая совпадает с внешней поверх-
поверхностью тела. Поэтому фактически поверхностный интеграл
берется только по этой части ше Внеся сюда значение би,
получим
cerpdco\
Будем считать, что узловые силы Р1' эквивалентны задан-
заданной внешней нагрузке, если работа этих сил Fve)r Pe на уз-
узловых перемещениях равна 6А* Это приводит к равенству
ctrpdco
D.16)
113
Учитывая блочную структуру матрицы ve — {v,- Vj ...}
в соотношении и = а\е, представим матрицу а также в блоч-
блочном виде а = [at at ...]. Тогда
где
p< = j afRdt+ j ojfpdco (r = i, /, ...). D.17)
Формула D.17) определяет вклад, который вносит данный
элемент в эквивалентные силы в узле г. Аналогично приводят-
приводятся к узловым силам нагрузки, приложенные к другим эле-
элементам (для тех элементов, которые находятся целиком вну-
внутри тела, второй член в D.17) будет отсутствовать). Суммируя
вклады отдельных элементов, найдем для каждого узла ма-
матрицу
рг=2р;- D.18)
е
Здесь знак 2 означает суммирование по всем элементам,
е
сходящимся в узле г.
Напомним, что в случае стержневых систем (см. § 3.6)
внеузловая нагрузка учитывалась введением матрицы уравно-
уравновешивающих сил Ре0 (матрицы, которая содержит реакции на
элемент от действия внеузловой нагрузки при полном закреп-
закреплении узлов). Здесь использован иной подход, при котором
внеузловая нагрузка заменяется статически эквивалентной
системой узловых сил Ре. При желании можно было бы и в
методе конечных элементов ввести матрицу уравновешиваю-
уравновешивающих сил Pj, полагая Р* = —Ре. Отметим, однако, что в отли-
отличие от стержневых систем матрица Ре0 может быть определе-
определена здесь лишь приближенно, поскольку ее компоненты за-
зависят не только от характера внешней нагрузки, но также и
от выбора аппроксимирующих функций, как это видно из
D.16).
§ 4.5. Определение узловых перемещений
Выполнив дискретизацию упругого тела, можно теперь со-
составить уравнения равновесия узлов и прийти к системе урав-
уравнений относительно перемещений v = {vj v2 ... v,,}, где п —
общее число узлов при принятой схеме дискретизации.
Если в узлах тела приложены сосредоточенные силы, то
из них можно образовать матрицу Р= {Р, Р2 ... Рп }• Ти-
114
повой элемент Рг этой матрицы представляет собой подматри-
подматрицу сил, действующих в узле г в направлении перемещений
vr.
Узловые силы, эквивалентные внеузловой нагрузке, так-
также объединим в матрицу Р = (Рг Р2 ... Рп}.
Уравнения равновесия для
каждого узла составляются теперь
точно так же, как и в случае
стержневых систем (см. § 3.8).
Объединяя все эти уравнения, по-
получим зависимость между внеш-
внешними узловыми силами и узловы-
узловыми перемещениями в виде
D.19)
Рис. 4.3
Здесь К — матрица жесткости всего тела, которая может
быть представлена в форме
. . . kln
D.20)
Типовая подматрица krs — 2k*s получается, как и прежде,
е
суммированием подматриц к% по всем конечным элементам,
содержащим одновременно узлы г и s.
Составление матрицы упругого тела поясним на простей-
простейшем примере. Пусть плоская область (рис. 4.3) идеализирова-
идеализирована совокупностью четырех конечных элементов (а, Ь, с, d).
Цифрами на рисунке обозначены номера узлов.
Запишем матрицы жесткости отдельных элементов в блоч-
блочном виде
кь =
к"
к"
"кзз
кс
*53
_ 43
3
к"
"•12
к"
К22
|>а
232
^35
Ks
Kb
5
ка
Kl3
^2 8
5
к34"
кС54
4
1
2 ;
3
3
5;
4
"к*
к?,
kft
кгг
kd
К52
kd
_К32
Из
kg3
[rb
К43
3
kd
2 5
kd
К55
kJ
К35
к%
[гЬ
k23~
kd
К53
[rd
кзз._
3
4
2
5
3
115
Цифры сбоку и снизу характеризуют здесь номера узлов,
обход которых для каждого конечного элемента осуществля-
осуществляется против часовой стрелки, начиная с наименьшего номера.
Матрица жесткости всего тела в соответствии с общим чис-
числом узлов имеет в блочной записи размер 5x5. Суммируя
подматрицы отдельных конечных элементов, имеющие одина-
одинаковые индексы, получим
If _
к a J-trb Ira Ira i Ub Ub n
к a ba -t-Ifrf ta _{_ hd n ud
91 l»oo*22 23 *^ 23 25
|,a -Llfft tra Л-bd Ьа ЛЛгЬ Л-Ьс AJbd ЬЬ -i-be Uc -i-\,d
Ol , 31 O? O? OO ¦ OO 00 О О O4 d4 О И АО
\rb Л itb _L IfC bft -tlfC ifC
«•41 w Л43 ' Л43 K44 'n44 K45
Сделаем некоторые пояснения к формированию матрицы
жесткости системы. В нашем случае узел 3, например, явля-
является общим для всех элементов. Поэтому подматрица к38
является суммой соответствующих подматриц всех четырех
элементов. Узлы J и 3 принадлежат элементам а и Ь, вследст-
вследствие чего kt з = k5s ¦+- к\3. Узлы 1 я 2 принадлежат вместе
только элементу а, так что к12 =¦ ка2. Наконец, такие узлы,
как 1 и 5, непосредственно не связаны между собой ни одним
из элементов, поэтому к16 =^0.
Вернемся к уравнению D.19). Как и в случае стержневых
систем, разобьем матрицу узловых перемещений v на две под-
подматрицы:
L vpj
В подматрицу vp включаются известные из условий за-
закрепления перемещения; все неизвестные перемещения состав-
составляют подматрицу va. Аналогично представляются и матрицы
сил
Р =
Если заданные перемещения vp ==- 0, то придем к урав-
уравнению
kaava = PafPa, D.21)
решение которого дает матрицу неизвестных узловых переме-
перемещений.
116
Матрица каа, как и ранее, получается из матрицы жест-
жесткости К вычеркиванием строк и столбцов, соответствующих
известным перемещениям. После определения узловых пере-
перемещений можно по формулам D.8) вычислить напряжения в
каждом конечном элементе.
§ 4.6. Связь метода конечных элементов
с методом Ритца
Выше метод конечных элементов рассматривался как обоб-
обобщение матричного метода перемещений для стержневых си-
систем на случай сплошных тел. Можно, однако, подойти к это-
этому методу с иных позиций, рассматривая его как специфиче-
специфическую форму метода Ритца. В самом деле, задаваясь характе-
характером изменения перемещений в пределах каждого конечного
элемента, мы тем самым задаемся приближенным полем переме-
перемещений по всему телу, что соответствует схеме метода Ритца
(см. §2.5). Специфика заключается здесь в том, что, во-пер-
во-первых, предполагаемый закон изменения перемещений задается
не сразу по всей области, а поэлементно, и, во-вторых, неиз-
неизвестными параметрами в методе конечных элементов являются
узловые перемещения (в классической схеме метода Ритца
неопределенные параметры не связываются с какой-либо фи-
физической интерпретацией). Рассматривая метод конечных
элементов с этой точки зрения, можно получить уравнения
для отыскания узловых перемещений путем минимизации пол-
полной энергии системы. При этом не требуется использовать пред-
предположение о том, что конечные элементы соединены между со-
собой лишь в узловых точках.
Итак, пусть тело представлено в виде совокупности конеч-
конечных элементов. Как и ранее, будем исходить из того, что для
каждого элемента известна матрица а, позволяющая аппрок-
аппроксимировать перемещения внутренних точек через узловые
перемещения: и = а\е.
По формулам Коши выразим деформации внутри элемента
через узловые перемещения е = pve, а в соответствии с за-
законом Гука имеем а = хе = xpve.
Вычислим потенциальную энергию деформации Vе, на-
накапливаемую в отдельном конечном элементе. Подставляя в
формулу
= — I eT adx
117
записанные выше выражения для матриц е и а, получим
V = -L Г (р \"}т хр vc dt =.-L (\е)т Г Г pr xp dTl ve.
Выражение, заключенное здесь в квадратные скобки,
представляет собой симметричную матрицу. Полагая
irxpdt, D.22)
запишем
Ue=— (\е)тке\е.
2,
D.23)
Если матрицы Vе и ке представить в блочной форме, то
к', к*. ... V,- . D.24)
Здесь i, j, ... — номера узлов, принадлежащих рассма-
рассматриваемому конечному элементу.
Пусть теперь v= {vlv2...vn}—• матрица-столбец узло-
узловых перемещений всего упругого тела, записанная в блочной
форме (п —общее число узлов). Для дальнейших рассужде-
рассуждений удобно в выражение для потенциальной энергии деформа-
деформации конечного элемента включить перемещения всех узлов
упругого тела и представить его в виде
к\
к°
2
K22
\п
v2
Последнее равенство будет тождественно выражению
D.24), если считать k's == 0, когда хотя бы один из узлов г,
s не относится к рассматриваемому конечному элементу.
Потенциальная энергия деформации, накопленная во всем
теле, U = 2(/е. После подстановки выражения для Vе и
118
суммирования получим
ц
где к„ =
к12
(г, s=l, 2, ... , п).
. К
Ч.П
_ _ vn_
Поскольку k's = 0. если хотя бы один из узлов г, s не
относится к данному конечному элементу, то фактически сум-
суммирование распространяется здесь лишь на те элементы, для
которых узлы г и s являются общими.
Введя обозначение
К =
k2i
• klrl
¦ k2n
¦ кпп _
представим теперь выражение для потенциальной энергии
деформации всего тела в краткой записи
?/= — vrKv. D.25)
2 v '
Выражение для U можно представить в несколько иной
форме, если учесть наложенные на тело связи. Как это делалось
и ранее, выделим в матрице v неизвестные перемещения va
и заданные перемещения vB. Выделяя также соответствующие
блоки в матрице К, будем иметь
vP.
= -у (vlк
Если, в частности, ve = 0, то потенциальная энергия
деформации, будет вычисляться по формуле
U = — Va
D.27)
Отметим, что матрицу каа можно получить из матрицы К
путем отбрасывания тех строк и столбцов, которые соответст-
соответствуют перемещениям vB.
Перейдем далее к вычислению потенциала внешних сил
П. Полагая, что на тело действуют поверхностные р и объем-
объемные R силы, а также узловые силы Р (в направлении переме-
перемещений v), будем иметь
П = —
J u'
где интегралы берутся по всему объему тела т и по той части
о)р его поверхности, на которой заданы нагрузки.
Преобразуем второе слагаемое в правой части равенства,
заменив интегрирование по объему тела суммой интегралов,
взятых по объемам отдельных конечных элементов:
X е Xе
Подставляя сюда равенства u — ave, получим
т е ^
Точно так же третье слагаемое в формуле для П приведем
к виду
f urpdw=2(ve)r J «rPd»,
где <ое — поверхность отдельного конечного элемента. По-
Поскольку нагрузки р заданы лишь на ыр, то в сумму войдут
только те элементы, часть поверхности которых совпадает с
в>р, и фактическое интегрирование будет выполия гься лишь по
этой части <¦>*.
Таким образом, для потенциала внешних сил приходим к
выражению
П = —vrp-
Введя обозначение
r/j arRdT + j arpdw\
RdtH- f arpdw,
перепишем этот результат в виде
П=г -vrP — 2
е
120
Учитывая блочную структуру матрицы а = lat aj ...],
имеем Ре = {Ре( Р/ ...}, где
Р,= f afRdx+ f ajpdco (r = i, /, ...).
Произведение
*"' 0 7* T
можно представить в виде
Pi
_P«
если считать, что Р, = 0, когда узел г не относится к рассма-
рассматриваемому конечному элементу. Тогда для потенциала внеш-
внешних сил запишем:
П = — vrP — [у
Вводя обозначения
Р2
я); Р-
окончательно получим
П = — vr(P + P). D.28)
Формально матрицы Рг образуются суммированием соот-
соответствующих матриц по всем конечным элементам, но факти-
фактически суммирование выполняется лишь по тем элементам, для
которых узел г является общим (для всех остальных элемен-
элементов Р* = 0).
Отметим, что из всех компонент матрицы Р + Р извест-
известными являются лишь те силы, которые действуют в направле-
121
нии неизвестных перемещений va. Остальные элементы ма-
матриц Р + Р представляют собой неизвестные реакции на тело
со стороны наложенных на него связей, действующие в на-
направлении vp. Разобьем Р и Р на соответствующие подматри-
подматрицы:
Учитывая также представление v = {va vp}, запишем
D.29)
В частности, в случае vp = О получаем отсюда выражение
, D.30)
в которое входят только известные силы.
Полная энергия системы V равна сумме V = U + П;
из D.27) и D.30) имеем
y = -^-v?kaava-v?<Pa + Pa). D.31)
Формула D.31) определяет V как функцию узловых пере-
перемещений va. Необходимым условием минимума полной энер-
энергии является равенство нулю ее первой вариации:
6V =^(Sv?kaava + Vqktta6va)-6v^
Подчеркнутые слагаемые равны между собой, ибо, бу-
будучи скалярными величинами, они получаются одно из дру-
другого путем транспонирования. Поэтому условие 6V = 0
можно записать в виде
Sv?(kaava-Pa-Pa) = 0.
Так как элементы матрицы 6va произвольны, то матрица
kaava — Pa — Pa должна быть нулевой. Отсюда выводим сле-
следующее матричное уравнение относительно va:
Мы снова пришли к уравнению D.21). Отметим, что обра-
образование матриц К и Р выполняется в обоих подходах по одним
и тем же формулам.
122
Записанное выше уравнение относится к случаю, когда
vp = 0. Если же заданные перемещения отличны от нуля, то
при вычислении полной энергии V следует исходить из выра-
выражений D.26) и D.29). В этом случае минимизация полной энер-
энергии по перемещениям va приводит к уравнению
kaava = Pa + Pa-vpkp«. D.32)
Равенство 61/ = 0 есть необходимое условие минимума
полной энергии системы. Покажем, что перемещения v, най-
найденные из решения системы D.21) или D.32), действительно
минимизируют V. Ограничившись случаем Vg = 0, будем
иметь для полной энергии выражение D.31). Рассмотрим да-
далее узловые перемещения \*а = va + Ava, которые отличают-
отличаются от перемещений va на некоторую произвольную величину
Ava. Таким перемещениям соответствует полная энергия си-
системы
Раскроем здесь скобки и найдем разницу:
Первые два слагаемых в правой части этого выражения
равны между собой, поскольку, являясь скалярными вели-
величинами, они получаются одно из другого путем транспониро-
транспонирования. С учетом этого имеем
V*-V = Av?(kaava-Pa-Pa) +~ Av?kaaAva.
Выражение в скобках равно нулю, поскольку перемещения
va удовлетворяют уравнению D.21). Отсюда приходим к сле-
следующему равенству:
Потенциальная энергия системы, определяемая как про»
изведение v?kaava/2, есть величина существенно положи-
положительная для любой матрицы узловых перемещений va, в том
числе и для матрицы Ava (если последняя отлична от нулевой).
Отсюда следует неравенство
V* — V > 0. D.33)
123
Таким образом, любым перемещениям у„, отличным от
vai соответствуют значения V* > V, что и требовалось дока-
доказать.
Следует отметить одно важное обстоятельство. Как гово-
говорилось в гл. 2, аппроксимирующие функции в методе Ритца
должны удовлетворять всем геометрическим связям. Это оз-
означает, в частности, что они должны быть непрерывными
функциями координат. Следовательно, метод конечных эле-
элементов можно рассматривать как метод Ритца лишь в том слу-
случае, если на границах между конечными элементами обеспе-
обеспечивается непрерывность перемещений. Конечные элементы,
которые дают непрерывное поле перемещений, называются сов-
совместными (или согласованными). Не всегда, однако, удается
выполнить условие совместности, вследствие чего в практике
нередко используются несовместные элементы. При переходе
от одного элемента к другому перемещения будут тогда пре-
претерпевать разрывы, и поэтому нельзя утверждать, что найден-
найденные узловые перемещения соответствуют минимуму полной
энергии системы.Тем не менее при выполнении определенных
условий (о которых будет сказано в § 6.4) решение в пределе
снова будет стремиться к точному, а в некоторых случаях не-
несовместные элементы позволяют получить даже более точные
результаты, нежели совместные.
§ 4.7. Коиечноэлементная форма метода
Канторовича—Власова
В изложенной выше трактовке в основу метода конечных элемен-
элементов был положен метод Ритца. Возможны различные модификации ме-
метода, которые в тех нли иных частных задачах могут дать более эконо-
экономичный алгоритм расчета. Рассмотрим один такой вариант, в основе
которого лежит метод Канторовича — Власова (см. § 2.6).
Пусть призматическое тело (рис. 4.4) ограничено плоскостями
z = 0 и z = /. Как и в § 2.6, будем обозначать торцовые поверхности
тела через «j и ш2, а его боковую поверхность — через ш3. Тело может
быть закреплено произвольным образом, но с одним ограничением: ес-
если имеется закрепление тела на боковой поверхности, то оно должно
осуществляться по всей длине тела. Участки поверхности, на которые
наложены геометрические связи, обозначим через <в1Ц, <в2Ц, шзи, а ос-
остальные участки (на которых заданы поверхностные нагрузки) — через
0IР, <о2Р, шз;). __
Разобьем все тело на конечные элементы сеткой поверхностей, об-
образующие которых параллельны оси г. Таким образом, каждый эле-
элемент представляет собой призматический брусок длиной /. На боковых
поверхностях смежных конечных элементов выберем прямые, парал-
параллельные осн г, которые будем называть узловыми линиями или просто
узлами. Перемещения точек, принадлежащих узловым линиям, при-
примем в качестве основных неизвестных; эти перемещения являются
функциями координаты г. Перемещения точек узловой линии г в нап-
124
равлении координатных осей обозначим через отХ (г), vry (г), vrz (г)
И составим из них матрицу
VTV B) I ¦
vrz (*) J
Рассмотрим далее типовой конечный элемент с узлами i, /,... При-
Примем, что перемещения их, иу, иг в каждом поперечном сечении элемен-
Рис. 4.4
та выражаются через его узловые перемещения, взятые в том же сече-
сечении, посредством зависимости
и (х, у, г) = а (х, у) \е (г).
D.34)
где
[их(х, у.
ии(х, у,
«г (*. У,
Vе (г) --
Через а (ж, у) в D.34) обозначена матрица, элементами которой яв-
являются выбранные функции координат х, у. Эта матрица имеет три
строки
[<**(*> У)
«у(х, у)
«г(х, у)
а число столбцов в ней равно числу компонент v*.
Итак, в рассматриваемом подходе осуществляется поэлементная
аппроксимация перемещений в плоскости поперечного сечения тела, а
основными неизвестными являются функции, зависящие от третьей ко-
координаты (перемещения узловых линий). Задача сводится теперь к
отысканию этих функций координаты г. Таким образом, мы приходим
к конечноэлементной формулировке метода Канторовнча-Власова.
125
Выразим деформации е= {ехх гуу ezz еху вуг ггх) через узловые
перемещения, воспользовавшись геометрическими соотношениями в
виде е = Lu. Учитывая выражение A.9) для матричного оператора L,
имеем
е=
- д/дх О 0 ~
О д/ду О
О 0 д/дг
д/ду д/дх О
О д/dz д/ду
_ д/дг 0 д/дх
д ах/дх
д ау/ду
О
д ау/дх-\- д ах/ду
даг/ду
daz/dx
'ах{х, у)
<*y(*> У)
„«*(*. У)
О ~
О
О
ау
_ «* _
где через ve = d\e/dz обозначена матрица-столбец, получаемая из v'
дифференцированием ее компонент по г.
Это равенство можно представить в следующей краткой форме:
D.35)
где Ро и рх — прямоугольные матрицы, составленные из строк матрицы
« н их производных по х, у:
Ро-
о -
о
«z
О
дах/дх
да,у/ду
О
/дх+ daxjdy
д а2 /ду
да21дх
Напряжения а = {ахх a,ly azz axy оиг огх) найдем по закону Гука:
а = хе = xpove + хРг\е.
Потенциальная энергия деформации рассматриваемого конечного
элемента
126
Подстановка выражений для матриц г и а дает
= 4" J
dT.
Заметим, что подчеркнутые члены в подынтегральном выражении
равны между собой, поскольку являются скалярными величинами и
получаются один из другого путем транспонирования.
Элементы матриц Р„, рх являются известными функциями коорди-
координат х, у. Выполнив интегрирование по площади Fe поперечного сече-
сечения конечного элемента, приведем выражение для Vе к виду
=т' f *(у')Г k"
О
Здесь через ко, kf н кеобозначены квадратные матрицы, вычисляе-
вычисляемые по формулам:
kS = J Po"xPodf; D.36)
Fe
'=J Pfx^df;
D.37)
k =
=J PUP
D.38)
Так же как и ранее, разобьем матрицы ($0, f}x на блоки в соответст-
соответствии е блочным представлением матриц Vе, Vе:
Po = iPoi Po; .J; Pi = [Pi; Pjj ••¦!•
Тогда из D.36)—D.38) придем к блочной структуре матриц kj.
kf и к":
"к" ке
К0,« K0,G ' • •
K0,/i КО,// • • •
K1,и K1,(j •¦ ¦
KiK
к<7
127
Типовые подматрицы вычисляются по следующим формулам (г,
• = ¦. /,...):
Если просуммировать вклады отдельных конечных элементов, то
получим потенциальную энергию деформации U всего тела. Рассуждая
так же, как в предыдущем параграфе, можно прийти к следующему
выражению для U:
"-¦И
(vrk0 v + vrk, v + 2v' k v) йг. D.39)
о
vt v2... vn); v= {v,v2...Vn) —матрицы-столбцы, в
которых перечислены перемещения и их производные по г для всех уз-
узловых линий тела (я — общее число узлов).
Квадратные матрицы к0, кх и к образуются из соответствующих
матриц для отдельных конечных элементов. Их типовые подматрицы по-
получаются по обычному правилу:
S=- ? Kg
'l-S5=^J "rS
Суммирование здесь ведется по всем конечным элементам, содержащим
одновременно узлы г, s (r, s = 1,2 п). Отметим, что матрицы к„ и
кх симметричны, поскольку это вытекает из симметрии матриц kj,
kf. Матрица к, вообще говоря, симметрией не обладает.
Если тело закреплено вдоль некоторых узловых линий, то следу-
следует уменьшить размеры всех матриц, фигурирующих в D.39), оставив в
матрицах v и v лишь перемещения свободных узлов и выделив соответ-
соответствующие подматрицы в k0, kj н к. Во избежание громоздкости обозна-
обозначений мы не будем здесь помечать эти уменьшенные в размерах матрицы
дополнительным индексом а, как это делалось ранее.
Перейдем теперь к вычислению потенциала внешних сил. Полага-
Полагаем, что на тело действуют объемные R = {RxRyftz) и поверхностные
Р ~ \PxPyPz] силы. Кроме того, считаем, что на боковой поверхности
тела вдоль узловых линий могут быть приложены погонные иагрузкн,
изменяющиеся по дли-не тела. Проекции на координатные оси погонной
нагрузки, действующей вдоль узловой линии г, обозначим через qrx (z)
Чгу (?)¦ qrz (г) и объединим их в матрицу-столбец,
[Чгх~
Ягу
128
Тогда потенциал внешних сил
П=— / JurRdT+f urpd(o + J' vTqdz J , D.40)
V ар ° /
где q = {q^-.-qn}.
Объемный интеграл в правой части этого выражения заменим сум-
суммой интегралов, взятых по объемам отдельных конечных элементов.
Учитывая, что в пределах каждого элемента перемещения и выража-
выражаются через узловые перемещения равенством u = ave, имеем
Выполнив далее интегрирование пе площади поперечного сечеиия
каждого элемента F", получим
j je)rQ?d2. D.41)
X е 0
Здесь через
обозначена матрица-столбец, элементы которой являются известными
функциями координаты г.
Если разбить матрицу а на блоки а = [а*а; ...] в соответствии с
блочной записью матрицы ve, то и матрица Q? будет представлена в
блочном виде:
Q? (*)=«&<*> От/И ¦••>.
где типовая подматрица
j TrR&F. D.42)
Fe
После выполнения в D.41) суммирования по всем конечным элемен-
элементам первое слагаемое в выражении для П будет представлено в форме
JurRdT= f
vrQT(z)dZ. D.43)
Здесь через Qt (г) =¦ {Qti (г) QTj (z)... QXfl (г) } обозначена матрица-
столбец, типовая подматрица которой
суммирование ведется по всем элементам, соединяющимся в узле г.
5 Зак. 651 129
Преобразуем второе слагаемое в формуле для П. Учитывая, что
<вр — <в1г) + <в2р + <i>3P> запишем
I u pd(i)= urpdco-)- urpdw+| urpd«.
> WIP "\p a:,P
Рассуждая аналогично предыдущему, получим
D.44)
где v @) и v (/) — значения матрицы v (г) при г = 0 и г= / соответст-
соответственно; Р @) и Р (/) — Матрицы-столбцы узловых сил, действующих в
торцовых сечениях н эквивалентных заданной там поверхностной на-
нагрузке. Эти матрицы можно получить в блочной форме:
Р @) - {Р1 @) Р2 @)... Р„ @)}; Р (/) — {Р, (/) Р2 (/)... Р„ (/)}.
Типовые подматрицы образуются путем суммирования вкладов отдель-
отдельных конечных элементов:
Pr@)=2p'@): Pi-W^SW 0"=i.2, ... , я)
Подматрицы Рсг @), Р/ (/) для отдельного конечного элемента вы-
вычисляются по формулам
Р? @)= J af p, d F; Р^(/) = \ arr p2 dF.,
где pj и р2 — матрицы-столбцы, которые содержат компоненты распре-,
деленной нагрузки на торцах 2= 0 и 2= / соответственно.
Матрица-столбец Ои (г) в последнем слагаемом формулы D.44) со-
содержит погонные нагрузки, которые действуют вдоль узловых линий
и эквивалентны поверхностной нагрузке, приложенной к боковой по-
поверхности тела. Эта матрица также имеет блочную структуру:
Qo>(?H={Q<olB) Q<o2(*) ¦¦¦<*«» W >
и вычисляется поблочно, по обычному правилу суммирования:
Вклад в эти узловые нагрузки будут давать лишь те конечные эле-
элементы, боковая поверхность которых имеет общую часть с боковой по-
поверхностью ш3р тела. Для таких элементов имеем
130
Матрица Рз содержит компоиенты поверхностной нагрузки на боковой
поверхности тела, а интегрирование ведется по той части контура по-
поперечного сечения конечного элемента, которая совпадает с контуром,
ограничивающим поперечное сечение тела.
После подстановки выражений D.43) и D.44) в D.40) получим
П= — [ \Т Q dz — vr @) Р @) — vr (О Р (/), D.45)
о
где Q (г) =Qa (г) + QT (г) + q (г).
С учетом D.39) и D.45) получаем следующее выражение для пол-
полной энергии системы V = U + П:
V =- Г ( ут ко v +- vr kt v + vr"k v —vr Q j dz —
о
-yT @) P @) -vr (/) P (/). D.46)
Таким образом, полная энергия системы представлена в виде функ-
функционала, зависящего от неизвестных узловых перемещений v (z) н их
производных v (z) по координате z. Функции v (z) должны быть выбра-
выбраны таким образом, чтобы этот функционал принимал минимальное зна-
значение. Для отыскания v (z) можно записать уравнения Эйлера вариа-
вариационной задачи и прийти, таким образом, к системе дифференциальных
уравнений относительно компонент матрицы v (z).
Мы имеем дело с минимизацией функционала вида
v,
который зависит от п функций vt (г), v2 (г),..., vn (г) и их производ-
производных по г. Внеинтегральный член представляет собой функцию от кра-
краевых значений v (z).
Как известно из курса вариационного исчисления, необходимым
условием минимума такого функционала является требование, чтобы
функции v z) удовлетворяли следующим уравнениям Эйлера:
dF d
dvx dz
dz V dv
dvn dz \ dvn
131
Все эти равенства можно объединить в одно:
dF d / dF \
~ т— \~тг- 1 — 0,
д\ az \ д\ }
если ввести матрицы
]F dF dF 1 dF f dF dF dF
F I JUL—{Jt!LJ*!L dF I
n j ' dv l дщ dv2 dvn j '
dv l Л»х ЛJ "" dvn
При этом функции v должны при г = 0 н z ¦= I принимать задан-
заданные значения, либо (если эти функции на концах интервала не заданы)
удовлетворять так называемым естественным граничным условиям ва-
рнациоиной задачи, т. е.
dF
av
dF_
dv
z =
z=
0
+
дФ
av(O)
дФ
av(/)
для г=
для z=l —r- + д. /ft =0-
av I z=/ av(/)
В общем случае на одном илн на обоих концах могут быть нзвест-
иы некоторые из функций v (г). Недостающие условия следует выби-
выбирать нз числа естественных граничных условий.
Обращаясь теперь к D.46), имеем
F =— vrk0 у-\ \Tkt v + vrlf v—vrQ;
Ф= —vr@) P @)—vr @ Р (/).
Таким образом,
dF ~ . dF
—-=kov + kv—Q; -^-=1
av av
так что матричная запись уравнений Эйлера будет
k0 v+(k—Тсг) V—k/v^Q. D.47)
Естественные граничные условия при г = 0 и г •= / соответственно
запишутся так:
kj v@)+T{rv@)= — Р@); k]v(/)+ltrv@ = P(O. D-48)
Следовательно, в рассматриваемом методе задачу можно свести к
интегрированию системы обыкновенных дифференциальных уравнений
второго порядка D.47) относительно узловых перемещений v (г). При
этом перемещения v (г) должны в торцовых сечениях принимать задан-
заданные значения либо удовлетворять там естественным граничным усло-
условиям D.48). Для интегрирования системы уравнений D.47) можно при-
применить различные численные методы [2]. Изложение некоторых мето-
методов, используемых в задачах строительной механики, можно найтн в
работе [19]. Рассмотренный выше подход нашел применение, в частно-
частности, в задачах нзгнба пластин, где ои известен под названием метода ко-
конечных полос [6].
132
ГЛАВА 5
КОНЕЧНЫЕ ЭЛЕМЕНТЫ СПЛОШНОЙ СРЕДЫ
Для решения плоской задачи теории упругости и для расчета трех-
трехмерных тел разработано много разнообразных конечных элементов.
Основное различие между ними заключается в характере аппроксима-
аппроксимации перемещений, а также в способе описания геометрии. Весьма пло-
плодотворным является нзопараметрический подход, в котором аппрокси-
аппроксимация перемещений и геометрии осуществляется с помощью одних и
тех же соотношений. Это позволяет построить одно-, дву- и трехмерные
конечные элементы произвольной конфигурации, в том числе криволи-
криволинейные, обеспечивающие совместность конечиоэлементной модели.
§ 5.1. Плоский треугольный элемент
В качестве первого примера рассмотрим простейший ко-
конечный элемент, применяемый для решения плоской задачи
теории упругости. Это треугольный элемент (рис. 5.1) с тремя
узлами, расположенными в вершинах треугольника. Узло-
Узловые перемещения для
такого элемента указа- у
ны на рисунке. Матри-
Матрицы перемещений для
каждого узла состоят из
двух компонент. Так,
для узла i имеем
44
кг
Рис. 5.1
При составлении мат-
матрицы Vе условимся обхо-
обходить узлы против часо-
часовой стрелки; тогда
Vе = {V: V; Vm }.
Точки элемента получают перемещения их, иу в направле-
направлении осей х, у. Поэтому матрица и имеет вид
u kJ
Для получения матрицы а, связывающей и и Vе, предпо-
предположим, что перемещения их и иу в пределах элемента ме-
меняются по простейшему закону
"* = /i + f2x + f3y; uy = /4 + f6x + fu у, E.1)
где / — некоторые постоянные. В вершинах треугольника
перемещения их и иу должны совпадать с узловыми переме-
перемещениями. Это дает шесть уравнений для определения кон-
133
стант /. Подставим в E.1) координаты узла i и приравняем
их и uv к vix и viy:
fi + hxi 4- /з«Л--= vts; fi + fbxt 4- /«*/* =* fij,.
Полагая значения х, у равными Xj, yh а затем хт, ут, за-
запишем аналогично оставшиеся четыре уравнения. Получен-
Полученная система будет содержать две независимые группы урав-
уравнений. В первую группу войдут постоянные flt /2, f а, а правые
части будут содержать узловые перемещения vix, Vjx, vmx:
/j 4- ftXi-r f3yt = vix; /, 4- ftXj 4 f zy, = vjx;
f I t r 4- f 4 71
/1 "Г /2-*m i I зУт — ym*-
Вторая группа будет содержать постоянные /,,, /5, /в и пе-
перемещения viy, Vjy, vmy. Решая первую группу уравнений,
приходим к следующим соотношениям:
, 1_ , ,
/2 —
1
2Fe
1
E.2)
где
i = «/у — Ут\ bj -= ут— у Г, Ьт — У; — у/,
m—xmyj; cj = xmyi — Xiym; cm ¦== Xjyj—Xj
E.3)
Выражения для /4, /5 и /6 можно получить соответственно
из формул для /,, /2 и /3, заменив в них yi3c, vjx, vmx на УгУ,
уУ!/> vmy Величина Fe, фигурирующая в этих соотношениях,
представляет собой площадь треугольника ijm и может быть
вычислена через координаты узлов с помощью определителя:
У,
У]
Ут
E.4)
Заметим также, что из E.3) и E.4) вытекает соотношение
2F' = d + Cj + cm. E.5)
Подставляя E.2) в первую из формул E.1), можно приве-
привести ее к виду
jx f
+ (сп -f- b
am у) v
E.6)
134
Последняя формула выражает перемещение их в любой точ-
точке элемента через его узловые перемещения. Аналогичное вы-
выражение получается и для перемещения иу. Представим'E.6)
и соответствующее выражение для иу в форме
Г"*Н"*Ь
где
IF
bi
>х + а>
0];
где
-»> 0 (с
Последние равенства можно переписать также в форме
a.v = text <*xj a.rrJ: «j, = lag( ayj aym\, E.7)
r x +- ar y) (/• =/, /, /n).
E.8)
E.9)
Эти формулы определяют искомую матрицу аппроксими-
аппроксимирующих функций
— 14.
которую можно представить в виде a = \щ а} ат\, где
Далее по D.7) вычисляем матрицу
-I
[<?аж/дл:
дау/ду
дау/дх -f 5а
С учетом E.7)—E.9) получим 0 = [04 fy f5,J, где
Л о
О a, (r = i,j,m).
E.10)
135
В данном случае элементы матрицы р не зависят от коор
динат. Это означает, что деформации (а следовательно, и на-
пряжения) в пределах рассматриваемого конечного элемента
постоянны; при переходе от одного элемента к другому они
изменяются скачком.
Теперь найдем матрицу жесткости элемента, пользуясь
формулой
Поскольку матрица 0 представлена в стандартной блочной
форме, то в соответствии с D.14), D.15) для матрицы жестко-
жесткости рассматриваемого треугольного элемента получим
ки кец
k% keif
kelm
Km
где типовая подматрица
sdT.
Подынтегральное выражение не зависит здесь от коорди-
координат и может быть вынесено за знак интеграла. В случае обоб-
обобщенного плоского напряженного состояния рассматриваемый
конечный элемент представляет собой пластину. Если его тол-
толщина постоянна и равна he, то объем элемента те будет равен
Fehe. Таким образом, в этом случае
k|s¦= F°h°$Try,$s (r, s = i, j, m).
E.11)
Формулой E.11) можно пользоваться для вычисления мат-
матрицы жесткости элемента как гладкой, так и конструктивно-
ортотропной пластины. В последнем случае матрица и опреде-
определяется согласно A.36), A.32), A.34) и перемножение матриц в
E.11) целесообразно выполнять на ЭВМ. Если же пластина не
имеет подкреплений, то удобнее получить элементы типовой
подматрицы k*s в аналитической форме. Представим для этого
матрицу упругости
1 и
1
О
A
0 1
°
-H)/2j
136
в виде двух слагаемых х = хе -f- хо, где
Е
Здесь G = Е/12 A + ц)] — модуль сдвига.
Тогда
1
ц
0
и-
1
0
0
0
0
у X(J = \J
О О 01
о о о|.
о о ij
= K/-S, ? Т" K/-S, G)
E.12)
E.13)
где
= F<
Г«оfc.
Подставляя в выражение для к%, е формулы для отдельных
подматриц, получаем
2А* [0 аг Ьт\ i-l
1
и-
_0
и-
1
0
0
0
0 .
X
X
2Fe
откуда
Ehe
$. е = •
4 (I—(X3) 7=*
Аналогично находим
агЬ3 aTas J
k,s.g = . E.15)
4Fe lbras brbs\
Отметим, что матрицы kers, e и k*s. а представляют собой
вклады, даваемые соответственно нормальными деформация-
деформациями и деформациями сдвига в матрицу к%.
Для того чтобы получить матрицу жесткости для случая
плоской деформации, следует принять he = 1 и заменить в
E.14) модуль упругости Е на Е1(\ — ц2), а коэффициент Пуас-
Пуассона ц, — на [*/A — \к) (см. § 1.2).
Коснемся далее вопроса о приведении внеузловых нагру-
нагрузок к эквивалентным узловым силам. Такое приведение долж-
должно выполняться в соответствии с D.16). Однако замена поверх-
поверхностной нагрузки узловыми силами часто осуществляется из
137
простых физических соображений, а формула D.16) исполь-
используется лишь для приведения объемных сил:
В блочной записи имеем
-pf
p;
где типовая подматрица
= i, /, /в).
Если, в частности, объемные силы постоянны, то можно по-
показать, что
Отсюда видно, что в рассматриваемом простейшем случае
постоянных объемных сил их равнодействующая поровну рас-
распределяется между узлами. В случае, когда объемные силы
переменны, можно приближенно воспользоваться этой же фор-
формулой, взяв значения Rx и Р у в центре тяжести треугольника.
Перемещения их и иу, определяемые выражениями E.1), из-
изменяются по линейному закону вдоль любой прямой в плоско-
плоскости ху, в том числе по сторонам треугольника. Линейная функ-
функция полностью определяется какими-либо двумя ее параметра-
параметрами. Значит, перемещения их и иу на каждой стороне треуголь-
треугольника будут однозначно определены, если известны их значе-
значения в узлах, лежащих на соответствующей стороне. Так как
узловые перемещения являются общими для соседних элемен-
элементов, то при переходе от одного элемента к другому перемеще-
перемещения не будут иметь разрыва. Следовательно, треугольные эле-
элементы с линейными полем перемещений относятся к катего-
категории совместных.
Недостатком рассмотренного элемента является то, что на-
напряжения в пределах треугольника постоянны, и поэтому для
получения достаточной точности решения часто приходится
использовать весьма густую сетку (особенно в областях с быст-
Г38
роменяющимся напряженным состоянием). Это может привес-
привести к системе уравнений слишком высокого порядка и соответ-
соответственно к чрезмерным затратам времени на решение задачи.
Тем не менее этот элемент широко используется, поскольку он
очень прост и позволяет идеализировать плоские тела доволь-
довольно сложной конфигурации.
§ 5.2. Совместный прямоугольный элемент
Другой конечный элемент, используемый в плоской задаче,
показан на рис. 5.2. Он представляет собой прямоугольник с
узлами в вершинах. Матрица узловых перемещений такого
элемента имеет восемь компонент. Обходя узлы против часовой
стрелки, запишем
Vе = {ViV7V,Vm},
где, как и ранее,
vr =
Для приближенного представления поля перемещений ко-
конечного элемента можно взять функции
их = h+ f*x + f3y + fiXy; uy = f5 + fex + f7y + f8xy,
E.16)
в которых содержится восемь постоянных. Для их определе-
определения можно так же, как и в случае треугольного элемента, за-
записать в каждом узле условия равенства перемещений их и
иу их узловым значениям. Мы опять придем к двум группам
уравнений, первая из которых позволяет выразить постоян-
постоянные fi--.fi через игх, а вторая — постоянные /5.../8 через vry
(г = i, j, l,m).
В итоге блоки матрицы а = [ага,а{ат] будут иметь такую
же структуру, как и в случае треугольного элемента:
E-17)
О ' '
где через tyT обозначены некоторые функции координат.
Покажем, что для отыскания функций i|v совсем необяза-
необязательно решать систему уравнений, как это делалось ранее, а
139
можно найти их путем подбора. Запишем прежде всего зависи-
зависимость u = fxve в развернутом виде:
\ь
uA [о *,\о
° 1
«ix
vJy
Отсюда вытекает следующее выражение для их:
Ус
vjx
РНС 5.2
Ux = _ . .. ,
Если положить здесь
fix =1. а смещения осталь-
остальных узлов равными нулю,
то будем иметь их = %.
Следовательно, г|)г — такая
функция координат х, у,
которая дает распределе-
распределение перемещений в элемен-
элементе при единичном смеще-
смещении узла / и при непод-
неподвижных остальных узлах.
Обобщая эти рассуждения,
приходим к заключению,
что каждая из функции г|зг
дает распределение пере-
перемещений в пластине при
единичном смещении (вер-
(вертикальном или горизон-
горизонтальном) узла г и при не-
неподвижных остальных уз-
узлах. В качестве примера
Рис- 53 на рис. 5.3. показан вид
функции i|jj.
Для того чтобы записать функции \рг, перейдем к системе
безразмерных координат ?, т), начало которой находится в
центре тяжести прямоугольника (см. рис. 5.2). Положим
I = 2 (х — хс)/а; т) = 2 (у — yc)lb,
140
где а, Ь — размеры сторон прямоугольника, а хс, ус — коор-
координаты его центра тяжести. Тогда новые координаты 1, ц бу-
будут на сторонах элемента принимать значения ±1. Для узлов
/, /, /, т они окажутся соответственно равными (—1, —1), A,
-1), A, 1), (-1, 1).
Учитывая, что перемещения согласно E.16) должны изме-
изменяться по линейному закону вдоль прямых х = const или у =
= const, можно функцииi|v искать в виде произведений A ±?) X
X(l ±ti). Условия в узлах будут удовлетворены, если поло-
положить
Ь = A - I) A - л)/4; Ь = A + I) A - л)/4;
= 0 -
ч)/4.
Все эти функции можно записать с помощью одного общего
выражения:
% = A + U) A + ти)/4 (г = г, /, /, т). E.18)
Вычислим далее матрицу р == [PiPjPiPrJ- По формуле D.7)
имеем
[dajdx
дау1ду
дау/дх + dajdyj
гдеая но, — соответственно первая и вторая строки матрицы
а.
Пользуясь соотношениями dx = (a/2)d?; Ay — (b/2)dTj и
учитывая блочную структуру матрицы а, для типовой подмат-
подматрицы pr получим
• 2 дфг
а д?
О
О -2-
Ch)
Подставляя сюда выражения для tyr, имеем
E.19)
141
где через ат (?) и Ът (ц) обозначены функции:
От = Лг A + 1Л)'Ь; Ьг = Ът A + т|гт|)/а.
E.20)
Вычислим теперь матрицу жесткости рассматриваемого
элемента для случая обобщенного плоского напряженного
состояния:
к// к// кц kin
ке„ кЬ ке
ке„ к'ш
Симм-
где
I 1
J J p?xP,dgdT,. E.21)
Так же как и в случае треугольного элемента, удобно раз-
разбить подматрицу kers на два слагаемых:
Здесь
krs— krs, Е Т krs. О*
1 1
к%.Е=^- J j P,r
abh
—« - l
l
s. a --
j j P,rxoP,d&iTb
где матрицы упругих коэффициентов иЕ н ха определены ра-
равенствами E.12). Подстановка выражений для *я, рг и ps в
формулу для k's, е дает:
' ' г, « -. Г1 (а 01
е _ abh С С 1 Г От 0 ат\ Е
-1—1 L J L0 0 Oj
U "* Ь ' 16(l-|j2)
X
142
Вычислим необходимые интегралы, учитывая E.20):
J ar(l)as(l)dl = -^ f 0+E,S)
-i -i
62 V з I'
Аналогично вычисляются интегралы по г\ от bT (ц) и от про-
произведения Ът (r\)bs (r\).
В итоге для krs, e имеем
4A-i
E.22)
где через у = bla обозначено отношение сторон элемента.
Подобным же образом находим
К/-». О —
dbh
Jt )t 2 [о ат Ьг\
'0
0
0
0
0
0
0'
0
1
X
откуда
,-Б.
. E.23)
Формулы E.22), E.23) относятся к случаю гладкой плас-
пластины. Для конструктивно-ортотропнои пластины следует в
E.21) подставить матрицу х, определенную в § 1.3, и восполь-
воспользоваться численным интегрированием. Но если подкрепля-
подкрепляющие элементы параллельны оси х, то в качестве матрицы уп-
упругости следует взять матрицу х0, определяемую равенст-
равенством A.32). В этом случае также нетрудно вывести аналитичес-
аналитические выражения для подматриц k*s подобно тому, как это дела-
делалось для гладкой пластины.
143
В рассмотренном прямоугольнике перемещения их, ии,
определяемые соотношениями E.16), изменяются по линейно-
линейному закону вдоль прямых х = const или у = const и, в частно-
частности, вдоль его сторон. Рассуждая так же, как и в случае тре-
треугольных элементов, заключаем отсюда, что введенные выше
прямоугольные конечные элементы являются совместными.
Заметим, что они совместны также с треугольными элемента-
элементами предыдущего параграфа, так как в обоих случаях переме-
перемещения вдоль сторон изменяются по линейному закону.
Представленный здесь прямоугольный элемент наряду с
треугольным является одним из простейших конечных эле-
элементов. При одинаковом числе узлов (т. е. при одинаковом по-
порядке системы разрешающих уравнений) он дает более точное
решение, чем при идеализации тела треугольными элементами.
Однако с помощью одних только прямоугольников можно
идеализировать лишь такие области, которые ограничены пря-
прямыми линиями, параллельными осямл:, у. Для более сложных
областей можно использовать прямоугольные элементы в со-
сочетании с треугольными, но это усложняет подготовку исход-
исходных данных. Поэтому для расчета тел произвольной конфигу-
конфигурации обычно применяют конечные элементы в виде четыреху-
четырехугольников произвольной формы. Примеры таких элементов
будут рассмотрены ниже.
В расчетах авиационных конструкций четырехугольные
(и, в частности, прямоугольные) элементы применяются как
составные компоненты при моделировании различных балок с
тонкими стенками (лонжеронов, нервюр, шпангоутов и т. п.).
Если изгиб происходит в плоскости стенки, то она будет нахо-
находиться в условиях обобщенного плоского напряженного состо-
состояния. Для упрощения исходных данных и снижения затрат
машинного времени желательно по высоте стенки брать толь-
только один элемент. Но рассмотренный выше прямоугольник не
подходит для этих целей, так как он плохо описывает состоя-
состояние чистого изгиба.
На рис. 5.4, а показана плоская прямоугольная пластина,
которая нагружена по боковым сторонам нормальными напря-
напряжениями, изменяющимися по линейному закону, так что
она находится в условиях чистого изгиба. Точное решение этой
задачи показывает, что взаимный угол поворота боковых гра-
граней равен 9 = Ma/(EJ)-, где J — ЛЬ3/12 — момент инерции по-
поперечного сечения пластины; М — изгибающий момент.
Пусть теперь прямоугольный конечный элемент с такими
же размерами находится в аналогичных условиях (рис. 5.4,6).
Поскольку вдоль каждой стороны перемещения изменяются
по линейному закону,.то все стороны элемента после деформа-
144
A/A©
Рис. 5.4
ции останутся прямыми. Можно показать [40], что взаимный
угол поворота 9е боковых сторон для рассмотренного выше
прямоугольного элемента будет равен
^ 45 Мд
SC48[A+3/(8y2)] EJ'
где у = Ыа.
Сопоставляя этот результат с точным, видим, что данный
конечный элемент дает заниженное значение угла поворота, т. е.
является слишком жестким. Источником чрезмерной жесткос-
жесткости конечного элемента при изгибе является деформация сдвига
гху. В точном решении гху — 0, а для конечного элемента
используемая аппроксимация перемещений приводит к появ-
появлению деформаций сдвига еху = 9е?. Конечно, можно полу-
получить хорошее решение, если моделировать пластину несколь-
несколькими элементами, но нас в данном случае интересует возмож-
возможность удовлетворительного воспроизведения состояния из-
изгиба с помощью одного элемента. В следующем параграфе бу-
будет рассмотрен несовместный элемент, удовлетворяющий это-
этому требованию. Другой способ исключения «ложного» сдвига
описан в § 6.6.
§ 5.3. Несовместный прямоугольный элемент
В предыдущих параграфах мы задавались характером изменения
перемещений внутри конечного элемента. Можно, однако, получить рас-
распределение перемещений, задавшись предварительно законом изменения
напряжений в пределах элемента. Воспользуемся таким подходом для
145
вывода жесткостных характеристик конечного элемента прямоуголь-
прямоугольной формы с четырьмя узлами в вершинах. Прн этом будем требо-
требовать, чтобы напряжения в пределах каждого элемента удовлетворяли
дифференциальным уравнениям равновесия (прн отсутствии объемных
сил).
Как известно (см. § 1.2), дифференциальные уравнения равновесия
будут тождественно удовлетворяться, если напряжения связаны с не-
некоторой функцией ф (функцией напряжений) соотношениями A.27).
При этом условие совместности деформаций будет в случае гладкой
пластины выполняться, если функция ф (х, у) является решением урав-
уравнения A.26).
Примем, что в пределах конечного элемента функция ф изменяется
по закону
Ф = с-^ + сгху + Сзу2 +
при котором уравнение A.26) удовлетворяется тождественно для лю-
любых значений постоянных c-^...Сь-
По A.27) находим
ахх = 2с3 + бСъУ, Оуу = 2сх + 6с4х; аху = — с2. E.24)
Отсюда видно, что используемый набор функций ф дает простей-
простейшие напряженные состояния (растяжение и изгиб в двух направлениях,
а также чистый сдвиг).
Пользуясь далее законом Гука для обобщенного плоского напря-
напряженного состояния, определим деформации:
()
хх = — (Охх—Wyy) = -j? B^3 + бСьУ—2ц СХ — 6ц с4 х);
j,j,=— (oyy — \iaxx)=— Bc1-\-6ctx—2ji c3—6|j, c& y);
?xy— q °ХУ ? C2-
Перемещения можно найти теперь нз уравнений Коши A.20):
дих диу diiy , дих
дх ду а дх ду "
Интегрируя найденные выражения для гхх и гуу соответственно по
х и у, будем иметь
«* = [2(с3 — |icj) х + 6съху —
Uy = [2 (q — цс3) у + 6ctxy — 3\1Сьу2 + g2(x)]/E,
где gi (у) и g2 (x) — произвольные функции.
Подстановка этих формул, а также выражения для еХу в третье со-
соотношение A.20) дает
Перепишем это равенство следующим образом:
146
В левой части полученного соотношения стоит функция только
х, а в правой — функция только у, н равенство возможно лишь в том
случае, когда обе функции равны некоторой константе. Обозначив эту
константу через с«, приравняем к ней поочередно каждую из функций.
Это дает два уравнения относительно g1 (у) н gt(x), интегрируя которые
находим
8i (У) = — Зад2 — A + Ц) сг у — сву + ст.
ё2 (*) = — Зс5дг2 — A + ц) с2х + свх + св,
где с-, н eg — постоянные интегрирования.
После подстановки полученных выражений в формулы для их и
иу имеем;
их = [2 (с3 - ii q) * + 6 сьху - 3 с4 (цх2 + уг) — A + ц) сгу-
— сву + c7l IE;
иу = [2 (с, — ц,с3) I/ + 6ctxy — Зс5 (лг2 + цу1) — A+ ц) с2дг +
Последним выраженням можно придать более простой вид
E.25)
«!, = /• + /•* + hy + fsxy - /4 (х* + fi«/2)/2,
если ввести новые произвольные постоянные: Д = с7/?; /2 = 2 (с3 —
— fiCl)/?; /? = — К» + ц) с2 + с«]/?; Л = W?; h = с8 / ?;
/« = — [A + Ц) с2 — св]/Е; /7=2 (сх — цса)/Е; fa = 6 Cl/?.
Функции E.25) отличаются от использованных в предыдущем па-
параграфе наличием дополнительных членов ft*2 + у3 и х2 + fiy2. Си-
Система уравнений, связывающих между собой произвольные постоян-
постоянные / и узловые перемещения, ие будет уже, как ранее, распадаться иа
две подсистемы, поскольку в выражениях для их и иу фигурируют об-
общие постоянные Л и ft- Это означает, что например, смещения узлов
вдоль оси х будут в общем случае вызывать в рассматриваемом конеч-
конечном элементе не только перемещения их, ио также и поперечные пере-
перемещения иу.
Исходя из вида функций E.25), можно и в этом случае путем под-
подбора записать общее выражение для подматриц аг (г = i, /, /, /я),
входящих в матрицу а = [а,-а7-агат].
Перейдем прежде всего к системе безразмерных координат ?, ц, по-
полагая, как и ранее, | = 2 (х — хе)/а; г\ = 2 {у—Ус)/Ь. Здесь по-
прежнему: а, Ь — размеры сторон прямоугольника; хс, ус — ко-
координаты его центра тяжести. В новых координатах выражения E.25)
примут внд
l ч +/; in -Yfl [-j
Ел—5-/4*(у i2+^vri2) ; E.26)
где у = Ь/а. Через /* здесь обозначены новые постоянные (например,
Я =(аЬ/4)и; П = (аЬН) /, и т. д.).
Пусть теперь один из узлов конечного элемента (скажем, узел г)
получил единичное смещение vrx = 1 вдоль оси х, а все остальные уз-
147
ловые перемещения равны нулю. Найдем распределение перемещений
их и иу, возникающее при этом в конечном элементе в соответствии с
формулами E.26). Перемещение их должно принимать единичное значе-
значение в узле г и обращаться в нуль во всех остальных узлах. В предыду-
предыдущем параграфе описана схема построения такой функции:
"*=— A + ёг 6) (И-*1гП)-
Отметим, что коэффициент /J, который согласно E.26) является
множителем перед произведением %х\, оказывается здесь равным 5rTjr/4.
Переходя к определению иу, замечаем прежде всего, что, как следует из
E.26), в выражение для uv обязательно должна входить функция ~62+
+цуПа с множителем — g-/J, т. е. выражение — g- %Ti\r (- ?2 + M-VH2)-
Кроме того, перемещение иу должно обращаться в нуль во всех
узлах, так как по условию отличным от нуля является лишь перемеще-
перемещение vrX. Функция же — g2 + цугJ во всех узлах принимает одинаковое
значение — + HY (поскольку координаты |, tj узлов равны ± 1).
Условие в узлах будет выполнено, если положить
Здесь к записанной выше функции добавлена постоянная величи-
величина, что не противоречит набору функций во втором равенстве E.26).
Аналогичные рассуждения показывают, что при единичном смеще-
смещении vry = 1 распределение перемещений дается равенствами
(l+b?)(I>
Таким образом, произвольное смещение узла г вызывает в конеч-
конечном элементе перемещения
Л) «V-«—Г"?' Чг I— 52+VT12 -т) vry;
Следовательно,
«,
4
ary
148
4" О +Ь Б) О +Чг ч)
(I +SrI) A +лгЧ)
Типовой блок рг матрицы р =
находим теперь по фор-
формуле
откуда получаем
a
2 дагу | 2 a^a.
Л.Л) ~^?
Ъ
Наконец, по формуле
1 1
J P^Ps-^-dl
E.28)
вычисляем типовую подматрицу жесткости. Представляя ее. как и преж-
прежде, в виде суммы двух слагаемых, имеем
Ks—Ks,
где
Eh
к«,я=;
¦)
^r*ls
E.29)
-1,6. 1
E.30)
Рассмотренные здесь конечные элементы являются несовместны-
несовместными. В самом деле, из E.26) следует, что при лг= const или у = const
перемещения изменяются по квадратичному закону. Квадратная пара-
парабола задается тремя параметрами, и узловые перемещения двух сосед-
соседних вершин прямоугольника не могут однозначно определить значе-
значения функций их и иу на прилегающих к ним стороиам. Следовательно,
равенство перемещений смежных элементов обеспечивается только в
узловых точках, а на линиях раздела элементов перемещения будут
претерпевать разрывы.
149
Тем не менее использование таких элементов позволяет получить
хорошую точность. Онн особенно удобны при моделировании балок, по-
поскольку обеспечивают точное представление состояния чистого изгиба.
§ 5.4. Внутренние узлы и подконструкции
До сих пор мы ограничивались случаем, когда узловые точ-
точки расположены на границе конечного элемента. Но это сов-
совсем необязательно. Рассмотрим конечный элемент, у которого
помимо обычных узлов на границе (будем называть их внеш-
внешними) имеются также внутренние узлы, принадлежащие толь-
только данному элементу. На рис. 5.5 показан пример такого
элемента. Здесь имеется восемь внеш-
внешних узлов (они являются общими для
данного элемента и смежных с ним)
и один внутренний.
Особенность внутренних узлов за-
заключается в том, что они непосред-
непосредственно связаны только с узлами,
принадлежащими данному конечному
элементу. Поэтому коэффициенты мат-
Рис- 5-5 рицы жесткости всей системы, отно-
относящиеся к внутренним узлам, бу-
будут просто совпадать с соответствующими коэффициентами
жесткости отдельных конечных элементов. Точно так же уз-
узловые силы во внутренних узлах конечного элемента не имеют
вкладов со стороны смежных элементов, т. е. они могут быть
вычислены еще до объединения конечных элементов. Все это
позволяет перемещения внутренних узлов каждого элемента
выразить через перемещения его внешних узлов и, таким об-
образом, исключить их из числа искомых параметров объединен-
объединенной системы.
Узловые перемещения конечного элемента с внутренними
узлами, которые мы будем обозначать через v, можно предста-
представить в виде
-[.
где ve — матрица-столбец, в которой перечисляются перемеще-
перемещения всех внешних узлов, а матрица v0 содержит перемещения
внутренних узлов. В представленном на рис. 5.5. примере мат-
матрица Vе будет включать в себя перемещения первых восьми
узлов, а матрица v0 — перемещения девятого узла.
150
В матрицах аир, связывающих перемещения и деформа-
деформации внутри элемента с v соотношениями
U =а\; 8= p~v,
также выделим соответствующие подматрицы:
Эти подматрицы имеют простой смысл. Так, столбцы матри-
матрицы а дают распределение перемещений в пределах элемента
при единичных смещениях внешних узлов, а столбцы матрицы
«о — распределение перемещений при единичных смещениях
внутренних узлов.
Пусть на элемент действуют объемные R и поверхностные
р силы. Матрица-столбец эквивалентных им узловых сил опре-
определится выражением
«/Rdt-f Jarpdo).
efi
Учитывая блочное представление матрицы а, получим отсю-
отсюда две подматрицы, которые мы обозначим через Ра и Ро:
Ра =
а
J c^Rdr -f J атpdo; Ро = J ojRdr + J ajpdo. E.31)
Первая из них содержит силы, приложенные к внешним узлам,
а вторая — к внутренним.
Наконец, в матрице жесткости элемента k= J p^xpdt так-
такте
же выделим соответствующие блоки:
1кГ ко]'
к
Здесь
ко = fP^pdt; кь = fP^Kpodr; ko= Гр?кройт. E.32)
Iе т« te
Теперь связь между узловыми силами и перемещениями
конечного элемента запишется так:
151
Через Р" и Ро обозначены здесь сосредоточенные силы, дей-
действующие на элемент во внешних и внутренних узлах соответ-
соответственно. Отсюда вытекают два равенства
E.33)
Второе из этих равенств позволяет выразить v0 через Vе:
v0 = ко1 (Ро + Ро) - коl kf, Vе. E.34)
Подстановка этого результата в первое соотношение E.33)
дает связь между перемещениями v* и узловыми силами:
(ka — kbko 'кь) ve =¦ Р* +¦ Ра — кьког (Ро + Ро). которую мож-
можно записать в стандартной форме D.13):
k" ve =Ре +-Ре.
Здесь
к" = ка — кь к—' к?; E.35)
Р- =Ра-к„ к. (Ро +Ро). E.36)
Формула E.35) позволяет вычислить матрицу жесткости ко-
конечного элемента, приведенную к перемещениям его внешних
узлов. Приведение сил к внешним узлам осуществляется при
этом по E.36).
Объединение конечных элементов выполняется далее обыч-
обычным образом. Матрица неизвестных перемещений будет те-
теперь включать лишь перемещения тех узлов, которые явля-
являются внешними для конечных элементов. Эти перемещения оп-
определяются в результате решения системы уравнений, а пере-
перемещения внутренних узлов при необходимости могут быть най-
найдены из E.34).
Использованные выше рассуждения можно применить к об-
образованию сложных конечных элементов из простейших. Выде-
Выделим часть тела, включающую в себя некоторое число простых
конечных элементов. Объединив эти элементы, можно сформи-
сформировать общую матрицу жесткости и матрицу узловых сил для
рассматриваемой части. В результате получим один сложный
конечный элемент, который затем можно обычным образом
объединять со смежными участками тела для формирования
разрешающей системы уравнений. Такой элемент называется
подконструкцией (или суперэлементом). Разбиение на подкон-
струкции применяется при расчете весьма сложных систем,
таких, как самолет в целом. При этом подконструкции могут
действительно соответствовать некоторым характерным отсе-
152
кам конструкции (крыло, фюзеляж и т. д.), но это необязатель-
необязательно.
Все узлы подконструкции можно разделить на «внешние»
и «внутренние». К внешним отнесем такие узлы, которые явля-
являются общими для соседних подконструкции, а к внутренним
— те, которые принадлежат только данной подконструкции.
Так, при идеализации крыла в виде подконструкции внешни-
внешними будут лишь те узлы, которые являются общими для крыла
и фюзеляжа. Перемещения внутренних узлов можно выра-
выразить через перемещения внешних подобно тому, как это было
сделано для конечного элемента с внутренним узлом. Тогда
разрешающая система уравнений будет включать в себя пере-
перемещения лишь тех узлов, которые являются для подконструк-
подконструкции общими.
Обозначим через Vе матрицу перемещений внешних, а че-
через v0 — внутренних узлов. Тогда матрица узловых переме-
перемещений подконструкции v будет представлена в виде
Матрицу узловых сил подконструкции Р запишем также в
блочной форме:
¦KMJ]
Здесь подматрицы Ро и Ро включают в себя соответственно
сосредоточенные силы и силы, эквивалентные распределенной
нагрузке, которые действуют во внутренних узлах. Подматри-
Подматрица Ра содержит силы во внешних узлах, эквивалентные рас-
распределенной нагрузке, а в Р" перечисляются сосредоточенные
силы, действующие на подконструкцию во внешних узлах.
Наконец, выделим соответствующие блоки в матрице жест-
жесткости подконструкции к:
k=f к к;
Отметим, что элементы матриц Ра и Ро> а также элементы
матрицы жесткости к находятся по обычному правилу суммиро-
суммирования вкладов отдельных конечных элементов, составляющих
подконструкцию.
153
Связь между узловыми силами и перемещениями запишет-
запишется теперь так:
Выражая далее перемещения внутренних узлов v0 через Vе,
приходим снова к соотношению keve = Ре 4- Р8, в котором
ке и 1>в определяются аналогично E.35), E.36):
Ье Ь Ь Ь—1 ЪТ. ре _р Ь Ь~ 1 Л) I pi
При этом
Использование подконструкций позволяет расчленить рас-
расчет сложных систем на отдельные этапы. Другое достоинство
метода подконструкций заключается в том, что конструктив-
конструктивные изменения в какой-либо
подконструкций требуют лишь
частичного пересчета, поскольку
матрицы жесткости всех осталь-
остальных подконструкций остаются
неизменными. Следует отметить,
однако, что введение подкон-
подконструкций существенно услож-
усложняет программирование.
Проиллюстрируем сказанное
на простейшем примере образо-
образования плоского четырехуголь-
четырехугольного конечного элемента про-
произвольной формы из четырех треугольных (рис. 5.6). Сумми-
Суммируя коэффициенты жесткости отдельных треугольников, обра-
образуем сначала матрицу жесткости к, которая будет иметь раз-
размер 10 X 10 (так как в каждом из пяти узлов имеется по две
степени свободы). В блочной форме матрица к имеет вид
кп к1г к13 к14 к15
кл к2г кзз кад к25
Рис. 5.6
154
Нижние индексы означают здесь, как обычно, номера уз-
узлов. Типовая подматрица,
krs- к\ + k»-f- к»Ч- к™ (r, s = 1,2,.... 5).
Выделяя в к необходимые блоки, имеем
к":
где
"к к« J
к —
кзх
13
кзз
K^ij *^42
к15
кз5
Для приведения матрицы жесткости к перемещениям внеш-
внешних узлов можно теперь воспользоваться формулой E.35).
В итоге получим блочную матрицу размером 4x4 вида
к" =
ke
K13
ke
K23
be
кзз
be
K43
ke
K24
K34
Здесь kers = krs — kr, 5кГ,5 к{5 (г, s = 1, 2, 3, 4).
Аналогично вычисляются и эквивалентные узловые силы.
Таким образом, мы получаем совместные четырехугольные
конечные элементы с восемью степенями свободы. Узловые
перемещения, найденные с помощью подобных элементов, бу-
будут такими же, как и при самостоятельном применении входя-
входящих сюда треугольников. Все же использование составных че-
четырехугольников имеет определенные преимущества. Во-пер-
Во-первых, сокращается количество исходной информации. В память
ЭВМ достаточно ввести координаты х, у всех внешних узлов,
а координаты внутренних можно определить для каждого эле-
элемента программным путем, пользуясь, например, формулами
t/4)/4.
у5 =
у а
Во-вторых, число узловых перемещений, подлежащих
отысканию из решения системы уравнений, уменьшается за
счет исключения перемещений внутренних узлов. Соответст-
Соответственно уменьшается и размер матрицы жесткости всей системы,
155
что приводит к экономии памяти. Последнее обстоятельство
может иметь существенное значение в тех случаях, когда реше-
решение системы уравнений выполняется с использованием одной
только оперативной памяти.
Процедуру исключения степеней свободы внутренних уз-
узлов можно рассматривать и с точки зрения минимизации пол-
полной энергии системы. Более подробно этот вопрос будет в нес-
несколько иной связи рассмотрен в следующем параграфе.
§ 5.5. Неузловые степени свободы
Добавление внутренних узлов позволяет улучшить жесткостные
характеристики конечных элементов и, следовательно, повысить точ-
точность решения. Улучшение характеристик получается за счет повыше-
повышения числа степеней свободы конечного элемента по сравнению со слу-
случаем, когда имеются только внешние узлы. Однако введение дополни-
дополнительных узлов требует полной перестройки матрицы аппроксимирую-
аппроксимирующих функций а. Удобнее взять за основу «базовый» конечный элемент с
одними только внешними узлами и добавить некоторые дополнитель-
дополнительные функции распределения перемещений, не связывая их с введением
новых узлов. Рассмотрим такой подход более подробно.
Пусть некоторый конечный элемент имеет узлы », /, ... н пусть для
него выбрана система аппроксимирующих функций, составляющих
матрицу а. Построим теперь новый конечный элемент, для которого
распределение перемещений внутренних точек определяется равенст-
равенством
и = «ve + «ос. E.37)
Здесь с — матрица-столбец некоторых постоянных, а матрица
а„ содержит выбранные заранее функции, определяющие дополнитель-
дополнительное распределение перемещений внутри конечного элемента при отсут-
отсутствии узловых перемещений. Каждая из этих функций, следовательно,
должна обращаться в нуль во всех узлах конечного элемента. Допол-
Дополнительные параметры (неузловые степени свободы) с не имеют здесь
ясного физического смысла. Их значения можно определить из усло-
условия минимума полной энергии системы.
Так как иеузловые степени свободы вызывают появление перемеще-
перемещений только в даииом конечном элементе, то минимизацию энергии по
параметрам, составляющим матрицу с, можно выполнить до объедине-
объединения конечных элементов.
Применяя обычным образом формулы Коши, для деформаций по-
получим соотношение
е = pv' + р0 с,
где матрица ро образуется из компонент матрицы «0 так же, как матри-
матрица Р образуется из компонент ос.
По закону Гука имеем также
0 =• у. е = у. (Pv* + Рос).
Потенциальная энергия деформации конечного элемента
156
откуда после подстановки выражений для в и о имеем
ив = Т J
Раскрывая здесь скобки н выполняя интегрирование, получаем
[(<)r К ve + (уУкьс+сгк?уЧ сг к„ с],
где введены матрицы, аналогичные E.32):
ko=J PrxpdT; kb=J р"гхр\,ат; ko= J pJxM*.
T« T« X»
Отметим, что ка есть матрица жесткости исходного конечного эле-
элемента, так что первое слагаемое в формуле для U* определяет энергию
деформации этого базового элемента. Подчеркнутые члены в формуле
для IIе, будучи скалярными величинами, получаются один из другого
путем транспонирования и поэтому равны между собой. С учетом этого
перепишем окончательно выражение для Vе так:
ие = ± [(^Т feo уе+ 2 (у*)Г Чс+сТ кв с].
Потенциал внешних сил, действующих иа конечный элемент,
Пе=—
где R и р — матрицы объемных н поверхностных сил; Р* — матрица
сосредоточенных сил в узлах элемента (второе слагаемое будет присут-
присутствовать лишь в том случае, если некоторая часть поверхности конеч-
конечного элемента совпадает с внешней поверхностью тела а>р).
Подставив в формулу для IF выражение E.37), получим
П«=— (v')r(Po+P*)-cTP0.
где матрицы-столбцы Ро и Ро определяются подобно E.31):
Ро= f aTRdT+f aTpd<u; P0=fajRdT+J ajpdto.
Xе <oe Xе <ae
Матрица Pa содержит компоненты узлоных сил, эквивалентных
виеузловой нагрузке, для базоного элемента.
Полная энергия Vе = Ue + Пе конечного элемента опреде-
определится теперь выражением
Условие минимума Vе приводит к равенству
dV/dc = О,
167
откуда приходим к следующему выражению для матрицы с:
c = k0-'(Po-lc?ve). E.38)
Подстановка этого результата в формулу для Vе позволяет выра-
выразить полную энергию элемента в функции одних только узловых пере-
перемещений ve. Учитывая симметрию матрицы к0, можно привести это
выражение к виду
ve= — Игк* ve-Иг(
где, подобно E.35) и E.36),
ие и и и — 1 ь 7\ п0 —- п |_ I. — I ¦
» КО RJ, Kq *?, Г Га »Ь Kg Г
Через Vo в формуле для Vе обозначена величина
которая ие зависит от узловых перемещений, т. е. представляет собой
некоторую константу. Поскольку потенциальная энергия всякой систе-
системы вообще определяется с точностью до произвольной постоянной, то
слагаемое Vo является несущественным и его можно опустить.
Матрица к* представляет собой матрицу жесткости конечного эле-
элемента с иеузловыми степенями свободы с, а Р* есть матрица-столбец
узловых сил, эквивалентных распределенной нагрузке.
Примеиим описаниый подход к построеиию прямоугольиого конеч-
конечного элемента с улучшенными жесткостиыми характеристиками, взяв
в качестве базового прямоугольник с линейным законом изменения
перемещений вдоль сторон (см. § 5.2). Для исходного элемента блоки
матрицы а=[а,а^а|От] определяются выражеиием E.17). Для построе-
построения нового элемента можно принять, например, что перемещения их,
иу изменяются в пределах конечного элемента по закону
их = ах^ + с, A - ?) A _ rf); иу ¦= а^ + с2 A - I2) (I - if).
E.39)
где ах и etj, — первая и вторая строки матрицы а.
Здесь в качестве дополнительной выбрана функция A — ?а)Х
ХA — г\2), которая на сторонах элемента ^при ? = ±1; ц = ±1) обра-
обращается в нуль. Следовательно, добавление таких функций ие нарушает
совместности конечных элементов. Однако по причинам, о которых бу-
будет сказано ниже (см. § 6.2), построенный таким образом конечный
элемент ведет себя практически так же, как и базовый, т. е. исполь-
использование выражений E.39) дает лишь незначительное улучшение жест-
костиых характеристик. Аналогичный результат получится и в том
случае, когда вместо A —?г) A —г\J взять, скажем, функцию
cos(n?/2) cos (ят)/2), которая также ие нарушает совместности конечных
элементов.
В работе [1] предлагается использовать следующее поле переме-
перемещений:
"х = «жуг + сх A - I2) + сг A - t]2);
иу = «» Vе + с3 A - I*) + ct {[- П2). E.40)
Здесь вводится четыре дополнительных параметра Су...с^. Функция
1 — |2 на сторонах т) = ± 1 ие обращается в нуль; точно так же
функция 1 —тJ ие равна нулю на сторонах % = ±1. Следовательно,
158
вдоль сторон прямоугольника перемещения уже ие будут изменяться
по линейному закону, как в случае базового элемента, и получаемые
таким путем конечные элементы оказываются несовместными.
Полагая с = {ct c2 ся с4), запишем:
!_«оу
1— ?2 1— 'п2 ° °
С 0 1-12 1—л2
В соответствии с формулами Коши находим матрицу ро:
даох/дх
Ро= <3<*oj//<3t/
_даОу/дх-\-даох/'дц
Подставляя далее
/%_
V)
0
= —4
Ер
На
0
0
// J
) ?/A-ц!
0
0
0
Tj/6
V?)
)
0
0
На
0"
0
G
0
Т]/6
0
третью формулу E.32), получим после интегрирования матрицу
16Л
G/Y
Gy
Для базового элемента матрица E была получена в блочной форме
Р — fPi PyPiPmJ. где рг определяется по E.19), E.20). С учетом этого
матрицу кь, определяемую вторым равенством E.32), представим также
в блочном виде:
.1
кь.>
кь.г
—кь.т-
где типовая подматрица
I. m).
Подставляя сюда выражения для pr, x и р0, после интегрирования
имеем
кь.г— —
2hlrr]r
0 G
GO
„2\ I
О J
159
Далее, пользуясь формулой E.35), вычисляем матрицу жесткости
ке. Напомним, что матрица ка представляет собой матрицу жесткости
базового элемента. В § 5.2 оиа получена в блочном виде и определиется
формулами E.13), E.22), E.23). К подобной же форме можно привести
и выражение для ке. В итоге для типовой подматрицы к% имеем:
ив
*rs,G 4
Полученный результат в точности совпадает с формулами E.29)—
— E.30) дли прямоугольного элемента с линейным полем напряжений,
рассмотренным в § 5.3. Таким образом, два различных подхода приво-
приводят в этом случае к одинаковым результатам. Этого и следовало ожи-
ожидать. Для аппроксимации перемещений по формулам E.26) и E.40)
используются в конечном счете одни и те же функции: 1, |, r\, g2, grj, t]2.
Причем множители перед |а и тJ в E.26) введены таким образом, чтобы
удовлетворялись дифференциальные уравнения равновесия, а в E.40)
эти множители находятся из условия минимума полной энергии. Но,
как отмечалось в § 2.3, минимизация полной энергии есть, по существу,
неявное удовлетворение дифференциальным уравнениям равновесия,
что и объясняет полученный выше результат.
§ 5.6. Четырехузловой изопараметрический элемент
Рассмотрим четырехугольный элемент произвольной формы
с узлами в вершинах (рис. 5.7, а). Поставим целью построить
систему аппроксимирующих функций, обеспечивающую сов-
совместность элементов. Для этого необходимо, чтобы вдоль каж-
каждой стороны элемента перемещения их, ии изменялись по линей-
линейному закону.
Введем прежде всего вспомогательный квадрат со сторо-
стороной, равной 2, и отнесем его к системе безразмерных коорди-
координат |, т), начало которой помещается в середине квадрата
(рис. 5.7, б). На сторонах квадрата переменные ?, т) принима-
принимают значения ± 1. Пусть требуется аппроксимировать в преде-
пределах квадрата какую-либо функцию Ф (|, т)), для которой из-
известны ее значения Фг, Ф;, Фг, Фт, в угловых точках. Такую
аппроксимацию удобно выполнить с помощью функций E.18)
я|?г = -i- (I +|r |) A +т|г г,) (г-/, /, /, m),
160
которые уже использовались ранее для аппроксимации пере-
перемещений в плоском прямоугольном конечном элементе. Функ-
Функция г|>г, определяемая таким образом, принимает единичное зна-
значение в узле г и обращается в нуль во всех остальных узлах,
изменяясь вдоль сторон квадрата по линейному закону. Функ-
Функции i|v называют иногда функциями формы [6].
Выражение
Ф (Б. л) = ~ О -Б) A -л) Ф*+-j О +I) A -
Рис. 5.7
дает такую аппроксимацию функции Ф, которая удовлетворя-
удовлетворяет условиям в узловых точках. При этом Ф (|, ц) изменяется
по линейному закону вдоль прямых | = const или tj = const,
в том числе вдоль сторон квадрата.
Поставим теперь в соответствие каждой точке квадрата не-
некоторую точку исходного четырехугольника, полагая х =
= х(%, г\), у = у (|, г)). В вершинах четырехугольника функ-
функции х (|, г)), у (|, л) должны совпадать с их узловыми значе-
значениями (т. е. с координатами узлов). Используя свойства аппро-
аппроксимации E.41), можно сразу записать искомые зависимости:
-Г A + Б) A + л)
4
4-0 -9 0
4
6 Зак. 651
, E.42)
161
Примем, например, 1=1. Тогда из E.42) получим
x = -L(l~4)xJ + -L(l+1])xl;
{l4)y+{l+4)i- E<43)
Эти соотношения определяют прямую в плоскости х, у.
При т) = — 1 имеем х = х}, у = у}, а при t] = 1 —х = xt,
у = у и следовательно, изменяя г\ от —1 до +1, получаем
одну из сторон четырехугольника. Рассуждая подобным об-
образом, нетрудно убедиться, что формулы E.42) действитель-
действительно дают отображение квадрата на рассматриваемый четырех-
четырехугольник.
Переходя далее к аппроксимации перемещений их, иу, бу-
будем также выражать их через переменные ?, г\. Это позволяет
получить функции с требуемыми свойствами:
их = ~ A -I) A -Л) vix + ± A +1) {1 -тО vJX +
+ ~(i+?)(i+n)%+4-(i-S)(i+q)<w E-44)
Рассмотрим, например, характер изменения перемещения
их вдоль стороны //, полагая снова g = 1. Из E.44) имеем
и* = ~ О -П) vjx + -i- A +ч) р„. E.45)
Отсюда видно, что во-первых, при т) = — 1 и г\ = 1 (т. е.
в узлах У и 0 перемещение их совпадает с vjx и vtx. Во-вторых,
формулы E.43) и E.45) определяют в пространстве х, у, их
прямую, заданную в параметрическом виде:
х = ах + а2ц; у = Ьг + Ь2ц; их = сг + с#\.
Это означает, что вдоль стороны // перемещение их изме-
изменяется по линейному закону. Аналогичные рассуждения пока-
показывают, что формулы E.45) обеспечивают аппроксимацию
перемещений внутри конечного элемента с линейным законом
изменения вдоль всех его сторон.
IG2
Полагая и = {их иу}\ \е = {v,VjV<vm}. где vr =
= {vrxvry}, представим E.44) в стандартной форме u = av'.
Здесь а = [a,a,-ajocml, где типовая подматрица аг включает
в себя функции E.18):
«
™
о
Перейдем далее к вычислению матрицы р = [р,Р7Р<Рш1-
Типовая подматрица рг образуется из строк матрицы аг по
формуле
откуда следует
даг
дх
дат
-•гг Г
-—
дх
дх
0
di|>r
а;
и
дагх
ду _
0
ду
дх _
E.46)
Входящие сюда производные -гр и -^ нельзя найти непо-
непосредственным дифференцированием, так как ifr не зависит в
явном виде от переменных х, у. На первый взгляд естествен-
естественным кажется воспользоваться правилом дифференцирования
сложных функций:
йд;
д|
,
ду
.
дг\
но это требует знания явной зависимости переменных ?, ц от
х, у, в то время как мы располагаем лишь обратной зависи-
зависимостью, выражаемой равенствами E.42).
Поэтому для вычисления требуемых производных восполь-
воспользуемся формулами
дх dl
+ ¦
ду dl
дх\
дх
дх
дг\
д$г ду
-г— —
ду от)
163
которые в матричной форме имеют вид
E.47)
Здесь через J (g, г)) обозначена так называемая матрица
Якоби:
J F. П> =
дт\ дт\
E.48)
элементы которой легко находятся по E.42). Поскольку функ-
функции в левой части E.47) также нетрудно найти из соотношения
E.18), то равенство E.47) можно использовать для определения
искомых производных:
E.49)
Здесь
матрицу J (I, л) входят функции:
Jl» ± [—A—п) хг + A-т0
о| 4
ОТ] 4
^_ = J_ [_A _t,)
о§ 4
a B
^ {[A|)У|A +
ОХ\ 4
Заметим, что фактическое вычисление матрицы жесткости
рассматриваемого элемента приходится выполнять на ЭВМ с
помощью численного интегрирования. При этом матрицу Р
требуется находить в отдельных точках области, положение
которых определяется используемым правилом интегрирова-
интегрирования. *В этих точках в соответствии с записанными выше фор-
164
мулами определяют матрицу J, а затем обратную к ней
матрицу J-1. В тех же точках по E.49) вычисляют матри-
dtb. d\b, . ... v
цу производных -^ и -z-{r=i, j, I; т), из которых может
быть сформирована матрица рг E.46).
Типовой блок k's матрицы жесткости ke находится по
формуле
где интегрирование ведется по объему Xе конечного элемен-
элемента. Удобно перейти к интегрированию по g, tj, поскольку
при этом получаются простые пределы. Можно показать
[6], что для этих переменных элементарный объем выра-
выражается так:
где h — толщина пластины, a |J (g, r\)\ — определитель
матрицы Якоби, называемой якобианом. Таким образом,
в случае обобщенного плоского напряженного состояния
матрицу k's находим по формуле
1 1
k«=/lJ S P^xPJj(?,ri)|dEdti. E.50)
— i —i
Интегрирование здесь, как уже было сказано, выполня-
выполняется численно на ЭВМ. Некоторые формулы численного
интегрирования, применяемые в методе конечных элемен-
элементов, будут приведены ниже.
Приведение распределенных нагрузок к узловым силам
выполняется обычным образом. Так, если в плоскости эле-
элемента действуют объемные силы R, то их заменяют узло-
узловыми по формуле
Полагая Р' = {Р'Р/Р* Рт} и переходя к интегрирова-
интегрированию по |, т] в плоскости элемента, придем к следующему
выражению для типовой подматрицы эквивалентных узло-
узловых сил:
E.51)
165
Здесь интегрирование также выполняется численно. Матрица
аг в точках интегрирования находится по формулам E.17),
E.18).
Получаемые таким образом конечные элементы являются
совместными. Характерной особенностью здесь является то,
что для задания перемещений их, щ, и координат х, у через
безразмерные координаты ?, т) используются одинаковые выра-
выражения. Это предполагает, в частности, что для определения ге-
геометрии конечного элемента требуется столько же парамет-
параметров (координат узлов хг, уТ), сколько параметров (узловых
перемещений vrx, vrlJ) необходимо для задания поля перемеще-
перемещений. Такие конечные элементы называются изопараметпричес-
кими. Если геометрия совместных элементов определяется
меньшим числом параметров, чем поле перемещений, то такие
конечные элементы называют иногда субпараметрическими.
В некоторых приложениях (например, при расчете оболочек)
используются также суперпараметрические элементы, в кото-
которых число параметров, определяющих геометрию, превышает
число узловых перемещений [6).
§ 5.7. Несовместный четырехугольный элемент
Рассмотренный в предыдущем параграфе конечный элемент явля-
является обобщением прямоугольного элемента с линейным изменением
перемещений вдоль сторон. Его можно было бы использовать при моде-
моделировании стеиок в балках переменной высоты, но ои, так же как и
прямоугольный элемент, неправильно воспроизводит состояние изги-
изгиба в своей плоскости, оказываясь чрезмерно жестким. Как уже гово-
говорилось в § 5.2, источником этого является ложная деформация сдвига
гху, которая в элементах данного типа всегда сопровождает чисто из-
гибные деформации. Один из приемов исключения ложного сдвига,
заключающийся в применении для матрицы жесткости специальной
схемы численного интегрирования, будет изложен в § 6.6. Здесь мы
воспользуемся другим способом, основанным на задании характера из-
изменения напряжений в пределах конечного элемента.
Итак, рассмотрим четырехугольный элемент с узлами в вершинах
(см. рис. 5.7, а). Элемент имеет восемь степеней освободи
ув={*г У] v/ vm},
где vr = {vTXvry}. Будем предполагать, что в пределах элемента ком-
компоненты напряжений изменяются по закону
°хх ~ ci "t" С$У» аю ~ ca "Т" <&Ч аху — *В.
где ct — некоторые постоянные.
Такие напряжения удовлетворяют дифференциальным уравнениям
равновесия при отсутствии объемных сил и условию совместности де-
деформаций и воспроизводят равномерное растяжение и изгиб в двух на-
правлениях, а также чистый сдвиг. Распределение перемещений их,
Чу будет представлено при этом формулами E.25):
и хг -4- и*
h
Введя матрицы и = {их иу); f = {fj^...fs}, представим эти
соотношения в виде
и = «*i, <5-52)
где через ее* обозначена матрица
[«П Г1^ ху 00 0 —(ц**+у*)/21
» = • С8-8»)
ау Л L0 ° ° -(•*2 + HS<2)/2 1 х у ху J
Свяжем далее параметры f с узловыми перемещениями Vе. Для
этого приравняем в узлах элемента перемещения их, иу к соответствую-
соответствующим узловым значениях:
h
х?+цу?
f*+f^r+fiyr+fsXrSr-h 1 -*, • E.54)
Всего мы имеем, таким образом, восемь уравнений {г = {, /, /,
т) относительно восьми постоянных f. Полученную систему уравне-
уравнений можно записать в форме
¦Л =у*, E.55)
где матрица z, имеющая размер 8X8, формируется исходя из выраже-
выражений E.54). Разрешай E.55) относительна f, аришдши к раввистау вида
где Q —т~1', обращение матрацы z выполяиется чнслеяяо иа ЭВМ.
Подстановка E.56) в E.52) приводит к обычаем зависимости и =
=• «Vе, где матрица а определяется как произведение
« = о*а. (S.5T)
По формуле D.7) вычисляем матрицу р. Строки ах, ау матрицы a
в соответствии с E.57) равны: лх = a*Q; «j, = «*Q, где a*, «' опре-
определены выражением E.53).
Матрица О. — числовая, так что формулу для ($ можно представить
в виде
Р = P*Q, E.58)
167
где
дау
О О О
О О 1
О1О
Х
о J
Подстановка E.58) в выражение D.11) приводит к следующей
формуле для матрицы жесткости:
где
E.59)
E.60)
Здесь, как и ранее, матрица х определяется по A.24).
Для выполнения интегрирования в E.60) удобно, как и в случае
изопараметричсского элемента, перейти к безразмерным параметрам
?, ц, полагая
х=Щг (I. rj) хт; у=Щг (I. TJ) Ут-
Суммирование здесь выполняется по четырем узлам элемента; функции
¦фг A, ч) даются равенством E.18). Узловые значения |г, т), парамет-
параметров |, tj назначаются в соответствия с рис. 5.7.
В соответствии с E.60) получаем расчетную формулу
E.61)
— I —I
где |J (g, tj) | — определитель матрицы E.48).
Получаемые таким образом конечные элементы являются несов-
несовместными. Оии могут быть использованы при решении плоской задачи
теории упругости наравне с описанными ранее элементами, а также
при моделировании различных балок с непараллельными поясами и тон-
тонкими стенками. При этом имеется в виду, что ось х (или ось у) ориен-
ориентирована вдоль оси балки. Если же балка произвольно ориентирована
относительно осей х, у, то сначала следует ввести соответствующую
местную систему координат х, у, для которой применимы исходные
формулы
0_- =
у ч
а--—с3.
Полученная в этих крордииатах матрица жесткости должна быть
затем преобразована в (матрицу в общей системе координат в соответ-
соответствии с обычной процедурой, описанной в § 3.2.
168
§ 5.8. Плоские изопараметрические элементы высших
порядков
Завершая рассмотрение плоских элементов, остановим-
остановимся сначала на конечном элементе с четырьмя сторонами
(в общем случае криволинейными), показанном на рис.
5.8, а. Элемент помимо четырех узлов в вершинах имеет
промежуточные узлы на сторонах. Координаты узлов за-
задаются в качестве исходных данных. Для удобства рассуж-
рассуждения все узлы пронумерованы от / до 8. При практиче-
практическом применении элемента каждому из этих восьми узлов
7
1
_8
1
%
Рис. 5.8
должен быть поставлен в соответствие его номер в общей
схеме нумерации узлов рассматриваемого тела.
Так же как и в случае изопараметрического элемента
с четырьмя узлами, введем вспомогательный квадрат со
стороной, равной 2 (рис. 5.8, б). Положение произвольной
точки внутри квадрата определим координатами ?, г\, кото-
которые изменяются от —1 до 1. На сторонах квадрата выбе-
выберем восемь точек в соответствии с числом узлов конечного
элемента. Четыре из них находятся в вершинах квадрата,
а четыре других — в серединах его сторон.
Построим для г=1, 2, ..., 8 такие функции фг(?> ЛЬ к0"
торые в точке г принимают единичное значение, а во всех
остальных узловых точках обращаются в 0. Их можно
получить [6], комбинируя использовавшиеся ранее функ-
функции A±|) A±т]) с функциями A—I2) {\±г\) и A—П2)Х
)
Функция A—?2) A—т]), например, равна нулю при
5=±1, а также при tj=1, т. е. во всех узловых точках,
кроме точки 2. Следовательно, можно сразу записать
169
Множитель Vg введен для того, чтобы в точке 2 выпол-
выполнялось равенство -ф2 == I -
Точно так же можно записать функции tyr для осталь-
остальных точек, расположенных иа серединах сторон квадрата:
Ъ (Б, п) =4" A~^2) (Hg); * ^4)
Рассмотрим далее функцию A—1)A—ц). Она равна
нулю при §=1 и при т] = 1, т. е. во всех узловых точках,
кроме точек /, 2, 8. Комбинируя ее с фг и г|>8, можно по-
построить функцию, которая обращается в нуль также и в
точках 2, 8. Удовлетворяя, кроме того, условию в точке /,
придем в результате к следующей функции i|>i:
4ч (Б, л)--J-(i-E) 0-л)-— О ~&) A -л)-
4 4
очча*)
Аналогичные рассуждения позволяют получить также
функции:
-ФзШ. -n)=-j-(i + i)(i—л)—^- (i-l2)(l-ri) -
—5"A—ч
ф5 (Б. ч) —|- A +1) (I + ч) --j-0 -I2) A +п> -
*,F.ч)—7-О-
—~-A-*12)<1-|).
Записанные выше формулы дчя фг(|, т)) можно пред-
представить в следующем обобщенном виде:
*, (Б. ч) = 36r'f~2 1Б? л? A +ir Б)
-Л? (l-^2) (I +rir Ч)-У A -Л2) (I + Б, Ю1- E-62)
Здесь |г, т]г — координаты узловых точек:
170
/
—1
—1
2
0
—1
3
1
—1
4
1
0
5
1
1
6
0
1
7
—1
1
8
—1
0
Если теперь требуется аппроксимировать в пределах квад-
квадрата какую-либо функцию Ф (I, ц), для которой известны ее
значения Фг в точках г — /, 2, ..., 8, то можно сразу записать
Как это видно из E.62), E.63), функция Ф (|, г\) будет
вдоль сторон изменяться по квадратичному закону. Квадрат-
Квадратная парабола вполне определяется тремя какими-либо парамет-
параметрами, так что значения Фг в трех точках, лежащих на стороне
квадрата, однозначно определяют закон изменения Ф (|, ц)
вдоль этой стороны.
Поставим далее в соответствие каждой точке квадрата не-
некоторую точку исходного элемента, полагая
х (|, п) = 2 *г & Л) х/, у (|, п)= 2 4V E, Л) У,. E-64)
/•=1 г=1
где хг, i/r — координаты узла г. При этом получится криволи-
криволинейная фигура, стороны которой проходят через заданные уз-
узловые точки. Положим, например, 1=1. Тогда из E.62),
E.64) получим
tj A +т)) д;5;
# = — ~ Ц A— Ц) Уз-h A — Цг) У4 — у
Эти два равенства дают уравнение стороны 3—5 конечного
элемента в параметрической форме. В них входят координаты
только тех трех узлов, которые принадлежат данной стороне.
Точно так же можно показать, что каждая сторона конечного
элемента, полученного на E.64), однозначно определяется ко-
координатами трех узлов, принадлежащих этой стороне. По-
Поскольку узлы являются общими для смежных элементов, то
отсюда следует, что смежные конечные элементы будут плотно
прилегать друг к другу, образуя сплошное тело.
Аналогичными формулами воспользуемся и для аппрокси-
аппроксимации перемещений:
и* = 2 *' №. Л) о™, и„ =. 2 4V ft» Л) vry. E.65)
Такая аппроксимация обеспечивает совместность конечных
элементов. В самом деле, координаты х*, у* точек элемента пос-
171
ле его деформации станут равными х* = х + их; у* = у +
+ иу, т. е. с учетом E.64) и E.65);
х* =
(I, Ц) (хг + vrx); у* - 2 Фг E. Л) (уг + Vrv)-
2
г=1
Величины x*r — xr + vrx; у' — ут -f vry представляют
собой координаты узлов деформированного элемента, и ра-
равенства
8 8
х* — 2 Фг (?• ч) К '< у* = Ъ Фг F. ц) у*
дают отображение квадрата на деформированный конечный
элемент. Но, как показано выше, такое отображение обеспечи-
обеспечивает непрерывность тела на границах между смежными эле-
элементами. Отсюда и следует свойство совместности криволиней-
криволинейных изопараметрических элементов.
Дальнейшие выкладки полностью аналогичны тем, которые
выполнялись выше для изопараметрического элемента с че-
четырьмя узлами. Типовой блок матрицы а = [а, а2... а81
имеет вид
О
а блоки матрицы Р = [pif^.-fU формируются из производных
от функций % по координатам х, у:
О
дх
О
дх
Эти производные находятся из равенства
дфг
__ J-I
а?
172
Здесь J-1 — матрица, обратная матрице Якоби:
~ дх ду
J (g, Л) =- f f
дх ду
дх\ дц
элементы которой определяются по формулам
дх 4. atr „. дх .
ду
г=1
8
д? дц **, дц
' ? ,~ j/r. "Т~ = ^ —— Уг-
r=l S ^ г = 1 ^
Производные от i|v по переменным |, т] равны:
-§^= 36»г1г»-2 [т,.A+Т|гП)Fг+26)_6гA_1Г^];
E.66)
ИМ1+ёг5)(т|г + 2т|)-т|гA-
При записи E.66) учтено, что для любого г справедливы ра-
равенства g? = gr, t)? = rjr.
Типовой блок матрицы жесткости вычисляется с помощью
численного интегрирования по формуле
f AP>Ps|J(g,Tj)|dgdTj (r,s=l,2 8),
-i -Ji
где |J (|, tj)| — определитель матрицы Якоби.
Изопараметрические элементы с восемью узлами позволя-
позволяют при одинаковом числе узловых перемещений получить
значительно лучшую точность, чем изопараметрические эле-
элементы с четырьмя узлами. Они особенно удобны для расчета
плоских тел с криволинейными границами. Их можно приме-
применять также для моделирования тонких стенок в плоских кри-
криволинейных брусьях типа шпангоутов (рис. 5.9).
Для той же цели можно с успехом использовать более прос-
простой изопараметрический элемент с шестью узлами, показан-
показанный на рис. 5.10, а. Этот элемент имеет две прямолинейных и
две в общем случае криволинейных стороны и получается из
восьмиузлового элемента путем удаления двух узлов, лежа-
173
щих на противоположных сторонах. Матрицу жесткости тако-
такого элемента можно получить точно так же, как и в предыдущем
случае, только в качестве г|)г (?, ti) (г = /, 2, ..., 6) следует
взять функции
v E, л) = ЪЦ
, n)-(i -I2)
где параметры |г, т]г определяются в соответствии с рис. 5.10, б.
Аппроксимация перемещений по формулам
«*=
г=\
6 5
/
1
1
V
11
Рис. 5.9
Рис. 5.10
приводит здесь к их линейному изменению вдоль прямолиней-
прямолинейных и к квадратичному относительно | — вдоль криволиней-
криволинейных сторон. Формулировка геометрии элемента осуществля-
осуществляется в соответствии с равенствами
у=
Аналогично могут быть построены и более сложные элемен-
элементы. На рис. 5.11, а показан, например, четырехугольный эле-
элемент с двенадцатью узлами. Помимо четырех узлов в угловых
точках на каждой стороне имеется по два промежуточных узла.
Поставим в соответствие этому четырехугольнику квадрат со
стороной 2 в координатах |, ц (рис. 5.11, б). Будем считать, что
промежуточные узлы квадрата расположены на расстоянии с0
от середин его сторон, так что их координаты равны: |г = ±с0,
т]г = ±1 или |г = ± 1, цг — ±с0- В угловых точках |г •=
= ±1, Лг = ±1- Как и в предыдущих случаях, можно подоб-
подобрать двенадцать функций г|)г (|, ц) таких, что каждая из них
имеет единичное значение в одном из узлов и обращается в нуль
174
в остальных узлах. Можно показать, что все эти функции дают-
даются единым выражением
*
E.67)
Исходя из формул л: = ЩгХг, у ~ Щгут, их =
иу =¦ StprDrj,, в которых суммирование ведется по всем узлам,
и пользуясь описанной выше процедурой, можно построить
матрицу жесткости данного конечного элемента.
12
а)
1
7 '
1
к
10
11
12
1
9 8
2
i.
3
M
7
6>
5'
it
1
б)
Рис. 5.11
Величину с0 берут обычно [6] равной Ч3. В работе [34]
рекомендуется для повышения точности результатов (в част-
частности, в динамических задачах) брать с0 = 1/V5.
Заметим, что изопараметрические элементы образуют ие-
иерархию, в которой элементы с узлами в вершинах рассматри-
рассматриваются как элементы первого, с одним промежуточным узлом на
каждой стороне —второго, с двумя промежуточными узлами—
третьего порядка и т. д.
§ 5.9. Деформация пространственного криволинейного
стержня
Для расчета лонжеронов и шпангоутов необходимо помимо
плоских элементов, моделирующих стенку, располагать также
конечными элементами для моделирования поясов. В поясе воз-
возникает продольная сила, которую будем считать равномерно
175
распределенной по площади его поперечного сечения. Это до*
пущение приемлемо для достаточно высоких балок, у которых
размеры поперечного сечения пояса малы по сравнению с вы-
высотой балки. Оно позволяет рассматривать вместо реального
пояса осевую линию, проходящую через центры тяжести его по-
поперечных сечений и наделенную жесткостью на растяжение-
сжатие. Изгибной жесткостью пояса будем пренебрегать,
учитывая, что она мала по сравнению с изгибной жесткостью
поперечного сечения балки в целом. Таким образом, мы при-
приходим к одномерной схематизации поясов, при которой все
величины, характеризующие напряженное состояние пояса,
зависят только от одной переменной (скажем, от дуговой коор-
координаты).
Прежде чем переходить к построению соответствующих ко-
конечных элементов, выведем формулу для расчета деформации
пространственного криволинейного стержня. Пусть уравнение
осевой линии стержня задано в параметрической форме
х = х {%); у = у (I); z = z (g). E.68)
Каждому значению параметра \ соответствует некоторая
точка М (х, у, г). В совокупности эти точки образуют простран-
пространственную кривую и параметр ? можно рассматривать как кри-
криволинейную координату на этой кривой.
Если дать параметру ? малое приращение d?, то получим
соседнюю с М точку N с координатами х + dx, у + dy, г +
+ dz, где их, dy, Лг определяются формулами
? ijf ? E.69)
d*?dg; d#jfd?; dz?dg
Ч dg d|
и представляют собой проекции отрезка MN на координат-
координатные оси. Длина
этого отрезка может быть с учетом E.69) подсчитана по форму-
формуле
ds = Adi, E.70)
где
Как видно из E.70), А представляет собой коэффициент,
на который нужно умножить приращение dg, чтобы получить
длину соответствующего отрезка рассматриваемой кривой.
176
Отрезок ds составляет с осями х, у, г углы, косинусы кото-
которых обозначим через ХЕж, Xiy, Х^г. Разделив dbc, Ay, 6z на ds,
находим:
, 1 их , 1 йу . 1 da
^*=ТГ; ^вя~Гм; ***-"Г~ЗГ-
Л dg Л dg Л а%
Предполагается, что отрезок ds имеет направление от точ-
точки М к точке N, т. е. в сторону возрастания параметра |.
Три величины E.72) определяют матрицу-строку
Х6 = 1*8^6,]. E.73)
Пусть далее точки кривой получают малые перемещения
их (I), иу (|), uz (|) в направлении осей х, у, г. Декартовы ко-
координаты деформированной кривой будут
х* = х + их; у* = у + иу; г* = г + uz.
Найдем параметр А* деформированной кривой, подставив
для этого х*, у*, х* вместо х, у, г в E.71):
л* =
w\ ^L siJ
Учитывая малость перемещений и их производных, будем
отбрасывать слагаемые, содержащие квадраты или произведе-
произведения этих величин. Тогда, с учетом E.71),
А* -л/Л* I 2( dx du* I dy Auy I йг du*
у \ dg dg -""-"¦-"¦
d|
Обозначив
iHH' E-74>
приведем это выражение к виду А * = A Vl + 2e.
Разложим vl + 2е в ряд по степеням е в соответствии с
формулой
и удержим в разложении лишь слагаемое первого порядка ма-
малости. Это дает
А* = A+г)А. E.75)
Длина ds* деформированного отрезка MN аналогично
E.70) будет
ds* = A*d% = A + е) Adt E.76)
177
Осевая деформация равна отношению (ds* — ds)/ds. Вно-
Внося сюда E.70) и E.76), убеждаемся, что введенная согласно
E.74) величина е есть не что иное, как искомая деформация
в точке М.
Если ввести матрицу-столбец перемещений u = {uxuyuz},
то формулу E.74) можно с учетом E.72), E.73) переписать
в виде
-т»«-т- E-77)
du fdus d«i/ d«2l -.
где через gr = \-^г -? -^\ обозначена матрица произ-
производных от перемещений по переменной \.
Выведем попутно формулу для вычисления углов поворота отрезка
ds при деформировании. Хотя здесь эта формула и не требуется, но в
дальнейшем она понадобится при построении конечных элементов
произвольных оболочек. Введем единичный вектор е^, направленный
вдоль отрезка dsoT точки М к точке N. Его проекции на оси х, у, г есть
направляющие косинусы отрезка ds, так что можно записать
где ех, еу, ег — орты осей х, у, г.
Пусть, далее, е0 — некоторый единичный вектор, ортогональный
вектору «g и заданный матрицей Я,„ = [Кох кОу XOz] своих направляю-
направляющих косинусов:
В результате деформации отрезок ds повернется и угол между ним
В вектором е0 будет отличаться от я/2 на величину, которую мы обозна-
чим fi>0. Будем считать ее положительной, если угол между е0 и единич-
единичным вектором е|, касательным к деформированной кривой в точке М,
становится острым. Косинус угла я/2 — ©0 можно иайти с помощью
скалярного произведения: cos (я/2 — щ) = е0 • в|, так как скаляр-
скалярное произведение двух векторов равно произведеиию их длин на коси-
косинус угла между ними.
Но cos (я/2 — w0) = sin w0, а поскольку соо — величина малая,
то можно принять sin щ ~ ш0. Отсюда приходим к равенству
Как известно, скалярное произведение двух векторов а = а^вх +
-*¦ -*-*-* -* -у
+ ауеу + azez; Ь — Ъхех + Ъуеу + Ъгег подсгштывается по формуле
178
Полагая eg =^1хех + Цуеу + Цгег, имеем
или в матричной форме
Г E.78)
где к* — 1^^5^|г] — матрица направляющих косинусов деформи-
деформированного отрезка ds*.
Проекции отрезка ds* на координатные оси могут быть иайдеиы
по формулам E.69), в которые вместо х, у, г должны быть подставлены
координаты деформированной кривой х + их, у + иу, г + иг'
^=dg; d^-jdfc d2= dg.
ds dg dg
Разделив этн проекции иа длину ds* == A + *)А&%, приходим с
учетом E.72) к выражениям:
Таким образом, для матрицы Х| получаем значение
1
По E.78) вычисляем
Произведение Х„^ есть скалярное произведение е0 • в|, ио векторы
е„ и е^ ортогональны и это произведение равно нулю. Пренебрегая ве-
величиной е по сравнению с единицей, приходим окончательно к выра-
выражению
1 du
o)o = "J->.o-dy • E-79)
§ 5.10. Одномерные конечные элементы
Рассмотрим семейство пространственных одномерных ко-
конечных элементов первого, второго и третьего порядков
(рис. 5.12, а, б, в). Геометрию элементов будем задавать коор-
координатами узлов, пользуясь при этом изопараметрической фор-
формулировкой для определения кривой, проходящей через эти
179
узлы. Введем вспомогательные отрезки прямой линии. Поло-
Положение текущей точки отрезка определим координатой %, ко-
которая отсчитывается от его середины и принимает на концах
значения ±1. Выполним отображение отрезков на конечные
элементы посредством соотношений
х = 2i|>r F) хт\ у = 2i|>r (I) ут; г = Zi|>r (?)гг, E.80)
где суммирование ведется по всем узлам конечного элемента.
Каждая из функций i|v (|) принимает единичное значение в
a)
Рис. 5.12
узле г и обращается в нуль в остальных узлах конечного эле-
элемента. Можно показать, что этим условиям удовлетворяют сле-
следующие функции:
для элемента первого порядка (г = /, 2)
1 " **;); E.81)
¦г(Э
для элемента второго порядка (г = /, 2, 3)
E.82)
для элемента третьего порядка (г = /, 2, 3, 4)
2?* B^1eg) V '
Через |г здесь обозначены точки вспомогательных отрез-
отрезков, отображающиеся в узлы конечных элементов. Для эле-
элемента первого порядка (рис. 5.12, а) |г = — 1, ga = 1; Для
элемента второго порядка (рис. 5.12, б) ?х = — 1, ga = 0, |3 —
= 1; для элемента третьего порядка (рис. 5.12, в) |t — — I,
52 = — с0, 53 = с0, lt—l. Параметр с0 выбирается так же,
как и в случае плоского изопараметрического элемента треть-
180
его порядка (см. § 5.8). Обычно берут с0 = 1/3; можно также
принимать с0 = 1/V5.
В соответствии с изопараметрической формулировкой за-
запишем далее закон аппроксимации перемещений u = {uxuyuz}
конечного элемента по узловым перемещениям:
и (?) = Щг (I) vr. E.84)
Здесь vr = {vrx vry vrz} — матрица перемещений узла г
в направлении координатных осей; суммирование выполняет-
выполняется по всем узлам конечного элемента.
По E.77) получаем выражение для продольной деформации
гдег|>/ Ш = ch|>r/d?-
Выражение для е можно также записать в виде е =
= Sprvri где
$Г~Ъ'ГЦ. E.85)
В поперечном сечении стержня возникает нормальное на-
напряжение а; по закону Гука для одноосного напряженного со-
состояния о = Ее. Таким образом, в этом случае в качестве х
следует брать скалярную величину Е.
По формуле D.15) вычисляем блоки kers матрицы жесткости
конечного элемента, которые будут здесь скалярными величи-
величинами. Так как dx = Fds =¦ FA&%, получаем
k%=E f Ffr^AUl. E.86)
Интегрирование здесь выполняется численно на ЭВМ. Для
элемента первого порядка можно получить и аналитическое
выражение для k%. В этом случае на основании E.80), E.81)
имеем
так что величина А E.71) будет представлять собой половину
длины I конечного элемента:
А = V(x, -*iJ + (л -УгГ + (*- Zi)V2 -1/2.
Согласно E.72) находим
%%г = (z2 — zj/l,
181
а матрицы рг в силу E.85) будут {$г =
лучим в случае F = const
. По E.86) по-
поЭтот результат совпадает с формулами C.19), полученными
для ферменного конечного элемента.
Отметим, что рассмотренные здесь конечные элементы сов-
совместны с плоскими изопараметрическими конечными элемен-
элементами соответствующих порядков.
§ 5.11. Трехмерные конечные элементы
Трехмерные конечные элементы используются для расчета
пространственных тел, имеющих трехосное напряженное со-
состояние (кронштейнов и т. п.). Простейшим пространственным
конечным элементом является тетраэдр с четырьмя узлами
<рис. 5.13), в пределах которого задается линейное поле пере-
перемещений:
и-х = к + /г* + 1гУ + /*г;
иу — h + fex + Uy + fez'
«г = fa + /ie X + кгУ + /12 г.
Здесь /i-../i2 — произвольные
постоянные. Приравнивая в узло-
узловых точках их, иу, uz к соответ-
РИС. 5.13 ствующим узловым перемещениям,
можно выразить постоянные / че-
через узловые перемещения Vе и по-
получить зависимость вида и = оте. Использование обычной
процедуры позволяет затем найти матрицу жесткости такого
элемента [6].
Для получения достаточной точности решения требуется
обычно применять весьма мелкое дробление тела на тетраэдры,
что приводит к большим затратам машинного времени. Поэто-
Поэтому такие конечные элементы не имеют большого распростране-
распространения, и останавливаться на них подробно не будем.
Рассмотрим далее восьмиузловой изопараметрический про-
пространственный конечный элемент, показанный на рис. 5.14, а.
Для описания его геометрии и аппроксимации перемещений
воспользуемся безразмерными координатами 5, т], ?, которые
изменяются от — 1 до 1 в пределах куба (рис. 5.14, б).
182
Рассуждая так же, как н в случае плоских элементов, вве-
введем систему функций
(I, П, О = -§¦
+ ЛгП) A + СгО. E.87)
каждая из которых принимает единичное значение в одной из
вершин куба (г = /, 2, ..., 8), обращаясь в нуль во всех осталь-
остальных вершинах и изменяясь линейно вдоль ребер.
С-1
Рис. 5.14
Следуя рассмотренной выше схеме построения изопарамет-
рических элементов, выполним отображение куба на рассмат-
рассматриваемый конечный элемент посредством соотношений
8 8 8
г=1 г=1 г=1
Подобным образом аппроксимируются и перемещения:
8 8 8
"*— 2 tyrVTX> ид = 2 $rvry> uz= 2 Фг°гг> E.89)
г—I г=1 r=l
где угя, vry, vrz — проекции перемещения узла г на координат-
координатные оси. Как и для всяких нзопараметрических конечных эле-
элементов, формулы E.88), E.89) обеспечивают совместность
элементов.
Полагая vr = {vr3?)TyVrz}\ ve = {ViV2...ve}, представим со-
соотношения E.89) в стандартной форме u = ave, где и =
= {uxUvuz}, а типовая подматрица матрицы а = {а1<яг..м^
равна
E.90)
183
Обозначая через е = {ежжег/уе22ежвег,2егя} матрицу-стол-
матрицу-столбец деформаций и пользуясь формулами Коши, запишем соот-
соотношение е = Pve. Типовой блок РГ матрицы Р = [рх Р2".р8]
формируется из производных от i|)r по координатам х, у, г:
о
о
о о
dtyr/dy О
О dijjr/i
dtyT/dx О
О
Необходимые производные можно найти через производные
от i|»r по переменным |, т|, ?:
дх
ду
дг _
а?
ал
Здесь J—l —матрица, обратная матрице Якоби
а.у Ду Зг
ag ag ag
ал- ay az
дх
которая составляется из величин
ar, ar,
ду дг
Производные от функций чрГ по координатам ?, tj, S равны:
184
Матрица жесткости элемента ке имеет 8x8 блоков V.U
(г, s = 1, 2,..., 8), которые можно найти с помощью числен-
численного интегрирования по формуле
i 1
k's= S J J firrxP.|J№, л. O|d?dr|dE.
-i —i —i
Здесь х — матрица упругости A.16) для трехмерного
напряженного состояния, а через |J (?, r\, ?)| обозначен оп-
определитель матрицы Якоби.
Взяв за основу рассмотренный конечный элемент, можно по-
получить и другие полезные элементы путем совмещения некото-
77
Рис. 5.16
рых узлов. Так, полагая в E.88), E.89) координаты и перемеще-
перемещения узлов б и 7 равными соответственно координатам и пере-
перемещениям узлов 2 и 3, придем к конечному элементу призма-
призматического вида (рис. 5.15). Возможны, конечно, и другие ва-
варианты.
Рассмотренную выше процедуру вычисления матрицы жест-
жесткости можно применить для построения и более сложных про-
пространственных изопараметрических элементов. На рис. 5.16
показан, например, двадцатиузловой пространственный
элемент с криволинейными гранями. Можно показать, что для
любого узла г — 1, 2, ..., 20 функция
Vr(i> л. ?)-¦
x
+с. о -г? ц? A+?г г) A+% л) A ~т -
185
принимает единичное значение в этом узле и обращается в нуль
во всех остальных узлах. Здесь каждая из переменных |, г), g
изменяется в пределах от — 1 до 1, причем узловым точкам со-
соответствуют следующие значения:
г ...
I, ¦ ¦ .
123456789 10
— 10 1 I 1 0—1—1—11
—1 —1 —I —I —I —I —1—I0 0
1 1 I О —1 —1 —I О 1 1
Продолжение
12 13 14 15 16 17 IS 19 20
I:::
11
! —I —I
0 0 I
—1 —1 I
О
1
1
1 ! О
1 1 I
О —I —I
—I —1
1 I
-I О
С использованием этих функций по формулам
20
2
20
2
2«
тУг\ 2=
описывается геометрия элемента, а с помощью соотношений
20
"*= 2 УгОгх
г=1
20 20
= 2 ¦г*1»; «2=2 ^г»
г=1 г=\
выполняется аппроксимация перемещений. Дальнейшие вы-
выкладки вполне аналогичны тем, которые приведены выше для
восышузлового элемента.
Применение таких элементов дает возможность моделиро-
моделировать тела сложной конфигурации с помощью относительно
небольшого числа элементов и получать при этом приемлемую
точность решения.Это оправдывает их использование, несмотря
на значительные затраты машинного времени на формирование
матрицы жесткости отдельного элемента.
§ 5.12. Численное интегрирование в методе
конечных элементов
Выше было представлено несколько конечных элементов,
для вычисления матриц жесткости которых приходится прибе-
прибегать к численному интегрированию. В связи с этим встает во-
вопрос о выборе экономичных схем численного интегрирования.
Поскольку интегрирование матрицы осуществляется интегри-
186
рованием каждого ее элемента, то достаточно рассмотреть
интегралы от скалярных функций вида
1 1
1 1 i
С /©d5, f f /(I, tOdgdri или f f </(E,4,
Начнем с простого интеграла
i
— i
Обычный способ приближенного интегрирования заключа-
заключается в следующем. В нескольких точках | = ?{, взятых на ин-
интервале интегрирования, вы-
вычисляют значения подынтег-
подынтегральной функции fi = / (?г).
Далее находят полиномиаль-
полиномиальную функцию ф (|), прохо-
проходящую через точки (?1$ /,),
Aй, ft), ¦¦¦ (рис. 5.17), и вы-
вычисляют интеграл J ф (?) d?,
величину которого принима-
принимают в качестве приближенного
значения интеграла от /(?).
численного интегрирования
имеющие вид
i
Рис. 5.17
В итоге получают формулы
(или квадратурные формулы),
E.91)
где п — число точек интегрирования; а,- — так называемые
весовые коэффициенты, значения которых зависят от количест-
количества и расположения точек интегрирования g,.
Точки ?г, в которых необходимо вычислять подынтеграль-
подынтегральную функцию, выбирают различными способами. Один из спо-
способов заключается в том, что интервал (—1,1) делят на несколь-
несколько равных отрезков, концы которых принимают в качестве точек
интегрирования. Получаемые при этом квадратурные формулы
носят общее название формул Ньютона—Котеса. В этом спо-
способе положение п точек ?г задают заранее, и в формуле E.91)
необходимо определить лишь весовые коэффициенты а,-. Их мож-
можно искать из условия, чтобы формула E.91) давала точный ре-
результат для следующих подынтегральных функций / (I):
1.1, 1г, ••¦, l"- Это дает столько уравнений, сколько необхо-
187
димодля определения at. Таким образом, л-точечная схема ин-
интегрирования Ньютона—Котеса дает точный результат для лю-
любого полинома степени не выше п — 1; эту максимальную сте-
степень называют порядком численного интегрирования. Отметим,
что частными случаями квадратур Ньютона—Котеса являются
формула трапеции (п = 2) и формула Симпсона (п = 3).
Другой способ заключается в том, что положения точек |4
не задают заранее. Их определяют из условия, чтобы квадра-
квадратурная формула E.91) при фиксированном числе л имела макси-
максимально высокий порядок. Здесь в качестве неизвестных высту-
выступают не только весовые коэффициенты аь но и значения ?г,
и можно потребовать, чтобы формула E.91) давала точный ре-
результат для функций 1, I, I2, ..., l2"-1. Получающиеся отсюда
2л уравнений позволяют найти 2л неизвестных at и ?г. Фор-
Формулы численного интегрирования, построенные таким спосо-
способом, имеют порядок 2л — 1 и носят название квадратурных
формул Гаусса. Интегрирование по Гауссу требует при одина-
одинаковой степени точности почти вдвое меньшего числа точек, чем
в случае использования формул Ньютона—Котеса. Вычисление
подынтегральных функций связано обычно со значительными
затратами машинного времени, вследствие чего формулы Нью-
Ньютона — Котеса в методе конечных элементов практически не
применяются.
Положения точек Гаусса определяются иррациональными
числами, но при использовании ЭВМ это не имеет существен-
существенного значения. Приведем некоторые значения at и |г [10]:
для п = 1 |j = 0; ах — 2;
для п = 2 ?а = — ?х = W% ai = аЛ = 1;
для п = 3 Б, = — l1 = V3/5; Б,«=0; аг = а3=5/9; аа = 8/9;
для п = 4 lt ¦ |х = 0,861 136 311 594 0492;
!, = _?, = 0,339 981 043 584 8646;
а1== ai^ о,347 854 845 137 4568;
ай^ а3 = 0,652 145 154 862 5432.
При вычислении интеграла
— 1 —I
188
от функции двух переменных можно принять сначала, что г\
= const, и проинтегрировать по |:
1 п,
f
где пх — число точек Гаусса в направлении 1.
Вторично? интегрирование по переменной г| дает
2
f S в«/Fь Ч)*1 = 2 °t f
= S °i 2 e
где na — число точек Гаусса в направлении г|. Отсюда при-
приходим к формуле интегрирования
п. л,
J
Координаты ?i, r\t точек Гаусса и весй at, aj совпадают с со-
соответствующими значениями для одномерного случая.
Подобные рассуждения позволяют получить аналогичную
формулу и для тройного интеграла:
(.!•{• Л, Л, Л,
где п1г пг, п3 — количество точек интегрирования, взятых в
каждом направлении.
Очень важным является вопрос о выборе числа точек ин-
интегрирования. Точность интегрирования будет тем выше, чем
больше этих точек, но с увеличением их числа возрастают за-
затраты машинного времени. Минимально допустимый порядок
интегрирования в трехмерном случае определяется требова-
требованием [6], чтобы интеграл
1 1 1
Л Л ii
где |J E, tj, ?)| — определитель матрицы Якоби, мог быть най-
найден точно. Это соответствует условию, чтобы формула интегри-
интегрирования позволяла точно вычислить объем конечного элемен-
та. Использование более низкого порядка интегрирования
недопустимо, ибо при этом исчезает сходимость конечноэле-
ментного решения к точному по мере сгущения сетки. Более
подробно об этом будет сказано в § 6.5. Обычно рекомендуется
при практических вычислениях увеличивать число точек Гаус-
Гаусса по сравнению с минимально допустимым. Аналогично фор-
формулируется подобное требование для двумерного н одномерно-
одномерного случаев. В табл. 5.1 приведены минимально допустимые
{/tiXn2Xn3}mln и рекомендуемые /iiXn,xn3 числа точек
Гаусса для тех конечных элементов, которые были рассмот-
рассмотрены выше.
Та&яица 5,1
Конечный
элемент
n,xnz*n3
2«2
2x2
JxJ
2*1
3X2
JxJ
Ut*1
2*2*2
2x2x2
3x3x3
Как уже сказано выше, при вычислении матрицы жесткости
метод интегрирования Гаусса оказывается наиболее экономич-
экономичным. Однако в других случаях иногда целесообразно использо-
использовать иные схемы интегрирования. Например, в динамических
задачах приходится рассчитывать так называемые матрицы
масс конечных элементов. Если точки интегрирования совпада-
совпадают с узлами конечного элемента, то матрица масс оказывается
диагональной, что очень важно для разработки экономичных
процедур динамического расчета конструкций. Подробнее во-
вопрос о вычислении матрицы масс конечных элементов будет
рассмотрен в гл. 9; здесь же в этой связи остановимся еще на
двух схемах численного интегрирования.
Первая из них, называемая методом интегрирования Мар~
нова [10], имеет обычный вид E.91). Отличительной чертой
метода Маркова является специфический выбор точек интег-
интегрирования. Две крайние точки всегда совпадают с концами от-
отрезка, а положение внутренних определяется (наряду с весо-
весовыми коэффициентами) так же, как и в методе Гаусса, т. е. из
условия, чтобы интегрирование было точным для полинома
максимально высокой степени. Заметим, что двухточечная схе-
схема Маркова совпадает с правилом трапеции, а трехточечная —
с правилом Симпсона. В четырехточечной схеме координаты
внутренних точек оказываются равными ±1/V5; при этом ин-
интегрирование дает точный результат для любого полинома от
? вплоть до пятой степени.
Метод Маркова может быть обобщен на дву- * трехмерный
случаи таким образом, чтобы точки интегрирования располага-
располагались только в углах и на сторонах квадрата или куба. Напри-
Например, для двумерного случая имеем
f \
где четыре точки интегрирования (?;, т);) всегда совпадают
с вершинами рассматриваемого квадрата, а остальные распола-
располагаются на его сторонах.
В табл. 5.2 даны координаты точек интегрирования и значе-
значения весовых коэффициентов в методе Маркова для некоторых
наиболее характерных случаев. Через р здесь обозначен поря-
порядок интегрирования, т. е. максимальный порядок полинома от
| (или полного полинома от ?, tj), для которого численное ин-
интегрирование оказывается точным.
В другой схеме, называемой методом интегрирования Эй-
Эйлера [10], используются значения не только самой подынте-
v
1
¦ 3
5
Ч
в-
Таблица
Элемент
одномерный
1
1
.'Л
3
1/5 5/6 ^5/61/6
двумерный
1
-1/t
г/з
-ф
ч
1
Г 2
V
1
-1/3 5/П
ь/п
fill
Ф
4
JT
5/12
1
п
1
/3- -1
5/12
А!
5/12
_, 1
\
1
'i
/в
г/з
-1/6
1
f
-Ф.
5/П
5/П
-11
1
гральной функции, но и ее первых производных. В частности,
двухточечная формула Эйлера для интеграла от функции од-
одной переменной имеет вид
I.
и дает точный результат для полинома от % до третьей степени
включительно.
Применительно к интегрированию функции / (|, tj) двух
переменных можно получить соответствующую четырехточеч-
четырехточечную формулу
192
1 1
¦ f% Г»
dfi
L V г,. Л!_, E.92)
3 fj ь ¦*, '
где /ь ^ , 4* — значения функции / (|, г}) и ее производных
в t-й вершине рассматриваемого квадрата, а ?;, тг|? — коорди-
координаты соответствующей вершины, равные ± 1 •
§ 5.13. О вычислении напряжений
После того как узловые перемещения найдены, по формуле
D.8) могут быть подсчитаны напряжения в любой точке конеч-
конечного элемента.
' Погрешность определения напряжений различна в разных
точках элемента. Наиболее точные значения получаются [32]
в точках Гаусса, соответствующих минимально допустимо-
допустимому порядку интегрирования. Но положение точек Гаусса оп-
определяется иррациональными числами, что доставляет боль-
большие неудобства при анализе результатов. На практике пред-
предпочитают, как правило, вычислять напряжения в узловых точ-
точках, хотя именно здесь погрешность в напряжениях оказывает-
оказывается наибольшей. *
При этом приходится иногда сталкиваться с двумя пробле-
проблемами. Первая связана с разрывным характером поля напряже-
напряжений. Если в узловой точке сходится несколько конечных эле-
элементов, то напряжения в ней, будучи подсчитаны согласно
D.8) независимо для каждого из элементов, окажутся различ-
различными. Особенно значительными эти различия могут быть в
случае простейших конечных элементов. Типичный характер
распределения напряжений, получаемый с помощью элемен-
элементов с линейным законом изменения перемещений, показан на
рис. 5.18, а сплошными линиями. Для сглаживания напряже-
напряжений здесь можно применить простое осреднение результатов,
получаемых в каждой узловой точке для отдельных конечных
элементов (штриховая линия). Осредненные напряжения ока-
оказываются и более точными, нежели полученные непосредствен-
непосредственно по D.8). Правда, заметное уменьшение погрешности проис-
происходит лишь во внутренних узлах, но не на границе, где обычно
как раз и возникают интересующие нас максимальные напря-
напряжения.
7 Зак. 651 193
Другая проблема возникает при использовании некоторых
типов изопараметрических конечных элементов высоких по-
порядков.. Напряжения, получаемые в соответствии с D.8), мо-
могут иметь тенденцию колебаться в пределах каждого элемента
относительно истинного решения (рис. 5.18, б). Здесь осред-
осреднение напряжений в узлах не всегда приводит к улучшению
результатов, в связи с чем для сглаживания напряжений при-
приходится прибегать к специальным процедурам [36, 39].
Различают общее (или глобальное) и местное (локальней
сглаживания. Обозначим через 5 вычисляемую по D.8) какую-
В)
Рис. 5.18
либо компоненту матрицы Напряжений а, подлежащую сгла-
сглаживанию, а через S — соответствующую сглаженную величи-
величину. При общем сглаживании [36] отыскивают узло-
узловые значения 5, которые обозначим через Sr. При этом в пре-
пределах каждого конечного элемента функция 5 аппроксими-
аппроксимируется через узловые значения так же, как для перемещений:
S = 2%S;. E.93)
Здесь г|)г — аппроксимирующие функции; суммирование
ведется по узлам конечного элемента. Значения ST находят из
условия, чтобы квадратичное отклонение S от 5, определяе-
определяемое выражением
= j(S-5JdT,
E.94)
было минимальным.
Процедура отыскания узловых значений Sr во многом по-
подобна процедуре определения узловых перемещений. Обозна-
Обозначим через ze = {SiSj...} матрицу-столбец, в которой пере-
перечислены значения ST, относящиеся к данному конечному эле-
194
менту (i, /, ... — номера узлов элемента). Зависимость E.93)
можно переписать в форме
S = ¦$?, E.95)
аналогичной записи и = а\е; через чр в E.95) обозначена мат-
матрица аппроксимирующих функций
.1. E.96)
Интегрирование по объему тела в E.94) заменим интегриро-
интегрированием по объемам отдельных конечных элементов:
Ф =* 2 J (S — SJ их=S J (S2 —2SS + Sa) dr. E.97)
Так как S — скалярная величина, то наряду с E.95) мож-
можно писать S = (ге)гфг. Это позволяет представить E.97) в
виде
Ф = 2 J [(ze)r ^г *z* — 2S (ze)r *г
или, иначе,
Ф - S [(z*)T D^z8 —
Фо.
E,98)
Здесь 0е и Ве — квадратная матрица и матрица-столбец,
определяемые формулами,
E.99)
= f
Через
обозначено слагаемое, не зависящее от искомых узловых зна-
значений функции S; суммирование в E.98) ведется по всем конеч-
конечным элементам.
Элементам матриц ТУ и Ве можно присвоить индексы в
соответствии с индексацией элементов матрицы ф E.96):
If,,...
Bi
ВГ,
7»
195
Эти элементы вычисляются по формулам
^rdn (r, s = /, /, ...). E.100)
Введем матрицу-столбец г = {SxSz...Sn}, в которой пере-
перечислены значения 5Г для всех узлов в порядке их нумерации
(п — общее число узлов). Подобно тому как это делалось при
вычислении потенциальной энергии деформации и потенциала
внешних сил конечноэлементной модели (см. § 4.6), выполним
суммирование в E.98), приведя выражение для Ф к виду
Ф = zrDz — 2zrB + Фо. E.101)
Элементы матриц D и В, имеющих размер соответственно
п X п и п х 1, определяются формулами
Drs = 2 D%; ВГ = SB?. E.102)
Суммирование в выражении для DTS выполняется по всем
конечным элементам, содержащим узлы г, s, а в выражении для
Вг — по всем конечным элементам, сходящимся в узле г.
Условие минимума функционала Ф приводит к равенству
Dz = В, E.103)
представляющему собой систему алгебраических уравнений
относительно узловых значений функции 5.
В описанной процедуре предполагалось, что пбрядок ап-
аппроксимации напряжений в пределах каждого конечного эле-
элемента соответствует порядку аппроксимации перемещений,
т. е. в E.93) используются те же функции г|>г, которые фигури-
фигурируют в матрице а. Такой подход дает более или менее удовлет-
удовлетворительные результаты лишь для конечных элементов пер-
первого порядка. Но для элементов высших порядков наиболее
эффективная процедура получается в том случае [36], если
в E.93) вместо г|>г берут функции \рг, соответствующие конеч-
конечному элементу, на один порядок ниже данного. При этом число
узлов, в которых вычисляются напряжения 5Г) не совпадает с
числом узлов, в которых определяются перемещения.
Так, на рис. 5.19 показаны участки плоских областей, иде-
идеализированных конечными элементами второго и третьего по-
порядков; узлы этих сеток отмечены кружочками. Те узлы, ко-
которые используются в процедуре сглаживания напряжений,
помечены крестиками. Для элементов второго порядка они сов-
совпадают с узлами в вершинах; в этом случае имеем аппроксима-
196
цию напряжений, соответствующую аппроксимации церемеще-
ний в элементах первого порядка:
..'.Для элементов третьего порядка также используются узлы
в вершинах, но помимо них на сторонах вводятся промежуточ-
промежуточное узлы A=0, ц = ± 1 и ? = ±1,11 = 0), не совпадающие с
узлами конечноэлементной модели. Это позволяет взять в ка-
Рис. 5.19
честве i|v функции E.62), посредством которых аппроксимиру-
аппроксимируются перемещения в элементах второго порядка:
Таким образом, для конечных элементов высших порядков
формулы E.99) и E.100) следует заменить формулами
DU =\ъЛ,df, B° = J5^rdr.
E.104)
Выполнение общего сглаживания поля напряжений связа-
связано с большими затратами машинного времени на формирование
и решение системы уравнений E.103), имеющей высокий поря-
порядок. Для их снижения можно выполнить сглаживание лишь в
197
некоторой области (или областях) тела, где ожидаются наи-
наибольшие напряжения; все конечные элементы за пределами
выбранной области при этом игнорируются. Для элементов
высших порядков можно пойти еще дальше, применив эту
процедуру к отдельно взятым конечным элементам. В этом слу-
случае приходим к так называемому местному (локаль-
(локальному) сглаживанию. Здесь вся проблема сводится
к отысканию для каждого конечного элемента матрицы-столб-
матрицы-столбца ге путем решения системы
ЕИг" = В", E.105)
причем матрицы ТУ и В" рассчитываются по E.104).
Местное сглаживание требует незначительных затрат ма-
машинного времени по сравнению с общим. Хотя оно не дает не-
непрерывного поля напряжений, но значительно улучшает ре-
результаты по сравнению с D.8) и может быть рекомендовано в
качестве практической процедуры. Сохраняющиеся здесь не-
небольшие скачки напряжений в узлах могут быть ликвидирова-
ликвидированы с помощью последующего осреднения напряжений. Получа-
Получаемое в Итоге поле напряжений, как правило, так же хорошо
согласуется с точным решением, как и при общем сглажива-
сглаживании.
Процедура сглаживания напряжений может применяться
в любых конечноэлементных моделях. Но особенно важное зна-
значение она приобретает при использовании конечных элемен-
элементов брусьев, пластин и оболочек, при построении которых учи-
учитываются деформации поперечного сдвига; примеры подобных
элементов даны в гл. 7, 8. Картина распределения напряжений,
получаемая с помощью этих элементов, оказывается часто со-
совершенно искаженной нз-за сильных колебаний результатов
относительно истинного решения, и их сглаживание является
здесь непременным условием получения корректных резуль-
результатов.
§ 5.14. Примеры расчета
Пример 1. Прямоугольная панель (рис. 5.20) длиной L =
= 5м и шириной ЗВ = 1,5м состоит из обшивки толщиной
h — 2 мм (?0 = 7' Ю4 МПа, ц = 0,3) и четырех продольных
поясов с одинаковой площадью поперечного сечения F =
= 1000 мм2 (?j = 2- 10s МПа). На одном конце панель закреп-
закреплена, а на другом нагружена двумя силами 2Р каждая, при-
приложенными к крайним поясам. Это — типичная задача о вклю-
включении в работу продольного набора. По мере удаления от на-
198
груженного края происходит включение в работу внутренних
поясов и соответствующая разгрузка наружных.
Для идеализации поясов использовались одномерные эле-
элементы первого порядка (см. § 5.10), а для обшивки — плоские
прямоугольные элементы с линейным законом изменения пере-
перемещений вдоль сторон
(cif. § 5.2) либо с линей-
линейным законом изменения
напряжений (см. § 5.3);
Отметим, что в данной
задаче оба элемента
дают практически оди-
одинаковые результаты.
Использованные ва-
варианты конечноэлемент-
ной идеализации панели
показаны на рис. 5.21.
В варианте (а) участок
обшивки между сосед-
соседними поясами моделиро-
моделировался одним слоем прямоугольных элементов, а в варианте
(б) — двумя. Число разбиений панели в продольном на-
направлении изменялось от п = 5 до п = 20.
На рис. 5.22 показано изменение по длине панели (? =
= x/L) величин ffx = Л^/Л^о и N2 — N2/No, где Nlt N2 — осе-
ZP
«а
«о
2Р
X
L
V,
1
\
\
Рис. 5.20
2Р
ZP
4
7,9
2P
i
t
i
4
Рис. 5.21
вые силы в сечениях наружных и внутренних поясов. На
рис. 5.23 представлен характер изменения относительных на-
напряжений в обшивке охх = ахх/а0 и axv = оху1а% вдоль
прямых, проведенных через середины соответственно внутрен-
внутреннего и наружного участков обшивки. Величины
l+3BA/D<pF)
199
N
2,4
2,0
%*
0,8
0
Л
\
/
/
/
/
/
-в/
\
\\
\
/
>
/
0,'
f1
\
У'
У
1
ч-
"^
Рис. .
-о*
-о-
0,6
5.22
1.2
0.8
1
1
1
\
\
(
/
/
r
\
r
\
o/
/
/
fc
j
V
<
>
Y
1
\
>>*
V
<^
1
-o—
5
«
1
представляют собой те зна-
значения силы в поясах и
нормального напряжения
азе* в обшивке, которые
возникли бы в поперечном
сечении панели при его
полном включении в рабо-
работу (ф = EJEO).
Сплошные линии полу-
получены при моделировании
панели по схеме (б) (см.
рис. 5.21) с параметром
п = 20; кружочками отме-
отмечены результаты, полу-
полученные на сетке (а) при
п = 10. Штриховые линии
соответствуют приближен-
приближенной аналитической методи-
методике расчета [8], согласно
которой силы в поясах Nlt
N2 и касательное напряже-
напряжение аху в обшивке опреде-
определяются выражениями:
Jxy
а -?±е-ах-
У}хи с ,
я
2 2GA
а — •
Рис 5.23
EFB
Нормальные напряже-
напряжения в обшивке здесь при-
принимаются равными нулю,
и вся нагрузка восприни-
воспринимается поясами. Так как
Иъ N2 отнесены по-преж-
по-прежнему к Л^о, то значения Nt
и ~N2 вдали от заделки не
равны 1. Следует отметить,
Е также, что в приближен-
приближенном методе расчета пред-
предполагается, что конструк-
конструкция имеет по всей длине
поперечные диафрагмы
200
(применительно к рассматриваемой панели — поперечные
стержни). Наличие поперечного стержйя на свободном
конце приводит к тому, что касательные напряжения оказы-
оказываются максимальными при х = 0, и включение внутренних
поясов в работу происходит быстрее, чем это получено в ко-
нёчноэлементном решении (где касательные напряжения на
свободном конце равны нулю).
Пример 2. Квадратная пластина с круглым отверстием
фис. 5.24, а) находится в условиях одноосного растяжения.
Радиус отверстия г составляет V20 стороны пластины. Нали-
Наличие двойной симметрии в этой задаче позволяет ограничиться
У
А
\
200
Рис. 5.24
рассмотрением лишь одной четверти пластины, закрепив ее
подходящим образом в узлах, расположенных на осях симмет-
симметрии (рис. 5.24, б). Расчет проводился с использованием четы-
четырехугольных изопараметрических конечных элементов перво-
первого и второго порядков. Применялась неравномерная в ради-
радиальном направлении сетка, более густая возле отверстия.
Значения максимального напряжения ахх, возникающего
в точке А :
Сетка 2X2 4x4 8x8
(а*х)тах/Я для элементов:
первого порядка .... 2,091 2,536 3,050
второго порядка .... 2,733 3,176 3,180
На рис. 5.25 сплошной линией показано распределение ахх
в сечении х = 0; штриховая линия соответствует аналитичес-
аналитическому решению для бесконечной пластины.
Пример 3. Круговое составное кольцо типа шпангоута
(рис. 5.26, а) нагружено двумя силами, приложенными по кон-
концам диаметра. Кольцо состоит из стенки высотой Я = 20 мм,
"ТЪлщиной h — 1 мм и двух поясов с площадью сечения F —
201
= 100 мм2 каждый (рис. 5.26, б). Средний радиус кольца г —
= 1 м, Е = 7-10* МПа, ц = 0.3.
Схема идеализации кольца представлена на рис. 5.26,в.
Как и в предыдущем примере, учитывается двойная симмет-
симметрия конструкции. Пояса моделируются одномерными элемен-
элементами, а стенка — плоскими элементами с четырьмя сторонами.
i
к
¦
/ i» \fi 2.2 У/г
Рис. 5.25
Рис. 5.26
Рассмотрены следующие три конечноэлементные модели:
1. Элементы первого порядка для поясов, четырехузловые
изопараметрические элементы для стенки;
2. Криволинейные элементы второго порядка для поясов,
шестиузловые изопараметрические элементы (см. § 5.8) для
стенки;
202
3. Элементы первого порядка для поясов, четырехуголь-
четырехугольные элементы с линейным полем напряжений (см. § 5.7) для
стенки.
Для различного числа разбиений п рассматриваемой чет-
четверти кольца значения радиального перемещения д точки
приложения силы, отнесенного к Pra/(EJ), где J =
=2,067 • 104 мм4 — момент инерции поперечного сечения коль-
кольца, следующие:
15
Ю
5
0
-5
-10
к 1
;
s /
1 2
X'
s
0 3
ч
0 1
9 8
о в'
Рис. 5.27
л 3 10 20 40
?УД/(Рл3) для модели:
1 . 0,0070 0,0423 0,0632 0,0718
2 0,0214 0,0728 0,0751 0,0753
3 ... 0,0673 0,0748 0,0754 0,0755
Как видно из этих результатов, модель / дает чрезмер-
чрезмерное завышение жесткости конструкции вследствие влия-
влияния ложных деформаций поперечного сдвига (см. § 5.2).
Даже при п = 40 погрешность определения Д составляет
~ 5%. Наилучшим образом воспроизводит работу этой кон-
конструкции модель 5, что обеспечивается полным исключением
ложных деформаций сдвига. Отметим, что аналитический
расчет кольца как рамы с учетом осевой силы и деформации
поперечного сдвига дает значение А = 0,07548 Pr3/(EJ).
На рис. 5.27 сплошной линией представлен закон измене-
изменения осевой силы N в наружном поясе, найденный аналитичес-
аналитически. Штриховые линии получены для модели 2 при п = 10 не-
непосредственным вычислением напряжений. Наблюдается силь-
сильное колебание значения N относительно истинного решения.
203
Максимальное значение N имеет погрешность порядка 30%,
хотя погрешность в перемещениях для этой сетки составляет
3,5%. Эти колебания отчетливо проявляются даже при весьма
густой сетке. Так, при п = 40 отклонение максимального
значения N от точного решения составляет ~ 2%, в то время
как погрешность в перемещениях не превосходит 0,3%. При-
Применение процедуры местного сглаживания, описанной в пре-
предыдущем параграфе, совместно с осреднением результатов ,в
узлах, позволяет полностью устранить эти колебания и полу-
получить значения N практически с той же погрешностью, что и
для перемещений (точки на рис. 5.27). Крестиками на графике
даны значения силы N, полученные на модели 3 в случае п =
— 10. Как видим, описанный в §5.7 плоский четырехугольный
конечный элемент с линейным полем напряжений весьма эф-
эффективен при моделировании тонких стенок.
ГЛАВА 6
КРИТЕРИИ СХОДИМОСТИ
Интуитивно кажется очевидным, что чем гуще сетка конечных
элементов, тем точнее получаемое решение. В действительности такая
сходимость приближенного решения к точному имеет место лишь при
использовании конечных элементов, удовлетворяющих определенным
требованиям. Вариационная трактовка метода конечных элементов
дает возможность ие только установить эти требования, ио и оценить
скорость сходимости решения к точному для различных конечных эле-
элементов.
§ 6.1. Предварительные замечания
Всякое упругое тело имеет бесконечно большое число сте-
степеней свободы. В методе Ритца деформированное состояние
тела определяется выбором нескольких параметров, которые
находятся из условия минимума полной энергии и выступают в
качестве степеней свободы тела. Ограничение числа степеней
свободы равносильно введению дополнительных внутренних
связей, что приводит к завышению жесткости тела по сравне-
сравнению с истинной. То же самое относится и к методу конечных
элементов, если используются совместные элементы. В этом
случае перемещения, получаемые методом конечных элементов,
будут в среднем меньше их точных значений.
При сгущении сетки число узловых перемещений (т.е. сте-
степеней свободы тела) увеличивается. Важно установить, при
каких условиях это будет сопровождаться улучшением реше-
решения, т. е. его сходимостью к точному. Существенное значение
204
имеет также скорость сходимости. При наличии высокой ско-
скорости сходимости можно получить удовлетворительное реше-
решение уже с достаточно грубой сеткой. Вопросы сходимости
часто исследуют численно на тестовых задачах, для которых
известно точное решение, а также путем сопоставления резуль-
результатов, найденных при различном разбиении тела на конечные
элементы. Но некоторые общие вопросы, касающиеся сходи-
сходимости, можно исследовать и теоретически.
При теоретическом анализе удобнее всего судить о сходимо-
сходимости по величине полной энергии системы. Если в пределе она
будет стремиться к своему точному значению, то перемещения,
деформации и напряжения также будут стремиться к своим
точным значениям в каждой точке тела.
Обозначим через и матрицу перемещений, найденных ме-
методом конечных элементов, а через и0 — матрицу перемеще-
перемещений, соответствующих точному решению задачи. Так как дей-
действительные перемещения и0 минимизируют полную энергию
системы V, то V (u) ^ V (и0).
Рассмотрим далее такое деформированное состояние тела,
составленного из конечных элементов, при котором узловые
перемещения совпадают с перемещениями соответствующих
точек тела, взятыми из точного решения. Обозначим матри-
матрицу получающихся при этом перемещений в пределах каждого
элемента через и*. Полная энергия системы, деформирбванной
подобным образом, будет удовлетворять неравенству V (u*) ^
^ V (и), так как при конечноэлементной идеализации минимум
полной энергии соответствует перемещениям и. Следователь-
Следовательно, имеем V (и*) ^ V (ц) ^ V (и0), и если в пределе V (и*)->-
-> V (и0), то подавно будет V (и) -> V (и0).
Таким образом, для доказательства сходимости конечное
элементной модели достаточно положить узловые перемещения
равными их значениям в точном решении и показать, что яри
уменьшении размеров конечных элементов полная энергия
такой системы будет стремиться к своему точному значению.
§ 6.2. Применение рядов Тейлора
к исследованию сходимости
Для сопоставления перемещений и* с и0 воспользуемся раз-
разложением и0 в ряд Тейлора. Напомним, что для функции / (х)
одной переменной разложение в ряд Тейлора в окрестности
точки х — х0 имеет вид
205
Зто разложение можно представить также как сумму
f(x) = Pn(x) + R(x).
Здесь полином
/ {Хо) + ... +
И л!
содержит первые члены разложения вплоть до (х — хо)я;
R (х) — остаточный член ряда. Для него справедлива оцен-
оценка \R (х)\ ^ М1п*\ где / — длина интервала, на котором про-
производится представление функции в виде ряда, а М — положи-
положительная константа, величина которой определяется максималь-
максимальным значением производной /<"+*> (х) на рассматриваемом ин-
интервале. С уменьшением длины интервала R (х) стремится к
нулю как in+1, т. е. приближение функции / (х) полиномом
Рп (х) будет тем лучше, чем выше степень этого полинома.
В дальнейшем выражение для Рп (х) будем записывать в
форме
Рп (х) = а, + агх + ...+апх",
где а0, аг,..., ап — некоторые коэффициенты, определяемые
значениями производных от функции/ (х) в точке х0.
Аналогично можно записать разложение Тейлора и для
функции нескольких переменных. Так, для двух переменных
имеем
}(х.у) - Рп{х, у) + R{x, у).
Здесь Р„ (х, у) содержит все'члены полинома степени п (т. е.
все члены вида xPy<i, где р + q = л), а также все полиномы
низших порядков. При этом условии для остаточного члена
R {х, у) справедлива оценка \R (х, у)\ ^ М/л+1, где / — ха-
рактерлый линейный размер области, в которой выполняется
разложение, а константа М зависит от максимальных значений
производных {п + 1)-го порядка от функции / (х, у) по коорди-
координатам х, у в рассматриваемой области. Подчеркнем, что если
в Рп (х, у) удержаны не все члены полинома степени п, то ос-
остаточный член будет в общем случае иметь порядок 1п, а не ?n+1.
Если f (х, у) — {Д (х, у) /2 {х, у)...} есть матрица-столбец,
то каждый ее компонент можно разложить в ряд Тейлора, при-
придерживаясь одинаковой степени точности:
L (х, у) = Рп, (х, у) + Ri (х, у); f2 (х, у) = Рпг (х, у) +
+ R2(x.y),....
Объединив все эти равенства, придем к разложению
f (х, у) = Р„ (х, у) + R (х, у),
306
где
. у)= {Ri(x,'y)Ra(x.
Рассмотрим теперь некоторый плоский конечный элемент.
Предположим, что для аппроксимации перемещений исполь-
используются полиномы относительно х, у, так что функции их, иу
определяются соотношениями
.' Мх (*> У) = До + сцх
и„ {х, у) = ba + bj.x + b& + М2 +btxy + bif+.... F. J)
Полагая u (x,y) — {их (х, у) иу (х, у)}, запишем эти соот-
соотношения в матричном виде
и (х,у) = Ао + Atx + Ку + Аэ*2, + AiXy + А^+..., F.2)
где Аг = {at bt).
Постоянные Аг выражаются через смещения узлов, и ра-
равенство F.2) можно представить в стандартной форме и (х, у) =
= а (х, у) Vе. Если конечный элемент имеет узлы i, /, ..., то
v* = {v,v,.v}; се (х, у) = [о,- (х, у) щ{х, у). Л.
Следовательно, можно записать
и (х, у) = 2аг (х, у) vr.
Здесь суммирование выполняется по всем узлам конечного
элемента. Если в качестве vr взять перемещения точек (xt,
уг) нз точного решения, то последнее равенство будет оп-
определять перемещения и* (х, у). Обозначая и° (хг, ут) = и*,
имеем
и* (х, у) = 2ar (jc, у) и». F.3)
Пусть, далее, п — наивысшая степень полного
содержащегося в аппроксимирующих функциях F.2). Разло-
Разложим истинные перемещения и° в ряд Тейлора в окрестности
какой-либо точки, принадлежащей конечному элементу, удер-
удерживая при этом также полные полиномы вплоть до степени п:
ц° (х, у) - Р„ (дс, у) + R (х, у). F.4)
Компоненты матрицы R (х, у) всюду в пределах элемента
не будут превышать величины порядка ln+1, где / — характер-
характерный размер элемента. Введя обозначения Р„ (яг, ут) = Р„г и
R (хг, Уг) — Rn из F-3) и F.4) получим
и* (х, у) = 2а, (х, у) Рпг + 2аг (х, у) Rr.
20?
Положив,
Р; (х, у) = Zar (х, у) Pnr; R* (х, у) = 2аг (х, у) Rr,
можно последнее равенство записать в виде
и* (х, у) = Р*п (х, у) + R* (х, у).
Здесь первое слагаемое дает интерполяцию полинома
Рц (*> У)> а второе — интерполяцию остаточного члена R (х,у)
по их узловым значениям. Аппроксимирующие функции со-
содержат по условию полные полиномы вплоть до степени п.
Поэтому интерполяция любой полиномиальной функции, по-
порядок которой не превосходит п, будет давать точный резуль-
результат. Отсюда следует, что Р« (х, у) = Рп (х, у), так что для
и* (х, у) приходим к выражению
и* (х, у) = Р„ (х, у) + R* (х, у).
Разность между истинными перемещениями и0 и перемеще-
перемещениями и* оказывается равной
и» - u* = R (х, y)-R* (х, у) =R(*. у) - Еаг (х, у) К
Таким образом, разность и0 — и* выражена через компо-
компоненты матрицы R (х, у), которые имеют порядок /rt+1. Следова-
Следовательно, эта разность также не превосходит величины порядка
ln+1 всюду в пределах области, занимаемой конечным элемен-
элементом. При уменьшении размеров конечного элемента (т. е. при
/-»-0)она будет стремиться к нулю, как /rt+1. Подобный же
анализ показывает, что при аппроксимации перемещений по-
полиномами степени п погрешность их первых производных по
л:, у будет иметь порядок /", вторых — ln~l и т. д.
Из приведенных рассуждений можно сделать следующие
выводы. Во-первых, скорость сходимости конечноэлементного
решения к точному будет тем выше, чем выше порядок полино-
полиномов, используемых для аппроксимации перемещений. Поря-
Порядок полиномов увеличивается, например, с увеличением числа
узлов конечного элемента. Во-вторых, разность и0 — и* будет
иметь порядок /л+1 лишь в том случае, если в аппроксимирую-
аппроксимирующих функциях F.2) представлены все члены полиномов степе-
степени п и ниже. Например, для п = 3 аппроксимирующие функ-
функции должны содержать члены х3, х*у, ху2, у3 с произвольными
множителями, а также все члены младших полиномов; тогда
ошибка в перемещениях будет иметь порядок I*. Отбрасыва-
Отбрасывание любого из записанных выше членов (или введение ограни-
ограничений на множители перед ними) приводит к понижению по-
208
рядка ошибки до Р. Если же для аппроксимации перемещений
используется, скажем, выражение вида
A0 + Atx+A2y-{-A3x2-
в котором отсутствует слагаемое с произведением ху, то ошиб-
ошибка будет иметь порядок /2 и скорость сходимости будет значи-
значительно ниже, чем при наличии этого слагаемого. Отметим так-
также, что полные полиномы степени п должны содержаться в вы-
выражениях для всех компонент перемещений. При использова-
использовании для отдельных компонент перемещений полиномов различ-
различной степени (что встречается, например, при расчете оболочек)
скорость сходимости будет определяться наименьшим поряд-
порядком аппроксимации.
Рассмотрим в качестве примера совместный плоский прямо-
прямоугольный конечный элемент (см. § 5.2), для которого перемеще-
перемещения задаются равенствами E.16):
и* = /i + /2* + hy + fiW, uy = h + /6* + f-гУ +
Здесь представлены полные полиномы первого и нулевого
порядков, и можно ожидать, что погрешность аппроксимации
перемещений будет порядка I2, где I — длина наибольшей сто-
стороны прямоугольника. Для улучшения характеристик эле-
элемента можно ввести неузловые степени свободы. В частности,
как говорилось в § 5.5, можно добавить к этим выражениям
функцию A — ?2) A — ц2) с произвольными множителями.
Безразмерные координаты ?, ц связаны с х, у линейными со-
соотношениями
I = 2 (х — хс)/а; ц = 2 (у - усIЬ,
где а, Ь — размеры сторон прямоугольника; хс, ус — коор-
координаты его центра тяжести. В итоге в выражениях для их,
иу появятся члены, содержащие квадраты координат. Но
множители перед х2 и у2 в каждом из выражений для их, иу не
произвольны, а равны между собой. Следовательно, мы не по-
получаем здесь полных полиномов второй степени, и поэтому по-
погрешность аппроксимации по-прежнему будет иметь порядок
Р. Таким образом, добавление функций A— |!) A — т]2) к ап-
аппроксимирующим функциям E.16) не должно привести к суще-
существенному улучшению конечного элемента, что и подтвержда-
подтверждается числовыми расчетами. В то же время добавление функций
A — |2), A — т}2) с произвольными множителями дает полные
полиномы второго порядка. Это приводит к конечному эле-
элементу с лучшими характеристиками, несмотря на то, что здесь
нарушается совместность элементов.
209
Если для аппроксимации перемещений в пределах конеч-
конечного элемента используются функции, отличные от полиноми-
полиномиальных, то для анализа сходимости можно разложить их в сте-
степенные ряды и воспользоваться затем предыдущими рассужде-
рассуждениями. Вернемся к прямоугольному конечному элементу с ап-
аппроксимирующими функциями E.16). Пусть к этим выраже-
выражениям добавляются функции cos (я?/2) cos (пц/2) с произволь-
произвольными множителями. Для исследования сходимости восполвк
зуемся разложением
Тогда имеем
cosv1\
Отсюда видно, что введение в E.16) функций cos (я|/2)х
X cos (пт]/2) равносильно использованию дополнительных функ-
функций типа A -г- |*).A—ч2), т. е. оно не сопровождается улучше-
улучшением сходимости по сравнению с базовым конечным элементом.
§ 6.3. Критерии сходимости совместных элементов
Сходимость перемещений не означает еще сходимости пол-
полной энергии системы
*= -j f eT odx — f ит Rdt — Г лт pdc
к ее точному значению. В матрицу деформаций 8 в соответст-
соответствий с формулами Коши входят первые производные от переме-
перемещений по координатам. Так как о" = xs, то и компоненты мат-
матрицы напряжений а также выражаются через эти производ-
производные. Следовательно, при сгущении сетки V (и*) -»- V (и0),
если не только сами перемещения, но и их первые производ-
производные совпадают в пределе с точными значениями. Сходимость
деформаций к точным значениям будет обеспечена, если пере-
перемещения представлены как полиномы по крайней мере первого
порядка. В общем случае трехмерного конечного элемента
должно быть
а3г + ...;
"и — К + Ьхх+ Ьгу + Ь3г + ...; F.5)
210
•Здесь а, Ь, с — независимые постоянные, а невыписанные
слагаемые могут произвольным образом зависеть от х, у, г.
Деформации будут при этом представлены полными полинома-
полиномами степени не ниже нулевой:
?хх — «1 + ...; Еуу — Ьг + ...; ezz = с3 + ...;
еж» = as + by + ...; ъуг = b3 + сг + ...; ezx = a3 -{- сх +
F,6)
Погрешность аппроксимации деформаций будет иметь поря-
порядок по крайней мере /\ т. е. она стремится к нулю при уменьше-
уменьшении размеров конечного элемента.
Формулами F.5) определяется минимальное требование,
необходимое для сходимости конечноэлементного решения к
точному в случае совместных конечных элементов 126 J. Таким
образом, для обеспечения сходимости достаточно, чтобы каж-
каждая компонента перемещения могла быть в пределах конечного
элемента представлена полиномом не ниже первой степени.
Это требование называют иногда условием полноты конечного
элемента.
Подчеркнем, что приведенные рассуждения применимы,
строго говоря, лишь к совместным конечным элементам. Если
элементы удовлетворяют условию полноты и совместны, то
при сгущении сетки сходимость конечноэлементного решения к
точному по энергии будет монотонной. Другими словами, при
сгущеиии сетки полная энергия системы будет уменьшаться,
оставаясь при этом выше своего точного значения. Можно по-
показать [26], что погрешность рассмотренных выше элементов
в энергии имеет порядок /2", где п — порядок полных полино-
полиномов в аппроксимирующих функциях. Если в выражении для
энергии деформации встречаются вторые производные от пере-
перемещений (это имеет место, например, для некоторых конечно-
элементных моделей пластин, работающих на изгиб, и оболо-
оболочек), то ошибка в энергии будет иметь порядок Ща-1).
Обращаясь к рассмотренным ранее конечным элементам,
вадим, что треугольный элемент с линейным полем перемеще-
перемещений (см. § 5.1) и совместный прямоугольный элемент (см. § 5.2)
удовлетворяют условию полноты. Это непосредственно следу-
следует из формул <5.1) и E.16) для перемещений их, иу, в которых
представлены полные полиномы первого и нулевого порядков.
Поскольку эти элементы являются также совместными, то
они обеспечивают монотонную сходимость решения к точному
при сгущении сетки. Погрешность аппроксимации перемеще-
перемещений убывает при этом в обоих случаях по крайней мере как
/2, где / — длина наибольшей стороны элемента. Как показы-
211
вают числовые расчеты, фактическая скорость сходимости у
прямоугольного элемента выше, чем у треугольного.
Выясним далее, удовлетворяют ли критериям сходимости
конечные элементы изопараметрического типа. Прежде всего
отметим, что эти элементы совместны. Следовательно, доста-
достаточно показать, что перемещения в пределах элемента описыва-
описываются полиномами степени не ниже первой. В частности, для
двумерных элементов должны быть справедливы разложения'
«* = а0 + Oi-H-a»*/ + •••; "» = b0 + Ьгх + b2y + ... F.7)
с независимыми коэффициентами аь bt.
Напомним, что в изопараметрических элементах для ап-
аппроксимации перемещений используются полиномы относи-
относительно переменных %, г\, которые представляют собой неорто-
неортогональные криволинейные координаты точек конечного эле-
элемента и связаны с х, у соотношениями
х = Щ, A, г)) хг; у = ltyr (|, г)) уг. F.8)
Здесь хг, уг — координаты узлов; я|зг (?, ¦*)) — полиномиаль-
полиномиальные функции. Суммирование в F.8) ведется по всем узлам ко-
конечного элемента.
Выражения для перемещений
их = ltyr (g, vt)vrx; uv = Щг (I, фгу F.9)
не зависят в явной форме от х, у и справедливость разложений
вида F.7) не очевидна.
Предположим [6], что узлы конечного элемента получают
смещения, равные
<>тх == а0 + аххт + a2yr; vry = b0 + bxxT + b2yr.
Если перемещения произвольной точки конечного элемента
с координатами х, у, найденные по F.9), окажутся при этом
равными
их = ао + агх + а2у; иу = Ьо + Ьхх + Ь*у, F.10)
то тем самым будет доказано, что изопараметрический элемент
может воспроизвести любое линейное поле перемещений и, сле-
следовательно, разложения F.7) справедливы.
Для доказательства F.10) подставим значения vrx в первое
из соотношений F.9):
"ж = ЩгA, ¦*)) (во + сцхг + а^уг) =
-=а0Щт (I, ц) + a^iprd, л) хг + а2 2% (?, х\) ут.
212
Но на основании F.8) это выражение можно переписать так:
их = а0 Щг (|, ц) + atx + а2у.
Аналогично приходим к соответствующей формуле для иу:
иу = b0 Щг (I, ц) + btx + b?y.
Сопоставляя эти выражения с F.10), заключаем, что пере-
перемещения конечного элемента действительно совпадают с тре-
требуемым полем, если только удовлетворяется условие
ЩгA, т,)= 1.
Чтобы доказать это равенство, предположим [33], что на-
начало системы координат х, у переместилось вдоль оси х на рас-
расстояние d. Тогда новая координатах произвольной_точки эле-
элемента станет* — х — d, а координаты узлов будутxr = xr^-d<
В новых координатах первое соотношение F.8) примет вид
х = 2tyr (I, t\) хг. Подставив сюда значения х и хг, будем иметь
х - d = Щг A, у]) (хт - d) - Щг (I, г\) хт - dZ% (I, Л)-
На основании F.8) получаем отсюда соотношение
d = d2afr (l, ц),
из которого и; следует справедливость равенства 2ч|;г (§, tj) =1.
Таким образом, мы доказали, что плоские изопараметри-
ческие элементы удовлетворяют условию полноты. Следова-
Следовательно, их использование обеспечивает монотонную сходимость
решения. Аналогично доказывается свойство полноты для одно-
и трехмерных изопараметрических конечных элементов.
Условие полноты формулируется иногда иначе [6], чем
это сделано выше. Элемент считается полным, если, во-пер-
во-первых, в аппроксимирующие функции включены его перемеще-
перемещения как жесткого целого и, во-вторых, если в элементе может
существовать однородное (т.е. не зависящее от координат) де-
деформированное состояние с произвольными компонентами де-
деформации.
Поясним эти условия подробнее. Предположим, что узлы
конечного элемента получают смещения, соответствующие
его перемещению в пространстве как абсолютно жесткого тела.
Если деформации, найденные по формуле 8 = Pve, окажутся
нулевыми, то это означает, что жесткие смещения точно пред-
представлены в используемых аппроксимирующих фунциях.
Второе требование основывается на следующих соображе-
соображениях. При уменьшении размеров конечных элементов измене-
изменения деформаций в пределах каждого из них будут все менее
существенными по сравнению с самими деформациями, т. е.
деформированное состояние будет приближаться к однородно-
однородному. Для сходимости решения необходимо, чтобы аппррксими-
213
рующие функции позволяли воспроизвести такое предельное
состояние. Это будет обеспечено, если можно подобрать значе-
значения узловых перемещений или констант в формулах типа F.1),
при которых деформации в пределах элемента будут постоянны.
Для большинства конечных элементов отмеченные два под-
подхода к определению полноты, по существу, совпадают, осо- ¦¦
бенио если в качестве компонент перемещений берутся их прб-
екции на декартовы оси координат, как это делалось выше.
В самом деле, допустим, что в невыписанных членах в F.5)
отсутствуют слагаемые, содержащие постоянные а0, alt...c2, ?3.
Тогда при выполнении соотношений F.5) автоматически удов^
летворяются условия жестких смещений и условие постоянства
деформаций. Но если какие-либо коэффициенты в полиномах
более высоких порядков связаны с этими постоянными, то усло-
условия жестких смещений н постоянства деформаций могут уже
не выполняться, хотя элемент является полным в том смысле,
что требование минимальности степени полинома удовлетво-
удовлетворено. Особенно существенно различие между двумя подхода-
подходами к определению полноты в том случае, когда компонентами
матрицы и являются проекции перемещений на криволиней-
криволинейные координатные оси, как это имеет место, например, прн рас-
расчете оболочек. Требования о жестких перемещениях и по-
постоянстве деформаций оказываются более трудновыполнимыми,
чем требование о минимальности степени полинома.
§ 6.4. Сходимость несовместных элементов
Обратимся теперь к несовместным элементам. Сходимость
решения к точному имеет место и в этом случае, если в пределе
(т.е. по мере сгущения сетки) в аппроксимирующих функциях
исчезают члены, создающие несовместность. Следовательно,
сходимость будет гарантирована, если несовместные конечные
элементы, во-первых, способны воспроизвести в пределе ли-
линейное поле перемещений и, во-вторых, оказываются прн этом
совместными. Обычно используют более жесткое требование, в
соответствии с которым должна обеспечиваться сплошность те-
тела в условиях линейного поля перемещений при любых разме-
размерах элемента, а не только в пределе.
Проверка выполнения последнего требования осуществля-
осуществляется с помощью группового тестирования [26]*. Пусть требу-
* В зарубежной литературе используется введенный Айронсом
термин «patch test», что в буквальном переводе означает «лоскутный
тест» — по-видимому, в связи с ассоциациями, вызываемыми видом
тестируемой области (см. рис. 6.1). В литературе на русском языке
можно встретить названия «кусочный тест», «выборочный тест», «пэтч-
тест». Мы предпочитаем термин «групповой тест» как наиболее coot- i
ветствующий существу дела.
214
ется проверить, будет ли давать сходимость некоторый несов-
несовместный конечный элемент. Рассматривается группа смежных
элементов исследуемого типа, составленных таким образом,
чтобы по крайней мере один узел оказался внутри полученной
области (рис. 6.1). Форма конечных элементов должна быть по
возможности произвольной. Далее принимается, что внешние
узлы, расположенные на границе этой области, получают пере-
перемещения, соответствующие линейному полю. Для плоских ко-
конечных элементов, например, узловые перемещения следует
брать равными
Vry — Ьо + fe^r + Ьгуг,
где хг, уг — координаты
типового внешнего узла.
В соответствии с
обычной процедурой ме- Рнс. 6.1
тода конечных элемен-
элементов можно теперь найти перемещения внутренних узлов,
координаты которых обозначим через ха, уа. Если окажется,
что эти перемещения совпадают с величинами
то групповой тест проходит. В этом случае использование не-
несовместных конечных элементов будет всегда обеспечивать схо-
сходимость решения.
Выполнение условий группового теста является достаточ-
достаточным, но ие необходимым условием сходимости [26J. Имеются
примеры конечных элементов, для которых групповой тест не
проходит, но которые тем ие менее обеспечивают сходимость
решения. Однако обычно конечный элемент считается непри-
непригодным к употреблению, если групповой тест для него не про-
проходит.
В изложенной трактовке групповое тестирование связано с при-
применением ЭВМ. Но во многих случаях можно проверить выполнение
условий этого теста более простыми средствами. Рассмотрим в качестве
примера несовместный прямоугольный конечный элемент с линейным
полем напряжений (см. § 5.3). Распределение перемещений определя-
определяется для этого элемента соотношениями E.25). Если принять в них
U — /в = 0, то все точки конечного элемента, в том числе узловые, бу-
будут находиться в условиях произвольного линейного поля перемеще-
перемещений. Постоянные / однозначно связаны с узловыми перемещениями,
так что справедливо и обратное: если поместить узлы в условия линей-
линейного поля перемещений, то постоянные/4 и /8 будут нулевыми, т. е. это
поле будет воспроизведено внутри элемента — групповой тест про-
проходит. То же самое относится и к четырехугольному элементу произ-
произвольной формы с линейным полем напряжений (см. §5.7).
215
Если элемент получен из базового введениям дополнительных не-
несовместных функций перемещений, то можно воспользоваться следую-
следующими рассуждениями. Перемещения в таком элементе определяются
равенством
и = eev' + а0С
Здесь первое слагаемое описывает перемещения в базовом элемент!
(который предполагается полным и совместным), а второе дает допой-
нительиое поле перемещений, нарушающее совместность конечных эле-
элементов; в узловых точках перемещения ее0С обращаются в нуль. Неуэ-
ловые степени свободы С выражаются через узловые перемещення V*
путем минимизации полной энергии конечного элемента (см. § 5.5).
Предположим, что в базовом элементе путем подходящего задания
узловых перемещений создано линейиое поле
U" л ^k I ^К ля I ^К л g I ^K /ш
где матрицы-столбцы Ао, At, A^, A3 содержат произвольно выбранные
постоянные. Если добавить к и функции а„С, то при тех же узловых
перемещениях получим поле перемещений в рассматриваемом несов-
несовместном элементе: ___
и = и + а0С.
Постоянные С, как уже говорилось, необходимо определить из ус-
условия минимума полной энергии элемента. Если при этом они окажут-
окажутся равными нулю, то это будет означать, что конечные элементы дан-
данного типа согласованно воспроизводят линейиое поле перемещений и,
следовательно, групповой тест будет проходить.
Выведем условие, при котором постоянные С обращаются в нуль.
Пользуясь формулами Коши, находим деформации в несовместном эле-
элементе ___
е = е + р0С.
Здесь матрица р0 содержит производные от элементов матрицы а„,
а компонентами матрицы в являются независимые постоянные величи-
величины, выражающиеся через элементы матриц А„, Aj, A2, А3. Подставляя
выражение для е в формулу
Ue = —
ыожио получить
е 1 С~т - С
2 J E J
Так как деформирование конечного элемента осуществляется путем
задания узловых перемещений, то потенциал Пс внешней нагрузки
равен нулю. Следовательно, минимизация полной энергии элемента
dUe
сводится к выполнению условия —qq- = 0, которое приводит к равен-
равенству
2J6
Постоянные С будут нулевыми, если
Так как матрицы хие содержат постоянные величины, то их мож-
можно вынести за знак интеграла. Так как полученное условие должно вы-
выполняться для любых компонент матрицы е и для любых упругих по'
стоянных материала, то его можно заменить равенством
J PcdT = O. F.1I)
Xе
Таким образом, групповой тест можно заменить проверкой усло-
условия, чтобы интегралы, взятые по объему конечного элемента от каждой
компоненты матрицы ее0, равнялись нулю.
В качестве примера возьмем прямоугольный конечный элемент,
рассмотренный в § 5.5. Для этого элемента поле перемещений опреде-
определяется равенствами E.40), а матрица
4
[На 0 0 0 I
0 0 0 т|/6|,
0 ц1Ь На 0 J
где а, Ь — размеры сторон прямоугольника. Учитывая, что
dt = (habl4) d|dt]
и что интегрирование по обеим переменным ?, t\ выполняется в преде-
пределах от —1 до 1, убеждаемся, что в случае постоянной толщины элемен-
элемента Л условие F.11) выполняется.
В другом примере в качестве базового возьмем плоский четырехуз-
ловой изопараметрический элемент (см. § 5.6), для которого коорди-
координаты х, у выражаются через переменные ?, г) посредством соотношений
*= 2i|>r (I, Г))хг; у = 2t|>r (|, т))уг,
где
а суммирование выполняется по всем узлам элемента.
По аналогии с предыдущим примером можно попытаться улучшить
жесткостиые характеристики элемента, вводя в выражения для пере-
перемещений
дополнительные функции-1 — ?2 и 1 — rf с произвольными множите-
множителями. В итоге получим несовместный элемент в форме произвольного
четырехугольника с перемещениями
u = 2eer vr -j- ав с,
217
где
о J;
_Г«Ч_Р~Б1
О 1 —
° 1
1 — П2 J
Для вычисления матрицы
Ро —
дх
ду
ду
необходимо составить предварительно матрицу Якобн
дх ду
дх ду
дц дц .
а
и выразить производные д^ф ^ через -^,
д
дх
д
ду
щ I
= J *
а
д%
а
дц
Учитывая, что
ду _ ду
дц ~ dl
дх дх
где |J| — определитель матрицы J, запишем
_а I
дх ~~ | J .
а^ а
дц
ду а_\
" ag дц у
_д {_( _^Lj_ дх
ду ~ \л\ дц ag + ag
218
В итоге
Ро =
имеем
2
Ml
—
1 ду
дц
0
дх
11ц~
п —
0
дх
0
Эх
дц
ду
~ ~дц
0
Эл:
ду
Так как dr *= Л | J j d?dt), то
•t —! —!
Внося сюда полученное выражение для ро, видим, что групповой
тест будет проходить, если каждый из интегралов
дх С С
dgdtj; I I
дц J J
j i
дц
J
дх
-I - i
1 l
JJ
An
~
обращается в нуль. Вообще говоря, эти интегралы не равны нулю даже
при постоянной толщине Л. Исключение составляет лишь случай, ког-
когда производные дх/д%, дх/дц, ду/дЦ и ду/дц постоянны. Можно пока-
показать, что этому требованию отвечают элементы в форме параллело-
параллелограмма (и, в частности, прямоугольника). Но для произвольного че-
четырехугольника групповой тест не проходит, и пользоваться подобны-
подобными конечными элементами нельзя.
В случае несовместных элементов уже нельзя ожидать, что
полная энергия системы будет всегда выше своего точного зна-
значения. Сходимость решения оказывается в этом случае, как
правило, немонотонной, т. е. при сгущении сетки полная энер-
энергия оказывается то выше, что ниже истинного значения. Не-
Нередко несовместные элементы позволяют получить при одина-
одинаковой сетке более точные результаты, нежели совместные.
Объясняется это тем, что совместные элементы всегда имеют
завышенную жесткость, а введение несовместных функций де-
делает их обычно более податливыми.
219
§ 6.5. Влияние иа сходимость численного
интегрирования
Выше негласно подразумевалось, что при вычислении по-
потенциальной энергии деформации
V = — ferxedx
интегрирование осуществляется точно. Так как, с другой сто-
стороны,
IIе =— veTkeve,
то это означает, что и вычисление матрицы жесткости по фор-
формуле
также выполняется с помощью точного интегрирования. Но,
как свидетельствуют многие примеры из предыдущей главы,
для определения ке нередко приходится прибегать к числен-
численному интегрированию. Это приводит к приближенному значе-
значению матрицы жесткости элемента. Последнюю можно рассмат-
рассматривать и как точную, но соответствующую уже некоторой дру-
другой системе аппроксимирующих функций. Вследствие этого в
конечноэлементной модели возникает дополнительная несов-
несовместность, даже если применяются так называемые «совмест-
«совместные» элементы. Сходимость такой модели к точному решению
требует особого обоснования.
Пусть конечный элемент при точном интегрировании удов-
удовлетворяет условию сходимости. Тогда при уменьшении его раз-
размеров компоненты матрицы е будут в пределах элемента стре-
стремиться к некоторым постоянным значениям. Обозначая эту
предельную матрицу с постоянными компонентами через е0,
запишем
е = е0 + Ае, F.12)
где матрица Де является функцией координат. В пределе
имеем Де->-0. Внося равенство F.12) в выражение для IIе,
представим его в виде
U* = Щ + V\ + U\,
220
где
-L z\ xe0 Jdt;
/|=— ("
Величина i/? представляет собой то значение, к которому
стремится Vе при уменьшении размеров конечного элемента,
и для обеспечения сходимости достаточно потребовать, чтобы
она вычислялась точно. Как видно из выражения для U%,
для этого необходимо, чтобы используемое правило интегри-
интегрирования позволяло в пределе точно находить объем конечного
элемента. Практически пользуются более простым правилом,
в соответствии с которым минимально допустимое число точек
интегрирования должно обеспечивать точное вычисление объ-
объема конечного элемента при любых его размерах, а не только
в пределе.
Вопрос о точности вычисления объема возникает в том слу-
случае, когда интегрирование выполняется в системе координат,
отличной от декартовой. Если элемент отнесен к локальной си-
системе координат ?, ц, ?, то элементарный объем будет равен
dx = |J| d?dTid?, где |J| — якобиан соответствующего преоб-
преобразования координат. Задача сводится к определению такого
правила интегрирования, которое, как минимум, обеспечива-
обеспечивает точное вычисление интеграла от |J(?, ц, ?)| по координа-
координатам |, г\, ?.
В случае изопараметрических конечных элементов функция
|J (i, Ц, ?)| представляет собой полином or ?, r\, ?, порядок ко-
которого можно легко установить. Например, для плоского че-
тырехузлового элемента (см. § 5.6) преобразование координат
определяется равенствами E.42):
Якобиан этого преобразования вычисляется по формуле
дх ди
дх ду
дц дц
дх ду ду дх
д\ дц д% дц
221
где производные от х, у по ?, ц даются равенствами
= 2t|f
or] 4
g at) 4
Отсюда видно, что в выражение для | J (|. ц)\ каждый из па-
параметров |, ц входит в степени не выше первой. Метод Гаус-
Гаусса дает точное значение интеграла
— 1
если f (|) представляет собой полином от § степени не выше
2п — 1, где п — число точек интегрирования. Следовательно,
для точного интегрирования ]J(|, ц)\ достаточно одной точки
Гаусса в каждом направлении. Подобным образом можно ус-
установить минимально необходимое число точек интегрирова-
интегрирования и для других конечных элементов. Для элементов с сов-
совместными аппроксимирующими функциями несовместность,
обусловленная приближенностью интегрирования, уменьша-
уменьшается с увеличением числа точек Гаусса. Практически применя-
применяют число точек Гаусса, рекомендованное в последнем столбце
табл. 5.1.
§ 6.6. Исключение ложных деформаций сдвига
с помощью численного интегрирования
В предыдущих рассуждениях предполагалось, что сгуще-
сгущение сетки сопровождается уменьшением всех размеров конеч-
конечного элемента. Иная ситуация возникает, когда при конечно-
элементной идеализации балки с тонкой стенкой последняя
моделируется по высоте одним конечным элементом. Сгущение
сетки сводится здесь к уменьшению продольных размеров ко-
конечных элементов, в то время как их поперечные размеры, оп-
определяемые высотой балки, не зависят от выбора сетки. Естес-
ственно, что при этом нельзя даже в пределе прийти к точному
(с позиции теории упругости) решению. Задача заключается в
получении приближенного результата, соответствующего, ска-
скажем, технической теории изгиба бруса.
Применительно к подобным элементам необходимо уточ-
уточнить понятие сходимости решения, которое может трактовать-
трактоваться здесь в двух различных смыслах. Во-первых, как и ранее,
222
должна быть обеспечена сходимость решения к правильному
ответу при сгущении сетки, т. е. при уменьшении продольных
размеров конечных элементов.
С другой стороны, если длина балки значительно превыша-
превышает ее высоту, то, как известно, ее сечения остаются практически
нормальными к изогнутой оси. Естественно потребовать, чтобы
с уменьшением высоты балки конечноэлементная модель вос-
воспроизводила такое поведение независимо от густоты сетки.
Тйлько в этом случае можно рассчитывать на успех при ис-
использовании реальных сеток.
Если поперечное сечение нормально к оси балки, то это оз-
означает, что деформация поперечного сдвига равна нулю (в дей-
действительности она может быть несколько отличной от нуля,
но ее порядок существенно меньше порядка продольной дефор-
деформации в крайних волокнах). Следовательно, при корректном
моделировании стеики должна быть обеспечена возможность
неограниченного уменьшения деформации поперечного сдвига
с уменьшением высоты конечного элемента или, что то же са^
мое, с увеличением его длины при фиксированной высоте.
Таким образом, при анализе применимости конечного эле-
элемента стенки следует оценить его поведение не только при бес-
бесконечном уменьшении (сходимость в обычном смысле), vlou при
неограниченном увеличении его длины (сходимость к балочному
решению).
Рбратимся для иллюстрации к совместному прямоуголь-
прямоугольному конечному элементу (см. § 5.2). Дифференцируя выраже-
выражения E.16) для перемещений в таком элементе, в соответствии
с формулами Коши имеем .
ди* , ¦ , дну
JLf+fy; %= —- =
f2+fiy; %
ox ay
F.13)
Примем для удобства, что начало координат находится в
центре прямоугольника, а ось х параллельна оси балки. При
уменьшении продольного размера элемента слагаемые, содер-
содержащие множителем координату х, будут давать все меньший
вклад в энергию деформации. Предельное деформированное со-
состояние элемента характеризуется величинами
ei«~/. + /«Sr, *l,~f,\ ь% ~ /з + h + /«tf. F-14)
где пять независимых параметров /2, /4, /7, /з + /в и /8 будут
определены из условия минимума полной энергии конечноэле-
ментной модели. .
223
Основное значение при изгибе балки имеет деформация
ъхх. Как видно из первого выражения F.14), ъхх в предельном
состоянии изменяется по высоте стенки по линейному закону,
что соответствует технической теории изгиба бруса. Помимо
гхх в конечноэлементной модели могут возникнуть постоян-
постоянная по высоте поперечная деформация ъуу (которая обычно
игнорируется в теории изгиба бруса) и деформация сдвига е^,
изменяющаяся по высоте по линейному закону. В действитель-
действительности распределение гху по высоте является параболическим,
но это расхождение с теорией может быть легко исправлено
введением корректирующего коэффициента при вычислении
матрицы жесткости. Таким образом, данный конечный элемент
обнаруживает приемлемое поведение при сгущении сетки.
Далее, предположив, что длина элемента возрастает, ис-
исследуем выражение для вху в F.13). С увеличением длины до-
доминирующее значение будет приобретать слагаемое ftx. Кон-
Константа /4 характеризует изгибную составляющую деформа-
деформации гхх в сечении, так что величина вху будет того же порядка,
что и гхх. Критерий сходимости к балочному решению не вы-
выполняется, и поэтому данный элемент, как уже отмечалось в
§ 5.2, практически непригоден для моделирования стенки.
Один путь исключения ложного сдвига рассмотрен в пре-
предыдущей главе. Он заключается в использовании несовмест-
несовместных функций перемещений в виде полных полиномов второго
порядка, вытекающих из линейного закона распределения на-
напряжений (см. § 5.3, 5.7) или содержащих неузловые степени
свободы (см. § 5.5). Но можно поступить иначе. Перепишем
выражения для деформаций в стандартной форме е = 2ргх
Xvr, где согласно E.19), E.20)
о
Как и ранее, типовой блок kers матрицы жесткости предста-
представим в виде суммы kers — krS) E + Ks, а- Здесь слагаемое
224
учитывает вклад линейных деформаций, а слагаемое
s. G=
— вклад деформации сдвига. Интегрирование в формуле для
krs, е будем, как и ранее, выполнять точно. Для вычисления же
krs, о применим численное интегрирование с одной точкой
Гаусса. Для этого нужно найти произведение рГисРз при
| = 0, г) = 0 и умножить результат на объем abh конечного
элемента. В итоге придем к выражению
k = Gh
K/-J, G *— ———
где по-прежнему у — отношение сторон прямоугольника.
uyi У
Рис. 6.2
По сути дела, мы принимаем здесь, что деформация сдвига
постоянна и равна своему значению при | =tj = 0 (илн х = у —
= 0). Тем самым выражение для ъху в F.13) неявно заменяет-
заменяется на
ху
— /3 Н~ /в-
Так как константа /3 + fe не связана с другими деформа-
деформациями, то в процессе минимизации полной энергии она может
принять любое значение, в том числе и сколь угодно малое.
Таким образом, критерий сходимости к балочному решению вы-
выполняется.
Заметим, что при одноточечном интегрировании исключа-
исключается не только слагаемое ftx, но также и слагаемое /gi/. Послед-
Последнее является посторонним с точки зрения теории изгиба бруса.
При конечной длине элемента постоянная /8 связана с дефор-
деформацией еуу и поэтому слагаемое f^y также дает вклад в ложный
сдвиг. Отметим также, что полученная здесь матрица kre#o
полностью совпадает с матрицей E.30) для конечного элемента
с линейным законом распределения напряжений.
8 Зак. 651 225
Подобный анализ можно приложить и к другим элементам,
предназначенным для моделирования стенки, в том числе изо-
параметрическим. В любом случае наилучшее воспроизведе-
воспроизведение жесткостных характеристик стенки достигается примене-
применением минимально допустимого порядка интегрирования для
кгв, о в сочетании с более точным интегрированием для кг8,я-
Если допустить, что вклад поперечной деформации еуу в
энергию пренебрежимо мал по сравнению с вкладом продоль-
продольной деформации гхх, то можно построить и более простые конеч-
конечные элементы (рис. 6.2) для моделирования стенок. Для них
узловыми параметрами являются смещения «*,., иут узловых
сечений вдоль координатных осей и углы поворота Фг этих се-
сечений. Для произвольного сечения
их (х, у) = и% (х) — у& (х); иу (х, у) = и°у (х),
где и%, и„ — перемещения точек, лежащих на осевой линии,
а Ф — угол поворота сечения.
Функции м$, и%, Ф обычным образом аппроксимируются по
их узловым значениям. При таком подходе гуу = -^ = О,
а вхх = е%х (х) — у% (х); еху = еху {х)\ где %(х) = -^ .
При вычислении вклада деформации сдвига еху в матри-
матрицу жесткости применяется минимально допустимый порядок
интегрирования, а для вклада ехх используется более точное
интегрирование. Такие элементы будут продемонстрированы в
гл. 8.
Подобный подход оказался весьма плодотворным и при по-
построении эффективных элементов пластин, работающих на из-
изгиб, а также оболочек. Этим вопросам посвящена следующая
глава.
226
ЧАСТЬ ГП
ПРИЛОЖЕНИЕ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ
К РАСЧЕТУ АВИАЦИОННЫХ КОНСТРУКЦИЙ
ГЛАВА 7
КОНСТРУКЦИИ В ВИДЕ ПЛАСТИН И ОБОЛОЧЕК
Пластины и оболочки широко применяются в конструкциях лета-
летательных аппаратов. Большинство методов их расчета основывается
на использовании гипотезы прямых нормалей. В методе конечных эле-
элементов такой подход наталкивается на серьезные трудности, связанные
с необходимостью обеспечения совместности конечных элементов. Эти
трудности можно обойти, если воспользоваться независимой аппрок-
аппроксимацией перемещений и углов поворота нормали. Благодаря этому
удается построить семейства конечных элементов изопараметрического
типа, пригодных для расчета иа изгиб пластин или моментных обо-
оболочек произвольной конфигурации.
§ 7.1. Предварительные замечания
Примерами пластин и оболочек как конструктивных эле-
элементов могут служить сплошное крыло малого удлинения или
топливный бак. Подобные тела можно идеализировать с помо-
помощью обычных трехмерных элементов, описанных в гл. 5. Но
такой подход оказывается неэкономичным, так как он приво-
приводит к конечноэлементной модели с большим числом степеней
свободы. Повышения эффективности расчета можно добиться
с помощью специальных конечных элементов, при построении
которых используются дополнительно гипотезы теории плас-
пластин и оболочек. Последние учитывают то обстоятельство, что
толщина мала по сравнению с габаритными размерами.
Использование соотношений теории пластин и оболочек по-
позволяет свести задачу к двумерной. Деформированное состоя-
состояние оболочки или пластины полностью определяется переме-
перемещениями срединной поверхности (или срединной плоскости)
и углом поворота прямолинейного отрезка до деформации
нормального к срединной поверхности (нормального отрезка
или просто нормали). Дискретизация тела сводится к разбие-
разбиению на конечные элементы срединной поверхности, а в качестве
основных неизвестных выступают узловые значения перемеще-
перемещений срединной поверхности и углов поворота нормали.
На рис. 7.1, а, б показаны возможные варианты конечноэле-
конечноэлементной идеализации крыла и бака. Крыло идеализируется с
8» 227
помощью произвольных четырехугольных, а также треуголь-
треугольных элементов. Для идеализации бака здесь применяется раз-
разбиение срединной поверхности на отдельные пояса. Роль уз-
узлов при этом выполняют узловые окружности, получаемые
при пересечении срединной поверхности с плоскостями, пер-
перпендикулярными оси бака. Такая идеализация возможна
лишь для оболочек вращения; она особенно удобна в случае
осесимметричного нагружения. При расчете оболочек общего
вида используют конечные элемен-
элементы треугольной или четырехуголь-
четырехугольной формы; их можно применять
и в случае оболочек вращения,
нагруженных произвольным об-
образом.
Для определения деформиро-
деформированного состояния конечного эле-
элемента необходимо выполнить ап-
аппроксимацию перемещений сре-
срединной поверхности и угла пово-
поворота нормали через узловые пере-
перемещения. При этом возможны два
пути. В одном варианте аппрок-
нормали осуществляется незави-
перемещений срединной поверх-
в использовании до-
Рис. 7.1
симация угла поворота
симо от аппроксимации
ности. Другой подход заключается
пущения о том, что нормаль и после деформации остается нор-
нормалью к деформированной срединной поверхности. Такое пред-
предположение оправдано для достаточно тонких пластин и обо-
оболочек; в этом случае выполняется аппроксимация только пере-
перемещений срединной поверхности, а угол поворота нормали вы-
выражается через производные от этих перемещений. Ниже бу-
будут представлены конечные элементы, полученные на основе
обоих вариантов.
§ 7.2. Основные соотношения теории изгиба пластин
Отнесем пластину к декартовой системе координат х, у, г,
совместив плоскость ху со срединной плоскостью пластины.
Перемещения точек срединной плоскости в направлении осей
х, у будем полагать равными нулю. Считая, что поперечное
перемещение их по толщине пластины постоянно, а тангенци-
тангенциальные перемещения их, иу изменяются по линейному закону,
имеем
«х = г&х (х, у); и у = гЪи (х, у); иг = uz (к, у). G.1)
228
Здесь &х (х, у) и Фу (х, у) — компоненты угла поворота нор-
нормального элемента. Как всегда, будем считать, что положитель-
положительные перемещения их, иу, и. совпадают с положительными на-
направлениями соответствующих осей. Принятые в G.1) поло-
положительные направления углов Фж, &у
указаны на рис. 7.2.
Найдем далее деформации, поль-
пользуясь формулами Коши A.7). Преж-
Прежде всего отметим, что
е„ = dujdz = 0.
Для компонент деформации слоя
пластины, параллельного срединной
плоскости, имеем
Рис. 7.2
G.2)
а для деформаций поперечного сдвига —
дих диг л
syz —¦
дг
dUy
дг
дх
оиг
~д~У~
дх
G.3)
Напряжения найдем теперь по формулам закона Гука. Учи-
Учитывая, что нормальные напряжения в площадках, параллель-
параллельных срединной плоскости, малы по сравнению с компонента-
компонентами ахх или оуу, положим azz = 0. Тогда напряжения ахх,
ауу> аху будут определяться по формулам обобщенного плос-
плоского напряженного состояния. Ограничиваясь случаем изот-
изотропного материала, имеем
G.4)
Касательные напряжения охг, оуг связаны с деформация-
деформациями поперечного сдвига равенствами
= Gsxz; ayz
Ge
Ух-
G.5)
229
Формулы G.2) —G.5) можно взять за основу при выводе
жесткостных характеристик конечных элементов, осуществи
ляя при этом независимую аппроксимацию функций иг,
¦дх и Oj, по их узловым значениям. Как следует из G.1), сов-
совместность перемещений обеспечивается, если каждая из этих
функций непрерывна на границах между элементами. Так же
как и в случае плоской задачи теории упругости, выполнить
это условие можно, например, с помощью изопараметрической
формулировки конечных элементов. Следовательно, здесь от-
открываются широкие возможности для введения конечных эле-
элементов произвольной формы, в том числе криволинейных. Но
применение подобных элементов к расчету тонких пластин до
последнего времени было ограниченным из-за чрезмерной жест-
жесткости элементов, которая обусловлена ложными деформациями
поперечного сдвига еж? и гу2, появляющимися при чистом изги-
изгибе пластины. В работе [38] показано, что и в случае изгиба пла-
пластин эффективным средством борьбы с ложными деформация-
деформациями поперечного сдвига является использование минимально
допустимого порядка интегрирования соответствующих чле-
членов при вычислении матрицы жесткости элемента. Несколько
конечных элементов, полученных таким способом, представле-
представлено в следующем параграфе. Они могут успешно использоваться
при расчете как тонких, так и сравнительно толстых пластин.
В другом способе построения конечных элементов пластины
принимают, что нормальный отрезок остается перпендикуляр-
перпендикулярным деформированной срединной поверхности. Такое допуще- ¦
ние, называемое гипотезой прямых нормалей, приемлемо в
случае достаточно тонких пластин, у которых толщина состав-
составляет не более V2(> от характерного размера в плане. Так как
угол между нормалью и срединной поверхностью остается пря-
прямым, то деформации exz и гуг оказываются равными нулю; из
G.3) имеем при этом
иям
v-7)
Подстановка этих равенств в G.2) приводит к выражениям
дх3 ду2 дхду
В этом варианте деформированное состояние конечного
элемента определяется единственной функцией иг (х, у). Ком-
Компоненты перемещения их, иу выражаются через иг по форму-
формулам
Ux<= —2 , Uu^=—2 -, G.8)
дх " ду
230
и теперь для выполнения совместности необходимо обеспечить
непрерывность не только самой функции uz, но и ее первых
производных по координатам х, у. Это существенно более слож-
сложная задача, чем выполнение условия непрерывности самой
функции. Обычно конечные элементы, построенные таким пу-
путем, оказываются несовместными, и их применение требует из-
известной осторожности. В дальнейшем будет рассмотрен пря-
прямоугольный элемент подобного типа, хорошо зарекомендовав-
зарекомендовавший себя в практических приложениях, а также более сложный
четырехугольный элемент.
В классической теории изгиба пластин принято напря-
напряженное состояние пластины характеризовать погонными из-
изгибающими Мхх, Муу и крутящим Мху моментами, действую-
действующими в ее сечениях;
ft/2 h/2
Мхх= J axxzdz; Mvv= j attyzdz;
— ft/2 —ft/2
ft/2
M*j,= \ axyzdz.
-h/2
При желании их можно вычислить по формулам, вытекаю-
вытекающим из G.2), G.4):
Здесь D = Eh3/ [12 A — ц.2)] — изгибная жесткость плас-
пластины.
§ 7.3. Изопараметрические конечные элементы
пластины
Рассмотрим конечный элемент с четырьмя узлами, имею-
имеющий в плане форму произвольного четырехугольника (рис. 7.3)
[38]. Обозначим через ы2Г, 0жг, Фуг значения функций иг, Фж,
&v в типовом узле г и введем матрицу
Vr = {и„^хг^уг}-
231
Обходя в определенном порядке узлы элемента, составим
матрицу
V = (vivyv,vm }.
Будем считать, что координаты хт, ут узлов элемента за-
заданы, а координаты текущей точки определим соотношениями
х = 2г|зг (I, i))xT; у = 2г|зг (I, ц)ут.
Здесь, как и в случае
четырехузлового изопара-
метрического элемента
плоской задачи теории уп-
упругости (см. § 5.6), функ-
функции г|зг (I, ц) E.18) зависят
от безразмерных перемен-
переменных ?, т), изменяющихся
от—1 до 1 и принимающих
в узлах значения ±1;
Рис. 7.3 суммирование выполняется
по всем узлам элемента.
Для аппроксимации функций иг, $х, #у воспользуемся
формулами
иг — 2i|3rMCT; *я = 2i|»P Ьхт\ bv = ЩтЬут. G.9)
В соответствии с равенствами G.2) и G.3) выразим дефор-
деформации через узловые перемещения:
дх
дх
,—г-
G.10)
G.11)
ду
232
Фигурирующие здесь производные от г|>г по координатам
х, у определяются соотношением
дх
~ду~_
где J — матрица Якоби:
J =
| 1
дЪ
дх ду
~dl W
дх ду
дц дц
Деформации гхх, еуу и гху, изменяющиеся по толщине
пластины по линейному закону, объединим в матрицу
6* = (р р р i
1°дгдг t-yy г'ху I•
В соответствии с G.10) связь е* с узловыми перемещениями
запишем в форме
е* = z2p;Vr, G.12)
где
0
дх
0- 0
0
0
G.13)
ду дх
Деформации поперечного сдвига объединим в матрицу
8 =
на основании G.11) имеем
где
дх
ду
G.14)
G.15)
2 33
Формулы G.12) и G.14) в совокупности дают следующую
связь между деформациями е = {е* е} и узловыми переме-
перемещениями:
е = 2prvr. G.16)
Здесь типовая матрица рг имеет вид
G.17)
Формулу G.16) можно переписать в стандартной форме
е = pve, полагая р = [0, р; р, рт].
Компоненты напряжения также сгруппируем в две матри-
матрицы
Соотношения упругости G.4) и G.5) можно представить тог-
тогда в форме
а* = х* ё*; а = G х е,
где
1 ц О
ц 1 О
о о —f
GЛ8)
Если объединить эти равенства и положить а = {а* а},
то получим связь а = хе, в которой
X =
о
Сх
"G.19)
По формуле
вычисляем типовой блок матрицы жесткости конечного эле-
элемента. Подставив сюда G.17) и G.19), приведем эту формулу
к виду
G.20)
234
Положим dr = |J| dgdrjdz, где |J| — определитель матри-
матрицы Якоби. Выполняя интегрирование по координате г в пре-
пределах от —Л/2 до Л/2, где Л — толщина пластины, имеем
к„=<3 f f/iprrp.|J|dEdn. G.22)
Отметим, что в общем случае пластнны переменной толщи-
толщины изгибная жесткость D является функцией координат х, у
(или I, л).
Интегрирование по координатам ?, tj приходится выпол-
выполнять численно. Прн вычислении k*s можно брать по две точки
Гаусса в каждом направлении, а для вычисления krs возьмем
одну точку Гаусса, что соответствует минимально допустимо-
допустимому порядку интегрирования. Как уже говорилось выше, это
необходимо для исключения ложных деформаций поперечного
сдвига.
Отметим еще одно обстоятельство. Считая, что нормаль-
нормальный отрезок при деформации пластины только поворачива-
поворачивается, но не искривляется, мы приходим к равномерному рас-
распределению напряжений ахг и ayz по толщине пластины, как
это видно из G.3) и G.5). Но в действительности поперечные
касательные напряжения распределяются по толщине нерав-
неравномерно. В случае пластины постоянной толщины они обра-
обращаются в нуль при 2 = ±Л^2, имея максимальное значение
при z = 0. Согласно элементарной теории изгиба тонких плас-
пластин напряжения ахг, ауг и соответствующие деформации из-
изменяются по толщине по квадратичному закону. При этом
вклад в матрицу жесткости от деформаций поперечного сдви-
сдвига оказывается несколько меньшим, чем по G.22). В связи с
этим вместо G.22) иногда используется формула
235.
Она отличается от G.22) тем, что вместо действительного
модуля сдвига здесь введена несколько меньшая величина G.
Последняя определяется из условия равенства удельной
энергии деформации при истинном и равномерном распреде-
распределениях поперечных касательных напряжений по сечению плас-
пластины. Если истинным считать квадратичный закон изменения
axz и 0у2> то G = 5G/6. Но в случае тонких пластин деформа-
деформации поперечного сдвига не играют решающей роли и подобное
уточнение матрицы krs не оказывает существенного влияний
на точность окончательных результатов.
Рис. 7.4
Подобным же образом можно ввести четырехугольные ко-
конечные элементы второго и третьего порядков (рис. 7.4). Соот-
Соотношения, полученные выше для элемента первого порядка,
остаются и здесь в силе. Отличие будет лишь в выражении для
функций г|>г (|, г]). Для элемента второго порядка должны ис-
использоваться функции E.62). Интегрирование в G.21) следует
выполнять при этом по трем точкам Гаусса для каждой из пе-
переменных ?, т], а в G.22) — по двум.
Для элемента третьего порядка выражение для ipr (?, tj)
дается равенством E.67), а интегрирование выражений для
k*s и krs должно выполняться соответственно по четырем и
трем точкам Гаусса в каждом направлении.
Узловые значения параметров \, tj определяются в соот-
соответствии с рис. 7.4.
§ 7.4. Несовместный прямоугольный элемент
пластины
Как уже говорилось ранее, в случае тонких пластин мож-
можно в качестве исходных соотношений взять формулы G.6)—
G.8), в соответствии с которыми напряженно-деформирован-
напряженно-деформированное состояние пластины определяется единственной функцией
236
uz (x, у)- Применим эти формулы для вывода матрицы жестко-
жесткости прямоугольного конечного элемента с четырьмя узлами
в вершинах, показанного на рис. 7.5. Стороны прямоугольни-
прямоугольника имеют размеры а, Ь и параллельны координатным осям х, у.
В качестве узловых перемещений возьмем, как и ранее,
смещения узлов игт в направлении оси г и углы поворота нор-
нормали $хт, ®ут:
vT = {игг $хг &уг}\
Матрица узловых перемещений элемента
Vе = {Vf \j V, Vm }
содержит двенадцать компонент. Для аппроксимации функ-
функции uz по этим узловым параметрам зададимся следующим
законом изменения прогиба в пределах прямоугольника [61:
Л + hx + f3y + /4*2
+ fioy3 + fu*y + fuxy*. G.23)
Здесь Д, /2, ...,/12 — постоянные, которые должны быть
выражены через узловые перемещения. В G.23) содержатся
полные полиномы от х, у вплоть до третьего порядка; члены
дЛ/ и ху3 взяты с таким расчетом, чтобы вдоль сторон прямо-
прямоугольника функция uz изменялась по кубическому закону.
Это обеспечивает непрерывность перемещения uz на границах
между элементами. В самом деле, закон деформирования, ска-
скажем, стороны, прилегающей к узлам i, /, характеризуется уз-
узловыми параметрами uzi, ftxi, uz3 и г^„-. Эти четыре пара-
параметра однозначно определяют кубическую параболу, а так
как узловые перемещения являются общими для смежных
элементов, то будет соблюдаться непрерывность ы2 вдоль сто-
стороны ij.
Однако полной совместности конечных элементов функция
G.23) не обеспечивает, поскольку при переходе к смежным
элементам возможен излом деформированной поверхности.
Так, например, производная dujdx, определяющая наклон
линий у = const, изменяется вдоль стороны /7 по кубическому
закону. Но из четырех параметров, необходимых для описа-
описания этого закона, лишь два (bxi и Ф^) являются общими
для смежных элементов, примыкающих к данной стороне
(рис. 7.6). Следовательно, непрерывность производных будет
соблюдаться только в узловых точках.
Связь постоянных f = {Д /2, .../12} с узловыми перемеще-
перемещениями можно получить, приравнивая в каждом узле значения
237
Рис. 7.5
«г. ** = —dujdx и fty = —dujdy к соответствующим уз-
узловым параметрам. Выразив f через Vе, можно в соответствии
с G.23) прийти к стандартному соотношению вида uz = ave.
Удобнее, однако, построить матрицу а непосредственно,
путем подбора. Для этого прежде всего представим ее в блоч-
блочной форме а = [а,- а,- а, ат}. Типовой блок аг представляет
собой матрицу-строку
и содержит три функ-
функции координат х, у:
аг = [аг1 аг2 аг31.
Первая из этих функ-
функций дает распределение
перемещения иг в эле-
элементе, когда поперечное
смещение узла г равно
единице, а все осталь-
остальные одиннадцать узло-
узловых перемещений равны
нулю. Функции аг2 и
аг3 определяют иг при
единичных значениях
углов #жг и $уг соответ-
соответственно. Следовательно,
функция <хп должна рав-
равняться единице в узле г
и нулю в остальных уз-
узлах, а ее производные
даТ1/дх и да.п/ду должны
во всех четырех узлах
обращаться в нуль.
Функции ап и агз вме-
вместе со своими первыми
производными равняются нулю во всех узлах, за исклю-
исключением узла г, где выполняются равенства дат2/дх = —1,
да.т3/ду = —1 (это соответствует единичным значениям углов
поворота Ож и 0„).
Для записи искомых функций удобно воспользоваться
безразмерными координатами g, tj, связанными с х, у соотно-
соотношениями
х = хс + (fl/2N; </ = J/c+ (Ы2)ц.
Здесь хе. Ус — координаты центра тяжести прямоуголь-
прямоугольника; переменные \, tj изменяются от —1 до 1, как показано
на рис. 7.5.
Рис. 7.6
238
Непосредственной проверкой можно убедиться, что функ-
функции
—i- г, A —Б) A -г,2);
«й=-—j||-(l —Б) A—п)A —Бя);
«18 = —j|- A —g) (l—^i) A —л2)
могут быть использованы в качестве компонент подматрицы
ос*. Действительно функция ап равна 1 в узле i, где g = ц =
= —1, и обращается в нуль в остальных узлах. Производные
же от а,ц по ?, tj во всех узлах равны нулю. Функции а,-.2 и аг 3
и их производные по |, г\ во всех узлах равны нулю, за иск-
исключением того же узла ?, где
dai2 _ 2 g«i2 , dai3 __ 2 dai3 _ ,
дх а д| йу Ь Л]
Отметим также, что содержащиеся здесь полиномиальные
функции от ?, т) соответствуют тому набору функций, который
представлен в G.23).
Аналогично подбираются и остальные функции, входящие
в матрицу а. В обобщенном виде выражение для типовой под-
подматрицы ат (г = I, /, /, т) можно записать так:
16
Ь-~т)гЛA-НД)A-л2)
о
- Е«) J- цг A + Ь I) A + Чг Л) A -Л2)]- G.24)
16 J
По G.7) выразим деформации через узловые перемещения:
дхду
239
Вводя матрицу в — {гхх гуу гху}, представим эти соотно-
соотношения в форме 8 = pve, где
дх2
д2 а
ду2
_ дхду _
Учитывая блочное представление матрицы ос, можно запи-
записать
Р = fPi Pj P( Pml-
Типовая подматрица |5Г определится равенством
рг = — zp;, G.25)
где
oz ar
If"
йу2
- 4
~?
4
ft»
8
_ дхду _
Подставив сюда выражение G.24) для матрицы осг, получим
~ Ъг I A +Tir Л) j-^- 1Г A Ч-ЗБгБ) A +г)г
Q*
_ аЬ
1
2о
G.26)
r — 2rj — Зт)гтJ)
240
Соотношения G.4), связывающие напряжения а —
= {ахх ayv аху) с деформациями е, в матричной записи име-
имеют вид а = хе, где
— ¦TijS1* G-27)
здесь и* дается первым равенством G.18).
По формуле
Pj: xPs d т (r,s = i,j,
вычисляем далее типовой блок матрицы жесткости. Полагая
dx = (ab/4)d?,dr\dz и подставляя в формулу для k*s соотноше-
соотношения G.25) и G.27), получим
1 1 ft/2
11 J
0а11 J
Выполнив интегрирование по г, приведем это выражение
к виду
k« = -T- f f ^P;r«*P;d&dr,. G.28)
Интегрирование в G.28) даже для пластины постоянной
толщины удобнее всего выполнять численно, используя по
две точки Гаусса в каждом направлении.
§ 7.5. Несовместный четырехугольный элемент
пластины
Будем снова исходить из гипотезы прямых нормалей. Если в ма-
матрицы узловых перемещений включены узловые значения прогиба и
углов поворота нормали, то тем самым в узловых точках задается не-
непрерывность функции uz и ее первых производных dujdx; диг1ду; меж-
между узлами эти величины могут вдоль сторон элементов претерпевать раз-
разрывы. Для уменьшения разрывов можно включить в число узловых
параметров старшие производные от uz по координатам х, у, обеспечи-
обеспечивая таким путем непрерывность этих производных в узловых точках.
Если толщина пластины изменяется скачкообразно, то этот подход не-
неприемлем, поскольку на линии, вдоль которой это происходит, вторые
производные от иг по х, у (имеющие смысл кривизн и кручения изогну-
изогнутой срединной поверхности) ие могут сохраняться непрерывными. Од-
Однако в случае плавного изменения толщины указанный прием вполне
оправдай.
241
Рассмотрим в качестве примера коиечиый элемеит в форме проиа-
вольиого четырехугольника с прямыми сторонами и четырьмя узлами
в вершинах (рис. 7.7). В число узловых параметров включим смешанную
i д2 иг
производную ф = d d '• Матрица перемещений элемента
будет иметь шестнадцать компонент — по четыре в каждом из узлов."
Закон изменения прогнба в пределах конечного элемента предста-
представим в форме
. «* = «*f. G.29)
/77 а Ь
Здесь f — матрица-столбец коэффици-
коэффициентов, число которых в соответствии с
количеством узловых параметров равно
шестнадцати:
Матрица-строка «* содержит полнно-
_ __ миальные функции от х, у, выбор кото-
Fhc- '•' рых может быть различным. Следуя [18]
примем, в частности,
«* = [1 х у х2 ху у2 л3 х*у ху* у3 х*у jcV ХУ3 *>У2 х^у3 хРу3).
G.30)
Первые десять компонент матрицы «* содержат полные полиномы
от х, у до третьего порядка включительно. Таков же порядок полных
полиномов у рассмотренного выше прямоугольного элемента, и можно
ожидать, что характеристики сходимости данного элемента будут та-
такими же, как и у прямоугольного; числовые расчеты подтверждают
это.
Исходя из условий в узлах, свяжем параметры f с узловыми пере-
перемещениями (г = i, /, I, m):
диг I
"z (хт, Ут) = иг Ъ
Г
дит
3*ит
G.31)
. -утг дхдУ
Это дает 16 соотношений, которые можно представить в форме
Tf = Vе,
где числовая матрица Т имеет размер 16 X 16 и формируется из эле-
элементов матрицы «* и ее производных в соответствии с G.29), G.31).
Выполнив обращение матрицы Т и обозначив
Q = Т-1, G.32)
242
приходим к выражению f = Qv", с помощью которого равенство G.29)
приводится к стандартной форме ц = «Vе с матрицей
« = «*Q.
G.33)
В соответствии с формулами
ду2
гху--2
устанавливаем связь между матрицей е = {ехх ъуу еху) и узловыми
перемещениями. Ее можно записать в обычной форме е = pve, где
Р=^—zp*Q; G.34)
д*а*
дх*
ду"-
2
_ дхду _
G.35)
Наконец, по формуле
ke= J 0г>ф
вычисляем матрицу жесткости элемента. Подставляя сюда G.27), G.34)
н учитывая, что dx = AxAyAz, после интегрирования по z получаем
ke=Qrk*Q,
G.36)
где
Интегрирование осуществляется здесь по площади четырехугольни-
четырехугольника.
Преобразование координат
с функциями
х =
r; у =
позволяет перейти к интегрированию по площади квадрата:
I i
— 1—1
J Dp*rn*
G.37)
Здесь |J| обозначает, как и ранее, якобиан преобразования координат:
дх дц ду дх
243
Прн вычислении к* по G.37) можно воспользоваться численным
интегрированием с тремя точками Гаусса для каждой из переменных
При моделировании крыла самолета пластиной часто можно огра-
ограничиться конечными элементами трапециевидной формы. Для них не
обязательно вводить координаты ?, tj, поскольку в случае, когда осно-
основания трапеции параллельны одной из координатных осей, удается
записать аналитические выражения для интегралов от полиномиаль-
полиномиальных функций [18].
Рассмотренный конечный элемент относится к категории несов-
несовместных. На его сторонах терпит разрыв даже сама функция uz. Тем
ие менее, как свидетельствуют числовые расчеты, он дает вполне при-
приемлемую точность, соизмеримую с точностью прямоугольного эле-
элемента.
§ 7.6. Учет внеузловой нагрузки.
Определение узловых перемещений
Если в узлах пластины действуют сосредоточенные силы
и моменты, то из них можно сформировать матрицу-столбец
Р= {Рх Р2...Р„}.
Здесь каждая подматрица Рг включает в себя поперечную
силу Ргт и два момента Мхг, Муг; их следует считать положи-
положительными, если они действуют в положительных направлени-
направлениях uzr, -&xr, ®ут соответственно. Если применяются элементы
с четырьмя степенями свободы в узле, то Рг будет содержать
четыре элемента. Четвертый элемент в Рг, соответствующий
параметру фг, не имеет физического смысла н его следует
всегда брать нулевым.
Кроме того, на пластину может действовать распределен-
распределенная поперечная нагрузка р (х, у), которую необходимо заме-
заменить эквивалентными узловыми силами и моментами. Замена
производится поэлементно из условия равенства работы на-
нагрузки р на перемещении иг работе эквивалентных узловых
сил Рг на перемещениях Vе. Повторяя рассуждения § 4.4, при-
придем к следующему выражению для Vе:
oJpdF. G.38)
ре
Здесь интегрирование ведется по площади F' конечного
элемента; через аи обозначена матрица функций, аппрокси-
аппроксимирующих перемещение иг через \е в соответствии с равенст-
равенством иг — аи\е.
Для конечного элемента с узлами i, /, ... блочное представ-
представление матрицы аи будет аи — [auiauj ...].
244
Подстановка этого равенства в G.38) позволяет записать
выражение для Ре в блочной форме Ре = {Pj Р*....}. Здесь
типовая подматрица Р« определяет вклад рассматриваемого
элемента в эквивалентные силы в узле г и вычисляется по фор-
формуле
ре
Если перемещения и углы поворота нормали аппроксими-
аппроксимируются независимо, как в случае-рассмотренных выше изопа-
раметрических элементов, То матрица аш имеет вид
«ur = №r 0 0]. G.40)
В этом случае в каждой подматрице Р« отличным от нуля
будет лишь первый компонент, т. е. узловая сила
P^=JtrpdF. G.41)
Fe
Таким образом, распределенная нагрузка заменяется здесь
одними лишь сосредоточенными узловыми силами, узловые
же моменты оказываются равными нулю. Интегрирование в
G.41) можно осуществить численно с использованием такого
же числа точек Гаусса, что и при вычислении матриц k?s (в
случае элементов с четырьмя сторонами следует положить
dF = |J| d? drj и интегрировать по параметрам ?, г\ в преде-
пределах от —1 до 1).
Если же при построении элемента применяется гипотеза
прямых нормалей, то матрица аиГ совпадает с матрицей с^
G.24). В этом случае все компоненты Рег будут отличны от ну-
нуля, т. е. при замене распределенной нагрузки эквивалентны-
эквивалентными узловыми силами появятся не только силы, но также и
моменты. Для прямоугольного элемента интегрирование в
формуле
Ь «« j
можно также осуществить методом Гаусса, взяв по две точки
в каждом направлении. Если нагрузка р постоянна, то точное
интегрирование дает следующие значения узловых сил:
6
-Ч-..
245
Для четырехугольного элемента с шестнадцатью степенями сво-
свободы следует пользоваться формулой
Pe = QrJ a*T p&F,
применяя замену координат с последующим интегрированием по 2 X 2
точкам Гаусса, либо прибегая к аналитическому интегрированию, если
элемент имеет форму трапеции. Отметим, что при этом появятся обоб-
обобщенные «силы», соответствующие узловым параметрам фг.
Выполнив для каждого элемента приведение распределен-
распределенной нагрузки к узловым силам, можно в каждом узле просум-
просуммировать вклады элементов и сформировать матрицу
?={?! Р2... Р„},
где типовая подматрица Рг — 2 Р« (суммирование ведется по
всем элементам, сходящимся в узле г).
Система уравнений, связывающих узловые перемещения
с узловыми силами, имеет вид
Kv = Р + "Р,
где К — общая матрица жесткости. Последняя формируется
по обычному правилу суммирования коэффициентов жестко-
жесткости с одинаковыми индексами: kr» = 2k*s (суммирование по
всем конечным элементам, соединяющим узлы г, s).
Для отыскания узловых перемещений необходимо учесть
связи, накладываемые на пластину опорными устройствами.
Обозначим, как и ранее, через vo матрицу, в которой содержат-
содержатся одни лишь неизвестные перемещения; известные же пере-
перемещения составят матрицу vp. Если vp = 0, то можно исклю-
исключить из матрицы жесткости строки и столбцы, соответствую-
соответствующие нулевым перемещениям, и прийти к системе уравнений
вида D.21) относительно неизвестных перемещений va.
В некоторых случаях связи нельзя считать абсолютно
жесткими, как, например, при расчете крыла. На крыло связи
накладываются в месте соединения его с фюзеляжем. Пере-
Перемещения узлов, в которых оно соединяется с фюзеляжем, стро-
строго говоря, не будут нулевыми. Они должны определяться из
расчета летательного аппарата в целом. Здесь удобно восполь-
воспользоваться методом подконструкций (см. § 5.4), рассматривая
эти узлы как внешние для крыла и исключая перемещения ос-
остальных узлов. Однако при выполнении приближенных рас-
расчетов можно считать фюзеляж абсолютно жестким, полагая
Vp = 0 и сводя, таким образом, задачу к решению системы
D.21).
246
§ 7.7. Основные соотношения для оболочек вращения
при осесимметричном нагружении
Рассмотрим оболочку, срединная поверхность которой об-
образована вращением вокруг оси произвольной плоской кривой
(рис. 7.8). Введем в плоскости меридиана систему координат
х, у, направив ось х вдоль оси оболочки. Предположим, что
уравнение кривой меридиана задано в параметрической форме
х = х (I), у = у (I). Для определения геометрических ха-
характеристик этой кривой можно воспользоваться полученны-
полученными в § 5.9 соотноше-
соотношениями, полагая в них э
2 = 0.
Элемент дуги ds свя-
связан с приращением па-
параметра I соотношением
ds = Adi, в котором
Рис. 7.8
. G.42)
Здесь и далее штрихом
отмечается дифференци-
дифференцирование по ?.
Направление касательной к меридиану будем характери-
характеризовать единичным вектором
или, что то же самое, матрицей его направляющих косинусов
К = IK, КУ G-43)
где в соответствии с E.72)
tX д > IV д ¦
G.44)
Через ех, еу в выражении для et обозначены орты коорди-
координатных осей х, у; вектор 7t направлен в сторону возрастания
параметра ?.
Помимо 7t введем также нормальный к меридиану вектор
еп с матрицей направляющих косинусов:
Ь„ = 1Ь„*Ь„у]- G-45)
247
Направление еп выберем таким образом, чтобы поворот et
до совмещения с еп по кратчайшему пути осуществлялся в ту
же сторону, что и поворот ех до совмещения с еу. Тогда
^пх — —\у', kny — Xtx. G.46)
Радиус кривизны меридиана R будем считать положитель-
положительным, если центр кривизны удален от меридиана в направле-
—»-
нии, противоположном направлению вектора еп. Значение R
может быть подсчитано по формуле, известной из аналитичес-
аналитической геометрии:
1 _ х' у"—у' х"
"~ (х'Чу*K12 '
которой с учетом G.42), G.44) можно придать вид
¦j=-^(hxy"-Kx")- G.47)
Угол Э между нормалью к меридиану и осью оболочки оп-
определим как угол, на который нужно повернуть ось у, чтобы
ее положительное направление совпало с положительным на-
направлением вектора et. Прн этом будем считать Э положитель-
положительным, если поворот происходит в сторону оси х; тогда
cos Э = — Кпх = Xls, sin Э = КпУ = Ktx. G.48)
При осесимметричном нагружении перемещения точек сре-
диииой поверхности будут иметь лишь составляющие в пло-
плоскости меридиана. В теории оболочек принято рассматривать
проекции перемещений на касательное и нормальное к мери-
меридиану направления. Эти составляющие мы обозначим через
ut, ы„, а соответствующие им компоненты поверхностной на-
нагрузки — через р„ рп. Их положительные направления бу-
будем считать совпадающими с направлениями векторов et, en.
Деформации срединной поверхности оболочки в меридио-
меридиональном и окружном направлениях, которые мы обозначим
через elf е2, связаны с перемещениями и., ип соотношениями
[14]
„ _ Aut ип _ 1 . ы„ г
1 d7+~T~~A t+T'
ei = -L(utcose+uns\nQ) = —(Ktyuti-Ktxun). G.49)
У У
Рассмотрим далее слой оболочки на расстоянии ? от сре-
срединной поверхности; отсчет положительных значений ? ус-
248
ловимся вести в положительном направлении еп. Все величи-
величины, относящиеся к этому слою, будем помечать дополнитель-
дополнительным верхним индексом ?. Считая, что толщина оболочки Л
значительно меньше радиуса кривизны R, и учитывая, что
|?| ^ Л/2, можно не делать различия между геометрическими
характеристиками срединной поверхности и слоя:
/?& да R; yt да у, А* да А; Цх = ltx; Цу = \у. G.50)
Перемещения слоя ы?, и\ определим равенствами
и}= ut + tfi; ы&= и G.51)
Деформации слоя получим, заменив в G.49) ut, un на ы^}
4 = ?j + SXiI e| = е2 + ^Хг. G.52)
где
у ^ °" „_ ^ а', у __ * a -QC 0 ==___ii. a /^7 53)
as Л # I/
Помимо ер, е| в оболочке возникает деформация попереч-
поперечного сдвига, которую мы обозначим через е13. Она равна изме-
изменению угла между нормалью и касательной к меридиану, и
ее можно найти как сумму двух углов, один из которых равен
А, а второй есть угол поворота касательной. Последний бу-
дем считать положительным, если угол между et и е„ становит-
становится острым; через перемещения срединной поверхности он вы-
выражается [14] как dMn/ds— utlR, так что для е13 имеем
В некоторых случаях удобнее вместо ut, и„ рассматривать
проекции перемещений на направления осей х, у; эти проек-
проекции мы обозначим через их, иу. Они связаны с и,, ип соотно-
соотношениями
N «* = Кх Щ + Кхип\ иу = %ty ut + Kytin- G.55)
Для определения деформации ej по перемещениям их, иу
можно воспользоваться общей формулой E.77), из которой
применительно к рассматриваемому случаю вытекает равен-
равенство
?1=4М'' G-56)
249
где и' означает производную по ? от матрицы и = {их иу}.
Для окружной деформации е2 на основании G.46), G.49) и
G.55) имеем
е2 = — иу. G.57)
Угол поворота касательной к меридиану через перемеще-
перемещения их, иу выражается на основании E.79) как -^%пи', так что
для деформации поперечного сдвига имеем
«и =-jbnii' +0. Г7.58)
Так же как и в случае изгиба пластин, здесь можно наме-
наметить два пути построения конечноэлементной модели оболоч-
оболочки. В первом варианте выполняется независимая аппрокси-
аппроксимация функций ut, un (или их, иу) я#, а е13 учитывается на-
наряду с е?, е| в матрице деформаций. Другой подход основан на
использовании гипотезы прямых нормалей, в соответствии с
которой следует положить е13 = 0. В этом случае аппрокси-
аппроксимируются лишь перемещения ut, un (или их, ии), а для вычис-
вычисления д используется одно из равенств
fl = 5r^,u', G.59)
вытекающих из G.54) или G.58) при е13 = 0; матрица дефор-
деформаций будет включать при этом лишь компоненты г\ и е|. Ни-
Ниже будут рассмотрены оба подхода.
Как говорилось в начале главы, при идеализации оболоч-
оболочки вращения ее срединную поверхность можно разбить на
пояса плоскостями, перпендикулярными ее оси. Эти пояса
будем рассматривать в качестве конечных элементов. Геомет-
Геометрия элементов обычно задается лишь координатами узлов (и,
возможно, значениями угла 9 в узлах), для определения же
самой кривой применяется приближенная аппроксимация.
Для оболочек простой геометрической формы (например, сфе-
сферической или круговой торовой) можно и не пользоваться
аппроксимацией, определяя все необходимые геометрические
параметры, исходя из точных соотношений. Однако в целях
унификации исходных данных даже в этих случаях предпо-
предпочитают обычно аппроксимировать реальную оболочку с помо-
помощью приближенных зависимостей.
250
i §7.8. Изопараметрические конечные элементы
оболочки вращения
Рассмотрим конечные элементы оболочки вращения изо-
параметрического типа. На рис. 7.9 представлены конечные
элементы первого, второго и третьего порядков, имеющие со-
соответственно два, три и четыре узла. Исходными данными для
них служат координаты узлов хт, ут и значения толщины Л
в узловых точках. Уравнение меридиана будем задавать при-
приближенными равенствами: х — Ъ$тхт\ у = Ъ$тут, где сумми-
суммирование ведется по всем узлам элемента. Функции *|эг (|) да-
даются равенствами E.81)—E.83).
к
VI
Согласно G.42), G.44) можно в любой точке вычислить
параметры
v\
—т" х; Ку = — у'-
где
х' = 2i|>;*r; у' - Щ'гуг.
Отметим, что для элемента первого порядка эти парамет-
параметры постоянны по длине образующей:
*; = Y lA*^-j{xi — *i)\ У' =\<У}—У^
А— ' /• X -
где / = У (х} — XiJ + (yj — у if — длина образующей эле-
элемента.
Каждый узел элемента имеет три степени свободы vr =
= {ихг иут йг}, так что для двухузлового элемента матри-
251
ца Vе = {уг Vj) содержит шесть перемещений, для трехузло-
вого — девять Vе = {vt \j vm} и т. д.
Для аппроксимации перемещений и угла поворота по уз-
узловым значениям воспользуемся изопараметрической форму-
формулировкой:
их = 2tyruxr; и v = Щгиуг\ Ь = ЩтЪт. G.60)
По формулам G.53), G.56)—G.58) выражаем параметры
деформации elf е2, %и %2, е13 через узловые перемещения.
Введя обозначения
-[¦:]• на-
представим эти зависимости в виде
G.61)
где
- _1_
т
— Фг
У
О
о
о о
о о
_1_
А
_!_
У
Рг-[~j-^»*;
G-62)
При записи последних соотношений учтены зависимости
G.43), G.45), G.46).
Матрицу деформаций е= {е? е| е13} на основании G.52),
G.61) можно представить в обычной форме в = 2prvr, где
G.63)
Нормальные напряжения, действующие в меридиональном
и окружном направлениях, обозначим через а?, а|, а попереч-
поперечное касательное напряжение — через а1а. Пренебрегая нор-
нормальным напряжением в площадках, параллельных средин-
срединной поверхности, запишем соотношения упругости
о\
= Ge1
где, так же как и в случае пластины, можно взять G = 5G/6 для
учета неравномерности напряжения а13 по толщине оболочки.
2 52
Отсюда получаем связь а = ие между матрицами а =
— {aial а1з} и е; ПРИ этом
и* О
J „2
о 5
f ] • G-64)
Далее вычисляем блоки матрицы жесткости
J
где dx = 2ra/dsdc; — /??
После подстановки в подынтегральное выражение G.63)
и G.64) и интегрирования по толщине оболочки в пределах от
—Л/2 до Л/2 можно получить
„ G.65)
J (В pf a* ps° + D Г/ и* р;) у A d 6; G.66)
— 1
5 $1?и, G.67)
где В •= ?/i/ A — ii2) — жесткость оболочки на растяжение.
Интегрирование в G.66), G.67) выполняется численно.
Для исключения ложного сдвига порядок интегрирования
в krSto должен быть минимально допустимым. Это соответст-
соответствует одноточечному правилу Гаусса в случае элемента с дву-
двумя, двухточечному для элемента с тремя и трехточечному —
для элемента с четырьмя узлами. Что касается krStE, то в слу-
случае трехузлового элемента здесь следует взять три точки Га-
Гаусса, четырехузлового — четыре, а для двухузлового доста-
достаточно и здесь без ухудшения точности ограничиться одной точ-
точкой. Отметим, что двухузловой элемент подобного типа впер-
впервые предложен в работе [41].
Приведение распределенных нагрузок к эквивалентным уз-
узловым осуществляется обычным образом. Типовая матрица,
характеризующая вклад данного конечного элемента в матри-
матрицу эквивалентных узловых сил в узле г, определяется ра-
равенством
253
где р —¦ [рх ру] — матрица поверхностных нагрузок в на-
направлений их, иу; аиг — матрицы функций, аппроксимирую-
аппроксимирующих перемещения срединной поверхности через узловые пе-
перемещения в соответствии с равенством
L «J
G.68)
интегрирование в выражении для Р, выполняется по средин-
срединной поверхности конечного элемента.
Как следует из {7.60),
"¦-4J? о]'
Учитывая, что dw ==• 2nyds = 2nyAd?,, приходим к выра-
выражению
Рх
Ру
0
G.70)
Интегрирование здесь можно выполнить так же, как и при
вычислении krs,G- Для двухузлового элемента результат
удобно записать в явном виде:
РхО
Руо
0
ал\)
Здесь рх1), ри0 — значения нагрузок рх, ру в середине
элемента (т. е. при | = 0), а у0 == {yt + yj)/2 — радиус со-
соответствующего параллельного круга.
Отметим, что в элементах рассматриваемого типа экви-
эквивалентные узловые силы не содержат компонент в направле-
направлении &г, т. е. узловые моменты, эквивалентные распределен-
распределенной нагрузке, оказываются здесь нулевыми.
§ 7.9. Двухузловой криволинейный конечный
элемент оболочки вращения
В данном параграфе рассматривается двухузловой конечный эле-
элемент с криволинейной образующей [24]. Предполагается, что помимо
координат узлов заданы также углы 9г, 6,-в узловых точках (рис. 7.10).
При выводе жесткостных характеристик элемента будем исходить из
предположения, что справедлива гипотеза прямых нормалей.
Прежде всего выполним аппроксимацию геометрии конечного эле-
элемента. Проблема заключается в приближенном задании уравнения об-
254
разующей по известным координатам узлов и значениям 6f, 6j. Это
уравнение будем искать в параметрической форме лс i= х (§L у = у (\),
Где параметр ?, изменяющийся от —1 до 1 при движении от узла i к
2s
узлу /, свяжем с дуговой координатой s соотношением ? = -г — 1.
Так как ds = (//2)d?, то параметр А равен 1/2, и на основании
G.44), G.48) имеем
х'— — sin 6; у' ——cos 6,
где штрих означает дифференцирование по \.
G.72)
«? л-
' ».ии
Рис. 7.10
Запишем теперь условия, накладываемые на функции jc (g), у (?)
в типовом узле элемента (г = «, /):
/ /
хAт)=хт; уAг)=Ут\ *' (?r) = — sin0r; У' (Sr) = — cos6r.
Этим условиям можно удовлетворить, взяв в качестве х (?), у (?)
полиномиальные функции третьей степени. Коэффициенты этих поли-
полиномов можно иайти так же, как это делалось в § 3.4 пря выводе уравне-
уравнения изогнутой оси бруса. В итоге придем к следующим выражениям
для искомых функции:
Здесь
G.-73)
xi ~f
Y=|y« — cose,- У) Ycos
а матрица а E) дается формулой C.35), которую мы представим в виде
-*¦>]• <7-74>
255
Пользуясь аппроксимацией G.73), можио получить все необходи-
необходимые геометрические параметры элемента. По G.44) находим для любой
точки меридиана значения %tx и ^ty-
btx=-y*'G): hu = ~yra). G.75)
Входящие сюда производные определяются соотношениями
lr0-l2) —~ (l + ErE)(l-36r|)] (r=i,i). G.76)
Кривизну меридиана вычисляем по G.47):
¦^=~(x"Xty-y"Xtx), G.77)
где
х"—а"\; у"=а"\; о""~[а, о?];
Представленными выше формулами можио пользоваться, когда из-
вестна длина I образующей элемента. Так как As = ~\/dx2 + dy2 =
= dg~l/*'2 + У'2, то по известным функциям х (?), у (?) ее можно най-
найти через интеграл
1= J Vx'*±y'*A\. G.78)
Однако в сами выражения для функций х — аХ; у =¦ а\ входит
величина /. Поэтому практически ее можно иайти с помощью последо-
последовательных приближений. В нулевом приближении матрицы-столбцы
X, Y сформируем, взяв в качестве I длину /0 хорды, соединяющей
узлы i, j:
После этого можио в соответствии с G.78) уточнить величину I.
Ограничиваясь первым приближением и применив для вычисления ин-
интеграла G.78) правило Симпсона, можно прийти к следующей формуле
для определения длины дуги I:
где
xJ—xi sinOj + sin 6j yj—yt
Qt3— - ; Q=3-^
256
Чтобы получить представление о точности предлагаемой аппрок-
аппроксимации, возьмем участок образующей сферической оболочки и заме-
заменим его приближенной кривой в соответствии с рассмотренными.выше
формулами. Приведем значения максимальной погрешности аппрок-
аппроксимации величины R для различных значений центрального угла, оп-
определяющего выделенную дугу:
Центральный угол, град . . 2 4 6 10 15
Максимальная ошибка, % . . 0,01 0,04 0,09 0,25 0,57
Как видно, погрешность незначительна даже для весьма больших
участков. Отметим, что если при определении / ограничиться нулевым
приближением, заменив длину дуги длиной хорды, то ошибка аппрок-
аппроксимации радиуса кривизны возрастает примерно в три раза по сравне-
сравнению с приведенными результатами.
Перейдем далее к аппроксимации перемещений, взяв за основу
компоненты щ, tin- При этом поставим себе целью получить возможно
более простой элемент, обладающий в то же время хорошими характе-
характеристиками сходимости. Как говорилось в предыдущей главе, скорость
сходимости конечноэлемеитной модели определяется минимальным по-
порядком аппроксимации компонент деформации в пределах конечного
элемента. В рассматриваемом случае деформации Е\, е| выражаются
через величины ех, ё2, Xi. Хг- Если последние представлены в пределах
элемента в виде полиномиальных фуикций от s (или от ?), то можно ожи-
ожидать, что скорость сходимости будет определяться наиболее низким
порядком аппроксимации этих величии. Потребуем, чтобы все четыре
функции е^ е», Xi. Хг были аппроксимированы в пределах элемента по-
полиномами от g первой степени. Этого можно добиться, если использо-
использовать при их вычислении различные аппроксимации перемещений Uj,
и„. Выбор типа аппроксимации определяется характером соотиошеиий,
связывающих et, ё2, хх или Хг с перемещениями.
Так, функция е2 выражается через перемещеиия второй формулой
G.49). Для того чтобы выразить ё2 через узловые перемещения, при-
примем, что в пределах элемента tif и ип изменяются по линейному закону,
т. е. воспользуемся аппроксимацией:
tr-
G.79)
где суммирование выполняется по двум узлам элемента (г =¦ г, /'). Под-
Подстановка G.79) в формулу для е2 дает
62=— 2 A +6Г I) («„• К,у -Н<„ hx);
Строго говоря, полученное выражение из-за наличия множителей
%tyly и Ъ-txly представляет собой сложную функцию от %, но для конеч-
конечных элементов малых размеров эти множители представляют собой
плавные и слабо изменяющиеся функции. Поэтому зависимость е2 (\)
близка к линейной, и можно ожидать, что при уменьшении размеров
элементов скорость сходимости будет соответствовать линейной ап-
аппроксимации е2.
Для вычисления
1 dut ип 2 Aut 1
ei=^T "^Г + ~= Т ~W +~r "n
9 Зак. 651 257
используем, для ип линейную аппроксимацию, а для и; — квадратич-
квадратичную. Квадратичная зависимость определяется тремя параметрами, в
связи с чем в дополнение к имеющимся узловым параметрам utt, utj
введем еще неузловую степень свободы с. Тогда зависимость щ(%) мож-
можно получить, добавляя в правую часть первого равенства G.79) слагае-
слагаемое A — %г)с. В итоге получим
„ 1 + 6г?
Подстановка этих соотношений в формулу для е1 дает
?,. utr
Объединив полученные выражения для е^ е2, представим их в ви-
виG.80)
где
2/?
¦ 'к,^ о
о_ *Д
G.81)
Через v,. = [щг Unz &A обозначена матрица перемещений узла
г в местной системе координат.
Переходя к аппроксимации /j, %2, начнем с функции yv2, которая
выражается через перемещения вторым равенством G.53). Принимая,
что угол поворота нормали О изменяется по | по линейному закону
имеем
Наибольшие затруднения вызывает аппроксимация функции
Согласно G.59) и первой из формул G.53) имеем
1
~А
d2»,, 1 d
d?2 Л d|
"t
G.82)
258
Прежде всего покажем, что в этом выражении можно опустить
вследствие малости второе слагаемое в правой части. На основании фор-
формулы el = ех + ?fa найдем значение деформации е\ в наиболее уда-
удаленном от срединной поверхности слое оболочки, т. е. при Z, = /i/2:
h I 2/i A*un . 2 d Г/ h
Так как оболочка предполагается тонкой, то слагаемое hlBR) в
круглых скобках мало по сравнению с единицей и его можно отбросить;
следовательно, второй член в правой части G.82) является также ма-
малым, тогда
4
Р
d2 un
G.83)
Так как %х есть производная по s от функции ¦& — —d«,,/ds -f-
то и выражение для ¦& можно упростить, полагая
d«n____2
ds
dg
G.84)
Примем далее, что перемещение ип изменяется по | по кубическо-
кубическому закону. При | = ±1 функция ип (I) должна совпадать с узловыми
значениями un,-, unj, а ее производная по ? иа основании равенства
G.84) должна в этих точках принимать значения — /д;/2 и —/д;/2. Ис-
Используя при аппроксимации ип те же функции G.74), которые встре-
встречались выше в матрице а, придем к соотношению
ir g) (I—
Тогда
Объединив полученные результаты для ^j^, %2, запишем
х=[Х|| = 2р;7г, G.85)
где
О
/2
О О
G.86)
Формулы G.80), G.85) позволяют в соответствии с G.52) получить
следующее выражение для матрицы деформаций е = {й еЕ):
где
G.87)
G.88)
259
Этот результат соответствует стандартной записи е = pv + Рс,
где v = {v,- v;-J; р = [рг в,].
Напряжения а = [а\ aij} связаны с деформадиями соотношением
а = хе, где
Е Г1 и!
1—U2 (.(Л lj
G.89)
Для получения матрицы жесткости элемента, имеющего неузлО-
вые степени свободы, необходимо вычислить предварительно матрицы
(см. §5.5):
В даином случае k<, будет представлять собой скалярную величи-
величину, а кь — матрицу-столбец. Учитывая блочное представление матри-
матрицы р, можно матрицы ка и kj, вычислять также поблочно:
Ks.a= J P,T*Psdx (г, s=i, /);
Xе
К,ь= J P^xpdt (r=[, /).
Подставим в подынтегральные выражения формулы G.88) и G.89).
Полагая далее Ах = 2nydsd? = n/yd|d? и выполняя интегрирование
по толщине оболочки, получим:
__ Т
I _
ко=л/ j" prx*p%dg. G.90)
— 1
Численное интегрирование в G.90) можно выполнить по трем точ-
точкам Гаусса.
Распределенные нагрузки р = {pj pn) заменяем эквивалентными
силами по формуле
_ i _
Р,.= п/ j aurp</dg ('¦=',/), G.91)
где через аиг обозначены блоки матрицы, связывающей перемещения
{н< ип] с узловыми перемещениями v= (v$Vj-}:
260
Придерживаясь той же степени точности, что и для деформаций,
воспользуемся здесь линейной аппроксимацией перемещений uj, цп:
тйгда аиг дается выражением G.69), где г|>г = A + ?г?)/2.
При таком подходе узловые моменты, обусловленные действием
распределенной нагрузки, будут отсутствовать. Интегрирование в G.91)
следует, как и в G.90), осуществить по трехточечному правилу Гаусса.
Исключение неузловой степени свободы выполним теперь в со-
соответствии с общими формулами E.35), E.38). Рассмотренный выше
способ приведения распределенной нагрузки ие дает силы, соответст-
соответствующей неузловому параметру с. Полагая в упомянутых формулах
Ро = 0 и переписывая их в блочной форме, имеем*
с = —Г-ЫТг.Ь*г. G.92)
к0
*«=*«.<.—Г-кг.ькГ.*- G-93)
Первая из этих формул позволяет после отыскания узловых пере»
мещений вычислить деформации, а затем и напряжения:
Равенство G.93) определяет четыре блока матрицы жесткости эле-
элемента к, приведенной к узловым перемещениям v = {v; Vj).
Чтобы перейти к перемещениям Vе = {v; v;-}, где
vr=iuxr uyr®r} ('' = ', /),
воспользуемся соотношениями
н,г=нЛ?. sin Qr-\-uyr cos 0r; unr=—uxr cos Qr-\-u,Jr sin 0r,
из которых вытекает матричное равенство vr = Xrvr с матрицей
sin Br cos 0r 0
-cosB,. sin6r 0| (»¦=*¦. /)• G.94)
0 0
Отсюда имеем связь v = kve, в которой
О
Применяя обычные преобразования
* Обозначение ке, употреблявшееся в § 5.5, заменено здесь на
к, поскольку данные результаты относятся к местной системе коорди-
координат.
26!
получим матрицу жесткости и матрицу эквивалентных сил е' o6"?* «с-
теме координат. Их отдельиые подматрицы определяются равенствами.
§ 7.10. Матрица жесткости шпангоута
В местах стыка днищ с обечайками баков, резкого излома
образующей и в других случаях применяется подкрепление
оболочек круговыми шпангоутами. Их жесткость должна
быть учтена при формировании общей матрицы жесткости
} конструкции. Каждый
Уо1 шпангоут рассматрива-
иУ1 ем как отдельный ко-
конечный элемент с одним
узлом (узловой окруж-
"хг „ ностью); узел распола-
располагаем в центре тяжести
его поперечного сечения
(рис. 7.11). Для вывода
жесткостных характери-
характеристик шпангоута воспользуемся соотношениями теорииjoh-
ких круговых колец при осесимметричном нагружении
Введем в поперечном сечении кольца систему координат
П ? совместив начало координат с центром тяжести попереч-
поперечного сечения, и обозначим через yoi радиус окружностипро-
• через центр тяжести поперечного сечения. Матрица
перемещений элемента включает в себя три компо-
компоненты:
ть
Рис. 7.11
= v,-
{u
положительные направления перемещений и угла поворота
"Т'Ги ^теорией тонких колец будем полагать
жить у & у о и тогда
е = (uyi
262
Последнюю формулу можно записать в стандартной форме
g as |W, полагая
Р = — [0 1 —х]}. G.95)
Считая, что отдельные волокна кольца не взаимодейству-
взаимодействуют друг с другом, связь между окружным напряжением а и
деформацией е запишем в виде а = Ег, как для одноосного
напряженного состояния. Таким образом, матрица к в данном
случае является скалярной величиной и совпадает с модулем
упругости Е.
Матрицу жесткости шпангоута найдем по обычной формуле
ке =
где Р — определяется по G.95). Подставляя вместо и модуль
упругости Е и полагая dt = 2nyoidF, где df — элемент пло-
площади поперечного сечения, получим
ке =кс =
п. лц
2пЕ
0 0 0
0 Fj 0
0 0 Jt
G.96)
Здесь Ft — площадь поперечного сечения шпангоута, а
Ji ~ [ rfdF — момент инерции этого сечения относительно
Pi
оси ?.
§ 7.11. Объединение конечных элементов.
Определение перемещений и напряжений
Объединение конечных элементов для гладкой оболочки
выполняется по обычным правилам. Несколько сложнее об-
обстоит дело в случае, когда конструкция подкреплена шпангоу-
шпангоутами. Пусть типовой конечный элемент в узле / соединен со
шпангоутом, как показано на рис. 7.12. Введем в этом месте
один общий узел, совпадающий с центром тяжести сечения
шпангоута. Его перемещения в осевом и радиальном направ-
направлениях вместе с углом поворота сечения шпангоута составят
матрицу
v,- = {uxi uyi ¦&;}.
Перед объединением конечных элементов необходимо при-
привести матрицу жесткости, а также матрицу эквивалентных уз-
263
ловых сил конечного элемента оболочки к данным перемеще-
перемещениям. В связи с этим матрицы жесткости и эквивалентных сил
элемента, отнесенные к его узловым перемещениям и обозна-
обозначавшиеся в § 7.8 и 7.9 через ке и Р% обозначим теперь через к
и Р, а сами узловые перемещения элемента обозначим через
v вместо Vе.
Учитывая, что сечение шпангоута не деформируется, мож-
можно получить следующую связь между компонентами матриц
V/ и у;:
G.97)
ч —
Здесь a,-, bt — расстояния вдоль координатных осей от центра
тяжести сечения шпангоута до края элемента оболочки
(рис. 7.12). Они счита-
считаются положительными,
если край элемента обо-
оболочки удален от центра
тяжести сечения шпан-
гоута в положительных
направлениях осей х, у,
и через координаты уз-
узлов вычисляются по
формулам щ = xt — xoi,
bi = г/г — yoi.
В матричной записи
G97)
Рис. 7.12
Г1 о
= 0 1
Loo
р с
формулы G.97) имеют
вид у; = ^-Vj, где
— щ
1
G.98)
Во всех остальных узлах конечного элемента оболочки
матрицы vr и \т совпадают, так что для этих узлов %т — еди-
единичные матрицы.
Применение стандартных преобразований кг = Хт~кХ, Ре =
= X Р позволяет получить искомые матрицы ке и Ре, приве-
приведенные к перемещениям шпангоута в узле i. Фактически пре-
преобразованию подлежат лишь подматрицы, связанные с узлом
264
i, поскольку в формулах
K/-S = A/- krg As; Pr = Аг Рг
матрицы аг, as для г, эф i являются, как уже сказано, еди-
единичными.
Такое преобразование должно быть выполнено для каждо-
каждого из элементов оболочки, связанных со шпангоутами, после
чего объединение конечных элементов можно осуществить
обычным образом:
к — Ske • Р~ = SP«
K-rs — "Vs1 r — г'
В тех узлах, где имеются шпангоуты, в диагональные эле-
элементы матрицы жесткости, соответствующие радиальному пе-
перемещению и углу поворота, в соответствии с G.96) добавля-
добавляются слагаемые 2ziEFily0t и 2nEJi/y0i.
Если помимо распределенных по поверхности нагрузок
действуют также силы и моменты, равномерно распределен-
распределенные по узловым окружностям, то из них следует дополнитель-
дополнительно сформировать матрицу Р, в которой
Рг = 2луг {qxr qyT mT},
где qXT, qyT — погонные значения осевой и радиальной нагру-
нагрузок; тт — погонный момент в рассматриваемом узле г. Поло-
Положительные направления qXT, qyr, mT совпадают с положитель-
положительными направлениями соответствующих узловых перемеще-
перемещений.
Узловые перемещения v = {vx v2 ...vn) определяются пу-
путем решения системы уравнений kv = Р + Р, из которой
предварительно должны быть исключены заданные переме-
перемещения.
После отыскания матрицы v будут известны узловые пе-
перемещения для каждого элемента. Если при этом элемент обо-
оболочки связан в узле i со шпангоутом, то полученную из реше-
решения системы матрицу v< следует при составлении матрицы Vе
умножить на матрицу Аг G.98).
Для элементов, описанных в § 7.8, по формуле
Ш'=*4
G.99)
265'
Определяются нормальные деформации в наиболее удаленных
от срединной поверхности точках. Далее могут быть найдены
напряжения
Такие расчеты выполняют для узловых точек каждого ко-
конечного элемента оболочки. Для улучшения точности могут
использоваться процедуры сглаживания, как это описано в
§5.13.
Для конечных элементов § 7.9 вычисления выполняются
аналогичным образом, но со следующими отличиями. Во-пер-
Во-первых, нужно перейти в каждом узле к перемещениям v в соот-
соответствии с равенством vr == Xrvr, где кг — матрица G.94). Во-
вторых, следует найти неузловой параметр с согласно G.92).
Наконец, в G.99) необходимо заменить vr на vr и добавить
слагаемое (ic.
Напряженное состояние оболочки можно характеризовать
погонными силами Nlt N2 и моментами Ми М2, которые свя-
связаны с напряжениями соотношениями:
ft/2 ft/2
#! = [ adS; iV2 j
-ft/2 -ft/2
ft/2 ft/2
Mx=\ a\lAV, Af2=f oi?d?.
— ft/2 -Л/2
Для их вычисления можно использовать равенства
N2
В сечении шпангоута возникают осевая сила iV и изгибаю-
изгибающий момент М, которые определяются через перемещения uyi,
¦ft,- (см. рис. 7.11) равенствами
N= l-uyi; М-—-Ъп
нормальное напряжение в сечении шпангоута может быть под-
подсчитано по формуле
N М
а =
Ft Jt
266
Знак минус перед вторым слагаемым поставлен потому, что
при положительной величине fy волокна с положительными
значениями г| будут сжаты.
§ 7.12. Деформации произвольной поверхности
Приступая к построению конечных элементов произволь-
произвольной оболочки, покажем предварительно, как можно найти де-
деформации заданной поверхности по известным перемещениям
ее точек.
Рассмотрим поверхность, заданную в параметрической фор-
форме х = х (?, г\), у = у (g, r\), z = z (I, ц). Каждой паре чисел
g, г| соответствует некоторая
точка поверхности. Если за-
зафиксировать параметр т), из- ^^^^д-линии
меняя при этом %, то полу-
получим на поверхности некото-
некоторую кривую. Такие кривые
можно построить для каждо- м???^Х~~~~*А-*^^*^~тнт
го значения х\; их совокуп-
совокупность называют ^-линиями.
Аналогично можно провести
на поверхности семейство кри- рис. 7.13
вых, вдоль которых параметр
| остается неизменным; это
семейство называют т}-линиями. Два семейства кривых обра-
образуют на поверхности координатную сетку (рис. 7.13), что дает
основание называть параметры %, г| криволинейными коорди-
координатами поверхности. Для расчета геометрических параметров
\- и ti-линий воспользуемся соотношениями, полученными в
§5.9.
Бесконечно малый отрезок g-линии, который мы обозначим
через dsg, связан с d| соотношением dsg = A |d?, аналогичным
E.70). Выражение для параметра A j можно получить по фор-
формуле E.71), заменив в ней обыкновенные производные по \
частными:
Аналогично определяется дифференциальный отрезок
n = A^Atx т]-линии. Здесь
S!67
Возьмем, далее, на поверхности произвольную точку М и
введем единичный вектор eg, касательный к \-линии в этой
точке. Его компоненты, представляющие собой направляющие
косинусы ?-линии, представим матрицей
Ц = [кЪх Ц„ кЪг]. G.102>
Для их вычисления воспользуемся формулами E.72), в
которых вместо А следует взять А g и перейти к частным про-
производным:
1 1 дх . ¦ \ ду , 1 дг ._ 1ЛОЧ
X ^1Г: **-=Trif GЛ03)
Точно так же можно ввести касательный к г|-линии единич-
ный вектор е„ с матрицей направляющих косинусов
К = ft,* Kv ^4x1, G.104)
где
. 1 дх _ « 1 ду . 1 дг .„ . ~_^
^ А) ' А\\ дг\ ' "ц от)
Так как векторы eg, е„ имеют единичную длину, то скаляр-
скалярные произведения
откуда вытекают матричные равенства
-> -»¦
Скалярное произведение eg • е„ будем обозначать буквой
у; в матричном представлении
7 = 4 Чг <7Л07>
Как известно, скалярное произведение двух векторов рав-
равно произведению их длин на косинус угла между ними. От-
Отсюда следует физический смысл у: это косинус угла Э между
направлениями \- и г|-линий в точке М (рис. 7.13). Если, в
частности, координатные линии взаимно ортогональны, то
7 = 0.
Для исследования деформации поверхности удобно в каж-
каждой ее точке взять два взаимно перпендикулярных направле-
ния, определив их единичными векторами elt e2 с матрицами
направляющих косинусов
^^ 1гс У 2м == lSC У z'*
Первое из направлений выберем совпадающим с направле-
нием ?-линии, так что ег = е6 или, что то же самое,
К = Ц. G.108)
Вектор е2, определяющий второе направление, можно ис-
искать в виде разложения по векторам е6, е„:
-A.il
Рис. 7.14
Для определения коэффициентов
ах, а2 необходимо, во-первых, ис-
использовать условие ортогональности:
ег • е2 — 0. Если учесть также, что
должно выполняться равенство е2»е2=
= 1, и воспользоваться соотноше-
соотношениями G.106), G.107), то для матрицы Я,2 получим значение
G.109)
Бесконечно малый отрезок dslt взятый в направлении elt
совпадает с ds6 : ds% = ds6 = A ?dg.
Чтобы переместиться вдоль е2 на бесконечно малое расстоя-
расстояние ds2 (рис. 7.14), необходимо дать такие приращения обоим
параметрам ^, tj, которые удовлетворяют соотношению
—A 6d? = A „dri cos Q = у A
При этом длина отрезка будет
G.110)
ds2 -
и с учетом предыдущего равенства получим
ds2 = УГ^у^А^ц. G.111)
Заканчивая описание геометрии поверхности, введем нор-
нормальный к ней единичный вектор е3, определив его с помощью
векторного произведения е 3 = ех X е2. Пользуясь правилом
перемножения векторов и принимая во внимание G.109), для
269
компонент матрицы направляющих косинусов к3 —
= [Xзх X3уХ32] можно получить значения:
G.112)
,,,*).
Отметим, что вектор е3 направлен в ту сторону, откуда по-
ворот ег по кратчайшему пути до совмещения с е2 наблюдается
происходящим против часовой стрелки. При этом тройка век-
->-»¦-»¦
торов е1( е2, es является правой.
Пусть, далее, точки поверхности получают перемещения
их (?, л). иу (?. *]), иг (&. л) в направлении осей х, у, z. Обо-
Обозначим через е11, е22 деформации отрезков dslt ds2, а через е12 —
изменение угла между ними. Для их вычисления снова обра-
обратимся к результатам, представленным равенствами E.77),
E.79). Эти результаты могут быть сформулированы здесь сле-
следующим образом. Деформация произвольной линии, имеющей
матрицу направляющих косинусов Xt, определяется выраже-
выражением
8 = ^77' Gл13)
а уменьшение угла между ее Положительным направлением и
нормальным к ней вектором с матрицей направляющих коси-
косинусов Хо — выражением
ш„ = Ь0 4^- G.114)
d s
Здесь и = {их иу uz}; ds — дифференциальный отре-
отрезок рассматриваемой линии.
Переходя в G.113) к частным производным du/ds1 и du/ds2
и заменяя %t на Хи Х2, получим
е11 = ~Z > е22 ¦= ^
е22 ¦ 2
Деформация сдвига е12 представляет собой сумму двух уг-
углов, один из которых есть поворот отрезка dst в направлении
ds2, а второй — поворот ds2 в направлении dst. Исходя из
G.114), имеем
е12 == —"— Т" ~ •
5S OS
270
Так как dsx =* A jdJj, то
du
l du
Далее, при переходе из точки М (?, г|) в соседнюю точку
поверхности вдоль отрезка ds2 параметры ?, г| получают при-
приращения, связанные между собой равенством G.110). Матри-
Матрица и получит при этом приращение
ди
du
дц
= — у
<Эи
Разделив это значение на ds2 = ]/ —-
выражение для частной производной
ди1 / у
1
), находим
ди . 1
Введем обозначения:
1 , du
Ч
1
+ -л—
ди
ди
G.115)
и воспользуемся соотношениями G.108) и G.109). Тогда
1
1-V'
¦(у
1
или в матричной форме
е22
е12
= р
Ч
G.116)
где
1-V2
о
. G.117)
yi-v2 _
В результате деформации поверхности изменятся углы
между вектором е3 и отрезками dslt ds2. Обозначим через ю1(
271
<в2 углы поворота отрезков ds1 и ds2 в направлении вектора
-¦¦
е3. Для их определения можно снова воспользоваться общей
формулой G.114), из которой следует, что
д и д и
dSi ' ds2
ди ди
Если подставить сюда значения производных —-, -г—, то
ds^ 5s2
можно получить расчетные формулы
L(o2j L^riJ
где
ди
ОТ)
Г =
о
1
I—и2
Г J
G.U8)
G.119)
G.120)
Формулы G.115)—G.120) решают задачу об определении
деформаций заданной поверхности.
§ 7.13. Конечные элементы произвольной оболочки
Рассмотрим конечные элементы четырехугольной формы.
На рис. 7.15 представлено семейство таких элементов, вклю-
включающее в себя элементы первого, второго и третьего порядков.
Пусть xr, yr, zr — координаты срединной поверхности в
типовом узле, h — толщина оболочки. Положение текущей
точки срединной поверхности определим соотношениями х —
— 2tyrxr; у = I.tyryr'> z = 2o|)rzr, где суммирование ведется по
всем узлам элемента. Функции o|v (%, г\) определены равен-
равенствами E.18), E.62), E.67).
Элемент первого порядка имеет прямые стороны, но так
как его узлы в общем случае не лежат в одной плоскости, он
будет искривлен в пространстве (закрученный четырехуголь-
четырехугольник). Элементы второго и третьего порядка имеют, вообще го-
говоря, криволинейные стороны.
Вычисляя производные
дх
_ V дУг Гг ¦ дх -
— 2л ,,. .лг> ~
о| дг\
дх
дг\
от)
272
и т. д., по G.100)—G.105) можно в любой точке срединной по-
поверхности рассчитать параметры Л $, Л„, у и компоненты ма-
матриц Ц, >,„.
В качестве узловых перемещений возьмем смещения ихг,
Uyr> Uzr узлов в направлении координатных осей и повороты
®xr, ®yr, ®zr нормали относительно этих осей:
где
vr = {ur *г },
ur = {usr uyr игт}; flr =
Рис. 7.15
Положительные направления перемещений и векторы по-
положительных углов поворота будем считать совпадающими с
положительными направлениями соответствующих осей.
Найдем далее перемещения
Рис. 7.16
точки, расположенной в узле г на vvr~ ~^~
расстоянии ? от срединной поверх-
поверхности; отсчет положительных зна-
значений ? будем вести в направле-
направлении вектора е3, нормального к
поверхности.
Отличие и? от ur обусловлено поворотом нормали в узле г.
Если некоторый вектор R поворачивается на угол д вокруг
оси, с которой он составляет угол ф (рис. 7.16), то конец век-
вектора совершит перемещение по дуге окружности радиуса
R sin ф (R — длина вектора R); величина перемещения бу-
будет ¦& R sin ф. Если угол поворота мал, то это перемещение
можно представить в виде вектора р, касательного к указан-
указанной окружности. Угловое перемещение можно изобразить
вектором й, длина которого равна #, а направление опреде-
273
ляется правилом правого винта; тогда вектор р будет представ-
-¦¦-¦¦ ->
лять собой векторное произведение р = # х R.
Применим этот результат к вычислению перемещений и,.
Последние относятся к точке, положение которой относитель-
относительно срединной поверхности определяется вектором ?е3г, где
езт — единичный вектор, нормальный к срединной поверхно-
поверхности в узле г. Введя вектор поворота нормали
zr ег,
найдем, что вектор перемещения, обусловленный этим пово-
поворотом, равен #г х ?е3г. Его первая компонента равна
t, (ftyrh з2.г — ®zrh3v,r)> а остальные получаются из этого вы-
выражения круговой заменой индексов х, у, г. Здесь К3х,г< ^зу.тг
Яз2Г — значения параметров G.112) в узле. г. В матричных
обозначениях можно записать
uE = ur + %U *r. G.121)
где
[
G.122)
Рассмотрим далее слой оболочки на расстоянии ? от сре-
срединной поверхности. Геометрию слоя в силу тонкостенности
оболочки можно отождествить с геометрией срединной поверх-
поверхности, полагая
4| = А 6; A t = А„; yt = у; Ц = ^', Ц = К- GЛ 23)
Перемещения uE == {ut u$ ы|} точек этого слоя будем
определять соотношениями
uE = 2i|)ruE. G.124)
Применяя формулы G.115)—G.116) к слою оболочки, нахо-
находим его деформации еЕ = {е^ е|2 г\2}:
8? = 8° ¦+¦ It, G.125)
где
8° = Г2ёгиг; 1 = T2grLr *r. G.126)
274
Здесь суммирование выполняется по всем узлам элемен-
элемента, матрица Г дается формулой G.117), а
Формулы G.126) можно записать и в форме
8° = 2p»vr; г = Sp;vr, G.128)
если положить
Р? = [Fgr 01; Р*. = [0 rgrLrl. G.129)
где нулевые подматрицы имеют размер 3x3.
Помимо деформаций слоя вЕ в оболочке возникают также
деформации поперечного сдвига 8 = {е]3 е23 }. Считая е13, е^
постоянными по толщине, определим их равенствами
Чз = *1 + «I*. ^23 = *2 + Ю2. G.130)
где #1( #2 — углы поворота нормали в направлении векторов
-*.-¦¦ -¦¦
elt e2, а (о1( ю2 — введенные ранее углы поворота векторов еи
-*¦ -*
е2 в направлении вектора е3.
Значения alt ю2 даются формулами G.118)—G.120). Под-
Подставив в них соотношения G.121) и G.124) при ? = 0, выра-
выразим эти углы через узловые перемещения:
шг. G.131)
Здесь Г — матрица G.120), а
1
G.132)
Для определения углов Фх, д2 выполним прежде всего
аппроксимацию матрицы ¦& — {®х #у Ог} по узловым зна-
значениям:
* = 2\|v»r. G.133)
Далее спроектируем #,., ду, #г (представив их в виде век-
векторов) на направления векторов еъ е2, которые имеют матри-
матрицы направляющих косинусов
V Ц\ К (
275
Принятые в G.130) положительные направления #ь #я
показаны на рис. 7.17, где двойными стрелками даны вектор-
векторные обозначения Olt #2. С учетом этого запишем ¦&! = ><2ф;
^2 = _Я,1д или, учитывая G.133),
где
G.134)
G.135)
Исходя из G.131) и G.134), для матрицы 8 получаем в
соответствии с G.130) выражение
8 = SPrVr, G.136)
в котором
Pr = [f gr iprL]. G.137)
Теперь можно объединить
матрицы ее и в и выразить
деформации г = {et e } через
узловые перемещения по-
посредством соотношения г =
= 2prvr, где рг определяет-
определяется равенством G.63).
Запишем далее соотношения упругости. Напряжения в слое
ot= {a\t a|a а\2}, так же как и в случае пластины, связаны
с е? законом Гука для обобщенного плоского напряженного
состояния:
Е -т G.138)
Рис. 7.17
где
ио =
1 ja
0 0
0
0
Поперечные касательные напряжения а = {сг13 аы} вы-
выражаются через е по формуле
G.139)
276
где х — единичная матрица размером 2x2; величину G мож-
можно взять равной 5G/6 с целью учета имеющей в действительно-
действительности место неравномерности напряжений а13, а23 по толщине
оболочки.
Полагая а— {а? а}, будем иметь из G.138), G.139) ра-
равенство а = хе, в котором
х =
О Gx
G.140)
Для вычисления типового блока матрицы жесткости
внесем в подынтегральное выражение равенства G.63) и
G.140). Положив
dt = dMs.dE = A bAJ/T^f dldr\dt,
выполним затем интегрирование по толщине оболочки. В ито-
итоге получим выражение для к^ в виде суммы трех матриц:
G.141)
,..n=f f
JiJ
1 1
j j
1 1
; G.142)
J
-i -
Поскольку матрица х единичная, в выражении для krs,o
она опущена. Заметим, что исходя из блочной структуры
G.129) матриц Р? и р*, можно выражения для к«,в и к„,о
представить в виде
L 0 0j
G.143)
где подматрицы kri и k"s, имеющие размер 3X3, определя-
определяются равенствами
k;s=[ f BQridgdr,; K. = L?\ f ^Qr.dgd4Lit G.144)
в которых
Ог.=вгГГгхвГьЛЕЛчугГ=у. G.145)
При численном интегрировании следует для исключения
ложных сдвигов использовать минимально допустимый поря-
порядок при вычислении krs,G', к матрицам k'rs и k"s должно быть при-
применено более точное интегрирование (см. табл. 5.1).
Отметим, что элемент оболочки рассматриваемого типа с
четырьмя узлами в вершинах описан в работе [23].
В заключение коснемся вопроса о приведении к узлам вне-
узловой нагрузки. Пусть р = {рх ру рг}—матрица проек-
проекций поверхностной нагрузки на координатные оси, а Р* —
матрица сил, действующих в узле г в направлении перемеще-
перемещений vr и эквивалентных этой нагрузке. Для вычисления Р'
можно получить выражение
G.146)
где аиг — типовая подматрица матрицы функций, аппрокси-
аппроксимирующих перемещения и = {их иу uz} через v* в соответ-
соответствии с равенством u = auve = 2aurvr.
Для рассмотренных элементов матрица аиГ имеет вид
[фг О 0 0 0 0"
0 \jv 0 0 0 0
0 0 фг О О О
Интегрирование в формуле для Р* осуществляется по то-
тому же правилу, что и при вычислении матриц k/s или k"s.
§ 7.14. Примеры расчета
Пример 1. Треугольное монолитное крыло жестко защем-
защемлено по части бортовой хорды (рис. 7.18, а) и нагружено по-
постоянным поперечным давлением р. Крыло имеет ромбовидный
профиль. Толщина с изменяется по размаху по линейному
278
закону, ее максимальное значение (в середине бортовой хор-
хорды) равно 40 мм, Е = 7 • 10* МПа; (х = 0,3.
Для идеализации использовались изопараметрические ко-
конечные элементы пластины первого порядка (см. §7.3). Схе-
1
1
1
1
1
1
1
к
l_v-
\
\
\
—.
0,Z 0,k 0,6 0,8 1,0 1,1
Рис. 7.19
х,и
ма идеализации дана на рис. 7.18, б; конечноэлементная мо-
модель содержит 59 конечных элементов и 78 узлов.
На рис. 7.19 сплошной линией показано изменение вдоль
заделки нормального напряжения azz в наружных слоях.
279
Штриховая линия дает закон изменения azz при полном за-
закреплении крыла по всей хорде. Представление о погрешности
решения можно получить, вычислив результирующий момент
напряжений azz в заделке; в полученном решении он состав-
составляет примерно 92% от момента, создаваемого относительно
оси х внешней нагрузкой. Следовательно, представленные на
рис. 7.19 напряжения найдены с погрешностью порядка 8%.
Пример 2. Стальная (Е =
= 2 • 105 МПа, (х = 0,3)
пологая коническая оболоч-
оболочка с жестким центром за-
защемлена по контуру и нагру-
нагружена равномерным давлени-
давлением р = 0,1 МПа (рис. 7.20).
N,kH/m
М,Н
30
20
10
m
\
/
-ч
/
><
s
ч
W
\
N2
\
\
/
J
}
ч
I
/
/
1
\
75 95 г,пн
Рис. 7.20
Рис. 7.21
Для расчета использован изопараметрический конечный эле-
элемент первого порядка, описанный в § 7.8. На рис. 7.21 показа-
показано изменение изгибающих моментов Мъ М2 и сил Nlt N2 в
срединной поверхности при разбиении оболочки на 25 конеч-
конечных элементов. Точками даны результаты, полученные по
теории оболочек [3]. Отметим, что использование конечных
элементов, описанных в § 7.9, позволяет получить аналогичные
по точности результаты при разбиении оболочки на 15 элемен-
элементов.
Пример 3. Круглая (на развертке) цилиндрическая па-
панель (рис. 7.22) жестко защемлена по контуру и нагружена
через жесткий центр силой Р. Радиус цилиндра R = Гм, ра-
радиус панели гх = 550,1 мм, радиус жесткого центра г0 =
= 66,1 мм, толщина панели h = 5 мм, Е = 1,96 • 105 МПа,
ц = 0,3.
Для идеализации конструкции использовались изопарамет-
рические элементы произвольной оболочки второго и третьего
порядков. Конструкция имеет двойную симметрию (относи-
(относительно плоскостей xz и yz), что позволяет ограничиться рас-
рассмотрением четверти панели. Схема ее идеализации представ-
представлена на рис. 7.23. Закрепления узлов на сторонах х = 0 и
280
у = О задавались исходя из условий симметрии. Наличие
жесткого центра может быть смоделировано различными спо-
способами. Можно, например, жесткий центр представить так
же, как и саму панель, в
виде совокупности конеч-
конечных элементов, но имею-
имеющих весьма большой мо-
модуль упругости или весьма
большую толщину. Здесь
использован другой под-
подход, в котором линия спая
панели с жестким центром
выступает в качестве од-
одной из границ области.
Перемещение соответствую-
соответствующих узлов по осям х и у,
а также углы поворота в
них относительно осей х,
у, z принимались равными
нулю. Что касается пере-
перемещений этих узлов в на-
направлении оси г, то все
они задавались равными 1.
Таким образом, расчет
проводился на единичное
смещение жесткого центра.
Сила Р/4, необходимая
для создания такого пере-
перемещения рассматриваемой
четверти панели, может
быть найдена из условия
равенства производимой
ею работы и потенциаль-
потенциальной энергии деформации
системы:
Рис. 7.22
Рис. 7.23
где v — матрица узловых
перемещений при единич-
единичном смещении центра;
К — общая матрица жесткости. Истинное перемещение
Жесткого центра от действия заданной силы Р:
281
На эту величину умножаются все перемещения и напряже-
напряжения, полученные в предположении о единичном смещении
жесткого центра.
Ф.
0,08
0,04
-ОМ
0,2
0,6
0,8
Рис. 7.24
п к
I1*
0,1
п
П 1
I
\
\
\
"V
а"
О4-О--
^;
¦0--0-
-а
-о— —
н
ft 2
0,5
0,8 Г/г,
Рис. 7.25
Результаты расчета (рис. 7.24, 7.25) получены при разбие-
разбиении на 45 E в окружном направлении, 9 — в радиальном)
конечных элементов второго порядка; через ог обозначена ра-
радиальная, а через сте — окружная компоненты напряжений
282
(г, 9 — полярные координаты в срединной поверхности пане-
панели, см. рис. 7.22). Напряжения отнесены к величине а0 =
= Р/Л2. При вычислении напряжений применялась процеду-
процедура местного сглаживания (см. § 5.13) с последующим осредне-
осреднением результатов в узловых точках.
На рис. 7.24 представлены нормальные напряжения в сре-
срединной поверхности панели, а на рис. 7.25 — значения нор-
нормальных напряжений, обусловленных действием изгиба, в
крайних волокнах. Сплошные и штриховые линии, полу-
полученные аналитическим путем [12], дают закон изменения на-
напряжений вдоль лучей 9 = я/2 и 9 = 0 соответственно; ко-
нечноэлементные результаты отмечены точками. Наиболее
напряженной является точка панели, расположенная на на-
наружной поверхности в месте стыка панели с жестким центром,
при 9 = я/2. Эквивалентное напряжение (по теории прочно-
прочности энергии формоизменения) получилось здесь равным при
данной сетке 0,690а0, что на 3,7% ниже точного значения
0,717а0. Величина w при той же сетке оказалась равной
0,417 RojE, что всего на 0,7% отличается от точного зна-
значения О,414#сто/?.
ГЛАВА 8
КАРКАСИРОВАННЫЕ ТОНКОСТЕННЫЕ КОНСТРУКЦИИ
Тонкостенные подкрепленные конструкции при относительно ма-
малом весе обладают высокими прочностными характеристиками, благо-
благодаря чему они иашлн широкое применение в авиации. Конечноэлемент-
ная модель подобной конструкции должна быть по возможности про-
простой, но в то же время она должна правильно воспронзводить наиболее
существенные особенности силовой работы. Как и в традиционных ме-
методах расчета, обшивку можно считать безмоментной. При моделиро-
моделировании лонжеронов, нервюр или шпангоутов следует учитывать дефор-
деформации поперечного сдвига. При этом необходимо заботиться об исклю-
исключении ложных деформаций поперечного сдвига, которые могут совер-
совершенно исказить жесткостные свойства конструкции в целом.
§ 8.1. Конечиоэлементная идеализация конструкции
Типичными представителями подкрепленных тонкостен-
тонкостенных конструкций являются крыло (рис. 8.1, а) и фюзеляж
(рис. 8.1,6) самолета. Они имеют относительно тонкую об-
обшивку и силовой набор (каркас), образованный такими эле-
элементами, как шпангоуты, лонжероны, нервюры, стрингеры.
Моделирование каркасированной конструкции набором ко-
конечных элементов можно осуществить различными способами;
283
конкретный выбор зачастую диктуется возможностями имею-
имеющихся вычислительных машин или программ.
Силовой каркас обычно разбивает обшивку на отдельные
панели, которые часто целиком моделируют одним конечным
элементом. Обшивка представляет собой тонкую оболочку,
и в принципе для идеализации панелей могут быть исполь-
использованы четырехугольные конечные элементы, описанные
в предыдущей главе. Однако тонкая обшивка работает в ос-
основном на растяжение-сжатие и сдвиг, слабо сопротивляясь
изгибу. Распределение напряжений по ее толщине можно счи-
Обшфа
Лонжерон
Стрингер
Шпангоут
ОдчшВка
Стрингер
Рис. 8.1
тать равномерным, что позволяет воспользоваться более про-
простыми конечными элементами безмоментной оболочки.
Если стрингеры, подкрепляющие обшивку, расположены
регулярно и достаточно часто, то проще всего «размазать» их
по обшивке и рассматривать последнюю как конструктивно-
ортотропную. При нерегулярном или редком расположении
стрингеров следует учесть дискретный характер подкрепле-
подкреплений. Изгибная жесткость стрингеров, как правило, невелика,
и для их идеализации подходят одномерные конечные элемен-
элементы с равномерным распределением нормальных напряжений
по сечению (см. §5.10).
Лонжерон представляет собой балку переменной высоты;
обычно он имеет тонкую стенку, работающую главным обра-
образом на сдвиг. Будем по длине разбивать лонжерон на отдель-
отдельные участки, рассматривая их как конечные элементы. При
этом достаточно учесть лишь те степени свободы, которые со-
соответствуют изгибу лонжерона в плоскости стенки и его про-
продольной деформации.
Один из возможных подходов к получению матрицы жест-
жесткости бруса, позволяющий учесть переменность высоты сече-
ния и влияние деформаций поперечного сдвига, изложен в
§ 3.7 применительно к элементу плоского кругового бруса.
Если жесткость лонжерона в пределах элемента постоянна,
а влияние деформации поперечного сдвига мало (лонжерон
С толстой стенкой), то можно воспользоваться результатами,
полученными в § 3.4 и 3.5. В этом случае матрица жесткости
в местной системе координат дается выражениями C.26), C.36)
и C.48).
Другой путь получения жесткостных характеристик эле-
элемента лонжерона основывается на независимой аппрокси-
аппроксимации перемещений и углов поворота подобно тому, как это
делалось в предыдущей главе при построении изопараметри-
ческих элементов изгибаемой пластины.
Можно, наконец, элемент лонжерона рассматривать как
составной. При таком подходе пояса идеализируются одно-
одномерными элементами, работающими на растяжение-сжатие,
а стенка — конечными элементами плоской задачи теории уп-
упругости. Во многих случаях такая модель наиболее естествен-
естественна, и она позволяет адекватно воспроизвести все особенности
работы лонжерона.
Нервюру также можно представить как тонкостенную
балку переменной высоты, и к ней в равной степени применимо
все то, что было сказано об идеализации лонжерона.
Шпангоут представляет собой криволинейный плоский
брус. Он может испытывать деформацию как в своей плоско-
плоскости, так и из плоскости, и зачастую ни одна из главных осей
инерции поперечного сечения не лежит в плоскости шпангоу-
шпангоута. Отметим, что в частном случае кругового шпангоута, ра-
работающего на изгиб в своей плоскости, можно для его идеа-
идеализации использовать элементы, рассмотренные в § 3.7.
§ 8.2. Конечные элементы безмоментной обшивки
Как говорилось выше, обшивку можно рассматривать как
безмоментную оболочку. Для вывода жесткостных характе-
характеристик конечных элементов обшивки воспользуемся соотно-
соотношениями, полученными в предыдущей главе для случая мо-
ментной оболочки произвольной формы. Эти соотношения уп-
упрощаются здесь, так как деформации в безмоментной оболочке
постоянны по толщине. В то же время будем учитывать при
вычислении матрицы жесткости возможное наличие конструк-
конструктивной ортотропии.
Рассмотрим семейство изопараметрических конечных эле-
элементов с четырьмя сторонами. Геометрия подобных элементов
показана на рис. 7.15. Основной исходной геометрической
285
информацией для элемента служат координаты xr, yr, zr его
узлов в общей системе координат. Положение текущей точки
срединной поверхности элемента определим соотношениями
а: — S^rX,., у =¦ ЩгУг, 2 — 2г|зг2г, где суммирование осуще-
осуществляется по всем узлам элемента. Функции г|зг (|, х\) даются
равенствами E.18), E.62) и E.67).
В соответствии с формулами §7.11 вычисляем геометри-
геометрические параметры:
где
I
обозначено
¦ —; Я
дх . .
1
1
У- 6-
iir; }
дц '
\т
1
^ ~~А~
1
dz
dz
Узловые перемещения возьмем в направлении координат-
координатных осей, тогда матрица перемещений типового узла будет
Vr = {Vrx Vry VTl}.
Аппроксимацию перемещений и = {их uv uz) внутри эле-
элемента осуществим в соответствии с изопараметрической фор-
формулировкой:
и = 2г|згуг. (8.0
Деформации е = {eu e22 &i2} определяются равенствами
G.115)—G.117).
Исходя из (8.1), приведем выражение для е к виду е =
= Sprvf, где
о
о
(8.2)
286
Связь между напряжениями а = {ап а22 а12} и деформа-
деформациями е запишем для общего случая конструктивно-орто-
тропной обшивки, подкрепленной системой ребер, располо-
расположенных параллельно друг другу с постоянным шагом. Для
приближенного определения ориентации ребер на поверхно-
поверхности обшивки поступим следующим образом. Пусть Хи у\, z°
и х\, у2, z\ — координаты
каких-либо двух точек, при-
принадлежащих любому из ре-
ребер или любой линии, парал-
параллельной ребрам. В примере,
показанном на рис. 8.2, эти
точки обозначены буквами
Мх и М2, причем точка Мг
взята здесь в одной из вер-
вершин четырехугольника. По-
Полагаем, что направление ре-
ребер жесткости совпадает с направлением вектора, соеди-
соединяющего точки Мг и 7W2. Обозначим через
^0;— Ох ^х г~ ои ц ~т~ Qz z
единичный вектор, имеющий направление от точки Мх к точ-
точке М2.
Компоненты е0 вычисляются через координаты /И,, М2 по
формулам
Рис- 8-2
о о
2— х\
/о
г° 7°
h = V(x°t -x°tJ + (у° -у°
Пусть, далее, 90 — угол, составляемый вектором е0 с ка-
касательной к g-линии. Направление касательной определяется
единичным вектором ех'-
-*-*-*-*¦
Ч = Н* ех + Чу еу + Чг ег-
Умножив скалярно е0 на еъ найдем косинус угла 80:
-*¦ ->
cos 90=^-^0 =
287
Чтобы вычислить sin 60, можно умножить скалярно е0 на
единичный вектор е2:
Введя в дополнение к
^ матрицу
представим полученные соотношения в форме
cos 60 = Ц %l; sin 60 = — (-
(8.3)
Теперь в соответствии с формулами § 1.3 можно построить
матрицу и, связывающую напряжения с деформациями соот-
соотношением о = не. Представим соотношения A.32), A.34) и
A.36) в виде
\i О
1 О
т =
Тх*Тг,
(8.5)
cos290 sin260 — sin 28,/
sin2 60 cos2 0O sin 260
sin 29O sin 290
2 2
cos 290
где
Здесь ?lt ?2 — модули упругости соответственно ребра и
обшивки; h — толщина обшивки; F — площадь сечения реб-
ребра; t—шаг ребер; входящие в матрицу Т значения sin 260
и cos 26O можно подсчитать через (8.4) по очевидным форму-
формулам:
sin 290 = 2 sin 0О cos 60; cos 20О = cos2 60 — sin2 80.
Для вычисления блоков матрицы жесткости элемента вос-
воспользуемся общим выражением
288
г
Учитывая, что dx = НА %А,У\ — у2А\Аг\, приведем по-
следнее выражение к расчетному виду
Ъ-sJ
Тх*
i4Vi—i
(8.7)
При численном интегрировании можно применить обычные
правила Гаусса (см. табл. 5.1).
Если обшивка гладкая, то в (8.7) следует опустить матри-
матрицы Т и Тг, а в матрице к* положить kF = 0. В итоге для слу-
случая гладкой обшивки имеем
(8.8)
— 1—1
причем здесь
1 |i
I* 1
0-0
о
о
Приведение распределенных сил к узловым осуществляет-
осуществляется обычным путем. Для подматрицы сил Р«, действующих в
типовом узле г в направлении перемещений vr, можно полу-
получить формулу
(8.9)
-l-i
где р= {рх ри pz}—матрица распределенных нагрузок.
Интегрирование здесь следует выполнять по тем же правилам,
что и в (8.8).
В заключение отметим, что жесткость отдельных панелей
обшивки может снижаться вследствие потери ею устойчиво-
устойчивости. Наличие начальных неправильностей приводит к тому,
что сдвиговая жесткость обшивки в областях с большой кри-
кривизной также оказывается ниже, чем это предсказывается без-
моментной теорией. Данные факторы могут быть учтены вве-
введением редукционных коэффициентов, на которые должны
быть умножены модули упругости Е и G соответствующих
конечных элементов; это согласуется с обычной расчетной
практикой, принятой в самолетостроении. Значения редук-
редукционных коэффициентов можно брать из справочной литера-
литературы, либо исходя из опыта проектных организаций.
Ю Зак. 651
289
§ 8.3. Конечные элементы изопараметрического типа
для лонжеронов
Как отмечалось выше, для идеализации лонжерона могут
быть использованы балочные элементы. В данном параграфе
рассматриваются балочные элементы изопараметрического ти-
типа с независимой аппроксимацией перемещений и угла пово-
поворота сечения. В отличие от балочных элементов, описанных
А-А
Рис. 8.3
в гл. 3, где под узлами понимались сечения элемента, здесь
узлами служат те же точки, которые являются узлами конеч-
конечных элементов обшивки; за узловые перемещения принима-
принимаются при этом линейные смещения узлов (рис. 8.3, а).
Исходная информация для элемента имеет стандартный
вид и включает в себя координаты узлов, а также упругие и
геометрические характеристики сечения. Для вывода матри-
матрицы жесткости используется местная система координат, оси
которой х, у лежат в плоскости стенки, а начало находится в
среднем сечении. Направление оси х определяется точками
290
/ и 2, которые делят пополам расстояния Нх и Я2 между пане-
панелями обшивки в крайних сечениях. Координаты этих точек
выражаются через координаты узлов: х1 = (х; + Xj)/2, у1 —
= (f/j + г/у)/2 и т. д.; длина элемента определяется по фор-
формуле
/ = Vixz-xtf + (Уг-Ух? + fe-ZiJ.
Расстояния между противоположными узлами обшивки так-
также могут быть найдены через координаты узлов, например:
#i -ViXf-Xi
При расчете жесткостных характеристик подобных эле-
элементов необходимо учитывать их податливость в поперечном
направлении, так как должна быть обеспечена независимость,
скажем, перемещений о.- и»- или о;- и v^. Здесь возника-
возникает затруднение, связанное с тем, что в технической теории из-
изгиба бруса поперечная податливость выпадает из рассмотре-
рассмотрения. Поэтому воспользуемся приближенной моделью, в кото-
которой сама стенка в поперечном направлении абсолютно подат-
податлива, а ее жесткость имитируется линейными упругими свя-
связями в виде стержней или пружин, которые связывают между
собой пояса лонжерона в узловых сечениях (рис. 8.3, а). Из
физических соображений ясно, что учет поперечной податли-
податливости не может существенно повлиять на результаты расчета
крыла в целом. Это дает оенование пользоваться подобной
моделью, назначая жесткость упомянутых пружин весьма
приближенно.
Рассмотрим вначале конечный элемент лонжерона с че-
четырьмя узлами i, j, I, m, показанный на рис. 8.3, а. Положе-
Положение центра тяжести произвольного сечения отмечено на ри-
рисунке буквой С, а его расстояние от оси х обозначено через ус.
В местной системе координат элемент имеет восемь степеней
свободы — по два смещения в каждом из узлов. Условимся
перечислять их в матрице узловых перемещений v в следую-
следующем порядке:
v ={Vi v;- v, vm}.
Здесь vr = {vr-v-} — матрица перемещений узла г (г = i,
U I, т).
Матрицу жесткости к элемента будем искать в виде суммы
двух матриц:
k=k'+k". (8.10)
10* ,.2Г".
Первая из них учитывает жесткостные характеристики
собственно бруса, а вторая — жесткостные характеристики
дополнительных упругих связей.
Переходя к вычислению к', обозначим через их, иу и О-
смещения в направлении осей х, у произвольной точки, ле-
лежащей на оси х, и угол поворота соответствующего сечения.
Для упрощения записи в этих обозначениях, а также далее в
обозначении деформаций и напряжений опущена черточка в
индексах х, у. Для функций их, иу и Ф воспользуемся неза-
независимой их аппроксимацией по узловым значениям:
их = 2%ихр; иу = Щриур; # = 2г|^р. (8.11)
Через ихр, иур, Фр здесь обозначены перемещения и пово-
повороты узловых сечений; их положительные направления пока-
показаны на рисунке. Индекс р, по которому выполняется сумми-
суммирование, принимает здесь значения / и 2.
Функции typ изменяются по длине элемента по линейному
закону
%® = ~(\+tpt) (P = l, 2),
где ? — безразмерная координата, имеющая в узлах /, 2 зна-
значения |х = —I, |2 = I и связанная с х соотношением | =
= 2x11.
Таким образом, здесь мы относим элемент бруса к шести
степеням свободы ихр, иур, Фр (р — 1, 2). Они связаны с пе-
перемещениями узлов v, очевидными соотношениями:
м*2= -j (vrx -f vm-); Uyi = -j (o,- + vm-);
^-=~(vm-x-vrx). (8.12)
11еремещения и*х, иу произвольной точки в текущем сече-
сечении, расположенной на расстоянии у от оси х, будем опреде-
определять равенствами
их=их—у~Ъ; Uy = uy. (8.13)
292
Согласно формулам Коши, имеем отсюда
д 2
диУ 2 ( d"* п м )
дх ' \ Al dW
дх ду
Чтобы выразить деформации через узловые перемещения,
подставим в последние равенства соотношения (8.11). Введя
матрицы узловых перемещений ир = {ихр иурдр}, запишем
где обозначено
-[i^»0]; К =[0 0-
Этот результат можно представить и в форме е = Ри, если
положить и = {и, и2}, е = {е,.,. еху}, р = [р, рг1, где
(8.15)
Связь между деформациями и напряжениями возьмем в
виде ахх — Егхх, аху = GeXJ/. Отсюда вытекает матричное
соотношение о = хе, в котором о = {ахх oxv), a
Н^Ч (8-16)
[о с\
Обозначая через к матрицу жесткости элемента бруса, от-
отнесенную к шести степеням свободы и, находим ее блоки:
я = jPp*PgCk (р, 9 =
Внося сюда (8.14)—-(8.16) и учитывая, что dx = dxdF
{dF — элементарная площадка в поперечном сечении), получим
к„. е = е j [F (ррот ps -y0 f/ р? - уе р°т р;)+/, р;7 p;i dx;
kP,.G=vG j?pppgdx. (8.18)
i
293
Здесь F, Jz — площадь поперечного сечения и его момент
инерции относительно оси г. В выражение для крч,в введен
дополнительно коэффициент v, учитывающий неравномер-
неравномерность распределения касательных напряжений аху по сечению.
Этот коэффициент зависит от формы поперечного сечения.
Так, для прямоугольного сечения он равен 5/6, для круглого—
9/10 и т. д. Для лонжерона можно брать в качестве v отноше-
отношение площади сечения стенки к F. Это соответствует предполо-
предположению, что поперечная сила воспринимается только стенкой
лонжерона, равномерно распределяясь по ее высоте.
Интегрирование в (8.18) осуществим по одноточечному пра-
правилу Гаусса. Если брус имеет постоянное сечение, то это соот-
соответствует точному вычислению кр,,я. Для матриц кр,,о од-
одноточечное интегрирование имеет минимально допустимый
порядок и позволяет исключить ложный сдвиг. С учетом (8.14)
получим в итоге
EFo
1
0
_ — Уо
—Уо
0
"О
о
о
0
О '
/ЕР/2
где Fo, Jo, y0 — значения F, J2, ye в среднем сечении элемен-
элемента (при х = 0).
Эти формулы относятся к случаю, когда пояса и стенки
лонжерона изготовлены из одного материала. Если же мате-
материалы различны, то их условно приводят к одному материалу.
Пусть Е — модуль упругости материала, к которому осу-
осуществляется приведение (например, материала стенки). Тог-
Тогда при вычислении площади сечения, его момента инерции и
статического момента вклад каждого элемента сечения (стен-
(стенки, поясов) должен быть умножен на редукционный коэффи-
коэффициент, равный отношению соответствующего модуля упру-
упругости к Е. Под величиной G в формуле для крч, а следует всег-
всегда понимать модуль сдвига материала стенки.
Приведем теперь полученную матрицу жесткости к восьми
узловым перемещениям конечного элемента v. Связь между
матрицами
и =¦ {uXJ uyl #! их2 иу2 Ф2};
iy Vfx %
u 1'Гу
294
на основании (8.12) может быть записана в форме и = км,
где Через к обозначена матрица вида
Ji-Р* ^ ° ° 1. (8.19)
Здесь типовая подматрица крг (р == 1,2; г = i, j, I, m)
может быть определена общим выражением
1/2 О
Ар,. —
О
1/2
О
• (8.20)
в котором г|г = —1 для г = /, т и г|г = 1 для г = /, /.
Искомая матрица к' получается далее с помощью обычного
преобразования V = кТкк. Учитывая, что матрица к представ-
представлена выше в блочной форме
выражение для к' представим также в блочном виде
'и к// к// к/т
к// к'ц к/т
к' =
Симм.
к„'!
где типовая подматрица
к' —
(8.21)
Здесь р = 1 при г — i, / и р = 2 при г =¦ I, т; аналогично,
q = 1 для s ~ i, j и q = 2 для s = /, /п.
Обратимся теперь к пружинным элементам. Жесткости
пружин будем считать одинаковыми и равными g0- Связь меж-
между перемещениями и - и соответствующими им узловыми си-
силами Р - (г = I, /, /, т) определится двумя равенствами:
go] Ul?l
go J|_*WJ
(8.22)
295
Исходя из этих равенств, можно записать выражение для
полной матрицы к", имеющей размер 8 х 8. В блочной форме
она имеет вид
к" =
kit
СИММ •
к"т
к-т
к'ш
к'тт
где
кц—kj'j — кд ~ к^цл— —k,y— —k/m — I I, (8
.23)
а подматрицы k/i, k"m, kfi, k"m— нулевые.
Суммируя матрицы к' и к", находим матрицу жесткости
конечного элемента в местной системе координат. Отдельные
ее блоки определяются как
krs = k/s + k"s {r, s =-i, j, I, tri).
(8.24)
Что касается значения g0, то, как говорилось выше, его
можно задавать сугубо приближенно. Можно, например, вы-
вычислить жесткость стенки при ее растяжении в поперечном на-
направлении и приравнять ее к суммарной жесткости пружин
2g0. Считая, что стенка имеет постоянную высоту Н =
= (//j + //2)/2, получаем следующую оценку для g0:
g0 = EMI
(8.25)
где hi — площадь сечения стенки плоскостью xz (h — толщи-
толщина стенки).
Заключительным этапом формирования матрицы жестко-
жесткости элемента лонжерона является переход к общей системе
координат х, у, г. Найдем прежде всего косинусы углов, сос-
составляемых осями х, у с осями х, у, г. Так как ось х проходит
через точки 1, 2, то для нее направляющие косинусы даются
равенствами:
Определим далее направляющие косинусы оси у. Выше
подразумевалось негласно, что направления // и 1т перпенди-
перпендикулярны оси х и лежат в одной плоскости. Однако из-за осо-
особенностей конструкции или разбиения обшивки на конечные
элементы, а также вследствие приближенного задания коор-
динат узлов может оказаться, что эти направления не явля
ются строго параллельными и перпендикулярными оси х. При
расчете жесткостных характеристик конечного элемента это
можно игнорировать, но возникают трудности с определением
направления оси у. Возможны различные пути разрешения
этой проблемы; мы поступим следующим образом.
Введем в рассмотрение точки а и Ъ, которые делят пополам
расстояния между узлами /, / и /, т соответственно. Их коор-
координаты: ха — (xt + xt)/2, ya = (yt + угI2 и т. д. Затем про-
проведем через данные точки плоскость, параллельную оси х, и
будем считать, что ось у параллельна этой плоскости. Тем са-
самым направление оси у будет однозначно определено даже в
том случае, когда узлы /, /, /, т не лежат в одной плоскости.
Как известно из аналитической геометрии, любую плос-
плоскость в пространстве можно задать линейным уравнением
Ах + By + Cz + D = 0. (8.26)
Коэффициенты А, В и С можно рассматривать как ком-
компоненты некоторого вектора, нормального к плоскости и оп-
определяющего, таким образом, ее ориентацию в пространстве.
Константа D характеризует перенос плоскости вдоль нормали
параллельно самой себе, и для нас она является несуществен-
несущественной.
Уравнение плоскости, проходящей через две точки с коор-
координатами ха, уа, га и хь, уь, гь параллельно прямой с направ-
направляющими косинусами %-хх, 1^ , %-г удобно записать в форме
равенства нулю определителя:
Х—Ха У—У а Z—Za
а Уъ—У а 2Ь — Za = 0-
К кг
Раскрыв определитель, придем к уравнению типа (8.26) с
коэффициентами
А = (Уь —Уа) кг — (Zb — Za) hu',
С - (хь-ха) к7у—(уъ -уа) К7х. (8.27)
Теперь мы можем рассмотреть пересечение двух плоско-
плоскостей, одна из которых нормальна к вектору с компонентами
А, В, С, другая же — « вектору с компонентами %~х, "к- , ^xz
(т. е. к оси х). Ясно, что ось у будет параллельна линии их
пересечения, так что направляющие косинусы оси у будут
совпадать с направляющими косинусами этой линии. Если
две плоскости заданы уравнениями
Ах + By -4 Сг + D = 0;
то направляющие косинусы линии их
равенствами
УУ
пересечения даются
(8.28)
Дальнейшие вычисления выполняются обычным образом.
Проектируя в каждом узле перемещения vrx, vry, vrz на на-
направления осей х, у, приходим к соотношениям вида vr =
{ }
в
X-
ХУ
с
х-
XZ
с
х-
XZ
А
X-
XX
¦ N —
> Jv z —
А
X-
XX
в
X-
ху
, у, р
где vr = {vrx vry vrt}, a
ъ К
(8.29)
Отсюда вытекает стандартная связь v = X\e между матри-
матрицами v = { VjVjV;Vm } и ve = {v;VjViVm }. Матрица X имеет здесь
блочно-диагональную форму
К, О
0
По формуле ke = V VX находим, наконец, матрицу жестко-
жесткости конечного элемента в общей системе координат. Для от-
отдельных ее блоков имеем
Ks=KKsK (8.зо)
Приведение распределенных нагрузок к узлам для данного
элемента рассматривать не будем, так как при расчете крыла
принято считать обычно, что вся распределенная нагрузка
(как воздушная, так и массовая) приложена к обшнвке.
Аналогично могут быть построены конечные элементы лон-
лонжерона второго и третьего порядков (рис. 8.3, б, в), для кото-
98
рых матрицы ке будут содержать соответственно 6 X 6 и 8 X 8
блоков k*s - Для вычисления последних справедливы приве-
приведенные выше формулы с некоторыми поправками. Так, в ка-
качестве г|)р нужно брать функции E.82)
*рF) - 35'Г2 I6p(» +6р6) —A — g»>l (Р=/, 2, 3)
2
для элементов второго и функции E.83)
Щ^- (р= /. 2, 3, 4)
для элементов третьего порядков (см. § 5.10). Значения |р да-
даны на рис. 8.3; параметр с0 = 1/3 или 1/]/5,
Связь координаты х с безразмерным параметром ? опреде-
определится выражением jc = Щрхр, в котором суммирование вы-
выполняется по трем точкам (р = /, 2, 3) для элемента второго и
по четырем (р = 1, 2, 3, 4) — для элемента третьего поряд-
порядков.
При вычислении кр,,я и км,в по (8.18) следует подставить
вместо их выражение
и применить для кр,,о минимально допустимый, а для kw,?
— обычный порядок интегрирования (см. табл. 5.1).
Формула преобразования (8.21) остается в силе и в этом
случае, причем значения индексов р, q должны выбираться в
зависимости от значений индексов г, s:
r(s) i или /
Р(Я) /
I или т п или /
2 3
k или g
4
В (8.20) r\rj= 1 для г = п, k и цг = —1 для г = t, g.
Матрица к" будет иметь блочную структуру, вид которой
проиллюстрируем на примере элемента второго порядка:
к" =
Симм.
ко
ко
0
0
ко
0
0
ко
кв
0
0
0
0
ко
0
0
0
0
-к0
к«
i
/
/
т
п
t
299
ГД€
go
Здесь жесткость пружин g0 — Ehll (ЗЯ3). _
Для элемента третьего порядка матрица к" имеет анало-
аналогичную структуру; значение g0 можно взять вдвое меньшим,
чем в (8.25).
Формулы (8.29), (8.30) также сохраняют свой вид. Направ-
Направляющие косинусы осей х, у определяют по координатам узлов
i, /, /, т, пользуясь соотношениями (8.27), (8.28).
§ 8.4. Составные конечные элементы лонжеронов
Будем теперь считать элемент лонжерона составленным
из конечных элементов поясов и стенки. На рис. 8.4, а пока-
показан элемент первого порядка с четырьмя узлами i, j, I, т. Так
же как и в случае элементов, описанных в предыдущем па-
параграфе, узлы совпадают с узлами конечных элементов обшив-
обшивки, срединная поверхность которой обозначена на рисунке
штрихпунктирными линиями.
Штриховыми линиями AtAi и AjAm на рисунке отмечены
осевые линии поясов, проходящие через центры тяжести их
поперечных сечений; верхний пояс отмечен индексом «в», ниж-
нижний — «н»; цифрами /, 2, 3, 4 отмечены угловые точки стенки.
Помимо координат узлов хТ, ут, гт (г = i, j, I, rri) исходная
информация для элемента включает в себя площади сечения
/*"„, FK верхнего и нижнего поясов, расстояния ав, Og от их
осевых линий до срединной поверхности обшивки, толщину h
стенки, ее высоты #{, Щ в крайних сечениях элемента, а так-
также упругие характеристики материалов (Ев, Ев—для поясов
и Е, G, ц — для материала стенки).
При вычислении жесткостных характеристик элемента
будем исходить из предположения, что от узла / к узлу / и от
узла / к узлу m перемещения точек изменяются по линейному
закону. Учитывая, что размеры сечений поясов малы по срав-
сравнению с высотой лонжерона, будем пренебрегать изменением
в них нормальных напряжений. Таким образом, мы считаем,
что пояса находятся в условиях одноосного напряженного
состояния с равномерным распределением напряжений по се-
сечению.
Вывод матрицы жесткости выполним сразу в общей систе-
системе координат х, у, г. Каждый узел имеет три степени свободы:
перемещения vrx, vry, vrz в направлении координатных осей.
300
Обозначим, как и ранее, через
Vе = {Vj \j V; Vm }
матрицу узловых перемещений элемента, в которой
vP = {vrx vry vTZ) (r = i, j, t, m).
Матрица жесткости к* рассматриваемого конечного эле-
элемента может быть получена как сумма трех матриц
ке = кв
к",
(8.31)
первые две из которых представляют вклады поясов, а по-
последняя — вклад стенки.
Рис. 8.4
Переходя к вычислению отдельных слагаемых, начнем с
верхнего пояса. Как уже говорилось, он представляет собой
одномерный элемент с равномерным распределением напря-
напряжений по сечению. Длину /в осевой линии пояса можно счи-
считать совпадающей с расстоянием между узлами i, I:
301
Направляющие косинусы этой линии считаем совпадающи-
совпадающими с направляющими косинусами прямой, соединяющей узлы
Кь *= (*i — xi)llB' ^г/в = (Ус — yt)HB\ Kb = {г,— г,I1в.
Здесь принято, что пояс имеет направление от узла I к узлу I.
Смещения точек Л,- и Лг в направлении координатных осей
обозначим через uix, uiy, uiz, ulx, uly, uh. Они не равны пере-
перемещениям узлов i, /, так как точки Л,- и Л( не совпадают с по-
последними.
Обозначим, далее, через vJ; = {ирх иру ирг} (р = i, I)
матрицы перемещений точек At, Л,, а через vB — {уг уг}~
матрицу перемещений верхнего пояса. Если пояс отнесен к
этим шести перемещениям, то его матрица жесткости будет
иметь вид
Г^ ?Х (8-з2)
к/, ки]
Отдельные подматрицы кв (р, q == i, I) имеют размер
3 X 3 и даются выражениями C.19), которые с учетом приня-
принятых здесь обозначений запишем так:
к~в '•в 'ъ е Е 1 в Г 1 в /о ЧЧЧ
РЯ — ; 5л =д ло ло> уэ.оо)
где ?* 1; ?, = I; X; = [Ххв Х„в Х„].
Приведем далее матрицу (8.32) к двенадцати узловым пе-
перемещениям vc. Исходя из линейного закона распределения
перемещений от узла / к узлу / и от узла / к узлу т, выразим
перемещения точек Ait Al через перемещения узлов t, /, /, т:
,, 71 _L VJX — v'x п ¦ о -. i_ °тх vlx „ /о ол\
Uix — Vix~i ав. "(я — у/зс-г ав. (8.с54)
Формулы для остальных компонент матрицы vB получа-
получаются из (8.34) заменой индекса х на у или г. Через Ни Н2 обо-
обозначены расстояния между узлами i, j и /, m, рассчитываемые
по формулам
*= ]/(^. -х;J + {у, -уtf + (г,--гг)а,
= V(xm- xtf + (ym- yif + (zm -г,J:
Шести соотношениям типа (8.34) можно придать привыч-
привычную форму vB = XB\e, если положить
^U?. tii о о 1
[о о vn vlm\
где
В /l % \ | . 1 В "в I
KU — М 7J— ) «3. Л/m = -7Т- *3
(8.35)
Здесь через 13 обозначена единичная матрица размером 3x3.
Выполнив преобразование кв = Х,вГ какв, получим иско-
искомую матрицу жесткости верхнего пояса размером 12 х 12.
Как обычно, представим ее в блочной форме
к?/ k?i
к?/
к// к?,
СИММ. kjjjm
Отдельные подматрицы можно записать в виде
вГГв
^s (г, s= i, j, I, m),
(8.36)
где
_ |* для г = i или /; _ Н
[I для г = / или т; \l
для s= i или у;
для s=/ или т.
Точно так же вычисляется матрица жесткости кн нижнего
пояса. Она имеет такую же структуру, что и кв, а отдельные
ее подматрицы
где
.(н)_»нГГн .н , . ¦ f v
KfS ЛрГ К-рд A,gS (', S I, J, 1, ГЛ.),
_ (/ для r = i или /; _| / для s = j
(8.37)
или
для r=l или m;
(m для s = / или /и.
303
Здесь, по аналогии с (8.33),
Л-хн Лжн A^,H A
EHFH
xn
(8.38)
Симм.
причем Кхв, kyil, KZH определяются соотношениями
In = V(Xm - X;)* + (*/m - ?,)« + (Zm - Z jf.
Матрицы %нг, %" в (8.37) даются равенствами
С/ =-J-1,; Cm= (l - -^-) I3- (8.39)
Переходя к конечному элементу стенки, начнем с опреде-
определения координат его узлов. Обозначим через alt a2 расстояния
соответственно от точки / до узла i и от точки 2 до узла /. Бу-
Будем считать, что отношение ах/а2 равно отношению aja^. Учи-
Учитывая, что ах + а2 = Я, — Н[, находим
fll - (Нг - Н{I A + ajaj; а2 = (Я, - H[)l (I + aJtQ.
Подобным же образом можно определить расстояния си,,
at от точек 3, 4 до узлов /, т:
а3 = (Я2 - Щ)/ A + аа/ав); а, = (Я2 - Я^)/ A + ajaj.
Теперь координаты точек /, 2, 3, 4 можно выразить через
координаты узлов i, j, I, m:
= I 1 I X; -\ Xi, Xo == X) +1 l
v .
Ht 1 '
Формулы для координат у и z получаются из этих равенств
соответствующей заменой обозначений.
Обозначим далее через их, иу, uz перемещения произволь-
произвольной точки стенки, через ихр, иур, uzP (р = J, 2, 3, 4) — их
узловые значения и введем матрицу перемещений конечного
элемента стенки
V = {Ut U2 U3 U4},
304
где Up = {ихр иур Uzp} — матрицы перемещений отдельных
узлов стенки. Через к обозначим матрицу жесткости конечно-
конечного элемента стенки, отнесенную к перемещениям v.
Для вывода к воспользуемся изопараметрической форму-
формулировкой элемента, аналогично выводу матрицы жесткости
конечного элемента обшивки в § 8.2.
Положение произвольной точки стенки определим безраз-
безразмерными координатами ?, tj: .
х = ЩРхр; у = Z%yp; г = 5typzp.
Здесь
Фр(&. Ц)=-тA+ЫH + ЪЧ) (р = 1, 2,3,4),
а суммирование ведется по четырем узлам стенки. Узловые
значения |р,'т)р параметров |, tj даны на рис. 8.4, б.
Далее могут быть вычислены параметры
где
. 1 дх . 1 ду . _ 1 Дг
Лцд: т —; Ацу=-д —, Л^г — —г —-.
Аппроксимация перемещений выполняется по формулам
Так как стенка лонжерона моделируется по высоте одним
конечным элементом, то необходимо позаботиться, чтобы в нем
правильно воспроизводилось состояние чистого изгиба, т. е.
следует исключить ложный сдвиг (см. § 5.2). Как говорилось
в § 6.5, этого можно добиться, применяя пониженный порядок
интегрирования при вычислении вклада поперечной дефор-
305
мации в матрицу жесткости. Поэтому в матрице е выделим
деформацию е^, полагая е = {е* е1а}, где е* = {еп е22}.
На основании G.116) имеем
8* = Г*
«I
J
где
ди
ди
I i ди , 1 « ди
л\ д\ лг\ &Ц
а матрицы Г* и Г содержат соответственно первые две и по-
последнюю строки матрицы Г G.117):
'-V2
о от r=_L_ 2 01,
1 -Vj' Vf=?
Через и = {ыж иу иг) обозначена матрица перемещений.
Далее выразим деформации через узловые перемещения
в форме е = 2 Эр ир, где
(8.40)
1
Напряжения о* = {а„ а?2} и а,2 связаны с деформация-
деформациями равенствами о* = х*8*, al2 = Gels, в которых
1-и* L^ lj
Их можно представить и в виде о = кг, полагая а= {о*а12},
о
Теперь можно найти отдельные блоки матрицы к:
306
Если учесть блочную структуру матриц рр, pq, x, то с
учетом равенства dx=hAiA-n j/^l —Y2d|dr] получим расчет-
расчетные формулы:
с, G»
(8.41)
Л Л
При вычислении матрицы kpq,a, представляющей собой
вклад деформации е12, воспользуемся одноточечным интегри-
интегрированием по Гауссу; это соответствует минимально допусти-
допустимому порядку интегрирования. Что касается кр9,в, то здесь
необходимо взять по две точки Гаусса для каждой из перемен-
переменных |, Г|. _
Матрица к отнесена к перемещениям точек /, 2, 3, 4. Пе-
Переход к перемещениям узлов i, /, /, т выполняется так же,
как и для конечных элементов поясов. Перемещения этих
точек выражаются через перемещения узлов по формулам:
jx—vix); ихг = v}s
(vis~- v}X);
«*з =Oj«4—j*- (vmx— Vix); uxi=vmx + -±-(vlx—vms);
остальные компоненты получаются из этих соотношений соот-
соответствующей заменой индексов.
Все эти равенства можно записать в форме v = %\e, где
\ \ ft П
О 0 Ui
_0 0 %ц л4(
Здесь
Э07
*3* == ( ' — ~Tf~ I *з>
\ /
(8.42)
Через 13 обозначена, как и выше, единичная матрица третьего
порядка. __
Далее воспользуемся формулой кст = № кА,. Переходя к
блочной форме
¦ СТ .СТ | СТ 1 СТ
К/,- К,у кц К/от
кст —
kw к/7
Симм.
можно получить следующее выражение для отдельных под-
подматриц:
кст уу» Г I /о доч
rs — ?i j?j ЛрР Kpg Лд8, \O.tof
Р Я
где г, s = i, j, I, т. Суммирование в (8.43) выполняется по
индексам р, q, значения которых должны выбираться в зави-
зависимости от индексов г, s:
г (s)... i или / / или т
р (q)... 1,2 3,4
Таким образом, определены отдельные вклады в матрицу
жесткости к* конечного элемента лонжерона. Блоки этой ма-
матрицы:
tfs -k,Bs+ k,Hs + k,cJ (r, s == i, j, I, m). (8.44)
Подобным же образом строятся и более сложные конечные
элементы второго и третьего порядков (рис. 8.4, в, г). В этом
случае пояса рассматриваются как одномерные элементы с тре-
тремя или четырьмя узлами. Аппроксимация геометрии и переме-
перемещений в них осуществляется с помощью функций
(!—?*)].
или
308
где для верхнего пояса индекс р принимает значения i, I, n
или i, I, n, k, а для нижнего — /, т, t или /, т, t, g. Узловые
значения параметра ? указаны на рис. 8.4. Матрицы жестко-
жесткости поясов в блочном виде будут иметь размер 3x3 или
4x4. Если отнести их к перемещениям узловых точек, ле-
лежащих на осевых линиях поясов, то они могут быть вычислены
по формуле E.86), которая с учетом принятых обозначений
примет вид
\
=?H f Fepjp,i4d&. (8.45)
Здесь А = Vx'' + у\ причем х' = Щ'„хр, у' = Ity'pyv, где
if'p = di|)p/di, а суммирование ведется по всем узлам пояса.
При расчете х', у' можно в качестве хр, ур брать координаты
соответствующих узлов конечного элемента вместо коорди-
координат узлов пояса. Матрица рг вычисляется по E.85). Интегри-
Интегрирование в (8.45) можно осуществлять по правилу Гаусса с тре-
тремя точками для элемента второго и с четырьмя — для элемен-
элемента третьего порядков.
К узловым перемещениям v* переходим так же, как и в пре-
предыдущем случае. Формулы (8.36), (8.37) остаются в силе, при
этом индексы р, q находятся в следующей зависимости от ин-
индексов г, s:
r(s) ( или / I или т п или / k wng
p'q) для пояса:
верхнего « I n k
нижнего / т t g
Помимо введенных ранее матриц (8.35), (8.39) здесь будут
фигурировать аналогичные матрицы для промежуточных уз-
узлов. Выражения для них можно получить из (8.35), (8.39),
подставляя вместо Нг или Н2 величины Н3 или Я4. Последние
вычисляются через координаты промежуточных узлов ана-
аналогично Я, и Н2.
Аппроксимация геометрии и перемещений стенки для
элемента второго порядка выполняется с помощью функций
ц)= Vp2 [Ego +S
Р= /. 2, ..., 6),
309
а для элементов третьего порядка — с помощью функций
Блоки матрицы к вычисляем по (8.41). При численном ин-
интегрировании в \lP4,b следует применять обычный, а в кро.о —
пониженный порядок интегрирования (см. табл. 5.1).
Приведение к к узловым перемещениям конечного элемен-
элемента лонжерона выполняется согласно (8.43), но здесь индексы
р, q определяются правилом:
г Is) i или / I или m я или t k или g
P(q) 1, 2 3, 4 5, 6 7,8
Появляющиеся здесь дополнительно матрицы Хрг опреде-
определяются аналогично (8.42).
§ 8.5. Двухузловой конечный элемент шпангоута
Рассмотрим теперь конечные элементы для моделирования
шпангоутов. Предполагается, что шпангоут представляет
собой плоскую криволинейную раму. Плоскость шпангоута,
проходящая через центры тяжести его поперечных сечений,
произвольно ориентирована относительно осей х, у, г. На по-
положение главных осей инерции поперечного сечения никаких
ограничений накладывать не будем.
В простейшем варианте конечноэлементной идеализации
шпангоута (рис. 8.5, а) используем набор прямолинейных
двухузловых конечных элементов (элементов первого поряд-
порядка). Как и в случае конечных элементов лонжеронов, узлы
совпадают с узлами конечных элементов обшивки (штрих-
пуиктирной линией отмечена срединная поверхность обшив-
обшивки).
Для каждого конечного элемента будем пользоваться мест-
местной системой координат х, у, г, начало которой помещается
в центре тяжести среднего сечения элемента. Оси х, у лежат
в плоскости шпангоута (рис. 8.5, б), причем ось х совпадает
с осью элемента. Предполагается, что ориентация плоскости
х, у относительно осей х, у, г определяется тремя узлами, два
из которых — узлы элемента i, j, а третий — какой-либо до-
дополнительный узел шпангоута п, не лежащий на прямой, сое-
соединяющей узлы I, /.
310
Направления осей х, у, z будем определять следующим об-
образом. Ось х всегда направляется от первого узла конечного
элемента ко второму (в последующем изложении считается,
что узел i — первый, а узел /—второй). Ось z направлена
в сторону поступательного движения правого винта, находя-
находящегося в точке п и вращающегося вместе с радиусом-вектором,
начало которого также лежит в точке п, при этом конец радиу-
радиуса-вектора должен находиться на оси х и двигаться в отри-
отрицательном ее направлении. Наконец, направление оси у долж-
должно быть взято таким, чтобы оси х, у, z образовывали правую
систему координат. Этих правил необходимо придерживать-
придерживаться, в частности, при вычислении центробежного момента инер-
инерции J-- сечения лонжерона.
В исходных данных для элемента помимо номеров i, j, n
должны быть также указаны площадь F поперечного сечения,
его моменты инерции /-, J- относительно осей у, z, центробеж-
центробежный момент инерции /—, жесткость сечения на кручение С/кр
и модули упругости Е, G. Если поперечное сечение шпангоута
образует вместе с обшивкой замкнутый контур, то это должно
быть соответствующим образом учтено при вычислении жест-
жесткости на кручение. Кроме того, должны быть заданы ко-
координаты у0, 20 точки сечения, лежащей на линии узлов i, j
(рис. 8.5, б). Наконец, следует задать параметры v-, v-, учи.
"бывающие неравномерность распределения по сечению пере-
перерезывающих сил в плоскостях ху и xz.
311
Пусть vTX, vry, vTZ — перемещения типового узла г в на-
направлении осей х, у, z, a #тх, ftry, ftrz — повороты соответст-
соответствующего сечения шпангоута. Тогда
vr = {vrx vry vrz $rx $ry &rz}.
Таким образом, конечный элемент шпангоута имеет две-
двенадцать степеней свободы:
Vе = {Vj V;}.
Положительные направления перемещений vr даны на
рис. 8.5, а; углы поворота сечения изображены в виде векто-
Рис. 8.6
ров с двойной стрелкой (их направления определяются пра-
правилом правого винта).
Обозначим далее через и-, и-, игг смещения произвольной
точки элемента, лежащей на оси х, в направлении местных осей
х, у, г, через 6-, 9^, 9- — повороты соответствующего сечения
относительно тех же осей, а через u-r, u-r, u-Zr, Q^r, 9-^, Q-r
(г = i, 0 — узловые значения этих величин (рис. 8.6).
Прежде всего найдем матрицу жесткости элемента, отне-
отнесенную к перемещениям v = {ut Uj}, где
«, = {«7, и- и- 9- 9- 9-).
Перемещения точек, не лежащих на оси х, не определяют-
определяются однозначно введенными перемещениями вследствие того,
что при кручении бруса его сечения не остаются плоскими, а
депланируют. Это затрудняет применение стандартного под-
подхода, использовавшегося ранее. Поэтому прежде чем перехо-
дить к аппроксимации перемещений, преобразуем формулу
для потенциальной энергии деформации
U — — i er xedr
2 .
2
и вытекающее из нее выражение для матрицы жесткости эле-
элемента
Предположим сначала, что кручение бруса отсутствует. Рас-
Растяжение и изгиб бруса сопровождаются появлением про-
продольной деформации е-- и деформаций поперечного сдвига
е--, г--. Этим деформациям соответствуют напряжения а- - =
Е % G
Полагая е = {е- е-- е--г); а = \а-х- о-- а--}, имеем 0 = хе, где
[? 0 01
0 G 0|-
0 0 GJ
Потенциальная энергия деформации в этом случае
U =± Je^xEdT =-1 j(?e^+ Gef^ + Ge|-)dT. (8.46)
Исходя из предположения о том, что сечения при изгибе
остаются плоскими, можно написать следующий закон рас-
распределения деформации е- - в поперечном сечении:
y (8-47)
где е' - — продольная деформация в центре тяжести сечения;
%- и%- — изменения кривизн осевой линии.
Заменив с!т произведением dfdx, где dF — элементарная
площадка в поперечном сечении, выполним интегрирование
в (8.46) по площади поперечного сечения с учетом соотноше-
соотношения (8.47). Памятуя о том, что у, z — центральные оси, при-
приходим к следующему выражении?:
u
= т J iEF («bJ
/7 Ц
-_ Y- у— -
UZ Ли Лг
Деформации е-- и е-- при интегрировании считались по-
постоянными в поперечном сечении, а для учета их неравномер-
неравномерности введены упоминавшиеся выше коэффициенты v- и v-,
зависящие от формы сечения.
Пусть теперь брус дополнительно испытывает кручение.
Как известно из курса сопротивления материалов, потен-
потенциальная энергия деформации, накапливаемая при кручении,
где %х — погонный угол закручивания. Объединяя это выра-
выражение с предыдущим, получаем формулу для потенциальной
энергии деформации бруса в общем случае пространственного
нагружения:
где
B-=EF; B- = v-GF; B-=
.
Выражение для U можно записать в матричном виде
{/=— (Vxsdx,
(8.48)
полагая e= {e^ e~ e~ /- x- xF);
S- 0 |
•л =
fi?
0 D-
(8.49)
Исходя из (8.48), выражение для матрицы жесткости эле-
элемента в местной системе координат можно вычислять в при-
привычной форме
jr (8.50)
если под Э — понимать матрицу, связывающую 8 с узловыми
перемещениями соотношением г — jjv. Вид матрицы 0 зави-
зависит от характера аппроксимации перемещений и будет опреде-
определен ниже.
При блочном вычислении матрицы жесткости к следует
представить матрицу 0 в виде р = [0,- 0^]; тогда отдельные
блоки матрицы (8.50) имеют вид
К* = J ?г »Ф8<? (Л s =», /). (8.51)
Выразим далее параметры деформации 8 через перемещения
и углы поворота сечения. Обозначим через и|, и|, и| переме-
перемещения произвольной точки, не лежащей на оси бруса, в на-
направлении осей х, у, z. Перемещения в поперечном сечении при
изгибе изменяются по закону:
-t/9-; u^u-; u^ = u-. (8.52)
Тогда
QUt Аи- АО- d8_
Xx *- л" J- У л- '
дх Ах Ах Ax
Сопоставляя это равенство с (8.47), видим, что введенные
выше параметры деформации е|-, х-, X; связаны с перемеще-
перемещениями зависимостями
d к_ d 0- d О-
dA: d л: d x
Для деформаций поперечного сдвигав--, е-- имеем
dui- dul d и—
¦* » — Г _ _ °2 >
дх ду Ах
ди\ ди\ аи- . _л.
е._ = __? J—JL s= __1.1- 0-. (8.54)
хг дх ^ дг Ах ^ » К '
315
Наконец, погонный угол закручивания
dO-
d х
(8.55)
Возвращаясь к аппроксимации перемещений конечного
элемента, запишем
"х = 2 ¦' иТг> = S *«¦ "Fr; "Г = s*r ujj
еГ = S Ф- %,; 6F = 2 Ъ вГг! 9Г * 2 *г eSV (8'56>
Здесь суммирование ведется по двум узлам элемента; ipr =
= A + lri)/2; безразмерная координата | = 2л;// принимает
в узлах значение |г = —1, \} = 1.
Переходя в формулах (8.53)—(8.55) к дифференцированию
по |, внесем в них соотношения (8.56). В итоге получим связь
параметров деформации е с узловыми перемещениями, кото-
которую в матричной записи можно представить в требуемом виде
в = 2prv,., где для г = i, j
0 if>'r
О О
О О
О О
О О
о о
о о
о
о
о
о
0
0
о ¦
о
о
о
о о
0
(8.57)
Через г|з; в (8.57) обозначена производная
Переходя далее в (8.51) к интегрированию по |, имеем
К>=-~
— 1
316
Подставляя сюда (8.49), (8.57) и пользуясь одноточечным
интегрированием, получим
о
о
о
о
о
о
о
о
о
Иг
о о
о о
В- О
О D-
^в- о % +
0
о
i?j«B_
4 г
О
(8.58)
Теперь приведем матрицу к к узловым перемещениям ve.
Вычислим прежде всего направляющие косинусы осей х, у, Г.
Считая, что ось х параллельна прямой, соединяющей узлы
(*, /, запишем
I = V (х,-х,)* + (yj-ytf + (г,-г,)« .
ж, Х , К^ можно рассматривать как ком-
компоненты единичного вектора е-, направленного вдоль оси х:
Три величины Я-ж, Х- ,
317
Здесь ех, еи, ег — орты общей системы координат.
Рассмотрим далее вектор
~R=-xnl ex + yni ey + zniez,
имеющий начало в узле t, а конец — в точке п. Для его ком-
компонент введены сокращенные обозначения
хП1 ~ хп — xt\ yni = Уп~ Уи zni = гп — Zj. (8.59)
Векторное произведение R х е~х дает некоторый вектор N,
совпадающий по направлению с осью г. Его компоненты оп-
определяются равенствами
Разделив их на длину
WЩЩ (8.61)
вектора Л^, получаем выражения для направляющих косину-
косинусов оси z:
, K~ =NZ/N. (8.62)
~> <»
Наконец, единичный вектор е- вдоль оси у найдем с помо-
J -*¦ -+
щью векторного произведения е- х е-, где е- — единичный
вектор с компонентами (8.62), направленный вдоль оси г. Учи-
Учитывая, что компоненты вектора е- есть направляющие косину-
косинусы оси у, приходим к равенствам
пух "гу хг гг ху> "уу пгг Чех l
(8-63)
Теперь выразим перемещения ut в узловом сечении i че-
через V;. Для этого нужно, во-первых, спроектировать переме-
перемещения v,- на направления местных осей координат. Если, да-
далее, известно перемещение и-х вдоль оси х произвольной точ-
точки сечения, то перемещение в центре тяжести сечения соглас-
согласно (8.52) будет
318
где у, г — координаты рассматриваемой точки. С учетом этого
можно найти требуемую связь между перемещениями ut и v*.
Введя матрицы
представим эту
«Д
u-t
Qxt
_ «а _
связь
*г
X-
0
0
0
в виде
' У о ^Г
—zo %¦
0
0
\
Это соотношение имеет обычную форму иг = A,ov,-, где
0
0
0
0
V
(8.64)
О
Подобным же образом в узле / имеет место зависимость
U; = ^ov;- Следовательно, связь между матрицами v =
и ve = {vj V/} можно записать в виде v = "k\e, где
О ^о
Использование формулы ке —№ кХ, завершает вычисление
матрицы жесткости рассматриваемого конечного элемента.
В блочном представлении
Г к'
где отдельные блоки
k» К]
(r,s = i,
(8.65)
319
§ 8.6. Криволинейные конечные элементы шпангоута
Теперь рассмотрим конечные элементы плоского шпангоу-
шпангоута второго и третьего порядков (рис. 8.7). Каждый узел имеет
шесть степеней свободы — три перемещения и три угла пово-
поворота:
Кривую, проходящую через узловые точки, зададим в па-
параметрической форме: х = 2г]5гл:г, у = 2г|)гг/г, г = 2лрггг, где
tyr (?) — встречавшиеся уже ранее функции E.82) или E.83).
Узловые значения параметра ? даны на рис. 8.7; суммирова-
суммирование выполняется по всем узлам элемента.
¦ %$
Дифференциальный отрезок ds кривой связан с d| соот-
соотношением E.70) ds = Аа%, а его направляющие косинусы
равны
JL йх ¦
A dg '
1 dy .
Т7Г
1 dz
где
В каждом поперечном сечении элемента введем местную
систему координат х, у, z с началом в центре тяжести сечения.
Оси х, у находятся в плоскости шпангоута, причем ось х яв-
является касательной к оси элемента в данном сечении.
Предполагаем, что в пределах конечного элемента размеры
поперечного сечения изменяются слабо. Тогда ось бруса и
проходящая через узловые точки кривая будут почти экви-
эквидистантны, и можно принять, что матрица %-х — [%-х Х^ К^]
направляющих косинусов оси дг совпадает с матрицей Ц =
= Г^1л ^!у ^lz\-
ЬТ = Ц. (8.66)
320
Направления осей у, г определим по тем же правилам, что
и в случае двухузлового элемента. Пусть хп, уп, zn — коорди-
координаты дополнительного узла п, определяющего в совокупности
с узлами i, j ориентацию плоскости шпангоута. В качестве
дополнительного может быть взят, в частности, промежуточ-
промежуточный узел элемента, если только он не лежит на одной прямой
с узлами i, j. Тогда компоненты матриц
могут быть найдены по (8.59)—(8.63). Отметим только, что здесь
в отличие от случая двухузлового элемента направляющие
косинусы местных осей, вообще говоря, не постоянны, а из-
изменяются с изменением параметра |.
Выразим далее параметры деформации
- | о ,
е — е— е— ?— у— у— у—
' X X X у X Z ™Х **у "Z /
через перемещения. Пусть u = {ux uv uz) — матрица пере-
перемещений центра тяжести произвольного сечения в направле-
направлении координатных осей, а 8= {Qx Qy 0Z}—матрица углов
поворота этого сечения относительно тех же осей.
Продольная деформация осевой линии может быть соглас-
согласно E.77) определена выражением
Пусть, далее, 0- = %-Jd, 0- = Х-в, 0- = кф — углы по
ворота плоскости сечения относительно местных осей коорди-
координат. Эти углы положительны, если соответствующие им век-
векторы направлены в сторону возрастания кординат х, у, г. Че-
Через со-, coj обозначим углы поворота касательной к осевой ли-
линии шпангоута относительно тех же осей. Будем считать их
положительными в том случае, когда углы между положитель-
положительным направлением касательной к оси шпангоута и осями г, у
становятся острыми (положительное направление касатель-
касательной совпадает с направлением оси х). На основании E.79) име-
имеем:
1 . du 1 . du
со— =— к ; со- -= — к .
у А г й% г А у А1
Деформации поперечного сдвига г--, е-- определяются вы-
выражениями
е = о 0—; е—=со—1-В—,
х у г г ' х г у ¦ у '
11 Зак. 651 321
в которых знаки проставлены в соответствии с правилами зна-
знаков для введенных выше углов. Отсюда приходим к соотно-
соотношениям
Можно показать, далее, что выражения для параметров
- ^~' ^г Даются Для криволинейного стержня формулами
X_ = _UXJ»; x_=_Lv^i: X_=_U_!±.(8.69)
Ajc A x Л* ' KV A v H ? Лг Л г H ? V 7
Переходя к аппроксимации перемещений и углов поворо-
поворота, запишем
и = 2i|)rur; в = Зд|)гег.
Здесь иГ1, вг — значения матриц и, в в узловых сечениях.
На основании (8.67)—(8.69) приходим к соотношению е ==
= 2frvT, где v"r = {ur6r}. a
0
К V
о
о
о
(8.70)
Здесь i|j; = di|3r/di.
Заменяя в (8.51) dx на Adt,, получаем расчетную формулу
(8.71)
— 1
для блоков матрицы жесткости к, отнесенной к перемещениям
vr. Матрица у, здесь дается формулой (8.49). Интегрирование
можно выполнить по трем точкам Гаусса для элементов вто-
второго и по четырем — для элементов третьего порядков. Для
повышения скорости сходимости решения можно выделить в
krs вклад деформаций поперечного сдвига к--, t--- и исполь-
использовать при его вычислении минимально допустимый порядок
322
интегрирования в соответствии с табл. 5.1. Если шпангоут
имеет переменное сечение, то входящие в матрицу х его гео-
геометрические характеристики удобно задать в узловых сечени-
сечениях, аппроксимируя их при этом подобно тому, как это дела-
делается для перемещений.
В заключение остановимся на переходе к узловым переме-
перемещениям конечного элемента v'. Пусть в некоторой точке М
сечения конечного элемента известны вектор поступательного
перемещения v == vxex + vyey + vzez и вектор поворота се-
чения ¦& = ®хех + ®уеу + bzez, где ех, еу, ez — орты общей
системы координат.
Рассмотрим другую точку N сечения, положение которой
относительно точки М определим вектором
Вектор поступательного перемещения точки N, который
мы обозначим через v*, выражается через перемещения точки
М равенством (см. §7.12) v* = v + ¦& X р. Отсюда можно
прийти к следующим выражениям для компонент вектора
(8.72)
Воспользуемся этими соотношениями для установления
связи между v и v'. Рассмотрим, например, сечение шпангоу-
шпангоута, содержащее узел г. Под точкой М будем понимать сам узел,
а под точкой Af — центр тяжести сечения. Если ут, zT — мест-
местные координаты узла г, то вектор рг в местной системе коорди-
координат х, у, z имеет проекции 0, —ут, —гт. Зная направляющие
косинусы осей у, г, вычисляем координаты вектора рг:
Рхг = -{Уг \х, г + 2г hx, л); Руг = — (^"г ^-уу, г + *Г^. г)'
Здесь дополнительный индекс г в обозначении направ-
направляющих косинусов указывает на то, что соответствующая ве-
величина должна быть взята в узле г.
11* 323
Понимая под v*, v*y, v* перемещения ихт, иут, uzr на основа-
основании (8.72) и тождеств 0ЖГ_= $тх, вут = i%y, 62Г = drz прихо-
приходим к соотношению вида vr = kTvT, в котором
(8.73)
h
0
— Pzr
Pur
Pzr
0
¦ Pxr
— Py,
Pxr
0
0
Пользуясь формулой
приводим отдельные блоки матрицы жесткости к общей систе-
системе координат.
§ 8.7. Заключительные замечания
Объединение конечных элементов при расчете тонкостен-
тонкостенной конструкции выполняется по общим правилам. Суммируя
подматрицы жесткости и сил с одинаковыми индексами соглас-
согласно равенствам
получаем матрицу коэффициентов и матрицу правых частей
в системе уравнений
К v = Р + Р,
где Р — матрица сосредоточенных узловых сил.
Для решения этой системы необходимо исключить из нее
известные перемещения. Если рассчитывается весь самолет
целиком, то система является свободной, и необходимо нало-
наложить на нее шесть связей, обеспечивающих неподвижность
самолета как жесткого целого (см. § 3.9). Исключая соответст-
соответствующие шесть перемещений, придем к системе
Кап Vo = Ра -[- Ра,
содержащей оставшиеся неизвестные перемещения. Матрица
Каа является невырожденной, и система уравнений допуска-
допускает решение. Отметим, что при наличии соответствующих про-
программ удобнее всего воспользоваться методом подконструк-
ций (см. § 5.4). Это облегчает подготовку и контроль исходных
данных, позволяет вносить изменения в конструкцию без из-
излишних затрат машинного времени, упрощает анализ полу-
полученных результатов.
.324
Однако подробная конечноэлементная модель самолета
может включать в себя десятки и даже сотни тысяч узловых
перемещений, в связи с чем полное решение такой задачи мо-
может оказаться невыполнимым на имеющихся ЭВМ. Поэтому
на практике часто выполняют поагрегатныи расчет, рассматри-
рассматривая, например, крыло как независимую конструкцию, не-
неподвижно закрепленную в местах соединения с фюзеляжем.
Соответствующие перемещения считаются нулевыми и исклю-
исключаются обычным образом из системы уравнений относительно
узловых перемещений крыла. Такой приближенный подход
согласуется с традиционными методами расчета авиационных
конструкций.
После отыскания узловых перемещений вычисляются на-
напряжения в отдельных конечных элементах. При этом для каж-
каждого конечного элемента по формуле типа v = fa?e находятся
узловые перемещения, соответствующие местной системе коор-
координат, а затем с помощью равенств е = Pv~, a = хе рассчиты-
рассчитываются напряжения. В некоторых случаях выводится допол-
дополнительная информация. Например, для конечных элементов
обшивки могут быть подсчитаны главные напряжения и опре-
определены их направления, в сечениях лонжеронов или шпан-
шпангоутов могут быть найдены интегральные характеристики на-
напряженного состояния (перерезывающие силы, изгибающие
моменты и т. п.).
Отметим, что подготовка исходных данных и анализ по-
полученных результатов являются наиболее трудоемкими эта-
этапами при выполнении практических расчетов по методу ко-
конечных элементов. Это обусловлено большим объемом инфор-
информации и тем, что эти этапы труднее всего поддаются автомати-
автоматизации. Поэтому еще при составлении конечноэлементной мо-
модели конструкции необходимо стремиться к наиболее просто-
простому ее описанию. Это достигается введением участков с регу-
регулярной сеткой конечных элементов, использованием симмет-
симметрии и другими средствами.
§ 8.8. Примеры расчета
Пример 1. Стреловидный кессон (угол стреловидности 45°).
имеющий четыре стальных пояса площадью сечения F =
== 240 мм2 каждый и дюралевую обшивку толщиной h =
— 1 мм (рис. 8.8), на одном конце нагружен поперечной си-
силой Р; на другом его пояса закреплены неподвижно. Верхняя
и нижняя панели обшивки подкреплены дюралевыми стрин-
стрингерами площадью сечения Fo = 40 мм2 каждый. Конструкция
ПВ Зак. 651 325
Рис. 8.8
6,Mlla
WO
80
60
20
' П
>**
У
—5
/
/
¦" о
\
k
\
S,5
i
1,0
i
if
i
„ lf.0 -
К l'"
t \
* 4
326
Рис. 8.9
включает в себя пять равномерно расположенных нервюр
толщиной 1 мм, перпендикулярных оси кессона; помимо них
имеется еще одна нервюра в сечении у заделки.
Р/2
n/p
М/Рг
0,5
О, к
0,3
0,2
0,1
О
-0,1
'0>Z0 W 20 30 НО 50 60 70 80 в'
Рис. 8.11
Для идеализации использованы конечные элементы вто-
второго порядка (рис. 8.9). При этом боковые стенки кессона
вместе с поясами рассматривались как лонжероны и идеали-
идеализировались конечными элементами, описанными в § 8.3, а
стрингеры моделировались одномерными элементами (см.
§5.10). Для обшивки использовались конечные элементы без-
ч
/
ч.
>
X
Г4
ч
N
>*
MB*
327
моментпой оболочки (см. § 8.2). Кривые на рис. 8.9 дают закон
изменения нормальных напряжений в поясах; кружочками и
крестиками отмечены значения напряжений, полученные экс-
экспериментально. Согласие результатов вполне удовлетвори-
удовлетворительное.
Пример 2. Круговой шпангоут (рис. 8.10) нагружен дву-
двумя равными противоположно направленными силами. Радиус
шпангоута г = 1 м, момент инерции и площадь поперечного
сечения ./ = 2,067 • 104 мм4, F = 220 мм2, ? = 7 • 104 МПа.
Эта задача уже рассматривалась ранее (см. § 5.13); здесь
для ее решения использованы описанные в § 8.5, 8.6 конечные
элементы шпангоута первого и второго порядков. На рис. 8.11
представлены зависимости осевой силы N = NIP и изгибаю-
изгибающего момента М — М1(Рг) от угла в, полученные аналити-
аналитически. Крестиками отмечены результаты, полученные при раз-
разбиении четверти кольца на 10 элементов первого порядка, кру-
кружочками — на 10 элементов второго порядка. Последние ре-
результаты получены с помощью местного сглаживания (см.
§5.12) значений N и М с последующим их осреднением по
смежным элементам. Непосредственное вычисление напряже-
напряжений (без сглаживания) обнаруживает здесь такие колебания
ях вокруг истинных значений, которые полностью искажа-
искажают действительную картину. Например, осевая сила N в уз-
узлах первого конечного элемента оказывается равной 11,44Р,
—5.75Р и 11,54/* вместо истинных значений 0; 0,039Р и
0.078/3 соответственно. Эти колебания, обусловленные влия-
влиянием ложных деформаций поперечного сдвига, полностью уст-
устраняются с помощью местного сглаживания, как это видно
из рис. 8.11.
328
ЧАСТЬ IV
ДИНАМИЧЕСКИЕ ЗАДАЧИ
ГЛАВА 9
СООТНОШЕНИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ
В ЗАДАЧАХ ДИНАМИКИ
Если нагрузки быстро изменяются во времени, то возникающие
при деформации тела инерционные силы могут играть существенную
роль, и их необходимо учитывать. Обобщение основных соотношений
метода конечных элементов на случай дннамического нагружения при-
приводит к понятию матрицы масс. Матрица масс имеет в принципе такую
же структуру, что и матрица жесткости, но в отличие от последней она
может быть представлена и в диагональной (или блочио-диагональ-
ной) форме, что важно для снижения затрат машинного времени и объ-
объема памяти ЭВМ. При надлежащей формулировке диагональная матрица
масс так же хорошо описывает распределение массы в конструкции,
как и «согласованная» матрица.
§ 9.1. Предварительные замечания
Пусть на тело действуют сосредоточенные Р, объемные R
и поверхностные р силы, зависящие от времени /. Перемещения
произвольной точки тела в направлении координатных осей
определим матрицей-столбцом и = и (х, у, г, t).
В соответствии с принципом Д'Аламбера будем рассматри-
рассматривать тело как находящееся в равновесии, добавляя при этом
к внешним силам силы инерции. Инерционные силы, действую-
действующие в направлении перемещений и на элементарный объем
dr., определяются матрицей — р ~ dr., где р — плотность ма-
материала. Разделив их на dr., получим силы, приходящиеся на
единицу объема. Обозначая матрицу этих сил через RHH и от-
отмечая дифференцирование по времени точками сверху, запи-
запишем
Rhh= —PU. (9.1)
Пусть, далее, тело разбито на конечные элементы. Рассмот-
Рассмотрим типовой элемент с узлами /, /, ...; матрица узловых пере-
перемещений будет
Vе = {Vt Vj ...},
где v,-, v;, ... —матрицы перемещений соответствующих уз-
узлов, являющиеся функциями времени.
329
Как и ранее, будем исходить из того, что перемещения и
и v<" связаны приближенной зависимостью
=a ve = [a; а-
(9.2)
где а — матрица аппроксимирующих функций.
Строго говоря, в динамических задачах простой зависи-
зависимости (9.2) записать нельзя, поскольку при одних и тех же
мгновенных значениях узловых перемещений деформирован-
деформированная форма конечного элемента может быть различной в зави-
зависимости от предшествующей истории движения. Но если раз-
размеры конечных элементов достаточно малы, то соотношения
вида (9.2) будут и в динамических задачах хорошо аппрокси-
аппроксимировать перемещения точек тела по их узловым значениям.
В задачах статики стержневых систем матричный метод
перемещений приводит к точному (в рамках технической тео-
теории бруса) решению. В случае динамического нагружения точ-
точное решение невозможно при указанном подходе даже для
стержневых систем. Желаемая точность может быть достигнута
путем разбиения стержней на более короткие участки, в пре-
пределах которых применяется приближенная аппроксимация
типа (9.2), но при этом исчезает различие между стержневыми
и непрерывными системами. Следовательно, в динамических
задачах целесообразно рассматривать стержневые системы с
общих позиций метода конечных элементов, как мы и будем
поступать в дальнейшем.
§ 9.2. Матричное уравнение движения конструкции
При статическом нагружении матричное уравнение рав-
равновесия конструкции имеет вид D.19). Соответствующее урав-
уравнение для случая динамического нагружения можно получить,
если добавить к внешним силам инерционные RIIH = —pu.
Заменяя их эквивалентными узловыми силами Р1Ш, получим
вместо D.19) равенство
Ку = Р+Р-ЬРи„. (9.3)
Элементы матрицы Рии перечисляются в том же порядке,
что и перемещения в матрице v. Если vlt v2, ..., vn —матрицы
перемещений отдельных узлов (п — общее число узлов конеч-
ноэлементной модели), то
330
V = {Vi V2...Vn}
и соответственно
*ин 1*ин,1 *ин,2 •• "ин,п »>
где РИН1г — матрица сил инерции для узла г.
Приведение инерционных сил к эквивалентным узловым
силам должно осуществляться так же, как это делалось ранее
для объемных сил. Напомним, что при действии объемных сил
R сначала выполняется их замена сосредоточенными силами
в пределах каждого элемента по формуле
Р*= ("arRdT.
Xе
В блочном виде Ре ==• {Р? Ре ... }, где типовая подматрица
р*= ja'Rdx
Xе
представляет собой вклад данного конечного элемента в экви-
эквивалентные силы в узле г. Далее осуществляется сложение в
узлах вкладов отдельных конечных элементов: Рг = Е Рег;
при этом суммирование выполняется по тем конечным элемен-
элементам, которые сходятся в узле г. Начнем с вычисления матрицы
Р*н узловых сил инерции для типового конечного элемента:
Так как и = а\е, то и = av^, где матрица \е содержит
вторые производные по времени от узловых перемещений ко-
конечного элемента (узловые ускорения). Таким образом,
Рин в — 5 Р«г « d т Vе .
Xе
Этот результат можно представить в виде
p^ = -mcve, (9.4)
где
т' = Ua'adt (9.5)
331
— квадратная симметричная матрица, называемая матрицей
масс конечного элемента; она имеет такой же размер, что и
матрица жесткости элемента ке.
Если записать матрицу а в виде a —[a; aj...], то придем
ч блочному представлению матрицы масс
те
ml. me..
где типовая подматрица
Г9.6)
Подматрица сил Р« в узле г определится теперь так:
Дополнив матрицу ускорений элемента Vе до полной ма-
матрицы v, придадим этому равенству вид
ре —
ин, г
Два последних равенства будут эквивалентны друг другу,
если считать m?s = 0, когда узел s не относится к данному
элементу.
332
Просуммировав вклады отдельных элементов, найдем под-
подматрицу
Суммирование здесь формально распространяется на все
конечные элементы, но фактически оно касается лишь тех из
них, которые сходятся в узле г.
Объединяя все подматрицы P,IH,r в матрицу Рин, запи-
запишем
р„„
• ин,
_ "ин.
1
2
п
m12
¦Щп
_mnl mn2
• tnn
где
mr.s = 2m«s (r, s = /, 2, ..., n).
(9.7)
Здесь суммирование ведется по тем конечным элементам,
которые имеют общие узлы r, s.
Полученный результат можно записать кратко в виде
Р„„=-Му (9.8)
Здесь через М обозначена квадратная симметричная матри-
матрица
m
n
• • • mm~
m21 m22 . . . m2n
_mn, m,,2
mlin_
называемая матрицей масс конструкции и образуемая из
матриц масс конечных элементов по правилу суммирования
333
(9.7). Последнее совпадает с правилом формирования матри-
матрицы жесткости конструкции из матриц жесткости отдельных
конечных элементов.
Внося (9.8) в (9.3), приходим к равенству
Mv + К v = Р + Р, (9.9)
которое и представляет собой матричное уравнение движения
конструкции, идеализированной по методу конечных элемен-
элементов. Оно заключает в себе систему обыкновенных дифференци-
дифференциальных уравнений относительно компонент матрицы v. Если
проинтегрировать эту систему, то получим матрицу v как
функцию времени. Затем по найденным узловым перемещениям
можно в любой момент времени вычислить напряжения в
каждом конечном элементе, пользуясь при этом теми же со-
соотношениями, что и в задачах статики.
Если на тело наложены внешние связи, то в систему урав-
уравнений (9.9) войдут лишь неизвестные перемещения и соответ-
соответствующие им силы. В этом случае при составлении матриц
К и М следует формировать лишь те строки и столбцы, кото-
которые соответствуют неизвестным перемещениям. Ранее такие
уменьшенные в размерах матрицы мы помечали дополнитель-
дополнительным индексом а. Здесь же для упрощения записи этот индекс
будем опускать. Заметим, что если тело не закреплено, то в
отличие от случая статического нагружения нельзя накла-
накладывать на него связи, фиксируя его положение в пространстве,
ибо это приведет к появлению динамических реакций, которые
в действительности отсутствуют. Как будет видно из дальней-
дальнейшего, отсутствие таких связей не приводит к каким-либо
трудностям при решении динамических задач.
Итак, в динамических задачах помимо матрицы жесткости
и матрицы эквивалентных узловых сил требуется вычисление
еще одной характеристической матрицы — матрицы масс.
К понятию матрицы масс можно прийти также рассматривая
кинетическую энергию системы. Кинетическая энергия эле-
элементарной массы, занимающей объем dx, равна -^ит updx,
где и — матрица скоростей. Отсюда следует, что кинетическая
энергия конечного элемента
^ )
334
Учитывая, что и = а\е, получаем
Т' = — (ve / Г р ат a d т Vе,
Xе
ИЛИ
Те = -^-(\е)т m' ve, (9.10)
где те — прежняя матрица масс конечного элемента (9.5).
Суммируя значения Те по всем конечным элементам, най-
найдем кинетическую энергию всей системы:
r=-vrMv, (9.11)
2 v
где М — введенная выше матрица масс конструкции.
При исследовании сходимости метода конечных элементов
в динамических задачах полезно основываться на вариацион-
вариационном принципе Гамильтона. Применительно к упругим сис-
системам он устанавливает, что при действии консервативных
нагрузок* истинное движение системы от момента времени
tx до момента t2 отличается от всех других тем, что интеграл
[(V-T)dt (9.12)
h
имеет стационарное значение. Здесь V = U + П — потен-
потенциальная, а Т — кинетическая энергии системы. Отметим
попутно, что равенство (9.9) можно получить как необходимое
условие стационарности функционала (9.12).
Так как кинетическая энергия всякой системы есть вели-
величина существенно положительная, то из (9.10), (9.11) следует,
что матрицы те и М положительно определенные: для любых
ненулевых матриц v' hv справедливы неравенства
(\е)Т те \е > 0, vrMv> 0.
Так же как и в случае матрицы жесткости, иногда бывает
удобно вычислить матрицу масс конечного элемента сначала
в некоторой местной системе координат, а затем уже перейти
к общей. Пусть v и \е — матрицы узловых перемещений эле-
* Сила называется консервативной, если совершенная ею работа
зависит лишь от начального и конечного положений точки ее прило-
приложения, но не от пути, пройденного этой точкой.
335
мента в местной и общей системах координат, a m и те — со-
соответствующие им матрицы масс элемента. Пусть, далее,, v
и \е связаны между собой соотношением v = к\е, где к — ма-
матрица преобразования координат. Кинетическая энергия ко-
конечного элемента может быть выражена через v:
Те — — v m v .
Так как v = к\е, то
Т* = — (к Vе )т in (к v") = — (ve )г кт in к ve.
Сопоставляя это выражение с (9.10), приходим к равенству
те == кт т к, (9.13)
посредством которого и осуществляется переход от m к те.
Формально этот результат аналогичен правилу преобразова-
преобразования матрицы жесткости конечного элемента, согласно которому
ке = кТкк. Следует отметить, однако, что при вычислении
матрицы гп в матрицу v должны быть включены все переме-
перемещения, в направлении которых происходит движение, в то
время как при вычислении матрицы к можно игнорировать
перемещения, связанные с движением тела как жесткого
целого (например, поперечные смещения узлов для стержнево-
стержневого элемента, работающего лишь на растяжение-сжатие).
При выводе уравнения (9.9) не были учтены силы неупру-
неупругого сопротивления (демпфирующие силы), которые иногда
приобретают существенное значение. Эти силы могут иметь
различную физическую природу (внутреннее трение в мате-
материале, трение в сочленениях агрегатов, сопротивление возду-
воздуха и т.п.) и соответственно различное математическое описа-
описание. Однако чаще всего принимают, что демпфирующие силы
независимо от их природы пропорциональны скоростям дви-
движения. Матрицу этих сил можно представить в виде произ-
произведения —Cv, где С — так называемая матрица демпфиро-
демпфирования, имеющая такой же размер, что и К или М. При учете
демпфирующих сил уравнение движения конструкции прини-
принимает вид
Mv + Cv + Kv = PrP. (914)
Что касается числовых значений элементов матрицы С, то
для их определения используются обычно экспериментальные
336
данные, получаемые путем исследования затухания собствен-
собственных колебаний конструкции. Учитывая приближенность
описания механизма демпфирования, часто (следуя Рэлею)
берут в качестве матрицы С линейную комбинацию матриц
К и М:
С = аК + ЬРЛ. (9.15)
Тогда задача сводится к экспериментальному определению
двух коэффициентов а и Ъ или даже одного из них, если
другой заранее берут равным нулю. Такой подход является
сугубо приближенным, но он все же позволяет воспроизвести в
общих чертах основные особенности реального поведения
конструкции (в частности, явление затухания собственных
колебаний).
В заключение параграфа коснемся вопроса об учете сосре-
сосредоточенных грузов, жестко связанных с телом. Пусть неко-
некоторый груз массой Мо закреплен в узловой точке г. Если в
матрицу vr входят одни лишь линейные смещения узла, то
матрица инерционных сил для рассматриваемого груза опре-
определится произведением —mrvr, которое учитывается при вы-
вычислении матрицы суммарных сил инерции в узле г:
Здесь тг — диагональная матрица, каждый из диагональных
элементов которой равен Мо. В результате появится допол-
дополнительное слагаемое в подматрице mrr матрицы масс конструк-
конструкции:
mrr = 2merr + m,.. (9.16)
Отсюда следует, что при наличии сосредоточенного груза
необходимо добавить его массу к тем диагональным элемен-
элементам общей матрицы масс, которые соответствуют его линейным
смещениям. Если бы, в частности, вся масса конструкции
была сосредоточена в узлах конечноэлементной модели, то
матрица масс оказалась бы диагональной и решение динамичес-
ской задачи на ЭВМ потребовало бы меньшего объема памяти
и затрат машинного времени.
Если в vr помимо линейных входят также угловые пере-
перемещения, то в матрице mr необходимо, вообще говоря, учесть
инерцию вращения груза. В том случае, когда центр массы
груза совпадает с узловой точкой, а направления главных
осей инерции груза совпадают с направлениями угловых пе-
перемещений (представленных в виде векторов), матрица тг
по-прежнему будет диагональной, причем ее элементами будут
337
масса и соответствующие динамические моменты инерции гру-
груза. В других же случаях (например, когда центр массы груза
не совпадает с узловой точкой) матрица mr не будет уже иметь
диагональной формы. Если основная масса конструкции за-
заключена в сосредоточенных грузах, жестко закрепленных в
узлах, а распределенной по объему конечных элементов мас-
массой можно пренебречь, то общая матрица М будет состоять
из отдельных подматриц, расположенных на главной диаго-
нали. Все остальные элементы матрицы М будут нулевыми,
т.е. она окажется блочно-диагональной.
Существуют методы, которые и для непрерывного распре-
распределения массы по объему тела позволяют получить матрицу
М в диагональной или блочно-диагональной форме; к их изло-
изложению теперь и перейдем.
§ 9.3. Согласованная и диагональная формулировки
матрицы масс
Матрица масс конечного элемента определяется формулой
(9.5). При выводе этой формулы предполагалось, что а — та же
матрица, по которой формируется матрица р, используемая
при вычислении ке согласно D.11). Если при этом в (9.5)
осуществляется, как и в D.11), точное интегрирование (или,
скажем, численное интегрирование по методу Гаусса доста-
достаточно высокого порядка), то получаемая таким путем матрица
те (соответственно и матрица М) называется согласованной.
Данный термин подчеркивает- согласованность формулировок
жесткостных и массовых характеристик конечноэлементной
модели. В случае согласованной формулировки матрица М
имеет такую же структуру, что и К. В частности, обе матрицы
имеют одинаковое расположение ненулевых элементов и тре-
требуют одинакового объема памяти ЭВМ для своего хранения.
Рассмотрим теперь выражения для ке и те с точки зрения
сходимости конечноэлементного решения к точному при сгу-
сгущении сетки. Подобно тому как это делалось в гл. 6, предпо-
предположим, что элементами матрицы v и v являются перемещения
и скорости узлов, совпадающие с соответствующими значе-
значениями из точного решения. При сгущении сетки потенциаль-
потенциальная энергия деформации Ue =-^ (\е)Т ке\е и кинетическая
энергия Те = - (ve)Tme \e типового конечного элемента будут
стремиться к своим точным значениям со скоростью, опреде-
определяемой порядком полиномов, фигурирующих соответственно
в матрицах р и а. Так как матрица р образуется из производ-
338
ных от элементов матрицы а, то она содержит полиномы бо-
более низкого порядка. Таким образом, скорость сходимости
конечноэлементного решения к точному решению динамичес-
динамической задачи будет определяться скоростью сходимости потен-
потенциальной энергии деформации.
Скорость сходимости решения не нарушится, если при вы-
вычислении матрицы масс по (9.5) понизить порядок полиномов
в матрице а, приведя его в соответствие с порядком полиномов
в матрице р. Можно также брать исходную матрицу а, но
зато понижать порядок интегрирования произведения рага,
заботясь лишь о точном вычислении полных полиномов той
степени, которая появляется в произведении {$гх|3. Последнее
обстоятельство может быть использовано для получения ма-
матрицы те (а следовательно, и матрицы М) в диагональной или
блочно-диагональной форме. Чтобы добиться этого, необхо-
необходимо [34] вместо правила Гаусса применить при расчете те
такую схему численного интегрирования (назовем ее для крат-
краткости схемой поузлового интегрирования), в которой точки
интегрирования совпадают с узлами конечного элемента.
В самом деле, обратимся к формуле (9.6):
Матрица аг содержит аппроксимирующие функции, ко-
которые равны нулю во всех узлах, кроме узла г, матрица же
as отлична от нулевой лишь в узле s. Таким образом, матрица
a^as в случае г =ф= s является во всех узловых точках нулевой,
и при поузловом интегрировании все подматрицы m*s ока-
окажутся нулевыми, за исключением диагональных подматриц
Кг'
В §5.12 описаны два метода, которые могут быть исполь-
использованы для поузлового интегрирования: метод Маркова и ме-
метод Эйлера. Первый из них пригоден для тех конечных эле-
элементов, у которых в узлах задаются значения функций, но не
их производных. Примерами могут служить четырехугольные
конечные элементы плоской задачи теории упругости, для ко-
которых матрицы аг имеют вид (см., например, § 5.2)
а произведение
339
представляет собой диагональную матрицу. Следовательно,
подматрицы тегг (а значит, и вся матрица те) будут иметь
диагональную структуру. Вычисление те сводится здесь к
вычислению интегралов типа
т,
и порядок схемы интегрирования Маркова в большинстве
случаев оказывается достаточным для сохранения скорости
сходимости. Отметим только, что для конечных элементов тре-
третьего порядка (см. рис. 5.11) промежуточные узлы должны быть
расположены в точках интегрирования Маркова. Это достига-
достигается использованием в формулах типа E.67) значения с0 —
Если в узлах задаются еще и производные от перемещений,
то необходимый порядок поузлового интегрирования может
быть достигнут применением метода Эйлера. Примером может
служить прямоугольный конечный элемент пластины при
изгибе, описанный в § 7.4; для него
где функции аг1 (?, т]), агг (|, т]), аг3 (|, т]) и их первые произ-
производные по !;, т) обращаются в нуль во всех узлах элемента, за
исключением узла г, в котором они равны:
даг2
дагЯ Ь
" дЪ ' дц 2
Нетрудно убедиться, что подматрица тегг получится в
этом случае, вообще говоря, полностью заполненной, т.е. для
подобных конечных элементов удается добиться (без потери
скорости сходимости) лишь блочно-диагональной структуры
матрицы т".
Поузловое интегрирование в том виде, как это описано
выше, имеет один существенный недостаток, связанный с на-
340
личием отрицательных весовых коэффициентов в формулах
интегрирования (см., например, последний столбец в табл. 5.2).
Соответствующие диагональные элементы матрицы масс (имею-
(имеющие теперь смысл сосредоточенных узловых масс) будут также
отрицательными. Это нежелательно и не только потому, что
затрудняется физическая интерпретация подобной замены
распределенной массы сосредоточенными узловыми массами.
При наличии отрицательных диагональных элементов ма-
матрица М перестает быть положительно определенной, что может
серьезно затруднить или сделать невозможным применение
тех численных процедур, в которых используется свойство по-
положительной определенности матрицы масс.
Можно, однако, поступить следующим образом. Для вы-
вычисления внедиагональных подматриц m«s будем по-прежнему
пользоваться поузловым интегрированием (иначе говоря,
брать эти подматрицы нулевыми). Для вычисления же диаго-
диагональных блоков тегг применим точное интегрирование, дру-
другими словами, возьмем их из согласованной матрицы масс.
Это не может ухудшить характеристик сходимости по сравне-
сравнению с обычным методом поузлового интегрирования, но ре-
решение будет сходиться теперь к неправильному ответу, по-
поскольку сумма полученных таким путем узловых масс не будет
равна массе конечного элемента. Для устранения этого де-
дефекта достаточно умножить полученную матрицу на соответ-
соответствующим образом подобранный скалярный коэффициент.
В итоге приходим к предложенному в работе [37] методу полу-
получения диагональной (или блочно-диагональной) матрицы масс
из согласованной, который будем называть методом выделе-
выделения диагонали. Как следует из изложенного, этот метод, так
же как и метод поузлового интегрирования, сохраняет скорость
сходимости решения. Кроме того, он гарантирует положитель-
положительную определенность матрицы масс.
Отметим, что для образования диагональной матрицы масс
можно было бы массу каждого элемента просто сосредоточить
в его узлах, поровну поделив ее между ними. При этом, однако,
скорость сходимости решения к точному может сильно сни-
снижаться по сравнению с согласованной формулировкой, осо-
особенно для сложных конечных элементов. На реальных сетках
этот способ приводит к ухудшению точности результатов, и
поэтому он чаще всего неприемлем. Исключение составляют
некоторые простейшие элементы типа стержневого с двумя
узлами или треугольного в плоской задаче, где все три метода
(поузлового интегрирования, выделения диагонали и распре-
распределения массы по узлам) приводят к одинаковым результатам.
341
§ 9.4. Матрицы масс конечных элементов
с линейными смещениями узлов
Переходя теперь к выводу выражений для матриц масс
тех конечных элементов, которые рассматривались ранее,
начнем с элементов, у которых узловыми параметрами являют-
являются одни лишь линейные перемещения; элементы могут быть
одно-, дву- или трехмерными. В случае изопараметрических
элементов перемещения выражаются через их узловые значе-
значения равенствами их = S^ruxr; иу = ^тиут\ и2 = 2iJ>ru2r.
Представляя эти соотношения в форме u = 2a,.vr> где и ==
= {их иу uz}, vr= {uXT иут игт), видим, что матрицы аг име-
имеют здесь вид
¦фг О 0 "
О i|»r 0 =^rl. (9.17)
О 0 ц»,_
где I — единичная матрица.
Для подматриц mers получаем в соответствии с (9.6) вы-
выражение
m«s = jpa^asdT = m;sI, (9.18)
где при постоянной плотности р материала скалярные величи-
величины m*s равны
m"rs= p fi})rt|)sdT. (9.19)
Переходя в (9.19) к безразмерным параметрам |, ц, t,
и пользуясь интегрированием по Гауссу того же порядка,
что и для соответствующей матрицы жесткости, придем к
согласованной матрице те.
Для вычисления интегралов (9.19) можно применить метод
Маркова, что дает mers — 0 (для г Ф s), merr = т*г\, т. е.
приводит к диагональной матрице те. Чтобы избежать по-
появления отрицательных значений величин т*гг (имеющих
смысл сосредоточенных узловых масс), воспользуемся вместо
этого методом выделения диагонали, в соответствии с которым
в согласованной матрице масс положим mers = 0 для г =/= s
и оставим лишь подматрицы mrr = rnerr\, где
Xе
342
Для того чтобы матрица те правильно воспроизводила
массу конечного элемента, сумма всех величин tn*F должна
иметь значение рте. Для получения требуемого результата
следует ввести множитель
Таким образом, диагональная матрица те определится
соотношениями
К,= ° (r^s): merr~Mer\\
Ме = pQ[ir; ц,- = \ ¦фг d т; ?2 = (9 21)
Г J 2(хг
В частности, в случае трехмерного конечного элемента
(dt = | J| d^ dr] d^, где | J| — якобиан преобразования коор-
координат)
lii 111
J J J J J J
(9.22)
для конечных элементов пластин, находящихся в условиях
обобщенного плоского напряженного состояния,
|ir= f f M?|J|d?dTi;T'= f J A | J f d & d л; (9-23)
для конечных элементов обшивки (безмоментной оболочки),
описанных в § 8.2,
1 1
J
(9.24)
Наконец, для одномерных конечных элементов (см. § 5.10),
где dx = FA&% (F — площадь сечения), имеем
1
fMdS; те= J Fi4di. (9.25)
— i
343
Если в узлах учитывается лишь по два перемещения (как,
например, в случае пластины, совершающей колебания в
своей плоскости), то отдельные подматрицы будут иметь раз-
размер 2x2. При расчете же, скажем, продольных колебаний
прямолинейного стержня достаточно учесть лишь продольное
перемещение, и в этом случае подматрицы mers будут скаляр-
скалярными величинами.
Для треугольного элемента с узлами в вершинах (см. § 5.1)
все узловые массы в (9.21) оказываются одинаковыми: Мег =
= pFh/3, где F — площадь треугольника; h — толщина эле-
элемента.
§ 9.5. Матрицы масс конечных элементов
изгибаемых пластин
В случае пластины, работающей на изгиб, узловыми пара-
параметрами наряду с поперечными смещениями игт срединной
плоскости являются также углы поворота нормали §хт, $ут.
Перемещения их, иу, иг произвольной точки могут быть здесь
определены соотношениями G.1):
их = гдх(х, у); и у = г&у (х, у); иг = иг (х, у).
Рассмотрим сначала конечные элементы изопараметричес-
кого типа с независимой аппроксимацией прогиба и углов по-
ворота нормали:
Понимая под и матрицу и = {иг их иу }, имеем
u = Tz2%vr, (9.26)
где
[1 О О
О z О
00 г
Таким образом, подматрицы аг для подобных элементов
определяются произведением
При вычислении согласованной матрицы масс элемента с
четырьмя сторонами положим dr. = |J| d? di| dz\ тогда
1 1 h/2
-! -! -h/2
344
Так как
¦1
0
0
0
2*
0
0"
0
2*
то после интегрирования по толщине приходим к выражению
it
(9-27)
где через Dh обозначена диагональная матрица вида
{
1 О О
О h2/\2 О
О О ft2/12
(9.28)
При выводе (9.27) в матрицу перемещений и были включены
не только нормальное перемещение иг, но также и тангенци-
тангенциальные перемещения их, «„, обусловленные поворотом нор-
нормального элемента при деформации пластины. Тем самым в
матрице масс учтена инерция вращения элементарных парал-
параллелепипедов, выделяемых из пластины плоскостями х = const
и у = const. Для тонких пластин можно пренебречь инерцией
вращения по сравнению с инерцией поступательного движения
параллелепипедов вдоль оси г; при этом матрица Dh в (9.27)
будет заменена на матрицу
[
1 0 0
0 0 0
0 0 0
Даже для достаточно толстых пластин инерция вращения
не слишком велика. Это позволяет, в частности, заменить в
случае пластины переменной толщины величину ft2/12 в ма-
матрице Dh ее значением при | = г\ — 0, что приводит к выра-
выражению
™U=<K <9-29)
Здесь Dj} — значение матрицы Dft в середине конечного эле-
элемента, а скалярный множитель
1 1
(9.30)
345
Диагональную матрицу масс те вычислим так же, как это
делалось в предыдущем параграфе. Для отдельных подматриц
получим тогда формулы, аналогичные (9.21), (9.23):
m's = 0 (г ф s); т'„ = Щ D°; (9.31)
it it
= | J hV\J\dldiY. Q = _i-j J h\J\dldr\. (9.32)
Рассмотрим далее прямоугольный конечный элемент, опи-
описанный в §7.4. Для него имеем: $х — —j2-; $у — —-?z-t
uz — 1>аТ\Т; матрицы ат даются выражением G.24).
Если пренебречь инерцией вращения, то отдельные под-
подматрицы согласованной матрицы масс те определятся выра-
выражением
1 1
Г Г haja.dldr\, (9.33)
r*~ 4
— 1 — 1
где интегрирование можно выполнять точно или по правилу
Гаусса 4x4.
Для приведения те к блочно-диагональному виду можно
воспользоваться поузловым интегрированием по методу Эйле-
Эйлера, что дает
f 6 alr ЬцТ~
(9.34)
Определители матриц (9.34) отрицательны; общая матри-
матрица М также может оказаться неположительно определенной.
Можно получить и положительно определенную матрицу, если
взять подматрицы merr из согласованной матрицы те и ввести
множитель, обеспечивающий точное воспроизведение массы
конечного элемента. Тогда придем к следующей матрице масс:
[3454 461а?г 4616лг ]
461 а ?г 80а* бЗа&^Лг • (9-35)
461 6tv бЗаЫгЦг 80b2 J
Рассмотрим еще четырехугольный элемент с шестнадцатью
степенями свободы, описанный в § 7.5. В число узловых па-
346
раметров этого элемента входит помимо поперечного смеще-
смещения и углов поворота смешанная производная от иг по х, г/:
ve = {viVjViVm}; vr = {uzr$xr#yr(t>r}(r=i, j, I, m).
Перемещение uz (x, у) произвольной точки срединной по-
поверхности определяется равенством uz (х, у) = ave, где а =
= a*Q. Здесь матрица-строка а* содержит 16 полиномиальных
функций, выбранных для аппроксимации поперечного сме-
смещения, а Q — квадратная матрица, связывающая узловые
перемещения Vе с коэффициентами при этих функциях.
Пренебрегая, как и в предыдущем случае, инерцией вра-
вращения, по формуле
те =
pQrJJ/ia>7a*cb:d(/Q (9.36)
можно вычислить согласованную матрицу масс данного ко-
конечного элемента. Интегрирование по площади четырехуголь-
четырехугольника в (9.36) можно выполнить, как и в случае матрицы жест-
жесткости, с помощью перехода к безразмерным координатам ?, tj.
Для элементов трапециевидной формы удается осуществить
и точное интегрирование [18].
Если в согласованной матрице (9.36) оставить лишь четыре
подматрицы т*г размером 4x4 каждая, лежащие на диаго-
диагонали, и заменить остальные элементы нулевыми, то после
умножения на подходящий скалярный множитель придем к
блочно-диагональной матрице вида
т% = 0 (г ф s); т'г = пт*„, (9.37)
где
Q = рт'/Af*. (9.38)
В знаменателе формулы (9.38) стоит величина, представляю-
представляющая собой сумму первого, пятого, девятого и тринадцатого
диагональных элементов матрицы (9.36), которые при переходе
к блочно-диагональной форме приобретают смысл сосредото-
сосредоточенных узловых масс. Введение нормирующего множителя
Q в (9.37) позволяет точно воспроизвести массу конечного
элемента. Объем элемента
может быть найден путем перехода к координатам ?, ц и ин-
интегрирования по площади квадрата. Отметим, что для этого
элемента появляются обобщенные «массы», соответствующие
узловым параметрам фг. Эти величины не имеют ясного физи-
физического смысла.
347
§ 9.6. Матрицы масс конечных элементов оболочек
Рассмотрим конечные элементы оболочки вращения (см.
§ 7.8) с независимой аппроксимацией перемещений срединной
поверхности их, иу и угла поворота нормали #: их = 2,tyriixr;
иу — 2tpruyr; # = 2t|)rGr. Касательное к меридиану ы| и
нормальное и|> перемещения произвольной точки на расстоя-
расстоянии ? от срединной поверхности выражаются через соответ-
соответствующие перемещения срединной поверхности равенствами
и} = ut + ?fl; u? = ип.
Так как их, иу связаны с ut, un соотношениями
их — Кх Щ + ^пхип', Ч-у = \уЩ + hnylln,
где htx, \у и Хпх, Кпу — направляющие косинусы касательной
и нормали к меридиану, то
«5=К
К
Таким образом
(9.39)
где
Г 1 О
Понимая под и матрицу u = {их ut}, выражение (9.39)
можно записать в виде u = 2arvr, где
ог = фгГс. (9.40)
Полагая в формуле (9.6) dx = 2nyAdldt,, получаем
1 h/2
m* =2яр f ifr^P» f T^
— 1 -ft/2
Так как Цх -f %\v — 1, то
1 0 fKtx
348
После интегрирования по толщине оболочки имеем
•—• 1
где
1 О
О 1
о о
О "I
о I
/t2/12J
(9.41)
(9.42)
Выражение (9.41) выведено с учетом инерции вращения.
Для оболочки переменной толщины можно, так же как и в
случае изгиба пластин, заменить величину Л2/12 в матрице
Dh ее средним значением (при I = 0), что приводит к выраже-
выражению вида (9.29), где
(9.43)
a Dg — значение матрицы Dh при % = 0.
Если пренебречь инерцией вращения, то вместо D% следует
взять матрицу
1" =
Еслив (9.43) выполнить интегрирование того же типа, что
и для соответствующей матрицы жесткости, то придем к со-
согласованной матрице масс конечного элемента.
Диагональную матрицу те вычислим по методу выделения
диагонали; это приводит к соотношениям
¦1
0
0
0
1
0
0"
0
0
M'^i
(9.44)
— 1
Рассмотрим, далее, семейство четырехугольных конечных
элементов произвольной оболочки (см. §7.13). Перемещения
349
u? = {«*«|w|} слоя оболочки, расположенного на расстоя-
расстоянии ? от срединной поверхности, выражаются через узловые
перемещения ur = {ихг uyr uzr} и углы поворота #г =
=¦ {&хг $уГ ¦&„} равенствами G.121) и G.124), из которых
вытекает соотношение
uS = Щг(иг + ?М>г) = ЩгЬуг, (9.45)
где vr = {ur #r>; Tr = [I3: ?1,].
Здесь I3 — единичная 3x3 матрица, а матрица Lr G.122)
содержит направляющие косинусы нормали к оболочке в
узле г. Выражению (9.45) можно придать вид u? = 2arvr,
где
ат = frTr. (9.46)
Таким образом,
h/2
j
—1—1 —h/2
Выполнив умножение TrTs и проинтегрировав результат
по толщине оболочки, получим
r=: (9-47)
где
Drg = rM _%__]. (9.48)
Если, как это делалось и ранее, заменить матрицу (9.48)
ее значением D?s при % = ц = 0, то будем иметь вместо (9.47)
выражение
где
i i
т * — |
Заменяя внедиагональные подматрицы m's нулевыми и
корректируя затем массу конечного элемента, придем к ма-
матрице т', определяемой соотношениями
350
i
— i —i
U=
=—— f f hAiAnVT^Ydldi\. (9.49)
2 Иг J^ J^
Отметим, что из-за наличия в D?r произведения L^Lr
получаемая согласно (9.49) матрица масс не является диаго-
диагональной. Если пренебречь инерцией вращения, то матрица
D?r заменится диагональной матрицей
,», П. О"
где нулевые подматрицы имеют размер 3x3.
§ 9.7. Матрицы масс конечных элементов бруса
Остановимся теперь на одномерных конечных элементах
для моделирования прямолинейных или криволинейных
брусьев.
Для расчета плоских и пространственных рам могут ис-
использоваться прямолинейные конечные элементы постоянного
сечения, описываемые технической теорией бруса; расчет
жесткостных характеристик элементов этого типа рассмотрен в
гл. 3 (§ 3.4, 3.5). В общем случае пространственного нагруже-
ния элемент имеет 12 степеней свободы — три перемещения и
три угла поворота в каждом из двух узлов i, j (см. рис. 3.8).
Так же как и в случае статического нагружения, отнесем эле-
элемент к местной системе координат, направив ось х вдоль оси
бруса, а оси у, z — по направлению главных осей инерции по-
поперечного сечения. Будем снова разбивать узловые переме-
перемещения на четыре группы, образуя из них матрицы va, vb,
vc, vd. Матрица
определяет осевую деформацию стержня, матрицы
* v, е.>
соответствуют изгибу элемента в плоскостях ху и хг, а ма-
матрица
определяет кручение элемента.
351
Группируя подобным же образом узловые инерционные
силы, придем к блочной структуре матрицы масс m рассматри-
рассматриваемого элемента в местной системе координат, аналогичной
структуре соответствующей матрицы жесткости C.25):
т —
ц, о
тс
О
(9.60)
Для определения матрицы шо, имеющей размер 2x2,
зададимся линейным законом изменения продольного пере-
перемещения игх по длине элемента:
,* *• = О + 6г 6)/2 (г = i, j).
Здесь | — безразмерная координата, отсчитываемая от се-
середины элемента и связанная с х соотношением 2х — A + 1I;
ее узловые значения |г = ±1.
Представляя матрицу то в виде
т.
[тИ,а т1},Л
тЛ,а тП,а\
и учитывая, что dx = Fdx = (Fld%)/2, по формуле
тгм = -^-[ pilv^Fdfc (r, s = ?, /)
находим отдельные ее элементы. Обозначим через qm = pf
величину, представляющую собой погонную массу элемента.
С помощью точного интегрирования приходим в случае q ==
= const к согласованной матрице та, определяемой равенством
mrs.a — -
12
(9.51)
Диагональную форму матрицы та можно получить с по-
помощью поузлового интегрирования либо по методу выделения
диагонали; оба способа дают здесь одинаковый результат
/nrr,a=qml/2.
(9.52)
,352
При изгибе в плоскости ху связь поперечного перемещения
и- с узловыми перемещениями дается равенством C.27), ко-
У
торое перепишем в виде
где vr,b = {y-
Блоки матрицы
имеющие размер 2x2, определяются формулой
и при точном интегрировании получаются равными
"A05 + 51Ш —~
т"'Ь 420~ i
~2
-?¦ A+75,1.)
(9.53)
В матрицу перемещений и в формуле и = аме включено
лишь поперечное смещение иг, т.е. инерция вращения здесь
не учитывается.
Применение поузлового интегрирования по схеме Эйлера
позволяет получить блочно-диагональную матрицу mb вида
^
(9.54)
Наконец, выделение диагональных блоков в согласованной
матрице (9.53) и последующая корректировка массы элемента
приводит к положительно определенной матрице, для которой
156
11/1,
].*
.55)
Аналогичным образом вычисляется матрица тс; ее отдель-
отдельные подматрицы определяются теми же выражениями (9.53)—
353
(9.55), но перед внедиагональными членами следует в них сме-
сменить отрицательный знак на положительный.
При закручивании стержня произвольного сечения про-
происходит, вообще говоря, не только поворот, но и депланация его
сечений. Будем, однако, пренебрегать инерционными силами,
вызванными продольными перемещениями точек сечения вслед-
вследствие депланации. Считая, что форма и размеры поперечного
сечения не изменяются, можно вычислить смещения и- и и-
произвольной его точки, обусловленные поворотом сечения на
угол 0-: и- = —гЭ-; и- = t/9-. Принимая для 9- линейный
закон изменения по длине стержня, для матрицы перемещений
{и-и-} будем иметь выражение
Hi 2*е-.
где o|v — функции E.81).
Обозначив
найдем по формуле
1
— 1 F
четыре элемента матрицы md. Точное интегрирование по
дает согласованную матрицу, для которой
(9.56)
где Jv = J (t/2 + г2) dF — полярный момент инерции попе-
F
речного сечения.
Диагональная матрица md дается соотношениями, анало-
аналогичными (9.52):
Я*.<*=0 (гфв); m^^J^lL. (9.57)
Итак, определены согласованная и блочно-диагональная
матрицы масс рассматриваемого элемента бруса в местной
системе координат. Переход к общей системе выполняется точ-
354
но так же, как и для матрицы жесткости. Можно, в частности,
воспользоваться формулой типа C.47). При поблочном вы-
вычислении матрицы
удобно пользоваться выражением
П1Г
mrs,d ^Od-
(9.58)
Здесь введены следующие обозначения для блоков матрицы "к:
= \\-Х 0]; hd=[0 *-й];
Все подматрицы в (9.59) имеют размер 1 х 3.
Рассмотрим, далее, конечные элементы лонжерона, описан-
описанные в § 8.3 (см. рис. 8.3). Так же как и при выводе матрицы
жесткости, вначале отнесем элемент к местной системе коор-
координат х, у и введем в каждом узловом сечении по три степени
свободы Up = {и— и—ftp). Пользуясь независимой аппрок-
аппроксимацией перемещений и-, и- и угла поворота ¦& сечения и
пренебрегая инерцией вращения, можно получить согласо-
согласованную матрицу масс т, определяемую соотношениями
= т*Ря I";
(9.60)
Г =
и отнесенную к указанным степеням свободы. Здесь F — пло-
площадь сечения лонжерона; интегрирование в (9.60) выполня-
выполняется с помощью подстановки
Перейдем теперь от трех перемещений ир = {и- и- ®р}
к линейным смещениям vt = {и,- v.- }, v^ = {vf- v.-} двух
355
точек, расположенных в данном узловом сечении на расстоя-
расстоянии ±Н/2 от оси л;:
Lvj- J
Здесь Xpr — матрицы, определяемые равенством (8.20). Со-
Соответствующее преобразование матрицы масс приводит к ма-
матрице т, отнесенной к линейным смещениям этих узловых то-
точек в местной системе координат. Последующее применение
метода выделения диагонали позволяет привести эту матрицу к
диагональной форме
Feu. (9.61)
Здесь I2— единичная 2x2 матрица; индексы г, s относятся
к узловым точкам, а индекс р — к соответствующим узловым
сечениям.
Остается j наконец, перейти к общей системе координат
х, у, z, в которой каждый узел имеет три степени свободы:
Vr = {Vrx Vry Vrz }.
Величины Мг в (9.61) представляют собой значения сосре-
сосредоточенных узловых масс. Так как эти узловые массы должны
сохраняться неизменными в любой системе координат, то мож-
можно сразу записать значения отдельных блоков матрицы масс
т":
merS = 0 {гфв); т% = МГ1» (9.62)
где 13 — единичная 3x3 матрица, а значения Мг определяются
соотношениями (9.61).
Эта же матрица масс может использоваться и для состав-
составного конечного элемента лонжерона (см. § 8.4), поскольку его
отличие от рассмотренного выше элемента касается главным
образом способа представления и расчета жесткостных ха-
характеристик, схема же аппроксимации перемещений в обоих
случаях примерно одна и та же.
Аналогичным образом находим выражения для матриц
масс и других конечных элементов подобного класса. Напри-
Например, для криволинейных конечных элементов шпангоута (см.
356
§ 8.6) может быть получена следующая диагональная матрица
те:
[ (9.63)
Здесь матрица Х,г определяется равенством (8.73). При вы-
выводе (9.63) не учитывалась инерция вращения и кручения
ГЛАВА 10
РАСЧЕТ ДИНАМИЧЕСКОГО ПОВЕДЕНИЯ КОНСТРУКЦИИ
Расчет динамического поведения конструкции заключается в оп-
определении перемещений и напряжений как функций времени. Динами-
Динамический расчет может в качестве предварительного этапа содержать
исследование собственных колебаний, в результате чего определяются
частоты и формы собственных колебаний конструкции; в некоторых
случаях эта информация представляет и самостоятельный интерес.
Другой подход заключается в прямом интегрировании матричного урав-
уравнения движения с помощью тех или иных численных процедур.
§ 10.1. Собственные колебания
Собственные (или свободные) колебания конструкции со-
совершаются при отсутствии внешних сил. Будем считать, что
демпфирующие силы отсутствуют. Полагая в (9.9) Р = Р =
= 0, получим уравнение
Mv + Kv = 0, A0.1)
решение которого можно искать в виде
v = W coswt, (Ю.2)
где со — круговая частота колебаний, а матрица-столбец W
содержит амплитудные значения перемещений и называется
формой колебаний. Это название оправдывается тем, что амп-
амплитудные значения узловых перемещений в совокупности с
равенствами типа u = ave = aW" cosat полностью опреде-
определяют форму деформированного тела при колебаниях. Кон-
Конструкция может совершать колебания с различными частота-
частотами; каждой частоте сог соответствует определенная форма
W*. Задача расчета собственных колебаний заключается в
отыскании всех или нескольких (обычно наименьших) частот и
соответствующих им форм колебаний.
357
Подставив A0.2) в A0.1), придем к уравнению
(К — co2M)W = 0. A0.3)
Это равенство можно рассматривать как систему линейных
однородных уравнений относительно элементов матрицы W.
Существует тривиальное решение этой системы W = 0, но
оно не представляет интереса, так как на основании A0.2)
получим в этом случае v = 0.
Однор дная система линейных алгебраических уравнений
может иметь и нетривиальное решение, если ее определитель
равеа нулю:
|К — ю2М| = 0. A0.4)
Значения со, удовлетворяющие условию A0.4), представляют
собой частоты собственных колебаний системы.
Каждой собственной частоте юг соответствует нетривиаль-
нетривиальное решение W* системы уравнений
(К — ©?M)Wf = 0. A0.5)
Так как определитель этой системы равен нулю, то между
уравнениями имеется линейная зависимость, т.е. одно из них
представляет собой линейную комбинацию остальных, и его
можно отбросить. В результате придем к системе из N — 1
уравнений относительно N неизвестных, содержащихся в ма-
матрице Wj. Одну из компонент матрицы Wt можно выбрать
произвольно, тогда остальные N—1 неизвестных будут най-
найдены путем решения оставшихся уравнений. Из приведенных
рассуждений вытекает, что формы колебаний могут быть оп-
определены лишь с точностью до постоянного множителя: число-
числовые значения компонент W,- зависят от выбранной величины
одной из них. Это видно и непосредственно из равенства
A0.5), которое не изменится от умножения W* на произволь-
произвольный скалярный множитель.
Отыскание значений скалярной величины К и соответствую-
соответствующих им матриц-столбцов X, удовлетворяющих уравнению
(А — ХВ)Х = 0, A0.6)
где А и В — квадратные матрицы порядка N, составляет пред-
предмет известной задачи линейной алгебры, называемой обобщен-
обобщенной проблемой собственных значений (термин «обобщенная»
употребляется в том случае, когда матрица В не единичная).
Значения К, для которых выполняется равенство
|А — Щ = 0, A0.7)
358
называются собственными значениями, а соответствующие им
матрицы X — собственными векторами* проблемы A0.6).
Таким образом, в методе конечных элементов задача о колеба-
колебаниях конструкции сводится к решению обобщенной алгебраи-
алгебраической проблемы собственных значений. При этом собственные
значения являются квадратами частот колебаний, а собствен-
собственные векторы определяют формы колебаний.
Перепишем A0.7) в развернутом виде
ап—
а12—
hbNl «Л/2
= 0.
Если раскрыть определитель, то придем к алгебраическому
уравнению степени N относительно X:
cn№-\-cn—i %N~l -f-... + схX-j-co = 0. A0.8)
Коэффициенты этого уравнения выражаются через элементы
матриц А и В.
Как известно, полином степени N имеет N корней, среди
которых могут быть и комплексные. Но если матрицы А и В
симметричны, то, как доказывается в линейной алгебре, все
N корней буду г действительными. Именно этот случай пред-
представляет для нас интерес, поскольку матрицы жесткости и
масс всегда симметричны.
Более того, если конечные элементы являются совместными
и используется согласованная формулировка масс, то матри-
матрица жесткости и матрица масс будут неотрицательно определен-
определенными; в этом случае среди корней уравнения A0.8) не будет
ни одного отрицательного. Точнее, для закрепленного тела
все корни будут положительными, а для свободной конструк-
конструкции появятся нулевые корни; число последних равно числу
степеней свободы тела как жесткого целого.
Использование несовместных конечных элементов или,
скажем, понижение порядка интегрирования при вычислении
матрицы жесткости, как это делается для исключения ложных
сдвигов, может привести к неположительно определенной
* Следуя терминологии линейной алгебры, будем пользоваться в
дальнейшем понятием вектора, отождествляя его с понятием матрицы-
столбца.
359
матрице жесткости; некоторые способы вычисления матрицы
масс также могут привести к потере положительной опреде-
определенности последней. В этих случаях отдельные корни урав-
уравнения A0.8) оказываются отрицательными. Однако их абсо-
абсолютные значения оказываются обычно весьма большими и
соответствуют спектру высоких частот, который вообще иска-
искаженно воспроизводится конечноэлементнои моделью и не имеет
существенного значения. Основные же (наиболее низкие)
частоты могут быть при достаточном сгущении сетки вычисле-
вычислены с необходимой точностью, так что и в этом случае конеч-
ноэлементная модель правильно воспроизводит наиболее су-
существенные особенности динамического поведения конструк-
конструкции.
Отметим, что практически для матриц большого размера
коэффициенты ct в A0.8) не вычисляются. Существуют другие,
более удобные для ЭВМ методы отыскания собственных зна-
значений и собственных векторов [1, 29].
§ 10.2. Ортогональность собственных форм колебаний
Рассмотрим два различных тона колебаний с частотами сог,
<tij и формами Wj, Wj. Умножив уравнение 1-го тона
KW* — afMWt = 0
на матрицу W/ слева, получим равенство
= 0. A0.9)
С другой стороны, умножая уравнение /-го тона
KWj — ©/MW, = 0
на Wf слева, имеем
? f = 0.
Транспонируем последнее равенство, принимая во внима-
внимание симметрию матриц К и М:
W^KW* — ©/WJMW, = 0.
Вычитая полученный результат из A0.9), приходим к ра-
равенству
(со? _ o)?)W[MWi = 0.
Если юг Ф coj, то отсюда следует соотношение
W/MWi = 0. A0.10)
360
Оно показывает, что формы колебаний ортогональны друг
другу относительно матрицы масс, и называется поэтому ус-
условием ортогональности собственных форм.
Из A0.9) и A0.10) следует, что собственные формы орто-
ортогональны также и по отношению к матрице жесткости:
wjKW, = 0. A0.11)
Эти результаты получены в предположении, что частоты
щ- и о); различны. На практике, однако, встречаются случаи
равных или весьма мало отличающихся («патологически близ-
близких») частот.
Если to,- = о);, то соответствующие им собственные векто-
векторы W,-, W;- могут и не удовлетворять условию ортогонально-
ортогональности A0.10). Но коль скоро найдены* два каких-нибудь линей-
линейно независимых вектора W,-, W;, то любые их линейные комби-
комбинации также могут быть взяты в качестве соответствующих
форм колебаний. Комбинируя W?, W;, можно всегда образовать
два вектора W,-, W/, удовлетворяющие условию ортогональЬъ-
сти A0.10). Возьмем, например, W* = Wb W,- = W; + aW,-
и определим скалярную величину а из условия
Wf MW{ = (W[+aWf) MWj = 0.
Это дает значение
а = — Vfj MW,/(Wf MWj).
Таким образом, и в случае кратных частот можно вести
вычисления таким образом, чтобы выполнялось условие A0.10);
в дальнейшем мы будем предполагать, что это условие выпол-
выполняется для любых двух форм колебаний WJ( W/.
Умножив теперь уравнение t-ro тона на wf слева, полу-
получим
^ [ = 0.
Отсюда имеем равенство
со/ = wrKWj/fwfMW,), A0.12)
* В случае кратной частоты ео$ в системе уравнений A0.5) будет
уже не одно, а два уравнения, линейно выражающихся через остальные
N — 2 уравнения, так что можно произвольно задаться двумя компо-
компонентами W. Различный выбор этих компонент будет приводить к раз-
различным собственным векторам, соответствующим со*.
12 Зак. 651 361
которое позволяет вычислить частоту колебаний щ, если из-
известна соответствующая форма W,-. Как говорилось выше,
формы колебаний определяются с точностью до произвольного
множителя. Поэтому умножением всех компонент вектора W4
на подходящий множитель можно всегда добиться выполне-
выполнения равенства
W?MW, = 1. A0.13)
Формы колебаний, удовлетворяющие условию A0.13),
называются нормированными. Для таких форм соотношение
A0.12) упрощается, принимая вид
ol = wfKWf. A0.14)
§ 10.3. Примеры расчета
Пример 1. Свободный стержень (рис. 10.1), имеющий дли-
длину /, площадь сечения F, погонную массу qm, совершает про-
продольные колебания. Ограничимся простейшей идеализацией
разбив его по длине на два стержневых элемента первого по-
порядка длиной 1Х — 1/2 каж-
гг дый- ПосколькУ каждый
q у3ел может смещаться
лишь в осевом направле-
направлении, полученная таким
образом модель имеет три
Рис шл степени свободы:
v = {vt v2 v3).
Для используемых конечных элементов матрица жестко-
жесткости дается согласно C.14) выражением
ir
где [е — длина элемента; матрица масс me совпадает с матри-
матрицей ~та в выражении (9.50). Используем сначала согласо-
согласованную формулировку масс; тогда в соответствии с (9.51)
имеем
362
Таким образом, матрицы жесткости и масс двух конечных
элементов, идеализирующих реальный стержень, будут
k<'>=-
-1 42' h [ —
12
1 2 |2
/ 2'
2 3
Здесь цифры снизу и сбоку указывают номера степеней
свободы, относящихся к соответствующим строкам и столб-
столбцам.
Далее формируем матрицу жесткости и матрицу масс всей
системы:
1
2 ¦
2
1
0
1
1
4
1
2
0
1
2
3
Матричное уравнение A0.3) принимает вид
2 1 0
4 1
/Єà 1—1 01
Поделив уравнение на
представим его в форме
6
1
w=o.
0 1 2_
и введя обозначение
[¦
A0.15)
A —2А,) — A+к) 0
-A+^) 2A —2Л,) —(
0 —A+Ь) A —2Х)
Если приравнять нулю определитель этой системы, придем
к уравнению относительно X:
X A _ 2Ь)B — к) = 0.
Трем корням Х-! = 0; кг — 1/2; Я,3 = 2 соответствуют сле-
следующие значения ю:
Wl = 0; щ = 3,mVEF/(qmP); a>a=b,928VEFl(qml2).
12* 3G3
Точные значения первых трех частот, полученные инте-
интегрированием дифференциального уравнения продольных коле-
колебаний стержня, равны
0^ = 0; щ = nVEF/(qml*); <o3 = 2nVEFI(qml2).
Приближенные значения со2 и со3 превышают точные на
10,2%. Такая большая ошибка связана с весьма грубой идеа-
идеализацией системы. Для получения более точного результата
необходимо разбить стержень на большее число конечных
элементов. Так, при разбиении стержня на 10 элементов оди-
одинаковой длины-ошибка в ю2 будет менее 0,5%.
Рис. 10.2
Найдем, далее, формы колебаний
соответствующие трем найденным значениям щ.
Положив в A0.15) 'к = Я,! = 0, для компонент Wx получаем
систему уравнений
Wn — W12 = 0;
— Wa = 0;
~Wl
—W
lt
W13 = 0.
Здесь независимыми являются лишь два уравнения (на-
(например, первое и второе; третье получается сложением пер-
первых двух). Приняв Wtl= 1, находим W12 = 1; W13 = 1.
Следовательно, нулевой частоте % = 0 соответствует форма
Wi = {111}, которая определяет поступательное движение
стержня как абсолютно жесткого тела вдоль своей оси.
Аналогично для Х2 = 1/2 находим W2 = {10 —1}, а для
b3=2-W3= {1-1 1}.
Последние два вектора определяют формы упругих про-
продольных колебаний рассматриваемого стержня (рис. 10.2).
364
Полученные формы колебаний не удовлетворяют условию
A0.13). Так, для Wx произведение
, [2 1 01ГП
"Mi i i :
= 2qml1 = qml.
Нормирование вектора Wx можно выполнить, разделив
его компоненты на Vqml. Таким образом, нормированный
вектор будет
I 1}.
Аналогично получаем нормированные векторы
Используем теперь для этой же задачи диагональную ма-
матрицу масс. На основании (9.52) имеем для типового конечного
элемента
общая матрица масс оказывается равной
Повторяя предыдущие выкладки, получим значения
= 2,828VEF/(qmn; щ = 4УEF/(gml%
которые ниже точных соответственно на 10 и 36%. Как видим,
для основного тона упругих колебаний диагональная матри-
матрица масс дает здесь такую же точность, что и согласованная.
Однако если при согласованной формулировке масс частоты
колебаний получаются всегда завышенными (для совместных
элементов), то при использовании диагональной матрицы они
оказываются, как правило, ниже точных значений.
Пример 2. Консольно закрепленная однородная балка
(рис. 10.3) длиной / имеет на конце сосредоточенный груз мас-
365
сой М„ и совершает изгибные колебания. Балку идеализиру-
идеализируем одним конечным элементом; массовый момент инерции гру-
груза примем равным нулю.
Матрица жесткости элемента балки есть матрица кь C.36):
EJ
I3
12
6/
-12
6/
6/
иг
¦Ы
2/2
2
-12
— 6/
12
— 6/
3
6/
2/г
-6/
4/г
4 "
а
Рнс. 10.3
Отбросим здесь первые
две строки и два первых
столбца, соответствующие
нулевым перемещениям. В
результате получаем матри-
матрицу жесткости системы
К=
—
I3
12 ~~6/
—б/ 4/*
6
—31
2/2
При согласованной формулировке масс в качестве тг
следует взять матрицу, определяемую по (9.53):
т°
420
156
22/
54
13/
22/
4/2
13/
— 3/г
2
54
13/
156
— 22/
3
-13/
—З/2
— 22/
4/г
4
1
2
3
4
Оставив строки и столбцы с номерами 3, 4 и добавив к
диагональному элементу с индексами C, 3) массу груза Мо,
получим матрицу масс системы
210 [ —И/ 2/2
где у = Mol(qml) — отношение массы груза к массе балки
366
Далее приравниваем нулю определитель матрицы К —
— ю2М, что приводит к уравнению для определения частот
35 A + 127)Ь2 — 6 A7 + 70?)*. + 3 = 0,
в котором через % обозначена безразмерная величина
420EJ
Если, например, масса груза равна массе балки, то у = 1;
в этом случае уравнение примет вид 455А,2 — 522А, + 3 = 0.
Наименьший корень этого уравнения Я,х = 5,776 • 10~3, что
соответствует частоте основного тона колебаний
В предельном случае y = О частотное уравнение будет
35А2 — 102Я, + 3 = 0; его корни Xt = 0,02972; Я, = 2,885.
Отсюда находим приближенные значения первых двух частот
колебаний консольной балки
= 3,533 VEJI{qml% щ
Они превышают соответствующие
@
на 0,47 и
Если
элемента
г = 3,51бУ?У/(9т/4); со2
= 34,81 У?//(<7т/4),
точные значения
= 22,03V?//(<7m/4)
58%.
использовать блочно-диагональную матрицу масс
балки
12
~6 /
1 0
0
0
6-/
-/ 0
определяемую равенствами (9.54), то получим уравнение
X2 + 6A + 4у)\~ 3 = О,
в котором обозначено
24EJ
В случае у = 1 находим отсюда ^ = 0,09%6, что соответ-
соответствует круговой частоте щ = 1,547 ~)/ЕЛ {дт^)- Эта величи-
величина на 0,7% ниже частоты колебаний балки с грузом, получен-
полученной с использованием согласованной формулировки масс.
367
Если груз отсутствует (у — 0), то корни частотного урав-
уравнения будут Я,х = 0,4641; к2 = —6,46. Первому из них соот.
ветствует частота колебания % = 3,337 VEJ/(qml*), что ниже
точного значения на 5,1%. Второй же корень Х2 оказался от-
отрицательным, так что частоту ю2 найти нельзя. Это произош-
произошло вследствие того, что матрица М не является положитель-
положительно определенной. Так же как и в предыдущих примерах, повы-
повышение точности результатов может быть достигнуто разбиением
балки на большее число элементов.
у///////////////////////////////
1 г з
N'32
/V=f8
Рнс. 10.4
Пример 3 [18]. Консольная пластинка (рис. 10.4) постоян-
постоянной толщины h, имеющая стреловидную форму в плане с уг-
углом стреловидности х, совершает поперечные колебания. Для
расчета использованы несовместные четырехугольные конеч-
конечные элементы с 16 степенями свободы (см. § 7.5); применялась
согласованная матрица масс (9.36). В табл. 10.1 для первых
пяти тонов даны в случае tg х = 0,5 значения частот щ, отне-
Таблица 10.1
Номер
Сетка
1
2
3
4
5
4,29 C,9)
10,60 E,2)
21,67A1,9)
24,98 A0,1)
41,95 C2,3)
4,29 C,9)
10,57 D,9)
21,44 A0,7)
24,64 (8,6)
41,12 B9,7)
4,27 C,4)
10,36 B,7)
20,29 D,8)
23,99 E,7)
35,34 A1,5)
4,26C,1)
10,23 A,5)
19,68 A,7)
23,50 C,5)
33,96 G,1)
368
Рис. 10.5
сенные к величине VD/(phA4), где?> = Eh3/[l2 A — ja2)]; A ~
характерный размер пластинки. В скобках в табл. 10.1 ука-
указана погрешность результата в процентах. Представленные
здесь данные получены для четырех различных разбиений
пластинки на конечные элементы (на рис. 10.4 через N обозна-
обозначено число степеней свободы конечноэлементнои модели). При
выборе конечноэлементнои модели следует стремиться к тому,
чтобы для каждого конечного элемента отношение сторон было
по возможности близким к единице,
так как в этом случае жесткостные и
массовые характеристики воспроизво-
воспроизводятся наилучшим образом. Это видно,
в частности, из результатов, представ-
представленных в табл. 10.1: сетка 2 дает менее
точные результаты, чем сетка 3, хотя
она имеет большее число степеней
свободы.
Пример 4. Оболочка вращения
(рис. 10.5), представляющая собой
жестко защемленный цилиндричес-
цилиндрический сосуд, закрытый полусфери-
полусферическим днищем такой же толщины, что и цилиндричес-
цилиндрическая часть, совершает осесимметричные колебания. Длина
и радиус цилиндра равны 500 мм, отношение толщины к радиу-
радиусу составляет 0,02; {х = 0,3; Е = 2 • 105 МПа; (> = 7,83 X
X 10~8 кг/м8. Результаты расчета получены с использованием
конечных элементов- первого порядка (согласованная форму-
формулировка масс без учета инерции вращения). С использованием
40 конечных элементов для частоты основного тона получено
значение ю = 1,041 • Ю7 с~\ что хорошо согласуется с дан-
данными других работ [351.
§ 10.4. Разложение движения по формам собственных
колебаний
Вернемся теперь к уравнению (9.9), описывающему при
отсутствии демпфирования вынужденные колебания конструк-
конструкции. Пусть в результате предварительного расчета найдены
частоты и формы собственных колебаний. Расположим соб-
собственные частоты в порядке возрастания с^ ^ со2 ^ cu3.-.;
соответствующие им формы колебаний обозначим через W,,
W2, W3... . Предполагаем, что для них выполняются соот-
соотношения
W,T MW; =
0
369
и соответственно соотношения
W[KW, = ( ° (l^/); A0.17)
\ а? (I ¦=}).
Матрицу узловых перемещений v (t) можно искать в виде
линейной комбинации векторов W,-:
v @=?х @ Wx+z, @ W2+ z9 (t) W3 + ...,
где zt (t) — зависящие от времени неизвестные пока коэффици-
коэффициенты разложения. В матричной форме последнее равенство
имеет вид
v (t) = H z @, A0.18)
где
H=[W1W2...I A0.19)
— прямоугольная матрица, столбцами которой являются соб-
собственные формы (так называемая модальная матрица), а
¦7(+\ = (г (/) 7 A\ \ A0 20Y
— матрица-столбец неизвестных функций времени. Количество
собственных форм, используемых в матрице Н, зависит от
желаемой точности расчета и возможностей используемой
ЭВМ. Обычно учитывается лишь несколько первых тонов ко-
колебаний.
Подстановка A0.18) в (9.9) дает равенство
MHz+KHz=P4-P.
Умножив его на Нг слева, получим
HrMHz-f HrKHz = FF(P-fP). A0.21)
Произведения НТМН и НГКН представляют собой квадрат-
квадратные матрицы, типовые элементы которых равны WfMW;- и
wTk\V/. В силу соотношений A0.16), A0.17) эти элементы
равны нулю для всех i Ф j, т.е. данные матрицы являются
диагональными. При этом матрица НТМН будет единичной,
а матрица НГКН, которую мы обозначим буквой й, будет
равна
0
Уравнение A0.21) принимает теперь вид
z + iiz = Q, A0.22)
где
Q = Hr(P+P). A0.23)
370
Система дифференциальных уравнений, заключающаяся
в равенстве A0.22), оказывается несвязанной. Каждая функ-
функция 2; (/) может быть найдена интегрированием уравнения
Zj + urfzj-Q,, A0.24)
где Qj {t) — i-й компонент матрицы-столбца Q:
Q,@*=wr(P + P). A0.25)
Интегрирование уравнений A0.24) можно осуществить чис-
численно; некоторые методы пошагового интегрирования описаны
ниже. Если зависимость внешних сил от времени имеет простое
аналитическое выражение, то можно воспользоваться и точ-
точным интегрированием. В случае со,- ф 0 решение уравнения
A0.24) может быть записано в виде
zt (t) - z, @) — sin сог / + Z; @) cos ш{ t +
со,-
t
+ — f Qt (т) sin [<o, (t —с)] dx. A0.26)
В.этом выражении последнее слагаемое есть частное ре-
решение уравнения A0.24), а первые два — общее решение соот-
соответствующего однородного уравнения, подчиненное начальным
условиям; zt @) и zt @) — начальные значения функции zt (t)
и ее первой производной.
Если со; = 0, то решение можно получить из A0.26) соот-
соответствующим предельным переходом:
_¦г)(Ь(т)<1т. A0.27)
В начальный момент времени t = 0 известны матрицы
v @) и v @), и чтобы выполнить численное интегрирование
уравнений A0.24) или воспользоваться равенствами A0.26),
A0.27), необходимо выразить через эти матрицы z,- @) и zt @).
Это можно сделать, исходя из равенства A0.18). Умножим его
на НГМ слева. Учитывая, что НТМН есть единичная матрица,
получим соотношение z (t) = HrMv (t), из которого вытекают
зависимости
z@)=HrMv@); z@)=H7'Mv@).
Отсюда находим требуемые выражения
z;@)=wf Mv@); zt@)-wrMv@). A0.28)
371
Формулы A0.26), A0.27) целесообразно использовать в том
случае, когда зависимость внешних сил от времени имеет вид
Р + Р=»Р0ф@, A0.29)
где ф (t) — скалярная функция времени, а матрица Ро от вре-
времени не зависит. При этом обобщенные силы Qt (t) = Q?<p (t),
где в силу A0.25) Q? = Wf Po.
Так как величины Q" не зависят от времени, то вычисление
интегралов в A0.26), A0.27) сводится к определению функ-
функций
* t
| ф (т) sin (to,- (t — x)]dx; j" (t — г) ф (т)Cт.
о о
Для зависимостей ф(/) простого вида можно записать ана-
аналитическое выражение этих функций. Например, при мгно-
мгновенном приложении внешней нагрузки имеем ф (t) = 0 при
t <; 0; ф (/) = 1 при t> 0 (под Ро понимается при этом ма-
матрица, содержащая окончательные значения внешних сил).
Тогда
Г* I
I ф (т) sin [to; (/—т)] dx= A —cosojj t);
J 4>i
о
В этом частном случае имеем
г-, (t) — z((O) sin w^ +Zj @) cos оог / +
(для сог=^0); A0.30)
у Q? t* (для сог = 0). A0.31)
Если zt @) = 0; Z; @) = 0, то из A0.30) ясно видно, что
наибольший вклад в разложение v (/) будут давать те формы
колебаний, которые соответствуют наименьшим частотам.
Колебания же с высокими частотами практически не возбуж-
возбуждаются при реальных силовых воздействиях. Это объясня-
объясняет, почему колебания с низкими частотами являются наибо-
наиболее важными и почему достаточно учесть в A0.19) лишь те
формы колебаний, которые соответствуют низшим частотам.
372
Если в процессе нагружения соотношение между отдельны-
отдельными компонентами матрицы сил изменяется, т.е. равенство
A0.29) не выполняется, то для отыскания z,- (/) удобнее вос-
воспользоваться численным интегрированием уравнений A0.24).
§ 10.5. О прямом интегрировании уравнений движения
Расчет собственных колебаний требует в случае систем
большого размера весьма больших затрат машинного времени.
Поэтому решение динамических задач методом разложения по
собственным формам целесообразно выполнять в том случае,
когда для получения приемлемой точности результатов доста-
достаточно ограничиться учетом лишь нескольких основных тонов
колебаний. Однако во многих случаях (например, при расчете
сложных стержневых или оболочечных конструкций) требует-
требуется учитывать большое число тонов собственных колебаний, и
метод разложения по собственным формам становится неэф-
неэффективным. В этих случаях более экономичным оказывается
прямое интегрирование дифференциального уравнения (9.14)
Mv + Cv + Kv = P A0.32)
с помощью той или иной численной процедуры. В уравнении
A0.32) узловые силы Р, эквивалентные внеузловой нагрузке,
включены для упрощения записи в матрицу Р.
Ограничимся рассмотрением методов интегрирования
шагового типа. В этих методах матрицы v,+1, vi + 1, \t+1,
относящиеся к некоторому моменту времени tt + i = tt -+- At
(At — шаг интегрирования), вычисляются через их значения,
найденные на предыдущих шагах.
Как уже говорилось выше, численное интегрирование мож-
можно применить и в методе разложения по собственным формам
при решении уравнений A0.24). С другой стороны, всякая
матрица v может быть единственным образом представлена в
виде разложения по формам собственных колебаний (если
включить в это разложение все формы). Процесс численного
интегрирования уравнения A0.32) можно понимать как неяв-
неявное пошаговое определение коэффициентов этого разложения,
являющихся функциями времени. То же самое, только в яв-
явной форме, делается и при интегрировании уравнений A0.24).
Таким образом, прямое интегрирование уравнения A0.32)
можно трактовать как неявное и одновременное выполнение
тех же вычислений, которые в методе разложения по собствен-
373
ным формам осуществляются раздельно для каждого тона
колебаний*.
Имеются, однако, и принципиальные различия между дву-
двумя указанными подходами к расчету динамического поведения
конструкции. Во-первых, в методе прямого интегрирования,
в отличие от метода разложения по собственным формам,
учитываются все без исключения тоны колебаний, в том числе
колебания с наивысшими частотами. Во-вторых, интегриро-
интегрирование выполняется здесь с одинаковым шагом по всем тонам,
в то время как для интегрирования каждого из уравнений
A0.24) шаг целесообразно выбирать различным.
Вообще говоря, шаг At при прямом интегрировании дол-
должен быть таким, чтобы с достаточной точностью воспроизво-
воспроизводились те колебания, которые играют наиболее существенную
роль в динамическом поведении конструкции, т.е. колебания с
относительно низкими частотами. Но обычно в спектре частот
конечноэлементной модели содержатся и весьма высокие ча-
частоты, и может оказаться, что выбранный шаг значительно
превосходит периоды соответствующих колебаний. Ясно, что
вклады колебаний с наивысшими частотами в динамическое
поведение конструкции будут в этом случае совершенно иска-
искажены, но это допустимо, поскольку, как было ранее сказано,
они не играют в целом сколько-нибудь существенной роли.
Однако важно, чтобы используемая процедура интегрирова-
интегрирования обеспечивала устойчивость процесса, когда шаг At как
угодно превосходит период колебания. Методы интегрирова-
интегрирования, удовлетворяющие этому требованию, называются безус-
безусловно устойчивыми. Для них единственным критерием вы-
выбора шага At является точность результатов.
На практике используются иногда и условно устойчивые
методы интегрирования, в которых устойчивость процесса
обеспечивается лишь в том случае, когда шаг At не превосходит
некоторого критического значения At*. Если же взять At>
> At*, то происходит стремительный рост численных значений
компонент матрицы v (t), которые уже после нескольких пер-
первых шагов могут достигать сколь угодно больших величин.
Чаще всего величина At* оказывается значительно меньше
того значения, которое необходимо для получения приемле-
приемлемой точности в безусловно устойчивых процедурах. Тем не
менее в отдельных случаях условно устойчивые процедуры
могут оказаться более экономичными, если на каждом шаге
* При выводе равенства A0.24) было принято, что отсутствует
демпфирование, так что, строго говоря, данные рассуждения относятся
к случаю, когда матрица С в A0.32) нулевая.
374
они требуют, как это часто бывает, меньшего числа арифме-
арифметических операций, чем безусловно устойчивые процедуры.
Существуют широко известные методы численного интегри-
интегрирования обыкновенных дифференциальных уравнений типа
Адамса, Рунге—Кутта и др. Однако они мало пригодны для
интегрирования систем высокого порядка, так как, будучи
условно устойчивыми, требуют тем не менее выполнения боль-
большого числа арифметических операций на каждом шаге. В свя-
связи с этим применительно к матричному уравнению видаA0.32)
разработано несколько специальных процедур; здесь будут
рассмотрены две из них.
§ 10.6. Метод центральных разностей
Обозначим через уг, v,-, v, значения матриц v (t), v (t).
v (t) в некоторый момент времени /,-. Матрицу перемещений
v (// Н- т) представим в виде разложения по степеням т. Огра-
Ограничиваясь членами, содержащими т2, получим приближенное
выражение
+ -y-v,. A0.33)
Полагая здесь т = —At, а затем т = At, будем иметь два
равенства
V/-l=Vj — Л^г + -у- V;; V; + 1 = V; + At\; -j — V,.
Складывая и вычитая эти соотношения, можно выразить
Vj и V,- через значения матрицы v (/) в моменты времени tt-t,
h, ti + l:
v, = ~-(Yi+i —vi-,); vi = ~^-(v^i — 2vt + v,-j)- A0-34)
Запишем теперь уравнение A0.32) в момент времени /{:
Mv,+Cv,+Kv,»^.
Если внести сюда приближенные зависимости A0.34), то при-
придем к уравнению для определения vf +1, которое можно запи-
записать в виде
(M+-y-CJvl+1*R,. A0.35)
где
-v,-1)+-~Cvj_1. A0.36)
375
Соотношения A0.34)—A0.36) совместно с начальными ус-
условиями дают процедуру пошагового интегрирования урав-
уравнения A0.32), известную под названием метода центральных
разностей [11. Равенства A0.34) можно рассматривать как фор-
формулы численного дифференцирования, симметричные относи-
относительно центральной точки t = tt; это объясняет название ме-
метода.
Так как в начальный момент времени t0 = 0 известны
v,, и vu, но не v.-,, то для выполнения первого шага следует
представить соотношения A0.35), A0.36) в иной форме. Вы-
Выразив на основании первого равенства A0.34) v._, через v0,
имеем
второе равенство A0.34) дает При этом
2
v0 = -— (v, — v0 — A/v0).
Внося последний результат в уравнение
Mv0 +• Cv0 + Kvo= Po,
получаем требуемое равенство для определения v,:
Mv,=-j- (р0—Kvo-cvo) + т (\0 + ы\0).
Метод центральных разностей весьма прост. Он особенно
удобен в том случае, когда матрица масс имеет диагональную
или блочно-диагональную структуру, а демпфирующими си-
силами можно пренебречь (или же когда матрица демпфирования
С пропорциональна матрице масс). Тогда решение системы
уравнений относительно vi + 1 становится тривиальным. Но
если некоторые узловые массы равны при этом нулю, то опре-
определение \i + 1 становится невозможным. В связи с этим иссле-
исследуем подробнее устойчивость метода центральных разностей.
Обратимся для этого к уравнениям типа A0.24), каждое из
которых можно трактовать как уравнение движения системы
с одной степенью свободы. В этих уравнениях не учитыва-
учитывается демпфирование, но, как показывают расчеты, это не ока-
оказывает существенного влияния на устойчивость процесса ин-
интегрирования. Кроме того, при исследовании устойчивости
можно принять правую часть уравнений равной нулю. Таким
образом, для определения области устойчивости процедуры
376
интегрирования будем применять ее к скалярному уравнению
типа
= O, A0.37)
точное решение которого может быть записано в виде
z (t) = сх cosiat -f сг sinat,
где clt c2 — произвольные постоянные, определяемые из на-
начальных условий. Это же решение можно представить и в эк-
эквивалентной комплексной форме
z (t) = Аеш + Ве~ш,
где А, В — комплексные постоянные.
Полагая в соответствии с методом центральных разностей
получаем из A0.37) соотношение
zt + l + zl-1 + (<a*AP — 2)zt = 0,
определяющее приближенное решение. Поставим себе целью
иайти такую функцию z (/), которая удовлетворяет условию
z(t + M) + z(t— At) + (@2Д/2 — 2) z (t) = 0 A0.38)
и является тем самым интегральной фуикцией для уравнения
A0.37), получаемой по методу центральных разностей. Будем
искать эту функцию в виде
где А — произвольная комплексная постоянная. Множитель
е*' описывает колебательное движение с круговой частотой
ц, а множитель evt характеризует изменение амплитуды коле-
колебания с течением времени; решение будет устойчивым (т.е.
невозрастающим) в случае v ^ 0.
Обозначив
A0.39)
будем иметь
z(t—Д*):=Ле<*+'»<'-д<>=— z(t).
я
Подставляя эти соотношения в A0.38), получим для q
квадратное уравнение, которое запишем в виде
<72 - 2aq + 1 - 0;
377
здесь через а обозначена величина
а = 1 — (<о2Д/2)/2. A0.40)
Отсюда находим два корня qu q2:
Qi,i = а ± Va2— 1. A0.41)
Так как для устойчивого решения v^O, то определение об-
области устойчивости сводится к отысканию тех значений At,
при которых модуль q, равный evA', не превосходит 1. Двум
корням qlt q2 соответствуют две функции z (t), удовлетворяю-
удовлетворяющие соотношению A0.38), и для обеспечения устойчивости
каждая из них должна оставаться ограниченной при t-*- oo.
Таким образом, необходимо потребовать, чтобы обе величины
qu q2 не превосходили по модулю 1.
В зависимости от величины шага At корни A0.41) могут
оказаться либо действительными, либо комплексно-сопряжен-
комплексно-сопряженными.
Предположим сначала, что шаг Д^ удовлетворяет условию
At ^. 2/@, так что а2 — 1 ^ 0. В этом случае имеем комплекс-
комплексно-сопряженные корни
qU2 = a± Ы, A0.42)
где через Ь обозначена действительная величина b = ~V\—-a3.
Так как a2 -f- b2 = 1, то по модулю оба корня qu q2 равны
единице. Отсюда следует, что для обоих частных решений, со-
соответствующих <7i и q2, величина v равна нулю, т.е. получае-
получаемое здесь приближенное решение, так же как и точное, опи-
описывает гармоническое колебание с постоянной амплитудой.
Из A0.39) следует теперь, что
ft,2= e±tvAI = cos \iAt ± i sin \iAt.
Сопоставляя это выражение с A0.42), видим, что частота
колебания в приближенном решении определяется равенством
cosp.A/ = а, т.е.
J(^) [A0.48)
Рассмотрим далее случай, когда выполняется условие а2 —
— 1 > 0, т.е. Arf > 2/@. Обозначив теперь через Ь величину
Ь — У а2 — 1, получим из A0.41) два действительных раз-
различных корня
<7i,2 =• а ± Ь.
Так как по теореме Виетта qxq2 =-1, то один из этих корней
больше 1, т.е. решение будет неустойчивым.
378
Итак, устойчивость метода центральных разностей обеспе-
обеспечивается лишь в том случае, когда шаг At не превосходит кри-
критического значения At*, равного
М* = 2/со = ТЫ,
A0.44)
где Т = 2я/(о — период колебания. При этом численное ре-
решение будет описывать колебательный процесс с той же амп-
амплитудой, что и в точном решении, но с круговой частотой ц
A0.43), отличной от to. На
рис. 10.6 дана зависимость
относительной погрешности
0,16
е, =
[1—Ш
1
X
I 2
от отношения At/T=<aAt/Bn).
Возвращаясь к общему
случаю матричного дифферен-
дифференциального уравнения A0.32),
можно заключить, что про-
процесс его интегрирования бу-
дет устойчивым при условии
At^T^Jn, A0.45)
0,08
-0.Й
'Z 0,16 0,10
Рис. 10.6
где Tmln — минимальный пе-
период собственных колебаний
данной системы. Если конечноэлементная модель содержит
конечные элементы малых размеров (с большой жесткостью и
малой массой), в ее спектре частот будут содержаться весьма
высокие значения <ог, которым соответствуют малые периоды
колебаний. Расчет такой системы методом центральных разно-
разностей может потребовать большого числа шагов из-за ограниче-
ограничения, накладываемого условием A0.45) на шаг At.
§ 10.7. Метод Ньюмарка
Метод Ньюмарка основан на следующих (независимых)
разложениях v (tt + т) и v {tt + т) в ряды по степеням т [1]:
= v4 +xvt + ¦— у» -far3 v4;
A0.46)
379
Здесь удержаны члены, содержащие матрицу v. Коэффи-
Коэффициенты аир выбираются таким образом, чтобы обеспечить
безусловную устойчивость процесса интегрирования; об
их численных значениях будет сказано ниже.
Полагая т = At и заменяя v,- приближенным отношением
(vi + 1 — Vi)/&t, приходим к равенствам
Л/2 .
1—v,). A0.47)
Найдем из первого равенства vt + г:
hir)^ <10-48>
Подстановка этого результата в выражение для vJ+1 дает
формулу
р
аД/ * - ¦« ¦ , _,-.¦«, —гК (Ю.49)
которая в совокупности с A0.48) составляет рекуррентные со-
соотношения метода Ньюмарка.
Для отыскания vl + 1 уравнение движения записывается
для момента t = ti + 1:
MvJ+1 -f Cvj+1 + Kvj+i = Pj+i-
После подстановки в это равенство соотношений A0.48),
A0.49) приходим к уравнению вида
AvJ + 1 = Rj + 1, A0.50)
в котором
A0-52>
Отметим, что метод Ньюмарка требует задания в начальный
момент времени t0 = 0 не только матриц v0, v0, но также и
380
матрицы v0. Обычно полагают v=0; можно также найти Mva
из уравнения движения, записанного для момента времени
/. = 0.
Для исследования точности и устойчивости метода Ньюмар-
ка обратимся снова к уравнению A0.37). Запишем примени-
применительно к этому случаю соотношения A0.47):
z,
A0.53)
= z, + Afe, + pA/ (z,+1—z,).
Получаемые по методу Ньюмарка функции z (tf), z(?),
z (f) будем искать в виде
z(Q-i41e<v+/M<; z@ = i4«e<v+/|l)'; z@=^3e(v+)', A0.54)
где i4lf Л 2, Л3 — некоторые комплексные постоянные.
Уравнение A0.37) должно удовлетворяться в моменты
времени t = tt, так что из равенства z\ + <o2Zj = 0 имеем сле-
следующую связь между постоянными Ах и А3:
А3 = —(о2Аг. A0.55)
Учитывая, что zi + 1 = qzt; zi + 1 = qz\; zi + 1 = qz\, где
7 определяется согласно A0.39), из второго равенства A0.53)
устанавливаем также, что
f) A0.56)
Наконец, первое равенство A0.53) дает с учетом A0.55)
и A0.56) квадратное уравнение относительно q, которое запи-
запишем в виде
Yi(l-<7)a-Y2(l-<7) + l=O. A0.57)
Здесь
^; ъ-V + T- <10-58>
Решая уравнение A0.57), находим два его корня:
, - Y2 ± У Т! -4Yi)- 0°-59)
Определим теперь значения параметров а, р, обеспечиваю-
обеспечивающие безусловную устойчивость метода. Потребуем для этого,
381
чтобы при Д/ -*- оо оба корня <7i и цг не превосходили по моду-
модулю 1. Отбрасывая в выражении для Yi второе слагаемое, имеем
Предположим сначала, что а ^ j flJ + jJ. Тогда получим
два комплексно-сопряженных корня <712 = «о ± boi, где
Условия устойчивости |<7i| ^ 1; |^2| ^ 1 сводятся к вы-
выполнению неравенства а§ + Н ^ 1, которое удовлетворяется
при Р > 1/2.
В случае же а <.— ф + —J оба корня qu q2 будут дейст-
действительными, причем один из них оказывается по абсолютной
величине больше 1.
Итак, метод интегрирования Ньюмарка будет безусловно
устойчивым, если
f(Г A0-60)
Более определенный выбор параметров а, р можно сде-
сделать, исследуя их влияние на точность решения. Возвра-
Возвращаясь к случаю конечных приращений А^, из A0.59) имеем
<7i,2 = а ± Ы,
где
а = 1 - v,/2Yi; Ь = Vl/Yi-(Y2/2YiJ.
Модули qlt q2 равны между собой и имеют значение
УЖТ~ь2 = Vi + A -
Так как 1^1 = ]e<v+t^> д'| = еУ**, то в обоих решениях,
соответствующих q1 и дг, величина v получается одинаковой;
она определяется равенством
= VI +A-
или
v=r—I_in[l+A — YsVyJ- A0.61)
382
Что касается величины ц, то она в этих двух решениях от-
отличается лишь знаком и определяется условием
1
(а±Ы),
откуда имеем
1
и = arccos
A0.62)
Влияние параметров а, р* на точность решения можно ха-
характеризовать двумя величинами elt e2. Первая из них ех =
ОД 0,16
Рис. 10.7
At/T
= (\х — оо)/<о дает относительную погрешность в определении
круговой частоты, а другая е2 = 1 — e2nv/n представляет
собой относительное уменьшение амплитуды колебания за
время t = 2я/ц, т.е. за одно полное колебание. Зависимости
ех и е2 от шага интегрирования при различных значениях а,
Р представлены соответственно на рис. 10.7 и 10.8, где через
а0 обозначена величина
A0.63)
Как видно из этих графиков, изменение параметра а более
существенно сказывается на величине elt причем наилучшая
точность достигается при а = а0. Именно это значение (или
несколько большее) следует употреблять в расчетах.
Величина е2 зависит главным образом от параметра р.
При р = 0,5 она равна нулю, т. е. амплитуда колебания
383
в численном решении сохраняется неизменной. При р > 0,5
амплитуда получается убывающей. В связи с этим можно гово-
говорить об искусственном демпфировании, присущем численной
процедуре метода Ньюмарка в случае р*>0,5. Оно проявляется
0,08 0,12 0,16 0,20 0,2* М/Т
Рис. 10.8
тем сильнее, чем больше шаг интегрирования в сравнении с
периодом колебания. Поэтому при использовании метода Нью-
Ньюмарка с параметром р* > 0,5 для интегрирования матричного
уравнения движения A0.32) колебания с высшими частотами
будут полностью подавляться,
в то время как в основных тонах
затухание будет проявляться
значительно слабее.
Можно брать р* > 0,5 и для
приближенного учета действи-
действительного демпфирования. Это
позволяет отбросить в исходном
уравнении и в расчетных фор-
формулах члены, содержащие мно-
множителем матрицу демпфирова-
демпфирования С и тем самым сэкономить
время вычислений. Поэтому ча-
часто используют [1] параметры
Р = 0,55; а = 0,28. Если же необходимости в введении ис-
искусственного демпфирования нет, то лучше брать значения р* =
= 0,5; а = 0,25, при которых достигается наивысшая точность
метода Ньюмарка.
Рис. 10.9
384
Пример. Жестко защемленная сферическая оболочка имеет
радиус кривизны 561 мм, диаметр основания 508 мм, толщину
10,4 мм (рис. 10.9); Е = 7,23 • 104 МПа; ц = 0,3; р = 2,8 X
X Ю-3 кг/м3. Оболочка мгновенно нагружается равномерным
давлением с максимальной интенсивностью р0 = 0,689 МПа.
На рис. 10.10 показано осевое перемещение w полюса и
меридиональное напряжение аг в вершине оболочки на ее на-
наружной поверхности в зависимости от времени t. Оболочка
щмм
6иМПа
-80
2,8 t,MKC
Рис. 10.10
ыла разбита на 30 кольцевых конечных элементов первого
орядка (см. § 7.8). Интегрирование осуществлялось методом
Ньюмарка с параметрами р = 0,5; а = 0,25. Шаг интегри-
интегрирования Д^ равнялся 1 • Ю-5 с, так что весь расчет потребовал
выполнения 320 шагов. Отметим, что применение метода цент-
центральных разностей в данной задаче потребовало бы осущест-
осуществления значительно большего (почти в 100 раз) числа шагов
из-за малой величины критического шага интегрирования.
Это связано с наличием в вершине оболочки конечных элемен-
элементов, имеющих весьма большую жесткость при малой массе.
В задачах такого рода метод центральных разностей менее
эффективен, чем безусловно устойчивые процедуры.
Представленные на рис. 10.10 результаты получены с ис-
использованием согласованной матрицы масс (9.43); они хорошо
совпадают с данными других работ [27]. Отметим, что приме-
применение в этой задаче диагональной матрицы масс (9.44) дает
i практически такие же результаты.
385
ЗАКЛЮЧЕНИЕ
В пособии изложены основы метода конечных элементов
в перемещениях применительно к линейным задачам. Метод
можно рассматривать как мощное современное средство проч-
прочностного расчета авиационных конструкций. В практике кон-
конструкторских бюро он используется на всех этапах создания
летательного аппарата, начиная с проработки и выбора сило-
силовой схемы изделия и кончая анализом результатов испытаний.
С его помощью выполняются расчеты как общей, так и местной
прочности, устойчивости силовых элементов, колебаний кон-,
струкции, температурных полей; он же помогает оценить влия-
влияние на прочность изделия различных производственных от-
отклонений.
Метод конечных элементов полностью ориентирован на
использование ЭВМ. Это обусловлено необходимостью выпол-
выполнения большого количества однотипных операций. Однако
есть два важных этапа расчета, плохо поддающихся автомати-
автоматизации и требующих больших затрат ручного труда — это,
во-первых, подготовка и ввод исходной информации и, во-
вторых, обработка и анализ результатов расчета.
Подготовка исходной информации начинается с составления
конечноэлементной модели, нумерации узлов и конечных эле-
элементов, вычисления координат узлов. Далее вся информация
должна быть соответствующим образом представлена и вве-
введена в машину. На этом этапе расчет практически неизбежно!
(если не говорить о простейших задачах) сопровождается зна-i
чительным количеством ошибок, которые впоследствии при-;
ходится выявлять всеми возможными средствами и исправлять.;
Поэтому важной задачей является изыскание возможностей
для максимального сокращения исходной информации. Боль-
Большие универсальные программы, реализующие метод конечных
элементов, обязательно предусматривают те или иные способы
такого сокращения. Однако независимо от этого инженер-
также должен стремиться к сокращению исходной информации
путем наиболее рациональной идеализации конструкции.
В качестве общих приемов здесь можно упомянуть использо-
использование симметрии, введение участков с регулярными сетками,
использование наиболее подходящих конечных элементов.
Простейшим способом представления результатов расчета
является вывод на печать перемещений и напряжений в харак--
терных точках (например, в узлах). При этом объем выводимой
информации оказывается часто настолько большим, что даже
простой ее просмотр требует значительного времени. В неко-
некоторых программах предусмотрены более эффективные способы
представления результатов, использующие, скажем, графо-
графопостроитель. Это может быть вычерчивание графиков интере-
интересующих нас величин, нанесение на чертеж конструкции ли-
линий равного уровня напряжений и т. п. Однако эти спо-
способы применимы лишь к конструкциям частного вида, так
<что до конца проблема представления результатов пока не
: решена.
Важным составным элементом анализа решения является
.оценка его достоверности. Ни в коем случае нельзя слепо до-
;верять машинным результатам: ответственность за правиль-
правильность решения задачи несет человек, а не машина. Здесь осо-
особое значение приобретают профессиональный опыт и квалифи-
квалификация расчетчика. Для подтверждения достоверности могут
использоваться экспериментальные данные, сопоставление с
результатами прежних расчетов аналогичных конструкций;
во многих случаях помогают проверки выполнения условий
¦ равновесия конструкции или отдельных ее частей. Подчас не-
незаменимым подспорьем оказывается оценка результатов с
помощью аналитических методов. Заметим, что по одной толь-
только этой причине неуместно противопоставлять численные мето-
методы расчета (в том числе метод конечных элементов) аналитиче-
аналитическим и умалять роль последних, с чем приходится иногда
сталкиваться.
Для практического осуществления расчетов необходимо
располагать соответствующими программами для ЭВМ, созда-
,ние которых связано со значительными затратами труда и вре-
времени. Считается, что на разработку комплекса программ по
методу конечных элементов с более или менее ш ирокими воз-
возможностями требуется от 10 до 100 человеко-лет. В настоящее
время в нашей стране созданы и успешно эксплуатируются
мощные вычислительные программы как общего назначения,
так и специально ориентированные на расчет авиационных кон-
конструкций. Наряду с этим во многих организациях создаются
относительно более простые программы, предназначенные для
расчета конструкций частного вида (скажем, оболочек враще-
вращения, пластинок и т.п.). Их эффективность обусловлена возмож-
возможностью задания минимальной информации, требующейся для
описания геометрии таких простых конструкций; сетка ко-
конечных элементов генерируется при этом автоматически.
В настоящем пособии вопросы реализации конечных эле-
элементов на ЭВМ не затронуты, поскольку они достаточно полно
освещены в литературе [1, 6, 15, 20, 25], где можно найти как
387
общие принципы организации вычислений, так и конкретные
примеры составления программ.
Для идеализации одной и той же конструкции могут быть
использованы различные конечные элементы. Выбор во многом
определяется той библиотекой конечных элементов, которая
имеется в данной программе; большую роль играют знания и
опыт расчетчика. В настоящее время широкое применение по-
получили конечные элементы изопараметрического типа, по-
позволяющие легко моделировать тела с криволинейными гра-
границами; именно поэтому в данной книге им уделено большое
внимание. При работе с ними приходится решать вопрос о
том, какие элементы лучше взять — простейшие элементы пер-
первого порядка или же более сложные многоузловые элементы
высших порядков. Здесь следует иметь в виду, что элементы
первого порядка позволяют получить достаточно точные зна-
значения напряжений лишь в центральной точке, но не в узлах.
Поэтому область эффективного применения элементов первого
порядка ограничивается, как правило, такими задачами, в
которых градиенты напряжений не слишком велики (например,
расчет крыла самолета без вырезов).
Однако во многих задачах (в частности, при расчете обо-
оболочек) напряженное состояние тела оказывается быстро изме-
изменяющимся, и тогда необходимо применять конечные элементы
более высоких порядков. Следует соблюдать определенную
осторожность, выбирая форму конечных элементов и положе-
положение узлов, с тем чтобы избежать обращения в нуль якобиана
преобразования координат. Не вдаваясь в подробности, от-
отметим, что такая опасность оказывается тем значительнее,
чем выше порядок элементов. Наилучшим компромиссом
является, по-видимому, использование элементов второго
порядка. Если при этом избегать слишком искривленных ко-
конечных элементов и помещать промежуточные узлы прибли-
приблизительно в серединах сторон, то корректное представление
жесткостных характеристик тела будет гарантировано.
На современном этапе развития техники все большее зна-
значение приобретают нелинейные задачи расчета конструкций
(учет больших перемещений, пластических деформаций, рас-
расчет закритического поведения силовых элементов и т.д.).
Применение метода конечных элементов в этих задачах [61
открывает широкие возможности для их практического реше-
решения. Следует, однако, отметить, что разработка теоретических
и практических аспектов приложений метода конечных эле-
элементов к нелинейным задачам еще далека от завершения, хотя
и в этой области налицо определенные успехи. Поскольку
расчет носит здесь итерационный характер, решение требует
388
существенно большей затраты машинного времени, нежели в
случае линейных задач. Совершенствование вычислительных
алгоритмов и развитие ЭВМ позволили уже сейчас преодолеть
многие трудности, и можно не сомневаться, что в скором вре-
времени станет доступным решение тех нелинейных задач, которые
выдвигаются на первый план потребностями практики.
СПИСОК ЛИТЕРАТУРЫ
1. Бате К., Вилсон Е. Численные методы анализа и метод конеч-
конечных элементов: Пер. с англ. — М., 1982.
2. Березин И. С, Жидков Н. П. Методы вычислений. М., 1962
т. 1, 2.
3. Бояршинов С. В. Основы строительной механики машин. М
1973.
4. Бирман 3. И., Лукашенко В. И., Тимофеев М. Т. Расчет тонко-
тонкостенных подкрепленных оболочек методом конечных элементов с при»
менением ЭЦВМ. Казань, 1973.
5. Гурьев Н. И., Поздышев В. Л., Старокадомская 3. М. Матрич-
Матричные методы расчета на прочность крыльев малого удлинения
М„ 1972.
6. Зенкевич О. Метод конечных элементов в технике: Пер. с англ —
М., 1975.
7. Кан С. И. Строительная механика оболочек. М., 1966.
8. Кан С. Н., Свердлов А. И. Расчет самолета иа прочность. М.,
1966.
9. Канторович Л. В., Крылов В. И. Приближенные методы выс-
высшего анализа. М.—Л., 1949.
10. Крылов В. И. Приближенное вычисление интегралов. М., 1967.
П. Лейбензон Л. С. Вариационные методы решения задач теории
упругости. М.—Л., 1943.
12. Леонов В. И., Хазанов X. С. К расчету искривленных круглых
пластин на нормальное сосредоточенное воздействие. — Науч. трУ
Куйбышевский авиац. ин-т, 1972, вып. 63, с. 22—32.
13. Метод конечных элементов в проектировании транспортных
сооружений//!. С. Городецкий и др. М., 1981.
14". Новожилов В. В. Теория тонких оболочек. Л., 1962.
15. Норри Д., де Фриз Ж. Введение в метод конечных элементов:
Пер. с англ. — М., 1981.
16. Образцов И. Ф. Вариационные методы расчета тонкостенных
авиационных конструкций. М., 1966.
17. Образцов И. Ф., Онанов Г. Г. Строительная механика скошен-
скошенных тонкостенных систем. М., 1973.
18. Полюдов М. В. Модель анизотропной неоднородной пластинки
из конечных элементов. — В кн.: Ученые записки ЦАГИ. М., 1978,
т. 9, с. 93—102.
19. Постное В. А. Численные методы расчета судовых конструк-
конструкций. Л., 1977.
20. Постное В. А., Хархурим И. Я. Метод конечных элементов в
расчетах судовых конструкций. Л., 1974.
21. Розин Л. А. Основы метода конечных элементов в теории уп-
упругости. Л., 1972.
22. Рублев А. Н. Лииейиая алгебра. М., 1965.
389
23. Савельев Л. М. Простой четырехугольный конечный элемент
произвольной тонкой оболочки. — В кн.: Вопросы прочности и дол-
долговечности авиационных конструкций. Куйбышев, 1979, с. 58—63.
24. Савельев Л. М. Простой криволинейный конечный элемент
оболочки вращения. — В кн.: Прочность, устойчивость и колебания
тонкостенных и монолитных авиационных конструкций. Казань,
1980, с. 86—92.
25. Сегерлинд Д. Применение метода конечных элементов: Пер. с
англ. — М., 1979.
26. Стренг Г., Фикс Дж. Теория метода конечных элементов: Пер.
с англ. — М., 1977.
27. Стриклин Дж. Статический и динамический расчеты геометри-
геометрически нелинейных оболочек вращения. — В кн.: Расчет упругих кон-
конструкций с использованием ЭВМ: Пер. с англ. — Л., 1974, т. 1, с. 272—
292.
28. Тимошенко С. П., Гудьер Дж. Теория упругости: Пер. с англ.
— М., 1975.
29. Фаддеев Д. К., Фаддеева В. Н. Вычислительные методы линей-
линейной алгебры. М.—Л., 1963.
30. Филин А. П. Прикладная механика твердого деформируемого
тела. М., 1975, т. 1; 1978, т. 2; 1981, т. 3.
31. Фихтенгольц Г. М. Основы математического анализа. М., 1968,
т. 2.
32. Barlow J. Optimal stress locations in finite element models. —
Int. J. Numer. Meth. Eng., 1976, vol. 10, №2, p. 243—251.
33. Cook JR. L. Concepts and applications of the finite element ana-
analysis. — N. y.: Wiley, 1974.
34. Fried /., Malkus D. S. Finite element mass matrix lumping
by numerical integration with no convergence rafe loss.— Int. J. Solids
and Struct,. 1975, vol. 11, №4, p. 461—466.
35. Galletly G. D., Mistry Y. The free vibration of cylindrical shells
with various end closures. — Nucl. Eng. and Des., 1976, vol. 30, № 2,
p. 249—268.
36. Hinton E., Campbell J. S. Local and global smoothing of discon-
tinious finite element functions using a least squares method— Int.
J. Numer. Meth. Eng., 1974, vol. 8, № 3, p. 461—480.
37. Hinton E., Rock Т., Zienkiewicz О. С A note on mass lumping
and relating processes in the finite element method. — Earthquake Eng.
and Struct. Dyn., 1976, vol. 4, № 3, p. 245—249.
38. Hughes T. J. /?., Tailor R. L., Kanoknukulchai W. A simple and
efficient finite element for plate bending.— Int. J. Numer. Meth. Eng.,
1977, vol. 11, № 10, p. 1529—1543.
39. Oden J. Т., Reddy J. N. Nate on an approximate method for
computing consistent conjugate stresses in elastic finite elements.— Inf.
J. Numer. Meth. Eng., 1973, vol. 6, № 1, p. 55—61.
40. Robinson J. A single element test. — Comput. Meth. Appl. Mech.
and Eng., 1967, vol. 7., № 2, p. 191—200.
41. Zienkiewicz 0. C, Bauer J., Morgan K., Onate E. A simple and
efficient element for axisymmetric shells. — Int. J. Numer. Meth. Eng.,
1977, vol. 11, № 10, p. 1545—1558.
39<j
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аппроксимация геометрии 254
— перемещений 133
Брус круговой 78
— прямой в местной системе коорди-
координат 59
в общей системе координат 61
Вариация напряжений 40
— потенциала внешних сил 31
дополнительного 32
— работы внешних сил 29
— — дополнительной 32
— энергии деформации 35
— дополнительной 35
Вариационный принцип Гамильтона 335
Лагранжа 39
Кастнльяно 42
Вектор нормальный 269
— собственный 359
Возможная работа внешних сил 30
Возможные деформации 35
— перемещения 30
Гипотеза прямых нормалей 230
Граничные условия 19
геометрические 19
естественные 48
— — статические 15
Групповой тест 214
Демпфирование искусственное 384
Деформация плоская 20
— линейная 14
— объемная 14
— сдвига 14
Дискретизация тела 106
Дискретная система 108
Закон Гука 17
для конструктивно-ортотропной
пластины 27
— — — обобщенного плоского напря-
напряженного состояния 22
— плоской деформации 22
Иерархия конечных элементов 175
Интеграл Мора 81
Интегрирование численное 186
порядок 188
— минимально допустимый 189
— — точки Гаусса 189
уравнений движения 373
устойчивость 374
— шаг 373
Колебания собственные 357
Компоненты деформации 14
— напряжения 13
— перемещения 14
Конструктивно-ортотропная пластина
23
Конечный элемент 107
— — базовый 156
нзопараметрическнй 166
Конечный элемент несовместный 149,
166
одномерный 179
прямоугольный 139
совместный 138
треугольный 133
трехмерный 182
четырехугольный 160
Конечноэлементиая идеализация кон-
конструкции 283
лонжерона 290. 300
оболочкк безмоыеитной 285
вращения 251. 254
произвольной 272, 280
пластины 201
тонкой 231, 236, 241. 278
подкрепленной пвнелн 198
шпангоута 201, 310, 320, 328
Координаты безразмерные 140, 182
— декартовы 13
местные 54
общие 54
— криволинейные 267
Коэффициенты весовые 187
Матрица аппроксимирующих функций
109
— демпфирования 336
— жесткости 51
вырожденная 92
конечного элемента 112
конструкции 89
ленточная структура 90
тела 51, 116
— масс 332
блочно-диагоиальная 341
диагональная 340
согласованная 338
конечного элемента 332
конструкции 333
— неотрицательно-определенная 359
— податливости 50
— положительно-определенная 335
— преобразовании координат 55
— Якобн 164
Метод Гаусса 188
— выделения диагонали 341
— Канторовича — Власова 46, 124
— конечных полос 132
— Маркова 191
— Ныомарка 379
— разложения по формам колебаний
369
— Ритца 43
— центральных разностей 375
— Эйлера 191
Минимизация полной энергии 43
— функционала 131
Напряжения в наклонных площадках
15
— касательные 13
— нормальные 13
Напряжение полное 13
Нормаль 230
— внешняя 15
Обобщенная проблема собственных
значений 358
Обобщенное плоское напряженное со-
состояние 20
391
Объединение конечных элементов 116,
253
Объем конечного элемента 111
— тела 29
Поверхность конечного элемента 113
— тела 15
Подкоиструкцня 152
Поле напряжений 197
— перемещений 216
Полином полный 207
Потенциал внешних снл 30
— дополнительный 32
Преобразование координат 54
Принцип возможных перемещений 38
— Д'Аламбера 329
— дополнительных виртуальных работ
41
Работа внутренних снл 33
— внешних снл 28
дополнительная 31
Ряд Тейлора 205
Сглаживание напряжений 193
— — местное 198
общее 194
Сдвиг ложный 145, 222
Силы внеузловые 74
— внешние 27
— внутренние 33
— демпфирующие 336
— инерционные 329
— объемные 13
— поверхностные 13
— реакции 74
— сосредоточенные 107
— узловые 51
— эквивалентные 107
Соотношения геометрические 16
— статические 14
— теории упругости 13
— физические 17
Стержневая система 49
Степени свободы 204
иеузловые 156
Степень полинома 206
Сходимость решения 204
критерии 210
для несовместных элементов
214
совместных элементов 210
— — монотонная 211
немонотонная 219
Сходимость решения, правило интег-
интегрирования 221
скорость 204
Теорема Клапейрона 29
— Максвелла 50
— Беттн 51
Узлы внешние 150
— внутренние 150
— конечного элемента 108
— подконструкцнн 153
Узловые лнннн 124
— окружности 228
— перемещения 108
Упругие постоянные Ляме 18
Уравнения Ляме 19
— равновесия узлов 87, 114
— Эйлера 48
Уравнение вариационное Кастнльяно
42
Лагранжа 38
Условие совместности деформаций 17
— полноты конечного элемента 211, 213
— ортогональности собственных форы
361
Ферменный элемент 58
Форма колебания 357
нормированная 362
Формулы Гаусса 188
— Кошн 16
— Ньютона — Котеса 187
Формула Остроградского — Гаусса 37
— Снмпсона 188
— трапеции 188
Функции аппроксимирующие 109
— формы 161
Частота колебания 357
Энергия кинетическая
конечного элемента 334
конструкции 335
— потенциальная полная 38
дополнительная 41
деформации 32
дополнительная 35
конечного элемента 117
конструкции 128
Якобиан преобразования координат 16?
OB, ЛМ.САВЕЛЪЕБ, Х.СХАЗАНОВ
МЕТОД
КОНЕЧНЫХ
ЭЛЕМЕНТОВ
в задачах
строительной механики
летательных
аппаратов
учебшм пособие
для вузов