Author: Образцов И.Ф. Савельев Л.М. Хазанов Х.С.
Tags: механика строительная механика авиастроение
Year: 1985
Text
И Ф. ОБРАЗЦОВ, Л, М. САВЕЛЬЕВ, X. С. ХАЗАНОВ
МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ в задачах строительной механики летательных аппаратов
Допущено Министерством высшего и среднего специального образования СССР в качестве учебного пособия для студентов авиационных специальностей вузов
МОСКВА «ВЫСШАЯ ШКОЛА» 198S
БВК-22.25-0-23 УДК_534/534
Рецензенты: кафедра строительной механики летательных аппаратов Казанского авиационного института им. А. Н. Туполева (зав. кафедрой — д-р техн, наук, проф. Ю, Г. Одинокое);; д-р техн, наук, проф. Л. А. Колесников (Харьковский авиационный институт им. Н. Е. Жуковского).
Образцов И. Ф., Савельев Л. М., Хазанов X. С.
0-23 Метод конечных элементов в задачах строительной механики летательных аппаратов: Учеб, пособие для студентов авиац. спец, вузов. — М.: Высш, шк;, 1985. — 392 с., ил.
В пер.: 1 р. 10 к.
В книге изложены общие принципы метода конечных элементов в перемещениях, его связь с вариационными принципами механики. Рассмотрены вопросы сходимости консчиоэлементного решения, способы построения матриц жесткости и матриц масс типовых конечных элементов, схемы ко-иечпоэлементной идеализации авиационных конструкций, их расчет на прочность и колебания. Приведены примеры расчетов.
„ 3606030000—335 ББК 22.25
О ---------------- 172—85
001(01)—85 531
Иван Филиппович Образцов
Леонид Макарович Савельев
Хацкель Соломонович Хазанов
МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ В ЗАДАЧАХ
СТРОИТЕЛЬНОЙ МЕХАНИКИ ЛЕТАТЕЛЬНЫХ АППАРАТОВ
Зав. редакцией К. И. Аношииа. Редактор Л. Н. Шатунова. Художник Н. Ю. Бабикова. Худ. редактор Т. А. Дурасова. Техн, редактор И. А. Балелина. Корректор В. В. Кожуткииа
ИБ № 4904
Изд. № ОТ-483. Сдано в набор 11.01.85. Подп. в печать 18.06.85. Т-04444.
Формат 84Х 108]/;2- Бум. кн.-жури. Гарнитура литературная. Печать высокая. Объем 20,58. усл, печ. л. 20,58. усл, кр.-отт. 19,16 уч.-изд. л. Тираж 6000 экз. Зак. № 651. Цепа I р. 10 к.
Издательство «Высшая школа», 101430. Москва. ГСП-4. Неглиниая ул., д. 29/14
Московская типография № 4 Союзполиграфпрома
при Государственном комитете СССР
но делам издательств, полиграфии и книжной торговли
129041, Москва, Б. Переяславская, 46
© Издательство «Высшая школа», 1985
ОГЛАВЛЕНИЕ
Предисловие............................................. 6
Введение ...... 9
Основные обозначения..................................... II
Часть I. Матричная формулировка соотношение теории упругости и задач строительиой механики стержневых систем
Глава 1. Основные соотношения теории упругости
§ 1.1. Определения и уравнения...................... 13
§ 1.2. Плоская задача ............................. 20
§ 1.3. Подкрепленная панель как конструктнвно-орто-тропная пластина ................................... 23
Глава 2. Вариационные методы теории упругости
§ 2.1. Работа внешних сил. Дополнительная работа ... 27
§ 2.2. Энергия деформации. Дополнительная энергия деформации ......................................... 32
§ 2.3. Вариационное уравнение Лагранжа . . ... 35
§ 2.4. Вариационное уравнение Кастнльяно .... 39
§ 2.5. Метод Ритца......... . . 43
§ 2.6. Метод Канторовича—Власова .... .46
Глава 3. Матричный метод перемещений для стержневых систем
§ 3.1. Понятие о матрице жесткости........... 49
§ 3.2. Преобразование координат.......... .54
§ 3.3. Ферменный элемент............... .58
§ 3.4. Прямой брус в местной системе координат . 61
§ 3.5. Прямой брус в общей системе координат .... 69
§ 3.6. Учет внеузловой нагрузки . . ........... 74
§ 3.7. Плоский круговой брус . . ........... 78
§ 3.8. Стержневая система .... ...........84
§ 3.9. Определение узловых перемещений . . 91
§ 3.10. Примеры расчета...................... . . .93
Часть II. Метод конечных элементов
Глава 4. Теоретические основы метода
§ 4.1. Дискретизация тела .... ............. 106
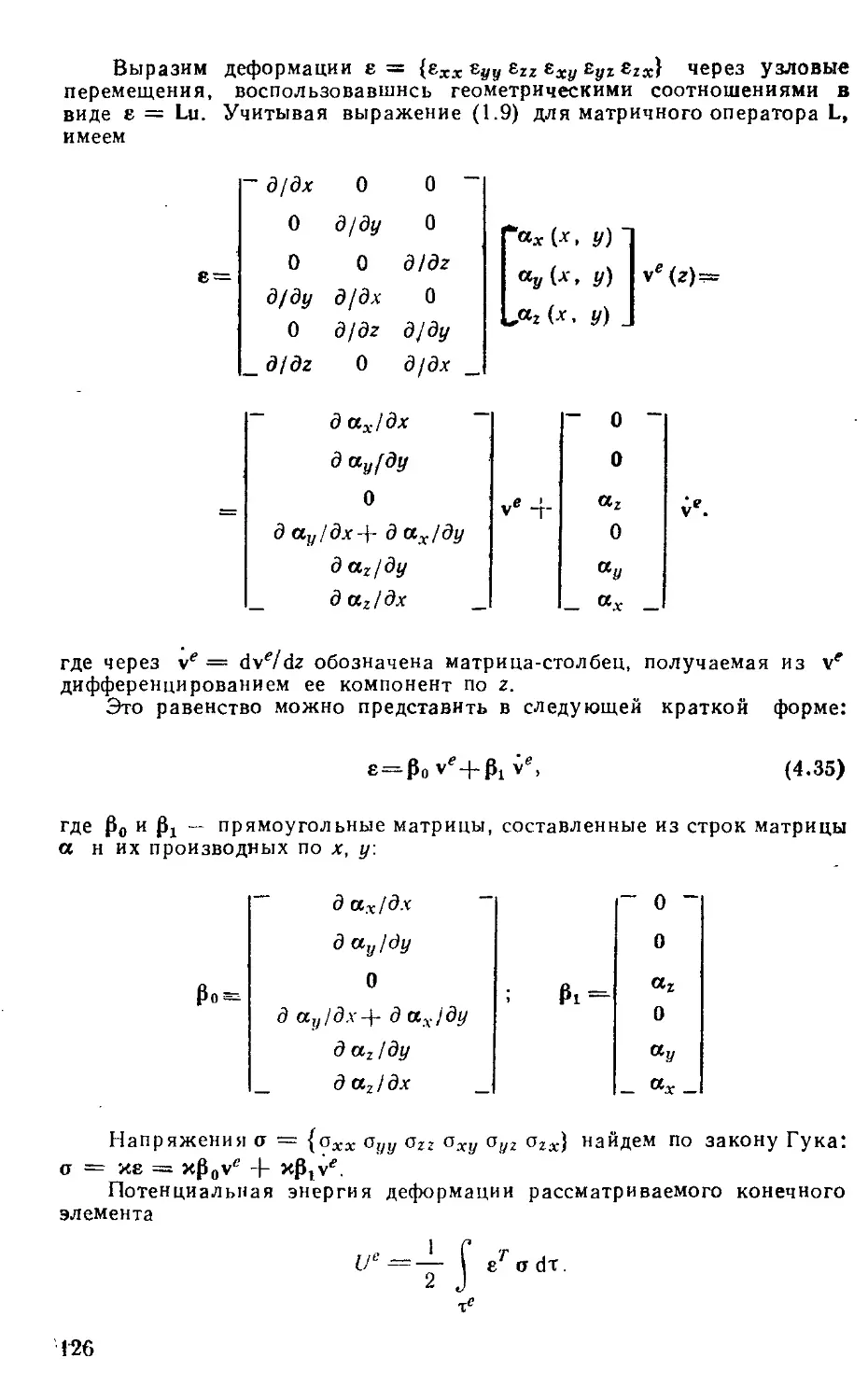
§ 4.2. Перемещения, деформации и напряжения в конечном элементе...................................... 108
§ 4.3. Матрица жесткости конечного элемента.........Ill
§ 4.4. Учет внеузловой нагрузки................... 113
§ 4.5. Определение узловых перемещений..............114
§ 4.6. Связь метода конечных элементов с методом Ритца 117
, § 4.7. Конечноэлементная форма метода Канторовича—
Власова .... 124
Глава 5. Конечные элементы сплошной среды
§ 5.1. Плоский треугольный элемент..................133
§ 5.2. Совместный прямоугольный элемент.............139
§ 5.3. Несовместный прямоугольный элемент...........145
§ 5.4. Внутренние узлы и подконструкцин.............150
§ 5.5. Неузловые степени свободы....................156
§ 5.6. Четырехузловой изопараметрический элемент .... 160
§ 5.7. Несовместный четырехугольный элемент.........166
§ 5.8. Плоские изопараметрические элементы высших порядков...........................................169
§ 5.9. Деформация пространственного криволинейного стержня............................................175
§ 5.10. Одномерные конечные элементы................179
§ 5.11. Трехмерные конечные элементы................182
§ 5.12. Численное интегрирование в методе конечных элементов........................................ . 186
§ 5.13. О вычислении напряжений.....................193
§ 5.14. Примеры расчета.............................198
Глава 6. Критерии сходимости
§ 6.1. Предварительные замечания....................204
§ 6.2. Применение рядов Тейлора к исследованию сходимости ...........................................205
§ 6.3. Критерии сходимости совместных элементов .... 210
§ 6.4. Сходимость несовместных элементов............214
§ 6.5. Влияние на сходимость численного интегрирования 220
§ 6.6. Исключение ложных деформаций сдвига с помощью численного интегрирования ........................ 222
Часть III. Приложение метода конечных элементов к расчету авиационных конструкций
Глава 7. Конструкции в виде пластин и оболочек
§ 7.1. Предварительные замечания....................227
§ 7.2. Основные соотношения теории изгиба пластин . . . 228
§ 7.3. Изопараметрические конечные элементы пластины 231
§ 7.4. Несовместный прямоугольный элемент пластины 236
§ 7.5. Несовместный четырехугольный элемент пластины 241
§ 7.6. Учет внеузловой нагрузки. Определение узловых перемещений.........................................244
§ 7.7. Основные соотношения для оболочек вращения при осесимметричном нагружении.........................247
§ 7.8. Изопараметрические конечные элементы оболочки вращения...........................................251
§ 7.9. Двухузловой криволинейный конечный элемент оболочки вращения..................................254
§ 7.10. Матрица жесткости шпангоута.................262
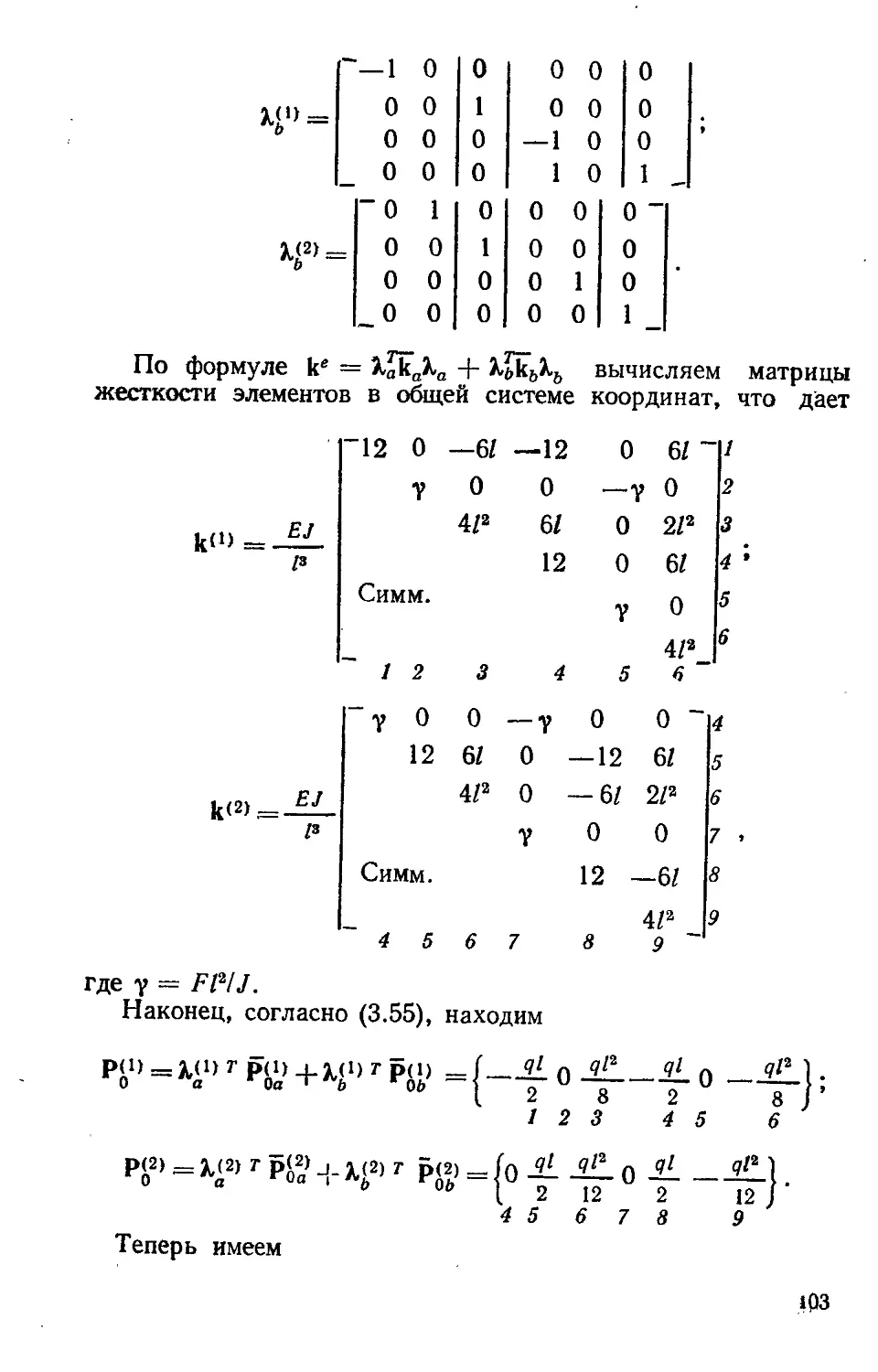
§ 7.11. Объединение конечных элементов. Определение перемещений и напряжений............................263
§ 7.12. Деформации произвольной поверхности.........267
§ 7.13. Конечные элементы произвольной оболочки. . . . 272
§ 7.14. Примеры расчета........................... . 278
Глава 8. Каркасированные тонкостенные конструкции
§ 8.1. Конечиоэлементная идеализация конструкции . . . 283
§ 8.2. Конечные элементы безмоментной обшивки .... Ивб
§ 8.3. Конечные элементы изопараметрического типа для . лонжеронов . . . ,.................................290
§ 8.4. Составные конечные элементы лонжеронов .... 300
§ 8.5. Двухузловой конечный элемент шпангоута .... 310
§ 8.6. Криволинейные конечные элементы шпангоута . . 320
§ 8.7. Заключительные замечания....................324
§ 8.8. Примеры расчета.............................325
Часть IV. Динамические задачи
Глава 9. Соотношения метода конечных элементов в задачах динамики
§ 9.1. Предварительные замечания...................329
§ 9.2. Матричное уравнение движения конструкции . . . 330
§ 9.3. Согласованная и диагональная формулировки матрицы масс......................................... 338
§ 9.4. Матрицы масс конечных элементов с линейными смещениями узлов...................................342
§ 9.5. Матрицы масс конечных элементов изгибаемых пластин ............................................ 344
§ 9.6. Матрицы масс конечных элементов оболочек .... 348
§ 9.7. Матрицы масс конечных элементов бруса ..... 351
Глава 10. Расчет динамического поведения конструкции
§ 10.1. Собственные колебания......................357
§ 10.2. Ортогональность собственных форм колебаний . . . 360
§ 10.3. Примеры расчета............................362
§ 10.4. Разложение движения по формам собственных колебаний ...........................................369
§ 10.5. О прямом интегрировании уравнений движения 373
§ 10.6. Метод центральных разностей................375
§ 10.7. Метод Ньюмарка.............................379
Заключение..............................................386
Список литературы.......................................389
Предметный указатель....................................391
ПРЕДИСЛОВИЕ
Создание прочных и надежных в эксплуатации машин высоким ресурсом работы, обладающих высокой экономично*, стью и минимальным весом, — это вопрос большой важности* на который постоянно обращается внимание в директивных, документах Коммунистической партии и Советского правительства. Его решение затрагивает множество проблем, среди которых важное место занимает проблема совершенствования методов расчета конструкций на прочность. Особенно это относится к конструкциям летательных аппаратов, где противоречие между требованиями прочности и минимального веса проявляется наиболее остро.
Ёурное развитие вычислительной техники приводит к определенной переоценке традиционных взглядов на исследование ’прочности летательных аппаратов, вызывая к жизни новые численные методы расчета. Среди методов, ориентированных 'на эффективное использование ЭВМ, наибольшее признание у нас в стране и за рубежом получил метод конечных элементов, обладающий целым рядом достоинств в сравнении с другими. методами.
Целью авторов данной книги было создание учебного пособия, содержащего доступное для студентов и в то же время достаточно строгое изложение метода конечных элементов в перемещениях с акцентом на его приложения к задачам строительной механики летательных аппаратов. При написании книги особое внимание было уделено методической отработке материала; учтен многолетний опыт преподавания метода конечных элементов на кафедрах строительной механики и прочности летательных аппаратов Московского и Куйбышевского авиационных институтов.
Пособие состоит из четырех частей. Первая часть имеет вводный характер. Здесь (главы 1, 2) дана краткая сводка уравнений теории упругости в матричной записи и изложены вариационные методы, составляющие теоретическую базу метода конечных элементов. В гл. 3 подробно описан матричный метод расчета стержневых систем в перемещениях. Используемые здесь принципы, алгоритмы, терминология во многом характерны и для метода конечных элементов. По этой причине расчет стержневых систем излагается иногда в рамках метода конечных элементов. Но между матричным методом перемещений стержневых систем и методом конечных эле*
ментов имеются и принципиальные различия. Например, при статическом расчете стержневых систем решение в рамках технической теории бруса получается точным. Поэтому расчет стержневых систем выделен в отдельную главу. Вообще говоря, изучение метода конечных элементов можно начинать сразу с чтения второй части книги, лишь по мере надобности обращаясь за справками к соответствующим главам первой части. Но усвоение метода существенно облегчится, если проработать сначала материал гл. 3 и приведенные здесь примеры расчета.
Во второй части, являющейся центральной, излагается собственно метод конечных элементов. Показана его связь.с методом Ритца (гл. 4), описаны некоторые конечные элементы сплошной среды (гл. 5), рассмотрены вопросы сходимости приближенного решения к точному (гл. 6). Для более глубокого понимания существа метода конечных элементов необходимо иметь хотя бы общую ориентировку в вопросах его сходимости. Именно такую ориентировку дает гл.6, не претендующая на математическую строгость, но содержащая зато доступное для инженера изложение этой темы.
В третьей части (главы 7, 8) рассматривается приложение метода конечных элементов к расчету характерных для летательных аппаратов конструктивных элементов — пластин, оболочек и тонкостенных подкрепленных систем типа фюзеляжа или крыла самолета. Основное внимание уделено здесь описанию подходящих конечных элементов для расчета тех или иных конструкций; их применение иллюстрируется примерами расчета.
Наконец, в четвертой части затрагиваются вопросы динамических расчетов конструкций летательных аппаратов. Значительное место отведено обоснованию эффективных способов представления массовых характеристик конструкции, обеспечивающих сокращение времени счета (гл. 9). В гл. 10 рассмотрен расчет собственных колебаний конструкции, а также расчет динамического поведения путем прямого интегрирования уравнений движения.
Учитывая, что книга предназначена для первоначального ознакомления с методом конечных элементов, авторы избрали способ изложения от простого к сложному. При этом неизбежны некоторые повторы, но, как показывает опыт преподавания, это оправдывается более быстрым и прочным усвоением метода. Чтобы облегчить читателю отбор наиболее важного материала, те места в книге, которые без ущерба для понимания существа дела можно пропустить прн первом чтении, напечатаны мелким шрифтом.
От читателя не требуется какой-либо дополнительной подготовки сверх обычной вузовской программы в объеме первых трех курсов. Необходимым условием усвоения материала является уверенное владение простейшим аппаратом матричной алгебры, язык которой используется на протяжении всей книги. Хотя пособие адресовано в первую очередь студентам авиационных институтов, оно может быть использовано для учебных целей и в других технических вузах, а также для самостоятельного изучения основ метода конечных элементов.
Общий замысел книги принадлежит И. Ф. Образцову. Им написаны введение, заключение, §2.6, 4.6, 4.7, 6.2, 6.3, 7.1, 7.2, 7.4, 7.5, а также осуществлено общее редактирование книги; §5.10—5.13, 7.7—7.9, 7.12, 7.13, 9.3 и 9.6 написаны Л. М. Савельевым, 9.5 и 10.3 — И. Ф. Образцовым и Л. М. Савельевым, §3.1—3.5, 3.8, 3.9, 5.1, 5.2, 5.6, 5.8 — X. С. Хазановым. Остальные параграфы написаны Л. М. Савельевым и X. С. Хазановым.
Авторы выражают свою признательность профессорам М. Б. Вахитову и Л. А.Колесникову, доценту Н. А. Шеломову и старшему научному сотруднику В. Ф. Снегиреву, внимательно ознакомившимся с рукописью и высказавшим много ценных замечаний, которые были учтены авторами и способствовали улучшению книги. Авторы благодарят инженеров Г. В. Канову и Л. К. Мещерякову за помощь в выполнении числовых расчетов, а также Т. Н. Верещагину, проделавшую большую работу по оформлению рукописи.
Авторы будут благодарны всем читателям, которые пришлют свои пожелания и замечания. Их следует направлять в издательство «Высшая школа» по адресу: 101430, Москва, ГСП-4, ул. Неглинная, 29/14.
Авторы
Основные уравнения теории упругости известны уже более полутора веков. Несмотря на это, количество задач, имеющих ।очное решение, относительно невелико. Для решения прак-1ПЧССКИХ проблем разработаны хорошо зарекомендовавшие < < бя методы сопротивления материалов и строительной механики. Однако эти методы применимы, как правило, лишь к телам простой конфигурации. Они зачастую оказываются бессильными, если требуется найти распределение напряжений и сложной реальной конструкции.
В этих условиях приходится либо упрощать до крайно-< in расчетную схему, сводя такой ценой всю проблему к решению одной из классических задач, либо обращаться к како-мулибо подходящему численному методу. Последний путь и настоящее время становится наиболее предпочтительным, поскольку успехи в развитии численных методов и в создании >ВМ делают его вполне осуществимым даже для таких сложных и нерегулярных систем, какими являются конструкции летательных аппаратов.
Существует много различных численных методов, пригодных для эффективного решения тех или иных частных задач. Начиная с конца 60-х годов предпочтение все больше отдается методу конечных элементов как наиболее гибкому и универсальному. По оценке специалистов этот метод будет в течение ближайших десятилетий служить основным расчетным ин-। 4>ументом при исследовании прочности конструкций летательных аппаратов. Отметим, что область применения метода конечных элементов не ограничивается задачами прочности; опа охватывает широкий круг разнообразных технических проблем, включая, например, задачи теплопередачи, расчета тираничного слоя и т. Д.
Применение метода конечных элементов способствует по-пышепию точности и надежности расчетов,а также автомати-i.iiiHH инженерного труда. Это дает большой экономический »>|н|« кт, поскольку влечет за собой сокращение сроков довод-| || и щелий, а в отдельных случаях позволяет даже отказать-....г проведения некоторых видов дорогостоящих прочностных испытаний.
Рождение метода конечных элементов относится ко второй ш>'1о1шпе 50-х годов нашего столетия. Базой для его появлении послужили предшествующие работы, среди которых осо
бое значение имели три направления: развитие методов расчета стержневых систем, применение метода конечных разностей и разработка вариационных методов решения задач теории упругости и строительной механики. Неоценимый вклад в эти исследования внесли советские ученые И. Г. Бубнов, Б. Г. Галеркин, Л. В. Канторович, В. 3. Власов, А. Р. Ржа-ницин, С. Г. Михлин и многие другие. Развитию и популяри: зации в СССР метода конечных элементов способствовали работы А. Ф. Смирнова, А. П. Филина, В. А. Постнова, В. Г. Корнеева, 3. И. Бурмана, Л. А. Розина, А. В. Александрова, Б. Я. Лащеникова, Н. И. Шапошникова и целого ряда других ученых.
Имеется несколько разновидностей метода конечных элементов: решение в перемещениях, в силах, смешанная формулировка, гибридный подход. Наибольшее распространение у нас в стране и за рубежом получил метод перемещений, поскольку он обладает целым рядом достоинств, среди которых можно отметить простоту, удобство реализации на ЭВМ, естественную приспособленность к анализу динамических проблем, Применительно к расчету пластин и оболочек, где создание эффективных конечных элементов в перемещениях длительное время наталкивалось на серьезные трудности, были разработаны и успешно использовались конечные элементы так называемого гибридного типа. Однако в конце 70-х годов эти трудности удалось в значительной степени преодолеть, что позволяет избежать применения сложных гибридных элементов.
В данном пособии рассматривается метод конечных элементов в перемещениях применительно к линейным задачам строительной механики летательных аппаратов. Не затрагиваются такие важные темы, как расчет на устойчивость или учет пластических деформаций. Можно, однако, надеяться, что материал пособия послужит достаточной базой для последующего самостоятельного изучения этих вопросов.
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
Для обозначения матриц, используется полужирный шрифт. Элементы матриц заключаются в квадратные скобки. Для экономяи места иногда применяется запись матрицы-столбца в строку; в этом случае используются фигурные скобки. Операция транспонирования матрицы отмечается верхним индексом «Г».
Наиболее часто встречающиеся обозначения:
В Eh!(\ — р2) —г- жесткость пластины или оболочки на растяжение D = £Л3/[12 (1 — р2)] — изгибная жесткость пластины, оболочки
е — единичный вектор
Е — модуль продольной упругости
G = Е7[2 (1 + р)] — модуль сдвига
Л — толщина пластины, оболочки
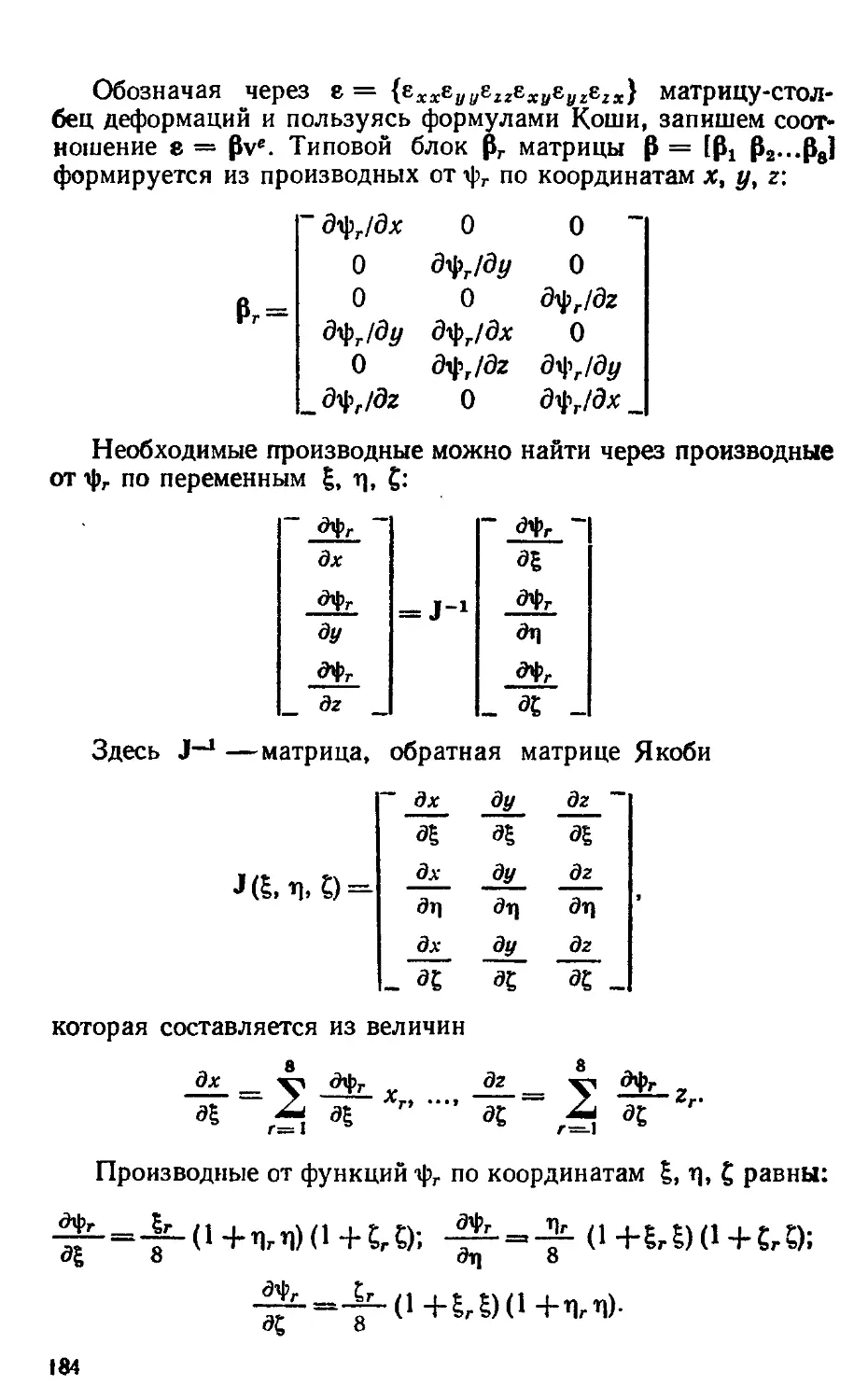
J; I J| — матрица Якоби и ее определитель
k, krS, kij — матрица жесткости конечного элемента, ее блоки /г, s — номера узлов) и скалярные компоненты (i, j — номера узловых перемещений) в местной системе координат
ke, k's, keij — то же, в общей системе координат
К, Krs, kjj — матрица жесткости конечноэлементной модели, ее блоки и скалярные компоненты
L — матричный дифференциальный оператор в соотношении е = = Lu
ш, mrs, mij — матрица масс конечного элемента, ее блоки н скалярные компоненты в местной системе координат
m'’, m®s, — то же, в общей системе координат
М, mfS, mij—матрица масс конечноэлементной модели, ее блоки и скалярные компоненты
р, рх, p,j, pz — матрица-столбец распределенных поверхностных нагрузок н ее компоненты
Р, Pr, Pt — матрица-столбец узловых сил конечного элемента, ее блоки (г — номера узлов) и скалярные компоненты (i — номера перемещений) в местной системе координат
Р*, Рег, Р\ —то же, в общей системе координат
Р, Pr, Pt — матрица-столбец узловых сил конечноэлементной модели, ее блоки н скалярные компоненты
Рг, Рег — матрица-столбец узловых снл конечного элемента, эквивалентных внеузловой нагрузке, и ее блоки
Р, Рг — матрица-столбец эквивалентных узловых сил конечноэлементной модели и ее блоки
Ро, Рог —матрица-столбец узловых сил, уравновешивающих внеузло-вую нагрузку, и ее блоки для элемента стержневой системы в местной системе координат
P^j, Pqa — то же, в общей системе координат
Ро. Рог—то же, для стержневой системы
Я, Ях, Яу, <7z — матрица-столбец, погонных нагрузок и ее компоненты
R, Rx, Ry, Rz — матрица-столбец объемных сил и ее компоненты t — время
Те, Т — кинетическая энергия конечного элемента и всего тела и, их, иу, uz — матрица-столбец перемещений произвольной точки тела и ее компоненты
Ue, U — потенциальная энергия деформации конечного элемента и всего тела
vr, vt — матрица-столбец перемещений узла г и ее скалярные компоие-ты (i — номер перемещения) в местной системе координат
vr, vi — то же, в общей системе координат
V, Vе — матрицы-столбцы узловых перемещений конечного элемента соответственно в местной и общей системах координат
v — матрица-столбец узловых перемещений конечиоэлементной модели
Vе, V — полная потенциальная энергия конечного элемента н всего тела
w — прогиб пластины
Wi—формы собственных колебаний конечноэлементной модели х, у, z — декартовы координаты
а — матрица аппроксимирующих функций (функций формы)
₽—матрица связи между деформациями и узловыми перемещениями 6—знак вариации
е—матрица-столбец деформаций т], £—безразмерные координаты
X — матрица упругих постоянных
1 — матрица преобразования координат
р — коэффициент Пуассона
Пе, П — потенциал внешних сил для конечного элемента и для всего тела
р — плотность материала
а — матрица-столбец напряжений
Iе, т—объем конечного элемента и всего тела
фг — аппроксимирующие функции (функции формы)
<ве, со — поверхность конечного элемента и всего тела
ЧАСТЬ I
МАТРИЧНАЯ ФОРМУЛИРОВКА СООТНОШЕНИЙ ТЕОРИИ УПРУГОСТИ И ЗАДАЧ СТРОИТЕЛЬНОЙ МЕХАНИКИ СТЕРЖНЕВЫХ СИСТЕМ
ГЛАВА 1
ОСНОВНЫЕ СООТНОШЕНИЯ ТЕОРИИ УПРУГОСТИ
Уравнения теории упругости лежат в основе любого метода расчета на прочность, в том числе метода конечных элементов. Так как при изложении последнего систематически применяются матричные обозначения, соотношения теории упругости представлены здесь в матричной форме. Особое внимание уделено записи физических соотношений для конструктивно-ортотропной панели, поскольку подобная расчетная схема часто используется для моделирования подкрепленной ребрами обшивки.
§ 1.1. Определения и уравнения
Отнесем исследуемое упругое тело к декартовым координатам х, у, z и обозначим через Rx, Ry, Rz — проекции на координатные оси объемных сил, приходящихся на единицу объема тела, рх, ру, р2—проекции поверхностных сил, приходящихся на единицу граничной поверхности тела.
Выделим из тела элементарный параллелепипед сечениями, параллельными координатным плоскостям (рис. 1.1). Обозначим компоненты напряжения в площадке, перпендикулярной оси х, через оузс, иху, gxz, в площадке, перпендикулярной оси у, — через оух, <зуу, oyz, а в площадке, перпендикулярной оси z, — через стгж, uzy, uzz. Первый индекс в этих обозначениях характеризует ориентацию площадки, д второй — направление действия соответствующей составляющей напряжения. Нормальные напряжения ихх, стуу, gzz считаются положительными, если оии направлены по внешней нормали к площадке. Положительные направления касательных напря--жений на грани принимаются совпадающими с положительными направлениями координатных осей, если внешняя нормаль к этой грани совпадает с положительным направлением соответствующей оси. Если же внешняя нормаль направлена противоположно соответствующей оси, то и положительные касательные напряжения в этой грани действуют в отрицательных направлениях двух других осей. Как известно, имеет
место следующее свойство парности касательных напряжений:
°xrj ~ °Ух> ауг ~~ °гу> °гх ~ °xz-
Рассмотрим произвольную точку М (х, у, г) упругого тела. Под действием внешних сил она переместится в положение /Ир Вектор полного перемещения ММХ можно разложить по координатным осям на три составляющие их, иу, ult называемые компонентами перемещения. Так как деформация тела совершается при сохранении непрерывности материала, то перемещения являются не-е прерывными функциями координат.
Деформация тела в каждой точке характеризуется величинами ехх, еуу, егг, е.ху, Еуг, Ezx- Первые три из них представляют собой относительные изменения длин бес-р 1 1 конечно малых отрезков,
первоначально (до деформации) параллельных осям х, у, г соответственно; они считаются положительными, если происходят удлинения отрезков, и отрицательными — в случае их укорочения. Последние три величины суть деформации сдвига, представляющие собой изменения углов между элементарными отрезками, первоначально параллельными тем координатным осям, которые указаны в нижних индексах. Деформации сдвига считаются положительными, если углы между отрезками, ориентированными в положительных направлениях координатных осей, становятся острыми.
Объемная деформация 0 представляет собой отношение изменения объема элементарного параллелепипеда к его пер. воначальному объему и может быть выражена как. сумма.
0 — Ё t у у + 6 Z г •
Исходными уравнениями для решения задач теории упругости являются статические, геометрические и физические соотношения.
Статические соотношения. Сюда относятся дифференциальные уравнения равновесия:
дахх । двух . ^ZX 1. р п.
дх 1 <>, дг -f- — и,
d<Jxy дх ... доуу _ ^zy дг 4-^=0;
дахг , д°уг , ^гг 4- Rz = 0
дх ду дг
(1.1)
й формулы для напряжений в наклонных площадках:
®пх °хх пх + ®Ух Пу .4* °zx^zl °пу — °ХУ ПХ 4" Оуу Пу 4" °z^rtzi °nz —®xz пх 4“ ®yz пу 'I" °zz Пг.
(1.2)
Здесь пх, tiy, пг — косинусы углов между внешней нормалью к наклонной площадке и координатными осями х, у, г; опх, ?пу, &nz — проекции полного напряжения в наклонной площадке на координатные оси.
Если наклонная площадка совпадает с граничной поверхностью <о упругого тела, то опж, апу, onz можно рассматривать как составляющие вектора поверхностной нагрузки, т. е. ®пх = Рх\ Оцу = Ру', Qnz —Pz- Поэтому для точек поверхности тела имеем
Рх— ^хх Пх-j~ <УуХ Пу -j-Ozx Пг, Ру ~ °ху Пх 4- °уу Пу -|- <5zy nz, Pz ~ ®хг Пх 4- ®yz Пу 4- ®zz Пг.
(1.3)
Равенства (1.3) устанавливают связь между поверхностными силами и компонентами напряжения вблизи поверхности тела и выражают так называемые статические граничные условия.
Введем следующие матрицы-столбцы:
Тогда равенства (1 1), (1.2) и (1.3) могут быть представлены матричными соотношениями
2^ + 2£'L+-^_ + R=0; (1.4)
дх ду дг
а,, =охпх + оуПу-Ьогп2, (1.5)
Р *= 0Х пх + Оу п,. + az п2 (1.6)
Геометрические соотношения устанавливают связь между компонентами деформации и компонентами перемещения. Если деформации и перемещения малы, то между ними имеет место линейная зависимость, выражаемая уравнениями Коши:
дих . S.V.V = д11У ч- », + дих
— дх дЧу . ду ду ' дну . дг ' (1.7)
— ди2 дг дг ди. дх
Эти соотношения можно представить одним матричным равенством
е = Lu, (1.8)
связывающим матрицы-столбцы деформаций
» - (₽.v.v В//» *21 е„2 Ггг)
и перемещений и — {их иу и2}.
Здесь и далее матрица, записанная в строку и заключенная в фигурные скобки, означает матрицу-столбец. Через L в (1.8) обозначен матричный дифференциальный оператор вида
Если из уравнений (1.7) исключить перемещения их иу и иг, то между компонентами деформации получим шесть дифференциальных соотношений, именуемых условиями совместности (или неразрывности) деформаций Сен-Венана:
й- t'xx . _ д' е-ху . д /dux,, d^iiz J де^-дД
ду1 дх- дхду дх \ дг дх ду 1
= 2 --2 *ЛХ-;
дудг
д': ччи , «гг д2 e?/z. д /де,/г
дг- дудг ду\ дх ду дг /
2 д2 е!Н1 .
дхдг
<52 е-л л,- д- ег х. д /дггх dexv । de„z \
d.v- дг- дхдг дг \ ду дг ' дх /
2 д~ дхду
(1.10)
Физические соотношения. Сюда относятся соотношения, устанавливающие связь между напряжениями и деформациями. В пределах упругости эта связь выражается законом Гу-ка, согласно которому компоненты деформации являются линейными функциями компонент напряжения. Для изотропного тела, т. е. тела, обладающего во всех направлениях одинаковыми упругими свойствами, закон Гука имеет вид:
1 — 10>х — Н(ого + ог1)1<
1°г«‘ — р(о,г+Ох.г)Г. (1.11)
1 fc'; т 1 [fzz- -р (оА.х+оет/)Г, 1 1
vиг— Kz.v—
G u G /
где Е — модуль упругости; G — модуль сдвига; р — коэффициент Пуассона; упругие постоянные материала Е, G и р связаны между собой равенством Е — 2 (1 4- р) G.
Введя матрицу-столбец напряжений
запишем <1.11) в форме одного матричного равенства
8 = Фо.
где
(1.12)
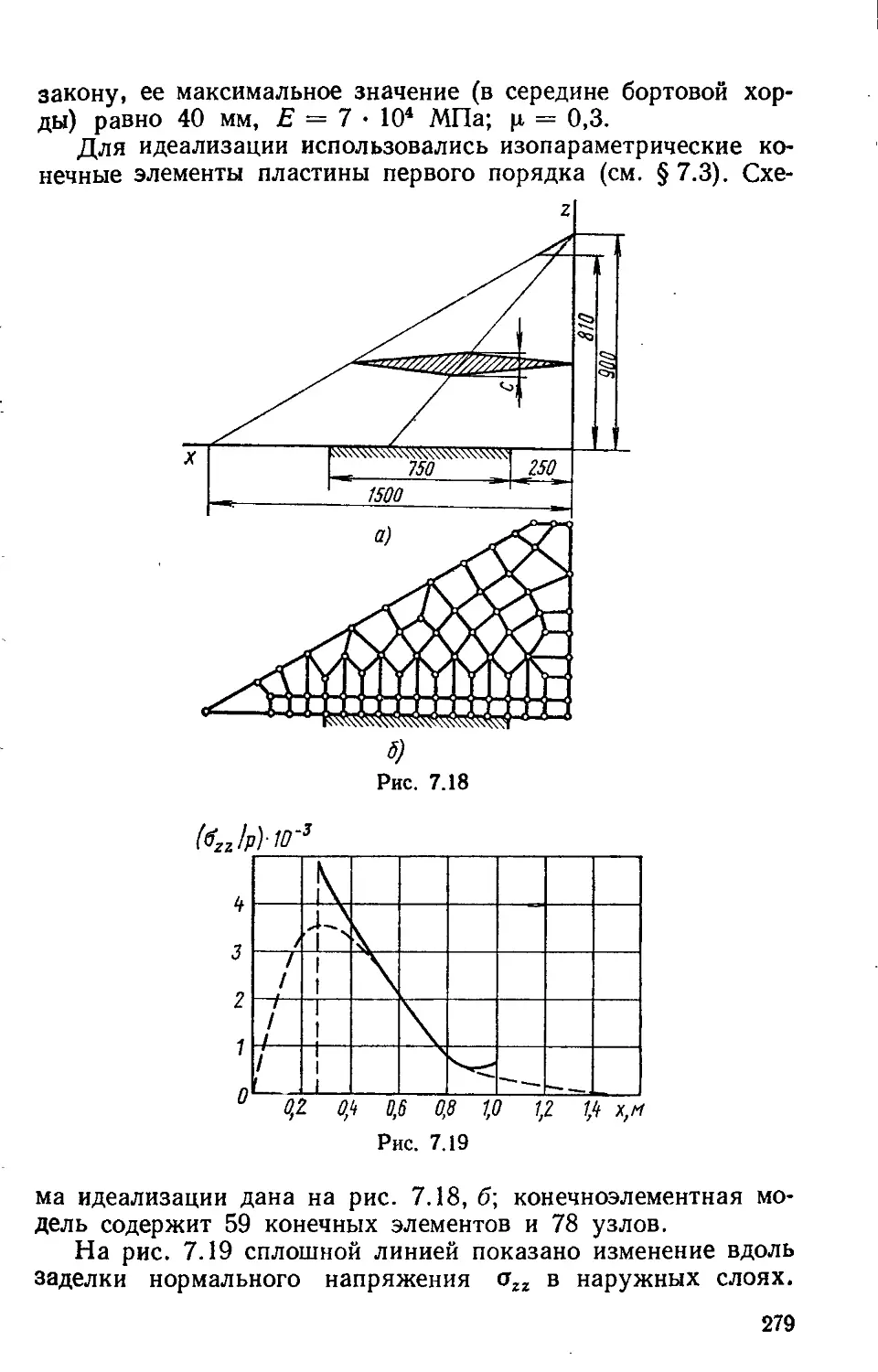
Ф= — Е
1 -н ~Р 1 -р -р
2 (1 Н-р) О
о
о 2 (1 + р) О
О О 2(1 + р)
. (1.13)
—р
—р
о
о
Разрешив уравнения (1.11) относительно напряжений, можно представить закон Гука в так называемой форме Ляме’.
°хх ~ 2Gexx + 10; оаа = 2Geyff + 10; a2Z = 2G ezz + 10;
= 6&xy'l Gyz ~ Gbyz't ®ZX ~ G&ZXf (1.14) где
— 2pG ___________р£_____
~ 1—2р ~ (1 + р) (1-2р) •
Константы G и 1 называются упругими постоянными Ляме.
В матричной записи соотношения (1.14) имеют вид
а = хе, (115)
“1—Р р Р —
Р 1—р Н 0
р р -Р
Е сч О ] сч <N | 04 - 1 ~ 0
(1+р)(1-2р) 0 0
0 0 1 —2р 2
(1.16)
Очевидно, что матрица х является обратной матрице Ф.
Совокупность дифференциальных уравнений равновесия (1.1), геометрических (1.7) и физических 1(1.11) или (1.14)]
соотношений образует систему из 15 уравнений, в которые входят 6 компонент напряжения, 6 компонент деформации и 3 компоненты перемещения. Таким образом, получается замкнутая система уравнений.
Решение этой системы можно искать либо «в перемещениях», либо «в напряжениях». В первом случае за основные неизвестные функции принимают перемещения и* (х, у, z), иу (х, у, г), t/2 (•*> У> 2)> а систему уравнений теории упругости сводят к трем уравнениям относительно этих функций. Для этого напряжения в дифференциальных уравнениях равновесия (1.1) выражают по закону Гука (1.14) через деформации, а последние по формулам Коши (1.7) — через перемещения. В результате получают уравнения Ляме:
GV2«x + (G + l)^- + /?x = 0;
G^UU + (G + Х)-^-+^=0; GV2Mz + (G+X)-^- + /?2=0, <3г
X
где
Q _ дих | | . ya „ J [ d2
dx dy dz ’ dx'1 dy'1 dz'1
K этим уравнениям необходимо присоединить граничные условия. Если на поверхности тела заданы перемещения, то граничные условия сводятся к требованию, чтобы в точках поверхности отыскиваемые функции uz приняли заданные значения н», иу, и*г. Такие условия называются геометрическими (или кинематическими). Однако чаще геометрические условия задаются лишь на части поверхности, а на остальной части задаются поверхностные нагрузки. Обозначим через <ои и wp соответствующие части поверхности тела (о. Тогда на ыр должны удовлетворяться статические граничные условия (1.3). Их следует также записать через перемещения, в результате чего они примут вид:
(2G-^- +xeVx+G(-^- +—Ь./ +
\ J \ dx dy ) !/
i /z ( t dllx ) „ „ .
+ ° -----Г Px>
\ дх dz
nx+ (2G-^- +xe)n!,+
\dx dy ) x \ dy
i /"* / C^m . <?«z \
+ GHJL+-T^-\ дг ду )
g(-^~ + 'Inx H-G f-^- + -^- k„ + \ дх ' дг }'\ dz dy J v
+ ^G-^-^nz=pz.
Другой подход заключается в том, что за основные неизвестные функции принимают напряжения. Для их отыскания следует в первую очередь использовать дифференциальные уравнения равновесия (1.1). К ним присоединяют условия совместности деформаций (1.10). Чтобы можно было ими воспользоваться, нужно выразить в них по закону Гука деформации через напряжения. Подобная замена после ряда преобразований с использованием уравнений равновесия (1.1) приводит к так называемым уравнениям Бельтрами-Мичелла 1281.
§ 1.2. Плоская задача
Существует широкий класс важных в практическом отношении задач, в которых перемещения, деформации и напряжения зависят лишь от двух координат — скажем, х и у. Этот класс задач под общим названием «плоская задача теории упругости>' подразделяется на плоскую деформацию и обобщенное плоское напряженное состояние.
Если в процессе нагружения все точки тела перемещаются только параллельно одной плоскости (плоскости ху, например), то соответствующее деформированное состояние называется плоской деформацией. Таким образом, для плоской деформации имеем мж=цх(х, у), и!1=и,,(х, у), uz—0. В соответствии с уравнениями Коши (1.7), деформации егг, &*г и гуг оказываются равными нулю, а из закона Гука (1.14) вытекает, что касательные напряжения оЖ2 и оу2 также равны нулю. Остальные компоненты деформации и напряжения являются функциями только координат х и у.
Если, далее, тонкая пластина, параллельная плоскости ху, нагружена объемными и по контуру—поверхностными силами, параллельными ее плоскости и равномерно распределенными по толщине, то имеем дело с обобщенным плоским напряженным состоянием. В этом случае можно пренебречь компо-
лентами напряжения агг, ахг и анг, а ахх, ауу и <зху считать постоянными по толщине:
°zz ~ axz ~ &yz ~ Oj
&хх &хх (^ //)> ®уу ° у у У}> ®ху °ху (-^i У} -
Из закона Гука (1.11) следует, что при обобщенном плоском напряженном состоянии деформации сдвига ехг = eyz — О, а остальные компоненты деформации представляются как функции только координат х и у.
Выпишем основные уравнения теории упругости применительно к плоской задаче. Из трех дифференциальных уравнений равновесия (1.1) остается два; в матричной записи они имеют вид
(1.17)
дх ду
Где Ож {Охх &ху}> Gy Gyy}' R {Rx Ry}-
Для напряжений в наклонных площадках имеем
&пх == Gxxflx 4" Oyxtly, ОцУ Gxyflx + ОууПу,
Матричная форма статических граничных условий
GXtlx + Gytly = Р,
(1.18) будет (1Л9)
где р = {рх ру}.
Из уравнений Коши (1.7) остаются только три соотношения
= —; еад=-^!- + —. (1.20)
дх т ду ху дх ду v '
Понимая под 8 и и матрицы 8= {еяа. eo exa}; и = = {«х«9}> этим соотношениям снова можно придать форму 8 = Lu, где матрица L имеет вид
д
дх
д ду
д ду д дх
(1.21)
Наибольшие упрощения получаются в условиях совместности деформаций (1.10), из которых остается только одно:
& । дР ёуу cP ъху
ду2 дх* дхду
Закон Гука по-прежнему можно записать в форме а — ~ хе или в форме 8 = Фо, где а = {охх ауу 0ху}. При этгом для плоской деформации имеем
1—р И 0 -
Е Х= — Р 1 — н 0 ; (1-22)
(1 +р) (1 -2ц) 0 о 1 —2ц
2
Г1-р — р 01
ф — ±±Л. Е —и 1 —р 0 (1.23)
0 0 2
напряженного состояния —
а для обобщенного плоского
"1 р 0
Е Р 1 0
1 — р2 0 0 1 —ц
2
(1-24)
1 ' 1 — р 0
Ф = — Е — ц 1 0
0 о 2(1+р)_
(1.25)
Отметим, что в случае плоской деформации нормальное напряжение o2Z отлично от нуля, но оно не имеет самостоятельного значения, поскольку выражается через охх и о11У по формуле о1г = р (охх + оУи).
Точно так же в обобщенном плоском напряженном состоянии деформация ег2 =И= 0 и может быть найдена через ехх и «vv:
&ZZ I 4" £уу)-
Решение плоской задачи теории упругости удобно выполнять в напряжениях. При постоянных объемных силах Rx, /?и оно сводится к отысканию некоторой функции <р (х, у), удовлетворяющей бигармоническому уравнению
д4 ф , 2 , д4Ф _ 0
дх4 дх2 ду2 ду'
(1.26)
Напряжения вычисляются через функцию <р посредством формул
d2 го д2(р д2 <р „ г» z.
ахх="~д^~; °х« ~Rxy-R„x.(l.27)
Помимо равенства (1.26) должны быть удовлетворены еще граничные условия (1.19) на боковой поверхности.
§ 1.3. Подкрепленная панель как конструктивноортотропная пластина
В летательных аппаратах часто встречаются подкрепленные ребрами пластины, воспринимающие нагрузки в своей плоскости. Ребра увеличивают жесткость пластины в соот-
ветствующем направлении. Если они расположены регулярно и достаточно часто, то их жесткость можно осреднить и заменить реальную панель гладкой пластиной, работающей в условиях обобщенного плоского напряженного состояния и имеющей различные упругие характеристики в продольном и поперечном направлениях. Такая
Рис. 1.2
пластина называется конструктивно-ортотропной. Статические и геометрические соотношения остаются для нее такими же, как и для изотропной пластины. Отличие будет в записи закона Гука.
Отнесем пластину к системе координат ц, направив ось 5 параллельно ребрам (рис. 1.2). Будем полагать, что все ребра имеют одинаковую площадь F и расположены равномерно с шагом t. Рассмотрим однородное (т. е. не зависящее от координат %, i|) деформированное состояние панели с компонентами еЕ5, и е При этом в ребрах возникает одноосное напряженное состояние, а пластина будет находиться в условиях обобщенного плоского напряженного состояния. Обозначив через ар напряжение в поперечном сечении ребра, а через <Tnil, Оъп — компоненты напряжения в пластине, свяжем эти напряжения с деформациями. Для ребра такая связь дается законом Гука для одноосного напряжен-
ного состояния
(1.28)
где Е, — модуль упругости материала ребер.
Для пластины же матрица напряжений а выражается через матрицу деформаций 8 посредством зависимости о — хе, где матрица х имеет вид (1.24). Это соответствует трем скалярным равенствам:
— £
= “ Г" (essH~ Pe^Tl)> 1-ц2
— Е„ . .
~ ~ (епп + реи);
• — г
е2
°Sn — "0 ,. . Г 65п>
20 + р)
(1.29)
где Е2 и р — модуль упругости и коэффициент Пуассона материала пластины.
Пусть, далее, эквивалентная гладкая пластина имеет такую же толщину h, что и действительная пластина, и в ней созданы такие же деформации еи, еЛ1) и е^, как и в реальной панели. Напряжения, возникающие в эквивалентной пластине, обозначим через Ogj, н и определим их из условия равенства сил, воспринимаемых подкрепленной панелью и этой пластиной. В частности, для нормальных сил в сечении £ = const имеем о % ith + opF = о j отсюда
=Ой+°р—
Остальные компоненты напряжения в эквивалентной пластине будут совпадать с соответствующими напряжениями в панели:
Из последних трех равенств с учетом (1.28) и (1.29) получаем:
=~£г1(1 + М «5? + цепп];
1—р
£
°пп = ~—(епп +
1 —р2
Ег
. 8Sn>
2(Ч~р)
где
kP= (1,30)
f о
В матричной записи эти соотношения примут вид
aQ = xQeQ, (1.31)
где <т0 = {а^а^ст^}; е0 = {в5gentle};
(1.32)
Зависимости (1.31), (1.32), определяющие упругое поведение конструктивно-ортотропной пластины, выведены в предположении об однородности деформированного состояния, но ими можно приближенно пользоваться и в случае переменного поля деформации.
Рис. 1.3
Найдем еще связь между напряжениями о = {ст^о^уст.^) и деформациями е. — {exxeyve.x}.} в произвольных осях х, у (рис. 1.3, а). Пусть ось g составляет с осью х угол 0, который будем считать положительным, если поворот оси х до совмещения с положительным направлением £ необходимо выполнить против часовой стрелки.
В соответствии с (1.18) проекции напряжений в произвольной площадке с внешней нормалью п на оси Л вычисляются по формулам
О'n J ° И
где и — косинусы углов между нормалью п и координатными осями £, Т).
Если нормаль к площадке совпадает с направлением оси х, то /г t = cos (x,£) — cos 0; /гп = cos (х,р) = — sin 0. Заменив в обозначениях о„ 6 и о„п индекс п на х, имеем для такой площадки
(УЛ Е — оg cos 0 — sin 0; ovn = cos 0 — oipi sin 0.
Проектируя эти компоненты на направления осей х и у (рис. 1.3, б), найдем нормальное и касательное напряжения в площадке, нормальной к осн х:
0ХХ = cos ® ~ а«ч s*r 6 ~ cos2 ® 4- sin2 6 — Ot., sin 20;
Охи — sin 0 -f o.vl] cos 0 = | (o.,j - ff„n) sin 20 -f
4- O;n COS 20.
Аналогично определяются компоненты напряжения в площадке с нормалью, параллельной оси у, у которой п 5 — sin 0, г* cos 0. Нормальное напряжение в этой площадке
<го ojj sin2 0 -f- er,,,, cos2 0-f оЕ)) sin 20.
Полученные формулы можно записать в виде одного матричного равенства
- cos20 sm20 — sin 20
XX sin2 0 cos2 0 sin 20
ии ( I a*in
!хи _ — sin 20 _ 2 sin 20 2 cos 20
которое устанавливает связь между напряжениями в двух координатных системах
где
(1.33)
о = Т о„.
cos2 0 sin20 — sin 20~
sin20 cos20 sin 20
— sin 20 — sin 20 cos 20
2 2 __
(1.34)
Матрицу деформаций е в системе координат х, у свяжем с 80 из условия равенства удельной энергии деформации в pacv
сматриваемых Двух координатных системах*:
1 т I т
2 ° 6 2 °0 ₽'°’
где индекс «7» обозначает транспонирование матрицы.
Внося сюда (1.33), получаем Тг е = aj е0. Это равенство должно соблюдаться для любых компонент матрицы о0, откуда следует, что
е0=Тге. (1.35)
Подставляя теперь (1.31) и (1.35) в (1.33), получим закон Гука для произвольной ориентации ребер:
а = Тх0 ТЛ е.
Это соотношение можно представить в стандартной форме о— хе, где
х = Тх0ТЛ (1.36)
ГЛАВА 2
ВАРИАЦИОННЫЕ МЕТОДЫ ТЕОРИИ УПРУГОСТИ
Вариационные принципы теории упругости позволяют свести проблему определения напряженно-деформированного состояния тела к задаче отыскания минимума того или иного функционала. На этом основаны различные прикладные методы расчета, в которых удается получить приближенное решение задачи, не прибегая к интегрированию системы дифференциальных уравнений теории упругости. Вариационные принципы составляют теоретический фундамент и метода конечных элементов, позволяя, в частности, обосновать его сходимость к точному решению.
§ 2.1. Работа внешних сил. Дополнительная работа
Рассмотрим упругое тело (рис. 2.1), находящееся в равновесии под действием п сил. Представим эти силы матрицей-столбцом
Р= (Р, Р2 ... Р, ... Р,,}
и введем матрицу перемещений
V = {и, 02 ... V; ... и;|}.
Здесь Vi есть проекция полного перемещения Д; (рис. 2.1) точки приложения силы Р,- на направление этой силы.
* Необходимые формулы для вычисления удельной энергии деформаций будут даны в следующей главе.
Вычислим работу, которую совершают силы Р в процессе деформирования тела. Будем полагать, что имеет место статическое нагружение, т. е. внешняя нагрузка возрастает настолько медленно, что можно не учитывать инерционные силы. Для линейно-упругого тела процесс деформирования является обратимым, а работа сил Р на перемещениях v не зависит от способа нагружения, а зависит лишь от окончательного значения этих сил. Поэтому при вычислении работы можно принять, что все силы возрастают одновременно от нуля до своего конечного значения, причем в процессе нагружения
Рис. 2.2
между ними сохраняется постоянное соотношение. Тогда для линейно-ynpyf-oro тела зависимость между силами Pt и соответствующими перемещениями и, будет линейной (рис. 2.2). Подчеркнем, что перемещение и,- вызвано действием всех сил.
Площадь под диаграммой, заштрихованная на рис. 2.2 вертикально, представляет собой работу At = PtVt/2, которую совершает сила Pt в процессе нагружения тела. Совершенно аналогично можно подсчитать работу, производимую другими силами. Суммарная работа, затраченная на деформирование тела,
" I
А = У At = — (Pi Vi + Р2 v2 + ... + Рп vn).
;=i z
Это выражение можно записать более кратко с использованием матричных обозначений:
Д=_1 p7v=J-vrP. (2.1)
2 2
Полученный результат выражает теорему Клапейрона, согласно которой работа, произведенная внешними силами при статическом деформировании линейно-упругого тела, равна полусумме произведений окончательных значений сил на окончательные значения соответствующих им перемещений.
Обобщим теорему Клапейрона на случай действия объемных R = {/?ж Kz} и поверхностных р = {рх ру pz} сил. Сначала рассмотрим бесконечно малые силы Reft и pdw, где dx и d.co — элементы объема и поверхности тела соответственно. Если перемещения точек тела представить матрицей и = — {их Uy uz}, то работа элементарных объемных сил будет равна u'Rdr/2, а поверхностных ur pdco/2. Последующее интегрирование дает полную работу, затраченную на деформирование тела:
Д =— f Jur Rdx-Ь ^u^pdtoY (2.2)
\т ° /
Здесь первый интеграл берется по всему объему, а второй — по поверхности рассматриваемого тела.
В дальнейшем нам потребуется выражение для приращения, которое получает работа А при возрастании сил от Р до Р + 6Р, где через 6Р = {6Pj 8Р2 ... 8Рп} обозначена матрица произвольных бесконечно малых приращений внешних сил. Соответствующие приращения перемещений определяются матрицей 6v = {6Oj би2 ... 6vn}.
Приращение АДг работы А; численно равно площади трапеции, заштрихованной на рис. 2.2 наклонными линиями:
А А I — Pi ЙЩ + 6Р; биг.
Для всей системы сил получаем отсюда
ДД = У ДЛ; ^6у7'РД — 6vr6P.
/^1 2
Первое слагаемое в правой части этого равенства является главной частью приращения АД и называется первой вариацией (или просто вариацией) работы внешних сил 6Д,
6Д = 6v7P. (2.3)
Если на тело действуют объемные и поверхностные силы, то
64 — J би7'Rdr j 6u7 pdw,
Т 4»)
где би - {биЛ. 6u/z 6wJ — матрица бесконечно малых при: ращений перемещений точек тела.
Формула для 64 выведена в предположении, что R и р получили приращения 6R и бр, а матрица би определяет действительные приращения перемещений, которые соответствуют такому возрастанию внешних нагрузок. Однако вариации сил 6R и бр в эту формулу не вошли, поэтому при вычислении 64 внешние нагрузки можно считать вообще неизменными, понимая при этом под элементами матрицы би некоторую произвольную систему бесконечно малых перемещений.
До сих пор речь шла о свободном теле. Если же на тело наложены связи, то его поверхность ы можно разбить на две части — ыр и юи, на которых заданы соответственно поверхностные нагрузки р и перемещения и. Для практических приложений полезно ограничиться такими функциями би, которые на ыи обращаются в нуль. Тогда выражение для 64 примет вид
64 = | 6urRdi 4- J би7*pdw, (2.4)
г
где поверхностный интеграл берется лишь по (ар.
Такие бесконечно малые перемещения би, которые удовлетворяют лишь требованию непрерывности внутри тела и согласуются с наложенными на него связями, называются возможными (иногда их называют также виртуальными). Любые возможные перемещения можно было бы действительно создать, прикладывая к телу, закрепленному заданным образом, некоторую систему бесконечно малых нагрузок, но связывать их с действительными приращениями внешних сил нет необходимости.
Из сказанного следует, что величину 64 можно трактовать не только как вариацию действительной работы А, но и как работу внешних сил на возможных перемещениях. Поэтому иногда 64 называют возможной (или виртуальной) работой внешних сил.
Введем далее в рассмотрение так называемый потенциал внешних сил П. В случае действия сосредоточенных сил
и представляет собой работу, необходимую для перемещения точек приложения сил Р в исходное положение, которое они занимали до деформации тела; значения сил при этом сохраняются неизменными.
Рассматривая величину П как функцию перемещений v, для вариации 6П запишем
6П = —б (vrP) = — 6vrP.
Сопоставляя этот результат с выражением (2.3) для 6А, видим, что
6П = -6Л, (2.6)
т, е. формально вариация потенциала внешних сил 611 отличается от вариации работы 6А лишь знаком. В действительности различие между ними является более глубоким; оно вытекает из определения величин А и П как функций от v согласно (2,1) и (2.5). Первое из указанных соотношений получено в предположении, что силы возрастают от нуля до своего конечного значения и поэтому в процессе нагружения сами являются функциями перемещений v. При записи же второго принято, что силы сохраняют свое окончательное значение и не зависят от перемещений.
Равенство (2.6) положим в основу определения функции II для случая произвольного нагружения тела. В соответствии с (2.6) под потенциалом внешних сил П будем понимать такую функцию от перемещений v, вариация которой совпадает по величине с виртуальной работой 6Л, отличаясь от нее знаком; внешние силы при варьировании П считаются неизменными. Тогда при действии объемных и поверхностных сил их потенциал с точностью до произвольной постоянной определится в соответствии с (2.4) выражением
П = —/ fu’ RdxH- [urpdo>\ (2.7)
U 4 )’
Рассмотрим теперь площадь слева от диаграммы Р, — эта площадь на рис. 2.2 заштрихована горизонтально. Обозначим ее через At и назовем дополнительной работой силы Р,- на перемещении и;. Хотя эта величина и не имеет физического смысла, она окажется в дальнейшем весьма полезной для формулирования некоторых важных теорем. В рассматриваемом случае линейно-упругого тела дополнительная работа At численно совпадает с действительной работой. At, но между ними все же остается принципиальное различие, вытекающее нз самого определения этих величин.
Запишем выражение для приращения ДЛ/, которое получает дополнительная работа Ai при возрастании нагрузки на величину
iPi ЛА/ = i jdP, -f- 6v/6Pi/2 Главная часть приращения 6Ai~ — vibPi Вариация дополнительной работы для всей системы сил
64*= vr6P=6Pr v
Сопоставляя это равенство с (2 3). видим существенное отличие в определениях 64 и 64”
При действии объемных и поверхностных сил вариация дополнительной работы
6.4* ur 6R di-j-J ur 6p do), (2.8)
т <0
где 6Rx=(6A’a. &Ru 8Rz], 6p= {6/>л. 6/>f/
По аналогии с функцией П можно ввести дополнительный потенциал внешних сил П* Определим его как такую функцию внешних нагрузок, вариация которой равна по- величине и обратна по знаку 64 * т е
6П*=—64*. (2 9)
перемещения при варьировании П* считаются постоянными и сохраняющими свое окончательное значение. Таким образом,
П* = - /j ur Rdr-|— f urpdo> j. (2.10)
' i o> /
§ 2.2. Энергия деформации. Дополнительная энергия деформации
Если к упругому телу приложить внешние силы, то, как было ранее сказано, они совершат некоторую работу, которая затрачивается исключительно на деформацию; других затрат энергии здесь нет При этом изменится потенциальная энергия положения внешних сил. При разгрузке за счет накопленной потенциальной энергии может быть совершена такая же работа, какая была затрачена на деформацию тела. Процесс здесь обратимый.
Вычислим потенциальную энергию, накопленную деформированным телом. Выделим для этого элементарный параллелепипед со сторонами dx, dy, dz и определим работу сил, действующих по граням этого элемента.
Примем сначала, что на элемент действуют лишь нормальные напряжения csXJC (рис. 2.3). Поскольку длина элемента при деформации возрастает на exx.dx, силы ovvd//dz в соответствии с теоремой Клапейрона произведут работу, равную
ov>,eA.<¥dxdydz/2 = о¥Л.еххс1т/2.
В общем случае объемного напряженного состояния работу напряжения ахх можно подсчитать по этой же формуле, 32
понимая подехл окончательное значение деформации, вызванное действием всех компонент напряжения.
Рассмотрим далее действие касательного напряжения
Как видно из рис. 2.4, сила o<(zdxdz производит работу иа перемещении ехийу. Эта работа равна
a,,/e,.f/dxd</dz/2 = ov?,eA.„dT/2.
Рассматривая аналогично все остальные компоненты напряженного состояния, найдем накопленную в элементе энер-
Рнс. 2.3
Рис. 2.4
гию, равную суммарной работе внутренних сил: d(7 “ ”Ь 4~ ^ху^хц 4“ Ч*
+ п.-л-Егзг) dT.
Вводя, как и прежде, матрицы напряжений и деформаций
® ~ х х&itU^z х у г® г х F. — {^х х&у г1Е хуС у гВг * }, перепишем это выражение в кратком виде
d U — — ат edr — ~ ет odr. 2 2
Величина
W =^-«1 <тте = — »та (2.11)
dr 2 2 4
представляет собой энергию деформации единицы объема упругого тела и называется удельной, энергией деформации. Потенциальная энергия деформации, накопленная всем телом,
U = f UZdT
Пользуясь законом Гука в форме (1.12), можно выразить величину W только через компоненты напряжения:
W = -у <тг Фсг = уу [ахх+о2Уи + —2р 1рхх оуу +
+ a0»azz+ffzzax*)4*2(l 4-р) (аХу +сг^г4-(Ггх)1> (2.12)
С другой стороны, запись закона Гука в форме (1.15) позволяет выразить удельную энергию деформации W только через компоненты деформации:
Рис. 2.5
W = у егхе = -у [Л9а +
4-2G (el* 4* %уу 4- efz) 4"
4-G(el,4-elz4-elA-)J. (2.13)
Из последней формулы, в частности, видно, что энергия деформации является величиной неотрицательной.
Предположим теперь, что напряжения <т и перемещения и получили бесконечно малые приращения
6о {6о** Ьоуу 5<Jzz d<Jyz S^zx).
би = {8их Ьиу buz}.
В соответствии с формулами Коши (1.7) деформации также получают некоторые приращения
5е 5=1 {беуy6t'zz6t’Xy6t’^26t’2Ji;).
На рис. 2.5 показана для линейно-упругого тела зависи мость между одноименными компонентами деформации е, и напряжения (i, / = х, у, z). Площадь под диаграммой заштрихованная вертикально, равна отнесенной к единице объема работе напряжения при деформировании тела (удельной энергии деформации):
Приращение ДИ7г?. этой работы при изменении напряжений и деформаций будет равно
4- -у боо- бео.
Суммарное изменение удельной энергии деформации, обус: ловленное действием всех компонент напряжения, определится как сумма
A W = 2А Г „ = бег a -f- — бег 6<т. 7 2
Главная часть этого приращения дает вариацию удельной энергии деформации 6U7 = бега. Если под би понимать возможные перемещения, то матрица бе будет определять возможные деформации, которые выражаются через компоненты би по формулам Коши. Тогда 6UZ следует трактовать как удельную работу действительных напряжений на возможных перемещениях.
Горизонтально заштрихованная площадь на рис. 2.5 определяет удельную дополнительную работу IF// напряжения оц. Если учесть все компоненты напряжения, то в сумме получим величину W*, которая называется удельной дополнительной энергией деформации. В случае линейно-упругого тела IF* совпадает по величине с IF. Вариация, же 6 IF* определяется соотношением 5 IF* = е7 6а, так как 6 IF«7 — е,д ба,} в соответствии с рнс. 2.5.
Интегрируя 6UT и б IF* по всему объему тела найдем вариации, энергии деформации и дополнительной энергии деформации:
б</=( 6ег абт; (2.14)
г
66/*=У er 6adr (2.15)
т
§ 2.3. Вариационное уравнение Лагранжа
Рассмотрим тело, находящееся в равновесии под действием внешних нагрузок R и р. Дадим точкам тела дополнительные возможные перемещения би = {8их 8ии &иг}. Этим возможным перемещениям соответствуют возможные деформации бв (бе^л у у
Вариация энергии деформации, согласно (2.14),
б (/ == J бе/ odr ~ | (ахх беХА. -f- Оуу teyU 4- о22 бе22 4~ т т
4~ ®ху $&ху 4- Gyz ^l/Z 4~ бе2х)^Т .
Преобразуем подынтегральное выражение следующим образом. Воспользовавшись сначала формулами Коши (1.7), запишем
&хх =»“ ’ “"Г" + ~Т~ @и^-
дх дг дх
Тогда Выражение для 6U можно представить в виде
W - ( (6«х) + а»й -7- (6и„) 4- а» -7- (6«J 4-
J ( дх ду дг
+ °х» [ “7" (6«9) + -7- (S«x)l + <ъД-7- (М + L дх ду J [ ду
4- -%- (б^)]4-ст^[— (6uJ 4- -у- (&U2) 1)ЙТ. дг J I дг дх JJ
Группируя члены, перепишем:
6l/=fta*-7- (fi«x)4-Ox»-T-(H)4-^ -7- W4 J [ дх дх дх
т
+ <г9х ~ (&«х) 4- ow (6ий) + ауг (6и2) +
4-ozx -7- (6иж) + <JZ9 —- (6м9) 4- °2z ~~r~ (&uz) 1 йт. дг дг ог J
Вводя матрицы
ddu _ ( дйих д6иу д&иг | дх I дх дх дх }
дби __( д6их д&иу d&uz 1
ду I ду ду ду )’
дби __| д&их д6иу дЬиг 1
дг 1 дг дг дг )’
а также учитывая введенные в § 1.1 матричные обозначения
<ГЖ = fax» аху °xz}’i ау ~ °уу оуг}'т az = {°zx azy °zz}r будем иметь
6(7 =
Используя преобразование типа д F д<Р dt Т dt dt ’
д&и
дх
дс>и . дои \, —~Оу+ —— оийт.
ду дг I
где f и <р —две любые дифференцируемые функции аргумента t, приведем это выражение к веду '
6t/=j’[^r(6u7X)+ -~№T<fyy+ -£-(6u4)](b-
_ f 6ur (4- 4- dT.
J \ dx dy dz J x
Первый интеграл заменим поверхностным, применяя формулу Остроградского—Гаусса, согласно котовой
+4r)d’= f(<?A+es«,+Q,".)d».
t/ \ g
t , w
где Qx, Q» и Qz — произвольные дифференцируемые функции, заданные в области т, а пх, пу и nz — направляющие, косинусы внешней нормали к поверхности со, ограничивающей эту область.
В результате получаем
6t/=J Sur (axnx+oyny + oznz)d<A —
&
— fsur/-^2- 4-JZ» 4--^£.'jdT. J \ dx dy dz } X
Так как на соы имеет место равенство Su = 0, то интегрирование в первом члене достаточно выполнить лишь по ®р. Тогда
St/= J Sur (<тх n х 4-(Ту «„ + <т2 raz) d®— “р
-f биг(-^ 4--^- + —(2.18)
J \ dx dy dz /
Поскольку предполагалось, что в исходном состоянии тело находится в равновесии, то напряжения должны удовлетворять уравнениям статики (1.4) и (1.6): дах I doy . da dx dy dz
R;
Oxtix + cyn„ 4- o/iz — p на (Яр.
Отсюда имеем
6t/ = f 6ur pdco + JStHRdr.
Wp t
Согласно (2.4), в правой части полученного выражения находится вариация работы внешних сил 6Л, и мы приходим окончательно к равенству
St/ = 6Л. (2.17)
Уравнение (2.17) выражает собой принцип возможных перемещений (принцип виртуальных работ) применительно к упругому телу, согласно которому работа внешних сил на возможных перемещениях равна вариации потенциальной энергии деформации.
Полагая в соответствии с (2.6) 6П = —6Л, приведем равенство (2.17) к виду 6 (U + П) = 0. Величина
(2.18)
называется полной потенциальной энергией системы, а равенство
SV = О (2.19)
называется вариационным уравнением Лагранжа.
Поскольку U и П вычисляются для равновесного состояния тела, уравнение (2.19) утверждает, что в состоянии равновесия полная энергия системы имеет стационарное значение. Исследуя знак второй вариации S2V, можно строго показать, что это стационарное значение является минимумом; мы для пояснения данного утверждения ограничимся простыми рассуждениями.
В самом деле, если тело, находящееся в состоянии устойчивого равновесия, под действием какого-либо внешнего воздействия несколько изменит свою форму, то после устранения этого воздействия оно снова займет первоначальное положение. При возвращении в исходное положение будет совершена работа, т. е. высвободится некоторое количество-потенциальной энергии. Значит, в соседнем положении тело обладает большей потенциальной энергией, чем в положении’ устойчивого равновесия.
Уравнение (2.19) получено в предположении, что тело находится в равновесии, так что это уравнение представляет собой необходимое условие равновесия тела. Покажем, что оно является также достаточным. Предполо-жим'для этого, что равенство SV — 0 выполняется; тогда име
ет место и равенство 8U — 6Д = 0. Записав выражение для 6С/ в виде (2.16) и вспомнив, что
6Л =«J 6urRdT -f- J 6urpdw, r <>,,
придем к уравнению
J биг (о х пх 4- в у пи 4- az пг —р) d« —
4--^" 4-4-rV1t =0.
J \ дх ду дг J r
(2.20)
Равенство нулю в (2.20) должно выполняться для любых функций 6«д., 6«v, 8uz, образующих матрицу би. Это возможно лишь в том случае, если равны нулю выражения, заключенные в (2.20) в круглые скобки. Отсюда вытекают дифференциальные уравнения равновесия (1.4) и статические граничные условия (1.6). Таким образом, если удастся найти перемещения, удовлетворяющие вариационному уравнению Лагранжа (2.19), то при этом автоматически будут удовлетворены уравнения равновесия, а также статические граничные условия.
Изложенные выше соображения позволяют сформулировать вариационный принцип Лагранжа: из всех перемещений, допускаемых наложенными на тело связями, в действительности имеют место такие, при которых полная энергия системы V минимальна.
§ 2.4. Вариационное уравнение Кастильяно
В предыдущем параграфе был установлен вариационный принцип для перемещений. Аналогичный принцип можно установить, рассматривая вариации компонент напряжения.
Пусть для упругого тела известны напряжения а, деформации е и перемещения и, возникающие при действии внешних нагрузок Кир. Напряжения а удовлетворяют дифференциальным уравнениям равновесия (1.4) и условиям на поверхности (1.6). Отметим, что на части Шр поверхности тела равенство (1.6) дает статические граничные условия, а на ыи оно выражает связь между напряжениями и реакциями на тело со стороны наложенных связей.
Предположим далее, что напряжения получили бесконечно малые приращения
{6ахх 6cr,Z!/ 6<J2Z &аХ!1 бо„г 6огк)
Вариации напряжения ба подчиним единственному требованию, чтобы новое напряженное состояние было также р а в н о в е с и ы м, т. е. чтобы удовлетворялись уравнения д д д
(®х+бох)4--^- (ав4-баа)4--— (<’z + 6ax)-f-R=0;
(ох + бо^пх + (СТй + 6ай)пу + (а24-6а2)п2=р + 6р. (2.21)
Здесь через бах, 5ай, бах обозначены матрицы
&ахх баух dazx
6ax = й^ху ; баУу ; бах = бахи
J^xz - _ бахх _
При записи условий равновесия (2.21) принято для общности, что изменение напряжений сопровождается изменением поверхностных нагрузок иа величину
бр = (6рхбрйбрх), объемные же силы предполагаются при варьировании напряжений неизменными.
Вычитая из (2.21) соотношения (1.4) и (1.6), найдем, что вариации напряжений удовлетворяют уравнениям
дбах д8аи дбсх
— J S- _1_ = 0; дх----------------ду-дг
(2.22)
6ax пх -J- 6ай пу-}~ бах пг = бр.
В результате изменения поверхностных сил дополнительная работа получит приращение
6Л*= J ит бр б<о.
<i>
Далее, варьирование напряжений приведет к изменению дополнительной энергии деформации U* иа величину
б£/*^= я ба бт^= J &°хх байй-|- ехх бахх4-X X
+ехи бЛху+вуг 6авх+ехх 6azx) бт.
Преобразуем выражение для &U* аналогично тому, хак это делалось при выводе вариационного уравнения Лагранжа. Подставляя формулы Коши (1.7) в подынтегральное выражение и группируя соответствующие члены, имеем
Г / дит „ диг . диг \
6£У J I Т“ {о«+Т' S+T" 6<г* dT*
J у дх ду дг j
где
du ( дих диу duz "l du / дих duy duz )
дх l дх дх dx )’ ду ( ду ду dy )’
ди ( дих ди у dut 1
дг l дг дг дг f
Применив далее формулу дифференцирования произведения, запишем
= f [ (ur fox)+~т~- (иТ 6оу) + ~~ (ит &rz) 1 dx —
у I дх ду № дг J
В силу первого равенства (2,22) второй интеграл здесь равен нулю. Заменяя первый интеграл поверхностным по формуле Остроградского—Гаусса, приходим к соотношению
dU* — J и' (6оя пх + 6ав Пу + да? пг) <ко ш
На основании второго соотношения (2.22) приведем этот результат к виду
6U* = J иГ бр d<o. к>
В правой части этого равенства стоит вариация дополнительной работы 64*, поэтому можно записать
6U* = 64*. (2.23)
Полученное соотношение выражает собой так называемый принцип дополнительных виртуальных работ. При выводе формулы (2.23) использовались формулы Коши (1.7), следствием которых являются уравнения совместности деформаций (1.10). Таким образом, исходное напряженное состояние неявно предполагалось не только статически возможным, ио и удовлетворяющим уравнениям совместности. Напряженное состояние, для которого удовлетворяются уравнения совместности деформаций, будем называть совместным. Из уравнения (2.23) следует, что для совместного напряженного состояния вариация дополнительной энергии деформации равна вариации дополнительной работы внешних сил.
Заменяя согласно (2.9) 64* на —6П*, придадим равенству (2.23) вид
6 (V* 4- П*) = 0.
Так как мы приняли, что 6R = 0, то в выражении (2.10) для П* останется лишь поверхностный интеграл:
П* — — J urpdtu. ш
Величину
V* = и* + П* (2.24)
будем называть полной дополнительной энергией системы.
Таким образом, мы приходим окончательно к уравнению
81-’* =0. (2.25)
Вариационное уравнение (2.25) устанавливает, что в действительном (т. е. совместном) напряженном состоянии полная дополнительная энергия системы имеет стационарное значение. Можно показать, что это стационарное значение есть минимум. Таким образом, минимальность V* является необходимым условием совместности напряженного состояния. Уравнение (2.25) является также и достаточным условием совместности, т. е. при выполнении равенства 6 V* ~ 0 уравнения совместности деформаций будут также удовлетворены. Строгое доказательство этого положения оказывается несколько громоздким, вследствие чего здесь не приводится.
На основании сказанного выше сформулируем вариационный принцип Кастильян о; из всех статически возможных напряженных состояний в действительности имеет место такое, для которого полная дополнительная энергия системы минимальна.
При практическом использовании вариационного уравнения Ка-стильяно во многих задачах оказывается возможным варьировать напряженное состояние таким образом, что поверхностные нагрузки на <йр остаются неизменными. В этом случае 6р •= 0 на <вр и выражение для П* принимает вид
П"= — J urpde>.
где матрица р содержит реакции на тело со стороны наложенных на него связей.
Если при этом на всей поверхности тела ш заданы статические граничные условия (<ви = 0) илн если перемещения на <ои равны нулю, то П* = 0, и мы приходим к уравнению 6(7* = 0. Для линейно-упругого тела, для которого U* — U, получаем известное начало наименьшей работы, или начало Кастильяно
6U=0.
Таким образом, в этом частном случае из всех статически возможных напряженных состояний в действительности имеет место такое, для которого потенциальная энергия деформации имеет минимальное значение.
Исходя из общей формулировки (2.25), можно вывести важную теорему. Пусть на тело действуют сосредоточенные силы
Р = {Р, P.t ... Рп)
н пусть этим силам соответствуют перемещения
V = {a, v2 ... On).
Тогда 6Л* — 6РГ V, и из (2.23) имеем 6(7* = 6Prv.
Если известно напряженное состояние, вызванное силами Р, то напряжения, а следовательно, и дополнительная энергия деформации U* будут известными функциями Р. Тогда можно записать
Сопоставляя два полученных выражения для 6U*, находим
AU* dU*
или vi=—(/»J,2........п).
Для линейно-упругого тела U = (7*, так что в этом случае
AU dU
— или Vi—----- fi=l,2....п).
dP dPt ’
Эти равенства, выражающие так называемую первую теорему Кастильяио, устанавливают, что перемещение точки приложения некоторой силы Pi в направлении этой силы равно для линейно-упругого тела частной производной от потенциальной энергии деформации по этой силе.
Располагая вариационными уравнениями Лагранжа и Кастильяно, можем теперь дать вариационную постановку задачи теории упругости: если задача решается в п е р вмещен и я х, то требуется найти такие перемещения и, которые непрерывны внутри тела, удовлетворяют геометрическим граничным условиям и минимизируют полную потенциальную энергию системы V; если задача решается внапряже-н и я х, то требуется найти такие напряжения а, которые удовлетворяют уравнениям равновесия и статическим граничным условиям и минимизируют полную дополнительную энергию системы V*,
§ 2.5. Метод Ритца
Метод Ритца приближенного решения задач теории упругости заключается в прямой минимизации полной энергии системы V. Следуя этому методу, перемещения будем искать в следующем виде:
их(х, у, z)=ux0(x, у, z) +-2 axkuxh(x, у, z);
kz= 1
Чу (х, у, z) = Uyo (X, у, Z) + 2 avk Uyh (x> y> z)< (2-26)
*=1
иг(х, у, z)=-uzQ(x, у, г)4- 2 auiuiiAx> У< z)-k=t
Здесь axh ayk и azh есть некоторые постоянные, подлежащие отысканию, остальные же величины представляют собой выбранные заранее подходящие функции координат. При этом функции цх0, «!/0, иг0 должны принимать заданные значения на части п>ц поверхности тела <о; все остальные функции должны на <ои обращаться в нуль. Тогда при любых значениях
постоянных а будут удовлетворяться геометрические граничные условия. Постоянные а подбирают таким образом, чтобы при выбранных функциях (2.26) полная энергия системы была минимальна.
Воспользуемся выражением для W в форме (2.13) и заменим в нем деформации через перемещения по формулам Коши:
Если теперь в это равенство подставить приближенные выражения для перемещений (2.26), то удельная энергия деформации IF будет представлена как известная функция координат х, у, z и постоянных a-. W = W (х, у, z, а). Как следует из (2.27), IF будет квадратичной формой относительно постоянных а.
После подстановки W в формулу U — J IFdx и интегри-т
рования по всему объему тела потенциальная энергия деформации окажется некоторой функцией относительно искомых постоянных U — U (а).
Для удобства дальнейших рассуждений представим зависимости (2.26) в следующей матричной форме:
где
и = и0 -f- и*а,
(2.28)
Через u', uj, uj здесь обозначены матрицы-строки вида и* = «л-2 «xml. а через ая, ав, ах — матрицы-столбцы
вида ая = {ах1агз ... ахт}.
Подставим далее заданные функции R = {/?* Ry Rz} и Р = {Рх Ри Рг}, а также перемещения в форме (2.28) в выражение для П и выполним интегрирование:
П«~/ Jurpd<o-}-[urRdTA«—(В04-агВ). (2.29)
Здесь
Во = J uJ pdu>-J-J uj Rdr, B= Ju*Tpd<i) 4- J u*rRdT.
Складывая V и П, найдем полную энергию системы V как функцию неизвестных параметров а:
V = (/(а) — (Во + аг В). (2.30)
В соответствии с уравнением Лагранжа (2.19) запишем необходимое условие минимума V:
SV = ди (а) — 6ат В = 0.
Вариацию потенциальной энергии деформации можно вычислить по формуле
Sa (а) = -^- дах1 + ... + -£- дау1+... + даа '+.... oaXi даух ” dazt
Вводя матрицу
dU ( ди дУ ди dU дУ ]
da ( даХ1 дахг даУ1 da2t да2т }’
представим выражение для St/ в форме
6t/ = 8aT —. da
Таким образом, условие 6У — 0 приводит к равенству
\ da J
В силу независимости элементов матрицы Sa получаем отсюда уравнение
— = В. (2.31)
da
Это матричное равенство заключает в себе систему алгебраических уравнений относительно искомых постоянных а. Общее число уравнений равно Зт, поэтому система является замкнутой. Как отмечалось выше, энергия деформации У является квадратичной функцией относительно параметров а, поэтому элементы матрицы dt//da содержат эти параметры в первой степени. Таким образом, система уравнений (2.31) будет линейной, и ее решение не представляет принципйаль-ных трудностей.
Коль скоро постоянные а найдены, выражения (2.26) или эквивалентное им (2.28) дают приближенное решение задачи.
По формулам Коши можно найти деформации, а затем по за* кону Гука — напряжения.
В заключение отметим, что в (2.26) для их, иу, uz совсем не обязательно брать одинаковое количество функций ихк, иук, игк. В любом случае минимизация полной энергии системы по всем параметрам а дает столько уравнений, сколько имеется этих параметров.
§ 2.6. Метод Канторовича—Власова
характером распределения проксимирующие функции
Как говорилось выше, в методе Ритца задаются приближенным перемещений внутри тела. Входящие в ап-постояиные подбираются из условия Минимума полной энергии системы. Подобная схема используется и в методе Канторовича—Власова, ио здесь вместо постоянных а вводятся неизвестные функции, зависящие от одной из координат. Минимизация полной энергии относительно этих функций приводит к системе обыкновенных дифференциальных уравнений, последующее интегрирование которых позволяет получить приближенное поле перемещений.
Подробности метода обсудим применительно к расчету тела, ограниченного плоскостями г = О и г = I (рис. 2.6). Площади граней в
этих плоскостях обозначим соответственно через н и2, а остальную часть поверхности тела —через ы3.
Для получения приближенного решения будем отыскивать перемещения в виде
т
их{х, у, г)=их0(х, у, г)4- 2 fxk (г) (*. У, г);
т
(х, у, г) —uw0 (х, у, г) 4- У fyk (г) u„k (х , у , г); k — I
т
«г(х,у,г)=и20(х,у,г)+ S fzk (г) “zft (х, у, г). (2.32)
I
Через /(г) обозначены здесь подлежащие Отысканию функции координаты г, а остальные функции выбирают заранее. При этом фуик» ции цло, Uyt, uty должны на ш, и шг обращаться в нуль. На той части <1>3, Где заданы перемещения, функции «Х0) Uy0) «го Должны принимать эти заданные значения, а функции ихк, иук, лц, — обращаться в нуль. В этом случае автоматически, т. е. для любых функций / (г), на. ы, будут удовлетворены геометрические граничные условия.
Подобно тому, как это делалось в методе Ритца, перемещения (2.32) можно представить К матричной форме
и (х, у, г) = uft (х, у, г) + и* (х, у, г) f (г). (2.33)
Здесь матрицы и0 и и* имеют такой же вид, как и в (2.23), а через t (г) обозначена матрица-столбец неизвестных функций
[*х (г) fy(z) fx И .
где »х(г) = "/«(г) ~ f Х2 (2) : fy (г) = (2) " fyz (2) ; Мг) = fzi (2) tzt (г)
хт (г) - -fym (г) - -fzm (г).
Подставим теперь приближенные выражения (2.32) в формулу (2.27) для удельной энергии деформации 1Г. Это позволяет получить W как функцию координат -х, у, г с известным характером зависимости от х и у. Потенциальная энергия деформации U определяется как интеграл U — $ W'dT, взятый по всему объему тела. Обозначим через т
F (г) площадь сечения тела плоскостью, перпендикулярной оси г. Тогда
I
i/=J / f f If/dxdi/jde.
0 \Р(г) /
Поскольку зависимость W от переменных х, у известна, то можно выполнить по этим координатам интегрирование и получить выражение для U в виде функционала типа
I
U — f Ф] (г, fxk, fyk> fzh> fxk> fyk< fzk^ • (2.34)
b
Штрихами обозначены здесь производные по г.
Найдем далее потенциал внешних сил
П—= — j ит Rdx— J иТ pda.
Т Юр
Для простоты дальнейших рассуждений считаем, что работа поверхностных сил иа гранях coj и <о2 равна нулю. Это возможно, если на Wj и ш2 отсутствует поверхностная нагрузка, либо если эти грани закреплены. Тогда
II——J иТ Rdt— У urpdco, х ®зр
где через а>зр обозначена та часть а>3, на которую не наложены связи. Подставим в правую часть этого равенства функции (2.33). После ин
тегрирования по координатам хну выражение для П может быть приведено к виду
I
П=-[ ФДг.^.^Д^бг, (2.35)
о
где Фг—некоторая функция, известным образом зависящая от г, • fxh (г). iyh (г), fzh (г).
Объединив (2,34) и (2.35), для полной энергии системы V = U +
•f-n получим
v=f ф(г. fxk, fvk, ftll, f-k, f-k. Ггк) Az (2.36)
о
где Ф == <1*! — Ф2.
Таким образом, полная энергия представлена как функционал, зависящий от неизвестных функций f (г). Необходимое условие минимума этого функционала заключается в требовании, чтобы функции I (z) удовлетворяли следующим уравнениям Эйлера:
дф Л Г дф \
------_------ ( ------ = 0;
dfxk Аг \ д[[.к )
дФ А { дф \
— | 1 = 0, д1цк------------------Az-df‘uk-)
дФ А [ дф \
------__----- |------- | -о.
Afik Аг /
Такие уравнения записываются для k = 1, 2, .... пт, в результате получается система Зт обыкновенных линейных дифференциальных уравнений второго порядка относительно Зт функций. Решение этой системы содержит 6т неопределенных постоянных, которые должны быть определены из граничных условий при г— 0 н г — I, т. е. на wt и ш2. Если в каком-либо из этих сечений перемещения равны нулю, то все функции f (г) должны здесь обращаться в нуль. Если же на перемещения не наложено никаких ограничений, то следует воспользоваться естественными граничными условиями вариационной задачи, которые для z=»/, например, записываются так.
аф
Се
= 0;
г=/
дФ
Afyk
= 0;
аФ
С* *=/
Таким образом, в рассмотренном методе совокупность уравнений теории упругости в частных производных приводится к системе обыкновенных дифференциальных уравнений,’ интегрирование которых осуществляется значительно проще. Приведение к обыкновенным дифференциальным уравнениям выполняется путем приближенной минимизации полной энергии.
Для практического использования метода Канторовича—-Власова удобнее отыскивать перемещения и (х, у, г) в виде
и (х, у, г) = ц0 (х. у. г) 4- и* (х, у) f (z), где функции и* зависят только от координат х, у.
Чаще всего метод Канторовича —Власова применяется в двумерных задачах. В этом случае приближенное распределение перемещений можно искать в форме
U (х, у) = Цо (х. у) + U* (у) f (X).
Отметим в заключение, что если функции и* удовлетворяют определенным условиям ортогональности, то система уравнений относительно функций f (г) получится несвязанной И ее интегрирование будет выполняться наиболее просто (9].
Г Л А В А 3
МАТРИЧНЫЙ МЕТОД ПЕРЕМЕЩЕНИЙ
ДЛЯ СТЕРЖНЕВЫХ СИСТЕМ
Стержневые системы широко применяются в конструкциях летательных аппаратов. Эффективным средством их расчета иа ЭВМ является метод перемещений в матричной формулировке. В терминологии и основных процедурах ои имеет много общего с методом конечных элементов. Жесткостиые характеристики стержней вычисляются здесь на основе соотношений технической теории бруса, и в рамках этой теории решение по.лучается точным.
§ 3.1. Понятие о матрице жесткости
Рассмотрим консольную балку, нагруженную силой на свободном конце (рис. 3.1). Вертикальное перемещение точки приложения силы, как известно, равно v = Pl3/(3EJ), где Е — модуль упругости; J—момент инерций поперечного сечения балки. Если перемещение v задано, то из этой формулы можно найти силу, необходимую для создания такого перемещения: Р = 3EJvll3 или
Р » kv, где k — ЗЕЛ1\
Величина k называется коэффициентом жесткости консольной балки. Если положить v — 1, то сила Р будет равна k. Отсюда вытекает физический смысл коэффициента жесткости: k есть сила, которую необходимо приложить на конце балки, чтобы его прогиб равнялся единице.
Пусть, далее, к балке приложены две силы, как показано на рис. 3.2. Используя известные методы сопротивления материалов, можно найти перемещения и, и v.t в направлении этих сил.
У. = б../5. + 612Р4; Vt = 621Р, 4- 62гЛ.
где (/, /' = I, 2) суть перемещение в направлении и, под действием единичной силы, направленной по Pj Величины б/у, называемые коэффициентами влияния, зависят от геоме-
трических параметров балки и от модуля упругости материала.
Запишем Связь между перемещениями и силами в матричной форме:
v = ДР. (3.1)
Здесь введены матрицы-столбцы сил и перемещений
а через Д обозначена так называемая матрица податливости би 61а ^21 &22
Рис. 3.1 Рис. 3.2
Если принять, что перемещения v известны, то из (3.1) можно найти силы Р, вызывающие эти перемещения: Р = = A-1v. Полагая к = Д-1, придадим последнему равенству вид Р = kv. Введенная здесь матрица к имеет размер 2x2 и называется матрицей жесткости рассматриваемой системы. Согласно теореме Максвелла о взаимности перемещений, справедливо равенство Sla — 6а1, т. е. матрица податливости Д является симметричной. Обратная к ней матрица к будет поэтому также симметричной.
Теперь рассмотрим общий случай, когда на произвольное упругое тело действует система т сил (рис. 3.3), которую представим матрицей
р= {Л ... Рт}.
Пусть перемещения точек приложения сил Р (в дальнейшем эти точки будем называть узлами) в направлении.этцх сил образуют матрицу ’
v = {uj и2 ... ит).
Здесь принято, что все перемещения v отличны от нуля. Если в некоторых из рассмотренных точек тело закреплено, то соответствующие элементы матрицы v будут равны нулю.
50
1 I
Предположим, что перемещения v заданы; тогда силы, необходимые для создания этих перемещений, определятся для линейно-упругого тела соотношением
Р « kv. (3.2)
Матрица к, связывающая силы Р с соответствующими им перемещениями v, называется матрицей жесткости рассматриваемого тела.
Представим (3.2) в развернутом виде
&11 &12 ••• &1/ ••• &lm
"Л "
Pl
• • • ^2m
Ьц &<2
ь.. ь.
... Kfj ••• кип
(3.3)
и выпишем t-ю строку этого матричного равенства:
Р{ — kil^l ki2V2 + ••• + kijVj + ... + klmVm.
Физический смысл коэффициента fe,-,- можно выяснить, по
лагая перемещение Vj = 1, а ными нулю; тогда Р Отсюда следует, что коэффициент жесткости kfj представляет собой силу, возникающую в узле i, когда перемещение о, равно единице, а все остальные перемещения равны нулю. Иначе говоря, если закрепить тело во всех узлах, кроме узла /, и приложить такую силу Pjt чтобы перемещение v} рав-
нялось единице, то реак-
ция на тело в узле i будет равна fe/y (при этом величина самой силы Pj определит значение коэффициента kjj).
Применяя теорему Бетти о взаимности работ, можно показать, что матрица жесткости всегда симметрична.
все остальные перемещения рав-
Рис. 3.3
Если силы Pt имеют произвольные направления, то удобно разложить эти силы по. координатным осям х, у, г и ввести для каждого узла i матрицу сил Р; = {Pix Piv Pi2). Тогда у< будет также матрицей-столбцом, элементы которой суть перемещения узла i по координатным осям: = = {pix viv vi2}. Связь между силами и перемещениями можно по-прежнему определить соотношением вида (3.3), только элементами ki? матрицы к, представляющей уже блочную матрицу, будут квадратные подматрицы размера 3, X 3.
Для практических вычислений удобнее иногда пользоваться сквозной нумерацией компонент узловых сил и перемещений. В этом случае силы Plx, Plv и Р12, действующие в узле 1, обозначаются соответственно через Ри Р2 и Р3; силы Р 2X1 Р2В и Р22, действующие в узле 2, — через Pt, Рй и Рв и т. д. При такой индексации элементы матрицы сил для узла i будут иметь номера 3/ — 2, 3/ — 1 и 3/, т. е.
Аналогично для перемещений имеем
v,=
LDiz J
У3«’-2
Уai .
Наконец, в самом общем случае, в каждом узле могут помимо сил действовать моменты относительно координатных осей. Тогда подматрицы Р; и v, будут состоять из шести компонент, которые мы условимся перечислять в следующем порядке:
Р| — {Рix Рiy P'lZ М ix Miy ;г }; Vi = {vixviy vi2 0ix Qiy егг),
(3-4)
где Mig и Qiq — момент и угол поворота относительно оси q (Я = х, у, z).
Если использовать сквозную нумерацию сил и перемещений, то вместо (3.4) следует писать
Pyi-i P«i-3 P&i-2 Pei-l Pei}’
V[— {Vfti-з Vei-i y6i-3 U<ti-2 vei-l V«i}‘
Положительные направления сил и моментов даны на рис. 3.4, а, линейных и угловых перемещений — на рис. 3.4, б;
моменты и угловые перемещения лредставляются векторами в соответствии с правилом правого винта.
Подматрица kf> будет иметь размер 6 X 61 Смысл отдельных элементов этой подматрицы можно выяснить, полагая, Как и ранее, всё перемещения (линейные и угловые) равными нулю, за исключением одного, которое берется равным единице. Так, коэффициент &ei_2. w_3 равен обобщенной силе Лц-г (т- е- моменту Mix). которая возникнет в узле I, если Р</-з='1 (т. е. vJz = 1), а остальные пять перемещений узла / и всё перемещения остальных узлов равны нулю.
Вычисление матриц жесткости отдельных конструктивных элементов, из которых состоит стержневая система, составляет важный этап ее расчета матричным методом перемещений. Узлами для элементов служат точки соединения их друг с другом. Для расчета матриц жесткости элементов могут применяться различные способы; мы остановимся на трех из них как наиболее простых и употребительных.
В простейших случаях можно исходить непосредственно из физического смысла коэффициентов жесткости; этот подход иллюстрируется ниже на примере прямолинейного стержня, работающего на растяжение-сжатие (ферменного элемента).
Другой способ получения связи между узловыми силами и узловыми перемещениями заключается в применении аналитического или численного интегрирования дифференциального уравнения, описывающего деформацию элемента; этот подход будет подробно рассмотрен в § 3.4 применительно к изгибу бруса.
Можно, наконец, с помощью известных методов сопротивления материалов найти сначала зависимость узловых пере
мещений от узловых сил, а затем обратить ее, разрешив относительно узловых сил. Детали этого варианта описаны в § 3.7 при вычислении матрицы жесткости криволинейного бруса.
§ 3.2. Преобразование координат
Если, как говорилось выше, в качестве компонент матриц Рь V/ принять проекции сил и перемещений на координатные оси, то элементы матрицы жесткости будут зависеть от принятой системы координат, выбор которой произволен. Для расчета конструкции применяют некоторую общую координатную систему. Однако для вычисления матриц жесткости отдельных конструктивных элементов может оказаться выгоднее воспользоваться местными системами координат. Для каждого конструктивного элемента местная система выбирается так, чтобы свести к минимуму вычислительную работу. В таких случаях после отыскания матрицы жесткости в местных координатах необходимо выполнить переход к общей системе координат.
Пусть х, у, z и х, у, z — соответственно местная и общая системы координатных осей. Обозначим через
P={PiP2... P„J; v = {v1v2... v’}
матрицу сил и матрицу узловых перемещений в местных, а через
Р = {Р1 ₽2 ••• Pm}; V = {Vj V2 ... vm} —
в общих координатах. Количество элементов в подматрицах Рь V, или Р,, V, определяется числом степеней свободы отдельного узла.
Выразим прежде всего v через v. Чтобы получить связь между перемещениями в двух системах координат, необходимо разложить перемещения v по направлениям перемещений v? Если перемещения (линейные и угловые) типового узла i в общей системе координат спроектировать на местные координатные оси, то придем к соотношениям, которые в матричной форме имеют вид
V/ = (3.5)
где 10 — матрица, составленная из косинусов углов между осями х, у, z и х, у, z.
Подобные соотношения могут быть записаны для веек узлов рассматриваемого тела. Сведем их в одно матричное равенство:
~Х0 0 .. О “ О Хо ... О
_ 0 0 ... Хо _
V1
Vt
Введя обозначение
(3.6)
представим последнее соотношение в форме
v~~ Kv.
(3.7)
Матрица К представляет собой матрицу преобразования координат. Отметим, что число диагональных блоков в (3.6) равно числу узлов тела (или рассматриваемого конструктивного элемента).
Придадим далее точкам тела возможные перемещения и обозначим через 6v матрицу-столбец возможных перемещений узлов, отнесенных к местной системе, а через 6v — к общей системе координат. На основании (3.7) эти матрицы связаны соотношением
6v = 16 v. (3.8)
Если узловые силы отнесены к местной системе координат то на возможных перемещениях они произведут работу (см. §2.1) 6vr Р; если же они отнесены к общей системе, то работа будет равна fivr Р. Поскольку работа не зависит от того, в какой системе координат производятся вычисления, то
6vr Р = 6vr Р.
Подставляя сюда (3.8), получим
6vr Р = № V Р,
откуда в силу независимости элементов матрицы Sv приходим к равенству
Р = V Р, (3.9)
которое устанавливает связь между матрицами сил Р и Р.
Пусть, далее, к — матрица жесткости в местных координатах; тЬгда согласно (3.2) имеем Р — Jkv. Учитывая (3.7), получим Р = kkv. Наконец, под-У становка последнего равенства в
(3.9) дает _
\ P = VkXv.
Эта формула связывает силы и перемещения В общей системе ко------- ординат в стандартной форме х Р = kv, где _
k = V кЛ. (3.10)
Таким образом, если матрица жесткости к в местной системе координат известна, то для вы-
числения матрицы жесткости в общей системе достаточно построить матрицу X и воспользоваться формулой (3.10). Матрица X имеет вид (3.6), и задача сводится к составлению матрицы Хо, конкретный вид которой зависит от того, какие перемещения (степени свободы) узлов учитываются при расчете.
В качестве примера покажем составление матрицы Хо для случая, когда в каждом узле рассматривается по три линейных перемещения в направлении координатных осей. На рис. 3.5 показаны проекции перемещения узла i на координатные оси двух систем — местной и общей.
Обе матрицы v{ и v{ будут состоять здесь из трех элементов:
Обозначим косинус угла между осью р (р =="х, у, г) местной системы и осью q (q = х, у, г) общей системы координат через ХР9. Проектируя перемещения vix, vly, vtz на ось х, получим
Vl~X = + = X0*Vi-
Аналогично выразим о,- и vt- через v,-:
У.- = k.-Vf, У.- = X.-V:. i у Оу” i г 0 2 г
В этих формулах обозначено:
^Ох~^хх^ху^хг^ ^9у~^ух^уу^уг^ ^Ог ~^гх^гу^г^ (311 Q
Заметим, что матрица к имеет блочно-диагональный вид (3.6) лишь в том случае, когда в матрицах v и v узловые перемещения перечисляются в одном и том же порядке:
v={v1v2... vm); v = {v1v2... vm).
При выводе матрицы жесткости в местных координатах иногда оказывается удобнее принять иной порядок расположения элементов матрицы v. В таких случаях X уже не будет иметь вид блочно-диагональной матрицы. Более подробно этот вопрос будет рассмотрен в § 3.5 при вычислении матрицы преобразования для пространственного бруса.
Отметим также, что в некоторых случаях удобно пользоваться криволинейной местной системой координат (см., например, § 3.7), для которой матрицы преобразования отдельных узлов будут отличаться друг от друга. Пусть тело имеет узлы 1, 2, ..., /и; через Хъ Х2, .... Х„ обозначим матрицы преобразования в соответствующих узлах. Если в обеих матрицах v и v последовательно перечисляются перемещения уз-
ДОВ 1,2, .... т, то матрица X будет иметь вид, подобный (3.6] но диагональные блоки здесь будут различными:
Подобным же образом строится матрица X и в случае, ког да в разных узлах тела учитывается различное число степене( свободы, т. е. когда матрицы v, имеют неодинаковый размер
Отметим в заключение, что, как вытекает из сути вывода преобразование к = ХгкХ справедливо не только при поворо те координатных осей, но и вообще при любой замене узловы: перемещений, представленной в форме v ~ Xv.
§ 3.3. Ферменный элемент
Ферменным элементом будем называть прямолинейный стержень, который присоединяется к другим конструктивны*, элементам посредством идеальных шарниров. Если к нему н<
приложены поперечны* нагрузки, то он буде1 испытывать лишь растя жение или сжатие. Выведем матрицу жесткости этого элемента, выбрав местные координаты таким образом, чтобы ось х совпадала с продольной осью стержня (рис. 3.6, а).
В рассматриваемом
Рис. 3.6 случае узлами являют-
ся концы стержня I, /, в которых действуют силы Рй и Рд, направленны* вдоль оси х. Перемещения этих узлов вдоль оси стержня обозначим через v.~ и v.~. Узловые силы и перемещения в местной системе координат образуют матрицы
р=Гр*1=Р*1
kJ lAd kJ k,v-
которые связаны зависимостью Р — kv или
|41
Для вычисления элементов матрицы жесткости к стержня предположим сначала, что узел i получил единичное перемещение в положительном направлении оси х, в то время как узел / остался неподвижным (рис. 3.6, б). В соответствии с физическим смыслом сила Р.-, создающая такую деформацию, совпадает численно с величиной Ъц, а реакция Р.~ в закрепленном узле / — с величиной кц-.
Р1х- = кп. (3.13)
Воспользуемся далее известной из сопротивления материалов формулой А/ = Pll(EF) для изменения длины стержня, нагруженного осевой силой Р (F — площадь поперечного сечения). Подставив сюда А/= vt- — \, Р = Pix — ^и, находим ka — EFH.
Из условия равновесия стержня следует равенство Р.-х — —Р{-, так что с учетом (3.13) имеем кц ——кц = = — EF/1.
Совершенно аналогично рассмотрим деформирование стержня по схеме рис. 3.6, в; это дает значения kjj = — кц — EFH.
Таким образом, матрица’жесткости ферменного элемента в местной системе координат оказывается равной
» /
Здесь для определенности указаны номера i, j строк и столбцов в соответствии с порядком расположения элементов в . матрицах Р и v.
Отнесем теперь ферменный элемент к общей системе координат (рис. 3.7). Пусть ось стержня составляет с осями х, у, 2 углы, косинусы которых равны
Чх = (xi - х№ = (У/ — — г,)//;
I - V(Xj - XiF + (уJ-уу + (г,-гУ. (3.15)
Перемещение каждого узла имеет составляющие по всем трем осям общей системы координат, поэтому матрица v< перемещений узла I будет иметь три элемента: .
V/ = {о(Л. Un, viz}.
Силы, действующие в узле I, образуют матрицу*
перемещения узла i на направление местной
оси х, полупим
Проектируя
vi* = Ч&* + Ч^ +
+ 4Vi*-
Матрица v,- перемещений узла I в местной системе координат состоит из единственного элемента v_, поэтому последнее равенство устанавливает требуемую связь между
перемещениями узла i в местных и общих координатах. Если обозначить через Хо матрицу
то оно примет стандартную форму v( — Xov{. Для стержня в целом получаем
о 1 fV£l Ы Loi0J[vJ
Обозначая через
V‘=[V/
1ЪД
* Здесь и далее верхним индексом «г» будем отмечать в общей системе координат те величины, которые относятся к отдельному конструктивному элементу (от англ, «element»). Так, Р^ будет означать матрицу сил, действующих в узле i иа рассматриваемый конструктивный элемент, в отличие от матрицы Р; внешних сил приложенных к узлу I конструкции. Ясно, что v' = V/.
матрицу узловых перемещений стержня в общей системе координат, представим это равенство в виде v да Xv*, где
Х^Г1® 0 1. (3.17)
[° 4J
Пользуясь, далее, формулой (3.10), вычислим матрицу жесткости к» ферменного элемента в общей системе координат:
°]— Г 1 ~’1] Г1® 0 1. 1° 41 1 L-1 1J 10 М
Выполнив перемножение матрицы, можно получить следующее блочное представление матрицы жесткости к*:
где все подматрицы
к ? = к|;« - ксц = - кеа = ~ XJ Хо (3.19)
имеют размер 3x3.
Если рассматриваемый стержень является элементом плоской фермы, то в общей системе координат каждый узел имеет перемещения лишь в направлении двух Осей (например, х н у). В этом случае матрицы vf и Р? состоят из двух элементов:
а матрица Хо равна
Х« -= IX-X-J. (3.20)
Матрица жесткости ке по-прежнему вычисляется по (3.18), но ее подматрицы (3.19) будут иметь размер 2X2.
§ 3.4. Прямой брус в местной системе координат
Рассмотрим прямолинейный брус, воспринимающий в общем случае все виды нагрузок (растяжение, изгиб в двух плоскостях и кручение). В качестве узлов i, j элемента возьмем его концы. Местные оси выберем так, чтобы ось х совпадала с продольной осью стержня, а оси у и г совпадали с главными центральными осями его поперечного сечения
В каждом узле будем рассматривать 6 перемещений (3 ли нейных и 3 угловых) и соответствующие им силовые факторы (рис. 3.8).
Матрицы сил и перемещений для всего бруса можно составить, как и раньше, перечислив сначала силы (перемещения) узла (, а затем узла /. Однако здесь удобнее расположить перемещения и силы в матрицах v и Р в ином порядке. При выбранной системе местных осей узловые силы распадаются на
четыре группы, которые можно рассматривать независимо друг
от друга. Силы Р(- и Pf - вызывают только осевую деформацию бруса и определяются перемещениями v.~ и v.~. Образуем из них соответствующие подматрицы, которые обозначим через ро и %-
Р =г " р-L
V v„ =
IV
Эти подматрицы связаны между собой равенством
(3.21)
где ка — некоторая квадратная матрица размером 2x2
Силы Р.-, Р.-, а также моменты М.-, М.- вызывают изгиб бруса только в плоскости ху и определяются только перемещениями v(~, vf- и углами поворота (С-, 9;. Составив из этих компонент подматрицы
связь между ними снова представим в форме
(3.22)
где кь — квадратная 4x4 матрица.
Аналогично образуем подматрицы сил и перемещений
определяющих изгиб бруса в плоскости хг; соответствующую матрицу жесткости обозначим через кс:
Pc=kcvc, (3.23)
Наконец, кручение подматрицы
стержня вокруг оси х характеризуют
Vd =
которые связаны соотношением
Pd = kdvd. (3.24)
Через kd здесь обозначена еще одна подлежащая отысканию матрица размером 2x2.
В совокупности формулы (3.21)—(3.24) дают связь между узловыми силами Р = {Ра Рь Рс Pd} и перемещениями v = = {vo v& vc yd) рассматриваемого конструктивного элемента. Объединим эти формулы общим равенством
(3.25)
Таким образом, при выбранном расположении компонент Р н v матрица жесткости к оказывается блочно-диагональной.
Переходя к вычислению отдельных блоков матрицы жесткости, начнем с матрицы ка. Эта подматрица связывает силы ₽о и перемещения va равенством (3.21). Перемещения и силы в матрицах vo и Ро расположены в том же порядке, что и в матрицах v и Р для ферменного элемента, и определяют они
Рис. 3.9
деформацию бруса вдоль оси. Поэтому подматрица ka совпадает с матрицей жесткости (3.14) ферменного элемента в местной системе координат:
_ ef [ 1 —11
ka=T' _i 1 (3-26)
Для вычисления подматрицы к6 необходимо рассмотреть изгиб бруса в плоскости ху (рис. 3.9,а). Пусть и-—прогиб бруса на расстоянии х от левого конца. Полагая £ = = 2x11— 1, введем безразмерную координату £, которая изменяется от —1 в узле i до +1 в узле /.
Если на концах бруса заданы поперечные смещения и углы поворота, то изогнутая форма бруса будет однозначно определена. Другими словами, в соответствии с технической теорией изгиба балки прогиб и- однозначно определяется узловыми перемещениями vft. В матричных обозначениях это означает существование равенства
«5(S) = a(l)vb, (3.27)
где a (£) — матрица-строка, четыре элемента которой являются функциями координаты Эта матрица будет в явной форме получена ниже, а сейчас перейдем к вычислению подматрицы к6, считая, что матрица a (&) известна.
Выпишем известные из курса сопротивления материалов дифференциальные соотношения для изгиба балки постоянной жесткости в плоскости ху:
d2 u-
—у.-
dx2
Q=™L^EJ-
dx
d3u-
____y_
dx3
АП d4«-
q=J^=EJ-—^ dx dx4
dQ dx
где J- — момент инерции поперечного сечения относительно
оси z; М — изгибающий момент в сечении балки; Q — перерезывающая сила; q — погонная поперечная нагрузка. Положительные направления Q и М показаны на рис. 3.9, б, а положительная нагрузка q действует по оси у. Такое правило знаков для М, Q и q при выбранной системе координат определяет положительные знаки в записанных выше формулах. Переходя к дифференцированию по %, перепишем данные соотношения в виде
4£У- 8EJ- ,,, rv о/4
Q~--------и- (£); . (3.28)
р У'•'°'' х р У у w 16/? J- ' .
Здесь и далее производные по £ отмечены штрихами.
На концах балки (при £ = =И и £ = 1) изгибающий момент и перерезывающая сила должны совпадать с их узловыми значениями. Учитывая направления сил и моментов, приведенные на рис. 3.9, запишем Pf-= Q (—I); М{- = = —М (— 1); Р,- ——Q (1); М.~ = М (1). Подстановка в эти равенства соотношений (3.28) дает
8EJ- т
4EJ-
(3.29)
8EJ- 4EJ-
Р.- =---------и-(\У М.- =--------и-(1).
1У р У ' ’ /г р У ' '
С учетом (3.27) получаем отсюда следующую связь между узловыми силами и узловыми перемещениями:
8EJ- _ 4EJ-
piy = -7Г- (“ ’) v<’ -------7^ «" (- 0 v„;
1 l' (3.30)
8EJ- 4EJ-
В матричной записи эти формулы имеют стандартный вид рь === kbvb, где
Г 8а'" (—1)
FI ' '
. . г — 4Z«"(—1)
I3 —8а'" (1)
(3.31)
4/а"(1)
Таким образом, для формирования матрицы кь необходимо определить матрицу-строку а (£) и воспользоваться формулой (3.31).
Для отыскания матрицы а (£) обратимся к последнему соотношению (3.28). Здесь рассматривается изгиб бруса под действием одних лишь узловых сил и моментов. Полагая в со-
IV
ответствии с этим q = 0, запишем и- (£) = 0. Решение этого однородного дифференциального уравнения имеет вид
и- (I) = q + СЛ + Сз£2 + с^3, (3.32)
где Clt .... С4 — произвольные постоянные, подлежащие определению из граничных условий. Последние заключаются в том, что на левом конце балки прогиб и- должен равняться du- 2 d"_
v(~, а угол поворота ~ должен равняться 9(.-;
аналогичные соотношения имеют место на правом конце. Таким образом, решение (3.32) необходимо подчинить следующим условиям:
(3.33)
Дифференцируя (3.32) по находим
и-у (?) = + 2Сз£ + ЗСД2.
На основании (3.33) приходим к уравнениям
Cj С2 С3 — С4 = У(.-; Сг + С2 + С3 4- С4 = ц;.-;
(3.34)
С2—2С3 4- ЗС4— — 0f-; Сг 2С3 4- ЗС4 = —- 9}- .
Решая эту систему, находим
с-=т(%-+вд+т(в-—W
с*=—г с» - ’») —г )
с>~—
С-"Т(%—“/,-)+Т(0.-.-+е/.-)-
После подстановки постоянных в (3.32) получим уравнение изогнутой оси бруса
и~у = Т (2VCy + Т (1 “ь + 53) 0Гг- +
+ 2-(2 + з^-?3)я -2- (I +1--F-?3) 0 4 ty 8 *
В матричной форме это выражение имеет требуемый вид и- = a (g) vb, где
а(?)=[-Ь(2-3? + В3) 4'<1-^-^ + ?3)^
L 4 8
^2_(2 + 3?-53) 4-(-1 -5 + ?2 + ?3)]- (3.35)
4 8 J
Дифференцирование последнего равенства дает
a"(?) = [j-? -L(-1+3S) —5-? -L(i4-3^;
т Г 3 3 . 3 3 .1
a (е) = — —I-------—1\-
v ' [ 2 4 2 4 J
По формуле (3.31) получаем искомую матрицу:
Г 12 6/ —12 6/"
f 6/ W 2Р (336)
I3 —12 —6/ 12 — 6/ v
6/ 2/2 —6/ 4Z2
Отметим, что в некоторых случаях (например, для тонкостенных балок) существенное влияние на перемещения может
оказать деформация поперечного сдвига, которая не учитывалась при выводе формулы (3.36). Значение матрицы жесткости бруса при изгибе, учитывающее деформацию сдвига, можно найти в книге [201.
Далее рассмотрим изгиб бруса в плоскости хг (рис. 3.10). В этой плоскости положительные узловые моменты (а также углы поворота) направлены по сравнению с предыдущим случаем (см. рис. 3.9) в противоположную сторону. В остальном
обе схемы идентичны. Повторяя предыдущие выкладки, найдем подматрицу
12 —61 — 12 —6Z
У__ — 61 6Z 2Z2 (3.37)
Р — 12 61 12 6Z
_-6Z 212 6Z 4Z2_
где J- — момент инерции сечення бруса относительно оси у.
। Рассмотрим, наконец, кручение бруса (рис. 3.11). Сечение /относительно сечения i закручивается на угол 9;.~— 9t.-t Из курса сопротивления материалов известно, что крутящий момент в сечении бруса М;.~, необходимый для создания такого угла закручивания, равен
кр
---9,-)=-££«Р-[— 1 1]Г°'71
,х I ' ,х ,х' I 1 I 9 - Г
L ix J
где G/HP — жесткость стержня на кручение. Из уравнения равновесия имеем также
о / Г 9,- -
-П[“
Объединяя эти соотношения в одно матричное равенство, получаем Pd == kdvd, где
kd =
б-/ кр I
(3.38)
— 1
Формулами (3.25), (3.26), (3.36), (3.37) и (3.38) определяется матрица жесткости бруса постоянной жесткости в местной системе координат.
§ 3.5. Прямой брус в общей системе координат
В общей системе координат матрицу Vе образуем, перечисляя, как обычно, сначала перемещения узла i, а затем — узла /. В свою очередь, в каждом узле условимся перечислять сначала линейные смещения, а затем угловые. Обозначим через v* и 0, матрицы линейных и угловых перемещений узла г:
Тогда матрица v, перемещений узла i будет
аналогичные обозначения введем для перемещений узла /.
Матрица узловых перемещений всего бруса в общей системе координат будет иметь следующую блочную форму:
Подобным же образом составим матрицу узловых сил Ре, перечисляя сначала силы и моменты в узле i, а затем в узле /.
Полагая
ГРЛ
(mJ
и пользуясь подобными обозначениями для узла /, запишем
р; р/
-р. _
мг
р;
_М>_
Выразим, далее, v через ve, используя введенные в § 3.2 обозначения:
^0х~ [Чх Ч^ ^xz ];
= ЧгГ».
Чг ”[Чх ^гу Чг]*
Проекция линейных перемещений узла i в общих координатах на местную ось х равна v(- = + '^yvty + Чг х
X viz = X0-vJ ’ аналогичное соотношение запишем для узла j'-v.- = ><0-Vj . Эти равенства устанавливают связь между перемещениями va и перемещениями vc:
1 1 й а* 1 1 — -Ко- 0 0 0- 1 1 CD < Ф < **•. # •». ♦».« 1 1
0 0 Чх 0
или в краткой записи Куе,
(3.39)
где через Ха обозначена прямоугольная 2 х 12 матрица
Выразим, далее, перемещения v& = {гл- 0,.j v.- 0д} через Vе. Проектируя перемещения v?, v* на направление оси у, находим
^ = Xo?v‘*; v/5 = 4?v/.
Если угловые перемещения, входящие в 0г, 0;, представить векторами и спроектировать их на направление оси г, то получим также
Объединяя все эти соотношения общим равенством
приходим к выражению
vb = Xbv', (3.41)
в котором
0 0 0 ~
0 V 0 0
— Oz (3.42)
0 0 ^'Off 0
о 0 0 хой_
Подобные рассуждения позволяют выразить также матрицы vc и vd через Vе посредством соотношений
vc = ve; (3.43)
vd = ^d v\ (3.44)
где
-Xo- 0 0 0 -
o 0 0
Off ; (3.45)
0 0 0
_0 0 0 x0-_
Г0 L- 0 0 1
= 1 0* 1 (3.46)
0 0 о к J
Отметим, что все подматрицы, в том числе нулевые, в формулах для Хь, кс и имеют размер 1 X 3.
Связь между v и ve можно записать в Виде одного равенства:
vb
_vd_
Введя обозначение
придадим этому равенству стандартную форму v = lve. Матрица жесткости бруса в общей системе координат может быть вычислена далее по формуле ke — Vkk.
Удобнее, однако, преобразовать эту формулу таким образом, чтобы избежать формирования полных матриц к и к. Для этого нужно в правой части равенства
выполнить перемножения блочных матриц; тогда
ке — ка Хд -|- Хй кь к# Кв -f- kd Xd. (3.47)
Отметим, что если общая система координат совпадает с местной, то матрицы v и Vе (или Р и Ре) отличаются лишь порядком перечисления компонент. В этом случае
Ко- = [1ОО]; X0-=tO 1 01; ^0- = [0 0 1]
и преобразование ке = ХгкХ будет заключаться в простой перестановке строк и столбцов матрицы к. В результате такой перестановки расположение элементов матрицы жесткости будет согласовано с порядком следования сил и перемещений в матрицах Ре и Vе.
Рассмотрим особо частный случай, когда брус является элементом плоской рамы. При этом каждый узел получает поступательное перемещение в направлении двух координатных осей и угловое перемещение в плоскости этих осей.
Если деформация бруса
происходит в плоскости ху V р
(рис. 3.12), то матрицы сил р,_ Ptg Я
и перемещений в местной си-
стеме координат имеют вид /7 - ® t ® jhx
Рис. 3.12
Матрица жесткости бруса в будет при этом равна
местной системе координат
к«Гк“ ° 1 [О кь]
(3.48)
'Г
; Vе =
где подматрицы ко и кь определяются формулами (3.26) и (3.36).
В общей системе координат матрицы сил и перемещений снова представим в форме
ре Д₽Г [Р/.
где, например, подматрицы сил и перемещений узла I определяются так:
P‘l fv’l
mJ [e,J
Матрицы сил и линейных смещений каждого узла имеют здесь по две компоненты:
S * =М, kJ KJ
Pi
а матрицы моментов и углов поворота состоят из единственной компоненты:
Обозначая через Хо-, Хо- матрицы
[Ч ЧП Ч “ [Ч Ч] <3-49>
и проектируя компоненты матрицы Vе на направления местных осей, получим
где
“00
vo = Kove; 0
0 01 0 1
х0- о ; о о
о о
о
о
к
I
о
О"
о о
1
(3.50)
Угловые перемещения 0iz и 0JZ прн повороте координат в плоскости изгиба не изменяются, поэтому на соответствующих местах матрицы, связывающей v и ve, стоят единицы. Матрицу ке можно вычислить по формуле
ке — Ха ко Ха Кь kfj
(3.51)
В частном случае, когда общая система координат для плоского бруса совпадает с местной, имеем
41 = II 01; 4-=[0 1].
§ 3.6. Учет внеузловой нагрузки
Выше получена связь между узловыми силами и узловыми перемещениями для бруса при отсутствии какой-либо внеузловой нагрузки. Рассмотрим случай, когда помимо узловых сил на брус действуют также внеузловые нагрузки (распределенные или сосредоточенные).
Отнесем сначала рассматриваемый конструктивный элемент к местной системе координат. Если узловые перемещения элемента равны нулю (концы стержня защемлены), то внеузло-вая нагрузка вызовет появление реакций в виде сил и моментов. Образуем из них подматрицы Р0о, Роь, Рос и Pod, соблюдая тот же порядок перечисления сил, что и в матрицах Ра, Рь, Рс, Pd. Таким образом, в подматрицу Р0о войдут реакции, действующие на стержень вдоль его оси; Роь и РЭс будут состоять из поперечных сил и моментов, действующих на концах стержня соответственно в плоскостях ху и xz\ наконец, в Pod войдут моменты относительно оси х. Объединив эти подматрицы, получим матрицу узловых сил, уравновешивающих при неподвижных узлах внеузловую нагрузку:
1*0 = (1*0а Р0Ь Pfic Pod I •
Положительные направления реакций примем совпадающими с положительными направлениями сил и моментов, указанными на рис. 3.8.
При вычислении матрицы Ро предполагалось, что узловые перемещения отсутствуют. Если же узлы бруса получают перемещения, определяемые матрицей v, то дополнительные узловые силы, необходимые для их создания, определятся, как и ранее, произведением kv. Таким образом, при наличии вне-узловой нагрузки матрицу узловых сил Р можно иайти по формуле
P = kv + Po. (3.52)
Перейдем к общей системе координат х, у, г. Для вычисления матрицы узловых снл Ре рассматриваемого бруса в общих координатах воспользуемся формулой (3.9), в которую подставим выражение (3.52). Это дает
Ре = Vkv+ VP0.
Учитывая, что перемещения v и Vе связаны соотношением v = lve, получаем
Р*= +vpo
Произведение Vkl дает матрицу жесткости ке бруса в общей системе координат. Введя также обозначение
Рео=^Ро, (3.53)
имеем
p» = keveH-P'. (3.54)
Равенство (3.54) определяет связь между узловыми силами и перемещениями в общей системе координат при наличии внеузловой нагрузки. Матрица Р« содержит компоненты узловых сил и моментов, уравновешивающих внешнюю нагрузку при Vе = 0 и отнесенных к общей системе координат. Учитывая блочное представление матриц Ро и X, формулу (3.53) можно привести к более удобному для практических вычислений виду:
Р*о = Роа + Роь + Ьс Рос + $ Pod. (3.55)
Компоненты матрицы Р„ располагаются в том же порядке, что и компоненты Ре. Поэтому равенство (3.54) может быть представлено в следующей блочной форме:
рЯ
P/J
kzz kz/ Cvf i Poz k£ kJ [vj [p‘.
Здесь Peoz и Ро/ — подматрицы сил, уравновешивающих внеузловую нагрузку, для узлов I и / соответственно. Так же как и в Pf, первые три элемента матрицы Ро,- — проекции силы, действующей в узле i, на координатные оси х, у, z, а последние три — моменты относительно этих осей. Аналогичным образом располагаются компоненты сил и моментов в подматрице Ро/.
Таким образом, при действии внеузловой нагрузки необходимо сформировать матрицу реакций Ро и по (3.55) найти матрицу Р*. Значения реакций, составляющие матрицу Ро, для многих встречающихся на практике видов нагружения имеются в справочной литературе. При отсутствии справочных данных можно вычислить их, пользуясь известными методами сопротивления материалов. Для наиболее часто встречающегося случая действия на брус поперечной нагрузки можно вывести простую формулу для расчета матрицы реакций.
Рассмотрим нагрузку, действующую в плоскости ху. Задача сводится к вычислению матрицы
РоЬ = IP - М - Р - М -). 06 V O.ty O.iz O./jz OJzf
Для решения этой задачи обратимся к дифференциальному уравнению изгиба бруса в плоскости ху (3.28):
» 16£/_
z
Общее решение этого уравнения имеет вид
«-(В) = «о(В) + С1 + С2? + С3 g2 + C4g’,
где и0 (5) — какое-либо частное решение неоднородного уравнения. Постоянные С4 ... С4 должны быть найдены нз условия полного закрепления бруса на концах: и- (—1) = 0; и- (1) = 0; (—1) = 0;
uL (1) = 0. и
у
Получаемая отсюда система уравнений относительно произвольных постоянных полностью совпадает с (3.34), если в правых частях заменить и -, и,- на —иа (—1), —иа (1), а /0 -/2, Z0.-/2 — на —(—1), i у j у “v v ' i z j z '•
—u’B (1) соответственно. Решив эту систему, представим выражение для и- (g) в виде
«-(g) =«о (I)— a(g)v0,
где матрица a (g) дается равенством (3.35), а через v0 обозначена матрица-столбец
(2 2 )
vo = |«o(-l) —«□( — !) «о (О “"НО]-
Для вычисления узловых сил, входящих в РоЬ, воспользуемся равенствами (3.29). Учитывая (3.31), для искомой матрицы получаем выражение
Роь = Р*-к& v0,
(3.56)
где
4£J_
р*---~{2uo(-l) -/«;(-!) —2«"' (1) /«;(!)}.
Итак, для вычисления Роь необходимо построить частное решение «о (5) Уравнения изгиба бруса, сформировать матрицы Р* и v0 и воспользоваться затем формулой (3.56). Проиллюстрируем эту процедуру иа двух примерах.
Рис. 3.13
Пример 1. По всей длине бруса действует распределенная поперечная нагрузка q — const (рис. 3.13, а). Частным решением уравнения изгиба будет функция
Z
Матрицы Р* и va оказываются равными
Р* =
1
дР — 8/1
8SAEJ- 1 z 8/1
Согласно (3.56), находим искомую' матрицу оЬ t 2 12 2 12 Г
(3.57)
Пример 2. Сосредоточенная сила S приложена на расстоянии ха от левого конца балки (рис. 3.13, б). Величине х0 соответствует безразмерная координата £0 = 2xjl — 1.
Здесь мы имеем два участка, для одного из которых —-1 ^ £ < £<>• а для другого 50 < g < 1; на каждом из иих поперечная нагрузка отсутствует. На первом участке принимаем и0 (g) = 0; тогда на втором частное решение должно при g = g0 обеспечивать непрерывность пере-
мещеиий и угла поворота, а также непрерывность изгибающего момента; при этом перерезывающая сила должна претерпевать скачок иа величину S. Для выполнения этих условий возьмем и0 (?) для второго участка в форме общего решения однородного уравнения, а именно:
«о (В) = с, + cg (6 - В») + с3 а ~ Во)2 + С4 (В - Во)3- >
Постоянные С, определяются условиями
«о(Во) = О; «ИВо) = О; «ИВо) = О; < (£0) = 3/»/(8£./_.);
последние два равенства вытекают из соотношения (3.28).
Отсюда находим Cj = С2 = С3 = 0; С4 = 5/У(48£У-) и оконча-
тельно выражение для и0 (?) получаем в виде
иа (£)=
0 при — 1 < £ < g0;
~ (В —Во)3 при ?0 < ? < I.
Пользуясь далее описанной выше процедурой, приходим к матрице
S
Роь=Т
—2(1—Во)2 (2-Но)
-1 (1 - Во)2 (1 + Во)
-2(1 + ?о)2(2-£о)
_ / (1 —Во) (1 + Во)2 _
Если, в частности, сила приложена в середине пролета, то ?0 = 0, в этом случае
Роь — {—S/2 —S//8 —S/2 S//8). (3.58)
§ 3.7. Плоский круговой брус
Рассмотрим плоский круговой стержень радиусом г, нагруженный силами в своей плоскости (рис. 3.14). Предполагаем, что одна из главных осей инерции поперечного сечеиия стержня также лежит в его плоскости. В качестве узловых возьмем перемещения и силы, показанные на рис. 3.14. На стержень может действовать также внеузловая нагрузка (на рис. 3.14 показано для примера действие распределенной радиальной нагрузки q). _
Матрица v, перемещений узла i включает в себя касательное и(1 и радиальное перемещения, а также угол поворота ц,3:
vf={pit f<2
матрица перемещений узла /:
Vj={V;l vj2 vis}.
Аналогично образуются матрицы узловых сил
СрМз}; р)= {Pji Pj2Pj3}•
Для всего элемента имеем,
Связь между матрицами Р и v при наличии внеузловой нагрузки дается соотношением (3.52). Для вычисления матриц к и Ро можно воспользоваться решением дифференциального уравнения изгиба кругового бруса. Мы, однако, продемонстрируем здесь другой подход, пригодный для случая бруса переменной жесткости. Запишем соотношение (3.52) в блочной форме:
отсюда следуют два равенства
P, = ki; Vi + kMVj+Poe; Р, = кя?; + к77У,+ Роу. (3.59)
Здесь через kr3 (г, s = = i, j) обозначены подматрицы жесткости_ размером 3 X 3, a POi и Ро; содержат силы, вызываемые внеузловой нагрузкой соответственно в узлах г нj при полном закреплении этих узлов.
Если положить Vj — О (узел j защемлен), то из первого равенству (3_59) получим Р£ = kttVi + Poi. Умножая это соотношение
Рис. 3.14
Т—1 слева на кх’х , имеем
к-1 p,. = 7i + k-> р0
Последний результат можно представить в виде vi= Aii Pi + voi.
где введены обозначения:
Aii = kt-: Уо>= к(-; Poj.
(3.60)
(3.61)
Полагая
611 612 613
®21 622 62з
-631 6 32 6зЗ_
Voi =
620 »
630 _
запишем (3.60) в скалярной форме:
vit = 6ц Ри -|-612 Р;2+ 613 Р;3+
Vi2 — ®21 622 Р12 + 623 Р13 + 62о!
vi3~ 631 Pii + 632 Р12 + 633 Р1з4-6зо.
Мы получили соотношения, которые устанавливают связь между перемещениями узла i и силами, действующими в этом узле, при защемленном узле /. Элементами 6mn матрицы A;i являются перемещения узла i от действия единичных сил, совпадающих по направлению с силами Pj; матрица же v0; определяет перемещения узла i от действия иеузловых нагрузок. Поскольку перемещения можно легко найти, пользуясь, например, известным методом Мора, то отсюда вытекает следующий способ отыскания матриц кц и Рог.
Защемив узел j и прикладывая единичные силы по направлению перемещений vh, v,-2, vis узла i, а также внеузловую нагрузку, вычислим по методу Мора элементы матриц Ai(- и v0;. Интересующие нас матрицы ki; и POj найдем затем, пользуясь соотношениями (3.61), нз которых следует, что
= Ро/——kjjVoj. (3.62)
Для отыскания остальных подматриц жесткости, а также матрицы Ро; можно воспользоваться условиями равновесия всего стержня в целом. Запишем, например, условие равенства нулю суммы проекций всех сил на направление перемещения v;1 (см. рис. 3.14):
Ph cos ip — Pi2 sin ip + Pji = 0,
где через Р'ц обозначена проекция результирующей внеузловой внешней нагрузки на направление v}l. Отсюда
Рц — ~Рц cos ip-|-Pi2 sin ip — Pj \.
Проектируя силы на направление vjt, находим аналогично
Рц — —Ph sin ip — Pi2 cos ip —Pj2.
Наконец, вычисляя сумму моментов относительно узла /, получим
Pj3= Ри г (1 — cos 40 + Рц r sin 1р — Р,з — Р/з •
В последних формулах через Р/2 обозначена проекция внеузловой нагрузки на направление перемещения vj2, а через Рц — ее момент относительно узла j (Рц, Рц н Р'ц считаются положительными, если они совпадают по направлению с иц, Vj2 и v}-3).
Полученные соотношения дают связь между силами в узлах i и j. В матричной форме их можно записать так:
Р^ = ЙР(-Р'., (3.63)
где
—cos ip Я = —sin тр |_г(1—cosip) 80 sin ip 0 £/i —cosip 0 1 P0j~ Р/2 r sin ip —IJ LP/3
Если в (3.63) внести формулы (3.59), то получим равенство к;; V,- + v; +₽о;= я (ki; Vf-|-k,j V;-|- Po;) — ₽oy. .
Это равенство должно выполняться при любых значениях узловых Перемещений, поэтому из него вытекают соотношения
kjy=:ftkfj; Poy=QPo^ Ро/* (3.64)
— —у
Совместно с равенством кг; = ку7, которое является следствием симметрии матрицы жесткости к, эти формулы позволяют вычислить все подматрицы жесткости по известной матрице к,-,-, а также матрицу
Ро7- по известной матрице Р0(. Вычисления по формулам (3.62) н (3.64) удобно выполнять численно с помощью ЭВМ, сформировав предварительно матрицы Л», v0(-, Я и Р'Оу-.
Перейдем к вычислению элементов матриц Л1(- и v0!-. В соответствии со сказанным выше рассмотрим действие на стержень единичных сил и внеузловой нагрузки. На рис. 3.15 даны эпюры изгибающих моментов в каждой единичной системе н от внеузловой нагрузки. Перемещение 6тп в направлении силы Pim от действия единичной силы, совпадающей по направлению с Рщ (tn, п-= 1, 2, 3), определяется интегралом Мора.
„ СI МтМп NmNn QmQn \
где Г, J — площадь поперечного сечения п его момент инерции относительно центральной оси, перпендикулярной плоскости кольца; М N и Q — изгибающий момент, осевая и перерезывающая силы в сечении стержня; Aq— коэффициент, зависящий от формы поперечного сечения.
Первое слагаемое в подынтегральном выражении учитывает изгиб, а два других — растяжение и поперечный сдвиг. Если пренебречь влиянием деформаций растяжения и сдвига, то вычисление перемещений несколько упрощается. Полагая, кроме того, момент инерции бруса постоянным н переходя к интегрированию по углу а посредством заме ны dZ = rda, имеем
3mn =-^у da. (3, 66)
о
Зависимости изгибающих моментов в единичных системах от угла а даны иа рис. 3.15. Подставляя их в формулу (3.66), находим:
. г3 Г 3 „ ф 1
6П=—— — (ф —simp)—sinifsin2— ;
bJ L z Z J
. <. 2г3 ф
61г — 6«f= —— sin4 —— ;
12 21 EJ 2 .
f3
б13 = 631 = — —— (ф — sin ф);
С. J
б22 = -—-Г (2ф —sin 2ф);
4EJ
2r* ib б2з= 632= — sin2 ;
622=^.
Если угол ф мал, то во избежание потери точности коэффициенты бц, ^13 и ^22 лучше вычислять по формулам:
2,-з . o2A-f-2_j
5n = VT-4>5 2 ~ Z2fe4-5H
Л = о (2й4-5)!
б13=—------ф3 (— 1)*-------------ф2*;
EJ т (2*4-3)! Т
2г3 о2*
полученным из предыдущих формул разложением функций в степенные ряды, либо вести счет с двойной точностью.
Перемещения узла i в направлении Р^, Pi3 и Р/Зот внеузловой нагрузки определяются формулой
е f / Мо Мл Nm Qa Qrn \
fimo-j — т ~ +kQ^^- dZ; (m= 1,2,3). (3.67) у \ cj tr * иг ]
Пренебрегая деформациями растяжения й сдвига, в случае постоянной жесткости получим отсюда
бто =—• [Мо Мт da (т= 1,2,3).
EJ J о
Для каждого конкретного типа виеузловой нагрузки можно найти
зависимость изгибающего момента Мо щения 6П1О.
Значения коэффициентов 6,пП и 6т0 при необходимости нетрудно уточнить, используя полные выражения для интеграла Мора (3.65) и (3.67). Если брус имеет переменное сечение, то интегрирование лучше выполнять непосредственно иа ЭВМ каким-либо численным методом (например, методом Симпсона).
Выше получена связь между узловыми силами и перемещениями рассматриваемого бруса в местных координатах. Отнесем теперь брус к общей системе координат х, у.
Пусть радиус-вектор rj, соединяющий центр кольца О с узлом I,
от угла ф и вычислить переме-
Рис. 3.16
составляет угол фг с осью х, а радиус-вектор rj — угол ф,- (рис. 3.16). Введем матрицы проекций узловых сил на координатные оси
Р?==
а также матрицы узловых перемещении
vJx viv 1л J
Проектируя перемещения v; иа направления перемещений vilt viz< vt3' устанавливаем связь vt- = Л.(Уг-, где
51Пфг —COS Ф; О cos ф; sin ф^ О
О 0 !
Аналогично, v; = 1;V;, где
sin ф; созф;
4 =
0
—COS Ip; 0 sin Ip; 0 0 1.
Связь между узловыми перемещениями v — {v£V;} и Vе = = {v$ v;} определится тогда равенством v — , в котором
1_Р‘ °1
[О Х;Г
По формуле к* — I? кХ вычисляем матрицу жесткости в общей системе координат. Учитывая, что матрица жесткости в местной системе координат получена в блочной форме
[к/ЛгЛ
L k/i kj/ J
удобно н матрицу к? представить в виде
kii 1 “ t! .
И ke I
«/» КЦ J
Выражение для типовой подматрицы k*s получим из соотношения к* ~ 1гкХ, представив входящие в него матрицы в блочной форме:
k*s — krs Xs (r, s = i, j).
Изложенный в этом параграфе способ построения матрицы жесткости можно применить и прн изгибе бруса нз своей плоскости, а также в общем случае пространственного нзгибз бруса (в том числе с произвольным расположением главных осей инерции поперечного сечеиия). Отличие будет лишь при вычислении коэффициентов податливости 6mn; в случае пространственного изгиба матрица жесткости к будет иметь размер 12X12.
§ 3.8. Стержневая система
Рассмотрим стержневую систему, отнесенную к некоторой системе координат х, у, г. Обозначим через v,- матрицу перемещений типового узла i. Число элементов этой матрицы (число степеней свободы узла) зависит от типа конструкции. Так, для пространственной фермы матрица V,- будет содержать три перемещения узла в направлении координатных осей
V/ = {Vix viv vi2}, а для плоской фермы — два перемещения
V,- = {vix vitt}.
В случае пространственной рамы матрица
V; = {Uix Viy Viz 0ix Oiy 0iz}
состоит из трех линейных смещений и трех углов поворота. Если же плоская рама нагружена силами в своей плоскости, то матрица
V; = {Ц;х и{!1 0;}
включает в себя два линейных смещения и угол поворота.
Матрицу внешних сил, действующих в узле i в направлении перемещений v,-, обозначим через Р,. Число элементов этой матрицы совпадает с числом степеней свободы узла; перечислять силы в матрице Р, всегда будем в том же порядке, в каком перемещения располагаются в матрице v;. Так, например, для пространственной рамы
Р< = {PixPiy PizMixMivMiz}.
где т — число узлов стержневой системы.
При отсутствии внеузловой нагрузки связь между матрицами Р и v может быть представлена в виде Р = Kv, где К — матрица жесткости системы.
Если же помимо узловых сил действуют внеузловые нагрузки, то можно рассуждать так же, как и в случае отдельного стержня. Предположим, что все узлы защемлены; тогда, в результате действия внеузловой нагрузки, со стороны наложенных связей возникнут силы реакции. Перечисляя реакции, действующие в узле /, в том же порядке, что и для матрицы Р,, образуем матрицу Ро/; число элементов этой матрицы совпадает, конечно, с числом степеней свободы узла. Для всей конструкции можно составить матрицу
Ро
_р01
Р«2
Pflm —
Если, далее, узлы имеют некоторые смещения v, то для их создания необходимо дополнительно приложить силы, величина которых зависит от жесткостных характеристик системы; матрица этих сил может быть вычислена как произведение Kv. Таким образом, связь между узловыми силами и узловыми перемещениями можно в общем случае записать ,так:
Р = Kv + Ро. (3.68)
Покажем теперь, как можно найти матрицы К и Ро, зная матрицы к® и Р® для отдельных конструктивных элементов, образующих систему. Запишем прежде всего уравнение (3.68) в блочной форме:
ku ... kj; ... klm
kjj ... к;• j ... k/n,
к к к
__Лт1 лпц лтт~
и выпишем его i-ю строку:
Р; = 1ч1У1 + ... + кг,у;- + ... + kimvm + PoS. (3.69)
Для вычисления подматриц кг1, ..., ktm, а также подматрицы Poi рассмотрим равновесие узла I. В качестве примера на рис. 3.17 показан узел плоской рамы со всеми сходящимися в нем стержнями. Выделим один из конструктивных элементов, соединяющихся в узле i (например, стержень 1). Рассматриваемый элемент соединяет узел i с некоторым другим узлом г. Пусть матрица жесткости этого типового элемента в общей системе координат равна ке. Силы Р® = {Р! Р£), действующие в узлах данного стержня, связаны с перемещениями Vе — {v,- vr} его узлов соотношением Р® = k®v® + PJ, где Р® = {Ро, Рог) — матрица реакций, возникающих в узлах элемента от внеузловой нагрузки при v® = 0.
Перепишем это соотношение в блочной форме:
рЯ= [к-, к;;1 рчкГр'о/ р*] [% ke,J LvJ [реОг
Отсюда получим выражение для матрицы сил, действующих в узле i на рассматриваемый элемент:
Р,=к?.У{ + к;,уг + Рео,-.
(3.70)
Соединим теперь все стержни; тогда из условия равновесия узла имеем Рг — 2 Ро где суммирование ведется по всем стержням, сходящимся в узле I. Подставляя сюда (3.70), получаем
Pi = 2 к« vt + Sk'r vr + 2 Р^. (3.71)
Для представленного на рис. 3.17 примера равенство (3.71) примет вид
Рг =(к#’ + М”+ М?’ +k‘/’)Vi + (k^’ +k)’’)vp +
+ к<3> vq + к/«> vg + Рй> + Рй* + Рй* + Рй\ (3.72)
где верхний индекс в скобках относится к номеру стержня.
У
Рис. 3.17
Сопоставим полученный результат с равенством (3.69). Прежде всего замечаем, что в (3.72) или для общего случая в (3.71) отсутствуют члены, содержащие перемещения тех узлов /, которые не связаны стержнем непосредственно с узлом I. Это означает, что соответствующие подматрицы кц являются нулевыми. Если узел / связан с узлом i одним стержнем (в рассматриваемом примере таковыми являются узлы q и s), то множителем при V; оказывается подматрица ку этого элемента, поэтому для таких узлов ку = ку. Если же узел / связан с узлом i несколькими элементами (узел р на рис. 3.17), то множителем при vj будет сумма подматриц ку элементов, соединяющих узлы i и j, т. е. в этом случае ку = Sky. Наконец, множитель при уг, являющийся диагональной подматрицей матрицы К, равен ку = Sky, где суммирование выполняется по всем элементам, сходящимся в узле I.
Из сказанного следует, что матрицу жесткости стержневой системы можно образовать из матриц жесткости разрозненных конструктивных элементов по следующему правилу: ktj = 0, если узлы I и / не связаны непосредственно никаким элементом; kf> = 2к?;-, если узлы i и / связаны несколькими элементами (суммирование выполняется по этим элементам); кн = 2к*ь где суммирование ведется по всем элементам, сходящимся в узле I. Все эти случаи можно объединить общей формулой
кг; = 2к?у (i, /=1, 2, .... т), (3.73)
где суммирование выполняется по всем конструктивным элементам, входящим в стержневую систему. При этом следует принимать для элемента кц = 0, если этот элемент не соединяет узлы i, j.
Таким образом, для получения матрицы жесткости стержневой системы можно все элементы матрицы жесткости каждого стержня
ке=Гк«кЯ
1^ kjJ
поместить в соответствующие ячейки общей матрицы жесткости (положение ячеек определяется нижними индексами) и произвести затем суммирование всех накладывающихся элементов.
Аналогичное правило суммирования получается и для вычисления матрицы Ро. Сравнивая последние слагаемые в (3.69) и (3.71), заключаем, что подматрицу Рог можно найти по формуле
Pw«SP*w, (3.74)
где суммирование ведется по всем конструктивным элементам, сходящимся в узле I.
Поясним схему формирования общей матрицы жесткости на примере плоской рамы (рис. 3.18).
Эта рама имеет четыре узла и включает в себя пять стержней. Матрицы жесткости стержней в общей системе координат представим в блочной форме:
k(1)__[kiv kivi. k<»>erMV kivi k(„ FkJ? kiq
[кй> к®J’ Lk?i’m’ LkH’ k$J’
k«»efHV k«’l. krn Jkfc’ k&”|
(MV кй’]’ "Iкй’ kft’j
Напомним, что нижние индексы i, j означают номера узлов данного стержня, а верхний индекс — номер стержня.
В соответствии с числом узлов рамы матрица жесткости системы К будет иметь 4x4 блоков. Подматрицы ki7 (t, j = •=» 1, 2, 3, 4) образуются путем суммирования всех подматриц
Рис. 3.19
жесткости отдельных элементов с одинаковыми нижними индексами. Так, подматрица к12 = кф + кН’- В итоге получим
К =
-кН» + кН’ + кН’ I кН’ + кН’ |кН’ кй’+кй’ |кИ’ + кИ’+ кИ’|О к&? (0 ’к^+к^з’
.0 № | к&
1 2 3
0 ~ !
кй» 2
к»» з
кй’+кП’_ 4
4
Некоторые подматрицы (например, к14) оказались нулевыми, так как соответствующие узлы непосредственно не связаны между собой стержнем.
Расположение нулевых подматриц в матрице жесткости К определяется порядком нумерации узлов. Нумеруя узлы определенным образом, можно иногда добиться того, чтобы все ненулевые подматрицы были сгруппированы вблизи главной диагонали, т. е. добиться ленточной структуры матрицы жесткости (рис. 3.19). Примеры такой нумерации узлов пока-
заны на рис. 3.20 для случая плоской рамы. Рассмотрим, например, узел 10 в схеме 3.20, а. Максимальный номер узла, с которым он связан непосредственно стержнем, — 16, минимальный — 4. Поэтому в десятой строке матрицы жесткости К (записанной в блочной форме) первая ненулевая подматри*-ца появится в четвертом, а последняя — в шестнадцатом столбцах. Выполняя подобные рассуждения для других узлов, можно убедиться, что все ненулевые подматрицы образуют ленту коэффициентов, ширина которой в данном примере постоянна и равна 13 подматрицам. Учитывая симметрию матрицы жесткости, можно говорить о полуленте, ширина ко-
а)
S)
Рис. 3.20
торой (включая диагональную подматрицу) равна 7. Поскольку в случае плоской рамы каждая подматрица имеет размер 3 х 3, фактическая ширина полуленты будет равна 21.
Ленточная структура матрицы жесткости обладает большими вычислительными достоинствами по сравнению со случаем полного заполнения. Во-первых, в памяти ЭВМ нет надобности хранить всю матрицу: достаточно иметь лишь те коэффициенты, которые заключены внутри полуленты. Поскольку ее ширина No часто значительно меньше размера матрицы N, то это позволяет достичь существенной экономии памяти, что весьма важно в задачах с большим числом степеней свободы. Во-вторых, все операции, в которых участвует матрица жесткости, можно выполнять только с теми элементами, которые ограничены шириной ленты; это значительно экономит время вычислений. Чем меньше ширина ленты, тем эффективнее будет решение задачи. Поэтому всегда следует тщательно продумывать порядок нумерации узлов. Так, в рассмотренном выше примере более удачной является схема нумерации узлов, показанная на схеме 3.20, б. Она приводит к ленточной матрице с шириной полуленты, равной 15.
§ 3.9. Определение узловых перемещений
До сих пор мы полагали, что зависимость (3.68) служит для определения сил Р, необходимых для создания известных перемещений V. Если же, наоборот, известны силы, действующие вузлах конструкции, то (3.68) можно рассматривать как систему алгебраических уравнений относительно перемещений V. - Если конструкция закреплена, то перемещения соответствующих узлов в направлении опорных связей равны нулю, остальные же перемещения подлежат отысканию. Все компоненты перемещений можно расположить таким образом, чтобы в матрице v сначала перечислялись все неизвестные, а затем — известные (нулевые) перемещения. Тогда матрица v будет представлена в блочной форме
vP ]
где матрица va содержит только неизвестные перемещения, а подматрица vp нулевая. Порядок перечисления сил в матрицах Р и Ро всегда должен строго соответствовать порядку следования перемещений в матрице v:
[Ра].
.P₽J’
р _ Г а ° [Рог.
р =
В Ра входят известные внешние силы, действующие в направлении перемещений уа. Подматрица Рр содержит силы, действующие по направлению наложенных связей и представляющие собой реакции опор.
Строки и столбцы матрицы жесткости К мы должны расположить в том же порядке, в котором силы и перемещения перечисляются в матрицах Р и v, т. е. матрица жесткости будет иметь следующую блочную структуру:
К __[ Каа Кар 1
L Кра Kpp J
Представляя уравнение (3.68) в развернутом виде и учитывая, что vB = 0, получим
Каа Кар] Va] ___[Ра]____[^Оа]
. Кра Крр J . О J [ Рр J [ Pop J
Отсюда следуют два матричных равенства:
KaaVa = Pa — Poa; (3.75)
Kpa Va = Pg — Pog. (3.76)
Решая уравнение (3.75), находим неизвестные перемещения va, а (3.76) позволяет найти реакции опор:
Рр — Kpava + Ро0.
Заметим, что практически нет необходимости производить перестановку элементов матриц Р, Ро и К. Матрицы Ра и Р0<х можно получить, вычеркнув в исходных матрицах Р и Ро элементы, соответствующие опорным связям; при этом вы-чернутые члены составят матрицы Р6 и Рор. Матрица Каа получится также вычеркиванием соответствующих строк и столбцов из полной матрицы К. Матрица Крр будет образована элементами, находящимися на пересечении вычеркнутых строк и столбцов, а матрица Кра — элементами на пересечении вычеркнутых строк и оставшихся столбцов.
Пользуясь аналогичными рассуждениями, можно рассмотреть и более общий случай, когда заданные перемещения vp не равны нулю. Тогда вместо (3.75) и (3.76) имеем
КааVa Pa Р oa KaSVp, Рр = KpaVa + KppVp + Ро0.
Если перемещения узлов найдены, то для любого конструктивного элемента будет известна матрица Vе перемещений в общей системе координат. Применяя формулу (3.7), можно найти узловые перемещения элемента в местных координатах v = lve, а по формуле Р = kv + Ро — вычислить узловые силы, действующие на элемент.
Мы рассмотрели случай, когда конструкция закреплена на опорах. Если система свободна, то непосредственно из уравнения (3.68) перемещения найти нельзя, так как матрица жесткости К для всей конструкции является вырожденной. Действительно, силы, действующие на свободную конструкцию, не могут быть произвольными; они должны удовлетворять уравнениям равновесия всей системы в целом. Таких уравнений будет 6 для пространственной и 3 для плоской стержневой системы. Таким образом, в случае пространственной конструкции 6 элементов матрицы Р — Ро в уравнении (3.68) определяются через остальные элементы, являясь некоторыми линейными комбинациями последних. Но тогда и соответствующие 6 элементов матрицы-столбца Kv будут также линейными комбинациями остальных. Это говорит о том, что строки матрицы жесткости связаны между собой линейными зависимостями. Определитель подобной матрицы равен нулю, т. е. матрица жесткости для свободного тела является вырожденной.
Это обстоятельство математически отражает тот факт, что перемещения свободного тела не определяются однозначно действующими на него силами, поскольку оно может получить произвольное перемещение в пространстве как жесткое тело (т. е. без деформации). Перемещение системы как жесткого целого можно устранить, закрепив ее статически определимым образом. В случае пространственной конструкции мы должны наложить 6 соответствующим образом ориентированных связей, а в случае плоской — 3. Дальнейший расчет выполняется так же, как и в случае закрепленной конструкции.
Изложенный метод расчета стержневых систем носит название матричного метода перемещений. В нем в качестве основных неизвестных принимаются перемещения узлов. Процедура матричного метода перемещений не зависит от того, является ли система статически определимой или неопределимой. Причем чем больше внешних связей наложено на систему, тем ниже порядок разрешающей системы уравнений (3.75), так как количество неизвестных в ней равно числу элементов матрицы va.
В заключение отметим, что для решения системы линейных алгебраических уравнений (3.75) могут быть использованы различные методы — как точные, так и итерационные. Чаще всёго применяется одна из разновидностей метода последовательного исключения неизвестных (метода Гаусса). Для достижения необходимой эффективности решения должны учитываться такие специфические свойства матрицы жесткости, как симметрия и ленточная структура. Подробное описание соответствующих процедур можно найти в книгах (1, 15, 20, 251.
§ 3.10. Примеры расчета
Пример 1. Ферменная конструкция (рис. 3.21, а) состоит из трех стержней, каждый из которых одним концом закреплен неподвижно, а другим связан шарнирно с остальными стержнями. К свободному узлу приложена горизонтальная сила S, направление которой указано на рисунке. Компоненты узловых сил и перемещений перенумеруем последовательно, как показано на рис. 3.21, б. Площади сечений F и модули упругости Е всех трех стержней примем одинаковыми. Поскольку узлы 1, 3 и 4 неподвижны, матрица неизвестных перемещений будет содержать всего две компоненты;
Матрица сил
Каа —
Матрица Каа. связывающая va и Ра, имеет вид ^33 ^34 ^43 ^44.
Для отыскания элементов этой матрицы рассмотрим прежде всего жесткостные характеристики стержней в местных
координатах. Для определенности будем принимать, что местная ось х направлена от узла с меньшим к узлу с большим номером.
Длины всех стержней, а также косинусы углов между местными н общими осями находим по формулам (3.15), получаем следующие значения:
Стержень . . . . .... 1 2 3
Xj — Xi . . . . . . . . 2а 0 а
У, — У1 . . . . а —а —а
1 . . . аУТ а аУ"2
X- 2/УТ 0 1/У "2
X-ху i/Уб —1 — 1/У"2
По (3.14) находим матрицы жесткости стержней в местных осях:
EF_ Г 1 -1].к-2)=^£Г 1 -11.
«И 5 L — 1 1J ’ "1-1 1J’
k<3) _ EF ' 1 — Г
а КГ [-1 1. '
Используя полученные значения Х-х, X- , выпишем матрицы
Л9 для каждого стержня в соответствии с (3.20):
М" = 12/1^5 1//5-]; Х<2> = [0 -1]; 1<з> = [1 - 1//2"].
Применяя формулы (3.18) и (3.19) к каждому стержню, получаем матрицы жесткости отдельных элементов в общей системе координат:
Х<0 т х<1) =
Л0 —
2/J/5 '
1/|/5~
[2/К5 1/К5 1 =
Г4/5 2/5 ' I 2/5 1/5
j_ Г4 2
5 2 1
EF
к(1) =-----_
5 И 5 а
~ 4 2
2 1
— 4 —2
т-2 —1
1 2
— 4 — 2~ 1
—2—1 2
4 2 3 :
2 \_4
3 4
х<2>г М2> =
~о о
к(2) — ££ 0 1
а 0 0
_0 -1
3 4
Х(3) ? Х(3) =
1’/И2
-1/К2"
- 1/Г2]= J _172
-1/2 1/2
Цифры внизу и сбоку матриц означают номера сил и перемещений.
Наконец, сформируем матрицу Каа. Для этого просуммируем соответствующие элементы матриц жесткости отдельных
стержней, стоящие на пересечении строк и столбцов с индексами 3 и 4. В результате получим
Каа =
EF Г 0,711 —0,174 13 а —0,174 1,442 J4 '
3 4
Согласно (3.75), система уравнений относительно неизвестных перемещений принимает вид
EF Г 0,711 — 0,1741 рз’ « [ — 0,174 1.442J [о4
Г — S’
L 0
Решая эту систему, находим
о3== —1,450
Sa
EF
о4 = —0,175 —
4 EF
Отрицательные знаки в этих формулах указывают на то, что узел 2 перемещается в отрицательных направлениях осей X, у.
Матрицы перемещений Vе в общей системе координат равны:
По формуле v=Xve , где
Хо 0 . о К
находим перемещения в местных координатах:
(1)__ 2/1^5 1 /]/~5 0 0 у(1) _ Sa О
О О 2/JZ5' 1/J/TJ ^L— 1,373
-(2) ГО —1 0 0 ,,, Sa [0,175 ]
[О 0 0—1] EF [ о ’
11=Г1/|/2“ -l/J/T о 0 1(3)
О О MV2 — 1/J/2J
= Sa Г ~ °’900 ]
EF О J ’
Наконец, по формуле Р = kv вычисляем узловые силы, действующие на каждый стержень вдоль его оси:
EF г 1 _ 1 I Sa Г о аКТ L—1 1 J EF [ — 1.373,
’ 0,6151
—0,615 J ’
= 5
p<2> = _£LI 1 — 1 1 Г0’175 l=s Г °>1751
a I — 1 1 J [EF [ 0 J [—0,175 J
p(s> _
— 1
1
Sa [ — 0,900'
EF о
—0,633
0,633
Как видно из рис. 3.6, а, для растянутого стержня первый элемент матрицы Р является отрицательным, а второй — положительным и наоборот. Таким образом, стержни 1 и 2 сжаты, а стержень 3 растянут; осевые силы в этих стержнях равны соответственно — 0,6155, —0,1755 и 0,6335.
Пример 2. Многоопорная балка постоянной жесткости (рис. 3.22, а) нагружена сосредоточенным моментом Мо. Момент инерции сечения балки относительно оси z равен J2; ось у совпадает с одной из главных осей инерции поперечного сечения.
В данном случае имеет место изгиб балки в плоскости хг/, и в каждом узле достаточно рассмотреть два перемещения — вертикальное и угол поворота. Узловые перемещения перенумеруем последовательно в соответствии с рис. 3.22, б. Неизвестными являются углы поворота е4, ve, v8; все остальные
перемещения равны нулю. Таким образом, матрица неизвестных узловых перемещений имеет вид
Va =
Матрица сил, действующих в направлении перемещений Va,
Р«
' Л'
Ру
L^J
О
-м0 о
Поскольку внеузло-вые силы отсутствуют, матрицы Ра и va связаны соотношением
Ра “ Каа^а, где
Для вычисления коэффициентов матрицы Каа рассмотрим сначала отдельные элементы балки в местных осях координат (рис. 3.23, а). Поскольку рассматриваются лишь перемещения изгиба в плоскости ху, матрицы узловых сил и перемещений каждого элемента совпадают с Рь и v6:
Р=РЬ={РГуМГгРГуМ1г\-, V = V6 ={р/-0/-П/-0/-},
а матрица жесткости к = кь определяется по (3.36).
Далее, общая система координат ху совпадает с местной системой ху для каждого элемента (рис. 3.23, б). Матрицы
сил и перемещений элемента в общей системе координат в рас сматриваемом случае имеют по четыре элемента:
ре ={pepe.J = jpei_iJpeiJpe/_iJpe.).
Vе = {Vf vj = {o2f-l V2i 02/-1 V2J-}.
Матрицы v и ve содержат одни и те же компоненты и притом в одинаковом порядке, поэтому матрицы жесткости в общей и местной системах координат совпадают. Учитывая это, имеем
Г 12 61 — 12 6Z1 1
к<1) — EJ 6Z 4Z2 — 6Z 2Z2 2 .
Р — 12 —6/ 12 — 6Z
6/ 2Z2 —6Z 4Z2
1 2 3
Г 12 6/ — 12 6Z - 3
к<2> - EJ 6/ 4Z2 —6Z 2/2 4*
Р — 12 —6/ 12 —6Z 5
6/ 2Z2 — 6Z 4Z2 6*
3 5 6*
Г 12 6/ — 12 61 ' 5
к(3) = EJ 6Z 4Z2 —6Z 2Z2 6*
Р — 12 —6Z 12 —6Z 7
6/ 2Z2 —6Z 4Z2 8*
5 6* 7 8*
Звездочкой'помечены те строки и столбцы, на пересечении которых находятся элементы, требуемые для формирования матрицы Каа- Суммируя эти элементы, находим
EJ ’ 8/2 2Z2 0 ' 4
2Z2 8/2 2Z2 6
0 2Z2 4Z2 8
4 6 8
2EJ
I
~4
1
О
1
4
1
О ’
1
2
Теперь система уравнений относительно va примет вид
1
4
1
4
1 О
О Г «4
1 и0 2
2EJ
I
О
-мй о
Решая систему, находим
Силы, действующие в концевых сечениях дем по формуле
Р== kv:
х i ff
р(О
il .^•7_
Мо
131
• 3“
I
—3
21
~ р(2)-iff
P^V Гу
м0
131
элементов, най-
— 9” — 21 .
9 ’
7/_
~ р(£)~| iff
п(3)
МФ
— /г _
м0 13/
6 -— 6/
6
_ о
Так как внеузловая нагрузка отсутствует, то в пределах каждого участка перерезывающие силы Q будут постоянны, а изгибающие моменты М изменяются по линейному закону. Эпюры Q и М представлены на рис. 3.24.
Пример 3. Рассмотрим плоскую раму (рис. 3.25, а). Горизонтальный стержень нагружен равномерной нагрузкой q, а в середине вертикального действует сосредоточенная сила ql. Оба стержня имеют одинаковые площадь F и момент инерции J поперечного сечения относительно оси, перпендикуляр-
ной плоскости рамы. Схема нумерации и положительные на-
правления узловых сил и перемещений показаны на рис. 3.25, б.
До сих пор при построении матрицы жесткости рамы учитывались осевые деформации стержней. Однако, как известно, влиянием осевых деформаций на перемещения в рамах можно пренебречь, если
размеры поперечных сечений стержней достаточно малы по сравнению с их длинами. Полагая удлинения стержней равными нулю, можно упростить расчет, так как это позволяет снизить число неизвестных. В самом деле, если считать стержни нерастяжимыми, то гори
Рис. 3.24
зонтальное перемещение
узла 2 следует приравнять к горизонтальному перемещению узла <?, а вертикальное — к вертикальному перемещению узла /.Так как узлы 1 и 3 неподвижны, то это равносильно требованию равенства нулю также и линейных перемещений узла 2. Таким образом, при использовании указанного упро
щения неизвестным остается единственное перемещение ve — угол поворота узла 2. Следовательно, матрица неизвестных перемещений состоит из одного элемента: va = [vel.
Поскольку внешний сосредоточенный момент в узле 2 отсутствует, то Ра = [Р6] = [01 и равенство Kaava = Ра — Роа принимает вид kwvt = — РОй.
Вычислим, далее, матрицы жесткости элементов 1 и 2 в местных координатах, направив местную ось х в первом случае от узла 1 к узлу 2, а во втором — от узла 2 к узлу 3. По (3.26) и (3.36) находим
к(1) —к(2) Кд — Ла _ EF ~ 1 1 — 1 — 1 1 1 J’
— 12 61 — 12 61 ~
кГ> 6/ 412 —61 2/2
i3 -12 - -61 12 —61
6/ 212 —61 412 _
Матрицы Ро содержат уравновешивающие внеузловую нагрузку силы в направлении перемещений v: Ро = {Р»о Роь}.
Подматрица Р0о включает в себя силы, действующие вдоль оси стержня. Так как внеузловые нагрузки вдоль осей х отсутствуют, то эти подматрицы для обоих стержней будут нулевыми. Подматрицы Роь для рассматриваемых нагрузок даются выражениями (3.57) и (3.58), где, учитывая направление нагрузок, следует сменить знаки на обратные и положить S = ql. В итоге имеем:
Роа = Роа’ = {0 0}; Р^ = {?//2 ql2/8 ql/2 —ql2/8}-, V$={ql/2 ql2/12 ql/2-ql2/12}.
Координаты узлов 1, 2 и 3 в общей системе координат равны соответственно (0, 0), (0, /) и (/, /). Пользуясь формулами (3.15), находим матрицы:
Ч7-1^Ч1"1=|° ч; V’-I-1 °1= ig-IW’-l1 °Ь’g-l’-;, Ч-
В соответствии с (3.50) составляем матрицы преобразования для каждого стержня:
Х,(1)_ [° 1 0 а | о о о
о о
0 1
0 о
о о
0 1
Г1 0 [о о
О | о 0 I о
а
— 1 о о
ООО
О О 1 ООО
ООО
ООО
— 10 0
10 1,
- о о о о
1 о о о
о 1 о о
0 0 О -ООО
О 1 о
О 0 1
По формуле ке = ХакаХа + ЦкьХь
жесткости элементов в общей системе
вычисляем матрицы координат, что дает
О
-12 0 —61 —12 О Ы~1
У 0 0 —у 0 2
к(1) = EJ Р 4/2 6/ 12 0 0 2/2 6/ 3 4 ’
Симм. У 0 5
/ 2 3 4 5 4Р 6 6
“ У 0 0 “У 0 0 ~ 4
12 6/ 0 — 12 6/ 5
к<2) = EJ Р 4/2 0 У -6/ 0 2/2 0 6 7 .
Симм. 12 - -6/ 8
4 5 6 7 8 4/2 9 9
где у = FPU.
Наконец, согласно (3.55), находим
12 3 4 5 6
J- Х<2) Т Р<2) = (о 0
° оь ( 2 12 2
4 5 6 7 8
12 J ‘
9
Теперь имеем
kM = Щ + k® = -%- (41* + 41*) = ;
/> -pm-L/wi = --^-4- —
roe—' oe oe 8 12
ql*
24
Подставляя kM и POe в уравнение £6et>6 = — РОв, находим ve = qP/(192EJ).
Матрицы перемещений элементов 1 и 2 в общей системе координат оказываются равными
vfD^lO 0 0 0 0 qP l(\92EJ)}\ v<2> = {О 0 qP/(\92EJ) 0 0 0}.
1 2 3 4 5 6 4 5 6 7 8 9
В местных координатах перемещения элементов равны: vV) = X<*) v<° = {0 0}; = v(1) = {0 0 0 qP/(\92EJ}-,
v<,2) = 1<2) v(2) = {0 0}; vP = 42) v<2> {<7/8/(192EJ) 0 0 0}.
Узловые силы в местных координатах могут быть найдены по формуле (3.52), из которой следуют соотношения
Р„ =ка va + РОа; Рь = kb vb + Роь.
Отсюда имеем р<1)=р<2) = {0 0};
+ 21* -Ы 4Р} +
---qP] = -^-{51 13/ 45 —10/};
(.2 8 2 8 J 96
pp=kpvP+PP = -^-— {6/ 4/2 —6/ 21*} +
192EJ Р
_q?_ _ql_--qP_ 1 jl. J()/ 45 _7q
I 2 12 2 12 / 96 1 1
Напомним, что расположение элементов в матрицах Рь определяется соотношением Рь = {Pz~ Mt- Pj- Al^-}.
Далее вычисляем распределение изгибающих моментов и перерезывающих сил по длине каждого стержня и строим соответствующие эпюры (рис. 3.26).
Матрицы P(a> и Р^’ оказались нулевыми, т. е. в полученном решении осевые силы в стержнях равны нулю вследствие принятого нами предположения о равенстве нулю вертикального, и горизонтального смещений узла 2. Такое предположение равносильно наложению связей на узел 2 (рис. 3.27, а).
Реакции наложенных опорных связей Р4 и Ръ (рис. 3.27, б) разгружают стержни, обеспечивая равенство нулю их осевой деформации. Эти реакции можно найти из условий равновесия узла 2 (рис. 3.27, в):
Р<=Р$- Р&=°- “ ?/= -0,469?/;
Рь-Р%+ Р<£ =° 4-^?/= 0,531?/.
Уо
Поскольку в действительности силы Р4 и Р5 отсутствуют, в узле 2 следует приложить равные им и противоположно направленные силы, которые вызовут появление осевых сил в стержнях рамы. Горизонтальная сила будет равна 0,469?/
(2)
6)
ар'2’
,(2) \гУ
и вызовет сжатие стержня 2, вертикальная сила составит 0,531?/ и вызовет сжатие стержня 1.
Данные примеры рассмотрены с иллюстративной целью. Преимущества матричного метода перемещений выявляются при расчете сложных многократно статически неопределимых систем; эти преимущества обусловлены однообразием вычислений, которые могут быть эффективно выполнены на ЭВМ.
ЧАСТЬ II
МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
ГЛАВА 4
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ МЕТОДА
Метод конечных элементов является мощным современным средством приближенного решения разнообразных задач математической физики, ориентированным на эффективное использование ЭВМ. В задачах теории упругости и строительной механики он позволяет распространить принципы расчета стержневых систем иа случай непрерывных тел н сложных конструкций. С другой стороны, его можно трактовать как специфическую форму метода Ритца, что дает ключ к теоретическому обоснованию метода конечных элементов.
§ 4.1. Дискретизация тела
Рассмотрим тело, нагруженное произвольным образом. С помощью сетки секущих плоскостей (или криволинейных поверхностей) разобьем его на отдельные части (рис. 4.1). Получаемые подобласти имеют хотя и малые, но все же конечные размеры, откуда и происходит их название «конечные элементы».
Таким образом, непрерывное тело представляется в виде совокупности конечных элементов, жесткостные свойства каждого из которых рассматриваются затем независимо от остальных. На границах между конечными элементами выбираются некоторые точки — узлы; перемещения узлов в направлении координатных осей (а иногда и производные от перемещений) принимаются в качестве основных неизвестных*.
Здесь можно сразу усмотреть аналогию с матричным методом перемещений для стержневых систем, в котором за основные неизвестные также принимают узловые перемещения. Однако в случае непрерывных тел возникает целый ряд затруднений, которые можно преодолеть лишь с помощью введения дополнительных гипотез.
Прежде всего встает вопрос о том, как найти перемещения (а следовательно, деформации и напряжения) внутри каждо
* Здесь рассматривается решение в перемещениях. Существует разновидность метода конечных элементов, в которой в качестве основных неизвестных принимают силы взаимодействия между элементами [4; 5]; возможна также смешанная формулировка.
го конечного элемента, зная перемещения принадлежащих ему узлов. Напомним, что в случае стержневых систем расчет базируется на использовании технической теории растяжения, изгиба и кручения бруса, которая и позволяет выразить перемещения и напряжения в любом сечении бруса через узловые перемещения. Для сплошного тела эта задача может быть решена приближенно, если сделать те или иные предположения о характере поля перемещений в элементе. Точнее, необходимо выбрать некоторую совокупность функций, которые позволяют аппроксимировать поле перемещений внутри конечного
элемента по известным узловым перемещениям. Выбор аппроксимирующих функций является одним из наиболее ответственных и важных этапов в методе конечных элементов. Если такой выбор сделан, то деформированное и напряженное состояние элемента будет однозначно определяться узловыми перемещениями. Поэтому под
конечным элементом сле
дует понимать не просто некоторую малую область тела, а область тела в совокупности с заданными в ней аппроксими-рающими функциями.
Вторая трудность возникает при объединении конечных элементов в единую систему. В расчете стержневых систем такое объединение производилось путем составления уравнений равновесия для узловых точек, в которых конструктивные элементы соединяются друг с другом. В сплошном теле число точек соединения между элементами бесконечно. Задаваясь распределением перемещений внутри каждого элемента, тем самым задаем и распределение напряжений во всех его точках, в том числе и в граничных. На границах раздела смежных элементов напряжения, найденные для каждого из них независимо, совпадать не будут. Следовательно, обеспечить выполнение условий равновесия на всей поверхности раздела не представляется возможным.
Чтобы обойти возникшее затруднение, можно напряжения, действующие по границе каждого элемента, условно заменить эквивалентными сосредоточенными узловыми силами; тогда уравнения равновесия узлов в направлении узловых перемещений могут быть составлены обычным образом. При этом эк-
бивалентные узловые силы определяются из условия^ чтобы производимая ими на узловых перемещениях работа равнялась работе действительных напряжений на перемещениях точек, граничной поверхности элемента.
Еще одна трудность связана с нагружением упругого тела распределенными поверхностными и объемными силами. Эти силы могут быть учтены также заменой их на эквивалентные в энергертическом смысле внешние узловые силы.
После введения указанных упрощений тело можно рассматривать как дискретную систему, т. е. как совокупность элементов, соединенных между собой в узловых точках. Разбиение конструкции на подобласти и выбор аппроксимирующих функций для каждой из них можно осуществить различными способами. При этом должны быть учтены особенности геометрии тела и обеспечена хорошая аппроксимация перемещений, деформаций и напряжений для всего тела в целом. В этом случае решение, полученное по методу конечных элементов, будет в пределе (при уменьшении размеров элементов) стремиться к точному. Более подробно вопрос о сходимости приближенного решения к точному будет рассмотрен в гл. 6.
§ 4.2. Перемещения, деформации и напряжения в конечном элементе
Рассмотрим типовой конечный элемент упругого тела, имеющий узлы I, /,... .Обозначим через v,, vy, ... матрицы перемещений соответствующих узлов. Количество элементов в этих матрицах зависит от характера задачи. Так, в случае пространственной задачи матрица vr обычно включает в себя три компоненты:
vr= vry .
.Vrz_
где vrx, vry, иТг — проекции перемещений узла г на координатные оси х, у, г (рис. 4.2). В плоской задаче компонентами матрицы vr будут vrx, vTy. В некоторых конечных элементах матрицы vr содержат помимо линейных также и угловые перемещения или производные от перемещений. Все узловые перемещения элемента образуют матрицу
Vе = {V/ Vy ... }.
Рассмотрим теперь произвольную точку внутри элемента. Перемещения этой точки в направлении координатных 108
осей образуют матрицу-столбец, которую рез и:
обозначим че-
и =
их
Uy
Uz
где их, Uy, uz — смещения рассматриваемой точки в направлении осей х, у, z (см. рис. 4.2). В плоской задаче матрица и содержит два элемента. Подчеркнем, что компоненты матрицы и представляют собой функции координат.
Как говорилось выше, в методе конечных элементов принимается допущение, согласно которому перемещения всех точек элемента однозначно определяются его узловыми перемещениями. В матричных обозначениях это означает существование равенства
и = ave.
(4.1)
Здесь а — прямоугольная матрица, в которой количество строк равно числу компонент матрицы и, а количество столбцов — числу компонент матрицы Vе. Элементами матрицы а являются некоторые функции координат (аппроксимирующие функции). Выбор подходящих функций, как отмечалось ранее, представляет собой важный этап в методе конечных элементов. Для некоторых элементов этот вопрос будет рассмотрен ниже. Здесь же мы будем предполагать, что аппроксимирующие функции уже известны.
Воспользовавшись формулами Коши, можно выразить деформации в каждой точке конечного элемента через его узловые перемещения. По формуле (1.8) имеем 8 — Lu, что с учетом (4.1) дает 8 = Lav®. Эту связь между 8 и Vе будем записывать в виде
е = ₽ve, (4.2)
где через р обозначена прямоугольная матрица
Р = La; (4.3)
число строк матрицы р равно числу компонент матрицы 8.
В общем случае пространственного тела, когда матрица и содержит три компоненты их, иу, uz, из зависимости (4.1) следует, что матрицу а можно представить в виде
а =
ах
«г/ •
(4-4)
В этой записи ах, ау, az — матрицы-строки, элементами которых являются известные аппроксимирующие функции. Матричный оператор L дается в этом случае выражением (1.9), так что согласно (4.3) имеем
д/дх- 0 0 ~ д ах/дх
0 <Э/ду 0 д а.у/ду
0 0 д/дг Г «»1 да,/дг
Р= La = д/ду д/дх 0 аУ = дау/дх + дах/ду
0 д/дг д/ду L azJ даг/ду-\- dayldz
_д/дг 0 д/дх __ _д az/dx + да.х/дг _
(4-5)
В плоской задаче компонентами и являются перемещения их, иу,' а матрица а имеет соответственно две строки
« = [“*]. (4.6)
.«» J
Матрица L в этом случае определяется выражением (1.21):
Гд/дх О
P = La =
О д/ду
д/ду д/дх
д ах/дх дау/ду дау/дх-\-дах/ду
(4.7)
Воспользуемся далее законом Гука в форме (1.15) о = = хе, где а — матрица-столбец напряжений; х — матрица упругих постоянных. Подставляя сюда соотношение е — Pve, имеем
о — x₽ve. (4.8)
Формулы (4.1), (4.2), (4.8) показывают, что при известной матрице аппроксимирующих функций а напряженное и деформированное состояние конечного элемента однозначно определяется узловыми перемещениями Vе.
§ 4.3. Матрица жесткости конечного элемента
Рассмотрим упругое равновесие деформированного конечного элемента. Внешними нагрузками для него являются напряжения, возникающие на его границе в результате взаимодействия со смежными элементами, объемные силы R и, возможно, поверхностные нагрузки р (если часть его поверхности совпадает с поверхностью, ограничивающей тело). Предположим, что узловые перемещения Vе получили произвольные бесконечно малые приращения, определяемые матрицей
6ve = {6V; 6vy- ... }.
Поскольку перемещения и точек элемента связаны с узловыми перемещениями равенством u = ave, то они получат приращения 6u — a6ve. Работу внешних нагрузок на перемещениях би обозначим через 8Ае, а изменение потенциальной энергии деформации конечного элемента — через f>Ue. Согласно принципу возможных перемещений (см. § 2.3) должно выполняться равенство б<7е = бЛе.
В соответствии со сказанным в §4.1 заменим напряжения (4.8) на поверхности элемента эквивалентными им сосредоточенными узловыми силами, действующими в направлении узловых перемещений:
Ре = {Р« Р? . . . },
где Р;, Р/, ... — матрицы сил для узлов г, /, .... Объемные R и поверхностные р силы также заменим эквивалентными узловыми силами Ре — {Р/ Р/...}.
Силы Рг + Ре будем считать эквивалентными действительным нагрузкам, если нх работа на перемещениях 6ve равна 6Ае, т. е. если выполняется равенство (см. §2.1)
бЛг = (буг)7'(Рг4-Рг). (4.9)
Подсчитаем теперь вариацию потенциальной энергии деформации &Ue. Так как деформации связаны с Vе соотношением е = pve, то изменение узловых перемещений вызовет приращение деформаций
бе = jJ6ve. (4.10)
По формуле (2.14) имеем
б Ue = J бег в dr,
где хе — объем занимаемый конечным элементом
Подставив в подынтегральное выражение (4.8) и (4.10), получим
6 t/e = j* (Р 6 ve)r хр ve dr = J (6ve)7’prxpv*dT.
В силу постоянства элементов матриц 6ve и Vе их можно вынести за знак интеграла:
6Уг = (6ус)гГу prxpdr
Vе.
Выражение, заключенное здесь в квадратные скобки, представляет собой квадратную матрицу. Ее элементы получаются интегрированием элементов симметричной матрицы рг хр. Введя обозначение
k*=j* prXpdT,
(4.U)
представим выражение для 8Ue в виде
= (6ve)r keve. (4.12)
Приравнивая (4.9) к (4.12) и учитывая независимость элементов матрицы 6ve, получаем
к' Vе = Рс + Ре.
(4.13)
Это соотношение связывает узловые силы с узловыми перемещениями в стандартной форме (3.2), поэтому матрицу ке, определяемую по (4.11), можно назвать матрицей жесткости конечного элемента. Из (4.11) видно, что при известной геометрии конечного элемента и заданных упругих характеристиках материала матрица жесткости вполне определяется выбором аппроксимирующих функций.
Матрица узловых перемещений имеет блочную структуру Vе— {v; Vj ...}. В соответствии с выражением 8 — pve матрицу р можно также разбить на блоки:
₽ = (Pi Р,
Тогда на основании (4.11) получим
~₽Г
ке
zip, ру ] dr.
Из этой записи вытекает следующее блочное представление матрицы жесткости конечного элемента:
(4.14)
где
k's=J р*хр,бт (г, s=i, j, . . .). (4.15)
У б ur р do»
§ 4.4. Учет внеузловой нагрузки
Выведем теперь формулу для вычисления матрицы Ре. Рассмотрим такой конечный элемент, часть поверхности которого совпадает с внешней поверхностью, ограничивающей тело.
Придадим узловым перемещениям бесконечно малые приращения Sv*; приращения перемещений би определятся при этом формулой би = a6ve Вычислим работу 8Ае объемных R и поверхностных р сил на перемещениях би. В соответствии с (2.4) имеем
б 6u7’Rdr4-
Первый интеграл в правой части этого выражения берется по объему элемента, а второй — по его поверхности. Подчеркнем еще раз, что нагрузка р действует лишь по той части поверхности элемента, которая совпадает с внешней поверхностью тела. Поэтому фактически поверхностный интеграл берется только по этой части ые Внеся сюда значение би, получим
б Ае = (б v')r / J arRdT-|-J arpdco \ те ые
Будем считать, что узловые силы Р1' эквивалентны заданной внешней нагрузке, если работа этих сил (6ve)r Ре на узловых перемещениях равна 6ЛС Это приводит к равенству
Ре —J arRdT-f~y arpdw (4.16)
tr ые
Учитывая блочную структуру матрицы ve = {vf v, ...} в соотношении u = ave, представим матрицу а также в блочном виде а = [аг ау ...]. Тогда
Ре = {Р? PJ где
P* = J aJ'RdrH- J aj’pcko (r — i, j, ...). (4.17)
Xе (j)e
Формула (4.17) определяет вклад, который вносит данный элемент в эквивалентные силы в узле г. Аналогично приводятся к узловым силам нагрузки, приложенные к другим элементам (для тех элементов, которые находятся целиком внутри тела, второй член в (4.17) будет отсутствовать). Суммируя вклады отдельных элементов, найдем для каждого узла матрицу
(4.18) е
Здесь знак S означает суммирование по всем элементам, е сходящимся в узле г.
Напомним, что в случае стержневых систем (см. § 3.6) внеузловая нагрузка учитывалась введением матрицы уравновешивающих сил Р® (матрицы, которая содержит реакции на элемент от действия внеузловой нагрузки при полном закреплении узлов). Здесь использован иной подход, при котором внеузловая нагрузка заменяется статически эквивалентной системой узловых сил Ре. При желании можно было бы и в методе конечных элементов ввести матрицу уравновешивающих сил Pj, полагая Р* = —Ре. Отметим, однако, что в отличие от стержневых систем матрица Ре0 может быть определена здесь лишь приближенно, поскольку ее компоненты зависят не только от характера внешней нагрузки, но также и от выбора аппроксимирующих функций, как это видно из (4.16).
§ 4.5. Определение узловых перемещений
Выполнив дискретизацию упругого тела, можно теперь составить уравнения равновесия узлов и прийти к системе уравнений относительно перемещений v = {vj v2 ... vn }, где n — общее число узлов при принятой схеме дискретизации.
Если в узлах тела приложены сосредоточенные силы, то из них можно образовать матрицу Р= (Pi Р2 Pn }• Ти
повой элемент Рг этой матрицы представляет собой подматрицу сил, действующих в узле г в направлении перемещений
Узловые силы, эквивалентные внеузловой нагрузке, также объединим в матрицу ₽ = {Рг Р2 ... Рп}.
Уравнения равновесия для каждого узла составляются теперь точно так же, как и в случае стержневых систем (см. § 3.8). Объединяя все эти уравнения, получим зависимость между внешними узловыми силами и узловыми перемещениями в виде
Kv = P + P. (4.19)
Здесь К — матрица жесткости 1 быть представлена в форме
всего тела, которая может
К=
кц кгх
к 12 к2-з
• к1п
• • к2„
(4.20)
к
кд2
. . к
•пп -
получается, как и прежде,
Типовая подматрица krs — Sk*s е суммированием подматриц k's по всем конечным элементам, содержащим одновременно узлы г и s.
Составление матрицы упругого тела поясним на простейшем примере. Пусть плоская область (рис. 4.3) идеализирована совокупностью четырех конечных элементов (а, Ь, с, d). Цифрами на рисунке обозначены номера узлов.
Запишем матрицы ном впде
отдельных элементов в блоч-
жесткости
’к“, К 1 2 ка *13 1 ’М. kt.
ка= м, .к?, 1 Lei *22 ка *3 2 2 ю и 2 ; 3 к® = кь L ?4, kta kb *43 3
Гкс *33 *35 кс ” *34 3 к22 kd *25
кс = кс *53 к5 5 кС 54 5 ; kd = kd *52 kd *55
кс _ *43 3 к4 5 5 к* 44 „ 4 4 kd LR32 2 kd *35 5
кь
*34
кь
*44
4
н3т
к53
kd
33 .J
к^у
з ;
4
5 .
3
Цифры сбоку и снизу характеризуют здесь номера узлов, обход которых для каждого конечного элемента осуществляется против часовой стрелки, начиная с наименьшего номера.
Матрица жесткости всего тела в соответствии с общим числом узлов имеет в блочной записи размер 5x5. Суммируя подматрицы отдельных конечных элементов, имеющие одинаковые индексы, получим
к^+н, ка *12 к?з к*3 К 1 4 0
к-м ba -4-W *22 1 *22 к?з “Ь Мз 0 kd К25
К31 1 Л31 к“2 +к^2 La -|_Lb 4-Ue 33~П33|Л33^П33 *34 ^*34 ^35^35
к?, 0 Мз ^43 к$4+кс44 кС45
_0 ks2 кзз + Мз кб4 kss^kjj-
Сделаем некоторые пояснения к формированию матрицы жесткости системы. В нашем случае узел 3, например, является общим для всех элементов. Поэтому подматрица k3S является суммой соответствующих подматриц всех четырех элементов. Узлы 1 и 3 принадлежат элементам а и Ь, вследствие чего kL з = k?3 + k?3. Узлы 1 и 2 принадлежат вместе только элементу а, так что к12 =• к?2. Наконец, такие узлы, как 1 и 5, непосредственно не связаны между собой ии одним из элементов, поэтому к18 — 0.
Вернемся к уравнению (4.19). Как и в случае стержневых систем, разобьем матрицу узловых перемещений v на две подматрицы:
В подматрицу vp включаются известные из условий закрепления перемещения; все неизвестные перемещения составляют подматрицу va. Аналогично представляются и матрицы сил
Если заданные перемещения vp — 0, то придем к уравнению
kaaVa = Pa I-Ра . (4.21)
решение которого дает матрицу неизвестных узловых перемещений.
Матрица каа> как и ранее, получается из матрицы жесткости К вычеркиванием строк и столбцов, соответствующих известным перемещениям. После определения узловых перемещений можно по формулам (4.8) вычислить напряжения в каждом конечном элементе.
§ 4.6. Связь метода конечных элементов
с методом Ритца
Выше метод конечных элементов рассматривался как обобщение матричного метода перемещений для стержневых систем на случай сплошных тел. Можно, однако, подойти к этому методу с иных позиций, рассматривая его как специфическую форму метода Ритца. В самом деле, задаваясь характером изменения перемещений в пределах каждого конечного элемента, мы тем самым задаемся приближенным полем перемещений по всему телу, что соответствует схеме метода Ритца (см. §2.5). Специфика заключается здесь в том, что, во-первых, предполагаемый закон изменения перемещений задается не сразу по всей области, а поэлементно, и, во-вторых, неизвестными параметрами в методе конечных элементов являются узловые перемещения (в классической схеме метода Ритца неопределенные параметры не связываются с какой-либо физической интерпретацией). Рассматривая метод конечных элементов с этой точки зрения, можно получить уравнения для отыскания узловых перемещений путем минимизации полной энергии системы. При этом не требуется использовать предположение о том, что конечные элементы соединены между собой лишь в узловых точках.
Итак, пусть тело представлено в виде совокупности конечных элементов. Как и ранее, будем исходить из того, что для каждого элемента известна матрица а, позволяющая аппроксимировать перемещения внутренних точек через узловые перемещения: u = ave.
По формулам Коши выразим деформации внутри элемента через узловые перемещения е = pve, а в соответствии с законом Гука имеем <т = Х8 = x0ve.
Вычислим потенциальную энергию деформации Ue, накапливаемую в отдельном конечном элементе. Подставляя в формулу
Ue = — f ет о dr 2 J
записанные выше выражения для матриц 8 и сг, получим
Выражение, заключенное здесь в квадратные скобки, представляет собой симметричную матрицу. Полагая
kc = J ргх₽с1т, (4.22)
запишем
f/c=-^-(ve)rkcve.
(4.23)
Здесь i, j, ... — номера узлов, принадлежащих рассматриваемому конечному элементу.
Пусть теперь v= {viV^.-Vn}—матрица-столбец узловых перемещений всего упругого тела, записанная в блочной форме (п —общее число узлов). Для дальнейших рассуждений удобно в выражение для потенциальной энергии деформации конечного элемента включить перемещения всех узлов упругого тела и представить его в виде
Последнее равенство будет тождественно выражению (4.24), если считать k‘s = 0, когда хотя бы один из узлов г, s не относится к рассматриваемому конечному элементу.
Потенциальная энергия деформации, накопленная во всем теле, U = 2[7е. После подстановки выражения для Ue и
суммирования получим
где krs = 2jk®s (г, s= 1, 2, ... , п). е
Поскольку k's = 0. если хотя бы один из узлов г, s не относится к данному конечному элементу, то фактически суммирование распространяется здесь лишь на те элементы, для которых узлы г и s являются общими.
Введя обозначение
kni кП2 • кпп _
представим теперь выражение для потенциальной энергии деформации всего тела в краткой записи
[7=J-vrKv. (4.25>
Выражение для U можно представить в несколько иной форме, если учесть наложенные на тело связи. Как это делалось и ранее, выделим в матрице v неизвестные перемещения va и заданные перемещения vB. Выделяя также соответствующие блоки в матрице К, будем иметь
U = — {vr I УГ]Г k““Lk“?_l
2 ₽ [ к₽а! к6($ J
Vg
Vp
= 4" k““ V“ + V« k“₽ Vp + V₽ k₽a V“ + VP kpfl Vp)' <4>26)
Если, в частности, ve = 0, то потенциальная энергия деформации, будет вычисляться по формуле
f/=4'v«k“aVa- <4,27)
Отметим, что матрицу каа можно получить из матрицы К путем отбрасывания тех строк и столбцов, которые соответствуют перемещениям vB.
Перейдем далее к вычислению потенциала внешних сил П. Полагая, что на тело действуют поверхностные р и объемные R силы, а также узловые силы Р (в направлении перемещений v), будем иметь
ит pdco^ ,
где интегралы берутся по всему объему тела т и по той части о)р его поверхности, на которой заданы нагрузки.
Преобразуем второе слагаемое в правой части равенства, заменив интегрирование по объему тела суммой интегралов, взятых по объемам отдельных конечных элементов:
J ur R dr =
Т е Xе
Подставляя сюда равенства u — ave, получим
JurRdT = 2<v‘!)7' f «rRdT т е
Точно так же третье слагаемое в формуле для П приведем к виду
J ur р dw = (ve)r У «rpdro, <ор е ые
где ю« — поверхность отдельного конечного элемента. Поскольку нагрузки р заданы лишь на юр, то в сумму войдут только те элементы, часть поверхности которых совпадает с Юр, и фактическое интегрирование будет выполни гься лишь по этой части ю®.
Таким образом, для потенциала внешних сил приходим к выражению
П = —vrp — 2 (v<!)r ( f arRdr-|-y arpdw e \ Xе (0₽
Введя обозначение
Pe = y arRdt перепишем этот результат в виде
П= -vI'P-2(vfP'
ат р dw,
Учитывая блочную структуру матрицы а = [аг а} имеем Рс = {Р? Р/ ...}, где
Pr=f «rRdx + J «rpdco (r = t, /, Xе <ae
Произведение
(v‘)rpe = [vrv/
можно представить в виде
если считать, что Р, = 0, когда узел г не относится к рассматриваемому конечному элементу. Тогда для потенциала внешних сил запишем:
П = -уГР-[угуг...уГ]2 е
р°
р|
_р«_
Вводя обозначения
Рг = 2 Рг (г ~ 1, 2, ... , n); Р {Р, Р2 ... Р„}, е
окончательно получим
П = — VT(P + P). (4.28)
Формально матрицы Рг образуются суммированием соответствующих матриц по всем конечным элементам, но фактически суммирование выполняется лишь по тем элементам, для которых узел г является общим (для всех остальных элементов Рг = 0).
Отметим, что из всех компонент матрицы Р + Р известными являются лишь те силы, которые действуют в направле
нии неизвестных перемещений va. Остальные элементы матриц Р + Р представляют собой неизвестные реакции на тело со стороны наложенных на него связей, действующие в направлении vp. Разобьем Р и Р на соответствующие подматрицы:
Ра]
Рр J ’
Учитывая также представление v = {va vp}, запишем
(р 1 Гр 1\ ~
“ + Г? =-v£(Pa + Pa)~ LPpJ LppJ/
-v^Pp+Pp). (4.29)
В частности, в случае vp = 0 получаем отсюда выражение
II = -vX(Pa + Pa), (4.30)
в которое входят только известные силы.
Полная энергия системы V равна сумме V = U + П; из (4.27) и (4.30) имеем
V = -у v£ ka„ va — v£(P„ + Pa)- (4.31)
Формула (4.31) определяет V как функцию узловых перемещений va. Необходимым условием минимума полной энергии является равенство нулю ее первой вариации:
6 V = ~ (б Уд касс Уд + Уд кдд 6 Уд) — 6 Уд(Рд + Рд) =0.
Подчеркнутые слагаемые равны между собой, ибо, будучи скалярными величинами, они получаются одно из другого путем транспонирования. Поэтому условие б/ = 0 можно записать в виде
6Va(kggVg -Pg Pg) = 0 .
Так как элементы матрицы 6va произвольны, то матрица kggVa — Pg — Pa должна быть нулевой. Отсюда выводим следующее матричное уравнение относительно va:
kaaVa = Pa + Pg.
Мы снова пришли к уравнению (4.21). Отметим, что образование матриц К и Р выполняется в обоих подходах по одним и тем же формулам.
Записанное выше уравнение относится к случаю, когда vp = 0. Если же заданные перемещения отличны от нуля, то при вычислении полной энергии V следует исходить из выражений (4.26) и (4.29). В этом случае минимизация полной энергии по перемещениям va приводит к уравнению
kaa Va = Pa -f- Pa-—Vp kjia- (4.32)
Равенство 61/ = 0 есть необходимое условие минимума полной энергии системы. Покажем, что перемещения v, найденные из решения системы (4.21) или (4.32), действительно минимизируют V. Ограничившись случаем v₽ = 0, будем иметь для полной энергии выражение (4.31). Рассмотрим далее узловые перемещения v„ = va + Ava, которые отличаются от перемещений va на некоторую произвольную величину Ava. Таким перемещениям соответствует полная энергия системы
V* = -у (ve + Л Vaf kaa (v„ + A va) -(vo + Л va)r (Pa + Pa).
Раскроем здесь скобки и найдем разницу:
V* —V = -7 Д va v“ + 4“ kaa A va +
+ — A Va kaa A Va — A Va (Pa + Pa)-
Первые два слагаемых в правой части этого выражения равны между собой, поскольку, являясь скалярными величинами, они получаются одно из другого путем транспонирования. С учетом этого имеем
Е* V = A Va (kaa Va Pa — Pa) 4—~ A v£ kaa A Va-
Выражение в скобках равно нулю, поскольку перемещения va удовлетворяют уравнению (4.21). Отсюда приходим к следующему равенству:
V* — V = -2-A v^ kaa A Va-
2 “
Потенциальная энергия системы, определяемая как про» изведение v£kaavo/2, есть величина существенно положительная для любой матрицы узловых перемещений va, в том числе и для матрицы Ava (если последняя отлична от нулевой). Отсюда следует неравенство
у* _ у о. (4.33)
Таким образом, любым перемещениям v„, отличным от va, соответствуют значения V* > V, что и требовалось доказать.
Следует отметить одно важное обстоятельство. Как говорилось в гл. 2, аппроксимирующие функции в методе Ритца должны удовлетворять всем геометрическим связям. Это означает, в частности, что они должны быть непрерывными функциями координат. Следовательно, метод конечных элементов можно рассматривать как метод Ритца лишь в том случае, если на границах между конечными элементами обеспечивается непрерывность перемещений. Конечные элементы, которые дают непрерывное поле перемещений, называются совместными (или согласованными). Не всегда, однако, удается выполнить условие совместности, вследствие чего в практике нередко используются несовместные элементы. При переходе от одного элемента к другому перемещения будут тогда претерпевать разрывы, и поэтому нельзя утверждать, что найденные узловые перемещения соответствуют минимуму полной энергии системы.Тем не менее при выполнении определенных условий (о которых будет сказано в § 6.4) решение в пределе снова будет стремиться к точному, а в некоторых случаях несовместные элементы позволяют получить даже более точные результаты, нежели совместные.
§ 4.7. Коиечноэлементная форма метода Канторовича—Власова
В изложенной выше трактовке в основу метода конечных элементов был положен метод Ритца. Возможны различные модификации метода, которые в тех нли иных частных задачах могут дать более экономичный алгоритм расчета. Рассмотрим один такой вариант, в основе которого лежит метод Канторовича — Власова (см. § 2.6).
Пусть призматическое тело (рис. 4.4) ограничено плоскостями 2 = 0 и z = /. Как и в § 2.6, будем обозначать торцовые поверхности тела через ец и ш2, а его боковую поверхность — через со3. Тело может быть закреплено произвольным образом, но с одним ограничением: если имеется закрепление тела на боковой поверхности, то оно должно осуществляться по всей длине тела. Участки поверхности, на которые наложены геометрические связи, обозначим через <o1U, <o2u> шзи> а остальные участки (на которых заданы поверхностные нагрузки) — через
W2P- шз;>- „ „
Разобьем все тело на конечные элементы сеткой поверхностей, образующие которых параллельны оси г. Таким образом, каждый элемент представляет собой призматический брусок длиной I. На боковых поверхностях смежных конечных элементов выберем прямые, параллельные осн г, которые будем называть узловыми линиями или просто узлами. Перемещения точек, принадлежащих узловым линиям, примем в качестве основных неизвестных; эти перемещения являются функциями координаты г. Перемещения точек узловой линии г в нап
равлении координатных осей обозначим через vrX (z), vry (г), vrz (г) И составим из них матрицу
vr (z) =
Чх (z)'
Vry (г)
Угг (z) _
Рассмотрим далее типовой конечный элемент с узлами i, j,,.. Примем, что перемещения их, иу, uz в каждом поперечном сечении элемен-
та выражаются через его узловые перемещения, взятые в том же сечении, посредством зависимости
и (х, у, г) = а (х, у) Vе (г).
(4-34)
где
ц(х, у, г) =
'их(х, у. г) ' иу (х, у, г)
Уг (х, у, г) .
'VI (г)' : Vе (г) = (г)
Через а (х, у) в (4.34) обозначена матрица, элементами которой являются выбранные функции координат х, у. Эта матрица имеет три строки
"ах(х, у)
а(х, у)— ау(х, у)
Уг(х, у)
а число столбцов в ней равно числу компонент Vе.
Итак, в рассматриваемом подходе осуществляется поэлементная аппроксимация перемещений в плоскости поперечного сечения тела, а основными неизвестными являются функции, зависящие от третьей координаты (перемещения узловых линий). Задача сводится теперь к отысканию этих функций координаты г. Таким образом, мы приходим к конечноэлементной формулировке метода Канторовнча-Власова.
Выразим деформации е = {е.хх гуу ъгг &Ху Еуг Ъгх} через узловые перемещения, воспользовавшись геометрическими соотношениями в виде е = Lu. Учитывая выражение (1.9) для матричного оператора L, имеем
~ д/дх О
О д / ду
О О
д/ду д/дх
О д/дг
_д/дг О
О
д/дг О
д/ду
*ах (х. У) у}
„<*г (х, у)
Vе (г)^
д/дх
где через ve = dv'Vdz обозначена матрица-столбец, получаемая из vf дифференцированием ее компонент по г.
Это равенство можно представить в следующей краткой форме:
е=Ро <е,
(4.35)
где Ро и Pj — прямоугольные матрицы, составленные из строк матрицы а н их производных по х, у.
д а,х/дх д ау/ду ~ о - 0
Р» = 0 д ау/дх-\- д ах/ду ; Pi = «Z 0
д az /ду «у
_ д а2/дх _ _ аж _
Напряжения а = {ожж оуу ozz ожу <Jyz ozx} найдем по закону Гука: о = хе = xpove + хргуг.
Потенциальная энергия деформации рассматриваемого конечного элемента
Ue ~ — f гг о dx.
2 J тс
Подстановка выражений для матриц е и а дает
Ue = у J (₽о ve+ Pi ve)T х (р0 v® + pt ;e) dx = t*
= ~ J {(ve)rp£xp0 v® + (vc)rp'fxpi ie +
Iе
+ (<е)грТхроуе+(?у p[ xpt ;®} dx.
Заметим, что подчеркнутые члены в подынтегральном выражении равны между собой, поскольку являются скалярными величинами и получаются один из другого путем транспонирования.
Элементы матриц Ро, рх являются известными функциями координат х, у. Выполнив интегрирование по площади Fe поперечного сечения конечного элемента, приведем выражение для Ue к виду
I
Ue — {(v®)r ко Vе + ( v0r к®1 v®4-2 ( ve)r к® v®} dz.
о
Здесь через к®, к? н к® обозначены квадратнце матрицы, вычисляемые по формулам:
ко Ро xPi> dF'f (4.36)
Fe
k®=J РГ *Pi dA; (4.37)
F®
k®=J tfxPidF. (4.38)
Fe
Так же как и ранее, разобьем матрицы р0, pt на блоки в соответствии е блочным представлением матриц v®, v®:
Po = lPoi Роу • •]: Pi = lPif Pjj ...J.
Тогда из (4.36)—(4.38) придем к блочной структуре матриц к£> kJ и к?:
"к® к® K0,ii К0,>; • •
к® к®
ко,ц- -
Типовые подматрицы вычисляются по следующим формулам (г, s= Г, /,...):
ko.rs = J Porx₽»»d^ k^.rs=J ₽J>₽ud^
Fe Fe
krs = j Por XP1S d^'
Fe
Если просуммировать вклады отдельных конечных элементов, то получим потенциальную энергию деформации U всего тела. Рассуждая так же, как в предыдущем параграфе, можно прийти к следующему выражению для U:
I
U~ ~ J (vr k0 v-f- vT kv v + 2vr k v) da. (4.39)
о
Здесь v = v2... vn); v = {v^a-.-Vn} —матрицы-столбцы, в
которых перечислены перемещения и их производные по г для всех узловых линий тела (п — общее число узлов).
Квадратные матрицы к0, Ц и к образуются из соответствующих матриц для отдельных конечных элементов. Их типовые подматрицы получаются по обычному правилу:
ко.гз — 2 k0,rs> ki.rs — 2k<i,rs> — 2 krs
e ее
Суммирование здесь ведется по всем конечным элементам, содержащим одновременно узлы г, s (г, s = 1,2. п). Отметим, что матрицы к0 и
kj симметричны, поскольку это вытекает из симметрии матриц kJ, kf. Матрица к, вообще говоря, симметрией не обладает.
Если тело закреплено вдоль некоторых узловых линий, то следует уменьшить размеры всех матриц, фигурирующих в (4.39), оставив в матрицах v и v лишь перемещения свободных узлов и выделив соответствующие подматрицы в k0, kj н к. Во избежание громоздкости обозначений мы не будем здесь помечать эти уменьшенные в размерах матрицы дополнительным индексом а, как это делалось ранее.
Перейдем теперь к вычислению потенциала внешних сил. Полагаем, что на тело действуют объемные R = {RxRyRz} и поверхностные Р ~ {РхРуРг} силы. Кроме того, считаем, что на боковой поверхности тела вдоль узловых линий могут быть приложены погонные нагрузки, изменяющиеся по длине тела. Проекции на координатные оси погонной нагрузки, действующей вдоль узловой линии г, обозначим через qrX (z) Чгу (z), qrz (г) и объединим их в матрицу-столбец,
<1 Г (г) — Чгу
L Ягг
Тогда потенциал внешних сил
(/ \
JurRdT+j* игрско +j vrqdz | , (4.40)
x &p о /
где q = {Ч1Ч2- -Чп).
Объемный интеграл в правой части этого выражения заменим суммой интегралов, взятых по объемам отдельных конечных элементов. Учитывая, что в пределах каждого элемента перемещения и выражаются через узловые перемещения равенством ц = ave, имеем
J ur R dx = (v^a^Rdr. T е те
Выполнив далее интегрирование по площади поперечного сечеиия каждого элемента Fe, получим
i
Jur RdT=2£ J(ve)rQrdz. (4.41)
т е 0
Здесь через
Q«(z) = J ат Rdf
Fe
обозначена матрица-столбец, элементы которой являются известными функциями координаты г.
Если разбить матрицу а на блоки a = [ага; ...] в соответствии с блочной записью матрицы Vе, то и матрица Qx будет представлена в блочном виде:
Q^(z)=[Q^(z) Q'.(z) ...},
где типовая подматрица
Q*r(z) = J afRdr. (4.42)
Fe
После выполнения в (4.41) суммирования по всем конечным элементам первое слагаемое в выражении для П будет представлено в форме
I
J urRdx = ( vrQT(z) dz. (4.43)
т О
Здесь через Qx (z) — {Qti (z) QTj (z)... Qtn (z) } обозначена матрица-столбец, типовая подматрица которой
Qtr(z) = SQxr(2) (r=l, 2, ...’, л); е
суммирование ведется по всем элементам, соединяющимся в узле г.
Преобразуем второе слагаемое в формуле для П. Учитывая, что сор = а>1;) + (о2Р + созР, запишем
J urp dco=J urpdw-|-J urpd&> + J urpd<o.
“p "1P °>2P ИЗР
Рассуждая аналогично предыдущему, получим
I
f u7'pd<o = v7'(0)P(0) + v7'(/)P(/)4 j v7'Qw(z) dc, (4.44) “p 0 '
где v (0) и v (Z) — значения Матрицы v (г) при г = 0 и г= / соответственно; Р (0) и Р (Z) — матрицы-столбцы узловых сил, действующих в торцовых сечениях н эквивалентных заданной там поверхностной нагрузке. Эти матрицы можно получить в блочной форме;
Р (0) - {Pi (0) Р2 (0)... Р,г (0)}; Р (/) « (Р, (Z) Р2 (Z)... Pn (Z)),
Типовые подматрицы образуются путем суммирования вкладов отдельных конечных элементов:
p,(0)=2pr(°); pr(o=2pr(z) (^1.2, ... , л)
е е
Подматрицы Р7 (0), Р/ (Z) для отдельного конечного элемента вычисляются по формулам
P’(O)=J afp.dA; Р;<//=[ a^d/7, Fe Fe
где pj и р2 — матрицы-столбцы, которые содержат компоненты распре-, деленной нагрузки на торцах г — 0 и г — I соответственно.
Матрица-столбец Q0J (г) в последнем слагаемом формулы (4.44) содержит погонные нагрузки, которые действуют вдоль узловых линий и эквивалентны поверхностной нагрузке, приложенной к боковой поверхности тела. Эта матрица также имеет блочную структуру:
(?)-= {Q«1 (2) Q.U2 (2) Qom (2)}
и вычисляется поблочно, по обычному правилу суммирования:
Q<o, (2)=2<4Л2)-е
Вклад в эти узловые нагрузки будут давать лишь те конечные элементы, боковая поверхность которых имеет общую часть с боковой поверхностью <озр тела. Для таких элементов имеем
s2
Q«r(2) = j arp3ds.
st
Матрица р3 содержит компоненты поверхностной нагрузки на боковой поверхности тела, а интегрирование ведется по той части контура поперечного сечения конечного элемента, которая совпадает с контуром, ограничивающим поперечное сечение тела.
После подстановки выражений (4.43) и (4.44) в (4.40) получим
I
П= — J vrQ dz — vT (0) Р (0) — vT (Г) Р (/), (4.45)
О
где Q (г) = QW (z) + QT (z) + q (z).
С учетом (4.39) и (4.45) получаем следующее выражение для полной энергии системы V = U + П:
I
V —у vr k0 v ki v + vr k v —vr QJ dz —
о
-vT (0) P (0)-vT (/) P (/). (4.46)
Таким образом, полная энергия системы представлена в виде функционала, зависящего от неизвестных узловых перемещений v (z) н их производных v (г) по координате г. Функции v (г) должны быть выбраны таким образом, чтобы этот функционал принимал минимальное значение. Для отыскания v (г) можно записать уравнения Эйлера вариационной задачи и прийти, таким образом, к системе дифференциальных уравнений относительно компонент матрицы v (г).
Мы имеем дело с минимизацией функционала вида
I
V — f F (v, V, г) dz-4-Ф(v (0), v (/)] ,
b
который зависит от п функций (г), и2 (г),..., vn (г) и их производных по г. Внеинтегральный член представляет собой функцию от краевых значений v (г).
Как известно из курса вариационного исчисления, необходимым условием минимума такого функционала является требование, чтобы функции v г) удовлетворяли следующим уравнениям Эйлера:
dF d / dF
dvx dz \ dvx
dF d / dF
dv2 dz \ dv2
dF dvn
d f dF dz \ dvn
Все эти равенства можно объединить в одно:
если ввести матрицы dF ( dF OF
ду ( dvt dv2
dF d { dF \
I—— 1=0 dv dz \ dv /
dF ] dF _( dF dF dF
dvn J dv ( dvt dv2 ' dvn
При этом функции v должны при г — 0 и z = I принимать заданные значения, либо (если эти функции на концах интервала не заданы) удовлетворять так называемым естественным граничным условиям вариационной задачи, т. е.
для z= I
dF I дФ
——--------------- о-
dv |z=o dv (0)
dF I . дФ
—— 4-------=0.
dv |z=z dv (I)
В общем случае на одном илн на обоих концах могут быть известны некоторые из функций v (г). Недостающие условия следует выбирать из числа естественных граничных условий.
Обращаясь теперь к (4.46), имеем
Ф= — vT (0) Р (0) — vT (/) Р (/).
Таким образом, dF ~ . dF . ~т
—— = k0 v+k V— Q; —r-=kxv + krv, dv dv
так что матричная запись уравнений Эйлера будет
k0 v-|-(k—"kr) V—k1’v=Q. (4.47)
Естественные граничные условия прн z — 0 и z = I соответственно запишутся так:
кх v (0)+кг v (0)= —Р (0); кх v (/) + кг v (Z) = р (/). (4.48)
Следовательно, в рассматриваемом методе задачу можно свести к интегрированию системы обыкновенных дифференциальных уравнений второго порядка (4.47) относительно узловых перемещений v (г). При этом перемещения v (г) должны в торцовых сечениях принимать заданные значения либо удовлетворять там естественным граничным условиям (4.48). Для интегрнровання системы уравнений (4.47) можно применить различные численные методы [2]. Изложение некоторых методов, используемых в задачах строительной механики, можно найти в работе [19]. Рассмотренный выше подход нашел применение, в частности, в задачах нзгнба пластин, где ои известен под названием метода конечных полос [6].
ГЛАВА 5
КОНЕЧНЫЕ ЭЛЕМЕНТЫ СПЛОШНОЙ СРЕДЫ
Для решения плоской задачи теории упругости и для расчета трехмерных тел разработано много разнообразных конечных элементов. Основное различие между ними заключается в характере аппроксимации перемещений, а также в способе описания геометрии. Весьма плодотворным является нзопараметрический подход, в котором аппроксимация перемещений и геометрии осуществляется с помощью одних и тех же соотношений. Это позволяет построить одно-, дву- и трехмерные конечные элементы произвольной конфигурации, в том числе криволинейные, обеспечивающие совместность конечиоэлементиой модели.
§ 5.1. Плоский треугольный элемент
В качестве первого примера рассмотрим простейший конечный элемент, применяемый для решения плоской задачи теории упругости. Это треугольный элемент (рис. 5.1) с тремя узлами, расположенными в вершинах треугольника. Узло-
вые перемещения для такого элемента указаны на рисунке. Матрицы перемещений для каждого узла состоят из двух компонент. Так, для узла i имеем
Vi=M.
.VigJ
При составлении матрицы Vе условимся обхо-
дить узлы против часо-о Рис 5 1
вой стрелки; тогда
Vе = {Vi V; Vm}.
Точки элемента получают перемещения их, иу в направле-
нии осей х, у. Поэтому матрица ц имеет вид
и =
Чу
Для получения матрицы а, связывающей и и Vе, предположим, что перемещения их и иу в пределах элемента меняются по простейшему закону
их = /i +f2x + f3y; uv = + f6x + f3y, (5.1)
где f — некоторые постоянные. В вершинах треугольника перемещения их и иу должны совпадать с узловыми перемещениями. Это дает шесть уравнений для определения кон
стант /. Подставим в (5.1) координаты узла i и приравняем их и иу к vix и viv:
f i + fixl + f зУГ= vin', ft + + feyi Viy.
Полагая значения x, у равными Xj, yJt а затем xm, ym, запишем аналогично оставшиеся четыре уравнения. Полученная система будет содержать две независимые группы уравнений. В первую группу войдут постоянные f2, f3, а правые части будут содержать узловые перемещения vtx, Vjx, vmx:
f\ ~b f 2х i f йУ t ~ vix\ ft H* f 2х i H" f зУ} ~ Vjx't
f 1 “b f 2х m 'b f зУт vmx-
Вторая группа будет содержать постоянные /4, /5, /в и перемещения viy, Vjy, vmy. Решая первую группу уравнений, приходим к следующим соотношениям:
/1 (и^х4-с, ^х-1-с’тУтх);
2.Г
f‘i'== е (&1 bj Vjx~F Ьт Vmx), (5.2)
zr
/з = “^Г (aiVix4-ajVjx+a,nvmx),
где cii хт — Xj, ctj Xf x}tl) cim — Xj х^,
Уj Ут* — Ут yti У1 {Jf-s
Ci= х1Ут—хтУГ, Cj = xmyi — Xiym\ cm = х,у}—х}у,. (5.3)
Выражения для /4, /5 и /6 можно получить соответственно из формул для /j, f2 и /з, заменив в них vtx, vjx, vmx на viff, Vjy, vmy. Величина Fe, фигурирующая в этих соотношениях, представляет собой площадь треугольника ijm и может быть вычислена через координаты узлов с помощью определителя:
2^=
1 xi У, 1 xi У]
Хт Ут
(5.4)
Заметим также, что из (5.3) и (5.4) вытекает соотношение
2F‘ = Ci + Cj + ст. (5.5)
Подставляя (5.2) в первую из формул (5.1), можно привести ее к виду
Ux IF+bi х+ai Vi*+ J + bjx + Vjx
Н” -f- bm ат у) (5.6)
Последняя формула выражает перемещение их в любой точке элемента через его узловые перемещения. Аналогичное выражение получается и для перемещения иу. Представим’(5.6) и соответствующее выражение для иу в форме
где
«л 1(Сг + Ь,х4-агг/) 0 (су4-6;х + asy) 0 ->
(ст+-Ьтх + ату) 0];
av=—(сг4-6гх + агг/) 0 (с} + Ь} х + а} у) -> 2.Г 0 (ст + z/)].
Последние равенства можно переписать также в форме
®.v &у ~ &yj (5.7)
где aXI. = [фг 01; ayr = [0 фг1; (5.8)
Фг = ттг(сг + 6гх + аг^) ('=г’> /. т)- (5-9)
Эти формулы определяют искомую матрицу аппроксимирующих функций
1ах аУ J которую можно представить в виде а = 1аг а} ат], где фг 0 1 0 ^’г.
Далее по (4.7) вычисляем матрицу да,х/дх дау/ду дау/дх -f- дих/ду _
С учетом (5.7)—(5.9) получим 0 = [0; 0, 0,„], где . R 01 аг Ь,
a,
(г= i, j, tn).
₽ =
(r = i, j, m).
о
(5.10)
В данном случае элементы матрицы Р не зависят от коор динат. Это означает, что деформации (а следовательно, и на. пряжения) в пределах рассматриваемого конечного элементг постоянны; при переходе от одного элемента к другому они изменяются скачком.
Теперь найдем матрицу жесткости элемента, пользуясь формулой
к" — рг хрбт.
te
Поскольку матрица Р представлена в стандартной блочной форме, то в соответствии с (4.14), (4.15) для матрицы жесткости рассматриваемого треугольного элемента получим
И- И
Ч/ ^im
k?- k?
л/7 Kym
ke • k* лт/
где типовая подматрица
kers= jp^zpA.
те
Подынтегральное выражение не зависит здесь от координат и может быть вынесено за знак интеграла. В случае обобщенного плоского напряженного состояния рассматриваемый конечный элемент представляет собой пластину. Если его толщина постоянна и равна he, то объем элемента т« будет равен Fehe. Таким образом, в этом случае
k£s— Fe/zepjxps (г, s = i, j, m). (5.И)
Формулой (5.11) можно пользоваться для вычисления матрицы жесткости элемента как гладкой, так и конструктивноортотропной пластины. В последнем случае матрица и определяется согласно (1.36), (1.32), (1.34) и перемножение матриц в (5.11) целесообразно выполнять на ЭВМ. Если же пластина не имеет подкреплений, то удобнее получить элементы типовой подматрицы krS в аналитической форме. Представим для этого матрицу упругости
р О
О 0 (1 —н)/2
в виде двух слагаемых и = ие 4- Хо, где
р ’ 1 у, 0* ГО 0 0‘
кЕ — - 1—у2 у 1 0 ; Xo = G ООО (5.12)
|_0 0 oj [_0 0 1J
Здесь G = Е/[2 (1 4- у)1 — модуль сдвига. Тогда
= к%, е 4- о>
(5.13)
где
krs, г = Fehe fir ке ₽s; к%. g = Fe he 0, Xq 0s.
Подставляя в выражение для подматриц, получаем
krS. £ формулы для отдельных
откуда
k*s Е = Eh<! Ь* bs Pbr as 1 4(1-и3) F* aTas J
Аналогично находим
ье ______ Ghe Г dr us aT bs
•rs» G ' I
4Fe brbs
(5.15)
Отметим, что матрицы k«, E и krS> g представляют собой вклады, даваемые соответственно нормальными деформациями и деформациями сдвига в матрицу k,s-
Для того чтобы получить матрицу жесткости для случая плоской деформации, следует принять he = 1 и заменить в (5.14) модуль упругости Е на £7(1 — у,2), а коэффициент Пуассона у, — на у/(1 — у) (см. § 1.2).
Коснемся далее вопроса о приведении внеузловых нагрузок к эквивалентным узловым силам. Такое приведение должно выполняться в соответствии с (4.16). Однако замена поверхностной нагрузки узловыми силами часто осуществляется из
простых физических соображений, а формула (4.16) используется лишь для приведения объемных сил:
= jj arRdx.
В блочной записи имеем
где типовая подматрица
Р‘— a^Rdx (r = z, /, т).
Xе
Если, в частности, объемные силы постоянны, то можно показать, что
Р* = J_p 3 Ш
Отсюда видно, что в рассматриваемом простейшем случае постоянных объемных сил их равнодействующая поровну распределяется между узлами. В случае, когда объемные силы переменны, можно приближенно воспользоваться этой же формулой, взяв значения Rx и /? „ в центре тяжести треугольника.
Перемещения их и и№, определяемые выражениями (5.1), изменяются по линейному закону вдоль любой прямой в плоскости ху, в том числе по сторонам треугольника. Линейная функция полностью определяется какими-либо двумя ее параметрами. Значит, перемещения их и иу на каждой стороне треугольника будут однозначно определены, если известны их значения в узлах, лежащих на соответствующей стороне. Так как узловые перемещения являются общими для соседних элементов, то при переходе от одного элемента к другому перемещения не будут иметь разрыва. Следовательно, треугольные элементы с линейными полем перемещений относятся к категории совместных.
Недостатком рассмотренного элемента является то, что напряжения в пределах треугольника постоянны, и поэтому для получения достаточной точности решения часто приходится использовать весьма густую сетку (особенно в областях с быст-
роменяющимся напряженным состоянием). Это может привести к системе уравнений слишком высокого порядка и соответственно к чрезмерным затратам времени на решение задачи. Тем не менее этот элемент широко используется, поскольку он очень прост и позволяет идеализировать плоские тела довольно сложной конфигурации.
§ 5.2. Совместный прямоугольный элемент
Другой конечный элемент, используемый в плоской задаче, показан на рис. 5.2. Он представляет собой прямоугольник с узлами в вершинах. Матрица узловых перемещений такого элемента имеет восемь компонент. Обходя узлы против часовой стрелки, запишем
Vе = {ViV} V;Vm),
где, как и ранее,
(г= i, /, /, zn).
Для приближенного представления поля перемещений конечного элемента можно взять функции
их = fi + f2x + f3y + ftxy; Uy = + fex + fcy -f- fsxy,
(5.16)
в которых содержится восемь постоянных. Для их определения можно так же, как и в случае треугольного элемента, записать в каждом узле условия равенства перемещений их и иу их узловым значениям. Мы опять придем к двум группам уравнений, первая из которых позволяет выразить постоянные fi-.. ft через vrx, а вторая — постоянные /5.../8 через vry (г = /, /, I, пг).
В итоге блоки матрицы а — [а2ауа(аго] будут иметь такую же структуру, как и в случае треугольного элемента:
где через фг обозначены некоторые функции координат.
Покажем, что для отыскания функций фг совсем необязательно решать систему уравнений, как это делалось ранее, а
можно найти их путем подбора. Запишем прежде всего зависимость u = ave в развернутом виде:
~ vix ~
Vty
Гмж1 =pi О 0 {Ф( 0 {Фт 0 1
[«J 1° Фн° Ф,Ю ф;]0 4>m] Vlx
Vly
Vmx
_ Уулу —
Отсюда вытекает следующее выражение для их:
их = + Ф;^х + ФАх + tymVmx-
Рнс. 5.2
Если положить здесь vix = 1, а смещения остальных узлов равными нулю, то будем иметь их = ф;. Следовательно, фг — такая функция координат х, у, которая дает распределение перемещений в элементе при единичном смещении узла i и при непод-
вижных остальных узлах. Обобщая эти рассуждения, приходим к заключению, что каждая из функции фг дает распределение перемещений в пластине при единичном смещении (вертикальном или горизонтальном) узла г и при неподвижных остальных узлах. В качестве примера на рис. 5.3. показан вид функции фг.
к системе
функции фг, перейдем
координат %, т], начало которой находится в
Рис. 5.3
Для того чтобы записать
безразмерных
центре тяжести прямоугольника (см. рис. 5.2). Положим
| = 2 (х — хс)/а; г] = 2 (у — ус)!Ь,
где a, b — размеры сторон прямоугольника, а хс, ус — координаты его центра тяжести. Тогда новые координаты т] будут на сторонах элемента принимать значения ±1- Для узлов i, j, I, т они окажутся соответственно равными (—1, —1), (1, -1), (1, 1), (-1, 1).
Учитывая, что перемещения согласно (5.16) должны изменяться по линейному закону вдоль прямых х = const или у = = const, можно функции фг искать в виде произведений (1 ±5) X X (1 ±т])- Условия в узлах будут удовлетворены, если положить
Ф. = (1 - §) (1 - п)/4; Ф, = (1 + &) (1 - п)/4;
Ф/ = (1 + §) (1 + ПИ; фт = (1 - §) (1 + т|)/4.
Все эти функции можно записать с помощью одного общего выражения:
Фг = (1 + (1 + ПгП)/4 (г = i, j, I, т). (5.18)
Вычислим далее матрицу ₽ = [₽<₽/₽г₽т1. По формуле (4.7) имеем
₽ =
dajdx дау/ду дау'дх + дах!ду
гдеаж иаа — соответственно первая и вторая строки матрицы а.
Пользуясь соотношениями dx = (a/2)d|; dy = (6/2) dr] и учитывая блочную структуру матрицы а, для типовой подматрицы ₽г получим
Подставляя сюда выражения для фг, имеем
(5.19)
где через аг (£) и Ьт (л) обозначены функции:
аг = Пг (1 + » ЬГ = Ъ(\ + т|гп)/а. (5.20)
Вычислим теперь матрицу жесткости рассматриваемого элемента для случая обобщенного плоского напряженного состояния:
k?,- k?z k?z кГ„ ке== ке„ kjz kj„, к» к?„, _Симм- к„1ОТ _ где
ке„= J₽rx₽sdT=-^- J j tfxM&dT). хе —1—1
(5.21)
Так же как и в случае треугольного элемента, удобно разбить подматрицу krS на два слагаемых:
krs— kf-s, Е ~Т krs, G*
Здесь
k‘s>£=^- j j tfxz-fWT);
—« _ 1
k%,0=^- j j p/’xoMIdt], — i — i
где матрицы упругих коэффициентов v.E н v.q определены равенствами (5.12). Подстановка выражений для v.e, ₽г и ₽s в формулу для k*s, е дает:
k'rs.E
X —
2
~bs о а*
О'
a, =
bs.
Ehab Г Г bT bs
16(1-н2) НДвоА
а° 1 dgdrj. aras J
Вычислим необходимые интегралы, учитывая (5.20):
f аг®<% = j' (i+U)d£=J3iL; J Ь .! b
f ar(|)ag(£)d£ = [ (1 +U)(i +U)d£ =
J J
— 1 —1
_ 2r]r t)s / j . £r \
ь2 \ 3 /'
Аналогично вычисляются интегралы по q от Ьг (q) и от произведения br (vi)bs (q).
В итоге для krs, е имеем
ке Eh ГгёЛЛ1+ПгПз/3) иБгЪ ]
rs'E 4(1—ц2) [|xqrgs (1/т)ПгПз(1 + £гиЗ)]’
(5.22)
где через у = b/а обозначено отношение сторон элемента. Подобным же образом находим
0
аг
X
о]1*
0
as dgdq =
ar bs bT bs
d£dq,
0
откуда
.e Gh Г(1/у)ПгПз(1 +lrU3) krs, G = —
4 L^rHs
?U,(1 +ПгПз/з)
. (5.23)
Формулы (5.22), (5.23) относятся к случаю гладкой пластины. Для конструктивно-ортотропной пластины следует в (5.21) подставить матрицу х, определенную в § 1.3, и воспользоваться численным интегрированием. Но если подкрепляющие элементы параллельны оси х, то в качестве матрицы упругости следует взять матрицу х0, определяемую равенством (1.32). В этом случае также нетрудно вывести аналитические выражения для подматриц krs подобно тому, как это делалось для гладкой пластины.
В рассмотренном прямоугольнике перемещения их, иу, определяемые соотношениями (5.16), изменяются по линейному закону вдоль прямых х = const или у = const и, в частности, вдоль его сторон. Рассуждая так же, как и в случае треугольных элементов, заключаем отсюда, что введенные выше прямоугольные конечные элементы являются совместными. Заметим, что они совместны также с треугольными элементами предыдущего параграфа, так как в обоих случаях перемещения вдоль сторон изменяются по линейному закону.
Представленный здесь прямоугольный элемент наряду с треугольным является одним из простейших конечных элементов. При одинаковом числе узлов (т. е. при одинаковом порядке системы разрешающих уравнений) он дает более точное решение, чем при идеализации тела треугольными элементами. Однако с помощью одних только прямоугольников можно идеализировать лишь такие области, которые ограничены прямыми линиями, параллельными осямх, у. Для более сложных областей можно использовать прямоугольные элементы в сочетании с треугольными, но это усложняет подготовку исходных данных. Поэтому для расчета тел произвольной конфигурации обычно применяют конечные элементы в виде четырехугольников произвольной формы. Примеры таких элементов будут рассмотрены ниже.
В расчетах авиационных конструкций четырехугольные (и, в частности, прямоугольные) элементы применяются как составные компоненты при моделировании различных балок с тонкими стенками (лонжеронов, нервюр, шпангоутов и т. п.). Если изгиб происходит в плоскости стенки, то она будет находиться в условиях обобщенного плоского напряженного состояния. Для упрощения исходных данных и снижения затрат машинного времени желательно по высоте стенки брать только один элемент. Но рассмотренный выше прямоугольник не подходит для этих целей, так как он плохо описывает состояние чистого изгиба.
На рис. 5.4, а показана плоская прямоугольная пластина, которая нагружена по боковым сторонам нормальными напряжениями, изменяющимися по линейному закону, так что она находится в условиях чистого изгиба. Точное решение этой задачи показывает, что взаимный угол поворота боковых граней равен 0 = MaJ(EJ\, где J — hb3/l2 — момент инерции поперечного сечения пластины; М — изгибающий момент.
Пусть теперь прямоугольный конечный элемент с такими же размерами находится в аналогичных условиях (рис. 5.4,6). Поскольку вдоль каждой стороны перемещения изменяются по линейному закону,.то все стороны элемента после деформа-144
ции останутся прямыми. Можно показать [40], что взаимный угол поворота 0е боковых сторон для рассмотренного выше прямоугольного элемента будет равен
де ______45______ Мд
S=48[(14-3/(8y2)] EJ ' где у = Ыа.
Сопоставляя этот результат с точным, видим, что данный конечный элемент дает заниженное значение угла поворота, т. е. является слишком жестким. Источником чрезмерной жесткости конечного элемента при изгибе является деформация сдвига 8яг,. В точном решении еху — 0, а для конечного элемента используемая аппроксимация перемещений приводит к появлению деформаций сдвига ъху = 0еКонечно, можно получить хорошее решение, если моделировать пластину несколькими элементами, но нас в данном случае интересует возможность удовлетворительного воспроизведения состояния изгиба с помощью одного элемента. В следующем параграфе будет рассмотрен несовместный элемент, удовлетворяющий этому требованию. Другой способ исключения «ложного» сдвига описан в § 6.6.
§ 5.3. Несовместный прямоугольный элемент
В предыдущих параграфах мы задавались характером изменения перемещений внутри конечного элемента. Можно, однако, получить распределение перемещений, задавшись предварительно законом изменения напряжений в пределах элемента. Воспользуемся таким подходом для
вывода жесткостных характеристик конечного элемента прямоугольной формы с четырьмя узлами в вершинах. При этом будем требовать, чтобы напряжения в пределах каждого элемента удовлетворяли дифференциальным уравнениям равновесия (прн отсутствии объемных сил).
Как известно (см. § 1.2), дифференциальные уравнения равновесия будут тождественно удовлетворяться, если напряжения связаны с некоторой функцией <р (функцией напряжений) соотношениями (1.27).
При этом условие совместности деформаций будет в случае гладкой пластины выполняться, если функция <р (х, у) является решением уравнения (1.26).
Примем, что в пределах конечного элемента функция <р изменяется по закону
ф = С±Х2 + С2Ху + СзУ2 + С4Х3+С51/3,
при котором уравнение (1.26) удовлетворяется тождественно для любых значений постоянных сг...Съ.
По (1.27) находим
охгс — 2с3 + 6съу, ауу = 2сх + 6с4х; <зху = — с2. (5.24)
Отсюда видно, что используемый набор функций <р дает простейшие напряженные состояния (растяжение и изгиб в двух направлениях, а также чистый сдвиг).
Пользуясь далее законом Гука для обобщенного плоского напряженного состояния, определим деформации:
ехХ=(<тхх—= “£ (2сз + 6с51/—2р — 6р. с4 х);
(ffyj, —ражж)=-|- (2C1 + 6c4x—2р с3—бр с5 у);
1 2(1 + р)
ЕХ»~ Q аху—— Е С2-
Перемещения можно найти теперь нз уравнений Коши (1.20): дих ди„ диу дих
~^Г = ехх’ ~1Г+~^=ех«-
Интегрируя найденные выражения для ехх и еуу соответственно по х и у, будем иметь
«х = [2(с3 — рс4) х + 6съху — Зрс4х2 + (у)]/Е;
«» = 12 (Cj — рс3) у + 6с4ху — 3pc5z/2 + g2(x)]/E,
где gi (У) и ёг (х) — произвольные функции.
Подстановка этих формул, а также выражения для еХу в третье соотношение (1.20) дает
I L , ( 1 Г ]_ 2(1 + р)
~ + Т 6с»х+ “^—-------------г---с2-
Е L d х J Е L d у J Е
Перепишем это равенство следующим образом: d я, Г d g. 1
-~+6С5х + (1+р)с2=- -ГГ+6с4р+(1 + р) с2 .
d х L d у J
В левой части полученного соотношения стоит функция только х, а в правой — функция только у, н равенство возможно лишь в том случае, когда обе функции равны некоторой константе. Обозначив эту константу через с8, приравняем к ней поочередно каждую из функций. Это дает два уравнения относительно gt (у) н g2(x), интегрируя которые находим
£1 (!/) = — Зад2 — 0 + И) Са У — се!/ + с7;
gi W = — 3cgx2 — (1 + р) с2х + с«х + с8,
где с7 н с8 — постоянные интегрирования.
После подстановки полученных выражений в формулы для их и иу имеем:
«х = (2 (с3 — р Cj) х + 6 аху — 3 с4 (рх2 + у2) — (1 + р) сгу—
— сву 4- с7] /£;
“у = (2 (П — рс3) у + 6с4ху — Зс5 (х2 + ру2) — (1+ р) с2х + + свх + Св]/Е.
Последним выражениям можно придать более простой вид
их = А + f2x + f зУ + ftxy — fa + £2)/2;
(5.25)
Uy = h + fax + fry + faxy — (X2 + py2)/2,
если ввести новые произвольные постоянные: А = с7/Е; f, = 2 (с3 — - рС1)/£; f3 = - 1(1 + р) с2 + св]/£; /4 = 6<%/£; /5 = с8 7 £; ft = — [(1 + И) с2 — св]/£; f7 = 2 (Ci — pcs)/£; f8 = 6 cJE.
Функции (5.25) отличаются от использованных в предыдущем параграфе наличием дополнительных членов рх2 -+- у3 и х2 + ру2. Система уравнений, связывающих между собой произвольные постоянные f и узловые перемещения, ие будет уже, как ранее, распадаться иа две подсистемы, поскольку в выражениях для их и иу фигурируют общие постоянные /4 и /8. Это означает, что например, смещения узлов вдоль оси х будут в общем случае вызывать в рассматриваемом конечном элементе не только перемещения их, ио также и поперечные перемещения Uy.
Исходя из вида функций (5.25), можно и в этом случае путем подбора записать общее выражение для подматриц ar (г = i, j, I, т), входящих в матрицу а = [а;а/цат].
Перейдем прежде всего к системе безразмерных координат £, т), полагая, как и ранее, £ = 2 (х— хс)/«; г) = 2 (у—ус)/Ь. Здесь по-прежнему: а, b — размеры сторон прямоугольника; хс, уе — координаты его центра тяжести. В новых координатах выражения (5.25) примут внд
«X=fj+f2^+f31l+f4 sn— v/sf— £2+ Y»l2) ;
uy^fs+ft, S+fJ n+fU’i— 4"; (5.26)
2 \ Y /
где у = b/a. Через f* здесь обозначены новые постоянные (например, ft = (ab/4)ft; fJ — (ab/4) fsH т. д.).
Пусть теперь один из узлов конечного элемента (скажем, узел г) получил единичное смещение vrx — 1 вдоль оси х, а все остальные уз
ловые перемещения равны нулю. Найдем распределение перемещений ия и Uy, возникающее при этом в конечном элементе в соответствии с формулами (5.26). Перемещение их должно принимать единичное значение в узле г и обращаться в нуль во всех остальных узлах. В предыдущем параграфе описана схема построения такой функции:
их^~~ (1 + Sr 5) (1 +Пг П)
Отметим, что коэффициент /J, который согласно (5.26) является миожителем перед произведением ji), оказывается здесь равным JjrT)r/4. Переходя к определению иу, замечаем прежде всего, что, как следует из
(5.26), в выражение для иу обязательно должна входить функция ~52+ 1 1 1
4-р.ут)2 с множителем — ^f*t, ч. е. выражение —§• ВгПг & + НУ1!2)-Кроме того, перемещение иу должно обращаться в нуль во всех узлах, так как по условию отличным от нуля является лишь перемеще-
ние vrX. Функция же — £2 + руг)2 во всех узлах принимает одинаковое
значение ~ + ру (поскольку координаты £, г) узлов равны ± I). Условие в узлах будет выполнено, если положить
«»= -4" ^г Пг (-7 S2+m2—~—Uy) • » \ Т у /
Здесь к записанной выше функции добавлена постоянная величина, что не противоречит набору функций во втором равенстве (5.26).
Диалогичные рассуждения показывают, что при единичном смещении vry = 1 распределение перемещений дается равенствами
“х= —4"6гПг(— 52+vn2—т); "» = 4-(>+SrS)О+ПгП)-о \ Y Y / ’
Таким образом, произвольное смещение узла г вызывает в конечном элементе перемещения
1 1 ! ц. и \
(,+Srs)(1+nrn)urx—— ^гПг-т1 S2+vn2---------т)»г»;
о \ т у /
«»= ~4-6г11г(-7 S2 + m2—f‘v')orx + 4-(l+SrS)(l+nrn)»rr 8 \ у у / 4
Следовательно,
«гх
«г»
-у (»+Ег£)(1+ПгП)
—~~f~£2+im2—~—~0 +SrS) (1 +пгп) _ 8 \ у у / 4
Типовой блок рг матрицы р = [PiPyPzPml находим теперь по формуле
д «гх дх
дагу ду
&ry j д дх ду
2 д атх а д£
догх Л)
2 д
Ь дц
2 д dry ,____2
а Ь
откуда получаем
-^(1+£Л) о
(5.28)
Наконец, по формуле
т UU
Рг *Ps — d£ dt]
вычисляем типовую подматрицу жесткости. Представляя ее. как и прежде, в виде суммы двух слагаемых, имеем
Vе__1Л । ь»
Krs— *rs, El *rs, G -
где
Eh
4 (1 —pi2)
/ 1 — p-2 \
V^r 5s H-------7- T)r »]s P^r »]s
\ о /
»]r»ls /, , 1 — P-2 „ . \
РПг^з -----H----------- Sr^s)
Y \ /_
(5.29)
.e Gh f~t]rT)3/y
r$-G 4 [ ^t)s
(5.30)
Рассмотренные здесь конечные элементы являются несовместными. В самом деле, из (5.26) следует, что при х = const или у = const перемещения изменяются по квадратичному закону. Квадратная парабола задается тремя параметрами, и узловые перемещения двух соседних вершин прямоугольника не могут однозначно определить значения функций их и иу на прилегающих к ним сторонам. Следовательно, равенство перемещений смежных элементов обеспечивается только в узловых точках, а на линиях раздела элементов перемещения будут претерпевать разрывы.
Тем не менее использование таких элементов позволяет получить хорошую точность. Они особенно удобны при моделировании балок, поскольку обеспечивают точное представление состояния чистого изгиба.
§ 5.4. Внутренние узлы и подконструкции
До сих пор мы ограничивались случаем, когда узловые точки расположены на границе конечного элемента. Но это совсем необязательно. Рассмотрим конечный элемент, у которого помимо обычных узлов на границе (будем называть их внешними) имеются также внутренние узлы, принадлежащие только данному элементу. На рис. 5.5 показан пример такого элемента. Здесь имеется восемь внешних узлов (они являются общими для данного элемента и смежных с ним) 7<Г ’ I и один внутренний.
\ о р Особенность внутренних узлов за-8 д 9 I ключается в том, что они непосред-
I____о--Aj ственно связаны только с узлами,
1°''^ 2 принадлежащими данному конечному
элементу. Поэтому коэффициенты мат-Рис- 55 рицы жесткости всей системы, отно-
сящиеся к внутренним узлам, будут просто совпадать с соответствующими коэффициентами жесткости отдельных конечных элементов. Точно так же узловые силы во внутренних узлах конечного элемента не имеют вкладов со стороны смежных элементов, т. е. они могут быть вычислены еще до объединения конечных элементов. Все это позволяет перемещения внутренних узлов каждого элемента выразить через перемещения его внешних узлов и, таким образом, исключить их из числа искомых параметров объединенной системы.
Узловые перемещения конечного элемента с внутренними узлами, которые мы будем обозначать через v, можно представить в виде
- Г Vе V —
Vo
где ve — матрица-столбец, в которой перечисляются перемещения всех внешних узлов, а матрица v0 содержит перемещения внутренних узлов. В представленном на рис. 5.5. примере матрица Vе будет включать в себя перемещения первых восьми узлов, а матрица v0 — перемещения девятого узла.
В матрицах а и Р, связывающих перемещения и деформации внутри элемента с v соотношениями
u = av; е = (Jv,
также выделим соответствующие подматрицы:
a = [aa0]; Р ==[Р Pol-
Эти подматрицы имеют простой смысл. Так, столбцы матрицы а дают распределение перемещений в пределах элемента при единичных смещениях внешних узлов, а столбцы матрицы а0 — распределение перемещений при единичных смещениях внутренних узлов.
Пусть на элемент действуют объемные R и поверхностные р силы. Матрица-столбец эквивалентных им узловых сил определится выражением
arRdr + J arpd<o.
t®
Учитывая блочное представление матрицы а, получим отсюда две подматрицы, которые мы обозначим через Ра и Ро:
aj Rdr + J pdw. (5.31)
t* ше te
Первая из них содержит силы, приложенные к внешним узлам, а вторая — к внутренним.
Наконец, в матрице жесткости элемента k = f prxpdt так-
Xе же выделим соответствующие блоки:
. |~ ка 1
[к£ ко]
Здесь
ко = f prxpdx; кь = J prxpodr; к0 = J pjxpodr. (5.32) Iе X? Xе
Теперь связь между узловыми силами и перемещениями конечного элемента запишется так:
Гка кь] [v‘1 _ ГРЧ ГРО"
I 7* II I ' I* | ,-ц •
|_кь koj LvoJ LpoJ [Ро
Ра = J arRdr 4- j arpd<o; Po = f
Через Р* и Ро обозначены здесь сосредоточенные силы, действующие на элемент во внешних и внутренних узлах соответственно. Отсюда вытекают два равенства
kov* + kbv0=P‘4-Pa, kbv‘4-k0v0=P0 + P0. (5.33)
Второе из этих равенств позволяет выразить v0 через Vе:
vo = ко’1 (Ро + Ро) - ко"1 к,Г Vе. (5.34)
Подстановка этого результата в первое соотношение (5.33) дает связь между перемещениями Vе и узловыми силами: (к0 — кько *кь) Vе =- ре +- Ра — кьк» * (Ро + Ро). которую можно записать в стандартной форме (4.13):
ке Vе =ре 4-ре .
Здесь
==ка—кь к0-[ к£; (5.35)
R =Ра-к„ к0“> (Ро +Р0). (5.36)
Формула (5.35) позволяет вычислить матрицу жесткости конечного элемента, приведенную к перемещениям его внешних узлов. Приведение сил к внешним узлам осуществляется при этом по (5.36).
Объединение конечных элементов выполняется далее обычным образом. Матрица неизвестных перемещений будет теперь включать лишь перемещения тех узлов, которые являются внешними для конечных элементов. Эти перемещения определяются в результате решения системы уравнений, а перемещения внутренних узлов при необходимости могут быть найдены из (5.34).
Использованные выше рассуждения можно применить к образованию сложных конечных элементов из простейших. Выделим часть тела, включающую в себя некоторое число простых конечных элементов. Объединив эти элементы, можно сформировать общую матрицу жесткости и матрицу узловых сил для рассматриваемой части. В результате получим один сложный конечный элемент, который затем можно обычным образом объединять со смежными участками тела для формирования разрешающей системы уравнений. Такой элемент называется подконструкцией (или суперэлементом). Разбиение на подконструкции применяется при расчете весьма сложных систем, таких, как самолет в целом. При этом подконструкции могут действительно соответствовать некоторым характерным отсе
кам конструкции (крыло, фюзеляж и т. д.), но это необязательно.
Все узлы подконструкции можно разделить на «внешние» и «внутренние». К внешним отнесем такие узлы, которые являются общими для соседних подконструкций, а к внутренним — те, которые принадлежат только данной подконструкции. Так, при идеализации крыла в виде подконструкции внешними будут лишь те узлы, которые являются общими для крыла и фюзеляжа. Перемещения внутренних узлов можно выразить через перемещения внешних подобно тому, как это было сделано для конечного элемента с внутренним узлом. Тогда разрешающая система уравнений будет включать в себя перемещения лишь тех узлов, которые являются для подконструкций общими.
Обозначим через Vе матрицу перемещений внешних, а через v0 — внутренних узлов. Тогда матрица узловых перемещений подконструкции v будет представлена в виде
v =
Vе
Уо .
Матрицу узловых сил подконструкции Р запишем также в блочной форме:
Р=
ре
Ро
Здесь подматрицы Ро и Ро включают в себя соответственно сосредоточенные силы и силы, эквивалентные распределенной нагрузке, которые действуют во внутренних узлах. Подматрица Ра содержит силы во внешних узлах, эквивалентные распределенной нагрузке, а в Ре перечисляются сосредоточенные силы, действующие на подконструкцию во внешних узлах.
Наконец, выделим соответствующие блоки в матрице жесткости подконструкции к:
Г кв к 1кб к0
Отметим, что элементы матриц Ра и Ро, а также элементы матрицы жесткости к находятся по обычному правилу суммирования вкладов отдельных конечных элементов, составляющих подконструкцию.
Связь между узловыми силами и перемещениями запишется теперь так:
Г К» К,] Г Vе О Р* 1 . ра 1
[kJ kojlvoj I ро] LpoJ
Выражая далее перемещения внутренних узлов v0 через Vе, приходим снова к соотношению keve = Ре -4- Р®, в котором ке и Р« определяются аналогично (5.35), (5.36):
к' = ko-kb k-> kJ; Р =Pa-kb k~> (Po + Po).
При этом
Vo = ko"' (Po+PoJ-k»-1 klve .
Использование подконструкции позволяет расчленить расчет сложных систем на отдельные этапы. Другое достоинство метода подконструкций заключается в том, что конструктив-
Рис. 5.6
ные изменения в какой-либо подконструкции требуют лишь частичного пересчета, поскольку матрицы жесткости всех остальных подконструкций остаются неизменными. Следует отметить, однако, что введение подконструкций существенно усложняет программирование.
Проиллюстрируем сказанное на простейшем примере образования плоского четырехуголь-
ного конечного элемента произвольной формы из четырех треугольных (рис. 5.6). Суммируя коэффициенты жесткости отдельных треугольников, образуем сначала матрицу жесткости к, которая будет иметь размер 10 X 10 (так как в каждом из пяти узлов имеется по две степени свободы). В блочной форме матрица к имеет вид
кн к12 к13 ки к22 к,3 к31 Кзг к33 k*i к42 к43 _k5i к52 км
км к15
kzi к25
кз4 к35
к44 к^
^64 ^55—
Нижние индексы означают здесь, как обычно, номера узлов. Типовая подматрица,
+ (г, 1,2,..., 5).
Выделяя в к необходимые блоки, имеем
где
ка кь] k? k0 J
kJ2 k13 kj<
k22 k24
кзл k33 k34
k42 k<3 kM_
k0 — [k^J.
Для приведения матрицы жесткости к перемещениям внешних узлов можно теперь воспользоваться формулой (5.35). В итоге получим блочную матрицу размером 4x4 вида
ке21 kti
-М,
ке к® Л13 ке14 -
кг "22 ке •*23
ке Л32 кв Кзз ке “34
ке К4 2 к* “43 к* «в —
Здесь kers = krs — kr, 5 к5,5 кГ, 5 (г, s = 1,2, 3, 4).
Аналогично вычисляются и эквивалентные узловые силы.
Таким образом, мы получаем совместные четырехугольные конечные элементы с восемью степенями свободы. Узловые перемещения, найденные с помощью подобных элементов, будут такими же, как и при самостоятельном применении входящих сюда треугольников. Все же использование составных четырехугольников имеет определенные преимущества. Во-первых, сокращается количество исходной информации. В память ЭВМ достаточно ввести координаты х, у всех внешних узлов, а координаты внутренних можно определить для каждого элемента программным путем, пользуясь, например, формулами х5 = (*! + Хг + х3 4- х^/4; Уъ = (t/T +• уг + Уз + Ул)/4.
Во-вторых, число узловых перемещений, подлежащих отысканию из решения системы уравнений, уменьшается за счет исключения перемещений внутренних узлов. Соответственно уменьшается и размер матрицы жесткости всей системы,
что приводит к экономии памяти. Последнее обстоятельство может иметь существенное значение в тех случаях, когда решение системы уравнений выполняется с использованием одной только оперативной памяти.
Процедуру исключения степеней свободы внутренних узлов можно рассматривать и с точки зрения минимизации полной энергии системы. Более подробно этот вопрос будет в несколько иной связи рассмотрен в следующем параграфе.
§ 5.5. Неузловые степени свободы
Добавление внутренних узлов позволяет улучшить жесткостные характеристики конечных элементов и, следовательно, повысить точность решения. Улучшение характеристик получается за счет повышения числа степеней свободы конечного элемента по сравнению со случаем, когда имеются только внешние узлы. Одиако введение дополнительных узлов требует полной перестройки матрицы аппроксимирующих функций а. Удобнее взять за основу «базовый» конечный элемент с одними только внешними узлами и добавить некоторые дополнительные функции распределения перемещений, не связывая их с введением новых узлов. Рассмотрим такой подход более подробно.
Пусть некоторый конечный элемент имеет узлы i, j, ... н пусть для него выбрана система аппроксимирующих функций, составляющих матрицу «. Построим теперь Новый конечный элемент, для которого распределение перемещений внутренних точек определяется равенством
u = ave + «ос. (5.37)
Здесь с — матрица-столбец некоторых постоянных, а матрица а0 содержит выбранные заранее функции, определяющие дополнительное распределение перемещений внутри конечного элемента при отсутствии узловых перемещений. Каждая из этих функций, следовательно, должна обращаться в нуль во всех узлах конечного элемента. Дополнительные параметры (неузловые степени свободы) с не имеют здесь ясного физического смысла. Их значения можно определить из условия минимума полной энергии системы.
Так как иеузловые степени свободы вызывают появление перемещений только в данном конечном элементе, то минимизацию энергии по параметрам, составляющим матрицу с, можно выполнить до объединения конечных элементов.
Применяя обычным образом формулы Коши, для деформаций получим соотношение
е = + р0 с,
где матрица ро образуется из компонент матрицы а0 так же, как матрица Р образуется из компонент «.
По закону Гука имеем также
о = Х8 = Z (Pv* + Рос).
Потенциальная энергия деформации конечного элемента
Ue = - J ег а <1т,
те
откуда после подстановки выражений для е и а имеем
= Kve)rpr+crpJ]x(₽ve + ₽oc)dT.
Раскрывая здесь скобки н выполняя интегрирование, получаем
Ve=-y [(ve)r ko у® + (у®)г kb с+ Сг к? у«+ сг ко с], где введены матрицы, аналогичные (5.32):
ko=j* 0rx0dx; kb=J prxpodx; к0 = J pJxPod-r. Xе Xе х®
Отметим, что ка есть матрица жесткости исходного конечного элемента, так что первое слагаемое в формуле для Ue определяет энергию деформации этого базового элемента. Подчеркнутые члены в формуле для Ue, будучи скалярными величинами, получаются один из другого путем транспонирования и поэтому равны между собой. С учетом этого перепишем окончательно выражение для Ue так:
ие = -у- [(у®)г ко Vе + 2 (v®)T kb С+ст ко с].
Потенциал внешних сил, действующих на конечный элемент,
П® =—/J urRdT+J urpd<«>-f-(v*)7'P®\ , \ Iе «>® )
где R и р — матрицы объемных и поверхностных сил; Р® — матрица сосредоточенных сил в узлах элемента (второе слагаемое будет присутствовать лишь в том случае, если некоторая часть поверхности конечного элемента совпадает с внешней поверхностью тела <ор).
Подставив в формулу для П® выражение (5.37), получим
П® = — (v*)T(Pa+P4)-cTP(„
где матрицы-столбцы Ра и Ро определяются подобно (5.31):
PO=J aTRdT+J arpd<o; ₽o = J a^RdT-f-j* agpdat. X® в>® X® ffl®
Матрица Pa содержит компоненты узловых сил, эквивалентных внеузловой нагрузке, для базового элемента.
Полная энергия V® — Ue + П® конечного элемента определится теперь выражением
V*=~ (уе)т ko у®—(v®)r (Ро + Р®) + ст к0 с+[(v®)r кь—Pj] с.
Л л
Условие минимума V® приводит к равенству dV®/dc = О,
откуда приходим к следующему выражению для матрицы с:
c=k0-1(P0-k£ve). (5.38)
Подстановка этого результата в формулу для Vе позволяет выразить полную энергию элемента в функции одних только узловых перемещений ve. Учитывая симметрию матрицы к0, можно привести это выражение к виду
Ve= у- (v‘)r k‘ ve -(ve)r (Р‘+ Рс) + Vo, где, подобно (5.35) и (5.36),
ke=ko-kb k“1 k£; Pe=Pa-kbk0-‘po.
Через Vo в формуле для Vе обозначена величина
Уо=— Pjk-‘ Ро/2,
которая не зависит от узловых перемещений, т. е. представляет собой некоторую константу. Поскольку потенциальная энергия всякой системы вообще определяется с точностью до произвольной постоянной, то слагаемое Уо является несущественным и его можно опустить.
Матрица кг представляет собой матрицу жесткости конечного элемента с иеузловыми степенями свободы с, а Ре есть матрица-столбец узловых сил, эквивалентных распределенной нагрузке.
Применим описанный подход к построению прямоугольного конечного элемента с улучшенными жесткостиыми характеристиками, взяв в качестве базового прямоугольник с линейным законом изменения перемещений вдоль сторон (см. § 5.2). Для исходного элемента блоки матрицы а=[а1-аув(ат] определяются выражением (5.17). Для построения нового элемента можно принять, например, что перемещения их, иу изменяются в пределах конечного элемента по закону
«х = ««Vе + с. (1 - g2) (1 - п2); иу = ayv* + с2 (1 - g2) (1 - if).
(5.39) где ах и ау — первая и вторая строки матрицы а.
Здесь в качестве дополнительной выбрана функция (1 — g2)X Х(1 — т)2), которая иа сторонах элемента кпри £ = ±1; т] — ±1) обращается в нуль. Следовательно, добавление таких функций не нарушает совместности конечных элементов. Однако по причинам, о которых будет сказано ниже (см. § 6.2), построенный таким образом конечный элемент ведет себя практически так же, как и базовый, т. е. исполь* зоваиие выражений (5.39) дает лишь незначительное улучшение жест-костиых характеристик. Аналогичный результат получится и в том случае, когда вместо (1 —g2) (1 —г])2 взять, скажем, функцию cos(ng/2) cos (лт]/2), которая также ие нарушает совместности конечных элементов.
В работе [1] предлагается использовать следующее поле перемещений:
«х = «xv* + (1 — g2) + с2 (1 — Т]2);
«» = a» ve + c3(l -g2) + c* (1-П2). (5.40)
Здесь вводится четыре дополнительных параметра ct...c4. Функция 1 — g2 иа сторонах 1) = ± I ие обращается в нуль; точно так же функция 1 —т]2 ие равна нулю иа сторонах g = ±1. Следовательно,
вдоль сторон прямоугольника перемещения уже не будут изменяться по линейному закону, как в случае базового элемента, и получаемые таким путем конечные элементы оказываются несовместными.
Полагая с — {сх с2 с3 с4), запишем:
1~£2
1 —т]2 0 0 ]
О 1— 1— т]2 ] ’
В соответствии с формулами
Коши находим матрицу 0О:
Ро
даох/дх доду/ду
аОу /дх -|- д аох /ду J
= —4
Ч/а
О
О
О
О
Т]/&
О
О
1/а
О ‘ Т]/&
О
Подставляя далее
£>/(1—ц2) О"
Е/(1 -ц2) О
О G
третью формулу (5.32), получим после интегрирования матрицу “?£/(!—ц2) ~
О
16Л
£7[у(1 —ц2)]
Для базового элемента матрица 0 была получена в блочной форме 0 — ЕР* P/PzPm). где 0г определяется по (5.19), (5.20). С учетом этого матрицу кь, определяемую вторым равенством (5.32), представим также в блочном виде:
кь =
кьл кь. j
*Ъ.1
—^Ъ.т—
где типовая подматрица
кь,г= [ 0^x00 йт (r = 7, j, I, т).
Xе
Подставляя сюда выражения для 0Г, имеем
х и 0о, после интегрирования
кь.г—
2А^т]г Г 0
з Um1—и2)
О G £ц/(1—ц2) GO О
Далее, пользуясь формулой (5.35), вычисляем матрицу жесткости к*. Напомним, что матрица ка представляет собой матрицу жесткости базового элемента. В § 5.2 оиа получена в блочном виде и определиется формулами (5.13), (5.22), (5.23). К подобной же форме можно привести и выражение для ке. В итоге для типовой подматрицы k®s имеем;
Ь® _Ь* I ь*
Krs“ Krs, *Vs, G»
^rs, E —
Eh 4(1—p2)
1 — pi2 3
Mr
ПгПз f.,1 —
т к 3
GA_p)rn»/T nrSel 4 Ur 4s Ld '
Полученный результат в точности совпадает с формулами (5.29)— — (5.30) дли прямоугольного элемента с линейным полем напряжений, рассмотренным в § 5.3. Таким образом, два различных подхода приводят в этом случае к одинаковым результатам. Этого и следовало ожидать. Для аппроксимации перемещений по формулам (5.26) и (5.40) используются в конечном счете одни и те же функции: 1, |, ц, £2, ц2.
Причем миожители перед £2 и т]2 в (5.26) введены таким образом, чтобы удовлетворялись дифференциальные уравнения равновесия, а в (5.40) эти множители находятся из условия минимума полной энергии. Но, как отмечалось в § 2.3, минимизация полной энергии есть, по существу, неявное удовлетворение дифференциальным уравнениям равновесия, что и объясняет полученный выше результат.
§ 5.6. Четырехузловой изопараметрический элемент
Рассмотрим четырехугольный элемент произвольной формы с узлами в вершинах (рис. 5.7, а). Поставим целью построить систему аппроксимирующих функций, обеспечивающую совместность элементов. Для этого необходимо, чтобы вдоль каждой стороны элемента перемещения их, ии изменялись по линейному закону.
Введем прежде всего вспомогательный квадрат со стороной, равной 2, и отнесем его к системе безразмерных координат £, т], начало которой помещается в середине квадрата (рис. 5.7, б). На сторонах квадрата переменные £, т) принимают значения ± 1. Пусть требуется аппроксимировать в пределах квадрата какую-либо функцию Ф (£, т|), для которой известны ее значения Фг, Фу, Ф;, Фт, в угловых точках. Такую аппроксимацию удобно выполнить с помощью функций (5.18)
%) (1 +чг ч) (г==1‘-/•1>т)> 4
которые уже использовались ранее для аппроксимации перемещений в плоском прямоугольном конечном элементе. Функция грг, определяемая таким образом, принимает единичное значение в узле г и обращается в нуль во всех остальных узлах, изменяясь вдоль сторон квадрата по линейному закону. Функции называют иногда функциями формы [6].
Выражение
ф (В. п) = 4~ <1 ф*+-т с1 + +
4 4
+4-0 +5) d + П) фг +_L (1 (1 + ф фт (5.41)
4 4
Рис. 5.7
дает такую аппроксимацию функции Ф, которая удовлетворяет условиям в узловых точках. При этом Ф (|, я) изменяется по линейному закону вдоль прямых £ = const или я = const, в том числе вдоль сторон квадрата.
Поставим теперь в соответствие каждой точке квадрата некоторую точку исходного четырехугольника, полагая х = — я)» у = у (£, л)- В вершинах четырехугольника функ-
ции х (I, я), У (В, Л) должны совпадать с их узловыми значениями (т. е. с координатами узлов). Используя свойства аппроксимации (5.41), можно сразу записать искомые зависимости:
х = 4-(1-^)(1-т>)^ + 4-(1+^) 0“П)*,+
4 4
+4- с1+§ о+n) *+4-d -в) и +п) хт-, 4 4
У~ 2. (1-1) (1-я) yt + 4- (144) (1 -Я) Уз +
4 4
4-4- 0 44) d 4-Т1) 4- 4- (!-4) (! 4-п) Ут- (5-42) 4 4
Примем, например, £ = 1. Тогда из (5.42) получим
х=Т "" Xi+Т х':
У = ~ О ~Я) Уз + -у U + Я) Уь (5.43)
Эти соотношения определяют прямую в плоскости х, у. При q = — 1 имеем х = xj, у = у}, а при т) = 1 —х = хг, у = уг; следовательно, изменяя q от —1 до +1, получаем одну из сторон четырехугольника. Рассуждая подобным образом, нетрудно убедиться, что формулы (5.42) действительно дают отображение квадрата на рассматриваемый четырехугольник.
Переходя далее к аппроксимации перемещений их, иу, будем также выражать их через переменные £, q. Это позволяет получить функции с требуемыми свойствами:
их = -1- (1 -В) (1 -q) vix + 2- (1 +1) (1 -q) vSx +
+4- <1 + % о+Я) «1х+4- (1 -В) (1 +я) vmx, 4 4
=4- а - в) (i-я) +4- о + в) а -я) «л, +
+ 4- (1 + В) (1 + q) v{„ + 4- (1 —l) (1 + q) vmy. (5.44)
Рассмотрим, например, характер изменения перемещения их вдоль стороны jl, полагая снова £ = 1. Из (5.44) имеем
«х = 4" С1 — Я) + 4" (* +Я) vix- (545)
Отсюда видно, что во-первых, при q = — 1 и q = 1 (т. е. в узлах j и Z) перемещение их совпадает с vjx и vtx. Во-вторых, формулы (5.43) и (5.45) определяют в пространстве х, у, их прямую, заданную в параметрическом виде:
х = аг + a2q; у = br + &2q; их = сг + c2q.
Это означает, что вдоль стороны jl перемещение их изменяется по линейному закону. Аналогичные рассуждения показывают, что формулы (5.45) обеспечивают аппроксимацию перемещений внутри конечного элемента с линейным законом изменения вдоль всех его сторон.
Полагая u = {их иу}\ ve = {v/vyvivro}, где vr = = {огжог9}, представим (5.44) в стандартной форме u = ave.
Здесь а = где типовая подматрица аг включает
в себя функции (5.18):
Перейдем далее к вычислению матрицы р « [P;P7PiPml-Типовая подматрица рг образуется из строк матрицы аг по формуле дагх дх о даг»
—
dary дагх _ дх ду _
откуда следует
дх
О
о
di|>r
- ду
д^г ду дт|>г дх _
(5.46)
дфг д-фг
Входящие сюда производные -£ и — нельзя наити непосредственным дифференцированием, так как фг не зависит в явном виде от переменных х, у. На первый взгляд естественным кажется воспользоваться правилом дифференцирования сложных функций:
chpr _ дфг д$ । _£Фг_ дт) . дфг ____________ д$г д£ дфг дт) .
дх д? дх дг) дх ’ ду ду дг) ду
но это требует знания явной зависимости переменных т] от х, у, в то время как мы располагаем лишь обратной зависимостью, выражаемой равенствами (5.42).
Поэтому для вычисления требуемых производных воспользуемся формулами
дфг _ дфг дх <h|>r ду . дфг______<h|?r дх difr ду
дх ду ’ дц дх дц ду дц
которые в матричной форме имеют вид
бфг аб афг
= J& n)
(5-47)
Здесь через J (£, я) обозначена так называемая матрица Якоби:
J а, п) =
дх aS дх _Л)
ду aS ду
_
(5.48)
элементы которой легко находятся по (5.42). Поскольку функции в левой части (5.47) также нетрудно найти из соотношения (5.18), то равенство (5.47) можно использовать для определения искомых производных:
афг ~ дх
дфг ду
аФг ~ as афг
_ *1 _
(5.49)
Здесь -^. = 11(14-^1)); (1+Jr |), а в
dS 4 Л) 4
матрицу J (£, я) входят функции:
“ = — (1—П) х4 + (1 —»]) Х/ + (1 +ч) Xi— (1 4-т]) хт];
Ofe 4
^==±[_(l_^)X|_(l+g)x> + (l+g)Xl +(l„g)XmI;
СП) 4
Л_ = _1_ [ —(J —Т]) у, + (1 —Т]) Уу + (1 +П) Уг—(1 +п) ут]-og 4
СП) 4
Заметим, что фактическое вычисление матрицы жесткости рассматриваемого элемента приходится выполнять на ЭВМ с помощью численного интегрирования. При этом матрицу 0 требуется находить в отдельных точках области, положение которых определяется используемым правилом интегрирования. “В этих точках в соответствии с записанными выше фор-
мулами определяют матрицу J, а затем обратную к ней
матрицу J-1. В тех же точках по (5.49) вычисляют матри-цу производных у1 и (r=i, j, т), из которых может
быть сформирована матрица 0Г (5.46).
Типовой блок матрицы жесткости ке находится по формуле
k's- f ₽rrx₽sdT, те
где интегрирование ведется по объему Xе конечного элемента. Удобно перейти к интегрированию по £, т), поскольку при этом получаются простые пределы. Можно показать [6], что для этих переменных элементарный объем выражается так:
dr=h| J(£, T])]d£drj,
где h — толщина пластины, a |J (g, т])| — определитель матрицы Якоби, называемой якобианом. Таким образом, в случае обобщенного плоского напряженного состояния матрицу k‘s находим по формуле
1 1
=h J *₽, IJ а. Т|) I dn. (5.50)
—. 1 1
Интегрирование здесь, как уже было сказано, выполняется численно на ЭВМ. Некоторые формулы численного интегрирования, применяемые в методе конечных элементов, будут приведены ниже.
Приведение распределенных нагрузок к узловым силам выполняется обычным образом. Так, если в плоскости элемента действуют объемные силы R, то их заменяют узловыми по формуле
Р arRdx.
Полагая Ре = {Р'Р/Р/Pm} и переходя к интегрированию по £, т] в плоскости элемента, придем к следующему выражению для типовой подматрицы эквивалентных узловых сил:
1 1
P, = /i S $ <R| J(M)l<^dr] — (5.51)
— 1 — 1
Здесь интегрирование также выполняется численно. Матрица аг в точках интегрирования находится по формулам (5.17), (5.18).
Получаемые таким образом конечные элементы являются совместными. Характерной особенностью здесь является то, что для задания перемещений их, щ, и координат х, у через безразмерные координаты £, г; используются одинаковые выражения. Это предполагает, в частности, что для определения геометрии конечного элемента требуется столько же параметров (координат узлов хг, уг), сколько параметров (узловых перемещений vrx, vry) необходимо для задания поля перемещений. Такие конечные элементы называются иэопараметричес-кими. Если геометрия совместных элементов определяется меньшим числом параметров, чем поле перемещений, то такие конечные элементы называют иногда субпараметрическими. В некоторых приложениях (например, при расчете оболочек) используются также суперпараметрические элементы, в которых число параметров, определяющих геометрию, превышает число узловых перемещений [6).
§ 5.7. Несовместный четырехугольный элемент
Рассмотренный в предыдущем параграфе конечный элемент является обобщением прямоугольного элемента с линейным изменением перемещений вдоль сторон. Его можно было бы использовать при моделировании стеиок в балках переменной высоты, но ои, так же как И прямоугольный элемент, неправильно воспроизводит состояние изгиба в своей плоскости, оказываясь чрезмерно жестким. Как уже говорилось в § 5.2, источником этого является ложная деформация сдвига еад, которая в элементах данного типа всегда сопровождает чисто из-гибные деформации. Один из приемов исключения ложного сдвига, заключающийся в применении для матрицы жесткости специальной схемы численного интегрирования, будет изложен в § 6.6. Здесь мы воспользуемся другим способом, основанным на задании характера изменения напряжений в пределах конечного элемента.
Итак, рассмотрим четырехугольный элемент с узлами в вершинах (см. рис. 5.7, а). Элемент имеет восемь степеней ©свободы
v<?= {*£ vy V/ vm),
где vr = {vrxvry}. Будем предполагать, что в пределах элемента компоненты напряжений изменяются по закону
°хх ~ сг °п = сэ ~ ft,
где с, — некоторые постоянные.
Такне напряжения удовлетворяют дифференциальным уравнениям равновесия при отсутствии объемных сил и условию совместности деформаций и воспроизводят равномерное растяжение и изгиб в двух на-166
правлениях, а также чистый сдвиг. Распределение перемещений их, ии будет представлено при этом формулами (5.25):
“х—/1+Ар:+/зУ+/«л;!/—fe---------
“р = /5+/в*+/?(/ +f»xy — ft —
Введя Матрицы u = {их иу}\ f= {fJa-.-fe}, представим эти соотношения в виде
и = a*f, (5.52)
где через а* обозначена матрица
[1 х у ху ООО
ООО —(х2 + цу2)/2 1 х у
-(gx2+j/2)/2 ху
(5.53)
Свяжем далее параметры f с узловыми перемещениями Vе. Для этого приравняем в узлах элемента перемещения их, иу к соответствующим узловым значениям:
fiJrfixr~\~f^yr-!rfircTyr — fe —°гх>
х^ + цу^
ft-i-fexT-f-fiyr~l~fexrlfr—h--Z------—vrjr (5.54)
«£
Всего мы имеем, таким образом, восемь уравнений (г = I, j, /, m) относительно восьми постоянных f. Полученную систему уравнений можио записать в форме
zf = < (5.55)
где матрица z, имеющая размер 8X8, формируется исходя из выражений (5.54). Разрешай (5.55) относительно f, ирикодим к равенству вида
f == «Vе, (5.56)
где ft —х-1; обращение матрицы г выполняется численно иа ЭВМ. Подстановка (5.56) в (5.52) приводит к обычной зависимости а = = где матрица а определяется как произведение
a = a*ft. (5.57)
По формуле (4.7) вычисляем матрицу 0. Строки аж, ау матрицы а в соответствии с (5.57) равны: ах = a*Q; ау = a*Q, где ах, <х*у определены выражением (5.53).
Матрица ft — числовая, так что формулу для р можно представить в виде
₽ = P*Q, (5.58)
где
да* дх
дау ду
"0 10 у 0 О О
ООО —цу О О 1
.0 0 1 0 0 1 0
— рх’
х О
да*у да* дх ду
Подстановка (5.58) в выражение (4.11) приводит к следующей формуле для матрицы жесткости:
ke = Qr k*Q,
(5.59)
где
k*= J (0*)тх0* dT< (5.60)
Здесь, как и ранее, матрица х определяется по (1.24).
Для выполнения иитегрировання в (5.60) удобно, как и в случае изопараметричсского элемента, перейти к безразмерным параметрам g, т), полагая
х=2фг (g, г,) хг; у=2фг (£, п) Ут-
Суммирование здесь выполняется по четырем узлам элемента; функции фг (1, О) даются равенством (5.18). Узловые значения gr, т), параметров т) назначаются в соответствии с рис. 5.7.
В соответствии с (5.60) получаем расчетную формулу
1 1
к*=Л$ $ (₽‘)rx₽*U(|.n)ld£dn. — 1 —- 1
(5.61)
где |J (g, t])| — определитель матрицы (5.48).
Получаемые таким образом конечные элементы являются несовместными. Они могут быть использованы при решении плоской задачи теории упругости наравне с описанными ранее элементами, а также при моделировании различных балок с непараллельными поясами и тонкими стенками. При этом имеется в виду, что ось х (или ось у) орнен-.тирована вдоль оси балки. Если же балка произвольно ориентирована относительно осей х, у, то сначала следует ввести соответствующую местную систему координат х, у, для которой применимы исходные формулы
о_._ + с2у; о- - =с3+<?2х; а--=с3.
Полученная в этих координатах матрица жесткости должна быть затем преобразована в матрицу в общей системе координат в соответствии с обычной процедурой, описанной в § 3.2.
§ 5.8. Плоские изопараметрические элементы высших порядков
Завершая рассмотрение плоских элементов, остановимся сначала на конечном элементе с четырьмя сторонами (в общем случае криволинейными), показанном на рис. 5.8, а. Элемент помимо четырех узлов в вершинах имеет промежуточные узлы на сторонах. Координаты узлов задаются в качестве исходных данных. Для удобства рассуждения все узлы пронумерованы от 1 до 8. При практическом применении элемента каждому из этих восьми узлов
должен быть поставлен в соответствие его номер в общей схеме нумерации узлов рассматриваемого тела.
Так же как и в случае изопараметрического элемента с четырьмя узлами, введем вспомогательный квадрат со стороной, равной 2 (рис. 5.8, б). Положение произвольной точки внутри квадрата определим координатами £, т], которые изменяются от —1 до 1. На сторонах квадрата выберем восемь точек в соответствии с числом узлов конечного элемента. Четыре из них находятся в вершинах квадрата, а четыре других — в серединах его сторон.
Построим для r= 1, 2, ..., 8 такие функции фг(£, т|)> к0" торые в точке г принимают единичное значение, а во всех остальных узловых точках обращаются в 0. Их можно получить [6], комбинируя использовавшиеся ранее функции (l±g) (IzfcT)) с функциями (1—£2) (1±л) и (1—л2)Х Х(1±£).
Функция (1—£2) (1—т|), например, равна нулю при ?=±1, а также при т]= 1, т. е. во всех узловых точках, кроме точки 2. Следовательно, можно сразу записать
Множитель % введен для того, чтобы в точке 2 выполнялось равенство ф2 = 1.
Точно так же можно записать функции фг для остальных точек, расположенных иа серединах сторон квадрата:
(£, п) =у (1 -<12) (1-+ (В, -П)=У (1 -n (14-11);
Ф.& ч)=у(М2)(1Ч).
Рассмотрим далее функцию (1—е)(1—т|). Она равна нулю при § = 1 и при г] = 1, т. е. во всех узловых точках, кроме точек 1, 2, 8. Комбинируя ее с ф2 и ф81 можно построить функцию, которая обращается в нуль также и в точках 2, 8. Удовлетворяя, кроме того, условию в точке 1, придем в результате к следующей функции фь
(I. w-= 4“ <1—0 - *1) - -г О -S2) (1 -л)-
4 4
-уО-п’Н!-?)-
4
Аналогичные рассуждения позволяют получить также функции:
ф3(£. п) =4 + £) <! -п)-4- -
4 4
4
Ф5(5.Ч)=4<1-|-^Н1+г1) -4(!-^)(1+П>-
4 4
-4 +£);
4
4 4
_4(i-r)2)(i_g).
4
Записанные выше формулы дтя фг(£, л) можно представить в следующем обобщенном виде:
фг (I, Л) = -36г4<~2 [У Тк2 (1 + 1Л) (1 + Пг П) -
-rtf (1 -I2) (I +Пг Ч)-& (I --П2) (1 + 1г 1)1- (5.62)
Здесь £г, т]г — координаты узловых точек:
г .... • 1 2 3 4 5 6 7 8
1г . -1 0 1 1 1 0 —1 —1
Пг • • • . . —1 —1 —1 0 1 1 1 0
Если теперь требуется аппроксимировать в пределах квадрата какую-либо функцию Ф (£, т])> для которой известны ее значения Фг в точках г — 1, 2, .... 8, то можно сразу записать
8
ф(?.п)= 2 Л)Ф,- (5.63)
г= I
Как это видно из (5.62), (5.63), функция Ф (£, т]) будет вдоль сторон изменяться по квадратичному закону. Квадратная парабола вполне определяется тремя какими-либо параметрами, так что значения Фг в трех точках, лежащих на стороне квадрата, однозначно определяют закон изменения Ф (£, т]) вдоль этой стороны.
Поставим далее в соответствие каждой точке квадрата некоторую точку исходного элемента, полагая
8 8
X (I, Т1) = 2 4>г (£, п) хг\ у(^,х}) = 2 (£, т|) уг, (5.64)
/•= 1 г= 1
где хг, уг — координаты узла г. При этом получится криволинейная фигура, стороны которой проходят через заданные узловые точки. Положим, например, |= 1. Тогда из (5.62), (5.64) получим
х= —т) (1—т|) Хз +(1 —II2) х4—П (1 +-Л) х5;
У = — ~ П (1—Л) //з+-(1 — Л2) У4 — у П (1 + п) Уь-
Эти два равенства дают уравнение стороны 3—5 конечного элемента в параметрической форме. В них входят координаты только тех трех узлов, которые принадлежат данной стороне. Точно так же можно показать, что каждая сторона конечного элемента, полученного на (5.64), однозначно определяется координатами трех узлов, принадлежащих этой стороне. Поскольку узлы являются общими для смежных элементов, то отсюда следует, что смежные конечные элементы будут плотно прилегать друг к другу, образуя сплошное тело.
Аналогичными формулами воспользуемся и для аппроксимации перемещений:
8 8
их = 2 п) «ч ==• 2 ч) vry- (5-65) Г =£ 1 гж 1
Такая аппроксимация обеспечивает совместность конечных элементов. В самом деле, координаты^*, у* точек элемента пос
ле его деформации станут равными х* = х + их; у* = у + + иу, т. е. с учетом (5.64) и (5.65);
8 8
х* = 2 4>г & Л) (xr + vrx); у*--^ фг (£, п) (Уг + vry). г=1 Г=1
Величины х‘ — xr + vrx, у* — уг + игу представляют собой координаты узлов деформированного элемента, и равенства
8 8
X* = 2 фг (L n) X*; у* = 2 Фг (5. П) У* Г=\ Г=1
дают отображение квадрата на деформированный конечный элемент. Но, как показано выше, такое отображение обеспечивает непрерывность тела на границах между смежными элементами. Отсюда и следует свойство совместности криволинейных изопараметрических элементов.
Дальнейшие выкладки полностью аналогичны тем, которые выполнялись выше для изопараметрического элемента с четырьмя узлами. Типовой блок матрицы а = [«j а2... а81 имеет вид
Фг О
О
Фг
а блоки матрицы Р = iPiP2---Psl формируются из производных от функций фг по координатам х, у.
дх
О
дфг
ду
О
дфг ду
дх _
Эти производные находятся из равенства
дх
ду
дфг д1 дфг
<Эг)
Здесь J-1 — матрица, обратная матрице Якоби:
JG,n)=
дх di дх Л]
ду di ду
Л]
элементы которой определяются по формулам
дх _ -у дф,. . дх _ у дфг
dg dg г’ Л) ' Л)
ду _ у дфг . ду __ у дфг
dg fa д1 Ут' Л] fa дц
Производные от фг по переменным g, т] равны:
-7^ = grjL.2- [t|« (1 + TJ) (gr+ 2g)—gr (1—T>«)];
„ 4 (5.66)
Ц(I + gr g) (tJr + 2т1)-т)г (1 -ga)].
Л] 4
При записи (5.66) учтено, что для любого г справедливы равенства g? = gr, T]r = Пг-
Типовой блок матрицы жесткости вычисляется с помощью численного интегрирования по формуле
k‘s = $ j М J (g« ’dldg d t) (r, s = l,2.........8),
— i —i
где |J (g, tj)| — определитель матрицы Якоби.
Изопараметрические элементы с восемью узлами позволяют при одинаковом числе узловых перемещений получить значительно лучшую точность, чем изопараметрические элементы с четырьмя узлами. Они особенно удобны для расчета плоских тел с криволинейными границами. Их можно применять также для моделирования тонких стенок в плоских криволинейных брусьях типа шпангоутов (рис. 5.9).
Для той же цели можно с успехом использовать более простой изопараметрический элемент с шестью узлами, показанный на рис. 5.10, а. Этот элемент имеет две прямолинейных и две в общем случае криволинейных стороны и получается из восьмиузлового элемента путем удаления двух узлов, лежа-
щих на противоположных сторонах. Матрицу жесткости такого элемента можно получить точно так же, как и в предыдущем случае, только в качестве фг (5, т]) (г = Л 2, 6) следует
взять функции
3?2 _2
п)=——ia? (1 +аг ю (1 п)—(1—а2) а -Нгли.
где параметры gr, т]г определяются в соответствии с рис. 5.10, б. Аппроксимация перемещений по формулам
приводит здесь к их линейному изменению вдоль прямолинейных и к квадратичному относительно | — вдоль криволинейных сторон. Формулировка геометрии элемента осуществляется в соответствии с равенствами
6 6
х= 2 П)*г', У — 2 ’l)Ут-
г~ 1 г= 1
Аналогично могут быть построены и более сложные элементы. На рис. 5.11, а показан, например, четырехугольный элемент с двенадцатью узлами. Помимо четырех узлов в угловых точках на каждой стороне имеется по два промежуточных узла. Поставим в соответствие этому четырехугольнику квадрат со стороной 2 в координатах л (рис. 5.11, б). Будем считать, что промежуточные узлы квадрата расположены на расстоянии с0 от середин его сторон, так что их координаты равны: = ±с0, т)г — ±1 или = ± 1, т]г = ±Со- В угловых точках %г — = ±1, Лг — ±1. Как и в предыдущих случаях, можно подобрать двенадцать функций фг (£, т]) таких, что каждая из них имеет единичное значение в одном из узлов и обращается в нуль
в остальных узлах. Можно показать, что все эти функции даются единым выражением
Ф,(5. П)
_(ёг+ёНть-+п)
4?гПг(1— с?)
(Пг2-eg) (1-ё2) + (У~С§) (1-n2)
1-2?ггЛ24-с? +
(5.67)
Исходя из формул х - .ЕфгХг, у = ^тут, их = 2фгугх, иу — ^^Ту, в которых суммирование ведется по всем узлам, и пользуясь описанной выше процедурой, можно построить матрицу жесткости данного конечного элемента.
Величину с0 берут обычно [6] равной V3. В работе [34] рекомендуется для повышения точности результатов (в частности, в динамических задачах) брать с0 = 1/V5.
Заметим, что изопараметрические элементы образуют иерархию, в которой элементы с узлами в вершинах рассматриваются как элементы первого, с одним промежуточным узлом на каждой стороне —второго, с двумя промежуточными узлами— третьего порядка и т. д.
§ 5.9. Деформация пространственного криволинейного стержня
Для расчета лонжеронов и шпангоутов необходимо помимо плоских элементов, моделирующих стенку, располагать также конечными элементами для моделирования поясов. В поясе возникает продольная сила, которую будем считать равномерно
распределенной по площади его поперечного сечения. Это до* лущение приемлемо для достаточно высоких балок, у которых размеры поперечного сечения пояса малы по сравнению с высотой балки. Оно позволяет рассматривать вместо реального пояса осевую линию, проходящую через центры тяжести его поперечных сечений и наделенную жесткостью на растяжение-сжатие. Изгибной жесткостью пояса будем пренебрегать, учитывая, что она мала по сравнению с изгибной жесткостью поперечного сечения балки в целом. Таким образом, мы приходим к одномерной схематизации поясов, при которой все величины, характеризующие напряженное состояние пояса, зависят только от одной переменной (скажем, от дуговой координаты).
Прежде чем переходить к построению соответствующих конечных элементов, выведем формулу для расчета деформации пространственного криволинейного стержня. Пусть уравнение осевой линии стержня задано в параметрической форме
X = X (£); у = у (g); z = z (g). (5.68)
Каждому значению параметра | соответствует некоторая точка М (х, у, г). В совокупности эти точки образуют пространственную кривую и параметр 5 можно рассматривать как криволинейную координату на этой кривой.
Если дать параметру 5 малое приращение d£, то получим соседнюю с М точку N с координатами х 4- dx, у 4- dy, г 4-+ dz, где dx, dy, dz определяются формулами
dx=-^M; dy=-^-d£; dz --£-dg (5.69)
d§ rig
и представляют собой проекции отрезка MN на координатные оси. Длина
ds = У dxa 4- dya 4- dz2
этого отрезка может быть с учетом (5.69) подсчитана по формуле
ds = 4d£, (5.70)
где
(5.71)
|/ Ug/ k dg/ \ dg /
Как видно из (5.70), А представляет собой коэффициент» на который нужно умножить приращение dg, чтобы получить длину соответствующего отрезка рассматриваемой кривой.
Отрезок ds составляет с осями х, у, г углы, косинусы которых обозначим через Xgx, Xgy, Xgz. Разделив dx, dy, dz на ds, находим:
Xgx= — —; Zgs,=—^=_LA-. (5.72)
6 A dg ’ w A dg 6 A dg v ' Предполагается, что отрезок ds имеет направление от точки М к точке IV, т. е. в сторону возрастания параметра £.
Три величины (5.72) определяют матрицу-строку
Xg = [X g-Д gyA gzl. (5.73)
Пусть далее точки кривой получают малые перемещения их (£), иу (£), uz (В) в направлении осей х, у, г. Декартовы координаты деформированной кривой будут
х* = х + их, у* = у + иу; г* = г + uz.
Найдем параметр А* деформированной кривой, подставив для этого х*, у*, х* вместо х, у, г в (5.71):
I2 । [Д(у+М
I L dg
d (z+uz) I3 dg J
Учитывая малость перемещений и их производных, будем отбрасывать слагаемые, содержащие квадраты или произведения этих величин. Тогда, с учетом (5.71),
dux , dy duy , dz duz \
dg dg dg + dg dg /’
Обозначив
l ( dx dux dy duy dz duz \ _ .v
( 7 ’
приведем это выражение к виду А * = A V1 + 2е.
Разложим V1 4- 2е в ряд по степеням е в соответствии с формулой
(1 +а)« = 1 -|- па 4- П(Я~1) cta+...
и удержим в разложении лишь слагаемое первого порядка малости. Это дает
Л* = (1+8) А. (5.75)
Длина ds* деформированного отрезка MN аналогично (5.70) будет
ds* = Л*^ == (1 + в) 4dg. (5.76)
Осевая деформация равна отношению (ds* — ds)/ds. Внося сюда (5.70) и (5.76), убеждаемся, что введенная согласно (5.74) величина е есть не что иное, как искомая деформация в точке М.
Если ввести матрицу-столбец перемещений u = {uxuyuz}, то формулу (5.74) можно с учетом (5.72), (5.73) переписать в виде
<5-77»
du fdux du„ d«2l ,
где через обозначена матрица произ-
водных от перемещений по переменной
Выведем попутно формулу для вычисления углов поворота отрезка ds при деформировании. Хотя здесь эта формула и не требуется, но в дальнейшем она понадобится при построении конечных элементов произвольных оболочек. Введем единичный вектор е^, направленный вдоль отрезка ds от точки Л1к точке N. Его проекции иа оси х, у, z есть направляющие косинусы отрезка ds, так что можно записать
где ех> еу, ег — орты осей х, у, г.
Пусть, далее, е0 — некоторый единичный вектор, ортогональный вектору eg и заданный матрицей АОг/ lOz] своих направляю-
щих косинусов:
е0 = ехХог/ еу+X-oz ez •
В результате деформации отрезок ds повернется и угол между ним В вектором ед будет отличаться от л/2 на величину, которую мы обозна-чим <оо. Будем считать ее положительной, если угол между е0 и единичным вектором eg, касательным к деформированной кривой в точке М, становится острым. Косинус угла л/2 — ®0 можно найти с помощью скалярного произведения: cos (л/2 — <оо) = е0 • е|, так как скалярное произведение двух векторов равно произведению их длин на косинус угла между ними.
Но cos (л/2 — <о0) = sin <о0, а поскольку <оо — величина малая, то можно принять sin <оо » ш0. Отсюда приходим к равенству
-> -> ©о — ^0 • •
Как известно, скалярное произведение двух векторов а = ахех + > —>•
+ ауеу + azez; b — bxex + byey + bzez подсчитывается по формуле a‘b—axbx-j-ay by-±-az bz.
Полагая ej ~^хех-}-Х^еу-1-Х^гег, имеем ю0= ХохХ|х + ХОд Х|у+Х02 Цг. или в матричной форме
<O0 = Xq Xg^*,
(5.78)
где X» = I^.gjAgjAgz] — матрица направляющих косинусов деформированного отрезка ds*.
Проекции отрезка ds* иа координатные оси могут быть найдены по формулам (5.69), в которые вместо х, у, г должны быть подставлены координаты деформированной кривой х + их, у + иу, г + иг-
de; d,-d-^±^dE1 d,._4£±^dt dg dg dg
Разделив этн проекции иа длину ds* = (1 + e)4dg, приходим с учетом (5.72) к выражениям:
= 1+е (4*+т dd“{ ); 1+8 (^+ л
1 *
Xt г “ I X. +
®г 1 + в \ *z А
duz \ dg Г
Таким образом, для матрицы Xg получаем значение
v___Ь_Л , _L
н- 1+в 14+ А dg
По (5.78) вычисляем
1 I. ,т 1 . du \
о>о— ~ I Хо X» + —- Хо —— )•
1+а \ 6 Л dg /
Произведение X0Xg есть скалярное произведение е0 • eg, ио векторы -*• ->
е0 и eg ортогональны и это произведение равно нулю. Пренебрегая величиной в по сравнению с единицей, приходим окончательно к выражению
1 i d“ “0= А Хо1Г-
(5.79)
§ 5.10. Одномерные конечные элементы
Рассмотрим семейство пространственных одномерных конечных элементов первого, второго и третьего порядков (рис. 5.12, а, б, в). Геометрию элементов будем задавать координатами узлов, пользуясь при этом изопараметрической формулировкой для определения кривой, проходящей через эти
узлы. Введем вспомогательные отрезки прямой линии. Положение текущей точки отрезка определим координатой g, которая отсчитывается от его середины и принимает на концах значения ±1. Выполним отображение отрезков на конечные элементы посредством соотношений
х = Sipr (5) хт; у = 2фг (ty ут\ г = Sip,. (g)zr, (5.80)
где суммирование ведется по всем узлам конечного элемента. Каждая из функций фг (£) принимает единичное значение в
I
Рис. 5.12
узле г и обращается в нуль в остальных узлах конечного элемента. Можно показать, что этим условиям удовлетворяют следующие функции:
для элемента первого порядка (г = 1, 2)
Ч>Л)="(1+и); (5.81)
для элемента второго порядка (г — 1, 2, 3)
4U£) = 3S?~2 [^(1 + ё^)-(1-Г)1; (5.82)
для элемента третьего порядка (г = 1, 2, 3, 4}
2ё?(2^-1- eg)
(5.83)
Через здесь обозначены точки вспомогательных отрезков, отображающиеся в узлы конечных элементов. Для элемента первого порядка (рис. 5.12, а) — — 1, |2 = 1; для элемента второго порядка (рис. 5.12, б) = — 1, ё2 — 0, £3 — = 1; для элемента третьего порядка (рис. 5.12, в) — — 1, |2 — — с0. Вз = с0, ^4=1. Параметр с0 выбирается так же, как и в случае плоского изопараметрического элемента треть-180
его порядка (см. § 5.8). Обычно берут с0 = 1/3; можно также принимать с0 = 1/V5.
В соответствии с изопараметрической формулировкой запишем далее закон аппроксимации перемещений u = {uxuyuz) конечного элемента по узловым перемещениям:
u (g) = (g) vr. (5.84)
Здесь vr — {vTX vTy оГ2)— матрица перемещений узла г в направлении координатных осей; суммирование выполняется по всем узлам конечного элемента.
По (5.77) получаем выражение для продольной деформации
е = 4' (Ю Ц Уг, /х
гдеф/ (£) = di|>r/dg.
Выражение для е можно также записать в виде е = = SPrvr, где
(5-85) /х
В поперечном сечении стержня возникает нормальное напряжение о; по закону Гука для одноосного напряженного состояния о = Ее. Таким образом, в этом случае в качестве х следует брать скалярную величину Е.
По формуле (4.15) вычисляем блоки k®s матрицы жесткости конечного элемента, которые будут здесь скалярными величинами. Так как dr — Fds — FA d£, получаем
kers—E ] Ftf^Att,. (5.86)
— I
Интегрирование здесь выполняется численно на ЭВМ. Для элемента первого порядка можно получить и аналитическое выражение для kers. В этом случае на основании (5.80), (5.81) имеем
JS=(x2-x1)/2; А.=(у2_^)/2; (г2-21)/2,
так что величина А (5.71) будет представлять собой половину длины I конечного элемента:
А = V(х2 -х^ + (уг -У1)г + (z2—Zi)2/2 =. 1/2.
Согласно (5.72) находим
= (Х2 — *1)/ZJ = (^2 — У1№', Чг = (Z2 — zi)/Z-
а матрицы ₽r в силу (5.85) будут ₽г = (&//) По (5.86) получим в случае F = const
& = (lr^EF/l) kjXj.
Этот результат совпадает с формулами (3.19), полученными для ферменного конечного элемента.
Отметим, что рассмотренные здесь конечные элементы совместны с плоскими изопараметрическими конечными элементами соответствующих порядков.
§ 5.11. Трехмерные конечные элементы
Трехмерные конечные элементы используются для расчета пространственных тел, имеющих трехосное напряженное состояние (кронштейнов и т. п.). Простейшим пространственным конечным элементом является тетраэдр с четырьмя узлами {рис. 5.13), в пределах которого задается линейное поле перемещений:
“х = А + М 4- f Зу + /*z;
иу = f5 + fex + /7г/ + f6z;
Uz == fg + /ю X + [пУ + /12 Z.
Здесь Л.../12 — произвольные постоянные. Приравнивая в узловых точках их, иу, uz к соответствующим узловым перемещениям, можно выразить постоянные / че-
рез узловые перемещения Vе и получить зависимость вида и = от®. Использование обычной процедуры позволяет затем найти матрицу жесткости такого элемента [61.
Для получения достаточной точности решения требуется обычно применять весьма мелкое дробление тела на тетраэдры, что приводит к большим затратам машинного времени. Поэтому такие конечные элементы не имеют большого распространения, и останавливаться на них подробно не будем.
Рассмотрим далее восьмиузловой изопараметрический пространственный конечный элемент, показанный на рис. 5.14, а. Для описания его геометрии и аппроксимации перемещений воспользуемся безразмерными координатами 5, т), £, которые изменяются от — 1 до 1 в пределах куба (рис. 5.14, б).
Рассуждая так же, как н в случае плоских элементов, введем систему функций
Фг (S, П. О = 4 О + ЧгЧ) (1 + U). (5.87)
каждая из которых принимает единичное значение в одной из вершин куба (г — 1, 2, 8), обращаясь в нуль во всех осталь-
ных вершинах и изменяясь линейно вдоль ребер.
Рис. 5.14
Следуя рассмотренной выше схеме построения изопарамет-рических элементов, выполним отображение куба на рассматриваемый конечный элемент посредством соотношений
8 8 8
х— 2 у= 3 z=2^zr. (5.88)
г=1 г=1 Г=1
Подобным образом аппроксимируются и перемещения:
8 8 8
2 Фг°«; «»= 2 Фг»г»; «z= 2 Фг»^. (5.89) Г=1 Г= 1 Г=1
где нгя, огв, vrz — проекции перемещения узла г на координатные оси. Как и для всяких нзопараметрических конечных элементов, формулы (5.88), (5.89) обеспечивают совместность элементов.
Полагая vr = Vе = {v1v2...ve}, представим со-
отношения (5.89) в стандартной форме u = ave, где и — = {t*x«B“z}, а типовая подматрица матрицы а = («!«,...а8] равна
Фг
Фг О
О
Фг.
(5.90)
Обозначая через е = {sxxEuue.2.zExuEyzEzx} матрицу-столбец деформаций и пользуясь формулами Коши, запишем соотношение 8 = ₽ve. Типовой блок рг матрицы Р = [рх р2...р8] формируется из производных от фг по координатам х, у, z:
dtyr/dx О О
О dtyr/dy О
О 0 dtyrldz
dtyr/dy dtyT/dx О О difr/dz д^г/ду _ dtyr/dz 0 д^\/дх
Необходимые производные можно найти через производные от 1|>г по переменным £, т), £:
дх
= J1 <?Фг
~sy~ dt)
д^г
_ Sz _
Здесь J—1 —матрица, обратная матрице Якоби
дх si, ду SI dz ~
J(L = дх ду dz
<5П ch) di)
дх Sy dz
- sz SI st, _
которая составляется из величин
д* _ V* дфг х . V
si £ si ........ ac r'
Производные от функций фг по координатам £, т], £ равны:
^=JL.(1+T]rr1)(l+U); _g^ = jL(l+g4)(l+SrS); dg 8 di) 8
M+U)(i+n,n)-
dg 8
Матрица жесткости элемента к® имеет 8x8 блоков k*s (г, s = 1, 2,..., 8), которые можно найти с помощью численного интегрирования по формуле
I I 1
ке — K/-S----
₽Гх₽з1 J& П. C)|dgdT]dS.
Здесь х — матрица упругости (1.16) для трехмерного напряженного состояния, а через |J (£, т], £)| обозначен определитель матрицы Якоби.
Взяв за основу рассмотренный конечный элемент, можно получить и другие полезные элементы путем совмещения некото
Рис. 5.16
рых узлов. Так, полагая в (5.88), (5.89) координаты и перемещения узлов 6 и 7 равными соответственно координатам и перемещениям узлов 2 и 3, придем к конечному элементу призматического вида (рис. 5.15). Возможны, конечно, и другие варианты.
Рассмотренную выше процедуру вычисления матрицы жесткости можно применить для построения и более сложных пространственных изопараметрических элементов. На рис. 5.16 показан, например, двадцатиузловой пространственный элемент с криволинейными гранями. Можно показать, что для любого узла г — 1, 2, ..., 20 функция
ЗЕ2 Tia С2_2
Фг G, п. О - ---[У £ (1+U) (1 + Пг п) X
X (1 -Hr Q-I? п? (1 + LS) (1 +пгп)(1-£2)-
--«(i+nrn)(i + U)(i-H-
-^2(1+U)(14- 0(1 — п2)]
принимает единичное значение в этом узле и обращается в нуль во всех остальных узлах. Здесь каждая из переменных £, 3, g изменяется в пределах от — 1 до 1, причем узловым точкам соответствуют следующие значения:
г...... 1 2 3 4 5 б 7 8 9 10
Ег.....—io 1 1 1 о—1—i—ii
Зг.....—1 —1 —1 —1 —1 —1 —1—10 о
gr..... 1 1 1 O—1—I—1O 1 1
Продолжение
г......11 12 13 14 15 16 17 18 19 20
1г..... 1—1—10 1 ! 1 0—1—1
Т)г.... О 0 11 1 1 1 1 1 I
t,r....—1—1 11 1 о —1 —I -I о
С использованием этих функций по формулам
20 20 20
* = 2 Фг*/ у= 2 ’biG-; z= 2 r=l r=l z — I
описывается геометрия элемента, а с помощью соотношений
20 20 20
2 «»= 2 № «.= 2
г—I г=1 Г=1
выполняется аппроксимация перемещений. Дальнейшие выкладки вполне аналогичны тем, которые приведены выше для восьмиузлового элемента.
Применение таких элементов дает возможность моделировать тела сложной конфигурации с помощью относительно небольшого числа элементов и получать при этом приемлемую точность решения.Это оправдывает их использование, несмотря на значительные затраты машинного времени на формирование матрицы жесткости отдельного элемента.
§ 5.12. Численное интегрирование в методе конечных элементов
Выше было представлено несколько конечных элементов, для вычисления матриц жесткости которых приходится прибегать к численному интегрированию. В связи с этим встает вопрос о выборе экономичных схем численного интегрирования. Поскольку интегрирование матрицы осуществляется интегри-
рованием каждого ее элемента, то достаточно рассмотреть интегралы от скалярных функций вида
1 1 I
j /ах j j /а,
или
/а, n. 9<ws.
Начнем с простого интеграла
$ f(IX
— I
Обычный способ приближенного интегрирования заключается в следующем. В нескольких точках £ = взятых на ин
тервале интегрирования, вычисляют значения подынтегральной функции ft = f (£f).
Далее находят полиномиальную функцию <р (£), проходящую через точки (Въ /,), (S2, /2), ... (рис. 5.17), и вы-1 числяют интеграл f <р (£) d£, —I величину которого принимают в качестве приближенного значения интеграла от /(£). В численного интегрирования
Рис. 5.17
итоге получают формулы квадратурные формулы),
(или
имеющие вид
* п
j £ CJ&).
(5.91)
где п — число точек интегрирования; аг — так называемые весовые коэффициенты, значения которых зависят от количества и расположения точек интегрирования £г.
Точки в которых необходимо вычислять подынтегральную функцию, выбирают различными способами. Один из способов заключается в том, что интервал (—1,1) делят на несколько равных отрезков, концы которых принимают в качестве точек интегрирования. Получаемые при этом квадратурные формулы носят общее название формул Ньютона—Котеса. В этом способе положение п точек задают заранее, и в формуле (5.91) необходимо определить лишь весовые коэффициенты at. Их можно искать из условия, чтобы формула (5.91) давала точный результат для следующих подынтегральных функций f (£): 1> &> &2, ^"“1. Это дает столько уравнений, сколько необхо-
димодля определения at. Таким образом, «-точечная схема интегрирования Ньютона—Котеса дает точный результат для любого полинома степени не выше п — 1; эту максимальную степень называют порядком численного интегрирования. Отметим, что частными случаями квадратур Ньютона—Котеса являются формула трапеции (п = 2) и формула Симпсона (п = 3).
Другой способ заключается в том, что положения точек не задают заранее. Их определяют из условия, чтобы квадратурная формула (5.91) при фиксированном числе п имела максимально высокий порядок. Здесь в качестве неизвестных выступают не только весовые коэффициенты гаг, но и значения и можно потребовать, чтобы формула (5.91) давала точный результат для функций 1, £, £2, ..., Получающиеся отсюда 2п уравнений позволяют найти 2п неизвестных гаг и £г. Формулы численного интегрирования, построенные таким способом, имеют порядок 2п — 1 и носят название квадратурных формул Гаусса. Интегрирование по Гауссу требует при одинаковой степени точности почти вдвое меньшего числа точек, чем в случае использования формул Ньютона—Котеса. Вычисление подынтегральных функций связано обычно со значительными затратами машинного времени, вследствие чего формулы Ньютона — Котеса в методе конечных элементов практически не применяются.
Положения точек Гаусса определяются иррациональными числами, но при использовании ЭВМ это не имеет существенного значения. Приведем некоторые значения at и £г [101:
для п = 1 = 0; Oj = 2;
для п = 2 = — Si = 1/УЗ; ах — а2 — Г,
для п — 3 Ь = — £i = V3/5; £2=0; аг = а3=5/9; аа = 8/9;
для га = 4 ----= 0,861 136 311 594 0492;
В3 = _ g2 = 0,339 981 043 584 8646;
= at = 0,347 854 845 137 4568;
ай = а3 = 0,652 145 154 862 5432.
При вычислении интеграла
( /(£, n)d^dn
от функции двух переменных можно принять сначала, что т] = — const, и проинтегрировать по
f f(l, n)d£= 2М&, П), — i <=i
где «1 — число точек Гаусса в направлении |.
Вторично? интегрирование по переменной л дает
f s aif<& П)*! = 2 а‘ f n)dn=
_ji=l 1=1 Jl
= 2fl' 2 a№ nj). r=l /=1
где na — число точек Гаусса в направлении г)- Отсюда приходим к формуле интегрирования
[ И (6, П) <1Ут) - 2 2 ai ai f П>)-— 1—1 i=i/=i
Координаты £г, т]> точек Гаусса и веса а1г aj совпадают с соответствующими значениями для одномерного случая.
Подобные рассуждения позволяют получить аналогичную формулу и для тройного интеграла:
$ f f f(L ть OdgdndC = S 2 2 Ы
J1J1J1 1=1/=!*=!
где nlt n2, n3 — количество точек интегрирования, взятых в каждом направлении.
Очень важным является вопрос о выборе числа точек интегрирования. Точность интегрирования будет тем выше, чем больше этих точек, но с увеличением их числа возрастают затраты машинного времени. Минимально допустимый порядок интегрирования в трехмерном случае определяется требованием [6], чтобы интеграл
f f j lJ(S. Ч. OldSd^dC, -i-i-i
где |J (£, т|, £)| — определитель матрицы Якоби, мог быть найден точно. Это соответствует условию, чтобы формула интегрирования позволяла точно вычислить объем конечного элемен
та. Использование более низкого порядка интегрирования недопустимо, ибо при этом исчезает сходимость конечноэлементного решения к точному по мере сгущения сетки. Более подробно об этом будет сказано в § 6.5. Обычно рекомендуется при практических вычислениях увеличивать число точек Гаусса по сравнению с минимально допустимым. Аналогично формулируется подобное требование для двумерного н одномерного случаев. В табл. 5.1 приведены минимально допустимые {/11 X и2 х и3}т1п и рекомендуемые njXngX/гз числа точек Гаусса для тех конечных элементов, которые были рассмотрены выше.
Таблица 5.1
Конечный элемент 1п1хПг’пз]т1п
° 2 2
3 3
1x1 2x2
2x2 3x3
2*1 3X2
3x3 ‘fXlf
1x1x1 2x2x2
2x2x2 3x3x3
Как уже сказано выше, при вычислении матрицы жесткости метод интегрирования Гаусса оказывается наиболее экономичным. Однако в других случаях иногда целесообразно использовать иные схемы интегрирования. Например, в динамических задачах приходится рассчитывать так называемые матрицы масс конечных элементов. Если точки интегрирования совпадают с узлами конечного элемента, то матрица масс оказывается диагональной, что очень важно для разработки экономичных процедур динамического расчета конструкций. Подробнее вопрос о вычислении матрицы масс конечных элементов будет рассмотрен в гл. 9; здесь же в этой связи остановимся еще на двух схемах численного интегрирования.
Первая из них, называемая методом интегрирования Маркова [10], имеет обычный вид (5.91). Отличительной чертой метода Маркова является специфический выбор точек интегрирования. Две крайние точки всегда совпадают с концами отрезка, а положение внутренних определяется (наряду с весовыми коэффициентами) так же, как и в методе Гаусса, т. е. из условия, чтобы интегрирование было точным для полинома максимально высокой степени. Заметим, что двухточечная схема Маркова совпадает с правилом трапеции, а трехточечная — с правилом Симпсона. В четырехточечной схеме координаты внутренних точек оказываются равными ± 1/V5; при этом интегрирование дает точный результат для любого полинома от % вплоть до пятой степени.
Метод Маркова может быть обобщен на дву- и трехмерный случаи таким образом, чтобы точки интегрирования располагались только в углах и на сторонах квадрата или куба. Например, для двумерного случая имеем
j $ /(£, rj)dgdTi^SaJ&.Th), — i—i
где четыре точки интегрирования (5ь т);) всегда совпадают с вершинами рассматриваемого квадрата, а остальные располагаются на его сторонах.
В табл. 5.2 даны координаты точек интегрирования и значения весовых коэффициентов в методе Маркова для некоторых наиболее характерных случаев. Через р здесь обозначен порядок интегрирования, т. е. максимальный порядок полинома от % (или полного полинома от £, ц), для которого численное интегрирование оказывается точным.
В другой схеме, называемой методом интегрирования Эйлера [10], используются значения не только самой подынте-
Таблица 5.2
Элемент
одномерный
двумерный
2/3
-1/6
2/3- -1/6
гральной функции, но и ее первых производных. В частности, двухточечная формула Эйлера для интеграла от функции одной переменной имеет вид
1
J f (g)dg == f (-1) +f (1) + -у- [f (-1)-f (1)]
и дает точный результат для полинома от £ до третьей степени включительно.
Применительно к интегрированию функции f (g, rj) двух переменных можно получить соответствующую четырехточечную формулу
j; 2^4-2^-
-т 2 * %-
где ft, ^ •. — значения функции f (l, ц) и ее производных
в Ай вершине рассматриваемого квадрата, a — координаты соответствующей вершины, равные ± 1.
§ 5.13. О вычислении напряжений
После того как узловые перемещения найдены, по формуле (4.8) могут быть подсчитаны напряжения в любой точке конечного элемента.
’ Погрешность определения напряжений различна в разных точках элемента. Наиболее точные значения получаются [32] в точках Гаусса, соответствующих минимально допустимому порядку интегрирования. Но положение точек Гаусса определяется иррациональными числами, что доставляет большие неудобства при анализе результатов. На практике предпочитают, как правило, вычислять напряжения в узловых точках, хотя именно здесь погрешность в напряжениях оказывается наибольшей.'
При этом приходится иногда сталкиваться с двумя проблемами. Первая связана с разрывным характером поля напряжений. Если в узловой точке сходится несколько конечных элементов, то напряжения в ней, будучи подсчитаны согласно (4.8) независимо для каждого из элементов, окажутся различными. Особенно значительными эти различия могут быть в случае простейших конечных элементов. Типичный характер распределения напряжений, получаемый с помощью элементов с линейным законом изменения перемещейий, показан на рис. 5.18, а сплошными линиями. Для сглаживания напряжений здесь можно применить простое осреднение результатов, получаемых в каждой узловой точке для отдельных конечных элементов (штриховая линия). Осредненные напряжения оказываются и более точными, нежели полученные непосредственно по (4.8). Правда, заметное уменьшение погрешности происходит лишь во внутренних узлах, но не на границе, где обычно Как раз и возникают интересующие нас максимальные напряжения.
Другая проблема возникает при использовании некоторых типов изопараметрических конечных элементов высоких порядков.. Напряжения, получаемые в соответствии с (4.8), могут иметь тенденцию колебаться в пределах каждого элемента относительно истинного решения (рис. 5.18, б). Здесь осреднение напряжений в узлах не всегда приводит к улучшению результатов, в связи с чем дЛя сглаживания напряжений приходится прибегать к специальным процедурам 136, 39].
Различают общее (или глобальное) и местное (локальнее) сглаживания. Обозначим через S вычисляемую по (4.8) какую-
Рис. 5.18
либо компоненту матрицы напряжений о, подлежащую сглаживанию, а через S — соответствующую сглаженную величину. При общем сглаживании (361 отыскивают узловые значения 3, которые обозначим через Зг. При этом в пределах каждого конечного элемента функция 3 аппроксимируется через узловые значения так же, как для перемещений:
3 = s^s;. (5.93)
Здесь — аппроксимирующие функции; суммирование ведется по узлам конечного элемента. Значения Sr находят из условия, чтобы квадратичное отклонение S от 3, определяемое выражением
Ф —J(S — 3)2<1т, (5.94)
т
было минимальным.
Процедура отыскания узловых значений Sr во многом подобна процедуре определения узловых перемещений. Обозначим через ге = {3*8/...} матрицу-столбец, в которой перечислены значения Sr, относящиеся к данному конечному эле
менту (i, j, ... — номера узлов элемента). Зависимость (5.93) можно переписать в форме
S = ф^ (5.95)
аналогичной записи u = ave; через ф в (5.95) обозначена матрица аппроксимирующих функций
ф = (ф<ф/...]. (5.96)
Интегрирование по объему тела в (5.94) заменим интегрированием по объемам отдельных конечных элементов:
Ф — S J (S — S)2 dr=2 J (S2 —2SS + S2) dr. (5.97) Xе Xе
Так как 5 — скалярная величина, то наряду с (5.95) можно писать 3 = (ге)гфг. Это позволяет представить (5.97) в виде
Ф = 2 J [(ze)r фг фг® — 2S (z®f фг + S2] dt т®
или, иначе,
Ф = 2 [(z®)r D®z® — 2(z®)rB®J + Фо. (5,98)
Здесь D5 и Ве — квадратная матрица и матрица-столбец, определяемые формулами,
D® = |ф^т; В® = ^фг&1г. (5.99)
Xе Xе
Через
Ф0 = 2 Js2dr
Xе
обозначено слагаемое, не зависящее от искомых узловых значений функции S; суммирование в (5.98) ведется по всем конечным элементам.
Элементам матриц D8 и Ве можно присвоить индексы в соответствии с индексацией элементов матрицы ф (5.96):
D‘u Detl ...
В-
Bet
D's - f
Эти элементы вычисляются по формулам
фгф5dr; В® = JS^dr (г, s = i, /, ...). (5.100) Xе Xе
Введем матрицу-столбец z = {S^..^}, в которой перечислены значения Sr для всех узлов в порядке их нумерации (п — общее число узлов). Подобно тому как это делалось при вычислении потенциальной энергии деформации и потенциалу внешних сил конечноэлементной модели (см. § 4.6), выполним суммирование в (5.98), приведя выражение для Ф к виду
Ф = zrDz — 2zrB 4- Фо. (5.101)
Элементы матриц D и В, имеющих размер соответственно n X пипх 1, определяются формулами
Drs = S Ders; Вт = SB®. (5.102)
Суммирование в выражении для Drs выполняется по всем конечным элементам, содержащим узлы г, s, а в выражении для Вт — по всем конечным элементам, сходящимся в узле г.
Условие минимума функционала Ф приводит к равенству
Dz = В, (5.103)
представляющему собой систему алгебраических уравнений относительно узловых значений функции S.
В описанной процедуре предполагалось, что порядок аппроксимации напряжений в пределах каждого конечного элемента соответствует порядку аппроксимации перемещений, т. е. в (5.93) используются те же функции фг, которые фигурируют в матрице а. Такой подход дает более или менее удовлетворительные результаты лишь для конечных элементов первого порядка. Но для элементов высших порядков наиболее эффективная процедура получается в том случае [36], если в (5.93) вместо фг берут функции фг, соответствующие конечному элементу, на один порядок ниже данного. При этом число узлов, в которых вычисляются напряжения Sr, не совпадает с числом узлов, в которых определяются перемещения.
Так, на рис. 5.19 показаны участки плоских областей, идеализированных конечными элементами второго и третьего порядков; узлы этих сеток отмечены кружочками. Те узлы, которые используются в процедуре сглаживания напряжений, помечены крестиками. Для элементов второго порядка они совпадают с узлами в вершинах; в этом случае имеем аппроксима
цию напряжений, соответствующую аппроксимации перемещений в элементах первого порядка:
Ф,(£, п) = 4-(l + U)(l+nrn)-
4
Для элементов третьего порядка также используются узлы в вершинах, но помимо них на сторонах вводятся промежуточное узлы (£=0, т) = ± 1 и £= ±1, н —0), не совпадающие с узлами конечноэлементной модели. Это позволяет взять в ка-
Рис. 5.19
честве фг функции (5.62), посредством которых аппроксимируются перемещения в элементах второго порядка:
Qt2 __О
Фг(?> п)= Ц.....[Stf(i+U)(i+nrn)-
4
(1 -¥) (1 + Пг t))- & (1 - п8) (1 + 1)1.
Таким образом, для конечных элементов высших порядков формулы (5.99) и (5.100) следует заменить формулами
IX — J ipdr; Ве = J dr;
Xе Xе
В, = J Si|)rdr. (5.104)
Xе Xе
Выполнение общего сглаживания поля напряжений связано с большими затратами машинного времени на формирование и решение системы уравнений (5.103), имеющей высокий порядок. Для их снижения можно выполнить сглаживание лишь в
некоторой области (или областях) тела, где ожидаются наибольшие напряжения; все конечные элементы за пределами выбранной области при этом игнорируются. Для элементов высших порядков можно пойти еще дальше, применив эту процедуру к отдельно взятым конечным элементам. В этом случае приходим к так называемому местному (локальному) сглаживанию. Здесь вся проблема сводится к отысканию для каждого конечного элемента матрицы-столбца ze путем решения системы
Dezc = Ве, (5.105)
причем матрицы 1У и Ве рассчитываются по (5.104).
Местное сглаживание требует незначительных затрат машинного времени по сравнению с общим. Хотя оно не дает непрерывного поля напряжений, но значительно улучшает результаты по сравнению с (4.8) и может быть рекомендовано в качестве практической процедуры. Сохраняющиеся здесь небольшие скачки напряжений в узлах могут быть ликвидированы с помощью последующего осреднения напряжений. Получаемое в Итоге поле напряжений, как правило, так же хорошо согласуется с точным решением, как и при общем сглаживании.
Процедура сглаживания напряжений может применяться в любых конечноэлементных моделях. Но особенно важное значение она приобретает при использовании конечных элементов брусьев, пластин и оболочек, при построении которых учитываются деформации поперечного сдвига; примеры подобных элементов даны в гл. 7, 8. Картина распределения напряжений, получаемая с помощью этих элементов, оказывается часто совершенно искаженной нз-за сильных колебаний результатов относительно истинного решения, и их сглаживание является здесь непременным условием получения корректных результатов.
§ 5.14. Примеры расчета
Пример 1. Прямоугольная панель (рис. 5.20) длиной L = = 5м и шириной ЗВ = 1,5м состоит из обшивки толщиной ft = 2 мм (Во = 7-104 МПа, р = 0,3) и четырех продольных поясов с одинаковой площадью поперечного сечения F = = 1000 мм2 (£\ — 2- 10s МПа). На одном конце панель закреплена, а на другом нагружена двумя силами 2Р каждая, приложенными к крайним поясам. Это — типичная задача о включении в работу продольного набора. По мере удаления от на-198
груженного края происходит включение в работу внутренних
поясов и соответствующая разгрузка наружных.
Для идеализации поясов использовались одномерные элементы первого порядка (см. § 5.10), а для обшивки — плоские
прямоугольные элементы с линейным законом изменения пере-
мещений вдоль сторон (см. § 5.2) либо с линейным законом изменения напряжений (см. § 5.3); Отметим, что в данной задаче оба элемента дают практически одинаковые результаты.
Использованные варианты конечноэлементной идеализации панели показаны на рис. 5.21. В варианте (а) участок обшивки между сосед
ними поясами моделиро-
вался одним слоем прямоугольных элементов, а в варианте (б) — двумя. Число разбиений панели в продольном направлении изменялось от п = 5 до п = 20.
На рис. 5.22 показано изменение по длине панели (| =
Рис. 5.21
вые силы в сечениях наружных и внутренних поясов. На рис. 5.23 представлен характер изменения относительных напряжений в обшивке ихх = охх/и0 и аху — оХу/ай вдоль прямых, проведенных через середины соответственно внутреннего и наружного участков обшивки. Величины
Р 4Р
No =---------------; о о = -----------
1+ЗВЛ/(4<рГ) 4<pF-|-3Bft
Рис. 5.22
Рис. 5.23
представляют собой те значения силы в поясах и нормального напряжения ахх в обшивке, которые возникли бы в поперечном сечении панели при его полном включении в работу (ф = Е^Ео).
Сплошные линии получены при моделировании панели по схеме (б) (см. рис. 5.21) с параметром п = 20; кружочками отмечены результаты, полученные на сетке (а) при п = 10. Штриховые линии соответствуют приближенной аналитической методике расчета [8], согласно которой силы в поясах Nlt N2 и касательное напряжение <Jxy в обшивке определяются выражениями:
А\ = .Р(1 +е~ахУ,
N2 = P (1—е~ах);
а — -01, “*
иху — h с >
2 2Gft а2 —-----.
EFB
Нормальные напряжения в обшивке здесь принимаются равными нулю, и вся нагрузка воспринимается поясами. Так как отнесены по-прежнему к АГ0. то значения и Л^2 вдали от заделки не равны 1. Следует отметить, также, что ном методе полагается, ция имеет поперечные
в приближеи-расчета пред-что конструк-по всей длине диафрагмы
(применительно к рассматриваемой панели — поперечные стержни). Наличие поперечного стержйя на Свободном конце приводит к тому, что касательные напряжения оказываются максимальными при х = 0, и включение внутренних поясов в работу происходит быстрее, чем это получено в ко-нёчноэлементном решении (где касательные напряжения на свободном конце равны нулю).
Пример 2. Квадратная пластина с круглым отверстием {рис. 5.24, а) находится в условиях одноосного растяжения. 'Радиус отверстия г составляет Ч20 стороны пластины. Наличие двойной симметрии в этой задаче позволяет ограничиться
Рис. 5.24
рассмотрением лишь одной четверти пластины, закрепив ее подходящим образом в узлах, расположенных на осях симметрии (рис. 5.24, б). Расчет проводился с использованием четырехугольных изопараметрических конечных элементов первого и второго порядков. Применялась неравномерная в радиальном направлении сетка, более густая возле отверстия.
Значения максимального напряжения охх, возникающего в точке А :
Сетка...........................2x2
(Охх)шах/Р для элементов: первого порядка .... 2,091
второго порядка .... 2,733
4X4 8x8
2,536 3,050
3,176 3,180
На рис. 5.25 сплошной линией показано распределение ахх в сечении х = 0; штриховая линия соответствует аналитическому решению для бесконечной пластины.
Пример 3. Круговое составное кольцо типа шпангоута (рис. 5.26, а) нагружено двумя силами, приложенными по концам диаметра. Кольцо состоит из стенки высотой Н = 20 мм, толщиной h — 1 мм и двух поясов с площадью сечения F —
= 100 мм2 каждый (рис. 5.26, б). Средний радиус кольца г = = 1 м, Е = 7-104 МПа, у. = 0,3.
Схема идеализации кольца представлена на рис. 5.26,в. Как и в предыдущем примере, учитывается двойная симметрия конструкции. Пояса моделируются одномерными элементами, а стенка — плоскими элементами с четырьмя сторонами.
Рассмотрены следующие три конечноэлементные модели:
1. Элементы первого порядка для поясов, четырехузловые изопараметрические элементы для стенки;
2. Криволинейные элементы второго порядка для поясов, шестиузловые изопараметрические элементы (см. § 5.8) для стенки;
3. Элементы первого порядка для поясов, четырехугольные элементы с линейным полем напряжений (см. § 5.7) для стенки.
Для различного числа разбиений п рассматриваемой четверти кольца значения радиального перемещения д точки приложения силы, отнесенного к Pr3/(EJ), где J = =2,067 • 104 мм4 — момент инерции поперечного сечения кольца, следующие:
Рис. 5.27
п.............................
EJb](Pr3) для модели:
1.........................
2.........................
3....................
3
0,0070 0,0214 0,0673
Ю
0,0423 0,0728 0,0748
20
0,0632
0,0751
0,0754
40
0,0718
0,0753
0,0755
Как видно из этих результатов, модель 1 Дает чрезмерное завышение жесткости конструкции вследствие влияния ложных деформаций поперечного сдвига (см. § 5.2). Даже при п = 40 погрешность определения Д составляет ~ 5%. Наилучшим образом воспроизводит работу этой конструкции модель 3, что обеспечивается полным исключением ложных деформаций сдвига. Отметим, что аналитический расчет кольца как рамы с учетом осевой силы и деформации поперечного сдвига дает значение Д = 0,07548 Pr3/(EJ).
На рис. 5.27 сплошной линией представлен закон изменения осевой силы N в наружном поясе, найденный аналитически. Штриховые линии получены для модели 2 при п — 10 непосредственным вычислением напряжений. Наблюдается сильное колебание значения N относительно истинного решения.
Максимальное значение N имеет погрешность порядка 30%, хотя погрешность в перемещениях для этой сетки составляет 3,5%. Эти колебания отчетливо проявляются даже при весьма густой сетке. Так, при п — 40 отклонение максимального значения N от точного решения составляет ~ 2%, в то время как погрешность в перемещениях не превосходит 0,3%. Применение процедуры местного сглаживания, описанной в предыдущем параграфе, совместно с осреднением результатов щ узлах, позволяет полностью устранить эти колебания и получить значения N практически с той же погрешностью, что и для перемещений (точки на рис. 5.27). Крестиками на графике даны значения силы N, полученные на модели 3 в случае п = = 10. Как видим, описанный в § 5.7 плоский четырехугольный конечный элемент с линейным полем напряжений весьма эффективен при моделировании тонких стенок.
ГЛАВА 6
КРИТЕРИИ СХОДИМОСТИ
Интуитивно кажется очевидным, что чем гуще сетка конечных элементов, тем точнее получаемое решение. В действительности такая сходимость приближенного решения к точному имеет место лишь при использовании конечных элементов, удовлетворяющих определенным требованиям. Вариационная трактовка метода конечных элементов дает возможность ие только установить эти требования, ио и оценить скорость сходимости решения к точному для различных конечных элементов.
§ 6.1. Предварительные замечания
Всякое упругое тело имеет бесконечно большое число степеней свободы. В методе Ритца деформированное состояние тела определяется выбором нескольких параметров, которые находятся из условия минимума полной энергии и выступают в качестве степеней свободы тела. Ограничение числа степеней свободы равносильно введению дополнительных внутренних связей, что приводит к завышению жесткости тела по сравнению с истинной. То же самое относится и к методу конечных элементов, если используются совместные элементы. В этом случае перемещения, получаемые методом конечных элементов, будут в среднем меньше их точных значений.
При сгущении сетки число узловых перемещений (т.е. степеней свободы тела) увеличивается. Важно установить, при каких условиях это будет сопровождаться улучшением решения, т. е. его сходимостью к точному. Существенное значение
имеет также скорость сходимости. При наличии высокой скорости сходимости можно получить удовлетворительное решение уже с достаточно грубой сеткой. Вопросы сходимости часто исследуют численно на тестовых задачах, для которых известно точное решение, а также путем сопоставления результатов, найденных при различном разбиении тела на конечные элементы. Но некоторые общие вопросы, касающиеся сходимости, можно исследовать и теоретически.
При теоретическом анализе удобнее всего судить о сходимости по величине полной энергии системы. Если в пределе она будет стремиться к своему точному значению, то перемещения, деформации и напряжения также будут стремиться к своим точным значениям в каждой точке тела.
Обозначим через и матрицу перемещений, найденных методом конечных элементов, а через и0 — матрицу перемещений, соответствующих точному решению задачи. Так как действительные перемещения и0 минимизируют полную энергию системы V, то V (u) V (и0).
Рассмотрим далее такое деформированное состояние тела, составленного из конечных элементов, при котором узловые перемещения совпадают с перемещениями соответствующих точек тела, взятыми из точного решения. Обозначим матрицу получающихся при этом перемещений в пределах каждого элемента через и*. Полная энергия системы, деформированной подобным образом, будет удовлетворять неравенству V (u*)
V (и), так как при конечноэлементной идеализации минимум полной энергии соответствует перемещениям и. Следовательно, имеем V (u*) V (ц) V (и0), и если в пределе V (и*)—>--> V (и0), то подавно будет V (и) V (и0).
Таким образом, для доказательства сходимости конечно-: элементной модели достаточно положить узловые перемещения равными их значениям в точном решении и показать, что при уменьшении размеров конечных элементов полная энергия такой системы будет стремиться к своему точному значению.
§ 6.2. Применение рядов Тейлора к исследованию сходимости
Для сопоставления перемещений и* с и0 воспользуемся разложением и0 в ряд Тейлора. Напомним, что для функции f (х) одной переменной разложение в ряд Тейлора в окрестности точки х — х0 имеет вид
f(x) =f (х0) +^Ч’ (ХО) /" (ХО) + ....
Это разложение можно представить также как сумму f (х) = Рп (х) + R (х).
Здесь полином
Рп (*) =f W + Г»(х0)
Н п!
содержит первые члены разложения вплоть до (х — х0)п; Z? (х) — остаточный член ряда. Для него справедлива оценка |/? (х)| еС М1п + \ где I — длина интервала, на котором производится представление функции в виде ряда, & М — положительная константа, величина которой определяется максимальным значением производной (х) на рассматриваемом интервале. С уменьшением длины интервала R (х) стремится к нулю как Jn+1, т. е. приближение функции / (х) полиномом Рп (х) будет тем лучше, чем выше степень этого полинома.
В дальнейшем выражение для Рп (х) будем записывать в форме
Рп (х) ^0 Д>х Н- •••"4^опхя,
где CL$t ап — некоторые коэффициенты, определяемые значениями производных от функции/ (х) в точке х0.
Аналогично можно записать разложение Тейлора и для функции нескольких переменных. Так, для двух переменных имеем
/ (х. У) = Рп (X, у) + R (X, у).
Здесь Р„ (х, у) содержит все'члены полинома степени п (т. е. все члены вида хруч, где р + q = л), а также все полиномы низших порядков. При этом условии для остаточного члена R (х, у) справедлива оценка |R (х, у)| М/п+1, где I — ха-
рактерный линейный размер области, в которой выполняется разложение, а константа Л1 зависит от максимальных значений производных (л + 1)-го порядка от функции / (х, у) по координатам х, у в рассматриваемой области. Подчеркнем, что если в Рп (х, у) удержаны не все члены полинома степени л, то остаточный член будет в общем случае иметь порядок а не /п+1.
Если f (х, у) = {Д (х, у) f2 (х, у)...} есть матрица-столбец, то каждый ее компонент можно разложить в ряд Тейлора, придерживаясь одинаковой степени точности:
Л (х, У) = Рм (х, у) + Rt (х, у); /2 (х, у) = Рлг (х, у) + + /?2 (х, у), ... .
Объединив все эти равенства, придем к разложению f (х, у) = Рп (х, у) + R (х, у),
где - • • •
Pn (х, у) = {Pnt (х, у) Рп2(х, у)...};
R (х, у) = {Ri(x, у) R2 (х, у)...}.
Рассмотрим теперь некоторый плоский конечный элемент. Предположим, что для аппроксимации перемещений используются полиномы относительно х, у, так что функции их, иу определяются соотношениями
' Рх (X, у) = а0 + а^х + а3хг + atxy 4- а^у2 +
иу(х, у) = ba + btx + b^y +b3x2+b^cy+ Ьъу2+... . (6.1)
Полагая и (х,у) — {их (х, у) иу (х, у}}, запишем эти соотношения в матричном виде
и (х,у) = Ао + Atx + А2р + А3Х2 + A4xz/ 4- Asjr24-..., (6.2) где Аг = {аг bi}.
Постоянные Аг выражаются через смещения узлов, и равенство (6.2) можно представить в стандартной форме и (х, у) = — а (х, у) Vе. Если конечный элемент имеет узлы t, /, ..., то
v* = {v£ Vj...}; а (х, у) = [а,- (х, у) а} (х, у}...].
Следовательно, можно записать
и (х, у) = 2аг (х, у) vr.
Здесь суммирование выполняется по всем узлам конечного элемента. Если в качестве vr взять перемещения точек (х„ ут) нз точного решения, то последнее равенство будет определять перемещения и* (х, у). Обозначая и® (хг, ут) = и®, имеем
И* (х, у) = 2аг (х, у) и?. (6.3)
Пусть, далее, п — наивысшая степень полного полинома; содержащегося в аппроксимирующих функциях (6.2). Разложим истинные перемещения и® в ряд Тейлора в окрестности какой-либо точки, принадлежащей конечному элементу, удерживая при этом также полные полиномы вплоть до степени п:
и® (х, у) = Рп (х, у) + R (X, у). (6.4)
Компоненты матрицы R (х, у) всюду в пределах элемента не будут превышать величины порядка ln+1, где I — характерный размер элемента. Введя обозначения Рп (хг, уг) = Рпг и R (xr, yr) = Rr, из (6.3) и (6.4) получим
и* (х, у) = 2а, (х, у} Рпг 4- 2аг (х, у) Rr.
Положив,
₽П (х, у) = 2аг (к, у) Рпг; R* (X, у) = 2аг (х, у) Rr, можно последнее равенство записать в виде
и* (х, у) = Рп (х, у) + R* (х, у).
Здесь первое слагаемое дает интерполяцию полинома Рп (х, у), а второе — интерполяцию остаточного члена R (х,у) по их узловым значениям. Аппроксимирующие функции содержат по условию полные полиномы вплоть до степени п. Поэтому интерполяция любой полиномиальной функции, порядок которой не превосходит п, будет давать точный результат. Отсюда следует, что Р£ (х, у) = Рп (х, у), так что для и* (х, у) приходим к выражению
“* (х, у) = Р„ (х, у) + R* (х, у).
Разность между истинными перемещениями и0 и перемещениями и* оказывается равной
u° — u* = R (х, у) — R* (х, у) = R(x, у) — Sar (х, у) Rr.
Таким образом, разность и0 — и* выражена через компо" ненты матрицы R (х, у), которые имеют порядок /п+1. Следов а' тельно, эта разность также не превосходит величины порядка /п+1 всюду в пределах области, занимаемой конечным элементом. При уменьшении размеров конечного элемента (т. е. при /—>0)она будет стремиться к нулю, как Zrt+1. Подобный же анализ показывает, что при аппроксимации перемещений полиномами степени п погрешность их первых производных по х, у будет иметь порядок 1п, вторых — /п-1 и т. д.
Из приведенных рассуждений можно сделать следующие выводы. Во-первых, скорость сходимости конечноэлементного решения к точному будет тем выше, чем выше порядок полиномов, используемых для аппроксимации перемещений. Порядок полиномов увеличивается, например, с увеличением числа узлов конечного элемента. Во-вторых, разность и0 — и* будет иметь порядок /,1+1 лишь в том случае, если в аппроксимирующих функциях (6.2) представлены все члены полиномов степени п и ниже. Например, для п = 3 аппроксимирующие функции должны содержать члены х3, х2у, ху2, у2 с произвольными множителями, а также все члены младших полиномов; тогда ошибка в перемещениях будет иметь порядок /4. Отбрасывание любого из записанных выше членов (или введение ограничений на множители перед ними) приводит к понижению по
рядка ошибки до Р. Если же для аппроксимации перемещений используется, скажем, выражение вида
Ло + Агх+А2у + А3х2 + А^у2 + +
+ А6х2у + Л,х«/2 + Agtf, в котором отсутствует слагаемое с произведением ху, то ошибка будет иметь порядок I2 и скорость сходимости будет значительно ниже, чем при наличии этого слагаемого. Отметим также, что полные полиномы степени п должны содержаться в выражениях для всех компонент перемещений. При использовании для отдельных компонент перемещений полиномов различной степени (что встречается, например, при расчете оболочек) скорость сходимости будет определяться наименьшим порядком аппроксимации.
Рассмотрим в качестве примера совместный плоский прямоугольный конечный элемент (см. § 5.2), для которого перемещения задаются равенствами (5.16):
их = Л + f2x + f3y + ftxy, иу = f5+ f6x + f-,y + fsxy.
Здесь представлены полные полиномы первого и нулевого порядков, и можно ожидать, что погрешность аппроксимации перемещений будет порядка I2, где I — длина наибольшей стороны прямоугольника. Для улучшения характеристик элемента можно ввести неузловые степени свободы. В частности, как говорилось в § 5.5, можно добавить к этим выражениям функцию (1 — £2) (1 — т]2) с произвольными множителями. Безразмерные координаты |, ц связаны с х, у линейными соотношениями
g = 2 (х — хс)/а; т] = 2 (у — ус)/Ь, где а, b — размеры сторон прямоугольника; хс, ус — координаты его центра тяжести. В итоге в выражениях для их, иу появятся члены, содержащие квадраты координат. Но множители перед х2 и у2 в каждом из выражений для их, иу не произвольны, а равны между собой. Следовательно, мы не получаем здесь полных полиномов второй степени, и поэтому погрешность аппроксимации по-прежнему будет иметь порядок Р. Таким образом, добавление функций (1— £2) (1 — ц2) к аппроксимирующим функциям (5.16) не должно привести к существенному улучшению конечного элемента, что и подтверждается числовыми расчетами. В то же время добавление функций (1 — g2), (1 — т]2) с произвольными множителями дает полные полиномы второго порядка. Это приводит к конечному элементу с лучшими характеристиками, несмотря на то, что здесь нарушается совместность элементов.
Если для аппроксимации перемещений в пределах конечного элемента используются функции, отличные от полиномиальных, то для анализа сходимости можно разложить их в степенные ряды и воспользоваться затем предыдущими рассуждениями. Вернемся к прямоугольному конечному элементу с аппроксимирующими функциями (5.16). Пусть к этим выражениям добавляются функции cos (л£/2) cos (лг|/2) с произвольными множителями. Для исследования сходимости воспользуемся разложением
, у2 , у4 cosv —-1--*—к-1------....
г 21 4!
Тогда имеем
л£ лп /. • л2 Е2 . \ (. л2 п2 . \
cos —— cos —— =11-------—1-... ||1-----— 4-... L
2 2 \ 8 Д 8 /
Отсюда видно, что введение в (5.16) функций cos (л£/2)х X cos (ix-q/2) равносильно использованию дополнительных функций типа (1 — |а) (1—т]2), т. е. оно не сопровождается улучшением сходимости по сравнению с базовым конечным элементом.
§ 6.3. Критерии сходимости совместных элементов
Сходимость перемещений не означает еще сходимости полной энергии системы
JerodT т
—J ur Rd? — J ur pd<o
* “р
к ее точному значению. В матрицу деформаций 8 в соответствий с формулами Коши входят первые производные от перемещений по координатам. Так как <r = хе, то и компоненты матрицы напряжений о также выражаются через эти производные. Следовательно, при сгущении сетки V (u*) V (и®), если не только сами перемещения, но и их первые производные совпадают в пределе с точными значениями. Сходимость деформаций к точным значениям будет обеспечена, если перемещения представлены как полиномы по крайней мере первого порядка. В общем случае трехмерного конечного элемента должно быть
их == а0 4- агх + щ + а3г 4- ...;
«а = ьо 4- М 4- М 4- bgZ 4- (6.5)
иг ~ с0 + сгх 4- СгУ 4- c3z 4-...........
•Здесь а, b, с — независимые постоянные, а невыписанные слагаемые могут произвольным образом зависеть от х, у, г. Деформации будут при этом представлены полными полиномами степени не ниже нулевой:
Схх “ Ч” •••» Egy ™ 6g Ч” . Czz = С, Ч~ •••»
Вху Да Ч~ 6g Ч~ • •6g Ч~ Cg Ч- -• •, ^zx Дз Ч- ^*1 Ч~•** -(6,6)
Погрешность аппроксимации деформаций будет иметь порядок по крайней мере I1, т. е. она стремится к нулю при уменьшении размеров конечного элемента.
Формулами (6.5) определяется минимальное требование, необходимое для сходимости конечноэлементного решения к точному в случае совместных конечных элементов 126]. Таким образом, для обеспечения сходимости достаточно, чтобы каждая Компонента перемещения могла быть в пределах конечного элемента представлена полиномом не ниже первой степени. Это требование называют иногда условием полноты конечного элемента.
Подчеркнем, что приведенные рассуждения применимы, строго говоря, лишь к совместным конечным элементам. Если элементы удовлетворяют условию полноты и совместны, то при сгущении сетки сходимость конечноэлементного решения к точному по энергии будет монотонной. Другими словами, при сгущении сетки полная энергия системы будет уменьшаться, оставаясь при этом выше своего точного значения. Можно показать [26], что погрешность рассмотренных выше элементов в энергии имеет порядок /2", где п — порядок полных полиномов в аппроксимирующих функциях. Если в выражении для энергии деформации встречаются вторые производные от перемещений (это имеет место, например, для некоторых конечноэлементных моделей пластин, работающих на изгиб, и оболочек), то ошибка в энергии будет иметь порядок
Обращаясь к рассмотренным ранее конечным элементам, видим, что треугольный элемент с линейным полем перемещений (см. § 5.1) и совместный прямоугольный элемент (см. § 5.2) удовлетворяют условию полноты. Это непосредственно следует из формул (5.1) и (5.16) для перемещений их, uv, в которых представлены полные полиномы первого и нулевого порядков. Поскольку эти элементы являются также совместными, то они обеспечивают монотонную сходимость решения к точному при сгущении сетки. Погрешность аппроксимации перемещений убывает при этом в обоих случаях по крайней мере как /2, где I — длина наибольшей стороны элемента. Как показы
вают числовые расчеты, фактическая скорость сходимости у прямоугольного элемента выше, чем у треугольного.
Выясним далее, удовлетворяют ли критериям сходимости конечные элементы изопараметрического типа. Прежде всего отметим, что эти элементы совместны. Следовательно, достаточно показать, что перемещения в пределах элемента описываются полиномами степени не ниже первой. В частности, для двумерных элементов должны быть справедливы разложения'
их = а0 + агх+а2у + ...; = 60 + b^x + М + ... (6.7)
с независимыми коэффициентами at, Ь{.
Напомним, что в изопараметрических элементах для аппроксимации перемещений используются полиномы относительно переменных g, т|, которые представляют собой неортогональные криволинейные координаты точек конечного элемента и связаны с х, у соотношениями
X = 2фг (£, Т|) Хг\ у = 2фг (£, Т|) уг. (6.8)
Здесь хг, уг — координаты узлов; фг (g, т|) — полиномиальные функции. Суммирование в (6.8) ведется по всем узлам конечного элемента.
Выражения для перемещений
«х = Ж (£, пКх! иу = Ж (g, т|)»гу (6.9) не зависят в явной форме от х, у и справедливость разложений вида (6.7) не очевидна.
Предположим [6], что узлы конечного элемента получают смещения, равные
vTX = а0 + a^r + a2yr-, vry = Ьв + Ьгхг + b2yr-
Если перемещения произвольной точки конечного элемента с координатами х, у, найденные по (6.9), окажутся при этом равными
их = аУ + аАх + а2у, иу = b0 + btx + bzy, (6.10) то тем самым будет доказано, что изопараметрический элемент может воспроизвести любое линейное поле перемещений и, следовательно, разложения (6.7) справедливы.
Для доказательства (6.10) подставим значения vrx в первое из соотношений (6.9):
«х = Ж(£. П) (а» + OiXr + а2уг) =
= а0Ж (£, Я) + а12фг(В, я) хг + а2 2% (g, т|) Уг-
Но на основании (6.8) это выражение можно переписать так: их = а0 2фг (g, я) + ЩХ + а2у.
Аналогично приходим к соответствующей формуле для иу: ии = b0 2фг (g, я) + М + b2y.
Сопоставляя эти выражения с (6.10), заключаем, что перемещения конечного элемента действительно совпадают с требуемым полем, если только удовлетворяется условие
(5. Я) = 1 •
Чтобы доказать это равенство, предположим [33J, что начало системы координат х, у переместилось вдоль оси х на расстояние d. Тогда новая координата х произвольной точки элемента станет х — х — d, а координаты узлов будут xr = xr—d. В новых координатах первое соотношение (6.8) примет вид х = (£, я) хг- Подставив сюда значения х и хг, будем иметь
х — d = 2фг (£, я) (хт — d) = (g, я) хт — (g, я)-
На основании (6.8) получаем отсюда соотношение d = (В, я).
из которого ц; следует справедливость равенства (£, я) =1.
Таким образом, мы доказали, что плоские изопараметрические элементы удовлетворяют условию полноты. Следовательно, их использование обеспечивает монотонную сходимость решения. Аналогично доказывается свойство полноты для одно-и трехмерных изопараметрических конечных элементов.
Условие полноты формулируется иногда иначе [6], чем это сделано выше. Элемент считается полным, если, во-первых, в аппроксимирующие функции включены его перемещения как жесткого целого и, во-вторых, если в элементе может существовать однородное (т.е. не зависящее от координат) деформированное состояние с произвольными компонентами деформации.
Поясним эти условия подробнее. Предположим, что узлы конечного элемента получают смещения, соответствующие его перемещению в пространстве как абсолютно жесткого тела. Если деформации, найденные по формуле в = Pve, окажутся нулевыми, то это означает, что жесткие смещения точно представлены в используемых аппроксимирующих фунциях.
Второе требование основывается на следующих соображениях. При уменьшении размеров конечных элементов изменения деформаций в пределах каждого из них будут все менее существенными по сравнению с самими деформациями, т. е. деформированное состояние будет приближаться к однородному. Для сходимости решения необходимо, чтобы аппроксими
рующие функции позволяли воспроизвести такое предельное состояние. Это будет обеспечено, если можно подобрать значения узловых перемещений или констант в формулах типа (6.1), при которых деформации в пределах элемента будут постоянны.
Для большинства конечных элементов отмеченные два подхода к определению полноты, по существу, совпадают, осо- бенио если в качестве компонент перемещений берутся их проекции на декартовы оси координат, как это делалось выше. В самом деле, допустим, что в невыписанных членах в (6.5) отсутствуют слагаемые, содержащие постоянные а0, аи...с2, с3. Тогда при выполнении соотношений (6.5) автоматически удовлетворяются условия жестких смещений и условие постоянства деформаций. Но если какие-либо коэффициенты в полиномах более высоких порядков связаны с этими постоянными, то условия жестких смещений и постоянства деформаций могут уже не выполняться, хотя элемент является полным в том смысле, что требование минимальности степени полинома удовлетворено. Особенно существенно различие между двумя подходами к определению полноты в том случае, когда компонентами матрицы и являются проекции перемещений на криволинейные координатные оси, как это имеет место, например, при расчете оболочек. Требования о жестких перемещениях и постоянстве деформаций оказываются более трудновыполнимыми, чем требование о минимальности степени полинома.
§ 6.4. Сходимость несовместных элементов
Обратимся теперь к несовместным элементам. Сходимость решения к точному имеет место и в этом случае, если в пределе (т.е. по мере сгущения сетки) в аппроксимирующих функциях исчезают члены, создающие несовместность. Следовательно, сходимость будет гарантирована, если несовместные конечные элементы, во-первых, способны воспроизвести в пределе линейное поле перемещений и, во-вторых, оказываются прн этом совместными. Обычно используют более жесткое требование, в соответствии с которым должна обеспечиваться сплошность тела в условиях линейного поля перемещений при любых размерах элемента, а не только в пределе.
Проверка выполнения последнего требования осуществляется с помощью группового тестирования [26]*. Пусть требу
* В зарубежной литературе используется введенный Айронсом термин «patch test», что в буквальном переводе означает «лоскутный тест» — по-видимому, в связи с ассоциациями, вызываемыми видом тестируемой области (см. рис. 6.1). В литературе на русском языке можно встретить названия «кусочный тест», «выборочный тест», «пэтч-тест». Мы предпочитаем термин «групповой тест» как наиболее соот- > ветствующий существу дела,
Рнс. 6.1
ется проверить, будет ли давать сходимость некоторый несовместный конечный элемент. Рассматривается группа смежных элементов исследуемого типа, составленных таким образом, чтобы по крайней мере один узел оказался внутри полученной области (рис. 6.1). Форма конечных элементов должна быть по возможности произвольной. Далее принимается, что внешние узлы, расположенные на границе этой области, получают перемещения, соответствующие линейному полю. Для плоских конечных элементов, например, узловые перемещения следует брать равными
Vrx ~ <*0 “Ь <hXr
Vry bfi “Ь Mr "Ь &ъУг1 где хт, ут — координаты типового внешнего узла.
В соответствии с обычной процедурой метода конечных элементов можно теперь найти координаты которых обозначим через ха, уа. Если окажется, что эти перемещения совпадают с величинами
Vsx = «о + atxa + агУа, иау == &0 + btxa + Ь^уа, то групповой тест проходит. В этом случае использование несовместных конечных элементов будет всегда обеспечивать сходимость решения.
Выполнение условий группового теста является достаточным, но ие необходимым условием сходимости [26). Имеются примеры конечных элементов, для которых групповой тест не проходит, но которые тем не менее обеспечивают сходимость решения. Однако обычно конечный элемент считается непригодным к употреблению, если групповой тест для него не проходит.
В изложенной трактовке групповое тестирование связано с применением ЭВМ. Но во многих случаях можно проверить выполнение условий этого теста более простыми средствами. Рассмотрим в качестве примера несовместный прямоугольный конечный элемент с линейным полем напряжений (см. § 5.3). Распределение перемещений определяется для этЬго элемента соотношениями (5.25). Если принять в них К = /в = 0, то все точки конечного элемента, в том числе узловые, будут находиться в условиях произвольного линейного поля перемещений. Постоянные f однозначно связаны с узловыми перемещениями, так что справедливо и обратное: если поместить узлы в условия линейного поля перемещений, то постоянные Д и fa будут нулевыми, т. е. это поле будет воспроизведено внутри элемента — групповой тест проходит. То же самое относится и к четырехугольному элементу произвольной формы с линейным полем напряжений (см. § 5.7).
Если элемент получен из базового введениемдополиительных несовместных функций перемещений, то можно воспользоваться следующими рассуждениями. Перемещения в таком элементе определяются равенством
u = ave + а0С.
Здесь первое слагаемое описывает перемещения в базовом элемент! (который предполагается полным и совместным), а второе дает дополнительное поле перемещений, нарушающее совместность конечных элементов; в узловых точках перемещения а0С обращаются в нуль. Неуэ-ловые степени свободы С выражаются через узловые перемещения Vе путем минимизации полной энергии конечного элемента (см. § 5.5).
Предположим, что в базовом элементе путем подходящего задания узловых перемещений создано линейное поле
и =А о + Ajx + А^ + AjZ, где матрицы-столбцы Ао, А3, А?, А3 содержат произвольно выбранные постоянные. Если добавить к и функции а0С, то при тех же узловых перемещениях получим поле перемещений в рассматриваемом несовместном элементе: .
u = и + а0С.
Постоянные С, как уже говорилось, необходимо определить из условия минимума полной энергии элемента. Если при этом они окажутся равными нулю, то это будет означать, что конечные элементы данного типа согласованно воспроизводят линейное поле перемещений и, следовательно, групповой тест будет проходить.
Выведем условие, при котором постоянные С обращаются в нуль. Пользуясь формулами Коши, находим деформации в несовместном элементе
в = в + р0С.
Здесь матрица 0О содержит производные от элементов матрицы а0, а компонентами матрицы в являются независимые постоянные величины, выражающиеся через элементы матриц Ао, Ар А2, А3. Подставляя выражение для в в формулу
ие-=~^- JerXBdT,
Xе можно получить
Ue = §гт хвс1т+ J егхро dTC-]--j- Ст J pjxpo drC. хе Xе хе
Так как деформирование конечного элемента осуществляется путем задания узловых перемещений, то потенциал Пс внешней нагрузки равен нулю. Следовательно, минимизация полной энергии элемента dUe
сводится к выполнению условия —&- = 0, которое приводит к равенству
J Ро XEdT-j- JpJxPo dxC = 0.
Xе Xе
Постоянные С будут нулевыми, если
J Ро xedx = 0.
Так как матрицы х и е содержат постоянные величины, то их можно вынести за знак интеграла. Так как полученное условие должно выполняться для любых компонент матрицы е и для любых упругих по' стоянных материала, то его можно заменить равенством
f pcdT = O. (6.11)
Xе
Таким образом, групповой тест можно заменить проверкой условия, чтобы интегралы, взятые по объему конечного элемента от каждой компоненты матрицы а0, равнялись нулю.
В качестве примера возьмем прямоугольный конечный элемент, рассмотренный в § 5.5. Для этого элемента поле перемещений определяется равенствами (5.40), а матрица
Ро=~4
1/а 0 0
0 0 Г)/Ь
о о
0 ?]/Ь
На 0 .
где а, b — размеры сторон прямоугольника. Учитывая, что
dx = (/ia6/4)d£dr]
и что интегрирование по обеим переменным 5, т] выполняется в пределах от —1 до 1, убеждаемся, что в случае постоянной толщины элемента Л условие (6.11) выполняется.
В другом примере в качестве базового возьмем плоский четырехузловой изопараметрический элемент (см. § 5.6), для которого координаты х, у выражаются через переменные т) посредством соотношений
х= StI> (g, Tj)xr; у = 2фг (£, т])уг, где
'Рг (5. П) = ~“ (1 + £г 5) (1 + Пг п).
4
а суммирование выполняется по всем узлам элемента.
По аналогии с предыдущим примером можно попытаться улучшить жесткостиые характеристики элемента, вводя в выражения для перемещений
цж = 2фгигх; uy = ^rvry
дополнительные функции •! — £2 и 1 — т]2 с произвольными множителями. В итоге получим несовместный элемент в форме произвольного четырехугольника с перемещениями
u = 2ar vr 4- ав с,
где
ГЧ’г 0 1 ,
«г = к с= (ct с2 с, с4),
l_O 'KJ
Г«ох1 р-£2 1-п2 ° О 1
а° L«oyJ [° О 1 — £2 1—Ч2]
Для вычисления матрицы
~ ^«01-
дх
₽0~ ду
deigif дОрх дх + ду
необходимо составить предварительно матрицу Якоби
дх ду К “ag дх ду dt] дт]
ду _ ду j-i_—!_ ап д%
IJI дх дх
_~~д^ "аГ_
где |J| — определитель матрицы J, запишем а 1 / ду д ду д \
дх । j । \ а^ ag ag а,? /’
a i f дх а дх а \
ay IJI \ а») ag ag а») /
В итоге имеем
₽о =
ду
О
Так как dr = Л | J ] d£dr), то
1 1
J Podr= J J h₽o|J | dgdq. т — 1 — 1
Внося сюда полученное выражение для ро, видим, что групповой тест будет проходить, если каждый из интегралов
f f
обращается в нуль. Вообще говоря, эти интегралы не равны нулю даже при постоянной толщине Л. Исключение составляет лишь случай, когда производные dx/dt, дх/дт\, ду/д£ и ду/дц постоянны. Можно показать, что этому требованию отвечают элементы в форме параллелограмма (и, в частности, прямоугольника). Но для произвольного четырехугольника групповой тест не проходит, и пользоваться подобными конечными элементами нельзя.
В случае несовместных элементов уже нельзя ожидать, что полная энергия системы будет всегда выше своего точного значения. Сходимость решения оказывается в этом случае, как правило, немонотонной, т. е. при сгущении сетки полная энергия оказывается то выше, что ниже истинного значения. Нередко несовместные элементы позволяют получить при одинаковой сетке более точные результаты, нежели совместные. Объясняется это тем, что совместные элементы всегда имеют завышенную жесткость, а введение несовместных функций делает их обычно более податливыми.
§ 6.5. Влияние иа сходимость численного интегрирования
Выше негласно подразумевалось, что при вычислении потенциальной энергии деформации
Vе =
е
интегрирование осуществляется точно. Так как, с другой стороны,
i
Ue =— veT ке Vе,
2
то это означает, что и вычисление матрицы жесткости по формуле
k® = J x₽dT те
также выполняется с помощью точного интегрирования. Но, как свидетельствуют многие примеры из предыдущей главы, для определения к® нередко приходится прибегать к численному интегрированию. Это приводит к приближенному значению матрицы жесткости элемента. Последнюю можно рассматривать и как точную, но соответствующую уже некоторой другой системе аппроксимирующих функций. Вследствие этого в конечноэлементной модели возникает дополнительная несовместность, даже если применяются так называемые «совместные» элементы. Сходимость такой модели к точному решению требует особого обоснования.
Пусть конечный элемент при точном интегрировании удовлетворяет условию сходимости. Тогда при уменьшении его размеров компоненты матрицы е будут в пределах элемента стремиться к некоторым постоянным значениям. Обозначая эту предельную матрицу с постоянными компонентами через е0, запишем
8 = е0 + Де, (6.12)
где матрица Де является функцией координат. В пределе имеем Де->-0. Внося равенство (6.12) в выражение для Ue, представим его в виде
U* = 6/® + (/®! + (/®2,
где
f ej XE0dT - ej xe0 f dx;
"V “ i)
te Iе
U\ = J eJxAedx; Ue2 —~~~ J ДетхДе6т.
Iе te
Величина {/* представляет собой то значение, к которому стремится U‘ при уменьшении размеров конечного элемента, и для обеспечения сходимости достаточно потребовать, чтобы она вычислялась точно. Как видно из выражения для для этого необходимо, чтобы используемое правило интегрирования позволяло в пределе точно находить объем конечного элемента. Практически пользуются более простым правилом, в соответствии с которым минимально допустимое число точек интегрирования должно обеспечивать точное вычисление объема конечного элемента при любых его размерах, а не только в пределе.
Вопрос о точности вычисления объема возникает в том случае, когда интегрирование выполняется в системе координат, отличной от декартовой. Если элемент отнесен к локальной системе координат я, С, то элементарный объем будет равен dx — |J| d|d^dC, где |J| — якобиан соответствующего преобразования координат. Задача сводится к определению такого правила интегрирования, которое, как минимум, обеспечивает точное вычисление интеграла от |J (|, я, 01 по координатам я, О
В случае изопараметрических конечных элементов функция |J (£, я, 01 представляет собой полином ог £, я, порядок которого можно легко установить. Например, для плоского четырехузлового элемента (см. § 5.6) преобразование координат определяется равенствами (5.42):
х=2-2(1 +1Л)(1 4-ПгП)хг; z/ = -J-2(J -)-|г|)(1 +ЯгП)/Л-
4 4
Якобиан этого преобразования вычисляется по формуле
дх ду
_ дх ду___________ду дх
дх ду <?Я dg дц ’
дц дц
где производные от х, у по £, я даются равенствами
V, 4L=-r2T’-<-l+^^x-
de, 4 dt] 4
-g- = 4- (1 + nr П) Уг, = 4 24r (1 + Sr I) Уг-
de, 4 dt] 4
Отсюда видно, что в выражение для 13 (|, г])| каждый из параметров 5, Л входит в степени не выше первой. Метод Гаусса дает точное значение интеграла
$ /(SMS.
—i
если f (5) представляет собой полином от § степени не выше 2п — 1, где п — число точек интегрирования. Следовательно, для точного интегрирования |J (£, rj) | достаточно одной точки Гаусса в каждом направлении. Подобным образом можно установить минимально необходимое число точек интегрирования и для других конечных элементов. Для элементов с совместными аппроксимирующими функциями несовместность, обусловленная приближенностью интегрирования, уменьшается с увеличением числа точек Гаусса. Практически применяют число точек Гаусса, рекомендованное в последнем столбце табл. 5.1.
§ 6.6. Исключение ложных деформаций сдвига с помощью численного интегрирования
В предыдущих рассуждениях предполагалось, что сгущение сетки сопровождается уменьшением всех размеров конечного элемента. Иная ситуация возникает, когда при конечноэлементной идеализации балки с тонкой стенкой последняя моделируется по высоте одним конечным элементом. Сгущение сетки сводится здесь к уменьшению продольных размеров конечных элементов, в то время как их поперечные размеры, определяемые высотой балки, не зависят от выбора сетки. Естес-ственно, что при этом нельзя даже в пределе прийти к точному (с позиции теории упругости) решению. Задача заключается в получении приближенного результата, соответствующего, скажем, технической теории изгиба бруса.
Применительно к подобным элементам необходимо уточнить понятие сходимости решения, которое может трактоваться здесь в двух различных смыслах. Во-первых, как и ранее,
должна быть обеспечена сходимость решения к правильному ответу при сгущении сетки, т. е. при уменьшении продольных размеров конечных элементов.
С другой стороны, если длина балки значительно превышает ее высоту, то, как известно, ее сечения остаются практически нормальными к изогнутой оси. Естественно потребовать, чтобы с уменьшением высоты балки конечноэлементная модель воспроизводила такое поведение независимо от густоты сетки. Только в этом случае можно рассчитывать на успех при использовании реальных сеток.
Если поперечное сечение нормально к оси балки, то это означает, что деформация поперечного сдвига равна нулю (в действительности она может быть несколько отличной от нуля, но ее порядок существенно меньше порядка продольной деформации в крайних волокнах). Следовательно, при корректном моделировании стеики должна быть обеспечена возможность неограниченного уменьшения деформации поперечного сдвига с уменьшением высоты конечного элемента или, что то же са-мое, с увеличением его длины при фиксированной высоте.
Таким образом, при анализе применимости конечного элемента стенки следует оценить его поведение не только при бесконечном уменьшении (сходимость в обычном смысле), но и при неограниченном увеличении его длины (сходимость к балочному решению).
Обратимся для иллюстрации к совместному прямоугольному конечному элементу (см. § 5.2). Дифференцируя выражения (5.16) для перемещений в таком элементе, в соответствии с формулами Коши имеем
дх ду
еху =/з+/в + Л (6.13)
ду дх
Примем для удобства, что начало координат находится в центре прямоугольника, а ось х параллельна оси балки. При уменьшении продольного размера элемента слагаемые, содержащие множителем координату х, будут давать все меньший вклад в энергию деформации. Предельное деформированное состояние элемента характеризуется величинами
~ /а + ftf, ^"U + f'+fd/, (6.14)
где пять независимых параметров /2, f4, f3 + /в и f8 будут определены из условия минимума полной энергии конечноэлементной модели.
Основное значение при изгибе балки имеет деформация е,хх. Как видно из первого выражения (6.14), е,хх в предельном состоянии изменяется по высоте стенки по линейному закону, что соответствует технической теории изгиба бруса. Помимо ехх в конечноэлементной модели могут возникнуть постоянная по высоте поперечная деформация е.уу (которая обычно игнорируется в теории изгиба бруса) и деформация сдвига еху, изменяющаяся по высоте по линейному закону. В действительности распределение еху по высоте является параболическим, но это расхождение с теорией может быть легко исправлено введением корректирующего коэффициента при вычислении матрицы жесткости. Таким образом, данный конечный элемент обнаруживает приемлемое поведение при сгущении сетки.
Далее, предположив, что длина элемента возрастает, исследуем выражение для е.ху в (6.13). С увеличением длины доминирующее значение будет приобретать слагаемое ftx. Константа характеризует изгибную составляющую деформации е,хх в сечении, так что величина е,ху будет того же порядка, что и ежж. Критерий сходимости к балочному решению не выполняется, и поэтому данный элемент, как уже отмечалось в § 5.2, практически непригоден для моделирования стенки.
Один путь исключения ложного сдвига рассмотрен в предыдущей главе. Он заключается в использовании несовместных функций перемещений в виде полных полиномов второго порядка, вытекающих из линейного закона распределения напряжений (см. § 5.3, 5.7) или содержащих неузловые степени свободы (см. § 5.5). Но можно поступить иначе. Перепишем выражения для деформаций в стандартной форме е — Sprx Xvr, где согласно (5.19), (5.20)
— (1 +ПгП) а
о
О
(1+ПгЛ) а
Как и ранее, типовой блок k®s матрицы жесткости представим в виде суммы k,s = krS) е + krSt о. Здесь слагаемое
krs, е — Рг He 0s dx
учитывает вклад линейных деформаций, а слагаемое krs, G = У Рг ^0 Ps dT
Xе
— вклад деформации сдвига. Интегрирование в формуле для krs, в будем, как и ранее, выполнять точно. Для вычисления же krs, о применим численное интегрирование с одной точкой Гаусса. Для этого нужно найти произведение ргХоРз ПРИ J- =*= 0, т) = 0 и умножить результат на объем abh конечного элемента. В итоге придем к выражению
IQs, о
Gh Г Г|г Пз/Т 4 L £гПз
ПгВз ?£Дз
где по-прежнему у — отношение сторон прямоугольника.
Рис. 6.2
По сути дела, мы принимаем здесь, что деформация сдвига постоянна и равна своему значению при £ = т) = 0 (илн х — у = = 0). Тем самым выражение для еЖ{, в (6.13) неявно заменяется на
ъху — /з + fe-
Так как константа f3 + fe не связана с другими деформациями, то в процессе минимизации полной энергии она может принять любое значение, в том числе и сколь угодно малое. Таким образом, критерий сходимости к балочному решению выполняется.
Заметим, что при одноточечном интегрировании исключается не только слагаемое ftx, но также и слагаемое [$. Последнее является посторонним с точки зрения теории изгиба бруса. При конечной длине элемента постоянная /8 связана с деформацией еу у и поэтому слагаемое f№y также дает вклад в ложный сдвиг. Отметим также, что полученная здесь матрица kre,e полностью совпадает с матрицей (5.30) для конечного элемента с линейным законом распределения напряжений.
Подобный анализ можно приложить и к другим элементам, предназначенным для моделирования стенки, в том числе изо-параметрическим. В любом случае наилучшее воспроизведение жесткостных характеристик стенки достигается применением минимально допустимого порядка интегрирования для krs, а в сочетании с более точным интегрированием для кг8,в*
Если допустить, что вклад поперечной деформации еуу в энергию пренебрежимо мал по сравнению с вкладом продольной деформации ежж, то можно построить и более простые конечные элементы (рис. 6.2) для моделирования стенок. Для них узловыми параметрами являются смещения wCT, иуг узловых сечений вдоль координатных осей и углы поворота этих сечений. Для произвольного сечения
их (X, у) = и% (х) — у® (х); иу (х, у) = < (х),
где «2, иу — перемещения точек, лежащих на осевой линии, а О — угол поворота сечения.
Функции иу, О обычным образом аппроксимируются по их узловым значениям. При таком подходе е,уу = = О,
а ежж = е°х (х) — у % (х); еху = гху (х); где х(х) = .
При вычислений вклада деформации сдвига еху в матрицу жесткости применяется минимально допустимый порядок интегрирования, а для вклада ежж используется более точное интегрирование. Такие элементы будут продемонстрированы в гл. 8.
Подобный подход оказался весьма плодотворным и при построении эффективных элементов пластин, работающих на изгиб, а также оболочек. Этим вопросам посвящена следующая глава.
ЧАСТЬ ГП
ПРИЛОЖЕНИЕ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ К РАСЧЕТУ АВИАЦИОННЫХ КОНСТРУКЦИЙ
ГЛАВА 7
КОНСТРУКЦИИ В ВИДЕ ПЛАСТИН И ОБОЛОЧЕК
Пластины и оболочки широко применяются в конструкциях летательных аппаратов. Большинство методов их расчета основывается на использовании гипотезы прямых нормалей. В методе конечных элементов такой подход наталкивается на серьезные трудности, связанные с необходимостью обеспечения совместности конечных элементов. Эти трудности можно обойти, если воспользоваться независимой аппроксимацией перемещений и углов поворота нормали. Благодаря этому удается построить семейства конечных элементов изопараметрического типа, пригодных для расчета иа изгиб пластин или моментных оболочек произвольной конфигурации.
§ 7.1. Предварительные замечания
Примерами пластин и оболочек как конструктивных элементов могут служить сплошное крыло малого удлинения или топливный бак. Подобные тела можно идеализировать с помощью обычных трехмерных элементов, описанных в гл. 5. Но такой подход оказывается неэкономичным, так как он приводит к конечноэлементной модели с большим числом степеней свободы. Повышения эффективности расчета можно добиться с помощью специальных конечных элементов, при построении которых используются дополнительно гипотезы теории пластин и оболочек. Последние учитывают то обстоятельство, что толщина мала по сравнению с габаритными размерами.
Использование соотношений теории пластин и оболочек позволяет свести задачу к двумерной. Деформированное состояние оболочки или пластины полностью определяется перемещениями срединной поверхности (или срединной плоскости) и углом поворота прямолинейного отрезка до деформации нормального к срединной поверхности (нормального отрезка или просто нормали). Дискретизация тела сводится к разбиению на конечные элементы срединной поверхности, а в качестве основных неизвестных выступают узловые значения перемещений срединной поверхности и углов поворота нормали.
На рис. 7.1, а, б показаны возможные варианты конечноэлементной идеализации крыла и бака. Крыло идеализируется с 8* 227
помощью произвольных четырехугольных, а также треугольных элементов. Для идеализации бака здесь применяется разбиение срединной поверхности на отдельные пояса. Роль уз-
лов при этом выполняют узловые окружности, получаемые при пересечении срединной поверхности с плоскостями, перпендикулярными оси бака. Такая идеализация возможна лишь для оболочек вращения; она особенно удобна в случае осесимметричного нагружения. При расчете оболочек общего
вида используют конечные элементы треугольной или четырехугольной формы; их можно применять и в случае оболочек вращения, нагруженных произвольным образом.
Для определения деформированного состояния конечного элемента необходимо выполнить аппроксимацию перемещений срединной поверхности и угла поворота нормали через узловые перемещения. При этом возможны два пути. В одном варианте аппрок
симация угла поворота нормали осуществляется независимо от аппроксимации перемещений срединной поверхности. Другой подход заключается в использовании допущения о том, что нормаль и после деформации остается нормалью к деформированной срединной поверхности. Такое предположение оправдано для достаточно тонких пластин и обо-
лочек; в этом случае выполняется аппроксимация только перемещений срединной поверхности, а угол поворота нормали выражается через производные от этих перемещений. Ниже будут представлены конечные элементы, полученные на основе обоих вариантов.
§ 7.2. Основные соотношения теории изгиба пластин
Отнесем пластину к декартовой системе координат х, у, г, совместив плоскость ху со срединной плоскостью пластины. Перемещения точек срединной плоскости в направлении осей х, у будем полагать равными нулю. Считая, что поперечное перемещение uz по толщине пластины постоянно, а тангенциальные перемещения их, иу изменяются по линейному закону, имеем
«х = 2®х (х, у)', иу = zfty (х, у); uz = uz (х, у). (7.1)
Здесь О',, (х, у) и (х, у) — компоненты угла поворота нормального элемента. Как всегда, будем считать, что положитель-
ные перемещения их, иу, и. совпадают с положительными направлениями соответствующих осей. Принятые в (7.1) поло-
жительные направления углов Ох, Оу указаны на рис. 7.2.
Найдем далее деформации, пользуясь формулами Коши (1.7). Прежде всего отметим, что
e2Z = duz/dz — 0.
Для компонент деформации слоя
пластины, параллельного срединной плоскости, имеем Рис- 7-2
— ди* ~ д&х • ₽ — duv -дх дх ’ w ду ду '
р диу । дих t д^у , ддх \ дх ду \ дх ду /
а для деформаций поперечного сдвига —
_ дих диг диг
дг дх х дх
Еуг = _*flL +
дг ду ду
(7-3)
Напряжения найдем теперь по формулам закона Гука. Учитывая, что нормальные напряжения в площадках, параллельных срединной плоскости, малы по сравнению с компонентами сгжж или вуу, положим ozz = 0. Тогда напряжения ахх, ауу> аху будут определяться по формулам обобщенного плоского напряженного состояния. Ограничиваясь случаем изотропного материала, имеем
Е Е
°ХХ ~ (ъхх 4-№уу)> ауу = - — (fiyy + Неля)">
* р* 1 — J1
°ху~ Gexy = еХу. (7.4)
* U ~Г Н/
Касательные напряжения axz, ayz связаны с деформациями поперечного сдвига равенствами
®acz = ^®kz> &yz = (j8j/z. (7«5)
Формулы (7.2) —(7.5) можно взять за основу при выводе жесткостных характеристик конечных элементов, осуществ-г ляя при этом независимую аппроксимацию функций uz, Qx и &у по их узловым значениям. Как следует из (7.1), совместность перемещений обеспечивается, если каждая из этих функций непрерывна на границах между элементами. Так же как и в случае плоской задачи теории упругости, выполнить это условие можно, например, с помощью изопараметрической формулировки конечных элементов. Следовательно, здесь открываются широкие возможности для введения конечных элементов произвольной формы, в том числе криволинейных. Но применение подобных элементов к расчету тонких пластин до последнего времени было ограниченным из-за чрезмерной жесткости элементов, которая обусловлена ложными деформациями поперечного сдвига еж? и е„г, появляющимися при чистом изгибе пластины. В работе [38] показано, что и в случае изгиба пластин эффективным средством борьбы с ложными деформациями поперечного сдвига является использование минимально допустимого порядка интегрирования соответствующих членов при вычислении матрицы жесткости элемента. Несколько конечных элементов, полученных таким способом, представлено в следующем параграфе. Они могут успешно использоваться при расчете как тонких, так и сравнительно толстых пластин.
В другом способе построения конечных элементов пластины принимают, что нормальный отрезок остается перпендикулярным деформированной срединной поверхности. Такое допуще- ‘ ние, называемое гипотезой прямых нормалей, приемлемо в случае достаточно тонких пластин, у которых толщина составляет не более от характерного размера в плане. Так как угол между нормалью и срединной поверхностью остается прямым, то деформации exz и гуг оказываются равными нулю; из (7.3) имеем при этом
-------_------------. (7.6) х дх v ду ' '
Подстановка этих равенств в (7.2) приводит к выражениям д* uz д* uz „ d2 uz . .
ХХ дх* т ду* У дхду ' '
В этом варианте деформированное состояние конечного элемента определяется единственной функцией иг (х, у). Компоненты перемещения их, иу выражаются через uz по формулам
и теперь для выполнения совместности необходимо обеспечить непрерывность не только самой функции uz, но и ее первых производных по координатам х, у. Это существенно более сложная задача, чем выполнение условия непрерывности самой функции. Обычно конечные элементы, построенные таким путем, оказываются несовместными, и их применение требует известной осторожности. В дальнейшем будет рассмотрен прямоугольный элемент подобного типа, хорошо зарекомендовавший себя в практических приложениях, а также более сложный четырехугольный элемент.
В классической теории изгиба пластин принято напряженное состояние пластины характеризовать погонными изгибающими Мхх, Муу и крутящим Л4Х1, моментами, действующими в ее сечениях;
Л/2 Л/2
Мхх = j <rxxzdz; МУу= j Gyyzdz-, — h/2 — ft/2
ft/2
Mxy — j" axy г d z.
—h/2
При желании их можно вычислить по формулам, вытекающим из (7.2), (7.4):
MXX = D
, .. Мх ду дх
Л1 =0-!—И-ху 2
<Ж ду
Здесь D = ЕЛ3/ [12 (1 — р2)1 — изгибная жесткость пластины.
§ 7.3. Изопараметрические конечные элементы пластины
Рассмотрим конечный элемент с четырьмя узлами, имеющий в плане форму произвольного четырехугольника (рис. 7.3) [381. Обозначим через «гг, йхг, ‘дуг значения функций иг, Ор в типовом узле г и введем матрицу
vr= {«»<>*, Op Д
Обходя в определенном порядке узлы элемента, составим матрицу
ve = {v,v/v/vm }.
Будем считать, что координаты хт, ут узлов элемента заданы, а координаты текущей точки определим соотношениями
х = 2фг (5, пК; У = 2фг (£, п)Уг-
Для аппроксимации функций формулами
Здесь, как и в случае четырехузлового изопара-метрического элемента плоской задачи теории упругости (см. § 5.6), функции фг (£, т|) (5.18) зависят от безразмерных переменных 1), изменяющихся от—1 до 1 и принимающих в узлах значения ±1; суммирование выполняется по всем узлам элемента. wz, 0я, ду воспользуемся
uz — 2фгы„; Од — 2фг дхт\ ду — (7.9)
В соответствии с равенствами (7.2) и (7.3) выразим деформации через узловые перемещения:
в» - - 2 Ьхт + 2 “аГ" М";
(7.11)
Фигурирующие здесь производные от х|?г по координатам х, у определяются соотношением
дх
дЪ,
<?Фг
где J — матрица Якоби:
~ дх ду ~
j= "Ц аГ
дх ду
<?Т) <?Т)
Деформации е,хх, и е.ху, изменяющиеся по толщине пластины по линейному закону, объединим в матрицу
е* = {ежж Ъуу &Ху}.
В соответствии с (7.10) связь 8* с узловыми перемещениями запишем в форме
8* = z2₽f‘vr, (7.12)
где “о 0 дх
• 1! 1 ° <? £ о •ч о, S' й) S' «= V 1 (7.13)
Деформации поперечного сдвига объединим в матрицу 8 — {&xz еУх), на основании (7.11) имеем
8 = Sprvr) (7.14)
где
Фг 0
дх
(7.15)
° Фг
L дУ
Формулы (7.12) и (7.14) в совокупности дают следующую связь между деформациями е = {е* е} и узловыми перемещениями:
в = 2prvr. (7.16)
Здесь типовая матрица рг имеет вид
г₽‘
(7.17)
Формулу (7.16) можно переписать в стандартной форме е — Pve, полагая Р — (р,- р; р{ рт].
Компоненты напряжения также сгруппируем в две матрицы
J* {ожх <?уу вХу}><* Ofyz}.
Соотношения упругости (7.4) и (7.5) можно представить тогда в форме
р ~ —
о* -------х* 8*; в = G v. в,
1 — р.2
где
II * X “1ц 0 ~ р 1 0 о о 2 ~ Г 1 0 ; х = [° 1
(7Л8)
Если объединить эти равенства и положить о — {о* о), то получим СВЯЗЬ О — Х8, в которой
X
Е * -----X*
1—р.2 о
о
Gx
(7.19)
По формуле
k®s = § РГ xPs d т (г, s = i, /, I, т)
Т?
вычисляем типовой блок матрицы жесткости конечного элемента. Подставив сюда (7.17) и (7.19), приведем эту формулу к виду
(7.20)
где
J2* dT;
те
кГ! = С J ^₽Л = С J #Мт.
Положим dr — |J| dgdTjdz, где |J| — определитель матрицы Якоби. Выполняя интегрирование по координате г в пределах от —Л/2 до Л/2, где Л — толщина пластины, имеем
k’fS= j j op;Tx*ps’|j|dgdn, — 1 —1
krs=G j pn,।j|dgdn. — 1 Jl
(7.21)
(7.22)
Отметим, что в общем случае пластины переменной толщины изгибная жесткость D является функцией координат х, у (или g, Т))-
Интегрирование по координатам g, т] приходится выполнять численно. Прн вычислении k*s можно брать по две точки Гаусса в каждом направлении, а для вычисления krs возьмем одну точку Гаусса, что соответствует минимально допустимому порядку интегрирования. Как уже говорилось выше, это необходимо для исключения ложных деформаций поперечного сдвига.
Отметим еще одно обстоятельство. Считая, что нормальный отрезок при деформации пластины только поворачивается, но не искривляется, мы приходим к равномерному распределению напряжений оЖ2 и <зуг по толщине пластины, как это видно из (7.3) и (7.5). Но в действительности поперечные касательные напряжения распределяются по толщине неравномерно. В случае пластины постоянной толщины они обращаются в нуль при z = ±Л/2, имея максимальное значение при z = 0. Согласно элементарной теории изгиба тонких пластин напряжения <тХ2, оуг и соответствующие деформации изменяются по толщине по квадратичному закону. При этом вклад в матрицу жесткости от деформаций поперечного сдвига оказывается несколько меньшим, чем по (7.22). В связи с этим вместо (7.22) иногда используется формула
1 1 ~ ~
krs = G J f Л₽Г₽з IJI d gdn.
-i —i
Она отличается от (7.22) тем, что вместо действительного модуля сдвига здесь введена несколько меньшая величина (j. Последняя определяется из условия равенства удельной энергии деформации при истинном и равномерном распределениях поперечных касательных напряжений по сечению пластины. Если истинным считать квадратичный закон изменения °xz и oyz, то G = 5G/6. Но в случае тонких пластин деформации поперечного сдвига не играют решающей роли и подобное уточнение матрицы krs не оказывает существенного влияния на точность окончательных результатов.
х
Рис. 7.4
Подобным же образом можно ввести четырехугольные конечные элементы второго и третьего порядков (рис. 7.4). Соотношения, полученные выше для элемента первого порядка, остаются и здесь в силе. Отличие будет лишь в выражении для функций (g, т])- Для элемента второго порядка должны использоваться функции (5.62). Интегрирование в (7.21) следует выполнять при этом по трем точкам Гаусса для каждой из переменных g, т], а в (7.22) — по двум.
Для элемента третьего порядка выражение для фг (g, т]) дается равенством (5.67), а интегрирование выражений для kr* и krs должно выполняться соответственно по четырем и трем точкам Гаусса в каждом направлении.
Узловые значения параметров g, т] определяются в соответствии с рис. 7.4.
§ 7.4. Несовместный прямоугольный элемент пластины
Как уже говорилось ранее, в случае тонких пластин можно в качестве исходных соотношений взять формулы (7.6)— (7.8), в соответствии с которыми напряженно-деформированное состояние пластины определяется единственной функцией
uz (x, у). Применим эти формулы для вывода матрицы жесткости прямоугольного конечного элемента с четырьмя узлами в вершинах, показанного на рис. 7.5. Стороны прямоугольника имеют размеры а, b и параллельны координатным осям х, у.
В качестве узловых перемещений возьмем, как и ранее, смещения узлов uzr в направлении оси г и углы поворота нормали '&ЛГ, $ут'.
{«zr ^уг }•
Матрица узловых перемещений элемента
Vе = {Vf V} V[ vm }
содержит двенадцать компонент. Для аппроксимации функции uz по этим узловым параметрам зададимся следующим законом изменения прогиба в пределах прямоугольника (61:
= fl + fiX + f3y + /4х2 + f5xy + f6y* + /,х3 + f^y +
+ W + fi^ + fnX*y + /12х/. (7.23)
Здесь /j, /2, ...,/12— постоянные, которые должны быть выражены через узловые перемещения. В (7.23) содержатся полные полиномы от х, у вплоть до третьего порядка; члены х?у и ху3 взяты с таким расчетом, чтобы вдоль сторон прямоугольника функция uz изменялась по кубическому закону. Это обеспечивает непрерывность перемещения uz на границах между элементами. В самом деле, закон деформирования, скажем, стороны, прилегающей к узлам i, /, характеризуется узловыми параметрами uzi, uz} и Ьх1. Эти четыре параметра однозначно определяют кубическую параболу, а так как узловые перемещения являются общими для смежных элементов, то будет соблюдаться непрерывность uz вдоль стороны ij.
Однако полной совместности конечных элементов функция (7.23) не обеспечивает, поскольку при переходе к смежным элементам возможен излом деформированной поверхности. Так, например, производная dujdx, определяющая наклон линий у = const, изменяется вдоль стороны jl по кубическому закону. Но из четырех параметров, необходимых для описания этого закона, лишь два (ftXj и •&ж/) являются общими для смежных элементов, примыкающих к данной стороне (рис. 7.6). Следовательно, непрерывность производных будет соблюдаться только в узловых точках.
Связь постоянных f — {/i /2, ,../12) с узловыми перемещениями можно получить, приравнивая в каждом узле значения
Рис. 7.5
Рис. 7.6
uz, = —duz/dx и — —duzldy к соответствующим узловым параметрам. Выразив f через Vе, можно в соответствии с (7.23) прийти к стандартному соотношению вида uz = ave.
Удобнее, однако, построить матрицу а непосредственно, путем подбора. Для этого прежде всего представим ее в блочной форме а = [а,- а> а, ат}. Типовой блок аг представляет собой матрицу-строку и содержит три функции координат х, у:
[«rl
Первая из этих функций дает распределение перемещения иг в элементе, когда поперечное смещение узла г равно единице, а все остальные одиннадцать узловых перемещений равны нулю. Функции аг2 и аг3 определяют иг при единичных значениях углов б’хг и $уг соответственно. Следовательно, функция аг1 должна равняться единице в узле г и нулю в остальных узлах, а ее производные даТ11дх и да.г1!ду должны во всех четырех узлах обращаться в нуль. Функции art и ar3 вместе со своими первыми во всех узлах, за исключением узла г, где выполняются равенства dar2/dx = —1, дат31ду = —1 (это соответствует единичным значениям углов поворота и bv).
Для записи искомых функций удобно воспользоваться безразмерными координатами £, т], связанными с х, у соотношениями
производными равняются нулю
X = хс + (а/2)1; у = ус4- (Ы2)х\.
Здесь хе, уе — координаты центра тяжести прямоугольника; переменные т| изменяются от —1 до 1, как показано на рис. 7.5.
Непосредственной проверкой можно убедиться, что функции
aa = Y<l-£)(1-T»)-T5(1"n)(1~52)~
О
= - ~ (1-5) (1 - п) (1 - £2);
10
а<з = -^-(1-£)(1-т))(1-п2)
10
могут быть использованы в качестве компонент подматрицы щ. Действительно функция аг1 равна 1 в узле i, где g = г| —
= —1, и обращается в нуль в остальных узлах. Производные же от аг1 по g, т] во всех узлах равны нулю. Функции ai2 и ai3 и их производные по g, г| во всех узлах равны нулю, за исключением того же узла i, где
da;2 _ 2 da;2 __ j. dct;3__2 da13 __ j
дх o dg ' dy b di]
Отметим также, что содержащиеся здесь полиномиальные функции от g, т] соответствуют тому набору функций, который представлен в (7.23).
Аналогично подбираются и остальные функции, входящие в матрицу а. В обобщенном виде выражение для типовой подматрицы ат (г — I, j, I, tn) можно записать так:
ar = [4“ + (1 + T)r ’l) + 4" +т1г +
+ 4-T)r n (1 н g) (1-^)1-^-gr(l + gr g) (14-T)r n) (1 -о I lb
-- w 14- -^1- (7-24)
I 10 J
По (7.7) выразим деформации через узловые перемещения:
ехх = —2
еии==— г
е — — 2z
д2 а „ == —г----------ve :
дх*
д* a , = — г-----------ve :
dj/2
d2 a ------V* . дхду
d2 иг дх*
д* uz
ду2
d2 uz п
----= —2z
дхду
Вводя матрицу е = {ежд; гуу еху}, представим эти соотношения в форме е = pve, где
д2 а ~ дх2
P=-Z д2 а Л/2 „ д2 а 2 _ дхду _
Учитывая блочное представление матрицы а, можно записать
Р = 1₽. ₽/ Р< PJ-
Типовая подматрица рг определится равенством
где
₽Г = — 2РЛ (7.25)
Р* = д2 аг ~ дх2 д2 аг ~ 4 а2 4 д2 аг~ д^2 д2 аг
ду2 Ь2 dt]2
О д2 аг 8 д2 аг
2
_ дхду _ _ ab д1дх\ _
Подставив сюда выражение (7.24) для матрицы аг, получим
---7 £г Б О + Пг П)
а3
—ПгПО + БЛ)
ь2
-Mi- (4 --3g2- Зт]2)
!- J- gr (1 +3grg) (i -к, n)
1
! J- gr т)г (gr-2g—3gr g2) I zo
0
__L(i-Hr g)(i + 3Tvn) z&
" Sr Пг (Пг — 2г)“3т)г Г]2)
2а
(7.26)
Соотношения (7.4), связывающие напряжения о = = К» ауу аху } с деформациями 8, в матричной записи имеют вид о = ие, где
Е *
X = ------- X*
1— J12
(7.27)
здесь х* дается первым равенством (7.18).
По формуле
к" = S ₽, *М т (r> s = г’ /•1’ т)
Xе
вычисляем далее типовой блок матрицы жесткости. Полагая dx = (aft/4)d£dr]dz и подставляя в формулу для k«s соотношения (7.25) и (7.27), получим
1 1 Л/2
к® ®~— f f Г г2 р*г х* р* d | d г] d г.
rs 4(1—ua) J J J Г s
— 1 _1 —h/2
Выполнив интегрирование по г, приведем это выражение к виду
1 1
к^=~ J Jnp7x*p;dUn-—1 —1
(7.28)
Интегрирование в (7.28) даже для пластины постоянной толщины удобнее всего выполнять численно, используя по две точки Гаусса в каждом направлении.
§ 7.5. Несовместный четырехугольный элемент пластины
Будем снова исходить из гипотезы прямых нормалей. Если в матрицы узловых перемещений включены узловые значения прогиба и углов поворота нормали, то тем Самым в узловых точках задается непрерывность функции иг и ее первых производных dujdx\ dujdy, между узлами эти величины могут вдоль сторон элементов претерпевать разрывы. Для уменьшения разрывов можно включить в число узловых параметров старшие производные от uz по координатам х, у, обеспечивая таким путем непрерывность этих производных в узловых точках. Если толщина пластины изменяется скачкообразно, то этот подход неприемлем, поскольку на линии, вдоль которой это происходит, вторые производные от иг по х, у (имеющие смысл кривизн и кручения изогнутой срединной поверхности) ие могут сохраняться непрерывными. Однако в случае плавного изменения толщины указанный прием вполне оправдай.
Рассмотрим в качестве примера конечный элемент в форме произвольного четырехугольника с прямыми сторонами и четырьмя узлами в вершинах (рис. 7.7). В число узловых параметров включим смешанную д2 иг
производную <р = . Матрица перемещений элемента
Vй{Vi Vj Vi vm)
будет иметь шестнадцать компонент — по четыре в каждом из узлов:
Vr — fair $xr$yr Фг}
Закон изменения прогиба в пределах конечного элемента представим в форме
Рис. 7.7
uz = a*t. (7.29)
Здесь f — матрица-столбец коэффициентов, число которых в соответствии с количеством узловых параметров равно шестнадцати:
f = {fl ft ...Лв).
Матрица-строка «* содержит полиномиальные функций от х, у, выбор которых может быть различным. Следуя [18] примем, в частности,
«* = [1 х у х2 ху у2 х3 х2у ху2 у3 х*у х2у2 ху3 х3:/2 х2у® хРу3].
(7.30)
Первые десять компонент матрицы «* содержат полные полиномы от х, у до третьего порядка включительно. Таков же порядок полных полиномов у рассмотренного выше прямоугольного элемента, и можно ожидать, что характеристики сходимости данного элемента будут такими же, как и у прямоугольного; числовые расчеты подтверждают это.
Исходя из условий в узлах, свяжем параметры f с узловыми перемещениями (г = i, j, I, tn):
диг I uz (хт> Ут) — игт‘> и=*г =
ax 'У — Уг
d2u2 дхду
=<Pr-'У=УТ .
(7.31)
Эго дает 16 соотношений, которые можно представить в форме
Tf = Vе,
где числовая матрица Т имеет размер 16 X 16 и формируется из элементов матрицы «* и ее производных в соответствии с (7.29), (7.31).
Выполнив обращение матрицы Т и обозначив
Q = Т-i,
(7.32)
приходим к выражению f = Qve, с помощью которого равенство (7.29) приводится к стандартной форме u = av" с матрицей
а = a*Q. (7.33)
В соответствии с формулами
д2 иг д2 иг д2 иг
хх дх2 уу ду2 ху дхду
устанавливаем связь между матрицей в = (едх еиа еж9} и узловыми перемещениями. Ее можно записать в обычной форме в = pve, где
Р = — гр* Q; (7.34)
d2a*
дх2
r*= д2«*
ду2
2^
_ дхду _
Наконец, по формуле
кг= J prxpdx
(7.35)
вычисляем матрицу жесткости элемента. Подставляя сюда (7.27), (7.34) и учитывая, что <1т = dxdydz, после интегрирования по z получаем
ke=Qrk*Q, (7.36)
где
k* =J J Dfi*T х* Р* dxdy. Интегрирование осуществляется здесь по площади четырехугольника.
Преобразование координат х = 2фгхг; у = 2фгуг с функциями
Фг (5. П) = -7~ (>+ЕгЕ) (1+ПгП) 4
позволяет перейти к интегрированию по площади квадрата:
1 I
k*= J J Ор*гх* Р*| J | d£dn.
(7.37)
Здесь |JJ обозначает, как и ранее, якобиан преобразования координат:
дх ди ду дх
' ' д£ дц Л)
При вычислении к* по (7.37) можно воспользоваться численным интегрированием с тремя точками Гаусса для каждой из переменных L *1-
При моделировании крыла самолета пластиной часто можно ограничиться конечными элементами трапециевидной формы. Для них не обязательно вводить координаты т], поскольку в случае, когда основания трапеции параллельны одной из координатных осей, удается записать аналитические выражения для интегралов от полиномиальных функций [18].
Рассмотренный конечный элемент относится к категории несовместных. На его сторонах терпит разрыв даже сама функция uz. Тем ие менее, как свидетельствуют числовые расчеты, он дает вполне приемлемую точность, соизмеримую с точностью прямоугольного элемента.
§ 7.6. Учет внеузловой нагрузки.
Определение узловых перемещений
Если в узлах пластины действуют сосредоточенные силы и моменты, то из них можно сформировать матрицу-столбец
Р= {Р, Р2 ...РП}.
Здесь каждая подматрица Рг включает в себя поперечную силу Pzr и два момента Мхг, Муг-, их следует считать положительными, если они действуют в положительных направлениях uzr, 'O'xr, соответственно. Если применяются элементы с четырьмя степенями свободы в узле, то Рг будет содержать четыре элемента. Четвертый элемент в Рг, соответствующий параметру <рг, не имеет физического смысла и его следует всегда брать нулевым.
Кроме того, на пластину может действовать распределенная поперечная нагрузка р (х, у), которую необходимо заменить эквивалентными узловыми силами и моментами. Замена производится поэлементно из условия равенства работы нагрузки р на перемещении uz работе эквивалентных узловых сил Ре на перемещениях Vе. Повторяя рассуждения § 4.4, придем к следующему выражению для Ре:
ре = Ja^pdF. (7.38)
Здесь интегрирование ведется по площади Fe конечного элемента; через au обозначена матрица функций, аппроксимирующих перемещение иг через Vе в соответствии с равенством uz — auve.
Для конечного элемента с узлами i, j, ... блочное представление матрицы ац будет аи = [а„гаи> ...].
Подстановка этого равенства в (7.38) позволяет записать выражение для Ре в блочной форме Ре = {Р® Р®....}. Здесь типовая подматрица Р« определяет вклад рассматриваемого элемента в эквивалентные силы в узле г и вычисляется по формуле
₽? = J <*TurPdF- (7-39)
Ее
Если перемещения и углы поворота нормали аппроксимируются независимо, как в случае-рассмотренных выше изопа-раметрических элементов, То матрица аиг имеет вид
aUr = N’r 0 0]. (7.40)
В этом случае в каждой подматрице Р« отличным от нуля будет лишь первый компонент, т. е. узловая сила
Рг,= p’rpdf- (7.41)
Ее
Таким образом, распределенная нагрузка заменяется здесь одними лишь сосредоточенными узловыми силами, узловые же моменты оказываются равными нулю. Интегрирование в (7.41) можно осуществить численно с использованием такого же числа точек Гаусса, что и при вычислении матриц k*s (в случае элементов с четырьмя сторонами следует положить dF = |J| d£ drj и интегрировать по параметрам £, т] в пределах от —1 до 1).
Если же при построении элемента применяется гипотеза прямых нормалей, то матрица аиГ совпадает с матрицей (7.24). В этом случае все компоненты Р® будут отличны от нуля, т. е. при замене распределенной нагрузки эквивалентными узловыми силами появятся не только силы, но также и моменты. Для прямоугольного элемента интегрирование в формуле
1 ।
Р® = J J «J" р d | d г]
-1 -1
можно также осуществить методом Гаусса, взяв по две точки в каждом направлении. Если нагрузка р постоянна, то точное интегрирование дает следующие значения узловых сил:
Для четырехугольного элемента с шестнадцатью степенями свободы следует пользоваться формулой
Pe = QrJ а*т pAF, Fe
применяя замену координат с последующим интегрированием по 2 X 2 точкам Гаусса, либо прибегая к аналитическому интегрированию, если элемент имеет форму трапеции. Отметим, что при этом появятся обобщенные «силы», соответствующие узловым параметрам <рг.
Выполнив для каждого элемента приведение распределенной нагрузки к узловым силам, можно в каждом узле просуммировать вклады элементов и сформировать матрицу
Р= {₽! Рг- Рп}.
где типовая подматрица Рг — 2 Р® (суммирование ведется по всем элементам, сходящимся в узле г).
Система уравнений, связывающих узловые перемещения с узловыми силами, имеет вид
Kv = Р + Р,
где К — общая матрица жесткости. Последняя формируется по обычному правилу суммирования коэффициентов жесткости с одинаковыми индексами: krs = 2k«s (суммирование по всем конечным элементам, соединяющим узлы г, s).
Для отыскания узловых перемещений необходимо учесть связи, накладываемые на пластину опорными устройствами. Обозначим, как и ранее, через vo матрицу, в которой содержатся одни лишь неизвестные перемещения; известные же перемещения составят матрицу vp. Если v& = 0, то можно исключить из матрицы жесткости строки и столбцы, соответствующие нулевым перемещениям, и прийти к системе уравнений вида (4.21) относительно неизвестных перемещений va.
В некоторых случаях связи нельзя считать абсолютно жесткими, как, например, при расчете крыла. На крыло связи накладываются в месте соединения его с фюзеляжем. Перемещения узлов, в которых оно соединяется с фюзеляжем, строго говоря, не будут нулевыми. Они должны определяться из расчета летательного аппарата в целом. Здесь удобно воспользоваться методом подконструкций (см. § 5.4), рассматривая эти узлы как внешние для крыла и исключая перемещения остальных узлов. Однако при выполнении приближенных расчетов можно считать фюзеляж абсолютно жестким, полагая Vp = 0 и сводя, таким образом, задачу к решению системы (4.21).
§ 7.7. Основные соотношения для оболочек вращения при осесимметричном нагружении
Рассмотрим оболочку, срединная поверхность которой образована вращением вокруг оси произвольной плоской кривой (рис. 7.8). Введем в плоскости меридиана систему координат х, у, направив ось х вдоль оси оболочки. Предположим, что уравнение кривой меридиана задано в параметрической форме х = х (£), у — у (£). Для определения геометрических характеристик этой кривой можно воспользоваться полученными в § 5.9 соотношениями, полагая в них 2 = 0.
Элемент дуги ds связан с приращением параметра £ соотношением ds = yld^, в котором
4 = + у'г. (7.42)
Здесь и далее штрихом
отмечается дифференци- Рис. 7.8
рование по £.
Направление касательной к меридиану будем характеризовать единичным вектором
et — Кх ех + Kv ev
или, что то же самое, матрицей его направляющих косинусов
— [Х(х (7.43)
где в соответствии с (5.72)
(7.44) Л Л
Через ех, еу в выражении для et обозначены орты координатных осей х, у, вектор et направлен в сторону возрастания параметра g.
Помимо et введем также нормальный к меридиану вектор еп с матрицей направляющих косинусов:
Х„ = 1ХпхХпД (7.45)
Направление еп выберем таким образом, чтобы поворот et до совмещения с еп по кратчайшему пути осуществлялся в ту же сторону, что и поворот ех до совмещения с еу. Тогда
Ъ'пх — ^ty', ^пу ~ \х- (7.46)
Радиус кривизны меридиана будем считать положительным, если центр кривизны удален от меридиана в направлении, противоположном направлению вектора еп. Значение R может быть подсчитано по формуле, известной из аналитической геометрии:
1 х' у"—у' х"
R / # 2 t / 2\ 3 / 2 ’
которой с учетом (7.42), (7.44) можно придать вид
(7.47)
Угол 0 между нормалью к меридиану и осью оболочки определим как угол, на который нужно повернуть ось у, чтобы ее положительное направление совпало с положительным направлением вектора et. Прн этом будем считать 0 положительным, если поворот происходит в сторону оси х; тогда
cos 0 = —А,пж = Х(!,, sin 0 = = Х;х. (7.48)
При осесимметричном нагружении перемещения точек срединной поверхности будут иметь лишь составляющие в плоскости меридиана. В теории оболочек принято рассматривать проекции перемещений на касательное и нормальное к меридиану направления. Эти составляющие мы обозначим через ut, ип, а соответствующие им компоненты поверхностной нагрузки — через р„ рп. Их положительные направления будем считать совпадающими с направлениями векторов et, еп.
Деформации срединной поверхности оболочки в меридиональном и окружном направлениях, которые мы обозначим через еь е2, связаны с перемещениями ut, ип соотношениями 1141
е2 = — (ut cos 04-«nsin0) = — (kts ut+klx ип). (7.49) У У
Рассмотрим далее слой оболочки на расстоянии £ от срединной поверхности; отсчет положительных значений t, ус
ловимся вести в положительном направлении еп. Все величины, относящиеся к этому слою, будем помечать дополнительным верхним индексом £. Считая, что толщина оболочки h значительно меньше радиуса кривизны R, и учитывая, что |£| С Л/2, можно не делать различия между геометрическими характеристиками срединной поверхности и слоя:
/?£ « Я; yt « у, « Л; X^ = Xtx; = (7.50)
Перемещения слоя определим равенствами
ul — ut + £0; ип. (7.51)
Деформации слоя получим, заменив в (7.49) ut, ип на tfih ик
4 = £j + SXn £> = £2 + £Хг. (7.52)
где
X2==_Lftcos0=_±lfl. (7.53) ds А у у
Помимо е|, е| в оболочке возникает деформация поперечного сдвига, которую мы обозначим через е13. Она равна изменению угла между нормалью и касательной к меридиану, и ее можно найти как сумму двух углов, один из которых равен О, а второй есть угол поворота касательной. Последний будем считать положительным, если угол между et и еп становится острым; через перемещения срединной поверхности он выражается [14] как d«n/ds — utlR, так что для е13 имеем
v+»=T-“;-4-“'+e- <7И>
В некоторых случаях удобнее вместо ut, ип рассматривать проекции перемещений на направления осей х, у, эти проекции мы обозначим через их, иу. Они связаны с ut, ип соотношениями
Wx = Xjj,. ut + Xnxun, иу — Ut XnyUn. (7.55)
Для определения деформации ех по перемещениям их, иу можно воспользоваться общей формулой (5.77), из которой применительно к рассматриваемому случаю вытекает равенство
где и' означает производную по £ от матрицы и = (их ии}. Для окружной деформации е2 на основании (7.46), (7.49) и (7.55) имеем
%^—Uy. (7.57)
у
Угол поворота касательной к меридиану через перемещения их, иу выражается на основании (5.79) как ^-Хаи', так что для деформации поперечного сдвига имеем
(7.58)
Так же как и в случае изгиба пластин, здесь можно наметить два пути построения конечноэлементной модели оболочки. В первом варианте выполняется независимая аппроксимация функций ut, ип (или их, иу) ий, а е,3 учитывается наряду с еу, е| в матрице деформаций. Другой подход основан на использовании гипотезы прямых нормалей, в соответствии с которой следует положить е13 = 0. В этом случае аппроксимируются лишь перемещения ut, ип (или их, иу), а для вычисления $ используется одно из равенств
А 1 • , 1
»------(7.59)
Л
вытекающих из (7.54) или (7.58) при е13 = 0; матрица деформаций будет включать при этом лишь компоненты и е|. Ниже будут рассмотрены оба подхода.
Как говорилось в начале главы, при идеализации оболочки вращения ее срединную поверхность можно разбить на пояса плоскостями, перпендикулярными ее оси. Эти пояса будем рассматривать в качестве конечных элементов. Геометрия элементов обычно задается лишь координатами узлов (и, возможно, значениями угла 0 в узлах), для определения же самой кривой применяется приближенная аппроксимация. Для оболочек простой геометрической формы (например, сферической или круговой торовой) можно и не пользоваться аппроксимацией, определяя все необходимые геометрические параметры, исходя из точных соотношений. Однако в целях унификации исходных данных даже в этих случаях предпочитают обычно аппроксимировать реальную оболочку с помощью приближенных зависимостей.
i § 7.8. Изопараметрические конечные элементы Оболочки вращения
Рассмотрим конечные элементы оболочки вращения изо-параметрического типа. На рис. 7.9 представлены конечные элементы первого, второго и третьего порядков, имеющие соответственно два, три и четыре узла. Исходными данными для них служат координаты узлов хг, ут и значения толщины h в узловых точках. Уравнение меридиана будем задавать приближенными равенствами: х — у = 2tyryr, где суммирование ведется по всем узлам элемента. Функции 4>г (£) даются равенствами (5.81)—(5.83).
Рис. 7.9
Согласно (7.42), (7.44) можно в любой точке вычислить параметры
Л ~У^х'2 4- у'2 ’ Кх = “г х'> ^ty = -j-/1 А
где х' = у' ==
Отметим, что для элемента первого порядка эти параметры постоянны по длине образующей:
2 ix I lv I
где I — У (xj — х{)2 + (yj — yi)2 — длина образующей элемента.
Каждый узел элемента имеет три степени свободы vr = «= (ижг иут бг), так что для двухузлового элемента матри-
ца ve = {v, vj} содержит шесть перемещений, для трехузлового— ДеВЯТЬ Vе = {v, Vj vm} и т. д.
Для аппроксимации перемещений и угла поворота по узловым значениям воспользуемся изопараметрической формулировкой:
их = 2фгижг; и у = 2yTuVT-, ft = S^rftr. (7.60)
По формулам (7.53), (7.56)—(7.58) выражаем параметры деформации Ej, е2, Xi. Xz, eis через узловые перемещения. Введя обозначения
е°=| 61
L ®2 .
Xi]
Хг1 ’
представим эти зависимости в виде
е°=2₽? vr;x = S ₽*vr;e13 = 2 ₽rvr, (7.61) где
[—г 4-• <7-62>
j Л /1 I
При записи последних соотношений учтены зависимости (7.43), (7.45), (7.46).
Матрицу деформаций е= {е£ е| е13) на основании (7.52), (7.61) можно представить в обычной форме е = S₽rvr, где
₽г.
(7.63)
Нормальные напряжения, действующие в меридиональном и окружном направлениях, обозначим через о£, о|, а поперечное касательное напряжение — через о13. Пренебрегая нормальным напряжением в площадках, параллельных срединной поверхности, запишем соотношения упругости
(еС +^1); = —— (е| + |хе£ ); о13 = Ge13,
1—|х2 1— Ц
где, так же как и в случае пластины, можно взять G = 56/6 для учета неравномерности напряжения о13 по толщине оболочки.
Отсюда получаем связь о = хе между матрицами а = = <*1з} И «; при ЭТОМ
X =
----х* О
1— и2 О G
И
1
(7.64)
Далее вычисляем блоки матрицы жесткости
Ms = j
te
где dx = 2ra/dsd£ — 2nyAdE>dt,.
После подстановки в подынтегральное выражение (7.63) и (7.64) и интегрирования по толщине оболочки в пределах от —Л/2 до Л/2 можно получить
k®s — kys. е 4“ k/-s(. g,
(7.65)
krs, E= 2л J (В 0“r x* 0S“ + D 07 x* 0;) у A d (7.66)
— 1
krs, c = 2nG ^^syhAdl, — 1
(7.67)
где В — Eh/ (1 — p2) — жесткость оболочки на растяжение. Интегрирование в (7.66), (7.67) выполняется численно.
Для исключения ложного сдвига порядок интегрирования в kfSto должен быть минимально допустимым. Это соответствует одноточечному правилу Гаусса в случае элемента с двумя, двухточечному для элемента с тремя и трехточечному — для элемента с четырьмя узлами. Что касается krs.£, то в случае трехузлового элемента здесь следует взять три точки Гаусса, четырехузлового — четыре, а для двухузлового достаточно и здесь без ухудшения точности ограничиться одной точкой. Отметим, что двухузловой элемент подобного типа впервые предложен в работе [411.
Приведение распределенных нагрузок к эквивалентным узловым осуществляется обычным образом. Типовая матрица, характеризующая вклад данного конечного элемента в матрицу эквивалентных узловых сил в узле г, определяется равенством
fa^pdco,
где р = lpx pj — матрица поверхностных нагрузок в направлений их, иу\ аиг — матрицы функций, аппроксимирующих перемещения срединной поверхности через узловые перемещения в соответствии с равенством
их иу
“иг
(7.68)
интегрирование в выражении для Р, выполняется по срединной поверхности конечного элемента.
Как следует из (7.60),
аиг=П’г
1 0 0
О 1 О
(7.69)
Учитывая, что dw =• 2ra/ds = 2nyAd£, приходим к выражению
1
Р*=2л J — 1
Рх
Ру О
ф,. z/Xdg.
(7.70)
Интегрирование здесь можно выполнить так же, как и при вычислении krs,G- Для двухузлового элемента результат удобно записать в явном виде:
Р^л/(/0
РхО
Руо 0
<7.71)
Здесь рх0, ри0 — значения нагрузок рх, ру в середине элемента (т. е. при £ = 0), а у0 = {у, + у,)12 — радиус соответствующего параллельного круга.
Отметим, что в элементах рассматриваемого типа эквивалентные узловые силы не содержат компонент в направлении 0г, т. е. узловые моменты, эквивалентные распределенной нагрузке, оказываются здесь нулевыми.
§ 7.9. Двухузловой криволинейный конечный элемент оболочки вращения
В данном параграфе рассматривается двухузловой конечный элемент с криволинейной образующей [24]. Предполагается, что помимо координат узлов заданы также углы 0,, 0,-в узловых точках (рис. 7.10). При выводе жесткостных характеристик элемента будем исходить из предположения, что справедлива гипотеза прямых нормалей.
Прежде всего выполним аппроксимацию геометрии конечного элемента. Проблема заключается в приближенном задании уравнения об
разующей по известным координатам узлов и значениям 0;, Qj. Это уравнение будем искать в параметрической форме х х (£), у = у (g), Где параметр g, изменяющийся от —1 до 1 при движении от узла i к 2s
узлу j, свяжем с дуговой координатой s соотношением g = -у — 1. Так как ds = (Z/2)dg, то параметр А равен 1/2, и на основании (7.44), (7.48) имеем
x'=-“-sin0; у'= -^-cos 0, (7.72)
где штрих означает дифференцирование по g.
Рис. 7.10
Запишем теперь условия, накладываемые на функции х (g), у (g) в типовом узле элемента (г = i, у):
х(£т)=хг'> У&г)=Уг', х' (£r) = -J-sin0r; у' (gr) = -£- cos 0Г.
Этим условиям можно удовлетворить, взяв в качестве х (g), у (g) полиномиальные функции третьей степени. Коэффициенты этих полиномов можно найти так же, как это делалось в § 3.4 пря выводе уравнения изогнутой оси бруса. В итоге придем к следующим выражениям для искомых функций:
x(g) = a(g)X; y(g) = a(g)Y. (7.-73)
Здесь
( I 1 1
X=(xj — sin0y Xj — siriOjk v * J
Y={yi cos0!‘ У} 4~cos0>}’
а матрица a (g) дается формулой (3.35), которую мы представим в виде «(£)=(«; (£)«;(§)];
+ -V 5r(l+5r I) (1- П]. (7.74)
L 4 4 J
Пользуясь аппроксимацией (7.73), можно получить все необходимые геометрические параметры элемента. По (7.44) находим для любой точки меридиана значения и
2 . 2
(7-75)
Входящие сюда производные определяются соотношениями
х' U) = a' X; у' U)=a' Y; а'=[а;аД:
“;(?) = ["Tgr(1“g2) Т^ + ^Н1--3^)] (7-76)
Кривизну меридиана вычисляем по (7.47):
1 4
— (x"Kty-y"ktx), (7.77)
£\ I
где х"-а" X; y"=a"Y; a"—[a'- а?];
“';=[““T5rg Таг+3|)]‘
Представленными выше формулами можно пользоваться, когда известна длина I образующей элемента. Так как ds = Д/dx2 + dy2 = = d§l/x'2 + у'2, то по известным функциям х (§), у (§) ее можно найти через интеграл
1 _________
/ = j’ Ух’г±у'‘М;. (7.78)
— 1
Однако в сами выражения для функций х — аХ; у = aY входит величина I. Поэтому практически ее можно найти с помощью последовательных приближений. В нулевом приближении матрицы-столбцы X, Y сформируем, взяв в качестве I длину /0 хорды, соединяющей узлы i, j:
4>= V (xj —хг)2 4-(у;—уг)2.
После этого можно в соответствии с (7.78) уточнить величину I. Ограничиваясь первым приближением и применив для вычисления интеграла (7.78) правило Симпсона, можно прийти к следующей формуле для определения длины дуги /:
I^(i+-VOT+Ql),
О где
Л „ xj—xi sinOi + sinOj Л „ у}—yi cosOj+cosOj
^ = 3“ 2 ’ Q>=3~ 2
Чтобы получить представление о точности предлагаемой аппроксимации, возьмем участок образующей сферической оболочки и заменим его приближенной кривой в соответствии с рассмотренными.выше формулами. Приведем значения максимальной погрешности аппроксимации величины /? для различных значений центрального угла, определяющего выделенную дугу:
Центральный угол, град . . 2 4 6 10 15
Максимальная ошибка, % . . 0,01 0,04 0,09 0,25 0,57
Как видно, погрешность незначительна даже для весьма больших участков. Отметим, что если при определении I ограничиться нулевым приближением, заменив длину дуги длиной хорды, то ошибка аппроксимации радиуса кривизны возрастает примерно в три раза по сравнению с приведенными результатами.
Перейдем далее к аппроксимации перемещений, взяв за основу компоненты ut, ип. При этом поставим себе целью получить возможно более простой элемент, обладающий в то же время хорошими характеристиками сходимости. Как говорилось в предыдущей главе, скорость сходимости конечноэлемеитной модели определяется минимальным порядком аппроксимации компонент деформации в пределах конечного элемента. В рассматриваемом случае деформации ®|, е2 выражаются через величины ef, е2, Xi, Xz- Если последние представлены в пределах элемента в виде полиномиальных функций от s (или от 5), то можно ожидать, что скорость сходимости будет определяться наиболее низким порядком аппроксимации этих величии. Потребуем, чтобы все четыре функции в!, е», Xi- Ха были аппроксимированы в пределах элемента полиномами от g первой степени. Этого можно добиться, если использовать при их вычислении различные аппроксимации перемещений ut, ип. Выбор типа аппроксимации определяется характером соотношений, связывающих 8t, е2, Xi или Ха с перемещениями.
Так, функция е2 выражается через перемещения второй формулой (7.49). Для того чтобы выразить е2 через узловые перемещения, примем, что в пределах элемента щ и ип изменяются по линейному закону, т. е. воспользуемся аппроксимацией:
utr, Un—E g unr< (7.79)
где суммирование выполняется по двум узлам элемента (г = i, j). Подстановка (7.79) в формулу для е2 дает
2 (1 -f~gr g) (U(r ^ty ^y
Строго говоря, полученное выражение из-за наличия множителей \tyly и представляет собой сложную функцию от В. ио для конечных элементов малых размеров эти множители представляют собой плавные и слабо изменяющиеся функции. Поэтому зависимость е2 (g) близка к линейной, и можно ожидать, что при уменьшении размеров элементов скорость сходимости будет соответствовать линейной аппроксимации е2.
Для вычисления
1 Allt , "п 2 dut . 1
1 A dg + R I dg R
используем, для ип линейную аппроксимацию, а для ut — квадратичную. Квадратичная зависимость определяется тремя параметрами, в связи с чем в дополнение к имеющимся узловым параметрам utt, utj введем еще неузловую степень свободы с. Тогда зависимость U/(£) можно получить, добавляя в правую часть первого равенства (7.79) слагаемое (1 — £2)с. В итоге получим
g ,ztr + (l— S2)r. «<п—-2 - unr.
Подстановка этих соотношений в формулу для gj дает
ei= -у Sg,. utr + ^~ S (1 + g) nn,.--v- с.
I z.[\ I
Объединив полученные выражения для gj, е2, представим их в виде
(7.80)
где
Через v,. = [utr Unz обозначена матрица перемещений узла г в местной системе координат.
Переходя к аппроксимации fa, fa, начнем с функции у2, которая выражается через перемещения вторым равенством (7.53). Принимая, что угол поворота нормали О изменяется по § по линейному закону
1 + ёг S
й,.,
2
имеем
Наибольшие затруднения вызывает аппроксимация функции j(i. Согласно (7.59) и первой из формул (7.53) имеем
1 d-f> 1 d2 и„ 1 d I ut \
X1=7 "dF= ~7F d£2 ~dT /
4 d2 un 2 d ! at \
~ dg2 + T "df J
(7.82)
Прежде всего покажем, что в этом выражении можно опустить вследствие малости второе слагаемое в правой части. На основании формулы 8j = Bj + £Х1 найдем значение деформации в наиболее удаленном от срединной поверхности слое оболочки, т. е. при £ = Л/2:
ь/9 h 1 2h
6?/2 = ei4-TX1 = —ип- —
d2 ип 2 d Г/ h \ dg2 +Т ~dT |Д 14"2/Г/ (
Так как оболочка предполагается тонкой, то слагаемое Л/(2Л?) в круглых скобках мало по сравнению с единицей и его можно отбросить; следовательно, второй член в правой части (7.82) является также малым, тогда
4 d2 ип
Х* Р dg2
(7.83)
Так как Х1 есть производная по s от функции О' = —d«n/ds ut!R,
то и выражение для О можно упростить, полагая
d«n 2 d«rt
ds I d£
(7.84)
Примем далее, что перемещение ип изменяется по § по кубическому закону. При £ = ±1 функция ип (|) должна совпадать с узловыми значениями uni, iinj, а ее производная по £ иа основании равенства (7.84) должна в этих точках принимать значения — /Ф;/2 и —/Фу/2. Используя при аппроксимации ип те же функции (7.74), которые встречались выше в матрице а, придем к соотношению
1 I
ип = ~ 2 (1 — gr g)2 (2-|r g) »nr + — 2gr (l-Чг S) (I-?2) .
$ о
Тогда
бН 1
Xl = -2 (Znr+ 2 (3£ + sr) • p I
Объединив полученные результаты для Х1, Хг, запишем X=JX1] = 2₽; Vr, (7.85) I.X2J
где
f) 6£rS ЗЖг
r,= /2 р
0 0 1 -I- Sr S ,
2у ‘У J
(7.86)
Формулы (7.80), (7.85) позволяют в соответствии с (7.52) получить следующее выражение для матрицы деформаций g = {gt g£):
8 = 8» + EX=23r7r + jk, (7.87)
где
₽, = ₽?Ж
(7.88)
Этот результат соответствует стандартной записи е = 0v + 0с, где v = {vf vy); 0= [0Z 0J.
Напряжения o=(o^ o|} связаны с деформациями соотношением о = хе, где
Е П и!
х = ------х*: х* = ; • (7.89)
1—и.2 [р, 1]
Для получения матрицы жесткости элемента, имеющего неузло-вые степени свободы, необходимо вычислить предварительно матрицы (см. §5.5):
ka= J 0rx0dx; kb= J 0rx0dx; Ло = J 0rx0dx.
Xе Xе Xе
В данном случае kg будет представлять собой скалярную величину, а к;, — матрицу-столбец. Учитывая блочное представление матрицы 0, можно матрицы ка и кь вычислять также поблочно:
krs.a = f 0/'x0sdx (г, s=i, j);
Xе
*r,b= f 0Г*₽<1т (^=«. /)• x‘
Подставим в подынтегральные выражения формулы (7.88) и (7.89). Полагая далее dx = 2npdsd£ = nZpd|dC и выполняя интегрирование по толщине оболочки, получим:
krs,a=n/ j (s0°r** ₽s° + D0;rx*0s*)yd£; — 1
кг>ь=л/ J 0°Г x* 0St/dg; — I
к0=л/ j 0Tx*0Bydg. (7.90)
Численное интегрирование в (7.90) можно выполнить по трем точкам Гаусса.
Распределенные нагрузки р= (р( рп) заменяем эквивалентными силами по формуле
Р,.= л/ j' aurppdg (г—/,/), (7.91)
где через аиг обозначены блоки матрицы, связывающей перемещения {щ ип} с узловыми перемещениями v= {v; vj}:
Придерживаясь той же степени точности, что и для деформаций, воспользуемся здесь линейной аппроксимацией перемещений u(, пп:
1 + Sr S „ 1 + Sr S
“ “(г! "n —S иПг;
itt = s
тогда аиг дается выражением (7.69), где фг = (1 + SrS)/2.
При таком подходе узловые моменты, обусловленные действием распределенной нагрузки, будут отсутствовать. Интегрирование в (7.91) следует, как и в (7.90), осуществить по трехточечному правилу Гаусса.
Исключение неузловой степени свободы выполним теперь в соответствии с общими формулами (5.35), (5.38). Рассмотренный выше способ приведения распределенной нагрузки ие дает силы, соответствующей неузловому параметру с. Полагая в упомянутых формулах Ро = 0 и переписывая их в блочной форме, имеем*
с = —^-Sk^vr, (7.92)
«0
krs —krf|(x ~ kr,bksj,. (7.93)
«о
Первая из этих формул позволяет после отыскания узловых пере* мещений вычислить деформации, а затем и напряжения:
o=xe=z (Sprvr4-₽0 с).
Равенство (7.93) определяет четыре блока матрицы жесткости элемента к, приведенной к узловым перемещениям v = {v, vj}.
Чтобы перейти к перемещениям Vе — {v, v7-}, где
vr ~{uxr ^r} — П, воспользуемся соотношениями
uir=iixl. sin 0Г + «У,. cos 0r; unr=—uxr cos 0,,-l-u,,,. sin 0r, из которых вытекает матричное равенство vr = Xrvr с матрицей
sin 0r
— cos 0,.
0
cos 0r 0
sin0r 0
0 1
/).
(7.94)
Отсюда имеем связь v = Xve, в которой
[К; 0 7
[о xj’
Применяя обычные преобразования
ke=XrkX; Ре=ктР,
* Обозначение кг, употреблявшееся в § 5.5, заменено здесь на к, поскольку данные результаты относятся к местной системе координат.
получим матрицу жесткости и матрицу эквивалентных сил в общей системе координат. Их отдельные подматрицы определяются равенствами.
k*s=^krsXs; Р>^РГ.
§ 7.10. Матрица жесткости шпангоута
В местах стыка днищ с обечайками баков, резкого излома образующей и в других случаях применяется подкрепление оболочек круговыми шпангоутами. Их жесткость должна быть учтена при формировании общей матрицы жесткости конструкции. Каждый шпангоут рассматриваем как отдельный конечный элемент с одним узлом (узловой окружностью); узел располагаем в центре тяжести его поперечного сечения (рис. 7.11). Для вывода жесткостных характери
стик шпангоута воспользуемся соотношениями теории тонких круговых колец при осесимметричном нагружении.
Введем в поперечном сечении кольца систему координат т), совместив начало координат с центром тяжести поперечного сечения, и обозначим через yoi радиус окружности, проходящей через центр тяжести поперечного сечения. Матрица узловых перемещений элемента включает в себя три компоненты:
ve = v; = {uxi и,ji flp};
положительные направления перемещений и угла поворота показаны на рис. 7.11.
В соответствии с теорией тонких колец будем полагать, что поперечное сечение шпангоута не деформируется. Тогда для 1 радиальное перемещение произвольной точки сечения определится равенством иу = иу1—трЭр. Такое перемещение сопровождается появлением окружной деформации е = иу1у, где у — радиус окружности, проходящей через рассматриваемую точку. В случае тонкого кольца можно положить у « yoi, тогда
е = (uyi — 4]®t}lyQi.
Последнюю формулу можно записать в стандартной форме g рус, полагая
₽ = —[0 1 -п1-
Уо1
(7.95)
Считая, что отдельные волокна кольца не взаимодействуют друг с другом, связь между окружным напряжением о и деформацией е запишем в виде а = Ее, как для одноосного напряженного состояния. Таким образом, матрица х в данном случае является скалярной величиной и совпадает с модулем упругости Е.
Матрицу жесткости шпангоута найдем по обычной формуле
ке = х Р d т,
где 0 — определяется по (7.95). Подставляя вместо х модуль упругости Е и полагая dr = 2npoidE, где d/7 — элемент площади поперечного сечения, получим
к' =
2лЬ~
Уо1
О 0
Ft О О 7г
(7.96)
О о
Здесь Fi — площадь поперечного сечения шпангоута, а Ji=j,T]2dF — момент инерции этого сечения относительно Ft оси £.
§ 7.11. Объединение конечных элементов.
Определение перемещений и напряжений
Объединение конечных элементов для гладкой оболочки выполняется по обычным правилам. Несколько сложнее обстоит дело в случае, когда конструкция подкреплена шпангоутами. Пусть типовой конечный элемент в узле i соединен со шпангоутом, как показано на рис. 7.12. Введем в этом месте один общий узел, совпадающий с центром тяжести сечения шпангоута. Его перемещения в осевом и радиальном направлениях вместе с углом поворота сечения шпангоута составят матрицу
V/ = {uxi uvi ft;}.
Перед объединением конечных элементов необходимо привести матрицу жесткости, а также матрицу эквивалентных уз
ловых сил конечного элемента оболочки к данным перемещениям. В связи с этим матрицы жесткости и эквивалентных сил элемента, отнесенные к его узловым перемещениям и обозначавшиеся в § 7.8 и 7.9 через ке и Ре, обозначим теперь через к и Р, а сами узловые перемещения элемента обозначим через v вместо Vе.
Учитывая, что сечение шпангоута не деформируется, можно получить следующую связь между компонентами матриц vt и vt:
И v; — И v t -4- Ь; Ф Л Л l Л I 1 P < 7
Myi = Uyi Ctt'&i,
(7.97)
ft; == &;.
Здесь at, bt — расстояния вдоль координатных осей от центра тяжести сечения шпангоута до края элемента оболочки
Рис. 7.12
(рис. 7.12). Они считаются положительными, если край элемента оболочки удален от центра тяжести сечения шпан-i: гоута в положительных 1/1 направлениях осей х, у, и через координаты узлов вычисляются по формулам at ~-= xt — xol, bt — У1 Уо1-
В матричной записи формулы (7.97) имеют ВИД V; = liVi, где
О
О Ь{ '
1 — at
О 1
(7.98)
Во всех остальных узлах конечного элемента оболочки матрицы vr и vr совпадают, так что для этих узлов — единичные матрицы.
Применение стандартных преобразований кг = V кХ, Ре = = Хг Р позволяет получить искомые матрицы ке и Ре, приведенные к перемещениям шпангоута в узле I. Фактически преобразованию подлежат лишь подматрицы, связанные с узлом
i, поскольку в формулах
= krg Х8; Рег = хГРг
матрицы 1Г, Xs для г, s =# t являются, как уже сказано, единичными.
Такое преобразование должно быть выполнено для каждого из элементов оболочки, связанных со шпангоутами, после чего объединение конечных элементов можно осуществить обычным образом:
krs = Sk«s; Pr = SP®.
В тех узлах, где имеются шпангоуты, в диагональные элементы матрицы жесткости, соответствующие радиальному перемещению и углу поворота, в соответствии с (7.96) добавляются слагаемые 2nEFily0t и 2nEJily0i.
Если помимо распределенных по поверхности нагрузок действуют также силы и моменты, равномерно распределенные по узловым окружностям, то из них следует дополнительно сформировать матрицу Р, в которой
Pf ~ 2lTi/r {^асг Яут mr},
где qxr, qVT — погонные значения осевой и радиальной нагрузок; пгг — погонный момент в рассматриваемом узле г. Положительные направления qXT, qyr, mT совпадают с положительными направлениями соответствующих узловых перемещений.
Узловые перемещения v = {vx v2 ...vn) определяются путем решения системы уравнений kv = Р + Р, из которой предварительно должны быть исключены заданные перемещения.
После отыскания матрицы v будут известны узловые перемещения для каждого элемента. Если при этом элемент оболочки связан в узле i со шпангоутом, то полученную из решения системы матрицу V; следует при составлении матрицы Vе умножить на матрицу 1г (7.98).
Для элементов, описанных в § 7.8, по формуле
л =S (7.99)
2 \ 2 /
определяются нормальные деформации в наиболее удаленных от срединной поверхности точках. Далее могут быть найдены напряжения
аИ А =—£ к* Г Б‘ ] h.
.0«]С=±'2 1— И2 ledE = ±-2-
Такие расчеты выполняют для узловых точек каждого конечного элемента оболочки. Для улучшения точности могут использоваться процедуры сглаживания, как это описано в §5.13.
Для конечных элементов § 7.9 вычисления выполняются аналогичным образом, но со следующими отличиями. Во-первых, нужно перейти в каждом узле к перемещениям v в соответствии с равенством vr = Xrvr, где — матрица (7.94). Во-вторых, следует найти неузловой параметр с согласно (7.92). Наконец, в (7.99) необходимо заменить vr на vr и добавить слагаемое 0с.
Напряженное состояние оболочки можно характеризовать погонными силами N2 и моментами Mlt Л42, которые связаны с напряжениями соотношениями:
h/2
Л\ = f a? dS;
— h/2
h/2
— h/2
h/2 h/2
— h/2 —h/2
Для их вычисления можно использовать равенства
л\] о *Ге11 Г^11 п
— В х* ; = D х* .
Md L^J i_m2 J [%2.
В сечении шпангоута возникают осевая сила N и изгибающий момент М, которые определяются через перемещения uyi, (см. рис. 7.11) равенствами
EFi EJt „
N =------ u,,i, M. ——
yoi J У ol
нормальное напряжение в сечении шпангоута может быть подсчитано по формуле
а =
N
Fi
П-
Знак минус перед вторым слагаемым поставлен потому, что при положительной величине волокна с положительными значениями г| будут сжаты.
§7.12. Деформации произвольной поверхности
Приступая к построению конечных элементов произвольной оболочки, покажем предварительно, как можно найти деформации заданной поверхности по известным перемещениям
ее точек.
Рассмотрим поверхность, заданную в параметрической форме х = х (g, г|), у = у (g, г|), z = z (g, г|). Каждой паре чисел
g, г| соответствует некоторая точка поверхности. Если зафиксировать параметр т], изменяя при этом g, то получим на поверхности некоторую кривую. Такие кривые можно построить для каждого значения ц; их совокупность называют g-линиями. Аналогично можно провести на поверхности семейство кри-
вых, вдоль которых параметр g остается неизменным; это
семейство называют ^-линиями. Два семейства кривых образуют на поверхности координатную сетку (рис. 7.13), что дает основание называть параметры g, г| криволинейными координатами поверхности. Для расчета геометрических параметров g- и 1]-линий воспользуемся соотношениями, полученными в §5.9.
Бесконечно малый отрезок g-линии, который мы обозначим через dsg, связан с dg соотношением dsg = A gdg, аналогичным (5.70). Выражение для параметра А $ можно получить по формуле (5.71), заменив в ней обыкновенные производные по g
частными:
(7.100)
Аналогично определяется дифференциальный отрезок dsn = A„dr| i]-линии. Здесь
(7.101)
Возьмем, далее, на поверхности произвольную точку М и введем единичный вектор е%, касательный к £-линии в этой точке. Его компоненты, представляющие собой направляющие косинусы Jj-линии, представим матрицей
= [Х6я biv Хб2]. (7.102>
Для их вычисления воспользуемся формулами (5.72), в которых вместо А следует взять А и перейти к частным производным:
^ = -4- — ; Ч»=4- —; ^г=-з—— • (7.103)
Точно так же можно ввести касательный к гр линии единич-ный вектор еп с матрицей направляющих косинусов
(7.104)
где
X,
<7-105)
ЛТ) ОТ] ЛТ) ОТ] ОТ]
Так как векторы е5, еп имеют единичную длину, то скалярные произведения
с5-^ = 1; еп-еп= 1, откуда вытекают матричные равенства
= ЦХ£ = 1. (7.106)
Скалярное произведение • еп будем обозначать буквой •у; в матричном представлении
(7-Ю7)
Как известно, скалярное произведение двух векторов равно произведению их длин на косинус угла между ними. Отсюда следует физический смысл у: это косинус угла 0 между направлениями и грлиний в точке М (рис. 7.13). Если, в частности, координатные линии взаимно ортогональны, то 7 = 0.
Для исследования деформации поверхности удобно в каждой ее точке взять два взаимно перпендикулярных направления, определив их единичными векторами ех, е2 с матрицами направляющих косинусов
Хх = [Х1ж Xjy XX2]j ^<2 = ^2Х ^2У ^2Z^.
Первое из направлений выберем совпадающим с направлением g-линии, так что ег = или, что то же самое,
Хх = Ц. (7.108)
Вектор е2, определяющий второе направление, можно искать в виде разложения по векторам ел:
^2 — Ui eg -f- вц.
Для определения коэффициентов ах, а2 необходимо, во-первых, использовать условие ортогональности: ех • е2 — 0- Если учесть также, что должно выполняться равенство е2*е2= = 1, и воспользоваться соотноше-
Рис. 7.14
ниями (7.106), (7.107), то для матрицы Х2 получим значение
_b_t-(_VKe-i-h4). (7.Ю9)
Бесконечно малый отрезок dsx, взятый в направлении ех, совпадает с ds6 : dsx — ds6 = A 5dg.
Чтобы переместиться вдоль е2 на бесконечно малое расстояние ds2 (рис. 7.14), необходимо дать такие приращения обоим параметрам Я. "П» которые удовлетворяют соотношению
—A 6dg = Andr| cos 0 = уЛлбг|. (7.110)
При этом длина отрезка будет
ds2 = Г(Лп<Ь1)2 - И 5<Ф2.
и с учетом предыдущего равенства получим
ds2 = V1 — у2Лпбт].
(7.Н1)
Заканчивая описание геометрии поверхности, введем нор-
мальный к ней единичный вектор е 3, определив его с помощью
—> “►
векторного произведения е 3 = ех X е2. Пользуясь правилом перемножения векторов и принимая во внимание (7.109), для
компонент матрицы направляющих косинусов Х3 = = [X зж X Зг/Х 32] можно получить значения:
^зх = 2~ ^"П2 Х1Ц,);
V1 —У
^Зу = ~|/| — у2~ ^’’Х “2)
^зг = 2~ (^6* "^ъу Xjj, Хпх).
1/1— У2
Отметим, что вектор е3 направлен в ту сторону, откуда по-ворот ег по кратчайшему пути до совмещения с е2 наблюдается происходящим против часовой стрелки. При этом тройка век-торов elt е2, ?з является правой.
Пусть, далее, точки поверхности получают перемещения их (£, л), иу (L *1), (В, л) в направлении осей х, у, г. Обо-
значим через еГ1, е22 деформации отрезков dSj, ds2, а через е12 — изменение угла между ними. Для их вычисления снова обратимся к результатам, представленным равенствами (5.77), (5.79). Эти результаты могут быть сформулированы здесь следующим образом. Деформация произвольной линии, имеющей матрицу направляющих косинусов Х{, определяется выражением
8 = Xt —, (7.113)
d s
а уменьшение угла между ее Положительным направлением и нормальным к ней вектором с матрицей направляющих косинусов Хо — выражением
®о = Хо4^-. (7.114)
d s
Здесь u = {их uv uz}; ds — дифференциальный отрезок рассматриваемой линии.
Переходя в (7.113) к частным производным du/dsr и ди/дз2 и заменяя X, на Х1Г Х2, получим
₽ _ 1 ди
е11 — Л1 -Г , ь22 — л2 -:
dst ds2
Деформация сдвига е12 представляет собой сумму двух углов, один из которых есть поворот отрезка dsr в направлении ds2, а второй — поворот ds2 в направлении dsr. Исходя из (7.114), имеем
. ди . ди е12 — Л2 —------- Г Аг —------ •
dsj ds2
Так как dsj A jdg, то дu _ 1 du ~д^
Далее, при переходе из точки М (g, т|) в соседнюю точку поверхности вдоль отрезка ds2 параметры г| получают приращения, связанные между собой равенством (7.110). Матрица и получит при этом приращение
_lJLd£ + — dT1 = (-yA±!L + _^)dt1. dg dt) * \ y л5 dg dt) J * 1
Разделив это значение на ds2 = /1 — yM^dr], находим выражение для частной производной
д и_______1 / у д и 1__________ д и \
ds2 ”1/1 —т2 \ dg dt) /
Введем обозначения:
1 1 du п 1 , du . е5 ~~ л > еч ~ ~л~ М) ~7 >
dg dr)
о 1 a du . 1 . du
e£n — ~д~ Лч + ~л~ ~—
dg dr)
и воспользуемся соотношениями (7.108) и (7.109). Тогда еи = е22 = - (у2 е5 + еп — уе5я);
1 —
ei2=="yfk^r (—2Teg + e5n)’ или в матричной форме 'бц” «22 _Е12_
(7.115)
«5 еп
(7.116)
= Г
где
Г =
О
1__
1 —у2
. (7.117)
О
О
7
1—у2
1
V1-Y2
поверхности изменятся углы
1
Т2 1—?2 2? V1-Y2
В результате деформации
между вектором е3 и отрезками dsj, ds2. Обозначим через <о1,
<о2 углы поворота отрезков dsx и ds2 в направлении вектора е3. Для их определения можно снова воспользоваться общей формулой (7.114), из которой следует, что
, д и ч , д и (01 — Л3 —-— , (02 — л3 —-— .
О<$2
„ du du
Если подставить сюда значения производных —, , то
vSj vSg можно получить расчетные формулы
(7.118)
где
= (7-И9)
dg di)
(7.120)
Формулы (7.115)—(7.120) решают задачу об определении деформаций заданной поверхности.
§ 7.13. Конечные элементы произвольной оболочки
Рассмотрим конечные элементы четырехугольной формы. На рис. 7.15 представлено семейство таких элементов, включающее в себя элементы первого, второго и третьего порядков.
Пусть xr, yr, zr — координаты срединной поверхности в типовом узле, h — толщина оболочки. Положение текущей точки срединной поверхности определим соотношениями х ~ = у — ^Tyr\ z = 2фг?г, где суммирование ведется по всем узлам элемента. Функции фг (£, т|) определены равенствами (5.18), (5.62), (5.67).
Элемент первого порядка имеет прямые стороны, но так как его узлы в общем случае не лежат в одной плоскости, он будет искривлен в пространстве (закрученный четырехугольник). Элементы второго и третьего порядка имеют, вообще говоря, криволинейные стороны.
Вычисляя производные
дх _ v d\pr , дх _ v drpr dg 24 dg ' r’ dr) 24 drj r
и т. д., по (7.100)—(7.105) можно в любой точке срединной поверхности рассчитать параметры А Ап, у и компоненты матриц
В качестве узловых перемещений возьмем смещения ихг, uvr, u-zr узлов в направлении координатных осей и повороты ^yr> &zr нормали относительно этих осей:
vr = {ur где
Ur = {uxr Uyr Uzr}', &r ~ {.®xr ® yr ®zr}-
Рис. 7.15
Положительные направления перемещений и векторы положительных углов поворота будем считать совпадающими с положительными направлениями соответствующих осей.
Найдем далее перемещения
"5-И, 4 "У (SV ’
- vZV- Я sin f
точки, расположенной в узле г на /xrvT
расстоянии t, от срединной поверх-ности; отсчет положительных зна-чений £ будем вести в направле-
нии вектора е3, нормального к Рис. 7.16
поверхности.
Отличие и£ от ur обусловлено поворотом нормали в узле т. Если некоторый вектор /? поворачивается на угол Ф вокруг оси, с которой он составляет угол <р (рис. 7.16), то конец вектора совершит перемещение по дуге окружности радиуса R sin <р (R — длина вектора /?); величина перемещения будет Ф R sin <р. Если угол поворота мал, то это перемещение можно представить в виде вектора р, касательного к указанной окружности. Угловое перемещение можно изобразить вектором О', длина которого равна &, а направление опреде
ляется правилом правого винта; тогда вектор р будет представлять собой векторное произведение р = # х
Применим этот результат к вычислению перемещений и,. Последние относятся к точке, положение которой относитель-—►
но срединной поверхности определяется вектором £е3г, где езт — единичный вектор, нормальный к срединной поверхности в узле г. Введя вектор поворота нормали
'&л.г ех ~Г 'ftyr £у fl1 zr е 2, найдем, что вектор перемещения, обусловленный этим поворотом, равен х £>е3г. Его первая компонента равна С (^г/Л sz,r — ^гг^зу.г), а остальные получаются из этого выражения круговой заменой индексов х, у, z. Здесь Х3х>г, Х3г/>г, Аз2,г — значения параметров (7.112) в узле. г. В матричных обозначениях можно записать
Ut ur ; £Lr #r, (7.121)
где
О
- ^3V,r
^3z,r 0 ^3x,r
^3y,r ^3X,r 0
(7.122)
^3z,r
Рассмотрим далее слой оболочки на расстоянии £ от срединной поверхности. Геометрию слоя в силу тонкостенности оболочки можно отождествить с геометрией срединной поверхности, полагая
4| = А 6; А S = Лл; ТС = у; (7.123)
Перемещения и? — {и| } точек этого слоя будем
определять соотношениями
и? = 2-фг11С. (7.124)
Применяя формулы (7.115)—(7.116) к слою оболочки, находим его деформации еЕ = {е^ е|2 е|2}:
8? = 8° + £Х, (7.125)
где
8° = TSgrur; X = TSgrLr #r. (7.126)
1
gr“ А1 31
1
Здесь суммирование выполняется по всем узлам элемента, матрица Г дается формулой (7.117), а
‘ 0 '
Лб .
и в форме
о Лп -
Формулы (7.126) можно записать 8° - Sft?vr; X = Sp;vr, если положить
₽? = [Гйг 01; = 10 rgrLr],
(7.127)
<Эт)
(7.128)
(7.129)
где нулевые подматрицы имеют размер 3x3.
Помимо деформаций слоя е£ в оболочке возникают также деформации поперечного сдвига 8 — {eJ3 е23 }. Считая е13, 823 постоянными по толщине, определим их равенствами
ем = + “f, 823 = 02 + со2, (7.130)
где О’з — углы поворота нормали в направлении векторов -> -> -> elt е2, a colt со2 — введенные ранее углы поворота векторов е19 —► —*
е2 в направлении вектора е3.
Значения ®х, ю2 даются формулами (7.118)—(7.120). Подставив в них соотношения (7.121) и (7.124) при £ — 0, выразим эти углы через узловые перемещения:
[“1l=rSgrUr- (7.131)
[<о2 J
Здесь Г — матрица (7.120), а 1 di|y 1 ~л~ Аз
Для определения углов 0,2 выполним прежде всего аппроксимацию матрицы О = {О* 0,г/ по узловым значениям:
й = 2фгФг. (7.133)
Далее спроектируем Фх, $у, (представив их в виде век-торов) на направления векторов elt е2, которые имеют матрицы направляющих косинусов
— ^Е’> ^2
---+ Ц)-
Принятые в (7.130) положительные направления Оа показаны на рис. 7.17, где двойными стрелками даны векторные обозначения й'г- С учетом этого запишем 0,1 = Z2O;
О или, учитывая (7.133),
(7.134)
где
~ —у 1 — - (— Ч~ ^-п)
L = У . (7.135)
—Ц
Исходя из (7.131) и (7.134), для матрицы е получаем в соответствии с (7.130) выражение
s = S₽rvr, (7.136)
в котором
₽Г = [çà фг L]. (7.137)
Теперь можно объединить матрицы 8е и 8 и выразить деформации 8 = {sE 8 } через узловые перемещения посредством соотношения 8 = = S₽rvr, где рг определяется равенством (7.63).
Запишем далее соотношения упругости. Напряжения в слое оС= {оЕ, оЕ2 ое2}, так же как и в случае пластины, связаны с 8е законом Гука для обобщенного плоского напряженного состояния:
<гЕ =-—^-7 «о8Е, (7.138)
1 —р.2 где
~ 1 р О
х0= Н 1 0
о о
L 2 J
Поперечные касательные напряжения о = {о13 оаз} выражаются через 8 по формуле
O—G Х8,
(7.139)
где х — единичная матрица размером 2x2; величину G можно взять равной 5G/6 с целью учета имеющей в действительности место неравномерности напряжений а13, а23 по толщине оболочки.
Полагая о = о}, будем
венство о = xs, в котором
х =
иметь из (7.138), (7.139) ра-
Е 1—ц2
О
х0 0
Gx
(7.140)
Для вычисления типового блока матрицы жесткости
krs=f P>Psdr Xе
внесем в подынтегральное выражение равенства (7.63) и (7.140). Положив
dx = dStdSjjdl; = А 1 — у2 dgdrjdl;,
выполним затем интегрирование по толщине оболочки. В итоге получим выражение для kers в виде суммы трех матриц:
k2s = krs,s + l<rs,D+ krs.o; (7.141)
Вргогхо₽;д6 ЛПК1 —Vs dgdTi;
1 1 _______________________
kfS,D = J J Dp*rxops Д£ Anyi— y2dgdt]; (7.142)
h Pr Ps Д? А К1 —Y2 dg dr].
Поскольку матрица x единичная, в выражении для kfS.o она опущена. Заметим, что исходя из блочной структуры (7.129) матриц Р? и р?, можно выражения для к«,в и к„,о представить в виде
0
о
0
0
0 1
krs, d —
0
(7.143)
где подматрицы к« и kfs, имеющие размер 3X3, определяются равенствами
k;s=j j BQ„dgdri; к;; = ь;j j DQ^dgdnU, (7.144)
в которых агв^Г^0ГёвА^АпУГ^. (7.145)
При численном интегрировании следует для исключения ложных сдвигов использовать минимально допустимый порядок при вычислении krs,o; к матрицам kf's и k"s должно быть применено более точное интегрирование (см. табл. 5.1).
Отметим, что элемент оболочки рассматриваемого типа с четырьмя узлами в вершинах описан в работе [23].
В заключение коснемся вопроса о приведении к узлам внеузловой нагрузки. Пусть р = {рх ру pz}—матрица проекций поверхностной нагрузки на координатные оси, а Р? — матрица сил, действующих в узле г в направлении перемещений vr и эквивалентных этой нагрузке. Для вычисления Р* можно получить выражение
Рг
1 1
«1г Р А% Ап У1 —у2 dg dT],
(7.146)
где аиг — типовая подматрица матрицы функций, аппроксимирующих перемещения u = {их иу uz} через Vе в соответствии с равенством u = auve = Saurvr.
Для рассмотренных элементов матрица аиГ имеет вид
Интегрирование в формуле для Р« осуществляется по тому же правилу, что и при вычислении матриц k/s или krs.
§ 7.14. Примеры расчета
Пример 1. Треугольное монолитное крыло жестко защемлено по части бортовой хорды (рис. 7.18, а) и нагружено постоянным поперечным давлением р. Крыло имеет ромбовидный профиль. Толщина с изменяется по размаху по линейному
закону, ее максимальное значение (в середине бортовой хорды) равно 40 мм, £ = 7 • 104 МПа; р = 0,3.
Для идеализации использовались изопараметрические конечные элементы пластины первого порядка (см. §7.3). Схе-
ма идеализации дана на рис. 7.18, б; конечноэлементная модель содержит 59 конечных элементов и 78 узлов.
На рис. 7.19 сплошной линией показано изменение вдоль заделки нормального напряжения агг в наружных слоях.
Штриховая линия дает закон изменения аг1 при полном закреплении крыла по всей хорде. Представление о погрешности решения можно получить, вычислив результирующий момент напряжений ст22 в заделке; в полученном решении он составляет примерно 92% от момента, создаваемого относительно
оси х внешней нагрузкой. Следовательно, представленные на рис. 7.19 напряжения найдены с погрешностью порядка 8%.
Пример 2. Стальная (Е =
= 2 • 105 МПа, р, = 0,3) пологая коническая оболочка с жестким центром защемлена по контуру и нагружена равномерным давлением р — 0,1 МПа (рис. 7.20).
Для расчета использован изопараметрический конечный элемент первого порядка, описанный в § 7.8. На рис. 7.21 показано изменение изгибающих моментов Мх, М2 и сил Nlf N2 в срединной поверхности при разбиении оболочки на 25 конечных элементов. Точками даны результаты, полученные по теории оболочек [3]. Отметим, что использование конечных элементов, описанных в§ 7.9, позволяет получить аналогичные по точности результаты при разбиении оболочки на 15 элементов.
Пример 3. Круглая (на развертке) цилиндрическая панель (рис. 7.22) жестко защемлена по контуру и нагружена через жесткий центр силой Р. Радиус цилиндра R — 1 М, радиус панели гг = 550,1 мм, радиус жесткого центра г0 = = 66,1 мм, толщина панели h = 5 мм, Е = 1,96 • 105 МПа, р, = 0,3.
Для идеализации конструкции использовались изопараметрические элементы произвольной оболочки второго и третьего порядков. Конструкция имеет двойную симметрию (относительно плоскостей хг и z/z), что позволяет ограничиться рассмотрением четверти панели. Схема ее идеализации представлена на рис. 7.23. Закрепления узлов на сторонах х = 0 и
у = 0 задавались исходя из условий симметрии. Наличие жесткого центра может быть смоделировано различными способами. Можно, например, жесткий центр представить так
же, как и саму панель, в виде совокупности конечных элементов, но имеющих весьма большой модуль упругости или весьма большую толщину. Здесь использован другой подход, в котором линия спая панели с жестким центром выступает в качестве одной из границ области. Перемещение соответствующих узлов по осям хну, а также углы поворота в них относительно осей х, у, z принимались равными нулю. Что касается перемещений этих узлов в направлении оси z, то все они задавались равными 1. Таким образом, расчет проводился на единичное смещение жесткого центра.
Сила Р/4, необходимая для создания такого перемещения рассматриваемой четверти панели, может быть найдена из условия равенства производимой ею работы и потенциальной энергии деформации системы:
4-i=;r к?,
где v — матрица узловых перемещений при единич
ном смещении центра;
К — общая матрица жесткости. Истинное перемещение Жесткого центра от действия заданной силы Р:
w=P/(4vTKv).
На эту величину умножаются все перемещения и напряжения, полученные в предположении о единичном смещении жесткого центра.
Результаты расчета (рис. 7.24, 7.25) получены при разбиении на 45 (5 в окружном направлении, 9 — в радиальном) конечных элементов второго порядка; через ог обозначена радиальная, а через <Jq — окружная компоненты напряжений 282
(г, 9 — полярные координаты в срединной поверхности панели, см. рис. 7.22). Напряжения отнесены к величине о0 = = Р/Л2. При вычислении напряжений применялась процедура местного сглаживания (см. § 5.13) с последующим осреднением результатов в узловых точках.
На рис. 7.24 представлены нормальные напряжения в срединной поверхности панели, а на рис. 7.25 — значения нормальных напряжений, обусловленных действием изгиба, в крайних волокнах. Сплошные и штриховые линии, полученные аналитическим путем [12], дают закон изменения напряжений вдоль лучей 0 = л/2 и 0 = 0 соответственно; конечноэлементные результаты отмечены точками. Наиболее напряженной является точка панели, расположенная на наружной поверхности в месте стыка панели с жестким центром, при 0 = л/2. Эквивалентное напряжение (по теории прочности энергии формоизменения) получилось здесь равным при данной сетке 0,690о0, что на 3,7% ниже точного значения О,717ао. Величина w при той же сетке оказалась равной 0,417 Ro0/E, что всего на 0,7% отличается от точного значения О,414/?сго/£.
ГЛАВА 8
КАРКАСИРОВАННЫЕ ТОНКОСТЕННЫЕ КОНСТРУКЦИИ
Тонкостенные подкрепленные конструкции при относительно малом весе обладают высокими прочностными характеристиками, благодаря чему они иашлн широкое применение в авиации. Конечноэлементная модель подобной конструкции должна быть по возможности простой, но в то же время она должна правильно воспроизводить наиболее существенные особенности силовой работы. Как и в традиционных методах расчета, обшивку можно считать безмоментной. При моделировании лонжеронов, нервюр или шпангоутов следует учитывать деформации поперечного сдвига. При этом необходимо заботиться об исключении ложных деформаций поперечного сдвига, которые могут совершенно исказить жесткостные свойства конструкции в целом.
§ 8.1. Конечиоэлементная идеализация конструкции
Типичными представителями подкрепленных тонкостенных конструкций являются крыло (рис. 8.1, а) и фюзеляж (рис. 8.1,6) самолета. Они имеют относительно тонкую обшивку и силовой набор (каркас), образованный такими элементами, как шпангоуты, лонжероны, нервюры, стрингеры. Моделирование каркасированной конструкции набором конечных элементов можно осуществить различными способами;
конкретный выбор зачастую диктуется возможностями имеющихся вычислительных машин или программ.
Силовой каркас обычно разбивает обшивку на отдельные панели, которые часто целиком моделируют одним конечным элементом. Обшивка представляет собой тонкую оболочку, и в принципе для идеализации панелей могут быть использованы четырехугольные конечные элементы, описанные в предыдущей главе. Однако тонкая обшивка работает в оо новном на растяжение-сжатие и сдвиг, слабо сопротивляясь изгибу. Распределение напряжений по ее толщине можно счи-
Рис. 8.1
тать равномерным, что позволяет воспользоваться более простыми конечными элементами безмоментной оболочки.
Если стрингеры, подкрепляющие обшивку, расположены регулярно и достаточно часто, то проще всего «размазать» их по обшивке и рассматривать последнюю как конструктивноортотропную. При нерегулярном или редком расположении стрингеров следует учесть дискретный характер подкреплений. Изгибная жесткость стрингеров, как правило, невелика, и для их идеализации подходят одномерные конечные элементы с равномерным распределением нормальных напряжений по сечению (см. §5.10).
Лонжерон представляет собой балку переменной высоты; обычно он имеет тонкую стенку, работающую главным образом на сдвиг. Будем по длине разбивать лонжерон на отдельные участки, рассматривая их как конечные элементы. При этом достаточно учесть лишь те степени свободы, которые соответствуют изгибу лонжерона в плоскости стенки и его продольной деформации.
Один из возможных подходов к получению матрицы жесткости бруса, позволяющий учесть переменность высоты сече-384
ния и влияние деформаций поперечного сдвига, изложен в § 3.7 применительно к элементу плоского кругового бруса. Если жесткость лонжерона в пределах элемента постоянна, а влияние деформации поперечного сдвига мало (лонжерон С толстой стенкой), то можно воспользоваться результатами, полученными в § 3.4 и 3.5. В этом случае матрица жесткости в местной системе координат дается выражениями (3.26), (3.36) и (3.48).
Другой путь получения жесткостных характеристик элемента лонжерона основывается на независимой аппроксимации перемещений и углов поворота подобно тому, как это делалось в предыдущей главе при построении изопараметри-ческих элементов изгибаемой пластины.
Можно, наконец, элемент лонжерона рассматривать как составной. При таком подходе пояса идеализируются одномерными элементами, работающими на растяжение-сжатие, а стенка — конечными элементами плоской задачи теории упругости. Во многих случаях такая модель наиболее естественна, и она позволяет адекватно воспроизвести все особенности работы лонжерона.
Нервюру также можно представить как тонкостенную балку переменной высоты, и к ней в равной степени применимо все то, что было сказано об идеализации лонжерона.
Шпангоут представляет собой криволинейный плоский брус. Он может испытывать деформацию как в своей плоскости, так и из плоскости, и зачастую ни одна из главных осей инерции поперечного сечения не лежит в плоскости шпангоута. Отметим, что в частном случае кругового шпангоута, работающего на изгиб в своей плоскости, можно для его идеализации использовать элементы, рассмотренные в § 3.7.
§ 8.2. Конечные элементы безмоментной обшивки
Как говорилось выше, обшивку можно рассматривать как безмоментную оболочку. Для вывода жесткостных характеристик конечных элементов обшивки воспользуемся соотношениями, полученными в предыдущей главе для случая моментной оболочки произвольной формы. Эти соотношения упрощаются здесь, так как деформации в безмоментной оболочке постоянны по толщине. В то же время будем учитывать при вычислении матрицы жесткости возможное наличие конструктивной ортотропии.
Рассмотрим семейство изопараметрических конечных элементов с четырьмя сторонами. Геометрия подобных элементов показана на рис. 7.15. Основной исходной геометрической
информацией для элемента служат координаты xr, yr, zT его узлов в общей системе координат. Положение текущей точки срединной поверхности элемента определим соотношениями х — 2фгхг, у — ^гуг, * ~ 2фг2г> где суммирование осуществляется по всем узлам элемента. Функции фг (£, т]) даются равенствами (5.18), (5.62) и (5.67).
В соответствии с формулами §7.11 вычисляем геометрические параметры:
. 1 дх . 1 ду . . \дг
di, ^g d% di
. 1 дх ._______1 ду ._______1 дг
т=^Ц,
где обозначено
^g — 1Х^Я ^-gy JtgJ;
Узловые перемещения возьмем в направлении координатных осей, тогда матрица перемещений типового узла будет
Vr — dri}.
Аппроксимацию перемещений u = {их uv uz} внутри элемента осуществим в соответствии с изопараметрической формулировкой:
и = 2фгуг. (8.1)
Деформации е, = {еп е22 е12} определяются равенствами (7.115)—(7.117).
Исходя из (8.1), приведем выражение для е к виду 8 » = S0rvr, где
р, gr, gr di
Г о!
р lAJ
(8.2)
О
[
j Связь между напряжениями а = {ахх о22 а12} и деформа-I циями 8 запишем для общего случая конструктивно-ортотропной обшивки, подкрепленной системой ребер, расположенных параллельно друг другу с постоянным шагом. Для приближенного определения ориентации ребер на поверхности обшивки поступим следующим образом. Пусть х®, у°, г® и х®, у2, — координаты
каких-либо двух точек, принадлежащих любому из ребер или любой линии, параллельной ребрам. В примере, Ц показанном на рис. 8.2, эти точки обозначены буквами и М2, причем точка Л4Х взята здесь в одной из вер-
шин четырехугольника. По- Рис- 8 2
лагаем, что направление ребер жесткости совпадает с направлением вектора, соединяющего точки Л4] и М2. Обозначим через
е0 — К)х ех е!1 ^Oz ez
единичный вектор, имеющий направление от точки Мх к точке М2.
Компоненты е0 вычисляются через координаты Л4,, М2 по формулам
х0_ „° ио_ О .0 0
Л х2 Л1 . л «2 «1 . » Z2—г1
Л0х — , > Лоу " , Л0г — ".- ’
/о = V (х° - X?)2 + (У® - У °)2 + (z° —— Z°)2 .
Пусть, далее, 0О — угол, составляемый вектором е0 с касательной к £-линии. Направление касательной определяется единичным вектором ех:
ei — Цх ех + еу ~Ь ег.
Умножив скалярно е0 на ех, найдем косинус угла 0О:
cos 0О — ех • е0 — ХОа. X,Oz.
Чтобы вычислить sin 0О, можно умножить скалярно е0 на единичный вектор е2:
sin 0О = е0 • е2 — .. — - [(—^-ох + Vi—У2
+ (—^оу + (— + ^nz) ^oz)
Введя в дополнение к ЦД, матрицу
Хо — [А,Ож koy A-ozli (8.3)
представим полученные соотношения в форме
cos0o = Z6A,J; sin0o=—-L^. (—+ (84)
V 1— 1г
Теперь в соответствии с формулами § 1.3 можно построить матрицу х, связывающую напряжения с деформациями соотношением о = хе. Представим соотношения (1.32), (1.34) и (1.36) в виде
х = —Tx*V, 1—н2
(8-5)
Г1+^ и 0 1 ' cos2 й0 sin2 0О — Sin 20о“
х* = И 1 0 ; т = sin2 0О cos2 0О sin 20о
0 0 sin 28О sin 290 cos 20о
2 J L 2 2
(8.6)
(1 -И2) Е^Р Е2 th
где
kp =
Здесь Elt Е2 — модули упругости соответственно ребра и обшивки; h — толщина обшивки; F — площадь сечения ребра; t—шаг ребер; входящие в матрицу Т значения sin 20о и cos 20о можно подсчитать через (8.4) по очевидным формулам:
sin 20о = 2 sin 0О cos 0О; cos 20о = cos2 0О — sin2 0О.
Для вычисления блоков матрицы жесткости элемента воспользуемся общим выражением
krs= J
те
Учитывая, что dx = hA n]/ 1 — T2d^dir), приведем последнее выражение к расчетному виду
= j рГТх*Тг M&VK'T^T'dldn. (8.7) — i—i
При численном интегрировании можно применить обычные правила Гаусса (см. табл. 5.1).
Если обшивка гладкая, то в (8.7) следует опустить матрицы Т и Тг, а в матрице х* положить kF = 0. В итоге для случая гладкой обшивки имеем
= S grr^TM^KT^dldn, (8.8)
-i —i
причем здесь
0
0
1—и
2
Приведение распределенных сил к узловым осуществляется обычным путем. Для подматрицы сил Рег, действующих в типовом узле г в направлении перемещений vr, можно получить формулу
1 1
p:=f ( Рфг -Т2 dgdT|, (8.9)
-1-1
где р = {рх ру pz} — матрица распределенных нагрузок. Интегрирование здесь следует выполнять по тем же правилам, что и в (8.8).
В заключение отметим, что жесткость отдельных панелей обшивки может снижаться вследствие потери ею устойчивости. Наличие начальных неправильностей приводит к тому, что сдвиговая жесткость обшивки в областях с большой кривизной также оказывается ниже, чем это предсказывается без-моментной теорией. Данные факторы могут быть учтены введением редукционных коэффициентов, на которые должны быть умножены модули упругости Е и G соответствующих конечных элементов; это согласуется с обычной расчетной практикой, принятой в самолетостроении. Значения редукционных коэффициентов можно брать из справочной литературы, либо исходя из опыта проектных организаций.
§ 8.3. Конечные элементы изопараметрического типа для лонжеронов
Как отмечалось выше, для идеализации лонжерона могут быть использованы балочные элементы. В данном параграфе рассматриваются балочные элементы изопараметрического типа с независимой аппроксимацией перемещений и угла поворота сечения. В отличие от балочных элементов, описанных
Рис. 8.3
в гл. 3, где под узлами понимались сечения элемента, здесь узлами служат те же точки, которые являются узлами конечных элементов обшивки; за узловые перемещения принимаются при этом линейные смещения узлов (рис. 8.3, а).
Исходная информация для элемента имеет стандартный вид и включает в себя координаты узлов, а также упругие и геометрические характеристики сечения. Для вывода матрицы жесткости используется местная система координат, оси которой х, у лежат в плоскости стенки, а начало находится в среднем сечении. Направление оси х определяется точками
I и 2, которые делят пополам расстояния Нг и Н2 между панелями обшивки в крайних сечениях. Координаты этих точек выражаются через координаты узлов: xr = (х; + xj)/2, i/j = = (у, + У])/2 и т. д.; длина элемента определяется по формуле
I = V (х2—х1)г + (уг~у1)2 + (z2 — zj2.
Расстояния между противоположными узлами обшивки также могут быть найдены через координаты узлов, например:
ffl “ V(X/—Xi)2 + (yj — yt)2 + (Zj—Zt)2.
При расчете жесткостных характеристик подобных элементов необходимо учитывать их податливость в поперечном направлении, так как должна быть обеспечена независимость, скажем, перемещений и,- и и - или и,- ио-. Здесь возника-ет затруднение, связанное с тем, что в технической теории изгиба бруса поперечная податливость выпадает из рассмотрения. Поэтому воспользуемся приближенной моделью, в которой сама стенка в поперечном направлении абсолютно податлива, а ее жесткость имитируется линейными упругими связями в виде стержней или пружин, которые связывают между собой пояса лонжерона в узловых сечениях (рис. 8.3, а). Из физических соображений ясно, что учет поперечной податливости не может существенно повлиять на результаты расчета крыла в целом. Это дает основание пользоваться подобной моделью, назначая жесткость упомянутых пружин весьма приближенно.
Рассмотрим вначале конечный элемент лонжерона с четырьмя узлами i, /, /, пг, показанный на рис. 8.3, а. Положение центра тяжести произвольного сечения отмечено на рисунке буквой С, а его расстояние от оси х обозначено через ус. В местной системе координат элемент имеет восемь степеней свободы — по два смещения в каждом из узлов. Условимся перечислять их в матрице узловых перемещений v в следующем порядке:
V ={V; V j V; vrn}.
Здесь vr = {vr-vr~}—матрица перемещений узла г (г = i, j, I, m).
Матрицу жесткости к элемента будем искать в виде суммы двух матриц:
k-k'-j-k". (8.10)
10*
29!
Первая из них учитывает жесткостные характеристики собственно бруса, а вторая — жесткостные характеристики дополнительных упругих связей.
Переходя к вычислению к', обозначим через их, иу и fl-смещения в направлении осей х, у произвольной точки, лежащей на оси х, и угол поворота соответствующего сечения. Для упрощения записи в этих обозначениях, а также далее в обозначении деформаций и напряжений опущена черточка в индексах х, у. Для функций их, иу и fl- воспользуемся независимой их аппроксимацией по узловым значениям:
их ~ 2фрижр; иу — ЛфрЦрр, fl = 2фрАр. (8.11)
Через ихр, иур, flp здесь обозначены перемещения и повороты узловых сечений; их положительные направления показаны на рисунке. Индекс р, по которому выполняется суммирование, принимает здесь значения 1 и 2.
Функции фр изменяются по длине элемента по линейному закону
фр® = у(1+М) (Р = 1. 2),
где 5 — безразмерная координата, имеющая в узлах 1, 2 значения — —1, £2 = 1 и связанная с х соотношением £ — = 2x11.
Таким образом, здесь мы относим элемент бруса к шести степеням свободы ихр, иур, flp (р = 1, 2). Они связаны с перемещениями узлов V, очевидными соотношениями:
«хх = у + Vi^' = + Vi^
«Х2= -j- (vlx 4- цт1); «Хй=у (%+%);
(8Л2>
Перемещения их, иу произвольной точки в текущем сечении, расположенной на расстоянии у от оси х, будем определять равенствами
их=их—у&, иу — иу.
(8.13)
Согласно формулам Коши, имеем отсюда 2 / dux - dO \ хх дх I к ds J
_ ди« I дц* _ 2 d“« а.
ВХ?— _ -Г — . —7J-
дх ду * dS
Чтобы выразить деформации через узловые перемещения, подставим в последние равенства соотношения (8.11). Введя матрицы узловых перемещений up = {ихр иур$р}, запишем
eix"^PsUp 1/^Ррир> Еху — ^Ррир> где обозначено
0 0 — I
Р₽=4т о Ol; р; = и J
?’-[° т
Этот результат можно представить и в форме е = Ри, если положить u = {u, u2), е — {ехх еЖ!Д 0 = [0, 02|, где
(8-14)
Рр =
(8.15)
Связь между деформациями и напряжениями возьмем в виде охх = Ее,хх, ахи — Gexy. Отсюда вытекает матричное соотношение а — хе, в котором о = {ахж оху), а
х=
(8.16)
Обозначая через к матрицу жесткости элемента бруса, отнесенную к шести степеням свободы и, находим ее блоки: kpff = J ₽px₽ffdr (р, 9 = 1, 2).
Внося сюда (8.14)—-(8.16) и учитывая, что dx = dxdF (dF —элементарная площадка в поперечном сечении), получим l^pg kptj, е -|- крр, о, (8.17)
кр,. Е = е J [F(0°рт 0“ -Уа 0£т 0? -ус 0°т 05)+Jz р;7 p;idx;
kpg.G =vG J £0p 0g dx. I
(8.18)
Здесь F, Jz — площадь поперечного сечения и его момент инерции относительно оси г. В выражение для кр,.о введен дополнительно коэффициент v, учитывающий неравномерность распределения касательных напряжений охи по сечению. Этот коэффициент зависит от формы поперечного сечения. Так, для прямоугольного сечения он равен 5/6, для круглого— 9/10 и т. д. Для лонжерона можно брать в качестве v отношение площади сечения стенки к F. Это соответствует предположению, что поперечная сила воспринимается только стенкой лонжерона, равномерно распределяясь по ее высоте.
Интегрирование в (8.18) осуществим по одноточечному правилу Гаусса. Если брус имеет постоянное сечение, то это соответствует точному вычислению кр,,в. Для матриц км,о одноточечное интегрирование имеет минимально допустимый порядок и позволяет исключить ложный сдвиг. С учетом (8.14) получим в итоге
"0 0
0 1Р1д
_0 /^/2
0 “
ЛР/2 •
Р/4 _
где Fo, Jo, у0 — значения F, Jг, уе в среднем сечении элемента (при х = 0).
Эти формулы относятся к случаю, когда пояса и стенки
лонжерона изготовлены из одного материала. Если же мате-
риалы различны, то их условно приводят к одному материалу. Пусть Е — модуль упругости материала, к которому осуществляется приведение (например, материала стенки). Тог
да при вычислении площади сечения, его момента инерции и статического момента вклад каждого элемента сечения (стенки, поясов) должен быть умножен на редукционный коэффициент, равный отношению соответствующего модуля упругости к Е. Под величиной G в формуле для кр?, о следует всегда понимать модуль сдвига материала стенки.
Приведем теперь полученную матрицу жесткости к восьми узловым перемещениям конечного элемента V. Связь между матрицами
U = {Uxl 'fl'i UX2 Uyi
v = It) - v- V- V.- V,- V,- V - V -1 I ‘X uiy )x jy lx ''ly mx my I
на основании (8.12) может быть записана в форме u = Xv, где Через X обозначена матрица вида
X = P Ш 0 0 (8.19)
I ) 0
Здесь типовая подматрица Xpr (p — 1,2; г = /, /, /, т)
может быть определена общим выражением
“1/2 0
Хрг — 0 1/2 , • (8.20)
_ —т]г/Яр 0 _
в котором = —1 для г = j, т и — 1 для г = i, /.
Искомая матрица к' получается далее с помощью обычного преобразования к'= ХгкХ. Учитывая, что матрица к представлена выше в блочной форме
__ кц к12
_ к21 к22
выражение для к' представим также в блочном виде
к а к,•/ к,/ к,т к// к// к/т к» к/т
Симм. кп'!т
где типовая подматрица
k;s-X^kPgX9s. (8.21)
Здесь р — 1 при г = i, j и р = 2 при г = I, nv, аналогично, q = 1 для s = z, j и q — 2 для s = I, т.
Обратимся теперь к пружинным элементам. Жесткости пружин будем считать одинаковыми и равными g0. Связь между перемещениями и- и соответствующими им узловыми силами Р - (г — I, j, I, т) определится двумя равенствами:
ГР.-1
Р-
go ~go
go go.
go —go Vly . go go . ьтй
L 1U J
(8.22)
Исходя из этих равенств, можно записать выражение для полной матрицы к7', имеющей размер 8 X 8. В блочной форме
она имеет вид _ _ _ _
~к,7 k"j ки к,"т
- _ к/, к/,
I» --- _ J
кН t ft ll klm
, СИММ• kmm
где
г.". — ь"-. — ь", _ Г"____й",— й". —О
— Л// “ к// — Л/nm— *4/ — — I Л
[О go
(8.23)
а подматрицы k,z, к"т, кд, к"т—нулевые.
Суммируя матрицы к' и к", находим матрицу жесткости конечного элемента в местной системе координат. Отдельные ее блоки определяются как
krs =kr's +k/s (г, s=i, j, I, tn). (8.24)
Что касается значения g0, то, как говорилось выше, его можно задавать сугубо приближенно. Можно, например, вычислить жесткость стенки при ее растяжении в поперечном направлении и приравнять ее к суммарной жесткости пружин 2g0. Считая, что стенка имеет постоянную высоту Н = = (Н1 + Н2)/2, получаем следующую оценку для g0:
go = Ehl/ (Нг + Я2),
(8.25)
где hl — площадь сечения стенки плоскостью xz (h — толщина стенки).
Заключительным этапом формирования матрицы жесткости элемента лонжерона является переход к общей системе координат х, у, г. Найдем прежде всего косинусы углов, составляемых осями х, у с осями х, у, г. Так как ось х проходит через точки 1, 2, то для нее направляющие косинусы даются равенствами:
=(z2—г,)//.
Определим далее направляющие косинусы оси у. Выше подразумевалось негласно, что направления ij и 1т перпендикулярны оси х и лежат в одной плоскости. Однако из-за особенностей конструкции или разбиения обшивки на конечные элементы, а также вследствие приближенного задания коор
динат узлов может оказаться, что эти направления не явля ются строго параллельными и перпендикулярными оси х. При расчете жесткостных характеристик конечного элемента это можно игнорировать, но возникают трудности с определением направления оси у. Возможны различные пути разрешения этой проблемы; мы поступим следующим образом.
Введем в рассмотрение точки а и Ь, которые делят пополам расстояния между узлами i, I и j, tn соответственно. Их координаты: ха = (хг + Xi)!2, уа = (у, + уг)/2 и т. д. Затем проведем через данные точки плоскость, параллельную оси х, и будем считать, что ось у параллельна этой плоскости. Тем самым направление оси у будет однозначно определено даже в том случае, когда узлы i, j, I, т не лежат в одной плоскости.
Как известно из аналитической геометрии, любую плоскость в пространстве можно задать линейным уравнением
Ах + By + Сг + D = 0. (8.26)
Коэффициенты А, В и С можно рассматривать как компоненты некоторого вектора, нормального к плоскости и определяющего, таким образом, ее ориентацию в пространстве. Константа D характеризует перенос плоскости вдоль нормали параллельно самой себе, и для нас она является несущественной.
Уравнение плоскости, проходящей через две точки с координатами ха, уа, га и хь, уь, гь параллельно прямой с направляющими косинусами А-х, Aj , А-* удобно записать в форме равенства нулю определителя:
х—ха У—У а е т
ХЬ—Ха Уъ—Уа 2Ь —Za = 0.
А- ХУ А-
Раскрыв определитель, придем к уравнению типа (8.26) с коэффициентами
А = (уь —уа) К-г — (zb — za) А-;
В = (zb—zo) А- — (хь - ха) к--,
С — (хь ха) (уь уа) к-х. (8.27)
Теперь мы можем рассмотреть пересечение двух плоскостей, одна из которых нормальна к вектору с компонентами А, В, С, другая же — к вектору с компонентами А-*, А- , А-* (т. е. к оси х). Ясно, что ось у будет параллельна линии их
пересечения, так что направляющие косинусы оси у будут совпадать с направляющими косинусами этой линии. Если две плоскости заданы уравнениями
Ах + By 4 Cz + D = 0;
^xxX + ^xi, f/+4a2 + d==0>
то направляющие косинусы линии их пересечения даются равенствами
K-v = Nv/N-,l- = Nz/N-,
Nx
(8.28)
Дальнейшие вычисления выполняются обычным образом. Проектируя в каждом узле перемещения vrx, vrv, vrz на направления осей х, у, приходим к соотношениям вида vr = = Xovr, где vr = {vrx vry vTZ}, a
(8.29)
Отсюда вытекает стандартная связь v = Xve между матрицами v = { V;VjV(vm } и ve = {viVj-VjVm }. Матрица X имеет здесь блочно-диагональную форму
По формуле ке = Хг кХ находим, наконец, матрицу жесткости конечного элемента в общей системе координат. Для отдельных ее блоков имеем
k?s=XjkrsX0. (8.30)
Приведение распределенных нагрузок к узлам для данного элемента рассматривать не будем, так как при расчете крыла принято считать обычно, что вся распределенная нагрузка (как воздушная, так и массовая) приложена к обшивке.
Аналогично могут быть построены конечные элементы лонжерона второго и третьего порядков (рис. 8.3, б, в), для которое
рых матрицы ке будут содержать соответственно 6 X 6 и 8 X 8 блоков k's- Для вычисления последних справедливы приведенные выше формулы с некоторыми поправками. Так, в качестве фр нужно брать функции (5.82)
3£2_ 2
=-[У(1+М)-(1-П1 (Р=Л 2, 3)
для элементов второго и функции (5.83)
(ё₽+ё)
2g’(2g«- 1-е?)
(р= /, 2, 3, 4)
для элементов третьего порядков (см. § 5.10). Значения даны на рис. 8.3; параметр с0 = 1/3 или 1/J/5.
Связь координаты х с безразмерным параметром £ определится выражением х = 2фрхр, в котором суммирование выполняется по трем точкам (р = 1, 2, 3) для элемента второго и по четырем (р = /, 2, 3, 4} — для элемента третьего порядков.
При вычислении кр,,£ и кр4,о по (8.18) следует подставить вместо dx выражение
dx = S-^x„d? йё
и применить для кот,о минимально допустимый, а для кр<?1£ — обычный порядок интегрирования (см. табл. 5.1).
Формула преобразования (8.21) остается в силе и в этом случае, причем значения индексов р, q должны выбираться в зависимости от значений индексов г, s:
r(s)..............i или j I или m n или t k или g
P(q) ............. i 2 3 4
В (8.20) т]г_= 1 Для r = n, k и т)г = —1 для r = t, g. Матрица k" будет иметь блочную структуру, вид которой проиллюстрируем на примере элемента второго порядка:
i j I m n t
k0 — k0 0 0 0 0 “ i
k0 0 0 0 0 i
k" = ko — ko 0 0 i
k# 0 0 m
Симм. ko — ko n
k0 _ i
где
к0 =
О О ‘
0 go.
Здесь жесткость пружин g0 — ЕМ/ (3//3). __
Для элемента третьего порядка матрица к" имеет аналогичную структуру; значение g0 можно взять вдвое меньшим, чем в (8.25).
Формулы (8.29), (8.30) также сохраняют свой вид. Направляющие косинусы осей х, у определяют по координатам узлов i, j, I, tn, пользуясь соотношениями (8.27), (8.28).
§ 8.4. Составные конечные элементы лонжеронов
Будем теперь считать элемент лонжерона составленным из конечных элементов поясов и стенки. На рис. 8.4, а показан элемент первого порядка с четырьмя узлами i, /, /, т. Так же как и в случае элементов, описанных в предыдущем параграфе, узлы совпадают с узлами конечных элементов обшивки, срединная поверхность которой обозначена на рисунке штрихпунктирными линиями.
Штриховыми линиями AjAi и AjAm на рисунке отмечены осевые линии поясов, проходящие через центры тяжести их поперечных сечений; верхний пояс отмечен индексом «в», нижний — «н»; цифрами /, 2, 3, 4 отмечены угловые точки стенки.
Помимо координат узлов хТ, уг, гг (г = i, j, I, т) исходная информация для элемента включает в себя площади сечения FB, Fa верхнего и нижнего поясов, расстояния ав, от их осевых линий до срединной поверхности обшивки, толщину h стенки, ее высоты Н{, Hi в крайних сечениях элемента, а также упругие характеристики материалов (£в, Ея—для поясов и Е, G, р. — для материала стенки).
При вычислении жесткостных характеристик элемента будем исходить из предположения, что от узла i к узлу j и от узла I к узлу т перемещения точек изменяются по линейному закону. Учитывая, что размеры сечений поясов малы по сравнению с высотой лонжерона, будем пренебрегать изменением в них нормальных напряжений. Таким образом, мы считаем, что пояса находятся в условиях одноосного напряженного состояния с равномерным распределением напряжений по сечению.
Вывод матрицы жесткости выполним сразу в общей системе координат х, у, z. Каждый узел имеет три степени свободы: перемещения vrx, vry, vrz в направлении координатных осей.
Обозначим, как и ранее, через
Vе = {v; V; V( Vm } матрицу узловых перемещений элемента, в которой vr = {vrx vry vrz} (г = i, /, I, m).
Матрица жесткости ke рассматриваемого конечного элемента может быть получена как сумма трех матриц
к« = кв + к“ + кст, (8.31)
первые две из которых представляют вклады поясов, а последняя — вклад стенки.
©
Рис. 8.4
Переходя к вычислению отдельных слагаемых, начнем с верхнего пояса. Как уже говорилось, он представляет собой одномерный элемент с равномерным распределением напряжений по сечению. Длину /в осевой линии пояса можно считать совпадающей с расстоянием между узлами i, I:
lB = V (.Xi — Xt)3 4- (yi—yt)2 + (z{ —Z;)2.
Направляющие косинусы этой линии считаем совпадающими с направляющими косинусами прямой, соединяющей узлы z, I:
^“хв в Х{)НВ, ^’Jb (Уг У()ИВ, ^zb (%l
Здесь принято, что пояс имеет направление от узла i к узлу I.
Смещения точек А, и Л; в направлении координатных осей обозначим через uix, uiy, uiz, ulx, uly, ulz. Они не равны перемещениям узлов i, /, так как точки А,- и Ai не совпадают с последними.
Обозначим, далее, через vJ; — {ирх иру upz} (р = i, I) матрицы перемещений точек Ait At, а через vB — {v, v(}— матрицу перемещений верхнего пояса. Если пояс отнесен к этим шести перемещениям, то его матрица жесткости будет иметь вид
кв
(8.32)
Отдельные подматрицы к® (р, q — i, I) имеют размер 3 X 3 и даются выражениями (3.19), которые с учетом принятых здесь обозначений запишем так:
(8.33)
/в
где gj = —1; h = 1; Xj = [Ххв XVB Хгв].
Приведем далее матрицу (8.32) к двенадцати узловым перемещениям Vе. Исходя из линейного закона распределения перемещений от узла i к узлу / и от узла I к узлу т, выразим перемещения точек A,, Ai через перемещения узлов i, j, I, пг:
= VJX~V^ ав, ulx^ vlx+ ав. (8.34)
/?1 П2
Формулы для остальных компонент матрицы vB получаются из (8.34) заменой индекса х на у или г. Через Н1г Н2 обозначены расстояния между узлами i, j и /, т, рассчитываемые по формулам
Hi = V (Xj —xt)2 + (у, —у,)2 + (г,-—z;)a,
H2 = V(xm — xt)2 4- (ym — yt)2 -'r (zm — z;)2:
Шести соотношениям типа (8.34) можно придать привычную форму vB = lBve, если положить
где
Гь?. Ц 0 0 1 лв —
О 0 Кц Kfm_
Хв / ] Ов \ I . IВ Св I . ii — I 1 *---) *31 ЛО' — ~ГГ~ *3’
\ 1 “1
п, в ___ /1 ав 1 1 . 1 в ___ ° в I
АЦ — I 1----7Г~ I '3> А/т----7Г~ *3-
\ **2 / “2
(8.35)
Здесь через 13 обозначена единичная матрица размером 3x3.
Выполнив преобразование кв = ХвГ кв1в, получим искомую матрицу жесткости верхнего пояса размером 12 х 12. Как обычно, представим ее в блочной форме
К// К// К// К/щ
k// к?от
кц kzBm Симм. к^ш:
Отдельные подматрицы можно записать в виде
к« = К% кр, KBgs (г, s — i, /, I, т), (8.36)
где
i для r = i или /;
I для г = 1 или /п;
i для s — i или
I для s=/ или т.
Точно так же вычисляется матрица жесткости кн нижнего пояса. Она имеет такую же структуру, что и кв, а отдельные ее подматрицы
к<£> = g,r к^ Ijs (г, s = I, /, I, т), (8.37)
где
(/ для г = i
Р== 7
[т для г =1
или /; j для s = i или /;
или /п; (т для s = / или т.
Здесь, по аналогии с (8.33),
кн — кр? —
Ен Ея » ?
I SP ь« ‘н
^хн hya Ахи ^zh
^-ун ^ZH
Симм. XzH
(8.38)
причем ХЛ.Н, кУя, Х.2Н определяются соотношениями
^хн = (Хт Х})НЯ, ^Ун = (Ут У))НЯ, ^zh ~ (%т
1н = У(хт— *у)2 + {ут — У})2 + (zm — Z;)2.
Матрицы X«r, X«s в (8.37) даются равенствами
<1Н _ ан I . <1Н ___________ (t °н \ I
Л<п/------г: *з> ”тт — 1 ~7. 1 *3-
^*2 \ /
(8.39)
Переходя к конечному элементу стенки, начнем с определения координат его узлов. Обозначим через alt а2 расстояния соответственно от точки 1 до узла i и от точки 2 до узла /. Будем считать, что отношение а1/а2 равно отношению aja^. Учитывая, что + а2 = Нг — Н{, находим
ах = (^i - Н{)1 (1 + ^/aj; а2 = - Hi)/ (1 + aB/aJ.
Подобным же образом можно определить расстояния Од, ал от точек 3, 4 до узлов /, т:
а3=(Н2- Н£/ (1 + ая/ав); а, = (Я2 - Н& (1 + aJcQ.
Теперь координаты точек 1, 2, 3, 4 можно выразить через координаты узлов i, j, I, т:
xt=(l----7г) *i + ~-x}-; х2=-^-хг+(1— 4т")*/;
\ «1 ' "1 “1 \ "1 1
г __! 1 _ а3 ) у | у . г _ а3 v ; (1 _ а4 \ „
хз ~~ I 1 „ I Xi т Хт, %4 — Х[ х I 1 „I Хт.
Формулы для координат у и z получаются из этих равенств соответствующей заменой обозначений.
Обозначим далее через их, иу, uz перемещения произвольной точки стенки, через ихр, иу]>, uzP (р — 1, 2, 3, 4) — их узловые значения и введем матрицу перемещений конечного элемента стенки
V = {Ut u2 u3 u4},
где Up = {ихр иур uzp} — матрицы перемещений отдельных узлов стенки. Через к обозначим матрицу жесткости конечного элемента стенки, отнесенную к перемещениям v.
Для вывода к воспользуемся изопараметрической формулировкой элемента, аналогично выводу матрицы жесткости конечного элемента обшивки в § 8.2.
Положение произвольной точки стенки определим безразмерными координатами тр .
х = 2фрхр; у = 2фр//р; г = 2фр?р.
Здесь
Фр (В. Л) =4-(1+ВРВ)(1 + г1рЯ) (Р = Л 2,3, 4),
а суммирование ведется по четырем узлам стенки. Узловые значения Вр/г]р параметров т) даны на рис. 8.4, б.
Далее могут быть вычислены параметры
У = Ч
где
~ Ре* Мр ^-т) = Рп* 4*1;
, 1 дх ' , 1 ду , , 1 дг
AE dl d%
, 1 дх , 1 ду 1 дг
Ац*----j —; АЧр — -j - ; г^г — -д —
% th) dt) % дт)
Аппроксимация перемещений выполняется по формулам цж = Si^pU^p, Uy = 2фрЦрр, uz = Si|)pUzp.
Так как стенка лонжерона моделируется по высоте одним конечным элементом, то необходимо позаботиться, чтобы в нем правильно воспроизводилось состояние чистого изгиба, т. е. следует исключить ложный сдвиг (см. § 5.2). Как говорилось в § 6.5, этого можно добиться, применяя пониженный порядок интегрирования при вычислении вклада поперечной дефор-
мации в матрицу жесткости. Поэтому в матрице е выделим деформацию е12, полагая 8 = {е* е12}, где е* = {еи е22}. На основании (7.116) имеем
«6
е* = Г* еп
-еЕп-
где
о _ 1 о. ди . о _ 1 1
eg —Ag-—, еп —т— л d£ Лп
du
4 дт) ’
е&п
1 „ du
1 . du -л--н —, Лп dij
а матрицы Г* и Г содержат соответственно первые две и последнюю строки матрицы Г (7.117):
Через и = {иЛ иу uz} обозначена матрица перемещений.
Далее выразим деформации через узловые перемещения в форме 8 = Spp Up, где
(8.40)
Xg
1 „ > J____
лц dt)
-ЛП_
Напряжения о* — {о,, о22) и о,2 связаны с деформациями равенствами о* = х*8*, о12 = Ge12, в которых
х* = & Г1 ]
1-На Ь 1J
Их можно представить и в виде о = хе, полагая о = (о*ст12},
Теперь можно найти отдельные блоки матрицы к: = j Рр «₽<г iP, Я -1, 2, 3, 4).
Если учесть блочную структуру матриц 0Р, рд, х, то с учетом равенства <1т=ЛЛ л 1 — Y2dgdrj получим расчетные формулы:
kpg == kpg> Е ~Ь kpg, G»
1 1
kw. Е = С f gj Г*г х* Г* g, Ai Дп d^dt), И -1-1
kpq,a = Gh j j g’'rrfg9 — у2 d£dn. (8.41)
При вычислении матрицы кР7.о, представляющей собой вклад деформации е12, воспользуемся одноточечным интегрированием по Гауссу; это соответствует минимально допустимому порядку интегрирования. Что касается кр?>£, то здесь необходимо взять по две точки Гаусса для каждой из переменных I, Г|. _
Матрица к отнесена к перемещениям точек 1, 2, 3, 4. Переход к перемещениям узлов i, j, I, т выполняется так же, как и для конечных элементов поясов. Перемещения этих точек выражаются через перемещения узлов по формулам:
их1—(Pjx ui«)> их2 — ®Jx 4” (vix V]x)>
ux3=Vix + ~ (Vmx—vlx); uxi =vmx + ~(vix—vmx);
H2 n2
остальные компоненты получаются из этих соотношений соответствующей заменой индексов.
Все эти равенства можно записать в форме v = Xve, где
0 0 “
х= ^2i 0 0
0 0 ^зг ^Зт
_0 0 ^4п» _
Здесь
Kli = fl--— )ls; Хи=-^13;
11 k Ht) 3
а __ аг t . j ___ (I °2 'l I
---~ 13> — 1 ~ I »3>
Hi \ /
-тН’з; хзт = -5-|3;
\ / “а
Ki = Ь; Кт Ч1 ~ 1з <8Л2) ”2 ' “2 /
Через 13 обозначена, как И выше, единичная матрица третьего порядка. _
Далее воспользуемся формулой kCT = V кХ. Переходя к блочной форме
~к?7 к?; к?; к& ~
кст== к// к/7 к% kctTm
__ СиММ. кщт_______
можно получить следующее выражение для отдельных подматриц:
k"=I]21PrkpgX9s, (8.43)
р я
где г, s = i, /, I, т. Суммирование в (8,43) выполняется по индексам р, q, значения которых должны выбираться в зависимости от индексов г, s:
г (s)... i или j I или пг
р (q)... 1,2 3,4
Таким образом, определены отдельные вклады в матрицу жесткости кг конечного элемента лонжерона. Блоки этой матрицы:
tfs -k?s+ k“ + k" (г, s = i, j, I, m). (8.44)
✓
Подобным же образом строятся и более сложные конечные элементы второго и третьего порядков (рис. 8.4, в, г). В этом случае пояса рассматриваются как одномерные элементы с тремя или четырьмя узлами. Аппроксимация геометрии и перемещений в них осуществляется с помощью функций
ЗЕ2 —2
ФР (В) = [Ш1 -ь £р £) — (1
или
(ёР + Е)
2g2(2g2-l-c2) ’
где для верхнего пояса индекс р принимает значения i, I, п или i, I, п, k, а для нижнего — /', т, t или /, т, t, g. Узловые значения параметра % указаны на рис. 8.4. Матрицы жесткости поясов в блочном виде будут иметь размер 3x3 или 4x4. Если отнести их к перемещениям узловых точек, лежащих на осевых линиях поясов, то они могут быть вычислены по формуле (5.86), которая с учетом принятых обозначений примет вид
i^=M f (8.45)
— 1 — 1
Здесь А = Ух’* + у*, причем х’ = 2фрхр, у' = ^'рур, где фр = dipp/dg, а суммирование ведется по всем узлам пояса. При расчете х', у' можно в качестве хр, ур брать координаты соответствующих узлов конечного элемента вместо координат узлов пояса. Матрица рг вычисляется по (5.85). Интегрирование в (8.45) можно осуществлять по правилу Гаусса с тремя точками для элемента второго и с четырьмя — для элемента третьего порядков.
К узловым перемещениям v« переходим так же, как и в предыдущем случае. Формулы (8.36), (8.37) остаются в силе, при этом индексы р, q находятся в следующей зависимости от индексов г, s:
r(s) ...........................i или / I или т п или t k или§
p'q) для пояса:
верхнего....................... i I п k
иижиего........................ / т t g
Помимо введенных ранее матриц (8.35), (8.39) здесь будут фигурировать аналогичные матрицы для промежуточных узлов. Выражения для них можно получить из (8.35), (8.39), подставляя вместо Нг или Н2 величины Н3 или Последние вычисляются через координаты промежуточных узлов аналогично Я, и Н2.
Аппроксимация геометрии и перемещений стенки для элемента второго порядка выполняется с помощью функций
ЗР—2
Фр(5, П)=-^--1^(1+М)(1+ПрП) -
4
-(1-Н(1+ПрП)1 (Р=Л 2,
а для элементов третьего порядка — с помощью функций
Блоки матрицы к вычисляем по (8.41). При численном интегрировании в крч,в следует применять обычный, а в кро.ц — пониженный порядок интегрирования (см. табл. 5.1).
Приведение к к узловым перемещениям конечного элемента лонжерона выполняется согласно (8.43), но здесь индексы р, q определяются правилом:
г Is)................................i или / I или m п или t k или g
plq)..................................... 1,2 3, 4 5, 6 7,8
Появляющиеся здесь дополнительно матрицы Хрг определяются аналогично (8.42).
§ 8.5. Двухузловой конечный элемент шпангоута
Рассмотрим теперь конечные элементы для моделирования шпангоутов. Предполагается, что шпангоут представляет собой плоскую криволинейную раму. Плоскость шпангоута, проходящая через центры тяжести его поперечных сечений, произвольно ориентирована относительно осей х, у, г. На положение главных осей инерции поперечного сечения никаких ограничений накладывать не будем.
В простейшем варианте конечноэлементной идеализации шпангоута (рис. 8.5, а) используем набор прямолинейных двухузловых конечных элементов (элементов первого порядка). Как и в случае конечных элементов лонжеронов, узлы совпадают с узлами конечных элементов обшивки (штрих-пуиктирной линией отмечена срединная поверхность обшивки).
Для каждого конечного элемента будем пользоваться местной системой координат х, у, z, начало которой помещается в центре тяжести среднего сечения элемента. Оси х, у лежат в плоскости шпангоута (рис. 8.5, б), причем ось х совпадает с осью элемента. Предполагается, что ориентация плоскости х, у относительно осей х, у, z определяется тремя узлами, два из которых — узлы элемента i, j, а третий — какой-либо дополнительный узел шпангоута п, не лежащий на прямой, соединяющей узлы I, /.
Направления осей х, у, z будем определять следующим образом. Ось х всегда направляется от первого узла конечного элемента ко второму (в последующем изложении считается, что узел i — первый, а узел /— второй). Ось z направлена в сторону поступательного движения правого винта, находящегося в точке п и вращающегося вместе с радиусом-вектором, начало которого также лежит в точке п, при этом конец радиуса-вектора должен находиться на оси х и двигаться в отри-
Рис. 8.5
дательном ее направлении. Наконец, направление оси у должно быть взято таким, чтобы оси х, у, z образовывали правую систему координат. Этих правил необходимо придерживаться, в частности, при вычислении центробежного момента инерции J-- сечения лонжерона.
В исходных данных для элемента помимо номеров I, j, п должны быть также указаны площадь F поперечного сечения, его моменты инерции J-, J- относительно осей у, г, центробежный момент инерции J—, жесткость сечения на кручение G/Kp и модули упругости Е, G. Если поперечное сечение шпангоута образует вместе с обшивкой замкнутый контур, то это должно быть соответствующим образом учтено при вычислении жесткости на кручение. Кроме того, должны быть заданы координаты у0, г0 точки сечения, лежащей на линии узлов i, j (рис. 8.5, б). Наконец, следует задать параметры v-, v-, учи. бывающие неравномерность распределения по сечению перерезывающих сил в плоскостях ху и xz.
Пусть игх, игу, vTZ — перемещения типового узла г в направлении осей х, у, z, a #rx, &rv, ,drz — повороты соответствующего сечения шпангоута. Тогда
Vr — Vry Vrz ^гх &Гу ^rz}-
Таким образом, конечный элемент шпангоута имеет двенадцать степеней свободы:
Vе = {v, vj.
Положительные направления перемещений уг даны на рис. 8.5, а; углы поворота сечения изображены в виде векто-
Рис. 8.6
ров с двойной стрелкой (их направления определяются правилом правого винта).
Обозначим далее через и-, и-, uz смещения произвольной точк1£элемента, лежащей на оси х, в направлении местных осей х, у, г, через 0-, 0-, 0- — повороты соответствующего сечения относительно тех же осей, а через и- , и- , и- , 0- , 0- , 0-
Г Хг Уг 2г1 Хг Уг 2г
(г = I, /) — узловые значения этих величин (рис. 8.6).
Прежде всего найдем матрицу жесткости элемента, отнесенную к перемещениям v = {uf u;}, где
иг = (“Г, и- и- 0- 0- 0-J.
Перемещения точек, не лежащих на оси х, не определяются однозначно введенными перемещениями вследствие того, что при кручении бруса его сечения не остаются плоскими, а депланируют. Это затрудняет применение стандартного подхода, использовавшегося ранее. Поэтому прежде чем перехо
дить к аппроксимации перемещений, преобразуем формулу для потенциальной энергии деформации
U — — f 8Г Х8(1т
V %
и вытекающее из нее выражение для матрицы жесткости элемента
ke = J Рг x0dr.
Xе
Предположим сначала, что кручение бруса отсутствует. Растяжение и изгиб бруса сопровождаются появлением продольной деформации е-- и деформаций поперечного сдвига 8--, е-~. Этим деформациям соответствуют напряжения о- - = = £е--: о-- — Ge--: а- - = Ge--.
хх’ ху ху’ хх хг
Полагая 8 = [е— е-- 8--|; ff — lozz a-- а--}, имеем <т = х8, где | Д'Л лу лх») | Ал "У АЛ ’
Г£ 0 01
о
.0
G 0 0 G
Потенциальная энергия деформации в этом случае
ч 4 J=Т f.(Esb+ О<% + (8.46)
т т
Исходя из предположения о том, что сечения при изгибе остаются плоскими, можно написать следующий закон распределения деформации е- - в поперечном сечении:
е«=е^ + ^ +УХ7, (8.47)
где е® - — продольная деформация в центре тяжести сечения; X- и Хг — изменения кривизн осевой линии.
Заменив dx произведением dFdx, где dF — элементарная площадка в поперечном сечении, выполним интегрирование в (8.46) по площади поперечного сечения с учетом соотношения (8.47). Памятуя о том, что у, z — центральные оси, приходим к следующему выражению:
и “т![£f ft)’ + £7?*?+£^xi+2£75i*;’fr+ I
+ GFv- e^ + GFv-e5-] dx.
Деформации e-- и e-- при интегрировании считались постоянными в поперечном сечении, а для учета их неравномерности введены упоминавшиеся выше коэффициенты v- и v-, зависящие от формы сечения.
Пусть теперь брус дополнительно испытывает кручение. Как известно из курса сопротивления материалов, потенциальная энергия деформации, накапливаемая при кручении,
t
где %- — погонный угол закручивания. Объединяя это выражение с предыдущим, получаем формулу для потенциальной энергии деформации бруса в общем случае пространственного нагружения:
4 ([ШГ + +D- +
I
+ D- & + D- ХЯ + 2D- %- %-1 dx, у лу 1 z г 1 У г "у лг] ’ где
B-=£F; B- = v-GF; B-=v-GF; л У У л л
D-=^GJW\ D- — EJ-; D- = EJ-\ D-- = EJ--.
X HP’ у y> Z Z9 yz yz
Выражение для U можно записать в матричном виде
U = ~ J ег xedx, (8.48)
i
полагая ё= {е5- г- г- Х^ Х?|;
- В- О I
ВУ I
В- ! О
z= 2_>1_ __ ’ (
_ 0 \С-у-г Ъ-г _
Исходя из (8.48), выражение для матрицы жесткости элемента в местной системе координат можно вычислять в привычной форме
k = J0rz0dx, (8.50)
i
если под 0 — понимать матрицу, связывающую 8 с узловыми перемещениями соотношением s = 0v. Вид матрицы 0 зависит от характера аппроксимации перемещений и будет определен ниже.
При блочном вычислении матрицы жесткости к следует представить матрицу 0 в виде 0 = [0,- 0J; тогда отдельные блоки матрицы (8.50) имеют вид
J 0гГ «0Д* (г, s = i, j). (8.51)
i
Выразим далее параметры деформации 8 через перемещения и углы поворота сечения. Обозначим через uj, и^, перемещения произвольной точки, не лежащей на оси бруса, в направлении осей х, у, z. Перемещения в поперечном сечении при изгибе изменяются по закону:
= +z0^— ?)-; = (8-52)
Тогда
du- _ d0- d0-
8^= -77- = + z—S- - У -=- •
dx dx dx dx
Сопоставляя это равенство с (8.47), видим, что введенные выше параметры деформации е®-, %-, х- связаны с перемещениями зависимостями
du- d 0- d 0-
= (8.53)
ax ax d x
Для деформаций поперечного сдвигав--, е-- имеем
dui. 8— — = L J х у _ 1 дх ди— । х d и— d х
ду
ди*. р.- — 2 J ди~ L * — (8.54)
хг дх 1 дг dx »'
Наконец, погонный угол закручивания
ХГ =
ае-
__X
d х
(8.55)
Возвращаясь к аппроксимации перемещений конечного элемента, запишем
"г=2 ’К “г,; “у - 2 tr ",т/ “г - »7/.
-2От;. °?-2Ч’го--, ег-.3 ♦,e-r. <s.sg)
Здесь суммирование ведется по двум узлам элемента; фг = = (1 + безразмерная координата | = 2x11 принимает в узлах значение g, = —1, g/ = 1.
Переходя в формулах (8.53)—(8.55) к дифференцированию по внесем в них соотношения (8.56). В итоге получим связь параметров деформации 8 с узловыми перемещениями, которую в матричной записи можно представить в требуемом виде в = 2prvr, где для г = I, j
ф; 0 0 0 0 0 ~
0 Фг 0 0 0 -J-ф, 2 4
__2_ ~ 1 0 0 0 0 Фг 0 0 Фг -i-ф, 2 0 0 0 (8.57)
0 _ 0 0 0 0 0 0 0 Фг 0 0 Фг _
Через ф/ в (8.57) обозначена производная
ф;
dipr __ 1
dg “ 2
Переходя далее в (8.51) к интегрированию по g, имеем
к~ j (г,s==f, /)-— 1
Подставляя сюда (8.49),
(8.57) и пользуясь одноточечным
интегрированием, получим
О
---В-
2 »
О
О
D в-
г 1 4 У
(8.58)
Теперь приведем матрицу к к узловым перемещениям ve. Вычислим прежде всего направляющие косинусы осей х, у, г. Считая, что ось х параллельна прямой, соединяющей узлы i, j, запишем
^=^—1/1)//; *Гг ==(*>—2/М;
l =V (Xj—Xi)2 + (yj — yi)2 + (Zj — 2t)2 .
Три величины Л-х, можно рассматривать как ком-
поненты единичного вектора е-, направленного вдоль оси х:
ех х ех + Ч у еУ + \ z ег-
Здесь ех, еу, ez — орты общей системы координат.
Рассмотрим далее вектор
R ~ xni вх -j- yni ^z>
имеющий начало в узле i, а конец — в точке п. Для его компонент введены сокращенные обозначения
xni ~ хп xi\ Уп1 ~ Уп Уг\ %п1 ~ (8.59)
—'► —1►
Векторное произведение R х ех дает некоторый вектор ЛГ, совпадающий по направлению с осью г. Его компоненты определяются равенствами
Мх~Уп1 2ni у' Ny-=zni А—ж xni к^-г;
^z~xni у Уп1 х- (8.60)
Разделив их на длину
W=VA^ + A/>+A/z* (8.61)
вектора N, получаем выражения для направляющих косинусов оси г:
hx =Nx/N, А- = ДГу/ДГ, А- = ЛГг/ЛГ. (8.62)
Наконец, единичный вектор е- вдоль оси у найдем с помощью векторного произведения е- х е-, где е- — единичный вектор с компонентами (8.62), направленный вдоль оси г. Учитывая, что компоненты вектора е- есть направляющие косинусы оси у, приходим к равенствам
А— —: А— А~ — А— А— • А— == А— А_ — А— А_ i ух zy xz zz ху' у у zz Чех ,vzx xz'
К- = А- А-----А- А- . (8.63)
'‘yz ,vzx ''‘ху "гу хх‘
Теперь выразим перемещения иг в узловом сечении i через Vi. Для этого нужно, во-первых, спроектировать перемещения Vi на направления местных осей координат. Если, далее, известно перемещение и-х вдоль оси х произвольной точки сечения, то перемещение в центре тяжести сечения согласно (8.52) будет
иГ = 4-^7+^0Г>
где у, г — координаты рассматриваемой точки. С учетом этого можно найти требуемую связь между перемещениями us и v^. Введя матрицы
представим эту связь в виде
Uxi 4 У о zo Vi*
Uyi 0 viy
Uzi — 0 Viz
Q~Xt 0
0 4- ®ly
_ 6«- _ _ 0 Ч-
Это соотношение имеет обычную форму иг = Xov,-, где
(8.64)
Подобным же образом в узле j имеет место зависимость U; == kovy. Следовательно, связь между матрицами v = {uf Uy) и v' = {vj vy} можно записать в виде v = kve, где
л _ Г ^0 0 j
I О М
Использование формулы ке —V к! завершает вычисление матрицы жесткости рассматриваемого конечного элемента. В блочном представлении
к* = ‘*0 1
к* к« I’ КЛ К/7 J
где отдельные блоки
к« = к© krs Л-о О'. s = i, j). (8.65)
§ 8.6. Криволинейные конечные элементы шпангоута
Теперь рассмотрим конечные элементы плоского шпангоута второго и третьего порядков (рис. 8.7). Каждый узел имеет шесть степеней свободы — три перемещения и три угла поворота:
Vf = {vrx ^ry ^rz 'б'гх ^ry
Кривую, проходящую через узловые точки, зададим в параметрической форме: х — 2фгхг, у — ^гУг, z = 2фг?г, где (g) — встречавшиеся уже ранее функции (5.82) или (5.83).
Узловые значения параметра g даны на рис. 8.7; суммирование выполняется по всем узлам элемента.
Дифференциальный отрезок ds кривой связан с dg соотношением (5.70) ds = Hdg, а его направляющие косинусы равны
, 1 dx , 1 d у ' , Id?
где
В каждом поперечном сечении элемента введем местную систему координат х, у, z с началом в центре тяжести сечения. Оси х, у находятся в плоскости шпангоута, причем ось х является касательной к оси элемента в данном сечении.
Предполагаем, что в пределах конечного элемента размеры поперечного сечения изменяются слабо. Тогда ось бруса и проходящая через узловые точки кривая будут почти эквидистантны, и можно принять, что матрица = [Х-ж X-J направляющих косинусов оси х совпадает с матрицей Xg = = Ц» kfczh
(8.66)
Направления осей у, z определим по тем же правилам, что и в случае двухузлового элемента. Пусть хп, уп, zn — координаты дополнительного узла п, определяющего в совокупности с узлами I, j ориентацию плоскости шпангоута. В качестве дополнительного может быть взят, в частности, промежуточный узел элемента, если только он не лежит на одной прямой с узлами I, j. Тогда компоненты матриц
Х- = [Х- X- X- 1; = X- X- 1
у I ух у у yz Г z I zx гу zz J
могут быть найдены по (8.59)—(8.63). Отметим только, что здесь в отличие от случая двухузлового элемента направляющие косинусы местных осей, вообще говоря, не постоянны, а изменяются с изменением параметра
Выразим далее параметры деформации
8- 14 X Х^Хг}
через перемещения. Пусть u = {их иу uz} — матрица перемещений центра тяжести произвольного сечения в направлении координатных осей, а 0 = {0Х 0У 0Z}—матрица углов поворота этого сечения относительно тех же осей.
Продольная деформация осевой линии может быть согласно (5.77) определена выражением
е- - - — 1- — . (8.67)
х х А х d g
Пусть, далее, 0- = V0, 0^ = 1-0, 0- = V0 — углы по ворота плоскости сечения относительно местных осей координат. Эти углы положительны, если соответствующие им векторы направлены в сторону возрастания кординат х, у, г. Через со-, со- обозначим углы поворота касательной к осевой линии шпангоута относительно тех же осей. Будем считать их положительными в том случае, когда углы между положительным направлением касательной к оси шпангоута и осями г, у становятся острыми (положительное направление касательной совпадает с направлением оси х). На основании (5.79) имеем:
со— у
1 л du А,—
А 2 dg
1 « du
со- — — 1--------
г -
А « dg
Деформации поперечного сдвига е,--, е,-- определяются выражениями
е = со--0—; е—=со—Ю-,
X у г г ’ X г у у ’
в которых знаки проставлены в соответствии с правилами знаков для введенных выше углов. Отсюда приходим к соотношениям
Т = Т Я + е-<М8)
Можно показать, далее, что выражения для параметров Х-, %-, Xj даются для криволинейного стержня формулами
1 . dO . 1 , d 0 1 , d 0
Xjc А d g ’ Х" A d g ’ Хг А d g ’ ( ’ )
Переходя к аппроксимации перемещений и углов поворота, запишем
и = 2фгиг; 0 = 2фг0г.
Здесь ur,, 0Г — значения матриц и, 0 в узловых сечениях.
На основании (8.67)—(8.69) приходим к соотношению е = = 2prvr, где vr = {ur0r}, а
ф'г X-ф' X-у
Ф'г хг о о
о
—Лфг хг
Дф,. X-
ф' X—
ф' X-
у
(8.70)
0 Фг
Здесь фг' = 6фг/6|.
Заменяя в (8.51) dx на Д6|,
получаем расчетную формулу
krs= рГхР5.Л6| (8.71)
— 1
для блоков матрицы жесткости к, отнесенной к перемещениям vr. Матрица х здесь дается формулой (8.49). Интегрирование можно выполнить по трем точкам Гаусса для элементов второго и по четырем — для элементов третьего порядков. Для повышения скорости сходимости решения можно выделить в кг., вклад деформаций поперечного сдвига е--, t--- и использовать при его вычислении минимально допустимый порядок
интегрирования в соответствии с табл. 5.1. Если шпангоут имеет переменное сечение, то входящие в матрицу х его геометрические характеристики удобно задать в узловых сечениях, аппроксимируя их при этом подобно тому, как это делается для перемещений.
В заключение остановимся на переходе к узловым перемещениям конечного элемента Vе. Пусть в некоторой точке М сечения конечного элемента известны вектор поступательного перемещения v == vxex -j- vyey + vzez и вектор поворота сечения Ф = ftxex + ®уеу + где ех, еу, ez — орты общей системы координат.
Рассмотрим другую точку N сечения, положение которой относительно точки М определим вектором
Р = Рх^х Py^y+pz^z-
Вектор поступательного перемещения точки N, который мы обозначим через v*, выражается через перемещения точки М равенством (см. § 7.12) v* =и х р. Отсюда можно прийти к следующим выражениям для компонент вектора V*'
V* =vx + $y р2 — й2 pj,;
vy = vu + fl’z Рх — Pzl (8.72)
и* + Py~®y Px-
Воспользуемся этими соотношениями для установления связи между v и Vе. Рассмотрим, например, сечение шпангоута, содержащее узел г. Под точкой М будем пониматьсам узел, а под точкой N — центр тяжести сечения. Если ут, zT — местные координаты узла г, то вектор рг в местной системе координат х, у, z имеет проекции 0, —ут, —zr. Зная направляющие косинусы осей у, z, вычисляем координаты вектора р2:
Рхг = - (уг \х, г + Zr г); Рг/г = — (Уг г + 2?г);
Pzr = (Уг г + zr г).
Здесь дополнительный индекс г в обозначении направляющих косинусов указывает на то, что соответствующая величина должна быть взята в узле г.
Понимая под v*, Vy, v* перемещения ихг, иуг, uzr на основании (8.72) и тождеств 0xr = ftrx, 0yr = i}r9, 02Г = 0>z приходим к соотношению вида vr = Xrvr, в котором
(8.73)
Пользуясь формулой krs ~ krs ^s, приводим отдельные блоки матрицы жесткости к общей системе координат.
§ 8.7. Заключительные замечания
Объединение конечных элементов при расчете тонкостенной конструкции выполняется по общим правилам. Суммируя подматрицы жесткости и сил с одинаковыми индексами согласно равенствам
k„ = 2k- Pr = 2P*r,
получаем матрицу коэффициентов и матрицу правых частей в системе уравнений
К v = Р + Р,
где Р — матрица сосредоточенных узловых сил.
Для решения этой системы необходимо исключить из нее известные перемещения. Если рассчитывается весь самолет целиком, то система является свободной, и необходимо наложить на нее шесть связей, обеспечивающих неподвижность самолета как жесткого целого (см. § 3.9). Исключая соответствующие шесть перемещений, придем к системе
Каа va = P<z P<z>
содержащей оставшиеся неизвестные перемещения. Матрица Каа является невырожденной, и система уравнений допускает решение. Отметим, что при наличии соответствующих программ удобнее всего воспользоваться методом подконструкций (см. § 5.4). Это облегчает подготовку и контроль исходных данных, позволяет вносить изменения в конструкцию без излишних затрат машинного времени, упрощает анализ полученных результатов.
Однако подробная конечноэлементная модель самолета может включать в себя десятки и даже сотни тысяч узловых перемещений, в связи с чем полное решение такой задачи может оказаться невыполнимым на имеющихся ЭВМ. Поэтому на практике часто выполняют поагрегатный расчет, рассматривая, например, крыло как независимую конструкцию, неподвижно закрепленную в местах соединения с фюзеляжем. Соответствующие перемещения считаются нулевыми и исключаются обычным образом из системы уравнений относительно узловых перемещений крыла. Такой приближенный подход согласуется с традиционными методами расчета авиационных конструкций.
После отыскания узловых перемещений вычисляются напряжения в отдельных конечных элементах. При этом для каждого конечного элемента по формуле типа v = lve находятся узловые перемещения, соответствующие местной системе координат, а затем с помощью равенств е = 0v, а = хе рассчитываются напряжения. В некоторых случаях выводится дополнительная информация. Например, для конечных элементов обшивки могут быть подсчитаны главные напряжения и определены их направления, в сечениях лонжеронов или шпангоутов могут быть найдены интегральные характеристики напряженного состояния (перерезывающие силы, изгибающие моменты и т. п.).
Отметим, что подготовка исходных данных и анализ полученных результатов являются наиболее трудоемкими этапами при выполнении практических расчетов по методу конечных элементов. Это обусловлено большим объемом информации и тем, что эти этапы труднее всего поддаются автоматизации. Поэтому еще при составлении конечноэлементной модели конструкции необходимо стремиться к наиболее простому ее описанию. Это достигается введением участков с регулярной сеткой конечных элементов, использованием симметрии и другими средствами.
§ 8.8. Примеры расчета
Пример 1. Стреловидный кессон (угол стреловидности 45°)> имеющий четыре стальных пояса площадью сечения F = == 240 мм2 каждый и дюралевую обшивку толщиной h = = 1 мм (рис. 8.8), на одном конце нагружен поперечной силой Р\ на другом его пояса закреплены неподвижно. Верхняя и нижняя панели обшивки подкреплены дюралевыми стрингерами площадью сечения Ло — 40 мм2 каждый. Конструкция
Рис. 8.8
включает в себя пять равномерно расположенных нервюр толщиной 1 мм, перпендикулярных оси кессона; помимо них имеется еще одна нервюра в сечении у заделки.
Для идеализации использованы конечные элементы второго порядка (рис. 8.9). При этом боковые стенки кессона вместе с поясами рассматривались как лонжероны и идеализировались конечными элементами, описанными в § 8.3, а стрингеры моделировались одномерными элементами (см. §5.10). Для обшивки использовались конечные элементы без-
моментной оболочки (см. § 8.2). Кривые на рис. 8.9 дают закон изменения нормальных напряжений в поясах; кружочками и крестиками отмечены значения напряжений, полученные экспериментально. Согласие результатов вполне удовлетворительное.
Пример 2. Круговой шпангоут (рис. 8.10) нагружен двумя равными противоположно направленными силами. Радиус шпангоута г = 1 м, момент инерции и площадь поперечного сечения J = 2,067 • 104 мм4, F = 220 мм2, Е = 7 • I04 МПа.
Эта задача уже рассматривалась ранее (см. § 5.13); здесь для ее решения использованы описанные в § 8.5, 8.6 конечные элементы шпангоута первого и второго порядков. На рис. 8.11 представлены зависимости осевой силы N — N/Р и изгибающего момента М = М/(Рг) от угла 0, полученные аналитически. Крестиками отмечены результаты, полученные при разбиении четверти кольца на 10 элементов первого порядка, кружочками — на 10 элементов второго порядка. Последние результаты получены с помощью местного сглаживания (см. §5.12) значений N и М с последующим их осреднением по смежным элементам. Непосредственное вычисление напряжений (без сглаживания) обнаруживает здесь такие колебания ях вокруг истинных значений, которые полностью искажают действительную картину. Например, осевая сила N в узлах первого конечного элемента оказывается равной 11,447, —5,757 и 11,547’ вместо истинных значений 0; 0,0397 и 0,0787 соответственно. Эти колебания, обусловленные влиянием ложных деформаций поперечного сдвига, полностью устраняются с помощью местного сглаживания, как это видно из рис. 8.11.
ЧАСТЬ IV
ДИНАМИЧЕСКИЕ ЗАДАЧИ
ГЛАВА 9
СООТНОШЕНИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ
В ЗАДАЧАХ ДИНАМИКИ
Если нагрузки быстро изменяются во времени, то возникающие при деформации тела инерционные силы могут играть существенную роль, и их необходимо учитывать. Обобщение основных соотношений метода конечных элементов на случай динамического нагружения приводит к понятию матрицы масс. Матрица масс имеет в принципе такую же структуру, что и матрица жесткости, но в отличие от последней она может быть представлена и в диагональной (или блочно-диагональной) форме, что важно для снижения затрат машинного времени и объема памяти ЭВМ. При надлежащей формулировке диагональная матрица масс так же хорошо описывает распределение массы в конструкции, как и «согласованная» матрица.
§ 9.1. Предварительные замечания
Пусть на тело действуют сосредоточенные Р, объемные R и поверхностные р силы, зависящие от времени t. Перемещения произвольной точки тела в направлении координатных осей определим матрицей-столбцом и = и (х, у, г, t).
В соответствии с принципом Д’Аламбера будем рассматривать тело как находящееся в равновесии, добавляя при этом к внешним силам силы инерции. Инерционные силы, действующие в направлении перемещений и на элементарный объем , „ <Э2п ,
от, определяются матрицей — р ат, где р — плотность материала. Разделив их на dr, получим силы, приходящиеся на единицу объема. Обозначая матрицу этих сил через RHH и отмечая дифференцирование по времени точками сверху, запишем
Кин= —ри- (9-0
Пусть, далее, тело разбито на конечные элементы. Рассмотрим типовой элемент с узлами i, j, ...; матрица узловых перемещений будет
Vе = {vz V; ... },
где Vi,Vj, ... —матрицы перемещений соответствующих узлов, являющиеся функциями времени.
Как и ранее, будем исходить из того, что перемещения и и Vе связаны приближенной зависимостью
u = а ve = |а; a.j ...]
(9.2)
где а — матрица аппроксимирующих функций.
Строго говоря, в динамических задачах простой зависимости (9.2) записать нельзя, поскольку при одних и тех же мгновенных значениях узловых перемещений деформированная форма конечного элемента может быть различной в зависимости от предшествующей истории движения. Но если размеры конечных элементов достаточно малы, то соотношения вида (9.2) будут и в динамических задачах хорошо аппроксимировать перемещения точек тела по их узловым значениям.
В задачах статики стержневых систем матричный метод перемещений приводит к точному (в рамках технической теории бруса) решению. В случае динамического нагружения точное решение невозможно при указанном подходе даже для стержневых систем. Желаемая точность может быть достигнута путем разбиения стержней на более короткие участки, в пределах которых применяется приближенная аппроксимация типа (9.2), но при этом исчезает различие между стержневыми и непрерывными системами. Следовательно, в динамических задачах целесообразно рассматривать стержневые системы с общих позиций метода конечных элементов, как мы и будем поступать в дальнейшем.
§ 9.2. Матричное уравнение движения конструкции
При статическом нагружении матричное уравнение равновесия конструкции имеет вид (4.19). Соответствующее уравнение для случая динамического нагружения можно получить, если добавить к внешним силам инерционные RHH = —pu. Заменяя их эквивалентными узловыми силами Рнн, получим вместо (4.19) равенство
Kv P P~P1!(I (9.3)
Элементы матрицы Рин перечисляются в том же порядке, что и перемещения в матрице v. Если Vj, v2, ..., vn —матрицы перемещений отдельных узлов (п — общее число узлов конечноэлементной модели), то
V = {Vi v2... vn}
и соответственно
^ИН {Рин,1 Рин,2 Рцн.П }>
где Рин.г — матрица сил инерции для узла г.
Приведение инерционных сил к эквивалентным узловым силам должно осуществляться так же, как это делалось ранее для объемных сил. Напомним, что при действии объемных сил R сначала выполняется их замена сосредоточенными силами в пределах каждого элемента по формуле
J ат Rd т.
В блочном виде Ре = {Рр Р‘' ... }, где типовая подматрица
Р,— J ос7' R d т
представляет собой вклад данного конечного элемента в экви-валентные силы в узле г. Далее осуществляется сложение в узлах вкладов отдельных конечных элементов: Рг = SP«; при этом суммирование выполняется по тем конечным элементам, которые сходятся в узле г. Начнем с вычисления матрицы Р®н узловых сил инерции для типового конечного элемента:
Рин= f arRH((dT = — Jarupdr.
Xе Xе
Так как u = ave, то и = avp, где матрица Vе содержит вторые производные по времени от узловых перемещений конечного элемента (узловые ускорения). Таким образом,
РРн — — рат a d т Vе .
Xе
Этот результат можно представить в виде
РиН = — тс Vе, (9.4)
где
тр == р a7' a d г (9.5)
Xе
— квадратная симметричная матрица, называемая матрицей масс конечного элемента; она имеет такой же размер, что и матрица жесткости элемента ке.
Если записать матрицу а в виде а — [ага^...1, то придем к блочному представлению матрицы масс
nie. пЕ.
и I/
те.. те..
Р п
где типовая подматрица
) Р ar a3 d Т (Г’ S “ /)•
Г9.6)
Подматрица сил Р« г в узле г определится теперь так:
Дополнив матрицу ускорений элемента Vе до полной матрицы v, придадим этому равенству вид
Ре =—fme. mc„... me 1
ин, г I rl г2 ml
Два последних равенства будут эквивалентны друг другу, если считать m£s = 0, когда узел s не относится к данному элементу.
Просуммировав вклады отдельных элементов, найдем подматрицу
Рин. Л = 2 р*н. (S [m% . m*„])
V1
V2
Суммирование здесь формально распространяется на все конечные элементы, но фактически оно касается лишь тех из них, которые сходятся в узле г.
Объединяя все подматрицы Рин,г в матрицу ₽ин, запишем
где
mrs = 2m* (г, s = /, 2, п). (9.7)
Здесь суммирование ведется по тем конечным элементам, которые имеют общие узлы г, s.
Полученный результат можно записать кратко в виде
Рин=—Mv (9.8)
Здесь через М обозначена! квадратная симметричная матрица
М =
t”n
m21
Ш12
m22
• m2n
mni m„2
•H1,| n-
называемая матрицей масс конструкции и образуемая из матриц масс конечных элементов по правилу суммирования
(9.7). Последнее совпадает с правилом формирования матрицы жесткости конструкции из матриц жесткости отдельных конечных элементов.
Внося (9.8) в (9.3), приходим к равенству
Mv + К v = Р + Р, (9.9)
которое и представляет собой матричное уравнение движения конструкции, идеализированной по методу конечных элементов. Оно заключает в себе систему обыкновенных дифференциальных уравнений относительно компонент матрицы v. Если проинтегрировать эту систему, то получим матрицу v как функцию времени. Затем по найденным узловым перемещениям можно в любой момент времени вычислить напряжения в каждом конечном элементе, пользуясь при этом теми же соотношениями, что и в задачах статики.
Если на тело наложены внешние связи, то в систему уравнений (9.9) войдут лишь неизвестные перемещения и соответствующие им силы. В этом случае при составлении матриц К и М следует формировать лишь те строки и столбцы, которые соответствуют неизвестным перемещениям. Ранее такие уменьшенные в размерах матрицы мы помечали дополнительным индексом а. Здесь же для упрощения записи этот индекс будем опускать. Заметим, что если тело не закреплено, то в отличие от случая статического нагружения нельзя накладывать на него связи, фиксируя его положение в пространстве, ибо это приведет к появлению динамических реакций, которые в действительности отсутствуют. Как будет видно из дальнейшего, отсутствие таких связей не приводит к каким-либо трудностям при решении динамических задач.
Итак, в динамических задачах помимо матрицы жесткости и матрицы эквивалентных узловых сил требуется вычисление еще одной характеристической матрицы — матрицы масс. К понятию матрицы масс можно прийти также рассматривая кинетическую энергию системы. Кинетическая энергия элементарной массы, занимающей объем dx, равна -^u7 updx, где и — матрица скоростей. Отсюда следует, что кинетическая энергия конечного элемента
Те — — ( р u7' u d т.
2 J
Xе
Учитывая, что и — те, получаем
Те = (ve )т J р аг a d т Vе,
Xе
ИЛИ
=-1-(v‘e )Г m've, (9.10)
где те — прежняя матрица масс конечного элемента (9.5).
Суммируя значения Те по всем конечным элементам, найдем кинетическую энергию всей системы:
Т — vT Mv, (9.11)
где М — введенная выше матрица масс конструкции.
При исследовании сходимости метода конечных элементов в динамических задачах полезно основываться на вариационном принципе Гамильтона. Применительно к упругим системам он устанавливает, что при действии консервативных нагрузок* истинное движение системы от момента времени tx до момента отличается от всех других тем, что интеграл
2
((V — T)dt (9.12)
о
имеет стационарное значение. Здесь V = U + П — потенциальная, а Т — кинетическая энергии системы. Отметим попутно, что равенство (9.9) можно получить как необходимое условие стационарности функционала (9.12).
Так как кинетическая энергия всякой системы есть величина существенно положительная, то из (9.10), (9.11) следует, что матрицы mf и М положительно определенные: для любых ненулевых матриц Vе и v справедливы неравенства
(уе)т пГ Vе > 0, vrM v > 0.
Так же как и в случае матрицы жесткости, иногда бывает удобно вычислить матрицу масс конечного элемента сначала в некоторой местной системе координат, а затем уже перейти к общей. Пусть v и ve — матрицы узловых перемещений эле
* Сила называется консервативной, если совершенная ею работа зависит лишь от начального и конечного положений точки ее приложения, но не от пути, пройденного этой точкой.
мента в местной и общей системах координат, a m и те — соответствующие им матрицы масс элемента. Пусть, далее,, v и Vе связаны между собой соотношением v = lve, где 1 — матрица преобразования координат. Кинетическая энергия конечного элемента может быть выражена через v:
Те — — v m v .
2
Так как v = lve, то
Те — (к Vе )т m (к v') = (ve )т кт m к ме.
Сопоставляя это выражение с (9.10), приходим к равенству
nTeVraX, (9.13)
посредством которого и осуществляется переход от ш к те. Формально этот результат аналогичен правилу преобразования матрицы жесткости конечного элемента, согласно которому ке = кткк. Следует отметить, однако, что при вычислении матрицы гп в матрицу v должны быть включены все перемещения, в направлении которых происходит движение, в то время как при вычислении матрицы к можно игнорировать перемещения, связанные с движением тела как жесткого целого (например, поперечные смещения узлов для стержневого элемента, работающего лишь на растяжение-сжатие).
При выводе уравнения (9.9) не были учтены силы неупругого сопротивления (демпфирующие силы), которые иногда приобретают существенное значение. Эти силы могут иметь различную физическую природу (внутреннее трение в материале, трение в сочленениях агрегатов, сопротивление воздуха и т.п.) и соответственно различное математическое описание. Однако чаще всего принимают, что демпфирующие силы независимо от их природы пропорциональны скоростям движения. Матрицу этих сил можно представить в виде произведения —Cv, где С — так называемая матрица демпфирования, имеющая такой же размер, что и К или М. При учете демпфирующих сил уравнение движения конструкции принимает вид
М vH-Cv + Kv = P Р (9.14)
Что касается числовых значений элементов матрицы С, то для их определения используются обычно экспериментальные
данные, получаемые путем исследования затухания собственных колебаний конструкции. Учитывая приближенность описания механизма демпфирования, часто (следуя Рэлею) берут в качестве матрицы С линейную комбинацию матриц К и М:
С = аК + ЫЛ. (9.15)
Тогда задача сводится к экспериментальному определению двух коэффициентов а и b или даже одного из них, если другой заранее берут равным нулю. Такой подход является сугубо приближенным, но он все же позволяет воспроизвести в общих чертах основные особенности реального поведения конструкции (в частности, явление затухания собственных колебаний).
В заключение параграфа коснемся вопроса об учете сосредоточенных грузов, жестко связанных с телом. Пусть некоторый груз массой Мо закреплен в узловой точке г. Если в матрицу vr входят одни лишь линейные смещения узла, то матрица инерционных сил для рассматриваемого груза определится произведением —mrvr, которое учитывается при вычислении матрицы суммарных сил инерции в узле г:
Ри„.г = 2 Реин, - mr vr.
Здесь mr — диагональная матрица, каждый из диагональных элементов которой равен Мо. В результате появится дополнительное слагаемое в подматрице тгг матрицы масс конструкции:
mrr = SnVr ф- m,.. (9.16)
Отсюда следует, что при наличии сосредоточенного груза необходимо добавить его массу к тем диагональным элементам общей матрицы масс, которые соответствуют его линейным смещениям. Если бы, в частности, вся масса конструкции была сосредоточена в узлах конечноэлементной модели, то матрица масс оказалась бы диагональной и решение динамичес-ской задачи на ЭВМ потребовало бы меньшего объема памяти и затрат машинного времени.
Если в vr помимо линейных входят также угловые перемещения, то в матрице mr необходимо, вообще говоря, учесть инерцию вращения груза. В том случае, когда центр массы груза совпадает с узловой точкой, а направления главных осей инерции груза совпадают с направлениями угловых перемещений (представленных в виде векторов), матрица тг по-прежнему будет диагональной, причем ее элементами будут
масса и соответствующие динамические моменты инерции груза. В других же случаях (например, когда центр массы груза не совпадает с узловой точкой) матрица mr не будет уже иметь диагональной формы. Если основная масса конструкции заключена в сосредоточенных грузах, жестко закрепленных в узлах, а распределенной по объему конечных элементов массой можно пренебречь, то общая матрица М будет состоять из отдельных подматриц, расположенных на главной диаго' нали. Все остальные элементы матрицы М будут нулевыми, т.е. она окажется блочно-диагональной.
Существуют методы, которые и для непрерывного распределения массы по объему тела позволяют получить матрицу М в диагональной или блочно-диагональной форме; к их изложению теперь и перейдем.
§ 9.3. Согласованная и диагональная формулировки матрицы масс
Матрица масс конечного элемента определяется формулой (9.5). При выводе этой формулы предполагалось, что а — та же матрица, по которой формируется матрица 0, используемая при вычислении ке согласно (4.11). Если при этом в (9.5) осуществляется, как и в (4.11), точное интегрирование (или, скажем, численное интегрирование по методу Гаусса достаточно высокого порядка), то получаемая таким путем матрица те (соответственно и матрица М) называется согласованной. Данный термин подчеркивает согласованность формулировок жесткостных и массовых характеристик конечноэлементной модели. В случае согласованной формулировки матрица М имеет такую же структуру, что и К. В частности, обе матрицы имеют одинаковое расположение ненулевых элементов и требуют одинакового объема памяти ЭВМ для своего хранения.
Рассмотрим теперь выражения для kf и mf с точки зрения сходимости конечноэлементного решения к точному при сгущении сетки. Подобно тому как это делалось в гл. 6, предположим, что элементами матрицы v и v являются перемещения и скорости узлов, совпадающие с соответствующими значениями из точного решения. При сгущении сетки потенциальная энергия деформации Ue = (ve)r keve и кинетическая энергия Те = -1 (ve)rme ve типового конечного элемента будут стремиться к своим точным значениям со скоростью, определяемой порядком полиномов, фигурирующих соответственно в матрицах 0 и а. Так как матрица 0 образуется из производ-338
ных от элементов матрицы а, то она содержит полиномы более низкого порядка. Таким образом, скорость сходимости конечноэлементного решения к точному решению динамической задачи будет определяться скоростью сходимости потенциальной энергии деформации.
Скорость сходимости решения не нарушится, если при вычислении матрицы масс по (9.5) понизить порядок полиномов в матрице а, приведя его в соответствие с порядком полиномов в матрице 0. Можно также брать исходную матрицу а, но зато понижать порядок интегрирования произведения рага, заботясь лишь о точном вычислении полных полиномов той степени, которая появляется в произведении 0гх0. Последнее обстоятельство может быть использовано для получения матрицы те (а следовательно, и матрицы М) в диагональной или блочно-диагональной форме. Чтобы добиться этого, необходимо [34] вместо правила Гаусса применить при расчете те такую схему численного интегрирования (назовем ее для краткости схемой поузлового интегрирования), в которой точки интегрирования совпадают с узлами конечного элемента.
В самом деле, обратимся к формуле (9.6):
Jp<«sdT.
Матрица аТ содержит аппроксимирующие функции, которые равны нулю во всех узлах, кроме узла г, матрица же as отлична от нулевой лишь в узле s. Таким образом, матрица ajas в случае г =/= s является во всех узловых точках нулевой, и при поузловом интегрировании все подматрицы nf окажутся нулевыми, за исключением диагональных подматриц тг<
В §5.12 описаны два метода, которые могут быть использованы для поузлового интегрирования: метод Маркова и метод Эйлера. Первый из них пригоден для тех конечных элементов, у которых в узлах задаются значения функций, но не их производных. Примерами могут служить четырехугольные конечные элементы плоской задачи теории упругости, для которых матрицы ar имеют вид (см., например, § 5.2)
ar =
Фг о О ф,.
а произведение
< «г
Ф? о о ф?
представляет собой диагональную матрицу. Следовательно, подматрицы m*r (а значит, и вся матрица те) будут иметь диагональную структуру. Вычисление те сводится здесь к вычислению интегралов типа
[ РФ? d т,
и порядок схемы интегрирования Маркова в большинстве случаев оказывается достаточным для сохранения скорости сходимости. Отметим только, что для конечных элементов третьего порядка (см. рис. 5.11) промежуточные узлы должны быть расположены в точках интегрирования Маркова. Это достигается использованием в формулах типа (5.67) значения с0 — = 1//5.
Если в узлах задаются еще и производные от перемещений, то необходимый порядок поузлового интегрирования может быть достигнут применением метода Эйлера. Примером может служить прямоугольный конечный элемент пластины при изгибе, описанный в § 7.4; для него
ССГ — [оСпОСгзОС?. 3],
где функции аг1 (£, т]), аг2 (£, -q), агз (£, т]) и их первые производные по £, т] обращаются в нуль во всех узлах элемента, за исключением узла г, в котором они равны:
а -^- = 0;
г* д£ dV
„ о. дагг _ а . даг2 _п.
— V, •-— , ————— —- V»
оё 2 ’ Л]
а — 0; = о- -^2- = — — .
Г3 dl dri 2
Нетрудно убедиться, что подматрица m®r получится в этом случае, вообще говоря, полностью заполненной, т.е. для подобных конечных элементов удается добиться (без потери скорости сходимости) лишь блочно-диагональной структуры матрицы tn'?.
Поузловое интегрирование в том виде, как это описано выше, имеет один существенный недостаток, связанный с на
личием отрицательных весовых коэффициентов в формулах интегрирования (см., например, последний столбец в табл. 5.2). Соответствующие диагональные элементы матрицы масс (имею-щие теперь смысл сосредоточенных узловых масс) будут также отрицательными. Это нежелательно и не только потому, что затрудняется физическая интерпретация подобной замены распределенной массы сосредоточенными узловыми массами. При наличии отрицательных диагональных элементов матрица М перестает быть положительно определенной, что может серьезно затруднить или сделать невозможным применение тех численных процедур, в которых используется свойство положительной определенности матрицы масс.
Можно, однако, поступить следующим образом. Для вычисления внедиагональных подматриц m*s будем по-прежнему пользоваться поузловым интегрированием (иначе говоря, брать эти подматрицы нулевыми). Для вычисления же диагональных блоков m«r применим точное интегрирование, другими словами, возьмем их из согласованной матрицы масс. Это не может ухудшить характеристик сходимости по сравнению с обычным методом поузлового интегрирования, но решение будет сходиться теперь к неправильному ответу, поскольку сумма полученных таким путем узловых масс не будет равна массе конечного элемента. Для устранения этого дефекта достаточно умножить полученную матрицу на соответствующим образом подобранный скалярный коэффициент. В итоге приходим к предложенному в работе [37] методу получения диагональной (или блочно-диагональной) матрицы масс из согласованной, который будем называть методом выделения диагонали. Как следует из изложенного, этот метод, так же как и метод поузлового интегрирования, сохраняет скорость сходимости решения. Кроме того, он гарантирует положительную определенность матрицы масс.
Отметим, что для образования диагональной матрицы масс можно было бы массу каждого элемента просто сосредоточить в его узлах, поровну поделив ее между ними. При этом, однако, скорость сходимости решения к точному может сильно снижаться по сравнению с согласованной формулировкой, особенно для сложных конечных элементов. На реальных сетках этот способ приводит к ухудшению точности результатов, и поэтому он чаще всего неприемлем. Исключение составляют некоторые простейшие элементы типа стержневого с двумя узлами или треугольного в плоской задаче, где все три метода (поузлового интегрирования, выделения диагонали и распределения массы по узлам) приводят к одинаковым результатам.
§ 9.4. Матрицы масс конечных элементов с линейными смещениями узлов
Переходя теперь к выводу выражений для матриц масс тех конечных элементов, которые рассматривались ранее, начнем с элементов, у которых узловыми параметрами являются одни лишь линейные перемещения; элементы могут быть одно-, дву- или трехмерными. В случае изопараметрических элементов перемещения выражаются через их узловые значения равенствами их = ^гихт; иу — 2tyrUj,r; и2 = Xtyrtizr. Представляя эти соотношения в форме u — 2a,.v,., где и = = {uxuyuz}, vr = {ихт uVT uzr}, видим, что матрицы аг имеют здесь вид
(9.17)
где I — единичная матрица.
Для подматриц nV. получаем в соответствии с (9.6) выражение
m>s
aTra3 dr = m's I,
(9.18)
где при постоянной плотности р материала скалярные величины m*s равны
mrs
(9.19)
Переходя в (9.19) к безразмерным параметрам £, ц, $ и пользуясь интегрированием по Гауссу того же порядка, что и для соответствующей матрицы жесткости, придем к согласованной матрице nV.
Для вычисления интегралов (9.19) можно применить метод Маркова, что дает m's = 0 (для г s), merr = m*rI, т. е. приводит к диагональной матрице nV. Чтобы избежать появления отрицательных значений величин пг*г (имеющих смысл сосредоточенных узловых масс), воспользуемся вместо этого методом выделения диагонали, в соответствии с которым в согласованной матрице масс положим nVs = 0 для г =# s и оставим лишь подматрицы ш,, = пге„\, где
<r = P J ФМт. (9.20)
Xе
Для того чтобы матрица те правильно воспроизводила массу конечного элемента, сумма всех величин т*г должна иметь значение рте. Для получения требуемого результата следует ввести множитель
Q = хе § 'Фг d-1. \ Xе /
Таким образом, диагональная матрица те определится соотношениями
т«= ° (г ¥= s); i;
(9.21)
В частности, в случае трехмерного конечного элемента (dr = | J| d| dr} d£, где | J| — якобиан преобразования координат)
(9.22)
для конечных элементов пластин, находящихся в условиях обобщенного плоского напряженного состояния,
для конечных элементов обшивки (безмоментной оболочки), описанных в § 8.2,
р,.= j’ h^r Лп )/1 — у2 d£drj;
‘1 — 1
1
Ы6.4п]/1- у2 d gd-q-— 1
(9.24)
Наконец, для одномерных конечных элементов (см. § 5.10), где dr = F/ld^ (F — площадь сечения), имеем
1 1
Иг= J /чр2 A d Е; F4d£. (9.25)
— 1 -11
Если в узлах учитывается лишь по два перемещения (как, например, в случае пластины, совершающей колебания в своей плоскости), то отдельные подматрицы будут иметь размер 2x2. При расчете же, скажем, продольных колебаний прямолинейного стержня достаточно учесть лишь продольное перемещение, и в этом случае подматрицы m*s будут скалярными величинами.
Для треугольного элемента с узлами в вершинах (см. § 5.1) все узловые массы в (9.21) оказываются одинаковыми: Мег — = pFh/З, где F — площадь треугольника; h — толщина элемента.
§ 9.5. Матрицы масс конечных элементов изгибаемых пластин
В случае пластины, работающей на изгиб, узловыми параметрами наряду с поперечными смещениями uzr срединной плоскости являются также углы поворота нормали $хт, &уг. Перемещения их, иу, иг произвольной точки могут быть здесь определены соотношениями (7.1):
ux — z$x(x, у); uy=z$y(x,y); uz^=uz(x, у).
Рассмотрим сначала конечные элементы изопараметричес-кого типа с независимой аппроксимацией прогиба и углов поворота нормали:
uz = гЭ'д. — Фу = 2лргФуГ.
Понимая под и матрицу u = {uz их иу }, имеем
где
Таким образом, подматрицы аг для подобных элементов определяются произведением
аг = а|)гТ2.
При вычислении согласованной матрицы масс элемента с четырьмя сторонами положим dr = |J| dg di| dz; тогда
1 1 h/2
§ a^asdT=p f TJ Tz d z % | J | d g d tj.
xe -1-1 —h/2
Так как
Г1
О О' г2 О
О г2.
то после интегрирования по толщине приходим к выражению
Л фг "Фе г>л I J J d gd T),
(9.27)
где через Dh обозначена диагональная матрица вида
’10 О"
О h2/\2 О .0 0 ft2/12
(9.28)
При выводе (9.27) в матрицу перемещений и были включены не только нормальное перемещение uz, но также и тангенциальные перемещения их, ид, обусловленные поворотом нормального элемента при деформации пластины. Тем самым в матрице масс учтена инерция вращения элементарных параллелепипедов, выделяемых из пластины плоскостями х = const и у = const. Для тонких пластин можно пренебречь инерцией вращения по сравнению с инерцией поступательного движения параллелепипедов вдоль оси г; при этом матрица Dh в (9.27) будет заменена на матрицу
’1 0
1'= 0 0
О' о о
— I
о
О
о о
Даже для достаточно толстых пластин инерция вращения не слишком велика. Это позволяет, в частности, заменить в случае пластины переменной толщины величину Л3/12 в матрице Dh ее значением при | — л = 0, что приводит к выражению
m;s=<D“-
(9.29)
Здесь D2 — значение матрицы Dft в середине конечного элемента, а скалярный множитель
юг*=р| J Zi^ipJJIdBdT).
(9.30)
Диагональную матрицу масс гпе вычислим так же, как это делалось в предыдущем параграфе. Для отдельных подматриц получим тогда формулы, аналогичные (9.21), (9.23):
m's — 0 (г ф s); пГг = Л1'Р°; (9.31)
i i
Hr = J J Л Ф’ | J | d| diy, Q — i —i
1
S pr
ft | J | d£ dtp
(9.32)
Рассмотрим далее прямоугольный конечный элемент, описанный в §7.4. Для него имеем: О',. = —fty = —~--г uz = ^>атут-, матрицы az даются выражением (7.24).
Если пренебречь инерцией вращения, то отдельные подматрицы согласованной матрицы масс те определятся выражением
mrS=-^Y~J J ftarasdgdT], -1 -1
(9.33)
где интегрирование можно выполнять точно или по правилу Гаусса 4x4.
Для приведения те к блочно-диагональному виду можно воспользоваться поузловым интегрированием по методу Эйлера, что дает
mzs = ° (^¥=s);
р abh 24
’ 6
alT
bl]r
(9.34)
air Ьцг
О О О О
Определители матриц (9.34) отрицательны; общая матрица М также может оказаться неположительно определенной. Можно получить и положительно определенную матрицу, если взять подматрицы merr из согласованной матрицы т* и ввести множитель, обеспечивающий точное воспроизведение массы конечного элемента. Тогда придем к следующей матрице масс:
те
rr
'3454 461a L 461ft Пг
461 a Ir 80a2 63а6|гт]г
461 ft т)г 63aftgrT)r 80ft2
(9.35)
Рассмотрим еще четырехугольный элемент с шестнадцатью степенями свободы, описанный в § 7.5. В число узловых па-
раметров этого элемента входит помимо поперечного смещения и углов поворота смешанная производная от иг по х, у-ve = {v; vy vi vm }; vr = {uzr ftxr ®yr q>r } (r = i, j, I, tn).
Перемещение uz (x, у) произвольной точки срединной поверхности определяется равенством uz (х, у) = ave, где а = = a*Q. Здесь матрица-строка а* содержит 16 полиномиальных функций, выбранных для аппроксимации поперечного смещения, a Q — квадратная матрица, связывающая узловые перемещения Vе с коэффициентами при этих функциях.
Пренебрегая, как и в предыдущем случае, инерцией вращения, по формуле
— р haTadxdy = pQr JJ ha*Ta* dxdi/Q (9.36)
можно вычислить согласованную матрицу масс данного конечного элемента. Интегрирование по площади четырехугольника в (9.36) можно выполнить, как и в случае матрицы жесткости, с помощью перехода к безразмерным координатам £, я-Для элементов трапециевидной формы удается осуществить и точное интегрирование [18].
Если в согласованной матрице (9.36) оставить лишь четыре подматрицы m*r размером 4x4 каждая, лежащие на диагонали, и заменить остальные элементы нулевыми, то после умножения на подходящий скалярный множитель придем к блочно-диагональной матрице вида
mrs = о (г #= s); m'r = Qm*r, (9.37)
где
Й = рт<Л4*. (9.38)
В знаменателе формулы (9.38) стоит величина, представляющая собой сумму первого, пятого, девятого и тринадцатого диагональных элементов матрицы (9.36), которые при переходе к блочно-диагональной форме приобретают смысл сосредоточенных узловых масс. Введение нормирующего множителя Q в (9.37) позволяет точно воспроизвести массу конечного элемента. Объем элемента
V = й dxdy
может быть найден путем перехода к координатам t| и интегрирования по площади квадрата. Отметим, что для этого элемента появляются обобщенные «массы», соответствующие узловым параметрам <рг. Эти величины не имеют ясного физического смысла.
§ 9.6. Матрицы масс конечных элементов оболочек
Рассмотрим конечные элементы оболочки вращения (см. § 7.8) с независимой аппроксимацией перемещений срединной поверхности их, uv и угла поворота нормали 0: их = ^гихг-, иу — StyrUyr; б1 = Shjv&r- Касательное к меридиану и нормальное перемещения произвольной точки на расстоянии £ от срединной поверхности выражаются через соответствующие перемещения срединной поверхности равенствами
«F = ut + и* = Un.
Так как их, uv связаны с ut, ип соотношениями
«х — Xix Uf 4* ^nxUn', Uy = ^fyUf 4“ KnyUn, где ktx, ktv и knx, kny — направляющие косинусы касательной и нормали к меридиану, то
«$ = Кх и} 4- й\ = ktx (ut + £й) -}- кпх ип = их+Кх £6",
— Ку и\ + Ку «„ = Ку (ut + + Ку un==uv + Ку
Таким образом
«Яр о ^Ж1 Ux
«Я 1° 1 и;
= TsStrv„ (9.39)
где
Vr = {«ХГ ««г <М; TS = [1 0 s Н .
l.v 1 feAtaJ
Понимая под и матрицу и= выражение (9.39)
можно записать в виде u = 2arvr, где
<*r = №- (9.40)
Полагая в формуле (9.6) dx = 2nyAd£dZ, получаем
1 Л/2
m;s = 2npj T[TtdSy4d§.
-Л/2
Так как 7^х 4- 7^у = 1, то
ТГТ£ =
~ 1 о Кх
о 1 ЬКу
&Кх
^Ку
После интегрирования по толщине оболочки имеем
mrS == 2яР j tr Dh yh A (9-41)
где
10 О'
0 1 0 (9.42)
.0 0 й2/12_
Выражение (9.41) выведено с учетом инерции вращения. Для оболочки переменной толщины можно, так же как и в случае изгиба пластин, заменить величину Л2/12 в матрице Dh ее средним значением (при g = 0), что приводит к выражению вида (9.29), где
1
щД = 2лр£ ifr yh A dg,
(9.43)
a D/? — значение матрицы DA при g = 0.
Если пренебречь инерцией вращения, то вместо DJI следует взять матрицу
1"
1 0 О' 0 1 о о о 0_
Еслив (9.43) выполнить интегрирование того же типа, что и для соответствующей матрицы жесткости, то придем к согласованной матрице масс конечного элемента.
Диагональную матрицу те вычислим по методу выделения диагонали; это приводит к соотношениям
m«s = 0 (r#=s); m*r = .'Vl*D°;
i
М‘ — р Q р,г; = 2л J yh A dg,
Q = -— f 0/Udg.
S р.г J
(9.44)
Рассмотрим, далее, семейство четырехугольных конечных элементов произвольной оболочки (см. §7.13). Перемещения
u£ = {uxUpUz} слоя оболочки, расположенного на расстоянии ? от срединной поверхности, выражаются через узловые перемещения ur = {ихт иут игт} и углы поворота = = {'б'хг’’З'уг'fl'zr} равенствами (7.121) и (7.124), из которых вытекает соотношение
цб = S^MUr + SMM = 5tyrTrvr, (9.45)
где vr = {ur fly); Tr = (I3: CLrl.
Здесь I3 — единичная 3x3 матрица, а матрица Lr (7.122) содержит направляющие косинусы нормали к оболочке в узле г. Выражению (9.45) можно придать вид = Sarvr, где
«Г = %ТГ. (9.46)
Таким образом,
т« rs
Л/2
J т:
— Л/2
ТДЯ^Гн^.
Выполнив умножение T,TS и проинтегрировав результат по толщине оболочки, получим
m*s=pj j 1—у2dgdn, (9.47)
— 1 —1
где
I_31 0 _
(9.48)
Если, как это делалось и ранее, заменить матрицу (9.48) ее значением D“s при | = q = 0, то будем иметь вместо (9.47) выражение
m;s=mrSDr°s’
где
mr*s = pf J Ч’г'М АЪ A KJ—VdSdr].
Заменяя внедиагональные подматрицы mjs нулевыми и корректируя затем массу конечного элемента, придем к матрице гл", определяемой соотношениями
mrs~0 (r=5^s); mrr^MrDrr> =
Hr = J J 1|>2,/1Д6Д„Ю— Y2 dfcdn;
Q =—— S р.г
(9.49)
Отметим, что из-за наличия в D“r произведения L'r Lr получаемая согласно (9.49) матрица масс не является диагональной. Если пренебречь инерцией вращения, то матрица D?f заменится диагональной матрицей
>3 01
0 0J ’
где нулевые подматрицы имеют размер 3x3.
1
§ 9.7. Матрицы масс конечных элементов бруса
Остановимся теперь на одномерных конечных элементах для моделирования прямолинейных или криволинейных брусьев.
Для расчета плоских и пространственных рам могут использоваться прямолинейные конечные элементы постоянного сечения, описываемые технической теорией бруса; расчет жесткостных характеристик элементов этого типа рассмотрен в гл. 3 (§ 3.4, 3.5). В общем случае пространственного нагружения элемент имеет 12 степеней свободы — три перемещения и три угла поворота в каждом из двух узлов i, j (см. рис. 3.8). Так же как и в случае статического нагружения, отнесем элемент к местной системе координат, направив ось х вдоль оси бруса, а оси у, z — по направлению главных осей инерции поперечного сечения. Будем снова разбивать узловые перемещения на четыре группы, образуя из них матрицы va, v6, vc, vd. Матрица
= {v.- vf-} определяет осевую деформацию стержня, матрицы
0<-2 v.- e.-}
соответствуют изгибу элемента в плоскостях ху и xz, а матрица
определяет кручение элемента.
Группируя подобным же образом узловые инерционные силы, придем к блочной структуре матрицы масс m рассматриваемого элемента в местной системе координат, аналогичной структуре соответствующей матрицы жесткости (3.25):
(9.60)
Для определения матрицы то, имеющей размер 2x2, зададимся линейным законом изменения продольного перемещения их по длине элемента:
«7 = S% vrx< ’Рг = С1 + Вг 1)/2 (г = I, /).
Здесь | — безразмерная координата, отсчитываемая от середины элемента и связанная с х соотношением 2х = (1 + £)/; ее узловые значения = ±1.
Представляя матрицу шо в виде
ша =
fill],а
и учитывая, что dx = Fdx = (F/d|)/2, по формуле
1
mrs,a = Yj (г, S = £, /)
— I
находим отдельные ее элементы. Обозначим через qm = pF величину, представляющую собой погонную массу элемента. С помощью точного интегрирования приходим в случае q == = const к согласованной матрице та, определяемой равенством
(9.51)
Диагональную форму матрицы ша можно получить с помощью поузлового интегрирования либо по методу выделения диагонали; оба способа дают здесь одинаковый результат
mrs,a~^ (r^=s); =</m 1/2. (9.52)
При изгибе в плоскости ху связь поперечного перемещения и- с узловыми перемещениями дается равенством (3.27), которое перепишем в виде
=2«r,bVr,b.
где vr,b = {и- ef-};
«г.ь (1 + U)42-U)! --v1 (1 + U) (1 ~£2)]
L 4 I о J
Блоки матрицы
m _ *"li,b ^ij,b fnb — _ — >
имеющие размер 2x2, определяются формулой
mrs.b^-^-J <,b«s,bdB — i
и при точном интегрировании получаются равными
*^*rs.b
__ Ят I 420
(105 + 51
—£-(35|r + 9|s)
_2_ (9Вг + 35 U
Y 0+71Л)
(9.53)
В матрицу перемещений и в формуле и = ave включено лишь поперечное смещение иг, т.е. инерция вращения здесь не учитывается.
Применение поузлового интегрирования по схеме Эйлера позволяет получить блочно-диагональную матрицу mb вида
Sr.,b = 0 (r^s); ^,ь = ^[ J, (9.54)
Наконец, выделение диагональных блоков в согласованной матрице (9.53) и последующая корректировка массы элемента приводит к положительно определенной матрице, для которой т„ ь = 0 (г =/= s); b = [ 78 (9.55)
r»,b \ т- „л 156 [ —Ц/Ег 2P J
Аналогичным образом вычисляется матрица mc; ее отдельные подматрицы определяются теми же выражениями (9.53)—
(9.55), но перед внедиагональными членами следует в них сменить отрицательный знак на положительный.
При закручивании стержня произвольного сечения происходит, вообще говоря, не только поворот, но и депланация его сечений. Будем, однако, пренебрегать инерционными силами, вызванными продольными перемещениями точек сечения вследствие депланации. Считая, что форма и размеры поперечного сечения не изменяются, можно вычислить смещения и- и и-произвольной его точки, обусловленные поворотом сечения на угол 6-: и- = —Z0-; и- = ув-. Принимая для 0- линейный закон изменения по длине стержня, для матрицы перемещений {и-и-} будем иметь выражение
где % — функции (5.81).
Обозначив
[—zl .
У J
найдем по формуле
1
«rs,d = -у- J J «s,d dF d?
— 1 F
четыре элемента матрицы md. Точное интегрирование по g дает согласованную матрицу, для которой
^=-^-(3+^5,), (9-56)
1^
где Jv = f (у2 + z2) dF — полярный момент инерции попе-F
речного сечения.
Диагональная матрица md дается соотношениями, аналогичными (9.52):
mrs,d=0(r^S); = (9.57)
Итак, определены согласованная и блочно-диагональная матрицы масс рассматриваемого элемента бруса в местной системе координат. Переход к общей системе выполняется точ-354
но так же, как и для матрицы жесткости. Можно, в частности, воспользоваться формулой типа (3.47). При поблочном вычислении матрицы
удобно пользоваться выражением
nirs = Xfla ГП„,О ХОа 4-Хоь тм.Ь ^ОЬ + ^Ос тгз,с 10с + Xod HlrSid Xod.
(9.58)
Здесь введены следующие обозначения для блоков матрицы X:
° 1
О
(9.59)
Все подматрицы в (9.59) имеют размер 1 х 3.
Рассмотрим, далее, конечные элементы лонжерона, описанные в § 8.3 (см. рис. 8.3). Так же как и при выводе матрицы жесткости, вначале отнесем элемент к местной системе координат х, у и введем в каждом узловом сечении по три степени свободы Up = {«— u—др). Пользуясь независимой аппроксимацией перемещений и-, и- и угла поворота О сечения и пренебрегая инерцией вращения, можно получить согласованную матрицу масс т, определяемую соотношениями
nipg = tnpq I"; tnpq -== р J % F dx; I
(9.60)
Г
1 О О’
О 1 о ООО
и отнесенную к указанным степеням свободы. Здесь F — площадь сечения лонжерона; интегрирование в (9.60) выполняется с помощью подстановки
Перейдем теперь от трех перемещений ир = {и-ри-р^р} к линейным смещениям v, = {v.-v.-}, vy = {у,-и,-} двух • л ]л / у
V.
точек, расположенных в данном узловом сечении на расстоянии -±.1112 от оси х:
Up = [Хрг
Здесь Хрг — матрицы, определяемые равенством (8.20). Соответствующее преобразование матрицы масс приводит к матрице т, отнесенной к линейным смещениям этих узловых точек в местной системе координат. Последующее применение метода выделения диагонали позволяет привести эту матрицу к диагональной форме
т„= 0 (r=#s); т„. = ЛГг12; Afr=pQpp;
Рр = f фр Fdx; £2 =—5— f F dx. (9.61) J S |ip J
Здесь I2— единичная 2x2 матрица; индексы r, s относятся к узловым точкам, а индекс р — к соответствующим узловым сечениям.
Остается, наконец, перейти к общей системе координат х, у, г, в которой каждый узел имеет три степени свободы:
Vr — {^гя ^ry ^rz }•
Величины Мг в (9.61) представляют собой значения сосредоточенных узловых масс. Так как эти узловые массы должны сохраняться неизменными в любой системе координат, то можно сразу записать значения отдельных блоков матрицы масс me:
uirs = 0 (r=/=s); merr = Л1Г13, (9.62)
где 13 — единичная 3x3 матрица, а значения Мг определяются соотношениями (9.61).
Эта же матрица масс может использоваться и для составного конечного элемента лонжерона (см. § 8.4), поскольку его отличие от рассмотренного выше элемента касается главным образом способа представления и расчета жесткостных характеристик, схема же аппроксимации перемещений в обоих случаях примерно одна и та же.
Аналогичным образом находим выражения для матриц масс и других конечных элементов подобного класса. Например, для криволинейных конечных элементов шпангоута (см.
§ 8.6) может быть получена следующая диагональная матрица ше:
m% = 0 (r=/= s); mrr = MrXrXr; M* = pQpr;
1 1
u = f Й = —L- f F4dg. (9.63)
J 2K J
— 1 —1
Здесь матрица Xr определяется равенством (8.73). При выводе (9.63) не учитывалась инерция вращения и кручения
ГЛАВА 10
РАСЧЕТ ДИНАМИЧЕСКОГО ПОВЕДЕНИЯ КОНСТРУКЦИИ
Расчет динамического поведения конструкции заключается в определении перемещений и напряжений как функций времени. Динамический расчет может в качестве предварительного этапа содержать исследование собственных колебаний, в результате чего определяются частоты и формы собственных колебаний конструкции; в некоторых случаях эта информация представляет и самостоятельный интерес. Другой подход заключается в прямом интегрировании матричного уравнения движения с помощью тех или иных численных процедур.
§ 10.1. Собственные колебания
Собственные (или свободные) колебания конструкции совершаются при отсутствии внешних сил. Будем считать, что демпфирующие силы отсутствуют. Полагая в (9.9) Р = Р = = 0, получим уравнение
Mv + Kv = 0, (10.1)
решение которого можно искать в виде
v = W cosco Z, (Ю-2)
где со — круговая частота колебаний, а матрица-столбец W содержит амплитудные значения перемещений и называется формой колебаний. Это название оправдывается тем, что амплитудные значения узловых перемещений в совокупности с равенствами типа u = ave = aWe coscoZ полностью определяют форму деформированного тела при колебаниях. Конструкция может совершать колебания с различными частотами; каждой частоте сог соответствует определенная форма W,. Задача расчета собственных колебаний заключается в отыскании всех или нескольких (обычно наименьших) частот и соответствующих им форм колебаний.
Подставив (10.2) в (10.1), придем к уравнению
(К —<o2M)W = O. (10.3)
Это равенство можно рассматривать как систему линейных однородных уравнений относительно элементов матрицы W. Существует тривиальное решение этой системы W — 0, но оно не представляет интереса, так как на основании (10.2) получим в этом случае v = 0.
Однор дная система линейных алгебраических уравнений может иметь и нетривиальное решение, если ее определитель равен нулю:
|К — w2M| = 0. (10.4)
Значения со, удовлетворяющие условию (10.4), представляют собой частоты собственных колебаний системы.
Каждой собственной частоте <ог соответствует нетривиальное решение W; системы уравнений
(К — 0>!M)W, = 0. (10.5)
Так как определитель этой системы равен нулю, то между уравнениями имеется линейная зависимость, т.е. одно из них представляет собой линейную комбинацию остальных, и его можно отбросить. В результате придем к системе из N — 1 уравнений относительно N неизвестных, содержащихся в матрице W;. Одну из компонент матрицы W,- можно выбрать произвольно, тогда остальные N—1 неизвестных будут найдены путем решения оставшихся уравнений. Из приведенных рассуждений вытекает, что формы колебаний могут быть определены лишь с точностью до постоянного множителя: числовые значения компонент W, зависят от выбранной величины одной из них. Это видно и непосредственно из равенства (10.5), которое не изменится от умножения W, на произвольный скалярный множитель.
Отыскание значений скалярной величины А и соответствующих им матриц-столбцов X, удовлетворяющих уравнению
(А — ХВ)Х = 0, (10.6)
где А и В — квадратные матрицы порядка N, составляет предмет известной задачи линейной алгебры, называемой обобщенной проблемой собственных значений (термин «обобщенная» употребляется в том случае, когда матрица В не единичная). Значения X, для которых выполняется равенство
|А — АВ| = 0,
(10.7)
называются собственными значениями, а соответствующие им матрицы X — собственными векторами* проблемы (10.6). Таким образом, в методе конечных элементов задача о колебаниях конструкции сводится к решению обобщенной алгебраической проблемы собственных значений. При этом собственные значения являются квадратами частот колебаний, а собственные векторы определяют формы колебаний.
Перепишем (10.7) в развернутом виде
#ц'—#12 — ^^12 ••• #1Л7'—
#21 #22*—^*^22 ••• #2W
= 0.
#W1 —M>Ni O.N2 — Mn?--- ONN—M>NN
Если раскрыть определитель, то придем к алгебраическому уравнению степени N относительно X:
cn № -j- CN—i № 1 .. -j- Ci X -j-Cg — 0.
(10.8)
Коэффициенты этого уравнения выражаются через элементы матриц А и В.
Как известно, полином степени N имеет N корней, среди которых могут быть и комплексные. Но если матрицы А и В симметричны, то, как доказывается в линейной алгебре, все N корней будут действительными. Именно этот случай представляет для нас интерес, поскольку матрицы жесткости и масс всегда симметричны.
Более того, если конечные элементы являются совместными и используется согласованная формулировка масс, то матрица жесткости и матрица масс будут неотрицательно определенными; в этом случае среди корней уравнения (10.8) не будет ни одного отрицательного. Точнее, для закрепленного тела все корни будут положительными, а для свободной конструкции появятся нулевые корни; число последних равно числу степеней свободы тела как жесткого целого.
Использование несовместных конечных элементов или, скажем, понижение порядка интегрирования при вычислении матрицы жесткости, как это делается для исключения ложных сдвигов, может привести к неположительно определенной
* Следуя терминологии линейной алгебры, будем пользоваться в дальнейшем понятием вектора, отождествляя его с понятием матрицы-столбца.
матрице жесткости; некоторые способы вычисления матрицы масс также могут привести к потере положительной определенности последней. В этих случаях отдельные корни уравнения (10.8) оказываются отрицательными. Однако их абсолютные значения оказываются обычно весьма большими и соответствуют спектру высоких частот, который вообще искаженно воспроизводится конечноэлементной моделью и не имеет существенного значения. Основные же (наиболее низкие) частоты могут быть при достаточном сгущении сетки вычислены с необходимой точностью, так что и в этом случае конечноэлементная модель правильно воспроизводит наиболее существенные особенности динамического поведения конструкции.
Отметим, что практически для матриц большого размера коэффициенты ct в (10.8) не вычисляются. Существуют другие, более удобные для ЭВМ методы отыскания собственных значений и собственных векторов [1, 29].
§ 10.2. Ортогональность собственных форм колебаний
Рассмотрим два различных тона колебаний с частотами со;, Шу и формами W,, Wj. Умножив уравнение i-ro тона
KW, — ®?MWf = о
на матрицу W, слева, получим равенство
WfKW; — ш/WyMWi = 0. (10.9)
С другой стороны, умножая уравнение /-го тона
KW; — ш/MWy = О
на Wf слева, имеем
WzrKWy — raJW,rMWy = 0.
Транспонируем последнее равенство, принимая во внимание симметрию матриц К и М:
WyKWz — ш/WfMWi = 0.
Вычитая полученный результат из (10.9), приходим к равенству
(ш? — ra?)Wj'MWi = 0.
Если ш, =Н= гоу, то отсюда следует соотношение
W/MWj = 0. (10.10)
Оно показывает, что формы колебаний ортогональны друг другу относительно матрицы масс, и называется поэтому условием ортогональности собственных форм.
Из (10.9) и (10.10) следует, что собственные формы ортогональны также и по отношению к матрице жесткости:
wjKWz = 0. (10.11)
Эти результаты получены в предположении, что частоты го,- и (О; различны. На практике, однако, встречаются случаи равных или весьма мало отличающихся («патологически близких») частот.
Если (»,•= <л}, то соответствующие им собственные векторы W,, W7 могут и не удовлетворять условию ортогональности (10.10). Но коль скоро найдены* два каких-нибудь линейно независимых вектора W,-, W>, то любые их линейные комбинации также могут быть взяты в качестве соответствующих форм колебаний. Комбинируя Wb W;, можно всегда образовать два вектора W,-, W/, удовлетворяющие условию ортогональности (10.10). Возьмем, например, W, = Wb W>- = Wj + aW,-и определим скалярную величину а из условия
Wf MW; = (Wf + aWf) MWj = 0.
Это дает значение
а = — Wj MW,/(Wr MW,).
Таким образом, и в случае кратных частот можно вести вычисления таким образом, чтобы выполнялось условие (10.10); в дальнейшем мы будем предполагать, что это условие выполняется для любых двух форм колебаний Wf, W7.
Умножив теперь уравнение i-ro тона на Wf слева, получим
WfKWf — (o/wfMWf = 0.
Отсюда имеем равенство
®,? = WzKW/^wrMWt), (10.12)
* В случае кратной частоты <аг в системе уравнений (10.5) будет уже не одно, а два уравнения, линейно выражающихся через остальные N — 2 уравнения, так что можно произвольно задаться двумя компонентами W. Различный выбор этих компонент будет приводить к различным собственным векторам, соответствующим ац.
которое позволяет вычислить частоту колебаний to;, если известна соответствующая форма W,-. Как говорилось выше, формы колебаний определяются с точностью до произвольного множителя. Поэтому умножением всех компонент вектора Wf на подходящий множитель можно всегда добиться выполнения равенства
w[mw, = 1.
(10.13)
Формы колебаний, удовлетворяющие условию (10.13), называются нормированными. Для таких форм соотношение (10.12) упрощается, принимая вид
«>? = W,rKWt. (10.14)
§ 10.3. Примеры расчета
Пример 1. Свободный стержень (рис. 10.1), имеющий дли' ну I, площадь сечения F, погонную массу qm, совершает продольные колебания. Ограничимся простейшей идеализацией, разбив его по длине на два стержневых элемента первого по
vt О (П Уг © (2) © v3
. I . l2
Рис. 10.1
рядка длиной = 1/2 каждый. Поскольку каждый узел может смещаться
лишь в осевом направлении, полученная таким образом модель имеет три степени свободы:
v = {ох о2 Уз).
Для используемых конечных элементов матрица жесткости дается согласно (3.14) выражением
।. EF
ке =------
1‘
1 —1
— 1 1
где Iе — длина элемента; матрица масс ш® совпадает с матрицей ша в выражении (9.50). Используем сначала согласованную формулировку масс; тогда в соответствии с (9.51) имеем
пг
<?т Г 6
2 11
1 2J
Таким образом, матрицы жесткости и масс двух конечных элементов, идеализирующих реальный стержень, будут
к( !)—_££. Г 1 1с(2> — Г 1 d2-
к [—1 d^’ ь L—i d<?’
12 2 3
m(O = Л”? Ь- [2 4/. m(2)~ JmJl. Г 2 П <
6 [ 1 2j/ 6 [1 2| 3
12 2 3
Здесь цифры снизу и сбоку указывают номера степеней свободы, относящихся к соответствующим строкам и столбцам.
Далее формируем матрицу жесткости и матрицу масс всей системы:
О 1 2 J 5
12 3
Матричное уравнение (10.3) принимает вид
1 —1 0
— 1 2 —1
0—1 1
Чт h 6
2 1 0|\
1 4 1 jw=O.
0 1 2JJ
Поделив уравнение на (£F//j) и введя обозначение
1 = ‘foJ*. со2 = Ю2
6Е 24EF
представим его в форме
(1 —21)
—(1 + ^) 0
-(1+1) 2(1—21)
-(1 +Х)
0
—(1 +^) (1—21)
W = 0.
(10.15)
Если приравнять нулю определитель этой системы, придем к уравнению относительно 1:
1(1— 21)(2 — 1) = 0.
Трем корням 12 = 0; 12 — 1/2; 13 — 2 соответствуют следующие значения со:
Ю1 = 0; со2 = 3,461VEF/(qmP); 6,928VEF/(qml2).
Точные значения первых трех частот, полученные интегрированием дифференциального уравнения продольных колебаний стержня, равны
Ю1 = 0; со2 = <о3 = 2nVEF/(qml2).
Приближенные значения со2 и со3 превышают точные на 10,2%. Такая большая ошибка связана с весьма грубой идеализацией системы. Для получения более точного результата необходимо разбить стержень на большее число конечных элементов. Так, при разбиении стержня на 10 элементов одинаковой длины-ошибка в со2 будет менее 0,5%.
Рис. 10.2
Найдем, далее, формы колебаний
W/ = {№п Wi2 Wi3}, соответствующие трем найденным значениям <ог.
Положив в (10.15) X = ^ = 0, для компонент Wj получаем систему уравнений
ТГц - U712 = 0;
~WU + 2U712 - U713 = 0;
-^12 + ^13 = 0.
Здесь независимыми являются лишь два уравнения (например, первое и второе; третье получается сложением первых двух). Приняв Wlt = 1, находим 1Г12 = 1; 1Г13 = 1. Следовательно, нулевой частоте coj = 0 соответствует форма Wi — {111}, которая определяет поступательное движение стержня как абсолютно жесткого тела вдоль своей оси.
Аналогично для Х2 = 1/2 находим W2 ={10 —1}, а для Х3= 2-W3 = {1 -1 1}.
Последние два вектора определяют формы упругих продольных колебаний рассматриваемого стержня (рис. 10.2).
Полученные формы колебаний не удовлетворяют условию (10.13). Так, для Wx произведение
1
4
1
0
1
2
1
1
1
1 1]-^А !
6
^Ят — Ят
Нормирование вектора Wt можно выполнить, разделив его компоненты на l/qml. Таким образом, нормированный
вектор будет
1
Wx
{111}.
Аналогично получаем нормированные векторы
{10—1}; W3=l/ —{1 — 1 1}.
V Ят1
Используем теперь для этой же задачи диагональную матрицу масс. На основании (9.52) имеем для типового конечного элемента
. gmi‘ Г» 0]
0 1J
общая матрица масс оказывается равной
1 о о
0 2 0
0 0 I
2
Повторяя предыдущие выкладки, получим значения
®2 = 2,828VEFl(qm^-, ю3 = 4]/EF/(gm/2),
которые ниже точных соответственно на 10 и 36%. Как видим, для основного тона упругих колебаний диагональная матрица масс дает здесь такую же точность, что и согласованная. Однако если при согласованной формулировке масс частоты колебаний получаются всегда завышенными (для совместных элементов), то при использовании диагональной матрицы они оказываются, как правило, ниже точных значений.
Пример 2. Консольно закрепленная однородная балка (рис. 10.3) длиной I имеет на конце сосредоточенный груз мас
сой Мо и совершает изгибные колебания. Балку идеализируем одним конечным элементом; массовый момент инерции груза примем равным нулю.
Матрица жесткости элемента балки есть матрица кь (3.36):
12 61 -12 61 1
6/ 4/2 — 6/ 2/2 2
/3 — 12 — 6/ 12 — 6/ 3 '
6/ 2/2 —6/ 4/2_ 4
1 2 3 4
Рнс. 10.3
Отбросим здесь первые две строки и два первых столбца, соответствующие нулевым перемещениям. В результате получаем матрицу жесткости системы
Г 12 — 6/1 2EJ Г 6 —3/1
/з [_€Z 4pJ- Р [_3Z 2/2J
При согласованной формулировке масс в качестве те следует взять матрицу, определяемую по (9.53):
156 22/ 54 — 13/ ~ 1
22/ 4/2 13/ —з/2 2
420 54 13/ 156 — 22/ 3
-13/ — З/2 — 22/ 4/2 4
1 2 3 4
Оставив строки и столбцы с номерами 3, 4 и добавив к диагональному элементу с индексами (3, 3) массу груза Л40, получим матрицу масс системы
М
/
420
<?тг / —22/
—22/
4/2
Гб(13 + 35у) —11/1
210 [ —11/ 2/2 J
где у= — отношение массы груза к массе балки
ft) .
Далее приравниваем нулю определитель матрицы К — — со2М, что приводит к уравнению для определения частот
35 (1 + 12у)Х2 — 6(17 + 70у)Х + 3 = 0, в котором через X обозначена безразмерная величина
4205/
Если, например, масса груза равна массе балки, то у = 1; в этом случае уравнение примет вид 455Х2 — 522Х + 3 = 0. Наименьший корень этого уравнения X, = 5,776 • 10_3, что соответствует частоте основного тона колебаний
= 1,558УЕУ/(?т/4).
В предельном случае у = 0 частотное уравнение будет 35Х2 — 102Х + 3 = 0; его корни Xj = 0,02972; Х2 = 2,885. Отсюда находим приближенные значения первых двух частот колебаний консольной балки
= 3,533VEJ/(<7m/4); <в2 = 34,81 УЕ//(<7т/4).
Они превышают соответствующие точные значения
= 3,516VEJ/(9m/4); <о2 = 22,03УЁ77О)
на 0,47 и 58%.
Если использовать блочно-диагональную матрицу масс элемента балки
nr =_22d
12
определяемую равенствами (9.54), то получим уравнение
X2 + 6 (1 + 4у)Х — 3 = 0,
в котором обозначено
X = со2 245/
В случае у = 1 находим отсюда Xj = 0,09966, что соответствует круговой частоте = 1,547 "VeJ! (</m/4). Эта величина на 0,7% ниже частоты колебаний балки с грузом, полученной с использованием согласованной формулировки масс.
Если груз отсутствует (у = 0), то корни частотного уравнения будут = 0,4641; Х2 — —6,46. Первому из них соответствует частота колебания coj = 3,337 ~VEJI(qmli), что ниже точного значения на 5,1%. Второй же корень Х2 оказался отрицательным, так что частоту со2 найти нельзя. Это произошло вследствие того, что матрица М не является положительно определенной. Так же как и в предыдущих примерах, повышение точности результатов может быть достигнуто разбиением балки на большее число элементов.
Рнс. 10.4
Пример 3 [18]. Консольная пластинка (рис. 10.4) постоянной толщины h, имеющая стреловидную форму в плане с углом стреловидности %, совершает поперечные колебания. Для расчета использованы несовместные четырехугольные конечные элементы с 16 степенями свободы (см. § 7.5); применялась согласованная матрица масс (9.36). В табл. 10.1 для первых пяти тонов даны в случае tg % = 0,5 значения частот ®i, отне-
Таблица 10.1
Номер Сетка
тона 1 1 3
1 4,29 (3,9) 4,29 (3,9) 4,27 (3,4) 4,26 (3,1)
2 10,60 (5,2) 10,57 (4,9) 10,36 (2,7) 10,23 (1,5)
3 21,67 (11,9) 21,44 (10,7) 20,29 (4,8) 19,68 (1,7)
4 24,98 (10,1) 24,64 (8,6) 23,99 (5,7) 23,50 (3,5)
5 41,95 (32,3) 41,12 (29,7) 35,34 (11,5) 33,96 (7,1)
сенные к величине 1/£>/(рЛЛ4), где О - £7i8/[12 (1 — ц2)1; А — характерный размер пластинки. В скобках в табл. 10.1 указана погрешность результата в процентах. Представленные здесь данные получены для четырех различных разбиений пластинки на конечные элементы (на рис. 10.4 через N обозначено число степеней свободы конечноэлементной модели). При выборе конечноэлементной модели следует стремиться к тому, чтобы для каждого конечного элемента отношение сторон было
по возможности близким к единице, так как в этом случае жесткостные и массовые характеристики воспроизводятся наилучшим образом. Это видно, в частности, из результатов, представленных в табл. 10.1: сетка 2 дает менее точные результаты, чем сетка <?, хотя она имеет большее число степеней свободы.
Пример 4. Оболочка вращения
(рис. 10.5), представляющая собой
жестко защемленный цилиндричес- Рис- 105
кий сосуд, закрытый полусфери-
ческим днищем такой же толщины, что и цилиндрическая часть, совершает осесимметричные колебания. Длина
и радиус цилиндра равны 500 мм, отношение толщины к радиусу составляет 0,02; р. = 0,3; Е = 2 • 105 МПа; р = 7,83 X X 10-8 кг/м8. Результаты расчета получены с использованием конечных элементов- первого порядка (согласованная формулировка масс без учета инерции вращения). С использованием 40 конечных элементов для частоты основного тона получено значение <о — 1,041 107 с-1, что хорошо согласуется с данными других работ 1351.
§ 10.4. Разложение движения по формам собственных колебаний
Вернемся теперь к уравнению (9.9), описывающему при отсутствии демпфирования вынужденные колебания конструкции. Пусть в результате предварительного расчета найдены частоты и формы собственных колебаний. Расположим собственные частоты в порядке возрастания a>j а>2 ®8...;
соответствующие им формы колебаний обозначим через W(, W2, W3... . Предполагаем, что для них выполняются соот-
ношения
W,T MWj = ( ° (г у);
I 1 («•=/)
(10.16)
и соответственно соотношения
W[KW; = (° (10.17)
| (t —j).
Матрицу узловых перемещений v (t) можно искать в виде линейной комбинации векторов W,:
v (/)=?! (/) Wi-f-22 (/) W2+ z3 (0 W3+ ...,
где Zt (t) — зависящие от времени неизвестные пока коэффициенты разложения. В матричной форме последнее равенство имеет вид
v(0=Hz(0, (10.18)
где
Н = [Wj W2 ...I (10.19)
— прямоугольная матрица, столбцами которой являются собственные формы (так называемая модальная матрица), а
z(/)= {?,(/) z, (/)...} (10.20)
— матрица-столбец неизвестных функций времени. Количество собственных форм, используемых в матрице Н, зависит от желаемой точности расчета и возможностей используемой ЭВМ. Обычно учитывается лишь несколько первых тонов колебаний.
Подстановка (10.18) в (9.9) дает равенство
MHz+KHz= Р4-Р.
Умножив его на Нт слева, получим
H7 MHz4-H7 KHz ^H' (P4 P) (10.21)
Произведения НТМН и НГКН представляют собой квадратные матрицы, типовые элементы которых равны WfMW; и W^KWy. В силу соотношений (10.16), (10.17) эти элементы равны нулю для всех t =Н= /, т.е. данные матрицы являются диагональными. При этом матрица НТМН будет единичной, а матрица НГКН, которую мы обозначим буквой Q, будет
равна
Q=-H'KH =
о
Уравнение (10.21) принимает теперь вид
z-f-S2z = Q, (10.22)
где
Q = Hr(P + 'P). (10.23)
Система дифференциальных уравнений, заключающаяся в равенстве (10.22), оказывается несвязанной. Каждая функция Zi (t) может быть найдена интегрированием уравнения
Zj + wf zt — Qit (10.24)
где Qi (f) — i-й компонент матрицы-столбца Q: Q. (Z)^Wl (P-4-P).
(10.25)
Интегрирование уравнений (10.24) можно осуществить численно; некоторые методы пошагового интегрирования описаны ниже. Если зависимость внешних сил от времени имеет простое аналитическое выражение, то можно воспользоваться и точным интегрированием. В случае со,- =/= 0 решение уравнения (10.24) может быть записано в виде
z£ (/) = z; (0) —— sin а>11 + z£ (0) cos <o£ t +
(Of
1
Wi
t
Qi (r) sin [«;(/ —т)](1т. о
(10.26)
В.этом выражении последнее слагаемое есть частное решение уравнения (10.24), а первые два — общее решение соответствующего однородного уравнения, подчиненное начальным условиям; г; (0) и z£ (0) — начальные значения функции z£ (t) и ее первой производной.
Если = 0, то решение можно получить из (10.26) соответствующим предельным переходом:
t
zi(t) = zi(O)t + Zi(0)+ j’(/ — T)Qi (T)dT. (10.27) b
В начальный момент времени t = 0 известны матрицы v (0) и v (0), и чтобы выполнить численное интегрирование уравнений (10.24) или воспользоваться равенствами (10.26), (10.27), необходимо выразить через эти матрицы г,- (0) и z£ (0). Это можно сделать, исходя из равенства (10.18). Умножим его на НГМ слева. Учитывая, что НТМН есть единичная матрица, получим соотношение z (/) = HrMv (/), из которого вытекают зависимости
z(0)=HrMv(0); z(0)=HrMv(0).
Отсюда находим требуемые выражения
z£ (0) = W[ М v (0); zj, (0) = Wf Mv (0). (10.28)
Формулы (10.26), (10.27) целесообразно использовать в том случае, когда зависимость внешних сил от времени имеет вид
Р + Р~Ро<р(0, (10.29)
где ср (0 — скалярная функция времени, а матрица Ро от времени не зависит. При этом обобщенные силы Q, (t) = Q“<p (f), где в силу (10.25) Q" = \¥Гр0.
Так как величины Q? не зависят от времени, то вычисление интегралов в (10.26), (10.27) сводится к определению функций t t
j ср (т) sin [со; (t — т)] dr; f (t — r) cp (t) dr. о b
Для зависимостей <p(/) простого вида можно записать аналитическое выражение этих функций. Например, при мгновенном приложении внешней нагрузки имеем ср (t) = 0 при t 0; ср (f) = 1 при t> 0 (под Ро понимается при этом матрица, содержащая окончательные значения внешних сил). Тогда
t
| <р (т) sin (/—т)] dr=---(1 —cos Wj /);
J о t J<P(t)(/ — r)dr=y . 0
В этом частном случае имеем
z<U)=zi(O) — sinco; / 4- Zj (0) cos «Д +
<0;
-b —i— Qf (1 --cosco; f) (для <0; 0); (10.30)
<of
гДО = ^(0)^+гг(0) + у Q?/2 (для <ог = О). (10.31)
Если zt (0) = 0; Z; (0) = 0, то из (10.30) ясно видно, что наибольший вклад в разложение v (/) будут давать те формы колебаний, которые соответствуют наименьшим частотам. Колебания же с высокими частотами практически не возбуждаются при реальных силовых воздействиях. Это объясняет, почему колебания с низкими частотами являются наиболее важными и почему достаточно учесть в (10.19) лишь те формы колебаний, которые соответствуют низшим частотам.
Если в процессе нагружения соотношение между отдельными компонентами матрицы сил изменяется, т.е. равенство (10.29) не выполняется, то для отыскания г,- (/) удобнее воспользоваться численным интегрированием уравнений (10.24).
§ 10.5. О прямом интегрировании уравнений движения
Расчет собственных колебаний требует в случае систем большого размера весьма больших затрат машинного времени. Поэтому решение динамических задач методом разложения по собственным формам целесообразно выполнять в том случае, когда для получения приемлемой точности результатов достаточно ограничиться учетом лишь нескольких основных тонов колебаний. Однако во многих случаях (например, при расчете сложных стержневых или оболочечных конструкций) требуется учитывать большое число тонов собственных колебаний, и метод разложения по собственным формам становится неэффективным. В этих случаях более экономичным оказывается прямое интегрирование дифференциального уравнения (9.14)
Mv + Cv -I- Kv = P (10.32)
с помощью той или иной численной процедуры. В уравнении (10.32) узловые силы Р, эквивалентные внеузловой нагрузке, включены для упрощения записи в матрицу Р.
Ограничимся рассмотрением методов интегрирования шагового типа. В этих методах матрицы vi + 1, vi+1, относящиеся к некоторому моменту времени tt + j == t, + At (At — шаг интегрирования), вычисляются через их значения, найденные на предыдущих шагах.
Как уже говорилось выше, численное интегрирование можно применить и в методе разложения по собственным формам при решении уравнений (10.24). С другой стороны, всякая матрица v может быть единственным образом представлена в виде разложения по формам собственных колебаний (если включить в это разложение все формы). Процесс численного интегрирования уравнения (10.32) можно понимать как неявное пошаговое определение коэффициентов этого разложения, являющихся функциями времени. То же самое, только в явной форме, делается и при интегрировании уравнений (10.24). Таким образом, прямое интегрирование уравнения (10.32) можно трактовать как неявное и одновременное выполнение тех же вычислений, которые в методе разложения по собствен
ным формам осуществляются раздельно для каждого тона колебаний*.
Имеются, однако, и принципиальные различия между двумя указанными подходами к расчету динамического поведения конструкции. Во-первых, в методе прямого интегрирования, в отличие от метода разложения по собственным формам, учитываются все без исключения тоны колебаний, в том числе колебания с наивысшими частотами. Во-вторых, интегрирование выполняется здесь с одинаковым шагом по всем тонам, в то время как для интегрирования каждого из уравнений (10.24) шаг целесообразно выбирать различным.
Вообще говоря, шаг А/ при прямом интегрировании должен быть таким, чтобы с достаточной точностью воспроизводились те колебания, которые играют наиболее существенную роль в динамическом поведении конструкции, т.е. колебания с относительно низкими частотами. Но обычно в спектре частот конечноэлементной модели содержатся и весьма высокие частоты, и может оказаться, что выбранный шаг значительно превосходит периоды соответствующих колебаний. Ясно, что вклады колебаний с наивысшими частотами в динамическое поведение конструкции будут в этом случае совершенно искажены, но это допустимо, поскольку, как было ранее сказано, они не играют в целом сколько-нибудь существенной роли. Однако важно, чтобы используемая процедура интегрирования обеспечивала устойчивость процесса, когда шаг Af как угодно превосходит период колебания. Методы интегрирования, удовлетворяющие этому требованию, называются безусловно устойчивыми. Для них единственным критерием выбора шага А/ является точность результатов.
На практике используются иногда и условно устойчивые методы интегрирования, в которых устойчивость процесса обеспечивается лишь в том случае, когда шаг А/ не превосходит некоторого критического значения Af*. Если же взять А/> > А/*, то происходит стремительный рост численных значений компонент матрицы v (t), которые уже после нескольких первых шагов могут достигать сколь угодно больших величин. Чаще всего величина Af* оказывается значительно меньше того значения, которое необходимо для получения приемлемой точности в безусловно устойчивых процедурах. Тем не менее в отдельных случаях условно устойчивые процедуры могут оказаться более экономичными, если на каждом шаге
* При выводе равенства (10.24) было принято, что отсутствует демпфирование, так что, строго говоря, данные рассуждения относятся к случаю, когда матрица С в (10.32) нулевая.
они требуют, как это часто бывает, меньшего числа арифметических операций, чем безусловно устойчивые процедуры.
Существуют широко известные методы численного интегрирования обыкновенных дифференциальных уравнений типа Адамса, Рунге—Кутта и др. Однако они мало пригодны для интегрирования систем высокого порядка, так как, будучи условно устойчивыми, требуют тем не менее выполнения большого числа арифметических операций на каждом шаге. В связи с этим применительно к матричному уравнению вида(10.32) разработано несколько специальных процедур; здесь будут рассмотрены две из них.
§ 10.6. Метод центральных разностей
Обозначим через v?, vit v, значения матриц v (t), v (t). v (/) в некоторый момент времени Матрицу перемещений v (if + т) представим в виде разложения по степеням т. Ограничиваясь членами, содержащими т2, получим приближенное выражение
v(6 + T)=v/4-TV, + -i-vi. (10.33)
Полагая здесь т — —А/, а затем т = А/, будем иметь два равенства
V;-l = V; — A/v; 4- —у— v;; v; + 1 = V; +A/v; 4-— Vi-
Складывая и вычитая эти соотношения, можно выразить V/ и V,- через значения матрицы v (/) в моменты времени /.„j, h > h +1 '
у/ = Т77(v;+i — vf-i); уг = —~ (vf+1—2у^уг_!). (10.34) 2Д/ A/'2
Запишем теперь уравнение (10.32) в момент времени t,:
MVi+Cv^Kv^P;.
Если внести сюда приближенные зависимости (10.34), то придем к уравнению для определения vf + 1, которое можно записать в виде
(М4-у-С)уг+1 = К;, (10.35)
где
R;=A/2(Pj-Kvi)4-M(2vi-viCv,-!. (10.36)
Соотношения (10.34)—(10.36) совместно с начальными условиями дают процедуру пошагового интегрирования уравнения (10.32), известную под названием метода центральных разностей [11. Равенства (10.34) можно рассматривать как формулы численного дифференцирования, симметричные относительно центральной точки t = t,; это объясняет название метода.
Так как в начальный момент времени t0 = 0 известны v0 и vu, но не V.-,, то для выполнения первого шага следует представить соотношения (10.35), (10.36) в иной форме. Выразив на основании первого равенства (10.34) v.., через v0, имеем
v-^vj — 2A/v0;
второе равенство (10.34) дает При этом
2
Vo = -CT (Vi —v0—A/vo).
A?2
Внося последний результат в уравнение
Mv0 4- Cv0 + Kv0— Ро,
получаем требуемое равенство для определения vp
Л/2
Mv, = -2- (Ро_ Kv0 -Cv0) + М (v0 + A7v0).
Метод центральных разностей весьма прост. Он особенно удобен в том случае, когда матрица масс имеет диагональную или блочно-диагональную структуру, а демпфирующими силами можно пренебречь (или же когда матрица демпфирования С пропорциональна матрице масс). Тогда решение системы уравнений относительно vi + 1 становится тривиальным. Но если некоторые узловые массы равны при этом нулю, то определение vi + 1 становится невозможным. В связи с этим исследуем подробнее устойчивость метода центральных разностей.
Обратимся для этого к уравнениям типа (10.24), каждое из которых можно трактовать как уравнение движения системы с одной степенью свободы. В этих уравнениях не учитывается демпфирование, но, как показывают расчеты, это не оказывает существенного влияния на устойчивость процесса интегрирования. Кроме того, при исследовании устойчивости можно принять правую часть уравнений равнрй нулю. Таким образом, для определения области устойчивости процедуры
интегрирования будем применять ее к скалярному уравнению типа
z + <o2z = ot (10.37)
точное решение которого может быть записано в виде
z (/) — Су coscut + с2 sinw^,
где clt с2 — произвольные постоянные, определяемые из начальных условий. Это же решение можно представить и в эквивалентной комплексной форме
z (!) = Ле1’®' + Be-'®',
где А, В — комплексные постоянные.
Полагая в соответствии с методом центральных разностей
Z| = (Zi + 1~ 2Zj + Zy-y),
получаем из (10.37) соотношение
zi + y + Zy_y + (<о2Д/2 — 2)гг = 0,
определяющее приближенное решение. Поставим себе целью иайти такую функцию z (/), которая удовлетворяет условию
z (t + AZ) + z (/ — ДО + (<о2Д/2 — 2) z (0 = 0 (10.38)
и является тем самым интегральной функцией для уравнения (10.37), получаемой по методу центральных разностей. Будем искать эту функцию в виде
z (0 == Aevt е‘& = Ае^+М,
где А — произвольная комплексная постоянная. Множитель е№ описывает колебательное движение с круговой частотой р, а множитель evt характеризует изменение амплитуды колебания с течением времени; решение будет устойчивым (т.е. невозрастающим) в случае v 0.
Обозначив
g = e<v+^)A«i (10.39)
будем иметь
z(t +Д0 = z=qz(f);
z(f—Д/)—=-L z(t). q
Подставляя эти соотношения в (10.38), получим для q квадратное уравнение, которое запишем в виде
q2 — 2aq +1=0;
здесь через а обозначена величина
а = 1 — (<о2А/2)/2. (10.40)
Отсюда находим два корня qlt q2:
41,2 — й ± Va2 — 1. (10.41)
Так как для устойчивого решения v<LO, то определение области устойчивости сводится к отысканию тех значений Д/, при которых модуль q, равный evAZ, не превосходит 1. Двум корням qlf q2 соответствуют две функции z (t), удовлетворяющие соотношению (10.38), и для обеспечения устойчивости каждая из них должна оставаться ограниченной при оо. Таким образом, необходимо потребовать, чтобы обе величины qlt q2 не превосходили по модулю 1.
В зависимости от величины шага Д/ корни (10.41) могут оказаться либо действительными, либо комплексно-сопряженными.
Предположим сначала, что шаг удовлетворяет условию Д/ 2/<о, так что а2 — 1 0. В этом случае имеем комплекс-
но-сопряженные корни
41,2 = а ± Ы, (10.42)
где через b обозначена действительная величина £> = V1—-а2. Так как а2 + Ь2 = 1, то по модулю оба корня qltq2 равны единице. Отсюда следует, что для обоих частных решений, соответствующих qx и q2, величина v равна нулю, т.е. получаемое здесь приближенное решение, так же как и точное, описывает гармоническое колебание с постоянной амплитудой.
Из (10.39) следует теперь, что
0112-= = cos рД/ ± i sin рД/.
Сопоставляя это выражение с (10.42), видим, что частота колебания в приближенном решении определяется равенством созрД/ = а, т.е.
1 /. <02 Д/2 \ г..А
р =----arccosll--------• (10.43)
r М \ 2 )
Рассмотрим далее случай, когда выполняется условие а2 — — 1 > 0, т.е. Д/ > 2/<о. Обозначив теперь через Ь величину b = Va2 — 1, получим из (10.41) два действительных различных корня
41,2 = а ±Ь.
Так как по теореме Виетта qxq2 — 1, то один из этих корней больше 1, т.е. решение будет неустойчивым.
Итак, устойчивость метода центральных разностей обеспечивается лишь в том случае, когда шаг А/ не превосходит критического значения А/*, равного
М* = 2/о = Т/л, (10.44)
где Т = 2л/(о — период колебания. При этом численное решение будет описывать колебательный процесс с той же амплитудой, что и в точном решении, но с круговой частотой р (10.43), отличной от (о. На рис. 10.6 дана зависимость относительной погрешности
II—<о 1
ei------------—л7~ X
<о соДг
от отношения Д//7’=(оА//(2л). Возвращаясь к общему случаю матричного дифференциального уравнения (10.32), можно заключить, что процесс его интегрирования будет устойчивым при условии
(10.45)
где TmIn — минимальный период собственных колебаний
данной системы. Если конечноэлементная модель содержит конечные элементы малых размеров (с большой жесткостью и малой массой), в ее спектре частот будут содержаться весьма высокие значения «г, которым соответствуют малые периоды колебаний. Расчет такой системы методом центральных разностей может потребовать большого числа шагов из-за ограничения, накладываемого условием (10.45) на шаг А/.
§ 10.7. Метод Ньюмарка
Метод Ньюмарка основан на следующих (независимых) разложениях v (tt + т) и v (/г + т) в ряды по степеням т [1]:
• >• • ••
V (ti +т) = vt 4-TVj + — Vi 4-ат3 vt-,
v(/i+t) = Vi4-Tvi4-pT2Vi. (10.46)
Здесь удержаны члены, содержащие матрицу v. Коэффициенты аир выбираются таким образом, чтобы обеспечить безусловную устойчивость процесса интегрирования; об их численных значениях будет сказано ниже.
Полагая т = AZ и заменяя v; приближенным отношением (v£ + 1 — уг)/Д/, приходим к равенствам
Vi+i = vf+&Vi4—у- Vi-|-aA/2(vJ+1—Vj);
Vi+i = Vi+AzVi+PAf(Vi+1—v’i). (10.47)
Найдем из первого равенства vJ + 1:
Vi+i = -7^- (Vi+i—vO---- v'i +(1 —4“1 Vi. (10.48)
аДР аД/ \ 2a /
Подстановка этого результата в выражение для V{+1 дает формулу
Vi+1=—^-(Vi+1-Vi)+(1-A]v- Lpi, (10.49)
аД/ \ а / 2 \ а /
которая в совокупности с (10.48) составляет рекуррентные соотношения метода Ньюмарка.
Для отыскания уг + 1 уравнение движения записывается для момента t = tt + г:
Mvi+1-f- С¥г+1 + Kvi+i = Pi+1.
После подстановки в это равенство соотношений (10.48), (10.49) приходим к уравнению вида
Av{ + i = Ri + i, (10.50)
в котором
А = К + -4;СЧ--у-М; (10.51)
аД/ ссД/2
Ri+1 = Р.+1 + М 1-4- Vi + -Ь. v'i +(J-1) v'i ] 4-
[ аД/2 аД/ \ 2а / J
+ cf-T7vi + (— -Hvi + y-f—<10-52> L аД/ \а / 2\а J ]
Отметим, что метод Ньюмарка требует задания в начальный момент времени t0 = 0 не только матриц v0, v0, но также и 380
матрицы v0. Обычно полагают v=0; можно также найти Mv0 из уравнения движения, записанного для момента времени t0 = 0.
Для исследования точности и устойчивости метода Ньюмарка обратимся снова к уравнению (10.37). Запишем применительно к этому случаю соотношения (10.47):
* А/2 "
Zi+1 = zt + Mzi 4—— Zi +aA/8 (zi+1 — Zj);
(10.53)
zi+i = Zj + A/zj + 0А/ (zi+1—z,).
Получаемые по методу Ньюмарка функции z (/), z(t), z (0 будем искать в виде
z(t)=A1e^+!Mt; z(t)—-A2e^v+c^t; г(1) = А3е^+‘^, (10.54)
где Alt А2, А3— некоторые комплексные постоянные.
Уравнение (10.37) должно удовлетворяться в моменты времени t = tlt так что из равенства гг + <o2Zi = 0 имеем следующую связь между постоянными Аг и А3:
А3 = —ал2А1. (10.55)
Учитывая, что zi + 1 = qzf, zi + 1 = qzt\ Zi + 1 = qzit где q определяется согласно (10.39), из второго равенства (10.53) устанавливаем также, что
Л2 = —Л1а>аА^0—ГТ)‘ (Ю.56)
Наконец, первое равенство (10.53) дает с учетом (10.55) и (10.56) квадратное уравнение относительно q, которое запишем в виде
Yi(l-<7)а-?2(1-<7) + 1 = 0. (10.57)
Здесь
т*=с,+^; Ь’Р + Т' <los8>
Решая уравнение (10.57), находим два его корня:
<71,2 = (2?i—у2 ± УТг—4?!). (10.59)
Определим теперь значения параметров а, 0, обеспечивающие безусловную устойчивость метода. Потребуем для этого,
чтобы при А/ -> оо оба корня q± и q2 не превосходили по модулю 1. Отбрасывая в выражении для Yj второе слагаемое, имеем
9i.2 = '^“[2a_"(P+y)± ]/ (P+v) ~4а ' ХС4 \ £ j Jr у £ j
Предположим сначала, что -|-(0 + у)2. Тогда получим два комплексно-сопряженных корня ql 2 = а0 ± boi, где
Условия устойчивости |</1| 1; |<у2| 1 сводятся к вы-
полнению неравенства а? + feo 1, которое удовлетворяется при 0 1/2.
В случае же а (0 + -^)2 оба корня qlt q2 будут действительными, причем один из них оказывается по абсолютной величине больше 1.
Итак, метод интегрирования Ньюмарка будет безусловно устойчивым, если
1 1 / 1 \2
а>т(р+т)- (10-60)
Более определенный выбор параметров а, 0 можно сделать, исследуя их влияние на точность решения. Возвращаясь к случаю конечных приращений А/, из (10.59) имеем
<71,2 = а ± bi, где _______________
а = 1 — Тг/гуг, b = У1/?1—-(Тг/г?!)2.
Модули qlt q2 равны между собой и имеют значение Уа2 + &2 = Vl + (1 -?2)/Т1.
Так как |</| = |e<v+4*> д<| = е*д<, то в обоих решениях, соответствующих qx и q2, величина v получается одинаковой; она определяется равенством
или
evA< = Vl + (1 — у2)/Т1
V~ "олТ" 1° 11
(10.61)
Что касается величины р, то она в этих двух решениях отличается лишь знаком и определяется условием
* — (а bi), V7+T2
откуда имеем
р = —J— arccos — ---= —— arccos —LtT?.'/2!.1}----. n 0.62)
)/a2-|-&2 Vl—О — Уг)/?!
Влияние параметров a, 0 на точность решения можно характеризовать двумя величинами ej, е2. Первая из них е2 =
= (р — <п)/<о дает относительную погрешность в определении круговой частоты, а другая е2 = 1 — е2ы>/ц представляет собой относительное уменьшение амплитуды колебания за время t — 2л/р, т.е. за одно полное колебание. Зависимости в! и е2 от шага интегрирования при различных значениях а, 0 представлены соответственно на рис. 10.7 и 10.8, где через а0 обозначена величина
1 / 1 \2
ао = 4(0 + 4- • (Ю.63)
4 \ 2 /
Как видно из этих графиков, изменение параметра а более существенно сказывается на величине Ej, причем наилучшая точность достигается при а = а0. Именно это значение (или несколько большее) следует употреблять в расчетах.
Величина е2 зависит главным образом от параметра 0. При 0 — 0,5 она равна нулю, т. е. амплитуда колебания
в численном решении сохраняется неизменной. При р > 0,5 амплитуда получается убывающей. В связи с этим можно гово-
Л24
Рис. 10.9
тем сильнее, чем больше шаг интегрирования в сравнении с периодом колебания. Поэтому при использовании метода Ньюмарка с параметром Р > 0,5 для интегрирования матричного уравнения движения (10.32) колебания с высшими частотами будут полностью подавляться, в то время как в основных тонах затухание будет проявляться значительно слабее.
Можно брать Р > 0,5 и для приближенного учета действительного демпфирования. Это позволяет отбросить в исходном уравнении и в расчетных формулах члены, содержащие множителем матрицу демпфирования С и тем самым сэкономить время вычислений. Поэтому часто используют [1] параметры
Р = 0,55; а = 0,28. Если же необходимости в введении искусственного демпфирования нет, то лучше брать значения Р = = 0,5; а = 0,25, при которых достигается наивысшая точность метода Ньюмарка.
Пример. Жестко защемленная сферическая оболочка имеет радиус кривизны 561 мм, диаметр основания 508 мм, толщину 10,4 мм (рис. 10.9); Е = 7,23 • 104 МПа; р. = 0,3; р = 2,8 X X Ю-3 кг/м3. Оболочка мгновенно нагружается равномерным давлением с максимальной интенсивностью р0 = 0,689 МПа.
На рис. 10.10 показано осевое перемещение w полюса и меридиональное напряжение Oj в вершине оболочки на ее наружной поверхности в зависимости от времени t. Оболочка
ыла разбита на 30 кольцевых конечных элементов первого орядка (см. § 7.8). Интегрирование осуществлялось методом Ньюмарка с параметрами Р — 0,5; а = 0,25. Шаг интегрирования А/ равнялся 1 • 10-® с, так что весь расчет потребовал выполнения 320 шагов. Отметим, что применение метода центральных разностей в данной задаче потребовало бы осуществления значительно большего (почти в 100 раз) числа шагов из-за малой величины критического шага интегрирования. Это связано с наличием в вершине оболочки конечных элементов, имеющих весьма большую жесткость при малой массе. В задачах такого рода метод центральных разностей менее эффективен, чем безусловно устойчивые процедуры.
Представленные на рис. 10.10 результаты получены с использованием согласованной матрицы масс (9.43); они хорошо совпадают с данными других работ [27]. Отметим, что применение в этой задаче диагональной матрицы масс (9.44) дает (практически такие же результаты.
ЗАКЛЮЧЕНИЕ
В пособии изложены основы метода конечных элементов в перемещениях применительно к линейным задачам. Метод можно рассматривать как мощное современное средство прочностного расчета авиационных конструкций. В практике конструкторских бюро он используется на всех этапах создания летательного аппарата, начиная с проработки и выбора силовой схемы изделия и кончая анализом результатов испытаний. С его помощью выполняются расчеты как общей, так и местной прочности, устойчивости силовых элементов, колебаний кон-, струкции, температурных полей; он же помогает оценить влияние на прочность изделия различных производственных отклонений.
Метод конечных элементов полностью ориентирован на использование ЭВМ. Это обусловлено необходимостью выполнения большого количества однотипных операций. Однако есть два важных этапа расчета, плохо поддающихся автоматизации и требующих больших затрат ручного труда — это, во-первых, подготовка и ввод исходной информации и, во-вторых, обработка и анализ результатов расчета.
Подготовка исходной информации начинается с составления конечноэлементной модели, нумерации узлов и конечных элементов, вычисления координат узлов. Далее вся информация должна быть соответствующим образом представлена и введена в машину. На этом этапе расчет практически неизбежно! (если не говорить о простейших задачах) сопровождается значительным количеством ошибок, которые впоследствии при-; ходится выявлять всеми возможными средствами и исправлять.; Поэтому важной задачей является изыскание возможностей для максимального сокращения исходной информации. Большие универсальные программы, реализующие метод конечных элементов, обязательно предусматривают те или иные способы такого сокращения. Однако независимо от этого инженер-также должен стремиться к сокращению исходной информации путем наиболее рациональной идеализации конструкции. В качестве общих приемов здесь можно упомянуть использование симметрии, введение участков с регулярными сетками, использование наиболее подходящих конечных элементов.
Простейшим способом представления результатов расчета является вывод на печать перемещений и напряжений в харак-^ терных точках (например, в узлах). При этом объем выводимой
информации оказывается часто настолько большим, что даже простой ее просмотр требует значительного времени. В некоторых программах предусмотрены более эффективные способы представления результатов, использующие, скажем, графопостроитель. Это может быть вычерчивание графиков интересующих нас величин, нанесение на чертеж конструкции линий равного уровня напряжений и т. п. Однако эти способы применимы лишь к конструкциям частного вида, так <что до конца проблема представления результатов пока не решена.
Важным составным элементом анализа решения является .оценка его достоверности. Ни в коем случае нельзя слепо доверять машинным результатам: ответственность за правиль-ность решения задачи несет человек, а не машина. Здесь особое значение приобретают профессиональный опыт и квалификация расчетчика. Для подтверждения достоверности могут использоваться экспериментальные данные, сопоставление с результатами прежних расчетов аналогичных конструкций; во многих случаях помогают проверки выполнения условий равновесия конструкции или отдельных ее частей. Подчас незаменимым подспорьем оказывается оценка результатов с помощью аналитических методов. Заметим, что по одной только этой причине неуместно противопоставлять численные методы расчета (в том числе метод конечных элементов) аналитическим и умалять роль последних, с чем приходится иногда сталкиваться.
Для практического осуществления расчетов необходимо располагать соответствующими программами для ЭВМ, создание которых связано со значительными затратами труда и вре-; мени. Считается, что на разработку комплекса программ по методу конечных элементов с более или менее ш ирокими возможностями требуется от 10 до 100 человеко-лет. В настоящее ; время в нашей стране созданы и успешно эксплуатируются . мощные вычислительные программы как общего назначения, так и специально ориентированные на расчет авиационных конструкций. Наряду с этим во многих организациях создаются относительно более простые программы, предназначенные для расчета конструкций частного вида (скажем, оболочек вращения, пластинок и т.п.). Их эффективность обусловлена возможностью задания минимальной информации, требующейся для описания геометрии таких простых конструкций; сетка конечных элементов генерируется при этом автоматически.
В настоящем пособии вопросы реализации конечных элементов на ЭВМ не затронуты, поскольку они достаточно полно освещены в литературе [1, 6, 15, 20, 25], где можно найти как
общие принципы организации вычислений, так и конкретные примеры составления программ.
Для идеализации одной и той же конструкции могут быть использованы различные конечные элементы. Выбор во многом определяется той библиотекой конечных элементов, которая имеется в данной программе; большую роль играют знания и опыт расчетчика. В настоящее время широкое применение получили конечные элементы изопараметрического типа, позволяющие легко моделировать тела с криволинейными границами; именно поэтому в данной книге им уделено большое внимание. При работе с ними приходится решать вопрос о том, какие элементы лучше взять — простейшие элементы первого порядка или же более сложные многоузловые элементы высших порядков. Здесь следует иметь в виду, что элементы первого порядка позволяют получить достаточно точные значения напряжений лишь в центральной точке, но не в узлах. Поэтому область эффективного применения элементов первого порядка ограничивается, как правило, такими задачами, в которых градиенты напряжений не слишком велики (например, расчет крыла самолета без вырезов).
Однако во многих задачах (в частности, при расчете оболочек) напряженное состояние тела оказывается быстро изменяющимся, и тогда необходимо применять конечные элементы более высоких порядков. Следует соблюдать определенную осторожность, выбирая форму конечных элементов и положение узлов, с тем чтобы избежать обращения в нуль якобиана преобразования координат. Не вдаваясь в подробности, отметим, что такая опасность оказывается тем значительнее, чем выше порядок элементов. Наилучшим компромиссом является, по-видимому, использование элементов второго порядка. Если при этом избегать слишком искривленных конечных элементов и помещать промежуточные узлы приблизительно в серединах сторон, то корректное представление жесткостных характеристик тела будет гарантировано.
На современном этапе развития техники все большее значение приобретают нелинейные задачи расчета конструкций (учет больших перемещений, пластических деформаций, расчет закритического поведения силовых элементов и т.д.). Применение метода конечных элементов в этих задачах [61 открывает широкие возможности для их практического решения. Следует, однако, отметить, что разработка теоретических и практических аспектов приложений метода конечных элементов к нелинейным задачам еще далека от завершения, хотя и в этой области налицо определенные успехи. Поскольку расчет носит здесь итерационный характер, решение требует
существенно большей затраты машинного времени, нежели в случае линейных задач. Совершенствование вычислительных алгоритмов и развитие ЭВМ позволили уже сейчас преодолеть многие трудности, и можно не сомневаться, что в скором времени станет доступным решение тех нелинейных задач, которце выдвигаются на первый план потребностями практики.
СПИСОК ЛИТЕРАТУРЫ
1. Бате К., Вилсон Е. Численные методы анализа и метод конечных элементов: Пер. с англ. — М., 1982.
2. Березин И. С., Жидков Н. П. Методы вычислений. М., 1962, т. 1, 2.
3. Бояршинов С. В. Основы строительной механики машин. М., 1973.
4. Бурман 3. И., Лукашенко В. И., Тимофеев М. Т. Расчет тонкостенных подкрепленных оболочек методом конечных элементов с применением ЭЦВМ. Казань, 1973.
5. Гурьев Н. И., Поздышев В. Л., Старокадомская 3. М. Матричные методы расчета на прочность крыльев малого удлинения. М„ 1972.
6. Зенкевич О. Метод конечных элементов в технике: Пер. с англ. — М., 1975.
7. Кан С. Н. Строительная механика оболочек. М., 1966.
8. Кан С. Н., Свердлов А. И. Расчет самолета иа прочность. М., 1966.
9. Канторович Л. В., Крылов В. И. Приближенные методы высшего анализа. М.—Л., 1949.
10. Крылов В. И. Приближенное вычисление интегралов. М., 1967.
11. Лейбензон Л. С. Вариационные методы решения задач теории упругости. М.—Л., 1943.
12. Леонов В. И., Хазанов X. С. К расчету искривленных круглых пластин на нормальное сосредоточенное воздействие. — Науч. тр./ Куйбышевский авиац. ин-т, 1972, вып. 63, с. 22—32.
13. Метод конечных элементов в проектировании транспортных сооружений/А. С. Городецкий и др. М., 1981.
Т4. Новожилов В. В. Теория тонких оболочек. Л., 1962.
15. Норри Д., де Фриз Ж. Введение в метод конечных элементов: Пер. с англ. — М., 1981.
16. Образцов И. Ф. Вариационные методы расчета тонкостенных авиационных конструкций. М., 1966.
17. Образцов И. Ф., Онанов Г. Г. Строительная механика скошенных тонкостенных систем. М., 1973.
18. Полюдов М. В. Модель анизотропной иеодиородиой пластинки из конечных элементов. — В ки.: Ученые записки ЦАГИ. М., 1978, т. 9, с. 93—102.
19. Постнов В. А. Численные методы расчета судовых конструкций. Л., 1977.
20. Постнов В. А., Хархурим И. Д. Метод конечных элементов в расчетах судовых конструкций. Л., 1974.
21. Розин Л. А. Основы метода конечных элементов в теории упругости. Л., 1972.
22. Рублев А. Н. Линейная алгебра. М., 1965.
23. Савельев Л. М. Простой четырехугольный конечный элемент произвольной тонкой оболочки. — В ки.: Вопросы прочности и долговечности авиационных конструкций. Куйбышев, 1979, с. 58—63.
24. Савельев Л. М. Простой криволинейный конечный элемент оболочки вращения. — В кн.: Прочность, устойчивость и колебания тонкостенных и монолитных авиационных конструкций. Казань, 1980, с. 86—92.
25. Сегерлинд Д. Применение метода конечных элементов: Пер. с англ. — М., 1979.
26. Стренг Г., Фикс Дж. Теория метода конечных элементов: Пер. с англ. — М., 1977.
27. Стриклин Дж. Статический и динамический расчеты геометрически нелинейных оболочек вращения. — В кн.: Расчет упругих конструкций с использованием ЭВМ: Пер. с англ. — Л., 1974, т. 1, с. 272— 292.
28. Тимошенко С. П., Гудьер Дж. Теория упругости: Пер. с англ. — М., 1975.
29. Фаддеев Д. К., Фаддеева В. Н. Вычислительные методы линейной алгебры. М.—Л., 1963.
30. Филин А. П. Прикладная механика твердого деформируемого тела. М., 1975, т. 1; 1978, т. 2; 1981, т. 3.
31. Фихтенгольц Г. М. Основы математического анализа. М., 1968, т. 2.
32. Barlow J. Optimal stress locations in finite element models. — Int. J. Numer. Meth. Eng., 1976, vol. 10, №2, p. 243—251.
33. Cook R. L. Concepts and applications of the finite element analysis. — N. y.: Wiley, 1974.
34. Fried I., Malkus D. S. Finite element mass matrix lumping by numerical integration with no convergence rafe loss.— Int. J. Solids and Struct,. 1975, vol. 11, №4, p. 461—466.
35. Galletly G. D., Mistry Y. The free vibration of cylindrical shells with various end closures. — Nucl. Eng. and Des., 1976, vol. 30, № 2, p. 249—268.
36. Hinton E., Campbell J. S. Local and global smoothing of discon-tinious finite element functions using a least squares method— Int. J. Numer. Meth. Eng., 1974, vol. 8, № 3, p. 461—480.
37. Hinton E., Rock T., Zienkiewicz О. C. A note on mass lumping and relating processes in the finite element method. — Earthquake Eng. and Struct. Dyn., 1976, vol. 4, № 3, p. 245—249.
38. Hughes T. J. R., Tailor R. L., Kanoknukulchai W. A simple and efficient finite element for plate bending.— Int. J. Numer. Meth. Eng., 1977, vol. 11, № 10, p. 1529—1543.
39. Oden J. T., Reddy J. N. Nate on an approximate method for computing consistent conjugate stresses in elastic finite elements.— Int. J. Numer. Meth. Eng., 1973, vol. 6, № 1, p. 55—61.
40. Robinson J. A single element test. — Comput. Meth. Appl. Meeh, and Eng., 1967, vol. 7., № 2, p. 191—200.
41. Zienkiewicz О. C., Bauer J., Morgan K., Onate E. A simple and efficient element for axisymmetric shells. — Int. J. Numer. Meth. Eng., 1977, vol. 11, № 10, p. 1545—1558.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аппроксимация геометрии 254 перемещений 133
Брус круговой 78 прямой в местной системе координат 59
----в общей системе координат 61
Вариация напряжений 40
— потенциала внешних сил 31
• дополнительного 32
— работы внешних сил 29
---------дополнительной 32
— энергии деформации 35
— — — дополнительной 35
Вариационный принцип Гамильтона 335
— — Лагранжа 39
• Кастнльяно 42
Вектор нормальный 269
— собственный 359
Возможная работа внешних сил 30
Возможные деформации 35
— перемещения 30
Гипотеза прямых нормалей 230
Граничные условия 19
— — геометрические 19
— — естественные 48
— •— статические 15
Групповой тест 214
Демпфирование искусственное 384
Деформация плоская 20
— линейная 14
— объемная 14
— • сдвига 14
Дискретизация тела 106
Дискретная система 108
Закон Гука 17
— — для конструктивно-ортотропной пластины 27
— — — обобщенного плоского напря* жеиного состояния 22
— — — плоской деформации 22
Иерархия конечных элементов 175
Интеграл Мора 81
Интегрирование численное 186
---- порядок 188
— * — — минимально допустимый 189
— — точки Гаусса 189
— —• уравнений движения 373
— — — — устойчивость 374
— —-----шаг 373
Колебания собственные 357
Компоненты деформации 14
— напряжения 13
— перемещения 14
Конструктивно-ортотропная пластина
23
Конечный элемент 107
— — базовый 156
----нзопараметрнческнй 166
Конечный элемент несовместный 149. 166
----одномерный 179
— — прямоугольный 139
----совместный 138
----треугольный 133
— — трехмерный 182
— — четырехугольный 160
Конечноэлементиая идеализация кое-струкции 283 ----лонжерона 290. 300 ----оболочкк безмоментной 285 ----вращения 251, 254 ----произвольной 272, 280 — — пластины 201 ----тонкой 231, 236, 241, 278 — — подкрепленной панели 198 ----шпангоута 201, 310, 320, 328 Координаты безразмерные 140, 182 — декартовы 13 — — местные 54 ----общие 54 — криволинейные 267 Коэффициенты весовые 187
Матрица аппроксимирующих функций 109
— демпфирования 336
— жесткости 51
----вырожденная 92
---- конечного элемента 112
----конструкции 89
---- ленточная структура 90 ----тела 51, 116
— масс 332
— — блочно-диагональная 341
---- диагональная 340
----согласованная 338
— — конечного элемента 332
----конструкции 333
— неотрицательно-определенная 359
— податливости 50
— положительно-определенная 335
— преобразовании координат 55
— Якобн 164
Метод Гаусса 188
— выделения диагонали 341
— Канторовича — Власова 46, 124
— конечных полос 132
— Маркова 191
— Ньюмарка 379
— разложения по формам колебаний 369
— Ритца 43
— центральных разностей 375
— Эйлера 191
Минимизация полной энергии 43
— функционала 131
Напряжения в наклонных площадках 15
— касательные 13
— нормальные 13
Напряженке полное 13
Нормаль 230
— внешняя 15
Обобщенная проблема собственных значений 358
Обобщенное плоское напряженное состояние 20
Объединение конечных элементов 116, 263 Объем конечного элемента 111 — тела 29 Сходимость решения, правило интегрирования 221 — — скорость 204
Поверхность конечного элемента 113 — тела 15 Подкоиструкцня 152 Поле напряжений 197 — перемещений 216 Полином полный 207 Потенциал внешних снл 30 — дополнительный 32 Преобразование координат 54 Принцип возможных перемещений 38 — Д’Аламбера 329 — дополнительных виртуальных работ 41 Теорема Клапейрона 29 — Максвелла 50 — Бетти 51 Узлы внешние 150 — внутренние 150 — конечного элемента 108 — подконструкцнн 153 Узловые лнннн 124 — окружности 228 — перемещения 108 Упругие постоянные Ляме 18 Уравнения Ляме 19 — равновесия узлов 87, 114 — Эйлера 48
Работа внутренних снл 33 — внешних снл 28 — дополнительная 31 Ряд Тейлора 205 Уравнение вариационное Кастнльяно 42 — — Лагранжа 38 Условие совместности деформаций 17 — полноты конечного элемента 211, 213 — ортогональности собственных форм
Сглаживание напряжений 193 — — местное 198 — — общее 194 Сдвиг ложный 145, 222 Силы внеузловые 74 — внешние 27 — внутренние 33 — демпфирующие 336 — инерционные 329 — объемные 13 — • поверхностные 13 — реакции 74 — сосредоточенные 107 361 Ферменный элемент 58 Форма колебания 357 — — нормированная 362 Формулы. Гаусса 188 — Коши 16 — Ньютона — Котеса 187 Формула Остроградского — Гаусса 37 — Симпсона 188 — трапеции 188 Функции аппроксимирующие 109
— узловые 51 — эквивалентные 107 Соотношения геометрические 16 — статические 14 — теории упругости 13 — физические 17 Стержневая система 49 Степени свободы 204 — — иеузловые 156 Степень полинома 206 Сходимость решения 204 — — критерии 210 для несовместных элементов 214 — совместных элементов 210 — — монотонная 211 — — немонотонная 219 — формы 161 Частота колебания 357 Энергия кинетическая — — конечного элемента 334 конструкции 335 — потенциальная полная 38 — — — дополнительная 41 деформации 32 дополнительная 35 конечного элемента 117 конструкции 128 Якобиан преобразования координат 165