БИБЛИОТЕКА СТУДЕНТА
В.В. Фриск
Mathcad
Расчеты и моделирование цепей на ПК
» I 11 i I к <•••. । • » прогр ммирования
J ly ii i и • i i| и ii . । и .i 11 и и । ’I .i ’ и i; v <4 теории qt ?гн *й
Result Format
Number Former Diaptajr Option» Un«Oi«el*u Tolerance
Дпм и< «И 1««е| l\Zlr»t.H<*n<J
УДК 621.3
ББК 32.88.01
Ф 89
В. В. Фриск
Основы теории цепей. Расчеты и моделирование с помощью пакета компьютерной математики Mathcad. — М.: СО-ЛОН-Прссс, 2006. — 88 с.: ил. — (Серия «Библиотека студента»)
ISBN 5-98003-242-8
Книга «Расчеты и моделирование с помощью пакета компьютерной математики Mathcad» является дополнением к курсу «Основы теории пеней» (ОТЦ) и предназначена для использования с учебными пособиями Фриск В. В.: «Основы теории цепей», «Лабораторный практикум на персональном компьютере», «Сборник задач с примерами применения персонального компьютера» и «Использование пакета Microwave Office для моделирования электрических цепей на персональном компьютере».
В ней приведены примеры расчета наиболее распространенных задач по ОТЦ и показано, как самостоятельно использовать персональный компьютер для автоматизации расчетов и математического моделирования электрических пеней.
Для студентов, бакалавров и аспирантов высших учебных заведений (университетов связи), инженерно-технических работников, также будет полезна учащимся техникумов и колледжей связи всех специальностей.
Рецензенты: А />. Мазепа, профессор (МАИ)
В, А. Сивов, доцент (ФГУП)
КНИГА - ПОЧТОЙ
Киши ищательства «СОЛОН-Пресс» можно заказать наложенным платежом (оплата при получении) по фиксированной цене. Заказ оформляется одним из двух способов:
I. Послан» от кринку или письмо по адресу: 123242, Москва, а/я 20.
2. Оформить таказ можно па сайте www.solon-press.ru в разделе «Книга — почтой».
Бесплатно высылается каталог издательства по почте.
При оформтенип така та следует правильно и полностью указать адрес, по которому должны бы и» высланы книги, а также фамилию, имя и отчество получателя. Жслак п»-по ука тан» ,!о11о'1нигелыю свой телефон и адрес электронной почты.
Чсрет Hiiicpiici Вы можете в любое время получигь свежий каталог излагельства «(’ОДОНПресс», считав сто с адреса www.solon-press.ru/kat.doc.
Но вопросам приобретения обращаться: ООО «АЛЬЯНС-КННГ\ КТК» 'Гел: (095) 258-91-94, 258-91-95, www.abook.ru
Сайт издательства «СОЛОН-Пресс»: www.solon-press.ru
E-mail: solon-avtor@coba.ru
ISBN 5-98003-242-8
© Фриск В. В., 2006
© Макет и обложка «СОЛОН-Пресс», 2006
Предисловие
Книга «Расчеты и моделирование с помощью пакета компьютерной математики Mathcad» написана применительно к четырем учебным пособиям Фриск В. В. «Основы теории цепей» (М.: Ра-диоСофт, 2002), «ОТЦ. Лабораторный практикум на персональном компьютере» (М.: СОЛОН-Р, 2002) и «ОТЦ. Сборник задач с примерами применения персонального компьютера» (М.: СО-ЛОН-Р, 2003). «ОТЦ. Использование пакета Microwave Office для моделирования электрических цепей на персональном компьютере» (М.: СОЛОН-Р, 2004).
Цель книги — помочь студентам в изучении дисциплины «Основы теории цепей» (ОТЦ) и побудить их к самостоятельному использованию персонального компьютера для автоматизации расчетов и математического моделирования электрических цепей.
Mathcad это многофункциональная интерактивная вычислительная система математики, позволяющая решать математические задачи как численно, так и аналитически. Особенно важно, что все это можно делать не прибегая к программированию. Формулы отображаются стандартными математическими символами, включая греческие буквы. В систему встроена двух- и трехмерная графика, есть возможность подключения к популярным офисным и конструкторским программам, возможен выход из программы прямо в Интернет.
Предполагается, что читатель имеет начальное представление об Mathcad и предварительные знания по курсу «Основы теории цепей».
Требование к программному обеспечению
Рекомендуется установить на свой персональный компьютер систему (пакет) компьютерной математики Mathcad самой последней версии (http://www.mathsoft.com/).
Посетить образовательный математический сайт «ЕХРопеп-ia.ru» (http://www.exponenta.ru/).
Требования к системе Mathcad 11 (12) Single-user Edition:
•	Windows 9<S SE, ME, NT 4.0 SP6, 2000 SP2, XP пли выше;
•	персональный компьютер с процессором Pent iuin/C eleron 233 MHz/300 MHz или выше;
3
Предисловие
•	минимум 96 MB RAM. 256 МВ или больше рекомендуется для повышения производительности;
•	CD-ROM или DVD-дисковод;
•	клавиатура и мышь или совместимые устройства;
•	SVGA-видеокарта и монитор;
•	по крайней мерс 150 МВ пространства на жестком диске.
Internet Explorer версии 5.5 или выше требуется для функционирования системы справки (Help) доступа к HTML-файлам в окне Resources, открытия и сохранения HTML-файлов и автоматической активации продукта. Нет необходимости в том, чтобы Internet Explorer был основным браузером. 1Е 6 может быть установлен с CD-диска Mathcad.
Рекомендуется прямое соединение с Интернет.
Excel, MATLAB, S-PLUS, Axum и SmartSketch-компоненты в Mathcad требуют наличия соответствующих версий этих продуктов.
Инсталляция пакета Mathcad обычно нс вызывает затруднений, если у вас достаточно оперативной памяти и много свободного места на жестком диске. Перед установкой не забудьте включить свой принтер.
После установки обязательно запустите Resource Center (Help/Resource Center) и пролистайте его по возможности не один раз. Информация, содержащаяся там, значительно расширю Ваш кругозор по применению данного пакета.
1 Расчет резистивных электрических цепей
Найдем с помощью Machcad общее сопротивление последовательно соединенных резисторов. На рис. 1.1 показан электронный лист программы. Здесь знак «:=» — знак присвоения, знак «=» служит для вывода результата. Для того чтобы вводить нижние индексы сопротивлений, следует использовать клавишу «[». Например, набрав на клавиатуре «R[l», на экране получим «Rj». Знак суммы можно ввести, щелкнув по соответствующей кнопке в панели Calculus рис. 1.2.
Так же просто можно вычислить общее сопротивление пяти параллельно соединенных резисторов (рис. 1.3).
Последовательное соединение резисторов
п ;= 5	- количество резисторов
R1 := 1	- сопротивление первого резистора, Ом
R2:= 2	- сопротивление второго резистора, Ом
R3:= 3	- сопротивление третьего резистора, Ом
:= 4	- сопротивление четвертого резистора, Ом
R = 5	- сопротивление пятого резистора, Ом
5’
П
R У R. R=15 • общее сопротивление, Ом к=1 к
Рис. /./
1 Расчет резистивных электрических цепей
Рис. 1.2
Параллельное соединение резисторов
R1
п := 5	- количество резисторов
r •= 1	- сопротивление первого резистора, Ом
r2:= 2	- сопротивление второго резистора, Ом
r := з - сопротивление третьего резистора, Ом
R4:= 4	- сопротивление четвертого резистора, Ом
r •- 5 - сопротивление пятого резистора, Ом
5’
R = 0.438 - общее сопротивление, Ом
Рис. 1.3
г
Преобразование звезды резисторов в треугольник
1
“Звезда"	“Треугольник"
R1 := 1 - сопротивление первого резистора звезды, Ом
R2 := 2 - сопротивление второго резистора звезды, Ом
R3 := 3 - сопротивление третьего резистора звезды, Ом
R2
R12 := R1 +R2 + R1 — R3
R3
R23 := R2 + R3 + R2 • —
R1
R1
R31 := R3 + R1 + R3-^>
R2
R12 = 3.667 - сопротивление ветви 1 - 2 треугольника, Ом
R23 =11	- сопротивление ветви 2-3 треугольника, Ом
R31 = 5.5	- сопротивление ветви 3 - 1 треугольника, Ом
Рис. 1.4
При преобразовании треугольника сопротивлений в эквивалентную звезду и обратно можно отказаться от использования нижних индексов (рис. 1.4 и 1.5).
Рассчитаем входное сопротивление R в параллельно-последовательной цепи рис. 1.6. Здесь резисторы R2 и R3 соединены параллельно, а резистор R1 подключен последовательно к ним.
1 Расчет резистивных электрических цепей
Преобразование треугольника резисторов в звезду
“Треугольник”
з R3
R2 2
“Звезда”
R12 := 1 - сопротивление ветви 1 - 2 треугольника, Ом
R23 := 2 - сопротивление ветви 2-3 треугольника, Ом
R31 := 3 ~ сопротивление ветви 3 - 1 треугольника, Ом
R12- R31
R1 ;=--------------- R1 = 0.5	- сопротивление первого резистора звезды, Ом
R12 + R23 + R31
R12  R23
R2 •=--------------- R2 = 0 333 ~ сопротивление второго резистора звезды, Ом
R12 + R23 + R31
R3 := ————————	R3 = 1	- сопротивление третьего резистора звезды, Ом
К12 + К23 + К31
Рис. 1.5
R1
R3
R1 := 1
- сопротивление первого резистора, Ом
R2 :=2
- сопротивление второго резистора, Ом
R3 := 3
- сопротивление третьего резистора, Ом
R := R1 +
R2R3
R2 + R3
R = 2.2 - входное сопротивление, Ом
Рис. 1.6
2 Законы Ома и Кирхгофа
•	Построим зависимость тока от сопротивления I(R) при постоянном напряжении U = 10 В. Будем считать, что сопротивление меняется от 0,5 до 6 Ом. Для задания области определения функции в Mathcad существует следующая конструкция:
К:=<первая точка>,<вторая точка>;<последняя точка>
где <первая точка>=0.5;
<вторая точка>=:0.6;
<последняя точка>=6.
Для построения графика нужно щелкнуть по соответствующим кнопкам панелей Math и Graph (рис. 2.1).
Рис. 2.1
Далее ввести имя аргумента «R» возле оси «X» и имя функции «I(R)» возле оси «У». Автоматически построится график зависимости тока от сопротивления. Щелкнув два раза на этом графике, его можно форматировать по своему усмотрению (рис. 2.2), например, сделать подписи к осям, щелкнув на закладке Labels (рис. 2.3). В результате получится искомая зависимость (рис. 2.4).
Если на графике не будут отображаться русские буквы, то щелкните мышкой на имени функции «I(R)» и установите шрифт с кириллицей (Суг).
•	Построим вольт-амперную характеристику (ВАХ) линейного резистивного элемента. Очевидно, что его ВАХ выражается следующей функцией
U(I) = R1.
2 Законы Ома и Кирхгофа
Formatting Currently Selected ... |X
X-Y Axes у Гасе$ Labels
Defaults
0 ;Lo.q S calef
0 Grid Lines
0 Numbered
0 Autoscale
0 Show Markers
0 Auto Grid
Number of Grids:
Q Log Scale 0 Grid Lines 0 Numbered 0 Autoscale О Show Markers 0 Auto Grid Number of Grids:
Axis Style
Q Boxed 0 Egual Scales
О Crossed
О None
Grid Colot... ]
OK ] [ Отмена
[ Справка j
Puc. 2.2
Puc. 2.3
Пусть ток I меняется в диапазоне 0...4 А. Вторую точку выберем равной 0,1 A, R = 100 Ом. В результате получим линейную характеристику, выходящую из начала координат (рис. 2.5).
10
и
R := 0.5, 0.6 ..6	- диапазон изменения
сопротивления, Ом
U _•= ю	- напряжение на резисторе, В
U
I(R) := —	- ток (закон Ома), А
R
Рис. 2.4
•	Построим ВАХ идеализированного независимого источника ЭДС Е = 8 В при изменении тока I в диапазоне 0...4 А с внутренним сопротивлением г = 2 Ом и нагрузкой R (рис. 2.6).
Из обобщенного закона Ома для замкнутой цепи нетрудно получить формулу ВАХ источника
U(l) = Е - rl.
Это уравнение прямой линии. Из построенного графика (рис. 2.6) хорошо видно, что в режиме холостого хода (I = 0), U = Е = 8 В. В режиме короткого замыкания (U = 0) ток равен току короткого замыкания
I = 1Кз = Е/г =8/2 = 4 А.
Если положить г = 0, то построится ВАХ идеального источника ЭДС (рис. 2.7).
И
2 Законы Ома и Кирхгофа
I := 0, 0.1 ..4	- диапазон изменения тока, А
R := 100	~ сопротивление резистора, Ом
U(I) = RI -ВАХ, В
Рис. 2.5
•	Построим ВАХ идеализированного независимого источника тока J = 4 А при изменении напряжения U в диапазоне 0...4 В с внутренней проводимостью g = 1 См и нагрузкой R (рис. 2.8). Из первого закона Кирхгофа для данной цепи нетрудно получить формулу ВАХ источника тока
I(U) = J - gU.
Это уравнение прямой линии. Из построенного графика (рис. 2.8) хорошо видно, что в режиме холостого хода (I = 0), U = J/g = 4 В. В режиме короткого замыкания (U = 0) ток 1 равен току источника тока I = J.
Если положить g = 0, то построится ВАХ идеального источника тока (рис. 2.9).
•	Построим зависимость мощности Р во внешнем резисторе R (рис. 2.6) при изменении этого сопротивления. Легко показать, что в этом случае мощность выражается следующий формулой
12
I
I := 0, 0.1 ..4
E :=8
г := 2
U(I) := E-r-I
- диапазон изменения тока, A
- ЭДС источника, В
-	внутреннее сопротивление источника ЭДС. Ом
-	ВАХ источника, В
Рис. 2.6
P=RP = r\_JL_
R -г г
будем считать, что
R = 0...Ю Ом — сопротивление нагрузки;
г — 2 Ом — внутреннее сопротивление источника ЭДС;
Е - S В — ЭДС источника;
I = E/(R + г) — ток (закон Ома для замкнутой цепи).
Как видно из полученного графика (рис. 2.I0) мощность имеет максимум. Для его точного нахождения возьмем первую ироизвод-
13
2 Законы Ома и Кирхгофа
Ток, А
Рис. 2.7
I ;= о, 0.1 . 4	- диапазон изменения напряжения, В
J := 4	- ток источника, А
g := 1	- внутренняя проводимость
источника тока, см
I(U):=J-gU ВАХ источника, А
Рис. 2.8
14
Рис. 2.9
ную от мощности по сопротивлению (рис. 2.11) и приравняем ее к нулю. Вычислим корень полученного уравнения с помощью функции root.
Выберем встроенную переменную TOOL = 10“6. Чем больше величина TOOL, тем быстрее будет сходимость, чем меньше, тем сходимость медленнее, но ответ будет более точным. Выберем точку начального приближения х = 1,5 Ом.
В результате автоматического расчета получим, что максимальная мощность равна 8 Вт при R = г = 2 Ом.
• В цепи рис. 2.12 найти сопротивление R, если величины Е, Rj и 1 известны.
Решение. Составим уравнение по второму закону Кирхгофа
HR. + R) = E.
Найдем R с помощью Mathcad. Введем полученное уравнение, знак равенства в котором вводится с помощью Boolean (рис. 2.13), далее вводится знак символьного равенства (рис. 2.14), ключевое слово solve, запятая и R. Щелкнув вне этой формулы, автоматически получим искомую формулу, т. с.
R = ^-LA.
/
15
2 Законы Ома и Кирхгофа
R := 0, 0.1 .. 10 - диапазон изменения сопротивления, Ом
Е := 8	- ЭДС источника, В
г = 2	- внутреннее сопротивление
источника ЭДС, Ом
/ Е \2
P(R) :=	------ • R - мощность, Вт
\ R + r /
Мощность, Вт
P(R)
Сопротивление, Ом
Найдем точку экстремума
f(R) := A P(R)
- первая производная мощность, Вт
х := 1.5
- начальное приближение, Ом
TOL := 10'6
- встроенная переменная
R := root (f(x), х) - решение уравнения f(x) = 0 r = 2	- точка экстремума, Ом
P(R) = 8	- максимальная мощность, Вт
Рис. 2.10
16
Рис. 2.11
Второй закон Кирхгофа
1  (R1 + R) = Е solve, R
-IR1 + Е
I
Рис. 2.12
Рис. 2.13
Рис. 2.М
17
3 Расчет разветвленных цепей постоянного тока
Для расчета разветвленных резистивных цепей постоянного тока разработано множество методов, например, уравнений Кирхгофа, контурных токов, узловых потенциалов, наложения и др. Математически они требуют решения некоторой линейной системы уравнений, например	такой, как (3.1).
\7ц • х,	+ ап	 х2	+ я13 • х3	= Е]
< я21 •	+ а22	• х2	+ а23  х3	= Е2	(3.1)
«31 '*1	+ «32	‘*2	+ «33 -*3	= £3
где ац, ..., азз — постоянные коэффициенты;
Е]..Е3 — правые части системы (внешние воздействия);
Xi, ..., хз — искомые неизвестные (токи, потенциалы и пр.).
Решать такие системы линейных уравнений можно разными способами, но методически лучше выбрать такой: перевести систему в матричную форму (3.2).
(7И а[2 а]3				
^21	@22	@23	Х2	=	е2	,	(3.2)
^@3]	@32	@33 >				
или
где
и решить с помощью команды Isolve. Перед расчетом присвоим переменной ORIGIN значение единицы, чтобы столбцы и строки матриц нумеровались, начиная с единицы.
• Рассмотрим пример. Определить все токи методом уравнений Кирхгофа в цепи (рис. 3.1), если Е = 12 В, R1 = 6 Ом, R2 = 4 Ом, R3 = 12 Ом.
18
Е := 12	- ЭДС источника, В
R1 := 6 - сопротивление первого резистора, Ом
R2 := 4 - сопротивление второго резистора, Ом
R3 := 12 - сопротивление третьего резистора, Ом
Решение системы линейных алгебраических уравнений
ORIGIN :=1 - начало нумерации столбцов и строк матрицы
4	1	1 '
R1 -R2 О
ч0 R2 -R3y
матрица коэффициентов
В :=
I := 1solve(A,B)
1.333
-1
-0.333
х.	У
1,:= 1.333	12:=-1	13:=-0.333 - токи, А
Проверка
о
В:=А1 В= 12 о
Рис. 3.1
19
3 Расчет разветвленных цепей постоянного тока
Запишем систему по методу уравнений Кирхгофа
/, 4 /2 + /, =0 < /?,/, - /?2/, = Е
/?2/2 - R3/3 =0
и переведем в матричную форму
( 1 1
Я, -R2 ч 0 R.
р
Е .0
Вес остальное, включая и проверку, сделаем с помощью Mathcad (рис. 3.1). Порядок ввода матрицы 3x3 показан на рис. 3.2.
Вычислив токи, легко составить баланс мощностей для данной схемы (рис. 3.3).
Как видно из этих расчетов, баланс сошелся.
Рис. 3.2
Баланс мощностей
Pi :=£•!., Pi := 16 мощность источника, Вт
Рр := (I^-RI +(I2)2 R2 +(I3)- R3
Рр = 16 - мощность приемников, Вт
Рис. 3.3
20
4 Расчет мгновенных токов и напряжений
Построим зависимость мгновенного значения синусоидального напряжения u(t) от времени t и рассчитаем его основные параметры. Пусть данное напряжение описывается следующим выражением
u(t) = Umsin(cot + \|/).
Задаваясь значениями амплитуды, частоты, начальной фазы и временным интервалом, можно рассчитать период, угловую частоту, действующее значение, размах и построить графики напряжения и действующего значения u(t) (рис. 4.1). Ввод греческих символов показан на рис. 4.2.
21
4 Расчет мгновенных токов и напряжений
Замените в данном электронном листе sin на cos и убедитесь в том, что при этой замене действующее напряжение останется прежним — 1,414 В.
• Рассмотрим математическую модель импульсного источника напряжения, например трапециида-льного (рис. 4.3).
Здесь
U — максимальное значение импульса;
Pi — начало переднего фронта;
Р2 — начало плоской вершины;
Рз — конец плоской вершины;
р4 — точка возвращения к исходному состоянию;
Т — период.
Перейдем от графического представления импульса к формульному (4.1).
О
	a}t + b}
U(t) = <	U
a2t + b2 О
О < / < /?, А t < Pi Pi^t < Pi, Pi<t<pA p,<t<T
(4.1)
где
U b = Ч - рл
Pi - Pi' 2 Pi - Pi
Pl - P\ Pl- Pl
22
Рис. 4.4
Рис. 4.5
Для ввода формулы (4.1) в электронный лист Mathcad следует использовать четыре раза команду Add Line (рис. 4.4). Ввод опе-
ратора if и знака < показан на рис. 4.4. и 4.5 соответственно.
Результат вычисления показан на рис. 4.6.
Задаваясь конкретными значениями параметров импульса, можно получить его график (рис. 4.6).
• Из трапсциидального импульса легко получить прямоугольный импульс ПОЛОЖИВ р2 = Р1 и Р4 = р3.
При этом формулу (4.1) можно заменить на более простую (4.2).
w(r) = <
О U О
о< К Р\ p2<t< р} Рь<1 <т
(4.2)
В результате получим прямоугольный импульс рис. 4.7.
Трапециидальное напряжение
и := 2.5	- максимальное значение, В
р1 := 0.1	- начало переднего фронта, с
р2 := 0.2	- начало плоской вершины, с
рЗ := 0.4	- конец плоской вершины, с
р4 := 0.5	- точка возвращения к
	исходному уровню, с
Т := 0.6	- период,с
t: = 0, 0.001 Т . Т	временной отрезок, с
О if 0 < t < р1
Ut _ U-р1 р2 - р1 р2 - р1 U if р2 t < рЗ
-Ut , U-p4 р4 - рЗ р4 - рЗ
if р1 < t < р2
if рЗ < t < р4
трапециидальное напряжение, В
Рис. 4.6
23
4 Расчет мгновенных токов и напряжений
Прямоугольное напряжение
и = 2.5
р1 := 0.1
р2 := 0.2
рЗ := 0.4
р4 := рЗ
Т := 0.6
t := 0, 0.001Т..Т
-	максимальное значение, В
-	начало переднего фронта, с
-	начало плоской вершины, с
-	конец плоской вершины, с
-	точка возвращения к исходному уровню, с
-	период,с
-	временной отрезок, с
u(t)=
0 if 0<t< р1
U if р2 < t < рЗ 0 if р4 < t < Т
прямоугольное напряжение, В
Рис. 4.7
• Исследуем форму тока в L-цепи, если к ней приложено пилообразное напряжение (рис. 4.8).
Для задания пилообразного напряжения разобьем временной интервал на три отрезка O...pj, P1...P2 и Р2...Т. На каждом отрезке напряжение будет представлено своей формулой (уравнением прямой линии at + b). Расчет коэффициентов а и b можно поручить компьютеру, используя функции slope и intercept (рис. 4.9).
Связь между током и напряжением на L представлена соответствующим интегралом. Как видно из рис. 4.8, форма тока не совпадает с формой приложенного напряжения.
Читателю предлагается взять этот интеграл «вручную» и сделать вывод о характере полученной зависимости тока от времени. Заметим, что при взятии этого интеграла с помощью Mathcad нужно
24
Пилообразное напряжение в L-цепи
i(t) L
а := 4 р1 := 0.25 р2 := 0.75 Т := 1
u(t)
- коэффициент, В/с
- точка окончания первого интервала, с - точка окончания второго интервала, с - период,с
0, 0.001-Т .. Т - временной интервал, с
u(t)=
at
-a-t+2 a t-4
if if if
р1 < t < p2
- напряжение на катушке, В
0)
0)
cu
10 := О
- начальное значение тока, A
L := 1
I(t) =1
- КП
- индуктивность, Гн
• J u(x)dx+I0 - ток в катушке, А о
Время, c
*
Рас. 4.8
25
4 Расчет мгновенных токов и напряжений
помнить о существовании константы интегрирования С (рис. 4.10).
Линейная регрессия y(t) = a*t + b
ORIGIN := 1
f 0 'I
VX := К 25	~ значение аргумента t
f
VX := H - значение функции y(t)
Вычисление коэффициентов а и b линейной регрессии
а := slope (VX, VY)
a = 4
b := intercept (VX, VY) b = 0
Puc. 4.9
Puc. 4.10
26
5 Вычисления с комплексными числами
В ОТЦ широко используются комплексные числа.
Z = а + j  b — комплексное число в алгебраической форме;
j =4-\ — мнимая единица;
Rc(Z) = а — действительная часть комплексного числа Z;
Im(Z) = b — мнимая часть комплексного числа Z;
Z = Z -eJ* — комплексное число в экспоненциальной форме;
Z = |Z| = w + Ь2 — модуль Z;
Ф = arg(Z) — фазовый угол (аргумент) Z.
Z = а - j • b — комплексно-сопряженное число.
В Mathcad встроены комплексные числа и операции над ними. Математики мнимую единицу обозначают буквой «i>, а в ОТЦ используют букву «j», чтобы нс спутать с током. Настроим отображение мнимой единицы. Командой Result... (рис. 5.1) вызовем окно Result Format и установим Imaginary value в I(J) (рис. 5.2).
Проведем проверку настройки. На клавиатуре наберем «lj=». Должно появиться «j=j».
Для упрощения откажемся от подчеркивания комплексных чисел в Machcad. Пример комплексных чисел приведен на рис. 5.3. Заметим, что для ввода мнимой единицы следует набирать «lj», а для ввода комплексно-сопряженного числа на клавиатуре нужно
р>| File Edit View Insert П ’ Ы О Ek vz
Tools Symbolics
Equation...
Normal
v iAnal
Tabs...

Puc. 5.1
27
5 Вычисления с комплексными числами
Result Format __________________ |SH|
Number Format. Display Options Unit Display Tolerance
Matrix display style	Automatic	v
[j Expand nested arrays
Imaginary value	ЦЦ] v-
Radix	Decimal	v'
[ OK | [ Отмена ] [ Справка
Рис. 5.2
Комплексные числа
j = j	- проверка мнимой еденицы
Z := 3+4 • j - комплексное число
Re(Z) = 3	- действительная часть
комплексного числа Z
lm(Z) = 4	- мнимая часть комплексного числа Z
|Z| = 5	" модуль комплексного числа Z
arg(Z) = 0 927 - аргумент (главное значение) комплексного числа Z, рад
arg(Z)	.	.
—— = 53.13 - аргумент (главное значение)
de9	комплексного числа Z, градус
Z = 3-4j
- комплексно-сопряженное число
Рис. 5.3
набрать «Z”», причем обозначаются комплексно-сопряженные числа с чертой сверху. При делении на deg происходит перевод радиан в градусы.
Ввод модуля показан на рис. 5.4.
Функции Re и*1т можно ввести с клавиатуры или с помощью кнопки «f(x)» (рис. 5.5).
• Отобразим комплексное число 1 = 5 — j4 и комплексно-сопряженное ему число на комплексной области в виде точек. Для этого введем комплексное число. Выведем комплексно-сопря-
28
Math jcj Д Calculator , g)
- <?
£] «/»
In log Г T x2 xY 9 /
it 4 5 6 x
+ 12 3 +
:= .	0	-	=
Puc. 5.4
женное число, используя знак равенства. Вставим график декартовой системы координат (рис. 5.6).
В открывшемся шаблоне графика возле оси «X» введите имена действительных частей чисел через запятую, а возле оси «У» имена мнимых частей. Щелкните вне графика.
Щелкните два раза на этом графике, чтобы отформатировать его, особенно trace 1 и trace 2, так, как это показано на рис. 5.7.
29
5 Вычисления с комплексными числами
Рис. 5.6
Formatting Currently Selected
X-YAxes Traces Labels Defaults
Legend	—Im^J^eight
“Trace 1 x's solid
traceT trace 4 trace 5 trace 6
trace 2
none none none
ШИ v dot
dadot Solid dot
jnct
—gwu-mag cya brn
blu v
lines lines lines
lines
red lines
I I Hide Arguments
0 Hide Legend
[ OK | [ Отмена ~] [ Применить j [ Справка ]
Puc. 5.7
Как видно из рис. 5.8, точки расположились симметрично относительно оси действительных чисел.
•	Найдем комплексную мощность пассивного двухполюсника, если комплексное напряжение и ток имеют вид U = —40 + J40 В, 1 = 2 + j4 А. Все вычисления показаны на рис. 5.9. Как видно из этого рисунка, баланс комплексных мощностей сошелся.
•	Построим диаграммы сопротивления и проводимости цепи с последовательным соединением резистивного и реактивного сопротивлений при изменении одного из этих параметров (рис. 5.10).
30
Комплексная плоскость
Re(I), Re(I) Действительная ось
Рис. 5.8
Комплексная мощность
I := 2 + 4 • j	- комплексный ток, А
I = 2 - 4j - комплексно-сопряженный ток, А
U ;= - 40 + 40 • j - комплексное напряжение, В
Si := U • I Si := 80 + 240j - комплексная мощность источника, ВА
Р := Re(Si)	Р = 80	- средняя мощность, Вт
Q := Im(Si)	Q = 240 - реактивная мощность, вар
|Si|= 252.982
Z:=y Z = 4 + 12j
-	полная мощность,BA
-	комплексное сопротивление двухполюсника, Ом
Э
Spr := (|1|) • Z Spr = 80 + 240j - комплексная мощность приемника, ВА
Рис. 5.9
31
5 Вычисления с комплексными числами
Диаграммы сопротивлений и проводимостей
R := 0, 0.1 ..100 - изменение сопротивления, Ом
X := 5	- реактивное сопротивление, Ом
Z(R) := R + j - X - комплексное сопротивление, Ом 1
Y(R) :=---- - комплексная проводимость, Ом
Рис. 5.10
При последовательном соединении элементов комплексное сопротивление равно
Z = R + jX.
Комплексная проводимость — это обратная величина сопротивления
Y = 1/Z.
При изменении резистивного сопротивления R геометрическим местом комплексного сопротивления будет прямая, параллельная действительной оси (рис. 5.11).
Читателю предлагается самому построить диаграмму сопротивления при отрицательном значении реактивного сопротивления X и сделать соответствующий вывод.
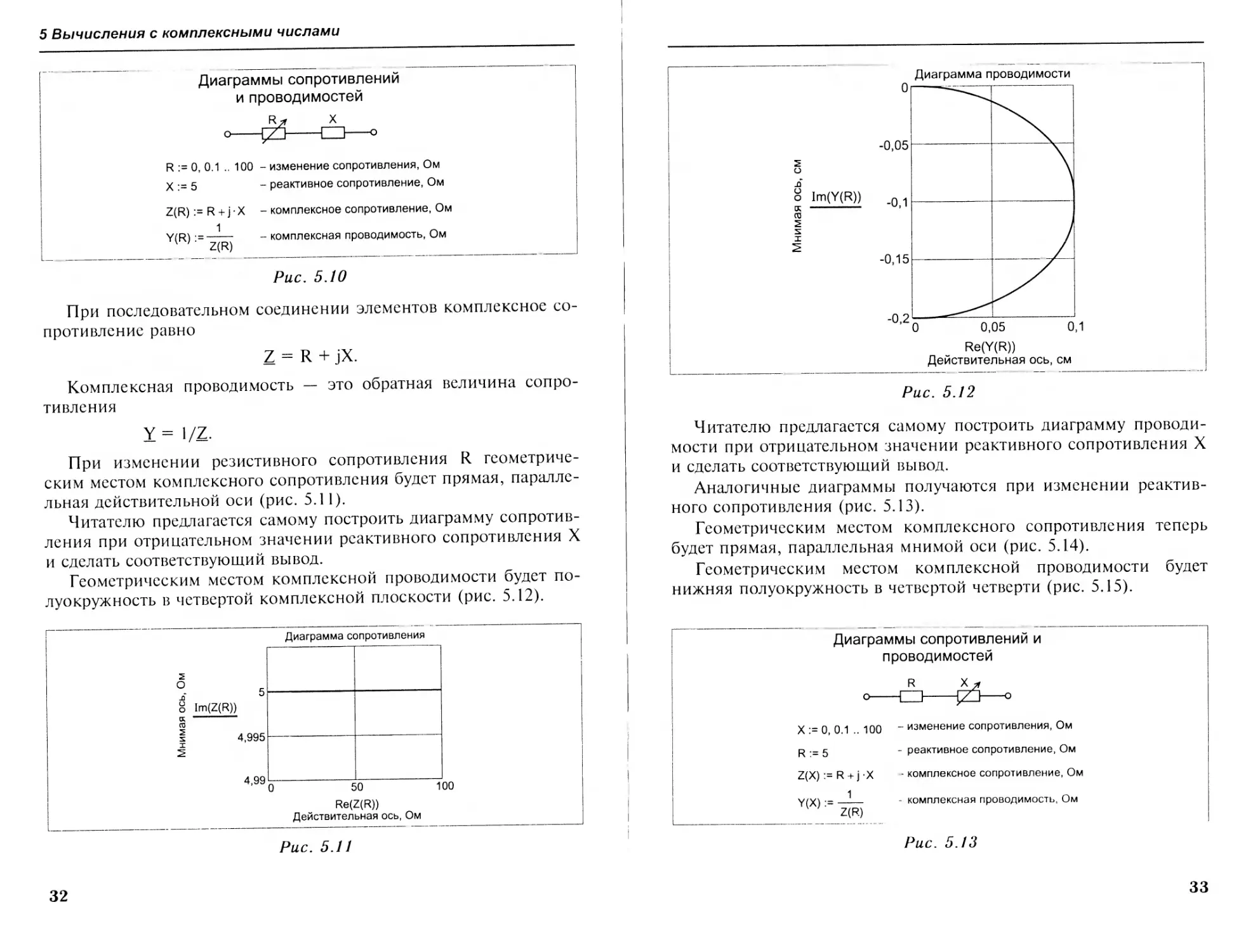
Геометрическим местом комплексной проводимости будет полуокружность в четвертой комплексной плоскости (рис. 5.12).
Диаграмма сопротивления
Re(Z(R)) Действительная ось, Ом
Рис. 5.11
32
Диаграмма проводимости
о lm(Y(R)) к ----------
го
S I
Re(Y(R))
Действительная ось, см
Рис. 5.12
Читателю предлагается самому построить диаграмму проводимости при отрицательном значении реактивного сопротивления X и сделать соответствующий вывод.
Аналогичные диаграммы получаются при изменении реактивного сопротивления (рис. 5.13).
Геометрическим местом комплексного сопротивления теперь будет прямая, параллельная мнимой оси (рис. 5.14).
Геометрическим местом комплексной проводимости будет нижняя полуокружность в четвертой четверти (рис. 5.15).
Диаграммы сопротивлений и проводимостей
X := 0, 0.1 .. 100	- изменение сопротивления, Ом
R := 5	- реактивное сопротивление, Ом
Z(X) :=R + jX Y(X) := — Z(R)	- комплексное сопротивление, Ом - комплексная проводимость, Ом
Рис. 5.13
33
5 Вычисления с комплексными числами
5
О
8 Im(Z(X))
СК ---------
га
S s X Z
Диаграмма сопротивления
Re(Z(X))
Действительная ось, см
Рис. 5.14
Рис. 5.15
Читателю предлагается самому построить диаграмму проводимости при отрицательном значении реактивного сопротивления X и сделать соответствующий вывод.
34
6 Частотные характеристики электрических цепей
С помощью системы Mathcad можно строить частотные характеристики электрических цепей с RLC-элементами RL-цепи (рис. 6.1).
Для зависимости модуля входного сопротивления и фазы от угловой частоты представлена на рис. 6.2, модуля передаточной функции напряжения Н(со) (АЧХ) и ее аргумента (ФЧХ) от угловой частоты на рис. 6.3.
RL - цепь
R
со := О, 0.1 .. 10
R := 1
L := 1
Z1(co) := R + j-co- L
Z2(co) :=j a) L
H(co) :=
Z2(co)
Z1(co)
диапазон частот, рад/с
-	сопротивление резистора, Ом индуктивность катушки, Гн
-	комплексное входное сопротивление. Ом
-	комплексное выходное сопротивление, Ом
-	комплексная функция передачи напряжения
Рис. 6.1
Рис. 6.2
35
6 Частотные характеристики электрических цепей
Угловая частота, рад/с
I агд(Н((о)) de9
Рис. 6.3
Аналогичные характеристики для RC-цепи (рис. 6.4) показаны на рис. 6.5, 6.6.
RC-цепь
со := 0, 0.1 .. 10	- диапазон частот, рад/с
R := 1	- сопротивление резистора, Ом
С := 1	- емкость конденсатора, Ф
Z1(w):=R—- комплексное входное сопротивление, Ом
Z2(w) := ——	- комплексное выходное
сопротивление, Ом
Н(о>) :=
Z2(o)
Z1(a>)
- комплексная функция передачи напряжения
Рис. 6.4
Рис. 6.5
36
Рис. 6.6
При построении частотных характеристик для RLC-цепи (рис. 6.8) блокируются встроенные единицы измерений (рис. 6.7).
Рис. 6.7
В результате получаются следующие характеристики (рис. 6.9).
Построим частотные характеристики реактивного последовательного LC-двухполюсника (рис. 6.11).
Как видно из рис. 6.11, при последовательном соединении катушки и конденсатора алгебраически складываются их реактивные сопротивления. Частотная характеристика сопротивления такого двухполюсника показана на рис. 6.12. Она пересекает ось угловой
37
6 Частотные характеристики электрических цепей
RLC-цепь
R := 350
- сопротивление резистора, Ом
С := 30 • 10'9	-- емкость конденсатора, Ф
L :=50- 10‘3
индуктивность катушки, Гн
т0= 2.582х104 - резонансная частота, рад/с
QV	з
f =-—	fn =4.109 х 10 - резонансная частота, Гц
и 2 л и
р ;= р= 1.291 х 103 - характеристическое
* и	сопротивление, Ом
Q :=£ Q = 3.689	- добротность
d := ^ d = 0.271	- затухание
3	3 з
со := 10-10, 10.5-10 ..50-10 - диапазон частот, рад/с
Z1(w) :=R+j'W L- -1-
(0' С
4/(«):= l^arg(Z1(M))
Z2(“) :=<jyc
lj, . Z2(co)
H(w)  Z1W
Ф(о>) := i|^-arg(H(<o))
-	комплексное сопротивление, Ом
-	фаза входного сопротивления,градус
-	комплексное выходное сопротивление, Ом
-	комплексная функция передачи напряжения
фаза передаточной функции, градус
Сопротивление, Ом
Рис. 6.8
СО
Угловая частота, рад/с
Рис. 6.9
38
Модуль
(и
Угловая частота, рад/с
Рис. 6.10
Реактивный LC-двухполюсник
со := 0, 0.05 ..2	- частотный диапазон, рад/с
L := 1	- индуктивность, Гн
С := 1	- емкость, Ф
соп:= ;-4— соО = 1 — резонансная частота, рад/с Тис
Х(ш) := со  L-- реактивное сопротивление, Ом
со • С
Z(<o) :=) Х(о>)
- комплексное сопротивление, Ом
- комплексная проводимость, См
Рис. 6.11
Рис. 6.12
39
6 Частотные характеристики электрических цепей
частоты при резонансной частоте ю0. Из этого рисунка хорошо видно, что в области ниже резонансной сопротивление двухполюсника имеет емкостной характер. В области выше резонансной частоты сопротивление двухполюсника имеет индуктивный характер.
Кривая частотной характеристики проводимости данного двухполюсника показана на рис. 6.13.
Частотная характеристика проводимости
Рис. 6.13
Читателю предлагается самому построить аналогичные частотные характеристики параллельного реактивного LC-двухполюсника.
40
7 Расчет переходных процессов
Включим постоянную ЭДС Е в RC-цепь (рис. 7.1). Построим зависимость напряжения на конденсаторе от времени u(t) при te [to, tn]. Будем считать, что до коммутации в цепи имели место нулевые начальные условия to = 0, u(to) = uo - 0. Как известно из ОТЦ, искомый процесс в такой цепи первого порядка описывается следующим линейным дифференциальным уравнением первого порядка с неизвестной функцией u(t):
du(f) 1 . . Е + -м(0 =—, at т т
где т = RC — постоянная времени цепи.
Решим это уравнение с помощью ключевого слова Given и функции odesolve (рис. 7.1).
Цепь первого порядка
u(t)
Е := 3	- ЭДС, В
т := 3	- постоянная времени цепи, с
tO := 0	- первая точка, с
иО := 0	~ напряжение при tO, В
tn := 3 • т Тп = 6 - последняя точка, с
N := 1000	~ количество точек
Given
d u(t) + Hffl. = - - дифференциальное уравнение dt т т
u(tO) = u0	- начальное условие, В
u: = Odesolve(t, tn)
Рис. 7.1
41
7 Расчет переходных процессов
Встроенная функция odesolve предназначена для решения дифференциальных уравнений линейных относительно старшей производной и записанных в общепринятой математической форме.
Эта функция решает дифференциальное уравнение методом Рунге—Кутты с фиксированным шагом. Для перехода на автоматический шаг нужно щелкнуть в рабочем документе по имени функции правой кнопкой мыши и выбрать в появившемся меню пункт Adaptive.
Обращение к функции имеет следующий вид
y:=Odesolve(t,tn,step) или y:=Odesolve(t,tn),
где у — имя искомой функции y(t);
t — переменная интегрирования;
tn — конец отрезка интегрирования;
step — шаг интегрирования.
Перед функцией odesolve необходимо поместить ключевое слово Given, затем ввести дифференциальное уравнение и начальные или граничные условия. В них следует использовать знак логического равенства (<Ctrl>+<=>). В записи производных можно использовать как оператор дифференцирования, так и «штрих» — знак производной (<Ctrl>+<F7>), например,
4-у(Г) или у'(Г).
at
В результате получим следующий график (рис. 7.2).
Рис. 7.2
42
Изменим начальное условие и0 < Е, например, введем ug = 2 В.
Получится график, такой как изображен на рис. 7.3.
Рис. 7.3
Из этого графика видно, что кривая напряжения начинается из точки 2 В и с течением времени возрастает, стремясь к установившемуся значению Е = 3 В.
Изменим начальное условие ug > Е, например, введем ug = 4 В.
Получим график, такой как изображен на рис. 7.4.
Как видно из этого графика, кривая напряжения начинается из точки 4 В и убывает, стремясь к установившемуся напряжению Е.
Измените начальное условие iig = Е, введите tig = 3 В. Получите график, такой как изображен на рис. 7.5.
Рис. 7.4
43
7 Расчет переходных процессов
Время, с
Рис. 7.5
Из этого графика видно, что при u0 = Е, переходной процесс отсутствует и сразу наступает установившейся режим.
• Построим зависимость тока разряда конденсатора в последовательной RLC-цепи (рис. 7.6) от времени. Дифференциальное уравнение, описывающее переходной процесс в такой цепи вто-
Цепь второго порядка
а := 0.1	- коэффициент затухания контура
со := 1 -^резонансная частота контура, рад/с
tn := 20	- конец отрезка интегрирования, с
N :=1000 - количество точек
Given
d2	d
— i(t) + 2 • a  — i(t)+2 • co2 i(t)=0 - дифференциальное dr	dt	уравнение
i(0)=0	i’(0) = -0.1	- начальные условия
i := Odesolve(t, tn)
Puc. 7.6
44
рого порядка (в электрическом RLC-контуре), как известно из отц, имеет следующий вид:
д'2/ , di	2 • а
---+ 2 • о - + со;. • / = О, dt dl	°
где
а — коэффициент затухания контура;
а>о — резонансная частота контура;
/(О — искомый мгновенный ток;
t — время.
Если выполняется условие а > <о0, то в контуре наблюдается апериодический процесс (рис. 7.7).
Если выполняется условие а < соо (а = 0,1), то в контуре наблюдается колебательный процесс (рис. 7.8).
Читателю предлагается самому определить, какой будет процесс при а = а>о?
•	Рассмотрим процессы в автогенераторе Ван-дер-Поля.
При £<< 1 (малая нелинейность) установившиеся колебания мало отличаются от гармонических (рис. 7.10).
При е>>1 (сильная нелинейность) установившиеся колебания становятся релаксационными (рис. 7.11).
•	Для расчета переходных процессов часто используется операторный метод. Система Mathcad предоставляет большие возможности для автоматизации этих расчетов.
Найдем с помощью Mathcad изображение единичной ступенчатой функции l(t)
К/) =
10
|1
при t < 0
при t > 0
Как видно из этой формулы, функция равна I, если t • 0; иначе она равна нулю.
45
7 Расчет переходных процессов
Рис. 7.8
Генератор Ван-дер-Поля
tn := 50	- конец отрезка интегрирования, с
е := 0.2	- параметр
N := 1000	- количество точек
Given
u”(t) _ e.(i _ uW^ u'G) ч u(t) = 0 - дифференциальное уравнение Ван-дер-Поля
u(0) = 0	u'(0) = 0.6	- начальные условия
u :=Odesolve(t, tn)
Рис. 7.9
Рис. 7.10
46
Рис. 7.11
Эта функция встроена в систему, обозначается Ф(х) и называется ступенчатой функцией Хевисайда (рис. 7.12).
Рис. 7.12
Для ввода этой функции и преобразования Лапласа используются кнопки, указанные на панелях (рис. 7.13).
Шелкнув вне рамки, получим следующий результат (рис. 7.14).
Читателю предлагается самому составить таблицу преобразования Лапласа от различных функций с помощью системы Mathcad. • Так же просто можно выполнить обратное преобразование Лапласа. Применим обратное преобразование Лапласа к изображению
47
7 Расчет переходных процессов
Рис. 7.13
1
ФЦ) laplace, t —> —
Рис. 7.14
Введем это изображение и с помощью кнопки invlaplace (обратное преобразование Лапласа) на панели Symbolic (рис. 7.15) получим ответ (рис. 7.16).
• Найдем напряжение U2(t) на выходе RC-цепи (рис. 7.17), если к цепи приложено линейно нарастающее напряжение uj(t) = kt.
Math
Symbolic	И
Modifiers assume substitute coeffs parfrac ztrans invztrans
|n| -
Puc. 7.15
Invlaplace, s—»	cos(t) + l-sin(t)
Puc. 7.16
48
План решения будет таков. Найдем операторную передаточную функцию напряжения H(s). Из нес, используя обратное преобразование Лапласа, получим переходную характеристику этой цепи
h(t) =
5
Для нахождения выходного напряжения применяем метол интеграла Дюамеля (рис. 7.17).
Интеграл Дюамеля
°—IF
u1(t)
u2(t)
У® invlaplace, s s
- обратное преобразование Лапласа
h(t) := exp	- nepex
u1(t) := k-t - входной сигнал
- переходная характеристика
u1(0) . h(t) ч-
£u1(x)j- h(t-x) dx
R-C - k- R- C- exp
• k - интеграл Дюамеля
u2(t) := RCk-RCexp
—— i • k - выходной сигнал
Puc. 7.17
Читателю предлагается самому, задавшись значениями R, С, к и временным интервалом, построить графики входного и выходного напряжений.
49
8 Расчет спектров
Рассмотрим линейный двухполюсник, к которому приложены два гармонических периодических (Т = 2л) напряжения с разными амплитудами и кратными частотами колебаний, например,
U|(t) = 8sin(2t) и U2(t) = 6sin(8t),
где t g [0, 2л].
Построим с помощью системы Mathcad два периода результирующего напряжения на входе этого двухполюсника u(t) = Ui(t) + U2(t) (рис. 8.1).
Негармонический сигнал
Т:=2-л	-период
t := 0, 0.01 . 2Т	- временной интервал
u(t) := 8sin(2t) + 6 • sin(8 • t) - периодический негармонический сигнал
Периодический негармонический сигнал
Рис. 8.1
Из этого рисунка хорошо видно, что результирующее напряжение u(t) периодическое, но имеет сложную, негармоническую форму.
• Как известно из ОТЦ, многие сигналы можно представлять в виде функций времени и в виде частотных и фазовых спектров. Построим с помощью системы Mathcad амплитудный спектр предыдущего негармонического сигнала, т. е. разложим его в тригонометрический ряд Фурье. Для расчета коэффициентов этого ряда добавим в электронный лист формулы Эйлера—Фу-
50
ръе (рис. 8.2). Заметим, что в литературе по ОТЦ постоянная составляющая обозначается как «Л()/2».
Строим график (дискретный спектр) обычным образом и только на закладке Traces в колонке Туре выбираем stem (рис. 8.3).
В результате получаим спектральную диаграмму, показанную на рис. 8.4.
Как и ожидалось, спектральные линии появились при к = 2 и 8 высотой 8 и 6 вольт соответственно.
Читателю предлагается самому изменить сигнал, например, к сигналу добавить постоянную составляющую
u(t) = 4 + 8sin(2t) + 6sin(8t).
Пронаблюдайте за изменением формы сигнала и появлением в спектре постоянной составляющей при к = 0 высотой 4 вольта.
• Построим дискретный амплитудный спектр прямоугольных импульсов амплитудой Um = 10 В, длительности timp = 0,2 мкс и периодом следования Т = I мкс. Один период такой последовательности импульсов показан на рис. 8.5.
0)1 :=	(1)1 = 1
А0:=у-[ u(t)dt J0
- угловая частота гармоники, рад/с
АО := 0 - постоянная составляющая, В
п :=1 .. 10
А(п) := y J u(t) cos(n <o1t)dt
- формулы Эйлера-Фурье
B(n) :=i- u(t) sin(n-<o1t)dt 1 •'0
C(n) := -/а(п)2+ B(n)2
k:=0..10
F(k) := I AO if k = 0	_ амплитудный
| C(k) if k > 0 дискретный спектр
Рис. 8.2
51
8 Расчет спектров
Рис. 8.3
Рис. 8.4
Для расчета коэффициентов тригонометрического ряда Фурье вновь воспользуемся формулами Эйлера—Фурье (рис. 8.6).
В результате получим дискретный амплитудный спектр (рис. 8.7). Из этого рисунка видно, что амплитуда гармоники, номер которой численно равен скважности Q, равна нулю.
Читателю предлагается самому изменить длительность импульса tjmp и проследить за изменениями в спектре и сделать соответствующий вывод.
52
Прямоугольные импульсы
Т := 1 -10'6 timp := 0.2 Ю 6
Um := 10
период следования, с
длительность импульса, с
- амплитуда импульсов, В
q •=...-I— Q = 5	- скважность
timp
Время, с
Рис. 8.5
col ;=?_2L {oi _ e 283 х 106 - угловая частота первой т	гармоники, рад/с
TOL := 10‘8
АО :=А- u(t) dt АО := 2	- постоянная
*	составляющая, В
п := 1..20
A(n) := yj u(t)-cos(nw1-t)dt
°	- формулы Эйлера-Фурье
B(n) := id u(t)-sin(n (o1t)dt 1 •'о
C(n) := yA(n)2 + B(n)2
k := 0..20	- номер гармоники
F(k):=|AO if k=0 амплитудный дискретный спектр |C(k) if k>0
Puc. 8.6
53
8 Расчет спектров
ПиГкПАТМК|Й ЯМППМТиПИк|Й гпгмгтп
Рис. 8.7
• Если сигнал непериодический (единичный импульс), то вместо тригонометрического ряда Фурье используют преобразование Фурье. Получают не линейчатый, а сплошной спектр. Данный спектр обычно называют спектральной плотностью. Построим спектральную плотность прямоугольного импульса амплитудой Um = 10 В, длительностью timp = 0,2 мкс (рис. 8.8).
Прямоугольные импульсы
timp := 0.2 -10’6	~ длительность импульса, с
Um := 10	~ амплитуда импульсов, В
-9
t := 0, 1 • 10 .. 2• timp - временной интервал, с
Время, с
Рис. 8.8
54
Для расчета плотности на интервале частот сое [0, соД используем двухстороннее преобразование Фурье (интеграл Фурье) (рис. 8.9).
сок := 2	сок = 6.283 х 10 7	- верхняя частота
timP	диапазона, рад/с
со := 0, 0.001 • сок .. сок - частотный диапазон, рад/с
TOL := 10’8
- точность вычисления
- timp
F(co) := u(t)e’J,0),tdt
- интеграл Фурье
S(co) := |Г(ю)|	- модуль спектральной плотности, Вс
Рис. 8.9
В результате получим АЧХ (модуль спектральной плотности) (рис. 8.10).
Рис. 8.10
Если известна спектральная плотность F(jco), то можно восстановить сам сигнал u(t) с помощью обратного преобразования Фурье «(/) = -l-j>(»e>“'J/.
2л \
Пусть спектральная плотность:
1 4 (Л (О' I /2(4(0
где а = 0,1 — коэффициент (рис. 8.11).
55
8 Расчет спектров
Обратное преобразование Фурье
а:=0.1	-параметр
сок := 12	верхняя частота диапазона, рад/с
со := 0, 0.001 сок..сок	- частотный диапазон, рад/с
F(co) :=---—~----------- спектральная плотность
1+а - со2 4-2 - j • со- а
S(co) := |F(co)|	- модуль спектральной плотности. Вс
Рис. 8.11
Если ввести формулу обратного преобразования так, как показано на рис. 8.12 с бесконечными пределами, то ресурсов компьютера может не хватить и u(t) не будет рассчитано.
Заменим бесконечность на 20 (рис. 8.13).
После такой замены можно получить график восстановленного сигнала (рис. 8.14).
Как видно из этого графика, сигнал представляет собой убывающее колебание вида
«(/) = e"a' sin(/).
F1 со 1 Ю 1 du)
8 - временной интервал, с
- предел интегрирования
- обратное преобразование Фурье
Рис. 8.12
56
-3
t := 0,1 • 10 ..8 - временной интервал, с
а •= 20	- предел интегрирования
U(t) := _L . I F(w) ei ("‘dw - обратное
Ja	преобразование Фурье
Рис. 8.13
•	Теперь найдем спектральную плотность «белого шума», т. е. плотность от сигнала, представляющего собой дельта-функцию 5(t).
СО при t = О
О при t ф 0
В системе Mathcad дельта-функция называется Dirac delta function и обозначается A(t). Как видно из рис. 8.15, спектральная плотность дельта-функции равна единице.
Белый шум
A(t)-e’j'“'ldt —> 1 - спектральная плотность >	дельта-функции
Рис. 8.15
Напомним, что для ввода бесконечности нужно нажать <Ctrl>+<Shift>+<Z>.
•	Рассмотрим колоколообразный видеоимпульс
u(t) = е U|-2, 2| с,
57
8 Расчет спектров
где t — время; a = 1 — коэффициент (рис. 8.16).
Колоколообразный импульс
t := -2, -1.9 ..2 - временной интервал, с
а := 1 - величина определяющая ширину импульса, 1/с
2
u(t) := еЧа	- колоколообразный импульс, В
U:=0.1	-уровень, В * I
Рис. 8.16
Рассчитаем длительность т этого импульса относительно уровня 0,1. Для этого нужно решить уравнение вида
e~(at)2 = U,
где U = 0,1 — уровень.
Как видно из рис. 8.16, это уравнение будет иметь два корня, т. к. график импульса пересекает уровень в двух местах. Разность этих корней и даст величину длительности т данного импульса. Продолжим расчеты в системе Mathcad (рис. 8.17).
Длительность импульса
ORIGIN := 1
.	-(Я'Х)2 ,,
f(x) := е =U - уравнение для расчета ширины импульса
I -1.5174271293851463509\
X := f(x) solve, х —> |	- решение уравнения
\ 1.5174271293851463509/
X, =-1.517 Х2 = 1.517 - корни уравнения
х := х2- X! т := 3.035	- длительность импульса, с
Рис. 8.17
58
Добавим к этим вычислениям расчет спектральной плотности данного импульса (рис. 8.18).
Спектральная плотность колокообразного импульса
F(co) :=J U(t)-e'j w t dt —> exp
- спектральная плотность, Вс
w := -7, -6.9 .. 7 частичный диапазон, рад/с
Рис. 8.18
Как и следовало ожидать, спектральная плотность F(co) получилась действительной, к тому же имеет колоколообразную форму.
Найдем ширину спектра на уровне 0,1 (рис. 8.19).
Ширина спектра
S(x) := F(x) = U -- уравнение для расчета ширины спектра
I -3.3911355242270962775 \
X := S(x) solve, х — >
\ 3.3911355242270962775 / решение уравнения
Х1 = -3.391	Х2 = 3.391	корни уравнения
wb = X2-X1	о)Ь = 6.782	ширина спектра, рад/с
Рис. 8.19
59
8 Расчет спектров
Читателю предлагается проверить утверждение, что чем больше длительность импульса, тем шире его спектр. Для изменения длительности импульса достаточно увеличить величину коэффициента а, например, взять а = 2.
•	Рассмотрим радиоимпульс с огибающей в виде предыдущего колоколообразного видеоимпульса
w(/) =е~(ш)2 cos(co0Z) , te[t1? t2] с, где / — время;
а = 1 1/с — коэффициент;
со о = 20 рад/с — частота заполнения;
tj = -1,517с, t2 = 1,517 с (рис. 8.20).
Рассчитаем спектральную плотность данного радиоимпульса (рис. 8.21).
Радиоимпульс
-2,-1.99 ..2	- временной интервал, с
соО := 20
а := 1
- частота заполнения видеоимпульса, рад/с
- величина определяющая ширину импульса, 1/с
t1 := -1.517
t2 := 1.517
u(t) :=
е’(а ’t)2 cos(w0 • t) if 11 < t < t2
- радиоимпульс, В
Puc. 8.20
60
Спектральная плотность радиоимпульса
rt2
F(co) := u(t)-e'J ‘” ldt - спектральная плотность, Вс Л1
w := -30, -29.9 .. 30 частотный диапазон, рад/с
Рис. 8.21
Как видно из полученного графика, спектральная плотность, в отличие от плотности видеоимпульса, имеетдва максимума. Читателю предлагается самому изменить частоту на «о = Ю рад/с и наблюдать, как данные максимумы переместятся на частоты — 10 и 10 рад/с.
•	Для нахождения спектра можно воспользоваться лапласовым изображением сигнала, в котором положить р = jco. Пусть сигнал представлен незатухающей косинусоидой
u(t) = cos(coot).
Его изображение по Лапласу имеет вид
Цр) =
Р
Рг + «о
Построим амплитудный (рис. 8.22) и фазовый (рис. 8.23) спектры этого сигнала.
Как видно из рис. 8.22 в спектральной плотности вместо обозначения мнимой единицы j программа выдала i. График модуля
61
8 Расчет спектров
Незатухающая косинусоида
<»0 := 2	- угловая частота рад/с
2 п2 р + (оО	- изображение
р := j o	- замена
F(<o) := L(p) — > i- -o2+ 4	- спектральная плотность
о := 0, 0.1 .. 4	- диапазон частот, рад/с
Рис. 8.22
Угловая частота, рад/с
Рис. 8.23
спектральной функции имеет разрыв при со = соо = 2 рад/с. Читателю предлагается изменить шачсние частоты на соц = I рад/с и наблюдать за изменениями графиков спектров.
• Рассмотрим прохождение сигнала через стационарную линейную систему спектральным методом. Пусть на вход этой системы действует экспоненциальный видеоимпульс
62
= l(r)e ct,
где с = 1 1/с — параметр сигнала;
1(Г) — единичная функция.
Найдем спектральную плотность S](jco) этого сигнала с помощью команды fourier (прямое преобразование Фурье) (рис. 8.24).
Прохождение сиглала через RC-цепь
s2ow) = s1aW)-Ha«)
с := 1 - параметр входного сигнала, 1/с u1(t) := O(t)-e‘c,t - входной сигнал,В
S1(w) := U1(t) fourier, t
- спектральная плотность входного сигнала, Вс
Рис. 8.24
Спектральная плотность на выходе такой системы будет равна произведению входного спектра на передаточную функцию системы
S2(j<o) = S|(jco) H(jco).
В качестве системы используем RC-цепь с передаточной функцией напряжения
Я(» = Н
1
1 + уюАС’
где RC = 0,5 с — постоянная времени цепи.
Реакцию, т. е. выходной сигнал u2(t) можно найти по команде invfourier (обратное преобразование Фурье) и float 4 (вывод 4 знаков) (рис. 8.25)
u2(t) = -I \S2(jw)e^dw.
RC := 0.5
UjaiRC
1592 Ф(1 t) (12 57 exp( 2
I invfourier, g) u2(t) := S1(w)-H(w)
| float 4
- постоянная времени RC-цепи, с
- функция передачи напряжения RC-цепи
t) 12.57 ехр( 1. t)) выходной сигнап, Н
Рис. 8.25
63
8 Расчет спектров
Рис. 8.26
На рис. 8.26 показаны входной (воздействие) и выходной (отклик) сигналы. Из этого рисунка видно, как RC-цепь «сглаживает» входной сигнал.
Читателю предлагается самому изменить параметр импульса на с = 2 и наблюдать за изменением отклика.
• Рассмотрим пример дискретного вейвлет-преобразования. Пусть исходный сигнал в виде вектора задан своими отсчетами (рис. 8.27).
п := 4 к:= 0.	В m := ,m Г 1 1	вейвлет-преобразование 2n-1 т = 15- номер последнего отсчета исходного сигнала
и :=	1 1 1 1 0.5	- исходный сигнал (вектор)
	0.5	
	0.5	
	0.5	
	0.5	
	0.5	
	0	
	0	
	0 < У	
Рис. 8.27
64
График этого исходного сигнала показан на рис. 8.28.
Рис. 8.28
Воспользуемся командой wave для вейвлет-преобразования.
В результате получим вейвлет-коэффициенты (рис. 8 29).
w := wave(u) - вейвелет - преобразование
w =
- вейвелет - коэффициенты
Рис. 8.29
По этим коэффициентам нетрудно построить вейвлет-спектр (рис. 8.30).
По вейвлет-коэффициентам восстановим исходный сигнал при помощи команды iwave — обратное вейвлет-преобразование (рис. 8.31).
По полученным отсчетам построим график восстановленного сигнала (рис. 8.32). Как видно, этот график совпадает с графиком, изображенным на рис. 8.28.
65
8 Расчет спектров
Рис. 8.30
z := iwave(w) - обратное вейвелет - преобразование
- восстановленный сигнал
Рис. 8.31
Рис. 8.32
66
9 Расчет параметров
четырехполюсников
Определим A-параметры четырехполюсника, образованного каскадным соединением двух одинаковых четырехполюсников, если A-параметры одного четырехполюсника равны:
Аи = 1 - j0,5; Ап = 50 - j 100 Ом; А21 = -j0,005 См; А22 = j0,5.
При каскадном соединении следует перемножить параметры соответствующих матриц соединяемых четырехполюсников (рис. 9.1).
Каскадное соединение четырехполюсников
ORIGN := 1
= 1 - j- 0.5
- А-параметры
= 50 - j  100 - Ом
= -j - 0.005 - См
A12
a22
1 - 0.5i	50- 100i
-5i x 10'3	0.5
A:=A1-A1 A =
0.25-1.25i	25-175i
-2.5 x 103-7.5 x 1Q3 -0.25 - 0.25i
Puc. 9.1
Построим |H(<o)| — АЧХ и arg(H(<o)) — ФЧХ нагруженного четырехполюсника (рис. 9.2), если
RH = 200 Ом; R = 100 Ом; L = 20 мГн; С = I мкФ.
Из ОТЦ известно, что
"* zli’
-|//(о>)|са,!Н
67
9 Расчет параметров четырехполюсников
где
R_ jtiiL
R ~J-
J + соС юС усоА
АЧХ и ФЧХ нагруженного четырехполюсника
со := 0.1, 102. 107	- диапазон частот, рад/с
А11(со):= 1- параметр А11
А12(со) := R--L + . Ц -Q- - параметр А12, Ом
со • С J  со • L
RH
Н(со) :=------—--------- - коэффициент передачи
А11 (со)- RH + А12(<о) напряжения
Рис. 9.2
При построении АЧХ и ФЧХ применим логарифмический масштаб по оси частот (рис. 9.3).
Formatting Currently Selected ... |$C]
X-Y Axes Traces Labels Defaults
0 Numbered
0 Autoscale
0 Show Markers
Number of Grids:
0 Log Scale
0 Grid Lines
0 Numbered
0 Autoscale
0 Show Markers
0 Auto Grjd
Number of Grids:
Axis Style 0 Boxed О Crossed О None
Grid Color...
[ OK j [ Отмена ]
Справка
Puc. 9.3
68
В результате получим АЧХ (рис. 9.4) и ФЧХ (рис. 9.5) нагруженного четырехполюсника.
Рис. 9.4
Угловая частота, рад/с
Рис. 9.5
• Рассмотрим автономную линейную систему с запаздывающей обратной связью. В этой системе в цепь обратной связи включено идеальное устройство задержки сигнала на время to (рис. 9.6). Комплексный коэффициент передачи напряжения такой системы равен
к	к
H(j(A) = -------------—- =	_____,= f7<l’<"’).
1 -f,Ke J‘"'" V27I -pA'cos((l)/0)
69
9 Расчет параметров четырехполюсников
Система с запаздывающей обратной связью
КО := 10	- коэфициент усиления
ро := -0.09 - коэффициент передачи обратной связи
tO := 0.1	- время запаздывания
АЧХ (модуль
Н(со) := —7=— ----— -.....--	_ коэффициента
V2 • V1 - ро • КО cos(cd • tO) передачи
системы)
Рис. 9.6
Построим АЧХ этой системы (рис. 9.7). Как видно из этого рисунка, АЧХ представляет собой периодическую кривую с чередующимися максимумами и минимумами.
Рис. 9.7
70
10 Расчет цепей с распределенными параметрами
С помощью системы Mathcad можно моделировать различные режимы работы нагруженной линии без потерь с волновым сопротивлением Zb, длиной /. В зависимости от величины сопротивления нагрузки Zh в линии могут возникать следующие режимы работы:
•	режим холостого хода (Zh = оо);
•	режим короткого замыкания (Zh = 0);
•	режим работы на согласованную нагрузку (Zh — Zb);
•	режим работы на несогласованную нагрузку (ZH * ZB).
Зададимся величинами сопротивлений, длиной волны и длиной линии, показанными на рис. 10.1. Используя уравнения длинной
Режим работы линии без потерь
ZH := 150	-- сопротивление нагрузки, Ом
ZB := 50	- волновое сопротивление, Ом
X := 1	- длина волны, м
I := X	- длина линии, м
р :=	- коэффициент фазы, рад/м
U2 = 0 if ZH = 0	- напряжение в конце линии, В
1 if ZH * 0
0 if ZH = оо ток в конце линии, А
yZ if ZH = ZB 4.0
otherwise ZH
U(y) = U2 cos(p • y) + j I2  ZB sin(p • у) - уравнения длинно линии, В
U2
l(y) := I2-cos(p-у) t j — sin(p у) уравнения 4 о
длинной линии, А
Рис. 10.1
71
10 Расчет цепей с распределенными параметрами
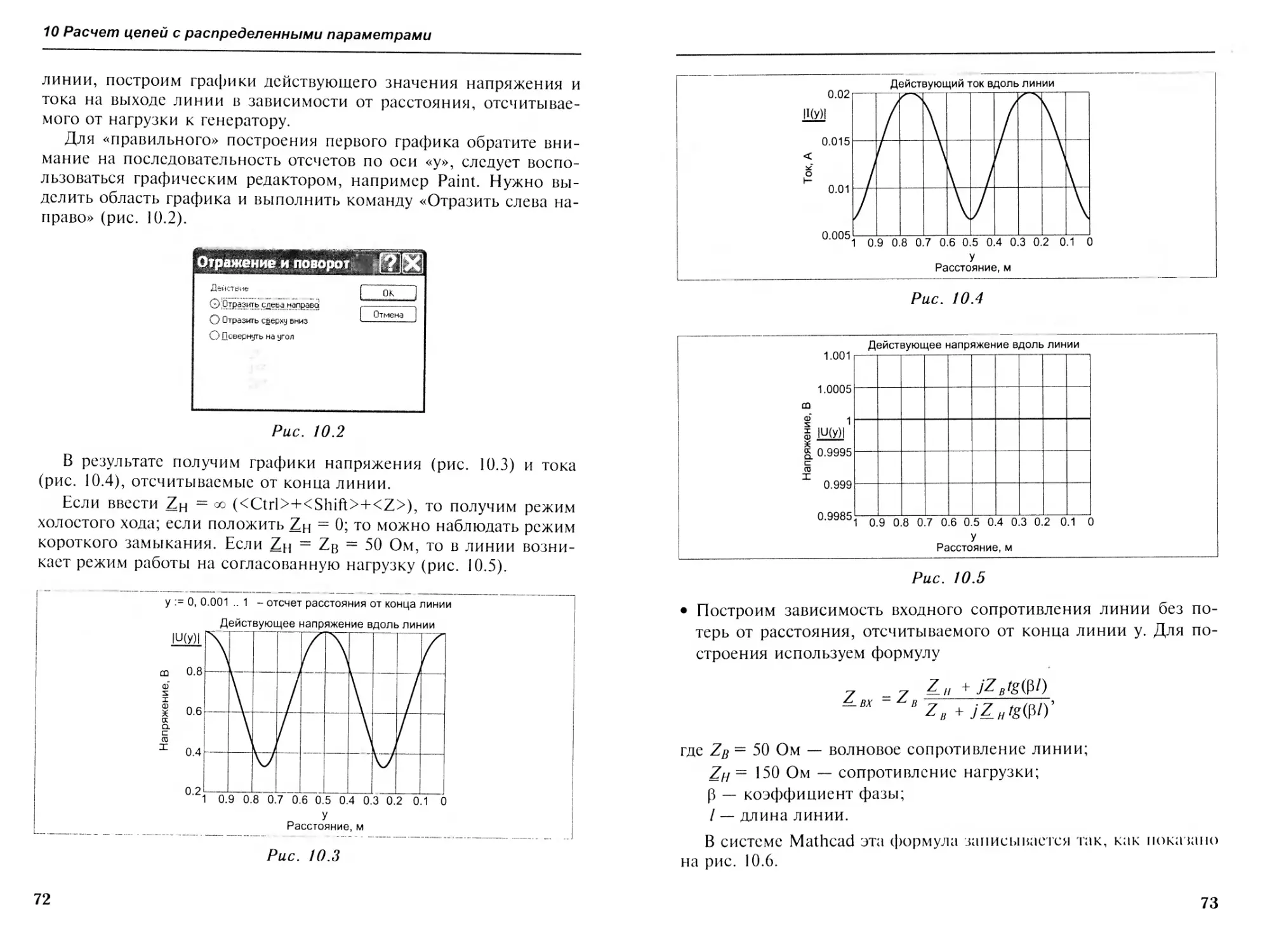
линии, построим графики действующего значения напряжения и тока на выходе линии в зависимости от расстояния, отсчитываемого от нагрузки к генератору.
Для «правильного» построения первого графика обратите внимание на последовательность отсчетов по оси «у», следует воспользоваться графическим редактором, например Paint. Нужно выделить область графика и выполнить команду «Отразить слева направо» (рис. Ю.2).
Отражение и поворот
I оГ J [ Отмена j
Действие
О -Отразить слева। направо!
О Отразить сверху вниз
О Повернуть на угол
Рис. 10.2
В результате получим графики напряжения (рис. 10.3) и тока (рис. 10.4), отсчитываемые от конца линии.
Если ввести Zh = °° (<Ctrl>+<Shift>+<Z>), то получим режим холостого хода; если положить Zh = 0; то можно наблюдать режим короткого замыкания. Если Zh = Zb = 50 Ом, то в линии возникает режим работы на согласованную нагрузку (рис. 10.5).
у Расстояние,м
Рис. 10.3
72
Рис. 10.4
у
Расстояние, м
Рис. 10.5
• Построим зависимость входного сопротивления линии без потерь от расстояния, отсчитываемого от конца линии у. Для построения используем формулу
7	_ 7 Lh +
~вх в zB+jzHtg^iy
где Zy = 50 Ом — волновое сопротивление линии;
Z}] = 150 Ом — сопротивление нагрузки;
р — коэффициент фазы;
/ — длина линии.
В системе Mathcad эта формула записывается так, как показано на рис. 10.6.
73
10 Расчет цепей с распределенными параметрами
Входное сопротивление линии без потерь
ZH := 150	- сопротивление нагрузки, Ом
ZB := 50	- волновое сопротивление, Ом
Л. := 1	- длина волны, м
1 ;=х	- длина линии, м
2тг
р :=	- коэффициент фазы, рад/м
ZBX(y) := ZB • -t j-- —' tan(P' У) - входное сопро-ZB + j-ZH tan(p-y) тивление, Ом
Рис. 10.6
График модуля входного сопротивления от расстояния у показан на рис. 10.7.
Рис. 10.7
Интересно построить зависимости резистивного (активного) входного сопротивления (рис. 10.8) и реактивного входного сопротивления от «у» (рис. 10.9).
Читателю предлагается самому изменить значение сопротивления нагрузки ZH = 50 Ом и сделать вывод о характере режима работы линии.
74
Рис. 10.8
у
Расстояние, м
Рис. 10.9
•	Перейдем к линии е потерями. Для этого в электронный лист добавим коэффициент затухания а и перепишем формулу входного сопротивления, заменив тангенсы на гиперболические тангенсы (рис. 10.10).
В результате получим зависимости полного сопротивления (рис. 10.11), резистивного сопротивления (рис. 10.12) и реактивного сопротивления (рис. 10.13) от расстояния у с учетом затухания в линии.
•	Рассмотрим режим в линии без потерь при согласовании короткозамкнутым шлейфом.
Пусть линия с волновым сопротивлением 7ц и длиной / нагружена резистивным сопротивлением Иц. В точках а Ь, находящихся на расстоянии /о от нагрузки, подключен короткозамкнутый шлейф длиной /у.
75
10 Расчет цепей с распределенными параметрами
Входное сопротивление линии с потерями
к-ZBX
- сопротивление нагрузки, Ом
- волновое сопротивление, Ом
-длина волны, м
- длина линии, м
- коэффициент ослабления, Нп/м
- коэффициент фазы, рад/м
- коэффициент распространения
ZH := 150
ZB := 50
X := 1
I :=Х
а := 0.4
Р:=^ y:=a+jp
ZBX(y) := ZB
ZH + ZB -tanh(y-y) ZB + ZH-tanh(yy)
- входное сопротивление, Ом
Рис. 10.10
Рис. 10.11
Зададимся сопротивлением нагрузки, волновым сопротивлением, длиной волны и длиной линии (рис. 10.14).
Целью расчета является нахождение расстояния подключения шлейфа /0 и длины шлейфа /s. Эти величины можно рассчитать по формулам, приведенным на рис. 10.15.
Для расчета действующего напряжения вдоль линии U(y) с подключенным шлейфом воспользуемся формулами, приведенными на рис. 10.16.
76
Расстояние, м
Рис. 10.12
Расстояние, м
Рис. 10.13
Согласование линии без потерь
ZH := RH
RB := 500	- волновое сопротивление
линии и шлейфа, Ом
YB :=-^j YB := 2 ИО'3 волновая проводимость, См
X := 1	длина волны, м
1 := X - длина линии, м
р := р ;= 6.283	- коэффициент фазы, рад/м
Рис. 10.14
11
10 Расчет цепей с распределенными параметрами
L01 :=Tatan(/l)
L02:=X.atan(-|f ]
L01 := 0.183
L02 :=-0.183
L0 := L01 if L01 > 0
L02 if L02 > 0 A L02 < L01
L0 = 0.183 — расстояние до t. a — b, м
Ls 1 =0.081
Ls 2 := — • atan
/-Jrhzb
\ RH-ZB
Ls 1 = -0.081
Ls := Ls1
Ls2
if Ls1 >0 Ls = 0.081 - длина шлейфа, м
if Ls2 >0 A Ls2 <Ls1
Puc. 10.15
ZBX(y) := ZB
ZH + jZBtan(Py)
ZB + j ZH-tan(0 y)
- входное сопротивление без шлейфа, Ом
YBX(y) := —-—
YBX(y)
входная проводимость без шлейфа, См
YBX(LO) = 2x10 \ 3.578j х 1 о 3	- входная проводимость в а - b без шлейфа, См
1	-3
YS(Ls) := ------------ YS(Ls) := -3.578jx 10	- входная проводимость в а - b шлейфа, См
j ZB - tan(p- Ls)
112
U2 := 1 I2 :=-4t7 - напряжение, В и ток, А в конце линии
UAB(y) := U2 • cos(p  y) 4- j • I2 ZB • sin([3 • у) - напряжение в линии до точек а - b
UAB(LO)
IAB := —~~—	- ток в линии в точках а - b
U(y) := UAB(y) if L0 > у >0
UAB(LO)• cos(p-у) + j • LAB-ZB-sin(p-y) if 1 > у > L0
- уравнение длинной линии, В
Рис. 10.16
В результате получим, что в линии слева от точек а—b будет существовать только падающая волна (рис. 10.17).
78
У
Расстояние, м
Рис. 10.17
Читателю предлагается самому доработать этот электронный лист, так чтобы можно было использовать комплексное сопротивление нагрузки линии.
• Проведем синтез несимметричной микрополосковый линии (НМЛ). Исходными данными для синтеза будут: частота f, толщина подложки h, относительная диэлектрическая проницаемость 8Г, волновое сопротивление Zb- Целью синтеза будет расчет ширины W полоски и длина волны X в линии. Исходные данные представлены на рис. 10.18.
Синтез несимметричной микрополосковой линии
h 1	толщина подложки
(диэлектрика), мм
ег:= 5	относительная диэлектрическая
проницаемость
ZB := 5	волновое сопротивление
линии, Ом
с:=3-108	- скорость света в свободном
пространстве, м/с
Рис. 10.18
79
10 Расчет цепей с распределенными параметрами
Необходимые расчетные формулы приведены на рис. I0.19, откуда видно, что помимо ширины полоски W, длины волны X в линии вычислена и величина Z/4, удобная при расчете четвертьволнового трансформатора.
Wdh := 1.715
- отношение W/h
W:=Wdh h W= 1.715	- ширина полоски, мм
eeff := —+ -------	— eeff = 3.707 - эффективная диэлектрическая проницаемость
2'J1 + 12"w
с	3
X :=-------- X-10 =51.936 - длина волны в линии, мм
—- — - 12.984	_ четверть длины волны в линии, мм
Рис. 10.19
С
80
11 Расчет полюсов передаточной функции фильтров
При синтезе фильтров нижних частот (ФНЧ) приходится выполнять довольно громоздкие вычисления. Поскольку алгоритм этих вычислений линейный, то его легко можно переложить на систему Mathcad.
• Рассчитаем полюсы передаточной функции Sj и количество реактивных элементов ФНЧ Чебышева. Исходные данные для этого расчета приведены на рис. ll.l.
ФНЧ Чебышева
f2 := 3.4	- граничная частота ПП, кГц
f3:=612	- граничная частота ПЗ, кГц
Да := 2.5 неравномерность ослабления в ПП, дБ
amin := 40 - минимальное ослабление в ПЗ, дБ
Рис. 11.1
К синтезу ФНЧ Чебышева
f3
Q3 := — Q3 = 1.8	- нормированная частота
е := J10°'1 Ла -1 е = 0.8822	- коэффициент неравномерности
А= 1.2848х104
1п(7а+7а- l)
n := ceil(N) п = 5
N = 4.5465
- число реактивных элементов фильтра
k= S(k)=___________________
~~Г|	- 0.0605 + 0.9691j
2	-0.1584 + 0.5989)
3	-0.1958
~4~	-0.1584-0.5989)
Т	- 0.0605 - 0.9691j
Рис. 11.2
81
11 Расчет полюсов передаточной функции фильтров
Здесь ПП — полоса пропускания, ПЗ — полоса задерживания. Расчетные формулы и результаты приведены на рис. 11.2.
• Аналогично можно рассчитать полюсы и количество реактивных элементов ФНЧ Баттерворта. Исходные данные для этого расчета приведены на рис. 11.3.
ФНЧ Баттерворта
f2 := 85	- граничная частота ПП, кГц
f3 := 115	- граничная частота ПЗ, кГц
Ла := 1.5	- неравномерность ослабления в ПП, дБ
amin := 10 - минимальное ослабление в ПЗ, дБ
Рис. 11.3
Изменив несколько формул так, как показано на рис. 11.4, получим полюсы передаточной функции и количество реактивных элементов фильтра.
К синтезу ФНЧ Баттерворта
Q3 ;= — Q3 = 1.3529 нормированная частота
q0.1  amm А:=--------------
в = 0.6423 коэффициент неравномерности
А = 21.8162
N.= _tog(A)_ 2log(S!3)
N = 5.099
п .= ceil(N)
n = 6	" число реактивных элементов фильтра
- полюсы передаточной функции
k = S(k) =
~П - 0.2786 + 1.0399[ ~2~ -0.7631 + 0.7613j
- 1.0399 + 0.2786j ~4~	- 1.0399-0.2786]
~5~	-0.7613-0.76Ilf
V - 0.2786 - 1 0399]
Рис. 11.4
82
•	Построим зависимость рабочего ослабления ФНЧ Баттерворта от нормированной частоты (рис. 11.5).
Q := 0, 0.0001 .. 3	- нормированая частота, f/f2
a(Q) := 10 - log (1 +e2 Q2 п) - рабочее ослабление
ФНЧ Баттервота
Рис. 11.5
•	Читателю предлагается самому повторить построение зависимости рабочего ослабления ФНЧ Чебышева от нормированной частоты (рис. 11.6).
Рабочее ослабление ФНЧ Чебышева
О := 0, 0.0001 ..3	- нормированая частота, f/f2
T5(Q) := 16 • Q5 - 20  Q3 + 5  Q - полином Чебышева
5-го порядка
а(Я) := 10 - log (l ь e2T5(Q)2) - рабочее ослабление
ФНЧ Чебышева, дБ
Рис. 11.6
83
Список использованных источников
1.	Фриск В. В. Основы теории цепей. — М.: РадиоСофт, 2002. 288 с.
2.	Фриск В. В. ОТЦ. Лабораторный практикум на персональном компьютере. — М.: СОЛОН-Пресс, 2002. 192 с.
3.	Фриск В. В. ОТЦ. Сборник задач с примерами применения ПК. - М.: СОЛОН-Пресс, 2003. 192 с.
4.	Фриск В. В. ОТЦ. Использование пакета Microwave Office для моделирования электрических цепей на персональном компьютере. — М.: СОЛОН-Пресс, 2004. 160 с.
5.	Основы теории цепей [Электрон, ресурс]: Поддержка и сопровожден^ учебного процесса по дисциплине ОТЦ для системы дистанционного самообразования. — М.: FR1SK.NE-WMAIL.RU, 1988-2005. - Режим доступа: World Wide Web. URL: http://frisk.newmail.ru/. — 24.02.2005.
6.	Mathcad [Электрон, ресурс]: Образовательный математический сайт Exponenta.ru. — Режим доступа: World Wide Web. URL: http://www.exponenta.ru/. — 24.02.2005.
7.	Mathcad 6.0 Plus. Руководство пользователя. Финансовые, инженерные и научные расчеты в среде Widows 95. — М.: Филинъ, 1996. 712 с.
84
Содержание
Предисловие.............................................1
I	Расчет резистивных электрических цепей................5
2	Законы Ома и Кирхгофа.................................9
3	Расчет разветвленных цепей постоянного тока..........IS
4	Расчет мгновенных токов и напряжений................21
4	Расчет мгновенных токов и напряжений................21
5	Вычисления с комплексными числами....................27
6	Частотные характеристики электрических цепей........35
7	Расчет переходных процессов..........................41
8	Расчет спектров......................................50
9	Расчет параметров четырехполюсников.................67
10	Расчет цепей с распределенными параметрами..........71
11	Расчет полюсов передаточной функции фильтров........81
Список использованных источников.......................84
Содержание.............................................85
85