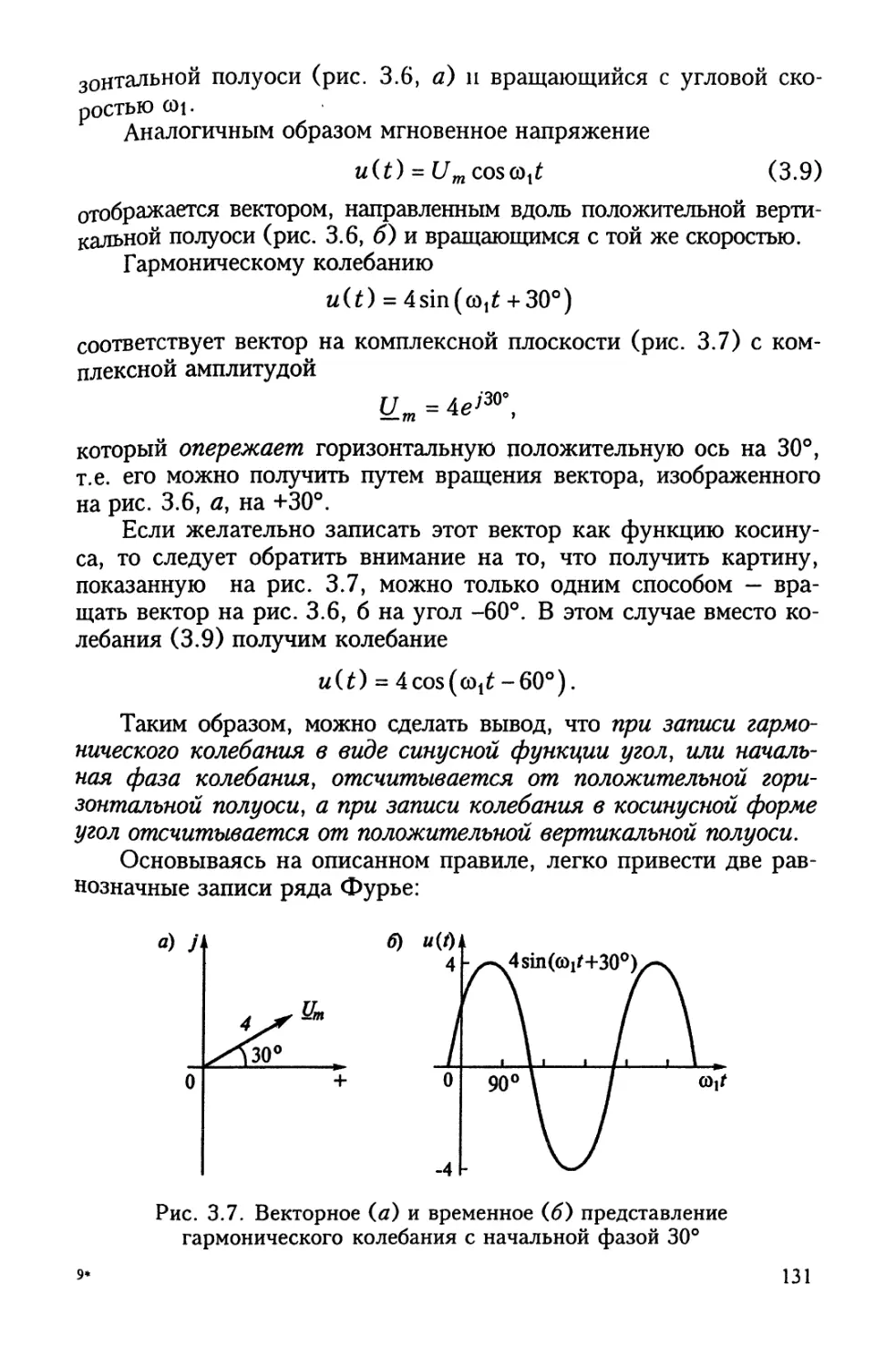
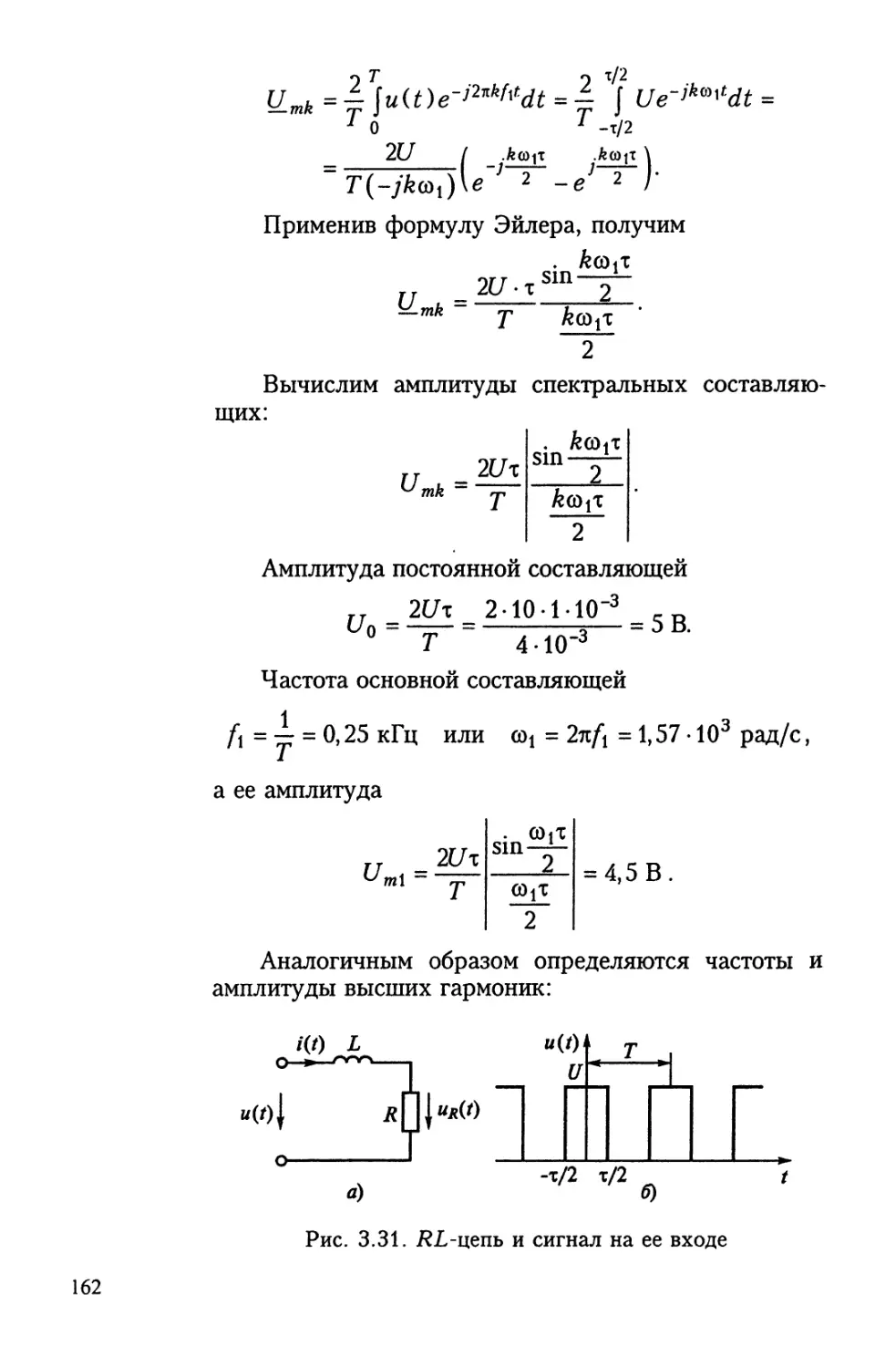
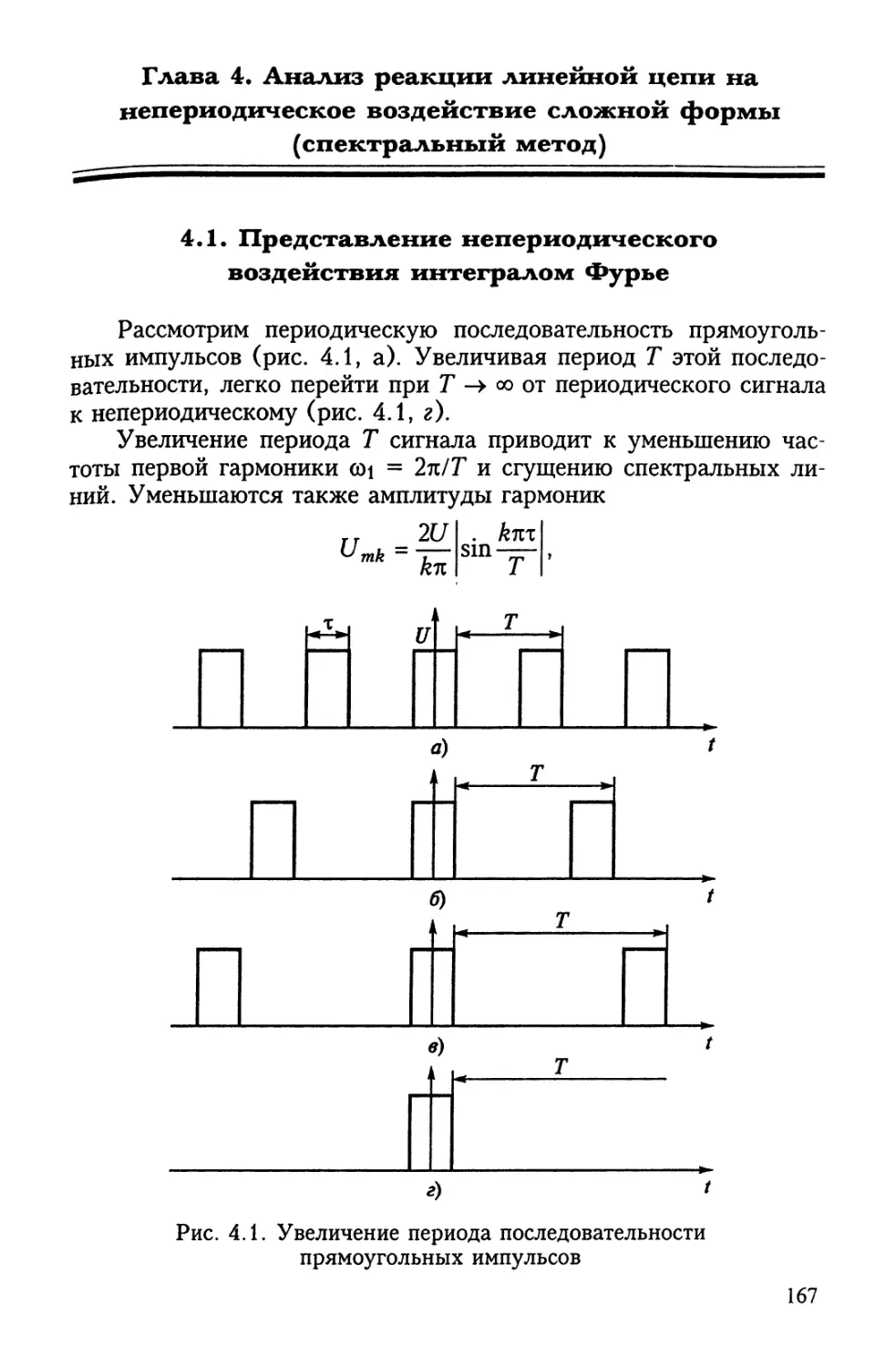
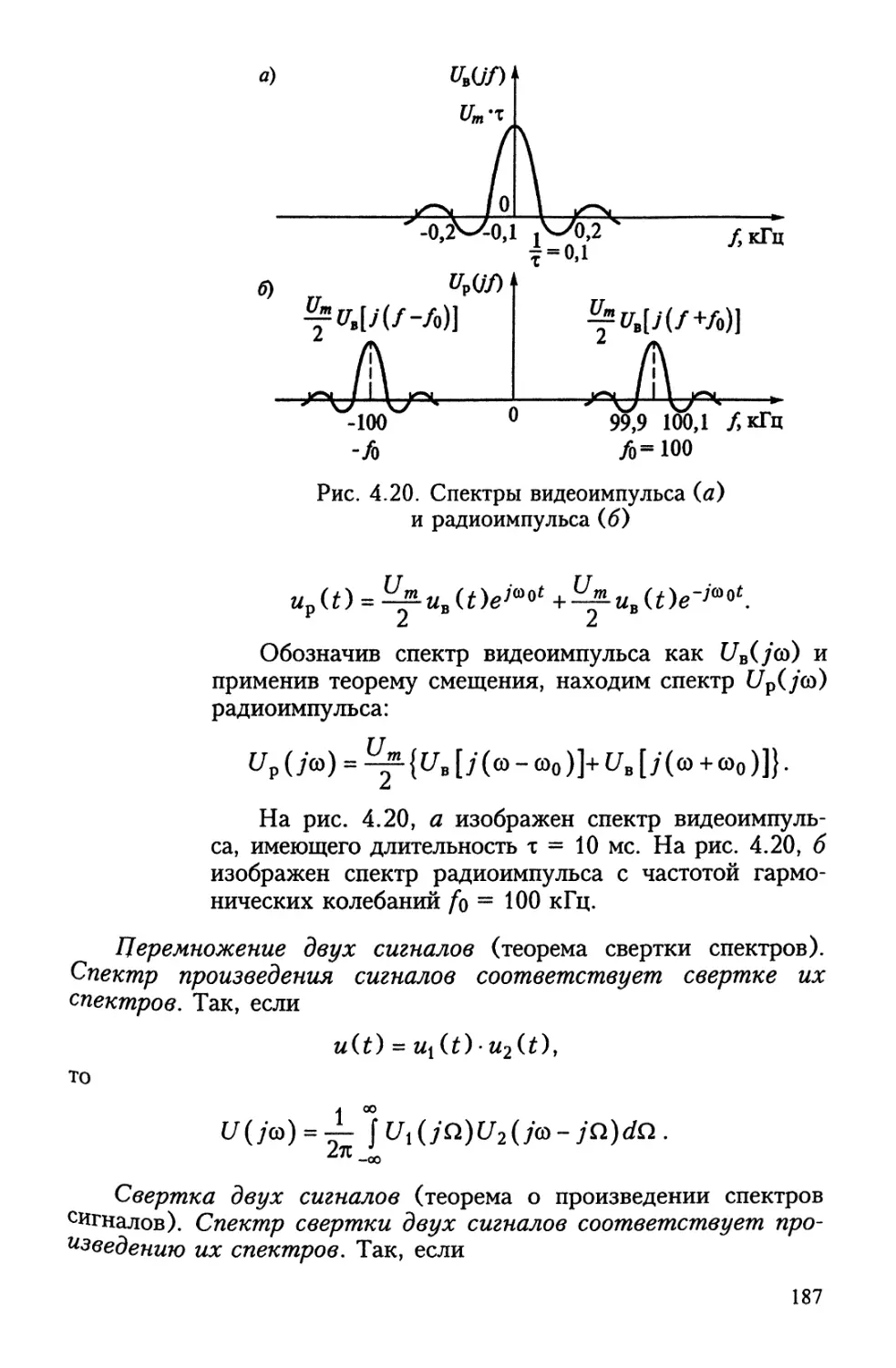
Author: Бакалов В.П. Журавлева О.Б. Крук Б.И.
Tags: электротехника электрическая связь информатика связь учебное пособие теоретические основы электротехники самообразование электрические цепи
ISBN: 5-93517-354-9
Year: 2007
И№1 ШИ ЦЕПЕЙ
Горячая линия-Телеком ИТ
. 0. Бакалов, 0.6. Журавлева, Ь. И. Крук
УДК 621.373 (075)
ББК 32.88
Б19
Рецензенты:
доктор техн, наук, профессор А. Е. Дубинин; доктор техн, наук, профессор
В. Ф. Дмитриков
Бакалов В. П., Журавлева О. Б., Крук Б. И.
Б19 Основы анализа цепей: Учебное пособие для вузов - М.: Горячая
линия-Телеком, Радио и связь, 2007. - 591 с: ил.
ISBN 5-93517-354-9.
Учебное пособие предназначено для самостоятельного изучения ос-
новных разделов теории цепей. В первой части пособия с единых позиций
рассматриваются вопросы анализа линейных, нелинейных и дискретных
цепей, находящихся под воздействием гармонических, периодических не-
гармонических, непериодических и дискретных колебаний. Вторая часть
пособия содержит материал об аналоговых и дискретных устройствах,
входящих в состав радио- и проводной аппаратуры связи: электрических
аналоговых и дискретных фильтрах, корректорах, генераторах, нелиней-
ных преобразователях.
Пособие может быть использовано как при традиционных, так и дис-
танционных технологиях обучения студентов. Оно представляет интерес
для студентов вузов и колледжей, обучающихся по специальностям связи
и информатики.
ББК 32.88
Адрес издатечьства в Интернет www rECHBOOK.RU
Учебное издание
Бакалов Валерий Пантелеевич
Журавлева Ольга Борисовна
Крук Борис Иванович
ОСНОВЫ АНАЛИЗА ЦЕПЕЙ
Учебное пособие
Лицензия ЛР № 071825 от 16.03.99 г.
Подписано к печати 02.09.2006. Формат 60 х 90 1/16.
Усл. печ. Лч 37. Изд. № 6314. Тираж 2000 экз. Заказ № 6972.
Отпечатано с готовых диапозитивов в ОАО ордена «Знак Почета»
«Смоленская областная типография им. В. И. Смирнова».
214000, г. Смоленск, проспект им. Ю. Гагарина, 2.
ISBN 5-93517-354-9 © В. П. Бакалов, О. Б. Журавлева, Б. И. Крук, 2007
© Оформление издательства «Горячая линия-Телеком», 2007
Предисловие
Дисциплина «Основы теории цепей» базируется, как извест-
но, «на двух китах» — анализе и синтезе. При этом раздел, опи-
сывающий анализ электрических цепей, является базовым для
подавляющего большинства дисциплин телекоммуникационных
специальностей.
Техническая революция, происходящая сейчас в сфере теле-
коммуникаций и информатики, предполагает органическое взаи-
модействие аналоговых и цифровых способов организации связи.
Подобное имеет место, например, в современных системах под-
вижной радиосвязи, в сетях проводного и радиодоступа, оптиче-
ских системах связи и др. Такие понятия, как фильтрация, гене-
рация, модуляция, выпрямление, корреляция, цифровая обработ-
ка и т.п., еще многие десятилетия останутся в арсенале специали-
стов радиотехники, связи и информатики. Более того, общая тео-
рия фильтров, генераторов, модуляторов, корректоров и других
устройств предполагает использование математических моделей
этих устройств и описание на их основе происходящих физиче-
ских процессов. Реализация данных моделей может быть осуще-
ствлена как на основе аналоговой (линейной и нелинейной), так
и на основе цифровой техники.
Материал предлагаемого читателю учебного пособия является
частью дисциплины «Основы теории цепей», которая изучается
студентами практически всех специальностей вузов и колледжей
радиотехники и связи. Он посвящен анализу реакций линейных,
нелинейных и дискретных цепей на различные воздействия и на
этой основе расчету различных узлов и устройств аналоговой и
цифровой аппаратуры связи.
Предлагаемый читателю материал, с одной стороны, пред-
ставляет собой теорию, использующую разнообразный и доста-
точно сложный математический аппарат. С другой стороны, это
первый материал, который закладывает фундамент в специаль-
ные знания студента.
При самостоятельном изучении материала, когда рядом нет
опытного преподавателя, традиционный учебник уже не является
самодостаточным средством для усвоения материала хотя бы по-
тому, что он написан в традиционной манере и предназначен для
использования при традиционной методике обучения.
Сегодня нет четких рекомендаций, каким должен быть учеб-
ник для самостоятельного изучения материала. Каждый автор
вынужден сам решать этот вопрос Поэтому в последние годы в
Дополнение к традиционным учебникам стали издаваться много-
численные учебные пособия для самостоятельной работы или для
3
дистанционного обучения. При всем многообразии и внешней не-
схожести этих пособий их объединяет одно — стремление авторов
изложить материал так, чтобы обучающийся мог самостоятельно
разобраться в дебрях математических формул, понять смысл су-
ществующих законов и правил, усвоить многочисленные алго-
ритмы и методы расчета.
Подобную попытку предприняли и авторы данного учебного
пособия. Учебное пособие состоит из двух частей. В первой из
них описаны методы анализа реакций разного рода цепей (линей-
ных, нелинейных, дискретных) на различные воздействия. Вто-
рая часть пособия посвящена анализу работы узлов и устройств
аналоговой и цифровой аппаратуры связи: фильтров, корректо-
ров, нелинейных преобразователей, генераторов.
То, что пособие предназначено для самостоятельного изучения
материала, в значительной мере определило язык и стиль построе-
ния книги. В качестве встроенных подзаголовков текста исполь-
зуются ключевые фразы, сразу же вводящие читателя в суть
предлагаемого материала, а в конце каждого раздела сформулиро-
ваны конечные цели изучения этого раздела. Текст книги насыщен
большим количеством иллюстративных примеров. Основные фор-
мулы приведены в рамках, привлекающих внимание обучаемого.
В конце глав даны контрольные вопросы и задания, упражнения с
ответами, способствующие самоконтролю усвоения материала.
Предложенная структура книги, а также стремление авторов
изложить материал ясно и доходчиво делают это учебное пособие
особенно полезным для системы дистанционного образования, где
основной упор ставится на самостоятельное приобретение знаний.
Данное учебное пособие является продолжением и дополнени-
ем комплекса учебной литературы, включающего учебник В.П. Ба-
калова, В.Ф. Дмитрикова, Б.И. Крука «Основы теории цепей»,
учебное пособие В.П. Бакалова, Б.И. Крука, О.Б. Журавлевой
«Основы теории цепей. Компьютерный тренажерный комплекс» и
учебное пособие М.Г. Виткова, Н.И. Смирнова «Основы теории
цепей. Лабораторный практикум».
Авторы признательны рецензентам: заведующему кафедрой
ТЭЦ Поволжской государственной академии телекоммуникаций и
информатики проф. А.Е. Дубинину, заведующему кафедрой ТЭЦ
Санкт-Петербургского государственного университета телекомму-
никаций проф. В.Ф. Дмитрикову за их замечания, способствую-
щие улучшению содержания книги.
Авторы
Вместо введения: задача анализа цепей
В.1. Элементы электрической цепи
Электрической цепью называют совокупность устройств,
предназначенных для прохождения тока и описываемых с помо-
щью понятий тока и напряжения. Электрическая цепь состоит из
источников (генераторов) и приемников электрической энергии.
Генераторы подразделяются на зависимые и независимые ис-
точники. К независимым источникам относятся батареи, аккуму-
ляторы, электрогенераторы, термоэлементы и другие преобразо-
ватели; к зависимым источникам — электронные лампы, транзи-
сторы, операционные усилители и другие активные элементы.
Независимые источники можно представить в виде двух моделей:
источника напряжений и источника тока.
Понятия электрического напряжения и электрического тока
являются одними из основных в анализе электрических цепей.
Каждая точка электрического поля характеризуется электри-
ческим потенциалом V. Разность потенциалов Vi и V2 двух то-
чек называется напряжением щ2.
U\2 — — V2.
В источнике электрической энергии, например, в таком, как
сухой элемент, в результате химических реакций появляется раз-
ность потенциалов между угольным стержнем и цинковым ста-
канчиком. Следовательно, между выводами от угольного стрежня
и цинкового стаканчика возникает напряжение.
В технике связи электрические напряжения получают от спе-
циальных электронных устройств, называемых генераторами, ко-
торые преобразуют электрическую энергию промышленной сети в
различные напряжения.
Напряжение на разомкнутых зажимах источника называется
электродвижущей силой (эдс) и обозначается буквой е.
Значение напряжения в любой заданный момент t называется
мгновенным и обозначается и = u(t). В системе СИ напряжение
и эдс измеряют в вольтах (В).
Под воздействием разности потенциалов (напряжения) ис-
точника в электрической цепи возникает электрический ток i —
упорядоченное движение электрических зарядов (ток проводимо-
сти в металлах, электролитах, газах; ток переноса в электроваку-
умных приборах и др.). Значение тока z(t) в любой заданный
момент t называется мгновенным и обозначается i = z(i). Изме-
ряется ток в амперах (А).
5
1 i
о---->
|"12
О-----
2
Электрическая
цепь
Являясь скалярной величиной,
напряжение u(t) может принимать
как положительные, так и отрица-
тельные значения. Для однозначного
Рис. В.1. Направления от-
счетов напряжения и тока
определения знака напряжения выби-
рают положительное направление его
отсчета, которое показывается стрел-
кой (рис. В.1). Для определенности будем считать, что положи-
тельное направление отсчета совпадает с направлением стрелки от
более высокого потенциала, т.е. «+», к более низкому, т.е. «—».
Ток i(t) также может принимать положительные и отрица-
тельные значения. Принято считать значение тока положитель-
ным, если движение положительно заряженных частиц совпадает
с заранее выбранным направлением отсчета тока.
В случае, показанном на рис. В.1, положительные направле-
ния отсчета напряжения и тока согласованы между собой, так
как положительное направление отсчета напряжения Ut2 соответ-
ствует направлению перемещения положительно заряженных час-
тиц от более высокого потенциала V\ к более низкому V2. Оче-
видно, ЧТО U12 = —«21-
Независимым источником напряжения называют идеализи-
рованный двухполюсный элемент, напряжение' на зажимах кото-
рого не зависит от протекающего через него тока. Условное обо-
значение источника напряжения показано на рис. В.2, а.
Источник напряжения полностью характеризуется своим за-
дающим напряжением иТ, или эдс ег. Внутреннее сопротивление
источника напряжения равно нулю.
Зависимость напряжения от тока носит название вольт-
амперной характеристики (ВАХ). У идеального источника на-
пряжения ВАХ представляет собой прямую, параллельную оси
токов (рис. В.З, а).
В.2. Идеальные источники напряжения (а и б) и тока (в)
и реальные (г и д)
6
Рис В.З. Вольт-амперные характеристики идеальных
источников напряжении («) и тока (б)
Независимым источником тока называют идеализирован-
ный двухполюсный элемент, ток которого не зависит от напря-
жения на его зажимах. Условное изображение источника тока
показано на рис. В.2, в. Источник тока полностью характеризу-
ется своим задающим током гг. Внутренняя проводимость источ-
ника тока равна нулю (внутреннее сопротивление бесконечно ве-
лико), и ВАХ представляет собой прямую, параллельную оси на-
пряжений (рис. В.З, 6).
Свойства реальных источников с конечным внутренним со-
противлением можно моделировать с помощью независимых ис-
точников напряжения и тока с дополнительно включенным рези-
стивным элементом с сопротивлением Rr или с проводимостью Gr
(рис. В.2, г и д). Напряжение и и отдаваемый ток i этих источ-
ников зависят от параметров подключаемой к ним цепи, а их
ВАХ имеют тангенс угла наклона а, пропорциональный Rr и Gr
соответственно (штриховые линии на рис. В.З).
Зависимый источник представляет собой четырехполюсный
элемент с двумя парами зажимов — входных и выходных. Вход-
Рис. В.4. Зависимые источники: ИНУН (а), ИТУН (б),
ИНУТ (в) и ИТУТ (г)
7
ные ток i\ и напряжение щ являются управляющими. Различают
следующие разновидности зависимых источников (рис. В.4): ис-
точник напряжения, управляемый напряжением (ИНУН); источ-
ник тока, управляемый напряжением (ИТУН); источник напря-
жения, управляемый током (ИНУТ); источник тока, управляе-
мый током (ИТУТ). На рис. В.4 показаны условные обозначения
зависимых источников различного типа.
В ИНУН (рис. В.4, а) входное сопротивление бесконечно
велико, входной ток Л = 0, а выходное напряжение иг связано с
входным щ равенством иг = Нищ, где Ни — коэффициент, харак-
теризующий усиление по напряжению зависимого источника. Ис-
точник типа ИНУН является идеальным усилителем напряжения.
В ИТУН (рис. В.4, 6) выходной ток 1г управляется входным
напряжением щ, причем = 0 и ток гг связан с щ равенством
i2 = НвЩ, где Нс — коэффициент, имеющий размерность прово-
димости.
В ИНУТ (рис. В.4, в) входным током it управляется выход-
ное напряжение иг', входная проводимость бесконечно велика;
«1 = 0, иг = HrU, где Hr — коэффициент, имеющий размерность
сопротивления.
В ИТУТ (рис. 8.4, г) управляющим током является Л, а уп-
равляемым г’г. Входная проводимость бесконечно велика; щ = О,
г’г = Hii\, где Hi — коэффициент усиления по току. ИТУТ явля-
ется идеальным усилителем тока.
Примером зависимого источника является операционный
усилитель (ОУ). Выпускаемые в виде отдельных микросхем
(рис. В.5,а) ОУ широко применяются в качестве зависимых ис-
точников электрической цепи.
Операционный усилитель имеет два входа: 1 — неинверти-
рующий и 2 — инвертирующий. При подаче напряжения щ на
вход 1 выходное напряжение иг имеет ту же полярность, что и
щ, а при подаче щ на вход 2 напряжение иг меняет свою поляр-
ность на противоположную.
Рис. В.5. Идеальный операционный усилитель (а)
и его схема замещения в виде ИНУН (б)
8
о
Рис. В.6. Резистивный (д), индуктивный (б) и емкостный (в)
элементы электрической цепи
Идеальный ОУ (рис. В.5, б) представляет собой ИНУН с
бесконечно большим коэффициентом усиления (Ни -> <ю), беско-
нечно большими входным сопротивлением и выходной проводи-
мостью.
Часто для анализа цепей с биполярными и полевыми транзи-
сторами используется модель ИТУН с конечным или соответст-
венно бесконечным входным сопротивлением.
Если источники электрической энергии называют активными
элементами, то приемники электрической энергии — пассивными
элементами: резистивным, индуктивным и емкостным.
Резистивным элементом называют идеализированный эле-
мент, обладающий только свойством необратимого рассеяния
энергии. Условное обозначение резистивного элемента показано
на рис. В.6, а. Вольт-амперная характеристика резистивного эле-
мента имеет вид
и = Ri или i = Gu. (B.l)
Коэффициенты пропорциональности R и G называются соот-
ветственно сопротивлением и проводимостью элемента и явля-
ются его количественной характеристикой. Они связаны обратной
зависимостью R = 1/G. Измеряют в системе СИ сопротивление
R в омах (Ом), а проводимость G в сименсах (См).
Если в ВАХ (В.1) сопротивление R постоянно, то ВАХ ли-
нейна (рис. В.7, а) и резистивный элемент является линейным.
Если же R зависит от протекающего через него тока или прило-
женного к нему напряжения, то ВАХ становится нелинейной и
резистивный элемент называется нелинейным.
Рис. В.7. Вольт-амперные характеристики линейного (д)
и нелинейного (б) резистивных сопротивлений
Индуктивным элементом называют идеализированный эле-
мент электрической цепи, обладающий только свойством накоп-
ления им энергии магнитного поля. Условное обозначение индук-
тивного элемента изображено на рис. В.6, 6.
Математическая модель, описывающая свойства индуктивно-
го элемента, определяется соотношением
Т = Li, (В.2)
где Т — потокосцепление, характеризующее суммарный магнит-
ный поток, пронизывающий катушку, измеряется в веберах (Вб);
L — индуктивность элемента, измеряется в генри (Гн).
Связь между напряжением на индуктивном элементе и током
в нем определяется согласно закону электромагнитной индукции
выражением
dT , di
= <вз)
Если величина L постоянна и не зависит от электрического
режима, то вебер-амперная характеристика (В.2) линейна и ин-
дуктивный элемент является линейным. Если же L зависит от то-
ка или напряжения, то вебер-амперная характеристика нелинейна
и индуктивный элемент будет нелинейным.
Из выражения (В.З) следует, что при протекании через ин-
дуктивный элемент постоянного тока i напряжение ui = 0 и ин-
дуктивный элемент эквивалентен в этом случае короткозамкнуто-
му участку цепи.
Емкостным элементом называется идеализированный эле-
мент электрической цепи, обладающий только свойством накап-
ливать энергию электрического поля. Условное обозначение ем-
костного элемента показано на рис. В.6, в.
Математическая модель, описывающая свойства емкостного
элемента, определяется кулон-вольтной характеристикой
q = Сис, (В.4)
где q — электрический заряд, измеряемый в кулонах (Кл); С —
емкость элемента, измеряемая в фарадах (Ф).
Между током и напряжением на емкостном элементе сущест-
вует связь, определяемая равенством
i = ^l = C^. (В.5)
at (it
Если величина С постоянная, то кулон-вольтная характери-
стика (В.4) линейна и емкостный элемент является линейным.
Если же параметр С зависит от электрического режима, то ха-
рактеристика (В.4) нелинейна.
10
R L
a)
6)
Рис. В.8 Простой (а) и сложный (б) узлы электрической цепи
а)
Рис. В.9. Ветвь (а) и контур (б) электрической цепи
Из выражения (В.5) следует, что при постоянном напряже-
нии ис ток i = 0 и емкостный элемент эквивалентен разрыву цепи.
Электрическая цепь представляет собой соединение активных
и пассивных элементов. Место соединения двух и более элемен-
тов называется узлом электрической цепи. Различают узлы про-
стые (место соединения двух элементов — рис. В.8, а) и слож-
ные (место соединения трех и более элементов — рис. В.8, б).
Обобщением понятия элемента как соединительного пути ме-
жду двумя узлами цепи является понятие ветви пути (рис. В.9, а).
Ветви, подсоединенные к одной паре узлов, образуют парал-
лельное соединение. Замкнутый путь между узлами 1 и 2 на
рис. В.9, б называется контуром.
Из данного параграфа мы узнали, что:
• Электрическая цепь — это совокупность соединенных меж-
ду собой источников и приемников электрической энергии. *
• Источники электрической энергии бывают независимыми и
зависимыми. Независимыми источниками являются источ- ,
ники напряжения и тока. Зависимые источники — это че- '
тырехполюсные элементы, входные ток и напряжение кото- ,
рых управляют выходными током и напряжением. Разли-
чают четыре типа зависимых источников: ИНУН, ЦНУТ, .
ИТУН, ИТУТ.
• Приемниками электрической энергии являются пассивные
элементы цепи — резистивные, индуктивные, емкостные. '
11
В.2. Воздействие и реакция
При любой конфигурации цепи и при любом составе ее эле-
ментов (см., например, рис. В. 10) задача анализа электрической
цепи заключается в расчете напряжений и токов в любых ее вет-
вях и элементах.
В теории электрических цепей принято называть все напря-
жения и токи, генерируемые источниками электрической энергии,
воздействиями, а напряжения и токи в пассивных элементах це-
пи — реакциями на эти воздействия.
При передаче сигналов через электрическую цепь использует-
ся представление цепи, показанное на рис. В.11.
Такое представление легко получить из рис. В. 10, если в ка-
честве входного воздействия uBX(i) рассматривать, например, на-
пряжение источника u(t), а в качестве реакции цепи (или выход-
ного напряжения пВых(0) — например, напряжение UR3(t) на ре-
зисторе R3. Остальная часть электрической цепи обозначена на
рис. В.11 в виде прямоугольника. Ясно, что в качестве входного
воздействия и выходной реакции цепи могут быть выбраны лю-
бые интересующие нас напряжения или токи.
Обычно система, предназначенная для передачи сигналов, со-
стоит из рада конкретных каскадно-соединенных электрических
цепей (рис. В. 12): каскадов усилителей, фильтров, корректоров,
участков кабельных линий связи и т.п. В этом случае источником
входного воздействия для определенной электрической цепи (на-
пример, цепи № 2 на рис. В. 12) является напряжение или ток на
выходе предыдущей цепи, которая может быть заменена при рас-
чете эквивалентным источником энергии (эквивалентным генера-
тором). Нагрузкой электрической цепи может служить входное
сопротивление последующей цепи. Подобная ситуация изображена
на рис. В. 13.
«вх(0 —
= и(0
цепь
Электри-
ческая
“вых(0 —
= «Яз(0
Рис. В. 10. Электрическая цепь
Рис. В.11. Передача сигнала
через электрическую цепь
12
Рис. В. 12. Система передачи электрических сигналов
Цепь № 1
заменена
эквивалентным
генератором
напряжения
Эл. цепь
№2
(линия
связи)
Цепь№3
заменена
ее входным
сопротивлением
Рис. В. 13. Включение электрической цепи между
источником и нагрузкой
Для линейных электрических цепей справедлив принцип су-
перпозиции или наложения, в соответствии с которым можно вы-
числить реакции цепи на каждое отдельно взятое воздействие, а
затем «наложить» эти реакции друг на друга, т.е. просуммиро-
вать их. Данный принцип широко используется на практике ин-
женерами. Например, при расчете усилительного каскада
(рис. В. 14) отдельно анализируют работу каскада в режиме по-
стоянного тока (статический режим), который определяется на-
пряжениями смещения Uq и питания С7Пит, и отдельно рассчиты-
вают напряжения и токи, обусловленные воздействием на усили-
тель входного сигнала uBX(t) (динамический режим). Полный
анализ состоит в «наложении» указанных режимов.
Самыми простейшими воздействиями являются напряжение
и ток, неизменные во времени, так называемые постоянное на-
пряжение и постоянный ток (рис. В. 15). Реальными генератора-
ми таких воздействий являются электрические батареи; аккуму-
ляторы; преобразователи переменных напряжений и токов в по-
стоянные.
VT
Рис. В. 14. Транзисторный усилительный каскад
13
u(t)
Kt)
U
О
О t
б)
Рис. В. 15. Постоянные во времени напряжение (а) и ток (б)
а) б)
Рис. В. 16. Гармонические напряжение (а) и ток (б)
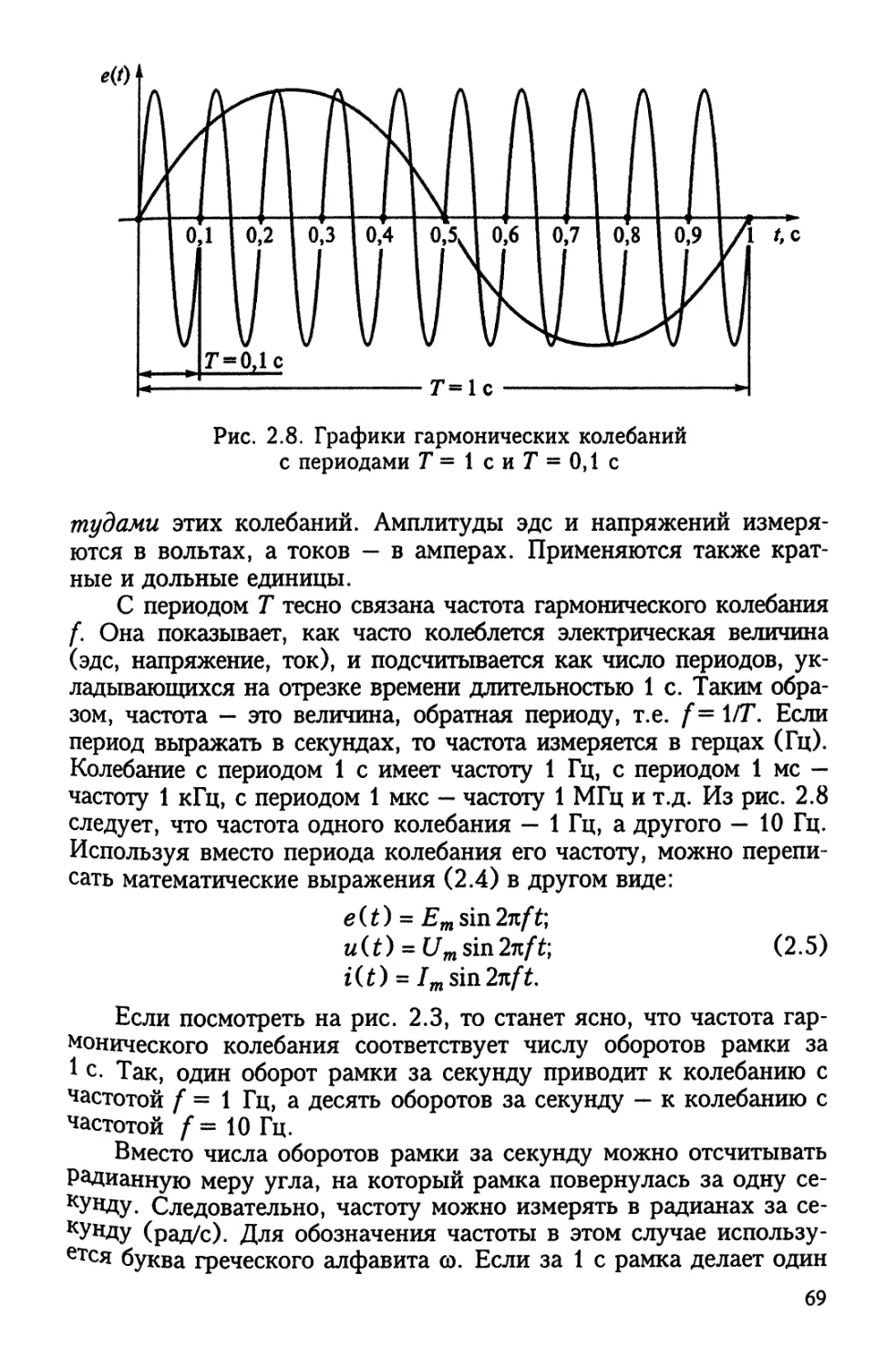
Переменные во времени воздействия (напряжения, токи) под-
разделяются на периодические и непериодические. Периодиче-
ское воздействие повторяет свою форму через строго заданный
промежуток времени — период Т.
К простейшим периодическим воздействиям относятся гармо-
нические напряжения и токи (рис. В. 16).
Рис. В. 17. Периодические воздействия сложной формы
14
u(t) или i(J)
в)
пп ппп п
t
Рис. В. 18. Непериодические воздействия:
а — одиночный импульс сложной формы;
б — непрерывное во времени воздействие;
в — случайная последовательность импульсов
Формы более сложных периодических воздействий, встре-
чающихся в технике, приведены на рис. В. 17: прямоугольная (с),
пилообразная (б), колоколообразная (в).
Примерами непериодического воздействия могут служить
(рис. В. 18): одиночный импульс сложной формы (а); напряже-
ние или ток, никогда не повторяющие своей формы (б); случай-
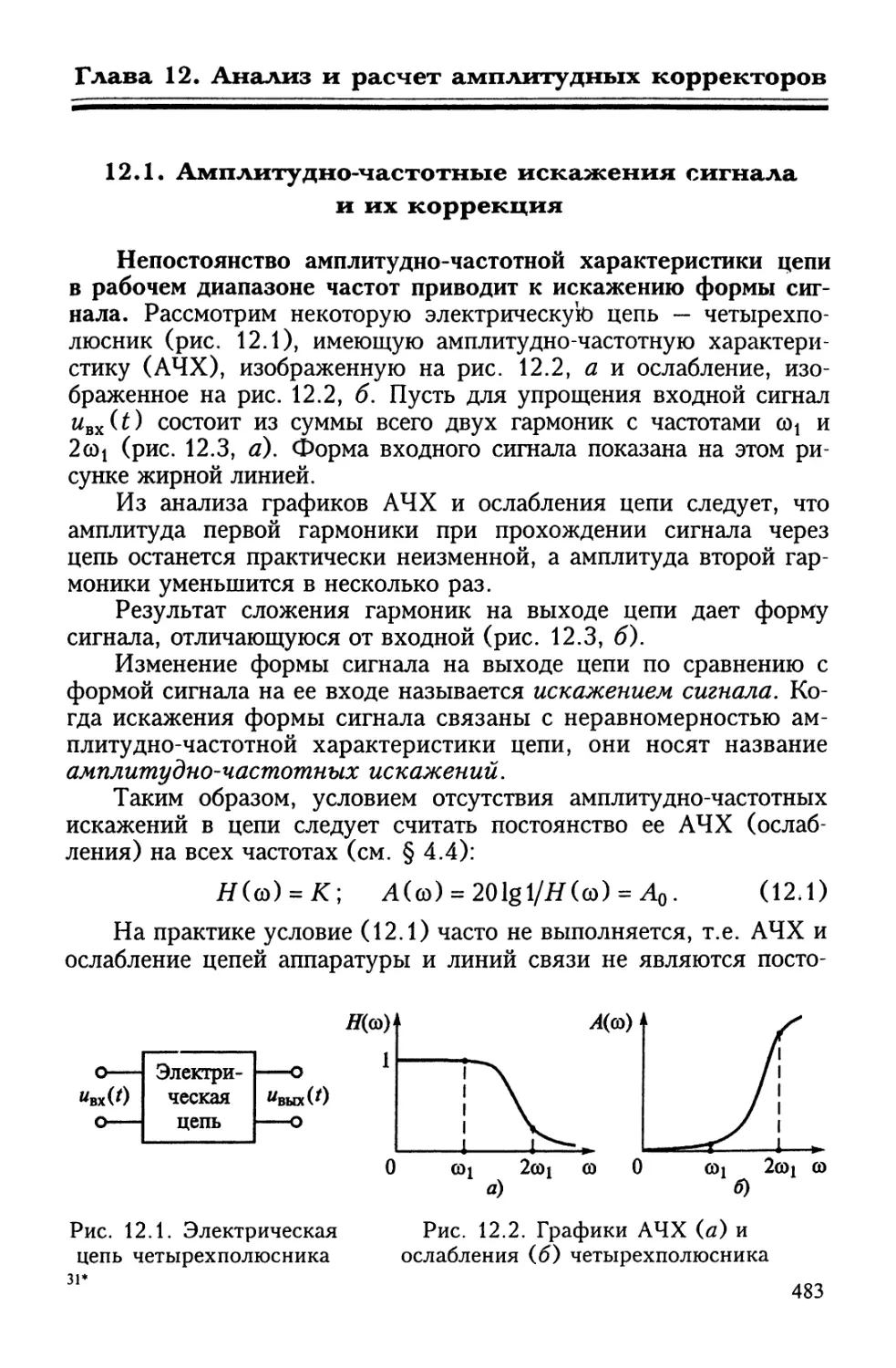
ная во времени последовательность импульсов (в).
С непериодическими воздействиями нам приходится сталки-
ваться постоянно. Микрофон преобразует звук в непериодиче-
ский сигнал сложной формы. Факсимильный аппарат анализиру-
ет изображение на бумаге и вырабатывает сложный непериодиче-
ский сигнал. Подобным образом действует телевизионная камера.
Телеграфный аппарат отправляет телеграммы с помощью сигна-
ла, состоящего из случайно чередующихся прямоугольных им-
пульсов. Следует заметить, что нести в себе информацию может
только непериодический сигнал. Периодический сигнал известен
заранее в любой момент времени и может служить лишь в каче-
стве испытательного или измерительного сигнала.
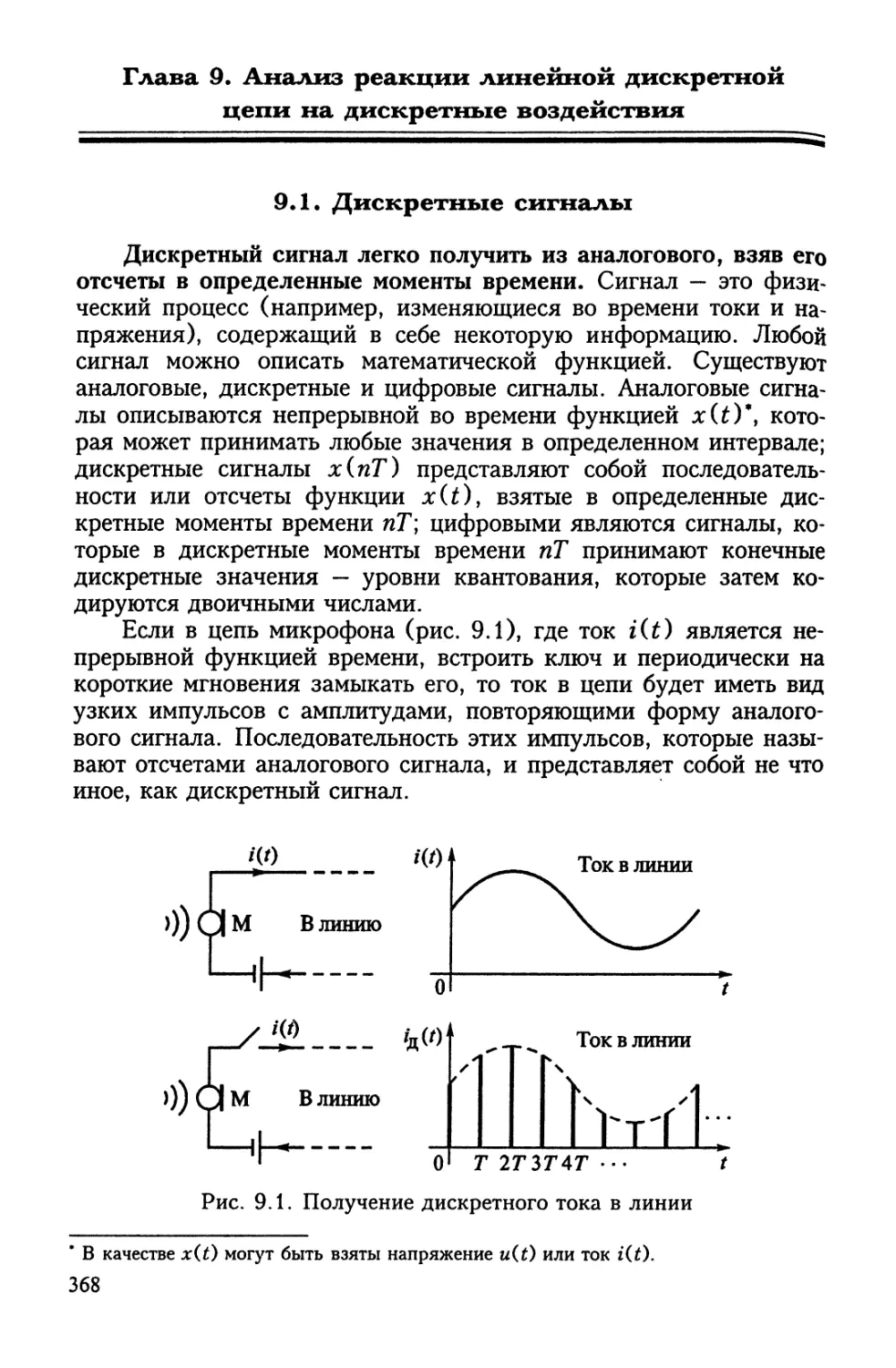
Особый статус имеют дискретные сигналы, которые можно по-
лучить из непрерывных путем их стробирования (дискретизации)
электронным ключом. Так поступают, например, в цифровой теле-
фонии или в цифровом телевидении, когда хотят перевести непре-
рывный (аналоговый) сигнал в цифровую форму.(рис. В. 19, а, б).
15
Ток в линии после
квантования
Д - шаг квантования
Рис. В. 19. Дискретизация и квантование непрерывного сигнала
Цифровые сигналы можно получить из дискретного сигнала
путем его квантования по уровню (рис. В. 19, в) с последующим
кодированием двоичными числами.
Подведем итоги параграфа:
• Инженер должен уметь определять реакцию цепи на воз- f
действие или сумму воздействий. ?
• Принцип суперпозиции позволяет рассчитывать реакцию I
линейной цепи на отдельные воздействия, а затем находить
полную реакцию как сумму отдельных реакций. |
• В качестве воздействий могут быть напряжения или токи, |
генерируемые источниками электрической энергии, а в ка- J
честве реакций — напряжения или токи в элементах элек- |
трической цепи. !
• Воздействия подразделяются на постоянные и переменные >,
во времени. ?
• Переменные во времени воздействия бывают периодические
и непериодические. |
• К простейшим периодическим воздействиям относятся гар- (
монцческие.
16
• Периодические сигналы сложной формы (прямоугольной, |
пилообразной и др.) используются в технике для целей ис- |
пытаний и измерений. |
• Только непериодический сигнал может нести в себе инфор-
мацию. §
В.З. Методы анализа цепей
Методы, применяемые для расчета реакции цепи на то или
иное воздействие, зависят от вида воздействия.
Если воздействие не зависит от времени, то говорят, что цепь
находится в режиме постоянного тока. При этом все индуктивно-
сти в цепи представляются, как известно, короткими замыкания-
ми (т.е. отрезками проводов), а все емкости — разрывами цепи.
Оставшиеся в эквивалентной схеме резистивные сопротивления
образуют чисто резистивную цепь. Нахождение напряжений и
токов в такой цепи от любых источников не представляет слож-
ностей. Методы расчета электрических цепей в режиме постоян-
ного тока хорошо описаны в литературе [1, 2]. С математической
точки зрения — это методы решения систем линейных алгебраи-
ческих уравнений с вещественными коэффициентами.
Неизменное во времени воздействие (т.е. постоянный ток или
постоянное напряжение) характеризуется только одним парамет-
ром — величиной или значением этого воздействия. Когда же в
качестве воздействия рассматривается гармоническое колебание,
то необходимо учитывать в общем случае три параметра — его
амплитуду, частоту и начальную фазу. Линейная электрическая
цепь обладает замечательным свойством: все ее реакции на гар-
моническое воздействие будут гармоническими и будут иметь ту
же частоту, что и воздействие. Таким образом, линейная элек-
трическая цепь не изменяет частоту гармонических колебаний в
ней. Кроме того, при наличии в цепи нескольких источников
гармонических напряжений и токов одной и той же частоты все
реакции цепи будут также гармоническими реакциями той же са-
мой частоты.
Следует заметить, что при гармоническом воздействии на ли-
нейную электрическую цепь расчет напряжений на элементах и
токов в ветвях усложняется. Дело в том, что реактивные элемен-
ты (индуктивность и емкость) оказывают влияние не только на
амплитуду гармонической реакции, но и изменяют ее начальную
фазу. Из трех параметров гармонического колебания (амплитуда,
частота и начальная фаза) два подвергаются изменению. Измене-
2-6972 17
Scan & DjVu Bookinqolz
ние амплитуды и начальной фазы гармонического колебания лег-
ко отразить в виде изменения длины и положения вектора на
комплексной плоскости. Действительно, у вектора, как и гармо-
нического колебания, может изменяться величина и фазовый
угол, отсчитываемый от какой-либо оси.
При заданной частоте гармонических колебаний в цепи воз-
действия представляются комплексными числами (или векторами
на комплексной плоскости при графическом изображении). Реак-
ции цепи будут представляться также комплексными числами, но
с другими амплитудами и начальными фазами. Задача анализа
цепи — найти эти амплитуды и начальные фазы.
Представление воздействий и реакций в виде комплексных
чисел позволяет использовать для расчета (анализа) цепи тот же
арсенал методов, который используется для цепей с постоянными
воздействиями, с той лишь разницей, что алгебраические опера-
ции производятся над комплексными числами. Стандартные ме-
тоды расчета линейной цепи сводятся обычно к решению систем
линейных алгебраических уравнений с комплексными коэффици-
ентами и комплексными переменными. Примеры анализа линей-
ных цепей при гармонических воздействиях даны в гл. 2.
При наличии в линейной электрической цепи нескольких ис-
точников гармонических колебаний разных частот расчет реакций
осуществляется методом наложения. Сначала находится реакция
цепи на каждое гармоническое воздействие в отдельности, а затем
полученные реакции складываются. Следует только помнить, что
сумма гармонических реакций разных частот дает в результате
периодическое колебание, которое по своей форме отличается от
гармонического. Анализ цепей с источниками гармонических ко-
лебаний разных частот рассматривается в гл. 3.
Тот факт, что периодическое воздействие сложной формы
можно представить в виде суммы гармонических колебаний раз-
ных частот, лежит в основе расчета цепей с источниками периоди-
ческих негармонических сигналов (например, последовательностей
прямоугольных, пилообразных, треугольных и тому подобных
импульсов). Из математики известно, что представление периоди-
ческой функции суммой гармонических колебаний называется
разложением этой функции в ряд Фурье. Таким образом, матема-
тический аппарат рядов Фурье — наиболее приемлемый аппарат
для представления периодических воздействий сложной формы.
Набор гармонических колебаний кратных частот, описываю-
щий периодический сигнал, называется спектром этого сигнала.
Анализ изменения спектра сигнала на выходе цепи по сравнению
со спектром входного сигнала позволяет сказать, как изменился
сам сигнал при прохождении его по цепи. Глава 3 посвящена
18
анализу линейных электрических цепей при воздействии на них
периодических сигналов сложной формы.
Адекватным математическим аппаратом для представления
непериодических воздействий является интеграл Фурье.
Два интегральных преобразования Фурье (прямое и обрат-
ное) позволяют по форме сигнала определять его комплексный
спектр, а по спектру — форму сигнала. Анализ электрической це-
пи при непериодическом воздействии сводится к нахождению
спектра реакции цепи на это воздействие, а затем и самой реак-
ции.
Расчет реакции линейной цепи с источниками непериодиче-
ских сигналов, называемый спектральным анализом, подробно
описан в гл. 4.
Обобщением интегральных преобразований Фурье являются
интегральные преобразования Лапласа, которые позволяют опре-
делять операторные изображения воздействий и, наоборот, фор-
му воздействий по их изображениям. Поэтому вместо спектраль-
ного анализа цепи может быть проведен операторный анализ,
суть которого состоит в отыскании сначала операторного изобра-
жения реакции, а затем с помощью обратного преобразования
Лапласа — реакции цепи на непериодическое воздействие. Мето-
ды операторного анализа изложены в гл. 5.
Существует прямой путь вычисления реакции цепи на воз-
действие, не прибегая к определению спектров или изображений
сигналов. В математике известны так называемые интегралы
свертки, которые дают возможность найти реакцию цепи на не-
периодическое воздействие путем прямого вычисления интеграла
свертки. Анализ линейных цепей с помощью интегралов свертки,
или временной метод анализа, изучается в гл. 6.
На практике часто встречаются случаи, когда в цепи проис-
ходят коммутации. Коммутацией принято называть любое изме-
нение параметров цепи, ее конфигурации, подключение или от-
ключение источников, приводящие к возникновению переходных
процессов. Анализ переходных процессов приведен в гл. 7. Этот
анализ может быть выполнен любым из трех методов: спектраль-
ным, временным или операторным.
Если цепь содержит нелинейные резисторы (диоды, тран-
зисторы), то чаще всего используют графоаналитические мето-
ды расчета. Как правило, в цепях с нелинейными элементами
не действует принцип суперпозиции. Ток нелинейного элемента
содержит гармоники, которых не было во входном сигнале.
Методам анализа нелинейных резистивных цепей посвящена
гл. 8.
2«
19
Подобно тому как аналоговые воздействия были представле-
ны преобразованиями Фурье и Лапласа, дискретные воздействия
представляются Z-преобразованием. Дискретные цепи описыва-
ются во временной области разностными уравнениями, а на ком-
плексной плоскости — передаточной функцией комплексного пе-
ременного Z. Расчет реакции дискретной цепи на дискретное воз-
действие может быть осуществлен как временным методом, так и
с помощью передаточных функций и Z-преобразования. Методы
анализа дискретных цепей описаны в гл. 9.
Во второй части книги на основании методов, рассмотренных
в первой части, описывается анализ различных узлов аппаратуры
связи: электрических фильтров (гл. И), амплитудных и фазовых
корректоров (гл. 12, 13), нелинейных преобразователей (гл. 14),
автогенераторов (гл. 15). Отдельная гл. 16 посвящена анализу и
расчету дискретных и цифровых фильтров.
Из данного параграфа мы узнали, что:
.чУ. ..> ............\ ..у .у-л?
Методы анализа цепи зависят от вида воздействия. *
Расчет реакции резистивной цепи в режиме постоянного
воздействия сводится к решению систем линейных уравне- |
ний с вещественными коэффициентами. i
Реакция цепи на гармоническое воздействие рассчитывается |
в результате составления и решения систем линейных урав- 1
нений с комплексными коэффициентами и переменными. |
Периодическое воздействие сложной формы можно пред- J
ставить как сумму гармонических колебаний кратных час- |
тот, разложив его в ряд Фурье. Расчет реакции цепи на та- |
кое воздействие производится методом наложения. |
Существует три метода анализа цепи на непериодическое \
воздействие сложной формы: спектральный, операторный, J
временной. »
Спектральный метод основан на применении преобразова- ।
ний Фурье. Вначале определяют спектр реакции цепи, а I
затем саму реакцию. £
В операторном методе используется интегральное преобра- *
зование Лапласа. Рассчитывается изображение реакции, а *
затем сама реакция. |
Временной метод позволяет сразу же определить реакцию |
цепи, используя интеграл свертки. |
Расчет реакции цепи на воздействие, изменяющееся скач- jj
кообразно, также может быть рассчитано временным, one- j
раторным или спектральным методами. S
20
• Для расчета реакций нелинейных резистивных цепей на по-
стоянное и гармоническое воздействия используются в ос-
новном графоаналитические методы.
• Для описания дискретных сигналов используется Z-преоб-
разование. Реакция дискретной цепи на дискретное воздей-
ствие рассчитывается либо с помощью разностных уравне-
ний, либо с использованием передаточных функций.
ЧАСТЬ 1. АНАЛИЗ РЕАКЦИИ ЦЕПЕЙ
НА РАЗЛИЧНЫЕ ВОЗДЕЙСТВИЯ
Глава 1. Анализ реакции линейной цепи
на постоянное воздействие
1.1. Постановка задачи
Рис. 1.1. Резистивная цепь с источ-
никами постоянных воздействий
Постоянные во времени воздействия на электрическую цепь
возникают при включении в эту цепь источников постоянного на-
пряжения и (или) источников постоянного тока. При таких воз-
действиях все индуктивности, находящиеся в электрической це-
пи, представляются на эквивалентной схеме короткими замыка-
ниями, а все емкости — разрывами цепи. Поэтому анализу под-
вергается цепь, состоящая только из резистивных элементов, т.е.
резистивная цепь. Примером такой цепи является цепь, показан-
ная на рис. 1.1 и содержащая независимый источник (генератор)
постоянного тока /гр независимый источник (генератор) пос-
тоянного напряжения Uy2 и
зависимый источник (гене-
ратор) напряжения Ur3.
Задачей анализа цепи
является расчет ее реакции
на заданные воздействия,
т.е. определение постоян-
ных токов в ветвях этой це-
пи и (или) постоянных на-
пряжений на резистивных
элементах.
Из данного параграфа
мы узнали, что:
• Постоянные во времени воздействия создаются включен-
ными в цепь независимыми и зависимыми источниками по-
стоянного напряжения и тока.
• Анализ реакции линейной резистивной цепи на постоянные
воздействия заключается в расчете токов в ветвях и напря-
жений на сопротивлениях цепи.
22
1.2. Расчет реакции линейной цепи с одним
источником воздействия
Определение эквивалентного сопротивления цепи осуществля-
ется «методом свертывания». На рис. 1.2 изображена линейная ре-
зистивная цепь с единственным источником постоянного напряже-
ния. Для расчета реакции цепи на это воздействие, т.е. для нахож-
дения токов ветвей и напряжений на элементах, используют после-
довательное «свертывание», а затем «развертывание» схемы с после-
дующим применением законов Ома и Кирхгофа [1, 2]. Под «сверты-
ванием» схемы понимается замена участков цепи их эквивалентны-
ми сопротивлениями. Поясним это на примере цепи на рис. 1.2.
Для определения эквивалентного сопротивления цепи относи-
тельно зажимов 1—2, к которым подключен источник напряже-
ния, будем «сворачивать» цепь, начиная с самых удаленных от
источника ветвей.
Сопротивления R& и Ry включены параллельно, и их можно
заменить одним сопротивлением R^y:
Re,-R^'
Сопротивления R3 и R4 также включены параллельно, по-
этому
р _ ^3-^4
Из схемы (рис. 1.2) видно, что сопротивления Rs и #67
включены последовательно и можно определить сопротивление
#34567:
#34567 = #34 + #5 + #67 •
Рис. 1.2. Линейная резистивная цепь с одним источником
постоянного напряжения
23
Сопротивления R2 и /?34567 включены параллельно, поэтому
^234567 =
^2^34567
+ Я34567
Окончательно определяем эквивалентное сопротивление цепи
как
*э = + ^234567 •
Пример 1.1. Определим эквивалентное сопротивление цепи, изо-
браженной на рис. 1.3, если Ri = 3,5 кОм, R2 =
= 3 кОм, R3 = Re = 2 кОм, Т?4 = 1?5 = 1 кОм.
Сопротивления Ra и Rs включены последова-
тельно. Заменяем их одним сопротивлением:
/?45 — R4 + Т?5 =1 + 1 — 2 кОм.
Параллельное соединение сопротивлений Re и
/?45 также заменяем одним сопротивлением:
D T?gT?45 2-2 . „
Т?456 = = -—- = 1 КОМ.
456 Я6 + Я45 2 + 2
Затем определяем сопротивление Т?з45б:
^3456 = -^3 + ^456 = 2 + 1 = 3 кОм.
Сопротивления R2 и /?3456 соединены параллель-
но, поэтому
^23456 =
#2-^3456
^2 + ^3456
3-3
3 + 3
= 1,5
кОм.
И наконец, определяем эквивалентное сопротив-
ление всей цепи относительно выходных зажимов ис-
точника напряжения:
Рис. 1.3. Линейная резистивная цепь
к примерам 1.1 и 1.5
24
R3 — Rj + R23456 = 3,5 + 1,5 = 5 кОм.
Пример 1.2. Определим эквивалентное сопротивление цепи, изо-
браженной на рис. 1.4, если Ri = 20 Ом, R5 = Rg =
= R2 = 10 Ом, R3 = R4 = 40 Ом.
Сопротивления R5 и Re соединены последова-
тельно:
R56 = R5 + R6 = 10 +10 — 20 Ом.
Сопротивления R3 и R4 соединены параллельно:
40-40 ~
—------ = 20 Ом.
40 + 40
р _ ^3^4
Сопротивления Rse
раллельно:
R34 также соединены па-
и
в _ ^56^34
^3456 ---------
20-20 ~
-------= 10 Ом.
Rs6 + -^34 20 + 20
Находим сопротивление R23456:
^23456 = ^2 + ^3456 =10 + 10 = 20 Ом.
Эквивалентное сопротивление цепи относительно
выходных зажимов источника тока найдем как со-
противление параллельного соединения Ri и R2-6:
R3 = ^1^23456 = 20;20 = 10 Ом
jRl + ^23456 20 + 20
Рис. 1.4. Линейная резистивная цепь
к примерам 1.2 и 1.6
На практике в цепях встречаются такие соединения элемен-
тов, которые нельзя свести только к последовательному или па-
раллельному. Рассмотрим в качестве примера соединение сопро-
тивлений звездой и треугольником (рис. 1.5). Уравнения, позво-
25
Рис. 1.5. Соединение сопротивлений звездой (а)
и треугольником (б)
ляющие осуществить переход от соединения сопротивлений звез-
дой к соединению треугольником, имеют вид [1,2]
^12 = R\+ R2 + ;
^з
R23 - R2 + R3 4—5 (11)
2?1з = Ri+ R3 + & -
к2
Обратный переход от соединения сопротивлений треугольни-
ком к соединению звездой можно осуществить, воспользовавшись
уравнениями
R{2 + R23 + *13
У"» <t2)
*М2 + ^23 + к13
^13^23
+ R23 + Rl3
Пример 1.3. Определим эквивалентное сопротивление цепи, изо-
браженной на рис. 1.6, а, если R\ = 1,7 кОм, R2 =
= R3 = 5 кОм, R5 = 10 кОм, = Re = 25 кОм.
В схеме, изображенной на рис. 1.6, а, сопротив-
ления R2, R3 и Rs соединены звездой. Преобразуем
это соединение сопротивлений в соединение тре-
угольником (рис. 1.6, б), используя уравнения (1.1):
R23 = R2+R3+^^- = 5 + 5 + — = 12,5 кОм;
23 2 3 R5 10
26
h ф ц
a)
ii Ф14
Рис. 1.6. Линейная резистивная цепь к примерам 1.3 и 1.7
R25 = R2 + Rs+^^- = 5 + 10 + ^- = 25 кОм;
2 * R3 5
R35 = Я3+Я5+^^. = 5 + 10 + ^-^ = 25 кОм.
1?2 5
В схеме на рис. 1.6, б сопротивления 7?д и R23, а
также 7?б и R35 соединены параллельно, поэтому
^425
•^356
K4R25 25 • 25 , „ -
4 i = ——— = 12,5 кОм;
R4 4" R25 25 + 25
^35-^6 25 • 25 . - с „
— - ——— = 12,5 кОм.
25 + 25
R35 + Кб
Сопротивления .R425 и 7?ззб соединены последо-
вательно, а с сопротивлением R23 — параллельно,
значит,
r, = (-^425 + ^356 )-^23 _ (12,5 + 12,5)12,5 _ g 2 KQM
^425 + K33q + R23 12,5 + 12,5 + 12,5
Эквивалентное сопротивление цепи относительно
выходных зажимов источника напряжения определя-
ется как
Кэ = 7?! + 7?'= 1,7 + 8,3 = 10 кОм.
Пример 1.4. Определим эквивалентное сопротивление цепи, изо-
браженной на рис. 1.7, а, если Ri = R2 = R3 = R4 =
= R5 = 10 Ом.
27
Рис. 1.7. Линейная резистивная цепь к примеру 1.4
Преобразуем треугольник, образованный сопро-
тивлениями 7?i, R3 и R4 (рис. 1.7, а), в звезду
(рис. 1.7, б), используя уравнения (1.2):
р R\R-$ _ 10 • 10 ~ 00 /~)м.
Ri - R~R3+Rt ' '
= RlR‘ о = = 3.33 Ом;
R\ + /?з +30
D R\R^ 10 10 о do
/?8 = —1 - = — = 3,33 Ом.
/?1 + /?з + /?4 30
В схеме на рис. 1.7, б сопротивления Rs и/?2, а
также Ry и Rs соединены последовательно; между
собой сопротивления Т?62 и Rys соединены парал-
лельно, и с сопротивлением Rs сопротивление Т?6275
соединено последовательно, поэтому эквивалентное
сопротивление цепи относительно зажимов источника
тока рассчитываем следующим образом:
р _ р . (#6 +-Кз)(^7 +^5) _
э 8 7?6 + R2 + R7 + R5
= 3 33 (3,33 +10)(3,33 + 10)
’ + 3,33 + 10 + 3,33 + 10
= 10 Ом.
Для расчета токов и напряжений в резистивных линейных
цепях с одним источником используют законы Ома и Кирхгофа.
Закон Ома применяется для ветви и для замкнутого контура. На
рис. 1.8, а изображена ветвь, содержащая п сопротивлений и
имеющая напряжение между узлами 1 и 2, равное разности на-
пряжений в этих узлах:
их2 = их-и2.
28
Un
Рис. 1.8. Ветви (а, б) и замкнутый контур (в) для
иллюстрации закона Ома
Ток в ветви определяется по закону Ома для участка цепи:
I = (13)
r1 + r2 + ... + r„ r9'\ v '
Положительное направление тока в ветви задается направле-
нием напряжения U\2-
На рис. 1.8, б изображена ветвь, содержащая п сопротивле-
ний и т источников постоянного напряжения. Закон Ома для та-
кой ветви имеет вид
U1 э + U г. +...— U г
I = _12---п-------! 4)
R1+R2+... + Rn
Напряжения Urt,..., Urm источников напряжения записыва-
ются в числителе (1.4) со знаком «плюс», если их направления
противоположны направлению тока, и со знаком «минус», если
их направления совпадают.
Ток в замкнутом контуре, изображенном на рис. 1.8, в, так-
же находится по закону Ома для замкнутой цепи:
I = Uv/R9. | (1.5)
Направление тока определяется направлением напряжения
источника.
Найдем токи в ветвях цепи на рис. 1.9, содержащей два сопро-
тивления R\ и Т?2> включенных параллельно, и источник пос-
тоянного тока /г-
Ток I в неразветвленной части цепи равен току источника
I = 1г- Для определения токов Л и I2 в ветвях цепи найдем на-
пряжение 1712 между узлами 1 и 2, используя закон Ома:
29
Рис. 1.9. Цепь для
определения токов в
параллельных ветвях
Тогда токи в каждой из параллель-
ных ветвей находим по формуле (1.3):
, _Ц\2 _ Т &2
1 Rt Rl+R2’
I = и*2 = I
2 ^2
(1.6)
Полученные выражения (1.6) назы-
вают формулами разброса тока по па-
раллельным ветвям.
Кроме законов Ома для анализа ли-
нейных цепей используются законы Кирхгофа.
Первый закон — закон токов Кирхгофа (ЗТК) гласит: алгеб-
раическая сумма токов ветвей, сходящихся в любом узле элек-
трической цепи, равна нулю. Математическая запись закона
п
k=\
(1.7)
где п — число ветвей, сходящихся в узле.
В уравнении (1.7) токи, одинаково ориентированные относи-
тельно узла, записывают с одинаковыми знаками. Например, то-
ки, входящие в узел, записывают со знаком «плюс», а выходя-
щие — со знаком «минус». Количество уравнений, которые сос-
тавляются по закону токов Кирхгофа (1.7), на единицу меньше
количества узлов в цепи: пузл — 1.
Запишем уравнения по закону токов Кирхгофа для схемы,
изображенной на рис. 1.1:
для узла 1 Ц -12 - /3 = 0;
для узла 2 12 - Ц -15 = 0;
для узла 3 -Ц +15 + /6 = 0.
Второй закон — закон напряжений Кирхгофа (ЗНК) гласит:
алгебраическая сумма напряжений ветвей в любом контуре
равна нулю'.
т
Z^=o,
k=\
(1.8)
где т — число ветвей, входящих в контур.
В уравнении (1.8) напряжения, направления которых совпа-
дают с обходом контура, берутся со знаком «плюс», а не совпа-
дающие — со знаком «минус». Количество независимых уравне-
ний, которые составляются по закону напряжений Кирхгофа (1.8),
рассчитывается по формуле пвет — (пузл — 1) — пИст> где пвет — чис-
30
ло ветвей в цепи; пИСт — число ветвей, содержащих источники то-
ка. Не составляют уравнения по закону напряжений Кирхгофа
для контуров, содержащих источники тока.
Запишем уравнения по закону напряжений Кирхгофа для
цепи, изображенной на рис. 1.1, выбирая направления обхода
контуров по часовой стрелке:
для левого нижнего контура I
/2^2 + _ ^з-^з +^т2 = 0;
для правого нижнего контура II
-liRi + I5R5 - ЦКб ~ Ur3 = 0.
Продолжим рассмотрение цепи, изображенной на рис. 1.2,
указав направления токов в ее ветвях (рис. 1.10). После ее «свер-
тывания» и определения эквивалентного сопротивления цепи R3
относительно зажимов источника напряжения найдем ток Ц, ис-
пользуя формулу закона Ома (1.5):
Л=^г/*э-
Ток I2 найдем по формуле разброса (1.6), имея в виду, что
сопротивления 7?г и /?345б7 включены параллельно:
г _ г -^34567
1 + -^34567
Ток /5 тоже можно найти по формуле разброса или по закону
токов Кирхгофа (1.7) для узла 3. Выберем закон токов Кирхгофа:
I5 = h~h-
Токи I3, Ц, Iq и /7 находим по формуле разброса (1.6):
Z3 = h nRin Л = Л r>R3n
Рис. 1.10. Линейная резистивная цепь с одним
источником напряжения
31
= 1
5 7?6 + T?7
Л = Л
Re
Re +R7
Для определения токов /4 и 1у можно также использовать
уравнения, составленные по закону токов Кирхгофа для узлов
4 и 5:
Л = Л ~Л>
Л = h -Ц-
Итак, мы рассчитали с помощью законов Ома и Кирхгофа
токи во всех ветвях цепи с одним источником постоянного на-
пряжения. Если мы захотим рассчитать напряжение между лю-
быми двумя узлами, то можем использовать закон Ома. Напри-
мер, для определения напряжения между узлами 3 и 2, т.е. С/32,
справедлива любая из следующих формул:
U32 = Л-^234567 = 12R2 = 15^34567 = ^Г р ^2р567---•
+ •'‘234567
Пример 1.5. Рассчитаем токи в ветвях цепи, изображенной на
рис. 1.3 (пример 1.1), если С/г = 10 В.
В примере 1.1 было рассчитано эквивалентное
сопротивление цепи R3 = 5 кОм. По закону Ома
(1.5) находим ток Ц:
г _ (/г _ Ю „ .
1 Ra 5 М '
По формуле разброса (1.6) находим ток I2:
/2 = Л = 2—2— = 1 мА.
^3456 + Ry 3 + 3
Ток /3 определим, используя закон токов Кирх-
гофа для узла 1:
13 =Ц-12 = 2-\ = 1 мА.
Токи Ц и /5 определим, используя формулу раз-
броса (1.6):
I _ г Re
3 R4 + R5 + Re
т т R4 + R5
I s — i ч
+ R5 + Rq
= 0,5
мА,
мА.
S + 1 + 2
Такое же значение тока /5 получается, если со-
ставить уравнение по закону токов Кирхгофа для
узла 2:
32
/5 = 73-74 = 1-0,5 = 0,5 мА.
Пример 1.6. Рассчитаем токи в ветвях цепи, изображенной на
рис. 1.4 (пример 1.2), если 7г = 1 А.
В примере 1.2 было рассчитано эквивалентное
сопротивление цепи 7?э = 10 Ом. Используя закон
Ома, найдем напряжение U23:
^23 = ^э =Ы0 = 10 В.
Рассчитаем токи 71 и I2 по закону Ома:
Ц = = 10 = 0 5 А>
1 7?! 20
/2=/^'^=0'5А'
•*'23456
Следует отметить, что токи It и I2 можно рас-
считать другим способом, используя формулу раз-
броса и закон токов Кирхгофа:
т _ т ^23456 _ 4 20 _ л с
1 Г *1+^23456 20 + 20 ’
12 =1Г-Ц =1-0,5 = 0,5 А.
А,
Найдем ток /5 по формуле разброса:
Г5 = 12-----^34------= 0 5-----20-----= 0 25 А
/?34 + /?5 + R$ 20 + 10 + 10
Для определения токов 1з и Ц составим уравне-
ние по закону токов Кирхгофа для узла 1:
/2-7з-/4-75=0.
Отсюда найдем сумму токов /3 и /4:
13 + Ц = 12 - /5 = 0,5 - 0,25 = 0,25 А.
Поскольку сопротивления R3 и /?4, стоящие в
параллельных ветвях, равны по величине, то будут
равны и токи, протекающие через них:
/3 = Ц = /з*/4 = = 0,125 А.
3 4 2 2
Такие же значения токов 1з и Ц можно полу-
чить, используя формулу разброса. Предлагаем чита-
телям убедиться в этом самостоятельно.
Пример 1.7. Рассчитаем токи в ветвях цепи, изображенной на
рис. 1.6 (пример 1.3), если (7г = Ю.В.
3-6972
33
В примере 1.3 было рассчитано R3 = 10 кОм. Ток
Ц найдем по закону Ома:
г 10 . .
''< = 10 = 1мА'
В схеме на рис. 1.6, б найдем напряжение (71з
по закону напряжений Кирхгофа (1.8):
(713 = UT-IiRi =10-1-1,7 = 8,3 В.
Тогда ток
Ьз
U13 8>3
Я23 12,5
= 0,664 мА.
Из уравнения, составленного по закону токов
Кирхгофа для узла 1, найдем суммарный ток 1ц, про-
текающий через параллельное соединение сопротив-
лений и R25, а также R35 и R&
/0 = Л -Лз = 1 -0,664 = 0,336 мА.
Используя формулу разброса, определим токи
Л и 1ь:
т _ т ^25
т __ т ^35
25
= 0,336 / , =0,168 мА,
25 + 25
25
= 0,336—-rz-= 0,168 мА.
25 + 25
В схеме на рис. 1.6, а из уравнений, составлен-
ных по закону токов Кирхгофа для узлов 1, 4 и 3,
найдем токи I2, Is и I3:
12=Ц-Ц=1- 0,168 = 0,832 мА,
15 = Ц - /б = 0,168 - 0,168 = 0 мА,
/3 = -16 + Ц = -0,168 +1 = 0,832 мА.
Из данного параграфа мы узнали, что:
• Для расчета реакции цепи с одним источником электриче- ;-
ской энергии сначала определяют путем «свертывания» ;
схемы эквивалентное сопротивление цепи относительно за-
жимов этого источника, а затем, последовательно «развер- j
тывая» схему, используют для расчета токов и напряжений г
в цепи законы Ома и Кирхгофа.
34
w* .WfeVW ШЛД. *W ,i §
На практике кроме последовательного и параллельного со-
единения сопротивлений встречается соединение сопротив-
лений звездой и треугольником.
Для расчета токов в параллельных ветвях удобно восполь-
зоваться формулой разброса.
В соответствии с законом токов, открытым Кирхгофом, ал-
гебраическая сумма токов ветвей, сходящихся в узле цепи,
равна нулю. Токи, одинаково ориентированные относитель-
но узла, записываются с одинаковыми знаками.
В соответствии с законом напряжений Кирхгофа алгебраи-
ческая сумма напряжений ветвей в контуре равна нулю.
Напряжения записываются со знаком «плюс», если их на-
правление совпадает с направлением обхода контура, и со
знаком «минус», если не совпадает.
f
I
I
£
1.3. Расчет реакции линейной цепи с несколькими
источниками воздействий
В основу одного из методов расчета положен принцип су-
перпозиции, суть которого заключается в следующем: если в
линейную цепь включены несколько источников постоянного
напряжения или тока, то реакция цепи равна сумме реакций от
каждого источника в отдельности. Данный метод получил назва-
ние метода наложения.
Используется следующий порядок расчета:
1. Произвольно выбирают направления токов в ветвях цепи.
2. Составляют так называемые частичные схемы, в которых ос-
тавляют только один источник, а остальные заменяют на их
внутренние сопротивления (напомним, что идеальный источ-
ник напряжения заменяется короткозамкнутой цепью, а иде-
альный источник тока — разрывом).
3. Рассчитывают частичные токи в ветвях каждой из частичных
схем, используя законы Ома и Кирхгофа.
4. Рассчитывают токи в ветвях исходной схемы как алгебраиче-
скую сумму соответствующих частичных токов. Частичные то-
ки записываются со знаком «плюс», если их направление сов-
падает с направлением тока в ветви исходной цепи, и со зна-
ком «минус», если направления частичного и исходного токов
противоположны.
Рассмотрим применение метода наложения на примере расче-
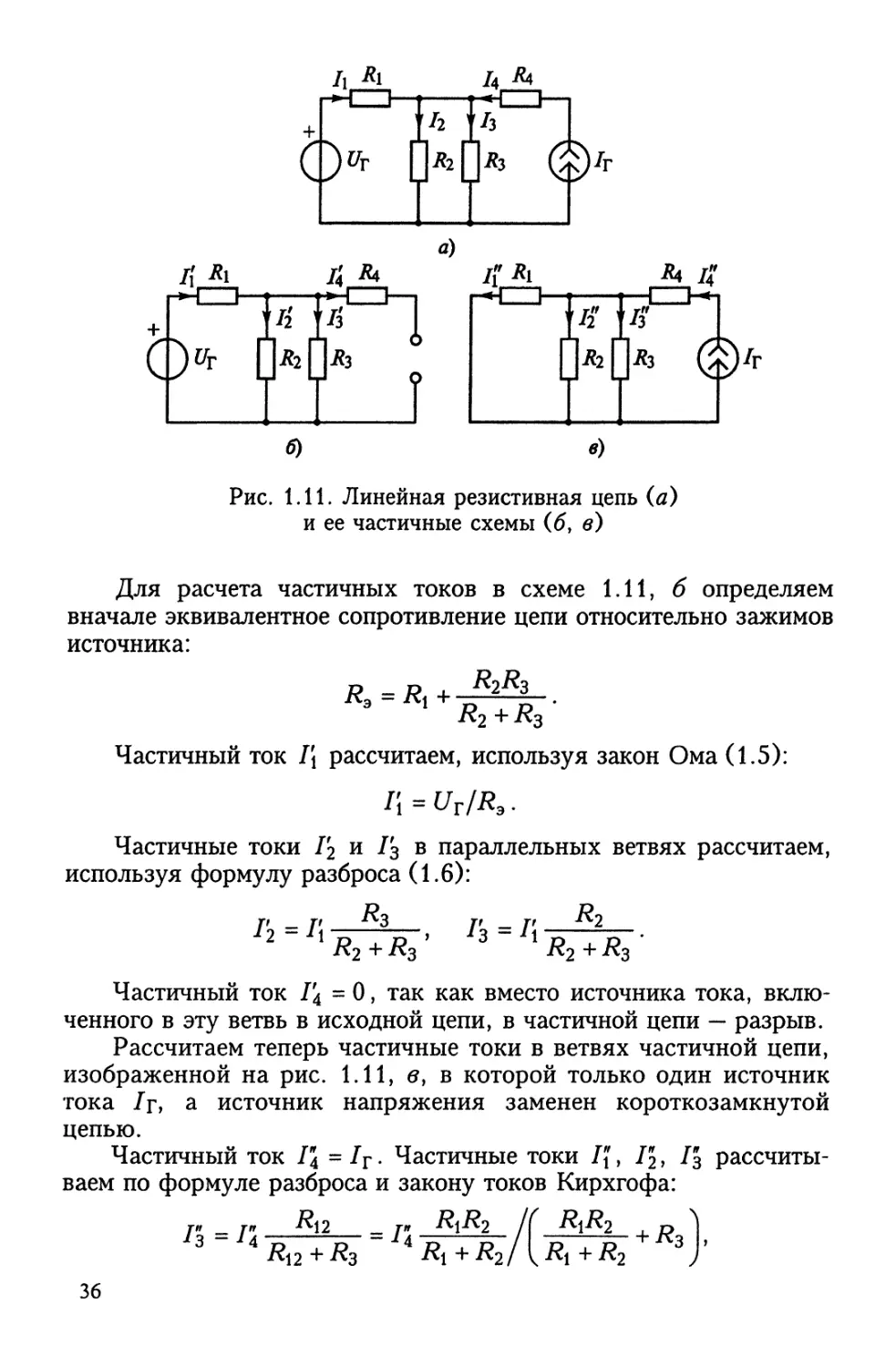
та токов в цепи, изображенной на рис. 1.11, а. Частичные схемы,
каждая из которых содержит только один источник напряжения
или тока, приведены на рис. 1.11, б или 1.11, в.
з»
35
Рис. 1.11. Линейная резистивная цепь (а)
и ее частичные схемы (б, в)
Для расчета частичных токов в схеме 1.11, б определяем
вначале эквивалентное сопротивление цепи относительно зажимов
источника:
D D ^2^3
R3 = R< + •„•* г, .
/?2 +^3
Частичный ток 1\ рассчитаем, используя закон Ома (1.5):
I'i=UT/R3.
Частичные токи Г2 и 1'з в параллельных ветвях рассчитаем,
используя формулу разброса (1.6):
/2=Л
R3
^2 + &3
/з = Д
R2
R2 + R3
Частичный ток /4 = 0, так как вместо источника тока, вклю-
ченного в эту ветвь в исходной цепи, в частичной цепи — разрыв.
Рассчитаем теперь частичные токи в ветвях частичной цепи,
изображенной на рис. 1.11, в, в которой только один источник
тока 1т, а источник напряжения заменен короткозамкнутой
цепью.
Частичный ток /4 = /г. Частичные токи Ц, Г2, /3 рассчиты-
ваем по формуле разброса и закону токов Кирхгофа:
г» _ тп -^12 _ тч R\R-2 ( R\R2 .o')
3 4Я12+Я3 47?i+7?2/1^i+^2 V
36
' T?13+/?2 Ri+R3/\Ri+R3 ZJ’
7? = 75-7$-75-
Токи в ветвях исходной цепи на рис. 1.11, а определяем как
алгебраическую сумму соответствующих частичных токов:
Л=д-Л, 12 = г2 + г2,
13=Г3+Г3, Ц=-Г4+Ц=1г.
Пример 1.8. Методом наложения рассчитаем токи в ветвях цепи,
изображенной на рис. 1.12, если C7ri = 120 В, (7гг =
= 40 В, /г = 60 мА, R\ = 4 кОм, R2 — 1 кОм, R3 =
- 3 кОм, R4 = 10 кОм.
В схеме на рис. 1.12 включены три источника и
истинное направление токов в ветвях неизвестно, по-
этому направления всех токов выбираются произ-
вольно.
Три частичные схемы изображены на рис. 1.13.
В каждой из них остается только один источник, а
остальные заменены их внутренним сопротивлением.
Рассчитаем частичные токи в ветвях каждой из этих
схем.
В частичной схеме на рис. 1.13, а частичные то-
ки 1\ и Г$ равны по величине и определяются по за-
кону Ома для контура:
л = л=^ = ^ = з° мА-
1\\ 4
Все остальные токи в частичной схеме равны ну-
лю, т.е.
1'2=^=Л=0.
В частичной схеме на рис. 1.13, б определяем
токи Г2 и Г3:
Рис. 1.12. Линейная резистивная цепь к примеру 1.8
37
Рис. 1.13. Частичные схемы к примеру 1.8
Г2 = Г3 = С/г2/(^2 + Яз) = 40/(1 + 3) = 10 мА.
Все остальные токи равны нулю:
Ц = Ц=Г5=0.
В частичной схеме на рис. 1.13, в рассчитываем
токи в ветвях, используя формулу разброса и при-
нимая во внимание, что I" = 0, так как сопротивле-
ние Rt закорочено. Получаем
Ц = Г5 = 1Г = 60 мА;
/т гт
2 = Л
/т тт
3 = У4
Я-з
r2 +r3
R2
r2 + R3
з
= 60-Лт
1 + 3
= 60—!-
1 + 3
= 45 мА;
= 15 мА.
Токи в исходной схеме на рис. 1.12 рассчитыва-
ем как алгебраическую сумму соответствующих час-
тичных токов:
Ц = /'i = 30 мА;
12 = Г2 -Г2 = Ю - 45 = -35 мА;
/3 = Г3 +/5 = 10 + 15 = 25 мА;
/4 = Ц = /г = 60 мА;
/5 = Л " = 30-60 = -30 мА.
Отрицательные знаки токов 12 и /5 означают, что
реальное направление этих токов противоположно
выбранному.
38
Для расчета токов в ветвях линейной резистивной цепи ис-
пользуют также метод токов ветвей, который базируется на
уравнениях, составленных для цепи по законам Кирхгофа. Не-
зависимые уравнения, составленные для цепи по законам Кирх-
гофа, объединяют в систему, решение которой дает токи ветвей.
Пример 1.9. Методом токов ветвей рассчитаем токи в цепи, изо-
браженной на рис. 1.14, если (7п = 100 В, Ur2 =
= 200 В, (7гз = 150 В, /г = 6 мА, R? = R3 - 20 кОм,
Т?4 = Т?5 = 10 кОм.
Схема на рис. 1.14 содержит четыре узла; это оз-
начает, что по закону токов Кирхгофа можно составить
три независимых уравнения. По закону напряжений
Кирхгофа можно составить пвет— (пузл — 1) — «ист =
= 6 — (4 — 1) = 2 уравнения.
Составим уравнения для узлов 1, 2 и 3, а также
для двух контуров: верхнего I и внешнего II, не со-
держащего источник тока /г- Контуры выбираем таким
образом, чтобы не проходить через ветвь с источником
тока, поскольку на его зажимах есть напряжение U,
которое является дополнительной неизвестной величи-
ной. Направление обхода каждого контура выбираем
по часовой стрелке. В результате получаем систему из
пяти уравнений с пятью неизвестными токами:
-/1-/4+/3 = 0;
^4 + ^5 + = 0>
Л-/2-/5 = 0;
if—J2—
-ЦКл + I5R5 + =0;
/2^2 + /з*з + ^Г1 “ ^г2 + ^Гз = 0.
Рис. 1.14. Линейная цепь к примеру 1.9
39
Подставляем в эту систему численные значения
сопротивлений схемы и напряжений источников и,
решая систему .уравнений, получаем значения токов в
ветвях:
=-6,25 мА; 12= 1,75 мА;
/3 = —4,25 мА; Z4 = 2 мА;
Z5 = —8 мА; Zg = Zp = 6 мА.
При расчете токов в сложных линейных цепях количество
уравнений, составляемых по законам Кирхгофа, бывает слишком
большим и решать систему линейно-независимых уравнений труд-
но. Поэтому были разработаны другие методы расчета цепей, а
законы Кирхгофа используются в основном для проверки пра-
вильности расчета.
Метод контурных токов основан на законе напряжений
Кирхгофа и позволяет уменьшить количество уравнений в сис-
теме до величины пвет — («узл — 1) — «ист* Порядок расчета токов
в ветвях цепи следующий:
1. Произвольно выбирают направления токов в ветвях.
2. Выбирают независимые контуры, а затем задают направления
условных токов, которые называют контурными токами.
3. Для каждого из выбранных контуров составляют систему ли-
нейных независимых уравнений по закону напряжений Кирх-
гофа. Решение этой системы уравнений позволит найти все
контурные токи.
4. Определяют токи в ветвях исходной цепи как алгебраическую
сумму контурных токов, протекающих по этой ветви.
Рассмотрим применение метода контурных токов для расчета
токов в ветвях цепи, изображенной на рис. 1.15.
Рис. 1.15. Линейная резистивная цепь
с несколькими источниками
40
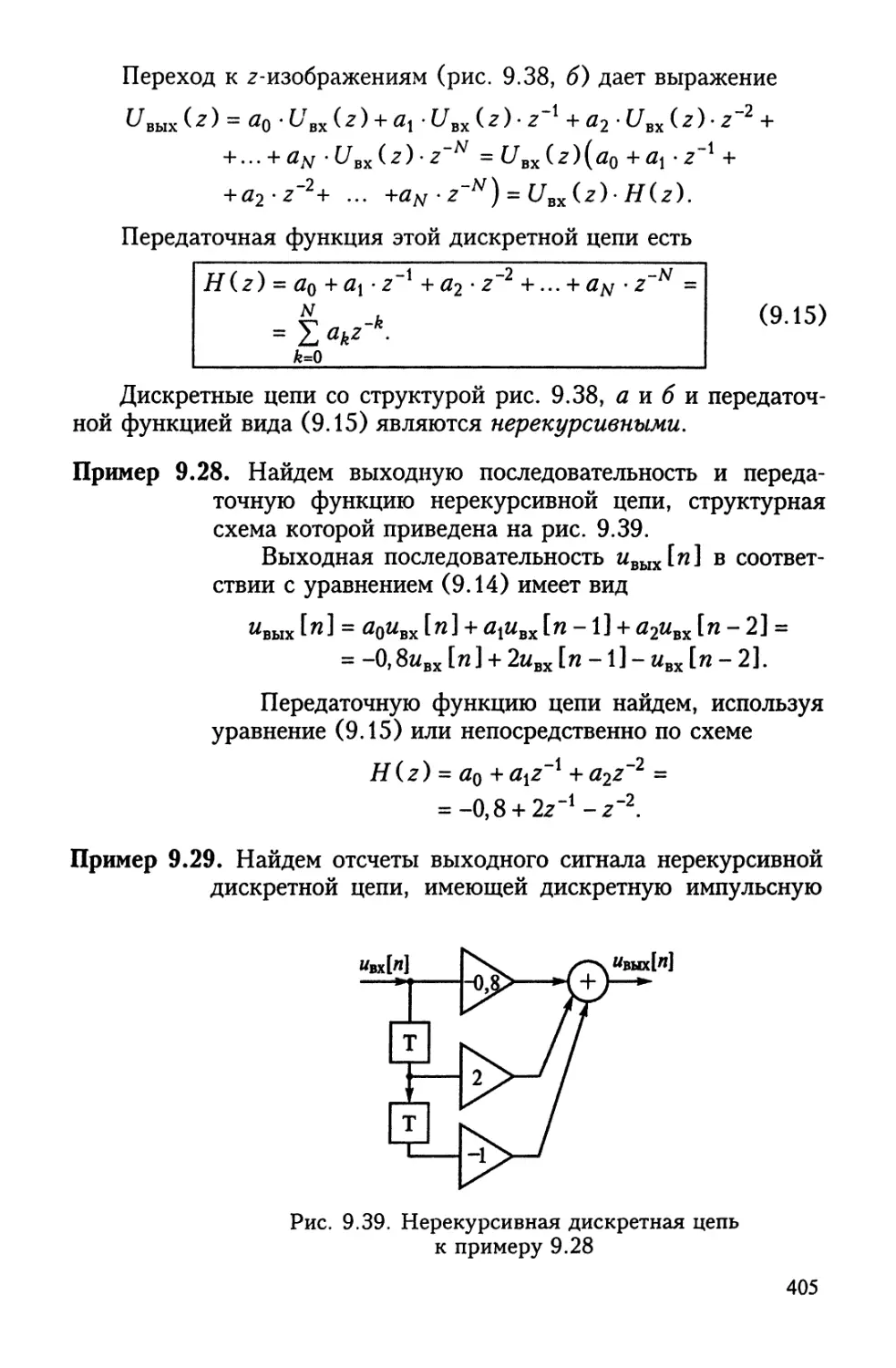
Направления токов в ветвях указываем произвольно, так как
их истинные направления неизвестны.
Выбираем два независимых контура I, II и направления кон-
турных токов IKi, 1К2, например, по часовой стрелке, как это пока-
зано на рис. 1.15. Ток источника тока 1г замыкаем по контуру III.
Из схемы видно, что контурный ток третьего контура 7кз оп-
ределяется током источника тока в этом контуре, т.е. /кз = 1г-
Поэтому систему уравнений составляем только для первого и
второго независимых контуров.
Правило составления уравнений основано на том, что каж-
дый контурный ток создает в рассматриваемом контуре свое на-
пряжение:
• собственное, определяемое данным контурным током и все-
ми сопротивлениями, входящими в контур;
• взаимное, определяемое смежными контурными токами и со-
противлениями ветви, являющейся смежной между контурами.
Для схемы на рис. 1.15 контурный ток 7К1 создает в первом
контуре собственное напряжение /К1(^2 + R3 + Ra), а контурные
токи /К2 и /кЗ внесут в этот же контур взаимные напряжения
-1*2^4 и -1x3^2- Знак «минус» означает, что контурный ток пер-
вого контура и контурные токи остальных контуров направлены
противоположно друг другу.
Аналогичным образом собственное напряжение, создаваемое
током /К2 во втором контуре, будет равно IK2(Ra + R5 + Re + R1X
а взаимные напряжения, создаваемые контурными токами сосед-
них контуров, будут равны -IkRa и -1кз^5-
По закону напряжений Кирхгофа алгебраическая сумма всех
внесенных в контур напряжений равна нулю. Поэтому оконча-
тельно система уравнений будет иметь вид
Ли (R2 + R3 + R4) ~ Лг-^4 “ ЛсЗ-^г - ^Г1 + С/г2 = 0;
-/к1/?4 + /к2 (/?4 + Т?5 + + -fy ) - /К3^5 ~^Г2 = 0-
Часто используют каноническую форму записи уравнений:
рК^11-/к2^2-4з/?13=^К1; (19)
Л1^21 + Лг^22 - ^кЗ-^23 = UK2-
В приведенных выше уравнениях использованы обозначения:
= R2 + R3 + R4, R-22 = Rt + R5 + Re + R7 — собственные со-
противления первого и второго контуров, равные сумме сопро-
тивлений всех ветвей, образующих каждый контур;
R\2 = R21 = Ra> R\3 - R2’ R23 = R5 — взаимные сопротивления,
равные общим сопротивлениям между рассматриваемым и сосед-
ними контурами;
41
L/K1 = Un -Un, Uk2 = Ur2 — контурные задающие напряжения,
равные алгебраической сумме напряжений источников, входящих
в каждый контур.
При составлении уравнений (1.9) пользуются правилами
знаков', собственное сопротивление всегда берется со знаком
«плюс»; взаимное сопротивление берется со знаком «плюс», если
контурные токи протекают через него в одном направлении, и со
знаком «минус» — если в разных направлениях; напряжение ис-
точника в правой части (1.9) берется со знаком «плюс», если его
направление противоположно направлению контурного тока, и со
знаком «минус» — если совпадает с ним.
В общем случае, когда резистивная цепь содержит т незави-
симых контуров, система уравнений в канонической форме име-
ет вид
41^11 + Лс2^12 +••• + 1ктВ\т = ик1;
. + 1К2^22 + •• + 1ктВ2т = Uk2;
.^к2^т2 ••• ^кт^тт = ^кт-
Из системы линейных уравнений (1.10) находят контурные
ТОКИ Л1, /К2, •••, /кт.
Для рассматриваемого выше примера из системы линейных
уравнений (1.9) находим контурные токи /К1 и /К2, используя
правило Крамера:
где Д =
-Т?21
-Т?12
/?22
/К1 -
А1
Д ’
Г _ Д2
/к2-Т
— главный определитель системы (1.9);
Д1, Д2 — определители, которые получены путем замены в Д
первого или второго столбцов на столбец свободных
членов в (1.9):
Д1 =
ик1 + /к3^13
U К2 + /к3^23
~^12
1?22
д2 =
7?п
-^21
UK1 + /к3^13
U к.2 + Лс3^23
Зная контурные токи, находим токи в ветвях цепи, исполь-
зуя принцип наложения. Если направление контурного тока сов-
падает с направлением тока в ветви, то последний берется со зна-
ком «плюс», если противоположно — со знаком «минус».
С учетом этого получаем
/1 = Zr; 12 = /К1 + Лез! /з = Ль
^4 = Л1 — /к2> /5 = Лс2 “ Лз> Л = /к2-
42
При использовании метода контурных токов следует учесть,
что если в цепи есть ветви с источниками тока, то независимые
контуры нужно выбирать так, чтобы в них эти ветви не входили.
Для учета действия этих источников их токи замыкаются через
ветви, не содержащие других источников тока.
Пример 1.10. Методом контурных токов рассчитаем токи в вет-
вях цепи, изображенной на рис. 1.16, если Ur =
= 100 В, /г = 1 А, Я1 = R3 = #4 = ЮО Ом, R5 =
= 50 Ом.
Выберем два независимых контура I и II, а ток
источника тока 1г замкнем через /?i, R2 (рис. 1.16).
Направления всех контурных токов возьмем против
часовой стрелки. Контурный ток /кз = Ir = 1 А. Для
первого и второго контуров запишем уравнения со-
стояния (1.9):
. 41 (^j + Я4 +14) -1*284 + 4з-^1 - 0;
. “41-^4 + 4г (*3 + -^4 ) - Ur-
Подставим в уравнения численные значения
Г/к1- 250 -/«2-100 = -100;
[-/к1 • 100 + 1к2 200 = 100
и найдем из этой системы уравнений контурные то-
ки. Получаем
/к1=-0,25А, /к2 =0,375 А.
Найдем токи в ветвях исходной цепи:
4 = 41 + 4з = -0,25 +1 = 0,75 А;
4 = 4г = 0,375 А;
Ц = 4г - 41 = 0,375 + 0,25 = 0,625 А;
4 = -41 = 0,25 А.
Л1 (Р Лз
Рис. 1.16. Линейная резистивная цепь к примеру 1.10
43
Пример 1.11. Методом контурных токов рассчитаем токи в ветвях
цепи, изображенной на рис. 1.17. Цепь содержит не-
зависимые источники задающего напряжения (7^ =
= 30 В и тока /г = 1 А, ИНУН с задающим напряже-
нием С7гг = HU\ = 2(Ji, сопротивления = R2 =
= R3 = 5 Ом.
В цепи на рис. 1.17 один независимый контур.
Левый контур содержит ветвь с источником тока, и
его контурный ток известен: 7К1 = /г - 1 А. Для пра-
вого независимого контура составим уравнение (1.10):
Ас2 (-^1 + #2 + ^3 ) - IjRi =иГ} - Ur2.
Напряжение зависимого источника
С/Г2 = HUt = .
Ток Ц можно записать через контурные токи
7к1 = /г и /кз:
А = Л- “Л<2>
тогда
иГ2=Н1гЪ-Н1к2Ь.
Окончательно получаем уравнение
^к2 (^ + /?2 + 7?з - HRi) = + Off ~ HIfR\ •
Находим контурный ток 1к2:
= ITRt+Uri-HIrR} = 1-5 + 30-2-1-5 =
к2 Ri+R2+R3-HRi 5+5+5-25
Зная контурные токи 1К\ и 1к2, определяем токи
в ветвях:
Л=/к1-/к2=1-5 = -4 А;
72 = /к2=5 А.
Рис. 1.17. Цепь с зависимым источником к примеру 1.11
44
Метод узловых напряжений (потенциалов) основан на за-
коне токов Кирхгофа и законе Ома и позволяет уменьшить ко-
личество уравнений в системе до (иузл — 1). Порядок расчета
токов в ветвях цепи следующий:
1. Произвольно выбирают направления токов в ветвях.
2. Заземляют один из узлов (называемый базисным); его потен-
циал поэтому становится равным нулю.
3. Составляют систему линейных независимых уравнений для уз-
лов цепи по закону токов Кирхгофа. Решение данной системы
позволяет найти напряжения (разность потенциалов) между
узлами.
4. Используя закон Ома для участка цепи, находят токи в ветвях
исходной цепи.
Рассмотрим применение метода узловых напряжений для
расчета токов в ветвях цепи, изображенной на рис. 1.15.
Направления токов в ветвях выбираем произвольно. Зазем-
ляем узел 4 (базисный узел). Это означает, что его потенциал ра-
вен нулю: Уд = 0.
Для узлов 1, 2 и 3 составляем систему линейных независи-
мых уравнений по закону токов Кирхгофа.
Правило составления системы уравнений следующее. По за-
кону токов Кирхгофа алгебраическая сумма токов в узле равна
нулю. Тогда в узле 1 сойдутся токи:
• собственный, определяемый потенциалом первого узла и про-
водимостями всех ветвей, подходящих к узлу:
у Г 1 । 1 1
11 R$ R&+ R1 J
• взаимные, определяемые потенциалами смежных узлов и про-
водимостями ветвей, соединяющих узлы:
( 1 > 1 1
2{ъ+вгу 3r6 + r7 r5
Напомним, что внутреннее сопротивление источника тока Rr
стремится к бесконечности, поэтому проводимость этой ветви
равна нулю и потенциал V4 равен нулю.
• узловой ток, образуемый источником напряжения или тока (в
данном случае -1г).
Взаимные токи всегда берутся со знаком «минус», а знак узло-
вого тока зависит от того, втекает он в узел или вытекает из него.
Узловой ток, образуемый источником напряжения (напри-
мер, такой имеется для узла 2 схемы на рис. 1.15), определяется
отношением напряжения источника к сопротивлению ветви, в ко-
торую этот источник включен.
45
Проводя рассуждения для узлов 2 и 3, аналогичные приведен-
ным выше, получим систему уравнений для схемы на рис. 1.15:
у _1_ +----i--- _у------!---=
I ^5 ^6 + fy ) ^6 + ^7
V2(— + — )-Уз— = 1г~иг —;
2 р р 3 р г г> р
к jf<2 К3 ) Кз К3
т/ 1 т/ 1 т/ Г 1 1 1 тт 1 тт 1
7?6 + R? ^3 1-^3 ^4 ^6 + ^7 J ^3 ^4
В канонической форме записи система уравнений имеет вид
'y1G11-y2G12-y3G13 = /yl;
• -VtG2i + У2С22 - y3G23 = Iy2; (1.11)
-ViG31 - V2G32 + V3G33 = /уз-
В уравнениях (1.11) использованы обозначения:
У1> У2, Уз — потенциалы узлов 1, 2 и 3 цепи;
~ 1 1^11’11 1
= °22=v^; G33=Wk^_
собственные проводимости узлов 1, 2 и 3, равные сумме прово-
димостей всех ветвей, подсоединенных к каждому из узлов;
1 1
Gi2 = G21 = 0; = G31 -—; G23 = G32 = — — взаимные
Щ + ^7 ^3
проводимости узлов 1 и 2, 1 и 3, 2 и 3, равные сумме проводи-
мостей всех ветвей, включенных между каждой парой узлов;
1 11
/У1=-7Г; /У2 =1г-иц—; 1у3 =иг— + иГ2— - задающие
Кз Кз К4
узловые токи узлов 1, 2 и 3, равные алгебраической сумме токов
всех источников, подключенных к каждому из узлов.
При составлении уравнений пользуются правилами знаков'.
собственные проводимости всегда берутся со знаком «плюс», вза-
имные проводимости всегда берутся со знаком «минус», задаю-
щие токи источников берутся со знаком «плюс», если они на-
правлены к узлу, и со знаком «минус» — если от узла.
В случае, когда резистивная цепь имеет п узлов, получаем
обобщенную систему уравнений в канонической форме. Если за-
землить n-й узел, т.е. Vn = 0, то имеем
ViGn - V2Gi2 -... - Vn.4Gi(n_t) = /у1;
-VjG21 + V2G22 -...-Уп_хС2(п.1) = Iy2; (j ^2)
[-VlGcn-t)! - V2G(n i)2 + V(„j)G(n-1 )(„-!) = /y(n-l)-
46
Из системы линейных уравнений (1.12) находят потенциалы
узлов Vi, V2, •••> V(n-i), используя, например, правило Крамера.
Для рассматриваемого выше примера из системы линейных
уравнений (1.11) находим потенциалы узлов 1, 2 и 3:
у1=А1; V2=A2. у = Аз
Д Д J Д
где Д — главный определитель системы уравнений (1.11):
—+ —-1— 0 _____<—
R$ ^6 + ^7 ^6 +
л л 1 1 1
Д = 0 —- + — ----
Т?2 R3 ^3
1 _J_ 1 1 1
^6 + Rj ^3 R3 R& Rf> + &7
Определители Дь Дг и Дз получают, заменяя в главном опре-
делителе соответствующий столбец на столбец задающих узловых
токов.
Зная потенциалы узлов, находим токи в ветвях цепи
(рис. 1.15), используя закон Ома (1.3), (1.4):
А
_у2-у4 у2.
2 r2 r2’
Уз-иг2. г _л.
R< ’ 5 R5'
г _у2-уз + [/Г1
3= R3 ’
г уз~У1
Rq + Ry
При использовании метода узловых напряжений (потенциа-
лов) следует учесть, что если в цепи есть ветвь с идеальным ис-
точником напряжения, то за базисный берут один из узлов, к ко-
торому подключена эта ветвь. При этом потенциал другого узла
будет сразу же известен. Он равен напряжению источника, взя-
тому со знаком «плюс» или «минус» в зависимости от полярности
источника постоянного напряжения. Уравнение по методу узло-
вых напряжений для такого узла составлять не нужно, но его по-
тенциал учитывается при составлении уравнений для других уз-
лов. Ток в ветви с идеальным источником нельзя рассчитать, ис-
пользуя закон Ома, так как его сопротивление равно нулю. По-
этому для расчета тока используют закон токов Кирхгофа после
расчета токов во всех других ветвях цепи.
Пример 1.12. Методом узловых напряжений рассчитаем токи в
ветвях цепи, изображенной на рис. 1.16, если €7г =
= 100 В, /г = 1 А, = 100 Ом, R3 = R4 = 100 Ом,
Т?5 = 50 Ом (см. пример 1.10).
47
Направления токов в ветвях показаны на рис. 1.16.
Заземлим узел 3. Это значит, что потенциал это-
го базисного узла равен нулю: V3 = 0.
Для узлов 1 и 2 составим уравнение (1.12):
VlGii - V2Gi2 = ^yl>
-V[G21 + V2G22 = ^у2-
Собственные проводимости узлов 1 и 2 определя-
ются по формулам
1 1 1
7?3 R4
611
= 0,03 См;
G22 = -77- + ~—Ь "тг” = 0,04 См.
** r> D
К3 К4 К5
Проводимость ветви с источником тока равна
нулю, поскольку его внутреннее сопротивление бес-
конечно велико. Поэтому в выражении для расчета
Gn только три слагаемых, хотя к узлу 1 подключены
четыре ветви.
Взаимные проводимости G12 и G21 между узлами
1 и 2 — это сумма проводимостей двух параллельных
ветвей:
G}2 = G21 = "77- + -77-- = 0,02 См.
R3 R±
Задающие узловые токи
Лч-Л+Угтг’2 А:
= “I А.
Подставляя значения Gn, G12, G21, G22, /yi и Ту 2
в систему уравнений, получаем
(Vt 0,03-V2 0,02 = 2;
I-Vi 0,02 + V2 -0,04 = -1
и находим потенциалы узлов
=75 В; V2 =12,5 В.
Определяем токи в ветвях исходной цепи, ис-
пользуя закон Ома:
48
=31 = 22 = 0,75 A;
Rt 100
V V+[/r 12,5-75 + 100 nQ7CA
----------------ioo---= 0’375 A;
/4=^ = Z2za5=0,625 A;
T?4 100
/5=^- = -^ = 0>25 A.
K5 3U
Полученные значения токов ветвей совпадают с
теми, которые были рассчитаны для этой же самой
цепи методом контурных токов при решении приме-
ра 1.10.
Пример 1.13. Методом узловых напряжений рассчитаем токи в
ветвях цепи, изображенной на рис. 1.18, если Un =
= 10 В, Ur2 = 4 В, /г = Ю мА, R\ = Rz = R3 = 2 кОм.
Заземляем узел 1: V\= 0. В цепи есть ветвь с
идеальным источником напряжения Urt, поэтому по-
тенциал узла 2 известен:
V2 = ^Г1 = ю в.
Для узла 3, потенциал которого неизвестен, со-
ставляем уравнение (1.12):
Отсюда находим V3:
Рис. 1.18. Цепь к примеру 1.13
4 - 6972
49
Зная потенциалы всех узлов, находим токи в
ветвях:
т у2 10 с Л
Z1 = -=г = — = 5 мА,
Я, 2
т V2-V3 Ю-13 . с .
/2=-^ = —= -1,5мА.
/3=^Ц±£1,1^=«. -, МЛ
/<3 2
Ток Ц нельзя рассчитать, используя закон Ома,
так как в ветви включен только идеальный источник
напряжения, внутреннее сопротивление которого
равно нулю. Для определения тока Ц используем за-
кон токов Кирхгофа для узла 2:
74 — 1^+12 = 5 -1,5 = 3,5 мА.
Метод эквивалентного генератора обычно применяется в том
случае, когда необходимо определить напряжение или ток в одной
ветви цепи. Метод основан на теореме об активном двухполюснике
[1, 2]. Вся цепь, кроме ветви, в которой нужно найти ток, заменяется
активным двухполюсником — эквивалентным генератором с задаю-
щим напряжением (7гэ или током /гэ и внутренним сопротивлением
7?э (рис. 1.19). Определив параметры эквивалентного генератора,
можно найти ток I в ветви с сопротивлением R. Для эквивалентного
генератора напряжения (рис. 1.19, б) по закону Ома получаем
'=7^м <113>
Для эквивалентного генератора тока (рис. 1.19, в), ис-
пользуя формулу разброса, имеем
Рис. 1.19. Активный двухполюсник (а) и эквивалентные генераторы
напряжения (б) и тока (в)
50
R3
Гэ R3 + R'
(1.14)
Алгоритм расчета тока в ветви цепи методом эквивалентного
генератора следующий:
Определяют напряжение (7гэ эквивалентного генератора на-
пряжения или ток /гэ эквивалентного генератора тока. На-
пряжение (7гэ равно напряжению на зажимах 1—Г активного
двухполюсника в режиме холостого хода: 1/гэ - Uxx- Ток 7гэ
равен току при коротком замыкании зажимов 1—1': /гэ = /кз-
Определяют внутреннее сопротивление эквивалентного генера-
тора R3. Оно равно сопротивлению пассивного двухполюсника
относительно разомкнутых зажимов 1—Г. Пассивный двухпо-
люсник получают в результате замены всех источников актив-
ного двухполюсника (рис. 1.19, а) их внутренними сопротив-
лениями.
Определяют искомый ток в ветви по закону Ома или по фор-
муле разброса:
1.
2.
3.
Цхх
Rg + R
(1.15)
I-J __
K3R3+R'
(1.16)
Пример 1.14. Методом эквивалентного генератора рассчитаем ток
/5 В цепи, изображенной на рис. 1.20, а, если Ur =
= 60 В, 1г = 10 мА, 7?1 = 5 кОм, R2 = 10 кОм,
R3 = 10 кОм, Т?4 = 15 кОм, R$ = 8 кОм.
Рис. 1.20. Линейная резистивная цепь к примеру 1.14
4*
51
1. Рассчитаем напряжение эквивалентного гене-
ратора. Для этого исключим из схемы на рис. 1.20, а
сопротивление R$ и определим напряжение холостого
хода Uхх (рис. 1.20, б). По закону напряжений
Кирхгофа для выбранного контура
Uxx + I3R3 ~ ЦК* = 0
или
Uxx = I4R4 - /3^з-
Находим токи /3 и I* для цепи на рис. 1.20:
Г - и?
3 R1+K3
-----= 4 мА, Ц = 1г = 10 мА.
5 + 10
Подставляем эти значения токов в выражение
для расчета (7ХХ и получаем
Uxx =1^4-13X3 =1015-410 = 110 В.
Напряжение эквивалентного генератора
[/Гэ=ихх=ио й.
Рассчитаем сопротивление эквивалентного гене-
ратора. Для этого в схеме на рис. 1.20, а заменяем
все источники их внутренними сопротивлениями.
Получаем схему, изображенную на рис. 1.20, в, из
которой определяем R3:
D ^1^3 D 5'10 . с 400 /Ч
Ra = 7— + R4 = -—- +15 = 18,3 кОм.
9 Ri+R3 4 5 + 10
Искомый ток I5 определяем по формуле (1.15):
т Uxx НО /ПЛ
h = 77——7 4,2 мА.
R э + R$ 18,3 + 8
2. Рассчитаем ток короткого замыкания /кз. Для
этого закоротим сопротивление R$. Получаем схему,
изображенную на рис. 1.20, г. По закону токов
Кирхгофа для узла 1 имеем
-Д +13 - /кз = О
или
^кз ~ Ц ~ Ц-
Токи /3 и Ц найдем, например, по методу узло-
вых напряжений. Выберем узел 1 как базисный:
Vi = 0. Для узла 2 запишем уравнение (1.12):
52
1 1 1
R3
RtrUri*h
Отсюда
Ur-^r + Ir
60 | + 10
= 1 1 Г
5 + 10 + 15
у, =__________
_L+_L _L
7?1 7?з
Находим токи /1 и I3:
r V!-V2+Ur -60 + 60 Л .
г = —1---1- =-----= 0 мА;
= 60 В.
5
1 Ri
т V2-Vi 60 „ д
I3 - —ь---L = — - 6 мА.
3 10 10
Ток короткого замыкания рассчитываем, под-
ставляя в выражение для определения 1КЗ значения
токов Ц и /з:
Лез - _ Л =6 мА.
Сопротивление эквивалентного генератора Rsr
остается равным 18,3 кОм, поскольку цепь не изме-
нилась.
Ток Is в ветви с сопротивлением Rs рассчитаем
по формуле (1.16):
Т Т Rs С 18,3 . „ А
Is = 1кз = 6-—г—- = 4,2 мА.
5 к R9+Rs 18,3 + 8
Получили такое же значение тока /5, что и при
расчете методом эквивалентного генератора напря-
жения.
Выбор метода эквивалентного генератора напря-
жения или тока для расчета тока в ветви определяется
тем, какую из величин проще рассчитать: Uxx или /кз-
Из данного параграфа мы узнали, что:
• Для расчета реакции цепи с несколькими источниками |
можно использовать методы наложения, токов ветвей, кон- |
турных токов, узловых напряжений (потенциалов), эквива- *
лентного генератора напряжения и тока. |
53
• Метод наложения заключается в составлении всех частич-
ных схем, содержащих только по одному источнику элек- |
трической энергии, расчете частичных токов в ветвях этих |
частичных схем и затем алгебраическом суммировании со- <
ответствующих частичных токов. J
• Метод токов ветвей требует составления системы линейных >
независимых уравнений по законам токов и напряжений J
Кирхгофа и решения этой системы относительно токов в |
ветвях цепи. Недостатком метода является большое число |
уравнений для сложных схем. |
• Методы контурных токов и узловых напряжений (потен- 1
циалов) позволяют уменьшить количество уравнений в сис- |
теме по сравнению с методом токов ветвей. В методе кон- |
турных токов составляется система линейных уравнений ।
для независимых контуров цепи, а в методе узловых на- |
пряжений (потенциалов) — для независимых узлов цепи. (
• Метод эквивалентного генератора применяется для расчета *
тока только в одной ветви цепи. Ток в этой ветви рассчи- !
тывается по напряжению холостого хода на разомкнутой 1
ветви или току короткого замыкания в закороченной ветви, |
величине эквивалентного сопротивления схемы относитель- |
но зажимов ветви и величине сопротивления ветви с ис- J
пользованием закона Ома. f
1.4. Коэффициент передачи резистивной цепи
Рассмотрим резистивную цепь с несколькими источниками
постоянного воздействия, изображенную на рис. 1.20, а. Часто
представляет интерес определение конкретной реакции цепи на
конкретное воздействие. Например, требуется определить ток Ц
как реакцию на постоянное воздействие (7г- В этом случае цепь
удобно представить в виде четырехполюсника, к входным зажи-
мам которого подключен интересующий нас источник постоянно-
го напряжения (7г, а к выходным зажимам — сопротивление, по
которому протекает интересующий нас ток, как это показано на
рис. 1.21, а или в общем виде — на рис. 1.21, б.
Зная конкретную реакцию цепи на конкретное воздействие,
можно ввести характеристику цепи, носящую название коэффи-
циента передачи цепи — это отношение реакции к воздействию.
Для цепи, изображенной на рис. 1.21, б, можно записать че-
тыре вида коэффициентов передачи.
1. Коэффициент передачи по напряжению
54
Рис. 1.21. Представление цепи из рис. 1.20, а
в виде четырехполюсника
Ни=^г- (117)
Ur
Это безразмерная величина, и она имеет ясный физический
смысл: показывает, во сколько раз цепь ослабила или усилила
напряжение генератора, подключенного к ее входу.
2. Коэффициент передачи по току
Я/=4- (118)
71
Эта величина также безразмерная и показывает, во сколько
раз цепь ослабила или усилила входной ток.
3. Передаточное сопротивление
HR=^. (1.19)
71
Эта величина измеряется в омах и имеет физический смысл
сопротивления.
4. Передаточная проводимость
(1.20)
иг
55
Эта величина измеряется в сименсах и имеет физический
смысл проводимости.
Если коэффициент передачи цепи заранее известен, то для
любого воздействия на цепь легко рассчитать ее реакцию на это
воздействие. Из уравнений (1.17)—(1.20) находим реакции цепи в
виде тока Ц и напряжения Uc
Ц=ЦН1 или Ц=итНа,
U4 = UrHv или U i = IXHR.
Отметим, что воздействием может быть не только постоянное
напряжение или ток соответствующих источников, но и ток в лю-
бом элементе цепи или напряжение на нем.
Далее из примеров будет видно, что значение любого коэф-
фициента передачи не зависит от величины напряжений и токов
на входе и выходе цепи, а определяется исключительно видом
схемы и значениями ее элементов.
Пример 1.15. Найдем коэффициент передачи по току и переда-
точное сопротивление цепи, приведенной в приме-
ре 1.14 (рис. 1.20, а), если воздействием в цепи явля-
ется источник постоянного тока /г = 10 мА, а реакци-
ей — ток в сопротивлении Rs или напряжение на нем.
При решении примера 1.14 методом эквивалент-
ного генератора был рассчитан ток, протекающий че-
рез сопротивление R5. Он равен 4,2 мА.
Коэффициент передачи по току найдем, восполь-
зовавшись формулой (1.18):
я, = 4 = ^.о,42.
Коэффициент передачи по току не имеет размер-
ности.
Для расчета передаточного сопротивления цепи
необходимо знать напряжение на сопротивлении R5.
Найдем его по закону Ома:
U5 =I5R5 = 4,2-8 = 33,6 В.
Передаточное сопротивление цепи находим, ис-
пользуя формулу (1.19):
„ Us 33,6 о
HR = -у5- = = 3,36 кОм.
Величина Hr имеет размерность сопротивления.
56
Пример
.16. Найдем коэффициент передачи по напряжению це-
пи, изображенной на рис. 1.22, если R\ = R2 = 2 кОм,
R3 = /?4 = 4 кОм.
Коэффициент передачи цепи, изображенной на
рис. 1.22, согласно (1.17) есть отношение напряже-
ния на выходе цепи к напряжению на входе:
Hu=U2IUx.
Напряжение на выходе цепи U2 — это напряже-
ние на параллельном соединении сопротивлений R3 и
Ri. Его можно записать как
U2 =/ •
R3 + &4
Напряжение на входе цепи
+к2+-^&Л
V ^3 + -*^4 J
Тогда коэффициент передачи по напряжению
j R3R4
и г _ У_2 -_____________+ Rj______
U\ т( п о ^3^4
V 2
или после преобразований и подстановки численных
значений сопротивлений
гт ___________R3R4___________ j.
U (Ri + R2)(R3+ Rt)+ R3R4 3
Как следует из последнего выражения, коэффи-
циент передачи резистивной цепи не зависит от вели-
чины приложенного воздействия и определяется толь-
ко параметрами элементов цепи. Для пассивной рези-
стивной цепи коэффициент передачи по напряжению
всегда меньше единицы.
R2
Рис. 1.22. Резистивная цепь к примеру 1.16
57
Пример 1.17. Найдем коэффициент передачи по напряжению ат-
тенюатора (делителя напряжения) в виде Т-образно-
перекрытой цепи, нагруженной на сопротивление Ro и
изображенной на рис. 1.23, если /?о=Ю кОм, R\ =
= 5 кОм, Т?2 = Ю кОм.
Коэффициент передачи по напряжению цепи, изо-
браженной на рис. 1.23, определяется в соответствии с
формулой (1.17) как отношение напряжения U2 на со-
противлении Ro к напряжению C7i на входе цепи:
ни=и2/их.
Из схемы на рис. 1.23 видно, что напряжение
U2— это напряжение в узле 2, a U\ — напряжение в
узле 1 при условии, что Vx = V2 = 0 (базисный узел).
Составим уравнения по методу узловых напряжений
(1.12) для узлов 2 и 3:
„ 1 тт ( 2 1 Л rr 1 Л.
—С/ 1 “77—U 2 1 “77—“77” 1^3 “77“ —
Ro Rx J Rq
1 1 (21)
-(/14--С72-4- + ^з + =°-
/?о R0 1^0 ^2 J
Из этой системы уравнений находим
ц _ц _______2RqR2 + Rq + R\R2__
2 ~ 1 3RXR2 + 2ВД + 2RqR2 + Ro '
Характерной особенностью аттенюатора, схема
которого изображена на рис. 1.23, является то, что
сопротивления Ro, Ri и R2 удовлетворяют условию
RxR2 = Rq •
Подставляя в выражение для расчета U2 вместо
Т?2 величину Ro/R\ и беря отношение U2 к U\, полу-
чаем коэффициент передачи Ну:
Рис. 1.23. Аттенюатор к примеру 1.17
58
H _U2 _ Ro _ 10 2
и их Ri + R0 5 + 10 3‘
Полученное значение коэффициента передачи оз-
начает, что на выход делителя напряжения поступает
только 2/3 входного напряжения.
Пример 1.18. Найдем коэффициент передачи по напряжению схе-
мы с операционным усилителем (рис. 1.24, а), кото-
рая носит название масштабного усилителя. Значения
элементов равны: = 100 Ом, = 1 кОм, Нус -> со,
где Нус — усиление операционного усилителя.
На рис. 1.24, б приведена его эквивалентная
схема, содержащая зависимый источник напряжения,
управляемый напряжением (ИНУН).
Составим уравнение по методу узловых напряже-
ний (1.12) для узла 3 эквивалентной схемы рис. 1.24, б:
( 1 1 \ I 1
иэ {^+1ГГи'Т-и21Г = ()-
V Щ ^2 7 Щ
Напряжение узла 2 равно напряжению зависимо-
го источника:
и2 = -НуСи3.
С учетом этого из уравнения, составленного для
узла 3, находим
тт __________-^2______тт
3" +(1 + Hyc)7?i 1
Тогда напряжение узла 2 определяем по формуле
R-,
Рис. 1.24. Масштабный усилитель (а) и его
эквивалентная схема (б) к примеру 1.18
59
Отсюда находим коэффициент передачи по напряже-
нию Нц масштабного усилителя:
Ни
U'2
их
r2
HycR2+(l + Hyc)Ri'
Поскольку коэффициент усиления операционно-
го усилителя Нус -> <ю, то
U2 = R2 = 1000
Ui Rx 100
= -10.
Полученное значение коэффициента передачи
означает, что напряжение на выходе усилителя в 10
раз больше, чем напряжение на его входе. Знак «ми-
нус» означает, что напряжение U2 находится в про-
тивофазе по сравнению с напряжением 171.
Из данного параграфа мы узнали, что:
• Отношение реакции резистивной цепи к воздействию назы-
вается коэффициентом передачи этой цепи.
• Различают коэффициенты передачи по напряжению и току,
а также передаточное сопротивление и передаточную про-
водимость.
• Реакцию резистивной цепи на любое воздействие можно
найти как произведение этого воздействия на соответст-
вующий коэффициент передачи.
Вопросы и задания для самоконтроля
1. В чем заключается задача анализа цепи?
2. Как рассчитываются линейные резистивные цепи с одним ис-
точником постоянного воздействия?
3. Найти показание амперметра в цепи, изображенной на
рис. 1.25, а, если (7г = 120 В, Ri = 10 кОм, R2 = R3 = Ri -
= 25 кОм, J?5 = 50 кОм.. Сопротивление амперметра Ra = 0.
4. Как преобразовать соединение сопротивлений звездой в соеди-
нение треугольником и наоборот?
5. Решить пример 1.3, преобразовав соединение треугольником
сопротивлений R3, Rs и Re в соединение звездой.
6. Сформулировать законы Кирхгофа и Ома.
7. Используя законы Ома и Кирхгофа, определить показания
вольтметра (7у в цепи, изображенной на рис. 1.25, б. Значе-
ния Ur и всех сопротивлений приведены в задании 3.
60
Рис. 1.25. Цепи к заданиям 3 («) и 7 (б) самоконтроля
8. Каков порядок расчета линейных резистивных цепей методом
наложения?
9. Методом наложения рассчитать токи в ветвях цепи, изобра-
женной на рис. 1.16, если Ur = 100 В, Ir = 1 A, Ri = R3 =
= R$ = 100 Ом, Rs = 50 Ом. Сравнить результаты расчета с
теми, которые были получены при решении примера 1.10.
10. В чем суть расчета цепей методом токов ветвей?
11. Решить задание 9 методом токов ветвей.
12. Каков порядок расчета реакции цепи методом контурных то-
ков?
13. Решить пример 1.13, используя метод контурных токов.
14. Каков порядок расчета реакции цепи методом узловых на-
пряжений (потенциалов)?
15. В чем заключается особенность расчета цепи методом узловых
напряжений, если в цепи есть ветвь, содержащая идеальный
источник напряжения?
16. Решить пример 1.14, используя метод узловых напряжений.
17. Как определяется реакция цепи методом эквивалентного гене-
ратора напряжения (тока)?
18. В примере 1.13 определить ток /3 методом эквивалентного ге-
нератора.
Рис. 1.26. Цепь к заданию 20 самоконтроля
61
19. Дать определение коэффициента передачи резистивной цепи.
20. Определить коэффициент передачи по напряжению цепи,
изображенной на рис. 1.26, если R\ = R2 = R3 = 10 Ом,
= 20 Ом.
21. Определить напряжение на выходе цепи, изображенной на
рис. 1.26, если (71 = 10 В.
Глава 2. Анализ реакции линейной цепи на
гармоническое воздействие
2.1. Математическое описание
гармонических колебаний
Во временной области гармоническое колебание представля-
ется синусоидой (косинусоидой). Еще в прошлом веке англий-
ский физик Майкл Фарадей обнаружил, что при перемещении
проводника в магнитном поле постоянного магнита на концах это-
го проводника появляется электродвижущая сила (эдс). Чем бы-
стрее проводник пересекает магнитное поле, тем больше значение
наводимой в нем эдс.
На рис. 2.1, а и б показан проводник, вращающийся в маг-
нитном поле равномерно с постоянным числом оборотов в мину-
ту. При этом он, естественно, с постоянной скоростью движется
по окружности, но с разной скоростью пересекает магнитное по-
ле. В точке 3, например, проводник пересекает магнитное поле с
максимальной скоростью, поэтому в нем наводится максимальная
эдс +Ет. Полярность ее определяется, как известно из школьного
курса физики, с помощью правила левой руки. В точке 7 эдс
также максимальна, но полярность ее противоположна: -Ет. В
точках 1 и 5 скорость пересечения магнитного поля проводником
равна нулю (проводник как бы «скользит» вдоль силовых линий)
и эдс на концах проводника отсутствует.
Простейший механический генератор эдс можно получить,
поместив внутрь постоянного магнита проволочную рамку, как
показано на рис. 2.2. Равномерное вращение рамки, например, с
2©
ю
8©
3
Ф
О
7
®4
05
©6
S
б)
Рис. 2.2. Простейший механиче-
ский генератор
^ис. 2.1. Вращение проводника
в магнитном поле
63
Рис. 2.3. Положения рамки в магнитном поле и графики
изменения эдс в течение полного оборота рамки
64
Рис. 2.4. Графики эдс генератора при разных начальных
положениях рамки в магнитном поле
помощью ручки вызовет появление на контактных кольцах пере-
менной по значению и полярности эдс. С помощью скользящих
по этим кольцам контактов (щеток) генератор подключается к
электрической цепи.
На рис. 2.3, а показаны последовательные положения рамки
в магнитном поле и график изменения эдс в течение одного пол-
ного оборота рамки. Сравнивая этот график с графиком функции
sin а, нетрудно установить, что они похожи и отличаются только
максимальными значениями: на графике эдс это значение равно
Ет, на графике синусоидальной функции — единице. График же
функции £msina полностью совпадает с графиком эдс. Это оз-
начает, что вырабатываемая механическим генератором эдс опи-
сывается математической функцией
e = £msina. (2.1)
Если начальное положение рамки изменить на четверть обо-
рота, а затем из этого положения вновь сделать полный ее обо-
рот, то получится график эдс в виде косинусоиды: е = £mcosa
(рис. 2.3, о). При смещении начального положения рамки на
произвольный угол полный ее оборот дает кривую эдс, занимаю-
щую промежуточное положение между синусоидой и косинусои-
дой (рис. 2.4).
Из математики известно, что для получения косинусоиды из
синусоиды в последней необходимо заменить аргумент а на аргу-
мент a + 90° (или в радианах на a + л/2), а для получения лю-
бой промежуточной между ними функции — на аргумент а + ср,
где в нашем случае <р — это начальный угол (еще говорят началь-
ная фаза) положения рамки.
Кривые, из которых при произвольном смещении верти-
кальной оси начала координат можно получить синусоиду или
5 - 6972 65
a)
Рис. 2.5. Схема генератора эдс (а) и графики гармонических
колебаний в схеме (б)
косинусоиду, называют гармоническими. Следовательно, си-
нусоида и косинусоида являются частными случаями кривых,
изменяющихся по гармоническому закону.
Напомним, что гармоническим законом описываются многие
физические явления, такие как незатухающие колебания маятни-
ка, незатухающие колебания струны и т.п.
Условное изображение генератора эдс на электрической
схеме показано на рис. 2.5, а. Если это генератор постоянной
эдс (аккумулятор, батарея от карманного фонаря и т.п.), то
около его изображения пишется прописная (заглавная) буква
Е, показывающая значение этой эдс, а если это генератор пе-
ременной эдс, то около него пишется строчная (малая) буква
е или е(£), означающая, что речь идет о мгновенных значени-
ях эдс в различные моменты времени.
Ток и напряжения на резисторах в цепи, изображенной на
рис. 2.5 а, повторяют все изменения эдс, и поэтому они тоже
имеют гармоническую форму (рис. 2.5, б).
Эдс, напряжения и токи, изменяющиеся в цепи по гармони-
ческому закону, называют обычно гармоническими колебаниями
соответственно эдс, напряжения и тока.
Время, за которое рамка совершает один оборот, соответству-
ет периоду гармонического колебания. Обозначается период бук-
вой Т. Так, если один оборот совершается за 1 с, то период коле-
бания равен 1 с, если за 0,1 с, то период равен 0,1 с.
Удобнее откладывать по оси абсцисс не значение аргумента
(угла поворота рамки) в градусах или радианах, а значение те-
кущего времени в долях периода либо в соответствующих едини-
цах времени (секундах, миллисекундах, микросекундах и др.).
66
Таблица 2.1. Значения эдс в различные моменты времени и угла
поворота рамки
0 0,125 0,25 0,375 0,5 0,625 0,75 0,875 1
/ в долях периода 0 -Т 8 3 у 8 5 'т* 8 зт 4 ь, г^|оо Т
а в град 0 45 90 135 180 225 270 315 360
а в рад 0 1 4я к я 5 4 Л 3 2Я 7 4я 2я
e(t) в до- лях Ет 0 0,707£т Е 0,707fm 0 -0,707Ет —Е™ L-'m -0,707Ет 0
Для этого нужно записать значение аргумента а через значения
текущего времени t:
а = 360°£Т (2.2)
или, используя радианную меру угла,
а = 2л|. (2.3)
Из (2.2) и (2.3) следует, что в те моменты, когда значение
времени t равно периоду колебания Т, угол а соответствует обо-
роту рамки на 360°, или 2л рад, т.е. полному обороту.
Предположим, что рамка в машинном генераторе на рис. 2.2
делает полный оборот за 1 с. Определим мгновенные значения
эдс e(t) = Em sin а в различные моменты времени t. Вычисления
сведем в табл. 2.1.
График функции e(t\ использующий данные табл. 2.1, по-
казан на рис. 2.6.
Рис. 2.6. График гармонического колебания с периодом 1 с
5*
67
Рис. 2.7. График гармонического колебания с периодом 0,1 с
Если период гармонического колебания Т имеет другое зна-
чение, из графика рис. 2.6 легко получить новый, изменяя мас-
штаб по оси абсцисс. Действительно, пусть один оборот рамки
совершается за десятую долю секунды, т.е. период Т = 0,1 с. В
этом случае на графике рис. 2.6 следует изменить числа, соответ-
ствующие значениям времени t в секундах, и записать вместо
числа 0,125 число 0,0125, вместо числа 0,25 — число 0,025 и т.д.
Это и есть изменение масштаба, поскольку тем же делениям оси
абсцисс стали соответствовать другие значения времени. Можно
также использовать более подходящие единицы измерения вре-
мени, например миллисекунды. Тогда у оси абсцисс указывается
новая единица измерения — мс, и все деления оси оцифровываются
в этих единицах (рис. 2.7).
Обратите внимание на то, как выглядит гармоническое колеба-
ние с периодом Т = 0,1 с, нарисованное в том же масштабе, в ко-
тором было изображено колебание с периодом Г = 1 с (рис. 2.8).
Синусоидальные колебания эдс, напряжения и тока можно
описать с учетом (2.1), (2.2) и (2.3) следующими математически-
ми функциями:
e(t) = Emsin^t;
u(t) = Umsin^t; (2.4)
i(t) = Zmsin^t
Величины Em, Um и Im равны максимальным значениям со-
ответствующих гармонических колебаний и называются ампли-
68
Рис. 2.8. Графики гармонических колебаний
с периодами Т=1сиТ = 0,1с
тудами этих колебаний. Амплитуды эдс и напряжений измеря-
ются в вольтах, а токов — в амперах. Применяются также крат-
ные и дольные единицы.
С периодом Т тесно связана частота гармонического колебания
f. Она показывает, как часто колеблется электрическая величина
(эдс, напряжение, ток), и подсчитывается как число периодов, ук-
ладывающихся на отрезке времени длительностью 1 с. Таким обра-
зом, частота — это величина, обратная периоду, т.е. f = 1/7. Если
период выражать в секундах, то частота измеряется в герцах (Гц).
Колебание с периодом 1 с имеет частоту 1 Гц, с периодом 1 мс —
частоту 1 кГц, с периодом 1 мкс — частоту 1 МГц и т.д. Из рис. 2.8
следует, что частота одного колебания — 1 Гц, а другого — 10 Гц.
Используя вместо периода колебания его частоту, можно перепи-
сать математические выражения (2.4) в другом виде:
e(t) = Emsin2nft;
u(t) = Umsin2nft; (2.5)
i(t) = Imsin2nft.
Если посмотреть на рис. 2.3, то станет ясно, что частота гар-
монического колебания соответствует числу оборотов рамки за
1с. Так, один оборот рамки за секунду приводит к колебанию с
частотой f = 1 Гц, а десять оборотов за секунду — к колебанию с
частотой f - 10 Гц.
Вместо числа оборотов рамки за секунду можно отсчитывать
Радианную меру угла, на который рамка повернулась за одну се-
кунду. Следовательно, частоту можно измерять в радианах за се-
кунду (рад/с). Для обозначения частоты в этом случае использу-
ется буква греческого алфавита со. Если за 1 с рамка делает один
69
оборот, т.е. поворачивается на 2л рад, то частота колебания рав-
на со = 2л рад/с (или 6,28 рад/с). Если за 1 с рамка совершает де-
сять оборотов, то частота со = 2л • 10 = 20л рад/с (или 62,8 рад/с).
Частота со, называемая угловой, частота f и период колебания
Т связаны соотношением
/* 2л
со = 2л/ = у-.
(2.6)
С учетом (2.6) синусоидальные колебания (2.5) могут быть
записаны в другой форме:
e(t) = Em sincoi;
u(t) = Um sin cot
i(t) = Im sin cot
Для перехода к косинусоидальным колебаниям необходимо к
аргументам функций добавить начальные фазы л/2:
e(i) = Emsin^2nft + = Em cos2k/Z;
u(£) = Um sin^Tc/t+ = Um cos2nft;
i(t) = Im sin(2nft + = Im cos2n/Z.
В гармонических колебаниях, занимающих промежуточное
положение между синусоидой и косинусоидой, начальные фазы
лежат в пределах -л/2 ... +л/2. В общем случае гармонические
колебания описываются функциями
e(i) = £msin(2n/’i+ фе) = Em sin(a>£ + <pe);
u(t) = Umsin(2nft + <pu) = Um sin(a>£+ <p„);
z(t) = Imsin(2iift + q>i) = Im sin(co£ + (pi),
(2.7)
где (ре, фи, Ф, — начальные фазы колебаний эдс, напряжения и
тока. Измеряются они в радианах или градусах.
На рис. 2.9 представлены те же колебания, что и на рис. 2.4,
но с той разницей, что кроме угла а в градусах из (2.2) по оси
абсцисс отложено также время в секундах. Колебание, которое
начинается раньше начала координат, имеет начальную фазу ф
со знаком «плюс», а колебание, которое начинается позже — на-
чальную фазу ф со знаком «минус». Первое называется опере-
жающим, а второе — отстающим или запаздывающим колебани-
ем. Следовательно, все опережающие колебания имеют положи-
тельные начальные фазы, а все запаздывающие — отрицательные
начальные фазы.
70
Рис. 2.9. Графики гармонических колебаний
с разными начальными фазами
Пример 2.1. Построим графики напряжения и(£) и тока i(t), за-
данные выражениями
u(.t) = 10sin(628t + л/3) В;
i(t) = 5sin(628£-л/6) A.
Для построения графиков гармонических коле-
баний w(i) и z(t) определим, используя (2.7), их ам-
плитуды Um, 1т и начальные фазы фи, ф/:
Um = 10 В; 1п = 5 А;
фи = л/3 = 60°; ф/ = -л/6 = -30°.
Напряжение u(t) — опережающее колебание, а
ток i(t) — запаздывающее колебание.
Период Т колебаний u(i) и i(t) найдем, исполь-
зуя (2.6):
_ 2л 2-3,14 А Л. .Л
Т = — =--------— = 0,01 с = 10 мс.
® 628
Найдем моменты времени и £10, при которых u(t)
и i(t) принимают значения, равные нулю. Из равенств
sin(628iao + я/3) = 0>
sin(628£i0 - л/6) = 0
получаем
tua = -т5тг = -1,67 мс,
“° 628
Й = °>83 мс-
’° 628
71
Графики u(t) и i(t) приведены на рис. 2.10.
Пример 2.2. Осциллограмма напряжения u(t) приведена на рис. 2.11.
Запишем выражение для мгновенного значения u(t)
и рассчитаем значение напряжения в момент времени
ti = 7712 с. Амплитуда колебания, изображенного на
рис. 2.11, Um = 1 В. Угловая частота со связана с пе-
риодом колебаний Т = 0,4 с выражением (2.6):
2л 2-3,14 ,с- /
со = — = ——— = 15,7 рад/с.
Г 0,4 Е
Начало синусоиды u(t) сдвинуто на 180° вправо
от начала отсчета времени, поэтому начальная фаза
<ра= -180°. Заметим, что график на рис. 2.11 можно
также рассматривать как синусоиду, сдвинутую на
180° влево от начала координат, т.е. сра = +180°.
Рис. 2.11. График гармонического напряжения
72
Выражение для мгновенного значения м(£) имеет вид
u(t) = sin(15,7i +180°), В.
Для определения значения u(t) в момент t = t\ = 7712
найдем вначале
2л , 2л Т л ЧЛО
co£i =---tt =------= — = 30.
1 Г 1 Г 12 6
Тогда
u(ti) =>sin(<o^ + 180°) = sin(30° + 180°) =
= sin 210° =-0,5 В.
Гармоническое колебание может быть представлено векто-
ром. Проделаем следующие геометрические построения. Нарису-
ем окружность и проведем через центр две перпендикулярные
оси. (рис. 2.12, а). Затем, вращая по кругу радиус, будем изме-
рять длину линии а, которую называют «линией синуса». Изме-
рения сведем в табл. 2.2, в которой будем указывать угол пово-
рота радиуса а и отношение длины линии а к радиусу R, т.е.
значение синуса этого угла. Если теперь по данным таблицы по-
строить график, то получится кривая, называемая синусоидой
(рис. 2.12, б). Ее амплитуда равна радиусу окружности. Это осо-
бенно хорошо видно, когда радиус повернут на 90°: его конец про-
ектируется в верхнюю точку синусоиды.
При других углах поворота конец радиуса проектируется в
другие точки, лежащие на синусоиде. Из условия sin а = a/R
легко определить ординаты этих точек:
а = R sin а.
Рис. 2.12. Соответствие вращающегося вектора
гармоническому колебанию
73
Таблица 2.2. Зависимость sin а от угла поворота вектора
а, град sin а = a/R а, град sin а = a/R
15 0,25882 195 -0,25882
30 0,50000 210 -0,50000
45 0,70711 225 -0,70711
60 0,86603 240 -0,86603
75 0,96593 255 -0,96593
90 1,00000 270 -1,00000
105 0,96593 285 -0,96593
120 0,86603 300 -0,86603
135 0,70711 315 -0,70711
150 0,50000 330 -0,50000
165 0,25882 345 -0,25882
180 0,00000 360 0,00000
Точно так же можно получить график, например, гармониче-
ской эдс. Если длину радиуса выберем равной Ет, а линию сину-
са обозначим малой (строчной) буквой е, то, вращая радиус и ри-
суя по данным таблицы график, получаем кривую гармонической
эдс, текущие ординаты которой зависят от угла поворота радиуса:
е = Ет sin а.
Вместо угла а можно откладывать на графике рис. 2.12, б
время t, за которое радиус повернулся на данный угол а. На-
помним, что эти величины связаны соотношением (2.3):
а = 2л + Фе = 2яД + фе ,
где фе в данном случае означает начальное положение, или началь-
ную фазу, радиуса перед его вращением; Т — время полного обо-
рота (на 360°) этого радиуса; f = 1/Т — частота вращения радиуса.
Если полный оборот совершается, к примеру, за 1 с, то кри-
вая эдс получится такой же, как на рис. 2.6 (или табл. 2.1), а ес-
ли за 0,1 с — то, как на рис. 2.7 или рис. 2.8.
Очевидно, что, изменяя начальное положение (начальную
фазу) радиуса и начиная вращение с этого положения, получаем
графики, аналогичные рис. 2.4. В качестве примера сошлемся на
рис. 2.9, где показана кривая гармонической эдс:
e(t) = Emsin^2nj;t + 30°^
для случая Т = 1 с.
74
Подведем некоторые итога. В математике существует понятие век-
тора. Это отрезок, который имеет длину и направление в простран-
стве. Радиус, который мы вращали, как раз и является вектором.
Отсюда следует важный вывод: кривая любого гармоническо-
го колебания (эдс, напряжения, тока) может быть заменена изо-
бражением вращающегося вектора. Длина этого вектора равна ам-
плитуде колебания, начальное положение вектора перед вращени-
ем определяется начальной фазой колебания; число его оборотов в
секунду зависит от частоты гармонического колебания. В качестве
положительного направления вращения векторов в теории элек-
трических цепей принято вращение против часовой стрелки.
Пример 2.3. Построим графики гармонических колебаний, соответ-
ствующие векторам U, вращающимся с одинаковой
частотой со, имеющим одинаковую длину_С7т, но раз-
ные начальные положения: U = (7OTZ0°, U = l7mZ90°,
(7 = C7mZ180°, l/ = (ZOTZ270°.
Векторы имеют одинаковую длину, т.е. амплиту-
ды всех гармонических колебаний равны Um- Оди-
наковая скорость вращения векторов указывает на
то, что гармонические напряжения имеют один и тот
же период Т = 2л/со.
Вектор C7 = (/mZ0° имеет нулевую начальную
фазу, т.е. расположен на горизонтальной оси
(рис. 2.13, а). Если этот вектор заставить вращаться
против часовой стрелки со скоростью <х>, то его про-
екцией на вертикальную ось будет гармоническое на-
пряжение u(t) = Um sin со t, график которого изобра-
жен на рис. 2ЛЗ, 6.
Вектор U = Um Z9O0 имеет начальную фазу 90° и
расположен на положительной части вертикальной
оси (рис. 2.14, а). Вращая этот вектор, получаем
гармоническое напряжение u(t) = C7msin(cot + 90°),
график которого изображен на рис. 2.14, б.
Рис. 2.13. Графики вектора CJmZO° (а)
и колебания C7msinco£ (б)
75
6)
Um
Um sin (cor+90°)
t
Рис. 2.14. Графики вектора C7mZ90° (в)
и колебания CJmsin(®t + 90°) (б)
в)
б) Um sin (©/+180°
Рис. 2.15. Графики вектора UmZ. 180° (а)
и колебания <7msin (art + 180°) (б)
Ф Um sin (©Г-90°)
Рис. 2.16. Графики вектора CJmZ270° (а)
и колебания UOTsin(©i — 90°) (б)
Вектор U = {7mZ180° имеет начальную фазу
180°, т.е. расположен на отрицательной части гори-
зонтальной оси (рис. 2.15, а). Вращая его, получаем
колебание u(t) = (7msin(©£ + 180°), график которо-
го изображен jja рис. 2.15, б.
Вектор U = UmZ 270° имеет начальную фазу
270° или -90°, т.е. расположен на отрицательной
части вертикальной оси (рис. 2.16, а). При вращении
получаем колебание u(t) = Uwsin(©t - 90°), график
которого изображен на рис. 2.16, б.
76
Разумеется, гармонические колебания могут _иметь начальные
фазы, не кратные 90°. В этом случае векторы U располагаются
между соответствующими осями.
Пример 2.4. Вектор напряжения, имеющий длину 5 В и началь-
ное положение 45° (рис. 2.17, а), вращается со ско-
ростью 10 оборотов в секунду. Построим график гар-
монического колебания, соответствующего этому век-
тору.
Амплитуда гармонического напряжения равна
длине вектора: Um = 5 В. Начальная фаза колеба-
ния сра = 45°. Частота гармонического колебания
/"=10 оборотов в секунду, значит, период колебания
Т = l/f = 0,1 с = 100 мс. График гармонического на-
пряжения
u(t) = 5sin| 2n-±-t + 45° |, В
I 0,1 J
изображен на рис. 2.17, б.
Рис. 2.17. Векторное и временное изображение
гармонического напряжения
цепи
Минаковыми
Может показаться странной попытка подменить статичную,
неподвижную кривую гармонического колебания изображением,
которое является динамичным, т.е. в котором присутствует дви-
жение. В самом деле, даже при анализе всего двух колебаний с
Разными частотами вместо того, чтобы спокойно рассматривать
график, подобный рис. 2.8, требуется призывать на помощь все
свое воображение, чтобы представить два вектора, имеющие раз-
ные длины, разные начальные положения да еще вращающиеся с
Разными скоростями. А если таких колебаний не два, а больше?
Почти неразрешимая задача.
Однако ситуация значительно упрощается, когда в электри-
действуют несколько гармонических колебаний с
частотами. В этом случае все векторы вращаются с
77
Рис. 2.18. Векторное пред-
ставление гармонических
колебаний
одинаковой скоростью. Это озна-
чает, что относительно друг друга
они остаются неподвижными.
Можно условиться отождествлять
каждое гармоническое колебание с
неподвижным вектором, имеющим
длину, равную амплитуде колеба-
ния, и угол поворота, равный на-
чальной фазе колебания.
Представление гармонических
колебаний с одинаковыми часто-
тами неподвижными векторами
иногда оказывается предпочтительнее изображения их в виде
графических зависимостей от времени. Действительно, когда гар-
монических кривых достаточно много, они накладываются друг
на друга и чтение их становится крайне неудобным. В то же вре-
мя анализ рисунка, на котором изображены несколько прямых
линий со стрелками на концах, особых затруднений не вызывает.
В качестве примера на рис. 2.18 показаны векторы, соответст-
вующие кривым гармонических колебаний из рис. 2.9.
Преимущество работы с векторами особенно проявляется, ко-
гда требуется сложить несколько гармонических колебаний с
одинаковыми частотами.
Пример 2.5. Сложим два гармонических колебания wi(£) =
= 10 sin (2 л/Y - 30°), В и u2(O = 20sin(2n^ + 60°), В.
Чтобы получить сумму этих колебаний, необхо-
димо выполнить трудоемкую операцию графического
суммирования кривых (рис. 2.19, а). Сложение век-
торов производится по правилам геометрии
(рис. 2.19, б). Построить же по результирующему
вектору гармоническую кривую — несложная задача.
Рис. 2.19. Сложение двух гармонических колебаний
78
В результате графического сложения двух векто-
ров получаем вектор итз = 22,4 Z 33,5°, В.
Гармоническое колебание
u(t) = щ(Л) + u2<.t) = 22,4sin(2Tt/Y + 33,5°), В
изображено на рис. 2.19, а.
Для удобства кривые и векторы можно изобра-
жать в разных масштабах, как это сделано на
рис. 2.19.
При анализе гармонических колебаний в электрических це-
пях широко используется понятие «фазовый сдвиг». Это разность
начальных фаз двух гармонических колебаний с одинаковыми
частотами. Например, для колебаний эдс
= £,OT1sin(27t/’t + (pel) и
e2(t) = Ет2 sin.(2nft + фе2)
фазовый сдвиг между ними
Ф = Фе1 - Фе2-
Если (ре1 = +30° и <pe2 = -30°, то ср = 60° (см. рис. 2.9). При
этом первое колебание опережает второе на 60°, а второе колеба-
ние, естественно, отстает от первого на 60°.
На графиках временных зависимостей (например, рис. 2.9)
фазовый сдвиг определяется как часть периода (в градусах, ра-
дианах или секундах), заключенная между началами двух гармо-
нических колебаний:
Ф = 360°^ = 2л^, (2.8)
где At — расстояние на оси времени между началами колебаний.
Фазовый сдвиг между реальными гармоническими напряже-
ниями и токами измеряется прибором, который называется фазо-
метром.
Сдвиг фаз между двумя гармоническими колебаниями с оди-
наковыми частотами удобно определять на векторных диаграм-
мах. Так, из рис. 2.18 хорошо видно, что векторы, представляю-
щие колебание et(t) и e2(t), отстоят друг от друга на угол 60°,
причем первый вектор опережает по фазе второй.
Пример 2.6. Заданы два гармонических колебания:
щ (t) = 4sin(cot + 30°), В,
u2 (£) = 4sin(cot +135°), В.
79
Рис. 2.20. Графики двух гармонических
напряжений с разными фазами
Построим графики этих колебаний, запишем и
построим векторы Umi и U m2 и определим сдвиг фаз
между этими векторами.
Графики и ufa) изображены на рис. 2.20 б, г.
Векторы U mi и U m2 можно записать в виде
и ml = 4Z30°, Um2 = 42135°.
Эти векторы изображены на рис. 2.20, а, в.
Сдвиг фаз между гармоническими колебаниями
<р = ф„2 - фи1 = 135° - 30° = 105°.
Напряжение w2(t) опережает nt(i) на 105° или, что
равнозначно, ut(i) отстает от и2(£) на 105°. Анало-
П1чный_вывод можно сделать, если сравнить векторы
U ml VI и m2 (рис. 2.20, а, в).
Символическое представление гармонического колебания —
это представление его вектором на комплексной плоскости.
Найдем решение уравнения х2 = —9. Получаем х = ±>/=9 = ±3>/й.
Величина 7Й обозначается /, т.е. j = >/И, и называется мнимой
единицей. Тогда можно записать решение уравнения х2 = —9 как
х = ±/3. Величины +/3 и —/3 называются мнимыми числами.
Они изображаются точками на вертикальной оси (рис. 2.21, б)
в противоположность вещественным числам, которые изобража-
ются точками на горизонтальной оси (рис. 2.21, а).
80
Вещественная
ось
_1__I__I--1-I—
-4 -2 0 2 4
а)
Мнимая
ось у 4"
J2-
0-
-2J-
Мнимая Комплексная
ось плоскость
4 = 2+73 =
= а +Jb
2 Вещественная
ось
Рис. 2.21. Вещественная
и мнимая оси
Рис. 2.22. Комплексная
плоскость
Сумма вещественного и мнимого чисел, например, 2 + /3, на-
зывается комплексным числом. Обозначается комплексное число
буквой с чертой под ней: А = а + jb. Здесь а — вещественная
часть комплексного числа А, т.е. а = Re[A]; b — мнимая часть
комплексного числа А, т.е. b = Im[A ].
Образованную вещественной и мнимой осями систему прямо-
угольных координат называют комплексной плоскостью (рис. 2.22).
На этой плоскости комплексное число А - 2 + /3 отображается
вектором, проекция которого на вещественную ось будет пред-
ставлять вещественное число а = 2, а проекция на мнимую ось —
мнимое число b = /3.
Поместим на комплексную плоскость вектор эдс (напря-
жения, тока) (рис. 2.23). Проекция этого вектора на ось абс-
цисс является вещественным числом. Она носит название ак-
тивной составляющей эдс (напряжения, тока) и обозначается
Ета (Uта, 1та)- Проекция же вектора на ось ординат — мни-
мое число. Называется такая проекция реактивной состав-
ляющей эдс (напряжения, тока) и обозначается Етр (Ump,
I тр).
Комплексное число, соответствующее нашему вектору,
обозначается Ет (Ujn, Ln) и записывается в виде
Е-т = Ета + ]Етр,
Um=Uma+jUmp; (2.9)
Lm ~ ^та + ]^тр-
Запись комплексного числа А = а + jb в виде суммы вещест-
венного и мнимого чисел называется алгебраической. Можно вы-
числить длину вектора, изображающего комплексное число. Она
называется модулем этого комплексного числа. Модуль всякого
комплексного числа есть положительное число (так как длина век-
Тора не может быть отрицательной). Он обозначается | А| = \а + jb\
или просто буквой А. Из рис. 2.24 видно, что по правилу прямо-
угольного треугольника (по теореме Пифагора)
6~6972 81
Рис. 2.23. Вектор эдс на
комплексной плоскости
।
!d=j4sin<p
<р = arctg b/a
О а=Лсо8ф
Рис. 2.24. Вектор А на
комплексной плоскости
А = |А| = у/a2 + Ь2.
Следовательно, для выражений (2.9) имеем
Ет = \Ет | = \]Ета + Етр,
Um=\Um\ = JuL+U2mp-> (2.10)
~ |Zm | = yj^ma + ^тр •
Угол <р между положительным направлением оси абсцисс и
вектором, изображающим комплексное число, называется аргу-
ментом комплексного числа (рис. 2.24):
tg<P = |; <p = arctg|.
Для векторов из (2.9) можно записать:
Фе = arctg
фи =arctg^2-; (2.11)
U та
ф, = arctg
* та
Из теоремы Пифагора можно установить связь между моду-
лем и аргументом комплексного числа, с одной стороны, и веще-
ственной и мнимой частями комплексного числа — с другой. Из
рис. 2.24 следует тригонометрическая форма записи комплексно-
го числа:
а = Лсозф; 6 = Asinф;
А = а + jb = АсоБф + уАвтф.
В соответствии с этим правилом можно записать для эдс (на-
пряжений и токов)
82
Еща ~~ Ет COS фр И
и та =итСОЗф„ И
1та = Ли COS ф; И
Е тр ~ Ent sin фр,
U/пр = Uт SIH фц,
1щр = ^т sill ф,.
Тогда комплексные выражения (2.9) могут быть представлены
через их модули и аргументы:
Ет = Ет cos фе + ]Ет sin фР;
Um = Umcos<pu + jUmsin<p„;
Lm = ЛпСО5ф,+ ;7т5тф/(
(2.12)
где модули Ет, Um, 1т и аргументы фе, фа, ф/ определяются по
формулам (2.10) и (2.11).
Известно, что длина вектора равна амплитуде гармониче-
ского колебания, а начальный угол его поворота равен началь-
ной фазе колебания. Таким образом, мы установили однознач-
ное соответствие между комплексным числом (рис. 2.23) и гра-
фиком гармонического колебания (рис. 2.9): модуль Ет (Um,
1т) комплексного числа представляет собой не что иное, как
амплитуду гармонического колебания эдс (напряжения, тока), а
аргумент фе (фи, ф;) комплексного числа — начальную фазу это-
го колебания.
Существует еще одна форма записи комплексного числа — пока-
зательная:
А = А(со$ф + /зшф) = AeJ<p. (2.13)
Правая часть данного выражения и называется показатель-
ной формой комплексного числа. Применительно к эдс, напря-
жениям и токам выражения (2.12) преобразуются в соответствии
с (2.13) в выражения вида
Р - р pj’fe-
±±т — ^тпу >
U = U
bLm ту »
Т = т
Lm 1тпУ
(2.14)
Величины Em, Um, 1_т называются комплексными амплиту-
дами гармонических колебаний и, как видно из (2.14), содержат
в себе сведения об амплитуде и начальной фазе гармонических
колебаний.
Зная комплексную амплитуду гармонического колебания,
легко восстановить его математическую зависимость от времени.
Замена гармонических колебаний комплексными числами
называется символическим представлением гармонических коле-
баний.
83
Существует формальная связь между комплексными ампли-
тудами Ет, Ujn, 1_т и мгновенными значениями e(i), w(t),
i(t). Будем вращать вектор Е_т, изображенный на рис. 2.23, в
положительном направлении (против часовой стрелки) с угло-
вой частотой со. Тогда в любой момент времени положение
вращающего вектора определится комплексной величиной
Eme1<at = Eme1(e>t+^ = Em cos (со£ + <ре) + ;EOTsin(<ot + cpe).
Первое слагаемое этого выражения отражает проекцию вра-
щающегося вектора на вещественную ось, а второе слагаемое —
на мнимую ось. Отсюда следует, что синусоидальная эдс е будет
определена как
е = Im [Ете^ ] = Im > ] = Ет sin (cot + <pe),
где Im - сокращенное обозначение слова Imaginarins (мнимый), а
косинусоидальная эдс е — по формуле
е = Re[Eme;W] = Re[Eme'(e>‘+<₽e)] = Ет cos (at + фв),
где Re — сокращенное обозначение слова Realis (действительный,
вещественный).
Пример 2.7. Запишем мгновенное значение напряжения u(i), за-
данного в виде Um = 10е?30°.
, Амплитуда гармонического колебания Um = 10 В,
начальная фаза <ри = 30°, поэтому мгновенное значение
w(£) = 10sin(27t/Y + 30°).
Пример 2.8. Найдем произведение двух комплексных напряжений:
Umi =10е>45°, Um2 = 20е;135°.
При умножении комплексных чисел их модули
перемножаются, а фазы складываются. Поэтому
Um3 = Umi -Um2 = 10е>45° • 20е;135° = 200е>18°°.
Пример 2.9. Найдем сумму двух комплексных напряжений:
Umt = 10е;45’ и Um2 = 20е;135°.
Для сложения двух комплексных чисел необхо-
димо записать каждое из них в алгебраической фор-
ме записи. В соответствии с (2.12) имеем
Umi = 10 cos 45° +/10 sin 45° = 7,07 + /7,07;
Um2 = 20cosl35°+ /20sinl35° =-14,14 +/14,14.
84
Складывая отдельно вещественные и мнимые части
Ц.пц И и_т2, получаем
итз = и т, + ит2 = (ъ 07 -14,14) + i (7,07 +14,14) =
= -7,07+ /21,21.
Преобразуем С7тч в показательную форму, ис-
пользуя (2.10) и (2.11):
. 21,21
С7МЗ = >/7,072 + 21,212е7аГГ -7-07 = 22,36е/108’4°.
Рассмотрим функцию w( t), представляющую сумму п гармо-
нических колебаний:
u(0 = (/misin(o^ + (p„1) + L7m2sin((oi + (pW2) + ...
...+Umn sin(<ot+ <рИ(1).
Основное свойство синусоидальной функции заключается в
том, что сумма произвольного числа синусоид одной и той же
частоты есть синусоида той же самой частоты. Таким образом,
колебание u(t) (2.15) можно записать в виде
u(t) = l7msin(<oi + <pu).
Каждое из гармонических колебаний в выражении (2.15)
может быть представлено комплексным числом в показательной
форме записи:
U = U е7ф"ь
У-пц >
ТТ =1/ р7Ф"2-
У-т2 и т2е >
ТТ = Г7 <»7Ф“»
—тп итпе
Сложение комплексных напряжений UjnV Ujn2........LLmn Дает
комплексное напряжение, которое представляет собой сумму си-
нусоид:
Пример 2.10. Найдем сумму двух гармонических напряжений:
^(^ = 20810(100^30°),
u2(t) = 15sin(100£-120°).
Представим гармонические напряжения в ком-
плексной форме записи, используя (2.14) и (2.12):
Umx =20е-730° =17,32-/10,.
С/Ш2 = 15е"7120° =-7,5-/12,9.
85
Комплексное напряжение
итз =итх +ит2 = 17,32-/10-7,5-/12,9 =
= 9,82 -/22,9 = 25е-7б6’9°.
Запишем мгновенное значение напряжения 17тз:
u3G) = 25sin(100£-66,9°).
Из данного параграфа мы узнали, что:
• График гармонического колебания определяет закон изме-
нения его во времени.
• Гармоническое колебание полностью описывается амплиту-
дой, частотой и начальной фазой.
• Амплитуда гармонического колебания определяет длину векто-
ра, начальная фаза колебания — угол поворота вектора, а час-
тота колебаний в герцах — число оборотов вектора в секунду.
• Гармонические колебания с одинаковыми частотами удобно
отображать неподвижными векторами.
• Разность начальных углов поворота двух векторов указыва-
ет на сдвиг фаз между двумя гармоническими колебаниями.
• Амплитуда гармонического колебания может отображаться
модулем комплексного числа, а начальная фаза этого коле-
бания — аргументом комплексного числа.
• Символическое представление гармонического колебания —
это представление его в виде комплексного числа либо век-
тора на комплексной плоскости.
2.2. Гармонические колебания в пассивных
элементах электрической цепи
При изображении на одном графике или на одной вектор-
ной диаграмме напряжения и тока необходимо использовать два
различных масштаба. Очень часто кривую гармонического тока и
кривую гармонической эдс или напряжения располагают на од-
ном графике (рис. 2.25), делая для этого две разметки верти-
кальной оси — одну разметку в вольтах для эдс или напряжения,
другую разметку в амперах для тока. Применяют также дольные
и кратные единицы (милливольты и киловольты, миллиамперы и
килоамперы и т.д.). Рассматривая такой график, нужно помнить,
что нельзя сравнивать высоту этих кривых — каждая начерчена в
своем масштабе и общая у них только ось времени.
Это же касается и векторов токов, эдс и напряжений, разме-
щенных на одной комплексной плоскости. Длины векторов из-
86
Рис. 2.26. Напряжение и ток в резисторе
меряются разными единицами, сравнивать можно только началь-
ные фазы колебаний (начальные углы положения векторов), и
измерять можно лишь сдвиги фаз между векторами.
Резистивный, индуктивный и емкостный элементы цепи ока-
зывают резистивное, индуктивное и емкостное сопротивления
гармоническому току. Исследуем цепь, состоящую только из одно-
го элемента, например резистора с сопротивлением R (рис. 2.26, а).
Это сопротивление называют резистивным. Пусть по этой цепи
протекает гармонический ток
i(t) = Zmsin(2Tt/’t + <pI). (2.16)
Форма напряжения на резистивном сопротивлении точно по-
вторяет форму тока, т.е. в те моменты, когда мгновенные значе-
ния тока равны нулю, мгновенные значения напряжения также
87
(2.17)
равны нулю, а когда мгновенный ток максимален, мгновенное
напряжение также максимально:
uR(t) = i(t)- R = Im Rsin(2nft + <?i) =
= UmRsin(2nft + <f>u).
Из выражения (2.17) следует, что амплитуда гармонического
напряжения зависит от амплитуды тока и значения сопротивле-
ния, а начальная фаза напряжения совпадает с начальной фа-
зой тока, т.е.
U mR — Im' &
Фи = Ф«-
(2.18)
И
Такие процессы называют совпадающими по фазе (рис. 2.26, б).
Из (2.18) следует, что отношение амплитуды гармонического
напряжения UmR к амплитуде гармонического тока 1т равно ре-
зистивному сопротивлению цепи R (измеряется в омах). Левое
равенство (2.18) представляет собой закон Ома для амплитуд
гармонических колебаний в резистивной цепи.
Рассмотрим теперь цепь, содержащую лишь один индуктив-
ный элемент с индуктивностью L (рис. 2.27, а). И пусть по нему
также протекает ток, описываемый выражением (2.16).
Если бы данный гармонический ток протекал по прямоли-
нейному проводу, то этот провод оказывал бы току только рези-,
стивное сопротивление. Однако стоит только провод свить в ка-
тушку, его сопротивление резко возрастет. По каким же причи-
нам катушка оказывает повышенное сопротивление току? И что
это за сопротивление, которое больше резистивного сопротивле-
ния провода?
При прохождении переменного электрического тока через
проводник вокруг последнего возникает переменный магнитный
поток, который наводит в витках этой же катушки переменную во
88
времени эдс. Эту наведенную эдс называют эдс самоиндукции и
обозначают е^.
т di
е --L
L dt
По второму закону Кирхгофа напряжение на зажимах цепи в
каждый момент равно по величине и противоположно по знаку
эдс, следовательно,
«г = ~eL
, di
или
(2.19)
Итак, напряжение на зажимах катушки пропорционально
скорости изменения тока. Медленные изменения тока вызывают
малое падение напряжения ul, а быстрые изменения — большое.
Подставим в (2.19) гармонический ток из (2.16):
uL(t) = L-^[lmsin(2nft + <рг)] =
= 27r/7Jmcos(27t/’i + <pi)= (2.20)
= 2nfLIm sin (2nft + ф i + 90° ) =
= UmLsin(2itft + <pu).
Мы использовали в (2.20) следующие обозначения:
UmL = ^fLIm I и I фц = фг+90°Т~| (2.21)
Величину
XL = 2nfL = oL, | (2.22)
связывающую в (2.21) амплитуды напряжения и тока, называют
индуктивным сопротивлением катушки индуктивности. Чем вы-
ше частота колебаний, т.е. чем больше скорость изменения тока,
тем больше индуктивное сопротивление катушки Xl (рис. 2.28,
б). Аналогичным образом оно зависит и от индуктивности
Рис. 2.28. Графики индуктивного сопротивления
89
(рис. 2.28, а). При подстановке частоты f в герцах и индуктивно-
сти L в генри сопротивление Xl измеряется в омах. Связь между
UmL и 1т (2.21) есть не что иное, как закон Ома для амплитуд
гармонических колебаний в индуктивном элементе.
Графики мгновенных значений тока г(£) и напряжения
ui(O, описываемые функциями (2.16) и (2.20), показаны на
рис. 2.27, б. Из этого рисунка и выражения (2.21) следует, что
начальная фаза напряжения на 90° больше начальной фазы то-
ка, т.е. ток отстает по фазе от напряжения на этот угол
(на четверть периода), а напряжение, наоборот, опережает ток
по фазе на 90°.
Перейдем к анализу цепи, состоящей из емкостного элемента
с емкостью С (рис. 2.29, а). Предположим, что по этой цепи
также протекает гармонический ток (2.16).
Ипользуем выражение (В.4):
rduc
l~c~dF
, 1
или аиГ = —idt.
с С
Интегрируя обе части последнего равенства, имеем
uc = -L \idt.
(2.23)
Подставим теперь в (2.23) выражение гармонического тока из
(2.16):
uc(t) = sia(2nft + cos(2itft + <?i) =
C 2nfC (2.24)
= -^-7^ Im sin(2n/Y + 9i -90°) = CrmCsm(27r/Y + <pu).
90
Рис. 2.30. Графики емкостного сопротивления
В (2.24) приняты обозначения
ИтС - 0 4г И Ф„ =9,-90°. (2.25)
Величину Z TtJ О
Хс =- с 2 1 nfC 1 ©С ’ (2.26)
связывающую амплитуды гармонических напряжения и тока в
(2.25), называют емкостным сопротивлением конденсатора. С
ростом частоты колебаний емкостное сопротивление конденсатора
гармоническому току падает (рис. 2.30, б). Аналогичным образом
ведет себя емкостное сопротивление Хс при изменении емкости
конденсатора (рис. 2.30, а). Если в (2.26) подставить частоту f в
герцах, а емкость С в фарадах, то получим сопротивление Хс в
омах. Связь между амплитудами гармонических напряжения Umc
и тока 1т представляет собой закон Ома для емкостного элемента.
Графики мгновенных значений тока i(t) и напряжения
uc(t), соответствующие формулам (2.16) и (2.24), приведены на
Рис. 2.29, б. Из рисунка и выражения (2.25) видно, что началь-
ная фаза напряжения на 90° меньше начальной фазы тока,
т-е. ток опережает по фазе напряжение на 90°, а значит, на-
пряжение отстает от тока на те же самые 90°.
Итак, индуктивное сопротивление растет с увеличением
Частоты, а емкостное — падает. Резистивное сопротивление
Огп частоты не зависит. Гармонические напряжения и ток на
Резистивном сопротивлении совпадают по фазе. На индук-
тивном сопротивлении ток отстает от напряжения на 90°, на
емкостном сопротивлении он опережает напряжение на 90°.
91
Рис. 2.31. Векторные диаграммы напряжения и тока
в резисторе, индуктивности, емкости
Комплексное сопротивление цепи состоит из резистивного и
реактивного (индуктивного и емкостного) сопротивлений. Пе-
рейдем от мгновенных значений тока (2.16) и напряжения (2.17) к
комплексным значениям по правилам, описанным в (2.14). Тогда
Lm=Ime^\ Um=Ume*«. (2.27)
Векторы, соответствующие этим комплексным числам, изо-
бражены на рис. 2.31, а.
Отношение комплексной амплитуды напряжения к комплекс-
ной амплитуде тока называют комплексным сопротивлением це-
пи и обозначают Z. Для цепи, состоящей из одного резистивного
сопротивления, получаем согласно (2.27) и (2.18)
(2.28)
Таким образом, комплексное сопротивление резистора явля-
ется положительным вещественным числом, его значения на ком-
плексной плоскости откладываются на положительной вещест-
венной полуоси (рис. 2.32, а).
Переходя от мгновенных значений (2.16) и (2.20) к ком-
плексным-амплитудам напряжения и тока в индуктивности, по-
лучаем
UmL=UmLe*«.
Сдвиг фаз между векторами напряжения и тока составляет,
как это следует из (2.21), 90° (рис. 2.31, б), причем ток отстает
от напряжения.
Комплексное напряжение цепи, состоящей из индуктивности,
Z£ = еЛ<₽«-ч>«) = 2nfLe>^ = >£ = jXL.
Lm * т
(2.29)
92
JXl
-JXc
в)
Рис. 2.32. Комплексные сопротивления резистора,
индуктивности, емкости
Замена в (2.29) выражения е;90° на j становится понятной,
если учесть, что е;90° = cos 90° + jsin 90° = j. Таким образом, ум-
ножение числа на j означает поворот вектора на 90°, а умноже-
ние на -] означает поворот на -90°.
Сравнение индуктивного (2.22) и комплексного (2.29) сопро-
тивлений индуктивности показывает, что на комплексной плоско-
сти индуктивное сопротивление катушки откладывают на поло-
жительной вертикальной полуоси (рис. 2.32, б), потому что эта
величина мнимая и положительная.
Запишем выражения комплексных амплитуд тока и напряже-
ния для цепи, содержащей емкость. Из (2.16) и (2.24) следует, что
где Umc и 1т, а также <ри и ср/ связаны соотношениями (2.25).
Векторы напряжения на емкости и тока в ней сдвинуты друг от-
носительно друга на -90°, при этом ток опережает напряжение
(рис. 2.31, в).
Комплексное сопротивление емкости найдем как
Lm Im 2nfC ](йС
= Хсе^°° =-jXc.
(2.30)
Здесь учтено, что е~}90° = cos 90° - j sin 90° = - j.
Очевидно, что комплексное сопротивление емкости является
мнимым отрицательным числом, на комплексной плоскости оно от-
кладывается на отрицательной вертикальной полуоси (рис. 2.32, в).
Мы уже знаем, что любое комплексное число, записанное в
алгебраической форме А = а + jb, имеет вещественную а и мни-
мую jb составляющие, а число, записанное в показательной форме
4 = — модуль А и аргумент (р.
Анализ выражений (2.28) — (2.30) показывает, что комплекс-
ное сопротивление резистора является вещественным и не содер-
93
Рис. 2.33. Последовательная 7?£-цепь и ее
комплексное сопротивление
жит мнимой составляющей, его аргумент равен нулю; комплекс-
ное сопротивление индуктивности, наоборот, является мнимым,
его аргумент равен +90°; комплексное сопротивление емкости
также мнимое, но аргумент его равен —90°.
Последовательное соединение R, L, С-элементов. Рассмот-
рим сначала последовательные RL- и 7?С-цепи, показанные на
рис. 2.33, а и 2.34, а. Комплексное сопротивление последователь-
ной 7?£-цепи в алгебраической форме содержит сумму положи-
тельного вещественного резистивного сопротивления R и положи-
тельного мнимого индуктивного сопротивления j'Xl (рис. 2.33, б):
Z.RL = R + ]XL,
где XL = 2nfL = a>L.
В показательной форме это сопротивление запишется в виде
ZRL=ZRLe^, (2.31)
где модуль Zrl называется полным сопротивлением последова-
тельной .RL-цепи, а аргумент <pz характеризует фазовый сдвиг
между током i и напряжением и ветви (рис. 2.33). Так как
Ф = Фи - ср,-, то угол ф всегда откладывается по направлению от
тока i к напряжению и. Причем ф/ > 0 (рис. 2.33, б), если он
откладывается в положительном направлении (против часовой
стрелки), и <pz < 0, если он откладывается в отрицательном на-
правлении (по часовой стрелке). Полное сопротивление Zrl и
аргумент фг подсчитываются, как это следует из рис. 2.33, б, по
формулам
ZRL = y]R2+Xl и ф2 = arctg
Пример 2.11. Определим комплексное сопротивление цепи, изо-
браженной на рис. 2.33, а, на частоте 50 Гц для
R = 10 Ом и L = 100 мГн.
Рассчитаем значение индуктивного сопротивле-
ния цепи, используя (2.29):
94
XL = 2nfL = 2-3,14-50 100-10'3 = 31,4 Ом.
Комплексное сопротивление RL-цепи
ZRL = R + jXL =10 + j31,4.
Полное сопротивление
ZRL = \]R2 + Xl = >/102 +31,42 = 32,95 Ом.
Аргумент комплексного сопротивления
. XL , 31,4 Q0
<Pz = arctg—= arctg^y- = 72,3°.
В показательной форме комплексное сопротив-
ление RL -цепи
ZRL = 32,95е;72’3° Ом.
Комплексное сопротивление последовательной 7?С-цепи в ал-
гебраической форме состоит из положительного вещественного ре-
зистивного сопротивления R и отрицательного мнимого емкостно-
го -]ХС (рис. 2.34, б):
Z = R-jXc,
у 1 1
где Хс =-^~сп=—^-
2nfC (оС
В показательной форме это комплексное число выглядит как
2ЛС = ZRCe™ , (2.32)
где ZRC = ^R2 + Хс — полное сопротивление последовательной
ЯС-цепи; <pz = arctg с — аргумент этого сопротивления.
R
Рис. 2.34. Последовательная ЯС-цепь
и ее комплексное сопротивление
95
Рис. 2.35. Треугольники
сопротивлений
Рис. 2.36. Комплексное
сопротивление 7?С-цепи
Комплексное сопротивление Zrc изображено на рис. 2.34, б
в виде вектора на комплексной плоскости. Там же показаны его
проекции на вещественную и мнимую оси.
Прямоугольный треугольник, составленный из резистивного,
реактивного и полного сопротивлений (рис. 2.35), называется
треугольником сопротивлений.
Пример 2.12. Определим комплексное сопротивление цепи, изо-
браженной на рис. 2.34, а, на частоте 5 кГц для
R = 100 Ом, С = 318 нФ.
Рассчитаем значение емкостного сопротивления
цепи:
Zc = -Д— =-----------Д---------5- = 100 Ом.
2л/С 2-3,14-5-103-318 -10’9
Комплексное сопротивление /?С-цепи
ZRC ]ХС = 100-/100 = 141е’у45° Ом.
Вектор комплексного сопротивления /?С-цепи
изображен на рис. 2.36.
Запишем комплексное сопротивление последовательной RLC-
цепи (рис. 2.37, а). Оно будет содержать положительное вещест-
венное резистивное сопротивление R (активная составляющая) и
мнимое сопротивление jX = j(XL-Xc) (реактивная составляю-
щая), знак которого будет зависеть от соотношения индуктивного
Xl и емкостного Хс сопротивлений. Следовательно,
ZRLC =R + j(Xl-Xc) = ZRLCe’*z , (2.33)
где ZR£C =7-R2+(A’£ -Xc)2 и <pz = arctg Xl ~X(?.
IX
Напомним, что значения Xl и Хс зависят от частоты и соот-
ветствующих элементов L и С, поэтому может случиться так, что
на определенной частоте и при определенных значениях L и С
значение Xl будет больше значения Хс, как это показано на
96
Рис. 2.37. Последовательная RLC-цепъ и треугольники
ее сопротивлений
рис. 2.37, б, при этом цепь будет носить индуктивный характер,
или, наоборот, значение Хс будет больше, чем Xl (рис. 2.37, в),
при этом цепь будет носить емкостный характер.
Из треугольника сопротивлений легко вычислить резистивное
и реактивное сопротивления, зная полное сопротивление и аргу-
мент <pz:
7? = Zrlc cos срz и X = - Хс = Z/гдс sin <pz.
Случай, когда реактивное сопротивление X = 0, т.е. Xl = Хс,
является особым. Когда это имеет место, то говорят, что в после-
довательной RLC-цепи возникает резонанс напряжений. Частота,
на которой индуктивное и емкостное сопротивления оказываются
равными, называется частотой резонанса напряжений. Ком-
плексное сопротивление всей 7?7.С-цепи равно при этом рези-
стивному сопротивлению R.
Пример 2.13. Определим активное (резистивное) и реактивное
сопротивления последовательной RLC-uenw., ком-
плексное сопротивление которой ZRLC = 14eJ75°, Ом.
Резистивное сопротивление
= Zrlc cos(pz = 14cos75° = 3,6 Ом.
Реактивное сопротивление
X = ZRLC sin<pz = 14sin75° = 13,5 Ом.
Х= 13,5 Ом
R = 3,6 Ом
Рис. 2.38. Треугольник сопротивлений
RLC-цепи
7 - 6972
. 97
Сопротивление X = Xl - Хс положительное, т.е.
Xl > Хс, треугольник сопротивлений такой цепи изо-
бражен на рис. 2.38.
Параллельное соединение R, L, С-элементов. При параллель-
ном соединении элементов (рис. 2.39) удобнее иметь дело не с со-
противлениями, а с проводимостями — резистивной G = 1/R, ин-
дуктивной BL = 1/XL и емкостной Вс = \/Хс , полной У = 1/Z и
комплексной У = 1/Z. Если при последовательном соединении
элементов складывались их комплексные сопротивления, то при
параллельном соединении складываются их проводимости.
Для параллельной BLC-цепи (рис. 2.39, а) ее комплексная
проводимость запишется в виде
Гис = G + )(Вс - BL) = , (2.34)
где G = 1/R — резистивная проводимость;
Вс = 2nfC = ©С — емкостная проводимость;
BL = l/(2itfL) = i/taiL) — индуктивная проводимость;
В = Вс - ВL — реактивная проводимость;
YRlc=№+(Bc-Bl)2 — полная проводимость;
В —В
Фу = arctg——- — аргумент комплексной проводимости.
G
Резистивную (активную) и реактивную проводимости можно
найти из треугольника проводимостей (рис. 2.39, б):
G = YrLc cos Фу и В = ВС-В£=УЛ£С sin фу.
Случай, когда реактивная проводимость В равна нулю, т.е.
когда Вс = BL, также представляет особый интерес. В этот мо-
мент в параллельной BLC-цепи наступает резонанс токов. По-
этому частота, на которой происходит совпадение реактивных
проводимостей ветвей, получила название частоты резонанса
токов. Комплексная проводимость всей цепи при резонансе ста-
новится равной резистивной проводимости G.
Рис. 2.39. Параллельная /?£С-цепь и треугольники
ее проводимостей
98
Пример 2.14. Определить комплексное сопротивление параллель-
ной RLC-цегт (рис. 2.39, а) на частоте f = 1 кГц для
R = 100 Ом, L = 10 мГн, С = 10 мкФ.
Элементы цепи соединены параллельно, поэтому
рассчитаем вначале комплексную проводимость
Yrlc, используя выражение (2.34).
Резистивная проводимость
G = 1 =-1-= 0,01 См.
R 100
Индуктивная проводимость
BL = тДт =-------------------Ч =0,016 См.
2itfL 2 - 3,14 • 103 • 10 • 10-3
Емкостная проводимость
Вс = 2nfC = 2 • 3,14 • 103 • 10 • 10~6 = 0,063 См.
Комплексная проводимость цепи
Yrlc = G + }(ВС - BL) = 0,01 + /(0,063-0,016) =
= 0,01+ /0,047 См.
Комплексное сопротивление цепи обратно про-
порционально комплексной проводимости, поэтому
Z = 1 = 1 = 1 =
~RLC Yrlc 0,01+ /0,047 0,048е'78°
= 20,8е’778° Ом.
Из данного параграфа мы узнали, что:
• Резистивные, индуктивные и емкостные элементы оказы-
вают гармоническому току сопротивления, причем индук-
тивные и емкостные элементы оказывают на каждой часто-
те различные сопротивления, сопротивление же резистив-
ного элемента не зависит от частоты.
• Значения резистивного сопротивления откладывают на ве-
щественной оси комплексной плоскости, значение индук-
тивного сопротивления — на положительной мнимой полу-
оси, а значение емкостного сопротивления — на отрица-
тельной мнимой полуоси.
• Комплексное сопротивление объединяет в себе сопротивле-
ния резистивных и реактивных элементов.
• Комплексное сопротивление может быть записано в двух ос-
новных формах — алгебраической и показательной.
7»
99
sX-Ot<’Wi '* s«< x .^.WRRW Г !>»Ш ♦ «w«vW5*5*4HJff
• Аргумент комплексного сопротивления цепи показывает |
угол сдвига фаз между напряжением и током в этой цепи. Е
• Модуль комплексного сопротивления цепи показывает й
соотношение между амплитудами напряжения и тока в в
этой цепи. В
2.3. Расчет реакций цепи в символической форме
При расчете реакций в цепи с одним источником использу-
ется следующий алгоритм действий:
1. Цепь, содержащую источник гармонических колебаний, преоб-
разуют, заменяя ее элементы их комплексными сопротивлени-
ями, а мгновенные значения эдс, токов и напряжений их ком-
плексными значениями.
2. Рассчитывают комплексные значения токов и напряжений в
ветвях, используя закон Ома и законы Кирхгофа.
3. Определяют соответствующие мгновенные значения токов и
напряжений в цепи.
Пример 2.15. Определим мгновенные значения тока и напряже-
ний на элементах цепи, содержащей источник гар-
монического напряжения и(t) = 10sin2000t, В, со-
противление R = 300 Ом, индуктивность L = 0,6 Гн
и емкость С = 0,625 мкФ (рис. 2.40).
В соответствии с порядком расчета реакции в це-
пи с одним источником заменяем элементы цепи их
комплексными сопротивлениями.
Анализируя выражение для мгновенного значения
напряжения u(t), определяем, что круговая частота
<в = 2000 рад/с, т.е. частота колебаний f = <в/(2л) =
= 318,3 Гц. Сопротивление R = 300 Ом остается не-
изменным. Индуктивность L = 0,6 Гн заменяется со-
противлением
ZL = jaL = /(2000-0,6) = /1200 Ом.
Рис. 2.40. Цепь с одним источником
гармонического напряжения
100
Рис. 2.41. Цепь с источником комплексного напряжения
и комплексными сопротивлениями
Емкость С = 0,625 мкФ заменяется сопротивле-
нием
zc = -4- = = -j--------------«= - j’8oo Ом.
-c jvC (DC 7 2000 0,625 10-6
Гармоническое напряжение u(t) = 10sin2000£
представим в показательной форме записи в виде
Um = 10e'°° В.
Ток i(i) заменяется на комплексный ток Lm, а
напряжения иц(Л), щ.(Л) и uc(t) заменяются ком-
плексными напряжениями UjnR, Umt и Umc соответ-
ственно.
В результате получаем схему, изображенную на
рис. 2.41.
Для определения тока и напряжений в этой схе-
ме рассчитаем вначале комплексное сопротивление
цепи Z относительно зажимов источника. Все сопро-
тивления включены последовательно, поэтому
Z = R + + Z_q = 300 + у 1200 — у800 =
= 300 + /400 Ом.
Отметим, что индуктивное и емкостное сопротив-
ления цепи частично компенсировали друг друга и что
реактивное сопротивление цепи меньше по величине,
чем сопротивление любого из реактивных элементов.
Фактически возможно полностью исключить на-
личие реактивного сопротивления в цепи, изменив
частоту генератора напряжения до выполнения усло-
вия Xl = Хс-
В рассматриваемом примере сопротивление цепи
имеет индуктивный характер, поскольку реактивная
составляющая комплексного сопротивления цепи
имеет знак «плюс».
101
Комплексный ток /т в цепи определим, исполь-
зуя закон Ома для комплексного напряжения U_m ис-
точника и комплексного сопротивления Z. Имеем
U 10е7°°
I — —У» — Avcr_____ д
-m Z 300 +/400 ’
Преобразуя комплексное сопротивление Z в по-
казательную форму для упрощения деления ком-
плексных чисел, получаем
10е7°°
т 500е;53°
= 0,02е-;53° А.
Амплитудное значение тока равно 0,02 А, а началь-
ная фаза равна -53°.
Напряжения на сопротивлениях цепи определя-
ем, умножая ток на соответствующие сопротив-
ления:
UmR = ImR = 0,02e-y53° • 300 = 6е-;53° В;
UmL ^ImjXL=Q,Q2e-^°-jl2Q0 =
= 0,02е~;53° • 1200е;9°° = 24е'37° В;
Umc =/от(-/Хс) = 0,02е->53в(-/800) =
= 16е";143’ В.
Ток Гт имеет начальную фазу (-53°), напряже-
ние UjnR имеет такую же начальную фазу, т.е. векто-
ры Ijn и UmR направлены по одной прямой на век-
торной диаграмме, изображенной на рис. 2.42.
Напряжение на индуктивности опережает ток на
90°, таким образом, UmL опережает вектор на гори-
зонтальной оси рис. 2.42 на 37°.
Напряжение на емкости отстает от тока на 90°, а
от горизонтальной оси на 143°.
Рис. 2.42. Векторная диаграмма напряжений
102
Отметим также, что сдвиг фаз между UjnL и U_mc
составляет 180°.
В соответствии с законом напряжений Кирхгофа
U-m = —mR + — гп£ + — тс ’
Последние два слагаемых представляют собой
сумму напряжений на индуктивности и емкости, и
этот суммарный вектор может быть направлен либо
по U_mL, либо по Umc в зависимости от того, какое из
этих напряжений больше по величине. В нашем слу-
чае он имеет направление UjnL-
Вектор UjnR может быть добавлен к сумме UjnL +
+ Umc, и результатом является вектор С/От, как пока-
зано на рис. 2.42.
Мгновенные значения тока и напряжений на эле-
ментах цепи можно записать в виде
i(£) = 0,02sin(2000£-53°) А;
uR(t) = 6sin(2000£-53°) А;
(^) = 24sin(2000^ + 37°) В;
wc (£) = 16sin(2000£ - 143°) В.
Векторная диаграмма часто бывает полезна при
объяснении и интерпретации результатов расчета.
Пример 2.16. Найдем токи и напряжения в цепи, изображенной
на рис. 2.43, если заданы значения Ri = 2 Ом, =
= 2 Ом, XL = 4 Ом, Хс = 2 Ом, Um = 9>/2е>°°, В.
Во-первых, определим комплексное сопротивле-
ние Za6 параллельного соединения резистора R2 и
емкостного сопротивления Хс'.
7 .Rl(-iXc') 2(-,2) .
R2-jXc 2-72 2j2e->15’
= >/2<Гу45° = 1-;, Ом.
Рис. 2.43. Схема для расчета токов и напряжений
в символической форме
103
а) б)
Рис. 2.45. Схемы для определения тока Lm
Сопротивление Zae можно представить в виде
Za6 = R&6 ~ ]-^аб-
Получаем эквивалентную схему, изображенную
на рис. 2.44.
Эквивалентное комплексное сопротивление цепи
определяется как
Zэ = + ]XL + Za(j = 2 + j4 + l-;l = 3 + ]3 Ом.
Ток (рис. 2.45) определяется по закону Ома:
U„ S-J2eir 9^’ ,i5-
3 + /3 ЗЛг'15
Токи Lmi и /m2 определяем по формулам разброса:
I . = I = Зе-745° • 2 =
-ml LmR2-jXc 2-j2
= 1,5^2е^ A;
2j2e~Ji5
1,-1 ~JXc = 3e_y45° • 2g~~'9° =
lm2 ~mR2-jXc 2V2e->45°
= l,5V2e->90° A.
Следует отметить, что согласно закону токов
Кирхгофа [jn\ + Zm2 = Lm- Векторная диаграмма то-
ков приведена на рис. 2.46.
104
Zml=l,5V2e>0°
Im2=l,5V2e-;90°v
Рис. 2.46. Векторная диаграмма токов
-Кяаб X (£тс»
Рис. 2.47. Векторная диаграмма напряжений
Определим напряжения на элементах цепи
(рис. 2.43):
UmRX =Lm Ri = 6<Н43° В;
UmL = I_m jXL = 3e-;45° • 4e'90° = 12e>45° B;
= Lm • —аб = 3<H45° • V2e->45’ = 3j2e~W° B.
Согласно закону напряжений Кирхгофа (рис. 2.47)
— mL +LLmRt +LLmsi6 - ILm
При расчете реакций в цепи с несколькими источниками все
методы, используемые для расчета в режиме постоянного тока,
применимы и к расчету цепей при гармоническом воздействии.
Методы наложения, узловых напряжений, контурных токов, эк-
вивалентного генератора используются для определения реакций
в цепи с несколькими источниками гармонических колебаний.
Расчет выполняется для символической формы записи токов,
напряжений и сопротивлений цепи.
Пример 2.17. Методом наложения определим токи в ветвях це-
пи, изображенной на рис. 2.48, если заданы значения
Rx = 2 Ом, XL = 4 Ом, Хс = 2 Ом, Um = 8е>°° В,
1тГ = 4V2e>45’ А.
Выберем направления токов в ветвях цепи
(рис. 2.48). Поскольку в схеме два источника, то ис-
тинные направления токов неизвестны, поэтому вы-
бираем их произвольно.
105
L, Л1 jXL ф
Рис. 2.48. Электрическая цепь с несколькими
источниками гармонических колебаний
Метод наложения основан на принципе супер-
позиции, согласно которому реакция линейной цепи
на сумму воздействий равна алгебраической сумме
реакций от каждого воздействия в отдельности.
Частичные схемы, в каждой из которых оставлен
только один источник, а другой заменен его внутренним
сопротивлением, изображены на рис. 2.49, а и 2.49, б.
Рассчитаем токи в первой частичной схеме
(рис. 2.49, а). Внутреннее сопротивление источника то-
ка равно бесконечности, поэтому 1т2=0. По закону Ома
г = т' 8 8
m -mi Rx+jXL-jXc 2 + j4-j2 2 + j2
= ._8 .= 2>/2e-/45° = 2-/2 A.
2j2e}i5
Рассмотрим вторую частичную схему (рис. 2.49, б).
Ток l"m2 равен току источника тока, т.е.
106
б)
Рис. 2.49. Частичные схемы
l"m2 = Zwr=4>/2e'45e=4 +j4 A.
Токи Гт и l’ml рассчитываем, используя формулу
разброса:
Г =1 г ~^Хс =
~тГ Ri+jXL -jXc
= 4>/2е745’—= -4/ А;
2>/2е;45
Г = I г Ri +Jxl _
-mi -тГ Rl+JxL-jXc
= 472^’4^= 4 +/8 А.
2%/2е;45 J
Токи в ветвях исходной схемы
Lm=L'm-Lm = 2-/2 + /4 = 2 + /2 А;
Zmi=Zmi+Imi = 2 - ;2 + 4 + ;8 = 6 + ;6 А;
1т2 = ~L'm2 + 1т2 = 1тГ =4 + ]4 А..
Пример 2.18. Методом узловых напряжений определим токи в
ветвях цепи, изображенной на рис. 2.48.
Заземляем узел 2. Потенциал этого узла равен
нулю: Vw2 = 0.
Для узла 1 составляем уравнение состояния:
Zml-Zll-Z«2-Z12=Zmyl-
В этом уравнении Уц — это собственная проводи-
мость узла 1, т.е. сумма проводимостей всех ветвей,
подсоединенных к узлу 1:
Y 1 1 - 1 1
—11 Ri+jXl ~]Хс 2 + у4 -/2
= 0,1 + /0,3, См;
У12 — взаимная проводимость узлов 1 и 2, совпа-
дающая в рассматриваемом примере с величиной Уц;
Lnyi — узловой ток узла 1:
Zmyl =^Tfe + “mr = 2+74+4 + ;4 =
= 4,8+ /2,4, А.
Из уравнения состояния находим потенциал пер-
вого узла:
107
И,., ’Vй = 12- /12, В.
Ln
Токи в ветвях находим по закону Ома:
J _ +£Zm _ -12 +J12 + 8 _ „ -2 А-
~т —r,+)Xl ’ ~'
г ^т\~^т2 12-/12 „ ._ .
1ml = = 6 +;6 А;
-jxc -]2
1т2 = 1тГ = 4 +j4 А.
Значения токов в ветвях цепи рис. 2.48 те же самые,
что и при расчете методом наложения.
Пример 2.19. Методом контурных токов определим токи в ветвях
цепи, изображенной на рис. 2.48.
Выберем направления обхода контуров в цепи
(рис. 2.50).
Контурный ток
Хтк2 = LrnT =4 + 74 А.
Для определения контурного тока /гак1 составляем
уравнение состояния:
LmKl ’ 211 +Хтк2 "212 = ^ткГ
В этом уравнении Zu — собственное сопротивление 1
контура, равное сумме сопротивлений всех ветвей,
образующих этот контур:
2ц = -^i + J^l ~ }ХС = 2 + /4 - ]2 =
= 2 + /2 Ом;
Z12 — взаимное сопротивление 1 и 2 контуров:
212 = ~]^с = “72 Ом;
Рис. 2.50. Электрическая цепь с двумя
источниками энергии
108
XZzbkI — контурное напряжение:
—тк1 = = 8 В.
Из уравнения состояния находим контурный ток
Г - —тк! тк2 £12 _ 8 -(4 + j4)•(-/2) _
-mK1~ £ц 2 +/2
= 2 +/2 А.
Зная контурные токи, находим токи ветвей:
Lm ~ LmKi = 2 + у2 А;
Iml = 1тк1 + 1тк2 = 2 + ;2 + 4 + /4 = 6 + /6 А;
1т2 ~ 1тк2 = 4 + /4 А.
Значения токов совпадают с теми, которые были по-
лучены при расчете цепи методами наложения и уз-
ловых напряжений.
Пример 2.20. Методом эквивалентного генератора определим ток
Imi в цепи, изображенной на рис. 2.48.
Разомкнем ветвь с емкостью и для определения
напряжения холостого хода CZmxx составим уравне-
ние по второму закону Кирхгофа:
—тхх + —тхх (Ri+jXL) = Um.
В режиме холостого хода ток Imxx = —LmV> по-
этому
£Zmxx ~ ~ Zmxx (*^1 + l^L ) ~
= 8-(-4-/4)(2 + /4) = /24 В.
Сопротивление эквивалентного генератора Z3
равно
Z3 = = 2 + у4 Ом.
Ток 1т\ найдем по формуле
г — ~уихх _ J24 _ у24 _
-т1~ Za-jXc~ 2 + У4-/2’ 2 + /2"
= 6 + ;6 А.
Получаем то же самое значение /mi, что и при
применении других методов расчета.
Из данного параграфа мы узнали, что
109
• Расчет реакций цепи на гармонические воздействия с приме- |
нением символической формы записи колебаний осуществля- |
ется теми же методами, что и расчет цепей постоянного тока: |
с помощью законов Ома и Кирхгофа; методами контурных |
токов, узловых напряжений, эквивалентного генератора.
2.4. Комплексные передаточные функции
Рассмотрим электрическую цепь, изображенную на рис. 2.51.
Нас может интересовать любая реакция цепи (напряжение или
ток в любом элементе или ветви цепи) на любое из приложенных
воздействий. Предположим, что воздействие создается источником
щ U), а реакцией является ток или напряжение на R3. В этом слу-
чае цепь удобно представить четырехполюсником, на входе которо-
го включен источник с заданным воздействием, а на выходе — ин-
тересующий нас элемент, например, как это сделано на рис. 2.52.
Рис. 2.51. Электрическая цепь с тремя источниками энергии
Рис. 2.52. Представление цепи на рис. 2.51
в виде четырехполюсника
1т1
О-*—
Четырех-
полюсник
1тЗ
Рис. 2.53. Символическое изображение напряжений
и токов в цепи рис. 2.51
110
Символическое изображение напряжений и токов на входе и
выходе четырехполюсника показано на рис. 2.53.
Важнейшей характеристикой линейной электрической цепи
является комплексная передаточная функция Н. Она определя-
ется отношением комплексной амплитуды реакции к комплексной
амплитуде воздействия.
В зависимости от того, что считается реакцией и воздействи-
ем, различают следующие виды передаточных функций.
1. Комплексный коэффициент передачи по напряжению
(2.35)
2. Комплексный коэффициент передачи по току
(2.36)
Lmi
3. Комплексное передаточное сопротивление
(2.37)
Lmi
4. Комплексная передаточная проводимость
(2.38)
У-т1
Комплексное число Н может быть представлено в показа-
тельной форме
Н = Не™,
где Н — модуль передаточной функции, а <р — ее аргумент.
Действительно, рассмотрим передаточную функцию
тт тт тт
= UmR3 = umR3e = UmR3 Ц<риЯз-чг11) = .фи
~и ~ ит1 ” umie^ " Uml -и .
Модуль передаточной функции
H»=UmR3/UmX (2.39)
Представляет собой отношение амплитуды напряжения гармони-
ческой реакции цепи к амплитуде напряжения гармонического
воздействия, т.е. показывает, во сколько раз амплитуда напряже-
ния гармонического колебания на входе цепи изменилась при
111
прохождении колебания через цепь. Поэтому величину Ни назы-
вают коэффициентом передачи по напряжению.
Аргумент передаточной функции
Ф« =ф«Дз -Ф»1 <2.40)
показывает изменение начальной фазы входного колебания на-
пряжения после передачи этого колебания по цепи и называется
фазовым сдвигом.
Знание комплексного коэффициента передачи цепи позволяет
вычислить реакцию цепи на гармоническое воздействие. Ампли-
туда реакции
а ее начальная фаза
Ф“Яз =Фгч'*’Фи'
Другими словами, чтобы найти амплитуду напряжения гармо-
нического колебания на выходе цепи, нужно амплитуду входного
напряжения гармонического колебания умножить на коэффициент
передачи по напряжению, а чтобы найти начальную фазу выходного
гармонического колебания, нужно к начальной фазе входного гар-
монического колебания добавить фазовый сдвиг, вносимый цепью.
В символической форме записи комплексная амплитуда гармо-
нического колебания на выходе цепи определяется из соотношения
U.R3=U„,-HU. (2.41)
Аналогичным образом вычисляют коэффициент передачи по
току
Hi — ^тз!^т\
и сдвиг фаз колебания тока
Фг ^Фгз-Фгр
полное передаточное сопротивление цепи
Hz ~ U/1т\
и фазовый угол этого сопротивления
Ф/ = Фи/?з Фгр
а также полную передаточную проводимость
Ну = m3/Н mi
и ее фазовый угол
ФУ ~ Фг'з ~ Фар
112
В общем виде можно записать
Комплексная амплитуда реакции
Комплексная амплитуда воздействия
Очевидно, что в схеме рис. 2.51 в качестве реакции может
выступать напряжение или ток в любом элементе или любой вет-
ви цепи, а в качестве воздействия использоваться не только на-
пряжения или токи источников, но и любые напряжения или то-
ки элементов (ветвей) цепи.
Пример 2.21. Найдем комплексный коэффициент передачи по
напряжению цепи, приведенной в примере 2.15, ес-
ли реакцией цепи является напряжение на емкости
uc(f).
При решении примера 2.15 воздействие было за-
писано в символической форме
Um = 10е;0° В.
Напряжение на емкости, т.е. реакция цепи, так-
же было определено:
и.с = 1бе-'113" в.
Комплексный коэффициент передачи
Н
_ —_ 16е 7143 _ j бе-/143°
" Um " 10е'°° ’
Коэффициент передачи по напряжению
Н = =1,6
показывает, что при прохождении по цепи амплитуда
воздействия увеличилась в 1,6 раза.
Сдвиг фаз
Фя„ =<РиС ~<Р« =-143°
показывает, что напряжение на емкости отстает от
входного колебания на 143°.
Пример 2.22. Найдем комплексный коэффициент передачи по
току цепи, изображенной на рис. 2.54, если /мг =
= 5еу90° А, Т?2 = Ю Ом, £ = 30 мГн, f = 50 Гц, реак-
цией цепи является ток в индуктивности.
8-6972
113
Рис. 2.54. Электрическая цепь с источником тока
Для расчета комплексного коэффициента пере-
дачи по току
—i = Lml/ LmV
необходимо определить ток в индуктивности. Ис-
пользуя формулу разброса, получаем
I = I =
-m2 ~^R2+j27tfL
г 10
-тГ 10+ /2-3,14-50-ЗОЮ'3
= 1тГ —— = 1тГ 0,73е“;43’2°.
-wr10 + /9,4 ~тТ
Комплексный коэффициент передачи по току
Очевидно, что комплексный коэффициент пере-
дачи цепи определяется значениями элементов цепи
Т?2, L и частоты f.
Пример 2.23. Найдем напряжение на индуктивности ui(t) в
цепи, приведенной в примере 2.22, если, комплексное
передаточное сопротивление Hz = 6,86е;46,8° Ом.
Амплитуда напряжения на индуктивности
UmL == 5 -6,86 = 34,3 В.
Начальная фаза напряжения на индуктивности
«Рид = <Pir+<Pz = 90°+ 46,8° = 136,8°.
Мгновенное значение напряжения
uL(t) = 34,3sin(314i +136,8°) В.
Из данного параграфа мы узнали, что:
114
, Комплексный коэффициент передачи цепи — это отношение
комплексной амплитуды реакции к комплексной амплитуде )
воздействия.
. В качестве реакции и воздействия могут быть выбраны лю-
бые интересующие нас токи и напряжения в элементах и
ветвях цепи.
. Коэффициент передачи по напряжению (току) показывает, ‘
во сколько раз изменилась амплитуда входного гармониче- *
ского напряжения (тока) при передаче его по цепи.
. Фазовый сдвиг, вносимый цепью, показывает изменение 3
начальной фазы входного гармонического колебания при
прохождении его по цепи. ’j
Вопросы и задания для самоконтроля
1. Какие колебания называются гармоническими?
2. Какие параметры характеризуют гармоническое колебание?
3. Как определяется величина и знак начальной фазы гармони-
ческого колебания по его графику?
4. Как связаны частота и период гармонического колебания?
5. Записать выражение для мгновенного значения тока, график
которого изображен на рис. 2.5, б, если период колебания
Т = 2 с. Определить значение тока в момент времени t\ = Т/8.
6. Построить в одной системе координат графики напряжений
ui(i) = 5sin(2n50£-45°), мг(£) — 3sin(2x50£+ 60°).
7. Какая связь между векторным и временным представлением
гармонических колебаний?
8. Построить векторы гармонических колебаний, приведенных в п. 6.
9. Построить в одной системе координат графики, гармонических
колебаний, которым соответствуют векторы Um\ = 5Z - 45° и
U „л =5/90°, вращающиеся с одинаковой частотой. Опреде-
лить сдвиг фаз этих колебаний.
10. Какая связь между параметрами комплексного и временного
представления гармонических колебаний?
И. Сформулировать закон Ома для резистивной, индуктивной и
емкостной цепей.
12. Какой сдвиг фаз между напряжением и током в резисторе
(емкости, индуктивности)?
13. Как рассчитывается комплексное сопротивление последова-
тельного соединения R, L, С-элементов?
14. Как рассчитывается комплексная проводимость параллельного
соединения/?, L, С-элементов?
8*
115
Рис. 2.55
Рис. 2.56
15. Определить комплексное сопротивление цепи, изображенной
на рис. 2.55, если
= 20 Ом, R2 = 40 Ом,
Xl = 30 Ом, Хс - 40 Ом.
16. Построить треугольник сопротивления цепи, изображенной на
рис. 2.55.
17. Какие методы используются для расчета цепей с источниками
гармонических колебаний?
18. Рассчитать токи в ветвях цепи, изображенной на рис. 2.55,
если на вход подается напряжение и kt) = 80,4 sin (со £ + 90°),
В. Построить векторную диаграмму токов.
19. Рассчитать ток /Ш2 в цепи, изображенной на рис. 2.56, мето-
дом наложения и методом эквивалентного генератора, если за-
даны сопротивления R = 10 Ом, Xl — 30 Ом, Хс= 20 Ом и
CJm = 10e>°’B,/mr=ey270’A.
20. Что такое комплексный коэффициент передачи? Какие виды
комплексных коэффициентов передачи известны?
21. Определить коэффициенты передачи в цепи примера 2.16, ес-
ли реакцией является 1_т2-
Глава 3. Анализ реакции линейной цепи на
периодическое воздействие сложной формы
3.1. Представление периодического
воздействия рядом Фурье
Из математического анализа известно, что периодическая не-
гармоническая функция f(t), удовлетворяющая условиям Дирих-
ле, т.е. имеющая на периоде Т конечное число разрывов первого
рода и конечное число максимумов и минимумов (что для реаль-
ных сигналов обычно выполняется), может быть разложена в ряд
Фурье:
= COS kOxt + bk SIR Oj = 2n/T,
2 л=1
где ak, bk — коэффициенты разложения, определяемые уравне-
ниями
2 т
dk= — (t)coskcoitdt;
о
? T
bk=-\f(t) sin k^tdt; (3.1)
* о
T
* 1 0
Применительно к периодическому гармоническому напряже-
нию u(t) в (3.1) можно использовать следующие обозначения:
оо и(i) = Uo + X (U'mk coskd)tt + UHmk sink<o UQ =±=\u(t)dt, 1 0 2 T U'mk = — ju(t)coska>itdt; 0 2T U"mk = — \u{t)sink<nxtdt. * 0 (3.2)
Напомним, что у периодического сигнала его значения по-
вторяются через равные промежутки времени, называемые пе-
риодом. Простейшим периодическим сигналом является гармони-
ческое колебание вида
117
u(t) = Um sin cot.
Естественно, что при разложении этого сигнала в ряд Фурье
последний будет содержать всего один член. Примером сложного
периодического сигнала может служить последовательность пря-
моугольных импульсов с периодом повторения Т (рис. 3.1, а).
Периодическая последовательность прямоугольных им-
пульсов, симметричная относительно начала координат, состо-
ит только из синусоид. Хотите убедиться в этом? Тогда взгля-
ните на рис. 3.1. В качестве исходной синусоиды нужно выбрать
такую, у которой период совпадает с периодом повторения Т пря-
моугольных импульсов (рис. 3.1, б):
2тг
их (t) = UmX sinG)xt = UmX sin 2nfxt = UmX sin — t.
Рис. 3.1. Последовательность прямоугольных
импульсов и образующие ее синусоиды
118
Следующая синусоида должна иметь частоту в три раза боль-
шую, а амплитуду — в три раза меньшую:
u3(t) = ^Umisin3(dxt = sin 671/1 i = |(7OT1sin^i.
«5 О «3 1
Сумма этих двух синусоид, т.е. их (t) + и3 (t), пока еще мало
похожа на прямоугольные импульсы (рис. 3.1, в). Но если мы
добавим к ним синусоиды с частотами в 5, 7, 9, И и т.д. раз
большими, то сумма всех этих колебаний
u(t) = (7mlsin®t£ + sin Зсо^ + ^f^sin5<»i£ +
3 5 (3.3)
+ ~y^sin 7©t£ + ^ур8П111а)1£ + •••.
будет не так уж сильно отличаться от прямоугольных импульсов
(рис. 3.1, гид). Таким образом, из (3.3) следует, что в случае
последовательности прямоугольных импульсов, симметричной
относительно начала координат, ряд Фурье (3.2) состоит толь-
ко из синусоидальных колебаний.
Ниже мы покажем, что для того, чтобы сигнал, сформирован-
ный из синусоид (3.3), совпадал с прямоугольными импульсами
также и по высоте, амплитуду основной синусоиды следует взять
СУот1 = (4/к)[/ = 1,27(7.
Таким образом, степень прямоугольности импульсов определя-
ется количеством синусоид со все более высокими частотами,
которые мы будем суммировать в (3.3).
Построения на рис. 3.1 носят скорее наглядный характер.
Воспользовавшись формулами (3.2), можно выполнить точные
вычисления.
Постоянная составляющая ряда Фурье
1 Т л Т/2 1 Т rr Т/2 rr т
U0=±$u(t)dt = ± $Udt-± $Udt = ^t ,-^t =
T о Т 0J Т т'/2 Т о Т т/2
= (7/2-(7 + (7/2 = О
равна нулю, т.е. она в данном сигнале отсутствует.
Амплитуды косинусоидальных гармоник
n Т п Т/2 q п .
\ u(t) cos ka^tdt-— \ Ucosk-tdt-— jUcosk—tdt=
Г о Г 0 Т Т Т/2 Т
2UT . k2it Т 2UT . k2n „ 2UT . k2n Т
=та51п~'г-та81"—r+T&sm~-7=
=—(sin kit-sin 2/m+sin kit)=0
kit
119
также равны нулю при любых значениях k, что означает их от-
сутствие в сигнале.
Амплитуды синусоидальных составляющих ряда Фурье
yT 9 о— 9 T 9—
U"mk =— {«(Osinfoo^dtjUsiak-tdt-— J Usink — tdt =
2UT k2nt T/2
COS--.....
T о
т
Т Т/2
2UT k2itt
+ 7Z77T-COS—;
Tk2it
и и
Tk2it
—(cos kit-l)+^-cos2kit-^-coskit.
kit kit kn
kit kit
При & = 1 U'mi=4U/it;
k = 2 U”m2=0;
k = 3 U’m3=4U/(3it)-,
k = * t/;4 = o;
k = 5 U’mk = 417/(5л) ИТ.Д.
Амплитуда U’ml обозначена в формуле (3.3) как амплитуда
первой (основной) гармоники Uml.
Может показаться, что представление периодических сигна-
лов в виде совокупности гармоник есть не более чем математиче-
ский прием и не имеет никакого отношения к реальности. Однако
это не так. Если бы вам удалось, например, подобрать струны с
частотами колебаний, кратными числам 1, 3, 5, 7, ..., и, распо-
ложив их рядом друг с другом, привести одновременно в движе-
ние так, чтобы амплитуды колебаний струн соотносились как
1 : (1/3) : (1/5) : (1/7) ..., то вы бы увидели, что форма кривой
звукового давления, создаваемого этими струнами совместно (а
значит, и форма тока, например, в цепи микрофона), была бы
прямоугольной.
Продолжим качественный анализ периодических несинусои-
дальных колебаний.
Пилообразный сигнал, симметричный относительно начала
координат, также состоит только из синусоид. Этот сигнал по-
казан на рис. 3.2, а. Радиолюбители знают, что подобную форму
имеет напряжение, развертывающее изображение на экране теле-
визора по строкам.
Чтобы сформировать пилообразный сигнал, нужно взять сна-
чала основную синусоиду или первую гармонику (рис. 3.2, б):
2тг
щ (£) = UmiSina)^ = (7mlsin27t/'1t = C7m1sin—t.
Амплитуду этой гармоники можно рассчитать по формуле
(3.2). Она равна
Umi = (2/it)U = 0,63517.
120
Рис. 3.2. Последовательность пилообразных импульсов
и образующие ее синусоиды
121
Затем следует использовать перевернутую синусоиду удвоенной
частоты и половинной амплитуды (рис. 3.2, в):
u2{t) = -^L!-sm2a>1£ = = -Цр-sin-y^,
а также синусоиды с утроенной, учетверенной и т.д. частотами
(рис. 3.2, г—е):
u(t) = (7mi sin — —-^-sin 2(0|( + —^-sin 3<В|( -
2 3 (3.4)
sin 4a) £ + Ii»lsin5a)1£ -....
4 5
Пример 3.1. Определим параметры синусоид, формирующих по-
следовательности прямоугольных (рис. 3.1, а) и пи-
лообразных (рис. 3.2, а) импульсов, имеющих ам-
плитуду U = 10 В и период Т = 20 мс.
а) Для формирования периодической последова-
тельности прямоугольных импульсов амплитуда ос-
новной синусоиды должна быть
Uml = 1,27(7 = 1,27-10 = 12,7 В.
Частота колебаний этой синусоиды обратно пропор-
циональна периоду:
Д =1 =-----L^ = 50 Гц.
Т 20 • 10’3
Круговая частота ан = 2nfi = 100л рад/с. Таким об-
разом, основная синусоида
щ (t) = (/„rtSinco^ = 12,7sinl00n( В.
Все последующие синусоиды в соответствии с (3.3)
должны иметь амплитуды в нечетное количество раз
меньшие, а частоты — в это же нечетное количество
раз большие, чем у основной синусоиды:
w3^) = ^Y1sin3®1i = 4,23sin300n( В;
О
W5(i) = ^^-sin5(Oii = 2,54sin500ni В;
О
M7(i) = ^’lsin7fi)1i = l,81sin700nt В
и Т.д.
Последовательность прямоугольных импульсов, изо-
браженных на рис. 3.1, а, — это сумма синусоид:
122
u(t) = 12,7 sin 100 тс£ + 4,23 sin 300 nt +
+2,54 sin 500 + 1,81 sin 700 + ....
Сигнал u(t) = щ (i) + u3 (Л) + u5 (t) + u7 (t) изобра-
жен на рис. 3.1, д.
6) Для формирования последовательности пило-
образных импульсов необходимо, чтобы амплитуда
основной синусоиды была, как мы уже знаем, равна
UmX = 0,635 (7 = 0,635 10 = 6,35 В.
Частота основной синусоиды
Д = у = 50 Гц, = 2itfi = 100л рад/с.
Таким образом,
щ (t) = 6,35sinl00nf В.
Последующие синусоиды в соответствии с (3.4) бу-
дут иметь вид
u2(t) = -^у^зт2со^ = -3,175sin200лt В;
u3(t) = ^^-sinScoti = 2,117sin300nt В;
О
u4 (t) = -^psnHco^ = -1,588 sin 400 л £ В
ит.д.
Последовательность пилообразных импульсов — это
сумма синусоид:
u(t) = щ (t) + u2(t) + u3(t) + Ui(t) + ....
Чем больше синусоид используется при формирова-
нии сигнала, тем ближе его форма к пилообразной.
Изменение начала координат превращает ряд, состоящий из
синусов, в косинусный ряд. Покажем на примере последователь-
ности прямоугольных импульсов, как изменение начала коорди-
нат превращает ряд, состоящий из синусов, в ряд, состоящий из
косинусов.
Рисунок 3.3, а отличается от рис. 3.1, а незначительно: мо-
мент наблюдения (т.е. начало координат) смещен вправо на чет-
верть периода последовательности прямоугольных импульсов.
Напомним, что колебание, которое начинается раньше нача-
ла координат, называется опережающим по отношению к коле-
123
Рис. 3.3. Последовательность прямоугольных импульсов,
смещенная на 774 относительно начала координат
банию, возникающему из начала координат, и характеризуется
появлением начальной фазы со знаком «плюс». Это означает,
что теперь вместо колебания (3.3) мы будем иметь дело с коле-
банием, опережающим по фазе данное колебание на л/2 рад или
на 90° (рис. 3.3, б):
ux(t) = Um{ sin(cotf + л/2).
Колебание утроенной частоты За>1 после переноса начала ко-
ординат получит сдвиг по фазе, равный Зя/2 рад, или 270°
(рис. 3.3, в):
u3(t) = ±Uml sin
Продолжая действовать таким образом, мы придем к форму-
ле для последовательности прямоугольных импульсов:
3 1
За>(£ + -^ л I.
124
+L^lsin[ 5®t£ + ^л1 + ^^5тГ7а)1£ + ^7tl+ (3.5)
-h^isinf9<ntt + ^n) + ^2L!-sin(lla>1£+ ^л1 + ---.
У \ ^/11 \ )
Применив к (3.5) тригонометрические формулы приведения
. ( п)
sin a + — = cos a;
k 2)
( 3 A
sinl р + -л I = -cosP;
. ( 5 } . f л^
sin у + — it = sin у + — = cosy;
X £л J X, Zu /
( 7 > ( 3 )
sin 5 +—it I = sin 5 +—л = -cosS;
{ 2 J { 2 J
f 9 A f it A
sin X + —я = sin X + — = cosl
I 2 J \ 2J
и т.д.
можно представить ряд (3.5) в виде суммы только косинусоид:
u(t) = (7т1со5со/ cos Зсо^ + ^^icos5a>1£ -
3 5 (3.6)
- cos 7a> t £ + cos 9a> 11 - cos 1 loo -J £ + • • •.
Периодические сигналы любой формы также состоят из
суммы синусоид или косинусоид; при этом нечетные сигналы
состоят только из синусоид, в то время как четные сигналы —
только из косинусоид. Впервые этот факт был доказан в 20-х
годах прошлого века французским математиком Ж. Фурье.
В табл. 3.1 приведены наиболее часто встречающиеся на
практике периодические последовательности импульсов и записа-
ны их представления в виде синусных или косинусных рядов. Из
таблицы видно, что нечетные функции содержат только синусои-
ды, а четные — только косинусоиды*.
Именно в честь французского математика приведенные в
таблице ряды называются рядами Фурье.
Наинизшая частота синусоидальных или косинусоидальных
компонент есть
Напомним, что четной называется функция, удовлетворяющая соотношению
XW) = х(О, нечетной — удовлетворяющая соотношению х(-1) = -x(t).
125
2л
СО. = —
1 т
или
Эта частота принадлежит основной составляющей, и она сов-
падает с частотой повторения сигнала. Таким образом, периоди-
Таблица 3.1. Ряды Фурье наиболее часто встречающихся сигналов
___________Ряд Фурье__________
С7ОТ1 cos© -^21 cos 3©jt +
+^1-cos5o1t-^y1cos7©|i+ ...;
(7mt = 4(7/л = 1,27(7
(7m । cos ©^t + —cos 3©7 +
+^ic°s5©,^...;
(7ml = 8(7/я2 = 0,8(7
Um j sin © (t - sin2©lt +
+^y7sin3©t( -sin4©,t + ••• i
(7ml = 2(7/л = 0,635(7_______
l/fl +~^1COS©1f +^yicos2©ti -
_^slcos4©<i + ^J-cos6©,i + ...
15 1 35 ’
...(-1 )^2+1 ~^”1' - cosfe©, t +...,
k - четные; Um f = 2U/n = 0,635(7;
(70 = (7/л = 0,3175(7_________
(70 +^^icos2©1t -•^icos4©tt +
О 10
+ “^C0S eojjt-...
v 7 k2 -1
k - четные; UmX = 4(7/л = 1,2717;
CT0 = 217/71 = 0,63517
J70 ^UmiCOSG)xt + Um2cos2(i)xt +
^Um3cos3oxt +...;
UQ=U/q; q = T/z;
„ _ 2U slnkn/q
kn/q
126
ческий сигнал с периодом в 1 мс имеет основную составляющую с
частотой /1 = 1 кГц.
Частоты остальных составляющих сигнала являются числа-
ми, кратными частоте основной составляющей. Эти составляющие
называются гармониками основной компоненты, и номер гармо-
ники определяется отношением ее частоты к частоте основной
составляющей. Так, в приведенном в предыдущем абзаце примере
гармониками основной составляющей в общем случае могут быть
вторая — с частотой 2 кГц, третья — с частотой 3 кГц, четвертая —
с частотой 4 кГц и т.д.
Кроме основной составляющей и высших гармоник в сигна-
ле может присутствовать постоянная составляющая. Посмотрите
на рис. 3.4, а и б. Нижний рисунок получен из верхнего вычита-
нием среднего значения сигнала, которое вычисляется, как из-
вестно, по формуле
_ Площадь под кривой за один период
0 Период'
Для последовательности прямоугольных импульсов, изобра-
женной на рис. 3.4, а, указанную площадь вычислить нетрудно,
поэтому
В случае, когда сигнал имеет сложную форму, площадь вы-
числяется с помощью интеграла из формулы (3.2):
Uo = ±[u(t)dt.
£о
Среднее значение сигнала Uq называют постоянной состав-
ляющей. Удаление постоянной составляющей из последователь-
ности прямоугольных импульсов на рис. 3.4, а приводит к после-
довательности, показанной на рис. 3.4, б.
а) Т = 20мс
\2U
б) 1 Т/2 1 1 t '
Г г
1 t '
Рис. 3.4. Последовательности прямоугольных импульсов
127
Поскольку гармонический состав последнего сигнала известен
(3.3), то гармонический состав однополярной последовательности
импульсов (рис. 3.4, а) будет отличаться только наличием посто-
янной составляющей Uq:
u(t) = U0 +Umisina>it + ^^IsinScDt + ^^sinSco^ + •••.
•J D
В двух предпоследних строках табл. 3.1 можно увидеть по-
стоянные составляющие у переменного напряжения, выпрямлен-
ного одно- и двухполупериодным выпрямителями.
Пример 3.2. Определим гармонический состав последовательности
треугольных импульсов, изображенных на рис. 3.5,
имеющих амплитуду U = 10 В и период Т = 10 мс.
Периодический сигнал на рис. 3.5 отличается от
сигнала во второй строке табл. 3.1 на величину по-
стоянной составляющей
Частота основной составляющей сигнала
/1 = i/T = 100 Гц или
©1 = 2nfi = 200л рад/с.
Амплитуда основной составляющей сигнала рас-
считывается по формуле, приведенной в табл. 3.1,
или по одной из формул (3.2):
Umi = 8U/n2 = 0,8(7 = 0,8-5 = 4 В.
Четная функция (рис. 3.5) содержит только коси-
нусоиды, амплитуды и частоты которых определяются
по формулам, приведенным во второй строке табл. 3.1.
Амплитуда и частота третьей гармоники:
Um3 = | = 0,44 В, 3®t = 600л рад/с.
Рис. 3.5. Последовательность треугольных импульсов
128
Амплитуда и частота пятой гармоники:
Um5 = = А = 0,16 В, 5cot = 1000л рад/с.
Амплитуда и частота седьмой гармоники:
Uml = = 4 = °’08 В> 7<°1 = 140071
49 49
и т.д.
Гармонический состав последовательности тре-
угольных импульсов (рис. 3.5) имеет вид
U(t) = Uq +UmiCOSG>it + Um3COS3(dit +
+ Um5 cosSwjt + Um7 cos 7(0^ =
= 5 + 4 cos 200л t + 0,44 cos 600л t +
+ 0,16 cos 1000лt + 0,08 cos 1400лt +... B.
Общая форма записи ряда Фурье содержит амплитуды и
начальные фазы гармоник. Мы наблюдали ранее, как изменение
начала координат (т.е. момента начала наблюдения) превращало
ряд синусов в ряд косинусов. Так, при переносе начала коорди-
нат на рис. 3.1, а вправо на четверть периода последовательности
прямоугольных импульсов (т.е. при переходе к рис. 3.3, а) изме-
нились начальные фазы основной составляющей и высших гар-
моник на величины, кратные л/2 рад (3.5).
Очевидно, если начало координат переносить на произволь-
ное расстояние вправо или влево, то начальные фазы основной
составляющей и гармоник в (3.5) будут принимать любые значе-
ния, а не только кратные л/2 рад. В этом случае ряд (3.5) преоб-
разуется в ряд
u(t} = t/mlsin(©^ + 01) + ^isin(3©^+ 93) +
О
+^1sin(5©1t + 95)+ ” ,
где Umi = 1,27(7; 0i, Оз, 65, ... — начальные фазы первой, третьей,
пятой и т.д. гармоник.
Для однополярной последовательности прямоугольных им-
пульсов, типа показанной на рис. 3.4, а, к данному ряду доба-
вится постоянная составляющая Uq = U/2.
Каждый сигнал, отличающийся от других по форме, имеет
свой сугубо индивидуальный гармонический состав, т.е. содержит
°сновную синусоиду и ее высшие гармоники со своими амплиту-
дами и начальными фазами. Поэтому в общем случае ряд Фурье
•г*Ля произвольного периодического сигнала записывается в форме
9-6972 1 29
u(t) = U0 +Umisin((j)]t + 0!) + {7m2sin(2a)|£ + 02) +
+ t/m3sin(3(o1^ + 03) + I7m4sin(4o)ii+ 04)+ (3.7)
+ €/т55ш(5(й^ + 05) + ••• = Uo + £ Umk sin(6<ot£ + 0* ),
k=\
где Umk — амплитуды Л-й гармоники; Qk — начальная фаза k-й
гармоники.
Мы уже знаем, что амплитуды некоторых гармоник могут
быть равны нулю, а фазы могут принимать любые значения, в
том числе и кратные л/2 рад — это зависит от формы сигнала (см.
табл. 3.1).
Форма записи ряда Фурье (3.7) получила название триго-
нометрической. Она справедлива для любого момента наблюде-
ния, т.е. для любого расположения начала координат.
Существуют две равноправные записи ряда Фурье в триго-
нометрической форме — через функцию синуса и через функ-
цию косинуса. Ряд Фурье с использованием функции синуса мы
уже записали в виде формулы (3.7). Чтобы заменить функцию
синуса на функцию косинуса, обратимся к гл. 2 этой книги.
Мгновенное напряжение
u(i) = 17msinco^ (3.8)
с частотой а>1 можно изобразить на комплексной плоскости как
вектор, направленный первоначально вдоль положительной гори-
«) J
Рис. 3.6. Векторное и временное представление
гармонических колебаний
130
зонтальной полуоси (рис. 3.6, а) и вращающийся с угловой ско-
ростью <01.
Аналогичным образом мгновенное напряжение
u(t) = Um coscot£ (3.9)
отображается вектором, направленным вдоль положительной верти-
кальной полуоси (рис. 3.6, б) и вращающимся с той же скоростью.
Гармоническому колебанию
u(t) = 4 sin (со^ + 30°)
соответствует вектор на комплексной плоскости (рис. 3.7) с ком-
плексной амплитудой
Um = 4е'30’,
который опережает горизонтальную положительную ось на 30°,
т.е. его можно получить путем вращения вектора, изображенного
на рис. 3.6, а, на +30°.
Если желательно записать этот вектор как функцию косину-
са, то следует обратить внимание на то, что получить картину,
показанную на рис. 3.7, можно только одним способом — вра-
щать вектор на рис. 3.6, б на угол -60°. В этом случае вместо ко-
лебания (3.9) получим колебание
w(t) = 4 cos (о/ -60°).
Таким образом, можно сделать вывод, что при записи гармо-
нического колебания в виде синусной функции угол, или началь-
ная фаза колебания, отсчитывается от положительной гори-
зонтальной полуоси, а при записи колебания в косинусной форме
угол отсчитывается от положительной вертикальной полуоси.
Основываясь на описанном правиле, легко привести две рав-
нозначные записи ряда Фурье:
9»
Рис. 3.7. Векторное (а) и временное (б) представление
гармонического колебания с начальной фазой 30°
131
оо
u(£) = U0 + sin(^<o1i+ 9*)
k=\
и
u(t) = UQ + ^Umkcos(k(»lt + (pk),
k=i
(3.10)
(3.11)
где угол k-й гармоники Qk отсчитывается от положительной гори-
зонтальной оси, а угол <р/> — от положительной вертикальной оси
комплексной плоскости.
Чтобы избежать путаницы, примем в дальнейшем в качестве
основной формы записи ряда Фурье формулу (3.11) и, кроме то-
го, будем иметь дело не с угловой частотой «ц, а с линейной час-
тотой fi в Гц, кГц, МГц, устанавливаемой на шкалах реальных
измерительных приборов, так что ряд Фурье будет иметь вид
u(t) = UQ + X Umk cos{2nkft + <pfe).
fe=i
(3.12)
Пример 3.3. Представим переменное напряжение, выпрямленное
двухполупериодным выпрямителем (пятая строка
табл. 3.1), рядом Фурье в тригонометрической форме
(3.12).
Из табл. 3.1 следует, что переменное напряжение
и(t) представлено рядом Фурье:
u(t) = Uo + —-^-cos 2<x>i£ — —cos 4cdj£ +
О ю
+ ^riCOS6(01£- ...(-l)^2+1-^i-COS/j<Btt+ ... ,
35 к — 1
k - четные.
Постоянная составляющая напряжения u(t) рас-
считывается по формуле Uо = 0,635(7.
Нечетные гармоники отсутствуют в ряде Фурье,
поскольку функция u(t) — четная.
Для расчета амплитуд четных гармоник необхо-
димо определить Umi — 1,27(7. Тогда амплитуда вто-
рой гармоники
(7т2 = ^ = М—0,42(7.
«3 о
Начальная фаза второй гармоники равна нулю: (рг = 0.
Амплитуда четвертной гармоники
(/,n4=%1='4F=0’()8C/-
132
Фаза четвертой гармоники ф4 = 180°, так как в
ряде Фурье перед слагаемым ((7ml/15)cos4o>i£ стоит
знак «минус».
Амплитуда шестой гармоники
U а = = о 0417
т6 35 35 ’ ’
а ее фаза, а также фазы десятой, четырнадцатой и
т.д. гармоник равны нулю.
Амплитуда восьмой гармоники
Um8 = = 0,02CZ,
ms 82-1 63
а ее начальная фаза, так же как и фазы гармоник с
номерами 12, 16, 20 и т.д., равна 180°.
Тригонометрическая форма ряда Фурье рассмат-
риваемого напряжения имеет вид
и(£) = 0,635(7 + 0,42(7 cosf 2л-2 ~£1 +
I Т J
+ 0,08 (7 cos I 2 л • 4 • +180° U 0,04 (7 cos | 2 я • 6 - - £ 1+
I Т ) I Т )
+ 0,02(7cosf 2л-8-—£ + 180° | + ... .
\ Т )
Уравнение (3.12) есть тригонометрическая форма ряда Фу-
рье. При анализе цепей часто удобно пользоваться комплексной
формой ряда Фурье, которая может быть получена из (3.12) с
помощью формулы Эйлера:
со5(2л^£ + ф J = - ) + e-7(2WtM*) ] =
? 1 (3-13)
_ ±e}2nkftt ej<pk +±e-j2nkfit ,e-m
2 2
Подставляя (3.13) в формулу (3.12), получаем
u(t) = Uo +1 f Umk -е™ +±fumk -e~™ е~^.
2 k=i 2 *=i
Изменяя порядок суммирования во втором слагаемом от
-оо до -1 и обозначая Uo = (7mo/2, приходим к следующему
выражению:
u(£) = ^ + lf Umk.e^k 2 (7m,.e-m.e>2^.
k=l /г=-оо
133
При записи w(i) учтен тот факт, что амплитуды спектраль-
ных составляющих Umk являются четными величинами, а фазы
ФА — нечетными. Это означает, что при замене индекса k на от-
рицательный индекс -k
U mk = U m(-k) К Ф-А = ~ ФА-
В последнем выражении u(t) произведение
U l e~JVk = U'- iU ’t.
u mk& u mk mk
представляет собой комплексную амплитуду C7WA k-й гармоники,
где Umk =ylU'^k + U% - амплитуда; <pA = arctg(U"mk/U'mk) - на-
чальная фаза k-й гармоники. Объединение всех слагаемых под
одной суммой дает запись ряда Фурье в комплексной форме
М) =1 £ U.ke™‘.
k=-<X)
(3.14)
Пример 3.4. Представим ряд Фурье, полученный в примере 3.3,
в комплексной форме, ограничив его восьмой гар-
моникой.
В соответствии с (3.14) значения постоянной со-
ставляющей и амплитуд гармоник уменьшаются в 2
раза по сравнению со значениями, которые были рас-
считаны в примере 3.3. Поэтому ряд Фурье в ком-
плексной форме имеет вид
. . .чяпо -/27t-8~t -»'2я-6~4
u(t) = 0, Oll/Л т +0,02Ue т +
1 1
..япо -;2я-4— t -
+ WUe~Jl80e т +0,21Ue т +
j2n-2~t ..one у2л-4~<
+ 0.3175С7 + 0,21Ue т + О,О4СЛ?;180 е т +
/2п-6-^4 .<япо ;2я-8-^
+ 0,02(7е т + 0,0Wt8Oe т .
Из данного параграфа мы узнали, что:
• Периодическая последовательность прямоугольных пилооб- J
разных, треугольных и других импульсов состоит из сину- i
соид кратных частот.
• Изменение начала координат может превратить ряд, со-
стоящий из синусоид, в косинусный ряд. |
134
. Периодические сигналы любой формы также состоят из си-
нусоид или косинусоид; при этом нечетные сигналы состоят
только из синусоид, в то время как четные сигналы — толь-
ко из косинусоид.
• Кроме основной составляющей и высших гармоник в сиг-
нале может присутствовать постоянная составляющая.
« Существуют две равноправные записи ряда Фурье в триго-
нометрической форме — через функцию синуса и через
функцию косинуса.
• Наиболее удобной для расчетов является комплексная фор-
ма ряда Фурье.
3.2. Спектры амплитуд и фаз периодических
колебаний
Набор гармоник, образующих ряд Фурье (3.12) в тригоно-
метрической форме, называют спектром периодического сигна-
ла, а наборы амплитуд Umk и начальных фаз <р* этих гармо-
ник — спектрами амплитуд и фаз. Каждую гармонику:
Uk (t) = Umk cos(2nkf{t + ср* )
можно отобразить двумя вертикальными линиями. Для этого на
одной оси частот необходимо отложить значение частоты этой
гармоники kfi и изобразить вертикальную линию высотой, рав-
ной амплитуде гармоники Umk', затем на другой оси частот на
частоте этой же гармоники kf\ изобразить вторую вертикальную
линию, равную по высоте начальной фазе гармоники <р&*.
Ряд Фурье (3.3) можно переписать в виде
ц(£) = (7,н1со5(2л/’1£-90о)-1-Ц*рСО5(2л-3/'1£-270о) +
+^lcos(27t • 5fit - 450°) + cos (2л lf\t - 630°) + (3.15)
+cos(2л • Щ -810°) + cos(2л • 1 lfxt - 990°) + •••.
Учитывая, что функция косинуса периодична с периодом
2л = 360°, т.е. ее значения повторяются через 360°, можно вы-
честь целое число периодов из фазы гармонических составляю-
щих. Тогда получим еще одну форму записи ряда (3.3):
Постоянную составляющую можно считать нулевой гармоникой, т.е. гармоникой
с номером k = 0.
135
и(t) = Umi cos(2л • fit - 90°) + cos(2л • 3ft - 270°) +
О
+cos (2л • 5 fit - 90°) + cos ( 2л • 1ft - 270°) + (3.16)
О /
+^lcos(2n-9/ii-90°) + ^lcos(2nll/’1^-270°) + -.
Эти ряды можно изобразить графически. Гармоники этого
сигнала, входящие в формулу (3.3), показаны на временных диа-
граммах рис. 3.1, б — д. Другой способ графического изображе-
ния составляющих ряда Фурье для сигнала на рис. 3.1, а приве-
ден на рис. 3.8, а — в. Амплитуды гармоник убывают по закону
1/п, где п — номер гармоники, а фазы гармоник изменяются по
закону пф1, где ф1 — фаза первой гармоники.
Для смещенной на четверть периода периодической последо-
вательности прямоугольных импульсов (рис. 3.3, а) формула ря-
да Фурье (3.6) может быть видоизменена, если вспомнить, что
знак «минус»-перед гармоническим колебанием означает поворот
колебания по фазе на 180°:
Рис. 3.8. Амплитуды и фазы гармоник сигнала (3.15) и (3.16)
136
a) Umk 4U it 4U | 3л 4U 15л 4U |7л 4t7 ,9* AU ... ,11л
0 50 Гц 150 Гц 250 Гц 350 Гц 450 Гц 550 Гц f
S) 4k 1180° il80° il80° — o° 1 o° 1 p° 1
0 50 Гц 150 Гц 250 Гц 350 Гц 450 Гц 550 Гц f
Рис. 3.9. Амплитуды и фазы гармоник сигнала (3.17)
u(t) = (7mlcos2n -fit + ^^ cos (2л • 3fat + 180°) +
О
+cos 2л • 5 fat + cos (2л • Ifat +180°) + (3.17)
+^1 cos 2л • 9 fat + cos ( 2л • 1 ifat +180°) + • ••.
Начальные фазы колебаний в ряде (3.17) поочередно прини-
мают значения 0 и 180°. Графическое изображение ряда (3.17)
дано на рис. 3.9, а и б.
Вертикальные линии на рис. 3.8 и 3.9 получили название
спектральных линий, а наборы этих линий, или, что то же, на-
боры амплитуд Umk и фаз ср* гармоник в (3.12), образуют спек-
тры амплитуд и фаз данного сигнала.
Пример 3.5. Построим спектр амплитуд и фаз выпрямленного на-
пряжения (строка 5 табл. 3.1), имеющего амплитуду
U = 10 В и период Т = 10 мс.
При решении примера 3.3 была получена триго-
нометрическая форма ряда Фурье, соответствующая
выпрямленному напряжению:
и<Л) = 0,635(7 + 0,42(7 cos^2n • 2 • у • +
+ 0,08(7 cos f 2л-4 ^ t + 180° | +
k Т )
+ 0,04(7cosf2л • 6 • -i- • t | +
I T )
+ 0,02(7cosf2л-8•^•( + 180° ] + ....
k T J
137
Частота основной составляющей сигнала определяет-
ся периодом колебаний:
Л = — =-------- = 100 Гц.
71 Т 10 10-3
В спектре сигнала отсутствуют нечетные гармоники,
так как само колебание является четной функцией.
Частоты высших гармоник с четными номерами крат-
ны этим номерам: частота второй гармоники равна
= 200 Гц, четвертой, шестой, восьмой гармоник —
400,600, 800 Гц соответственно и т.д.
Постоянная составляющая
Uo = 0,635(7 = 6,35 В.
Амплитуды четных гармоник спектра в соответ-
ствии с выражениями, полученными для ряда Фу-
рье, имеют следующие значения:
(7т2 = 0,42(7 = 4,2 В; Umi = 0,081/ = 0,8 В;
(7т6 = 0,04(7 = 0,4 В; Um8 = 0,02(7 = 0,2 В
и т.д.
Фазы гармоник поочередно принимают значения
0 и 180°.
Umk
6
6,35 В
5
4
3 -
2 -
1 -
(Г 100 200
Фл»
180
°»?в 0,4 В
I !
400 600
«)
180°
0,2 В —
___I_______►
800 /Гц
180°
0°
100 200
0
0°
400 600 800 / Гц
б)
Рис. 3.10. Спектры амплитуд и
фаз выпрямленного напряжения
138
Спектры амплитуд и фаз приведены на рис. 3.10,
а и б.
Радиоинженерам хорошо знакомы приборы (они называются
анализаторами спектров), которые откликаются на каждую гар-
монику, входящую в состав сигнала сложной формы.
Таким образом, спектр амплитуд — это набор амплитуд
гармоник Uo, Um\, Um2, Um3, ... (включая постоянную и ос-
новную составляющие), входящих в ряд Фурье, записанный в
тригонометрической форме (3.12), а спектр фаз — это набор
начальных фаз <pi, 92, <рз, ••• этих гармоник. Комплексные ам-
плитуды Ujnk из (3.14) образуют комплексный спектр сигнала
u(t).
Анализ спектрального (гармонического) состава периодиче-
ских сигналов — это вычисление амплитуд Umk и начальных
фаз фа гармонических составляющих ряда Фурье. Обычно для
вычисления указанных величин используется форма записи ряда
Фурье (3.2):
u(t) = Uq +U'micos2'Kfit + C7^Jlsin2n/‘1i + U'm2cos Aicfit +
+ U'm2sin.4itf\t + U'm3cos6nfit + U”m3sm6n/\t + ••• =
= uo + £ (U'mk cos + U"mn sin 2nkfit).
A=1
(3.18)
Покажем, что форма записи (3.18) эквивалентна форме запи-
си (3.7). Сделаем это с помощью стандартного тригонометриче-
ского преобразования:
Umk sin(2nkfit + Qk) = Umk sin 0^ cos 2nkf\t + Umk cos 0* sin 2nkf\t.
Обозначая
U mk — UrnksinQ^ И Umh — Umk COS0£, (3.19)
приходим к равенству
Umk sin(2itkfxt + Qk ) = U'mk cos 2nk/\t + sin 2nkf\t. (3.20)
Применяя равенство (3.20) к ряду (3.7), сразу же получаем
Ряд (3.18).
Преобразование (3.20) хорошо иллюстрируется геометриче-
ски (рис. 3.11). Слагаемое U'mk cos2nkftt представляется векто-
ром с амплитудой U'mk = Umk sin0*, направленным вдоль положи-
тельной вертикальной оси. Напротив, слагаемое U’mk sin 2nkfxt —
вектором с амплитудой U”mk = Umk cos 0^, расположенным вдоль
положительной горизонтальной оси. Сумма двух векторов дает
139
Рис 3.11. Векторная диаграмма колебания
третий вектор, соответствующий гармоническому колебанию
L^sin^/it + e*).
Пример 3.6. Рассмотрим в качестве примера сигнал, ряд Фурье
которого содержит постоянную составляющую, ос-
новную составляющую (первую гармонику) с часто-
той 1 кГц и вторую гармонику с частотой 2 кГц. Ряд
Фурье (3.2) имеет вид
u(t) = 18 + 40 cos 2я *1000?-30 sin 2я> 10001-
- 24 cos 2л • 2000£ +10 sin 2л • 20001.
Необходимо представить этот ряд в тригономет-
рической форме (3.10):
м(£) = 18 + t7mlsin(2K lOOOi + 0()+ , .
+ U т2 sin (2л • 2000t + 02)
10 20 30 40
-40 - /2 = 2000 Гц
Рис. 3.12. Векторы гармонических колебаний
а)
140
или в форме (3.11):
u(t) = 18 + (7m|COs(2n• lOOOt + (pj) + 2п)
+Um2cos(2n 1000£ + <р2).
Представляя гармонические колебания
-30 sin 2л•1000t и 40 cos 2л • 1000t
векторами, направленными вдоль косинусной и си-
нусной осей соответственно (рис. 3.12, а), вычисляем
суммарный вектор:
Umx = -30 + /40 = 50еу126,87°.
Точно так же рассчитываем вектор С/от2 (рис- 3.12, б),
представляющий вторую гармонику:
= 10-/24 = 26е";67’38°.
В соответствии с равенством (3.20) мы получили
амплитуды Umi, Um2, углы 0i и 02 и поэтому можем
записать тригонометрическую форму (3.21) ряда
Фурье:
u(t) = 18 + 50sin (2л lOOOt + 126,87°) +
+ 26sin(2n-2000t-67,38°).
Углы epi и ф2 в (3.22) отсчитываются от поло-
жительной вертикальной оси и получаются путем вы-
читания 90° из углов 91 и Э2-
Ф, =126,87° -90° = 36,87° и
Ф2 = -67,38°-90° = -157,38°.
Таким образом, для формы записи (3.22) имеем
u(t) = 18 + 50соз(2л-1000£ + 36,87°) +
+ 26 cos (2л-2000/-157,38°).
Umk
60
40
20’18
50
126
1 2 X кГц
180
36,87
1_
0 1
/кГц
0
-180 г
-157,38
Рис. 3.13. Спектры амплитуд и фаз сигнала (3.22)
141
Поскольку мы договорились, что для изображе-
ния спектра сигнала всегда будем использовать вы-
ражения (3.12), то можем сказать, что спектр ампли-
туд в данном случае состоит из трех спектральных
линий высотой 18, 50 и 26 единиц (например, мил-
ливольт), расположенных на частотах 0; 1 и 2 кГц, а
спектр фаз — из двух спектральных линий, высота
которых выражена в градусах 36,87° и —157,38°, на
частотах 1 и 2 кГц. Спектр данного сигнала изобра-
жен на рис. 3.13.
Из приведенных выше рассуждений следует, что для анализа
спектрального состава сигнала достаточно знать, как вычислять
величины Uq, U’mnH U"mn в выражении (3.18).
Из формул (3.2) мы знаем, что постоянная составляющая
ряда Uq вычисляется как среднее значение функции:
u0 =^\u(t)dt. * 0 (3.23)
Коэффициенты U'mk и U"mk вычисляются как средние взве-
шенные значения с весами cos/eco^ и sin ka^t соответственно:
2 т Umk = ~ \u(t)c,Qsktoxtdt\ Т о (3.24)
2 т Umk = 7Г /W(t)sin kayxtdt. T о (3.25)
Поскольку Umk = U'mk - jU”mk, то
2 т 2т
Umk = — | и (t) cos 2nkf\tdt - j— jи (t )sin 2nkf{tdt.
' о •* о
Применяя формулу Эйлера
cos 2nk/\tdt - j sin 2nkfxt = е~}2кк^,
получаем окончательно выражение для комплексного спектра сиг-
нала:
Umk=^u(t)e-^dt.
1 о
(3.26)
Пример 3.7. Рассмотрим периодическую последовательность пря-
моугольных импульсов, показанную на рис. 3.4, а:
142
utt) = <
2U для 0 t -j,
О для -j < t < T.
Т/2
О
Она имеет постоянную составляющую, равную в со-
ответствии с (3.23) Uq = U. Коэффициенты U'mk вы-
числяются по формуле (3.24):
2 Ч2 4/7
U’mk = z; / 2(7c.os2nkf{tdt = -—-—sir
mk Т I 71 2nkf{T
4U ( . 2МГ J
2nkf{T V 2 J
AU . , л , Л
= ——sin ял = 0 для всех л#0.
2nk
Здесь было учтено, что f\ - ИТ.
Коэффициенты U’mk вычисляются по формуле
(3.25):
U'mk = /2(7sm2nkfjdt = -^^cos2nkfj\Tl2=
-4(7Г 2nk/\T Л 2U ,ч
2nk t 2 ) nkv 7
Выражение cosnk удовлетворяет соотношению
для нечетных k,
для четных k.
cos itk = I J
+1
Поэтому
u'mk =
4/7
nk
О
для нечетных k,
для четных k.
Форма ряда Фурье (3.18) будет содержать только
синусоиды с нечетными гармоническими частотами:
u(t) = U + ^•sin2n/’1t + ^-sin6nf\t +^¥-sialOnf\t +
л Зл 5л
4/J 00 4/7
+ —— 8ш14л/’1/ + ••• = U+ -т— sin2nkftt,
'К Л=1,3,5,... kn
что, естественно, с точностью до постоянной состав-
ляющей U совпадает с полученным ранее выражени-
ем (3.3).
143
Переход к форме ряда Фурье (3.12) дает
u(t) = U + ^-cos(27t/’1i -90°) +
ТС
+ ^cos(2n • 3fxt - 270°) +
Зтс
+ -^-cos(2n •5/’1£-450°) + (3.27)
5л
+ ^cos(2n-7/;t-630o) + - =
7тс
= 17 + £ 4r-cos(27tVi^-^-90°).
£=1,3,5,...
Спектр такого сигнала без постоянной составляющей
был показан на рис. 3.8.
Пример 3.8. Представим спектр (3.27) сигнала из примера 3.7 в
комплексной форме.
Комплексный спектр периодической последова-
тельности прямоугольных импульсов рассчитывается
по формуле (3.26):
э т о т/2
Umk = ju(t)e~j2nk^dt = + f 2Ue-}2*kfitdt =
7о т о
kn
Функция е~}жк имеет значения
е-;п£ _ ( 1 при четном k,
~ (-1 при нечетном k.
Это значит, что комплексный спектр Umk существует
только для нечетных гармоник:
Umk ~ = ^-e~^k90° при k = 1, 3,5,7,....
~тк kit kit
Заметим, что в спектре Ujnk нет постоянной со-
ставляющей Uq, которая рассчитывается по формуле
(3.23) и равна U.
Полученный комплексный спектр Umk соответст-
вует спектрам амплитуд и фаз, изображенным на
рис. 3.8.
На спектр сигнала влияет не только форма сигнала, но и
его параметры. Лучше всего рассмотреть это влияние на кон-
кретном примере, а проще всего — на примере периодической по-
144
сдедовательности прямоугольных импульсов. В достаточно общем
случае эта последовательность изображена на рис. 3.14, а. Пери-
од повторения импульсов обозначен Т', а отношение периода к
длительности импульсов т' называют скважностью и обозначают
q = T4x'.
Вычисление коэффициентов ряда Фурье в тригонометриче-
ской форме по формулам (3.23) — (3.25) приводит нас к записи
(см. табл. 3.1)
u (t) = l/0 + Umi cos 2лД£ + Um2 cos 2л • 2ftt +
+ Um3 cos 2л • 3f\t + Um4 cos 2л • 4/^ + •••,
где Uo = U/q и
Umk= — • sin(fe7t^), £ = 1,2,3,.... (3.28)
<7 kn/q
Рис. 3.14. Периодическая последовательность прямоугольных
импульсов со скважностью q = 3 и ее спектр
Ю-6972
145
Спектр амплитуд такой периодической последовательности со
скважностью q = 3 изображен на рис. 3.14, б.
При значениях k, кратных скважности q импульсной после-
довательности, функция sin kit/q принимает нулевые значения и
гармоники с этими номерами имеют нулевые амплитуды (в нашем
примере с k = 3, 6, 9, ...). Частота первой гармоники определяет-
ся по формуле
/;=£.
Для гармоник с номерами k, для которых амплитуда Umk по-
ложительная, фазовый угол <pk равен нулю; для гармоник же с
номерами k, для которых величина Umk окажется отрицатель-
ной, фазовый угол принимает значение 180° (рис. 3.14, в).
Рис. 3.15. Последовательность прямоугольных импульсов
со скважностью q = 5 и ее спектр
146
Рассмотрим влияние на спектр последовательности прямо-
угольных импульсов таких ее параметров, как период и длитель-
ность импульса.
От величины периода зависит прежде всего частота основной
гармоники, т.е. ее местоположение в спектре. Если мы будем, на-
пример, увеличивать период импульсной последовательности
(рис. 3.15, а), то частота первой гармоники (/i=l/T*) будет
уменьшаться. Это приведет к сгущению спектральных линий
(рис. 3.15, б и в). Скважность импульсов будет также увеличи-
ваться с ростом периода (в нашем примере q = 5), следовательно,
обращаться в нуль будут гармоники с более высокими номерами,
кратными q (k = 5, 10, 15, ...). Амплитуды всех гармоник умень-
шатся.
С другой стороны, если период последовательности оставлять
неизменным (например, Г'), а длительность импульсов, скажем,
Рис. 3.16. Влияние длительности импульсов
на спектр сигнала
10*
147
Рис. 3.17. Влияние длительности импульсов и периода
их повторения на спектр сигнала
уменьшать (например, до величины т", как на рис. 3.16, а), то
первая гармоника не будет менять свое местоположение в спектре
сигнала. С ростом же скважности в нуль будут обращаться, как и
ранее, гармоники с номерами, кратными q (на рис. 3.16, б с k =
= 5, 10, 15, ...).
На рис. 3.17, показан случай, когда подверглись изменению
и период, и длительность импульса. Предлагаем читателям про-
анализировать данную ситуацию самостоятельно.
Хотя мы проанализировали довольно частные примеры, ха-
рактерное поведение спектра наблюдается и для других видов пе-
риодических импульсных последовательностей. Оно заключается
в следующем:
• при увеличении периода последовательности Т частота первой
гармоники /1 уменьшается и спектральные линии сгущаются;
наоборот, при уменьшении периода частота первой гармоники
увеличивается и спектральные линии становятся реже;
148
, чем короче импульсы в последовательности, тем медленнее убы-
вают с ростом номера п амплитуды гармоник; наоборот, чем шире
импульсы, тем быстрее убывают амплитуды высших гармоник.
Пример 3.9. Найдем спектр последовательности прямоугольных
импульсов, изображенных на рис. 3.18.
Сигнал, изображенный на рис. 3.18, имеет сле-
дующие параметры: амплитуда U = 10 В, длитель-
ность импульса т = 10 мс, период повторения им-
пульсов Т = 40 мс, скважность q = Tlx = 4. Спектр
этого сигнала в форме (3.18) имеет вид
u(t) = (Jo + UmXcos2nf]t -+-С7от2cos2n• 2fxt +
+ Um3 cos 2л • 3f\t + C7m4 cos 3л • 4/jt +....
Постоянная составляющая
Uo = - = = 2,5 B.
Я 4
Частота первой гармоники
fi = 1/Г = 100 Гц.
Частоты высших гармоник кратны 100 Гц.
Амплитуды первых шести гармоник, рассчиты-
ваемые по формуле (3.28)
Umk = — •sinp/7t—) , k = 1, 2, 3, 4,5,6,
q kn/q
имеют следующие значения:
(7ml = 4,5B; (Jm2 = 3,18 В; С/от3 = 1,5В;
(7m4 = 0B; (7от5=0,9В; С/тб = 1,06В.
Фазы первой, второй, третьей гармоник равны
0°, фазы пятой и шестой гармоник равны 180°, так
как при расчете Ujn5 и Um6 получены отрицательные
Рис. 3.18. Последовательность прямоугольных
импульсов со скважностью q = 4
149
£U.b
5
4
3
2
1
4,5 В
2,5 В
3,18 В
1,5 В
1,06 В
0
ф£Вп
180 -
100 200 300 400 500 600 700 /Гц
а)
180° 180°
0° 0° 0°
4----> I
О
100 200 300 400 500 600 700 f Гц
6)
Рис. 3.19. Спектр последовательности прямоугольных
импульсов со скважностью q = 4
значения. Амплитуды и фазы последующих гармоник
рассчитывают аналогичным образом. Причем амплиту-
ды гармоник, кратных скважности q, т.е. четвертой,
восьмой, двенадцатой, шестнадцатой гармоник и т.д.,
равны нулю. Спектры амплитуд и фаз сигнала, изо-
браженного на рис. 3.18, приведены на рис. 3.19.
Из данного параграфа мы узнали, что:
• Набор гармоник, образующих ряд Фурье в тригонометри-
ческой форме, называют спектром периодического сигнала,
а наборы амплитуд и начальных фаз этих гармоник — спек-
трами амплитуд и фаз.
• Анализ спектрального (гармонического) состава периодиче-
ских сигналов — это вычисление амплитуд Umk и началь-
ных фаз <рй гармонических составляющих ряда Фурье.
• На спектр сигнала влияют не только его форма, но и дли-
тельность импульсов, и период.
3.3. Анализ реакции линейной цепи методом
суперпозиции (наложения)
Пусть к последовательному колебательному контуру, изо-
браженному на рис. 3.20, подключен источник, вырабатывающий
150
Рис. 3.20. Последователь-
ный колебательный
контур с источником
периодического сигнала
Рис. 3.21. Последовательность
прямоугольных импульсов
периодическую последовательность прямоугольных импульсов
(рис. 3.21), ряд Фурье которой имеет вид
и(Л) = Ц- + У -p^sin koit. (3.29)
2 Л=1, 3, 5,... kit
Колебательный контур (рис. 3.20), на который подается сумма
гармонических напряжений (3.29), можно представить последо-
вательностью частичных схем, каждая из которых содержит источ-
ник гармонического напряжения только одной частоты (рис. 3.22).
Используя принцип суперпозиции, запишем результирующий ток
в исходной цепи как сумму токов ik частичных схем:
i(t) = i0(t) +
Л-1, з, 5, ...
Найдем также результирующее напряжение на резисторе в
контуре как сумму напряжений URk частичных схем:
Рис. 3.22. Замена источника периодического сигнала
источниками гармонических сигналов
151
(3.30)
u7?(i) = M/?o+ Z uRk{t).
Л=1, 3, 5. ...
Расчет цепи от отдельных гармонических составляющих на-
пряжения проводится в символической форме. При этом нужно
иметь в виду, что на Л-й гармонике сопротивление индуктивности
^Lk - ka>\L, а сопротивление емкости Xck = i/ka>iC.
Таким образом, для определения реакции цепи на периодиче-
ский сигнал необходимо просуммировать реакции этой цепи на
каждую из гармонических составляющих сигнала в отдельности.
Пример 3.10. Определим напряжение на резисторе uR(t) в по-
следовательном колебательном контуре, на который
подается последовательность прямоугольных импуль-
сов (рис. 3.21). Параметры элементов контура и сиг-
нала заданы: R = 2 Ом; L = 0,704 мГн; С - 4 мкФ;
U = 5 В; Т = 1 мс; т = 0,5 мс.
Найдем параметры постоянной и гармонических
составляющих сигнала (рис. 3.21), представленного
рядом Фурье (3.29). Частота первой гармоники
®1 =у" = 6,28 103 рад/с, или f\ = 1 кГц.
Частоты третьей, пятой и т.д. гармоник равны
соответственно: Зел = 18,84 рад/с; З/t = 3 кГц; 5<»i =
= 31,4 рад/с; 5/1 = 5 кГц; ... .
Постоянная составляющая
CJ0=y = 2,5B.
Амплитуды четных гармоник равны нулю. Ам-
плитуды нечетных гармоник рассчитываются по
формуле (3.2):
rr 2U
Umk=~kn' поэтому
(7 =12 (7 =12 (7 =12.
ml л’ т3 Зя’ m5 5л
Ряд Фурье сигнала имеет вид
и (t) = 2,5 +—sin 2л • 1 000 £ + 22 sin 2л • 3000£ +
я Зя
+ 12sin2л-5000£ + 12sin2n -7000£ + ....
5л 7л
Определим резонансную частоту ©о и /о контура
(рис. 3.20):
152
Ю0 -ILC 7o,7O4 1O’3
------= = 18,84 IO3 рад/с;
•4 IO"6
/о=^ = 3 кГц.
Резонанс в контуре наступает на частоте третьей
гармоники входного напряжения.
Добротность контура
<ОрД
R
1
(HqCR
= 6,63.
Определим гармонические составляющие тока в
цепи и напряжения на резисторе в каждой из схем,
изображенных на рис. 3.22.
Схема последовательного колебательного контура
с источником постоянного напряжения Uq = (772 =
= 2,5 В приведена на рис. 3.23. В этой цепи сопротив-
ление индуктивности равно нулю, а сопротивление
конденсатора равно бесконечности, поэтому го — 0;
ия0 = 0-
В цепи, изображенной на рис. 3.24, в контур
включен источник напряжения, соответствующий на-
пряжению первой гармоники. Синусоидальное на-
пряжение
щ\Л) = —SintOjt
ТС
заменено на комплексное (Ю/л)е/0°. На частоте f\ =
= 1 кГц (<oi = 6,28-10J рад/с) сопротивление индук-
тивности
/(Otl = /6,28 • 103 • 0,704 • 10"3 = /4,42 Ом,
а сопротивление емкости
Il j 4,42 Ом"7.39,8 Ом
—•—О—О
JO
Рис. 3.23. Контур с
источником постоянного
напряжения
2 0м|
тс I
(/1 = 1 кГц)
Рис. 3.24. Контур с
источником напряжения
первой гармоники
153
__L_ =-------1------ = -/39,8 Ом.
/®tC /6,28 • 10J • 4 • 10-6
Комплексное сопротивление цепи
Z = R + j( a>iL--^-} = 2- /35,38 = 35,44e''87° Ом.
k J
Определим комплексные значения тока It и нап-
ряжения С/рр
^(‘М^эо^мА;
35,44с 'и
= /„,-« = 180с'87’ мВ.
Это соответствует составляющей синусоидального на-
пряжения (3.30) в исходной цепи:
uR] (i) = 180sin(2Tr-1000£+ 87°) мВ.
На третьей гармонике синусоидальный источник
«3(£) = —sin3o>i£
Зтг
в цепи с гармоническим напряжением (рис. 3.22) за-
меняется . источником комплексного напряжения
(10/Зл)е7 . В результате имеем цепь, изображенную
на рис. 3.25.
На частоте З/i = 3 кГц (3o>i = 18,84 рад/с) в це-
пи наступает резонанс напряжений. Сопротивления
индуктивности и емкости равны по величине и про-
тивоположны по знаку:
/3coi£ = /13,26 Ом; 1/( /Зс^С) = -/13,26 Ом.
Комплексное сопротивление цепи Z = R = 2 Ом.
Ток
I3 J 13,26 Ом']'13,26 Ом
47^4.
( 2 0мПйз
V-Z Diz LJ
(3/! = ЗкГц) Т
& >22,1 Ом'^ Ом
(5Л = 5 кГц)
Рис. 3.25. Контур с
источником напряжения
третьей гармоники
Рис. 3.26. Контур с
источником напряжения
пятой гармоники
154
Zm3 = 1° е?°7 2 = 530е7°° мА.
oil /
Напряжение на резисторе UmR3 равно входному
напряжению:
= М)6с'" В или
uR3 (t) = 1,06sin 2л • 30001 В.
На пятой гармонике синусоидальный источник
Ю • г ,
u5(£) = —sinocoji
5л
заменяется источником комплексного напряжения
(10/5л)е;О° (рис. 3.26).
На частоте 5/1 = 5 кГц (5о>1 = 31,4 рад/с) сопро-
тивления индуктивности и емкости равны соответст-
венно
= /22,1 Ом и
._ * _ = -/8 Ом.
а)
0 1
1.0
1,06
в)
0,089
------I----1-----А-----►
3 4 5 6 /кГц
3 4 р 6 /кГц
-82
Рис. 3.27. Спектры амплитуд и фаз входного
напряжения и напряжения на резисторе
в колебательном контуре
155
Комплексное сопротивление цепи
Z = R + j(5(diL - —| = 2 + /14,1 = 14,24е;82° Ом.
Эй^С J
Ток 1_т5 рассчитаем по формуле
Im5 = J0 е>°714,24е;82° = 44,6е“>82’ мА.
5л /
Напряжение на резисторе
UmR5 =/от5 •/? = 89,2е-;82’мВ,
что соответствует в (3.30) слагаемому
uR5 (t) = 89,2sin(2л -5000t -82°) В.
Таким образом, ряд Фурье напряжения на рези-
сторе u/?(t) имеет вид
uR (t) = 0,18 sin ( 2л • 1000£ + 87° ) +
+ 1,06 sin ( 2л • 30001) +
+ 0,089 sin (2л • 50001 - 82°) + ... В.
Спектры амплитуд и фаз этого напряжения изо-
бражены на рис. 3.27, б, в.
Анализ спектра UmRk показывает, что колеба-
тельный контур выделил третью гармонику из вход-
ной последовательности и подавил остальные гармо-
ники, т.е. явление резонанса можно использовать
для выделения отдельных гармоник из периодиче-
ского несинусоидального сигнала.
Из данного параграфа мы узнали, что:
• Чтобы определить реакцию линейной цепи на периодиче- I
ский сигнал произвольной формы, нужно просуммировать I
реакции этой цепи на гармонические составляющие сигнала. I
3.4. Расширение понятия комплексной передаточной
функции. Спектральный анализ цепи
Комплексная передаточная функция цепи на какой-либо час-
тоте вычисляется как отношение комплексной амплитуды реакции
на этой частоте к комплексной амплитуде воздействия на этой же
частоте.
156
При подключении цепи к источнику периодического напря-
жения комплексная передаточная функция цепи принимает раз-
личные значения на частотах гармоник. Сравнение спектров ам-
плитуд и фаз реакции и воздействия позволяет рассчитать коэф-
фициенты передачи и фазовые сдвиги в цепи для каждой гармо-
нической составляющей периодического сигнала.
Пример 3.11. Сравним спектры амплитуд (рис. 3.27) входной по-
следовательности прямоугольных импульсов u(t) и
напряжения ur(£) на резисторе колебательного кон-
тура из примера 3.10, чтобы определить коэффици-
енты передачи по напряжению цепи на частотах гар-
моник.
В соответствии с (3.29) и рис. 3.27, а постоянная
составляющая Uo в спектре напряжения u(t) равна
2,5 В, амплитуды первой, третьей и пятой гармоник
имеют значения:
1/и1 = 3,2В, (7m3 = l,06B, t/m5=0,64 В.
Постоянная составляющая в спектре напряжения
wr(£) на резисторе (рис. 3.27, б) равна нулю, а ам-
плитуды нечетных гармоник равны соответственно
^=0,18 В, £4^=1,06 В, UmR5 =0,089 В.
Коэффициенты передачи по напряжению HURk
на частотах гармоник рассчитаем по формуле
‘ = 0,1, 3,5.
u mk
На частоте f = 0 кГц получаем HURo - 0/2,5 = 0.
На частоте f = 1 кГц (частота основной составля-
ющей) HUR{ = 0,18/3,2 = 0,056.
Рис. 3.28. Коэффициенты передачи по напряжению
на резисторе R на частотах гармоник
157
На частоте f = 3 кГц (третья гармоника) HUR3 =
= 1,06/1,06 = 1.
На частоте f = 5 кГц (пятая гармоника) HUR3 =
= 0,089/0,64 = 0,14.
На рис. 3.28 приведен график зависимости ко-
эффициента передачи контура от частоты гармоник.
На частоте резонанса коэффициент передачи макси-
мален и равен 1. На частотах первой и пятой гармо-
ник коэффициент передачи резко уменьшается.
Пример 3.12. Найдем коэффициенты передачи по напряжению на
емкости HUCk на частотах гармоник периодической
последовательности прямоугольных импульсов, коле-
бательного контура в примере 3.10.
Определим комплексные амплитуды и мгновенные
значения напряжения на емкости на частотах гармоник,
воспользовавшись результатами расчета в примере 3.10.
На частоте f = 0 кГц имеем постоянную состав-
ляющую Uсо = 2,5 В.
На частоте первой гармоники f = 1 кГц
= х„1 f-7-У = 0,09е/87’ 39,8е->9»- =
= 3,5е_у3’В или
ыС1 (i) = 3,5sin(2л • 1000t - 3°) В.
На частоте третьей гармоники f = 3 кГц
и^3 = (-J = 0,53г'°’ Шбе-'9»- =
= 7,01е~}9°° В или
01 2 3 4 56 /кГц 01 2 34 56 / кГц
а) 6)
Рис. 3.29. Спектры амплитуд входной
последовательности прямоугольных импульсов
и напряжения на емкости контура
158
uC3(t) = 7,01 sin(2л • 3000t - 90°) В.
На частоте пятой гармоники f = 5 кГц
= 0,0446е-;82° Se-790’ =
—тс5
= 0,35е ;172° В или
иС5 (t) = 0,35 sin ( 2л • 50001 -172°) В.
Ряд Фурье напряжения ис( О имеет вид
ис(.t) = 2,5 + 3,5sin(2л • 10001 - 3°) +
+ 7,01sin(2n-3000£-90°) +
+ 0,35 sin (2л • 50001 -172°) + ... В.
Сравнивая спектры амплитуд Um(k(£>\)
UmC(kQ>i) (рис. 3.29) входного сигнала u(t) и
пряжения на емкости uc(t), получаем значения
эффициента передачи по напряжению на емкости
Umck
Umk
и
на-
ко-
HuCk
на частотах 0; 1; 3 и 5 кГц:
Н
"2,5 ’
7 01
Ни„ = Т77 = 6,63;
Сз 1,06
График зависимости
3 5
Н = ±2 = 1,09;
с' 3 2
ГТ 0,35 л е
"Л64"0'5'
коэффициента передачи
контура от частоты Д приведен на рис. 3.30. На час-
тоте резонанса контура /о = 3/1 =3 кГц коэффици-
ент передачи имеет максимальное значение НиСз =
UmCk
Umk
6,63 (б)
1
5
6 /, кГц
Рис. 3.30. Коэффициенты передачи по напряжению
на емкости на частотах гармоник
159
= 6,63, равное добротности Q контура. На первой и
пятой гармониках значение HuCk гораздо меньше.
Комплексная передаточная функция по напряжению на резисто-
ре последовательного колебательного контура (рис. 3.20) имеет вид
fj _ ~mRk Lmk ' R_______________________
~тк Lmk\R+jk^L- .
J
_______R________
R + j ] ka><.L - -I
3 v kc^C J
Модуль комплексной передаточной функции (или коэффици-
ент передачи по напряжению) на частотах гармоник
Н _ UmRk _ R
URk ~ Umk ~
(3.31)
m rv
LR2+ L-
V k®iC)
показывает, во сколько раз изменяются амплитуды каждой гар-
монической составляющей периодического сигнала на входе цепи
при его прохождении через цепь.
Аргумент комплексной передаточной функции (или фазовый
сдвиг)
ka^L-—^—
^uRk ~ ~tyUmk = — HTCtg — - (3.32)
показывает изменение начальных фаз каждой гармонической со-
ставляющей входного периодического сигнала после передачи его
по цепи.
Аналогичным образом можно определить комплексную переда-
точную функцию по напряжению на емкости на частотах гармоник:
. 1
rr _ — mck _ 1 k(S>\C
~uCk ~ ~П ( 1 А
3 JfecojC )
и комплексную передаточную проводимость:
Г 1
и _ Lmk _ 1
"у* - ТТ----------7---------7-у
—тк R + j I k(i>iL - -—— I
3 V )
160
Зная значения комплексной передаточной функции цепи - на
частотах гармоник периодического воздействия, можно вычис-
лить реакцию цепи на это воздействие.
Задача определения изменения спектра периодического воз-
действия произвольной формы при прохождении его по цепи на-
зывается задачей спектрального анализа цепи. Для расчета
спектра реакции цепи необходимо определить спектр воздейст-
вия, разложив периодический сигнал в ряд Фурье, вычислить
комплексную передаточную функцию цепи на частотах гармоник,
а затем найти спектр реакции, умножив спектр воздействия на
комплексную передаточную функцию.
Комплексные амплитуды гармоник напряжения на резисторе
в последовательном колебательном контуре рассчитываются по
формуле
(3.33)
Чтобы вычислить амплитуды гармоник реакции, необходимо,
в соответствии с (3.31) и (3.33), амплитуды гармоник воздейст-
вия умножить на значения коэффициента передачи для этих гар-
моник. Чтобы вычислить начальные фазы гармоник реакции це-
пи, необходимо в соответствии с (3.32) и (3.33) к начальным фа-
зам гармоник воздействия прибавить фазовые сдвиги, вносимые
цепью на этих гармониках.
Амплитуды гармоник напряжения на резисторе в последова-
тельном колебательном контуре
U тцк = Umk ' HuRk > & = 0, 1, 3, 5, ... ,
а их начальные фазы
Фит/fy = ФитЛ + Фи/?А •
Зная спектры амплитуд и фаз реакции, можно рассчитать ре-
акцию цепи, воспользовавшись ее представлением в виде ряда
Фурье в тригонометрической (3.10) или комплексной (3.14) фор-
ме, и установить, как изменилась форма воздействия при переда-
че его по цепи.
Пример 3.13. Определим спектр амплитуд напряжения на рези-
сторе в цепи, изображенной на рис. 3.31, а, на вход
которой поступает периодическая последовательность
прямоугольных импульсов (рис. 3.31, б), если заданы
R = 50 Ом, £ = 10 мГн, U = 10 В, т = 1 мс, Т = 4 мс.
Найдем комплексный спектр входного сигнала
а(£), воспользовавшись (3.26):
11 -6972
161
9 Т “с/ 2
Umk = 4 = 4 J Ue-i^dt =
1 0 1 -т/2
__ 2CJ / _ .feCQfT .ZeCOiT \
Г(-/Л©1)\е } 2 -e 2 /’
Применив формулу Эйлера, получим
. k(£>tT
2t/-TSm~2~
“2~
спектральных составляю-
^Lmk р
Вычислим амплитуды
щих:
тт 2Ux
U mk ~ гр,
. k(i>\T
sin ‘
_______2
k(£>xX
2
Амплитуда постоянной составляющей
тт 2Ux 210110"3 со
U Q — — Q — Э 13.
т 4-10-3
Частота основной составляющей
ft = у = 0,25 кГц или ©j = 2nfi =1,57 103 рад/с,
а ее амплитуда
TT 2Ut
ml ”* p
. CDiT
sin—-—
____2_
COtT
~r
= 4,5B.
Аналогичным образом определяются частоты и
амплитуды высших гармоник:
Рис. 3.31. 7?£-цепь и сигнал на ее входе
162
При ft = 2 2f\ = 0,5 кГц, Um2 = 3,18 В;
ft = 3 3/i = 0,75 кГц, Um3= 1,5 В;
ft = 4 4/i = 1 кГц, = 0 В;
ft = 5 5/i = 1,25 кГц, Um5 = 0,9 В;
ft = 6 6/i = 1,5 кГц, Um6= 1,06 В;
ft = 7 7/i = 1,75 кГц, Um7 = 0,64 В;
ft = 8 8/1 = 2,0 кГц, Um8 = 0 В;
ft = 9 9/1 = 2,25 кГц, = 0,5 В;
ft = 10 Ю/i = 2,5 кГц, = 0,64 В
Спектр амплитуд Umk входного сигнала изобра-
жен на рис. 3.32, а. Огибающая спектра амплитуд
прямоугольных импульсов изменяется по закону
|sinx/x|; нули спектра расположены на частотах,
кратных 1/т = 1 кГц (четвертая, восьмая, двенадца-
тая и т.д. гармоники),.
Комплексная передаточная функция цепи
(рис. 3.31) определяется по формуле
Н = —mRk - -т^ ' R
Umt I^R + jk^L)
R
— г- в К
^R2+(kalL)2
Вычислим коэффициенты передачи цепи на час-
тотах гармоник при k = 0, 1, 2, 3, ..., 10 по формуле
Н - R - 50
URk ~ 7/?2+(^)2 " ^2500 +246,5ft2 ‘
При ft = 0 Hurq - 1;
ft = 1 Hurx ~ 0,95;
ft = 2 Hurz = 0,85;
ft = 3 Hur$ = 0,73;
ft = 4 Hur± ~ 0,62;
ft = 5 HUR5 = 0,54;
ft = 6 HUR6 = 0,47;
ft = 7 Huri — 0,41;
ft = 8 Hur% = 0,37;
ft = 9 ~ 0,33;
ft = 10 = 0Д
163
J______I_____I_____I______I_____I_____I______I_____L
0 0,25 0,5 0,75 1 1,25 1,5 1,75 2 2,25 2,5 f кГц
6)
5 '
4 -
3 -
2 -
1 -
0+
\2,7
°>49 2>5 0,26 0,17 0,19
0,25 0,5 0,75 1 1,25 1,5 1,75 2 2,25 2,5 кГц
e)
Рис. 3.32. Спектры амплитуд последовательности
прямоугольных импульсов и напряжения на резисторе
в 7?£-цепи и коэффициенты передачи цепи
График зависимости коэффициента передачи
/?£-цепи от частоты изображен на рис. 3.32, б.
Спектр амплитуд UmRk напряжения на резисто-
ре, рассчитываемый в соответствии с (3.33):
UmRk = ^mk ’ HuRk >
принимает значения
UmRQ = 5 В; = 4,3 В; UmR2 = 2,7 В;
UmR$ = 1,1 В; = 0 В; = 0,49 В;
= 0,5 В; UmRi = 0,26 В; UmR% = 0 В;
= 0,17 В; UmR\Q = 0,19 В
и приведен на рис. 3.32, в.
164
Из данного параграфа мы узнали, что:
. Задача спектрального анализа цепи состоит в определении
того, как изменился спектр входного периодического сиг-
нала при передаче его по цепи.
. Чтобы вычислить комплексные амплитуды гармоник напря-
жения (тока) на элементе цепи, необходимо комплексные
амплитуды гармоник входного напряжения (тока) умно-
жить на значения комплексного коэффициента передачи
для этих гармоник.
• Зная изменение спектра периодического сигнала при пере-
даче по цепи, можно вычислить по формулам Фурье изме-
нения формы сигнала.
Вопросы и задания для самоконтроля
1. Из каких тригонометрических функций можно сформировать
периодический сигнал?
2. Что такое постоянная и основная составляющие, гармоники
сигнала?
3. Какие формы ряда Фурье используют для описания перио-
дических сигналов?
4. Записать ряд Фурье (3.4) в тригонометрической и комплекс-
ной формах, ограничившись третьей гармоникой.
5. Что такое спектр амплитуд и спектр фаз периодического сиг-
нала?
6. Периодический сигнал задан рядом Фурье в форме
u(t) = 10 + 20cos27C-50£ + 30sin2K-50£-
- 10cos27t-100£-10sin27t 100t
Представить этот ряд в тригонометрической форме (3.10).
7. Рассчитать и построить спектр амплитуд периодической по-
следовательности прямоугольных импульсов, изображенных
на рис. 3.4, б, используя выражение для комплексного спек-
тра сигнала.
8- Каким образом длительность периодических импульсов, пери-
од их следования и скважность влияют на спектр сигнала?
9. Как определить реакцию цепи на периодическое воздействие?
Ю. Определить параметры седьмой гармоники напряжения на ре-
зисторе в примере 3.10.
И. Как рассчитывается комплексная передаточная функция цепи,
на вход которой поступает периодический сигнал?
165
12. Каков физический смысл коэффициента передачи и фазового
сдвига цепи на частотах гармоник?
13. Сформулировать задачу спектрального анализа цепи при пе-
риодическом воздействии.
14. Как рассчитывается спектр реакции цепи на периодическое
воздействие?
15. Рассчитать спектр Ujnik напряжения на индуктивности коле-
бательного контура в примере 3.10. Записать выражение
wr(t).
Глава 4. Анализ реакции линейной цепи на
непериодическое воздействие сложной формы
(спектральный метод)
4.1. Представление непериодического
воздействия интегралом Фурье
Рассмотрим периодическую последовательность прямоуголь-
ных импульсов (рис. 4.1, а). Увеличивая период Т этой последо-
вательности, легко перейти при Т -> оо от периодического сигнала
к непериодическому (рис. 4.1, г).
Увеличение периода Т сигнала приводит к уменьшению час-
тоты первой гармоники <Bi = 2я/Т и сгущению спектральных ли-
ний. Уменьшаются также амплитуды гармоник
в) 1
Т
г) '
Рис. 4.1. Увеличение периода последовательности
прямоугольных импульсов
167
Umk
Umk
Umk
0 <0i 2o>i
4«ц 6<»i
a)
8<di co
0 <01 3<D|
6<oi 9<oi
12<»i co
J____I I , ( 1 I , I___________________L
0 4g>i 8<0i 12<oi
16<»i <o
Рис. 4.2. Спектры амплитуд периодических последовательностей
импульсов с разными периодами
поскольку остающаяся неизменной энергия сигнала распределя-
ется теперь между возросшим числом гармоник и, естественно,
доля каждой гармоники в общем сигнале падает (рис. 4.2).
При Т -> оо периодическая последовательность импульсов пе-
реходит в одиночный импульс (рис. 4.1, г). В спектре такого сиг-
нала вместо отдельных гармоник будет бесконечно большое число
синусоидальных колебаний с бесконечно близкими частотами и
бесконечно малыми амплитудами. Другими словами, в любой
бесконечно узкой полосе частот есть синусоидальное колебание
бесконечно малой амплитуды.
Сравнивать между собой бесконечно малые величины не-
удобно, поэтому вместо амплитуд Umk (рис. 4.2) по оси ординат
откладывают величину (C7mfe-T)/2, которая при увеличении пе-
риода Т остается неизменной. Введем новые обозначения для
осей ординат на рис. 4.3: U= Umk (Т/2). В новых коорди-
натах спектры сигналов (рис. 4.1) выглядят так, как показано на
рис. 4.3, а—г. Спектр непериодического сигнала является в об-
щем случае не дискретным, а непрерывным (сплошным).
Для комплексного спектра введенное на рис. 4.3 обозначение
примет вид
(4.1)
В гл. 3 была получена пара преобразований (3.26) и (3.14),
позволяющих найти спектр периодического сигнала Ujnk и вос-
становить периодический сигнал u(t) по его спектру:
168
Рис. 4.3. Переход к спектральной плотности
прямоугольного импульса
= | Е (4.2)
k=-<x>
э т/2
Umk =4 f u(t)e-^dt. (4.3)
1 -Т/2
Получим подобную пару преобразований для непериодическо-
г° сигнала, изображенного на рис. 4.1, г. Для этого нужно в вы-
169
ражении (4.3) устремить период Т к бесконечности и совершить в
формулах (4.2) и (4.3) предельные переходы.
Сначала выразим из (4.1) комплексную амплитуду U_mk в ви-
де LLmk ~ (U ‘ ty/T и подставим ее в (4.2) и (4.3). Перепи-
шем теперь эти выражения в виде
u(t) = ^ f U(jk^)e>k^ (4.4)
Ж k=-n
и
Т/2
U(jko>i) = J u(t)e~}k&itdt. (4.5)
-T/2
В выражении (4.4) учтено, что Т = 2n/o>i. Затем устремим
период к бесконечности (Т -> со). Гармоники будут сгущаться и
дискретная частота п«н перейдет в текущую частоту со, а значе-
ние частоты первой гармоники coi будет стремиться к бесконечно
малой величине do.
После предельного перехода получаем из (4.5) и (4.4)
U(jo) = f u(t)e-imtdt, -00 (4.6)
u(t) = ^- \U(jo) e,0>tdo. -00 (4.7)
Уравнения (4.6) и (4.7) являются основными в теории спек-
тров непериодических сигналов, причем (4.6) называется пря-
мым, а (4.7) — обратным преобразованием Фурье (интегралом
Фурье).
Если вместо частоты о использовать частоту f, то эти урав-
нения примут вид
U(jf)= ^uCOe-^dt,
________-00____________
u(t)= K\U(jf)e^ftdf.
(4.8)
(4.9)
Из данного параграфа мы узнали, что:
““ Ы
Сигнал и его Фурье-изображение связаны парой инте- |
гральных преобразований, называемых преобразованиями i
Фурье. ,
170
4.2. Спектральные плотности амплитуд и фаз
непериодических колебаний
Величина (/(/со) в (4.6) или U(jf) в (4.8) называется ком-
плексной спектральной плотностью непериодического сигнала
M(i). Она может быть записана в показательной и алгебраической
формах:
(/(/со) = [/((о)е--,<,,(со) = (/'(со)-/(/''(со) (4.10)
и содержит в себе сведения о спектральной плотности ампли-
туд и(Ф) и спектральной плотности фаз ф(со) сигнала, где
величины (/'(со) и (/"(со) определяются формулами
00
(/'(со) = J u(t)cos(otdt,
-% (4.11)
(7"(со) = J u(t')sin(otdt.
Определим физический смысл преобразования Фурье (4.7).
Для этого подставим в выражение (4.7) вместо (/(/со) его значе-
ния из (4.10):
иа) = 4-1и(о)е^-^(й =
2л Jo
= — [ (/(co)cos(cot-<р) с/со+ /— Г (/(co)sin(co/-ф) (/со .
2л 2л
Учитывая, что (/(со) — четная, а синус — нечетная функция
частоты, интеграл от второго слагаемого равен нулю. Следова-
тельно, интеграл Фурье (4.7) имеет вид
«(/) = —f(/(co)cos(cot-9) с/со . (4.12)
п о
Отсюда следует важнейший вывод о том, что непериодиче-
ский сигнал может быть представлен пределом суммы (интег-
ралом) бесконечно большого числа гармонических колебаний с
бесконечно малыми амплитудами (1/л)(/(со) и начальными фа-
зами ф = ф(со), причем разность частот соседних гармоник
бесконечно мала'. Дсо = с/со. Это означает, что спектр непериоди-
ческого сигнала является сплошным или непрерывным.
Определим спектральную плотность прямоугольного импуль-
са> изображенного на рис. 4.4. Для расчета его комплексной спек-
тральной плотности воспользуемся преобразованием Фурье (4.6):
171
Рис. 4.4. Прямоугольный импульс
-т/2 0 т/2 t
оо т/2
[/(»= f u(t)e-i(atdt= jUe~]atdt =
-оо -т/2
= _£_е->‘Т/2 2U е^-е-^12
-ja) _т/2 со 2/
(4.13)
Уравнение (4.13) удобнее преобразовать к виду
17 (/со) = [/т81ПЮ.Т/2, (4.14)
так как это выражение содержит функцию sina/a, поведение
которой хорошо известно: эта затухающая функция максималь-
на и равна 1, когда a = 0; она принимает нулевые значения при
a = ±kit.
График комплексной спектральной плотности прямоугольно-
го импульса изображен на рис. 4.5. В тех областях частот, где
функция U(,]<£>) положительна, спектральная плотность фаз ср(со)
равна нулю; там же, где (7(/со) отрицательна, спектральная
Рис. 4.5. Спектральная плотность прямоугольного импульса
172
Рис. 4.6. Спектральные плотности (спектры) амплитуд (а)
и фаз (б) прямоугольного импульса
плотность фаз равна ±180°. Поэтому на графиках можно изобра-
зить отдельно спектральную плотность амплитуд (/(со) — модуль
|С/(;со)| и спектральную плотность фаз ср (со) (рис. 4.6).
Пример 4.1. Определим спектральную плотность амплитуд пря-
моугольного импульса, изображенного на рис. 4.7,
если т = 1 мс, U = 10 В.
Комплексную спектральную плотность прямо-
угольного импульса (рис. 4.7) определим, используя
прямое преобразование Фурье (4.6):
и(0
U
От/
Рис. 4.7. Прямоугольный импульс
173
U(j(o) = X\Ue-^fdt =
о
t
0
. COT
sin—
= (Ут---£-e 2
cot/2
Полученное выражение U(j(£)) отличается от
комплексной спектральной плотности (4.14) прямо-
угольного импульса, изображенного на рис. 4.4,
множителем е'-'“т/2, учитывающим запаздывание сиг-
нала (рис. 4.7) на т/2 и влияющим только на спек-
тральную плотность фаз.
Спектральная плотность амплитуд — это модуль
комплексной спектральной плотности, поэтому
U((h) = Ut
. сот
sin—
_____2_
сот/2
Обратим внимание на то, что спектральная плот-
ность амплитуд (/(со) прямоугольных импульсов,
изображенных на рис. 4.4 и 4.7, рассчитывается по
одной и той же формуле. Это означает, что графики
спектральной плотности амплитуд импульсов также
совпадают (рис. 4.6, а).
Построим график Для этого прежде всего
рассчитаем значение спектральной плотности ампли-
туд на нулевой частоте, которое равно площади пря-
моугольного импульса:
(/(О) = U • т = 10 1 = 10 мВс.
Рис. 4.В. Спектральная плотность амплитуд
прямоугольного импульса
174
Частоты f, на которых спектральная плотность
обращается в нуль, можно найти из соотношения
2л/т ,
' = ±кл.
2
Эти частоты равны kit, т.е. 1; 2; 3 кГц и т.д. На
частотах 1,5 и 2,5 кГц лепестки функции при-
нимают максимальные значения, равные соответст-
венно 2 и 1,3 мВ с. График спектральной плотности
амплитуд приведен на рис. 4.8.
Пример 4.2. Найдем комплексную спектральную плотность тре-
угольного импульса, изображенного на рис. 4.9, на
частоте f = 200 Гц, если U = 10 В, т = 5 мс.
Сигнал u(t) можно записать следующим образом:
Г 0
u(t) = •
при t < 0,
при 0 i С т.
I t
Комплексную спектральную плотность импульса
(рис. 4.9) рассчитываем, используя формулу (4.6):
U(/co) = \—te~jatdt.
о т
Берем интеграл по частям и получаем
\—^—r—dt =
о т
-ll
-jat
U(j<£>) = — t - .
т -/со 0
= -^-Г(1 + /®т)е’;шт-1]-
со т L J
На частоте f = 200 Гц комплексная спектральная
плотность
4 л f т L
Рис. 4.9. Треугольный импульс
175
равна 8е;90 , т.е. спектральная плотность амплитуд рав-
на 8 мВ с, а спектральная плотность фаз равна 90°.
Из прямого преобразования Фурье легко определить спек-
тры типовых, часто встречающихся в технике импульсов. Рас-
смотрим некоторые из них.
Импульс включения. При анализе переходных процессов в
электрических цепях используется импульс включения (единичная
функция) (рис. 4.10), который возникает при подключении к це-
пи источника постоянного напряжения:
««) = (’
((7 при £ > 0.
Строго говоря, эта функция не удовлетворяет условиям ин-
тегрирования по Фурье, поэтому воспользуемся следующим при-
емом: умножим ее на «гасящий» множитель e'at, а затем после
интегрирования перейдем к пределу при а -> 0:
(/(;©) = °]ue~ate~jatdt = ule^^dt = -У—.
о о а + У®
Совершая предельный переход, получаем спектральную плот-
ность импульса включения:
JCD (О
1/(Г)м
и----------------------------
Рис. 4.10. Импульс включения
Рис. 4.11. Спектры амплитуд (а) и фаз (б) импульса включения
176
«(0 = 5(0
Ща>)
1
0
a)
Рис. 4.12. 3-импульс (а) и его спектр (б)
Спектральная плотность амплитуд при этом С7(со) = U/m, а
спектральная плотность фаз <р(а>) = -90°. Графики (/(со) и <р(со)
показаны на рис. 4.11.
8-импульс. Этот импульс является математической моделью
очень узкого и большого по амплитуде импульса (рис. 4.12, а):
6(4) = (” пРи('0; (4.15а)
(0 при других значениях t,
удовлетворяющего условию
ОО
J 8(t)dt - 1 (т.е. площадь его равна единице). (4.156)
-00
Для нахождения спектра 3-импульса воспользуемся прямым
преобразованием Фурье
(/(/©) = j b(t)e~}<otdt = j 3(t)coscot dt-j J3(i)sincoi dt.
-OO -00 -00
Так как второе слагаемое равно нулю (в силу нечетности по-
дынтегрального выражения), то
(/(/©) = j 3(£)coscot dt. (4.16а)
-00
В силу свойства (4.15а) 3-импульса подынтегральное выра-
жение существует только при t - 0, а это означает, что согласно
(4.156) U{j(a) - 1. График спектра 3-импульса приведен на
рис. 4.12, 6.
Обратное преобразование Фурье для 8-импульса имеет вид
3(() = ^7(/(/а>)е>‘с/со.
2л Л
Так как спектр 3-импульса (/(/со) = 1, то
3(i) = -L f (4.166)
12 — 6972
177
и(0 /7(со) = 2л8(®)<
1 —
0 t 0 ©
a)
Рис. 4.13. Постоянное напряжение (л) и его спектр (б)
Постоянное напряжение U = 1 В существует во все момен-
ты времени, а не только при £ > 0.
Учитывая взаимозаменяемость параметров t и со [1], выраже-
ние (4.166) можно переписать в виде
5(со) =
Сравнивая его с выражением для спектра постоянного на-
пряжения
(/(» = ]ue-jatdt= e~ja>tdi,
-ОО -00
приходим к выводу, что (7(У<в) = 2л5(со).
Таким образом, спектр постоянного напряжения (рис. 4.13, 6)
равен нулю на всех частотах, кроме со = О, где iKj®) обращается
в бесконечность.
Экспоненциальный импульс. Переходные процессы в цепях с
одним реактивным элементом описываются экспоненциальной
функцией (рис. 4.14, а)
u(t) = Ue~at при £ > 0.
Спектральная плотность этого импульса
U(j(0) = lue-ate-}<i>tdt = = -jJL----^/arct^/a),
о a + ;co Va2 + со2
где спектр амплитуд
а спектр фаз
/ X .со
ср (со) = -arctg — .
a
178
Рис. 4.14. Экспоненциальный импульс (а) и его спектры
амплитуд (б) и фаз (в)
Графики U(a>) и <р(<о) показаны на рис. 4.14, бив.
Пример 4.3. Найдем значение комплексной спектральной плотно-
сти импульса, изображенного на рис. 4.15, на часто-
тах, равных нулю ИО] = 10° с-1. На отрезке време-
ни от нуля до т = 5 мкс функция u(t) имеет вид
u(t) = Ue~at = 80е_2’81°6' В.
Определим комплексную спектральную плот-
ность импульса (рис. 4.15) по формуле (4.6):
(/(» = f u(t)e~}0>tdt = ]ue-ate~^fdt =
-00 о
= [ 1 - e-(a+/w)t ]
а + ](£>
12*
179
Рис. 4.15. Экспоненциальный импульс
Рассчитаем значение U(](£>) на частоте © = 0:
С/(;0) =
80
2,8 106
। _ е-2,810б-510-6
= 28,6е}0°.
Спектральная плотность амплитуд (7(0) на час-
тоте со = 0 равна 28,6 В с; спектральная плотность
фаз ф(0) равна 0°.
На частоте (о = 10° с-1 имеем
80
j _ е-(2,8106+/10'
|6)-510’6 I _
U (J106) =------g------д
2,8 • 106 +/106 L
= 26,9 Ю-6^'21’8’.
Спектральная плотность амплитуд на частоте
©1 = 10° с-1 равна 26,9 мкВ-c, а спектральная плот-
ность фаз равна -21,8°.
Покажем, что в отличие от прямоугольного им-
пульса спектральная плотность импульса, изобра-
женного на рис. 4.15, вообще не имеет нулей ни при
каких конечных значениях частоты ©.
Действительно, для того чтобы U(ja>) была рав-
на нулю, необходимо, чтобы выполнялось равенство
1 _ еЧа+/®)т = 0
ИЛИ
е-аг.е->т =1
Используя формулу Эйлера, запишем систему
уравнений:
I e-at cos ют = 1;
[e-ax sin сот = 0.
Эта система уравнений несовместна.
180
Для вычисления спектров при различных преобразованиях
сигналов можно воспользоваться теоремами о спектрах. Оста-
новимся на физической интерпретации основных теорем спек-
трального анализа.
Спектр суммы сигналов (теорема линейности). Если сигналы,
спектры которых известны, суммируются, то для вычисления ре-
зультирующего спектра можно воспользоваться теоремой линейно-
сти: спектр суммы сигналов равен сумме спектров этих сигналов.
Итак, если
u(t) = c1M1(t) + a2w2(t) +... + anan(t),
то
U (/со ) = axUx (/со) + a2U2 (/<о) + ...+ anUn .
Сдвиг сигнала во времени (теорема запаздывания). Часто
при обработке сигнала приходится осуществлять его задержку на
время to:
n(t) = Wi(t-t0).
В этом случае спектр задержанного сигнала умножается на
множитель е"1 °:
U(jei) = U(a))e~}<f = U1 = Ux (со)е-'(в’‘о"<₽1).
При запаздывании сигнала на время to его спектральная
плотность амплитуд остается неизменной, а спектральная
плотность фаз изменяет свой наклон на величину со to.
Пример 4.4. Определим спектральные плотности амплитуд и
фаз прямоугольного импульса, изображенного на
рис. 4.16, а.
Комплексная спектральная плотность прямоу-
гольного импульса, симметричного относительно оси
ординат (рис. 4.4), рассчитывается по формуле (4.14):
ТТ / . \ тт sin (® т/2)
UM’U'~^/2 '
Сигнал на рис. 4.16 задержан на время, равное
длительности импульса to = т. Тогда по теореме за-
паздывания комплексная спектральная плотность
этого импульса имеет вид
(J(/co) =
со т/2
Спектральная плотность амплитуд (7(со) импуль-
сов, изображенных на рис. 4.4 и рис. 4.16, а, рас-
считывается по одной и той же формуле:
181
u(t)
U
От Зт t
амплитудный (б) и фазовый (в) спектры
с-(ю>.сч5'"(ю52)
сот/2
а спектральная плотность фаз <р(ю) импульса на
рис. 4.16, а рассчитывается по формуле
<р(со) = arg(sin(a>T/2))-coT,
где arg(sin®x/2) — аргумент синусоидальной функции.
Графики спектральной плотности амплитуд U(f)
и фаз <p(f) сигнала на рис. 4.16, а приведены на
рис. 4.16, бив.
Дифференцирование и интегрирование сигнала. Если сиг-
нал ui(t) подвергается дифференцированию
u(i) =
at
182
то его спектр умножается на оператор /со:
I/ (/со) = /со(71(/со)-м1(0),
где wi(0) — значение сигнала wi(i) в момент времени t = 0.
При интегрировании сигнала
t
u(.t) = f щ (t)dt
-00
его спектр делится на/со (при условии (7(0) = 0):
^(/<о) = -?-171(/й>).
7 со
Пример 4.5. Найдем спектр сигнала, полученного в результате диф-
ференцирования экспоненциального импульса u\(t) =
= lie"™ (при t > 0), если U = 10 В, а = 103 с"1.
Рис. 4.17. Импульс u(t) = -Uae~at (а)
и его спектры амплитуд (б) и фаз (в)
183
Комплексная спектральная плотность экспонен-
циального импульса определяется выражением
1/10®) = -^.
а + усо
Дифференцирование сигнала приводит к умно-
жению его спектра на /со, поэтому комплексная спек-
тральная плотность (7(/со) сигнала
и<Л) = = -Uae~at
dt
рассчитывается по формуле
(7(/со) = /со • (Л (/со) - (0) = U
а + /со а + ;со
Спектральные плотности амплитуд (7(со) и фаз
ср(со) равны соответственно:
С/(й)) = _£=^= = _±==;
Va2 +со2 V106 +со2
ср (со) = 180° - arctg— = 180° - arctgl0"3co.
а
Графики сигнала w(t) = ~(7ae-at и спектральных
плотностей (7(f) и cp(f) приведены на рис. 4.17.
Изменение масштаба сигнала (теорема подобия). Пусть сиг-
нал ui(t) имеет спектр (7i(/co). Изменение масштаба по шкале
времени
u(t) = Ux(at)
приводит к изменению масштаба спектра по шкале частот:
а \ a J
Сжатие сигнала во времени приводит к расширению его
спектра и, напротив, растяжение сигнала — к сужению спектра.
Другими словами, чем короче импульс, тем шире его спектр.
Пример 4.6. Построим графики спектральных плотностей ампли-
туд прямоугольных импульсов, имеющих одинаковую
амплитуду U, но разные длительности т: а) т = 2 мс,
б) т = 4 мс, в) т = 1 мс (рис. 4.18).
Ранее было установлено, что спектральная плот-
ность амплитуд U(f) прямоугольного импульса из-
184
(7(7). В-мс,
2
и(/),В
1
-1 0 1 /, мс -1 -0,5 0 0,5 1 /, кГц
-2-10 1 2 t, мс -1 -0,5 0 0,250,5 1 /,кГц
<5)
U(f), В-мс
«(О, В,
1
-0,500,5 /, мс -1
О
«)
1 f, кГц
1
Рис. 4.18. Прямоугольный импульс и его спектр при
длительности импульса 2 мс (а), 4 мс (б) и 1 мс (в)
меняется по закону |sina/a|. Значение U(f) на ну-
левой частоте равно площади импульса (7(0) = (7-т,
а нули функции U(f) располагаются на частотах,
кратных величинам 1/т.
Для импульса, имеющего параметры U = 1 В и
т = 2 мс, получаем (7(0) = (7-т = 2 Вмс, нули рас-
положены на частотах 0,5; 1; 1,5 кГц и т.д. График
спектральной плотности амплитуд такого импульса
изображен на рис. 4.18, а.
Увеличение длительности импульса в 2 раза
(т = 4 мс) приводит, в соответствии с теоремой подо-
бия, к сужению спектра в 2 раза. Это означает, что
нули спектра (7(/) располагаются на частотах, крат-
ных 1/т = 0,25 кГц, а значение (7(0) = (7-т = 4 В мс.
График спектральной плотности амплитуд импульса,
имеющего параметры (7 = 1 В и т = 4 мс, изображен
на рис. 4.18, б.
Уменьшение длительности импульса в 2 раза (т =
= 1 мс) по сравнению с исходным приводит к расши-
рению спектра, т.е. нули располагаются на частотах
1; 2; 3 кГц и т.д., а значение спектра на нулевой час-
185
тоте L/(0) = 1 Вмс. График U(f) прямоугольного
импульса с параметрами U = 1 В и т = 1 мс изобра-
жен на рис. 4.18, в.
Смещение спектра сигнала (теорема модуляции). Эта теоре-
ма является двойственной (дуальной) по отношению к теореме
запаздывания. Если спектр сигнала щ(Л) сместить вниз или вверх
по шкале частот на величину <оо> т.е.
= Ut [/(со + соо)].
то это соответствует умножению сигнала на комплексную гармо-
нику с частотой coo:
«(t) = щ (t)e±}e>ot.
Другими словами, при умножении сигнала на гармоническое
колебание с частотой о>о спектр сигнала смещается по шкале
частот на величину о>о.
Пример 4.7. Найдем спектр радиоимпульса, изображенного на
рис. 4.19, б.
Радиоимпульс можно получить как произведение
видеоимпульса прямоугольной формы (рис. 4.19, а)
и гармонического колебания u(t) - L7mcoso)ot:
Up(t) = UB(t)UmCOS(i>ot.
Воспользовавшись формулой Эйлера
cosco0£ = ^(e}<aot + e~J®ot),
получаем
д) ив(0 1
Um------------
О х t
б) ир(б 1
Рис. 4.19. Видеоимпульс (а) и радиоимпульс (б)
186
Рис. 4.20. Спектры видеоимпульса (а)
и радиоимпульса (б)
Мр(О = +^-ива)е~^.
Обозначив спектр видеоимпульса как (7В(/®) и
применив теорему смещения, находим спектр (7р(/со)
радиоимпульса:
tfp(/®) = ^{tU/(a>-G>o)]+ ^в[/(ю + ®о)]}-
На рис. 4.20, а изображен спектр видеоимпуль-
са, имеющего длительность т = 10 мс. На рис. 4.20, б
изображен спектр радиоимпульса с частотой гармо-
нических колебаний fo = 100 кГц.
Перемножение двух сигналов (теорема свертки спектров).
Спектр произведения сигналов соответствует свертке их
спектров. Так, если
uCt) = щ<Л)и2<ЛХ
то
^(» = 4- JUx(jQ.)U2(J<o-jQ.)d£l.
-00
Свертка двух сигналов (теорема о произведении спектров
сигналов). Спектр свертки двух сигналов соответствует про-
изведению их спектров. Так, если
187
u(t) = J щ(х)и2(Л-x)dx ,
-00
TO
U(jd)) = U2 (jco).
Пример 4.8. Вычислим свертку двух экспоненциальных видеоим-
пульсов ui(t) = Uie~att и U2(t) = U2e~a2t двумя
способами: а) прямым нахождением интеграла сверт-
ки, б) с помощью теоремы о произведении спектров
сигналов.
а) Интеграл свертки двух заданных экспоненци-
альных функций имеет вид
00
u(t) = j Ui(x)u2(t-x)dx =
= f CJ1e-aiV[j2e-a2(t-T)jx =
“2-“1 -L
Графики сигналов щ(х) и U2(t-x), образующих
подынтегральное выражение свертки функций, изоб-
ражены на рис. 4.21. Произведение этих сигналов
отлично от нуля только в промежутке 0 < т < t, по-
этому интеграл свертки
M(t) = p-(«l-a2)xjT =
a2-ai о
= _£j£2_(e-ait_e-a2t)
a2 - at
б) Воспользуемся теоремой о произведении спек-
тров двух сигналов. Комплексные спектральные
плотности l/j(/co) и U2(ja>) экспоненциальных сиг-
налов ui(t) и w2(t) равны соответственно
£Л(;со) =——*т~, и2(](й) = —U2. .
v 7 cq + ;со ' 1 a2 + ja>
Произведение комплексных спектральных плот-
ностей Ut(j(o) и (72(/со) — это спектр свертки сиг-
налов. Найдем
U (/со) = C/f (/со) • U2 (j(i) ) = т-U2—__
V V 7 V 7 (a1+7co)(a2 + jco)
f
188
Рис. 4.21. Графики экспоненциальных функций
Определим сигнал u(t) по его комплексной спек-
тральной плотности, воспользовавшись выражением
(4.6):
u(i) = J_ | и=
-00
и}и2 °? .
2я Jo (ai + ;®)(а2 +;<»)
Разложив на простые дроби подынтегральное вы-
ражение
________1________= 1 Г 1__________1
(aj + /и)(а2 +/(£>) а2-аДа1+/в) a2+/coj’
получаем
.(Й.ВД. ljU------------------
а2-а! 2nJxXai+j(i) a2+;<oj
Воспользовавшись известной формулой, уста-
навливающей связь между экспоненциальным им-
пульсом и его комплексной спектральной плотно-
стью, получаем
w(t) = _^2_(e-«l‘_e-a2<))
a2 -at
что, конечно же, совпадает с выражением для опреде-
ления интеграла свертки, рассчитанным прямым путем.
Между спектрами непериодического и периодического сиг-
налов существует связь: графики модуля спектральной плотно-
сти непериодического сигнала и огибающей дискретного спектра
аналогичного периодического сигнала совпадают по форме и от-
личаются только масштабом. Из уравнения (4.1)
о
Umk=ju(Jk<^ (4.17)
189
следует, что если периодически повторять одиночный импульс, то
амплитуды Umk и фазы <рл получающегося при этом дискретного
спектра можно определить, заменив в комплексной спектральной
плотности (Я/со) одиночного импульса текущую частоту со на
значения частот гармоник ka>i и пронормировав эту плотность
относительно величины полупериода. Таким образом,
2
=уЩ/со) присо = ^со1.
Если мы будем периодически с периодом Т повторять прямо-
угольный импульс, изображенный на рис. 4.4, то в соответствии
с (4.17) можно записать выражение для комплексного спектра
Umk периодической последовательности прямоугольных импуль-
сов, вытекающее непосредственно из спектральной плотности
(4.14) одиночного прямоугольного импульса при замене частоты
со на &coi:
„ _2U т sin(^co1x/2)
-mk fto1X/2 ’
(4.18)
Используя понятие скважности q — Т/т последовательности
прямоугольных импульсов и учитывая, что ©1 = 2л/Т, получаем
комплексный спектр
. kit
тт 2U SinV 2U . kit
Umk =-----. I = -7— sm .
q kn/q kit q
(4.19)
Пример 4.9. Построим спектр амплитуд последовательности пря-
моугольных импульсов, полученных повторением
одиночного импульса, изображенного на рис. 4.7
(пример 4.1), с периодом Т = Зт. Параметры прямо-
угольного импульса (рис. 4.7) остаются неизменны-
ми: U = 10 В, т = 1 мс.
Спектр амплитуд Umk периодической последова-
тельности прямоугольных импульсов определяется в
соответствии с (4.19):
тт 2U sm(kit/q) 2U . kit
Umk =--------= — sin— .
q kit/q kit q
Этот спектр является дискретным, его огибаю-
щая изменяется по закону
sin(&7t/<7)
kit/q
190
Рис. 4.22. Спектр амплитуд последовательности
прямоугольных импульсов
а нули расположены на частотах гармоник, номера k
которых кратны скважности q.
Рассчитаем постоянную составляющую и ампли-
туды первых семи гармоник спектра. Найдем вначале
частоты гармоник:
Л = МТ = 1/G-103) = 0,333 кГц;
fl = 2f\ = 0,67 кГц; f3 = 1,0 кГц; Д = 1,333 кГц;
f5 = 1,673 кГц; f6 = 2,0 кГц; f7 = 2,333 кГц.
Для расчета спектра необходимо знать скваж-
ность q импульсов:
q = T/x = 3.
Постоянная составляющая спектра
Uq = —= -^ = 6,67 В.
q з
Амплитуды гармоник спектра рассчитываются по
формуле
тт 2U . kit
kit
20
= —lsin& • 60°
и равны соответственно:
С7т1 = 5,52 В; Um2 = 2,76 В; Um3 = 0 В;
Umi = 1,38 В; Um5 = 1,10 В; Um& = 0 В;
Um7 = 0,79 В.
График спектра амплитуд приведен на рис. 4.22.
Сравнивая его с графиком спектральной плотности
амплитуд (рис. 4.8) непериодического импульса, лег-
ко убедиться, что спектральные линии вписываются
в огибающую, которая имеет такую же форму, что и
спектр одиночного прямоугольного импульса, но зна-
191
чения дискретных отсчетов отличаются от значении
соответствующих спектральных плотностей.
Из данного параграфа мы узнали, что:
• Спектр непериодического сигнала является непрерывным;
он состоит из бесконечно большого числа частотных со-
ставляющих с бесконечно близкими смежными частотами и
с бесконечно малыми амплитудами.
• Чем короче импульс любой формы, тем шире его спектр.
• Запаздывание сигнала приводит лишь к изменению наклона
характеристики спектра фаз.
• Для смещения спектра по шкале частот необходимо «запол-
нить» сигнал гармоническим колебанием.
• Операция свертки сигналов ведет к перемножению их спек-
тров.
• Дискретный спектр «вписывается» в огибающую непрерыв-
ного спектра.
4.3. Еще раз о комплексных передаточных
функциях и частотных характеристиках цепи
Комплексная передаточная функция цепи — это важнейшая
характеристика линейной электрической цепи в частотной об-
ласти. Электрическую цепь удобно изображать в виде четырех-
полюсника (рис. 4.23), на входные зажимы (1 — Г) которого по-
дается воздействие в виде напряжения u\(t) или тока
имеющих комплексные спектральные плотности UtCjat) и /1(/<в),
а реакция цепи снимается с выходных зажимов (2 — 2') также в
виде напряжения U2(t) или тока гг(£), имеющих комплексные
спектральные плотности (УзС/®) и /2(7®). Комплексная переда-
точная функция определяется как отношение комплексной
спектральной плотности реакции цепи к комплексной спек-
тральной плотности воздействия.
»2<0
-*—О2
I «2(0
I 02(7©)
----оз'
Рис. 4.23. Четырехполюсник
192
в зависимости от типов воздействия и реакции различают
^дующие виды комплексных передаточных функций:
комплексная передаточная функция по напряжению
(4.20)
комплексная передаточная функция по току
(4.21)
комплексное передаточное сопротивление
ЯгОю)”Хи): (4.22)
комплексная передаточная проводимость
(4.23)
Функции Ни{]<о) и Hi(]'(£>) являются безразмерными вели-
чинами, a Hz(j<o) и Яу(/а>) имеют соответственно размерности
сопротивления и проводимости.
Комплексные передаточные функции цепи определяются на
каждой частотной составляющей непериодического воздействия'
сложной формы.
Представление непериодических сигналов в форме интеграла
Фурье (4.6) и (4.7) позволяет применить к бесконечно малым
гармоникам, составляющим их спектр, методы анализа, рассмот-
ренные в гл. 2 и 3. В частности, законы Ома и Кирхгофа для
спектров будут иметь вид
/(/®) = -^| = (/(/®)У(;®); ЕЛ(;®) = 0; ЕВДМ
*=1 л=1
где /(/<»), — спектры токов и напряжений ветвей соответ-
ственно; Z(J<b) и У(/<в) имеют смысл комплексных сопротивле-
ний и проводимостей ветвей.
Законы Ома и Кирхгофа для спектров позволяют распро-
странить рассмотренные ранее методы анализа цепей при гармо-
нических и периодических несинусоидальных воздействиях на
непериодические сигналы.
Пример 4.10. Найдем комплексную передаточную функцию по
напряжению последовательного колебательного кон-
тура, изображенного на рис. 4.24.
13 - 6972 1 93
i(t) R L
о—»—I 1—-o
«101 ==c|“2(0
Рис. 4.24. Последовательный колебательный контур
Комплексная передаточная функция по напря-
жению в цепи, изображенной на рис. 4.24, есть от-
ношение комплексных спектральных плотностей на-
пряжения на емкости и входного напряжения:
UcU®) __
Комплексную спектральную плотность тока К jo)
в цепи рассчитывают, используя закон Ома для
спектров:
К = = .
Z (/со) R + /со£ + 1/(/<оС)
Подставляя в выражение для расчета
Huctjto), получаем
Яц О®) = л. (4.24)
cV 7 Я + /(®1-1/®С)
Очевидно, что комплексная передаточная функ-
ция Нис{]а>) зависит только от частоты и параметров
цепи. Этот вывод справедлив и для любых других
передаточных функций.
Как всякую комплексную величину, Я(/®) можно предста-
вить в показательной форме:
Я(/ю) = |Я(/®)|е;<₽(<0) = Я(®)еу<(,(й)).
Модуль Я(со) комплексной передаточной функции называет-
ся амплитудно-частотной характеристикой цепи (АЧХ), а ар-
гумент комплексной передаточной функции <р(со) = аг§Я(/со)
называется фазо-частотной характеристикой цепи (ФЧХ).
Амплитудно-частотная характеристика цепи определяет сте-
пень изменения спектральной плотности амплитуд входного сиг-
нала при передаче его по цепи.
Фазо-частотная характеристика цепи определяет степень из-
менения спектральной плотности фаз входного сигнала при пере-
даче его по цепи.
194
Пример 4.11. Найдем АЧХ и ФЧХ цепи, изображенной на
рис. 4.24 (пример 4.10), если R = 2 Ом, L = 0,704 мГн,
С = 4 мкФ.
АЧХ и ФЧХ последовательного колебательного
контура определим, воспользовавшись (4.24):
. _____________1
UC 7(<о21С-1)2 + (со/?С)2
Фя(®)=- 90° + arctg
Подставляя в НиС((а) и фя(со) параметры R, L,
С и значение со = 2л/’, получаем
и.с (/) = . ' ‘ ----------
7(111 10~9/’2-1) + 2,53 10’9/’2
Фя (Л = -90° - arctg 2,21 • 10"3/ - 20 • 1031
Графики АЧХ HuC{f) и ФЧХ фя(/) приведены
на рис. 4.25.
Из этих графиков следует, что, например, на
частоте f = 3 кГц (резонансная частота контура) ам-
плитуда напряжения на конденсаторе возрастает в
Рис. 4.25. АЧХ и ФЧХ последовательного
колебательного контура
6,3 раза, а фаза напряжения на конденсаторе изме-
няется на -90° по сравнению с амплитудой и фазой
входного напряжения. Аналогичным образом можно
на каждой частоте определить изменение спектраль-
ного состава сигнала при передаче его по цепи.
В ряде случаев частотные характеристики цепи могут изме-
няться в довольно широких пределах, поэтому более удобно их
оценивать в логарифмическом масштабе. С этой целью для оцен-
ки АЧХ вводят понятие логарифмической амплитудно-частот-
ной характеристики (ЛАХ):
/C = 201g/f((o).
(4.25)
Значения величины К оцениваются в децибелах (дБ). В ак-
тивных цепях величину К также называют логарифмическим
усилением. В пассивных цепях вместо коэффициента усиления
используют понятие ослабления цепи (А):
А = 201g ' 1 1 Lh(co) ]’
(4.26)
которое также оценивается в децибелах.
Пример 4.12. Определим пределы изменения логарифмической
амплитудно-частотной характеристики цепи, если ее
АЧХ Я(ы) принимает значения от 1 до 10000.
Для определения значений ЛАХ воспользуемся
выражением (4.25). Значению Ж со) = 1 соответству-
ет К = 201gZZ(co) = 0 дБ. Значению Ж со) = 10 000
соответствует К = 201g (10 000) = 80 дБ. Характери-
стику, изменяющуюся от 0 до 80 дБ, легко изобра-
зить графически.
Из данного параграфа мы узнали, что:
• Частотная характеристика показывает, как ведет себя цепь |
на разных частотах: АЧХ показывает изменение амплитуды |
каждой частотной составляющей входного сигнала при пе-
редаче по цепи; ФЧХ показывает сдвиг фаз каждой час- |
тотной составляющей. |
• Логарифмические частотные характеристики удобны для ?
специалистов, так как логарифмические характеристики из- |
меняются в менее широких пределах, чем АЧХ. |
196
4.4. Спектральный анализ цепей при
непериодических воздействиях
Представление непериодического сигнала в виде суммы
бесконечного количества гармонических колебаний с бесконеч-
но малыми амплитудами позволяет применить известные частот-
ные методы анализа цепей при синусоидальных воздействиях к
расчету линейных электрических цепей при непериодических
воздействиях произвольной формы. Предположим, задана элек-
трическая цепь, в которой нужно определить реакцию в виде то-
ков гк(0 или напряжений мк(0 ветвей на непериодическое воз-
действие wi(t). Для решения такой задачи необходимо прежде
всего найти комплексную спектральную плотность воздействия
[/1(;со), воспользовавшись прямым преобразованием Фурье (4.6),
и комплексные сопротивления ветвей ZK(/co). Теперь можно най-
ти спектральные плотности реакций цепи /к(/со) или UK(jo),
применив для расчета любой известный метод: законы спектра
напряжений или токов Кирхгофа, методы свертывания, наложе-
ния, контурных токов, узловых напряжений или эквивалентного
генератора. Затем спектры реакций /к(/<») или UK( jo) преобра-
зуются в мгновенные значения токов zK(i) или напряжений uK(i)
ветвей с помощью обратного преобразования Фурье (4.7).
Пример 4.13. Определим напряжение unit) на резисторе в схеме,
изображенной на рис. 4.26, на вход которой подается
импульс включения (рис. 4.27).
Заменим импульс включения его комплексной
спектральной плотностью (см. с. 176):
JG)
а электрическую цепь на рис. 4.26 представим в виде
цепи, изображенной на рис. 4.28.
Рис. 4.26. Электрическая
цепь с источником непери-
одического сигнала
t
Рис. 4.27. Импульс
включения
197
Рис. 4.28. Замена импульса включения его
Комплексной спектральной плотностью
Рассчитаем комплексную спектральную плот-
ность Ur(J®), используя разные методы расчета
электрических цепей.
Согласно методу узловых напряжений имеем
уравнение
и2 (/®)( = и (/®)• -L
jfC ](»L, KJ К
из которого определяем комплексную спектральную
плотность напряжения второго узла:
U (/со) = LL. I. = U L '
2U ’ R R + 2ja>L R + 2j®L
Из схемы (рис. 4.28) очевидно, что
С4(/®) = (40®) =
U-L
R + 2ja>L
Воспользуемся теперь методом контурных токов
для определения комплексной спектральной плотно-
сти тока 4(/®)- Составим систему уравнений состо-
яния для двух контуров:
I к 1 ( /®) ( # + /® L) -/к2 ( ]'а ) • jсо L = U (> );
-41 О®)• J<oL + 4г (/®)(Я + /со!) = 0.
Из второго уравнения системы выразим 41(/<о):
41 (/®) = 4г О®)
Подставляя полученное выражение /К1(/<о) и
(7(/со) = U/j(£) в первое уравнение системы, получаем
198
, ,. x_ U-L
d2 -э r D •
R + ]2g)LR
Поскольку /К2(/а>) = /2(700), то по закону Ома
найдем комплексную спектральную плотность напря-
жения Ur(jo>):
Выражение UrCjo), полученное с применением
метода контурных токов, совпадает с Ur(j'g)), полу-
ченным методом узловых напряжений.
Проверим также, можно ли использовать метод
эквивалентного генератора для расчета Ur(jg)). Для
этого найдем комплексную спектральную плотность
напряжения холостого хода С7/?хх(/о). Напряжение
холостого хода равно напряжению на индуктивно-
сти, значит, равны и их комплексные спектральные
плотности, поэтому
Сопротивление эквивалентного генератора
2эг(/<о)=
Э1ЧУ ' R + JoL
Комплексная спектральная плотность тока IrCjo)
рассчитывается в соответствии с методом эквивалент-
ного генератора по формуле
I (= ^^хх L
RU Zэг ( jа) +R ~ R2 + j2R($L
Комплексная спектральная плотность напряжения
как и следовало ожидать, имеет тот же самый вид,
что и при расчете любым другим методом.
По известному выражению комплексной спек-
тральной плотности напряжения Ur(Jq>) можно най-
ти мгновенное значение самого напряжения UR^t),
применив преобразование Фурье (4.7):
199
Рис. 4.29. График реакции цепи на импульс включения
-00
Однако поскольку полученное выражение Ur(Jg))
после простейшего преобразования приобретает вид
^Л(/со) =
U/2 U'
R
2L + J0>
а + /со ’
то нетрудно заметить, что это есть комплексная спек-
тральная плотность экспоненциального импульса, т.е.
тт R t
uR(t) = U' e-at =ув 2L.
График напряжения uR(t), являющегося реакци-
ей цепи (рис. 4.26) на воздействие u(t) в виде им-
пульса включения, приведен на рис. 4.29.
Для определения реакции цепи в виде четырехполюсника
при воздействии на входе цепи непериодического сигнала ис-
пользуют комплексную передаточную функцию цепи. Как было
установлено в § 4.3, комплексная передаточная функция по на-
пряжению (4.20) — это отношение комплексных спектральных
плотностей реакции и воздействия в цепи:
Ни (/со) =
^2 О)
СЛО©)’
Зная комплексную спектральную плотность воздействия
171(/со) и комплексную передаточную функцию цепи,
легко найти комплексную спектральную плотность (Уз (/со) реак-
ции цепи:
С72(7<о) = ^1 (/®) • Ни (/со j.
(4.27)
200
Аналогичным образом, используя соотношения (4.21), (4.22)
и (4.23), можно определить любую реакцию четырехполюсника
(рис. 4.23) на непериодическое воздействие:
(72(>(о) = /1(;а))-Я2(;со);
/2(» = /1(»-Я,(»;
72(/©) = £71(»Яу(».
Все величины в уравнении (4.27) являются комплексными и
могут быть записаны в показательной форме:
С72 (<о)е><р2(е>) = ^(ш)^^ .Ни(<о)е^"(в,)
При этом уравнение (4.27) можно представить совокупностью
двух уравнений:
(J2 (со) = (Л (©)•#„ (со), (4.28)
Ф2(о>) = <Р1(а>) + <1>я(й)), (4.29)
из которых следует, что спектральная плотность амплитуд
реакции цепи равна произведению спектральной плотности ам-
плитуд (71(®) воздействия и АЧХ Ни(а>) цепи, а спектральная
плотность фаз <рг(®) реакции цепи равна сумме спектральной
плотности фаз <pi(a>) воздействия и ФЧХ <ря(а>) цепи.
После определения комплексной спектральной плотности
С72(усо) реакции цепи по формулам (4.27) или (4.28), (4.29) сама
реакция u2(i) четырехполюсника может быть найдена с помощью
обратного преобразования Фурье (4.7) или по таблицам.
Пример 4.14. Найдем комплексную спектральную плотность на-
пряжения UR(t) в цепи, изображенной на рис. 4.26,
при воздействии u(t) в виде импульса включения
(рис. 4.27).
Комплексная спектральная плотность U(ja)) им-
пульса включения
«<«)=(,°. при5;°„;
[U при t О,
как известно, имеет вид
(7(;со) = (7/(/со).
Найдем комплексную передаточную функцию
цепи на рис. 4.26, используя выражение
(4.20):
201
Hur ( Jw) ~
. R - ]<£>L
UrU<o) ^R + jmL
w \ R + joL)
j(oL
R + /2<в£
Комплексная спектральная плотность Ur(jg>)
реакции uR(t) цепи рассчитывается по формуле
(4.27):
UL
R + /2со£ ’
Выражение для расчета (JR(jco) совпадает с
формулой комплексной спектральной плотности, по-
лученной при решении ранее той же самой задачи
другим способом (см. пример 4.13).
Пример 4.15. Найдем спектральную плотность амплитуд С/г (со)
выходного сигнала в цепи, изображенной на
рис. 4.30, на вход которой подается прямоугольный
импульс (рис. 4.31). Параметры сигнала и элементов
цепи заданы: U = 4 В, т = 250 мкс, R = 5 Ом,
С = 25 мкФ.
Определим вначале комплексную спектральную
плотность входного прямоугольного импульса, ис-
пользуя преобразование Фурье (4.6):
1/1 (/со) = J u^e-^^t = ]ue~J(atdt =
_ (j . Tsin((OT/2) ^-Дшт/2)
сот/2
«1(/)|
о
Рис. 4.30. 7?С-цепь
0 т t
Рис. 4.31. Прямоугольный
импульс
202
Спектральная плотность амплитуд
(Л(со) = U т
sin(G>t/2)
со т/2
принимает значение, равное площади импульса U-i =
= 1 В мс на нулевой частоте, и значения, равные ну-
лю на частотах fk = k/т, т.е. кратных 4 кГц. График
Ux(f) приведен на рис. 4.32, а.
Найдем теперь комплексную передаточную функ-
цию цепи, изображенной на рис. 4.30. В соответст-
вии с (4.20) имеем
н( 1(й} = ВД = /(»[1/(>С)] = 1
u 7 /(>)[2Я + 1/(/®С)] l + jZRCa»
АЧХ 7? С-цепи
Н (е)_ 1 - 1
° V1 + 47?2С2со2 >/1 + 62,5 10"9со2
уменьшается от единицы до нуля с ростом частоты.
График зависимости Н( f) изображен на рис. 4.32, б.
Рис. 4.32. Спектры амплитуд входного сигнала (а),
АЧХ цепи (б) и выходного сигнала (в).
203
Спектральную плотность амплитуд U2C0)) вы-
ходного сигнала найдем, используя (4.28):
С/2(о) = [/1(<о)Я„(<о) = Ут х
сот/2
1 _ 8sin(125 • 10~6<о)
Х V1 + 4Я2С2®2 <в>/1 + 62,5 • 10~9<о2 '
График (72(f) приведен на рис. 4.32, в.
Безыскаженная передача сигналов через линейную цепь
возможна только при равномерной АЧХ и линейной ФЧХ цепи.
Спектральный метод является достаточно эффективным и нагляд-
ным при анализе передачи сигналов через линейную систему. Он
позволяет оценить частотные искажения в канале связи, требова-
ния к характеристикам электрической цепи. Особенно важно оп-
ределить требования к АЧХ и ФЧХ цепи с точки зрения искаже-
ния формы сигнала. Определим условия неискажаемой передачи
сигнала через линейную систему. Предположим, что на входе ли-
нейной цепи (четырехполюсника) действует сигнал щ(Л) опреде-
ленной формы (рис. 4.33). На выходе в результате прохождения
сигнала через четырехполюсник с комплексной передаточной
функцией Й(/со) амплитуда сигнала может измениться, и сигнал
вследствие конечности скорости его распространения может за-
паздывать относительно входного воздействия на io- Однако
важно, чтобы при этом не изменилась форма сигнала. Таким об-
разом, условие безыскаженной передачи можно сформулировать
с помощью равенства
u2(t) = Xw1(t-t0), (4.30)
где К — некоторая вещественная постоянная; to — время задерж-
ки (запаздывания) выходного сигнала относительно входного.
Применив к (4.30) прямое преобразование Фурье и учтя свойство
линейности и теорему запаздывания, перепишем условие (4.30) в
частотной области:
204
и2и<й) = Ки^]Ъ)е-}а,1°. (4.31)
Так как комплексная передаточная функция цепи с учетом (4.5)
должна быть
Я(» = = Ке^»,
^10“)
То отсюда получаем требование к АЧХ и ФЧХ неискажающей
цепи:
Н((ц) =-К = const; (4.32)
ф(со) =-cot0, (4.33)
т.е. для того, чтобы линейная цепь не искажала форму сигнала,
ее АЧХ должна быть равномерной (рис. 4.34, а), а ФЧХ — ли-
нейной (рис. 4.34, б).
Условие безыскаженной передачи во всем частотном диапа-
зоне можно выполнить лишь для резистивных цепей*. В цепях с
реактивными элементами условия (4.32) и (4.33) можно обеспе-
чить лишь в ограниченном частотном диапазоне соо (на рис. 4.34
показано штриховой линией).
Из данного параграфа мы узнали, что:
Расчет спектров реакций цепи выполняется теми же мето-
дами, что и расчет цепи синусоидального тока.
От спектров реакции к их мгновенным значениям можно
перейти с помощью обратного преобразования Фурье.
Спектр сигнала на выходе цепи находится как произведе-
ние спектра входного сигнала и комплексной передаточной
функции цепи.
Линейная цепь, имеющая равномерную АЧХ и линейную
ФЧХ, не искажает форму сигнала, проходящего через нее.
Вопросы и задания для самоконтроля
1- Как рассчитывается комплексная спектральная плотность не-
периодического сигнала?
2- Как восстановить непериодический сигнал по его комплексной
спектральной плотности?
3- Что такое спектральная плотность амплитуд и спектральная
плотность фаз?
Если пренебречь зависимостью сопротивлений резистивных элементов от частоты.
205
4. Рассчитать комплексную спектральную плотность и построить
график (7(<о) прямоугольного импульса, изображенного на
рис. 4.7, если U = 5 В, т = 200 мкс.
5. Рассчитать спектральную плотность амплитуд экспоненциаль-
ного импульса тока г(£) = 0,75е-4 1о7< (при i > 0) на частоте
f = 10 МГц.
6. Доказать теорему линейности на примере суммирования двух
экспоненциальных импульсов.
7. Какие изменения произойдут в спектрах амплитуд и фаз пря-
моугольного импульса, изображенного на рис. 4.16, а, если
его задержать по времени на т/2?
8. Сформулировать теоремы дифференцирования и интегрирова-
ния сигнала.
9. Как изменится график спектральной плотности амплитуд пря-
моугольного импульса, если его длительность уменьшить в
три раза?
10. Сформулировать теорему модуляции, теоремы свертки спек-
тров и сигналов.
11. Как связаны между собой спектры непериодического и перио-
дического сигналов?
12. Построить графики спектральных плотностей амплитуд пря-
моугольного импульса амплитудой U = 1 В, длительностью
t = 5 мс и последовательности прямоугольных импульсов с
параметрами U = 1 В, т = 5 мс, Т = 25 мс.
13. Как определяется комплексная передаточная функция цепи?
14. Как изменится график АЧХ цепи, изображенной на рис. 4.24,
если параллельно конденсатору подключить нагрузку, рав-
ную R7
15. Какие методы используются для расчета реакции цепи на не-
периодическое воздействие?
16. Рассчитать комплексную спектральную плотность напряжения
Ur(J(£>) в цепи, изображенной на рис. 4.26, если вместо ин-
дуктивности L включить емкость С. Воздействием u(t) явля-
ется импульс включения (рис. 4.27).
17. Сформулировать условия безыскаженной передачи сигналов
через линейную цепь.
Глава 5. Анализ реакции линейной цепи
на непериодическое воздействие
сложной формы (операторный метод)
5.1. Представление непериодического
воздействия интегралом Лапласа
Переход в гл. 4 от временных представлений напряжений
u(t) и токов :(t) к спектральным плотностям U (jo) и I(jo)
позволил при расчете реакций цепи заменить решение дифферен-
циально-интегральных уравнений решением комплексных алгеб-
раических уравнений, что существенно проще. Действительно, в
цепи на рис. 5.1 реакция в виде напряжения на емкости izc(t)
может быть найдена из решения дифференциального уравнения
/?C^^ + MC(i) = ur(i).
at
Переходя к спектральным плотностям, можно записать
joRCUc(j®) + Uc (» = UT (jo).
Откуда
Uc(jG>)=
CU 7 i + joRC
Для различных видов воздействия ur(t) можно определить их
спектры и вычислить спектральную плотность реакции Uc(jo).
При переходе к временному представлению реакции uc(t)
необходимо вычислять интеграл (4.7):
uc(i) = ± J
271 1 + ]®RC
Рис. 5.1. ЯС-цепь Рис. 5.2. Комплексная плоскость
оператора р = а + /со
207
В гл. 4 мы представляли воздействие в виде интеграла Фу-
рье (4.7):
= J U(jG>)eje,tdG). (5.1)
-00
Существует также другое представление воздействия в виде
интеграла Лапласа.
Заменим в интеграле (5.1) оператор /со оператором р = а + /со,
значения которого представляют собой точки на комплексной
плоскости (рис. 5.2).
В интеграле Фурье область изменений переменной /со рас-
пространялась от —/со до +/оо. Область изменения переменной
р = а + /со будет лежать от а - /со до а +/со. Очевидно также, что
]
Тогда вместо интеграла (5.1) можно записать выражение
1 а+;оо "»<«> = i j 2^7 а-/оо (5.2)
Аналогично для тока
4 а+/оо = —: f I(p)eptdp. 2nJ а-/® (5.3)
Выражения (5.2) и (5.3) описывают представление напряже-
ния и тока (как воздействия, так и реакции) в виде интеграла
Лапласа.
Подстановка оператора р вместо /со в интеграл (4.6)
t/(;co)= e-i^dt 0 (5.4)
или интеграл
0 (5.5)
приводит к следующим выражениям:
(7(p)=fw(i)e-^di; о (5.6)
I(p) = e~ptdt. (5.7)
0
208
В выражениях (5.4) и (5.5) нижние пределы интегрирования
взяты равными нулю. Тем самым заранее предполагается, что напря-
жения и токи отсутствуют при t < 0. Это не слишком жесткое огра
ничение, накладываемое на сигналы, поскольку всегда можно вы-
брать такое начало отсчета, ранее которого сигналы не существуют.
Выражения типа (5.6) и (5.7) получили название прямого
преобразования Лапласа. Оно позволяет по временной форме
сигнала определить его изображение по Лапласу. Выражения
(5.2) и (5.3) называются -обратным преобразованием Лапласа.
Оно дает возможность перейти от изображения к оригиналу, т.е.
к временному представлению сигнала.
Для сокращенной записи преобразований (5.2), (5.3) и (5.6),
(5.7) используют знак соответствия
Таблица 5.1. Преобразования Лапласа сигналов, используемых при
анализе цепей
№ п/п м(£)или Kt) U(р)или I(p)
1 Kt) VP
2 А A/p
3 8(f) 1
4 e±at l/(p?a)
5 l-e~at a p(p + a)
6 sinco0t <0p 2 2 p +C0o
7 COS(00t p 2 2 p +®0
8 e~at sin G)Ot COq (p + a)2+®o
9 e"af cos<»ot p + a (p + a)2 -ьсоо
_ 10 t 1/p2
И t” n! p”+1
12 e~attn n\ (p + a)"+1
209
u(t) =' U(/?);
i(i) .= 1{р).
Преобразования Лапласа для простейших функций рассчита-
ны и сведены в справочные таблицы. Для теоретических и экспе-
риментальных исследований характеристик электрических цепей
и передачи сообщений по каналам связи используют испытатель-
ные сигналы в форме единичной функции 1(£) и единичной им-
пульсной функции 5(£) (функция Дирака), а также гармониче-
ские импульсы включения, уровни постоянных напряжений, пря-
моугольные импульсы, экспоненциальные сигналы и т.д. Ориги-
налы и изображения сигналов, наиболее часто применяемых при
анализе электрических цепей, приведены в табл. 5.1.
Определим изображения некоторых функций, оригиналы ко-
торых приведены в этой табл. 5.1.
Пример 5.1. Найдем изображение напряжения в форме единичной
функции!(£), которое соответствует включению по-
стоянного напряжения, равного 1 В, в момент t = 0.
Напряжение u(t) = l(i), изображенное на рис. 5.3,
можно представить как
a(t) (0 при t<0,
(1 при с > 0.
Преобразование Лапласа напряжения tz(t) рас-
считаем, используя выражение (5.6):
Полученное изображение напряжения в форме
единичной функции
соответствует выражению, приведенному в строке 1
табл. 5.1
и(0
1
0
t
Рис. 5.3. Напряжение в форме единичной функции
210
Любое произвольное постоянное напряжение,
подключенное в момент времени t = 0, может быть
получено путем умножения единичной функции на
соответствующую константу А, т.е. u(t) = А l(i).
Изображение такого напряжения приведено в строке
2 табл. 5.1:
Пример 5.2. Найдем изображения напряжения в форме экспо-
ненциальной функциям^) = e~at.
Согласно (5.6) изображение экспоненциального
напряжения имеет вид
U(p) = =
О о
= - 1 е -(Р+а У _ *
-(Р + а) о Р + а
или в сокращенной форме
-at 1
р + а’
что соответствует выражению, приведенному в стро-
ке 4 табл. 5.1.
Пример 5.3. Найдем изображение тока i(i) = cosco0i.
Воспользуемся формулой Эйлера и представим
косинусоидальную функцию cos co0i в виде
cos<B0i =
Изображение 7(р) гармонического тока полу-
чим, используя прямое преобразование Лапласа
(5.7) и разложение cosa>0i на две экспоненциальные
функции:
I(p) = Ji(t)e-^dt = + e~ja>ot)e~pldt =
о о2
= 1 "[ e-(p-W) Udt + - 1е~<р+™>) £di.
nJ n J
z 0 z 0
Рассчитав сумму двух приведенных выше интег-
ралов, получим
14*
211
rt 4 If 1. 1 'l p
Up) = d ——+—;— = ?r..>
2{p-JG)Q p + JG)q J p'+(i)o
или
* • p
COS COOE .= —T2-—7,
p +g>0
что соответствует выражению в строке 7 табл. 5.1.
Аналогичным образом, используя преобразование Лапласа
(5.6) или (5.7), можно найти изображения синусоидального и ко-
синусоидального сигналов, амплитуды которых затухают по экс-
поненциальному закону (строки 8 и 9 в табл. 5.1), единичной
импульсной функции
sen = !» 4м
(О при t *0
(строка 3 в табл. 5.1), а также типовых сигналов и их комбина-
ций (строки 5, 10, И, 12 табл. 5.1), применение которых будет
показано в следующих параграфах.
Свойства преобразований Лапласа. Математическим опе-
рациям над оригиналами соответствуют определенные операции
над изображениями, называемые свойствами преобразований
Лапласа. Они облегчают нахождение изображений сложных
сигналов и вычисление искомых оригиналов по найденным изо-
бражениям. Свойства преобразований Лапласа применимы к
любым сигналам (токам и напряжениям), рассматриваемым в
этой главе.
Умножение на константу. Если оригинал u(t), имеющий
изображение U(p), умножается на постоянный коэффициент
А, то изображение тоже умножается на этот же самый коэффи-
циент:
Au(t) = A-U(p). (5.8)
Аналогично
A i(t) = А 1(р).
Это свойство легко доказать, взяв преобразование Лапласа
(5.6) или (5.7) от функции A u(t) njiaA iU).
Свойство линейности можно записать в виде
п п
lLakukU)= ±akUk(p),
k=i k=i
(5.9)
212
w n
iakik(t) = XakIk(p)>
k=i k=i
(5.10)
где dk ~ постоянные коэффициенты.
Свойство легко доказать, если применить к левой части пря-
мое преобразование Лапласа (5.6) или (5.7)
Приведенные выше формулы означают, что преобразование
Лапласа суммы нескольких оригиналов есть сумма преобразова-
ний Лапласа каждого из оригиналов.
Пример 5.4. Найдем изображение напряжения
u(t) = 10 + 5e"4t +12sin5i + 8e-2t cos5£.
Для нахождения изображения U(p) воспользуем-
ся данными табл. 5.1 (строки 2, 4, 6, 9) и свойствами
линейности и умножения на константу. Получим
(7(р) = 10 + _5_ + _12^_ + _._8_(£±.2). =
{Р) р р + 4 р2 + 52 (р + 2)2+52
= 10 5 60 8р + 16
р р + 4 р2 + 25 р2 + 4р + 29
Дифференцирование оригинала (теорема дифференцирования)
и'(t) .= pU(р) - ы(0). (5.11)
Эта математическая операция означает, что для нахождения пре-
образования Лапласа производной от оригинала необходимо изо-
бражение оригинала умножить на оператор р и вычесть началь-
ное значение оригинала.
Для доказательства подставим и'(Л) в выражение для опре-
деления прямого преобразования Лапласа (5.6):
Ju'(t)e-^t = =
О 0
= “je-^duCt).
о
После интегрирования по частям получаем
fe~ptdu(t) = e~pt • u(t)lo + р $u(t)e~ptdt = pU(p)-u(0).
о о
Если начальное значение оригинала равно нулю, т.е.
& ( 0) = 0, то
213
u'U) .= pU(p).
Аналогично
i'(t) = pl(p)- i(0)
при ненулевых начальных условиях,
i'(i) .= pl(p)
при г(0) = 0.
Другими словами, операция дифференцирования во времен-
ной области заменяется простой операцией умножения изображе-
ния на оператор р в операторной области.
Интегрирование оригинала (теорема интегрирования)
\u(t)dt .= , о Р (5.12)
о Р (5.13)
Эта математическая операция показывает, что для нахожде-
ния преобразования Лапласа определенного интеграла от ориги-
нала необходимо разделить изображение оригинала на оператор
р, т.е. операция интегрирования оригинала во временной области
заменяется простой операцией деления изображения на р в опе-
раторной области.
Данную теорему доказывают, используя свойство дифферен-
цирования оригинала.
Применение теорем дифференцирования и интегрирования
оригинала позволяет переходить от интегродифференциальных
уравнений для оригинала к более простым алгебраическим урав-
нениям, записываемым для изображений, и дальнейшему опреде-
лению оригинала по найденному изображению.
Пример 5.5. Найдем изображение напряжения, имеющего форму
косинусоиды u(t) = cosco0£, если известно, что нап-
ряжение щ (t) = sin<о0£ имеет изображение (7i(p) =
= соо/(р2 +соо) (см. строку 6 в табл. 5.1).
Определим производную функции = sino>0£.
Получим
u'i (.t) = со0 cos<n0i.
Воспользуемся теоремой дифференцирования
(5.11) и получим изображение функции w'j(i):
u\(t) = p-Ui (р) - щ (0)
214
или
u\(t) =’ 0)02 -0.
р + соо
Найдем также изображение функции ci)0cosa>o<>
применив свойство умножения на константу:
О>0 COSC00t= (DqU (р),
где U(р) — изображение оригинала cosco0£.
Сравнивая два последних выражения, находим
изображение U(p) напряжения u(t) = cos<B0t:
Р +®о
или
. . Р
cos coo £ •= —г,
р +®о
что согласуется со строкой 7 табл. 5.1.
Теорема запаздывания
u(t±to) = U(p)e±pt°.
(5.14)
Эта математическая запись означает, что сдвиг оригинала
u(t) по оси времени на ±t$ приводит к умножению изображения
U(р) на экспоненту e±pt°.
Теорема легко доказывается, если осуществить замену пере-
менной т = £±£0 и взять преобразование Лапласа (5.6) функции
м(т).
Подобное соотношение можно записать и для оригинала
i(t). В дальнейшем будем рассматривать свойства преобразова-
ний Лапласа главным образом для напряжения u(t).
Пример 5.6. Найдем изображение экспоненциального напряже-
ния (рис. 5.4, а):
u(t) = [e~at ПРИ
[0 при t > tQ.
и (Л) как сумму двух
Представим напряжение
напряжений (рис. 5.4, б):
f
“1U)= о
при t < 0;
215
u2(i) = H’at0 e'a('_'o) при t > t0;
[О при t < t0.
Изображение t/i(p) напряжения щ(Л) имеет
вид (строка 4 табл. 5.1)
Напряжение w2(t) с учетом теоремы запаздыва-
ния (5.14) имеет изображение
р-«<0
U2(p) = -~----
р + а
На основании свойства линейности
щ(Л) + и2(Л) = Ui(p) + U2(p)
получаем изображение U(p) напряжения, показан-
ного на рис. 5.4, а:
Ui(p) = —-----L^Le-r>to =_l_[i_e-(p+«)*o]
р + а р + а р + а
Этот же результат получается, если найти пря-
мое преобразование Лапласа непосредственно для за-
данного напряжения:
u(t) = [e~at при
(0 при t > t0-
Имеем
*0
U(p)= [e-o-'e-^dt^
о
_ 1 е-(.Р+аУ ° _ * [j _ е-(р+а)*о ]
р+а 0 р+а
«(/)
1
о
u(t) — е'а1
I е-<М>
4)
u(f)
6)
t
а)
Рис. 5.4. Напряжение в форме
экспоненциального импульса
216
Теорема смещения
U (р±а) = и<Л)е*а*. (5.15)
Эта теорема констатирует, что если оригинал u(t} умножает-
ся на е*”*, то изображение этого произведения получается заме-
ной р в изображении U(p) оригинала u(t) на р±а. Причем а
может быть как действительной, так и комплексной величиной.
Теорема (5.15) следует непосредственно из прямого преобра-
зования Лапласа, если в (5.6) вместо uit) подставить и<Л)е*.
Пример 5.7. Найдем изображение синусоидального напряжения,
амплитуда которого затухает по экспоненциальному
закону
щ (() = e~at sincooi.
Из табл. 5.1 следует, что оригиналу u(t) = sin со о t
соответствует изображение СЧр) = сОр/( Р2 + ®о) • По
теореме смещения (5.15) умножение sin со о t на e~at
приводит к замене в U(p) оператора р на р + а, по-
этому изображение С71(р») сигнала имеет вид
соо
+ а)2 +<»о
что согласуется со строкой 8 в табл. 5.1.
(/1(р) = -
(Р
Теорема подобия (изменение масштаба независимого пере-
менного)
w(ai).= -(/f^\
а \а)
(5.16)
где а — постоянный вещественный коэффициент. Эта теорема ус-
танавливает, что изменению масштаба оригинала по оси времени
соответствует изменение масштаба изображения. Причем умно-
жение времени t на коэффициент а ведет к делению изображения
и переменной р на тот же самый коэффициент а.
Теорема доказывается следующим образом. Находим прямое
преобразование Лапласа (5.6) для оригинала u(at):
fu(at)e ptdt = —fe ^u(at)d(.at) = —i/f—Y
о <4 a \aj
Пример 5.8. Найдем изображение U(p) экспоненциального нап-
ряжения u(t) = e~2at, если известно изображение
экспоненциального напряжения = e~at:
217
е at =—-— (см. табл. 5.1).
р + а
По теореме подобия (5.16) с учетом того, что
а = 2, получаем
Щр) = 1(7/2] = 1—— = —
v а Ча/ 2 £ + а р + 2а
2
Найдем теперь изображение (7(р), используя
преобразование Лапласа (5.6):
U(p) = °\e-2ate-Ptdt =-!e-(^2a)t
о р + 2а
= __L_
о P + 2a‘
Получили тот же самый результат, что и при
применении теоремы подобия.
Теорема свертки
t t
U\{pyU2(p) Jwi(^-t)u2(t)</t = |м1(т)и2(^-т)(/т. (5.17)
о о
Эта теорема устанавливает, что умножению изображений в
области переменной р соответствует свертка оригиналов во вре-
менной области.
Пример 5.9. Найдем изображение (7(р) свертки двух напряже-
ний:^ (£) = 1(£), u2(.t) = e~at.
Изображения напряжений щ(Л) и u2(t) приве-
дены в табл. 5.1:
1(0 = 1 = (/,(?);
р
По теореме свертки изображение U(p) свертки
оригиналов имеет вид
(/(р) = (/,(р) (7г(р)= 1
р(р + а)
Найдем также изображение свертки оригиналов
напряжений щ(Л) и a2(i), используя прямое пре-
образование Лапласа. Для этого определим вначале
функцию свертки:
218
u(t) = /«j(t)u2(i-t)Jt = fl • e a(f t)<7t = — (1-e a/).
о о a
Преобразование Лапласа (5.6) оригинала напря-
жения u(t)
U(p) = = ---L_
о a p + a
1
p(p + a)
совпадает с изображением, полученным с применени-
ем теоремы свертки.
По полученному изображению 1/(р) легко найти
спектр сигнала. Для этого заменяем р на /со и полу-
чаем комплексную спектральную плотность
U (» =
1
/со(/со + а)
Сопоставление свойств и теорем преобразований Лапласа и
Фурье, рассмотренных в гл. 4, показывает, что при замене опера-
тора р на /со и наоборот теоремы и свойства преобразований Лап-
ласа и Фурье переходят друг в друга. А это означает, что спектры
непериодических сигналов можно вычислить с помощью прямого
преобразования Лапласа и его свойств и теорем. В свою очередь,
физическая интерпретация теорем спектрального анализа позволяет
понять физический смысл теорем операционного исчисления.
Переход от изображений к сигналам. Для нахождения сиг-
нала по его изображению можно использовать обратное преобра-
зование Лапласа (5.2) и (5.3). Однако обычно такой подход до-
вольно трудоемок, и на практике используют более простые спо-
собы. Проще всего применить справочные таблицы, устанавли-
вающие соответствие между оригиналами и их изображениями
Для типовых воздействий в электрических цепях, например, мож-
но использовать табл. 5.1.
Пример 5.10. Найдем сигнал u(t), изображение U(p) которого
задано в виде
10 15 20
р рг р + 3
По табл. 5.1 и с учетом постоянных коэффици-
ентов определяем в выражении для U(p) оригиналы
каждого из слагаемых:
219
— = 10-1(£),
Р
-Ц- = 15г,
р
= 20e“3t.
р + 3
Применяя теорему линейности, получаем напря-
жение u(t):
и(г) = 10 + 15г + 20е-3*.
Пример 5.11. Найдем воздействие z(t), изображение которого
задано в виде
/(р)=8£±30.
р2 + 25
Представим выражение /(р) в виде суммы двух
дробей:
/(р) = 8-—#...... + б-
р2 +(5)2 р2 +(5)2
По табл. 5.1 находим
-~-Р-—=- = cos5i (строка 7),
р2+(5)2
—------х- = sin 5г (строка 6).
р2+(5)2
Применяя свойства линейности и умножения на кон-
станту, получаем оригинал тока
г(г) = 8соз5г + б5т5г.
Использование таблиц при переходе от изображения к сигна-
лам удобно, но не всегда удается представить изображение в виде
совокупности табличных величин. Поэтому для определения инте-
гралов токов и напряжений (5.2), (5.3) применяют теорему раз-
ложения, которая позволяет операцию интегрирования заменить
на операцию суммирования, что значительно упрощает расчеты.
Теорема разложения. Большинство изображений напряже-
ний и токов, используемых в теории цепей, могут быть представ-
лены в виде отношения двух полиномов:
220
_ а-Р" +«,-|Р”4 + +<!0 ,, ,яч
где Яп> an-i, • ••, «о. bm, bm.it.... bo - вещественные коэффициенты,
причем F^p) и F2(p) не имеют общих корней; степень полинома
числителя п меньше степени полинома знаменателя т, т.е. дробь
р}(р)/Р2(р) — рациональная.
Представим знаменатель дроби (5.18) в виде произведения
сомножителей:
F2(p) = bm(p-pl)(p-p2) ...(Р-Рт),
где Pi, р2> •••> Рт ~ полюсы знаменателя изображения U(p) или
корни характеристического уравненияF2(p) = 0.
Тогда изображение напряжения U(p) можно разложить на
простые дроби:
u(p)=
^г(р) k^p-Pk
(5.19)
Коэффициенты разложения А^ в (5.19) в соответствии с тео-
рией функций комплексного переменного определяются по фор-
муле
Fi(pk) j-.,, ч dF2(p)
Ak = ч > где F2 (pk) =.........
F2 (pk) dP
p=Pk
С учетом того, что изображению А^/{р - Pk) в (5.19) соответ-
ствует оригинал AkePkt (см. табл. 5.1), на основании свойства ли-
нейности преобразования Лапласа получаем оригинал напряжения
u(t) = f Il(Pk)ePkt
^F2'(pk)
(5.20)
Это общая форма теоремы разложения, которая позволяет
найти оригинал напряжения по его изображению в виде (5.20)
Для случая простых корней.
Если среди полюсов изображения напряжения (5.18) имеют-
ся комплексно-сопряженные корни = -а ± /со, то получаются
Два сопряженных слагаемых, сумма которых равна удвоенному
значению действительной части:
u(£) = 2Re ' Fi(pi) сР<<1 .F1(P\) J
Формулы, аналогичные (5.20) и (5.21), можно использовать
также для определения оригинала тока по его изображению.
221
Пример 5.12. Найдем оригинал напряжения w(t), изображение
которого имеет вид
ЗОр + 30
Р2+Зр
Для заданного изображения U (р) = Fi (p)/F2(p)
имеем
Fi(p) - ЗОр+ 30; F2(p) = p2 + 3p.
Найдем F2'(p) = 2р + 3. Корни уравнения F2(p) =
= 0 равны соответственно
pi =0; р2 = -3.
Определяем
Л (Pi) = 30; F1(p2) = -60;
^2'(P1) = 3; F2(p2) = -3.
По теореме разложения (5.20) находим оригинал
напряжения:
?2 (Pi) F2(p2)
= 3Oe/o.f + Z6Oe-3t = lo + 2Oe-3t
3 -3
Пример 5.13. Найдем оригинал напряжения u(.t), изображение
которого имеет вид
u(p)= Л+26-г
р + 6р + 34
Для заданного изображения имеем
Л(р) = 2р + 26;
F2(p) = р2 +6р + 34.
Корни уравнения F2(p) = 0 комплексно-сопря-
женные:
Pi,2 =-3±/5.
Находим fi(pi) иГ2'(Р1):
F( (pi) = 2 (-3 + /5) + 26 = 20 + /10;
F2'(p) = 2p + 6;
F2'(p1) = 2(-3 + ;5) + 6 =/10.
222
Для нахождения оригинала напряжения восполь-
зуемся формулой (5.21):
и(Л) = 2Re[-F1^^ e^l = 2Re[-
/2'(Pi) J L ^10
/10
-3'.<Д5'] =
= 2Re|_(l-/2)e- -e?5f J =
= 2e-3<Re[e>s/-2e>(5t+9°O)] =
= 2e-3f cos 5t + 4e-3< sin 5£.
Из данного параграфа мы узнали, что:
• Преобразование Лапласа является обобщением преобразо- 1
вания Фурье. Заменой оператора /о на оператор р и на- |
оборот осуществляется переход от одного преобразования к ч
другому. j
• Спектральная плотность сигнала — это сечение его изобра-
жения по Лапласу вдоль мнимой оси комплексной плоско- 4
сти. Это означает, что спектры сигналов могут быть вы- |
числены с помощью прямого преобразования Лапласа и, |
наоборот, физический смысл теорем операционного исчис- |
ления раскрывают теоремы о спектрах. |
5.2. Законы Ома и Кирхгофа
в операторной форме
Применение преобразований Лапласа и его свойств к непе-
риодическим сигналам позволяет преобразовать интегральные и
дифференциальные соотношения между напряжениями и токами
на элементах цепи в алгебраические соотношения. Рассмотрим
электрическую цепь, содержащую только пассивные элементы
(рис. 5.5, а). На эту цепь воздействует напряжение и(£), а в це-
пи протекает ток i(£). Только на резистивных элементах цепи
напряжения и токи связаны простым алгебраическим уравнением.
На емкостных и индуктивных элементах напряжения и токи свя-
заны интегродифференциальным преобразованием.
Пусть U(p) и Др) представляют собой преобразования Ла-
пласа напряжения w(£) и тока г(£) в цепи, изображенной на
Рис. 5.5, а. В операторной схеме замещения (рис. 5.5, б) вели-
чина Z(p), называемая операторным сопротивлением цепи,
°пределяется как отношение изображения напряжения к изобра-
жению тока:
223
б)
а)
Рис. 5.5. Пассивная /?£С-цепь и ее операторная схема замещения
Кр)
ко
u(t)
Z(p)~R
а) Ф
Рис. 5.6. Сопротивление и его операторная схема замещения
Z(p) = U(P^
{р) W
Величина Y(р), обратная операторному сопротивлению, на-
зывается операторной проводимостью цепи:
У(р) = —-— = УУеУ
Z(p) U(p)
Определим операторные сопротивления каждого из трех ос-
новных элементов цепи.
Сопротивление. Мгновенные значения напряжения и тока в
сопротивлении (рис. 5.6, а) связаны соотношением
w(t) = 7?i(i). (5.22)
Применяя преобразование Лапласа к левой и правой частям
уравнения (5.22), получаем
U(p) = RI(p).
(5.23)
Выражение (5.23), устанавливающее связь между изображе-
ниями напряжения U(p) и тока 1(р) в сопротивлении, представ-
ляет собой закон Ома в операторной форме для сопротивления.
Операторное сопротивление Z(p) в схеме замещения
(рис. 5.6, б), полученное из уравнения (5.23):
Z("’ = W = R’
это просто значение сопротивления R.
224
Индуктивность. Мгновенные значения напряжения и тока в
индуктивности (рис. 5.7, а) связаны соотношением (В.З):
uL(t) = L^-. (5.24)
at
Применяя преобразование Лапласа к левой и правой частям
уравнения (5.24) и учитывая теорему дифференцирования (5.11),
получаем
UL(p) = pLI(p)-Li(O). (5.25)
Отсюда
/( ) = ^(р)^«оТ~1 (5 26)
_______pL_______
Выражения (5.25) и (5.26), устанавливающие соотношения
между изображениями напряжения U(p) и тока 1(р), — это за-
кон Ома в операторной форме для элемента индуктивности.
На рис. 5.7, б приведена операторная схема замещения ин-
дуктивности, составленная на основании анализа выражения
(5.26). В этой схеме индуктивность L заменяется операторным
сопротивлением Z(p) = pL и последовательно с ним включается
источник £г(0), направление которого совпадает с направлением
тока. Величину £г(0), характеризующую энергию магнитного
поля, запасенную в индуктивности к моменту времени t = 0, на-
зывают еще расчетной эдс.
В случае, когда начальное значение тока в индуктивности
равно нулю: г(0) = 0, уравнения закона Ома (5.25) и (5.26) уп-
рощаются:
CTL(p) = pLZ(p) = Z(p)/(p),
Ul(p\ (5.27)
pL Z(p) ’
и в операторной схеме замещения (рис. 5.7, в) индуктивность L
заменяется только на операторное сопротивление Z(p) = pL, а
источник £г(0) отсутствует.
рис. 5.7. Индуктивность (а) и ее операторные схемы замещения (б, в)
15-6972
Если в Z(p) заменить р на /со, то получим комплексное со-
противление индуктивности Z(/co) = ju>L.
Емкость. Мгновенные значения тока и напряжения в емко-
сти (рис. 5.8, а) связаны соотношением (В.4):
i(.t) = C^^-. (5.28)
at
Применяя преобразование Лапласа к левой и правой частям
уравнения (5.28) и учитывая теорему дифференцирования (5.11),
получаем
I(p) = pCUc(p)-Cuc(O) (5.29)
или
ос(р)-^
(5.30)
Выражение (5.30) — это закон Ома в операторной форме для
элемента емкости.
На рис. 5.8, б приведена операторная схема замещения емко-
сти, соответствующая (5.30). В этой схеме емкость С заменяется
операторным сопротивлением Z(p) = i/pC, и последовательно с
ним включается источник расчетной эдс UcW)/p, направление
которого противоположно направлению тока. Величина ис^}/р
характеризует энергию электрического поля, запасенную в емко-
сти к моменту времени t = 0.
В случае, когда начальное значение напряжения на емкости
равно нулю: ис(0) = 0, закон Ома (5.30) принимает вид
Цр) =
UcW UcM
1/(рС) “ Z(p)
(5.31)
и в операторной схеме замещения (рис. 5.8, в) емкость С заменя-
ется только операторным сопротивлением Z(p) = 1/рС, а источник
Uc(ff)/p отсутствует.
КО
Цр)
Рис. 5.8. Емкость (а) и ее операторные схемы замещения (б, в)
Цр) мс(0)=0
226
Рис. 5.9. /?£С-контур (а) и его операторная схема замещения (б)
Если в Z(p) заменить р на /со, то получим комплексное со-
противление емкости = 1//шС.
Подобно законам Ома (5.23), (5.26), (5.30) для элементов сопро-
тивления, индуктивности и емкости можно получить законы Кирх-
гофа в операторной форме для изображений токов в узлах и изобра-
жений напряжений в контурах разветвленной электрической цепи.
Первый закон Кирхгофа
т
24(р) = о.
Второй закон Кирхгофа
п
X^k(p) = 0.
Л=1
(5.32)
(5.33)
Например, операторная схема замещения цепи, содержащей
элементы сопротивления, индуктивности и емкости, включенные
последовательно (рис. 5.9, а), приведена на рис. 5.9, б. Уравне-
ние по второму закону Кирхгофа в операторной форме для этой
схемы имеет вид
U(p) = RI(p) + pU(p)-Li^ + ^-I(p) + ^^-.
рС р
Изображение тока
L/(p) + Zz-(O)-^^
----------г,--. (5.34)
R + pL + \/(pC)
Выражение Z(p) = 7? + р£ + 1/(рС), стоящее в знаменателе
формулы (5.34), — это операторное сопротивление цепи, изобра-
женной на рис. 5.9.
При нулевых начальных условиях, т.е. при г(0) = 0,
ис(0) = 0, из (5.34) получаем более простое выражение закона
Ома в операторной форме:
15*
227
(5.35)
Замена p на /со в операторном сопротивлении Z(p), изобра-
жении тока /(/?) и изображении напряжения U(.p) приводит к
комплексному сопротивлению Z(/co) = R + ja>L + 1/(/<оС) и ком-
плексным спектральным плотностям тока Z(/co) и напряжения
(7(/<о). Таким образом, законы Ома и Кирхгофа в операторной
форме записи (5.35), (5.33), (5.32) имеют такой же вид, как и
для спектральных плотностей (см. гл. 4), а также комплексных
амплитуд (см. гл. 2) и постоянных напряжений и токов (см. гл. 1).
Пример 5.13. Найдем операторное сопротивление RLC-цепи, к ко-
торой в момент времени t = 0 подключается источ-
ник напряжения a(t). Параметры элементов цепи
(рис. 5.10, а) имеют следующие значения: R = 1 кОм,
L = 30 мГн, С = 0,5 мкФ.
По операторной схеме замещения (рис. 5.10, б),
составленной для нулевых начальных условий, т.е.
wc (0) = 0, (0) = 0, определяем операторное со-
противление цепи:
Z(D}= U(P) = 1 + RPL = p2RLC + pL + R
I(p) рС R + pL p2LC + pRC
Заметим, что замена р на /со в Z(p) приводит к
комплексному сопротивлению цепи:
Z( со) - * + _ (z? - co2Z?£C) + /со£
" /соС + R + /со£ ~ -co2£C + j<s>RC
Подставляя в выражение Z(p) значения R =
= 103 Ом, £ = 30-10-3 Гн, С = 0,5 -10"6 Ф, получаем
х 15»2+3•104р +109
Z (p) =.^-5-5-----—.
10 3p2 + 5 102p
Рис. 5.10.7?£С-цепь с нулевыми начальными условиями (л)
и ее операторная схема замещения (б)
228
Кример 5.14. Найдем операторное сопротивление цепи, изобра
женной на рис. 5.11, а и имеющей параметры R =
= 1 кОм, L = 30 мГн, С = 0,5 мкФ, а также нулевые
начальные условия.
Операторная схема замещения цепи приведена
на рис. 5.11, 6. Все элементы в схеме включены па-
раллельно, поэтому определим вначале операторную
проводимость цепи:
v/ ч 1 1 п p2RLC + pL + R
У (р) = — + —- + рС = -—г-------.
R pL pRL
Операторное сопротивление цепи
Z(o}= 1 ______
Y (р) p2RLC + pL + R
Подставляя в выражение Z(p) значения R, L и
С, получаем
7, ч 3-107р
15р2+ 3 104р + 109
а)
Рис. 5.11. RLC-контур (а) и его операторная
схема замещения (б)
Пример 5.15. Найдем изображение Щр) тока г3(£) в цепи, при-
веденной на рис. 5.12, а, после переключения ключа
из положения 1 в положение 2. Заданы параметры
элементов цепи: R = 1 Ом, L = 100 мГн, С = 100 мкФ,
U\ = 10 В, С/2 = 16 В. Известны также значения на-
пряжения на емкости и тока в индуктивности в мо-
мент времени t = 0: uc(0) = 10 В, ij(0) = 10 А.
В схеме на рис. 5.12, а — ненулевые начальные
условия, поэтому при составлении операторной схемы
замещения цепи используем схемы, изображенные на
рис. 5.7, б и 5.8, б. Кроме того, постоянное напряже-
ние U2 источника заменяем его изображением
U2(p) = U2/p, используя выражения, приведенные в
229
Рис. 5.12. RjLC-цепь с ненулевыми начальными
условиями (а) и ее операторная схема замещения (б)
строке 2 табл. 5.1. Операторная схема замещения
изображена на рис. 5.12, б.
Составим уравнения по законам Кирхгофа (5.32)
и (5.33) в операторной форме:
Л(/’) = ^(р) + Л(р)>
Ц(р)рЬ +I3(p)R = — + Lii(0),
р
I Рс р
Из этой системы уравнений находим изображе-
ние тока в сопротивлении:
т ( р2ЬСис(0) + рЬц(0) + и2 _
3{Р)~ p3RLC + p2L + pR
_ 10р2+105р + 16 105
р3 +104р2 + 105р
Из данного параграфа мы узнали, что:
• Законы Ома и Кирхгофа для изображений записываются в
такой же форме, как для спектральных плотностей, ком-
плексных амплитуд и постоянных напряжений и токов.
• Операторные и комплексные сопротивления элементов цепи
получают друг из друга заменой переменных /со и р.
5.3. Операторный метод расчета реакции цепи
Переход от оригиналов сигналов к их изображениям и от
схем во временной области к операторным схемам замещения
позволяет рассчитывать реакцию цепи на непериодическое воз-
230
действие произвольной формы. Алгоритм операторного метода
расчета реакции сложной цепи заключается в следующем.
Схему сложной цепи во временной области заменяют оператор
ной схемой замещения. Для этого:
а) все напряжения и (Л) на элементах цепи заменяют их изоб-
ражениями U(p);
б) все токи i(t) в ветвях цепи заменяют их изображениями Кр);
в) напряжения и токи источников сигналов заменяют их изоб-
ражениями (см. § 5.1);
г) пассивные элементы цепи заменяют их операторными сопро-
тивлениями (см. § 5.2);
д) начальная энергия, запасенная в емкостях и индуктивно-
стях, т.е. ненулевые начальные условия, учитываются введени-
ем в схему дополнительных источников расчетных эдс LiL(0) и
wc(0)/p (см. § 5.2).
2. В операторной схеме замещения определяют изображения то-
ков в ветвях или напряжений на элементах. Для этого можно
использовать любые стандартные способы расчета электриче-
ских цепей: методы контурных токов, узловых напряжений,
эквивалентного генератора и т.д. Все математические преобра-
зования в области оператора р производятся в алгебраической
форме, а не в интегродифференциальной, как в реальном вре-
мени. Это существенно облегчает расчет.
3. Переходят от изображений токов и напряжений к их оригина-
лам, используя обратное преобразование Лапласа, таблицу со-
ответствия оригиналов и изображений или теорему разложе-
ния, как это было показано в § 5.1.
Пример 5.16. В цепи, изображенной на рис. 5.13, а, ключ замы-
кается в момент времени t = 0. Начальное напряже-
ние на емкости«с(0) = 0, начальный ток в индук-
тивности г’1 (0) =U/(Ri + R2). Найдем изображение
/3(р) тока, протекающего в ветви с емкостью: а) ме-
Рис. 5.13. RLC-цеиъ (а)
и ее операторная схема замещения (б)
231
годом контурных токов, б) методом узловых напря-
жений.
Составляем операторную схему замещения
(рис. 5.13, б). Токи ij, i2, &з заменяем их изображени-
ями 12^рУ> 1з(р)> напряжение U источника —
изображением (7(р) = U/p. Незаряженную емкость С
заменяем операторным сопротивлением \/рС, индук-
тивность — операторным сопротивлением pL и вклю-
ченным последовательно с ним источником (0).
а) Метод контурных токов.
Выбираем два контура и обозначаем оператор-
ные изображения контурных токов 1к\(р) и 1к2(р).
Составляем уравнения для контуров:
IKi(p)(Ri + R2+pL)-IK2(p)-R2= — + Lii(0),
Р
_^к1(р)-^2 +-^К2(Р)Г^2 +-тЙ = О-
I k J
Из системы уравнений находим изображение
второго контурного токаI^tp):
j (р\ =________pR2CLi\ (0) + UR2C__
p2LCR2+p(RiR2C + L) + Rl+R2
Из операторной схемы замещения следует, что
изображение тока в ветви с емкостью
/з(р) = /к2(р)-
б) Метод узловых напряжений.
В операторной схеме замещения (рис. 5.13, б)
заземлим узел 1: U^p) = Ои запишем уравнение для
расчета изображения напряжения узла 2:
гт , / 1 1 U/p + Lit(0)
tb(p)\---------+ — + рС = —— 2 .
2 /?! +pL R2 ) Rx+pL
Отсюда
U 2 ( Р ) = -Г-,-Д2[^*рЦ(0)]---------
p\_p2LCR2+p(RlR2C + L) + Ri+R2]
Изображение тока Щр) в ветви с емкостью
j (д') - ^2 (р) ____pR2CLi\ (0) + UR2C____
зУР)~ \/рС ~ p2LCR2+p(RlR2C + L) + Rl+R2
232
совпадает с полученным методом контурных то-
ков, и представляет собой отношение двух полиномов.
Переход от изображения сигнала к оригиналу позволяет по-
лучить мгновенные значения токов или напряжений на элементах
реальной цепи.
Хотя операторный метод теоретически может быть использо-
ван для получения реакции линейной цепи любого порядка, т.е. с
любым количеством реактивных элементов, тем не менее на прак-
тике накладываются ограничения из-за громоздкости математиче-
ских преобразований. Операторный метод обычно применяют для
расчета цепей первого и второго порядков, в которых полиномы,
стоящие в числителе и знаменателе изображения, сравнительно
легко могут быть разложены на сомножители, чтобы можно было
воспользоваться теоремой разложения или таблицами.
Пример 5.17. Найдем ток i(t) в цепи первого порядка, изобра-
женной на рис. 5.14, а. К /?£-цепи, имеющей пара-
метры R = 6 Ом, L = 3 Гн, подключен источник сту-
пенчатого напряжения величиной 17 = 30 В. В схеме
нулевые начальные условия, т.е. i(0) = 0.
В соответствии с порядком операторного метода
расчета реакции цепи составим прежде всего опера-
торную схему замещения. Для этого заменяем ток
i(t) его изображением 1(р), напряжение U источни-
ка — изображением Ujp = 30/р, индуктивность L —
операторным сопротивлением pL. Операторная схема
замещения изображена на рис. 5.14, б.
Далее найдем изображение тока 1(р), используя '
закон Ома:
R + pL
Преобразуем 1(р) к табличному виду
R p(p + R/L)
Рис. 5.14. /?Л-цепь при воздействии на нее импульса (а)
включения и операторная схема замещения (б)
233
Изображению а/[р(р + а)] соответствует ориги-
нал )-e~at (табл. 5.1, строка 5). В выражении для
расчета Кр) постоянная затухания а = R/L равна
2 [1/с], а константа U/R равна 5 А.
Мгновенное значение тока
Заметим, что в момент времени t = 0 ток
г(0) = 5-5е"20 = О,
что соответствует условию задачи.
Пример 5.18. Найдем ток г(£) и напряжение uc(i) для t > 0 в
цепи первого порядка, изображенной на рис. 5.15, а.
Заданы параметры цепи: R = 4 Ом, С = 1/12 Ф, а
также напряжение источника гармонического импуль-
са включения u(t) = 40 sin 4/. Емкость в момент вре-
мени t = 0 не заряжена, т.е. ис (0) = 0.
В соответствии с алгоритмом операторного метода
расчета реакции цепи составляем операторную схему
замещения (рис. 5.15, б). Ток i(i) и напряжение
Uc^t) заменяем их изображениями 1(р) и С7с(р), ем-
кость — операторным сопротивлением. Изображение
напряжения и (Л) источника имеет вид (см. табл. 5.1)
(7(р) = 160/(Р2 +16).
В схеме нулевые начальные условия цс(0) = 0,
поэтому источника ис(0)/р в операторной схеме нет.
Для единственного контура операторной схемы
замещения записываем уравнение по второму закону
Кирхгофа:
Kt) _R
Рис. 5.15. PC-цепь при воздействии на нее
гармонического импульса включения (а)
и ее операторная схема замещения (б)
234
-J,. М(р)
к Р'-' J
или после подстановки численных значений
(, 12А 160
к Р ) р2 +16
Отсюда находим
/ (г,) = 160Р = 40Р
(/?2 + 1б)(4р + 12) (р2+1б)(/? + 3)
Воспользовавшись разложением /(р) на простые
дроби (5.19) и (5.21), получим
З2е;36,9° 4,8
р2+16 р + 3
Первое и второе слагаемые являются изображе-
ниями табличных синусоидальной и экспоненциаль-
ной функций соответственно. Поэтому мгновенное
значение тока i(t) в реальной цепи имеет вид
i(t) = 8sin(4£ + 36,9°) -4,8e~3t.
Изображение напряжения на емкости
тт / \ т( \ 1 480
Напряжение на емкости uc(t) в реальной цепи
также рассчитывается с применением теоремы раз-
ложения и таблиц и имеет вид
uc (t) = 24 sin (it - 53,10) +19,2е ~3t.
В выражениях i(t) и uc(t) первое слагаемое —
это синусоидальная функция 9 частотой 4 рад/с, ко-
торая обусловлена тем, что в цепь включен источник
синусоидального напряжения той же самой частоты.
Начальные фазы тока и напряжения на емкости от-
личаются от фазы напряжения источника, но общая
синусоидальная форма и частота сохраняются.
Экспоненциальная компонента вида e~at в вы-
ражениях для расчета i(t) и u(i) имеет постоянную
затухания а = 3, которая зависит от параметров цепи
а = 1//?С.
235
Из данного параграфа мы узнали, что:
Изображения токов и напряжений в операторных схемах
замещения рассчитываются теми же методами, что и реак-
ция в цепях, находящихся под постоянным или гармониче-
ским воздействием: методами наложения, контурных токов,
узловых напряжений, эквивалентного генератора.
Операторный метод заключается в расчете изображений
сигналов и переходе к мгновенным значениям токов и на-
пряжений на элементах цепи.
5.4. Операторные передаточные функции
Операторные передаточные функции используются при ана-
лизе и синтезе электрических цепей при нулевых начальных ус-
ловиях. Рассмотрим линейный четырехполюсник с реактивными
элементами, изображенный на рис. 5.16. Мгновенные значения
воздействия (тока i[(t) или напряжения щ(0) связаны с мгно-
венными значениями реакции (тока i2(t) или напряжения u2(t))
интегродифференциальными уравнениями. При переходе от ори-
гиналов сигналов к их изображениям Ц(р), Ut(p), I2(p), U2(p)
операции дифференцирования и интегрирования в соответствии с
теоремами преобразований Лапласа заменяются операциями ум-
ножения и деления. При этом отношение изображения реакции к
изображению воздействия имеет алгебраическую форму. Это оз-
начает, что реакцию цепи сравнительно просто найти для любого
воздействия произвольной формы.
Операторная передаточная функция определяется как от-
ношение изображения реакции цепи к изображению воздейст-
вия. В соответствии с этим определением различают операторные
передаточные функции по напряжению Ни(.р) и току Hi(p),
операторные передаточные сопротивление Hz(p) и проводимость
Ну(р):
й(0 4(0 W 4(р)
Рис. 5.16. К определению операторных передаточных
функций четырехполюсника
236
(5.36)
Замена р на /со в уравнениях (5.36) приводит к выражениям
для расчета комплексных передаточных функцийН(/со), кото-
рые подробно рассматриваются в § 3.4 и 4.3 и используются для
спектрального (частотного) анализа электрических цепей при не-
периодических воздействиях сложной формы.
Для пассивных линейных цепей операторную передаточную
функцию можно представить как дробно-рациональную функцию
с вещественными коэффициентами:
Н(с)_ апрп +а„-1рп^ +... + а1р + а0 (5 37)
Ьтрт + +... + blp + b0'
Степени полиномов числителя и знаменателя в (5.37) зависят
от числа реактивных элементов пассивной цепи. Причем степень
полинома числителя не превышает степень полинома знаменате-
ля, т.е. п < т.
Другая форма записи операторной передаточной функции
имеет вид
и (п \ = н (Р-Ро\)(р-Ро2)-(Р-Роп)
{Р)' (p-PiKp-p2)...(p-pm) ’
где р01, р02,..., р0„ — нули; р2, •••, рт — полюсы передаточной
функции; Н = ап!Ьт.
Полюсы передаточной функции располагаются в левой полу-
плоскости комплексной переменной р. На расположение нулей
ограничений нет.
Передаточная функция цепи определяется структурой цепи и
не зависит от вида воздействия. Полюсы и нули передаточной
Функции также зависят только от параметров элементов цепи.
Пример 5.19. Найдем передаточную функцию по напряжению
.RC-цепи, изображенной на рис. 5.17, а и имеющей
параметры R = 4 Ом, С = 1/40 Ф.
Операторная схема замещения изображена на
рис. 5.17, б. Для этой схемы операторная передаточ-
ная функция по напряжению, определяемая в соот-
ветствии с (5.36), имеет вид
Hu(p) = U2(p)/Udp).
237
R
o—4 I о
«1(01 C== I «2(0
о —о
a)
I(P) *
О-»—I I -t о
<4(p)| ^== |t/2(p)
о......... —о
б)
Рис. 5.17. /?С-цепь (а) и ее операторная схема
замещения (б)
Поскольку изображение выходного напряжения
U2(p) = Кр) 1/рС, а изображение входного напря-
жения Ui(р) = 1(р) (R + 1/рС), то
Я (р) =_________=________
ЛР) R + i/pC pRC + 1
Подставляя в Ни(р) значения R = 4 Ом и С =
= 1/40 Ф, находим
Н„(р) = 10/(р + 10).
Полученная передаточная функция является
дробно-рациональной функцией (5.37)
&1Р + Ьо
с вещественными коэффициентами ао=1О, &i=l,
b0 = 10. Степени полиномов числителя и знаменателя
равны соответственно п = 0, т = 1, единственный по-
люс функции р\ = -10 лежит в левой полуплоскости
переменной р.
Заменяя в выражении для Ни(р) р на jo, полу-
чаем комплексную передаточную функцию цепи:
Яи(/(о) = 10/(/<о + 10).
Пример. 5.20. Найдем передаточное сопротивление цепи, изо-
браженной на рис. 5.18, а и имеющей параметры
Ct = 1,5 Ф, С2 = 0,5 Ф, L = 4/3 Гн, R = 1 Ом. Эта
схема в теории цепей называется фильтром Баттер-
ворта третьего порядка с нагрузкой 1 Ом.
Операторная схема замещения цепи изображена
на рис. 5.18, 6. Для определения передаточного со-
противления (5.36)
Hz(p) = U2(p)/I(p).
238
Рис. 5.18. RLC-цепъ с тремя реактивными элементами (а)
и ее операторная схема замещения (б)
—о
r\u2(p)
—о
необходимо найти изображение реакции U2(p). Вос-
пользуемся методом узловых напряжений и запишем
систему уравнений для изображений U^Cp) и U2(p)
напряжений узлов:
^(p)fpC1+3-'|-C/2(p)J- = /(p);
pL) pL
-и^Р^ + иЛР)[^- + РС2+ъ} = °-
pL \pL KJ
Решение этой системы уравнений относительно
U2(p) имеет вид
U2(p) =
Нр)
р3 + 2р2 + 2р +1
Передаточное сопротивление цепи
^2(р)_ 1
Z(p) р3 + 2р2 + 2р +1
Зная передаточную функцию Н(р) цепи, можно найти изоб-
ражение реакции цепи, используя (5.36):
U2(p) = Ui(p)Hu(p), 11 U2(p) = I{(p)Hz(p)-, | (5.38)
Л (р) = Л (p)Hdpl~] | h(p) = Ut (P)HY (p). | (5.39)
Переход от изображения U2(p) или /2(р) к оригиналам
w2(i), i2(t) позволяет найти мгновенные значения реакции цепи
на воздействие произвольной формы.
Пример 5.21. Найдем изображение U2(p) и реакцию u2(t) цепи,
изображенной на рис. 5.17, а (пример 5.19), если
входное воздействие «f(£) = 20 В. Напряжение Wj(t)
подключается в момент t = 0; цепь имеет нулевые на-
чальные условия.
239
Передаточная функция цепи была найдена при
решении примера 5.19:
Изображение U^Cp) воздействия ut(t) определя-
ем по табл. 5.1:
тт / \ 20
Udp) = ~-
Р
Их (5.38) находим
ГТ т \ ТТ т \ и т \ 20 10 200
</2(р)-с/'(,,)я-(₽)=77^о=й^о)’
Разложим U2(p) на простые дроби, используя
(5.19):
тт т \ 20 20
U2{p) = — 77-
р р +10
Оригинал каждого из слагаемых в изображении
172(р) находим по табл. 5.1. В результате получаем
реакцию — мгновенное значение напряжения на вы-
ходе цепи:
u2(i) = 2O-2Oe"lot.
Пример 5.22. Найдем реакцию u2(t) цепи, изображенной на рис.
5.19, а на воздействие Uj(i) = 20sinl0£. Напряжение
Ut(t) подключается к цепи с нулевыми начальными
условиями в момент времени t = 0. Параметры це-
пи: R = 20 Ом, £ = 2 Гн.
Изображение U\(p) воздействия щ&) определя-
ем по табл. 5.1:
тТ г \ 20 10 200
Составляем операторную схему замещения, изо-
браженную на рис. 5.19, б.
Находим операторную передаточную функцию
по напряжению:
н (с}-и2(р) 1(Р) К -
и{Р’~и^р)~ I(p)(R + pL)~
= R = 20 = 10
R + pL 20 + 2p p + 10
240
L
a)
Рис. 5.19. RL-цепь (а) и ее операторная схема
замещения (б)
Заметим, что две совершенно разные цепи (рис. 5.17
и 5.19) имеют одинаковую передаточную функцию
или, при замене р на /со, одинаковые частотные ха-
рактеристики.
Изображение [^(р) реакции цепи находим, ис-
пользуя (5.38):
2000
(р + 10)(р2 +100 )
Применив теорему разложения (5.20), получаем
реакцию u2(t) цепи:
u2(t) = 10е~* В * 10' + 10V2sin(10£-45°).
Из данного параграфа мы узнали, что:
• Операторную и комплексную передаточные функции полу- |
чают друг из друга путем замены переменных р на /со или |
/со на р. I
• Реакция цепи на воздействие произвольной формы опреде- |
ляется в результате перемножения изображения воздейст- |
вия на операторную передаточную функцию и перехода к |
оригиналу этого произведения. |
5.5. Связь со спектральным методом
В гл. 4 было показано, что спектральный или частотный ме-
тод расчета реакции цепи мреакц(^) или греакц(£) на непериодиче-
ское воздействие ивозд(^) или гвозд(£) произвольной формы за-
ключается в определении комплексной спектральной плотности
^возд(/а>) или /ВОЗд(/со) воздействия с помощью преобразования
Фурье (4.6) и комплексных сопротивлений цепи, расчете
16 - 6972
241
комплексных спектральных плотностей (7пеакц(/<») или •^pe.iKu(jO))
реакции цепи любым известным методом (контурных токов, узло-
вых напряжений и т.п.) и переходе к мгновенным значениям ре-
акции Цреакц (t) или 1реакц (t) с помощью обратного преобразова-
ния Фурье (4.7).
Аналогичным образом при расчете реакции цепи на воздейст-
вие произвольной формы операторным методом вначале опреде-
ляют изображение воздействия (/ВОзд(р) или /Возд(р), применяя
преобразование Лапласа (5.6) или (5.7) и операторные сопротив-
ления Z(p) цепи. Затем в операторной схеме замещения рассчи-
тывают изображения реакций (/реакц(р) или /реакц(р) и переходят
к напряжениям м^акцС^) и токам г^акцСО с помощью обратного
преобразования Лапласа (5.2) или (5.3), таблиц или теоремы
разложения (5.20).
Изображения (7(р), /(р) и комплексные спектральные плот-
ности U(jсо), /(/со) сигналов переходят друг в друга при замене р
на /со и наоборот. Операторные Z(p) и комплексные со-
противления цепи идентичны при замене переменных. Отметим
также, что операторная и комплексная передаточные функции
Н(р) и H(j&) одной и той же цепи тоже получаются одна из
другой путем замены переменных р на /со. Это означает, что опе-
раторный и спектральный методы — это два равнозначных метода
решения одной и той же проблемы: расчета реакции цепи на воз-
действие сложной формы.
Из данного параграфа мы узнали, что:
• Операторный и спектральный методы расчета реакции цепи |
на непериодическое воздействие сложной формы выполни-
ются по одному и тому же алгоритму и могут быть замене- ,1
ны один на другой.
Вопросы и задания для самоконтроля
1. Что такое оригинал и изображение сигнала? Как они связаны
между собой?
2. Какая связь существует между преобразованиями Лапласа и
преобразованиями Фурье?
3. Найти изображение напряжения u(t) = 1 -e~20t, используя
преобразование Лапласа.
4. Найти комплексную спектральную плотность напряжения u(t) = 2t.
5. Какой физический смысл имеют свойства и теоремы преобра-
зований Лапласа?
242
g Доказать свойство линейности преобразований Лапласа и тео-
рему запаздывания.
у Определить изображение сигналов a) u(t) = 6; б) u(t) =
= 8sin4t; в) u(t) = 2S(t) + 3, используя табл. 5.1.
g Найти изображение сигнала в форме треугольного импульса
u(t) =
ft
(о,
0 < t < х,
t > т,
используя свойства преобразований Лапласа.
9. Как перейти от изображения сигнала к его оригиналу?
10. Найти оригиналы сигналов, имеющих изображения
а) = 6)
р + 4 pz+9
л г) U(p) = 2 16 17 18
р +16 р + 2р + 5
И. Найти оригинал сигнала, имеющего изображение
/(р) = 8г±зо
р2+25
используя теорему разложения. Сравнить ответ с решением
примера 5.11.
12. Как определяется операторное сопротивление цепи?
13. Какой вид имеет операторная схема замещения элемента ин-
дуктивности (емкости)?
14. Сформулировать закон Ома в операторной форме для элемен-
тов сопротивления, индуктивности, емкости.
15. Найти операторное сопротивление цепи, изображенной на
рис. 5.20.
Рис. 5.20. RLC-цепь
16. Записать уравнения по законам Кирхгофа в операторной
форме для цепи, изображенной на рис. 5.20.
17. Каков алгоритм операторного метода расчета реакции цепи?
18. Как рассчитывается изображение тока или напряжения в раз-
ветвленной цепи?
19- Найти ток i(t) в последовательном колебательном контуре
(рис. 5.9, а), имеющем параметры R = 6 Ом, L = 0,5 Гн, С =
и*
243
= 0,1 Ф. Источник ступенчатого напряжения U = 30 В вклю-
чается в цепь в момент t = 0, причем г(0) = 0, =
20. Что такое операторная передаточная функция?
21. Как рассчитать реакцию цепи на воздействие произвольной
формы, используя операторную передаточную функцию?
22. Найти Ни(р) последовательного колебательного контура, ес-
ли реакцией является напряжение на емкости.
Глава 6. Анализ реакции линейной цепи
на непериодическое воздействие
сложной формы (временной метод)
6.1. Испытательные сигналы
Для расчета характеристик электрических цепей во времен-
ной области используются испытательные сигналы в форме еди-
ничной функции и 5-импульса. Напомним, что воздействие в ви-
де единичной функции определяется как (рис. 6.1)
К) (0 при4<0; (6.0
(1 при £ > 0.
Импульс включения величиной U (рис. 6.2) можно записать
через единичную функцию как u(t) =U 1(0, т.е.
и(Н-/° при t < 0;
uyi)-\U при £ > 0.
Единичная функция, задержанная по времени на величину т
(рис. 6.3), определяется как
1((_т) = |0 при(<т;
(1 при t т.
Другим испытательным сигналом является воздействие в виде
5-функции (4.15а):
5(0 = (" "Ри1"0’
(О при других значениях t.
Рассмотрим импульс напряжения м(О длительностью т и ам-
плитудой 1/т, изображенный на рис. 6.4, а. Заметим, что площадь
импульса равна единице. Напряжение и (О можно представить как
сумму двух импульсов включения, показанных на рис. 6.4, бив.
КО
1---------
О t
Рис. 6.1. Единичная
функция
«(О
U
О t
Рис. 6.2. Импульс
включения
величиной U
1(,--0 л
1------------
От t
Рис. 6.3. Единичная
функция, задержанная
на т
245
Рис. 6.4. Импульс напряжения длительностью т и амплитудой 1/т
Импульс включения на рис. 6.4, б описывается выражением
щ (t) = (1/т) • 1 (£) при t > 0, а импульс включения на рис. 6.4, в —
сдвинутый на время т по сравнению с Uj(£) — описывается вы-
ражением а2 (£) = -( 1/т)-1(£-т) при t > т. Импульс напряжения
(рис. 6.4, а) запишется как
w(£) = iq(t) +u2(i) = ————. (6.2)
т
Устремим к нулю длительность импульса т и найдем предел
функции u(t). В результате получим, что (рис. 6.5)
.. 1(£)-1(£-т) dl(t) ,,z,4 zc
8(£) = 1ип-------------= —-— = l(t), (6.3)
т-»о т at
т.е. 8-импульс есть производная от единичной функции.
Не следует думать, что производная единичной функции
1(0 равна нулю, как производная константы. На самом деле
функция 1(0 имеет разрыв в момент времени t = 0, поэтому в
точке разрыва производная отличается от нуля (обращается в
бесконечность).
Площадь 8-импульса равна, как мы знаем, единице:
J 6(t)dt = J d]Xt)dt = \(t)\Z> = 1(оо)-1(-оо) = 1-0 = 1.
Если единичная функция смещена во времени на т, т.е.
1(£-т), то функция 8(£-т) тоже смещена на время т (рис. 6.6)
и может быть определена как
5(0
оо
о
От/
Рис. 6.5. 6-импульс
Рис. 6.6. 5-импульс,
смещенный на т
246
ИЛИ
1G -т)
dt
S(t - т) =
О
S(t - т) = < 00
О
при t < т;
при t = т;
при t > т.
(6.4)
Площадь смещенной 5-функции также равна единице:
J 5(i-t)di = 1.
-00
Отметим фильтрующее свойство 5-функции, определяемое
равенством
J/-(05(i-T)dt = /(t).
-00
Найдем изображение 6-импульса (6.3). Изображение функ-
ции 1(£) равно 1/р (см. пример 5.1). По теореме запаздывания
изображение функции Ki-т) равно (1/р)е~рх. Тогда изображе-
ние Д(р) 8-импульса с учетом свойства линейности имеет вид
Д(р) = lim —(1 = lim——.
т-»0 рх т->0 р
В итоге получаем Д(р) = 1 (см. табл. 5.1).
В реальных условиях 8-импульс, практически неосуществи-
мый, заменяется видеоимпульсом конечной амплитуды и конеч-
ной длительности, причем импульс можно сделать очень узким,
сохранив его площадь равной единице, так что различие реакций
Цепи на этот импульс и 8-импульс будет небольшим.
Рассмотренные единичная функция и 5-импульс используют-
ся в качестве испытательных (тестовых) сигналов по двум причи-
нам. Во-первых, в области реального времени t при определении
нормированных характеристик электрических цепей, рассчиты-
ваемых как отношение реакции цепи к величине ступенчатого воз-
действия или площади импульсного воздействия, удобно исполь-
зовать входные сигналы, величина или площадь которых равны
единице. Во-вторых, как будет показано ниже, расчет реакции це-
пи на непериодическое воздействие произвольной формы сводится
к определению суммы реакций цепи на испытательные единичные
стУпенчатые или импульсные воздействия, с помощью которых
аппроксимируется исходный сигнал.
247
Из данного параграфа мы узнали, что:
<• -^W гу у *? vft > < ##4 Ж
• Испытательными сигналами являются единичная функция
и 6-импульс.
6.2. Импульсная характеристика цепи
Импульсная характеристика цепи вычисляется как обратное
преобразование Фурье (Лапласа) от комплексной (оператор-
ной) передаточной функции. В § 4.3 описаны различные типы
комплексных передаточных функций. Зная комплексные спек-
тральные плотности или операторные изображения входных воз-
действий и комплексные передаточные функции цепи, можно из
(4.20)—(4.23) найти комплексные спектральные плотности или
операторные изображения реакций цепи на соответствующие воз-
действия. Для комплексных спектральных плотностей:
^реакц ( 7® ) = возд ( j®) ’ Hu ( JO ) J (6.5)
^реакц ( 7® ) = ^возд ( J®) ’ H7 ( JCO ) J (6.6)
^реакц ( J®) = ^возд ( 7® ) ’ Hy ( J®) J (6.7)
^реакц ( 7^) = ^возд (j®) ' Hi(jo) • (6.8)
Для операторных изображений:
^реакц (Р) = ^возд (Р ) ' Ни ( Р ) > (6.9)
^реакц ( Р ) = ^возд ( Р ) * Hz ( Р ) > (6.10)
^реакц (Р) = ^возд (Р) * Ну (Р) > (6.11)
^реакц (Р ) = ^возд (Р) ’ Н{ (р ) . (6.12)
Любая комплексная или операторная передаточная функция
полностью характеризует свойства электрической цепи. Если вы-
числить обратное преобразование Фурье от комплексных переда-
точных функций или обратное преобразование Лапласа от опера-
торных передаточных функций, то полученные оригиналы, т.е.
временные функции, будут также полностью описывать свойства
цепи. Эти временные характеристики цепи получили название
импульсных характеристик цепи:
A„(i) = ГЯ„(/<в)е;®‘</<0 или Au(t) =f Hu(p)eptdp
-оо ATI] a-jao
248
импульсная характеристика цепи по напряжению;
hzM = у- J Яг(У<о)е7<”'(/со или hz(t) = у-- j Hz(p)eptdp
-оо д-.уоо
_ импульсное сопротивление цепи;
hy = Т" I (]G))eJ0>td(£> или hY (i) = 77^-7 f Hy(p)eptdp
-00 a—y'oo
- импульсная проводимость цепи;
/z/i) = 77- f Hj(yco)e7Mf</co или/г,(0 = —^-7 f Hi(p)eptdp
2^-oo 2^7 a-/о©
- импульсная характеристика по току.
Импульсная характеристика цепи — это характеристика,
численно равная реакции цепи на воздействие в виде 5-импуль-
са при нулевых начальных условиях. Представим, что в качестве
мгновенного воздействия используется 5-импульс напряжения
В § 4.2 и 5.1 мы определили, что комплексная спектраль-
ная плотность и операторное изображение 8-импульса равны еди-
нице: 17Возд(/со) = 1 и (7возд(р) = 1- Подставим эти значения в (6.5)
и (6.9):
(/реакц(/®) = На(У<й); (6.13)
^реакц (Р) = Ни (р) . (6.14)
Применяя к обеим частям равенств (6.13) и (6.14) обратные
преобразования Фурье и Лапласа соответственно, мы получаем и
в том и в другом случае:
^реакц ( ) = ( ^ ) •
Это выражение свидетельствует о том, что функция, числен-
но равная реакции цепи на 5-импульс, как раз и является им-
пульсной характеристикой цепи hit).
Заметим, что в общем случае под импульсной характеристи-
кой цепи понимают отношение реакции цепи на любое импульс-
ное воздействие (а не только 5-импульс) к «площади воздейст-
вия» при нулевых начальных условиях. Но поскольку площадь 5-
импульса равна единице, то именно это воздействие и используют
При вычислении импульсных характеристик цепей.
Импульсная характеристика цепи может быть вычислена
спектральным или операторным методом. Для нахождения ха-
рактеристики h(t) спектральным или операторным методом сна-
249
чала определяют Hijai) или Н(р), а затем переходят к оригина-
лу либо с помощью обратных преобразований Фурье или Лапла-
са, либо применяя теоремы разложения.
Пример 6.1. Найдем спектральным и операторным методами им-
пульсные характеристики huc(t), hyit) цепи, изо-
браженной на рис. 6.7, а и имеющей параметры
R = 1 кОм, С = 1 мкФ.
а) Спектральный метод.
Для расчета импульсных характеристик цепи
(рис. 6.7) подаем на ее вход напряжение в виде 5-им-
пульса и(t) = 5(t). Комплексная спектральная плот-
ность и операторное изображение 8-импульса равны
единице (см. § 4.2 и 5.1), т.е.
С7(/со) = 1 и U(p) = l.
В соответствии с выражениями (6.5) и (6.7) ком-
плексная передаточная функция цепи, когда реакцией
является напряжение на емкости, определяется как
=______I_______L = J__________1_____= 1оз____L_
7? + 1/(;соС) /а>С RC joi + l/tRC) yco + lO3
а комплексная передаточная функция цепи, когда
реакцией является ток, определяется как
Яу(;'ю) = и^ = /°'ю) = я^Ьс) =
_ j(O _ 1 1
~ Я[/й) + 1/(ЯО] " R ~ R2C[j«> + 1/(RC)] '
= 10'3----—=-.
jo) +103
Для определения импульсных характеристик
huc(t) и hy(t) можно взять обратное преобразование
и(/)| с==|мс(0
О--------1—0
а)
U(p)=l
I(P) R
Рис. 6.7. RC-цепь к примеру 6.1 (а) и ее операторная
схема замещения (б)
250
Фурье (4.7) выражений Н tlc(jG)) и Яу(/со). Однако,
как было показано в § 3.2, комплексную спектраль
ную плотность 1/( /со +103) имеет экспоненциальный
импульс е~103', а комплексную спектральную плот
ность, равную единице, имеет 5-импульс. Поэтому с
учетом теоремы линейности сразу же получаем им
пульсные характеристики /?С-цепи:
h (i) = JL е-^с = 10зе-ю3г.
RC
hY(t) = ^-8(t)—l-e-t/RC =10-35(О-е-,0Ч
R R2C
б) Операторный метод.
Найдем теперь эти же самые импульсные харак-
теристики huc(t) и hy(t) операторным методом. Для
этого по операторной схеме замещения, изображен-
ной на рис. 6.7, б, находим изображения тока 1(р) и
напряжения на емкости Uc(p):
Пр1_ UM _иМ им
Я + 1/(рС) R Р2С[р + 1/(КС)]
Из (6.11) и (6.9) следует, что при воздействии
на цепь (рис. 6.6, а) 5-импульса, имеющего изобра-
жение (7(р) = 1, операторные передаточные функции
цепи будут
Яу(р) =
Др)
U(p)
= 10'3
Яис(р) =
Мр)
U{p)
= 103
1
р + 103
1
р + 103 ’
Для определения импульсных характеристик
hy(t) и huc(t) перейдем от изображений Ну(р) и
Нис{р) к оригиналам, используя табл. 5.1 и свойство
линейности. Получаем
hY(.t) = 10"35(£)-е"1<)3‘.
251
huc(t) = 103е 1()3f.
Импульсные характеристики hy(t) и Л«С(О це-
пи, рассчитанные операторным методом, совпадают с
соответствующими характеристиками цепи, рассчи-
танными спектральным методом.
Отметим, что импульсная характеристика Лу(()
содержит два слагаемых — импульсную составляю-
щую и экспоненциальную. Первое слагаемое
10"38(£) означает, что в момент времени t = 0 в ре-
зультате воздействия на цепь 8-импульса ток заряда
конденсатора мгновенно достигает бесконечно боль-
шого значения, при этом напряжение на емкости при
t = 0 мгновенно изменяется до конечной величины
\/RC = 103. Второе слагаемое — экспоненциальная со-
ставляющая — определяет процесс разряда конденса-
тора через короткозамкнутый вход (так как 8(t) = О
при t > 0, то это соответствует короткому замыканию
входа).
Пример 6.2. Найдем спектральным и операторным методами им-
пульсные характеристики hiL(t), hiR.2(t) цепи, изо-
браженной на рис. 6.8,а и имеющей параметры
Ri = R2= 100 Ом, L = 100 мГн.
а) Спектральный метод.
Комплексные передаточные функции
HiR2(ja) цепи, изображенной на рис. 6.8, а, когда
реакцией цепи является ток в индуктивности и ток в
сопротивлении R2, соответственно имеют вид
И = =____^2___=R2_______1____=
lL /?2+/coL L j(^ + R2/L
/со + 10
Рис. 6.8. /?£-цепь к примеру 6.2 (а)
и ее операторная схема замещения (б)
252
H- j®1' 1
I/?2 /(/co) R2 + yco£ L jo> + R2/L
= l-103---^r.
jo +103
Импульсные характеристики hjL(t) и hiR^t) це-
пи можно получить, взяв обратное преобразование
Фурье от выражений Н|Д(/со) и HiR2{j(o) или вос-
пользовавшись переходом от спектральных плотно-
стей типовых сигналов к самим сигналам, как это
было использовано в примере 6.1. В результате
hiL(t) = 103е_1°3(;
= 8 (^) - 103е'1(,3/.
Численно hiL(t) равна току в индуктивности, а
hiR-f-t) — току в сопротивлении R2 при воздействии
на цепь 5-импульса. Заметим, что сумма этих токов
в параллельных ветвях цепи равна величине воз-
действия 8(t), т.е. выполняется закон токов Кирх-
гофа.
6) Операторный метод.
По операторной схеме замещения, изображенной
на рис. 6.8, б, находим изображения токов Ii(p) и
lR2(p) и операторные передаточные функции HiL(p)
и HiR2(.p) -.
г^Р) I(p) R2+pL L p + R2/L
= Ю3—Цн
р + 103
Н (-п} = ^i^P). — Р^ = 1 _ ^2 1 _
tR^P) I(p) R2+pL L p + R2/L
= 1 -103——т.
р + 103
Применение к HiL(p) и HiR2(p) обратного пре-
образования Лапласа или использование табл. 5.1
соответствий изображений и оригиналов сигналов
приводят к тем же самым выражениям для импульс-
ных характеристик hiL(t), hiR/.t), что и при опера-
торном методе расчета:
r2
253
hi{ (t) = lO3e'lo3f;
//,R2(i) = 8(^-lO3e"lo3z.
Из данного параграфа мы узнали, что:
4 *' < <?W *с» < *♦ |чч* * < *'•&*#**» уШё
• Импульсная характеристика цепи численно равна реакции
цепи на 5-импульс.
• Для расчета импульсной характеристики цепи используется
обратное преобразование Фурье или Лапласа от комплекс-
ной или операторной передаточной функции.
• Вычислить импульсную характеристику можно, используя
спектральный или операторный методы.
6.3. Анализ реакции цепи с помощью
интеграла наложения
Использование импульсной характеристики h(t) позволяет
определить реакцию цепи на воздействие произвольной формы.
Обратимся к выражениям (6.5) — (6.12), которые позволяют най-
ти спектральные плотности или операторные изображения реак-
ций на воздействие любой формы. Напомним, что порядок расче-
та следующий: от мгновенных значений воздействий переходят с
помощью прямых преобразований Фурье или Лапласа к их спек-
тральным плотностям или операторным изображениям, затем вы-
числяют спектральные плотности или операторные изображения
реакций и, наконец, используя обратные преобразования Фурье
или Лапласа, определяют мгновенное значение реакции. В этом
алгоритме неизбежными шагами является использование прямых
и обратных преобразований Фурье или Лапласа.
Можно избежать перехода в частотные или операторные об-
ласти, если воспользоваться известными теоремами о свертке
функций, или, по-другому, о произведении спектров или изобра-
жений (§ 4.2 и 5.1). Применяя эту теорему к (6.5) — (6.12), по-
лучаем
00 ^реакц () = J ^возд х)t/т, -00 (6.15)
00 ^реакц ( ) = J ^возд ) (1х, (6.16)
254
00
^реакц(^)“ J ^возд ( ) б/т, (6.17)
-00
00
^'реакц(^)= f ^во.чд — т)(7т. (6.18)
-00
Анализ формул (6.15) — (6.18) показывает, что для вычисле-
ния реакции цепи нужно знать ее импульсную характеристику
hit) и форму входного воздействия. Интегралы подобного типа
являются интегралами свертки двух функций; их еще называют
интегралами наложения. Если начало отсчета времени совпадает
с началом воздействия, то нижний предел интегрирования в
формулах (6.15) — (6.18) берется равным нулю. В качестве верх-
него предела используют текущее время наблюдения t:
t.
/реакц (^) = J/возд (,t)^(£ — т)</т
О
(6.19)
или другая форма:
/реакц (*>= j/возд (^-t) А(т)б?Х. 0 (6.20)
Интеграл наложения (6.19) можно также получить, если ап-
проксимировать входное воздействие /’ВОзд^) серией прямоуголь-
ных импульсов длительностью di, как это показано на рис. 6.9.
Реакция цепи на k-Й прямоугольный импульс равна реакции
цепи на единичное импульсное воздействие, умноженной на пло-
щадь этого импульса:
/реакц£ —/возд£ Лт)(/т.
Используя принцип наложения, получаем суммарную реак-
цию цепи на серию прямоугольных импульсов в виде (6.19).
Запись интеграла наложения является общей для любых ти-
пов воздействий, реакций и импульсных характеристик.
Рис. 6.9. Аппроксимация воздействия серией
прямоугольных импульсов
255
Физический смысл интеграла свертки заключается в том, что
воздействие /’возд(т) как бы взвешивается с помощью функции
Л(£-т): чем медленнее убывает со временем h(t), тем большее
влияние на реакцию оказывают более удаленные от момента наб-
людения значения входного воздействия.
Для того чтобы выходной сигнал не искажался, импульсная
характеристика цепи должна стремиться к 5-функции.
В физически реализуемой цепи реакция не может возникнуть
раньше воздействия. Это означает, что импульсная характеристи-
ка цепи должна удовлетворять условию Л(£) = О при t < 0. Кро-
ме того, для физически реализуемой устойчивой цепи должно
выполняться условие абсолютной интегрируемости импульсной
характеристики:
|\h(t)|d£ < оо.
Пример 6.3. Найдем напряжение на емкости Uc(t) в ЯС-цепи,
изображенной на рис. 6.7, а, на вход которой посту-
пает ступенчатое воздействие
И(^)-/5В при £ > 0;
при £ < 0.
В примере 6.1 была определена импульсная ха-
рактеристика данной цепи:
Лис(£) = 103е-1°3<.
Для нахождения реакции цепи на ступенчатое
воздействие воспользуемся интегралом наложения
(6.19). Получаем
t t Я, V
uc(t) = \u(x)huc (t-x)dx = |5- 103e"10 =
о о
= 5(l-e-,o3O B.
Рис. 6.10. Графики воздействия и реакции к примеру 6.3
256
Графики воздействия u(t) и реакции и с it) при-
ведены на рис. 6.10.
Пример 6.4. Найдем ток zj?2(t) в сопротивлении R2 цепи, изо-
браженной на рис. 6.8, а, на вход которой поступает
воздействие
zr(t)= 5е
1г (t) = 15e’21°3f А при t> 0;
[0 при t < 0.
В примере 6.2 была определена импульсная ха-
рактеристика данной цепи:
hiR (t) = 5(i)-103e-1°3f.
Реакцию цепи рассчитаем, используя интеграл
наложения (6.19):
t
iR.2 it) = |гг (т)-Л1/?2 (t-x)dx =
о
= J5 • e-2,°3x - t) - 10V,()3(t-T) ] dx
0
или
iy?2(£)= |5e-210 x6(t -x)dx-
o
-f5e-21o3t-lO3e-lo3<elo3xrfT.
о
Первый интеграл в последнем выражении в соответ-
ствии с фильтрующим свойством 5-функции
$ f(t)S(t-x)dt ~ fix)
-00
равен 5е-21°3*. Второй интеграл равен -5e~21°3f+
+ 5е-103<
Поэтому ток в ветви с сопротивлением R2 рас-
считывается как
iR2 it) = 10е-2 ,°3л -5е-1°3‘ А.
Если непериодический сигнал, поступающий на вход элек-
трической цепи, задан различными функциями на нескольких
интервалах времени, то реакция цепи на такое воздействие оп-
ределяется отдельно на каждом временном интервале, где
17 - 6972
257
функция непрерывна. Реакция цепи на каждом последующем ин-
тервале учитывает реакции цепи на предыдущих интервалах вре-
мени. Существует также остаточная реакция цепи после прекра-
щения воздействия.
Пример 6.5. Найдем напряжение на емкости в 7?С-цепи,
изображенной на рис. 6.7, а, на вход которой посту-
пает воздействие (рис. 6.11):
!5 В при 0 < t < 1 мс;
10 В при 1 < t < 2 мс;
0 при 0 2 мс.
Импульсная характеристика данной цепи была
определена в примере 6.1:
hllc (t) = Ю3е"10\
Напряжение iz(i) непрерывно на трех времен-
ных интервалах: 0 < £ < 1 мс, 1 < t < 2 мс и t > 2
мс. Поэтому реакцию цепи licit) определяем для
каждого интервала времени отдельно, используя ин-
теграл наложения (6.19).
На интервале 0 < t < 1 мс
wc(£) = \u(x)huc it - т)с?т = J5 • 1О3е-10 (t~x)dx =
о о
= 5-5е-1°3< В.
На интервале 1 < t < 2 мс
110"3 Ч. ч
uc(t) = J 5-1О3е"10 (t~x)dx +
о
+ f 10-103е"1о3и-т)(/т = 10-18,6е"1о3‘В.
Рис. 6.11. Графики входного воздействия
и реакции к примеру 6.5
258
На интервале £ > 2 мс
iio-3 , ,
ыс(£) = f 5-1О3е"10 (t~x)di +
о
2Ю “3 (
+ f 10 • 103е_1°3(г_т)</т = 55,Зе-1<)3/ В.
1-10'3
График напряжения u^it) изображен на рис. 6.11.
Из рисунка видно, что воздействие u(t) имеет скач-
ки напряжения в моменты времени 0; 1; 2 мс, равные
соответственно 5; 5 и —10 В. Напряжение на емкости
изменяется плавно и не имеет никаких скачков.
Кроме того, реакция цепи ис(£) существует и после
того как действие напряжения на входе цепи u(t)
закончилось: на интервале времени £ > 2 мс напря-
жение uc(t) уменьшается до нуля по экспоненци-
альному закону.
Из данного параграфа мы узнали, что:
• Для определения реакции цепи на воздействие произволь- .
ной формы используют интеграл наложения или свертки.
• Для вычисления реакции цепи нужно знать ее импульсную '
характеристику и форму входного воздействия.
• Если входное воздействие задается разными функциями на »
нескольких участках времени, то реакция цепи рассчитыва- “
ется отдельно на каждом временном интервале, в пределах
которого функция непрерывна. При расчете необходимо
учитывать реакцию цепи на предыдущих интервалах.
6.4. Переходная характеристика цепи
Переходная характеристика цепи — это характеристика,
численно равная реакции цепи на единичное ступенчатое воз-
действие при нулевых начальных условиях. Возьмем в качест-
ве испытательного сигнала единичное ступенчатое воздействие
мвозд.(£) = 1(£)• В § 4.2 и 5.1 было установлено, что комплекс-
ная спектральная плотность воздействия 1(£) имеет вид
Uт возд. ( /со ) = !/(/©), а операторное изображение Uт возд. (р) = 1/р •
Подставив эти значения в формулы (6.5) и (6.9), получаем ком-
плексную спектральную плотность и операторное изображение
реакции цепи:
17. 259
Ц,еакц(Л0) = Л-ЯЛ>); (6.21)
7 со
С7реакц(р) = ^Я„(р). (6.22)
По теореме об интегрировании сигнала деление спектра на /со
или деление изображения на р соответствует интегрированию
оригинала, а оригиналом передаточной функции является им-
пульсная характеристика, поэтому
t.
U^^it} = jhit}dt. (6.23)
О
Характеристика цепи, численно равная реакции цепи (6.23)
на единичное ступенчатое воздействие, и есть переходная харак-
теристика. Обычно ее обозначают git}. Связь между переход-
ной и импульсной характеристиками цепи определяется выраже-
нием
t.
git} = \hit}dt
о
(6.24)
или ______________
hit} = g'it}?\ (6.25)
Если переходная характеристика имеет разрыв (скачок), т.е.
в цепи ненулевые начальные условия g(0) ф 0, то импульсная и
переходная характеристики цепи связаны соотношением
/z(£) = g'(?;) + g(0)6(£). (6.26)
Пример 6.6. Найдем переходную характеристику gy(£) RC-
цепи, изображенной на рис. 6.7, а.
В примере 6.1 была определена импульсная ха-
рактеристика /?С-цепи
hYit} = ±Mt}-----\-e-t/(RC).
R R2C
Переходную характеристику цепи gyit} опреде-
ляем по формуле (6.24):
t it 1 f ,z .
gyit} = \hYit}dt = — \bit}dt---— [e^^dt =
о Rq R Cq
-L + Lp-^RC) * _±e-t/(RC)
R R о R
260
Подставляя в gy(£) значения параметров элемен-
тов цепи из примера 6.1, т.е. R = 1 кОм, С = 1 мкФ,
получаем
gY (t) = Ю-3 е"10\
Пример 6.7. Найдем переходную характеристику giL(t) RL-
цепи, изображенной на рис. 6.8, а.
В примере 6.2 была определена импульсная ха-
рактеристика цепи
Р —--t
Aj, = L .
L L
Переходная характеристика цепи giL(t) рассчи-
тывается по формуле (6.24):
t t п ^2 f ^2 f
giL(t) = \hiL(t)dt = j-2-е L dt = \-e L .
о о L
Подставляя в giL(t) значения параметров эле-
ментов цепи из примера 6.2, получаем
giL(t) = i-e-io3t.
Переходная характеристика giL(t) численно рав-
на значению тока, протекающего через индуктив-
ность при ступенчатом воздействии величиной 1 А на
входе цепи, но является безразмерной величиной,
поскольку представляет собой отношение реакции
i£(£) к воздействию zr(i) = 1 (t).
Переходную характеристику можно найти операторным ме-
тодом. Для нахождения характеристики g(t) операторным мето-
дом сначала определяют операторную передаточную функцию
цепи Н(р), затем делят ее на р, а потом переходят к оригиналу
g(t) с помощью обратного преобразования Лапласа, таблиц со-
ответствия оригиналов и изображений либо применяя теорему
разложения.
Пример 6.8. Найдем операторным методом переходную характе-
ристику gy(t) RC-цепи, изображенной на рис. 6.7, а,
когда реакцией цепи является ток.
Операторная передаточная функция Ну(р) RC-
цепи есть отношение изображения тока Кр) к изо-
бражению воздействия U(p):
261
HY(p) =
Up) _ u(p)
u(p} [R + ~^c]u(p}
pc
1 + pRC
Разделив HY(p) на p, получим изображение пе-
реходной характеристики Gy(p):
Г ( V. С - 1 1
y4>) 1 + pRC R' p + l/(RC)
Изображению 1/[р + Г(7?С)] соответствует экспо-
нента e~f RC, поэтому переходная характеристика
gy(t) имеет вид
gy(t)=-U-'/<RC>.
JLX
Подставляя в gy (£) значения R = 1 кОм и С =
= 1 мкФ, как в примерах 6.1 и 6.6, получаем
gY(t) = 10~3
что, естественно, совпадает с выражением для расче-
та gy(i) той же самой цепи, полученным из им-
пульсной характеристики в примере 6.6.
Пример 6.9. Найдем переходную характеристику цепи gu(i),
изображенной на рис. 6.7, а, когда реакцией являет-
ся напряжение на емкости. Параметры элементов це-
пи равны соответственно R = 1 кОм, С = 1 мкФ.
Операторная передаточная функция цепи
Н Пр) У(рС) _
’ЛР)- U(p) - I(p)[R + i/(pC)]~
1 1
" RC p + l/(RC)
Разделив Ни(р) на р, получим изображение пе-
реходной характеристики Gu(p)\
Gu(p)=RC' p[p + l/(RC)]'
Полученное изображение Gu(p) является таб-
личным (табл. 5.1, строка 5), и ему соответствует пе-
реходная характеристика
gu(t) =
262
Пример 6.10. Найдем переходную характеристику g„(£) RL-це
пи, изображенной на рис. 6.12.
Операторная передаточная функция цепи рассчи-
тывается по формуле
И„(р)=
IW-R
р + R/L
2[p + R/(2L)]'
Разделив Ни(р) на р, получаем изображение пе-
реходной характеристики цепи Gu(p):
G (р) =_____P + R/L___
ЛР) 2p[p + R/(2L)]
Для перехода к оригиналу, т.е. непосредственно
к переходной характеристике цепи gu(t), используем
теорему разложения (5.20). Обозначим F/p) = р +
+ R/L, F2(p) = 2р[р + R/(2L)], F2(p) = 4р + R/L.
Найдем корни знаменателя Gu(p). Они равны
Р! = 0, р2 = -R/(2L). Значения F/pt) = R/L, F2(pi) =
= R/L, Р\(р2) = R/(2L), F2(p2) = -R/L позволяют
найти переходную характеристику gu(t) цепи:
-A,
= l-0,5e 21 .
F\(P2)cP2t_
KM
Рис. 6.12. FL-цепь к примеру 6.10
Как переходные, так и импульсные характеристики цепей
являются нормированными временными характеристиками устой-
чивых линейных электрических цепей. При t -> со значения пере-
ходной характеристики приближаются к величине, характеризую-
щей относительную реакцию электрической цепи в режиме посто-
янного воздействия.
263
Из данного параграфа мы узнали, что:
; z tW- , <<:, 7 м < zA ' > WW4 г-^
• Нормированная характеристика цепи, численно равная ре- j
акции цепи на единичное ступенчатое воздействие при ну-
левых начальных условиях, называется переходной харак- |
теристикой. |
• Для расчета переходной характеристики достаточно взять |
интеграл от импульсной характеристики цепи. |
• Переходную характеристику можно вычислить оператор-
ным методом. Для этого определяют операторную переда-
точную функцию цепи, делят ее на р и затем переходят к |
оригиналу, используя обратное преобразование Лапласа, ?
таблицы или теорему разложения. I
6.5. Анализ реакции цепи с помощью
интеграла Дюамеля
Зная переходную характеристику, можно вычислить реак-
цию цепи на воздействие любой формы. В § 6.3 было показано,
что реакция цепи на непериодическое воздействие произвольной
формы рассчитывается с помощью интеграла наложения (6.19):
t
^реакц ( £ ) = J^возд ( Т ) Л ( £ — Т ) (/т.
О
Подставим под знак интеграла вместо импульсной характери-
стики hit-т) выражение (6.26), устанавливающее связь между
импульсной и переходной характеристиками:
hit) = g'(t) + g(0)8(£),
в котором переменную t заменим на t — т. Получаем
t t
«реакц^)= \u3O3^x)g'it-x)dt+ Jg(0)uBO3fl (t)5G - т)(/т.
О О
С учетом фильтрующего свойства 5-функции имеем
t
Jg (0) г/возд ( т) 8 (£ — т) с/т = g (0) г/возд (£).
о
В результате получаем формулу для расчета реакции цепи на
заданное непрерывное воздействие по известной переходной ха-
рактеристике цепи:
264
t
реакц — ( 0)Мвозл /^возд )S (^ — T ) </x.
0
(6.27)
Это выражение называют интегралом Дюамеля.
Другая форма интеграла Дюамеля получается, если соотно-
шение (6.26) /?(£) = g'(t) + g(0)8(i), в котором t заменено на т,
подставить в формулу (6.20) для расчета реакции цепи:
t
реакц (^) = J^возд — Т ) А ( Т ) </т.
0
(6.28)
Тогда получаем
-
реакц (^) ~ g (0 ) ^возд (£ ) + У^Возд (.t — Т)g (т)б(т.
0
Еще две формы интеграла Дюамеля приводим здесь без вы-
вода:
реакц (^возд (0)^(0 + t ju^Mgtt-xydx; 0 (6.29)
реакц ( — ^возд ( 0 ) t) + t \u'303Jl{t-x}g{x)dx. 0 (6.30)
В уравнениях (6.29) и (6.30) ивозд(т) и м'В03Д(£-т) — это
производные функции, описывающей входное воздействие, в ко-
торых затем переменная t заменена на т либо t - т.
Интеграл Дюамеля может быть также получен в результате
аппроксимации воздействия ступенчатыми функциями и приме-
нения принципа наложения. Воздействие произвольной формы,
изображенное на рис. 6.13, представим как сумму ступенчатых
воздействий, сдвинутых относительно друг друга на время Дт.
Ступенчатое воздействие в момент времени t = 0 можно записать
как Uo • 1 (t), в момент времени t = Дт — как (Ui - Uq) • l(i - Дт).
Рис. 6.13. Аппроксимация воздействия суммой
ступенчатых функций
265
Аналогичным образом можно записать ступенчатые воздействия во
все другие моменты времени, кратные Ат. Тогда воздействие
мвозд^)> представляющее собой сумму ступенчатых воздействий,
математически записывается как
«возд^) = Ц> 1(£)+£АС4 Ht-kbx),
k=i
где ДС/^ =Uk -U^; п — число участков аппроксимации.
Найдем реакцию цепи на каждое ступенчатое воздействие,
входящее в ивозд (£). В § 6.4 было установлено, что реакцией це-
пи на единичное ступенчатое воздействие l(t) является переход-
ная характеристика git) цепи. Поэтому
“реакц(О) = U0 git) = Мвозд(0)£(£);
“реакц<^) = (^1 -U0)-git-&x) = bUfgit-Ьх);
«реакц (2Ат) = (U2 - Ux) git- 2Дт) = Д(/2 • git - 2Дт);
Чрегкц^х) = (Uk - Uk_i)-git-kM) = MJk git-k&x).
Результирующая реакция цепи на сумму ступенчатых воздей-
ствий определяется по принципу наложения:
^реакц it) = МВ03д ( 0 ) g (t) + У, A Ufa 'git — k&X ).
k-l
При Ат -> 0 имеем k&x -> т. Кроме того, умножив и разделив
величину стоящую под знаком суммы, на Ат, получаем, что
(АС^/Ат)-Ат стремится в пределе при Ат -> 0 к и'возд ix)dx, а ре-
акция цепи рассчитывается по формуле
t
^реакц it) — ^Возд ( 0 ) git) + У^возд i^) git — Т ) dx ,
О
совпадающей с одной из форм интеграла Дюамеля (6.29).
Другая форма интеграла Дюамеля (6.30) получается из пре-
дыдущей путем замены переменной t - т на новую переменную
Tj, изменения порядка интегрирования и возвращения к прежнему
значению т для переменной, по которой ведется интегрирование.
Формы интеграла Дюамеля (6.27) и (6.28) можно получить,
интегрируя по частям выражения, стоящие в уравнениях (6.29) и
(6.30). Выбор формы интеграла Дюамеля при расчете реакции
цепи определяется удобством и простотой выражений.
Пример 6.11. Найдем напряжение на емкости Ucit) в 7? С-цепи
(рис. 6.7, а), на вход которой поступает ступенчатое
воздействие (рис. 6.10):
266
„(() = [5В при«>0;
(О при t < 0.
В примере 6.9 была рассчитана переходная харак-
теристика /?С-цепи с элементами R = 1 Ом, С = 1 мкФ:
gu(t) = i-e-t(RC) =l-e-’°3f.
Реакцию 1?С-цепи на ступенчатое воздействие
найдем, используя интеграл Дюамеля, рассчитывае-
мый в форме (6.29):
t
uc(t) = u(0)glftt) + p/'(i:)gM(£ -x)dx =
о
= 5(l_e-io3/) + j(5)'[1_e-io3(f-o]rft
0
Поскольку производная от константы равна нулю,
то интеграл тоже равен нулю, и в результате имеем
uc(t) = 5(1-е"1о3О В.
Полученное выражение совпадает с уравнением
для расчета uc(t), выполненного в примере 6.3 с
помощью интеграла наложения в той же самой цепи
и при том же самом воздействии.
При расчете цепей с помощью интеграла Дюамеля необхо-
димо учитывать все скачки воздействия, а также выполнять ин-
тегрирование отдельно на каждом интервале времени, где функ-
ция воздействия непрерывна. В уравнениях (6.27) — (6.30)
функция, соответствующая воздействию мВ03д(£), является непре-
рывной функцией времени. Если г/возд(£) — кусочно-непрерыв-
ная функция, т.е. имеет скачки напряжения не только при t = 0,
но и в другие моменты времени tk, то эти скачки рассматривают
как дополнительные ступенчатые воздействия, реакция на кото-
рые вычисляется как произведение величины скачка на переход-
ную характеристику цепи, т.е. Дмвозд ) • g(t - tk).
Для расчета реакции цепи на воздействие, заданное кусочно-
непрерывной функцией, определяют число участков интегрирова-
ния, на которых функция непрерывна и дифференцируема, а за-
тем для каждого из выделенных участков записывают уравнения
(6.27) — (6.29) или (6.30) с учетом реакции предыдущих участ-
ков. Реакцию цепи рассчитывают также на интервале времени, на
котором воздействие в цепи уже прекратилось.
267
Рис. 6.14. График входного воздействия
Пусть на вход цепи, имеющей переходную характеристику
gy(t), воздействует напряжение, график которого изображен на
рис. 6.14. Найдем реакцию цепи на это воздействие, используя
интеграл Дюамеля (6.29).
Выделим три интервала времени, на которых функция u(t) не-
прерывна и дифференцируема: на интервале 0 < t < напряжение
n(i) = Wi(t); на интервале < t < t2 напряжение u(t) = u2(t);
на интервале t2 < t < <» напряжение iz(t) = 0. Отметим также, что
u(t) имеет скачки: в момент времени t=Q скачок и(0) = щ (0) = Uo ;
в момент времени £ = скачок utt^) = u2(.t^)в момент
времени t = t2 скачок u(t2) = Q-u2(t2).
Реакция цепи (ток) на интервале времени 0 < t < в соответ-
ствии с (6.29) имеет вид
t
i(t) = C0gy(O + (t-x)dx.
о
На интервале времени < t < t2
i(t) = Uogy(t)+ ju'i(x)gy(t- x)dr+
о
t
+ [w2(£i)-“i(£i)]gy(£-£i)+ \u'2(x)gy (t-x)dx.
ti
На интервале времени t2 < t < °°
i(t) = Uogy (t) + fu’(x)gy (t-x)dx +
о
+ [iz2(^i)_Mi(^i)]gy (t -) +
<2
+ J U2(x)gy(t -x)dx - U2(t2)gy (t -12).
<1
Пример 6.12. Найдем напряжение на емкости Uc(t) в 7?С-цепи
(рис. 6.7, а), на вход которой поступает напряжение
(рис. 6.11)
268
5 В при 0 < t < 1 мс;
u(t) = 10 В при 1 < t < 2 мс;
О при £ > 2 мс.
Переходная характеристика 7?С-цепи с элементами
R = 1 кОм, С = 1 мкФ была вычислена в примере 6.9:
gn(t) = 1 -е"((яс) = 1 -е-1°3'.
Используя интеграл Дюамеля (6.29), записываем
реакцию цепи на интервале времени 0 < t < 1 мс:
t
uc(.t) = u(O)gu(t)+ Ju'(T)g(i -x)dx.
о
Поскольку напряжение u(t) постоянно на ин-
тервале времени от 0 до 1 мс, то его производная
u'(t) равна нулю, поэтому
uc(t) = 5(1 - в-10'3*) В.
На интервале времени 1 < t < 2 мс
uc(t) = a(0)g„(£)+ Jw'(T)g(t-T)dT +
0
t
+ Au(i1)gu(t-t1) + Jiz'(t)g(t - x)dx.
В выражении для uc(t) использованы обозна-
чения: Au(ij) — скачок входного напряжения в мо-
мент времени = 1 мс (он равен 5 В); gu(t-ti) —
переходная характеристика цепи, учитывающая за-
держку на время tt = 1 мс = 10”J с. Напряжение
u(t) постоянно при 0 < t < и < t < 2, поэтому
производные и'(х) и интегралы в уравнении для рас-
чета Uc(t) равны нулю.
В результате получаем
uc(t) = M(O)gtz(^ + Aiz(i1)g„(f-^1) =
= 5(1_е-ю^) + 5[1_е-ю3(мо-з)] =
= 10-18,6е-1°3‘ В.
На интервале времени t > 2 мс
tt
uc(t) = u(0)gu(t)+ $u'(x')g(t-x)dx +
о
+ Aw(t1)g„(£-£1) +
269
ti
+ Ju'(i:)g(£ - т)dx + Au(£2)gM (t ~t>)-
t\
Интегралы равны нулю, так как м'(т) =0, время
t2 = = 2 мс = 2 • 10-3 с, поэтому
uc(t) = u(Q) gu(t) + &u(ti)gu(t - +
+ Ди(t2)g,j (t -t2) = 5(l-e"lo3f) +
+ 5[1_e-io3(t-io-3)]_1()[1_e-io3(t-2.io-3)] =
= 55,Зе-1°3< В.
Выражения для вычисления реакции цепи uc(t)
на каждом временном интервале, где функция вход-
ного воздействия непрерывна и интегрируема, совпа-
дают с выражениями, полученными в примере 6.5
при решении этой же самой задачи путем примене-
ния интеграла наложения.
Пример 6.13. Найдем значение напряжения на индуктивности
Мд (О в PL-цепи (рис. 6.15) в моменты времени,
равные 0,5; 1,5; 3 мс, если на вход цепи поступает
напряжение, изображенное на рис. 6.16 и имеющее
параметры Uo = 2 В, = 1 мс, t2 = 2 мс.
Переходную характеристику цепи найдем опера-
торным методом. Для этого запишем вначале опера-
торную передаточную функцию Ни(р):
Hu(p) = pL/(R + pL).
Разделив Ни(р) на р, получаем изображение пе-
реходной характеристики G„(p):
Gu{p) = H-u^ =---------.
р p + R/L
Используя табл. 5.1, находим переходную харак-
теристику
R
О 1 I—|—о
о 1 о
0 t2 t, мс
Рис. 6.16. График воздействия
к примеру 6.13
Рис. 6.15. 7?£-цепь
к примеру 6.13
270
g„(O = e-(R/I)f =е-1о3/.
Запишем функции, соответствующие воздейст-
вию u(t) (рис. 6.16) на интервалах времени
О < t < 11, t\ « i <t2, t2 < oo.
На интервале времени от 0 до t\ напряжение
u(t) постоянно и равно Uo.
На интервале времени от до t2 u(t) — это
прямая линия, которой соответствует математическое
выражение
и = at + b.
Коэффициенты а и b находим из условий и = [70 при
t = tt, и = 0 при t = t2. Получаем
Up _ Upt2 _ Up{t2-t)
~t'2. ^2 ^2 _
На интервале времени от t2 до oo значение на-
пряжения равно нулю. В результате имеем
и(Л) =
^р(^2 ~t)
^2 “Л
О
при 0 < t < ti,
при ti < t < t2,
при t2 < t < 00.
Заметим также, что в момент времени t = 0 на-
пряжение u(t) имеет скачок, равный Uq, а в момен-
ты времени и t2 скачков нет, т.е. Дм(^) = О,
Дм(£2) = 0.
Для вычисления напряжения на индуктивности в
момент времени t = 0,5 мс найдем реакцию цепи на
интервале 0 < t < t\, используя интеграл Дюамеля
(6.29):
t
uL(t) = и(0)gu(t) + \u'(x)gu (t -x)dx =
о
= С7ог.(4) = 2<Г1Л
При t = 0,5 • 10-3 с имеем
uL (t) = 2е-1о3 °’51(г3 = 0,74 В.
Для вычисления напряжения на индуктивности в
момент времени t = 1,5 мс найдем реакцию цепи на
интервале времени t\ < t < t2:
271
Z1
uL(t) = u(O)g„(t) + ]u'(x)gtl(t -x)dx +
о
t.
+ ju'(T)g„ (t -x)dx =
t [T
= UQgu(t)+ j-—°-gu(t-x)dx =
tt C2 - Ct
= 2e-1°3< + f -2OOOe-lo3(t-T)JT =
MO-3
=-2 + 7,44е~10Ч
При t = 1,5 • IO-3 с имеем
uL(t) = -2 + 7,44e-103 ,’510’3 =-0,33 B.
Для вычисления напряжения на индуктивности в
момент времени t = 3 мс найдем реакцию цепи на ин-
тервале времени < t < 00:
t
uL(t) = u(Q)gu(t)+ \u'(x)g(t-x)dx +
о
+ $u'(x)g(t-x)dx = -2,67е-10\
При t = 3 мс имеем uL (t) = -0,13 B.
Из данного параграфа мы узнали, что:
• Для определения реакции цепи на непериодическое воздей-
ствие произвольной формы используют интеграл Дюамеля.
• Для вычисления реакции цепи нужно знать ее переходную
характеристику и форму входного воздействия.
• Если воздействие задано кусочно-непрерывной функцией,
имеющей скачки, то реакция цепи рассчитывается отдельно
на каждом интервале времени, на котором функция непре-
рывна и дифференцируема, с учетом реакции на предыду-
щих интервалах.
Вопросы и задания для самоконтроля
1. Какие испытательные сигналы используются для расчета ха-
рактеристик электрических цепей? Почему применяются имен-
но эти сигналы?
272
2 Как связаны единичная функция и 5-импульс?
3 Что такое импульсная характеристика цепи?
4 Как связаны импульсная характеристика и операторная пере-
даточная функция цепи?
5 Какие методы применяются для расчета импульсных характе-
ристик?
6. Определить импульсную характеристику последовательной
RL-цепи (рис. 6.15), когда реакцией цепи является:
а) напряжение на сопротивлении;
б) напряжение на индуктивности.
7. Как рассчитать реакцию цепи на воздействие произвольной
формы, используя импульсную характеристику?
8. Получить выражение для расчета реакции цепи путем ап-
проксимации входного воздействия прямоугольными импуль-
сами.
9. Каков физический смысл интеграла наложения?
10. Как рассчитывается реакция цепи, если воздействие задано
различными функциями на нескольких интервалах времени?
И. Найти напряжение uR(t) на сопротивлении в последователь-
ной /?£-цепи (рис. 6.15), на вход которой в момент времени
t= 0 поступает напряжение u(t) в форме прямоугольного
импульса амплитудой Uo и длительностью Указание: ис-
пользуйте импульсную характеристику, полученную в п. 6.
12. Что такое переходная характеристика цепи?
13. Как связаны переходная и импульсная характеристики цепи?
14. Определить переходные характеристики последовательной
RL-цепи (рис. 6.15), когда реакцией цепи являются:
а) напряжение на сопротивлении;
б) напряжение на индуктивности.
15. Какие методы применяются для расчета переходных характе-
ристик?
16. Операторным методом найти переходные характеристики
guR(t) и gU£(O последовательной jRZ-цепи. Сравнить с ре-
зультатами, полученными при решении задачи п. 14.
17. Как рассчитать реакцию цепи на воздействие произвольной
формы, используя переходную характеристику?
18. Вывести формулу интеграла Дюамеля (6.29) для расчета ре-
акции цепи по известной переходной характеристике. Ука-
зание: при выводе используйте соотношение (/реакц/р) ~
= ивозл,(р) Н(р) = [H(p)/p] p UB03:i\p), теоремы свертки и
дифференцирования и правила дифференцирования интегра-
ла по параметру t.
19. Решить задачу п. И, используя переходную характеристику
цепи, полученную в п. 14. Сравнить результаты.
18 - 6972
273
20. Найти напряжение на емкости ис (t) в последовательной /?С-
цепи (рис. 6.7), на вход которой поступает напряжение, изо-
браженное на рис. 6.17. Даны: R = 100 Ом, С = 25 мкф,
Uо = 10 В, if = 2 мс. Указание: использовать для расчета ин-
теграл Дюамеля.
Рис. 6.17. Форма воздействия к заданию 20
Глава 7. Анализ реакции линейной цепи при
коммутациях (переходные процессы)
7.1. Законы коммутации
Когда в цепи, содержащей реактивные элементы, происхо-
дят внезапные изменения, такие как подключение или отключе-
ние с помощью ключей источников тока и напряжения или из-
менение параметров пассивных элементов цепи, то это приводит
к плавному изменению энергетического состояния цепи. Проис-
ходит это потому, что согласно принципу непрерывности энергия
электрического и магнитного полей в емкости и индуктивности не
может измениться мгновенно (скачком). Должен пройти опреде-
ленный промежуток времени, прежде чем режим работы цепи по-
сле переключения можно будет считать установившимся, т.е. та-
ким, при котором токи и напряжения не зависят от времени или
являются периодическими функциями времени. Именно для та-
ких воздействий рассматривались ранее все методы анализа элек-
трических цепей. Процесс, происходящий в цепи от момента пе-
реключения ключа до установившегося состояния, называют пе-
реходным процессом. В этой главе мы будем анализировать ра-
боту электрических цепей в переходном режиме, при котором
токи и напряжения изменяются непериодически.
Любое изменение параметров цепи или ее конфигурации,
приводящее к возникновению переходных процессов, называется
коммутацией. Будем считать, что коммутация осуществляется с
помощью идеального ключа (рис. 7.1), сопротивление которого в
замкнутом состоянии равно нулю, а в разомкнутом состоянии —
бесконечно велико. Направление замыкания (рис. 7.1, а), размы-
кания (рис. 7.1, б) или переключения (рис. 7.1, в) ключа будем
показывать стрелкой.
Теоретически можно считать, что коммутация происходит
мгновенно в момент времени t = 0. Удобно ввести еще два обо-
значения времени: t = 0_ — это момент времени непосредственно
перед коммутацией; t = 0+ — это первый момент времени непо-
средственно после коммутации. Хотя в математических выраже-
а) б) в)
Рис. 7.1. Ключи на замыкание (а), размыкание (б), переключение (в)
18*
275
ниях моменты времени 0_ и 0+ можно рассматривать как t = О,
поскольку разница между ними пренебрежимо мала, тем не менее
введение таких обозначений времени является полезным при ана-
лизе цепей, в которых происходит коммутация.
Законы коммутации связаны с непрерывностью изменения
энергии магнитного поля катушки индуктивности WL = Li2/2 и
энергии электрического поля емкости Wc = Си2/2. Если бы в
первый момент времени после коммутации ток в индуктивности
гд (0+) изменился скачком от одного значения до другого, то на
индуктивности появилось бы бесконечно большое напряжение:
Ul(0+) = £^±l,
at
что лишено физического смысла.
Поэтому первый закон коммутации гласит, что в первый
момент времени непосредственно после коммутации ток в ин-
дуктивности остается таким же, каким он был в момент
времени непосредственно перед коммутацией, а затем плавно
изменяется:
iL<0j = tL(0-).l (7.1)
Если бы в первый момент времени после коммутации на-
пряжение в емкости мс(0+) изменилось скачком от одного зна-
чения до другого, то через емкость протекал бы бесконечно
большой ток:
ic(0+) = C^M,
at
что также лишено физического смысла.
Поэтому второй закон коммутации гласит, что в первый
момент времени непосредственно после коммутации напряже-
ние на емкости остается таким же, каким оно было в момент
времени непосредственно перед коммутацией, а затем плавно
изменяется:
ис(.0+) = ЦС(0Э~| (7.2)
Заметим, что в отличие от тока в индуктивности и напряже-
ния на емкости токи в сопротивлении и емкости, а также напря-
жения на сопротивлении и индуктивности могут изменяться скач-
ком в момент коммутации.
Следует также иметь в виду, что в резистивных цепях пере-
ходных процессов нет. Цепь мгновенно переходит в момент ком-
мутации из одного устойчивого состояния в другое.
Из данного параграфа мы узнали, что:
276
Мгновенные подключения или отключения источников
энергии либо мгновенные изменения параметров цепи, со-
держащей реактивные элементы, приводят к возникнове-
нию переходных процессов.
Два закона коммутации являются основой расчета переход-
ных процессов. Законы коммутации связаны с принципом
непрерывности изменения энергии электрического и маг-
нитного полей.
Ток в индуктивности и напряжение на емкости не могут из-
меняться скачком. В первый момент времени непосредствен-
но после коммутации они сохраняют те же самые значения,
которые были до коммутации, а затем плавно изменяются.
I*
7.2. Расчет начальных условий в
моменты коммутации
При расчете переходных процессов необходимо знать зна-
чения токов и напряжений на всех элементах цепи в первый мо-
мент времени непосредственно после коммутации. Значения то-
ка в индуктивности г£(0+) и напряжения на емкости Uq(0+) в
момент коммутации называются независимыми начальными ус-
ловиями. Если до коммутации ток в индуктивности г£(0.) и на-
пряжение на емкости izc(O-) были равны нулю, т.е. конденсатор
не был заряжен, в нем не была запасена энергия электрического
поля, а в катушке не была запасена энергия магнитного поля, то
согласно законам коммутации (7.1) и (7.2) в первый момент вре-
мени непосредственно после коммутации эти ток и напряжение не
изменяются: i£(0+) = i£(0_) = 0, ис(0+) = «с(0_) = 0. Это означа-
ет, что при нулевых начальных условиях в момент £ = 0+ индук-
тивность равносильна разрыву цепи, а емкость равносильна ко-
роткому замыканию. На рис. 7.2 изображены схемы замещения
емкости и индуктивности в момент t = 0+ при нулевых началь-
ных условиях.
Если до коммутации в конденсаторе была запасена энергия
электрического поля, а в катушке запасена энергия магнитного
Рис. 7.2. Схемы замещения С (а) и L (б) в момент t = 0+
при нулевых начальных условиях
277
+ «с(О-)
с4= ~
/=о+
Рис. 7.3. Схемы замещения С (а) и L (б) в момент t = 0+
при ненулевых начальных условиях
поля, т.е. мс(0_) * 0 и i£(0_)*0, то в первый момент времени
непосредственно после коммутации в цепи будут ненулевые на-
чальные условия-.
«с<°+) = * 0. гЛ°+) = г7(0_) * 0.
При ненулевых начальных условиях в момент времени t = 0+
индуктивность равносильна источнику постоянного тока 1Г = ,
а емкость равносильна источнику постоянного напряжения U^ =
= uq(0_). Схемы замещения емкости и индуктивности в момент
t = 0+ при ненулевых начальных условиях изображены на рис. 7.3.
При расчете переходных процессов обязательно требуется
знание независимых начальных условий, поскольку эти условия
характеризуют энергию магнитного и электрического полей, запа-
сенную в индуктивности и емкости к моменту коммутации.
Значения токов в емкости ic(0+) и сопротивлении г'д(0+),
напряжений на индуктивности «д(0+) и сопротивлении Ur(Q+), а
также производных этих величин в первый момент времени непо-
средственно после коммутации называются зависимыми началь-
ными условиями. Для их определения используются законы Ома
и Кирхгофа.
Пример 7.1. Найдем значения токов и напряжений на всех эле-
ментах цепи, изображенной на рис. 7.4, а в момент
времени t = 0+. Ключ в момент t = 0 замыкается.
Значения эдс и сопротивлений R\ и R2 заданы:
щ =20 В, R] = 4 Ом, R2=6 Ом.
До коммутации ключ был разомкнут, поэтому
все токи и напряжения в цепи в момент t = 0_ были
равны нулю:
= г'/,(0_) = iyj2(0_) = 0;
Мд/О.) = мс(0_) = uL(0_) = г/д2(0_) = 0.
Эквивалентная схема замещения цепи в момент
t = 0+ показана на рис. 7.4, 6. Незаряженный кон-
денсатор заменен короткозамкнутой цепью, а индук-
тивность заменена разомкнутой цепью. Заметим, что
для нашего анализа нет необходимости знать значе-
278
Рис. 7.4. Цепь к примеру 7.1 (л) и ее схема
замещения в момент времени t = 0+ (б)
ния С и L. В цепи на рис. 7.4, 6 только один контур
и только один ток, протекающий через последова-
тельно соединенные источник напряжения щ и со-
противления Rt и R2. По второму закону Кирхгофа
или закону Ома он равен
Согласно законам коммутации (7.1) и (7.2) имеем
г£(0+) = г£(0_) = 0;
пс(0+) = пс(0_) = 0.
Напряжения на сопротивлениях в момент време-
ни t = 0+ определяются по закону Ома:
“Kt(0+) = i/?1(0+)J?1 =2-4 = 8 В;
= '^2 = 2 • б = 12 В.
Напряжение на индуктивности W£,(0+) будет та-
ким же, как на сопротивлении /?2> поскольку эти
элементы включены параллельно:
u£(0+) = Ur2(0+) = 12 В.
Подчеркнем, что полученные значения токов и
напряжений на элементах цепи (зависимые и незави-
симые начальные условия) справедливы только для
одного очень краткого момента времени t = 0+ непо-
средственно после коммутации. В дальнейшем с те-
чением времени они изменяются.
Пример 7.2. В схеме, изображенной на рис. 7.5, а, ключ пере-
ключается из положения 1 в положение 2. Заданы
значения напряжений 1^=16 В, и2 = 10 Ви значе-
ния сопротивлений R^ = 2 Ом, R2 = 3 Ом. Известны
также значения напряжений на емкостях и тока в ин-
279
дуктивности в момент времени непосредственно пе-
ред коммутацией: Mq(0-) = 0 В, Wc2(0_) = 6 В
г£(0_) = 2 А. Найдем значения токов и напряжений
на всех элементах цепи в момент времени t = 0+.
Схема замещения цепи в первый момент времени
непосредственно после коммутации t = 0+ приведена
на рис. 7.5, б. В ней незаряженный конденсатор С,
заменен короткозамкнутой цепью, заряженный кон-
денсатор С2 заменен источником напряжения величи-
ной «с(О-) = 6 В, катушка заменена источником тока
величиной гд(0_) = 2 А. В соответствии с законами
коммутации (7.1) и (7.2) имеем
аС1(0+) = иС1(0_) = 0;
ыС2(0+) = мс2(°-) = 6 В;
г£(0+) = г£(0_) = 2 А.
Напряжение w/?i(0+) на сопротивлении Rx най-
дем из уравнения, составленного по закону Кирхго-
фа для левого контура. Получаем
м«1(0+) = Щ ~ wc2(0+) = 16-6 = 10 В.
Ток в емкости Сх будет таким же, что и в сопро-
тивлении Rx:
гс( (0+) = irx (0+) = —s— = -у = 5 А.
Ток в емкости С2 найдем, используя первый за-
кон Кирхгофа:
ic2 (0+) = icx (0+) - ц(0+) = 5 - 2 = 3 А.
Напряжение на сопротивлении R2
а) 6)
Рис. 7.5. Цепь к примеру 7.2 (а) и ее схема замещения
в момент времени t = 0+ (б)
280
Ur2(0+) - i^+) • #2 = 2 • 3 = 6 В.
Напряжение на индуктивности М/,(0+) определя-
ем из уравнения, составленного по второму закону
Кирхгофа для правого контура:
«i,(0+) = wC2(0+)-ггЛ2(0+) = 6-6 = 0 В.
Из данного параграфа мы узнали, что:
-............ <-......>.i, .... ....—.......—.... . .
. Начальные условия — это значения токов и напряжений на $
элементах цепи в первый момент времени после коммута- *
ции. Начальные условия бывают нулевыми и ненулевыми. ’
. Независимые начальные условия — это значения тока в ин- g
дуктивности и напряжения на емкости в момент коммута- ;
ции. Для их определения используют законы коммутации. S
• Все остальные токи и напряжения на элементах цепи, а
также их производные в момент коммутации называются J
зависимыми начальными условиями. Для их определения J
используют законы Ома и Кирхгофа. $
• При нулевых начальных условиях в момент коммутации f
емкость заменяется короткозамкнутой цепью, а индуктив- *
ность — разрывом. При ненулевых начальных условиях в |
момент времени t = 0+ емкость заменяется источником на- »
пряжения UT = Uq(0_), а индуктивность — источником тока *
1г = *l(0-) • i
7.3. Расчет установившихся реакций в цепи
Переходный процесс — это переход цепи из одного устано-
вившегося состояния в другое. Состояние или режим работы це-
пи, при котором все напряжения и токи в ней имеют установив-
шиеся (постоянные или гармонические) значения, называется
установившимся или принужденным. Обычно для установивше-
гося режима используется обозначение времени £ -> оо. Следует
иметь в виду, что t -> со является только математическим симво-
лом, означающим, что проходит достаточно долгое время, прежде
чем напряжения u(t) и токи i(.t) в цепи примут установившиеся
значения. В дальнейшем при расчете реакций цепи в установив-
шемся режиме будем использовать другие обозначения принуж-
денных составляющих напряжения и тока: ыпр, гпр.
Вновь обратимся к известным соотношениям между мгно-
венными значениями токов и напряжений в емкости и индуктив-
ности:
281
Рис. 7.6. Схемы замещения С (а) и L (б) в установившемся
режиме постоянного тока
duc(t)
dt
Заметим, что в установившемся режиме постоянного тока на-
пряжение на емкости uc(t) и ток в индуктивности i^it) являются
постоянными величинами, поэтому их производные равны нулю.
Таким образом, принужденные составляющие тока, протекающего
через емкость, и напряжения на индуктивности также равны нулю:
^Спр — 0 >
мДпр ~ 0 •
(7.3)
(7.4)
Условия (7.3) и (7.4) означают, что в установившемся режи-
ме постоянного тока емкость равносильна разрыву цепи, а индук-
тивность равносильна короткому замыканию. На рис. 7.6 изо-
бражены схемы замещения емкости и индуктивности в цепи по-
стоянного тока в установившемся режиме.
В установившемся режиме гармонического тока напряжения
и токи на индуктивном и емкостном элементах также являются
гармоническими.
Пример 7.3. Найдем принужденные составляющие токов и напря-
жений на каждом элементе цепи постоянного тока, изо-
браженной на рис. 7.7, а, если U[ = 30 В, R^ = 10 Ом,
R2 = 5 Ом.
Схема замещения электрической цепи при t <»
приведена на рис. 7.7, б. При ее составлении учтено,
что в установившемся режиме емкости Ct и С2 заме-
нены разрывами в цепи (рис. 7.6, а), а индуктивности
Li и L2 — короткозамкнутыми цепями (рис. 7.6, б).
Из схемы рис. 7.7, б очевидно, что принужденные
составляющие токов в емкостях равны нулю: iqnp =
= ic2np = 0, а принужденные составляющие токов в со-
противлениях 7?! иЯ2, а также в индуктивностях Lx и
L2 имеют одинаковое значение, определяемое по закону
Кирхгофа для единственного замкнутого контура цепи:
282
/YY\
Ci 4=c2
6)
Рис. 7.7. Цепь к примеру 7.3 (я) и ее схема
замещения при t -> оо (б)
z/?tnp - г/?2пр “ гйпр - г12пр ”10 + 5” 2
Напряжения на индуктивностях равны нулю:
^Zinp “ ^Z,2nP ” 0 *
Напряжения на сопротивлениях определяются по
закону Ома:
w7?inp ~ (riiip ' Ri -2*10-20 В,
^/?2пР = ^2пР ^2 = 2 • 5 = 10 В.
Напряжения на обеих емкостях равны по вели-
чине и имеют то же самое значение, что и напряже-
ние на сопротивлении R2:
иС\пр — ^Сгпр “ ^Т?2ПР “ Ю В’
Установившийся режим постоянного тока в цепи, в которой
происходит коммутация, существует не только при t -> оо, но и до
коммутации. При расчете токов и напряжений на элементах цепи
До коммутации емкость, так же как и при t оо, заменяется раз-
рывом, а индуктивность — короткозамкнутой цепью (рис. 7.6).
Пример 7.4. В цепи, изображенной на рис. 7.8, в момент времени
t = 0 происходит мгновенное переключение ключа из
положения 1 в положение 2. Найдем токи и напря-
жения на всех элементах цепи в первый момент вре-
мени непосредственно после коммутации t = 0+ ив
установившемся режиме при t -> оо. В схеме заданы:
Ux = 10 В, U2 = 15 В, 7?! = 2 Ом, R2 = 3 Ом.
283
a)
R\____________*2 tt2(0-) / = 0-
+t'c1(E) * U(0-)4
UA W-)! И£(0.)6 1исг(0.)
~f I "IM>->
Рис. 7.8. Цепь к примеру 7.4 (а) и ее схемы замещения
при t = 0_ (б), t = 0+ (в), t -» оо (г)
Первоначально ключ находился в положении 1,
в цепи был включен источник постоянного напряже-
ния U\. Значит, до коммутации (t = 0_) в цепи был
установившийся режим, при котором емкости Q и
С2 заменяются разрывами, а индуктивность L — ко-
роткозамкнутой цепью (рис. 7.8, б).
Из схемы, изображенной на рис. 7.8, б, следует,
что в момент времени до коммутации t = 0_ токи че-
рез емкости равны нулю: = 0, а ток
через индуктивность, так же как и токи через сопро-
тивления и R2, рассчитываются по закону Ома:
iL(0_) = iR,<0_> = .„/О.) = -Й- = i = 2 А.
+ £\>2 Z + Э
284
Напряжение на емкости С2 равно нулю: Wc2(0_) =
= 0, поскольку параллельно этой емкости включена
короткозамкнутая ветвь, которой была заменена ин-
дуктивность. Напряжение на индуктивности также
равно нулю: uL(0_) = 0. Напряжение на емкости Ct
такое же, как на сопротивлении R?:
wq(O-) = «д2(0_) = iR2(0_) R2 = 2-3 = 6 В.
На сопротивлении напряжение
мЛ1(0_) = 1Л1(0_) Л1 = 2-2 = 4 В.
В первый момент времени непосредственно после
коммутации t = 0+ заряженная емкость Q заменяет-
ся источником напряжения, незаряженная емкость
С2 — короткозамкнутой цепью, а индуктивность —
источником тока (рис. 7.8, в).
Согласно законам коммутации (7.1) и (7.2) имеем
iL(0+) = г£(0_) = 2 А;
«с/°+) = «q(O-) = 6 В;
иС2(0+) = ыс2<0-) = °-
Кроме того, поскольку в момент коммутации
ключ находится в положении 2, то в цепи включен
источник U2 = 15 В вместо источника Ui = 10 В, ко-
торый был до коммутации.
Из уравнения по закону напряжений Кирхгофа,
составленного для левого контура схемы на рис. 7.8, в,
находим напряжение на сопротивлении R\:
u«1(0+) = CZ2-MC1(0+) = 15-6 = 9 В.
Ток в сопротивлении R\ найдем по закону Ома:
Ч«.) = ^^ = | = 4,5 А,
1х\ Z
Напряжение на индуктивности «£,(0+) осталось
равным нулю, поскольку параллельно включенная
незаряженная емкость С2 заменена короткозамкну-
той ветвью:
«l(0+) = wc2(0+) = 0-
Напряжение на сопротивлении Т?2 будет таким
же, как на заряженной емкости Q:
285
ыя2(0+) = ыс/0+) = 6 В.
Ток через сопротивление R.2
.я2(0.) = ^^ = | = 2 А.
К2 о
По закону токов Кирхгофа имеем
iCi(0+) = iR1(0+) - гЛ2(0+) = 4,5-2 = 2,5 А;
г'с2(0+) = гд2<0+) - *£<0+) = 2 - 2 = О А.
В установившемся режиме, который вновь на-
ступает в цепи после окончания переходного процес-
са, т.е. при t -> 00, емкость вновь заменяется разры-
вом, а индуктивность — короткозамкнутой цепью.
Схема, соответствующая этому режиму работы цепи,
изображена на рис. 7.8, г. Принужденные состав-
ляющие токов и напряжений на всех элементах, обу-
словленные действием источника постоянного на-
пряжения U2, рассчитывают, используя закон Ома:
_ • _ и2 15 о ..
lJ?inp - гК2пр - г£пр ~ & + & - 2 + 3 ~ А’
гС]пр = ^С2пр = О,
мС2пр = О,
^/?inp = *Rinp ’ — 3-2 = 6 В,
^Qnp = ^Я2пр = (к2пр ’ ^2 = 3 • 3 = 9 В.
Таким образом, за время переходного процесса
токи iL(t) и г’д2(^) увеличиваются от 2 до 3 А, на-
пряжения uq{ (t) и UR2(t) возрастают от 6 до 9 В,
ток iRX (t), наоборот, уменьшается от 4,5 до 3 А, ток
г'с2(О — от 2,5 А до нуля, напряжение URX(t) падает
от 9 до 6 В, а ток ic2(t) и напряжения гс2(^) и
Ul (t) вообще не меняются, оставаясь все время рав-
ными нулю. Кроме того, следует иметь в виду, что в
момент коммутации t = 0 произошли скачки напря-
жения urx (от 4 до 9 В), тока гд, (от 2 до 4,5 А),
тока icx (от 0 до 2,5 А). Все остальные токи и на-
пряжения своих значений в момент коммутации не
изменили.
В примерах, которые были рассмотрены выше, рассчитыва-
лись установившиеся реакции на постоянные воздействия. Одна-
286
в цепи могут быть и источники гармонического напряжения
0ди тока, например u(t) = (7wsin(co£+ <р). При расчете реакции
цепи на гармоническое воздействие в установившемся режиме ем-
кости не заменяются на разрывы в цепи, а индуктивности не за-
меняются на короткозамкнутые цепи, как это было в цепях по-
стоянного тока. При гармоническом воздействии необходимо учи-
тывать комплексные сопротивления емкости Zc = l/(/coC) и ин-
дуктивности ZL = /со£.
Из данного параграфа мы узнали, что:
• Переходный процесс представляет собой переход цепи из '•
одного установившегося состояния в другое. 2
• Установившиеся режимы в цепи существуют до коммута- ;
ции, т.е. при t = 0_, и при t -> оо. J
. В установившемся режиме в цепи постоянного тока емкость j
равносильна разрыву в цепи, а индуктивность равносильна д
короткозамкнутой цепи. 2
7.4. Расчет переходных реакций в цепях
первого порядка
Расчет переходных процессов в электрических цепях сво-
дится к решению дифференциальных уравнений для мгновенных
значений токов или напряжений на элементах цепи. Для состав-
ления таких уравнений чаще всего используются законы Кирх-
гофа. Порядок дифференциального уравнения соответствует по-
рядку цепи. Цепи первого порядка содержат один реактивный
элемент — индуктивность или емкость, цепи второго порядка со-
держат два разнотипных реактивных элемента — и индуктив-
ность, и емкость. Могут быть цепи более высокого порядка.
Решение дифференциального уравнения относительно тока
или напряжения в цепи составляет сущность классического ме-
тода расчета переходных процессов.
Переходные процессы в RL-цепях первого порядка. Приме-
ним классический метод для расчета переходных процессов в це-
пях, содержащих последовательно соединенные сопротивление R
и индуктивность L, для трех случаев:
• при коротком замыкании /?£-цепи;
• при включении в TJL-цепь источника постоянного напряже-
ния U;
287
Рис. 7.9. Короткое за-
мыкание ЛЛ-цепи
• при включении в /?Л-цепь источ.
ника гармонического напряжен^
u(t) = Um sin (cot + ф„).
Короткое замыкание RL-цепи.
Рассмотрим 7?£-цепь, присоединен-
ную к источнику постоянного на-
пряжения, которая в момент комму-
тации t = О замыкается накоротко в
результате переключения ключа из
положения 1 в положение 2 (рис. 7.9).
Составим уравнение по закону напряжений Кирхгофа для
контура, образовавшегося после коммутации при t = 0+:
uL(t) + uR(t) = О
или
+ Ri(t) = Q. (7.5)
at
В короткозамкнутом контуре нет источников напряжения,
поэтому правая часть уравнения (7.5) равна нулю. Полученное
дифференциальное уравнение первого порядка является однород-
ным. Его решение
i(t) = iCB (t) = Aept (7.6)
представляет собой свободную составляющую тока, обусловлен-
ную тем, что к моменту коммутации в катушке индуктивности
была запасена энергия магнитного поля.
В выражении (7.6) р — корень характеристического уравне-
ния, соответствующего дифференциальному уравнению (7.5):
pL + R = 0.
Отсюда получаем
Величина т = 1/|р| = L/R называется постоянной времени
RL-цена. Она измеряется в секундах.
Подставляя р - - R/L или т = L/R в уравнение (7.6),. получаем
-*t _L
iCB(t) = Ае L = Ае т.
Постоянную интегрирования А найдем из начальных усло-
вий. До коммутации ключ в цепи (рис. 7.9) находился в положе-
нии 1, индуктивность в установившемся режиме равносильна ко-
роткозамкнутой цепи, поэтому в момент времени t = 0_ имеем
288
i(0->4
По закону коммутации (7.1) ток в индуктивности не может
измениться скачком, поэтому в первый момент времени непосред-
ственно после коммутации
£(0+) = К0.) = И.
К
Уравнение (7.6) для момента времени t = 0 имеет вид
i(0) = Ае° или = А.
R
Подставляя найденные значения А и р в уравнение (7.6), по-
лучаем, что ток в индуктивности при коротком замыкании RL-
цепи изменяется по экспоненциальному закону:
R R
Анализ экспоненциальной функции е~*!х показывает, что при
t = 0 она принимает значение е° =1, при этом ток i(t) имеет
максимальное значение U/R.
= е"1
= е'2
= е~3
= е~4
Теоретически экспонента никогда не достигнет нулевого зна-
чения. Однако на практике можно считать, что функция близка
к нулю уже между интервалами времени Зт...4т. За это время
ток, протекающий через индуктивность, уменьшается до 5...2%
от своего максимального значения. График тока i(t) изображен
(7.7)
При t = т
t = 2т
t = Зт
t = 4т
e~t/x
е~^х
e~tlx
e~t/x
= 0,367,
= 0,135,
= 0,05,
= 0,02,
г(т) = 0,367(17/1?);
г(2т) = 0,135 (U/R);
i(3i) = 0,05 (U/R);
i(4x) = 0,02(U/R).
Рис. 7.10. Ток в короткозамк-
нутой 1?£-цепи
Рис. 7.11. Напряжение на индук-
тивности в короткозамкнутой
1?!,-цепи
19 - 6972
289
на рис. 7.10. Как видно из приведенного выше анализа и графи-
ка на рис. 7.10, переходный процесс теоретически длится беско-
нечно долго. Практически можно считать, что он заканчивается
при £пп = Зт... 4т. Величина £пп называется временем переходно-
го процесса.
Физический смысл переходного процесса, происходящего в
короткозамкнутом RL-контуре, заключается в том, что с течением
времени энергия магнитного поля, накопленная в катушке индук-
тивности до коммутации WL = [Li2(0_)]/2, постепенно рассеива-
ется, превращаясь в сопротивлении R в тепло, поэтому ток в RL-
цепи приближается к нулю.
Напряжение на индуктивности
UL(t) = £^2 = -[/e“.
at
График зависимости напряжения на индуктивности от време-
ни ив короткозамкнутой RL-цепи изображен на рис. 7.11.
Пример 7.5. Найдем ток г(t) в цепи, изображенной на рис. 7.12,
для двух значений сопротивления R2\ а) /?2 = ЮОм,
б) R2 = 20 Ом, если заданы 17 = 10 В, R\ = 10 Ом,
L = 100 мГн.
Дифференциальное уравнение, составленное для
цепи (рис. 7.12) при t > 0 (ключ замкнут), имеет вид
£^£2 + /?2i(O = 0.
at
Решением этого однородного дифференциального
уравнения является свободная составляющая тока
t
i(t) = iCB(t) = Aept = Аех. (7.9)
Корень p характеристического уравнения
pL + R2 = 0
для двух разных значений R2 равен соответственно:
(7.8)
Рис. 7.12. /?£-цепь к примеру 7.5
290
\ ^2 Ю . пл -j
а) р = —-4 =--------т = -100 с ,
К L 100 Ю’3
хч /?2 20 плл -j
б) р = —=-----------5- = -200 с 1.
к L 100 Ю’3
Постоянная времени т = 1/|р| также имеет разные
значения для разных R2:
а) т = Дт = -Д- = 0,1 с = 10 мс,
|р| 100
б) т = Дт = -Д- = 0,005 с = 5 мс.
|р| 200
Постоянную А в уравнении (7.9) найдем из на-
чальных условий. Для момента времени t = 0 имеем
i(0) =Ле° = А.
Чтобы определить ток г(0) в момент коммута-
ции, найдем вначале ток в схеме в момент времени
до коммутации t = 0_. Ключ находится в разомкну-
том состоянии. Индуктивность в цепи постоянного
тока равносильна закоротке, поэтому
г(0_)=
U
+ R2
Для разных значений R2 имеем:
a)i(OJ = io7io = 0'5 А'
« -10720 “°'ЗЗА
По закону коммутации (7.1) ток в индуктивности
не может измениться скачком, значит г(0+) = i(0_).
Поэтому для случая а) получаем А = г(0) = 0,5 А,
для случая б) А = г(0) = 0,33 А.
Рис. 7.13. Ток в индуктивности 7?£-цепи,
изображенной на рис. 7.12
19*
291
В результате ток в короткозамкнутой 7?£-цепи на
рис. 7.12 определяется (7.9) как
а) г(£) = О,5е“,о°' А,
б) i(t) = O,33e'2oot А.
Графики:(t), построенные для случаев а) и б),
приведены на рис. 7.13. Заметим, что переходный
процесс в случае 6) заканчивается в 2 раза быстрее
(inn = Зт = 15мс), чем в случае a) (tnn = Зт = 30мс).
Включение в RL-цепь источника постоянного напряжения.
К изображенной на рис. 7.14 .RL-цепи при замыкании ключа в
момент времени t = 0 подключается источник постоянного на-
пряжения U. Составим уравнение по закону напряжений Кирх-
гофа для контура в первый момент времени непосредственно по-
сле коммутации t = 0+:
uR(t) + uL(t) = U.
В дифференциальной форме имеем
L^^ + Ri{t) = U. (7.10)
at
Полученное неоднородное дифференциальное уравнение пер-
вого порядка, описывающее переходный процесс в цепи, имеет
решение, содержащее две составляющие тока:
i(O = inp + ia,(t). (7.11)
Второе слагаемое гсв(£) — это уже известная нам свободная
составляющая тока, которая определяется в результате решения
однородного уравнения, полученного из (7.10) путем замены
правой части на нуль:
r di(t)
Is *
dt
+ Ri(t) = 0.
Рис. 7.14. Включение в
/?£-цепь источника по-
стоянного напряжения
Это уравнение совпадает с уравнением (7.5), и его решение
нам известно (см. (7.6)):
гсв (£) = Ле~^х,
L где постоянная времени т = L/R.
Первое слагаемое гПр в уравнении
(7.11) — это принужденная состав-
ляющая тока, вызванная наличием в
схеме источника постоянного напряже-
ния U. Принужденную составляющую
292
Znp можно найти как частное решение уравнения (7.10). Но
обычно гПр находят в результате расчета цепи в установившемся
режиме. При t -> оо индуктивность в цепи (рис. 7.14) заменяется
короткозамкнутой цепью и принужденная составляющая тока оп-
ределяется как
U
г"Р R-
Полное решение уравнения (7.10) имеет вид
i(t) = inP + iCB = + Ae~t/x. (7.12)
IX,
Постоянную интегрирования А определяем из начальных ус-
ловий. До коммутации ключ в цепи на рис. 7.14 был разомкнут и
тока в цепи не было: i(0_) = 0. Поскольку по закону коммутации
(7.1) ток в индуктивности в момент времени t = 0+ сохраняет то
же самое значение, которое было в момент t = 0_, то
i(0+) = i(0_) = 0.
Для момента времени t = 0+ уравнение (7.12) имеет вид
i(0+) = inp + Ае°.
Отсюда
^ = i(0+)-inP = “. (7.13)
К
Подставляя полученное значение А в выражение (7.12), по-
лучаем закон изменения тока в RL-цепи при подключении ее к
источнику постоянного напряжения:
или
i(i) = £(l-e-^). (7.14)
R
Обобщая все вышесказанное, с учетом (7.12) и (7.13) можно
для расчета тока в переходном режиме использовать формулу
*(*) = *пР + *cb (*) = *пР + [i(0+) - inp]e~t/T- (7.15)
Построим график изменения тока во времени в переходном
режиме в цепи на рис. 7.14. В первый момент времени непосред-
ственно после коммутации t = 0+ из выражения (7.14) имеем
i(0+) =(U/B)(1 -е°) = 0.
293
Рис. 7.15. Ток (л) и напряжение (б) на индуктивности при
подключении к /?Л-цепи источника постоянного напряжения
При t = z г(т) = (1//Д)(1-е'1) = 0,632(0//?);
t = 2т г(2т) = (U/R)(i-e~2) = 0,865(U/R);
t = Зт г(3т) = (О/Я)(1 - е~3) = 095(U/R);
t = 4т г(4т) = (О/Я)(1 -е-4) = 0,98(U/R).
При времени t = Зт переходный процесс достигает 95% от
своего установившегося значения, а при t = 4т — достигает 98%
от установившегося значения, и поэтому переходный процесс на
практике можно считать закончившимся за время £пп = Зт...4т.
График i(t) изображен на рис. 7.15, а. Здесь же изображе-
ны принужденная и свободная составляющие тока. В момент
коммутации ток в индуктивности равен нулю, а затем он плавно
нарастает до установившегося значения U/R.
Напряжение на индуктивности пропорционально ско-
рости изменения тока, протекающего через нее:
iL(t) = L^^- = L~~e-t/x =ие~^.
at R L
График uL(t) изображен на рис. 7.15, б. В момент времени
t= 0 напряжение г/д (0) изменяется скачком от 0 до U, а затем
плавно уменьшается по экспоненте. В установившемся режиме
напряжение на индуктивности равно нулю, так как при t -> оо
индуктивность равносильна короткозамкнутой цепи.
Пример 7.6. Найдем напряжение на сопротивлении «#(£) в це-
пи, изображенной на рис. 7.14, если U = 10 В, R =
= 10 Ом, L = 100 мГн.
По закону Ома напряжение uR(t) = i(t) R. Для
определения i (t) составляем дифференциальное
уравнение (7.10):
294
L^^- + Ri(t) = U
at
и находим его решение (7.11);
i ( i) = znp + zCB (t).
Принужденная составляющая тока (при t -> оо)
inp = U/R = 10/10 = 1 А.
Свободная составляющая тока
iCB(t) = Ае~^х.
Постоянную интегрирования найдем из (7.13):
А-
Постоянная времени
Ток i(t) в цепи находим как
i(t) = г„р + zCB (Л) = i„p + Ae~t/x = 1 - lf?"100f.
Напряжение на сопротивлении uR(t) имеет вид
uR(t) = i(t) -J? = 10(l-e-100f), В.
Для построения графика uR(t) рассчитаем значе-
ния напряжения в моменты времени t = 0, т, 2т, Зт, оо.
При t = 0 uR(0) = 0;
£ = т = 10мс «Л(т) = 10(1-е-1) = 6,32 В;
t = 2т = 20 мс uR(2т) = 10(1 -е-2) = 8,65 В;
t = Зт = 30 мс ur(3t) = 10(1-е-3) = 9,5 В;
t ->00 «дпр = Ю В.
Рис. 7.16. График u^tt) к примеру 7.6
295
График Ur (t), изображенный на рис. 7.16, на-
чинается от нуля в момент коммутации и за время
переходного процесса tnn = 30 мс достигает 95%
(9,5 В) от установившегося значения и^пр = 10.
Включение в RL-цепь источника гармонического напряже-
ния. К изображенной на рис. 7.17 RL-цепи в момент коммутации
(i = 0) подключается с помощью ключа источник гармонического
напряжения u(t) = Umsin.(at + фы). Дифференциальное уравне-
ние, составленное с использованием закона напряжений Кирхгофа,
имеет вид
L^l + Ri(t) = u(t).
at
Решение однородного уравнения — это свободная составляю-
щая тока:
zCB(i) = Aept = Ае~1^.
Частное решение имеет вид (см. гл. 2)
*пр= 'I....--------=sin(coi + <р„ - <pz) = Imsin (cot + <pf),
V/?2+(coL)2
, aL
где <Pi = <p„ - (pz = <Pu ~ arctg —.
К
Tok i{t} в цепи, изображенной на рис. 7.17, определяется по
формуле
i(t) = Aip + хсв(£> = /msm(cot + 9,) + Ae~tlx.
Постоянную интегрирования А находим из начальных усло-
вий. В момент времени t - 0+ ток г(0) равен нулю (нулевые на-
чальные условия), так как ток в индуктивности скачком не меня-
ется, поэтому
г(0) = 1т зтф,- +А = 0.
Отсюда
Рис. 7.17. Включение в
.RL-цепь источника сину-
соидального напряжения
А = -/Отзтф^.
В результате получаем
i(t) = Im sin(cot + ф,)-/т8тф1-е_^т.
Постоянная времени т, как и пре-
жде, равна L/R.
График зависимости i(t) изо-
бражен на рис. 7.18. Ток i(t) изме-
296
Рис. 7.18. Ток в 7?£-цепи, подключенной к источнику
синусоидального напряжения
няется от нуля в момент коммутации до установившегося зна-
чения
гПр = /msin(G)t + <pt).
На рисунке показаны также графики принужденной и сво-
бодной составляющих тока.
Переходные процессы в RC-цепях первого порядка. Приме-
ним теперь классический метод расчета переходных процессов в
цепях первого порядка, содержащих последовательно соединен-
ные сопротивление R и емкость С для трех случаев:
• при коротком замыкании RC-цепи;
• при включении в RC-цепь источника постоянного напряжения U;
• при включении в RC-цепь источника гармонического напряже-
ния u(t) = {7msin(coi + Фи).
Короткое замыкание RC-цепи (.разряд конденсатора). В
схеме на рис. 7.19 RC-цепь с помощью ключа в момент коммута-
ции замыкается накоротко.
Составим уравнение по закону напряжений Кирхгофа для
контура при t = 0+:
Un(t) + uc(t) = 0 или Ri(t) + Uc(t) = 0.
С учетом того, что ток и напряжение
отношением
в емкости связаны со-
i(t) = C
duc(t)
dt
имеем
RCd-^- +uc(t) = Q. (7.16)
at
Дифференциальное уравнение (7.16)
является однородным, и его решение
представляет собой свободную состав-
Рис. 7.19. Короткое
замыкание RC-цепи
i(t)
297
ляющую напряжения на емкости, изменяющуюся по экспоненци-
альному закону:
ис (t) = иСсв(Л) = Aept = Ae~f'^. (7.17)
Принужденная составляющая напряжения на емкости равна
нулю: wcnp(£) = 0.
Корень р характеристического уравнения, соответствующего
дифференциальному уравнению (7.16)
р7?С + 1 = 0,
определяется элементами R и С цепи:
P = ~~RC
Постоянная времени /?С-цепи т = 1/|р| = RC.
Постоянную интегрирования А в (7.17) найдем из начальных
условий. До коммутации 7?С-цепь была подключена к источнику
постоянного напряжения, емкость была заряжена до напряжения
U, т.е. ис(0_) = U. По закону коммутации (7.2) в первый момент
времени непосредственно после коммутации t = 0+ имеем
uc(0+) = uc(0-) = U.
Подставляя найденное значение Uq(0+) в уравнение (7.17),
получаем
uc(Q) = U = A.
Окончательно находим
uc(t) = Ае^ = Ue~^RC.
Напряжение на емкости плавно уменьшается от величины U
до нуля за время tnn = Зт = 3RC. Емкость разряжается на сопро-
тивление R. График uc(t) изображен на рис. 7.20, а.
Рис. 7.20. Напряжение' на емкости («) и ток при коротком
замыкании (б) ЯС-цепи
298
Ток в цепи
i(t) = cduc{t) = ~е~^
d t I\>
имеет знак «минус», т.е. его направление противоположно на-
правлению напряжения на емкости.
В момент коммутации ток изменяется скачком от нуля до ве-
личины (-U/R), а затем плавно изменяется по экспоненте до ну-
ля. График ic(t) изображен на рис. 7.20, 6.
Пример 7.7. Найдем напряжение на емкости в цепи, изображен-
ной на рис. 7.21, если U= 10 В, Rt = R2 = R3 = 10 Ом,
С = 10 мкФ.
Дифференциальное уравнение для правого кон-
тура в схеме на рис. 7.21 в первый момент времени
непосредственно после коммутации t = 0+ имеет вид
z(t) + uc(t) = 0
или
я3с^^2+ис(*) = о.
dt
Решением этого уравнения является свободная
составляющая напряжения на емкости:
UC (t) = иСсв (г) = Ae~t/l.
Постоянная времени т = 7?3С = 10 • 10 • 10-6 = Ю^с =
= 0,1 нс.
Постоянную интегрирования А найдем из на-
чальных условий. До коммутации ключ был разомк-
нут, емкость представляла собой разрыв и напряже-
ние на ней было такое же, как на сопротивлении R2:
uc(0_)=U п R2 = 10 -10 = 5 В.
с Ri+R2 10 + 10
По закону коммутации
Рис. 7.21. /?С-цепь к примеру 7.7
299
Рис. 7.22. Напряжение на емкости к примеру 7.7
wc(0+) = ис(0_) = 5 В.
Для момента времени t = 0+ имеем
Uc(ff) = А или А = 5В.
Напряжение на емкости изменяется по закону
нс(£) = , В.
График Uc(t) изображен на рис. 7.22. Напря-
жение на емкости в момент коммутации сохраняет то
же самое значение, которое было до коммутации, т.е.
5 В, а затем по экспоненте стремится к нулю. Время
переходного процесса составляет 0,3...0,4 мс.
Включение в RC-цепь источника постоянного напряжения
U (заряд конденсатора). Для схемы, изображенной на рис. 7.23,
в которой к последовательно соединенным сопротивлению R и
емкости С подключается при замыкании ключа источник посто-
янного напряжения U, составим уравнение по второму закону
Кирхгофа для момента времени t = 0+:
uR(t) + Uc(t) = U или Ri(t) + Uc(t) = U.
С учетом соотношения i(t) = C(duc(t)/dt) получаем
ЯС^^ + ис(£) = (Л (7.18)
dt
Решение неоднородного дифференциального уравнения
(7.18) содержит две составляющие — принужденную и свобод-
ную:
uc(t) = иСпр + uCcB(t).
Свободная составляющая напряжения на емкости имеет вид
uCcB(t) = Aept,
где р — корень характеристического уравнения:
300
pRC + 1 = 0,
т.е. p = -\/RC 1/c.
Постоянная времени RC-цепи
т = Дт = RC с.
hl
Таким образом, свободная со-
ставляющая определяется как
Рис. 7.23. Включение в RC-
цепь источника постоянного
напряжения
“Сев (i) = Ле = Ae~flRC
Принужденную составляющую напряжения на емкости «спр
найдем, анализируя цепь на рис. 7.23 в установившемся режиме.
При £-> оо ключ замкнут, а емкость равносильна разрыву цепи,
поэтому напряжение
“Спр ~ <
т.е. конденсатор заряжается до величины напряжения источника
за время переходного процесса.
Общее решение дифференциального уравнения (7.18) имеет
вид
uc(t) = иСпр + Ae~tfx. (7.19)
Постоянную интегрирования А находим из начальных усло-
вий. Для первого момента времени непосредственно после комму-
тации справедлив закон коммутации (7.2): Uc(0+) = Uc(0~)
Напряжение на емкости до коммутации Uq($_) было равно
нулю, так как источник не был включен в цепь, поэтому
ис(0+) = ис(0-) = 0.
Из уравнения (7.19) при t = 0+:
«с<0+) = “спР + Л
находим
Л = мс(0+) - мСпр = 0-U = -U.
Подставляя значения Л, т и испр в (7.19), получаем закон
изменения напряжения на емкости в ДС-цепи при подключении
ее к источнику постоянного напряжения:
uc(t) = U-Ue~^c =(/(1-е’яс). (7.20)
Обобщая вышесказанное, можно для расчета напряжения на
элементе цепи в переходном режиме использовать формулу
301
Рис. 7.24. Напряжение (а) и ток (б) на емкости при заряде конденсатора
«(£) = unp +[u(0+)-unp]e t/x. (7.21)
Построим график изменения напряжения на емкости во вре-
мени в переходном режиме, анализируя выражение (7.20). В пер-
вый момент времени непосредственно после коммутации t = 0+
напряжение «с(0) = (7(1 -е°) = 0. При t = т, 2т, Зт, 4т получаем
ис(т) = 0,632(7, wc(2т) = 0,865(7, мс(3т) = 0,95(7, ис(4т) = 0,98(7.
График uc(t) изображен на рис. 7.24, а.
Ток в цепи
i(t) = cdu^t) = U~
dt £ъ
На рис. 7.24, б изображен график тока i(t).
В момент коммутации ток через емкость скачком изменяется
от нуля до максимального значения U/R, а затем по экспоненте
плавно уменьшается до нуля.
Пример 7.8. Найдем напряжение на емкости и ток, протекающий
через нее в цепи, изображенной на рис. 7.25, если
(7= 10 В, R = 10 Ом, С = 10 мкФ. Ключ в момент
коммутации переключается из положения 1 в поло-
жение 2.
Уравнение по закону напряжений, составленное
для контура в момент времени непосредственно после
коммутации t = 0+ (ключ в цепи на рис. 7.25 нахо-
дится в положении 2), имеет вид
их<Л) + Uc(t) = U
или (7.18):
RCducU)^ uc(t) = U.
dt с
Решением этого неоднородного дифференциаль-
ного уравнения является (7.19):
302
Рис. 7.25. ЯС-цепь к примеру 7.8
uc(t) = иСпр + Ae~t/x.
Принужденная составляющая напряжения на ем-
кости испр -<7 = 10 В, поскольку за время переход-
ного процесса конденсатор заряжается до величины
напряжения источника.
Свободная составляющая
“Сев = Ae~tlx.
Постоянная времени т = RC =10•10• 10-6 = 10-4 с =
= 0,1 мс. Время переходного процесса £Пп = Зт...4т =
= 0,3...0,4 мс.
Для определения постоянной интегрирования А
запишем начальные условия. До коммутации ключ в
цепи находился в положении 1, источник напряжения
не был подключен к JSC-цепи, поэтому zzc(O_) = O.
По закону коммутации (7.2)
“с(0+) = ис(0_) = 0.
Тогда для момента времени t = 0+ имеем
мс(0) = иСпр + Ае°.
Отсюда
А = wc(0)-«ClIp = -10 В.
Окончательно получаем закон изменения напря-
жения на емкости при заряде конденсатора:
licit) = мСпр + Ае~^х = 10-10e-1°4f В.
Ток в емкости найдем, используя соотношение
dt R
Получаем
i(i) = e-lo4< А.
303
uc(t), В i(t), A
e) (5)
Рис. 7.26. Напряжение (а) и ток (б) через емкость
к примеру 7.8
Графики зависимостей uc(t) и г(£) изображены
на рис. 7.26. Напряжение на емкости не может изме-
няться скачком. В момент коммутации (t = 0) оно
равно нулю, так же как и до коммутации, а затем
плавно увеличивается до величины U = 10 В. Неза-
ряженная емкость в момент коммутации равносильна
короткому замыканию, поэтому при t = 0 происхо-
дит скачок тока до величины
г(0)Л = 1А,
R
а затем ток плавно уменьшается по экспоненте до
нуля, поскольку при t -> оо емкость равносильна
разрыву.
Включение в RC-цепь источника гармонического напря-
жения. Предлагаем читателям самостоятельно убедиться, что
при включении в /?С-цепь источника синусоидального напря-
жения u(t) = (7msin(co£+ ф„) (рис. 7.27) напряжение на емко-
сти имеет вид
ыс(£) = иСпр +мСсв(£) = £/ sin <o£ + (pu+<p-^ -
, 2 (7.22)
- Umc sin^(pa + <p - J е~Л/т,
1 i rj 1
C oC mc coC 7t?2 + (1/coC)2 *
Ток, протекающий через емкость, определяется как
г(£) = - 1тс sin(co£+ фи + ф) +
304
R
Рис. 7.27. Включение в /?С-цепь источника
синусоидального напряжения
г 1 • ( 71 —tlx
При расчете переходных процессов в сложных цепях с од-
ним реактивным элементом следует придерживаться приведен-
ного выше порядка расчета RL- и /?С-цепей. Обобщая все, что
было написано о расчете переходных процессов при коротком за-
мыкании RL- и RС-цепей и подключении к ним источника на-
пряжения, можно привести следующий алгоритм расчета слож-
ных цепей первого порядка-.
1. По законам Кирхгофа составляем систему интегродифферен-
циальных уравнений.
2. Преобразуем их в дифференциальное уравнение первого по-
рядка относительно искомого тока i(.t) или напряжения
uc(t).
3. Записываем выражение для свободной составляющей тока или
напряжения:
гсв (t) = Aept, uCB(.t) = A^ept,
где p — корень характеристического уравнения, соответствую-
щего дифференциальному уравнению.
Определяем постоянную времени т = 1/|р|.
4. Находим принужденную составляющую тока гпр или напряжения
«пр, рассчитывая цепь в установившемся режиме при t -><ю.
5. Определяем постоянную интегрирования:
А — z(0+) ^пр> = — ипр.
Предварительно необходимо найти начальные условия, т.е.
значение тока (напряжения) в момент времени t = 0+. Для оп-
ределения тока в индуктивности г’д(0+) и напряжения на ем-
кости ис(0+) используем законы коммутации (7.1) и (7.2), для
определения значений любых других токов или напряжений
составляем уравнения по законам Кирхгофа или рассчитываем
схемы замещения, приведенные в § 7.2.
6. Записываем выражение для тока или напряжения:
20-6972 305
i(t') ^пр + ^св (— ^пр А& t
u(.t) = ипр + uCB(t) = иар +Aiept.
7. Строим графики i(t) wmu(t).
Пример 7.9. Найдем ток ii(t) в цепи, изображенной на рис. 7.28,
если U = 10 В, Ri = R2 = 5 Ом, С = 10 мкФ.
Расчет будем проводить в соответствии с приве-
денным выше алгоритмом.
Составляем систему уравнений по законам Кирх-
гофа для момента времени t = 0+:
ii(t) = i2(t) + i3(t),
• Rj + i2(t) R2 = U,
ii(t)Ri +uc(t) = U.
Учтем также, что
uc(t) = ji3(t)dt.
О
Преобразуя уравнения в системе, получаем диф-
ференциальное уравнение
rxr2C^1 + (Pj + R2 (t) = U.
at
В результате решения этого неоднородного диф-
ференциального уравнения находим
Zj ( £ ) = Zjnp + Z|CB (t) .
Свободная составляющая тока
zt(i) = Aept.
Корень р найдем из характеристического уравнения
р • R\R2C + (R\ + R2) = 0.
Л1 6(0
6(0
Рис. 7.28. Цепь первого порядка к примеру 7.9
306
r=0+
и
Рис. 7.29. Схема замещения при t = 0+ к примеру 7.9
Получаем
n = _-R.t+7?2 =____5+_5__= 4•104 1
Р RiR2C 5-510 IO"6 с'
Постоянная времени
г = JL = - С = = 0,25-10"4 с = 25 мкс.
|р| Ri+R2 4 104
Принужденную составляющую iinp находим при
t -> оо. В установившемся режиме ключ в цепи замк-
нут, но емкость равносильна разрыву, поэтому
• _ и 10 .
г1пр-д1+я2"5+5
Для определения А в свободной составляющей
тока найдем значение тока в первый момент
времени непосредственно после коммутации t = 0+.
До коммутации ключ в цепи был разомкнут, поэтому
напряжение на емкости было равно нулю: ис(0-) = 0.
По закону коммутации Uc(Q+) = uc(Q_) = Q, т.е. ем-
кость равносильна короткому замыканию (см. § 7.2).
Схема замещения цепи в момент времени t = 0+ изо-
бражена на рис. 7.29.
В этой схеме ij(0+) = ?з(0) = U/R^ = 10/5 = 2 А.
Тогда постоянная интегрирования
А = i\ (0+) - ii пр = — - =
UR2 = 10-5
Ri(Rt +R2) 5(5 + 5)
Окончательно имеем
• • • U UR2 pt _
zlnp + itcB ~ Ri+Ri+ R^Ri + R^
= i + eil0it A.
20*
307
6(0, A
2
1
_J___i___i___i__i „
0 25 50 75 100 /, мкс
Рис. 7.30. График тока q(t) к примеру 7.9
График тока ij(i) изображен на рис. 7.30. До
коммутации ток ц(Л) был равен U/(R\ + R2} = 1 А.
В момент коммутации происходит скачок тока от 1
до 2 А. Затем ток плавно затухает по экспоненте до
принужденного значения, равного 1 А, за время пе-
реходного процесса = Зт...4т = 75...100 мкс.
Для цепей с одним реактивным элементом можно использо-
вать другой, более простой способ расчета переходных процессов,
при котором нет необходимости составлять и решать дифферен-
циальное уравнение, т.е. можно опустить пп. 1, 2, 3 в приведен-
ном алгоритме.
Для цепей первого порядка можно сразу же записать реше-
ние в виде (7.15) или (7.21):
i(t) = гпр + Ae~t/x = inp +[г(0+) - гПр]е-</т
ИЛИ
u (t) — Пдр + — и Пр + £ м(0+) и пр J •
Здесь т = 1/|р|.
Корень р характеристического уравнения можно найти, не
составляя дифференциального уравнения. Достаточно найти со-
противление Z цепи, разорвав ее в любом месте, где протекает
ток, и заменив /со на р.
Приравняв Z(p) к нулю и решив полученное уравнение от-
носительно р, находим корень характеристического уравнения.
Кроме того, для цепей первого порядка можно сразу же оп-
ределить постоянную времени т.
Для /?£-цепи
Для /?С-цепи
т = R3C.
308
В этих формулах R3 — внутреннее сопротивление эквива-
лентного генератора, образованного цепью относительно реактив-
ного элемента.
Принужденные составляющие тока гпр или напряжения иПр,
а также постоянные интегрирования А или Ai определяем так
^е, как описано в пп. 4 и 5 общего алгоритма расчета переход-
ных процессов. Зная гпр, А, х или ггПр, Д, т, записываем законы
изменения тока i(t) или напряжения и Ct) от времени и строим
графики.
Пример 7.10. Найдем корень р характеристического уравнения и
постоянную времени т для цепи, изображенной на
рис. 7.28 в примере 7.9, без составления дифферен-
циального уравнения.
Сопротивление Z цепи на рис. 7.28 относительно
зажимов источника имеет вид
7 „ . R2 A/(j(oC)
- 1 я2+1/(>сг
Заменив /со на р и приравняв Z к нулю, получаем
2(р) = *1 +
R2A/(pC)
т?2 1/(рО
= 0
или, приведя к общему знаменателю,
Z(-o) = &&£Р + R\+R2 _ 0
CR2p + l
Отсюда имеем
pR\R2C + (Rt + R2) = 0
или
Р = ~
+ -^2
R\R2C
Получили точно такое же выражение для расчета
корня характеристического уравнения, как и в при-
мере 7.9.
Постоянную времени т найдем по формуле
т = R3C.
Эквивалентное сопротивление цепи R3 относи-
тельно емкости С найдем по схеме пассивного двух-
полюсника (рис. 7.31):
о _ 7?! • R2
э Rt+R2'
309
Ri
Рис. 7.31. Схема пассивного резистивного
двухполюсника к примеру 7.10
Постоянная времени
т = R3C =
R1R2 Q
R\ + R%
что совпадает с выражением для расчета т в приме-
ре 7.9.
Пример 7.11. Найдем ток i(t) и напряжение на индуктивности в
цепи, изображенной на рис. 7.32, если U = 48 В,
= R2 = 12 Ом, L = 120 мГн.
До коммутации при t = 0_ ключ был замкнут,
индуктивность в установившемся режиме равносиль-
на короткозамкнутой цепи, поэтому
г(0_) = U/Ri = 48/12 = 4 A, uL(t) = 0.
Ток i(t) — это ток, протекающий через индук-
тивность, поэтому по закону коммутации (7.1) можем
определить его значение в первый момент времени
непосредственно после коммутации t = 0+:
г(0+) = г(0_) = U/Ri = 4 А.
Индуктивность равносильна источнику тока.
Схема замещения исходной цепи в момент времени
t = 0+ изображена на рис. 7.33.
Рис. 7.32. Цепь к Рис. 7.33. Схема замещения
примеру 7.11 к примеру 7.11
310
Рис. 7.34. График тока (а) и напряжения на
индуктивности (б) в цепи- рис. 7.32
Напряжение на индуктивности uL(0+) рассчита-
ем из уравнения, составленного по закону напряже-
ний Кирхгофа:
uL(0+) = U - i(0+)(JR1 + R2) = 48 - 4 • 24 = -48 В.
В установившемся режиме при t -» со ключ ра-
зомкнут, индуктивность равносильна короткозамкну-
той цепи, поэтому
. U 48 =2
12 + 12
м£пр ~ О-
Постоянная времени
L L 120 -10-3 _
т = — =--------=---------= 5 мс.
R3 Rx+R2 24
Ток i(t) в цепи в соответствии с (7.15) можно
записать в виде
г(£) = гпР+Ле_‘Л = гпр +[г(0+) - =
= 2 + 2е-'/510’3 А;
= Ы£Пр+[ц£(0+)-и1пр]е’</т =
=-48е-^510^ В.
Графики i(t) и uL(t) изображены на рис. 7.34.
Из данного параграфа мы узнали, что:
• Переходные процессы в цепях первого порядка, содержа- *
щих один реактивный элемент, рассчитываются путем со- f
ставления и решения дифференциального уравнения перво- <
го порядка относительно неизвестных тока и напряжения.
311
• Ток или напряжение в переходном режиме имеют принуж-
денную и свободную составляющие.
• Принужденная составляющая тока или напряжения опре-
деляется в результате расчета цепи в установившемся ре-
жиме.
• Свободная составляющая тока или напряжения в цепях
первого порядка изменяется по экспоненциальному закону.
• Скорость убывания (или нарастания) экспоненты зависит
от постоянной времени цепи т, определяемой параметрами
цепи. Переходный процесс можно считать закончившимся
за время, равное Зт...4т.
• Постоянная интегрирования, стоящая перед экспонентой,
определяется как разность значений тока (напряжения) в
момент коммутации и в установившемся режиме.
7.5. Расчет переходных реакций в цепях
второго порядка
Расчет переходных процессов в цепях, содержащих два
разнотипных реактивных элемента, сводится к составлению и
решению дифференциального уравнения второго порядка отно-
сительно неизвестных тока или напряжения. Применим класси-
ческий метод для расчета переходных процессов в последова-
тельном колебательном 7?£С-контуре для двух случаев:
• при разряде емкости на /?£-цепь;
• при включении RLC-цепи на постоянное напряжение.
Разряд емкости на RL-цепь. Прежде чем составлять диффе-
ренциальное уравнение для расчета переходного процесса в цепи,
изображенной на рис. 7.35, определим значения тока i(t) и на-
пряжения на емкости uc(t) и индуктивности uL(t) в моменты
времени t = 0_, t = 0+ и t -> <ю.
До коммутации при t = 0_ ключ находится в левом положе-
нии (рис. 7.36, а), емкость была подключена к источнику напря-
жения и заряжена. Напряжение на емкости в установившемся
Рис. 7.35. Разряд емкости на /?£-цепь
312
a) 6) в)
Рис. 7.36. Схемы замещения цепи на рис. 7.35
в моменты времени t = 0_ (a), t = 0+ (б) и t -> оо (в)
режиме до коммутации wc(0_) = (7. Ток в /?£-цепи г(0_) и на-
пряжение на индуктивности и/,(0_) были равны нулю: г(0_)= О,
Mt(0_) = 0.
В первый момент времени непосредственно после коммутации
t = 0+ (рис. 7.36, б) ключ переключается вправо и заряженная
емкость ведет себя как источник напряжения ис(0+) = ис(0_) = U.
Индуктивность, ток через которую до коммутации был равен ну-
лю, равносильна разрыву, поэтому г(0+) = г(0_) = 0, uL(0+) =
= -ис(0¥) = -U. Значения напряжения на емкости ис(0+) и тока
в индуктивности г(0+) являются независимыми начальными ус-
ловиями, которые были определены по законам коммутации.
Напряжение на индуктивности Ui(Q+) является зависимым на-
чальным условием, и для его определения использовали закон
Кирхгофа.
В установившемся режиме при t -> оо (рис. 7.36, в) емкость
равносильна разрыву, а индуктивность — закоротке, поэтому
принужденная составляющая напряжения на емкости равна ну-
лю: испр = 0. Равны нулю также принужденные составляющие
тока: гпр = 0 и напряжения на индуктивности: М£Пр = 0.
В переходном режиме ключ в цепи на рис. 7.35 находится в
правом положении, емкость разряжается через 7? £-цепь. Схема
разряда емкости изображена на рис. 7.37.
Уравнение по закону напряжений Кирхгофа для контура на
рис. 7.37 имеет вид
uL(t) + uc(.t) + uR(t) = Ъ
R i(t)
Рис. 7.37. Цепь разряда емкости на RL-цепь в переходном режиме
313
/,ч r di(t)
или с учетом того, что (с) = L—-—,
at
uc(t) + L^l + Ri(t) = Q.
at
(7.23)
Кроме того, поскольку ток и напряжение на емкости связаны
.Z.4 ^duc(t)
соотношением lit)-С——, получаем
ис (t) + + RCdUc}t} = О
с dt2 dt
или в окончательной форме
d2uc(t) Rduc(t) uc(t) _0
dt2 L dt + LC ’ ’
Получили дифференциальное уравнение второго порядка от-
носительно неизвестной реакции — напряжения на емкости.
Дифференциальное уравнение (7.23) является однородным,
поэтому принужденная составляющая напряжения равна нулю:
«Спр =0-
Решением уравнения (7.23) является свободная составляю-
щая напряжения на емкости:
uc(t) = uCcB(t) = A{eP{t + A2eP2t. (7.24)
Для нахождения рх и р2 составим характеристическое урав-
нение, соответствующее дифференциальному уравнению (7.23):
Р2+тР + 7^ = 0. (7.25)
Такое же уравнение можно получить другим путем. Запишем
комплексное сопротивление контура, изображенного на рис. 7.37,
разорвав его в любом месте:
Z = R + ja>L + 1/(/соС).
Заменим /со на р:
Z{p) = R + pL+-^- = Q.
pC
После преобразований получаем
2 R 1 Л
314
цТ0 совпадает с уравнением (7.25).
Корни /?! и р2 характеристического уравнения (7.25) опреде-
ляются как
(7.26)
R ( R Г 1
Р1’2 2L±\\2L/ LC
Характер свободной составляющей напряжения зависит от
вида корней р\ и Р2- Если подкоренное выражение в (7.26)
больше нуля, то корни р\ и р2 вещественные и разные (обозначе-
ны точками 1 на комплексной плоскости на рис. 7.38) и переход-
ный режим в цепи называется апериодическим. Если подкорен-
ное выражение в (7.26) меньше нуля, то корни р\ и р2 комплекс-
но-сопряженные:
R I1 ( R
где а = R/(2L) — коэффициент затухания контура; юсв = - а2 —
частота свободных колебаний; «>0 = {/^LC — резонансная часто-
та контура. Они обозначены на рис. 7.38 цифрой 2, а переход-
ный режим в этом случае называется колебательным. Точка 3
на рис. 7.38 соответствует случаю, когда подкоренное выраже-
ние равно нулю, корни р\ и р2 вещественные и равные. Пере-
ходный режим в цепи при этом называется критическим.
Рассмотрим порядок расчета переходных процессов в RLC-
колебательном контуре для каждого из трех перечисленных ре-
жимов.
Апериодический процесс. Если подкоренное выражение в
(7.26) больше нуля, то это означает, что выполняется неравенство
fA? 1
UzJ > LC
или
(7.27)
+/
1 3 1
2*
о +1
Рис. 7.38. Расположение корней характеристического
уравнения на комплексной плоскости
315
где ^L/C — характеристическое сопротивление контура.
При выполнении условия (7.27) корни р\ и характери-
стического уравнения являются вещественными и разными. На-
пряжение на емкости uc(t) имеет только свободную составляю-
щую, определяемую в соответствии с (7.24):
uc(t) = Alep't+A2eP2t.
Для нахождения двух постоянных интегрирования А\ и Д2
составим еще одно уравнение:
= AxPxePit + A1P2eP2t (7 28)
at
и используем начальные условия. Как было установлено ранее, в
момент времени t = 0+ по законам коммутации
wc(0+) = «с(0-> = I/;
г(0+) = г(0_) = 0.
Поскольку через все элементы колебательного контура
(рис. 7.37), в том числе и через емкость, протекает один и тот же
ток, то
г-(0+) = =о.
dt <=о+
Отсюда находим производную напряжения в момент t = 0+.
Она равна нулю
duc<$+) _ 0
dt
Подставляя значения t = 0, wc(0+) = Um duQ^^/dt = 0 в
выражения для расчета uq<J) и ductCl/dt, получаем
[At+A2 = U,
U1P1 + А2р2 = 0.
Откуда
д =__^2_; д (7.29)
Р1-Р2 Р1-Р2
В результате напряжение на емкости определяется выраже-
нием
ис (t) = ——— (-p2ePxt + p\eP2t).
Pi~P2
Ток в контуре
i(t) = = C(AxpiePxt + Д2»2еР29- (7.30)
at
316
разряде емкости
Напряжение на индуктивности
uL(t) = = LC{Axple^ + A2p2eP2t}. (7.31)
at
Каждая из найденных реакций цепи uc(t), i(t), uL(t) в
апериодическом режиме определяется как сумма двух экспонент.
Графики зависимости этих величин от времени изображены на
рис. 7.39.
В момент времени график uc(t) имеет точку перегиба,
модуль тока |i(t)| принимает максимальное значение, а напряже-
ние на индуктивности uL(t) равно нулю. В момент времени t2
график тока i(t) имеет точку перегиба, а напряжение uL(t) дос-
тигает максимального значения. Значения времени и t2 нахо-
дят из условий di(t)/dt = 0 и duL(t)/dt = 0:
tx=—-—ln^; i2=2£i. (7.32)
Pi~P2 Pi
Колебательный процесс. Если подкоренное выражение в
(7.26) меньше нуля, то выполняется неравенство
[Я/(2£)]2 <1/(ZC)
или
R<2y[L/C. (7.33)
317
При выполнении условия (7.33) корни рх и характерис-
тического уравнения являются комплексно-сопряженными (7.26).
Подставляя в выражение (7.24) для расчета напряжения
емкости
wc(t) = + A2eP2t
комплексно-сопряженные корни (7.26) = -а + ja>CB, Р2 = -а.~
-](дсв, получаем
uc(t) = Ae~at sin(coCBt + <p). (7.34)
Запишем также производную duc(t)/dt, так как в (7.34) две
неизвестные величины — А и <р:
^U<dt^ = ^[_а^п(<йсв^ + (Р) + ®свС08((йсв^ + ф)]- (7.35)
Используя начальные условия в контуре, которые были опре-
делены при расчете апериодического процесса,
при t = 0+ ыс(0+) = (7, — =0,
dt f=o+
получаем систему уравнений для определения Л и ср:
p4sin<p = U,
[H(-asin(p + a>CBcos(p) = 0.
Отсюда
, со . со р» . (7
tga = —(p = arctg—А = ——.
a a sm ф
Подставляя найденные значения А и ф в (7.34), можно полу-
чить формулу для расчета напряжения на емкости u^it) в коле-
бательном режиме. Для нахождения тока и напряжения на ин-
дуктивности достаточно взять производные i(t) = C(duc(t)/dt),
uL(t) = L(di(t)/dt).
Анализ выражения (7.34) показывает, что в цепи возникают
затухающие синусоидальные колебания с частотой сосв. Графики
Uc(t), i(t), uL(t) изображены на рис. 7.40. Колебания возни-
кают в результате периодического преобразования электрического
поля в магнитное и наоборот, причем в сопротивлении R проис-
ходят потери энергии. Величина Т - 2тг/сосв называется периодом
свободных колебаний, а величина 1/а называется постоянной
времени колебательного контура.
Критический процесс. Если подкоренное выражение в (7.26)
равно нулю, то выполняется равенство
318
Рис. 7.40. Графики «с Q), i(t), Ul<J) при
колебательном разряде емкости
При выполнении условия (7.36) корни характеристического
уравнения являются вещественными и равными
R
P,2=-Tl=~^.
Подставляя в выражение (7.24) для расчета напряжения на
емкости корни= р2 = -а, получаем
мс(О = (Л1 +Л2^)е~а<. | (7.37)
Производная напряжения на емкости по времени имеет вид
=(A2-aA1-aA20e~af- (7.38)
at
Для известных начальных условий uq(0+) = U и duc(S>+)/dt =
= 0 в момент времени t = 0+ из уравнений (7.37) и (7.38) форми-
руем систему
319
Mi = <Л
|Л2 - ccAj = 0.
Решая ее, находим постоянные интегрирования At = П
А2 = clU . В результате напряжение на емкости (7.37) становится
равным
uc(t) = U(l + at)e~at.
Ток в цепи и напряжение на индуктивности определяются как
.Z.X ^duc(t) г.ч r di(t)
dt L dt
Графики uc(t), i(t), uL(.t) качественно повторяют графики
апериодического процесса, изображенные на рис. 7.39.
Пример 7.12. Найдем напряжение на емкости в цепи, изображен-
ной на рис. 7.35, для трех случаев:
10 В, R = 20 Ом, L = 100 мГн, С = 1333 мкФ;
(2) U = 10 В, R = 20 Ом, L = 100 мГн, С = 1000 мкФ;
(3) U = 10 В, R = 20 Ом, L = 100 мГн, С = 200 мкФ.
Напряжение на емкости uc(t) имеет только сво-
бодную составляющую «ссв(^> вид которой зависит
от корней характеристического уравнения (7.25), ко-
торые определяются по формуле (7.26):
R If R ? Г
Р1'2 2L"K2lJ LC
Рассчитаем корни р12 для всех трех случаев.
Случай (/).
20
P12 =---------г ±
2 100 1Q-3_______________
V20>21
± --------------------_!------- = -100 ± 50.
VI2- юо -Ю"3; юо • Ю"3 • 1ззз ю-6
Корни pt = -150 и р2 = -50 являются вещест-
венными и разными, т.е. в цепи апериодический пе-
реходный процесс.
Случай (2).
Корни pi = р2 = -100 вещественные и равные,
т.е. в цепи критический переходный процесс.
Случай (3).
Корни pi = -100 + /200 и р2 = -100 - /200 ком-
плексно-сопряженные, т.е. в цепи колебательный пе-
реходный процесс.
320
Найдем начальные условия в момент времени
t = 0+, которые являются неизменными для любого
типа переходного процесса. До коммутации емкость
была заряжена до величины напряжения источника
ис(0-) =U = 10 В, а ток в цепи был равен нулю:
г(0) = 0. По законам коммутации Ис(0+) = uq(0_) =
= (7 = 10 В, г(0+) = г(0_) = 0.
Найдем также du^+)/dt, которая равна г(0+)/С = 0.
В случае апериодического переходного процесса
в цепи напряжение u^it) определим по формуле
(7.24):
ис (t) = Atep,t + A2eP2t.
В выражении для u^it) две неизвестные вели-
чины At иА2, поэтому используем также выражение
(7.28) для производной напряжения по времени:
duc(t)/dt = А^е^ +A2p2eP2t.
Для момента времени t = 0+ имеем
(U = At + А2,
|0 = Ахрх +А2р2.
Отсюда находим (7.29):
A UP2 = Ю (-50) _ 5.
1 Pi~Pz -150-(-50)
= Ю-С-150) .
2 р{-р2 (-150)-(-50)
Подставляя найденные значения А2, pt и р2
в выражение для Uc(t), получаем закон изменения
напряжения на емкости при ее разряде на RL -цепь в
апериодическом режиме:
uc(t) = -5e-150t + 15е 5(К В.
График UqU) изображен на рис. 7.41, а. Время
t1( соответствующее точке перегиба графика, рассчи-
тываем по формуле
=—-—In^- = — 1 — In—-^- = 11 10"3 с = 11 мс.
Р\~Рг Pi -150 + 50 -150
Время переходного процесса £пп = 4т = 4 (2L/R) =
= 40 мс.
В случае критического переходного процесса на-
пряжение на емкости uc(t) определим по (7.37):
21 - 6972
321
Рис. 7.41. Графики Uc(t) в апериодическом (а),
критическом (б) и колебательном (в) режимах
к примеру 7.12
uc(t) = (At + A2t)e at.
Значения величин At и А2 найдем, используя
начальные условия:
At = U = 10;
А2 = at/ =-100 10 =-103.
Закон изменения напряжения на емкости в кри-
тическом режиме имеет вид
wc(i) = (10- 103i)e~100t В.
График uc(t) изображен на рис. 7.41, б. Время
переходного процесса £пп = 4т = 4 • 1/1 а I = 40 мс.
322
В случае колебательного переходного процесса
напряжение на емкости определяем по формуле
(7.34):
uc(t) = Ae af sin(wCBi+ ф).
Величины А и (р находим из начальных условий:
. со#.!. 1 200
Ф = arctg -& = arctg — = 63 ,
А = —= -^ = 11,2.
ЗШф Sin 63
Закон изменения напряжения на емкости в коле-
бательном режиме имеет вид
ис<Л) = ll,2e-lootsin(2OO£+ 63°) В.
График uc(t) изображен на рис. 7.41, в. Пери-
од свободных колебаний
2тг 2л о
Гсв = — = = 31 • 10’3 с = 31 мс.
св сосв 200
Постоянная времени цепи
т = т—-т = —— = 10 • 10’3 с = 10 мс.
|а| 100
Время переходного процесса
= 4т = 40 мс.
Включение RLC-цепи на постоянное напряжение. Рассмот-
рим подключение ЯЛС-контура к источнику постоянного напря-
жения U.
Напряжение на емкости при заряде конденсатора в схеме,
изображенной на рис. 7.42, в отличие от z/c(t) в RZ, С-контуре,
рассмотренном ранее, содержит не только свободную, но и при-
нужденную составляющие.
Принужденная составляющая напряжения «спр = U. В случае
вещественных и разных корней р\
и р2 характеристического уравне-
ния свободная составляющая оп-
ределяется уравнением (7.24):
wCcB(t) = AxePit +A2eP2t.
Рис. 7.42. Включение RLC-
цепи на постоянное напряжение
Корни рх и р2 такие же, как
и при разряде конденсатора.
21*
323
Напряжение на емкости имеет следующий вид:
UC (i) = “с пр + “Сев ) = и + AiePit + A2eP2t. (7.39)
Производная напряжения по времени
dUC^~ = AiPteP,f + A2Pzep2t <7.40)
Найдем постоянные интегрирования At и А2. Для этого опре-
делим прежде независимые и зависимые начальные условия в мо-
мент времени t = 0+. До коммутации ключ был разомкнут и на-
пряжение на емкости Uc(0_) и ток г(0_) были нулевыми. В пер-
вый момент времени непосредственно после коммутации по зако-
нам коммутации (7.1) и (7.2) имеем нулевые начальные условия:
Г г(0+) = КО.) = 0;
[ uc(Q+) = мс(0_) = 0.
Кроме того, так как i(t) = C(duc(t)/dt), то
duc(Q+) = 0
dt
Подставляя найденные значения г/с(0+) и duc(S)+)/dt в
уравнения (7.39) и (7.40), получаем
(U + Ai = А2 = 0;
(А1Р1 + А2р2 = 0.
Откуда
Pl - Р2 Pl- Р2
Сравнивая полученные выражения для Aj и А2 с соответст-
вующими величинами (7.29) при разряде емкости, нетрудно заме-
тить, что их знаки изменились на противоположные.
Таким образом, свободные составляющие при заряде конден-
сатора изменяются по таким же законам, что и при разряде, но
противоположны по знаку.
Напряжение на емкости в схеме заряда конденсатора имеет вид
uc(t) = иСпр + uCcB(t) = U + У'Р? ePit ep2t.
Р1-Р2 Р1"Р2
Ток, протекающий в цепи,
г(£) = с — с - = C- '^2 (ePlt -eP2t).
dt рх - p2
Напряжение на индуктивности
324
Рис. 7.43. Графики Uc(t), i(t), uL(t) при апериодическом
заряде конденсатора
uL(t) = -p^Y
at P\~Pi
Графики изменения напряжения на емкости Uc(t), тока iit)
и напряжения на индуктивности &£,(£) при заряде емкости в по-
следовательном колебательном контуре изображены на рис. 7.43.
Переходный процесс в цепи является апериодическим.
Если корни р\ и р2 характеристического уравнения ком-
плексно-сопряженные, то переходный процесс в цепи колебатель-
ный. Свободная составляющая напряжения или тока определяет-
ся по формуле (7.34), и графики uc(t), i(t), uL(t) имеют вид
затухающей синусоиды. Если корни pt и р2 вещественные и
равные, то переходный процесс в цепи будет критическим. Сво-
бодная составляющая любого напряжения или тока определяется
по формуле (7.37), а графики зависимости напряжений и тока во
времени имеют такой же характер, как и при апериодическом
режиме (рис. 7.43).
Пример 7.13. Найдем напряжение на емкости в цепи, изображенной
на рис. 7.42, если U = 10 В, R = 20 Ом, L = 100 мГн,
С = 200 мкФ.
Напряжение на емкости есть сумма принужден-
ной и свободной составляющих:
UC(t) = «Спр +uCcB(t).
Принужденная составляющая определяется по
схеме в установившемся режиме при £—><». При
325
этом индуктивность равносильна короткозамкнутой
цепи, а емкость — разрыву, поэтому емкость заряжа-
ется до величины напряжения источника, т.е.
“СпР = U = 10 В.
Вид свободной составляющей зависит от корней
характеристического уравнения
Z(p) = « + pi+^ = 0.
Рс
Корни этого уравнения для заданных значений R,
L и С будут комплексно-сопряженными pi2 =-а+/а>св:
Pi = -100 + /200;
р2 = -100 - /200.
В цепи колебательный переходный режим, по-
этому в соответствии с (7.34) имеем
ыСсв = Ae~at sin(a>CB£ + ср) = Ле-100* sin(200£ + <р).
Для определения неизвестных А и (р составим
еще одно уравнение и используем начальные усло-
вия. Производная напряжения по времени (7.35)
dUCd^ = sin (03 св^ + <Р) + а>св cos (сосв£ + <р) ].
В момент времени t = 0+ напряжение на емкости
и ток в индуктивности по законам коммутации со-
храняют те же значения, которые были до коммута-
ции, когда ключ был разомкнут:
uc(Q+) = ыс(0_) = 0;
г(0+) = г(0_) = 0.
Через емкость и индуктивность в последователь-
ном контуре протекает один и тот же ток. Поскольку
• z,4 „duc(t)
i\t) = С—5----, то
dt
с/цс(0+) _ г(0+) _ 0
dt С
В первый момент времени после коммутации
t = 0+
ис(0+) = «СпР + «Ссв(0+) = + z4sin<p = 0,
326
Рис. 7.44. Напряжение на емкости при заряде
конденсатора к примеру 7.13
—- • = 4(-asin<p + coCB cos<p) = 0.
at
Из этих двух уравнений находим
, <осв , 200 „00
Ф = arctg—— = arctg-— = 63 ;
а 100
Л и 10
А = —:— =---------= -11,2.
sma sin 63
В результате получаем закон изменения напря-
жения на емкости в контуре (рис. 7.42) при колеба-
тельном переходном процессе:
uc(t) = иСар + Ae~at sin(<nCBt + ф°) =
= 10 -11,2е -loot sin (200t + 63°), В.
Сравнивая полученное выражение для определе-
ния uc(t) при заряде конденсатора в последова-
тельном колебательном контуре с выражением ис&)
при разряде конденсатора в контуре с теми же самы-
ми параметрами (пример 7.12, случай 3) видим, что
свободная составляющая отличается только знаком,
но при заряде конденсатора есть еще принужденная
составляющая.
График uc(t) изображен на рис. 7.44.
Пример 7.14. Найдем ток ^(t) в цепи, изображенной на
рис. 7.45, если U = 20 В, = 100 Ом, R2 = 100 Ом,
L = 100 мГн, С = 1 мкФ.
До коммутации ключ был разомкнут, конденса-
тор в установившемся режиме заменяется разры-
вом, поэтому
= г2(0-) = »з(0-> = 0;
wc(0_) = U = 20 В, uL(0_) = 0.
327
Рис. 7.45. Цепь второго порядка к примеру 7.14
В установившемся режиме после коммутации
(£ -> оо) ключ замкнут, вместо емкости — разрыв,
вместо индуктивности — короткозамкнутая цепь, по-
этому
(7 20 п . . п
imp - *3np ~ Ri+R2~ 200 " 0,1 А’ 12пр " °’
UR2 20 100 _Л
Ucnp'Ri+R2~ 200 °В’ М£пр-°-
Составим уравнения по законам Кирхгофа при
замкнутом ключе:
Riii(t) + uc(t) = U;
• -uc(t)+ ui(t) + R2i3(t) = 0;
i\(t) = i2(t) + i3(t).
Учтем также, что
i2(t) = C-U<j~; uL(t) = L&^.
at at
Найдем значения тока ^(t) и его производной
di\(t)/dt в момент времени t = 0+. Независимые на-
чальные условия определяем по законам коммутации:
г3(0.) = Ж) = 0;
«с(0+) = «с(0_) = U = 20 В.
Зависимые начальные условия — ток г\(0+) и
производную ditto+)/dt — находим из первого урав-
нения системы:
( 20^20 =()
1 * R, 100
Для определения производной тока в момент
t = 0+ продифференцируем первое уравнение системы:
328
„ di, it) duc(t) л
7?i —— + —Ц— = 0.
dt dt
Отсюда
dijit) 1 ducit)
dt R{ dt
С другой стороны,
duc<$+) _ i2j0+) _ Q
dt C
так как по закону токов Кирхгофа
г2(0+) = А(0+) - г3(0+) = 0.
Таким образом,
dt
Составим характеристическое уравнение. Для
этого разорвем ветвь, содержащую индуктивность, и
запишем комплексное сопротивление Zijat) цепи от-
носительно этого разрыва. Заменив /со на р и при-
равняв Zip) к нулю, получаем
После преобразований имеем
1 , ^2 +^1 _ л
RiC) RtLC
9
р +р
или
Р2 + 1,1Ю4р + 0,2-108 =0.
Корни квадратного уравнения
Pi = -2300, р2 = -8700
вещественные и разные, т.е. в цепи имеет место апе-
риодический переходный процесс. Поэтому свобод-
ную составляющую тока записывают в виде:
Чсв it) = AiePit + A2eP2t.
Ток it) содержит две составляющие — прину-
жденную и свободную:
329
«1(0, A
0,1
0 0,5 1 1,5 2 г, мс
Рис. 7.46. График ц (£) в цепи к примеру 7.14
А (О = Опр + Осв d) = п U в + А^ + А2еП* =
+ £<2
= а,\ + Ахе-2Ж(+А2е-^.
Запишем также производную тока:
^2 = p1A1^f + p2A2e«f.
at
Для определения постоянных интегрирования
At и А2 используем начальные условия it(0+) = 0,
di\{Q+)/dt = 0. Составляем систему уравнений для
t = 0+:
р + -41 + А2 = it(0+);
Kt + к2
л л diAQA
Pl-Af + PlAl --Т7--
dt
или
(0,1 + А| + А2 — 0;
(-2300At-8700A2 = 0.
Отсюда
Aj =-0,136; А2 = 0,036.
Подставляя найденные значения г"1пр, At, А2, Р\
и р2 в общее выражение для расчета тока, получаем
it (£) = 0,1 - 0,136е~2300< + 0,ОЗбе"8700' А.
График тока i\{t) изображен на рис. 7.46.
Переходные процессы в цепях можно рассчитывать, ис-
пользуя преобразование Лапласа. Расчет изображения тока или
напряжения в операторной схеме замещения и дальнейший пере-
ход к мгновенным значениям сигналов составляет сущность one-
330
упорного метода расчета переходных процессов в цепях пер
вого и второго порядка. В гл. 5 подробно изложены вопросы по
строения операторных схем замещения, методы расчета изобра
,кений в этих схемах и способы получения оригинала по изобра
#ению функции. Поэтому ниже приведем только порядок расче-
та переходных процессов операторным методом.
Последовательность расчета:
1. Определяют независимые начальные условия — напряже-
ние на емкости wc(0+) и ток в индуктивности г^(0+), используя
законы коммутации.
2. Составляют операторную схему замещения. Для этого все
напряжения w(i) и токи i(t) заменяют их изображениями U(p)
и Кр). Напряжения и токи источников сигналов заменяют их
преобразованиями Лапласа (§ 5.1). Пассивные элементы цепи за
меняют их операторными схемами замещения — индуктивность
заменяют ее операторным сопротивление pL и последовательно с
ним включенным источником Li£(0+), емкость заменяют ее опе-
раторным сопротивлением 1/рС и последовательно с ним вклю-
ченным источником (/с(0+)/р.
3. В операторной схеме замещения определяют изображения
токов Z(p) в ветвях или напряжений U(p) на элементах, исполь-
зуя законы Ома, Кирхгофа, метод наложения или любые другие
известные методы расчета цепей (§ 5.2).
4. Переходят от изображений токов 1(р) и напряжений U(p)
к мгновенным значениям i(t), u(t), используя таблицы соответ-
ствия сигналов и их изображений (например, табл. 5.1) или тео-
рему разложения (§ 5.1).
Пример 7.15. Найдем ток из примера 7.14, используя опе-
раторный метод расчета переходных процессов.
Независимые начальные условия определяем по
законам коммутации:
uc(0+) = uc(0_) = U = 10 В;
г3(0+) = г’з(О-) = 0.
Операторная схема замещения цепи, изображен-
ной на рис. 7.45, приведена на рис. 7.47. Напряже-
ние источника U заменено его изображением U/p', ем-
кость С заменена последовательным соединением опе-
раторного сопротивления 1/рС и источника Uc<$+)Ip>
индуктивность L заменена операторным сопротивле-
нием pL, а источник Аг^(О+) отсутствует, так как
ток г£(0+) = г3(0+) равен нулю.
331
h(p) (2) ЫР)
Рис. 7.47. Операторная схема замещения цепи,
изображенной на рис. 7.45
Для расчета изображения 13(р) в схеме (рис. 7.47)
воспользуемся методом узловых напряжений. Зазем-
лим узел 1:
V,(p) = 0.
Для второго узла составим уравнение
у2(ру[-±-+рс+
1 А
R2 + pL J
U 1 | цс(0+)
Р Ri Р
рс,
решением которого является
v2 („) = ___U(UpR,C)(R^pL)
p[p2RtLC + p(L + RtR2C) + R, + K2]
Изображение тока
/ (р) = 2гМ =
R2+pL
_Uji+pRjC)
RxLCp p +Р|-Л + -^ +—-----------L
L, jvjV j
l + 10~4p
RXLC
= ?.in6_______1 + 1U P________= 2• 106
p(p2 + l,1104p + 0,2108) F2(p)'
Обратите внимание, что полином второй степени,
стоящий в знаменателе, совпадает с левой частью ха-
рактеристического уравнения при классическом ме-
тоде. Знаменатель имеет три корня:
Pi = 0; Р\ - -2300; р2 = -8700.
Для определения мгновенного значения тока
z3(i) применим теорему разложения (5.20):
332
^i(Pt) g/>i'
f-2 (Pi)
i3(O = 2106[-^4^4ew/
L^(Po)
+ ДДД e',2t = o, 1 - 0,1 le'2300' + 0,04e~8700', A.
F2(P2)
Принужденная составляющая тока (или напряжения) суще-
ствует в том случае, когда в выражении для изображения сигнала
один из корней знаменателя равен нулю.
Операторный метод удобно использовать при расчете цепей
высокого порядка, когда достаточно сложно определять постоян-
ные интегрирования в классическом методе.
Из данного параграфа мы узнали, что:
При расчете переходных процессов классическим методом
составляют и решают дифференциальное уравнение для
мгновенного значения тока или напряжения.
Ток или напряжение в переходном режиме содержат при-
нужденную и свободную составляющие. Принужденная со-
ставляющая обусловлена действием источников энергии, а
свободная составляющая — запасом электрической или маг-
нитной энергии в реактивных элементах.
В цепях первого порядка (с одним реактивным элементом)
переходный процесс носит апериодический характер. В це-
пях второго порядка (с двумя независимыми реактивными
элементами) вид свободной составляющей зависит от кор-
ней характеристического уравнения. Если корни вещест-
венные и разные, то процесс апериодический, если корни
вещественные и кратные, то процесс критический, если кор-
ни комплексно-сопряженные, то процесс колебательный.
Постоянные интегрирования, входящие в выражения для
свободных составляющих тока или напряжения, определя-
ются из начальных условий в момент коммутации.
Величина, обратно пропорциональная модулю корня харак-
теристического уравнения (или модулю его вещественной
части в случае комплексно-сопряженных корней), называ-
ется постоянной времени цепи. Переходный процесс прак-
тически заканчивается за время, в три-четыре раза большее
постоянной времени цепи.
При расчете переходных процессов операторным методом
составляют операторную схему замещения цепи, любым из-
вестным методом определяют в ней изображения токов и
напряжений, а затем по таблицам или теореме разложения
переходят к мгновенным значениям сигналов.
£
333
Вопросы и задания для самоконтроля
1. Почему в электрической цепи возникают переходные процес-
сы? Каковы условия их возникновения?
2. Сформулировать законы коммутации.
3. Какие условия в электрической цепи называются независимы-
ми (зависимыми) начальными условиями?
4. Каковы схемы замещения емкости и индуктивности в момент
коммутации при нулевых (ненулевых) начальных условиях?
5. Определить начальные условия в цепи, изображенной на
рис. 7.48, при:
а) замыкании ключа;
б) размыкании ключа.
6. Какой режим работы цепи называется установившимся?
7. Каковы схемы замещения емкости и индуктивности при t -> оо?
8. Определить принужденные составляющие токов и напряжений
на всех элементах цепи, изображенной на рис. 7.48.
9. В чем суть классического метода расчета переходных процессов?
10. Какой вид имеет свободная составляющая в цепи первого
порядка?
11. Как определяется постоянная интегрирования в цепи первого
порядка?
12. Как определяется постоянная времени в цепи первого по-
рядка?
13. Чему равно время переходного процесса?
14. Чем отличается напряжение на емкости при заряде и разряде
конденсатора в последовательной 7?С-цепи?
15. Докажите справедливость выражения (7.22) для определения
напряжения на емкости при включении в ЛС-цепь источника
гармонического напряжения.
16. Какова последовательность расчета переходных процессов в
цепях первого порядка?
17. Найти ток i(t) в цепи, изображенной на рис. 7.32, при замы-
кании ключа.
Рис. 7.48. Цепь к заданиям 5 и 8
Рис. 7.49. Цепь к заданию 18
334
Рис. 7.50. Цепь к заданию 23 Рис. 7.51. Цепь к заданию 24
18. Найти напряжение на емкости Uc(t) в цепи, изображенной на
рис. 7.49, если 17 = 25 В, Rt = 20Ом, R? = 50м, С = 25 мкФ.
19. От чего зависит вид свободной составляющей тока или напря
жения в цепи второго порядка?
20. Как определяются постоянные интегрирования, входящие в
свободную составляющую в цепи второго порядка?
21. Какой процесс называется апериодическим (критическим, ко-
лебательным)?
22. Каков порядок расчета переходных процессов в цепях второго
порядка классическим методом?
23. Найти напряжение на емкости в цепи, изображенной на
рис. 7.50, если 17 = 125 В, R = 100 Ом, L = 40 мГн, С = 1 мкФ.
24. Найти ток в сопротивлении R в цепи, изображенной на
рис. 7.51, если U = 30 В, R = 100 Ом, L = 1 Гн, С = 16 мкФ.
25. В чем суть операторного метода расчета переходных процессов?
26. Решить пример 7.11, используя операторный метод расчета.
27. Решить пример 7.13, используя операторный метод расчета.
Глава 8. Анализ реакции нелинейной резистивной
цепи на постоянное и гармоническое воздействия
8.1. Нелинейные резистивные элементы
и их сопротивления постоянному
и гармоническому токам
Сопротивление нелинейного резистивного элемента не явля-
ется постоянной величиной — оно зависит от протекающего че-
рез него тока или от приложенного к нему напряжения. Напом-
ним, что для линейного резистивного элемента характерна ли-
нейная связь между током i и напряжением и (рис. 8.1), а для
нелинейного резистивного элемента — нелинейная связь (рис. 8.2).
Сопротивление нелинейного резистивного элемента (НЭ) не яв-
ляется постоянным, а зависит от того, в какой точке ВАХ оно
определяется. На рис. 8.3 изображена ВАХ нелинейного элемен-
та. Можно определить сопротивление как
= и/i = U0/Iq ,
где Uo — приложенное к нелинейному элементу постоянное на-
пряжение; 10 — протекающий через нелинейный элемент посто-
янный ток. Это сопротивление постоянному току (или статиче-
ское). Оно зависит от приложенного напряжения.
Пусть на нелинейный элемент действует сумма постоянного
напряжения Uo и гармонического Umcosa>t, причем амплитуда
Um гармонической составляющей достаточно мала (рис. 8.3), так
что тот небольшой участок ВАХ, в пределах которого действует
гармоническое напряжение, можно считать линейным. Проекти-
руя каждое мгновенное значение гармонического напряжения на
ВАХ и отображая результат проекции на плоскости «ток — вре-
мя», получаем зависимость тока от времени. В силу того, что вы-
бран линейный участок ВАХ, ток, протекающий через нелиней-
Рис. 8.1. ВАХ линейного
резистивного элемента
336
Рис. 8.2. ВАХ нелинейного
резистивного элемента
({ЫЙ элемент, повторит по
форме напряжение: i(t) =
~ Iq + ЛйСО5<в£ (рис. 8.3).
Отношение амплитуды
гармонического напряже-
ния Um к амплитуде гар-
монического тока 1т (на
графике это отношение
приращения напряжения
дм к приращению тока
дг) называют дифферен-
циальным (динамическим)
сопротивлением нелиней-
ного элемента, которое,
по сути, является сопро-
тивлением нелинейного
элемента гармоническо-
му току малой амплитуды'.
Рис. 8.3. Определение статического и
динамического сопротивлений по ВАХ
^диф ~~ UmlIm ~ &и/ bi.
Обычно переходят к пределу этих приращений и определяют
дифференциальное сопротивление в виде 7?диф = du/di. Часто
удобно пользоваться понятием дифференциальной крутизны
(проводимости):
^диф = 1/^диф = di/du. (8.1)
Наиболее распространенными приборами с нелинейным рези-
стивным сопротивлением являются ламповые и полупроводниковые
приборы (диоды, транзисторы и т.п.), используемые в радиотехни-
ке для преобразования и усиления сигналов. На рис. 8.4 приведе-
ны ВАХ типовых нелинейных резисторов и их условные обозначе-
ния: полупроводникового (рис. 8.4, а) и туннельного (рис. 8.4, б)
диодов; биполярного (рис. 8.4, в) и полевого (рис. 8.4, г) транзи-
Рис. 8.4. ВАХ полупроводникового (а) и туннельного (б) диодов,
биполярного (в) и полевого (г) транзисторов
22-6972
337
сторов. Здесь w6o, i6 и iK — соответственно напряжение, приложен-
ное к участку «база — эмиттер», и токи базы и коллектора биполяр-
ного транзистора; w )H и ic — соответственно напряжение, приложен-
ное к участку «затвор — исток», и ток стока полевого транзистора.
Приборы, имеющие падающие участки ВАХ (рис. 8.4, б), на-
зываются приборами с отрицательным сопротивлением, так как
^-диф du/di < 0.
Из данного параграфа мы узнали, что:
• Нелинейные двухполюсные резистивные элементы (полу-
проводниковые и электронные диоды) характеризуются не-
линейной вольт-амперной характеристикой — зависимостью
тока (реакции) от приложенного напряжения (воздействия).
• Нелинейные четырехполюсные резистивные элементы (тран-
зисторы, электронные лампы, тиристоры) описываются се-
мействами нелинейных вольт-амперных характеристик.
• Сопротивление нелинейного резистивного элемента посто-
янному току называется статическим. Оно зависит от вели-
чины приложенного к нелинейному резистору постоянного
напряжения.
• Сопротивление нелинейного элемента переменному току
малой амплитуды называется дифференциальным или ди-
намическим. Оно зависит от амплитуды приложенного пе-
ременного напряжения.
• Часто используют понятие дифференциальной крутизны
(проводимости) — это величина, обратная дифференциаль-
ному сопротивлению.
8.2. Расчет реакции нелинейной резистивной
цепи на постоянное воздействие
Рассчитать нелинейную цепь в режиме постоянного тока —
значит найти токи и напряжения на всех нелинейных и линей-
ных элементах. Расчет нелинейных цепей, ВАХ нелинейных эле-
ментов (НЭ) которых заданы графически или описываются
сложными функциями, проводят графоаналитическими методами.
Суть этих методов состоит в составлении системы аналитических
уравнений, которые затем решаются графически. Точки пересе-
чения графиков дают искомое решение.
Для расчета цепи, содержащей один НЭ, естественно приме-
нить метод эквивалентного генератора, при этом линейная цепь
338
Рис. 8.5. Замена линейной цепи (а) эквивалентным
генератором напряжения (б) или тока (в)
относительно зажимов НЭ заменяется эквивалентным генерато-
ром напряжения или тока (рис. 8.5).
Напомним, что параметры эквивалентного генератора опреде-
ляют следующим образом: (7ХХ — напряжение холостого хода на
зажимах активного линейного двухполюсника (АЛД) при отклю-
ченном НЭ; R3 — эквивалентное сопротивление пассивного двух-
полюсника, когда все задающие напряжения и токи источников
АЛД равны нулю; IK3 = Uxx/R3 — ток АЛД при коротком замы-
кании его зажимов.
Ток в НЭ и напряжение на нем находятся из системы, со-
стоящей всего из двух уравнений. Так, применяя закон напряже-
ний Кирхгофа (ЗНК) к схеме рис. 8.5, б, получаем
UK + IKR3-UXX =0. (8.2)
Дописывая к данному равенству уравнение НЭ 1И = Г(ин), по-
лучаем систему из двух уравнений. Решить данную систему мож-
но графическим путем, построив график прямой
4=-^- + ^ (8.3)
и график ВАХ гн =Г(ын) нелинейного элемента. Точка пересе-
чения графиков дает значение тока /н и напряжения UH на НЭ
(рис. 8.6).
Все остальные токи и напряжения на линейных элементах
можно найти, используя законы Кирхгофа.
Рис. 8.6. Определение тока и напряжения на НЭ
22»
339
Пример 8.1. Рассчитать ток, протекающий через нелинейный эле-
мент в цепи, изображенной на рис. 8.7. Заданы: ВАХ
НЭ 4 =Г(мн) (рис. 8.8), = R2 = 2 кОм, U = 1 В,
Iq = 0,5 мА.
Для построения прямой (8.3) рассчитаем напря-
жение холостого хода между узлами 1 и 2 (при от-
ключении НЭ), эквивалентное сопротивление пас-
сивного двухполюсника и ток короткого замыкания
(при закороченном НЭ):
Uxx = U +10 • R2 = 1 + 0,5 • 2 = 2 В;
Rs = R2 - 2 кОм;
U 2
/кз = ± = 1 мА.
кз R3 2
Строим график прямой (8.3) по аналогии с гра-
фиком, изображенным на рис. 8.6. Точка пересече-
ния этой прямой с ВАХ НЭ (рис. 8.8) дает значения
тока /н = 0,7 мА, протекающего через НЭ, и напря-
жения UH = 0,5 В на нем.
Рис. 8.8. Определение тока
через НЭ к примеру 8.1
Рис. 8.7. Цепь с НЭ
к примеру 8.1
Для расчета цепи, содержащей несколько НЭ, используют
эквивалентные преобразования схемы. Суть эквивалентных пре-
образований состоит в замене участков цепи с параллельным или
последовательным соединением ветвей одной эквивалентной вет-
вью путем суммирования их токов или напряжений. Речь здесь
идет о суммировании ординат или абсцисс заданных характери-
стик ветвей цепи. Этот метод особенно эффективен в случае цепи
с одним источником: цепь представляется источником и одним
эквивалентным нелинейным элементом.
Пусть два НЭ с уравнениями (ВАХ) ti=Fi(wi) и i2 =
= F2(u2) включены параллельно (рис. 8.9). Поскольку приводи-
340
Рис. 8.10. Графическое
сложение токов
Рис. 8.9. Параллельное
соединение двух НЭ
Рис. 8.12. Графическое сложение
напряжений
Рис. 8.11. Последовательное
соединение двух НЭ
мне ниже рассуждения справедливы не только для режима по-
стоянного, но и для режима переменного тока, в дальнейшем бу-
дем использовать для обозначений напряжений и токов малые
(строчные) буквы.
Необходимо найти уравнение НЭ, эквивалентного данному
соединению элементов. Так как элементы соединены параллель-
но, то щ = и2 = и, а по первому закону Кирхгофа i = q + i2. Вы-
полним сложение токов графически, как показано на рис. 8.10.
Задаемся значением напряжения. При этом значении напряжения
находим токи НЭ и суммируем их. Задаемся новым значением
напряжения и опять суммируем токи. Таким образом находим се-
рию точек, соединяя которые получаем ВАХ эквивалентного НЭ.
Рассмотрим последовательное соединение НЭ (рис. 8.11). В
данном случае ц = г2 = г, а и = щ + и2. Процесс определения
ВАХ НЭ показан на рис. 8.12. Заметим, что рассмотренные пре-
образования применимы и в случае, когда последовательно или
параллельно соединены несколько нелинейных, а также линей-
ных элементов.
Пример 8.2. Рассчитать напряжения и токи в цепи, схема которой <
изображена на рис. 8.13, где U = 5 В, R = 500 Ом, а
ВАХ НЭ заданы графиками на рис. 8.14.
341
Рис. 8.13. Цепь
к примеру 8.2
Рис. 8.15. Построение ВАХ эквивалентного
двухполюсника и определение токов к примеру 8.2
Рис. 8.14. ВАХ двух НЭ
к примеру 8.2
Поскольку ВАХ заданы графиками, то при ре-
шении воспользуемся графическими построениями.
Найдем ВАХ i = F32(и) двухполюсника, эквивалент-
ного параллельному соединению линейного сопро-
тивления R и НЭг- Для этого перенесем ВАХ НЭг на
новый рисунок и построим ВАХ линейного элемента
(рис. 8.15, а). На этом же рисунке показана эквива-
лентная ВАХ i = Fa2(и). Перенесем эту эквивалент-
ную ВАХ и ВАХ НЭ] на рис. 8.15, 6 и найдем ВАХ
эквивалентного двухполюсника г = F3i (и), который
присоединяется к зажимам источника.
По рис. 8.15, б по кривой i = F31(zz) находим,
что напряжению и = 5 В соответствует ток i = 16 мА,
по кривой i = Fi (и) — напряжение на НЭ] = 2,8 В
и по кривой i = F32 (и) — напряжение на параллель-
ном соединении R и НЭг и2 - 2,2 В. Зная это напря-
жение, по графикам рис. 8.15, а находим iR = И мА и
Z2 = 5 мА.
342
Пример 8.3. На рис. 8.16, а показана подключенная к источнику
напряжения цепь из трех резистивных НЭ. Сумми-
рование ординат характеристик элементов 2 и 3, со-
единенных параллельно, дает эквивалентную харак-
теристику 2 — 3 (рис. 8.16, б). Суммируя абсциссы
последней с абсциссами кривой 1, получаем эквива-
лентную характеристику нелинейной цепи F3. Из
графиков рис. 8.16, б можно, задаваясь напряжени-
ем на входе, получить токи и напряжения ветвей.
Рис. 8.16. Цепь (а) к примеру 8.3 и ВАХ
ее нелинейных элементов (б)
Если вольт-амперные характеристики двухполюсных НЭ за-
даны не графически, а аналитически, причем функции i = F(u)
достаточно простые, то для расчета нелинейных цепей составляют
систему уравнений состояния цепи, которую решают аналитиче-
ски или численными методами.
Уравнения состояния цепи обычно составляют на основании
законов Кирхгофа. Методика составления уравнений остается та-
кой же, как и в случае линейных резистивных цепей, но допол-
нительно появляются уравнения вида iK = FK (ик) для НЭ.
Составим, например, систему уравнений состояния для цепи,
схема которой изображена па рис. 8.17. Пусть ВАХ нелинейного
элемента описывается выражением
о
н “
при UH < 0;
при U„ > 0.
(8.4)
Зададимся положительными направлениями напряжений и
токов. Цепь содержит один независимый контур (7) и один неза-
висимый узел (1). Уравнения, записанные по закону токов Кирх-
гофа (ЗТК) и ЗНК, имеют следующий вид:
Л+^02-4=0; (8.5)
343
/(7?! + (7Н - С/©1 ~ 0 • (8.6)
К этим уравнениям дописываем уравнение (8.4). Неизвест-
ными в данной системе уравнений являются напряжение UH н
токи Ц и /н. Всего три неизвестных. Для их отыскания состав-
лено три уравнения. Как видим, процесс составления системы
уравнений такой же, как и в случае линейной цепи. Однако про-
цесс решения полученной системы, которая содержит нелинейное
уравнение, может существенно затрудниться. Для большинства
относительно сложных цепей аналитического решения системы
уравнений может и не существовать. Тогда приходится прибегать
к численным методам решения.
Пример 8.4. Рассчитать ток 1Я и напряжение UH на нелинейном
элементе, а также ток в цепи, изображенной на
рис. 8.17, если заданы значения = 1 кОм, U0l =
= 14 В, /02 = Ю мА, а = IO’5 А/В.
Предположим вначале, что решение системы
уравнений (8.5), (8.6), (8.4) существует при UH >0.
Тогда уравнение НЭ имеет вид
ZH=at/H2. (8.7)
Выразим из уравнения (8.5) ток Ц = 1Я - Z02 и под-
ставим его в уравнение (8.6). В результате этой опе-
рации получим
1яК1-102П1+ия -UOi=Q. (8.8)
Подставив в (8.8) выражение (8.7), определим урав-
нение относительно неизвестного напряжения на не-
линейном двухполюснике:
С/2 +-^-ия - ^i+^ot = 0 (8.9)
aRt olR\
Рис. 8.17. Цепь с нелинейным элементом
к примеру 8.4
344
Отсюда имеем
2a7?i
' 1 . ^02^1 + ^01
4а2/?2 а/?!
(8.10)
Подставляя в (8.10) заданные значения а0,
(7oi и /о2> получаем UH = 20 В.
Второе решение уравнения (8.9) даст U„ < 0.
Это решение не подходит, так как применялось урав-
нение НЭ, справедливое при UH > 0.
Допустим теперь существование решения систе-
мы уравнений (8.5) — (8.6) при t/H<0. Согласно
уравнению НЭ (8.4) /н=0. Тогда из уравнения
(8.8) имеем
Ull=I02Ri+U0 = 24 В > 0,
а это противоречит условию (/н < 0.
Таким образом, остается первое решение (8.10):
UH =20 В. Найдем остальные неизвестные. Из (8.7)
имеем In = aU$= 10~5 -202 = 4 мА, а из (8.5) /, =
= 7Н “ ^02 = МА.
В данном примере получено аналитическое ре-
шение системы нелинейных уравнений. Если бы
ВАХ нелинейного элемента описывалась более слож-
ной функцией, то этого достичь не удалось бы.
Можно составлять уравнения состояния цепи методом узло-
вых напряжений (потенциалов).
Рассмотрим в качестве примера схему, изображенную на
рис. 8.18. Пусть ВАХ нелинейных элементов описываются выра-
жениями I = а С/3 для элемента НЭ1 и I = рС72 для элемента
НЭ2. В схеме имеется зависимый источник (ИТУТ) с током
h=Hih.
Приняв узел 4 за базисный, имеем три независимых узла: 1,
2 и 3. Токи ветвей выражаются через узловые напряжения Uit
U2 и Uз следующим образом:
Л=(Я1-Я2)С1; /2 = аСУ23;
I3=U3G3; 74=р(Я1-Я3)2; (8.11)
/5=Я,/1 = Я,С)(171-1/2).
Составим уравнения для узлов 1, 2 и 3 по ЗТК:
Л +Л = Л)!
* -~J\ + /2 -^5 “
. /3-74-75=0.
345
Рис. 8.18. Цепь с нелинейными элементами
и зависимым источником тока
Подставив в эти уравнения значения токов из (8.11), по-
лучим
' +Р(СГ1 -U3)2= 10-,
-(<7(-(72)Gi(l-Hj) + at723 = 0; (8.12)
-(Ui -и2)С^ + U3G3 -₽((/!-U3)2 = 0.
Уравнения узловых напряжений получены в виде системы
трех нелинейных уравнений с тремя неизвестными узловыми на-
пряжениями. Можно уменьшить число уравнений, если из перво-
го уравнения выразить U2 через и U3 и исключить его из
двух остальных уравнений. В результате получим систему двух
нелинейных уравнений с двумя неизвестными напряжениями уз-
лов 1 и 3.
Решить данную систему уравнений можно одним из числен-
ных методов (например, известным из математики методом Нью-
тона — Рафсона). Определив узловые напряжения, можно вы-
числить токи и напряжения ветвей.
Рассмотрим порядок расчета резистивных цепей, если в их
состав входят нелинейные четырехполюсники, которые описыва-
ются нелинейными уравнениями, связывающими напряжения и
токи на его входе ( щ, z'j) и выходе ( и2, i2):
ut =f1(zt,w2);
z2 =F2(z1(u2).
На рис. 8.19 показана схема включения нелинейного четы-
рехполюсника, а на рис. 8.20 — семейство его входных (а) и вы-
ходных (6) ВАХ.
По ЗНК для входной и выходной цепей схемы рис. 8.19
можно записать
346
К} /1
Четырехполюсный
нелинейный
элемент
<2
Рис. 8.19. Схема включения нелинейного четырехполюсника
Рис. 8.20. Определение токов и напряжений на входе (а)
и выходе (б) четырехполюсника
(7Г1 = ДТ?! + и Ur2 = I2R2 + U2.
Решая эти уравнения относительно токов Ц и /2> получаем
уравнения
U1 . и г _
и J "
Т?2 Т?2
которые называются уравнениями нагрузочных прямых.
На рис. 8.20 построены графики этих прямых и графических
входных и выходных ВАХ четырехполюсного НЭ. Точки пересече-
ния нагрузочных прямых и ВАХ определяют режимы постоянного
тока (рабочие точки) на входе и выходе четырехполюсного НЭ.
Из данного параграфа мы узнали, что:
• Для определения токов в ветвях и напряжений на элементах
нелинейной цепи при постоянном воздействии используют
графоаналитические методы: составляют систему аналитиче-
ских уравнений и решают ее графически.
• Часто для расчета цепей с одним нелинейным элементом ис-
пользуют метод эквивалентного генератора. Ток и напряже-
ние на нелинейном элементе определяются в точке пересече-
ния ВАХ и нагрузочной прямой эквивалентного генератора.
347
$3? > ij* >> * «r >>s <s л V?4 " ' W * & #* ^***«8^
• Для расчета токов и напряжений в цепях с несколькими не-
линейными элементами используют законы Кирхгофа для
графических построений.
• Если вольт-амперные характеристики нелинейных элементов
заданы аналитически, то для расчета цепи составляют сис-
тему уравнений состояния цепи и решают ее аналитически
или численными методами.
8.3. Аппроксимации вольт-амперных характеристик
нелинейных резистивных элементов
Аппроксимация вольт-амперных характеристик нелинейных
элементов — это замена табличных значений или графической
кривой аналитическим выражением. Как правило, ВАХ нели-
нейных элементов получают экспериментально, поэтому чаще
всего они заданы в виде таблиц или графиков. Чтобы иметь дело
с аналитическими выражениями, приходится прибегать к аппрок-
симации.
На рис. 8.21 приведена ВАХ нелинейного элемента. Пусть к
нелинейному элементу приложено постоянное напряжение Uo и
гармоническое напряжение Um cosot.
Увеличение постоянного напряжения Uo приведет к смеще-
нию на рис. 8.21 гармонического напряжения вправо, а уменьше-
ние Uо — к смещению гармонического напряжения влево. В свя-
зи с этим постоянное напряжение Uq назвали напряжением сме-
щения, а точку на ВАХ с координатами (Uo, 10) — рабочей
точкой. Таким образом, выбор рабочей точки на ВАХ связан с
изменением напряжения смещения U$.
При подаче на нелинейный элемент гармонического напря-
жения рабочая точка будет перемещаться по ВАХ в такт с изме-
нением мгновенного значения гармонического напряжения.
Очевидно, что аппроксимировать (т.е. описывать аналитиче-
ски) нужно только тот участок ВАХ, по которому перемещается
рабочая точка.
Часто в качестве аппроксимирующего ВАХ выражения ис-
пользуют степенной полином:
i = а0 +at(n -Uo) + a2(u -U0)2 + ... + aN(u -U0)N. (8.13)
Определить коэффициенты a0, сц, ..., aN полинома (8.13)
можно различными способами. Наиболее распространенным спо-
собом является интерполяция (метод выбранных точек), при ко-
торой коэффициенты а0, аь ..., aN находятся из равенства
348
Рис. 8.21. Построение графика тока в нелинейном элементе
значений полинома (8.13) и аппроксимируемой ВАХ в выбран-
ных точках {узлах интерполяции).
Пример 8.5. Аппроксимировать экспериментальную зависимость
тока базы i6 от напряжения между базой и эмитте-
ром ыбэ для биполярного транзистора, заданную в
табл. 8.1.
Известно также, что напряжение смещения Uq =
= 0,6 В и что амплитуда гармонического напряжения
на входе транзистора не превышает 0,2 В, т.е.
Um < 0,2 В.
Экспериментальные точки из табл. 8.1 показаны
на графике рис. 8.22 кружочками, соединенными
штриховой линией.
Можно потребовать, чтобы значения степенного по-
линома совпадали со значениями тока i6 для всех шести
значений напряжения и6э, указанных в таблице. В этом
Таблица 8.1. Экспериментальная ВАХ биполярного
транзистора
^бэ > В 0,4 0,5 0,6 0,7 0,8 0,9
гб, мА 0,05 0,07 0,1 0,175 0,3 0,53
349
Рис. 8.22. Графики к примеру 8.5
случае необходимо выбрать степенной полином пятой
степени (так как он содержит шесть коэффициентов):
i6 =a0+ai(u63-UQ) + a2(u63-U0)2 +
+ аз(м6э-^о)3 +а4(мбэ-^о)4 + (8.14)
+ а5(м6э -Ц))5
и составить систему уравнений. Первое уравнение
получаем, подставляя в (8.14) значения м6э = 0,4 В
и гб = 0,05 мА:
0,05 = ao + ai(0,4-[/o) + a2(0,4-(70)2 +
+a3(0,4-(70)3+ a4 (0,4-С70)4+a5(O,4-(7o)5.
Второе уравнение получаем, подставляя в (8.14) зна-
чения Ыбэ = 0,5 В и г'б = 0, 07 мА:
0,07 = ао +а1(0,5-{/о) + а2(0,5-С/0)2 +
+a3(O,5-Uo)3 +a4(O,5-Uo)4 +a5(O,5-Uo)5.
Третье уравнение получаем, подставляя в (8.14) зна-
чения «бэ = 0,6 В и гб = 0,1 мА:
0,1 = <Xq + ос j ( 0,6 — C7q ) + a 2 (0,6 — C7q ) +
+ a3 (0,6-t/0 )3 +a4(0,6-t/0)4 + a5(O,6-(7o)5.
350
Четвертое уравнение получаем, подставляя в (8.14)
значения и63 = 0.7 В и г6 = 0,175 мА:
O,175 = ao + a)(O.7-t/o) + a2(O,7-17o)2 +
+ a3(0,7-t/0)3 +a4(0,7-Uo)* + a5(0,7-(70)5 •
Пятое уравнение получаем, подставляя в (8.14) зна-
чения ибэ = 0,8 В и г6 = 0,3 мА:
0,3 = осд + ctj (0,8 — Uo) + а3 (0,8 — Uq ) +
+a3(O,8-C7o)3 + a4(O,8-(7o)4 + a5(0,8-(/o)5
И наконец, шестое уравнение получаем, подстав-
ляя в (8.14) значения гг6э = 0,9 В и г6 = 0,53 мА:
0,53 = cig + otj (0,9 - Uо) + а3 (0,9 — Uq ) +
+a3(0,9-(То)3 +a4(O,9-(7o)4 +a5(O,9-(/o)5.
Учитывая, что Uq=0,6, получаем окончательно
следующую систему:
0,05 = а0 - 0,2aj + 0,04а2 - 0,008а3 +
+ 0,0016а4 -0,00032а5;
0,07 = а0 -O.laj +0,01а2 -0,001а3 +
+ 0,0001а4 -0,00001а5;
0,1 = а0;
< 0,175 = а0 + 0,1а4 +0,01а2 +0,001а3 + (8.15)
+ 0,0001а4 +0,00001а 5;
0,3 = а0 + 0,2aj + 0,04а2 + 0,008а3 +
+0,0016а4 +0,00032а5;
0,53 = ао + 0,3aj + 0,09а2 + 0,027а3 +
+ 0,0081а 4 + 0,00243а 5.
Решение системы уравнений (8.15) даст искомые
значения коэффициентов а0, at, а2, а3, а4 и а5,
при которых ток базы г6 (8.14) будет совпадать во
всех узлах интерполяции со значениями тока из
табл. 8.1. По формуле (8.14) можно вычислить лю-
бые промежуточные значения тока и построить точ-
ный график аппроксимирующей функции.
Заметим, что решение системы уравнений, со-
стоящей из шести уравнений с шестью неизвестными,
в настоящее время не представляет заметных трудно-
стей. Для этих целей существуют программы не
только для персональных компьютеров, но и для
микрокалькуляторов.
351
Однако нет необходимости аппроксимировать
ВАХ вне интервала 0,4 В < < 0,8 В, так как мы
знаем, что сигнал на входе транзистора не выходит
за эти пределы (действительно, м6э = Uo ~Um = 0,4 В
и и6а = Uo +Um = 0,8 В). Кроме того, можно вы-
брать меньше узлов интерполяции (например,
ыбз=0,4; 0,6; 0,8 В), что позволит уменьшить сте-
пень аппроксимирующего полинома до второй:
ifi = «о + а1 (ыбэ ~ ^о) + а2 (ыбэ _ Uo)2.
Система уравнений будет состоять всего из трех
уравнений и содержать три неизвестные:
0,05 = а0 -0,2а! + 0,04а2,
• 0,1 = а0,
0,3 = а0 +0,2а! + 0,04а2.
Решение этой системы дает а0=0,1мА, at =
= 0,625 мА/B, а2 = 1,875 мА/B2. Кривая тока
i6 = 0,1+ 0,625(мбэ - 0,6) +1,875(ибэ-0,6)2 (8.16)
проходит через три экспериментальные точки
(рис. 8.22).
В табл. 8.2 приведены для сравнения значения
тока базы ц, вычисленные из (8.16). Из рисунка и
таблиц видно, что экспериментальные точки доста-
точно плотно «ложатся» на кривую (8.16).
Таблица 8.2. Расчетная вольт-амперная характеристика
^бэ > В 0,4 0,5 0,6 0,7 0,8 0,9
Значения г6, мА из (8.16) 0,05 0,05625 0,1 0,18125 0,3 0,45625
Если к нелинейному элементу приложено гармоническое на-
пряжение с большой амплитудой, то вольт-амперную характери-
стику этого нелинейного элемента заменяют отрезками прямых
линий. Прежде всего следует уточнить, что понимается под боль-
шой амплитудой гармонического напряжения. На рис. 8.23 кру-
жочками, соединенными штриховой линией, показана эксперимен-
тальная зависимость тока базы i6 от напряжения м6э, полученная
для транзистора КТ-306. Кроме того, известно, что напряжение
смещения выбрано равным Uo =0,3 В, а гармонический сигнал,
также подводимый к нелинейному элементу, имеет амплитуду
Um = 0,6 В (рис. 8.23).
352
Рис. 8.23. Построение графика тока в НЭ при воздействии
гармонического колебания большой амплитуды
Из графика видно, что когда мгновенное значение гармони-
ческого напряжения изменяется от -0,3 до -0,6 В, напряжение на
участке «база — эмиттер» становится отрицательным и ток базы
отсутствует (г6 = 0), т.е. транзистор закрыт. По-видимому, в
данном случае как раз и можно говорить о большой амплитуде
сигнала на входе транзистора.
С некоторым приближением можно считать, что ВАХ транзис-
тора имеет два участка: первый — там, где ток базы 16 = 0 (при
ибэ < 0) и транзистор закрыт; второй — там, где ток базы растет с
ростом напряжения “бэ и, следовательно, транзистор открыт. При
этом можно пренебречь «кривизной» вольт-амперной характерис-
тики и заменить ее на втором участке прямой линией. На рис. 8.23
аппроксимирующая участок ВАХ прямая линия изображена сплош-
ной линией. Такой же сплошной линией показана зависимость тока
базы от времени, полученная путем проекции гармонического на-
пряжения на аппроксимирующую участок ВАХ прямую линию.
Для сравнения штриховой линией показан реальный ток базы, про-
текающий через нелинейный элемент с экспериментальной ВАХ.
Поскольку отличие этих кривых незначительное, можно считать
замену участка ВАХ прямой линией вполне приемлемой.
Уравнение прямой линии имеет вид у = Кх, где К — коэф-
фициент, определяющий наклон прямой. Смещение прямой па-
23 - 6972
353
раллельно самой себе вправо на величину Хо по оси абсцисс оцц
сывается выражением
у = К (х - XQ).
Наклон аппроксимирующей участок ВАХ прямой линии оп-
ределяется крутизной 5, а смещение по оси и6з — напряжением
отсечки U0TC. Аппроксимирующая всю ВАХ функция задается
параметрически для двух участков напряжения ы6э (рис. 8.23):
j = Г0 ПРИ “бэ < t/отс!
бэ [5(и6э - Uorc) при и6з > U
отс-
(8.17)
Для экспериментальных данных, приведенных на рис. 8.23,
крутизна 5 определяется приращением тока ig к приращению на-
пряжения ыбэ и составляет 4 мА/B, а напряжение отсечки С70тс =
= 0,5 В.
Пример 8.6. Аппроксимировать график ic = F(u3K) зависимости
тока стока от напряжения между затвором и исто-
ком для полевого транзистора (рис. 8.24), на вход ко-
торого подается напряжение иЗИ (t) = -3 + 3cos ot, В.
Транзистор работает в режиме большого сигнала,
поэтому его ВАХ аппроксимируется двумя прямыми
линиями. По графику ic=F(u3K) находим напря-
жение отсечки Umc = -2 В. По аналогии с (8.17) в
диапазоне изменения напряжения мзи < -2 В ток
стока ic равен нулю. Когда напряжение изи стано-
вится больше Umc, то крутизна 5 аппроксимирую-
щей прямой рассчитывается по формуле
~ ^с/( ^ЗИ ^ОТС ) •
Подставляя в эту формулу значения мзи и ic на
границе рабочего диапазона, т.е. мзи =0, ic = 4 мА,
получаем 5 = 2 мА/В.
/с>мА
-3-2-10 12 йзи> В
Рис. 8.24. Вах полевого транзистора к примеру 8.6
354
Таким образом, аппроксимирующая ВАХ функ-
ция имеет вид
i Г0 при изи < UOTC;
~ отс ) При U3H > Umc
ИЛИ
. (О при изи < -2 В;
1с [2(изи + 2) при мзи > -2 В.
Из данного параграфа мы узнали, что:
• Для получения аналитического выражения для вольт-ампер- /
ной характеристики, заданной таблично или графически,
используется аппроксимация. (
• При воздействии на нелинейный элемент гармонического {
сигнала малой амплитуды используют аппроксимацию рабо- *
чего участка ВАХ степенным полиномом.
• При воздействии на нелинейный элемент гармонического сиг- д
нала большой амплитуды используют аппроксимацию ВАХ ‘
отрезками прямых линий (кусочно-линейная аппроксимация).
8.4. Расчет спектрального состава тока
в резистивном нелинейном элементе
при гармоническом воздействии
За счет нелинейности ВАХ происходит искажение формы
тока, протекающего через нелинейный элемент при воздействии
на него гармонического напряжения;
новной составляющей появляются
высшие гармоники. Рассмотрим схе-
му усилительного каскада на бипо-
лярном транзисторе (рис. 8.25), на
входе которого действует напряжение
Мбэ> состоящее из напряжения сме-
щения Uо и гармонического напря-
жения с амплитудой Um. Под дейст-
вием входного напряжения в цепи
коллектора транзистора протекает
коллекторный ток гк. Зависимость
коллекторного тока от напряжения
на участке «база — эмиттер» является
проходной вольт-амперной характе-
ристикой.
в спектре тока помимо ос-
Рис. 8.25. Усилитель на
биполярном транзисторе
23*
355
Рис. 8.26. Линейный режим работы транзисторного усилителя
Рис. 8.27. Нелинейный режим работы транзисторного усилителя.
Искажение формы тока из-за нелинейности ВАХ
На рис. 8.26 изображены проходная ВАХ транзисторного
каскада, зависимость во времени напряжения на входе каскада
«бЭ(£) и зависимость во времени коллекторного токагк(£). На-
пряжение смещения Uo и амплитуда гармонического напряжения
Um выбраны на рисунке таким образом, что рабочая точка не
выходит за пределы линейного участка ВАХ. В результате кол-
356
.[екторный ток будет содержать постоянную составляющую /0 и
Гармоническую составляющую с амплитудой [,„.
Иная картина будет наблюдаться, если напряжение смещения
Uo уменьшить и тем самым выбрать рабочую точку на нижнем,
нелинейном, участке ВАХ (рис. 8.27). Форма тока исказится, ток
перестанет быть гармоническим. Дальнейшее уменьшение напря-
жения смещения С'о приведет к еще большему искажению формы
тока (рис. 8.28).
Рис. 8.28. Работа транзисторного усилителя
в режиме нижней отсечки тока
357
Рис. 8.30. Одностороннее и двухстороннее ограничения
напряжения с помощью диодных ограничителей
Из теории спектрального анализа сигналов известно, что лю-
бой периодический сигнал может быть представлен рядом Фурье
(см. гл. 3). Это значит, что коллекторный ток гк складывается из
постоянной составляющей, основной составляющей с частотой
входного сигнала и высших гармоник:
гк = А) +£УтбСО5(/г<в£ -ф^), Л = 1,2,3.... (8.18)
k
Искажения формы сигнала из-за нелинейности ВАХ называ-
ют нелинейными искажениями. Если перед нами стоит задача
усилить сигнал без искажений (например, при воспроизведении
речи, музыки, изображения и т.п.), то следует выбирать такой
режим работы (напряжение смещения и амплитуды сигналов),
чтобы не выходить за пределы линейного участка ВАХ.
Наоборот, стремление преобразовать сигнал с помощью не-
линейного элемента, например, не дать мгновенному значению
сигнала превысить некоторый заранее установленный порог, при-
водит к необходимости работать в режиме больших нелинейных
искажений.
На рис. 8.29 изображена вольт-амперная характеристика дио-
да. Приближенно можно считать, что при воздействии на диод
напряжения в «прямом направлении» (правая полуплоскость ри-
сунка) через него будет протекать ток, т.е. р-п переход диода бу-
дет открыт, а при воздействии напряжения в «обратном направ-
лении» (левая полуплоскость рисунка) ток практически протекать
не будет, т.е. р-п переход диода будет закрыт.
На практике широко применяются схемы диодных ограничи-
телей напряжения (рис. 8.30). Здесь диод выполняет роль венти-
358
ля: в открытом состоянии его сопротивление мало (десятки Ом),
в закрытом состоянии — очень велико (сотни МОм). Эти свойст-
ва диода позволяют аппроксимировать его ВАХ кусочно-линей-
ной функцией (рис. 8.31). Напряжением смещения Uq регули-
руют порог ограничения.
Состав спектра тока в нелинейном элементе при аппрокси-
мации ВАХ степенным полиномом определяется степенью поли-
нома и его коэффициентами. Ограничимся рассмотрением поли-
номов со степенью не выше третьей.
График полинома первой степени
i = а0 +a.t(u-U0) (8.19)
представляет собой прямую а0, параллельную оси абсцисс, и на-
клонную прямую а(ы с коэффициентом наклона eq, смещенную
по оси абсцисс на величину Uq. Регулируя величины а0, «1 и
Uq, можно перемещать аппроксимирующую прямую вниз, впра-
во и влево и менять ее наклон.
Для определения амплитуд гармоник тока подставим в (8.19)
выражение для напряжения, приложенного к нелинейному эле-
менту u(t) = Uo +Um coscot:
i = а0 +ai((70 +Umcosot-U0) = а0 + «Дп coscot.
359
Сравнивая это выражение с рядом Фурье
i = IQ +Im\ coscot + Zm>cos2cot + Zm3 cos3co< +...,
видим, что IQ = a0; Imi = aiC,„; Im2 = 1тз = ••• = 0. Таким обра-
зом, при аппроксимации ВАХ полиномом первой степени ток со-
держит кроме постоянной составляющей Zo только основную
(первую) гармонику, совпадающую по частоте с приложенным
гармоническим напряжением. Высшие гармоники в спектре тока
отсутствуют, нелинейных искажений нет.
График полинома второй степени
i = a0 + a( (и -(/o) + a2(w-Cro)i 2 (8.20)
содержит в дополнение к графику полинома первой степени
квадратичную параболу а2п2, смещенную по оси абсцисс на ве-
личину Uo. Квадратичный член служит для аппроксимации сла-
бой нелинейности ВАХ параболического типа.
Подставляя в (8.20) напряжение u(t) = Uo +Um coscoi, по-
лучаем:
i = a0 +at(7m coscoi + a cos2 cot =
, f i 1 A
= a0 + alm coscot + a2CZ„ I - + - cos 2coi I =
x0 +|a2t7^ + aiC/mcoscot + |a2(72 cos2cot =
= Io + Zm) cos cot + Im2 cos 2cot.
Это выражение показывает, что если вольт-амперная характери-
стика нелинейного элемента имеет нелинейность, описываемую
квадратичной параболой, то в спектре тока, протекающего через
такой нелинейный элемент, появляется при воздействии на него
постоянного и гармонического напряжений вторая гармоника с
частотой 2со.
Для описания нелинейности ВАХ более высокого порядка
используется полином третьей степени:
i = a0 + a1(u-(70) + a2(u-(70)2 + a3(u-U0)3,
в котором добавляется так называемая кубическая парабола
а3п3, смещенная по оси абсцисс на величину Uq .
Подстановка напряжения u(t) = Uo +Um coscoi в этот поли-
ном дает
i = <х0 + щит cos G)t+ a2U„ cos2 cot + a3U„ cos3 cot = a0 +
, (j i A , г з j
+ a((7m cos cot + a.2Um I 2 + 2 COS J +аз^т I coscot + — cos 3cot
360
«О "* л +1 "* . ®3^-' т
2 J \ 4
1 2
coscoi + -ct2U,n cos 2ut +
1
+-a3Lr;‘ cos3cof = 70 + ImX
cos (of + Im2 cos 2coi + Im3 cos 3(ol,
где постоянная составляющая
/О " a0 + 2a2^m
и амплитуды гар-
Э о 17 14
МОНИК 1тХ =О.хит+-ази^,1т2 = ^а2ит И Im3 =-CL3U .
Из приведенных примеров видно, что наличие в ВАХ нели-
нейностей высокого порядка приводит к появлению высших гар-
моник в спектре тока. Количество гармоник в спектре тока
равно степени полинома, описывающего нелинейность ВАХ.
Постоянная составляющая и амплитуды четных гармоник оп-
ределяются коэффициентами полинома при четных степенях,
а амплитуды нечетных гармоник — коэффициентами полинома
при нечетных степенях. Это означает, что, если ВАХ аппрокси-
мируется полиномом только с четными степенями, в спектре тока
будут присутствовать постоянная составляющая и четные гармо-
ники. При аппроксимации ВАХ полиномом с нечетными степеня-
ми спектр тока будет содержать только нечетные гармоники.
Пример 8.7. Рассчитать спектральный состав тока базы биполяр-
ного транзистора для данных примера 8.5. Построить
спектр тока.
В рабочем диапазоне напряжений 0,4 В < и6э < 0,8 В
ВАХ транзистора была аппроксимирована полиномом
второй степени (8.20):
i6 = а0 + ах(и6э-и0) + а2(ибэ-и0)2.
Коэффициенты полинома были определены в примере
8.5 (см. формулу (8.16)):
а0 = 0,1 мА; ах = 0,625 мА/B; Г°’ 1т1
а2 = 1,875 мА/В2.
Рассчитаем значения по-
стоянной составляющей и
амплитуды первой и второй
гармоник тока, воспользо-
вавшись вышеприведенными
формулами:
0,15.:
0,1
0,05 т
0 со 2со Зсо со
Рис. 8.32. Спектр тока
к примеру 8.7
/0 = а0+^а2и2т = 0,1 + | 1,875 0,22 =0,1375 мА;
361
Im\ = a^m = 0.625 • 0,2 = 0,125 мА;
I m2 = fa’2m = | • 1,875 • 0,22 = 0,0375 mA.
Спектр тока (рис. 8.32) содержит постоянную
составляющую 10 и две гармоники с амплитудами
1ml И 1т2
Спектр тока при кусочно-линейной аппроксимации ВАХ за-
висит от угла отсечки. Напомним, что при больших амплитудах
гармонического напряжения, подводимого к нелинейному элемен-
ту, практически нет смысла учитывать небольшую кривизну ВАХ
(так называемую слабую нелинейность). В тех случаях, когда не-
линейный элемент работает как вентиль (есть ток или нет тока),
используют кусочно-линейную аппроксимацию ВАХ (рис. 8.33):
i = (°, тт \ npnu^Umc; (821)
[5(м-(Уотс) прии>17отс.
График тока при этом имеет вид косинусоидальных импуль-
сов с отсечкой. Половина той части периода в радианах (или гра-
дусах), в течение которой протекает ток, называется углом от-
сечки. Он обозначен на рис. 8.33 буквой 0.
Из графика рис. 8.33 можно вычислить угол отсечки 0. При
a>t = 0 напряжение u(t) = Uo +Um coscot = Uo +Um cos0 = Umc.
Откуда
Рис. 8.33. Построение графика тока при
кусочно-линейной аппроксимации ВАХ
362
cos0 = ^22—^0 и 0 = arccos ——c- U(>. (8.22)
U m U m
Последнее равенство показывает, что угол отсечки можно изме-
нить, меняя напряжение смещения 170, амплитуду гармоническо-
го сигнала Um или выбирая параметр Umc аппроксимирующей
функции (8.21).
Периодическую последовательность импульсов тока на рис. 8.33
можно разложить в ряд Фурье:
i = /0 + Imi costoi + Im2 cos2©t + Im3 cos3cd£ +....
Опуская процедуру нахождения коэффициентов ряда Фурье и
отсылая любознательного читателя к стандартным учебникам [1,
2], приведем окончательный результат.
Постоянная составляющая и амплитуды гармоник тока вы-
числяются по формуле
Imk = SUmyk(Q), k = 0, 1, 2, 3, ..., (8.23)
где функции yfe(0) называются функциями Берга (в честь круп-
ного российского радиотехника академика А.И. Берга). Они за-
висят от угла отсечки, и их значения для разных углов отсечки
приводятся в справочниках. Графики нескольких функций Берга
представлены на рис. 8.34.
Чтобы получить максимальные амплитуды гармоник, следует
выбирать 0 = 180°/^! так как при таких углах отсечки функции
Берга у^(0) принимают максимальные значения.
Таким образом, амплитуды спектральных составляющих
тока в нелинейном элементе при кусочно-линейной аппрокси-
мации его ВАХ зависят от угла отсечки. Количество гармоник
при этом бесконечно большое. Чем меньше угол отсечки (т.е.
чем уже импульс), тем медленнее убывают амплитуды гармо-
ник тока.
363
Пример 8.8. Рассчитать постоянную составляющую и амплитуды
первой и второй гармоник в спектре тока стока поле-
вого транзистора для данных примера 8.6.
По данным примера 8.6 напряжение смещения
Uо = -3 В, амплитуда гармонического напряжения
U„, = 3 В, напряжение отсечки UOTC = -2 В, крутиз-
на S = 2 мА/В.
По формуле (8.22) рассчитываем угол отсечки:
0 = arccos —ОТ1--— = arccos ---t = 70°.
Um 3
Для угла отсечки 0 = 70° определяем по графи-
кам, приведенным на рис. 8.34, функции Берга:
уо(О) = У2<©> = 0.22, У1(0) = О,33.
Постоянную составляющую и амплитуды гармо-
ник тока рассчитываем, используя формулу (8.23):
/0 = 5(7ту0(0) = 2-3-0,22 = 1,32 мА;
Imi = SU^te) = 2-3-0,33 = 1,98 мА;
Im2 =S<7mY2(G) = 2- 3-0,22 = 1,32 мА.
Амплитуды других гармоник в спектре тока
можно рассчитать аналогично, выбрав в справочнике
соответствующие функции Берга.
При воздействии на нелинейный элемент суммы гармониче-
ских колебаний возникают спектральные составляющие с ком-
бинированными частотами. Сигнал, состоящий из суммы двух
гармонических колебаний с различными частотами (Dj и со2 и ам'
плитудами Uml и 1/от2:
и (t) = Umi cos со + Um2 cos co2t,
называется бигармоническим воздействием. Спектр бигармониче-
ского воздействия изображен на рис. 8.35, а.
Пусть на вход НЭ, ВАХ которого аппроксимирована поли-
номом второй степени
i = F(u) = а0 +a1(w-l/0) + a2(u-t/0)2,
поданы напряжение смещения Uo и бигармонический сигнал
u(t). Подстановка напряжения и = Uo + Umi cos со + Um2 cos®2i
в выражение для ВАХ позволяет определить ток в цепи НЭ в виде
i(.t) = a0 coscoti + at(7OT2 cosco2f + a.£Jmi cos 2 со +
+ 2aJJmiUm2 cos cos co2^ + a2t/^2 cos2 co2i.
Используя тригонометрические формулы
364
Um2
Umt
^ + ^U2mi+u\)
СИ Umt
''т[ ''m2
0 (01-©2
(02 <°1 CD
a)
* ‘ <X] ^6n2
" ’ al Um[ 0-2 Umi Umi
(02 <Oj 2(02 <0i+(02 2(0i <0
Рис. 8.35. Спектры бигармонического напряжения (л)
и тока (б) в нелинейном элементе
cos 2 v = - (1 + e°s 2v|/)
и
cosigjcosvg2 = (</2)[cos(i|/1 + \|/2) + cos(vi “'Иг)]»
получаем:
i(t)= a0++y-(^t+a1[/miCos<B1i +
+ O.\Um2 COS <02^ + 2^Г— COS 2(B^ + COS 2(O2t +
+ a2C/mll7OT2COs(©1 +©2)^ + a2^ml^m2COs((01-C02)^
(8.24)
Спектральный состав тока в цепи с НЭ показан на рис. 8.35, б.
Принципиально новым по сравнению с воздействием на НЭ
одного гармонического колебания здесь является появление спек-
тральных составляющих с комбинационными частотами со1 + со2
и a>i - <х>2 • Если ВАХ нелинейного элемента аппроксимирована в
общем случае полиномом степени N, то в спектральном составе
тока будут присутствовать составляющие с комбинационными
частотами pcoj ± qa2, причем p + q = ЛГ, где р n q — целые поло-
жительные числа (О, 1, 2, ...). Так, например, при аппроксима-
ции ВАХ нелинейного элемента полиномом третьей степени в со-
ставе спектра тока присутствуют комбинационные частоты, при-
веденные в табл. 8.3.
В общем случае входное воздействие можно представить бес-
конечной суммой
u(t) = U0 + f,Umkcos((i)kt-q>k).
&=1
365
Таблица 8.3. Комбинационные частоты при аппроксимации ВАХ
нелинейного элемента полиномом третьей степени
Значения q Частоты спектральных составляющих " при значениях р
0 1 2 з
0 со = 0 2а>! 3(0 ( '
1 а>2 а>! ±<Х>2 2(0! ± (02
2 2(0 2 COj ± 2сО2 —
3 Зсо2 — — —
В зависимости от степени М аппроксимирующего полинома
(8.13) в спектре тока, протекающего через нелинейный элемент,
появляются комбинационные частоты вида
рал\ ±qa>2 ±яо3 +... + ka>k + ..., где р +<? + $ + ... + & + ... = .V
(р, q, s, k — целые положительные числа). Например, при воз-
действии на НЭ с ВАХ в виде полинома второй степени суммы
трех гармонических колебаний в спектре тока, помимо постоян-
ной составляющей и первых двух гармоник каждой частоты, при-
сутствуют комбинационные частоты coj ±<ю25 ± ®з > а>2±(Эз-
При аппроксимации полиномом третьей степени дополнительно
появляются третьи гармоники За»!, За>2 > За>3 и комбинационные
частоты типа (Oj ± <в2 ± со3; 2(0j ± со3; (ot ± 2со3 и т.д.
Из данного параграфа мы узнали, что:
• Форма тока, протекающего через нелинейный элемент при |
гармоническом воздействии, отличается от гармонической |
из-за нелинейности ВАХ. Такое искажение формы тока на- 3
зывается нелинейным искажением. |
Спектр тока, протекающего через нелинейный элемент при
гармоническом воздействии, содержит постоянную состав-
ляющую, первую гармонику и высшие гармоники.
При аппроксимации ВАХ нелинейного элемента степенным
полиномом количество гармоник в спектре тока равно сте- ।
пени полинома. |
• При кусочно-линейной аппроксимации ВАХ нелинейного ®
элемента в спектре тока содержится бесконечное количест- |
во гармоник. Их амплитуды зависят от угла" отсечки. §
• Спектр тока, протекающего через нелинейный элемент под воз-
действием суммы гармонических колебаний, содержит постоян- |
ную составляющую основную и высшие гармоники, а также ;
спектральные составляющие с комбинационными частотами. *
366
Вопросы и задания для самоконтроля
1. Какие резистивные элементы называются нелинейными?
2. Определить статическое и динамическое сопротивления нели-
нейного элемента, имеющего ВАХ, изображенную на рис. 8.22.
3. Какие методы используют для расчета нелинейных цепей в
режиме постоянного тока?
4. Рассчитать ток, протекающий через нелинейный элемент в
схеме рис. 8.36, а, если заданы 7?t = R2 = 2 кОм, Ux =2 В,
U2 = 8 В, ВАХ НЭ приведена на рис. 8.36, б.
5. Рассчитать ток I в схеме рис. 8.37, а, если R - 0,5 кОм, U = 2 В,
ВАХ НЭ1 и НЭг приведены на рис. 8.37, б.
6. Каким образом формируются уравнения состояния нелиней-
ных резистивных цепей?
7. Каков порядок расчета резистивных цепей с нелинейными че-
тырехполюсниками ?
8. Какие существуют виды аппроксимации ВАХ нелинейных эле-
ментов?
9. Аппроксимировать ВАХ НЭ, изображенную на рис. 8.8, в ра-
бочем диапазоне 0 < ип < 1 В при CJ0 = 0,5 В.
10. Аппроксимировать ВАХ НЭ, изображенную на рис. 8.8, если
к НЭ приложено напряжение ип (t) = coscot.
И. Рассчитать амплитуды спектральных составляющих тока в за-
дании 9. Построить спектр тока.
12. Рассчитать постоянную составляющую и амплитуды спек-
тральных составляющих 1тХ и 1т2 тока в задании 10. По-
строить спектр тока.
13. Построить графики тока биполярного транзистора,
ВАХ которого изображена на рис. 8.23, если заданы следую-
щие значения u63(e)t):
a) w63(cot) = 0,3 + 0,2coscot; б) w63(cot) = 0,3 + 0,4coscot;
в) ц6з (cot) = 0,7 + 0,05coscot.
Рис. 8.37. Схема (д) и ВАХ нели-
нейного элемента (б) к заданию 5
Рис. 8.36. Схема (д) и ВАХ нели-
нейного элемента (б) к заданию 4
Глава 9. Анализ реакции линейной дискретной
цепи на дискретные воздействия
9.1. Дискретные сигналы
Дискретный сигнал легко получить из аналогового, взяв его
отсчеты в определенные моменты времени. Сигнал — это физи-
ческий процесс (например, изменяющиеся во времени токи и на-
пряжения), содержащий в себе некоторую информацию. Любой
сигнал можно описать математической функцией. Существуют
аналоговые, дискретные и цифровые сигналы. Аналоговые сигна-
лы описываются непрерывной во времени функцией x(t)*, кото-
рая может принимать любые значения в определенном интервале;
дискретные сигналы х(пТ) представляют собой последователь-
ности или отсчеты функции x(t), взятые в определенные дис-
кретные моменты времени пТ; цифровыми являются сигналы, ко-
торые в дискретные моменты времени пТ принимают конечные
дискретные значения — уровни квантования, которые затем ко-
дируются двоичными числами.
Если в цепь микрофона (рис. 9.1), где ток i(t) является не-
прерывной функцией времени, встроить ключ и периодически на
короткие мгновения замыкать его, то ток в цепи будет иметь вид
узких импульсов с амплитудами, повторяющими форму аналого-
вого сигнала. Последовательность этих импульсов, которые назы-
вают отсчетами аналогового сигнала, и представляет собой не что
иное, как дискретный сигнал.
Рис. 9.1. Получение дискретного тока в линии
‘ В качестве x(i) могут быть взяты напряжение u(f) или ток i(t).
368
В отличие от аналогового сигнала z(t) дискретный сигнал
можно обозначить гл(£). Однако чаще его обозначают i(nT),
заменяя непрерывное время t дискретными моментами пТ, сле-
дующими строго через интервал Т. Используются и более крат-
кие обозначения: г[п] и г„. Причем во всех этих записях п —
целое число, принимающее как положительные, так и отрица-
тельные значения. Так, на рис. 9.1 при п < 0 дискретный сигнал
in(t) = i(nT) s 0. При п = 0 значение г (ОТ) равно значению
сигнала г(б) в момент времени i = 0. При п > 0 отсчеты г («Г)
повторяют форму сигнала z(t), так как их амплитуды равны
значениям аналогового сигнала в моменты времени пТ.
Дискретные сигналы можно задавать графиками, как это по-
казано на рис. 9.1, формулами, например, гд(£) = sinpn/nT), в
виде таблиц дискретных значений или в виде комбинации этих
способов. Рассмотрим примеры некоторых дискретных сигна-
лов, полученных из типовых аналоговых сигналов.
Пример 9.1. Единичная функция 1(£) приведена на рис. 9.2, а.
Соответствующий ей дискретный сигнал 1[п] назы-
вается ступенчатой последовательностью и определяет-
ся следующим образом:
1Ы = (* “Р""»0:
[0 при п < 0.
Такая последовательность приведена на рис. 9.2, б.
Рис. 9.2. Единичный ступенчатый аналоговый (а)
и дискретный (б) сигналы
Пример 9.2. 5-импульс в аналоговой области приведен на рис. 9.3.
Дельта-последовательность, или дискретный 8-импульс,
определяется выражением
S[”] = {o
при п = 0;
при п ф 0.
Последовательность 3[п], приведенная на
рис. 9.3, б, принимает единственное значение, рав-
369
24-6972
5(0 51л]
8[Л 5[л-2]
0 t -2-1012»
a) S)
-2-1012 п
О
Рис. 9.3. Аналоговый (а)
и дискретный (6 и в) 5-импульс
ное 1, при п = 0. Этот сигнал можно сдвинуть на k
интервалов (рис. 9.3, в):
б[Л-н=(1 пРи" = *;
(0 при п * k.
Математическая запись любого дискретного сигнала может
быть представлена в виде последовательности дискретных 5-
импульсов с весовыми коэффициентами, равными отсчетам и[Л]
аналогового сигнала u(t) в точках kT'.
и[п] = £ u[fc]5[n-£].
Дискретный сигнал можно получить из аналогового периоди-
ческим замыканием ключа на очень короткие моменты времени
(рис. 9.4).
Дискретные отсчеты аналогового сигнала нужно брать с та-
кой частотой, чтобы по ним можно было однозначно восстано-
вить исходный сигнал. Интервал времени Т, через который от-
считываются значения аналогового сигнала i(t), называется ин-
тервалом дискретизации. Обратная величина МТ (обозначим ее
Л) называется частотой взятия отсчетов или частотой дискре-
тизации.
Отсчеты аналогового сигнала следует брать с такой частотой
(или через такой интервал времени), чтобы успевать отследить
все, даже самые быстрые, изменения сигнала. Иначе при восста-
новлении этого сигнала по дискретным отсчетам часть информа-
ции будет потеряна и форма
восстановленного сигнала бу-
дет отличаться от формы ис-
ходного (рис. 9.5). Если обра-
титься к схеме рис. 9.1, то это
означает, что звук на приеме
будет восприниматься с иска-
жениями.
•о
Дискретный
сигнал
«[лТ]
о
Рис. 9.4. Получение дискретного
сигнала из аналогового
370
Рис. 9.5. Исходный аналоговый сигнал (а) и аналоговый сигнал,
восстановленный по его дискретным отсчетам (б)
Для сигналов с ограниченным спектром, т.е. для тех сигна-
лов, у которых спектральная плотность локализована в опреде-
ленной полосе частот, существуют более конкретные рекоменда-
ции по выбору интервала дискретизации Т (или, что то же, час-
тоты дискретизации fa). Эти рекомендации будут даны в § 9.2
после изучения спектров дискретных сигналов.
Аналоговые сигналы после их дискретизации можно обра-
батывать на компьютере. Если задано напряжение на входе цепи
wBX(£) и нужно найти напряжение на ее выходе wBbIX(t), мы
можем сделать это, воспользовавшись интегралом свертки (6.19):
t
[uex(x)h(.t-x)dx. (9.1)
о
Заменим непрерывные сигналы в формуле (9.1) их дискрет-
ными отсчетами. Чтобы не вносить путаницы, время t заменим
дискретными значениями пТ, а время т — дискретными значе-
ниями тТ. Тогда интеграл придется заменить суммой и выраже-
ние (9.1) запишется в виде
ивых(пТ) = £ u3X(mT)h[(n -m)T]
m=0
(9.2)
Вместо непрерывного сигнала ивх (t) мы будем иметь дело с дис-
кретным сигналом ивх(тТ) и вместо непрерывной импульсной
характеристики h(О — с дискретной импульсной характеристикой.
Поскольку любой отсчет сигнала — это число, то формулу (9.2)
можно запрограммировать на компьютере. Останется лишь ввести
24*
371
числа, соответствующие всем дискретным отсчетам wBX (тпТ) и
h[(n-m)T], и он вычислит отсчеты выходного напряжения
«вых Выражение (9.2) на языке вычислительной техники
называется алгоритмом вычисления выходного сигнала.
Таким образом, аналоговые сигналы можно обрабатывать с
помощью компьютера. Однако не следует думать, что отсчеты
сигналов вносятся в компьютер с клавиатуры. Их можно вводить
в компьютер и выводить из него непосредственно. На рис. 9.6
показано, как это делать. Непрерывный сигнал uBX(t) подается
на ключ, на выходе которого образуются дискретные отсчеты
uBX(nT). Но их еще нельзя ввести в компьютер. Сначала нуж-
но перевести амплитуды отсчетов в двоичный код — ведь только
такой код понимает компьютер. Выполняет эту операцию кодер.
Скажем, если отсчет имеет величину 30 В, то запись числа 30 в
двоичном 8-разрядном коде будет такой: 00011110. Закодиро-
ванные в двоичном коде отсчеты на рисунке обозначены
Йвх(пГ).
Вычислительные средства (ВС) могут представлять собой
универсальный компьютер, специализированное микропроцессор-
ное устройство или что-нибудь в этом роде. Главное состоит в
том, что в его памяти записаны программа вычисления, например
выражение (9.2), и отсчеты импульсной реакции цепи. Следова-
тельно, в результате работы программы компьютер будет выда-
вать закодированные в двоичном коде отсчеты й вых (пТ). Деко-
дер преобразует код в амплитуду, и на его выходе появляются дис-
кретные отсчеты выходного напряжения г/вых^Т). Интерполятор
(ИНТ) восстанавливает функцию между отсчетами. В итоге на
выходе системы мы имеем аналоговый сигнал ивых(Л).
Рис. 9.6. Устройство (а) и компьютерная
обработка (б) аналогового сигнала
372
Устройство, состоящее из ключа и кодера и преобразующее
непрерывный (аналоговый) сигнал в двоичный код (или, что то
же, в цифровой сигнал), называют аналоге цифровым преобразо-
вателем (АЦП). Обратное преобразование выполняет цифро-
аналоговый преобразователь (ЦАП), содержащий декодер и ин-
терполятор.
Как видим, компьютер или вычислительное устройство могут
сыграть роль реальной цепи. И хотя самой физической цепи мо-
жет и не быть в наличии, а задана она будет лишь в виде отсче-
тов импульсной реакции и программы вычислений, мы будем на-
блюдать на выходе описанной системы такое же выходное на-
пряжение ивых(£), как и на выходе реальной цепи.
Из данного параграфа мы узнали, что:
• Дискретные сигналы могут представлять собой отсчеть.
аналогового сигнала в определенные дискретные моменты
времени.
• Интервал дискретизации, т.е. интервал времени между
дискретными отсчетами, выбирают таким образом, чтобы
по взятым отсчетам можно было как можно точнее восста-
новить исходный аналоговый сигнал.
«г
>5.
•«s
• Дискретные отсчеты аналогового сигнала, переведенные в
двоичный код, легко обрабатывать на компьютере по за-
данным формулам и алгоритмам.
9.2. Спектры дискретных сигналов
Дискретный сигнал имеет периодический спектр. Формулы
для расчета спектра дискретного сигнала можно получить из
формул преобразования Фурье для аналогового сигнала. В со-
ответствии с принципом неопределенности сигнал, имеющий ог-
раниченную протяженность во времени, обладает неограни-
ченным по полосе спектром (рис. 9.7, а). И наоборот, сигнал с
ограниченным спектром имеет бесконечную протяженность во
времени (рис. 9.8, а). Как следует из этих рисунков, аналоговый
сигнал и ограниченной, и бесконечной протяженности во времени
имеет сплошной спектр.
Как мы знаем из гл. 3, если сигнал и(Л) является периоди-
ческим, то спектр его — дискретный, т.е. теперь вместо U(jf)
используют отсчетыU_[п]. Эта ситуация показана на рис. 9.7, б.
Период сигнала равен длительности сигнала Тс. Интервал дис-
кретизации спектра по частоте F определяется, как известно, пе-
риодом сигнала, в данном случае F - 1/Тс .
373
Рис. 9.7. Спектры аналогового сигнала с ограниченной длительностью
Рис. 9.8. Спектры аналогового (а) и дискретного (б)
сигналов бесконечной протяженности во времени
В соответствии с принципом дуальности можно сказать: если
периодическим является спектр, то дискретным будет сигнал
(рис. 9.8, 6). Обозначая период повторения спектра fa, получаем
интервал дискретизации сигнала Т = l/fa .
Формулы прямого и обратного преобразований Фурье для
дискретных сигналов получают из формул (4.8) и (4.9) для ана-
логовых сигналов, заменив непрерывное время t на дискретные
значения пТ:
U(jf) = £ и[п]е~^пТ; П=-СО (9.3)
u[n] = ^UUf)e^nTdf. /д о (9.4)
374
В формулах (9.3) и (9.4) использовано обозначение иМ = и(пТ).
Пример 9.3. Рассчитаем спектр дискретного сигнала, состоящего
из одного отсчета и[п] = [а; 0; 0; 0; ...].
Воспользуемся формулой (9.3), в которую под-
ставим значения и[п\ заданного сигнала:
U (jf) = f и [п ] e~i2*fnT = ае~^от = а.
72=—ОО
Пример 9.4. Рассчитаем спектр экспоненциальной дискретной
функции ы[ц] = 0,5”, п > 0.
График дискретной функции и[п] приведен на
рис. 9.9, а ее отсчеты можно записать в виде последо-
вательности и(п]= {1; 0,5; 0,25; 0,125; 0,0625; ...}.
Спектр дискретной экспоненты рассчитаем по
формуле (9.3):
U(jf) = f u[n]e~’2nfhT = f 0,5”е~^пТ =
72=-OO 72=0
= J (о, 5е->2я/г)” =----i—T7r,
п=о 1-0,5е-^
где для суммирования ряда использована формула
^уп =1 + у + у2 + у3 +... =——.
п=0 1 У
Получим выражение для расчета спектра ампли-
туд U(f), используя формулу Эйлера (е>х = cosx +
+/sinx):
X(f) = "j----------------------------------Г •
41 - о, 5 cos (-2л/Т)р + [0,5sin(-2n/T)]
Для построения графика будем задавать значения
f от 0 до 1 /Т с шагом 0,1/Т и рассчитывать U(f).
0 1 2 3 4 t0 0,1/Т 0,5/Т 1/Т /
Рис. 9.9. Дискрет- Рис. 9.10. Спектр амплитуд
ная функция к примеру 9.4
к примеру 9.4
375
График спектра амплитуд U(f} экспоненциаль-
ной дискретной функции м[п] = 0,5" приведен на
рис. 9.10.
Как видно из графика, спектр дискретного сиг-
нала сплошной и периодический с периодом = 1/Т.
При выборе интервала дискретизации сигнала нужно не до-
пустить наложения спектров, приводящего к искажению формы
сигнала. Обратимся вновь к рис. 9.7. Когда дискретизации под-
вергается спектр, это приводит к периодическому повторению
сигнала. На рис. 9.11 показаны случаи выбора разных интерва-
лов дискретизации спектров. При слишком редкой дискретизации
спектра происходит наложение сигналов из разных периодов
друг на друга. При этом форма периодической последовательно-
сти будет отличаться от формы одиночного сигнала.
Когда дискретизации подвергается сигнал (рис. 9.12 и 9.13),
то периодически повторяется спектр сигнала. При неудачном вы-
Рис. 9.11. Наложение сигналов при редкой
дискретизации спектров
Рис. 9.12. Наложение спектров при редкой дискретизации
сигнала ограниченной длительности
376
Рис. 9.13. Наложение спектров при редкой дискретизации
сигналов бесконечной длительности
боре интервала дискретизации будет иметь место наложение друг
на друга спектров из разных периодов повторения, т.е. искаже-
ние формы спектра.
Вывод: все наложения (сигналов или спектров) происходят
из-за неудачного — слишком редкого — интервала дискретизации
(соответственно спектра или сигнала). Это приводит к появлению
ошибок наложения или, другими словами, искажений формы
сигнала (либо спектра), на каждом периоде.
Сравнивая рис. 9.8 и 9.13, можно убедиться, что спектр дис-
кретного сигнала содержит в себе (в самом первом периоде)
спектр исходного аналогового сигнала. Если с помощью фильтра
нижних частот подавить все «боковые» спектры и выделить толь-
ко «основной» спектр, то на выходе фильтра будет восстановлен
аналоговый сигнал. Чтобы эта процедура не была «испорчена»,
периодически повторяемые спектры не должны пересекаться, т.е.
не должно быть наложения спектров.
На рис. 9.6 устройство, восстанавливающее непрерывный
сигнал из дискретного, было названо интерполятором. Оно по
известным (отсчетным) значениям непрерывной функции вычис-
ляет все промежуточные значения. В математике подобная опера-
ция называется интерполяцией.
Итак, если пропустить дискретный сигнал и[пТ] через
фильтр нижних частот с граничной частотой полосы пропускания
Ёгр, то фильтр подавит все «боковые» спектры и не внесет ника-
ких изменений в «основной» спектр. Значит, на его выходе поя-
вится непрерывный сигнал u(t). Таким образом, фильтр нижних
частот с частотой среза jFrp может играть роль интерполятора.
Непрерывный сигнал можно однозначно восстановить по
дискретным отсчетам, взятым через интервалы времени, обрат-
но пропорциональные удвоенной ширине спектра. В 1933 г. в
377
работе «О пропускной способности «эфира» и проволоки в элек-
тросвязи» В.А. Котельников доказал теорему, ставшую основопо-
лагающей в теории и технике цифровой связи. Она гласит: если
непрерывный сигнал u(t) имеет спектр, ограниченный часто-
той FTf, то он может быть полностью и однозначно восста-
новлен по его дискретным отсчетам, взятым через интервалы
времени
т.е. с частотой
/д = 2-Frp-
Мы не приводим полную математическую формулировку тео-
ремы, а также ее доказательство, а лишь ограничиваемся указа-
нием сути теоремы. Однако справедливость ее легко усматривает-
ся из рис. 9.8 и 9.13. Частота дискретизации непрерывного сиг-
нала не должна быть меньше удвоенной ширины спектра:
/д > 2Frp, иначе произойдет наложение спектров (рис. 9.13) и бу-
дет невозможно с помощью фильтра нижних частот выделить
спектр исходного непрерывного сигнала.
Пример 9.5. Рассчитаем интервал дискретизации и минимально
допустимую частоту дискретизации сигнала, спек-
тральная плотность которого равна нулю при значе-
ниях частоты выше 100 кГц.
Из условия задачи следует, что граничная часто-
та спектра Frp = 100 кГц. Тогда в соответствии с тео-
ремой Котельникова имеем интервал дискретизации
1 1 -
Т = —— =----------т = 5 мкс.
2Frp 2100103
Минимально допустимая частота дискретизации
/д = 2^ = 2-100= 200 кГц.
Пример 9.6. Определим дискретные отсчеты сигнала длительно-
стью tu = 3 мс, приведенного на рис. 9.16, а, если в
качестве граничной частоты спектра Frp принять
значение 3/tu, выше которого все значения спек-
тральной плотности уменьшаются более чем в 10 раз
по сравнению с максимальным.
Хотя сигнал конечной длительности имеет беско-
нечный спектр частот, однако почти всегда можно
определить граничную частоту спектра таким обра-
зом, чтобы отсекание частот, превышающих Ггр,
привело к пренебрежимо малым изменениям энергии
исходного сигнала. Такое условие задано в примере.
378
Рис. 9.14. Аналоговый (а) и дискретный (б)
сигналы к примеру 9.6
Граничная частота спектра
3 3
Frp = « = 1 кГц.
р tu 3-103
Интервал дискретизации
Т = —= 0,5 мс.
2Frp 21-103
Берем, отсчеты сигнала, приведенного на
рис. 9.14, а, через интервал времени Т = 0,5 мс и по-
лучаем последовательность и[п] = {0; 2; 3,2; 4; 1;
0,3; 0}, изображенную графически на рис. 9.14, б.
Спектры дискретных периодических сигналов являются пе-
риодическими и дискретными. Для их расчета используется
дискретное преобразование Фурье. Мы уже отмечали, что раз-
витие вычислительной техники привело к появлению компьютер-
ных методов обработки сигналов. При этом как сигнал, так и его
спектр необходимо перед вводом в вычислительное устройство
представлять в виде отсчетов, т.е. в виде чисел.
В формулах (9.3) и (9.4) один из компонентов уже является
дискретным. Остается только заменить в этих формулах остав-
шуюся непрерывную переменную /"дискретными значениями.
Так, например, из формул (3.26) и (3.14) после замены вре-
мени t на пТ, можно получить формулы
г , г , -/2яи?п2-
U[m] = £ и[п]е N;
п=0
и[п] = £ U[m]eJ N.
™ m=0
(9.5)
(9.6)
379
Рис. 9.15. Спектр дискретного
периодического сигнала
(9.7)
Следует заметить, что при этом периодический сигнал u(t)
стал дискретным сигналом ы(пТ) или и[п], а значит, дискрет-
ный спектр U[m] начал периодически повторяться (рис. 9.15).
Суммирование дискретных составляющих спектра U[яг] в фор-
муле (3.14) следует теперь вести не в бесконечных пределах, а на
периоде, где укладывается N отсчетов. Значит, индекс суммиро-
вания т в формуле (9.6) будет изменяться отяг = 0дояг = Л/-1.
На периоде повторения Тс дискретного сигнала и[п] также
укладывается М отсчетов, включая нулевой отсчет. Интеграл в
(3.26) заменяется суммой с индексом суммирования п, изменяю-
щимся от п = 0 до п = N - 1. Переменная dt в этой формуле при
переходе от интеграла к сумме заменяется на Т, так что отношение
T/Tc=l/N, так как Тс = NT. Частота дискретизации fa=NF.
Отсюда вытекают соотношения
rr. 1 fl
Т = —— и F = ——
NF NT
Произведение FT можно заменить величиной 1/N.
Выражения (9.5) и (9.6) называются прямым и обратным
дискретным преобразованием Фурье.
Формулы дискретного преобразования Фурье (ДПФ) удобны
для расчетов на компьютере.
Пример 9.7. Рассчитаем ДПФ дискретного периодического сиг-
нала, заданного тремя отсчетами: и[п] = {0; 1; 2}.
Для расчета воспользуемся формулой ДПФ (9.5):
_ , . , -/2я00-1 г , ->2я10-1 г , -у2л-2-О~
(7[0] = и[0]е 3+ы[1]е 3+и[2]е 3 =
= 0 + 1 + 2 = 3;
1 1 1
-/2л 01— ->2л11-4 -/2л-21-4
C7[l] = w[0]e 3+ы[11е 3+w[2]e 3 =
= 0 + 16-/120»+2е-/240».
С7 [ 2] = 0е-/°° +1е-/240° + 2е-/480°.
Поскольку
380
Рис. 9.16. Дискретный периодический сигнал (а)
и его спектр (б) к примеру 9.7
-/120° _ _ 1 _ ;2/З -;240° _ _ 1. >/3
~е 2 7 2 ’ 6 ~ 2+;Т’
[J[l] = 1(-3 + ;\/3) = 1,74е'150’,
U [ 2 ] = j (-3 - />/3) = 1,74е'210’.
Графики заданного дискретного периодического
сигнала и[п] и рассчитанного дискретного периодиче-
ского спектра амплитуд U[т] приведены на рис. 9.16.
Пример 9.8. Рассчитаем значения дискретного сигнала и[п],
ДПФ которого имеет вид U[m] = {0; 1; 0; 1}.
Значения дискретного сигнала и[п] будем рас-
считывать по формуле (9.6):
.6л '
.71
м[0] = 1[1/[0]е>°° + C/[l]e>0°+t/[2]e>0°+(7[3]e>0O] =
4
= -(0 + 1 + 0 + 1) = 0,5;
4
г/[1] = -1С7[0]^0О+(/[1]Л+(7[2]е-'я+{У[3]еУТ =
4
= 4(0 + ;1 + 0-/1) = 0;
4
гЯ2]Л[сЛО]е'о°+<7[1к>’ +Ul2]e'2* +17[31е'3п] =
4
=—(0-1+0-1) = -0,5;
4
ы[3]=Я(/ [01е>0° +U [1]е^ +и[2]е'3п+1ЛЗ]е^ ]=
4
= |(0-/+0+/) = 0.
.9тс
381
«[л]
0,5
-0,5
Рис. 9.17. Дискретный периодический
сигнал к примеру 9.8
График последовательности и[п] = {0,5; 0; —0,5;
0} приведен на рис. 9.17. Сигнал и[п] — дискретный
и периодический.
Из данного параграфа мы узнали, что:
• Спектр дискретного сигнала является непрерывным и пе-
риодически повторяется. Период его повторения обратно
пропорционален интервалу дискретизации.
• Формулы для расчета спектра дискретного сигнала полу-
чаются из формул для спектра аналогового сигнала путем
замены непрерывного времени на дискретное, а интеграла —
на сумму.
• При редкой дискретизации сигнала происходит явление,
известное под названием «наложение спектров».
• Аналоговый сигнал с ограниченным спектром можно одно-
значно восстановить по его дискретным отсчетам, взятым с
частотой, не меньшей, чем удвоенное значение максималь-
ной частоты спектра.
• Дискретный периодический сигнал имеет периодически по-
вторяющийся дискретный спектр.
• Для расчета спектра дискретного периодического сигнала
используют прямое дискретное преобразование Фурье.
• Дискретный периодический сигнал можно восстановить по
его дискретному периодическому спектру, воспользовав-
шись обратным дискретным преобразованием Фурье.
9.3. ^преобразование дискретного сигнала
Подобно преобразованию по Лапласу аналогового сигнала
существует z-преобразование дискретного сигнала. Дискретный
сигнал и его спектр описываются формулами (9.4) и (9.3). Про-
изведем в формуле (9.3) замену:
382
e]2nfT _ z
Тогда формула примет вид
L/(z)= X ulnVz'”.
п=-<х>
(9.8)
Выражение (9.8) получило название z-преобразования или z-
изображения дискретного сигнала иМ. Если начать суммиро-
вание с п = 0, то выражение
U(z)= £ и[п]г ”
п-0
(9.9)
есть одностороннее z-преобразование. Оно применяется для сиг-
налов uln} =0 при п < 0.
Можно указать на связь z-преобразования с преобразованией
Лапласа дискретного сигнала
U(p)= f и[п]е~рпТ,
п-0
которое легко получить из (9.3), положив j2nf = р.
Очевидно, что z = ерТ или р = — Inz.
Эти формулы устанавливают связь между точками в плоско-
стях р = а + ja> и г = х + jy (рис. 9.18).
Если положить а = 0, то мы будем перемещаться по оси /со в
плоскости р. При переходе в z-плоскость точки мнимой оси /со
будут располагаться на единичной окружности z = е;<эГ. Причем
точка /0 на /?-плоскости переходит в точку z = +1 на веществен-
ной оси z-плоскости, а точки ±/0,5сод — в точку z = -1. Это оз-
начает, что точки отрезка [-/0,5<од; /0,5сод ] ^-плоскости проекти-
руются в точки на единичной окружности z-плоскости. Так как
Рис. 9.18. Связь между точками в р- и z-плоскостях
383
функция e±jnT периодическая, то последующие отрезки осн /щ
на /?-плоскости такой же длины будут вновь проектироваться на
единичную окружность.
Точкам левой /2-полуплоскости соответствуют точки внутри
единичной окружности z-плоскости, а точкам правой p-полуплос-
кости — точки вне этой окружности.
Пример 9.9. Рассчитаем z-преобразование дискретного сигнала
и[п], имеющего вид
[°
и[п] = И
О
при п < 0;
при п = 1, 2, 3;
при п > 3.
Воспользовавшись формулой (9.9), получаем
т г/ ч -1 -2 -3 Z2+Z + l
t7(z) = z,+z‘J + zi>=-5— •
zJ
Пример 9.10. Найдем z-преобразование l/(z) дискретного экспо-
ненциального сигнала и[п} = е~апТ.
Подставив значение и[п] в формулу (9.9), полу-
чим
U(z)=fu[n]z~n = ^е-°-пТ -z~n = f (e"“rz-1)”.
n=0 n-0 n=0
Из теории рядов следует, что при выполнении
условия |e-arz-1|<l сумма ряда U(z) равна
1/(1 -e-arz-1) или
(7(z) = z/(z-e-ar).
Z-преобразование (7(z) дискретного сигнала
и[п] определено только для области z, в которой
jy
Рис. 9.19. Область сходимости к примерам 9.10 и 9. И
384
степенной ряд (9.9) сходится. Эта область сходимо
сти включает в себя все значения z, находящиеся
вне некоторого круга на комплексной z плоскости,
радиус которого г0 называется радиусом сходимо
сти (рис. 9.19), т.е. при г0 < Ы < <» ряд сходится. В
области сходимости существует взаимно-однознач-
ное соответствие между U(z) и и[п], т.е. каждому
и[п] соответствует одно, и только одно U(z), опре-
деленное для \z\ > г0, и наоборот.
Пример 9.11. Определим радиус сходимости для z-преобразова-
ния сигнала, заданного в примере 9.10.
Как уже было установлено, z-преобразование сиг-
нала и[п] = е~апТ имеет вид
(7(z) = z/(z-e"aT).
Нуль функции U(z) будет в точке г0 =0, по-
люс — в точке гп = е-аГ. Следовательно, радиус
сходимости г0 = е~аТ, а функция (7(z) сходится при
|z| > е~аТ.
Окружность, имеющая радиус сходимости
г0 = е~аТ, приведена на рис. 9.19. Область сходимости
находится за пределами этой окружности.
Пример 9.12. Найдем z-преобразование сигнала и[п] = Аап,
п > 0. Этот дискретный сигнал показан на рис. 9.20
для трех различных значений а: а = 0,8; а = 1; а =
= -0,8.
В соответствии с (9.9) z-преобразование такого
дискретного сигнала
(7(z) = А£ЛГ". (9.10)
n-Q
Из математики известно, что этот ряд сходится к
функции
U(z) = ——г = А —, (9.11)
1-az’1 z — a
если |az-1| < 1 или Izl > а.
Функция (7(z) имеет нуль при z = 0, а ее полюс
z„ = а лежит на окружности радиусом Ro = а, огра-
ничивающей область сходимости.
На рис. 9.20 показано расположение нуля и по-
люса функции U(z) в z-плоскости при различных а.
25 - 6972
385
и[л] — Аап
а = -0,8
_ 1
0
-0,8Л --
I ;t; t; г.-
4 j 6 1 S 1 10 п
-Д-0,8
£ z-плос-
Х\ кость
/1
/ zO = o
. *„—0,8
Рис. 9.20. Дискретные сигналы и расположение нуля
и полюса их z-преобразования к примеру 9.12
Для нахождения дискретного сигнала по его z-изображению
можно воспользоваться обратным ^-преобразованием (подобно
тому, как мы пользуемся обратным преобразованием Лапласа):
и[п] = -^—:$U(z)zn~'dz,
2nj
где интегрирование ведется по замкнутому контуру в z-плоскости.
Другой способ заключается в том, чтобы разложить функцию
U(г) в степенной ряд по степеням z-1. Тогда коэффициенты
при степенях z-t будут, в соответствии с формулой (9.9), отсче-
тами дискретного сигнала и[п].
Пример 9.13. Найдем дискретный сигнал и[п], которому соот-
ветствует z-преобразование U(z) = 1/(1 - 0,5z-1).
Воспользуемся разложением функции (l-ty)'1 в
ряд \ + q + q2 + q3 + ....
386
Для заданного z-преобразования q = 0,5z 1, по
этому запишем г-преобразование в виде
C7(z) = 1 + 0,5z-1 + 0,25z"2 + 0,125z’3 + ....
Сравнивая полученное выражение с общей фор-
00
мул ой z-преобразования (7(z) = £x[n]z-”, записы-
п=0
ваем последовательность
и[п]= {1; 0,5; 0,25; 0,125;
Общий член этой последовательности и[п] = 0,5",
п > 0.
Пример 9.14. Найдем отсчеты дискретного сигнала по его z-
преобразованию:
30z2
гт/ \ 5
U (z) = —5------=----<-----<---.
6z2-z-l <1 -1_1 -2
6 6
Для разложения функции U(г) в степенной ряд
по степеням z-1 выполним деление числа 5 на много-
член [l-(l/6)z-1 — (l/6)z~2]. В результате получим
частное 5 + (5/6)z-1 + (35/36)z-2 +.... Отсчеты дис-
кретного сигнала
х[0] = 5; х[1] = -|; х[2] = и т.д.
6 36
Процедура деления здесь не приведена из-за ее
громоздкости, хотя выражения полиномов, стоящих в
числителе и знаменателе Utz'), не слишком сложные.
Более эффективным способом нахождения и\п!
по известному £7(z) является способ, подобный ме-
тоду разложения на простейшие дроби в преобразо-
ваниях Лапласа.
Пример 9.15. Найдем общий член и„ дискретного сигнала и[п],
которому соответствует z-изображение, заданное в
примере 9.14:
U(z) =
30z2
6z2 - z - 1
5
. 1-1 1-2
6 6
Функция Utz) имеет полюсы в точках z^ = и
z2 = -1/3 или, что то же, в точках zf1 = 2 и z2j = -3.
25*
387
Разложим Lr(z) на сумму простых дробей:
(/U) 5 —
[ 1 111 +^z 1 1
I 2 А 3 J
3 2
2 3
Коэффициенты в числителях каждой дроби вычис-
ляются по формулам разложения:
(9.12)
5 fl-iz'1!
I 2 J
l-iz-Hfl + l^1
2 Д 3
5 fl+^z-1)
I 3 J
l-^z’^fl + ^z-1
2 Д 3
z-,=2
= 3;
= 2.
г’’=-3
Подобно тому, как формула (9.11) представляет
сумму ряда (9.10), простые дроби в (9.12) являются
суммами рядов
3 £ (1/2)" z~" и
72=0
2£ (-1/3)” z“".
n=0
Поскольку z-преобразование — это линейная опе-
рация, то последовательность и[п] состоит из суммы
двух последовательностей:
(IV г 1
м[п] = 3 — +2 —х > п>0.
После выполнения операции возведения в сте-
пень п получим отсчеты дискретного сигнала
u[0] = 5; w[l] = 5/6; и[2] = 35/36 и т.д.
Так же как и для преобразований Лапласа и Фурье, суще-
ствуют теоремы для z-преобразования. Приведем наиболее ваЖ'
ные теоремы одностороннего z-преобразования.
388
и[п + 1]
Рис. 9.21. Дискретный сигнал (а) и его сдвиг влево (6)
на один интервал дискретизации
-1 О
Теорема линейности {суперпозиции). Сумме дискретных
сигналов соответствует сумма их z-изображений. Если дискрет-
ным сигналам щ[п] и и21п] соответствуют г-изображения U\ (z)
и U2{z), то
ащ[п] + Ьи2[п] = aUi(z) + bU2(z),
где а тлЬ — некоторые числа.
Доказательство теоремы выполните самостоятельно, ис-
пользуя выражение (9.9) для расчета z-изображения дискрет-
ного сигнала.
Теорема опережающего сдвига. Если дискретному сигналу
и[п] соответствует одностороннее z-преобразование U(z), то
сигналу и[п + 1], сдвинутому влево на один интервал дискре-
тизации, соответствует z-преобразование z{U(z)-а[0]).
Математическая запись теоремы имеет вид
и[п + 1] = z(t/(z)-u[01).
Чтобы доказать теорему, воспользуемся основным выражени-
ем (9.9) для расчета z-преобразования дискретных сигналов и[п]
и ufn +1], а также графиками, приведенными на рис. 9.21:
U(z) = X ufn]z~n = u[0] +u[llz-1 + u[2]z~2 + ...;
n-0
U’(z) = luln +l]z~n = u[l] + u[2]z~1 + u[3]z~2 + ....
72=0
Сравнивая U(z) и t7'(z), получаем U'{z) = z{U(z)-u[01),
что и требовалось доказать.
Очевидно, что теорема опережающего сдвига выполняет ту
же самую роль, что и теорема дифференцирования для преобра-
зований Лапласа.
Теорема задержки. Математическая запись теоремы имеет вид
ufn - N]l[n - NJ = z~N U(z), Af>0.
389
Ф1
U(z)=—^—
1-z 1
1[л-N]
^(7) = -^.
1-z'1
-2 -1 О
1 2 3 4 5 и
-2 -1 О
« й •-----------
1 N-l N N+1 п
Рис. 9.22. Дискретный единич-
ный скачок
Рис. 9.23. Дискретный единичный
скачок, задержанный на ЛГ интер-
валов дискретизации
1
1
В теореме задержки 1[п] — это дискретные отсчеты функции
единичного скачка (рис. 9.22):
![«] = ('
(О при п < О,
а 1[п-ЛЧ — это дискретные отсчеты функции 1[п], задержан-
ной на Af интервалов дискретизации (рис. 9.23):
(1 при п > N.
Доказательство вытекает из основного выражения (9.9) для
z-преобразования:
= u[0]z'N +u[1]z^+1UM[2F(n+2) + ...=
= z~N (u[0] + w[l]z-1 + u[2]z“2 +...) =
= z~N-U(z).
При доказательстве учтено, что единичная ступенчатая
функция обращается в нуль при отрицательных значениях ее ар-
гумента, т.е. при п < N.
Теорема умножения на ап. Математическая запись теоремы
имеет вид
апи[п] = u(a 1z).
Теорема умножения на п
г , . dU(z)
n-ulnl = -z-----------------------.
az
Теоремы умножения дискретного сигнала
можно также доказать, используя формулу
проделать это самостоятельно.
Теорема свертки. Свертке дискретных
/г[п] соответствует произведение их ^-преобразований:
и[п\ на ап и на п
(9.9). Предлагаем
сигналов и[п] и
390
и[п] * h[n] = £ u[m]h[n-m] = U(z)H(z).
m-Q
Эту теорему мы приводим здесь без доказательства. При не-
обходимости с ним можно познакомиться в специальной литера-
туре по дискретным и цифровым сигналам и цепям.
Пример 9.16. Найдем z-преобразование дискретного 3-импульса,
задержанного на ЛГ интервалов дискретизации.
Найдем вначале 2-преобразование дискретного 8-
импульса 8[п] (рис. 9.3), используя выражение (9.9):
= £8[п]г-я =1.
п=0
Используя теорему задержки, найдем z-изобра-
жение сигнала 8[п-АГ]:
U(z) = z~N -U^tz) = z~N.
На рис. 9.3, в приведен также график задержан-
ного 8-импульса для частного случая N = 2.
Пример 9.17. Найдем z-преобразование функции:
и[п] = an~Mi[n - N].
В примере 9.4 мы уже находили, что z-преоб-
разование сигнала ап имеет вид (9.11) (7(z) =
= 1/(1 -<2Z-t).
Используя теорему задержки, получаем
a”-wl[n-Ar] = —-----г.
1-az’1
При а - 1 имеем
1[п-АГ]= z-Af/(l-z-1).
Графики дискретных сигналов 1[п-.У] и
a"-Afl[n - АЛ] приведены на рис. 9.23 и 9.24.
а»-*1(л-ЛГ]
1
1- az 1
-2 -1 О
1 КЛГ-1 N N+1 п
Рис. 9.24. Дискретный сигнал к примеру 9.17
391
Пример
9.18. Найдем z-преобразование дискретной последова-
тельности и[п] = пап, w > 0.
Поскольку z-изображение последовательности ап
известно из (9.11), то, используя теорему умножения
на п, получаем
[/(z) = _zAf
az у
1
1 - az~l
(i-az 1 )2
Пример 9.19. Найдем z-преобразование дискретной последова-
тельности из N отсчетов единичной амплитуды
(рис. 9.25):
«[»] = (! ч>во«"<лг;
(0 при п > N.
Сигнал и[п] можно представить как разность
двух сигналов:
и[п] = 1[и]-1[п -АГ].
Из теорем линейности и задержки легко полу-
чить z-преобразование
l-z'N
17(2) = ?—^,
1-z"1
что совпадает с формулой для частичной суммы гео-
метрической прогрессии
oo N-1
U(z) = £u[n]z-n= Yz~n.
n-Q n=Q
Пример 9.20. Вычислим z-преобразование свертки дискретных
сигналов ut[n]= {1; 1; 1; 0; 0; 0; ...} и U2tn]= {0; 0;
1; 1; 0; 0; ...}.
Найдем z-преобразование сигнала щЬг], исполь-
зуя формулу (9.9):
Ui (z) = £ щ [n]z~n = 1 + z-1 + z"2.
n=0
Ил]
Г
-2 -1 0
1 2 й ЛГ-1 л
Рис. 9.25. Дискретный сигнал к примеру 9.19
392
Найдем z-преобразование сигнала u2[nl:
C/2(z) = S w2[n]2’_" = z-2 + z-3.
и=0
Вычислим z-преобразование свертки сигналов
щ [ п ] и и2 [ п ], используя теорему свертки
щ [п]*ы2[«] = C7i(z) (72(z) =
= (1 + z-1 + z-2)(z-2 + z-3) = z-2 + 2z-3 +2Z-4 + z-5.
В табл. 9.1 дана сводка z-преобразований наиболее часто
встречающихся дискретных последовательностей. Эти табличные
сведения также могут быть использованы для расчета z-преобра-
зований сигналов и перехода от z-преобразований к дискретным
сигналам.
Таблица 9.1. Краткая таблица односторонних z-преобразований
Дискретный сигнал и[п], п > 0 z-преобразование U(z) = u[n]z~n п=0
И[П1 = 8М = (1 (0 при п ф 0 U(z) = l
ам»1[п-м = [* "Р" *»"»(), (0 при n<N C7(z) = z-Af/(i-z-1)
и(п]= ап U (z) = 1/(1-az-1)
и[п] = А U(z) = —Ц- 1 — z-1
и[п] = п U (z) = 1ч2 (1-z-1)2
и[п] - пап rrr \ U(z) = - 7-5- (1-az-1)2
и[п] = ап cosrcO rr/ ч 1-acosOz-1 U{Z) = : 5—у 1 -2acos0z +a z
и[п] = ап sinn0 тт/ 4 asin0z-1 U (z) = 5 5—7 1 - 2a cos Qz + az
u[n] = (eJn2n/T при«>0, (0 при п < 0 t/(z) = r 1 _ ei^fr . z-\
393
Пример 9.21. Найдем общий член дискретного сигнала и[п], ко-
торому соответствует z-изображение
11 —
U(z) = -^--------.
б б
Разложение функции (7(z) на простые дроби
приводит к выражению
тт( ч с 3 2
U ( 2 ) = 6 Н-z- Н-з-.
1 >! 1
2 3
Используя теорему линейности и находя в табл. 9.1
дискретные сигналы, соответствующие каждому из
слагаемых в выражении U(z), получаем
(1 V ( 1 \я
и[и] = 68[п] + 3 — +2 =
И при п = 0;
= < т" ( п"
3 - + 2 при и > 0.
[ V2J k 3J
По этой формуле легко подсчитать значение и[п]
для любого п. Аналогичным образом разложение
У Т / \ 1 Т * >2 —.1 Л
U(.2) =-------— = -z -2 +
1-z’1
приводит к последовательности
3
1 -z-1
1
и[п] = -8[п-1]-28[п] + 3 = < 2
3
при п - 0;
при п = 1;
при п > 1.
Из данного параграфа мы узнали, что:
Z-изображение дискретного сигнала играет такую же роль, '
как и изображение по Лапласу для аналогового сигнала. |
По z-изображению дискретного сигнала можно найти сам |
сигнал, разложив, например, z-изображение в степенной ряд. |
Свойства z-преобразований определяются теоремами ли- |
нейности (суперпозиции), опережающего сдвига, задержки, 1
умножения на а” и п, свертки, подобными теоремам для i
преобразований Лапласа. ч
394
9.4. Нерекурсивная дискретная цепь
и ее реакция на дискретное воздействие
Дискретная цепь — это устройство, которое преобразует
одну дискретную последовательность в другую. Сигнал на вы-
ходе аналоговой цепи находят из интеграла свертки (наложения)
по входному сигналу и импульсной характеристике. Формула ин-
теграла свертки описывается выражением (9.1). Это выражение
можно назвать математической моделью аналоговой цепи.
При переходе к дискретным сигналам используют выражение
дискретной свертки (9.2). Обозначим в этом выражении
мвых[и] = ивых(пТ), ивх[т] = ивх(тТ) и
h[n - т] = h[(n - т) Т].
Тогда оно запишется в виде
п п
Ывых[га1= £ uBX[m\-h[n-m]= h[m] uBX[n-m\ =
т=0 т=0
= Л[0]ивх[п] + /г[1]пвх[п-1] +
+ h[21- ивх[п - 2] + ... + h[n] • ивх [0].
(9.13)
Пример 9.22. Рассчитаем значения выходной последовательности
wBbIX[n] цепи, имеющей дискретную импульсную ха-
рактеристику Л[п] = {-1; 1; 2}, если входная последо-
вательность имеет вид ивх[п] = {-2; 1; 2: -1}. Графики
ивх[п] и h[n] приведены на рис. 9.26.
Пользуясь формулой (9.13), рассчитаем значе-
ния выходной последовательности пвых[га]:
«вхИ
Л [я]
Рис. 9.26. Графики входного дискретного
сигнала (д) и дискретной импульсной
характеристики (б) цепи к примеру 9.22
395
Рис. 9.27. Дискретный сигнал на выходе цепи
к примеру 9.22
^вых [0] = А [ 0 ] • авх [0] = (-1) • (-2) = 2;
мвых[1] = h [0] • uBX [1] + Ml] • wBX [0]
= (-1)1 + 1(-2) = -3;
ивых[4] = M0]uBX[4] + Ml]zzBX[3] + M2]uBX[2] +
+М3] • ывх [1] + М4] • wBX [0] = (-1)0 +
+1 (-1) +2-2+ 0 1 + 0-(-2) = 3.
Аналогичным образом рассчитываем пвых[5] =
= — 2; ивых[6] = 0. Все остальные отсчеты иЯЫУ[п]
равны нулю.
График дискретного сигнала мвых[п] приведен
на рис. 9.27.
Вычисления по формуле (9.13) можно выполнить также с
помощью простого устройства. Запишем последовательности чи-
сел пвх[п] и Л [-и] на отдельных полосках бумаги, как показа-
но на рис. 9.28. На обеих полосках пометим маленькими стре-
лочками точки п = 0. Обратим внимание на то, что /г[-п] явля-
ется обратной последовательностью относительно h[n], так что
она строится в обратном направлении от п = 0. Будем сдвигать
нижнюю полоску относительно верхней в направлении стрелки.
Вычисление суммы произведений стоящих друг против друга чи-
сел при каждом сдвиге дает последовательность wBbIX[n].
Выбирая те или иные значения А [и], получаем дискретные
модели различных цепей. Таким образом, формула дискретной
свертки является универсальной, пригодной для описания любых
цепей.
396
л = 0
♦_______________
им[л]{О О 0-2 1 2-1 О О О)
Л [-л] ( 0 0 0 2 1 -1 О 0 }-*-
— 4^1
п = 0
Произведение ООО 4_Н> ООО
Сумма произведений = 3 = иВых[4]
л = 0
________t_______________
Мл] (о 0 0-2 1 2-1 0 0 о)
Л[-л] ( 0 0 0 2. 1 -1 0 0 }-*-
Uo
Произведение 0 0 0 2 0 0
Сумма произведений = 2 = «МО]
Рис. 9.28. Вычисления по формуле дискретной свертки
Пример 9.23. На вход цепи поступает сигнал в виде дискретного
5-импульса. Рассчитаем выходные последовательно-
сти мвых[п] цепей, имеющих дискретные импульс-
ные характеристики
a) hln] = {1; 1; 0; 0; ...};
б) hln] = {1; -1; 0; 0; ...};
в) hln] = 2е~п!2.
Графики дискретного 8-импульса 5[п] и им-
пульсных характеристик а), б), в) приведены на рис.
9.29 и рис. 9.30 соответственно.
Рассчитываем значения ивых[п], используя фор-
п
мулу (9.13): ЦВьпДя1= S h[m]uBX In - т], в которой
т=0
ивх1п] = 5[n] = {1; 0; 0; 0; ...}.
Для цепи, имеющей дискретную импульсную ха-
рактеристику
a) hln] = {1; 1; 0; 0; ...}, получаем
«вых [0J = Л[0]-8[0] = 1 -1 = 1;
мвых(1] = Л[0]-5[1] + Л[1]-5[0] = 10 + 11 = 1;
ивых[2] =/г[0]-5[2] + Л[1]-5[1] + Л[2]-8[0] =
= 10 + 10 + 01 = 0;
397
5 И
1
0 12 3л
Рис. 9.29. Дискретный S-импульс к примеру 9.23
«выХ[3] = /г[0]-5[3] + /г[1]-5[2] + Л[2]-5[1] +
-ьЛ[3] - 8(0] = 0.
Все остальные значения нвых [п] будут также ну-
левыми.
Для цепи с импульсной характеристикой
б) Л[п]= {1; —1; 0; 0; ...} получаем
мвых 10] =/г[0]-8[0] = 1-1 = 1;
мвьгх[1] = Л[0] 8[1] + ЛЕИ-8[0] =
= 10 + (-1)-1 =-1;
нвых 12] = /г[0]-8[2] + ЛЕ1]-8[1] + ЛЕ2] 8[0] =
= 0.
Остальные значения ывых[п] равны нулю.
Для цепи с импульсной характеристикой
в) h[n} = 2e~n2= {2; 1,22; 0, 74; 0,45; 0,27; ...}
получаем
«выхЮ] = Л[0]-8[0] = 2;
«вЫХ[И = М0]-5[1] + Л[1]-8[0] = 1,22;
«выХ [2] = ЛЕО]-8[2] + М11 - 8 [1 ] 4-Л [2] - 8 [0] =
= 0,74.
Все остальные отсчеты выходной последователь-
ности мвых [ п ] повторяют соответствующие отсчеты
дискретной импульсной характеристики Л[п], так же
А [л]
А [л]
А [л]
2
0 123л 0 1234л 0 1234л
Рис. 9.30. Дискретные импульсные характеристики
к примеру 9.23
как и в двух предыдущих случаях а) и б). Этот вы-
вод очевиден, так как импульсная характеристика —
это реакция цепи на 5-импульс.
Графики мвых[п] будут такими же, как графики
/г[п] на рис. 9.30.
Анализ формулы (9.13) показывает, что в ней выполняется
всего три действия: умножение, сложение и задержка. На
рис. 9.31 эти действия представлены в виде элементов структур-
ной схемы. Операцию умножения дискретного сигнала uBX(n] на
число К можно представить в виде усилителя с коэффициентом
усиления К. На его выходе получаем сигнал ивых [п] = К • izBX [п].
Сложение чисел естественно отобразить на схеме в виде суммато-
Лвх[л] |>>^Ивых[л] ~ ^Ивх[л]
ИвхИ «вых[и] = «вх(я] + а ит[п -1]
а)
«вх[л]
дивх[«-1]
ИвыхИ — Ивх[л~1]
б)
Т
«)
Рис. 9.31. Умножитель (а), сумматор (б)
и элемент задержки (в) дискретной цепи
“вхИ
Ивых[л] — ИВХ[Л 1]
Ивх[л]
1
Ивых[л] — Ивх[л 1]
-2 -10
1 2 3 4 5 п
Ивх[я]
ИвхИ
1
«вых[я] — «вх[я 3] ‘
1 -
ЗТ
Явых[я]— иВх[Л 3]
-2 -10
п -2-ю
1 2 3 4 5 6 л
2 3 4 5 6 я
1 2 3 4 5
Рис. 9.32. Задержка дискретного сигнала при прохождении
через элементы задержки
399
ра. Получение отсчета uBX[n-i] = ивх[пТ-Т] из ивх[п] = ивх(пТ)
можно связать с задержкой последнего на время Т, т.е. на один
«такт».
Действие элемента задержки поясняется на рис. 9.32.
Алгоритм вычислений дискретного сигнала raBMX[”]> описы-
ваемый выражением (9.13), можно представить в виде структур-
ной схемы. Подобные структурные схемы называют нерекур-
сивными дискретными цепями.
Пример 9.24. Составим структурную схему цепи, дискретная им-
пульсная характеристика которой дана в задаче 9.22,
т.е. h[n]= {-1; 1; 2} (рис. 9.26).
В соответствии с алгоритмом (9.13) и с учетом
заданных значений характеристики h[n] структур-
ная схема цепи приведена на рис. 9.33. По этой схе-
ме несложно определить выражение для выходной
последовательности ивых [ п ] = -ивх [ п ] + ивх [ п -1 ] +
+2ивх[п - 2].
ивх[л]
Рис. 9.33. Дискретная цепь к примеру 9.24
Вывод: в отличие от аналоговых цепей, которые представля-
ют собой соединение элементов, например R, L и С, дискретная
цепь — это структурная схема алгоритма вычислений выходной
последовательности по входной. Она состоит из элементов за-
держки, сумматоров и усилителей (умножителей).
Передаточная функция дискретной цепи — это отношение z-
изображений дискретных сигналов на ее входе и выходе. Рас-
смотрим один из элементов дискретной цепи — элемент задержки
(рис. 9.32). Сигнал на его входе ивх [га], а на выходе ивых[га] =
= ивх[га-1]. Напомним, что z-изображения дискретных сигналов
ивых[га] и ивх[га] имеют вид
*ЛыХ<г)= Е «выхЬ] 2’"; (7BX(z)= % uBX[n]-z~”.
п=0 w=0
400
t4x(z) П С4ых(2) = Um(z) H(z) = C4x(z) • z-1
----». z-i---------------
H(z) = z'1
Рис. 9.34. Передаточная функция элемента задержки
Тогда, воспользовавшись теоремой задержки, можно записать z-
преобразование для равенства ивых[п] = ивх [п - 1]:
UBbtx(z) = UBX(z)-z~l.
Отношение z-изображений выходного и входного дискрет-
ных сигналов называют передаточной (или системной) функ-
цией дискретной цепи
H(z):
Тогда
UB№X{z) = UBX{z)H{z).
В таком случае передаточная функция элемента задержки
(рис. 9.34)
H(z) = z-1.
Обратимся теперь к выражению (9.13). На основании теоре-
мы свертки z-преобразование дискретной свертки равно произве-
дению z-преобразований дискретных сигналов:
^вых [т/} = У. й[т]' ивх [п — т] ?= Uвых (z) — Н[z') ‘UBX(.z).
Из последнего выражения видно, что z-преобразование дискрет-
ной импульсной реакции h[n\ есть передаточная функция
H(z) дискретной цепи:
H(z) = fh(n)-z~n.
п=0
Пример 9.25. Найдем импульсную характеристику и передаточную
функцию нерекурсивной дискретной цепи (рис. 9.35),
выходная последовательность которой задана выра-
жением ивых [п] = 4ывх [п] -1,5ывх [п -1].
Отсчеты дискретной импульсной характеристики
k[n] — это отсчеты wBbIX[«], рассчитанные при ус-
ловии, что на вход цепи подается дискретный 5-
импульс, т.е. ивх[и] = 5[«]= {1; 0; 0; ...}:
26 - 6972
401
«вх[«1
«ВЫхМ = 4иВх[л]_1,5иВх[Л~1)
Рис. 9.35. Z-изображение дискретной цепи
к примеру 9.25
Л[0] = 48(0]-1,58[-1] = 4,1-1,5-0 = 4;
Л[1] = 48[1]-1,58[0] =-1,5;
kin] = 0 при п > 1.
Таким образом, отсчеты дискретной импульсной
характеристики h[nl = {4; -1,5} соответствуют коэф-
фициентам усиления усилителей в схеме (рис. 9.35).
Для нахождения передаточной функции Н(г)
возьмем z-преобразование дискретной импульсной
характеристики:
H(z)= fh[n]z-n = A[0]z° + /z[l]z-1 = 4-1,5г'1.
n=0
Другой способ нахождения передаточной функ-
ции H(z) заключается в том, чтобы определить г-
изображение выходной последовательности, а затем
найти H(z) как отношение 17вых(г) и L7BX(z):
(7BbIX(z) = 4t/BX(z)-l,5t7BX(z)z-1
ИЛИ
C/BMX(z) = l/BX(z)(4-l,5z-,) = ^Bx(2)^(z).
Очевидно, что H(z) = 4 - l,5z-1. Z-изображение
нерекурсивной дискретной цепи с такой передаточ-
ной функцией приведено на рис. 9.36.
Рис. 9.36. Дискретная цепь к примеру 9.25
Явых(г) = 4 £4x(z) -1,5 Um(z)z
-1
Я(г) = 4 -1,5г-1
402
<4x(z)
H(z) — -1 + z"1 + 2z‘2
Jt«z)z-l| 2Um(z)z'2
\UBla(z) = UBX(z)H(z) =
'---* = ~ Um(z) + UBX(z)z~l + 2 Um(z)z'2
Рис. 9.37. Z-изображение дискретной цепи
к примеру 9.26
Пример 9.26. Найдем отсчеты выходного сигнала г/вых[п] нере-
курсивной дискретной цепи, 2-изображение которой
приведено на рис. 9.37, а входной сигнал ивх1п] =
= {-2; 1; 2; -1}.
Найдем z-изображение входного сигнала ивх[п]:
UBX(z) = Y uBX[n]z~n = uBX[0] +wBX[l]z-1 +
+uBX [ 2] z 2 + ивх [3]z 3 =
= -2 + z"1 + 2z-2 - z"3.
Передаточная функция цепи (рис. 9.37) H(z) =
= -1 + z"1 + 2z-2. Она находится непосредственно по
схеме либо как z-изображение дискретной импульс-
ной характеристики h[n] = {-1; 1; 2}.
Найдем z-изображение выходного сигнала:
UBBlx{z) = UBX{z)H{z) =
= (-2 + z-1 +2z-2 —z-3)(—1 + z-1 +2z-2) =
= 2 - 3z-1 - 5z~2 + 5z'3 + 3z~4 - 2z-5.
Коэффициенты при z в отрицательных степенях в
этом выражении являются отсчетами выходного сиг-
нала ивых [«] (рис. 9.27):
«вых[я! = {2; -3; -5; 5; 3; -2}.
Пример 9.27. Найдем передаточную функцию нерекурсивной
дискретной цепи, входная и выходная последова-
тельности которой имеют вид
ивх{п] ={1; 0; 1; 2}; пвых[п] = {0; 1; 2; 1}.
26*
403
Z-изображения последовательностей
UBX (z) = У wBX [nJ - z~n = 1 + z~2 + 2z~3;
DA Jgggi DA •
n-0
UBbK(z)= EMBbixW- z~” = z-1+ 2z~2 + z~3.
n=0
Следовательно, передаточная функция
Я(г) = ^вых(^) _ г"1 + 2z~2 + z~3
UBX(z) i + z~2 + 2z~3
Разделив числитель передаточной функции на
знаменатель, можно представить H(z) в виде
H(z)= 2 akz~k = z”1 +2z-2 -4z‘4 -4z"5 +4z-6 + ....
л=о
Рассмотрим структуру дискретной цепи, подобную рис. 9.33,
но содержащую ЛГ элементов задержки. Она приведена на
рис. 9.38, а и 6. Здесь коэффициенты усиления «о- а1> а2..
аы представляют собой отсчеты дискретной импульсной реакции
h[n], т.е.
а0 = А[0], = All], ..., Ддг = А[Л7].
Из структуры рис. 9.38, а следует, что
а) б)
Рис. 9.38. Нерекурсивная дискретная цепь (а) и ее z-изображение (б)
404
Переход к z-изображениям (рис. 9.38, б) дает выражение
^вых ( ^ ) «о ' вх вх ( £ ) * £ + Д2 ’ Uвх ( ^ ) ' ^ +
+ ... + aN -UBX(z) • z~N = UBX(.z)(a0 +at z"1 +
+ a2-^~2+ ••• +a/v z~N) = UBX(z)- H(z).
Передаточная функция этой дискретной цепи есть
H(z) = а0 +<?! • z-1 + а2 • z~2 + ... + aN z~N =
= Е ak?
k=0
(9.15)
Дискретные цепи со структурой рис. 9.38, а и 6 и передаточ-
ной функцией вида (9.15) являются нерекурсивными.
Пример 9.28. Найдем выходную последовательность и переда-
точную функцию нерекурсивной цепи, структурная
схема которой приведена на рис. 9.39.
Выходная последовательность мвых[п] в соответ-
ствии с уравнением (9.14) имеет вид
мвых W= #омвх [я] + atnBX[« -1] + а2ивх [п - 2] =
= -0,8г/вх [п] + 2ивх [и -1]- ивх [п - 2].
Передаточную функцию цепи найдем, используя
уравнение (9.15) или непосредственно по схеме
H(z) = а0 +а^~х +a2z~2 =
=-0,8 + 2z-1-z-2.
Пример 9.29. Найдем отсчеты выходного сигнала нерекурсивной
дискретной цепи, имеющей дискретную импульсную
Рис. 9.39. Нерекурсивная дискретная цепь
к примеру 9.28
405
Рис. 9.40. Нерекурсивная дискретная цепь
к примеру 9.29
реакцию h[n] = {1; -0,6; -1,5; 1}, при воздействии
на нее дискретного сигнала нвх [п] = {1; 0; 1; 0}.
Отсчеты дискретной импульсной характеристи-
ки — это коэффициенты усиления а0 = 1; а.\ - -0,6;
«2 = -1,5; «з=1- Структурная схема нерекурсивной
дискретной цепи с заданной импульсной характери-
стикой приведена на рис. 9.40.
Выходной дискретный сигнал нвых[п] найдем,
используя выражение (9.15):
Ывых [и] = йоывх [и] + й1мвх [я - 1] + «2МВХ [» - 2] +
+ яЗмвх [я -3] = wBX [и]-0,6мвх[п -1] -
-1,5ывх [п - 2] + ивх [п - 3].
Отсчеты сигнала wBbIX[n] найдем, подставляя
значения ивх[п] в полученное разностное уравнение:
^вых 10 ] “ UBX [ 0 ] “ 1,
«вх(л]
ИвыхИ
Рис. 9.41. Входной (а) и выходной (б) сигналы
дискретной цепи к примеру 9.29
406
мвых 115 = uBX[l]-0,6wBX[0] = 0-0,61 = -0,6;
izBbIX[2] = wBX[2]-0,6wBX[l]-l,5uBX[0] =
= 1-0,60-1,51 = -0,5;
uBbIX[3] = wbx[3]-0,6wbx[2]-1,5ubx[1] + mbx[0] =
= 0-0,6-1-1,5 0 + 1 = 0,4.
Аналогичным образом рассчитываем wBbIX[4] =
= -1,5; ивых[5] = 1; wBbIX[6] = 0. Все остальные от-
счеты также равны нулю.
Таким образом, выходная последовательность
mbxIw1= {1; -0,6; -0,5; 0,4; -1,5; 1}. Графики wBX[n]
и мвых[и] приведены на рис. 9.41.
Из данного параграфа мы узнали, что:
• Структурная схема, реализующая алгоритм дискретной *
свертки, называется дискретной цепью. Она состоит из [
масштабных усилителей, сумматоров и элементов задержки. 4
• Дискретный сигнал на выходе любой цепи можно рассчи- ?
тать, используя уравнение дискретной свертки. Для расчета |
нужно знать отсчеты дискретного входного сигнала и дис- ’
кретной импульсной характеристики цепи. |
• Передаточная функция дискретной цепи — это отношение >
z-изображения сигнала на выходе цепи к z-изображению J
сигнала на входе. .1
• Передаточная функция и импульсная характеристика дис- <
кретной цепи связаны парой z-преобразований. J
9.5. Рекурсивная дискретная цепь и ее реакция
на дискретное воздействие
Сигнал на выходе рекурсивной цепи формируется из отсче-
тов как входного, так и выходного сигнала, поэтому такая цепь
кроме прямых связей содержит также обратные связи. Рассмот-
рим дискретную цепь, показанную на рис. 9.42, а и б.
Как следует из рис. 9.42, а, выходной сигнал
мвых [^ ] = UBX [п ] + biUBbIX [п — 1 ] + &2mbmx (и — 21+ (9 16)
________+.. > + Ьдг^вых ].
Формула (9.16) позволяет вычислить текущий отсчет ивых[п]
выходного сигнала не только по текущему отсчету ивх [ п ] вход-
ного сигнала, но и по предыдущим (задержанным) N отсчетам
407
i=l
0
Рис. 9.42. Рекурсивная дискретная цепь (а)
и ее г-изображение (б)
ивых I л -1 ], ^вых [ п - 2 ], ..., мвых [ п - N ] выходного сигнала. По-
добные формулы в отличие от (9.14), где используются текущий
и задержанные отсчеты только входного сигнала, в математике
получили название рекурсивных. Поэтому и цепь, реализующая
алгоритм (9.16), называется рекурсивной.
Z-преобразование выражения (9.16) имеет вид
ВЫХ ( Z ) = U ЪХ ( % ) + Ь\ t/BbIX ( Z ) • Z + &2 UВЫХ (z) • Z + Zg j -J у
+...+bN-Um(z)-z~N.
Эта же запись следует непосредственно из рис. 9.42, б.
Передаточную функцию рекурсивной цепи получаем из (9.17):
408
и< 2} =1 1
1 h 7’1 h Г'2 h N К
1-OfZ -о2-г -...-oNz \-^bk-z~k
k=t
(9.18)
Пример 9.30. Структурная схема рекурсивной дискретной цепи
приведена на рис. 9.43. Найдем передаточную функ-
цию, импульсную характеристику и реакцию цепи
на дискретное воздействие wBX [п] = {1; —1; 1}.
Передаточную функцию цепи Н(г) найдем, ис-
пользуя формулу (9.18):
H(z) =----J-------------------------------=- =
1-612 ~b2Z
k=i
1
1 - 2z-1 + 2z~2 ’
Для нахождения дискретной импульсной харак-
теристики h[n} рассчитаем реакцию цепи мвых[п] на
дискретный 5-импульс, т.е. на сигнал uBX[n] = 5[п] =
= {1; 0; 0; ...}. С учетом формулы (9.16) получаем,
что дискретная импульсная характеристика цепи
(рис. 9.43) имеет вид
h[n] = + + =
= 8 [ п J + 2wBbIX [ п “ 1 ] ~ 2zzBbjX 21.
Отсчеты Л[п] равны соответственно Л[0] = 1;
Л[1] = 2; h[2] = 2; Л[3] = 0 и т.д.
Для расчета реакции цепи мвых [п ] на сигнал wBX [п ]
также воспользуемся разностным уравнением (9.16):
^ВЫХ [^1 = ^вх 1^1 + ^1^ВЫХ “ 1] + ^2^ВЫХ — 2] —
= ивх[п] + 2мвых[п-1]-2мвых[п-2].
Рис. 9.43. Рекурсивная дискретная цепь к примеру 9.30
409
Найдем отсчеты мвых[я]:
^ВЫХ 10 ] — ^вх [О] = 1 ,
ггвых[1] = ивх [1] + 2мвых [0] = -1 + 21 = 1;
^вых 12 ] zzBX 12 ] + 2ziBBjx Ill 2uBbIX [ 0 ]
= 1 + 21-2-1 = 1;
^вых [ 3] = ивх [ 3 ] + 2аВЬ1Х [ 2 ] — 2ивых [ 1 ] =
= 0 + 2-1-21 = 0;
^вых 14 ] = —2 , ^Вых 15 ] = —4 , ^вых 16 ] = —4 и т.д.
Если выход дискретной цепи рис. 9.38, а подключить ко вхо-
ду цепи, изображенной на рис. 9.42, а, то полученная цепь будет
описываться уравнением
410
wBbIX[n] = «о uBX[n] + at ивх [п -1] + а2 • ивх[п - 2] +
+ ... + aN • мвх[?г-N]+Z>! • ивых [п -1 ] +
+ Ь2 •цВЬ1Х[?г-2] + ... + Ьлг -цвых [и - N].
(9.19)
Для получения передаточной функции Н(г) можно либо
выполнить z-преобразование выражения (9.19), либо перемно-
жить передаточные функции (9.15) и (9.18) каскадно включен-
ных структур:
-1 -2 -Ь!
H(z\ = а^+а\ 2 1 +д2 -z * +... + aN-z
1 - z~l -b2 -z~2 - ,..-bN z~N
n h
I akz-k
k=o_______
n i,'
1 - X iv”‘
k=0
(9.20)
Можно изменить порядок каскадного включения нерекурсив-
ной и рекурсивной цепей на обратный. Получится схема, пока-
занная на рис. 9.44, а. Передаточная функция этой новой струк-
туры, естественно, будет по-прежнему описываться выражением
(9.20), а временной алгоритм — формулой (9.19). Заметим, что
на выходах параллельных элементов задержки будут одни и те
же сигналы. Следовательно, реально необходимо иметь лишь
один из двух элементов задержки. Соответствующая эквива-
лентная дискретная цепь изображена на рис. 9.44, б; она назы-
вается канонической. Так как схема рис. 9.44, б содержит и ре-
курсивную часть, в литературе ее часто также называют рекур-
сивной дискретной цепью.
Пример 9.31. Определим передаточную функцию цепи, приве-
денной на рис. 9.45.
Рис. 9.45. Z-изображение рекурсивной
дискретной цепи к примеру 9.31
411
Для рекурсивной цепи с прямыми и обратными
связями (рис. 9.45) запишем коэффициенты усиле-
ния усилителей:
а0 = 1; «j = 1,5; а2 = -2; а3 = 0,5;
61=-1; b2 = 1; Ь3 = -1,5.
Определим передаточную функцию цепи (рис. 9.45),
подставляя значения коэффициентов усиления в вы-
ражение (9.20):
д (2) = Др + + о2г~2 + йзг~3 =
1 - bjZ'1 - b2z~2- b3z~3
1 + 1,5г’1 -2z~2 + 0,5z~3
1+ z-t-z~2+l,5z-3
Пример 9.32. Найдем реакцию дискретной цепи на воздействие
uBX [n] = {1; -Г, 1; -1}, если передаточная функция
tr/ ч l-z-1+z-2
цепи имеет вид H(z) =-------------------;т.
l-0,5z" + 0,5z-2
Составим структурную схему дискретной цепи с
заданной передаточной функцией (рис. 9.46). Ко-
эффициенты усиления известны: с0 = 1; а^ = -1;
а2 = 1; bi = 0,5; b2 = -0,5.
Найдем выходной сигнал мвых[п] цепи, исполь-
зуя уравнение (9.19) или непосредственно по схеме:
“вых Ед1 = д0ывх [и] + й1мвх Ед -11 + Д2«вх IД - 2] +
+b\uВых Ед 11 + ^2^вых Ед 2] двх Ед 1 Двх Ед 11 +
+ wBX [п - 2] + 0,5мвых [п -1 ] - 0,5мвых [п - 2].
Рассчитаем отсчеты ывыхЕдЬ
Двых Е 0 ] — ивх Е0] = 1,
^вых El 1= Двх Е1 ] — двх Ео ] + 0,5ивых Ео] =
=-1-1 + 0,5-1 = -1,5;
Рис. 9.46. Рекурсивная дискретная цепь к примеру 9.32
412
^вых 12] — WBX [2] WBX [ 1 ] + ывх [0] + 0,5zzBbIX [ 1 ]
-0,5мвых [0] = 1 +1 +1 + 0,5(-1,5) = 2,25.
Аналогичным образом рассчитываем мвых[3] =
= -1,125, «вых [4] = 1,3125 и т.д.
Рекурсивная дискретная цепь устойчива, когда полюсы ее
передаточной функции находятся на z-плоскости внутри окруж-
ности с радиусом, равным единице. Дискретная цепь считается
неустойчивой, если ограниченное по амплитуде входное воздейст-
вие вызывает на ее выходе бесконечно нарастающий отклик. На-
оборот, дискретная цепь устойчива, когда отклик на ограни-
ченное воздействие также ограничен.
Известно, что у устойчивой аналоговой цепи полюсы переда-
точной функции располагаются в левой полуплоскости комплекс-
ной переменной р. При переходе от аналоговой цепи к дискретной
и замене преобразования Лапласа ^-преобразованием точки левой
полуплоскости p-плоскости переходят в точки, лежащие внутри
единичной окружности z-плоскости (рис. 9.18). Таким образом,
полюсы передаточной функции устойчивой дискретной цепи
располагаются внутри единичной окружности z-плоскости.
Пример 9.33. Определим устойчивость цепей, имеющих переда-
точные функции:
б) Я2(г)=
l-2z~
Полюс передаточной функции
H1(z) = (l-z-1)/(l-0,3z’1)
найдем, приравняв знаменатель Я((г) к нулю:
1-0.3Z’1 =0.
Получаем полюс z^ = 0,3, который находится
внутри единичной окружности z-плоскости. Это оз-
начает, что цепь устойчива.
Передаточная функция
H2(z) = (l-z-i)/(l-2z~i)
413
имеет полюс в точке гр’ = 2; такая цепь неустойчива.
Полюсы передаточной функции
1-z’2
Н3 (z) =----------------у
1-1,82-’ +0,97г'2
являются комплексно-сопряженными гр’ =0,9 + /0,4
и гр’= 0,9 -/0,4. Поскольку эти полюсы лежат
внутри единичной окружности (их модули |гр’| =
= |гр’| < 1), то данная дискретная цепь устойчива.
Примером неустойчивой цепи служит цепь с пере-
даточной функцией
1-г'2
Я4 (г) =----------------=-,
1-2,4г'1 + 1,69г'2
у которой гр’= 1,2+ /0,5, гр’= 1,2-/0,5 и |гр’| =
= |гр’|>1.
Пример 9.34. Дискретная цепь имеет передаточную функцию
Я5(г) =
=__________(1-2г~’ + г'2)(1- 0,707г'1 + г'2)______.
(1 + 0,777г'1 + 0,3434г'2) (1 + 0,01877г'1 + 0,801г'2 )
Ее полюсы zjp = 0,586е±?131,6° и гр4 = О.вЭЗе1790’60
также лежат внутри области устойчивости. Заметим,
что на нули таких ограничений нет: они оказались в
Рис. 9.47. Расположение полюсов в плоскости z (а) дис-
кретной цепи (б) к примеру 9.35
414
точках г = 1 (двойной нуль) и е±;69’3°, т.е. лежат на
единичной окружности.
Пример 9.35. Дискретная цепь описывается передаточной функ-
цией
Н6 (z) =---------1 0,1317 ------------? (9.21)
1-1,785г'1 +1,202z’2 - 0,2853г-3
с полюсами Zj6)= 0,544 и = 0,731е1/0,544, Рас-
положение полюсов в плоскости z показано на
рис. 9.47, а. Здесь же приведена структурная схе-
ма цепи. Цепь устойчива.
Пример 9.36. Рассчитаем сигнал явых[п] на выходе дискретной
цепи, имеющей передаточную функцию =
= (1-z-,)/(l-0,3z-1) (см. пример 9.33, а), если на
вход подается сигнал ивх[я] = {3; 2; 1}.
Воспользуемся выражениями (9.19) и (9.20) для
нахождения выходного сигнала ивых[я] в рекурсив-
ной дискретной цепи с прямыми и обратными связями:
^ВЫХ t 1 = ^O^BX I + ^l^BX — 1 ^1^ВЫХ IД — 11 =
— Пвх [и 1 — Явх — 1 ]4* 0, ЗнВ|>|Х [fl — 1 ].
Рассчитаем значения выходного сигнала, под-
ставляя значения ивх[п] в выражение для цныу [я].
Получаем выходную последовательность мвык[я] =
= {3; -0,1; -1,03; -1,31; -0,39; -0,11; -0,03; -0,01; ...}.
Таким образом, отклик ивых [я] цепи с передаточной
функцией Hi (г) на ограниченное воздействие также
ограничен, т.е. цепь является устойчивой.
Вывод: полюсы передаточной функции устойчивой дискрет-
ной цепи лежат внутри единичной окружности z-плоскости. Не-
рекурсивные цепи всегда устойчивы.
Замена переменной z в передаточной функции дискретной
цепи на функцию, зависящую от нормированой частоты Q, по-
зволяет получить частотные характеристики цепи. При переходе
от преобразования Фурье к z-преобразованию была сделана за-
мена:
= z
Для перехода от передаточной функции Жг) к частотной
характеристике H(jf) необходимо произвести обратную за-
мену:
z = .
415
Обычно вводят в рассмотрение нормированную частоту
Q. = f T = flfx - С учетом этого формула (9.20) примет вид
Я(/Я) = я(еу2яП) =
_ д0 + + д2е~74яП + ••• + a^e~j2nNn _
1 - bie~j2nn - b2e~j4nn -... - Ь^е~}2к1^п
_ (д0 + ах cos2rcQ + д2 cos4nQ +... + aN cos2kNQ) - (9.22)
(1 -b\ cos2nQ — b2 cos4лЯ-... -bN cos2n)VQ) +
-j ( Д( sin 2лЯ + д2 sin 4nQ +... + aN sin 2лЛ/Я)
+j (bi sin 2nQ. + b2 sin 4лЯ +... + b^ sin 2nNQ)
Из (9.22) легко получить амплитудно-частотную и фазо-
частотную характеристики дискретной цепи. В частности, ам-
плитудно-частотная характеристика будет представлена выра-
жением
Я(Я) = |Я(/Я)| = (Др +Д1СО5 2лЯ + Д2СО8 4лЯ + ... )2 +
2 (1 -biCos2itQt-b2 cos4лЯ-... ) + +(д( зш2лЯ +д2зш4лЯ + ... )2
x 2 , + (bi sin 2лЯ + b2 sin 4лЯ +...)
а фазо-частотная характеристика — выражением
ф(й) = arctg
Д1 sin 2лЯ + д2 sin 4nQ +... + д^ sin 2itNQ
д0 + Д1 cos2kQ + д2 cos4лЯ + ... + aN cos2nNCl
- arctg
bi sin 2лЯ + b2 sin 4nQ +... + fyy sin 2nNQ
1 - bi cos 2лЯ - b2 cos 4 лЯ - ...~bN cos2izNQ
Пример 9.37. Рассмотрим цепь, приведенную на рис. 9.47, б и
описываемую передаточной функцией (9.21). Под-
становка в (9.21) z = дает
Я(Я) =
__________________0,1317 ____________
1(1-1,785 cos 2лЯ +1,202 cos 4лЯ - 0,2853 cos 6лЯ )2 + ’
у+(1,785 sin 2лЯ -1,202 sin 4nQ + 0,2853 sin блЯ )2
На рис. 9.48 изображен график АЧХ ЖЯ) этой
цепи. Как и следовало ожидать, амплитудно-частот-
ная характеристика дискретной цепи является перио-
дической функцией (так как Я (/Я) есть преобразо- <
вание Фурье от дискретной импульсной характери-
416
Рис. 9.48. АЧХ дискретной цепи к примеру 9.37
стики). Ее период равен = 1/Т или Q = /д • Т = 1.
АЧХ используется в диапазоне частот от 0 до 0,5/д
(или до Q = 0,5).
Пример 9.38. Найдем частотную характеристику дискретной цепи
с импульсной характеристикой h[n} = {1,5; 1; 0,5}.
Запишем передаточную функцию H(z) цепи, вое-
00
пользовавшись формулой H(z) = lLh[n]z~n. Полу-
чим H(z) = 1,5 + z-1+0,5z-2 — передаточную функ-
цию нерекурсивной цепи.
Найдем АЧХ цепи, подставляя в формулу (9.23)
значения коэффициентов усиления а0=1,5; «1=1;
а2 = 0,5:
(«o+fliCos2itQ + a2c°s47rn)2 +
ri = 2 =
у-ь (sin 2ftQ + «2 sin 4%Q)2
(1,5 + cos 2nQ + 0,5 cos 4 л Q)2 +
у+( sin 2лП + 0,5 sin 4nQ )2
График АЧХ изображен на рис. 9.49.
Рис. 9.49. АЧХ дискретной цепи к примеру 9.38
27 - 6972
417
Пример 9.39. Изменим коэффициенты усиления в предыдущем
примере. Выберем я0 = а2 = 1 > а\ = ~2- Вновь найдем
выражение Н(й) и построим график его амплитудно-
частотной характеристики.
Заменим в формуле для Я(й), полученной в
примере 9.38, значения коэффициентов а0> а\ и а2.
Получим
Я(О)- М “ 2c°s27tQ + cos4ttQ)2+
у + ( -2 sin 2nQ + sin 4nQ )2.
График АЧХ изображен на рис. 9.50.
Рис. 9.50. АЧХ дискретной цепи
к примеру 9.39
Из данного параграфа мы узнали, что:
g
• В отличие от нерекурсивных цепей, где каждый текущий 8
отсчет выходного сигнала вычисляется по текущему и за- j
держанным отсчетам только входного сигнала, в рекурсив- I
ных цепях текущий отсчет выходного сигнала вычисляется I
по текущему отсчету входного сигнала и задержанным от- |
счетам выходного сигнала. |
• Рекурсивные цепи обязательно имеют обратные связи в от- |
личие от нерекурсивных цепей, содержащих только прямые 1
связи. |
• Нерекурсивные цепи всегда устойчивы. Рекурсивные цепи |
устойчивы, только когда полюсы их передаточных функций j
располагаются внутри единичной окружности на плоскости г. |
• Амплитудно-частотные и фазо-частотные характеристики |
дискретных цепей получают, как обычно, из передаточных |
функций, заменяя переменную z функцией частоты Q. g
418
9.6. Типовые звенья дискретных цепей
Рекурсивные дискретные цепи, содержащие один или два
элемента задержки, являются типовыми звеньями, из которых
можно сформировать любую сложную дискретную цепь. В ли-
тературе типовыми звеньями дискретных цепей считаются звенья
первого и второго порядков. Они получаются из общей структу-
ры рис. 9.44, если оставить в ней только один либо два элемента
задержки.
На рис. 9.51, а показано звено первого порядка с передаточ-
ной функцией
я(г) =
1 - djz-1
и АЧХ
(д0 + ах cos 2лО)2 + sin 2лО)2
(1 - bi cos2nfi)2 + (6) sin 2nQ)2
Типовое звено второго порядка изображено на рис. 9.51, б.
Его передаточная функция
Рис. 9.51. Типовые звенья первого (а)
и второго (б) порядков
27*
419
д(г) = Др + aiz'1 +a2z~2
1 -b\Z~x -b2z~2
и АЧХ
Я(П) =
( а0 + а\ cos 2лП + а2 cos 4лП )2 + (а\ sin 2nQ + а2 sin 4nQ)2
у (1 - 6i cos 2nQ - b2 cos 4nQ)2 + (bt sin 2kQ + b2 sin4nQ)
2 ‘
Пример 9.40. Построим график АЧХ звена первого порядка, у
которого а0 = 1, а\ = 0.
Передаточная функция такого звена первого по-
рядка
1 — 1-biZ 1
Амплитудно-частотная характеристика
1
Н(П) = ---------------------------- -
7(1 - 6t cos 2nQ)2 + (6t sin 2nQ)2
1_________________
71 + 62 - 2bi cos 2n£l
Поскольку полюс zn передаточной функции
H(z) равен bit то для того, чтобы цепь была устой-
чивой, необходимо выбирать значения 6( такими,
чтобы выполнялось условие |6t| < 1.
На рис. 9.52 приведены графики АЧХ, постро-
енные для значений 6t = 0,5 и Ь\ = -0,5.
Рис. 9.52. АЧХ звена первого порядка
к примеру 9.40
420
Рис. 9.53. АЧХ звена второго порядка
к примеру 9.41
Пример 9.41. Найдем передаточную функцию и построим гра-
фик АЧХ звена второго порядка (рис. 9.51, б) при
а0 = а2 - 1, at = ~2, bj = 0,2 и Ь2 = -0,4.
Передаточная функция такого звена
)- ао + a^z~X + fl2z~2 _ 1 ~ 2г-> + г~2
1 - Ьхг~1 - b2z~2 1 - 0,2z-1 + 0,4z-2
Как указывалось ранее, рекурсивную цепь с пря-
мыми и обратными связями можно представить как
каскадное соединение рекурсивной цепи с передаточ-
ной функцией и нерекурсивной цепи с пере-
даточной функцией Я2 (г). В нашем случае, для зве-
на второго порядка,
Ht(2) =--------1------5-, H2(z) = i-2z~1+z~2,
1-0,2г’1 + 0,4z~2
H(z) = ffi<z)H2(z).
График АЧХ для H2(z) уже был построен и
приведен на рис. 9.50. АЧХ рекурсивной
цепи рассчитывается по формуле
Я, (Я) = -------------1----------=.
(1 - 0,2 cos 2nQ + 0,4 cos 4лЯ) +
y+(0,2sin2n£l - 0,4sin 4лЯ)2
Графики (Q), H2 (Q) и Я(Я) = Я2(Я)
изображены на рис. 9.53.
Типовые звенья могут соединяться каскадно (рис. 9.54, а);
при этом их передаточные функции перемножаются:
ff(z) = Hi(z)H2(z)H3(z),
421
Рис. 9.54. Каскадное (а) и параллельное (б) соединение типовых
звеньев и включение в цепь обратной связи (в)
где Hi, Н2, Н3 — передаточные функции звеньев.
При параллельном соединении звеньев (рис. 9.54, б) общая
передаточная функция определяется как
Я(г) = Я1(г) + Я2(г) + Я3(г).
Соединение, показанное на рис. 9.54, в, называют включени-
ем цепи Н2 в обратную связь цепи Hi, причем _
Следует иметь в виду, что все соединения, изображенные на
рис. 9.54, справедливы не только для типовых звеньев, но и для
любых других структур.
Пример 9.42. Найдем передаточные функции при различных спо-
собах соединения рекурсивной и нерекурсивной це-
пей, имеющих
Hi(z) =--------г и H2(z) = 0,2 + z-1 +z~2.
1-0, Зг-1 2
При каскадном соединении этих цепей
H(z) = Hi (z) • Н2 (г) = 0,2 +
l-0,3z-1
422
при параллельном соединении
H(z) = Ht(z) + H2(z) =
_ 1,2 + 0,94г '* + О,7г'2 - 0,Зг'3 .
1-О.Зг'1
при включении цепи Н2 в обратную связь цепи Hi
и( ^(г)
Н{2} 1-Я((г)Я2(г)
=________1,25
1-1,625г'1 -1,25г'2
Пример 9.43. Найдем передаточную функцию дискретной цепи,
изображенной на рис. 9.55.
Цепь, приведенная на рис. 9.55, представляет
собой каскадное соединение типовых звеньев первого
и второго порядков. Передаточная функция соедине-
ния имеет вид
Я (г ) = Д° + giz l • а'° + а'12' + a'2Z~2
1-bi-z'1 1 - biz'1 - b2z'2
Подставляя в выражение для H(z) заданные
значения коэффициентов усиления «о = 1, а\ = 0,5,
bi = -1 и а'о = 0,5, а\ = 1,5, «2 = -1,2, Ь\ = -0,2,
Ь2 = 0,4, получаем
. 0,5 + 1,75г'1 -0,45г'2 -6г'3
Ж г ) = —--- ;---------------5—.
1 + 1,2г" -0,2г'2-0,4г'3
Рис. 9.55. Каскадное соединение типовых звеньев
к примеру 9.43
423
Из данного параграфа мы узнали, что:
• Типовые звенья дискретных цепей первого и второго по-
рядка представляют собой рекурсивные цепи с прямыми и
обратными связями, в которых имеются только один или
два элемента задержки.
• Типовые звенья можно соединять каскадно и параллельно,
а также включать в цепь обратной связи.
Вопросы и задания для самоконтроля
1. Почему нельзя выбирать большой интервал дискретизации
сигнала (или спектра)?
2. Как нужно выбирать интервал дискретизации сигнала, чтобы
можно было однозначно восстановить непрерывный сигнал по
его дискретным отсчетам?
3. Как рассчитывается спектр дискретного периодического сиг-
нала?
4. Как рассчитывается /-изображение дискретного сигнала?
5. Как вычисляются значения выходной последовательности дис-
кретной цепи?
6. Как связаны передаточная функция и импульсная характери-
стика дискретной цепи?
7. Какие цепи называются нерекурсивными и рекурсивными?
8. Вычислить реакцию дискретной цепи с импульсной характе-
ристикой Л [я] на входной дискретный сигнал ивх [я]:
а) А[я]= {2; 1; 0,5}, ивх[п] = {0,5; 0,5};
б) h[n} = {2; 2; 2}, авх[я] = {1; 1; 1}.
9. Найти /-преобразование дискретных сигналов
а) и[п] = {3; 2; 1};
г 1 (1, я-четное,
б) ulnl = { ’
(0, я-нечетное;
( 1X"
в) и[п] = 1 2 I ’ п 0-
10. Найти дискретные сигналы я [я], имеющие /-преобразования
a) U(/) = 1 + 2/-1 + 4/-3;
б) [/(/) = -£-.
/ - 2
11. Найти дискретное преобразование Фурье прямоугольного им-
пульса, заданного четырьмя единичными отсчетами.
424
Рис. 9.56. Дискретные цепи к заданиям 14, 15, 16
12. Найти ДПФ дискретного сигнала и[п] = {0,5; 0,25; 0,0625}.
Построить спектр амплитуд и спектр фаз дискретного сигнала.
13. Найти отсчеты дискретных сигналов и[п], имеющих спектры
a) U(m) = {4; 0; 0; 0};
б) U(m)= {0; 4; 0; 0}.
14. Записать разностные уравнения для дискретных цепей, струк-
турные схемы которых приведены на рис. 9.56.
15. Записать передаточные функции цепей, приведенных на
рис. 9.56, и определить их импульсные характеристики.
16. Рассчитать отсчеты ивых[0], нвых[1] и мвых[2] выходных
сигналов цепей, приведенных на рис. 9.56, если входной сиг-
нал — ступенчатая последовательность wBX[n]= 1[п]= {1; 1;
1; 1; •••}.
17. Составить структурные схемы, записать разностные уравне-
ния и определить импульсные характеристики цепей, переда-
точные функции которых имеют вид
а) Н(г) = 5-Г[ + 3z~2;
425
18.
19.
20.
6) H(z) =——г;
1 - 2г'1
ч ,,, X 2 3
в) H(z) =-----г +----г.
1 - 2z-1 1 + z~{
Определить устойчивость цепей, имеющих передаточные
функции, приведенные в задании 17.
Определить передаточную функцию цепи, если на ее входе и
выходе действуют дискретные сигналы uBX[n] = {1; 0; 0; 0; 1;
0; 0; 0; 1; ...}, мвых[п] = {1; 0; 1; 0; 1; 0; ...}.
Найти импульсные характеристики дискретных цепей, имею-
щих передаточные функции
а) Я(г) = 1/(1 -z-1);
6) Я(г)= 1+/ * •
’-к1
Составить структурную схему каскадного соединения этих
цепей, определить для нее передаточную функцию и записать
разностное уравнение.
Найти передаточную функцию дискретной цепи с импульсны-
ми характеристиками
a) h[n] = {1; -1};
б) Л[п] = 0,2”, 0<п<ЛГ-1.
22. Определить передаточные функции и АЧХ дискретных цепей,
имеющих разностные уравнения:
а) мВЬ1Х[п] = ывх[и]-0,5мвх[п-1];
6) ^вых [ 1 = ^вх IЯ ] + 0, Змвых ( П - 1 ].
21.
ЧАСТЬ 2. АНАЛИЗ И РАСЧЕТ УЗЛОВ
АППАРАТУРЫ СВЯЗИ
Глава 10. Анализ поведения линейных
четырехполюсников на комплексной плоскости
10.1. Комплексные и операторные передаточные
функции нагруженного четырехполюсника.
Условия их физической реализуемости
Передаточная функция четырехполюсника — это отношение
изображения реакции цепи к изображению воздействия. Элек-
трическую цепь любой сложности, имеющую две пары зажимов
для подключения к источнику и приемнику электрической энер-
гии, в технике связи называют четырехполюсником. Зажимы, к
которым подключается источник, называют входными, а зажимы,
к которым присоединяется приемник (нагрузка), — выходными.
В общем виде четырехполюсник изображают, как показано
на рис. 10.1. К входу четырехполюсника 1—Г подключен источ-
ник электрической энергии с комплексной амплитудой напряже-
ния (Jmr и внутренним сопротивлением Z^. К выходным зажи-
мам 2—2' присоединена нагрузка с сопротивлением ZH. К вход-
ным зажимам приложено напряжение с комплексной амплитудой
С/т1, к выходным — с комплексной амплитудой Um2- Через
входные зажимы протекает ток с комплексной амплитудой /от1,
через выходные зажимы — с комплексной амплитудой 1т2. Заме-
тим, что в роли источника и приемника электрической энергии
могут выступать другие четырехполюсники.
На рис. 10.1 использованы символические обозначения на-
пряжений и токов. Это означает, что анализ электрической цепи
проводится для гармонического колебания определенной частоты.
Рис. 10.1. Включение четырехполюсника между
генератором и нагрузкой
Электрическая
цепь
(четырех-
полюсник)
427
Ни = ит2/итГ,
Ну ~
Для данйого гармонического колебания можно определить пере-
даточную функцию нагруженного четырехполюсника, которая
будет представлять собой отношение комплексной амплитуды вы-
ходной электрической величины к комплексной амплитуде вход-
ной электрической величины.
Если входным воздействием считать напряжение генератора с
комплексной амплитудой НтГ, а реакцией четырехполюсника на
это воздействие — напряжение с комплексной амплитудой Um2
или ток с комплексной амплитудой 1т2, то получаются ком-
плексные передаточные функции общего вида'.
(10.1)
(10.2)
В частных случаях, когда заданными воздействиями являются
напряжение на входных зажимах четырехполюсника или ток,
протекающий через эти зажимы, получают следующие четыре
разновидности передаточных функций нагруженного четырехпо-
люсника:
Ни = — комплексный коэффициент передачи по на-
пряжению (для активных четырехполюсников, на-
пример усилителей, он носит название комплексного
коэффициента усиления по напряжению);
Hj = LmnlLm\ ~ комплексный коэффициент передачи по току (для
активных цепей — коэффициент усиления по току);
Н.2 = Um2/lmi ~ комплексное передаточное сопротивление;
Ну = Lna/H-mi ~ комплексная передаточная проводимость.
Часто в теории цепей используют нормированную или рабо-
чую передаточную функцию четырехполюсника:
(10.3)
которая получается путем нормирования (10.1) множителем
o,5^7ZF-
Комплексный коэффициент передачи нагруженного четы-
рехполюсника позволяет определить изменение амплитуды и
фазы гармонического воздействию! при прохождении его через
четырехполюсник. Мы уже представляли ранее комплексную ве-
личину Н в показательной форме:
H = \H\eiv = Не^, (10.4)
где Н = |Я| — модуль комплексной передаточной функции
(АЧХ), а <р — ее аргумент (ФЧХ).
428
Рассмотрим комплексный коэффициент передачи по напря-
жению:
lt — — m2
и ит.
(10.5)
Подставляя в (10.5) запись комплексных действующих зна-
чений
Um2=Um2e^ и Uml=Umie^,
получаем
тт _ Um2eJ4>'>2 _ Um2 е1 (<Рн2_Фи1)
Umie^ UmX
Из сравнения этого выражения с (10.4) видно, что
_ Um2
и Г/
U ml
И фи = фи2~ «Pul-
Т.е. модуль комплексного коэффициента передачи по напряже-
нию (или комплексного коэффициента усиления по напряжению)
показывает, во сколько раз изменяется амплитуда гармонического
колебания напряжения на выходе нагруженного четырехполюс-
ника по сравнению с аналогичным значением на его входе, а ар-
гумент этой функции определяет сдвиг фаз между гармонически-
ми колебаниями напряжения на входе и выходе.
Точно так же можно найти
и ф/ = ф»2 - Ф«1-
Все сказанное выше о коэффициенте передачи по напряже-
нию справедливо и для коэффициента передачи по току.
Частотные характеристики нагруженного четырехполюсника
показывают его поведение на разных частотах. Перепишем вы-
ражение (10.4) в виде
Я(» = Жсо)еу<₽(ш). (10.6)
Напомним, что функция частоты Ж со) называется ампли-
тудно-частотной характеристикой цепи (АЧХ). Она показы-
вает, какие изменения в амплитуды гармонических колебаний
вносит четырехполюсник на каждой частоте.
Функция частоты ср (со) называется фазо-частотной харак-
теристикой цепи (ФЧХ). Соответственно эта характеристика
показывает, какой фазовый сдвиг приобретает гармоническое ко-
429
лебание - каждой частоты при прохождении через четырехпо-
люсник.
Комплексную передаточную функцию Н(/со) можно пред-
ставить также в алгебраической форме:
= ReH(ja>) + /1шЯ(/со),
где ИеЯ(/со) = H(a>)coscp(co); 1тЯ(/со) = H(co)sin<p(<o);
Я(<о) = y][ReH(j(£>)]2 +[ImH(j©)]2;
Пример 10.1. Определим комплексный коэффициент передачи по
напряжению АЧХ и ФЧХ четырехполюс-
ника, изображенного на рис. 10.2, а.
Согласно (10.5) запишем
И.О®)
Найдем комплексную функцию на вы-
ходе четырехполюсника:
IJ ( йл \ = Т ( im1 О®) 1 = (/®)
m2(j ) ”»W;(oC R + i/jtoC jtoC l+j(>)RC'
Подставив ит2(](а) в формулу для Ни(/со), полу-
чим комплексную передаточную функцию:
Рис. 10.2. ЛС-четырехполюсник (а)
и его АЧХ (б) и ФЧХ (в)
430
Я„ (/со) = 1/(1 +/<оЯС).
АЧХ четырехполюсника
Я„ (<о) = 1/71+ (<оЯС)2;
ФЧХ четырехполюсника
<ри (о) = - arctg oRC.
Изменяя частоту со от 0 до оо, можем изобразить
графики АЧХ и ФЧХ цепи (рис. 10.2, б и в).
АЧХ и ФЧХ цепи можно представить
единым графиком, если построить зави-
симость комплексной передаточной функ-
ции Н(](п) от частоты ш на комплексной
плоскости. При этом конец вектора
Я (/со) опишет некоторую кривую, кото-
рая называется годографом комплексной
передаточной функции (рис. 10.3).
Напомним еще раз, что часто спе-
циалисты имеют дело с логарифмической
амплитудно-частотной характеристикой (ЛАХ):
К = 201яЯ(юГ
Значения величины К оцениваются в децибелах (дБ). В актив-
ных цепях, содержащих усилители, величину К называют еще
логарифмическим усилением. Для пассивных цепей вместо ко-
эффициента усиления вводят понятие ослабления цепи:
Л = 201§Ъ7-^’ (Ю.7а)
Я(со)
} |Я(а>)°0; <р(°о)=0
'+
Я(0)’ '.У Н(<о)
Рис. 10.3. Годограф
комплексной переда-
точной функции
которое также оценивается в децибелах.
В теории электрических цепей применяется понятие рабочего
ослабления:
1
Лр = 201§яД^)-
(10.76)
Пример 10.2. Известно, что модуль коэффициента передачи по
напряжению цепи принимает следующие значения:
При f=Q H(.f) - I;
/=1кГц Ж/) =0,3;
f=2 кГц Ж/) =0,01;
/=4кГц H(f) =0,001;
f=8 кГц Ж/Э =0,0001.
431
Рис. 10.4. Ослабление четырехполюсника
к примеру 10.2
Изобразим график ослабления четырехполюсника.
Значения ослабления цепи, рассчитанные по
(10,7а), приведены в таблице.
f, кГц 0 1 2 4 8
A(f), дБ 0 12 40 60 80
График А( f) приведен на рис. 10.4.
Операторная передаточная функция цепи — это рациональ-
ная дробь с вещественными коэффициентами. Если вместо ком-
плексных сопротивлений емкости 1//<оС и индуктивности jcoL
иметь дело с операторными сопротивлениями емкости 1/рС и ин-
дуктивность pL, то в выражении Я(у'со) нужно заменить /© на р.
Операторная передаточная функция цепи Н(р) может быть
записана в общем виде как дробно-рациональная функция с ве-
щественными коэффициентами:
Я (о) = апрп+ап-\Рп~Х+ + (№ +ао = ^(р)
bmpm + + - + bip + b0 v(p)
или в виде
Н(п\=Н (P-Poi)(P-Po2)-(p-Pon)
{Р)~ (p-PlHp-p2)...(p-pm) ’
(10.8)
(10.9)
где Роь Р02> >Роп ~ нули; Р1> Р2> ’Рт ~ полюсы передаточ-
ной функции; Н = ап/Ьт .
Заменив в (10.8) оператор р на/со, вновь получим комплекс-
ную передаточную функцию цепи
Я(/со) = Ж©)е;<|,(о)),
где АЧХ цепи
432
Я(о) = l(flo-fl2<o2 + Q4^4- )2+(a1co-a3co3 + a5co5-...)2-
(t>o-Ьцш? +д4<в4 -...)2 +(bt<£>-b$f)3 +b&)5 -...)2
(10.10)
ФЧХ цепи
„(В) =
(л0 -а2со2 +я4(о4 -...)
(bQ -t>2®2 +ь4©4 - ...)
(10.11)
Учитывая, что Жсо) является иррациональной функцией,
обычно при анализе и синтезе цепей имеют дело с квадратом АЧХ:
|2 _ Ср(О2” 4- С](О2”~2 +... + Сп 1й>2 + Сп
|^(?<0)| d0G)2m + di(j32m 2 +...+ </„!©2 +dm.’
(10.12)
где коэффициенты с* и получаются путем объединения ко-
эффициентов при одинаковых степенях переменной со.
Пример 10.3. Найдем операторную передаточную функцию и
квадрат АЧХ четырехполюсника, изображенного на
рис. 10.5, а.
Операторная передаточная функция этого четы-
рехполюсника
Н Гг)- 22^ - pl+Vpc
и{Р) Zl(p) + Z2(p) R + pL + 1/pC
p2+\/LC н р2+а0
р2 + pR/L + 1/LC р2 + btf> + b0 ’
где Н = 1; а0 = 60 = 1/LC; = R/L.
Корни числителя этой рациональной дроби, т.е.
нули передаточной функции,
Р01’02 = ±у?Ес-
Корни знаменателя, или полюсы передаточной
функции,
R ж • П
На рис. 10.5, б показано расположение нулей и
полюсов функции при 1/(£С) > /?2/(4£2).
По теореме Виета
28-6972
433
Рис. 10.5. Цепь («), полюсы и нули передаточной
функции (б) и АЧХ (в) к примеру 10.3
нАр) =
(Р-РО1)(Р~РО2)
(Р-Р1)(Р"Р2) ’
Амплитудно-частотная характеристика определя-
ется из Ни(р) путем замены р на /со и вычисления
модуля полученной функции:
|Я„(/со)| = Яи(со) =
[ (о0—со2)2
(д0-со2)2 +(М)2
Квадрат АЧХ запишется в виде
|Яа(/со)|2=Н2(со) =
со4 + qco2 + с2
со4 - 2аосо2 + йр
со4 + (б2 - 260 )со2 + 6р
со4 +J1C02 +б?2'
где Ci = -2а0 =-2/(.LC);
с2 = а% =1/(LC)2;
di = bl -2b0 = (R/L)2 - 2/(LC);
d2=b$ = 1/(ZC)2.
АЧХ цепи Ж co) изображена на рис. 10.5, в.
434
Операторная передаточная функция цепи и квадрат ее АЧХ
обладают определенными свойствами. Эти свойства получили
название условий физической реализуемости (УФР). Перечислим
основные свойства У ФР операторных передаточных функций и
квадрата АЧХ пассивных четырехполюсников.
1. Передаточная функция является дробно-рациональной
функцией с вещественными коэффициентами. Вещественность ко-
эффициентов объясняется тем, что они определяются элементами
схемы.
2. Полюсы передаточной функции располагаются в левой по-
луплоскости комплексной переменной р. На расположение нулей
ограничений нет. Докажем это свойство на примере передаточной
функции Hv(p) = U2(p)/U\{p). Выберем входное воздействие
Mj(t) = 5(t) или в операторной форме С7(р) = 1. Изображение
выходного напряжения U2(p) = Ui(p)Hu(p) в этом случае чис-
ленно равно Ни(р), т.е.
и2 (р) = Н. (р) = ------ =
Р +Ьт_хрт 1+... + bip + b0
=w(p)= Д + А2 + + Ат
(Р-Р\)(р-Р2)-(Р-Рт) Р-Р1 Р-Р2 Р-Рт’
где w(p) — полином числителя передаточной функции; А{, А2, ...,
Ат — коэффициенты разложения дробно-рациональной функции
на сумму простых дробей.
Перейдем от изображения С72(р) к оригиналу u2(t):
u2(t) = AiePit + A2eP2t +... + AmePmt, (10.13)
где в общем случае pt- = о, + /а»,-.
В пассивных и устойчивых активных четырехполюсниках ко-
лебания на выходе четырехполюсника после прекращения воз-
действия должны иметь затухающий характер. Это означает, что
в (10.13) вещественные части полюсов р, должны быть отрица-
тельными (а, <0), т.е. полюсы должны находиться в левой по-
луплоскости переменной р.
3. Степени полиномов числителей передаточной функции и
квадрата АЧХ не превышают степеней полиномов знаменателей,
т.е. п < т. Если бы это свойство не выполнялось, то на беско-
нечно больших частотах АЧХ принимала бы бесконечно боль-
шое значение (так как числитель рос бы с увеличением частоты
быстрее знаменателя), т.е. цепь обладала бы бесконечным уси-
лением, что противоречит физическому смыслу.
4. Квадрат АЧХ является четной рациональной функцией
переменной <о с вещественными коэффициентами. Это свойство
28»
435
с очевидностью вытекает из способа получения квадрата АЧХ
по передаточной функции.
5. Квадрат АЧХ не может принимать отрицательных и беско-
нечно больших значений при со > 0. Неотрицательность |(/со)|2
следует из свойств квадрата модуля комплексной величины. Ко-
нечность значений АЧХ на реальных частотах объясняется так
же, как и в свойстве 3.
Из данного параграфа мы узнали, что:
• Операторная передаточная функция записывается в общем |
виде как дробно-рациональная функция с вещественными |
коэффициентами. I
• Полюсы передаточной функции пассивной цепи находятся ।
в левой полуплоскости комплексной переменной р. |
• Степень полинома в числителе передаточной функции не |
превышает степени полинома знаменателя. |
• Комплексная передаточная функция получается из опера- 1
торной передаточной функции в результате замены опера-
тора р на /<о. I
• При анализе и синтезе цепей обычно имеют дело с квад- |
ратом амплитудно-частотной характеристики.
• Квадрат АЧХ — это четная рациональная функция частоты |
с вещественными коэффициентами. При положительных |
частотах квадрат АЧХ принимает только положительные |
конечные значения. I
10.2. Расчет передаточных функций цепей
с обратной связью. Устойчивость цепей
В большинстве цепей с зависимыми источниками имеется по
крайней мере два пути прохождения сигнала: прямой (от входа к
выходу) и обратный (с выхода на вход). Обратный путь прохож-
дения сигнала реализуется с помощью специальной цепи обрат-
ной связи (ОС). Таких путей, а значит, и цепей ОС может быть
несколько. Наличие в цепях с зависимыми источниками ОС при-
дает им новые ценные качества, которыми не обладают цепи без
ОС. Например, с помощью цепей ОС можно осуществить темпе-
ратурную стабилизацию режима работы цепи, уменьшить нели-
нейные искажения, возникающие в цепях с нелинейными элемен-
тами, и т.д.
Любую цепь с обратной связью можно представить состоящей
из двух четырехполюсников (рис. 10.6).
436
Суммирующее
звено Усилитель
Рис. 10.6. Цепь с обратной связью
Активный линейный четырехполюсник с передаточной функ-
цией по напряжению Нус(р) является усилителем. Его иногда
называют основным элементом цепи и говорят, что он образует
канал прямого усиления.
Пассивный четырехполюсник с передаточной функцией по
напряжению Нос(р) называется цепью обратной связи. На входе
цепи осуществляется суммирование входного напряжения uBX(i)
и напряжения обратной связи иос (t).
Выведем формулу передаточной функции по напряжению
цепи, изображенной на рис. 10.6. Пусть на вход подается напря-
жение uBX(t). Его операторное изображения UBX(p). На выходе
цепи возникает напряжение ивых(£). В соответствии с рис. 10.6
его операторное изображение
^вых(р) = [^вх(р) + С/ос(р)]Нус(р). (10.14)
Операторное изображение (70С(р) можно записать через пе-
редаточную функцию Нос (р) Депи обратной связи:
^ос(р) = ^вых(р)Яос(р).
Тогда выражение (10.14) можно переписать в виде
f/вых (р) = рвх (р) + С^вых (р) • Яос (р)] • Яус (?)
или
^вых(р)[1-Яос(р) Нус(р)] = [7вх(р) Нус(р). (10.15)
Операторная передаточная функция по напряжению цепи с
ОС (рис. 10.6).
Н(р) = =------нус(Р)------ (10 1б)
{Р) uBM t-Hyc(p) Hoc(pY
Пример 10.4. На рис. 10.7 изображена цепь на операционном уси-
лителе (ОУ), предназначенная для масштабирования
437
напряжения. Найдем переда-
точную функцию этой цепи.
Мы уже находили пере-
даточную функцию этой це-
пи ранее. Теперь получим ее
как передаточную функцию
цепи с обратной связью, ис-
пользуя формулу (10.16).
Цепью обратной связи
на схеме рис. 10.7 служит Г-
образный делитель напряже-
ния, составленный из рези-
стивных сопротивлений Ro и
Рис. 10.7. Цепь
к примеру 10.4
Выходное напря-
жение усилителя Uт2 поступает на вход цепи ОС;
напряжение ОС U_m3 снимается с резистора R{. Пе-
редаточная функция по напряжению цепи ОС
Воспользуемся формулой (10.16) и учтем, что
входное напряжение Umi и напряжение обратной свя-
зи U_m3 не суммируются, а вычитаются. Тогда полу-
чим передаточную функцию масштабного усилителя:
Н = = 1/f 1
- 1 + ЯиЯос /{Ни Ro+Rj’
где Ни — коэффициент усиления ОУ
Учитывая, что в реальных ОУ значение Ни » 1,
окончательно имеем
Пример 10.5. Звено на ОУ с частотно-зависимой ОС представле-
но на рис. 10.8. Найдем передаточную функцию это-
го звена.
Чтобы проанализиро-
вать прямой путь прохож-
дения сигнала и путь про-
хождения сигнала в цепи
ОС, необходимо восполь-
зоваться методом наложе-
ния. Для этого следует по-
очередно исключать источ-
ники входного напряжения
и напряжения обратной свя-
Рис. 10.8. Цепь
к примеру 10.5
438
зи, заменяя их внутренним сопротивлением. В случае
идеальных источников напряжения их внутреннее
сопротивление равно нулю. Напряжение Uit прило-
женное к звену, ослабляется входной цепью, пред-
ставляющей собой Г-образный делитель напряжения
с сопротивлениями Z( и Zo в плечах. Передаточная
функция по напряжению такого делителя
а„=у»з/и», =Zo/(z„+z,).
Цепь обратной связи также является Г-образным
четырехполюсником с передаточной функцией
S„t=K„2/K.3 = Z1/(Zo + 21).
Коэффициент усиления ОУ НуС = -Ни.
В соответствии с формулой (10.16) получаем пе-
редаточную функцию звена
тт _ тт —ус _ Z0______________~Ни_____ _
— —вх j _ нуснос z0 + zt । #______Zi__
“zo + zt
Zo + Z, 7{hu zo+zj
Учитывая, что Hu » 1, находим
H = -Z0/ZP
Данное звено может выполнять различные функ-
ции в зависимости от вида сопротивлений Zo и Zt.
При Zo = Rq и Zj = /?! звено превращается в инвер-
тирующий масштабный усилитель; при Zo = 1//соС и
Z, = R — в интегратор; при Zo = R и Zt = 1/jaC —
в дифференциатор.
Пример 10.6. Звено второго порядка с регулируемым коэффици-
ентом усиления представлено на рис. 10.9, а. Найдем
передаточную функцию этого звена.
Анализ прохождения входного сигнала и сигнала
в цепи ОС показывает, что звено имеет входную
цепь, изображенную на рис. 10.9, б, и цепь ОС, по-
казанную на рис. 10.9, в. Передаточные функции
этих цепей можно получить матричным методом, на-
пример рассматривая каждую цепь как каскадное со-
единение соответствующих Г-образных четырехпо-
люсников.
Для входной цепи
439
Рис. 10.9. Звено второго порядка (д), входная цепь (б)
и цепь обратной связи (в) к примеру 10.6
Нвх(р) = 1/(р2Н2С2+ЗрНС + 1). (10.17)
Для цепи ОС
Нос (Р) = < ч f —------• (10.18)
p2R2C2+3pRC + l
С учетом (10.16) получим передаточную функ-
цию звена
нЮ*н„(.р)- ,„г <>о«9)
1-Нус (?)««.(?)
Коэффициент передачи усилителя Нус(р) = К.
Тогда, подставляя (10.17) и (10.18) в (10.19), после
преобразования имеем
= p2R2C2+pRC(3-K) + l
Обратная связь бывает отрицательной и положительной. По
годографу петлевого усиления можно судить о типе обратной
связи. Переходя в (10.16) от оператора р к оператору /<о, полу-
чаем комплексную передаточную функцию
= (.vl <10-20)
^твх(7®) 1 -f^yc (У®)НОС (у<й)
Произведение Нус(;<в)Нос(/со) = Нр(/о) представляет со-
бой комплексную передаточную функцию усилителя и цепи об-
ратной связи при условии, что обратная связь разорвана
440
Рис. 10.10. Цепь с разорванной обратной связью
(рис. 10.10). Функцию Яр(/со) называют передаточной функ-
цией по петле ОС или петлевым усилением. Введем понятия
положительной и Отрицательной обратной связи. Эти понятия
играют заметную роль в теории цепей с обратной связью.
Предположим вначале, что передаточные функции Яус, Яос,
Яр не зависят от частоты и являются вещественными числами.
Такая ситуация возможна, когда в цепи отсутствуют LC-элемен-
ты. При этом Яр может быть как положительным, так и отрица-
тельным числом. В первом случае сдвиг фаз между входным и
выходным напряжениями или, другими словами, сдвиг фаз по
петле обратной связи равен нулю или 2Н, k = 0, 1,2, ... . Во вто-
ром случае, когда Яр < 0, сдвиг фаз по этой петле равен ±л или
±(2£-1)л.
Если в цепи с обратной связью сдвиг фаз по петле равен нулю,
то обратная связь называется положительной, если же сдвиг фаз
равен ±л, то такая обратная связь называется отрицательной.
Передаточную функцию можно изобразить в виде
векторов и показать их на комплексной плоскости. При положи-
тельной обратной связи этот вектор находится на положительной
Рис. 10.11. Годографы петлевого усиления
441
вещественной полуоси, а при отрицательной обратной связи — на
отрицательной вещественной полуоси. Кривая, которую описыва-
ет конец вектора при изменении частоты со (рис. 10.11), называ-
ется, как мы уже знаем, годографом.
Представление Яр(;со) в виде годографа позволяет опреде-
лить вид обратной связи в случае частотно-зависимой обратной
связи. Обратная связь называется положительной, если годо-
граф Яр(/со) лежит в правой, и отрицательной — если в левой
полуплоскости комплексной плоскости. Отрицательная ОС при-
меняется для стабилизации коэффициента усиления, подавле-
ния паразитных сигналов, коррекции частотных характеристик;
положительная ОС может являться причиной неустойчивости
цепи.
Цепь является устойчивой, если годограф петлевого усиле-
ния не охватывает точку с координатами (1,;0). Введем понятия
устойчивой и неустойчивой цепи. Цепь называется устойчивой,
если свободные колебания с течением времени стремятся к нулю.
В противном случае цепь называется неустойчивой. Из теории
переходных процессов следует, что цепь является устойчивой, ес-
ли корни характеристического уравнения лежат в левой полу-
плоскости комплексной переменной р. Если корни такого уравне-
ния лежат в правой полуплоскости, то цепь является неустойчи-
вой, т.е. она находится в режиме самовозбуждения. Таким обра-
зом, для определения условий устойчивости цепи достаточно най-
ти характеристическое уравнение и его корни. Как видим, усло-
вия устойчивости можно определить и не вводя понятие обратной
связи. Однако здесь возникает ряд проблем. Дело в том, что вы-
вод характеристического уравнения и определение его корней яв-
ляются громоздкой процедурой, особенно для цепей высокого
порядка. Введение понятия обратной связи облегчает получение
характеристического уравнения или даже дает возможность обой-
тись без него. Крайне важно и то, что понятие обратной связи
адекватно физическим процессам, возникающим в цепи, поэтому
они становятся более наглядными. Глубокое понимание физиче-
ских процессов облегчает работу по созданию автогенераторов,
усилителей и т.д.
Рассмотрим цепь (рис. 10.6) и выведем ее характеристиче-
ское уравнение. Пусть uBX(t) = 0 и, значит, (7вх(р) = 0. Тогда из
(10.15) следует
(7вых(р)[1-Нус(р)Яос(р)] = 0. (10.21)
Здесь {7Вых(р)*0 (в противном случае цепь нельзя считать
возбужденной), и поэтому равенство (10.21) выполняется при ус-
ловии
442
1-Яус(р)Яос(р) = 0. (10.22)
Если записать передаточную функцию основной цепи в виде
Нус{р) = да1(р)/и1(р), а цепи ОС - Яос (р) = да2(р)/о2(р), то
уравнение (10.22) перепишется следующим образом:
»i(p)»2(p)-^i(p)^2(p). Q
«1(р)и2(р)
Это равенство выполняется при
ui(p)^2(p)-®i(p)^2(p) = 0- (10.23)
Выражение в левой части этого равенства является полино-
мом, поэтому (10.23) можно записать в общем виде:
Ьтрт +Ьт.1рт'1 +... + bip + b0 =0. (10.24)
Это и есть характеристическое уравнение цепи.
Корни уравнения (10.24) в общем случае являются ком-
плексными величинами
Pb Р2> ->Pk’-,Pm<
где Pk= ak+ /®* • Зная корни характеристического уравнения,
можно записать выходное напряжение:
мвых (^) = AiePit + A2ewt +... + AmePmt. (10.25)
Чтобы напряжение авых(() не возрастало безгранично, всем
корням pi, р2, ... ,рт характеристического уравнения необходи-
мо иметь отрицательные вещественные части, т.е. корни должны
располагаться в левой полуплоскости комплексной переменной
р = а + /со. Цепь с ОС, обладающая такими свойствами, называ-
ется абсолютно устойчивой.
При исследовании цепей с обратной связью могут возникать
две проблемы. Если проектируемая цепь должна быть устойчи-
вой, то необходимо располагать критерием, который по виду
функций Яус(р) и Нос{р) позволял бы судить об отсутствии
корней характеристического уравнения в правой полуплоскости
р. Если обратная связь используется для создания неустойчивой
автоколебательной цепи, то следует убедиться, что корни уравне-
ния (10.24) расположены, наоборот, в правой полуплоскости.
При этом необходимо иметь такое расположение корней, при ко-
тором самовозбуждение происходило бы на требуемой частоте.
Рассмотрим критерий устойчивости цепи, названный крите-
рием Найквиста и позволяющий судить об устойчивости цепи с
обратной связью по свойствам разомкнутой цепи (рис. 10.10).
443
Передаточная функция разомкнутой цепи, или петлевое уси-
ление, Яр(/©) = Яус(/©)ЯОС(/©) входит в характеристическое
уравнение (10.22):
1-Яр(/©) = 0. (10.26)
Если найдется такая частота со, для которой конец вектора
Яр (/со) попадает в точку с координатами (1, /0), то это будет
означать, что выполняется условие (10.26), т.е. на этой частоте в
цепи произойдет самовозбуждение. Значит, по годографу можно
определить, устойчива цепь или нет. Для этого используется кри-
терий Найквиста, который формулируется следующим образом:
если годограф передаточной функции разомкнутой цепи не ох-
ватывает точку с координатами (1,/0), то при замкнутой
цепи обратной связи цепь является устойчивой. В том случае,
когда годограф Яр(©) охватывает точку (1, /0), цепь неустойчи-
ва. На рис. 10.11 показаны годографы трех цепей с положитель-
ной обратной связью (цифра 1 соответствует годографу устойчи-
вой цепи).
Пользуясь критерием Найквиста, получим условия самовоз-
буждения цепи с ОС. Запишем выражение Яр(/©) в виде
Яр (/©) = |Яус (;©)||Я0С (;©)|е^фус(<а)+ф“(<в)1,
Яус(/©)||Яус (/©)|> 1
Яус(©)Яос(©)>1.
где |ЯУс(/©)|, |Яос(/©)| — модули передаточных функций;
<рус(©), фоеСсо) — фазовые сдвиги соответственно в основ-
ном элементе и в цепи ОС.
Условия пересечения годографом оси абсцисс Не[Яр(/©)]
при |Яр(/©)| > 1 можно записать в виде двух условий:
1) условия (уравнения) баланса фаз <рус (©) + фос(©) = 2nk,
где k = 0, 1, 2, ...;
2) амплитудного условия
или
Выполнение неравенства соответствует режиму возникнове-
ния колебаний с нарастающей амплитудой, что характерно для
начального этапа самовозбуждения. Выполнение равенства
Яус(©)Яос(©) = 1 соответствует режиму генерации гармониче-
ского напряжения на частоте с постоянной амплитудой и носит
название баланса амплитуд.
Как будет показано ниже, уравнение баланса фаз позволяет
определить частоту, на которой происходит самовозбуждение це-
пи с ОС, а уравнение баланса амплитуд дает возможность опре-
делить величину амплитуды мвых(£) генерируемого колебания с
частотой ©0 в стационарной режиме.
444
Пример 10.7. Исследуем устойчивость цепи, изображенной на
рис. 10.9, а. В ней можно выделить усилительный
элемент с передаточной функцией Нус = К и цепь
обратной связи (рис. 10.9, в) с передаточной функ-
цией (10.18)
Нос (р) - 2 2 7 >
р т + Зрх +1
где т = RC.
Кроме того, напомним, что на усилитель сигнал
поступает через входную цепь (рис. 10.9, б), переда-
точная функция которой (см. (10.17))
Нвх (р) = -уг ------- •
р х + Зрх +1
Получим характеристическое уравнение цепи
1-Яус(р)Яос(р) = 0
или
_____Р1_____= 0.
р2х2 + Зрх +1
Откуда окончательно находим
р2х2 + (3 - Юрх +1 = 0.
Корни этого характеристического уравнения
-(3-К) х±х/(3-Ю2х2-4х2
Pi,2 =------------~2-------------= -а ± ;сос
зависят от коэффициента усиления усилителя К.
Расположение корней р\ и р2 на плоскости ком-
плексного переменного р для разных коэффициентов
усиления и соответствующие графики свободных ко-
лебаний в цепи показаны на рис. 10.12.
Устойчивость данной цепи можно исследовать и
с помощью критерия Найквиста. Комплексная пере-
даточная функция разомкнутой цепи
Нр (;<о) = Яус ( /®)Я0С (» = —2'2^"^----7 =
-сот + /Зсот +1
. (п . Зсот
7(1 - со2т2)2 +9со2т2
445
«2c(0 = ^Sin((Oc/+ 0)
♦ Л»
Pl =М
Р2 = -М к
а
в)
Рис. 10.12. Расположение корней на плоскости р
и графики свободных колебаний к примеру 10.7
K = 3
На рис. 10.11 приведены годографы ус-
тойчивой (К = 2, кривая 1) и неустойчивой (К = 3,
кривая 2; К = 4, кривая 3) цепи.
Из данного параграфа мы узнали, что:
• Передаточная функция цепи, охваченной обратной связью, |
зависит от коэффициента усиления усилителя и передаточ- |
ной функции цепи обратной связи. |
• Обратная связь бывает отрицательной и положительной. |
Об этом легко судить по годографу петлевого усиления: на |
тех частотах, где годограф лежит в левой комплексной по- J
луплоскости, обратная связь отрицательная, а на тех часто- |
тах, где годограф лежит в правой полуплоскости, — поло- |
жительная. !
446
л». ..... "' > <><> г*^ »,,^..Л
• Цепь является устойчивой, если свободные колебания с те- (
чением времени стремятся к нулю. Усилитель с обратной 1
связью является устойчивым, если годограф петлевого уси- |
ления не охватывает точку на комплексной плоскости с ко- |
ординатами (1,/0). |
Вопросы и задания для самопроверки
1. Что такое комплексная передаточная функция? Какие виды
комплексных передаточных функций четырехполюсника из-
вестны?
2. Определить коэффициент передачи по напряжению Яи(/<о),
АЧХ и ФЧХ цепи, изображенной на рис. 10.2, а, если выход-
ным напряжением является напряжение на резисторе R. По-
строить графики АЧХ и ФЧХ.
3. Определить коэффициент передачи по напряжению при холо-
стом ходе и коэффициент передачи по току при коротком за-
мыкании для П-образного четырехполюсника, в продольную
ветвь которого включена индуктивность L, а в поперечные
ветви — емкость С.
4. Определить ослабление, вносимое цепью рис. 10.2, а, при R =
= 31,8 кОм и Хс = 10 кОм.
5. Что такое операторная передаточная функция? Как она связа-
на с комплексной передаточной функцией? Как определить
нули и полюсы операторной передаточной функции?
6. Определить операторную передаточную функцию, комплекс-
ный коэффициент передачи по напряжению, АЧХ и квадрат
АЧХ последовательного колебательного контура, изображенно-
го на рис. 10.5, а, если выходным напряжением U_2 является
напряжение на емкости С. Построить график АЧХ цепи.
7. Перечислить основные свойства операторных передаточных
функций пассивных цепей.
8. Как рассчитывается передаточная функция цепи с обратной
связью?
9. Доказать, что операторная передаточная функция дифферен-
циатора на операционном усилителе равна (—pRC). Построить
график АЧХ такого дифференциатора.
10. Рассчитать передаточную функцию каскадного соединения
цепей, изображенных на рис. 10.2, а и 10.7. Построить гра-
фик АЧХ полученной цепи.
11. Определить передаточную функцию цепи, изображенной на
рис. 10.13.
447
Ci
Рис. 10.13. Цепь к заданиям И и 14
12. Что такое годограф петлевого усиления? Как по годографу
определить тип обратной связи?
13. Как формулируется критерий устойчивости Найквиста? Для
каких цепей он используется?
14. Определить комплексную передаточную функцию Яр(/а>)
разомкнутой цепи, изображенной на рис. 10.13. Исследуйте
зависимость устойчивости цепи от величины коэффициента
усиления К.
Глава 11. Анализ и расчет электрических фильтров
11.1. Типы и характеристики фильтров
Электрический фильтр — это устройство, которое практиче-
ски не ослабляет спектральные составляющие сигнала в заданной
полосе частот и существенно подавляет спектральные состав-
ляющие вне этой полосы. Полоса частот, в которой ослабление
мало, называется полосой пропускания. Полоса частот, в которой
ослабление велико, называется полосой непропускания (задержи-
вания). Между этими полосами находится переходная область.
По расположению полосы пропускания на шкале частот раз-
личают следующие фильтры:
нижних частот (ФНЧ), в которых полоса пропускания рас-
полагается на шкале частот от со = 0 до некоторой граничной час-
тоты со = соп, а полоса непропускания (задерживания) — от часто-
ты со = со3 до бесконечно больших частот (рис. 11.1, а);
верхних частот (ФВЧ) с полосой пропускания от частоты
со = соп до бесконечно больших частот и полосой непропускания
от частоты со = 0 до со = со3 (рис. 11.1, б);
полосовые (ПФ), в которых полоса пропускания <оп1...соп2
располагается между полосами непропускания О...со31 и соз2...да
(рис. 11.1, в);
Рис. 11.1. Ослабление разных типов фильтров:
НЧ (а), ВЧ (б), ПФ (в) и ЗФ (г)
29-6972
449
заграждающие (режекторные) (ЗФ или РФ), в которых ме-
жду полосами пропускания O...coni и а>п2...оо находится полоса
непропускания <»я1 ...соз2 (рис. 11.1, г);
многополосные, имеющие несколько полос пропускания.
На рис. 11.1, а — г показаны также условные обозначения
фильтров каждого типа в соответствии с ГОСТом.
В соответствии с используемой элементной базой к настоя-
щему моменту выделились несколько классов фильтров. Исто-
рически первыми (и все еще наиболее широко применяемыми)
являются пассивные фильтры, содержащие элементы L и С.
Они носят название LC-фильтров.
Во многих случаях на практике требовалась крайне высокая
избирательность (различие ослаблений в полосах пропускания и
непропускания в десятки тысяч раз). Это привело к появлению
фильтров с механическими резонаторами: кварцевых, магнитост-
рикционных, электромеханических.
По-видимому, самые значительные достижения в области
теории и проектирования фильтров связаны с успехами микро-
электроники. Требования микроминиатюризации радиоэлек-
тронной аппаратуры заставили отказаться от использования ин-
дуктивностей, которые имеют большие габаритные размеры,
особенно на низких частотах, и не поддаются исполнению в
микроминиатюрном виде. Появились активные 7?С-фильтры,
состоящие из резисторов, конденсаторов и активных приборов
(например, транзисторов). Эти фильтры могут быть выполнены
в виде микромодульной конструкции или интегральной схемы.
Применение активных /?С-фильтров ограничивается пока срав-
нительно небольшим диапазоном частот до десятков (иногда со-
тен) килогерц.
Разработка цифровых систем связи и достижения в облас-
ти цифровых вычислительных машин стимулировали создание
фильтров на базе элементов цифровой и вычислительной тех-
ники — цифровых фильтров. В силу специфики элементной
базы фильтров не будем далее упоминать о них, хотя расчет
таких фильтров производится методами теории электрических
цепей. Заинтересованные читатели могут обратиться к специ-
альной литературе по цифровым фильтрам.
Характеристика ослабления определяет избирательность
фильтра. В идеальном случае (идеальный фильтр) характеристи-
ка рабочего ослабления (10.76), например, для ФНЧ имеет вид,
показанный на рис. 11.2, а. С рабочим ослаблением связана ра-
бочая амплитудно-частотная характеристика (АЧХ): |.Нр(/а>)| =
= е-Ар(а>) pja рИС и 2, б изображена АЧХ идеального фильтра
нижних частот.
450
Реальные фильтры (т.е.
фильтры, состоящие из реаль-
ных элементов) имеют харак-
теристики рабочего ослабле-
ния и амплитудно-частотную,
отличные от идеальных.
Требования к электриче-
ским характеристикам фильт-
ров задаются в виде допусти-
О------1—-
co„ <о
а)
Рис. 11.2. Графики рабочего
ослабления (а) и АЧХ (б)
идеального ФНЧ
мых пределов изменения этих
характеристик. Так, рабочее ослабление в полосе пропускания не
должно превышать некоторого максимального допустимого зна-
чения Лр тах, а в полосе непропускания не должно быть ниже
некоторого минимально допустимого значения Apmin. Нетрудно
изобразить эти требования графически, как это сделано на
рис. 11.3, а. На этом рисунке соп и со3 — граничные частоты по-
лос пропускания и непропускания.
Зная требования к Ар, можно пересчитать их в требования к
АЧХ или, как это принято в теории фильтров, в требования к
квадрату АЧХ (рис. 11.3, б):
|Wp(y<B)|2=- Уиртах, 0<ю<(Оп1 e-2Apmin, ф>(0з
Характеристики проектируемых фильтров должны «уклады-
ваться» в эти требования (рис. 11.3, а и б).
Помимо требований к частотной зависимости рабочего ослаб-
ления (а значит, и к АЧХ) могут задаваться также требования к
фазо-частотной характеристике фильтра (скажем, допустимые от-
клонения от линейного закона) и величине нелинейных искаже-
ний (обусловленных, например, наличием железа в катушках ин-
дуктивности). Могут предъявляться требования и к другим ха-
рактеристикам и параметрам фильтра. Ниже будем учитывать
только требования к рабочему ослаблению и АЧХ.
Идеальные частотные характеристики фильтра (рис. 11.2, а)
заведомо нереализуемы. Частотные характеристики реальных
фильтров могут лишь приближаться к ним с той или иной степе-
нью точности в зависимости от сложности схемы фильтра.
Функция фильтрации. В общем виде электрические фильт-
ры описываются передаточной функцией вида (10.8):
Яр(р)=
+ ап-\Рп~х +... + ахР + ао
bmPm + bm-tp”1"1 +... + btp + bQ
(11.1)
Квадрат амплитудно-частотной характеристики таких фильтров
(см. (10.12))
29*
451
Рис. 11.3. Графики рабочего ослабления (а)
и квадрата АЧХ (б) реального ФНЧ
I И ( ,-т\|2 _ Cpto2” + С1Ю2"~2 + - + Cn_jG)2 4- С„
р d0©2m + </1©2m-2 +... + </m_i<»2 + dm
и, следовательно, рабочее ослабление
Jpg)2”* + djO2”8-2 +... + <im_ico2 + dm '
Ср©2” + q© 2/1-2 +... + c„_i©2 + c„ ,
(11.2)
(11.3)
Ap =101g
могут при надлежащем выборе степени полинома (порядка
фильтра) и коэффициентов d^ удовлетворить заданным требова-
ния (рис. 11.3).
В теории фильтров принято иметь дело не с обычной уг-
ловой частотой ©, а с нормированной частотой Q = ©/©н, где
©н — нормирующая частота. Обычно в качестве нормирующей
частоты выбирают граничную частоту полосы пропускания
©п, так что Qn = ©п/©н = <оп/©п = 1 •
В теории электрических фильтров вместо формул (11.2) и
(11.3) используют другие, также универсальные для любого типа
1яр<7’п)|г - 1+еу(п)'
Ap(Q) = 101g[l + e2i|/2(Q)
(11.4)
(11.5)
Функция \|/2(Q) называется функцией фильтрации. В общем
случае — это дробно-рациональная функция с вещественными ко-
эффициентами (в частости, полином), удовлетворяющая условиям
-1 < \|/(Q) < 1 в полосе пропускания и |y(Q)| » 1 в полосе не-
пропускания фильтра.
В зависимости от вида функции фильтрации получают раз-
личные типы фильтров. Если в качестве функции фильтраций
452
используют полиномы, то фильтры называются полиномиальны-
ми. Среди полиномиальных фильтров широкое использование
нашли фильтры Баттерворта и Чебышева. Если y(Q) —
дробно-рациональная функция (10.8), например дробь Золотаре-
ва, то получают фильтр Золотарева. Все эти три типа фильтров
будут рассмотрены в этой главе.
Низкочастотный фильтр является основой для получения
других типов фильтров. Следует отметить, что имеет смысл под-
робно изучать только фильтры нижних частот, так как другие
типы фильтров (верхних частот, полосовые и заграждающие) мо-
гут быть легко получены из ФНЧ с помощью замены переменной
(частоты). Для этого во всех выражениях, содержащих перемен-
ную Q, нужно произвести замену переменной таким образом,
чтобы характеристики ФНЧ (AP(Q) и |Яр(/О)|2) перешли в
характеристики соответствующего фильтра. Подобная замена пе-
ременной Q называется преобразованием частоты, а исходный
ФНЧ — фильтром НЧ-прототипа.
Преобразование частоты позволяет установить соответствие
между частотами полос пропускания и непропускания НЧ-прото-
типа и частотами фильтра верхних частот (полосового или заграж-
дающего), а также преобразовать схему ФНЧ в схему ФВЧ (ПФ
или ЗФ). Более подробно вопросы, связанные с преобразованием
частоты, будут рассматриваться ниже.
Из данного параграфа мы узнали, что:
• Электрический фильтр — это устройство, которое практиче- |
ски не ослабляет спектральные составляющие сигнала в за- |
данной полосе частот и значительно ослабляет (подавляет) i
все спектральные составляющие вне этой полосы. *
• По расположению полосы пропускания по шкале частот |
различают фильтры нижних и верхних частот, полосовые, |
заграждающие (режекторные) и многополосные фильтры. *
• Основными частотными характеристиками фильтра явля- J
ются рабочее ослабление и квадрат АЧХ. Чем больше кру- }
тизна характеристики ослабления фильтра и чем меньше !
ослабление в полосе пропускания, тем лучше избиратель- f
ность фильтра. {
• Тип фильтра, его передаточная функция и частотные ха- |
рактеристики однозначно определяются функцией фильт-
рации. )
• Низкочастотный фильтр-прототип является основой для <
получения остальных типов фильтров путем преобразова- ।
ния частоты. *
453
11.2. Анализ фильтров нижних частот Баттерворта,
Чебышева и Золотарева
Фильтры Баттерворта нижних частот имеют пологую харак-
теристику рабочего ослабления в полосе пропускания. Если в
выражениях, описывающих квадрат АЧХ фильтра (11.4) и его
рабочее ослабление (11.5), в качестве функции фильтрации ис-
пользуются полиномы Баттерворта = Bm(Q) = Qm (по
имени автора, предложившего использовать их для «конструи-
рования» частотных характеристик фильтра), то такие фильтры
называются фильтрами Баттерворта.
Из формул (11.4) и (11.5) следует, что для фильтров Баттер-
ворта на частоте Q = О значение квадрата АЧХ равно единице, а
рабочего ослабления — нулю. С ростом частоты квадрат АЧХ
фильтра Баттерворта уменьшается и падает до нуля на бесконечно
большой частоте. Рабочее ослабление плавно растет до бесконечно
большого значения. Таким образом, выражения (11.4) и (11.5)
приближенно воспроизводят характеристики идеального фильтра.
Чтобы эти характеристики «вписывались» в предъявляемые к
фильтру требования (рис. 11.3), необходимо иметь рабочее ос-
лабление (11.5) в полосе пропускания, меньшее Ар тах, а в поло-
се непропускания — большее Apmin. Первому условию можно
удовлетворить, если потребовать на граничной частоте полосы
пропускания (Г2 = 1) выполнения равенства Ap(Q)q=i = Apmax
или |ЯР (/О)|о=1 = е~2А? гаах. Отсюда с учетом (11.5) или (11.4)
имеем 1 + е2 = е2АР тах и s2 = е2А? тах -1. Вычисленный таким спо-
собом коэффициент е:
£ = Уе2лртах -1 (П.6)
называется коэффициентом неравномерности ослабления в по-
лосе пропускания фильтра.
В формуле (11.6) величина Ар шах имеет размерность непер.
Если воспользоваться значениями Ар тах в децибелах, то
g = У1Оо>1ЛР max -1, (11.7)
С учетом введенных обозначений квадрат АЧХ фильтра Бат-
терворта запишется в виде
|ЯР(Д2)|2 = l/(l + £2Q2m). (11.8)
Эта функция удовлетворяет свойствам квадрата АЧХ реаль-
ных четырехполюсников, и поэтому ей можно сопоставить физи-
чески осуществимый электрический фильтр.
454
Рис. 11.4. Графики рабочего ослабления (а)
и квадрата АЧХ (б) фильтров Баттерворта
Рабочее ослабление фильтра Баттерворта
Лр =-|1п(1+ е2П2т) Ни; Ар = 101g(l + e2Q2n2) дБ. (11.9)
Крутизна частотных характеристик (11.8) и (11.9) зависит от
степени т (порядка фильтра).Чем больше степень т, тем выше
крутизна характеристик. На рис. 11.4, а, и б показаны графики
рабочего ослабления и квадрата АЧХ фильтра Баттерворта для
различных т. Таким образом, для удовлетворения требований в
полосе непропускания необходимо выбрать соответствующий по-
рядок фильтра т. Его легко определить из условия: на гранич-
ной частоте полосы непропускания Q3 Ap(Q3) > Apmin или
|Нр (у^)|п=Оз е 2Ар min • С учетом этого условия получим 1 +
+E2Q|m > е2^р min, откуда Qlm (е2Ар min — 1)/е2. Логарифмируя
обе части неравенства, придем к выражению
_2Ар min _ ।
2ти1пО3 > In-----=----.
е2
Из него находим окончательно
m > In m*n — 1 k e2 J /21nQ3.
(11.10)
Величина Ар min входит в формулу в неперах. Если вычис-
лять ее в децибелах, то
.q0,1Ap min _ j
lg •у -
21gQ3
(11.11)
455
Передаточную функцию фильтра Баттерворта можно полу-
чить из (11.8), если положить /Q = р:
|Яр(р)|2 = Нр(р)Яр(-р). ‘ (11.12)
1 + s (-Р2)
и разложить знаменатель полученной функции на произведение
сомножителей.
Вычислим корни знаменателя, т.е. полюсы функции
Яр(р)Яр(-р), отдельно для четных и нечетных значений т.
Для четных значений т
1-г2р2т=0 и pk = k = 1, 2.2т.
Так как
-1 = e^2k = cos(2& - 1)л + /sin(2& -1)л,
имеем
, _______ 4 .(2£-1)л
= 1 1 е'^Г.
(11.13)
1 С 2k-l . . 2k-i
Pk = =7= COS —---Л + 1 Sin —-7C
^[z\ 2m J 2m
1, 2, ..., 2т.
Для нечетных значений m
\ ( k k \
Pk=-^i= COS — Л+7'sin — Л , k=i, 2,
’Уе V m mJ
..., 2m.
Выражение (11.12) примет вид
1
Яр (р)Яр (-р) = —---------—---------.
£ (P~Pi)(p-P2)-(p-P2m)
Половина полюсов функции Яр(р)Яр(-р) лежит в левой
полуплоскости комплексной переменной р и может быть отнесена
к передаточной функции реализуемого фильтра Яр(р). Другая
половина полюсов, являясь зеркальным отражением первой, рас-
полагается в правой полуплоскости и относится к Яр(-р).
Построенная из полюсов, лежащих в левой полуплоскости,
передаточная функция фильтра Баттерворта является полиноми-
альной передаточной функцией типа (11.1):
^Р ~ Н т , _1_ _L h п , А ’
Р +Рт-1Р +... + Е»1Р + О0
где Я = 1/s.
456
Пример 11.1. Найдем выражения для частотной характеристики
и передаточной функции фильтра нижних частот
Баттерворта, удовлетворяющего следующим требова-
ниям: Лртах = 3 дБ; Apmin = 12,2 дБ; fa = 159 кГц;
/3 = 318 кГц.
Определим нормированную частоту П3 = f3/fn = 2
и по формуле (11.7) коэффициент неравномерности
ослабления s = V100,1’3 -1 = 1. Порядок фильтра най-
дем согласно (11.11):
т > lg(100112’2 - l)/(21g2) > 1,98.
Возьмем т = 2. Тогда в соответствии с (11.8) и
(11.9)
|Нр(/О)|2 = 1/(1 + Q4); Ар = 101g(l + Q4).
Найдем передаточную функцию фильтра Яр(р).
Значения полюсов функции Нр(р)|2 = Нр(р)Н(-р) =
= 1/(1 + р4) вычислим из формулы (11.13): Р\ =
= 0,707 + /0,707; р2 =-0,707 + /0,707; р3 = -0,707 -
-/0,707; р4 = 0,707 - /0,707. Расположение полюсов
в комплексной плоскости показано на рис. 11.5, а.
По теореме Виета из полюсов в левой полуплос-
кости р2 и р3 формируем передаточную функцию
„ , X ________1_______ 1
Р р е(р-Р2)(р-Рз) р2 +1.41Р + 1 ‘
Рис. 11.5. Расположение полюсов ФНЧ
Баттерворта (а) и Чебышева (б)
Используя введенное ранее обозначение Вт(С1) = Пт поли-
нома Баттерворта, можно представить частотные характеристики
(11.8) и (11.9) фильтра Баттерворта в следующей форме:
457
|/7p(jQ)|2 = l/[l + e2^(Q)];
Ар(Я) = |1п[1 + е2В2 (Я)] Нп; >
Ap(fi) = 101g[l + s2B2 (Я)] дБ.
(11.14)
Фильтры Баттерворта называют также фильтрами с максималь-
но плоским ослаблением в полосе пропускания (рис. 11.4, а).
Фильтры Чебышева имеют равноволновую характеристику
рабочего ослабления в полосе пропускания. Если в качестве
функции фильтрации в (11.4) и (11.5) использовать полином Че-
бышева, обозначаемый^ (Я) = Тт (Я), то формулы (11.14) при-
мут вид
|Яр(/Я)|2 = 1/[1 + е2Т2(Я)];
Ар(Я) = |1п[1 + г2Т2 (Я)] Нп; >
Ар(Я) = 101g[l + £2Т2(Q)] дБ,
(11.15)
где Тт(Я) — полином Чебышева степени (порядка) яг; е — ко-
эффициент неравномерности, определяемый (11.6) или (11.7).
Фильтры с частотными характеристиками (11.15) называют
фильтрами Чебышева. Проанализируем частотные характери-
стики фильтра Чебышева. Для этого вначале рассмотрим свойст-
ва полиномов Тт(Я). Ниже приведены шесть первых полиномов
Чебышева:
Г0(Я) = 1; Тз(Я) = 4Я3 - ЗЯ;
Т1(Я) = Я; Тд (Я) = 8Я4 - 8Я2 +1; (11.16а)
Т2(О) = 2Я2-1; Т5 (Я) = 16Я5 - 20Я3 + 5Я.
Любой полином Чебышева при яг > 2 может быть вычислен
по рекуррентной формуле Тт(Я) = 2Я7'т_1 (Я)-Тт_2(Я). Таким
образом, выражения (11.15) удовлетворяют общим выражениям
(11.1) — (11.3) характеристик полиномиальных фильтров.
Существует единая тригонометрическая форма записи поли-
номов Чебышева в интервале -1 < Я < 1:
Tm(Q.) = cos яг arccos Я. (11.166)
Действительно, То (Я) = cos 0arccos Я = 1; 7} (Я) = cos 1 arccosЯ =
= Я; Т2 (Я) = cos2arccosЯ = 2cos2 arccosЯ-1 = 2Я2-1. Вне ин-
тервала -1 < Я< 1 полиномы ТТО(Я) также представляются в
тригонометрической форме:
Тт (Я) = ch т Arch Я. (11.16в)
458
Рис. 11.6. Графики полинома Чебышева (а) и рабочего ослабления
ФНЧ Чебышева четвертого порядка (б)
Анализ поведения полиномов Чебышева показывает, что в
интервале —1 < Q < 1 угол arccos Q изменяется от -п (при П =
-1) до 0 (при О. = 1), поэтому полином TOT(Q) = cos/и© ровно т
раз принимает значения, равные нулю, и т + 1 раз достигает
значений, равных +1 или —1 и чередующихся друг с другом. Вне
интервала -1 < Q < 1 полином Tm(Q) согласно формуле (11.16в)
монотонно возрастает. В качестве примера на рис. 11.6, а изо-
бражен график полинома Чебышева T4(Q), т.е. полинома чет-
вертого порядка.
В соответствии с (11.15) рабочее ослабление АР(П) фильтра
Чебышева на тех частотах Q, где полином Тт(С1) обращается в
нуль, также обращается в нуль. На частотах, на которых Tm(Q)
равен ±1, рабочее ослабление достигает величины
Ар = 101g(l + s2) = 101g(l + 10°’1Лр max -1) = Ар max.
С ростом значений полинома Тт(С1) на частотах Q > 1 рабо-
чее ослабление Ap(Q) также монотонно растет. На рис. 11.6, б
приведен график рабочего ослабления фильтра Чебышева четвер-
того порядка.
Фильтры Чебышева называют также фильтрами с равновол-
новой характеристикой ослабления в полосе пропускания.
459
Рис. 11.7. Графики квадрата АЧХ
фильтров Чебышева
На рис. 11.7 показаны
частотные зависимости квад-
рата АЧХ фильтра Чебыше-
ва для различных значений
т, полученные для |/7р(/П)|2
из (11.15). Подобные зави-
симости могут быть построе-
ны для рабочего ослабления
фильтра.
Чтобы характеристики
фильтра отвечали требова-
ниям в полосе непропуска-
ния, необходимо выбрать
порядок фильтра т из условия |Нр (/О)|д=£1 < е-2ЛР . Для
полосы непропускания ТОТ(П) определяется формулой (11.16в),
следовательно,
1 + е2 ch2 т Arch Q3 > е2л₽ min.
Отсюда ch яг Arch Q3 >
lg2Apmjn _ ।
“~2
Далее m ArchQ3 > Arch7(е2Лрт'п —l)/e2
Arch^ g2^pmin
Е2
Arch Q3
и m >
В этой формуле величина Ар mjn измеряется в неперах. При
использовании единицы децибел порядок фильтра вычисляется
из выражения
Сравнивая частотные характеристики фильтров Баттерворта
и Чебышева, следует указать, что полиномы Чебышева являются
полиномами наилучшего приближения. Это означает, что при
одинаковом значении т из всех полиномиальных фильтров, ос-
лабления которых в полосе пропускания не превышают Ар тах >
наибольшие значения ослабления в полосе непропускания имеет
фильтр Чебышева. В частности, рабочее ослабление фильтра Че-
бышева в полосе непропускания может превышать (и весьма зна-
чительно) рабочее ослабление фильтра Баттерворта при равных
значениях т и Ар тах • Однако характеристика рабочего ослабле-
ния фильтра Баттерворта имеет в полосе пропускания монотон-
ный характер и легче поддается корректированию для устранения
искажений передаваемых сигналов.
460
Выбор типа полиномиальных фильтров определяется кон-
кретными условиями их применения в аппаратуре связи и радио-
технических устройствах.
Для получения передаточной функции фильтра Чебышева
поступим аналогично тому, как делали это для фильтров Баттер-
ворта. Заменим оператор j'Q. на оператор р и перейдем от функ-
ции |Яр(/И)|2 к функции
|Яр(р)|2=Яр(р)Яр(-р) = 1/[1 + 6гГ2(р>)].
Представим полином Tm(Q) в виде (11.166) и найдем полю-
сы функции) Яр (/?)|2, решив уравнение
е2 cos2 т arccos (р//) + 1 = 0. (11.17)
Поскольку согласно (11.16а) коэффициент при старшем чле-
не полинома Чебышева Tm(Q) равен 2ОТ-1, то коэффициент при
старшем члене полинома в левой части приведенного выше урав-
нения равен е222(т-1).
Как можно доказать, корни уравнения (11.17) определяются
аналитически следующим выражением:
k = 1, 2, ..., 2т, (11.18)
, . 2Л-1 . , 2Л-1
рк = shy sin ——л + jchycos—-—п,
2т 2т
1 1
где у = —Arsh-.
т е
Из корней в левой полуплоскости составляются сомножители
и по теореме Виета строится передаточная функция
фильтра
И, (р) = н ------------,
Р +Ьт_1Рт'+... +biP + bo
где Я = 1/(£2’”-1).
Пример 11.2. Построим передаточную функцию фильтра Чебы-
шева второго порядка (т = 2), рабочее ослабление в
полосе пропускания (от 0 до 159 кГц) которого не
превышает Ар тах = 3 дБ. Граничная частота полосы
непропускания 318 кГц.
Коэффициент неравномерности е такого фильт-
ра согласно (11.7) равен 1. Рабочее ослабление на
частоте Q3 =318/159 = 2 составляет Ap(Q)n=2 =
= 101g(l + ch22Arch2) = 17 дБ, что почти на 5 дБ пре-
вышает рабочее ослабление на этой же частоте фильт-
ра Баттерворта второго порядка (см. пример 11.1).
461
Расчет полюсов функции Нр (р)Нр (-р) по фор-
мулам (11.18) дает величины: рх = 0,322 + /0,777;
р2 = 0,322 - /0,777; р3 = -0,322 - /0,777; р4 =
= -0,322 + /0,777. Расположение полюсов в ком-
плексной плоскости показано на рис. 11.5, 6.
Передаточная функция фильтра
1 pW| £/2(р-р4)(р-р3) р2 + 0,645р +0,707
В заключение отметим, что для полиномиальных фильтров в
справочниках составлены весьма полные таблицы полюсов и ко-
эффициентов передаточных функций для различных величин
Лр max и т. Порядок же фильтров т определяется по специальным
графикам, исходя из заданных величин Ар max, Ар min и Q3.
Фильтры Золотарева имеют всплески ослабления в полосе
непропускания. Частотные характеристики полиномиальных
фильтров, описываемые выражениями (11.1) — (11.3), имеют мо-
нотонный характер в полосе непропускания. В частности, рабочее
ослабление таких фильтров монотонно возрастает по мере удале-
ния от полосы пропускания (рис. 11.4, а и 11.6, б).
При «жестких» требованиях к частотным характеристикам
(малая переходная область между полосами пропускания и не-
пропускания и большая величина рабочего ослабления в полосе
непропускания) порядок фильтра т может получиться очень
большим даже в случае применения полинома Чебышева. Это
приведет к существенному усложнению фильтра и к излишнему
«расходу» элементов.
В таких случаях целесообразно применять фильтры со
всплесками рабочего ослабления в полосе непропускания
(рис. 11.8, а). На частотах всплеска По,!, и т.д. рабочее ос-
Рис. 11.8. Графики рабочего ослабления (а)
и квадрата АЧХ (б) фильтра со всплесками ослабления
462
давление фильтра стремится к бесконечности; за счет этого воз-
растает крутизна характеристики ослабления в переходной облас-
ти. Соответственно АЧХ фильтра на частотах £2те1, Оад2 и т.д.
будет обращаться в нуль (рис. 11.8, б).
Для выполнения указанных условий в выражениях (11.2) —
(11.3) используют рациональные дроби вида
\Н (/п)12 Jq2>i-Q2)(Q«2-Q2)-. (Q^-Q2).
р ' d0Q2m + dtQ2m~2 + ...+ dm_tQ2 + dm
(11.19)
д (с)\- 1 in d()Q + d\Q, + ... +dm_\Cl + dm z..
4(n)-2,n( (1120)
Действительно, когда £2 принимает значения £2ooi> £2«>2>
|Яр(/£2)|2 = 0 и Ар(£2) -> оо.
Передаточная функция таких фильтров является дробно-
рациональной:
н ( ч ? (jP2 + n^i)(p2+n«2)-(p2 + ^J
Р 6mpm + bm_1pm-1+... + 61p + &0
(11.21)
и кроме полюсов р1г р2, ,рт имеет нули:
Pot = ±;£2да1; р02 = ±/£2„2; рОп = ±;О«,П.
Фильтры со всплесками рабочего ослабления называют еще
фильтрами с нулями передачи.
Среди фильтров со всплесками ослабления наиболее широкое
распространение получили фильтры, построенные на основе дро-
бей Чебышева и Золотарева. Чтобы получить частотные характе-
ристики фильтра на основе дробей Чебышева, нужно в формулах
(11.14) или (11.15) использовать в качестве функции фильтрации
дробь Чебышева. Обозначая ее Фт (£2), получаем
|Яр(/£2)|2 = 1/[1 + 82Ф2(£2)];
Ар(£2) = -^1п[1 + е2Фт(£2)] Нп; •
Ар(£2) = 101g[l + е2Ф„(£2)] дБ.
(11.22)
В качестве примера укажем дробь Чебышева пятого порядка,
для которой построены графики Ар(£2) и |Яр(/£2)|2 на
рис. 11.8, а и б:
Ф5(£2) =
+ ctj£2^ + cl 2£2
(я2! -q2)(q22 -q2) ’
463
где а0, ai и а2 — коэффициенты, связанные с частотами вспле-
ска Яда1 и Яда2.
Очевидно, что подстановка этой дроби в (11.22) приведет по-
сле некоторых преобразований к выражениям общего вида
(11.19)и(11.20).
В полосе пропускания дробь Чебышева ведет себя так же, как и
полином Чебышева, т.е. рабочее ослабление фильтра носит равно-
волновый характер. На частотах всплеска Я^ и Я^ дробь Чебы-
шева обращается в бесконечность, что приводит к бесконечно
большому рабочему ослаблению.
Следует отметить, что дробь Чебышева является дробью наи-
лучшего приближения. Это означает, что фильтр на основе дроби
Чебышева на любой частоте полосы непропускания имеет боль-
шее значение рабочего ослабления по сравнению с фильтрами на
основе других дробей (и полиномов как частных случаев дробей)
при прочих равных условиях (при одинаковых порядках т, при
таком же количестве и расположении частот всплеска и тех же
величинах Ар тах ).
Частным случаем дробей Чебышева являются дроби Золота-
рева:
Rm(Q) = -O2)/(q2v -Q2)], (11.23)
V
где -1)/(Яоу “1)]> ^ = 1, 2, ... ,(m-S)/2, значение
v
S равно нулю для четных т и равно единице для нечетных пг,
т — порядок дроби; Яо^, — нули и полюсы дроби, связан-
ные соотношением Яюу = Я3/Я07 .
Используя в качестве функции фильтрации в (11.14) и
(11.15) дроби Золотарева, получаем
|Нр(/Я)|2 = 1/[1 + 82Я2 (Я)]; Лр(Я) = |1п[1 + е2Я2 (Я)] Нп; > Лр(Я) = 101§[1 + 82/?2 (Я)] дБ. (11.24)
Из формул (11.23) и (11.24) следует, что нули функции АР(Я)
совпадают с нулями дроби Золотарева, а всплески функции
АР(Я) — с полюсами этой же дроби. Нули и полюсы дроби Золо-
тарева можно рассчитывать, однако обычно их определяют по ката-
логам для операторных передаточных функций ФНЧ. На рис. 11.9
показан график АР(Я) для фильтра Золотарева пятого порядка.
Дроби Золотарева так же, как и полиномы Чебышева, дают
равноволновую характеристику рабочего ослабления фильтра в
464
полосе пропускания. Од-
нако в полосе непропуска-
ния у фильтров Золотаре-
ва значения всех миниму-
мов рабочего ослабления
оказываются одинаковыми
и равными значению рабо-
чего ослабления на частоте
Q3. Такие фильтры назы-
вают также фильтрами с
изоэкстремальными харак-
теристиками рабочего ос-
лабления.
Рис. 11.9. График рабочего ослабле-
ния фильтра Золотарева 5-го порядка
Фильтры с характеристиками Золотарева можно рассматри-
вать как частный случай фильтров с характеристиками Чебыше-
ва, когда значения минимумов ослабления фильтра в полосе не-
пропускания выравнены, а число всплесков — максимально воз-
можное при выбранном значении т.
Из данного параграфа мы узнали, что:
• В фильтрах Баттерворта нижних частот функцией фильт-
рации является полином Баттерворта. Эти фильтры харак- *
теризуются максимально плоским ослаблением в полосе
пропускания. Чем больше порядок фильтра, тем выше кру- ?
тизна его частотных характеристик. Ч
• Фильтры Чебышева — это фильтры с равноволновой коле- 1
бательной характеристикой ослабления в полосе пропуска- «
ния и более крутой, чем у фильтров Баттервората, харак- J
теристикой ослабления в полосе непропускания. Функцией J
фильтрации здесь является полином Чебышева.
• В фильтрах со всплесками ослабления функцией фильтра-
ции являются дроби Чебышева и дроби Золотарева.
Фильтры Золотарева — это фильтры со всплесками ослаб- >
ления в полосе непропускания. В полосе пропускания эти \
фильтры имеют равноволновую характеристику рабочего
ослабления.
11.3. Расчет и построение схем электрических
фильтров нижних частот
Электрический фильтр может быть сконструирован в виде
пассивного четырехполюсника из индуктивностей и емкостей.
30-6972
465
ZBX1 (?)
Рис. 11.10. Пассивный LC-фильтр,
включенный между генератором
и нагрузкой
Любые из рассмотренных
выше фильтров, как поли-
номиальные, так и со
всплесками ослабления, в
зависимости от особенно-
стей их применения могут
быть реализованы либо в
виде пассивных ZC-цепей,
либо в виде активных RC-
цепей.
Пассивные jLC-фильт-
ры обычно представляют собой реактивный лестничный четырех-
полюсник, включенный между генератором с активным внутрен-
ним сопротивление Rr и нагрузкой с активным сопротивлением
RK (рис. 11.10). Входное сопротивление реактивного четырех-
полюсника, нагруженного на сопротивление RH, обозначено на
рис. 11.10 Zbxi(p).
Если фильтр со стороны зажимов 1 — Г рассматривать как
двухполюсник, образованный реактивным четырехполюсником и
нагрузкой RH, то, зная выражение ZBXi(p), можно реализовать
данный двухполюсник одним из известных в теории цепей мето-
дов синтеза двухполюсников. Таким образом, задача реализации
фильтра сводится к реализации двухполюсника по его заданному
входному сопротивлению. Идея данного подхода принадлежит С.
Дарлингтону, и метод реализации фильтров называется методом
Дарлингтона.
На входе фильтра имеет место несогласованность, которую
можно оценить, введя в рассмотрение коэффициент отражения
ст(р) =
Rr+ZBxl(p)
Решая (11.25) относительно ZBXi(p), получаем
1 + о(р)
(11.25)
(11.26)
В (11.26) неизвестным является коэффициент отражения
о(р). В свою очередь, коэффициент отражения о(р) связан с
передаточной функцией Нр(р) = w(p)/u(p) следующим соотно-
шением:
а(р)о(-р) = 1-Нр(р)Нр(-р) =
_ u(p)v(-p)-w(p)w(-p) (11.27)
о(р)и(-р)
466
Из (11.27) следует, что знаменатель у о(р) такой же, как и
у Яр(р): им является полином о(р). Остается найти нули пра-
вой части выражения (11.27) и половину из них «приписать» по-
линому числителя о(р). Последний формируется из нулей по
теореме Виета.
Пример 11.3. Реализуем фильтр нижних частот Баттерворта вто-
рого порядка из примера 11.1 в виде пассивной LC-
схемы. Внутреннее сопротивление генератора 1 кОм.
В примере 11.1 была получена передаточная функ-
ция Баттерворта второго порядка Нр(р) = 1/(р2+1,41/2+1)
для нормированных значений частоты Q = со/со н =
= со/(2л • 159 • 103) = со/106, где <вн = <вп = 2itfn. Реа-
лизация нормированной передаточной функции при-
ведет к схеме с нормированными-Значениями реак-
тивных элементов (обозначим их L, С), которые за-
тем необходимо денормировать для получения ре-
альных значений.
В соответствии с (11.27)
р2 +1,41р +1 р2 -1,41/2 + 1
=_____________________________
(р2 +1,41/2+ 1)(/22 - 1,41р +1)
Нули ЭТОЙ функции /201,02,03,04 = 0- Полином чис-
лителя а(р) в соответствии с теоремой Виета равен
(P-Poi)-(P-Po2) = Р2- Отсюда <?(/?) =р2/(р2+1,41/2+1).
Согласно (11.26)
z (р) = 1 о3 1~Р2/(р2 +1,41/2 + 1) = 1,41- 103/2 + 103
1 + р2/(р2 + 1,41/2 + 1) 2р2+ 1,41/2 + 1
Реализацию двухполюсника с входным сопро-
тивлением ZBXi(p) осуществим разложением в цеп-
1 к 1,41 мГн
^вх1 (?)
Рис. 11.11. Схема пассивного £С-фильтра
к примеру 11.3
30*
467
ную (лестничную) дробь [1]. Представим ZBxl(p) =
= 1/УВХ1(р) и проведем разложение проводимости:
1 -й этап _2р2 +1,41р +1 1,41 • 103р +103 .
2р2 +1,41р 1,4110-3р ’
1
2-й этап
_1,41103р + 103 1_________.
1,41-103р 1,41 103р ’
103
3-й этап
Процесс разложения закончен. Входное сопро-
тивление ZBxl(p), представленное цепной дробью,
имеет вид
ZBX1(p) = pC + l/(pL + l/GH) =
=_____________1______________
1,41 • 10’3р +----—=•
К 1,41103р + 1/10-3
Схема двухполюсника, входное сопротивление
которого соответствует данной цепной (лестничной)
дроби, приведена на рис. 11.11. Нормированные зна-
чения элементов С = 1,41 • 10-3, L = 1,41 • 103. Актив-
ная проводимость нагрузки не нормируется и равна
GH = 10-3 См, т.е. сопротивление нагрузки RK = 1 кОм.
Денормировать значения элементов можно следующим
образом. Комплексная проводимость нормированной
емкости /QC = j(co/<bh)C = j’QC, откуда ненормиро-
ванное значение емкости С = С/<он = 1,41 Ю-3/106 =
= 1,41-10-9 Ф = 1,41 нФ.
Подобным образом комплексное сопротивление
нормированной индуктивности /QL = / (со/<вн)£ = jQL
или L = £/сон = 1,41 • 103/106 = 1,41 • IO’3 Гн = 1,41 мГн.
Аналогично рассмотренному примеру решается задача реализа-
ции фильтра любого порядка. Например, полиномиальный ФНЧ
пятого порядка (т = 5) реализуется в виде одной из двух схем, по-
казанных на рис. 11.12, а и б. Количество реактивных элементов
468
Рис. 11.12. Пассивные LC-фильтры нижних
частот пятого порядка
=Т=С2 =i=c4
о
определяется порядком фильтра т. Отличие фильтра Баттервор-
та от фильтра Чебышева будет заключаться в этом случае только
в разных значениях реактивных элементов, получаемых в про-
цессе реализации соответствующих передаточных функций.
По подобной схеме осуществляется и реализация передаточ-
ных функций фильтров со всплесками затухания (Чебышева или
Золотарева). Разложение входного сопротивления таких фильт-
ров в цепную дробь приведет к схемам, содержащим резонансные
контуры, в которых резонансы происходят на частотах ,
Qoo2, .... Наличие этих контуров и обеспечивает бесконечно
большое затухание на частотах всплеска.
Так, ФНЧ пятого порядка со всплесками затухания на часто-
тах Qooi и Ооог реализуется в виде одной из схем, приведенных
на рис. 11.13, а и б. И в первой, и во второй схемах контуры рас-
считаны на резонансные частоты и В первой схеме в
параллельных контурах происходят резонансы токов; сопротив-
ления контуров принимают бесконечно большие значения. В ре-
зультате на частотах резонансов и DW2 наблюдается «обрыв»
продольных ветвей фильтра и сигнал от генератора в нагрузку не
поступает, т.е. фильтр вносит бесконечно большое ослабление.
Во второй схеме в последовательных контурах происходят резо-
нансы напряжений; сопротивления контуров обращаются в нуль.
Таким образом, здесь на частотах и Qoo2 поперечные ветви
«закорачивают» нагрузку и сигнал на выход фильтра не поступа-
ет. Таким образом, имеет место бесконечно большое ослабление.
Рис. 11.13. Схемы ФНЧ пятого порядка со всплесками ослабления
469
Электрический фильтр, не содержащий индуктивностей, —
это чаще всего усилитель, охваченный частотно-зависимой об-
ратной связью, построенной на резистивных и емкостных эле-
ментах. Фильтры, представляющие собой комбинацию пассивной
ЯС-цепи и активного элемента, называют активными RC-
фильтрами. В качестве активного элемента чаще всего использу-
ют операционные усилители с двумя входами: инвертирующим и
неинвертирующим.
Реализация передаточных функций фильтров на активных ЯС-це-
пях осуществляется следующим образом. Заданную функцию Нр(р)
порядка т разбивают на произведение передаточных функций не
выше второго порядка, т.е. Яр(р)=Яр1(р)Яр2(р)...Яр^(р).
Каждую передаточную функцию Яр,(р) реализуют в виде ARC-
звена первого или второго порядка. Схему ARC-фильтра полу-
чают путем каскадного соединения звеньев.
Пример 11.4. Пусть задана передаточная функция полиномиаль-
ного фильтра Чебышева пятого порядка:
н( ) =____________________________0,0628________________
?Р р5 +0,397р4 +1,415р3 +0,543р2 +0,408р+0,0628 ’
Полюсы этой функции (корни знаменателя): р^ =
= -0,177; р2.3=-0,143±/0,597; р4>5=-0,0547±/0,966.
Вещественный полюс рх дает по теореме Виета со-
множитель первого порядка (р - р\) = р + 0,177; пер-
вая пара комплексно-сопряженных полюсов р2 и
р3 — сомножитель второго порядка (р~Р2)(р~Рз)-
= р2 + 0,286р + 0,377; вторая пара полюсов р4 и р5 —
сомножитель (р - р4) • (р - р5) = р2 + 0,1 Юр + 0,936.
Тогда
нр(р)=
=0,0628=
(р+0,177 )(р2+0,286р+0,377)(р2+0,110р+0,93б)
0,177 0,377__________0,936
р+0,177 р2+0,286р+0,377 р2+0,110р+0,936
= Яр1(р)Яр2(р)Яр3(р).
Таким образом, фильтр Чебышева пятого поряд-
ка может быть реализован двумя звеньями с переда-
точными функциями второго порядка и одним зве-
ном с передаточной функцией первого порядка.
В практике проектирования активных ЯС-фильтров исполь-
зуется большое число схем, реализующих передаточные функции
470
a)
Рис. 11.14. Схемы активных /?С-фильтров
первого и второго порядков. Один из способов построения таких
схем показан на рис. 11.14, а. Пассивная часть схемы представ-
лена в виде цепи из элементов R и С. Между зажимами 2 и 3
включен операционный усилитель, в котором использован инвер-
тирующий вход. Примером такой пассивной /?С-цепи является
схема, приведенная на рис. 11.14, б. Передаточная функция изо-
браженного на рис. 11.14, б активного 7?С-фильтра может быть
получена любым из методов теории цепей и имеет вид
Н (п) - ^^(р) __________________________ (1128)
р(Ю Щ(р) У5(У1 + У2 + Уз + У4) + У3У4’
Для реализации в виде такой цепи полиномиального фильт-
рового звена второго порядка с передаточной функцией
----Г (11'29)
Ь2р +61Р + 60
нужно выбрать проводимостиyj, У3 и У4 активными: Gf, G3 и
G4, а проводимости У2 и У5 — емкостными: рС2 и рС5. Тогда
(11.28) запишется в следующей форме:
Нр (р) = —7---------~G1G3-------------. (11.30)
Р p2C5C2+pC5(G1+G3+G4) + G3G4
Сопоставление коэффициентов при р в соответствующих сте-
пенях и свободных членов из (11.30), выраженных через элемен-
ты фильтра, с заданными числовыми значениями коэффициентов
при р и свободных членов из (11.29) позволяет определить зна-
чения элементов фильтра.
Пример 11.5. Реализуем фильтр нижних частот Баттерворта вто-
рого порядка из примера 11.1 в виде активной RC-
цепи.
Передаточная функция НЧ фильтра Баттерворта
второго порядка была получена ранее: Нр(р)=
471
Рис. 11.15. Активный 7?С-фильтр к примеру 11.5
=1/(р2 +1,41р+1). Для сопоставления с ней переда-
точной функции (11.30) представим последнюю в ви-
де, когда коэффициент при р2 равен 1:
rr / \ _ -G\G3 1
р [Р) ~ С,С. „2 G1+G3+G4 G3G4'
р и С2 С2С5
Приравнивая коэффициенты при р и свободные
члены этих передаточных функций, получаем три урав-
нения с пятью неизвестными^ Gt, G3, G4, С2 „и_ С5:
G\G3IC2C5 =1; (Gi+G3+G4)/C2=1,41; G3G4/C2C5=1.
Следует учесть, что в уравнения входят норми-
рованные значения емкостей С2 и С5, так как коэф-
фициенты передаточной функции фильтра Баттервор-
та получены для нормированной частоты £1 = (о/сон,
где <он=а>п=2л/’п=2л159 103=106 рад/с.
Поскольку искомых величин больше, чем урав-
нений, зададимся частью из них. Выберем приемле-
мые значения проводимостей Gt, G3 hG4, например
Gi = G3 = G4 =10-3 См, т.е. Rt = R3 = K4 = 1 кОм.
Далее из второго уравнения легко получить С2 =
=(G1+G3+G4)/l,41 = 2,128-10-3, а из первого и треть-
его уравнений — С5 = G^G/JC^ = 0,47 • 10~3. Денорми-
рованные значения емкостей С2 = C->las„ = 2,13 нФ,
С5 =С5/сон =0,47 нФ.
Схема фильтра приведена на рис. 11.15.
Реализация фильтров со всплесками ослабления, передаточ-
ные функции которых описываются выражением (11.21), осуще-
ствляется так же, как и реализация полиномиальных фильтров.
Передаточная функция (11.21) разбивается на произведение про-
стейших (первого и второго порядков) передаточных функций; по-
следние реализуются в виде фильтровых ЛС-звеньев первого и вто-
рого порядков, соединяемых каскадно в общую схему фильтра.
472
Для реализации передаточных функций второго порядка с
нулем передачи: Hpi(р) = (р2 + а0)/[р2 + Ьхр + b0) используются
специальные фильтровые АЯС-звенья.
Более подробно методику синтеза активных ЯС-фильтров со
всплесками ослабления можно изучить, обратившись к специаль-
ной литературе.
Из данного параграфа мы узнали, что:
• Полиномиальные фильтры нижних частот могут быть по- I
строены в виде пассивных LC- или активных ЯС-цепей. i
• Пассивные LC-фильтры нижних частот рассчитываются по (
методу Дарлингтона: к реактивному LC-четырехполюснику
подключают нагрузку, определяют входное сопротивление
полученного двухполюсника и реализуют этот двухполюс-
ник в виде схемы Кауэра. 1
• Для реализации активных фильтров обычно используют |
типовые ЯС-звенья с операционными усилителями, охва-
ценными обратной связью. Сравнение требуемой переда- (
точной функции фильтра с передаточной функцией актив- j
ного ЯС-звена позволяет определить значения элементов Я ।
и С в схеме фильтра. |
11.4. Переход к фильтрам верхних частот,
полосовым и заграждающим
Для перехода от фильтра нижних частот к фильтрам других
типов используют преобразование шкалы частот. Для синтеза
фильтров верхних частот (полосовых заграждающих) можно бы-
ло бы заново повторить все выкладки, примененные к фильтрам
нижних частот. Однако такой подход нерационален. Обычно для
расчета ФВЧ, ПФ и ЗФ используют преобразование шкалы час-
тот ФНЧ-прототипа.
На рис. 11.16 приведены характеристики ослабления фильт-
ров: нижних частот (а), верхних частот (б), полосового (в) и за-
граждающего (г). Для ФНЧ эта характеристика построена как
для положительных, так и для отрицательных частот. Шкала
частот для каждого фильтра помечена для удобства буквенными
обозначениями: «н.ч», «в.ч», «п.ф», «з.ф».
Из рис. 11.16, а и б видно, что характеристика ослабления
ФНЧ в отрицательной области частот повторяет характеристику
ФВЧ. Преобразовать характеристику ФНЧ в характеристику
ФВЧ можно с помощью замены переменной
473
Рис. 11.16. Графики рабочего ослабления фильтров нижних частот
(о), верхних частот (б), полосового (в) и заграждающего (г)
(11.31)
где соп — граничная частота полосы пропускания ФНЧ и ФВЧ.
Действительно, такое преобразование частоты приводит к соот-
ветствию: частоты ©н ч = -оо частоте ©в ч = 0; частоты сон ч = -®п
частоте шв ч = ©п; частоты ©н ч = 0 частоте ©в ч = оо.
Чтобы из характеристики ФНЧ получить характеристику
ПФ (рис. 11.16, в), необходима замена переменной
®н.ч = ®п.ф — ®о/®п.ф = п.ф — ®о)/®п.ф = 22)
= <»о(®п.ф/юо-юо/в>п.ф),
'н.ч
где ©о = > ®П1 и ®п2 — граничные частоты по-
лосы пропускания ПФ; ю31 и ©з2 — граничные частоты полосы
непропускания ПФ.
Преобразование частоты (11.32) приводит к соответствию часто-
ты ®н.ч = -°0 частоте ©п ф = 0; частоты ©н ч = 0 частоте ©п ф = ©0;
частоты ©н ч = оо частоте ©п ф = оо.
Характеристику (рис. 11.16, г) заграждающего фильтра мож-
но получить из характеристики ФНЧ, применяя преобразование
частоты
474
юо • 0>3.ф
(11.33)
Схема пассивного LC-фильтра любого типа получается пу-
тем преобразования схемы низкочастотного фильтра-прототипа.
Замена переменных (11.31) и (11.32) в выражении для квадрата
АЧХ |Яр(/<о)|2 фильтра нижних частот приводит при реализа-
ции этой функции к преобразованию схемы ФНЧ в схемы ФВЧ
и ПФ. Индуктивное сопротивление ФНЧ /<х>нч£нч переходит
при преобразовании частот (11.31) в сопротивление:
УСОн.Ч-^-Н.Ч = ] (— ®п/®в.ч )-^н.ч = ®п/( J®B.4^-H.4 ) ~ 1/( У^В.чСв.Ч ) >
т.е. в емкостное сопротивление ФВЧ, где Св ч = .
Емкостная проводимость
ЧСН ч = ] (—®п/®В.Ч )(^Н.Ч = ®п/(/®В.чСн.Ч ) = 1/0®В.Ч-^В.Ч )
переходит в индуктивную проводимость фильтра ВЧ с индуктив-
ностью £вч = Сн ч/(0^.
Преобразование частоты (11.32) приводит к замене индук-
тивного сопротивления ФНЧ
г • г ®0 г • г 1
У^н.ч^н.ч ” /®п.ф^н.ч + • ^Н.Ч “ 7ЮП.ф^П.ф1 + п
7®п.ф 7®п.ф^п.ф1
сопротивлением последовательного контура в ПФ с элементами
^п.ф! = ^Н.Ч И ^п.ф1 = у(®п^н.ч)-
Емкостная проводимость ФНЧ
./^н.ч^н.ч = У^п.фСн.ч “Сн.ч = /<Юп.фСп.ф2 7
7®п.ф 7^п.ф-^п.ф2
заменяется в ПФ проводимостью параллельного контура с эле-
ментами Спф2 = Снч и 1пф2 = 1/(®оСнч).
Нетрудно убедиться также, что индуктивный элемент ФНЧ
преобразуется в ЗФ в параллельный колебательный контур с ре-
зонансной частотой соо, а емкость ФНЧ — в последовательный
колебательный контур с той же резонансной частотой.
Пример 11.6. Рассчитаем полосовой фильтр с характеристиками
Баттерворта, удовлетворяющий требованиям: Ар тах =
= 3 дБ; Apmin = 12,2 дБ; fa1 = 1241 кГц; /п2 =
= 1400 кГц; /з! = 1168,5 кГц; fa2 = 1486 кГц.
Для решения поставленной задачи нужно сначала
построить низкочастотный фильтр-прототип, а затем с
помощью преобразования частоты перейти к ПФ.
475
Рис. 11.17. Схема полосового LC-фильтра
к примеру 11.6
1,41 мГн 6’?пФ
6,0 мкГн
1к
о
Пересчитаем требования ПФ (рис. 11.16, в) в
требования к НЧ-прототипу (рис. 11,16, а). Вос-
пользуемся формулой (11.32): /0 = V/ni/n2 = >//з1/з2 =
= 1734,4 кГц; /п = fn2 = fn2 =159 кГц;
/з =/’з2-/о//з2 =f32-f3i = 318 кГц. В качестве нор-
мирующей частоты выберем fH = fn. Тогда нормиро-
ванные частоты Qn = 1 и = /з/7п = 2. Итак, требо-
вания к НЧ-прототипу запишем в виде Ар тах = 3 дБ;
Ар min = 12,2 дБ; /„ = 159 кГц (Qn = 1); f3 = 318 кГц
(Q3 = 2).
В примере 11.1 для такого НЧ-фильтра были
получены квадрат АЧХ 1Яр (/Q)j2 = 1/(1 + Q4), ра-
бочее ослабление Ап = lOlgCl + Q4) и передаточная
функция Яр (р) = 1Др2 +1,41р +1).
В примере И.о это фильтр оыл реализован в
виде схемы, изображенной на рис. 11.11 с элемен-
тами LH 4 = 1,41 мГн и Сн ч = 1,41 нФ.
При переходе к требуемому полосовому фильтру
необходимо индуктивность продольного плеча LH 4
фильтра НЧ-прототипа заменить последовательным
контуром с элементами Ln.$i = £н.ч =1,41 мГн и
СП.Ф1 = 1/[(2#о )2 А,.,] = 6 • 10-f2 Ф = 6,0 пФ.
Вместо емкости Сн ч в поперечном плече поло-
сового фильтра будет включен параллельный кон-
тур с элементами Сп.ф2 = Сн.ч = 1,41 нФ и La ф2 =
= 1/[(2nf0 )2 Сн ч] = 6 • 10-6 Гн = 6 мкГн.
Схема искомого полосового фильтра приведена
на рис. 11.17.
Для получения схемы активного Я С-фильтра любого типа
необходимо вначале преобразовать передаточную функцию
ФНЧ-прототипа. В активных ЯС-фильтрах для того, чтобы пе-
рейти от передаточной функции ФНЧ-прототипа к передаточным
функциям ФВЧ и ПФ, следует осуществить замену комплексной
переменной р. Из (11.31) получаем для ФВЧ
476
7®Н.Ч — ®п/у®в.4
или /QH ч = 1//QB ч , (11.34)
где QH ч = (Вн.ч/Ип и QB ч = сов.ч/а>п •
Заменяя в (11.34) оператор jQ на оператор р, запишем пре-
образование переменной р в выражении нормированной по часто-
те передаточной функции ФНЧ-прототипа:
(11.35)
второго по-
(11.36)
Рн.Ч ~ 1/Рв.Ч •
Передаточная функция полиномиального звена
рядка ФНЧ имеет вид
-------Г-------Г-
Ь2Рн.ч +&1Рн.ч +Ь0
Замена переменной (11.35) в этом выражении приводит к пе-
редаточной функции полиномиального звена второго порядка
ФВЧ:
Рв.ч
Яр (рВ'Ч) — Н , 2 , ,
&0Рв.ч+&1Рв.ч+&2
(11.37)
Для реализации звена с передаточной функцией (11.37) мо-
жет быть использована схема рис. 11.14, 6, в которой следует вы-
брать проводимости У2 и У3 активными, т.е. У2 = G2 и У5 = G5, а
проводимости У1, У3 и У4 — емкостными, т.е. Yt = pQ; У3 = рС3
и У4 = рС4. Подставляя эти значения проводимостей в выраже-
ние (11.28), получаем передаточную функцию
~Pb.hQ(^3
Яр (рв.ч) = Н ------------(11.38)
РВ.4С3С4 + pG3 (С4 + С3 + С4) + G2G5
АДС-звена ФВЧ второго порядка, схема которого дана на
рис. 11.18. Значения элементов схемы будут найдены, если при-
равнять коэффициенты из (11.37) и (11.38) при соответствующих
степенях р.
Для перехода от НЧ-прототипа к полосовому фильтру вос-
пользуемся (11.33):
/®н.ч ~ (®о — ®п.ф )/j®п.ф или = (fig— ПП ф)/уОпф, (11.39)
где = сон ч/оп; £^п.ф = ®п.ф/®п, Оо = соо/соп.
Вводя переменную р = jQ. и учитывая, что р2 =-Q2, нахо-
дим из(11.39)
Рн.ч ~ (Рн.ч «О )/Рп.ф •
(11.40)
Такая замена переменной рнч в (11.36) приводит к переда-
точной функции полосового фильтра
477
Рис. 11.18. Активный RC-
фильтр верхних частот
Рис. 11.19. Активный RС-
полосовой фильтр
Рп.ф
Нр ( Рп.ф ) Н ф + ф + ф + 6,рп ф + ’
(11.41)
где &4 = b2; b3 = b{; b2 = 262Qq + b0; b\= b^l; b'Q = 62^о •
Видим, что при переходе к ПФ порядок передаточной функ-
ции удваивается. Передаточную функцию (11.41) можно разбить
на произведение передаточных функций второго порядка и каж-
дую из них реализовать отдельной ARC-схемой.
Запишем передаточную функцию ПФ второго порядка:
2 (11.42)
^2п.фРп.ф "* "1п.фРп.ф ®0п.ф
Подобную передаточную функцию имеет ЛДС-схема, изображен-
ная на рис. 11.14, б при Yi =G1( У2 = G2, У5 = G5 и У3 = рС3,
У4 = рС±. Действительно, из (11.28) находим
Wp(Pn.*) = Tec v <,,'43)
Рп.фСзС4 + Рп.фСз (C3 + C4) + G5 (Gj + G2 )
Элементы схемы фильтра (рис. 11.19) определяются сопос-
тавлением (11.42) и (11.43).
Из данного параграфа мы узнали, что:
• Для перехода от низкочастотного прототипа к высокочас- J
тотным, полосовым и заграждающим фильтрам используют !>
преобразование частоты.
• В пассивных LC-фильтрах из схемы НЧ-прототипа сразу :
же получают схему требуемого фильтра, а в активных RC- J
фильтрах сначала преобразуют передаточную функцию.
478
11.5. Анализ фильтров с механическими
резонаторами
Аналоговые фильтры могут использовать различные механи-
ческие резонаторы. В многоканальных системах передачи разде-
ление каналов по частоте осуществляется с помощью полосовых
фильтров. Чтобы сигналы одного канала не попадали в другой,
ПФ должны иметь высокую избирательность. Добротность резо-
нансных контуров таких фильтров Q > 20 ... 25/’0/(/п2 — /п1) Так,
для фильтра с fo = 62 кГц и полосой пропускания - fni =
= 4 кГц Q > 300, в то же время для фильтра с fQ = 106 кГц и
/п2-/п1 = 4кГц Q > 1500.
В радиосвязи используются еще более высокие частоты (де-
сятки и сотни мегагерц), и для построения избирательных
фильтров нужны резонаторы с добротностью в тысячи и десятки
тысяч единиц. Такие значения добротности никогда не обеспечи-
ваются в ZC-резонаторах (их добротность не превышает сотен
единиц), поэтому в фильтрах применяют высокодобротные меха-
нические резонаторы, пьезоэлектрические, магнитострикционные
и электромеханические.
В пьезоэлектрических фильтрах роль резонатора выполняет
пластинка, вырезанная специальным образом из материала, обла-
дающего пьезоэлектрическим эффектом (например, из кристалла
кварца). Пьезоэффект кварцевой пластинки заключается в появ-
лении на ее поверхностях электрических зарядов при механиче-
ском воздействии на пластинку. Существует и обратный пьезо-
эффект — возникновение механических колебаний пьезопластин-
ки при помещении ее в переменное электрическое поле.
Если пьезопластинку поместить между металлическими об-
кладками и подать на обкладки переменное напряжение, то
пластинка начнет совершать механические колебания. На по-
верхностях пластинки возникнут электрические заряды, и во
внешней цепи потечет ток. При совпадении частоты переменно-
го напряжения и частоты собственных колебаний пластинки
возникнет механический резонанс, амплитуда колебаний дос-
тигнет максимума, и ток во внешней цепи будет максимальным.
Таким образом, механический резонанс в кварцевой пластине
подобен резонансу напряжений в последовательном колебатель-
ном контуре.
Эквивалентная схема пьезоэлектрического (в частности, квар-
цевого) резонатора (рис. 11.20) помимо эквивалентных индук-
тивности L и емкости С резонатора содержит емкость кварцедер-
жателя Ск, т.е. обкладок, между которыми помещена кварцевая
пластинка.
479
Рис. 11.20. Пьезоэлектрический
фильтр и его эквивалентная схема
Рис. 11.21. Мостовая схема
кварцевого фильтра
Пьезоэлектрические фильтры с кварцевыми резонаторами на-
зывают кварцевыми. Добротность кварцевых резонаторов дости-
гает 10...20 тыс. ед. Кварцевые фильтры могут быть построены
по мостовой схеме (рис. 11.21).
Магнитострикционные фильтры строятся на основе резо-
наторов из ферромагнитного материала, обладающего магнитост-
рикционным эффектом (например, из сплава никеля с кобаль-
том). Магнитострикционный эффект состоит в том, что стержень
из ферромагнетика, помещенный в переменное магнитное поле,
изменяет свои геометрические размеры. Обратный эффект — из-
менение магнитной проницаемости стержня при механическом
воздействии на него. Если, например, никель-кобальтовый стер-
жень поместить внутрь катушки индуктивности, создающей пере-
менное магнитное поле, его геометрические размеры начнут ме-
няться. При этом будет меняться и его магнитная проницаемость.
В катушке индуктивности наведется эдс, направленная против
эдс генератора и уменьшающая ток во внешней цепи. При меха-
ническом резонансе амплитуда колебаний стержня будет макси-
мальной, а ток во внешней цепи — минимальный. Таким образом,
механический резонанс магнитострикционного стержня подобен
резонансу токов параллельного колебательного контура.
Эквивалентная схема резонатора приведена на рис. 11.22 и
включает в себя элементы LM и См эквивалентного резонатору
контура, а также индуктивность До, учитывающую рассеяние
магнитного потока при замыкании его через воздух.
Добротность магнитострикционных резонаторов ниже, чем
кварцевых, и составляет 5... 10 тыс. ед. Магнитострикционные
фильтры строятся по мостовой схеме (рис. 11.23).
В электромеханических фильтрах резонаторами являются
металлические тела (диски, шарики, стержни, пластинки), соеди-
Рис. 11.22. Эквивалентная схема резонатора
480
Рис. 11.23. Мостовая
схема магнитострикцион-
ного фильтра
Рис. 11.24. Электромеханический
фильтр
ненные металлическими связками. На рис. 11.24 изображен трех-
резонаторный стержневой электромеханический фильтр. Возбуж-
даются колебания в фильтре с помощью входного магнитострик-
ционного преобразователя (МСП); снимаются колебания с выхо-
да фильтра с помощью выходного МСП. Электромеханические
фильтры являются также высокодобротными.
Кроме рассмотренных существуют и другие типы фильтров:
фильтры с переключаемыми конденсаторами, кварцевые фильтры
на поверхностных акустических волнах (ПАВ) и др. С некоторы-
ми из них можно ознакомиться в [4] и специальной литературе.
Из данного параграфа мы узнали, что:
• Для получения фильтров с высокой добротностью исполь-
зуются пьезоэлектрические, магнитострикционные и элек- |
тромеханические резонаторы. |
• Механический резонанс в кварцевой пластине пьезоэлек- |
трического фильтра подобен резонансу напряжений в по- 1
следовательном колебательном контуре. |
• Механический резонанс магнитострикционного стержня по-
добен резонансу токов в параллельном колебательном кон- |
туре- |
• Пьезоэлектрические и магнитострикционные фильтры стро- •
ятся по мостовой схеме. л
• В электромеханических фильтрах резонаторами являются
металлические тела, соединенные металлическими связками.
Вопросы и задания для самоконтроля
1. Что такое электрический фильтр? Какие типы фильтров суще-
ствуют?
2. Характеристика рабочего ослабления фильтра изображена на
рис. 11.3. Определить тип фильтра.
31 -6972
481
3. Какой вид имеют функции фильтрации фильтров Баттерворта.
Чебышева, Золотарева?
4. Привести графики Ap(Q) ФНЧ третьего порядка Баттервор
та, Чебышева и Золотарева.
5. Рассчитать коэффициент неравномерности ослабления в полосе
пропускания и порядок фильтра Баттерворта, удовлетворяю-
щего требованиям Ар тах = 2 дБ; Apmin = 25 дБ; fa = 15 кГц;
f3 = 26 кГц.
6. Найти выражение для передаточной функции ФНЧ Баттервор-
та, удовлетворяющего требованиям, приведенным в задании 5.
7. Рассчитать порядок и найти операторную передаточную функ-
цию ФНЧ Чебышева, удовлетворяющего требованиям А„ тах =
= 1,25 дБ; Ар min = 30 дБ; fn = 105 кГц; Д = 2,5 105 кГц.
8. Привести LC-схемы фильтров, имеющих характеристики, изо-
браженные на рис. 11.4.
9. Привести LC-схему фильтра, характеристика которого изо-
бражена на рис. 11.3.
10. Привести £С-схему ФНЧ Золотарева, а также график зави-
симости его рабочего ослабления от частоты.
11. Каков алгоритм расчета фильтров методом Дарлингтона?
12. Реализовать ФНЧ Баттерворта третьего порядка, имеющего
передаточную функцию Яр(р) = 1/(р3 + 2р2 + 2р +1), в виде
пассивной £С-схемы. Внутреннее сопротивление генератора
Rr = 1.
13. Какие фильтры называются активными ЯС-фильтрами?
14. Какие передаточные функции имеют У?С-фильтровые звенья
первого и второго порядков? Как получить передаточную
функцию фильтра более высокого порядка?
15. Реализовать активный ЯС-фильтр, имеющий передаточную
функцию, приведенную в задании 12.
16. Как осуществить переход от ФНЧ к ФВЧ, ПФ, ЗФ?
17. Доказать, что при переходе от ФНЧ к ЗФ индуктивность
фильтра-прототипа преобразуется в параллельный контур в
ЗФ, а емкость — в последовательный контур.
18. Привести схемы LC-фильтров, имеющих характеристики, изоб-
раженные на рис. 11.16, б, в, г.
19. Рассчитать ФВЧ с максимально плоской характеристикой ос-
лабления, удовлетворяющий требованиям Артах =1,5 дБ;
Ар min = 20 дБ; <в3 = 106 с’1; <оп = 2 • 106 с1.
20. Как осуществляется переход от схемы НЧ-прототипа к схемам
ФВЧ и ПФ в активных 7?С-фильтрах?
21. Какие высокодобротные механические резонаторы использу-
ются для построения фильтров?
482
Глава 12. Анализ и расчет амплитудных корректоров
12.1. Амплитудно-частотные искажения сигнала
и их коррекция
Непостоянство амплитудно-частотной характеристики цепи
в рабочем диапазоне частот приводит к искажению формы сиг-
нала. Рассмотрим некоторую электрическу'ю цепь — четырехпо-
люсник (рис. 12.1), имеющую амплитудно-частотную характери-
стику (АЧХ), изображенную на рис. 12.2, а и ослабление, изо-
браженное на рис. 12.2, 6. Пусть для упрощения входной сигнал
цвх(£) состоит из суммы всего двух гармоник с частотами и
2©! (рис. 12.3, а). Форма входного сигнала показана на этом ри-
сунке жирной линией.
Из анализа графиков АЧХ и ослабления цепи следует, что
амплитуда первой гармоники при прохождении сигнала через
цепь останется практически неизменной, а амплитуда второй гар-
моники уменьшится в несколько раз.
Результат сложения гармоник на выходе цепи дает форму
сигнала, отличающуюся от входной (рис. 12.3, б).
Изменение формы сигнала на выходе цепи по сравнению с
формой сигнала на ее входе называется искажением сигнала. Ко-
гда искажения формы сигнала связаны с неравномерностью ам-
плитудно-частотной характеристики цепи, они носят название
амплитудно-частотных искажений.
Таким образом, условием отсутствия амплитудно-частотных
искажений в цепи следует считать постоянство ее АЧХ (ослаб-
ления) на всех частотах (см. § 4.4):
Ж(в) = /С; A(®) = 201gl/H(co) = Ао. (12.1)
На практике условие (12.1) часто не выполняется, т.е. АЧХ и
ослабление цепей аппаратуры и линий связи не являются посто-
Рис. 12.2. Графики АЧХ (а) и
ослабления (б) четырехполюсника
483
Рис. 12.1. Электрическая
цепь четырехполюсника
31»
Рис. 12.3. Сигналы на входе (а) и выходе (б) цепи
явными. Эти цепи практически всегда вносят амплитудно-частот-
ные искажения в передаваемый сигнал. Устранить подобные ис-
кажения полностью не удается, но их можно уменьшить до вели-
чин, допустимых соответствующими нормами. Для этих цепей
применяются амплитудные корректоры.
Амплитудный корректор — это четырехполюсник, который
включается каскадно с цепью. Его задача заключается в том, что-
бы дополнить АЧХ цепи или ее рабочее ослабление до постоян-
ной величины на всех частотах рабочего диапазона. Вне рабочего
диапазона АЧХ цепи может иметь любую форму.
На рис. 12.4 изображена цепь, работающая между генерато-
ром с внутренним сопротивлением и нагрузкой RK. Рабочий
коэффициент передачи этой цепи в соответствии с (10.3)
Для достижения условий безыскаженной передачи между це-
пью и нагрузкой включен амплитудный корректор (рис. 12.5).
Чтобы режим работы цепи не нарушался, входное сопротивление
Рис. 12.5. Каскадное включение
цепи и корректора
Лн
Рис. 12.4. Нагруженная
электрическая цепь
484
корректора должно равняться соп-
ротивлению нагрузки. Очевидно,
только при этом условии напря-
жение на выходе цепи будет равно
U_m2, как и в схеме рис. 12.4 до
включения корректора.
Если обозначить напряжение
на выходе каскадного соединения
цепи и корректора U 'т2, то рабо-
чий коэффициент передачи такого
соединения запишется в виде
Рис. 12.6. Ослабление цепи,
корректора и их каскадного
соединения
Н ( /ml = т2 1^г
р<; )- и.г К'
Разделим и умножим это выражение на Um2 и представим
его в виде произведения двух сомножителей:
Яр (><о) = [ J# f тИ] = ЯРц (»• Як (».
к ОщГ УКн Д О m2 7
Первый сомножитель представляет рабочий коэффициент пе-
редачи цепи (рис. 12.4), а второй — коэффициент передачи по
напряжению корректора. Тогда для АЧХ каскадного соединения
можно записать
Яр(со) = Ярц(о))Як(<о).
Ослабление, вносимое каскадным соединением цепи и коррек-
тора, вычисляется путем сложения ослаблений цепи и корректора:
A(co)=201g 1 x=201g 1 +201g.^-L =лрц((й)+Ак((о).
Яр (со) Ярц (со) Як(со) F
Из рис. 12.6 видно, что корректор должен вносить ослабле-
ние, дополняющее ослабление цепи в рабочей полосе частот
сон...сов до постоянной величины Ао.
Из данного параграфа мы узнали, что:
• Если цепь имеет различные значения амплитудно-частотной 1
характеристики на разных частотах, т.е. неодинаково ос- j
лабляет гармонические составляющие входного сигнала, то Г
форма сигнала на выходе цепи будет искажена. |
• Задача амплитудной коррекции заключается в том, чтобы t
дополнить амплитудно-частотную характеристику цепи или ’
ее рабочее ослабление до постоянной величины на каждой ,
частоте в рабочем диапазоне. .
• Для коррекции АЧХ и рабочего ослабления используют
амплитудные корректоры. <
485
12.2. Анализ схем
амплитудных корректоров
Рис. 12.7. Т-перекрытый
корректор
Пассивные амплитудные коррек-
торы строят, как правило, в виде
симметричной Т-перекрытой схемы.
Симметричный Т-перекрытый четырех-
полюсник приведен на рис. 12.7. Со-
противления Zj и Z2 выбираются об-
ратными, т.е. Zj • Z2 = Rq . Если такой
четырехполюсник нагрузить на сопро-
тивление Rq, то его входное сопротив-
ление окажется равным также Ro.
ция по напряжению схемы
формуле
Комплексная передаточная функ-
рис. 12.7 может быть вычислена по
уу — —м2 _ *0
—К tZml 21 + Ro
или Нк (j со) = ——.
Операторная передаточная функция по напряжению имеет
вид
Вычислим ослабление, вносимое корректором:
Ак (о) = 201g—1— = 201g к \ СО ✓ <. ^1(» Ro ’
(12.2)
(12.3)
Данная формула показывает, что, зная поведение Zt на раз-
ных частотах, можно определить частотную зависимость ослабле-
ния Ак.
Пример 12.1. Схема двухполюсника Zj в продольном плече
корректора изображена на рис. 12.8, а. Построим
график частотной зависимости ослабления корректо-
ра Ак (со).
Построим вначале график частотной зависимости
сопротивления реактивного двухполюсника ^(со),
образованного элементами Ц, Ct, L2 и С2. На нуле-
вой частоте индуктивное сопротивление равно нулю,
а емкостное — бесконечности, поэтому Х](0)->-<».
Двухполюсник имеет три резонанса, причем пер-
вый — резонанс напряжений на частоте ©t, второй —
резонанс токов на частоте со2, третий — снова резо-
нанс напряжений на частоте со3. Это значит, что
486
a)
Рис. 12.8. Схема двухполюсника в продольном плече
корректора (в), сопротивление ее реактивной части (б),
полное сопротивление двухполюсника (в) и ослабление
корректора (г)
Xt (©!) = Xi (®3) = 0, Xt (со2)При о —> оо со-
противление Xj (со) также бесконечно большое
(рис. 12.8, б).
Сопротивление Z], стоящее в продольном плече
корректора, содержит помимо реактивных элементов
активное сопротивление Rt (рис. 12.8, а). Поэтому
на частотах, равных 0, со2 и оо, на которых реактив-
ное сопротивление (со) стремится к оо, полное со-
противление IZJ двухплюсника ограничено величи-
ной Ri (рис. 12.8, в).
Ослабление корректора Ак(со) рассчитывается
по формуле (12.3) и зависит от значений ^(со)].
487
График Ак(со) повторяет по форме график |Zj (со)|.
На частоте резонанса токов со2, а также на частотах
со = 0 и со —> со ослабление корректора Ак(со) дости-
гает своего максимального значения:
max ~ 201g 1 ,+^
На частотах резонанса напряжений cot и со3 зна-
чение Ак(со) равно нулю (рис. 12.8, г).
Пример 12.2. Задано ослабление Арц((о) цепи, подлежащей кор-
рекции (рис. 12.9, а). Приведем схему корректора,
выравнивающего характеристику этой цепи до значе-
ния Ао.
Находим требуемую характеристику ослабления
Ак(со) корректора из условия Ак(со) = Ло - Арц(со).
График Ак (со) приведен на этом же рис. 12.9, а.
По характеристике Ак(со) строим графики час-
тотной зависимости полного сопротивления [Zj (со)| и
Рис. 12.9. Схемы и графики к примеру 12.2
488
реактивного сопротивления (<в) продольного пле-
ча корректора (рис. 12.9, б и в).
Из графиков рис. 12.9, бив следует, что двух-
полюсник Д имеет три реактивных элемента и одно
активное сопротивление. В схеме два резонанса: пер-
вым наступает резонанс напряжений на частоте ®1(
вторым — резонанс токов на частоте а>2 • Таким усло-
виям удовлетворяет двухполюсник Zt, изображенный
на рис. 12.9, г. Двухполюсник Z2 в поперечном пле-
че корректора является обратным двухполюснику Z}.
Схема корректора приведена на рис. 12.9, д.
На практике широко используются типовые звенья пассив-
ных корректоров первого и второго порядков. Звенья первого
порядка содержат по одному реактивному элементу в двухполюс-
никах Zj и Z2. На рис. 12.10, а изображено такое звено с двух-
полюсником Zt, состоящим из параллельного соединения элемен-
тов и Ct.
Операторное сопротивление двухполюсника Zj
(124)
Если подставить выражение (12.4) в формулу (12.2), то по-
лучим операторную передаточную функцию звена:
tf (D\- + _ P + 1/-R1C) _ p + ctj
1 + (р +1/ R\Ci) Ro + p + a2
P CiRQRi
где a( = -7777- и a 2 = .
Частотная характеристика ослабления данного звена
Рис. 12.10. Звено первого порядка (а) и его рабочее ослабление (б)
489
2 2
л f \ -mi со +аэ
Ак (со) = 101g—-= 1
СО + (*1
показана на рис. 12.10, 6.
Максимальное значение ослабления корректора
Л max = 20 lg^^-.
(12.5)
На рис. 12.11, а изображено звено первого порядка с двух-
полюсником Zlf состоящим из параллельного соединения R\ и
Ц. Операторная передаточная функция этого звена
Я,(р) =
Rr,
R$ + R\
P + R\/L\ _иР + а-\
р । RoRi Р + ^21
А (Ко +R\)
RqRi . тт Rq
где ci] = —5-; а2 = z ” ‘ ; Н = ——.
Zi ( Rq + Ri) Rq + R{
Частотная характеристика ослабления звена
показана на рис. 12.11, б.
Максимальное значение ослабления корректора
Дс max = 20 lg|l + R{/Rq I.
(12.6)
Звенья второго порядка содержат по два реактивных эле-
мента в двухполюсниках Zx и Z2. На рис. 12.12, а изображено
звено, содержащее последовательный колебательный контур и
сопротивление R\ в продольной ветви корректора. Операторная
передаточная функция такого звена
Рис. 12.11. Звено первого порядка (а) и его рабочее ослабление (б)
490
Рис. 12.12. Звено второго порядка (а) и его рабочее ослабление (б)
р +—-р +----- 9 э
н (п\- Ro____________Ltct - Т,Р +а1Р + <°0
нлр)~Rh+ъ ад 1 ~%2+W(a2’
P + цс.
2 г г т т
где cq = cog =Т7г; Н = -5—^5-; а2 = щН.
L>\ JUjCj -Kq + rCj
Частотная характеристика ослабления звена
показана на рис. 12.12, б.
Максимальное значение Ак тах по-прежнему рассчитывается
по формуле (12.6).
На рис. 12.13, а изображено еще одно звено второго порядка
с двухполюсником Zj, представляющим собой параллельный ко-
лебательный контур. Операторная передаточная функция звена и
частотная характеристика ослабления (рис. 12.13, б) имеют вид
р2 +—-—р + —-— 2 2
и (п\ £1С1 -Г+сцр + оо
ЛР) ~ p2 + R^Ri p + _L_ ’ Р2 +а2Р + ^ ’
Р C^RqRx Р ЦСх
. . . (<»о-со2)2+а2О)2
Ак (со) = 101g—2--Ц------—
(coq—со2) +а2а>2
1 Rq + R\ 2
гдеа1 = вд:а2 = с?ад;сй0 = ад-
491
Рис. 12.13. Звено второго порядка (а) и его рабочее ослабление (6)
Значение Лктах на графике рис. 12.12, б рассчитывается
по формуле (12.6).
Пример 12.3. Определим элементы в поперечном плече корректо-
ра (рис. 12.10, а), имеющего элементы Ro = 600 Ом,
= 2400 Ом, Ci = 60 нФ. Рассчитаем и построим
частотную зависимость ослабления корректора AK(f)
в диапазоне частот 0...8 кГц.
Элементы сопротивления Z2 в поперечной ветви
должны быть обратны сопротивлению Z{.
Из теории двухполюсников известно, что для
обратных двухполюсников Zj • Z2 = Rq. Отсюда
R -R° -
6002
2400
= 150 Ом,
L2 = Ct • R$ = 60 • IO’9 • 6002 = 21,6 мГн.
Значения Ак(со) рассчитываем по формуле
(12.5) или по общей формуле (12.3), применимой
для корректора любого типа. Например, на частоте
f = 0 получаем
Рис. 12.14. Ослабление корректора к примеру 12.3
492
Лтах = Ак (0) = 101g = 201g^-^ =
af Rq
ОЛ1 600 + 2400 < о no к
= 20 --------= 13’98 дБ-
oUv
Остальные значения AK(f) рассчитывают анало-
гично. По результатам расчета простроен график
Ак(/’), изображенный на рис. 12.14.
Помимо Т-перекрытой схемы корректора (рис. 12.7) приме-
няют также другие схемы, изображенные на рис. 12.15.
Передаточные функции, которые реализуются Т-перекры-
тым корректором, можно реализовать и элементарными четы-
рехполюсниками, схемы которых приведены на рис. 12.16. На-
пример, для четырехполюсника на рис. 12.16, а операторная пе-
редаточная функция
Я(р) =
u2(p)Ъ
и^р)
рассчитывается так же, как и для корректора, построенного по Т-
перекрытой схеме (см. (12.2)). Цепи с элементарными четырех-
полюсниками применяют в случаях, когда не требуется согласо-
вание между генератором, корректором и нагрузкой.
В качестве активных звеньев амплитудных корректоров
обычно используют схемы на операционных усилителях. Кро-
ме пассивных схем ам-
плитудных корректо-
ров применяют актив-
ные схемы. Активные
амплитудные корректо-
ры строятся в общем
случае с применением
RC- и /?£С-элементов,
которые называют
ARZ-цепями. Сущест-
вует большое количест-
Рис. 12.15. Схемы пассивных амплитуд-
ных корректоров
Рис. 12.16. Схемы пассивных амплитудных корректоров
493
Рис. 12.17. Схемы активных амплитудных корректоров
во разновидностей активных звеньев, эквивалентных по переда-
точной функции пассивным амплитудным корректорам. Две схе-
мы таких активных звеньев изображены на рис. 12.17. Их пере-
даточные функции выражаются соответствующими формулами:
(12.7)
(12.8)
Если в схеме рис. 12.17, а в качестве двухполюсника Z вы-
брать последовательное соединение резистора R и емкости С, то
передаточная функция (12.7) звена примет вид
Я,(Р) = -
R' R^R+jc
= -Я[(р + а!)/(р + а2)],
R2R
RxR2 + R\R
1
P+ C(R2 + R)
1 1 r2r
гдеа1 RC’ “2 C{R2+R),H Ri(R2 + R)'
Частотная характеристика ослабления данного звена, также как
и у пассивного звена первого порядка, вычисляется по формуле
Данная функция при увеличении частоты имеет монотонно
возрастающий характер от величины Ак(0) = 201g(7?1//?2) Д° ве-
494
Рис. 12.18. Ослабления кор-
ректоров с одним реактивным
элементом: 1 — схемы рис.
12.17, а с последовательной
/гС-цепью в качестве двухпо-
люсника Z; 2 — схемы рис.
12.17, б с емкостью С в каче-
стве двухполюсника Z
Рис. 12.19. Ослабления коррек-
торов с двумя реактивными эле-
ментами: 1 — схемы рис. 12.17 с
последовательной L С-контуром
в качестве двухполюсника Z; 2 —
схемы рис. 12.17 с параллель-
ным LC-контуром в качестве
двухполюсника Z
личины Ак (оо) = 201g (R + R2)/(RR2)]. Если выбрать R{ < R2
и R = RxR2/(R2 - jRi ), то ослабление будет изменяться от Ак(0)
до нуля, оставаясь отрицательным (рис. 12.18, кривая 1).
Выберем в схеме 12.17, б в качестве двухполюсника Z ем-
кость С. Тогда передаточная функция (12.8) этого звена при-
мет вид
1
И (п\_ _ гг Р + <Х1
к(Р) R2 + l/(pC) ~ > + а2’
1 R\ + R2
I№ai‘(R, + R2)C'a^Rfi--H‘-RT-
Частотная характеристика ослабления
Ак (©) = 101g 2^2 2а2 2ч •
Н (аг + а/)
При увеличении частоты данная функция имеет монотонно
убывающий характер от Ак(0) = 0 до AK(oo)=201g[/?2/(/?1+/?2)]
(рис. 12.18, кривая 2).
Если в качестве двухполюсника Z выбрать последовательный
LC-контур, то частотная характеристика ослабления будет иметь
вид, показанный на рис. 12.19, кривая 1. При выборе в качестве
двухполюсника Z параллельного LC-контура частотная характе-
ристика ослабления будет иметь обратный характер, как показано
на рис. 12.19, кривая 2.
Несмотря на то что рассмотренные схемы могут содержать ин-
дуктивности, они имеют ряд преимуществ по сравнению с пассивны-
ми амплитудными корректорами. Так, число реактивных элементов
495
вдвое меньше, а ослабление, вносимое каскадным соединением цепи
и корректора, близко к нулю. Последнее важно также потому, что
дополнительное ослабление за счет применения пассивного коррек-
тора, как правило, приходится компенсировать с помощью уси-
лителя, т.е. общая схема все равно оказывается активной.
Пример 12.4. Определим передаточную функцию амплитудного
корректора, построенного по схеме рис. 12.17, б, в
которой в качестве двухполюсника Z выбран после-
довательный колебательный £С-контур. Рассчитаем
и построим частотную характеристику ослабления
Лк(/’) корректора в диапазоне частот от 0 до fB =
= 100 кГц для элементов контура = 20 кОм,
R2 = 10 кОм, L = 200 мГн, С = 1,268 нФ.
Операционный усилитель в схеме рис. 12.17, б
включен по неинвертирующей схеме. Поэтому пере-
даточная функция корректора определяется по фор-
муле (12.8), в которой Z(p) = pL + 1/(рС):
wK(p)=
R\ + Z(р) _ R\ + R2 + pL + ^1{рС)
Ri + Z(p) R2+pL + l/(pC)
2 R{ + /?2 1
p
2 &2 1
P + ~LP + ~LC
Частотная характеристика ослабления
Лк(со)=201ён^)
=101g
I £ J
В формулах Нк(р) и Лк(ю) величина 1/(£С) —
это квадрат резонансной частоты Qq £С-контура.
Для заданных значений £ и С имеем
<£>о - --------о ~ 0> 394 • 1010 (рад/с)2.
£С 200 10"3 1,268 IO-9 F
Резонансная частота f0 = 1/(2ть/£С) = 10 кГц.
Рассчитаем значения AK(f) на частотах, равных ну-
лю (/о = Ю кГц и fB = 100 кГц):
AK(0) = 101g
(1/£С)2
(1/£С)2
= 101gl = 0 дБ,
496
ЛК(/),ДБ
Рис. 12.20. Ослабление корректора к примеру 12.4
Л(/о) = 2О1§Ъ-Т^- = 2О1§77ГГ^ = -9.54 ДБ,
К) + 1U + ZU
( 1 2? 2(R2}2
+ сов г
AM) = 101g, \LC У-------7-^-"-<2 = -4-1 ДБ-
( 1 2 2 ( Rl R2
{lc b) b( l J
Аналогичным образом можно рассчитать ослаб-
ление Ак(/") на любой частоте в рабочем диапазоне.
График AK(f) изображен на рис. 12.20.
Из данного параграфа мы узнали, что:
• Пассивный амплитудный корректор представляет собой на- 5
груженный симметричный Т-перекрытый четырехполюс- *
ник, в продольное и поперечное плечи которого включены 1
обратные двухполюсники. д
• Ослабление, вносимое в цепь амплитудным корректором, .
полностью определяется поведением на оси частот реактив- I
ного сопротивления двухполюсника в продольном плече его
Т-схемы. «
• Для построения корректора с требуемой характеристикой
ослабления часто используют типовые звенья первого и
второго порядков.
• Активные амплитудные корректоры строятся на схемах с •
операционными усилителями.
• Передаточные функции типовых звеньев активных ампли- I
тудных корректоров совпадают с передаточными функция- <•
ми типовых звеньев этого же порядка пассивных амплитуд- <
ных корректоров.
32-6972
497
12.3. Расчет пассивных амплитудных корректоров
Расчет пассивного амплитудного корректора сводится к опре-
делению значений элементов двухполюсников в его плечах. При
расчете пассивного амплитудного корректора исходными данными
являются: частотная характеристика ослабления цепи Apil(co), под-
лежащая коррекции в диапазоне частот он ... сов; точность коррек-
ции ДА в этом же диапазоне частот; сопротивление нагрузки 7?0.
Вначале определяют частотную характеристику амплитудного
корректора Ак(со). Для этого необходимо задать характеристику
ослабления Ао каскадного соединения цепи и корректора. Эта
характеристика должна быть постоянной, не зависящей от час-
тоты, причем ее величину принимают несколько большей, чем
максимальное ослабление цепи:
Ао = шах Арц + Аь (12.9)
где Aj = 1 ... 2 дБ.
Частотная характеристика ослабления амплитудного коррек-
тора вычисляется по формуле
Ак(о>) = Ао - Арц((о). (12.10)
На рис. 12.6 в качестве примера показаны характеристики
ослабления цепи Арц(<в), ослабления Ао каскадного соединения
цепи и корректора, а также ослабления Ак(о>) корректора.
Следующим этапом расчета амплитудного корректора являет-
ся выбор схемы корректора. Выбирают такую схему, которая в
диапазоне частот сон ... сов имеет нужный характер частотной за-
висимости ослабления. Например, для реализации частотной за-
висимости Ак (со), приведенной на рис. 12.6, можно использовать
амплитудный корректор, в котором двухполюсник Z[ состоит из
параллельного соединения емкости Ct и резистора (рис. 12.10).
Выбрав схему корректора, приступают к ее расчету. При
этом часто используется метод интерполирования. Согласно
этому методу задаемся числом точек интерполирования, равным
числу элементов в двухполюснике Zt. С учетом формулы
(12.3) составляется система уравнений вида
AK(coi) = 201g 1 +
AK(co2) = 201g 1 +
Ак (соя ) = 201g 1 -ь
Zt(/(ot,x1,x2,...,x„ )/R0]
Z1(jO)2,X1,X2,...,X„)/R0
Zt(ja„,xltx2.....xn)/R0
где xif...,xn значения параметров элементов двухполюсника Zr
Решение данной системы и дает значения которые яв-
ляются параметрами индуктивностей, емкостей и резисторов.
498
Особенностями расчета является то, что, во-первых, пара-
метры элементов могут быть отрицательными, а во-вторых, точ-
ность коррекции может не удовлетворять заданным требованиям.
Обычно приходится данный расчет повторять. Если параметры
элементов получились отрицательными, то следует изменить либо
величину Aj в формуле (12.9), либо положение точек интерполя-
ции. Если параметры элементов получились в конце концов по-
ложительными, то проверяется точность аппроксимации (коррек-
ции). Для этого по формуле (12.3) рассчитывается ослабление
корректора Акр(со) и проверяется выполнение неравенства
|Акр (со) - Ак (се>)| < ДА.
При выполнении неравенства расчет на этом заканчивается.
В противном случае необходимо снова повторить расчет, меняя
точки интерполяции, до получения равноволновой характеристи-
ки погрешности. Если при равноволновом характере погрешности
требования к точности не выполняются, то необходимо либо уве-
личить число элементов в двухполюснике, либо поделить Ак(со)
пополам и построить корректор в виде каскадного соединения
двух четырехполюсников.
Методика синтеза активных ARZ-корректоров такая же, как
и описанная выше методика расчета пассивных амплитудных
корректоров. Отличие заключается в том, что характеристика ос-
лабления Ао каскадного соединения цепи и корректора выбира-
ется близкой к нулю.
Пример 12.5. В табл. 12.1 задана частотная характеристика ос-
лабления цепи Арц(/). Рассчитаем элементы ампли-
тудного корректора, если Ао = 12 дБ и Ro = 200 Ом.
Воспользуемся формулой (12.10) и рассчитаем
ослабление корректора AK(f) = A0-Apti(f) в диа-
пазоне частот от 0 до 50 кГц.
Результаты расчета Ак(/) приведены в табл. 12.2,
а на рис. 12.21 изображены графики ослаблений
А) и Ак(/).
Таблица 12.1. Ослабление цепи к примеру 12.5
f, кГц 0 5 10 15 20 25 30 35 40 45 50
Ли, дБ 11,9 11,0 10,0 8,5 7,2 5,8 4,3 3,4 2,5 1,8 1,1
Таблица 12.2. Ослабление корректора к примеру 12.5
/, кГц 0 5 10 15 20 25 30 35 40 45 50
Ак, дБ 0,1 1,0 2,0 3,5 4,8 6,2 7,7 8,6 9,5 10,2 10,9
32*
499
Рис. 12.21. Ослабление цепи, корректора и их
каскадного соединения к примеру 12.5
Частотная характеристика ослабления AK(f)
на рис. 12.21 может быть получена с помощью кор-
ректора, реализованного по схеме рис. 12.11, в кото-
рой двухполюсник Zj состоит из параллельного со-
единения элементов L, и .
Найдем из формулы (12.6):
Ri =/?о(1О°’О5Лктах -1).
Значение Ак тах = 10,9 дБ на частоте f = 50 кГц
берем из табл. 12.2. Получаем
Rx = 200 (1О0’0510’9 -1) = 500 Ом.
Для расчета Ц выбираем узел интерполяции:
fi =25кГц, AKi(fi) = 6,2 дБ. Подставляем эти дан-
ные в формулу (12.3) или
2 2
л„(и,) = ю18
ti ^<Bi+(X2
Получаем значение Ц = 2 мГн.
Значения параметров элементов R2 и С2, обра-
зующих обратный двухполюсник Z2, рассчитываем
по формулам
R2 =
Rl
Rx
с2 =
А
Ro'
И
Получаем R2 = 80 Ом и С2 = 0,05 мкФ. Отметим,
что расчетная характеристика ослабления корректора,
500
вычисляемая по формуле (12.3), точно совпадает с тре-
буемой только на частотах f\ = 25 кГц и fmax = 50 кГц.
Используя каскадное соединение различных типовых звеньев
корректоров, можно получить частотные зависимости ослабления
Ак(а>) любой сложности. На рис. 12.22 изображена схема слож-
ного корректора, построенного на основе типовых схем (рис. 12.13),
и его рабочее ослабление. Изменением характеристик типовых
схем добиваются получения требуемой характеристики амплитуд-
ного корректора.
Рис. 12.22. Сложный корректор (а) и его ослабление (б)
Из данного параграфа мы узнали, что:
• Исходными данными при расчете корректора являются 4
частотная характеристика ослабления цепи, точность кор-
рекции в рабочем диапазоне частот и сопротивление на-
грузки.
501
... ..WWS<;
• При расчете амплитудного корректора вначале определяют
его частотную характеристику, затем выбирают схему кор-
ректора и рассчитывают значения элементов двухполюсни-
ков в продольном и поперечном плечах.
Вопросы и задания для самоконтроля
1. Почему происходят искажения сигнала на выходе цепи?
2. Сформулировать условие отсутствия амплитудно-частотных
искажений в цепи.
3. Каким образом корректируются частотные характеристики цепей?
4. По какой схеме можно построить пассивный амплитудный
корректор?
5. Как рассчитывается передаточная функция Т-перекрытого кор-
ректора и вносимое им ослабление?
6. Схема двухполюсника Z2 в корректоре приведена на рис. 12.8, а.
Получить схему двухполюсника Z<. Построить график частот-
ной зависимости ослабления Ак(а>) корректора.
7. Какие схемы типовых звеньев пассивных корректоров из-
вестны? Какой вид имеют частотные характеристики вноси-
мого ими ослабления?
8. Доказать, что частотная характеристика ослабления Ак(со)
звена, изображенного на рис. 12.10, имеет вид (12.5), а макси-
мальное значение ослабления рассчитывается по формуле
^к max “ 201g|l + /?1/7?0|.
9. Доказать, что операторная передаточная функция элементар-
ного четырехполюсника, изображенного на рис. 12.16, б, соот-
ветствует передаточной функции корректора (см. (12.2)).
10. Какие амплитудные корректоры называют активными?
И. Получить передаточную функцию и частотную характеристику
ослабления активного звена корректора, изображенного на рис.
12.17, б, в котором в качестве двухполюсника Z выбран парал-
лельный LC-контур. Подтвердить, что график рабочего ослаб-
ления Ак (со) такого корректора — это кривая 2 на рис. 12.19.
12. Каков порядок расчета пассивного амплитудного корректора?
13. Рассчитать элементы, образующие двухполюсник Zx ампли-
тудного корректора, частотная зависимость ослабления Ак(/)
которого приведена в табл. 12.3, а значение 7?0 = 200 Ом.
14. Зачем применяют каскадное соединение типовых звеньев кор-
ректоров?
Таблица 12.3. Ослабление корректора к заданию 13
Л кГц 0 5 10 15 20 25 30 35 40 45 50
А, дБ 15,6 10,5 6,3 4,0 2,7 1,9 1,4 1,1 0,9 0,7 0,6
502
Глава 13. Анализ и расчет фазовых корректоров
13.1. Фазо-частотные искажения сигнала
и их коррекция
Нелинейность фазо-частотной характеристики цепи приво-
дит к искажению формы сигнала. Рассмотрим электрическую
цепь — четырехполюсник (рис. 13.1), имеющую рабочую фазовую
постоянную В(<й) = -ф(со), изображенную на рис. 13.2, а, и ха-
рактеристику группового времени прохождения (ГВП) irp (со),
являющуюся производной от рабочей фазовой постоянной, — на
рис. 13.2, б. Входной сигнал uBX(t) состоит из суммы двух гар-
моник с частотами cot и 2coj (рис. 13.3, а). Форма входного сиг-
нала изображена на этом рисунке жирной линией.
Анализ графиков фазовой постоянной и ГВП цепи показыва-
ет, что фаза первой гармоники почти не меняется при прохожде-
нии сигнала через цепь, а фаза второй гармоники существенно
увеличивается.
В результате сложения гармоник на выходе цепи получается
сигнал, форма которого отличается от входной (рис. 13.3, б).
Искажения формы сигнала при прохождении его по цепи,
обусловленные нелинейностью рабочей фазовой постоянной (фа-
зо-частотной характеристики — ФЧХ) цепи или непостоянст-
вом группового времени прохождения, называются фазо-частот-
ными искажениями.
Условием отсутствия фазо-частотных искажений в цепи сле-
дует считать линейность рабочей фазовой постоянной В (со) и
ФЧХ цепи (рис. 13.4, а):
Рис. 13.2. Графики рабочей фазовой
постоянной (а) и группового времени
прохождения (б) цепи
Рис. 13.1. Электрическая
цепь в виде четырех-
полюсника
503
Рис. 13.3. Сигналы на входе (а) и выходе (б) четырехполюсника
Производная от рабочей фазовой постоянной — это групповое
время прохождения, которое для неискажающей цепи
, , ч б?В(ю) ,
0®) = —-------= А)
ао
(13.2)
должно быть постоянным на всех частотах (рис. 13.4, б).
В реальных цепях условия (13.1) и (13.2) обычно не выпол-
няются, т.е. ФЧХ не является линейной, а ГВП — не постоянно.
Такие цепи вносят фазо-частотные искажения в передаваемый
сигнал. Для уменьшения подобных искажений до допустимых
значений применяют фазовые корректоры.
Фазовый корректор — это четырехполюсник, включаемый кас-
кадно с цепью и дополняющий фазовую характеристику цепи до
лйнейной. Вместо корректирования частотной характеристики фа-
зы можно выравнивать характеристику группового времени прохо-
ждения так, чтобы она была постоянной на всех частотах рабочего
диапазона. Фазовый корректор не должен искажать АЧХ цепи.
На рис. 13.5 для достижения условий безыскаженной пере-
дачи между генератором и нагрузкой включено каскадное соеди-
нение цепи с ФЧХ, подлежащей коррекции, и корректора. Вход-
ное сопротивление фазового корректора должно равняться сопро-
тивлению нагрузки, чтобы условия работы цепи не изменялись по
сравнению с теми, в которых находится цепь, включенная между
генератором и нагрузкой в отсутствие корректора.
Рис. 13.4. Графики рабочей фазовой постоянной (й) и ГВП (б) цепи,
не вносящей фазо-частотных искажений
504
Рис. 13.5. Каскадное включение цепи и корректора
Рабочая передаточная функция цепи, изображенной на рис. 13.5,
Умножим и разделим это выражение на U_m2 и представим
его в виде произведения передаточных функций цепи Нрц(/со) и
корректора Нк (усо):
„ ( . ч (2Um2 [ЁГУ Um2 "I
k ИтГ V^h Д SZW2 J
= Нрц(/(о)Нк(».
Фазо-частотная характеристика каскадного соединения цепи
и корректора
ср (со) = <рц (©) + <рк (®)
(13.3)
вычисляется как сумма ФЧХ цепи и корректора.
Из рис. 13.6 видно, что фазовый корректор должен допол-
нять фазовую постоянную (ФЧХ) цепи в рабочей полосе частот
сон...сов до линейной зависимости (рис. 13.6, а) либо дополнять
групповое время прохождения цепи до постоянной величины i0 в
том же рабочем диапазоне частот (рис. 13.6, б). За пределами
рабочего диапазона ФЧХ и ГВП могут иметь любую форму.
Рис. 13.6. Коррекция фазовой постоянной (ФЧХ) (а) и ГВП (б) цепи
505
Из данного параграфа мы узнали, что:
• Нелинейность фазо-частотной характеристики цепи, или, |
другими словами, неодинаковое запаздывание различных I
гармонических составляющих сигнала при передаче его по
цепи, приводит к искажению формы сигнала.
• Задача коррекции заключается в том, чтобы дополнить фа- j
зо-частотную характеристику цепи до линейной или харак- £
теристику группового времени прохождения до постоянной |
величины на всех частотах рабочего диапазона.
• Для коррекции ФЧХ и ГВП каскадно с цепью включают
фазовый корректор. *
13.2. Анализ схем фазовых корректоров
Пассивные фазовые корректоры строятся по симметричной
мостовой схеме. Фазовые корректоры должны иметь постоянное
входное сопротивление и постоянное ослабление, которые не за-
висят от частоты. Таким условиям удовлетворяют симметричные
мостовые четырехполюсники (рис. 13.7), у которых сопротивле-
ния Zj и Z2 реактивные и взаимно-обратные, т.е.
' Z.2 = ^0 и
Такие четырехполюсники имеют с обеих сторон одинаковые
характеристические сопротивления
Zlc = ' Zl2 ~ ^0 >
поэтому их легко согласовывать с внутренним сопротивлением
генератора и сопротивлением нагрузки.
Рабочее ослабление мостового симметричного согласованно
включенного четырехполюсника с взаимно-обратными сопро-
тивлениями Zf и Z2 равно нулю на всех частотах: А(со) = 0,
Рис. 13.7. Мостовая схема фазового корректора
506
т.е. эта схема не вносит никакого дополнительного ослабления
сигнала.
Операторная передаточная функция по напряжению схемы
рис. 13.7 имеет вид
и (р) = ^_
к(р) R.^zx(Py
(13.4)
Комплексная передаточная функция по напряжению схемы
рис. 13.7, в которой Zt и Z2 — реактивные двухполюсники, мо-
жет быть вычислена по формуле
(13.5)
Нетрудно видеть, что модуль передаточной функции (13.5)
равен единице, а аргумент и ГВП вычисляются по формулам
фк(®) = -2arctg^-,
______________Rq
Вк(оз) = 2arctg^-,
______________Rq
z s_JB(o))_ 2/Rq dX{
” d<s> = ^(ад,)2^-
(13.6)
(13.7)
(13.8)
Формулы (13.6), (13.7) и (13.8) показывают, что фазо-
частотная характеристика, фазовая постоянная и характеристика
группового времени запаздывания корректора зависят только от
вида двухполюсника .
На практике используются типовые звенья пассивных фазо-
вых корректоров первого и второго порядков.
На рис. 13.8, а изображена схема фазового корректора первого
порядка, в котором двухполюсником Zt является индуктивность
Zi (р) = pL, а двухполюсником Z2 — емкость Z2 (р) = 1/(рС).
Рис. 13.8. Фазовый корректор первого порядка (а),
его фазовая постоянная (ФЧХ) (б) и ГВП (в)
507
Операторная передаточная функция этого корректора в соот-
ветствии с (13.4) имеет вид
if (п \ = ~~~ а1 (1 ч q\
Ro+pL p + Ro/L p + a,’ Q ‘9)
где oq = Ro/L.
Рабочая фазовая постоянная В (co) и ГВП в соответствии с
формулами (13.7) и (13.8)
Вк(со) = 2arctg(co/ai); (13.10)
ar + af (13.11)
Графическое изображение данных характеристик показано
на рис. 13.8, бив.
На рис. 13.9, а изображена схема фазового корректора второго
порядка с двухполюсником , состоящим из последовательного
соединения элементов Ц и Ct, т.е. Z\ (р) = pLx + 1/(рС1) •
Операторная передаточная функция такого корректора в со-
ответствии с (13.4) имеет вид
н _ ^p-pBi-l/CpCt) р2-(<o0/Qn)p + g>o
/?о +рЦ +l/(pCi) p2+(<o0/Qn)p + ®o ’
где ©о = 1/(LtCt); Qn = I/^oqRqCi) — добротность полюса переда-
точной функции.
Комплексная передаточная функция корректора получается
при р = У со:
(13.12)
<0о-(0 +Д®о/Оп)<0
Модуль функции равен единице, а рабочая фазовая постоян-
ная В (со) и ГВП irpCw) вычисляются в соответствии с (13.7) и
(13.8) по формулам
Рис. 13.9. Фазовый корректор второго порядка (а),
его рабочая фазовая постоянная (ФЧХ) (б) и ГВП (в)
508
Вк(а>) = п + 2arctg[Qn(co2 -соо)/(со0со)
/ 0,0 - _2<QoQn(<o2+<Oo)
Оп(®2(0о) +©о®2
(13.13)
(13.14)
Графики зависимостей Вк(со) и tTA($) фазового корректора
второго порядка приведены на рис. 13.9, бив.
Если известны коэффициенты передаточной функции соо, Qn и
нагрузка Ro, то параметры элементов корректора рассчитываются
по формулам
.Ci=1/(Qn/?o(»o); (13.15)
Ц = QM&Q. (13.16)
Пример 13.1. Фазовый корректор (рис. 13.8, а) имеет элементы
Ц = 100 мГн, Rq = 500 Ом. Рассчитаем и построим
графики частотных зависимостей фазовой постоян-
ной BK(f) и группового времени прохождения
trp (f) в диапазоне частот от 0 до 10 кГц.
Фазовая характеристика В (со) рассчитывается
по формуле (13.10), поэтому
BK(/) = 2arctg(2%/L1/B0).
ГВП irp(co) рассчитывается по формуле (13.11),
поэтому
t (f\ -
rpU}"47t2/-2Z?+jR02-
Подставляя в выражения для Вк(/) и tTp(f)
значения Ц = 100 • 10“3 Гн и Ro = 500 Ом, получаем
о п 4. 2nfLi „ . 2-3,14-100-Ю-3,
Вк (f) = 2arctg-^-l = 2arctg---—-----------f =
OUU
= 2arctgl,256 10’7;
m 2B0£t 2-500-100-10'3
rpZ' 4tc2/’2£2+Bo 4-3,142-1002-10'6/’2+5002
100
0,394/2+25-104‘
Таблица 13.1. Расчет фазовой постоянной и ГВП
к примеру 13.1
f, кГц 0 1 2 4 6 8 10
Вк, рад 0 1,8 2,38 2,75 2,88 2,94 2,98
tm, мкс 400 155 96 55 38 29 24
509
Рис. 13.10. Графики рабочей фазовой постоянной
(ФЧХ) (л) и ГВП (б) к примеру 13.1
Результаты расчета BK(f) и tTp(f) в диапазоне
частот f =0...10 кГц приведены в табл. 13.1, а гра-
фики — на рис. 13.10, а и б.
Пример 13.2. Схема фазового корректора приведена на рис. 13.9, а.
Рассчитаем и построим графики частотных зависимо-
стей фазовой постоянной BK(f) и ГВП в
диапазоне частот 0... 10 кГц для двух случаев:
1) Rq = 600 Ом; Ц = 36 мГн, €\ = 0,025 мкФ;
2) Rq = 600 Ом; Ц = 36 мГн, Ct = 0,05 мкФ.
Фазовая характеристика Вк(<в) корректора рас-
считывается по формуле (13.13), а ГВП trp (со) — по
формуле (13.14), поэтому
Вк (/) = * + 2arctg[Qn (4л2/2 - cojj )/(<о02л/’)];
t цу. 2(ОоОп(4л2/~2-ко^)
₽ О2(4л2/’2 -coq)2 +(0о4л2/’2
где coq = lAliQ); Qn = 1/( cooWi).
Рассчитаем значения сод и Qn для двух случаев
задания параметров элементов корректора:
1) ---------«=0,11-1O10 (рад/с)2;
° АЛ 36-10-3-0,025-Ю-6 F
Q =_____1__= ____________= 2 •
п т07?0С1 Тод! 105 -600- 0,025 Ю’6
2) al =-------5-J-------- = 0,056 • Ю10 (рад/с)2;
° 36 10-3 0,05 10'6 F
Qn = ..—-----------F =1,41.
VO56 105 • 600 • 0,05 10"6
510
Подставляя значения coo и Qn в выражения для рас-
чета и £гр(/), рассчитываем эти характери-
стики в диапазоне частот 0...10 кГц и заносим резуль-
таты расчета в табл. 13.2 для случая 1) и в табл. 13.3
для случая 2).
Поскольку график trp(co) имеет максимум
(рис. 13.9, в), то для определения частоты этого мак-
симума берем производную и, приравняв ее
к нулю, находим
®max=coO#-Qn’-l (13.17)
ИЛИ /max = (<Оо/(2я))аД/4 - - 1 = О ДЛЯ ПврВОГО СЛу-
чая (Qn = 2) и fmax = 2,42 кГц для второго случая
(Qn=l,4D.
В общем случае анализ выражения (13.17) пока-
зывает, что при Qn > 43 ГВП имеет максимум на
частоте f = 0, а при Qa < л/3 = 1,73 — на частоте
fпах •
Значение trp max рассчитывается по формуле
/ ___1 2Qn <о\
Для второго случая, когда Qn = 1,41, имеем
(гр max =144 мкС. Следует также отметить, что при
Qn » 1 формулы (13.17) и (13.18) существенно уп-
рощаются:
®тах “ (гр max = “• (13.19)
®0
Таблица 13.2. Расчет фазовой постоянной и ГВП
к примеру 13.2 (случай 1)
f, кГц 0 2 4 5,3 8 10
Вк, рад 0 1,44 2,59 3,14 4,11 4,35
(гр . МКС 120 106 73,5 60 34,8 26,2
Таблица 13.3. Расчет фазовой постоянной и ГВП
к примеру 13.2 (случай 2)
f, кГц 0 1 2,42 3,76 6 8 10
Вк, рад 0 0,77 2,0 3,14 4,35 4,87 5,19
irp, мкс 120 117 144 120 57,6 30,8 18,9
511
Рис. 13.11. Графики рабочей фазовой постоянной
(ФЧХ) (а) и ГВП (б) к примеру 13.2
Графики зависимостей Вк(а>) и irp(<°) Для двух
случаев приведены на рис. 13.11 (обозначены циф-
рами 1 и 2).
Мостовая схема не всегда удобна в реализации, так как явля-
ется уравновешенной. Существует ряд эквивалентных схем в ви-
де неуравновешенной схемы, как показано на рис. 13.12. Заме-
тим, что на практике добротность полюса больше единицы и по-
этому чаще используется схема рис. 13.12, а, что удобно, так как
она не содержит связанных индуктивностей с заданным коэффи-
циентом связи. Неуравновешенные схемы по сравнению с мосто-
выми содержат вдвое меньше элементов.
Активные схемы фазовых корректоров получают из фильт-
ровых звеньев на операционных усилителях. Помимо пассивных
фазовых корректоров применяют активные фазовые корректоры.
Кроме пассивных R С- или ЯХС-элементов схемы активных кор-
ректоров содержат операционные усилители. Существуют актив-
ные фазовые звенья первого и второго порядков. На рис. 13.13
Рис. 13.12. Неуравновешенные схемы фазовых корректоров
512
приведена схема фильтрового звена на операционном усилителе.
Передаточная функция этого звена вычисляется по формуле
Як(р)=
р-1/(^С)_ p-gt
p + l/(BtC) р + а/
(13.20)
где aj = 1/(В(С).
Выражение (13.20) аналогично формуле для расчета переда-
точной функции пассивного фазового корректора (13.9), т.е. схе-
ма, приведенная на рис. 13.13, — это активный корректор перво-
го порядка.
Фазовые характеристики В (со) и ГВП данного звена, так же
как у пассивного корректора первого порядка, вычисляются по
формулам
Вк(со) = 2arctg(co/a1);
^гр ( ® ) —
2a 1
2 2 *
СО +СХ1
График Вк(<в) монотонно нарастает от Вк(0) = 0 до
Вк(оо) = л, а график £гр(со) монотонно убывает от trp(0) = 2/aj
до trp(oo) = 0. На рис. 13.14 показаны графики Вк (со) и irp(со),
построенные для разных значений aj активного корректора пер-
вого порядка.
На рис. 13.15 приведена еще одна схема активного фазового
корректора, также построенная на основе активного фильтрового
звена. Если в схеме рис. 13.15 задать В3 = пВ2, В4 = пВ2/(п-1),
п > 1, то передаточная функция, рассчитанная, например, с по-
мощью метода узловых напряжений, будет иметь вид
(13.21)
(сравни с
Это передаточная
Bl +Z(p)
функция фазового корректора
фазовый корректор
первого порядка
постоянной (ФЧХ) (д) и ГВП (б)
фазового корректора первого порядка
33-6972
513
Рис. 13.16. Графики рабочей фазовой
постоянной (ФЧХ) (а) и ГВП (б)
фазового корректора второго порядка
Рис. 13.15. Звено активно-
го фазового корректора
Если в качестве двухполюсника Z выбрать емкость, то пере-
даточная функция (13.21) примет вид (13.20):
н (п} - R\-VpC p-i/(/?iC)_. р-сч
к^7 ^t+1/рС р +1/(^0) р + а/
т.е. схема на рис. 13.15 — это схема фазового корректора первого
порядка.
Когда в качестве двухполюсника Z используется последова-
тельный £ С-контур, то получается передаточная функция фазо-
вого корректора второго порядка:
2 R£ 1
Н Р Р LC + LC Р2~(юо/Оп)Р + <Оо
к{Р)~\2 R£+A_~~P2^/Qn)P^20’
Р И LC LC
где <»о = 1/(£С); Qn = l/(a>o.RiC) — добротность полюса переда-
точной функции.
Графики частотных зависимостей Вк(<в) и trp(co) данного
корректора, полученные для разных значений Qn, приведены на
рис. 13.16.
Хотя активные ARZ-фазовые корректоры имеют индуктив-
ность, но преимуществом их по сравнению с пассивными кор-
ректорами является меньшее количество элементов при том же
порядке передаточных функций.
Пример 13.3. Определим передаточную функцию фазового кор-
ректора, построенного по схеме рис. 13.15, в которой
в качестве двухполюсника Z используется парал-
лельный £С-контур. Рассчитаем и построим качест-
венно частотную характеристику ГВП £rp(f) коррек-
тора в диапазоне частот 0...5 кГц для элементов цепи
= 37,5 Ом, £ = 36 мГн, С = 1,6 мкФ.
514
Найдем сопротивление Z(p) параллельного
LC-контура:
,= Р^1/(рС) PL
pL + l/(pC) p2LC + \
Подставив Z(p) в формулу (13.21), получим
передаточную функцию фазового корректора
Н(п) = Ri~Z(P) = Ri~pL/(p2LC + i) =
Ri+Z(p) Rx+pL/(p2LC + i)
. Р2-(<ао/Оп)Р + <00(
p2+(©o/Qn)p + a>o’
где ®о = 1/(ЬС); Qn = ©07?iC.
ГВП рассчитывается по формуле (13.14), в кото-
рой со = 2л/:
2©0Qn(4n2/2+©р)
Q„(4л2/2 - coq ) + ©о • 4л2f2
Находим значения ©р и Qn:
®0 = 0,416 104 рад/с; /0 = 0,662 кГц;
Qn = ©0Я1С = 0,416 104-37,5-1,6 10”6 = 0,25.
Поскольку Qn < V3 , то находим значения ©тах
и тах по формулам (3.17) и (3.18):
®тах = ®0 “ Qn — 1 =
= 0,416-1047V4-0,252 -1 = 4,16-103 рад/с;
4р(/)> мС
3
2
1
0 1 2 3 4 5 f кГц
Рис. 13.17. График ГВП корректора
к примеру 13.3
515
/max = = 0,662 кГц; trp max = 3,7 MC.
Рассчитываем значения £гр(/) на частотах Д =
= 0 и /2 = 5 кГц по формуле (13.14). Получаем
£гр(/1) = 1,92 мс и ^Гр(/г) = 0,12 мс.
График зависимости tTp(f) приведен на рис. 13.17.
Из данного параграфа мы узнали, что:
• Существуют пассивные и активные фазовые корректоры. ?
• Пассивный фазовый корректор представляет собой натру- |
женный симметричный мостовой четырехполюсник с вза-
имно-обратными двухполюсниками в его плечах. |!
• Типовые звенья фазового корректора первого порядка со- <
держат по одному реактивному элементу (£ или С) в каж- |
дом плече моста, а звенья второго порядка — по два разно- }
родных реактивных элемента (£ и С). *
• Активные фазовые корректоры строятся на схемах с опера- \
ционными усилителями, RC- или ЛВС-элементами. |
13.3. Принципы расчета фазовых корректоров
Расчет фазовых корректоров — весьма трудоемкая опера-
ция, она требует применения компьютеров. При синтезе фазо-
вых корректоров задаются характеристика ГВП корректируемой
цепи, сопротивление нагрузки Ro, точность коррекции и диапа-
зон частот <он ...®в, в котором осуществляется коррекция. Внача-
ле определяют требуемую характеристику фазового корректора.
Для этого задают постоянное значение ГВП tQ, которое должно
быть несколько больше максимального значения ГВП цепи
(рис. 13.6, б):
^0 = max *"
Затем любым способом определяют площадь 5К под характери-
стикой требуемого ГВП корректора, например, площадь можно
рассчитать по формуле
|^(<о)(/со = fdBK(o>) = Вк(оо)-Вк(0).
о__________о_______________________
После этого приближенно можно определить число фазовых
звеньев второго порядка, необходимых для коррекции, так как
516
О COfll ®02 ®03 <004 ®
Рис. 13.18. Графики ГВП фазовых звеньев и корректора
площадь под кривой группового времени фазового звена второго
порядка равна 2л:
п = 1,15к/2л.
В данной формуле коэффициентом 1,1 учитывается то, что
не вся площадь под характеристикой фазового звена попадает в
диапазон коррекции.
Зная число звеньев, задаемся в первом приближении их па-
раметрами <в0£ и Qak, k = 1, ..., п. Для начала частоты распре-
деляются равномерно, добротность определяют из условия тре-
буемой величины группового времени звена на частоте omaxfe.
Эта величина выбирается на 10...20% меньше, чем требуемое
групповое время корректора на этой частоте. Из сказанного и
формулы (13.17) следует
Qnk = ’ ^гр max k >
где т = 0,8...0,9.
На рис. 13.18 показаны характеристики ГВП четырех фазо-
вых звеньев, требуемая и реальная характеристики ГВП коррек-
тора.
Далее с применением компьютерных программ решается оп-
тимизационная задача в общей постановке:
max|£K/©)-£K(co,QnJfe,toOA)| = ттш е [®н,сов].
Если полученный минимум меньше или равен требуемой точ-
ности коррекции, то по заданным Qnb, и Rq рассчитывают
элементы L]k и мостовой схемы фазового звена (рис. 13.9, а).
Остальные элементы находят из условия, что двухполюсники Za
и Zb обратные:
^2k = -^oQk> ^2k = ^\k!^0 •
Если полученная точность коррекции не удовлетворяет требова-
ниям, то увеличивают число звеньев и повторяют расчет также с
помощью компьютера.
517
Из данного параграфа мы узнали, что:
• При расчете фазовых корректоров вначале по заданной -
ГВП определяют требуемую характеристику корректора, 1,
затем число фазовых звеньев и рассчитывают параметры их ’
элементов. Расчет проводят до тех пор, пока не получат за- j
данную точность коррекции в рабочем диапазоне частот. :
Вопросы и задания для самоконтроля
1. Сформулировать условия безыскаженной передачи сигнала.
2. Почему происходят фазо-частотные искажения?
3. Что такое групповое время прохождения?
4. По рис. 13.6 пояснить, как работает фазовый корректор.
5. Каким образом строятся пассивные фазовые корректоры?
6. Как рассчитываются передаточные функции Нк{р), фазовые
характеристики Вк(<в) и ГВП £гр(со) мостовых фазовых кор-
ректоров первого и второго порядков?
7. Как изменится график ^гр(/) в примере 13.1, если индуктив-
ность Lj уменьшить в 2 раза?
8. Определить параметры элементов фазового корректора второго
порядка (рис. 13.9) по заданным коэффициентам передаточной
функции ©о = 0,416 • 104 с'1, Qn = 0,25 и Ro = 600 Ом.
9. Каким образом строятся активные фазовые корректоры?
10. Доказать, что операторная передаточная функция Нк(р)
корректора, изображенного на рис. 13.13, имеет вид (13.20).
И. Каким образом на основе схемы рис. 13.15 получить фазовые
корректоры первого и второго порядков?
12. Как изменится график tTp(f) в примере 13.3, если сопротив-
ление Bp 1) увеличить в 4 раза; 2) увеличить в 10 раз;
3) уменьшить в 2 раза?
13. Каков алгоритм расчета фазовых корректоров?
Глава 14. Анализ нелинейных преобразователей
14.1. Стабилизаторы постоянного напряжения
Для поддержания постоянства (стабилизации) напряжения
питания активных электрических цепей при возможных колеба-
ниях первичного питающего напряжения и изменениях сопро-
тивления нагрузки используются устройства, получившие на-
звание стабилизаторов постоянного напряжения. Схема про-
стейшего стабилизатора приведена на рис. 14.1, а. В него входят
генератор первичного питающего напряжения, задающее напря-
жение Ur которого под воздействием дестабилизирующих факто-
ров может меняться относительно его среднего значения, и ста-
билитрон, подсоединенный параллельно нагрузке. Внутреннее
сопротивление генератора Rr и сопротивление нагрузки RH счи-
таются чисто резистивными.
При анализе работы стабилизатора цепь, внешнюю по отно-
шению к стабилитрону, заменим эквивалентным генератором с
задающим напряжением Uo и внутренним сопротивлением Rq.
После этой замены схема анализируемой цепи преобразуется в
схему рис. 14.1, б. На этой схеме через UH обозначено напряже-
ние на зажимах нагрузки, которое совпадает с напряжением в
рабочей точке стабилитрона (рис. 14.1, а). Зная последнюю,
можно найти токи в ветвях исходной цепи: Ir = (Ur - UH)/Rr,
Iv.= Un/R-ii, 1ц=1г~ 1я-
Рисунок 14.2 показывает, что рабочая точка стабилитрона
изменяется вдоль прямой, практически параллельной оси орди-
нат, с изменением как задающего напряжения эквивалентного ге-
нератора (рис. 14.2, а), так и его внутреннего сопротивления
(рис. 14.2, б). Тем самым решается задача стабилизации напря-
жения на зажимах нагрузки, поскольку оно незначительно меня-
ется при изменении в широких пределах первичного питающего
напряжения Ur и сопротивления нагрузки RH.
Рис. 14.1. Схема стабилизатора (а) и замена его внешней
цепи эквивалентным источником (б)
519
О Ua UOi UO2 и
а)
Рис. 14.2. Постоянство напряжения стабилитрона при изменении
напряжения (а) и сопротивления (б) эквивалентного генератора
Естественно, что эффект стабилизации достигается ценой
рассеяния энергии в стабилитроне и резисторе Rr-
Из данного параграфа мы узнали, что:
У.»?.! .........'Л'" 4 ..>х
....................Й
• Стабилизаторы предназначены для поддержания постоян-
ным напряжения питания в электрических цепях.
• Изменение первичного напряжения питания цепи и сопро- й
тивления нагрузки в широких пределах вызывает лишь не-
значительные колебания напряжения на стабилитроне. j
14.2. Резонансные усилители
и умножители частоты
Нелинейный резонансный усилитель содержит колебатель-
ный контур, настроенный на частоту первой гармоники тока.
Рассмотрим вначале процессы в линейном усилителе с резистив-
ной нагрузкой (рис. 14.3, а). Это позволит лучше уяснить отли-
чия от него нелинейного резонансного усилителя. Будем пола-
гать, что ВАХ iK = F(u63), т.е. зависимость тока коллектора от
напряжения на участке «база — эмиттер», достаточно точно пред-
ставляется кусочно-линейной функцией вида (8.21). На входе НЭ
транзистора действует напряжение
ыбэ = Uo + Um cosat,
не выходящее за пределы линейного участка. Тогда ток в цепи
коллектора
ZK — S (М(5э - U ОТС ) — *$*(Uо + Uт cos at — Uотс) —
= S(UQ - UOTC ) + SUm cos at = Io. + Im\ cosat
будет, как и входное напряжение, гармоническим (рис. 14.3, б).
Определим коэффициент полезного действия (КПД) линей-
ного усилителя. Ток коллектора создает на резисторе нагрузки
520
Рис. 14.3. Линейный резистивный усилитель (а)
и графический анализ его работы (б)
RH падение напряжения iKRn, которое является выходным сиг-
налом с амплитудой Um вых. КПД усилителя есть отношение по-
лезной активной мощности
1
п — Г ГТ
-‘ПОЛ ~ 2 1 т вых
к активной мощности, потребляемой от источника питания
-^ПИТ = Л)^пит> т-е-
_ Рцол _ т вых
~ п ~ *)Г ГТ
____-‘пит___О1-7 пит
Из рис. 14.3, б видно, что 1т1 <10. Если при этом учесть,
что Um вых < UmT, то получим КПД ц < 0,5, т.е. коэффициент по-
лезного действия линейного усилителя не может превышать 50%.
Вольт-амперная характеристика гк = F(u6a) реальных транзис-
торов является нелинейной (на рис. 14.3, б она показана штрихо-
вой линией), поэтому форма тока в цепи коллектора при гармони-
ческом воздействии на усилитель будет отличаться от гармониче-
ской. В коллекторной цепи оказываются постоянная составляющая,
а также первая, вторая и последующие гармоники частоты сигнала.
Чтобы количественно оценить степень искажения сигнала на
выходе усилителя, вводят коэффициент гармоник, который опре-
деляется отношением среднеквадратического уровня всех высших
гармоник к амплитуде первой гармоники тока:
= m2 "* ^тЗ ^т4 + • •/^т\ •
521
Пример 14.1. Рассчитаем коэффициент гармоник усилителя на
биполярном транзисторе, спектр тока базы которого
был рассчитан в примере 8.7.
ВАХ транзистора, была аппроксимирована поли-
номом второй степени, поэтому в спектре тока есть
только постоянная составляющая 10 = 0,1375 мА и
две гармоники, имеющие амплитуды Imi = 0,125 мА
и 1т2 = 0,0375 мА. Коэффициент гармоник рассчита-
ем по формуле
kT = = I m2/1 ml = = 0,3 .
Vj 1
Рис. 14.4. Резонансный
усилитель
Так работает усилитель в линейном
режиме, который в большинстве случа-
ев и используется на практике. Между
тем достаточно мощные усилители вы-
годно использовать в нелинейном ре-
жиме работы, поскольку, как будет по-
казано ниже, они имеют более высокий
КПД.
Нелинейный резонансный усили-
тель изображен на рис. 14.4. На входе
его действует переменное напряжение
UmCQS(i>t и постоянное напряжение
смещения (70, причем амплитуда Um
переменного напряжения велика, так
что напряжение пбэ «выходит» за рам-
ки линейного участка (см. рис. 8.33).
Ток в цепи коллектора имеет форму
косинусоидальных импульсов с отсеч-
кой. Резонансный контур настроен на частоту первой гармоники
тока, т.е. на частоту входного сигнала со. Сопротивление парал-
лельного контура на этой частоте велико, а на частотах гармоник
2со, Зсо, ... мало, так что высшие гармонические составляющие
практически не влияют на форму выходного сигнала мвых и
вых ~ Ди1-^0э ~ )>
где Imi — амплитуда первой гармоники тока коллектора гк; 7?Оэ —
сопротивление параллельного контура на резонансной частоте (о.
Выходное напряжение
“вых (t) = S итух (0) 2?оэ cos (at = Um вых cos (oY
практически оказывается косинусоидальным (т.е. гармоническим).
522
Вычислим КПД нелинейного резонансного усилителя. Мощ-
ность, потребляемая от источника, Рпит=Л)^пит=5уо(6)Сгт1/Пит-
Полезная активная мощность в колебательном контуре
•^пол =(W т вых = (1/2)5СУшУ1(0)С/твь1Х.
Отсюда
_ 71(9) т вых
2уо(О)’ <4ИТ ‘
В мощных усилителях обычно стремятся максимально ис-
пользовать источник питания и получают С7ОТВЫХ ®(7ПИТ, поэтому
КПД _________________
г]»yt (е)/2у0 (е).
Исследования показывают, что с уменьшением 0 отношение
У1(0)/уо(6) растет, т.е. КПД увеличивается, но одновременно
падает амплитуда первой гармоники. Считается, что оптималь-
ным значением является 0 = 90°, при этом отношение функций
Берга равно 1,517. Это соответствует КПД около 76%.
Таким образом, нелинейный резонансный усилитель работает в
более выгодном энергетическом режиме по сравнению с линейным
усилителем.
Пример 14.2. Рассчитаем КПД резонансного усилителя, если
угол отсечки 0 = 70° (см. пример 8.8).
В примере 8.8 по графикам рис. 8.34 были опре-
делены значения функций Берга:
уо(0) = О,22; у1(0) = О,33.
КПД нелинейного резонансного усилителя
П = Yi (0 )/2у0 ( 0) = 0,33/2 • 0,22 = 75%.
Резонансный умножитель частоты — это тот же резонанс-
ный усилитель, но настроенный в резонанс на одну из высших
гармоник. Схема резонансного умножителя частоты отличается от
нелинейного резонансного усилителя (рис. 14.4) только тем, что
колебательный контур в выходной цепи настраивается на частоту
одной из высших гармоник входного сигнала.
Амплитуда выходного сигнала умножителя при кусочно-
линейной аппроксимации
U т вых = SRo9Umy k ® >
а выходной сигнал
^вых ( ) = т вых COS k(iyt
523
имеет частоту в k раз больше, чем у входного сигнала
wBX (i) = Um cosa>t.
При больших k функции у&(6) имеют небольшие значения
(см. § 8.4), поэтому важно выбрать угол отсечки 0, при котором
значение соответствующей функции Берга максимально. Сущест-
вует оптимальный угол отсечки 0ОПТ = 180°/&, при котором ам-
плитуда выходного напряжения получается наибольшей.
Умножители частоты применяют в радиотехнике для получе-
ния высокочастотных стабильных колебаний, когда в распоряже-
нии имеется стабильный низкочастотный генератор. Если откло-
нение частоты со, генерируемое низкочастотной схемой, составля-
ет До, то относительная нестабильность частоты равна Дсо/со. В
умножителе частоты вместо частоты со + До получаем частоту
k(a + Дсо), а относительная нестабильность ^Дсо/Лсо остается та-
кой же, как и у низкочастотного генератора.
Из данного параграфа мы узнали, что:
• Сигнал на выходе транзисторного усилителя с резистивной |
нагрузкой из-за нелинейности ВАХ отличается от гармони- |
ческого. Коэффициент гармоник позволяет оценить степень |
искажения сигнала. |
• Если вместо резистивной нагрузки включить параллельный |
колебательный контур, настроенный на частоту первой гармо-
ники тока, то получим нелинейный резонансный усилитель, g
Выходное напряжение нелинейного резонансного усилителя
является гармоническим. Нелинейный резонансный усилитель |
имеет более высокий КПД по сравнению с линейным. ।
• Резонансный усилитель, колебательный контур которого ।
настроен на одну из высших гармоник, является резонанс- I
ным умножителем частоты. |
14.3. Ограничители мгновенных и амплитудных
значений сигнала
Ограничитель мгновенных значений «обрезает» значения
сигнала, превышающие заданный порог, а ограничитель ампли-
тудных значений поддерживает постоянной амплитуду колеба-
ния. К ограничителям мгновенных значений предъявляются сле-
дующие требования. Если мгновенное значение входного сигнала
превышает заданное значение, называемое порогом ограничения,
то значение выходного сигнала должно оставаться неизменным.
Различают ограничения снизу, сверху и двухстороннее. Ограни-
524
Рис. 14.5. Графический анализ работы резонансного усилителя
чение снизу наглядно демонстрирует рис. 8.33. Таким образом, в
схеме на транзисторе можно совмещать функции усилителя и ог-
раничителя, если амплитуда входного сигнала «выходит» за
рамки линейного участка ВАХ (рис. 8.33), а в цепи коллектора
включена резистивная нагрузка (рис. 14.3, а). Порог ограниче-
ния можно регулировать напряжением смещения Uo.
Ограничение сигнала сверху и двухстороннее ограничение
можно также осуществить на транзисторном резистивном каскаде
(рис. 14.3, а), если ВАХ iK = F(u6a) будет иметь вид, показан-
ный на рис. 14.5. Ограничение происходит за счет верхней от-
сечки тока, двухстороннее ограничение — за счет нижней и верх-
ней отсечки тока гк. Указанная характеристика = F(u63) тран-
зистора получается при использовании существенно пониженного
напряжения коллекторного питания ипит. Идеализация характе-
ристики достигается применением кусочно-линейной аппроксима-
ции тремя отрезками прямых.
Пример 14.3. На вход усилителя (рис. 14.3, а) поступает напряже-
ние u(t) = U0+UmcosG)t = l + l,5cos(i>t, В. Проходная
ВАХ iK=F(u63) транзистора изображена на рис. 14.6
штриховой линией. Построим график тока гк(£).
525
Рис. 14.6. Двухстороннее ограничение тока
(к примеру 14.3)
Аппроксимируем ВАХ транзистора тремя отрез-
ками прямых. Усилитель работает в режиме двух-
стороннего ограничения тока. График тока гк(£) по-
строен с использованием метода проекций и приведен
на рис. 14.6.
Ограничители мгновенных значений могут строиться на схе-
мах с диодами, ВАХ которых могут быть также аппроксимиро-
ваны отрезками прямых. На рис. 14.7 приведены схемы диод-
ных ограничителей снизу (а), сверху (б) и двухстороннего (в).
В этих схемах сигнал появляется на выходе, если диод закрыт.
Мейяя величину пороговых напряжений, можно осуществлять
ограничение на разных уровнях. Для правильной работы схемы
необходимо, чтобы сопротивление резистора R было во много
раз больше дифференциального сопротивления диода в откры-
том состоянии.
R
R
О—I I о
+ 2£VD+
wbx(O нвых(0
Чгор
-о—
а)
wbx(O мвых(О
Цаор
О ? ----О
WBx(0 О
Cfcopl
- +?
О .........
WVD2+
+ ивых(О
4iop2
----5
в)
Рис. 14.7. Диодные ограничители сигнала: снизу («),
сверху (6), двухсторонний (в)
526
Задача ограничителя амплитудных значений состоит в том,
чтобы из сигнала с переменной амплитудой получить на его вы-
ходе колебание с постоянной амплитудой. Такая операция мо-
жет быть выполнена с помощью нелинейного резонансного уси-
лителя (рис. 14.4), работающего в режимах нижней и верхней
отсечек тока. При этом будут получаться почти прямоугольные
импульсы, подобные приведенным на рис. 14.5. Гармоническое
же колебание с постоянной амплитудой выделяется колебатель-
ным контуром, настроенным на частоту сигнала со.
Ограничители мгновенных значений применяются, напри-
мер, когда необходимо из синусоидального сигнала получить
импульсы, близкие к прямоугольному. Ограничители амплитуд-
ных значений широко используются для устранения паразитных
изменений амплитуды сигнала, которые могут возникнуть при
передаче сигнала.
Из данного параграфа мы узнали, что:
• В ограничителях мгновенных значений выходное напряже-
ние остается постоянным, когда входной сигнал превышает
значение, называемое порогом ограничения. Различают ог-
раничения сигнала снизу, сверху и двухстороннее.
• Для ограничения мгновенных значений сигнала используют
транзисторные резистивные усилители и схемы с диодами.
• Для ограничения амплитудных значений используют нели-
нейные резонансные усилители.
__________________________________________________________
14.4. Выпрямители переменного тока
Выпрямитель — прибор, превращающий переменное напря-
жение (ток) в постоянное напряжение (ток). Подадим на вход
цепи (рис. 14.8), состоящей из последовательного соединения
диода и резистора RH, гармоническое напряжение. Когда подава-
емое на диод напряжение таково, что его анод положителен по
отношению к катоду, в цепи течет ток. Форма тока — синусои-
дальная в течение первой половины периода. Когда полярность
VD
О В Форма выходного
напряжения
Рис. 14.8. Диодный выпрямитель и напряжения
на его входе и выходе
527
Рис. 14.9. Выпрямитель с вход-
ным трансформатором и про-
стейшим фильтром
напряжения меняется на проти-
воположную, анод становится
отрицательным по отношению к
катоду и тока в цепи нет.
Напряжение на резисторе
RH пропорционально току и по-
этому представляет собой по-
следовательность однополярных синусоидальных импульсов.
Рис. 14.10. Преобразование
переменного напряжения в
постоянное в схеме рис. 14.9
Этот
процесс называется выпрямлением.
Приложенное напряжение изменяется по закону синуса; в
первом полупериоде диод работает в режиме прямого смещения,
а в следующем полупериоде — в режиме обратного смещения (см.
рис. 8.29). Только при прямом смещении диода через него проте-.
кает ток. Падением напряжения на диоде в этот период времени
пренебрегают.
Поскольку выпрямитель проводит ток только в течение одной
половины периода приложенного напряжения, то и называется он
полуволновым выпрямителем.
Очевидно, что в выпрямителе, изображенном на рис. 14.8,
выходное напряжение не является постоянным, как это требуется
в цепях питания для электронной аппаратуры.
Исследование формы сигнала показывает наличие пульсаций
напряжения. Для того чтобы сгладить эти пульсации и получить
напряжение питания требуемого постоянного уровня, параллель-
но сопротивлению Rn подключают емкость С (рис. 14.9), т.е. ис-
Входот
выпрямителя
с конденсато-
ром
Рис. 14.11. Селективный фильтр Рис. 14.12. АЧХ селективного
фильтра
528
Рис. 14.13. Двухполупериодный выпрямитель (а)
и выпрямленное напряжение не его выходе (б)
Рис. 14.14. Мостовой выпрямитель с фильтром
пользуют схему простейшего фильтра. Значение емкости должно
быть большим (500...5000 мкФ). Выпрямленные импульсы заря-
жают емкость до напряжения, близкого к максимальному значе-
нию, создаваемому выпрямителем (рис. 14.10). Из-за больших
значений емкости С постоянная времени R„C будет тоже боль-
шой по сравнению с периодом приложенного напряжения.
Напряжение на сопротивлении поэтому уменьшается не по
закону синуса, а по экспоненциальному закону в соответствии с
уравнением
uRh =ите'^**с\
Падение напряжения может быть уменьшено для данной на-
грузки увеличением значения С.
Напряжение на выходе выпрямителя, когда используется
один конденсатор, не является гладким, но может рассматривать-
ся в виде малых пульсаций напряжения, наложенных на сравни-
тельно большое постоянное напряжение C/const. Это постоянное
напряжение и является требуемым напряжением, а переменное
пульсирующее напряжение должно быть устранено.
Чтобы уменьшить пульсации до приемлемого уровня, необ-
ходимо использовать селективный фильтр, который будет подав-
лять пульсирующее напряжение, но не будет значительно ослаб-
лять постоянную составляющую. Схема такого фильтра приведе-
на на рис. 14.11. Емкость представляет очень малое сопротивле-
34-6972
529
ние переменным составляющим и очень большое сопротивление
постоянной составляющей напряжения. Обычно используется ем-
кость в несколько тысяч микрофарад. Амплитудно-частотная ха-
рактеристика фильтра показана на рис. 14.12.
Схема двухполупериодного выпрямителя показана на рис. 14.13, а,
а график выпрямленного напряжения (£) на рис. 14.13, 6.
Схема мостового выпрямителя с фильтром изображена на
рис. 14.14.
Из данного параграфа мы узнали, что:
• Для преобразования переменного (гармонического) напря-
жения в постоянное используют схемы с диодами. Разли-
чают одно- и двухполупериодные, а также мостовые вы-
прямители.
• Для сглаживания пульсаций выпрямленного напряжения
используют различные фильтры нижних частот.
14.5. Преобразователи частоты
Преобразователи частоты служат для переноса спектра сиг-
нала вверх или вниз по шкале частот. При передаче электриче-
ских сигналов на расстояние часто требуется переносить спектр
сигнала вверх или вниз по шкале частот. Такой перенос спектра
называется преобразованием частоты. Необходимость в преобра-
Рис. 14.15. Транзисторный
преобразователь частоты
зовании частот возникает, например,
в случаях, если спектр сигнала, ко-
торый можно передать, расположен
на шкале частот значительно ниже по-
лосы пропускания системы передачи.
В качестве преобразователя час-
тоты может быть использован усили-
тельный каскад на транзисторе с ко-
лебательным контуром (рис. 14.15).
Предположим, что нужно перенести
вверх по шкале частот на значение со
гармоническое низкочастотное коле-
бание с частотой Q:
un(t) = UmacosQt.
Подадим на вход нелинейного
резонансного усилителя кроме этого
колебания также высокочастотное ко-
лебание с частотой со:
530
%(<о)
Рис. 14.16. Спектр низкочастотного напряжения на входе преобразо-
вателя частоты (а) и спектр тока в нелинейном элементе (б)
ua(t) = [7m(B coscot.
Амплитуды напряжений смещения Uq, низкочастотного Uma
и высокочастотного Um(0 колебаний выберем так, чтобы работать
на участке ВАХ, который достаточно точно аппроксимируется
полиномом второй степени
4 = F(u6a) = a.o+ai(u63-Uo) + a2(u63-Uo)2. (14.1)
Напряжение на участке «база — эмиттер»
“бэ = ^0 + UmQCOSflt + Ume) coscot.
После подстановки этого выражения в зависимость (14.1) в
формуле для тока появляются в соответствии с (8.24) гармониче-
ские колебания с частотами Q, со, 2Q, 2со и с суммарной и разно-
стной комбинационными частотами со + О и со - Q.
Колебательный контур резонансного усилителя настроен на
частоту со + Q и выделяет из спектрального состава тока колебание
^о>+С1 (t) = ОС 2Um<& COS ( СО + ) t.
Выделенное колебание тока создает на резонансном сопротивле-
нии контура ROa падение напряжения
^вых (t) = СХ 2RqJJmco COS ( CO + Q ) t = Um+Q ( CO + ) t,
которое и является выходным сигналом преобразователя частоты.
В реальных системах связи передаваемый низкочастотный
сигнал не является гармоническим, а имеет сложный спектр
Un (со) (рис. 14.16, а), т.е. состоит из суммы гармонических ко-
лебаний с частотами , Q2> ....
34*
531
Если этот сигнал вместе с высокочастотным колебанием
ыга(£) подать на нелинейный элемент, то в спектре тока /к(о>)
(рис. 14.16, б), протекающего через НЭ, будут присутствовать
полезные продукты преобразования — комбинационные частоты
со + П1( co + Q2> й) + ^з> ••• • Чтобы отфильтровать токи с этими
частотами, недостаточно воспользоваться одиночным колебатель-
ным контуром, поскольку он не сможет обеспечить хорошую
фильтрацию полезных продуктов преобразования. Его можно за-
менить в схеме рис. 14.15 обычной резистивной нагрузкой, а на
выходе схемы включить электрический фильтр с характеристикой
ослабления, обеспечивающей необходимую степень подавления
несущего колебания с частотой <в.
Приведем еще несколько практических схем преобразовате-
лей частоты. На рис. 14.17 представлены диодные преобразова-
тели: однотактный (а), двухтактный или балансный (б) и коль-
Рис. 14.17. Диодные преобразова-
тели частоты: однотактный (а),
двухтактный (б), кольцевой (в)
Рис. 14.18. Транзисторный
балансный преобразователь
частоты
532
цевой (в), работающие в режиме больших амплитуд колебания
частоты со, т.е. в режиме аппроксимации ВАХ диодов кусочно-
линейными функциями. Схема балансного транзисторного пре-
образователя частоты показана на рис. 14.18.
В балансных и кольцевых преобразователях гораздо меньше
побочных продуктов преобразования; тем самым значительно об-
легчаются требования к фильтру, выделяющему полезные коле-
бания.
Из данного параграфа мы узнали, что:
• Перенос спектра сигнала по шкале частот осуществляется с
помощью преобразователей частоты.
• В качестве преобразователя частоты используется резо-
нансный усилительный каскад на транзисторе либо схемы
на диодах.
Вопросы и задания для самоконтроля
1. По графикам рис. 14.3 и 14.5 пояснить принцип работы рези-
стивного и резонансного нелинейных усилителей. Сравнить их
КПД.
2. На вход резонансного усилителя (рис. 14.4) поступает гармо-
ническое колебание частотой 50 кГц. Как получить на выходе
напряжение частотой 150 кГц? Каким должен быть при этом
угол отсечки и как добиться оптимального значения 0?
3. Построить качественно графики напряжений ывых(£) в схемах
ограничителей рис. 14.7, а — в.
4. По графику рис. 14.10 пояснить принцип работы выпрямите-
ля, схема которого изображена на рис. 14.9.
5. Как сгладить пульсации напряжения на выходе выпрямителя?
6. Какой спектр имеет бигармоническое воздействие? Каков
спектральный состав тока в цепи с НЭ, на который подано би-
гармоническое воздействие?
7. Какие комбинационные частоты будут в спектре НЭ, если его
ВАХ аппроксимирована полиномом четвертой степени?
8. Каким образом можно перенести спектр сигнала по шкале
частот?
Глава 15. Анализ генераторов гармонических
колебаний
15.1. Физические процессы в генераторах
гармонических колебаний
Генераторы — это устройства, в которых без посторонних
воздействий самостоятельно возникают электрические колеба-
ния. Генераторы используются в радиотехнике и связи для по-
лучения электромагнитных колебаний. В зависимости от формы
колебаний различают генераторы гармонических и негармониче-
ских (прямоугольных, пилообразных, импульсных и т.п.) коле-
баний.
В качестве активных элементов в генераторах применяют
электронные лампы, биполярные и полевые транзисторы и др.
Различие в элементной базе пассивной части схемы генератора
позволяет вести речь о LC-генераторах или о /?С-генераторах.
На рис. 15.1, а показан параллельный колебательный кой-
тур, состоящий из элементов L, С и G. Если контуру сообщить
некоторое количество энергии, то в нем возникнут свободные
гармонические колебания. Из-за наличия резистивной проводи-
мости G в контуре имеются потери и колебания будут затухаю-
щими, т.е. напряжение на контуре будет иметь вид затухающей
синусоиды (рис. 15.1, б):
uK(t) = UmKe~at sin(<oc£+ <р),
где UmK — начальная амплитуда напряжения на контуре; а — ко-
эффициент затухания контура; о>с = ~ а2 — частота свобод-
ных колебаний; <г»о — резонансная частота контура; ср — началь-
ная фаза колебания.
д) б)
Рис. 15.1. Параллельный колебательный контур (а)
и график затухающих колебаний в этом контуре (б)
534
Чтобы превратить такой контур
в генератор незатухающих гармо-
нических колебаний, нужно возме-
щать в нем потери, т.е. пополнять
контур энергией. Энергию в конту-
ре можно пополнять, например, за
счет собственных колебаний, сня-
тых с контура и усиленных усили-
телем. Работающая на таком прин-
ципе схема автогенератора показана
на рис. 15.2 (источник питания обо-
значен на схеме (7П). Она состоит
из биполярного транзистора, в кол-
лекторную цепь которого включен
колебательный контур. С помощью
трансформатора напряжение сни-
Рис. 15.2. Генератор с
трансформаторной
обратной связью
мается с контура и подается на
вход (участок «база — эмиттер») транзистора.
Причиной возникновения колебаний в автогенераторе явля-
ются флуктуации тока в элементах реальной схемы за счет теп-
лового движения электронов в активных элементах и резисторах,
дробового эффекта в активных элементах и т.д., а также за счет
внешних помех. Флуктуации тока гк, протекающего через кон-
тур, вызывают флуктуации напряжения на контуре wK. Спектр
этих случайных флуктуаций весьма широк и содержит состав-
ляющие всех частот.
Составляющие напряжения ик с частотами, близкими к резо-
нансной частоте контура ®о> будут иметь наибольшую амплиту-
ду, так как модуль комплексного эквивалентного сопротивления
контура является наибольшим и равным R = i/G именно на этой
частоте со0. Выделенное на контуре синусоидальное с частотой
©о напряжение через цепь обратной связи, образованную транс-
форматором, передается на вход транзистора, создавая напряже-
ние мбэ. Это напряжение вызовет увеличение коллекторного тока
гк, что, в свою очередь, приведет к увеличению напряжения на
контуре ик. Как следствие этого, увеличатся напряжение обрат-
ной связи иос и напряжение цбэ и, значит, вновь увеличатся
коллекторный ток и напряжение на контуре ик и т.д. Таким об-
разом, в замкнутой системе автогенератора самовозбуждаются
колебания частоты, близкой к резонансной частоте контура <в0.
Очевидно, важным условием возникновения колебаний явля-
ется то, что фаза напряжения ибэ должна быть такой, чтобы уве-
личение напряжения ик вызывало увеличение коллекторного то-
ка iK и тем самым новое увеличение ик. Это условие и есть усло-
535
вие баланса фаз. Баланс фаз достигается правильным включени-
ем вторичной обмотки трансформатора. При переполюсовке об-
мотки трансформатора возрастание напряжения на контуре ик
приведет к уменьшению коллекторного тока, т.е. баланс фаз на-
рушится и самовозбуждения не произойдет.
Обратная связь (ОС), при которой выполняется баланс
фаз, является положительной обратной связью. В противном
случае обратная связь отрицательная. Самовозбуждение авто-
генератора возможно только при наличии положительной об-
ратной связи.
Пока амплитуда напряжения ибэ была мала, работа происхо-
дила на линейном участке вольт-амперной характеристики тран-
зистора. С увеличением амплитуды колебаний на контуре возрас-
тает напряжение обратной связи иос и, значит, входное напряже-
ние транзистора ыбэ. При этом все сильнее сказывается нелиней-
ность ВАХ транзистора. Наконец, при достаточно больших ам-
плитудах колебаний ток коллектора гк перестает увеличиваться,
напряжения на контуре мк, обратной связи woc и входное и6э
стабилизируются и в автогенераторе устанавливается стационар-
ный динамический режим с постоянной амплитудой колебаний и
частотой генерации, близкой к резонансной частоте колебательно-
го контура соо. Таким образом, стационарные колебания в ав-
тогенераторе устанавливаются только благодаря наличию не-
линейности вольт-амперной характеристики транзистора.
Из данного параграфа мы узнали, что:
• Устройство, содержащее резонансный усилитель с транс-
форматорной обратной связью, является генератором гар-
монических колебаний.
• Колебания в генераторе возникают без внешних воздейст-
вий, их причиной являются флуктуации тока в элементах
цепи.
• Из-за нелинейности вольт-амперной характеристики актив-
ного элемента в генераторе устанавливается стационарный
режим с постоянной амплитудой гармонических колебаний.
• Частота колебаний совпадает с резонансной частотой коле-
бательного контура.
536
15.2. Типы генераторов гармонических колебаний
Любой генератор — это усилитель, охваченный положи-
тельной обратной связью. Рассмотренный выше генератор со-
держит трансформатор и называется генератором с трансфор-
маторной обратной связью, так как через трансформатор на-
пряжение с выхода транзисторного усилительного каскада попа-
дает на его вход. Можно сказать, что трансформатор представля-
ет собой цепь обратной связи. Транзисторный усилительный кас-
кад есть не что иное, как нелинейный резонансный усилитель.
Таким образом, автогенератор с трансформаторной обратной свя-
зью можно изобразить в виде усилителя, охваченного обратной
связью (рис. 15.3). Обобщенная схема на рис. 15.3 справедлива и
для других типов генераторов.
Недостатком схем LC-генераторов с трансформаторной об-
ратной связью является наличие двух индуктивно связанных ка-
тушек. Поэтому на практике используют схемы LC-генераторов с
автотрансформаторной обратной связью, в которых напряжение
ОС снимается с части колебательного контура. Такая схема изоб-
ражена на рис. 15.4, а. Она известна также под названием схемы
индуктивной трехточки. Элементы С, Ц и L2 образуют коле-
бательный контур: резистор R6 является элементом цепи автома-
тического смещения, через который протекает постоянная состав-
ляющая тока базы; конденсатор Сб предотвращает попадание на-
пряжения питания Un на базу и влияет на постоянную времени
цепи автосмещения. На рис. 15.4, б приведена эквивалентная
схема индуктивной трехточки по переменному току, т.е. цепи пи-
тания и смещения на рисунке не показаны.
Обычно полагают, что входное сопротивление транзистора
настолько велико, что током базы можно пренебречь. В этом слу-
чае, как видно из рис. 15.4, б, элементы С, Lt и L2 образуют
трехэлементный колебательный контур, в котором сначала про-
исходит резонанс токов, а затем резонанс напряжений в контуре
CL2. Усилительный каскад со сложным колебательным контуром
Нелинейный резонансный
усилитель
Активный
элемент
Колебательная
система
Цепь обратной
связи
J
Рис. 15.3. Обобщенная схема автогенератора
537
Рис. 15.4. Генератор — индуктивная трехточка (а)
и его эквивалентная схема по переменному току (б)
в коллекторной цепи транзистора является нелинейным резо-
нансным усилителем.
Цепью обратной связи в этой схеме служит делитель напря-
жения, образованный индуктивностью Lt и индуктивностью L2.
Действительно, напряжение, снимаемое с выхода усилительного
элемента (транзистора), приложено к колебательному контуру
или, что то же, к ветви Ц (рис. 15.4, б). Напряжение обратной
связи снимается с индуктивности L2 и подается на вход усили-
тельного элемента. Усилительный каскад на одном транзисторе
поворачивает фазу сигнала на 180°. Для соблюдения баланса фаз
цепь обратной связи также должна вносить фазовый сдвиг 180°.
Это и происходит на самом деле. Ток в ветви CL2 из-за емкост-
ного характера ее сопротивления опережает напряжение на кон-
туре uK(t) на 90°. В свою очередь, напряжение иж (t) на индук-
тивности L2 опережает этот ток еще на 90°. Таким образом,
сдвиг фаз между напряжениями wK(i) и ыос(£) составляет 180°.
На сравнительно низких частотах, где реализация £С-конту-
ров становится затруднительной из-за больших габаритов и мас-
сы, низкой добротности и невозможности перестройки, исполь-
зуют 7?С-автогенераторы. Они также представляют собой комби-
нацию усилителя и пассивной ЛС-цепи для создания обратной
связи.
На рис. 15.5, а показана схема такого генератора — однокас-
кадный транзисторный усилитель, между входом и выходом ко-
торого включен лестничный пассивный RС -четырехполюсник.
Для возникновения генерации колебаний необходимо, чтобы
напряжение обратной связи, подаваемое на вход генератора, не-
прерывно возрастало. Это возможно только тогда, когда усиление
усилительного каскада больше ослабления, вносимого цепью об-
538
Рис. 15.5. 7?С-генератор с лестничной обратной связью (а)
и зависимость сдвига фаз от частоты в цепи обратной связи (б)
ратной связи. Кроме того, должно выполняться условие баланса
фаз. Последнее означает, что поскольку один каскад транзистор-
ного усилителя вносит сдвиг фаз, равный 180°, то цепь обратной
связи также должна вносить сдвиг фаз 180°, чтобы общий сдвиг
фаз равнялся 0° (или 360°).
Однако простейшее RC-звено вносит сдвиг фаз, не превы-
шающий 90°. Поэтому необходимо взять число звеньев не меньше
трех. Зависимость сдвига фаз от частоты RC-цепи из трех звень-
ев показана на рис. 15.5, б. Элементы /?С-цепи рассчитывают
так, чтобы на частоте генерации получить сдвиг фаз 180°.
В стационарном режиме кроме баланса фаз выполняется
также и баланс амплитуд, т.е. усиление усилительного каскада
становится равным ослаблению цепи обратной связи, так что ам-
плитуда напряжения цепи обратной связи, а значит, и выходного
остается постоянной.
На рис. 15.6 изображен еще один 7?С-автогенератор, нося-
щий название автогенератора с мостом Вина. Это усилитель с
Рис. 15.6. 1?С-генератор с мостом Вина (а)
и его схема с разомкнутой обратной связью (б)
539
коэффициентом усиления Н(со) = К; между его выходом и вхо-
дом включена ЯС-цепь обратной связи. Как и в других генерато-
рах, для самовозбуждения колебаний необходимо, чтобы усиле-
ние усилителя К было бы больше ослабления, вносимого в вы-
ходной сигнал усилителя 7?С-цепью обратной связи. Усилитель
не изменяет фазу сигнала. Следовательно, чтобы обратная связь
была положительной и выполнялся баланс фаз, цепь обратной
связи также не должна изменять фазу сигнала.
Из данного параграфа мы узнали, что:
• Автогенератор любого типа состоит из усилителя и цепи
положительной LC- или 7?С-обратной связи.
♦ В LC-генераторе с трансформаторной обратной связью на-
пряжение с выхода транзисторного усилительного каскада
подается через трансформатор на его вход.
• В LC-генераторе с автотрансформаторной обратной связью,
называемом индуктивной трехточкой, напряжение обратной
связи снимается с одной из катушек индуктивности трех-
элементного колебательного контура.
♦ В 7?С-генераторе с лестничной обратной связью и транзи-
сторным усилителем напряжение обратной связи снимается
с выхода РС-цепи.
• В 7?С-генераторе с мостом Вина напряжение обратной свя-
зи снимается с параллельной 7?С-цепи.
15.3. Анализ условий возникновения
колебаний в генераторе
Самовозбуждение генератора происходит только в том слу-
чае, если усиление колебания в усилителе превышает ослабле-
ние его в цепи обратной связи и если сдвиг фазы колебания в
усилителе и цепи обратной связи кратен 360°. Анализ различ-
ных схем автогенераторов показывает, что все они могут быть
представлены обобщенной структурой, показанной на рис. 15.7, а
(см. § 10.2). При этом избирательная система (LC- и 7?С-цепи)
может быть включена либо в схему усилителя, либо в схему цепи
обратной связи. Задача избирательной системы — отфильтровать
ненужные гармонические составляющие, возникающие из-за не-
линейности ВАХ, и обеспечить тем самым условия самовозбуж-
дения автогенератора только на частоте генерации.
На рис. 15.7, б изображена обобщенная схема автогенератора
с разомкнутой цепью ОС. На входе усилителя действует гармо-
540
Рис. 15.7. Обобщенная структурная схема автогенератора
с замкнутой (л) и с разомкнутой (б) обратной связью
ническое напряжение с комплексной амплитудой Цтвх. Усили-
тель изменяет амплитуду и начальную фазу колебания и форми-
рует напряжение с комплексной амплитудой Цотвых. Коэффици-
ент усиления усилителя Нус равен отношению амплитуды вы-
ходного напряжения к амплитуде входного напряжения:
Яус=^вых (15.1)
V твх
Усилитель добавляет к начальной фазе входного гармониче-
ского напряжения фазовый сдвиг <рус.
Цепь ОС ослабляет сигнал, действующий на ее входе, до ве-
личины Umoc. Коэффициент передачи цепи обратной связи
Яос=?^. (15.2)
U т вых
Фазовый сдвиг, вносимый этой цепью, составляет величину ф^.
Для того чтобы после замыкания цепи обратной связи в гене-
раторе происходило самовозбуждение колебаний, необходимо,
чтобы на частоте генерации сог амплитуда гармонического на-
пряжения на выходе схемы рис. 15.7, б была больше амплитуды
гармонического напряжения на входе схемы, т.е.
Яо=^->1, (15.3)
где Но — коэффициент передачи обобщенной схемы автогенера-
тора с разомкнутой обратной связью.
Преобразуем выражение (15.3):
тт тос Umoc Сетевых , /<<-
н° = й— = U—~й— (15,4)
т вх т вых т вх
С учетом (15.1) и (15.2) получим
Я0(сог) = Яус(сог)Яос(<йг)>1.1 (15.5)
541
Выражение (15.5) является фундаментальным в теории автоколе-
баний; оно применимо к любому типу генератора.
Таким образом, для самовозбуждения автогенератора не-
обходимо, чтобы на частоте генерации усиление усилителя
превышало ослабление, вносимое цепью обратной связи, т.е.
^ус(юг)-^ос((0г) >1- (15.6)
Условие (15.5) или (15.6) является необходимым, но недос-
таточным. Кроме него должен выполняться баланс фаз, т.е. сов-
падение начальных фаз гармонических напряжений на входе и
выходе схемы рис. 15.7, 6. Такое совпадение наступает, когда
суммарный сдвиг фаз, вносимый усилителем и цепью обрат-
ной связи, равен нулю или кратен 360°:
фо (<вг) = Фус (<ог) + Фос (<ог) = I (15.7)
где k = 0, 1, 2, ... .
Таким образом, сдвиг фаз в цепи обратной связи зависит от
сдвига фаз в усилителе и дополняет его до 360°.
Генератор с трансформаторной обратной связью. Усили-
тельным (активным) элементом в генераторе с трансформаторной
обратной связью является усилительный каскад на одном тран-
зисторе с колебательным контуром в коллекторной цепи. На
рис. 15.8, а показана вольт-амперная характеристика транзистора,
представляющая зависимость тока коллектора 4 от напряжения
на участке «база — эмиттер» ыбэ.
При выборе постоянного напряжения смещения Uo и отсут-
ствии переменного напряжения на входе транзисторного усили-
тельного каскада (рис. 15.2) на участке «база — эмиттер» дейст-
вует напряжение ы6э = (7&0 = Uo. В цепи коллектора транзистора
протекает постоянный ток гк = 7к0. Предположим теперь, что на
входе транзисторного каскада появилось гармоническое напряже-
ние с небольшой амплитудой ит6э, так что рабочая точка, сме-
щаясь под действием переменного напряжения, остается все вре-
мя на линейном участке ВАХ. В этом случае в цепи коллектора
наряду с постоянным током будет протекать переменный ток.
Из-за линейного характера рабочего участка ВАХ перемен-
ный ток в цепи коллектора будет гармоническим и будет иметь ту
же частоту, что и напряжение на участке «база — эмиттер». Если
постоянно увеличивать амплитуду ит6э гармонического напря-
жения на входе транзистора (рис. 15.8, б), то наступит момент,
когда рабочая точка, перемещаясь под действием переменного
напряжения, начнет «захватывать» нелинейный участок ВАХ.
Ток коллектора перестанет тогда быть гармоническим. Помимо
542
Рис. 15.8. Линейный (а) и нелинейный (б)
режимы работы усилителя
первой гармоники, имеющей ту же самую частоту, что и входное
напряжение, появятся высшие гармоники.
В случае, когда коллекторный ток транзистора является гар-
моническим (рис. 15.8, а), напряжение, создаваемое этим током
на колебательном контуре, будет также гармоническим с ампли-
тудой UmK = 1тк • Z, где Z — полное сопротивление контура на
частоте гармонического колебания.
Коэффициент передачи (усиления) усилителя определяется
отношением амплитуды выходного напряжения к амплитуде
входного напряжения (рис. 15.7, б):
543
Um вых _ UmK _ 1тк ' %
Umix U mfe Ujnte
Отношение амплитуды гармонического колебания тока к ам-
плитуде гармонического колебания напряжения (при условии,
что эти амплитуды малы) называется дифференциальной крутиз-
ной 5диф вольт-амперной характеристики транзистора:
диф -
V тбэ
(15.8)
Пока рабочая точка не выходит за пределы линейного участка
ВАХ, дифференциальная крутизна остается постоянной.
Таким образом, коэффициент передачи усилителя Нус равен
произведению дифференциальной крутизны ВАХ в рабочей точке
5даф и полного сопротивления колебательного контура Z на час-
тоте гармонического колебания:
U ус — •5диф^-
(15.9)
При больших амплитудах ит6э напряжения на входе тран-
зистора (рис. 15.8, б) ток коллектора перестает быть гармониче-
ским и определение дифференциальной крутизны из (15.8) теря-
ет смысл. Обычно вместо дифференциальной крутизны исполь-
зуют понятие средней крутизны, или крутизны по первой гармо-
нике, т.е. отношение амплитуды первой гармоники коллектор-
ного тока к амплитуде входного напряжения. Обозначим ам-
плитуду первой гармоники ImKi- Тогда вместо (15.8) будем
иметь
(15.10)
Если колебательный контур построен таким образом, что его
резонансная частота
f =______
2%jLC
совпадает с частотой первой гармоники тока коллектора, то пол-
ное сопротивление контура на этой частоте будет максимальным
и равным R = 1/G, а на частотах, отличных от резонансной, оно
будет уменьшаться. При больших добротностях Q колебательного
контура его полное сопротивление станет настолько малым для
всех высших гармоник тока, начиная со второй, что эти гармони-
ки не создадут практически никакого напряжения на контуре.
544
Амплитуда напряжения на контуре будет определяться только
амплитудой первой гармоники тока: UmK = ImKi R.
Коэффициент передачи усилительного каскада в этом случае
определится как
Яус =^ж=/^1^ = 5ср.Л (15.11)
m вх тбэ U тбэ
Данное выражение справедливо только для резонансной частоты
/р. На других частотах при достаточно высокой добротности
контура коэффициент усиления усилителя резко уменьшается.
Следовательно, самовозбуждение генератора может произойти
только на частоте резонанса колебательного контура, т.е. частота
генерации fT = fp.
Цепь обратной связи в генераторе на рис. 15.2, ослабляющая
сигнал, подводимый к усилителю, представляет собой трансформа-
тор с первичной обмоткой, имеющей индуктивность L, вторичной
обмоткой с индуктивностью Loc и взаимной индуктивностью М.
Из теории трансформатора известно, что напряжение, наво-
димое первичной обмоткой во вторичной, зависит от взаимной ин-
дуктивности М:
irdii
В свою очередь, напряжение на первичной обмотке (т.е. на кон-
туре) зависит от ее индуктивности L:
ик = L—
к dt
Следовательно, напряжение на вторичной обмотке можно выра-
зить через напряжение на колебательном контуре:
Мос=^«к- (15.12)
JL/
Наличие связи (15.12) между мгновенными значениями на-
пряжения позволяет сразу же установить связь между амплиту-
дами этих напряжений:
Коэффициент передачи цепи обратной связи, как это сле-
дует из рис. 15.7, б
яос _ U тъс = м
Uт вых ^тк L ’
35-6972
545
Он не зависит от частоты и поэтому одинаков на всех частотах.
Условие самовозбуждения генератора (15.5) или (15.6) при-
мет в данном случае вид
В реальных схемах генераторов выполнение условия (15.14)
обеспечивают изменением взаимной индуктивности М. Поэтому
данное условие записывают обычно в виде
Величина
(15.15)
называется критическим коэффициентом взаимной индукции.
Колебания в генераторе могут возникнуть только при обрат-
ной связи с М > Мкр.
Второе условие возникновения колебаний (15.7) означает,
что в схеме генератора должен выполняться баланс фаз. Извест-
но, что однокаскадный усилитель (усилитель на одном транзи-
сторе) «переворачивает» сигнал, т.е. вносит сдвиг фаз 180°. Что-
бы сдвиг фаз в цепи обратной связи дополнял сдвиг фаз в усили-
теле до 360°, т.е. равнялся также 180°, необходимо переполюсо-
вать вторичную обмотку трансформатора таким образом, чтобы
напряжение на ней было перевернуто относительно напряжения
на первичной обмотке.
Пример 15.1. Рассчитаем значение коэффициента передачи цепи
обратной связи Н^, при котором наступает самовоз-
буждение автогенератора (рис. 15.2), а также частоту
генерации fT, если заданы параметры элементов кон-
тура L = 100 мкГн, С = 0,1 мкФ, R = 20 кОм и сред-
няя крутизна ВАХ транзистора 5ср = 4 мА/В.
Из условия (15.6) следует, что самовозбуждение
автогенератора наступает при
Рассчитаем коэффициент передачи усилителя Нус (сог)
по формуле (15.11):
Hvc(cor) = 5ГР •/? = 4 • 20 = 80.
jV \ 1 / vp
546
Найдем Я0(. (<вг):
Нос М > %......7.х = ± = 0,0125.
ЯУ(.(сог) 80
Самовозбуждение автогенератора наступает при
Яос(®г) > 0,0125.
Частотой генерации колебаний является резо-
нансная частота колебательного контура, поэтому
2ny[LC ~ 2.3,147 100 Ю-6 0,110“6 ~ 5° КГЦ‘
Пример 15.2. Рассчитаем значение критического коэффициента
взаимной индукции автогенератора (рис. 15.2), если
заданы параметры элементов контура L = 100 мкГн,
R = 10 кОм и коэффициент передачи усилителя
Яус((ог) = 20.
Рассчитаем вначале крутизну ВАХ транзистора.
Из формулы (15.11) имеем
ЭЛ
5ср = Яус(<ог)/Я = ^= 2мА/В.
Критический коэффициент взаимной индукции
рассчитаем по формуле (15.15):
L 100 10’6 . г
MKD = —ТТ =------5-------о = 5 мкГн.
р 5срЯ 2-Ю-3-10-103
Колебания в контуре могут возникнуть только
при М > 5 мкГн.
Пример 15.3. Рассчитаем крутизну характеристики транзистора,
при которой наступит самовозбуждение автогенера-
тора (рис. 15.2), если заданы емкость и сопротивле-
ние контура С = 10 нФ, R = 5 кОм, добротность
контура Q = 10, а также взаимная индуктивность
М = 100 мкГн.
Из теории параллельного колебательного конту-
ра известно, что
Q = /?p/p,
где Яр — сопротивление контура на резонансной час-
тоте; р — характеристическое сопротивление контура
р=Ж
Зная значения Q = 10, Rp = R = 5 кОм, С = 10 нФ,
находим значение L :
35*
547
, R2C 25 IO6 10 IO'9 __ „
L =----2" =-------775-------- =2,5 мГн.
102
Для расчета крутизны BAX транзистора восполь-
зуемся условием самовозбуждения (15.14). Получаем
с L 2,5 10'3 с
5,.о > „ =--------------д = 5 мА/В.
р RM 5 • 103 • 10 • 10-6
Крутизна 5ср проходной ВАХ транзистора должна
быть больше 5 мА/B, чтобы наступило самовозбуж-
дение автогенератора.
Генератор с автотрансформаторной обратной связью (ин-
дуктивная трехточка). В данной схеме генератора (рис. 15.4)
усилительный каскад собран на одном транзисторе, в коллектор-
ную цепь которого включен трехэлементный колебательный кон-
тур из элементов L2 и С. Ток базы транзистора обычно при-
нимается равным нулю, т.е. входное сопротивление транзистора
считается достаточно большим и, следовательно, транзистор не
влияет на работу контура.
Из теории реактивных двухполюсников известно, что на час-
тоте
/р = , 1(Т \т (15.16)
2ityJ(L\ + L2 )С
в данном колебательном контуре возникает резонанс токов, пол-
ное сопротивление становится максимальным и равным R = i/G.
Эта частота и выбирается в качестве частоты генерации: fT = fp.
Усиление транзисторного каскада на резонансной частоте
определяется, как и в схеме с трансформаторной обратной
связью, формулой (15.11):
Яус(сог) = ^ср"^Г| (15.17)
где 5Ср — средняя крутизна ВАХ в рабочей точке, совпадающая с
дифференциальной крутизной 5диф при малых амплитудах гар-
монического напряжения на входе транзистора.
Коэффициент передачи цепи обратной связи (рис. 15.7, б)
тт _ ^тос _ ^тос
ос~ и ~ и ‘
т вых тк
Напряжение обратной связи, подаваемое на вход транзисто-
ра, снимается с индуктивности Л2 и имеет амплитуду /т2 * •
Амплитуду напряжения на входе усилителя, или, что то же, на
548
колебательном контуре, можно вычислить по формуле 1т1 соЦ
Тогда
_ Ьп2 ^L2
ОС “ г г •
*ml
На частоте резонанса токов (15.16), которая и является час-
тотой генерации сог, амплитуды токов в реактивных ветвях рав-
ны по величине, т.е. = Im2. Следовательно,
Яог(сог) = 41-
__________М
(15.18)
Условие самовозбуждения (15.6) запишется с учетом (15.17)
и (15.18) в следующем виде:
ScpR>^-.
_______L2
Данное условие позволяет подобрать такое отношение индуктив-
ностей Ц и L2, при котором в генераторе могут возникнуть гар-
монические колебания. Частота генерации подстраивается соглас-
но (15.16) изменением величины емкости С.
Усилительный каскад на одном транзисторе вносит сдвиг фаз
180°. Для самовозбуждения генератора такой же сдвиг фаз долж-
на вносить цепь обратной связи. Это и происходит на самом деле,
поскольку токи в реактивных ветвях контура в момент резонанса
токов находятся в противофазе и, значит, напряжения на индук-
тивных элементах Ц и L2 также находятся в противофазе.
Пример 15.4. Рассчитаем минимальное значение коэффициента
передачи Яус(сог) усилителя, при котором происхо-
дит самовозбуждение автогенератора, схема которого
приведена на рис. 15.4, б, а также частоту генерации
fr, если заданы параметры элементов контура Ц =
= 15 мкГн, L2 = 6 мкГн, С = 0,1 мкФ.
Рассчитаем коэффициент передачи цепи обрат-
ной связи Яос(<вг) по формуле (15.18):
Н0с(сог) = ^ = Д = 0,4.
jLj 13
Из условия самовозбуждения автогенератора (15.6)
получаем
Рассчитаем значение
549
___1 = _L_ = 25
Яос(®г) 0>4
Самовозбуждение автогенератора может наступить
только при Яус(сог) > 2,5.
Частоту генерации рассчитаем, используя фор-
мулу (15.16):
fr 2n^Li+L2)C
1_______________________
2л7(15 + 6)-10"6 -0,1 -10"6
= 100 кГц.
RC-генератор с лестничной цепью обратной связи. Схема
генератора изображена на рис. 15.5, а. В цепь коллектора тран-
зистора включено резистивное сопротивление RK. Усиление тран-
зисторного каскада на любой частоте равно произведению сред-
ней крутизны ВАХ в рабочей точке и сопротивления коллектор-
ной цепи:
ЯуС ~ •
Транзисторный каскад вносит сдвиг фаз 180°.
По-прежнему считаем входное сопротивление транзистора
настолько большим, что он не влияет на работу цепи обратной
связи.
Из теории черытехполюсников известно, что передаточная
функция лестничной цепи, изображенной на рис. 15.5, а, описыва-
ется выражением
Яос =
тос
(^ШВЫХ
-I--------------5----!------------------т- (15-19)
7(1 - 5со2Т?2С2 )2 + ®2Т?2С2 (б - (o2R2C2 )2
Необходимо, чтобы цепь обратной связи вносила на частоте
генерации фазовый сдвиг 180°. Можно показать, что это про-
изойдет, если выбрать частоту генерации
(ог = J6/(RC~
Подставив данную формулу в (15.19), легко убедиться, что
передаточная функция цепи обратной связи будет
|Н0С(фг) = 1/29."
Тогда из (15.6) получим условие самовозбуждения на час-
тоте <ог:
ScpRK > 29, (15.20)
550
т.е. для возникновения в RС генераторе колебаний усиление
транзисторного каскада должно быть больше 29 единиц.
Пример 15.5. Рассчитаем значение сопротивления R* в коллек-
торной цепи, при котором произойдет самовозбужде-
ние автогенератора (рис. 15.5, а), а также частоту
генерируемых колебаний, если заданы параметры эле-
ментов цепи обратной связи С = 200 пФ, R = 20 кОм
и средняя крутизна ВАХ транзистора 5ср = 65 мА/В.
Из условия самовозбуждения (15.20) найдем
значение RK:
29 29
>5ср 65-10-3
= 446 Ом.
Для того чтобы произошло самовозбуждение ав-
тогенератора, необходимо, чтобы RK было больше
446 Ом.
Частота генерации fT рассчитывается по формуле
f -J6 г
/г = „ =-------------5--------тт = 97 кГц.
2nRC 2-3,14-20-Ю3-200 10"12
RC-генератор с мостом Вина. Схема генератора дана на
рис. 15.6, а. Усилитель, выполненный на транзисторах или опе-
рационном усилителе, имеет независимый от частоты коэффици-
ент передачи К. Между выходом и входом усилителя включен
четырехполюсник обратной связи в виде /?С-цепи. Схема генера-
тора с разомкнутой обратной связью приведена на рис. 15.6, б.
Коэффициент передачи четырехполюсника обратной связи име-
ет вид
Яос =
UfnBUX
Л
+ (oCjl?! —
(15.21)
(В1?2С1 J
Поскольку усилитель не вносит фазового сдвига, для вы-
полнения условия баланса фаз требуется, чтобы цепь обратной
связи также не вносила никакого фазового сдвига. Известно,
что 7?С-четырехполюсник на рис. 15.6, б вносит нулевой сдвиг
фаз на частоте
в>г = 1/-\/7?iJ?2CiC2 •
На этой частоте будет происходить генерация колебаний.
Подстановка выражения для <вг в (15.21) дает значение ко-
эффициента передачи цепи обратной связи на частоте генерации:
551
Яос(®г)- R с-
1 + ~ +-7Г-
/?2 G
Условие самовозбуждения на частоте генерации сог примет вид
! С2
В2 Q
(15.22)
Если выбрать = R2 и Q = С2, то условие возникновения
колебаний упростится: К > 3. В этом случае гармонические ко-
лебания с частотой сог возникнут в генераторе, когда усиле-
ние усилителя будет больше 3 единиц.
Пример 15.6. Рассчитаем значение емкости С2 в цепи обратной
связи автогенератора (рис. 15.6, а) и частоту генера-
ции /г, если заданы параметры элементов R\ = 20 кОм,
R2 = 10 кОм, С) = 7 нФ и коэффициент усиления
усилителя К = 4.
Значение емкости С2 найдем из условия само-
возбуждения (15.22):
, с2
Q
Отсюда
c2<Cj к-t-
\ ^2
A ] = 7.f4-1-2!Г| = 7 нФ.
I Ю)
Для того чтобы произошло самовозбуждение автоге-
нератора, необходимо, чтобы емкость С2 была мень-
ше 7 нФ.
Частота генерации рассчитывается по формуле
г 1
R\R2CiC2
=-------1------Ц---------°Т =16 кГц-
2 • 3.14V20 -10 • 106 • 7 • 7 • 10’18
Из данного параграфа мы узнали, что:
Для возникновения колебаний в генераторе необходимо,
/-у1'1 VWA1XJ./1 AVKZVA ЧУАЛАЛХАХА AJ Л VrAA4/|^V4 A Л A V'V-ZV/A ATAVZ )
чтобы усиление усилителя превышало ослабление цепи об- |
ратной связи на частоте генерации и сумма фазовых сдви- |
гов, вносимых в сигнал усилителем и цепью обратной связи |
на частоте генерации, равнялась или была кратна 360°. |
552
• Колебания в LC-генераторе с трансформаторной обратной 1
связью возникают на частоте резонанса колебательного f
контура усилителя, когда значение взаимной индуктивно |
сти трансформатора превышает критическое значение, а |
напряжения на первичной и вторичной обмотках транс J
форматора находятся в противофазе. >
• Возникновение колебаний в генераторе с автотрансформа
торной обратной связью происходит на частоте резонанса
токов сложного колебательного контура, когда коэффици- J
ент усиления усилителя больше отношения индуктивностей |
в колебательном контуре, при этом напряжения на индук- j
тивных элементах всегда находятся в противофазе. |
• Возникновение колебаний в 7?С-генераторе с лестничной I
цепью обратной связи происходит при условии, что усиле- |
ние усилителя больше 29 единиц. |
• Самовозбуждение генератора с мостом Вина происходит то- |
гда, когда усиление усилителя больше 3 единиц при уело-
вии, что все сопротивления и емкости в цепи обратной свя- i
зи имеют одинаковые величины.
15Л. Анализ работы генератора
в стационарном режиме
Усиление нелинейного усилителя зависит от амплитуды
входного гармонического напряжения. В усилителях на транзи-
сторе передаточная функция определяется, как было показано
выше, выражением
Hyc=ScpRH, (15.23)
где 1?н — сопротивление нагрузки
усилителя (резонансное сопротивле-
ние контура, коллекторное сопро-
тивление и т.п.).
Средняя крутизна 5Ср зависит
от амплитуды напряжения на входе
транзистора Um бэ и от положения
рабочей точки (70. На рис. 15.9 по-
казана типичная ВАХ транзистора
iK = F (а6э ). Пусть рабочая точка
выбрана на середине линейного
участка характеристики (U0=Uq).
При увеличении амплитуды напря-
Рис. 15.9. Выбор рабочей
точки в середине линейного
участка и на нижнем загибе
ВАХ транзистора
553
Рис. 15.10. Средняя крутизна ВАХ при выборе рабочей точки
в середине ВАХ (а) и на нижнем ее загибе (б)
Рис. 15.11. Колебательные характеристики генератора
для двух положений рабочей токи на ВАХ:
в середине участка (а) и на ее загибе (б)
жения ит6э средняя крутизна, пока мы находимся в пределах
линейного участка характеристики, остается неизменной. Затем
средняя крутизна ВАХ падает (рис. 15.10, а).
Если выбрать рабочую точку (Uq=Uq) на нижнем загибе
характеристики гк =Г(г/бэ), где средняя крутизна мала, то по
мере увеличения амплитуды ит6э будут охватываться участки
характеристики с большей крутизной и, следовательно, 5ср(17т6э)
будет расти. После прохождения участка с наибольшей крутиз-
ной дальнейшее увеличение приводит к уменьшению средней
крутизны (рис. 15.10, б).
Из выражения (15.23) следует, что усиление транзисторного
усилителя также зависит от амплитуды напряжения на входе
транзистора и от положения рабочей точки. На рис. 15.11, а и 6
показаны графики Яус в зависимости от амплитуды Uтвх = ит6э
для двух положений рабочей точки на ВАХ, соответствующих
рис. 15.9.
Амплитуда установившихся гармонических колебаний в ге-
нераторе определяется графически точкой пересечения кривой
усиления усилителя Hyc(UmBX) и прямой линии l/ffOc(G>r). Ус-
ловие (15.6)
554
Яуг(сог)Я0, (cor) > 1
соответствует появлению в генераторе гармонических колебаний с
нарастающей амплитудой. Смена знака в этом неравенстве на об-
ратный, т.е. Яус (сог)Яос (сог) < 1, будет означать, что гармони-
ческие колебания в генераторе затухают по амплитуде. Устано-
вившемуся (стационарному) режиму соответствует равенство
Яус(юг)Яос(<ог) = 1. | (15.24)
Кроме того, на частоте генерации должен выполняться баланс
фаз: Фус(сог) + Фос(®г) = 2я.
Равенство (15.24) удобно иллюстрировать графически. Сна-
чала строится график зависимости усиления усилителя Нус от
амплитуды UmBX сигнала на его входе (рис. 15.11), а затем про-
водится прямая линия на уровне 1/Яос(шг). Перпендикуляр,
опущенный из точки пересечения линий на ось абсцисс, указыва-
ет на установившееся (стационарное) значение амплитуды С7^вх
гармонического колебания на входе усилителя.
На рис. 15.11, 6 прямая линия 1/Я0С(<вг) пересекает кривую
усиления в двух точках В и С, которым соответствуют две устано-
вившиеся (стационарные) амплитуды колебаний 1/„вх1 и ^твх2 •
Установившийся режим работы генератора называется ус-
тойчивым, если отклонение амплитуды UmBX от установившего-
ся значения U*mBX с течением времени будет уменьшаться.
Рассмотрим установившийся режим в точке А на рис. 15.11, а.
Уменьшение амплитуды напряжения UmBX, т.е. отклонение UmBX
влево от значения U*mBX, приведет к выполнению неравенства
Яус>1/Яос.
В результате амплитуда колебаний будет увеличиваться и при-
ближаться к установившемуся значению. При увеличении ампли-
туды напряжения (7твх, т.е. при отклонении UmBX вправо от
С/^вх> будет выполняться неравенство
НуС < VНос
и амплитуда UmBX уменьшится, вновь приближаясь к установив-
шемуся значению U^BX.
Точка В на рис. 15.11, б соответствует неустойчивому уста-
новившемуся режиму, так как отклонение амплитуды UmBX от
установившегося значения U*mBX в сторону уменьшения ведет в
силу неравенства
Нус < ^-/Нос
555
к дальнейшему уменьшению амплитуды U„IBX и в конечном сче-
те к срыву колебаний, а отклонение амплитуды UmBX от уста-
новившегося значения U*nBX в сторону увеличения вызовет
дальнейший ее рост, так как
// ус > У^ОС >
и переход в следующее установившееся состояние, отмеченное
точкой С. Установившееся состояние в точке С является устой-
чивым, в чем легко убедиться с помощью рассуждений, анало-
гичных приведенным выше.
Можно заметить, что справедливо следующее утверждение:
пересечение прямой линии с кривой усиления
НуС((7ОТвх) дает устойчивое установившееся значение ампли-
туды гармонических колебаний на входе усилителя U*mBX, если
касательная к кривой Hyc(UmBX) в стационарной точке имеет
отрицательный угол наклона, и неустойчивое — если угол на-
клона касательной является положительным.
По графикам на рис. 15.11 определяют амплитуду установив-
шегося гармонического колебания на входе усилителя. Для того
чтобы определить амплитуду установившегося гармонического ко-
лебания на выходе усилителя, или, что то же, на выходе генера-
тора (рис. 15.7), нужно амплитуду напряжения на входе усили-
теля умножить на коэффициент усиления усилителя Яус(сог) в
установившемся режиме:
Пример 15.7. Рассчитаем амплитуду стационарного колебания на
выходе автогенератора (рис. 15.2), если заданы L =
= 100 мкГн, М = 10 мкГн, G = 0,2 10~3 См, а также
график зависимости Scp(Um6B) — рис. 15.12.
Рассчитываем коэффициент передачи цепи об-
ратной связи по формуле (15.13):
Рис. 15.12. График к примеру 15.7
556
U ( \ M 10 Л4
Яос(®г)- L - 100 -0,1.
Определим коэффициент передачи усилителя,
при котором в автогенераторе существуют стационар-
ные колебания:
Яус (®г) =-------= 7“ = Ю •
' //„(Мг) 0,1
Из условия (15.23) находим значение стационар-
ной средней крутизны:
с* /\ ^ус(®г)
\Р(®Г) = —-------
^н
= 7/yc(cor)G =100,210"3 =
= 2 мА/В.
По графику 15.12 определяем амплитуду стацио-
нарного колебания на входе усилителя:
^бэ = 1,2 в.
Рассчитываем амплитуду стационарного колеба-
ния на выходе автогенератора:
^твых = ^тбэ'^ус (®г) = 1,2 • Ю = 12 В.
Пример 15.8. Определим амплитуду стационарного колебания на
выходе автогенератора (рис. 15.4, б), если заданы
индуктивности Ц = 15 мкГн, L2 = 5 мкГн и колеба-
тельная характеристика (рис. 15.13) автогенератора.
Рассчитаем коэффициент. передачи цепи ОС
Нос(сог) автогенератора по формуле (15.18):
ЯОС(®Г) = ^ = 4 = 0’33-
Рис. 15.13. Колебательная характеристика
к примеру 15.8
557
Из баланса амплитуд находим коэффициент пе-
редачи усилителя:
ЯУс(в>г) = ;=7Г^ = 3-
} ЯО(. (сог) 0,33
По колебательной характеристике (рис. 15.13)
определяем амплитуду стационарного колебания
на входе усилителя. Следует отметить, что прямая
1/Яос(сог) пересекает колебательную характери-
стику в точке С, причем этот режим является ус-
тойчивым, поэтому
^63= 0,6 В.
Амплитуда стационарного колебания на выходе
автогенератора определяется по формуле
Um вых = Um 6э ' Нус (<1>г ) = 0,6 • 3 = 1,8 В.
Из данного параграфа мы узнали, что:
• Усиление нелинейного усилителя на транзисторе зависит от
амплитуды напряжения на входе транзистора и от положе-
ния рабочей точки на проходной ВАХ.
• Если рабочая точка находится в середине линейного участ-
ка ВАХ транзистора, то усиление усилителя плавно умень-
шается с увеличением амплитуды сигнала на входе. Если
рабочая точка находится на нижнем загибе ВАХ, то с уве-
личением амплитуды сигнала на входе усилителя его уси-
ление вначале нарастает до максимального значения, а за-
тем уменьшается.
• Амплитуда стационарного гармонического колебания на |
входе усилителя определяется точкой пересечения колеба- I
тельной характеристики с прямой линией Нус = I
Амплитуда стационарного гармонического колебания на I
выходе генератора вычисляется как произведение ам- I
плитуды колебания на входе усилителя и коэффициента I
усиления усилителя на частоте генерации. I
• Установившийся режим работы генератора является устой- I
чивым, если касательная к колебательной характеристике в |
стационарной точке имеет отрицательный наклон; и наобо- I
рот, при положительном наклоне установившийся режим — |
неустойчивый. |
558
15.5. Мягкий и жесткий режимы
самовозбуждения
Режим самовозбуждения генератора, при котором колеба-
ния возникают и срываются при одном и том же значении Яос,
называется мягким, а режим самовозбуждения, при котором
колебания возникают при большем значении Нос, а срываются
при меньшем значении Нос, называется жестким. Будем менять
величину Яос и наблюдать за процессом возникновения колеба-
ний. Этот процесс зависит также от выбора рабочей точки на
вольт-амперной характеристике (напряжения смещения Яо).
Выбору рабочей точки в области наибольшей крутизны (на-
пряжение смещения Uq на рис. 15.9) соответствует график
ЙуС((Ливх)> показанный на рис. 15.11, а.
На рис. 15.14, а изображены несколько прямых, соответст-
вующих различным значениям Нос.
При Яос = Яос1 колебания в автогенераторе возникнуть не
могут, поскольку Яус < 1/Яос, значит, любые случайные флук-
туации напряжения wBX будут быстро затухать.
Увеличение Яос до значения Яос2 приводит к условию
Яус = 1/Яос. Дальнейшее увеличение Яос усиливает неравенство
Яус > 1/Яос, и, таким образом, начиная с Яос > Яос2 в автогене-
раторе возникают незатухающие гармонические колебания с соот-
ветствующими установившимися амплитудами на входе усилителя
Umax- С увеличением Яос установившаяся амплитуда Я«вх гар-
монических колебаний плавно нарастает. Уменьшение Яос вызовет
плавное уменьшение значений установившейся амплитуды (7„вх.
а) б)
Рис. 15.14. Колебательная характеристика (а) и напряжение
на входе усилителя (б) при мягком режиме самовозбуждения
559
1'рафик зависимости установившейся амплитуды (7„,вх rap
ионического колебания на входе усилителя от коэффициента пе
редачи Нт. цепи обратной связи приведен на рис. 15.14, б. Та
кой режим самовозбуждения, при котором амплитуда колебаний
плавно нарастает с увеличением //ос, называется мягким, режи-
мом самовозбуждения.
Если рабочую точку выбрать на нижнем загибе ВАХ, как
это сделано на рис. 15.9, при Uq=Uq, то график Нус((7твх)
будет иметь вид, показанный на рис. 15.15, а.
При значениях а¥О(., равных Нос1, Нос2 и Нос3, наличие ма-
лых флуктуаций напряжения и6э не приведет к установившемуся
режиму работы генератора, поскольку при этих значениях Яос
будет иметь место неравенство Нус < \/Н0(..
Только начиная с Hoc=Hoci, когда Нус > 1/Я0С, малые
флуктуации амплитуды напряжения ы6э начинают быстро расти,
пока не установится устойчивое стационарное значение амплиту-
ды колебаний (7^вх • Дальнейшее увеличение Нос ведет к плавно-
му росту амплитуды установившегося в генераторе колебания.
При плавном уменьшении коэффициента передачи цепи об-
ратной связи амплитуда (7^вх установившегося гармонического
колебания будет также плавно уменьшаться. Колебания сорвутся
при значении Нос = НОС2, меньшем Нос4, когда перестанет выпол-
няться условие Нус > 1/Я0С. На рис. 15.15, б дан график изме-
нения стационарной амплитуды U*mm в зависимости от Нж. Та-
кой режим, когда колебания возбуждаются при большем значе-
нии Нос, а срываются при меньшем значении Яос, называется
жестким режимом самовозбуждения.
Рис. 15.15. Колебательная характеристика (а) и напряжение
на входе усилителя (б) при жестком режиме самовозбуждения
560
Рис. 15.16. Автогенератор с цепью автоматического смещения
Достоинством мягкого режима самовозбуждения является
плавное изменение амплитуды (7^вх при изменении коэффициента
передачи Нос. Достоинством жесткого режима является высокий
КПД за счет работы с отсечкой коллекторного тока.
Можно объединить достоинства мягкого и жесткого режимов
самовозбуждения, если ввести в автогенератор цепь автоматиче-
ского смещения R6 Cq (рис. 15.16, а). Исходное смещение Uq
выбирают таким, чтобы рабочая точка находилась на участке
наибольшей крутизны ВАХ, что соответствует мягкому режиму.
При нарастании амплитуды колебаний UmBX в цепи базы за счет
нелинейности ВАХ i6 = F(ufy) будет происходить детектирова-
ние колебаний. Возрастание постоянной составляющей тока базы
160, которая на активном сопротивлении R6 создает напряжение
76о • Вб > приведет к уменьшению результирующего напряжения
смещения Uq - R6 и, как результат, к сдвигу рабочей точки
влево (рис. 15.16, б) к нижнему загибу вольт-амперной характери-
стики гк =F (мбэ). Переходный процесс заканчивается (при соот-
ветствующей величине Rq ) установлением жесткого стационарного
режима с более высоким КПД.
Из данного параграфа мы узнали, что:
• При выборе рабочей точки в середине линейного участка |
ВАХ режим самовозбуждения генератора называется мяг- |
ким. При выборе рабочей точки на нижнем загибе ВАХ f
режим самовозбуждения называется жестким. |
36 — 6972
561
• При мягком режиме самовозбуждения колебания возникают |
и срываются при одном и том же значении коэффициента |
передачи цепи обратной связи. |
• При жестком режиме самовозбуждения колебания возни- |
кают при большем значении, а срываются при меньшем |
значении коэффициента передачи цепи обратной связи. 1
• Преимуществом мягкого режима самовозбуждения является |
плавное изменение амплитуды колебаний при изменении |
глубины обратной связи Яос. Преимуществом жесткого ре- I
жима самовозбуждения является высокий КПД. Достоинства |
мягкого и жесткого режимов можно объединить, введя в ав- |
тогенератор цепь автоматического смещения. j
Вопросы и задания для самоконтроля
1. Каким образом в автогенераторе (рис. 15.2) возникают стацио-
нарные гармонические колебания?
2. Пояснить принцип работы автогенератора по рис. 15.3.
3. Какие типы автогенераторов существуют? Как работают эти
генераторы?
4. Сформулировать условия самовозбуждения автогенераторов:
а) с трансформаторной обратной связью; б) индуктивной трех-
точки; в) 7?С-генератора с лестничной цепью обратной связи;
г) 7?С-генератора с мостом Вина.
5. Проверить, произойдет ли самовозбуждение автогенератора
(рис. 15.2), если L = 200 мкГн, М = 50 мкГн, Rp = 10 кОм,
5ср = 1 мА/В.
6. Является ли цепь на рис. 15.4, б автогенератором, если Нус =
= 2,5, Ц = 30 мкГн, L2 = 10 мкГн?
7. Рассчитать значение крутизны характеристики транзистора,
при котором произойдет самовозбуждение 7?С-автогенератора с
лестничной цепью обратной связи, если RK =0,5 кОм.
8. Как рассчитывается частота генерируемых колебаний в автоге-
нераторах разных типов?
9. Рассчитать частоту генерации колебаний в 7?С-генераторе с
мостом Вина, если Ct = С2 = 7 нФ, 7?t = R2 = 10 кОм.
10. Какими будут графики зависимости средней крутизны (или
коэффициента передачи усилителя) от напряжения на входе
усилителя при разных положениях рабочей точки на ВАХ (в
середине линейного участка и на нижнем загибе)?
И. Сформулировать условия баланса амплитуд и баланса фаз в
установившемся режиме.
562
//ус
40
30
12. Каким образом по колебатель-
ной характеристике (рис. 15.11)
определяется амплитуда стаци-
онарных колебаний?
13. Определить амплитуду ста- _
ционарного колебания на вы- | ______
ходе ЛС-генератора с лест- о 0,4 0,6 0,8//тбЭ,в
ничной цепью обратной свя-
зи, если 5ср = 14,5 мА/B, Rp = Рис. 15.17. Колебательная
= 2 кОм, колебательная харак- характеристика к заданию 13
теристика изображена на
рис. 15.17.
14. При каких условиях режим самовозбуждения автогенератора
является мягким (жестким)?
15. В чем отличие мягкого режима самовозбуждения автогенера-
тора от жесткого режима? Пояснить по графикам рис. 15.14 и
15.15.
16. Каким образом объединить достоинства мягкого и жесткого
режимов самовозбуждения?
36*
Глава 16. Анализ и расчет дискретных фильтров
16.1. Расчет параметров и реализация рекурсивных
дискретных фильтров нижних частот
Дискретная цепь может осуществлять фильтрацию сигнала.
При расчете дискретных частотных фильтров нужно найти такие
коэффициенты передаточной функции (9.15), (9.18) или (9.20),
частотная характеристика которой удовлетворяла бы нормам ос-
лабления фильтра в полосах пропускания и непропускания
(рис. 16.1, а). Определение коэффициентов — это задача аппрок-
симации. Известен целый ряд методов ее решения. Наиболее
распространенным является следующий метод. Сначала рассчи-
тывают аналоговый НЧ-прототип и получают его передаточную
функцию Н(р), затем путем замены комплексной переменной
р = Ф{г} переходят от Н(р) к передаточной функции дискрет-
ной цепи H(z).
Использование стандартного преобразования z = ерТ или
р = (1/T)lnz не приведет к дробно-рациональной функции. По-
этому для ФНЧ применяют билинейное преобразование
Рис. 16.1. Графики АЧХ и ослабления дискретного (а)
и аналогового (б) фильтров
564
1 - z 1 z - 1
Р = У------zr = Y — 7-
1 + z 1 z + 1
(16.1)
(у — некоторый постоянный множитель), которое является пер-
вым приближением стандартного преобразования при разложении
его в ряд Тейлора:
1 1 2
Р ~ 7‘пг = 77
к т т
г-1 1 (г-1)3 1 (г-1)5
г + 1 + 3(г + 1)3 +5(2 + 1)5 +
(16.2)
Из разложения (16.2) следует, что необходимо выбирать
у = 2/Т. Однако далее мы покажем, что удобнее брать другие
значения коэффициента у.
Билинейное преобразование (16.1) переводит все точки из
левой полуплоскости переменной р в точки на единичной окруж-
ности плоскости г. Так что, если была устойчива аналоговая
цепь, будет устойчивой и дискретная. Подтвердим эти утвержде-
ния на примере.
Пример 16.1. Найдем положения точек на г-плоскости, соответ-
ствующих следующим значениям переменной р:
Р\=-^', Р2 =-2 +/2; р3 = ;2.
Из формулы (16.1) найдем выражение для рас-
чета г:
7-1±Р.
у-р'
Подставляя в эту формулу значение полюса р =
= Pi = -2, лежащего в левой полуплоскости плоско-
сти р, получаем
Поскольку у — число вещественное и положи-
тельное, то числитель (у - 2) меньше знаменателя
(у+ 2) и, значит, г < 1, т.е. точка г лежит внутри
единичной окружности, что говорит об устойчивости
цепи.
При р = р2 = -2 + j2 получаем
z=iz2 + /2
Г + 2-;2
Найдем модуль комплексной величины г:
565
У(7-2)^2;
V(7 + 2)2 + 22 '
Он меньше единицы, поскольку модуль числите-
ля меньше модуля знаменателя, т.е. точка z также
лежит внутри единичной окружности.
При р = р3 = /2 получаем
z= Y + /2_Jp74/2arctg7
У - /2 7у2 + 4
Модуль z равен единице, т.е. точка р = /2, ле-
жащая на мнимой оси плоскости р, переходит в точ-
ку на единичной окружности плоскости z при ис-
пользовании билинейного преобразования.
Следует иметь в виду, что частотная характеристика аналого-
вого фильтра определена на всей положительной полуоси частот,
в то время как у дискретного фильтра она имеет тот же смысл
только до частоты 0,5/д, затем она периодически повторяется
(см. рис. 9.48). Ясно, что шкала частот дискретного фильтра ока-
зывается деформированной относительно шкалы частот аналого-
вого фильтра. Соответствие этих шкал легко установить из били-
нейного преобразования (16.1). Перепишем его в виде
z = I±£.| (16.3)
У-Р
Обозначим во избежание путаницы нормированную частоту
для аналогового фильтра-прототипа Qa, обычную (т.е. ненорми-
рованную) частоту для дискретного фильтра будем, как и ранее,
обозначать буквой f, а нормированную — буквой Q. Теперь за-
меним в (16.3) комплексную переменную р на ;Qa, а комплекс-
ную переменную z на е-'2*/7' = ei21ta и установим соответствие
между частотами f (или Q) и Qa:
1 На
g/2it/T _ _ У + /Qa _ е} аГС 8 у
о —о — # — о •
у-;яа
Отсюда легко получить, что
itfT = 7tQ = arctg —
У
ИЛИ
566
(16.4)
При изменении частоты f от 0 до 0,5/д (или нормированной час-
тоты Q от 0 до 0,5) нормированная частота Па в шкале анало-
гового прототипа будет пробегать значения от 0 до бесконечно-
сти (рис. 16.1, б).
Во многих справочниках по расчету фильтров граничная
частота полосы пропускания принимается равной Qan = 1. Что-
бы частота fn (или Пп) дискретного фильтра соответствовала в
(16.4) Пап =1 (рис. 16.1, б), коэффициент у нужно взять рав-
ным
1 1
Y tgTl/пГ tgTtfV
(16.5)
Пример 16.2. Рассчитаем дискретный ФНЧ с параметрами /"д =
= 8 кГц, /п = 1 кГц, f3 = 3 кГц, ДА = 1,4 дБ, Amin =
= 40 дБ.
По формуле (16.5) находим у = 1/tgn 0,125 =
= 2,414214 и по формуле (16.4) определяем норми-
рованную граничную частоту полосы непропускания
Паз аналогового НЧ-прототипа:
= 2,414214 tg л 0,375 «5,82.
Тем самым произведен пересчет требований, предъяв-
ленных к дискретному фильтру (рис. 16.1, а), в тре-
бования к аналоговому НЧ-прототипу (рис. 16.1, б).
По требованиям к аналоговому ФНЧ-прототипу известными
методами находят его передаточную функцию. Исходными дан-
ными для расчета являются требования к НЧ-пототипу. По ним,
пользуясь любым справочником, рассчитывают передаточную
функцию фильтра-прототипа.
Пример 16.3. Для Паз = 5,82, Amjn = 40 дБ и ДА = 1,4 дБ, поль-
зуясь справочником Э. Христиана, Е. Эйзенмана
«Таблицы и графики по расчету фильтров» (М.:
Связь, 1975), находим, что
Н(р) =
=_______________1,732052______________ (16.6)
(р +1,200937 )(р2 +1,200937? +1,442249)'
567
Для перехода от аналогового фильтра-прототипа к дискрет-
ному используют замену переменных (16.1):
1 — г-1
Р = Т:---q--
1 + z
Пример 16.4. От передаточной функции (16.6) аналогового
фильтра-прототипа перейдем к передаточной функ-
ции H(z) дискретного фильтра.
Подставим в выражение (16.6) значение
1 — г-1
р = 2,414214 —Ц-.
и 1 + г-1
Получим
1 + г-1
Н (z ) = 1,732052------—------------г х
3,615151-1,213278г-1
/. _<\2
Х 10,1699-8,77236г-1 +4,371362г-2 '
Дискретный фильтр можно реализовать в виде кас-
кадного соединения типовых звеньев первого и второго
порядков. Для этого функцию Н(г) перепишем в виде:
\ , ,опЛ„0,2766 + 0,2766г-1
H1Z) = 1,732052-!-------!----:—х
1-0,33561г-1
0,09833 + 0,19666г-1 + 0,09833г-2
1-0,86258г-1 + 0,42983г-2
Схема фильтра, имеющего такую передаточ-
ную функцию, приведена на рис. 16.2. Амплитуд-
но-частотная характеристика А (Q) = -201g Ж £1),
Рис. 16.2. Схема дискретного фильтра к примеру 16.4
568
Рис. 16.3. Ослабление фильтра
к примерам 16.4 (кривая 1) и 16.5 (кривая 2)
рассчитанная на основании формул для АЧХ типо-
вых звеньев, показана на рис. 16.3 (кривая 1).
Аналогичным образом производится расчет фильтров со
всплесками ослабления (нулями передачи).
Пример 16.5. Найдем передаточную функцию дискретного
фильтра НЧ с АЧХ, равноволновой в полосе пропус-
кания и со всплеском ослабления в полосе задер-
живания. Параметры фильтра: = 32 кГц; fn =
= 6 кГц; /з = 8,8 кГц; ДА = 1,5 дБ; Amin = 30 дБ.
Определяем нормированные частоты:
Qn = 6 • 103/(32 • 103) = 0,1875 и
Я3 =8,8-103/(32 103) = 0,275.
Далее по формулам (16.5) и (16.4) находим
у = ctg я • 0,1875 = 1,496606 и
Qa3 = 1,496606 • tg я • 0,275 = 1,7523.
По справочнику рассчитываем
Н(р) = 0,129302х
х_____________р2+3,865161____________
Х (р + 0,510162)(р2 + 0,38086р + 0,980233)
и с помощью подстановки
1-г-1
» = 1,496606 i-Ц-
к 1 + Z’1
569
переходим к H(z)\
H(z) = 0,103788
1 + г'1
1-0,491558г’1
X
1 + 0,53246г’1 + г’2
Х 1 - 0,664682г’1 + 0,699215г’2 ’
Амплитудно-частотная характеристика A(Q) =
= -20IgH(Q) такого фильтра показана на рис. 16.3
(кривая 2).
Из данного параграфа мы узнали, что:
• При переходе от требований дискретного фильтра к требо
ваниям к аналоговому ФНЧ-прототипу устанавливается со- J
ответствие шкал частот: при изменении нормированной час- ।
тоты дискретного фильтра от 0 до 0,5 нормированная час- |
тота аналогового прототипа изменяется от нуля до веско- I
нечности. *
• Передаточную функцию аналогового фильтра-прототипа g
определяют по справочникам. Исходными данными при I
этом являются ослабление в полосе пропускания и непро- j
пускания, а также значение нормированной частоты на
границе полосы непропускания. |
♦ Для получения передаточной функции дискретного фильт- |
ра Жг) в передаточной функции фильтра-прототипа Н(р) |
осуществляют замену переменной р, которая связана с пе- |
ременной г билинейным преобразованием. *
• Дискретный фильтр реализуется как каскадное соединение I
типовых дискретных звеньев. j
16.2. Расчет параметров и реализация
нерекурсивных дискретных фильтров
нижних частот
При построении нерекурсивных дискретных фильтров по
заданным частотным характеристикам рассчитывают дискрет-
ную импульсную характеристику фильтра, которая и определя-
ет структуру дискретной цепи. Если известны требуемые частот-
ные характеристики Я(/О) фильтра, то для реализации нере-
курсивного фильтра с импульсной характеристикой Л [и], равной
нулю везде, кроме 0 < п < N -1, поступают следующим образом.
Амплитудно-частотную характеристику фильтра H(Q) и фазо-
570
частотную характеристику <p(Q) дискретизируют, разбивая час-
тотный интервал Q = 0 — 1 на N равных интервалов. В резуль-
тате получают последовательность отсчетов АЧХ и ФЧХ на N
частотах £l = m/N, т.е. H_[m/N], 0 < т < N - 1. Подставляя эту
последовательность в формулу обратного дискретного преобразо-
вания Фурье (9.6), получаем выражение для дискретной им-
пульсной характеристики Л[п] фильтра:
(16.7)
0<п<ЛГ-1.
Полученные отсчеты дискретной импульсной характеристики
hln} являются коэффициентами усиления й0> й1> •••> aN-\ в схе-
ме нерекурсивного фильтра, приведенной на рис. 9.38, а.
Пример 16.6. Найдем импульсную характеристику hln] фильтра
нижних частот, имеющего граничную частоту полосы
пропускания Q = 0,1, и АЧХ, приведенную на
рис. 16.4. Импульсную характеристику будем рас-
считывать для значения N = 30.
В формуле (16.7) для расчета hln} использу-
ются комплексные значения передаточной функции.
Если выбрать значения H[m/N], показанные на
рис. 16.4 (Hlm/N] = 1 в полосе пропускания и
Hlm/N] = 0 в полосе непропускания), и фазу пе-
редаточной функции arg/flm/JV], равную нулю, то
передаточная функция будет иметь заданные значе
ния в точках Q = m/N, но очень сильно отличаться
от требуемой формы на частотах Q между этими
точками.
Гораздо лучшие результаты получаются, если
выбрать arg//[m/A/J = -2лО(ЛГ/2)|п=т . Выбор та-
кой фазы эквивалентен тому, что Hlm/N] = (-!)”’
Я(П)
Требуемая Я(О)
1/N
0,1
0,5
0,9 1 Q
Рис. 16.4. Дискретизация АЧХ дискретного
фильтра к примеру 16.6
Рис. 16.5. АЧХ дискретного
фильтра к примеру 16.6
Рис. 16.6. Дискретная импульсная характеристика
фильтра к примеру 16.6
вместо 1 в полосе пропускания. Такой передаточной
функции соответствует АЧХ, изображенная на
рис. 16.5. Подстановка значений H[m/N] в формулу
(16.7) позволяет получить выражение для расчета
/г[п]:
/г[п] = —(_e-J2jc3n/30 + e-j'2n2n/30 _ g-j2m/30 +
. 1 ^}2яп/30 , ^j2n2n/30 ^j2n3n/30)
т 1 с т tz с I.
График конечной импульсной характеристики
h{n} изображен на рис. 16.6.
Для реализации фильтра с такой импульсной характеристи-
кой по схеме рис. 9.38, а потребуется 30 усилителей и 29 элемен-
тов задержки, т.е. схема довольно громоздкая. Схема с обратны-
ми связями, реализующая АЧХ, изображенную на рис. 16.4, бу-
дет иметь гораздо меньше элементов. Однако достоинством нере-
курсивных фильтров с конечной импульсной характеристикой
является то, что они всегда устойчивы и, кроме того, обеспечи-
вают линейные фазовые характеристики.
572
Из данного параграфа мы узнали, что:
• Для реализации нерекурсивного фильтра используют еле- |
дующий алгоритм: дискретизируют заданные частотные ха- |
рактеристики фильтра; по их отсчетам с помощью обратно- i
го дискретного преобразования Фурье получают дискрет-
ную импульсную характеристику фильтра и по ней состав-
ляют схему дискретной цепи. |
• Преимущества нерекурсивных фильтров: они устойчивы и я
имеют линейную фазовую характеристику. |
16.3. Переход к дискретным фильтрам верхних
частот, полосовым и заграждающим
Расчет высокочастотных, полосовых и заграждающих дискрет-
ных фильтров также сводят к определению передаточной функции
аналогового фильтра-прототипа. Требования к любому типу фильтра
преобразуются в требования к аналоговому ФНЧ-прототипу. За-
тем рассчитывается аналоговый прототип, как это показано выше,
и с помощью замены переменных переходят от Н(у) к H(z).
Конечно, формулы замены переменных уже не такие, как
для ФНЧ. Они приведены для разных типов фильтров в
табл. 16.1. Требования к дискретным фильтрам графически изо-
бражены на рис. 16.7.
Рис. 16.7. Требования к дискретным высокочастотным,
полосовым и режекторным фильтрам
573
Таблица 16.1. Формулы замены переменных для различных типов
фильтров
Дискретный фильтр Граничные частоты Формула замены Параметр
НЧ II II к « а а 1-z-1 P = Y . .j 1 + z 1 Y = ctgnQn
ВЧ О D ы д 11 II ^5^ 1 + z-1 P=T1-Z- у = ctgnQn
ПФ Ч^Ч^ ч^ ч2! II II II II в *2 -S S3 а а а а 1 - 2az-1 + z~2 Y = ctgn(Qn2-Qnl) a = cosTC(fln2 + Qnl)
P T 1-z-2
COS7t(Qn2-Qnl)
ЗФ а Э D D & а я п и и и to"** w"** ш'*' н**' fe** Sa"*' 1 - z~2 Y = ctgn(Qn2-Qnl) a cos7c(nn2+flni)
41 - 2az-1 + z~2
cosn(nn2 -Qnl)
Дискретный фильтр Связь между частотами Граничные частоты аналогового фильтра
НЧ Qa = у tg TtQ ^аз = Y tg7lfi3
ВЧ Па = YCtgTtQ ^аз =YCtgnQ3
ПФ _ а - cos 2nQ Qa = Y—r-r sin 2nQ £^аз = П1Й1(|£2аз|>|^аз|)> где п, a-cos2nQ31 83 sin 2лОз1 Q, a-cos2nn32 аз sin 2я£2з2
ЗФ Л sin 2kQ Л/ □аз = г где £Уаз = у Г^аз = Y nin( |Оаз | > |^аз 1) > sin 2nQ31
W J а - cos 2rcQ a - cos 2nQ31 sin 2лОз2 a - cos 2лОз2
Пример 16.7. Определим передаточную функцию дискретного
полосового фильтра с параметрами: /д = 140 Гц;
574
/ni - 15,5 Гц; fn2 = 30 Гц; f3i = 7,75 Гц; Л2 = (50 Гц;
Д/1 = 0,5 дБ; Amin = 40 дБ.
Определяем:
Qnl = 15,5/140 = 0,110714; Яп2 = 30/140 = 0,214286;
Яз1 = 7,75/140 = 0,055357; Оз2 = 60/140 = 0,428571;
у = ctg[n • (0,214286 - 0,110714)] = 2,964087;
cos £л (0,214286 + 0,110714)" .
L J= 0,551433;
^аз
Q’a3
“ cos [л (0,214286- 0,110714)
э Ол/ЛО70,551433-cos2л-0,055357 „ „о
= 2,96408/-----:—-————— ---------» -3,38;
sm 2л • 0,055357
n nt/лот0-551433-cos2л -0,428571 n n_
-- 2*, Уи4ио/ _ Z4 z ГЧ ГЧ Г* l-T Z У, У/^,
sin 2л • 0,428571
= min(3,38; 9,92) «3,38.
По данным Qa3 = 3,38, ЛА = 0,5 дБ и Amin = 40 дБ
из справочника находим
^аз
Н(р) = 0,484123 J-----------х
р2 + 0,412569? +1,144123
___________1___________
Х?2 +0,996024? + 0,437016'
Передаточную функцию H(z) найдем, исполь-
зуя подстановку
? = 2,9640871-2 0,551433 zX+z2
к 1 - г’2
и разлагая каждый из двух полиномов четвертой
степени (в знаменателе H(z)) на множители (поли-
номы второй степени):
H(z) = 0,0035652
__________1 -г 2__________
1 -0,703705г-1 + 0,684397г’2
X
х___________1 —г 2___________>
Х1-1,155395г’1 + 0,741638г'2’
х 1 _ 2 ~2
Х1 - 0,378998г-1 + 0,860199г’2
*___________1 - г’2__________
Х 1 - 1,479492г’1 + 0,907562г’2 '
575
Из данного параграфа мы узнали, что:
Для расчета дискретных фильтров верхних частот, полосо-
вого и режекторного используют следующий алгоритм: пе-
ресчитывают требования к любому типу фильтра в требо-
вания к аналоговому ФНЧ-прототипу; рассчитывают пере-
даточную функцию прототипа; переходят к передаточной
функции дискретного фильтра, используя замену перемен-
ных; строят схему дискретного фильтра как каскадное со-
единение типовых звеньев дискретной цепи.
4
I
16.4. Особенности реализации дискретных
фильтров с помощью цифровых схем
Дискретная цепь — это структурная схема алгоритма вычис-
лений, цифровая цепь — это воплощение данного алгоритма в
виде аппаратных и программных средства, т.е. в виде цифровых
схем.
Приведенные на рис. 9.44 и 9.6 операции можно осуществить
с помощью элементов цифровой или вычислительной техники.
Первые представляют собой выпускаемые промышленностью ин-
тегральные микросхемы, позволяющие задерживать, складывать
и умножать сигналы, последние — это компьютеры либо микро-
процессорные устройства.
Характерно, что и те и другие средства работают с цифровы-
ми сигналами (см. рис. 9.6), т.е. с отсчетами, представленными в
двоичном коде. В этом случае любая конкретная цепь (например,
рис. 9.44) может быть реализована либо с помощью устройства,
собранного из интегральных микросхем, либо в виде программы
в компьютере или в микропроцессорном устройстве.
Заметим, что представление чисел в двоичном коде из-за ог-
раниченности разрядности цифровых устройств выполняется не-
точно. Операция умножения отсчетов цифрового сигнала на чис-
ло также выполняется неточно из-за округления или усечения ре-
зультата. Это приводит к ошибкам при восстановлении непре-
рывных сигналов. Существует только один путь уменьшения этих
ошибок — увеличение количества разрядов в двоичном коде.
В цифровом фильтре хранение и обработка чисел (представ-
ленных, как мы уже знаем, в двоичном коде) осуществляются в
устройствах (элементах памяти, умножителях, сумматорах) с ко-
нечным числом разрядов. Поэтому расчет цифрового фильтра
помимо определения передаточной функции H(z) фильтра и его
576
структурной схемы (см. выше) включает в себя также расчет раз-
рядностей АЦП и ЦАП (см. рис. 9.6) и разрядностей резисторов
оперативной памяти (умножителей, сумматоров).
Кроме того, при расчете цифрового фильтра предусматрива-
ют расчет масштабных множителей, вводимых в схему для пре-
дотвращения переполнения регистров фильтра, а также проверку
устойчивости фильтра. Более подробно с расчетом цифровых
фильтров можно ознакомиться в книге «Цифровые фильтры в
электросвязи и радиотехнике» под ред. Л.М. Гольденберга (М.:
Радио и связь, 1982).
Из данного параграфа мы узнали, что:
• В цифровом фильтре хранение и обработка отсчетов, пред- |
ставленных в двоичном коде, осуществляются с помощью |
цифровой и вычислительной техники. 8
• В цифровых фильтрах необходимо учитывать ошибки ок-
ругления, возникающие из-за применения цифровых уст-
ройств с конечным числом разрядов. Э
Вопросы и задания для самоконтроля
1. В чем суть задачи аппроксимации и метода ее решения для
дискретных фильтров?
2. Какое билинейное преобразование применяется при расчете
дискретных фильтров?
3. Почему при использовании билинейного преобразования ус-
тойчивой аналоговой цепи соответствует устойчивая дискрет-
ная цепь?
4. Докажите, что дискретная цепь неустойчива, если полюс пере-
даточной функции соответствующей аналоговой цепи лежит в
правой полуплоскости плоскости р, т.е. р = а + job, а > 0.
5. Что такое конечная (и бесконечная) импульсная характери-
стика?
6. Какая импульсная характеристика у нерекурсивных (у рекур-
сивных) фильтров: конечная или бесконечная?
7. Как рассчитать нормированную частоту аналогового фильтра-
прототипа, если известна нормированная частота дискретного
фильтра?
8. Как изменяется нормированная частота аналогового фильтра-
прототипа при изменении частоты дискретного фильтра от 0
ДО 0,5/д?
37-6972
577
9. Рассчитайте нормированную частоту аналогового фильтра-
прототипа, соответствующую частоте 4 кГц при граничной час-
тоте полосы пропускания 2 кГц?
10. Как осуществить переход от передаточной функции аналого-
вого фильтра к передаточной функции дискретного фильтра?
И. Как составить структурную схему дискретного фильтра, реа-
лизующего полученную передаточную функцию?
12. Как построить график АЧХ дискретного фильтра с рассчи-
танной передаточной функцией?
13. Каков алгоритм реализации фильтра с конечной импульсной
характеристикой?
14. Как перейти от передаточной функции к дискретной им-
пульсной характеристике фильтра?
15. Какой вид имеет структурная схема фильтра с конечной им-
пульсной характеристикой?
16. Каков порядок расчета дискретного фильтра верхних частот
(полосового, режекторного)?
17. Какие формулы замены переменных (р и z) используются при
расчете дискретного фильтра верхних частот (полосового, ре-
жекторного)?
18. Как рассчитать нормированную частоту аналогового дискрет-
ного фильтра верхних частот (полосового, режекторного), ес-
ли известна соответствующая частота дискретного фильтра?
19. В чем отличие цифровой и дискретной цепей?
20. Почему возникают ошибки при восстановлении непрерывного
сигнала по его цифровому представлению? Как их умень-
шить?
предметный указатель
Автогенератор с мостом Вина 539
Амплитуда 68
— комплексная 83
— спектральных составляющих 363
Анализ операторный 19
— спектральный 19
Баланс амплитуд 444
— фаз 444
Воздействие 12
Время переходного
--процесса 290
Выпрямитель 527
Гармоники 127
Генераторы 534
- с автотрансформаторной ОС 548
- с трансформаторной ОС 537, 542
Годограф 431
Двухполюсник активный 50
Дифференцирование
- оригинала 213
— сигнала 182
Емкость 226
Зажимы входные 427
- выходные 427
Закон Кирхгофа 30
— коммутации второй 276
- коммутации первый 276
— напряжений Кирхгофа 30
— Ома 28, 88, 90
— токов Кирхгофа 30
Избирательность фильтра 450
Изменение масштаба сигнала 184
Изображение сигнала 209
Импульс включения 176
— экспоненциальный 178
Индуктивная трехточка 537
Индуктивность 225
Интеграл Дюамеля 265
- наложения 255
- свертки 19
- Фурье 19
Интегрирование оригинала 214
— сигнала 182
Интервал дискретизации 370
Искажения
- амплитудно-частотные 483
— нелинейные 358
— сигнала 483
— фазо-частотные 503
Источник напряжения
независимый 6
зависимый 7
— тока независимый 7
----зависимый 8
Колебания стационарные 536
— гармонические 66
Коммутация 275
Комплексная
— передаточная функция 111
— спектральная плотность 171
Контур И
Корректоры амплитудные 484
— амплитудные активные 493
- амплитудные пассивные 486, 489
— фазовые 504
— фазовые активные 512
- фазовые пассивные 506
Коэффициент
- неравномерности ослабления 454
- передачи по напряжению 111, 112
----по току 111, 112
----цепи 54
Крутизна дифференциальная 337
Метод Дарлингтона 466
— интерполяции 348
— контурных токов 40
— наложения 35
— операторный 231, 331
- расчета классический 287
— токов ветвей 39
- узловых напряжений 45
— эквивалентного генератора 50
Напряжение 5
— мгновенное 5
— отсечки 354
— смещения 348
Напряжения
— контурные задающие 42
Начальные условия зависимые 278
----независимые 277
----ненулевые 278
----нулевые 277
Обратная связь отрицательная 441
----отрицательная 536
----положительная 441, 536
Обратная связь
----трансформаторная 537
579
37*
Ограничитель
— мгновенных значений 524
— амплитудных значений 524
Одностороннее
— z-преобразование 383
Оригинал 209
Ослабление цепи 196, 431
— рабочее 431
Ошибки наложения 377
Перемножение двух сигналов 187
Переходный процесс 19, 275, 281
- режим апериодический 315
--колебательный 315
--критический 315
Полиномы Баттерворта 454
— Чебышева 458
Полоса непропускания 449
— пропускания 449
Полюсы
— передаточной функции 413
Постоянная времени 288
— составляющая 127
Постоянное напряжение 178
Потенциал 5
Правила знаков 42, 46
Преобразование Лапласа
--обратное 209
--прямое 209
— Фурье обратное 170
--прямое 170
-----дискретное 380
--прямое дискретное 380
--обратное дискретное 38
— частоты 453
— шкалы частот 473
Преобразователи частоты 530
Принцип наложения 13
— суперпозиции 13
Проводимости взаимные 46
— собственные 46
Проводимость комплексная
— передаточная 111, 193
— операторная 224
— элемента 9
Процесс апериодический 315
— колебательный 317
— критический 318
Рабочая точка 348
Реакция 12
Режим работы принужденный 28
— переходным 287
--установившийся 281
— самовозбуждения жесткий 560
--мягкий 560
Резонанс напряжений 97
Резонанс токов 98
Ряд Фурье 18, 125
Самовозбуждение 536, 540
Свертка двух сигналов 187
— дискретная 395
Свойства
- преобразований Лапласа 212
Свойство линейности 212
Сдвиг сигнала во времени 181
Сжатие сигнала во времени 184
Скважность 145
Смещение спектра сигнала 186
Соединение последовательное 94
— параллельное 98
Сопротивление 224
— дифференциальное 337
— комплексное 92
--передаточное 111,193
- операторное 223
— отрицательное 338
— гармоническому току 337
— полное 94
— постоянному току 336
— эквивалентное 23
— элемента 9
Сопротивления взаимные 41
— емкостные 91
— индуктивные 89
— комплексные 92
— резистивные 87
- собственные 41
Составляющая тока
--принужденная 292
--свободная 288
Спектр 18
- амплитуд 135, 137, 139
- дискретного сигнала 379
— непериодического сигнала 168
— периодического сигнала 135
— произведения сигналов 187
— свертки сигналов 187
— суммы сигналов 181
- фаз 135, 137, 139
580
Спектральная плотность
---амплитуд 171
- - фаз 171
Спектральные линии 137
Схема замещения операторная 223
Теорема дифференцирования 213
— задержки 389
Теорема запаздывания 215
— Котельникова 378
— линейности 181, 391
— модуляции 186
— опережающего сдвига 389
— подобия 184, 217
— разложения 220
— свертки 218, 390
— смещения 217
— суперпозиции 389
— умножения на п 390
Ток электрический 5
— мгновенный 5
Токи задающие узловые 46
— контурные 39
Треугольник сопротивлений 96
Узел электрической цепи 11
-----простой И
-----сложный И
Узлы интерполяции 348
Умножение на константу 212
Умножитель
— частоты резонансный 523
Уравнение дифференциальное
— однородное 288
---неоднородное 292
Уравнения
— нагрузочных прямых 347
Усиление
— логарифмическое 196, 431
— петлевое 441
Усилитель
— нелинейный резонансный 520
Фазовый сдвиг 112
Фильтры электрические 449
— Баттерворта 453, 454
— Золотарева 453, 462
— кварцевые 480
— магнитострикционные 480
— НЧ-прототипа 453
— пьезоэлектрические 479
— со всплесками ослабления 462
— Чебышева 453, 458
— электромеханические 480
Формулы разброса 30
Функция
— комплексная передаточная 192, 428
----по напряжению 193
----по току 193
— передаточная 401
----операторная 236, 432
Функция передаточная
----нормированная 428
----рабочая 428
— системная 401
Функция фильтрации 451
Характеристика
— группового времени прохождения 503
— ослабления 450
— цепи амплитудно-частотная 194, 429
----логарифмическая 196
----импульсная 248
----переходная 259
----фазо-частотная 194, 429, 503
Цепь дискретная 395
----нерекурсивная 400
— неустойчивая 442
— с обратной связью 436
— рекурсивная с ОС 412
---с прямыми и обратными связями 412
— устойчивая 442, 444
— электрическая 5
Частота дискретизации 370
— нормированная 452
— резонанса напряжений 97
---- токов 98
Частоты комбинационные 365
Четырехполюсник 427
Числа вещественные 80
— комплексные 81, 83
— мнимые 80
ЭДС самоиндукции 89
Эквивалентное сопротивление 23
Эквивалентный генератор
— напряжения 50
---- тока 50
Электродвижущая сила 5
Элемент задержки 400
— емкостный 10
— индуктивный 10
— резистивный 9
----линейный 9
----нелинейный 9
5-импульс 177
7?С-генератор
— с лестничной обратной связью 550
— с мостом Вина 551
581
Список литературы
Основная
1. Бакалов В.П., Дмитриков А.Ф., Крук Б.И. Основы теории цепей:
Учебник для вузов. М.: Радио и связь, 2000. — 670 с.
2. Бакалов В.П., Воробиенко П.П., Крук Б.И. Теория электрических
цепей: Учебник для вузов. — М.: Радио и связь, 1998. — 444 с.
3. Бакалов В.П., Крук Б.И., Журавлева О.Б. Основы теории цепей.
Компьютерный тренажерный комплекс: Учебное пособие для ву-
зов: — М.: Радио и связь, 2002. — 200 с.
4. Белецкий А.Ф. Теория линейных электрических цепей. — М.: Ра-
дио и связь, 1986. — 544 с.
5. Воробиенко П.П. Теория линейных электрических цепей: Сб. за-
дач и упражнений. — М.: Радио и связь, 1989. — 328 с.
6. Шебес М.Р., Кублукова М.В. Задачник по теории линейных элек-
трических цепей: Учебное пособие для вузов. — М.: Высшая шко-
ла, 1990. — 544 с.
Дополнительная
7. Андреев Б.С. Теория нелинейных электрических цепей. — М.: Ра-
дио и связь, 1982. — 280 с.
8. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электри-
ческих цепей и электроники: Учебник для вузов. — М.: Радио и
связь, 1989. — 526 с.
9. Баскаков С.И. Радиотехнические цепи и сигналы. — М.: Высшая
школа, 1988.
10. Баскаков С.И. Радиотехнические цепи и сигналы. Руководство к
решению задач. — И.: Высшая школа, 1987.
И. Гольденберг Л.М., Матюшкин Б.Д., Поляк М.Н. Цифровая об-
работка сигналов: Справочник. — М.: Радио и связь, 1985.
12. Гоноровский И.С. Радиотехнические цепи и сигналы. — М.: Ра-
дио и связь, 1986.
13. Жуков В.П., Карташев В.Г., Николаев А.М. Задачник по курсу
«Радиотехнические цепи и сигналы»: Учеб, пособие для студентов
вузов спец. «Радиотехника» — М.: Высшая школа, 1986.
14. Сиберт У.М. Цепи, сигналы, системы: В 2 ч.: Пер. с англ. — М.:
Мир, 1988.
15. Цифровые фильтры в электросвязи и радиотехнике /Под. ред.
Л.М. Гольденберга. — М.: Радио и связь, 1985.
582
Ответы
Глава 1
3. 1Л = 0,48 мА.
7. (7у=15В.
20. Я = 0,5.
21. U2 =5 В.
Глава 2
5. i(t) = 0,25sin(jrt); i(^) = 0,177 А.
9. <р = 135°.
15. Z = 40,2e-;31°.
17. 7m]=2e;59°A; Im, =.№'"• Л; I.* = 1,2е/,,2!° А.
18. 7.2 = le'w.
20.
4.
6.
7.
Я, =0,707; Ну =0,167 См.
Глава 3
u(t) = Umi cos^coit+ -^^ + ^yicos^2®^+ j^ +
+ ^Mcosf Зй) t +
3 к 2 )
u(t) = 2 е]2к^ + ^mi e^e12*'2^ +
2 4
Т T .Зл у у .3я
। Umi e~^ е’2п'2^ + + —wl e-H*3ht +
6 " 6
т т • Я г г »3?С
I ^m1 с~’?2с-У2я-2/,1< [ Umi e~7TсУ2я/1<
4 2
u (t) = 10 + 36,1 sin (2л • 50£ + 33,7°) +14,1 sin (2rc • 100£ + 225°).
rr < О C 7
Umn = — для n = 1, 3, 5, 7,....
nn
10. uR1 (t) = 0,018sin(2л-7000^88,5°), В.
15. uL (О = 2,5 + 0,4sin(2n • 1 OOOt +177°) +
+ 7,03 sin (2л • 3000£ + 90°) + 0,99 sin ( 2л • 5000t + 8°), В.
Глава 4
. rr/ • 4 sinlO 4(0 -;l(T4a> t>
4. U(jg>) =---------------e1 Вмс
v 7 10-4co
583
5. /(co) = 10“8 А с.
14. Н(](й) = -г--==--------
V(2-co2LC) +Я2со2С2
16. СГд(Уш)= U .
-co RC - ]2a>
Глава 5
3 UM-^y
4. = —-^e'180’.
CO
7. а)Щр)Л; б)Щр) = т^-; B)C7(p) = fc3.
p p +16 p
8. и(р) = ^--е-Рх~е~Р\
P P P
10. a) u(t) = 6e-4z; 6) u(t) = 4cos3i; в) u(t) = 5sin4£;
r) iz(i) = e-t sin2t
15 Z(v) = P2R&LC + pL(Ri+ R2) + R1R2
pR^RiC + R\ +1?2
19. i(i) = 7,5e-2*-7,5e"10t, A.
22.
Hur (?) = -5--------•
cVF' p2LC + pRC + \
Глава 6
6. а)Авя(О = 6) hUL (t) = 5(t)-^e^R L^.
11 и (f) - приО^г^,
и. ^u;-|^b_(R/LX(_ti)_e_(W] при^<оо
14. a)g„R(£) = 1-е_(Л1)‘; 6) gU£ (i) =
20 zx\_ f5103i-12,5+12>5e-4OOt npnOcicJi,
UC [5103i1-10-2,5e"4OO(M,)+12,5e-4OOZ при^>^.
Глава 7
5. a)A(0+)=i2(0+)=ic(0+)=2 A; i£(0+)=i3(0+)=0; zzc(O+)=O.
6)ir(0+)=i3(0+)=5 A; fc(0+)=i2(0+)=-5A; ыс(0+)=10 B.
8. ^Inp = ^Lnp = ^3np = 5 А, &2пр = ^Cnp = ^/?inp = ^Lnp =
wCnp = w/?2nP = Ю B.
584
17. г(£) = 4 - 2e-100f, А.
18. ыс(7) = 5 + 20е?-’°4', В.
23. ис<Л) = 1,25• 106te"5000f, В.
24. iR(t) = 0,l(4e-500f -е-125' ), А.
Глава 8
2. Rq =6 кОм; /?даф =1,9 кОм.
4. /н = 2,7мА.
5. 7 = 2,25 мА.
9. i(uH) = 0,7 + l,5(u-0,5) + 0,2(u-0,5)2.
..л •/ v [0, и < 0,25 В,
ю. 1(uk)-|2(m_0 25)i м>0 25 в
И. /0 = 0,725 мА; /т1 = 0,75 мА; 1т2 = 0,025 мА.
12. 9 = 75,5°; 70 = 0,6 мА; Imi = 0,9 мА; 1т2 = 0,5 мА.
13. а) и6э(а>7) = 0,3 + 0,2coscoi; б) ибэ(со7) = 0,3 + 0,4coso>£;
в) UfeCcot) = 0,7 + 0,05 cos at.
Глава 9
8. а) ивых[п] = {1; 1,5; 0,75; 0,25}; б) ивых[п] = {2; 4; 6; 4; 2}.
9. a) (/(z)=3+2z~1+z_3; б) U(z)=—^-5-; в) U(z)=-----------—7.
1-z-2 1-0,5г-2
10. а) и[п] = {1; 2; 0; 4}; б) и[п] = 2”, п>0.
И. U[m] = {3; 0;0;0}.
12. U[m] = {5,6; 2,5; 1,9; 2,5};
arg 17[т] = {0; -0,464; 0,0464}.
13. а) и[п] = {0,25; 0,25; 0,25; 0,25};
б) |м(п]| = {0,25; 0,25; 0,25; 0,25}, argwtn] = {0; тс/2; л;-л/2}.
14. а) ивых[п]=«вх[п]-0,5г/вх[п-1]+2«вх[п-2];
б) wBbIX [n]=wBX [w]+0,5zzBbiX [w—1]—пвых [п—2],
в) мвых[я]=2ивх[n]+l,5wBX [n-l]+wBX[п-2]-
-0,5ивых[п-1]+0,5ивых[п-2].
15. а) Жг) = 1-0,5г'1 + 2z-2, h[nl = {1;-0,5; 2};
б) H(z) =-------Ц----7, h[n] = {1; 0,5; -0,75; -0,875;...};
1-0,52-’ +z~2 1
585
?4-1 Sz 1 4* 2?
в) Я(г) = +-±£__, h[n] = {2; 0,5; 1,75; -0,625;
1 + 0,52-’-0,5z-2 1 ’
16. а) ывых[п] = {1; 0,5; 2,5}; б) мвых [nj = {1; 1,5; 0,75};
в) “вых [я! = {2; 2,5; 4,25}.
17. a) wBbIX[n]=5uBX[n]-uBX[«-l]+3wBX[n-2], Mn]={5; -1; 3};
6) “выхГп1=2“вх1п1+2“выхС“_11, h[nl = 2 2n ={2; 4; 8; 16;...};
в) “вых [“3=5“вх (n]-4uBX [п-1 ]+ ивых[п—11+2ивых[п-2],
/г[п]={5; 1; И; 13;...}.
18. а) устойчивая; б) неустойчивая; в) неустойчивая.
19. Я(2) = 1 + 2*2.
20. а) й[п]=1, п>0;
б)Л[п]=Р’/ kn V’ H(z)=------------------2;
(3/2*, п>0; l-l,5z-’+0,5z-2
“вых [“] = “вх [“1+“вх [“- 1]+1,5мВых [п-1]-0,5мвых [“-2].
21. а) Ж2) = 1 - 2“’; б)Я(2> =-------г.
1-0,22-’
22. а) H(z) = 1-0,52-’; Я(О) = Д 25 - cos 2лО;
б)Я(2) =-----!---Г; Я(О) = -=_=£------------
1 - 0,32"’ V1,09-0,6cos2kQ
Глава 10
2- И,(/т) = гЙ?^-; Я. (ш) = , *?*? ;
1 + 7®ЯС >/1 + (соЯС)2
<р (со) = 90° - arctgco.RC.
3. Я(/си) =-----.
v 7 1-(о21С
4. А = 12 дБ.
6. Н(р) = !-------;
p2LC + pRC + \
^(LC)2+G)2(R2C2-2LC) + i
И. H(p) = -2------------- K(i + PR2C2)------------
р C\C2R\R2 + p{R\C\ + R2C2 + ^1^2 “ KR^2 ) +1
14. Яр(/со) = —5------------,
p w ’ -(h2RxR2CxC2 + ;© (RXCX + R2C2 + RXC2 ) +1
586
Глава 11
2. ФНЧ Чебышева пятого порядка.
5. е = 0,765; т = 6.
6. Нр(р)=
=_______________________1,3076_______________________
[(p2+0,5413p+l,094)(p2+l,479jP+l,094)](p2+2,02p+l,094)'
7 о и / \ 0, 433
7. m=3; Нп(р)=.
р р2+0,9064р2+1,1608р+0,433
12. Li =1; С = 2; £3 = 1.
Глава 12
2 _1_____ 1
11 Н (о] = R* + ? ^(Д+.К2)С LC _ н р2 + а1;> + <Вр
Rt р2+р L + ± р2 + а2р + <⧑
р Р R2C LC
13. 7?!=1кОм; С] =51 нФ.
Глава 13
8. Lj = 36 мГн; С\ =1,6 мкФ; L2 = 0,58 Гн; С\ = 0,1 мкФ.
Глава 15
5. Да.
6. Нет.
7. 5ср > 58 мА/В.
9. fr = 2,27 кГц.
13- Юговых =И,6 В.
ОГЛАВЛЕНИЕ
Предисловие ...................................................... 3
Вместо введения: задача анализа цепей ............................ 5
В. 1. Элементы электрической цепи ............................ 5
В.2. Воздействие и реакция .................................. 12
В.З. Методы анализа цепей.................................... 17
ЧАСТЬ 1. Анализ реакции цепей на различные воздействия .......... 22
Глава 1. Анализ реакции линейной цепи на постоянное воздействие 22
1.1. Постановка задачи ...................................... 22
1.2. Расчет реакции линейной цепи с одним источником
воздействия ................................................ 23
1.3. Расчет реакции линейной цепи с несколькими источниками
воздействий ................................................ 35
1.4. Коэффициент передачи резистивной цепи................... 54
Вопросы и задания для самоконтроля .......................... 60
Глава 2. Анализ реакции линейной цепи на гармоническое
воздействие ..................................................... 63
2.1. Математическое описание гармонических колебаний ........ 63
2.2. Гармонические колебания в пассивных элементах
электрической цепи ......................................... 86
2.3. Расчет реакций цепи в символической форме ............. 100
2.4. Комплексные передаточные функции ...................... 110
Вопросы и задания для самоконтроля ......................... 115
Глава 3. Анализ реакции линейной цепи на периодическое
воздействие сложной формы ...................................... 117
3.1. Представление периодического воздействия рядом Фурье... 117
3.2. Спектры амплитуд и фаз периодических колебаний ........ 135
3.3. Анализ реакции линейной цепи методом суперпозиции
(наложения) ............................................... 150
3.4. Расширение понятия комплексной передаточной функции.
Спектральный анализ цепи .................................. 156
Вопросы и задания для самоконтроля ......................... 165
Глава 4. Анализ реакции линейной цепи на непериодическое
воздействие сложной формы (спектральный метод) ................. 167
4.1. Представление непериодического воздействия
интегралом Фурье .......................................... 167
4.2. Спектральные плотности амплитуд и фаз непериодических
колебаний ................................................. 171
4.3. Еще раз о комплексных передаточных функциях и частотных
характеристиках цепи ...................................... 192
4.4. Спектральный анализ цепей при непериодических
воздействиях .............................................. 197
Вопросы и задания для самоконтроля ......................... 205
588
Глава 5. Анализ реакции линейной цепи на непериодическое
воздействие сложной формы (операторный метод) ................ 207
5.1. Представление непериодического воздействия
интегралом Лапласа ....................................... 207
5.2. Законы Ома и Кирхгофа в операторной форме ............ 223
5.3. Операторный метод расчета реакции цепи ............... 230
5.4. Операторные передаточные функции ..................... 236
5.5. Связь со спектральным методом ........................ 241
Вопросы и задания для самоконтроля ........................ 242
Глава 6. Анализ реакции линейной цепи на непериодическое
воздействие сложной формы (временной метод)................... 245
6.1. Испытательные сигналы ................................ 245
6.2. Импульсная характеристика цепи ....................... 248
6.3. Анализ реакции цепи с помощью интеграла наложения .... 254
6.4. Переходная характеристика цепи........................ 259
6.5. Анализ реакции цепи с помощью интеграла Дюамеля ...... 264
Вопросы и задания для самоконтроля ........................ 272
Глава 7. Анализ реакции линейной цепи при коммутациях
(переходные процессы) ......................................... 275
7.1. Законы коммутации .................................... 275
7.2. Расчет начальных условий в моменты коммутации ........ 277
7.3. Расчет установившихся реакций в цепи ............... 281
7.4. Расчет переходных реакций в цепях первого порядка..... 287
7.5. Расчет переходных реакций в цепях второго порядка .... 312
Вопросы и задания для самоконтроля ........................ 334
Глава 8. Анализ реакции нелинейной резистивной цепи на
постоянное и гармоническое воздействия........................ 336
8.1. Нелинейные резистивные элементы и их сопротивления
постоянному и гармоническому токам ....................... 336
8.2. Расчет реакции нелинейной резистивной цепи на постоянное
воздействие .............................................. 338
8.3. Аппроксимация вольт-амперных характеристик нелинейных
резистивных элементов .................................... 348
8.4. Расчет спектрального состава тока в резистивном нелинейном
элементе при гармоническом воздействии ................... 355
Вопросы и задания для самоконтроля ........................ 367
Глава 9. Анализ реакции линейной дискретной цепи на дискретные
воздействия................................................... 368
9.1. Дискретные сигналы ................................... 368
9.2. Спектры дискретных сигналов .......................... 373
9.3. Z-преобразование дискретного сигнала ................. 382
9.4. Нерекурсивная дискретная цепь и ее реакция на дискретное
воздействие .............................................. 395
9.5. Рекурсивная дискретная цепь и ее реакция на дискретное
воздействие .............................................. 407
589
9.6. Типовые звенья дискретных цепей ..................... 419
Вопросы и задания для самоконтроля ....................... 424
ЧАСТЬ 2. Анализ и расчет узлов аппаратуры связи .............. 427
Глава 10. Анализ поведения линейных четырехполюсников
на комплексной плоскости ..................................... 427
10.1. Комплексные и операторные передаточные функции
нагруженного четырехполюсника. Условия их физической
реализуемости ............................................ 427
10.2. Расчет передаточных функций цепей с обратной связью.
Устойчивость цепей ....................................... 436
Вопросы и задания для самоконтроля ....................... 447
Глава 11. Анализ и расчет электрических фильтров ............. 449
11.1. Типы и характеристики фильтров ..................... 449
11.2. Анализ фильтров нижних частот Баттерворта,
Чебышева и Золотарева .................................... 454
11.3. Расчет и построение схем электрических фильтров
нижних частот ............................................ 465
11.4. Переход к фильтрам верхних частот, полосовым
и заграждающим............................................ 473
11.5. Анализ фильтров с механическими резонаторами ....... 479
Вопросы и задания для самоконтроля ....................... 481
Глава 12. Анализ и расчет амплитудных корректоров ............ 483
12.1. Амплитудно-частотные искажения сигнала и их
коррекция................................................. 483
12.2. Анализ схем амплитудных корректоров ................ 486
12.3. Расчет пассивных амплитудных корректоров ........... 498
Вопросы и задания для самоконтроля ....................... 502
Глава 13. Анализ и расчет фазовых корректоров ................ 503
13.1. Фазо-частотные искажения сигнала и их коррекция .... 503
13.2. Анализ схем фазовых корректоров..................... 506
13.3. Принципы расчета фазовых корректоров ............... 516
Вопросы и задания для самоконтроля ....................... 518
Глава 14. Анализ нелинейных преобразователей ................. 519
14.1. Стабилизаторы постоянного напряжения ............... 519
14.2. Резонансные усилители и умножители частоты ......... 520
14.3. Ограничители мгновенных и амплитудных значений
сигнала .................................................. 524
14.4. Выпрямители переменного тока ....................... 527
14.5. Преобразователи частоты ............................ 530
Вопросы и задания для самоконтроля ....................... 533
Глава 15. Анализ генераторов гармонических колебаний ......... 534
15.1. Физические процессы в генераторах гармонических
колебаний................................................. 534
15.2. Типы генераторов гармонических колебаний ........... 537
590
15.3. Анализ условий возникновения колебаний в генераторе . 540
15.4. Анализ работы генератора в стационарном режиме....... 553
15.5. Мягкий и жесткий режимы самовозбуждения ............. 559
Вопросы и задания для самоконтроля ........................ 562
Глава 16. Анализ и расчет дискретных фильтров ................. 564
16.1. Расчет параметров и реализация рекурсивных дискретных
фильтров нижних частот................................... 564
16.2. Расчет параметров и реализация нерекурсивных дискретных
фильтров нижних частот................................... 570
16.3. Переход к дискретным фильтрам верхних частот, полосовым
и заграждающим .......................................... 573
16.4. Особенности реализации дискретных фильтров с помощью
цифровых схем............................................ 576
Вопросы и задания для самоконтроля ........................ 577
Предметный указатель .......................................... 579
Список литературы ............................................. 582
Ответы......................................................... 583