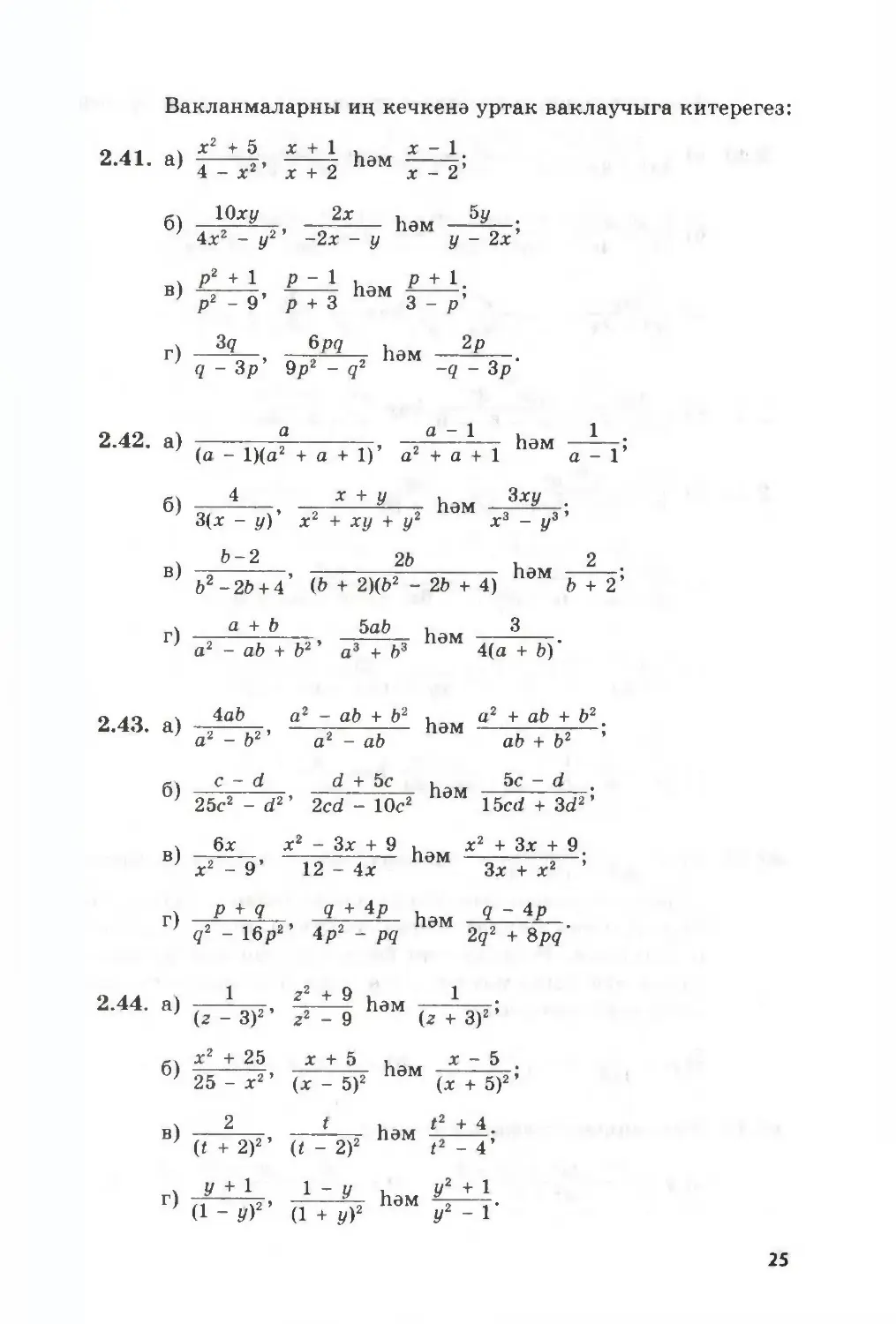Author: Мордкович.А.Г.
Tags: математика алгебра алгебра дәреслеге алгебра китабы
ISBN: 978-5-346-02021-9
Year: 2013
Text
AflΓβθ08 * 2 КИСӘК • МӘСЬӘЛӘЛӘР ЖЫЕНТЫГЫ
Ике кисәктә
2 кисәк
Гомуми белем бирү
учреждениеләре ечен
МӘСЬӘЛӘЛӘР ҖЫЕНТЫГЫ
А.Г. Мордкович редакциясендә
Москва 2012
Россия Федерациясе
Мәгариф һәм фән министрлыгы
тарафыннан тәкъдим ителгән
ХӘТЕР
УДК 373.167.1:512
ББК 22.141я721
А47
Авторлары:
А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина,
Е. Е. Тульчинская
Алгебра. 8 класс. В 2 ч. Ч. 2. Задачник для учащихся
общеобразовательных учреждений / [А. Г. Мордкович и др.] ;
под ред- А. Г. Мордковича. — 14-е изд., доп. — М. : Мнемозина,
2012. — 280 с.: ил.
ISBN 978-5-346-02021-9
Алгебра. 8 класс. Ике кисәктә. 2 кисәк. Гомуми белем бирү
А47 учреждениеләре өчен мәсьәләләр җыентыгы / [А.Г. Мордкович
Һ.6.]; Русчадан Р.С. Вафина тәрҗ.— «Татарстан Республикасы
«ХӘТЕР» нәшрияты» ҖЧҖ, 2013. — 280 б. : рәс. б-н
ISBN 978-5-94113-422-9
Мәсьәләләр җыентыгы дәреслеккә тулысынча туры килә. Һәр
параграфта катлаулана бару тәртибендә урнаштырылган күнегүләр
системасы сыйныфта дәресләрдә эшләү өчен дә, өй эшләре өчен дә,
мөстәкыйль эшләр өчен дә җитәрлек.
УДК 373.167.1:512
ББК 22.141я721
Учебное издание
Мордкович Александр Григорьевич,
Александрова Лидия Александровна,
Мишустина Татьяна Николаевна и др.
АЛГЕБРА
8 класс
В двух частях
Часть 2
ЗАДАЧНИК
для учащихся общеобразовательных учреждений
(перевод с русского на татарский)
Редакторы Ф.Ш. Шакурова, корректоры Е.Ю. Мурзина
Компьютерда битләргә салучысы Ю.М. Эстис
Оригинал макеттан басарга кул куелды 21.06.2013.
Форматы 60x90l∕lβ. Офсет кәгазе № 1. «Школьная» гарнитурасы.
Офсет басма. Басма табагы 17,5. Тиражы 2030 экз. Заказ С-1532.
420111, Казан, Тельман ур., 5. Тел. (843) 264-67-96.
Хатлар өчен: 420014, Казан, Кремль, а/я 54.
«Татмедиа» ААҖ филиалы — «Идел-ПРЕСС» полиграфия-нәшрият комплексы.
420066, Казан, Декабристлар урамы, 2.
ISBN 978-5-346-02021-9 (ч. 2)
ISBN 978-5-346-02019-6 (общ.)
ISBN 978-5-94113-422-9
© «Мнемозина», 1998
© «Мнемозина», 2012, с изменениями
© Оформление. «Мнемозина», 2012
Все права защищены
© Татарчага тәрҗемә, Татарстан
Республикасы «ХӘТЕР» нәшрияты,
2013
УКЫТУЧЫ ӨЧЕН КЕРЕШ СҮЗ
«Мнемозина» нәшрияты тарафыннан гомуми белем бирү мәктәбе¬
нең 8 нче сыйныфында алгебра курсын укыту өчен чыгарыла торган
укыту-методик комплект* составына түбәндәге китаплар керә:
Программы. Математика. 5—6 классы. Алгебра. 7—9 классы.
Алгебра и начала математического анализа. 10—11 классы / авт.-сост.
И.И. Зубарева, А.Г. Мордкович;
А.Г. Мордкович. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник;
А.Г. Мордкович и др. Алгебра. 8 класс. В 2 ч. Ч. 2. Задачник;
А.Г. Мордкович. Алгебра. 8 класс. Методическое пособие для
учителя;
Л.А. Александрова. Алгебра. 8 класс. Контрольные работы / Под
ред. А.Г. Мордковича;
Л.А. Александрова. Алгебра. 8 класс. Тематические проверочные
работы в новой форме / Под ред. А.Г. Мордковича;
Л.А. Александрова. Алгебра. 8 класс. Самостоятельные работы /
Под ред. А.Г. Мордковича;
Е.Е. Тульчинская. Алгебра. 8 класс. Блицопрос;
В.В. Шеломовский. Электронное сопровождение курса «Алгеб¬
ра-8» / Под ред. А.Г. Мордковича.
Сезнең кулыгызда әлеге комплектның икенче китабы - мәсьәләләр
җыентыгы**. Мәсьәләләр җыентыгын аерым китап итеп чыгару укыту¬
чыларны класста эшләү һәм өй эше биремнәре өчен башка чыганак¬
лардан җитәрлек кадәр материал белән тәэмин итәрлек күнегүләр
системасы төзергә мөмкинлек бирде.
Барлык параграфларда да (6 нчы «Кабатлау» бүлегеннән тыш)
күнегүләр икешәр блокка тупланып бирелә. Беренчесе (аркылы сы¬
зыкка кадәр) - ике база дәрәҗәсендәге: телдән (ярым телдән) һәм
уртача авырлыктагы (мондый биремнәрнең сул ягында О тамгасы куел¬
ган) биремнәрне; икенчесе (аркылы сызыктан соң) уртачадан авыррак
* УМК турында тулырак мәгълүматны www.mnemozina.ru һәм
www.ziimag.narod.ru сайтларыннан табарга мөмкин.
** Дәреслек һәм мәсьәләләр җыентыгы гына татар теленә тәрҗемә
ителгән (ред.).
3
һәм тагын да катлаулырак (мондый биремнәрнең сул ягында • тамга¬
сы куелган) биремнәрне үз эченә ала. Икенче, өченче һәм дүртенче
дәрәҗәдәге күнегүләрнең күпчелегенә җаваплар бирелгән. Дүртенче
дәрәҗә күнегүләрнең күбесе укытучы өчен ярдәмлектә тикшерелә.
һәр номердагы биремнәр билгеле бер санда: йә бер, йә ике (а)
һәм б)), йә дүрт (а), б), в), г)). Алар барысы да бер номер эчендә
бер типта, шуңа күрә класста а) һәм б) биремнәрен эшләү, ә өйгә в)
һәм г) биремнәрен биреп җибәрү тәкъдим ителә.
һәр бүлек (6 нчы бүлектән тыш) ике варианттагы «Өй контроль
эше» белән тәмамлана. Укучылар аны әлеге теманы өйрәнү барышында
эшли барырлар һәм, әзер булгач, укытучыга тикшерергә бирерләр
дип уйлыйбыз.
Укучылар белән барлык күнегүләрне дә чишәргә тырышу кирәкми.
Аларның саны артык күп, укытучының сайлап алу мөмкинлеге булсын
өчен, бу махсус шулай эшләнде. Сайлап алу классның әзерлегенә һәм
укытучының үз методик карашларына бәйләнгән, шунлыктан беркадәр
иҗатка да урын кала.
Укытучыларның игътибарын тагын шуңа юнәлтәсе килә: шушы
басмадан башлап, мәсьәләләр җыентыгында «Иң гади комбинаторика
мәсьәләләре. Вариантларны карап чыгу. Вариантлар агачы» (авторы —
П.В. Семёнов) дигән Кушымта бирелә башлаячак. Ул зур булмаган
биш кисәктән тора, һәм аларның һәркайсы дәреслек һәм мәсьәләләр
җыентыгының тиңдәшле бүлеге материалына таяна.
Безнең карашка, мәктәп баласы (һәм укытучылар) өчен шун¬
дый өр-яңа уку материалын мәктәп математика курсыннан аерырга
ярамый. Яңа (стохастик) укытуны безнең ил мәктәпләрендә эзгә
салынган укыту традицияләре белән кушып алып барырга кирәк.
Шул сәбәпле, Кушымтаның күпчелек мәсьәләләрендә (алар барысы
50 — җыентыкның һәр бүлегенә 10 ар өстәмә мәсьәлә) дәреслекнең
һәм мәсьәләләр җыентыгының 1 — 5 нче бүлекләрендә өйрәнелгән
материал (алгебраик вакланмалар, квадрат тамырлар, парабола һәм
гипербола, квадрат тигезләмәләр, тигезсезлекләр) файдаланыла.
Авторлар
КАБАТЛАУГА МӘСЬӘЛӘЛӘР
Иң рациональ юл белән исәпләгез:
1. а) 47 -15 + 53 15; в) 9,3 • 34 + 16 ■ 9,3;
6)29-72-29-22; г) 8,3 ■ 18 - 18 • 5,8.
2∙ a>l+2l+1l+1l= в) ⅛-l+⅛)∙14j
6)3∣-2∣-5-7ι г) (12∣ + 24∣ - 16⅛) : 2.
3. Табыгыз:
а)45тәнЗ%; в) 15 тән 2%;
б) 12 дән 125 %; г) 250 дән 206 %.
4. Түбәндәге шарт буенча b ны табыгыз:
a) b санының 30% ының 30% ы 7,2 гә тигез;
б) b санының 24% ының 25% ы 2,94 кә тигез;
в) b санының 80% ының 38% ы 136,8 гә тигез;
г) b санының 70% ының 35% ы 0,98 гә тигез.
5. Кайсы зуррак:
а) 52 санының 25% ымы яки 212 санының 2,5% ымы;
б) 83 санының 41% ымы яки 20 санының 15% ымы;
в) 16 санының 12% ымы яки 160 санының 1,2% ымы;
г) 72 санының 3% ымы яки 13 санының 0,5% ымы?
6. Санлы аңлатманың кыйммәте нульгә тигез икәнлеген ис¬
батлагыз:
а)
(3.25-3^):0,2-14
2,5 • 0,01 - 0,1
б)
2-5 - 1 : ⅛
о 1о
1,4 : 0,1 - 2
5
7. Аңлатманың мәгънәсе юк икәнлекне исбатлагыз:
θi2 • 5 - 4 .
б) 1>43÷1
(0,4 0,01) : 0,25 + 0,384 - 0,4'
Аңлатманы гадиләштерегез:
8.
a) a5 ∙ a7;
б) с3 ■ с4; в) г2 ■ г9; г) р6 ■ р3.
9.
a) a3b5 ■ aib7∙,
6) c4d7 ∙ c8d3;
в) m9n2 ■ n3m3∙,
г) p2q1 ■ p3q6.
10.
а) (г2)4;
б) (а6)2; в) (х5)6; г) (d3)3.
11.
a) (a3)2 ∙ a5;
б) (d4)3 ∙ d2∙, в) (∕β)2 • /4;
г) (х4)4 • х3.
12.
a) <χ3>2 ∙
a' χ2 . χ3 ’
б) (х4)2 - х3. в) (X3)3 .
х5 ■ (х3)2 ’ X2 • X4 ’
г)
(x3)s
(X2)4 ■ X3
13.
Исәпләгез:
a) 136 ∙ 28 .
, 265 ’
g4 711 ■ 911. 428∙38.
635 ’ 64 ’
г)
126
З5 • 45 ‘
14.
Аңлатмаларның кыйммәтләрен табыгыз:
v 253 ■ 142 . ω 122 ■ 353 . в) 363 ■ 152 .
7 49 ∙ 106 ’ ’ 282 ∙ 154 ’ , 184 ∙ 103 ’
г)
224 ■ З3
62 ∙ 1212,
Аңлатмаларны гадиләштерегез:
15. a) 12а - (Ь - 2а); в)5Ь + (-Ь-5);
б) (2х + Зу) - (х - 2у); г) (Зх - 5y) + (-Зх + у).
16. a) 3α + 2α(α - 3); в) 4x - 3x(x + 1);
б) 5a(a - 2b) - 2b(4a + b); г) 2x2(x + 1) + x2(χ - 3).
17. а) (х - 4)(х + 5); в) (х + 4)(-x + 2);
6)(x-1)(2х + 3); r)(3x-2)(x-l).
18. Бердәйлек булып торучы аңлатмаларны күрсәтегез:
а) (a - 3)(a + 7) = (3 - a)(7 + a);
б) (a - 3)(a - 7) = (3 - a)(7 - a);
в) (a - 3)(a + 7) = (3 - a)(-7 - a);
r) (a - 3)(a - 7) = ~(a + 3)(-7 + a).
6
Аңлатманы кыскача тапкырлау формулаларын кулланып
үзгәртегез:
19. a) (a - b)(a + Ь); в) (1 - 5)(1 + &);
б) (a - 2)(а + 2); г) (3α - b)(3a + Ь).
20. a)(3x-l)(3x +1); в) (10p + 7g)(7g - 10р);
б) (1 Зт - lln)(13τn + lln); г) (4 - 5p)(5ι∕ + 4).
21. а)(а + 2)2; б) (3b -1)2; в)(х-8)2; r)(l+4p)2.
22. а) (4т + 5п)2; б)(2з-ЗО2; в) (9p - 7g)2; r)(8r+lls)2.
23. а) (х + 3)(x2 - Зх + 9);
б) (2α - 35)(4α2 + 6ab + 952);
в) (х + l)(x2 - х + 1);
г) (7y2 - l)(49y4 + 7y2 + 1).
24. Бердәйлекне исбатлагыз:
(a - 2)(a2 + 2a + 4) - (a + c)(a2 - ас + c2) + (с + 2)(c2 - 2с + 4) = 0.
Кыскача тапкырлау формулаларын кулланып исәпләгез:
25. а) 69-71; 6)42 -38; в) 89 91; г) 58 62.
26. а) 212; б) 592; в) 822; г) 682.
Тапкырлаучыларга таркатыгыз:
27. а) 2d2 + 2cd; в) r3s4 + r4s3j
б) npi - mpi∙, г) 20a3x - 15a4x2.
28. a)x2-y2∙, б)х2-4у2; в)х2-9; г) 1 - 25г/2.
29. а) 12z2 - 9kz + 4пг - 3kn∙, в) Зх - 2x2 + Зу - 2ху;
б) a2 - ab - Ьс - с2; г) 20z2fe + 2z - 5⅛ + 1.
30. а) a2 + 4a + 4; в) 16t2 + 8fs2 + s4;
б) 9x2 - бхт. + т2; г) b4 - 16b2c + 64с2.
Вакланманы кыскартыгыз:
31 ЯЧ «2 + Д . 3p + 6g . ч 8m - 8ra. r∖ 3x3 + Зху2
a3 + a2’ p2 + 2pq, 9n - 9m ’ 6yx2 + бу3
qo . a2 + 4a + 4 . ⅛2 - 8⅛ + 16.
32. а) —; в) ;
’ а + 2 ’ k - 4
б) Зга - m г) р - 2g
9ra2 - бпт + m2 ’ p2 - 4pg + 4g2
7
Вакланмаларны кыскартыгыз:
. b2 - 25
33∙ a) b ■ g''
2zn - 3 . , t2 - 36. . 5⅛ - 2Z
4m2 - 9’ ’ 6 + t ’ Г 25⅛2 - 4Z2 ’
4p2 - 2p + 1. в) 9 + 12z + 16z2.
8p3 + 1 * 27 - 64z3 ’
27α3 + 8. , 5 + 2т
2 + За ’ ; 125 + 8zn3'
9x2 - 6x + 1. . 4m2 - 9n2
9x2 - 1 ’ 9n2 - 12тп + 4тг ’
16α2 - 25⅛2 . 36⅜2 + 12s⅜ + ⅜2
16a2 + 40ab + 2562 ’ , s2 - 36t2
36. Координаталар турысында санлы аралыкны сурәтләгез,
аны атагыз һәм, тигезсезлек тамгаларын кулланып, аның
аналитик моделен языгыз. Бирелгән аралыкта ятучы иң
кечкенә бөтен санны табыгыз:
а)(2;+~); б)(-~;6]; в)[1;5]; г) [4; 10).
37. Координаталар турысында санлы аралыкны сурәтләгез,
аны атагыз һәм, тигезсезлек тамгаларын кулланып, аның
аналитик моделен языгыз. Бирелгән аралыкта ятучы бар¬
лык бөтен саннарны табыгыз:
а)(-2;5); б) [4; 8); в)[-1;4); г)(4,5;6).
38. Координаталар яссылыгында А(2; 4) һәм В(2; 7) нокталарын
билгеләгез. Якларының берсе АВ кисемтәсе булган квадрат
төзегез. Квадрат түбәләренең координаталарын табыгыз.
Шундый ничә квадрат төзергә мөмкин?
39. Координаталар яссылыгында А(2; 4) һәм С(7; -1) ноктала¬
рын билгеләгез. Диагонале АС кисемтәсе булган квадрат
төзегез. Квадрат түбәләренең координаталарын табыгыз.
40. а) Координаталар яссылыгында Р(-1; 2) ноктасын билге¬
ләгез. Ординаталар күчәренә карата бирелгән ноктага
симметрик ноктаны табыгыз.
б) Координаталар яссылыгында К(3; -1) ноктасын билге¬
ләгез. Абсциссалар күчәренә карата бирелгән ноктага
симметрик ноктаны табыгыз.
41. а) Координаталар яссылыгында А(-3; 3) ноктасын һәм
х = -2 турысын сурәтләгез. Төзелгән турыга карата бирелгән
ноктага симметрик ноктаны табыгыз.
8
б) Координаталар яссылыгында С(4; -2) ноктасын һәм
у = 1 турысын сурәтләгез. Төзелгән турыга карата бирелгән
ноктага симметрик ноктаны табыгыз.
42. а)С(2; 4) һәм D(l; 5) нокталары бирелгән. Абсцисса¬
лар күчәренә карата CD турысына симметрик турыны
төзегез.
б)Е(-1; 4) һәм F(2∙, -2) нокталары бирелгән. Ордината¬
лар күчәренә карата EF турысына симметрик турыны
төзегез.
43. у = х — 5 функциясенең графигын төзегез.
Билгеләгез:
а) аргументның нинди кыйммәтендә у = -3 тигезлеге
үтәлә;
6) x = -3 ноктасында функциянең кыйммәте нинди;
в) аргументның нинди кыйммәтләрендә функция уңай
кыйммәтләр ала;
г) аргументның нинди кыйммәтләрендә функция 3 тән
кечерәк кыйммәтләр ала;
д) функция үсәме, әллә кимиме.
44. у = - х + 4 функциясенең графигын төзегез.
Билгеләгез:
а) аргументның нинди кыйммәтендә у = 0 тигезлеге үтәлә;
б) х = -1 ноктасында функциянең кыйммәте нинди;
в) аргументның нинди кыйммәтләрендә функция тискәре
кыйммәтләр ала;
г) аргументның нинди кыйммәтләрендә функция 5 тән
кечерәк кыйммәтләр ала;
д) функция үсәме, әллә кимиме.
45. у = 2х + 3 функциясенең графигын төзегез.
Билгеләгез:
а) аргументның нинди кыйммәтендә у = 7 тигезлеге үтәлә;
б) х = -2 ноктасында функциянең кыйммәте нинди;
в) аргументның нинди кыйммәтләрендә функция тискәре
кыйммәтләр ала;
г) аргументның нинди кыйммәтләрендә функция 3 тән зур¬
рак кыйммәтләр ала;
д) функция үсәме, әллә кимиме.
9
46. у = -Зх + 2 функциясенең графигын төзегез.
Билгеләгез:
а) аргументның нинди кыйммәтендә у = -4 тигезлеге үтәлә;
б) х = 3 ноктасында функциянең кыйммәте нинди;
в) аргументның нинди кыйммәтләрендә функция уңай
кыйммәтләр ала;
г) аргументның нинди кыйммәтләрендә функция -1 дән
зуррак кыйммәтләр ала;
д) функция үсәме, әллә кимиме.
47. Функцияләр графикларының кисешү ноктасын табыгыз:
а) у = 2x - 1 һәм у = 5 - х; в) у = 2х + 3 һәм у = Зх + 2;
б) у = 0,5x - 1 һәм у = —х - 4; г) у = -Зх + 4 һәм у = 2x - 1.
48. у = х2 функциясенең графигын төзегез.
Табыгыз:
а) аргументның кыйммәтләре -3; 1; 2 булганда функциянең
кыйммәтләрен;
б) функциянең кыйммәтләре 0; 1; 9 булганда аргументның
кыйммәтләрен;
в) функциянең [-2; 0) кисемтәсендәге иң зур һәм иң кечкенә
кыйммәтләрен;
г) парабола белән у = 4 турысының кисешү ноктасы коорди-
наталарын.
49. у = -х2 функциясенең графигын төзегез.
Табыгыз:
а) аргументның кыйммәтләре -3; -2; 1 булганда функциянең
кыйммәтләрен;
б) функциянең кыйммәтләре 0; -1; -4 булганда аргументның
кыйммәтләрен;
в) функциянең [-1; 3] кисемтәсендәге иң зур һәм иң кечкенә
кыйммәтләрен;
г) у = -х2 параболасы белән у = 2х турысының кисешү нокта¬
лары координаталарын.
50. Тигезләмәне график юл белән чишегез:
а)х2 = х + 2; в)х2 = 2х + 3;
б)х2 = -х + 6; r)x2 = -3x.
51. Функция у = /(х) формуласы белән бирелгән, биредә
f(x) = 2x-6.
a) f(-1), /(0), ДЗ) не табыгыз.
б) f(2x) = 4 тигезләмәсен чишегез.
10
52. Функция у = f(χ) формуласы белән бирелгән, биредә ∕r(x) = х2.
a) 7(-l)> /(0), /(3) не табыгыз.
б) = 1 тигезләмәсен чишегез.
[-x2, 3 < х < 1 булганда,
□3. у ∣
[х - 2, 1 < х ≤ 4 булганда,
функциясенең графигын төзегез.
Тигезләмәне чишегез:
54. a) 19х-Зх + 4х = 80; в) 20х - 13х - 12х = 6;
б) 0,17x - 13 = 10 - 0,29х; г) 8х + 0,77 = 4,61 - 8х.
55. а) (х + 1)(х + 2) - (х + 3)(х + 4) = 0;
б) (х - 2)(х - 3) - (х - 1)(х - 4) = 0;
в) 10х2-(2х-3)(5х-1) = 31;
г) 12x2-(4x-3)(3x + 1) = -2.
56. a)9x2-1-(3x-2)2 = 0j
б)(2х-3)2-2х(4 + 2х)=11;
в) х + (5x + 2)2 = 25(1 + х2);
г) (4x - 3)(3 + 4x) - 2x(8x - 1) = 0.
57. Тигезләмәләр системасын график юл белән чишегез:
у = Зх - 2,
у = X - 3,
а)
у = -х + 6; В)
у = —2х + 3;
у = 2х - 1,
у = Зх + 1,
б)
⅛.,-,4i Г>‘
У = -х + 5.
Тигезләмәләр системасын чишегез:
[Зх - 2у = 12,
4х + Зу - Ю,
58. а)
. в)
х + 2у = -4;
х - 2у = -3;
Зх - У = 4’ г)
х - У = 3.
б)
2х + зу = Ю;
Зх - 4у = 7.
Зх + 4</ = 55,
Зх -5у = 14,
59. а)
7х - У = 56;
х + 2у = 1;
9х + ЗУ = 21,
Зх - 2у = -12,
б)
бх + 4у - 13;
5x + 4j∕ = -4.
11
60. Аралары 350 км булган А һәм В шәһәрләреннән бер үк ва¬
кытта бер-берсенә каршы ике мотоцикл юлга чыга. Хәрәкәт
башланып 3 сәг үткәннән соң, аларның очрашуга кадәр
20 км үтәселәре кала. Әгәр бер мотоциклчының тизлеге
икенчесенең тизлегеннән 10 км/сәг кә артык булса, аларның
тизлекләрен табыгыз.
61. Бер кисәк электр үткәргече икенчесеннән 54 м га озынрак.
Ике кисәктән дә 12 шәр м кисеп алганнан соң, икенче кисәк
беренчесеннән 4 тапкыр кыскарак булып калган. Башта һәр
кисәктә ничә метр үткәргеч булган?
62. Универмагка 150 палас китерәләр. Шуларның 20% ы —
кулдан, ә калганнары фабрикада эшләнгән. Китерелгән
паласларның ничәсе фабрикада эшләнгән?
63. А пунктыннан В пунктына 60 км/сәг тизлек белән мо¬
тоциклчы юлга чыга. 30 минуттан соң В пунктыннан
аңа каршы икенче мотоциклчы кузгала, аның тизлеге
50 км/сәг. Әгәр А һәм В пунктлары арасы 162 км булса, оч¬
рашуга кадәр икенче мотоциклчы күпме вакыт сарыф итәр?
64. Катер елганың агымы уңаена 5 сәг, аннан соң агымга каршы
3 сәг бара. Әгәр елганың агым тизлеге 3 км/сәг һәм барысы
126 км юл үтелгәне билгеле булса, катерның үз тизлеген та¬
быгыз.
65. Аралары 30 км булган А һәм В пунктларыннан бер үк ва¬
кытта бер-берсенә каршы ике җәяүле юлга чыга, һәм алар
3 сәг 45 мин тан очрашалар. Әгәр беренче җәяүле икенчесен¬
нән 2 сәг алданрак чыккан булса, очрашу икенчесе юлга
чыкканнан соң 2,5 сәг узгач булыр иде. Җәяүлеләрнең
тизлекләрен табыгыз.
66. Ике сорт корыч ватыгының берсендә никель 5%, ә икенче¬
сендә 40% ны тәшкил итә. 30% ы никель булган 140 т корыч
табу өчен, бу ике сорт корычны күпмешәр алырга кирәк?
67. Ике эшче бергәләп 1020 деталь эшли. Беренче эшче 15 көн,
икенчесе 14 көн эшләгән. Әгәр беренчесе 3 көн эчендә икен¬
чесе 2 көндә эшләгәннән 60 детальгә күбрәк эшләсә, һәр
эшче ничә деталь эшләгән?
68. Икеурынлы санны аның цифрлары суммасына бүлгәннән
соң, өлеш 7 гә, калдык 3 кә тигез була. Әлеге сан цифрлар¬
ның урыннарын алыштырганнан соң, аннан 36 га кимрәк
сан килеп чыга. Бу санны табыгыз.
12
1
БҮЛЕК
АЛГЕБРАИК
ВАКЛАНМАЛАР
§1 . ТӨП ТӨШЕНЧӘЛӘР
Аңлатма алгебраик вакланма буламы:
, 1 .3a2 ,. 10x2+4x-7.
1∙1. a)5fe2j б) 8
∖ c2. 1,∖ 3 o
в) b2' > 9т - 5 ’
1.2. a) 7-a2,.+ 4i
14
Р2
в) 3t - γj^,
б) ^ +2g∕÷15 - 5Л
6nm + 3m2n2 9
r> 7n - 12τn 1
Үзгәрешленең нинди кыйммәтләре өчен алгебраик
аңлатманың мәгънәсе юклыгын билгеләгез:
1.3. а) —б) 1⅛J
’ a + 5 ’ 4 + 1Ос
. Зх - 9. . 15m + 4
1 + х ’ r' 4m + 15’
Qjf2
1∙4∙ а> x(x + 2)j
8u2
В) У (У- D’
45z3 + 5 .
°, 3z(23z + 69),
72t2 - 17
Г) 2i(15t-60)'
1 _ . 3α2 + 5
1,5∙ a> (a + 2)(а + 3)’
31c2
в) (с + 12)(e - 19)’
8⅛3 + 14 .
(2b - 7)(3fe + 9)’
99d2 - 53
r' (3d - 4)(5d + 45)'
13
1.6. Бирелгән алгебраик аңлатма өчен үзгәрешленең мөмкин
табылган кыйммәтләрен табыгыз:
a) 4χ2 - 2x - 3 . х 17s + 1 .
’ (х - 3)(x + 3)’ ? (з - 2)(2 + з)’
g∖ 35р - 24, . t2 + 41 — 1
р2 - 16 ’ ' t2 - 36 ‘
1.7. Түбәндәге шарт үтәлгәндә мәгънәсе була торган алгебраик
аңлатмалар уйлап табыгыз:
а) х ≠ 3; в) г ≠ -4, z ≠ -7, z ≠ 0;
б) у ≠ 0, у ≠ 12; г) х - теләсә нинди сан.
Үзгәрешленең алгебраик аңлатманы нульгә тигез итә
торган кыйммәтләрен табыгыз (әгәр шундый кыйммәтләр
була алса):
1.8. а)
Qr2
1∙9∙ а)
б)
б)
х2 + 1.
х2 ’
. 2х + 6
в>
г)
х + 1
х2 + 1*
х2 - 4.
х - 2 ’
х(х + 3).
b, (х + З)2 ’
ч х(х + 1)
г)
Алгебраик аңлатманың кыйммәтен табыгыз:
√c — 2
1.10. а) —-— , х = 3 булганда;
б)
(t - 7)2
2s
, t = 4, s = -1 булганда;
в)
у + 6
У-2
у = 4 булганда;
г) (2y + 3)2 ’ x = 2, y = ~2 бУлганДа-
1.11. а) (р2++8] , Р = -2 булганда;
(1 + 4s)2 4 . . ,
б) —х-— , t = 4, s = -1 булганда;
ΔSt
ч s2 - 1 1 _
в) ~∑⅛Γ, s = 2 булганда;
х - 5у
Г) „2 _ „2 > х = 2, у = -2 булганда.
X у
14
ol.l2. a - 2b = 3 булганда, аңлатманың кыйммәтен табыгыз:
a) 2Ь - а;
. 4Ь - 2а
≡) 3 ,
б) 2a - 4Ь;
г) —l-
2a - 4Ь
Мәсьәлә шартында сурәтләнгән хәлнең математик моде¬
лен төзегез:
01.13. Туристлар урман сукмагы буйлап 6 км, ә аннан соң,
тизлекне 1 км/сәг кә арттырып, шоссе буйлап 10 км
баралар. Барлык юлны алар 3,5 сәгатьтә үтәләр.
01.14. Катер агым тизлеге 2 км/сәг булган елга буйлап хәрәкәт
итә. Ул агым уңаена 18 км, ә агымга каршы 14 км юл үтә
һәм барлык юлга 1 сәг 20 мин вакыт сарыф итә.
01.15. А пунктыннан аннан 120 км ераклыктагы В пунктына
таба бер үк вакытта ике автомобиль юлга чыга. Аларның
берсенең тизлеге икенчесенең тизлегеннән 20 км/сәг кә
зуррак һәм шунлыктан ул В пунктына 1 сәг кә алдарак
килеп җитә.
01.16. ТТТаҺәрдән 40 км ераклыктагы авылга таба йөк машинасы,
ә 10 минуттан соң тизлеге йөк машинасы тизлегеннән
20 км/сәг кә зуррак булган җиңел машина юлга чыга.
Авылга алар икесе бергә килеп җитәләр.
01.17. Ике туристлар базасыннан бер үк вакытта туристларның
ике группасы юлга чыга һәм алар елга буенда очрашырга
тиеш була. Бу урынга кадәр беренче группага 12 км, ә
икенчесенә 10 км барырга кирәк. Беренче группаның
тизлеге икенчесенең тизлегеннән 1 км/сәг кә кимрәк, һәм
ул очрашу урынына 1 сәг кә соңрак килеп җитә.
Мәсьәләне математик модельләштерүнең өч этабын аерып
күрсәтеп чишегез:
01.18. Үз тизлеге 30 км/сәг булган моторлы көймә елганың
агымы уңаена 18 км һәм агымга каршы 42 км араны
үтә. Әгәр көймә агым уңаена да, агымга каршы да бер үк
вакыт сарыф иткән булса, елганың агым тизлеге нинди?
01.19. Автобус 160 км араны автомобиль 280 км араны үтүгә
сарыф иткән вакытта үтә. Әгәр автобусның тизлеге
автомобиль тизлегеннән 30 км/сәг кә кимрәк булса, бу
тизлекне табыгыз.
15
1.20. -, —, -⅞ булса,
У У У
а) х > 0, у > 0;
б) х > 0, у < 0;
в) х < 0, у > 0;
г) х < 0, у < О
вакланмаларының тамгаларын билгеләгез.
1.21. Исбатлагыз, үзгәрешленең теләсә нинди кыйммәтләре
өчен:
.5 „
a) д2 + _ вакланмасының кыйммәте уңай;
-3
б) ∣j2 + вакланмасының кыйммәте тискәре;
_ч (х-3)2
в) —7 — вакланмасының кыйммәте тискәре түгел;
d т о
. (У - 6)2
г) TΓ,^2—о вакланмасының кыйммәте уңай түгел.
Алгебраик вакланманың кыйммәтен табыгыз:
, nn . (3α - b)2
1.22. a) —, а = 4, ь = -2 булганда;
,. c6 - 1
°/ tj4 + 2 • с = -2, d = 1 булганда;
π, (χ - УҮ
a, x2 + yi > х = 3, у = 4 булганда;
, 2тп
, mr+^3 . т = 2, п = -1 булганда.
1 24 я1 "L→i
(α + ьу , a = 4, b = -2 булганда;
61 c3 +-gf∙
' c2d +^2 > с = -2, d = 10 булганда;
X2 +j∕2
х4 ,x=13,y = 12 булганда;
г) n4
' m3τ^~^rn∏2 , m ~ 2’ n = “1 булганда.
16
1.24. Үзгәрешленең нинди кыйммәтләре өчен алгебраик
вакланманың мәгънәсе барлыгын билгеләгез:
а)
Зх2 .
х2 + 3’
в)
X2 - 1.
х2 + 5’
15⅛ + 1
b2(b2 + 1)’
8т - 3
r) m2(m2 + 4)‘
3x2 + 2x + 5 . . 17s2 + 24s + 1 .
(Зх - l)(2x + 5)’ В) (44s + 1)(3 2s - 3),
9y2 - 5y + 4 . 52r2 + 13r - 5
(5y - 3)(31 + 93«/)’ ' (5r _ i5)(9r _ 25)'
1.26. а) (“_+^2;
в) ^-2-7i
’ (с + 3)2’
fix - ⅛2÷12 .
4∂2 - 4Ь + 1’
. 27nt3 - 15
’ 4m2 + 36m + 81’
1 27 а) 7g2 ~ § •
L , (a + 8)(α - 9)(a + 17)’
73c3 - 8 .
B) (4c - 2)(7c + 8)(13c + 39)’
101⅛3 - 58t>2 + 5 .
θ, (25 + l)(3b + 4)(3fe - 8)’
. d3 + 4d2 + 8d - 16
r, (d + l)(4d + 4)(7d + 5)'
< 28 а) ЗЬ + 2
1.ZS. а) 3b(3δ.2)2,
ч 2« - 1 .
B) 2s(2s + 1)2’
14⅛2 +14 .
, (⅛2 - 9)(⅛2 + 1)’
. 8m2 + 16
(m2 + 2)(m2 - 4)’
1.29. а) a2(3a _ 9)(a + 17),
. 73c2
b, C3(c + 8)(13c - 39)’
fi 3⅛ + 4
0j (2b + l)(9b2 - 16)’
1 2d-1
r, (4d2 - l)(7d + 5)'
1.30. Үзгәрешленең нинди кыйммәтләре өчен ———ττ~
m(m + 1)(т - 2)
алгебраик вакланмасы нульгә әйләнә, ниндиләре өчен
мәгънәсе булмый?
17
1.31. Үзгәрешленең теләсә кайсы кыйммәтләре өчен дә
алгебраик вакланманың нульгә тигезлеген исбатлагыз:
4 (a + 2)2 - 4(α + 1) - a2 9 + x(x - 6) - (х - З)2
а) ; б) ^Тз •
1.32. Үзгәрешленең теләсә кайсы кыйммәтләре өчен дә
алгебраик вакланманың мәгънәсе булмавын исбатлагыз:
2х - 5 .
а) (х - 3)(x2 + Зх + 9) - x(x2 + 3) + 3(9 + х)’
3α - 1
tυ 2(4 - a) - (α + 2)(α2 - 2α + 4) + α(α2 + 2)‘
01.33. 5a - 10& = 18 булудан чыгып, аңлатманың кыйммәтен
табыгыз:
, „ z>ι 7,2 . 8b - 4a. ∖ a2 - 4ab + 4b2
а)За-6Ь; б) в) —θ-; г) — .
01.34. Зх - 9y = 1 булудан чыгып, аңлатманың кыйммәтен
табыгыз:
. „ . 12у - 4х
а) х - Зу; в) —;
О
б) —^5-; г) (9ι∕2 - вху + х2) • 3.
х — оу
ol.35. ү = 3 булудан чыгып, аңлатманың кыйммәтен табыгыз:
Ь
a
а)
,x b . a + b, , b + 2a
б) - в) —— г)
’ а ’ b 'а
х 1
01.36. — = — булудан чыгып, аңлатманың кыйммәтен табыгыз:
У 5
а)
2у’
х + у
б)
X
, X - У
г) •
’ У
≡) ⅛
01.37. Вакланманың кыйммәтен табыгыз:
а) x = 0,2 булганда; б) 3x 8—, = 0,4 булганда.
a + 2b „ c-
—-— = 7 булудан чыгып
ь
табыгыз:
аңлатманың кыйммәтен
∖ a
а) ь
-x 2a -b . 2a + 3b, . 4b - а
б) ~2Γ' в) —ъ-’ г)
18
x ~ 3 и
•1.39. — = 12 булудан чыгып, аңлатманың кыйммәтен
У
табыгыз:
. X. 2x + У.
а) у’ б) Зу ’
В> г) ⅛ji.
х 2х
01.40. п ның бирелгән вакланманы натураль санга әверелдерә
торган барлык кыйммәтләрен табыгыз:
. п + 3 2п + 5
а) ; б) ;
п п
, 6 - п , 45 - 7п
в) ; г)
п п
1.41. Бирелгән математик модель ярдәмендә сурәтләнә торган
реаль хәлне уйлап табыгыз:
,12 12
a) ,i-i;
’ х х + 1
, 20 25
в) — = т
х х + 1
fi, 24 - 16 •
’ х+ 2 х - 2’
М 10 4- 9 _ О
) х - 2 х + 2 3∙
§ 2. АЛГЕБРАИК ВАКЛАНМАНЫҢ
ТӨП ҮЗЛЕГЕ
2.1. Алгебраик вакланманың төп үзлеген кулланып, *
символын түбәндәге тигезлекләрне дөрес итә торган
алгебраик яки санлы аңлатма белән алыштырыгыз:
,46 * .
a) 7 21α,
, т2 *
в) — = т—;
п 5гп
fζλ α2.
б) Т =
Г) = ⅛
p2s *
2.2. Бирелгән тигезлек бердәйлек буламы:
a) = —≡-;
х + у хп + уп
, a - Ь а2 - аЬ
в) - 2 ;
a а2
_, с с + S
б) - = ;
d d + s
, тх + п т + n,ct
г) - 1
qχ + р я + р
2.3. Вакланманы кыскартыгыз:
, 15α∂. й 14A2Z
а) 12te∙ 6> TW ’
144xy. 135p3g2
в) 63yz ’ 25<z2p '
19
2.4. Вакланманы кыскартыгыз:
4(a - ⅛).
а) 5(α - b)2'
13(x + 4)3 .
6) 26x(x + 4)’
8(fe + Z)2.
В) 9(⅛ + Z)3 ’
48m(2m - n)3
r' 60n(2m - n)3 '
Аңлатманың кыйммәтен табыгыз:
24
2.5. a)
43
б) ⅛!
Ч 712.
в) γιo ’
ч 63
Г) 62∙
2.6.
ч θ4.
а)
кч 24 •
б) 2?-
. 625
в) -jr;
г)
З3
54 ‘
o2.7.
Исәпләгез:
. 33 ∙ 124.
а) 35.42’
„ 147 ■ 282.
°) 7э . 2< ’
. 625 ∙ 153
В) 5’ 3 ;
г)
115 56
25 ∙ 555
2.8.
Вакланманы 56 ваклаучысына китерегез:
. 5а
а) т;
26m
б) И2’
. 3⅛
в) т;
г)
27t
168'
2.9.
Вакланманы 36α ваклаучысына китерегез:
ч 2b.
а) за
5an
б) 36a2
ч 7s∙
В) 36’
г)
9d
108ad'
2.10. Вакланманы 14znn ваклаучысына китерегез:
. 58Z . ,4 1 . ч 27mk . . 3
a 28lmn, 2n, В 42m2n, Г 7т'
2.11. Вакланманы 24x2y ваклаучысына китерегез:
1 йч 15x2 . 2х. 22a2y2
а) 8ху’ б) 120x3∕ В) 3y, Г) 48x2j∕3'
2.12. Бирелгән аңлатмаларны бер үк төрле вакланмалы алгеб¬
раик вакланмалар рәвешендә языгыз:
a) 1θ*- һәм 7у2; в) 3m2 һәм
б) Юу2 һәм г) ү— һәм 10b.
20
Бирелгән аңлатмаларны бер үк төрле вакланмалы алгеб¬
раик вакланмалар рәвешендә языгыз:
2.13. a) x һәм 5х; в) 9α2 һәм α ;
7 х-у a + 9
б) һәм (х - у); г) (5 - Ь) һәм
2.14. a) —һәм (а + Ъ); в) (a - b) һәм a b ;
’ a + b a - Ъ
б) x Һәм х2 - ху + у2; г) x + θ һәм х2 + 2х + 4.
' х + у э я ■> > χ _ 2
Бирелгән алгебраик вакланмаларны иң кечкенә уртак
ваклаучыга китерегез:
o <e . 5a . lb. . Id , 43c.
2.15. a) y һәм в) - һәм —,
,4 3a2 , 5ab . 8t2 . 7x2
б) — һәм —, г) — һәм —.
о in х b , 3. λ 5 , 2 ,
2.1 θ. а) n һәм , в) rt, һәм ,
3a a 2b 5b
c, 7 , 11 . 13a , 5a
б) 12с ҺӘМ 8? Г) 48d ҺӘМ 54d∙
2.!7. а) J һәм в) һәм
-х a , b . х 3c2 , t2
б) w һәм 2^’ г) it һәм τ^c-
n 1 o . a + b , a - b' χ3-x. у + 2.
2.18. а) —-— һәм в) —— һәм —
5a 10b ’ 12u 4х
б)
7d3 , 5c3 .
60с ҺәМ 36d,
г)
2n3 , 7m2
77=—т ҺӘМ 77=—.
27 т2 ЗОп
2.19. а) - һәм -^-r∙, в) һәм ;
a 2ab ’ Зп бтп
Ях 5 + р , 4р х т + п , т2
б) һәм г) ;— һәм —5-
b3 b2 n3 п2
21
Бирелгән алгебраик вакланмаларны иң кечкенә уртак
ваклаучыга китерегез:
2.20. a) ξ- һәм ≡-⅛⅛5
5j∕ у2
в) Зс һәм c + d.
2d2 6ad
б) һәм ∏⅛
15x1/ 5x2ι∕2
г) -⅞- һәм ⅛
4x2ι∕ 5ху*
2.21. a) τ-g82.3 һәм —;
15α2b3 10a⅛2
4 11c 4с .
В) 28p⅛31 Һ 35p⅛,
б) ⅛ һәм
63zn2n4 36τn3n3
г) V - x һәм 8У + 5χ2.
7 24x2ι∕3 60x4y
2.22. а) -Ц- һәм 1^;
a + b а
в) — һәм —-—;
b Ь - с
б) ⅛ һәм 1;
ai а - 4
г) һәм *±3.
X + у xi
2.23. а) — һәм —— ;
a a(a - 1)
∙>⅛i¾ һ’“
c(c - d) с
б) £±А һәм
с - 1 c(c - 1)
г) — һәм —У-—.
у(у + X) У + X
2.24. а) А һәм -^-+b ;
2a a(a - Ь)
в) 7 ~ П . һәм
m(m + n) 3m
б) a-≤ һәм -a + 1 ;
a2 a(a - 1)
г) һәм ^-⅛2.
m(m + 2) т2
2.25. а) һәм ;
Зх - 3 6х - 6
. 5х , 9у .
в) о ≡- һәм -—- - ;
8х + 8у 4х + 4у
6) -b~l Һәм
ab + 2a 2b + b2
\ х - 3 r, у - 3
г) -у Һәм -г у.
X2 - ху ху - у
2.26.
а)
һәм
т - 8 т + 8
в)
һәм
q - 10
3g .
q + 10’
б)
Й^һәм^)= г>
* —÷,- һәм √—ir-.
y(x - 1) y(x + 1)
22
2.27.
a)
- -,3c ,2 Һәм j + 3,2>
cd + d2 cd - d2
в)
х - 2
χy - У
һәм
2У
ХУ + У
2.28.
2.29.
2.30.
2.31
2.32.
2.33.
2.34.
б)
а)
б)
а)
б)
а)
б)
а)
б)
а)
б)
а)
б)
4 - 2x + χ2
2х -
15
т - п
15а
2a + Ь
x2
һәм
һәм
1
(х - У)2
һәм
2х + х2
16
п - т
65 .
-2а - 5’
к 1 .
ПЭМ . .2 j
(у - ху
15m 17n
(а - 5)2 ҺӘМ -(5 - а)2
7х
х2 - 4
8у
У2 - 9
х - У
32а
һәм
һәм
һәм
(z - t)8
11а
α3 + δ3
Зх + 1
г3 - 27
а - b
5α + 55
У3
х2 ~ У2
г)
в)
г)
в)
г)
.2
һәм
X
.2
х + 2
х - 2
5
3 - у
49
(х - У)2'
һәм
һәм
һәм
һәм
һәм
в)
г)
в)
48
Зр - у
һәм
11
q - Зр’
4s
-2t - 3s
25 р
(Р - ?)2
3k
-(I - ⅛)2
т - п
т + п
, 8t
һәм - —.
2t + 3s
һәм
һәм
һәм
7т
-т - п
Р
(Р + 9)2
425
(z - t)7
1
а + 5’
х - 3
х2 + Зх + 9’
а2
α2 - 52’
г)
в)
г)
в)
x2 - ху + у2. ,
X2 - ху
Бердәйлекне исбатлагыз:
. 4,5α2 + 0,5α5 _ а
a' 40,5α2 - 0,552 9а - 5
б)
7а
(а + 5)12
105
53 - 8
1 - бу
t3 + у3
бу .
(9 - Р)2 ’
81
(⅛ - О2 ‘
5тп '
т2 - п2’
, Зп
һәм -i 5-.
mi - и
һәм
һәм
һәм
ху
х2 - у2
Р - Я.
р + q,
95
(а + 5)14'
1
Ь - 2’
һәм — ≥
i2 - ty + у
һәм x + ;
2х - 2у
*2÷t*+∕ һәм -⅛.
zt + z2 z2 - t2
24,5x2 - 0,5y2 _ 7x + у
3,5x2 - 0,5xy
х
23
Вакланманың кыйммәтен табыгыз:
o2.35. a) ,9*a ~ 3j⅜, х = 0,5, у = 0,25 булганда;
12xj∕ - 4у
6) Λζ,2^ 4<^һ ’ a = ~2’4’ b = 0,2 бУлганДа;
12fe2 - 6ab
в) 16fft2 ~ 4 —, т = 1,5, п = -4,5 булганда;
' 6т - Зп
. 30⅛Z - 15⅛2 , 1 , 1 ,
Г) 4Ы-8^~’*=5’ l= 6 буЛГаНДа'
o2.36. a) 0 25^ 2 β^25y2 > х + Зу = 8, х - Зу ≠ 0 булганда;
б) ∩ o22 + ∩‰a> a ~ 2b = 5, a + 2b ≠ 0 булганда.
∖J9oU
Вакланмаларны иң кечкенә уртак ваклаучыга китерегез:
2.37
, b 7 , a
а) 2a2' 6ab ҺӘМ 3b2 ’
о. 2Z , 5
б) 3t, һәм —;
s2 st
4 3km k2 , kl .
в) _ .q » ~τ~1 ПЭМ . о ,
, 5∕3 2lm 4m3
г) —5∙, Бтп һәм —5-.
’ m2 ∏2
2.38. a) -½-, һәм -—t-∙, в) һәм ~
s + Z t s а2 За а +
б) (mπl nV ~ ^эм (m + л); г) —^эм (b + α)∙
(т + n) т ' ,' ’ а - Ь 2а
2.39. а) —5-, һәм —; в) —p-, —s- һәм —;
' х + у х - у ху р - q р + q pq
-, l + x + x2x + 2, „ ,У-5_, У2-У +
б) χ-2 , 7^7 Һәм 2х; г) y71, 5у һәм
ч л a <a⅛ 3a⅛ a2 , b2 .
(а - b)(a + b), а + b ЭМ а - b'
б) 2 4-o⅛> Һәм ^±5;
c2 - 25 с + 5 с - 5
с - 1 с2 , , 4
В) _ г»\ > 77 ПЭМ —■«
(с - 2χc + 2) с-2 с + 2
24
Вакланмаларны иң кечкенә уртак ваклаучыга китерегез:
2.41.
а)
х2 + 5
4 - х2’
Л Т 1 η
Һәм
х + 2
х - 1.
х - 2’
б)
Юху
4x2 - у2’
2х
-2х - у
һәм
.
У - 2х’
в)
p2 + 1
р2 - 9’
Зд брд
д - Зр’ 9p2 - д2
һәм
2р
-9 - Зр‘
2.42. а) —4 -, 2a 1 1 һәм -⅛
(α - l)(α2 + a + l) a2 + a + 1 a - 1
б) г Х + У t Һәм -⅛⅛
3(х - у) х2 + ху + у2 х3 - у3
в) b~2 2b һ 2
b2-2b + 4, (b + 2)(t>2 - 2b + 4) Ь + 2’
г) 2 a∖b һ2, һәм —3
a2 - ab + b2 a3 + b3 4(a + Ь)
2.43. а)
4ab
а2 - Ь2’
a2 - ab + b2
a2 - ab
һәм
а2 + ab + b2.
ab + b2 ’
2.44.
б)
с - d
25e2 - d2 ’
d + 5с . 5с - d .
2cd - 10c2 15cd + 3d2'
6х х2 - Зх + 9 । х2 + Зх + 9
—з —— пәм — ;—
х2 - 9 12 - 4х Зх + х2
һәм oξ-4p
2 - 16p2 4p2 - pq 2q2 + Spq
а)
1
(2 - 3)2 ’
4^1 һәм
z2 - 9
1 .
(z + З)2 ’
б)
х2 + 25
25 - х2 ’ (х - 5)2
һәм
(х + 5)2
в)
(t + 2)2 ’ (t - 2)2
Һәм t -t-4;
t2 - 4
Р - 1
р + 3
һәм γ~⅛
3 - р
2
t
У + 1
1 - У
г)
(1 - У)2 ’ (1 + у)2
, y2 + 1
һәм -.
У2 - 1
25
Вакланмаларны иң кечкенә уртак ваклаучыга китерегез:
2.45. а)
2тп
3n2 - Зт2’
т2 , п2 .
m2 - 2mn + n2 ӘМ m2 + 2mn + n2 ’
,, 2mn (т + n)2 (m - п)2
3n2 - 3m2' -m2 + 2mn - п2 ӘМ 2тп + т2 + п2’
ч 5x⅛ х2 h 3⅜2
7 2y2 - 2x2 ’ χ2 + 2ху + у2 х2 - 2xy + у2 ’
ч 6х (х - З)2 , х2 + 6х + 9
7 5x2 - 45’ -х2 - 6х - 9 ПӘМ х2 + 9 - 6x'
п ч c + 6b 2Ь , с ,
' , ас + 2bc - 6аЬ - За2’ a + 2b ҺӘМ с - За’
,, За - b 2а + с , 6α2 .
4α + 2с’ 6α + 2Ь ӘМ 6α2 + 2ab + 3αc + bc,
у - 5z, х + 2у ху - Юуг - 5хг + 2у2’
а - 1 а + с , a - b
a2 - ab + be - ас’ 2b - 2а ҺӘМ За - 3c'
*) ~ 2ts
•2.47. Әгәр ЗдЗ _ a2b _ 4afr2 вакланмасында а һәм Ь үзгәреш-
леләрен тиңдәшле рәвештә ра һәм pb белән алыштырсак,
бирелгәненә бердәй тигез аңлатма килеп чыгуын
исбатлагыз. Исбатланган бердәйлектән файдаланып,
түбәндәге кыйммәтләр өчен бирелгән вакланманың
кыйммәтен табыгыз:
ч 5 , 4
а) а = үүз» Ь = —б) a = 65, Ь = 52.
•2.48. Функциянең графигын төзегез:
= X3 - 4x2 + 2х - 8. _ х8 - 4х2 + 2х - 8
х2 + 2 ’ θ7 У х - 4
26
§ 3. ВАКЛАУЧЫЛАРЫ БЕРТӨРЛЕ БУЛГАН
АЛГЕБРАИК ВАКЛАНМАЛАРНЫ
КУШУ ҺӘМ АЛУ
Алгебраик вакланмаларны кушу яки алуны эшләгез:
3.1. а) | ÷ |;
в) — - -^-∙
, 12 12’
б)^;
’ Р Р
. m , 3
r) — + -.
n n
3.2. a) ⅞→ ⅛S
4х 4х
π1 48p8 _ 23p8.
f 5n 5n ’
б) Ξ≡J∕ _ 2L.
’ 14 14’
∖ c , d - c
Г) 25 25 '
o о x a + b a - 2b.
3.3. a) 9
Ga Ga
. 2a - b , a + b
B) 125 1 125 ’
,x 19 - 10x , 3x - 19
6) x2 + χ2 ;
4 7m + 2n 7m - 3n
Г) n≡ n≡ ∙
44 . 7p-13 2p-3.
3,4∙ a) 10p 10p ’
3x + 7y 3x - 4y.
B) 24y 24j∕ ’
-. 5 - 7a _ b - a.
°’ 2ab 2ab '
. 2x - 3c , 2x + 5c
r) . + .
4cx 4cx
oκ . a2 - 1 2a - 1.
O∙∂∙ a) q О >
α3 α3
. 2 - 353 , 52 - 2
≡> Ы + 5^ ’
fi. x2+2x-3 3-x.
} 2x2 2x2 ’
2 - 3y2 + у _ 2 + y2
r, 3y2 3y2 ,
3.6. a) Ц;
a - 2 a - 2
в) -1- +
в) У + 7 у + 7’
Λ∖ c J. 2 ∙
c + 2 c + 2’
. m 8
r' m - 8 m - 8’
3.7. a) + ⅛5
' 3 + p 3 + p
в) ;
, q - 4 q - 4
61 a ~ 1 - 1 ∙
' a - 2 a - 2’
X 6 + У + 1
г) У + 7 у + Т
27
Алгебраик вакланмаларны кушу яки алуны эшләгез:
3.8. а)
7
Z
в)
t
3
2-7
2-7’
3 - t 3
- t'
б)
t
2
г)
-А- + -
5-2 2
2
t - 2 1
2 - t'
- 5’
3.9. а)
У
5
X
1
У + 5
-у - 5’
в)
1 + х -
х - 1’
б)
2y +
У - 3 .
г)
Зх + 5 ,
2х
у + 3
-у - 3’
-х-5 '
х + 5'
03.10. а)
2т
2п
в)
Зс
3d
т - п
п - т’
с + d -
d - с'
X2
ху .
P9 +
q2
б)
X + у
-у - х’
г)
Р - У ' <7
- P^
o3.ll. а)
с2
81
144
Ь2
2(с + 9)
2(с + 9)’
в)
5(12 - Ь)
5(12 - Ь)'
а2 - 3
6
15 - d2
10
б)
а(а - 3)
а(а - 3)’
г)
d(5 + d)
d(d + 5)'
03.12. а)
У
. 4 .
7 .
t
У2 - 16
у2 - 16’
в)
49 - t2
49 - t2 ’
б)
100
9x2
г)
121
25x2
Зх - 10
Зх - 10’
5х + 11
5х + 11’
03.13. а)
2г
6
в)
3t
21
9 - г2
9 - 22’
49 - t2
49 - t2 ’
б)
х2 + 1
ху - У2
y2 + 1 .
У2 - ху’
г)
Рг
Р2 - РУ
g2 - 2
РУ - Р2 ’
03.14. а)
22
64
t2
100
(2 + 8)2
(2 + 8)2 ’
в)
(t + Ю)2
(t + Ю)2 ’
а2
81x2
49c2
Ь2
б)
(Эх - а
)2 (a - 9x)2 ’
г)
(b - 7c)2
(7c - Ь)2 ‘
28
03.15. Бердәйлекне исбатлагыз:
b2 2b2 + 1 2(2b2 + 1)
b2 + 1 + b2 + 1 b2 + 1
3c2 + 4 2(c2 + 2) c2 + 3 = 1
2c2 +3 2c2 + 3 + 2c2 + 3 1'
Аңлатманы гадиләштерегез:
3.16.
х2 + 12х 36 .
х2 - 36 х2 - 36’
б) х2 - у2 х2 - у2'
х2 + у2 _ 2ху .
в) χ2 _ y2 χ2 _ у2’
λ У3 + 8
г) У2 - 4 у2 - 4'
3.17.
α2 _ 6д - 9.
a - 3 a - 3 ’
б)
c2 + 100 20c
с - 10 + 10 - с’
b2 10⅛ + 25.
b + 5 b + 5 ,
d2 + 49 14d
7 - d + d - 7’
3.18.
n2 + п п + 4 .
n3 - 8 п3 - 8’
х2 + 2 _ 3 .
1 + х3 1 + х3’
zn2 + 9 3zn
m3 +27 т3 + 27’
3j∕2 - 1 у2
8y3 - 1 + 8y3 - Г
3.19.
Аңлатманы гадиләштерегез һәм аның кыйммәтен
табыгыз:
. a2 - 58 6 1 o ,
а) ——— - -—- , a = 12 булганда;
a — о a — о
б) cc _ θc + c lθ4 , с = -3,5 булганда;
, b2 - 108 , 8 , „ _ e,
В) ^ΓΓlδ~ + ГЙО ’ b = 3’5 б 7УлганДа!
r> ~ι + + Γ⅛T ’ x = 4'1 булганда.
-L г X J- + X
29
3.20. Аңлатманы гадиләштерегез һәм аның кыйммәтен табыгыз:
x -x2 + 5x . 41x2 - 2x 1 _
a) + 6χ.1- , х = - булганда;
б) m^T27 + -^T27 ’m = ~3’5 буЛГаНДа;
. 4c2 - 8с 2c + 5c2 2 e,
в) ~3^2 - ^2^3Γ ’ С = 9 бУлганДа;
,n2 + re + l а + 3
г) гез_8 - ’п = ~4 булганда-
Аңлатманы гадиләштерегез:
3.21. а)
9x2
12х
4
9x2 - 4
(Зх - 2)(3x + 2)
9x2 - 4 ’
25a2
Юа
1
б)
25a2 - 1
(5a - l)(5a + 1)
1 - 25a2
100d2 160d 9 - 100t∕ .
3.22. a) 100d2 _ 9 (3 _ 10d)(1θd + з) + ιood2 - 9’
49 56а + 33 49a2
б) 49a2 - 16 (7a - 4)(-7a - 4) 16 - 49a2 ’
х2 — 3 5x-l x + 6
3.23. а) (х _ 2)4 (х _ 2)< (х - 2)4
8zn2 + Зт - 2 5т - 7 4т - 9
θ) 4τn2 + 4zn + 1 -4τn2 - 4аг - 1 (1 + 2m)2'
а2 2ab № .
3∙24∙ a> (a - b)2 b2 - 2ab + a2 (a - b)(b - а)’
У2 . х2 2ху__
f (-х - г/)2 х2 + 2xy + у2 (х + y)(-x - у)'
3.25. а) (Ь _ 4)(5 _ i>) + (4 _ b)(5 _ bγ
б) (3 - a)(2 - a) + (a - 3)(α - 2)‘
30
3.26. Дөрес тигезлек килеп чыгарлык итеп, * тамгасы урынына
аңлатма языгыз:
a) 2 - За + 2 - За ^ 1* В) 2y + 5 + 2y + 5 - 1;
f-. 5х - 4 _ * _ ө. . 4⅛ - 7 * „
х - 2 х - 2 ^ П 8b + 9 8b + 9 ~ d,
3.27. Үзгәрешленең барлык мөмкин табылган кыйммәтләре
x2-3 5x-l,x + 6
ӨЧеН (х - 2)4 “ (х - 2)4 + (х - 2)4 а«латмась1НЬ1й УЧаи
кыйммәтләр алуын исбатлагыз.
3.28. Үзгәрешленең барлык мөмкин табылган кыйммәтләре
2 - у2 7 -бу 4 - у
өчен - ∣-r - ⅛ - ⅛- аңлатмасының тискәре
\У ~ а) \У ~ °) \У ~ о)
кыйммәтләр алуын исбатлагыз.
3.29. Бердәйлекне исбатлагыз:
х3 + y3 3xy2 - y3 Зху2 _ х3
(х - y)2 + (у - х)2 + 2ху - х2 - у2 (х - у)2 ‘
§ 4. ВАКЛАУЧЫЛАРЫ ТӨРЛЕ БУЛГАН
АЛГЕБРАИК ВАКЛАНМАЛАРНЫ
КУШУ ҺӘМ АЛУ
Алгебраик вакланмаларны кушу яки алуны эшләгез:
4.1. a) | + |;
б)|-
_7_.
32’
в)
4
49
6.
7’
г)
13
100
20
4.2. a) ∣ + f;
6.
6’
в)
?♦
л.
4’
г)
с
10
4'
. „ , х 2х
d,. зъ
6т
m.
т
5т
4.3. а) 5 +
’> 28
" 4’
в)
~7~~ ^
^ 11’
г)
42
6 •
. . . х - 1 , х + 1 .c + 5,2c + 9
4.4. а) — + —; в) ~ + —- -
31
Алгебраик вакланмаларны кушу яки алуны эшләгез:
4.5. а)
b - 2 2b + 1.
5 15 ’
в)
51 - s 3s - 1.
14 7 ’
б)
5 - 4g _ 2g + 5.
6 10 ’
г)
Р - 5 . Р - 1
20 12 ‘
4.6. а)
о а
в)
"sj*H
1
co | ⅛
б)
п _ 4m2.
2т Зп ’
г)
2p + <£_
5g 2p'
4.7. а)
Зс - 5 3d - 2.
с d ’
в)
7 - 5r _ 8 - 5s.
r s ’
б)
8а - 15 + 13 - 125.
2а ЗЬ ’
г)
9 - 5z + 5 + 41
5z 41
4.8. а)
х _ 1.
1у у'
в)
l + ±-i
а 5а
б)
а За.
125 45’
г)
5у_2у_.
8х 24х'
4.9. а)
4m - 5 _ zn + 2.
3m2 m2 ’
в)
Зг - 8 г - 1.
5z2 z2 ’
б)
7p + 1 + 2p - 3.
Зр 9р
г)
8-91 _ 1 + 4
22t 111 '
4.10. а)
х - 4 + 2_,
5х Зх’
в)
3 _ 6 + 2а.
5a 13а
б)
п + 4 _ m - 2.
8п 8т ’
г)
р + 4 _ д + 8
12p 12g
o4.ll. а)
Зс + 5d с - 3d.
35cd 2 led ’
в)
4d + 7 _ 2d + 5.
14d2 10d2 ’
б)
9 - 2α _ 2α + 1.
35α2 15a2 ’
г)
2т + Зп т + 6п
21mn 15тп
32
Алгебраик вакланмаларны кушу яки алуны эшләгез:
4.12. a) - + ⅛
a аЬ
. £ _ А.
В У yt'
fλ 2t_ _ Зх.
) ху yt,
Г)
P<7 qs
4.13. a)
ab ас
в)
’ ху уг
,, 2m - п , 5n - 2k
о) ÷ , ;
тп nk
. Зг + 2t t + 3s
Г) 2t St ■
4.14. a) χ2 + y2 - х;
X
B)3z÷ 1 ⅛⅛
б) 2s - <⅛⅛
0
4.15. a) (2α + 1) - 3;
9b2 - 4
в> + (2 - 3b*
ои
6) A + 36 + 4;
г) a - 1 + у-.
4a
4.16. a) -⅛ +
x2 X
, т + 1 Зт - 1
В) т
5 10α - 1
б) а 5a2 ’
г) L±⅛ + 8.
Г) 2y3 у
4.17. а) У-^ ÷ ⅛
’ ху y2
. a - 3b , b + а
в) Γ~ + —5“
ab а2
d + 9 d - 3
б) 3d - d2 ’
, с + 4 с + 4
г) . , .
4с с2
04.18. а) —
тгп. тгг
. У - 1 _ 2 + X.
В) χy2 χ2y ’
б) ?2 + 3t + z - 2∙
3z2t 2z2 ’
ч m3 - 3n2 _ m - 5
’ 3m3n2 5m3 ’
33
o4.19. Аңлатманы гадиләштерегез:
ху ~ У
х
ху - X _ х2 - у2.
у ху
б) 12 +
4р Р2 .
<7 Зд2’
в)
Зтп + 2n2 _ т + 2n + тп - 2п.
тп т п
г)
25⅜2 _ 10⅛ 9
2α2 a
θ4.20. Аңлатманы гадиләштерегез һәм үзгәрешленең бирелгән
кыйммәтләре өчен аның кыйммәтен табыгыз:
. 12x + 5u 5u-4x 1 1 _
a) —-2 —— , х= -х, У = т булганда;
4xzι∕ 5ху* ә
e,. 2п + Зтп 9τn - 2п 2 1 e,
б) = ? "= 2 булгаяда-
Аңлатманы гадиләштерегез:
1 9
04.21. а) —
’ г + 2 3z
4 1 2 .
В) 2t - 1 5t,
f-, 2a + Ь Ь_,
’ ба-b 2а
ч 7n + 2k , п
г) Ч .
9n - 2k 2k
o4.22. a) 4α Ч ;
a - 1
≡)V+33 -2b;
,λ 1 2-За.
’ a - 2
^⅛5÷b + 3,
χ2 + u2
o4.23. a) х + у ;
y χ-y
ч a2 + b2 . .
в) , + а Ъ;
а + Ь
x2 + y2 φ
β)≈-i∕-
a2 +b2
г) , а Ь.
а + b
o4'24∙ >>!÷α(Λl)'
в) 3d - d∙
с(с + 3) с ’
fn b + a + fr2
' 2α α(α-fc),
ч п2 т - п
т(т + п) Зт '
34
Аңлатманы гадиләштерегез:
04.25.
a)
с + 1 с2 - 3 .
в)
x2 ι у + 2х
с + 3 с(с + 3)’
у(у + х) У + X ’
б)
а - 2 а + 2
г)
4 - т т - 2
а2 а(а - 2)’
m(m + 2) т2
04.26.
а)
2 + 2 •
в)
3 3
α(α + b) ' b(a + b)'
χ(χ - у) у(х - у)’
б)
У + с + У - а .
с(с + а) а(с + а)’
г)
У - X У - а
х(х - а) а(х - а)'
04.27.
а)
У х
в)
9t Р
х(х + у) у(х + у)’
p(3t - р) t(3t - р)'
б)
т + 2п п
п(т + п) т(т + п) ’
г)
а 2а - Ъ
b(a - b) a(a - b)'
04.28.
а)
с- + 2 •
b(c - 2b) 2b - с'
в)
6 +-g-;
а(а - 2) 2 - а
б)
c + b •
г)
9n l т
b(c - b) c(b - с)’
m(3n - т) n(m - Зп)'
04.29.
а)
х + У X - у
в)
т п
т - п т + п ’
б)
G ~ 3 CL + 2 β
а + 3 а - 2’
г)
р + 2 р + 6
р + 1 р + 3'
04.30.
а)
с - d с + d
2d(c + d) 2d(c - d),
в)
х + У х-у
4х(х - у) 4х(х + у)’
б)
х + 4у х-у
г)
d - с + 2с - d
3c(2c + d) 3c(c + d)
5у(х + у) 5у(х - 4у)’
04.31.
а)
х2 - 3xy ι у
b - 2пг m2 - 5bm
(х + у)(х - у) х-у’
В)
b + т (b - m)(b + m),
б)
а - Зс + a2 + Зс2
а - с (а - с)(а + с)’
г)
3d d2 - 20d
d + 4 (d-4)(d + 4)'
35
Аңлатманы гадиләштерегез:
04.32.
-6х - 3 2
a)
(2x-3)(2x + 3) 3-2х’
6α + 1 2α
б)
(2α + l)(2α-l) -2а-1’
15х - 15г/ 4
в)
(5х - Зг/)(5х + Зу) 1 -Зу -
5х’
4 -18х Зх
г)
(3x-2)(3x + 2) 2-Зх’
04.33.
а)
4t> ι а - Ь
в)
с + 2 8
(а - 5)(a + 5) ' a(a + 5),
c(c-2) (c-2)(c + 2),
б)
3-х х- 2 .
г)
а + 5 а + 4
(а - 3)(а + 3) а(-а - 3)
(х - l)(x + 1) х(1 - х)’
04.34.
Зс 6
Зт ι 2
а)
(с-2)2 с-2’
в)
(т + 5)2 ' т + 5’
a2 а + b .
х + у l х2
б)
(а - 5)2 2(а - Ь)’
г)
3(х - г/) (х - г/)2 ’
04.35.
а)
a2 + ЗаЬ а
2ab + 2b2 2b,
в)
с _ 4cd + с2 .
3d 3d2 + 3cd,
35 +a ι 52
п m - 2п
9a a2 - 3ab’
Г)
m2 + 2mn tmn
04.36.
а)
а - 12 + а .
2а - 8 а - 4’
в)
У-27 ι 4г/ .
6 - 2г/ 3 - у'
б)
х - 1 х - 2
Г)
с - 2 с - 6
Зх - 12 2х-8’
6с + 4 15с + 10
o4.37.
а)
2 - а 2 - 5 .
в)
d + 3 с - 3
a2 - ab ab - 52 ’
cd + d2 cd + c2 ’
б)
5 + 2а _ а + 25 .
a2 + ab b2 + ab'
Г)
3p + q 3q + р
p2 -pq pq-q2'
04.38.
а)
25 1
1 - 52 1 + 5’
в)
2а 1
а2 - 9 а + 3 ’
б)
36 + с2 с .
с2 - 36 с - 6’
г)
2 5гп - 4
т - 4 т2 - 16’
36
Аңлатманы гадиләштерегез:
04.39. а)
Юх
16-х2
5
в)
12и
п2 - 49
6
х - 4’
7 - п
б)
6x2 -15х
+ 25 , х
г)
2г 1
4-Зг
.522 + 32г + 16
4x2 - 25 5 - 2х’
9г2 - 16
04.40. а)
1-х
у-1 .
3 + с
3 + d
х2 - ху
У2 ~ ху'
в)
2 z7 1
- са
d2 - cd’
р - д
+ 2q ;
Зт + п
⅛n
б)
2p2 + 2pq
p2 - д2
г)
9m2 - 3/7171 9m2 - п2 ’
o4.41. а)
У
х + у .
а + b
а
(х - уУ
У2 - ху'
в)
a2 - ab
(Ъ - а)2 ’
9р + 63
8
Зг + 7
2
б)
(-Р - 9)2
р + 9’
г)
(-2 - 7)2
2 + 7'
Бердәйлекне исбатлагыз:
12х + бу бу - 4х _ (бу + 4хҮ .
θ4,42∙ 20x2p 25xp2 - I Юхр J ’
2п + Зт 9т - 2п _ (Зт - 2п}2
12mn2 18m2n I бтп )
5
2 + Зу у - 3
У-2
У + 2
04.43. а)
Юу
3p3 9p2
бу2
Зр3
abc -
β3 abc - b3
abc - с3
б)
a2b
— + 5 +
Ъгс
с2 а
- 0.
Аңлатманы гадиләштерегез:
АЛА ∖ 3fn + 4 , 3
4.44. а) ——- + -——;
9т - 4 4 - бт
j-. х - 12а 4а
} х2 - 16a2 4ах - х2 ’
3 За + 25 .
2b - 6a + 9β2 - b2 ’
с - 30d 10d
c2 - 100d2 10cd - c2 ‘
4 45 a) 4a _ За2 + 8a + 4. , 8p2 - 9xp + x2 _ 9y ,
а + 2 (а + 2)2 ’ (х - у)2 у - х’
,. 7n2 + тп - 8∕τt2 _ 8т . . 5 + 1⅜ - бр2 2р
m2 - 2mn + n2 п - т’ Г ⅛,2 + бр + 1 Зр + 1
37
Аңлатманы гадиләштерегез:
4.46. a) 2*2 + 1 - т;
х3 - 1 х2 + х + 1
6c2 + 48 _ Зс
с3 + 64 с2 - 4с + 16
бу 1 .
б) у3 +8 у+ 2’
1 9⅜
г) b - 3 b3 - 27’
. , , , ., c3 - d3. . m3 + n3 2 2
4.47. a) c2 - cd + d2 j~, в) τn2 - тп - п2;
’ с + d т - п
_ γ∙3 I 7/3
∕7θ — № - % + У
б) — -—ТГ - а - Ь; г) x2 + xυ + и2 + х~ У-
a2 - ab + b2 х + ху + У
4.48. а)
α2 - ab + b2 a2 + a⅜ + ⅛2.
а - b а + b ’
m2 - 2mn + 4n2 + m2 + 2mn + 4n2.
i т - 2п т + 2п
9x2 - Зху + y2 9x2 + Зху + у2.
в) Зх - у Зх + у
4Z2 + 6Zfe + 9⅛2 4Z2 - 6lk + 9⅛2
Г) 2Z + 3⅛ 2Z - 3⅛
4.49. а) 1 - -Д- - -⅛
a3 + 1 а + 1
fi1 с 1 27 .
с2 + Зс + 9 с - 3 с3 - 27’
_ 2d - 1 2d .
В) 1 4d2 - 2d + 1 2d + Г
1 Ь 12_
г) b + 2 b2 - 2b + 4 b3 + 8'
4.50.
. 3b2 + 2Ь + 4
а) ь3 -Т-
1 - 2Ь 3_.
b2 + b + 1 b - 1’
б)
а - 2
а2 + 2а + 4
6a + 1
а3 - 8 а - 2
38
Аңлатманы гадиләштерегез:
. κι v 2mn , 2m 1
4.51. а) — - + — - ;
m3 + n3 mi - пг т - п
2xy _ 2x 1
X3 - у3 x2 - у2 х + у
4'52' a> (b - 5)2 ~ b2 - 25 + (b + 5)2 ’
1 2 1
(2m - 5n)2 25n2 - 4m2 (5n + 2m)2
Бердәйлекне исбатлагыз:
3a(16 - За) 3(1 + 2а) 2 - 9а _ 1
‘ ' 9α2 - 4 2 - За За + 2 ^ За + 2’
х + 2y х -2y 2y2 _ 2y
4∙54∙ x2 + 2xy + y2 ~ x2 -y2 + (x + y)(x2 - у2) ~ X2 - у2'
455 I 2 4 = ±
’ ’ 2z2 + 5z 25 - Юг 4z2 - 25 5г'
-4 ≈fi 1 . 1 . 2 4 8 16 = 32
' 1-а 1 + а 1 + α2 1 + α4 1 + α8 1 + a,β 1 - а32'
§5. АЛГЕБРАИК ВАКЛАНМАЛАРНЫ
ТАПКЫРЛАУ ҺӘМ БҮЛҮ.
АЛГЕБРАИК ВАКЛАНМАНЫ
ДӘРӘҖӘГӘ КҮТӘРҮ
Алгебраик вакланмаларны тапкырлау һәм бүлүне эшләгез:
5.1. а)
77
17.
б)
12 .
18.
в)
20
2_.
г)
13
•
34 '
33’
25 ‘
35’
9
40’
64
■ 128
5.2. а)
6х
у.
5 .
7_.
lie
5d.
7m
. 3
б)
в)
г)
19
5 ’
4α
9b,
12
’ 13’
6
5t
5.3. а)
5х
6
: х;
б)
25
12у
■ у;
в)
19t
20
: t;
г)
z :
5z
27’
39
Аңлатманы гадиләштерегез:
5.4. a) :
За,
Ь ’
в)
1 2х
) 1 3 /
б)
_4₽
, _ч_.
2p'
г)
5с . (
2d ‘ 1
15сЛ
d /
5.5.
а)
д2 .
6 ■
⅜ б)
О
24
Ь2
' 36’
в)
п24 . п39.
28 ‘ 56 ’
. zn5 100
г) 10
5.6.
а)
12x5
55
. 6x2 .
■ 5 ’
в)
16 .
5d3
12.
d4 ’
б)
4
Зу3
18’
г)
36с12
49
7
’ 6с15 ’
5.7.
а)
⅛2
χy
χy.
a2b'
в)
a3b
с
с2 .
a4b2 ’
б)
т3 .
cd
m2n,
cd ’
г)
p2q2
Z
. pV
‘ г2 ’
5.8.
а)
3m1ι
г . m2n,
в)
а9 .
а11 .
с
' Зс ’
8b3
1051° ’
б)
X3
6у'°
Зу9.
' х11 ’
г)
5c2x
а
15а
' c3x^
5.9.
а) бтх
ab .
в)
4ab2
• Qc2m2∙,
2mx2 ’
Зст3
б)
15<∕3
. 25y2.
' 4х ’
г) 9ху :
3x2y
ab
5.10. a)
4x3y2
Р
: 6х4у5;
в) : 36х3у4;
а
б)
т
17α2d2
• 34а2</8;
r^8^5∙ 6p2n≡∙
5.11. a)
х-У
4 .
ч 2m - 3n 7s
в) = т: —;
4а
х - у
7 2т - Зп
a + Ь .
а + Ь,
15p +12y . 15p +12g
°)
8
8х ’
13р ' 13
40
Аңлатманы гадиләштерегез:
5.12. a)
За + 46 . 4Ь + За.
в)
г)
44 с3
52с
8x2
7с + 9t
13p3
16x2 ’
1 39р12
9d + 7с’
15τn + •
12ab
19Z + 8
in 4п + 15т’
8 + 19⅜
15∂2
б)
5.13.
а)
16u - 13ι> . 13ι> - 16а.
в)
98p - 1
.7q . 17g - 98р .
21
Р
4
16т
б)
45т -
п с
г)
64г - 15s 18с
23с
п - 45т ’
9c2
15s - 64r'
5.14.
а)
с + d
с - d .
в)
т(т -
n) p2(p + q).
c(c + d),
с - d
p(p + q) т - п
б)
а - Ъ
3(α - 6)
г)
а + Ь
а + b
с + d
α(c + d)’
2b(a - ।
b) ’ 2b2(a-b)'
5.15.
а)
х + У
(х - у);
в) (а + Ь)
2a + b.
х - У
а + b
б)
Зх + у
х - у
: (2х + уУ;
г) (а - b)2
а - b
а - 2Ь
5.16.
а
а3
т3 - т
2 У2
а)
В)
х2 - 3j
с Зх - 9
У
τni - т
б)
а + а2
п2
г)
Юс2
5
п
3 + За ’
b2 -b3
’ b - b2 ’
5.17.
а)
гх + г2
. x + r.
в)
ху
Р+ Р2.
X2
X
Р2 + р3
x2y2
б)
тх + ту a2b
г)
6а
Зап
ab2
4x + 4y,
п2 - п
’ 2п - 2’
o5.18.
а)
⅛> - Р
г_ . 8p - 2p2 .
в)
с3 - с2
1 + d2.
у - х
х - У
d3 + d
с - с2
б)
а - b
3q-q2
6q - 2q2 .
b - а ’
г)
X + X3
п - п2
. х2 + 1
' п3 - п2 '
41
Аңлатманы гадиләштерегез:
- 1Q a x2 - У2 *У . , с2 - 49 . 2с + 14.
o5.19. а) —- ; в) . ———,
Зху х - у 10cd 5d
5α2 . 5а . , Ь - d 3bd
° а2 - 16 ' a + 4’ Г) d ' b2 -d2'
o5.20. a) • (х3 + y3)∙,
х + у
б) (a3 + b3) : (a2 - ab + b2)∙,
в) —--—- ∙ (n2 + пт + тп2);
n3 - m3
г) (p3 - <73) : (Р - q)-
θ5∙21∙ a> в> fn •
б) (8a3 + 1) : — ~ 2a +-L г) ■»' . (m≈ + 4m + 16).
п 3
05.22.
а)
х2 - Юх + 25
Зх + 12
2х - 10.
х2 - 16’
1 - а д2 + 4a⅛ + 4⅛2 .
’ 4a + 8Ь ' 3 - За
с2 - 25 Зс + 18.
В) с2 + 12с + 36 ’ 2с + 10’
г)
5m - 10n . 4n2 - 4mn + т2
т - 5 15 Зт
Алгебраик вакланманы дәрәҗәгә күтәрүне эшләгез:
42
5.27. Үзгәрешлеләрнең бердәйлекне дөрес итә торган мөмкин
табылган кыйммәтләрен табыгыз:
Аңлатманы гадиләштерегез:
05.28.
а)
-■1
й |Н
w I to
∖2
,
в)
/ от \5 /
1 a 1 1
1 C4 7
с7
a5∂2
у
[ Р \
3 (
2 ∖2
P2 I.
fx6P8Y .
x10i
μl3
б)
lx3 J
.x3 J
г)
1 zs J '
г1
i
05.29.
а)
[ 18fl∩
1 1163 J
С 22b4∖
’ 1 9a2 /
в)
35ax2
12b2ι∕
8ab .
21xι∕ ’
б)
17x2ι
5а
У : (
' 34xy2∖
< 25a2 /
г)
< 27c3 Λ
k 4t>2 J
=(-
45c5 '⅝
326 /
05.30.
а)
[ 2р<
1 Зта2'
I2 9zn2a2.
) 4p3q7 ’
в)
( 2x3yi
I 5a2b
)3 [
25a463 λ
24xV3 )
б)
50α4⅛,
63m9n8
. f 5a2⅛3 Ү.
’ (зтп2п5 J
г) 1
, Wp2q2
< За3
■г
( 25p3q3
1 27a6 .
05.31.
а)
9a
5y3 За2.
, 3b by ’
в)
28a2 . 21x4
27x3 ' 45</
х8 .
20 уа'
б)
25a3⅜3 .
14x2ι∕4
21xy3 8xy2 -
10a2b2 15ab,
г) ■
45τn4 56n3
49n2Z 27aι2
. 20m2n
63i2 ’
05.32.
а) |
' x2
^2a3
чЗ
f 4a4 Ү.
в)
, 2a2Y
k b3 J
( ь2 У.
l-2a3) ’
8-2a863J
J )
∣5 ( 4awb4 У
9x7ι∕β
4
Я λ3
а8 ]
б) I
∣'l с9 ) ’
г) 1
. а12 ;
27x5j∕4 J
43
Аңлатманы гадиләштерегез:
5.33.
a)
б)
α2 - 1 9a - 96.
а - b а2 + а
в)
г)
(х + 4)2
Зх - 9
b2 + 46с .
6 + 6 ’
х2 - 9 .
Зх + 12’
62 - 16с2
26 + 12
(У - 5)2 .
Зу + 18 ’
2г/-10.
У2 -36’
5.34.
а)
х2 - 16 .
х + 4.
в)
m2 - п2
Зги2 .
8x2
4х
9т
т - п
(У - 5)2
1у2
(с + 2)2
с2 - 4
б)
У
У2 - 25’
г)
2c2
4с
5.35.
x2y
15г/ + 6.
m2n
5тп
а)
25г/2 - 4
Зхг/2 ’
в)
64n2 - 9
Sn + 3
7 - 2х
4x2 - 49
24c2d
5 - Зр
б)
22a2b2
Had3 ’
г)
9p2 - 25
12cd3 '
5.36.
а)
г2 - 25 .
z2 - Зг
г + 5 .
9 - г2 ’
в)
6d - 6с
с + р
с2 + ср.
с2 - d2 ’
5p2 - 5q2
P2 - 2pg .
3x2 - Зу2
. (р - X)2
б)
5p - 10g
(9 - Р)2 ’
г)
ху + Зу2
9г/ + Зх
5.37.
x2 - 6х + 9 х2 - 9
25-г/2
Юг/2
а)
9x3
9х ’
в)
25г/
у2 - Юг/ + 25’
б)
4c2 + 4с + 1 2d - 2с.
г)
3 - 6a
2a2 - а
c2d - cd2 4c2 - 1 ’
1 - 6a + 9a2 1 - 9a2
5.38.
а)
a3 + b3
а - b'
в)
2x2 + 4x
. х + 2.
a2b - ab2
а + b’
x3 - 8
’ х - 2’
х2 + 3x +
(x3 + у3)
X + У
б)
х + 3
Г)
х2 - ху + у2
5.39.
а)
х2 - 1 . х2 - 2x + 1.
в)
z2 + 6г +
9 . Зг + 9
х3 + 1 ’
х2 - х + 1 ’
г3 + 27
' z2 - Зг + 9’
t3 + 8
4t + 9
У3 -8
У + з
б)
12i2 + 27f t2 - 2t + 4’
Г)
У2 -9 у
2 + 2г/ + 4'
44
Аңлатманы гадиләштерегез:
e .r, 4 a2 - 6а + 9
5∙40∙a> l f
2а - 6.
ь2 -1;
. 52 - 65 + 9 27 + 853.
В 452 - 65 + 9 ' 6 - 2Ь ’
c3 - 8rf3 4d2 - с2 .
6) 2c + 4d ‘ (2d - с)2'
(rn - I)2 . 1 - m2
r) 4 + 4m3 ' (2m + 2)2 ’
a) 1~lθfl2 ∙ 4a - 1
а) 4a2 + Юа + 25 ’ 8a3 - 125’
64a3 - 2753 952 - 16a2
б) (4а - 35)2 ' 16a2 + 12a5 + 952 ’
в) 4 ~ 9c2 • 2 - Зс .
В 9c2 - 12с + 16 ' 27c3 + 64’
125p3 + 8<73 . 25p2 - 10p¾r + 4</2
г) (5p + 2q)2 ’ 4q2 - 25p2 ‘
a) x ~ 3 х2 - 4 х2 + Зх + 9.
2х + 4 х3 - 27 х2 - 2х
б) fl2 ~ 16 ab ~ ∙ a ~ 4.
2а - а2 а2 + 8а + 16 45 ’
. Ь2 - 105 + 25 . 52 - 25 5 + 5.
В' 55 - 10 ’ 25 - 52 ' 55 ’
, a3 + 8 . a2 + 4a + 4 . а2 - 2а + 4
За - 6 a2 - 2a а2 - 4
f54(5 - е)2 У . (52(5 - с)?
5∙43∙ аЦа'(с - a) J : U3(a-c)J ’’
( a2 + ab V 7 5 - a "⅛3.
I ab2 - 53 J la2 + 2a5 + 52 J ’
в)
( а2 (а - 5)
∣4x4 (a - х)3
п
х6 (х - а)5
а3 (5 - а)2
г)
х2 - 4xι∕ + 4ι∕2 j2 ( х + у ү
х2 + ху J t 2ху - х2 )
45
5.44. Бердәйлекне исбатлагыз:
. a4 - 64a⅛3 a2 - b2 . a3 + 4a2⅛ + 16a⅛2 _ a + Ь.
a a2 - 2aft + b2 a2b - 16b3 ab + 452 a - b'
х3г + 125z . х3 - 25х х + 4г . х - 4г _ г_
6' х2 - 16z2 ' х2 - 8хг + 16z2 х2 - 5х + 25 ’ х - 5 ^ х
5.45. Аңлатманың кыйммәтен табыгыз:
a) -γξ- : л 122χ3 г ∙ a 22χ2⅞- ’ x = 2,7845, у = -13,8471
2х - у 4x2 - j∕2 6x2 + Зху
булганда;
б) a2 + a а2 + а За* + 6a3 + 3a^ a _ 1 234 567 890
’ 2a -8 2a + 8 а2 - 16
булганда.
5.46. Үзгәретилеләрнең барлык мөмкин табылган кыйммәтләре
өчен аңлатманың бер кыйммәт алуын исбатлагыз:
Γ2x2t∕3 Ү . I x6ys 8x - 8y Ү
а) х + у J ’ ∣4x2 - у2 х2 + 2ху + У2 λ
f a - 3 √ . f 9 - a2 . a2b + 3a∩
б) I 3a26 J ' I 18a3b ' 2а - 6 Л
§6. РАЦИОНАЛЬ АҢЛАТМАЛАРНЫ
РӘВЕШҮЗГӘРТҮ
Аңлатманы гадиләштерегез:
46
o6.3. a) (V ~ πM∑ + 1)5
6) ∣3 + j⅜o uυa ;
∖ υ) 2u + 6υ
o6.4. а) (2 + -Ц-1 : ¾ + 3*;
I t + 1J 12t + 8
( 5р А р - 3
б) I/" 7T2 J: ?72;
в)
z-3
г + 3
z2 Y
3 - г)’
06.5. a) [ — — λ∣ • * y ;
\Х - У х + у) x + lly
г) μ--2Λik⅛
ГЧ? - 5 4) q - 5
в)
V ху х) X - у
. cd - d2 f с d
c2 + d2 1с + d с - d)'
06.6. a) +
11 + с J 1 - с2
в)
3d + 1
2d + 2
6d - 6.
d + 1 ’
⅛ + 3
b3 + 9Ъ
Ь + 3
Ь-3
b - 3\
b + 3/
х2 — 9
Г) 2x2 + 1
6x + 1
х - 3
6x - 1 '⅜
х + 3 /
06.7. a) f - + 1.-тп ;
∖n2 - тп т2 - тп) п + т
г2 - 25 1
г + 3 ' г2 + 5г
г + 5 .
г2 - Зг’
∖ ( st 4. t s + t.
В) ls2 - t2 2t - 2s) ' 2t ’
За + b b - а . a2 - b2
a2b - ab2 ab За - b ’
о6.8. Аңлатманың кыйммәтен табыгыз:
а)
2m + 1
2m - 1
2m - 1A
2m + 1)
4m
Ют - 5
т = — булганда;
б) —] ∙ ~~+ %ab + α , a = 23 һәм b = 33 булганда.
∖b - a b + aj 2a2
47
Бердәйлекне исбатлагыз:
, + _L_
06.9. a) *∑J' =
1 _ 1 У
х + у X - у
2 _ х - 2
б) х х2 - х = 1
3 । * + 3 4
X х2 - X
1 1
X- У х + У _ У.
1 + 1 х’
X + У X - У
1 _ 4^_х_
х - 1 х2 - х _ 2
2 _ х + 2
х - 1 х2 - х
06.10. a) f+ £±5] . <+ 5« + °2 +5
∖,5α -1 a + 1J 1 - 5a a + 1
= a - 1;
⅛ - 3
7b - 4
⅛ - ЗЛ
b-4j
7⅛ - 4 b2 - 14
9b - 3b2 4 - b
Аңлатманы гадиләштерегез:
6.11. а) —т - ~2—а т : ^¾
’ \а + Ь a2 + 2ab + b2 ) ∖a + b
а2 \
a2 - b2 )’
z - 2 . ( 2 z2 + 4 2_ '∣
б) 4z2 + 16z + 16 ' V2z - 4 2z2-8 z2 + 2zΛ
,. ,.1 Л 10m2 -A ι 30m2 - 15m , 8 - 2m
6.12. а) а о & ∙ —о—я *^ 7’
’ \3 + 2m ) 8m3 + 27 2m - 1
fq 9n2 '∣ 27n3 + 1 9л - 3
6, I 3n + lJ'βn-9n2 3n-2'
9л + 27 ГЗл + 9? . Г 1 2 1 \
a Зл2 - л3 \ л — 3 J 13л - 9 9 - л2 л2 + Зл/
fi, ( 2 , 6? 4 . L 4p2 + q2
’ ∖2p - q q2 - 4p2 2p + qJ ' [ 4p2 - q2 )'
⅛ - 4 . I 80k 2k k - 16Λ _ 6⅛ + 4 .
•6.14. a) k _ 2 ∙ ∣^fe3 _ 8 + k2 + 2k + 4 2- k ) (4 - ⅛)2 ’
б)
m - л 2m m + л
(т + л)2 т2 - л2 (т - л)2
8тл2 2 л2
т4 - л4 л2 - т2
48
Бердәйлекне исбатлагыз:
6.15.
6.16.
6.17.
6.18.
8y2 +2j∕ _ 2у + 1 А _ Г + 2у + 1
8<∕3 -1 4j∕2 +2y + l) 2у
y2 + 9 + У
27 - Зу2 Зу + 9
з A
y2 - 3yJ
z z2 z2 + 2z^ι
2 - 2 ~ z3 + 8 г - 2 )
⅜ l 1
2у + Зх 2у - Зх
4y2 +lgj4
-"^r+2y '
(3y+^]j
■ 3y2 ' /
z2 - 2z + 4
4
4y2 - 9x2
1 = 2ι∕ - 1
2<∕ 2i∕ + l'
У
= gy'+M
z2 +
2z + 4 * * * *
г - 2
4
бу9 **,
8y3 + 27x3
= Зх + 2у.
Аңлатманың кыйммәтен табыгыз:
2-0 ( I УЛ -⅛A- ■ -4⅛τ2°11
•6.19. 5 + (j-2<J 41o,-lo≈+α 1 - So, 2« +«
a = -3,2746 булганда.
f⅛2 - 2⅛ + 4 2b2 + b _ ⅛ + 2 A . 4 Λi-⅛-,
•6.20. 4fc2 _ 1 b3 + 8 2b2 - b I ‘ b2 + 2fc 3 - 6Ь ’
7
Ъ - — булганда.
Z IӘ
•6.21.
1
2x + 1
з l 3 "I (2 4*^-l
8x3 + 1 4x2 - 2x + 1J Ч 2x + l>,
х = -2,123 булганда.
6.22. Алыштырып куегыз һәм аңлатманы гадиләштерегез:
ах + Ьх
a + х х - b
ab -
булганда.
a - b
•6.23. х > 2 булган теләсә нинди кыйммәтләр өчен
( x + 1 + 4 _ 2l ∙ x + 4 _ χ2 ~ 5х + 3
I 2х х + 3 ) х + 3 2х
аңлатмасының кыйммәте тискәре сан икәнен исбатлагыз.
•6.24. а үзгәрешлесенең мөмкин табылган теләсә нинди кыйм¬
мәтләре өчен
12a - 4α2 + 1 . ( 4 6a - 9 "⅛
2a + 3 2a - 3 ’ ∖ 4a2 - 9 8a3 + 27 J
аңлатмасының бер үк кыйммәт алуын исбатлагыз.
49
§7. РАЦИОНАЛЬ ТИГЕЗЛӘМӘЛӘР ТУРЫНДА
БЕРЕНЧЕ ТӨШЕНЧӘЛӘР
Үзгәрешленен, нинди кыйммәте өчен алгебраик вакланма
нульгә тигез:
7.1.
а)
б)
х + 1 .
х2 + 1’
. Зх + 12.
≡) 4 ’
г)
2х ?
х2 + 2
7.2.
а)
Зх + 1.
х + 3 ’
в)
6х - 18.
х-2 ’
б)
(x + 3)(x-l).
Зх
г)
(х + 4)(х - 5)?
X
7.3.
а)
х2 + Зх.
2 ’ б)
х*
4x2 -
6х +
_1.
3 ’
. х2 - 4х.
В) ’
г)
4 - 9x2 ?
6х - 4
7.4.
x - 4 . fix
х2 + 1.
-х X2
г)
х2 + 2?
2х
а)
x2 - 4х’
X
>
в) х2 + 2х’
7.5.
Тигезләмәне чишегез:
. 2x + 5 n.
а) ■ 2 = 0;
в)
3x~± = 0;
4
б)
х(х - 2) _
х2 + 4
г)
х(х + 1) _ 0
х2 +1
7.6.
а)
=°:
4х
в)
5x + 2 = 0.
5х
б)
(2x + 3)(х - 5)
Зх + 2
= 0;
г)
(2x - 1)(х + 3)
2x + 1
= 0.
7.7.
а)
m2 + 5zn _ θ.
5 ’
в)
n2 - 9n _ θ.
9
б)
р2 + 4р
2 - р = °;
г)
q2 - 16ςr
? + 4 =0∙
7.8.
а)
х2 - 100 = 0.
х2 + 100
в)
=0;
г2 + 36
б)
1T÷5 =0;
4xz
г)
9xL≤ =0.
Зх
50
Тигезләмәне чишегез:
o7.9.
a)
х2 - 4х
4х
= 0;
в)
х2 + 5х
5х
= 0;
б)
х2 + Зх
5х + 15
= 0;
г)
х2 - 7х
Зх - 21
= 0.
o7.10.
а)
х2 - 25
Зх + 15
= 0;
в)
х2 - 49
4х - 28
= 0;
б)
х2 - 36
х2 + 6х
= 0;
г)
х2 - 64
8х - х2
= 0.
07.11.
а)
ti - 81
t2 + 9
= 0;
в)
У4 -16
У2 + 4
= 0;
б)
a3 - 4α
а + 2
= 0;
г)
9d - d3
d - 3
= 0.
7.12.
а)
2x + 1
5
= 1;
в)
Зг - 14
2
= -1;
б)
Ю-Зу
4у
= -2;
г)
2Л + 9
5t
= 4.
7.13.
а)
а
4.
в)
Зе
7.
а - 3
5’
с - 1
3’
б)
6 - а _
2υ - 1 ^
4.
3’
г)
s + 2 _
3s - 5 ~
5
4'
7.14.
а)
За + 75
5
_ 6а + 42.
5 ’
в)
8г + 3 _
7
. Юг
7
б)
х2 + 2х
х2 + 1
_ 2x + 1.
х2 + 1’
г)
х2 - Зх
х2 + 2
= 4 -
X2
Зх
+ 2
7.15.
а)
X2
X
в)
X2
2х
х + 3
х + 3’
3- х ~
3-х
б)
5y2 -1
У
= у2 +3.
У
г)
3t2 + 5 .
t
_ 9 + 2t2
t
51
Тигезләмәне чишегез:
07.16. а)
х2 - 2 _ 2
в)
х2 + 1 2
х + 2 х + 2’
х - 1 х - 1’
б)
X2 -х
г)
2х х2
х + 1 х + 1’
2 - х 2 - х
07.17. а)
х2 - 1 = Зх - 1.
х - 3 х - 3 ’
в)
х2 + 3 = 2х + 3.
X X
б)
х2 - 15 _ 10 .
г)
16 + 3x2 4x2
х + 5 х + 5’
х - 4 х - 4
07.18. а)
х2 - 8х _ 4х - 36.
х - 6 х - 6 ’
в)
х2 + 16х _ 6х - 25
х + 5 х + 5
б)
4х - 1 _ х + 5.
х - 2 ^ х - 2’
г)
7х + 4 _ Зх - 8
х + 3 х + 3
07.19. а)
a _ α - 3 1.
4 5 ^ 1,
в)
с Зс - 1 _
7 14
б)
Р Р + 12 1.
г)
2 - q q 1
5 15 3’
5 20 4'
07.20. а)
4 _ х + 8 _ 5.
х 2х 6’
в)
х - 20 5 = 2.
4х х 3’
б)
J- + -*- = l5
2х х +1 2
г)
х 2 1
х- 2 Зх 3
07.21. а)
—Ц + -~ = 1;
х + 2 х - 2
в)
1 + x - 1-
х - 3 х + 3
б)
2x3 _ р.
г)
Зх 5 $
х - 1 х + 1
х - 2 х + 2
Мәсьәләне математик модельләштерүнең өч этабын
аерып күрсәтеп чишегез:
07.22. А һәм В шәһәрләре арасы 50 км. А шәһәреннән В га
велосипедчы, ә 2 сәг 30 мин тан соң мотоциклчы юлга
чыга. Велосипедчыга караганда 2,5 тапкыр зуррак тиз¬
лек белән барып, мотоциклчы В га велосипедчы белән
бергә килеп җитә. Велосипедчының һәм мотоциклчының
тизлекләрен табыгыз.
52
07.23. А пунктыннан автобус, ә 15 минуттан соң шул ук юнә¬
лештә, тизлеге беренче автобус тизлегеннән 1,2 тапкыр
3УРРак булган икенче автобус чыга һәм беренчесен А
дан 45 км ераклыкта куып җитә. Беренче автобусның
тизлеген табыгыз.
07.24. Катер агым уңаена 12 км һәм агымга каршы 4 км юл
үтеп, барлык юлга 2 сәг вакыт сарыф итә. Әгәр агым
тизлеге 4 км/сәг булса, катерның үз тизлеген табыгыз.
07.25. Көймә агым уңаена 18 км һәм агымга каршы 6 км юл
үтеп, барлык юлга 4 сәг вакыт сарыф итә. Әгәр агым
тизлеге 3 км/сәг булса, көймәнең үз тизлеген табыгыз.
07.26. А һәм В шәһәрләре арасы 400 км. А дан В га йөк маши¬
насы, ә 2 сәгатьтән соң тизлеге аныкыннан 1,5 тапкыр
зуррак булган җиңел машина юлга чыгалар. Әгәр йөк
машинасы В га җиңел машинадан 1 сәг 20 мин соңга
калып килеп җитсә, аның тизлеген табыгыз.
07.27. А һәм В пунктлары арасы 100 км. А дан В га автобус, ә
8 минуттан соң тизлеге автобус тизлегеннән 1,2 тапкыр
зуррак булган мотоциклчы юлга чыгалар. В пунктына ав¬
тобус мотоциклдан 12 минутка соңга калып килеп җитә.
Мотоциклчының тизлеген табыгыз.
Тигезләмәне чишегез:
7.28.
а)
2x2 -1 = χ.
X
в)
3≡L^=2x5
X
б)
⅛L+2 =3х;
х + 1
г)
½⅛=5x.
х - 2
7.29.
а)
3x2 +_1 _ χ +
2х
в)
=х-2;
6х
б)
2x2 - 5 _ χ _ р
х + 1
г)
⅛L≤3 = χ + 2.
х - 2
7.30.
а)
х3 - 25x _ Q.
5х + 25
в)
36 х - X3 _ Q.
6х - 36
б)
У4 -256 =о
2уг +
г)
625 - yi _
3y2-15y
53
Тигезләмәне чишегез
7.31. a)
б)
х2 + 4х
х + 2
с - 2 =
с + 3
- 2χ.
3 ’
с + 3.
с - 2’
в)
г)
х2 - 5х
х-1
х - 2 _
х + 2
_ 7х.
9 ’
х + 3
х - 4'
7.32. а)
Зх
х + 3
3;
в)
х + 3
И н
1 1
со сэ
II
ГС
х-1 ’
х + 1
б)
а - 1
4а - 5
- { 2a ~
Ua -
1Y.
δj ’
г)
гь-if
lb + 3J
= fe + 1
b + 3’
7.33. а)
3
25
х +
1
х - 4
х2 - 16
х + 4
>
19
х + 1) +
X
3
б)
(х - 5)(.
х + 1
х -
5’
в)
1
26
X +
4
х - 5
х2 - 25
X +
5
9
г)
14
6
X
(х - 3)(х + 2) '
х + 2
х -
3‘
7.34. a)
x2 + Зх х + 12
2(x-3) 6
Зх .
х - 3’
X2 - X X
В) 3(х + 2) х + 2
х + 6.
12 ’
61 - - 6 = 1 + 2x∙
х х(х + 2) х + 2 ’
.1 5 х - 7
г) = .
х х(5 - х) 5 - х
6
х + 3
7.35. а)
8 .
х2 - 4’
в)
18 .
х2 - 9’
б)
Зх + 27 + 3
Зх - х2 х
4х
3 - х
= 0;
г)
5x + J? _ 16 + 2х
х - 2 х х2 - 2х
4
х + 2
X
х - 3
7∙36∙ ∙> ⅛τs+⅛⅛ *
У + 2 4 _ 1 .
°⅛2-7j∕ (7 - у)2 у-7’
. d + 5 d - 4 _ _9_.
В) 5d - 20 4d + 20 ~ 20’
. 2а - 2 _ a - 2 a - 1
a2 - 36 a2 - 6a a2 + 6a
54
•7.37. Тигезләмәне чишегез:
a) c + 2 - c ~5 = c + 25 .
c2 - 5c 2c2 - 50 2c2 - 50’
8y-l _ 1 = у
°, бу - 3 1 - 4у2 2у + 1;
4(d + 9) + d + 3 _ d - 3 .
, 5d2 - 45 5d2 - 15d d2 + 3d’
. 1 2х - 5 1
Г) 4х - 6 18 - 8x2 2x2 + Зх “°’
7 qc 4 , 12d - 7 , d - 3
• .do. a) а ның пәм вакланмаларының аермасын
1 гә тигез итә торган кыйммәтләре бармы?
, 186 + 2 , 156 + 1
о) 6 ның b _ 4 һәм вакланмаларының аермасын
3 кә тигез итә торган кыйммәтләре бармы?
•7.39. а) 6 = -0,5 һәм а ниндидер кыйммәт алганда,
a 1 - 36 алгебраик аңлатмасы 3⅛ кыйммәтен ала.
5
а ның кыйммәте шул ук һәм 6 = — булганда, әлеге
аңлатманың кыйммәте нинди булыр?
1 с - 2
б) х = -- һәм с ниндидер кыйммәт алганда, —— • х -
о 3
- 4х алгебраик аңлатмасы 1 кыйммәтен ала. с ның
кыйммәте шул ук һәм х = -11 - булганда, әлеге
3
аңлатманың кыйммәте нинди булыр?
•7.40. а) у = -3 һәм п ниндидер кыйммәт алганда, n * * • у +
О
+ 1 ,y2 + y3 алгебраик аңлатмасы -21 кыйммәтен
5 1
ала. п ның кыйммәте шул ук һәм у = - булганда,
О
әлеге аңлатманың кыйммәте нинди булыр?
s - 9
б) z = -2 һәм з ниндидер кыйммәт алганда, 4 - ∙z +
+ 8 * 2 ∙ z2-z3 алгебраик аңлатмасы 16 кыйммәтен
ала. s ның кыйммәте шул ук һәм z - 0,5 булганда,
әлеге аңлатманың кыйммәте нинди булыр?
55
§8. ТИСКӘРЕ БӨТЕН
КҮРСӘТКЕЧЛЕ ДӘРӘҖӘ
Түбәндәге аңлатманы уңай күрсәткечле дәрәҗә рәвешендә
языгыз:
8.1. a) З-8; б) 13'2; в) 5’2; г) 27 4.
8.2. а) а 5; б) -⅛ в) d 3; г) -⅛-.
с t
8.3. a) (α →)- 6)(7-⅛f= в) (1 - а)’3; г)
8.4. Исәпләгез:
a) 4 ∙ ⅛j б) 6 • З-8; в) 2 ∙ ⅛ г) 3 ∙ 9 2.
2 i 5 1
Тискәре күрсәткечле дәрәҗәнең билгеләмәсен кулланып,
8.5.
вакланманы дәрәҗәләр тапкырчыгышы рәвешендә
күрсәтегез:
а)
«> ⅛
а
х n .
в) —;
т
Рг
r, F∙
8.6.
а)
(t - а)2
(⅛ + ιr .
6) </,-<>-
в) <!∑⅛
с + d
(п - тг
(т + n)^3
8.7.
2, 4, 8, 16, 32, 64, 128, ∣, -, 1, ⅛
2 4 8 32
санның дәрәҗәсе рәвешендә күрсәтегез:
1
— саннарын
1 Zo
а) 2;
б)
1
2’
8.8. 3, 9, 27, 81, 243, ∙^-, саннарын санның
3 У 27 81 243
дәрәҗәсе рәвешендә күрсәтегез:
а) 3; б)
О
8.9. Бирелгән санны ниндидер гади санның дәрәҗәсе рәвешен¬
дә күрсәтегез:
„х 1 . 1 . х 1 . χ 1
> 729’ б) 343’ В) 625’ Г) 1024'
8.10. 10 санының дәрәҗәсе рәвешендә күрсәтегез:
а) 0,1;
б) 0,0001;
в) 0,01;
г) 0,00001.
56
8.11. Саннарны кими бару тәртибендә языгыз:
M∣r∙ йШйП
б) 31, З3, 3°, З 2;
в) 5^2, 52, 5’1, 5°;
о ЙГ- ЙГ- ЙГ- ЙГ-
Аңлатманың кыйммәтен табыгыз:
08.12. а) (64 • 4~5)2; б) в) (128 ■ 2 е)2; г) -⅛r
o8.13. a) (-∣j ∙ 10 1 + (4)0 - (-2)3 - (-5) 2 ∙ (-5)3;
б) -(∣) ∙ (2)^1 - (£) - (-0,5)-2 + (2,5)^1 ∙ (2,5)2;
в) (I) ∙ (4)^1 - (-∣ j + (-0,6) ≡ ∙ (-0,6)4 - (4е)0;
г) (-0,5)^8 ∙ (2)"l - (-2,7)0 - (-2)3 ∙ 1,2 - (I) ∙
Гамәлләрне эшләгез һәм, кирәк табылганда, дәрәҗәләрнең
тискәре күрсәткечләре булмаган рәвешләргә китерегез:
8.14. a) а2 ■ а~3; б) b4 ∙ b 5; в) d ∙ d~2∙, г) m"5 ∙ τn^1.
8.15. a) ft6: А-1; б) l2: Г1; в) х3 : х"4; г) у : y^3.
8.16. а) 2а2: (|а); в) |/n7: (⅛A
б) l,2x^2: (4х 5); г) 8r5: (∣r^τ )•
o8.17. a) 2m-2n3∙.
б) 0,5α⅛^2 • (4а’3Ь3);
в) ⅛r2sβ∙ (l∣*-*s-2)
г) 16p^⅛3 : [ур-3?2
57
Гамәлләрне эшләгез һәм, кирәк табылганда, дәрәҗәләрнең
тискәре күрсәткечләре булмаган рәвешләргә китерегез:
8.18. a) (α2 - 1) • а1;
б) (Z3 - Z2) ∙ l~2∙,
в) (b - b3) ■ b 2∙,
г) (τn5 - mi) ■ т~5.
8.19. a) ab~1 + a~1b∙,
б) c~ld2 - c2d1∙,
в) p2q2 (p-2 - q~2)∙,
г) mn~2 - m 2n.
o8.20. a) (b1 + a~1) ■ (а + Ь)’1;
в) (m~2 + zι^2) : (пг2 + п2);
б) (x"2 - у-2) : (х - у);
/ -1 Λ~2
г) (ab~2 + a~2b) ∙ •
( 1 1V
o8.21. a) (b1 + α1) ■ ~ + ^rJ ;
6) ((»- +<'): (⅛ - ⅛)Γ
8.22. Аңлатманы дәрәҗә рәвешендә күрсәтегез һәм үзгәреш-
ленең бирелгән кыйммәтендә аның кыйммәтен табыгыз:
. fc5(b-4)2
a) .,-2 A
b ib
b = 3 1 булганда; б)
(n^5)3n
∏-2n1°
, п = 4 булганда.
Аңлатманы гадиләштерегез:
8.23. a) (⅛±⅛
(x + l)-1)
(х + 1Ү1 2
I 3 J + х2 - 1’
б)
х + 10
5х + 25
-<*+5>-,H⅛4
10
х2 - 25’
8.24. a) 2-*~5<a÷2)-1i б) (x2-D1-3
5(4-α2)"1-l 3(x - 1) - (х + I)"1
8.25. Аңлатманың кыйммәтен табыгыз:
, 3x^2 Зх-2 „ _
а) — - х = 0,5 булганда;
2 - х 2 2 + х 2
Q γ~ 1 Q ∙y∙-1
б) ∏—ΣT - о . r-ι' > x = 0>2^1 булганда.
Ct X ct Т X
Аңлатманың кыйммәтен табыгыз:
О θβ v 2x(2 - х)1 3 -
8.Zb. a) , х = — булганда;
58
3x(2 -¾)-ι 5
υ-, ' -, x = — булганда.
2 - 1Ү 7
I 3χ J
2x^1 - y-ι
8.27. a) - i t У = 3-1 булганда;
y x
x^1 - 3j∕~1
6) x1 + 3^Γ, J = 4^1 булганда.
X^1 - 3y'1 -r
8.28. a) λ,.2 _ g ~ ∙ x-ij — = 2^1 булганда;
x^1 + 2y1
6) x-2 _ 4 JT ■ χl, = 5"1 булганда.
8.29. Тигезләмәне чишегез:
a) 4x^2 - 4x1 = -1;
б) х 4 + 16 = 8x-z;
в) 9x 2 + 6x 1 = -1;
г) x^4 + 81 = 18x^2.
Бердәйлекне исбатлагыз;
( У2 (xy ' - 1)2 y2 (x^2 + y~2) ¾ . 1 - x~1y _ х - у
I x(l + x~1y)2 x(xy~1 + x~1y)J ’ xy~1 + 1 х + y’
f a^n + ⅜~π _ Д-" - b^" Y1 _ a~nbn - b~na"
∖α^n - b~n a~n + b~n ) 4
( a~n - b~" Y1 f a~n + b~n Y' _ 2a~n b2"
I α^2" - a~nb'" + b~2n J + lα^2n + a~nb~n + b~2n J b2π - a2"
ӨЙ КОНТРОЛЬ ЭШЕ № 1
1 нче вариант
-1 м a - 8
1. Үзгәрешленең нинди кыйммәтләре өчен — үх?
∖CL + ()(d ~ 1^)
алгебраик аңлатмасы нульгә тигез, ә ниндиләре өчен
кыйммәтләре юк?
2. Вакланманы кыскартыгыз:
а2 - ac + 2ab + b2 - Ъс
ab - c2 + ас + b2
59
3. Аңлатманың кыйммәтен табыгыз:
a2 - 4⅛2 - 5a + 10⅛ д _ 1 9 b _ θ 55 булганда,
(a + 2b)2 - 25
4. Аңлатманы гадиләштерегез:
2 4 + 4р
9р - 12g 9p + 12g 16g2 - 9p2 ‘
5. Аңлатманы гадиләштерегез:
8А + А2 + 16 . 16 - А2
15А2 + ЗА ’ 25A2 - 1'
6. Аңлатманы гадиләштерегез:
1 + 1
a b + с (1 ⅛2 + c2 - а2
11 Л 2bc
а Ь + с
7. Аңлатманың кыйммәтен табыгыз:
8. Аңлатманы гадиләштерегез:
(c1 + d^1)^1 ∙ f-¾- - -⅛Λ
Vd 2 с 2 J
( 2ab a - ⅜ λi 2a + Ь
kα2-∂2 2a + 2Ь , а + Ь Ь-а
аңлатмасының кыйммәте аңа кергән үзгәрешлеләрнең
кыйммәтләренә бәйле түгел икәнен исбатлагыз.
10. Математик модельләштерүнең өч этабын аерып күрсәтеп,
мәсьәләне чишегез.
Катер елга агымы уңаена 21 км араны агымга каршы шул
араны үткәннән 15 минутка тизрәк үтә. Әгәр елганың агым
тизлеге 1 км/сәг булса, катерның үз тизлеге нинди?
2 нче вариант
1. Үзгәрешленең нинди кыйммәтләре өчен ———γj
алгебраик аңлатмасы нульгә тигез, ә ниндиләре өчен
кыйммәтләре юк?
60
2. Вакланманы кыскартыгыз:
x2 + zx - zy + y2 - 2xy
ху - y2 + zx + z2
3. Аңлатманың кыйммәтен табыгыз:
—(χ ~ 2у)2 ~ 49— , х = 3,5, у = °>75 булганда.
х2 - 4y2 + 7х + 14у
4. Аңлатманы гадиләштерегез:
1 1 _ За
6а -46 6а + 46 + 9α2 - 462'
5. Аңлатманы гадиләштерегез:
ЗЬу + бу - 56 - 10 62 - 4
7yb - 14y ‘ 9y2 - 25'
6. Аңлатманы гадиләштерегез:
х + у _ х - у
х- у х +у . х2У2
X + у + х - у ’ (х + у)2 + (х - УҮ
х - У X + у
7. Аңлатманың кыйммәтен табыгыз:
a2 - 2α + 1
а - 3
((a + 2)2 - a2
I 4α2 - 4
, a = -0,01 булганда.
a2 - a)
8. Аңлатманы гадиләштерегез:
(χ-≈-i,-≈)∙ (⅛-7r) ■
Г 6 6 - 6 . 26-6 _ 6
1б2 - зб б2 + 66 J' б2 + 66 6 -6
аңлатмасының кыйммәте аңа кергән b үзгәрешлеләрнең
кыйммәтләренә бәйле түгел икәнен исбатлагыз.
10. Математик модельләштерүнең өч этабын аерып күрсәтеп,
мәсьәләне чишегез.
Моторлы көймә елга агымы уңаена 16 км араны агымга
каршы шул араны үткәннән 12 минутка тизрәк үтә. Әгәр
елганың агым тизлеге 2 км/сәг булса, көймәнең үз тизлеге
нинди?
61
2
БҮЛЕК
У =√x ФУНКЦИЯСЕ.
КВАДРАТ ТАМЫРНЫҢ ҮЗЛЕКЛӘРЕ
§9. РАЦИОНАЛЬ САННАР
N, Z, Q хәрефләрен һәм ∈, ∈ тамгаларын кулланып,
түбәндәге раслауларны языгыз:
9.1. а) -8 — бөтен сан;
б) -12 — рациональ сан;
в) 79 — натураль сан;
г) 15 — бөтен сан.
9.2. а) -10 натураль сан түгел;
б) -5,7 бөтен сан түгел;
в) 0 натураль сан түгел;
х 2 _
г) — бөтен сан түгел.
1о
Түбәндәге раслауларның дөреслеген билгеләгез:
9.3. а) 12 ∈ N; б) -3 ∈ Q; в) -γf ∈ Z;
9.4. а) 37 2 Z; б) -5 g N; в) ⅛ ∈ N;
г) 0 ∈ N.
r> 1«<?•
9.5. a) 5 ∈ [3; 7];
б) 8 ∈ [2; 6];
в) 12 ∈ [12; +«>);
г) 45 ∈ (-∞j 45).
9.6. а) 14,9 ∈ [13; 15];
в) -17 ∈ (-17; 8];
б) 0 е (-1; 1);
г) 25,001 ∈ [0; 25].
9.7. а) 23 £ (22; 23);
в) -19 g (0; 19);
б) 45 ≡ [0; 45];
г) 84 £ [0; 100].
62
9.8. a) (2; 4) ⊂ [1; 5]; в) [7; 9] с (6; 10);
б) [1; 6] ⊂ (0; 4); г) [0; 8] С (0; +∞).
9.9. а) [1; 3] <Z [2; 4]; в) (-3; +∞) <Z [0; +~);
б) [12; 42] а [10; 50]; г) [3; 4] (Z [5; 7].
9.10. -1,2 һәм -1,1 саннары бирелгән.
а) икесеннән дә зуррак булган бөтен санны;
б) икесеннән дә кечерәк бөтен саны;
в) алар арасындагы бөтен санны;
г) аларның икесеннән дә 2 гә зуррак булган натураль
санны күрсәтегез.
График сурәтен ясагыз.
Бирелгән санга кире санны һәм бирелгән санга капма-
каршы санны күрсәтегез:
9.11. а) 3; б) -12; в) 8; г) -7.
9.12. а) 1; в) в) |; г) -≤.
9.13. а) Натураль саннар;
б)тискәре саннар;
в) бөтен саннар;
г) рациональ саннар күплегенең берничә элементын
атагыз.
9.14. а) Натураль саннар һәм бөтен саннар күплекләренең;
б) рациональ саннар һәм натураль саннар күплекләренең;
в) бөтен саннар һәм рациональ саннар күплекләренең;
г) уңай саннар һәм бөтен саннар күплекләренең берничә
уртак элементын атагыз.
Чиксез периодик унарлы вакланма рәвешендә языгыз:
09.15.
X 3
а) й;
6> ⅛
в)
5 .
99’
г)
2
15
09.16.
. 29
а)
6) ⅜5
в)
53.
12’
г)
78
11
63
Чиксез периодик унарлы вакланма рәвешендә языгыз:
9.17. а) 6,335;
9.18. a) 1;
б) 0,48;
б) 35;
в) 7,31;
в) 108;
г) 91,856.
г) 572.
Гади вакланма рәвешендә языгыз:
9.19. а) 0,(3); б) 0,(15); в) 0,(6);
г) 0,(108).
09.20. а) 15,(3);
б) 2,(14);
в) 7,(2);
г) 23,(25).
09.21. а) 0,0(24);
б) 0,00(3);
в) 0,0(6);
г) 0,00(18).
o9.22. а) 1,6(1);
б) 2,03(5);
в) 3,9(12);
г) 0,7(72).
9.23. [1; 5] кисемтәсе бирелгән. Күрсәтегез:
а) бу кисемтәдә ятучы уңай санны;
б) бу кисемтәдә ятучы рациональ санны;
в) бу кисемтәдә ятмаучы бөтен санны;
г) бу кисемтәдә ятмаучы рациональ санны.
9.24. (-2,5; 1,7) интервалы бирелгән. Күрсәтегез:
а) бу интервалда ятучы бөтен санны;
б) бу интервалда ятучы уңай санны;
в) бу интервалда ятмаучы тискәре бөтен санны;
г) бу интервалда ятмаучы уңай рациональ санны.
9.25. (-4; 12) интервалы бирелгән. Күрсәтегез:
а) бу интервалда ятучы нинди дә булса саннар күплеген;
б) бу интервалда ятмаучы нинди дә булса саннар күпле¬
ген;
в) бу интервалга кергән һәм аның очларыннан тигез ерак¬
лыкта ятучы уңай санны;
г) бу интервалда ятмаучы һәм аның бер очыннан 2 бе¬
рәмлектән артык булмаган ераклыкта торган рациональ
санны.
9.26. Бирелгән саннарга кире һәм капма-каршы саннарны
күрсәтегез:
а) 0,35; б) -1,12; в) 3,7; г) -5,32.
64
9.27. Чиксез периодик унарлы вакланма рәвешендә языгыз:
а) |;
«X 12. ч 17. ч 13
” 35 В> 2~Г Г) bΓ
Гади вакланма рәвешендә языгыз:
9.28. а) 0,15(3);
6)0,7(27); в) 0,15(63); г) 0,3(306).
9.29. а) 1,52(3);
6)2,1(61); в) 6,12(8); г) 0,3(36).
§10. ТИСКӘРЕ БУЛМАГАН САННАН
КВАДРАТ ТАМЫР ТӨШЕНЧӘСЕ
10.1. Тигезлекнең дөрес икәнлеген исбатлагыз:
a) √36 = 6;
в) √25 = 5;
б) √121 = 11; г) √196 = 14.
10.2. Тигезлекне тикшерегез:
a) √49 = 7;
в) √100 = 10;
«> Д = 1,5;
r>7b∣∙
10.3. Тигезлекнең ни өчен дөрес түгеллеген аңлатыгыз:
a) √25 = -5;
в) √100 = 10,1;
б) √36 = 6,5; г) √-81 = -9.
Исәпләгез:
10.4. a) √4j
в) 749;
6) 725;
Г) 7i∙
10.5. а) 7144;
в) 7225;
б) 7169;
г) ТзбТ.
10.6. а) 70,36;
б) 70-04; в) 70,64; г) 7θ,81.
10.7. а) Д;
б) J⅝i
‘4'1
65
10.8. Исәпләгез:
10.9. Натураль саннарның квадрат таблицасыннан файдаланып
исәпләгез:
а) 71156; б) 71521; в) 71024; г) 71849.
10.10. Аңлатманың мәгънәсе бармы:
а) 7^1;
б) -7-9?
в) 7(тзТ;
10.11. а нинди кыйммәтләр алганда аңлатманың мәгънәсе була:
а) Та; б) Ja?; в) Т=а; г)
Исәпләгез:
10.12. а) (Тб/; б) (Д) ; в) (7W; г) (JJ) .
10.13. а) (-7Й)2; б) -(Т21)2; В) -(-72)2; г) -7(-3)2.
10.14. а) (2Тз)2; б) (зТ?)2; в) (47∏)2; г) (βj2↑.
( ТзҮ Г1ү. f7δY ( 4 ү
10.15. a) -⅛- ; б) [~f= ; в) ⅛- ; г) -τ= •
10.16. а) (7з)6; б) (з72)4; в) (-7∏Λ г) (7δ)6.
10.17. а) 7з + Тзб;
б) 744 + 725;
10.18. a) 7iθ + 7100;
б) 749 + 7о;
в) 77 + 781;
Г) 77 - 79.
в) 7121 - Тб4;
г) 781 + 71.
66
Исәпләгез:
10.19. a) √64 ∙ √4j в) √49 ■ 7100;
б) 7121 • 79; г) 725 • 7225.
10.20. а) | • 70,36; в) -7 ∙ 70,04;
О
б) o,2 • 71600; г) - • Тооо;
5
Тигезләмәне чишегез:
10.21. a) x2 = 4; б) х2 = 16; в) х2 = 9; г) х2 = 25.
10.22. а) х2 = 5; б) х2 = 11; в) х2 = 13; г) х2 = 17.
10.23. а) |х2 = 75; в) |х2 = 24;
б) 4x2 - 28 = 0; г) Зх2 - 78 = 0.
10.24. Тигезсезлекне канәгатьләндерә торган кимендә бер бөтен
х санын күрсәтегез:
а) х > 72; б) 2х < 73; в) х > 7^; г) Зх < 7∏∙
10.25. Тигезсезлекне канәгатьләндерә торган өч бөтен санны
күрсәтегез:
а) 2х > 7б; в) Зх < 72;
б) 2х < 77; г) 5x > 710-
10.26. Түбәндәге мәйданнары буенча квадратның ягын табыгыз:
а) 64 см2; б) 100 см2; в) 2,25 см2; г) 17 м2.
10.27. Үзгәрешленең кыйммәтләре нинди булганда тигезлек дөрес:
а) у[х =11; в) yfx =1,1;
√- 9 ,— 7
χ = «; г) 7^ = д?
ol0.28. Аңлатманың кыйммәтен табыгыз:
а) 7б - 2α, а = 1 булганда;
б) yj5b2 + 10fe + 9, b = 2 булганда;
в) 7^ - 2с, с = 1,5 булганда;
г) y∕d3 - d2, d = 5 булганда.
67
010.29. Аңлатманың кыйммәтен табыгыз:
a) y∣2a - b, a = 4, b = 7 булганда;
б) √p + 11
р = 25, q = 16 булганда;
в) y]m - 4п, т = 33, п = 2 булганда;
s = 225, t = 25 булганда.
Исәпләгез:
в) -0,03 • 710 000 +
71б;
10.30. а)
7225 + 37121;
_?д5_+ /I;
7361 * 4
б)
г)
_А__ [Z;
√256 ' 64
10.31.
а)
7 V 169
в)
1
2 , 1— - 1;
\ 16
б)
8 ■ , 5— + 3;
V 16
г)
л 1
4 • ./5—.
4 V 49
10.32.
а)
- • 7196 + 1,5 •
2 v
70,36;
в) 3,6 • 7θ,25 +
— • 7256;
32 x
б)
0,5 ∙ 70,04 + -
v 6
• 7144;
г) 2,5 ∙ 7θ,24 -
- ∙ J^225.
2 v
Араларында түбәндәге сан урнашкан янәшә килүче ике
бөтен санны сайлап алыгыз:
10.33. а) 714;
в) Т0?8; г) -√28.
10.34.
а)
-√0,3ι
б) Т325;
в) 7105;
г) -7238.
10.35. Тигезсезлекне канәгатьләндерә торган иң зур бөтен санны
табыгыз:
а) х < 7^; б) 2х < у/1;
в) х < 73;
г) Зх < 72.
68
10.36. Түбәндәге саннан зуррак булган иң кечкенә бөтен санны
табыгыз:
a) 77; б) 710; в) y∣G2∙, г) ∕l03.
10.37. Бу аралыкка ничә бөтен сан керә:
а) [1; 75];
в) [-73; 7б ];
б) (-72; 7з);
Г) (77; 7)?
Квадрат тамыр билгеләмәсен кулланып, тигезләмәне
чишегез:
10.38. a) Jx - 1 = 3; в) y∣x + 2 = 5;
б) √4x + 1 = 7; г) 77x - 1 = 1.
10.39. а) 7289 - х2 = 8; в) 725 - х2 = 0;
б) 7х2 + 144 = 13; г) y∣x2 - 144 = 5.
10.40. Квадратлар таблицасын һәм микрокалькулятор куллан¬
мыйча исәпләгез:
а) 72116; б) 74225; в) y∣9801∙, г) 75329.
•10.41. Квадрат тамырның кыйммәте бөтен сан түгел икәнен
исбатлагыз:
а) 78467; б) 72215; в) 72113; г) 71228.
10.42. Исәпләгез:
а) 777; б) 7б4; в) 7716; г) 3yfl25.
10.43. Исбатлагыз:
а) 71000 = Ю; в) 7θ,θθl = 0,1;
б) 73,375 = -; г) T7τ7 = 74.
2
69
§11. ИРРАЦИОНАЛЬ САННАР
11.1. Бирелгән сан иррациональ буламы:
a) /9; б) 712; в) 718;
г) 725?
11.2. Нисбәтләрнең дөреслеген тикшерегез:
а) 6,1 < Т38 < 6,2; в) 4,4 < 720 < 4,5;
б) 10,5 < 71Й < Ю,6; г) 21,5 < 7⅛63 < 21,6.
11.3. 7? саны нинди бөтен саннар арасында ята?
11.4. 4 һәм 5 саннары арасында ятучы өч иррациональ санны
табыгыз.
Саннарны чагыштырыгыз:
11.5. а) 7? һәм 3; в) 75 һәм 2;
б) y∣17,3 һәм 4; г) 710 һәм 3,16.
11.6. а) -712 һәм -4; в) -719 һәм -4,5;
б) -725,6 һәм -5; г) -yfS7 һәм -6,1.
oll.7. Исбатлагыз:
а) 6 + 72 һәм 6 - 72 иррациональ саннарының суммасы
рациональ сан була;
б) 2 + y∣~3 һәм 2 - 73 иррациональ саннарының тапкыр¬
чыгышы рациональ сан була;
в) 3 + 2 7δ һәм 3-2 y∣^5 иррациональ саннарының
суммасы рациональ сан була;
г) 7? ~ T≡7 һәм 7? + 72? иррациональ саннарының
тапкырчыгышы рациональ сан була.
011.8. а) Суммалары рациональ сан булган ике иррациональ
санга мисал китерегез.
б) Суммалары иррациональ булган ике иррациональ санга
мисал китерегез.
oll.9. а) Тапкырчыгышлары рациональ сан булган ике ирра¬
циональ санга мисал китерегез.
б) Тапкырчыгышлары иррациональ булган ике ирраци¬
ональ санга мисал китерегез.
70
oil.10. Рациональ саннан квадрат тамыр иррациональ сан була
дигән раслау дөресме?
oll.ll. Рациональ саннан квадрат тамыр:
а) бөтен сан;
б) чиксез булмаган унарлы вакланма;
в) периодик булмаган чиксез унарлы вакланма;
г) периодик чиксез унарлы вакланма булган очракларга
мисаллар китерегез.
011.12. Бирелгән санның ни өчен иррациональ сан булуын
аңлатыгыз:
a) 5 + √3j б) 7 - 72; в) 1 + √8j г) 3 - √5.
11.13. Рациональ һәм иррациональ саннарның суммасы ирра¬
циональ сан икәнен исбатлагыз.
11.14. Рациональ (нульгә тигез булмаган) һәм иррациональ
саннарның тапкырчыгышы иррациональ сан икәнен
исбатлагыз.
11.15. Әйтик, I— рациональ сан, a — иррациональ сан булсын.
Бу сан рациональ санмы, әллә иррациональ санмы:
a) г + а; б) а2; в) 2а; г) г2 - а2?
•11.16. у = √2 • х функциясенең графигында абсциссасы да,
ординатасы да бөтен саннар булган бары бер генә нокта
барлыгын исбатлагыз. Бу функциянең графигын төзегез.
•11.17. y=4⅛ ■ х + 7з функциясенең графигында абсциссасы
да, ординатасы да бөтен саннар булган бары бер генә
нокта барлыгын исбатлагыз. Бу функциянең графигын
төзегез.
§12. РЕАЛЬ САННАР
КҮПЛЕГЕ
12.1. а) Натураль саннар;
б) иррациональ саннар;
в) бөтен саннар;
г) реаль саннар күплегенең берничә элементын атагыз.
71
12.2. Әгәр бу мөмкин булса:
а) рациональ саннар һәм реаль саннар күплекләренең;
б) бөтен саннар һәм реаль саннар күплекләренең;
в) иррациональ саннар һәм реаль саннар күплекләренең;
г) натураль саннар һәм иррациональ саннар күплекләренең
берничә уртак элементын атагыз.
12.3. Ни өчен координаталар турысындагы барлык саннар
күплеге белән барлык рациональ саннар күплеге ара¬
сындагы тиңдәшлекне үзара беркыйммәтле дип атап
булмый? Турының һәр ноктасына билгеле бер сан
тиңдәш булсын өчен, рациональ саннар күплегенә нинди
саннарны өстәргә кирәк?
Саннарны чагыштырыгыз:
12.4. а) 7,5 һәм 7,498;
в) 54,46 һәм 54,64;
б) 3,1416 һәм 3,14159; г) 1,2112 һәм 1,2121.
12.5. а) -0,25 һәм -0,26;
б) -5,123 һәм -5,1231;
12.6. а) 3,(7) һәм у;
б) 0,(1) һәм |;
12.7. а) 4,8 һәм /29;
б) —/10 һәм -3,16;
в) -27,36 һәм -27,63;
г) -7,3434 һәм -7,4343.
в) 6,(3) һәм ¾
г) 4,(2) һәм ⅛
5
ч Го ь 71.
в) -√3 һәм “ту!
г) /45 һәм 5,9.
12.8. Бу тигезлекләрдә х зурракмы, әллә у мы:
а) х - у = 3; в) х - у = /7;
б) х - у = -0,01; г) х - у = -/з?
12.9. a < b икәне билгеле, a - b аермасы түбәндәге сан була
аламы:
а) 6,08; б) -5; в) 0; г) 3,72?
12.10. а (а + 2) һәм (a - 3)(а + 2) аңлатмалары бирелгән, а ның
бирелгән кыйммәтләре өчен бу аңлатмаларны исәпләмичә
генә чагыштырыгыз:
а) а = 2; б) а = —/3; в) а = 3,23; г) a = -/5.
72
012.11. Түбәндәге шартлар буенча х Һәм у саннарын чагыш¬
тырыгыз:
а) х = у - 5; в)у + 3 = х + 2 ∙J^2∙,
б) х ÷ 1 = 2у, у > 1; г) у - х = 1 + у2.
12.12. а) т һәм п — бер тамгалы саннар;
б) т һәм п — төрле тамгалы саннар булса, тп тапкыр¬
чыгышының һәм өлешенең тамгасы нинди булыр?
012.13. α>0, b>0, c<0, d<0 икәне билгеле. Бу аңлатманың
тамгасы нинди:
a) abed; б) —; в) r) aΨcids1
с bd ’
012.14. Саннар турысында А һәм В нокталары (рәс.1) белән 1,3,
2,5, π, — саннарының икесен билгеләгәннәр. Кайсы
π
сан — А ноктасына, ә кайсысы В ноктасына туры килә?
А В
• •—I—• ' • • • ►
0 1 2 3 4 5 6 7
Рәс. 1
С D
• • -ч—. • •—н. • ►
-3-2-10 1 2 3 4
Рәс. 2
012.15. Саннар турысында С һәм D нокталары (рәс.2) белән
λ∕δ, -1,2, 0,5π, саннарының икесен билгеләгәннәр.
Кайсы сан С ноктасына, ә кайсысы D ноктасына туры
килә?
Саннарны үсә бару тәртибендә языгыз:
12.16. a) √5, 0, ⅛ в) ≡ 0,3, 0,5;
О о
б) π, 3, 3,1; г) -3,2, -√16, -3.
12.17. a) 2π, 6,3, 5,81; в) f, 1,5, 1,6;
б)о, --⅛, -у; r)-0,5, -^, -1.
73
12.18. a) pq > 0; б) p2q <0; в) ~ < 0; г) ~ > 0
икәне билгеле булса, р һәм q саннарының уңаймы яки
тискәреме икәнен ачыклагыз.
12.19. a > 2 икәне билгеле. Аңлатманың тамгасы нинди:
а) За - 6; в)
б) г) (a - 2)(1 - а)?
12.20. b < 3 икәне билгеле. Аңлатманың тамгасы нинди:
a) (b - 1)2(∂ - 3);
в) 14 - 4Ь;
λ, b~4∙
б) 3-5’
b2 + 1 ?
(b - 7)(3 - 5)
12.21. a) s < 1;
в) 1 < s < 4;
б) s > 4; г) s > 5
икәне билгеле булса (s - l)(s - 4) аңлатмасының тамгасы
нинди?
12.22. Саннар турысында К, L һәм М (рәс.З) нокталары
билгеләнгән. Әгәр аларның координаталары түбәндәге
саннар булса, бу нокталарга тиңдәш координаталарны
атагыз:
a) -√3, -2, в) √5, 2,5, &
б) √3, -j=, 1;
г) √20, 4,5,
-• • •-
KLM
Рәс. 3
§13. у =√x ФУНКЦИЯСЕ, АНЫҢ ҮЗЛЕКЛӘРЕ
ҺӘМ ГРАФИГЫ
13.1. у = λ∕χ функциясенең графигын төзегез.
График ярдәмендә табыгыз:
а) х = 4; 7; 16 булганда у ның кыйммәтләрен;
б) у = 0; 1; 3 булганда х ның кыйммәтләрен;
в) [0; 4] кисемтәсендә функциянең иң зур һәм иң кечкенә
кыйммәтләрен;
г) х ның нинди кыйммәтләрендә функция графигының
У = 1 турысыннан өстә һәм у = 1 турысыннан аста ятуын.
74
13.2. у - yJχ функциясенең графигы буенча табыгыз:
а) х = 0; 1; 2- булганда у ның кыйммәтләрен;
б) у = 2; 2,5; 4 булганда х ның кыйммәтләрен;
в) [1; 9] кисемтәсендә функциянең иң зур һәм иң кечкенә
кыйммәтләрен;
г) х ның нинди кыйммәтләрендә функция графигының
У = 2 турысыннан өстә һәм у = 2 турысыннан аста ятуын.
13.3. у = --√x функциясенең графигын төзегез.
График ярдәмендә табыгыз:
а) х = 1; 2 ; 9 булганда у ның кыйммәтләрен;
б) у = 0; -2; -4 булганда х ның кыйммәтләрен;
в) [2; 4] кисемтәсендә функциянең иң зур һәм иң кечкенә
кыйммәтләрен;
г) х ның нинди кыйммәтләрендә функция графигының
у= -2 турысыннан өстә һәм у = -2 турысыннан аста ятуын.
13.4. Төзүләрне эшләмичә генә, түбәндәге нокталарның у = Jx
функциясе графигында яту-ятмавын әйтегез:
а)А(2;Т2); в) С(6,25; 2,5);
б) В(1; 0); г) О(-9; 3).
13.5. Төзүләрне эшләмичә генә, түбәндәге нокталарның у = -■√x
функциясе графигында яту-ятмавын әйтегез:
а) А(144;-12); в) С(3; -7з);
б) В(-4; 2); г) .0(2,25; 1,5).
у = y[χ функциясенең иң зур һәм иң кечкенә кыйм¬
мәтләрен табыгыз:
13.6. а) [0; 1] кисемтәсендә;
б) (3; 9] ярыминтервалында;
в)[1; 4] кисемтәсендә;
г) [4; 7) ярыминтервалында.
13.7. а) [0; +oo) нурында;
б) [2; +∞) нурында;
в) [9; +∞) нурында;
г) [5; +∞) нурында.
75
13.8. у = -\[х функциясенең иң зур һәм иң кечкенә кыйм¬
мәтләрен табыгыз:
а) [0; 4] кисемтәсендә;
б) [3; +∞) нурында;
в) [1; 9] кисемтәсендә;
г) (2; 9] ярыминтервалында.
Тигезләмәне график юл белән чишегез:
013.9.
a) y∣x = х;
б) y[x = 6 - х;
в) yfx = 2;
г) √x = -х2.
013.10. a) -√x = х - 2;
б) -λ∕x = 2 - Зх.
Тигезләмәләр системасын график юл белән чишегез:
у = -V*.
У =
013.12. а)
1 .
у = -х - 4;
Г 2
б)
1
У = —X
2
13.13 . у = f(x) функциясе бирелгән, биредә f(χ) = y∣^^c- Табыгыз:
a) /(9), f[∣} Д6,25);
б) f(α), Д-a), f(2a)∙,
в) f(a + 1), Я2 - a), f(2a - 1);
г) Яа) + 1, Я2а) - 1, f(a - 3) + 1.
013.14. Бирелгән: f(x) = y[χ, биредә g(x) = х\ Исбатлагыз:
a) f(x4) = g(x); б) (f(x))8 = g(χ2).
013.15. f(x) = √x икәнлеге билгеле. Тигезләмәне чишегез-
a) f(x - 1) = 3; б) Я2х) = 4.
76
13.16. Графигы түбәндәге рәсемдә сурәтләнгән функциянең
графигы кайсы аралыкта өскә таба кабарынкы,
Рәс. 6 Рәс. 7
013.17. у = f(x) функциясе бирелгән, биредә
Лх) =
-х2, х < 0 булганда,
у[х, х ≥ 0 булганда.
a) f(-2), /(0), /(1) не табыгыз.
б) у = /(х) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
77
013.18. у = f(x) функциясе бирелгән, биредә
f(x) =
х-2, -2≤x≤l булганда,
--Jx, 1 < х < 9 булганда.
a) f(~2), /(1), /(4), /(9) не табыгыз.
б) у = f(x) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
13.19. У - функциясе бирелгән. Әгәр күрсәтелгән аралыкларда
түбәндәге шартлар үтәлсә, х үзгәрешлесе кайсы аралыкта
ятар:
a) ymin = 0, ymaκ = 1; в) <∕min = 0, ymta = 3;
б) Z∕min 2, Ут&х 4, г) i∕n∣in 1, У так ~ б.
у = \[х функциясе бирелгән. Әгәр түбәндәге шартлар
үтәлсә, у үзгәрешлесе кайсы аралыкта ятар:
13.20.
а) х ∈ [0; 9];
в) х ∈ [1; 4];
б) х ∈ [4; +°°);
г) х ∈ [9; +∞).
13.21.
а) х ∈ [2; 4];
в) х ∈ [3; 9];
б) х ∈ (4; 7];
г) х ∈ [1; 5).
13.22. у = y[x функциясе бирелгән. Әгәр түбәндәге шартлар
үтәлсә, х үзгәрешлесе кайсы аралыкта ятар:
а) У ∈ [1; 3]; в) у ∈ [2; 4];
б) у ∈ [2; +°°); г) у ∈ [3; +∞)7
13.23. у = -√x функциясе бирелгән. Әгәр ниндидер аралыкта
түбәндәге шартлар үтәлсә, х үзгәрешлесе шул аралыкта
ятар:
a) ‰ιn = -3, утлх = 0; б) ymin = -2, утлх = -1?
у = у[х функциясенең графигыннан файдаланып, у үзгә-
решлесен канәгатьләндерә торган аралыкны языгыз:
13.24.
а) 0 ≤ х ≤ 4;
б) 2 < х < 9;
в) 4 <
г) 3 <
х ≤ 9;
х <
: 4.
13.25.
а) х > 1;
в) X <
4;
б) 0 < х ≤ 5;
г) 0 ≤
х <
10.
78
У -\х функциясенең графигыннан файдаланып, х үзгә-
решлесен канәгатьләндерә торган аралыкны языгыз:
13.26. а) 0 < у ≤ 2;
б) 1 < у < 4;
в) 1 ≤ у < 3;
г) 2 < у < 3.
13.27. а) у > 1;
б) у < 3;
в) у < 2;
г) У > 1.
13.28. у = -yjχ функциясенең графигыннан файдаланып, у үзгә-
решлесенең кайсы аралыкта ятуын билгеләгез:
а) х е [1; 3];
б) х ∈ [4; +°°);
в) х ∈ [2; 4];
г) х ∈ [1; +∞).
13.29. Функциянең графигын төзегез:
а) у = 2√xj
в) у = 0,5 у/х;
б) у = -0,5 \[х;
г) у = -2 √x.
•13.30. Тигезләмәне график юл белән чишегез:
a) 2√x = х;
б) 2√x = 3 - х.
•13.31. Функциянең графигын төзегез:
а) у = √-xj
б) у = -√-x.
•13.32. Тигезләмәнең графигын төзегез:
а) х = у2;
б) (у - x2)(<∕2 - х) = 0.
§14. КВАДРАТ
Исәпләгез:
ТАМЫРНЫҢ ҮЗЛЕКЛӘРЕ
14.1. a) √4 • 9;
б) √16 ■ 25;
в) √49 • 81;
г) √64 ■ 36.
14.2. a) √0,01 • 0,09;
б) √0,36 • 0,49;
в) √0,04 • 1,21;
г) √0,81 0,81.
79
Исәпләгез:
014.3. a) √25 ∙ 16^9; в) √81 ∙ 100 ∙ 4;
б) √0,64 ■ 0,36^9; г) √0,01 • 81 ■ 0,25.
, Гл 4^. . Γ^9 49.
Ol4.7. a) 5∣l-g ∙ 25, bH116 81,
б) -/з— . 2—; г) ./б— • 2—.
' V 16 25’ , У 16 81
14.8. a) √4τj б) √5≡! в) √Fj
14.9. a) 7F; б) √(-2)8j в) √2π^j
014.10. a) √34 • 52; б) √26 • 74; в) √72 • З6;
г) √67.
г) √(-5)2.
г) √24 ∙52.
014.11
81 25.
16 ’
9 16
25 ■ 49
36
49 121
ΓL21- 256
У 25•100 '
Квадрат тамырның үзлекләрен кулланып, квадратлар
таблицасы ярдәмендә аңлатманың кыйммәтен табыгыз:
14.12. а) 7115600; б) ^577 600; в) 7608 400; г) √902500.
14.13. а) 720,25; б) 743,56; в) 796,04; г) Т37,21.
14.14. Аңлатманың кыйммәтен табыгыз:
a) Ja2, а = 15 булганда;
б) 2∖[a*, а = 7 булганда;
в) ~3y[b^, Ъ - 2 булганда;
г) &7у^, у = -2 булганда.
80
Аңлатманы гадиләштерегез*:
14.15. a) √9αlβ!
б) √36b8j в) √49c4j
г) √81d6.
14.16.
a) -5∖∣4x2∙,
в) -0,l√100z8j
б) -3√9∕j
г) -√0,25Z2.
г) λ∕pV0∙
14.17.
a) √x2y4j
б) √z6t8! в) √m12ra16j
014.18.
a) √25α4bi4
в) √36zn2ra8!
« >∣⅛P,V∙.
г) J-r18s2.
N 4
014.19.
. 1 4a2.
а) V ⅛6 ’
. 149a18
В) V 81&® ’
fi. ∕169a18.
. / 576a12
, V 25∂3° ’
r, N 25b2β ‘
Квадрат тамырның үзлекләрен кулланып, санлы
аңлатманың кыйммәтен табыгыз:
014.20. а) √32 ∙ √ 2;
в) √63 ■ y∣7∙,
б) √45 • 75;
г) √10 ∙ √90.
014.21. а) √‰3 • 7^2;
в) √θj ∙ √Γθ;
б) √2^8 ∙ √0J;
г) √4^5 ∙ √50.
014.22. а) √0,05 ∙ √45j
б) √1,92 • √3j
в) √2J • 7К2;
г) √16,9 • ТОЛ.
0X4.23. .)
√108. γ∏7 4 √999
61 √∏' в| Т52; rl √1TT∙
014.24. а)
√50
б) в) г)
√192 √242 √27
* Бу параграфта үзгәрешлеләр бары тик уңай кыйммәтләр генә ала дип
кабул ителгән.
81
014.25. Исәпләгез:
014.26. Аңлатманың кыйммәтен иң уңайлы юл белән табыгыз:
a) √132 - 122; в) √412 - 402;
б) √252 - 242; г) √852 - 842.
14.27. Исбатлагыз:
б) √b = ⅛ ∙ √169bj
в) >∕c = 77 ∙ √225c,
Аңлатманың кыйммәтен табыгыз:
14.28. a) √82 + 152;
в) √52 + 122;
б) √1452 - 1442;
г) √3132 - 3122.
14.29. a) √72,52 - 71,52;
в) √98,52 - 97,52;
б) √6,82 - 3,22;
г) √21,82 - 18,22.
14.30. a) J16s,,∑724∖
V 1о4
. 1 98
bj V 1762 - 1122’
fi. / 1492 - 762 .
V 4572 - 3842’
1145,52 - 96,52
\ 193,52 - 31,52 ■
14.31. Квадратлар таблицасын һәм микрокалькулятор куллан¬
мыйча исәпләгез:
a) √4356j б) √8464j в) √3844s г) √9025.
82
14.32. √60 ≈ 7,7 тигезлегеннән чыгып, аңлатманың якынча
кыйммәтен исәпләгез:
а) ТЬТб; б) √240j в) √6000j г) √540.
14.33. √f90 ≈ 9,5 тигезлегеннән чыгып, аңлатманың якынча
кыйммәтен исәпләгез:
a) √810j б) √360 + 2; в) √2250j г) √9000 - 4.
14.34. Түбәндәге шартлардан чыгып, у[ху аңлатмасын квадрат
тамырлар тапкырчыгышы рәвешендә күрсәтегез:
а) х > 0, у > 0; б) х < 0, у < 0.
14.35. Үзгәрешл ел әрнең бирелгән тигезлекне дөрес итә торган
ике пар кыйммәтен, дөрес итми торган ике пар кыйммәтен
сайлап алыгыз:
a) y∣a + b = y[a + y/b; в) yja - b = y[a - yfb;
б) y[ab = ay/b; г) y[ab = ab.
•14.36. f(x) = -y[χ икәне билгеле. Исбатлагыз:
a) f(4x) = 2f(x)∙, в) ∕(0,01x) = 0,lftx);
б) ftχ4) = - (ftx))4; Г) f(x5) = x2∕(x).
§15. КВАДРАТ ТАМЫР АЛУ
ОПЕРАЦИЯСЕ КЕРГӘН
АҢЛАТМАЛАРНЫҢ РӘВЕШЕН ҮЗГӘРТҮ
Тапкырлаучыны тамыр тамгасы астыннан чыгарыгыз:
15.1. a)√9 ∙3j б) √2 144;
15.2. a) Д, 5)
15.3. a) <9 j1¾ ⅛
15.4. a) J12; б) √20j
в) √36 • 5; г) √196 • 7.
. Γβ~ 4 I^225
≡ V 49’ rH"2-∙
ч /6-49 , /144-3
В) √ 121 ’ Г) √ 7 -25’
в) Т32; г) √54.
83
Тапкырлаучыны тамыр тамгасы астыннан чыгарыгыз:
15.5. a) √
15.6. а) |
15.7. а)
15.8. a) J
015.9. Аңл
a) А
б) А
Тап
15.10. a) >j
15.11. a) λ∣
15.12. a) x
15.13. a) x
15.14. a) yj
015.15. а)
Тап
15.16. а) 2
15.17. а)-
r275j б) 7363; в) √675j г) √108.
√45j б) -√120j в) —>/200; г) -√150.
2 10 5
r8^ _ [40. 4 I 54 . 4 1 243
27’ б) V 63’ В) V 125’ Г) V 128'
ГТ. «ч Г7Г. а 17™. л 7~™
1—; б) «10—; в) . 1—; г) «/1—.
12 ’ N 8 ’ У 32 , У 81
атмаларның кыйммәтләрен чагыштырыгыз:
= 3√50, В = 2 √98j в) А = 4748, В = 5>/27;
= зД, в«|748; r)A=∣√80,B = 2jg.
кырлаучыны тамыр тамгасы астыннан чыгарыгыз*:
^4а; б) 725b; в) y∣16c∙, г) ∖∣49d.
Га3; б) y∣b3∙, в) 7Z; г) >Jdn.
Ixliy2∙, б) >jx8t9∙, в) y∣m21nlβ∙, г) y∣p10ql3.
/100х3; б) √32ι∕4; в) y∣96z5∙, г) 750t10.
Γm3^. ач Γ*r∙ Ч ∕81c6. . ∣32c7
п3 ’ б) V 8<∕3 ’ в) V а3 ’ Г) ∖ 9fe6 '
150m4n3. ∕9⅛ ч 172a6⅛7. 127x11y13
9r4 ’ V 4z2 ’ В' V 49y8 ’ r, ∖ 25ιc6 '
кырлаучыны тамыр тамгасы астына кертегез:
73; б) 572; в) 117б; г) 7Tθ∙
ЗТ8; б) -1173; в) -1зТ5; г) -6y[2.
* Бу параграфта үзгәрешлеләр бары тик уңай кыйммәтләр генә ала дип
кабул ителгән.
84
Тапкырлаучыны тамыр тамгасы астына кертегез:
15.18.
а| 1'
/32;
2 ГГ7
б) --715;
О
в)
г)1'
/35.
15.19.
a) x>l
(12;
б) </Тз2;
в) г
г) ^7
И.
15.20.
а) а2
\(7;
б) -Ь 710;
в) с2 711»
г) -d
7з.
015.21. а)-Зх2^|; в) -5mβy∣5m∙,
б) 4x⅛√O,5xz∕5 г) ⅛pJ^~∙
015.22. Саннарны үсә бару тәртибендә языгыз:
a) 6, 2√8, 5, √26j в) 4, 3√2, 4∣, √19j
б) 2, √7, 2√3, 3; г) 1, ∣√3, 0,7.
о ∆
Аңлатманы гадиләштерегез:
15.23. a) 2√x + зТх - 5√xj
б) 5λ∕α + 3λ∕⅛ - ∙ja + 2y/b;
в) Jz - 3λ∕z + 9y[z∙,
г) 8√c + y∣d - y[d - 4,/с.
015.24. a) √216 - 2√6j
б) √20 + 7125;
015.25. a) 5√3 - √300 - y∣27∙,
б) 2√125 + 2√20 - -√80j
2
015.26. a) √9α + √25a - √36aj
б) 5√3∑ + ∣√12x - 10√0,03xj
в) √5b - 2√20b - 3√80b!
г) 3√2^ - √8^ + 0,l√200y.
в) √125 + 7 Тб;
г) √32 - √128.
в) 3√5 + √20 + ^80;
г) 3√12 + 2√3 - -λ∕27.
3
85
Аңлатманы гадиләштерегез:
015.27. a) χ∕α3b +
oCl
б) Tτn^ + 4mTrn^ - m24rn∖
в) 2ayJa7b - ja9b∙,
г) √81d3 - 5dyfd + -√4dr.
d
015.28. a) (6√12 - √7δ) ∙ √3j
б) (зТб - 2√2θ) ∙ √5j
в) (√32 + 2√18) ∙ √2j
г) (2√50 - 5√2) ∙ √2.
015.29. a) JxUa - Тх);
б) 'lmnA4m + Тп);
в) (Тс + Td) • у[с;
г) Up - y∣q)∙ >∣pq.
O15.30. a) (√50 + Тб) : √2j
в) (Т12 - Т1б) : 73;
б) (12√45 - 6√2θ) : 3√5j
г) (4√75 + 2√12) : 2√3.
015.31. a) (2 + √3)(√3 - 1);
в) (3 - Tδ)(δ + Тб);
б) (5 + Т15 )(Тз - Тб);
г) (3 + √21)(√3 - √7).
015.32. a) (α + Tb)(2α - зТб);
в) (Тх - 2y)(2√x + у);
б) (2√a - бТзь)(2Та + Тзб);
г) (Тгй - 2Tra)(Tm - Тп).
Гамәлләрне кыскача тапкырлау формулаларын кулланып
эшләгез:
15.33. a) (√7 - √5)(√7 + Тб);
б) (7 - 5√2)(7 + 5√2)5
в) (Тб + T2)(T6 — Т2);
г) (8 + ЗТ7)(8 - ЗТ7).
15.34. a) (α + √b)(a - Tb);
б) (Vx - Vy)(Tx + Ту);
в) (Тх - l)(Tx + 1);
г) ~ Jq)Usp + ТТ).
86
a) (Vα + 4b)2;
б) (√χ - 3>fy)2;
a) (√2 + 4)2;
6) (√5-1)2j
a) (2√3 - 3√2)2j
6) (√6 + √12)2∙,
15.35.
15.36.
015.37.
015.38.
15.39.
15.40.
015.41.
015.42.
015.43.
015.44.
b) (yfrn - Jn) ;
r) (∙7F + 2>∕x) .
в) (2 + √17)2j
γ) (3-√8)2∙
в) (3√5 - 5√3Λ
γ) (√14 +√8)2.
a) (y∣^m - yJ^n)(m + jmn + n);
6) (c + yJctyc2 - >[d + d);
в) (√r - 2√n)(r + 2y∕^rn + 4n);
r) (2√^ + 3f)(4s-6<7s + 9<2).
Аңлатманы ваклаучыда иррациональлектән котылдыры
гыз:
β4 х 2 . у ,42
’ 77i б) 3√2, В) Л’ Г) 5^'
a) -rL-i 6) в) уХ-; г) ⅛⅜∙.
x∣a + b ∙Ja2-9 y∣c - d √ 4 - b2
a∖ 4α fl2ft • x c2 . , 9a2bc
а) ~г=; б) ,—в) -т=; г)
√2^ √a∂≈ √27a63c
87
Аңлатманы ваклаучыда иррациональлектән котылдыры¬
гыз:
015.45. а) —≡-7=5 б) fl2---⅛i в) Ц=; г) 2∙⅛!^3a.
x + √ι∕ a - √6 2s + √3r √3a - 5b
015.46. а)
1
в)
2
∖J (1 + 3 -2
3-√2x-l,
б)
У-З
г)
3-6
√4 - у + 1’
2 - yjb + 1
015.47. а)
√P - √<7
4 + 2√t+t.
θ) rt Γ~ ’
2 + √t
x - 3∙s∕x +9
в) —j= ;
√x - 3
a + 2yfab + 4b
Г) √^ + 2√6
Уртак тапкырлаучыны җәя тышына чыгару юлы белән
аңлатманы тапкырлаучыларга таркатыгыз:
015.48. а) 5 + -/б; б) yJb - Ь; в) 3 - y∣3∙, г) yfa + а.
015.49. а) 10 + 5√3j
б) 8 - 4√2ι
в) 20 + 60√7j
г) 45 - 9 √5.
015.50. а) /10 - √6;
б) 2 + √6 - √2j
в) ∖J 14 + 35;
г) 7 + √14 - √7.
15.51. а) a - 2>/а;
б) √3b - Ь;
в) у/a ~ 2a;
г) a + y∣cιb.
015.52. а) a + Ь + у]а + Ь; в) 3a - 3b - 2 yja - b;
б) ∙ja2 - b2 - Ja + Ь; г) ay∣a - b + yja2 - b2.
88
015.53. Квадрат тамырның, билгеләмәсен һәм үзлекләрен кул¬
ланып, группалау юлы белән аңлатманы тапкыр¬
лаучыларга таркатыгыз:
a) aja + bjb + ajb + bja;
б) 2 + bja - 2jab - Jb;
в) ajb - Ja + Jab - 1;
г) ab + aja + bjb + Jab.
Квадратлар аермасы формуласын кулланып, аңлатманы
тапкырлаучыларга таркатыгыз:
015.54. a) а2 - 5; б) 25 - р; в) 11 - Ь2; г) т - 100.
015.55. a) Ь - 3; б) 16г - 5; в) a - с; г) 7 - 641.
Аңлатманы икебуынның квадраты рәвешендә күрсәтегез:
015.56.
a) 1 - 2 Jp + р;
в) с - 2 Jed + d;
б) х + 6y Jx + 9у2;
г) q + 4pjq + 4p2.
015.57.
a) 49α - 14 Jab + Ь;
в) 9m - 6Jmn + п;
б) 3c2 + 10c√3 + 25;
г) 2a + 2b J~2a + Ь2.
015.58.
a) 4 + 4√3 +3;
в) 2 + 2√2 +1;
б) 3 - 2 √2; г) 7 - 4 √3.
Вакланманы кыскартыгыз:
15.59. а)
» в
1 “
1
σ∖
CO ≈∙
1 +
O'
h3 CO '
в)
c2 - 11 .
с - √1Γ
г)
b + √21
21-ft2 ’
15.60. а)
х - 9 т- п .
в)
9- √f∖
Jr + Js
г— ’ о) /— Γ,
√7 + 3 Jm -y∣n
t - 81 ’
г)
Г - S
015.61. а)
sjx - 4√fy .
9х - 16у
в)
25a - 49ft
5λ∕a + 7λ∕ft ’
121α2 - 144ft.
9 Jab - 4λ∕c
б)
12√ft - Ila ’
1)
16с - Slab
89
Вакланманы кыскартыгыз:
015.62.
1-/2
√2 + √6
1 - √3
√6 + /З
а)
1— 1— ’ θ)
√3 - √6
1 + √3 '
’ В) 1— 1—»
√2-√6
г) Г—
√2 + 1
015.63.
а)
√io - √6
√15 - 3 ’
в)
/15 - √6
5 - √10
б)
√15 + √iθ.
√21 + √14 ’
г)
√18 + /12
√15 + √lθ'
015.64.
а)
4a + 4√3
3 - а2 '
в)
х - 25 .
3√x +15’
б)
χ - У
г)
>1тп + п
/бу - /бх
т - п
015.65.
а)
х + 2/ху + у.
/х + /у
в)
∕s - /г .
г - 2/rs + s
б)
х2 - бх/у + 9у _
з/у - х
г)
5/ 3a ÷ -J 5b
За + 5b + J 60ab
015.66.
а)
х + 4/ху + 4у'
х - 4у
в)
x2 - 25y
x2 + 5y - x∕20y
б)
2a + 6yJ 2ab + 9Ь
ба - 27b
; г)
6x2y - 2xy2
3x + у - y∣ 12xy
015.67.
а)
// + √b7. ~
г- г ' б>
√α + √b
х/х - 8.
/х - 2 ’
4 √^^-√dr
в) l- ;
с + y∣cd + d
27 + а/а
r' г-
3 ÷ √a
015.68. Аңлатманы гадиләштерегез:
11/х - 2y∣y + 2∖fx - з/у /х - /у .
4>∕x 4∖lx 4л/х
б)
г) 2/с - ∙Jd 8/с + 6∖fd + \[с - 3∖∕d
δVc 5>∕c 5∖lc
90
Аңлатманы гадиләштерегез:
015.69.
015.70.
b)^--7⅛-5
√c + 9 √c + 9
. d , 14√d + 49
г) ^7= + —7= •
у/d + 7 + 7
015.71.
015.72.
015.73.
015.74.
Тигезлекне тикшерегез:
а) Ц= + = 20;
5 + 2√6 5 -2√6
6 6 _ 144.
7 - 4√3 7 + 4√3 √3 ’
≡,√b + wfc = 30^
Г) 9 + 4√5 9-4√5 " 2^‘
91
015.75. Бердәйлекне исбатлагыз:
4y[ab y∣a - 2y[b _ a + 4b.
a> a - 4b + + 2√b α ~ 4b’
2 УУ — 3∙J~b 12γ∕ αb 4α + 9b
2√α + 3√b 9b-4α 4a - 9b'
Аңлатманы гадиләштерегез:
015.76.
015.77. а)
х - 16 . Ух + 4.
8x ’ 4√x
г - 25 . √z + 5.
-3λ∕z ’ 9-z ’
5 - Уу . Ту .
Уу У-25’
3c - 3d Ус + Ур
с + y[cp 6y[d - бУс
015.78. а)
х - 10-Ух + 25 . 2λ∕x - 10.
3λ∕x+12 ’ х - 16 ’
1-а а + 4y[ab + 4b ι
4yfa + 8yJb 3 - зУУ
в) с — 25 зУс + 18.
с + 12λ∕c + 36 2y[c + 10
015.79.
з« + зУ?.
12√7 + 8’
6) f Ух - 2y∕y + 1 1 ху
t ууу Ух J Ух - Уу
92
015.80. a)
б)
015.81. a)
б)
α- 16 1 _ √a + ⅜ .
λ∕a + 3 a + 4λ∕a a - 3∙fa
1 - 2√⅛ b + 3√⅜ . 3 + √⅛
2√b + 1 4∂ - 1 4λ∕⅛ + 2'
15.82. Әгәр a < 0 икәне билгеле булса, тапкырлаучыны тамыр
тамгасы астыннан чыгарыгыз:
а) a 712; б) -а>/5; в) За.у/2; г) -2a 7?-
Аңлатманы гадиләштерегез:
15.83.
а) (√6 + √δ)2 - 7120; в)
(√2
+ √iδ)2 - 30;
б) √60 + (√3 - √5)7 г)
(6-
√2)2 + 3√32.
15.84.
а) (√3 + √2 + 1)2; в)
(√6
+ √2 - 1)2;
б) (√5-√2-1)2; г)
(√3
- √2 + 5)2.
15.85.
а>
б) O,1√14O-J∣-JJ1
γ,i∕⅛ + 2^I-∕I-Aj∙
15.86.
а) 3J— + 6√0^6 - ТбО;
б) 5√20 - lδJ∣ + 5√0^8!
в) 10√0,18 - 2Ji - 3√5θ5
г) 20√0,27 - 5√0,12 + 7√0,03.
93
Тигезлекнең дөреслеген исбатлагыз:
15.87. a) √3 + 2√2 = 1 + √25
б) √23-4√15 = 2√5 - √3j
в) 2 - √3 = TΓ→√3!
г) √5 + 3√2 = >∣23 + 6√10.
15.88. а) (3 + 2√2)(1 - √2)2 = 1;
б) (√3 -l)2(4 + 2√3) = 4;
в) (7 + 4√3)(2 - √3)2 = 1;
г) (√2 -3)2(ll + 6√2) = 49.
15.89. а) (1 - √2) =3-2λ∕2 икәнлеген исбатлагыз. Шуның
нигезендә √3 - 2λ∕2 = 1 -V2 икәнлеген исбатларга мөм-
кинме?
б) (√2 - 1)2 = 3 - 2√2 икәнлеген исбатлагыз. Шуның
нигезендә √3 - 2√2 = √2 - 1 икәнлеген исбатларга
мөмкинме?
15.90. a) √28 - 10√3 = √3 - 5; б) √28 - 10√3 = 5 - √3 тигез-
лекләренең кайсы дөрес? Җавапны аңлатыгыз.
15.91. Бердәйлекне исбатлагыз:
94
Аңлатманы гадиләштерегез:
i к 04 ∖ 9x ∙ 4
15.94. a) —7= τ= ∙ -. τ=i
2slx - y/у Ьх-У 6x+3√xy
б) ∙Jmn3 т - п ' ∙Jmn + п
~Jm - ∙Jn &п4т
Аңлатманың кыйммәтен табыгыз:
15.96. а) х2 - 2xy[2 + 2, х = y∕^2 + 1 булганда;
б) 2a2 - 8aJ~2 + 16, a = 5 ^2 булганда;
в) y2 + 2y y∣3 + 3, у = 4
√3
булганда;
г) 3b2 + 2Ь у/з + 1, ь = 3 у^З булганда.
15.97. a) 2α2 - ab - b2, a = λ∕δ + 1 һәм b = y∣^5 - 1 булганда;
б) 2a2 - 5ab + 2b2, a = λ∕β + λ∕δ һәм b = ∙Jβ - λ∕5 булганда.
95
15.98. А һәм В санлы аңлатмаларның кыйммәтләрен чагыш¬
тырыгыз:
а) А = —4 + —4 5 В = ТЗО;
3√3 - 5 3√3 + 5
б) А = Ц= Ц=; В = √245
4 + 2√5 4 -2√5
\ Л θ ■ 3 d Гп
в) А = —т= 1—r- ; в = √ з,
2√6-3 2√6+3
г) А = ⅛ Ц=; В = √2.
2+3√2 2-3√2
Аңлатманы гадиләштерегез:
•15.100. a) √7 + 4√3j в) √7 - 4√3j
б) √3 - 2√2j г) √3 + 2√2.
15.101. Аңлатманың кыйммәтен табыгыз:
а = y∣~2 + yj^3, х = 0,2(13) булганда.
15.102. Аңлатманың кыйммәтен табыгыз:
1 + ax"1 α~1 . ax^1 . -2
a"1x"1 a lx - ax1 х - a
a = -2,785, х = λ∕13 - 1 булганда.
15.103. Бердәйлекне исбатлагыз:
96
Тигезлекне тикшерегез:
•15.104. a) √9 - 4√5 + √14 - 6√5 = 1;
б) √11 - 4√7 + √16^6√7 = 1.
•15.105. - 6 +J⅛≈- + £_~ 4√2
l√2 + √6 + 4√2 √2 - y∣β _ 4J2 j
•15.106. Аңлатманы гадиләштерегез ∖10 + 8y2 + 7θ + 4λ∕2 .
§16. РЕАЛЬ САННЫҢ МОДУЛЕ
Исәпләгез:
16.1.
а) |6|;
б)|-2|; в)|-4|;
r)∣25∣.
16.2.
а) |-2,5б|;
б)|1,7|; в)|5,09|;
r)∣-3,75∣.
16.3.
a) ∣√2-1∣5
6)∣√3-5∣j в) ∣√8 - 4|;
г) ∣√5 - 2|
16.4.
а)|9|2;
б)|-2|2; в)|-5|2;
r)∣8∣2.
16.5.
Тигезлек дөресме:
а)|3| = |-3|; в)|-7| = |7|;
б)-|2| = |2|; г) ∣-10∣ = -|10|?
Аңлатманың кыйммәтен табыгыз:
16.6. a) ∣α∣ + 3, a = 7 булганда;
б) |5| + √3 , b = -y∣3 булганда;
в) ∣i>∣ - 2, b = 0 булганда;
г) √2 - ∣d∣, d = ~∖fz булганда.
016.7. a)∣α∣ + 1, a = √2 -1 булганда;
б) ∣α∣ + 2, a = 2 - √5 булганда;
в) √3 - ∣α∣, a = √3 - 1 булганда;
г) ∣α∣ - √3 , a = - 2 булганда.
97
016.8. Аңлатманың кыйммәтен табыгыз:
a)∣α∣ + ∣b∣, α=l- y∣^2, Ь = 3 - y∣2 булганда;
б) |х + у\, х = 2 yp7 - 5, у = - 3 булганда;
B)∣t∣-∣z∣, t = 2 - y]^5, z = y[5 - 1 булганда;
г) ∖z - t∣, z = 2 л/з - 3, t = 2 - у[з булганда.
16.9. у = |х| функциясенең графигын төзегез. График ярдәмендә
табыгыз:
а) х = 5; 0; -2,5 булганда у ның кыйммәтләрен;
б) у = 7; 3; 1 булганда х ның кыйммәтләрен;
в) [-4; -1] кисемтәсендә функциянең иң зур һәм иң
кечкенә кыйммәтләрен;
г) функция кимегәндә һәм үскәндә х ның кыйммәтләрен.
16.10. у = -|х| функциясенең графигын төзегез. График
ярдәмендә табыгыз:
а) х = -6; -1; 4 булганда у ның кыйммәтләрен;
б) у = -8; -6; 0 булганда х ның кыйммәтләрен;
в) әгәр х ∈ [-1; 4] булса, у үзгәрешлесенең нинди аралык¬
та ятуын;
г) функция кимегәндә һәм үскәндә х ның кыйммәтләрен.
у = |х| функциясенең иң зур һәм иң кечкенә кыйммәтләрен
табыгыз:
16.11. а) [-1; 1] кисемтәсендә;
б) (-4; 2) интервалында;
в) [2; 7] кисемтәсендә;
г) (-2; 1) интервалында.
16.12. а) [0; +∞) нурында;
б) (-1,5; 7] ярыминтервалында;
в) [-2; +∞) нурында;
г) [-3; 1) ярыминтервалында.
16.13. у = |х| һәм у = 3 функцияләренең графикларын төзегез.
а) Функция графикларының кисешү нокталарының абс¬
циссаларын табыгыз.
б) у = |х| функциясе графигының у = 3 турысыннан аста
яткан өлешен аерып күрсәтегез.
в) х ның нинди кыйммәтләрендә у = ∣χ∣ функциясе өчен
у < 3 шарты үтәлә?
г) х ның нинди кыйммәтләрендә |х| > 3 шарты үтәлә?
98
16.14. у = ∣χ∣ функциясенең графигын төзегез. График буенча
табыгыз:
а) х ның нинди кыйммәтләрендә у - 2;
б) х ның нинди кыйммәтләрендә у > 2, у < 2;
в) х ның нинди кыйммәтләрендә 2 < у < 5;
г) у ның нинди кыйммәтләрендә х < -2.
16.15. у = -∣χ∣ функциясенең графигын төзегез. График буенча
табыгыз:
а) х ның нинди кыйммәтләрендә у = -4;
б) х ның нинди кыйммәтләрендә у > -4, у < -4;
в) у ның нинди кыйммәтләрендә х > 4;
г) х ның нинди кыйммәтләрендә -4 ≤ у ≤ -1 шарты үтәлә?
16.16. Тигезләмәне график юл белән чишегез:
a)∣x∣ = -χ2j в) |х| = х2;
б) ∣X∣ = y[χ∙, г) ∣X∣ = -у/х.
16.17. у = ∣χ∣ Һәм у = Ь функцияләренең графикларын төзеп,
тигезләмәне чишегез:
а) |х| > Ь, Ь = 5 булганда; в) ∣x∣ < b, Ь = 4 булганда;
б) ∣x∣ ≤ b, b = 1 булганда; г) ∣x∣ ≥ b, Ь = 2 булганда.
016.18. у = f{χ) функциясе бирелгән, биредә
Дх) =
|х|, х < 0 булганда,
х2, х ≥ 0 булганда.
a) /(-2), ДО), Д5) не табыгыз.
б) у = Дх) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
f(x) = j
016.19. у = f(χ) функциясе бирелгән, биредә
|х|, -3 ≤ х ≤ 3 булганда,
6 - х, х > 3 булганда.
a) Λ-3), ДЗ), Д4,5) не табыгыз.
б) у = Дх) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
016.20. у = f(x) функциясе бирелгән, биредә
|х|, х < 1 булганда,
Дх) = r-
√x,х > 1 булганда.
a) /(4), Д-1), ДО) не табыгыз.
б) у = Дх) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
99
16.21.
Тигезләмәне чишегез:
а) |х - √3∣ = 0;
б) |х + 7| = 0;
в) ∣x + λ∕δ∣ = 0;
г) |х - 6| = 0.
16.22 . а) |х| = 5,5;
б) ∣x∣ = 1;
в) |х| = 3;
г) |х| = 0,2.
016.23. а) |х - 11 = 2;
б) |х — 51 = 4;
в) |х — 71 = 5;
г) |х - 11| = 9.
016.24. a) ∣x + 2,5∣ = 1;
в) ∣x + 0,75∣ = 3,75;
б) ∣x-lf∣ = 2;
6 I
16.25. Аңлатманы гадиләштерегез λ∕(χ ~ 3)2,
а) х - 3 ≥ 0 булганда; б) х - 3 < 0 булганда.
16.26. Аңлатманы гадиләштерегез √ (х + 5)2,
a) х + 5 > 0 булганда; б) х + 5 < 0 булганда.
Аңлатманы гадиләштерегез:
016.27. а) 7 (1 - √3)2;
б) 7(2 - √3)2;
016.28. a) √(4 - 2√5)2j
б) √(π - З)2;
Тигезләмәне чишегез:
16.29. a) ∣2x - 11 = 3;
б) |1 + Зх| = 2;
16.30. a) ∣0,2x - 2| = 3,6;
б) |3 - l,5x∣ = 2,5;
в) J (√5 - З)2;
г) 7(з - √β)2.
в) 7(б - З7б)2;
г) √(4 - π)2.
в) |2 + 2х| = 6;
г) ∣4x + 11 = 5.
в) |2 - 3,5x∣ = 6,2
г) ∣0,4x + 1| = 2,3
100
Аңлатманы гадиләштерегез:
√
16.31. а) -
x2 - 4x + 4. √χ^ + Юх + 25
x~2 х + 5
x + 3 ■ iλ — х - 6
б)7
16.32. а) 2
б) 4
•16.33. а) λ∕
б) 7
в) 7
г) 7
-— ’ 17 r-⅞-
х2 + 6х + 9 √x2 _ 12χ + 36
+ √5 - 7 G/б - з)2; В) V (2 - √7 )2 +77 + 2;
+ √6 - 7(7б - 2)2; г) √7√lδ - 4)2 - √Γδ - 4.
(5 - √30)2 + J(6 - √3θ)%
(4 - 2√3)2 + J(З - 2√3)2;
(б - √42)2 + J(7 - √42)2;
(З - 2√2)2 + 7(2 - 2√2)2.
•16.34. Аңлатманы гадиләштерегез ,^ -l*l ^t^*,
Зх2 - Зх
а) х < 0 булганда; в) х > 1 булганда;
1 Q
б) 0 < х < 1 булганда; г) - ≤ χ ≤ £ булганда.
J 4
•16.35. Аңлатманы гадиләштерегез ———1LJ7∣
b2 - Ъ + 1 - ∣b∣,
a) b < 0 булганда; в) ь > 1 булганда;
б) 0 < b < 1 булганда; г) 5 < ь < 6 булганда.
•16.36. Аңлатманы гадиләштерегез √x2 + 4χ + 4 _ λ∕χ2 _ θx + 9
а) х < -2 булганда;
б) -2 < х < 3 булганда;
в) х > 3 булганда;
r)-7≤x≤-4 булганда.
•16.37. Аңлатманы гадиләштерегез:
∖∣x2 - 4x + 4 + ∙Jx2 + 2x + 1
а) х < -1 булганда;
б) -1 < х < 2 булганда;
2Vx≡ _ Юх + 25,
в) 2 < х < 5 булганда;
г) х > 5 булганда.
101
Тигезләмәләр системасын график юл белән чишегез:
у = 1*1»
у = -1*1»
16.38. а)
у = 0,5х + 3; В)
1
у = -х - 4;
y 3
у = 2х - 3,
У = х - 1,
б)
II г>
у = -1*1;
у = 1*1-
у = 3|х|,
у = ||*1»
•16.39. а)
2 б
2
[у = * ;
У = ⅛∙
Тигезсезлекне график юл белән чишегез:
•16.40. a) ∣x∣ ≥ 3; в) -|х| < 4;
б) х2 > ∣x∣; г) y[χ ≥ |х|.
•16.41. a) ∣x∣ ≤ -х + 4; в) |х| > -х + 4;
б) |х| > х - 2; г) -|х| > 3 - х.
Функциянең графигын төзегез:
•16.42. а) у = х|х|; б) у = у + 1; в) у = щ; г) у = щ.
•16.43. а) у = λ∕x2^ + х; в) у = y[x^ - х;
б) у = Зх - |2х - 4|; г) у = |х - 31 + 2х.
•16.44.
а) у = 2|х|;
б) У = -||*1;
О
в) у = 0,5∣x∣;
г) у = -3|х|.
ӨЙ КОНТРОЛЬ ЭШЕ № 2
1 нче вариант
1. а) — не периодик унарлы вакланма рәвешендә языгыз.
15
б) 1,2(34) не гади вакланма рәвешендә языгыз.
2. Калькулятор ярдәменнән башка исәпләгез: >/54756.
102
3. a =
2 + √5
—~j= һәм b = 4,5 саннарын чагыштырыгыз.
2 — -J 5
4. Аңлатманы гадиләштерегез:
a) 5√18 + 7√50 - 3O√25 б) -^ΞΞ=, a>O,b>O булганда.
sj 125α' и
5. Вакланманы кыскартыгыз:
а)
pjp+gjg - pJq - <?Ур.
p√p - qjq + pjq - qjp
б)
4x - 12λ∕xy + 9 у
7 4x3 - ∖∣9x2y
6. Функциянең графигын төзегез һәм [0; 8] кисемтәсендә
аның иң кечкенә һәм иң зур кыйммәтләрен табыгыз.
а) у = у[х; б) у = -|х|.
7. Тигезләмәләр системасын график юл белән чишегез.
У = 'Jx,
у - 0,5х.
8. Аңлатманы гадиләштерегез
Jc — 7 Jd 7 Jc + Jd ) с + d
Jed - d Jed - с J Jc - Jd
9.
Аңлатманы гадиләштерегез
√ 10 < х < λ∕20 булганда.
√x2 - 6x + 9 + √x2 - Юх + 25,
2 нче вариант
а)
— не периодик унарлы вакланма рәвешендә языгыз.
б) 0,2(31) не гади вакланма рәвешендә языгыз.
2.
Калькулятор ярдәменнән башка исәпләгез:
√126736.
3 а = —т= т= һәм b = 5,5 саннарын чагыштырыгыз.
3-2√2 3 + 2√2
Аңлатманы гадиләштерегез:
a) 3√27 + 5√75 - 35√3s б)
√48x7y5 *
∙j3x3yl2
х > 0, у > 0 булганда.
5. Вакланманы кыскартыгыз:
а)
mjm+njn + m∙jn + njm
mjm - njn + mjn - njm
б)
9х + 24 Jxy + 16у
λ∕ 9x5 + >∕16x4!∕
103
6. Функциянең графигын төзегез һәм [4; 7] кисемтәсендә
аның иң кечкенә һәм иң зур кыйммәтләрен табыгыз:
а) у = -y∣χ∙, б) у = |х|.
7. Тигезләмәне график юл белән чишегез: y[x = 2 - х.
8. Аңлатманы гадиләштерегез:
9. Аңлатманы гадиләштерегез: >/л
√7 < х < √15 булганда.
Ja Jb } ∙Jab
- √ab a - √ ab ) ∙Jb + ∙√ a
:2 - 4x + 4 + Vx2 - 8х + 16,
3
БҮЛЕК
КВАДРАТИК ФУНКЦИЯ,
у = у ФУНКЦИЯСЕ
§17. у = far2 ФУНКЦИЯСЕ,
АНЫҢ ҮЗЛЕКЛӘРЕ ҺӘМ ГРАФИГЫ
Бирелгән у = kx2 функциясе өчен k коэффициентының
кыйммәтен табыгыз:
17.1. а) у = 2х2; б) у = -8х2; в) у = 7х2; г) у = -х2.
17.2. а) у = 0,2х2; в) у = -1,85х2;
ү.2 ү.2
б) у = --s-; г) у = .
О Of
17.3. Функциянең графигын схема рәвешендә сурәтләгез:
а) у = -0,2х2; б) у = Юх2; в) у = -1,8х2; г) у = | х2.
Функциянең графигын төзегез һәм аның кайда кимегә¬
нен, кайда үскәнен күрсәтегез:
17.4. а) у = Зх2; б) у = -4х2; в) у = -2х2; г) у = 5x2.
17.5. а) у = -1,5х2; 6)ι∕=∣x2j в) у = 2,5х2; r)ι∕=-∣x2.
Бер үк координаталар системасында бирелгән функ¬
цияләрнең графикларын төзегез һәм төзелгән гра¬
фикларның үзара урнашуы турында нәтиҗә ясагыз:
17.6. а) у = х2 Һәм у = -х2; в) у = 3,5x2 һәм у - -3,5х2;
б) у = 0,5x2 һәм у = -0,5х2; г) у = ~х2 һәм у = х2.
Ә ә
17.7. а) у = х2 Һәм у = 2х2; в) у = l,5x2 һәм у = 2,5х2;
б) у = -0,5x2 һәм у = -Зх2; г) у = х2 һәм у - -х2.
О
105
17.8. Функцияләрнең графикларын төземичә генә әйтегез,
аларның графиклары бер үк координаталар системасында
һәм үзара ничек урнашкан:
а) у = 105x2 һәм у = - 105х2;
б) у = -3,165x2 һәм у = 3,165x2.
17.9. Функциянең графигын төзегез:
а) у = 2х2; в) у = Зх2;
б) у = 0,5х2; г) у = 0,2x2.
Төзелгән графикның һәм у = х2 функциясе графигының
үзара урнашуы турында нәрсә әйтергә мөмкин?
17.10. Функциянең графигын төзегез:
а) у = -1,5х2; в) у = -2,5х2;
б) у = -Зх2; г) у = -0,5x2.
Төзелгән графикның һәм у = -х2 функциясе графигының
үзара урнашуы турында нәрсә әйтергә мөмкин?
17.11. у = kx2 функциясенең графигы:
а) беренче һәм икенче чирекләрдә;
б) өченче һәм дүртенче чирекләрдә урнашырлык итеп,
k санын сайлап алыгыз.
17.12. у = 2x2 функциясенең графигын төзегез. График ярдәмендә
билгеләгез:
а) х = 0; 1; -2 булганда, функциянең кыйммәтләрен;
б) у = 0; 2; 8 булганда, аргументның кыйммәтләрен;
в) [-2; 1] кисемтәсендә функциянең иң зур һәм иң
кечкенә кыйммәтләрен;
г) әгәр у ∈ [2; 8] булса, х үзгәрешлесенең нинди аралык¬
ларда урнашуын.
17.13. у = -х2 функциясенең графигын төзегез. График ярдәмендә
билгеләгез:
а) х = 0; -2; 3 булганда, функциянең кыйммәтләрен;
б) у = 0; -4; -9 булганда, аргументның кыйммәтләрен;
в) (-3; 1] интервалында функциянең иң зур һәм иң
кечкенә кыйммәтләрен;
г) әгәр у ∈ [-4; -1) булса, х үзгәрешлесенең нинди ара¬
лыкларда урнашуын.
106
17.14. у = 0,5x2 функциясенең графигын төзегез.
а) х ның кыйммәтләре нинди булганда, функциянең
кыйммәте 2 гә тигез була?
б) Графикның у < 2 шартына туры килгән өлешен аерып
күрсәтегез. Бу шарт х ның нинди кыйммәтләре өчен
үтәлә?
в) у > 2 шарты х ның нинди кыйммәтләре өчен үтәлә?
г) функциянең нинди кыйммәтләре х ≤ -2 шартына туры
килә?
17.15. у = -Зх2 функциясенең графигын кулланып табыгыз:
а) х ның нинди кыйммәтләре өчен у = -3;
б) х ның нинди кыйммәтләре өчен у > -3; у ≤ -3.
17.16. Бу нокта у = -220x2 функциясенең графигында ятамы:
а) А(1; -220); в) С(—3; 1320);
б) В(4; -880); г) D(l,5; -495)?
17.17. Параболаның түбәндәге нокта аша үтүе билгеле булса,
у = kx2 параболасы тигезләмәсендә k коэффициентын
табыгыз:
а) М(2; 20); б) N(-3; 27); в) 10); г) L(4; -96).
17.18. Графигы түбәндәге рәсемдә сурәтләнгән у = kx2 пара¬
боласының тигезләмәсен языгыз:
а) рәс. 8; в) рәс. 10;
б) рәс. 9; г) рәс. 11.
107
17.19. Графигы түбәндәге рәсемдә сурәтләнгән функция астан
чикләнгән була аламы? Әгәр булса, функциянең иң
кечкенә кыйммәтен табыгыз:
а) рәс. 12; в) рәс. 14;
б) рәс. 13; г) рәс. 15.
17.20. Графигы түбәндәге рәсемдә сурәтләнгән функция өстән
чикләнгән була аламы? Әгәр булса, функциянең иң зур
кыйммәтен табыгыз:
а) рәс. 16; в) рәс. 18;
б) рәс. 17; г) рәс. 19.
108
109
17.21. Графигы түбәндәге рәсемдә сурәтләнгән функция чик¬
ләнгән була аламы:
а) рәс. 20; в) рәс. 22;
б) рәс. 21; г) рәс. 23?
17.22. Схема рәвешендә түбәндәге функциянең графигын тө¬
зегез:
а) астан чикләнгән;
б) астан һәм өстән чикләнгән;
в) өстән чикләнгән;
г) астан да, өстән дә чикләнмәгән.
17.23. у = 2x2 функциясенең иң кечкенә һәм иң зур кыйммәтлә¬
рен табыгыз:
а) [-2; 2] кисемтәсендә; в)[-3;-1]кисемтәсендә;
б) (-3; 1] ярыминтервалында; г) [1; +∞) нурында.
110
17.24. у = -0,5x2 функциясенең иң кечкенә һәм иң зур кыйм¬
мәтләрен табыгыз:
а) (-3; 2] ярыминтервалында; в) [-1; 4] кисемтәсендә;
б) (-2; 1) интервалында; г) (-∞j 2] нурында.
17.25. у = | х2 функциясенең иң кечкенә һәм иң зур кыйммәт-
3
ләрен табыгыз:
а) (3; 6) интервалында; в) (-°°; 3) ачык нурында;
б) [-3; 0] кисемтәсендә; г) [-1; 4) ярыминтервалында.
17.26. Функцияләр графикларының кисешү нокталарын табы¬
гыз:
а) у = х2 һәм у = 2х; в) у = -Зх2 һәм у = -Зх;
б) у = -0,5x2 һәм у = 2; г) j∕ = - х2 һәм у = 3.
3
Тигезләмәне график юл белән чишегез:
017.27. a) х2 = х + 2;
в) -Зх2 = Зх - 6;
б) |х2 = х + 4;
г) -х2 = 2х - 3.
017.28. a) 5x2 = 5х - 6;
в) х2 = -х - 8;
б) 4х2= 2Х + 2;
г) -0,5x2 = 0,5х + 3.
Тигезләмәләр системасын график юл белән чишегез:
017.29. а)
б)
II II II
Н to to
*= *• н
* м
в)
г) ■
II II II II
⅛ ⅛ ⅛
1 2
—
2 ’
2;
-X2,
-5.
У =
6;
У =
2x2,
у =
1 2
—X ,
017.30. а)
в)
ZJ
3
У =
4х;
У =
-х;
У =
-х2,
У =
2x2,
б)
г) ■
х +
У + 6 = 0;
У +
2х - 4 = 0.
У =
1 2
-х ,
У =
Зх2,
017.31. а)
8
в)
у =
Vx;
У =
-Vx;
у -
0,5x2,
У =
χ∣,
б)
г)
1 2
У =
И;
У =
—х2.
3
111
017.32. Тигезләмәләр системасын график юл белән чишегез:
1 2
У = ~7x ,
У = 0,5x2,
а)
4 в)
у = х - 1;
у = 2х - 2
У = -4|х|, .
у = -∣3χ∣,
б)
0 2 ГМ
у = -2xl∙,
У = -x2∙
График ысул ярдәмендә тигезләмәләр системасының
чишелешләре санын билгеләгез:
017.33.
а)
У =
У =
2x2,
х + 4;
в)
У
У
=
0,5x2,
1,5х;
б)
У =
1 2
зх ’
г)
У
=
1 2
-х ,
4
У =
-л/х;
У
=
х| .
017.34.
а)
II II
⅛
-4x2,
1;
в)
У
У
=
Зх2,
х - 3;
б)
У =
У =
1 W | >->
г)
У
У
=
-2x2,
4х.
17.35. у = f(x) функциясе бирелгән, биредә Дх) = 2x2. Табыгыз:
а) ДО), Д1), Д-3), /(£);
б) f(a), f(4a), ∕(-2α), Д-0,5а);
в) Да + 1), f(b - 2), f(x - 3), f(x + 9);
г) f(a) + 1, f(x) - 2, f(a) + Ь, f(x) - а.
17.36. у = Дх)функциясе бирелгән, биредә Дх) = -4x2. Табыгыз:
а) /(1), Д-2), ДО), /(I);
б) Да), f(-a), f(-2a), f(5a);
в) f(a + 2), Да - 3), Дх - 1), Дх + 6);
г) Да) + 1, Дх) - 5, Дх + 2)-1, Дх - с) + d.
Түбәндәге шарт үтәлсә, у = Зх2 функциясенең графигы
ярдәмендә у үзгәрешлесе яткан аралыкны табыгыз:
017.37. а) 0 < х < 1; б) -2 < х <. О; в) 1 < х < 2; г) -1 < х < 1.
017.38. а) х > 0; б) х < -1; в) х < 0; г) х > 1.
112
017.39. Түбәндәге шарт үтәлсә, у = τ∙ х2 функциясенең графигы
О
ярдәмендә х үзгәрешлесе яткан аралыкны (аралыкларны)
табыгыз:
а) у > 3; б) | < у < 3; в) у < 3; г) 3 ≤ у < 12.
017.40. Түбәндәге шарт үтәлсә, у = -х2 функциясенең графигы
ярдәмендә х үзгәрешлесе яткан аралыкны (аралыкларны)
табыгыз:
а) у < -4; б) -4 ≤ у < -1; в) у > -4; г) -9 < у < -4.
017.41. у = /(х) функциясе бирелгән, биредә
[ 2x2, -1 ≤ х ≤ 1 булганда,
f(x) = )
[2, 1 < х < 6 булганда.
a) /(-1), Д6), Д1) не табыгыз.
б) у = f(x) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
017.42. у = f(x) функциясе бирелгән, биредә
-2x, -4 ≤ х < 0 булганда,
Д*) = 1 2 _ . _ _
-θx , θ < х < 3 булганда.
a) Д-4), /(0,5), ДЗ) не табыгыз.
б) у = f(x) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
017.43. у = f(x) функциясе бирелгән, биредә
f(x) =
-3x2, -1 ≤ х ≤ 0 булганда,
Vx, 0 < х ≤ 4 булганда.
а) ДО), /(2), /(4) не табыгыз.
б) у = f(x) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
017.44. у = f(x) функциясенең графигын төзегез, биредә
Дх) =
2x2, -2 ≤ х ≤ 0 булганда,
Зх + 2, х > 0 булганда.
График ярдәмендә табыгыз:
а) Д-2), ДО), Д1);
б) Дх) = 2, Дх) = 0, Дх) = 8 булганда, х ның кыйммәтләрен.
113
017.45. у = f(x) функциясенең графигын төзегез, биредә
-0,5x2, -4 ≤ х ≤ 0 булганда,
f(x) = r-
-\!х, 0 < х ≤ 4 булганда.
График ярдәмендә табыгыз:
а) Д-1), ЛО),
б) f(χ) = -2, f(x) = 0, /(х) = -8 булганда, х ның кыйм¬
мәтләрен.
Лх) =
017.46. у = f(x) функциясенең графигын төзегез, биредә
—∣x∣, -4 ≤ х ≤ 2 булганда,
0,5x2, 2 < х < 4 булганда.
График ярдәмендә табыгыз:
а) Л-2), /(2), /(4);
б) f(χ) = -1, f(x) = 2, f(x) = 4,5 булганда, х ның кыйм¬
мәтләрен.
17.47. A — [-1; 1] кисемтәсендә у - Зх2 функциясенең иң зур
кыйммәте, ә В — [-1; 1] кисемтәсендә у = х2 функ¬
циясенең иң зур кыйммәте булсын. А һәм В ны чагыш¬
тырыгыз. График сурәтен ясагыз.
17.48. С — [—1;0] кисемтәсендә у = 4x2 функциясенең иң зур
кыйммәте, ә D — [1; +∞) нурында у = 3 + х функциясенең
иң кечкенә кыйммәте булсын. С һәм D ны чагыштырыгыз.
График сурәтен ясагыз.
17.49. М — [2; 5] кисемтәсендә у = 2х функциясенең иң кечкенә
кыйммәте, ә N — (~°°; 0] нурында у = -5x2 функциясенең
иң зур кыйммәте булсын. М һәм N ны чагыштырыгыз.
График сурәтен ясагыз.
17.50. L — [0; +∞) нурында у = l,8x2 функциясенең иң кечкенә
кыйммәте, ә К — [-1; 0] кисемтәсендә у = -Зх + 1
функциясенең иң кечкенә кыйммәте булсын. L һәм К ны
чагыштырыгыз. График сурәтен ясагыз.
17.51. Р — [0; +∞) нурында у = -702x2 функциясенең иң зур
кыйммәте, ә Q — [-2; 1] кисемтәсендә у = х2 функциясенең
иң кечкенә кыйммәте булсын. Төзүләр үткәрмичә генә,
Р һәм Q ны чагыштырыгыз.
114
17.52. а) Бер үк координаталар системасында у = 0,5x2 парабо¬
ласын һәм у = х + 4 турысын төзегез.
б) Төзелгән функция графикларының кисешү нокталары
абсциссаларын һәм ординаталарын табыгыз.
в) Параболаның турыдан астарак яткан өлешен билгеләгез,
г) ) х ның кыйммәтләре нинди булганда, у = 0,5x2 пара¬
боласы у = х + 4 турысыннан аста урнаша?
17.53. а) Бер үк координаталар системасында у = 2x2 парабола¬
сын һәм у = -2х + 4 турысын төзегез.
б) Төзелгән функция графикларының кисешү нокталары
абсциссаларын һәм ординаталарын табыгыз.
в) Параболаның турыдан өстәрәк яткан өлешен билгеләгез,
г) х ның кыйммәтләре нинди булганда, у = 2x2 парабола¬
сы у = -2х + 4 турысыннан өстә урнаша?
17.54. а) у = -2x2 һәм у = 2х - 4 функцияләре графикларын
кулланып, х ның нинди кыйммәтләрендә турының пара¬
боладан астарак ятуын билгеләгез.
б) у = -х2 һәм у = 2х функцияләре графикларын кулланып,
х ның нинди кыйммәтләрендә турының параболадан
өстәрәк ятуын билгеләгез.
17.55. а) у = ⅛ х2 һәм у = х функцияләре графикларын кулла-
О
б) у = -х2 һәм у = 2х - 3 функцияләре графикларын кул¬
ланып, —х2 > 2х — 3 тигезсезлеген чишегез.
17.56. у = f(x) функциясе бирелгән, биредә f(x) = 2x2. Табыгыз:
а) /(-х); б) f(x2y, в) f(x3)∙, г) /(-х2).
17.57. у = f(x) функциясе бирелгән, биредә f(x) = l,5x2. Табыгыз:
а) /(х2); б) Д2х2); в) /(-х2); г) f(-2x2).
17.58. у = f(x) функциясе бирелгән, биредә f(x) = ~4x2. Табыгыз:
a) f(x2Y, б) f(2x2)∙, в) Д-Зх2); r) ∕(x3).
•17.59. у = f(x) функциясе бирелгән, биредә ∕(x) = х2. Аргументның
нинди кыйммәтләрендә ∕(x 4- 1) = Г(Х + 4) тигезлеге
үтәлә?
•17.60. у = /(х) функциясе бирелгән, биредә f(x) = 2х2.
Аргументның нинди кыйммәтләрендә 4∕(χ + 3) = f(2x) -
— 24 тигезлеге үтәлә?
115
•17.61. у = f(x) функциясе бирелгән, биредә f(x) = -х2. Аргу¬
ментның нинди кыйммәтләрендә f(x - 3) = f(x + 5)
тигезлеге үтәлә?
•17.62. у = f(x) функциясенең графигын төзегез, биредә
f(x) =
х + 3, -4 ≤ х ≤ -1 булганда,
2x2, -1 < х ≤ 1 булганда,
-х + 3, 1 < х ≤ 3 булганда.
График ярдәмендә билгеләгез, р ның нинди кыйммәтлә¬
рендә f(x) = р функциясе:
а) бер тамыр; в) өч тамыр;
б) ике тамыр; г) дүрт тамыр ала?
•17.63. у = f(x) функциясе бирелгән, биредә
/(*) =
-х - 4, -4 ≤ х ≤ -2 булганда,
-0,5x2, -2<x≤2 булганда,
-2, 2<x<3 булганда.
a) ∕r(-2), /(2), /(2,4) не табыгыз.
б) у = f(x) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
•17.64. у = f(x) функциясе бирелгән, биредә
Лх) =
-х2, -3 ≤ х ≤ -1 булганда,
-1, -1 < х < 0 булганда,
Vx, 0 < х ≤ 2 булганда.
a) f(-2,5), f(-0,5), ∕,(4), ∕(Vδ - з) не табыгыз.
б) у = f(x) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
•17.65. Функциянең графигын төзегез:
. 2x3 + 2x2
4 ’ = х + 1 ;
. 3x3 - Зх2
= х - 1 •
1 3 2 2
,. -0,5x3 + х2
6|’’ х-2 ;
х - ^χ
ч 3 3
г) и = -
’ i, х + 2
•17.66. Тигезләмәнең графигын төзегез:
а) (у - х)(у - х2) = 0;
в) (у - 3x2)(y - 5) = 0;
б) (-2x2 + y)(y + 1) = 0; г) (у - 4x2)(5x2 + у) = 0.
116
§ 18. у = у ФУНКЦИЯСЕ, АНЫҢ ҮЗЛЕКЛӘРЕ
ҺӘМ ГРАФИГЫ
18.1. Кире пропорциональлек коэффициентын әйтегез:
. 1. fa 2. . 1 . . 3
а) У = -> б) у = в) у = т)у=
А А ил А
18.2. Функциянең графигын төзегез һәм аның кайда кимегәнен,
кайда үскәнен күрсәтегез:
а) У = б) у = в) у = г)у=
18.3. Бер үк координатлар системасында бирелгән функциянең
графигын төзегез һәм төзелгән графикларның үзара
урнашуы турында нәтиҗә ясагыз:
а) У = | һәм у =
б) У = | һәм у =
2 2
В) у = - һәм у =
, з , з
Г) у = - һәм у =
k
18.4. у = — функциясенең графигы:
а) беренче һәм өченче чирекләрдә;
б) икенче һәм дүртенче чирекләрдә урнашырлык итеп,
k санын сайлап алыгыз.
2
18.5. у = — функциясенең графигын төзегез. График ярдәмендә
билгеләгез:
а) х = 1; —2; 4 булганда, у ның кыйммәтләрен;
б) у = -1; 2; -4 булганда, х ның кыйммәтләрен;
в) 2^ кисемтәсендә функциянең иң зур һәм иң кечке¬
нә кыйммәтләрен;
г) әгәр у ∈ [-2; -1] булса, х үзгәрешлесенең нинди ара¬
лыкларда урнашуын.
117
18.6. у = функциясенең графигын тезегез. График ярдә¬
мендә билгеләгез:
а) х = -3; 1; 6 булганда, у ның кыйммәтләрен;
б) у = 3; -1; -6 булганда, х ның кыйммәтләрен;
в) [-3; -1] кисемтәсендә функциянең иң зур һәм иң
кечкенә кыйммәтләрен;
г) әгәр у ∈ [-3; булса, х үзгәрешлесенең нинди ара¬
лыкларда урнашуын.
4
18.7. а) у = — функциясенең графигын төзегез,
х
б) х ның кыйммәтләре нинди булганда, функциянең
кыйммәте 2 гә тигез була?
в) Графикның у > 2 шартына туры килгән өлешен аерып
күрсәтегез. Бу шарт х ның нинди кыйммәтләре өчен
үтәлә?
г) у < 2 шарты х ның нинди кыйммәтләре өчен үтәлә?
18.8. а) у = — функциясенең графигын төзегез,
х
б) Аргументның кыйммәтләре нинди булганда, функ¬
циянең кыйммәте 1 гә тигез була.
в) х ның нинди кыйммәтләре өчен у > 1?
г) х ның нинди кыйммәтләре өчен у < 1?
18.9. Бу нокта у = — функциясенең графигында ятамы:
а)А(1;68); в) С(-2; 34);
б) В(5; 13); г) В(-4; -17)?
18.10. Графигы түбәндәге нокта аша үтүе билгеле булса, кире
пропорциональлек формуласын языгыз:
а) М(3; 7); в) Х(-4; 19);
б) М-0,2; 12); г) L(2,5; 8).
2
18.11. у = — функциясенең иң кечкенә һәм иң зур кыйммәт-
X
ләрен табыгыз:
а) [-2; -1] кисемтәсендә; в) (-∞j -1] нурында;
б) [1; 4) ярыминтервалында; г) (1; 2) интервалында.
118
18.12. у = функциясенең иң кечкенә һәм иң зур кыйммәт¬
ләрен табыгыз:
а) [-4; -2] кисемтәсендә; в) [2; +∞) нурында;
б) (1; 4) интервалында; г)(—4; -2] ярыминтервалында.
18.13. Функцияләр графикларының кисешү нокталарын табы¬
гыз:
2 3
а) у = — һәм у = 2х; в) у = —— һәм у = -Зх;
5 4
б) у = — һәм у - -5; г) у = — һәм у = 1.
X %
Тигезләмәне график юл белән чишегез:
018.14. а) - = 2; б) -- = 3 - х; в) - = -1; г) -- = 1 - х.
X X X X
018.15. a) = -≡5 б) 3 = |х|; в) ∣ = ≡; г) = |х|.
X Δ X х О X
018.16. а) - = х2; б) - = 7х; в) -- = 2х2; г) - = √x.
х х х х
Тигезләмәләр системасын график юл белән чишегез:
5
3
018.17. а)
У ~ х' в)
У = х’
у = -5;
у = -1;
4
3
б)
У х' г) -
у = —,
X
у = х + 3;
у = х + 4.
4
8
018.18. а)
У ~ х' в)
У = -»
х
У = о,5х2;
у = х2;
1
2
У - ~~,
У =
б)
х г) -
х
у =
у = 2√x.
График ысул ярдәмендә тигезләмәләр системасының
чишелешләре санын билгеләгез:
_ 2
1
018.19. а) \У ~ х’ в) <
У = “х’
2х - Зу - 6 = 0;
х - 5у = 0;
з
4
б) × Г)
У = -»
х
X - 2у - 2 = 0;
Зх - 4у + 12
119
2
018.20. у = — Һәм у = 0,5x функцияләренең графиклары ярдә¬
мендә:
а) х ның нинди кыйммәтләрендә турының гиперболадан
аста урнашуын билгеләгез;
2
6) 0,5х > — тигезсезлеген чишегез.
х
2
018.21. у = Һәм у = -2х функцияләренең графиклары ярдә¬
мендә;
а) х ның нинди кыйммәтләрендә турының гиперболадан
өстә урнашуын билгеләгез;
О 2
о) ~2х < — тигезсезлеген чишегез,
х
018.22. у = ⅛ функциясе бирелгән. Табыгыз:
a) ΛD, f(-2), /(0,3),
б) ∕(-α), ∕(-2a), ∕(3x), /(-х);
в) /(a + 1), f(b - 3), /(х + 1), /(х - 10);
г) Да) + 1, f(x) - 2, Лх - 2) + 1, f(x +7)-1.
018.23. у = f(x) функциясе бирелгән, биредә f(x) = . Табыгыз:
а) Л-D, Я-3), f (I), f (|);
б) Λ3a), Λ6a), Λ-2x), ∕f-∣x∖
\ О /
в) f(a - 2), ЛЬ + 4), Лх - 1), Лх + 2);
г) Лх) - 4, Λ2x) + 1, Лх -1) + 2, 2f(x + 3)-1.
018.24. у = f(x) функциясенең графигын төзегез, биредә
Λχ) =
2 1 й
—, х < -1 булганда,
х
2x2, -1 ≤ х < 1 булганда.
График ярдәмендә табыгыз:
а) Л-2), Л-D, Л1);
б) Лх) ~ 2, Лх) = о, Лх) = I булганда, х ның кыйммәтләрен.
Ci
120
018.25. у = f(x) функциясенең графигын төзегез, биредә
∕(x) =
4 1 -
—, х ≤ -1 булганда,
х
——x2, -1 < х < 1 булганда.
2
График ярдәмендә табыгыз:
а) Л-4), /(-1), /(1);
б) ∕(x) = -2, /(х) = 0, /(х) = булганда, х ның кыйм¬
мәтләрен.
з
18.26. A — у = — кисемтәсендә [1; 3] функциясенең иң зур
кыйммәте, ә В — у = х2 кисемтәсендә [-1; 1] функ¬
циясенең иң кечкенә кыйммәте булсын. А һәм В ны
чагыштырыгыз. График сурәтен ясагыз.
18.27. С — у = нурында [1; +∞) функциясенең иң кеч¬
кенә кыйммәте, ә D — у = 2x2 функциясенең [0; 1]
кисемтәсендә иң кечкенә кыйммәте булсын. С һәм D ны
чагыштырыгыз. График сурәтен ясагыз.
78
18.28. Р — у = — кисемтәсендә [1; 7] функциясенең иң зур
кыйммәте, ә Q — у = -103x2 функциясенең [-5; 4]
кисемтәсендә иң зур кыйммәте булсын ди. Төзүләр үт¬
кәрмичә генә, Р һәм Q ны чагыштырыгыз.
18.29. Түбәндәге шарт үтәлсә, У = ~ функциясенең графигын
кулланып, х үзгәрешлесе яткан аралыкны табыгыз:
a) 1 < у < 3; в) -2 < у < -1;
б) у < -2; г) у > 6.
4
18.30. у = f(x) функциясе бирелгән, биредә ∕r(x) = —. Табыгыз:
а)/(х2); б) |Дх3 4 * *); в) г) √(x8).
121
4
18.31. у = f(x) функциясе бирелгән, биредә f(x) = Табыгыз:
1 2
а) /2(х); б) 7⅛ в) /3(х); г) "7u)'
•18.32. Тигезсезлекне график юл белән чишегез:
4 4
а) — > 2х - 2; б) 0,5x - 1 > —.
х х
4
•18.33. у = f(x) функциясе бирелгән, биредә f(x) = —. Тигезлекне
исбатлагыз:
f(x + 1) - f(x - 1) = -∣ f(x + 1) ∙ f(x - 1).
з
• 18.34. у - f(x) функциясе бирелгән, биредә f(x) = —. Тигезлекне
исбатлагыз:
f(x + 2) + Д2 - х) = -4f(x2 - 4).
• 18.35. у = f(x) функциясе бирелгән, биредә f(x) = Аргументның
түбәндәге тигезлек үтәлә торган кыйммәтен табыгыз:
Дх + 3) = 2Дх + 5).
• 18.36. у = f(x) функциясе бирелгән, биредә
f(x) =
-iχ2, -3 ≤ х ≤ 0 булганда,
λ∕x, 0 < х < 4 булганда,
8 л r
—, х > 4 булганда.
х
a) Д-3), Д1), ∕(√33 - 1) не табыгыз.
б) у = Дх) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
•18.37. Функциянең графигын төзегез:
х - 3 -х +2
а) у = —;——5 в) у = ———;
w х2 - Зх х2 - 2х
1 _ 2
2х + 2. . _ 3* 3
$ - x2 + х’ Г х2 + 2х ’
•18.38. Тигезләмәнең графигын төзегез:
а) ху = 3; в) ху = 6;
б) (ху - 1) (у - 3) = 0; г) (ху - 2) (ху + 5) = 0.
122
§19. ӘГӘР у = f(x) ФУНКЦИЯСЕНЕҢ
ГРАФИГЫ БИЛГЕЛЕ БУЛСА,
у = f(x + /) ФУНКЦИЯСЕНЕҢ ГРАФИГЫН
НИЧЕК ТӨЗЕРГӘ
Бер үк координаталар системасында функциянең гра¬
фигын төзегез:
19.1.
а) у = х2 Һәм у = (х + I)2;
б) у = х2 һәм у = (х - З)2;
в) у = х2 Һәм у = (х - 2)2;
г) у = х2 Һәм у = (х + 4)2.
19.2.
а) У = v һәм у - Л
Л Л ut
1 , 1
6)ι∕ = һәм у - ,
Л Л Т Zj
. 1 . 1
в) у - һәм у - ,
Л л т о
. 1 , 1
г) У = һәм у - _.
х х - 5
19.3.
а) у = Vχ Һәм у = yJx + 2;
б) у = уГх Һәм у = √x - 1;
в) у = Vχ Һәм у = у!х + 4;
г) у = у/х һәм у = у/х - 2.
19.4.
а) у = |х| һәм у = х - 3|;
б) у = |х| Һәм у = х + 5;
в) у = |х| Һәм у = |х + 1|;
г) у = |х| һәм у = |х - 4|.
19.5. Нинди функциянең графигы килеп чыгар, әгәр:
а) у = Зх2 параболасын Ох күчәре буйлап 4 берәмлеккә
сулга күчерсәк;
7
б) у = гиперболасын Ох күчәре буйлап 3 берәмлеккә
уңга күчерсәк;
в) у = Vx функциясенең графигын Ох күчәре буйлап
2 берәмлеккә уңга күчерсәк;
г) у = |х| функциясенең графигын Ох күчәре буйлап
1 берәмлеккә сулга күчерсәк?
19.6. Нинди функциянең графигы килеп чыгар, әгәр:
а) у = ~ х2 параболасын Ох күчәре буйлап 0,5 берәмлеккә
О
уңга күчерсәк;
2
б) у = — гиперболасын Ох күчәре буйлап 3 берәмлеккә
сулга күчерсәк;
в) у = —|х| функциясенең графигын Ох күчәре буйлап
4 берәмлеккә уңга күчерсәк;
г) у = -у/х функциясенең графигын Ох күчәре буйлап
1,5 берәмлеккә сулга күчерсәк?
123
Функциянең графигын төзегез һәм аның кайда кимегәнен,
кайда үскәнен күрсәтегез:
19.7. а) у = 2(x + I)2; в) у = 3(х - 5)2;
б) у = - (х - З)2; г) у = -4(x + 2)2.
lβ.8. а) „ . _А_; 6)i,= -⅛ .),= ⅛ r)i, = -7li.
19.9. а) у = Vx - 3; б) у - -Vx + 4; в) у - >∕x - 1; г) у = -Vx - 2.
19.10. а) у = |х + 3|;
в) у = |х - 2|;
б) у = -|х - 4|;
г) у = -|х + 1|.
019.11. а) 24 рәсемдә;
в) 26 рәсемдә;
б) 25 рәсемдә;
г) 27 рәсемдә сурәтләнгән
у = a(x + Z)2 параболасының тигезләмәсен языгыз.
124
ol9.12. a) 28 рәсемдә; в) 30 рәсемдә;
б) 29 рәсемдә; г) 31 рәсемдә сурәтләнгән
у = ~∙Jx + I яки у = -√χ + I функциясен күрсәтегез.
019.13. а) 32 рәсемдә;
б) 33 рәсемдә;
в) 34 рәсемдә;
г) 35 рәсемдә сурәтләнгән
у = ; гиперболасының тигезләмәсен языгыз.
Рәс. 32
Рәс. 33
125
019.14. Графигы
a) 36 рәсемдә; в) 38 рәсемдә;
б) 37 рәсемдә; г) 39 рәсемдә сурәтләнгән
126
019.15. у = 2(x - 1)2 функциясенең иң кечкенә һәм иң зур кыйм¬
мәтләрен табыгыз:
а) [0; 2] кисемтәсендә; в) [0; +∞) нурында;
б) (—°°; 1] нурында; г) [1; 2] кисемтәсендә.
019.16. у = -5(x + 4)2 функциясенең иң кечкенә һәм иң зур кыйм¬
мәтләрен табыгыз:
а) [-5; -3] кисемтәсендә; в) (-5; -3) интервалында;
б) [-4; +∞) нурында; г) (-°°; 0] нурында.
019.17. у = —-— функциясенең иң кечкенә һәм иң зур кыйм-
х - 3
мәтләрен табыгыз:
а) [4; 7] кисемтәсендә; в) [4; +∞) нурында;
б) (—°°; 1] нурында; г) (3; 7] ярыминтервалында.
2
019.18. у = ~ x + 2 Функциясенең иң кечкенә һәм иң зур кыйм¬
мәтләрен табыгыз:
а) [-4; -3] кисемтәсендә; в) (-2; 0] ярыминтервалында;
б) [2; +∞) нурында; г) [-1; 0] кисемтәсендә.
019.19. у = \х + 4 функциясенең иң кечкенә һәм иң зур кыйм¬
мәтләрен табыгыз:
а) [-3; 0] кисемтәсендә; б) [5; +∞) нурында.
019.20. у = -√x - 1 функциясенең иң кечкенә һәм иң зур кыйм¬
мәтләрен табыгыз:
а) [2; 5] кисемтәсендә; б) [1; 4) ярыминтервалында.
019.21. у = |х + 2| функциясенең иң кечкенә һәм иң зур кыйм¬
мәтләрен табыгыз:
а) [-2; 0] кисемтәсендә; в) (-°°; 3] нурында;
б) [-3; +∞) нурында; г) [1; 4] кисемтәсендә.
019.22. у = 2(x - I)2 функциясенең графигын төзегез.
а) х = -1; 0; 1 булганда, у ның кыйммәтләрен табыгыз.
б) у = 2; 8; 0 булганда, х ның кыйммәтләрен табыгыз.
в) Функциянең үсү һәм кимү аралыкларын күрсәтегез.
г) Параболаның симметрия күчәре тигезләмәсен языгыз.
127
019.23. у = -∣ (х + 2)2 функциясенең графигын төзегез.
а) х = -2; 0; 2 булганда, у ның кыйммәтләрен табыгыз.
б) у = 0; -1; -4 булганда, х ның кыйммәтләрен табыгыз,
в) Функциянең үсү һәм кимү аралыкларын күрсәтегез,
г) Параболаның симметрия күчәре тигезләмәсен языгыз.
019.24. у =
функциясенең графигын төзегез.
а) х = -2; 0; 2 булганда, у ның кыйммәтләрен табыгыз.
б) у = 6; -1; -6 булганда, х ның кыйммәтләрен табыгыз.
в) Функцияне монотонлыкка тикшерегез.
г) Гиперболаның асимптоталары тигезләмәләрен языгыз.
019.25. у = 6 функциясенең графигын төзегез.
х - 2
а) х = -1; 0; 3 булганда, у ның кыйммәтләрен табыгыз.
б) у = 3; -1; -2 булганда, х ның кыйммәтләрен табыгыз.
в) Функцияне монотонлыкка тикшерегез.
г) Гиперболаның асимптоталары тигезләмәләрен языгыз.
019.26. у = \/х + 4 функциясенең графигы ярдәмендә табыгыз:
а) х = -4; 0; 5 булганда, у ның кыйммәтләрен;
б) у = 1; 0; 3 булганда, х ның кыйммәтләрен;
в) [-3; 0] кисемтәсендә функциянең иң кечкенә һәм иң
зур кыйммәтләрен;
г) аргументның 0 < у < 3 шартын канәгатьләндерә торган
кыйммәтләрен.
019.27. у = |х + 1| функциясенең графигын төзегез. График
ярдәмендә табыгыз:
а) х = -1; 0; 4 булганда, у ның кыйммәтләрен;
б) у = 1; 0; 5 булганда, х ның кыйммәтләрен;
в) функциянең үсү һәм кимү аралыкларын;
г) аргументның у ≤ 1 шартын канәгатьләндерә торган
кыйммәтләрен.
019.28. у = |х - 2| функциясенең графигын төзегез. График
ярдәмендә табыгыз:
а) х = -3; 0; 1 булганда, у ның кыйммәтләрен;
б) у = 1; 0; 4 булганда, х ның кыйммәтләрен;
в) функциянең үсү һәм кимү аралыкларын;
г) аргументның у > 2 шартын канәгатьләндерә торган
кыйммәтләрен.
128
Тигезләмәне график юл белән чишегез:
019.29.
а) (х - 2)2 * = х;
в) (х - 2)2 = -х;
б) (х + 3)2 = 1;
г) (х + 5)2 = 4.
019.30.
a) 2(x - I)2 = 2х + 2;
в) -(x + 2)2 = х;
б) -4(x + З)2 = -х;
г) 2(x - 2)2 = 8.
019.31.
а) = 2;
W
1
н
1 co
ьэ
II
2
б) x÷l =Х!
1
н
| 00
оо
II
→
1
н
019.32.
а) х - 1 "
в) |х| = ;
х + 2
б) = √x +1;
7 х - 2
г) √x = ■ 4 .
’ х - 2
у = /(х) функциясе бирелгән, биредә
019.33.
019.34.
-х, -2 ≤
∕(x)= 2
3(x - З)2,
a) /(-1); /(2); /(4)
х < 2 булганда,
2 < х ≤ 4 булганда,
не табыгыз.
б) у - f(x) функциясенең графигын төзегез,
в) Функциянең үзлекләрен санап чыгыгыз.
у = f(x) функциясе бирелгән, биредә
2
f(χ) = < х + 1 ’
-3 ≤ х < -1 булганда,
-х2, -1 < х ≤ 2 булганда.
а) /(-1,5); /(-1); /(2) не табыгыз.
б) у = /(х) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
19.35.
Функциянең графигын
а) у = х2 - 2x + 1;
б) у = х2 + 4х + 4;
төзегез:
в) у = х2 + Юх + 25;
г) у = х2 - 6х + 9.
19.36. а) у = -х2 + 8х - 16;
б) у = 14х - х2 - 49;
19.37. а) у = Зх2 + 24х + 48;
б) у = 2x2 - 20х + 50;
в) у = -х2 + 12х - 36;
г) у =■ 4х - х2 - 4.
в) у = 20x - 2x2 - 50;
г) у = 4x2 + 56х + 196.
129
Функциянең графигын
төзегез:
19.38.
а) у = >J(χ ~ 4)2;
в) y = √(x-l)2j
б) I/ = √(x + 6)2;
г) у = ∕(x + I)2.
19.39.
а) у = y∣x2 - 2x + 1;
в) у = y∣x2 + 4х + 4;
б) у = 7х2 + Юх + 25;
г) у = y[x2 - 6х + 9.
19.40.
у = √x2 + 2x + 1 функциясенең иң кечкенә һәм иң зур
кыйммәтләрен табыгыз:
а) [-2; 2] кисемтәсендә; в) (-∞j 3] нурында;
б) [0; +∞) нурында; г) [-5; 0] кисемтәсендә.
19.41.
у = y∣x2 - Юх + 25 функциясенең иң кечкенә һәм иң зур
кыйммәтләрен табыгыз:
а) [4; 7] кисемтәсендә; в) [2; +∞) нурында;
б) (—°°; 5] нурында; г) [-1; 6) ярыминтервалында.
19.42.
А —[-5; -3] кисемтәсендә
у = -3(x + 4)2 функциясенең иң
3
зур кыйммәте, ә В — [1; +∞) нурында у = — функциясенең
х
иң зур кыйммәте булсын. Кайсы зуррак: А мы, әллә В
мы? График сурәтен ясагыз.
19.43. М — [-4; -2] кисемтәсендә у = 5(x + З)2 функциясенең иң
кечкенә кыйммәте, ә N — [0; 1] кисемтәсендә у - 2х + 3
функциясенең иң зур кыйммәте булсын. Кайсы зуррак:
М мы, әллә N мы? График сурәтен ясагыз.
19.44. К — (-°°; -3] нурында у = функциясенең иң
X + Δ
зур кыйммәте, ә L — (-°°; 1] нурында у = -Зх + 2
функциясенең иң кечкенә кыйммәте булсын. Кайсы
зуррак: L мы, әллә К мы? График сурәтен ясагыз.
19.45. Р — [-6; -4] кисемтәсендә у = -(x + 5)2 функциясенең
иң зур кыйммәте, ә Q — [0; 2] кисемтәсендә
у = -2(x - I)2 функциясенең иң зур кыйммәте булсын. Р
һәм Q ны чагыштырыгыз. График сурәтен ясагыз.
19.46. Тигезләмәне график юл белән чишегез:
а) | х - 2| = х2; в) |х — 3∣ = √x - 1;
б) | х + 1| = -2х2; г) |х + 5| = -х - 1.
130
Тигезләмәне график юл белән чишегез:
19.47.
a) 7⅜γ = -0,5(x + I)2;
б) -Ц = 2(x - З)2;
в) -⅛τ = -4(χ + З)2;
X + о
Г) ⅛ =-5(x-D2.
19.48.
a) y∣x + 3 = -1 - х;
в) у/х - 1 = 3 - х;
б) λ∕x - 2 = х - 4;
г) √x + 4 = х + 2.
19.49.
а) (х - I)2 = |х - 3|;
в) (х + I)2 =
б) √x + 2 = ——;
х - 1
г) ∣x + 1∣ = √x + 3.
•19.50.
a) λ∕x2 - 4x + 4 = -2(х - 2)2;
в) yjx2 + 6х + 9 = (х + З)2;
б) √x2 - 2x + 1 =
г) y∣x2 + 4х + 4 = -х.
Тигезләмәләр системасын график юл белән чишегез:
У = (х - 2)2,
у = -(X + I)2,
19.51. а)
в)
У = Х-,
у = х - 1;
У = 2(x + I)2,
[у = -(x-3)2,
б)
г)
У = Зх;
[у = х - 5.
у = '∣χ - з.
у = √x + 4,
•19.52. а)
в)
У = (X - З)2;
у = -2х + 2;
У = (х - 2)2,
у = 0,5(x + I)2,
61
у - Vx2 - 8х + 16;
у = √x2 + 2x + 1.
19.53. Тигезләмәләр системасының ничә чишелеше бар:
1
.4
У х-2’
У = о’
а)
в)
х + 2
X
y ~ 3’
|у = -2х - 1;
б)
_ 2
У х + 3’ г)
4
У ~ х - 2’
[х-у = 7;
х + у = 2?
131
•19.54. Тигезләмәләр системасының ничә чишелеше бар:
. \у = —⅛ \у = 2(χ -1)2,
а) х - 3 б) s r
ι∕=∣x + 2∣j b∕ = √x + 27
•19.55. а) у = 2х - 2 һәм у = —функцияләренең график-
X
лары буенча билгеләгез, х ның нинди кыйммәтләрендә
б) у = λ∕x + 1 һәм у = х - 1 функцияләренең графиклары
буенча билгеләгез, х ның нинди кыйммәтләрендә
x>∕x + 1 ≤ х - 1.
19.56. у = f(χ) функциясенең графигын төзегез, биредә
l-2x - 2, -3 ≤ х ≤ 1 булганда,
f(x) = I I—
[√x + 1, 1 < х < 5 булганда.
Функциянең графигы ярдәмендә табыгыз:
a) f(-2,8), /(3,84), /(0);
б) х ның нинди кыйммәтләрендә /(х) = 0, ∕(x) = 2, /(х) = 4.
•19.57.
у = /(х) функциясе бирелгән, биредә
|>/х + 3, -3 ≤ х ≤ 1 булганда,
∕(x) = 1
∣2(x - I)2, 1 < х < 3 булганда.
а) у = /(х) функциясенең графигын төзегез.
б) р ның нинди кыйммәтләрендә /(х) = р тигезләмәсенең
бер тамыры, ике тамыры була?
•19.58. Функциянең графигын төзегез:
а) у = ү(х - 2)2; в) у = ^-γ(x ~ З)2;
§20. ӘГӘР у = /(х) ФУНКЦИЯСЕНЕҢ
ГРАФИГЫ БИЛГЕЛЕ БУЛСА,
у = /(х) + т ФУНКЦИЯСЕНЕҢ ГРАФИГЫН
НИЧЕК ТӨЗЕРГӘ
20.1. Бер үк координатлар системасында функцияләрнең гра¬
фигын төзегез:
а) у - х2 һәм у = х2 + 2; в) у = х2 һәм у = х2 + 5;
б) у = х2 һәм у = х2 - 1; г) у = х2 һәм у = х2 - 3.
132
Бер үк координаталар системасында функцияләрнең
графигын төзегез:
20.2. а) у = — Һәм у = — +2; в) у = - Һәм у = - - 4;
х х х i, х ’
б) у = — һәм у = - - 3; г) у = - һәм у = — +1.
х я х х i, х
20.3. а) у = ~j^χ Һәм у = - 2; в) у = Vx һәм у = Vx - 4;
б) у = ∙Jχ Һәм у = 4х +3; г) у = 4х һәм у - Jx + 1.
20.4. а) у - |х| Һәм у = ∣x∣ + 1; в) у = |х| һәм у = |х| - 2;
б) у = |х| һәм у = |х| - 3; г) у = |х| һәм у = |х| + 2.
20.5. Нинди функциянең графигы килеп чыгар, әгәр:
а) у = 2x2 параболасын Оу күчәре буйлап 3 берәмлеккә
өскә күчерсәк;
9
б) у = — гиперболасын Оу күчәре буйлап 1 берәмлеккә
аска күчерсәк;
в) у = \Гх функциясенең графигын Оу күчәре буйлап
2 берәмлеккә аска күчерсәк;
г) у = | х| функциясенең графигын Оу күчәре буйлап
4 берәмлеккә өскә күчерсәк?
20.6. Нинди функциянең графигы килеп чыгар, әгәр:
a) у = -0,5x2 параболасын Оу күчәре буйлап 1 берәмлеккә
аска күчерсәк;
б) у = -8 гиперболасын Оу күчәре буйлап 4 берәмлеккә
өскә күчерсәк;
в) у = —7х функциясенең графигын Оу күчәре буйлап
3 берәмлеккә өскә күчерсәк;
г) у = —|х| функциясенең графигын Оу күчәре буйлап
2 берәмлеккә аска күчерсәк?
Функциянең графигын төзегез:
20.7. а) у = 2x2 + 3;
б) у = -х2 - 4;
в) у = 4x2 - 5;
г) у = —Зх2 + 2.
20.8. а) у = | х| + 4; в) у = | х| - 2;
б) у = —|х| - 1; г) у = -1 х| + 3.
133
Функциянең графигын төзегез:
20.9.
а) у = Vx + 5;
б) у = -Vx - 3;
в) у = √x - 2;
г) у = -л/х + 4.
20.10. а) у = | +4;
6)ι∕= - 1;
в) у = | - 3;
Г) У = + 3.
o20.ll. а) 40 рәсемдә;
б) 41 рәсемдә;
в) 42 рәсемдә;
г) 43 рәсемдә сурәтләнгән
у = ах2 + т параболасының тигезләмәсен языгыз.
Рәс. 41
У,
1
L
X
-2,
-4
Рәс. 42
Рәс. 43
134
θ20.12. a) 44 рәсемдә; б) 45 рәсемдә; в) 46 рәсемдә; г) 47 рәсемдә
⅛ . ,
сурәтләнгән у = — + т гиперболасының, тигезләмәсен
языгыз.
o20.13. а) 48 рәсемдә; б) 49 рәсемдә; в) 50 рәсемдә; г) 51 рәсемдә
135
θ20.14. a) 52 рәсемдә;
б) 53 рәсемдә;
в) 54 рәсемдә;
г) 55 рәсемдә сурәтләнгән
функция графигының тигезләмәсен языгыз.
o20.15. у = 2x2 - 5 функциясенең иң кечкенә һәм иң зур кыйм¬
мәтләрен табыгыз:
а) [-1; 1] кисемтәсендә; в) [-2; 1] кисемтәсендә;
б) [0; +∞) нурында; г) (-«>; 2] нурында.
136
2
θ20.16. и = — - 2 функциясенең иң кечкенә һәм иң зур кыйм-
х
мәтләрен табыгыз:
a) [1; 2] кисемтәсендә; в) [-2; -0,5] кисемтәсендә;
б) (-∞5 -1] нурында; г) [2; 5) ярыминтервалында.
020.17. у = -Зх2 + 4 функциясенең иң кечкенә һәм иң зур кыйм¬
мәтләрен табыгыз:
а) [-1; 1] кисемтәсендә; в)(-3; 1) интервалында;
б) (-2; +∞) ачык нурында; г) [-1; 0] кисемтәсендә.
020.18. у = + 1 функциясенең иң кечкенә һәм иң зур кыйм¬
мәтләрен табыгыз:
a) [1; 3] кисемтәсендә; в) (-∞j -1] нурында;
б) [1; +∞) нурында; г) [-4; -2] кисемтәсендә.
o20.19. у = Vx - 2 функциясенең иң кечкенә һәм иң зур кыйм¬
мәтләрен табыгыз:
a) [1; 4] кисемтәсендә; в) [4; 9] кисемтәсендә;
б) [4; +∞) нурында; г) [1; +∞) нурында.
θ20.20. у = -у/х + 1 функциясенең иң кечкенә һәм иң зур кыйм¬
мәтләрен табыгыз:
а) [0; 1] кисемтәсендә; в) [1; 9] кисемтәсендә;
б) (1; 9] ярыминтервалында; г) [4; 9) ярыминтервалында.
020.21. у = |х| - 4 функциясенең иң кечкенә һәм иң зур кыйм¬
мәтләрен табыгыз:
а) [2; 6] кисемтәсендә; в) (-∞j 0] нурында;
б) [-1; +∞) нурында; г) [-4; 5] кисемтәсендә.
020.22. у = -|х| + 2 функциясенең иң кечкенә һәм иң зур кыйм¬
мәтләрен табыгыз:
а) [-2; -1] кисемтәсендә; в) [-1; 2] кисемтәсендә;
б) [-3; 1) ярыминтервалында; г) (-<»; 1] нурында.
020.23. у = 0,5x2 - 2 функциясенең графигы ярдәмендә табыгыз:
а) х = -1; 0; 2 булганда, функциянең кыйммәтләрен;
б) у = 0; у = -2; у = 6 булганда, аргументның кыйм¬
мәтләрен;
в) функциянең иң кечкенә кыйммәтен;
г) аргументның у < 0; у > 0 булгандагы кыйммәтләрен.
137
θ20.24. у = —x2 + 9 функциясенең графигы ярдәмендә табыгыз:
а) х = -3; 0; 1 булганда, функциянең кыйммәтен;
б) у = 9; у = 5; у = 0 булганда, аргументның кыйммәтләрен;
в) функциянең иң зур кыйммәтен;
г) аргументның у > 0, у < 0 булгандагы кыйммәтләрен.
020.25. у = —Ух + 2 функциясенең графигы ярдәмендә табыгыз:
а) х = 0; 1; 9 булганда, функциянең кыйммәтен;
б) у = 1; у = 0; у = -2 булганда, аргументның кыйммәтләрен;
в) функциянең кыйммәтләре күплеген;
г) аргументның у > 0, у < 0 булгандагы кыйммәтләрен.
020.26. у = √x - 1 функциясенең графигы ярдәмендә табыгыз:
а) х = 0; 1; 4 булганда, функциянең кыйммәтен;
б) у = -1; у = 0; у = 1 булганда, аргументның кыйммәтләрен;
в) функциянең кыйммәтләре күплеген;
г) аргументның у < 0, у > 0 булгандагы кыйммәтләрен.
4
o20.27. у = — + 2 функциясенең графигы ярдәмендә табыгыз:
а) х = -4; -2; 1 булганда, функциянең кыйммәтен;
б) у = 3; 0; -2 булганда, аргументның кыйммәтен;
в) у < 0, у > 0 булганда, аргументның кыйммәтләрен;
г) функция графигының асимптоталары тигезләмәләрен.
020.28. у = - 3 функциясенең графигы ярдәмендә табыгыз:
а) х = -3; 2; 6 булганда, функциянең кыйммәтен;
б) у = 0; —1; 3 булганда, аргументның кыйммәтен;
в) у > 0, у < 0 булганда, аргументның кыйммәтләрен;
г) функция графигының асимптоталары тигезләмәләрен.
020.29. у = ∣x∣ - 1 функциясенең графигын төзегез. График
ярдәмендә табыгыз:
а) х = 0; -2; 3 булганда, у ның кыйммәтен;
б) у = 3; 0; -2 булганда, х ның кыйммәтләрен;
в) у < 0, у > 0 булганда, х ның кыйммәтләрен;
г) функциянең иң кечкенә кыйммәтен.
o20.30. у = -|х| + 3 функциясенең графигын төзегез. График
ярдәмендә табыгыз:
а) х = -4; 0; 1 булганда, у ның кыйммәтен;
б) у = 3; 0; -2 булганда, х ның кыйммәтләрен;
в) у > 0, у < 0 булганда, х ның кыйммәтләрен;
г) функциянең иң зур кыйммәтен.
138
Тигезләмәне график юл белән чишегез:
020.31. а) х* 2 * * + 1 =
X
б) — - 5 = -х;
х
o20.32. a) -√x + 4 = Зх2;
б) |х| - 3 =
В) X2 + 1 =
X
г) - - 2 = х.
X
в) 7х - 1 = —;
х
г) -∣x∣ + 2 = 0,5(x - 2)2.
/(х) =
o20.33. у = /(х) функциясе бирелгән, биредә
-х2 + 2, -2 ≤ х ≤ 1 булганда,
х, 1 < х ≤ 4 булганда.
а) /(-1,5); /(1); Д4) не табыгыз.
б) у - Дх) функциянең графигын төзегез.
в) График буенча х ның нинди кыйммәтләрендә /(х) = 2,
∕(x) = 1, /(х) = -2 икәнлеген билгеләгез.
020.34. у - f(x) функциясе бирелгән, биредә
Дх) =
-3x2 + 2, -1 ≤ х ≤ 1 булганда,
з
—, 1 < х ≤ 3 булганда.
a) /(-1); ∕f∣J5 ДЗ) не табыгыз.
б) у = Дх) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
20.35. А — [1; 3] кисемтәсендә у = — - 2 функциясенең иң зур
кыйммәте, ә В — [-4; 3] нурында у = 1 - х функциясенең
иң кечкенә кыйммәте булсын. А һәм В ны чагыштырыгыз.
График сурәтен ясагыз.
2
20.36. К — (~°°; -1] нурында у = - 1 функциясенең иң
зур кыйммәте, ә L — [3; 5] кисемтәсендә у = (х - 4)2
функциясенең иң кечкенә кыйммәте булсын. L һәм К ны
чагыштырыгыз. График сурәтен ясагыз.
139
Тигезләмәне график юл белән чишегез:
20.37. .>!" * 3'2 - 2’ в) ? = ~2χ2 + 3∙
I» - 1; [у - 3;
б)
У = - + 1- .
X г)
ci
1
τr∣ Н
1
II
У = 3;
У = -1∙
20.38. а)
4≡
II
Н 1 rs□
н-*
W
у = -х2 - 2,
у + 5х - 1 = 0;
5х - Зу = 0;
y = -- + ι>
у = 0,5x2 - 3,
б)
х г)
у = -уГх - 1;
у = √x + 3.
20.39. у = f(x) функциясе бирелгән, биредә
1, -4 < х ≤ -2 булганда,
_ -0,5x2 + 3, -2 < х < 2 булганда,
—, 2 < х < 4 булганда,
а) /(-2); ДО); Д4) не табыгыз.
б) у = Дх) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
•20.40. у = Дх) функциясе бирелгән, биредә
Дх) =
2, -5 ≤ х ≤ -3 булганда,
∣χ∣ - 1, -3 < х < 1 булганда,
л/х-1, 1 ≤ х ≤ 5 булганда.
а) Д-5); Д1); f(— + 11 не табыгыз.
I 4 )
б) г/ = Дх) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
•20.41. Функциянең графигын төзегез:
а) у = √≡χ - 1; б) у = -7=x + 1.
140
•20.42. а) у = -x2 + 4 һәм у = х + 2 функцияләренең графикларын
кулланып, х + 2 ≤ -х2 + 4 тигезсезлеген чишегез.
б) у = х2 - 2 һәм у = -|х| + 4 функцияләренең графикларын
кулланып, х2 - 2 < -|х| + 4 тигезсезлеген чишегез.
§21. ӘГӘР у = f(x) ФУНКЦИЯСЕНЕҢ
ГРАФИГЫ БИЛГЕЛЕ БУЛСА,
y=f(x+∣) +т ФУНКЦИЯСЕНЕҢ ГРАФИГЫН
НИЧЕК ТӨЗЕРГӘ
Бер үк координаталар системасында функцияләрнең
графигын төзегез:
21.1. а) у = х2 һәм у = (х + 2)2 + 1;
б) у = х2 Һәм у = (х - З)2 + 2;
в) у = х2 Һәм у = (х + 5)2 - 4;
г) У - X2 Һәм
у = (х - 6)2 - 3.
21.2.
а) у = 1
X
һәм
У=-^- -4;
y х + 2
б) у = 1
X
һәм
1 Q.
у - —7 - 3;
y х - 1
В) у = 1
X
һәм
1 -L Q.
у = . + 3
i, х - 5
г) у = 1
X
һәм
y=χ1+2 ÷1∙
21.3. а) у = 2χ2 һәм у = 2(x - 2)2 - 2;
б) У = ҺӘМ у _ + 2;
х t, х - 2
в) y = ~~2χ2 һәм у = -2(x + 2)2 + 2;
г) У = I һәм у = —Ц - 2.
x y х + 2
021.4. a)y= √J һәм у= _ 1.
б) y = "|х| һәм у = -|х - 1| + 4;
В) У - һәм у _ _JX + 1 + 2;
r)jZ = 1*1 һәм у = ∣x + 2| - 1.
141
o21.5. Нинди функциянең графигы килеп чыгар, әгәр:
а) у = 2,5x2 параболасын 3 берәмлеккә сулга һәм
4 берәмлеккә аска күчерсәк;
4
б) у = гиперболасын 2 берәмлеккә уңга һәм
1 берәмлеккә өскә күчерсәк;
в) у = 4х функциясенең графигын 1 берәмлеккә сулга
һәм 2 берәмлеккә өскә күчерсәк;
г) у = |х| функциясенең графигын 3 берәмлеккә уңга һәм
1 берәмлеккә аска күчерсәк?
o21.6. Нинди функциянең графигы килеп чыгар, әгәр:
а) у = -|х2 параболасын 2 берәмлеккә уңга һәм
О
3 берәмлеккә өскә күчерсәк;
3
б) у - — гиперболасын 1 берәмлеккә сулга һәм
2 берәмлеккә аска күчерсәк;
в) у = -y[χ функциясенең графигын 4 берәмлеккә сулга
һәм 2 берәмлеккә аска күчерсәк;
г) у = —|х| функциясенең графигын 6 берәмлеккә уңга һәм
3 берәмлеккә өскә күчерсәк?
021.7.
Функциянең графигын төзегез:
а) у = (х + I)2 - 2;
б) у = -(х + 3)2 + 1;
в) у = — (х - 4)2 + 3;
г) у = (х - 2)2 - 5.
021.8.
а) у = 2(x + 5)2 - 3;
в) У = -4(x - 2)2 - 1;
б) у = -3(x - I)2 + 4;
г) у = 0,5(x + 4)2 + 1
021.9.
а) </ - +2;
X + ә
≡^=xt4-15
б) У - r ч + 4;
X о
r^=-χ-l -1∙
o21.10.
а) у = + 2;
в) у = - 4 - 1;
х -1
х - 5
б) У - x + 3 4;
г) у = + 3.
’ y х + 3
142
o21.ll. а) у = √x + 1 + 2; в) у = √x - 1 - 1;
б) у = |х + 3| - 4; г) у = |х - 2| + 3.
021.12. а) 56 рәсемдә; в) 58 рәсемдә;
Рас. 58 Рэе. 59
143
o21.13. a) 60 рәсемдә; б) 61 рәсемдә; в) 62 рәсемдә; г) 63 рәсемдә
⅛
сурәтләнгән у = —+ l + т гиперболасының тигезләмәсен
языгыз.
o21.14. a) 64 рәсемдә; б) 65 рәсемдә; в) 66 рәсемдә; г) 67 рәсемдә
144
021.15. у = 2(x - 1)2 + 3 функциясенең иң кечкенә һәм иң зур
кыйммәтләрен табыгыз:
а) [0; 1] кисемтәсендә; в) [1; 2] кисемтәсендә;
б) [1; +∞) нурында; г) (-∞j 0] нурында.
Q
021.16. υ = - - 3 функциясенең иң кечкенә һәм иң зур
х + 1
кыйммәтләрен табыгыз:
а) [0; 2] кисемтәсендә; в) [2; 5] кисемтәсендә;
б) [0; +∞) нурында; г) (-°°; -2] нурында.
021.17. у = y∣x + 2 - 3 функциясенең иң кечкенә һәм иң зур
кыйммәтләрен табыгыз:
а) [-2; 2] кисемтәсендә; в)[23; 34) ярыминтервалында;
б) (0; 1) интервалында; г) [3; +∞) нурында.
o21.18. у = -(x - З)2 + 4 функциясенең графигы ярдәмендә:
а) у = 0, у > 0, у < 0 булганда, аргументның кыйммәтләрен
табыгыз;
б) функциянең үсү һәм кимү аралыкларын билгеләгез;
в) функциянең иң кечкенә кыйммәтен күрсәтегез;
г) параболаның симметрия күчәре тигезләмәсен языгыз.
021.19. у = —- 1 функциясенең графигы ярдәмендә:
х + 2
а) у = 0, у > 0, у < 0 булганда, аргументның кыйммәтләрен
табыгыз;
б) функциянең үсү аралыкларын билгеләгез;
в) гиперболаның симметрия үзәген күрсәтегез;
г) гиперболаның асимптоталары тигезләмәләрен языгыз.
o21.20. у - >∣x + 1 - 2 функциясенең графигы ярдәмендә табыгыз:
а) функциянең билгеләнү өлкәсен;
б) функциянең кыйммәтләре күплеген;
в) графикның координата күчәрләре белән кисешү нокта¬
лары координаталарын;
г) аргументның у > 0, у < 0 булгандагы кыйммәтләрен.
145
o21.21. у = ∣x - 2∣ - 3 функциясенең графигын төзегез. График
ярдәмендә табыгыз:
а) функциянең иң кечкенә кыйммәтен;
б) функциянең үсү һәм кимү аралыкларын;
в) у = 0, у > 0, у <0 булганда, х ның кыйммәтләрен;
г) функциянең кыйммәтләре күплеген.
021.22. у = 5 - |х + 2| функциясенең графигын төзегез. График
ярдәмендә табыгыз:
а) функциянең иң зур кыйммәтен;
б) функциянең үсү һәм кимү аралыкларын;
в) у = 0, у > 0, у < 0 булганда, х ның кыйммәтләрен;
г) функциянең кыйммәтләре күплеген.
o21.23. у = f(x) функциясе бирелгән, биредә
∣-3(x + 2)2 - 1, -3 < х < -1 булганда,
f(x) = 1
[4x, -1 < х ≤ 1 булганда.
у = f(x) функциясенең графигын төзегез һәм р ның нинди
кыйммәтләрендә /(х) = р тигезләмәсенең
а) бер тамыры; в) өч тамыры булуын;
б) ике тамыры; г) тамырлары булмавын билгеләгез.
021.24.
у = /(*)
Дх) =
функциясе бирелгән, биредә
2
+ 2, х < -1 булганда,
-2х - 2, х ≥ -1 булганда.
а) /(-2); /(-1); /(0,25) не табыгыз.
б) у = /(х) функциясенең графигын төзегез.
в) ) График буенча х ның нинди кыйммәтләрендә /(х) =1,
/(х) = 0, /(х) = -2 икәнлеген билгеләгез.
21.25. у = /(х) функциясенең графигын төзегез һәм укыгыз,
биредә:
[(x + 2)2 + 2, -3 ≤ х ≤ -1 булганда,
а) /(х) = k jl 1.2 jr 1 1 ,
((x + 1)2 + 1, х > -1 булганда.
f. . _ ∫√x + 4 - 1, -4 ≤ х < 0 булганда,
{-х +1, х > 0 булганда.
21.26. Башта тулы квадрат аерып алып, аннан соң у = a(x + I)2 +
+ т рәвешенә китереп, функциянең графигын төзегез:
а) у = х2 + 2х + 3; в) у = х2 + 6х + 10;
б) у = х2 - 4x + 1; г) у = х2 - 14х + 51.
146
Функциянең графигын төзегез:
21.27. а) у = х2 - 10х + 24; в) у = х2 - 4х;
б) у = х2 + 8х + 7; г) у = х2 - 6х + 5.
•21.28. а) у = 2x2 - 4х + 5; в) у - -4x2 + 8х - 10;
б) у = -3x2 + 6x - 1; г) у = 2x2 - 8х + 6.
•21.29. у = f(x) функциясенең графигын төзегез һәм укыгыз, биредә:
-3(x + 2)2 + 3, -3 < х ≤ -1 булганда,
f(x) =
0, -1 < х ≤ 0 булганда,
2
+ 2, х > 0 булганда.
§22. у = ах2 + Ьх + с ФУНКЦИЯСЕ,
АНЫҢ ҮЗЛЕКЛӘРЕ ҺӘМ ГРАФИГЫ
22.1. Түбәндәге функцияләрнең кайсылары квадратик:
а) у = 3x2 + 5x + 6; в) у = 5x2 - 7х;
б) у = Зх - 1; г) у = 9х?
22.2. Квадратик функцияләрнең a, b һәм с коэффициентларын
атагыз:
а) у = 7x2 - Зх - 2; в) у = 8x2 - 2х;
6)i/=|x’ + l; HJ∕=∣x + ∣-⅛χ2∙
22.3. ax2 + Ьх + с квадрат өчбуынын төзегез:
a) a = 2, b = -1, с = 4; в) a = 9, b = -3, с = -1;
б) a = -1, b = 7, с = 0; г) a = 1, b = 0, с = 5.
22.4. Төзүләр ясамыйча әйтегез, параболаның тармаклары кая
(өскә яки аска) юнәлгән:
а) у = 3x2 - 7x + 1; в) у = -7x2 + х - 2;
б) у = -5x2 + 2х + 0,5; г) у = 6x2 + 9x + 1.
022.5. Параболаның симметрия күчәре булып торган турының
тигезләмәсен языгыз:
а) у = 2x2 - х + 1; в) у = 7x2 + 12х + 4;
б) у = -5x2 + 2х - 2; г) у = -x2 + 2x + 1.
o22.6. Парабола түбәсенең координаталарын табыгыз:
а) у = 4x2 + 8х - 1; в) у = -x2 + х - 1;
б) у = -Зх2 - 6х + 2; г) у = 5x2 - 10х + 4.
147
Функциянең графигын
o22.7. а) у - x2 + 4x + 5;
б) у = -χ2 + 2х - 3;
022.8. а) у = х2 + 6х;
б) у = -х2 + 2х;
o22.9. а) у = 2x2 + 4х;
б) у = -Зх2 + 12х;
o22.10. а) у = 3x2 + 6x + 1;
б) у = -2x2 + 8х - 5;
o22.ll. а) у = (х - 2)(х + 4);
б) у = -5х(х + 2);
төзегез:
в) У = -х2 + 2х + 2;
г) у = х2 - 4χ + 1.
в) У = х2 - 6х;
г) У = -х2 - 4х.
в) У = 3χ2 - 12х;
г) У = -4x2 - 8х.
в) у = -Зх2 + 6х + 2
г) у = 2x2 - 4х + 3.
в) у = (2 - χ)(χ - 6);
г) у = Зх(2 + х).
022.12. а) у = (х + 2)2 - 2х + 2;
б) у = —(х - I)2 + 4(x - 1) + 5;
в) у = 6х + (х - 2)2;
г) у = (х + I)2 - 6(x +1) + 8.
022.13. Функциянең иң кечкенә кыйммәте 1 гә тигез булса,
с коэффициентының кыйммәтен табыгыз һәм у = х2 -
- 6х + с функциясенең графигын төзегез.
022.14. Функциянең иң зур кыйммәте 2 гә тигез булса, с ко¬
эффициентының кыйммәтен табыгыз һәм у = -х2 +
+ 4х + с функциясенең графигын төзегез.
022.15. у = 2x2 + 4x - 1 функциясенең иң кечкенә һәм иң зур
кыйммәтләрен табыгыз:
а) [-1; 0] кисемтәсендә; в) [0; 5] кисемтәсендә;
б) [-2; +∞) нурында; г) (-∞j -3] нурында.
022.16. у = -х2 + 2х + 3 функциясенең иң кечкенә һәм иң зур
кыйммәтләрен табыгыз:
а) [0; 2] кисемтәсендә; в) [1; 2] кисемтәсендә;
б) (-оо; 1] нурында; г) [2; +∞) нурында.
022.17. у = 3x2- 12x + 1 функциясенең иң кечкенә һәм иң зур
кыйммәтләрен табыгыз:
a) [1; 4] кисемтәсендә; в) [0; 4] кисемтәсендә;
б) (1; 4] ярыминтервалында; г)[0;4)ярыминтервалында.
148
022.18. у = x2 + 4x - 5 функциясенең графигын төзегез. График
ярдәмендә билгеләгез:
а) х = —3; 0; 1 булганда, функциянең кыйммәтен;
б) у = —8; —5; 0 булганда, аргументның кыйммәтләрен;
в) функциянең иң кечкенә кыйммәтен;
г) функциянең үсү һәм кимү аралыкларын;
д) у > 0, у < 0 булганда, аргументның кыйммәтләрен.
022.19. у = -2x2 + 4х + 6 функциясенең графигын төзегез. График
ярдәмендә билгеләгез:
а) х = —2; 0; 3 булганда, функциянең кыйммәтен;
б) у = -10; 6; 0 булганда, аргументның кыйммәтләрен;
в) функциянең иң зур кыйммәтен;
г) функциянең үсү һәм кимү аралыкларын;
д) у > 0, у < 0 булганда, аргументның кыйммәтләрен.
Функцияне монотонлыкка тикшерегез:
022.20. а) у = (х - 2)2;
б) у = 2x2 + 1;
в) у = - (х + I)2;
г) у = 4 - Зх2.
022.21. а) у = х2 + 6х - 2;
б) у = 4 - х2 + Зх;
в) у - 7 + 4х - 2х2;
г) у = 3 + 2x2 + 8х.
022.22. Квадратик функциянең х лар күчәре белән кисешү нок¬
талары координаталарын табыгыз:
а) у = х2 - 6х + 5; в) у = 2x2 + 8х + 6;
б) у = -0,5x2 + 2х + 6; г) у = -х2 + 8х - 7.
022.23. Тигезләмәнең ничә тамыры булуын билгеләгез:
а) -х2 + 4х + 5 = 0; в) 2x2 - 6x + 1 = х - 2;
б) -2x2 - 4x + 1 = -- ; г) -х2 + 2x + 1 = -.
х х
o22.24. у = -х2 + 6х - 5 функциясенең графигыннан файдаланып,
х ның нинди кыйммәтләрендә тигезсезлекнең үтәлүен
билгеләгез:
а) у > 0; б) у ≤ 3; в) у < 0; г) у > -5.
022.25. у = 2x2 + 8х + 6 функциясенең графигыннан файдаланып,
х ның нинди кыйммәтләрендә тигезсезлекнең үтәлүен
билгеләгез:
а) у > 0; б) у < 6; в) у < 0; г) у ≥ 6.
149
o22.26. Тигезләмәләр системасының ничә тамыры булуын билге¬
ләгез:
[ у - 2x2 - 6x + 1, ( у = -Зх2 + 12х - 5,
*,W=S∙ В)Ь = -5;
I у = х2 - 2x, ∫ у -- -4x2 + 4х + 2,
б) [ 2x - 3z∕ = 0; Г) ] Зх - 2у = 0.
022.27. a) ∕(x) = 2x2 - 5х + 3 икәне билгеле булса, f(x6) ны
табыгыз.
б) f{x) = ~х2 + 2х - 4 икәне билгеле булса, f(-x - 1) ны
табыгыз.
022.28. а) Әгәр у = х2 + 4х + с функциясе графигының ординаталар
күчәрен А(0; 2) ноктасында кисеп үтүе билгеле булса,
с коэффициентының кыйммәтен табыгыз.
б) Әгәр у = х2 + 4х + с функциясе графигының ординаталар
күчәрен В(0; 4) ноктасында кисеп үтүе билгеле булса,
с коэффициентының кыйммәтен табыгыз.
022.29. а) Әгәр у = ах2 + 4х + 5 функциясе графигының абс¬
циссалар күчәрен М(-10; 0) ноктасында кисеп үтүе
билгеле булса, а коэффициентының кыйммәтен табыгыз,
б) Әгәр у = ах2 + 4х - 8 функциясе графигының абс¬
циссалар күчәрен N(4; 0) ноктасында кисеп үтүе билгеле
булса, а коэффициентының кыйммәтен табыгыз.
o22.30. а) Әгәр у = х2 + Ъх + 4 функциясе графигының симметрия
күчәре булып х = 1 турысы торса, Ъ коэффициентының
кыйммәтен табыгыз.
б) Әгәр у = 2x2 + Ъх - 3 функциясе графигының симметрия
күчәре булып х = -4 турысы торса, Ъ коэффициентының
кыйммәтен табыгыз.
22.31. у = х2 - 4х + 5 функциясенең (3; 12) аралыгында үсә
баручы икәнлеген исбатлагыз.
22.32. у = х2 + 6х - 7 функциясенең (-8; -5) аралыгында кими
баручы икәнлеген исбатлагыз.
22.33. у = /(х) функциясе бирелгән, биредә ∕(x) = х2 - 4х + 3.
Чагыштырыгыз:
а) /(2) һәм /(2,0137); в) /(1,999) һәм /(2);
б) /(||) һәм /[||]; г) /(49,7) һәм /(49,69).
150
22.34. у = f(x) функциясе бирелгән, биредә f(x) = -χ2 - 6х + 7.
Чагыштырыгыз: / 25λ
a) /(-2,43) һәм /(-3); в) ) һәм /(-3);
б) /(-59,9) һәм /(-60); г) /(-0,99) һәм /(1,1).
22.35. у = f(x) функциясе бирелгән, биредә ∕(x) = 2x2 + 4x - 1.
Чагыштырыгыз:
a) ∕(V2) һәм /(-1); в) /(-1) һәм /(—>/s);
б) /(-12,473) һәм /(-12,472); г) ∕(√2) һәм ∕(√3).
22.36. у = f(x) функциясе бирелгән, биредә ∕(x) = 5x2 + Зх - 2.
Табыгыз:
а)/(2х); б) ∕(x - 1); в) /(х3); г) 2∕(3x).
22.37. у = /(х) функциясе бирелгән, биредә ∕(x) = -2x2 + х - 4.
Табыгыз:
а) /(-х); б) /(х + 5); в) /(-х2); г) 3∕(2x).
•22.38. у = /(х) функциясе бирелгән, биредә ∕(x) = 2x2 - Зх + 12.
Аргументның нинди кыйммәтендә ∕(x - 1) = ∕(χ + 1)
тигезлеге үтәлә?
•22.39. у = f(x) функциясе бирелгән, биредә ∕(x) = -х2 + 4х - 3.
Аргументның нинди кыйммәтендә ∕(2x + 3) = 4/(х - 2)
тигезлеге үтәлә?
•22.40. Тигезләмәләр системасының чишелешләре санын бил¬
геләгез:
∫ у = -х2 + 6x - 4, ∫ у = -х2 - 2х + 4,
) I 2х - у + 3 = 0; В) ] х - 2у = 0;
_ [ у = Зх2 - 6х - 4, [ у = 2x2 + 8х + 6,
б) ( г) ∣
[у-2х-4 = 0; ’ 1 Зх - 2y + 1 = 0.
Функциянең графигын төзегез һәм укыгыз:
22.41.
У = <
[2x2 + 4х - 1,
[х - 1, х > 0
-2 ≤ х ≤ 0 булганда,
булганда.
22.42.
У = \
[х + 1, х < 0
[-x2 + 2х + 3,
булганда,
х ≥ 0 булганда.
22.43.
У =
' 2x2 + 4x + 1,
[-3(x - 2)2, 1
х ≤1 булганда,
< х ≤ 3 булганда.
22.44. у =
-3x2 +6x + 4, 0≤x<2 булганда,
4
—, 2 < х ≤ 4 булганда.
151
Функциянең графигын төзегез һәм укыгыз:
•22.45. у =
•22.46. у =
1 X 1 «
—, х≤-1 булганда,
х
х2, -1 < х ≤ 1 булганда,
∣x + 2∣, 1 < х ≤ 5 булганда.
2 1 л
—, х < -1 булганда,
х
4 - 3x2, -1 ≤ х ≤ 1 булганда,
|х - 2|, х > 1 булганда.
2
•22.47. а) у = x2 - 2x - 1 һәм у = — функцияләре графикла¬
ры ярдәмендә х ның нинди кыйммәтләрендә түбәндәге
тигезсезлекнең үтәлүен билгеләгез:
х2 - 2x - 1 <
X
б) у = -х2 + 6х - 3 һәм у = —функцияләре графикла-
X Zu
ры ярдәмендә х ның нинди кыйммәтләрендә түбәндәге
тигезсезлекнең үтәлүен билгеләгез:
-х2 + 6х - 3 > —
х - 2
• 22.48. Әгәр у = ах2 — (а + 6)х + 9 функциясе графигының
симметрия күчәре булып х = 2 турысы торса, а ко¬
эффициентының кыйммәтен табыгыз.
• 22.49. с коэффициенты нинди кыйммәт алганда, у = х2 + 6х + с
параболасының түбәсе координаталар башыннан
5 берәмлек ераклыгында була?
• 22.50. b һәм с коэффициентларының нинди кыйммәтләрендә
А(1; -2) ноктасы у = х2 + Ъх + с параболасының түбәсе
була?
• 22.51. Әгәр А(1; -2) ноктасы у = ах2 + Ъх + с параболасының
түбәсе булса һәм парабола ординаталар күчәрен В(0; 2)
ноктасында кисеп үтсә, а, Ъ һәм с коэффициентларының
кыйммәтләрен табыгыз.
• 22.52. Әгәр у = х2 + Ъх + с функциясенең графигы (0; 8) һәм
(3; -1) нокталары аша үтсә, Ъ һәм с коэффициентларының
кыйммәтләрен табыгыз.
152
• 22.53. Әгәр у = x2 + Ъх + с функциясенең графигы (1; 6) һәм
(-1; -2) нокталары аша үтсә, b һәм с коэффициентларының
кыйммәтләрен табыгыз.
• 22.54. Нинди квадратик функциянең графигы К(-2; 3), Д-1; 0),
М(0; -9) нокталары аша үтә?
• 22.55. Нинди квадратик функциянең графигы А(2; 3), В(0; 1),
С(3; 2) нокталары аша үтә?
§23. КВАДРАТ ТИГЕЗЛӘМӘЛӘРНЕ
ГРАФИК ЮЛ БЕЛӘН ЧИШҮ
Тигезләмәне график һәм аналитик юллар белән чишегез:
023.1.
а) х2 - 2х = 0;
б) -х2 + 6х = 0;
в) х2 + 4х = 0;
г) -х2 - 8х = 0.
023.2.
а) х2 - 4 = 0;
б) -х2 + 1 = 0;
в) х2 - 9 = 0;
г) -х2 + 16 = 0.
023.3.
a) 2x2 - 2 = 0;
в) 0,5x2 -2 = 0;
б) -Зх2 + 6х = 0;
г) х2 - 2х = 0.
Тигезләмәне график юл белән чишегез:
023.4.
а) х2 + 2х - 3 = 0;
б) х2 - 4х + 3 = 0;
в) х2 + 4х - 5 = 0;
г) х2 - 2х - 3 = 0.
023.5.
а) х2 - х - 2 = 0;
б) х2 - Зх - 4 = 0;
в) х2 + Зх + 2 = 0;
г) х2 + х - 6 = 0.
023.6.
а) -х2 + 6х - 5 = 0;
б) -х2 - Зх + 4 = 0;
в) -х2 - 6х - 8 = 0;
г) -х2 + х + 6 = 0.
023.7.
а) х2 - 5х + 6 = 0;
б) -х2 - х + 6 = 0;
в) х2 - х - 6 = 0;
г) -х2 - 5х - 6 = 0.
023.8.
Тигезләмәнең тамырлары булмавын исбатлагыз:
a) Зх2 - 6х + 11 = 0; в) х2 + 2х + 4 = 0;
б) х2 - Зх + 5 = 0; г) 2x2 + 5х + 9 = 0.
o23.9. Турыпочмаклыкның мәйданы 8 см2, ә буе иңеннән 2 см
га зуррак икәне билгеле булса, аның якларын табыгыз.
153
θ23.10. Турыпочмаклыкның периметры 14 дм, ә мәйданы 12 дм2
икәне билгеле булса, аның якларын табыгыз.
o23.ll. Турыпочмаклы өчпочмакта гипотенуза 5 см, ә бер катет
икенчесеннән 1 см га зуррак булса, бу катетларны
табыгыз.
23.12. Квадрат тигезләмәне берничә юл белән чишегез:
а) х2 - 6х + 8 = 0; в) х2 - 2х - 8 = 0;
б) х2 + 2х - 8 = 0; г) х2 + 6х + 8 = 0.
Тигезләмәнең ничә тамыры барлыгын ачыклагыз:
23.13. a) 2x2 - Зх + 1 = 0; в) 2x2 -5х +
б) х2 + 6х + 9 = 0; г) 2x2 - Зх +
2 = 0;
2 = 0.
23.14. a) -2x2 - 7х + 3 = 0; в) 2x2 + 5х +
б) -х2 + 4х - 4 = 0; г) 2x2 - 5х -
5 = 0;
3 = 0.
•23.15. р ның нинди кыйммәтләрендә х2 - 2х +
сенең бер тамыры була?
1 = Р
тигезләмә-
•23.16. р ның нинди кыйммәтләрендә х2 + 2х +
сенең тамырлары булмый?
3=р
тигезләмә-
•23.17. р ның нинди кыйммәтләрендә х2 - 4х +
сенең ике тамыры була?
4=р
тигезләмә-
•23.18. р ның нинди кыйммәтләрендә х2 + 4х -
6=р
тигезләмә-
сенең кимендә бер тамыры була?
•23.19. р ның нинди кыйммәтләрендә х2 + 6х + 8 = р тигезлә¬
мәсенең:
а) тамырлары булмый;
б) бер тамыры була;
в) ике тамыры була?
23.20. Турыпочмаклык формасындагы участокны әйләндереп
алган койманың озынлыгы 20 м га тигез. Участокның
мәйданы 24 м2 булса, аның буен һәм иңен табыгыз.
23.21. Турыпочмаклы өчпочмакның мәйданы 6 см2 ка тигез.
Катетларның берсе икенчесеннән 4 см га зуррак булса,
аларның озынлыкларын табыгыз.
23.22. Турыпочмаклы өчпочмакта катетларның берсе икен¬
чесеннән 1 м га озынрак һәм гипотенузадан 1 м га кыс¬
карак. Бу өчпочмак якларының озынлыкларын табыгыз.
154
23.23. Гади вакланманың санаучысы ваклаучысыннан 2 гә
кимрәк, ә аларның тапкырчыгышы 15 булса, бу
вакланманы табыгыз.
23.24. Җәяүле урман сукмагы буйлап 2 км һәм, тизлеген
2 км/сәг кә арттырып, шоссе буйлап 3 км бара. Әгәр
барлык юлга 1 сәг вакыт сарыф итсә, җәяүленең һәр
участоктагы тизлеген табыгыз.
ӨЙ КОНТРОЛЬ ЭШЕ № 3
1 нче вариант
1. Бер үк координаталар системасында у = 2x2 һәм у = -2x2
функцияләренең графигын төзегез; төзелгән графикларның
үзара урнашуы турында нәтиҗә ясагыз.
2. Өстән чикләнгән; астан чикләнгән функцияләргә мисаллар
китерегез.
3. [0; 5] кисемтәсендә у = -√x - 1 + 3 функциясенең иң кечке¬
нә һәм иң зур кыйммәтләрен табыгыз.
4. у = 4x2 - 5 функциясенең графигын төзегез.
5. у = х2 + 6х + 2 функциясенең графигын төзегез.
6. ↑(x) = 2x2, g(x) = - икәнлеге билгеле, х ≠ 0 булганда
f(2x4) = 2g | —1 икәнен исбатлагыз.
ух8 √
7. Тигезләмәләр системасын график юл белән чишегез:
\ху = 2,
}χ2 + у = -1.
8. у = f(x) функциясе бирелгән, биредә
[ 2x2 + 4x + 2, -2 ≤ х < 0 булганда,
∕(x) = < r-
[√x + 2, х > 0 булганда.
а) /(-3); /(0); /(9) ны табыгыз.
б) у = /(х) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
5
9. у = 2 - —- функциясен монотонлыкка тикшерегез.
X 4^ £
155
10. р ның нинди кыйммәтләрендә -χ2 + 4х + 6 = р тигезлә¬
мәсенең:
а) тамырлары булмый;
б) бер тамыры була;
в) ике тамыры була?
2 нче вариант
9 о
1. Бер үк координаталар системасында у = — Һәм и =
х y х
функцияләренең графигын төзегез; төзелгән графикларның
үзара урнашуы турында нәтиҗә ясагыз.
2. Өстән чикләнгән; астан чикләнгән функцияләргә мисаллар
китерегез.
3. [—1; 2]кисемтәсендә у = — 2(x — I)2 функциясенең иң кечкенә
һәм иң зур кыйммәтләрен табыгыз.
4
4. у = — + 2 функциясенең графигын төзегез.
5. у = х2 - 4х + 7 функциясенең графигын төзегез.
3
6. f(x) = --, g(x) = Зх2 икәнлеге билгеле, х ≠ 0 булганда
f[ —- | = g(x3) икәнен исбатлагыз.
k x° J
7. Тигезләмәләр системасын график юл белән чишегез:
∫ у = -х2 + 3,
[ у = -у/х - 1.
8. у = /(х) функциясе бирелгән, биредә
∕(x) =
∣x + 1| -1, х < 1 булганда,
2x2 -8x + 7, l<x≤4 булганда.
a) Д-3); /(1); f(9) ны табыгыз.
б) у = f(x) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
9.
3 Л
у = - 4 функциясен монотонлыкка тикшерегез.
10. р ның нинди кыйммәтләрендә -х2 + 6х — 2 =р тигезләмәсенең:
а) тамырлары булмый;
б) бер тамыры була;
в) ике тамыры була?
156
БҮЛЕК
КВАДРАТ
ТИГЕЗЛӘМӘЛӘР
§24. ТӨП ТӨШЕНЧӘЛӘР
24.1. Квадрат тигезләмә буламы:
a) x2 + Зх + 1 = 0; в) 2x2 + Зх - 7 = 0;
б) 5x3 - х2 + 4 = 0; г) х3 - х - 6 = 0?
Тигезләмәне ах2 + Ъх + с = 0 рәвешенә китерегез һәм
өлкән коэффициентны, икенче коэффициентны һәм
ирекле буынны күрсәтегез:
24.2. a) 4x2 + 5х - 1 = 0;
в) -х2 - х = 0;
б) 15x2 = 0;
г) 8 - 9x2 = 0.
24.3. a) 7x2 + 12х - 5 = 0;
©
II
ιn∣∞
1
*
| Ь-
1
сч
н
(N | Ю
б) 4*2+п»0;
г) -4x2 - 7х + 16 = 0.
24.4. a) (Зх + l)(2x - 3) + 4(х - 2) = 5(4 - Зх);
б) 12 - 6(х + 3) - 7х = (х - 2) (х + 3);
в) (2х + 10) (х - 1) + 5(х - 2) = 2(7 + х);
г) 1 + 3(2x - 4) + (2х - 1) (3 - 2х) = 8.
24.5. a) 2(x + 6) (х - 6) + 3(x + 6) = х2 - 5х;
б) 25 - х2 + 2(х - 5) = 4(х - 5).
24.6. а) 4(4 - Зх)2 - 2(4 - Зх) = 12 - х;
б) х2 - 49 - 3(x + 7) = 2(x - 7)2.
157
Квадрат тигезләмәләр төзегез:
24.7. а) Өлкән коэффициент 8 гә тигез, х алдындагы коэф¬
фициент 5 кә тигез, ә ирекле буын 1 гә тигез;
б) өлкән коэффициент -12 гә тигез, х алдындагы коэф¬
фициент 3 кә тигез;
в) өлкән коэффициент 1 гә тигез, ә ирекле буын 4 кә
тигез;
г) өлкән коэффициент 9 га тигез, х алдындагы коэф¬
фициент -2 гә тигез, ә ирекле буын 3 кә тигез.
24.8.
а) Өлкән коэффициент 1
фициент -1 гә тигез;
б) өлкән коэффициент —
„ 1
циент -3-7 гә тигез, ә
4
гә тигез, х алдындагы коэф-
гә тигез, х алдындагы коэффи-
« 1 з
ирекле буын 1 - кә тигез;
5
в) өлкән коэффициент 6 га тигез, ә ирекле буын 3,5 кә
тигез;
7
г) ) өлкән коэффициент гә тигез, х алдындагы коэф-
13
λ 4 e, λ 1
фициент 4 — кә тигез, ә ирекле буын -4 — гә тигез.
7 3
Түбәндәге квадрат тигезләмәләрнең кайсылары ките-
релгән тигезләмә? Тигезләмә китерелгән квадрат
тигезләмә булсын өчен нинди рәвешүзгәртүләр эшләргә
кирәк? Бу үзгәртүләрне эшләгез.
24.9. а) х2 - 4х + 35 = 0;
б) -15x2 + 4х - 2 = 0;
24.10. а) -х2 + 31х - 6 = 0;
б) -∣*2÷⅛=o5
в) 12 - х2 + Зх = 0;
г) 18 - 9х + х2 = 0.
b)-2∣x2-∣x-4⅛=O5
г) х2 - 7х + 16 = 0.
Түбәндәге квадрат тигезләмәләрнең кайсылары тулы
квадрат тигезләмә? Тулы квадрат тигезләмәне чишегез.
24.11. а) х2 + 14х - 23 = 0; в) -х2 + х = 0;
б) 16x2 -9 = 0; г) х + 8 - 9x2 = 0.
24.12. a) Зх2 - 12х = 0; в) -2x2 + 14 = 0;
б) х2 + 2х = 0; г) 3 - х2 + х = 0.
158
24.13. а) Тулы китерелгән;
б) тулы китерелмәгән;
в) тулы булмаган китерелгән;
г) тулы булмаган китерелмәгән квадрат тигезләмә төзегез.
24.14. Исбатлагыз:
а) 3 саны х2 - 4х + 3 = 0 тигезләмәсенең тамыры була;
б) -7 саны 2x2 + х - 3 = 0 тигезләмәсенең тамыры булмый;
в) -5 саны 2x2 - Зх — 65 = 0 тигезләмәсенең тамыры
булмый;
г) 6 саны х2 - 2х + 6 = 0 тигезләмәсенең тамыры булмый.
24.15. Исбатлагыз:
а) 5 һәм -5 саннары Зх2 - 75 = 0 тигезләмәсенең тамыры
була;
б) 0 һәм -7 саннары 2x2 + 14х = 0 тигезләмәсенең тамыры
була;
в) 12 һәм -12 саннары 0,5x2 - 72 = О тигезләмәсенең
тамыры була;
г) 0 һәм 6 саннары Зх2 - 18х = 0 тигезләмәсенең тамыры
була.
Тигезләмәләрне чишегез:
24.16. а) х2 + 5х = 0;
б) 2x2 - 9х = 0;
в) х2 - 12х = 0;
г) Зх2 + 5х = 0.
24.17.
а) -х2 + 8х = 0;
б) Зх - х2 = 0;
в) -χ2 + 7х = 0;
г) 19х - х2 = 0.
24.18.
а) х2 - 9 = 0;
б) х2 - 5 = 0;
в) х2 - 64 = 0;
г) х2 - 10 = 0.
024.19.
a) -2x2 + 50 = 0;
б) -Зх2 + 4 = 0;
в) -5х2 + 45 = 0;
г) -9x2 + 13 = 0.
24.20.
a) Зх2 + 7 = 0;
б) 6x2 = 0;
в) 4x2 + 17 = 0;
г) 15x2 = 0.
159
Тигезләмәләрне чишегез:
24.21.
a) (х - 2) (х + 4) = 0;
б) (х + 3,5) (х - 7) (х2 + 9) = 0;
в) (х + 2,8) (х + 1,3) = 0;
г| (∙-iX'^l)<**1>∙∙∙
o24.22.
а) х2 + 12х + 36 = 0; в) x2 - 1бх + 64 = 0;
б) 4x2 - 28х + 49 = 0; r) 9x2 + 30х + 25 = 0.
024.23.
a) 4x2 - Зх + 7 = 2x2 + х + 7;
б) (2х + 3) (Зх + 1)= Их + 30;
в) 1 - 2х + Зх2 = х2 - 2x + 1;
г) (5х - 2) (х + 3) = 13(х - 2).
o24.24.
а) = х; В) _ *2+-≡ = 0;
6)≡⅛i + ≡ = oj r)⅛l-⅛l = -l.
о 5 3
o24.25.
Рәттән килүче ике натураль санның тапкырчыгышы
аларның кечерәгеннән 2 тапкыр зуррак. Бу саннарны
табыгыз.
o24.26.
Рәттән килүче ике натураль санның тапкырчыгышы
аларның кечерәгенең квадратыннан 1,5 тапкыр зуррак.
Бу саннарны табыгыз.
o24.27.
Туры почмакның түбәсеннән аның яклары буйлап тиз¬
лекләре 5 см/с һәм 12 см/с булган ике материаль нок¬
та хәрәкәт итә башлый. Күпме вакыттан соң алар
арасындагы ераклык 52 см га тигез булыр?
o24.28.
Әгәр квадраттан мәйданы 59 см2 булган өчпочмак кисеп
алсак, мәйданы 85 см2 булган кисәк кала. Квадратның
ягын табыгыз.
o24.29.
Квадратның мәйданы түгәрәк мәйданыннан 12 см2 га
зуррак. Әгәр түгәрәк мәйданы 36 см2 булса, квадратның
ягын табыгыз.
160
o24.30. Үз тизлеге 15 км/сәг булган катер агым уңаена 36 км,
агымга каршы 24 км юл үтеп, барлык юлга 4 сәг вакыт
сарыф итә. Агымның тизлеге нинди?
24.31. Бирелгән тигезләмә р параметрының нинди кыйм¬
мәтләрендә тулы булмаган квадрат тигезләмә була?
Параметрның табылган кыйммәте белән тигезләмәне
чишегез.
a) 6x2 + (р - 1)х + 2 - 4р = 0;
б) (р - 2)x2 + Зх + р = 0;
в) 3x2 - (2р + 3)х + 2 + р = 0;
г) (6 - p)x2 + (2p + 6)(х + 12) = 0.
24.32. р параметрының нинди кыйммәтләрендә
(2p - 3)x2 + (Зр - 6)x + р2 - 9 = 0 тигезләмәсе:
а) китерелгән квадрат тигезләмә;
б) тулы булмаган китерелмәгән квадрат тигезләмә;
в) тулы булмаган китерелгән квадрат тигезләмә;
г) сызыкча тигезләмә була?
24.33. р параметрының нинди кыйммәтләрендә:
a) х2 + рх + 24 = 0 тигезләмәсенең 6 га тигез булган тамыры;
б) 2x2 + рх + 68 = 0 тигезләмәсенең 17 гә тигез булган
тамыры;
в) х2 + рх - 35 = 0 тигезләмәсенең 7 гә тигез булган
тамыры;
г) Зх2 + рх - 54 = 0 тигезләмәсенең 9 га тигез булган
тамыры була?
24.34. р параметрының нинди кыйммәтләрендә:
а) х2 - 8х + р = 0 тигезләмәсенең 4 кә тигез булган тамыры;
б) 4x2 - 24х + р = 0 тигезләмәсенең 0 гә тигез булган тамыры;
в) х2 + 15х + р = 0 тигезләмәсенең 10 га тигез булган
тамыры;
г) 6x2 + ЗОх + р = 0 тигезләмәсенең -5 кә тигез булган
тамыры була?
Тигезләмәнең сул ягын тапкырлаучыларга таркатып чи¬
шегез:
24.35.
а) х2 - 8х + 15 = 0;
б) х2 - 12х + 20 = 0;
в) х2 - 4х + 3 = 0;
г) х2 + 6х + 8 = 0.
24.36.
а) х2 + Зх - 10 = 0;
б) 2x2 - 5х + 2 = 0;
в) х2 + 9х + 14 = 0
г) 4x2 - 4х - 3 = 0.
161
24.37.
Аңлатмаларның кыйммәтләре а ның нинди кыйммәт¬
ләрендә тигез:
a) α2 + 6a һәм 3a2 - а; в) 3a2 + 2a һәм 4a2 - 5a;
б) 5a2 - 12 һәм a2 - 4; г) 7a2 - 9 һәм a2 + 9?
24.38.
Тигезләмәне чишегез:
а) (Зх - 1) (х - 9) = (х + З)2;
б) 2x - (х + I)2 = Зх2 - 5;
в) (Зх - 4)2 - (5х + 2) (2х + 8) = 0;
г) 6x2 - (х + 2)2 = 4(4 - х).
24.39.
. х - 2 _ х + 2. . х - 3 х + 3 _ „
Э х-3 х + З’ В х + 3 х-3 ’
x-2 x + 2 51 . 2x + l,2x-l o _
б> « + 2 ' х-2’33; Г) 2x-l , 2x÷1"2∙5∙
§25. КВАДРАТ ТИГЕЗЛӘМӘЛӘРНЕҢ
ТАМЫРЛАРЫ ФОРМУЛАЛАРЫ
Квадрат тигезләмәнең дискриминантын табыгыз:
25.1.
а) х2 + 5х - 6 = 0; в) х2 - 7х - 4 = 0;
б) х2 - 1,3х + 2 = 0; г) х2 - 2,4x + 1=0.
25.2.
а) 3x2 + 2х - 1 = 0; в) 4x2 - 5х - 4 = 0;
б) -х2 + 4х + 3 = 0; г) -2x2 + 5х + 3 = 0.
Квадрат тигезләмәнең тамырлары санын билгеләгез:
25.3.
а) х2 - 8х - 84 = 0; в) х2 - 22х - 23 = 0;
б) 36x2 - 12x + 1 = 0; г) 16x2 - 8x + 1 = 0.
25.4.
а) х2 + Зх + 24 = 0; в) х2 - 2х + 5 = 0;
б) х2 - 16х + 64 = 0; г) х2 + 6х + 9 = 0.
Тигезләмәне чишегез:
25.5.
а) х2 - 5х + 6 = 0; в) х2 + 6х + 8 = 0;
б) х2 - 2х - 15 = 0; г) х2 - Зх - 18 = 0.
25.6.
а) х2 + 42х + 441 = 0; в) х2 - 34х + 289 = 0;
б) х2 + 8х + 7 = 0; г) х2 + 4х - 5 = 0.
25.7.
а) 2x2 + Зх + 1 = 0; в) 5x2 - 8х + 3 = 0;
б) Зх2 - Зх + 4 = 0; г) 14x2 + 5х - 1 = 0.
25.8.
а) 4x2 + 10х - 6 = 0; в) Зх2 - 8х + 5 = 0;
б) 25x2 + 10x + 1 = 0; г) 4x2 + х + 67 = 0.
162
Тигезләмәне чишегез:
25.9. a) 3x2 + 32x + 80 = 0;
б) 100x2 - 160x + 63 = 0;
25.10. a) -x2 - 5x + 14 = 0;
б) -3x2 - 2x + 5 = 0;
25.11. a) x2 = 2x + 48;
б) 6x2 + 7x = 5;
25.12. a) -x2 = 5x - 36;
б) -3x2 + 8 = 2x;
25.13. a) x2 + 7x + 2 = 0;
6) 2x2 + 3x - 1 = 0;
25.14. a) x2 + 2x - 7 = 0;
6) 2x2 - 4x - 1 = 0;
o25.15. a) 2x2 + 10x + 12 = 0;
6) -3x2 + 18x - 24 = 0;
в) 5x2 + 26x - 24 = 0;
r) 4x2 - 12x + 9 = 0.
в) -x2 + 26x - 25 = 0;
r) -5x2 - 9x + 2 = 0.
в) x2 = 4x + 96;
r) 2x2 - 2 = 3x.
в) 25 = -26x - x2;
r) -5x2 = 9x - 80.
в) x2 - 5x + 3 = 0;
r) 5x2 - x - 1 = 0.
в) x2 + 6x + 3 = 0;
r) 5x2 - 10x + 1 = 0.
в) 6x2 - 18x - 60 = 0;
r) -4x2 - 16x + 84 = 0.
025.16.
a) 0,6x2 + 0,8х - 7,8 = 0;
λ 4 2 7 3
в) —х2 х
5 5 2
= 0;
б) ⅛x2 - х + 1 = 0;
4
г) 0,2x2 - 10х +
125 = 0.
025.17.
a) ⅛ х2 + х + у = 0;
’ 3 4
в) х2 + Зх - 1
= 0;
б) х2 + 5x + 2 i =0;
. 2 5 1
r)x2- πx- θ
= 0.
025.18.
a) 6x(2x + 1) = 5x + 1;
в) 8x(l + 2х) = -
1;
б) 2х(х - 8) = -х - 18;
г) x(x - 5) - 1 -
4х.
o25.19. a) (x - 2)2 = 3x - 8;
6) (3x - 1) (x + 3) + 1 = x(l + 6x);
в) 5(x + 2)2 = -6x + 44;
r) (x + 4) (2x - 1) = x(3x + 11).
o25.20. Тигезләмәнең p параметры нинди кыйммәт алганда бер
тамыры була:
а) х2 - рх + 9 = 0; в) х2 + рх + 16 = 0;
б) х2 + Зрх + р = 0; г) х2 - 2рх + Зр = 0?
163
o25.21. р параметрының теләсә нинди кыйммәтләрендә Зх2 — рх -
-2 = 0 тигезләмәсенең ике тамыры булуын исбатлагыз.
025.22. Квадраты үзеннән 56 га зуррак булган натураль санны
табыгыз.
025.23. Турыпочмаклыкның бер ягы икенчесеннән 5 см га
зуррак, ә мәйданы 84 см2. Турыпочмаклыкның якларын
табыгыз.
025.24. 120 санын берсе икенчесеннән 2 тапкыр кечерәк булган
саннар тапкырчыгышы рәвешендә күрсәтегез.
025.25. Турыпочмаклы өчпочмакның мәйданы 180 м2. Бер
катеты икенчесеннән 31 м га зуррак булса, бу катетларны
табыгыз.
o25.26. Квадрат картоннан киңлеге 3 см булган тасма кисеп
алалар. Калган өлешнең мәйданы 70 см2. Картонның
баштагы үлчәмнәрен табыгыз.
025.27. Рәттән килүче ике натураль санның тапкырчыгышы
аларның суммасыннан 271 гә зуррак. Бу саннарны
табыгыз.
025.28. Рәттән килүче ике натураль санның суммасы 1201 гә
тигез. Бу саннарның квадратлары аермасы ничәгә тигез?
o25.29. Квадратлары суммасы 1589 булган рәттән килүче өч
натураль санны табыгыз.
025.30. Турыпочмаклы өчпочмакның гипотенузасы катетларның
берсеннән 32 см га, икенчесеннән 9 см га зуррак.
Өчпочмакның якларын табыгыз.
o25.31. Турыпочмаклы өчпочмакта бер катет гипотенузадан
8 см га, ә икенче катеттан 4 см га кечерәк. Гипотенузаны
табыгыз.
025.32. Рәттән килүче ике натураль санның квадратлары
суммасы аларның тапкырчыгышыннан 307 гә зуррак. Бу
саннарны табыгыз.
025.33. Рәттән килүче ике натураль санның квадраты аларның
квадратлары суммасыннан 840 ка зуррак. Бу саннарны
табыгыз.
164
θ25.34. Банкка акча салучы күпмедер еллык процентка
10 000 сум акча кертә. Беренче ел ахырында банк еллык
процентны 5% ка арттыра. Әгәр акча кертүче банкта
акчасын ике ел саклаганнан соң 11 550 сум акча алса, ул
аны нинди процентка салган булган?
025.35. Завод бер данәсе 2500 сумнан миксерлар чыгара. Яңа
җитештерү технологияләрен кертә барып, эшләнмәнең
бәясен берничә ай эчендә ай саен бер үк процентка
киметү планлаштырылган була. Әмма икенче айда
эшләнмә бәясе пландагыдан 10% ка күбрәк төшә. Әгәр
миксерның бәясе ике айдан соң 1800 сумга калса, аны ай
саен ничә процентка киметү каралган була?
Тигезләмәне чишегез:
25.36. а) x2 + 3√2x +4 = 0; в) x2 - 3√5x - 20 = 0;
б) 4x2 + 4λ∕3x +1 = 0; г) 4x2 - 2^7 х +1 = 0.
25.37. a) (2х - 1) (2x + 1) + x(x - 1) = 2x(x + 1);
б) (3x + I)2 - х(7х + 5) = 4;
в) (Зх - 1) (Зх + 1) - 2x(l + 4х) = -2;
г) (2x + I)2 + 2 = 2 - 6x2.
пе оо ч х2 - х 2х + 4 X 2x2 + х 4х - 2
25.38. а) —— = —-—; в) —-— = ——;
3 5 5 3
6)⅛^ - 6х = 5; =
25.39. Бирелгән тигезләмәләр арасыннан р параметрының
теләсә кайсы кыйммәтендә ике тамыры булганнарын
күрсәтегез:
а) х2 + рх = 0; в) х2 + рх + 5 = 0;
б) х2 - рх - 5 = 0; г) рх2 - 2 = 0.
25.40. Волейбол чемпионатында барысы 66 уен уйналган. Әгәр
һәр команда һәр башка команда белән берәр уен уйнаса,
чемпионатта ничә команда катнашкан?
165
25.41. Мәктәпне тәмамлаганнан соң, берничә классташ үзара
фотолар алышырга җыенган (һәркем һәркем белән). Әгәр
барысы 210 фото таратылган булса, ничә укучы фотолар
алышкан?
25.42. Икеурынлы сан уйлаганнар. Бу санның квадратына 36
ны кушкач, уйланылган саннан 20 тапкыр зуррак сан
килеп чыккан. Нинди сан уйлаганнар?
25.43. А пунктыннан бер үк вакытта, берсе — төньякка,
икенчесе - көнчыгышка таба, йөк машинасы һәм
җиңел машина юлга чыга. Җиңел машинаның тизлеге
йөк машинасы тизлегеннән 20 км/сәг кә зуррак. 1,5
сәгатьтән соң алар арасындагы ераклык 150 км була. Бу
машиналарның тизлекләрен табыгыз.
25.44. Хезмәт хакын бер-бер артлы ике тапкыр күтәргәннән соң,
ул баштагысыннан 32% ка арта. Әгәр икенче тапкырында
беренчесеннән 2 тапкыр артык процентка күтәрсәләр,
беренче күтәрүнең ничә процент булганын табыгыз.
•25.45. Тигезләмәне чишегез:
а) х2 + (у[х) -2 = 0; в) х2 - з(-/х) -4 = 0;
б) х2 + (λ∕x - 2)2 -4 = 0; г) х2 + (λ∕x + 3) -15 = 0.
25.46. р параметры кергән тигезләмәләрне чишегез:
а) х2 - (2р - 2)х + р2 - 2р = 0;
в) х2 - (1 - p)x - 2p = 2p2∙,
. 2 , SP + 2 . Р Л
г) х2 + — х + - = 0.
6 о
•25.47. р параметрының x2-px+p-2 = 0 тигезләмәсе бер генә
тамыр ала торган кыйммәтләре юк икәнен исбатлагыз.
•25.48. Тигезләмәне чишегез:
а) х2 + 5х — = 0;
х
б) ⅛ - 7х + 12 = 0;
в) х2 + ⅛ - 6 = 0;
г) х • |х| + 7х + 12 = 0.
166
§26. РАЦИОНАЛЬ ТИГЕЗЛӘМӘЛӘР
Тигезләмәне чишегез:
4
_ λ 24
o26.1. а) Зх + - =7;
в) х - 10 = —;
X
6) 2χ2 ~ 10 -4 = 0;
х + 5
r) 4÷∣ = 2∙
x2 + 1
o26.2. a) χ2 + 3x + * ^-3- = 2х;
’ 2 8
б) Зх + 1 _ 4х - х2 _ х2 - 4
3 12 9
026.3. a) - ⅛1 = 1;
8 5
gx Зх + 4 _ х2 + 4х - 3 _ 1
’ 5 3
026.4. а) -≤- = χ2 ^⅛
х + 1 х + 1
х - х2 _ -20 .
В) 5-х 5-х’
,. χ2 ~ = x ■
j х-3 х-3’
ч Зх2 - х 2
Г) 1-х ^l-χ∙
o26.5. a) 3χ2 ~ 14* = ——;
х - 4 4 - х
x 2x2 _ -7х + 6.
В) х - 2 - 2 - х ’
g∖ -2x2 + 6 _ 11х .
х + 6 6 + х’
V X2 + X _ 6
х + 3 3 + х
е λ х2 + 4х 2х + 3.
θ26β'a> х + 2 3 1
в) χ2 ~ 5 = 7x + 10∙
' х -1 9 ’
б) 5х - 3 _ 2х - 3.
х-3 х ’
ч 2х + 3 Зх + 2
Г) x + 2^' х •
026.7. a) -≠- =
х2 - 3 х
в) √- = 15
х2 + 2 х
б) 4x + 1 _ Зх - 8.
х-3 х + 1 ’
г) ~ 1 _ Зх + 4
х + 7 х - 1 '
пп a ч X + 1 X - 2 1
026.8. а) - - = 1;
х + 5 х - 5
Зх 4^ 3 х 1
х + 2 х - 2 “ ’
,, Зх - 9 , х + 6 о.
б) + - 3;
х - 1 х + 1
,2x-21x + 3 г
Г> x + 3 ' ,-3 = 5∙
167
Тигезләмәне чишегез:
o26∙9∙ *) 7(⅛ - 7⅛ = 3; ≡> ⅛⅛ + 7⅛ = 1;
б) 3χ - — - 3 \ 5х 20 _ 4
х - 1 х х2 - х’ Гх + 2 x2+2x х
Л 2х - 7 х + 2 _ х + 6
026.10. a) χ 4 χ + 1 (x-4)(x + i)'
fi. 6 х _ 3 .
0j (5 - х)(х + 1) х + 1 х - 5’
х - 1 28 Зх .
В) х + 3 + (х + 3)(x - 4) ^ х - 4’
2х _ х - 1 _ 10
Г) х + 2 х - 3 (3- x)(x + 2)'
o26.ll. a) + -Ц = -уЦ;
х - 1 х + 1 х2 - 1
д. х 6 _ Зх + 35.
х - 5 х + 5 х2 - 25 ’
1 %x + 30 _ 5 .
х + 3 x2-9 х - 3 ’
. 2 , х 20 - Зх
х - 4 х + 4 x2-16
026.12. a) а ның нинди кыйммәтләрендә -—һәм ——у- вак-
а + 2 a + 5
ланмаларының кыйммәтләре тигез?
„ За + 9 , 2а -13
б) а ның нинди кыйммәтләрендә ——- һәм ga^b^5^
вакланмаларының кыйммәтләре суммасы 2 гә тигез?
Д* ψ У 1
o26.13. а) Үзгәрешленең һәм ——- вакланмаларының
X X 4^
кыйммәтләре суммасын 1 гә тигез итә торган кыйммәтләре
бармы?
1 — Зх х + 5
б) Үзгәрешленең нинди кыйммәтләрендә ——- һәм
4х - 3 х + 2
вакланмаларының аермасы аларның тапкырчыгышына
тигез була?
168
Тигезләмәләрне яңа үзгәрешле кертү юлы белән эшләгез:
026.14. а) х4 - 17x2 + 16 = 0;
б) х4 + Зх2 - 10 = 0;
в) х4 - 10x2 + 25 = 0;
г) х4 + 5x2 - 36 = 0.
026.15. а) 4x4 - 37x2 + 9 = 0;
б) 9x4 + 32x2 - 16 = 0;
в) 16x4 - 25x2 + 9 = 0;
г) 9x4 - 32x2 - 16 = 0.
026.16. а) x6 - 7x3 - 8 = 0;
б) xβ - 9x3 + 8 = 0;
в) xβ + 7x3 - 8 = 0;
г) xβ + 9x3 + 8 = 0.
Тигезләмәләрне чишегез:
. 5 , = 14
' х-2 x2 -4x + 4,
б) —-— + —-— = 5
, Зх + 1 9x2 + 6x + 1
1 2 +1 = 15
В х - 3 х2 - 6х + 9’
r)-2- + - =
5x + 1 25x2 + 10x + 1
9R 1 Я a⅛
1
1
8
х + 2
х2 - 2х
х3 - 4х
2
1
5
б)
х2 - Зх
х - 3
х3 - 9х
7
х + 4
Зх2 - 38
в)
х + 1
2 - 2х
х2 - 1 ’
26.19. а)
б)
в)
г)
2х - 5 х + 2 + х - 5
х2 - Зх х2 + Зх х2 - 9
8x + 4 + 4 _ 5x - 1 .
x3+l х + 1 x2-x + l,
α2 + 56 3a + 2 = 5 .
a3 + 8 a2 - 2a + 4 a + 2’
16 - a2 _ 2a + 1 _ 2 .
8a3 + 1 4a2 - 2a + 1 2a + 1’
х + 3 3 1
9x2 + Зх + 1 + 27x3 - 1 Зх - 1'
169
Тигезләмәләрне чишегез:
•26.20. a) - - = 1 :
16x2 - 9 16x2-24x + 9 4x2 + 3x
б) 18 1 _ 6
4x2 + 4x + 1 2x2 - х 4x2 - 1’
. х + 3 3 - х _ 2
4x2 - 9 4x2 + 12х + 9 2х - 3’
. 1 + 2х 2x - 1 _ 8
Г)6х2-3х 14x2+7x 12x2-3'
aι х + 1 1— х - 2 .
’ х3 - 3x2 + x- 3 x4-l х3 - Зх2 - х + 3’
25 8х + 29 _ 18х + 5.
4x2 + 1 16x4 - 1 8x3 + 4x2 + 2х + 1’
. х2 - 2x + 4 + х2 + 2х + 4 _ 2х + 2.
В' х3 - 2x2 + 4х - 8 х3 + 2x2 + 4x + 8 х2 - 4’
. 5 2 = 1
Г х3 - 2x2 - 2x + 1 х3 - 4x2 + 4x - 1 х2 - 1’
Тигезләмәләрне яңа үзгәрешле кертү юлы белән эшләгез:
26.22. a) (Зх - 4)2 - 5(3х - 4) + 6 = 0;
б) 3(2x + I)2 + 10(2x + 1) + 3 = 0;
в) (5x + I)2 - 3(5x + 1) - 4 = 0;
г) 2(7x - 6)2 + 3(7x - 6) + 1 = 0.
26.23. а) (х2 + 2x)2 - 2(x2 + 2х) - 3 = 0;
б) 2(x2 + 3)2 - 7(x2 + 3) + 3 = 0;
в) (x2 + I)2 - 6(x2 + 1) + 5 = 0;
г) 2(x2 + 4x)2 + 17(x2 + 4х) + 36 = 0.
26.24. а) (х2 - 9)2 - 8(x2 - 9) + 7 = 0;
б) (х2 - 4x + 4)2 + 2(x - 2)2 = 3;
в) (х2 - 3x)2 + 3(x2 - Зх) - 28 = 0;
г) 2(x2 + 2x + I)2 - (х + I)2 = 1.
170
Тигезләмәләрне яңа үзгәрешле кертү юлы белән эшләгез:
26.25. а) 48 - 14x^1 + χ~2 _ θ.
б) 9(x + 2)^2 - 6(x + 2)^1 + 1 = 0;
в) 24 - 10x'1 + Х'2 = 0;
г) 16(x - 3)^2 + 8(χ - 3)-ι + 1 = 0.
•26.26. а) (х2 - Зх + 1) (χ2 - Зх + 3) = 3;
б)
= 2,9;
в) (х2 - 5x + 7)2 - (х - 2)(х - 3) = 1;
, х2 + х - 5
г) ~
+ 4 = 0.
∙z J- V _ К
•26.27. a) x2 + х + 1 = —-1» ;
X2 + х + 3
6)≠^--⅛12L÷2=i
x2-x + l x2-x-2
г) + - = - .
х2 - Зх + 3 х2 - Зх + 4 х2 - Зх + 5
•26.28. a) x(x - l)(x - 2)(х - 3) = 15;
б) х2 + -⅛ + X + - = 4;
X2 X
в) (х + l)(x + 2)(x + 3)(х + 4) = 3;
D2(x-+⅛)
- 7
+ 9 = 0.
§27. РЕАЛЬ ХӘЛЛӘРНЕҢ
МАТЕМАТИК МОДЕЛЬЛӘРЕ БУЛАРАК
РАЦИОНАЛЬ ТИГЕЗЛӘМӘЛӘР
o27.1. Велосипедчы 18 км ны билгеле бер тизлек белән, ә калган
6 км ны баштагыдан 6 км/сәг кә кимрәк тизлек белән
бара. Әгәр ул барлык юлга 1,5 сәг вакыт сарыф итсә,
юлның беренче өлешендә велосипедчының тизлеге нинди
булган?
171
027.2. Беренче җәяүле 6 км, ә икенчесе 5 км юл үтә. Беренчесенең
тизлеге икенче җәяүленекенә караганда 1 км/сәг кә
кимрәк. Әгәр беренче җәяүле юлда икенчесенә караганда
30 мин ка күбрәк булса, аның тизлеген табыгыз.
027.3. 30 км араны беренче чаңгычы икенчесеннән 20 мин ка
тизрәк үтә. Беренче чаңгычының тизлеге икенчесенең
тизлегеннән 3 км/сәг кә зуррак була. Һәр чаңгычының
тизлеге нинди?
027.4. Вакланманың санаучысы ваклаучысыннан 1 гә ким. Бу
вакланмага аңа кире булган вакланманы кушкач, 2 —
килеп чыга. Баштагы вакланманы табыгыз.
027.5. Бер үк вакытта бер үк шәһәрдән икенчесенә ике ав¬
томобиль юлга чыга. Беренче автомобильнең тизлеге
икенчесенең тизлегеннән 10 км/сәг кә зуррак, шунлык¬
тан ул тиешле урынга икенчесеннән 1 сәг алданрак барып
җитә. Шәһәрләр арасындагы ераклык 560 км булса, һәр
автомобильнең тизлеген табыгыз.
o27.6. А шәһәреннән аннан 100 км ераклыктагы В шәһәренә
шәһәрара автобус юлга чыга. Һава шартлары уңайсыз
булу сәбәпле, ул расписаниедә билгеләнгәннән
10 км/сәг кә кимрәк тизлек белән бара һәм В пунктына
30 мин ка соңга калып килеп җитә. Расписание буенча
автобус нинди тизлек белән барырга тиеш була?
027.7. Велосипедчы билгеле бер тизлек белән авылдан чыгып,
аннан 32 км ераклыктагы станциягә юнәлә. Кире кайт¬
канда, ул 1 км/сәг кә артыграк тизлек белән бара һәм
кире юлга баргандагыдан 8 мин кимрәк вакыт сарыф итә.
Велосипедчы станциягә нинди тизлек белән бара?
027.8. Тизлеген 10 км/сәг кә арттырып, поезд 720 км араны
үтү өчен кирәкле вакытны 1 сәг кә кыскарта. Поездның
баштагы тизлеген табыгыз.
027.9. Велосипедчы шәһәрдән турбазага кадәрле 16 км араны
билгеле бер тизлек белән үтә. Кире кайтканда, ул тизле¬
ген 4 км/сәг кә киметә. Барып кайту өчен велосипедчы
2 сәг 20 мин вакыт сарыф итә. Аның турбазадан шәһәргә
кайткандагы тизлеген табыгыз.
172
θ27.10. Автобус А пунктыннан В пунктына 40 км ны даими тиз¬
лек белән үтә. Кире кайтканда, тизлеген 10 км/сәг кә
киметә һәм кире юлга 20 мин күбрәк вакыт сарыф итә.
Автобусның баштагы тизлеген табыгыз.
027.11. 18 км лы араны үтү өчен, велосипедчы җәяүлегә караган¬
да вакытны 1 сәг 48 мин ка азрак тота, чөнки ул 1 сәг тә
җәяүлегә караганда 9 км га артыграк юл үтә. Велосипед¬
чы һәм җәяүленең тизлекләре нинди?
027.12. Авылдан шәһәргә бер үк вакытта автомобиль һәм мото¬
цикл юлга чыга. Шәһәрдән авылга кадәр ераклык 90 км.
Әгәр автомобильнең тизлеге 15 км/сәг кә зуррак булса
һәм ул шәһәргә мотоциклдан ярты сәгатькә алдарак ки¬
леп җитсә, автомобиль һәм мотоцикл нинди тизлекләр
белән хәрәкәт иткәннәр?
027.13. Автовокзалдан аннан 40 км ераклыктагы аэропортка
экспресс-автобус юлга чыга. Автобус кузгалып 10 мин
үткәннән соң, аэропортка такси китә. Таксиның тизлеге
автобусныкыннан 20 км/сәг кә артыграк. Әгәр алар аэро¬
портка бер үк вакытта килеп җитсәләр, таксиның һәм
автобусның тизлекләрен табыгыз.
027.14. Автомашиналар колоннасы складтан елга портына 60 т
йөк ташырга тиеш була. Һава шартларына карап, һәр
машинага уйланылганнан 0,5 т га кимрәк йөк төйиләр
һәм шунлыктан колоннага тагын дүрт өстәмә машина
бирәләр. Башта колоннада ничә машина була?
027.15. Остаханә билгеле бер вакытка 5400 пар аяк киеме эшләп
чыгарырга тиеш була. Көненә 30 парга артыграк эшләп,
ул планны 9 көнгә алданрак үти. Заказ ничә көндә
үтәлгән?
o27.16. Моторлы көймә агым уңаена 5 км һәм агымга каршы
6 км юл үтеп, барысы 1 сәг вакыт сарыф итә. Елганың
агым тизлеге 3 км/сәг. Көймәнең агым уңаена тизлеген
табыгыз.
173
027.17. Мәктәпнең яшь натуралистлар түгәрәгенә йөрүчеләр, ка¬
терга утырып, дару үләннәре җыярга китәләр. Елганың
агымы уңаена 35 км үтеп, алар өч сәгатьлек тукталыш
ясыйлар һәм аннан кире кайталар. Әгәр барлык сәяхәт
7 сәг кә сузылса һәм елганың агым тизлеге 3 км/сәг
булса, катерның акмый торган судагы тизлеген табыгыз.
027.18. Моторлы көймә агым уңаена 54 км һәм агымга каршы
42 км юл үтеп, моның өчен акмый торган суда 96 км
үткән кадәр вакыт сарыф итә. Әгәр елганың агым тизлеге
3 км/сәг булса, көймәнең акмый торган судагы тизлеген
табыгыз.
027.19. Туристның байдаркада күл буйлап 24 км һәм елгада
агымга каршы 9 км үткән вакыты аның агым уңаена
45 км араны үткән вакытына тигез. Әгәр елганың агым
тизлеге 2 км/сәг булса, турист күлдә нинди тизлек белән
йөзгән?
o27.20. Катер агым уңаена 27 км һәм агымга каршы 42 км
ара үтеп, агым уңаена агымга каршы барганнан 1 сәг
кә азрак вакыт сарыф итә. Әгәр елганың агым тизлеге
3 км/сәг булса, катерның агымга каршы тизлеге нинди?
027.21. Ишкәкченең агымга каршы 3 км һәм агым уңаена
3 км араны узган вакыты салның агым уңаена 4 км
араны йөзеп узган вакытка тигез. Көймәнең үз тизлеге
6 км/сәг. Елганың агым тизлеген табыгыз.
o27.22. Ял итүчеләрне йөртүче теплоход А пристаненнан В га
таба агым уңаена китә. В да ярты сәгать туктап торган¬
нан соң, ул кире китә һәм А дан кузгалып киткәннән
башлап 8 сәг вакыт узгач, яңадан А га кайта. Әгәр А һәм
В пристаньнары арасы 36 км, ә елганың агым тизлеге 2
км/сәг булса, теплоходның үз тизлеген табыгыз.
027.23. Моторлы көймә агым уңаена 6 км, аннан соң күл буйлап
10 км юл уза һәм моның өчен 1 сәг вакыт сарыф итә. Әгәр
елганың агым тизлеге 3 км/сәг булса, катер күлдә нинди
тизлек белән барган?
027.24. Катер 210 км араны агым уңаена агымга каршы йөз¬
гәннән 4 сәг кә тизрәк үтә. Әгәр елганың агым тизлеге
3 км/сәг булса, катерның үз тизлеген табыгыз.
174
027.25. Моторлы көймә агымга каршы 20 км һәм күлдә 14 км
араны үтә һәм күлдә елга буйлап йөзгәннән 1 сәг вакыт
кимрәк була. Елганың агым тизлеге 4 км/сәг. Көймәнең
агымга каршы баргандагы тизлеген табыгыз.
027.26. Ике басуның гомуми мәйданы 20 га. Беренче басудан
550 т, икенчесеннән 540 т бәрәңге җыеп алалар. Берен¬
че басуның 1 гектарыннан икенчесенең 1 гектарыннан
алганга караганда 10 т га кимрәк уңыш алынса, һәр
басуның 1 гектарыннан күпме бәрәңге алганнар?
027.27. Токарь билгеләнгән вакытка 120 деталь эшкәртергә тиеш
була. Яңа кискеч кулланып, ул бер сәгатьтә 20 гә күбрәк
деталь кыра башлый һәм эшен 1 сәг кә алдан бетерә. Ул
план буенча 1 сәгатькә ничә деталь эшләргә тиеш була?
027.28. Бригада билгеләнгән вакытка 120 эшләнмә әзерләргә
тиеш була. Ләкин ул бер көнгә планда күрсәтелгәннән
2 гә артыграк эшләнмә ясый һәм эшне 3 көнгә алдан
төгәлли. План буенча бригада бер көнгә ничә деталь ясар¬
га тиеш була?
27.29. Гади вакланманың ваклаучысы санаучысыннан 3 кә зур¬
рак. Санаучыга 7 не, ә ваклаучыга 5 не кушканнан соң,
вакланма | гә арта. Бу вакланманы табыгыз.
27.30. Кыскармый торган гади вакланманың санаучысы ваклау¬
чыдан 5 кә кечерәк. Санаучыны 2 гә киметеп, ваклау¬
чыны 16 га зурайтканнан соң, вакланма гә кими. Бу
О
вакланманы табыгыз.
27.31. Гади вакланманың санаучысы ваклаучысыннан 1 гә ким.
Санаучыдан да, ваклаучыдан да 1 не алганнан соң, вак¬
ланма — гә кими. Бу вакланманы табыгыз.
12
27.32. А пунктыннан чыгып 2 сәг барганнан соң, автобус 30 мин
ка тоткарлана һәм, В га расписание буенча килеп җитү
өчен, тизлеген 5 км/сәг кә арттыра. Әгәр А һәм В пункт¬
лары арасы 260 км булса, автобусның баштагы тизлеген
табыгыз.
175
27.33. Велосипедчы шәһәрдән туристлар базасына кадәр 30 км
юл үтә. Кире кайтканда, ул 2 сәг шундый ук тизлек белән
бара, аннан соң тизлеген 3 км/сәг кә арттыра һәм кире
кайту өчен баргандагыдан 6 мин ка азрак вакыт сарыф
итә. Велосипедчы кайту юлын нинди вакытта уза?
27.34. Велосипедчы ВС маршрутын 2 сәг тә узарга уйлый. Әмма
С пунктына 6 км калгач, каршы исүче җил аркасында,
ул тизлеген 3 км/сәг кә киметә һәм С га уйлаганына ка¬
раганда 6 мин ка соңга калып килә. ВС маршрутының
озынлыгы нинди?
27.35. Җәяүле С пунктыннан М пунктына кадәр араны 3 сәг тә
уза. Кире кайтканда, ул беренче 16 км ны шул ук тиз¬
лек белән бара, аннан соң тизлеген 1 км/сәг кә киметә
һәм шунлыктан кире кайтуга С дан М га баргандагыдан
4 минут артыграк вакыт сарыф итә. С һәм М пунктлары
арасы нинди озынлыкта?
27.36. Поезд 54 км араны узарга тиеш була. 14 км ны узгач, ул
семафор янында 10 мин ка тоткарлана. Аннан соң тизле¬
ген 10 км/сәг кә арттыра һәм билгеләнгән урынга 2 мин
ка соңга калып килеп җитә. Поездның баштагы тизлеген
табыгыз.
27.37. А һәм В станцияләре арасы 240 км. В дан А юнәлешендә
поезд чыга. 30 мин тан соң А дан аңа каршы тизлеге бе¬
ренче поезд тизлегеннән 12 км/сәг кә зуррак булган икен¬
че поезд кузгала. Әгәр алар А һәм В арасындагы юлның
уртасында очрашсалар, бу поездларның тизлекләрен
табыгыз.
27.38. Пристаньнар арасындагы елга юлы 21 км. Бер пристань¬
нан икенчесенә киткән катер, тукталышка 30 мин вакыт
сарыф итеп, 4 сәг тән соң кире кайта. Әгәр елганың агым
тизлеге 2,5 км/сәг булса, катерның тизлеген табыгыз.
27.39. Туристның байдаркада агымга каршы 15 км һәм агым
уңаена 14 км юл узуга киткән вакыты аның күлдә
30 км араны йөзгән вакытына тигез. Елганың агым тизлеге
1 км/сәг булса, туристның күлдәге тизлеген табыгыз.
176
27.40. 180 туристны йөртү өчен берничә автобуска заказ бирә¬
ләр. Әмма 2 автобус килеп җитми, ә туристлар көткәннән
8 гә артык булып чыга. Шунлыктан аларны һәр автобус¬
ка уйланылганнан 17 кешегә күбрәк итеп утырталар, һәр
автобуска ничә турист утыртылган?
27.41. Тракторчылар бригадасы билгеләнгән вакытка 1800 га
җир сөрергә тиеш була. Көн саен планны 25 га га арт¬
тырып үтәп, билгеләнгән вакытка 4 көн кала, бригада
планны үтәп кенә калмый, ә тагын өстәмә 200 га җир
сөрә. План буенча бригаданың көнлек нормасы нинди
була?
•27.42. Ике шәһәр арасы 44 км. Бу шәһәрләрдән бер үк вакытта
бер-берсенә каршы ике җәяүле юлга чыга һәм 4 сәг тән
соң алар очрашалар. Әгәр аларның берсе икенчесеннән
44 мин ка алданрак чыкса, алар юлның нәкъ уртасында
очрашырлар иде. Һәр җәяүле нинди тизлек белән барган?
•27.43. Велосипедчы 96 км араны алдан уйлаганнан 2 сәг кә
тизрәк уза. Шуның белән бергә, ул һәр сәгать эчендә үзе
1 сәг 15 мин та үтәргә планлаштырган кадәр юл узган.
Велосипедчы нинди тизлек белән барган?
•27.44. 80 г алтыны булган алтын белән көмеш эретмәсенә 100 г
алтын өстиләр. Нәтиҗәдә эретмәдәге алтын 20% ка арта.
Эретмәдә ничә грамм көмеш бар?
•27.45. 5 кг цинкы булган бакыр һәм цинк эретмәсенә 15 кг цинк
өстиләр һәм эретмәдәге цинк 30% ка арта. Әгәр башта
эретмәдә бакыр цинкка караганда артыграк булган булса,
эретмәнең баштагы авырлыгын табыгыз.
§ 28. КВАДРАТ ТИГЕЗЛӘМӘ ТАМЫРЛАРЫНЫҢ
ТАГЫН БЕР ФОРМУЛАСЫ
28.1. Тигезләмәләрне чишегез:
а) х2 - 14х + 33 = 0; в) х2 + 12х - 28 = 0;
б) х2 - 10х - 39 = 0; г) х2 + 12х + 35 = 0.
177
028.2.
Тигезләмәләрне чишегез:
а) х2 + 34х + 280 = 0;
б) х2 - 16х - 132 = 0;
в) х2 - 24х + 108 ⅛= 0;
г) х2 + 26х - 120 = 0.
028.3.
a) 9x2 - 20х - 21 = 0;
б) 7x2 + 6х - 1 = 0;
в) 5x2 + 8х - 4 = 0;
г) 5x2 - 4х - 1 = 0.
028.4.
а) х2 - 2х - 1 = 0;
б) х2 + 4x + 1 = 0;
в) х2 + 2х - 2 = 0;
г) х2 - 6х + 7 = 0.
028.5.
a) 4x2 - 8x + 1 = 0;
б) 9x2 + 12x + 1 = 0;
в) 4x2 - 12х + 7 = 0;
г) 25x2 + 10х - 4 = 0.
028.6.
, х + 3 2х + 3
а) x _ з = x ;
б) 3* + 1 _ *211 = 1;
х + 2 х - 2
, х + 2 Зх - 2
В) x-2^ 2х ’
.3x + 2 х + 2 ,
г) = 1.
х - 3 х + 3
θ28.7. Турыпочмаклыкның мәйданы 675 см2 га тигез. Әгәр
якларының берсе икенчесеннән 30 см га кечерәк булса,
турыпочмаклыкның якларын табыгыз.
θ28.8. Квадрат биттән киңлеге 6 см га тигез булган тасма кисеп
алганнар. Калган өлешнең мәйданы 135 см2. Бу битнең
баштагы үлчәмнәрен табыгыз.
o28.9. Берсе икенчесеннән 6 га зуррак булган ике натураль
санның тапкырчыгышы 187 гә тигез. Бу саннарны табы¬
гыз.
028.10. Әгәр турыпочмаклыкның бер ягы икенчесеннән 14 см га
зуррак, ә диагонале 34 см булса, аның мәйданын табыгыз.
o28.ll. Мотоциклчы юлга 6 мин ка соңга калып чыккан. Вакы¬
тында килеп җитү өчен, ул тизлеген 10 км/сәг кә арттыр¬
ган. Әгәр барлык юл 30 км га тигез булса, мотоциклчы
нинди тизлек белән барган?
028.12. Катер 36 км араны билгеле бер вакытта үтәргә тиеш була,
ләкин ул 12 минутка соңга калып чыга һәм, вакытында
килеп җитү өчен, расписаниедә каралганнан 6 км/сәг
кә зуррак тизлек белән бара. Катер нинди тизлек белән
барган?
o28.13. Ике автобус бер үк вакытта А пунктыннан аннан 48 км
ераклыктагы В пунктына юнәлә. Автобусларның берсе,
икенчесеннән 4 км/сәг кә тизрәк барып, В га 10 мин ка
иртәрәк килеп җитә. Автобусларның тизлекләрен табыгыз.
178
028.14. Поезд семафор янында 24 мин ка тоткарлана һәм, стан¬
циягә вакытында килеп җитү өчен, калган 195 км ны
баштагыдан 10 км/сәг кә артыграк тизлек белән барырга
мәҗбүр була. Поездның баштагы тизлеген табыгыз.
o28.15. 400 км араны тизйөрешле поезд товар поездыннан 1 сәг
кә тизрәк уза. Әгәр товар поездының тизлеге тизйөрешле
поезд тизлегеннән 20 км/сәг кә кимрәк булса, һәр
поездның тизлеген табыгыз.
o28.16. А һәм В станцияләре арасындагы юлның уртасында поезд
10 мин ка тоткарлана. В станциясенә вакытында килеп
җитү өчен, машинистка поездның баштагы тизлеген
12 км/сәг кә арттырырга туры килә. Әгәр станцияләр
арасы 120 км булса, поездның баштагы тизлеген табыгыз.
028.17. Катер елганың агымы уңаена 8 км һәм агымга каршы
4
16 км юл үтеп, барлык юлга - сәг вакыт сарыф итә. Әгәр
О
катерның үз тизлеге 20 км/сәг булса, аның агым уңаена
тизлеге нинди булыр?
o28.18. Моторлы көймә елганың агымы уңаена 7 км һәм агымга
каршы 10 км юл үтеп, агым уңаена агымга каршы бар¬
ганнан 0,5 сәг кимрәк вакыт сарыф итә. Көймәнең үз
тизлеге 12 км/сәг булса, аның агымга каршы тизлеген
табыгыз.
Тигезләмәләрне чишегез:
28.19. a) χ2 - 52х - 285 = 0;
б) 3x2 + 130х - 133 = 0;
в) х2 + 108х - 2413 = 0;
г) 17x2 - 128х - 64 = 0.
28.20. a) χ2 - 4√3x + 12 = 0; в) x2 + 6√2x + 18 = 0;
б) х2 + 2√5x - 20 = 0; г) x2 - 4√2x + 4 = 0.
28.21. a) χ2 - 2(p - l)x + р2 - 2р - 3 = 0;
б) х2 + 2(р + 1)х + р2 + 2р - 8 = 0;
в) х2 - 2(p - l)x + р2 - 2р - 15 = 0;
г) х2 + 2(p + 3)x + р2 + 6р - 7 = 0.
179
Тигезләмәләрне чишегез:
•28.22. a) χ2 — 2px + p2 — 1 = 0;
б) pχ2 - 4x + 1 = 0;
в) x2 - 4px + 4p2 - 1 = 0;
г) px2 - 12x ÷ 4 = 0.
•28.23. а) (р - 4)x2 + (2р — 4)х + р = 0;
б) pχ2 + 2(р + 1)х + р + 3 = 0.
28.24. А һәм В шәһәрләре арасы 120 км. А дан чыгып 2 сәг бар¬
ганнан соң, мотоциклчы шлагбаум янында 6 мин ка тот¬
карлана. В га вакытында килеп җитү өчен, ул тизлеген
12 км/сәг кә арттыра. Мотоциклчы нинди тизлек белән
бара башлый?
28.25. Велосипедчы шәһәрдән фермага кадәр 40 км юл үтә. Кире
кайтканда, башта 2 сәг шул ук тизлек белән бара һәм
20 мин туктап тора. Тукталыштан соң ул тизлеген
4 км/сәг кә арттыра һәм кире кайтуга да баргандагы
кадәр үк вакыт сарыф итә. Тукталыштан соң велосипед¬
чы нинди тизлек белән бара?
28.26. Ел башында завод аена 800 эшләнмә чыгара. Ел дәва¬
мында ул продукция чыгаруны ике тапкыр бер үк
процентка арттыра. Әгәр ел ахырында бер айга 1152
эшләнмә чыгарылса, завод продукция чыгару күләмен
ничәшәр процентка арттырган?
28.27. Университет ике ел дәвамында студентлар кабул итүне
бер үк процентка арттыра. Әгәр кабул ителүчеләр саны
2000 кешедән 2880 гә җитсә, студентлар кабул итү ел
саен ничә процентка арткан?
28.28. 2800 м3 суы булган буаны чистарту өчен, барлык суны
билгеләнгән вакытка насослар белән суыртып бетерү
каралган була. Насосларны көтелгәннән азрак санда
җибәрүләре аркасында, көн саен фаразланган нормадан
20 м3 га азрак су суырталар. Билгеләнгән вакыттан бер
көн узганнан соң, әле 100 м3 су суыртасы кала. Башта
суны ничә көндә суыртып бетерергә уйлаганнар?
180
§ 29. ВИЕТ ТЕОРЕМАСЫ
29.1. Бирелгән квадрат тигезләмәләрнең кайсысында тамырлар
суммасы -6 га, ә тамырлар тапкырчыгышы -11 гә тигез:
a) х2 - 6х + 11 = 0;
б) х2 + 6х - 11=0;
в) х2 - 11х - 6 = 0;
г) х2 + 11х - 6 = 0?
Тигезләмәләрне чишмичә генә, тамырлары булу-булмавын
билгеләгез. Тамырлары булган тигезләмәләрдә аларның
суммасын һәм тапкырчыгышын табыгыз:
29.2. а) х2 + 2х - 5 = 0;
б) х2 - 15х + 16 = 0;
в) х2 - 19x + 1 = 0;
г) х2 + 8х + 10 = 0.
29.3. a) 2x2 + 9х - 10 = 0;
б) 5x2 + 12х + 7 = 0;
в) 19x2 - 23х + 5 = 0;
г) 3x2 + ИЗх -7 = 0.
29.4. а) х2 - 6 = 0;
б) 2x2 + Зх = 0;
в) х2 + 5х = 0;
г) 7x2 - 1 = 0.
29.5. a) 0,2x2 - 4х - 1 = 0;
в) х2 - λ∕δx +1 = 0;
б) √3x2 - 12x - 7√3 = 0;
г) ∣x2 + 2х - 1 = 0.
Тамырлар формуласын кулланмыйча гына, квадрат ти¬
гезләмәләрнең тамырларын табыгыз:
29.6. а) х2 + Зх + 2 = 0;
б) х2 - 15х + 14 = 0;
в) х2 + 8х + 7 = 0;
г) х2 - 19х + 18 = 0.
29.7. а) х2 + Зх - 4 = 0;
б) х2 - 10х -11 = 0;
в) х2 - 9х - Ю = 0;
г) х2 + 8х - 9 = 0.
29.8. а) х2 + 9х + 20 = 0;
б) х2 - 15х + 36 = 0;
в) х2 + 5х - 14 = 0;
г) х2 - 7х - 30 = 0.
θ29.9. Бирелгән тамырлары буенча квадрат тигезләмә төзегез:
a) x1 = 4; х2 = 2;
б) x1 = 3; х2 = -5;
в) x1 = -8; Х2 - 1;
г) x1 = -6; х2 = _2.
181
o29.10. Бирелгән тамырлары буенча квадрат тигезләмә төзегез:
a) x1 = 2,5; х2 = -2; в) x1 = -2,4; х2 = -1,5;
2. 1 1. . 3 1 2
б) x1 = -; χ2 = -1 -; г) x1 = -; χ2 = -1 -.
o29.ll. х2 + Ьх - 8 = 0 квадрат тигезләмәсенең:
а) тамырлары булмавы;
б) тигез тамырлар алуы;
в) төрле тамгалы төрле ике тамыры булуы;
г) бер үк тамгалы төрле ике тамыры булуы мөмкинме?
o29.12. x1 һәм х2 — ах2 + Ьх + с = 0 квадрат тигезләмәсенең
тамырлары булсын. Табыгыз:
а) әгәр a = 2, x1 = 3, x2 = -0,5 булса, Ь һәм с ны;
б) әгәр b = -1, x1 = 3, х2 = -4 булса, а һәм с ны;
в) әгәр с = 4, x1 = -2, х2 = -0,25 булса, а һәм Ъ ны;
г) әгәр b = 6, x1 = 3, х2 = -4 булса, а һәм с ны.
029.13. р параметрының нинди кыйммәтләрендә x2 + (p2 + 4p-
- 5)х - р = 0 квадрат тигезләмәсенең тамырлары суммасы
нульгә тигез була?
029.14. р параметрының нинди кыйммәтләрендә x2 + Зх + (р2 -
- 7р + 12) = 0 квадрат тигезләмәсенең тамырлары
тапкырчыгышы нульгә тигез була?
Квадрат өчбуынны тапкырлаучыларга таркатыгыз:
029.15.
а) х2 - 11х + 24;
б) х2 - 2х - 15;
в) х2 + 7х + 12;
г) х2 + Зх - 10.
029.16.
а) -х2 + 16х - 15;
б) -х2 - 8х + 9;
в) -х2 + 5х - 6;
г) -х2 + 7х + 8.
029.17.
a) Зх2 + 5х - 2;
б) 6x2 + 5x + 1;
в) 5x2 + 2х - 3;
г) 15x2 - 8x + 1.
029.18.
a) -Зх2 - 8х + 3;
б) -5x2 + 6х - 1;
в) -2x2 + 9х - 4;
г) —4x2 — Зх + 85.
029.19.
Вакланманы кыскартыгыз:
х + 4 . х +1 .
х2 + 7х + 12’
х2 +4х + 3’
Зх2 - 10х + 3.
61 x∙-3x ■
. 5x2 + х - 4
г) i •
X2 + X
182
Вакланманы кыскартыгыз:
o29.20. a)
хг - 1
. 2x2 + 7х - 4.
В) х= - 16 ’’
9x2 - 1 .
, Зх2 - 8х - 3’
4x2 - 1
Г) 2x2 - 9х - 5‘
029.21. a) χ3i ~θ*+⅛
х2 + 7х - 30
6x2 - 19х + 13.
В) 2х2 + 7х - 9 ’
6x2 + 7х - 3.
, 2 - х - 15x2 ’
. 21x2 + х - 2
Г) 2 + 5x-3x2'
o29.22. Аңлатманы гадиләштерегез:
. ( 1 + 5 + 2x "⅛ • x ■
a,lx + 2 х2 -х-6 х-3) 2х + 1’
( 2 10 3x λ∣ . Зх + 2
6)∖x + l + x2-3x-4 х - 4 J 3
Тигезләмәне чишегез:
029.23.
а)
б)
029.24.
а)
б)
029.25.
а)
б)
х2 + 1 2
3
х - 3’
х2 - 4х + 3
х - 1
18 _ х2
- 7
6
х - 8 х2 -
7х - 8
х + 1'
х2 + 14 ,
10
Зх
х2 - х - 2
х + 1
х - 2’
6 Зх
х!
2 + 20
х - 4 х + 2
х2 -
- 2х - 8’
х2 - 5
х + 3
, 2х + 2
+
х2 - Зх + 2
х - 1
х - 2
2x2 + 9х ,
Зх + 2
2х + 3
х2 - х - 6
х + 2
х-3
29.26. Тамырлар формуласын кулланмыйча гына, квадрат ти¬
гезләмәләрнең тамырларын табыгыз:
а) х2 - 88х + 780 = 0; в) х2 - 26х + 105 = 0;
б) х2 - 26х + 120 = 0; г) х2 + 35х - 114 = 0.
183
29.27. Әгәр a + b + с = 0 булса, ax2 + bx + с = О тигезләмәсенең
1 гә тигез булган тамыры барлыгын исбатлагыз.
29.28. Виет теоремасын һәм 29.27 нче күнегүдәге раслауны
кулланып, тигезләмәнең тамырларын табыгыз:
a) 13x2 + 18х -31 = 0; в) 6x2 - 26х + 20 = 0;
б) 5x2 - 27х + 22 = 0; г) Зх2 + 35х - 38 = 0.
29.29. Әгәр a - b + с = 0 булса, ах2 + Ьх + с = 0 тигезләмәсенең
-1 гә тигез булган тамыры барлыгын исбатлагыз.
29.30. Виет теоремасын һәм 29.29 нчы күнегүдәге раслауны
кулланып, тигезләмәнең тамырларын табыгыз:
a) Зх2 + 18х + 15 = 0; в) llx2 + 17х + 6 = 0;
б) 67x2 - 105х - 172 = 0; г) 14x2 - 37х - 51 = 0.
Тамырлары түбәндәге саннар булган квадрат тигезләмә
төзегез:
29.31. a) x1 = √2, x2 = -√2j в) x1 = √7, x2 = -√7j
б) x1 = 3-/5, х2 = -3^5; г) x1 = 9y∣2, x2 = -9y[2.
29.32. a) χ1 = 3 + √2, х2 = 3 - √2j
б) x1 =
в) x1 = 2 + y∣5, х2 = 2 - у[5;
Аңлатманы тапкырлаучыларга таркатыгыз:
29.33.
а) х + (jy[χ + 8;
б) х - 7√x - 18;
в) х - 12λ∕x + 35;
г) х + 3√7 - 40.
29.34.
a) 7x + 23√x + 16;
б) Зх3 - Юхл/х + 3;
в) 9x + 4√rx - 5;
г) 2x3 - 5x√x + 2.
29.35.
а) х4 - 13x2 + 36;
б) -2x6 + 9x3 - 4;
в) -х4 + 20x2 - 64;
г) 15x8 - 8x3 + 1.
184
29.36. Квадрат өчбуынны тапкырлаучыларга таркатыгыз:
а) х2 - 12х + 24; в) x2-6x÷ 1;
б) 4x2 - 4х - 1; г) 4x2 - 12х + 7.
Вакланманы кыскартыгыз:
29.37.
х - 5y[x - 14
Э) x-2√7-85
2x + 11√7 - 6
х + 3 y∣^x - 18 ’
29.38.
б)
а)
x4 - 10x2 + 9.
х2 - 2х - 3 ’
х3 - 4х
xr~-~3xr- 4’
х3 + 5x2 - 4х - 20,
х2 + Зх - 10 ’
в)
'3 + χ2 _ 4χ _ 4
х2 + Зх + 2
б)
х3 - 2x2 - 16х + 32,
х2 - 6х + 8
х3 - Зх2 - х + 3
х2 - 2х - 3
•29.39. x1 һәм х2 — х2 - 9х - 17 = 0 квадрат тигезләмәсенең
тамырлары булсын. Тигезләмәне чишмичә генә исәпләгез:
a) x2l + х|; б) x2x2 + x1x2 .
•29.40. x1 һәм х2 — 3x2 + 8x - 1 = 0 квадрат тигезләмәсенең
тамырлары булсын. Тигезләмәне чишмичә генә исәпләгез,
a) x21 + х|; б) xfx2 + x1x22.
•29.41. х2 - (2p2 - р - 6)x + (8p - 1) = 0 тигезләмәсе бирелгән. Аның
тамырлары суммасы -5 икәне билгеле, р параметрының
кыйммәтен табыгыз.
•29.42. х2 - (р + l)χ + (2p2 - 9р - 12) = 0 тигезләмәсе бирелгән.
Аның тамырлары тапкырчыгышы -21 икәне билгеле.
р параметрының кыйммәтен табыгыз.
•29.43. р параметрының ниндидер кыйммәтләрендә 2px2 + (р2 -
- 9)х - 5р + 2 = 0 квадрат тигезләмәсенең тамырлары
капма-каршы саннар була. Бу тамырларны табыгыз.
•29.44. р параметрының ниндидер кыйммәтләрендә 2px2 + 5х +
+ р + 1 = 0 квадрат тигезләмәсенең тамырлары үзара кире
саннар була. Бу тамырларны табыгыз.
•29.45. х2 + (Зр - 5)x + (Зр2 - Ир - 6) = 0 квадрат тигезләмәсе
бирелгән. Аның тамырларының квадратлары суммасы 65
кә тигез, р параметрының кыйммәтен һәм тигезләмәнең
тамырларын табыгыз.
185
•29.46. 2x2 — 15x + p = 0 тигезләмәсенең тамырлары аермасы
2,5 кә тигез, р параметрының кыйммәтен һәм тигезләмәнең
тамырларын табыгыз.
•29.47. 2x2 - 14х + р = 0 квадрат тигезләмәсенең бер тамыры
икенчесеннән 2,5 тапкыр зуррак, р параметрының кыйм¬
мәтен һәм тигезләмәнең тамырларын табыгыз.
29.48.
•29.49.
Аңлатмаларны гадиләштерегез:
х + 12 . ( х - 3 9 А.
а) х3 - 9x ' Ьх2 + 5х - 3 9 - х2 /
( За - 1 _ 9α '∣ 15a3 - 60a
θ ∖ a2 - 4 3a2 + 5a - 2/ 12a + 1
( 4 a + 1 A 15a - 12.
a) I. 5a2 + a - 4 9(5a - 4)) a + 7
5(a + 4) φ f 9(a - 1) _ (2a - 7)2 A
a - 1 ∖ 3a + 4 3a2 + a - 4√
o29.50. Бердәйлекне исбатлагыз:
a lx + 2 x2+5x + 6 х + 3 J 3 3 + х
,, f 2x + 1 + 4 A. x + 3
' lx - 3 x + 1 x2 - 2x - 3√ 2x + l 3-x
Тигезләмәне чишегез:
r2 1 а
•29.51. a) -—≡ — + q 21° 10 = 1;
x2 - 7x + 10 3x2 - 12
g, 2x2 8 _ j
, 2x2 + x - 3 2x2 - 3x - 9
29 52 a) lθx + x ~ 1 _ 21 .
29.5Z. a) 2u14 2χ + 3 6χ2+5χ. 6>
g. 4 + x - 2 _ 2x + 1
’ 6x2 - 13x + 6 + 6x - 4 ^ 10x - 15'
29 53 a) + -1 — = %x —;
29 .53. a) 6χ 4 6χ2+5χ-6 4x + 6,
8x - 1 + x - 1 _ 2x + 1
10x2 -19x+6 10x-4 4x-6'
186
•29.54. Тигезләмәне чишегез:
, х-1 х + 3 _ 4x -1
a х2 - 2х - 3 х2 - 2x - 8 2x2 - 6х - 8’
2 х _ Зх + 1
2x2 - х-1 x2-x-2 Зх2 - 3'
29.55. х = 2007 булганда, аңлатманың кыйммәтен табыгыз:
а)
-θ-+4+ 2дИ
х - 3 x2-5x + 6 х - 2)
2x + 1 _ х - 12.
3 9 - Зх’
I" 2x + 1 4 1∖ х + 3 - х
lx + 3 + x-l х2 + 2x - 3j 2x + 1 + 6 + 2x'
§30*. ИРРАЦИОНАЛЬ ТИГЕЗЛӘМӘЛӘР
Тигезләмәне чишегез:
30.1. a) √x + 2 = 3;
в) λ∕χ - 5 = 9;
б) √4x + 1=3;
г) √7x -1=3.
30.2. a) √χ2 - 1 = 2;
в) √3 - 2x2 = 1;
б) √4x2 +5=3;
г) √6 + 5x2 = 2.
оЗО.З. a) √4x2 + 5х - 2 = 2;
в) √23 + Зх - 5x2 = 3;
б) √23x - 14 - Зх2 = 0;
г) √5x2 + 22х - 15 = 0.
О30.4. а)
2х + 3
х-1
= 2;
б)
х+ 5
4x - 1
х - 4
Зх + 1
= 3.
o30.5. Тигезләмәнең тамырлары юклыгын исбатлагыз:
a) √5- х +2 = 0; в) √3x - 1 +1 = 0;
б) √x - 4 + √x2 - 3 = 0; г) √x - 8 + 3 = √16 - х.
187
оЗО.б. Тигезләмәне чишегез:
a) y∣7x - 4 = λ∕5x + 2;
б) λ∕2x - 5 = y∣ 4х - 7;
в) y∣3x + 4 = y∣5x + 2;
г) √3x + 1 = √2x - 3.
Тигезләмәләрне яңа үзгәрешле кертү юлы белән эшләгез:
o30.7. а) х - 6√x +8 = 0;
б) х — 5-Тх +6 = 0;
в) х - 7λ∕x + 12 = 0;
г) х - 3y[x +2 = 0.
o30.8. а) х + у[х = 30;
в) х + yfx = 12;
б) х - 4λ∕x - 12 = 0;
г) х - 3>/х - 18 = 0.
o30.9. a) √x - -^ = 1;
√ X
, Г 6 1
в) √x —== = 1;
7 х
б) √x + 3 =
√ X
. Г . 32
г) √x + 4 = —г=.
у/ x
o30.10. a)(5x - 1) + √5x - 1 = 12;
б) (2х + 3) + √2x + 3 = 2;
в) (7x + 4) - √7x + 4 = 42;
r)(12x - 1) + √12x - 1 = 6.
Тигезләмәне чишегез:
o30.ll. a) y∣7 - Зх = х + 7;
б) 73 - х = Зх + 5;
в) 715 + Зх = 1 - х;
г) 734 - 5х = 7 - 2х.
o30.12. a) √8 - 2х = х;
б) 75 - х = х + 15;
в) 73 + 2х = х - 6;
г) 71 ~ 5х = 7 + х.
o30.13. а) -7 х - 4 + х = 6;
б) 5x - √3x + 4 =2;
в) y∣ 5х + 1 + 1 = 2х;
г) 77 - Зх + 3 - х = 0.
188
Тигезләмәләрнең тигезкөчле булуын ачыклагыз:
30.14. a) yj х + 1 = 2 һәм х - 2 = 1;
б) ^2x + 1 = 3 һәм х2 = 16;
в) ^5 - х = 3 һәм х2 = 16;
г) λ∕3x + 4 = 5 һәм 2(х - 3) = 15 - х.
30.15. a) y∣х + 1 = 3 һәм х2 - 7х - 8 = 0;
б) \[х = х - 2 һәм х2 = 5х — 4;
в) ^7 - х = —2 һәм х2 + 4х + 8 = 0;
г) V 4x + 1 = х - 1 һәм х2 — 12х + 36 = 0.
Тигезләмәне чишегез:
30.16. a) λ∕4x + 3 = 7 4x2 + 5х - 2;
б) 76x2 - 2x + 1 = λ∕3x + 2;
в) 7 2x2 + Зх - 1 = 7 5x - 1;
г) λ∕8x - 3 = 7 х2 + 4x + 1.
30.17. a) 7 x2 + 2x + 5 = y∣ х2 - Зх + 10;
б) 7δx2 - Зх + 1 = 73x2 - 4х + 2;
в) 73x2 + 5x - 1 = 72x2 + 2х - 3;
г) 7 θx2 + х ~ 15 = 7 х2 - х + 1.
30.18. a) 72x2 + Зх + 1 = х + 1; в) 7 x2 + х + 1 = х + 2;
б) 75x2 - Зх + 2 = х - 3; г) 7Зх2 + х + 30 = х - 5.
30.19. a) y∣x + 1 = 2 + 7х - 19;
б) 7x + 8 = 77x + 9 - 1;
в) 7х - 13 = 7х + 8 - 3;
г) 73x - 5 = 1 + 7х - 2.
189
Тигезләмәне чишегез:
30.20. a) λ∕15 - х + √3 - х = 6; в) ∙⅛∕x - 1 - λ∕β - х = 1;
6) -JЗх + 7 - ^x + 1 = 2; г) у] х — 2 + ^х + 3 = 2.
30.21. a) √4 - 2x + √2 + х = √2xj
б) yjx + 7 = >/Зх + 19 - y∣x + 2;
в) √3x + 1 + y∣x - 4 = 2-Ух;
г) λ∕x - 2 + 7^ + 3 = λ∕6x - 11.
30.22. a) √x + 1 - √9 - х = √2x - 12;
б) х + 1 + -J 4х + 13 = у]Зх + 12;
в) √2x + 5 + √5x + 6 = √12x + 25;
г) y∣2x + 3 - у] 4 - х = у]7 - х.
•30.23. а) (х2 + 1) + 2√x2 + 1 = 15;
в) 2(x2 - 9) + 3 √x2 - 9 -5 = 0;
х-1-2
х-1 -6
•30.24. а)
Зх + 2 2х-3
2x-3 +V Зх + 2
б) J-¾ - 2,5 = 3J1- —;
I х-1 ∣2x + l _ ю
\ 2x + l + У х-1 - ^3 ’
г) 4. 3--
190
ӨЙ КОНТРОЛЬ ЭШЕ № 4
1 нче вариант
1 τ3 2x2 * + 5х - 7
1. Вакланманы кыскартыгыз: χ2 _ gχ + γ •
2. Тигезләмәне чишегез:
а) 2(х + 4) - х(х - 5) = 7(х - 8);
б) 6x4 + х2 — 1 = 0.
3. k ның, аны куйгач x2 - 2fex + k - 3 = 0 тигезләмәсе бер
генә тамыр ала торган кыйммәте булмавын исбатлагыз.
4. Тигезләмәне чишегез:
-2- + 1 - = 2.
Зх + 1 9x2 + 6x + 1
5. Автомобиль, озынлыгы 300 км булган А һәм В арасын
үтеп, кире борыла һәм тизлеген 12 км/сәг кә арттыра.
Нәтиҗәдә ул кире юлга А дан В га баргандагыдан 50 мин
ка кимрәк вакыт сарыф итә. Автомобильнең баштагы
тизлеген табыгыз.
6. x1 һәм х2 — 2x2 - 9х - 12 = 0 тигезләмәсенең тамырлары
булсын. Тигезләмәне чишмичә генә табыгыз:
a) x2x2 + xjx2! б) — + —; в) х* + х®.
Х1 %2
7. х2 + (t2 - 3t - ll)x + 6t = 0 тигезләмәсе бирелгән.
Аның тамырлары суммасы 1 гә тигез, t параметрының
кыйммәтен һәм тигезләмәнең тамырларын табыгыз.
8. Тигезләмәне чишегез:
х - 1 = y∣2x2 - Зх - 5.
2 нче вариант
х2 + 9х + 8
1. Вакланманы кыскартыгыз: gχ2 + gx + с
2. Тигезләмәне чишегез:
а) х(х + 3) - 4(x - 5) = 7(x + 4)-8.
б) 2x4 - 9x2 + 4 = 0.
191
3. k ның аны куйгач x2 - 2kx + 2k + 3 = 0 тигезләмәсе бер
генә тамыр ала торган кыйммәтләрен табыгыз.
4. Тигезләмәне чишегез:
1 13х - 4
= 4.
2х - 1 4x2 - 4x + 1
5. Автобуслар хәрәкәтенең яңа расписаниесе төзелгәч,
автобусның 325 км араны үтүгә сарыф итә торган
вакыты 40 мин ка кыскарган. Әгәр аның тизлеге иске
расписаниедә күрсәтелгәннән 10 км/сәг кә артыграк булса,
яңа расписаниедә автобуска нинди тизлек каралган?
6. x1 һәм х2 — 3x2 - 4x - 1 = 0 тигезләмәсенең тамырлары
булсын. Тигезләмәне чишмичә генә табыгыз:
a) x2x2 + x1x2! б) ⅛ + —; в) х® + х®.
Xi Хг
7. х2 + (4fe - l)x + (⅛2 - k + 8) = 0 тигезләмәсе бирелгән. Аның
тамырлары тапкырчыгышы 10 га тигез, k параметрының
кыйммәтен һәм тигезләмәнең тамырларын табыгыз.
8. Тигезләмәне чишегез:
•7 х2 + Зх + 3 = 2x + 1.
5
БҮЛЕК
ТИГЕЗСЕЗЛЕКЛӘР
* тамгасын
§31. САНЛЫ ТИГЕЗСЕЗЛЕКЛӘРНЕҢ
ҮЗЛЕКЛӘРЕ
Дөрес тигезсезлек килеп чыгарлык итеп,
< яки > тамгасы белән алыштырыгыз:
31.1.
а) 5,6 * 5,56;
б) -2,4 * -2,39;
в) 6,79 * 6,8;
г) -0,1 * -0,11.
31.2.
a) -≤ * Л
’ 5 7
3 , 5
б) - *
’ 4 9
ч 7 . 9 .
в) 11 13’
г) - — * -1.
17 3
31.3.
9
а) ^ * 0,41;
5
в) -1,7 * -1|;
б) -2∣ * 2,2;
г) ⅛ . 0,25.
31.4.
а) 0,4 * 1;
3
7
в) 2,56 *2^-;
6)-l∣ *-1,82;
6
г) -0,13 *
31.5. а) 3,7 + 1,02 * 4,26 + 0,5;
б) -3,1 + 3,5 * 2,1 - 2,59;
в) 5,9 - 1,45 * 2,8 + 1,9;
г) 7,31 - 2,33 * 3,11 + 1,88.
31.6.
a> 1+I*Φ
, 5 3 2
б) -1— *
’ 6 4 5
в) 2— * н 1—;
’ 7 14 2
г) -- -2—* -2—.
’ 5 6 2
193
31.7.
Санлы аңлатманың кыйммәтен нуль белән чагыштырыгыз:
а) (-1.21)2; в) (-5,74)4;
б) (—3,41)7; г) (-9,85)3.
31.8.
а) -| • (-45,14);
В) -1,7 : Ң|);
б) -2 у • 54,235;
4
г) ⅛ • (-21,489).
31.9.
ч 2 j3.
a) 5 + 4’
б) 2,35 - 2
4
, 5 1.
В) 13 2’
, 4.3
Г) 11 7’
Түбәндәге җөмләләрне математика телендә языгыз:
31.10. a) а һәм Ь саннарының суммасы аларның тапкыр¬
чыгышыннан зуррак;
б) т санының квадраты п саныннан кечерәк;
в) k һәм I саннарының ярымсуммасы аларның өчләтелгән
аермасыннан кечерәк;
г) өчләтелгән р саны р санының кубыннан зуррак.
31.11. a) t һәм з саннарының аермасы аларның чагыштыр¬
масыннан зуррак;
б) т һәм п саннары суммасының квадраты аларның аер¬
масыннан зур түгел;
в) k һәм I саннары квадратлары аермасы аларның ике-
лэтелгән суммасыннан кечерәк;
г) эзлекле килүче ике натураль санның тапкырчыгышы
аларның зуррагының квадратыннан кечерәк түгел.
a < Ь икәне билгеле. Дөрес тигезсезлек килеп чыгарлык
итеп, * тамгасын < яки > тамгасы белән алыштырыгыз:
31.12. a) -5α * -5Ь; в) 0,lα * 0,15;
e∙∖ л Ь ч ci , Ь
б) - * —; г) — * —.
’ 6 6 ’ 7 7
31.13. a) a - 4 * Ь - 4; в) a + 1,8 * Ь + 1,8;
б) a + 7,3 * Ь + 7,3; г) a - 125 * Ь - 125.
31.14. Тигезсезлекләрдәге т һәм п саннарының кайсы зуррак
икәнен ачыклагыз:
а) т + 12 < п + 12; в) -0,3 - т > -0,3 - п;
б) 3,5 - т > 3,5 - п; г) 4,9 + т < 4,9 + п.
31.15. Түбәндәгеләр билгеле булса, х ның тамгасы нинди булыр:
а) 5х < Зх; в) 9х > 2х;
б) -4х < 4х; г) -45х > -Зх?
194
31.16. т > п икәне билгеле. Санлы тигезсезлекләрнең нинди
үзлекләренә таянып, бу тигезсезлек дөрес дип әйтергә
мөмкин:
а) -7т < -7п; в) — > р
б) 1 - т < 1 - п; г) 5тп + 13 < 5п + 13.
31.17. Әгәр түбәндәге тигезсезлек дөрес булса, a > Ь дип расларга
мөмкинме:
a) a - 8 > Ь - 8; в) 12 - a > 12 - Ъ;
б) 3α > 3b; г) ∣ > |?
31.18. Әгәр түбәндәге тигезсезлек дөрес булса, х < у дип
расларга мөмкинме:
а) 2 - х > 2 - у; в) -41 + х < -41 + у;
б) -3,5x > -3,5i/; г) ~ >
31.19. а, Ь, с, d — уңай саннар, шул ук вакытта a > b, d < Ь,
^1111 « й
с > а. —, —, -, — саннарын үсә бару тәртибендә языгыз.
a b с а
Тигезсезлекләрне буынлап кушыгыз:
31.20. а) 13 > 5 һәм 8 > 1; в) 19 > 12 һәм 3,5 > 2;
б) -1,5 < -0,2 һәм -2 < 3,5; г) -0,1 < 1 һәм -2,8 < 4.
31.21. а) 5 > 2 һәм -3 < 1;
б) 7,5 < 11,7 һәм -4,7 > -5,8;
в) 0,2 < 3 һәм 2,8 > 1,7;
г) -3,9 > -7,2 һәм 6,5 < 14,7.
31.22. Әгәр а > 2 булса, тигезсезлекнең дөрес булуын исбатлагыз:
а) За > 6; в) 0,5α > 1;
б) -2а < -4; г) -1,5а < -3.
31.23. Әгәр т < 4,5 булса, тигезсезлекнең дөрес булуын исбат¬
лагыз:
a) ~ < 0,9;
Ә
б) -^ > -1,5;
О
в) р < 3;
г> -оЬ > -50∙
031.24. Әгәр Ь > 0,5 булса, тигезсезлекнең дөрес булуын исбат¬
лагыз:
a) 2Ь + 4 > 5;
б) -6Ь + 8 < 5;
в) 4,5b - 3,25 > -1;
г) -7Ь - 2 < -5,5.
195
031.25. Әгәр п < 3 булса, тигезсезлекнең дөрес булуын исбат¬
лагыз:
, п 2 1.
а) 7 + 7 <~Г
f'∖ — 4- 2 5 .
6) 6 + 9 18’
031.26. Исбатлагыз:
.2. w
। to∣a
∞∣a l
1 w∣ω
Л
v 1
00 1 н* to
θH
а) әгәр a > 2, b >
б) әгәр a<2b,b
в) әгәр а > 3, b >
3 булса, 3α + 5b > 21 була;
< с булса, 2а < 4с була;
5 булса, 2a + 4Ь > 26 була;
г) әгәр a > 5b, b > 2с булса, 3α ≥ 30c була.
031.27. Бу раслау дөресме:
а) әгәр а >
б) әгәр а <
в) әгәр а >
г) әгәр а <
■ 3, b > 5 булса, ab > 15 була;
2, b < 3 булса, ab < 6 була;
• 4 булса, а2 > 16 була;
6 булса, α2 < 36 була?
031.28. Бу раслау дөресме:
а) әгәр a >
1 булса, ® < 6 була;
б) әгәр a <
4
2 булса, — > 2 була;
в) әгәр a <
15
: 5 булса, — > 3 була;
г) әгәр a >
7 булса, < 2 була?
o31.29. k > 3, 1 >
бәяләгез:
а) 2k + 3/;
б) -⅛ - 1;
- 7 икәне билгеле. Аңлатманың кыйммәтен
в) k + 1,5/;
г) -4fe — 51.
031.30. р > 2, s < 5 икәне билгеле. Аңлатманың кыйммәтен бәяләгез:
а) р - 2s;
б) 4s - 2р;
в) s - Зр;
г) Зр - 6s.
031.31. т > 1, п > 4 икәне билгеле. Аңлатманың кыйммәтен
в) 3 - 2т - 5п;
г) 7m + 6n + 1.
бәяләгез:
а) т + п + 4;
б) 12 - 4п - Зт;
o31.32. х > 6, у < 12 икәне
билгеле. Аңлатманың кыйммәтен
бәяләгез:
а) х - 5 - 2у;
в) 5х - у + Ю;
б) 14 - 2х + Зр;
г) 16 - Зу + 4х.
196
31.33. Бирелгән а саныннан зуррак һәм Ь саныннан кечерәк
сан сайлап алыгыз. Раславыгызны икеле тигезсезлек
рәвешендә языгыз:
a) a = 3, Ь = 8; в) a = -2,5, Ь = 7,8;
б) a = -5, Ь = -3; г) a = -6, Ь = -2.
o31.34. 10 < a < 16 икәне билгеле. Аңлатманың кыйммәтен
бәяләгез:
а) 0,5а; в) -За;
б) а - 16; г) 2a + 1.
031.35. 2,6 < λ∕7 < 2,7 икәне билгеле. Аңлатманың кыйммәтен
бәяләгез:
a) 2√7j б) 2 + 2√7; в) -√7j г) 3 - √7.
031.36. 2,8 < √8 < 2,9 һәм 3,3 < √∏ < 3,4 икәне билгеле.
Аңлатманың кыйммәтен бәяләгез:
a) √8 + √∏5 в) √8 + 2√llj
б) √8 - 711; г) 3√8 - √∏.
031.37. 8 < a < 10 һәм 1 < Ь < 2 икәне билгеле. Аңлатманың
кыйммәтен бәяләгез:
1 1 , a
a) 4α + Ь; б) a - -=b^, в) ab; г) -•
4 £ υ
o31.38. α>b + 3, b+l>7 икәне билгеле, a > 9 икәнен ис¬
батлагыз.
Үзгәрешлеләрнең теләсә нинди кыйммәтләре өчен
тигезсезлекнең дөрес булуын исбатлагыз:
o31.39. а) 3(x + 1) + х < 4(2 + х); в) 2y2 - бу + 1 > 2V⅛ ~ 3>;
б) т(т + п)> тп; г) c2 - d2 > '2d-2 ~ Е
o31.40. а) x2 + 2xy + у2 > 0; в) 2pq < p2 + cl ’
б) 9∕n2 + бтп ≥ -n2∙, г) 4c2 + 6d2 ^2c
031.41. а) 2x > 2(x - 4) - a2;
б) z(z + 1) + 5 ≥ 1 - 3z;
в) 4y2 -Зу> Щ 1);
г) i("÷5)'3≥3t-4.
031.42. а) (х + l)(x - 4) > (х + 2)(х - 5);
б) (t - 3)(f + 4) < (t - 1)(£ + 2);
в) (a + 2)(a + 6) < (a + 5)(a + 3);
г) (b - 4)(b + 6) < (b - 3)(i> - 1).
197
Үзгәрешлеләрнең теләсә нинди кыйммәтләре өчен
тигезсезлекнең дөрес булуын исбатлагыз:
o31.43. a) (7 + 2d)(7 - 2d) < 49 - d(4d + 1), биредә d < 0;
б) (2q - 3)(<7 -3)>(q- 1)(<7 - 8).
д2 ^2
o31.44. a) _ , ≥ 1, ab > 0 булганда;
∆ab
б) 25г + 1 < -10, г < 0 булганда;
9
в) у + — >6, у>0 булганда;
г) п + — ≤ -8, п < 0 булганда.
п
o31.45. a) + p ≤2, pq < 0 булганда;
(т + п)2 „ „
б) —< m2 + п2.
Икебуынның квадратын аерып алу юлы белән тигезсез¬
лекне исбатлагыз:
031.46. а) х2 - 6х + 14 > 0; в) у2 + 70 > 16у;
б) а2 + 10 > -6а; г) b2 + 20 > -8Ь.
o31.47. a) (s - 4)(2 - s) < 2; в) (a + 1)(3 - а) < 5;
б) z2 + 6zt + 10⅛2 ≤ 0; г) m2 - 12mn + 40n2 ≤ 0.
31.48. Саннарны чагыштырыгыз:
а) 2,8 һәм y∣8∙, в) λ∕10 һәм 3,4;
б) у[з һәм 1,7; г) y∕7 һәм 2,7.
а һәм b саннарын чагыштырыгыз:
31.49. a) a = √5, b = ∣√8j в) α = √8, Ъ = |713;
ә ә
б) a = √3, b = ^√2j г) a = √7, b = ∣√19.
6 5
•31.50. a) a = √2 + √7, b = √5 + 2;
б) α = 2 + √TT, b = √5 + 710;
в) a = ∖J~7 + λ∕δ, Ъ = 3 + у[3;
г) a = л/з + >∕15, b = 4 + \[2.
198
•31.51. а һәм b саннарын чагыштырыгыз:
a) а =
√37 -
√14,
b = 6 - л/
Тб;
б) α =
√∏ -.
Ло,
b = √6 -
Л;
в) а =
√17 -
√15,
b = Л -
Л;
г) а = ■
√ιo -.
Л,
ь = √ιi -
√6∙
в) 7α > 5с
г) ^ > -?
b а
в) ху2 < 0 булса, х < 0;
г) — >0 булса, х > 0?
У
Исәпләүләрне эшләмичә генә, санлы аңлатмаларны ча¬
гыштырыгыз:
31.52. а) 15,4 : 3,5 һәм 15,4 : 3,4; в) 238 • 2 һәм 237 • 2;
б) -22,1 • 2,5 һәм -22 • 2,5; г) -5,2 : 4,3 һәм -5,1 : 4,3.
31.53. а) 1,8 : 2,7 һәм 1,82 • 2,7; в) 492 ■ 0,3 һәм 492 : 0,3;
б) 32,5 • 0,5 һәм 32,5 : 0,5; г) 8,34 : 1,1 һәм 8,34 • 1,1.
31.54. k > I икәнлегеннән чыгып, саннарны үсә бару тәртибендә
урнаштырыгыз:
0,2 + k;l;l- 12; k; k + 2,6; I - 1,45.
31.55. Түбәндәгеләрдән чыгып, a > Ь дип әйтергә мөмкинме:
а) За + 12 > 3b + 10;
б) ⅛ > 2;
ь
31.56. Бу раслаулар дөресме:
a) x2y > 0 булса, у > 0;
X
б) ~у2 > 0 булса, х > 0;
•31.57. Бу раслаулар дөресме:
2
а) х > 1 булса, 3 < а < 5;
CL — О
б) —< 1 булса, а > 3;
a z
в) —> 2 булса, 2 < а < 6;
CL Δ
г) < 3 булса, а > 5?
•31.58. а һәм Ь — бер үк тамгалы саннар икәне билгеле булса,
5α l2⅛ _
ти; + -7— > 4 тигезсезлеген исбатлагыз.
ЗЬ 5а
•31.59. Тигезсезлекне исбатлагыз:
a) a2 + 2b2 + 2ab + 2Ь + 2 > 0; б) (a + b) (~ + ∣) ≥ 4.
199
Тигезсезлекне исбатлагыз:
•31.60. a) 2a2 + b2 + c2 ≥ 2a(b + с);
б) (х2 - y2)2 > 4xy(x - у)2.
•31.61. a3 + 1 ≥ a2 + a, a > -1 булганда.
• 31.62. y[a + ∖∣b > y∣a + Ь, а > 0, Ь > 0 булганда.
• 31.63. y]a2 + b2 <a + b, a>0, b>0 булганда.
• 31.64. λ∕(α + c)(b + d) ≥ ∖[ab + y[cd, a>0, b>0, c>0, d>0
булганда.
• 31.65. + r^ > Ja + ∖∣b, a > 0, Ь > 0 булганда.
§32. ФУНКЦИЯЛӘРНЕ
МОНОТОНЛЫККА ТИКШЕРҮ
32.1. Графигы:
200
a) 72 рәсемдә; б) 73 рәсемдә; в) 74 рәсемдә; г) 75 рәсемдә
сурәтләнгән функция кими баручы буламы?
201
32.3. Графигы:
a) 76 рәсемдә; в) 78 рәсемдә;
032.4. у = 2x - 5 функциясенең үсә баручы икәнен исбатлагыз.
θ32.5. у = 7 - 13х функциясенең кими баручы икәнен исбатлагыз.
Функцияне монотонлыкка тикшерегез:
32.6. а) у = 2х + 3; в) у = х - 2;
б) у = 5 - 4х; г) у = 1 - 2х.
32.7. а) у = 2х2; в) у = 0,5х2;
б) у = -х2; г) у = -2x2.
032.8. а) у = |; б) у = в) у = 3 - |; г) у = ½- 1.
202
o32.9.
o32.10.
32.11.
32.12.
32.13.
32.14.
33.1.
33.2.
33.3.
Функцияне монотонлыкка тикшерегез:
а) у = у[х; в) у= -у[х;
б) у = √x - 3; г) у = 2 + √x.
а)у = |х|; б) ι∕ =-|х|; в) у = |х| + 2; r)y = ∣x-l∣.
у = f(x) функциясе бирелгән, биредә
х, х < 0 булганда,
7(х) = 1
—, х > 0 булганда.
1х
a) f(-2), /(1), 7(5) не табыгыз.
б) у = /(х) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
у = f(x) функциясе бирелгән, биредә
2x2, -1 ≤ х ≤ 0 булганда,
7(х) = г-
√x, х > 0 булганда.
a) f(-l), /(0), 7(4) не табыгыз.
б) у = 7(х) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
у = f(x) функциясе бирелгән, биредә
7(χ) =
з
—, -1 ≤ х < 0 булганда,
х
|х|, 0 ≤ х ≤ 6 булганда.
a) 7(^^3), 7(θ), 7(θ) не табыгыз.
б) у = 7(х) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
а) у = х2 + Jx + 1 функциясенең [0; +∞) нурында үсүен;
б) у = - х2 функциясенең (0; +∞) ачык нурында кимүен
исбатлагыз.
§33. СЫЗЫКЧА ТИГЕЗСЕЗЛЕКЛӘРНЕ ЧИШҮ
a түбәндәге кыйммәтләрне алса, ул2а + 3>7а~17 тигез¬
сезлегенең чишелеше булырмы:
a) 2; б) 6,5; в) -√2j г) √18?
-1, 7, √5, ү саннарының кайсысы Зх > х + 2 тигез¬
сезлегенең чишелеше була?
9x + 1 > 7х тигезсезлегенең теләсә нинди ике чишелешен
табыгыз.
203
33.4.
Тигезсезлекне чишегез һәм аның чишелешләре күплеген
координаталар турысында күрсәтегез:
а) х + 1 > 0; в) х + 2,5 < 0;
б) х - 3 ≤ 0; г) х - 7 ≥ 0.
33.5.
а) 2х > 8;
б) 4х < 12;
в) 5х > 25;
г) 7x ≤ 42.
33.6.
а) Их > -33;
б) -8х > 24;
в) —6х > -12;
г) 13x ≤ -65.
33.7.
а) Зх + 2 > 0;
б) -5х - 1 < 0;
в) 4х - 5 < 0;
г) —6х + 12 > 0.
33.8.
а) 2х + 3 > 7;
б) -Зх + 4 < 13;
в) -5х - 1 > 24;
г) -х - 8 < 19.
33.9.
а) 5(х + 2) > 4;
б) -2(х - 3) ≤ 5;
в) 6(x - 1) < 11;
г) -3(x + 4) ≥ -2.
o33.10. a) a ның нинди кыйммәтләрендә 5a - 3 икебуыны уңай
кыйммәтләр ала?
б) Ъ ның нинди кыйммәтләрендә 23b +11 икебуыны
тискәре кыйммәтләр ала?
o33.ll. а) с ның нинди кыйммәтләрендә 13с - 22 икебуыны
тискәре булмаган кыйммәтләр ала?
б) d ның нинди кыйммәтләрендә 2d + 4 икебуыны уңай
булмаган кыйммәтләр ала?
033.12. а) т ның нинди кыйммәтләрендә 5m + 8 икебуыны 2 дән
зуррак кыйммәтләр ала?
б) п ның нинди кыйммәтләрендә 7n + 1 икебуыны 1 дән
кечерәк кыйммәтләр ала?
o33.13. а) р ның нинди кыйммәтләрендә 9р - 2 икебуыны
Зр + 4 икебуыныннан кечерәк булмаган кыйммәтләр ала?
б) q ның нинди кыйммәтләрендә 11g + 3 икебуыны
5q - 6 икебуыныннан кечерәк кыйммәтләр ала?
Тигезсезлекләрне чишегез:
033.14. а) 2а - 11 > а + 13;
в) 6 - 4с > 7 - 6е;
б) 8Ь + 3 < 9Ь - 2;
г) 3 - 2х < 12 - 5х.
033.15. а) 2d - 5 > 3 - d;
в) 6п - 2 < 7п + 8;
б) Зт + 17 ≤ т - 13;
г) р + 4 ≥ 12 + 9р.
204
Тигезсезлекләрне чишегез:
033.16. a) -2x + 12 > 3x - 3; в) 5z - 14 < 8z - 20;
б) 6z∕ + 8 ≤ Юу - 8; г) 3t + 5 ≥ 71 - 7.
o33.17. a) 10x + 9 > -3(2 - 5x);
6) -(6y + 2) + 3(y - 1) > 0;
в) 2(3 - 2z) + 3(2 - z) ≤ 40;
г) -(81 -2)- 2(1 - 3) > 0.
o33.18. a) 2(x + 1) - 1 < 7 + 8x; в) -2(4z + 1) < 3 - lOz;
6) 3 - lly ≤ -3(y - 2); г) 4 - 31 > -4(21 + 2).
o33.19. a) 8 + 6p < 2(5p + 4);
6) -(6y + 2) + 6(y - 1) ≥ 0;
в) 2(3 - 4g) - 3(2 - 3<γ) ≤ 0;
r) 7 - 16r ≤ -2(8r -1) + 5.
o33.20. a) 4(α + 1) + 3α > 7a + 2;
6) 7b - 3 ≥ 7(1 + b)∙,
в) 4(2 + 3z) + 3(4 - 4z) > 0;
r) 5(4d -3) + 5(3 - 4d) < 0.
33.21. a) ⅛ > 1; 6) -⅞ > 0; в) ⅛ > 2; r) ~ < 0.
4 о 11 5
λλ λλ 4 3x + 2 ^ 4 5x - 7 λ
33.22. a) —- < 0; в) —- > 0;
ә 4
β>-v>'∙ ∙')'Ttrι-
33.23. a) ⅛ ‘ > 1; в) ~ < IS:
6) 12-9x r) 23-5x < J
7 11 ’
033.24. a) + > 7; b)∣-∣≤1j
Δ о О 4
б) у - с > 3; г) - 2d < 0.
33.25. Координаталары түбәндәге тигезсезлекне канәгатьләндерә
торган нокталарны координаталар яссылыгында күрсә¬
тегез:
а) у < 2x + 1;
б) у > Зх - 5;
в) у < 0,5х - 2;
г) у ≥ х + 2.
205
33.26. а) Үзгәрешл ел әрнең нинди кыйммәтләрендә Зх + 8 һәм
х + 12 аңлатмаларының тапкырчыгышы икенче тапкыр¬
лаучының өчләтелгән квадратыннан зуррак?
б) Үзгәрешлеләрнең нинди кыйммәтләрендә 2х + 5 һәм
8х - 15 аңлатмаларының тапкырчыгышы 4х - 3 аңлатмасы
квадратыннан кечерәк?
Тигезсезлекләрне чишегез:
33.27. a) α(α - 2) - a2 > 5 - 3a;
б) 3x(3x - 1) - 9x2 < Зх + 6;
в) 5g2 - 5g(ι∕ + 4) > 100;
г) 7c(c - 2) - c(7c + 1) < 3.
33.28. a) 0,2zn2 - 0,2(zn - 6)(τn + 6) > 3,6/п;
б) (12n - l)(3n + 1) < 1 + (6п + 2)2;
в) (2p - 5)2 - 0,5jp < (2p - l)(2p + 1) - 15;
г) (4g - 1)2 > (2g + 3)(8g - 1).
λo λλ „ 2a - 1 5a - 2 2b - 1 3 - b o
33.29. а) „ < в) — — < 2;
О d fJ о
,λ o с + 1 с - 1 . d - 1 d + 1
6) 2c-~2~< ~з“; Г) ~3~~d > “7-
33.30. а) ½±± - *θ 2 < 2 +
37 - За _ 2г - 7
б) - + 9 < — 2z;
1-121÷3,
’ 2 8
. 8y + 5 5 . Зу - 2 ι
г) 1 < о + У-
4 3
Тигезсезлекнең иң зур бөтен чишелешен табыгыз:
33.31. а) 4(х - 7) - 2(х + 3) < 9; б) 5(x - 1) + 7(х + 2) < 3.
33.32.
v 2x - 1 5х + 7
Зх + 2 2х - 4 _
б> “5 Г" ≈∙ 7'
Тигезсезлекнең иң кечкенә бөтен чишелешен табыгыз:
33.33. а) 7(х + 2) - 3(х - 8) > 10; б) 3(х - 2) - 4 > 2(х + 3).
oo „ . . 2х - 3 9 - 4x 1 Зх - 2 4x + 1
33.34. а) —-— + —-— < 1; б) —— + —> 1.
Ә О 4 О
206
•33.35. Елга ярында лагерь корыр алдыннан туристлар елга буй¬
лап һәм аның кушылдыгы буйлап көймәдә 10 км йөзеп
киләләр, аларга юлның бер өлешен агым уңаена, бер
өлешен агымга каршы йөзәргә туры килә. Әгәр алар юлга
ике сәгатьтән кимрәк вакыт сарыф итсәләр, көймәнең үз
тизлеге 5 км/сәг, ә елганың һәм аның кушылдыгының үз
тизлеге 1 км/сәг булса, туристларның агым уңаена нинди
юл үткәнен табыгыз.
•33.36. Бакчачылар бистәдән станциягә кадәр 10 км юл үтәләр.
Башта алар 4 км/сәг тизлек белән баралар, аннан соң
тизлекләрен 2 км/сәг кә арттыралар. Алар, бистәдән чы¬
гып 2 сәг үткәннән соң, станциядән кузгалып китә торган
поездга өлгерү өчен, бакчачылар 4 км/сәг тизлек белән
нинди ераклыкны узарга мөмкиннәр?
•33.37. А бистәсеннән В бистәсенә бару өчен, шоссе буйлап
С пунктына кадәр барырга, аннан авылара юлга боры¬
лырга кирәк. А дан С га кадәр ара С дан В га кадәрле
арадан 15 км га озынрак. Мотоциклчының шосседагы
тизлеге 50 км/сәг, ә авылара юлдагысы 40 км/сәг, һәм ул
А дан В га кадәр барлык юлга өч сәгатьтән кимрәк вакыт
сарыф итә. А белән С арасы, әгәр ул бөтен сандагы дистә
километрларда үлчәнсә, барысы ничә километр булыр?
•33.38. А пунктыннан аннан 240 км ераклыктагы В пунктына
54 км/сәг тизлек белән автобус юлга чыга. Ул китеп
берникадәр вакыт узгач, аның артыннан 90 км/сәг тиз¬
лек белән җиңел машина китә. В га килеп җиткәннән
соң, җиңел машина шундук кире борыла. Ул А пунктын¬
нан нинди ераклыкта автобус белән очрашыр?
§34. КВАДРАТ ТИГЕЗСЕЗЛЕКЛӘРНЕ ЧИШҮ
o34.1. у = х2 - 4х + 3 функциясенең графигын төзегез. График
ярдәмендә тигезсезлекне чишегез:
a) х2 - 4х + 3 > 0;
б) х2 - 4х + 3 < 0;
в) х2 - 4х + 3 < 0;
г) х2 - 4х + 3 > 0.
θ34.2. Тигезсезлекне чишегез:
а) х2 - 6х - 7 > 0;
б) х2 + 2х - 48 < 0;
в) х2 + 4х + 3 ≥ 0;
г) х2 - 12х - 45 < 0.
207
Тигезсезлекне чишегез:
o34.3. a) -x2 + 6x - 5 < 0;
б) -x2 - 2x + 8 > 0;
в) -х2 + 16х - 28 > 0;
г) -х2 + 4х - 3 < 0.
o34.4. a) 2x2 - х - 6 > 0;
б) 3x2 - 7x + 4 < 0;
o34.5. a) -5x2 + 4x + 1 > 0;
б) -2x2 - 5x + 18 < 0;
o34.6. a) (х - 2)(x + 3) > 0;
б) (x + 5)(x + 1) ≤ 0;
o34.7. a) (2 - x)(x + 1) > 0;
б) (x - 3)(4 - x) < 0;
в) 2x2 + Зх + 1 < 0;
г) 5x2 - Их + 2 > 0.
в) -6x2 + 13х + 5 < 0;
г) -Зх2 + 5х - 2 > 0.
в) (х + 7)(х - 5) < 0;
г) (х - 4)(х - 6) > 0.
в) (1 - х)(х - 2) < 0;
г) (3 - х)(5 + х) > 0.
o34.8. a) (2x + l)(3x + 2) < 0;
б) (3 - 4x)(2x - 5) < 0;
в) (7x + 3)(4x - 1) > 0;
г) (1 - 2x)(3 + х) < 0.
o34.9. a) 6x2 > 5x - 1;
б) -5x2 < 6 - Их;
в) -2x2 + х < -6;
г) 5x2 > 4 - 8х.
o34.10. a) x2 - 6x + 9 < 0;
б) -х2 + 12х - 36 > 0;
в) х2 - 16х + 64 > 0;
г) -х2 + 4х - 4 < 0.
034.11. a) 25x2 + ЗОх + 9 > 0;
б) -9x2 + 12х - 4 < 0;
o34.12. а) Зх2 + х + 2 > 0;
б) 5x2 - 2x + 1 > 0;
o34.13. a) -7x2 + 5х - 2 < 0;
б) -Зх2 - Зх - 1 < 0;
034.14. а) х2 - 2х - 1 > 0;
б) -4x2 + 2x - J ≤ 0;
4
034.15. а) х2 - 36 > 0;
б) х2 + 7 < 0;
в) -4x2 + 12х - 9 > 0;
г) 36x2 + 12x + 1 < 0.
в) 7x2 - х + 3 < 0;
г) 2x2 + 5х + 10 < 0.
в) -2x2 + Зх - 2 > 0;
г) -5x2 - х - 1 > 0.
в) -х2 - 2х + 2 < 0;
г) 2x2 + 2х - 1 > 0.
в) х2 - 25 < 0;
г) х2 + 15 > 0.
o34.16. a) 4x2 - 9 < 0;
б) 16 - 25x2 < 0;
в) 25x2 - 36 > 0;
г) 64 - 49x2 > 0.
034.17. а) х2 < 100;
б) 4x2 > 25;
в) х2 > 625;
г) 16x2 < 47.
034.18. а) х2 - 5х > 0;
б) х2 + 0,5х < 0;
в) х2 + 8х < 0;
г) х2 - 2,3х > 0.
208
o34.19. Тигезсезлекне чишегез:
a) x2 > 25х; в) x2 < 36х;
б) 0,3x2 < 0,6х; г) 0,2x2 > 1,8х.
034.20.
х ның нинди кыйммәтләрендә:
a) 2x2 +
б) -х2 -
5х + 3 өчбуыны уңай кыйммәтләр ала;
1
36
өчбуыны тискәре булмаган кыйммәтләр
1
3
ала?
o34.21. а) х2 - 5х - 6 < 0 тигезсезлегенең ничә бөтен санлы
чишелеше бар?
б) x2 - 6x ≤ 7 тигезсезлегенең ничә бөтен санлы чишелеше
бар?
o34.22. а) х2 + 7x ≤ 30 тигезсезлегенең иң кечкенә бөтен санлы
чишелешен табыгыз;
б) Зх - χ2 > -40 тигезсезлегенең иң зур бөтен санлы
чишелешен табыгыз.
х ның нинди кыйммәтләрендә аңлатманың мәгънәсе
барлыгын ачыклагыз:
034.23.
а)
√X2 - 8х + 7;
в) ∙Jx2 - 6х + 5;
б)
>∕-x2 + Зх + 4;
г) √2 + х - х2.
034.24.
а)
∖[^x2∙,
в) y∣9χ2 - 1;
б)
1
г) 1
√16χ2 - 81 ’
√4 - 25х2
034.25.
а)
√2χ - х2;
в) y∣5x - χ2;
б) (TKx2 - 2х) *; г) (√3x2 - 12x)^1.
o34.26. a) √(J^∑ 3)(x + 2); в) √(x + 5)(4 - х);
б) (V(x^^ 1)(2 - х))'*; г) (√Γx-6)(2x + 3))"1.
o34.27. a) V(χ2 _ 5x + g)-ι.
6) Vb2x* + 5x - 2)'1;
в) √(x2 - х - 12)^1;
г) √(⅞x2 - Юх - 3)^1.
209
Тигезсезлекне чишегез:
34.28. a) 5x2 > 2х; б) ∣ х2 > 12; в) 4x ≤ -х2; г) ~x2> L
Δ о У
34.29. a) 2x(3x - 1) > 4x2 + 5х + 9;
б) Зх2 + 40х + 10 < 43 - х(х - 11).
34.30. a)⅜ + ∣-12<O5 6) ⅛ ÷ ⅜ > ⅜∙
34.31. а) x4 + 16x2 - 17 < 0; в) x4 + 6x2 - 7 > 0;
б) ι∕4 + 12ι∕2 - 64 ≥ 0; г) z4 + Зг2 - 28 < 0.
1 Ч
34∙32' “> * - 1, ÷ 12 > °i »> 42τV∑7 < °;
6> х2 - х - 20 У °’ г) 2х" + 15 - х2 < °’
34.33. Тигезсезлекләр тигезкөчлеме:
б) х2 + 6х - 16 < 0
в) х2 - 6х + 8 > 0
һәм ~i—- 77 > 0;
х2- 5х - 14
һәм х2 + 6х - 16 ≤ 0;
һәм (x2 - 6x + 8)^1 > 0;
34.34. а) х2 + 5х - 8 < 0 тигезсезлегенең ничә бөтен санлы
чишелеше бар?
б) 15 — х2 + 10x ≥ 0 тигезсезлегенең ничә бөтен санлы
чишелеше бар?
34.35. а) х2 + 10х < -12 тигезсезлегенең иң кечкенә бөтен санлы
чишелешен табыгыз.
б) 3x2 + 5x ≤ 4 тигезсезлегенең иң зур бөтен санлы
чишелешен табыгыз.
34.36. р параметрының нинди кыйммәтләрендә Зх2 - 2рх - р +
+ 6 = 0 квадрат тигезләмәсенең:
а) төрле ике тамыры бар;
б) бер тамыры бар;
в) тамырлары юк?
210
34.37. р параметрының нинди кыйммәтләрендә 2x2 — 2рх + р +
+ 12 = 0 квадрат тигезләмәсенең:
а) төрле ике тамыры бар;
б) бер тамыры бар;
в) тамырлары юк?
34.38. р параметрының нинди кыйммәтләрендә х2 + брх + 9 = 0
квадрат тигезләмәсенең:
а) төрле ике тамыры бар;
б) бер тамыры бар;
в) тамырлары юк?
34.39. р параметрының нинди кыйммәтләрендә түбәндәге тигез¬
ләмәнең реаль тамырлары булмый:
a) (р - l)x2 - 4х + 5 = 0;
б) (р - 15)x2 + 4рх -3 = 0;
в) (2p + 3)x2 - 6х + 8 = 0;
г) (Зр - 5)x2 - (6р - 2)х + Зр - 2 = 0.
34.40. р параметрының нинди кыйммәтләрендә түбәндәге тигез¬
ләмәнең реаль тамырлары була:
а) х2 - 6x + р2 = 0; в) х2 - 4х - 2р = 0;
б) х2 - 12рх - Зр = 0; г) х2 + 2рх + р + 2 = 0.
34.41. р параметрының нинди кыйммәтләрендә түбәндәге тигез¬
ләмәнең реаль тамырлары була:
a) Зрх2 - брх + 13 = 0;
б) (1 - 3p)x2 - 4х - 3 = 0;
в) рх2 - Зрх -2 = 0;
г) (р - l)x2 - (2р - 3)х + р + 5 = 0.
34.42. р параметрының нинди бөтен кыйммәтләрендә (х - 2) х
× (х - р) < 0 тигезсезлегенең бөтен санлы өч чишелеше
була?
•34.43. р параметрының нинди кыйммәтләрендә x2 ≤ 9p2 тигез¬
сезлегенең бөтен санлы бер чишелеше була?
34.44. Турыпочмаклыкның буе иңеннән 2 см га зуррак. Әгәр
мәйданы 224 см2 тан артып китмәсә, бу турыпочмаклык¬
ның буе нинди озынлыкта?
211
34.45. Квадратның параллель булмаган ике ягын 6 см га һәм 4
см га озайталар. Әгәр килеп чыккан турыпочмаклыкның
мәйданы квадратның икеләтелгән мәйданыннан кечерәк
булса, квадратның ягы күпмегә тигез булган?
•34.46. Туристларның ике группасы турбазадан үзара туры
почмак ясаучы юнәлешләрдә чыгып китә. Беренче группа
4 км/сәг, икенче группа 5 км/сәг тизлек белән бара.
Алар үзара радио аша бәйләнеш тоталар, әмма аралашу
мөмкинлеге 13 км дан артык булмаган арада гына була.
Әгәр икенче группа беренчесеннән 2 сәг кә соңрак чыкса,
туристлар икенче группа чыгып күпме вакыт үткәнче
бәйләнештә була алалар?
§35. РЕАЛЬ САННАРНЫҢ
ЯКЫНЧА КЫЙММӘТЛӘРЕ
Бирелгән санның якынча кыйммәтләрен киме һәм ар¬
тыгы буенча 0,1 гә кадәр төгәллек белән табыгыз:
35.1. а) 2,734;
б) 1,2(5);
б) ∣2-√7∣j
в) 3,9(42);
в) ∣12-√3∣5
г) 3,9(62).
ч 45
Г) 49'
35.2. а) ,
Бирелгән
санның якынча
кыйммәтләрен
киме һәм
артыгы буенча 0,01 гә кадәр
төгәллек белән табыгыз:
035.3. аһ
/3;
б) √2 - 1;
в) 5 - √7j
Г) 3*
035.4. а) ,
/5;
б) √11 - 3;
в) 6 - √8j
г) —•
’ 19
035.5. а) ’
/11;
б) ∣2-√1O∣5
в) ∣5 - √2∣j
Г) Я.
17
035.6. Бирелгән
санның якынча
кыйммәтләрен
киме һәм
артыгы буенча 0,001 гә кадәр төгәллек белән табыгыз:
а) -
/15;
б) √19 - 6;
в) 1-/8;
r>⅞∙
o35.7. Гадиләштерегез һәм 0,1 гә кадәр төгәллек белән исәпләгез:
a) √18 + √8 + √32; б) √ 48 + √12 - √75.
o35.8. Гадиләштерегез һәм 0,01 гә кадәр төгәллек белән исәпләгез:
a) √27 + √75 - √147j
б) 0,5√200 - √98 + ∣√162.
212
35.9. Якынча тигезлекнең хатасын бәяләгез:
a) √2 ≈ 1,4; б) π ≈ 3,14; в) J ≈ 1,57;
г) √3 ≈ 1,73.
35.10. Гадиләштерегез һәм 0,1 гә кадәр төгәллек белән исәпләгез:
a) 0,l√200 - 2√0,08 + 4√0^5 - 0,4√5δj
б) 5J - - i√20 + √500 - 0,2^3125;
V 5 2
в) √176 - 2√⅞ - √891 + 71584;
г) 71,25 - —7245 + 7180 - 780.
•35.11. Гадиләштерегез һәм 0,1 гә кадәр төгәллек белән исәпләгез:
а) >/з - y∣29 - 1275 ; б) ∖j5 - 713 + 7^8 .
§ 36. САННЫҢ СТАНДАРТ РӘВЕШЕ
10 санының дәрәҗәсе рәвешендә күрсәтегез:
36.1. а) 100;
б) 10000;
в) 1000;
г) 10000000.
36.2. а) 0,001;
б) 0,1;
в) 0,00001;
г) 0,0001.
Санны стандарт рәвешендә
күрсәтегез:
языгыз һәм
аның тәртибен
36.3. а) 2300;
б) 75000;
в) 12;
г) 620000.
36.4. а) 0,0035;
б) 0,00007;
в) 0,00024;
г) 0,91.
36.5. а) 350 • Ю2;
б) 0,67 • Ю3;
в) 85 • Ю4;
г) 0,015 • Ю2.
36.6. а) 0,73 • Ю5;
б) 512 • Ю3;
в) 0,43 • Ю4;
г) 3900 • Ю4.
Гамәлләрне эшләгез (җавапны стандарт рәвештә языгыз):
o36.7. a) (0,2 • Ю5) • (1,4 • Ю-2); в) (3,7 ∙ 101) • (7 • Ю8);
б) (2,4 ∙ 103) • (0,5 • Ю"3); r) (5,2 • Ю14) • (3 ∙ 10^8).
036.8. а) 0,2 • Ю5 + 1,4 • 10е; в) 5,2 • Ю3 - 0,5 ∙ Ю2;
б) 7,8 ∙ Ю1 + 7 ■ Ю2; г) 6,1 • 10^3 - 9 • 10^4.
213
Гамәлләрне эшләгез (җавапны стандарт рәвештә языгыз):
_ _ _ .1,5 10 23 . λ 4,8 10’4
036.9. a) 0 θ6 10.9, в) 0,24 10 17 ,
2,7 ■ Ю15 . 1,44 ■ 10 7
б) 3,6 10^5 ’ Г> 1,8 10' ‘
036.10. а)
(2,89 ∙ 10^5) ■ (0,2 ∙ 103)-
3,4 10 9
0,25 ■ Ю15
) (0,45 ∙ Ю9) • (3 ■ Ю*3) 2 ’
6,3 Ю20 .
В) (0,15 ■ Ю11 *) • (4,2 Ю16)’
(2 • Ю4)’3 ■ (9,6 • Ю7)
Г 0,24 ■ Ю20
o36.ll. а һәм Ъ саннарын чагыштырыгыз:
a) a = (1,4 ∙ 10"2) • (5 ∙ 101) һәм b = 0,006;
б) a = 3g6 * * * * 1θθ һәм b = 0,001;
в) a = (4,2 • Ю5) • (2 • Ю2) һәм b = 700000000;
г) a = 9.107 һәм b = 70∙
036.12. b санының тәртибе 2 икәне билгеле. Бу санның тәртибе
нинди:
a) 100b; б) 0,1b; в) 10b; г) 0,001b?
036.13. т санының тәртибе -4 икәне билгеле. Бу санның тәртибе
нинди:
a) 10т; б) 0,01m; в) 1000m; г) 10000m?
36.14. Мисыр фиргавене Хеопсның коллары тарафыннан төзел¬
гән пирамиданың массасы якынча 7,231 • Ю6 т. Шундый
массаны ташу өчен һәрберсенең йөк күтәрүчәнлеге 64 т
лы ничә вагон кирәк булыр иде?
36.15. Санның стандарт рәвешен кулланып языгыз:
а) бер тәүлектә 86400 с;
б) 100 км биеклектә атмосфера басымы 0,000024 мм тер.
баг.;
в) 1 кал 0,00419 кДж гә тигез;
г) 1 с тигез 0,0002778 сәг.
•36.16. х санының тәртибе 6 икәне билгеле. Бу санның тәртибе
нинди булырга мөмкин:
а) х2; б) х5; в) -/х; г) ½
214
•36.17. т санының тәртибе -4, ә п санының тәртибе 3 икәне
билгеле. Бу санның тәртибе нинди булырга мөмкин:
а) пт; б) т + п; в) 10n + т; г) 0,1m + 10п?
•36.18. s санының тәртибе 2, ә t санының тәртибе 4 икәне
билгеле. Бу санның тәртибе нинди булырга мөмкин:
a) st; б) 100s + t; в) 0,01s + t; г) 0,1st?
•36.19. Саннарның тапкырчыгышы, өлеше һәм суммасының
тәртибен табыгыз:
а) 3,252 ■ Ю9 һәм 2,165 • Ю9;
б) 4,435 • 10 7 һәм 7,098 • 10 7;
в) 8,389 • Ю5 һәм 9,762 • Ю4;
г) 7,987 ∙ 10 β һәм 3,157 ∙ 10^5.
ӨЙ КОНТРОЛЬ ЭШЕ № 5
1 нче вариант
_ Зх + 5 10 - Зх 2х + 7 148
1. Тигезсезлекне чишегез: — 1- - > —- —
7 5 3 41
2. Икебуынның квадратын аерып алу юлы белән, х үзгә-
решлесенең теләсә нинди тискәре булмаган кыйммәт¬
ләре өчен х3 - 8xVx + 18 > 0 тигезсезлеге үтәлүен
исбатлагыз.
3. Тигезсезлекне чишегез:
4x2 + х
3
5х - 1 c х2 + 17
6 9
4. Координаталар яссылыгында координаталары у < -Зх +
+ 1 тигезсезлеген канәгатьләндерә торган нокталар күплеген
сурәтләгез.
5. Аңлатманың х нинди кыйммәтләр алганда мәгънәсе була:
√x2 - 7х + 12 - 22x + 1 ?
v х2 + 2х
6. у = Дх) функциясе бирелгән, биредә
Ах) =
2 т «
—, х < -1 булганда,
х
|х| - 3, -1 ≤ х < 6 булганда.
a) А-5), Aθ)> АП не исәпләгез.
б) у = Aχ) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
215
7. 0,1 гә кадәр төгәллек белән исәпләгез:
4√3 + √48 - 2√75.
8. Саннар тапкырчыгышының тәртибен табыгыз:
2,345 • Ю2 һәм 3,564 ∙ 10^5 *.
2 нче вариант
1. Тигезсезлекне чишегез: ~ - 1-1∕x -t..1l < _х ~ 1 _ 13 ~ x
3 6 3 2 '
2. Икебуынның квадратын аерып алу юлы белән, х үзгә-
решлесенең теләсә нинди тискәре булмаган кыйммәтләре
өчен х3 - 10x√x + 26 > 0 тигезсезлеге үтәлүен исбатла¬
гыз.
Зх2 + х 2 - 7x Зх2 + 17
3. Тигезсезлекне чишегез: —j— $— —£q—•
4. Координаталар яссылыгында координаталары у > 2х + 4
тигезсезлеген канәгатьләндерә торган нокталар күплеген
сурәтләгез.
5. Ух2 + 9х + 14 - * + 2
х2 - 4х + 3
аңлатманың х нинди кыйм¬
мәтләр алганда мәгънәсе була.
6. у = f(x) функциясе бирелгән, биредә
∫x2-2, х<-2 булганда,
Λ^) - [2∣x∣-2, -2<x<6 булганда.
a) ∕(-7), ДО), /(5) не исәпләгез.
б) у = Дх) функциясенең графигын төзегез.
в) Функциянең үзлекләрен санап чыгыгыз.
7. 0,1 гә кадәр төгәллек белән исәпләгез:
2√5 - √125 + 0,5√20.
8. Саннар тапкырчыгышының тәртибен табыгыз:
4,115 ■ Ю3 һәм 1,234 ∙ 10 β.
6
БҮЛЕК
ЙОМГАКЛАУ
Бирелгән функциянең, графигын характерлагыз һәм аны
төзегез:
1- а) у = 2х2; б) у = -¾ в) у = х2; г) у =
X о X
О \ 3 1 X 5 6
2. а) у = - - 1; в) у =
X X Δ
б) у = —(х + I)2; г) у = Зх2 - 4.
3. а) у = 0,5(x - 2)2 - 4; в) у = 9 - (х + I)2;
б) У = 7⅛ + 1; г) У = “з ^ 4'
4. Түбәндәге параллель күчерү юлы белән табылган квадратик
функциянең тигезләмәсен языгыз:
а) у = x2 параболасын 5 берәмлеккә сулга;
б) у = х2 параболасын 1 берәмлеккә аска;
в) у = х2 параболасын 1 берәмлеккә уңга һәм 3 берәмлеккә
өскә;
г) у = х2 параболасы түбәсен (2; -4) ноктасына.
5. Түбәндәге параллель күчерү юлы белән табылган квадратик
функциянең тигезләмәсен языгыз:
а) у = 2x2 параболасын 4 берәмлеккә уңга һәм 3 берәмлеккә
өскә;
б) у = х2 параболасы түбәсен (-3; 2) ноктасына;
в) у = х2 параболасын 1 берәмлеккә сулга һәм 4
берәмлеккә аска;
г) у - l,5x2 параболасы түбәсен (2; 1) ноктасына.
Килеп чыккан функциянең графигын төзегез.
217
6. у = — функциясе графигын түбәндәгечә параллель күчерү
х
нәтиҗәсендә табылган гиперболаның тигезләмәсен языгыз:
а) 2 берәмлеккә уңга;
б) 3 берәмлеккә өскә;
в) 3 берәмлеккә сулга һәм 1 берәмлеккә өскә;
г) 1 берәмлеккә уңга һәм 2 берәмлеккә аска.
Рәс. 82 Рәс. 83
218
Рәс. 86
Рас. 87
9. Парабола түбәсенең координаталарын билгеләгез һәм
бирелгән параболаның симметрия күчәре тигезләмәсен
төзегез:
а) у = х2 - 4х + 5;
б) у = -Зх2 - 6х;
в) у = -2x2 + 12х - 10;
г) у = 2x2 - 8х.
219
10. a) x = -3 турысының у = ax2 + (а - 5)х + 10 параболасының
симметрия күчәре икәне билгеле булса, а параметрының
кыйммәтен табыгыз.
б) х = 2 турысының у = ах2 - (а + 9)х - 15 параболасының
симметрия күчәре икәне билгеле булса, а параметрының
кыйммәтен табыгыз.
11. а) М(2; -8) ноктасы b һәм с ның нинди кыйммәтләрендә
у = 2x2 + Ьх + с параболасының түбәсе була?
б) N(-4; 3) ноктасы b һәм с ның нинди кыйммәтләрендә
у = -Зх2 + Ьх + с параболасының түбәсе була?
12. у = 0,5x2 - х - 1,5 функциясенең графигын төзегез. График
ярдәмендә табыгыз:
а) функциянең үсү һәм кимү аралыкларын;
б) функциянең иң кечкенә кыйммәтен.
13. у = -х2 + 8х - 12 функциясенең графигын төзегез. График
ярдәмендә табыгыз:
а) функциянең иң зур кыйммәтен;
б) функциянең кыйммәтләре күплеген.
14. у = х2 — 6х функциясенең графигын төзегез. График ярдә¬
мендә табыгыз:
а) х2 — 6х = -5 тигезләмәсенең тамырларын;
б) х2 - 6х > 0 тигезсезлегенең чишелешен.
15. Квадратик функциясе түбәндәге тигезләмә белән бирелгән:
а) у = 12 - Зх2; в) у = -(x - I)2 + 4;
б) у = 0,5(x - 2)2; г) у = 2x2 - 4х + 5.
Графикны төземичә генә билгеләгез:
1) парабола түбәсе координаталарын;
2) параболаның симметрия күчәрен;
3) функциянең үсү һәм кимү аралыкларын;
4) функциянең иң кечкенә һәм иң зур кыйммәтләрен;
5) функциянең кыйммәтләре күплеген.
16. Квадратик функция графигыннан файдаланып, х ның
нинди кыйммәтләрендә y = 0, у>0, у<0 шарты үтәлүен
билгеләгез:
а) у = -2x2 + 12х - 10; в) у = Зх2 + 12х + 9;
б) у = 0,5(x + 5)2 - 8; г) у = -(x - 2)2 + 9.
220
17. Бирелгән аралыкта функциянең иң кечкенә һәм иң зур
кыйммәтләрен табыгыз:
а) [-3; -1] кисемтәсендә у = 2x2 + 4х - 6;
б) [-7; -4] кисемтәсендә у - -- (х + 4)2;
3
в) [-1; +∞) нурында у = Зх2 - 6;
г) (0; 4) интервалында у = -2x2 + 8х.
18. Тигезләмәләр системасын график юл белән чишегез:
fy = (x + 3)2-3, ∣ι∕ = 2x + 5,
\у = х + 6; [у = -х2 + 8х - 3;
\у = -х2 - 4х, (у = х2 - 6х + 6,
[у = (х + I)2 - 1; \у = -(χ - 4)2 + 2.
19. Квадрат тигезсезлекне
a) 0,5(x + З)2 - 8 > 0;
б) -3x2 + 6x + 9 ≥ 0;
20. а) х2 + 4х + 4 > 0;
б) Зх2 - 6х + 5 > 0;
график юл белән чишегез:
в) ∣(x - I)2 - 4 ≤ 0;
г) -2x2 - 6х + 8 < 0.
в) -х2 + 6х - 9 > 0;
г) -2x2 + 4х - 7 > 0.
21. а) т ның нинди кыйммәтләрендә 2x2 - 8х + 5 = т
тигезләмәсенең бер тамыры, ике тамыры була, тамырлары
булмый?
б) k ның нинди кыйммәтләрендә -3x2 - 12x - 7 = k
тигезләмәсенең бер тамыры, ике тамыры була, тамырлары
булмый?
22. у = — функциясенең графигын төзегез. График буенча
билгеләгез:
a) [1; 6] кисемтәсендә функциянең иң зур һәм иң кечкенә
кыйммәтләрен;
б) у > 1 булганда, аргументның кыйммәтләрен.
23. у = функциясенең графигын төзегез. График буенча
X — 3
табыгыз:
а) гиперболаның симметрия үзәге координаталарын;
б) функциянең монотонлык аралыкларын.
221
24. у = + 3 функциясенең графигын төзегез. График буенча
табыгыз:
а) гиперболаның асимптоталарын;
б) функциянең кыйммәтләре күплеген.
25. у = - 2 функциясе графигыннан файдаланып табы-
X + о
гыз:
а) функциянең билгеләнү өлкәсен һәм кыйммәтләре күп¬
леген;
б) функциянең монотон аралыкларын;
в) гиперболаның симметрия үзәге координаталарын;
г) гиперболаның асимптоталарын.
26. Функция формула белән бирелгән:
. 1 , . , 2
а)+ 4; »> У = -775.
б) У = -j4τ + 5; г> У = 777 - 2∙
Графикны төземичә генә билгеләгез:
1) функциянең билгеләнү өлкәсен;
2) функциянең кыйммәтләре күплеген;
3) функциянең монотон аралыкларын;
4) гиперболаның симметрия үзәге координаталарын;
5) гиперболаның асимптоталарын.
k
27. Түбәндәге нокта аша үтүе билгеле булса, у = — гипербо¬
ласының формуласын языгыз:
28. А ноктасы бирелгән функциянең графигында ятамы:
а) У = y⅛ Ж-3,9; 100);
б) у = -х2 - >/2х + 15, a(-V2; 15);
1 R
≡) y = ~d⅛ a<0=
Г) У = у + x√7,
A(-√7j 6).
222
29. Бирелгән аралыкта функциянең иң зур һәм иң кечкенә
кыйммәтләрен табыгыз:
a) [1; +∞) нурында у = ;
4
б) [0; 3] кисемтәсендә у = 1;
g
в) [-4; -1] кисемтәсендә у = — - 2;
г) (3; 7] ярыминтервалында у = + 1.
X ~ о
30. а) у = x2 - 6x - 7 функциясенең [-1; 2] кисемтәсендә кимүен
һәм [4; 6] кисемтәсендә үсүен исбатлагыз.
б) у = —х2 + 2х + 5 функциясенең [1; 4] кисемтәсендә
кимүен һәм [-3; 0] кисемтәсендә үсүен исбатлагыз.
31. Монотонлык үзлегеннән файдаланып, бирелгән аралыкта
функциянең иң зур һәм иң кечкенә кыйммәтләрен табыгыз:
. ^1 . √3^∣ 6 , 1
a) —j=, -т- кисемтәсендә у = — + 1;
L√3 * J χ
б) [√5j √β] кисемтәсендә у = ~l,5x2 + 6х;
в) [0; 7з] кисемтәсендә у = 5
г) [-3; -л/б] кисемтәсендә у = (х + З)2 - 5.
32. Тигезләмәләрне график юл белән чишегез:
= х - 5;
в) 2х - 6 = -
х + 1’
г) - + 2 = -
х
х - 2
33. Тигезләмәләр системасын график юл белән чишегез:
У = -0,5x2 + 2x + 1,
У = х2 - 2х - 4.
223
34. Бирелгән функциянең графигыннан файдаланып, χ Ның
нинди кыйммәтләрендә y = m,y>m,y<m шарты үтәлүен
билгеләгез:
а) У - χ _ 1 4, т - 0;
6 o
6)i∕= х_2> т = 3;
в) у = $ + 3, т = 0;
Q
г) У = r , 9 + 2, т = 2.
X Т Ci
35. Тигезсезлекне график юл белән чишегез:
a)χ≡2+l≤0i B)∕1+2>0i
6>-χ5+l <1; r>-χ-3 11∙
36. Бирелгән гиперболаның симметрия күчәрен төзегез Һәм
тигезләмәләрен языгыз:
4 4 4 4
а) </ = -; б) у = ——; в) у = - + 3; г) у = —— - 1.
Л Л, Ct Д. Л- Т
Функциянең билгеләнү өлкәсен табыгыз һәм аның гра¬
фигын төзегез:
37. а) у = √x + 4;
в) у = -∙√x + 1;
б) у = √x + 6;
г) у = у/х - 2 - 2.
38. а) у = V-x;
в) у = уГ-х + 2;
б) у = √3 - х;
г) у = -√2 - х.
39. Бирелгән аралыкта функциянең иң зур һәм иң кечкенә
кыйммәтләрен табыгыз:
а) [4; +∞) нурында у = yfx ;
б) [0; 3] кисемтәсендә у = -Vx + 2 ;
в) (0; 4] ярыминтервалында у = -уГх + 4;
г) [6; 9] кисемтәсендә у = √x - 3 + 1.
40. у - Vx + 4 - 1 функциясенең графигын төзегез. График
буенча билгеләгез:
а) координаталар күчәрләре белән кисешү нокталарын;
б) у < 0, у > 0 булганда аргументның кыйммәтләрен;
в) әгәр z∕mln = 1, ι∕max = 3 булса, х ның нинди аралыкта
булуын;
г) 0 < х ≤ 5 булганда функциянең кыйммәтләрен.
224
41. у = -√x - 1 + 2 функциясенең графигын төзегез. График
буенча билгеләгез:
а) функциянең билгеләнү өлкәсен һәм кыйммәтләре күп¬
леген;
б) [5; 10] кисемтәсендә функциянең иң зур һәм иң кечкенә
кыйммәтләрен;
в) y(x) = 1 тигезләмәсенең тамырларын;
г) у(х) < 0 тигезсезлегенең чишелешен.
42. Тигезләмәләрне график юл белән чишегез:
a) Vx - 3 =1; в) 3 - л/х + 2 = 0;
б) -√x + 1 = 4 - 2х; г) √x + 3 = |х + 1.
О
43.
Тигезләмәләр системасын график юл белән чишегез:
[у = х2 - 6х + 5, У = ~^x + 1 ~ 1>
а) / , л б) 2
[у = √x 3 4; Г = χ - Г
44. Бирелгән функциянең графигыннан файдаланып, х ның
нинди кыйммәтләрендә у > Ъ, у < Ь тигезсезлеге үтәлүен
билгеләгез:
а) у = √x + 3 - 1, Ь = 0; в) у = -Vx +2, Ь = 0;
б) у = -Vx - 1, Ь = -2; г) у = >/х +3, Ь = 5.
Функциянең графигын төзегез:
45. а) у = |х|;
в) у = |х| - 3;
б) у = |х + 11;
г) у = |х - 3| + 1
46. а) у = -|х|;
в) у = -|х - 2|;
б) у = -|х + 4| - 2;
г) у = 2 - |х|.
47. у = |х - 4| - 5 функциясенең графигын төзегез. Табыгыз:
а) функциянең иң кечкенә кыйммәтен;
б) функциянең монотонлык араларын;
в) функциянең нульләрен;
г) у > 0, у < 0 булганда аргументның кыйммәтләрен.
48. у = —|х + 3| + 4 функциясенең графигын төзегез. Табыгыз:
а) функциянең иң зур кыйммәтен;
б) функциянең монотонлык араларын;
в) функциянең нульләрен;
г) у > 0, у < 0 булганда аргументның кыйммәтләрен.
225
49. Функциянең иң зур һәм иң кечкенә кыйммәтләрен табы¬
гыз:
a) [-V2; 1] кисемтәсендә у = |х|;
б) [-V2; 1] кисемтәсендә у = -|х + 41;
в) [-1; \[з] кисемтәсендә у = -|х| + 5;
г) [2; Vδ] кисемтәсендә у = |х - 1| - 3.
50. Тигезләмәне график юл белән чишегез:
а)|х-2|-4 = 0; в)3-|х+1| = 0;
б) |х + 3| = 5; r)∣x-4∣ = 3.
51. Тигезләмәләр системасын график юл белән чишегез:
б)
I у = 2x2 - 8х + 3,
\у = -|х - 2| - 2;
8
У х + 2’
у = |х + 4| - 4;
I у = 0,5x - 1,
∙, u = -|х -31 + 2;
r) l⅛ = √JT1,
\у = М - i∙
52. Тигезсезлекне график юл белән чишегез:
a) |х - 1| - 2 ≥ 0; в) 4 - |х - 2| > 0;
6)∣x÷ 1|<1; r)∣x-4∣≥2.
53. Функциянең графигын төзегез:
а) у = Vx2"; в) у = V(χ ^ З)2;
б) у = >∕x2 + 10х + 25; г) у = -√x2 - 8х + 16.
54. а) у = /(х) функциясе бирелгән, биредә Дх) = Зх2 - 2х + 5.
Табыгыз: ДО), /(-3), f(2t), Дх + 2).
б) у = Дх) функциясе бирелгән, биредә Дх) = -4x2 + Зх - 1.
Табыгыз: Д1), Д-2), ДЗх), Дх - 1).
55. а) у = Дх) функциясе бирелгән, биредә Дх) = √χ - 1.
Табыгыз: Д1), Д8), Д0,5х), Дх2 + 1).
б) у = Дх) функциясе бирелгән, биредә Дх) = √χ + 4.
Табыгыз: ДО), Д-2), Д4х), Дх2 + 4х).
56. а) у = Дх) функциясе бирелгән, биредә Дх) = х2 - Зх + 2.
х ның нинди кыйммәтләрендә Дх + 2) = Дх - 1) тигезлеге
үтәлә?
б) у = Дх) функциясе бирелгән, биредә Дх) = х2 - 5х + 6.
х ның нинди кыйммәтләрендә Дх + 1) = Дх - 3) тигезлеге
үтәлә?
57. а) у = Дх) функциясе бирелгән, биредә Дх) = √χ - 1. х ның
нинди кыйммәтләрендә Дх2 - 2х) = Дх + 4) тигезлеге үтәлә?
226
б) у = Дх) функциясе бирелгән, биредә f(x) = >Jx + 4. х ның
нинди кыйммәтләрендә f(x2 — 5x) = f(x - 5) тигезлеге үтәлә?
58. а) у = /(х) функциясе бирелгән, биредә ∕(x) = х ның
нинди кыйммәтләрендә f(x2 - 1) = ДЗх2 - Зх) тигезлеге үтәлә?
б) у = Дх) функциясе бирелгән, биредә Дх) = χ ү. х ның
нинди кыйммәтләрендә Дх2 - 2х) = Дх - 2) тигезлеге үтәлә?
59. а) у = Дх) функциясе бирелгән, биредә Дх) = х2 — 8х - 9.
х ның нинди кыйммәтләрендә Дх + 1) < Дх - 2) тигезлеге
үтәлә?
б) у = Дх) функциясе бирелгән, биредә Дх) = х2 - 6х + 8.
х ның нинди кыйммәтләрендә Дх - 4) ≥ Дх + 2) тигезлеге
үтәлә?
60. а) у = Дх) функциясе бирелгән, биредә Дх) = x2+7x+12.
х ның нинди кыйммәтләрендә Дх + 3) > ДО) тигезлеге
үтәлә?
б) у = Дх) функциясе бирелгән, биредә Дх) = х2 - 4х + 3.
х ның нинди кыйммәтләрендә Дх - 1) ≤ Д1) тигезлеге
үтәлә?
61. у = х2 - 6x + 1 функциясенең монотонлыгыннан файдаланып,
у(а) һәм y(b) ны чагыштырыгыз:
a) a = 3, Ъ = 1,72; в) a = 4, b = 3√2j
б) a = 3 - √2, b = 3 + 72; г) a = 0,8, b = 5.
62. у = /(х) функциясенең графигын төзегез һәм аның
үзлекләрен санап чыгыгыз:
х2 + 2, 1 ≤ х ≤ 2 булганда,
а) Дх) =
—, 2 < х < 6 булганда.
х
б) Дх) =
х < -1 булганда,
-Зх2 +3, -l≤x<2 булганда.
63. у = f(x) функциясе бирелгән, биредә
Дх) =
х2 - 4, -3 < х < 0 булганда,
-2x2 +4x-4, 0<x≤3 булганда.
а) Д-2), ДО), ДЗ) не табыгыз.
б) А(-1; -3), В(1; -3), С(1; -2) ноктасының функциянең
графигында ятуын белегез.
в) Бирелгән функциянең графигын төзегез.
227
64. у = f(x) функциясенең графигын төзегез, биредә
fx2 + 4х + 3, х < -1 булганда,
Дх) = ∏ 1 . 1 ,
[-xz +1, х > -1 булганда.
График ярдәмендә р ның нинди кыйммәтләрендә
/(х) = р тигезләмәсенең бер тамыры, ике тамыры, өч тамы¬
ры булуын билгеләгез.
65. Графигы а) 88 рәсемдә; б) 89 рәсемдә сурәтләнгән у = Дх)
•66. Тигезләмәнең графигын төзегез:
a) (ху - 6)(√x + 4 + у) =0; в) (у - 2x2 + l)(xy + 8) = 0;
б) (у + х2 - 3)(y2 - х) = 0; г) (√χ2^ - y)(x2 - 4х + у) = 0.
•67. у = /(х) функциясенең графигын төзегез, биредә :
х2 - 4, х ≤ -2 һәм х > 2 булганда,
-(x2 - 4), -2 < х < 2 булганда.
-(x2 - 9), -3 ≤ х ≤ 3 булганда,
х2 - 9, х < -3 һәм х > 3 булганда.
a) Дх) =
б) Дх) =
Модульнең билгеләмәсеннән чыгып, кисәкле функцияне
У = |Лх)| рәвешендә күрсәтегез.
•68. у = Дх) функциясен кисәкле функция рәвешендә күрсәтегез
һәм графигын төзегез:
а) Дх) = |х2 - 11; б) Дх) = -∣χ2 - 4|.
228
Функциянең графигын төзегез:
•69. а) у = (х + 4) 1∙,
б) y= [τ∙ 1 V;
l√(χ - З)2 )
в)у= (√ΓΓ2Γ25
г) у = f~r⅜-1 —Л .
V√X2 + + J
-n ∖ ^χ2 - 2x + 1.
•70. а) у = χ _ ι ;
6) У = 'χ + J (X2 2х 3);
в) у = + 2
'''x*~+ 4х + 4
Г)У= ⅛¾2 + 6*'5>'
∣λ " о|
—, 4 3
.71. a)9=lχp 4s≈∣x + 1∣∙
в)у= ⅛ ~3; г)у= '∣⅛
•72. а) у = 2x∣x∣ + 2;
б) у = -2x2 -
в) у = ~x∣x∣ + 2х2;
. 1*1
r>"=⅛+l∙
•73. Тигезләмәне график юл белән чишегез:
О
a) + 0,5x2 4x0 - 0;
х + 2
∙y∙2 Л
б) 2x - 4 + — ⅛ = 0.
(х - 2)0
Тигезләмәне чишегез:
74. a) x2 + 6x = 0;
б) -3x2 = 18х;
в) -х2 - 12χ = 0;
г) 4x2 = 28х.
75. a) 3x2 - 27 = 0;
б) 18 - 6x2 = 0;
76. a) -5x2 = 0;
б) 32 + 8x2 = 0;
в) 24 - 6x2 = 0;
г) 5x2 - 30 = 0.
в) (Зх + 4)2 = 0;
г) -4x2 = 40.
77. a) 6x2 - 13x - 15 = 0;
б) -5x2 - 27х + 56 = 0;
в) 9x2 + 40х + 16 = 0;
г) -Зх2 + 16х + 75 = 0.
78. а) -х2 + 4х - 1 = 0;
б) 4x2 - 10х + 5 = 0;
в) х2 + 6х + 2 = 0;
г) -5x2 - 6x + 1 = 0.
79. a) 4x2 + 28х + 49 = 0;
б) -Зх2 - 24х - 49 = 0;
в) -25x2 + 80х - 64 = 0;
г) 2x2 - 8х + 11 = 0.
80. а) (х - l)(x - 2) = (Зх + 2)(3 - х) + 2;
б) (х + 4)(4x - 3) = х2 + 5х + 4;
в) х2 + х + 12 = 2(x + 1)(х - 5);
г) 19 - (х - 6)(2x + 1) = (х - 5)(x - 1).
229
81. Тигезләмәне чишегез:
, 8x2 + х 15.
а) —8^^ = 32’
,. 2x2 - Зх , 9х + 2 3 - 2x2 .
б) ~τ~~+ = —б~’
. 10x2 - Зх 7.
В) 2 = 5’
. 7х + 15 6x2 + 1 3 - 6x2
г) __
82. Ике уңай санның берсе икенчесеннән 4 кә зур. Әгәр
аларның тапкырчыгышы 96 булса, бу саннарны табыгыз.
83. Турыпочмаклыкның бер ягы квадрат ягыннан 3 тапкыр
зур, ә икенче ягы 8 см га кечкенә. Әгәр квадратның
мәйданы турыпочмаклык мәйданыннан 54 см2 га зуррак
булса, квадратның мәйданын табыгыз.
84. Турыпочмаклы җир участогы озынлыгы 80 м булган койма
белән әйләндереп алынган. Участокның мәйданы 175 м2.
Аның якларын табыгыз.
85. Турыпочмаклы өчпочмакның гипотенузасы 17 см, ә ка¬
тетларның берсе икенчесеннән 7 см га кечерәк. Өч¬
почмакның мәйданын табыгыз.
86. Турыпочмаклы өчпочмакның гипотенузасы катетларның
берсеннән 2 см га, ә икенчесеннән 16 см га зуррак.
Өчпочмакның якларын табыгыз.
87. Ике квадратның яклары 3 һәм 4 саннарына пропорцио¬
наль. Әгәр икенче квадратның ягын 2 см га кечерәйтеп, бе¬
ренче квадратның ягын 2 см га зурайтсалар, килеп чыккан
квадратларның мәйданнары аермасы 35 см2 га тигез була.
Бу квадратларның якларын табыгыз.
88. Турыпочмаклы өчпочмакның периметы 48 см, ә гипотену¬
засы 20 см. Өчпочмакның катетларын табыгыз.
89. Турыпочмаклыкның диагонале 34 см, ә периметры 92 см.
Турыпочмаклыкның мәйданын табыгыз.
90. у = х2 - 10x ÷ с параболасының түбәсе с ның нинди
кыйммәтләрендә координаталар башыннан 13 берәмлек
кисемтә ераклыкта урнаша?
91. у = ах2 + 6х — 5 параболасының түбәсе а ның нинди
кыйммәтләрендә координаталар башыннан 5 берәмлек
кисемтә ераклыкта урнаша?
230
92. а) Квадратик у = ax2 + bx + с функциясенең графигы
D(3; -2), /(0; 4), K(2; -4) нокталары аша үтсә, а, Ъ, с ның
кыйммәтләрен табыгыз.
б) Квадратик у = x2 + рх + q функциясенең графигы А(2; -3),
В(-3; 7) нокталары аша үтсә, р һәм q ның кыйммәтләрен
табыгыз.
Тигезләмәне яңа үзгәрешле кертү юлы белән чишегез:
93. а) x4 - 2x2 - 8 = 0; в) x4 - Их2 + 18 = 0;
б) 2x4 - 19x2 + 9 = 0; г) 3x4 - 13x2 + 4 = 0.
94. а) (х2 + 3)2 - 7(x2 + 3) + 12 = 0;
б) 3(6x2 - x)2 - 4(6x2 - х) + 1 = 0;
в) 2(x2 - I)2 - 13(x2 - 1) - 24 = 0;
г) (х2 - 4x)2 + 9(x2 - 4х) + 20 = 0.
Тамырлары бирелгән саннар булган квадрат тигезләмә
төзегез:
95. a) x1 = -9, х2 = 4; в) x1 = -7, х2 = _3;
,4 1 2. 5 2
6)x1= x2=-3, r)x1= -, x2=-.
96. a) Xι,2 = 2 ±>/3; в) х1>2 = -3 ±>/5;
3 ± √7 ч -1 ± √Ii
б) Xι,2 = —л—; г) x1,2 = .
2 о
97. а) — + — не исәпләгез, биредә x1 һәм х2 — Зх2 - 2х - 6 = 0
тигезләмәсенең тамырлары.
б) xf + х2 не исәпләгез, биредә x1 һәм х2 — x2 + x- 5 = 0
тигезләмәсенең тамырлары.
98. a) x2 + x22 = 13 икәне билгеле, биредә Xi һәм х2 — х2 + Ьх +
+ 6 = 0 тигезләмәсенең тамырлары, b ны табыгыз.
б) J- + — = 1 икәне билгеле, биредә Xi һәм х2 — х2 + х +
Xi х2 2
+ с = 0 тигезләмәсенең тамырлары, с ны табыгыз.
99. а) -х2 + Их + q = 0 квадрат тигезләмәсенең тамырлары
аермасы 3 кә тигез, q параметрының кыйммәтен табыгыз,
б) Зх2 — 18х + с = 0 квадрат тигезләмәсенең бер тамыры
икенчесеннән 5 тапкыр зуррак, с параметрының кыйммәтен
табыгыз.
231
•100. а) Әгәр x2 - (m - l)x + (4m2 — 45τn — 8) = 0 тигезләмәсенең
тамырлары тапкырчыгышы 28 гә тигез булса, т пара¬
метрының кыйммәтен табыгыз.
б) Әгәр х2 - (3m2 + 16zn - 8)х + (гп + 9) = 0 тигезләмәсенең
тамырлары суммасы 4 кә тигез булса, т параметрының
кыйммәтен табыгыз.
101. Квадрат өчбуынны тапкырлаучыларга таркатыгыз:
а) х2 + 22х - 23; в) -х2 + 18х - 77;
б) -Зх2 - 8х + 3; г) 7x2 + 9х + 2.
102. Вакланманы кыскартыгыз:
. х2 + 2х - 63. . 8х - х2
a' 49 - х2 ’ х2 - Зх - 40’
θχ2 + x ∖ 5x2 - 12х + 4
6x2 - 17х - 3’ l j 25x2 - 4
103.
Аңлатманы гадиләштерегез:
, 4 - a , а . . 1 + х
а) + . ; в)
а 4 + а х
_ χ + 2.
1 + х’
б)
2 - с _ 2 + с.
2 + с 2 - с'
г)
3
3 + у
104.
а)
4a a - 1.
в)
12х
5<÷ti
a2 - 1 а + 1’
х2 -
2b - 5 1
т + 2 1
б)
b2 - 5b 5 - b'
г)
3zn2 ■
- Зт т - 1’
105.
а)
х2 - 9 х2 - 4 .
в)
х - х2 2х + 10.
2x + x2 5x + 15,
25 -
х2 х2 - 1 ’
б)
4y2 . У .
г)
а
6a2
у2 - 4 у + 4 ’ у - 2’
а + 6
' а2 + 36 + 12a'
106.
а)
∕κz, ь\2
(5“ Ь) 25a2-b2'
в* b2 - 16 ^~ 8Ь + 16);
б)
4αx + 4a2 + х2 .
+ ах);
г) (Зху - у2) • У2 - 9χ2
Зх ’ ’
Зу
232
Аңлатманы гадиләштерегез:
ιn7 яЛ_ь ъ ⅛2÷9V(3-⅛)2.
ιu'∙ _ з ъ + 3 9-b2J 3b + b2'
у2 + 5 у . Г 5 У2 + 25 _ 5 λ
, (i∕-5)2 4≈∕ + 5 y2 -25 5-у/
1∩R QX x + 4° ∙ f Х ~ 4 16 \
, X3 - 16x ■ кЗх2 + Их - 4 16 - X2 /
fn у3 - у ( у -1 i_J
, У-4 ∖2y2 +3y + l y2 -1J∙
4,r4,r, , ( 1 , m +1 4m2 + 2т +Р
1 . 1
,, 1,2 - 4m 8m3 - 1 1 + 2m ) ’ 4m -
2 + 6р Г 1 + 1 . 1 + 3p 1
р 1 2 - 6p 27p3 - 1 ‘ 1 + 3p + 9p2 }
2’
110. Үзгәрешленең мөмкин табылган барлык кыйммәтләре өчен
дә, аңлатманың кыйммәте үзгәрешле кыйммәтенә бәйле
булмавын исбатлагыз:
с + 5
а) с2 - 64
4 12 λ 4
с + 8 c2 + 16с + 64 √ 8 - с ’
б)
P- + “
1х - 7 х2 - 14х + 49
х2 - 49 _ 7х - 21
2х - 7 х - 7
Тигезләмәне чишегез:
_ 7 5х .
х х + 1’
х + 5 _ 50
5 - х х2 - 25’
. а) —
X2 + X
, х 5 _ 10 - х
В' х - 2 х + 2 х2 - 4
3 _ 6 _ Зх - 7
х х2 - Зх 3 - х
112. а)
х2 - 4х + 3
13 - 7х
1 - х
3
х - 3’
61 8 + 1~3x = 4
х2 - 6х + 8 2-х х - 4’
113. а) 2х + | -5 = 0;
б) Зх - 2χ-1 -1 = 0;
в) Зх + — + 10 = 0;
х
г) 4x + 5 - 6x1 = 0.
233
114.
Тигезләмәне яңа үзгәрешле кертү юлы белән чишегез:
а) ~—Ъ о - x2 + 2х = 0;
х2 - 2х - 2
б)
х + 6(x2 - 2)
х2 - 2 х
(x2 - 4x)2 х2 - 4х’
х - 3 + х2 + 10х + 27
х2 + 10х + 27 х - 3
Мәсьәләне чишегез:
115. Сәяхәт барышында туристларның көймә белән тау елгасы
агымы буйлап 54 км һәм тагын күлдә 6 км барган вакыты
салның шушы елга буйлап 21 км йөзгән вакытына тигез.
Әгәр көймәнең үз тизлеге 12 км/сәг булса, елганың агым
тизлеген табыгыз.
116. Катерның елга агымына каршы 8 км һәм тагын агым
уңаена 30 км барган вакыты аның күлдә 36 км барган ва¬
кытына тигез. Әгәр елганың агым тизлеге 2 км/сәг булса,
катерның үз тизлеген табыгыз.
117. Велосипедчы шәһәрдән турбазага керү борылышына кадәр
24 км ны бер тизлек белән бара, ә борылыштан соң тизле¬
ген 3 км/сәг кә киметә һәм турбазага кадәр тагын 6 км юл
үтә. Әгәр ул барлык юлга 2 сәг 40 мин вакыт сарыф итсә,
велосипедчының борылышка кадәрге тизлеген табыгыз.
118. Автоузышчы раллида, машинасы ватылу сәбәпле, 4 мин
вакытын югалта, ә аннан соң калган 120 км юлда, тизлеген
20 км/сәг кә артырып, югалткан вакытын кире кайтара.
Аның баштагы тизлеген табыгыз.
119. Кыяга менүчеләр ярышында 10 м озынлыктагы трасса¬
да ике спортчы ярыша; берсенең тизлеге икенчесенең
тизлегеннән 0,2 м/с ка зуррак. Әгәр аларның берсе финиш¬
ка икенчесеннән 2,5 с ка алданрак җитсә, спортчыларның
тизлекләрен табыгыз.
120. N шәһәреннән аннан 60 км ераклыктагы М шәһәренә ав¬
тобус, ә шуннан соң 20 мин вакыт үткәч, тизлеге автобус
тизлегеннән 40 км/сәг кә артыграк булган җиңел машина
юлга чыгалар. Әгәр автобус М шәһәренә җиңел машина¬
дан 12 мин ка соңрак килеп җитсә, аларның тизлекләрен
табыгыз.
234
121. А пунктыннан аннан 20 км ераклыктагы В пунктына ав¬
тобус, ә шуннан сон, 7 мин вакыт үткәч, тизлеге автобус
тизлегеннән 20 км/сәг кә артыграк булган йөк машинасы
юлга чыгалар. Әгәр йөк машинасы В пунктына автобустан
3 мин ка алданрак килеп җитсә, аларның тизлекләрен та¬
быгыз.
Исәпләгез:
122. а) 23 ∙ 25 • (2 2)4;
,. 38 9-g.
б) (34)-2 ’
в) (5^1)4 • 59,5-2;
(7-2 )3 . 7-7
Г) 49^6
123. а)
5^4 ■ 156 .
(з-6)-8 ’
б)
43 ■ 14-3 .
7-5 . 27 ’
. З5 • 6~6 .
в) (23)-4 ’
8-3 ■ Ю5
56 ∙ 2^2 '
124. Аңлатманың кыйммәтен табыгыз:
m6(m2)5 п к. к
а) -.—=—, т = 0,5 булганда;
rrr3m7
(a2b
б) / 3 42 ⅜-4 , α = 15, & = 5 булганда;
(α^3 у Ь 4
/I ( I-3
в) \ „— , п = 10 булганда;
zΓ47i1°
(cdλ V2
Г) (c-H2(d-3)^8 ’ С = 6, d = 3 булГанда-
125. Аңлатманы гадиләштерегез:
. ( х х + 2 . 1
a lx2-2x + l х2 + х - 2√ (2х - 2)~2 ’
б)
У + 2
У2 - У - θ
■ (Зу - 9)2.
У
у2 - бу+ 9
Иррациональ тигезләмәне чишегез:
126. a) √x + 4 = 3; в) √3χ - 1 = 2√2j
б) = 3; г) x∣^ΞI = 2.
Мх + 2 \ 6 - х
127. a) √x2 - 5х = 6; в) + бх = 4;
б) Vx2 - 5x + 5 = 1; г) Vχ2 + 5х + 2 = 4.
235
Иррациональ тигезләмәне чишегез:
128. а) 4х = 2 - х; в) 7х + 2 = х;
б) 77-х = х - 1; г) 712 - х = х.
129. a) 27x - 1 - 7х + 4 = 1;
б) 7х + 3 - √2x - 1 = 73х - 2;
в) 7х + 6 - 2√x - 2 = 1;
г) 7x + 1 - 7х — 2 = 72х - 5.
130. a) √2x2 + 8х + 7 - 2 = х; в) √2x2 + 8x + 1 - х = 3;
б) х + 72x2 - 7х + 5 =1; г) х + 72x2 - 8x + 1 = 3.
Тигезләмәне яңа үзгәрешле кертү юлы белән чишегез:
•131. а) х2 + 2x - 2∖∕x2 + 2х = 3;
б) х2 + 6х + 24 = lθ7x2 + 6х.
•132. a) 72-х + ■■ ■4 = 2;
√2 - х + 3
б) . 3 + 2√x + 1 = 5.
√x + 1 + 1
•133. a) 10√x2 - х - 1 - 3 .. = 7;
7х2 — х — 1
б) 2√x2 - 9х + 23 - 5 = - 3
√x2 - 9х + 23
134. Аңлатмаларның кыйммәтләрен чагыштырыгыз:
a) 7192 һәм -—— ——;
7-4√3 7 + 4√3
б) 3 + 2√2 һәм 77 + 710;
в) 7198 һәм —y⅛ 7J——;
5√2 - 7 5√2 + 7
г) 2Tδ + 3 һәм 710 + 719.
236
135. Аңлатманы гадиләштерегез һәм аның кыйммәтен табыгыз:
a) + 4λ^- , т = булганда;
+ 4 т - 16 У
б) , п = булганда.
√n-5 ∏ -25 4
136. Аңлатманы гадиләштерегез:
Л + 3.
1 - х ’
б) (2 + √b) - 2√b + 2
k√b - 1
г) [l + 2√^-^^¼-√^).
I √α+l√
137. Бердәйлекне исбатлагыз:
138. х үзгәрешлесенең мөмкин табылган барлык кыйммәтләре
өчен дә аңлатманың кыйммәте х ка бәйле булмавын
исбатлагыз:
ar3√ξ-x⅛-2y' [^2ΛtlY' .-pL.
× 3 х ' х - 4 * ∖ Vx - 2 / ∖Γx - 1
139. Аңлатманың кыйммәтөн табыгыз!
a) V(3√2 - 2√5)2 + 3√2j
б) V(2 - √7)2 + 7⅛T√f)r.
в) √(2√15 - 3√7)2 - 3√7j
г) 7(√ιo - 3)2 + 7(√1^Z 4)2.
237
•140. Тигезләмәне чишегез:
a) x2 - δ(Vx) - 6 = 0; в) x2 + (Vx - з)2 -9 = 0;
б) x2 + √(x + 1)2 - 3 = 0; г) x2 + √(χ - 3)2 -9 = 0.
Тигезсезлекне чишегез:
141. а) 3 + 2х < -4;
в) 2 + 5х > -3;
г) 1 - 2х < 3.
б) 1 - Зх > 2;
142.
. х - 2 ч Зх-5.
а) 12 ’ 15 ’
, 2 + х ~ Зх-1
■’ 10 =■ 15 •
б) 3 - 2х < 2х + 7.
’ 9 6 ’
. Зх - 1 . 3 — 5х
Г) 8 > 20
143. a) (х - 3)(x + 3) > x2 + 5x - 4;
б) (х + 4)2 ≤ x2 + 6x + 10;
в) (3 - 2x)(3 + 2x) ≤ 10 - 4x2 + 5х;
г) (1 - 3x)2 > 9x2 + Зх - 8.
144. a) q ның нинди кыйммәтләрендә x2 + 5x + q = 0 тигез¬
ләмәсенең тамырлары булмый? q ның шундый иң кечкенә
бөтен кыйммәтен күрсәтегез.
б) q ның нинди кыйммәтләрендә x2-7x+q=0 тигез¬
ләмәсенең ике тамыры була? q ның шундый иң зур бөтен
кыйммәтен күрсәтегез.
145. a) а ның нинди кыйммәтләрендә ах2 + 6х - 3 = 0 тигез¬
ләмәсенең ике тамыры була?
б) а ның нинди кыйммәтләрендә ах2 + 5х + 15 = 0 тигез¬
ләмәсенең тамырлары булмый?
\ 3 - р u 5 - 2р
14b. а) р ның —-— һәм ——— вакланмаларының аермасы
4 18
тискәре булгандагы иң кечкенә бөтен кыйммәтен табыгыз.
, 5 - 2⅛ , 9 + 2k
б) к ның —-— һәм —-— вакланмаларының суммасы
4 о
уңай булгандагы иң зур бөтен кыйммәтен табыгыз.
Тигезсезлекне чишегез:
147. а) х2 + Зх + 2 < 0;
б) -х2 - х + 12 ≤ 0;
в) х2 - 7х + 12 > 0;
г) -х2 + Зх + 4 > 0.
148. a) 2x2 - 9x + 4 ≥ 0;
б) -9x2 - 8x + 1 > 0;
в) 3x2 - 4x + 1 ≤ 0;
г) -2x2 + х + 1 < 0.
238
149. a) x2 - 81 ≤ 0; б) -χ2 > 4x; в) 121 ≤ x2; г) x2 - 2x < 0.
150. a) 4x2 - 12x + 9 > 0;
б) -2x2 + x - 1 < 0;
в) 9x2 - 6x + 1 < 0;
г) x2 - 2x + 5 < 0.
Үзгәрешленең нинди кыйммәтләрендә аңлатманың мәгъ¬
нәсе барлыгын табыгыз:
151. a) √4x - 9; б) , ;
√5 - 7х
152. a) √x2 - Зх; б) . 1 ;
√12 - Зх2
в) 73 - 9х; г) . 1
√5x + 3
в) √36 - х2; г) , 1
√4x2 - 8х
153. a) √x2 - 8х + 15;
б) √(-x2 +9x-2O)^15
154. a) ∖∣(x2 + 8x + 16)^1;
б) y∣(-x2 + 2x - З)-1;
∖ √3 - 5x - 2x2 .
.!55. а> - ;
б) >∕3x2 - х - 14 .
в) √(x2 + 7х + 12) 1;
г) √-x2 - Их - 28.
в) Vx2 + бх + 10;
г) V-x2 + 2x - 1.
. √2 - 5х - Зх2 .
в> —й—•
. √3x2 - 4х - 15
г) —т^Гх •
156. Функциянең билгеләнү өлкәсен табыгыз:
а) у = yj2x + 8; в) у = V(θx - 18)-1;
б) у = , 1 .г) у = √10 + Зх - х2.
У √10x2 - Зх - 1
157. k ның кыйммәте нинди булганда:
a) 5x2 — kx + 5 = 0 тигезләмәсенең ике тамыры була;
б) 3x2 + 2⅛x - (ft - 6) = 0 тигезләмәсенең тамырлары була;
в) 3x2 + 2⅛x + 12 = 0 тигезләмәсенең тамырлары булмый;
г) 2x2 -fex + fe + 6 = 0 тигезләмәсенең тамырлары бердән
артмый.
158. Математик модельләүнең өч этабын аерып, мәсьәләне
чишегез.
а) Турыпочмаклыкның бер ягы икенчесеннән 3 см га зуррак,
ә мәйданы 70 см2 дан артыграк. Турыпочмаклыкның
кечерәк ягы нинди озынлыкта булырга мөмкин?
б) Турыпочмаклы өчпочмакның бер катеты икенчесеннән
5 см га кечерәк, ә бу өчпочмакның мәйданы 25 см2 дан
артыграк. Зур катет нинди озынлыкта булырга мөмкин?
239
КУШЫМТА
ИҢ ГАДИ КОМБИНАТОРИКА МӘСЬӘЛӘЛӘРЕ.
ВАРИАНТЛАРНЫ КАРАП ЧЫГУ. ВАРИАНТЛАР АГАЧЫ
«Алгебраик вакланмалар» бүлегенә
П.1. d үзгәрешлесенең кыйммәтен -5 тән 4 кә кадәр саннар
„ d(4 + d2 ⅛
арасыннан аларны да кертеп сайлап алалар. -√ L
d3 (16 - d<j
вакланмасының кыйммәте ничә d кыйммәте өчен:
а) билгеләнми; в) тискәре;
б) нульгә тигез түгел; г) уңай?
П.2. а үзгәрешлесенең кыйммәтен 0 дән 9 га кадәр саннар
арасыннан аларны да кертеп сайлап алалар.
а2 (а2 - 4)
а) —— вакланмасының кыйммәте ничә а үзгәреш¬
лесенең кыйммәте өчен билгеләнми?
Вакланманы гадиләштерегез һәм вакланма кыйм¬
мәтенең:
б) бөтен булмаган сан; в) икеурынлы сан; г) җөп сан
булу ихтималын табыгыз.
П.З. Вакланма кыйммәтләре таблицасын тутырыгыз (әгәр
вакланманың t ның тиңдәшле кыйммәтендә мәгънәсе
булмаса, сызыкча куегыз):
t
-6
-5
-4
-3
-2
-1
0
1
2
3
CO ®
1 1
Таблицаның беренче юлындагы t үзгәрешлесенең кыйм¬
мәтен очраклы сайлап алганда, вакланма кыйммәтенең:
а) тискәре сан;
б) бөтен сан;
в) 0 саныннан 3 тән кимрәк ераклыктагы сан булу их¬
тималы нинди?
П.4. Вакланманың санаучысы 1 гә, 3 кә, 7 гә яки 10 га тигез,
ә ваклаучысы санаучыдан 2 гә яки 5 кә кечерәк.
а) Ничә вакланманың ваклаучысы 5 кә тигез?
240
б) Табылган барлык гади вакланмаларны унарлы вак¬
ланма рәвешендә языгыз һәм тәртипкә салынган сан¬
нар рәтен төзегез.
в) Табылган рәтнең күләмен һәм колачын табыгыз.
г) Бирелгән саннар бүленешенең түгәрәк диаграммасын
төзегез.
П.5. Вакланманың ваклаучысын -10, -4, 4, 10 саннары ара¬
сыннан сайлап алалар, ә санаучысы сайлап алынган
ваклаучының квадратыннан 3 кә аерыла.
а) Вакланманың мөмкин табылган санаучыларын языгыз,
б) Барысы ничә вакланма төзергә мөмкин?
в) Табылган барлык уңай саннарны языгыз.
г) Иң зур тискәре санны күрсәтегез.
Мөмкин табылган барлык вариантларны сайлап алуны нинди дә булса
алым ярдәмендә эшләү уңай. Иң киң таралган алымнарның берсе — вари
антлар агачы дип йөртелә торганы. Аны конкрет мисалда күрсәтеп узар-
2х — у
быз. вакланмасын карыйк. Әйтик, аның х үзгәрешлесе 1, 2, 3
X + У
кыйммәтен, ә у үзгәрешлесе 3 яки 4 кыйммәтләрен алгандагы кыйммәтен
табарга кирәк булсын. Башта х ны сайлап алуны сурәтлибез (рәс. 90).
х кыйммәтләренең һәркайсы өчен у ның ике (3 яки 4) кыйммәтенең
берсен сайлап алырга мөмкин. Моны 91 нче рәсемдәгечә сурәтләү уңай.
Рәс. 91
Хәзер санлы вакланмаларның кыйммәтләрен исәплисе генә кала. 92
нче рәсемдә йомгаклау күрсәтелгән (кайбер арадаш исәпләүләр төшереп
калдырылган).
241
Рас. 92
Вариантлар агачы дәфтәрдә бик күп урын ала. Әмма анда вариант¬
ларны сайлап алу уч төбендәге кебек ачык күренә. Вариантлар агачын
астан өскә дә, үзәктән ян-якларга таба да ясарга була, барысын бергә
таблицаларга җыярга да мөмкин.
2х - у
X + у
х = 1
х = 2
х = 3
у = 3
г/ = 4
у = з
у = 4
J∕ = 3
у = 4
2
1
°
2
2
I.f
' >р а үзгәрешлесе 2 яки 4, b үзгәрешлесе 2, 3 яки 4
(1Ь U
’тләреналса, вакланмасы кыйммәтләренең
b - a
: агачын ясагыз. Ничә очракта вакланманың
ьнәсе булмый?
һәм Ь ның кыйммәтләрен очраклы сайлаганда, ваклан-
тмәтенең:
■ он кечкенә булу ихтималын исәпләгез.
Әгәр /г, п, т үзгәрешлеләренең һәркайсы -1 яки 2 кыйм-
⅛ + п + т
мәтләрен алса, вакланмасы кыйммәтләренең
⅛(n - т)
вариантлар агачын ясагыз.
Үзгәрешлеләр кыйммәтләрен очраклы сайлаганда, вак¬
ланма кыйммәтенең:
а) билгеләнмәве;
б) бөтен сан;
в) уңай сан булу ихтималы нинди?
242
П.8. Мәктәпне тәмамлаучы укучы А, В, С шәһәрләренең
берсендәге федераль, техник яки педагогик универ¬
ситетларының физика яки математика факультетына
керергә җыена. Әгәр:
а) В шәһәрендә федераль университет булмаса;
б) А шәһәренең педагогика университетында физика фа¬
культеты булмаса;
в) техник университет бары С шәһәрендә генә булса һәм
анда математика факультеты булмаса;
г) барлык шәһәрләрдә дә - бу университетлар, ә универ¬
ситетларда күрсәтелгән факультетлар булса, универ¬
ситет һәм факультет сайлап алуның вариантлар ага¬
чын ясагыз.
П.9. Укытучы киләсе дәрестә өй эше мисалларын чишү өчен
такта янына башта Айсылуны, аннан соң Таһирны чакы¬
рачагын әйтә. Такта янында җавап биргән өчен, кагыйдә
буларак, 2, 3, 4 яки 5 билгесе куела.
а) Айсылу һәм Таһир алачак билгеләрнең вариантлары
агачын ясагыз.
б) Айсылу һәм Таһир алачак билгеләрнең ничә вариан¬
ты бар?
в) Бары тик «дүртле »ләр һәм «бишле »ләр генә алына
торган ничә вариант бар?
г) « Икеле »ләрсез ничә вариант бар?
Кайбер очракларда вариантлар агачы 6, 7, 8 һәм 9 мисаллардагы ке¬
бек симметрияле булмаска да мөмкин. Бер мисал карап китик.
Үтә күренмәле булмаган пакетта бер үк үлчәмдәге бер кара һәм ике
ак шар ята. Карамыйча гына бер шарны алалар. Әгәр ул ак булса, аны
кире пакетка салалар. Әгәр кара булса, анысын өстәлгә куялар. Ике
тапкыр алганнан соң, пакеттагы шарлар составының вариантлар ага¬
чын ясарга кирәк. Җавап 93 нче рәсемдә бирелә.
КАА
Беренче тапкыр алганнан соң КАА
Икенче тапкыр алганнан соң КАА АА АА
Рәс. 93
243
•П.10. Өстәлдә цифрлы ягы өскә караган нәкъ бертөсле 4 вак
акча ята. Аларның өчесе чын, ә берсе ялган акча, аның
икенче ягында рәсеме юк. Карамыйча гына бер-бер арт¬
лы өч акча алалар. Чын акчаны янчыкка салалар, ә ял¬
ганын ташлыйлар.
а) Өстәлдәге акчалар составының вариантлар агачын
ясагыз.
б) Янчыкка бернинди акча керми калу ихтималы нинди?
в) Янчыкка нәкъ 2 сум өстәлү ихтималы нинди?
« у - √x функциясе. Квадрат тамырның үзлеге» бүлегенә
П.11. * ∈ ■ язылышында * урынына -19, -0,(19), ξj,
л/19 саннарының берсен, ә ■ урынына саннар күп¬
лекләре символлары: N, Z, Q ның берсен куярга
мөмкин. Дөрес һәм дөрес булмаган төрле раслаулар ки¬
леп чыга, мәсәлән: -19 ∈ N, -0,(19) ∈ Q һ.б.
а) Беренче урында V19 торган ничә раслау килеп чыга?
б) Төрле раслаулар төзүнең вариантлары агачын
төзегез.
в) Барысы ничә раслау килеп чыга?
г) Алар арасында ничә дөрес раслау бар?
17 /—
П.12. * £ ■ язылышында * урынына -3, 0,(317), —, √3
саннарының берсен, ә ■ урынына — саннар күплекләре
символлары: N, Z, Q ның берсен куярга мөмкин.
Дөрес һәм дөрес булмаган төрле раслаулар килеп чыга,
мәсәлән: -3 ∈ N, >/з £ Q һ.б.
а) Соңгы урында Z торган ничә раслау килеп чыга?
б) Төрле раслаулар төзүнең вариантлары агачын
төзегез.
в) Барысы ничә раслау килеп чыга?
г) Алар арасында ничә дөрес раслау бар?
∏.13. * Ω ■ язылышында * урынына —^25, -^2,5, ^0,25
саннарының берсен, Ω урынына ∈ яки £ тамгасын, ■
урынына саннар күплекләре символлары: Q яки R ны
куярга мөмкин.
а) Шундый раслаулар төзүнең вариантлары агачын
төзегез.
б) £ символы кергән ничә раслау булыр^
244
в) Барысы ничә раслау килеп чыга?
г) Алар арасында ничә дөрес раслау бар?
П.14. а) 123 456 789 санының теләсә кайсы цифрлары арасы¬
на өтер куярга мөмкин. Бу вакытта ничә унарлы вак¬
ланма килеп чыга?
Өтер куйганнан соң:
а) миллионнан зур; б) йөздән кечкенә; в) вакланмалы
өлеше 0,3 тән зуррак булган сан килеп чыгу ихтима¬
лы нинди?
П.15. Аңлатмаларның кыйммәтләре таблицасын тутыры¬
гыз (әгәр вакланманың t ның тиңдәшле кыйммәтендә
мәгънәсе булмаса, сызыкча куегыз):
t
0
1
2
3
4
5
6
7
8
9
1
CD
CM
1
+
Таблицаның беренче юлындагы t үзгәрешлесенең кыйм¬
мәтен очраклы сайлап алганда, аңлатма кыйммәтенең:
а) булмау;
б) бөтен сан булу;
в) икедән зур сан булу ихтималы нинди?
П.16. V∏ + 1 аңлатмасы бирелгән, п үзгәрешленең кыйммәте
0 дән 99 га кадәр, һәм алар да кергән бөтен саннар ара¬
сыннан очраклы сайлап алына.
а) Бирелгән аңлатма барлыгы ничә кыйммәте алырга
мөмкин?
б) Алар арасында ничә бөтен сан бар?
в) Алар арасында ничә иррациональ сан бар?
г) Алар арасында җидедән зуррак ничә сан бар?
∏.17. √n + 1 аңлатмасы бирелгән, п үзгәрешленең кыйммәте
0 дән 99 га кадәр, һәм алар да кергән бөтен саннар ара¬
сыннан очраклы сайлап алына. Бу вакытта аңлатма
кыйммәтенең:
а) билгеләнмәү;
б) уннан кечкенә булу;
в) (7; 10) интервалында яту;
г) [2; 6] кисемтәсендә яту ихтималы нинди?
245
П.18. Модульләре 11 дән кечкенә һәм шул ук вакытта нульгә
тигез булмаган саннар карала.
а) Барысы ничә шундый сан бар?
б) Алар арасында ничә тискәре сан бар?
в) Алар арасында модульләре 7 дән зуррак ничә сан бар?
г) Алар арасында (-10; -1) аралыгындагы ничә сан бар?
П.19. Түбәләре А(0; 0), В(0; 3), С(9; 3), В(9; 0) булган турыпоч¬
маклыкта координаталары бөтен саннар булган барлык
нокталарны билгелиләр.
а) Барысы ничә нокта билгеләнгән (яклар өстендә яту¬
чы нокталарны да кертеп)?
б) Шундый ничә нокта турыпочмаклыкның якларында
түгел, ә эчендә ята?
в) Шундый ничә нокта у = Jx функциясенең графи¬
гында ята?
г) Шундый ничә нокта у = 4х функциясенең графи¬
гыннан өстәрәк ята?
Π.20. ACEG квадратында А түбәсеннән Е түбәсенә, бары тик
өскә һәм уңга таба гына хәрәкәт итеп, билгеләнгән сы¬
зыклар аша үтәргә кирәк (рәс. 94).
Рәс. 94
a) G ноктасы аша узучы барлык юлларны языгыз.
б) Н ноктасы аша ничә юл уза?
в) В ноктасы аша ничә юл уза?
г) Барлыгы ничә шундый юл бар?
«Квадратик функция, у функциясе» бүлегенә
П.21. [0; 4] кисемтәсендә у - 0,5x2 функциясенең графигын
сурәтләгез. Бөтен сан координаталы ничә нокта:
а) бу графикта урнаша;
б) графиктан астарак һәм абсциссалар күчәреннән
өстәрәк ята;
246
в) графиктан өстәрәк һәм у = 5 турысыннан астарак ята;
г) графиктан астарак һәм у = 0,5х турысыннан өстәрәк
ята?
П.22. Координаталары натураль сан булган ничә нокта бу
функциянең графигында ята:
а) У = б) у = В) у = г) у = ¾
П.23. Бөтен сан координаталы ничә нокта:
а) у = - функциясенең графигыннан астарак һәм коор-
X
динаталарның беренче чирегендә*;
5
б) у = — функциясенең графигыннан өстәрәк һәм коор-
динаталарның өченче чирегендә*;
в) у = функциясенең графигыннан астарак һәм ко-
ординаталарның икенче чирегендә*;
9 9
г) у = - һәм у = — функцияләре графиклар арасын-
х х
да (координата күчәрләрендәге нокталар керми) ята?
П.24. Контроль эш өчен у = ах2 + Ьх + с рәвешендәге төрле
квадрат функцияләр төзиләр, а коэффициентын 2 һәм
3 саннары арасыннан, b һәм с коэффициентларын -3
һәм -4 саннары арасыннан ирекле сайлап алалар (бер
үк төрле булырга да мөмкиннәр). Шундый квадрат
функцияләр төзүнең вариантлар агачын ясагыз,
а) Барысы ничә шундый функция төзергә мөмкин?
б) Алар арасында b = с булган ничә функция бар?
в) Алар арасында a, b һәм с коэффициентлары төрлечә
парлашкан ничә функция бар?
П.25. Контроль эш өчен и = —-— + b рәвешендәге төрле квад-
х + а
рат функцияләр төзиләр.
а һәм b коэффициентларын -1, 1, 2 саннары арасын¬
нан ирекле сайлап алалар (бер үк төрле булырга да
мөмкиннәр).
а) Шундый квадрат функцияләр төзүнең вариантлар
агачын ясагыз.
б) Барысы ничә шундый функция төзергә мөмкин?
в) Алар арасында a ≠ Ь булган ничә функция бар?
* Координата күчәрләрендә түгел.
247
г) Әгәр k коэффициентын -3 һәм 3 саннары арасыннан
k
ирекле сайлап алсалар, у = χ + a + & рәвешендәге
ничә функция төзеп була?
П.26. у = -х2 + с параболасы тигезләмәсендә с коэффициентын
-1, 1, 2, 3, 4 саннары арасыннан очраклы сайлап ала¬
лар. Бу параболаның:
а) координаталарның дүртенче чиреген кисеп үтмәү;
б) у = √10 турысыннан астарак яту;
в) абсциссалар күчәрен ике ноктада кисеп үтү;
г) у = 2 турысы белән кимендә бер уртак ноктасы булу их¬
тималы нинди?
∏.27. k коэффициентын -2, -1, 1, 2, 3 саннары арасыннан оч-
k
раклы сайлап алалар, у = — функциясе графигының:
а) беренче һәм икенче координата чирекләрен кисеп үтү;
б) координаталар башына карата симметрияле булу;
в) (-1, -2) ноктасы аша үтү;
г) бөтен сан координаталы нәкъ ике ноктасы булу ихти¬
малы нинди?
∏.28. b коэффициентын -5, -4, ..., 3, 4 саннары арасыннан оч¬
раклы сайлап алалар, y = x2 + bx функциясе графигының:
а) координаталар башы аша үтү;
б) ординаталар күчәренә карата симметрияле булу;
в) ике координатасы да уңай булган нокталары булу;
г) ике координатасы да тискәре булган нокталары бул¬
мау ихтималы нинди?
П.29. Бөтен сан координаталы ноктаны, ул у = 2x2 функция¬
се графигыннан өстәрәк һәм у = 9 турысы графигыннан
астарак ятарлык итеп сайлап алалар. Бу ноктаның:
а) абсциссалар күчәреннән өстә;
б) ординаталар күчәрендә;
в) ординаталар күчәреннән сулда;
г) у = 7 турысыннан өстә яту ихтималы нинди?
П.ЗО. АСКМ турыпочмаклыгында А түбәсеннән К түбәсенә,
бары тик өскә һәм уңга таба гына хәрәкәт итеп, билге¬
ләнгән сызыклар аша үтәргә кирәк (рәс. 95). Барысы
ничә юл:
а) М түбәсе аша уза;
б) Н ноктасы аша уза;
248
«Квадрат тигезләмәләр» бүлегенә
П.31. Контроль эш өчен х2 + Ъх + с = 0 рәвешендәге төрле ква¬
драт тигезләмәләр төзиләр. Ъ коэффициентын -2, -4 һәм
-6 саннары арасыннан, с коэффициентын 4 һәм 9 санна¬
ры арасыннан ирекле сайлап алалар.
а) Шундый квадрат тигезләмәләр төзүнең вариантлар
агачын ясагыз.
б) Барысы ничә шундый тигезләмә төзергә мөмкин?
в) Алар арасында дискриминанты нульгә тигез булган
ничә тигезләмә бар?
г) Алар арасында кимендә бер тамыры булган ничә
тигезләмә бар?
П.32. Контроль эш өчен ax2 + bx + 1 = 0 рәвешендәге төрле
квадрат тигезләмәләр төзиләр, а коэффициентын 4, 8
һәм 9 саннары арасыннан, Ъ коэффициентын 2, 4 һәм 6
саннары арасыннан ирекле сайлап алалар.
а) Шундый квадрат тигезләмәләр төзүнең вариантлар
агачын ясагыз.
б) Барысы ничә шундый тигезләмә төзергә мөмкин?
в) Алар арасында дискриминанты нульгә тигез булган
ничә тигезләмә бар?
г) Алар арасында кимендә бер тамыры булган ничә
тигезләмә бар?
П.ЗЗ. Тамырлары x1 һәм х2 алдан бирелгәндә, квадрат тигезләмә
түбәндәгечә төзелә. Башта (х - xi)(x - х2) тапкырчыгы¬
шын төзиләр. Аннан соң, җәяләрне ачып, тиңдәш бу¬
ыннарны берләштерәләр. Килеп чыккан тигезләмәне
нульгә тигезлиләр. Тамырларын түбәндәгечә сайлап
алып, ничә квадрат тигезләмә төзергә мөмкин:
249
a) Xi тамырын 1, 2 саннарыннан, ә x2 не 5, 6 саннарыннан;
б) Xi тамырын 1, 2, 3 саннарыннан, ә х2 не 4, 5, 6 сан¬
нарыннан;
в) ике тамырны да, әгәр тамырларны тигез итеп алу да
мөмкин булса, 2, 3, 4 саннарыннан;
г) ике тамырны да, әгәр тамырларны төрле итеп алу
тиеш булса, 2, 3, 4 саннарыннан?
П.34. ах2 + Ъх + с = 0 рәвешендәге тигезләмәләр өчен дис-
криминантның кыйммәтләре таблицасын тутырыгыз;
Тигезләмә
№ 1
№2
№3
№4
№5
№6
№ 7
№8
№9
№ 10
а
3
7
9
-1
4
-1
4
-3
-1
1
ь
7
7
6
0
5
6
7
-5
2
3
с
4
2
1
3
2
-8
4
4
-1
0
D
а) Тамырлары булмаган;
б) бердәнбер тамыры булган;
в) кимендә бер тамыры булган тигезләмәләр нинди про¬
центлы ешлыкта?
П.35. а) Мәсьәләләр җыентыгының 162 битен ачыгыз. 25.2 -
25.7 биремнәренең һәрберсендә квадрат тигезләмәнең
тамырлары санын билгеләгез. Нәтиҗәләрне табли¬
цаның икенче юлына кертә барыгыз һәм шунда ук
ал арны гомумиләштерегез.
2 тамыры булган
тигезләмәләр саны
1 тамыры булган
тигезләмәләр саны
Тамырлары булмаган
тигезләмәләр саны
б) Үткәрелгән үлчәүләрнең күләме нинди?
в) Тамырлары булмаган тигезләмәләрнең процентлы
ешлыгы нинди?
П.36. Үзгәрешле х ка карата тигезләмә ах + — + с = 0 рәве-
х
шендә, биредә a, Ь коэффициентлары - 1 дән 5 кә кадәр
натураль саннар (тигез булулары да мөмкин), с коэффи¬
циенты 6 га яки 7 гә тигез.
а) Шундый рәвешле тигезләмә төзүнең вариантлар ага¬
чын ясагыз.
250
б) Шундый рәвештәге ничә төрле тигезләмә төзергә
мөмкин?
в) Алар арасында a = b булган ничә тигезләмә бар?
г) Алар арасында с = 2а булган ничә тигезләмә бар?
П.37. у = ∖∣x + а функцияләре графиклары арасыннан, бире¬
дә a — [-2; 2] кисемтәсеннән ниндидер бөтен сан, оч¬
раклы рәвештә берсен сайлап алалар. Сайлап алынган
графикның:
а) абсциссалар күчәрен кисү;
б) ике координата күчәрен дә кисү;
в) (0; 1) ноктасы аша үтү;
г) ордината күчәрен кисмәү ихтималы нинди?
П.38. Баһадир юллар чатындагы ташта менә нинди язу укы¬
ган: «Сулга, турыга яки уңга барсаң - шундый ук чат¬
ларга җитәрсең, ә аларның һәркайсыннан тагын шун¬
дый чатларга килерсең, әмма барыбер утыз тугызынчы
патшалыкка эләгерсең».
а) Баһадир утыз тугызынчы патшалыкка ничә юл белән
барып җитә ала?
б) Бер тапкыр сулга һәм ике тапкыр уңга борылып китә
торган юллар ничә?
в) Бер тапкыр уңга һәм ике тапкыр сулга борылып китә
торган юллар ничә?
г) Бары ике генә тапкыр борыла торган юллар ничә?
П.39. Х-файл «Минем документлар» директориеның берен¬
че баскычтагы А, В, С яки D папкаларында. А папка¬
сында икенче баскыч АА, АВ, АС папкалары бар. В һәм
D папкаларына да икенче баскыч өчәр «аспапка»: ВА,
ВВ, ВС, DA, DB, DC, ә С папкасына СВ, СА, СС, CD,
СЕ керә. Икенче баскычтагы һәр папка үз эченә өченче
баскыч 7 шәр папканы, ә ВС папкасы исә 8 папканы
ала. Өченче баскыч папкаларына файллар гына керә.
«Юзер» Х-файлны барлык папкалардагы барлык файл-
лардан турыдан-туры сайлап алырга булган.
а) Файлга кадәр барып җитү юлларына тиңдәшле вари¬
антлар агачын схематик рәвештә күрсәтегез.
б) А папкасыннан файлга ничә юл белән барып җитәргә
була?
в) «Минем документлар» папкасыннан файлга ничә юл
белән барып җитәргә була?
251
г) Кирәкле файлның С папкасында булу ихтималлыгы
ничәгә тигез?
•П.40. Елганың сул ягында - өч авыл, ә уң ягында ике турба¬
за урнашкан. Елга аша биш урында чыгарга мөмкин.
Турбазалардан авылларга һәм авыллардан турбазаларга
бару юлларының вариантлар агачларын ясагыз. Ничә
юл белән:
а) үзең яшәгән авылдан нинди дә булса турбазага барып
кире кайтырга;
б) үзең яшәгән турбазадан нинди дә булса авылга барып
кире икенче турбазага кайтырга мөмкин?
«Тигезсезлекләр» бүлегенә
∏.41. a > b тигезсезлегендә а һәм b урынына 1, 2, 3, 4 яки 5
саннарын куярга мөмкин.
а) Барысы ничә санлы тигезсезлек барлыкка килер?
б) Ничә очракта табылган тигезсезлек дөрес булмый?
в) Ничә очракта a > b тигезсезлеге дөрес була?
г) Ничә очракта a > b + 2 тигезсезлеге дөрес була?
П.42.
П.43.
* Ω ■ язылышында * урынына ∖∣2 яки Vδ не, Ω уры¬
нына < яки > тамгасын, ә ■ урынына 1, 2 яки 3 не ку¬
ярга мөмкин. Төрле тигезсезлекләр, мәсәлән, V2 > 1,
√5 < 2 һ.б. килеп чыгачак.
а) Шундый тигезсезлекләр төзүнең вариантлары агачын
төзегез.
б) Барысы ничә тигезсезлек килеп чыга?
в) < тамгасы кергән ничә раслау тигезсезлек булыр?
г) Алар арасында ничә дөрес тигезсезлек бар?
* Ω ■ язылышында * урынына √2, √3 яки √5 не, Ω
урынына ≤ яки ≥ тамгасын, ә ■ урынына 1,5, 1,7 яки
2,3 не куярга мөмкин. Төрле тигезсезлекләр, мәсәлән,
√2 > 1,5, √5≤ 2,3 һ.6. килеп чыгачак.
а) Шундый тигезсезлекләр төзүнең вариантлары агачын
төзегез.
б) Барысы ничә тигезсезлек килеп чыга?
Очраклы сайлап алынган:
в) > тамгалы тигезсезлекнең дөрес булмау;
252
∏.44.
∏.45.
∏.46.
∏.47.
∏.48.
∏.49.
г) ≤ тамгалы тигезсезлекнең дөрес булу ихтималы нинди?
у = f(x) функциясе у = ~Jax + b тигезлеге белән
бирелгән, а коэффициентын -2, -1, 1, 2 яки 3 санна¬
рыннан, b кушылучысын 2, 3, 4 яки 5 саннарыннан сай¬
лап алалар.
а) Шундый функцияләр төзүнең вариантлары агачын
төзегез.
б) Барысы ничә шундый функция табарга мөмкин?
Очраклы сайлап алынган функциянең:
в) үсә баручы;
г) кими баручы функция булу ихтималы нинди?
3 < 2х < 43 тигезсезлегенең чишелеше булып торучы
ирекле бөтен санны сайлап алалар. Сайлап алынган
санның:
а) җөп; в) бишкә кабатлы;
б) өчкә кабатлы; г) икеурынлы сан булу ихтималы
нинди?
|3х| < 8 тигезсезлегенең чишелеше булып торучы ирекле
бөтен санны сайлап алалар. Сайлап алынган санның:
а) х < -1; в) х > -1;
б) |х + 1| > 0; г) ∣x∣ < ∖∣2 тигезсезлегенең дә
чишелеше булу ихтималы нинди?
х2 + 5х - 14 < 0 тигезсезлегенең чишелеше булып тору¬
чы ирекле бөтен санны сайлап алалар. Сайлап алынган
санның:
а) х2 < 1; в) х2 ≥ 4;
б) х2 < 3; г) 5х + х2 ≥ 0 тигезсезлегенең дә
чишелеше булу ихтималы нинди?
48 - 13х - х2 > 0 тигезсезлегенең чишелеше булып тору¬
чы ирекле бөтен санны сайлап алалар. Сайлап алынган
санның:
а) х2 > 0, в) х2 < 101;
б) х2 + 10x ≤ 0; г) 4x2 - 20х + 21 < 0 тигезсезле¬
генең дә чишелеше булу ихтималы нинди?
Мәсьәләләр җыентыгының форзацында икеурынлы
саннарның квадратлары таблицасы китерелгән. Шушы
таблица буенча анда язылган барлык саннарның беренче
цифрларын тапканнар.
а) Бирелгәннәр рәтенең күләме нинди?
б) Нәтиҗәләр таблицасын тутырыгыз:
253
Сан квадратының беренче
цифры
1
2
3
4
5
6
7
8
9
Ничә тапкыр очрады
в) «5» цифрының процентлы ешлыгы нинди?
г) Мода ничәгә тигез һәм аның процентлы ешлыгы нин¬
ди?
•П.50. А, В, С, D нокталары - квадратның түбәләре. Очлары бу
нокталарда булган өч кисемтә үткәрергә кирәк (нинди
тәртиптә үткәрелүе әһәмиятле түгел). Түбәндәге очрак¬
ларда мәсьәләнең ничә чишелеше бар:
а) барлык кисемтәләр дә квадратның яклары буйлап
үткәрелә;
б) кисемтәләрнең берсе -АС диагонале, калган икесенең
уртак нокталары юк;
в) кисемтәләрнең берсе - BD диагонале, калган икесенең
уртак нокталары бар;
г) барысы ничә чишелеше бар?
ҖАВАПЛАР
1 НЧЕ БҮЛЕК. 1.18.2км/сәг. 1.19.40км/сәг. 1.20. a)+,+,+;б)-,+;в)
14 1
г) +, -. 1.22. а) 98; б) 21; в) г) 1.23. а) 3; б) -±;
2Ә I Ә
.) ⅛ г) -2,5.
рендә; б) b ≠
1.24. а), в) Үзгәрешлеләрнең теләсә нинди кыйммәтлә-
х ≠ -2,5; б) у
1.26. a) a ≠ 1; б)
булганда; г) т ≠ 0 булганда. 1.25. a) х ≠ i;
3
о 1 1 Q 7
≠ -3; В) s ≠ s ≠ -; г) г ≠ 3; г ≠ 2-.
5 ≠ —; в) с ≠ -3; г) т ≠ -4,5. 1.27. a) a ≠ -8; a ≠ 9;
2
0
д ≠ 17; б) b ≠ --;
2
b ≠ -1—; 6 ≠ 2-; в) с ≠ с ≠ -1|; с ≠ -3; г) d ≠ -1;
3 3 2 7
5 2 1
d ≠ 1.28. a) b ≠ 0; b ≠ ⅜ б) k ≠ -3; k ≠ 3; в) s ≠ 0; s ≠ г) т ≠ 2;
7 3 2
т ≠ -2. 1.29. a) a ≠ 0; a ≠ 3; a ≠ -17; б) b ≠ -b ≠ 1^; b ≠ -1^;
2 3 3
115
в) с ≠ 0; с ≠ -8; с ≠ 3; г) d ≠ —; d ≠ —-; d ≠ 1.30. т = 1 булганда
2 £ (
нульгә әйләнә; m = 0, т = -1, т = 2 булганда мәгънәсе юк. 1.33. а) 10,8; б) 2;
1 4 1 1
в) -4,8; г) 3,6. 1.34. a) i; б) 18; в) -⅛ г) -. 1.35. а) -3; б) в) 4;
3 15 з 3
1 1 5 4
г) 2⅛. 1.36. a) ⅛ б) 6; в) г) 1.37. а) 6; б) -6,8. 1.38. а) 5; б) 4,5;
3 10 2 ә
1 1 22
в) 13; г) -0,1. 1.39. а) 15; б) 10-; в) —; г) —. 1.40. a) 1 һәм 3; б) 1 һәм 5;
в) 1; 2; 3; г) 1; 3; 5. 2.7. а) 144; б) 128; в) 225; г) 0,2. 2.35. а) 1,5; б) -4;
в) -2; г) -4,5. 2.36. a) 1; б) 2. 2.47. а), б) —. 3.10. а) 2; б) х; в) 3; г) q.
o-- Xc~9 ≡Λα + 3∙ X12 + b. 45-d o1o. 1 . Qv 1∩.
3.11. а) —-—; б) ; в) —-—; г) —-—. 3.12. а) -; б) -Зх - 10,
2 a 5 д у - 4
1 2 х + У 3 Р + 9
в) г) 11 - 5х. 3.13. а) ; б) в) ; г)
о*, ч 2~8 «X д + 9х. . £-10 . 7c + b х + 6.
3∙14∙ а) ТТ8; б) T≡9√ в) ГГТо; г) 77→∙ 3∙16∙ а) х-6’
б) χ2 + ху в) г) y2 ~ 2y +∙3.17. а) д - 3; б) с - 10; в) b + 5;
х + у х + У у - 2
1 х — 1 1 2д + 1
г) 7 -d. 3.18. a) —Ц; б) 2x -; в) -у-; г) y -■ 3.19. а) 20;
п - 2 x2-x + l т + 3 ⅛yi * * + 2y + 1
255
б) -7,5; в) -6,5; г) 5,1. 3.20. а) |; б) -2; в) |; г) 3.21. a) ~ς|;
4 о О оХ + Z
βl 5a - 1 „ „„ , 10d + 3 7а - 4 „ „„ , x + У. гч 4т
б) ₽ т- 3.22. а) —-—-; б) - -■ 3.23. а) > б) - -.
5a +1 10d - 3 7 а + 4 ’ х - у 2m +1
3. 24. а) 1; б) 1. 3.25. а) —Ц; б) —Ц-. 3.26. а) 6 - 6а; б) Зх; в) -Зу - 4;
Ь - ә а - 3
г) 28b + 20. 4.11. а) б) 4(1Ч в) г)
4.18.,)224^
тп
2z + 3Z. х + 2y t 5m2 - 3n2
б) 6zt ' В) x2j∕2 1 Г) 15τn2n2 '
4. 19. а) у - х; б)
(6g + p)2
3g2 ’
в) г) 4.20. а) 45; б) 4.21. a) z 4 б)
П 4(1 4 oZ∖Z + Δ)
(2a - b)2
2α(6α - Ь)’
в) г) <2n~3V∖ 4.22. а) <2а - 1)2; б) -⅛
bj 5t(2t -1) 2A(9n-2⅛) а-1 а-2
в)
Ь + 3
~J⅛-. 4.23. а)
2b-l
-W-; б) -⅛ в) Ы. г) __2^_ 4.24. а) -Ц;
х- у х- у а + b а + b а-1
_gl+ ⅛2..., в) d. γj гп7 4 25 а) 1. б)
°' 2а(а - Ь) с + 3 Зт(т + п) с
4 - 6a
a2(a - 2)’
1 £i-^; г) -½5—— 4.26. а) ⅛ б) —; в) -—; г) . 4.27. а) ~—~
в) у m2(m + 2) ab ас ху ах ’ ху
б) в)
0, гпп
3t + р
pt
а-Ь
г)^Г
4.28. а) |; б)
ь
+ с . 3 . Зп + т
в) —; г)
Ьс а тп
x2 + y2 10a . m2
4∙2θ∙ а) x^-y2' (a+ 3)(2-a)’ т2
mL. г) ≡f .
- П2 (р + 1)(р + 3)
4.3θ∙ d(c2 - d2)' б *) (х + z∕)(4ι∕ - х)’ В) х2 - у2 ’ (2с + d)(c + d)
ч х~ У. «л 2a ■ ч b + m
4.31∙ a^x + u, а + c' В Ь - т
∖ 2d Л И Ч 1 «ч 2α +1
Г) d - 4 3 ' Э) 2х + 3’ б) 2α - 1
1 Зх - 2 а + Ь 2 с - 2
в) з^-5х’ Г) Зх + 2' ^∙33. a) α(α _ ⅛j 6) χ^χ + ^j, в) c(c + 2)’
4 . „ . . 12 - Зс . ,, a2 +b2 . 5тп + 10. 4x2 - у2
r) ^(a^3)' ’ ’ Я (с - 2)2 ’ 2(a - b)2 ’ (m + 5)2 ’ 3(х - у)2 ‘
4.35- а) ⅛= 6> ξ(⅛j= в> -ТГс' Г) 4^⅛4∙36∙ а) 1= б) 4=
ч r'> ⅛∙ 4∙37∙а) б)
в) 2 lθ ab
6 . ч 1 ч 3
б) В а-3’Г т + 4
. 4.39. а)
b - а .
~ττi в)
з . . Р + Я . „„ , 1 .
,> г) • 4.38. а) , »
cd pq 1 - b
5_. ω 2х - 5. 6 .
х + 4’ 2х + 5’ В п + 7’
256
ил, г -χ . .λ 4 . ^ . -v г • ч , о от — п
г) — 4.40. а) » б) —— в) ; г) .
За-4 ’ ху ’ 2p(p-q) , cd , 3m(3m + п)
. .. ч х2 я» р-9 62 . a-7 1
44l∙al^v^' ∙∙l-Ji^5-ir>∏ττF-4∙44-a'-⅞,>⅞i
X - 4α . 1 с - 10d . . а - 2 7п
x(x + 4а)’ В 2(3α + 6), Г c(c + 10d)' * ‘ a а + 2’ n-m’
в)
х + У.
X - у'
Г) Зр + Г
4.46. а) —Ц; б)
х - 1
У+2 3 . Ь-3
у2 - 2у + 4’ В с + 4’ r¼2 + 36 + 9
4.47. а)
2d3
с + d'
ОлЗ
4∙48∙ a> "Γ⅛ б)
a2 - b2
б) —-2 .2; в)
ai - ab + b2
2m3 54 х3
m2 - 4n2 ’’ В) 9x2 - у2' Г)
2n3
; г)
т - п
2x3
X2 + ху + у2'
16f3
4∕2 - 9⅛2 ‘
4.49. а)
a(a - 1).
a3 + 1
6 2 - 2d . 4 . „ 2(⅛-l) 2(α - 2)
c2+3c + 9 8d3+f 62 - 26 + 4 4" 62 + 6 + l’6 a2 + 2a + 4'
4.51. а)
m2 + тп + n2.
m3 + п3
б)
х2 - ху + у2
у3 - х3
4.52. а)
100
(6 - 5)2 (6 + 5)2 ’
б) 7о √∖θ7o √r∖T∙ 5∙14∙ а> 7: б) V в) «р; г) Ь. 5.18. а)
(2m - 5n)2 (2zn + 5n)2 с 3 2
б) -2; в) ~;г) -пх. 5.19. а) б) -≡-; в) г)
а х а - 4 4с
5.20. а) х2 - ху + у2; б) a + 6; в) —; г) p2 + pq + q2. 5.21. а)
п - т
a + 6
a2 + ab + 62 ’
2
б) n(2a + 1); в) -; г)
X ~ о
в)
3(c-5)
2(с + 6)’ Г
15
2п - т
х^
. 5.28. а)
(Г
5.22. .) <£7 ?><»■-■«>■ б) 1±2⅛
X3 г x20u27
б) —; в) г) —. 5.29. а) 4а6;
р 6 z17
,. 5ax 10а2х »24 κ „п . 93 . ,λ 6n7 . х
б) —-—; в) —: г) 5.30. а) ——; б) : в) —:
2y 96y2 56c2 a2p 35a264m3 15a2y
г) -12pq. 5.31. а) 2ау; б) 2у; в) г) 6t. 5.32. а) б) -⅛ в)
9 a 86
64a10 .
62° ’
9 ’
г)
X13J∕12
За24
. 5.33. а) ———; б)
а
(y-5Xy-6)
(х + 4Хх + 3)
г)
26
6 - 4с
5.35. а)
со. » х-4 -» 7y(y-5). m(τn + n)
5.34. а) —; б) в)
у(5у - 2)’ б) ^2a(2x + 7)’ В) 5(8∏ - 3)’ г)
9
. 2(c + 2)
’ Г) c(c-2),
2с
d2(3p + 5)’
6
; в)
5.36. а) <5-~*χ3 + *∖ б) Р(Р^-, в) -
p-q
2
6с . ч 9(x + у) κvr ч X - з .
c + d'r y(x-y)' ' 'β x2(x + 3),
257
б)
2(2c + 1) . 2y(5 + у) 3(1 + За) α2 - ab + b2
cd(l - 2с)’ В 5(5 - у) ’ Г α(3α-l)' ∙ ∙ a ab
б)
1 2x . 4 , „ _ „„ , 1 „ t + 2 , 1
⅛ в) √Vi77T г) (х + ■ 5∙39' a) Γ∑r б) ЧГ’ в) з;
г)
У-2
у-3'
(3 - a)(b + 1)
5∙4θ∙ а) 2(b2 + b + 1) ’ б)
c2 + 2cd + 4d2 v (3 - b)(2b + 3)
2 ; В) 2 5
г) —. 5.41. а) (5 - 2a)(l + 4a); б) -(4a + 35); в) (Зе + 2)(3c + 4);
1 - т + т2
1 4b2 5 - b a(a - 2)
г) 2q - 5р. 5.42. а) ^χ, б) в) —; г) 5.43. а) (с - а)’;
а4 (а - х)2 . (х - 2y)(x + у)
*^ • n | • р 1
bs(b + a)2(b - а)’ (а - b)2 ’ х5
2 1
5.45. а) б) -.
6.1. а) ⅛ б) ——в) - * 4; г) θ∙2. а) 5(х + у); б)
6с у о о t
в) 3(a - Ь); г) 6∙3∙ а) m - л; б) в) - q<∙2p + q^; г) -у. 6.4. а) ¾
a δ р ∆ ⅛
61 pi в| ~τh∙г) ’■ β'5' *, 7⅛i в ⅛ ” xu'∙г) 7⅛' 6∙6∙a, 1 - c'∙
«■> ⅛r, β∙ β7∙∙, ^1≈ 6, ⅛ ,l l; r, j⅛∙ β∙8∙,, 7i
а(Ь — а) 2
б) 5,6. 6.11. а) -⅛ ; б) - ■ . 6.12. а) 1 - 2тл; б) 2 - Зл.
о + а 4(г + 2)
6.13. а) б) “• 6.14. а) б) 1. 6.19. |. 6.20. 6.21. 1.
6.22. а + Ь. 7.9. а) 4; б) 0; в) -5; г) 0. 7.10. а) 5; б) 6; в) -7; г) -8.
7.11. а) +3; б) 0; 2; в) ±2; г) 0; -3. 7.12. а) 2; б) -2; в) 4; г) 0,5. 7.13. а) -12;
б) 2; в) -3,5; г) 3. 7.16. а) 2; б) 0; в) -1; г) 0. 7.17. а) 0; б) 5; в) 2; г) -4.
7 3
7.18. а) — г) Тамырлары юк. 7.19. а) -32; б) ; в) -27; г) —. 7.20.
а)—г) Тамырлары юк. 7.21. а) 0,4; б) 0,2; в) 6; г) -22. 7.22. 12 км/сэг,
30 км/сэг. 7.23. 30 км/сэг. 7.24. 8 км/сэг. 7.25. 6 км/сэг. 7.26. 40 км/сэг.
2
7.27.60 км/сэг. 7.28. а) ±1; б) в) ±2; г) 0,3. 7.29. а) 1; б) ±2; в) 6; г) ±3. 7.30.
3
а) 0; 5; б) 4; в) -6; 0; г) -5. 7.31. а) -8; 0; б) -0,5; в) 0; 19; г) ⅛ 7.32. а) -5; 0;
б) в) 0; 9; г) 7.33. а) 3; б) 4; в) 1; г) 2. 7.34. а) -3; б) 1; в) 2;
5 3
г) 6.7.35. а) 0; б)-3; в) 0; г)-2.7.36. а)Тамырлары юк; б) -7; в) 40; г)тамырлары
юк. 7.37. а) б) тамырлары юк; в) г) тамырлары юк. 7.38. а) ~;
3 3
258
6) -∣. 7.39. а) б) 34. 7.40. а) б) -8.12. а) б) 25; в) |;
1 2b s4
г) 8.13. а) 13,7; б) -3,5; в) 25,9; г) 2,35. 8.17. a) 4m; б) в) —;
г) 28p⅛. 8.20. a) ⅛ б) в) г) a3 + b3. 8.21. а) -±-;
ab x2y2 mlni ab
б) st(s - t)∙ 8.22. а) 9; б) ⅛. 8.23. а) (х - I)’1; б) (х + 5)^1. 8.24. а) а - 2;
1о
б) (1 - x)^1. 8.25. а) ⅛ б) 8.26. а) 6; б) 5. 8.27. а) б) 8.28. а)
2111 ә 7 ә
б) 8.29. а) 2; б) ±|; в) -3; г) ±|.
У Z о
2 НЧЕ БҮЛЕК. 9.15. а) 0,(27); б) 0,(24); в) 0,(05); г) 0,1(3). 9.16. а) 4,8(3);
б) 3,(7); в) 4,41(6); г) 7,(09). 9.20. a) 15∣∙, б) 2^; в) 7§; г) 23∣∣.
3 УУ У УУ
9.21. а) τ⅛S б) ⅛! в) ⅛ г) -⅛. 9.22. a) ⅛ б) 2-|-; в) 3≡⅛5
1ОӘ 30U Io OθU 18 320 330
г) 1|. 9.25. в) 4; г) 5 яки 13. 9.26. а) 2®; -0,35; б) -||; 1,12; в)
-3,7; г) ; 5,32. 9.27. а) 0,(285714); б) 0,3(426571); в) 0,(809523);
р) 0,9(286714). 9.28. .) ⅛ 6) ⅛ в) ⅛ г) 9.29. .) ≡1
б) 299’ В) 6225’ Г) ПО 10'28' а) 4; б) 75 В) 11 Г) 1°' 10'29’ й) 1; б) “2;
в) 5; г) 3^. 10.30. а) 48; б) 1; в) 1; г) 10.31. a) 4∣∣s б) 21; в) 1,5;
3 8 13
г) 3∣. 10.32. а) 7,9; б) 2,1; в) 2,3; г) -3. 10.33. а) 3, 4; б) 6, 7; в) 0, 1;
г) -6, -5. 10.34. а) -1, 0; б) 18, 19; в) 10, 11; г) -16, -15. 10.35. а) 2;
б) 1; в) 1; г) 0. 10.36. а) 3; б) 4; в) 8; г) 11. 10.37. а) 2; б) 3; в) 4; г) 4.
2
10.38. а) 10; б) 12; в) 23; г) 10.39. а) ±15; б) ±5; в) ±5; г) ±13.
10.40. а) 46; б) 65; в) 99; г) 73. 10.42. а) 3; б) 4; в) 6; г) 5. 11.15. а),
в) Иррациональ саннар; б), г) рациональ дә, иррациональ дә булырга
мөмкин. 12.11. а) х < у; б), в) х > у, г) х < у. 12.13. а)—в) +; г) -.
12.14. а) А(1,3); б) B(π). 12.15. a) С|--1; б) D(√δ), 12.16. а) 0; ⅛ 7б;
\ 4 J 6
б) 3; 3,1; л; в) 0,3; 0,5; -; г) -3,2; -710; -3. 12.17. а) 5,81; 2л; 6,3;
6
259
б) ^τ
√2 7
0; в) 1,5; 1,6;
г) -1; ; -0,5. 12.18. а) бер тамгалы;
б) q < 0; р ≠ 0; в) төрле тамгалы; г) q ≠ 0, р > 0. 12.19. а)—в) +; г) -.
12.20. а), б), г) -; в) +. 12.22. a) K(-2)∙, ь(-Тз);
L(l); м(Тз); в) 2 К^; m(2>5>! r) *(Т20); L(4,5); Λ7{yj∙
13.9. а) 0; 1; б) 4; в) 4; г) 0. 13.10. а) 1; б) 1. 13.11. а) (0; 0), (1; 1);
б) (1; 1); в) (0; 0), (1; 1); г) чишелешләре юк. 13.12. а) (4; -2); б) (0; 0), (4; -2).
13.15. а) 10; б) 8. 13.17. а) -4, 0, 1. 13.18. а) -4, -1, -2, -3. 13.19. а) [0; 1];
б) [4; 16]; в) [0; 9]; г) [1; 25]. 13.20. а) [0; 3]; б) [2; +°°); в) [1; 2]; г) [3; +∞).
13.21. а) [Т2; 2]; б) (2; Т?]; в) [ТЗ; з]; г) [1; Тб). 13.22. а) [1; 9];
б) [4; -К»); в) [4; 16]; г) [9; +∞). 13.23. а) [0; 9]; б) [1; 4]. 13.24. а) 0 ≤ у ≤ 2;
б) 72 < у < 3; в) 2 < у ≤ 3; г) Тз < у < 2. 13.25. а) у > 1; б) 0 < у < Тб;
в) 0 < у < 2; г) 0 < у < Т10. 13.26. а) 0 < х < 4; б) 1 < х < 16;
в) 1 < х < 9; г) 4 < х < 9. 13.27. а) х > 1; б) 0 < х < 9; в) 0 < х < 4;
г) х > 1. 13.28. а) [-ТЗ; - 1]; б) (-°о; -2]; в) [-2; -Тй]; г) (-°°; -1].
13.30. а) 0; 4; б) 1. 14.3. а) 60; б) 1,44; в) 180; г) 0,45. 14.7. а) ⅛
15
б) 2,8; в) г) 3,5. 14.10. а) 45; б) 392; в) 189; г) 20. 14.11. а) 11,25;
Зо
б) в) -ψj∙, г) 3,52. 14.18. а) 5а2б3; б) lyPβ<713! в) бгап4; г) ^r9s.
, . , 2а 13α9 . 7a9 . 24aβ , . . o en . t- , ∏1 ∖ on
14.19. а) —; б) -=τrr', в) —-; г) ——. 14.20. а) 8; б) 15; в) 21; г) 30.
b3 5615 9&3 5Ь13
14.21. а) 2,6; б) 1,4; в) 1; г) 15. 14.22. а) 1,5; б) 2,4; в) 1,8; г) 2,6. 14.23. а) 2,5;
б) 3; в) 1,5; г) 3. 14.24. а) |; б) в) г) 1-. 14.25. а) ⅛ б) з|;
5 о 11 3 1о о
17
в) ½⅛ г) 3. 14.26. а) 5; б) 7; в) 9; г) 13. 14.28. а) 17; б) 17; в) 13; г) 25.
Зо
14.29. а) 12; б) 6; в) 14; г) 12. 14.30. а) 8,5; б) ⅛ в) г) -⅛.
ЗУ Уо 13Ә
14.31. а) 66; б) 92; в) 62; г) 95. 14.32. а) 0,77; б) 15,4; в) 77; г) 23,1.
14.33. а) 28,5; б) 21; в) 47,5; г) 91. 14.34. а) Тх ∙ Т7; б) Tξx ∙ √≡p.
5m2n∖∕2n 3xJy
15.9. а) А > В; б) А < В; в) А > В; г) А < В. 15.15. а) 5 б) -√*j4
Зг Зг
β<Λ⅛ 15.21. .) -Л?! 5) √S⅛; .) -√USSΛ
7yi 5w3
260
г) y∣5pq. 15.22. а) 5; V26; 2^8; 6; б) 2; >/7; 3; 2>/3; в) 4; Зл/2; л/19; 4^;
г) о,7; 2^3; 2^.- 1.15.24. a) 4√6∙, б) 7√5j в) 12√5∙, г) -4√2. 15.25. a) -8√3;
б) 12√5∙, в) 9\/5; г) 6>/з. 15.26. а) 27а; б) бТЗх; в) -15>/5Ь; г) 2j2y.
5
15.27. а) -а
о
√∑b∙, б) 4m2Vm; в)
a4 Jab; г) 10dJd.
15.28. а) 21; б) -5;
в) 20; г) 10. 15.29. a) Jax - х; б) mjn + njm; в) с + Jed; г) pjq - qjp.
15.30. 5 + √3∙ б) 8; 2 - √5∙, г) 12. 15.31. а) 1 + 73; б) -2>/5; в) 10 - 2 Тб;
r)-4√3. 15-32,a)2α2 - ajb - ЗЬ;б)4а - 8√3αb - 15b; в)2х - 3yjx - 2y2;
г) т - 3√mπ + 2п. 15.37. а) 30 - 12√6j б) 18 + 12√2ι в) 120 - 30Т15;
г) 22 + 8√7. 15.38. a) mJm - nJn; б) c3 + dJd; в) rJr - 8nJn;
г) 8s>∕s+27t. 15.41. a) 2√2aj б) в) —; г) —аЬс.
о с b
15.42. а) 57*~5⅜ б) + ; в) 3^ + 3^- г) ~
X - У (а - b)2 т - п ' (p-q)i '
15.43. a) √7+√3! б) ^θ2 ; в) 2√3(√5 - 2); г) 6(3√2 + 2√3).
15.44. а) 2 - Тз; б) 3^9~; в) 3 + 2√2∙, г) ∙6 + 5Л 15.45. а) ~ ^1.
i y х2 - у ’
б) а + √b∙, в) β⅛-⅜i г) -(5b + √3^). 15.46.a) ^3 + 2; 6)1- √Γ^∙
4s2 - Зг α - 1 3
3 + √2x-l г)2+ √bTl. 15.47. a) б) ⅛⅛ в) ⅛± 2L
5 — X Р Ч t*L ли
r) 2-4^ • 15.48. a) √δ(√5+l)j б) √b(l - √b)∙, в) √3<√3 - 1);
г) √^(1 + √^). 15.49.a) б(2 + Тз); б) 4(2 - √2)j в) 2θ(l + 3√f)5 г) 9<5 - √δ).
1550∙a) √2(√5 - 7з);б) √2(√2 + √3 - 1); в) √7 (√2 + √5)∙, г) √7(√7 + √2 - 1).
15.51. a) √α(√α - 2); б) 7b(√3 - %/b); в) √a(l - 2ja); г) √a(√a + √b).
15.52. а) √a + b(√a + b + 1); б) Ja→b(JJ~^b - 1); в) Ja - b(⅛Ja - Ь - 2);
г) -Va - b(a + ∙Ja + b). 15.53. а) (a + b)(Ja + Jb); б) (2 - Jb) (1 - Jab);
в) (Jab - 1) (Ja + 1); г) (b + Ja) (а + Jb). 15.54. а) (a - Vδ)(a + V5);
б) (5 - J^p)(b + Jp∖, в) (√∏ - b)(√∏ + b); г) (√m - lθ)(√m + Ю).
261
15.55. a)(77 - 7з)(77 + V3)∙,6)(4Vz - 7δ)(47z + 75);в)(77 - y[c)(x∣a + 7c);
г) (√7 - 8√t)(√7 + 8√t). 15.56. a) (1 - √pΓ; б) (77 + 3j∕)'; в) (7c - 77)';
г) (√g+2p)2. 15.57. a) (тТа-Тб)2; б) (сТз + δ)2; в) (зТй - 77)2;
г) (777 + b)2. 15.58. a) (7з + 2/; б) (77 - 1/ ; в) (√2 + 1)2; г) (2 - √3)2.
15.61. а) —j=~i T' 6) ~^12^ + 11а): в) 5^“ -777; г) f-—=.
37x + 4√ι∕ 47с + 9√αb
15.62. а) -⅛J б) 77; в) г) 7з. 15.63. a) J|; б) Д; в) J|; г) J∣.
4 √x + √u
15.64. a) ~; б) f÷7
7з - а Л
б) 3y∣y - х; в) r ‰’,
y∕S - ∖Jr
6) 777 + з77 . в) * + 5√y.
з(777 - з77)’ х - бТу
15.65. а) 77 + 77!
1
7з7 + 5 77
г)
г)
15.66. а)
77 + 277
77 - 277’
2ху(ТЗх + 77)
777 - 77
15.67. a) α - 'Tab + b;
б) х + 277 + 4; в) 7с - 77; г) 9 - з77 + а. 15.68. а) б) — —;
5 λ∕7
в) -^-∙, г) + 2'⅛-. 15.69. а) 1; б) 1; в) -1; г) -1. 15.70. а) 77 + 3;
12 √c
б) 7с - Ю; в) 77 - 9; г) 77 + 7. 15.71. a) ⅛⅛ б) . в) HL÷½.
∖∣xyz ∖lmnr \lcdm
. „ ч 5(77 - 1) . х ч 6
15∙72∙ а) 77(77-5)’ б) 77(77 ÷T7)', В) 77(77 -2)’
d
r) y∣c(4c - 77)
15.73. а) б) —⅛=J В) г) -γ=. 15.76. a) ~∙,
о y∣ pq <ij- √ cd √x
г)
15.77. а)
77-4
277 : б) *
(5 - 7z)(3 + 77)
7√7 . ч 7с + 77 _ 7ft о. (77 - 5)(77 - 4). (ι + 77)(77 + гТь)
b'-K7Λ « ,6) П i
в) 3!7 ~⅛ г> г-15 r^∙ 15∙79' ,> ⅛^i δ, ■й'- 15∙80∙ - 1;
б) 15-81.а) б) 6λf ^ -∙ 15∙82,a) -71275^j б) 7б7; в) -T18Tr;
∖Jc + yJd и — й ½o 1
г) T28αr. 15.83. а) 11; б) 8; в) 2; г) 38. 15.84. а) 6 + 2Тб + 2Тз + 272;
262
6)8-2√10 -2√5 +2√2j b)9+4√3 -2√6 -2√2j r)41-2√6 + 12√3 -12√2.
15.85 . a) -2Тб; б) -|Т35; b) ⅛ r) 15.86. a) -|Т15; 6) эТб;
в) -13√2ζ г) 5,7√3. 15.90. Дөрес, б). 15.94. а) б) т. 15.95. a) r- 1
х y∣a - y∕b
б) 15.96. а) 1; б) 36; в) 16; г) 100. 15.97. a) бТб + 2; б) 39.
15.98. а) А < В; б) А < В; в) А > В; г) А < В. 15.99. а) б) -.
х - √2 а
15.100. а) 2 + ТЗ; б) Т2 - 1; в) 2 - ТЗ; r) Т2 +1. 15.101. -1. 15.102. 1.
15.106. 4 + √2. 16.7. а) Т2; б) Тб; в) 1; г) 2 - 2√3. 16.8. а) 2; б) 8 - зТ7;
в) -1; г) зТз - 5. 16.23. а) -1; 3; б) 1; 9; в) 2; 12; г) 2; 20. 16.24. а) -1,5;
5 1 1 1
-3,5; б) 3-; в) 3; -4,5; г) 1; 16.29. а) -1; 2; б) -1; в) -4; 2;
66 3 / > , / > 3 / , .
Л 1 к. 1 1Λ QA О ОО 1 11 ∖ θ 82 13 33 . в. o. , 1
г) -1,5, 1. 16.30. а) -8; 28; б) —, —; в) -—; —; г) —; ——. 16.31. а) ±1;
о о 5 оэ 4 4
б) ±1; в) ±1; г) ±1. 16.32. a) 2√5 - 1; б) 6; в) 2√7; г) -2√H). 16.33. а)—г) 1.
ол 1 х ÷ 1 х Зх — 1 v х + 1 Q,ς х b(b — 1)
16 .34..) б) в) г) sjjj-π. 16.35.a) v7τ-
5) -Ц-: в) —Ц-; г) τ-‰-. 16.36. а) -5; 5) 2x - 1; в) 5; г) -5. 16.37. а> -9;
б) 2х - 7; в) 4х - 11; г) 9. 16.38. а) (6; 6); (-2; 2); б) (1; -1); в) (3; -3); (6; -6);
г)чишелешләре юк. 16.39. а)(0; 0); (3; 9); (-3; 9); б)(0; 0); (4; 2). 16.40. а)х<-3;
х ≥ 3; б) х < -1; х > 1; в) -∞ < х < +°°; г) 0 ≤ х < 1. 16.41. а) х < 2;
б) -∞ < х < +<х>; в) х > 2; г) чишелешләре юк.
3 НЧЕ БҮЛЕК. 17.27. а) -1; 2; б) -2; 4; в) -2; 1; г) -3; 1. 17.28. а)—г)
Тамырлары юк. 17.29. а)(1; 2); (-1; 2); б) (Тб; б); (-Тб; б); в) (2; 2); (-2; 2);
г) (Тб; -б); (-Тб; -б). 17.30. а) (0; 0); (2; 8); б) (3; -9); (-2; -4); в) (0; 0);
(3; -3); г) (-2; 8); (1; 2). 17.31. а) (4; 2); (0; 0); б) (0; 0); (2; 2); (-2; 2);
в) (0; 0); г) (0; 0); (3; 3); (-3; 3). 17.32. а) (2; 1); б) (0; 0); (-2; -8);
(2; -8); в) (2; 2); г) (0; 0); (-3; -9); (3; -9). 17.33. а) 2; б) 2; в) 2; г) 3.
17.34. а) Чишелешләре юк; б) 1; в) чишелешләре юк; г) 1. 17.37. а) [0; 3],
б) [0; 12); в) (3; 12); г) [0; 3]. 17.38. а) (0; +°°); б) [3; +°°); в) [0; +°°); г) (3; +°°)∙
17.39. а) х < -3; х > 3; б) -3 < х < -1; 1 < х < 3; в) -3 < х < 3; г) -6 ≤ х < -3;
3 ≤ х ≤ 6. 17.40. а) х < -2; х > 2; б) -2 < х < -1; 1 < х ≤ 2; в) -2 < х ≤ 2;
263
г) -3 < х ≤ -2; 2 ≤ х < 3. 17.44. б) f(x) = 2, х = -1 булганда; Дх) = О,
х = О булганда; Дх) = 8, х = ±2 булганда. 17.45. б) f(x) = -2, х = -2,
х = 4 булганда; f(x) = О, х = О булганда; f(x) = -8, х = -4 булганда.
17.46. б) f(x) = -1, х = ±1 булганда; f(x) = 2 х ның андый кыйммәтләре
юк; Дх) = 4,5, х = 3 булганда. 17.47. А > В. 17.48. С = D. 17.49. М > N.
17.50. L < К. 17.51. Р = Q. 17.52. г) -2 < х < 4. 17.53. г) х < -2; х > 1.
17.54. а) -2 < х < 1; х > 1; б) х < -2; х > 0. 17.55. а) 0 < х < 3;
б) -3 < х < 1. 17.56. а) 2х2; б) 2х4; в) 2х6; г) 2x4. 17.57. а) 1,5х4; б) 6х4;
в) 1,5х4; г) 6x4. 17.58. а) -4х4; б) -16х4; в) -36х4; г) -4xβ. 17.59. -2,5.
17.60. -2. 17.61. -1. 17.62. а) -1 < р < 0; б) р = 2; в) р = 0; г) 0 < р < 2.
17.63. a) Д-2) = -2, Д 2) = -2, f(2, 4) = -2. 17.64. а) Д-2,5) = -6,25, Д-0,5) = -1,
Д4) булмый, f(Vδ - з) = -1. 18.14. а) 1; б) -1; 4; в) -4; г) -1; 2.
18.15. а) Тамырлары юк; б) 1; в) ±3; г) -2. 18.16. а) 1; б) 4; в) -1; г) 1.
18.17. а) (1; -5); б) (-4; -1); (1; 4); в) (-3; -1); г) (-3; 1); (-1; 3).
18.18. а) (-2; 2); б) (1; -1); в) (2; 4); г) (1; 2). 18.19. а) 2; б),
в) чишелешләре юк; г) 2. 18.20. б) -2 < х < 0; х > 2. 18.21. 6) -1 < х < 0;
х > 1. 18.22. г) f(a) + 1 = /(х) - 2 = 4 f(x-2) + l =
U X X с»
f(x + 7) - 1 = -^Ц. 18.23. г) f(x - 4) = ∕(2x) + 1 = *-½∙,
Z(x-l) + 2 = 2f(x + 3) - 1 = -i5*3c∙ 18.24. а) Л-2) = 1,
Д-1) = 2, Д1) = 2; б) Дх) = 2, х = ±1 булганда; Дх) = 0, х = 0 булганда;
= 1 > х = ~4 булганда; ±⅛. 18.25. а) Д-4) = -1; Д-1) = -4; Д1) = —
б) Дх) = -2, х = -2 булганда; Дх) = 0, х = 0 булганда; Дх) = -|, х = 1
һәм х = -8 булганда. 18.26. А > В. 18.27. С < D. 18.28. Р > Q. 18.29.
а> 12; 6]; б) (-3; 0); в) (-6; -3]; г) (0; 1]. 18.30. а) р-; б) р-; в) 4х;
r) ~⅛. 18.31. а) ⅛ б) ≡J в) ⅛ г) -≡. 18.32. а) х < -1, 0 < х < 2;
× xi 4 х6 *
б) -2 < х < 0> х > 4. ι8.35. -1. 18.36. а) Д-З) = -3; Д1) = 1; ∕(√33 - 1) =
= 19.11. в) у = 3(х + 2)2; г) j∕ = -∣(x-4)2. 19.12. а)
= √x - 2; в) у = -√x + 4. 19.13. в) у = —г) у =
19-14. в) у = -|х - 4|; г) у = ∣x + 3|. 19.15. а), г) i∕min = 0, ут„ = 2;
б^’ в) !∕min = 0, !∕max булмый. 19.16. a) j∕mιn = -5, ym∞ = 0; б)—г) ymin
264
булмый, ι∕mix = 0. 19.17. a) j∕mln = 1, ∕∕max = 4; б) ∕∕min = -2, ι∕max булмый;
в) //min булмый, ∕∕max = 4; г) ∕∕mln = 1, ι∕max булмый. 19.18. ymin = 1,
//max = 2; б) ∕∕mln = --, I∕raax булмый; в) j∕min булмый, ∕∕n,ax = -1;
г) j∕min — 2, утлх — —1. 19.19. a) ∕∕min = 1, yma× ~ 2; б) //min = 3, ym∣>×
булмый. 19.20. a) ∕∕min = -2, ∕∕max = -1; б) ∕∕mln булмый, ∕∕max = 0.
19.21. a) ymln = 0, ∕∕max = 2; б) j∕mln = 0, j∕max булмый; в) ∕∕min = О,
∕∕max булмый; г) ∕∕mln = 3, j∕πtax = 6. 19.22. г) х = 1. 19.23. г) х = -2.
19.24. г) х = -1; у = 0. 19.25. г) х = 2; у = 0. 19.26. г) -4 < х < 5.
19.27. г) -2 < х < 0.19.28. г) х < 0; х > 4.19.29. а) 1; 4; б) -4; -2; в) тамырлары
юк; г)-3; -7.19.30. а) 3; 0; б) тамырлары юк; в) -1; -4; г) 0; 4. 19.31. а) -2;
б) -2; 1; в) -1; г) 0; 4. 19.32. а) 2; б) 3; в) -3; г) 4. 19.33. а) /(-1) = -|,
/(2) = 1, /(4) = 3. 19.34. а) /(-1,5) = 4, /(-1) = -1, /(2) = -4. 19.40. a) ∕∕min = О,
//max = 3; б) J∕nlln = 1, ⅛∕max булмый; в) ∕∕nl,n = О, J∕max булмый;
г) //min ~ О, //max — 4. 19.41. a) ∕∕min = θ* //max = 2, б) //min - θ* //max
булмый; в) ∕∕min = 0, ∕∕mlχ булмый; г) ∕∕min = 0, ym,κ = 6. 19.42. А < В.
19.43. M<N. 19.44. К > L. 19.45. Р = Q. 19.46. а) -2; 1; б) тамырлары юк;
в) 2; 5; г) -3. 19.47. а) -3; б) 4; в) -4; г) 0. 19.48. а) -2; б) 6; в) 2; г) 0. 19.49.
а) -1; 2; б) 2; в) 1; г) -2; 1. 19.50. а) 2; б) 2; в) -4; -3; -2; г) -1. 19.51.
а) (1; 1); (4; 4); б) чишелешләре юк; в) (0; -1); (-3; -4); г) (1; -4); (4; -1).
19.52. а) (3; 0); (4; 1); б) (0; 4); (3; 1); в) (0; 2); г) (-1; 0); (-3; 2); (1; 2). 19.53.
а)—в) 2; г) чишелешләре юк. 19.54. а) 3; б) 2. 19.55. а) 0 < х < 2; х > 3;
б) х > 3.19.56. a) /(-2,8) = 3,6, /(3,84) = 2,2, /(0) = -2; б) /(х) = 0, х = -1 булганда,
∕(x) = 2, х = -2, х = 3 булганда, ∕(x) = 4, х = -3 булганда. 19.57. б) р = 0, 2 <
< р ≤ 8 булганда, бер тамыр; 0 < р ≤ 2 булганда, ике тамыр. 20.11. в) у = -2x2 -
Q 1 /—
- 2; г) у = х2 - 7. 20.12. в) у = - + 1; г) У = 3. 20.13. в) у = √x - 1;
х *
г) у = ~∙Jx + 3. 20.14. в) у = |х| + 2; г) у = — ∣x∣ - 1. 20.15. а) -5, -3; б)
∕∕mi∏ = -5, //max булмый; в) -5, 3; г) ∕∕min = -5, ∕∕max булмый. 20.16. a) -1, 0;
б) //min = -4, ∕∕maχ булмый; в) -6, -3; г) ∕∕n,in булмый, ∕∕raaχ = “1.
20.17. a) 1, 4; б) <∕mln булмый, ym,x = 4; в) ∕∕mln булмый,
2
‰» = 4; Г) 1, 4. 20.18. а) 0, б) ∕∕min = 0, //max булмый;
О
в) //min булмый, //max = 2; Г) 1,25, 1,5. 20.19. a) ∕∕min = -1, //max = 0;
б) //min = 0, //max буЛМЫЙ; В) ∕∕min = 0, у n,ax = 1; Г) ∕∕mln = ~1,
//max булмый. 20.20. а) О, 1; б) ∕∕min = -2, //„,., булмый;
в) 0, -2; г) ∕∕mln булмый, ⅜∕maχ = -1∙ 20.21. а) -2, 2; б) ∕∕mιn = -4,
//max булмый; в) j∕min = -4, ι∕maχ булмый; г) -4, 1. 20.22. а) О, 1;
265
б) -1, 2; в) 0, 2; г) ymin булмый, ymax = 2. 20.23. в) ymin = -2;
г) У < 0, -2 < х < 2 булганда; у > 0, х < -2, х > 2 булганда. 20.24. в) ymax = 9;
г) у > О, -3 < х < 3 булганда; y>0,x<-3,x>3 булганда. 20.25. в) (-∞∙, 2]; г) у > О,
О < х < 4 булганда; у < 0, х > 4 булганда. 20.26. в) [-1; +«>); г) у < О,
О < х < 1 булганда; у > 0, х > 1 булганда. 20.27. в) у < 0, -2 < х < О
булганда; у > 0, х < -2, х > 0 булганда; г) х = 0; у = 2. 20.28. в) у > 0, -2
< х < 0 булганда; у < 0, х < -2, х > 0 булганда; г) х = 0; у = -3. 20.29.
в) у < О, -1 < х < 1 булганда; у > 0, х < -1, х > 1 булганда; г) ymin = -1.
20.30. в) у > 0, -3 < х < 3 булганда; у < 0, х < -3, х > 3 булганда; г) 3.20.31. а) 1;
б) 1; 4; в) -1; г) 1; -3. 20.32. а) 1; б) -4; в) 4; г) 0; 2. 20.33. а) /(-1,5) = -0,25,
/(1) = 1, /(4) = 4; в) /(х) = 2, х = 0 булганда һәм х = 2 булганда, ∕(x) = 1, х = ±1
булганда, /(х) = -2, х = -2 булганда. 20.34. a) /(-1) = -1,/
о
if, /(3) = 1.
о
20.35. А > В.20.36. К > L. 20.37. а) (1; 1); (-1; 1); б) (1; 3); в) (0; 3); г) (-4; -1).
20.38. а), в) Чишелешләре юк; б) (1; -2); г) (4; 5). 20.39. a) /(-2) = 1, /(0) = 3,
/(4) = 1|. 20.40. a) /(-5) = 2, /(1) = 0, /(2) = 1, ∕(⅞ + 1) = j∙
20.42. а) -2 < х < 1; б) -2 < х < 2. 21.5. а) у = 2,5(x + З)2 - 4;
б)у = ^-г + 1; в) y = √x + 1 +2;г)у = |х-3|-1.21.6.а) y = -½(x-2)2 + 3;
х - 2 о
б) у = - 2; в) у = -√x + 4 - 2; г) у = -|х - 6| + 3. 21.12. а) у = -2(х +
+ 2)2 + 2; б) у = (х - З)2 - 5; в) у = -3(x - 4)2 + 9; г) у = | (х + З)2 - 3.
Ci
21.13. a)y=7⅛1 +2j6)y=-7⅜1 -3;в)у=7^ +2=γ^=⅛ "1∙
21.14. а) у = √x + 1 - 1; б) у = -|х - 2| + 4; в) у = -√x - 1 + 2;
г) у = |х - 3| + 1. 21.15. а) 3, 5; б) ymln = 3, ymax булмый; в) 3, 5;
Г) J∕min = 5, ymax булмый. 21.16. а) -2, 0; б) j∕mln булмый,
ymax = 0; в) -2,5, -2; г) j∕π,ln = -6, ymax булмый. 21.17. а) -3, -1;
б) Утах» J∕min булмыйлар; в) ym⅛ = 2, ym.x булмый; г) ymln = Vδ - 3,
Утах булмый. 21.18. а) у = 0, х = 1, х = 5 булганда; у > О, l<x<5 булганда;
y<0, x<l, х>5 булганда; б) (-∞j 3] да функция кими, [3; +∞) да үсә;
в) 4; г) х = 3. 21.19. а) у = 0, х = 4 булганда; у > 0, -2 < х < 4 булганда;
у < 0, х < —2, х > 4 булганда; б) (^^ooj ~2) һәм (—2; +∞) да функция кими;
в) (-2; -1); г) х = -2, у = -1. 21.20. а) [-2; +°°); б) [0; +«»); в) (0; -1),
(3; 0); г) у > 0, х > 3 булганда; y<0, -l<x<3 булганда. 21.21. а) -3; б) (-»; 2]
да функция кими, [2; +∞) да үсә; в) у = 0, х = -1, х = 5 булганда;
у > 0, х < -1, х > 5 булганда; у < О, -1 < х < 5 булганда; г) [-3; +∞).
266
21.22. a) 5; б) (-оо; -2] да функция кими, [-2; +∞) да үсә; в) у = О,
х = -7, х = 3 булганда; у > О, -7 < х < 3 булганда; y<O, х < -7, х > 3 булганда;
г) (—оо; 5]. 21.23. а) -1 < р < 4; б) р = -1, р = -4; в) -4 <р < -1; г)р < -4, р > 4.
21.24. а) Д-2) = О, Д-1) = О, ДО,25) = -2,5; в) Дх) = 1, х = -3 булганда; f(x) = О,
x = -l,x =-2 булганда; Дх) =-2, х = О, х = -1,5 булганда. 21.26. a)<∕ = (x+ 1)2 + 2;
б) у = (х - 2)2 - 3; в) у = (х + 3)2 + 1; г) у = (х - 7)2 + 2. 22.5. а) х =
б) х = |; в) х = г) х = 1. 22.6. а) (-1; -5); б) (-1; 5); в) (1; -Н
5 7 4)
г) (1; -1). 22.13. с = 10. 22.14. с = -2. 22.15. а) -3, -1; б) j∕mln = -3,
<∕n>.x булмый; в) -1, 69; г) yπlln = 5, <∕m.x булмый. 22.16. а), в) 3, 4;
б) <∕min булмый, ym.x = 4; г) <∕mln булмый, j∕max = 3.
22.17. а)—г) -11, 1. 22.18. в) -9; д) у > 0, х < -5, х > 1 булганда;
у < 0, -5 < х < 1 булганда. 22.19. в) 9; д) у > 0, -1 < х < 3 булганда; у < 0, х < -1,
х > 3 булганда. 22.20. a) (-∞∙, 2] да кими, [2; +∞) да үсә; б) (-оо; 0] да
кими, [0; +∞) да үсә; в) (-°°; -1] да үсә, [-1; +°°) да кими;
г) (-оо; 0] да үсә, [0; +∞) да кими. 22.21. a) (-∞∙, -3] да кими, [3; +∞) да
үсә; б) (-оо; 1,5] да үсә, [1,5; +∞) да кими; в) (-∞∙, 1] да үсә, [1; +∞) да
кими; г) (-оо; -2] да кими, [-2; +∞) да үсә. 22.22. а) (1; 0), (5; 0); б) (6;
0), (-2; 0); в) (-3; 0), (-1; 0); г) (1; 0), (7; 0). 22.23. а), в) ике; б), г) еч.
22.24. а) 1 < х < 5; б) х < 2, х > 4; в) х < 1, х > 5; г) 0 < х < 6. 22.25. а) х < -3,
х > -1; б) -4 < х < 0; в) -3 < х < -1; г) х < -4, х > 0. 22.26. а)—г) ике.
22.27. a) 2x10 - 5x5 + 3; б) -х2 - 4х - 7. 22.28. а) с = 2; б) с = 4. 22.29. а) а = 0,35;
б) а = -0,5. 22.30. a) b = -2; б) Ь = 16. 22.33. а) Д2) < Д2.0137);
б) zl О1< 411в) Λ1∙999> > Л2); г) /(49’7) > Л49.69). 22.34. а) Д-2,43) <
< Д-З); б) Д-59,9) > Д-60); в) /(-у) < Д-З); г) Д-0,99) > /(1,1).
22.35. a) ∕(√2) > Д-1); б) Д-12,473) > Д-12,472); в) Д-1) < /(-Тб);
г) f(√2) < ∕(√3). 22.36. a) 20x2 + 6х - 2; б) 5x2 - 7х; в) 5xβ + Зх3 - 2;
г) 90x2 + 18x - 4. 22.37. a) -2x2 - х - 4; б) -2x2 - 19х - 49; в) -2x4 - х2 - 4;
г) -24x2 + 6х - 12. 22.38. 22.39. 22.40. а) Чишелешләре юк; б), в) ике;
4 о
г) чишелешләре юк. 22.47. а) -1 < х < 0, 1 < х < 2; б) 0 < х < 2, 3 < х < 5.
22.48. а = 2. 22.49. с = 5; с = 13. 22.50. b = -2; с = -1. 22.51. а = 4; Ь = -8;
с = 2. 22.52. Ь = -6; с = 8. 22.53. b = 4; с = 1. 22.54. у = -Зх2 - 12х - 9.
9 7
22.55. у = -→2 + ⅛x + 1. 23.1. а) 0; 2; б) 0; 6; в) -4; 0; г) -8; 0. 23.2. а) -2;
о о
267
2; б) -1; 1; в) -3; 3; г) -4; 4. 23.3. а) -1; 1; б) 0; 2; в) -2; 2; г) -6; 0.
23.4. а) -3; 1; б) 1; 3; в) -5; 1; г) -1; 3. 23.5. а) -1; 2; б) -1; 4; в) -1; -2;
г) -3; 2. 23.6. а) 1; 5; б) -4; 1; в) -2; -4; г) -2; 3. 23.7. а) 2; 3; б) -3; 2;
в) -2; 3; г)-2; -3. 23.9. 2 см һәм 4 см. 23.10. Здм һәм 4 дм. 23.11. Зсм һәм 4 см.
23.12. а) 2; 4; б) 2; -4; в) 4; -2; г) -2; -4. 23.13. а) 2; б) 1; в) 2; г) тамырла¬
ры юк. 23.14. а) 2; б) 1; в) тамырлары юк; г) 2. 23.15. р = 0. 23.16. р < 2.
23.17. р > 0. 23.18. р > -10. 23.19. а) р < -1; б) р = -1; в) р > -1. 23.20. 6 м
Q
Һәм 4 м. 23.21. 2 см һәм 6 см. 23.22. 3 м, 4 м, 5 м. 23.23. —• 23.24. 4
5
км/сэг, 6 км/сэг.
4 НЧЕ БҮЛЕК. 24.19. а) ±5; б) ±^; в) ±3; г) ±~-. 24.22. а) -6; б) 3,5;
о 3
в) 8; г) -124.23. а) 0; 2; б) ±3^3; в) О; г) тамырлары юк. 24.24. а) 0; 9;
О Δ
б) 0; |; в) 0; -3; г) ±2. 24.25.1 һәм 2. 24.26. 2 һәм 3. 24.27. 4 с. 24.28. 12 см.
О
24.29. 4\/з см. 24.30. 3 км/сэг. 24.31. а) р = 1, х = ±—; р = 0,5, х = ⅛>
3 1*
х = 0; б) р = 0, х = 0, х = 1,5; в) р = -1,5, чишелешләре юк; р = -2, х = 0,
х = ; г) р = -3, х = 0. 24.32. а) р = 2; б) р = ±3; в) р = 2; г) р = 1,5.
24.33. а) р = -10; б) р = -38; в) р = -2; г) р = -21. 24.34. а) р = 16; б) р = 0;
в) р = -250; г) р = 0. 24.35. а) 3; 5; б) 10; 2; в) 3; 1; г) -4; -2. 24.36. а) -5;
2; б) 0,5; 2; в) -2; -7; г) -0,5; 1,5. 24.37. а) 0; 3,5; б) ±√2j в) 0; 7;
г) ±√3. 24.38. а) 0; 17; б) ±1; в) 0; -68; г) ±2. 24.39. а) 0; б) ±4; в) 0;
г) ±1,5. 25.15. а) -2; -3; б) 2; 4; в) -2; 5; г) -7; 3. 25.16. а) 3; -4∣I
О
б) 2; в) 2,5; -у; г) 25. 25.17. а) ~3 б)-4,5; -0,5; в) ~3 ; г)
4 Δ 2 о
-4- 25.18. а) 4; б) 6; 1,5; в) -0,25; г) ЦД. 25.19. а) 3; 4; б) 2;
4 4а 2
1 4
±; в) -6; 0,8; г) -2. 25.20. а) ±6; б) 0; в) ±8; г) 0; 3. 25.22. 8. 25.23. 7 см,
12 см. 25.24. 10 һәм 12 яки -12 һәм -10. 25.25. 9 м, 40 м. 25.26. 10 × 10.
25.27. 17 һәм 18. 25.28. 49. 25.29. 22, 23, 24. 25.30. 33 см, 56 см, 65 см.
25.31. 20 см. 25.32. 17 һәм 18. 25.33. 20 һәм 21. 25.34. 5%. 25.35. 10%.
25.36. a) -4z∙, -2>/2; б) ■ ∙^3-? в) -V5; 4-75; г)
о . /77
25.37. а) —— ; б) -1,5; 1; в) 1; г) тамырлары юк. 25.38. а) -0,8; 3;
6
268
б) -1; 13; в) 2; |; г) -1; 25.39. б). 25.40. 12 команда. 25.41. 15
О
укучы. 25.42. 18. 25.43. 60 км/сэг, 80 км/сэг. 25.44. 10%. 25.45. а) 1; б) 2;
в) 4; г) 3. 25.46. а) р; р - 2; б) |; в) р + 1; -2р; г) 25.48. а) 1;
3 2 Δ о
-2; -3; б) 3; 4; ~7 8 ~2^i в) 1; -1; г) 7 • 26.1. а) 1; 1|; б) -3; 5;
в) -2; 12; г) -1; 1. 26.2. а) 0; 3; б) 14; -2. 26.3. а) 6; -2,8; б) -3; 0,8.
26.4. а) 6; б) -2; в) -4; г) -|. 26.5. а) |; б) |; в) |; г) 2. 26.6. а) -6;
1; б) -3; 1; в) -3,5; 5; г) -4; -1. 26.7. а) 3; -1; б) -23; 1; в) 1; 2; г) -27;
-1. 26.8. а) -10; 3; б) -3; 4; в) 0; 4; г) -6; 5. 26.9. а) -1; б) |; в) 3;
г) 2,8. 26.10. а) 5; б) 9; в) -4; г) 4. 26.11. а) -з|; б) -1; в) 2,5; г) 3.
26.12. а) 0,5; 1; б) 2. 26.13. а) юк; б) 1; -3. 26.14. а) ±1; ±4; б) ±72;
в) ±75; г) ±2. 26.15. а) ±|; ±3; б) ±|; в) ±|; ±1; г) ±2. 26.16. а) 2; -1;
Δ о 4
1 2
б) 1; 2; в) 1; -2; г) -2; -1. 26.17. а) -5; 4; б) -±; 0; в) -2; 6; г) ±^. 26.18. а) 3;
Δ о
б) ~* в) -2,2; 6; г) -1,5. 26.19. а) ±3; б) 20; в) ±1; г) 0,5. 26.20. а)
Тамырлары юк; б) 7 в) 0; -6; г)тамырлары юк. 26.21. а) б) ±1;
10 3 8
7 2 3 2 5 11
в) тамырлары юк; г) 2; 4. 26.22. а) 2; —; б) -2; ; в) —; ; г) —; —.
3 3 Ә Ә ( 14
26.23. а) ±1; -3; б) 0; в) 0; ±2; г) -2. 26.24. а) ±710; ±4; б) 3; 1; в) 4;
-1; г) 0; -2. 26.25. а) б) 1; в) 1; г) 7. 26.26. а) 3; 0; б) 2; -
8 6 6 4 Δ
в) 2; 3; г) -1 ± Тб; 1; -5. 26.27. а) 1; -2; б) 0; 1; в) -4; -2; ±1; г) 1; 2.
oβ . 3 ± 721. , -3 ± 75. 1 . -5 ± 713 , о 1 о, 1 1 о ,
26.28. а) - ; б) - ; 1; в) ; г) 2; —. 27.1. 12 км/сэг.
2 2 2 2
3
27.2. 4 км/сэг. 27.3. 15 км/сэг һәм 18 км/сэг. 27.4. —. 27.5.
4
80 км/сэг, 70 км/сэг. 27.6. 50 км/сэг. 27.7. 15 км/сэг. 27.8.
80 км/сэг. 27.9. 12 км/сэг. 27.10. 40 км/сэг. 27.11. 15 км/сэг,
6 км/сэг. 27.12. 60 км/сэг һәм 45 км/сэг. 27.13. 80 км/сэг, 60 км/сэг.
27.14. 20 машина. 27.15. 36 кон. 27.16. 15 км/сэг. 27.17. 18 км/сэг.
269
27.18. 24 км/сәг. 27.19. 8 км/сәг. 27.20. 21 км/сәг. 27.21.
3 км/сәг. 27.22. 10 км/сәг. 27.23. 15 км/сәг. 27.24. 18 км/сәг. 27.25.
10 км/сәг. 27.26. 50 т, 60 т. 27.27. 40 деталь. 27.28. 8 эшләнмә.
27.29. ∣. 27.30. ∣. 27.31. 27.32. 40 км/сәг. 27.33. 2 сәг 24 мин.
о о 4
27.34. 30 см. 27.35. 18 км. 27.36. 50 км/сәг. 27.37. 48 км/сәг,
60 км/сәг. 27.38.12,5 км/сәг. 27.39. 6 км/сәг. 27.40. 47 кеше. 27.41. 75 га.
27.42. 5 км/сәг, 6 км/сәг. 27.43. 16 км/сәг. 27.44. 120 г. 27.45. 25 кг.
28.2. а)-20;-14; б)-6; 22; в) 6; 18; г)-30; 4. 28.3. а) -1; 3; б)-1; |; в)-2; |;
г) -1; 1. 28.4. a) 1 ± V2; б) -2 ± 73; в) -1 ± 73; г) 3 ± √2. 28.5. а) 2 ±
5 2
б) ~2i∕⅛i в) 3±„ Г) ~1* . 28.6. а) 3 ± 3√2; б) 3 ± >/5; в) 6 ± 4√2s
о Δ ә
г) -6 ± 3√3. 28.7. 15 см, 45 см. 28.8. 15 см х 15 см. 28.9. 11 һәм 17.
28.10. 480 см2. 28.11. 60 км/сәг. 28.12. 36 км/сәг. 28.13.
32 км/сәг, 36 км/сәг. 28.14. 65 км/сәг. 28.15. 80 км/сәг,
100 км/сәг. 28.16. 60 км/сәг. 28.17. 24 км/сәг. 28.18.
10 км/сәг. 28.19. а) -3; 55; б) 1; -441; в) -127; 19; г) 8; -~⅛.
28.20. а) 2%/3; б) -√5 ± 5; в) -3√2j г) 2√2 ± 2. 28.21. a) р + 1; р - 3;
б) -р - 4; 2 - р; в) р - 5; р + 3; г) 1 - р; -7 - р. 28.22. a) -р ± 1; б)р = 0,
1
х=-;р
<0, 0<p<4, х = 2 ± y∣4 - р; р > 4, тамырлары юк; в) 2p ± 1;
г) р = о, х =
p<0, 0<p≤9, х =
6 ± 2√9-р
Р
р > 9, тамырлары юк.
р
28.23. а) р = 4, х = -1; р ≠ 4, х = -1, х =
б) р = 0, х = -1,5; р < 0,
0 <р < 1, х =
-(p±i)±√iT7
р > 1, тамырлары юк. 28.24. 60 км/сәг.
Р
28.25. 16 км/сәг. 28.26. 20%. 28.27. 20%. 28.28. 14 көн. 29.9. a) х2 - 6х +
+ 8 = 0; б) х2 + 2х - 15 = 0; в) х2 + 7х - 8 = 0; г) х2 + 8х + 12 = 0;
29.10. а) х2 - 0,5х - 5 = 0; б) 6x2 + 5х - 6 = 0; в) x2 + 3,9х + 3,6 = 0;
г) 15x2 + 16х - 15 = 0. 29.11. а), б), г) юк; в) әйе. 29.12. a) Ь = -5;
с = -3; б) a = -1; с = 12; в) a - -8, b = -14; г) a = 6, с = -72. 29.13. р = 1.
29.14. р = 3, р = 4. 29.15. a) (х - 3)(х - 8); б) (х - 5)(х + 3);
в) (х + 3)(х + 4); г) (х + 5)(x - 2). 29.16. a) -(x - 15)(x - 1); б) -(x + 9) х
х (х - 1); в) -(x - 3)(х - 2); г) -(x - 8)(x + 1). 29.17. a) (Зх - 1)(х + 2);
б) (2x +l)(3x + 1); в) (5x - 3)(x + 1); г) (Зх - l)(5x - 1); 29.18. a) -(x + 3×3x - 1);
270
6) -(5x - l)(x - 1); в) -(2x - l)(x - 4); г) -(x + 5)(4x - 17). 29.19. а)
х
. 2x - 1
г) Г
х - 5
.29.21. а)
——-. 29.20. a) 2x + 7;
х х - 1
х - 5 2х + 3 .
ΓΓιo5 б) -5ΓΓ2, в)
.. Зх - 1
б) τττ= в>
6х - 13
2х + 9 : Г)
2x - 1.
х - 4 ’
7х - 2
2 - х '
Зх - 1 ,
б) ; в)
7⅛ г)
29.22. а) —≡-; б) 29.23. а) 2; -1; б) 1; 23. 29.24. а) 3,5; б) 0,5.
X — о X 4
29.25. а) б) -|. 29.26. а) 10; 78; б) 6; 20; в) 5; 21; г) -38; 3. 29.28. а) 1;
2 3
-2—; 6)1; 4⅛ в) 1; 3⅛ г) 1; -12-. 29.30. а)-1;-5; б)-1; 2^; в)-1;
13 5 3 3 67
г) -1; зЛ. 29.31. а) х2 - 2 = 0; б) х2 - 45 = 0; в) х2 - 7 = 0;
11 14
г) х2 - 162 = 0. 29.32. а) х2 - 6х + 7 = 0; б) x2 - х - 1 = 0; в) x2 - 4x - 1 = 0;
г) 49x2 + 56х + 13 = 0. 29.33. a) (√x + 2)(√x + 4); б) (√^ - 9)(√x + 2);
в) (√^ - 7)(√x - 5); г) (√^ + 8)(√x - 5). 29.34. a) (√^ + l)(7√x + 1б);
б) (x√x - з)(3х7х - 1); в) (√^ + l)(9>∕x - 5); г) (x√x - 2)(2x√x - 1).
29.35. а) (х - 2)(х + 2) (х - 3) (х + 3); б) -(x3 - 4)(2x3 - 1);
в) -(x - 2)(x + 2)(x - 4)(х + 4); г) (5x3 - l)(3x3 - 1). 29.36. a) (χ - 6 + 2√3) ×
X (х - 6 - 2Тз); б) (2х -1 + √2)(2x -1-5/2); в) (х - 3 + 2√2)(x - 3 - 2√2)j
г) (2х - 3 + √2)(2x - 3 - √2). 29.37. а) ^ б) (х - 1)(х + 3);
√x - 4
в) —i; г) 2 • 29.38. а) х + 2; б) х + 4; в) х - 2; г) х - 1.
√x - 3 х + 1
29.39. а) 115; б) -153. 29.40. а) —; б) -. 29.41. р = -0,5. 29.42. р = 3,
9 9
р = 1,5. 29.43. • 29.44. -2; -0,5. 29.45. р = -2 х = 4 булганда,
2
x = 7; р = 4 — х = -1 булганда, х = -8. 29.46. р = 25 х = 5 булганда, х = 2,5.
О
29.47. р = 20 х = 2 булганда, х = 5. 29.48. а) 2x б) -15° ■ 29.49. а)
х2 За - 1
5 - а Ял + 4 1
3UT1); 6) a _ 2 ∙ 29∙51∙ а) -з|; б) -1. 29.52. а) 2; 73; б) 2; -18,5. 29.53.
а) 9; б) 29.54. а) 8; б) тамырлары юк. 29.55. а) б) |. 30.3. а) -2; |;
* о zi 4
2 1
б) 7; -; в) 2; -1,4; г) 0,6; -5. 30.4. а) -4; б) в) 11; г) -0,5. 30.6. а) 3;
271
б) тамырлары юк; в) 1; г) тамырлары юк. 30.7. а) 4; 16; б) 4; 9; в) 9; 16;
г) 1; 4. 30.8. а) 25; б) 36; в) 9; г) 36. 30.9. а) 25; б) 9; в) 9; г) 16. 30.10. а)
2; б) -1; в) у; г) у. 30.11. а) -3; б) -1; в) -2; г) |. 30.12. а) 2; б) -11;
23 9 1
в) 11; г) -3.30.13. а) 5; б) —; в) —; г) тамырлары юк. 30.16. а) 1; б) 1; ; в) 1;
z⅛D 4 О
г) 2. 30.17. а) 1; б) -1; в) -2; г) -2; 30.18. а) 0; -1; б) тамырлары юк;
2 5
в) -1; г) тамырлары юк. 30.19. а) 35; б) 1; в) 17; г) 2; 3. 30.20. а) -1; б) 3;
-1; в) 5; г) тамырлары юк. 30.21. а) 2; б) 2; в) 4—; г) 6. 30.22. а) 7; 8;
о
б) -1; в) 2; г) 3. 30.23. a) ±272; б) 3; в) ±710; г) 101. 30.24. а) 2,8; -1,1;
б) 1,4; в)±1|; г)
5 НЧЕ БҮЛЕК. 31.4. а) >; б)—г) < . 31.5. а), в), г) <; б) >. 31.6. а), б) >; в),
Ь 4- /
г) <. 31.10. а) а + b > ab; б) т2 < п; в) —— < 3(k + Z); г) Зр > р3.
31.11. a) t - s > б) (т + n)2 < т - л; в) k2 - l2 < 2kl; г) л(л + 1) > (л + I)2.
s
31.17. а), б), г)Эйе;в)юк. 31.18. a)—r)θfte.31.19. i; -; i; -. 31.21.а)6>-1;
с a b d
б) 12,2 < 17,5; в) 5,8 > 1,9; г) 10,4 < 21,9. 31.27. а) Әйе; б) юк; в) әйе;
г) юк. 31.28. а) Әйе; б), в) юк; г) әйе. 31.29. a) 2k + 31 > 27; б) -k - I < -10;
в) А + 1,5/ > 13,5; г) -4А - 5Z < -47. 31.30. а) р - 25 > -8; б) s - Зр < -1;
в) 4s - 2р < 16; г) Зр - 6s > -24. 31.31. а) т + п + 4 > 9; б) 12 - 4п - Зт < -7;
в) 3 - 2т - 5п < -19; г) 7m + 6n + 1 > 32. 31.32. а) х - 5 - 2у > -23;
б) 14 - 2х + Зу < 38; в) 5х - у + 10 > 28; г) 16 - Зу + 4х > 4.
31.34. а) 5 < 0,5а < 8; б) -6 < а - 16 < 0; в) -48 < -За < -30;
г) 21 < 2α + 1 < 33. 31.35. а) 5,2 < 2√7 < 5,4; б) 7,2 < 2√7 + 2 < 7,4;
в) -2,7 < -√7 < -2,6; г) 0,3 < 3 - √7 < 0,4. 31.36. а) 6,1 < 78 + 711 < 6,3;
6)-0,6< 78 - 711 <-0,4; в) 9,4 < 78 +2711 <9,7;г)5<зТ8 - 711 <5,4.
31.37. а) 3 < а + + Ь < 4,5; б) 7 < а - ∣ b < 9,5; в) 8 < ab < 20; г) 4 < - <10.
4 z if
31.48. а) 2,8 < 7в; б) 7з > 1,7; в) 710 < 3,4; г) 77 < 2,7. 31.49. а) Тб <
< | 78; б) Тз > 72; в) 78 < | 713; г) 77 > | 719. 31.50. а), б) а < Ь;
Ә О о э , , ,
в), г) а > Ь. 31.51. а) а > Ь; б)—г) а < Ь. 31.54.1 - 12; I - 1,45; Z; A; k + 0,2;
А + 2,6. 31.55. а)—г) Юк. 31.56. а), г) Юк; б), в) әйе. 31.57. а) Әйе; б) юк;
272
в) әйе; г) юк. 32.8. а), г) (-°°5 θ) да кими, (0; +°o) Да Ycθ! бЬ в> a (~°°; °)
да үсә, (0; +∞) да кими. 32.9. а), г) [0; +∞) да үсә; б) [0; +∞) да кими; в)
[3; +oo) Да үсә. 32.10. а), в) (-~; 0] да кими, [0; +∞) да үсә; б) (-∞5 0] да
үсә, [0; +∞) да кими; г) (-«>; 1] да кими, [1; +∞) да үсә. 32.11. a) f(-2) = -2,
f(l) = 1, Д5) = -• 32.12. а) /(-1) = 2, ДО) = 0, /(4) = 2. 32.13. а) Д-З) булмый,
5
ДО) = о, Д6) = 6. 33.10. а) а > |; б) b < 33.11. а) с ≥ 1—; б) d < -2.
33.12. а) т > -1,2; б) п < О. 33.13. а) р > 1; г) q < -1,5. 33.14. а) а > 24;
б) Ъ > 5; в) с > 0,5; г) х < 3. 33.15. a) d > 2∣J б) т < -15; в) п > -10;
г) р < -1. 33.16. а) х < 3; б) у > 4; в) г > 2; г) t < 3. 33.17. а) х < 3;
2 θ
б) у < -1|; в) Z > -4; г) t < 0,8. 33.18. а) х > -1; б) у > -θ! в) z < 2,5;
г) t > -2,4. 33.19. а) р > 0; б) у — теләсә нинди сан; в) q < 0; г) г — теләсә
нинди сан. 33.20. а) а — теләсә нинди сан; б) чишелешләре юк; в) г — теләсә
1 3
нинди сан; г) чишелешләре юк. 33.21. а) а > 1 —; б) b < 4,8; в) с > 1 —; г) d < 0.
3 о
2 1 1
33.22. а) а > -—; б) х ≤ 1»! в) х > 1,4; г) х > ~∙ζ∙ 33.23. а) х > 2;
3 о &
12 6
б) х < -4 i; в) X < 19 =-∖ г) х > 2,4. 33.24. а) а > 8,4; б) с < -3 -; в) Ь > -12;
У о •
г) d > 0. 33.26. а) х < -12; б) 2γy. 33.27. а) а > 5; б) х > -1; в) у < -5;
г) с > -|. 33.28. а) т < 2; б) п > в)р > 2; г) q < ⅛. 33.29. а) а >
а 5 15 11
14 5
б) с < γ∙ в) Ь < 4—; г) d < 33.30. а), в) х — теләсә нинди сан; б),
г) чишелешләре юк. 33.31. а) х = 21; б) х = -1. 33.32. а) х = 0; б) х = -80.
33.33. а) х = -6; б) х = 16. 33.34. а) х = 0; б) х = 1. 33.35. 6 км дан 10 км га.
33.36. 4 км дан азрак. 33.37. 20 км, 30 км, 40 км, 50 км, 60 км яки 70 км.
33.38.180 км дан күбрәк. 34.1. а) х < 1; х > 3; б) 1 < х < 3; в) 1 < х < 3; г) х < 1;
х > 3. 34.2. а) х < -1; х > 7; б) -8 < х < 6; в) х < -3; х > -1; г) -3 < х < 15.
34.3. а) х < 1; х > 5; б) -4 < х < 2; в) 2 < х < 14; г) х < 1; х > 3.
34.4. а) х < -1,5; х > 2; б) 1 < χ < 1|; в) -1 < х < -0,5; г) х < 0,2; х > 2.
3
34.5. а) -0,2 < х < 1; б) х < -4,5; х > 2; в) х < -|; х > 2,5; г) ≡ < x < 1.
34.6. а) х < -3; х > 2; б) -5 < х < -1; в) -7 < х < 5; г) х < 4; х > 6.
34.7. а) -1 < х < 2; б) х < 3; х > 4; в) х < 1; х > 2; г) -5 ≤ х < 3.
273
34.8. a) -— < х < —; б) х < 0,75; x > 2,5; в) х < х > 0,25; г) х < -3;
3 2 7
х > 0,5. 34.9. а) х < |; х > |; б) х < 1; х > 1|; в) х ≤ -1|; х > 2;
г)х<-2; х ≥ —. 34.10. а) х = 3; б) чишелешләре юк; в) х— теләсә нинди сан;
5
2
г) х ≠ 2. 34.11. а) х — теләсә нинди сан; б) х ≠ —; в) чишелешләре
О
юк; г) х = —. 34.12. а), б) х — теләсә нинди сан; в), г) чишелешләре
6
юк. 34.13. а), б) х — теләсә нинди сан; в), г) чишелешләре юк.
34.14. а) х < 1 - >/2; χ > 1 + ^2; б) -∞ < х < +°°; в) х < -1 - л/з;
х > -1 + >/3; г) χ < .~1~^∙ х > ~1 + ^θ. 34.15. а) х < -6; х > 6; б) чи-
2 2
телешләре юк; в) -5 < х < 5; г) х — теләсә нинди сан. 34.16. а)
2 2 г- 4 .4 , 6 6,1l<vχ1l
-Q < x < 6) x < -7;x > е в) x < -7; x > 7; r) -17 < x ≤ 17∙
о о 55 5 5 < 7
34.17. а) -10 < х < 10; б) х < -2-; х > 2∣j в) х < -25; х > 25;
2 2
г) < X < 34.18. а) х < 0; X > 5; б) -0,5 < х < 0;
4 4
в) -8 < х < 0; г) х < 0; х > 2,3. 34.19. а) х < 0; х > 25; б) 0 < χ < 2;
в) 0 ≤ х ≤ 36; г) х < 0; х > 9. 34.20. а) х < -1,5, х > -1; б) х = 34.21. а) 6;
б) 9. 34.22. а) -10; б) 7. 34.23. а) х < 1, х > 7; б) -1 ≤ х ≤ 4; в) χ < 1,
9 9 1
х > 5; г) х < -2, х > 1. 34.24. а) -3 < х < 3; б) х < х > ^; в) х < --,
12 2 1
х > -; г) ~~ < х < 34.25. а) 0 ≤ х ≤ 2; б) х ≤ 0, х > -; в) 0 ≤ χ ≤ 5-
О О э о
г) х < 0, х > 4. 34.26. а) х < -2, х > 3; б) 1 < х < 2; в) -5 < χ < 4;
г) х < -1,5, х > 6. 34.27. а) х < 2, х > 3; б) 0,5 < х < 2; в) х < -3, х > 4;
г) -3 < х < -∣∙ 34.28. а) х < 0, х > 0,4; б) х < -2√6, х > 2>/б; в) -4 < χ < 0;
√3 √3 33
г) х < —т"» х > 34.29. а) х < -1, х > 4,5; б) —— < х < 1.
о о 4
9
34.30. а) -8 < х < 6; б) х < -4, х > -■ 34.31. а) -1 < х < 1; б) х < -2,
х > 2; в) х < -1, х > 1; в) -2 ≤ х < 2. 34.32. а) х < 3, х > 4; б) -4 < χ < 5;
в) х < -7, х > 6; г) -3 < х < 5. 34.34. а) 8; б) 7. 34.35. а) -8; б) 0.
34.36. а) р < -6; р > 3; б) р = —6; р = 3; в) -6 < р < 3. 34.37. а) р < -4; р > 6;
б) р = 6; р = -4; в) -4 < р < 6. 34.38. а) р < -1; р > 1; б) р = -1; р = 1;
274
в) -1 < р < 1. 34.39. а) р > 1,8; б) ~ < р < 3; в) р > -⅛ г) р < 0,6.
4 16
34.40. а) -3 < р < 3; б) р < -—; р ≥ 0; в) р > -2; г) р < -1; р > 2.
34.41. а) р < 0; р > у; б) р < у в) р < p > 0; г) р < -1; р > 2.
34.42. р = -2; р = 6. 34.43. -— < р < 34.44. 2 см дан зуррак, 16 см дан
О О
азрак. 34.45. 12 см дан зуррак. 34.46. 1 саг тән кимрәк. 35.3. а) 1,73; 1,74;
б) 0,41; 0,42; в) 2,35; 2,36; г) 0,66; 0,67. 35.4. а) 2,23; 2,24; б) 0,31; 0,32;
в) 3,17; 3,18; г) 0,78; 0,79. 35.5. а) 3,31; 3,32; б) 1,16; 1,17; в) 3,58; 3,59;
г) 0,7; 0,71. 35.6. а) 3,872; 3,873; б) -1,642; -1,641; в) -1,829; -1,828; г)
0,157; 0,158. 35.7. а) 12,7; б) 1,7. 35.8. а) 1,73; б) 1,41. 35.10. а) 0,8; б) 11,2;
в) 3,3; г) 4,5. 35.11. а) 1,24; б) 0,73. 36.7. а) 2,8 102; б) 1,2-10°; в) 2,59 ∙ 108 *;
г) 1,56 Ю10. 36.8. а) 1,42- 10е; б) 5,15 103; в) 7,0078 102; г) 7 10 3.
36.9. а) 2,5 ■ 1013; б) 7,5 1019 *; в) 2 ∙ 10 * * * *14; г) 8 ∙ 10^11. 36.10 *. а) 1,7 106;
б) 5 • 10 30; в) 10 м; г) 5 10 26. 36.11. а) а > Ь; б) а > Ь; в) а < Ь; г) а < Ь.
36.12. а) 4; б) 1; в) 3; г) -1. 36.13. а) -3; б) -6; в) -1; г) 0. 36.14. 112985.
36.16. а) 12 һәм 13; б) 30, 31, 32, 33, 34; в) 3; г) -7 яки -6. 36.17. а) -1
яки 0; б) 3; в) 4; г) 4. 36.18. а) 6 яки 7; б) 4 яки 5; в) 4 яки 5; г) 5 яки 6.
36.19. а) 18, 0, 9; б) -13, -1, -6; в) 10, 0, 5; г) -10, -1, -5.
6 НЧЫ БҮЛЕК. 10. а) а = -1; б) а = 3. 11. а) b = -8, с = 0; б) Ь = -24,
с = -45. 18. а) (-5; 1), (0; 6); б) (-3; 3), (0; 0); в) (2; 9), (4; 13); г) (2; -2), (5; 1).
19. a) (-∞j -7) и (1; +°°); б) [-1; 3]; в) [-3; 5]; г) (-■»; -4) и (1; +∞). 20. а)
(_оо; -2) ∖j (-2; +°о); б) (-°°; +°°); в) х = 3; г) чишелешләре юк. 21. а) тп = -3
булганда бер тамыр, т > -3 булганда ике тамыр, т < -3 булганда тамырлары
юк; б) k = 5 булганда бер тамыр, ⅛ < 5 булганда ике тамыр, k > 5 булганда
тамырлары юк. 31. a) <∕n>ι∏ = 1 - 6-*/3, j∕max = 1 - 4-ТЗ; б) j∕min = 6\/б - 9,
yma× = 6>/5 — 7,5; в) i/min = 2>/з — 2, ι∕max — 4; г) ytnιn = —5, j∕max — 10 — 6∙7β.
32. а) 2, 6; б) -1, 4; в) 0, 2; г) -3, 1. 33. а) (-2; -5), (1; 2,5), (4; 1);
б) (-2; 4), (1; -5), (3; -1)∙ 34. а) у = 0, х = 2 булганда, y>0, 1 < х < 2 булганда,
у < 0, х < 1 һәм х > 2 булганда; г) у = -2, х = 0 булганда, у > -2, х < -2 һәм
X > 0 булганда, у < -2, -2 < х < 0 булганда. 35. а) [-4; 2); б) (-«; -6) и (-1; +~);
в) (_оо; -1) U (1; +оо); г) [0; 3). 36. г) у = X + 1, у = -X - 3.42. а) 4; б) 3; в) 7; г) -3; 6.
43. а) (3; -4), (4; -3); б) (-1; -1), (θ! -2). 44. а) у > 0, х > -2 булганда, у < 0,
-3 < х < 2 булганда; r)j∕<5,0<x<4 булганда, у > 5, х > 4 булганда. 50. а) -2,6;
275
б) -8, 2; в) -4, 2; г) 1, 7. 51. а) (1; -3), (3; -3); б) (-6; -2), (-4; -4), (2; 2);
в) (0; -1), (4; 1); г) (1; 0), (2; 1). 52. a) (-°°; -1] и [3; +~); б) (-2; 0);
в) (-2; 6); г) (—~; 2] и [6; +∞). 56. а) 1; б) 3,5. 57. а) -1, 4; б) 1, 5. 58. а) 0,5;
б) 2. 59. а) х < 4,5; б) х < 4. 60. а) х < -10 һәм х > -3; б) 2 < х < 4.
61. a) ι∕(3) <{/(1,72); б) у (3 - √2) = {/(3 + Т2); в) y(4) < y (зТг); г) {/(0,8) >
> ι∕(5). 64. р > 1 һәм р < -1 булганда бер тамыр, р = ÷1 булганда ике тамыр,
-1 < р < 1 булганда өч тамыр. 73. а) -4, 2; б) -4. 77. а) , 3; б) -7, 1,6;
6
в)-4, r)-3, 8∣. 78. а)2±ТЗ; б) 4 5 * 7 *■—; в) -3 ± 77; г) ~3 ⅜-VH.,
9 3 4 5
79. а) -3,5; б) тамырлары юк; в) 1,6; г) тамырлары юк. 80. а) -0,5, 3; б) -4,
1|; в)-2, 11;г)-1,б|. 81. а) |; б)-1, в)-0,4, 0,7; г) -|,
О о z* о О ОО
82. 8, 12. 83. 81 см2. 84. 5 м, 35 м. 85. 60 см2. 86. 26 см, 24 см, 10 см.
87. 15 см, 20 см. 88. 12 см, 16 см. 89. 480 см2. 90. с = 37, с = 13. 91. а = -1.
92. а) а = 2, Ь = -8, с = 4; б) р = -1, q = -5. 93. а) ±2; б) ±3, ±√0^5∙,
в) ±3, ±72; г) ±2, ±^. 94. а) 0, ±1; б) ±|, в) ±3; г) 2. 97. а) -1;
3 о о ∆
б) -16. 98. а) Ь = ±5; б) с = -2. 99. a) q = -28; б) с = 15. 100. а) т = 12;
б)т=-6.107.а) Ц-3; б) -Ц. 108.a) ≡*flj б) —ζ-. 109∙a) —7—;
Ъ у -5 х2 2y + 1 2m +1
б) --. 111. а) 1; б) 2,5; в) 0; г) -1|. 112. а) 11; б) 1|. 113. а) |, 2;
Р о < о 2
9 1 Q 11
б) -≤, 1; в) -3, ±; г) -2; 7. 114. а) ±1, 3; б) -1, 2, -1 7, 1 в) ±1, 3, 5;
о 3 4 о 2
г) -3, -8. 115. 6 км/сэг. 116. 18 км/сэг. 117. 12 км/сэг. 118. 180 км/сэг.
119. 0,8 м/с, 1 м/с. 120. 90 км/сэг, 50 км/сэг. 121. 40 км/сэг, 60 км/сэг.
123. а) ||; б) 3⅛ в) 211; г) 124. а) 256; б) |; в) 0,01; г) 27.
о! 1о о 20 Ә
125. а) 4; б) 126. а) 5; б) -11; в) 3; г) 5∣. 127. а) -4, 9; б) 4, 1;
27 о о
4 4
в) -8, 2; г) -7, 2. 128. а) 1; б) 3; в) 2; г) 3. 129. а) 5, 1 -; б) 1; в) 3, 7-;
г) 3. 130. а) -1; б) 1; в) 2; г) -2. 131. а) -1 ± 710; б) -8, 2; -3 ± зТб.
132. а) 1; б) 3. 133. а) -1, 2; б) 2, 7. 135. а) б) -|. 136. а) 1 - 7х;
О о
б) 4 - Ь; в) 77 - 1; г) 1 - а. 139. а) 275; б) 1; в) -2715; г) 1. 140. а) 6;
6)1, ≥L√K∙
2 ’
в) 3; г) 3, -2. 142. а)
о | 7 9
-оо; 1— ; б) [-1,5;+°о); в) -оо; 2—
7 J \ о
276
r) f И; +oo). 143. а) (-со; -1); б) (-ос; -3]; в) [-∣J ÷∞) r) (-∞! 1>∙
\ 25 / &
144. a) q > 6∣, q = 7; б) q < 12∣, q = 12. 145. а) а > -3; б) а > -•
146. а)р = 4; б) ⅛ = 16. 147. а) (-2; -1); б) (-«; -4] и [3; +~); в) (-∞! 3) и
и (4; +оо); г) [-1; 4]. 148. a) (-∞! 0,5] и [4; +~); б) [-1; в) [θJ 1].
Г) (-оо; -0,5) и (1; +∞). 152. а) (-<
г) (-°0; 0) u (2; +∞). 153. а) (-°°;
и (-3; +оо); г) [-7; -4]. 154. a) (-°c
»; 0] и [3; +°°); б) (-2; 2); в) [-6; 6];
3] и [5; +°о); б) (4; 5); в) (-∞! -4) и
,. -4) ⅛j (“4; +оо); б) чишелешләре юк;
в) оо; +оо); г) х = 1. 155. а) [-3; 0) и (0; 0,5]; б) (-
-2,5) и
и (-2,5; -2] и
в) [-2; 0)
—оо; -1- и[3; 3,5) и
3 _
и (3,5; +<×>). 156. а) [-4; +~); б) (-∞! -0,2) и (0,5; +°°); в) (6; +∞)j
г) [-2; 5]. 157. a) k < -10 һәм k > 10; б) k ≤ -6 һәм Һ > 3; в) -6 < k < 6;
г) -4 ≤ k < 12. 158. а) 7 см дан зуррак; б) 10 см дан зуррак.
КУШЫМТА, ∏.l. а) 3; б) 7; в) 5; г) 2. П.2, а) 2; б) 0; в) 0,7; г) 0,3.
П.З.
t
-6
-5
-4
-3
-2
-1
0
1
2
3
Вакланма
2
2,5
4
—
-2
-0,5
0
0,25
0,4
—
а) 0,2; б) 0,4; в) 0,7. П.4, а) икенең; б) -1,5; -1; -0,25; 1,25; 1,4; 2; 3;
3,5; в) мода 8, киңлеге 5; г) 45" лы 8 сектор. П.5, а) 13, 19, 97, 103;
б) 8; в) 3,25, 4,25, 9,7, 10,3; г) -3,25. П.6, а) | б) 0,5. П.7, а) 0,5;
б) 0,25; в) 0,125. П.9, б) 16; в) 4; г) 9. П.10, б) 6; в) 0; г) 0,75. П.11, а) 3;
в) 12; г) 4. П.12, а) 4; в) 12; г) 8. П.13, б) 6; в) 12; г) 6. П.14, а) 8; б) 0,25;
в) 0,25; г) 0,875.
П.15.
в) 0,5; г) 0,33. П.18, а) 20; б) 10; в) 6; г) 8. П.19, а) 40; б) 16; в) 4; г) 14.
П.20, a) AHGFE; 6)AHGFE, AHOFE, AHODE; в) 3; г) 6. П.21, а) 3; б) 12;
277
в) 10; г) 8. П.22, а) 1; б) 2; в) 4; г) 6. П.23, а) 5; б) 8; в) 3; г) 4. П.24, а) 8; б) 4;
в) 2. П.25, б) 9; в) 6; г) 18. П.26, а) 0; б) 0,8; в) 0,8; г) 0,6. П.27, а) 0;
б) 1; в) 0,2; г) 0,4. П.28, а) 1; б) 0,1; в) 1; г) 0,6. П.29, а) 1;
б) 0,4; в) 0,3; г) 0,15. П.30, а) 1; б) 6; в) 4; г) 10. П.31, б)
6; в) 2; г) 3. П.32, б) 9; в) 2; г) 4. П.ЗЗ. а) 4; б) 9; в) 6; г) 3.
П.34.
Тигезләмә
№1
№2
№3
№4
№5
№6
№7
№8
№9
№ 10
D
1
-7
0
12
-7
4
-15
73
0
9
а) 30%; б) 20%; в) 70%.
П.35, а)
2 тамыры булган
тигезләмәләр саны
1 тамыры булган
тигезләмәләр саны
Тамырлары булмаган
тигезләмәләр саны
W W / и
/ 6
/// 3
б) 20; в) 15%. П.36, б) 50; в) 10; г) 5. П.37, а) 1; б) 0,6; в) 0,2; г) 0,4.
П.38, а) 27; б) 3; в) 3; г) 12. П.39, б) 21; в) 99; г) —. П.4О. а) 50; б) 300.
9
П.41, а) 25; б) 10; в) 10; г) 3. П.42, б) 12; в) 3; г) 6. П.43, б) 18; в) -;
г) —. П.44, б) 20; в) 0,6; г) 0,4. П.45, а) 0,5; б) 0,35; в) 0,2; г) 0,6.
18
П.46, а) 0,2; б) 0,8; в) 0,6; г) 0,6. П.47, а) 0,3; б) 0,3; в) 0,7; г) 0,6.
П.48, а) 0,95; б) 0,55; в) 0,7; г) 0,1.
П.49, а) 81; б)
Сан квадратының беренче
цифры
1
2
3
4
5
6
7
8
9
Ничә тапкыр очрады
16
12
10
8
9
7
8
5
6
в) |; г) ||. П.50, а) 4; б) 2; в) 8; г) 20.
ЭЧТӘЛЕК
Укытучы өчен кереш сүз 3
Кабатлауга мәсьәләләр 5
1 бүлек. АЛГЕБРАИК ВАКЛАНМАЛАР
§ 1. Төп төшенчәләр 13
§ 2. Алгебраик вакланманың төп үзлеге 19
§ 3. Ваклаучылары бертөрле булган
алгебраик вакланмаларны кушу һәм алу 27
§ 4. Ваклаучылары төрле булган
алгебраик вакланмаларны кушу һәм алу 31
§ 5. Алгебраик вакланмаларны тапкырлау һәм бүлү.
Алгебраик вакланманы дәрәҗәгә күтәрү 39
§ 6. Рациональ аңлатмаларны рәвешүзгәртү 46
§ 7. Рациональ тигезләмәләр турында беренче төшенчәләр ... 50
§ 8. Тискәре бөтен күрсәткечле дәрәҗә 56
Өй контроль эше № 1 59
2 бүлек, у = √x ФУНКЦИЯСЕ. КВАДРАТ ТАМЫРНЫҢ ҮЗЛЕКЛӘРЕ
§ 9. Рациональ саннар 62
§10. Тискәре булмаган саннан квадрат тамыр төшенчәсе 65
§11. Иррациональ саннар 70
§12. Реаль саннар күплеге 71
§ 13. у = y∣χ функциясе, аның үзлекләре һәм графигы 74
§14. Квадрат тамырның үзлекләре 79
§15. Квадрат тамыр алу операциясе кергән
аңлатмаларның рәвешен үзгәртү 83
§16. Реаль санның модуле 97
Өй контроль эше № 2 102
279
3 бү лек. КВАДРАТИК ФУНКЦИЯ, у = - ФУНКЦИЯСЕ
§ 17. у = kx2 функциясе, аның үзлекләре һәм графигы 105
∣i
§ 18. у = — функциясе, аның үзлекләре һәм графигы 117
§ 19. Әгәр у = f(x) функциясенең графигы билгеле булса,
у = f(x + Z) функциясенең графигын ничек төзергә 123
§ 20. Әгәр у = f(x) функциясенең графигы билгеле булса,
у = f(x) + т функциясенең графигын ничек төзергә 132
§21. Әгәр у = f(x) функциясенең графигы билгеле булса,
у = f(x + I) + т функциясенең графигын ничек төзергә .. .141
§ 22. у = ах2 + Ъх + с функциясе, аның үзлекләре һәм графигы . 147
§ 23. Квадрат тигезләмәләрне график юл белән чишү 153
Өй контроль эше №3 155
4 бүлек. КВАДРАТ ТИГЕЗЛӘМӘЛӘР
§ 24. Төп төшенчәләр 157
§ 25. Квадрат тигезләмәләрнең тамырлары формулалары 162
§26. Рациональ тигезләмәләр 167
§27. Реаль хәлләрнең математик модельләре буларак
рациональ тигезләмәләр 171
§ 28. Квадрат тигезләмә тамырларының тагын бер формуласы. .177
§ 29. Виет теоремасы 181
§ 30*.Иррациональ тигезләмәләр 187
Өй контроль эше №4 191
5 бү лек. ТИГЕЗСЕЗЛЕКЛӘР
§31. Санлы тигезсезлекләрнең үзлекләре 193
§ 32. Функцияләрне монотонлыкка тикшерү 200
§ 33. Сызыкча тигезсезлекләрне чишү 203
§ 34. Квадрат тигезсезлекләрне чишү 207
§ 35. Реаль саннарның якынча кыйммәтләре 212
§ 36. Санның стандарт рәвеше 213
Өй контроль эше №5 215
6 бүлек. ЙОМГАКЛАУ 217
Кушымта 240
Җаваплар 255
280
ИКЕУРЫНЛЫ САННАРНЫҢ КВАДРАТЛАРЫ ТАБЛИЦАСЫ
0
1
2
3
4
5
6
7
8
9
1
121
144
169
196
225
256
289
324
361 '
2
441
484
529
576
625
676
729
784
841
3
961
1024
1089
1156
1225
1296
1369
1444
1521
4
1681
1764
1849
1936 2025
2116
2209
2304
2401
5
2601
2704
2809
2916
3025
3136
3249
3364
3481
6
3721
3844
3969
4096
4225
4356
4489
4624
4761
11
7
5041
5184
5329
5476
5625
5776
5929
6084 6241
1
8
6561
6724
6889
7056
7225
7396
7569
7744
1
•
7921
9
8281
8464
8649
[_^—j
8836
9025
9216
9409
р !
9604 9801
L_ 1—
Алгебра
2 КИСӘК
ӘСЬӘЛЭЛӘР ҖЫЕНТЫГЫ