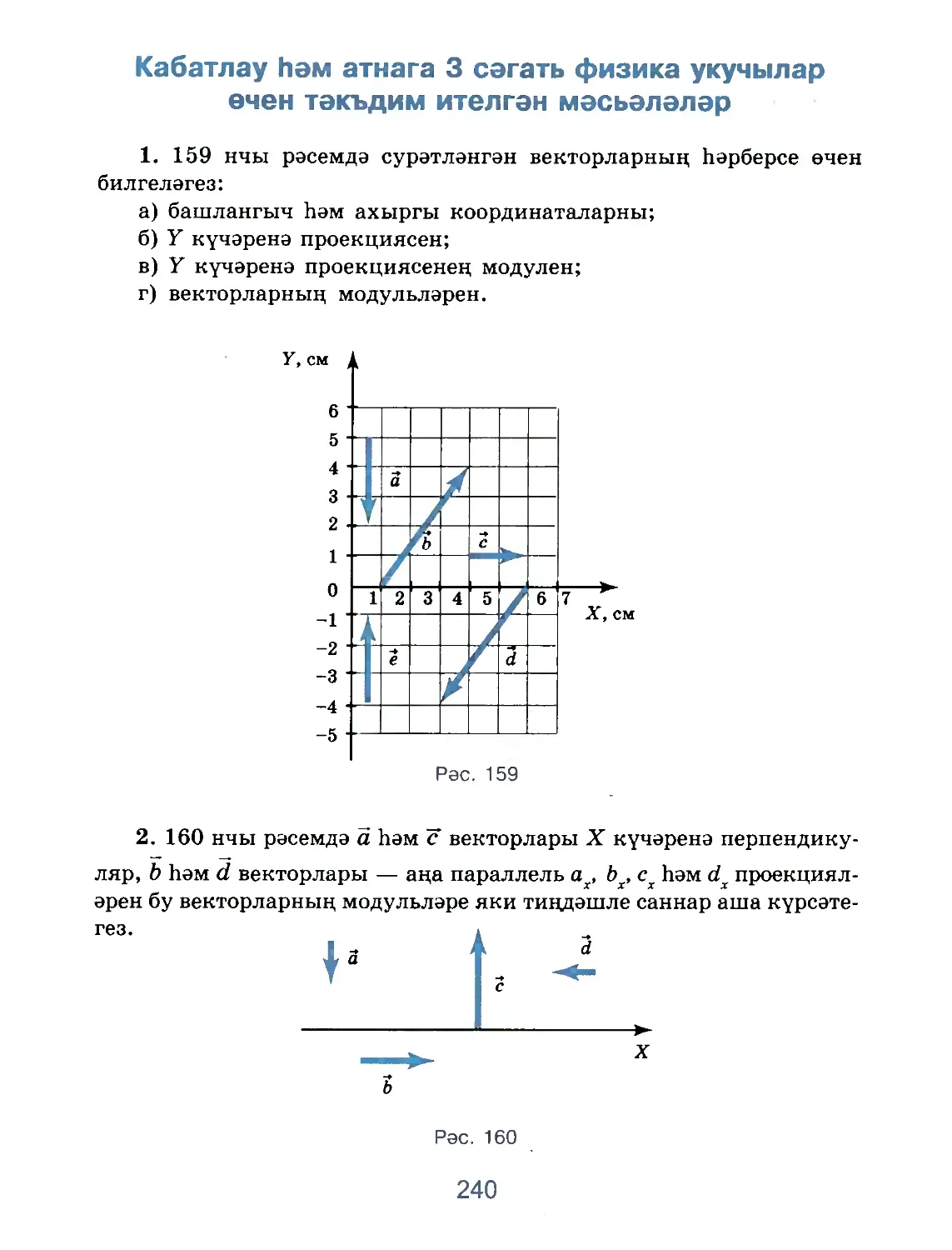
Text
А. В. Перышкин, Е.М.Гутник
ФИЗИКА
СЫЙНЫФ
ТАТАР ГОМУМИ УРТА БЕЛЕМ
МӘКТӘПЛӘРЕ ӨЧЕН ДӘРЕСЛЕК
Россия Федерациясе Мәгариф министрлыгы
тарафыннан рөхсәт ителгән
Тәрҗемә Татарстан Республикасы
Мәгариф министрлыгы тарафыннан расланган
врофа
Москва
2003
ТаРИХ
Казан
2003
УДК 373.167.1:53
ББК 22.3я72
П27
Перышкин А. В., Гутник Е. М.
Физика. 9 кл.
Учеб, для общеобразоват. учреждений. — 6-е изд., стереотип.
Москва, Дрофа, 2003
Перышкин А. В., Гутник Е. М.
П27 Физика. 9 сыйныф.: Татар гомуми белем мәкт. өчен д-лек / Русчадан
Р. С. Вафина тәрҗ. — Казан: ТаРИХ, 2003. — 256 б., рәс. б-н.
ISBN 5-94113-168-2 (ТаРИХ)
ISBN 5-7107-7916-4 (Дрофа)
Әлеге китап А. В. Перышкинның «Физика. 7 сыйныф», «Физика. 8 сыйныф» дәреслекл-
әренең дәвамы булып тора. Ул төп мәктәпнең физика курсын төгәлли һәм төп белем минимумы
таләпләренә туры килә.
Дәреслеккә түбәндәге төп бүлекләр керә: «Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт
законнары», «Механик тирбәнешләр һәм дулкыннар. Тавыш», «Электромагнитик кыр», «Атом
һәм атом төшенең төзелеше. Атом төше энергиясен куллану».
Китапта танылган педагог һәм методист Александр Васильевич Перышкин материалла¬
ры файдаланылды. Дәреслек ачык, кыска һәм аңлаешлы төзелеше белән аерылып тора.
7 һәм 8 нче сыйныфларда алынган белемнәр нигезендә материал югарырак дәрәҗәдә өйрәтелә.
Җентекләп аңлатылган һәм рәсемнәр ярдәмендә күрсәтелгән демонстрацион тәҗрибәләр,
физиканың хәзерге программасы тәкъдим иткән мәсьәләләр шулай ук яңа дәреслекнең
өстенлеге булып тора.
Дәреслек Федераль экспертлар советы тарафыннан югары бәяләнде һәм Россия Федераци¬
ясе Мәгариф министрлыгы тарафыннан тәкъдим ителде. Дәреслекләрнең Федераль комплек¬
тына кертелде.
Учебное издание
Перышкин Александр Васильевич, Гутник Елена Моисеевна
ФИЗИКА
9 класс
Учебник для татарских общеобразовательных учреждений
(перевод с русского на татарский язык)
Редакторы Г. Нуретдинова. Компьютерда биткә салучысы 3. Мадьярова
Корректоры Л. Фазуллина
Нәшриятка 184 нче номерлы лицензия 16.04.1997 бирелде. Оригинал-макеттан басарга кул
куелды 25.08.03. Тиражы 18100 д. Заказ № 0316100.
Татарское Республиканское издательство «Хәтер» (ТаРИХ)
420014, Казань, Кремль, а/я 54.
ООО «Дрофа», 127018, Москва, Сущевский вал, 49.
Отпечатано в полном соответствии с качеством предоставленных
диапозитивов в ОАО «Ярославский полиграфкомбинат»
150049, Ярославль, ул. Свободы, 97.
ISBN 5-94113-168-2 (ТаРИХ) ∣⅜∏g⅝^∣ © θOO «Дрофа», 2003
ISBN 5-7107-7916-4 (Дрофа) ” © Татарчага тәрҗемә, ТаРИХ, 2003
КЕРЕШ
Сез бу уку елында төп мәктәп физика курсының иң соңгы тема¬
ларын өйрәнәчәксез.
9 нчы сыйныфта сезгә, яңа белемнәр алу белән беррәттән, алган
белемнәрне киңәйтергә һәм тирәнтенрәк өйрәнергә туры килер.
«Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары» дигән
беренче бүлекне өйрәнгәндә, сез алган белемнәрегезгә бигрәк тә еш
мөрәҗәгать итәрсез.
Беренче карашка, бу бүлектә сез инде 7 нче сыйныф физика¬
сында өйрәнгән сораулар урын алган кебек. Мәсәлән, механик хәрәкәт
һәм аның чагыштырма булуы, инерция законы, җисемнәрнең үзара
тәэсир итешүе һәм аларның тизлекләре үзгәрүгә сәбәпче буларак —
көч, бөтендөнья тартылуы һәм башкалар шундыйлардан.
Ә чынлыкта исә бу бүлекнең материалы, сезнең белемнәрегезне
киңәйтеп, аларны тагын да югарырак яңа баскычка — законнар бас¬
кычына күтәрә. Мәсәлән, сез 7 нче сыйныфта тигез хәрәкәтне
өйрәнгән булсагыз, 9 нчы сыйныфта тигез булмаган хәрәкәтне
өйрәнергә керешәчәксез (элек аның турында искә генә алынды).
Бу темага бәйләп, сез бик мөһим физик зурлык — тизләнеш
белән танышырсыз, аның барлыкка килүенә нәрсә сәбәп булуын
белерсез, җисемнәрнең ни өчен кайвакыт туры сызык буйлап хәрәкәт
итүен һәм башка бик күп күренешләрне аңларсыз.
Шулай ук механиканың иң төп нигезе — Ньютонның өч зако¬
ны белән, импульс саклану законы, бөтендөнья тартылу законы белән
танышырсыз һәм аларны әйләнә-тирәдә бара торган төрле күренеш¬
ләрне аңлату өчен кулланырга өйрәнерсез.
Бу бүлекне уңышлы үзләштерү өчен, сезгә вектор зурлыклар,
аларның проекцияләре һәм модульләре турында элементар төшен¬
чәләр кирәк булыр. Аларны сез геометрия дәресләрендә өйрәнгән
идегез.
Сезгә боларны геометрия дәреслекләре буенча кабатлау кирәк
булмас, чөнки кирәкле математик материал, кыска һәм аңлаешлы
3
Кереш
формада, физика дәреслегенең шул параграфында урнаштырылган.
Шуңа күрә һәрбер укучы бу теманы үзләштерә ала.
Әмма мәсьәләләр чишкәндә хаталар килеп чыкмасын өчен, сезгә
векторларның, аларның модульләренең һәм тиешле күчәргә бул¬
ган проекцияләренең билгеләнешен, кайсы очракта проекциянең —
уңай, ә кайсында тискәре дип саналуын тиз арада һәм ныклап истә
калдырырга кирәк. Шулай ук мәсьәлә чишү үрнәкләрен дә игъти¬
бар белән өйрәнегез.
Икенче, өченче һәм дүртенче бүлекләрдә, нигездә, сезнең өчен
гадәти булган математик исәпләүләр кулланыла.
Беренче бүлектә өйрәнгән белемнәрегез калган өч бүлек матери¬
алын үзләштерү өчен дә кирәк булыр. Мәсәлән, тизләнеш турында¬
гы мәгълүмат механик тирбәнешләр һәм алмаш электр тогы, элек-
тромагнитик кырның барлыкка килүе һәм электромагнитик дул¬
кыннарның нурланышы кебек әһәмиятле күренешләрне өйрәнергә
ярдәм итәр.
Ньютонның икенче һәм өченче законнарын белү сезгә матдә
атомының төзелешен өйрәнү буенча ясалган тәҗрибәләрне аңларга
булышыр. Ә инде импульс саклану законы ярдәмендә сез, мәсәлән,
атом төше бүленгәндә кисәкчекләрнең ни өчен төрле якка таралу¬
ларын аңлата алырсыз.
Шулай итеп, алда санап үтелгән законнарның механикада гына
түгел, физиканың башка бүлекләрендә дә кулланыла алуына конк¬
рет мисалларда ышанырсыз.
I бүлек
ҖИСЕМНӘРНЕҢ ҮЗАРА ТӘЭСИР ИТЕШҮ
[ҺӘМ ХӘРӘКӘТ ЗАКОННАРЫ
§ 1. Материаль нокта.
Ис®[П] системасы
Безне чолгап алган дөньяда һәрнәрсә өзлексез хәрәкәт итә.
Хәрәкәт, гомумән алганда, табигатьтәге теләсә нинди үзгәреш ул.
Механик хәрәкәт — хәрәкәтнең иң гади төре булып санала.
7 нче сыйныфның физика курсыннан белгәнегезчә, җисрЗпнең
вакыт узу белән башка җисемнәргә карата пространствода уры¬
нын үзгәртүе аның механик хәрәкәте дип атала.
Җисемнәрнең механик хәрәкәте белән бәйле булган төрле фәнни
һәм гамәли мәсьәләләр чишкәндә, бу хәрәкәтне сурәтли белергә, ягъни
теләсә кайсы вакыт мизгелендә җисемнең торышын, хәрәкәтнең
траекториясен, тизлеген, үтелгән юлын һәм башкаларны билгели
белергә кирәк.
Мәсәлән, Җирдән башка бер планетага оч¬
кыч аппарат җибәргәнче, галимнәр бу плане¬
таның очкыч килеп төшкән мизгелдә Җиргә
карата кайда булачагын исәпләргә тиешләр.
Ә моның өчен вакыт узу белән әлеге планета¬
ның юнәлеше һәм тизлек модуле ничек үзгә¬
рүен һәм нинди траектория буенча хәрәкәт
итүен ачыклыйлар.
Математика курсыннан белгәнегезчә, нок¬
таның торышын координаталар турысы яки
турыпочмаклы координаталар системасы (рәс.
1) белән бирергә мөмкин. Ә менә үлчәмнәре
булган җисемнең торышын ничек бирергә?
5
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Чөнки бу җисемнең һәр ноктасы үз координатасы белән билгеләнә.
Үлчәмнәре булган җисемнең хәрәкәтен сурәтләгәндә башка сорау¬
лар да туа. Мәсәлән, пространствода күчеп йөрүче җисем шул вакытта
үз күчәре тирәсендә дә әйләнсә, аның тизлеге нинди булыр? Чөнки
җисемнең төрле нокталарының тизлекләре модуле буенча да, юнәле¬
ше буенча да бер төрле үк булмый. Мәсәлән, Җирнең тәүлеклек әйләнүе
вакытында аның диаметраль капма-каршы нокталары капма-каршы
юнәлештә хәрәкәт итәләр, ә инде күчәргә якынрак урнашкан нокта¬
ның тизлеге кимрәк була.
Үлчәмнәре булган җисем хәрәкәтенең координатасын, тизлеген
һәм башка характеристикаларын ничек итеп бирергә соң? Моның
өчен бик күп очракларда реаль җисемнең хәрәкәте урынына мате¬
риаль ноктаның, ягъни бу җисем массасына ия булган ноктаның
хәрәкәтен тикшерү кабул ителгән.
Материаль нокта өчен координата, тизлек һәм башка физик зур¬
лыкларны төгәл билгеләргә мөмкин, чөнки ул үз күчәре тирәсендә
әйләнә алмый һәм аның үлчәмнәре дә юк.
Табигатьтә материаль нокталар юк. Материаль нокта — бик күп
мәсьәләләр чишүне гадиләштерергә һәм шул ук вакытта җитәрлек
төгәл нәтиҗәләр алырга мөмкинлек бирүче төшенчә ул.
Җисемнең үлчәмнәрен (димәк, формасын һәм әйләнүен дә) исәпкә
алмаслык булган очракларда гына аны материаль нокта дип санар¬
га мөмкин, чөнки әлеге мәсьәләне чишү шартларында зур әһәми¬
яткә ия түгел.
Җисемнең нокталары уза торган аралар аңың үлчәмнәре белән
чагыштырганда бик күпкә зур булган очракларда һәр җисемне дә
диярлек материаль нокта дип исәпләргә була.
Мәсәлән, Кояш тирәсендәге хәрәкәтләрен өйрәнгәндә, Җирне һәм
башка планеталарны материаль нокталар дип саныйлар. Бу очрак¬
та тәүлеклек әйләнеше нәтиҗәсендә планеталардагы төрле нокта¬
ларның хәрәкәтләрендәге аерымлыклар еллык хәрәкәтне сурәтләү¬
че зурлыкларга тәэсир итми.
Ләкин планетаның тәүлеклек әйләнеше белән бәйләнгән мәсьәлә¬
ләрне (мәсәлән, Җир шарының төрле урыннарында Кояш чыгу, вакы¬
тын билгеләгәндә) чишкәндә, планетаны материаль нокта дип санау
мәгънәсез булыр иде, чөнки мәсьәләнең җавабы бу планетаның
үлчәмнәренә һәм үз өслегендәге нокталарның хәрәкәт тизлегенә бәйле.
6
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Әгәр, мәсәлән, Мәскәүдән Новосибирски-
га очучы самолетның уртача тизлеген исәп¬
ләргә кирәк булса, самолетны материаль нок¬
та дип исәпләү урынлы булачак. Ә инде очып
баручы самолетка тәэсир итүче һаваның кар¬
шылык көчен исәпләгәндә, самолет — мате¬
риаль нокта түгел, чөнки каршылык көче
аның үлчәмнәренә һәм формасына бәйле.
Еш кына, җисемнең үлчәмнәрен ул үткән
юл белән чагыштырырга мөмкин булганда да,
Рәс. 2
хәрәкәт итүче җисемне материаль нокта дип кабул итәләр. Мәсәлән, та¬
мызгыч куелган кечкенә арбаның (рәс. 2) барлык нокталары да (көпчәк
нокталарыннан тыш) теләсә кайсы вакыт мизгелендә бертөрле
хәрәкәт итәләр. Мондый хәрәкәт йөреш1 хәрәкәте дип атала. Шуңа
күрә, арбаның хәрәкәтен сурәтләргә (ягъни вакыт узу белән тизлекнең,
юлның һ.б. ничек үзгәрүен билгеләргә) кирәк булса, аның бер генә нокта¬
сын тикшерү дә җитә. Шунлыктан мәсьәләне чишү дә гадиләшә.
Тикшерелә торган мәсьәлә шартларында җисемнец үлчәмнәрен
исәпкә алмаслык булса, ул материаль нокта дип атала.
Турысызыклы хәрәкәте вакытында җисемнең торышын билгеләү
өчен бер генә координаталар күчәре дә җитә.
Моны тамызгыч куелган арба мисалында аңлатыйк (рәс. 2). Арба
блок аша уздырылган җепнең бер очына бәйләнгән. Җепнең икен¬
че очына йөк эленгән. Җепне тартучы әлеге йөкнең авырлыгы тәэ¬
сирендә, арба өстәл буенча турысызыклы хәрәкәт итә.
Арбаның хәрәкәт траекториясе буйлап, аның торышын бил¬
геләргә мөмкинлек бирүче линейка урнаштырылган (бу очракта арба
белән тамызгычны, йөреш хәрәкәте ясаганлыктан, материаль нокта
дип санарга мөмкин). Бу тәҗрибәдә линейканы исәпләү җисеме дип,
ә аның шкаласын координаталар күчәре дип кабул итү уңайлы.
(Исегезгә төшерәбез, исәпләү җисеме дип пространствода бу җисемгә
1 Турысызыклы хәрәкәт тә, кәкресызыклы хәрәкәт тә йөреш хәрәкәте
була ала. Мәсәлән, күзәтү тәгәрмәченең кабинасы йөреш хәрәкәте ясый.
Йөреш хәрәкәтенең төп билгесе булып, бу җисемнең ике ирекле ноктасы
аша үтә дип уйланылган теләсә нинди турының беренче юнәлешкә парал¬
лель булып калуы тора.
7
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
карата башкаларының торышы үзгәрүне билгеләү җисеме атала.)
Арба белән тамызгычның торышы линейканың нуль бүлеменә ка¬
рата билгеләнә.
Ә инде без арбаның ниндидер вакыт аралыгында үткән юлын,
яки аның хәрәкәт тизлеген исәпләргә теләсәк, безгә линейкадан тыш,
вакыт үлчәү приборы — сәгать тә кирәк булачак.
Бу очракта әлеге прибор ролен тамызгыч үти: аңардан тигез вакыт
аралыкларында тамчылар тамып бара. Кранны боргалап, тамчылар¬
ның, мәсәлән, 1 с интервал белән тамуына ирешергә мөмкин. Линейка¬
да тамчы эзләре арасының санын белеп, вакытны билгеләргә була.
Алдагы мисаллардан күренгәнчә, хәрәкәт итүче җисемнең теләсә
кайсы вакыт мизгелендәге торышын, хәрәкәт төрен, җисемнең
тизлеген һәм хәрәкәтнең башка характеристикаларын белү өчен,
исәпләүләр җисеме, аның белән бәйләнгән координаталар систе¬
масы (яки, җисем туры буенча хәрәкәт итсә, бер координаталар
күчәре) һәм вакыт исәпләү приборы кирәк.
Координаталар системасы, аныц белән бәйләнгән исәпләү
җисеме һәм вакыт үлчәү приборы исәп системасын төзиләр,
һәм җисемнең хәрәкәте шул системага карата тикшерелә.
Билгеле, күп кенә очракларда без хәрәкәт итүче җисемнең
теләсә кайсы вакыт мизгелендә координаталарын турыдан-туры
үлчи алмыйбыз. Мәсәлән, хәрәкәт итүче автомобильнең, океанда
йөзүче лайнерның, очып баручы самолетның, артиллерия пушка¬
сыннан чыккан снарядның, үзебез күзәтә торган төрле күк җи¬
семнәренең һ.б. бик зур араларга сузылган юлына үлчәү линей¬
касы салып кую яки сәгать тоткан күзәтүчеләр бастырып тору
берәүнең дә кулыннан килми.
Шулай да физика законнарын белү — төрле исәп системала¬
рында, аерым алганда Җир белән бәйле системаларда хәрәкәт итүче
җисемнәрнең координаталарын билгеләргә мөмкинлек бирә.
? Сораулар
1. Материаль ноктаның массасы буламы? Аның үлчәмнәре буламы?
2. Материаль нокта нәрсә ул — реаль объектмы, әллә абст¬
ракт төшенчәме?
8
/ бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
3. «Материаль нокта» төшенчәсе нинди максатларда кулла¬
ныла?
4. Гадәттә нинди очракларда хәрәкәт итүче җисемне матери¬
аль нокта буларак тикшерәләр?
5. Мисал китерегез: кайчан бер үк җисемне бер очракта мате¬
риаль нокта дип санарга була, ә икенче очракта булмый?
6. Нинди хәрәкәте вакытында җисемне, аның үткән юлы белән
үлчәмнәре чагыштырырлык дәрәҗәдә булса да, материаль нокта
дип карарга мөмкин?
7. Нәрсәне материаль нокта дип атыйлар?
8. Нинди очракта хәрәкәт итүче җисемнең торышын бер коор-
динаталар күчәре белән билгеләргә мөмкин?
9. Исәп системасы дип нәрсәгә әйтәләр?
$ 1 нче күнегү
1. Автомобильне материаль нокта дип әйтеп буламы: ул 2 сәгатьтә
уртача 80 км/сәг тизлек белән хәрәкәт иткән юлның озынлыгын
исәпләгәндә? Ул икенче автомобильне узып киткәндә?
2. Самолет Мәскәүдән Владивостокка оча. Хәрәкәтне күзәтүче
диспетчер; самолеттагы пассажир самолетны материаль нокта дип
саный аламы?
3. Машинаның, поездның яки башка транспорт чарасының тиз¬
леге турында сөйләгәндә гадәттә исәпләү җисемен күрсәтмиләр. Бу
очракта исәпләү җисеме буларак нәрсә күз алдында тотыла?
4. Малай, җирдән торып, сеңлесенең карусельдә әйләнүен күзәтә.
Карусельдән төшкәч, сеңлесе өйләрнең дә, агачларның да, малай¬
ның да аның яныннан тиз-тиз узып китүләре турында сөйли. Ма¬
лай исә үзенең өйләр һәм агачлар белән хәрәкәтсез торуын, ә сең¬
лесенең хәрәкәт итүен аңлата. Малай һәм кыз хәрәкәтне нинди
исәпләү җисемнәренә карата күзәткәннәр? Бәхәстә кемнең хаклы
икәнен аңлатыгыз.
5. Бу очракларда хәрәкәт нинди исәпләү җисеменә карата тик¬
шерелә: а) җилнең тизлеге 5 м/с; б) бүрәнә елга агымы уңаена йөзә,
шуңа күрә аның тизлеге нульгә тигез; в) елга буйлап агучы бүрәнәнең
тизлеге елганың агымы тизлегенә тигез; г) хәрәкәт итүче велосипед
көпчәгенең теләсә кайсы ноктасы әйләнә ясый; д) Кояш иртән көнчы¬
гыштан чыга, көн буе күк йөзе буйлап хәрәкәт итә һәм кич көнба¬
тышта бата.
9
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
§ 2. Күчеш
Җисемнәрнең хәрәкәтенә карата мәсьәләләрнең бик күбендә
без моңарчы «юл» дип аталучы физик зурлык белән эш иттек.
Җисемнең билгеле бер вакыт аралыгында үткән траектория¬
сенең барлык бүлемтекләре суммасын юлның озынлыгы дип ал¬
дык.
Юл — скаляр зурлык (ягъни юнәлеше булмаган зурлык).
Кеше эшчәнлегенең төрле сфераларында (мәсәлән, җир өсте
һәм һава транспортының диспетчерлар хезмәтендә, космонавти¬
када, астрономиядә һ.б.) төрле гамәли мәсьәләләрне чишү өчен,
вакытның билгеле бер мизгелендә хәрәкәт итүче җисемнең кай¬
да булырга тиешлеген исәпләргә кирәк була.
Күп кенә очракларда, хәтта җисемнең бу вакыт эчендә күпме
юл үтүен белсәк тә, мондый мәсьәләне чишеп булмавына игъти¬
бар итик. Моның өчен 3 нче а рәсемен карыйбыз.
Әйтик, безгә ниндидер җисемнең (аны материаль нокта дип
алырга мөмкин) О ноктасыннан башлап хәрәкәт итүе һәм 1 сә¬
гатьтә 20 км юл үтүе билгеле, ди.
О ноктасыннан чыгып 1 сәг үткәч, җисемнең кайда булуын
билгеләү өчен, безгә аның хәрәкәте турында мәгълүмат җитми.
Җисем, мәсәлән, төньяк юнәлешендә турысызыклы хәрәкәт итеп,
О ноктасыннан 20 км ераклыктагы А ноктасына эләгергә мөмкин
(нокталар арасындагы ераклык аларны тоташтыручы туры буен¬
10
I булек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
ча үлчәнә). Шулай ук ул, О ноктасыннан 10 км ераклыктагы В
га җиткәч, көньякка борылып кире О ноктасына кайтырга да
мөмкин, аның үткән юлы бу вакытта да 20 км га тигез. Туры
сызык буенча көньяк-көнчыгышка таба — С ноктасына, ә рәсем¬
дәге кәкресызыклы траектория буенча D ноктасына барганда да
ул шулкадәр үк\юл үтәр иде.
Бирелгән вакыт мизгелендә җисемнең пространстводагы то¬
рышын исәпләү өчен кертелгән күчеш дигән физик зурлык әлеге
аныксызлыкны ачыкларга ярдәм итә.
Җисемнең башлангыч торышын аның соңгы торышы белән
тоташтыручы вектор зңисемнең (материаль ноктаның)
күчеше дип атала.
Билгеләмә буенча күчеш — вектор зурлык (ягъни юнәлешле
зурлык). Ул юл шикелле үк, ләкин өстенә ук куелган хәреф s
белән тамгалана. Юл кебек үк, СШда күчеш метрларда үлчәнә.
Күчешне үлчәү өчен башка озынлык берәмлекләре дә, мәсәлән
километр, миль һ.б. кулланыла.
3 нче б рәсемдә 20 км юлны төрлечә узган җисемнең күчеш
векторлары күрсәтелгән: төньякка таба турысызыклы ОА траек¬
ториясе буенча ( soa векторы); көньяк-көнчыгышка таба турысы¬
зыклы ОС траекториясе буенча ( soc векторы); кәкресызыклы OD
траекториясе буенча ( sod векторы). Ә инде В ноктасына барып,
кире кайту өчен 20 км юл узганда, җисемнең күчеш векторы
нульгә тигез була.
Күчеш векторын белү — аның юнәлешен һәм модулен белү
дигән сүз.
Башлангыч торышын һәм күчеш векторын белгәннән соң, җи¬
семнең торышын төгәл билгеләргә мөмкин. Мәсәлән, О ноктасын¬
нан чыккан җисемнең күчеш векторы төньякка юнәлгән һәм аның
1 Исегезгә төшерәбез, СИда (Халыкара берәмлекләр системасында) ки¬
лограмм (кг) массаның төп, ягъни ирекле сайлап алынган берәмлеге бу¬
лып тора, озынлыкныкы — метр (м), вакытныкы — секунд (с). Төп берәм¬
лекләр аша аңлатылганнары чыгарылма берәмлекләр дип атала. СИда
чыгарылма берәмлеккә мисал итеп 1 м/с, 1 кг/м3 һ.б. күрсәтергә була.
11
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
модуле 20 км икәне билгеле булса, без җисемнең А ноктасында
икәнлеген ышанып әйтә алабыз (рәс. 3, б).
Шулай итеп, күчеш сызымда озынлыгы һәм юнәлеше күр¬
сәтелгән ук рәвешендә бирелсә, күчеш векторын башлангыч
торышка куеп, җисемнең соңгы торышын табарга мөмкин.
? Сораулар
1. Җисемнең башлангыч торышын (£о=О) һәм t вакыт аралы¬
гында үткән юлын белгәндә, аның t вакыт мизгелендәге торышын
һәрвакытта да билгеләп буламы? Җавапны мисаллар белән нигез¬
ләгез.
2. Җисемнең (материаль ноктаның) күчеше дип нәрсә атала?
3. Җисемнең башлангыч торышын (fo=O) һәм t вакыт аралы¬
гында күчеш векторын белгәннән соң, аның t вакыт мизгелендәге
торышын төгәл билгеләп буламы? Җавапны мисаллар белән нигез¬
ләгез.
$ 2 нче күнегү
1. Машина йөртүче спидометр буенча нинди физик зурлыкны
билгели: үткән юлнымы яки күчешнеме?
2. Машинаның спидометры буенча билгеле бер вакыттагы күчеш
модулен билгеләп булсын өчен, ул бу вакыт эчендә ничек хәрәкәт
итәргә тиеш?
§ 3. Хәрәкәт итүче җисемнең
координаталарын билгеләү
Алдагы параграфта беркадәр күчеш ясаган җисемнең торы¬
шын, күчеш векторын башлангыч торышка куеп, график юл белән
табу мөмкинлеге турында сөйләгән идек инде. Әмма күпчелек оч¬
ракларда җисемнең торышын исәпләргә, ягъни аның координа¬
таларын табарга кирәк була.
Геометрия курсыннан белгәнебезчә, исәпләүләрне векторлар
белән түгел, ә аларга тиңдәш скаляр зурлыклар — векторларның
координата күчәрләренә проекцияләре һәм вектор модульләре яки
12
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
аларның проекцияләре (ягъни юнәлешсез зурлыклар — уңай яки
тискәре саннар) белән эшлиләр.
Башлангыч торышының координатасы һәм күчеш векторы
билгеле булган хәрәкәт итүче җисемнең координатасын исәплик.
Моның өчен бер мәсьәлә чишәрбез.
Ике катер елгада капма-каршы юнәлештә хәрәкәт итә, һәм
алар П пристаненнан көнчыгышка таба 100 км да очрашалар
(рәс. 4). Хәрәкәтләрен дәвам итеп, берсе t вакыт эчендә очрашу
урыныннан көнчыгышка таба — 60 км га, ә икенчесе көнбатыш¬
ка таба 50 км га күчә. Очрашып t вакыт узганнан соң, һәр катер¬
ның пристаньга карата координаталарын һәм алар арасындагы
ераклыкны табыгыз.
Катерлар хәрәкәтенә параллель итеп, X координаталар күчәрен
үткәрик. Күчәрне көнчыгышка юнәлтәбез, ә аның башлангычын
(х = 0) пристаньга куябыз, пристань — исәпләү җисеме булсын
(чөнки мәсьәләдә катерларның торышын пристаньга карата бил¬
геләргә кирәк).
Күчеш векторларын (вхһәм s2) х күчәренә проекцияләп, slχ һәм
s2χ кисемтәләрен табабыз, алар бу векторларның проекцияләре бу¬
лып тора.
Геометрия курсыннан белгәнебезчә, вектор белән күчәрнең юнә¬
лешләре бертөрле булса, вектор — уңай дип, ә капма-каршы бул¬
са, тискәре дип исәпләнә.
Димәк, бу очракта slχ> 0, ә s2χ< 0.
13
I бу лек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Проекция — векторның ахыргы һәм башлангыч координата-
ларының аермасына тигез, сез моны инде беләсез.
Бу очракта x1 һәм х2 нокталары — s1 һәм ¾ векторлары очла¬
рының координаталары, ә х0 ноктасы — ике векторның да баш¬
лангыч координатасы. Шуңа күрә
Slx = xι ~ Х0’ (1)
S2x ~ Х2~ x0' (2)
(1) һәм (2) тигезләмәләреннән x1 һәм х2 не табабыз:
xi = x0+six> (3)
x2=x0+s2χ∙ (4)
Билгеле булганча, ике җисем арасындагы ераклык I аларның
координаталары аермасының модуленә тигез:
I = | x1 — х2|. (5)
Без ээләнелә торган x1 һәм х2 координаталарын исәпләү өчен
формулалар таптык. Ә менә (3) һәм (4) тигезләмәләрендәге x0, slχ
һәм s2χ символлары урынына нинди саннар куярга соң?
Мәсьәләнең шарты буенча, катерлар пристаньнан 100 км ерак¬
лыкта очрашалар, димәк, Ox0 кисемтәсенең озынлыгы 100 км га
тигез. 4 нче рәсемнән x0 координатасының уңай х ярымкүчә-
рендә икәнлеген күрәбез, димәк, х0 > 0. Шуңа күрә х0 = 100 км.
Хәзер slχ һәм s2χ ның нәрсәгә тигез икәнен карыйк. X күчәрен
катерларның күчеш векторларына параллель үткәргәнлектән, slχ
һәм s2χ кисемтәләренең озынлыгы s*1 һәм ^s2 векторлары озынлы¬
гына тигез (алар өстендә төзелгән турыпочмаклыкның капма-кар¬
шы яклары буларак), ә бу исә һәр проекциянең модуле тиңдәш
векторның модуленә тигез дигән сүз.
Катерларның t вакыт эчендә күчкән ераклыклары (60 км һәм
50 км) аларның күчеш векторларының модульләре була (мәсьәлә
шартында нинди дә булса вектор зурлыкларның санча кыйммәтлә¬
ре дигәндә, нәкъ менә аларның модульләре күздә тотыла).
Димәк, slχ проекциясе модуле 60 км га, ә s2χ проекциясе моду¬
ле 50 км га тигез.
slχ проекциясе уңай булганлыктан, slχ = 60 км дип язарга
мөмкин. Ә инде s2χ символы тискәре санны күрсәтә. Димәк,
s„ = -50 км.
2х
14
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Хәзер без мәсьәләнең шартын язып, аны чишә алабыз.
Бирелгән:
х0 = 100 км
s1 = 60 км
s„ = -50 км
2х
Чишү:
xι = xo+siχ5
Х2= x0+s2x^
I =∖xχ - х2|;
x1-7
х2 — ?
I - Ч
x1 = 100 км+60 км = 160 км;
х2 = 100 км - 50 км = 50 км;
I = 160 км - 50 км|= 110 км.
Җавап: x1 = 160 км, х2 = 50 км, Z = 110 км.
? Сораулар
1. Исәпләүләр нинди зурлыклар белән исәпләнә: вектор зурлык¬
лар беләнме, скаляр беләнме?
2. Нинди шарт үтәлгәндә векторның күчәргә проекциясе уңай,
нинди шарт үтәлгәндә — тискәре?
3. Башлангыч торышының координатасы һәм күчеш векторы
буенча җисемнең координатасын исәпләү өчен тигезләмә языгыз.
$ 3 нче күнегү
1. Мотоциклчы, кечкенә күпер аша чыгып, юлның турысызык¬
лы өлеше буенча хәрәкәт итә. Күпердән 10 км ераклыкта урнаш¬
кан светофор янында ул велосипедчыны очрата. Очрашып 0,1 сәг
үткәннән соң, мотоциклчы светофордан 6 км га, ә велосипедчы 2 км
га күчә (икесе дә туры сызык буйлап капма-каршы юнәлештә
хәрәкәтләрен дәвам итәләр).
Күперне исәпләү җисеме итеп алып һәм мотоциклчы хәрәкәте
ягына юнәлтеп, X күчәрен сызыгыз. Бу күчәрдә светофорның коор¬
динатасын (хс), мотоциклчының (хм) һәм велосипедчының (хв) ко-
ординаталарын (очрашудан соң 0,1 сәг үткәч) билгеләгез. Күчәрдән
өстә велосипедчы (¾) һәм мотоциклчының (⅛) күчеш векторларын
сызыгыз, ә күчәрдә бу векторларның проекцияләрен (sbx Һәм smx)
билгеләгез.
15
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Очрашып 0,1 сәг узганнан соң мотоциклчының һәм велоси¬
педчының координаталарын һәм алар арасындагы ераклыкны та¬
быгыз.
2. Малай җир өстеннән 1 м биеклектә кулы белән туп тотып
тора. Аннары ул тупны вертикаль юнәлештә югарыга чөя. Нинди¬
дер t вакыт эчендә туп башлангыч торышыннан 2,4 м га югары
менәргә һәм шул ноктадан 1,25 м га түбән төшәргә өлгерә (рәс. 5).
Рәс. 5.
Рәсемнән файдаланып билгеләгез: а) тупның башлангыч торы¬
шының координатасы х0 не; б) t вакыт эчендә тупның күчеш век¬
торы St ның проекциясе з ны; в) ыргытканнан соң t вакыт узгач,
тупның координатасы xt ны.
§ 4. Турысызыклы
тигез хәрәкәт вакытында күчеш
Җисемнең координаталарын табуга карата алда каралган ми¬
сал һәм мәсьәләләрдә күчеш векторы (ягъни аның модуле һәм юнә¬
леше) билгеле иде.
Ә күчеш векторы билгесез булганда нишләргә?
Иң гади очрак — турысызыклы тигез хәрәкәт итүче җисемнең
күчеш векторын исәпләү формуласын табуны карыйк (җисем туры¬
16
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
сызыклы траектория буйлап хәрәкәт итә һәм тигез вакыт арала¬
рында тигез юл үтә).
Билгеләмә буенча, турысызыклы тигез хәрәкәттә тизлек —
векторлы даими зурлык, ул теләсә кайсы вакыт аралыгында
ясалган күчешнең бу вакытка чагыштырмасына тигез.
(1) формуласыннан турысызыклы тигез хәрәкәт өчен күчешне
табарга була:
s = υt. (2)
Векторлы зурлыкларны (күчеш, тизлек, көч һ.б.) табуга карата
күпчелек мәсьәләләрне чишкәндә, бу зурлыкларның бер-берсенә
карата ничек урнашуын белергә кирәк. Аерым алганда, моны век¬
торлар формасында язылган тигезләмәләрдән күрергә мөмкин.
Мәсәлән, (1) һәм (2) формулалары турысызыклы тигез хәрәкәт ва¬
кытында тңзлек һәм күчеш векторларының бер үк якка юнәлгәнен
күрсәтә. '
Ләкин күчешне исәпләү өчен, векторларның күчәргә проекция¬
ләре кергән формулалар кулланыла:
sx = vxt∙ (3)
Проекциянең тамгасы буенча аңа тиңдәшле векторның сайлап
алынган күчәргә карата ничек юнәлгәнен без инде әйтә алабыз. Ә
инде турысызыклы хәрәкәткә карата мәсьәләләр чишкәндә күчеш
һәм тизлек векторларының юнәлеше безне кызыксындырмый икән,
аларның модульләре кергән формуланы кулланырга мөмкин:
s - υt. (4)
(4) формуласы сезгә күптән таныш — физикадан һәм математи¬
кадан мәсьәләләр чишкәндә, сез аны еш кулландыгыз. Тик s хәре¬
фен сез үтелгән юл дип билгеләдегез. Алайса ни өчен хәзер s — ул
күчеш векторының модуле дибез?
Эш шунда ки, бер үк юнәлештә хәрәкәт иткәндә, җисемнең нин¬
дидер вакыт аралыгында башкарган күчеш векторы модуле бу
җисемнең шул вакыт арасында үткән юлына тигез.
17
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Бу раслауның дөреслегенә 3 нче рәсемгә карап ышанырга
мөмкин. Җисем үз хәрәкәтенең юнәлешен үзгәртмәгән очракларда
(О ноктасыннан А ноктасына һәм О ноктасыннан С ноктасына
хәрәкәт иткәндә) күчеш векторы модуле үтелгән юлга тигез. Әгәр
инде җисемнең хәрәкәт юнәлеше үзгәрсә (О ноктасыннан В га күчеп,
кире кайтканда һәм О ноктасыннан D га кәкресызыклы траектория
буенча күчкәндә), үтелгән юл күчеш векторы модуленнән зуррак
булып чыга.
6 нчы рәсемдә җисем турысызыклы тигез хәрәкәт иткәндә, тиз¬
лек v векторы модуленең вакыт t га бәйлелеге графигы күрсәтелгән
(калын сызык). Мондый графиклар белән сез инде 7 нче сыйныф¬
ның физика дәресләрендә очрашкан идегез (ул вакытта алар тиз¬
лекнең вакытка бәйлелеге графиклары дип атала иде).
Бу очракта җисемнең t1 вакыт эчендә ясаган күчеш векторы¬
ның модуле s түбәндәге формула буенча исәпләнә:
s = v1i1∙
Ләкин υ1f1 тапкырчыгышы санча кыйммәте буенча буялган ту¬
рыпочмаклыкның мәйданына да тигез, чөнки υ1 һәм i1 кисемтәләре
(ягъни Oυ1 һәм Ot1 дияргә дә була) — бу турыпочмаклыкның чиктәш
яклары.
Шулай итеп, җисем турысызыклы тигез хәрәкәт иткәндә, күчеш
векторы модуле сан ягыннан — тизлек графигы, Ot күчәре,
күзәтүнең башлангыч һәм ахыргы мизгелләренә тиңдәш бул¬
ган нокталардан (бу очракта О һәм t1 нокталарыннан) бу
күчәргә торгызылган перпендикулярлар арасындагы турыпоч¬
маклык мәйданына тигез була. Еш кына бу мәйданны тизлек
графигы асты мәйданы диләр.
Күпчелек мәсьәләләрне чишкәндә векторларның модульләре
белән генә түгел, проекцияләре белән дә эш итәргә туры килгән¬
лектән, тизлек векторлары проекцияләренең графикларын карап
үтик.
Моның өчен тагын бер тапкыр катерларның капма-каршы юнә¬
лешләрдә турысызыклы тигез хәрәкәте турындагы мәсьәләне искә
төшерик (§ 3, рәс. 4). Әйтик, катерлар күрсәтелгән күчешләрен яса¬
ган t вакыт аралыгы 2 сәг кә тигез булсын, ди. 2 сәг тә беренче
18
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
катер 60 км га, икенчесе 50 км га күчә. Димәк, беренче катерның
тизлек векторы модуле 30 км/сәг, икенчесенеке 25 км/сәг.
Беренче катерның тизлек һәм күчеш векторларының проекция¬
ләре уңай, ә икенчесенең — тискәре булганлыктан, vlχ = 30 км/сәг,
slχ = 60 км, υ2χ = -25 км/сәг, s2x = -50 км.
Күргәнебезчә, проекция графикларында модульләр генә түгел,
тамгалар да чагылыш таба (рәс. 7). Беренче катерның тизлек векто¬
ры проекциясенең графигы тизлек күчәренең уңай кыйммәтләре
өлкәсендә, ә икенчесенең тискәре кыйммәтләр өлкәсендә урнашкан.
Шуны ук санча зурлыклары күчеш векторлары проекцияләренә тигез
булган турыпочмаклыклар турында да әйтергә мөмкин.
Ф Сораулар
1. Турысызыклы тигез хәрәкәтнең тизлеге дип нәрсәне атый¬
лар?
2. Хәрәкәт тизлеге векторының проекциясе билгеле булса, ту¬
рысызыклы тигез хәрәкәт итүче җисемнең күчеш векторы проек¬
циясе ничек табыла?
3. Нинди шарт үтәлгәндә, җисемнең ниндидер вакыт аралы¬
гында ясаган күчеш векторы модуле аның шушы вакыт эчендә уз¬
ган юлына тигез була?
4. Тигез хәрәкәт вакытында күчеш векторы модуленең санча
кыйммәте тизлек графигы асты мәйданына тигез икәнлеген ис¬
батлагыз.
5. 7 нче рәсемдә сурәтләнгән графиклар ике җисемнең хәрәкәте
турында нинди мәгълүмат бирә?
19
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
£ 4 нче күнегү
1, /Гизлек векторы модуленең графигы Ot күчәре астында (ягъ-
н^тХзлек күчәренең тискәре кыйммәтләре өлкәсендә) урнаша ала¬
мы? Тизлек векторы проекциясе графигы?
2. Турысызыклы тигез хәрәкәт итүче өч автомобильнең тизлек
векторлары проекцияләренең вакытка бәйлелеге графикларын төзе¬
гез: ике автомобиль бер юнәлештә, ә өченчесе аларга каршы хәрәкәт
итә. Беренче автомобильнең тизлеге — 60 км/сәг, икенчесенең —
80 км/сәг, өченчесенең — 90 км/сәг.
/
§ 5. Турысызыклы тигез тизләнешле хәрәкәт.
Тизләнеш
Сез 7 нче сыйныфта даими тизлек белән баручы җисемнәрнең
механик хәрәкәтен өйрәндегез. Бу тигез хәрәкәт дип атала.
Хәзер без тигез булмаган, ягъни тигезсез хәрәкәтне өйрәнүгә
күчәбез. Тигезсез хәрәкәтнең барлык төрләре арасыннан иң гадиен —
турысызыклы тигез тизләнешле хәрәкәтне өйрәнергә керешербез,
бу очракта җисем туры сызык буйлап хәрәкәт итә, ә тизлек векто¬
рының проекциясе теләсә нинди тигез вакыт араларында бертөрле
үзгәрә (тизлек векторы модуле үсәргә дә, кимергә дә мөмкин).
Мәсәлән, күтәрелеп китү полосасында хәрәкәт итүче самолетның
тизлеге теләсә кайсы 10 с эчендә — 15 м/с ка, теләсә кайсы 5 с та —
7,5 м/с ка, һәр секундта 1,5 м/с ка һ.б. артса, ул вакытта самолет
тигез тизләнеш белән хәрәкәт итә.
Бу очракта самолет тизлеге дигәндә, моменталь тизлек, ягъни
траекториянең һәр конкрет ноктасында аңа тиңдәш булган ва¬
кыт мизгелендәге тизлек күз алдына тотыла (моменталь тизлек¬
нең тагын да төгәлрәк билгеләмәсе өлкән сыйныфларның физика
курсында бирелер).
Тигез тизләнеш белән хәрәкәт итүче җисемнәрнең моменталь
тизлеге төрлечә үзгәрергә мөмкин: кайбер очракларда — тизрәк,
кайберләрендә — әкренрәк. Мәсәлән, уртача егәрлектәге гадәти пас¬
сажир лифтының тизлеге — һәр секундта 0,4 м/с ка, ә тиз йөрешле
лифтныкы 1,2 м/с ка арта. Мондый очракларда җисемнәр төрле
тизләнеш белән хәрәкәт итә, диләр.
Нинди физик зурлыкның тизләнеш дип аталуын тикшерик.
20
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Тигез тизләнеш белән хәрәкәт итүче җисемнең тизлеге t вакыт
аралыгында υθ дән v га кадәр үзгәрде, ди. υ0 — җисемнең башлан¬
гыч тизлеге, ягъни вакыт исәпләү башлангычы итеп алынган t0 = 0
мизгелендәге тизлек. Ә и — җисемнең t0 = 0 дән башланган t вакыт
аралыгы ахырындагы моменталь тизлеге. Ьәрбер вакыт берәмлеге
эчендә тизлек υ~ и° зурлыгына үзгәрә барган. Бу чагыштырма a
символы белән тамгалана һәм тизләнеш дип атала:
→ _ v - υ0
a--~Γ-
(1)
Тизлек үзгәрешенең бу үзгәреш ясалган вакытка чагыштыр¬
масы җисемнең тигез тизләнешле хәрәкәте вакытындагы тиз¬
ләнеше дип атала.
Тигез тизләнешле хәрәкәт — даими тизләнеш белән хәрәкәт
итү дигән сүз.
Тизләнеш — вектор зурлык, ул модуле белән генә түгел, юнәле¬
ше белән дә характерлана.
Тизләнеш векторының модуле — тизлек векторы модуленең
һәрбер вакыт берәмлеге эчендә ничек үзгәрүен күрсәтә. Тизләнеш
зуррак булган саен, җисемнең тизлеге тизрәк үзгәрә.
СИ системасында тизләнеш берәмлеге итеп, хәрәкәт итүче җи¬
сем тизлегенең 1 с вакыт эчендә 1 м/с ка үзгәрә торган тизләнеше
алынган: 1-rzc = 1 м/с2.
1с
Димәк, СИда тизләнеш берәмлеге метр квадрат секундка (м/с2)
дип йөртелә.
Тизләнешнең башка берәмлекләре дә кулланыла, мәсәлән, 1 см/с2.
Турысызыклы һәм тигез тизләнеш белән хәрәкәт итүче җисем¬
нең тизләнешен тизлек һәм тизләнеш векторларының проекциялә¬
ре кергән тигезләмә ярдәмендә исәпләргә мөмкин:
a = . (2)
x t
Тизләнеш исәпләүне конкрет мисалларда карарбыз.
8 нче а рәсемдә таудан тигез тизләнеш белән төшүче чана
күрсәтелгән.
21
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Рәс. 8
8 нче а рәсемдә таудан тигез тизләнеш белән төшүче чана
күрсәтелгән.
Чананың АВ арасын 4 с та үтүе билгеле. Аның А ноктасындагы
тизлеге 0,4 м/с, ә В ноктасында 2 м/с (чана материаль нокта дип
алынган).
Чананың АВ арасын нинди тизләнеш белән үтүен исәплик.
Бу очракта вакытны исәпләү башлангычы итеп, чананың А нок¬
тасын узу вакытын алырга кирәк, чөнки, мәсьәләнең шарты буенча,
тизлек векторы модуленең 0,4 м/с тан 2 м/с ка кадәр үзгәрүе нәкъ
менә шушы мизгелдән исәпләнә башлый.
Хәзер, чананың хәрәкәт тизлеге векторына параллель итеп, шул
ук якка юнәлгән X күчәрен үткәрәбез. Аңа р һәм v векторларының
башларын һәм ахырларын проекциялибез. Килеп чыккан υ0χ һәм υχ
кисемтәләре и һәм υ векторларының X күчәренә проекцияләре була¬
лар. Алар икесе дә уңай. Шуңа күрә аларны тиңдәшле векторларының
модульләренә тигез дип яза алабыз: υ0χ = 0,4 м/с, vχ = 2 м/с.
Мәсьәләнең шартын язабыз һәм аны чишәбез.
Бирелгән: Чишү:
υn = 0,4 м/с
v = 2 м/с a _ υχ ~ υ°*
f=4c x t
Uχ - 2
2 м/с - 0,4 м/с
4 с
м/с
= 0,4 - = 0,4 м/с2,
с
а =
Җавап: aχ = 0,4 м/с2.
Тизләнеш векторының X күчәренә проекциясе уңай булды,
димәк, тизләнеш векторы X күчәре һәм чананың хәрәкәт тизлеге
белән бер үк юнәлештә.
22
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Әгәр тизлек һәм тизләнеш векторлары бер якка юнәлгән булса,
тизлек арта.
Хәзер икенче мисалны карыйбыз: чана, таудан төшеп җитеп,
горизонталь CD участогы буенча хәрәкәт итә (рәс. 8, б).
Ышкылу көче тәэсир итү нәтиҗәсендә, чананың тизлеге өзлек¬
сез кими бара һәм D ноктасында ул туктый, ягъни тизлеге нульгә
тигез була. С ноктасында чананың тизлеге 1,2 м/с булуы һәм аның
CD арасын 6 с та үтүе билгеле.
Чананың бу очрактагы тизләнешен исәплик, ягъни аның тизле¬
генең һәрбер вакыт берәмлеге эчендә күпмегә үзгәрүен табыйк.
Вакытны исәпләү башлангычы итеп чананың С ноктасын үтү
мизгелен алабыз. Ул чагында, башлангыч тизлек векторының мо¬
дуле 1,2 м/с ка, ә соңгысыныкы нульгә тигез була.
CD кисемтәсенә параллель итеп X күчәрен үткәрәбез һәм аны,
рәсемдә күрсәтелгәнчә, чананың хәрәкәт юнәлеше буйлап салабыз.
Бу вакытта хәрәкәтнең теләсә кайсы мизгелендә тизлек векторы¬
ның X күчәренә проекциясе уңай һәм тизлек векторы модуленә тигез
була. Аерым алганда, £0= 0 булганда, υ0x = 1,2 м/с, t = 6 булганда, υχ = 0.
Бирелгәннәрне язып, тизләнешне исәплибез.
Бирелгән:
υ0χ= 1,2 м/с
и = 0
/= 6 с
Чишү:
vχ - υox .
ar = — — ,
x t
0 -1,2 м/с
a = „ = -0,2 м/с2.
x 6 с
aχ — ?
Җавап: aχ = -0,2 м/с2.
Күргәнебезчә, тизләнешнең X күчәренә проекциясе — тискәре
зурлык. Бу — тизләнеш векторы а ның X күчәренә капма-каршы,
шулай булгач, хәрәкәт тизлегенә дә каршы юнәлгәнен күрсәтә. Шуңа
күрә чананың тизлеге кимегән.
Шулай итеп, хәрәкәт итүче җисемнең тизлек һәм тизләнеш век¬
торлары бер үк якка юнәлсә, тизлек векторы модуле үсә, капма-
каршы юнәлсә — кими.
Сораулар
1. Турысызыклы тигез тизләнешле хәрәкәт нинди төрле
хәрәкәт була: тигезме, тигезсезме?
2. Тигезсез хәрәкәтнең моменталь тизлеге нәрсә ул?
23
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
3. Нәрсәне тигез тизләнешле хәрәкәтнең тизләнеше дип атый¬
лар?
4. Нинди хәрәкәт тигез тизләнешле хәрәкәт дип атала?
5. Тизләнеш векторы модуле нәрсәне күрсәтә?
6. Тизләнеш берәмлеге итеп нәрсә алына?
7. Нинди очракта хәрәкәт итүче җисемнең тизлек векторы
модуле үсә; кими?
$ 5 нче күнегү
1. Бер үк вакыт аралыгында беренче автомобильнең тизлек век¬
торы модуле υ1 дән υ'κa, ә икенчесенең v2 дән и ка үзгәрә (тизлекләр
бертөрле масштаблар белән 9 нчы рәсемдә сурәтләнгән). Кайсы ав¬
томобиль бу вакыт эчендә зуррак тизләнеш белән барган? Кайсысы¬
ның тизлеге тизрәк арткан?
-,> fl = i2
ι>1 V
v2
υ
Рәс. 9
2. Самолет күтәрелеп китү алдыннан күпмедер вакыт тигез тиз¬
ләнеш белән хәрәкәт итә. Әгәр 30 с эчендә аның тизлеге 10 м/с тан
55 м/с ка кадәр артса, тизләнеше нинди булган?
3. Билгеле бер арада поездның тизлеге 12 с эчендә 6 м/с ка арт¬
са, тизләнеше нинди булыр?
j 6. Турысызыклы тигез тизләнешле хәрәкәт
вакытында тизлек. Тизлекнең графигы
Турысызыклы тигез тизләнешле хәрәкәт вакытында тизләнеш
векторының X күчәренә проекциясе
n Vχ - v0x
x t
(1)
формуласы белән исәпләнүен без инде беләбез.
24
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
t0 = 0 дән башлап исәпләнгән t вакыт аралыгының ахырында
хәрәкәт итүче җисем ирешкән D тизлегенең υχ проекциясен (1) фор¬
муласы аша күрсәтәбез:
a t = и - υn , (2)
v = vn +a t.
Шулай итеп, башлангыч тизлек векторының υ0χ проекциясен
һәм тизләнеш векторының aχ проекциясен белгәннән соң, күзәтү
башлаган мизгелдән, ягъни £о=О дән исәпләнгән теләсә нинди ва¬
кыт аралыгы t ахырында җисемнең моменталь тизлеге векторы¬
ның υχ проекциясен (2) формуласы буенча исәпләп була.
Әгәр башлангыч мизгелдә җисем тикторышта, ягъни v0 — 0 бул¬
са, бу очрак өчен (2) формуласы түбәндәге рәвешне ала:
υx = a=ct • (3)
Тигез тизләнешле хәрәкәт вакытында тизлек векторы проекция¬
сенең вакытка бәйлелеген график рәвештә күрсәтик.
Математикадан безгә сызыкча функция у = kx + Ъ билгеле, би¬
редә х — аргумент, k — даими коэффициент, Ь — ирекле буын. Бу
функциянең графигы туры сызык була.
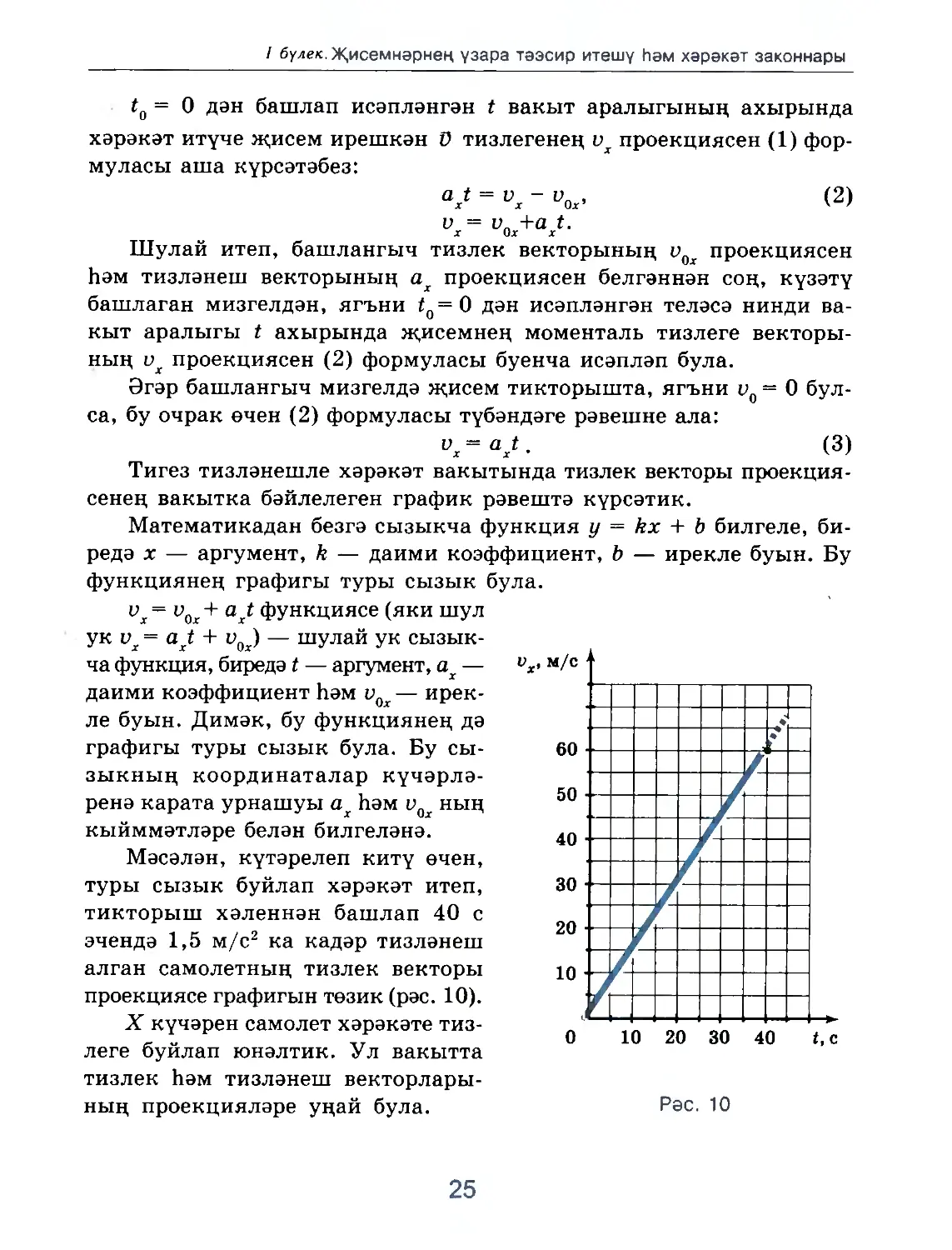
υχ = υ0χ + at функциясе (яки шул
ук υχ = at + υ0χ) — шулай ук сызык¬
ча функция, биредә t — аргумент, ах —
даими коэффициент һәм υ0χ — ирек¬
ле буын. Димәк, бу функциянең дә
графигы туры сызык була. Бу сы¬
зыкның координаталар күчәрлә¬
ренә карата урнашуы aχ һәм υ0χ ның
кыйммәтләре белән билгеләнә.
Мәсәлән, күтәрелеп китү өчен,
туры сызык буйлап хәрәкәт итеп,
тикторыш хәленнән башлап 40 с
эчендә 1,5 м/с2 ка кадәр тизләнеш
алган самолетның тизлек векторы
проекциясе графигын төзик (рәс. 10).
X күчәрен самолет хәрәкәте тиз¬
леге буйлап юнәлтик. Ул вакытта
тизлек һәм тизләнеш векторлары¬
ның проекцияләре уңай була.
Рәс. 10
25
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Туры сызыклы графикны төзү өчен аның теләсә нинди ике нок¬
тасының координаталарын (ягъни t һәм пж) белү җитә, t га ике ирекле
кыйммәт биреп, υχ = at формуласы буенча υχ ның тиңдәш кыйммәт¬
ләрен табарга мөмкин.
Мәсәлән, t0 = 0 булганда, υ0χ = 0; t = 40 с булганда, vχ= 1,5 m∕c2×
× 40 с = 60 м/с. Беренче ноктаның координаталары графикның
координаталар башлангычы аша үтүен күрсәтә.
Хәзер башлангыч тизлек нульгә тигез булмаган очрак өчен шуңа
охшаш график төзик (тизлек модуле, беренче очрактагы кебек үк,
арта).
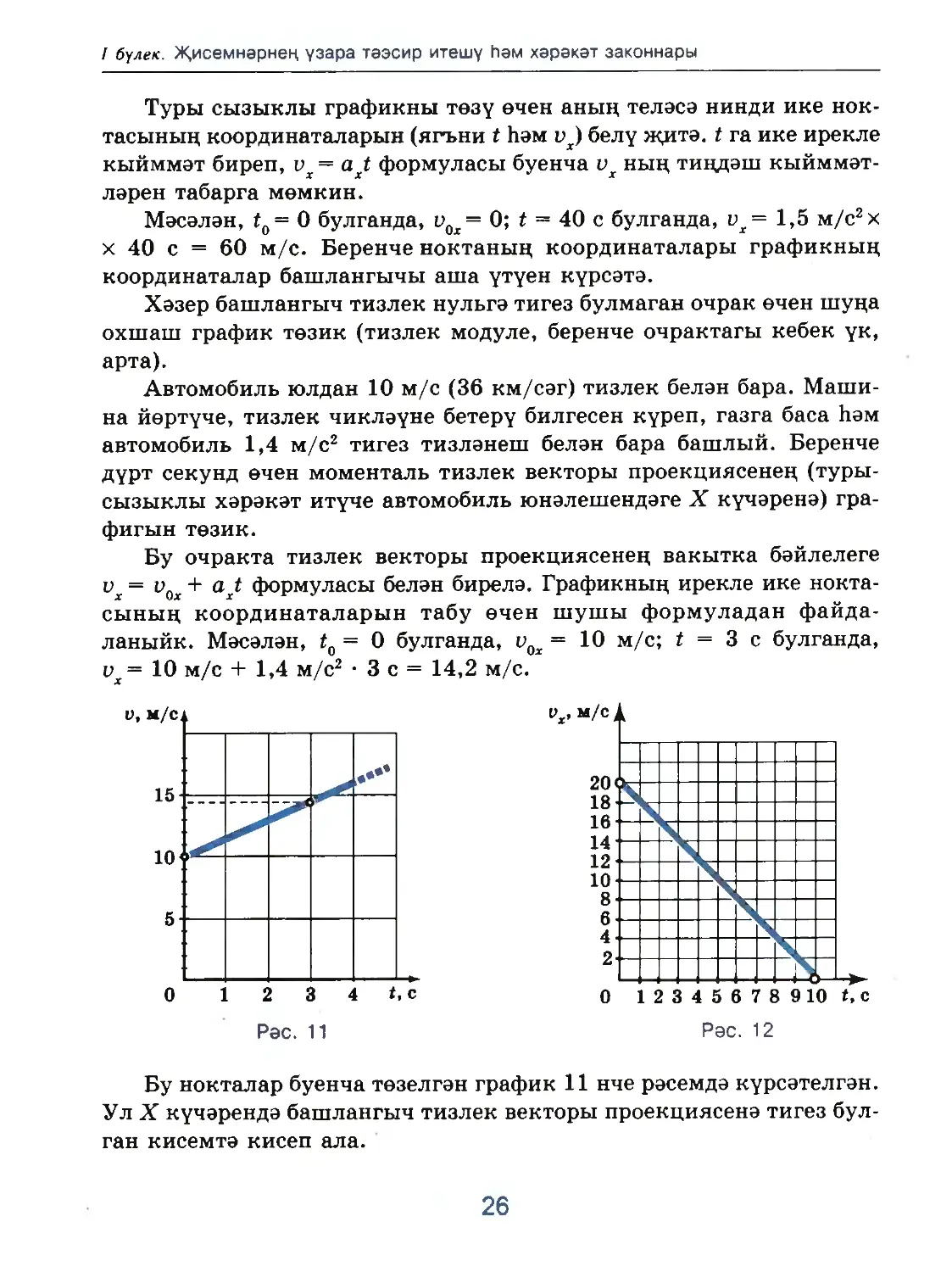
Автомобиль юлдан 10 м/с (36 км/сәг) тизлек белән бара. Маши¬
на йөртүче, тизлек чикләүне бетерү билгесен күреп, газга баса һәм
автомобиль 1,4 м/с2 тигез тизләнеш белән бара башлый. Беренче
дүрт секунд өчен моменталь тизлек векторы проекциясенең (туры¬
сызыклы хәрәкәт итүче автомобиль юнәлешендәге X күчәренә) гра¬
фигын төзик.
Бу очракта тизлек векторы проекциясенең вакытка бәйлелеге
υx = vox + axt формуласы белән бирелә. Графикның ирекле ике нокта¬
сының координаталарын табу өчен шушы формуладан файда¬
ланыйк. Мәсәлән, t0 = 0 булганда, υ0χ = 10 м/с; t = 3 с булганда,
υχ = 10 м/с + 1,4 м/с2 • 3 с = 14,2 м/с.
Бу нокталар буенча төзелгән график 11 нче рәсемдә күрсәтелгән.
Ул X күчәрендә башлангыч тизлек векторы проекциясенә тигез бул¬
ган кисемтә кисеп ала.
26
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Ә хәзер башлангыч тизлек нульгә тигез булмаган, ә тизлек век¬
торы модуле вакыт узу белән кимегән очракны карыйк.
Мәсәлән, автомобильне йөртүче 20 м/с (72 км/сәг) тизлек белән
барганда тормоз педаленә баса. Нәтиҗәдә автомобиль, 2 м/с2 тизлә¬
неш белән хәрәкәт итеп, 10 с тан сон, туктый.
Тизлек 20 м/с булган тормозлау мизгелен вакыт исәпләү баш¬
лангычы итеп алыйк.
Бу очракта графиктагы ике ноктаның координаталары анык
булганлыктан, тизлек векторы проекциясенең кыйммәтләрен
исәпләүнең кирәге калмый: t0 = и булганда, ι>0χ = 20 м/с; t = 10 с
булганда, υχ = 0. Тиңдәшле график 12 нче рәсемдә сурәтләнгән.
Күргәнебезчә, тизлек модуле буенча кимесә, график t күчәренең
уңай юнәлеше белән җәенке почмак төзи.
Ф Сораулар
1. Әгәр а) башлангыч тизлек векторы проекциясе һәм тизлә¬
неш векторы проекциясе; б) тизләнеш векторы проекциясе һәм баш¬
лангыч тизлекнең нульгә тигез булуы билгеле булса, турысызыклы
тигез тизләнешле хәрәкәтнең моменталь тизлек векторы проек¬
циясен исәпләү өчен формула төзеп языгыз.
2. Башлангыч тизлек: a) нульгә тигез; б) нульгә тигез булма¬
ганда, тигез тизләнешле тизлек векторы проекциясенең графигы
нинди була?
3. Графиклары 11 нче һәм 12 нче рәсемнәрдә күрсәтелгән
хәрәкәтләр нәрсә белән охшаш һәм нәрсә белән аерыла?
£ 6 нчы күнегү
1. Хоккейчы, кәшәкә белән алкага җиңелчә генә сугып, аңа 2 м/с
лы тизлек бирә. Әгәр алка, бозга ышкылу нәтиҗәсендә, 0,25 м/с2
тизләнеш белән шуса, сугып җибәрелгәннән соң 4 с узгач нинди
тизлек белән барыр?
2. Велосипедчы тикторыш хәленнән 0,2 м/с2 тизләнеш белән кузга¬
лып китә. Күпме вакыт узганнан соң аның тизлеге 2 м/с булыр?
3. Турысызыклы тигез тизләнешле хәрәкәтнең түбәндәге очрак¬
лары өчен бер үк координаталар күчәрендә тизлек векторы проек¬
циясенең (башлангыч тизлек векторы белән бер үк юнәлештәге X
күчәренә) графикларын төзегез:
27
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
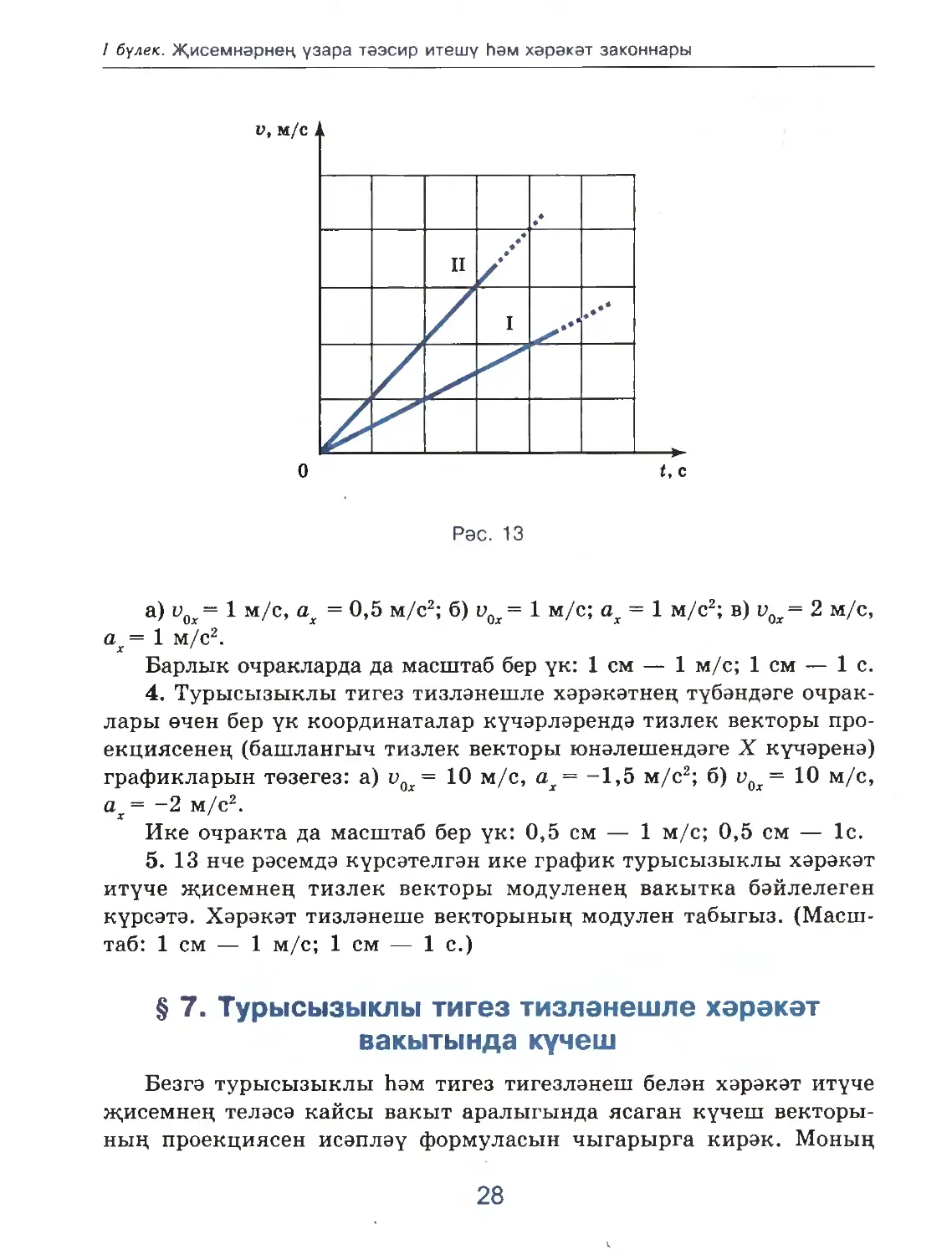
Рәс. 13
a) v0x= 1 м/с, ах = 0,5 м/с2; б) υ0χ= 1 м/с; ax = 1 м/с2; в) v0χ = 2 м/с,
aχ = 1 м/с2.
Барлык очракларда да масштаб бер үк: 1 см — 1 м/с; 1 см — 1 с.
4. Турысызыклы тигез тизләнешле хәрәкәтнең түбәндәге очрак¬
лары өчен бер үк координаталар күчәрләрендә тизлек векторы про¬
екциясенең (башлангыч тизлек векторы юнәлешендәге X күчәренә)
графикларын төзегез: a) υ0χ = Ю м/с, ax= -1,5 м/с2; б) υ0χ= 10 м/с,
a = -2 м/с2.
Ике очракта да масштаб бер үк: 0,5 см — 1 м/с; 0,5 см — 1с.
5. 13 нче рәсемдә күрсәтелгән ике график турысызыклы хәрәкәт
итүче җисемнең тизлек векторы модуленең вакытка бәйлелеген
күрсәтә. Хәрәкәт тизләнеше векторының модулен табыгыз. (Масш¬
таб: 1 см — 1 м/с; 1 см — 1 с.)
§ 7. Турысызыклы тигез тизләнешле хәрәкәт
вакытында күчеш
Безгә турысызыклы һәм тигез тигезләнеш белән хәрәкәт итүче
җисемнең теләсә кайсы вакыт аралыгында ясаган күчеш векторы¬
ның проекциясен исәпләү формуласын чыгарырга кирәк. Моның
28
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
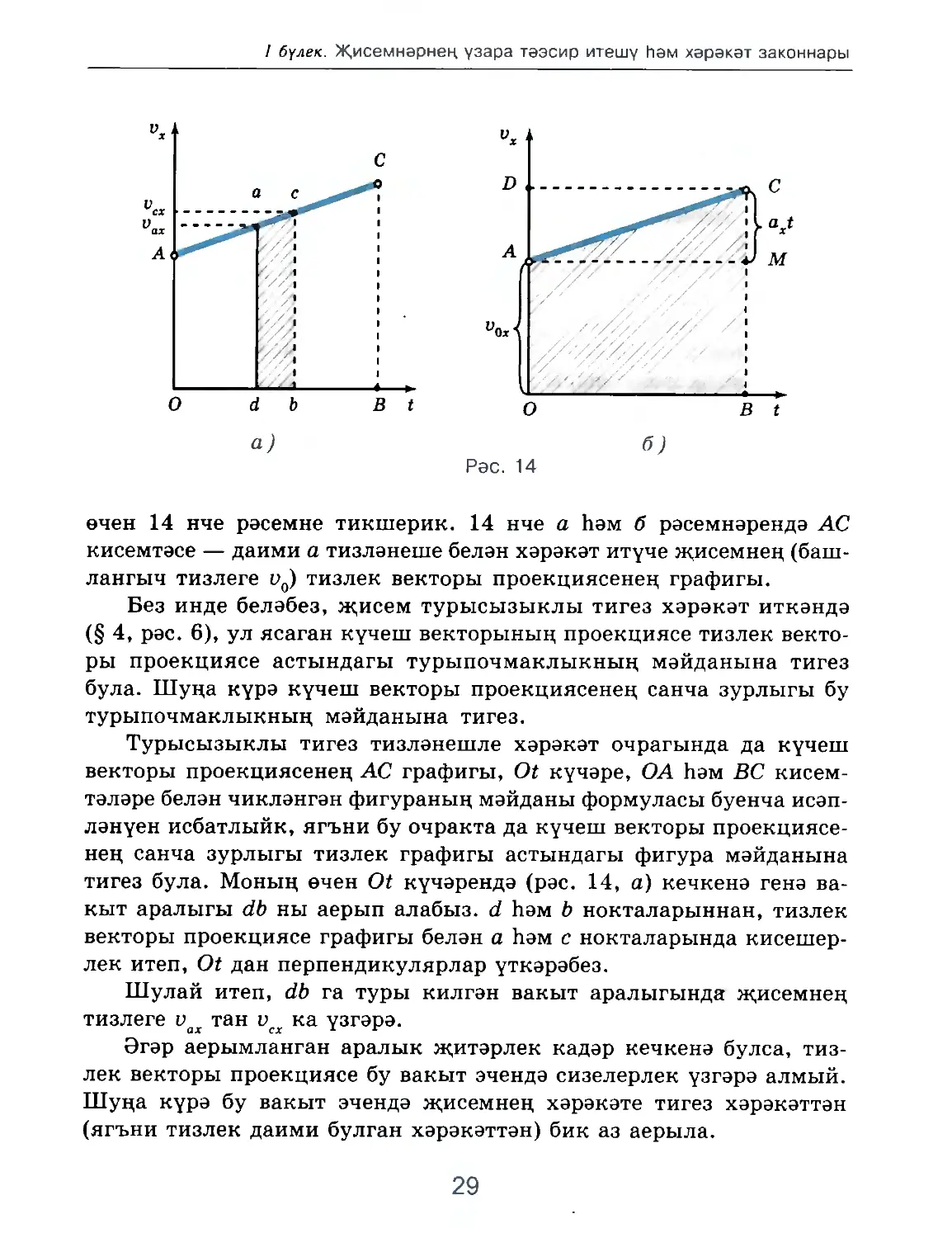
өчен 14 нче рәсемне тикшерик. 14 нче а һәм б рәсемнәрендә АС
кисемтәсе — даими а тизләнеше белән хәрәкәт итүче җисемнең (баш¬
лангыч тизлеге υ0) тизлек векторы проекциясенең графигы.
Без инде беләбез, җисем турысызыклы тигез хәрәкәт иткәндә
(§ 4, рәс. 6), ул ясаган күчеш векторының проекциясе тизлек векто¬
ры проекциясе астындагы турыпочмаклыкның мәйданына тигез
була. Шуңа күрә күчеш векторы проекциясенең санча зурлыгы бу
турыпочмаклыкның мәйданына тигез.
Турысызыклы тигез тизләнешле хәрәкәт очрагында да күчеш
векторы проекциясенең АС графигы, Ot күчәре, ОА һәм ВС кисем¬
тәләре белән чикләнгән фигураның мәйданы формуласы буенча исәп¬
ләнүен исбатлыйк, ягъни бу очракта да күчеш векторы проекциясе¬
нең санча зурлыгы тизлек графигы астындагы фигура мәйданына
тигез була. Моның өчен Ot күчәрендә (рәс. 14, а) кечкенә генә ва¬
кыт аралыгы db ны аерып алабыз, d һәм b нокталарыннан, тизлек
векторы проекциясе графигы белән а һәм с нокталарында кисешер¬
лек итеп, Ot дан перпендикулярлар үткәрәбез.
Шулай итеп, db га туры килгән вакыт аралыгында җисемнең
тизлеге vaχ тан vcχ ка үзгәрә.
Әгәр аерымланган аралык җитәрлек кадәр кечкенә булса, тиз¬
лек векторы проекциясе бу вакыт эчендә сизелерлек үзгәрә алмый.
Шуңа күрә бу вакыт эчендә җисемнең хәрәкәте тигез хәрәкәттән
(ягъни тизлек даими булган хәрәкәттән) бик аз аерыла.
29
I бүлек. Җисемнәрнең узара тәэсир итешү һәм хәрәкәт законнары
Андый очракта графикның ас бүлемтеген — горизонталь дип, ә
abed полосасын турыпочмаклы дип санарга мөмкин. Димәк, бу по¬
лоса мәйданының санча кыйммәте db кисемтәсенә тиңдәш вакыт
эчендә ясалган күчеш векторының проекциясенә тигез.
ОАСВ трапециясенең барлык мәйданын шундый полосаларга
бүлгәләп бетерергә мөмкин. Димәк, ОВ кисемтәсенә тиңдәш вакыт
эчендә ясалган күчеш векторы проекциясенең санча кыйммәте ОАСВ
трапециясе мәйданына тигез һәм аның мәйданын табу формуласы
буенча исәпләнә. 14 нче б рәсемнән күренгәнчә, ОАСВ трапециясе¬
нең мәйданы s — ОАМВ турыпочмаклыгы һәм ACM турыпочмак¬
лы өчпочмагы мәйданнары суммасына тигез:
S = ОА-ОВ + үСМ-АМ.
Шулай булгач, t вакыт эчендә җисем ясаган күчеш векторы¬
ның проекциясе sχ ны да шушы формула буенча табарга мөмкин
(әгәр кисемтәләрнең һәркайсы тиңдәш берәмлекләрдә, ягъни тиз¬
лек һәм вакыт берәмлекләрендә бирелсә).
ОА = υ0χ, OB = AM = t, CM = aχt булганлыктан, күчеш векторы¬
ның проекциясен табу формуласын болай язалар:
sx = ‰∙⅛ + ⅜∙<M ∙t ,
ЯКИ -2
αχt
«х = υ0xt + — ■
Шулай итеп, тигез тизләнешле хәрәкәт вакытында күчеш век¬
торының проекциясен исәпләү өчен формула чыгарылды.
Җисем модуле буенча кими барган тизлек белән хәрәкәт иткәндә
дә, күчеш векторының проекциясен шушы формула буенча исәплиләр,
тик бу очракта тизлек һәм тизләнеш векторлары капма-каршы
юнәлгәнлектән, проекцияләренең тамгалары төрле була.
Сораулар
1. 14 нче a рәсемнән файдаланып, тигез тизләнешле хәрәкәттә
күчеш векторы проекциясенең санча кыйммәте ОАСВ фигурасы
мәйданына тигез икәнен исбатлагыз.
2. Җисем турысызыклы тигез хәрәкәт иткәндә, аның күчеш
векторы проекциясен исәпләү өчен тигезләмә языгыз.
30
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
£ 7 нче күнегү
1. Велосипедчы таудан даими 0,5 м/с2 тизләнеш белән 5 с эчендә
төшеп җитә. Төшә башлаганда аның тизлеге 18 км/сәг булса, тау¬
ның озынлыгын табыгыз.
2. 15 м/с тизлек белән баручы поезд тормозлый башлаганнан
соң 20 с узгач туктый. Тормозлану даими тизләнеш белән барган
дип фаразлап, поездның 20 с эчендәге күчешен табыгыз.
§х8. Башлангыч тизлеге булмаган турысызыклы
тигез тизләнешле хәрәкәт вакытында
җисемнең күчеше
Тигез тизләнеш белән хәрәкәт итүче җисемнең башлангыч тиз¬
леге О0 нульгә тигез булгандагы күчеш векторы проекциясен исәпләп
карыйк. Бу очракта
тигезләмәсе түбәндәгечә языла:
»х= ≠ • (1)
(1) тигезләмәсенә sχ һәм aχ проекцияләре урынына күчеш һәм
тизләнеш векторларының s һәм а модульләрен куеп язабыз. Бу
вакытта S һәм 3 векторлары бер үк юнәлештә булганлыктан, алар-
ның проекцияләренең дә тамгалары бер төрле була. Шуңа күрә век¬
тор модульләре өчен тигезләмәне болай язарга мөмкин:
at2
2
(2)
(2) формуласыннан күренгәнчә, башлангыч тизлеге булмаган
турысызыклы тигез хәрәкәт вакытында, күчеш векторының модуле
бу күчеш ясалган вакыт аралыгының квадратына туры пропорцио¬
наль була.
Бу — хәрәкәт башлану мизгеленнән алып хәрәкәт вакыты п тап¬
кыр артканда, күчеш п2 тапкыр арта дигән сүз.
31
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Мәсәлән, хәрәкәт башланганнан алып ниндидер ti вакыт эчендә
җисем sι = ^tι күчеше ясаса, t2 = 2t1 вакыт эчендә (f1 башланган
CL 2
мизгелдән исәпләп) — ул s2 = ∙ 4f1 = 4s1 күчеше; t3 = 3t1 вакыт эчен-
d
дә s3 = ∙ 9tl2 = 9s1; tn = ntl вакыт эчендә sn = n2s1 күчеше ясый (п —
2
натураль сан).
—
0t1 ij=2t1 <3=3i1 t4=4t1 tβ-5t1
О1А 3 В 5 С 7 D 9 Е
⅛ ⅜ * - ■ ⅜ — 4 ⅜-
-→-
0 s1 4s1 9s1 16s1 25s1
8
Рәс. 15
Башлангыч тизлеге булмаган турысызыклы тигез тизләнешле
хәрәкәт вакытында күчеш векторы модуленең вакытка мондый
бәйлелеге 15 нче рәсемдә ачык күренә, биредә ОА, ОВ, ОС, OD, ОЕ
кисемтәләре — җисемнең t1, t2= 2t1, t3=3tl, ti=4t1 һәм i5=5⅛1 ва¬
кытлары эчендә ясаган күчешләренең модульләре (s1, s2, s3, s4, s5).
Рәсемнән,
ОА : ОВ : ОС : OD : ОЕ = 1 : 4 : 9 : 16 : 25 (3)
икәнлеген күрәбез, ягъни хәрәкәт башланганнан исәпләнгән ва¬
кыт аралыклары tl белән чагыштырганда бөтен сан тапкыр арт¬
са, тиңдәшле күчешләр саннарның квадратлары рәте кебек арта.
15 нче рәсемдә тагын бер закончалык күренә:
ОА : AB : ВС : CD : DE = 1 : 3 : 5 : 7 : 9, (4)
ягъни эзлекле килүче тигез вакыт аралыкларында (һәрберсе tl гә
тигез) җисем ясаган күчеш векторының модульләре эзлекле килү¬
че так саннар чагыштырмасында була.
32
I бүлек. Җисемнәрнең узара тәэсир итешү һәм хәрәкәт законнары
(3) һәм (4) закончалыклары бары тик тигез тизләнешле хәрәкәткә
генә хас. Шуңа күрә аларны хәрәкәт тигез тизләнешлеме, түгелме
икәнен ачыклау өчен кулланырга мөмкин.
Мәсәлән, җисем хәрәкәтенең беренче 0,03 с эчендә — 2 мм, икенче
0,03 с эчендә — 6 мм, өченче 0,03 с эчендә 10 мм юл үтә. Бу
хәрәкәтнең тигез тизләнешле булу-булмавын ачыклыйк.
Моның өчен икенче һәм өченче вакыт аралыкларында җи¬
сем ясаган күчешнең беренчесеннән күпмегә зур икәнен табыйк:
- М—= з; 10 мм = 5. Димәк, 2 мм: 6 мм: 10 мм = 1:3:5. Чагыштыр-
2 мм 2 мм
малар эзлекле так саннар рәте булганлыктан, җисемнең хәрәкәте
тигез тизләнешле дибез.
Бу очракта җисемнең хәрәкәте тигез тизләнешле икәнлеге (4)
закончалыгы нигезендә ачыкланды.
Шуны ук (3) закончалыгы нигезендә дә күрсәтергә мөмкин иде.
Шарттан билгеле булганча, f1=0,03 с эчендә җисем s1=2 мм
ераклыкка, i2=2⅛1 = 0,06 с эчендә s2=2 мм + 6 мм = 8 мм га, ә
t3 = 3f1 = 0,09 с эчендә s3= 2 мм + 6 мм + 10 мм = 18 мм га күчә (t1,
t2 һәм t3 хәрәкәт башланудан алып исәпләнә).
ττ s2 8мм . s, 18мм _
Димәк, — = = 4 , -2- = = 9.
s1 2мм s1 2мм
Шулай итеп, s1: s2: s3 = 1 : 4 : 9, ягъни хәрәкәт тигез тизләнешле.
(3) һәм (4) закончалыклары шулай ук кайбер мәсьәләләрне
чишкәндә дә кулланыла.
Сораулар
1. Җисем тикторыштан башлап тигез тизләнешле хәрәкәт
иткәндә, аның күчеш векторы проекциясе һәм модуле нинди форму¬
лалар буенча исәпләнә?
2. Җисем тикторыштан башлап хәрәкәт иткәндә, хәрәкәт ва¬
кыты п тапкыр артса, күчеш векторының модуле ничә тапкыр
артыр?
3. Тикторыштан башлап тигез тизләнеш белән хәрәкәт итү¬
че җисемнең хәрәкәт вакыты ∕1 белән чагыштырганда бөтен сан
тапкыр артса, күчеш векторларының модульләре нинди чагыштыр¬
мада булыр?
33
/ булек.. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
4. Әгәр җисем тикторыштан башлап тигез тизләнеш белән
хәрәкәт итсә, аның тигез вакыт араларында ясаган күчеш вектор¬
ларының модульләре бер-берсенә нинди чагыштырмада булуын язы¬
гыз.
5. (3) һәм (4) закончалыкларын нинди максатларда кулланыр¬
га мөмкин?
$ 8 нче күнегү
1. Станциядән кузгалып киткән поезд беренче 20 с дәвамында
тигез тизләнеш белән турысызыклы хәрәкәт итә. Хәрәкәт башлануы¬
ның өченче секундында ул 2 м юл узган. Поездның беренче се¬
кундта ясаган күчеш векторы модулен һәм тизләнеш векторы
модулен табыгыз.
2. Тикторыштан башлап, тигез тизләнеш белән хәрәкәт итүче
автомобиль, тизләнүенең бишенче секундында 6,3 м юл үтә. Би¬
шенче секундның ахырында автомобильнең тизлеге нинди булган?
/ § 9.уХәрәкәтнең чагыштырмалыгы
7 нче^сыйныфта физика курсында механик хәрәкәтнең чагыш-
тырмалылыгы хакында әйтелгән иде. Хәзер бу мәсьәләне җен¬
текләбрәк тикшерик һәм хәрәкәтнең чагыштырмалылыгы нидән
гыйбарәт икәнен күрсәтик. Моның өчен мәсьәлә чишәбез.
V =19 м/с
кеш.җ.кар '
V =1 м/с
кеш.ваг.кар '
LOIOJ
V =20 м/с
ваг.җ.кар '
Рәс. 16
Кеше вагон буйлап поезд хәрәкәтенә каршы атлый (рәс. 16).
Поездның җир өслегенә карата тизлеге 20 м/с, ә кешенең вагонга
карата тизлеге 1 м/с. Кешенең җиргә карата нинди тизлек белән
һәм нинди юнәлештә хәрәкәт итүен ачыклагыз.
34
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Болай фикер йөртәбез. Әгәр кеше вагон буйлап бармаса, ул 1 с
эчендә поезд белән бергә 20 м ераклыкка күчәр иде. Әмма ул шул
ук вакытта поезд йөрешенә каршы 1 м юл узган. Шунлыктан 1 с
вакыт эчендә ул поезд хәрәкәте юнәлешендә җиргә карата 19 м гына
күчә. Димәк, кешенең җир өслегенә карата тизлеге 19 м/с ка тигез
һәм поезд тизлеге белән бер үк юнәлештә. Шулай итеп, поезд белән
бәйле исәп системасында кеше 1 м/с тизлек белән, ә җир өслегендәге
нинди дә булса әйбер белән бәйле исәп системасында 19 м/с тизлек
белән хәрәкәт итә.
Без тизлекнең чагыштырма булуын, ягъни бер үк җисемнең төрле
исәп системаларындагы тизлеге санча кыйммәте буенча да, юнә¬
леше буенча да төрле булырга мөмкин икәнен күрдек.
Хәзер икенче мисалны карап үтәрбез. Җиргә вертикаль төшүче
вертолетны күз алдыгызга китерегез. Аның винтындагы теләсә кай¬
сы, мәсәлән, А ноктасының траекториясен тикшерик (рәс. 17). Вер¬
толетка карата бу нокта һәрвакыт әйләнә буенча хәрәкәт итә, рәсемдә
ул тоташ сызык белән күрсәтелгән. Җирдән күзәтеп торучы өчен
шушы ук нокта винт сыман траектория (пунктир сызык) ясый.
Бу мисалның асылы шул, хәрәкәтнең траекториясе дә чагыш¬
тырма, ягъни бер үк җисемнең траекториясе төрле исәп система¬
ларында төрлечә булырга мөмкин.
Моннан юлның да чагыштырма зур¬
лык булуы килеп чыга, чөнки юл — җи¬
семнең тикшерелә торган вакыт аралы¬
гында узган барлык траектория бүлемтек¬
ләренең озынлыклары суммасы. Бу
бигрәк тә физик җисемнең, бер исәп сис¬
темасында хәрәкәт итеп, икенчесендә тик
торган очракларда ачык күренә. Мәсәлән,
хәрәкәт итүче поездда утырып торган
кеше Җир белән бәйле исәп системасын¬
да s юлы үтә, ә поезд белән бәйле систе¬
мада аның юлы нульгә тигез.
Шулай итеп, хәрәкәтнең чагыш¬
тыр малылыгы тизлек, траектория,
юл һәм аның башка характеристика-
Рәс; -17
35
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
ларының чагыштырма булуында, ягъни төрле исәп система¬
ларында төрле булуларында чагыла.
Бер үк җисемнең хәрәкәтен төрле исәп системаларында тикшерү
мөмкинлеген аңлау Галәмнең төзелеше турындагы карашларның
үсешендә гаять зур роль уйный.
Әле борынгы заманнарда ук кешеләр йолдызларның төнлә, Кояш
көндез хәрәкәт иткән кебек, күк йөзендә көнчыгыштан көнбатышка
таба дугалар буенча күчүен һәм тәүлек эчендә Җир тирәли тулы
әйләнеш ясавын күзәткәннәр. Шуңа күрә күп гасырлар буена —
Дөньяның үзәгендә хәрәкәтсез Җир тора, ә барлык күк җисемнәре
аның тирәсендә әйләнә дип уйланылган. Дөньяның мондый система¬
сы геоцентрик (грек сүзе «гео» «җир» дигәнне аңлата) дип аталган.
II гасырда Александрия галиме Клавдий Птолемей геоцент¬
рик системада яктырткычларның һәм планеталарның хәрәкәте ту¬
рында мәгълүмат туплый һәм шактый ук төгәл таблицалар төзи.
Бу таблицалар буенча күк җисемнәренең үткәндәге һәм киләчәктә¬
ге торышын билгеләргә, Ай һәм Кояш тотылуларның вакытын ал¬
дан әйтергә һ.б. мөмкинлек бирә.
Әмма вакытлар узу белән, астрономик күзәтүләрнең төгәллеге
таләп ителә башлагач, планеталарның исәпләп табылган һәм
күзәтелә торган торышларында аермалар күзәтелә. Төрле дөресләү-
төзәтүләр Птолемей теориясен катлауландыра һәм бутый гына.
Дөньяның геоцентрик системасын алыштыру зарурлыгы туа.
Галәм төзелеше турында яңача карашлар XVI гасырда поляк
галиме Николай Коперник тарафыннан җентекләп эшкәртелә. Ул
Җир һәм башка планеталар Кояш тирәсендә һәм шул ук вакытта
үз күчәрләре тирәсендә дә әйләнә дип исәпли. Мондый система ге-
лиоцентрик дип атала, чөнки аның үзәге итеп Кояш (грекча «ге¬
лиос») кабул ителә.
Шулай итеп, гелиоцентрик исәп системасында күк җисемнәре¬
нең хәрәкәте — Кояшка карата, ә геоцентрик системада Җиргә ка¬
рата тикшерелә.
Коперник системасы ярдәмендә Кояшның Җир тирәли тәүлек¬
лек күренмә хәрәкәтен ничек аңлатып була соң? 18 нче рәсемдә схе¬
ма рәвешендә бер ягыннан кояш нурлары белән яктыртыла торган
Җир һәм тәүлек буе Җирнең бер урынында торучы кеше (күзәтүче)
сурәтләнгән. Җир белән бергә әйләнеп, ул яктырткычларның күчеш¬
ләрен күзәтә.
36
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Җир шары аны Төньяк (N) һәм Көньяк
(S) географик полюсларында «тишеп» үтүче
уйланма күчәр тирәсендә әйләнә. Ук Җир¬
нең көнбатыштан көнчыгышка таба әйләнү
юнәлешен күрсәтә.
18 нче а рәсемдә Җир шарының кү¬
зәтүчене караңгы төнге яктан Кояш яктыр¬
та торган көндезге якка алып чыккан
вакыты сурәтләнгән. Әмма күзәтүче, Җир
белән бергә аның күчәре тирәсендә көнба¬
тыштан көнчыгышка таба 200 м/с1 тизлек
белән әйләнүенә карамастан, бу хәрәкәтне
сизми (без дә сизмибез бит!). Шуңа күрә аңа
Кояш үзе горизонттан күтәрелә һәм көн
буена көнчыгыштан көнбатышка таба (рәс.
18, б) — Җир әйләнешенә каршы хәрәкәт
итә кебек тоела. Кичен, әйләнүче җир
күзәтүчене акрынлап күләгәле өлкәгә күчерә
башлаганда (рәс. 18, в), ул Кояшның гори¬
зонт артына киткәнен «күзәтә». Аннан соң
ул инде йолдызларның төн буена көнчы¬
гыштан көнбатышка хәрәкәт итүен күрә
(рәс. 18, г).
Шулай итеп, Кояш һәм йолдызларның
күренмә әйләнүе, ягъни көн белән төн алы¬
шыну, Коперник системасында Җирнең үз
күчәре тирәсендә әйләнүе белән аңлатыла.
Җир шары тулы әйләнеш ясый торган ва¬
кыт тәүлек дип атала.
Иртә,
кояш чыгышы
Көндез
Төн
Рәс. 18
Гелиоцентрик система, күп кенә фәнни һәм гамәли мәсьәләләрне
чишү өчен, геоцентрик системага караганда аеруча уңышлы булып
чыга.
Шулай итеп, хәрәкәтнең чагыштырма булуы турындагы белемнәр
Галәмнең төзелешенә яңача карарга мөмкинлек бирә. Ә бу, үз чира-
'Җир өстендәге нокталарның күчәргә карата әйләнү тизлеге бу урын¬
ның киңлегенә бәйле: ул нульдән (полюсларда) алып 465 м/с ка (экватор¬
да) кадәр арта.
37
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
тында, бераздан җисемнәрнең Кояш системасындагы хәрәкәтләрен
сурәтләгән физик законнарны ачарга һәм мондый хәрәкәтнең
сәбәпләрен аңлатырга ярдәм итә.
Сораулар
1. Тизлек чагыштырма, хәрәкәт траекториясе чагыштырма, юл
чагыштырма дигән расламалар нәрсәне аңлата?
2. Тизлекнең, хәрәкәт траекториясенең һәм үткән юлның ча¬
гыштырма зурлыклар булуын мисалларда күрсәтегез.
3. Кыскача әйтеп бирегез, хәрәкәтнең чагыштырма булуы нидән
гыйбарәт?
4. Гелиоцентрик һәм геоцентрик системаларның төп аермасы
нәрсәдә?
5. Гелиоцентрик системада Җирдәге көн белән төннең алышы¬
нуын аңлатыгыз (рәс. 18).
£ 9 нчы күнегү
1. Елгадагы су ярга карата 2 м/с тизлек белән ага. Елгада агып
баручы салның ярга карата тизлеге нинди? Елгадагы суга карата?
2. Кайбер очракларда җисемнең тизлеге төрле исәп системала¬
рында бер төрле булырга мөмкин. Мәсәлән, поезд вокзал бинасы
белән бәйле исәп системасында да, юл буенда үсеп утырган агачка
бәйле исәп системасында да бер үк тизлек белән хәрәкәт итә. Бу
хәрәкәтнең чагыштырмалылыгы турындагы расламага каршы кил¬
миме? Җавапны аңлатыгыз.
3. Нинди шартларда хәрәкәт итүче җисемнең тизлеге ике исәп
системасына карата бер төрле була?
4. Җирнең тәүлеклек әйләнүе нәтиҗәсендә, Мәскәүдә үз фати¬
рында урындыкта утырып торган кеше җир күчәренә карата
900 км/сәг тизлек белән хәрәкәт итә. Бу тизлекне пуляның писто¬
леттан чыгу тизлеге (200 м/с) белән чагыштырыгыз.
5*1. Торпедалар катеры, көньяк киңлекнең алтмышынчы па¬
раллеле буйлап, коры җиргә карата 90 км/сәг тизлек белән бара.
Бу киңлектә Җирнең тәүлеклек әйләнү тизлеге 223 м/с. Әгәр катер
а) көнчыгышка; б) көнбатышка таба хәрәкәт итсә, аның тизлеге
нәрсәгә (СИ) тигез һәм кая юнәлгән?
’Йолдызчык белән катлаулырак мәсьәләләр билгеләнгән.
38 7
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
§ 10. Инерциаль исеп системалары.
Ньютонның беренче законы
Сезгә инде хәрәкәт законнарының берсе — инерция законы
билгеле. Бу закон буенча җисемнәр (материаль нокталар), аларга
башка җисемнәр тәэсир итмәгәндә, тикторыш хәлендә булалар яки
турысызыклы тигез хәрәкәт итәләр (ягъни тизлекләрен үзгәрешсез
саклыйлар).
Инерция законының асылы беренче тапкыр итальян галиме
Галилео Галилейның XVII гасырда чыккан бер китабында сурәт¬
ләнә.
Моңа кадәр фәндә күп гасырлар буена борынгы грек галиме Ари¬
стотельнең һәм аның шәкертләренеңфикерләре өстенлек итә.
Аристотель карашынча, тышкы тәэсир булмаганда, җисем тикто¬
рыш хәлендә генә була, ә инде ул даими тизлек белән хәрәкәт итсен
өчен, аңа икенче җисем өзлексез тәэсир итеп торырга тиеш.'-'
^Галилей исә тышкы тәэсирләр булмагкнда^җисем, тикторышта
булуы өстенә, турысызыклы тигез хәрәкәт итәргә дә мөмкин дигән
нәтиҗәгә килә. Ә аның хәрәкәтен дәвам иттерү өчен куела торган
көч җисемгә куелган башка көчләрне, мәсәлән ышкылу көчен, ти¬
гезләргә генә тотыла^
Хәрәкәтнең сәбәпләренә караган мондый фикерләрне Галилей-
га кадәр дә кайбер галимнәр әйткән була. Галилей, аларның идеялә¬
рен тәнкыйть күзлегеннән анализлап, дөрес нәтиҗәләргә килә һәм
аларны конкрет күренешләрне аңлату
өчен куллана. Аның гаять әһәмиятле
казанышы булып — гасырлардан килгән
ялгышларны төзәтеп, фәннең үсешенә
зур этәргеч бирүе тора.
XVII гасырның ахырында инглиз
галиме Исаак Ньютон Галилей нәти¬
җәләрен гомумиләштерә, инерция зако¬
нын формалаштыра һәм аны өч закон¬
ның беренчесе рәвешендә механиканың
(җисемнәрнең хәрәкәте һәм тәэсир ите¬
шүе турындагы фән) нигезенә сала.
Шуңа күрә аны Ньютонның беренче
законы дип атыйлар.
39
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Рәс. 19
Ньютон инерция законын болай әйтеп бирә: «Һәрбер җисем, үзенә
куелган көчләр ярдәмендә бу хәлен үзгәртергә мәҗбүр ителгәнче,
үзенең тикторыш хәлен яки турысызыклы тигез хәрәкәтен сакла¬
вын дәвам итә».
Ләкин, вакыт узу белән, Ньютонның беренче законының бар¬
лык исәп системаларында да үтәлмәве ачыклана.
Моңа 19 нчы рәсемдә сурәтләнгән тәҗрибә ярдәмендә ышанырга
мөмкин. Башта арба Җиргә карата турысызыклы һәм тигез хәрәкәт
итә (рәс. 19, а). Бер шарчык арбаның горизонталь өслегендә ята, ә
икенчесе арбада җепкә эленеп куелган, һәр ике шарчыкка верти¬
каль тәэсир итүче көчләр тигезләшкән, ә горизонталь буенча аларга
бернинди көчләр дә тәэсир итми (бу очракта һава каршылыгын исәпкә
алмаска мөмкин).
Арбаның Җиргә карата теләсә нинди тизлек белән (ι>1, υ2, υ3 һ.б.)
хәрәкәте вакытында да шарчыклар арбага карата тикторыш хәлендә
булалар.
Әмма арба ком өстенә терәлгәч (рәс. 19, б), аның тизлеге тиз
генә кими, нәтиҗәдә арба туктый. Арба тормозлана башлауга, ике
шарчык та хәрәкәткә килә, ягъни, аларны этүче бернинди көч бул¬
мауга да карамастан, арбага карата үз тизлекләрен үзгәртәләр.
Димәк, Җиргә карата туктый башлаган арба белән бәйле исәп
системасында инерция законы үтәлми.
Шулай булгач, инерция законына Ньютон биргән әйтелешкә бу
законның барлык исәп системалары өчен дә дөрес булмавын өстәргә
кирәк. Шундый күрсәтүдән башка Ньютон формулировкасы тәмам¬
ланмый һәм бик үк төгәл булмый (чөнки инерция законының теләсә
нинди исәп системаларында да үтәлүе турындагы ялгыш төшенчәгә
40
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
китерә). Шунлыктан, хәзерге заман күзаллауларыннан чыгып, Нью¬
тонның беренче законын түбәндәгечә әйтәләр:
башка җисемнәр тәэсир итмәгәндә, җисемнәр үзләренең
тизлекләрен үзгәрешсез саклый торган исәп системалары бар.
Шуны истә тотарга кирәк: Ньютонның беренче законында сүз
материаль нокта итеп кабул ителә торган җисемнәр турында бара.
Инерция законы үтәлә торган исәп системалары — инерциаль
системалар дип, үтәлми торганнары инерциаль булмаган система¬
лар дип атала.
Җисемнәрнең сез 9 нчы сыйныфта өйрәнә торган хәрәкәт һәм
тәэсир итешү законнары инерциаль исәп системалары өчен форма-
лаштырылган, бу очракта әлеге законнар иң гади рәвештә була.
Шуңа күрә, мәсьәләләр чишү өчен теге яки бу законны куллану ал¬
дыннан, хәрәкәт яки тәэсир итешү бара торган исәп системасының
инерциаль булу-булмавын белергә кирәк.
Шулай да тикшерелә торган барлык күренешләр өчен дә һич¬
шиксез инерциаль булган исәп системасы табу мөмкин түгел.
Гелиоцентрик системаны иң югары төгәллек дәрәҗәсендәге инер¬
циаль система дип алырга була. Бу система күк механикасы һәм
космонавтика мәсьәләләрендә кулланыла.
9 нчы сыйныфта тикшерелә торган мәсьәләләрдә Җир өслегенә
карата тикторыш хәлендә яисә турысызыклы тигез хәрәкәт итә тор¬
ган теләсә нинди җисем белән бәйле исәп системаларын шулай ук
инерциаль дип санарга мөмкин.
Ә инерциаль системаларга карата тизләнеш белән хәрәкәт итүче
системалар инерциаль булмый.
Инерциаль һәм инерциаль булмаган системаларның саны чик¬
сез күп. ∙4⅛7
араулар
1. Җисемгә башка җисемнәр тәэсир итмәсә, ул ничек хәрәкәт
итә?
2. Җисем турысызыклы тигез хәрәкәт итә. Бу вакытта аның
тизлеге үзгәрәме?
41
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
3. XVII гасырга кадар җисемнәрнең тикторышы һәм хәрәкәте
турында нинди карашлар хөкем сөргән?
4. Галилейның җисемнәр хәрәкәте турындагы күзаллаулары
Аристотельнекеннән ни белән аерыла?
5. 19 нчы рәсемдә сурәтләнгән тәҗрибә ничек үткәрелә һәм
нинди нәтиҗәләр ясала?
6. Ньютонның беренче законы ничек әйтелә (хәзерге әйтелеш
формасы )?
7. Нинди исәп системалары — инерциалъ дип, ниндилэре инер¬
циалъ булмаган дип атала?
8. Җиргә карата тикторышта яисә турысызыклы тигез
хәрәкәт итә торган җисемнәр белән бәйле исәп системаларын
күпчелек очракларда инерциалъ дип санарга мөмкинме?
9. Нинди дә булса инерциалъ системага карата тизләнеш белән
хәрәкәт итүче исәп системасы инерциалъ буламы?
$ 10 нчы күнегү
Турысызыклы тигез хәрәкәт итүче поезддагы өстәлгә җиңел
хәрәкәтләнә торган уенчык автомобиль куелган. Поезд акрыная баш¬
лагач, автомобиль, бернинди тышкы тәэсирдән башка, үзенең җиргә
карата тизлеген саклап, алга тәгәри.
а) Җир белән бәйле исәп системасында; б) турысызыклы тигез
хәрәкәт итүче поезд белән бәйле исәп системасында; в) туктала ба¬
ручы поезд белән бәйле исәп системасында инерция законы үтәләме?
Бу очракта җирне инерциаль система дип санарга мөмкинме?
поездны?
§11. Ньютонның икенче законы
Җисемнәрнең тигез тизләнешле хәрәкәтләрен өйрәнгәндә, без
аларның ни өчен тизләнеш белән хәрәкәт итүләрен, ягъни тизлә¬
неш барлыкка килүнең сәбәбен тикшермәдек.
Бу сорауга җавап бирү өчен җисемнең тизлеге үзгәрүгә, димәк,
тизләнешнең барлыкка килүенә көч сәбәпче булуын искә төшерергә
кирәк.
Берничә көч тәэсир иткәндә, бу көчләрнең бердәй тәэсир итүче¬
се нульгә тигез булмаган очракта, ул тизләнеш белән хәрәкәт итә
42
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
(бердәй тәэсир итүче нульгә тигез булса, җисем турысызыклы ти¬
гез, ягъни тизләнешсез хәрәкәт итә).
Тизләнешне көч тудыра, шуңа күрә бу ике зурлык арасындагы
микъдари бәйләнеш бар дип уйлау бик табигый.
Тормыш тәҗрибәсенә таянып әйтә алабыз: җисемгә куелган
көчләрнең бердәй тәэсир итүчесе зуррак булган саен, җисем зур¬
рак тизләнеш ала. Мәсәлән, футболчы кырдагы тупка никадәр
көчлерәк типсә, туп шулкадәр зуррак тизләнеш ала һәм футболчы¬
ның аягы белән тәэсир итешкән вакыт (секундның йөзенче өлешлә¬
ре) эчендә зуррак тизлек алып өлгерә (туп алган тизлек турында
аның нинди ераклыкка барып төшүенә карап фикер йөртәбез).
Күпсанлы күзәтү һәм тәҗрибәләр тагын шуны күрсәтә: җи¬
семнәргә тәэсир итүче көчләр бертигез булганда, тизләнеш бу җи¬
семнәрнең массаларына бәйле.
Шома горизонталь өстәл өстендәге бер үк үлчәмдәге алюминий
һәм җиз (җизнең массасы алюминийныкыннан өч тапкыр диярлек
артык) цилиндрлар ята дип күз алдыгызга китерегез.
Әгәр дә без көч белән тәэсир итеп, цилиндрларны кузгатып
җибәрергә тырышсак, кечерәк массалы (ягъни алюминий) цилиндр
зуррак тизләнеш, димәк, зуррак тизлек ала һәм нәтиҗәдә җиз ци¬
линдрдан ераграк тәгәри.
Билгеле инде, цилиндрлар белән ясалган әлеге тәҗрибә бертигез
көчләр тәэсир иткәндә, зуррак массалы җисемнәрнең кечерәк тизлә¬
неш алуына кире каккысыз исбатлау була алмый. Чөнки җиз ци¬
линдрга алюминиена караганда зуррак ышкылу һәм тәгәрәү көчләре
тәэсир иткәнлектән дә, аның кечерәк тизләнеш алуы да мөмкин
(димәк, бәрү көче бер үк булганда, җиз цилиндрга куелган бердәй
тәэсир итүче көч алюминийга куелганга караганда зуррак, ә тизлә¬
неш нәкъ менә бердәй тәэсир итүчегә бәйле).
Ниндидер көч куелган җисемнең тизләнеше аның массасына
бәйле икәнен исбатлау өчен, ышкылу көчләре мөмкин кадәр ти¬
гезләшкән тагын бер тәҗрибәне тикшерик.
20 нче а рәсемдә өсләренә кечкенә тамызгычлар һәм икешәр
җилләткеч урнаштырылган җиңелчә арбалар сурәтләнгән (җилләт¬
кечләр бертигез егәрлектәге үз батареялары белән эшли). Әйтик,
арбаның җилләткечләр һәм тамызгыч белән гомуми массасы бил¬
геле булсын, ди.
43
1 бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Рәс. 20
Арбага блок аша үткәрелгән җепнең бер очы бәйләнгән. Җеп¬
нең икенче очына зур булмаган йөк асылган. Бу йөк хәрәкәт итүче
арбага тәэсир итә торган ышкылу көчен тигезләү өчен кирәк.
Арбаны 20 нче а рәсемдә күрсәтелгәнчә урнаштырабыз. Арба¬
ның хәрәкәт траекториясе буенча кәгазь тасма сузабыз. Кранны ачып,
җилләткечләрне кабызабыз. Аларның винтлары, һава белән тәэсир
итешеп, арбаны ниндидер даими көч белән өстәл кырыендагы чиклә¬
гечкә юнәлтә. Бу вакытта кәгазь тасмада тигез вакыт аралыкларын-
да (Т) тамган тамчыларның эзләре калып бара.
Арба туктагач, җилләткечләрне туктатабыз һәм тасмадагы күр¬
ше тамгалар арасын үлчибез. Үлчәүләр бу:ераклыкларның эзлекле ки¬
лүче так саннар чагыштырмасында икәйһн (1 : 3 : 5 : 7 : 9...) күрсәтә.
Димәк, даими көч тәэсирендә арба тигез тизләнеш белән хәрәкәт
итә (§8).
44
1 бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Арбаның тизләнешен исәпләү өчен, аның күчеш векторының
модулен (з) (ягъни тасмадагы иң кырый тасмалар арасын) үлчибез.
Аннан соң күрше тамга араларының санын яки, икенче төрле,
арба хәрәкәтләнгәндәге Т вакыты араларын санап чыгабыз, t = Тп
формуласы буенча, арбаның s ераклыгына күчү вакытын (t) таба-
, αf2
быз. 8 =
2
формуласыннан тизләнеш модулен чыгарабыз (a -
2s
t2)
һәм исәплибез.
Хәзер, 20 нче б рәсемдәге кебек, герләр ярдәмендә хәрәкәт итүче
системаның (арба, җилләткечләр, тамызгычлар һәм җепкә эленгән
йөктән торучы) массасын ике тапкыр арттырыйк (бу вакытта, җеп¬
нең асылынып торган очына, арткан ышкылу көчен тигезләү өчен
тагын бер гер өстәлә).
Тәҗрибәне яңадан кабатлыйбыз. Тизләнешне исәпләп, алдагы
тәҗрибәнең тизләнеше белән чагыштырабыз: бер үк зурлыктагы
көч тәэсир иткәндә, массасы ике тапкыр артык булган система ике
тапкыр кечерәк (ягъни ) тизләнеш ала.
Без карап узган һәм күп кенә башка тәҗрибәләрдән күренгәнчә,
җисемнәргә бер үк даими көч белән тапшырыла торган тизлә¬
нешләр бу җисемнәрнең массаларына кире пропорциональ була.
Әлеге эксперименталь җайланма ярдәмендә җисемнең тизләне¬
ше белән җисемгә тизләнеш бирә торган көч арасындагы микъдари
бәйләнешләрне исәпләргә мөмкин.
Моның өчен соңгы тәҗрибәдә өстәлгән герне алып, системаны
беренче тәҗрибәдәге кебек калдырабыз (рәс. 20, в). Тик бу юлы ар¬
баны хәрәкәткә китерүче бер генә җилләткечне ялгыйбыз, нәтиҗәдә
арбага ике җилләткеч ялгаган вакыттагыдан ике тапкыр кимрәк
көч тәэсир итә (арбага а тизләнеше бирә).
Үлчәүләр һәм исәпләүләр күрсәткәнчә, көчне ике тапкыр ки¬
меткәндә, тизләнеш тә ике тапкыр кими, ягъни „ гә тигез булып
кала (арбаның массасы үзгәрмәгәндә).
Димәк, хәрәкәт итүче даими массалы җисемнең тизләнеше бу
тизләнешне тудыручы көчкә туры пропорциональ була.
45
I бу лек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Җисемнең массасы, аның хәрәкәтенең тизләнеше, җисемгә куел¬
ган һәм бу тизләнешне тудыра торган көчләрнең бердәй тәэсир
итүчесе арасындагы микъдари бәйләнешләр Ньютонның икенче
законы дип атала. Ньютонның икенче законы болай әйтелә:
җисемнең тизләнеше аңа куелган көчләрнең бердәй тәэсир итү¬
чесенә туры пропорциональ һәм җисем массасына кире пропор¬
циональ.
Шуны истә тотарга кирәк: Ньютонның икенче законында, бе-
ренчесендәге кебек үк, хәрәкәте инерциаль исәп системасында кара¬
ла торган материаль нокта җисем дип алына.
Ньютонның икенче законының математик формуласы түбән¬
дәгечә языла:
α=l. (1)
т
Без монда тизләнеш векторының җисемгә куелган көчләрнең
бердәй тәэсир итүчесе векторы белән бер үк юнәлештә икәнен күрәбез.
Икенче законны скаляр рәвештә болай язып була:
ax = , (2)
т
яки
F
a=t , (3)
т
биредә ax һәм Fχ — тизләнеш һәм көч векторларының X күчәренә
пропорциясе, ә а һәм F — бу векторларның модульләре.
Көчнең нъютоннарда (Н) үлчәнүен сез инде беләсез.
Ньютонның икенче законы ярдәмендә көч берәмлегенә билгеләмә
биреп карыйк. Моның өчен (3) формуласыннан көч модулен күр¬
сәтәбез:
F = та. (4)
(4) формуласы буенча, масса берәмлеккә (1 кг) тигез һәм тизлә¬
неш берәмлеккә (1 м/с2) тигез булса, көч тә берәмлеккә (1 Н) тигез
була.
СИда 1 кг массалы җисемгә үзенең тәэсир итү юнәлешендә
1 м/с2 тизләнеш тапшыручы көч — көч берәмлеге итеп алынган.
46
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Бу кыйммәтләрне (4) формуласына куеп, аларның берәмлекләре
арасындагы бәйләнешне табабыз:
1 Н = 1 кг • 1 м/с2 = 1 кг • м/с2.
Сораулар
1. Җисемнең тизләнеп хәрәкәт итүенә нәрсә сәбәп була?
2. Җисемгә куелган көч зуррак булган саен, бу көч тапшырган
тизлекнең дә зуррак булуына тормыштан мисаллар китерегез.
3. 20 нче рәсемнән файдаланып, нинди тәҗрибәләр куелуы һәм
алардан нинди нәтиҗәләр килеп чыгуы турында сөйләгез.
4. Ньютонның икенче законы ничек укыла? Ул нинди матема¬
тик формула белән бирелә?
5. Тизләнеш векторының һәм җисемгә куелган көчләрнең бердәй
тәэсир итүчесе векторының юнәлеше турында нәрсә әйтеп була?
6. Көч берәмлеген масса һәм тизләнеш берәмлекләре аша күр¬
сәтегез.
£ 11 нче күнегү
1. Велосипедчы белән велосипедның гомуми массасы 50 кг бу¬
лып, ул таудан 0,8 м/с2 тизләнеш белән төшсә, велосипедка нинди
көч тәэсир итә?
2. Хәрәкәт башланып 20 с үткәч, электровозның тизлеге 4 м/с
ка җитә. Электровозның массасы 184 т булса, аңа тизләнеш бирүче
көчне табыгыз.
3. Массалары тигез булган ике җисем тиңдәшле рәвештә
0,08 м/с2 һәм 0,64 м/с2 тизләнеш белән хәрәкәт итә. Җисемнәргә тәэ¬
сир итүче көчләр модульләре буенча тигезме? Беренче җисемгә 1,2 Н
көч тәэсир итсә, икенче җисемгә тәэсир итүче көч нинди зурлыкта?
4. Массасы 0,5 кг булган су астындагы тупка тәэсир итүче авыр¬
лык көче 5 Н, Архимед көче 10 Н, ә хәрәкәткә уртача каршылык
көче 2 Н булса, ул нинди тизләнеш белән калкып чыгар?
5. Боҗра һәм сетка аша үткән баскетбол тубы башта авырлык
көче тәэсирендә аска таба — арта баручы тизлек белән, ә, идәнгә
бәрелгәннән соң, өскә таба кими баручы тизлек белән хәрәкәт итә.
Аска таба хәрәкәтләнгәндә, тупның тизләнеш, күчеш һәм тизлек
векторлары авырлык көченә карата ничек юнәлгән? өскә таба
хәрәкәтләнгәндә?
47
1 бу лек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
6. Ниндидер җисем даими тизләнеш белән турысызыклы хәрәкәт
итә. Бу җисемнең хәрәкәтен сыйфатлаучы нинди зурлык һәрвакыт¬
та да аңа куелган көчләрнең бердәй тәэсир итүчесе белән бер үк
юнәлештә була, ә нинди зурлыклар бердәй тәэсир итүче белән кап¬
ма-каршы юнәлештә булырга мөмкин?
§ 12. Ньютонның өченче законы
Без бер җисемнең икенчесенә берьяклы гына тәэсир итә алма¬
вын беләбез. Җисемнәр һәрвакыт үзара тәэсир итешәләр. Мәсәлән,
кадак какканда чүкеч кенә кадакка тәэсир итми, кадак та, үз чира¬
тында, чүкечкә тәэсир итә, нәтиҗәдә чүкеч туктап кала.
Ике җисемнең бер-берсенә тәэсир итү көчләре турында нәрсә
әйтергә мөмкин?
Бу сорауга җавап бирү өчен тәҗрибәләр карап үтик.
21 нче рәсемдә бер-берсенә эләктерелгән ике динамометр
сурәтләнгән, ал арның берсе вертикаль терәк С га беркетелгән. Икенче
динамометрны тарткач, икесенең дә пружиналары тартыла, һәм алар
капма-каршы якларга юнәлгән эластиклык көчләре F1 һәм F2 белән
бер-берсенә тәэсир итә башлыйлар. Бу вакытта динамометрларның
күрсәтүләре бертөрле була, димәк, F1 һәм F2 көчләренең модульләре
тигез.
Әгәр уң яктагы динамометрны көчлерәк тартсак, икесенең дә
күрсәтүләре бер үк зурлыкка артыр, ягъни тагын үзара тигез бу¬
лырлар. Димәк, бу очракта динамометрлар модульләре буенча тигез
көчләр белән тәэсир итешәләр.
Рәс. 22
48
I бүлек Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Тәэсир итешү ераклыктан булганда да, җисемнәр бер-берсенә
модуле буенча тигез көчләр белән тәэсир итәләр. Моны раслаучы
тәҗрибәне 22 нче рәсемдә күрәбез. Биредә сурәтләнгән ике арбаны
вертикаль таянычларга беркетелгән динамометрлар тотып тора.
Әгәр бер арбага — магнит, икенчесенә корыч борыс куйсак, ике
арба да, үзләренә куелган җисемнәр белән бергә, бер-берсенә каршы
хәрәкәт итә башлый. Ике арбаның да хәрәкәткә килүе җисемнәр¬
нең тәэсир итешүен күрсәтә: борыс кына магнитка тартылып кал¬
мый, магнит та борыска тартыла.
Бер-берсенә каршы хәрәкәтләнү — үзара тәэсир итешүче җи¬
семнәргә куелган көчләрнең капма-каршы юнәлүе турында сөйли.
Арбаларның хәрәкәте нәтиҗәсендә динамометр пружиналары тар¬
тыла башлый. Пружиналарның эластиклык көчләре җисемнәрнең
тартылу көчләре белән тигезләшкәч, арбалар туктый. Бу вакытка ди¬
намометрларның күрсәтүе бер төрле була, димәк, магнит белән борыс
бер-берсенә модульләре буенча тигез көчләр белән тартылалар.
Хәзер үзара тәэсир итешүче җисемнәрнең хәрәкәте барышында
тәэсир итешү көчләре үлчәнә торган тәҗрибәне карыйк (хәрәкәтне
нәкъ менә шушы көчләр тудыра).
Рәс. 23
23 нче рәсемдә роликлы конькида йөрүче ике малай сурәтләнгән.
Аларның һәркайсы бер үк бауның бер очыннан тарта һәм әкренләп
кулларын күчерә барып, бауның уртасына якынаялар. Бу вакытта,
бауның уртасына куелып, аның ике яртысын тоташтыручы дина¬
мометрлар бердәй көчләрне күрсәтә.
^Әлеге һәм башка бик күп тәҗрибәләрдән күренгәнчә,
ике җисемнец бер-берсенә тәэсир итү көчләре модульләре буен¬
ча тигез һәм юнәлешләре буенча капма-каршы.*
49
1 бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Бу закон Ньютон тарафыннан ачыла һәм Ньютонның өченче
законы дип атала.
Математик рәвештә аны болай язалар:
χ = →2.
«Минус» тамгасы көчләрнең капма-каршы юнәлүен күрсәтә.
Без күзәтә торган җисемнәрнең теләсә кайсының хәрәкәтен,
кешенең җирдән басып баруымы ул, диңгездәге корабның йөзүеме,
кошлар очуымы һ.б. Ньютон законнары ярдәмендә аңлатырга
мөмкин.
Мәсәлән, атлап баручы кеше аяклары белән җирдән этелеп ки¬
түе, ягъни Җир белән тәэсир итешүе аркасында хәрәкәт итә. Кеше
белән Җир бер-берсенә модульләре тигез, юнәлешләре буенча кап¬
ма-каршы көчләр белән тәэсир итешә һәм үзләренең массаларына
кире пропорциональ тизләнешләр ала. Җирнең массасы кешенеке
белән чагыштырганда гаять зур булганлыктан, аның тизләнеше нуль
диярлек, ягъни ул тизлеген үзгәртми. Ә кеше исә Җиргә карата
хәрәкәт итә.
Шунысы мөһим: җисемнәрнең үзара тәэсир итешүе нәтиҗәсендә
туган көчләрнең табигате бер үк төрле. Мәсәлән, Җир белән Ай
бер-берсе белән бөтендөнья тартылу көчләре тәэсирендә тартыла, ә
корыч борыс белән магнитка (рәс. 22) магнит көчләре тәэсир итә.
Сез инде беләсез, таянычта яткан предметлар Җиргә тартылу
көче тәэсирендә беркадәр үзләре кысылалар һәм асларындагы тая¬
нычны да кысалар (гадәттә бу деформацияләр үтә кечкенә була һәм
без аны сизмибез дә). Нәтиҗәдә җисемнәрнең үзендә дә, таянычта
да эластиклык көчләре туа һәм шул көчләр тәэсирендә җисем һәм
таяныч үзара тәэсир итешә.
Таянычка куелган һәм вертикаль рәвештә түбәнгә юнәлгән көчне —
җисемнең авырлык көче Р, ә җисемгә куелган һәм вертикаль рәвештә
югарыга юнәлгән көчне таянычның реакция көче N диләр. Алда
әйтелгәнчә, бу ике көч тә эластиклык көче була.
Шуны истән чыгармаска кирәк: Ньютонның өченче законында
әйтелгән көчләр беркайчан да бер-берсен тигезләми, чөнки алар төрле
җисемнәргә куелган. (Модульләре буенча тигез һәм юнәлеше кап¬
ма-каршы булган ике көч, бер үк җисемгә куелган булсалар гына,
бер-берсенә тигезләшәләр. Ул вакытта аларның уртак тәэсир итүче¬
50
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
ләре нульгә тигез, һәм җисем дә тигезләнеш торышында була, ягъ¬
ни я тик тора, я турысызыклы тигез хәрәкәт итә.)
? Сораулар
1. 21, 22 һәм 23 нче рәсемнәрдән файдаланып сөйләгез, аларда
сурәтләнгән тәҗрибәләр ничек үткәрелә һәм алар буенча нинди
нәтиҗәләр ясала?
2. Ньютонның өченче законы ничек укыла? Математик рәвештә
ничек языла?
3. Җир өстендә йөрүче кеше белән тәэсир итешүдән Җир нинди
тизләнеш ала? Җавабыгызны нигезләгез.
4. Ике җисемнең тәэсир итешүе нәтиҗәсендә туган көчләрнең
табигате бертөрле икәнен күрсәткән мисаллар китерегез.
5. Ни өчен җисемнәрнең тәэсир итешүе вакытында туган
көчләрнең тигезләнеше турында сөйләү урынсыз?
$ 12 нче кунегу
1. 24 нче рәсемдә такта өстендә таш ята. Дәфтәрегезгә бу рәсем¬
не күчереп алыгыз һәм Ньютонның өченче законы буенча үзара
тигез булган ике көчне уклар белән күрсәтегез. Бу нинди көчләр?
Исемнәрен атагыз.
2. Динамометр Д 100 Н һәм аннан зур булмаган көчләрне үлчәргә
исәпләнгән булса, 25 нче рәсемдә ул чик үлчәүдән артмыймы?
3. 26 нчы а рәсемдә җепләр белән тоташкан ике арба сурәтләнгән.
Ниндидер F көче тәэсирендә арбалар a = 0,2 м/с2 тизләнеш белән
хәрәкәт итә башлый.
51
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
а) Җеп тиңдәшле рәвештә икенче һәм беренче арбаларга тәэсир
итә торган F2 Һәм F1 көчләренең X күчәренә проекцияләрен табыгыз.
(Ышкылуны исәпкә алмагыз.)
б) Әгәр арбаларның урынын 26 нчы б рәсемдәгечә алыштырып
куйсак, F1 һәм F2 көчләренең проекцияләре нәрсәгә тигез булыр?
в) 26 нчы рәсемдәге очракларның кайсысында арбалар арасын¬
дагы җеп ныграк тартылган?
г) Арбалар нинди F көче тәэсирендә хәрәкәткә килә? Көчнең про¬
екциясен табыгыз.
§ 13. Җисемнәрнең ирекле төшүе
Җисемнәрнең авырлык көче тәэсирендәге хәрәкәте ирекле
төшү дип атала.
Җисемнәрнең көндәлек тормышыбызда без күзәтә торган төшүе,
төгәлрәк уйлаганда, ирекле түгел, чөнки җисемнәргә, авырлык
көченнән тыш, һаваның каршылык көче тәэсир итә. Әмма каршы¬
лык көче авырлык көченә караганда исәпкә алмаслык дәрәҗәдә кеч¬
кенә булса, җисемнең хәрәкәте иреклегә бик нык якыная (мәсәлән,'
авыр кечкенә шома металл шар төшкәндә).
Җисемнәр һавасыз пространствода, мәсәлән һавасы суыртып
алынган көпшә эчендә, ирекле төшәләр.
Җир өслеге тирәсендәге һәр җисемгә тәэсир итүче авырлык көче
даими булганлыктан, ирекле төшүче җисем даими тизләнеш белән,
ягъни тигез тизләнеш белән хәрәкәт итәргә тиеш (бу Ньютонның
икенче законыннан килеп чыга).
Тәҗрибәләр бу нәтиҗәне раслый. 27 нче рәсемдәге ирекле төшүче
шарчыкны, хәрәкәт башланган мизгелдән алып, һәр 0,1 с саен фото¬
га төшереп торганнар1.
1 Мондый фотоларны стробоскопик метод белән ясыйлар. Караңгыда
ирекле төшүче шарчыкны тигез вакыт аралыклары саен кыска вакытлы
яктылык белән яктырталар. Кабыныш мизгелләрендә шарчыкның торы¬
шы фотоаппарат пленкасында сурәтләнеп кала. Фотоаппарат затворы шар
төшеп җиткәнче ачык тора.
52
1 бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Алда әйтелгәнчә, турысызыклы тигез
тизләнеш белән хәрәкәт итүче җисем
ясаган күчешнең векторларының модуль¬
ләре эзлекле килүче так саннар чагыштыр¬
масында була (§ 8). Шарчыкның
27 нче рәсемдәге тиңдәшле күчешләре нәкъ
менә шундый рәт төзи:
8χ * * S3 * ' ss
≈ 4,9 см : 14,1 см : 24 см : 35 см: 45 cm ≈
≈ 1 : 3 : 5 : 7 : 9.
Шулай итеп, шарчыкның эзлекле кил¬
үче тигез вакыт араларында ясаган күчеш
векторы модульләре чагыштырмасы шар¬
чыкның ирекле төшкәндә тигез тизләнеш
белән хәрәкәт итүен белдерә.
27 нче рәсемдә шарчыкның хәрәкәт баш¬
ланганнан алып 0,5 с эчендә 1,23 м юл
үткәнлеге күренә, һәм башлангыч тизлеге
at2
нульгә тигез, s = —— формуласын кулланып,
2
бу бирелгәннәр буенча, шар хәрәкәтенең тиз¬
ләнеш векторы модулен исәпләргә мөмкин:
_ 2. _ 1,23 м 2,46 м 9
“ = .!=2(0,5 c)≡ = 0,25 c≈=8,84m∕c-
≈ 9,8 м/с2.
Шарчыкның ирекле төшүе 9,8 м/с2 тиз¬
ләнеш белән бара.
Рәс. 27
Ә башка җисемнәр, мәсәлән мамык кисәге, аяк киеменнән буша¬
ган катыргы тартма, агач мәрҗән, нинди тизләнеш белән төшәләр
соң? Икенче төрле әйткәндә: җисемнәрнең ирекле төшү тизләнеше
аларның тыгызлыгына, массасына, формасына бәйлеме"!
Бу сорауга җавап бирү өчен, мондый тәҗрибә ясыйбыз. 1,5 м
тирәсе озынлыгындагы пыяла көпшә алабыз. Аның бер башы ябык,
икенчесенә кран куелган (рәс. 28). Көпшәгә вак акча, кош каурые,
бөке кисәге, ярма, ягъни төрле формадагы һәм төрле массалы җи-
53
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Рәс. 28
семнәр кертелгән. Көпшәнең һавасын суыртып, кра¬
нын ябалар. Әйләндереп каплагач, андагы барлык
җисемнәрнең дә, бертөрле хәрәкәт итеп, бер үк ва¬
кытта төпкә төшүен күрербез. Вакытның теләсә кай¬
сы мизгелендә барлык бу предметларның моменталь
тизлекләре бертөрле була, димәк, алар бер үк тизлә¬
неш белән хәрәкәт итәләр.
Шулай итеп, җисемнәрнең җирнең бирелгән уры¬
нында бердәй тизләнеш белән төшүе ирекле
төшүнең үзенчәлеге булып тора.
Бу тизләнеш ирекле төшү тизләнеше дип атала.
Ирекле төшү тизләнеше g хәрефе белән тамгалана
(латинча gravitas — «гравитас» — «авырлык» сүзе¬
нең беренче хәрефе).
Ирекле төшүче шарчыкның стробоскопии фото¬
сы буенча без ирекле төшү тизләнешенең 9,8 м/с2
икәнен таптык, g зурлыгын тагын да зуррак төгәллек
белән (мәсәлән, 0,0001 м/с2 ка кадәр) билгели торган
ысуллар бар. Ләкин физиканың мәктәп курсындагы
мәсьәләләрдә нәтиҗәнең зур төгәллеге таләп ителми,
гадәттә 9,8 м/с2 кыйммәтен, хәтта 10 м/с2 кыйммәтен
дә кулланалар.
Безнең мисалда ирекле төшүче җисемнең хәрәкәте
башлангыч тизлексез тигез тизләнешле булганлыктан,
тизлек һәм күчеш векторлары проекцияләре vx = axt
Cl t2
Һәм sx= x формулалары буенча исәпләнә. Әмма aχ
урынына ирекле тизләнешнең проекциясен белдергән
gχHbi куялар, шуның белән ирекле төшүче теләсә кайсы җисемнең
ирекле төшү тизләнеше белән хәрәкәт итүен ассызыклыйлар. Фор¬
мулалар түбәндәгечә языла:
, g t
υx=gxt һәм s1 = % .
54
I бүлек. Җисемнәрнең у запа тәэсир итешү Һәм хәрәкәт законнары
Җисем түбәнгә таба хәрәкәт иткәндә, ирекле
төшү тизләнеше, тизләнеш һәм күчеш векторла¬
ры бер үк якка юнәлгән, шуңа күрә аларның про¬
екцияләре бер үк тамгага ия була.
Барлык җисемнәрнең дә массалары, форма¬
лары һәм үлчәмнәре нинди булуга карамастан,
ирекле төшүләре бер үк төрле дигән нәтиҗә, бе¬
ренче карашка, безнең көндәлек тәҗрибәгә кар¬
шы килә кебек. Без бер үк биеклектән төшүче
авыррак җисемнәрнең җиңелләренә караганда
җиргә тизрәк җитүенә күнеккәнбез.
Чынлыкта исә, бернинди каршылык та юк. Без
бит җисемнәрнең һавада төшүен күзәтәбез, ә ул,
төшүче җисемгә ниндидер көч белән тәэсир итеп,
хәрәкәткә каршылык күрсәтә.
Әгәр без, мәсәлән, кечкенә авыр шарчыкның һавада төшүен тик¬
шерәбез икән (рәс. 29), һава каршылыгын исәпкә алмаска мөмкин.
Чөнки ул шарга тәэсир итүче авырлык көче белән чагыштырганда
чиксез кечкенә, шунлыктан шар ирекле төшә дип әйтә алабыз.
Рәсемнән күренгәнчә, авырлык көче белән һава
каршылыгының бердәй тәэсир итүчесе (Fιu) (ул
шарга тизләнеш бирә) авырлык көченнән (Гшав)
әллә ни аерылмый, шуңа күрә шарчык g га якын
тизләнеш белән хәрәкәт итә.
Ә инде һавада мамык кисәгенең төшүен
(рәс. 30) берничек тә ирекле төшү дип атап бул¬
м. карш.
F м.
Рәс. 30
мый, чөнки бу очракта каршылык көче авырлык көченең шактый
зур өлешен тәшкил итә һәм бердәй тәэсир итүче көч (Fm ) авырлык
көченнән (Fiλ ав) күпкә ким. Шуңа күрә мамык кисәге һавада ирекле
төшүгә караганда күпкә ким тизләнеш белән төшә.
Ирекле төшүнең тигез тизләнешле хәрәкәт булуы турындагы
нәтиҗәгә беренче булып XVI гасыр ахырында Галилей килә. Ул
җисемнәрнең төшүен тәҗрибә юлы белән, авыр җисемнәрне мана¬
радан ыргытып карап тикшерә. Бу тәҗрибәләр җисемнәрнең, масса¬
ларына бәйсез рәвештә, җиргә бер үк вакытта диярлек төшеп җитү¬
ен күрсәтә.
55
I бүлек. A∏' У ∙ΛH∈*{.kl√4∙. ∖ '.зрй T<∕3i∕Mi ИГӨШУ Һ<М ..∙.∙≡∙c⅛υ∙ ..∙ ir√i< !H<J∣ )b;
Авырлык көче тәэсирендә җисемнәрнең нинди тизләнеш белән
хәрәкәт итүен белгәч, Ньютонның икенче законы нигезендә, масса¬
сы т булган теләсә нинди җисемгә тәэсир итүче авырлык көче век¬
торы модулен табу формуласын язарга мөмкин:
Fb= 9,8 м/с2 • т . (1)
(1) формуласын 7 нче сыйныф физикасында бирелгән формула
белән чагыштырыгыз:
Fb = 9,8 Н/кг • т . (2)
Бу ике формула 9,8 коэффициенты янындагы берәмлекләре белән
генә аерыла. 9,8 Н/кг ның шул ук 9,8 м/с2 икәнен исбат итик.
11 нче параграфта 1 Н = 1 кг • м/с2 икәне күрсәтелгән иде.
Димәк, 1 Н / кг = 1 КГ М / С =1 м / с2, ягъни 9,8 Н/кг = 9,8 м/с2,
к r
шулай булгач, (1) һәм (2) формулалары үзара эквивалент.
Сораулар
1. Җисемнәрнең ирекле төшүе дип нәрсә атала?
2. 27 нче рәсемдә сурәтләнгән шарчыкның ирекле төшүе тигез
тизләнешле икәнен ничек исбатларга?
3. 28 нче рәсемдәге тәҗрибә нинди максат белән куела һәм
аннан нинди нәтиҗә ясала?
4. Ирекле төшү тизләнеше нәрсә ул?
5. Ни өчен мамык кисәге тимер шарчыкка караганда кечерәк
тизләнеш белән төшә?
6. Ирекле төшүнең тигез тизләнешле хәрәкәт икәнлеге ту¬
рында нәтиҗәгә беренче булып кем килә?
$ 13 нче куны
1. Таш кисәге кое төбенә 2 с тан соң төшеп җитә. Коеның тирән¬
леген табыгыз.
Й, 80 см биеклектәге өстәлдән карандаш идәнгә төшә. Аның
төшеп җитү вакытын табыгыз (g ≈ 10 м/с2).
3. Кечкенә корыч шарчык 45 м биеклектән төшә. Төшү вакы¬
ты күпме дәвам иткән? Хәрәкәтенең беренче һәм соңгы секундында
шарчык нинди күчеш ясаган? (g ≈ 10 м/с2.)
I бүлек. Җисемнәрнең үзара гәэсир итешү һәм хәрәкәт законнары
§ 14 Вертикаль рәвештә югарыга ыргытылган
җисемнең хәрәкәте
Авырлык көче Җирдәге барлык җисемнәргә дә тәэсир итә: тик-
торыштагыларына да, хәрәкәт итүчеләренә дә, Җир өслегендәгелә-
ренә дә, аңа якын урнашканнарына да.
Җиргә ирекле төшүче җисем тигез тизләнеш белән тизләнеп
хәрәкәт итә, чөнки аның тизлеге авырлык көче һәм ирекле төшү
тизләнеше белән бер үк юнәлештә.
Югарыга ыргытылган җисем, һава каршылыгы булмаганда, авыр¬
лык көче тәэсирендә барлыкка килгән даими тизләнеш белән хәрәкәт
итә. Тик бу очракта ыргыту вакытында җисемгә бирелгән башлан¬
гыч тизлек v0 өскә, ягъни авырлык көченә һәм ирекле төшү тиз¬
ләнешенә капма-каршы юнәлгән. Шуңа күрә җисемнең тизлеге
кими (һәр секундта — ирекле төшү тизләнеше модуленә тигез
булган 9,8 м/с зурлыгына).
Билгеле бер вакыттан соң җисем иң югары биеклегенә ирешә,
ниндидер мизгелгә туктап кала, ягъни тизлеге нульгә тигезләшә.
Җисем ыргыту вакытында никадәр зуррак башлангыч тизлек алса,
аның күтәрелү вакыты да шулкадәр күбрәк була һәм, туктаганчы,
ул зуррак биеклеккә менеп өлгерә.
Аннары авырлык көче тәэсирендә җисем тигез тизләнеш белән
төшә башлый.
Җисемнәрнең югарыга таба хәрәкәтләренә карата мәсьәләләр
чишкәндә, бу вакытта аңа авырлык көче генә тәэсир итсә, башлан¬
гыч тизлеге v0 булган тигез тизләнешле турысызыклы хәрәкәт фор¬
мулаларын кулланалар, тик aχ кына gχ ка алыштырыла:
s t2
vx= υ0x + Sxt һәм sjr= v0xt + —
Монда җисем югарыга таба хәрәкәт иткәндә тизлек векторы белән
ирекле төшү тизләнеше векторының капма-каршы юнәлгән булуын
исәпкә алалар, аларның проекцияләре һәрвакыт төрле тамгаларга ия була.
Әгәр, мәсәлән, X күчәре вертикаль рәвештә өскә, ягъни тиз¬
лек векторы буенча юнәлсә, vχ > 0 була, димәк, vχ = v, ә gχ < 0,
димәк, gχ = -g = -9,8 м/с2 (биредә и — моменталь тизлек векторы
модуле, ә g — тизләнеш векторы модуле).
57
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Әгәр X күчәре вертикаль рәвештә аска юнәлсә, υχ < 0, ягъни υχ = -и,
ә gχ > 0, ягъни gx = g = 9,8 м/с2.
? Сораулар
1. Вертикаль рәвештә югарыга ыргытылган җисемнең күтәре¬
лүе вакытында аңа авырлык көче тәэсир итәме?
2. Ышкылу булмаганда, югарыга ыргытылган җисем нинди тиз¬
ләнеш белән хәрәкәт итә? Бу вакытта җисемнең хәрәкәт тизле¬
ге ничек үзгәрә?
3. Ышкылу көче исәпкә алынмаслык булганда, югарыга ыргы¬
тылган җисемнең иң зур күтәрелү биеклеге нәрсәгә бәйле?
4. Җисемнең югарыга таба хәрәкәте вакытында аның момен¬
таль тизлеге һәм ирекле төшү тизләнеше векторлары проекциялә¬
ренең тамгалары турында нәрсә әйтергә мөмкин?
$ 14 нче күнегү
Теннис шарын 9,8 м/с2 башлангыч тизлек белән вертикаль
рәвештә югарыга ыргыталар. Күпме вакыттан соң өскә күтәрелүче
тупның тизлеге нульгә кадәр кимер? Бу вакытта ул ыргытылган
урыныннан нинди күчеш ясап өлгерер?
§ 15. Бөтендөнья тартылу законы
Җирнең тартуы белән кеше әле бәләкәй вакытыннан ук таны¬
ша башлый. Идәнгә төшеп киткән уенчык, егылып төшкәндә бәрелгән
кул яки аяк аны җисемнәрнең Җиргә тартылуы белән таныштыра.
Җирнең тартуы тәэсирендә җисемнәр төшеп китәләр, бу төшүне
тоткарлаучы терәкләргә басым ясыйлар, бауларны тарттыралар.
Хәтта иң кечкенә, күзгә күренми торган атом да Җиргә тартыла.
Тәҗрибәләр Җирнең үзен әйләндереп алган барлык җисемнәрне дә
үзенә тартуын күрсәтә, бу тарту көче ерактан да тәэсир итә ала.
Шунлыктан, фән өчен кызыклы һәм әһәмиятле булган сораулар
туган. Мәсәлән, галимнәрне тагын нинди җисемнәрнең шундый ук
җисемнәрне үзенә тарта алу сәләте бар дигән сорау кызыксындыра.
Үзе тирәсендә тарту көче тудыра алучы җисемнең нинди аерым
үзенчәлекләре булырга тиеш? Бу көчнең зурлыгы нәрсәгә бәйле?
Җисемнәрнең тартылуы белән бәйле мондый бик күп сораулар¬
га җавапны XVII гасырның икенче яртысында Ньютон ачып бирә.
58
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт закойнары
λ⅛ 1
Күп еллар дәвамында җисемнәрнең, аерым алганда, Айның Җир
тирәли һәм планеталарның Кояш тирәли хәрәкәтен өйрәнеп, Нью¬
тон үтә дә кыю фикергә килә: Галәмдәге барлык җисемнәр үзара
бер-берсен тарталар, ди ул.
Барлык җисемнәр арасындагы үзара тартылу бөтендөнья тар¬
тылуы дип аталган. Бөтендөнья тартылу көчләрен икенче төрле
гравитация көчләре дип йөртәләр.
Ньютонның төп ачышы — җисемнәрнең үзара тартылуы ту¬
рындагы даһи фаразларында гына түгел, ул әлеге үзара тәэсирләр¬
нең законын, дөресрәге, ике җисем арасындагы гравитация көчен
исәпләү формуласын чыгаруга ирешә.
Бөтендөнья тартылу законы болай әйтелә:
теләсә нинди ике җисем үзләренең массаларына туры пропор¬
циональ һәм алар арасындагы ераклыкның квадратына кире
пропорциональ көч белән бер-берсенә тартылалар:
биредә F — массалары m1 һәм т2 һәм бер-берсеннән г ераклыгында
булган җисемнәр арасындагы гравитацион тартылу көче векторы¬
ның модуле.
G — гравитация даимие (константасы) дип аталып йөртелә
торган коэффициент.
Әгәр m1 = m2 = 1 кг һәм r = 1 м булса, формуладан күренгәнчә, грави¬
тация даимие G сан ягыннан F көченә тигез. Башкача әйткәндә, гравита¬
ция даимиенең санча кыйммәте бер-берсеннән 1 м ераклыкта урнашкан
1 әр кг массалы ике җисемнең тартылу көченә (F) тигез. Үлчәүләр ниге¬
зендә:
G = 6,67 . Ю11 H.m2∕kγ2.
Бу формула өч очракта бөтендөнья тартылу көчен төгәл исәпләргә
мөмкинлек бирә: 1) җисемнәрнең үлчәмнәре алар арасындагы ерак¬
лыктан исәпкә алмаслык дәрәҗәдә кечкенә (рәс. 31, а); 2) ике җи¬
сем дә бериш һәм шарсыман формада (рәс. 31, б); 3) тәэсир итешүче
көчләрнең берсе — шар, аның үлчәмнәре һәм массасы бу шарның
өслегендә яки аңа якын урнашкан икенче җисем (ирекле формада)
үлчәмнәреннән һәм массасыннан күпкә зуррак (рәс. 31, в).
Тикшерелгән очракларның өченчесе бу Җир өслегендә яткан теләсә
нинди җисемнең Җиргә тартылу көчен формула буенча исәпләү өчен
59
I булек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Икенче
җисем
Беренче
б)
Рәс. 31
җисем
нигез булып тора. Бу вакытта җисемнәр арасындагы ераклык итеп
Җирнең радиусын алырга кирәк, чөнки аның өслегендә яки аңа якын
урнашкан барлык җисемнәрнең дә үлчәмнәре Җир радиусы белән
чагыштырганда исәпкә алмаслык дәрәҗәдә кечкенә.
Ньютонның өченче законы нигезендә ике җисем модульләре бу¬
енча тигез һәм юнәлешләре буенча капма-каршы көчләр белән тәэ¬
сир итешәләр. Димәк, әгәр алмагач ботагында асылынып торган алма
Җиргә 1,5 Н көч белән тартыла икән, Җир дә бу алмага 1,5 Н көч
белән тартыла дигән сүз.
Алма ботагыннан өзелеп төшсә, ике көч тә — Җир һәм алма —
бер-берсенә каршы (мәсәлән, йолдызларга карата) үзләренең масса¬
ларына кире пропорциональ тизләнешләр белән хәрәкәт итәләр.
Җирнең массасы алма массасыннан күп тапкырлар зур булган¬
лыктан, аның тизләнеше нульгә тигез диярлек. Алма исә ирекле
төшү тизләнешенә тигез булган тизләнеш белән (һава каршылыгын
исәпкә алмаслык булса) Җиргә таба хәрәкәт итә (төшә).
? Сораулар
1. Бөтендөнья тартылуы дип нәрсәне атыйлар?
2. Бөтендөнья тартылу көчләре башкача ничек атала?
3. Бөтендөнья тартылу законын кем һәм кайчан ачкан?
4. Бөтендөнья тартылу законы ничек укыла?
5. Бөтендөнья тартылу законын чагылдыручы формуланы языгыз.
6. Нинди очракларда бу формуланы гравитация көчләрен исәпләү
өчен кулланырга мөмкин?
7. Җир агачта асылынып торган алмага тартыламы?
60
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
9 15 нче күнегү
1. Тартылу көче күренешенә мисаллар китерегез.
2. Космик станция Җирдән Айга очып бара. Бу вакыт эчендә
аның Җиргә тартылу көче векторының модуле ничек үзгәрә? Айга
тартылу көченең? Ай белән Җир арасының уртасында вакытта стан¬
циянең ал арга тартылу көчләре модульләре тигез булырмы, әллә
юкмы? Өч җавапны да нигезләгез. (Җир массасының Айныкыннан
81 тапкыр диярлек зуррак икәне билгеле.)
3. Кояшның массасы Җир массасыннан 330 000 тапкыр зуррак
икәне билгеле. Кояшның Җирне үзенә тарту көче Җирнең Кояш¬
ны үзенә тарту көченнән 330 000 тапкыр зуррак дип әйтү дөресме?
Җавапны нигезләгез.
4. Малай ыргыткан туп берникадәр вакыт өскә күтәрелә. Бу
вакытта аның тизлеге, кими барып, нульгә тигезләшә. Аннан соң
арта баручы тизлек белән туп аска төшә. Аңлатыгыз: а) тупның
өскә; аска таба хәрәкәтендә аңа Җир тарту көче тәэсир итәме;
б) өскә күтәрелгәндә тупның тизлеге кимүгә; аска төшкәндә тизлек
артуга нәрсә сәбәп була; в) ни өчен туп өскә таба хәрәкәт иткәндә
аның тизлеге кими, ә аска төшкәндә — арта?
5. Җирдә басып торган кеше Айга тартыламы? Тартылса, ул кай¬
сысына көчлерәк тартыла: Айгамы, әллә Җиргәме? Ай бу кешегә
тартыламы? Җавапны нигезләгез.
§ 16. Җирда һәм башка күк җиеемнөреад® ирекле
тизләнеше
Җисемнәрнең Җиргә тартылуы — бөтендөнья тартылу законы¬
ның бер очрагы ул. Җирдә яшәүчеләр өчен бу көчнең әһәмияте
искиткеч зур.
М тп
Массасы т булган җисемнең Җиргә тартылу көче F = G ү-,
Rx
бу җисемгә тәэсир итүче авырлык көче Fas = gm нан берникадәр
аерыла (бу аерымлык — Җирнең тәүлеклек әйләнүе нәтиҗәсендә
төгәл инерциаль система була алмавына бәйле). Ләкин бу көчләр
арасындагы аерымлык аләрның һәркайсыннан күп тапкырлар
кимрәк булганлыктан, аларны якынча тигез дип санарга мрмкин.
61
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Димәк, Җир өслегендә яки аның тирәсендәге теләсә нинди т
массалы җисем өчен:
mg ≈ A
-ГЬҖ
(1) формуласыннан күренгәнчә, Җир өслегендәге яки аның тирәсен¬
дәге җисемнең тоткарсыз төшү тизләнеше Җирнең радиусына (ягъни
Җирнең үзәге белән бу җисемгә кадәр ераклыкка) һәм массасына бәйле.
32 нче а рәсемдәге шикелле, җисемне Җир өслегеннән һ биекле¬
генә күтәргәндә, бу җисем белән Җирнең үзәге арасы Rχ+h булыр.
Мж
Ул вакытта g≈G~ никадәр зуррак булса, g шулкадәр ке-
⅛+λ)
черәк һәм җисемнең авырлык көче азрак була. Димәк, җисемне
Җир өслегеннән югарырак күтәргән саен, аңа тәэсир итүче авырлык
көчехготкарсыз төшү тизләнеше кимү хисабына кими-бара. Ләкин
бу кимү гадәттә бик зур түгел, чөнки җисемнең күтәрелү биеклеге
Җир радиусы белән чагыштырганда исәпкә алынмаслык дәрәҗәдә
кечкенә. Мәсәлән, 80 кг массалы альпинист 3 км биеклегендәге
тауга күтәрелгәндә, аңа тәэсир итүче авырлык көче нибары 0,7 Н га
(яки 0,09 % ка) кими. Шуңа күрә, Җир өстеннән зур булмаган биек¬
лектәге җисемнәрнең авырлык көчләрен исәпләү өчен, күпчелек
очракларда ирекле төшү тизләнешен 9,8 м/с2 дип алалар, зур булма¬
ган кимүне исәпкә алмыйлар. Авырлык көчен дә түбәндәге формула
буенча исәплиләр:
F = 9,8 м/с2 • т.
g коэфициентының кыйммәтләре (димәк, авырлык көченең дә
кыйммәтләре) бу урынның Җир шарындагы географик киңлегенә
дә бәйле. Ул экваторда 9,78 м/с2 тан алып полюсларда 9,83 м/с2 ка
кадәр үзгәрә, ягъни полюсларда экватордагыдан әз генә артыграк.
Бу аңлашыла да, чөнки Җир нәкъ шар формасында түгел. Ул по¬
люсларда бераз янчелгәнрәк (рәс. 32, б), шуңа күрә Җир үзәгеннән
полюсларга кадәр ара Rn экваторга кадәрге ара R3 дан кечерәк. Ә
62
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
бөтендөнья тартылу законы нигезендә, җисемнәрнең арасы кечерәк
булган саен, аларның бер-беренә тартылуы зуррак була.
(1) формуласында Җирнең массасы һәм радиусы урынына тиң¬
дәшле рәвештә нинди дә булса планетаның яки аның иярчененең
массасын һәм радиусын куеп, әлеге күк җисемнәренең өслегендәге
ирекле төшү тизләнешен якынча исәпләп табарга мөмкин. Мәсәлән,
Айдагы ирекле төшү тизләнеше болай исәпләнә:
MJR∖ нисбәте Мҗ//?2җ нан алты тапкыр кимрәк икәне исәпләнгән.
Шуңа күрә Айда ирекле төшү тизләнеше дә, җисемнәрнең Айга тар¬
тылуы да Җирдәгедән алты тапкыр кимрәк. Мәсәлән, массасы
60 кг булган кеше Җиргә 588 Н, ә Айга 98 Н көч белән тартыла.
? Сораулар
1. Җисемнәрнең Җиргә тартылуы бөтендөнья тартылуының
бер күренеше дип әйтү дөресме?
2. Җисемне Җир өстеннән ераклаштырганда, аңа тәэсир итүче
авырлык көче ничек үзгәрә?
3. Әгәр җисем Җир өстеннән артык зур биеклектә булмаса, аңа
тәэсир итүче авырлык көчен нинди формула белән исәплиләр?
4. Кайсы очракта бер үк җисемгә тәэсир итүче авырлык көче
зуррак була: җисем Җир шарының экватор өлешендә вакыттамы,
әллә полюсларының берсендәме? Ни өчен?
5. Айдагы ирекле төшү тизләнеше турында сез нәрсәләр беләсез?
63
I бүлек. Җисемнәрнең үзара тәэсир итешү Һәм хәрәкәт законнары
£ 16 нчы күнегү
1. Массасы 2,5 кг; 600 г; 1,2 т; 50 т булган җисемгә тәэсир
итүче авырлык көче нәрсәгә тигез? (g ≈ 10 м/с2)
2. Массасы 64 кг булган кешегә тәэсир итүче авырлык көчен
якынча исәпләгез (g ≈ 10m∕c2).
Җир шары бу кешегә тартыламы? Тартылса, бу көч якынча
күпмегә тигез?
3. Беренче совет ясалма иярчене 1957 елның 4 октябрендә җи¬
бәрелгән. Әгәр Җирдә аңа 819,3 Н лы авырлык көче тәэсир иткән
булса, аның массасын табыгыз.
>4уҖир өслегеннән 5000 км ераклыкта очып йөрүче космик ра¬
кетага тәэсир итүче авырлык көчен Fm = 9,8 м/с2-т формуласы белән
исәпләп буламы (биредә т — ракетаның массасы)? Җирнең радиу¬
сы якынча 6400 км. Җавапны аңлатыгыз. Бу формула белән
исәпләнмәсә, сез әлеге очракта нинди формула тәкъдим итәр иде¬
гез?
⅛5∕ Карчыга Җир өстеннән4 ниндидер бер биеклектә озак вакыт
хәрәкәтсез тора ала. Аңа авырлык көче тәэсир итми дип әйтү дөрес¬
ме? Әгәр карчыга канатларын җыйса нәрсә булыр?
∣6§ ** Җирдән космик ракета старт ала. Җирдән нинди ераклыкта
ракё’ганьщ авырлык көче стартка кадәргедән 4 тапкыр кимрәк бу¬
лыр? 9 тапкыр кимрәк?
§ 17. Нептун һөм Плутон планеталарының ачылуы
(өстәме уку өчен )
Бөтендөнья тартылу законы һәм Ньютон законнары ярдәмендә
Кояш системасындагы планеталарның хәрәкәт траекторияләре бил¬
геләнә һәм, бик күп еллар алга, аларның теләсә кайсы вакыт момен¬
тындагы координаталары исәпләп куела. Моның өчен элек бөтенд¬
өнья тартылу законы буенча Кояш һәм конкрет планета арасында¬
гы гравитацион тәэсир итешү көче исәпләнелә. Аннары, Ньютон¬
ның икенче законы ярдәмендә, бу планетаның Кояш тирәсендә
хәрәкәт итү тизләнешен исәплиләр. Тизләнеш буенча хәрәкәтне сур¬
әтләүче башка зурлыклар, шул исәптән координаталар да билгеләнә.
Шул ук вакытта Кояш системасындагы башка планеталарның
да әлеге планетаның хәрәкәтенә тәэсире исәпкә алына.
64
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Планеталарның шушы юл белән исәпләнгән орбиталары һәм
теләсә нинди вакыт мизгелендәге торышлары астрономик күзәтүләр
нәтиҗәләре белән раслана.
1781 елда инглиз астрономы Уильям Гершель күзәтүләр юлы
белән Кояш системасының җиденче планетасын ача, аңа Уран дип
исем бирәләр.
Башка барлык планеталар кебек, Уран өчен дә орбита билгеләнә
һәм алдагы елларда аның торышларын күрсәткән таблица төзелә.
Уранның хәрәкәтен күпьеллык күзәтүләр нәтиҗәсендә, XIX га¬
сырның беренче яртысында галимнәр аның чынбарлыктагы орби¬
тасы белән исәпләнгәненең туры килмәвенә тәгаен ышаналар. Уран
артында тагын ниндидер планета булып, ул үзенә Уранны тарта һәм
шуның белән аның хәрәкәтенә йогынты ясый дигән фикер туа.
Инглиз галиме Джон Адамс һәм француз галиме Урбен
Леверье Уран хәрәкәтендәге тайпылышлар буенча, бөтендөнья тар¬
тылу законына нигезләнеп, фаразлардагы планетаның урынын һәм
үлчәмнәрен исәпләп табалар.
Адамс эшен беренче булып төгәлли һәм обсерваторияләрнең бер¬
сенә яңа планетаны эзләүне сорап мөрәҗәгать итә. Аның координа-
таларын ул инде теоретик исәпләүләр ярдәмендә тапкан була. Шул
ук обсерваториягә шундый ук үтенеч белән Леверье да мөрәҗәгать
итә. Әмма ниндидер сәбәп белән планетаны эзләү билгесез вакытка
кичектерелә.
Шул вакытта Леверье, Уран артында дип фараз ителгән плане¬
таның төгәл координаталарын күрсәтеп, Берлин обсерваториясенең
яшь хезмәткәре Иоганн Галлега хат язып җибәрә.
1846 елның 23 сентябрендә Галле, хатны алуга, күзәтүләргә ке¬
решә һәм шул ук төндә Леверье күрсәткән урыннан нибары ярты
градус кына авышлыкта яңа планетаны таба.
Биш көннән соң Леверье Берлин обсерваториясе директорын¬
нан котлау хаты ала. «Сезнең исемегез бүгеннән башлап бөтен¬
дөнья тартылу законының хаклыгына ышанырга мөмкин саналган
иң күренекле раслау белән бәйле булачак»,— диелгән була әлеге хатта.
Леверье тәкъдиме белән планетаны Нептун дип атыйлар.
Нәм бары тик берничә ел үткәч кенә, фән дөньясында Джон
Адамсның да Нептун планетасы ачудагы хезмәте бәяләнә.
Бөтендөнья тартылу законына да нигезләнгән исәпләүләр һәм
шул юнәлештәге асторномик күзәтүләр ярдәмендә, Ц930 елның
65
1 бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
18 февралендә Кояш системасының тагын бер планетасы — Плутон
ачыла. Ул Кояштан Нептунга караганда өч тапкыр диярлек ераг¬
рак. Бу планеталарның теоретик юл белән, ягъни физика законна¬
рына нигезләнеп эшләнгән исәпләүләр ярдәмендә генә ачылуын ас-
сызыклап күрсәтү өчен, Нептун һәм Плутон планеталары «каләм
очында» ачылган, диләр.
§ 1 Турысызыклы һәм кәкресызыклы хәрәкәт
Көчнең җисемгә тәэсир итүе кайбер очракларда бу җисемнең
бары тик тизлек векторы модулен генә, ә кайберләрендә юнәлешен
үзгәртүгә китерә. Моны мисалларда күрсәтик.
33 нче а рәсемдә өстәлдәге А ноктасында ятучы шарчык
күрсәтелгән. Ул резин шнурның бер очына бәйләнгән. Шнурның
икенче очы өстәлгә О ноктасында беркетелгән. Әгәр шарны В нокта¬
сына күчерсәк, шнур тартылачак. Бу вакытта шарга тәэсир итүче
һәм аны башлангыч торышына кайтарырга омтылучы эластиклык
көче F барлыкка килә. Әгәр шарны хәзер ычкындырсак, ул F көче
тәэсирендә тизләнеш белән А ноктасына таба хәрәкәт итәчәк. Бу
очракта шарнъщ тизлеге траекториясенең теләсә кайсы нокта¬
сында (мәсәлән, С ноктасында) эластиклык көче һәм бу көч тәэси¬
рендә барлыкка килгән тизләнеш белән бер үк юнәлештә була. Бу
вакытта бары тик тизлек векторы модуле генә үзгәрә, ә тизлек век¬
торының юнәлеше үзгәрешсез кала, һәм шарчык турысызыклы
хәрәкәт итә.
66
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Хәзер тикшерелә торган мисалда шарчык эластиклык көче тәэ¬
сирендә кәкре сызык буенча хәрәкәт итә (ягъни аның траекториясе
кәкре сызык рәвешендә). 33 нче б рәсемдә резин шнурга эленгән
шул ук шар А ноктасында ята. Шарны В ноктасына таба этәрәбез,
ягъни ОА кисемтәсенә перпендикуляр юнәлгән башлангыч тизлек
бирәбез. Әгәр шарга бернинди дә көч тәэсир итмәсә, инерция күре¬
неше нигезендә, ул бу тизлекнең зурлыгын һәм юнәлешен саклар
иде. Ләкин, В га таба хәрәкәт итеп, ул О ноктасыннан ераклаша
һәм шнурны бик аз гына тарта. Шунлыктан шнурда аны элекке
озынлыгына һәм шул ук вакытта О ноктасына кире кайтарырга
омтылучы эластиклык көче F хасил була. Бу көч тәэсирендә шар¬
чык тизлегенең юнәлеше хәрәкәтенең һәр мизгелендә берникадәр үзгәрә,
шунлыктан шар кәкресызыклы АС траекториясе буенча хәрәкәт итә.
Траекториянең һәр ноктасында (мәсәлән, С ноктасында) шарчыкның
тизлеге и һәм көч F кисешүче турылар буйлап юнәлгән: тизлек —
траекториягә орынма буенча, ә көч О ноктасына таба.
Әлеге мисаллар җисемгә куелган көч тәэсиренең, тизлек һәм
көч векторларының юнәлешенә бәйле рәвештә, төрле нәтиҗәләргә
китерүен күрсәтә.
Әгәр җисемнең тизлеге һәм аңа куелган көч бер туры буйлап
юнәлсә, җисем турысызыклы хәрәкәт итә, әгәр алар кисешүче
сызыклар буйлап юнәлсә, җисем кәкресызыклы хәрәкәт итә.
Киресен раслау да дөрес: җисем кәкресызыклы хәрәкәт ясый
икән, димәк, аңа тизлек юнәлешен үзгәртеп торучы ниндидер көч
тәэсир итә, шул ук вакытта һәрбер нок¬
тада көч һәм тизлек кисешүче туры¬
лар буйлап юнәлә.
Кәкресызыклы траекторияләр чик¬
сез күп санда. Ләкин бик күп кәкре
сызыклар, мәсәлән ABCDEF сызыгы
(рәс. 34), төрле радиустагы әйләнә ду¬
галары күплеге рәвешендә бирелергә
мөмкин.
Шуңа күрә җисемнең кәкресызык¬
лы хәрәкәтен өйрәнү аның әйләнә бу¬
енча хәрәкәтен өйрәнүгә кайтып кала.
67
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Сораулар
1. 33 нче a рәсем буенча сорауларга җавап бирегез: нинди көч
тәэсирендә шарчык тизлек ала һәм В ноктасыннан А ноктасына
таба хәрәкәт итә? Бу көч нәрсә нәтиҗәсендә хасил була? Шар¬
ның тизлеге, тизләнеше һәм аңа тәэсир итүче көч ничек юнәлгән?
Шарчык нинди траектория буйлап хәрәкәт итә?
2. 33 нче б рәсем буенча сорауларга җавап бирегез: ни өчен шнурда
эластиклык көче барлыкка килә, һәм ул шнурга карата ничек
юнәлгән? Шарның тизлеге һәм шнурның аңа тәэсир итүче элас¬
тиклык көче ничек юнәлгән? Шар ничек хәрәкәт итә: туры сызык
буйлапмы, кәкре сызык буйлапмы?
3. Нинди шартларда көч тәэсирендәге җисем — турысызыклы,
ниндиендә кәкресызыклы хәрәкәт итә?
> 17 нче күнегү
1. Шарчык өстәлнең горизонталь өслегендә А ноктасыннан В
ноктасына тәгәри (рәс. 35). В ноктасында шарга F көче белән тәэ¬
сир итәләр. Нәм ул С ноктасына таба тәгәри башлый. F көче 1, 2, 3
һәм 4 уклары белән күрсәтелгән юнәлешләрнең кайсысы буенча
тәэсир иткән?
2. 36 нчы рәсемдә шар хәрәкәтенең
траекториясе күрсәтелгән. Түгәрәкләр шар¬
чыкның һәр секунд саен торышын билге¬
ли. 0—3; 4—6; 7—9; 10—12; 13—15; 16—19
бүлемтекләрендә шарга көч тәэсир иткәнме?
Әгәр итсә, ул тизлек векторына карата ничек
1(
2
A 4 В
Өстәл
3 X
(өстән күренеш) С
68
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
юнәлгән? Ни өчен шар борылу алдындагы хәрәкәт юнәлешенә карата
7—9 бүлемтегендә шар — сулга, 10—12 бүлемтегендә уңга борылган?
3*. 37 нче рәсемдә ниндидер җисем хәрәкәтенең ABCDE траек¬
ториясе күрсәтелгән. Кайсы бүлемтекләрдә җисемгә һичшиксез көч
тәэсир иткән? Траекториянең башка бүлемтекләрендә хәрәкәт
иткәндә, җисемгә нинди дә булса көч тәэсир иткән булуы мөмкинме?
Барлык җавапларны да нигезләгез.
§ 1 &. Җисемнең әйлә^® буйлаи даи^и
модульле тизлек белек хәрәкәт®
Кәкресызыклы траекториянең теләсә кайсы ноктасында момен¬
таль тизлекнең бу ноктага орынма буйлап юнәлүенә тәҗрибәдә күреп
ышанырга мөмкин (рәс. 38).
Әгәр тиз әйләнә торган кайрау ташын корыч предметны якын ки¬
терсәк, аның астыннан очкыннар чәчри башлар. Болар — кайрала тор¬
ган предметка ышкылу сәбәпле, таштан ыч¬
кынып киткән кызган вак кисәкчекләр.
Алар ычкынып китү мизгелендә алган тиз¬
лекләре белән очалар.
Кисәкчекләрнең хәрәкәт юнәлеше,
димәк тизлек векторы да, алар хәрәкәт
иткән әйләнәгә орынма юнәлеше белән
тәңгәл килә.
Вектор зурлыкларның модуле һәм юн¬
әлеше белән характерланганын без инде
беләбез. Бу ике характеристиканың берсе
генә үзгәрсә дә, вектор үзгәрә.
Җисем әйләнә буенча хәрәкәт иткәндә тизлек векторының модуле
үзгәрергә яки даими калырга да мөмкин, ләкин тизлек векторының юнә¬
леше һичшиксез үзгәреп тора.
Юнәлеше өзлексез үзгәреп тору аркасында, әйләнә буенча хәрәкәт
итүче җисемнең тизлек векторы — үзгәрешле зурлык була (модуле
буенча тизлек үзгәрүгә яки үзгәрмәүгә карамастан).
Димәк, әйләнә буенча хәрәкәт һәрвакыт тизләнеш белән бара.
Җисем әйләнә буенча даими модульле тизлек белән хәрәкәт
иткәндә, аның тизләнешенең юнәлешен табыйк. Моның өчен 39
69
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
нчы рәсемгә игътибар итәрбез. Анда г
радиуслы әйләнә буенча хәрәкәт итүче
җисем (материаль нокта) сурәтләнгән.
Бик аз вакыт аралыгы t эчендә җисем
А ноктасыннан аңа бик якын урнашкан
В ноктасына күчә. Бу очракта АВ дуга¬
сы белән АВ хордасы аермасын исәпкә
алмаска һәм җисем хорда буенча хәрә¬
кәт итә дип кабул итәргә мөмкин. Әмма
җисемнең А һәм В нокталарындагы υ0
һәм v тизлекләренең юнәлешләре бер¬
төрле түгел.
Җисем хәрәкәтенең тизләнеше бу
формула буенча исәпләнә:
_ υ-υ0 (1)
а •
t
Тизләнеш векторы тизлекләрнең геометрик аермасына (U - v0)
тигез булган вектор белән бер юнәлештә. Бу векторны табу өчен v
векторын, үзенә параллель итеп, А ноктасына күчерәбез һәм тизлек
векторларының очларын, υ0 дән и га юнәлтеп, кисемтә белән тоташ¬
тырабыз. Бу (D - v0) векторы булды. Аның әйләнә эченә юнәлүе
ачык күренә.
Өлкән сыйныфларның физика курсында вакыт аралыгы t нульгә
омтылганда, АС кисемтәсенең, һаман кыскара барып, ноктага якын¬
лашуы исбат ителә. Тизләнеш векторы бу очракта әйләнә үзәгенә
юнәлә. Шуңа күрә даими модульле тизлек белән әйләнә буенча
хәрәкәт итүче җисемнең тизләнеше үзәккә омтылучы тизләнеш
дип атала. Үзәккә омтылучы тизләнеш теләсә кайсы ноктада
әйләнәнең радиусы буенча аның үзәгенә омтыла.
Үзәккә омтылучы тизләнеш векторының модуле түбәндәге фор¬
мула буенча табыла:
υ2
αγ=-. (2)
γ г
биредә αγ — даими модульле тизлек υ белән г радиуслы әйләнә буен¬
ча хәрәкәт итүче җисемнең үзәккә омтылучы тизләнеш векторы¬
ның модуле.
70
I бу лек. Җисемнәрнең үзара тәэсир игешү һәм хәрәкә* ’•
> 1 39 нчы рәсем ярдәмендә үзәккә омтылучы тизләнеш векто¬
рының модулен исәпләргә мөмкин, υ0, v һәм (υ0 - υ0) векторлары
белән төзелгән өчпочмакның АОВ өчпочмагына охшаш булуын¬
нан файдаланыйк. Өчпочмакларның охшашлыгы аларның тигезь¬
янлы (ОА = ОВ — бер үк әйләнәнең радиуслары, ∣υ0∣ = ∣υ∣— җисем¬
нең тизлек модуле барлык нокталарда да бертөрле) һәм түбә янын¬
дагы почмаклары а тигез булуыннан (үзара перпендикуляр яклар
арасындагы почмаклар: υ0 ± ОА, υ ± ОВ, чөнки v0, v — орынмалар, ә
ОА һәм ОВ — орыну ноктасында үткәрелгән радиуслар) килеп чыга.
Өчпочмаклар охшаш булгач, аларның тиңдәш яклары пропор¬
циональ:
(3)
биредә ∣p-υ0∣- җисемнең бик аз вакыт аралыгындагы (t) тизлек
үзгәреше векторының модуле, ә. ∣υ∣— җисемнең әйләнә буенча
хәрәкәт тизлеге векторы модуле. АВ — җисемнең t вакыты эчендә
∣υ∣ тизлеге белән хәрәкәте вакытында ясаган күчеш векторы моду¬
ле. Димәк,
AB = ∖v∖∙t. (4)
(3) формуласында АВ ны ∣υ∣√ га алыштырабыз:
∣υ-υ0∣ ∣v∣ ∣i>-4)∣ ∣υ∣2
-ГП = — , ЯКИ j ' =
∣υ∣√ r t г
(5)
= ∣α∣ икәнен исәпкә алып, (5) формуласын үзгәртәбез:
t
rι ∣υ∣2 υ2
∣α∣ = —, яки, икенче төрле язсак: a = —.
τ∙ * У*
1 Бу тамга белән өстәмә материал билгеләнә, ул физиканы атнага
3 сәгать укыту программасына исәпләнгән.
71
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Даими модульле тизлек белән хәрәкәт итүче җисем траектория¬
сенең барлык бүлемтекләре дә әйләнә дугалары булсын (рәс. 34).
Ул вакытта бу траекториянең теләсә кайсы ноктасында җисемнең
тизләнеше тиңдәшле әйләнәнең үзәгенә юнәлер һәм аны (2) форму¬
ласы буенча исәпләргә мөмкин булачак.
F
Ньютонның икенче законы буенча (а=—) тизләнеш һәрвакыт¬
та
та да үзен китереп чыгаручы көч белән бер үк юнәлештә була. Бу
үзәккә омтылучы тизләнеш өчен дә дөрес.
Димәк, әйләнә буенча даими модульле тизлек белән хәрәкәт
итүче җисемгә тәэсир итә торган көч һәрбер ноктада әйләнә ра¬
диусы буенча аның үзәгенә юнәлә.
Бу көч үзәккә омтылучы көч дип йөртелә. Ньютонның икенче
законына һәм (2) формуласына нигезләнеп, үзәккә омтылучы көч
векторының модуле түбәндәге формула буенча исәпләнә:
Fγ=-^∙ (6)
\ Һәрбер конкрет очракта үзәккә ом-
• тылучы көч ролен төрле көчләр үти.
Мәсәлән, бауның бер очына бәйләнгән
/ таш (рәс. 40) бауның эластиклык көче
тәэсирендә әйләнә; Кояш тирәсендә —
планеталар һәм планеталар тирәсендә
аларның иярченнәре бөтендөнья тар¬
тылу көче тәэсирендә әйләнеп йөри; ав¬
томобиль көпчәкләренең юлга ышкы¬
лу көче исәбенә борыла.
Санап үтелгән әлеге көчләр бу очракларда үзәккә омтылучы көч
булып тора. Аларның тәэсире нәтиҗәсендә, җисемнең тизлек юнәле¬
шен үзгәртүче тизләнеш барлыкка килә һәм шуның аркасында җи¬
сем әйләнә яки аның дугасы буйлап хәрәкәт итә.
Сораулар
1. Әйләнә буйлап хәрәкәт итүче җисемнең моменталь тизлеге
әйләнәнең һәр ноктасында аңа орынма юнәлешендә булганын нин¬
ди тәҗрибә исбатлый?
72
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
2. Даими модульле тизлек белән әйләнә буенча хәрәкәт итүче
җисемнең тизләнеше кая юнәлгән? Бу тизләнеш ничек атала?
3. Үзәккә омтылучы тизләнеш векторы модулен нинди форму¬
ла буенча исәплиләр?
4. Үзәккә омтылучы көч ничек юнәлгән? Бу көч векторының
модулен ничек исәпләргә мөмкин?
$ 18 нче күшегү
1. Кер юу машинасы киптерү режимында эшләгәндә, әйләнү
күчәреннән 21 см ераклыктагы барабанның өслеге бу күчәр тирә¬
сендә 20 м/с тизлек белән хәрәкәт итә. Барабан өслеге нокталары¬
ның тизләнешен табыгыз.
2. Сәгатьнең секундлык теленең очы әйләнү үзәгеннән R = 2 см
ераклыкта булса, аның хәрәкәт тизләнешен исәпләгез. (Радиусы R
булган әйләнә озынлыгы I = 6,28/? формуласын кулланып исәпләнә.)
3. Сәгать теленең чик ноктасының тизләнеше бу телнең урта
ноктасы тизләнешеннән ике тапкыр зуррак икәнен исбатлагыз
(әйләнү үзәге белән телнең очы уртасындагы нокта).
4. Сәгатьнең минутлык һәм секундлык телләре уртак үзәк тирә¬
сендә әйләнәләр. Үзәктән алып телләрнең очларына кадәрге аралар
бертөрле. Бу очларның тизләнешләре чагыштырмасын табыгыз.
Кайсц телнең очы зуррак тизләнеш белән хәрәкәт итә?
5. Җирнең массасы 6 ∙ Ю24 кг, ә Ай массасы 7 ∙ Ю22 кг. Ай Җир
тирәсендә радиусы 384 000 км лы әйләнә буенча хәрәкәт итә дип алып
исәпләгез: а) Җир белән Ай арасындагы тартылу көчен; б) Айның
Җир тирәли хәрәкәте вакытында үзәккә омтылу тизләнешен; в) Ай¬
ның Җиргә карата хәрәкәт тизлеге модулен. (G = 6,67 ∙J,O^11H ∙m2∕kγ2.)
§ 20. Җирнең ясалма иярченнәре
Тагын бер тапкыр 33 нче б рәсемне тикшерик. Әгәр шарны этеп
ж,ибәреп, башка аңа кагылмасак, ул ниндидер дуга ясар да туктап
калыр. Шарның тукталуына сәбәп булып, хәрәкәткә комачаулаучы
һәм аның тизлеген киметүче ышкылу һәм һаваның каршылык
көчләре тора.
Туктатучы көчләрне киметкәндә, шарчык, туктап калганга кадәр,
О ноктасы тирәсендә бер яки берничә әйләнеш ясап өлгерә (бу оч-
73
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Рәс. 41
ракта шнур О ноктасына шарның хәрәкәтенә комачауламаслык итеп
беркетелә).
Әгәр без хәрәкәткә каршылык күрсәтүче барлык көчләрне дә
бетерә алсак, шар О ноктасы тирәли йомык кәкре, мәсәлән әйләнә
буйлап мәңге әйләнеп торыр иде. Бу вакытта шарның тизлек юнә¬
леше, әйләнә үзәгенә юнәлгән көч тәэсирендә, өзлексез үзгәрер иде.
Планеталарның Кояш тирәсендә һәм иярченнәрнең планеталар
тирәсендә әйләнүе мондый хәрәкәтнең үрнәге булып тора.
Җирнең ясалма иярченнәрен (ҖЯИ) җибәрү һәм аларның
хәрәкәте турында җентекләбрәк аңлатыйк.
Җисемнең Җирнең ясалма
иярчене була алу шартларын
аңлау өчен, 41 нче рәсемне ка¬
рыйк. Ул — Ньютон ясаган рә¬
семнең копиясе. Бу рәсемдә Җир
шары, ә аның өстендә биек тау
ясалган, тау башыннан горизон¬
таль юнәлештә, модуле буенча
төрле тизлек биреп, ташлар ыр¬
гыталар.
Рәсем астына болай язылган:
«Ыргытылган таш авырлык көче
тәэсирендә турысызыклы юлын¬
нан авыша һәм, кәкре траектория
' ясап, ниһаять, Җиргә төшә. Әгәр
зуррак тизлек белән ыргытсаң —
ераграк барып төшә». Бу фике¬
рен дәвам итеп, Ньютон шундый нәтиҗәгә килә: һаваның каршы¬
лыгы булмаганда һәм җитәрлек зур тизлек бирелгәндә, җисем Җиргә
бөтенләй төшмәскә мөмкин, ә Җир өстеннән даими ераклыкта ка¬
лып, түгәрәк траекторияләр ясаячак. Мондый җисем Җирнең ясал¬
ма иярчене булып китә.
Иярченнең хәрәкәте — ирекле төшүгә мисал булып тора, чөнки
ул бары тик авырлык көче тәэсирендә генә бара. Әмма иярчен, үзе
хәрәкәт иткән әйләнәгә орынма буенча юнәлгән җитәрлек кадәр зур
тизлеккә ия булганлыктан, Җиргә егылып төшми.
Димәк, ниндидер җисем Җирнең ясалма иярчене булсын өчен,
аны Җир атмосферасы тышына чыгарырга һәм ул хәрәкәт итәчәк
74
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
әйләнәнең орынмасы буйлап юнәлгән билгеле бер тизлек бирергә
кирәк.
Җир өслегеннән алып, һава каршылыгы инде гамәлдә булмый
торган иң кечкенә биеклек — 300 км лар тирәсе. Шуңа күрә
гадәттә аларны Җир өслегеннән 300—400 км биеклектә җи¬
бәрәләр.
Җир тирәсендә әйләнә буенча хәрәкәт итеп, аның ясалма ияр¬
чене булсын өчен, җисемгә нинди тизлек бирергә кирәклеген исәпли
торган формула чыгарыйк.
Иярченнең хәрәкәте бары тик авырлык көче тәэсирендә генә
бара. Бу көч аңа ирекле төшү тизләнешен (g) бирә, ә ул бу очрак¬
та үзәккә омтылу тизләнеше ролен үти.
Үзәккә омтылучы тизләнешне исәпләү формуласын без инде
беләбез:
биредә υ — җисемнең г радиуслы әйләнә буенча хәрәкәт итү тиз¬
леге.
Димәк, иярчен өчен
y2 2
§ = — ∙ υ2=gr ,
υ=∕gr. (1)
(1) формуласы буенча табылган тизлек — җисемгә Җир
үзәгеннән г ераклыгындагы әйләнә буенча аның тирәли әйләнүе
өчен бирелергә тиеш.
Бу тизлек (түгәрәк буенча) беренче космик тизлек дип
атала.
Әгәр иярченнең Җир өслегеннән биеклеге һ Җир радиусы белән
чагыштырганда бик аз булса, аны исәпкә алмаска һәм г = R* дип
алырга мөмкин. Җир өслеге тирәсендә ирекле төшү тизләнешен
g0 дип алырбыз.
Ул вакытта Җир өслеге тирәсендә хәрәкәт итүче иярченнең
беренче космик тизлеген исәпләү формуласы болай языла:
v = λ⅛Λ* - (2)
75
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт-законнары
Җир радиусын 6400 км (яки 6,4 ∙106 м), ә g = 9,8 м/с2 дип алып,
бу тизлекне исәплибез:
и = V9,8 м/с2 • 6,4 ∙ 106m ≈ 7,9 ■ Ю3 м/с = 7,9 км/с.
Әгәр инде иярченнең Җир өслегеннән биеклеге зуррак булса,
16 нчы параграфтагы кебек, Җир үзәгеннән ирченгә кадәр ара һәм
һ биеклегендәге ирекле төшү тизләнеше g түбәндәге формулалар
буенча исәпләнә:
Mκ
r=Rκ + h, g≈G •
_йҗ + һ
Бу очракта беренче космик тизлекне исәпләү өчен (1) формула¬
сы түбәндәгечә языла:
яки
\ + h (3)
(3) формула буенча теләсә кайсы планета иярчененең беренче
космик тизлеген исәпләргә мөмкин: Җирнең массасы һәм радиусы
урынына тиешле планетаның массасы һәм радиусы куела.
(3) формуласыннан күренгәнчә, иярчен җибәрелә торган һ
биеклеге никадәр зуррак булса, түгәрәк орбита буенча хәрәкәте
өчен аңа шулкадәр азрак тизлек бирергә кирәк (чөнки һ —
ваклаучыда).
Мәсәлән, Җир өслегеннән 300 км биеклектә беренче кос¬
мик тизлек якынча 7,8 км/с ка, ә 500 км да 7,6 км/с ка тигез.
Әгәр Җир өслегеннән һ биеклегендә җибәрелгән җисемгә би¬
релгән тизлек бу биеклеккә тиңдәшле беренче космик тизлектән
зуррак булса, аның орбитасы эллипс була (рәс. 41, тышкы траек¬
тория). Тизлек зуррак булган саен, эллипс сузынкырак була. Икен¬
че космик тизлек дип аталучы 11,2 км/с тизлек бирелсә, җисем
Җир тартуын җиңә һәм космик киңлеккә китә.
Иярченнәрне җибәрү өчен ракеталар кулланыла (§ 23). Ракета
двигательләре авырлык көченә һәм һаваның каршылык көченә
каршы эш эшләргә һәм иярченгә тиешле тизлекне бирергә тиешләр.
76
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
1957 елның 4 октябрендә Советлар Союзында, кешелек тари¬
хында беренче булып, Җирнең ясалма иярчене җибәрелә. Диамет¬
ры 58 см һәм массасы 83,6 кг булган шар формасындагы иярчен
һәм йөртүче ракета озак вакытлар Җир өслегеннән берничә йөз
километр биеклектә очып йөрделәр.
1961 елның 12 апрелендә дөньяда беренче очучы-космонавт, без¬
нең ватандашыбыз Юрий Алексеевич Гагарин «Восток» корабль-
иярченендә космик очыш ясады.
Хәзерге вакытта һәр елны фәнни-тикшеренү һәм гамәли мак¬
сатларда: теле- һәм радиоэлемтә, атмосфераны тикшерү, һава торы¬
шын фаразлау һ.б. өчен йөзләрчә иярчен җибәрелә.
Сораулар
1. Каршылык көчләре булмаганда, җисемнең аның хәрәкәт тиз¬
леге юнәлешен үзгәртүче көч тәэсирендә йомык траектория буен¬
ча чиксез озак әйләнеп йөри алуына мисаллар (астрономиядән) ки¬
терегез.
2. Ни өчен авырлык көче тәэсирендә Җир тирәли әйләнүче ияр¬
ченнәр Җиргә егылып төшми?
3. Иярченнең Җир тирәли әйләнүен ирекле төшү дип атап бу¬
ламы?
4. Физик җисем Җирнең ясалма иярчене булсын өчен нәрсә
эшләргә кирәк?
5. Җир өслеге тирәсендә түгәрәк орбита буенча хәрәкәт итүче
иярченнең беренче космик тизлеген исәпләү өчен формула чыгары¬
гыз.
6. Беренче космик тизлеккә; икенче космик тизлеккә ия булган
иярчен ничек хәрәкәт итә?
$ 19 нчы күнегү
1. Җирнең ясалма иярчене Җир өслегеннән 2600 км биек¬
лектәге түгәрәк орбита буенча хәрәкәт итә. Аның тизлеген табы¬
гыз. (Мҗ= 6 • Ю24 кг; Лҗ= 6,4 • Ю6 м; G = 6,67 • Ю11 H∙ m2∕kγ)
2. (/6гәр Ай өслеге тирәсенә түгәрәк орбитага ясалма иярчен җи¬
бәрелсә, ул 1,67 км/с тизлек белән хәрәкәт итәр иде. Ай өслегендә
ирекле төшү тизләнеше 1,6 м/с2 булса, Айның радиусын табыгыз.
77
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
§ 21. Җисемнең импульсы
Ньютон законнары җисемнәрнең үзара тәэсир итешүенә һәм
хәрәкәтенә кагылышлы төрле гамәли мәсьәләләрне хәл итәргә
булыша. Мәсәлән, мондый мәсьәләләрнең күбесе, җисемгә тәэсир
итүче барлык көчләр дә билгеле булганда, аның тизләнешен табу
белән бәйле. Ә аннан соң тизләнеш буенча башка зурлыклар да та¬
была (моменталь тизлек, күчеш Һ.6.).
Әмма еш кына җисемгә тәэсир итүче көчләрне табу гаять кыен
була. Шунлыктан бик күп мәсьәләләрне чишү өчен тагын бер мөһим
физик зурлыкны — җисемнең импульсын кулланалар.
Җисем массасы белән аның тизлеге тапкырчыгышына ти¬
гез булган зурлыкны җисемнең импульсы р дип атыйлар.
p=τnυ .
Импульс — вектор зурлык. Җисемнең импульс векторының юнә¬
леше һәрвакыт хәрәкәт тизлеге векторы юнәлеше белән туры килә.
p = mv булганлыктан, СИда импульс берәмлеге итеп, 1 м/с тиз¬
лек белән хәрәкәт итүче 1 кг массалы җисемнең импульсы алына.
Димәк, СИда җисем импульсы берәмлеге 1 кг-м/с.
Исәпләүләрдә векторлар проекциясе тигезләмәсе кулланыла:
Px = mυx.
Тизлек векторының сайлап алынган X күчәренә карата юнәле¬
шенә, димәк, аның проекциясе тамгасына бәйле рәвештә, импульс
векторы проекциясе уңай да, тискәре дә булырга мөмкин.
Латинчадан тәрҗемә иткәндә, «импульс» сүзе (impulsus) «этәр¬
геч» дигәнне аңлата. Кайбер китапларда «импульс» термины уры¬
нына «хәрәкәт микъдары» дигән термин кулланыла.
Бу зурлык фәнгә чама белән Ньютон тарафыннан хәрәкәт закон¬
нары ачылган вакытларда килеп керә (XVII гасыр ахырында).
вр Сораулар
•
1. Җисемнең импульсы дип нәрсәне атыйлар?
2. Импульс һәм хәрәкәт итүче җисем тизлеге векторларының
юнәлеше турында нәрсә әйтергә мөмкин?
3. Импульс берәмлеге итеп нинди зурлык кабул ителгән?
78
/ бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
20 нче күнегү
1. Ьәркайсының массасы 0,2 кг булган ике уенчык машина,
туры сызык буйлап, бер-берсенә каршы хәрәкәт итә. Аларның Җиргә
карата тизлекләре 0,1 м/с. Машиналарның импульслары тигезме?
Импульс векторы модульләре тигезме? Траекторияләренә параллель
булган бер үк X күчәренә һәр машинаның импульсы проекциясен
табыгыз.
2. Массасы 1 т булган автомобильнең тизлеген 54 км/сәг тән
72 км/сәг кә үзгәрткәндә, аның импульсы (модуле буенча) күпмегә
үзгәрер?
§ 22. Импульс саклану законы
Җисемнәр үзара тәэсир итешкәндә, импульслары үзгәрергә
мөмкин. Моңа бик гади тәҗрибәдә ышанырга була.
Рәс. 42
42 нче а рәсемдә бер үк массалы ике шарчык күрсәтелгән. Алар
параллель җепләргә бер-берсенә орындырып эленгәннәр.
Уңдагы шарчыкны ниндидер почмакка авыштыралар да ычкын¬
дыралар (рәс. 42, б). Ул, элекке торышына кайтып, хәрәкәтсез сул
шарчыкка бәрелә һәм туктап кала. Аннан соң сул шарчык хәрәкәткә
килә һәм шул ук почмакка авыша (рәс. 42, в).
Бу очракта шунысы ачык, үзара тәэсир итешү нәтиҗәсендә һәр
шарның импульсы үзгәрә: уң шарның импульсы күпмегә кимесә,
сулыныкы шулкадәр арта.
Әгәр ике яки берничә җисем үзара гына тәэсир итешсәләр (ягъ¬
ни тышкы көчләр тәэсиренә дучар ителмәсә), бу җисемнәр йомык
система тәшкил итәләр.
79
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Йомык системага кергән һәр җисемнең импульсы алар үзара
тәэсир итешкәндә үзгәрергә мөмкин.
Ләкин йомык системаны тәшкил итүче җисемнәрнең им¬
пульсларының векторлы суммасы вакыт узу белән бу җисемнәр¬
нең теләсә нинди хәрәкәтләре һәм тәэсир итешүләре вакытында
да үзгәрми.
Импульс саклану законы әнә шуннан гыйбарәт.
Импульс саклану законы Ньютонның икенче һәм өченче законна¬
рыннан чыгарыла. Моны күрсәтеп үтәбез. Гадилек өчен ике генә җи¬
семнән — массалары ml һәм т2 булган шарлардан торган системаны ка¬
рыйк. Алар туры буйлап бер юнәлештә ц һәм
υ2 тизлекләре белән хәрәкәт итә (рәс. 43).
Һәр шарга да тәэсир итүче авырлык
көчләре өстәл өслегенең эластиклык көче
белән тигезләшкән. Димәк, бу көчләрнең тәэсирен исәпкә алмаска
мөмкин. Хәрәкәткә каршылык көче дә бик аз, аның да тәэсирен
исәпләмибез. Шулай итеп, шарлар йомык система тәшкил итәләр,
ягъни бары тик үзара гына тәэсир итешәләр дип санарга мөмкин.
43 нче рәсемнән күренгәнчә, икенче шар зуррак тизлек белән тәгәри
(аның тизлек векторы озынрак ук белән билгеләнгән). Шуңа күрә күпме¬
дер вакыттан соң ул беренчесен куып җитә, һәм алар бәрелешәчәкләр.
Бик кыска арада (i) булып узган бәрелешү вакытында, беренче һәм
икенче шарларда тиңдәшле рәвештә Fl һәм F-, көчләре барлыкка ки¬
лер. Көчләрнең тәэсире нәтиҗәсендә шарларның тизлекләре үзгәрер.
Тәэсир итешүдән соң тизлекләрне υ{ һәм υ'2 дип билгелик.
Ньютонның өченче законы нигезендә, Fi һәм F2 көчләре модуль¬
ләре буенча тигез һәм капма-каршы юнәлгәннәр:
Fl=-F2∙ (1)
Ньютонның өченче законы буенча көчләрнең һәркайсын масса
белән бу шарларның үзара тәэсир итешүе вакытында туган тизлә¬
нешләре тапкырчыгышына алыштырырга мөмкин:
τn1αl = -m2a2 ∙ ^)
80
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
Тизләнешен түбәндәге тигезлекләрдән исәплибез:
(3)
(4)
(2) тигезлегендә тизләнешләрне аларның (3) һәм (4) тигезләмә¬
ләрендәге тиңдәш аңлатмалары белән алыштырабыз:
(5) тигезләмәсенең ике ягын да t га кыскартабыз:
τn1(υ1,-υ1) = -zn2(υ2'-υ2),
яки
mxυ'x-mxυx = -m2υ2 + m2υ2. (6)
(6) тигезлегендәге буыннарны башкача группалыйбыз: lς
m1vx + m2υ2 = mxvx + m2υ2. (7)
(7) тигезләмәсенә mv = р аңлатмаларын куеп язабыз:
P∣+P2 = Pi + p2∙ <8)
(7) һәм (8) тигезләмәләренең сул яклары — шарларның тәэсир
итешүдән соңгы суммар импульсы, ә уң яклары — тәэсир итешүгә
кадәрге суммар импульсы.
Димәк, үзара тәэсир итешү вакытында һәр шарның импульсы
үзгәрсә дә, тәэсир итешүдән соң аларның импульсларының век¬
торлы суммасы тәэсир итешүгә кадәрге кебек булып калды.
(7) һәм (8) тигезләмәләре импульс саклану законының матема¬
тик язылышы булып тора.
Безнең бу курста бер туры буенча хәрәкәт итүче җисемнәрнең
генә тәэсир итешүләре каралганлыктан, импульс саклану законын
скаляр формада язу өчен бер генә тигезләмә җитә, аңа вектор зур¬
лыкларның X күчәренә проекцияләре керә:
√n∣+ m2⅛x = mxυxx + m2υ2x . (9)
81
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
J> Сораулар
1. 42 нче рәсемдә сурәтләнгән тәҗрибә ничек куела һәм нәрсәне
аңлата?
2. Берничә җисем йомык системаны тәшкил итәләр дигән рас¬
лама нәрсәне аңлата?
3. Импульс саклану законын әйтеп бирегез.
4. Ике җисемнән торган йомык система өчен җисемнәрнең мас¬
салары һәм тизлекләре кергән импульс саклану законын тигезләмә
рәвешендә языгыз. Бу тигезләмәгә кергән һәр символның нәрсәне
аңлатуын аңлатыгыз.
$ 21 нче күнегү
1. Кеше күл өстендәге хәрәкәтсез көймәдә утыра. Ниндидер бер
мизгелдә, ул торып, көймәнең койрык өлешеннән алгы өлешкә килә.
Бу вакытта көймә нишләр? Бу күренешне импульс саклану законы
нигезендә аңлатыгыз.
2. Массасы 35 т булган тимер юл вагоны шул ук юлда торучы
28 т массалы хәрәкәтсез вагонга килеп бәрелә һәм аның белән авто¬
мат рәвештә тоташа. Тоташканнан соң, алар туры буенча 0,5 м/с
тизлек белән хәрәкәт итә башлыйлар. Тоташканга кадәр 35 т лы
вагонның тизлеге нинди булган?
§ 23. Реактив хәрәкәт. Ракеталар
Импульс саклану законының дөреслеген раслаучы берничә ми¬
сал карап үтик.
Һава тутырылган шарның бәйләп куелган җебен чишкәннән соң
ничек хәрәкәт итә башлавын күргәнегез бардыр инде.
Бу күренешне импульс саклану законы ярдәмендә аңлатырга
мөмкин.
Шарның тишеге бәйләп куелган вакытта, шар, үз эченә туты¬
рылган һавасы белән бергә, тикторышта була һәм аның импульсы
нульгә тигез.
Тишек ачылып китүгә, аннан шактый ук зур тизлек белән кы¬
сылган һава агымы бәреп чыга. Хәрәкәт итүче һаваның хәрәкәт
юнәлешендә беркадәр импульсы була.
Импульс саклану законы нигезендә, ике җисемнән — шарчык¬
тан һәм аның эчендәге һавадан торган системаның суммар импуль¬
82
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
сы, һава чыкканчыга кадәр булып калырга, ягъни нульгә тигез бу¬
лырга тиеш. Шуңа күрә шарчык һава агымына каршы юнәлештә
хәрәкәт итә башлый. Ул импульсы модуле буенча һава агымы им¬
пульсына тигез булган тизлек ала. Шар белән һаваның импульс век¬
торлары капма-каршы юнәлгән. Нәтиҗәдә, үзара тәэсир итешүче
җисемнәрнең суммар импульслары нульгә тигез булып кала.
Шарчыкның хәрәкәте реактив хәрәкәткә мисал булып тора.
Җисемнән аерылып киткән нинди дә булса кисәкчекнең хәрәкәт
итүе нәтиҗәсендә җисем үзе капма-каршы юнәлгән импульс алса,
аның хәрәкәте реактив хәрәкәт була.
Рәс. 44
Рәс. 45
44 һәм 45 нче рәсемнәрдә сурәтләнгән тәҗрибәләр реактив
хәрәкәтне газ агынтысы гына түгел, су агынтысы да китереп чыгара
алуын күрсәтә.
44 нче рәсемдә өске башы — бүрәнкә белән, ә аскысы бөгелгән
пыяла көпшә белән тоташтырылган резин көпшә күрсәтелгән. Ул
вертикаль торышыннан су агынтысына капма-каршы якка авыша.
Үзенең авыш торышыннан ул өске башы беркетелгән булганга гына
агымга каршы кузгалып китми.
Сегнер тәгәрмәче (рәс. 45) дип аталучы җайланманың әйләнүе
дә реактив хәрәкәт принцибына нигезләнгән. Конус формасындагы
83
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
савыттан аңа тоташкан бөгелгән көпшә аша агып чыгучы сыеклык
савытны бу көпшәнең бөгелешләренә каршы якка әйләндерә.
Хәтта кайбер тереклек ияләре, мәсәлән сигезаяк һәм кальмар¬
лар, реактив хәрәкәт нигезендә күченеп йөриләр.
Сез инде беләсез, реактив хәрәкәт принцибы авиациядә һәм кос¬
монавтикада киң кулланылыш таба. Космик пространствода җи¬
сем тәэсир итешә алырлык һәм шуның аркасында үзенең тизлек
юнәлешен һәм модулен үзгәртә алырлык мохит юк. Шуңа күрә кос¬
мик очышлар өчен бары тик реактив очу аппаратлары, ягъни раке¬
таларны гына кулланып була.
Йөртүче ракета дип аталучы, ягъни Җирнең ясалма иярченнә¬
рен, космик корабльләрне, планетара автомат станцияләрне һәм баш¬
ка файдалы йөкләрне космоска чыгару өчен кулланыла торган ра¬
кеталарның төзелешен һәм аларның ничек җибәрелүен карап үтик.
Теләсә кайсы ракетада, төзелеше нинди булуга да карамастан,
һәрвакыт тышча һәм оксидлаштыручы ягулык була. 46 нчы рәсемдә
ракетаның аркылы кисеме бирелгән. Ракетаның тышчасына фай¬
далы йөк (бу очракта космик корабль), приборлар бүлеге һәм двига¬
тель (яну камерасы, насослар һ.б.) керә.
Ракетаның төп массасын оксид¬
лаштыргыч белән ягулык тәшкил итә
(оксидлаштыргыч ягулыкның януын
тәэмин итү өчен кирәк, чөнки космос¬
та кислород юк).
Ягулык һәм оксидлаштыргыч на¬
сослар ярдәмендә яну камерасына би¬
релә. Ягулык, янып, югары темпера¬
туралы һәм югары басымлы газга әве¬
релә. Яну камерасын космик простран-
стводагы белән басымнар аермасы га¬
ять зур булу сәбәпле, газлар, куәтле таш¬
кын булып, сопло дип аталучы махсус
формадагы киңәюле торба аша яну ка¬
мерасыннан тышка ыргыла. Сопло
агымның тизлеген арттыру өчен кирәк.
Газ агышының чыгу тизлеген ни
өчен арттыралар? Чөнки ракетаның
тизлеге шушы тизлеккә бәйле. Моны
Ягулык багы
Насослар
Яну камерасы
Сопло
Космик корабль
Приборлар
бүлеге
Оксидлаштыр¬
гыч багы
Рәс. 46
84
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
импульс саклану законы ярдәмендә
күрсәтергә мөмкин.
Гадирәк фикер йөртү өчен, хәзергә
ракета йомык система хасил итә дип
уйлыйк (ягъни аңа Җир тарту көченең
тәэсирен исәпләмибез).
Стартка кадәр ракетаның импуль¬
сы нульгә тигез булганлыктан, сакла¬
ну законы нигезендә, хәрәкәт итүче
тышча белән аннан чыгучы газның сум¬
мар импульсы да нульгә тигез булырга
тиеш. Шулай булгач, тышчаның им¬
пульсы һәм аңа капма-каршы юнәлгән
газ агымы импульсы модульләре буен¬
ча тигез булырга тиеш. Димәк, сопло-
дан чыгучы газның тизлеге никадәр зур
Космик корабль
III баскыч
II баскыч
I баскыч
Рәс. 47
булса, ракета тышчасының тизлеге шулкадәр зуррак була.
Газ чыгу тизлегеннән тыш, ракетаның тизлеген билгели торган
башка факторлар да бар.
Без югарыда бербаскычлы ракетаның төзелеш һәм эш принци¬
бын карап үттек. Баскыч — ракетаның ягулык белән оксидлаш¬
тыргыч баклары һәм двигатель урнашкан өлеше ул.
Космик очышларда гадәттә күпбаскычлы — тагын да зуррак
тизлекләрне тәэмин итүче һәм бербаскычлыга караганда ераграк
очышлар өчен билгеләнгән ракеталар кулланыла.
47 нче рәсемдә өчбаскычлы ракетаның схемасы бирелгән. Бе¬
ренче баскычның ягулыгы белән оксидлаштыргычы тулысынча янып
беткәч, ул автомат рәвештә ташлап калдырыла һәм икенче баскыч¬
ның двигателе эшли башлый.
Кирәксезгә әйләнгән баскычны ташлап калдыру юлы белән раке¬
таның гомуми массасын киметү ягулык белән оксидлаштыргычны эко¬
номияләргә һәм ракетаның тизлеген арттырырга мөмкинлек бирә.
Икенче баскыч та шулай ук ташлап калдырыла.
Әгәр космик корабльне Җиргә кире кайтару яисә башка плане¬
тага җибәрү күздә тотылмаса, өченче баскыч, беренче икесе кебек
үк, ракетаның тизлеген арттыру өчен хезмәт итә. Ә инде корабль
каядыр төшәргә тиеш булса, ул төшү алдыннан корабльнең тизле¬
ген киметү Өчен кулланыла. Бу очракта ракетаны, сопло алда бу¬
85
I бүлек Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт законнары
лырлык итеп, 180° ка әйләндерәләр. Ул чагында ракетадан ыргы¬
лып чыгучы газ аның хәрәкәт тизлегенә каршы юнәлгән импульс
бирә һәм, тизлекне киметеп, ракетаны утыртырга булыша.
Космик очышлар өчен ракеталарны куллану идеясе XX гасыр
башларында рус галиме, уйлап табучы, укытучы Константин Эду¬
ардович Циолковский тарафыннан тәкъдим ителә. Циолковский
ракеталарның хәрәкәт теориясен эшли, ал арның тизлекләрен исәпләү
формуласын чыгара һәм күпбаскычлы ракеталар куллануны берен¬
че булып тәкъдим итә.
Ярты гасыр үткәч, Циолковский идеясе Сергей Павлович Ко¬
ролев җитәкчелегендәге совет галимнәре тарафыннан үстерелә һәм
тормышка ашырыла.
tf Сораулар
1. Импульс саклану законына нигезләнеп аңлатыгыз, ни өчен
кабартылган шар үзеннән чыгучы кысылган һава агымы юнәлешенә
капма-каршы хәрәкәт итә?
2. Җисемнәрнең реактив хәрәкәтенә мисаллар китерегез.
3. Ракеталар ни өчен кирәк?
4. 46 нчы рәсемнән файдаланып, теләсә нинди космик ракета¬
ның төп өлешләрен санап чыгыгыз.
5. Ракетаның эш принцибын аңлатып бирегез.
6. Ракетаның тизлеге нәрсәгә бәйле?
7. Күпбаскычлы ракеталарның бербаскычлылардан өстенлеге
нидән гыйбарәт?
8. Космик корабльне утырту ничек башкарыла?
$ 22 нче күнегү
1.2 м/с тизлек белән йөзүче көймәдән ишкәкче аның хәрәкәтенә
каршы якка 8 м/с горизонталь тизлек белән 5 кг массалы ишкәкне
ыргыта. Әгәр көймә белән ишкәкченең гомуми массасы 200 кг бул¬
са, ыргытудан соң көймә нинди тизлек белән хәрәкәт иткән?
2. Ракета моделе тышчасының массасы 300 г, аның эчендәге
дарының массасы 100 г, ә газлар соплодан 100 м/с тизлек белән
чыксалар, бу модель нинди тизлек алыр? (Газ чыгу вакыты — мо¬
менталь дип алына.)
II бүлек
МЕХАНИК ТИРБӘНЕШЛӘР ҺӘМ ДУЛКЫННАР.
ТАВЫШ
§ 24. Тирбенү хәрәкәте
Тигезсез хәрәкәтнең бер төре — тигез тизләнешле хәрәкәт белән
сез таныштыгыз инде.
Тигезсез хәрәкәтнең тагын бер төрен — тирбәнү хәрәкәтен тик¬
шереп үтик.
Тирбәнү хәрәкәте безне чолгап алган дөньяда бик киң таралган.
Тегү машинасы энәсенең, таган, сәгать маятнигы, рессорлар өстен¬
дәге вагонның һәм башка бик күп җисемнәрнең хәрәкәте тирбәнүгә
мисал булып тора. 48 нче рәсемдә сурәтләнгән җисемнәр, тигезлә¬
неш торышыннан чыгарылганнан соң, тирбәнү хәрәкәте ясый ала¬
лар (авыштыргач яки ОО' сызыгыннан тайпылдыргач).
/ Металл
линейка
Тиски
Бу җисемнәрнең хәрәкәтләрендә аерымлыклар бик күп. Мәсәлән,
җепкә эленгән шарчык — кәкре сызык буйлап (рәс. 48, а), резин
шнурдагы цилиндр (рәс. 48, б) туры сызык буйлап хәрәкәт итә; ли¬
87
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
нейканың өске башы (рәс. 48, е), кылның урта ноктасы башка нок¬
таларына караганда (рәс. 48, г) зуррак авышлык ясап тирбәнә. Бер
үк вакыт эчендә кайбер җисемнәр икенчеләренә караганда күбрәк
сандагы тирбәнешләр ясый.
Ләкин, күптөрле булсалар да, бу хәрәкәтләрнең бик әһәмиятле
бер уртак сыйфатлары бар: билгеле бер вакыт аралыгыннан соң
теләсә кайсы җисемнең хәрәкәте кабатлана.
Чыннан да, шарчыкны тигезләнеш торышыннан бераз авышты¬
рып, аннары ычкындырсак, ул, тигезләнеш торышыннан узып ки¬
теп, каршы якка авыша, туктап тора һәм хәрәкәт башланган урын¬
га кире кайта. Бу тирбәнештән соң икенчесе, өченчесе һ.б. беренче¬
сенә охшаш тирбәнешләр кабатлана.
48 нче рәсемдә сурәтләнгән башка җисемнәрнең хәрәкәтләре дә
кабатланучан.
Хәрәкәтнең кабатлану вакыты тирбәнешнең периоды1 дип ата¬
ла. Шуңа күрә тирбәнү хәрәкәте периодик була, диләр.
Шулай итеп, тирбәнү хәрәкәтен хәрәкәтнең башка төрләреннән
аера торган төп билге булып аның периодиклыгы санала.
48 нче рәсемдә сурәтләнгән җисемнәрнең хәрәкәтендә, перио¬
диклыктан тыш, тагын бер уртак билге бар: тирбәнү периодына ти¬
гез булган вакыт эчендә теләсә кайсы җисем тигезләнеш торышы
аша ике тапкыр узып китә (капма-каршы юнәлешләрдә хәрәкәт итеп).
Без нәкъ менә шундый тирбәнешләрне өйрәнербез.
Сораулар
1. Тирбәнү хәрәкәтенә мисаллар китерегез.
2. Тирбәнү хәрәкәте периодик була дигән сүзне ничек аңлый¬
сыз?
3. Тирбәнү периоды нәрсә ул?
4. 48 нче рәсемдә сурәтләнгән җисемнәргә, периодиклыктан баш¬
ка тагын нинди уртак билге хас?
*« Тирбәнешләр периоды» терминының мәгънәсе 26 нчы параграфта
төгәлрәк күрсәтелер.
88
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
§ 25. Ирекле тирбәнешләр.Тирбәнү системалары.
Маятник
49 нчы рәсемдә сурәтләнгән тишекле шарчык шома корыч кылга ки-
дертелгән һәм пружинага эләктерелгән, ә пружинаның икенче очы верти¬
каль терәккә беркетелгән. Шарчык кыл буйлап иркен шуып йөри, чөнки
ышкылу көчләре аның хәрәкәтенә тәэсир итәрлек дәрәҗәдә түгел, бик аз.
Шарчык О ноктасында торганда (рәс. 49, а), пружина деформацияләнмәгән
(сузылмаган да, кысылмаган да), шунлыктан аңа горизонталь юнәлештә
бернинди көч тә тәэсир итми. О ноктасы — шарның тигезләнеш торышы.
Шарны В ноктасына күчерик (рәс. 49, б).
Бу вакытта пружина сузыла һәм анда
эластиклык көче F3jl в хасил була. Гук
законы буенча, бу көч тайпылышка (ягъ¬
ни шарның тигезләнеш торышыннан
авышуына) пропорциональ һәм аңа кап¬
ма-каршы якка юнәлгән. Димәк, шар уң
якка тайпылганда, аңа тәэсир итүче көч
сул якка — тигезләнеш торышына таба
юнәлгән.
Шарны җибәрсәк, ул эластиклың көче
тәэсирендә тизләнеш белән сулга, О нок¬
тасына таба күчә башлый. Эластиклык
көченең һәм бу көч тудырган тиз¬
ләнешнең юнәлешләре шарның тизлек
юнәлеше белән туры килә. Шуңа күрә, О
ноктасына якынайган саен, шарның тиз¬
леге арта бара. Һәм, пружинаның дефор¬
мациясе кимегәнлектән, эластиклык көче
кими төшә (рәс. 49, в).
Билгеле булганча, һәрбер җисем, әгәр
аңа көчләр тәэсир итмәсә яки көчләрнең
Рәс. 49
бердәй тәэсир итүчесе нульгә тигез булса, үзенең тизлеген саклап
калу үзлегенә ия. Шунлыктан шар тигезләнеш торышына җиткәч
(рәс. 49, г, биредә эластиклык көче нульгә тигез) туктап калмый, ә
сул якка үтеп китә.
О ноктасыннан А га хәрәкәт иткәндә, пружина кысыла. Аңарда
кабаттан эластиклык көче барлыкка килә, һәм ул бу очракта да
89
// бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
тигезләнеш торышына юнәлгән була (рәс. 49, д, ё). Эластиклык
көче, шарның хәрәкәт тизлегенә каршы юнәлгәнлектән, аның
хәрәкәтен киметә. Нәтиҗәдә А ноктасында шар туктый. О ноктасы¬
на юнәлгән эластиклык көче үз тәэсирен дәвам итә, шунлыктан шар
яңадан хәрәкәткә килә һәм АО бүлемтегендә аның тизлеге үсә бара
(рәс. 49, е, ж, з).
Шарның О ноктасыннан В ноктасына хәрәкәте нәтиҗәсендә,
пружина сузыла һәм тагын эластиклык көче барлыкка килә, ул
тигезләнеш торышына юнәлгән була һәм шарның хәрәкәтен тук¬
тап калганчыга кадәр киметә (рәс. 49, з, и, к). Шулай итеп, шар
тулы тирбәнеш ясый. Ьәм траекториясенең һәрбер ноктасында (О
ноктасыннан башка) аңа пружинаның тигезләнеш торышына
юнәлгән эластиклык көче тәэсир итә.
Тигезләнеш торышына кире кайтаручы көч тәэсирендә җисем
үзеннән-үзе тирбәнешләр ясарга мөмкин. Беренче тапкыр көч без пру¬
жинаны сузып эш башкаргач барлыкка килде, чөнки аңа күпмедер
энергия тапшырылды. Тирбәнешләр шушы энергия хисабына ясал¬
ды да.
Энергиянең башлангыч запасы хисабына гына була торган
тирбәнешләр — ирекле тирбәнешләр дип атала.
Ирекле тирбәнүче җисемнәр һәрвакыт башка җисемнәр белән
тәэсир итешәләр, һәм алар белән бергә тирбәнүләр системасы дип
йөртелә торган системалар барлыкка китерәләр. Моны аңлатып үтик.
Без тикшергән мисалда тирбәнүләр системасына шар, пружина
һәм пружинаның сул очы беркетелгән терәк керә. Бу җисемнәрнең
үзара тәэсир итешүе нәтиҗәсендә, шарны тигезләнеш торышына кай¬
таручы көч хасил була.
50 нче рәсемдә шар, җеп, штатив һәм Җирдән (Җир рәсемдә
күрсәтелмәгән) торучы тирбәнүләр системасы сурәтләнгән. Бу оч¬
ракта ирекле тирбәнешләрне шар ике көч: авырлык көче һәм җеп¬
нең эластиклык көче тәэсирендә ясый. Аларның бердәй тәэсир итү¬
чесе тигезләнеш торышына юнәлгән.
Ирекле тирбәнешләр ясарга сәләтле булган җисем система¬
лары тирбәнү системалары дип атала.
90
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
Барлык тирбәнү системаларына хас булган төп уртак үзлекләр¬
нең берсе — аларда системаны тотрыклы тигезләнеш торы¬
шына кайтаручы көчләр барлыкка килә.
Тирбәнү системалары — бик киң төшенчә, һәм ул төрле күре¬
нешләргә карата кулланыла. Без карап узган тирбәнү системалары
маятниклар дип атала. Берничә типтагы маятниклар була: җепле
(рәс. 50), пружиналы (рәс. 51) һ.б.
Гомуми очракта, үзенә куелган көчләр тәэсирендә хәрәкәтсез
нокта янында яки күчәр тирәсендә тирбәнешләр ясаучы каты
җисемне маятник дип атыйлар.
Тирбәнү хәрәкәтен без пружиналы һәм җепле маятниклар миса¬
лында өйрәнербез.
? Сораулар
1. 49 нчы рәсемне карап әйтегез, шар В; С; О; D; А нокталарын¬
да булганда, аңа пружинаның эластиклык көче тәэсир итәме?
2. 49 нчы рәсемнән файдаланып аңлатыгыз, ни өчен О нокта¬
сына теләсә кайсы яктан якынайганда, шарның тизлеге арта, ә
О ноктасыннан теләсә кайсы якка ерагайганда — кими?
3. Ни өчен шар тигезләнеш торышына җитү белән туктап
калмый?
91
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
4. Нинди тирбәнешләрне ирекле тирбәнешләр диләр?
5. Тирбәнүләр системасы нәрсә ул?
6. Маятник дип нәрсә атала?
7. Пружиналы маятник дип аталган тирбәнү системасына
нәрсәләр керә? җепле маятник системасына?
$ 23 нче күнегү
1. 52 нче рәсемдә системаларның кайсылары тирбәнүләр систе¬
масы була, ә кайсылары — булмый?
Шар горизонталь
өслектә
Шар касә
төбендә
Шар кабарынкы
өслектә
Рәс. 53
Рәс. 52
2. 53 нче рәсемдә өч резин шнурга эленгән
металл диск сурәтләнгән. Әгәр дискны верти¬
каль күчәр тирәсендә бераз борганнан соң ыч¬
кындырып җибәрсәк, ул берникадәр вакыт әле¬
ге күчәр тирәли, я сәгать теле уңаена, я сәгать
теленә каршы юнәлештә борылгалап торыр.
Аңлатыгыз: а) дискның тирбәнүләре нинди көч
тәэсирендә бара; б) әгәр диск шнурга үзенең
авырлыгы белән тәэсир итмәсә, бу көч барлык¬
ка килер идеме; в) бу тирбәнү системасына нин¬
ди көчләр керә; г) бу система маятникмы?
92
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
§ 26. Тирбәнү хәрәкәтен характерлаучы зурлыклар
54 нче рәсемдәге ике бертөрле маятникның тирбәнешләрен ча¬
гыштырыйк. Беренче маятник ныграк авышып тирбәлә, ягъни аның
чик торышлары тигезләнеш торышыннан икенче маятникныкына
караганда ераграк була.
Тирбәнүче җисемнең тигезләнеш, торышыннан иң зур авы¬
шуы (модуле буенча) тирбәнешләрнең амплитудасы дип атала.
Рәс. 54
Рәс. 55
Биредә кечкенә амплитудалы (рәс. 55), АВ дугасының озынлы¬
гын АВ кисемтәсенә һәм хәтта СВ ярымхордасына тигез дип алыр¬
лык очракларны тикшерербез. Шуңа күрә җепле маятникның
тирбәнүләр амплитудасы итеп дуганы яки бу кисемтәләрнең берәр¬
сен кабул итәргә мөмкин. Беренче маятникның тирбәнүләр ампли¬
тудасы —O1A1 гә яки O1B1 гә, икенчесенеке O2A2 гә яисә O2B2 гә тигез
була (рәс. 54). Гадәттә амплитуданы А хәрефе белән билгелиләр һәм
озынлык берәмлекләрендә — метрларда (м), сантиметрларда (см)
һ.б. үлчиләр. Амплитуданы шулай ук яссы почмак берәмлекләрендә,
мәсәлән, градусларда үлчәргә мөмкин, чөнки әйләнә дугасына бил¬
геле бер үзәк почмак, ягъни түбәсе әйләнә үзәгендә (бу очракта О
ноктасында) булган почмак тиңдәш була.
Пружиналы маятникның тирбәнешләр амплитудасы (рәс. 49)
ОВ яки ОА кисемтәсе озынлыгына тигез.
Тирбәнүче җисем, тирбәнүләр башланганнан алып, дүрт ампли¬
тудага тигез юл үтсә, ул бер тулы тирбәнеш ясый. Мәсәлән, беренче
шарның O1 дән B1 гә, аннан соң B1 дән A1 гә һәм яңадан O1 гә
хәрәкәте бер тулы тирбәнеш тәшкил итә.
93
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
Бер тулы тирбәнеш ясау өчен сарыф ителгән вакыт тирбә¬
нешнең периоды дип атала.
Тирбәнешләр периоды гадәттә Т хәрефе белән билгеләнә һәм СИда
секундлар белән (с) үлчәнә.
Аркылы борыска ике маятник эләбез: берсе озынрак, икенчесе
кыска булсын. Аларны тигезләнеш торышыннан бер үк ераклыкка
авыштырабыз да ычкындырабыз. Озыны белән чагыштырганда,
кыска маятникның бер үк вакыт эчендә күбрәк тирбәнешләр яса¬
вын күрербез.
Бер вакыт берәмлегендә ясалган тирбәнешләр саны тирбә¬
нешләр ешлыгы дип атала.
Ешлык v («ню») хәрефе белән билгеләнә. Ешлык берәмлеге итеп
бер секундка бер тирбәнеш кабул ителгән. Немец галиме Генрих
Герц хөрмәтенә бу берәмлек герц (Гц) дип аталган.
Әгәр маятник, мәсәлән, бер секундка 2 тирбәнеш ясаса, аның
тирбәнүләр ешлыгы 2 Гц (яки 2-), ә тирбәнүләр периоды (бер тулы
С
тирбәнешнең вакыты) 0,5 с ка тигез. Тирбәнешнең периодын табу
өчен, бер секундны шул бер секунд эчендә ясалган тирбәнешләр са¬
нына, ягъни ешлыкка бүләргә кирәк:
Шулай итеп, тирбәнешләр периоды Т һәм тирбәнешләр ешлыгы
v түбәндәгечә бәйләнгән:
m 1 1
Т - — , яки v = — •
V Т
Төрле озынлыктагы маятникларның ничек тирбәнүләреннән
чыгып, шундый нәтиҗәгә киләбез: җепле маятникның ирекле тир¬
бәнешләре периоды һәм ешлыгы аның җебенең озынлыгына бәйле.
Маятникның җебе озынрак булса, тирбәнешләр периоды зуррак һәм
94
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
ешлыгы кечерәк була. (Бу бәйлелекне без 3 нче лаборатор эштә тик¬
шерербез.)
Ирекле тирбәнешләрнең ешлыгы тирбәнүләр системасының
үз ешлыгы дип атала.
Җепле маятник кына түгел, теләсә нинди башка тирбәнүләр сис¬
темасы да ирекле тирбәнешләрнең шул система параметрларына
бәйле булган билгеле бер үз ешлы¬
гына ия. Мәсәлән, пружиналы маят¬
никның ирекле тирбәнешләр ешлы¬
гы йөкнең массасына һәм пружи¬
наның катылыгына бәйле.
Хәзер түбәндәгечә хәрәкәтләнә
торган ике бертөрле маятникның
тирбәнешләрен карыйк (рәс. 56). Бер
үк вакыт мизгелендә сул маятник сул
чик торышыннан — уңга таба, ә уң маятник уң чик торышыннан
сулга таба хәрәкәтләнә башлый. Икесе дә бер үк ешлык (ж;епләрнең
озынлыклары тигез) һәм бер үк амплитуда белән тирбәнәләр. Әмма бу
тирбәнешләр бер-берсеннән аерыла: теләсә кайсы вакыт мизгелендә
маятникларның тизлекләре капма-каршы якларга юнәлгән. Бу оч¬
ракта маятникларның тирбәнешләре капма-каршы фазаларда бара,
диләр.
54 нче рәсемдәге маятниклар да бер үк ешлык белән тирбәнә.
Аларның тизлекләре теләсә кайсы вакыт мизгелендә бертөрле
юнәлгән. Бу очракта маятниклар бер -үк фазаларда тирбәнә, диләр.
Тагын бер очракны карыйк. 57 нче а рәсемдә сурәтләнгән миз¬
гелдә ике маятникның да тизлекләре сулга юнәлгән. Әмма күпме¬
дер вакыттан соң (рәс. 57, б) алар төрле якларга юнәлерләр. Бу
очракта тирбәнешләр билгеле бер фазалар аермасы белән бара, диләр.
'95
II бу лек. Механик тирбәнешләр һәм дулкыннар. Тавыш
Фаза дип йөртелүче физик зурлык ике яки берничә җисемнең
тирбәнүләрен чагыштыру өчен генә түгел, бер җисемнең тирбәнеш¬
ләрен сурәтләү өчен дә кирәк.
Фазаны теләсә кайсы вакыт мизгеле өчен исәпләү формуласы
бар, тик сез аны югары сыйныфларда өйрәнерсез.
Шулай итеп, тирбәнү хәрәкәте амплитуда, ешлык (яки пе¬
риод) һәм фаза белән характерлана.
? Сораулар
1. Тирбәнешнең амплитудасы, периоды, ешлыгы дип нәрсә ата¬
ла? Бу зурлыкларның һәркайсы нинди хәреф белән билгеләнә һәм
нинди берәмлекләрдә үлчәнә?
2. Бер тулы тирбәнеш нәрсә ул?
3. Тирбәнешләрнең периоды белән ешлыгы арасында нинди ма¬
тематик бәйләнеш бар?
4. Маятникта тирбәнешләрнең а) ешлыгы; б) периоды аның
җебенең озынлыгына ничек бәйләнгән?
5. Тирбәнүләр системасының үз ешлыгы дип нәрсәгә әйтәләр?
6. Әгәр ике маятник: а) капма-каршы фазаларда; б) бер үк фа¬
заларда тирбәнсә, теләсә кайсы вакыт мизгелендә аларның тиз¬
лекләре бер-берсенә карата ничек юнәлер?
$ 24 нче күнегү
1. 49 нчы рәсемдә сурәтләнгән пружиналы маятник ирекле тирбә¬
нешләр ясый. Бу хәрәкәтне тасвирлаучы нинди зурлыклар (амплиту¬
да, ешлык, период, тизлек, бу тирбәнешләрне ясауга сәбәпче көч) —
даими, ә ниндиләре үзгәрешле була? (Ышкылуны исәпкә алмагыз.)
⅛. Йөз метрлы тимер юл күперенең тирбәнүләр ешлыгы 2 Гц.
Бу тирбәнешләрнең периодын табыгыз.
3. Тимер юл вагонының вертикаль тирбәнешләре периоды 0,5 с.
Вагон тирбәнешләренең ешлыгын табыгыз.
4. Тегү машинасының энәсе бер минут эчендә 600 тулы әйләнеш
ясый. Энәнең тирбәнешләр ешлыгын герцларда исәпләгез.
5. Пружинадагы йөкнең тирбәнешләр амплитудасы 3 см га ти-
113
гез. -^Т; -^Т', -±Т; 1Т вакыт эчендә йөк тигезләнеш торышыннан
күпме ераклыкка китәр?
96
// бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
6. Пружинадагы йөкнең тирбәнешләр амплитудасы 10 см, еш¬
лыгы 0,5 Гц. Йөк 2 с эчендә күпме юл үтәр?
7. 58 нче рәсемдә тирбәнүче маятниклар пары күрсәтелгән. Нинди
очракларда маятниклар бер-берсенә карата бер үк фазаларда; капма-
каршы фазаларда тирбәнә?
Рәс. 58
§ 27. Гармоник тирбәнешләр
Табигатьтә һәм техникада гармоник тирбәнешләр дип йөртелү¬
че тирбәнешләр киң таралган.
Тирбәнүче ноктаның тайпылышына пропорциональ һәм тай¬
пылышка каршы юнәлгән көч тәэсирендә була торган тирбәнешләр
гармоник тирбәнешләр дип атала.
ч Белгәнебезчә, пружиналы маятникның
тирбәнүләре дә шундый көч 'тәэсирендә
килеп чыга (§ 25), шуңа күрә алар билгеле
бер шартларда гармоник тирбәнүләргә ми¬
сал булып тора (атап әйткәндә, аларга ыш¬
кылу көче сизелерлек тәэсир итмәсә).
59 нчы рәсемдә сурәтләнгән тәҗрибә
ярдәмендә, тирбәнүче пружиналы маятник
координатасының вакыт узу белән нинди
Рәс. 59
97
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
закон буенча үзгәрүен һәм бу бәйлелекнең графигын ачыкларга
мөмкин.
Әлеге тәҗрибәдә йөк буларак, төбендә тишеге булган бик зур
булмаган савыт (мәсәлән, бүрәнкә) алына, ә аның астына озын кәгазь
тасма салына. Алдан ком тутырылган (яки буяулы сыекча салын¬
ган) савытка тирбәнү хәрәкәте бирәләр. Әгәр тасманы тирбәнүләр
яссылыгына перпендикуляр юнәлештә даими тизлек белән күчерә
барсак, анда дулкынсыман комлы юл калыр. Юлның һәр ноктасы тир¬
бәнүче йөкнең шул нокта өстеннән узган торышына туры килә.
60 нчы рәсемдә бу кәкренең гомуми күренешен күрәсез. Ул сину¬
соида дип атала (өлкән сыйныфларның математика курсында әле¬
ге графикларга охшаш булган у = sin х һәм у = cos х тибындагы функ¬
цияләрнең (х — үзгәрешле зурлык) графикларын өйрәнерсез). Маятник¬
ның тигезләнеш торышларына туры килгән нокталар аша — вакыт күчә¬
ре t, ә аңа перпендикуляр итеп тайпылышлар күчәре х үткәрелгән.
Тигезләнеш торышыннан ике якка да йөкнең иң зур тайпы¬
лышлары — модульләре буенча бер үк һәм А га тигез. Бу — тир¬
бәнешләрнең амплитудасы.
Маятник хәрәкәтне координатасы х =А булган чик ноктадан
башлый. Периодка (Т) тигез вакыт эчендә маятник тулы тирбәнеш
ясый: тигезләнеш торышыннан узып китеп, координатасы х = -А
булган каршы чик ноктага җитә, анда бик азга туктала, тизлек юнә¬
лешен капма-каршыга үзгәртеп, кирегә юнәлә һәм, тигезләнеш торы¬
шыннан тагын бер тапкыр узып, хәрәкәт башланган ноктага әйләнеп
кайта. Аннан соң икенче тирбәнеш башлана.
Әгәр тәҗрибә барышында маятник тирбәнеп торган t вакыты
үлчәп алынган булса, бу вакытны тирбәнешләр санына бүлеп, пери¬
98
11 бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
одны (Т) табарга мөмкин: Т = —. Периодны белгәч, тирбәнешләр
N
1
ешлыгын исәпләп була: v = — .
График теләсә кайсы вакыт мизгелендә йөкнең якынча коорди-
натасын табарга мөмкинлек бирә. Мәсәлән, беренче тирбәнеш баш¬
ланып, ∣∙ Т вакыт узгач, йөк x1 координаталы ноктада булган.
Әгәр нинди дә булса җисем координатасының вакытка бәйлелеге
графигы синусоида (косинусоида) булса, ягъни вакыт үтү белән
координатасы синус (косинус) законы буенча үзгәрсә, бу очракта
координата да, җисем дә гармоник тирбәнешләр ясый, диләр.
Физик зурлыкныц вакыт эчендә синус яки косинус законы
буенча бара торган периодик үзгәрешләре гармоник тирбәнешләр
дип атала.
61 нче рәсемдә алда тикшерелгәнгә охшаш тәҗрибә җепле маят¬
ник белән үткәрелә. Бу тәҗрибә ярдәмендә җепле маятник өчен дә
координатаның вакытка бәйлелек
графигы синусоида икәнен, ягъни
аның тирбәнешләренең дә гармо¬
ник икәнен күрсәтергә мөмкин.
Җепле маятник кечкенә ампли¬
туда1 белән ышкылусыз тирбәлүче
материаль нокта булса һәм аның
белән эленү ноктасы арасындагы
ераклык үзгәрмәсә, аның тирбә¬
нешләрен теоретик яктан гармоник
тирбәнешләр дип кабул итәргә
мөмкин. (Бары шушы шартларда
гына ноктаны тигезләнеш торышы-
ЧЗсегезгә төшерик, маятник хәрәкәте траекториясен туры сызык дип
исәпләргә мөмкин булса, амплитуда кечкенә диләр (§ 26). Амплитуданың
бу шартны канәгатьләндерүче санча кыйммәте чишелә торган мәсьәләдә
нинди төгәллек таләп ителүенә бәйле. Күпчелек гамәли мәсьәләләрдә
8° тан артмаган амплитуданы кечкенә диләр.
99
// бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
на кайтаручы көч тайпылышка туры пропорциональ була һәм шу¬
ның нәтиҗәсендә тирбәнешләр гармоник закон — синус яки коси¬
нус үзгәрешләре законы буенча ясалалар. Моны исбатларга мөмкин.)
Элену ноктасыннан үзгәрешсез ераклыкта тирбәлә торган
материаль нокта математик маятник дип атала.
Математик маятник — модель ул, чынбарлыкта андый маят¬
никлар булмый.
Чынбарлыкта гармоникка якын тирбәнешләрне авыр (корыч)
шарчык ясый: ул озынлыгы бу шар диаметрыннан күпкә озынрак,
җиңел һәм аз сузылучан җепкә эленә, аның амплитудасы кечкенә,
ышкылу шулай ук бик аз булырга тиеш.
Җисем гармоник тирбәнешләр ясаганда, аның координатасы
гына түгел, көч, тизләнеш, тизлек кебек зурлыклары да синус яки
косинус законы буенча үзгәрә. Бу әлеге зурлыкларның икешәрләп
туры пропорциональ бәйлелектә булуларын күрсәтүче формула һәм
Fx
законнардан килеп чыга: мәсәлән, F = -kx (Гук законы), a - —
x т
(Ньютонның икенче законы). Бу формулалардан күренгәнчә, җи¬
семнең тайпылышы иң зур булган кырый нокталарда көч һәм тиз¬
ләнеш иң зур кыйммәтләрен ала, ә җисем тигезләнеш торышында
вакытта нульгә тигез була. Димәк, җисемнең тигезләнеш торышы
тирәсендәге тирбәнү хәрәкәте — турысызыклы хәрәкәткә иң якы¬
ны, ә кырый торышлары янында турысызыклыдан кискен аерыла.
Ә инде тизлеккә килгәндә, киресенчә, кырый торышларда ул
нульгә тигез, ә җисем тигезләнеш торышын үткән вакытта иң зур
кыйммәтенә ирешә.
? Сораулар
1. 59 нчы рәсем буенча аңлатыгыз, андагы тәҗрибә нинди мак¬
сат белән куела, ничек үткәрелә һәм нинди нәтиҗәләр алына.
2. 60 нчы рәсемдә сурәтләнгән кәкре сызык ничек атала? ОА
һәм ОТ кисемтәләре нәрсәне аңлата?
3. Нинди тирбәнешләр гармоник дип атала?
4. 61 нче рәсемдә сурәтләнгән тәҗрибә ярдәмендә нәрсәне
күрсәтергә мөмкин?
100
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
5. Математик маятник нәрсә ул?
6. Нинди шартларда җепле маятник гармоникка якын булган
тирбәнешләр ясый?
7. Җисем гармоник тирбәнешләр ясаганда, аңа тәэсир итүче
көч, аның тизләнеше һәм тизлеге ничек үзгәрәләр?
§ 28. Тирбәнү хәрәкәте вакытында энергия
әверелеше. Сүнә баручы тирбәнешләр
Тагын бер тапкыр пружинага беркетелгән шарның тирбәнешлә¬
ренә әйләнеп кайтыйк (рәс. 49). Шарны тигезләнеш торышыннан (О
ноктасы) В ноктасына күчерик. Бу вакытта без, пружинаның элас¬
тиклык көчен ж,иңеп, эш эшлибез. Сузылган пружина потенциаль
энергиягә Еп ия. Шар О ноктасына якынайган саен, деформациясе
кими. Тиңдәшле рәвештә потенциаль энергиясе дә кими бара. Шул
ук вакытта шарның тизлеге арта бара, димәк, кинетик энергия Ек
дә арта.
Әйтик, тирбәнү системасының хәрәкәте вакытында ышкылу
көчләрен ж,иңүгә тотылган энергия югалтулары исәпкә алынмас¬
лык аз булсын, ди. Ул чагында, энергия саклану законы нигезендә,
шарның тигезләнеш торышыннан үтү вакытындагы кинетик энер¬
гиясе тирбәнү системасының башлангыч мизгелендәге — шарның
иң кырый ноктадагы потенциаль энергиясенә тигез була. ВО юлын¬
дагы теләсә кайсы арадаш торыш өчен потенциаль һәм кинетик
энергияләр суммасы — даими зурлык, ул тирбәнү системасының
башлангыч потенциаль энергиясе запасына тигез. Бу энергияне
без системага, пружинаны сузып, шарны О ноктасыннан В га
күчергәндә бирдек.
Шулай итеп, хәрәкәт вакытында энергия югалтулары булмаса,
тирбәнешләр үзеннән-үзе чиксез озак дәвам итәр һәм амплитудасы
даими — О В га тигез булыр иде.
Әмма чынбарлыкта энергия югалуы һәрвакыт була. Энергия,
мәсәлән, ышкылу көчен һәм һава каршылыгын ж,иңү эшенә тоты¬
ла. Икенче төрле әйткәндә, механик энергия акрынлап эчке энергиягә
күчә, шунлыктан тирбәнешләр амплитудасы акрынлап кими һәм
күпмедер вакыттан соң хәрәкәт туктый. Мондый тирбәнешләр сүнә
торган тирбәнешләр дип атала.
101
// булек. Механик тирбәнешләр һәм дулкыннар. Тавыш
Тирбәнүче җисемгә каршылык зуррак булган саен, амплитуда
тизрәк кими һәм тирбәнүләр тизрәк туктый. Мәсәлән, тирбәнешләр
һавада шактый озак дәвам итәргә мөмкин, ә суда бик тиз сүнәләр.
Сораулар
1. Нинди шартларда шарның О ноктасыннан узгандагы кине¬
тик энергиясе аның В ноктасындагы потенциаль энергиясенә ти¬
гез була (рәс. 49, б, г)?
2. Әгәр энергия югалулары бөтенләй юк дип исәпләсәк, юлның
теләсә кайсы ноктасында шарның кинетик һәм потенциаль энер¬
гияләре суммасы турында нәрсә әйтергә мөмкин (рәс. 49)? Моны
нинди закон буенча расларга була?
3. Реаль шартларда тирбәнү хәрәкәте энергия югалтуларын¬
нан башка була аламы?
4. Вакыт узу белән сүнә баручы тирбәнешләрнең амплитудасы
ничек үзгәрә?
5. Маятникның тирбәнешләре кайда тизрәк тукталыр: һава¬
дамы, әллә судамы? (Башлангыч энергия запасы икесендә дә тигез.)
£ 25 нче күнегү
1. 49 нчы рәсемдә сурәтләнгән горизонталь пружиналы маят¬
никны читкә тарталар һәм җибәрәләр. Таблицада бу маятникның
тирбәнү хәрәкәтен характерлаучы зурлыклар бирелгән. Алар юл¬
ның күрсәтелгән бүлемтекләрендә ничек үзгәрә? 1 нче таблицаны
дәфтәрегезгә күчереп сызыгыз һәм тутырыгыз.
1 нче таблица
Маятник
хәрәкә¬
тенең
юнәлеше
Элас¬
тиклык
көче,
F
эл.
Ц. ∙ H⅛λ'∙'
Тиз¬
лек, V
∙'ibc∙'i <
Потен¬
циаль
энер¬
гия, Е
Кине¬
тик
энергия,
Е
к
Тулы механик
энергия, £тул
реаль
шарт¬
ларда
(ышк. бар)
идеаль
шарт¬
ларда *
(ышк. юк)
В дан 0 га
О дан А га
1 ’
■ .β ; t.√∙ t⅛
? с.
А дан 0 га
,KL- ',.'
} '! ': Λ,λ . ? '■
О дан В га
■
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
2. 62 нче рәсемдә А һәм В нокталары арасында ышкылусыз
тирбәнә торган җепле маятник күрсәтелгән. В ноктасында чагында
бу маятник 1 горизонталенә, ягъ¬
ни үзенең иң түбәнге торышы¬
на карата 0,01 Дж гә тигез бул¬
ган потенциаль энергиягә ия.
Шарның а) А һәм О нокталарын¬
дагы потенциаль энергиясе; б) В,
О һәм А нокталарындагы кине¬
тик энергиясе; в) В, D, О, С һәм
А нокталарындагы тулы механик
энергиясе нәрсәгә тигез?
§ 29. Мәҗбүри тирбәнешләр
Әлегә кадәр без ирекле тирбәнешләрне, ягъни энергиянең баш¬
лангыч запасы хисабына бара торган тирбәнешләрне тикшердек.
Ирекле тирбәнешләр һәрвакыт сүнә торган була, чөнки
тирбәнү системасына башта бирелгән энергия тулысы белән ыш¬
кылу һәм тирәлекнең каршылык көчләрен җиңүгә тотылып бетә
(механик энергия эчке энергиягә әверелә). Шуңа күрә ирекле тир¬
бәнешләр практикада кулланылмый диярлек.
Тирбәнешләр сүнмәсен өчен, энергия югалтуларны тирбәнеш¬
нең һәр периоды саен яңартып торырга кирәк. Моның өчен тир¬
бәнүче җисемгә периодик рәвештә үзгәреп торучы көч белән тәэ¬
сир итәргә мөмкин. Мәсәлән, таганны тирбәнүләр тактына һәрва¬
кыт этеп торып, тирбәнешләрне сүндерми калып була.
Җисемнең периодик үзгәреп торучы тышкы көч тәэсирендә
ясаган тирбәнешләре мәҗбүри тирбәнешләр дип атала.
Бу тирбәнешләрне тудыручы, периодик үзгәрә торган тышкы
көч мәҗбүр итүче көч дип атала.
Тикторыштагы таганга периодик рәвештә үзгәреп торучы тыш¬
кы көч белән тәэсир иткәндә, күпмедер вакыт дәвамында мәҗбүри
тирбәнешләрнең амплитудасы үсә, һәр амплитуда алдан булганы¬
II бу лек. Механик тирбәнешләр һәм дулкыннар. Тавыш
на караганда зуррак була бара. Таганның ышкылу көчен җиңүгә
югалган энергиясе аңа читтән бирелгән энергия белән тигез¬
ләшкәч (мәҗбүр итүче көчнең эше хисабына), амплитуданың
үсүе туктый.
Күпчелек очракларда мәҗбүри тирбәнешләрнең даими еш¬
лыгы шунда ук түгел, тирбәнеш башланып бераз вакыт үткәч
урнаша.
Мәҗбүри тирбәнешләрнең амплитудасы белән ешлыгы үз¬
гәрүдән туктагач, тирбәнешләр урнашты, диләр.
Урнашкан мәҗбүри тирбәнешләрнең ешлыгы мәҗбүр итүче
көчнең ешлыгына тигез.
Мәҗбүри тирбәнешләрне тирбәнү системасы булмаган җи¬
семнәр дә ясый ала. Мәсәлән, тегү машинасының энәсе, эчке яну
двигателенең пешкәге һ.б. Мондый җисемнәрнең тирбәнешләре
шулай ук мәҗбүр итүче көч ешлыгында була.
Мәҗбүри тирбәнешләр сүнмиләр. Алар мәҗбүри итүче көч
тәэсире туктагач кына сүнә.
Сораулар
1. Ирекле тирбәнешләр сүнми торган була аламы? Ни өчен?
2. Тирбәнешләр сүнми торган булсын өчен нәрсә эшләргә кирәк?
3. Нинди тирбәнешләр мәҗбүри дип атала?
4. Мәҗбүр итүче көч нәрсә ул?
5. Нинди очракта тирбәнешләр урнашты, диләр?
6. Урнашкан мәҗбүри тирбәнешләр ешлыгы һәм мәҗбүр итү¬
че көч ешлыгы турында нәрсә әйтергә мөмкин?
7. Тирбәнү системасы булмаган җисемнәр мәҗбүри тирбә¬
нешләр ясый аламы? Мисаллар китерегез.
8. Мәҗбүри тирбәнешләр кайчанга кадәр дәвам итә?
£ 26 нчы күнегү
1. 52 нче рәсемне карап әйтегез, кайсы җисемнәр ирекле тирб¬
әнешләр; мәҗбүри тирбәнешләр ясый ала? Җавапны нигезләгез.
2. а) Тирбәнү системасында мәҗбүри тирбәнешләр; б) тирбәнү
системасы булмаган системада ирекле тирбәнешләр була аламы?
Мисаллар китерегез.
104
П бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
§ 30. Резонанс
1 Бу параграф материалына турыдан-туры кагыла торган тарихи
вакыйганы искә төшерик.
1908 елда Петербургта, өстеннән марш атлап (ягъни «бер аяктан
атлап») кавалерия эскадроны үткәндә, Фонтанка аша салынган Ми¬
сыр күпере (Египетский мост) бик көчле тирбәлә башлый һәм җи¬
мерелеп төшә.
Ни өчен бу очракта күпернең мәҗбүри тирбәнешләр амплитуда¬
сы шундый зур була? Авария булдырмау мөмкин иде микән?
Бу сорауларга җавап бирү өчен, мәҗбүри тирбәнешләр ампли¬
тудасы белән мәҗбүр итүче көчнең үзгәрү ешлыгы арасындагы бәйле-
лекне тикшерик.
63 нче рәсемдә уртак шнурга эленгән ике маятник сурәтләнгән.
2 маятнигының озынлыгы үзгәрешсез, бу озынлыкка ирекле тирбә¬
нешләрнең билгеле бер ешлыгы (ягъни маятникның үз ешлыгы)
туры килә. 1 маятнигының озынлыгын җепләрнең очларын тарт¬
калап үзгәртергә мөмкин. Маятникның озынлыгын үзгәрткәндә,
тиңдәшле рәвештә аның үз ешлыгы да үзгәрә.
Рәс. 63 Рәс. 64
Әгәр 1 маятнигын тигезләнеш торышыннан авыштырып ычкын¬
дырсак, ул ирекле тирбәнешләр ясый. Бу хәл шнурның тирбәлүенә
китерә, нәтиҗәдә 2 маятнигына, эленү ноктасы аша, мәҗбүр итүче
көч тәэсир итә башлый. Ул модуле һәм юнәлеше буенча 1 маятнигы
ешлыгында периодик рәвештә үзгәреп тора. Бу көч тәэсирендә
2 маятнигы мәҗбүри тирбәнешләр ясый башлый.
Әгәр 1 маятнигының озынлыгын акрынлап киметсәк, аның тир¬
бәнешләр ешлыгы, димәк, 2 маятнигына тәэсир итүче мәҗбүри
көчнең үзгәрү ешлыгы да арта һәм 2 маятнигының үз ешлыгына
якыная бара. Шул ук вакытта 2 маятнигының урнашкан мәҗбүри
105
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
тирбәнешләре амплитудасы үсәчәк. Маятникларның озынлыклары
тигезләшкәч, ягъни мәҗбүр итүче көчнең ешлыгы v 2 маятныгы-
ның үз ешлыгы v0 белән тәңгәлләшкәч, ул иң зур кыйммәтенә
ирешәчәк. Маятниклар бер үк фазаларда тирбәнәчәкләр.
1 маятнигының озынлыгын моннан соң да, кыскартканда, көч¬
нең мәҗбүр итүче ешлыгы 2 маятнигының үз ешлыгыннан артып
китә. Ул вакытта аның тирбәнешләр амплитудасы кими башлый.
Бу тәҗрибә нигезендә түбәндәге нәтиҗәгә килергә мөмкин:
мәҗбүр итүче көчнең ешлыгы v белән тирбәнү системасының
үз ешлыгы vθ тигезләшкәч, урнашкан мәҗбүри тирбәнешләр амп¬
литудасы үзенең иң зур кыйммәтенә ия була. Резонанс күренеше¬
нең асылы шуннан гыйбарәт.
Резонанс күренешен 64 нче рәсемдәге тәҗрибәдә дә күзәтергә
мөмкин. Бер үк шнурга дүрт маятник эленгән. 1 һәм 3 маятникла¬
рының озынлыклары тигез. 3 маятнигының ирекле тирбәнүләре
тәэсирендә башка маятниклар мәҗбүри тирбәнешләр ясый. 1 маят¬
нигы тирбәнешләренең амплитудасы 2 һәм 4 маятниклары тирбә¬
нешләренең амплитудаларыннан күпкә зур икәне күзәтелә. Бу оч¬
ракта 1 маятнигы 3 маятнигы белән резонанста тирбәлә.
Ни өчен мәҗбүр итүче көч тудырган, урнашкан тирбәнешләр
амплитудасы, бу көчнең үзгәрүләре ешлыгы белән тирбәнү система¬
сының үз ешлыгы туры килгәч кенә, үзенең иң зур кыйммәтенә ия
була? Эш шунда ки, бу очракта мәҗбүр итүче көчнең юнәлеше теләсә
кайсы вакыт мизгелендә тирбәнүче җисемнең хәрәкәт юнәлеше белән
туры килә. Шулай итеп, мәҗбүр итүче көчнең эше хисабына тирбәнү
системасының энергиясен тулыландыру өчен иң уңайлы шартлар
туа. Мәсәлән, таганны ераккарак җибәрү өчен, без аны тәэсир итүче
көч юнәлеше белән таганның хәрәкәт юнәлеше туры килерлек итеп
этәрәбез.
Шуны онытмаска кирәк: резонанс төшенчәсе бары тик мәҗбүри
тирбәнешләргә карата гына кулланыла.
Хәзер җимерелгән күпер очрагына әйләнеп кайтыйк. Күрәсең,
күпергә периодик тәэсир итүче мәҗбүри көчнең («бер аяктан ат¬
лап» барган ат тоякларының) ешлыгы очраклы рәвештә бу күпер¬
нең үз ешлыгы белән туры килгән һәм амплитуда зураеп киткән.
106
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
Күпергә кергәндә ятлыларга бер аяктан бармаска кушылса, авария
булмый калыр иде.
Резонанс бик күп төрле күренешләрдә кайчакта — уңай, ә кай-
чакта тискәре роль уйный. Аерым алганда, иң аз периодик көч
белән мәҗбүри тирбәнешләрнең билгеле бер колачын ясатканда моны
истә тотарга кирәк. Мәсәлән, зур кыңгырауның авыр теленә бу тел¬
нең үз ешлыгы белән тәэсир иткәндә чагыштырмача аз көч куеп та
кузгатып җибәреп була. Резонанста тәэсир ителмәсә, зуррак көч куеп
та кирәкле нәтиҗәне алып булмый.
Резонансның зыянлы күренешенә дә мисаллар китерик. Мәсәлән,
рессор тирбәнүләренең үз ешлыгы белән тәгәрмәчләрнең рельслар
тоташкан урыннарга бәрелү ешлыгы очраклы туры килгәндә, тимер
юл вагоны бик көчле селкенә башлый, пароходлар дулкын вакы¬
тында көчле тирбәнә һ.б.
Резонансның зыян китерүен булдырмаска тырышалар,. Мәсәлән,
аерым өлешләре периодик хәрәкәтләр ясый торган күп кенә завод
станокларын массив нигезгә урнаштыралар, ул станокның гомуми
тирбәнешен булдырмау өчен ярдәм итә.
? Сораулар
1. 63 нче рәсемдә сурәтләнгән ике маятник белән тәҗрибә нин¬
ди максат белән һәм ничек үткәрелә?
2. Резонанс дип аталучы күренеш нидән гыйбарәт?
3. 64 нче рәсемдәге маятникларның кайсысы 3 маятнигы белән
резонанста тирбәнә? Сез моны нинди билгеләр буенча белдегез?
4. Нинди тирбәнешләргә резонанс төшенчәсе кулланыла: ирек¬
ле тирбәнешләргәме, әллә мәҗбүриләренәме?
5. Бер очракта резонанс күренешенең — файдалы, икенчесендә
зыянлы булуына мисаллар китерегез.
$ 27 нче күнегү
1. 64 нче рәсемне карап, җавап бирегез:
а) 1,2 һәм 4 маятниклары нинди тирбәнешләр ясый: иреклеме,
әллә мәҗбүриме?
б) 1,2 һәм 4 маятникларына мәҗбүри таэсир итүче көч нәрсә
аркасында барлыкка килә?
107
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
в) 3 маятнигы тирбәнешләре ешлыгы белән чагыштырганда, 1, 2,
4 маятникларының үз ешлыклары нинди?
г) Ни өчен 1 маятнигы 3 маятнигы белән резонанста тирбәнә, ә 2
һәм 4 маятниклары резонанста тирбәнми?
2. Малай барганда чиләктәге су көчле чайкала башлый. Малай
йөрешен әкренәйтә һәм чайкалу туктый. Ни өчен шулай була?
3. Таганның үз ешлыгы 0,5 Гц. Чагыштырмача аз көч куеп,
таганны ныграк тирбәндерү өчен, аны нинди вакыт аралыгы саен
этеп торырга кирәк?
§ 31. Тирбәнешләрнең тирәлектә таралуы.
Дулкыннар
65 нче рәсемдә күрсәтелгән тәҗрибәне карыйк. Озын пружина¬
ны җепләргә элеп куялар. Кул белән аның сул очына сугалар (рәс.
65, а). Сугудан, пружинаның берничә уралмасы якыная, эластик-
а)
б)
в)
Рәс. 65
лык көче барлыкка килә, аннары әлеге көч тәэсирендә бу уралмалар
тарала башлый. Маятник тигезләнеш торышын үтеп киткән кебек,
уралмалар да, тигезләнеш торышын үтеп, таралуларын дәвам итәләр.
Нәтиҗәдә пружинаның шушы урынында бераз сирәгәю хасил була
(рәс. 65, б). Әгәр пружинаның очына ритм белән суксак, һәр сугуда,
уралмалар якынаеп — тыгызлык, аннан соң, бер-береннән ерагаеп,
сирәклек хасил итәр. Шулай итеп, пружина уралмалары үзләренең
тигезләнеш торышлары янында тирбәләләр. Бу тирбәнешләр, акрын¬
лап, пружина буйлап уралмадан уралмага күчә башлый. Пружина
буйлап, 65 нче в рәсемдәгечә, тыгызлану һәм сирәгәюләр тарала.
108
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
Икенче төрле әйткәндә, пружина буйлап, аның сул очыннан
уңына таба ярсыну, ягъни тирәлекнең халәтен характерлый торган
кайбер физик зурлыкларның үзгәрешләре күчә.
Безнең очракта бу ярсыну — вакыт узу белән пружинада эластик¬
лык көченең, тирбәнүче уралмалар хәрәкәте тизлегенең һәм тизләне¬
шенең, аларның тигезләнеш торышыннан тайпылышының үзгәрүе ул.
Пространствода үзләренең барлыкка килү урыныннан ера¬
гаеп тарала торган ярсынулар дулкыннар дип атала.
Бу билгеләмәдә йөгерек дулкыннар дип йөртелә торган дулкын¬
нар турында сөйләнелә. Без нәкъ менә шундый дулкыннарны
өйрәнербез. Йөгерек дулкыннарның (табигате төрле булса да) төп
үзлеге булып, пространствода таралганда энергия күчерүе санала.
Мәсәлән, пружинаның тирбәнүче уралмалары энергиягә ия.
Күрше уралмалар белән тәэсир итешеп, бу уралмалар үз энергиясе¬
нең бер өлешен аларга бирә, шул сәбәпле пружина буйлап механик
ярсыну (деформация) тарала, ягъни йөгерек дулкын хасил була.
Әмма бу вакытта пружинаның һәр уралмасы үзенең тигезлә¬
неш торышы тирәсендә генә тирбәлә һәм пружина тулысынча үз
урынында кала.
Шулай итеп, йөгерек дулкында матдә күчмичә генә энергия күчә.
Бу темада без эластиклык йөгерек дулкыннарны гына тикше¬
рербез, аларның аерым очрагы булып тавыш тора.
Эластик дулкыннар — эластик тирәлектә тарала торган
механик ярсынулар ул.
Башкача әйткәндә, тирәлектә эластик дулкыннарның барлыкка
килүе деформация нәтиж,әсендә анда эластиклык көчләре хасил булу
белән бәйләнгән. Мәсәлән, нинди дә булса металл ж,исемгә чүкеч
белән сукканда, аңарда эластик дулкын барлыкка килә.
Эластик дулкыннардан тыш, дулкыннарның башка төрләре дә
бар, мәсәлән, сыеклык өслегендәге дулкыннар, электромагнитик дул¬
кыннар була (соңгысы турында 58 нче параграфта сөйләнә).
Дулкынсыман процесслар физик күренешләрнең барлык
өлкәләрендә диярлек очрый һәм шунлыктан аларны өйрәнү зур
әһәмияткә ия.
109
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
Ф Сораулар
1. Нәрсәне дулкын диләр?
2. Теләсә нинди табигатьле йөгерек дулкыннарның төп үзлеге
нидән гыйбарәт?
3. Йөгерек дулкында матдә күчәме?
4. Эластик дулкын нәрсә ул?
5. Эластик булмаган дулкын төрләренә мисаллар китерегез.
§ 32. Буй Һәм аркылы дулкыннар
Пружинада дулкын хасил булганда, уралмалар дулкын таралу
юнәлешендә тирбәнә иде (§ 31, рәс. 65).
Тирбәнешләре дулкын таралу юнәлешендә булган дулкын¬
нар буй дулкыннар дип атала.
Буй дулкыннардан тыш, аркылы дулкыннар да була. Шундый
тәҗрибәне тикшерик. 66 нчы а рәсемдә бер очы беркетелгән резин
шнур күрсәтелгән. Икенче очына вертикаль яссылыкта тирбәнү
хәрәкәте бирәләр (горизонталь урнашкан шнурга перпендикуляр
итеп). Шнурда барлыкка килгән эластиклык көчләре аркасында,
тирбәнешләр шнур буйлап тарала. Анда дулкыннар барлыкка килә
(рәс 66, б), тик шнур кисәкчекләренең тирбәнеше дулкын таралу
юнәлешенә перпендикуляр була.
Тирбәнешләре дулкын таралу юнәлешенә перпендикуляр бул¬
ган дулкыннар аркылы дулкыннар дип атала.
110
II бу лек. Механик тирбәнешләр һәм дулкыннар. Тавыш
Буй һәм аркылы дулкыннар хасил була торган тирәлектә кисәк¬
чекләрнең хәрәкәтен дулкын машинасы (рәс. 67) ярдәмендә
күрсәтергә мөмкин. 67 нче а рәсемдә — аркылы дулкын, ә 67 нче б
рәсемдә буй дулкын сурәтләнгән. Ике дулкын да горизонталь юнә¬
лештә тарала.
Дулкын машинасында бер генә рәт шарчыклар күрсәтелгән. Әмма,
аларның хәрәкәтен күзәтеп, дулкыннарның өч үлчәнешле тоташ
Рәс. 67
тирәлекләрдә ничек таралуын аңларга була (мәсәлән, каты, сыек яки
газсыман матдәнең берникадәр күләмендә).
Моның өчен һәр шарчыкны рәсем яссылыгына перпендикуляр
урнашкан матдәнең вертикаль катламындагы бер кисәге дип күз
алдына китерегез. 67 нче а рәсемнән күренгәнчә, аркылы дулкын
таралганда бу катламнар, шарчыклар шикелле үк вертикаль юнә¬
лештә тирбәнеп, бер-берсенә карата күчеш ясыйлар. Шуңа күрә ар¬
кылы механик дулкыннар күчеш дулкыннары була.
Ә инде буй дулкыннар, 67 нче б рәсемендә сурәтләнгәнчә, кысы¬
лу һәм сирәгәю дулкыннары. Бу очракта тирәлек катламнарының
деформациясе аларның тыгызлыгы үзгәрүдән гыйбарәт, димәк, буй
дулкыннар — чиратлашып килүче тыгызланулар һәм сирәгәю¬
ләр ул.
Катламнар күчкәндә, бары тик каты җисемнәрдә генә эластик¬
лык көчләре хасил була. Сыеклыкларда һәм газларда чиктәш кат¬
ламнар, эластиклык көчләренең каршы тәэсирен сизмичә, бер-бе¬
ренә карата иркен шуышалар. Эластиклык көче булмагач, сыеклык
һәм газларда эластик дулкыннарның барлыкка килүе дә мөмкин
түгел. Шуңа күрә эластик аркылы дулкыннар бары тик каты җи¬
семнәрдә генә тарала ала.
Кысылганда һәм сирәгәйгәндә (ягъни җисем бүлемтекләренең
күләмнәре үзгәргәндә), эластиклык көчләре каты җисемнәрдә дә, сы¬
еклык һәм газларда да хасил була. Шуңа күрә эластик буй дул¬
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
кыннар теләсә нинди тирәлектә — каты, сыек һәм газсыман
тирәлекләрдә тарала ала.
Ф Сораулар
1. Нинди дулкыннар буй дулкын дип атала? аркылы дулкын
дип? Мисаллар китерегез.
2. Аркылы яки буй дулкынның кайсысы күчеш дулкыны була;
кысылу һәм сирәгәю дулкыны була?
3. Нинди тирәлектә эластик аркылы дулкыннар тарала ала;
нинди тирәлектә эластик буй дулкыннар тарала ала?
4. Ни өчен эластик аркылы дулкыннар сыеклыкларда һәм газ¬
ларда тарала алмый?
§ 33. Дулкын озынлыгы.
Дулкыннарның таралу тизлеге
Аркылы дулкын таралганда, ноктадан ноктага тирбәнешләр тап¬
шырылу барышын җентекләбрәк тикшерик. Моның ечен 68 нче
рәсемне карыйбыз, биредә, һәр 1/4 Т вакыты саен, аркылы дулкын
таралу процессының төрле стадияләре күрсәтелгән.
68 нче а рәсемдә номерланган шарчыклар чылбыры сурәтләнгән.
Бу модельдә шарчык — тирәлек кисәкчәгенең символы. Шарчык¬
лар арасында, тирәлек кисәкчекләре арасындагы кебек үк, тәэсир
итешү көчләре бар дип исәпләрбез, мәсәлән, шарчыкларны бер-бер-
сеннән аз гына ераклаштырганда, тартылу көче барлыкка килә.
Әгәр беренче шарчыкка тирбәнү хәрәкәте бирсәк, ягъни аны ти¬
гезләнеш торышыннан өскә һәм аска таба хәрәкәтләнергә мәҗбүр
итсәк, үзара тәэсир итешү көчләре нәтиҗәсендә, чылбырдагы һәр
шарчык, берникадәр соңга калып (фаза күчеше белән), беренче шар¬
чыкның хәрәкәтен кабатлый. Шарчык беренчесеннән ераграк бул¬
ган саен бу соңга калу зуррак булыр. Мәсәлән, дүртенче шарның
беренчесеннән 1/4 тирбәнешкә соңга калуы күренә (рәс. 68, б). Чөнки,
беренче шарчык максималь тайпылып, тулы тирбәнеш юлының 1/4
өлешен үткәндә, дүртенче шарчык тигезләнеш торышыннан хәрәкәтен
башлый гына әле. Җиденче шарчыкның хәрәкәте беренчесеннән 1/2
тирбәнешкә (рәс. 68, в), унынчысының 3/4 тирбәнешкә (рәс. 68, г)
соңга кала. Унөченче шарчык беренчедән бер тулы тирбәнешкә со¬
ңара (рәс. 68, д), ягъни аның белән бер үк фазаларда була. Бу ике
шарчыкның хәрәкәтләре нәкъ бертөрле (рәс. 68, е).
112
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
0
ΩΩΩΩΩΩΓ⅛ΩΩ∣^fF>∣TnT)∣T^∣T⅝∣T<iT⅞T
Рәс. 68
Бер ук фазаларда тирбәнүче һәм бер-берсенә иц якын нокта¬
лар арасындагы ераклык дулкын озынлыгы дип атала.
Дулкын озынлыгы грек хәрефе λ («лямбда») белән билгеләнә.
Беренче һәм унөченче шарчыклар (рәс. 68, е), икенче һәм ундүртен¬
че, өченче һәм унбишенче шарчыклар һ.б. арасы, ягъни бер үк фа¬
заларда тирбәнүче, бер-беренә иң якын урнашкан шарчыклар ара¬
лары дулкын озынлыгына (λ) тигез була.
68 нче рәсемнән күренгәнчә, тирбәнү процессының беренче шар¬
чыктан унөченчесенә, ягъни дулкын озынлыгы кадәр арага таралу
вакыты беренче шарчыкның тулы бер тирбәнеш ясау вакытына, ягъ¬
ни тирбәнү периоды Т га тигез була.
Димәк,
λ = υT,
биредә υ — дулкын тизлеге.
Тирбәнешләр периоды ешлык белән Т = бәйлелегендә (§ 26) бул¬
ганлыктан, дулкын озынлыгын тизлек һәм ешлык аша күрсәтеп була:
113
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
Шулай итеп, дулкын озынлыгы бу дулкыннарны тудыручы тир¬
бәнешләр чыганагының ешлыгына (яки периодына) һәм дулкын¬
ның таралу тизлегенә бәйле.
Дулкын озынлыгы формулаларыннан дулкынның тизлеген та¬
бып була: χ
V = — яки υ = λv.
т
Дулкын тизлеген табу формулалары аркылы дулкыннар өчен
дә, буй дулкыннар өчен дә дөрес. Буй дулкыннар таралганда, дул¬
кынның озынлыгын 69 нчы рәсем буенча күз алдына китереп була.
Анда пешкәкле торбаның кисеме сурәтләнгән. Пешкәк зур булма¬
ган амплитуда белән торба буйлап тирбәнә. Аның хәрәкәте торбаны
тутырган һава катламнарына күчә. Тирбәнү процессы, акрынлап,
һавада сирәгәюләр һәм тыгызланулар ясап, уңга күчә.
Рәсемдә дулкын озынлыгы λ га тәңгәл килүче ике кисемтә үрнәге
бирелгән. Анда 1 һәм 2 нокталарының бер үк фазаларда тирбәнүче
иң якын нокталар булуы ачык күренә. Шуны ук 3 һәм 4 ноктала¬
ры турында да әйтергә мөмкин.
Торбада пешкәкнең
һәм һава кисәкчекләре
хәрәкәтенең юнәлеше
Буй дулкыннарның
таралу юнәлеше
Рәс. 69
Сораулар
1. Дулкын озынлыгы дип нәрсә атала?
2. Дулкын озынлыгы нинди хәреф белән билгеләнә?
3. ДСүпме вакыт эчендә тирбәнү процессы дулкын озынлыгына
тигез булган юл уза?
114
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
4. Аркылы һәм буй дулкыннарның таралу тизлеген һәм дулкын
озынлыгын нинди формулалар буенча исәпләргә мөмкин? ).'
5. 69 нчы рәсемдә кайсы нокталар арасы буй дулкынның озын¬
лыгына тигез була?
$ 28 нче күнегү
1. Океанда дулкынның озынлыгы 270 м, ә аның тирбәнешләр
периоды 13,5 с булса, ул нинди тизлек белән тарала?
2. Дулкынның таралу тизлеге 340 м/с, ешлыгы 200 Гц булган¬
да, аның озынлыгын табыгыз.
3. Көймә 1,5 м/с тизлек белән таралучы дулкыннар өстендә чай¬
кала. Ике янәшә сырт арасы 6 м. Көймәнең тирбәнешләр периодын
табыгыз.
§ 34. Тавыш чыганаклары.
Тавыш тирбәнешләре
Рәс. 70
Тирбәнешләр һәм дулкыннар турында алган белемнәребез та¬
выш тирбәнешләрен өйрәнергә мөмкинлек бирә.
Безне чолгап алган тавышлар дөньясы искиткеч күптөрле — кеше
һәм музыка тавышы, кошлар сайравы һәм умарта кортлары безел¬
дәве, күк күкрәү һәм урманның җилдә шаулавы, машина, самолет
һ.б. тавышы.
Бу тавышларның барысы өчен дә уртаклык булып, аларны ту¬
дыручы җисемнәрнең, ягъни тавыш чыганакларының тирбәнүе тора.
Моңа гади тәҗрибәләрдә ышанырга мөмкин.
70 нче рәсемдә тискига беркетелгән
сыгылмалы металл линейка сурәтләнгән.
Әгәр линейканың билгеле бер озынлыкта
калдырылган өске рлешенә тирбәнү хәрә¬
кәте бирелсә, ул тавыш чыгара башлаячак
(тирбәнүче линейканың чик торышлары
пунктир белән күрсәтелгән). Бу очракта
тавыш чыганагының тирбәнүе ачык
күренә.
Хәзер 71 нче рәсемне карыйк. Очлары
беркетелгән нәзек кыл тавыш чыгара.
Кылның тигезсез сызыклары һәм уртада
115
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
калынайган кебек тоелуы аның тирбәнүен күрсәтә. Аның урта өле¬
шенә (биредә тирбәнүләр амплитудасы иң зур) кәгазь тасманың бер
очын тидергәндә, кылның периодик этәрүләреннән бу тасма си-
кергәләп торыр. Кыл тынып калгач, тасма да тирбәнүдән туктар.
72 нче рәсемдәге прибор камертон дип атала. Ул — урталай
бөгелгән металлдан гыйбарәт. Бу очракта камертон резонаторлы
тартмага беркетелгән (§ 40 та тулырак өйрәнелер).
Камертонга бәләкәй чүкеч белән сукканда, ул тавыш чыгара.
Камертон тармакларының тирбәнүе сизелми. Әмма камертонга җепкә
эленгән нәни шарчыкны (мәсәлән, төймә яки мәрҗән) якын ките¬
реп, тирбәнешләрне сизәргә мөмкин. Шарчык периодик рәвештә сел¬
кенеп торыр — бу камертон тармакларының тирбәнүе турында сөйли.
Рәс. 71
Тавыш чыгарып торган камертонның тирбәнүен башкача да
күзәтергә була. Моның өчен камертонның бер тармагына энә бер¬
кетеп, аның очын корымлы пыяла буйлап йөртәбез. Камертонда
тавыш юк икән — пыялада туры сызык эзе кала (рәс. 73, а). Тавыш
чыгаручы камертон исә пыялада дулкынсыман сызык ясый (рәс.
73, б). Бер тулы тирбәнешкә бу сызыкта бер чыгынты белән бер
батынкы тиңдәш була.
73 нче б рәсемдә сурәтләнгән сызык синусоидага бик якын.
Шулай итеп, тавыш чыгаручы камертонның һәр тармагы гармоник
тирбәнешләр ясый.
Төрле тәҗрибәләрдән күренгәнчә, теләсә кайсы тавыш чыганагы
һичшиксез тирбәнә (күп очракта тирбәнешләрне гади күз белән күреп
116
II бу лек. Механик тирбәнешләр һәм дулкыннар. Тавыш
булмаса да). Мәсәлән, кешеләр һәм күпчелек хайваннарның тавыш¬
лары аларның тавыш җепселләре тирбәнеше нәтиҗәсендә, ә тынлы
музыка кораллары, сирена тавышы, җил сызгыруы, күк күкрәү исә
һава массаларының тирбәнеше аркасында килеп чыга.
Ләкин тирбәнүче һәрбер җисем дә тавыш чыганагы була ал¬
мый. Мәсәлән, җепкә яки пружинага эленгән йөкнең тирбәнеше
тавыш чыгармый. 70 нче рәсемдәге металл линейканы тискида
өскәрәк күтәртеп, өстәге ягын озынайтканда, ягъни тирбәнешләр
ешлыгын 20 Гц тан кимрәк булырлык итеп калдырганда, ул та¬
выш чыгарудан туктый.
Тикшеренүләр күрсәткәнчә, кешенең колагы 20 Гц тан алып
20 000 Гц ка кадәр ешлыктагы механик тирбәнешләрне тавыш
итеп кабул итә. Шунлыктан ешлыклары шушы диапазонда бул¬
ган тирбәнешләр тавыш тирбәнешләре дип атала.
Ешлыклары 20 000 Гц тан артып киткән механик тирбә¬
нешләр — ультратавыш, 20 Гц тан кимрәк булганнары инфра¬
тавыш тирбәнешләре дип атала.
Шунысын билгеләп үтәргә кирәк тавыш диапазонының әлеге
чикләре — шартлы чикләр, чөнки алар кешеләрнең яшенә һәм
аларның тавыш аппаратларының шәхси үзенчәлекләренә бәйле.
Гадәттә, олыгая барган саен, кабул ителә торган тавышларның
югарыгы чиге шактый түбәнәя, кайбер картрак кешеләр ешлыгы
6000 Гц тан түбән булган тавышларны гына ишетә. Балалар исә,
киресенчә, 20 000 Гц тан да югарырак ешлыклы тавышларны
ишетергә сәләтле.
Ешлыгы 20 000 Гц тан югары һәм 20 Гц тан түбән тавыш¬
ларны кайбер хайваннар ишетә.
? Сораулар
1. 70— 72 нче рәсемнәрдәге тәҗрибәләр турында сөйләгез. Алар-
дан нинди нәтиҗә чыга?
2. Барлык тавыш чыганакларының да нинди уртак үзлеге бар?
3. Нинди ешлыктагы механик тирбәнешләр тавыш тирбәнеш¬
ләре була һәм ни өчен?
4. Нинди тирбәнешләр ультратавыш тирбәнешләре дип ата¬
ла? инфратавыш тирбәнешләре дип?
117
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
£ 29 нчы күнегү
Ни өчен без очып йөрүче черки тавышын ишетәбез, ә кошның
очуын ишетмибез?
§ 35. Тавышның югарылыгы һәм тембры
Гитарада яки балалайкада төрле ике кылның тавышын чыгарыйк.
Без төрле тавышлар ишетербез: берсе — түбәнрәк, икенчесе — югары¬
рак. Ир-атлар тавышы хатын-кызныкына караганда түбәнрәк, бас та¬
вышы тенордан түбәнрәк, сопрано альттан югарырак була.
Тавыш югарылыгы нәрсәгә бәйле? Моңа җавап бирү өчен
тәҗрибәләр ясыйбыз.
74 нче рәсемдә уртак күчәргә утыртылган тешле металл диск¬
лардан торучы прибор сурәтләнгән. Дисклардагы тешләр саны
төрлечә. Приборны әйләндерә башлыйлар һәм, дискларның берсенә
Рәс. 74
юка катыргы пластинка белән
орынгач, тавыш ишетелә. Бу та¬
вышның чыганагы булып тирбән¬
үче пластинка тора. Диск әйлән¬
гәндә, аның һәр теше пластинка¬
ны этеп җибәрә, чираттагы батын¬
кы урынны узганда, пластинка
турая. Нәтиҗәдә тирбәнү хәрәкәте
ясала.
Диск тизрәк әйләнгән саен,
пластинканың тирбәнешләр еш¬
лыгы зуррак һәм ул чыгарган та¬
выш та югарырак була.
Әгәр приборны даими тизлек белән әйләндереп, пластинканы
төрле дискларга орындырып карасак, төрле югарылыктагы тавыш¬
лар ишетелер, дискта тешләр саны никадәр күп, ягъни пластинка¬
ның тирбәнешләр ешлыгы никадәр зур булса, тавыш шулкадәр югары
булыр.
75 нче рәсемдә төрле югарылыктагы тавышлар чыгаручы ике
камертонның энә эзләре күрсәтелгән. Ике камертонны да, корым¬
ланган пыяла пластиналар буйлап (энә очы белән орынып), бер үк
тизлек белән йөртә. Өскесе — югарырак тавышлы камертонның эзе.
118
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
Бу эзләрне чагыштырып, югары тавышлы камертонның тирбәнешләр
ешлыгы зуррак икәнен күтәбез.
Тикшерелгән тәҗрибәләр нигезендә әйтергә була: тавышның
югарылыгы тирбәнүләр ешлыгына бәйле, тавыш чыганагының
тирбәнешләр ешлыгы зуррак булган саен, ул чыгарган тавыш
югарырак була бара.
Без камертонның гармоник (синусоидаль) тирбәнешләр ясавын
беләбез. Бу тирбәнешләргә билгеле бер аныкланган ешлык кына хас.
Гармоник тирбәнешләр тирбәнешләрнең иң гади төре санала. Ка¬
мертон тавышы — чиста тон ул.
Бер генә ешлыктагы гармоник тирбәнешләр ясаучы тавыш
чыганагы чиста тон дип атала.
Башка чыганакларның тавышлары (мәсәлән, төрле музыкаль ко¬
раллар, кешеләр, сирена тавышы һ.б.) — төрле ешлыктагы гармоник
тирбәнешләр җыелмасы, ягъни чиста тоннар җыелмасы булып тора.
Мондый катлаулы тавышның иң түбән (ягъни иң кечкенә) еш¬
лыгы — төп ешлык дип, ә аңа тиңдәшле билгеле бер югарылыкта¬
гы тавыш төп тон дип атала (кайвакыт тон гына диләр). Катлау¬
лы тавышның югарылыгы аның төп тонының югарылыгы белән
билгеләнә.
Катлаулы тавышның калган барлык тоннары обертоннар дип
атала. Бу тавышның барлык обертоннары ешлыгы аның төп тоны
ешлыгыннан бөтен сан тапкыр зуррак (шунлыктан аларны югары
гармоник тоннар дип тә атыйлар).
Обертоннар тавышның тембрын, ягъни бер чыганакның тавыш¬
ларын икенчесенекеннән аерырга мөмкинлек бирүче сыйфатын бил-
119
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
гели. Мәсәлән, рояль белән скрипканың тавышларын, хәтта төп тон¬
нарының ешлыгы бер үк булган очракта да бутамыйбыз. Бу тавыш¬
ларның аермасын обертоннарның төрле җыелмалары билгели (төрле
чыганакларның обертоннар җыелмасы обертоннар саны, аларның
амплитудасы, алар арасындагы фазалар күчеше, ешлыклар спектры
белән аерылырга мөмкин).
Шулай итеп, тавышның югарылыгы аның төп тонының
ешлыгы белән билгеләнә, төп тонның ешлыгы никадәр зур бул¬
са, тавыш шулкадәр югарырак була.
■ Тавышның тембры аның обертоннар җыелмасы белән билгеләнә.
Ф Сораулар
1. 74 нче рәсемдәге тәҗрибә нинди максат белән куела? Тәҗри¬
бәнең ничек үтүе һәм нинди нәтиҗә алынуы турында сөйләгез.
2. Камертонның тирбәнүче тармакларының эзләрен алу тәҗри¬
бәсе ничек үткәрелгән (рәс. 75)? Бу тәҗрибә нәрсәне раслый?
3. Тавыш югарылыгы нәрсәгә бәйле?
. 4. Чиста тон дип нәрсәне атыйлар?
5. Төп тон һәм обертон дип нәрсәгә әйтәләр?
6. Тавышның тембры дип нәрсә атала?
7. Тавыш югарылыгы нәрсә белән билгеләнә?
и 8. Тавыш тембры нәрсә белән билгеләнә?
£ 30 нчы күнегү
1. Кайсы бөҗәк: төклетура, черки һәм чебен, очканда, канатла¬
рын ешрак җилпи? Ни өчен шулай уйлыйсыз?
2. Циркуляр пычкы әйләнгәндә, аның тешләре һавада тавыш
дулкыннарын тудыра. Аның белән тыгыз калын такта кисә башла¬
салар, пычкының буш йөрештәге тавышы ничек үзгәрер? Ни өчен?
3. Гитараның кылы, ныграк тартылган саен, югарырак тавыш
чыгара. Нава температурасын шактый арттырганда, гитара кылла¬
ры тавышының югарылыгы ничек үзгәрә? Җавапны аңлатыгыз.
§ 36. Тавышның катылыгы
Тавышның катылыгы нәрсәләргә бәйле икәнен ачыклау өчен
72 нче рәсемгә кире кайтыйк. Камертонның бер тармагына җепкә
эленгән кечкенә шарчыкны терәп диярлек якынайталар, икенчесенә
120
// булек. Механик тирбәнешләр һәм дулкыннар. Тавыш
чүкеч белән җиңелчә генә сугалар. Ике тармак та тирбәнә башлый.
Акрын гына тавыш ишетелә. Шарчык тирбәнүче тармактан бераз
читкә этәрелә. Аннан соң камертонның тавышын сүндерәләр һәм
катырак итеп тагын сугалар. Бу юлы камертон көчлерәк яңгырый
һәм шарчык та күбрәккә этәрелә — димәк, тармакның тирбәнешләр
амплитудасы зуррак дигән сүз.
Әлеге һәм башка тәҗрибәләр түбәндәге нәтиҗәне ясарга мөмкин¬
лек бирә:
тавышның катылыгы тирбәнешләр амплитудасына бәйле: тир¬
бәнеш амплитудасы зуррак булган саен, тавыш катырак була.
Тикшерелгән тәҗрибәдә ике тавышның да — акрынының да,
катысының да — ешлыгы бер төрле, чөнки аларның чыганагы —
бер үк камертон. Ә инде төрле ешлыктагы тавышларны чагыш¬
тырган булсак, тирбәнешләр амплитудасыннан тыш, катылыкка
йогынты ясый торган тагын бер факторны тикшерергә булыр иде.
Чөнки кеше колагы төрле ешлыктагы тавышларны төрлечә сизә.
Амплитудалары бер үк булганда, ешлыгы 1000 Гц тан 5000 Гц ка
кадәр булган тавышларны катырак итеп кабул итәбез. Шуңа күрә,
мәсәлән, амплитудалары бер үк булса да, 1000 Гц ешлыктагы ха¬
тын-кыз тавышы безнең колаклар өчен 200 Гц ешлыктагы ир кеше
тавышыннан катырак булып ишетелә.
Тавышның катылыгы аның дәвамлылыгына һәм тыңлаучының
шәхси үзенчәлекләренә дә бәйле.
Тавышның катылыгы — ишетү тойгысының барлык тавышлар¬
ны, бик зәгыйфьләреннән алып иң катысына кадәр, шкала буенча
урнаштырырга мөмкинлек бирүче субъектив сыйфаты ул.
Тавышның катылыгын үлчәү берәмлеге сон дип атала.
Практик мәсьәләләрдә тавышның катылыгын тавышның ка¬
тылык дәрәҗәсе белән сыйфатлыйлар, ул фоннарда, ә кайбер оч¬
ракларда белларда (яки белның унынчы өлешләре — децибеллар-
да) үлчәнә.
Газеталар актарганда 20 дБ тирәсе катылыктагы тавыш ише¬
телә; будильник сәгать кыңгыравының катылыгы — 80 дБ тирәсе,
реактив самолет моторының тавышы 130 дБ катылыкта була (мон¬
дый катылыктагы тавыш колакны авырттыра).
121
// бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
Каты тавышлар, бигрәк тә шау-шуның (тонның югарылыгы,
тембры катылыгы төрлечә булган тавышларның тәртипсез сумма¬
сы) системалы рәвештә тәэсир итеп торуы кеше сәламәтлегенә тискә¬
ре йогынты ясый.
Шау-шулы районнарда бик күп кешеләрдә тавыштан авыру бил¬
геләре күренә: югары нерв ярсынуы, тиз аручанлык, югары артери¬
аль басым. Шуңа күрә зур шәһәрләрдә тавышны киметү өчен махсус
чаралар күрергә, мәсәлән, автомобильләрнең тавыш сигналларын
тыярга туры килә.
? Сораулар
1. 72 нче рәсемдә сурәтләнгән тәҗрибә нинди максат белән
куела һәм ничек -үткәрелә?
2. Тавыш чыганагындагы тирбәнешләр амплитудасын ки¬
меткәндә, тавышның катылыгы ничек үзгәрә?
3. Әгәр тавыш чыганакларының тирбәнү амплитудалары бер
төрле булса, кеше колагы 500 Гц һәм 3000 Гц ешлыктагы тавыш¬
ларның кайсысын катырак итеп сизәр?
4. Тавышның катылыгы нәрсәгә бәйле?
5. Тавышның катылык берәмлекләрен һәм катылык дәрәҗәләрен
атап күрсәтегез.
6. Каты тавышларның системалы тәэсир итүе кешенең сәла¬
мәтлегенә нинди йогынты ясый?
§ 37. Тавышның таралуы
Рәс. 76
Тавышны безнең колакларыбыз кабул
итә. Тавыш чыгаручы җисем (чыганак) һәм
колак (тавышны кабул итүче) арасында та¬
выш тирбәнешләрен чыганактан кабул итү¬
чегә тапшыра торган матдә була. Күбесенчә,
мондый матдә ролен һава үти. Һавасыз про-
странствода тавыш тарала алмый. Һәм тәҗ¬
рибәләр бу сүзне раслый да. Аларның бер¬
сен карап үтик (рәс. 76). Һава насосының
калпагы астына кыңгырау урнаштыралар
һәм челтәргә ялгыйлар. Аннан соң насос
белән һаваны суырта башлыйлар. Һава
122
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
сирәкләнгән саен, тавыш әкренәя бара һәм, ниһаять, бөтенләй тына.
Ә инде яңадан һава тутыра башлагач, кыңгырау тавышы да ишетелә
башлый.
Шулай итеп, сирәклэндерелгэн һавада тавыш начар тарала һәм
һавасыз пространствода бөтенләй таралмый.
Тавыш һавада гына түгел, башка җисемнәрдә дә тарала. Моны
да тәҗрибәдә күрергә була. Өстәлнең бер башында ятучы кесә сәга¬
тенең бик әкрен текелдәвен, колакны өстәлнең икенче башына куеп,
ачык итеп ишетергә мөмкин.
Җир яки тимер юл рельслары буйлап тавышның ерак-ераклар-
га таралуы яхшы билгеле. Колакны җиргә яки рельсларга куеп,
еракта баручы поезд тавышын яки атлар чабуын ишетергә мөмкин.
Әгәр без су астында ташны ташка бәрәбез икән, бу тавышны
яхшы ишетәбез. Димәк, тавыш суда да тарала. Судагы балык яр
буендагы кешеләрнең сөйләшү һәм аяк тавышын ишетә — бу ба¬
лыкчыга яхшы билгеле.
Тәҗрибәләр күрсәткәнчә, каты җисемнәр тавышны төрлечә
үткәрә. Эластик җисемнәр — яхшы үткәрүчеләр. Күпчелек метал¬
лар, агач, газлар, шулай ук сыеклыклар эластик җисемнәргә керә
һәм шунлыктан тавышны әйбәт үткәрәләр.
Йомшак һәм күзәнәкле җисемнәр — тавышны начар үткә¬
рүчеләр. Мәсәлән, кесәдә яткан сәгатьнең йомшак тукыма эчендә
булганлыктан, тавышы ишетелми дә.
Нинди дә булса бинаны чит тавышлардан саклау өчен, стеналар¬
ны, идән һәм түшәмнәрне тавышны начар үткәрә торган материал¬
лар (киез, паласлар, прессланган бөке, пычкы чүбе, күзәнәкле таш¬
лар) белән каплыйлар. Тавыш дулкыннары, ал арга килеп кергәч
сүнәләр. Мондый җисемнәрдә тирбәнү хәрәкәте энергиясе эчке энер¬
гиягә әверелә — җисемнәр җылыналар.
Шулай итеп, тавыш барлык эластик — каты, сыек һәм газсы-
ман җисемнәрдә тарала, әмма һавасыз пространствода тарала
алмый.
Ф Сораулар
1. 76 нчы рәсемдә сурәтләнгән тәҗрибә нинди максат белән
эшләнә? Тәҗрибәнең ничек үткәрелүе һәм нинди нәтиҗә ясалуы
турында аңлатыгыз.
123
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
2. Тавыш газларда, сыеклык һәм каты җисемнәрдә тарала ала¬
мы? Җавапны мисаллар белән раслагыз.
3. Нинди җисемнәр тавышны яхшырак үткәрә: эластигымы,
әллә күзәнәклесеме? Мисаллар китерегез.
4. Биналарга ничек итеп тавыш изоляциясе ясыйлар, ягъни алар-
ны чит тавышлардан саклыйлар?
$ 31 нче күнегү
1. Айдагы көчле шартлау тавышы Җирдә ишетелергә мөмкин-
ме? Җавапны нигезләгез.
2. Ике очына сабын савытлары бәйләп куелган җеп — «теле¬
фон» ярдәмендә, хәтта пышылдап та, төрле бүлмәләрдән торып
сөйләшергә мөмкин. Бу күренешне аңлатыгыз.
§ 38. Тавыш дулкыннары. Тавышның тизлеге
Билгеле булганча, тавыш пространствода ниндидер эластик тирә¬
лек булганда гына тарала. Тирәлек тавыш чыганагының тирбәнеш¬
ләрен кабул итүчегә, мәсәлән, кешенең колагына тапшыра. Икенче
төрле әйтсәк, чыганакның тирбәнешләре үзен әйләндереп алган ти¬
рәлектә тавыш ешлыгындагы эластик дулкыннар тудыра. Колакка
килеп кергәч дулкын, барабан пәрдәсенә тәэсир итеп, аны тавыш
чыганагы ешлыгына туры килгән ешлыкта тирбәндерә. Барабан
пәрдәсенең тирбәнүе сөякләр системасы аша ишетү нервлары очла¬
рына бирелә, аларны ярсытып, тавыш ишетү тойгысын уята.
32 нче параграфта дә газларда һәм сыеклыкларда бары тик буй
дулкыннар булдырырга гына мөмкин диелгән иде. Һавада тавыш,
мәсәлән, буй дулкыннар белән, ягъни чыганактан башланган һава
тыгызланулары һәм сирәкләнүләре белән тапшырыла.
Башка барлык механик дулкыннар кебек, тавыш дулкыны да
пространствода мизгел эчендә түгел, ә билгеле бер тизлек белән та¬
рала. Иң гади күзәтүләр моңы раслый. Мәсәлән, без тавыш буларак
кабул иткән һава тирбәнешләре яшен яктыртуы белән бергә туса да,
без башта яшенне күрәбез һәм күпмедер вакыттан соң гына күк
күкрәгәнен ишетәбез. Эш шунда ки, яктылык тизлеге искиткеч зур
(300 000 км/с), шунлыктан аның яктыртуын без шул ук мизгелдә
күрәбез. Ә яшен белән бергә барлыкка килгән күк күкрәү тавышы¬
124
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
на, шул урыннан күзәтүчегә кадәр араны узу өчен, сизелерлек t ва¬
кыты кирәк була.
Тавыш барлыкка килгән вакыттан алып (яшенне күргән вакыт),
күзәтүчегә ишетелгән вакыт арасы t ны һәм тавыш чыганагы белән
күзәтүче арасы s ны үлчәп, тавыш тизлеге υ ны табарга мөмкин:
s
v = -.
t
Тавыш тизлеген төгәл итеп диярлек беренче тапкыр 1822 елда
француз галимнәре билгели. Ара ераклыгы билгеле булган ике пункт¬
та туплардан аталар. Ике пунктта да атканда ут күренү вакыты
белән ату тавышы ишетелгән вакытны үлчиләр. Һавада 20 °C темпе¬
ратурада тавыш тизлеге 340 м/с.
Тавыш тизлеге тавыш тарала торган тирәлекнең үзлекләренә
бәйле. Галимнәр тарафыннан тавыш тизлеген төрле тирәлекләрдә
билгеләү юллары эшләнгән. Кайбер тирәлекләрдәге тавыш тизлеге
2 нче таблицада бирелә.
2 нче таблица
Төрле тирәлекләрдә тавышның тизлеге, м/с (t = 20 °C)
Су
1483
Агач (чыршы)
5000
Кургаш
2160
Корыч
5000—6100
Бакыр
4700
Пыяла
5500
Тавыш — дулкын булганлыктан, тавыш тизлеген билгеләү өчен
s
V = Т
формуласыннан тыш, сезгә билгеле булган и = — һәм v = vλ
(§ 33) формулаларын да кулланырга мөмкин.
Сораулар
1. Кеше колагындагы барабан пәрдәсе, тавыш килеп кергәч, нин¬
ди ешлыкта тирбәлә?
2. һавада; суда таралучы тавыш нинди дулкын була: буй дул¬
кынмы, әллә аркылымы?
3. Тавыш дулкынының мизгел эчендә түгел, ә күпмедер тизлек
белән таралуына мисал китерегез.
125
// бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
4. Тавышның һавадагы тизлеге кайсы гасырда һәм ничек үлчәнә?
5. Һава температурасы 20 °C булганда, андагы тавыш нинди
тизлек белән тарала?
6. Тавышның тизлеге аның нинди тирәлектә таралуына бәйлеме?
g 32 нче күнегү
1. Тавыш чыганагы 0,002 с периоды белән суда 2,9 м озынлыгын¬
дагы дулкыннар тарата. Тавышның суда таралу тизлеген табыгыз.
2. Ешлыгы 725 Гц булган тавыш дулкынының һавада, суда һәм
пыяладагы озынлыгын табыгыз.
3. Озын металл торбаның бер башына чүкеч белән бер тапкыр
сугалар. Сугу тавышы торбаның икенче башына металл буенча; торба
эчендәге һава буенча таралырмы? Икенче башта торучы кеше сугу
тавышын ничә тапкыр ишетер?
4. Тимер юлның туры сызыклы бүлемтеге янындагы кеше ерак¬
тан килүче паровоз сыбызгысы чыгарган парны күреп ала. Пар күре¬
неп 2 с узгач, ул сыбызгы тавышын ишетә, ә 34 с узгач, паровоз үзе
килеп җитә. Паровозның тизлеген табыгыз.
5*. Күзәтүче секунд саен сугып тора торган кыңгыраудан ерак¬
лаша. Баштарак сугу белән чыңлау туры килеп бара. Аннан туры
килми башлый. Соңыннан, кыңгыраудан ниндидер ераклыкта, сугу
белән чыңлау тагын туры килә. Бу күренешне аңлатыгыз.
§ 39. Тавыш кайтарылу. Кайтаваз
Сезнең һәрберегез кайтаваз дигән та¬
выш күренеше белән таныш инде. Кай¬
таваз тавышның төрле киртәләрдән — зур
биналарның стеналарыннан, урманнан,
биек аркаларның эчке стеналарыннан
(рәс. 77) кайтарылуы нәтиҗәсендә бар¬
лыкка килә.
Ни өчен без кайтавазны кечкенә фа¬
тирларыбызда ишетмибез? Анда да бит
тавыш стена, түшәм, идәннәрдән кайта¬
рылырга тиеш.
Чынлыкта без, кайтарылган тавыш
әйтелгәненнән аерым ишетелсә генә, кай¬
126
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
тавазны ишетәбез икән. Моның өчен бу ике тавышның колактагы
барабан пәрдәсенә тәэсир итү вакытлары арасындагы аерма 1/15 с
тан ким булмаска тиеш.
Хәзер исәпләп карыйк: әгәр сез стенадан 3 м ераклыкта тора¬
сыз икән, сезнең кискен әйтелгән кыска тавышыгызның күпме ва¬
кыттан соң кире стенадан кайтарылуы ишетелер икән?
Тавыш 340 м/с тизлек белән стенага һәм кирегә таба 6 м ара
үтәргә тиеш. Моңа t = s/v вакыты кирәк:
t = бм/340 м/с ≈ 1/50 с.
Бу очракта колак кабул итә торган — әйтелгән һәм кайтарылган
тавышлар арасы кайтавазны ишетү өчен кирәкле булган вакыттан күпкә
ким. Моннан тыш, кайтаваз барлыкка
килүгә бүлмәдәге мебель, пәрдәләр һәм z'' ∙⅛∣ ∕ s'"
кайтарылучы тавышны өлешчә йота тор- I Sj⅞∖∕
ган башка әйберләр дә комачаулый. Шуңа 3
күрә мондый биналарда кешеләр сөй- 4 v Г
ләшүен һәм башка тавышларны кайтаваз
бозмый, алар аермачык ишетелә. Рәс. 78
Әмма зур залларда сөйләүченең тыңлаучыга турыдан-туры һәм
стеналар, түшәмнәр, башка предметлардан кайтарылып килеп җиткән
тавышлары аерым ишетелә, чөнки еш кына алар арасындагы вакыт
1/15 с тан зур була. Нәтиҗәдә һәрбер иҗек сузыла, икенчесенә кушы¬
ла һәм сөйләм аңлаешсызга әйләнә. Тыңлаучылар аз булган залда
кайтаваз бигрәк тә нык күзәтелә, чөнки ул бөтенләй диярлек йотыл¬
мый. Зур заллар һәм аудиторияләрнең ишетелү үзлекләрен яхшырту
өчен, стеналарны тавышны йотучы материаллар белән каплыйлар.
Тавышның шома өслекләрдән кайтарылу үзлегенә нигезләнеп
рупорлар — түгәрәк яки турыпочмаклы кисемле киңәеп киткән тор¬
балар эшләнгән (рәс. 78). Рупор кулланганда, тавыш дулкыннары
бөтен якларга да чәчелми, тар бәйләм хасил итә һәм шуның арка¬
сында тавышның егәрлеге үсә һәм ул ерак араларга тарала.
Ультратавыш кайтарылу күренешенең техникада һәм терек та¬
бигатьтә кулланылышы турында 41 нче параграфта сөйләнер.
J> Сораулар
1. Кайтаваз нәрсә нәтиҗәсендә барлыкка килә?
2. Ни өчен кайтаваз мебель белән тулган кечкенә бүлмәдә түгел,
ә зур, яртылаш буш залда күзәтелә?
127
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
3. Зур залның тавыш ишетелү үзлекләрен ничек яхшыртып була?
4. Рупор кулланганда, ни өчен тавыш ераккарак тарала?
§ 40. Тавыш резонансы
I Белгәнебезчә, мәҗбүр итүче көчнең ешлыгы белән тирбәнү сис¬
темасының үз ешлыгы тәңгәл килсә, урнашкан мәҗбүри механик
тирбәнешләр амплитудасы иң зур кыйммәтенә ирешә. Бу күренеш
резонанс дип атала (§ 30.)
Мәсәлән, шактый авыр җепле маятникны да, (рәс. 79) аңа бик
зәгыйфь һава агымы белән периодик рәвештә аның үз ешлыгы белән
тәэсир итеп торып, көчле чайкалдырырга
мөмкин. Нава агымы юнәлеше һәрвакыт
маятник хәрәкәте юнәлешендә булырга
тиеш.
Тавыш дулкыннары да резонанс ките¬
реп чыгарырга сәләтле. Моны 80 нче
рәсемдәге тәҗрибәдә күзәтергә мөмкин.
Анда үз ешлыклары бер үк булган ике
камертон сурәтләнгән, алар резонатор тар¬
тмаларына беркетелгән һәм бер-берсеннән
берникадәр ераклыкта урнаштырылган.
Бер камертонны тирбәндереп җибәрәләр. Бераздан соң кул белән
тотып сүндерәләр. Әмма тавыш һаман ишетелеп тора. Монысын инде
икенче камертон чыгара. Аңа да кул белән орынсак, тавыш бөтенләй
сүнә. Икенче камертонны беркем дә ярсытмады, шуңа күрә ул бе¬
ренче камертоннан күчкән һава тирбәнешләре (тавыш дулкыннары)
белән ярсытылган дигән нәтиҗә ясыйбыз.
Әгәр балавыз кисәкчеге беркетеп, икенче камертонның ешлы¬
гын үзгәртсәк, ул беренче камертон тирбәнешләренә җавап бирмәс,
ягъни без аның тавышын ишетмәбез.
Әгәр рояль капкачын ачып, педальгә баскан килеш ниндидер
югарылыкта каты итеп дәшсәк, рояль шул ук югарылыктагы та¬
выш белән җавап бирер. Рояльнең барлык кыллары арасыннан,
әйтелгән тавыш югарылыгына көйләнгән бердәнбер кыл яңгырар.
Бу күренеш тавыш резонансы дип атала.
Тавышка кушылучы (резонанслана торган) җисем резонатор дип
атала. Тавыш чыгарырга сәләтле һәрбер җисем резонатор була ала.
128
// бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
Камертонны тирбәндерәләр икән, димәк, эш эшләнә, ягъни ка¬
мертонга берникадәр энергия запасы бирелә.
һавада тавыш тирбәнешләрен ярсытып, камертон энергия са¬
рыф итә. Вакыт узу белән, тавыш чыгаручы камертонның энергия
запасы азая, тавышның катылыгы да кими.
Тавышны көчәйтү өчен камертоннарны еш кына билгеле бер
үлчәмдәге резонатор тартмаларына урнаштыралар (рәс. 80). Ка¬
мертон тавыш чыгарганда, тартмадагы һава баганасы да тирбәнә
башлый. Бу багана камертон тирбә- Jill _
нешләре белән резонанста тирбәнә. I |
Мондый тартмасы (резонаторы) бул- I I
ган камертонның тавышы көчлерәк, \/
әмма озак дәвам итми (энергия сак- \
лану законы нигезендә). l"—*⅛-''—
Музыка коралларында резона-
тор ролен корпусларының бер өле-
ше уйный. Мәсәлән, гитара, скрип- Рәс. 80
ка һәм башка кыллы инструментларда резонатор ролен декалар үти.
Резонаторлар инструмент чыгарган тавышны көчәйтәләр һәм
аңа үзенчәлекле төсмер — тембр да бирәләр, шуның аркасында бер
инструментны икенчесеннән аерып була. Тавышның тембры резо¬
наторның формасы белән үлчәмнәренә генә түгел, аның нинди агач¬
тан эшләнүенә дә, хәтта нинди лак белән каплануына да бәйле. Тембр
кылның нинди материалдан эшләнүе, шома яки үрелгән булуы белән
дә билгеләнә.
Кеше һәм күпчелек хайваннарның тавыш чыганагы булып, үзен¬
чәлекле кыллар — тавыш җепселләре тора. Үпкәдән килә торган
һава агымы тәэсирендә тавыш җепселләре тирбәнә һәм бик акрын
тавыш чыгара. Бу тавыш табигый резонаторлар — бугаз һәм авыз
куышлыгы аша үтеп көчәя һәм һәр кешенең тавышына хас булган
теге яки бу тембр рәвешен ала. Тавыш тембры буенча, күрмичә дә,
үзебез белгән кешеләрне таныйбыз.
Сораулар
1. Тавыш резонансы күренешенә мисаллар китерегез.
2. Ни өчен камертоннарны резонатор тартмаларына урнаш¬
тыралар?
129
// бу лек. Механик тирбәнешләр һәм дулкыннар. Тавыш
3. Музыкаль инструментларда кулланыла торган резонатор¬
лар нинди роль уйный?
4. Кеше тавышының чыганагы булып нәрсә тора?
■ 5. Тавышның тембры нәрсәләргә бәйле?
§41. Ультратавыш һем инфратавыш
(өстәмә уку өчен)
Ешлыгы 20 000 Гц тан артык булган механик тирбәнешләр —
ультратавышлар, ә 20 Гц тан ким булганнары инфратавышлар
дип атала. Ультратавышларны һәм инфратавышларны кеше кола¬
гы кабул итә алмый, без ал арны ишетмибез.
Күп төрле ешлыклар өчен югары сизгерлектәге тавыш кабул
иткечләр уйлап табылгач, табигатьтә инфра- һәм ультратавышлар¬
ның ишетелә торган тавышлар кебек үк киң таралганлыгы билгеле
булды. Ал арны коры җирдә, һавада һәм судагы тереклек ияләре
нурландыра һәм кабул итә, үзара «сөйләшү» өчен файдаланыла икән.
Этләр, мәсәлән, 40 кГц ешлыктагы ультратавышларны кабул итә.
Моннан дрессировщиклар юста файдалана: этләргә кешеләр ишетми
торган командалар бирәләр.
Диңгезләргә куелган ультратавыш кабул иткечләр планктонның
«йөзмә утрауларын» табарга булыша. Бу планктонда ишкәгаяклы
нәни кыслачыклар, аякларын аякка ышкып, ультратавыш чыгара¬
лар икән.
Ультратавыштан ярканатлар да файдалана. Табигать фәне бел¬
гечләре аларның үтә начар күрүен белгәннәр — алар бөтенләй ди¬
ярлек сукыр. Бу хайваннар ничек итеп үз юлларындагы каршы¬
лыкларны белә һәм кап-караңгыда ауларга сәләтле соң? Сәбәп шун¬
да — ярканатлар ультратавыш дулкыннары чыгарырга һәм кабул
итәргә сәләтле икән. Ярканат чыгарган ультратавыш дулкыннары
төрле каршылыклардан һәм бөҗәкләрдән кайтарыла, һәм ул үзе үк
аларны кабул итә (ярканатларның колаклары бик зур). Кайтарыл¬
ган дулкынның кайдан килүенә карап, ярканат автомат рәвештә бу
каршылыкның юнәлешен билгеләп өлгерә. Бу аңа шундук ориент¬
лашырга һәм ауларга мөмкинлек бирә. Ультратавыштан дельфин¬
нар, тирән судагы балыклар һәм кайбер башка тереклек ияләре дә
шулай файдалана.
130
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
Югары ешлыктагы махсус нурландыргычлар ярдәмендә дә ульт¬
ратавыш дулкыннарын чыгарырга мөмкин. Ультратавышның тар
параллель бәйләме таралу барышында
бик аз киңәя. Шуңа күрә ультратавыш
дулкынын кирәкле юнәлештә нурлан¬
дырып була.
Ультратавышның юнәлешле тар
бәйләмнәре, мәсәлән, диңгез төбенең
тирәнлеген үлчәү өчен кулланыла
(рәс. 81). Моның өчен судно төбенә уль¬
тратавышны нурландыручы һәм кабул
итүче приборлар урнаштырыла. Нур-
ландыргыч диңгез төбе юнәлешендә
кыска (0,001 с дәвамында) сигналлар
җибәрә. Ә прибор һәр сигналның би¬
релү вакытын язып бара. Күпмедер ва¬
кыттан соң бу сигнал диңгез төбеннән
кайтарылып, кабул иткечкә әйләнеп
кайта. Сигналны кабул итү мизгеле шулай ук язып алына. Шулай
итеп, сигнал җибәрү мизгеленнән алып, аны кабул итү мизгеленә
кадәрге t вакыты эчендә сигнал, v тизлеге белән таралып, диңгез
төбе тирәнлегеннән ике тапкыр артык юл 2Һ үтә:
2h = υt.
Моннан диңгез төбенең тирәнлеген исәпләү кыен түгел:
Объектка кадәр ераклыкны исәпләүнең бу методы эхолокация
дип атала. Шунысын өстәргә кирәк: һавада ультратавыш локация-
сенең эффекты зур түгел, чөнки газларда бу ешлыктагы дулкыннар
бик тиз сүнә.
Ультратавыш коелма детальләрдәге төрле дефектларны — ярык¬
лар, һава куышлыклары һ.б. эзләп табу өчен дә кулланыла. Бу ме¬
тод ультратавыш дефектоскопиясе дип атала. Аның асылы
түбәндәгедән гыйбарәт: тикшерелә торган детальгә кыска ультрата¬
выш сигналлары җибәрелә. Алар, деталь эчендәге бериш булмаган
дефектлы урыннардан кайтарылып, кабул иткечкә керә. Дефект
131
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
булмаган урыннардан сигналлар деталь аша кайтарылусыз диярлек
узып чыга һәм кабул иткечкә кабат кайтмый.
Ультратавыш кайбер авыруларга диагноз кую һәм дәвалау өчен,
медицинада киң кулланыла. Диагноз кую өчен ультратавыш белән
тикшерүләр (УЗИ) органнарның һәм тукымаларның гадәттән тыш
(патологик) үзгәрешләрен хирург катнашыннан башка күреп алыр¬
га ярдәм итә. Бу тикшерүләр ешлыгы 0,5 тән 15 МГц ка кадәрле
ультратавыш дулкыннарының үзлегенә нигезләнгән: алар, составы
һәм тыгызлыгы төрле булган тукымаларның чикләреннән аз-азлап
кайтарылып, бу тукымалар аша үтеп чыгарга сәләтле.
Ультратавыш белән дәвалау исә, кайбер ешлыктагы бу дулкын¬
нарның тукымаларга механик, җылылык һәм физик-химик тәэсир
итә алуына нигезләнгән: шулар нәтиҗәсендә организмда матдә ал¬
машу процесслары һәм иммунитет реакцияләре активлаша.
Инфратавыш кайвакыт диңгездә килеп чыга, бу очракта аны
«диңгез тавышы» диләр. Гадәттә аны давыл вакытында суның пе¬
риодик рәвештә кысылуы һәм сирәгәюе китереп чыгара.
Инфратавыш дулкыны, без ишетә торган диапазондагы тавыш
кебек үк, суда һавадагыга караганда 5 тапкыр тизрәк тарала. Шун¬
лыктан «диңгез тавышын» ишетергә сәләтле диңгездәге тереклек
ияләре — медузалар, кысласыманнар, диңгез борчалары һ.б. — да¬
выл буласын бик күпкә алдан сизәләр.
Ишетелә торган тавыш белән чагыштырганда, инфратавыш һавада
да, суда да аз йотыла һәм шунлыктан бик ерак араларга тарала
(берничә йөз километрларга). Шуңа күрә аны файдалану мөмкин¬
лекләре зур. Мәсәлән, хәрби хезмәттә инфратавышны куллану уңай
нәтиҗәләр бирә. Аны махсус приборлар белән тотып, ерактан атучы
артиллериянең урынын төгәл билгеләргә мөмкин. Инфратавышны
балык тоту промыселенда да кулланалар. Балык тоту суднолары,
махсус кабул итү җайланмалары ярдәмендә, инфратавыш чыгаручы
яки аны кайтаручы балык көтүләрен тиз эзләп табалар.
§ 42. Тавыш интерференциясе
Ике чыганактан килүче тавыш дулкыннарын кушуны күрсәткән
тәҗрибәне карыйк (рәс. 82).
Тавыш чыганаклары булып, ТГ тавыш генераторына (звуковой
генератор — ЗГ) ялганган K1 һәм К2 көчәйткечләре (громкоговори-
132
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
Рәс. 82
тель) хезмәт итә. Тавыш көчәйткеч нурландырган тавыш, М микро¬
фонына эләгеп, электр тирбәнешләренә әверелә. Бу тирбәнешләрне
түбән ешлыклар көчәйткече ТЕК (УНЧ — усилитель низкой часто¬
ты) көчәйтә, ә гальванометр Г исәпкә ала.
Тавыш көчәйткечләрне микрофоннан 1—1,5 м ераклыкка ур¬
наштырабыз (82 нче рәсемдә бу ара сакланмаган). Көчәйткечләр белән
микрофон арасына демонстрацион метр куелган. Тавыш генерато¬
рына башта K1 көчәйткечен ялгыйбыз. Генераторны ялгап, аны
1000 Гц ешлыкка, ягъни 34 см тирәсе озынлыкка көйлибез.
Түбән ешлыклар көчәйткече көйләгечен кулланып, гальванометр¬
ның тавыш генераторын ялгаганда авышкан угын шкаланың урта¬
сыннан еракка күчмәслек итеп көйлибез.
Тавыш генераторыннан K1 көчәйткечен өзеп, К2 көчәйткечен
ялгыйбыз. Гальванометр угының беренче очрактагы кебек үк бүлем¬
теккә күчүен күрәбез. Димәк, тавыш көчәйткечләр нурландыра тор¬
ган бер үк ешлыктагы дулкыннарның амплитудалары да тигез була.
Хәзер ике көчәйткечне дә берьюлы ялгыйбыз. Бу вакытта галь¬
ванометрның угы шкаланың соңгы бүлемтегенә кадәр авыша, ягъ¬
ни аның күрсәтүләре тавышны аерым-аерым көчәйткечләр чыгар¬
ганнан күпкә зур.
Гальванометр күрсәтүләренең артуы шуны аңлата; тавыш дул¬
кыннары, М ноктасында кушылып, берсен-берсе көчәйтәләр, ягъни
суммар тавыш дулкынының амплитудасы һәр аерым тавыш дул¬
кыны амплитудасыннан зуррак.
Хәзер икенче көчәйткечне (К2), демонстрацион метр буйлап күче¬
реп, микрофонга якынайтабыз (рәс. 83, а). Ул чагында гальванометр¬
ның угы нуль ягына авыша башлый. Көчәйткеч белән микрофон
133
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
арасындагы ераклык якынча 17 см га (ягъни тавыш дулкыны озын¬
лыгының яртысына) кимегәч, гальванометр нульне күрсәтә.
Димәк, тавыш көчәйткечләр белән микрофон болай урнашкан¬
да, М ноктасына җиткән тавыш дулкыннары теләсә кайсы мизгелдә
бер-берсен сүндерәләр, ягъни М ноктасында суммар дулкын ампли¬
тудасы нульгә тигез була.
Рәс. 83
83 нче а рәсемнән күренгәнчә, 1 дулкынының М ноктасына кадәр
үткән юлы 2 дулкынының шул ук ноктага кадәрге юлыннан d зур¬
лыгына артыграк. Ераклыклар аермасы d ике дулкын йөрешенең
аермасы дип атала. Бу аерма дулкын озынлыгының яртысына ти¬
гез булса, бер үк фазаларда нурлана торган 1 һәм 2 дулкыннары М
ноктасына теләсә кайсы мизгелдә капма-каршы фазаларда килеп
җитә (рәс. 83, а).
Графикка карап (рәс. 83, б), тирбәнешләре капма-каршы фаза¬
ларда була торган тигез амплитудалы 1 һәм 2 дулкыннарын М нок¬
тасында кушканда, суммар дулкын амплитудасының теләсә кайсы
вакыт мизгелендә нульгә тигез, ягъни минималь икәнен күрәбез.
Икенче репродукторны (К2) микрофонга тагын да якынайта бар¬
сак, гальванометр күрсәткечләре үсә башлар һәм d йөреш аермасы
134
// бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
34 см га, ягъни дулкын озынлыгына тигез булып калгач, иң зур
кыйммәтенә ирешер. Рәсемнән күренгәнчә, дулкыннар бу очракта
М ноктасына бер үк фазаларда килә һәм гальванометр күрсәтүләре
буенча фикер йөртсәк, теләсә кайсы мизгелдә бер-берсен көчәйтә.
Бу очракта суммар тавыш дулкынының амплитудасы М нок¬
тасына килүче һәр ике дулкынның амплитудасыннан ике тапкыр
зуррак. Бу 84 нче б рәсемдәге графикта ачык күренә.
α>
Рәс. 84
К2 репродукторын микрофонга тагын да якынайта барып,
түбәндәге закончалыкны күрәбез:
— әгәр йөреш аермасы так сандагы ярымдулкын озынлыклары-
λ λ, λ
на тигез булса (1 —, з —, 5 — Һ.6.), дулкыннар М ноктасына теләсә
∆ 2
кайсы мизгелдә капма-каршы фазаларда килә һәм бер-берсен
сүндерәләр (суммар дулкын амплитудасы нульгэ тигез);
— әгәр йөреш аермасы бөтен сандагы дулкын озынлыкларына
тигез булса (λ, 2λ, 3λ, 4λ Һ.6.), дулкыннар М ноктасына теләсә кайсы
мизгелдә бер үк фазаларда килә һәм бер-берсен көчәйтәләр {суммар
дулкын амплитудасы бер дулкынның икелэтелгэн амплитудасы¬
на тигез).
135
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
Бу закончалык үтәлсен өчен мәҗбүри шарт бар: тавыш чыга¬
наклары бер үк ешлык белән тирбәнергә һәм тирбәнешләрнең фа¬
залар аермасы вакыт узу белән үзгәрмәскә тиеш. Мондый чыганак¬
лар һәм алар нурландырган дулкыннар когерент дип атала.
Без тавыш дулкыннарын кушуның нәтиҗәсен микрофон куел¬
ган М ноктасында гына тикшердек. Әгәр без, ике репродукторны да
баштагы урыннарында калдырып, микрофонны төрле юнәлешләрдә
күчереп йөртсәк, тавыш чыганаклары алдындагы пространствода
вакыт узу белән үзгәрми торган картина — тирбәнеш амплитудала¬
ры максимумнары һәм минимумнарының чиратлашуы барлыкка
килер. Димәк, кайбер нокталарда (аларга дулкыннар һәрвакыт
бердәй фазаларда килеп җитә) тавыш дулкыннары һәрвакыт иң
зур амплитуда белән тирбәлә. Шул сәбәпле бу нокталарда иң каты
тавыш була. Кайбер нокталарда (дулкыннар бирегә капма-каршы
фазаларда килә) тирбәнүләр амплитудасы нульгә тигез. Шуңа күрә
бу урыннарда тавыш юк. Пространствоның калган нокталарында
тирбәнешләр амплитудасы 1 һәм 2 дулкыннарының амплитудалар
суммасыннан кечерәк була. Шулай да һәрбер ноктага вакыт узу
белән үзгәрми торган үз амплитудасы туры килә.
Тирбәнү амплитудасының максимум һәм минимумнарының
пространствода вакыт узу белән үзгәрмәслек булып таралып урна¬
шуы интерференция күренеше дип атала. Интерференция күрене¬
ше когерент чыганаклар дулкыннарын кушканда гына күзәтелә.
Пространствода дулкыннар кушылган вакыт дәвамында
суммар тирбәнеш амплитудаларының даими таралып урна¬
шу күренеше интерференция дип атала.
Пространствода ике когерент тавыш дулкыны кушылудан ин¬
терференция күренеше килеп чыгуына тыңлап карап ышанырга
мөмкин. Моның өчен тавыш чыгаручы ике репродукторны аудито¬
рия ягына боралар, һәрбер тыңлаучы, бер колагын каплаган килеш
акрын гына я уңга, я сулга таба борылып, тавышның көчәюен яки
акрынаюын ишетер. Бу тыңлый торган колакның кайсы зонага —
интерференциянең максимумына яки минимумына эләгүе белән бәйле.
Интерференция күренеше — дулкыннарның барлык төрләренә
дә: эластик, электромагнитик, су өстендәге дулкыннарга һ.б. хас
күренеш.
136
11 бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш
Сораулар
1. 82—84 нче рәсемнәр буенча тавыш дулкыннарын кушу тәҗри¬
бәсенең ничек үткәрелүен кыскача аңлатыгыз.
2. Ике дулкынның йөреш аермасы нәрсә ул?
3. 82—84 нче рәсемнәрдәге тәҗрибә нәтиҗәсендә нинди закон¬
чалык ачыклана?
4. Нинди дулкыннар когерент була?
5. Интерференция күренеше нәрсә ул һәм аны нинди чыганак¬
лар китереп чыгара?
6. Нинди күренеш интерференция дип атала?
7. Интерференция күренешен ишетеп буламы?
8. Нинди дулкыннарга интерференция күренеше хас?
Ill бүлек
ЭЛЕКТРОМАГНИТИК КЫР
§ 43. Магнит кыры һәм аның график сурәте
8 нче сыйныф физикасыннан без электр тогының магнит кы¬
рын тудыруы турында беләбез. Магнит кыры, мәсәлән, токлы ме¬
талл үткәргеч тирәсендә була. Ә токның үзен үткәргеч буйлап юнә¬
лешле хәрәкәт итүче электроннар тудыра. Ток электролит эремәсе
аша үткән чакта да магнит кыры барлыкка килә. Бу очракта, уңай
яки тискәре корылып, бер-берсенә каршы хәрәкәт итүче ионнар ко¬
рылма йөртүчеләр булып тора.
Электр тогы — корылмалы кисәкчекләрнең юнәлешле хәрәкәте
булганлыктан, магнит кырын уңай яки тискәре корылмалы
'хәрәкәт итүче кисәкчекләр тудыра, дип әйтә алабыз.
Исегезгә төшерәбез, Ампер гипотезасы буенча, электроннар
хәрәкәте нәтиҗәсендә җисемнең атом һәм молекулаларында боҗ¬
ралы токлар туа.
85 нче рәсемдә бу элементар боҗралы токларның магнит эчендә
бертөрле ориентлашуы күрсәтелгән. Шуңа күрә шундый һәрбер ток
тирәсендә хасил булган магнит кырларының да юнәлешләре бертөр¬
ле. Бу кырлар, магнитның эчендә һәм тирәсендә кыр тудырып, бер-
берсен көчәйтәләр. ∣
Рәс. 85
138
Ill бүлек. Электромагнитик кыр
Магнит сызыгының
юнәлеше
_ -⅞-τ~N ⅜rjL ⅛⅛ '
I
Магнит сызыгы а)
Магнит кырын яхшылабрак күз алдына китерү өчен, без магнит
сызыкларыннан файдаланырбыз (аларны магнит кыры сызыклары
дип тә атыйлар)1. Исегезгә төшерәбез, магнит сызыклары — маг¬
нит кырына кертелгән бик вак магнит уклары тезелеп урнаша
дип уйланылган уйланма сызыклар ул.
Пространствоның магнит кыры булган теләсә кайсы ноктасы
аша магнит сызыгын үткәрергә мөмкин.
86 нчы а, б рәсемдә туры яки кәкре магнит сызыкларының ни¬
чек үткәрелүе күрсәтелгән: сызыкның теләсә кайсы ноктасында
үткәрелгән орынма бу ноктага урнаштырылган магнит угы күчәре
белән тәңгәл килә.
Магнит сызыклары йомык була. Мәсәлән, токлы туры үткәргеч¬
нең магнит сызыклары — үткәргечкә перпендикуляр урнашкан
яссылыкта ятучы концентрик әйләнәләрдән гыйбарәт.
Шул ук рәсемнәрдән күренгәнчә, магнит сызыгының нинди дә
булса ноктасына куелган магнит угының төньяк полюсны күрсәткән
юнәлешен, шартлы рәвештә, магнит сызыгы юнәлеше итеп алалар.
147H4e параграфта бу сызыкларга төгәлрәк исем һәм билгеләмә бирелер.
139
Ill бүлек. Электромагнитик кыр
Пространствоның магнит кыры көчлерәк булган өлкәләрендә
магнит сызыкларын бер-беренә якынрак, башка урыннарга кара¬
ганда куерак итеп күрсәтәләр. Мәсәлән, 87 нче рәсемнең сул өле¬
шендә сурәтләнгән кыр көчлерәк.
Шулай итеп, магнит сызыкларының сурәтләнеше буенча маг¬
нит кырының юнәлеше турында гына түгел, зурлыгы турында да
(пространствоның кайсы нокталарында кыр магнит угына зуррак,
кайсысында кечерәк көч белән тәэсир итә) фикер йөртергә мөмкин.
Ф Сораулар
1. Магнит кырын нәрсә тудыра?
2. Даими магнитның магнит кырын нәрсә тудыра?
3. Магнит сызыклары нинди сызыклар ул?
4. Сызыклары туры; кәкре булган магнит кырында магнит ук¬
лары ничек урнаша?
5. Магнит сызыгының нинди дә булса ноктасында бу сызык¬
ның юнәлеше итеп нәрсә алына?
6. Пространствоның бер өлкәсендәге кырның икенче кырдан
көчлерәк икәнен магнит сызыклары ярдәмендә ничек күрсәтәләр?
7. Магнит кыры сызыклары рәсеме буенча нәрсәләр турында
белергә мөмкин?
£ 33 нче күнегү
1. 88 нче рәсемдә токлы үткәргечнең ВС бүлемтеге сурәтләнгән.
Аның тирәсендәге яссылыкларның берсендә бу ток тудырган магнит
кыры сызыклары күрсәтелгән. А ноктасында магнит кыры бармы?
140
Ш бүлек. Электромагнитик кыр
2. 88 нче рәсемдә А, М, N нокталары сурәтләнгән. Аларның кай¬
сысында ВС үткәргече буйлап агучы токның магнит кыры магнит
угына иң зур көч; иң аз көч белән тәэсир итә?
§ 44. Бериш булмаган һәм бериш магнит кыры
89 нчы рәсемдә сурәтләнгән даими туры магнитның магнит сы¬
зыклары рәсемен тикшерик. 8 нче сыйныф физикасыннан без маг¬
нит сызыкларының, төньяк полюстан чыгып, көньяк полюска керү¬
ен беләбез. Магнит эчендә алар көньяк полюстан төньякка юнәлгән.
Магнит сызыкларының башы да, ахыры да булмый: алар я йомык,
я, рәсемдәге урта сызык кебек, чиксезлектән чиксезлеккә баралар.
Магнитның тышында магнит сызыклары аның полюслары тирә¬
сендә куерак урнаша. Димәк, полюслар тирәсендә кыр иң көчле
була, ә полюслардан ерагайган саен, көчсезләнә бара. Магнит угы
полюска никадәр якынрак урнашса, аңа магнит кыры шулкадәр
зуррак көч белән тәэсир итә (модуле буенча). Магнит сызыклары
кәкрәйгән булганлыктан, укка тәэсир итүче көчнең юнәлеше дә нок¬
тадан ноктага үзгәрә бара.
Шулай итеп, туры магнит кыры бу кырга кертелгән магнит
угына кырның төрле нокталарында модуле һәм юнәлеше буенча
141
Ill бүлек. Электромагнитик кыр
Рәс. 91
төрле көчләр белән тәэсир итәргә мөмкин. Мондый кыр бериш
булмаган кыр дип атала1. Бериш булмаган магнит кыры сызыкла¬
ры кәкре була, аларның куелыгы ноктадан ноктага үзгәреп тора.
Токлы туры үткәргеч тирәсендәге кыр да бериш булмаган маг¬
нит кырына мисал булып тора. 90 нчы рәсемдә мондый үткәргеч¬
нең сызым яссылыгына перпендикуляр урнашкан өлеше сурәт¬
ләнгән. Үткәргечнең кисеме түгәрәк белән билгеләнгән. Нокта ток¬
ның сызым артыннан безгә таба юнәлгәнен күрсәтә (нокта ток юнә¬
лешен билгеләүче укның очын аңлата, ә инде ток бездән сызым арты¬
на китсә, укның койрыкчасы сыман, хач тамгасы куела).
Рәсемнән күренгәнчә, токлы туры үткәргеч тудырган кырның
магнит сызыклары концентрик әйләнәләрдән гыйбарәт, аларның
аралары үткәргечтән ерагайган саен арта бара.
Пространствоның ниндидер чикләнгән өлкәсендә бериш, ягъни
теләсә кайсы ноктасында магнит угына тәэсир итү көче модуле
һәм юнәлеше буенча бер үк булган магнит кырын тудырырга
мөмкин.
91 нче рәсемдә соленоид, ягъни чыбык уралган цилиндрик кәтүк
аша ток узганда, аның эчендә барлыкка килүче бериш кыр
күрсәтелгән. Әгәр солиноидның озынлыгы аның диаметрыннан
күпкә зур булса, соленоид эчендәге кырны бериш дип исәплиләр
(соленоид тышындагы кыр бериш түгел, аның магнит сызыклары
'Бериш һәм бериш булмаган кырларга төгәлрәк билгеләмә 47 нче па¬
раграфта бирелер.
142
Ill бүлек. Электромагнитик кыр
× × ×
× × ×
× × ×
Рәс. 92
Рәс. 93
туры магнитныкы кебек диярлек урнашкан). Бу рәсемнән без бе¬
риш магнит кырының магнит сызыклары бер-беренә параллель һәм
бер үк куелыкта урнашкан икәнен күрәбез.
Даими туры магнит эченең урта өлешендәге кыр да бериш була
(рәс. 89).
Магнит кырын түбәндәгечә сурәтлиләр: әгәр бериш магнит кыры
сызыклары сызым яссылыгына перпендикуляр урнашып, бездән
сызым эченә юнәлсә, аларны — хачлар белән (рәс. 92), ә сызым
яссылыгыннан безгә таба юнәлсә, нокталар белән (рәс. 93) билге¬
лиләр. Ток очрагындагы кебек, һәрбер хач — безгә юнәлгән укның
койрыгы, ә нокта безгә таба очучы укның очы (ике рәсемдә дә ук
юнәлеше магнит сызыклары юнәлеше белән тәңгәл килә).
Сораулар
1. Туры магнит кыры сызыкларының юнәлеше һәм формасы
турында нәрсә әйтә аласыз?
2. Туры магнит тирәсендә; токлы туры үткәргеч тирәсендә;
озынлыгы диаметрыннан күпкә зур булган соленоид эчендә нинди
магнит кыры — беришме, бериш булмаганмы барлыкка килә?
3. Бериш булмаган; бериш магнит кырының төрле ноктала¬
рында магнит угына тәэсир итүче көчнең модуле һәм юнәлеше
турында нәрсә әйтергә мөмкин?
4. Бериш булмаган һәм бериш магнит кырларында сызыклар¬
ның урнашу рәсемнәрен чагыштырыгыз.
5. Сызым яссылыгына перпендикуляр юнәлгән магнит кыры
сызыкларын ничек күрсәтәләр?
143
Ill бүлек. Электромагнитик кыр
34 нче күнегү
1. 94 нче рәсемдә токлы үткәргеч уралма һәм бу ток тудырган
магнит кырының сызыклары сурәтләнгән.
Рәс. 94
а) Рәсемдәге А, В, С һәм D нокталары арасында кыр магнит угына
модуле буенча тигез көч белән тәэсир иткәннәре бармы? (AC=AD,
АЕ = BE.) Булса, бу нокталарны күрсәтегез.
б) A, В, С һәм D нокталарының кайсысында кыр магнит угына
иң зур көч белән тәэсир итә?
2. 94 нче рәсем буенча билгеләгез: токлы уралма тудырган бе¬
риш булмаган магнит кырында магнит угына тәэсир итү көчләре
модуле буенча да, юнәлеше буенча да тигез булган нокталар табарга
мөмкинме? Булса, дәфтәрегезгә 94 нче рәсемгә охшаш рәсем ясагыз
һәм анда шундый нокталарның кимендә ике парын күрсәтегез.
§ 45. Токның юнәлеше һәм аның магнит кыры
сызыкларының юнәлеше
95 нче рәсемдә сызым яссылыгына перпендикуляр булган ток¬
лы үткәргеч тирәсендәге магнит сызыкларының ничек урнашуы
күрсәтелгән.
144
Ill бүлек. Электромагнитик кыр
Рәсемнән күренгәнчә, үткәргечтәге токның юнәлешен үзгәртү
белән, барлык магнит уклары да 180° ка борыла. Әмма һәр ике оч¬
ракта да укларның күчәрләре магнит сызыклары орынмалар буен¬
ча урнаша.
Бу тәҗрибә ярдәмендә, токның магнит кыры сызыкларының
юнәлешләренең үткәргечтәге ток юнәлешенә бәйле икәнен белдек.
Әлеге бәйлелекне борау кагыйдәсе (яки уң винт кагыйдәсе) дип
йөртелүче гади кагыйдә белән күрсәтеп була. Ул болай әйтелә:
әгәр борауның йөреш хәрәкәте юнәлеше үткәргечтәге ток юнә¬
леше белән туры килсә, борау сабының әйләнү юнәлеше токның
магнит кыры сызыклары юнәлеше белән тәңгәл килә (рәс. 96, 97).
Борау кагыйдәсе ярдәмендә, токның юнәлеше буенча бу ток ту¬
дырган магнит кыры сызыкларының юнәлешен, ә магнит кыры
сызыкларының юнәлеше буенча — кырны тудыручы ток юнәлешен
билгеләргә мөмкин.
Борау сабының әйләнү һәм
магнит сызыклары юнәлеше
Борауның йөреш хәрәкәте '
һәм ток юнәлеше
Рәс. 96
Борауның
йөреш хәрәкәте
Борау сабының әйләнү
Ток юнәлеше
Рәс. 97
145
Ill бүлек. Электромагнитик кыр
Соленоидның магнит кыры сызыклары юнәлешен билгеләү өчен
икенче кагыйдә кулланыла, аны уң кул кагыйдәсе дип тә атыйлар.
Кагыйдә болай әйтелә:
әгәр соленоидны уң кул белән, дүрт бармакны уралмалардагы
ток юнәлеше буенча куеп тотсак, читкә караган баш бармак
соленоид эчендәге магнит кыры сызыкларының юнәлешен
күрсәтер (рәс. 98).
Солениод уралмаларында
ток юнәлеше
Рәс. 98
Сез инде соленоидның магнит кыры белән даими туры магнитның
кырлары охшаш икәнен беләсез (рәс. 89 һәм 91). Соленоид, магнит
шикелле үк, полюсларга ия: аның магнит сызыклары чыккан очы —
төньяк полюсы дип, ә кергән очы көньяк полюсы дип атала.
Соленоид тагы ток юнәлешен белгәннән соң, уң кул кагыйдәсе
буенча аның эчендәге магнит сызыклары юнәлешен, димәк, магнит
полюсларын билгеләргә мөмкин.
Киресенчә, соленоид эчендәге магнит сызыклары юнәлешен яки
аның магнит полюсларын белеп, соленоид уралмаларындагы ток
юнәлешен билгеләп була.
Токлы ялгыз уралма үзәгендә магнит кыры сызыкларының
юнәлешен белү өчен дә уң кул кагыйдәсен кулланырга мөмкин.
? Сораулар
1. Үткәргечтәге ток юнәлеше белән аның магнит кыры сызык¬
лары юнәлеше арасындагы бәйлелекне нинди тәҗрибә ярдәмендә
күрсәтеп була?
2. Борау кагыйдәсен әйтегез.
3. Борау кагыйдәсе ярдәмендә нәрсәне билгеләп була?
4. Соленоид өчен уң кул кагыйдәсен әйтегез.
5. Уң кул кагыйдәсе ярдәмендә нәрсәне билгеләргә мөмкин?
146
Ill бүлек. Электромагнитик кыр
£ 35 нче күнегү
1. 99 нчы рәсемдә металл чыбыктан ясалган турыпочмаклык
аша үтүче ток юнәлеше ук белән күрсәтелгән. Рәсемне дәфтәрегезгә
күчерегез һәм, борау кагыйдәсен кулланып, аның һәр ягы тирәсендә
берәр магнит сызыгы сызыгыз. Ук белән юнәлешен күрсәтегез.
Рәс. 100
2. 100 нче рәсемдә токлы үткәргеч тирәсендәге магнит кыры
сызыклары күрсәтелгән. Үткәргечләр түгәрәк рәвешендә сурәтләнгән.
Рәсемне дәфтәрегезгә күчерегез һәм, борау кагыйдәсен кулланып,
үткәргечләрдәге ток юнәлешен шартлы билгеләр белән күрсәтегез.
3. Эченә корыч кендек кертелгән кәтүк аша (рәс. 101) күрсәтелгән
юнәлештә ток уздыралар. Барлыкка килгән электромагнитның по¬
люсларын билгеләгез. Аның полюсларын ничек итеп үзгәртергә
мөмкин? . . ,
Рәс. 101
4. Әгәр кәтүк аша ток узганда рәсемдә күрсәтелгән магнит по¬
люслары барлыкка килсә (рәс. 102), кәтүктәге ток юнәлешен һәм
ток чыганагының полюсларын билгеләгез.
Рәс. 102
5. Дагасыман электромагнит чорнауларының уралмаларында¬
гы ток юнәлеше уклар белән күрсәтелгән (рәс. 103). Электромагнит¬
ның полюсларын билгеләгез.
14/
Ill бүлек. Электромагнитик кыр
6. Токлары бер үк юнәлештә булган параллель үткәргечләр бер¬
беренә тартыла, ә бер үк юнәлештә хәрәкәт итүче параллель элект¬
рон бәйләмнәре этеләләр. Бу очракларның кайсысында үзара тәэ¬
сиргә — электр көчләре, ә кайсысында магнит көчләре сәбәп була?
Ни өчен шулай уйлыйсыз?
*
§ 46. Магнит кырын аның электр тогына тәэсире
буенча белү. Сул кул кагыйдәсе
8 нче сыйныф физикасы буенча сез инде беләсез: магнит кы¬
рына кертелгән һәм аның магнит сызыклары белән тәңгәл
килмәгән теләсә нинди токлы үткәргечкә бу кыр ниндидер көч
белән тәэсир итә.
Мондый көчнең булуын 104 нче а рәсемдәге җайланма ярдә¬
мендә күрсәтергә мөмкин. Бу тәҗрибәне кабат искә төшерик.
АВ үткәргече бөгелүчән чыбык үткәргечләргә эленгән, ә алар
реостат һәм ялгагыч аша ток чыганагына тоташтырылган. Үткәргеч
дагасыман магнитның полюслары арасына, ягъни магнит кырына
урнаштырыла.
Ялгагычны тоташтыргач, чылбырда электр тогы барлыкка килә
һәм үткәргеч хәрәкәт итә башлый (рәс. 104, б).
Магнитны алып куйсак, токлы үткәргеч ялгагычны тоташтыр¬
ганда хәрәкәт итми. Димәк, магнит кыры, токлы үткәргечкә нин¬
дидер көч белән тәэсир итеп, аны башлангыч торышыннан тайпыл -
дыра.
Пространствоның билгеле бер өлешендә магнит кырын табу
өчен, магнит кырының токлы үткәргечкә тәэсирен кулланырга
мөмкин.
Билгеле, магнит кырын компас ярдәмендә табу күпкә уңайрак.
Әмма магнит кырының бу кырдагы компас угына тәэсире, асылда,
кырның элементар электр токларына тәэсиренә кайтып кала. Бу
токлар компас угы эшләнгән магнитлы җисемнең атом һәм моле¬
кулаларында була.
Шулай итеп, магнит кыры электр тогы тарафыннан туды¬
рыла һәм үзенең электр тогына тәэсире буенча беленә.
Магнит кырындагы токлы үткәргечкә тәэсир итүче көчнең юнә¬
леше нәрсәләргә бәйле икәнен ачыклыйк. Тәҗрибәләр күрсәтүенчә,
148
Ill бүлек. Электромагнитик кыр
токның юнәлешен үзгәрткәндә, үткәргечнең хәрәкәт юнәлеше дә,
димәк, аңа тәэсир итүче көчнең юнәлеше дә үзгәрә (рәс. 104, в).
Токның юнәлешен үзгәртмичә генә, магнит полюсларын (ягъни
магнит кыры сызыкларының юнәлешен) алыштырып куйган оч¬
ракта да көчнең юнәлеше үзгәрә.
Димәк, үткәргечтәге токның юнәлеше, магнит кыры сызыкла¬
рының юнәлеше һәм үткәргечкә тәэсир итүче көчнең юнәлеше үзара
бәйләнгәннәр.
Рәс. 104
149
Ill бүлек. Электромагнитик кыр
Магнит кырындагы токлы үткәргечкә тәэсир итүче көчнең юнә¬
лешен сул кул кагыйдәсе буенча билгеләргә мөмкин. Үткәргечнең
магнит кыры сызыкларына перпендикуляр яссылыкта урнашкан иң
гади очрагы өчен бу кагыйдә түбәндәгечә әйтелә:
әгәр сул кулны, магнит кыры сызыклары уч төбенә перпенди¬
куляр керерлек, ә дүрт бармак ток юнәлешен күрсәтерлек итеп
куйсак, 90° ясап читкә караган баш бармак үткәргечкә тәэсир
итүче көчнең юнәлешен күрсәтер (рәс. 105).
Рәс. 105
Уңай ионнарның
хәрәкәт юнәлеше
Рәс. 106
Сул кул кагыйдәсен кулланганда шунысы мөһим: электр чыл¬
бырының тышкы өлешендәге (ягъни ток чыганагы тышындагы)
токның юнәлеше итеп ток чыганагының уңай полюсыннан тискә¬
ресенә таба юнәлеше алына (рәс. 106). Икенче төрле әйткәндә, сул
кулның дүрт бармагы электроннарның электр чылбырындагы
хәрәкәтенә каршы юнәлгән булырга тиеш. Электролит эремәсе ке¬
бек үткәрүчән тирәлекләрдә электр тогын ике тамгалы корылма¬
ларның да хәрәкәте тудыра. Димәк, сул кулның дүрт бармагы юнә¬
леше бу очракта корылган кисәкчекләрнең хәрәкәт юнәлеше белән
тәңгәл килә.
Сул кул кагыйдәсе ярдәмендә магнит кыры эчендә хәрәкәт итү¬
че тискәре яки уңай корылган аерым бер кисәкчеккә кырның тәэ¬
сир итү көче юнәлешен билгеләргә мөмкин.
150
Ill бүлек. Электромагнитик кыр
Рәс. 107
Кисәкчек магнит сызыкларына перпендикуляр яссылыкта
хәрәкәт итә торган иң гади очракта бу кагыйдә болай әйтелә:
Әгәр сул кулны уч төбенә магнит кыры сызыклары перпен¬
дикуляр керерлек, ә дүрт бармак уңай корылган кисәкчек
хәрәкәте буенча (яки тискәре корылган кисәкчек хәрәкәтенә
каршы) юнәлерлек итеп куйсак, 90° ка читкә караган баш бар¬
мак кисәкчеккә тәэсир итүче көчнең юнәлешен күрсәтер (рәс.
107—109).
Сул кул кагыйдәсен кулланып, магнит кырындагы токлы
үткәргечкә яки хәрәкәт итүче корылмалы кисәкчеккә тәэсир итә
торган көч юнәлешен билгеләргә мөмкин. Алай гына да түгел, бу
кагыйдә буенча без ток юнәлешен (магнит кыры сызыкларының
һәм үткәргечкә тәэсир итүче көчнең юнәлешләре билгеле булса),
магнит сызыклары юнәлешен (ток белән көчнең юнәлешләре билге¬
ле булса), хәрәкәт итүче кисәкчек корылмасының тамгасын (маг¬
нит сызыкларының, көчнең һәм кисәкчек тизлегенең юнәлешләре
буенча) һ.б. билгели алабыз.
Рәс. 108
Рәс. 109
151
Ill бүлек. Электромагнитик кыр
Рәс. 110
Шунысы игътибарга лаек: әгәр үткәргечтәге токның юнәлеше
яки кисәкчекнең тизлеге магнит индукциясе сызыгы белән тәңгәл
килсә яки аңа параллель булса, магнит кырының токлы үткәргечкә
яки хәрәкәт итүче корылмалы кисәкчеккә тәэсире нульгә тигез була
(рәс. 110, а, б).
? Сораулар
1. Магнит кырындагы токлы үткәргечкә тәэсир итүче көчнең
булуына нинди тәҗрибә ясап ышанырга мөмкин?
2. Магнит кырының барлыгы ничек беленә?
3. Магнит кырында токлы үткәргечкә тәэсир итүче көчнең
юнәлеше нәрсәгә бәйле?
4. Магнит кырындагы токлы үткәргеч өчен; бу кырда хәрәкәт
итүче корылган кисәкчек өчен сул кул кагыйдәсе ничек әйтелә?
5. Электр чылбырының тышкы өлешендәге ток юнәлеше итеп
нәрсә кабул ителә?
6. Сул кул кагыйдәсе буенча нәрсәне билгеләп була?
7. Нинди очракта магнит кырының токлы үткәргечкә яки
хәрәкәт итүче корылган кисәкчеккә тәэсир итү көче нульгә ти¬
гез?
152
Ill бүлек. Электромагнитик кыр
$ 36 нчы күнегү
1. Чылбырны ялгаганнан соң җиңел алюминий көпшә кайсы
якка таба тәгәрәр (рәс. 111)?
Рәс. 111
2. 112 нче рәсемдә ток чыганагы белән тоташтырылган ике изо¬
ляциясез үткәргеч һәм җиңел алюминий көпшә АВ сурәтләнгән.
Бу җайланма тулысы белән магнит кырын¬
да урнашкан. Әгәр АВ көпшәсе аша үтүче
ток белән магнит кырының тәэсир итешүе
нәтиҗәсендә бу көпшә үткәргечләр буйлап
рәсемдәге юнәлештә тәгәрәсә, АВ көпшәсен¬
дәге токның юнәлешен билгеләгез. Ток чы¬
ганагының кайсы полюсы уңай, ә кайсысы
тискәре?
3. Магнитларның полюслары арасына
үткәргеч урнаштырылган. Ал арның һәркайсының хәрәкәт юнәле¬
шен билгеләгез.
4. 114 нче рәсемдә магнит кырында v тизлеге белән хәрәкәт итү¬
че тискәре корылган кисәкчек сурәтләнгән. Дәфтәрегездә шундый
Рәс. 112
(рәс. 113) токлы дүрт
Рәс. 113
ук рәсем ясагыз һәм кырның бу кисәкчеккә тәэсир итү көче юнә¬
лешен ук белән күрсәтегез.
153
Ill бүлек. Электромагнитик кыр
Рәс. 114
5. Магнит кыры и тизлеге белән хәрәкәт итүче кисәкчеккә F көче
белән тәэсир итә (рәс. 115). Кисәкчекнең корылмасы нинди тамгалы?
§ 47. Магнит кырының индукциясе
Сезнең күбегез бәлки игътибар иткәндер, кайбер магнитлар про-
странствода башкаларына караганда көчлерәк кырлар тудыра.
Мәсәлән, 116 нчы рәсемдә күрсәтелгән беренче магнитның кыры
икенчесенең кырыннан көчлерәк. Чынлап та, өстәлдә чәчелгән ка¬
дакларга кадәр ераклыклары бер үк булса да, беренче магнитка тар¬
тылу көче кадакларның авырлык көчен җиңү өчен җитәрлек бул¬
ган, ә икенчесенә тартылу көче — җитмәгән.
Магнит кырын нинди зурлык белән характерларга соң?
Г Магнит кыры — магнит кыры индукциясе (яки магнит ин¬
дукциясе) дип атала һәм В символы аша билгеләнә торган век¬
торлы физик зурлык белән характерлана^
Моның нинди зурлык икәнен ачыклыйк.
Без инде магнит кырының аңа кертелгән токлы үткәргечкә бил¬
геле бер көч белән тәэсир итүен беләбез.
Токлы АВ үткәргеченең турысызыклы өлешен, магнит сызык¬
ларына перпендикуляр итеп, магнит кырына (рәс. 117) урнашты¬
рыйк. Үткәргечнең ток зурлыгы I нең юнәлеше һәм магнит полюс¬
ларының урнашуы рәсемдәгечә булганда, үткәргечкә тәэсир үтүче F
көче, сул кул кагыйдәсе буенча, аска таба юнәлә. F көчен тигезләү
өчен үлчәүнең уң тәлинкәсенә өстәлгән герләрнең авырлыгын
исәпләп, бу көчне табарга мөмкин.
Тәҗрибәләр күрсәткәнчә, бу көчнең модуле магнит кырының үзенә
бәйле — көчлерәк магнит үткәргечкә зуррак көч белән тәэсир итә.
154
Ill булек.. Электромагнитик кыр
Рәс. 116
2
Моннан тыш, магнит кырының үткәргечкә тәэсир итү көче бу
үткәргечнең озынлыгына I һәм андагы ток зурлыгына I пропор¬
циональ.
F көче модуленең үткәргеч озынлыгы I белән ток зурлыгы I
F
чагыштырмасы (ягъни ) — даими зурлык. Ул үткәргечнең озын-
лыгына да, андагы ток зурлыгына да бәйле түгел. чагыштырмасы
II
кырга гына бәйле һәм аның санча характеристикасы булып тора.
Шушы зурлык магнит индукциясе векторының модуле итеп
кабул ителә дә инде:
F
в~п (1)
Шулай итеп, магнит индукциясе векторының модуле В —
магнит сызыкларына перпендикуляр урнашкан токлы үт¬
кәргечкә магнит кырының тәэсир итү көче модуленың F бу
үткәргечтәге ток зурлыгы I һәм аның озынлыгы I га чагыш¬
тырмасына тигез.
(1) формуласы буенча бериш магнит кыры индукциясен исәпләргә
мөмкин.
155
Ill бүлек. Электромагнитик кыр
СИда магнит индукциясе берәмлеге Югославия электротехнигы
Никола Тесла хөрмәтенә тесла (Тл) дип атала.
(1) формуласы ярдәмендә магнит индукциясе берәмлеге белән
СИдагы башка зурлыкларның берәмлекләре арасындагы бәйләнеш¬
не табарга мөмкин:
1Тл = 1-2—
А ■ м
Моңа кадәр без, магнит кырларын график сурәтләү өчен, шарт¬
лы рәвештә магнит сызыклары яисә магнит кыры сызыклары дип
аталган сызыклардан файдаландык (§ 43). Хәзер исә бу сызыклар¬
ның атамасын ачыклап, төгәлрәк билгеләмә бирә алабыз.
Магнит сызыкларының төгәл атамасы —t магнит индукциясе
сызыклары (яки магнит кыры индукциясе сызыклары^
Магнит кырындагы сызыкларныц һәр ноктасына орынма
магнит индукциясе векторының юнәлеше белән туры килсә, ул
магнит индукциясе сызыклары дип атала.
Рәс. 118
Магнит индукциясе сызыкларының бу билгеләмәсен 118 нче
рәсем ярдәмендә ачыкларга мөмкин. Биредәге нокталы түгәрәк —
сызым яссылыгына перпендикуляр урнашкан токлы үткәргечне
күрсәтә. Үткәргеч тирәсендәге әйләнә — үткәргечтәге ток тудырган
магнит кыры индукциясе сызыкларының берсе.
Күргәнебезчә, әйләнәнең теләсә кайсы ноктасыннан үткәрелгән
орынмалар магнит индукциясе векторлары белән тәңгәл киләләр.
Хәзер, «магнит индукциясе» терми¬
ны ярдәмендә, бериш һәм бериш
булмаган магнит кырларына 43 нче
параграфтагыга караганда төгәлрәк
билгеләмә бирик. Моның өчен 119—
121 нче рәсемнәрне тикшерәбез.
119 нчы рәсемдә сурәтләнгән бериш
магнит кырының (аның магнит индук¬
циясе сызыклары үзара параллель һәм
бер үк ешлыкта) ирекле сайлап алын¬
ган барлык нокталарында да магнит ин¬
дукциясе векторы В модуле һәм юнә¬
леше буенча бертөрле.
156
Ill бүлек. Электромагнитик кыр
Рәс. 119
Рәс. 120
Рәс. 121
Бу кырны бериш булмаган ике кыр: даими туры магнит кыры
(рәс. 120) һәм үткәргечнең турысызыклы өлеше буйлап узучы ток¬
ның кыры (рәс. 121) белән чагыштырабыз.
Бериш булмаган кырларда, беришләреннән аермалы буларак,
магнит индукциясе векторының ноктадан ноктага үзгәрүе ачык
күренә. Мәсәлән, бериш булмаган ике кырда да, 1 ноктасыннан
2 ноктасына күчкәндә, магнит индукциясе векторы — модуле буен¬
ча үзгәрә, 1 ноктасыннан 3 ноктасына күчкәндә — юнәлеш буенча, ә
2 ноктасыннан 3 ноктасына күчкәндә исә магнит индукциясе векто¬
ры модуле буенча да, юнәлеше буенча да үзгәрә.
Әгәр барлык нокталарында да магнит индукциясе В бертөрле
булса, магнит кыры бериш дип атала. Башка очракларда бериш
булмаган кыр дип йөртелә.
Кырның бирелгән ноктасында магнит индукциясе никадәр зур¬
рак булса, бу ноктада кыр магнит угына яисә хәрәкәт итүче электр
корылмасына шулкадәр зуррак көч белән тәэсир итә.
Сораулар
1. Магнит кырының санча характеристикасы булып саналган
векторлы зурлык ничек атала һәм нинди символ белән билгеләнә?
157
Ill бүлек. Электромагнитик кыр
2. Бериш магнит кырында индукция векторының модуле нинди
формула буенча исәпләнә?
3. Магнит индукциясе берәмлеге итеп нәрсә кабул ителгән? Бу
берәмлек ничек атала?
4. Магнит индукциясе сызыклары дип нәрсәне атыйлар?
5. Нинди очракта магнит кыры бериш дип, нинди очракта бе¬
риш булмаган дип атала?
6. Магнит кырының бирелгән ноктасында магнит угына якй
хәрәкәт итүче корылмага тәэсир итүче көч бу ноктаның магнит
индукциясенә ничек бәйле?
£ 37 нче күнегү
1. Бериш магнит кырына, магнит индукциясе сызыкларына пер¬
пендикуляр итеп, туры үткәргеч урнаштыралар. Аның аша 4 А лы
ток уза. Әгәр кыр үткәргечнең һәр 10 см озынлыгына 0,2 Н көч
белән тәэсир итсә, аның индукциясен табыгыз.
2. Индукциясе В булган магнит кырына токлы үткәргеч кертәләр.
Бераз вакыттан соң үткәргечтәге ток зурлыгын 2 тапкыр киметәләр.
Бу вакытта магнит кырының В индукциясе үзгәрерме? Ток зурлы¬
гының кимүе нинди дә булса башка физик зурлыкның үзгәрүенә
китерәме? Китерсә, бу нинди зурлык һәм ул ничек үзгәрә?
§ 48. Магнит агышы
122 нче а рәсемдә бериш магнит кырындагы үткәргеч контур
сурәтләнгән. Магнит кырындагы контур аша магнит агышы Ф яки
магнит индукциясе^ векторы агышы үтеп чыга дип сөйләү кабул
ителгән.
Билгеләмәсе буенча (ул өлкән сыйныфлар физика курсында би¬
релә), контур аша үтүче магнит агышы бериш магнит кырының
индукциясе векторы модуленә һәм бу контур белән чикләнгән
мәйданга пропорциональ була. Моннан тыш, магнит агышы контур
яссылыгының магнит индукциясе сызыкларына карата ничек ур¬
нашуына бәйле.
Әйтик, контур белән чикләнгән мәйдан аша үтүче магнит кыры
индукциясе үсеп китте, ди. Бу хәл, мәсәлән, магнит кырын тудыру¬
чы ток зурлыгының артуы яки контурның башка бер көчлерәк кырга
күчүе нәтиҗәсендә булырга мөмкин.
158
Ill бүлек. Электромагнитик кыр
Магнит агышы индукциягә пропорциональ булганлыктан, ул п
тапкыр артканда (122 нче а, б рәсемнәрендәге кебек, B1 кыйммә¬
теннән B2 = nB1 гә кадәр), бу контурның з мәйданы аша үтүче маг¬
нит агышы да шул тапкыр ук артыр.
Индукциясе B1 булган шул ук магнит кырында зуррак S' (рәс.
122, в) мәйданы аша үтүче магнит агышы, S' мәйданы S тан ничә
тапкыр зуррак булса, S мәйданы (рәс. 122, а) аша үтүче магнит
агышыннан шул тапкыр зуррак була.
Әгәр контур яссылыгы магнит индукциясе сызыкларына пер¬
пендикуляр булса (рәс. 122, а), контур белән чикләнгән S мәйданы
аша узучы магнит агышы Ф бирелгән B1 индукциясе өчен макси¬
маль була.
Контурны ОО' күчәре тирәсендә әйләндергәндә аның аша узучы
магнит агышы кими (косинус законы буенча) һәм, контур яссылыгы
магнит индукциясе сызыкларына параллель урнашканда, нульгә
әйләнә (рәс. 122, г). Бу очракта магнит индукциясе сызыклары кон¬
тур яссылыгы аша түгел, ә аның өстеннән шуып узалар дияргә була.
159
Ill бүлек. Электромагнитик кыр
Рәс. 123
Шулай итеп, магнит индукциясе
векторы В ның модуле яки контур
мәйданы s үзгәргәндә, шулай ук контур¬
ны әйләндергәндә, ягъни магнит кыры
индукциясе сызыкларына карата кон¬
турның ориентлашуы үзгәргәндә, кон¬
тур мәйданы аша узучы магнит агы¬
шы үзгәрә.
Әгәр әйләнүче контурның теләсә нинди торышында магнит ин¬
дукциясе сызыклары контур яссылыгында ята һәм аның мәйда¬
нын кисеп үтми (рәс. 123) икән, бу очракта агыш үзгәрми: теләсә
кайсы мизгелдә ул нульгә тигез.
? Сораулар
1. Бериш магнит кырына кертелгән яссы контурның мәйданы
аша узучы магнит агышы нәрсәләргә бәйле?
2. Әгәр мәйдан да, контурның ориентлашуы да үзгәрмәсә, маг¬
нит индукциясен п тапкыр үзгәртүдән магнит агышы ничек үзгәрә?
3. Контур магнит индукциясе сызыкларына карата ничек ори¬
ентлашканда, аның мәйданы аша узучы магнит агышы максималь?
нульгә тигез?
4. Әгәр контур әйләнгәндә магнит индукциясе сызыклары я аның
аша узып чыга, я өстеннән шуып үтә икән, магнит агышы үзгәрәме?
$ ЗВ нче күнегү
Корыч кендекле үткәргеч кәтүк K1 даими ток чыганагы чылбы¬
рын реостат R һәм ялгагыч К белән бер-бер артлы тоташтырыла
(рәс. 124). Кәтүкнең K1 уралмалары
аша узучы электр тогы аның тирәсен¬
дәге пространствода магнит кыры ту¬
дыра. K1 кәтүге кырына шундый ук
К2 кәтүге дә урнаштырыла.
К2 кәтүге аша узып чыгучы маг¬
нит агышын ничек итеп үзгәртергә
мөмкин? Барлык вариантларны да тик¬
Рәс. 124
шерегез.
160
П1 бүлек. Электромагнитик кыр
§ 49. Электромагнитик индукция күренеше
Билгеле булганча, электр тогы
тирәсендә һәрвакыт магнит кыры
була. Электр тогы белән магнит
кыры бер-берсеннән аерылгысыз.7
Ә менә электр тогы, алдарак
әйтелгәнчә, магнит кырын «тудыра»
икән, моңарга кире күренеш була ал¬
мыймы? Магнит кыры ярдәмендә
электр тогын «тудырып» булмыймы?
XIX гасыр башында бик күп га¬
лимнәр бу мәсьәләне чишәргә ты¬
рышкан. Инглиз галиме Майкп
Фарадей да шул юнәлештә эш алып
барган. «Магнит күренешен электр¬
га әверелдерергә»,— үзенең көндәле¬
Майкл Фарадей
(1791-1867)
генә бу сүзләрне ул 1822 елда язып куя. Фарадейга әлеге проблеманы
хәл итү өчен 10 еллык тырыш хезмәт кирәк була.
Фарадейның ничек итеп «магнит күренешен электрга әверелде¬
рергә» ирешүен белү өчен, аның кайбер тәҗрибәләрен хәзерге при¬
борларны кулланып эшләп карыйк.
161
Ill бүлек. Электромагнитик кыр
Гальванометрга тоташтырылган кәтүк эченә (рәс. 125, а) магнит
керткәндә, гальванометрның угы авыша — бу кәтүк чылбырында
индукцион ток хасил була. Үткәргечтәге индукцион ток, гальваник
элементтан яки аккумулятордан алынган ток кебек үк, электрон¬
нарның тәртипле хәрәкәте ул. «Индукцион» атамасы аның килеп
чыгу сәбәбен генә аңлата.
Магнитны кәтүктән чыгарган вакытта гальванометр угы яңадан
авыша, әмма бу юлы — капма-каршы якка. Димәк, кәтүктә капма-
каршы юнәлештәге ток хасил була.
Магнитның кәтүккә карата хәрәкәте туктагач, ток та бетә. Димәк,
кәтүк чылбырындагы ток магнитның кәтүккә карата хәрәкәте ва¬
кытында гына була.
Тәҗрибәне бераз үзгәртергә мөмкин. Хәрәкәтсез магнитка кәтүкне
кидерәбез һәм салдырабыз (рәс. 125, б). Нәкъ элеккечә, кәтүкнең
магнитка карата хәрәкәте вакытында чылбырда яңадан ток барлык¬
ка килә.
Рәс. 126
126 нчы рәсемдә ток чыганагына тоташтырылган А кәтүге
күрсәтелгән. Бу кәтүк гальванометр белән тоташкан С кәтүге эченә
куелган. А кәтүгенең чылбырын ялгаган һәм өзгән вакытта, С
кәтүгендә индукцион ток барлыкка килә.
А кәтүгендә ток зурлыгын үзгәртеп яисә бу кәтүкләрне бер-бе¬
ренә карата хәрәкәтләндереп тә, С кәтүгендә индукцион ток булды¬
рырга мөмкин.
Тагын бер тәҗрибә ясыйбыз. Магнит кырына үткәргечле яссы
контур кертеп, аның очларын гальванометрга тоташтырабыз (рәс.
162
Ill бүлек. Электромагнитик кыр
127, а). Контурны борганда, гальванометр анда ток барлыкка килү¬
ен күрсәтә. Шулай ук контур янында яки аның эчендә магнитны
әйләндерсәк тә, ток хасил була (рәс. 127, б).
Карап үтелгән барлык тәҗрибәләрдә дә, үткәргеч биләгән мәйдан
аша үтүче магнит агышы үзгәргәндә, индукцион ток барлыкка
килде.
125 нче а, б һәм 126 нчы рәсемнәрдәге очракларда магнит агы¬
шы магнит кыры индукциясе үзгәрү хисабына үзгәрде. Чынлап та,
магнитның яки кәтүкнең бер-беренә карата хәрәкәте вакытында
(рәс. 125, а, б), кәтүк кырның магнит индукциясе зуррак яки азрак
булган өлкәләренә эләкте (чөнки магнит кыры бериш түгел). А кәтүге
чылбырын ялгаганда яки өзгәндә исә, бу кәтүк тудырган магнит
кыры индукциясе кәтүктәге ток зурлыгы үзгәрү хисабына үзгәреп
торды.
Магнит кырында үткәргеч контурны (рәс. 127, а) яки контурга
карата магнитны (рәс. 127, б) әйләндергәндә магнит агышының
үзгәрүе — магнит индукциясе сызыкларына карата бу контурның
ориентлашуы үзгәрү хисабына булды.
Шулай итеп, йомык үткәргеч контуры аша узучы магнит
агышының һәрбер үзгәреше вакытында бу үткәргечтә электр
тогы барлыкка килә, һәм ул магнит агышының үзгәрүе бары¬
шында булып тора.
Менә шушы электромагнитик индукция күренеше була да инде.
Электромагнитик индукцияне ачу — XIX гасырның беренче
яртысындагы иң мөһим фәнни казанышларның берсе. Ул электро-
163
Ill бүлек. Электромагнитик кыр
техника һәм радиотехника фәннәренең барлыкка килүенә һәм үсе¬
шенә этәргеч була.
Электромагнитик индукция күренешенә нигезләнеп, куәтле
электр энергиясе генераторлары төзелә (киләсе параграфта сөйләнер).
Аларны уйлап табуда һәм төзүдә төрле илләрнең галимнәре һәм
техниклары катнаша. Безнең ватандаш галимнәребез — Эмилий
Христианович Ленц, Борис Семенович Якоби, Михаил Иосифо¬
вич Доливо-Добровольский һәм башкалар да электротехника үсе¬
шенә лаеклы өлешләрен кертәләр.
Сораулар
1. 125—127 нче рәсемнәрдәге тәҗрибәләр нинди максат белән
куела? Алар ничек үткәрелә?
2. Нинди шарт үтәлгәндә барлык тәҗрибәләрдә дә гальвано¬
метрларга ялганган кәтүктә индукцион ток барлыкка килә?
3. Электромагнитик индукция күренеше нидән гыйбарәт?
4. Электромагнитик индукция күренеше ачылуның әһәмияте
нәрсәдә?
£ 39 нчы күнегү
1. 124 нче рәсемдәге К2 кәтүгендә ничек итеп кыска вакытлы
индукцион ток тудырырга мөмкин?
0'0'
а) б) в) г) д)
Рәс. 128
2. Тимерчыбык боҗра бериш магнит кырына кертелә (рәс. 128).
Боҗра янындагы кечкенә уклар: а һәм б очрагында боҗраның маг¬
нит индукциясе сызыклары буенча туры хәрәкәтен, ә в, г һәм д
очракларында 00'күчәре тирәсендә әйләнүен күрсәтә. Бу очраклар¬
ның кайсысында боҗрада индукцион ток туарга мөмкин?
164
Ill бүлек. Электромагнитик кыр
§ 50. Алмаш электр тогын алу
Тагын бер кат даими магнитны кәтүккә карата күчерү юлы белән
кәтүктә индукцион ток табу мисалын тикшерик (рәс. 125, а). Тик
хәзер берничә секунд дәвамында магнитны өскә һәм аска хәрә¬
кәтләндереп торырбыз. Ьәм без гальванометр угының нуль бүлем¬
тегеннән әле бер, әле икенче якка авышуын күрәбез. Димәк, кәтүктәге
индукцион ток зурлыгының модуле һәм бу токның юнәлеше пери¬
одик үзгәреп тора.
Вакыт узу белән модуле һәм юнәлеше периодик рәвештә
үзгәрә торган ток алмаш ток дип атала.
Безнең йортларның яктырту челтәрендә һәм промышленность¬
ның бик күп тармакларында нәкъ менә алмаш ток кулланыла.
Хәзерге вакытта алмаш ток алу өчен, нигездә, электромеханик
индукция генераторлары, ягъни механик энергияне электр энер¬
гиясенә әверелдерү җайланмалары файдаланыла. Ал арның эше элек-
тромагнитик индукция күренешенә нигезләнгәнгә күрә, индукцион
диләр.
Яссы контур эчендә магнитны әйләндергәндә, бу контурда ин¬
дукцион ток хасил булу 49 нчы параграфта тикшерелгән иде (рәс.
127, б). Алмаш токның электромеханик генераторы шушы прин¬
ципта эшли. Алмаш ток генераторының контурга охшаш хәрәкәтсез
өлеше статор дип, ә әйләнүче өлеше, ягъни магнит, ротор дип
атала. Куәтле промышленность генераторларында даими магнит
урынына электромагнит кулланыла.
129 нчы а рәсемдә промышленность генераторы статорының
төзелеше күрсәтелгән. Статор — цилиндр формасындагы корыч ста-
нинадан гыйбарәт (станина — машинаның төрле эшче узеллары,
механизмнарын һ.б. монтажлап куя торган төп өлеше). Аның эчке
өлешенә уентылар ясала һәм аларга юан бакыр үткәргечләр салы¬
на. 129 нчы рәсемдә үткәргечнең бер генә уралмасы күрсәтелгән, ә
чынлыкта, статорда алар бик күп. Нәкъ менә бу үткәргечләрдә, алар
аша узучы магнит агышы үзгәргәндә, алмаш электр тогы индук¬
ция л әнә.
Магнит кырын ротор тудыра (рәс. 129, б). Ротор — электромаг¬
нит ул, аның катлаулы формадагы корыч кендегенә чорнау киде-
165
Ill бүлек. Электромагнитик кыр
Рәс. 129
релгән һәм чорнау аша даими ток ага. Бу чорнауга ток икенче бер
даими ток чыганагыннан щеткалар һәм балдаклар аша бирелә.
129 нчы в рәсемдә сез алмаш ток генераторының тулы схема¬
сын күрәсез. Роторның магнит кыры индукциясе сызыкларының
якынча урнашуы пунктир сызык белән билгеләнгән. Роторны нин¬
ди дә булса тышкы механик көч белән әйләндергәндә, ул тудырган
магнит кыры да әйләнә. Ул чакта статор чорнаулары аша уза торган
магнит агышы периодик рәвештә үзгәрә һәм нәтиҗәдә чорнауларда
даими ток индукцияләнә.
Җылылык электростанцияләрендә генераторның роторы — пар
турбинасы ярдәмендә, гидроэлектростанцияләрдә су турбинасы ярдә¬
мендә әйләндерелә.
166
Ill бу лек. Электромагнитик кыр
130 нчы а рәсемдә — куәтле гидрогенераторның тышкы күре¬
неше, ә 130 нчы б рәсемдә схематик рәвештә аның төзелеше
күрсәтелгән; биредә 1 — статор, 2 — ротор, 3 — су турбинасы.
Күргәнебезчә, гидрогенератор роторында магнит полюслары бер
генә пар түгел, ә берничә пар. Полюс парлары күбрәк булган саен,
ротор бер үк тизлек белән әйләнгәндә, генератор эшләп чыгарган
алмаш электр тогының ешлыгы зуррак була. Гадәттә су турбинала¬
рының әйләнү ешлыгы зур түгел, шунлыктан стандарт ешлыктагы
Рәс. 131
ток алу өчен күп полюслы роторлар кулланыла.
Россиядә һәм башка күп кенә илләрдә промышленность һәм
яктырту челтәре өчен кулланыла торган алмаш токның стандарт
ешлыгы 50 Гц ка тигез. Бу — 1 с
эчендә ток 50 тапкыр бер якка һәм
50 тапкыр икенче таба якка ага
дигән сүз. Кайбер илләрдә (мәсәлән,
АКШта) алмаш токның стандарт еш¬
лыгы 60 Гц ка тигез.
Алмаш ток генераторы эшләп
чыгарган ток зурлыгы вакыт эчендә
гармоник закон буенча (ягъни синус яки косинус законы буенча)
үзгәрә. 131 нче рәсемдә ток зурлыгы i нең вакыт t буенча үзгәрү
графигы күрсәтелгән.
Сораулар
1. Нинди электр тогы алмаш дип атала? Аны нинди гади
тәҗрибә ярдәмендә алырга мөмкин?
2. Алмаш электр тогы кайда кулланыла?
3. Хәзерге вакытта иң күп таралган алмаш ток генераторы¬
ның эше нинди күренешкә нигезләнгән?
4. Промышленность генераторының төзелеше һәм ничек эшлә¬
ве турында сөйләгез.
5. Җылылык электростанциясендә; гидроэлектростанциядә ге¬
нераторның роторы нәрсә белән хәрәкәткә китерелә?
6. Ни өчен гидрогенераторда күп полюслы роторлар кулланы¬
ла?
7. Россиядә һәм башка илләрдә кулланыла торган промышлен¬
ность тогының стандарт ешлыгы нинди?
167
Ill бүлек. Электромагнитик кыр
40 нчы күнегү
1. Россия электростанцияләре
ешлыгы 50 Гц булган алмаш ток
җитештерә. Бу токның периодын
табыгыз.
I 1 2. Графигы буенча (рәс. 132) ток
зурлыгы i тирбәнешләренең перио¬
дын, ешлыгын һәм амплитудасын
табыгыз^
§51. Электромагнитик кыр
Электромагнитик индукция күренеше 1831 елда Майкл Фара¬
дей тарафыннан ачыла.
Шул ук елда Англиядә булачак галим Джеймс Клерк Макс¬
велл туа. Ул ясаган гаять әһәмиятле фәнни ачыш электромагнитик
индукциянең асылын тирәнрәк аңларга мөмкинлек бирә.
Джеймс Максвелл
(1831—1879)
Электромагнитик индукция күрене¬
ше буенча, йомык үткәргеч контур аша
узучы магнит агышын үзгәрткәндә, бу
үткәргечтә индукцион ток хасил була.
Үткәргечтә электр кыры булган оч¬
ракта аның буенча ток узуын без белә¬
без.
Димәк, Фарадей тәҗрибәләрендә йо¬
мык үткәргеч контур аша үтүче үзгәреш¬
ле магнит кыры анда электр кырын ту¬
дырган һәм инде аның тәэсирендә ин¬
дукцион ток барлыкка килгән.
Магнит кыры үзгәрү нәтиҗәсендә
электр кыры барлыкка килә дигән фа¬
раз галимнәрдә шактый ук сораулар ту¬
дыра. Мәсәлән, бу кыр хәрәкәтсез электр
корылмалары тудырган кырдан аерыла¬
мы? Бу кыр бары тик үткәргечтә генә барлыкка киләме, әллә аның
тирәсендәге пространствода да буламы? Аның барлыкка килүендә
токлы йомык үткәргеч нинди дә булса роль уйныймы?
168
Ill бүлек. Электромагнитик кыр
Әлеге һәм башка сорауларга җаваплар, Максвелл тарафыннан
электромагнитик кыр теориясе эшләнгәч, 1865 елда табыла. Ул моны
теоретик рәвештә исбатлый:
магнит кырының вакыт узу белән булган һәрбер үзгәреше
алмаш электр кыры тууга сәбәп була, ә электр кырының ва¬
кыт узу белән булган һәрбер үзгәреше алмаш магнит кырын
тудыра.
Бер-берсен тудыра торган алмаш электр һәм магнит кырлары
бердәм электро магнитик кырны төзи.
Электромагнитик кырның чыганагы булып, тизләнеш белән
хәрәкәт итүче электр корылмалары тора.
Чынлап та, электр һәм магнит кырлары электр корылмалары
тирәсендә килеп чыга, шул ук вакытта электр кыры — теләсә нинди
исәп системасында да, ә магнит кыры үзенә карата корылмалар
хәрәкәт иткән системада була (бу даими магнит кырына карата да
дөрес, чөнки әлеге кыр электроннарның атом эчендәге хәрәкәте,
ягъни элементар электр токлары аркасында килеп чыга).
Даими тизлек белән хәрәкәт итүче корылмалар тирәсендә
(мәсәлән, даими ток уза торган үткәргеч тирәсендә) даими магнит
кыры туа.
Ә инде электр корылмалары тизләнеш белән хәрәкәт итсә, мәсәлән
тирбәнсә, алар тудырган электр кыры периодик үзгәреп тора. Ал¬
маш электр кыры пространствода алмаш магнит кырын тудыра, ә
анысы, — үз чиратында, алмаш электр кырын һ.б.
Алмаш электр кыры өермәле дип атала, чөнки аның көч сы¬
зыклары, магнит кыры индукциясе сызыклары кебек, йомык урна¬
ша. Бу аны хәрәкәтсез корылмалы җисемнәр тирәсендә була торган
электростатик (даими үзгәрми торган) кырдан аерып тора. Элек¬
тростатик кырның көч сызыклары уңай корылмалардан башлана
һәм тискәреләрендә бетә.
Электромагнитик кырның ачылуы индукцион ток килеп чыгу
механизмын детальләп аңлатырга мөмкинлек бирде. Индукцион ток
алу буенча барлык тәҗрибәләрдә дә (§ 49) йомык үткәргеч контуры
аша узучы магнит агышы ничек итеп булса да үзгәрде. Бу вакытта
Максвелл теориясе буенча өермәле электр кыры туды һәм аның
169
Ш бүлек. Электромагнитик кыр
тәэсирендә үткәргечтә һәрвакыт була торган ирекле корылмалар
юнәлешле хәрәкәткә килде. Бу очракта гальванометр белән ялган¬
ган үткәргеч пространствоның әлеге өлешендә барлыкка килгән
электр кырын билгеләүче индикатор ролен генә үти. Электр кыры
үткәргечнең булу-булмавына бәйле түгел.
Максвелл теориясе ачылып 22 ел үткәч кенә, ул фаразлаган элек-
тромагнитик кырны эксперименталь юл белән табалар. Электромагни-
тик кыр теориясе иң бөек фәнни ачышларның берсе булып санала,
фән һәм техника үсешендә аның ролен бәяләп бетереп тә булмый.
Сораулар
1. Электромагнитик кыр теориясен кем һәм кайчан ача, аның
асылы нидән гыйбарәт?
2. Электромагнитик кырның чыганагы булып нәрсә хезмәт итә?
3. Өермәле электр кырының көч сызыклары электростатик кыр¬
ныкыннан ни белән аерыла?
4. Электромагнитик кырның булуы турындагы белемнәргә
таянып, индукцион ток барлыкка килү механизмын аңлатыгыз.
$41 нче күнегү
126 нчы рәсемдәге тәҗрибәдә ялгагычны тоташтыргач, А кәтүге
аша узучы токның зурлыгы ниндидер вакыт аралыгында үсеп китә.
Бу вакытта С кәтүге чылбырында кыска вакытлы ток барлыкка килә.
А һәм С кәтүкләрендә токлар барлыкка китерүче электр кырлары
бер-берсеннән аерыламы? Әгәр С кәтүге белән гальванометр булмаса,
ялгагычны тоташтырган мизгелдә бу кырлар булыр идеме?
§ 52. Электромагнитик дулкыннар
Максвелл теориясеннән шундый бер нәтиҗә килеп чыга: тиз
алмашынучан электромагнитик кыр пространствода аркылы дул¬
кыннар рәвешендә таралырга тиеш. Өстәвенә бу дулкыннар җи¬
семнәрдә генә түгел, вакуумда да булырга мөмкин. Бары тик теоре¬
тик нәтиҗәләргә генә таянып, Максвелл электромагнитик дулкын¬
нарның вакуумда 300 000 км/с, ягъни яктылык тизлеге белән та¬
ралырга тиешлеген исәпләгән (яктылык тңзлеге моннан элегрәк та¬
былган була инде).
17«
Ill бүлек. Электромагнитик кыр
Сез инде беләсез, механик дулкыннарда, мәсәлән тавыш дулкын¬
нарында, энергия тирәлек кисәкчекләренең берсеннән икенчесенә
тапшырылып күчә. Бу вакытта кисәкчекләр тирбәнә башлый, ягъ¬
ни аларның тигезләнеш торышыннан тайпылышы периодик рәвештә
үзгәрә. Тавышны тапшыру өчен матди тирәлек булу шарт.
Электромагнитик дулкыннарның җисемдә генә түгел, вакуумда
да таралуы шундый сорау тудыра: электромагнитик дулкында тир¬
бәнешләрне нәрсә ясый, ягъни анда нинди физик зурлыклар перио¬
дик рәвештә үзгәрә?
Электро магнитик дулкын — бер-берсен тудыра һәм про-
странствода тарала торган алмаш электр һәм магнит кыр¬
лары системасы ул.
Магнит кырының санча характеристикасы булып магнит ин¬
дукциясе векторы В тора.
Электр кырының төп санча характеристикасы булып — электр
кырының көчэнешлелеге дип аталган һәм Е хәрефе белән бил¬
геләнгән вектор зурлык хезмәт итә. Электр кырының нинди дә бул¬
са ноктадагы көчәнешлеге Е кырның бу ноктада урнашкан уңай
берәмлек корылмага тәэсир итү көченә тигез.
Магнит һәм электр кырлары үзгәрә
дип әйтәбез икән, бу — тиңдәшле
рәвештә магнит кыры индукциясе век¬
торы В һәм электр кыры көчәнешлеле-
ге векторы Е үзгәрә дигән сүз.
Электромагнитик дулкында нәкъ
В һәм Е векторларының модульләре
һәм юнәлешләре периодик рәвештә
үзгәреп тора, ягъни тирбәнәләр.
133
нче рәсемдә электромагнитик дулкындагы электр кыры
көчэнешлелеге векторы Е һәм магнит кыры индукциясе векторы В
бер үк вакыт мизгелендә сурәтләнә. Аны Z күчәре юнәлешендә тара¬
лучы дулкынның «моменталь рәсеме» дип санарга мөмкин. В һәм
Е векторлары аша теләсә кайсы ноктада үткәрелгән яссылык —
171
Ill бүлек. Электромагнитик кыр
дулкын таралу юнәлешенә перпендикуляр, һәм бу дулкынның ар¬
кылы булуын күрсәтә.
Тирбәнешләр периодына тигез булган вакыт эчендә дулкын, Z
күчәре буйлап, үз озынлыгы кадәр күчә. Дулкын озынлыгы λ, аның
тизлеге с һәм периоды Т арасындагы нисбәтләр механик дулкыннар
өчен чыгарылган иде, алар электромагнитик дулкыннар өчен дә
дөрес:
λ = сТ = у
Максвелл электромагнитик дулкыннар булу ихтималын фәнни
яктан нигезләп кенә калмый, җитәрлек кадәр интенсив дулкыннар
табу өчен кирәкле шартларын да күрсәтә. Мондый дулкыннарны
табуның төп ысулларын карап үтик.
Үткәргечтә тирбәнүче электроннар тудырган алмаш электр кыры
бу үткәргеч тирәсендә алмаш магнит кырын барлыкка китерә,
нәтиҗәдә пространствода яңадан алмаш электр кыры хасил була
һ.б. Мондый периодик рәвештә үзгәреп торучан электромагнитик
кыр, электромагнитик дулкын хасил итеп, тирбәнүче корылмалар¬
дан барлык якларга тарала.
Шулай итеп, электромагнитик дулкыннар электр корылмала¬
рының тизләнеп хәрәкәт итүе вакытында барлыкка килә.
Максвелл теориясеннән тагын бер нәтиҗә чыга: электр кыры
көчәнешлелеге Е тизрәк үзгәргән саен, барлыкка килүче магнит
кырының индукциясе В зуррак була, ә инде магнит индукциясенең
тизрәк үзгәрүе көчәнешлелеге зуррак булган электр кыры тудыра.
Димәк, приборлар ярдәмендә чыганактан берникадәр ераклыкта
теркәп калырлык интенсив электромагнитик дулкын барлыкка
китерү өчен, Е һәм В векторларының тирбәнешләре югары ешлык¬
та булырга тиеш (секундка 100 000 һәм аннан да күбрәк тирбә¬
неш).
1888 елда немец галиме Генрих Герц электромагнитик дулкын¬
нарны алуга һәм теркәүгә ирешә. Герц тәҗрибәләре нигезендә элек-
тромагнитик дулкыннарның Максвелл тарафыннан теоретик фараз-
ланган барлык үзлекләре дә ачыкланып раслана.
Хәзер инде без әйләнә-тирәбездәге барлык пространствоның төрле
ешлыктагы электромагнитик дулкыннар белән шыгрым тулганын
беләбез.
172
Ill бүлек. Электромагнитик кыр
Хәзерге вакытта барлык электромагнитик дулкыннар озынлык¬
лары (тиңдәшле рәвештә, ешлыклары) буенча алты диапазонга бүленә
(рәс. 134).
яктылык
Рәс. 134
Диапазоннарның чикләре шартлыча гына билгеләнә, шуңа күрә,
рәсемнән күренгәнчә, күпчелек очракта күрше диапазоннар бер-бер-
сен бераз каплый.
Төрле ешлыктагы электромагнитик дулкыннар бер-берсеннән
үтеп керү сәләте, матдәдә таралу тизлеге, күренмә булуы, төсе һәм
башка үзлекләре буенча аерыла.
Электромагнитик дулкыннарны алу гаять зур фәнни һәм гамә¬
ли әһәмияткә ия. Моңа бер диапазон — радиодулкыннар мисалында
гына да ышанырга була, алар телевизион һәм радиоэлемтәдә, ра¬
диолокациядә (объектларны эзләп табу һәм аларга кадәр ераклык¬
ларны үлчәү өчен), радиоастрономиядә һәм эшчәнлекнең башка
сфераларында кулланыла.
Электромагнитик дулкыннарның тагын бер диапазоны —
күренмә яктылыкның табигате һәм аны өйрәнү тарихы турынд а
төшенчә алдагы ике параграфта бирелер.
Сораулар
1. Максвелл теориясеннән электромагнитик дулкыннарга ки
рата нинди нәтиҗәләр килеп чыга?
2. Электромагнитик дулкында нинди физик зурлыклар перио¬
дик рәвештә үзгәрә?
Ill бүлек. Электромагнитик кыр
3. Электромагнитик дулкыннар өчен дулкын озынлыгы, тизле¬
ге, тирбәнүләр ешлыгы һәм периоды арасында нинди нисбәтләр дөрес?
4. Нинди шарт үтәлгәндә, электромагнитик дулкынңарның ин¬
тенсивлыгы теркәп куярлык дәрәҗәдә була?
5. Электромагнитик дулкыннарны беренче булып кем һәм кай¬
чан ала?
6. Электромагнитик дулкыннарның 2—3 диапазонына мисал¬
лар китерегез.
7. Электромагнитик дулкыннарны куллануга мисаллар ките¬
регез.
$ 42 нче күнегү
1. Радиодулкыннар нурландыра торган антеннада корылмалар¬
ның тирбәнү периоды 10^7 с ка тигез. Бу радиодулкыннарның еш¬
лыгын табыгыз.
2. 1896 елда рус галиме A. С. Попов үзе төзегән радиосигналлар
тапшыргычы һәм алгычы ярдәмендә дөньяда беренче радиограмма¬
ны җибәрә. Ул «Генрих Герц» дигән ике генә сүздән тора. Әгәр ра¬
диосигналлар тапшыргыч белән алгыч арасын якынча 8,3 ∙ 10^7 с
эчендә үткән булса, радиограмма нинди ераклыкка җибәрелгән?
Искәрмә. Радиосигналлар — кыска вакыт аралыгында Ю2 нан
Ю9 кГц ка кадәр ешлык диапазонында нурландырыла торган элек-
тромагнитик дулкыннар ул.
3. Халыкара килешү буенча һәлакәт сигналы SOS радиодулкын¬
нарының озынлыгы 600 м булса, кораблар аны нинди ешлыкта
җибәрә?
4. Җирдән Айга җибәрелгән радиосигнал, Ай өслегеннән кайта¬
рылып, Җиргә кире кайтырга мөмкин. Радиосигнал ярдәмендә Җир
белән Ай арасын үлчәү юлын тәкъдим итегез.
Күрсәтмә. Мәсьәлә ультратавыш локациясе ярдәмендә диңгез
тирәнлеген үлчәү алымы белән чишелә (§ 41).
5. Җир белән Ай арасындагы ераклыкны тавыш яки ультратавыш
дулкыннары ярдәмендә үлчәргә мөмкинме? Җавапны нигезләгез.
§ 53. Яктылык интерференциясе
8 нче сыйныфта яктылыкның таралуын, кайтарылуын һәм сы¬
нуын өйрәнсәк тә, аның табигатен белү мәсьәләсен куймадык. Хәзер,
174
Ill бүлек. Электромагнитик кыр
электромагнитик дулкыннарнрг өйрәнүгә бәйләп, бу сорауга җавап
эзләп карыйк.
Яктылыкның табигате турында борынгы заманнардан бирле ике
караш яши. Кайбер галимнәр яктылыкны дулкын дип исәпли, икен¬
челәре исә — кисәкчекләр (корпускулалар) агышы, ди. Ләкин XIX
гасырның башларына кадәр боларның икесе файдасына да ышан¬
дырырлык раслаулар булмый.
1802 елда инглиз галиме Томас Юнг ике чыганактан килүче
яктылык бәйләмнәрен кушу тәҗрибәсен ясый. Нәтиҗәдә вакыт үтү
белән үзгәрми торган чиратлашып килүче $кты һәм караңгы поло¬
салар таба. Юнг полосалар килеп чыгу күренешен яктылык интер¬
ференциясе дип атый һәм тәҗрибә нәтиҗәләрен дөрес итеп аңла¬
тып бирә.
Сез инде тавыш дулкыннарының интерференциясе белән таныш.
Бу күренешнең асылын исегезгә төшерик.
Ике когерент дулкын (бер үк ешлыктагы һәм фазалар аермасы
даими) кушылганда, интерференция дип атала торган күренеш,
ягъни пространствода тирбәнеш амплитудаларының вакыт бу¬
енча үзгәрми торган бүленеше барлыкка килә.
Бу — пространствоның кайбер нокталарында тирбәнешләрнең
амплитудасы һәрвакыт максималь дигән сүз. Әлеге нокталарга ике
чыганактан да теләсә кайсы вакыт мизгелендә тирбәнешләр бер үк
фазаларда килә һәм шуңа күрә һәрвакыт бер-берсен көчәйтә.
Икенче нокталарда тирбәнешләр минималь амплитуда белән яса¬
ла. Бу нокталарга исә, чыганаклардан нинди ераклыкта урнашуына
карап, тирбәнешләр һәрвакыт капма-каршы фазаларда килеп җитә
һәм бер-берсен көчсезләндерә. (Ә инде тирбәнеш амплитудалары тигез
булганда, бу дулкыннар һәрвакыт бер-берсен тулысынча сүндерә.)
Башка нокталарда тирбәнешләрнең амплитудалары шулай ук
даими — кыйммәтләре иң кечкенәдән алып иң зурына кадәр арада
була.
Интерференция күренеше дулкынсыман (ягъни периодик) про¬
цессларга гына хас булганлыктан, Юнг тәҗрибәсе яктылыкның
дулкын үзлекле икәнен кире каккысыз дәлилли.
Юнг тәҗрибәсен мәктәп физика кабинетларында эшләү бик кат¬
лаулы. Шунлыктан яктылык интерференциясе күренешенең гадирәк
тәҗрибәсен карап үтик.
П5
Ill бүлек. Электромагнитик кыр
135 нче а рәсемдә тоткалы тимерчы¬
бык боҗра сабын элпәсе белән каплан¬
ган. Караңгырак бүлмәдә элпәгә нинди
дә булса яктылык (мәсәлән, сары төстәге)
төшерсәк, анда горизонталь урнашкан
сары һәм кара полосалар күренер. (Сары
төс алу өчен спиртовка ялкынына натрий
хлоридына манылган мамык кисәге кер¬
тергә мөмкин.)
Полосалар килеп чыгуның сәбәбен
135 нче б рәсемнән аңларга тырышыйк.
Ул урта өлештәге сабын элпәсенең ян¬
нан күренешен зурайтып күрсәтә. Аска
таба элпә киңәя. Бу сабын эремәсенең
авырлык көче тәэсирендә аска агып
төшүе белән бәйле.
Әйтик, элпәнең А ноктасына якты¬
лык дулкыны төшә, ди. Яктылыкның
бер өлеше алгы өслектән А ноктасында
кайтарыла, ә бер өлеше — арткы өслек¬
тән В ноктасында, элпәдән чыкканда С ноктасында кайтарыла.
А һәм С нокталарыннан чыгучы дулкыннар — когерент, ягъни
бер үк ешлыкка һәм фазаларның даими аермасына ия, чөнки алар-
ны бер үк дулкын тудыра. Бу дулкыннарның фазалар аермасы,
мәсәлән, ABC йөреше аермасының яктылык дулкыны озынлыгын¬
нан ничә тапкыр зуррак булуына бәйле. Ә йөреш аермасы элпәнең
яктылык төшкән урындагы калынлыгына бәйләнгән.
Әйтик, берничә кисемдә, элпәнең калынлыгына бәйле рәвештә,
А һәм С нокталарыннан чыккан дулкыннарның фазалары бер үк
булсын, ди. Кушылганда бу дулкыннар бер-берсен көчәйтәләр. Димәк,
элпәнең бу урынында без ачык сары сызык күрербез.
Башка кисемнәрдә элпәнең калынлыгы үзгәрәк, мәсәлән, А һәм
С нокталарыннан дулкыннар капма-каршы фазаларда чыгачак. Бу
очракта дулкыннар бер-берсен сүндерә, һәм без элпәдә караңгы по¬
лоса күрәбез.
Шулай итеп, әгәр яктылык интерференциясе күренеше күзәтелә
икән, димәк, яктылык — дулкыннар агышы дигән сүз.
176
Ill бүлек. Электромагнитик кыр
Юнг яктылыкның дулкын икәнлеген исбатлап кына калмый,
бу дулкынның озынлыгын да үлчи.
Төрле төстәге яктылыкларга дулкын озынлыкларының төрле
интерваллары туры килүе билгеле булган. Дулкын озынлыгының
иң зур кыйммәтләре кызыл төстә: 7,6 ∙ 10^7 м дан 6,2∙ 10^7 м га кадәр.
Тирбәнешләрнең ешлыгы дулкын озынлыгына кире пропорцио¬
наль булганлыктан, кызыл төскә башкалар белән чагыштырганда
иң кечкенә ешлыклар туры килә: 4,0∙ Ю14 Гц — 4,8∙ Ю14 Гц.
Дулкын озынлыгы кимү (ә ешлыклар арту) төсләрнең түбәндәге
тәртибендә: кызыл, кызгылт сары, сары, яшел, күксел, зәңгәр, миләүшә.
Бу рәттә миләүшә төс — иң кыска дулкынлы, аның дулкын озын¬
лыклары 4,5∙10^7 м — 3,8∙10^7 м интервалында, аларга ешлык¬
ларның 6,7∙ Ю14 Гц — 8,0- Ю14 Гц интервалы туры килә.
Шулай итеп, яктылыкның Юнг тарафыннан алынган интерфе¬
ренция күренешләре яктылыкның дулкын табигатьле булуы турын¬
дагы карашларны раслый.
Шул ук вакытта, физика фәненең үсеше нәтиҗәсендә, XIX га¬
сырның ахырында эксперименталь фактларның тулы бер рәте ачы¬
ла, аларны исә яктылыкның корпускуляр табигатенә нигезләнеп
кенә аңлатып була.
Шуңа күрә хәзерге вакытта дулкын теориясе дә, корпуску¬
ляр теория дә дөрес дип таныла.
Бу ике теория, бер-берсен тулыландырып, бик күп физик күре¬
нешләрне аңларга мөмкинлек бирә.
Сораулар
1. Яктылыкның табигатенә карата элек-электән нинди ике
караш яшәгән?
2. Юнг тәҗрибәсенең мәгънәсе нәрсәдә, бу тәҗрибә нәрсәне ис¬
батлаган һәм кайчан ясалган?
3. 135 нче а рәсемдәге тәҗрибә ничек үткәрелә?
4. 135 нче б рәсемнән файдаланып аңлатыгыз, ни өчен сабын
элпәсендә чиратлашкан полосалар барлыкка килә?
5. 135 нче а рәсемдәге тәҗрибә нәрсәне исбатлый?
6. Төрле төстәге яктылык дулкыннарының ешлыгы (яки дул¬
кын озынлыгы) турында нәрсә әйтергә мөмкин?
177
Ш бүлек. Электромагнитик кыр
§ 54. Яктылыкның электромагнитик табигате
XIX гасыр башында, тәҗрибәләр юлы белән, яктылык табигате¬
нең дулкын үзлеге турындагы карашлар раслана. Бу вакытта га¬
лимнәр механик дулкыннардан башка дулкыннарны белми әле.
Шунлыктан яктылык, тавыш шикелле үк, механик эластик дулкын
дип саналган.
Без инде беләбез, эластик дулкыннар бары тик матдәләрдә генә
килеп чыгарга мөмкин, чөнки матдә кисәкчекләре генә простран-
ствода таралучы эластик тирбәнешләр ясый (тавышның вакуумда
тарала алмавын раслый торган тәҗрибәне исегезгә төшерегез).
Димәк, әгәр яктылык эластик дулкын икән, аның таралуы өчен
тирәлек кирәк.
Ләкин безгә йолдызлардан килүче яктылык космик простран-
ствоның матдәләр булмаган өлкәләре аша үтә. Яктылыкның таби¬
гатенә карата дулкын карашлы галимнәр, бу фактны исәпкә алып,
галәмнең барлык пространствосы ниндидер күренмәс эластик тирә¬
лек белән тулган дигән фараз тәкъдим итәләр. Бу тирәлекне алар
яктылык йөртүче эфир дип атыйлар (эфирның булуы турындагы
идея инде XVII гасырда ук билгеле була). Яктылык нәкъ менә шушы
эфирда тарада дип уйланыла.
Шул ук вакытта яктылык йөртүче эфир турындагы фаразлар
күп кенә каршылыклар һәм бәхәсле сораулар да тудыра. Мәсәлән,
XIX гасырның икенче унъеллыгы ахырында яктылыкның аркылы
дулкын булуы ачыклана. Эластик аркылы дулкыннарның бары тик
каты җисемнәрдә генә барлыкка килүе билгеле. Моннан яктылык
йөртүче эфирның каты җисем булуы килеп чыга.
Билгеле инде, планеталар һәм башка күк җисемнәре каты эфир
аша ничек итеп каршылыксыз хәрәкәт итәләр, дигән сорау туа.
XIX гасырның икенче яртысында Максвелл теоретик юл белән
электромагнитик дулкыннар булу мөмкинлеген, аларның матдә
эчендә генә түгел, вакуумда да тарала алуын исбатлагач, яктылык
тарала торган махсус тирәлек турындагы фаразларның кирәге кал¬
мый. Максвелл теориясе буенча электромагнитик дулкыннар —
яктылык дулкыннары кебек үк, аркылы дулкыннар һәм вакуумда
300 000 км/с, ягъни яктылык тизлеге белән таралалар.
Яктылык дулкыннарының һәм электромагнитик дулкыннарның
гомуми үзлекләргә (аркылы дулкыннар булуы һәм вакуумда бер үк
тизлек белән таралулары) ия булуыннан чыгып, Максвелл, якты-
178
Ill бүлек. Электромагнитик кыр
лык — электромагнитик дулкыннарның аерым очрагы, дигән фи¬
кергә килә.
Физика фәненең үсеше бу фикерне раслый. Күренмә якты¬
лыкның электромагнитик дулкыннарның бик кечкенә диапазо¬
ны гына икәне ачыкланды: дулкын озынлыклары 3,8∙ 10^7 м дан
7,6-10^7 м га кадәр яки ешлыклары 4,0∙ Ю14 Гц тан 8,0∙ 1014 Гц
ка кадәр (рәс. 134).
Электромагнитик нурланышның ешлыгын арттырган вакытта,
аның корпускуляр үзлекләре, ягъни кисәкчекләр агышына хас бул¬
ган үзлекләре күбрәк, ә дулкын үзлекләре азрак чагыла. Электро-
магнитик дулкыннарның барлык диапазоннары арасыннан корпус¬
куляр үзлекләрне иң ачык чагылдыручысы — гамма-нурланыш (ул
да 134 нче рәсемдә күрсәтелгән).
Электромагнитик нурланышның кисәкчекләре фотоннар яки
квантлар дип атала. Гамма-квантлар турында сез алдагы бүлектә
күбрәк өйрәнерсез.
? Сораулар
1. XIX гасыр башында галимнәр яктылыкны нинди дулкын рәве¬
шендә күз алдына китергәннәр?
2. Яктылык йөртүче эфир турындагы фараз нәрсә өчен кирәк
була?
3. Яктылыкның табигате турында Максвелл нинди фараз
әйтә? Бу фикергә яктылык белән электромагнитик дулкыннар¬
ның нинди уртак үзлекләре нигез булып тора?
4. Электромагнитик нурланыш кисәкчеге ничек дип атала?
IV бүлек
АТОМ ҺӘМ АТОМ ТӨШЕНЕҢ ТӨЗЕЛЕШЕ.
АТОМ ТӨШЕ ЭНЕРГИЯСЕН КУЛЛАНУ
§ 55. Радиоактивлык — атомнарның катлаулы
төзелешен раслаучы факт
Барлык җисемнәр дә бик вак кисәкчекләрдән тора дигән фараз-
л аул ар борынгы грек фәлсәфәчеләре Левкипп һәм Демокрит тара¬
фыннан 2500 еллар элек үк әйтелгән була. Бу кисәкчекләрне атом¬
нар, ягъни бүленмәс дип атаганнар. Мондый атама белән атомның иң
вак, иң гади, инде бүленми торган кисәкчек икәнен ассызыклап
күрсәтергә тырышканнар.
Әмма XIX гасырның урталарыннан башлап, атомның бүленмәс -
леге турындагы күзаллауларны шик астына куя торган эксперимен¬
таль фактлар күренә башлый. Аларның нәтиҗәләре — атом төзеле¬
шенең катлаулы булуы һәм алар составына электр корылмалы ки¬
сәкчекләр керүе мөмкин, дигән фикер тудыра.
1896 елда француз физигы Анри Беккерель ачкан радиоактив¬
лык күренеше — атом төзелешенең катлаулы булуын раслаучы иң
ачык дәлил.
Беккерель химик элемент уранның үзлегеннән (тышкы тәэ¬
сирләрдән тыш) моңарчы билгеле булмаган күренмәс нурлар чыга¬
руын ача, аларны соңыннан радиоактив нурланыш дип атыйлар.
Радиоактив нурланыш гадәттән тыш үзлекләргә ия булганлык¬
тан, бик күп галимнәр аны өйрәнүгә керешә. Уранның гына түгел,
башка кайбер химик элементларның да (мәсәлән, радий) үзлеклә¬
реннән радиоактив нурлар чыгаруы билгеле була. Кайбер химик
элемент атомнарының үзлегеннән нурландыра алу сәләтен радио¬
активлык дип атый башлыйлар (латин сүзләреннән radio — нур¬
ландырам һәм activus — тәэсир итүчән).
180
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
1899 елда инглиз галиме Эрнест
Резерфорд җитәкчелегендә үткәрелгән
тәҗрибә нигезендә, радийның радиоак¬
тив нурланышы — бериш түгел, ягъни
катлаулы төзелешле икәнлеге ачыкла¬
на. Бу тәҗрибәнең ничек үткәрелүен
тикшерик.
136 нчы а рәсемдәге калын стеналы
кургаш савытның төбенә радий бөртеге
салынган. Радий чыгарган радиоактив
нурланыш бәйләме, тар канал аша чы¬
гып, фотопленкага эләгә (радийның нур¬
ланышы барлык якларга да юнәлә,
ләкин ул калын кургаш катламы аша
үтә алмый). Фотопластинканы ачыгайт-
кач, анда — нәкъ бәйләм эләккән урын¬
да — кара тап күренгән.
Аннан соң тәҗрибәне үзгәртәләр
(рәс. 136, б): бәйләмгә көчле магнит
кыры белән тәэсир итәләр. Бу очракта
ачыгайтылган пластинкада өч тап бар¬
лыкка килгән: беренчесе — үзәк тап —
шул ук урында, ә калган икесе үзәк тап¬
тан төрле якларга тайпылган була. Әгәр
магнит кырындагы агышлар элекке
юнәлешеннән тайпыла икән, димәк, алар
корылган кисәкчек агышлары дигән сүз.
Рәс. 136
Төрле якларга тайпылу кисәкчекләрдәге электр корылмаларының
төрле тамгалы икәнен күрсәтә. Бер агышта — бары тик уңай ко¬
рылган кисәкчекләр генә, икенчесендә тискәреләр генә була. Ә үзәк
агыш — электр корылмасы булмаган нурланыш.
Уңай корылган кисәкчекләрне — альфа-кисэкчеклэр, тискәре
корылганнарын — бета-кисэкчеклзр, ә нейтральләрен гамма-кисэк-
чеклэр яки гамма-квантлар дип атаганнар (кыскача а-кисәкчек,
р-кисәкчек һәм ү-кисәкчек, шулай ук ү-квант яки фотон дип билге¬
лиләр).
Беркадәр вакыттан соң, бу кисәкчекләрнең төрле физик харак¬
теристикаларын һәм үзлекләрен (электр корылмасын, массасын һ.б.)
181
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
өйрәнеп, шундый нәтиҗәгә киләләр: fi-кисәкчек-электрон, ә а-кисэк-
чек гелий элементының тулысынча ионлашкан атомы (ягъни ике
элетронын да югалткан гелий атомы) икән. Шулай ук ү-нурла-
нышның — ^лектромагнитик нурланышның бер төре, төгәлрәге,
бер диапазоны икәнлеге ачыклангащ (рәс. 134).
Радиоактивлык күренеше, ягъни матдәнең үзлегеннән α-, β- һәм
γ-кисәкчекләр нурландыруы, башка эксперименталь фактлар белән
беррәттән, матдәнең атомнары катлаулы төзелешле дигән фаразлар
өчен нигез булып тора.
? Сораулар
1. 1896 елда Беккерель ясаган ачыш нидән гыйбарәт?
2. Кайбер химик элемент атомнарының үзлегеннән нурланды¬
ра алу сәләтен ничек атыйлар?
3. Схемасы 136, а, б рәсемнәрдә күрсәтелгән тәҗрибә ничек
үткәрелә? Аның нәтиҗәсе буенча нәрсә ачыклана?
4. Радиоактив нурланыш составына керүче кисәкчекләр ничек
дип аталалар? Бу кисәкчекләр нәрсәдән гыйбарәт?
5. Радиоактивлык күренеше нәрсәне раслый?
§ 56. Атом модельләре. Резерфорд тәҗрибәсе
Радиоактивлык күренеше атом составына тискәре һәм уңай
корылган кисәкчекләр керә дигән фаразны нигезли (§55). Моннан
тыш, атомның тулаем алганда нейтраль икәнлеге дә билгеле.
Әлеге һәм башка фактларга нигезләнеп, инглиз физигы Джозеф
Джон Томсон 1903 елда атом төзелешенең иң беренче модельлә¬
реннән берсен тәкъдим итә. Томсон күзаллавы буенча, атом — шар
формасында, аның бөтен күләме буенча тигез бүленеп уңай корыл¬
ма урнашкан. Бу шар эчендә — электроннар, һәр электрон үзенең
тигезләнеш торышы тирәсендә тирбәнү хәрәкәте ясый. Шарның уңай
корылмасы, модуле буенча, электроннарның суммар тискәре корыл¬
масына тигез, шунлыктан тулаем алганда атомның электр корыл¬
масы нульгә тигез.
Атом төзелешенең Томсон тәкъдим иткән моделе эксперимен¬
таль тикшеренүләр таләп итә. Аерым алганда, уңай корылманың
атомның тулаем күләмендә даими тыгызлык белән бүленүен тик¬
шерү әһәмиятле була. Шуңа күрә 1911 елда Резерфорд, үзенең хез-
182
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
Рәс. 137
мәттәшләре белән берлектә, атомнарның төзелешен һәм составын
тикшерү буенча төрле тәҗрибәләр үткәрә.
Бу тәҗрибәләрнең ничек үткәрелүен аңлау өчен, 137 нче а, б рәсем¬
нәрне карыйк. Аларның икесендә дә а-кисәкчекләр нурландыручы
радиоактив матдә Р салынган кургаш савыт С сурәтләнә (а-кисәк-
чекләр — уңай электр корылмалы кисәкчекләр, корылмасы — икелә-
телгән электрон корылмасы модуленә тигез). Бу савыттан (х-кисәкчекләр
тар канал аша 15 000 км/с тирәсе тизлек белән чыгалар.
а-кисәкчекләрне турыдан-туры күзәтү мөмкин булмаганлыктан,
аларның юлына пыяла экран Э куела. Экран юка итеп махсус матдә
белән каплана, һәм аңа а-кисәкчек бәрелгән урыннарда кабынып
китүләр күзәтелә. Аларны микроскоп М ярдәмендә күзәтеп тора¬
лар. Кисәкчекләрне болай теркәү сцинтилляцияләр (кабынышлар)
методы дип атала.
Бу җайланма тулысы белән һавасы суыртып алынган савытка
урнаштырыла (а-кисәкчекләр һава молекулалары белән бәрелешеп
читкә таралмасын өчен).
183
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
Әгәр а-кисәкчекләрнең юлында каршылыклар булмаса, алар
экранга тар, җиңелчә киңәеп киткән бәйләм булып төшә (рәс. 137,
а). Ул чагында экрандагы барлык кабынып китүләр бергә кушыла
һәм зур булмаган яктылык табы хасил итә.
Ә инде а-кисәкчекләрнең юлына тикшерелә торган металлдан
юка фольга Ф куелса, матдә белән тәэсир итүче, а-кисәкчекләр, төрле
юнәлешләрдә почмаклар β ясап, таралып китә (рәсемдә өч почмак:
β , β2 һәм β3 почмаклары гына күрсәтелгән).
Экран 1 торышында булганда, иң куп кабынышлар экранның
үзәгендә урнаша. Димәк, а-кисәкчекләрнең төп өлеше фольга аша
үзенең элекке юнәлешен үзгәртмичә диярлек (кечкенә почмакларга
таралып) үтеп чыга. Экран үзәгеннән читкәрәк киткән саен, кабы¬
нышлар азая бара. Димәк, таралу почмагы β зурайган саен, бу поч¬
макларга таралган кисәкчекләр саны кискен кими.
Экранны микроскобы белән бергә фольга тирәсендә күчереп йөртеп,
шундый нәтиҗә табыла: кисәкчекләрнең бик аз сандагылары — 90°
ка якын (экранның бу торышы 2 дип билгеләнгән) почмакка, ә кайбер
ялгыз кисәкчекләр 180° тирәсенә авышкан, ягъни алар, фольга белән
тәэсир итешеп, кирегә ыргытылганнар (3 торышы).
а-кисәкчекләрнең нәкъ менә шундый зур почмакларга таралу
очрагы Резерфордка атомнар төзелешен аңлау өчен иң әһәмиятле
мәгълүматны бирә. Тәҗрибә нәтиҗәләрен анализлап, ул шундый
йомгак ясый:
а-кисәкчекләрнең мондый зур авышуы атом эчендә гадәттән
тыш көчле электр кыры булган очракта гына мөмкин. Мон¬
дый кырны гаять кечкенә (атом белән чагыштырганда) күләмдә
тупланган корылма гына тудыра алуы исәпләнә.
Электрон массасы а-кисәкчек массасыннан якынча 8000 тап¬
кыр кечерәк булганлыктан, атом составына кергән электроннар
а-кисәкчекнең хәрәкәт юнәлешен сизелерлек үзгәртә алмыйлар.
Шуңа күрә бу очракта а-кисәкчек белән атомның уңай корылган
өлеше арасындагы электрик этешү көчләре турында гына сүз алып
барырга мөмкин. Атомның уңай корылган өлеше массасы а-кисәк-
чек массасыннан күпкә зуррак.
Шулардан чыгып, Резерфорд атомның төш (планетар) моделен
тәкъдим итә (сез аны 8 нче сыйныф физика курсыннан беләсез инде).
Бу модель буенча, атомның үзәгендә уңай корылган һәм атом күләме¬
184
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
нең бик аз өлешен алып торган төш урнашкан. Төш тирәсендә масса¬
лары төш массасыннан күп тапкырлар кечерәк булган электроннар
хәрәкәт итә. Төшнең корылмасы модуле буенча электроннарның сум¬
мар корылмасына тигез булганлыктан, атом — электрик нейтраль.
Алда сурәтләнгән тәҗрибәләр нигезендә, Резерфорд атом төшләре¬
нең үлчәмнәрен бәяли ала. Атом массасына бәйле рәвештә, төшнең
диаметры Ю14 — 10^15 м тирәсе, ягъни
атомнан дистә яки йөз меңнәр тапкыр
кечерәк була (атом диаметры 10“10 м ти¬
рәсе).
138 нче рәсем а-кисәкчекләрнең
матдә атомнары аша үтү процессын төш
моделе күзлегеннән чыгып аңлата. Бу
рәсемдә төштән нинди ераклыкта очып
үтүләренә карап, а-кисәкчекләр траекто¬
риясенең ничек үзгәрүе күрсәтелгән. Төш
тудырган электр кырының көчәнешлелеге (Е), димәк, а-кисәкчеккә
тәэсир итү көче дә, төштән ераклашкан саен, шактый тиз кими бара.
Шуңа күрә кисәкчек төшкә бик якын узганда гына аның очу юнә¬
леше көчле үзгәрә.
Төшнең диаметры атом диаметрына караганда күпкә зур бул¬
ганлыктан, атом эченнән узучы а-кисәкчекләрнең күбрәк өлеше
төштән ерактарак үтә. Биредә төш тудырган кырның этү көче кимрәк
була һәм а-кисәкчекнең юнәлешен сизелерлек үзгәртә алмый. Ьәм
бик аз кисәкчекләр генә төшнең яныннан — көчле кыр өлкәсеннән
үтә һәм алар зур почмакларга этеләләр. Резерфорд тәҗрибәләреннән
шундый нәтиҗәләр алынган иде дә.
Шулай итеп, а-кисәкчекләрнең таралуын тикшерүче тәҗрибәләр
нигезендә Томсонның атом моделе яраксыз дип табыла, атом төзе¬
лешенең планетар моделе күрсәтелә һәм атом төше диаметрлары¬
ның тәртибе исәпләнә.
? Сораулар
1. Томсон тәкъдим иткән модель буенча атомны ничек сурәтләп
була?
2. 137 нче рәсем буенча а-кисәкчекләрнең таралуын тикшерү
тәҗрибәсе турында сөйләгез.
185
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
3. а-кисэкчекләрнең, фольга белән тәэсир итешеп, зур почмак¬
ларга авышуы нигезендә Резерфорд нинди нәтиҗә ясый?
4. Резерфорд тәкъдим иткән төш моделе буенча атом төзеле¬
шен аңлатыгыз.
5.138 нче рәсем буенча төш моделенә нигезләнеп, а-кисэкчекләр¬
нең матдә атомы аша ничек үтүен аңлатыгыз.
§ 57. Атом төшләренең
радиоактив әверелешләре
1903 елда (әле атом төше ачылганга кадәр) Эрнест Резерфорд
һәм аның хезмәттәше, инглиз химигы Фредерик Содди а-таркалу
(ягъни а-кисәкчекләрнең үзлегеннән нурланышы) вакытында ра¬
диоактив радий элементының икенче бер химик элементка — ра¬
донга әверелүен күрәләр.
Радий һәм радон — физик һәм химик үзлекләре буенча аеры¬
лучы бөтенләй төрле матдәләр. Радий — металл, гадәти шартларда
ул каты хәлдә була, ә радон — инерт газ. Бу химик элементларның
Д.И.Менделеев таблицасында үз урыннары бар. Аларның атомнары
массасы, төш корылмасы, электрон сүрүләрендәге электроннар саны
белән аерылып тора. Алар химик реакцияләргә төрлечә керәләр.
Төрле радиоактив препаратлар белән үткәрелгән башка тәҗ¬
рибәләр күрсәткәнчә, бер химик элементның икенчесенә әверелүе
а-таркалу вакытында гына түгел, ^-таркалуда да була икән.
1911 елда Резерфорд тарафыннан атомның төш моделе тәкъдим
ителгәннән соң (уңай корылган төш һәм аның тирәсендә хәрәкәт
итүче электроннар), радиоактив әверелешләр вакытында нәкъ менә
төшнең үзгәрешләр кичерүе бәхәскә урын калдырмый. Чыннан да,
әгәр үзгәрешләр электрон сүрүгә генә кагылса (мәсәлән, бер яки бер¬
ничә электрон югалу), атом, башка төрле физик һәм химик үзлекләргә
ия булган икенче элемент атомына түгел, шул ук элементның ионына
әверелер иде.
Радий атомы төшенең радон атомына әверелүе белән бара тор¬
ган а-таркалу реакциясе болай языла:
282≡Ra → 2‰Rn + 4He , (1)
биредә 2g®Ra — радий атомы төше, 2g∣Rn — радон атомы төше, 4He —
а-кисәкчек яки гелий атомы төше (ягъни атом- төшләре Д.И.Мен¬
делеев таблицасындагы ауомнар кебек үк тамгд^ана).
186
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
Хәрефле тамганың алдына куелган югарыгы сан — масса саны
дип, ә түбәндәгесе корылма саны (яки атом номеры) дип атала.
61 нче параграфта масса һәм корылма саннарының билгеләмә¬
ләре һәм шартлы билгеләре китерелә, ал арның физик мәгънәсе аңла¬
тыла, аларны табу юллары күрсәтелә.
Хәзергә алар турында түбәндәгеләрне белү җитә:
Бирелгән химик элемент атомы төшенең бөтен саннарга кадәр
төгәллек белән алынган масса саны — массаның бу төш массасын¬
дагы атом берәмлекләре санына тигез. (Исегезгә төшерәбез, масса¬
ның атом берәмлеге (кыскача м.а.б.) углерод 1^C атомы массасы¬
ның 1/12 енә тигез.)
Бирелгән химик элемент атомы төшенең корылма саны — бу
төш корылмасындагы элементар электр корылмалары санына
тигез. (Исегезгә төшерәбез, элементар электр корылмасы — модуле
буенча электрон корылмасына тигез булган иң кечкенә уңай яки
тискәре электр корылмасы ул.)
Болай дип әйтергә дә була: корылма саны — төшнең элемен¬
тар электр корылмаларында күрсәтелгән корылмасы ул.
Бу ике сан — масса һәм корылма саннары — һәрвакыт бөтен
һәм уңай саннар була. Аларның исемнәре булмый, чөнки алар төш
массасының һәм корылмасының берәмлек үлчәмнәрдән ничә тап¬
кыр зуррак икәнен күрсәтәләр.
(1) язылышы радий атомы төшенең, а-кисәкчек нурландыруы
нәтиҗәсендә, якынча массасының дүрт атом берәмлеген һәм ике
элементар корылмасын югалтып, радон атомы төшенә әверелүен
күрсәтә.
Бу язылыштан күренгәнчә, радиоактив таркалу процессында
масса саны һәм корылма саклану законнары үтәлә: таркала торган
радий атомы төшенең масса саны (226) һәм корылмасы (88), тиңдәш¬
ле рәвештә, таркалудан соң барлыкка килгән радон һәм гелий атом¬
нары төшләренең масса саннары суммасына (222 + 4 = 226) һәм
корылмалары суммасына (86 + 2 = 88) тигез.
Шулай итеп, Резерфорд һәм Содди ясаган ачыштан яңа нәтиҗә —
атом төшләренең катлаулы составлы булуы, ягъни ниндидер ки¬
сәкчекләрдән торуы килеп чыга. Моннан тыш, радиоактивлыкның —
кайбер атом төшләренең, үзеннэн-үзе кисәкчекләр нурландырып, баш¬
ка төрле төшләргә әверелү сәләте икәне ачыкланды.
187
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
Радиоактивлык күренеше нигезендә, галимнәр төшнең катлау¬
лы төзелешле булуын таныдылар.
Сораулар
1. а-таркалу нәтиҗәсендә радий ничек үзгәрә?
2. а- яки β-mapκaπy нәтиҗәсендә радиоактив химик элемент¬
лар ничек үзгәрә?
3. Радиоактив таркалу вакытында атомның нинди өлеше —
төшме, әллә электрон сүрүме үзгәрешләр кичерә? Ни өчен шулай
уйлыйсыз?
4. Радийның а-таркалу реакциясен языгыз һәм бу язылышта¬
гы һәр символның нәрсә аңлатуын сөйләгез.
5. Элементның хәрефле тамгаланышы алдындагы саннар ни¬
чек дип атала?
6. Масса саны; корылма саны нәрсәгә тигез?
7. Радийның а-таркалу реакциясе мисалында корылма (яки ко¬
рылма саны) һәм масса саны саклану законнарының мәгънәсен
аңлатыгыз.
8. Резерфорд һәм Содди ясаган ачышлардан нинди яңа нәтиҗә
килеп чыккан?
9. Радиоактивлык нәрсә ул?
$ 43 нче күнегү
1. Түбәндәге элементларның атом төшләре массасын (м.а.б., бөтен
саннарга кадәр) һәм корылмасын (элементар корылмаларында) та¬
быгыз: углерод 1^C5 литий ®Li; кальций *°Са.
2. Алдагы мәсьәләдә саналган һәрбер химик элементның ато¬
мында ничә электрон бар?
3. Литий ∣Li атомы төшенең массасы водород }Н атомы төше
массасыннан ничә тапкыр зуррак икәнен (бөтен саннарга кадәр
төгәллек белән) билгеләгез.
4. Бериллий ®Be атомының төше өчен билгеләгез: а) масса са¬
нын; б) төшнең массасын м.а.б. ендә (бөтен саннарга кадәр төгәллек
белән); в) төш массасының углерод 1θC атомы массасының 1/12
еннән ничә тапкыр зуррак икәнен (бөтен саннарга кадәр төгәллек
белән); г) корылма санын; д) төшнең корылмасын элементар электр
188
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
корылмаларында; е) атомдагы барлык электроннарның суммар ко¬
рылмасын элементар электр корылмаларында; ж) атомдагы элект¬
роннар санын.
5. Масса саны һәм корылма саклану законнарын кулланып,
түбәндәге р-таркалу реакциясе нәтиҗәсендә хасил булган X химик
элементы атомы төшенең масса санын һәм корылмасын табыгыз:
1JC→X+>,
биредә θe — З-кисәкчек (электрон).
Бу элементны Д.И.Менделеев таблицасында эзләп табыгыз. Ул
ничек атала?
§ 58. Кисәкчекләрне тикшерүнең
эксперименталь методлары
Төш физикасын тагын да үстерү өчен (мәсәлән, атом төшләре¬
нең төзелешен тикшерү өчен) махсус җайланмалар булдыру, алар
ярдәмендә төшләрне һәм төрле кисәкчекләрне теркәү һәм аларның
үзара тәэсир итешүләрен өйрәнү ихтыяҗы туа.
Кисәкчекләрне теркәүнең бер ысулы — сцинтилляция методы
турында 56 нчы параграфта сөйләнде. Ләкин бу метод тиешле
төгәллекне тәэмин итә алмый, чөнки экрандагы кабынышларны са¬
нау, күбесенчә күзәтүченең күрү сәләтенә кайтып кала. Моннан тыш,
озакка сузылган күзәтүләр алып
бару да уңайсыз, чөнки күзләр
тиз арый.
Кисәкчекләрне санау өчен
камилрәк прибор — Гейгер
счетчигы 1908 елда уйлап та¬
была.
Бу приборның төзелеше
һәм эш принцибы 139 нчы
рәсемдә күрсәтелә. Гейгер счет¬
чигы катод ролен үтәүче металл
цилиндрдан (тискәре корылган
электрод) һәм аның күчәре буй¬
лап тарттырылган нәзек чыбык
189
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
— анодтан (уңай электрод) тора. Катод һәм анод R каршылыгы
аша югары көчәнеш чыганагына (200 — 1000 В) тоташтырыла һәм
шуның аркасында электродлар арасында көчле электр кыры бар¬
лыкка килә.
Ике электродны да сирәкләндерелгән газ (гадәттә аргон) туты¬
рылган герметик пыяла көпшә эченә урнаштыралар.
Газ ионлашмаганда, көчәнеш чыганагы булган электр чылбы¬
рында ток булмый. Ә инде стеналары аша көпшәгә газ атомнарын
ионлаштырырга сәләтле берәр кисәкчек эләксә, көпшәдә беркадәр
санда электрон-ион парлары хасил була. Электроннар һәм ионнар
тиңдәшле электродларына юнәлә.
Әгәр электр кырының көчәнешлелеге җитәрлек кадәр зур бул¬
са, электроннар, газ молекулалары белән бәрелүләр арасында, шак¬
тый энергия туплыйлар һәм шулай ук газ атомнарын ионлашты¬
ралар: ионнар һәм газларның яңа буыны барлыкка килә, алар да
ионлаштыру процессында катнаша һ.б. Көпшәдә электрон-ион таш¬
кыны барлыкка килә һәм нәтиҗәдә чылбырдагы ток зурлыгы кыс¬
ка вакытка кинәт арта, R каршылыгында көчәнеш тә шулай арта.
Көчәнешнең счетчикка кисәкчек эләгүен аңлатучы бу импульсын
махсус җайланма теркәп (регистрацияләп) өлгерә.
Каршылык R зур булу (Ю9 Ом тәртибендә) сәбәпле, ток узган
мизгелдә көчәнешнең төп өлеше шунда төшә, шунлыктан анод белән
катод арасында көчәнеш кискен кими һәм бушану автомат рәвештә
туктала (чөнки яңа электрон-ион парлары ясау өчен бу көчәнеш
җитми). Счетчик чираттагы кисәкчекне теркәргә әзер дигән сүз.
Гейгер счетчигы нигездә электроннарны теркәү өчен хезмәт итә,
әмма ү-квантлар өчен яраклы модельләре дә бар.
Гейгер счетчигы үзе аша кисәкчекнең үтү фактын терки генә.
Микродөньяны тикшерү өчен 1912 елда уйлап табылган Вильсон
камерасы дип аталган приборның мөмкинлекләре зуррак (рәс. 140).
Вильсон камерасы пыяла капкачлы (LL) тәбәнәк пыяла цилиндр¬
дан (СС) гыйбарәт (рәсемдә цилиндрның кисеме бирелгән). Цилиндр
эчендә пешкәк Р йөри ала. Камераның төбендә кара төстәге тукыма
FF була. Бу тукыма су һәм спирт катнашмасы белән чылатыла,
шунлыктан камераның һавасы сыеклык парлары белән туендырыл¬
ган була.
Пешкәк тиз генә аска күчкәндә, камерадагы һава һәм парлар
киңәя, аларның эчке энергиясе кими, температура төшә.
190
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
Фотоаппарат
Яктылык
нурлары
бәйләме
Юка тәрәзә
Гадәти шартларда бу күренеш парларның конденсациясен (то¬
ман төшүне) китереп чыгарыр иде. Әмма Вильсон камерасында бу
хәл була алмый, чөнки конденсация төшләре дип йөртелүче кисәк¬
чекләр (тузан бөртекләре, ионнар һ.б.) алдан ук суыртып алына.
Шуңа күрә камерада температура кинәт түбәнәйгәндә, парлар үтә
туенган хәлгә килә, ягъни алар үтә тотрыксыз халәткә күчә һәм
камерада хасил булган теләсә нинди конденсация төшләре, мәсәлән,
ионнар белән конденсацияләнә.
Тикшереләсе кисәкчекләр камерага юка тәрәзә аша кертелә (кай¬
вакытта кисәкчекләр чыганагын камера эченә дә урнаштыралар).
Зур тизлек белән газ аша үтеп, кисәкчекләр үз юлында ионнар ха¬
сил итә. Бу ионнар конденсация төшләренә әверелә, ал арда бик вак
тамчылар рәвешендә парлар конденсацияләнә (су пары күбесенчә —
тискәре ионнарда, этил спирты парлары уңай ионнарда куера). Ки¬
сәкчекнең барлык юлы буйлап, тамчылардан торучы нәзек эз (трек)
барлыкка килә һәм хәрәкәт траекториясен күрергә мөмкин була.
Вильсон камерасын магнит кырына урнаштырганда корылган
кисәкчекләрнең траекторияләре кәкрәя. Кәкрәю юнәлеше буенча
кисәкчек корылмасының тамгасын, ә кәкрелек радиусы буенча аның
массасын, энергиясен, корылмасын билгеләп була.
Камерада треклар озак сакланмый, чөнки камера стеналары
җылысы белән һава җылына, һәм тамчылар парга әйләнә. Яңа эзләр
191
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
алу өчен электр кыры ярдәмендә ионнарны бетерергә, һаваны пешкәк
белән кысарга, кысылудан җылынган һаваның суынуын көтәргә һәм
яңадан киңәйтергә кирәк.
Вильсон камерасында кисәкчекләрнең трекларын, гадәттә,
күзәтеп кенә калмыйлар, фотога да төшерәләр. Моның өчен камера¬
ны 140 нчы рәсемдә күрсәтелгәнчә, сул яктан көчле яктылык бәйләме
белән яктырталар.
Төш физикасы һәм элементар кисәкчекләр физикасы өлкәсендә
Вильсон камерасы ярдәме белән күп кенә әһәмиятле ачышлар ясалды.
1952 елда уйлап табылган куыклы камера Вильсон камерасы¬
ның бер төре булып тора. Ул Вильсон камерасы принцибы белән
эшли, тик анда үтә туенган пар урынына кайнау ноктасыннан юга¬
рырак җылынган сыеклык (мәсәлән, сыек водород) файдаланыла.
Корылган кисәкчек бу сыеклык эченнән хәрәкәтләнгән вакытта, аның
траекториясе буйлап пар куыклары рәте хасил була. Куыклы каме¬
ра Вильсон камерасына караганда кызурак эшли.
Сораулар
1. 139 нчы рәсем буенча Гейгер счетчигының төзелеше һәм эш
принцибы турында сөйләгез.
2. Гейгер счетчигы нинди кисәкчекләрне теркәү өчен кулланы¬
ла?
3.140 нчы рәсем буенча Вильсон камерасының төзелеше-һәм эш
принцибы турында сөйләгез.
4. Магнит кырына урнаштырылган Вильсон камерасы ярдәмендә
Кисәкчекләрнең нинди характеристикаларын билгеләп була?
5. Куыклы камераның Вильсон камерасыннан өстенлеге нәрсәдә?
Бу приборлар нәрсә белән аерыла?
§ 59. Протон ачылу
Атом төшләренең катлаулы төзелешле булуы ачыклангач, алар-
ның нинди кисәкчекләрдән торуын өйрәнү мәсьәләсе килеп баса.
1913 елда Резерфорд, барлык химик элемент атомнарының төше
составына керүче кисәкчекләрнең берсе — водород атомы төше, дигән
фаразын тәкъдим итә.
Мондый фаразлауның нигезендә шушы чорда тәҗрибә ярдәмендә
алынган кайбер фактлар ята. Аерым алганда, химик элементларда
192
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
атом массаларының водород атомы массасыннан бөтен сан тапкыр
зуррак икәне билгеле була.
1919 елда Резерфорд а-кисәкчекләр белән азот атомы төшләре¬
нең тәэсир итешүен тикшерә.
Бу тәҗрибәдә гаять зур тизлек белән очучы а-кисәкчек азот ато¬
мы төшеннән ниндидер кисәкчекне бәреп чыгара. Резерфорд фике-
ренчә, бу кисәкчек водород атомы төше була, һәм ул аны протон
дип атый (грекча protos — беренче). Әмма бу кисәкчекләр сцинтил¬
ляция методы белән тикшерелгәнгә күрә (ягъни экранга эләккән
кисәкчекләрнең кабынып китүе), азот атомы төшеннән нинди кисәк¬
чек чыгуын төгәл билгеләп булмый.
Берничә ел үткәч, а-кисәкчек белән азот атомы төшенең тәэсир
итешү реакциясе Вильсон камерасында үткәрелгәч кенә, азот атомы
төшеннән, чынлап та, протон чыгуы раслана.
Вильсон камерасының үтә күренмәле түгәрәк тәрәзәсеннән, хәтта
гади күз белән дә, анда хәрәкәт итүче кисәкчекләрнең трекларын
(траекторияләрен) күрергә мөмкин (рәс. 141).
Рәсемдә җилпәзә кебек тара¬
лучы туры сызыклар күренә. Бу —
а-кисәкчекләрнең камера про-
странствосында азот атомы төш¬
ләренә бәрелмичә үткән эзләре.
Әмма бер а-кисәкчекнең эзе, нин¬
дидер «сәнәк» ясап, икегә аеры¬
лып китә. Бу — аерылу ноктасын¬
да а-кисәкчек азот атомы төше
белән тәэсир итешкән һәм нәтиҗә¬
дә кислород һәм водород атомна¬
рының төшләре хасил булган дигән сүз. Вильсон камерасын магнит
кырына куеп, трекларның авышу характеры буенча нәкъ менә шушы
төшләр хасил булуын ачыклаганнар.
Азот төшенең, а-кисәкчекләр белән тәэсир итешеп, кислород һәм
водород хасил итү реакциясе болай языла:
1*N + *He → 187O + }Н ,
биредә }Н символы белән протон тамгалана, ягъни массасы якынча
1 м.а.б. булган (төгәлрәге, 1,0072765 м.а.б.) һәм уңай корылмалы
элементар корылмага (ягъни электр корылмасы модуленә) тигез
Рәс. 141
193
IV бүлек. Атом Һәм атом төшенең төзелеше. Атом төше энергиясен куллану
булган водород атомы төше. Протонны 11p символы белән дә тамга¬
лыйлар.
Соңга таба а-кисәкчекнең башка элемент атом төшләре белән
тәэсир итешүе тикшерелә: бор (Вг), натрий (Na), алюминий (А1),
магний (Mg) һ.б. Нәтиҗәдә а-кисәкчекләрнең тикшерелгән барлык
төшләрдән дә протон бәреп чыгарулары ачыклана. Бу күренеш про¬
тоннар барлык химик элемент атомнарының да төш составына
керә, p,vltl әйтү өчен нигез булып тора.
? Сораулар
1. Резерфордның 1919 елда ясаган тәҗрибәсе турында сөйләгез.
2. Вильсон камерасында кисәкчек трекларының фоторәсеме
нәрсә турында сөйли (рәс. 141)?
3. Водород атомы төше башкача ничек атала һәм нинди сим¬
вол белән тамгалана? Аның массасы һәм корылмасы нинди?
4. а-кисәкчекләрнең төрле элемент атомнарының төшләре
белән тәэсир итешүен тикшерә торган тәҗрибәләр төшләрнең
составы турында нинди фаразлар ясарга мөмкинлек бирә?
4 44 нче күнегү
Азот һәм гелий төшләре тәэсир итешүдән кислород һәм
водород төшләре хасил булган төш реакциясенең язылышын
тикшерегез. Тәэсир итешүче төшләрнең суммар корылмасын
хасил булган төшләрнең суммар корылмасы белән чагышты¬
рыгыз. Нәтиҗә ясагыз, бу тигезләмәдә электр корылмасы сак¬
лану законы үтәләме?
§ 60. Нейтрон ачылу
Атом төшләре нинди кисәкчекләрдән тора, дигән сорауга про¬
тонның ачылуы гына тулы җавап була алмый. Атом төшләре про¬
тоннардан гына тора дип уйлау үзе үк каршылыкка китерә.
Бериллий (®Ве) атомының төше мисалында бу каршылыкны
аңлатырга тырышыйк.
Әйтик, ®Ве төше протоннардан гына тора, ди. Нәр протонның ко¬
рылмасы бер элементар корылмага тигез булганлыктан, төштәге про¬
тоннар саны корылма санына, бу очракта дүрткә тигез булырга тиеш.
194
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
Ә инде бериллий төше чынлап та дүрт протоннан гына торса,
аның массасы якынча 4 м.а.б. нә тигез булыр иде (чөнки һәр про¬
тонның массасы якынча 1 м.а.б.).
Әмма бу бирелгәннәргә каршы килә, чөнки бериллий атомы төше¬
нең тәҗрибәләр нәтиҗәсендә табылган массасы 9 м.а.б. нә тигез.
Шулай итеп, атом төшенә протоннардан тыш тагын ниндидер
кисәкчекләр керүе ачык аңлашыла.
Резерфордның бу турыда 1920 елда әйтелгән фаразы буенча,
төштә протон массасына якын булган, электрик яктан нейтраль ки¬
сәкчек булырга тиеш.
30 нчы еллар башында моңарчы билгесез булган нурлар ачыла.
Алар бериллийны а-кисәкчекләр белән бомбага тотканда хасил була
һәм шунлыктан бериллий нурланышы дип атала башлый.
1932 елда инглиз галиме Джеймс Чедвик (Резерфордның шәкер¬
те) бериллий нурланышының якынча протон массасына тигез мас¬
салы һәм электрик яктан нейтраль кисәкчекләр агышы икәнен Виль¬
сон камерасында үткәрелгән тәҗрибәләр ярдәмендә исбатлый.
Тикшерелә торган кисәкчекләрдә электр корылмасының булма¬
вы аларның, мәсәлән, электр кырында да, магнит кырында да тай¬
пылмавыннан килеп чыга. Ә аларның массасын башка кисәкчекләр
белән тәэсир итешүе буенча бәяләргә мөмкин.
Бу кисәкчекләрне нейтроннар дип атаганнар. Нейтронны θn
дип тамгалау кабул ителгән. Төгәл итеп үлчәүләр нейтрон массасы¬
ның 1,0086649 м.а.б.нә, ягъни протон массасыннан бик азга гына
артык икәнен күрсәтте. Күп очракларда нейтрон массасын (протон
массасы кебек үк) 1 м.а.б. итеп алалар. Шуңа күрә нейтрон симво¬
лы алдыннан берәмлек куела. Астагы нуль электр корылмасы бул¬
мауны аңлата.
? Сораулар
1. Атом төшләре протоннардан гына тора дип уйлау нинди
каршылыкка китерә? Моны мисалда аңлатыгыз.
2. Массасы якынча протон массасына тигез һәм электрик як¬
тан нейтраль кисәкчек булуы турындагы фаразны беренче булып
кем әйтә?
3. Бериллий нурланышының нейтроннар агышы икәнен кем һәм
кайчан исбатлый?
195
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
4. Нейтроннарда электр корылмасы булмавын ничек исбат¬
лыйлар? Аларның массасын ничек бәялиләр?
5. Нейтрон ничек тамгалана? Аның массасын протон массасы
белән чагыштырыгыз.
§ 61. Атом төшенең составы.
Масса саны. Корылма саны
Нейтрон ачылу вакыйгасы атом төшенең төзелешен өйрәнүгә
этәргеч бирә.
Нейтрон ачылган 1932 елда ук, совет физигы Дмитрий Дмит¬
риевич Иваненко һәм немец физигы Вернер Гейзенберг тарафын¬
нан төш төзелешенең протон-нейтронлы моделе тәкъдим ителә
һәм соңыннан аның дөреслеге тәҗрибәләр юлы белән раслана.
Протоннар һәм нейтроннар нуклоннар (латин сүзе nucleus —
төш) дип атала. Бу терминны кулланып, атом төшләре нуклоннар¬
дан тора дияргә мөмкин.
1
Төштәге нуклоннарның гомуми саны масса саны дип атала
һәм А хәрефе белән тамгалана.
Масса саны химик элементның хәрефле тамгаланышы алдын¬
нан өскә куела. Мәсәлән, азот 1*N өчен масса саны А = 14, тимер
2∣Fe өчен А = 56, уран 2g∣U өчен А = 235.
Масса саны А (ягъни төштәге нуклоннарның гомуми саны) —
массаның атом берәмлекләрендә алынып берәмлеккә кадәр
түгәрәкләнгән төш массасына (т) тигез икәне аңлашыла (чөнки
һәр нуклонның массасы якынча 1 м.а.б. нә тигез). Мәсәлән, азот
өчен А = 14, т ≈ 14 м.а.б., тимер өчен A = 56, т ≈ 56 м.а.б. һ.б.
' Төштәге протоннар саны корылма саны дип атала һәм Z
хәрефе белән тамгалана.
Мәсәлән, азот 1*N өчен Z = 7, тимер ^Fe өчен Z = 26, уран 2θgU
өчен Z = 92 һ.б. Мисаллардан күренгәнчә, корылма саны химик эле¬
ментның хәрефле тамгаланышы алдында аска куела.
196
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
һәр протонның корылмасы элементар электр корылмасына ти¬
гез. Шуңа күрә корылма саны (ягъни төштәге протоннар саны)
төшнең элементар электр корылмалары белән алынган корылма¬
лар санына тигез була. Һәрбер химик элемент өчен корылма саны
Д.И.Менделеев таблицасында атом (тәртип) номерына тигез.
'■ Теләсә кайсы химик элементның төше гомуми рәвештә zX дип
тамгалана (X — химик элементның символы).
Гадәттә, төштәге нейтроннар санын N хәрефе белән билгелиләр
(азотның химик символы белән бутамагыз). Масса саны А төштәге
протоннар һәм нейтроннарның гомуми санын аңлатканлыктан,
A = Z + N дип язарга мөмкин.
Ф Сораулар
9
1. Протоннар һәм нейтроннар бергә ничек атала?
2. Нәрсәне масса саны диләр һәм нинди хәреф белән билгелиләр?
3. Атом массасының санлы кыйммәте (м.а.б.) һәм аның масса¬
сы турында нәрсә әйтергә мөмкин?
4. Төштәге протоннар саны ничек дип атала һәм нинди хәреф
белән билгеләнә?
5. Корылма саны элемент символының кайсы ягына куела?
6. Теләсә кайсы химик элемент өчен корылма саны, төшнең ко¬
рылмасы (элементар электр корылмаларында белдерелгән) һәм
Д.И.Менделеев таблицасындагы тәртип номеры турында нәрсә
әйтергә мөмкин?
7. Теләсә кайсы химик элементның төшен гомуми рәвештә ни¬
чек билгеләү кабул ителгән?
8. Төштәге нейтроннар санын нинди хәреф белән тамгалыйлар?
9. Масса саны, корылма саны һәм төштәге нейтроннар саны
үзара ничек бәйләнгән?
£ 45 нче күнегү
1. Бериллий 4 Be атомы төшендә ничә нуклон бар? Анда ничә
протон, ничә нейтрон бар?
2. Калий is К атомы өчен билгеләгез: а) корылма санын; б) протон¬
нар санын; в) төш корылмасын (элементар электр корылмаларында);
197
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
г) электроннар санын; д) Д.И.Менделеев таблицасындагы тәртип номе¬
рын; е) төшнең масса санын; ж) нуклоннар санын; з) нейтроннар са¬
нын; и) төшнең массасын (м.а.б. ндә берәмлеккә кадәр түгәрәкләп).
3. Д.И.Менделеев таблицасы ярдәмендә билгеләгез, кайсы химик
элемент атомының: а) төшендә 3 протон бар; б) 9 электроны бар?
§ 62. Изотоплар
• Атом төзелешенең протон-нейтронлы моделе нигезендә, XX га¬
сырның беренче ике унъеллыгында ачылган кызыклы эксперимен¬
таль фактлар аңлатып бирелде.
Бу чорда бик күп галимнәр радиоактив элементларның үзлеклә¬
рен өйрәнү белән шөгыльләнә. Эш барышында төрле тәҗрибәләр
үткәрелә, шул исәптән атом төшләренең массалары үлчәнә. (Дөрес¬
рәге, ионнарның массасы үлчәнә, әмма бу очракта, төшнең, ионның
һәм атомның массаларын бер үк дип алырга мөмкин, чөнки атом¬
дагы барлык электроннарның массасы төш массасыннан исәпкә
алынмас дәрәҗәдә кечкенә.) Кайбер очракларда бер үк химик эле¬
ментта төш массасы төрле булган атомнар очрый. Мәсәлән, уран
атомының берничә төре табыла, аларның төш массалары якынча
234 м.а.б., 235 м.а.б., 238 м.а.б. һәм 239 м.а.б. нә тигез. Бу атом¬
нарның химик үзлекләре бер үк төрле. Алар химик реакцияләргә
бер үк төрле керәләр һәм бер үк кушылмалар хасил итәләр.
Химик үзлекләрнең бер үк төрле булуы бу атомнарның бары¬
сында да электрон сүрүдәге электроннар саны тигез, димәк,
төшләрнең корылмасы да тигез икәнлекне аңлата.
Әгәр атом төшләренең корылмасы бер үк төрле икән, димәк, бу
атомнар, чыннан да, бер үк химик элементныкылар (массалары үзгә
булса да) һәм Д.И.Менделеев таблицасында бер үк тәртип номеры¬
на ияб ягъни бер үк урынны алып торалар. Моннан бер химик эле¬
ментның барлык төрләре өчен дә атама килеп чыга: изотоплар
(грек сүзләре isos — бертөрле һәм topos — урын).
Изотоплар — бирелгән химик элементның атом төшләре¬
нең массасы буенча аерыла торган төрләре ул.
Төшнең протон-нейтронлы моделе ачылгач кына (ягъни изотоп¬
лар ачылганнан соң ике дистәгә якын ел үткәч), бер үк корылмалы
198
/V бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
атом төшләренең массалары ни өчен тигез түгеллеген аңлатуга
ирешәләр. Изотоп атомнарының төшендә протоннар саны бер үк,
ләкин нейтроннар саны төрлечә булуы ачык күренә. Моны водород
изотоплары мисалында аңлатыйк.
Водородның өч изотобы бар: [Н (протий), ijH (дейтерий) һәм ®Н
(тритий). Н изотобының төшендә нейтрон булмый, анда бары тик
бер протон гына бар. Тиңдәшле рәвештә, аның корылмасы элемен¬
тар электр корылмасына тигез (астагы сан), ә массасы — 1 м.а.б.
тирәсе (өстәге сан). Дейтерий (^H) төше составына ике кисәкчек
керә: протон һәм нейтрон. Шунлыктан дейтерий массасы 2 м.а.б.
тирәсе була. Тритий төше өч кисәкчектән тора: бер протон һәм ике
нейтроннан. Ь.әм тритий массасы якынча 3 м.а.б. була.
Табигатьтә изотоплар булу сәбәпле, Д.И.Менделеев таблицасын¬
да күпчелек химик элементларның чагыштырма атом массалары
вакланмалы сан белән аңлатыла. Химик элементлар гадәттә бер¬
ничә изотоп катнашмасыннан тора, шунлыктан бу элементтагы бар¬
лык изотопларның да атом төше массаларының уртача кыйммәте
күбесенчә вакланмалы сан була. Мәсәлән, хлорның 100 атомында
уртача 75 атомның массасы 35 м.а.б. һәм 25 атомның массасы 37
м.а.б. була (массалар берәмлеккә кадәр түгәрәкләнгән). Бу очракта
атом массасының уртача кыйммәте болай исәпләнә:
35 а.е.м. -75 + 37 а.е.м. -25 _
т = == 35,5 а.е.м.
100
? Сораулар
1. Изотоплар нәрсә ул?
2. Изотоп атомнары төшләренең охшашлыгы нәрсәдә?
3. Бертөрле корылмалы һәм төрле массалы төшләр булу төшнең
протон-нейтронлы моделенә нигезләп ничек аңлатыла?
4. Водород изотоплары турында сөйләгез.
5. Ни өчен Менделеев таблицасында күпчелек химик эле¬
мент атомнарының массасы вакланмалы санга тигез? Ми¬
саллар китерегез.
199
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
£ 46 нчы күнегү
Ике химик элемент 224 U һәм 2g40Th ның атом төшләре составын
чагыштырыгыз. Ал арда нәрсә уртак һәм алар нәрсә белән аерыла¬
лар? Аларның химик үзлекләре бертөрлеме? Ни өчен?
§ 63. Альфа- һәм бета-таркалу.
Күчеш кагыйдәсе
Радиоактив элемент атомының төше, а-таркалу вакытында башка
химик элемент атомының төшенә әверелеп, а-кисәкчек нурланды¬
ра. Радий радонга әверелә торган а-таркалу реакциясен искә төше¬
рик:
f86Ra → ^6R∏ + 42He.
Күргәнебезчә, радий атомы төшеннән а-кисәкчек (4He) бүленеп
чыгу нәтиҗәсендә, радийның корылмасы ике элементар корылмага
кими. Нәтиҗәдә радон атомы төше хасил була, ә аның корылма
саны радий тешенекеннән ике берәмлеккә кимрәк. Һәрбер химик
элементның корылма саны аның Д.И.Менделеев таблицасындагы
тәртип номеры белән тәңгәл килә. Димәк, радон таблица башл¬
ангычына радийга караганда ике шакмакка якынрак урнашкан. Бу
нәтиҗәне а-таркалуга дучар булган башка химик элементларга ка¬
рата да кулланырга мөмкин. Аны а-таркалу өчен күчеш кагыйдәсе
дип атыйлар:
бер химик элементның а-таркалуы вакытында хасил булган
икенче элемент Д.И.Менделеев таблицасының башына таба
беренчел урыннан ике шакмакка якынрак урнаша.
Шулай итеп, күчеш кагыйдәсе радиоактив таркалу кичергән
беренчел элементның һәм шул таркалу нәтиҗәсендә хасил булган
элементның Д.И.Менделеев таблицасында үзара ничек урнашула¬
рын билгели.
β-τapκaлy өчен дә күчеш кагыйдәсен чыгарырга мөмкин. Тик
башта Р-кисәкчек нурландыручы атом төше эчендә нинди процес¬
слар баруын белергә кирәк.
200
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
Радиоактив элемент атомының төше β-τapκaлy вакытында элек¬
трон (яки β-κπcθκ4eκ) һәм антинейтрино дип аталучы нейтраль
кисәкчек нурландыра1 * *.
Бары тик протоннар һәм нейтроннардан гына торучы уңай ко¬
рылган төштә тискәре корылган электрон кайдан килеп чыга соң?
Чынбарлыкта, билгеле бер шартлар булганда, төштәге нейтрон про¬
тонга, электронга һәм антинейтронга әверелә икән. Төштән элек¬
трон белән антинейтрино чыгып китә, ә протон кала. Нәтиҗәдә
төштәге протоннар саны бергә арта. Димәк, β-τapκaлy нәтиҗәсендә
хасил булган атомның корылма саны (Z) һәм Д.И.Менделеев таб¬
лицасындагы тәртип номеры беренчесеннән бергә артык була.
Шуңа күрә ft-таркалу өчен күчеш кагыйдәсе түбәндәгечә әйтелә:
бер химик элементның ft-таркалуы вакытында хасил булган
икенче элемент Д.И.Менделеев таблицасында беренчел элемент¬
тан соң килгән шакмакта (ягъни таблица азагына таба бер
шакмакка якынрак) урнаша.
β-τapκaлyгa мисал итеп, массив калий изотобының кальцийга
әверелү реакциясен алырга була:
t°K→4°Ca+>+°V.
Биредә °е символы белән — электрон ф-кисәкчек), ә °V сим¬
волы белән антинейтрино тамгаланган. Күргәнебезчә, беренчел
төшнең масса саны (бу очракта 40) β-τapκaлy вакытында үзгәрми.
Бу аңлашыла да, чөнки масса саны төштәге нуклоннар санына тигез
(§ 61), ә нуклоннар саны β-τapκaлy вакытында үзгәрми. Бары тик
бер нейтрон урынына бер протон барлыкка килә.
Күчеш кагыйдәсенең гомуми язылышы (ягъни теләсә нинди
элемент өчен) түбәндәгечә:
а-таркалу өчен:
tX→t42Y+⅛
1 Антинейтрино, нейтрино шикелле үк, җиңел (бәлки, массалары юк¬
тыр да!), электрик нейтраль кисәкчекләр, аларның үтеп керү сәләтләре
искиткеч көчле: алар, мәсәлән, Җир шары аша җиңел үтеп чыгалар. «Ней¬
трино» — итальян теленнән «бәләкәй нейтрон» яки «нейтрончык» дип
тәрҗемә ителә.
201
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
Р-таркалу өчен: ^x→zAγ++ ov _
а- һәм Р-таркалулар өчен күчеш кагыйдәсен, бер-берсенә бәйсез
рәвештә, 1913 елда Америка физигы Казимиж Фаянс һәм Англия
физигы Фредерик Содди бәян иткән.
а- һәм З-таркалу еш кына ү-нурланыш белән бара.
Сораулар
1. Радиоактив элементның а-таркалуы вакытында төш ни¬
чек үзгәрә?
2. а-таркалу реакциясенә мисал китерегез.
3. Ни өчен радонның атом номеры радийның атом номерыннан
ике берәмлеккә кимрәк?
4. а-таркалу өчен күчеш кагыйдәсе ничек әйтелә?
5. ft-таркалуга дучар булган атом төше ничек үзгәрә? Бу ва¬
кытта нинди кисәкчекләр нурлана? Төшнең корылмасы ничек үзгәрә
һәм ни өчен?
6. ft-таркалу өчен күчеш кагыйдәсен әйтегез.
7. ft-таркалу вакытында төшнең масса саны үзгәрәме? Ни өчен?
8. Күчеш кагыйдәсенең гомуми язылышы нинди?
9. а- һәм ft-таркалулар вакытында еш кына нинди нурланыш
була?
£ 47 нче күнегү
1. Уран изотобының 2g®U а-таркалуы нәтиҗәсендә нинди хи¬
мик элемент хасил була. Бу реакцияне языгыз.
2. Ничә Р-таркалу нәтиҗәсендә торий атомы 2gθTh төше уран
2∣jU атомы төшенә әверелә?
202
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
§ 64. Төш көчләре
Атом төшләре протоннар һәм нейтроннардан тора дигән фараз
бик күп эксперименталь фактлар белән раслана. Бу атом төше төзе¬
лешенең протон-нейтронлы моделенең дөреслеген күрсәтә.
Ләкин шундый сорау туган: ни өчен төшләр уңай корылган
протоннар арасындагы электростатик этешү көчләре тәэсирендә
аерым нуклоннарга таркалмый икән?
Исәпләүләр күрсәтүенчә, нуклоннар гравитацион яки магнетик
табигатьле тартылу көчләре хисабына бергә тотылып тора алмый¬
лар, чөнки бу көчләр электростатик көчләрдән күп тапкырлар
кимрәк.
Атом төшләренең тотрыклылыгы турындагы сорауларга җавап
эзләп, галимнәр мондый фаразлау тәкъдим итә: төштәге барлык
нуклоннар арасында ниндидер аерым бер төр тартылу көчләре тәэ¬
сире бар, алар протоннар арасындагы электростатик этешү көч¬
ләреннән күп тапкырлар зуррак. Аларны төш көчләре диләр.
Төш көчләре турындагы бу фараз дөрес булып чыга. Шул ук
вакытта төш көчләренең якыннан тәэсир итүчән икәне ачыклана:
10^15 м арада алар электростатик үзара тәэсирдән 100 тапкыр тирә¬
се зуррак, әмма инде 10“14 м арада исәпкә алынмаслык дәрәҗәдә
кечкенә була. Икенче төрле әйткәндә, төш көчләре төшнең үз
үлчәмнәре белән чагыштырырлык араларда гына тәэсир итә.
Сораулар
1. Атом төшләре протоннар һәм нейтроннардан тора дигән
фаразга бәйле рәвештә нинди сорау килеп туа? Бу сорауга җавап
бирү өчен галимнәргә нинди яңа фаразлау тәкъдим итәргә туры
килә?
2. Төштәге нуклоннар арасындагы тартылу көчләре ничек дип
атала һәм аларга нинди үзенчәлекләр хас?
$ 48 нче күнегү
Сез ничек уйлыйсыз, төштәге нуклоннар арасында гравитаци¬
он тартылу көчләре (ягъни бөтендөнья тартылу көчләре) тәэсир
итәме?
203
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
§ 65. Бәйләнеш энергиясе. Масса дефекты
Төшне аерым, үзара тәэсир итешми торган (ирекле) нуклоннарга
бүлгәләү өчен, төш көчләрен җиңү эшен эшләргә, ягъни төшкә бил¬
геле күләмдә энергия бирергә кирәк. Киресенчә, ирекле нуклоннар¬
ны төшкә туплаганда шундый ук энергия бүленеп чыга (энергия
саклану законы буенча).
Төшне аерым нуклоннарга таркату өчен кирәкле булган ми¬
нималь энергия төшнең бәйләнеш энергиясе дип атала.
Төшнең бәйләнеш энергиясе зурлыгын ничек итеп билгеләргә
мөмкин?
Бу энергияне исәпләп табуның иң гади юлы күренекле галим
Альберт Эйнштейн тарафыннан ачылган масса һәм энергиянең
үзара бәйләнеше законына нигезләнә.
Әлеге закон буенча, кисәкчекләр системасының т массасы белән
бу системаның тикторыш энергиясе, ягъни эчке энергиясе Ео ара¬
сында туры пропорциональ бәйлелек бар:
E0=mcz, (1)
биредә с — яктылыкның вакуумдагы тизлеге.
Димәк, әгәр кисәкчекләр системасының тикторыш энергиясе
нинди дә булса процесслар нәтиҗәсендә Δ Ео 1 зурлыгына үзгәрә икән,
ул бу система массасының ∆τn зурлыгына тиңдәшле үзгәрешен дә
китереп чыгара һәм әлеге зурлыклар арасындагы бәйләнеш түбәндәге
тигезлек белән күрсәтелә:
яки '
ΔE0 = ∆znc2. (3)
Шулай итеп, ирекле нуклоннар төшкә бәрелгәндә энергия бүле¬
неп чыгу аркасында (энергияне бу вакытта нурланган фотоннар алып
китә), нуклоннар массасы да кимергә тиеш.
1Γpeκ хәрефе Δ («дельта») белән физик зурлыкның үзгәрешен билге¬
лиләр, ул үзгәрешле зурлыкның символы алдына куела.
204.
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
Икенче төрле әйтсәк, төшнең массасы һәрвакыт аны төзегән
нуклон массалары суммасыннан кечерәк.
Төш массасы ∆m белән аны төзегән нуклоннарның суммар мас¬
сасы арасындагы аерма болай языла:
∆m∙ = (Zmp + Nmn)- Mτ f (4)
биредә Mτ — төш массасы, Z һәм N — төштәге протоннар һәм нейт¬
роннар саны, ә тр һәм тп — ирекле протон һәм нейтрон массасы.
(4) формуласында ∆τn зурлыгы масса дефекты дип атала.
Масса дефектының булуы күп санлы тәҗрибәләр белән раслана.
(3) формуласын кулланып, мәсәлән, бер протоннан һәм бер ней¬
троннан торучы дейтерий ≡ Н (авыр водород) атомы төшенең бәйләнеш
энергиясен Ео, ягъни төшне протонга һәм нейтронга таркату өчен
кирәкле энергияне исәплик.
Моның өчен иң элек дейтерий атомы төшенең массасын һәм
нуклон массаларының ∆m якынча кыйммәтләрен тиңдәшле табли¬
цалардан алып, бу төшнең масса дефектын исәплибез. Таблица
мәгълүматлары буенча протон массасы якынча 1,0073 м.а.б., нейт¬
ронныкы — 1,0087 м.а.б., дейтерий төшенеке — 2,0141 м.а.б. Димәк,
∆τn = (1,0073 м.а.б. + 1,0087 м.а.б.) - 2,0141 м.а.б. = 0,0019 м.а.б.
Әгәр без бәйләнеш энергиясен джоульләрдә табарга теләсәк, мас¬
са дефектын килограммнарда алырга кирәк. 1м.а.б. = 1,6605 ∙10^27
кг икәнен исәпкә алып табабыз:
∆τn = l,6605∙ Ю27 кг 0,0019 = 0,0032 Ю 27 кг.
Масса дефектының бу кыйммәтен (3) формуласына куябыз:
ΔE0 =0,0032 ∙10^27κr∙ (2,9979-108 J2 = 0,0288 Ю11 К^М-м =
= 0,0288 Ю’11 Дж.
Теләсә нинди төш реакциясе вакытында үзара тәэсир итешүче
һәм шушы тәэсир нәтиҗәсендә хасил булган төшләрнең һәм кисәк¬
чекләрнең массалары билгеле булса, (3) формуласы белән бу реак¬
ция барышында бүленеп чыккан яки йотылган энергияне исәпләп
табарга мөмкин.
• 205
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
Сораулар
1. Төшнең бәйләнеш энергиясе дип нәрсә атала?
2. Теләсә нинди төшнең масса дефектын исәпләү формуласын
языгыз.
3. Төшнең бәйләнеш энергиясен масса дефекты буенча исәпләү
формуласын языгыз.
ман тарафыннан ачыла.
Рәс. 142
§ 66. Уран төшләренең бүленүе
Нейтроннар белән бомбага тотканда уран төшләренең бүленү
күренеше 1939 елда немец галимнәре Отто Ган һәм Фриц Штрасс-
Бу күренешнең механизмын карыйк.
142 нче а рәсемдә — уран ( 29325U) атомы
төшенең шартлы сурәте. Артык нейтрон
йотып, төш тәэсирләнә һәм, деформация¬
ләнеп, сузынкы формага керә (рәс. 142, б).
Төштә көчләрнең ике төре тәэсир итү¬
ен без инде беләбез: протоннар арасын¬
дагы электростатик этешү көчләре —
алар төшне җимерергә омтыла һәм бар¬
лык нуклоннар арасындагы төш көчләре
— аларның тартылу көче аркасында төш
таркалмый. Тик төш көчләре — якын
арада тәэсир итүче көчләр, шунлыктан
сузынкы төштә алар инде бер-берсеннән
артык ераклашкан кисәкләрне тотып
тора алмый. Электростатик этешү көчләре тәэсирендә, төш ике
кисәккә бүленә, һәм алар, ике якка гаять зур тизлек белән очып
китеп, бу вакытта 2—3 нейтрон нурландыралар (рәс. 142, в).
Шулай итеп, төшнең эчке энергиясенең бер өлеше очып тара¬
лучы кыйпылчыкларның һәм кисәкчекләрнең кинетик энергия¬
сенә күчә. Кыйпылчыклар тирәлектә тиз тормозланалар һәм алар¬
ның кинетик энергиясе тирәлекнең эчке энергиясенә (ягъни аны
төзегән кисәкчекләрнең үзара тәэсир итешү һәм җылылык энергия¬
ләренә) әверелә.
206
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
Берьюлы бик күп сандагы уран төшләре бүленгәндә, уранны
әйләндереп алган тирәлекнең эчке энергиясе, димәк, аның темпера¬
турасы да бик нык арта (ягъни тирәлек җылына).
Шулай итеп, уран төшләренең бүленү реакциясе вакытында
тирәлеккә энергия бүленеп чыга.
Атом төшләрендә тупланган энергия иксез-чиксез. Мәсәлән, 1 г
урандагы барлык төшләр дә бүленсә, 2,5 т нефть янганда аерылып
чыккан кадәр энергия бүленеп чыгар иде.
? Сораулар
1. Уран төшләрен нейтроннар белән бомбага тотканда бүленү
күренеше кайчан ачыла?
2. Ни өчен төшнең бүленүе ул нейтронны йоту тәэсирендә де¬
формацияләнгәч кенә башланып китә?
3. Төшнең бүленүе нәтиҗәсендә нәрсәләр хасил була?
4. Төш бүленгәндә аның эчке энергиясенең бер өлеше нинди энер¬
гиягә әверелә?
5. Уран төше кисәкчекләре тирәлектә тормозланганда, аның
кинетик энергиясе нинди төр энергиягә әверелә?
6. Уран төше бүленү реакциясе ничек бара: энергия тирәлеккә
бүленеп чыгамы, әллә, киресенчә, йотыламы?
§ 67. Чылбырлы реакция
Атом электростанцияләрендә атом төшенең эчке энергиясен
электр энергиясенә әверелдерү өчен, төш бүленүнең чылбырлы ре¬
акцияләреннән файдаланалар.
Уран изотобы 29325 U атомы төшләренең чылбырлы бүленү реак¬
циясен тикшерик. 143 нче рәсемдә өстә — уран атомының төше,
нейтрон эләккәннән соң ул, өч нейтрон нурландырып, ике кисәккә
бүленгән. Бу нейтроннарның икесе — тагын ике төшнең бүленү
реакциясен китереп чыгарган, бу юлы инде дүрт нейтрон аерылган.
Алар, үз чиратында, дүрт төшне бүлгәннәр һәм инде бусында тугыз
нейтрон нурланган һ.б.
Чылбырлы реакция барсын өчен, һәрбер төш бүленгәндә 2—3
нейтрон барлыкка килүе һәм аларның икенче төшләрне бүлгәләүдә
катнаша алуы кирәк.
207
IV бүлек. Атом һәм* атом төшенең төзелеше. Атом төше энергиясен куллану
Рәсемдә күрсәтелгән чылбырлы реакция схемасында уран кисә¬
гендәге ирекле нейтронның гомуми саны вакыт узу белән ташкын
сыман арта. Тиңдәшле рәвештә, төшләрнең бүленүләре саны да, ва¬
кыт берәмлегендә бүленеп чыккан энергия дә кинәт арта. Шуңа күрә
мондый реакция шартлау характерында була (ул атом бомбасы
эчендә бара).
Вакыт узу белән ирекле нейтроннар саны кими бара торган
икенче вариант та бар. Бу очракта чылбырлы реакция туктала.
Димәк, мондый реакцияне дә электр энергиясен җитештерүдә
кулланып булмый.
Тыныч максатларда вакыт узу белән ирекле нейтроннар саны
үзгәрми торган чылбырлы реакция энергиясен генә кулланырга
Нейтроннар санын ничек итеп һәрвакыт даими калдырырга була?
Бу проблеманы хәл итү өчен, чылбырлы реакция бара торган уран
кисәгендә нинди факторларның ирекле нейтроннар санын арттыра
яки киметә алуын белергә кирәк.
Шундый факторларның берсе булып уранның массасы тора. Эш
шунда: төш бүленгәндә нурландырылган һәр нейтрон да башка
төшләрне бүлүдә катнаша алмый (рәс. 143). Әгәр уран кисәгенең
массасы (димәк, үлчәмнәре дә) артык кечкенә булса, бик күп нейт¬
роннар, үз юлларында төш очратырга өлгермичә дә, бу кисәктән очып
чыгалар, ягъни бу нейтроннар реакцияне дәвам итү өчен кирәк бул¬
208
/V бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
ган яңа буын нейтроннар тудыруда катнашмый. Бу очракта чыл¬
бырлы реакция туктый. Реакция тукталмасын өчен, уран массасын
критик дип аталучы билгеле бер кыйммәткә кадәр арттырырга кирәк.
Ни өчен массаны арттырганда чылбырлы реакция булу ихтима¬
лы арта? Кисәкнең массасы зуррак булган саен, аның үлчәмнәре дә
зурая һәм нейтроннар үтә торган юл да озыная. Бу вакытта нейт¬
роннар белән төшләрнең очрашу мөмкинлеге үсә. Тиңдәшле рәвештә,
төш бүленү һәм нейтрон нурландыру саннары да арта.
Уранның билгеле бер критик массасында төшләр бүленүдән
хасил булган нейтроннар саны югалган нейтроннар санына
(төшләр тарафыннан бүленмичә генә йотылган һәм кисәктән
чыгып киткән) тигез була.
Шуңа күрә аларның гомуми саны үзгәрешсез кала. Бу очракта
чылбырлы реакция, туктамыйча һәм шартлау характерында бул¬
мыйча, озак вакытлар дәвам итәргә мөмкин.
Чылбырлы реакция була ала торган иц аз уран массасы
критик масса дип атала.
Әгәр уранның массасы критик массадан артып китсә, ирекле
нейтроннар саны кинәт арта һәм чылбыр реакциясе шартлау ки¬
тереп чыгара, ә кимесә — ирекле нейтроннар җитмәү сәбәпле, ре¬
акция туктый.
Нейтроннар югалуны (төшләргә бәрелмичә ураннан атылып чы¬
гуны), уран массасын арттыру хисабына гына түгел, махсус кайтар¬
гыч тышча ярдәмендә дә киметергә мөмкин. Моның өчен уран ки¬
сәген нейтроннарны әйбәт кайтара торган (мәсәлән, бериллий)
матдәдән эшләнгән тышча эченә урнаштыралар. Бу тышчадан кай¬
тарылып, нейтроннар уранга кире керергә һәм төшләрне бүлүдә кат¬
нашырга мөмкин.
Массадан һәм кайтаргыч тышчадан тыш та, чылбырлы реак¬
циянең барышына йогынты ясый торган берничә фактор бар.
Мәсәлән, әгәр уран кисәгендә башка химик элемент катнашма¬
лары артык күп булса, алар нейтроннарның күпчелек өлешен йота
һәм реакция туктала.
Реакция барышына йогынты ясый торган тагын бер фактор —
уранда нейтрон акрынайткычлары булу. Мәсәлән, уран-235 төшләре
209
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
күбесенчә акрын нейтроннар тәэсирендә бүленә, ә төшләр бүленгәндә
җитез нейтроннар хасил була. Җитез нейтроннарны акрынайткач,
уран-235 төшләре аларның күбрәк өлешен эләктереп ала һәм алар
яңадан бүленә. Акрынайткычлар сыйфатында графит, су, авыр су
(аның составына дейтерий — водородның масса саны 2 гә тигез
булган изотобы керә) һәм башка матдәләр файдаланыла. Бу матдәләр
нейтроннарны йотмый диярлек, бары акрынайталар гына.
Шулай итеп, чылбырлы реакция бару мөмкинлеге уран массасы,
андагы катнашмаларның микъдары, тышча һәм акрынайткыч булу
һәм башка факторлар белән билгеләнә.
Шар формасындагы уран-235 кисәгенең критик массасы якын¬
ча 50 кг га тигез. Уранның тыгызлыгы бик зур булганлыктан, бу
кисәкнең радиусы 9 см гына тәшкил итә.
Акрынайткыч һәм кайтаргыч тышча кулланып һәм катнашма¬
лар микъдарын киметеп, уранның критик массасын 0,8 кг га кадәр
киметүгә ирешәләр.
Ф Сораулар
1. 143 нче рәсемнән файдаланып, чылбырлы реакция барышы¬
ның механизмын аңлатыгыз.
2. Уранның критик массасы нәрсә ул?
3. Уранның массасы критик массадан ким булса, чылбырлы ре¬
акция барамы? Ни өчен?
4. Уранның массасы критик массасыннан күбрәк булса, чыл¬
бырлы реакция ничек бара? Ни өчен?
5. Уран кисәгендә ирекле нейтроннар санын нинди факторлар
хисабына арттырырга һәм шуның белән чылбырлы реакция булды¬
рырга мөмкин?
§ 68. Теш реакторы.
Атом тешләренең эчке энергиясен электр
энергиясенә әверелдерү
Төш реакторы — идарә ителешле төш реакциясен тормышка
ашыручы җайланма ул.
Төш реакциясе белән идарә итү — урандагы ирекле нейтроннар¬
ның арту тизлеген көйләү һәм аларның санын даими калдырудан
210
IV булек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
гыйбарәт. Бу очракта чылбырлы реакция, туктамыйча һәм шарт¬
лау характерын алмыйча, кирәк кадәр вакыт дәвам итә ала.
Реакторның төзелешен һәм эш принцибын тикшерик. Анда бүле¬
нүче матдә сыйфатында (аны ягулык, шулай ук төш ягулыгы да диләр),
нигездә, уран-235 кулланыла. Табигый уранда бу изотоп чылбыр ре¬
акциясе өчен җитәрлек түгел (0,7% кына), шуңа күрә табигый уран¬
ны баеталар, ягъни андагы уран-235 не 5% ка җиткерәләр.
Уранның бу изотобы белән эшли торган реакторны акрын нейт¬
роннарда эшләүче төш реакторы диләр. Бу — уран-235 нең акрын
нейтроннар тәэсирендә эффектив бүленүе сәбәпле шулай атала. Төшләр
бүленгәндә күбесенчә җитез нейтроннар хасил булганлыктан, аларны
акрынайтырга кирәк була. Моның өчен әлеге ягулык белән эшләүче
реакторда нейтроннарны акрынайткыч кулланыла.
Рәс. 144
144 нче а рәсемдә акрын нейтроннарда эшләүче реакторның төп
өлешләре күрсәтелгән. Актив зонага уран кендекләр рәвешендәге
төш ягулыгы (алар рәсемдә күрсәтелмәгән) һәм нейтроннарны ак¬
рынайткыч, бу очракта су урнаштырыла.
Ьәрбер уран кендекнең массасы критик массадан кечерәк, шуңа
күрә бер генә кендектә чылбырлы реакция була алмый (бу хдаеф-
сезлек максатында махсус шулай эшләнә). Реакция барлык уран
кендекләрне дә актив зонага тыгып бетергәч, ягъни уран массасы
критик кыйммәтенә ирешкәч башлана.
211
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
Актив зона нейтроннарны кайтара торган матдә катламы (кай¬
таргыч) һәм нейтроннар белән башка кисәкчекләрне тоткарлый
торган саклагыч бетон тышча белән әйләндереп алынган.
Реакция белән нейтронны эффектив йота торган көйләгеч кен¬
декләр идарә итә. Ал арны актив зонага тулысынча тыгып бетергән
очракта чылбырлы реакция бара алмый. Реакторны эшләтеп җибәрү
өчен көйләгеч кендекләрне акрынлап чыгаралар, реакция башлан¬
гач чыгару туктала.
Бу реакция процессында хасил булган нейтроннар һәм төш кый-
пылчыклары, зур тизлекләр белән таралып, суга килеп эләгәләр, анда
кислород һәм водород атомнарына кинетик энергиянең бер өлешен
биреп акрынаялар. Бу вакытта су җылына, ә акрынайган нейтрон¬
нар күпмедер вакыттан соң яңадан уран кендекләргә эләгәләр һәм
төшләрне бүлүдә катнашалар.
Реакторның актив зонасы трубалар ярдәмендә җылы алмаштыр-
гыч белән тоташа һәм беренче йомык контурны төзи. Бу контурда су
әйләнешен насослар тәэмин итә. Ә актив зонада атом төшләренең эчке
энергиясе хисабына җылынган су, җылы алмаштыргыч аша үтеп, икенче
контурның уралма трубаларындагы суны җылыта һәм парга әйләндерә.
Шулай итеп, актив зонадагы су нейтроннарны акрынайтып кына
калмый, җылылыкны алып китүче җылы йөрткеч ролен дә үти.
144 нче б рәсемдә пар энергиясен электр энергиясенә әверелдерә
торган җайланмаларның схемасы күрсәтелгән. Пар турбинаны
әйләндерә, ә ул, үз чиратында, электр тогы генераторының роторы¬
на әйләнү хәрәкәте бирә. Эшләгән пар, конденсаторга эләгеп, суга
әверелә. Аннан соң цикл яңадан кабатлана.
Шулай итеп, атом электростанцияләрендә электр тогы алганда,
энергиянең түбәндәге әверелешләре бара: уран атомы төшләрнең
эчке энергиясенең бер өлеше —> нейтроннар һәм төш кыйпылчык-
ларының кинетик энергиясе → суның эчке энергиясе парның эчке
энергидсе —> суның эчке энергиясе → парның кинетик энергиясе →
турбина роторының һәм генератор роторының кинетик энергиясе
—> электр энергиясе.
Сораулар
1. Төш реакторы нәрсә ул?
2. Төш реакциясе белән идарә итү нидән гыйбарәт?
3. Реакторның төп өлешләрен санап чыгыгыз.
212
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
4. Актив зонада нәрсәләр урнашкан?
5. Һәр уран кендек массасының критик массадан ким булуы ни
өчен кирәк?
6. Көйләгеч кендекләр ни өчен кирәк? Алардан ничек файдала¬
налар?
7. Реакторның беренче контурында су нинди икенче функцияне
(нейтроннарны акрынайтудан тыш) үти?
8. Икенче контурда нинди процесслар бара?
9. Атом электростанцияләрендә электр тогы алу процессында
нинди энергия әверелешләре була?
§ 69. Атом энергетикасы
Кешелек алдында торган иң мөһим проблемаларның берсе —
энергия чыганакларын табу проблемасы. Энергия куллану шулкадәр
тиз үсә, хәтта бүгенге көнгә билгеле булган ягулык запаслары ча¬
гыштырмача кыска вакыт эчендә бетәргә дә мөмкин.
Мәсәлән, күмернең ышанычлы саналган запаслары — якынча
350 елга, нефтьнең — 40 елга, табигый газның 60 елга гына
җитәрлек.
«Энергетик ачлык» проблемасын яңартылучан дип йөртелүче
чыганаклар энергиясе дә (су, җил, кояш, диңгез дулкыннары, Җир¬
нең тирән катлаулары җылылыгы) хәл итә алмый, чөнки алар без¬
нең ихтыяҗның иң күбе 5—10% ын гына канәгатьләндерә. Шуңа
күрә XX гасыр урталарында энергиянең яңа чыганакларын эзләп
табу зарурлыгы туа.
Хәзерге вакытта энергия белән тәэмин ителешкә төш энергети¬
касы лаеклы өлеш кертә. 1940 елга кадәр күпчелек галимнәрдә төш
физикасы фәнни кызыксыну гына уята, аның гамәли кулланылы¬
шы исәпкә алынмый. Мәсәлән, 1937 елда Резерфорд төш энергия¬
сен беркайчан да гамәли файдалану өчен җитәрлек итеп алып бул¬
маячак дип саный.
Әмма 1942 елда ук АКШта Энрико Ферми җитәкчелегендә бе¬
ренче төш реакторы төзелә. Европадагы беренче реактор 1946 елда
Советлар Союзында Игорь Васильевич Курчатов җитәкчелегендә
сафка баса.
1954 елда безнең илебездә (Обнинск шәһәрендә) дөньяда берен¬
че атом электростанциясе (АЭС) төзелеп бетә. Аның егәрлеге зур
213
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
булмый — 5000 кВт кына. Хәзерге заман АЭСларының егәрлеге
йөзләрчә тапкыр артыграк.
АӘСларның башка төрдәге электростанцияләрдән өстенлеклә¬
ре күп. Аларның төп өстенлеге — АЭСның эшләве өчен бик аз микъ¬
дардагы ягулык кирәк. (1 г уранда тупланган энергиянең 2,5 т нефть
янгандагы энергиягә тигез булуын искә төшерегез.) Шуңа күрә атом
электростанцияләрен эксплуатацияләү җылылык станцияләреннән
күпкә арзан (чөнки аларда ягулыкны чыгару һәм транспортлау өчен
чыгымнар бик зур).
Дөрес, җылылык станцияләрен (ТЭС) төзү арзангарак төшә. Шуңа
күрә бүгенге көнгә атом һәм җылылык станцияләренең бәяләрен
чагыштырып була. Әмма киләчәктә атом энергетикасы файдалы¬
рак булачак.
АЭСның икенче өстенлеге (дөрес эксплуатацияләгәндә) — алар¬
ның ТЭСлар белән чагыштырганда экологик яктан чиста булуын¬
нан гыйбарәт. Билгеле, АЭС калдыкларында радиоактив газлар һәм
кисәкчекләр була. Әмма алардагы радиоактив төшләрнең (радио-
нуклидларның) күпчелек өлеше, радиоактив булмаганнарга әвере¬
леп, бик тиз таркала. Ә инде озак яшәүчән радионуклидларның саны
һәм аларның нурланыш куәте чагыштырмача зур түгел. Шунлык¬
тан АЭС төзелгән районнарда яшәүче халык өчен өстәмә радиация
йөкләнеше табигый радиация фоныннан процентның унынчы өлеш¬
ләре кадәр генә артып китә.
Күмер ягып эшләүче электр станцияләре исә әйләнә-тирә мо-
хиткә озак яшәүчән радионуклидлар чыгаручы төп чыганакларның
берсе булып тора. Чөнки күмердә һәрвакыт радиоактив матдәләр¬
нең микрокатнашмасы була, алар, яну продуктлары белән бергә
чыгып, якын тирәлеккә утыра һәм ТЭС тирәсендәге көлле кырлар¬
да туплана.
Мәсәлән, Екатеринбургтан 80 км ераклыктагы Рефта ТЭСының
көлле кырларында аның эшчәнлеге дәверендә 7 кг га кадәр уран,
торий, радий һәм башка радиоактив изотоплар тупланган.
Моннан тыш, ТЭСларда кулланыла торган органик ягулыкта
(күмер, нефть, газ) 1,5 тән 4,5% ка кадәр күкерт була. Ягулык ян¬
ганда хасил булган күкерт ангидриды, фильтрлар һәм чистарту си¬
стемалары аша үтсә дә, өлешчә атмосферага чыгарыла. Анда атмос¬
фера дымы белән кушылып, сульфат кислотасы хасил итә һәм яңгыр¬
лар белән бергә җиргә ява. Мондый кислота яңгырлары үсемлекләргә
214
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
коточкыч зыян китерә, туфракның структурасын боза һәм составын
үзгәртә (аны элекке хәленә кайтару өчен берничә йөз ел кирәк).
Елгалар энергиясен куллану да күңелсез экологик нәтиҗәләргә
китерә. Моңа бик зур җир мәйданнарын югалту (сусаклагычлар
төзелү һәм шуның аркасында сазлыклар барлыкка килү), елгалар¬
ны буып куеп, балыкларны һәлак итү һ.б. керә.
Кояш һәм җил энергиясен файдаланып, кирәкле зур егәрлектә¬
ге электростанцияләр төзү өчен дә шактый иркен территорияләр
кирәк икән.
Төш энергетикасына алда саналган негатив күренешләр кагыл¬
мый. Әмма бу — АЭСлар бернинди дә җитди проблемалар тудыр¬
мый икән дигән сүз түгел әле.
Хәзерге вакытта төш энергетикасына квалификацияле тәнкыйть
аның принципиаль өч проблемасы тирәсенә тупланган: атом төш
коралы таралуга булышлык күрсәтү, радиоактив калдыклар һәм
аварияләр булу ихтималы.
Беренче проблема бөтендөнья бердәмлеге кысаларында гына хәл
ителә ала. Аны хәл итүгә, аерым алганда, ООН каршындагы Атом
энергиясе буенча халыкара агентлыкның (МАГАТЭ) эшчәнлеге зур
өлеш кертә. Ул 1957 елда оешкан, атом-төш коралын таратмау һәм
төш энергиясен тыныч максатларда дөрес куллануның торышын
тикшерә.
Радиоактив калдыкларны зарарсызландыру, нигездә, өч мәсьә¬
ләне хәл итүгә кайтып кала: 1) реактор эшләгәндә хасил булган
калдыкларны киметү максаты белән, технологияләрне камилләш¬
терү; 2) консолидацияләү (ягъни бергә туплау, бәйләү) һәм әйләнә-
тирәгә таралу куркынычын киметү өчен, калдыкларны эшкәртү; 3)
төрле типтагы каберлекләр төзү юлы белән калдыкларны ышаныч¬
лы изоляцияләү.
Бу бурычларны үтәү өчен, барлык АЭСларның да проектларын¬
да сыек калдыкларны каты хәлгә әверелдерүче җайланмалар эшләү
каралган. Санкт-Петербург, Тверь һәм башка бик күп АЭСларда алар
инде эшли, калганнарында эксперименталь тикшерү уза яки гамәлгә
кертелергә әзерләнгән.
Моннан тыш, төш ягулыгын кабат эшкәртү заводларында калдык¬
ларны пыялага әверелдерәләр. Газсыман калдыклар чистартыла.
Санап кителгәннәрдән тыш, радиоактив калдыклар проблема¬
сын чишү юнәлешендә башка чаралар да күрелә. Ә инде АЭСлар-
215
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
ның куркынычсызлыгына килгәндә, МАГАТЭның бу өлкәдәге эшчән-
легенә куркынычсызлык стандартларын эшләү (АЭС урнаштыру өчен
урын сайлауга, проектлаштыруга, эксплуатацияләүгә һ.б. кагыла),
МАГАТЭ әгъзасы булган илләргә консультацияләр бирү (мәсәлән,
аварияләр очрагында МАГАТЭга керүче илләргә ярдәм итү, үсеп
килүче илләргә иминлек мәсьәләләрен хәл итү буенча булышлык
итү һәм башка аспектлар буенча) керә.
Атом станцияләрендә булып узган аварияләрне анализлау, про¬
филактика буенча киңәшләр бирү, куркынычсызлыкны анализлау¬
ның заманча методларын гамәлгә кертү һәм башка бик күп чара¬
лар белән дә МАГАТЭ экспертлары шөгыльләнә. Бу чаралар бөтен¬
дөнья АЭСларының иминлек дәрәҗәсен күтәрүгә булышлык итә.
Сораулар
1. Нәрсәләргә бәйле рәвештә XX гасыр уртасында энергиянең
яңа чыганакларын табу зарурлыгы туа?
2. АЭСның ГЭСтан төп ике өстенлеген атагыз.
3. Хәзерге заман атом энергетикасының принципиаль өч про¬
блемасын атагыз.
4. Атом энергетикасы проблемаларын хәл итүгә мисаллар ки¬
терегез.
§ 70. Радиациянең биологик тәэсире
Радиоактив нурланышның билгеле бер шартларда тере организм¬
нарның сәламәтлегенә куркыныч тудыруы һәркемгә билгеле. Ра¬
диациянең тереклек ияләренә тискәре йогынтысы ни сәбәпле килеп
чыга соң?
Эш шунда:()а-, β- һәм ү-кисәкчекләр матдә аша үткәндә, молеку¬
ла һәм атомнарыннан электроннар бәреп чыгарып, аны ионлашты¬
ралар. 'Тере тукыманың ионлашуы бу тукыманы төзүче күзә¬
нәкләрнең тереклек эшчәнлеген боза, ә бу тулаем организмның сәла¬
мәтлегенә тискәре йогынты ясый.
Радиациянең ни дәрәҗәдә һәм нинди характерда тискәре йогын¬
ты ясавы берничә факторга бәйләнгән, мәсәлән, бу җисемгә ионлашты¬
ручы кисәкчекләр агышы белән нинди энергия бирелә, бу җисемнең
массасы нинди һ.б. Кеше үзенә тәэсир итүче кисәкчекләрдән никадәр
216
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
күбрәк энергия алса һәм аның массасы никадәр кечерәк булса (ягъни
һәрбер масса берәмлегенә зуррак энергия туры килсә), радиация алучы
кешенең организмы шулкадәр җитдирәк зарарлана.
Нурланучы матдә (аерым алганда, организм тукымалары)
тарафыннан үзенә йотылган һәм масса берәмлегенә исәпләнгән
ионлаштыручы нурланыш энергиясе — йотылган нурланыш
дозасы (D) дип атала.
Йотылган нурланыш дозасы D җисем тарафыннан йотылган энер¬
гия Е саны белән җисем массасы т чагыштырмасына тигез:
Е
D = — (1)
т
СИда йотылган нурланыш дозасы булып 1 грэй (1 Гр) санала.
Е
D = — формуласыннан 1 Гр =
т
1 Дж
1 кг
икәне килеп чыга. Димәк, 1 кг .
массалы җисемгә 1 Дж нурланыш энергиясе туры килсә, йотылган
нурланыш дозасы 1 Гр га тигез дигән сүз.
Билгеле бер очракларда (мәсәлән, тереклек ияләренең йомшак
тукымаларын рентген яки ү-нурланыш белән нурландырганда), йо¬
тылган дозаны рентгеннар (Р) белән үлчәргә мөмкин: 1 Гр якынча
100 Р га тигез.
Шунысы бәхәссез: йотылган нурланыш дозасы никадәр зуррак
булса, организмны бу нурланыш шулкадәр күбрәк зарарлый (башка
шартлар бер үк булганда).
Ләкин ионлаштыручы нурланыш нәтиҗәсендә күрелгән зарар¬
ны дөрес итеп бәяләү өчен, шулай ук, йотылган дозалары тигез
булганда, нурланыш төрләренең төрле зурлыктагы биологик эф¬
фект ясавын да исәпкә алырга кирәк.
Теләсә нинди ионлаштыручы нурланышлар китереп чыгарган
биологик эффектларны рентген яки ү-нурланыш эффекты белән ча¬
гыштырып бәялиләр. Мәсәлән, йотылган дозалар бер үк булганда, а-
нурланыш тәэсирендә биологик эффект ү-нурланыш эффектыннан
20 тапкыр күбрәк, җитез нейтроннарның эффекты ү-нурланышка
караганда 10 тапкыр артык, Р-нурланыш белән ү-нурланышның
биологик эффектлары тигез.
217
IV бүлек.. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
Шунлыктан а-нурланышның сыйфат коэффициенты (К) —
20 гә, җитез нейтронның — 10 га, ү-нурланышның (рентген һәм
З-нурланышныкы кебек) — 1 гә тигез дип исәпләнә.
Шулай итеп, сыйфат коэффициенты К бу тор нурланыш-
ныц тере организмга тәэсире нәтиҗәсендә радиация куркыны¬
чы ү-нурланыш тәэсире белән чагыштырганда ничә тапкыр
зуррак икәнне күрсәтә (йотылган дозалар тигез булганда).
Бер үк дозада йотылган төрле нурланышлар төрле биологик эф¬
фект ясаганлыктан, бу эффектларны үлчәү өчен эквивалент доза
(Н) дип аталучы берәмлек кертелгән.
Эквивалент доза Н йотылган доза D белән сыйфат коэффициен¬
ты К тапкырчыгышына тйгез:
H=D∙K. (2)
Эквивалент доза йотылган доза белән бер үк берәмлекләрдә дә
үлчәнергә мөмкин, ләкин аны үлчәү өчен махсус берәмлекләр дә
бар. Халыкара берәмлекләр системасында эквивалент доза берәм¬
леге булып зиверт (Зв) хезмәт итә. Шулай ук аның өлеш берәм¬
лекләре: миллизиверт (мЗв), микрозиверт (мкЗв) һ.б. да кулла¬
ныла.
(2) формуласыннан аңлашылганча, рентген, ү- һәм р-нурланыш-
лар өчен 1 Зв (К = 1 булганнар өчен) 1 Гр йотылган дозага тигез, ә
нурланышның башка барлык төрләре өчен 1 Гр дозаны бу нурла¬
нышның сыйфат коэффициентына тапкырларга кирәк.
Тере организмга ионлаштыручы нурланыш тәэсирен бәя¬
ләгәндә, кайсы органның сизгерлеге нинди икәнен дә искә алыр¬
га кирә. Мәсәлән, эквивалент доза бер үк булганда, үпкәдә рак
авыруы килеп чыгу ихтималы калкансыман биздәгегә караганда
зуррак була.
Икенче төрле әйткәнчә, һәрбер органның һәм тукыманың бил¬
геле бер радиация хәвефе коэффициенты бар (үпкә өчен ул 0,12 гә,
ә калкансыман биз өчен 0,03 кә тигез).
Йотылган һәм эквивалент дозалар нурландыру вакытына да
бәйле (ягъни нурланыш белән тирәлекнең тәэсир итешү вакыты¬
на ). Башка барлык шартлар да бертөрле булганда, нурландыру ва¬
кыты зуррак булган саен, бу дозалар да арта, ягъни вакыт эчендә
туплана.
218
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
Радиациянең табигый фоны дигән төшенчә дә бар. Радиацион
фонның чыганаклары булып космик нурланышлар, Җир астында¬
гы радиоактив матдәләр һ.б. тора. Әлеге табигый фонның тәэсире
нәтиҗәсендә кеше ел саен 2∙10~3 Гр га тигез булган доза ала. Мон¬
дый доза сәламәтлеккә тискәре йогынты ясамый.
Радиоактив препаратлар һәм башка нурланыш чыганаклары белән
эшләүче белгечләр өчен мөмкин саналган чик доза — елга 0,05 Гр.
Радиациядән саклану чараларын да белергә кирәк. Радиоактив
препаратларны кулга тотып карау катгый тыела — аларны озын
саплы махсус кыстыргычлар белән тоталар.
а-нурланыштан саклану аеруча җиңел, чөнки аның үтеп керү-
чәнлеге түбән һәм ул, мәсәлән, кәгазь бите, кием, тире белән дә то¬
тылып кала. Шул ук вакытта организм эченә үтеп кергән а-кисәк-
чекләр (ризык, һава, ачык яралар аша) зур куркыныч тудыра.
р-нурланышның үтеп керүчәнлеге зуррак булганлыктан, аннан
саклану да кыенрак. Р-нурланыш һавада 5 м араны үтә ала; ул орга¬
низм тукымаларына да үтеп керергә сәләтле (якынча 1—2 см га).
Бу нурланыштан саклагыч чара булып, мәсәлән, берничә миллиметр
калынлыктагы алюминий хезмәт итәргә мөмкин.
γ-нурланыш тагын да зуррак үтеп керә алу сәләтенә ия, ул кургаш
яки бетонның калын катламы белән тоткарлана. Шуңа күрә ү-радио-
актив препаратларны калын стеналы кургаш контейнерларда саклый¬
лар. Шул сәбәпле төш реакторында кешеләрне ү-нурлардан һәм төрле
кисәкчекләрдән (а-кисәкчекләр, нейтроннар, төш бүленү кыйпылчык-
лары һ.б.) саклый торган калын бетон катлам кулланалар.
Сораулар
1. Радиациянең тереклек ияләренә негатив тәэсире нидән гый¬
барәт?
2. Йотылган нурланыш дозасы дип нәрсә атала? Ул нинди фор¬
мула буенча билгеләнә һәм нинди берәмлекләрдә үлчәнә?
3. Әгәр башка барлык шартлар бер үк булса, нинди доза орга¬
низмга күбрәк зыян ясый: зуррагымы, әллә кечерәгеме?
4. Ионлаштыручы нурланышның төрле төрләре тере организмда
нинди зурлыктагы биологик эффект тудыра? Мисаллар китерегез.
5. Нурланышның сыйфат күрсәткече нәрсәне күрсәтә? α-, β-, ү-
һәм рентген нурланышы өчен ул нинди зурлыкларда?
219
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
6. Нурланышның эквивалент дозасы дип аталган зурлык ни
сәбәпле һәм нәрсә өчен кертелә? Ул нинди формула буенча исәпләнә
һәм нинди берәмлекләрдә -үлчәнә?
7. Ионлаштыручы нурланышның тере организмга тәэсирен
бәяләүдә тагын нинди ике факторны исәпкә алырга кирәк (энергия,
нурланыш төре һәм җисем массасыннан башка)?
8. Радиоактив кисәкчекләр һәм нурланышлар тәэсиреннән сак¬
лану чаралары турында сөйләгез.
§ 71. Радиоактив изотопларны
табу һәм куллану
(өстәмә уку өчен)
Табигатьтә очрый торган радиоактив изотоплар табигый
изотоплар дип атала. Мәсәлән, уранның, торийның табигый
радиоактив изотоплары була. Әмма күпчелек химик элемент¬
лар табигатьтә тотрыклы (ягъни радиоактив булмаган) хәлендә
генә очрый.
1934 елда француз галимнәре Ирен һәм Фредерик Жолио-
Кюрилар радиоактив изатопларны ясалма юл белән — төш реак¬
цияләре нәтиҗәсендә алу мөмкинлеген ачыклыйлар. Мондый
изотоплар ясалма дип атала.
Соңрак барлык химик элементларның да ясалма изотоплары
табыла. Хәзерге вакытта якынча 2000 радиоактив изотоп билге¬
ле, тик аларның 300 е генә — табигый изотоплар.
Ясалма радиоактив изотопларны табу өчен, гадәттә, төш ре¬
акторлары һәм элементар кисәкчек тизләткечләре кулланыла.
Мондый элементлар җитештерүгә специальләшкән сәнәгать
тармагы да бар.
Хәзерге вакытта радиоактив изотоплар фәнни һәм гамәли эш-
чәнлекнең төрле сфераларында (техника, медицина, авыл хуҗа¬
лыгы һ.б.) киң кулланыла. Бу эшләрдә тамгалы атомнар мето¬
ды дип аталучы ысул кулланыла.
Бу методның асылын медицинада кулланыла торган мисал
буенча аңлатыйк. Кешенең канына бик аз (сәламәтлек өчен за¬
рарсыз) микъдарда билгеле бер радиоактив элемент кертелә һәм
ул кан белән организм буйлап тарала. Аннан соң әлеге эле¬
220
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
ментның радиоактив нурланышы, бу кеше тирәсендә куелган
приборлар ярдәмендә, төрле юллар белән теркәлеп барыла.
Нәтиҗәдә, мәсәлән, нинди дә булса эчке органның рәсемен алыр¬
га мөмкин. Бу рәсем буенча органның үлчәмнәре һәм форма¬
сы, аның төрле өлешләрендә изотопларның югары яки түбән
концентрациясе турында фикер йөртергә мөмкин. Шулай ук
эчке органнарның радиоизотопларны нинди тизлек белән туп¬
лавына яки чыгаруына карап, аларның функциональ хәлен
(ягъни эшчәнлеген) бәяләп була. Барлык бу фактлар авыруга
дөрес диагноз куярга ярдәм итә.
Тамгалы атомнар методы ярдәмендә шулай ук кан әйләнеше
системасы эшендәге төрле үзгәрешләрне тикшерәләр, шешләрне
табалар (чөнки нәкъ менә аларда кайбер радиоизотоплар тупла¬
на), организмда матдәләр алмашын өйрәнәләр. Бу метод ярдәмендә,
мәсәлән, чагыштырмача кыска гына вакыт эчендә кеше организ¬
мының тулысынча яңаруы билгеле булды. Бу бары тик кан соста¬
вына керә торган тимергә генә кагылмый, чөнки организмда ти¬
мер запаслары беткәннән соң гына ул аны ризыктан үзләштерә
башлый.
Медицинада радиоактив изотоплар диагностикада гына түгел,
кайбер авыруларны, мәсәлән, рак шешләрен, базед авыруын һ.б.
дәвалауда кулланыла.
Бик аз дозада гына кулланылганга күрә, радиацион диагнос¬
тика һәм дәвалау вакытында радиоизотопларның организмга
нурланыш тәэсире пациентлар өчен куркыныч түгел.
Тамгалы атомнар методы авыл хуҗалыгында да кулланыла.
Аның ярдәмендә төрле ашламаларның үсемлекләр тарафыннан
ничек үзләштерелүен, аларның үсемлекләрнең үсүенә һәм уңышы¬
на ничек йогынты ясавын өйрәнәләр.
Техникада тамгалы атомнарны, мәсәлән, двигательдәге кай¬
бер частьларның тузу дәрәҗәсен билгеләү өчен кулланалар.
Тамгалы атомнардан тыш, радиоизотопларны куллануның баш¬
ка ысуллары да бар. Чагыштырмача бик аз дозадан да төрле
микробларның, бөҗәк личинкаларының һ.б. һәлак булуы мәгълүм.
Бу исә медицина инструментларын стерильләштерү, продуктлар¬
ны консервлау, чәчүлекләрдә корткычларны юк итүдә радиоизо¬
топларны кулланырга мөмкинлек бирә.
221
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
§ 72. Термотеш реакциясе
Сез инде XX гасыр урталарында яңа энергия чыганакларын эзләп
табу проблемасы туганын беләсез. Шул сәбәпле галимнәрнең игъти¬
барын термотеш реакцияләре җәлеп итә.
Йөзләрчә миллион тәртибендәге градус температура ас¬
тында җиңел төшләрнең (водород, гелий һ.б. кебек) кушылу
реакциясе термотөш реакциясе дип атала.
Югары температура төшләргә җитәрлек кадәр зур кинетик
энергия бирү өчен кирәк: шушы шарт үтәлгәндә генә төшләр, элек¬
трик этешү көчләрен җиңеп, төш көчләре тәэсире зонасына эләк¬
кәнче якыная алалар. Ә инде мондый якын араларда төшләрнең
тартылу көчләре электрик этешү көчләреннән күпкә артып китә
һәм шунлыктан төшләр синтезы (ягъни кушылу, берләшү) гамәлгә
ашырыла.
66 нчы параграфта уран мисалында авыр атомнарның бүле¬
нүе вакытында энергия аерылып чыгу мөмкинлеген күрдек. Җи¬
ңел төшләр очрагында энергия кире процесста — аларның синте¬
зы вакытында аерылып чыга. Җиңел төшләр синтезы реакциясе
авыр төшләр бүленү реакциясенә караганда энергетик яктан отыш¬
лырак та әле (әгәр бер нуклонга туры килә торган энергияләрне
чагыштырсак).
Термотөш реакциясенә мисал итеп водород изотоплары (дейте¬
рий һәм тритий) кушылуны күрсәтергә мөмкин, нәтиҗәдә гелий
хасил була һәм нейтрон нурлана:
1Н + ?Н → ⅛e + o∏
Бу — галимнәр тормышка ашырган беренче термотөш реакция¬
се. Ул термотөш бомбасында бара һәм идарә ителми торган (шарт¬
лау) характерда була.
Алда билгеләп үтелгәнчә, термотөш реакцияләрендә бик күп
микъдардагы энергия аерылып чыга. Әмма бу энергияне тыныч
максатларда куллану өчен идарә ителүле термотөш реакцияләрен
ясый белергә кирәк. Мондый реакцияләрне гамәлгә ашыруда төп
222
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
кыенлыкларның берсе — җайланма эчендә югары температуралы
плазма (тулысынча диярлек ионлашкан газ, аның эчендә төшләр
синтезы бара) булдырып тору. Плазма җайланманың стеналарына
тияргә тиеш түгел, югыйсә стеналарның парга әйләнүе мөмкин. Плаз¬
маны чикләнгән пространствода, стеналардан билгеле бер ераклык¬
та тотып тору өчен, хәзерге вакытта бик көчле магнит кырларын
кулланалар. Тик әле бу методка камиллек җитеп бетми.
Термотөш реакцияләре Галәмнең эволюциясе, аерым алган¬
да, андагы химик матдәләрнең әверелешләре процессында мөһим
роль уйный.
Кояшта бара торган термотөш реакцияләре барышында Җирдә
яшәүчеләргә тереклек бирүче энергия аерылып чыга.
? Сораулар
1. Нинди реакцияне термотөш реакциясе диләр?
2. Ни өчен термотөш реакциясе бик югары температураларда
гына барырга мөмкин?
' 3. Кайсы реакция энергетик яктан файдалырак (бер нуклонга
исәпләнгәндә): җиңел төшләр синтезымы яки авыр төшләр бүле¬
нүме?
4. Термотөш реакциясенә мисал китерегез.
5. Термотөш реакцияләрен тормышка ашырудагы төп кыен¬
лыкларның берсе нидән гыйбарәт?
6. Җирдә тереклекнең яшәвендә термотөш реакцияләре нинди
роль уйный?
§ 73. Элементар кисәкчекләр. Антикисәкчекләр
(өстәмә уку өчен)
Төрле матдәләрнең атомнары төзүче кисәкчекләрне — элект¬
рон, протон һәм нейтронны — элементар кисәкчекләр дип атаган¬
нар. «Элементар» сүзе бу кисәкчекләр — беренчел, иң гади, башка¬
ча бүленми һәм үзгәрми дигәнне күздә тоткан.
Әмма тиздән бу кисәкчекләрнең барысының да үзгәрмәс түгел
икәне беленгән. Алар барысы да үзара тәэсир итешкәндә бер-
берсенә әверелергә сәләтле.
223
ιv бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
Шуңа күрә хәзерге заман физикасындагы «элементар кисәкчекләр»
термины, гадәттә, үзенең төгәл мәгънәсендә түгел, ә материянең атом
да яки атом төше дә булмаган иң вак кисәкчекләренең зур төркемен
атап йөртү өчен кулланыла (протонны исәпкә алмаганда, протон —
водород атомы төше булса да, элементар кисәкчекләргә керә).
Хәзерге вакытта 350 дән артык элементар кисәкчек билгеле. Бу
кисәкчекләрнең үзлекләре искиткеч күп төрле. Алар бер-берсеннән
массасы, электр корылмасының тамгасы һәм зурлыгы, яшәү вакы¬
ты (ягъни кисәкчекнең оешу мизгеленнән алып аның нинди дә булса
башка кисәкчеккә әверелү мизгеле арасы), үтеп керә алу сәләте (ягъни
матдә аша уза алу сәләте) һәм башка сыйфатлары белән аерыла.
Мәсәлән, күпчелек кисәкчекләр — «кыска гомерле», секундның
миллионнан ике өлешеннән артык яшәми, ә атом төшеннән читтә
яшәүче нейтронның уртача яшәү вакыты — 15 мин.
Элементар кисәкчекләрне тикшерү өлкәсендә 1932 елда бик мөһим
ачыш ясала: Америка физигы Карл, Дейвид Андерсон магнит кыры¬
на урнаштырылган Вильсон камерасында билгесез кисәкчек эзен таба.
Эзенең характеры буенча (кәкрелек радиусы, бөгелү юнәлеше һ.б.) га-
ζ, Кургаш
Рәс. 145
лимнәр аның уңай корылган электрон¬
га охшаш кисәкчек булуын билге¬
ләгәннәр. Бу кисәкчекне позитрон дип
атаганнар.
Шунысы кызык: позитронның бу¬
лу ихтималын эксперименталь юл бе¬
лән ачылуына бер ел кала инглиз га¬
лиме Поль Дирак теоретик рәвештә
фаразлап әйткән була (ул уйлап тап¬
кан тигезләмәдән нәкъ менә шундый
кисәкчек булуы килеп чыга). Моннан
тыш, Дирак аннигиляция (юкка чыгу) һәм электрон-позитрон
пары туу дип йөртелүче процессларны да алдан күрә. Электрон
белән позитронның очрашып, ү-квантка (фотонга) әверелеп юкка
чыгуы аннигиляция була. Ә ү-квантның нинди дә булса массив төш
белән бәрелүеннән электрон-позитрон пары туа.
Бу ике процессны да тәҗрибәдә беренче тапкыр 1933 елда
күзәтүгә ирешә, ү-нурлар кургаш пластина аша үткән вакытта кур¬
гаш атомы белән ү-квантлар бәрелешүе нәтиҗәсендә электрон һәм
позитрон хасил була. 145 рәсемдә аларның треклары сурәтләнгән.
224
IV бүлек. Атом һәм атом төшенең төзелеше. Атом төше энергиясен куллану
Бу тәҗрибә магнит кырына урнаштырылган Вильсон камерасында
бара. Трекларның бер үк кәкрелек радиуслары — кисәкчек масса¬
ларының тигезлеге, ә төрле якларга кәкрәюе электр корылмалары¬
ның капма-каршы тамгалары турында сөйли.
1955 елда тагын бер антикисәкчек — антипротон (аның бу¬
луы да Дирак теориясеннән килеп чыга), ә бераз соңрак антинейт¬
рон ачыла. Антинейтрон, нейтрон кебек үк, электр корылмасыз, тик
аның антикисәкчек икәнлеге бәхәссез, чөнки ул аннигиляциядә һәм
нейтрон-антинейтрон пары туу процессында катнаша.
Антикисәкчекләр табу мөмкинлеге галимнәрне антиматдә ясау
идеясенә алып килә. Антиматдәнең атомнары түбәндәгечә төзелергә
тиеш була: атомның үзәгендә — антипротоннар һәм антинейтрон¬
нардан торучы тискәре корылган төш, ә төш тирәли позитрон әйләнеп
йөри. Тулаем алганда, атом нейтраль. Бу фикер эксперименталь
юл белән раслана. 1969 елда Серпухов шәһәрендә совет физиклары
протон тизләткече ярдәмендә антигелий атомы төшләрен таптылар.
Хәзерге вакытта барлык билгеле элементар кисәкчекләрнең дә
диярлек антикисәкчекләре табылды.
Бер-берсе белән төш көчләре ярдәмендә тәэсир итешә ала торган
элементар кисәкчекләр адроннар дип атала.
Адрон төркемнәре гаять күп санлы. Адроннарга, мәсәлән, про¬
тон һәм нейтрон керә.
1964 елда барлык адроннарның тагын да беренчелрәк кисәк¬
чекләрдән — кварклардан торуы турында фараз тәкъдим ителә.
Мәсәлән, протон һәм нейтрон составына өчәр кварк керә. Кварклар
„2 1
вакланмалы корылмага ия дип тә фаразлыйлар: θe һәм θe-
XX гасырның 60 нчы еллары ахырында — 70 нче еллары ба¬
шында үткәрелгән экспериментларның нәтиҗәләре адроннар эчендә
кварклар булуын раслый.
Хәзерге вакытта кварклар чын элементар кисәкчекләр, ягъни
материянең беренчел элементы булып исәпләнә.
Адроннардан аермалы буларак, төш көчләре ярдәмендә тәэсир
итешми торган кисәкчекләр дә бар. Мондый кисәкчекләр лептон¬
нар дип атала. Лептоннар төркеменә алты кисәкчек (аларның берсе —
электрон) һәм алты тиңдәш антикисәкчек керә.
Лептоннар, кварклар кебек үк, чын элементар кисәкчекләр бу¬
лып санала.
22б
ЛАБОРАТОР ЭШЛӘР
*
1 нче лаборатор эш
Башлангыч тизлексез
тигез тизләнешле хәрәкәтне тикшерү
/вариант
Эшнең максаты: Борыс хәрәкәтенең тигез тигезләнешле булуына
ышану, аның тизлеген һәм моменталь тизлеген табу.
Җиһазлар: җисемнәрнең хәрәкәтләрен өйрәнү приборы, озын¬
лыгы 300 мм һәм киңлеге 20 мм булган миллиметрлы һәм күчер¬
геч кәгазь тасмалар, муфталы һәм кыстыргычлы штатив.
226
Лаборатор эшләр
Приборның төзелеше һәм эшләү тәртибе
146 нчы а рәсемдә сурәтләнгән прибор үзара тоташкан
ике өлештән (өске 1а һәм түбәндәге 16) торучы улактан
гыйбарәт. Улакның өске өлешендә тирбәткеч (2, вибратор)
урнашкан.
Тирбәткечнең суккыч (3) куелган хәрәкәтчән өлеше бар
(рәс. 146, б).
Борыска 4 кәгазь һәм күчергеч тасмалар (5) беркетелә.
Бу тасмалар тирбәткечнең хәрәкәтчән өлешендә суккыч
астыннан уздырылалар һәм кыскычлар (6) белән кысып
куелалар.
Тирбәткечне алмаш ток челтәренә тоташтырып, кноп¬
кага (7) баскач, хәрәкәтчән өлеш Т = 0,12 с интервалы белән
тирбәнә башлый. Кәгазьне ычкындыру белән, борыс улак
буйлап шуып китә. Тасмада нокталар рәвешендә суккыч¬
ның бәргән эзләре кала (рәс. 147).
1 иче бирем. Борысның авыш яссылык буйлап тигез
тизләнеш белән хәрәкәт итүен ачыклагыз.
Теоретик нигезләүләр
Хәрәкәтнең тигез тизләнү характерында булуына,
мәсәлән, түбәндәге закончалык ярдәмендә ышанырга
мөмкин:
Si:s2:s3:...sn 1:4:9:...: n2,
биредә s1≈s2ιs3ι...sn— борысның, хәрәкәт башланудан алып,
t1, t2=2t1, t3=3t1 ^л=п^1 вакыт аралыкларында ясаган күчеш
векторлары модульләре (§ 8 не карагыз).
Күрсәтелгән закончалык үтәлсә, хәрәкәт — тигез тизлә¬
нешле дигән сүз.
Эшкә күрсәтмәләр
1. Дәфтәрегездә үлчәү һәм исәпләү нәтиҗәләрен язып
бару өчен 3 нче таблицаны күчереп сызыгыз.
Рәс. 147
3 нче таблица
t, с
о
0,02
0,04
90*0
90*0
0,08
0,10
0,12
0,14
0,16
0,18
0,20
cq
О
0,26
0,28
0,30 J
S, мм
0
227
Лабоаратор эшләр
2. Эшләү өчен җайланманы 146 нчы а рәсем буенча җыегыз.
3. Тирбәткечне электр челтәренә ялгагыз, кнопкага (7) басыгыз
һәм аны, кыскычны (6) ычкындырып, борыс төшеп туктаганчы ба¬
сып торыгыз.
4. Кәгазь тасманы ычкындырыгыз. Андагы нуль ноктасы белән
башка тамгалар араларын үлчәгез. Алар 0,02 с, 0,04 с, 0,06 с, ..., 0,3 с
мизгелләренә туры килүче s1, s2, s3,..., s15 ераклыклары булыр. Нәти¬
җәләрне 3 нче таблицага языгыз.
5. -∣∣∙, -∣p ..., чагыштырмаларын исәпләгез, нәтиҗәләрне бөтен
саннарга кадәр түгәрәкләгез.
6. Исәпләү нәтиҗәләрен, түбәндәге тигезләмәнең уң ягын язып
бетереп, чагыштырмалар рәте рәвешендә языгыз:
s1: s2: s3: s4: s5: s6: s7: s8: s9: s10: s11: s12: s13: s14: s15= 1: ..., биредә
S1 8, , ,
бу очракта s1 урынына - 1, s, урынына 2 3 не һ.б. язу күздә тотыла.
sι S1
7. Борыс хәрәкәтенең характеры турында нәтиҗә ясагыз.
2 нче бирем. Борысның хәрәкәт тизләнешен билгеләгез.
1. 8 =
at1
2
формуласыннан а ны s һәм t аша күрсәтегез.
2. Экспериментлар юлы белән алынган саннарны кулланып, тиз¬
ләнешнең кыйммәтен ике тапкыр исәпләп карагыз: мәсәлән, i10= 0,2
с һәм аңа туры килгән s10 белән, аннары t15= 0,3 һәм аңа туры кил¬
үче s15 белән, (t һәм s ның кечерәк кыйммәтләрен алу тәкъдим
ителми, чөнки кыйммәтләр кечерәк булган саен, табылган тизлә¬
нешнең хатасы да зуррак була.)
3. Тизләнешнең уртача кыйммәтен (ayp) табыгыз.
3 нче бирем. Төрле вакыт мизгелләрендә борысның моменталь
тизлеген табыгыз һәм моменталь тизлек белән вакыт арасындагы
бәйлелек графигын төзегез.
1. и = at формуласы буенча хәрәкәт башланып, 0,1, 0,2, 0,3 с
узган мизгелләрдә борысның моменталь тизлекләрен табыгыз.
2. Табылган кыйммәтләр буенча борысның моменталь тизлеге
модуле белән вакыт арасындагы бәйлелек графигын төзегез.
Өстәмә бирем. Борысның х координатасының хәрәкәт башлан¬
гычыннан башланган t вакытына бәйлелеге графигын төзегез.
228
Лаборатор эшләр
Графикны төзү өчен 3 нче таблицадан файдаланыгыз, исәп баш¬
лангычы итеп хәрәкәт башлану мизгелен һәм аңа тиңдәш булган
координатаны алыгыз (to=O һәм xo=O).
Борыс туры сызык буйлап бер генә юнәлештә хәрәкәт иткән¬
лектән, s1, s2, s3, ..., s15 ераклыклары хәрәкәт итүче җисемнең 0,02 с,
0,04 с, 0,06 с, ... 0,3 с интерваллары ахырындагы х , x2, х3, ... ,x15
координаталары булып тора.
Искәрмә. Графикны биеклеге 25 см һәм киңлеге 18 см булган
миллиметрлы кәгазьдә эшләргә, вакытны абциссалар күчәре буй¬
лап, 10 мм да — 0,02 с масштабы белән салырга (ординаталар
күчәреннән кыскарак) киңәш ителә.
II вариант
Эшнең максаты: шарчыкның хәрәкәт тизләнешен һәм цилиндр¬
га бәрелү алдыннан моменталь тизлеген табу.
Җиһазлар: 1,4 м озынлыктагы металл лаборатория улагы, 1,5—
2 см диаметрлы металл шарчык, металл цилиндр, метроном (сый¬
ныфка бер), үлчәү тасмасы, акбур кисәге.
Теоретик нигезләүләр
Шарчыкның турысызыклы авыш яссылык буйлап тигез тизлә¬
неш белән тәгәрәп төшүе билгеле.
Тигез тизләнеш вакытында үтелгән юл, башлангыч тизлек бул¬
маганда, түбәндәге формула белән табыла:
моннан
α = ∙⅛∙ . (2)
t2
Тизләнеш билгеле булганда, моменталь тизлекне түбәндәге фор¬
мула буенча табалар:
v = at. (3)
Әгәр шарчыкның, хәрәкәт башлангычыннан алып, цилиндрга
бәрелеп туктаганга кадәрге вакытын (t) һәм бу вакыт эчендә үткән
юлын (з) үлчәп тапсак, (2) формуласы буенча аның тизлеге а ны, ә
(3) формуласы буенча моменталь тизлеге υ ны исәпләргә мөмкин.
229
Лабоаратор эшләр
Вакыт аралыгы t метроном ярдәмендә үлчәнә. Метрономны ми¬
нутына 120 тапкыр сугарлык итеп көйлиләр, димәк, бер-бер артлы
килүче сугулар арасы 0,5 с ка тигез була. Метрономның шарчык
хәрәкәт итә башлаган моменттагы сугуы нульгә тигез дип исәпләнә.
Улакның түбәнге өлешендә шарчыкны тоткарлау өчен цилиндр
урнаштыралар. Цилиндрның урынын шарчыкның бәрелү вакыты
метрономның өченче яки дүртенче сугу вакытына туры килерлек
итеп сайлыйлар. Ул вакытта хәрәкәт вакытын (t) t = 0,5n форму¬
ласы буенча исәпләргә мөмкин, биредә п — метрономның сугулар
саны (нуль сугуын исәпләмичә) яки хәрәкәт башланганнан алып тук¬
талганга кадәр 0,5 с лы вакыт аралыклары саны.
Шарчыкның башлангыч торышы акбур белән тамгалана. Тук¬
талганга кадәр үткән юлын (з) сантиметрлы тасма белән үлчиләр.
Эшкә күрсәтмәләр
1. Җайланманы 148 нче рәсем буенча җыегыз. (Авышлыкны
шарчык улак озынлыгын метрономның кимендә дүрт сугуы ара-
2. 4 нче таблицаны дәфтәрегезгә күчереп сызыгыз.
4 нче таблица
Метроном¬
ның сугулар
саны п
Юл
з,м
Хәрәкәт
вакыты t, с
t = 0,5 • п
Тизләнеш
2S / 2
a = -р-, м/с2
■■■ ” ■
Моменталь
тизлек
υ = at, м/с
1 * Λ . ^Hf⅞⅞Z∙'
230
Лаборатор эшләр
3. Метрономның өч яки дүрт сугуы вакытында шарчыкның
үткән юлын (з) үлчәгез һәм 4 нче таблицага языгыз.
4. Шарчыкның хәрәкәтләнү вакытын (i), тизләнешен һәм ци¬
линдрга бәрелгәндәге моменталь тизлеген исәпләгез. Табылган нәти¬
җәләрне таблицага языгыз.
£ 2 нче лаборатор эш
Ирекле төшү тизләнешен үлчәү
Эшнең максаты: җисемнәрнең хәрәкәтләрен өйрәнү приборы
ярдәмендә ирекле төшү тизләнешен үлчәү.
Җиһазлар: җисемнәрнең хәрәкәтләрен өйрәнү приборы, озын¬
лыгы 300 мм һәм киңлеге 20 мм булган миллиметрлы һәм күчер¬
геч кәгазь тасмалар, муфталы һәм кыстыргычлы штатив.
Приборның төзелеше һәм эшләү тәртибе
Прибордагы (рәс. 149) йөккә (1) миллиметрлы бүлемнәре булган
озын кәгазь тасма (2) беркетелгән, аның өсте күчергеч кәгазь тасма¬
сы белән капланган. Тасма белән йөк өстән кыстыргыч (7) белән
тотылып тора.
Система бөтенләе белән штативка (6)
беркетелгән улакта (5) тотылып тора. Улак¬
ка шулай ук тирбәткеч (3) куелган.
Кыстыргычны ычкындыргач, йөк баш¬
лангыч тизлексез ирекле төшә башлый
һәм үзе белән кәгазь тасманы да тарта.
Тирбәткечнең хәрәкәтчән өлеше (аны
кнопкага басып алдан ялгыйлар) тирбәлә
башлый һәм хәрәкәт итүче тасмада
Т = 0,02 с вакыт аралыгы саен тамгалар
ясый (рәс. 150).
Теоретик нигезләүләр
Нуль тамгасы белән теләсә кайсы баш¬
ка тамга арасын үлчәп, йөкле тасманың
t = пТ вакыты эчендә нинди з юлы үтүен
исәпләргә мөмкин, биредә п — күрсәтел¬
гән тамгалар арасындагы интерваллар
саны.
Рәс. 149
231
Лабоаратор эшләр
Юлны (s) һәм бу юлны узу өчен киткән вакытны (t)
белгәннән соң, ирекле төшү тизләнешен түбәндәге формула
буенча исәпләргә мөмкин:
2s
«=Г ■
Эшкә күрсәтмәләр
1. Җайланманы 149 нчы рәсемдә күрсәтелгәнчә җые¬
гыз.
2. 5 нче таблицаны дәфтәрегезгә күчереп сызыгыз
5 нче таблица
Хәрәкәт
вакыты
t = пТ, с
Юл
8, ММ
Юл 8, М
Ирекле төшү
тизләнеше
g = 2 s∕t2, м/с2
3. Тирбәткечне электр челтәренә ялгагыз, кнопкага (S)
басыгыз, аннан соң, кнопканы борыс туктаганчы җибәрми
торып, кыстыргычны ычкындырыгыз.
4. Кирәкле үлчәүләрне һәм исәпләүләрне эшләгез. Нәти¬
җәләрне 5 нче таблицага языгыз.
5. Үзегез исәпләп тапкан d кыйммәте белән 9,8 м/с2 ка
тигез булган чын кыйммәтнең аермасын табыгыз. Бу аер¬
маның чын g кыйммәтенең нинди өлеше (процентларда)
булуын исәпләгез.
ψ 3 нче лаборатор эш
Җепле маятник тирбәнешләре периодының һәм еш¬
лыгының маятник озынлыгына бәйлелеген тикшерү
Эшнең максаты: җепле маятник тирбәнешләре перио¬
дының һәм ешлыгының аның озынлыгына ничек бәйлән¬
гәнен ачыклау.
Җиһазлар: муфталы һәм кыстыргычлы штатив, 130
см озынлыктагы җеп бәйләнгән шарчык һәм бу җепкә
кидерелгән резина кисәге, секундлык угы булган сәгать
яки метроном. (Резина кисәге (мәсәлән, бозгыч) җеп шта¬
РӘС. 150
232
Лаборатор эшләр
тив аягыннан шумасын өчен һәм маятникны кирәкле озынлыгына
тиз һәм төгәл урнаштыру өчен кулланыла. Җепне резина аша энә
ярдәмендә үткәрәләр).
Эшкә күрсәтмәләр
1. Үлчәүләрне һәм исәпләүләрне язып бару өчен, дәфтәрегезгә 6
нчы таблицаны күчереп сызыгыз.
6 нчы таблица
2. Маятник асылган резина кисә¬
ген, 151 нче рәсемдә күрсәтелгәнчә,
штатив кыстыргычына беркетегез. Бу
маятникның озынлыгы, 6 нчы табли¬
цада күрсәтелгәнчә, беренче тәҗрибә
өчен 5 см га тигез булырга тиеш. Ма¬
ятникның озынлыгын, рәсемдәге ши¬
келле — эленү ноктасыннан шарның
уртасына кадәр үлчәгез.
3. Беренче тәҗрибә өчен, шарчың -
ны тигезләнеш торышыннан аз гына
(1—2 см) амплитуда белән авыштыры¬
гыз һәм ычкындырып җибәрегез. Ма¬
ятник 30 тулы тирбәнеш ясаган вакыт аралыгын (t) үлчәгез. Үлчәү
нәтиҗәләрен 6 нчы таблицага язып куегыз.
233
Лабоаратор эшләр
4. Калган дүрт тәҗрибәне дә берейчесе шикелле үк үткәрегез.
Тик һәр тәҗрибәдә маятникның озынлыгын (Z) 6 нчы таблицада
күрсәтелгән зурлыкта итеп алыгыз.
5. Биш тәҗрибәнең һәрберсе өчен маятник тирбәнешләренең
периодын (Т) исәпләгез һәм 6 нчы таблицага языгыз.
1 N
6. Биш тәҗрибәнең һәрберсе өчен v = яки v = формуласы
буенча маятник тирбәнешләренең ешлыгын исәпләгез. Нәтиҗәләр¬
не 6 нчы таблицага язып куегыз.
7. Маятникның ирекле тирбәнүләре периодының һәм ешлыгы¬
ның аның озынлыгы белән ничек бәйләнгәнлеге турында нәтиҗәләр
ясагыз. Нәтиҗәләрне язып куегыз.
8. Сорауларга җавап бирегез: әгәр а) тирбәнешләр периоды баш¬
та 0,3 с, озынлыгын үзгәрткәч 0,1 с булса; б) тирбәнешләр ешлыгы
башта 5 Гц, үзгәрткәннән соң 3 Гц ңа кадәр кимесә, маятник озын¬
лыгын арттырганнармы яки киметкәннәрме?
Өстәмә бирем
Биремнең максаты: маятник озынлыгы белән тирбәнешләр пе¬
риоды арасында нинди математик бәйләнеш булуын ачыкларга.
Эшкә күрсәтмәләр
1. Дәфтәрегезгә 7 нче таблицаны күчереп сызыгыз.
7 нче таблица
2. 6 нчы таблицадагы саннардан файдаланып, 7 нче таблицада¬
гы периодлар һәм озынлыклар чагыштырмаларын исәпләгез һәм
язып куегыз (периодлар чагыштырмасын исәпләгән нәтиҗәләрне
бөтен саннарга кадәр түгәрәкләргә).
3. 7 нче таблицаның дүрт баганасындагы нәтиҗәләрне чагыш¬
тырыгыз һәм алар өчен уртак закончалыкны табарга тырышыгыз.
Шулар нигезендә, түбәндәге биш тигезлек арасыннан маятник озын¬
лыгы I белән тирбәнешләр периоды Т арасындагы бәйләнешне иң
дөрес күрсәтүче тигезлекләрне сайлап алыгыз:
234
Лаборатор эшләр
биредә к 2, 3, 4, 5 кыйммәтләрен ала; мәсәлән,
4. Түбәндәге биш раслама арасыннан дөресен сайлап алыгыз.
Маятник озынлыгын 4 тапкыр арттырганда, аның тирбәнешләр
периоды: а) 4 тапкыр арта; б) 4 тапкыр кими; в) 2 тапкыр арта;
г) 2 тапкыр кими; д) 16 тапкыр арта.
£ 4 нче лаборатор эш
Электромагнитик индукция күренешен өйрәнү
Эшнең максаты: электромагнитик индукция күренешен өйрәнү.
Җиһазлар: миллиамперметр, уралма кәтүк, дугасыман магнит,
ток чыганагы, сүтелмә электромагниттагы тимер кендекле кәтүк,
реостат, ачкыч, тоташтыру үткәргечләре, электр тогы генераторы
моделе (сыйныфка бер).
Эшкә күрсәтмәләр
1. Уралма кәтүкне миллиамперметр клеммаларына ялгагыз.
2. Магнитның бер полюсын кәтүккә якын китерегез, берничә
секунд туктатып торыгыз да, яңадан, кәтүк эченә кертеп үк якынай¬
тыгыз (рәс. 152), бу вакыт эчендә миллиамперметр күрсәтүләрен
күзәтеп барыгыз. Язып куегыз, магнитны кәтүккә карата хәрәкәт
иттергәндә, кәтүктә индук¬
цион ток барлыкка килде¬
ме? Туктатып торганда ток
булдымы?
3. Язып куегыз, магнит¬
ны хәрәкәт иттергәндә кә¬
түк аша узучы магнит агы¬
шы Ф үзгәрдеме? туктатып
торганда?
4. Алдагы җавапларга таянып, нәтиҗә ясагыз һәм язып куегыз,
нинди шартларда кәтүктә индукцион ток барлыкка килде?
235
Лабоаратор эшләр
5. Ни өчен, магнитны кәтүккә якынайтканда, бу кәтүк аша узу¬
чы магнит агышы үзгәрде? (Бу сорауга җавап бирү өчен түбәндәгеләр¬
не исегезгә төшерегез, беренчедән, магнит агышы Ф нинди зурлык¬
ларга бәйле һәм, икенчедән, даими магнитның магнит кыры индук¬
циясе векторының В модуле бу магнит тирәсендә һәм аннан ерак-
тарак бертөрлеме.)
6. Миллиамперметр угының нуль бүлемтегеннән кайсы якка авы¬
шуы буенча кәтүктәге токның юнәлешен белергә мөмкин.
Тикшереп карагыз, кәтүккә магнитның бер үк полюсын якы¬
найтканда һәм ерагайтканда, кәтүктәге индукцион токның юнәле¬
ше бер үк булырмы.
7. Миллиамперметрның угы шкаладагы чик кыйммәтнең яр¬
тысыннан кимрәккә авышырлык тизлек белән магнит полюсын
кәтүккә якынайтыгыз.
Шушы ук тәҗрибәне магнитны тизрәк хәрәкәтләндереп кабат¬
лап карагыз.
Кәтүк аша узучы магнит агышы Ф кайсы очракта тизрәк үзгәрде:
магнит кәтүккә карата тизрәк хәрәкәт иткәндәме, акрынрагында¬
мы?
Кәтүк аша узучы магнит агышы тизрәк үзгәргәндәме, әллә ак-
ранрак үзгәргәндәме модуле буенча зуррак ток барлыкка килә?
Соңгы җавап нигезендә нәтиҗә ясагыз һәм язып куегыз: кәтүктә
барлыкка килүче индукцион ток зурлыгының модуле бу кәтүк аша
узучы магнит агышы Ф үзгәрешләренең тизлегенә ничек бәйләнгән?
8. 153 нче рәсем буенча тәҗрибә өчен җайланманы җыегыз.
Рәс. 153
236
Лаборатор эшләр
9. Түбәндәге очракларда уралма
кәтүктә 1 индукцион ток барлыкка
килү-килмәвен тикшерегез:
а) кәтүк 2 кертелгән чылбырны
ялгаганда һәм өзгәндә;
б) кәтүк 2 аша даими ток уз¬
ганда;
в) реостатның шудырмасын ти¬
ешле якка күчерү юлы белән, кәтүк
2 аша уза торган ток зурлыгын арт¬
тырганда һәм киметкәндә.
10. 9 нчы пунктта санап үтелгән
очракларның кайсыларында кәтүк
Рәс. 154
1 аша узучы магнит агышы үзгәрә? Ни өчен үзгәргәнен аңлатыгыз.
11. Генератор моделендә (рәс. 154) электр тогы хасил булуын
күзәтегез. Магнит кырында әйләнүче рамда ни өчен индукцион ток
барлыкка килүен аңлатыгыз.
£ 5 нче лаборатор эш
Трекларның фоторәсеме буенча уран атомы төше бүленүне өйрәнү
Эшнең максаты: уран атомы төше бүленү мисалында импульс
саклану законының дөреслегенә ышану.
Җиһазлар: уран атомы төшенең нейтрон тәэсирендә бүленгәндә
фотоэмульсиядә барлыкка килгән корылган кисәкчекләрнең трек¬
лары фоторәсеме (рәс. 155), үлчәү линейкасы.
Рәс. 155
237
Лабоаратор эшләр
Аңлатмалар. Бу фоторәсемдә сез ике кыйпылчыкның трекла¬
рын күрәсез, алар нейтронны эләктереп алган уран атомы төшенең
бүленүе нәтиҗәсендә барлыкка килгәннәр. Уран төше ук белән
күрсәтелгән g ноктасында булган. Треклардан күренгәнчә, уран төше
кыйпылчыклары капма-каршы юнәлешләрдә очып киткән (сул трек¬
тагы сынган урын — кыйпылчыкның фотоэмульсиядәге берәр атом¬
ның төше белән бәрелешүе нәтиҗәсе).
1 нче бирем. Импульс саклану законыннан чыгып аңлатыгыз:
уран атомы төше бүленүдән барлыкка килгән кыйпылчыклар ни
өчен капма-каршы якка юнәлә?
2 нче бирем. Уран төше кыйпылчыкларының Д. И. Менделеев
таблицасының урта тирәсендәге ике төрле химик элемент атомна¬
рының төшләре икәне билгеле (мәсәлән, барий, ксенон Һ.6.).
Уран бүленү реакциясенең мөмкин табылган бер вариантын сим¬
волик рәвештә түбәндәгечә язып була:
92^U + qTI —> 5θBa ^∣^ гХ “Ь 2 , θ∏,
биредә гХ символы — ниндидер химик элемент атомы төше.
Корылма саклану законыннан һәм Д. И. Менделеев таблицасын¬
нан файдаланып, аның нинди элемент икәнлеген ачыклагыз.
6 нчы лаборатор эш
Г Әзер фоторәсемнәр буенча корылмалы кисәкчекләрнең
трекларын өйрәнү
Эшнең максаты: корылган кисәкчекләр хәрәкәтенең характе¬
рын аңлату.
Җиһазлар: Вильсон камерасыннан, куыклы камерадан һәм фо-
тоэмульсиядән алынган корылмалы кисәкчекләрнең треклары фо¬
торәсемнәре.
Аңлатмалар. Бу лаборатор эшне үтәгәндә түбәндәгеләрне истә
тотарга кирәк:
а) кисәкчекнең энергиясе зуррак булган саен (тирәлекнең ты¬
гызлыгы азрак булган саен), трекның юлы озынрак була;
б) кисәкчекнең корылмасы зуррак һәм тизлеге азрак булган
саен, трекның киңлеге зуррак була;
в) корылмалы кисәкчек магнит кырында хәрәкәт иткәндә, трек
кәкре булып чыга, бу очракта кисәкчекнең массасы һәм тизлеге зур¬
238
Лаборатор эшләр
рак булган саен һәм корылма зурлыгы белән
магнит кыры индукциясе модуле кечерәк,
трекның кәкрелек радиусы зуррак була;
г) кисәкчек кәкрелек радиусы зуррак
булган трекның ахыргы очыннан кәкрелек
радиусы кечерәк булган трек ахырына таба
хәрәкәт итә (хәрәкәт барышында кәкрелек
радиусы кими бара, чөнки тирәлекнең кар¬
шылыгы аркасында кисәкчекнең тизлеге ак¬
рыная).
1 нче бирем. Сезнең алдагы өч фото¬
рәсемнең (рәс. 156, 157, 158) икесендә маг¬
нит кырында хәрәкәт итүче кисәкчекләрнең
треклары сурәтләнгән. Кайсыларында икә¬
нен күрсәтеп, җавапны нигезләгез.
2 нче бирем. Вильсон камерасында хә¬
рәкәт итүче а-кисәкчекләрнең трекларын
карап, сорауларга җавап бирегез (рәс. 156):
а) а-кисәкчекләр нинди юнәлештә хә¬
рәкәт иткән?
б) а-кисәкчек трекларының озынлыкла¬
ры якынча бертөрле. Бу нәрсә турында сөйли?
в) Хәрәкәт барышында трекның калын¬
лыгы ничек үзгәргән? Бу нәрсәне аңлата?
3 нче бирем. 157 нче рәсемдә магнит
кырына урнашкан Вильсон камерасындагы
а-кисәкчекләрнең треклары фоторәсеме би¬
релгән. Бу фоторәсем буеча билгеләгез:
Рәс. 156
Рәс. 157
Рәс. 158
а) а-кисәкчекнең хәрәкәте вакытында кәкрелек радиусы һәм
трекның калынлыгы ни өчен үзгәргән?
б) Кисәкчекләр кайсы якка таба хәрәкәт иткән?
4 нче бирем. 158 нче рәсемдә магнит кырына урнашкан куыклы
камерадагы электронның трегы фоторәсеме бирелгән. Бу фоторәсем
буенча билгеләгез:
а) Ни өчен трек спираль формасында?
б) Электрон кайсы юнәлештә хәрәкәт иткән?
в) Нинди сәбәп аркасында 158 нче рәсемдәге электрон трегы
157 нче рәсемдәге а-кисәкчекләр трекларыннан озынрак?
239
Кабатлау һәм атнага 3 сәгать физика укучылар
өчен тәкъдим ителгән мәсьәләләр
1. 159 нчы рәсемдә сурәтләнгән векторларның һәрберсе өчен
билгеләгез:
а) башлангыч һәм ахыргы координаталарны;
б) У күчәренә проекциясен;
в) Ү күчәренә проекциясенең модулен;
г) векторларның модульләрен.
2. 160 нчы рәсемдә а һәм с векторлары X күчәренә перпендику¬
ляр, Ь һәм d векторлары — аңа параллель aχ, bχ, cχ һәм dχ проекциял¬
әрен бу векторларның модульләре яки тиңдәшле саннар аша күрсәте¬
гез. д
d
Ь
Рәс. 160
240
Мәсьәләләр
3. 161 нче рәсемдә А ноктасыннан В ноктасына күчкән шарчык¬
ның траекториясе сурәтләнгән. Табыгыз:
а) шарчыкның башлангыч һәм соңгы торышларының коорди-
наталарын;
б) шарчык күчешенең проекцияләрен ∣sχ∣hθM∣sJ;
в) күчеш проекцияләренең модульләрен ∣sχ | һәм |в |;
г) күчеш модулен ∣ s |.
Рәс. 161
4. Катер пристаньга карата А (-8; -2) ноктасыннан В (4; 3) нок¬
тасына күчә. Координаталар башлангычын пристаньга куеп, сызы¬
мын сызыгыз, анда А һәм В нокталарын күрсәтегез. Катерның күче¬
шен (АВ) табыгыз. Катер үткән юл ул ясаган күчештән зуррак була
аламы? Күчештән кечерәк? күчешкә тигез? Җавапларны нигезләгез.
5. Турысызыклы хәрәкәт итүче җисемнең координаталарын табу
өчен х = x0 + sχ формуласы кулланылуы билгеле. Турысызыклы ти¬
гез хәрәкәт итүче җисемнең теләсә кайсы вакыт мизгелендәге коор-
динатасы х = x0 + υχt тигезләмәсе белән табылганын исбат итегез, би¬
редә х0 һәм υχ — даими зурлыклар, ә t — үзгәрешле.
6. X күчәре буйлап 5 м/с тизлек белән турысызыклы хәрәкәт
итүче җисемнең координатасын табу өчен тигезләмә языгыз. Күзәтү
башланганда, аның координатасы 3 м га тигез булган.
7. Пассажир һәм товар поездлары параллель юллардан бара.
Вокзал бинасына карата пассажир поездының хәрәкәте xπ = 260 - 10£
тигезләмәсе, товар поездыныкы xτ= -100 + 8t тигезләмәсе белән би¬
релә. Вокзалны һәм поездларны материаль нокта итеп алып,
X күчәрендә аларның күзәтү башлангандагы торышларын күрсәте¬
гез. Күзәтү башланып күпме вакыт үткәннән соң, поездлар очра¬
241
Мәсьәләләр
шырлар? Очрашу урынының ктордина-
тасы нинди? X күчәрендә очрашу уры¬
нының торышын күрсәтегез. X күчәрен
рельсларга параллель дип санарга.
8. Туристлар елга буйлап салда
йөзәләр. 162 нче рәсемдә туристлар тук¬
талышына карата (О ноктасы) сал ко-
ординатасының вакытка бәйле рәвештә
үзгәрүе күрсәтелгән. Күзәтү башлангы¬
чы — салны суга төшереп, хәрәкәтне
башлау вакытына туры килә.
Сал суга кайчан төшерелгән: елга
агымына карап, тукталыштан югы-
рыракмы, түбәнрәкме? Тукталыштан
югарырак яки түбәнрәк булса, ничә
метрга?
Салның башлангыч координата-
сын һәм хәрәкәт тизлеген табыгыз һәм
координатаның вакытка бәйлелеге
Рәс. 162
графигын төзегез.
9. Малай тау башындагы тикторыш хәленнән туры сызык буен¬
ча һәм тигез тизләнеш белән чанада шуып төшә. Хәрәкәт башла¬
нып 2 с үткәч, аның тизлеге 3 м/с ка җитә. Хәрәкәт башланганнан
алып күпме вакыт узгач, малайның тизлеге 4,5 м/с ка тигез булыр?
Ул бу вакыт эчендә күпме юл узар?
10. s =v0t + ~- формуласын s = ⅛j^u ■ t рәвешенә үзгәртегез.
2
11. s = υ0t + һәм a = v° v формулаларыннан а = форму-
ласын чыгарыгыз.
12. 27 нче рәсемдә, тикторыш хәленнән башлап, тигез тизләнеш
белән төшкән шарчыкның һәр 0,1 с саен алган торышлары күр¬
сәтелгән. Барлык алты торышның да координаталары линейканың
уң читендәге сызыклар белән билгеләнгән. Рәсемнән файдаланып,
шарчыкның беренче 0,3 с эчендәге уртача тизлеген һәм аның бу
араны үтү ахырындагы моменталь тизлеген табыгыз.
242
Мәсьәләләр
13. Ике лифт — гадәти һәм тиз йөрешле лифтлар — бер үк
вакытта хәрәкәткә килеп, бер үк вакыт аралыгында тигез тизләнеш
белән хәрәкәт итәләр. Тиз йөрешле лифтның тизләнеше гадәти лифт¬
ныкыннан 3 тапкыр артык булса, аның бу вакыт эчендә үткән юлы
гадәти лифт үткән юлдан ничә тапкыр артыграк? Тиз йөрешле лифт¬
ның тизлеге бу вакыт ахырына гадәти лифтныкыннан ничә тапкыр
артык булыр?
14. 163 нче рәсемдә тизләнә баручы лифт тизлегенең вакытка
бәйлелеге графигы бирелгән. Бу графикны дәфтәрегезгә күчереп
сызыгыз һәм шушы ук координаталар күчәрләрендә тиз йөрешле
лифт тизлегенең шундый ук графигын төзегез. Аның тизләнеше
гадәти лифт тизләнешеннән 3 тапкыр зуррак.
15. Автомобиль турысызыклы хәрәкәт итә. Автомобиль тизлеге
векторы проекциясенең вакытка бәйлелеге СИ системасында
υχ = 10 + 0,5£ тигезләмәсе белән күрсәтелә. Автомобильнең тизләне¬
шен, башлангыч тизлегенең модулен һәм юнәлешен табыгыз. Аның
тизлек векторы модуле ничек үзгәрә?
16. Кәшәкә белән сукканнан соң, алка (шайба) 5 м/с башлангыч
тизлек ала һәм 1 м/с2 тигезләнеш белән боз өстеннән шуа башлый.
Алканың тизлек векторы проекциясенең вакытка бәйлелеге тигез¬
ләмәсен языгыз һәм аңа тиңдәшле графикны төзегез.
17. Турысызыклы хәрәкәт итүче җисемнең координатасын исәп¬
ләү өчен х = х 0+ s χ тигезләмәсе кулланыла. Турысызыклы тигез тиз¬
ләнешле хәрәкәт иткәндә, җисемнең теләсә кайсы вакыт мизгелен¬
дәге координатасы x-xθ+υθ t + ciχt тигезләмәсе буенча табылганын
243
Мәсьәләләр
исбатлагыз, биредә x0, υ0χ һәм ах — даими зурлыклар, ә t — үзгәреш¬
ле зурлык.
18. Чаңгычы таудан туры сызык буйлап, даими 0,1 м/с2 тизләнеш
белән шуып төшә. Әгәр аның башлангыч координатасы белән тизлеге
нульгә тигез булса, хәрәкәтенең тизлек векторы проекциясенә һәм
вакыт координатасына бәйлелеген күрсәтүче тигезләмәләрне языгыз.
19. Велосипедчы шоссе буйлап җиргә карата модуле 40 км/сәг
булган тизлек белән туры сызыклы хәрәкәт итә. Аңа параллель юнә¬
лештә автомобиль бара. Аның велосипедчыга карата тизлегенең
модуле а) 0; б) 10 км/сәг; в) 40 км/сәг; г) 60 км/сәг булса, җиргә
карата булган хәрәкәт юнәлеше һәм тизлек векторының модуле
турында нәрсә әйтергә мөмкин?
20. Катерның суга карата тизлеге су агымының ярга карата
тизлегеннән 5 тапкыр зуррак. Катерның ярга карата хәрәкәтен тик¬
шереп, аның агым уңаена бару тизлегенең агымга каршы тизле¬
геннән ничә тапкыр зуррак икәнен белегез.
21. Малай массасы 3,87 г һәм күләме 3∙10^3 м булган шарчык¬
ны тотып тора. Кулдан ычкындырып җибәргәннән соң, шар нишләр?
22. Корыч шар, горизонталь өслектән тигез тәгәрәп барып,
хәрәкәтсез алюминий шарга бәрелә, нәтиҗәдә алюминий шар бер¬
никадәр тизләнеш ала. Бу вакытта корыч шарның тизләнеш моду¬
ле нульгә тигез булырга мөмкинме? Алюминий шар тизләнешеннән
зуррак яки кечерәк булырга? Җавапларыгызны нигезләгез.
23. М һәм R — Җир шарының массасы һәм радиусы, gn —
Җир өслегендә, ә g — һ биеклегендә ирекле төшү тизләнешләре.
G-M*
g (Вҗ+ һ)2
һәм g0 =
GM*
Rk
формуларыннан файдаланып, g
Sp ∙ Rκ
(Яҗ+ Λ)2
формуласын чыгарыгыз.
24. 164 нче рәсемдәге 1 һәм 2
шарчыкларының массалары тигез.
Алар г һәм 2г озынлыгындагы
җепләргә бәйләнгән һәм әйләнәләр
буйлап модуле буенча бер үк v тиз¬
леге белән хәрәкәт итәләр. Шар¬
чыкларның үзәккә омтылу тизлә¬
нешләрен һәм җепләрнең тарты¬
лу көчләрен чагыштырыгыз.
Рәс. 164
244
Мәсьәләләр
25. Әйләнә буенча хәрәкәт вакытында үзәккә омтылу тизләнеше
v2 ё ∙ R2
а -— һәм 23 нче мәсьәләне чишкәннән соң табылган g = -=?—⅛
Y∙o∙ г (⅛ + һ)2
формулалары буенча Җир өслегеннән һ биеклегендә беренче космик
, I -
тизлекне исәпләү формуласын u=-J табыгыз.
у хьҗ + Һ
26. Җир радиусының уртача кыйммәте 6400 км, ә Җир өсте тирә¬
сендә ирекле төшү тизләнеше 9,8 м/с2. Шулардан гына файдаланып,
Җир өслегеннән 3600 км биеклектә беренче космик тизлекне табыгыз.
27. 4 с дәвамында ирекле төшкән җисемнең тизлек проекциясе
векторының вакытка бәйлелеге графигын төзегез (υ0= 0, g = 10 м/с2).
28. 0,3 кг массалы җисем тикторыш хәленнән 3 с дәвамында
ирекле төшә. Төшүнең беренче секунды эчендә аның импульсы
күпмегә үзгәрә? икенче секунд эчендә?
29. 27 нче мәсьәләне чишү өчен төзегән графигыгыз ярдәмендә
ирекле төшүче җисемнең импульсы тигез вакыт араларында бер үк
зурлыкка үзгәргәнен күрсәтегез.
30. Күләмнәре тигез булган алюминий һәм бакыр шарлар тикто¬
рыш хәленнән һәм бер үк биеклектән 2,5 с дәвамында төшәләр. Берен¬
че секундның ахырына кайсы шарның импульсы зуррак була һәм
ничә тапкыр зуррак? икенче секундның ахырына? Җавапны нигезләгез.
31. Бертөрле ике бильярд шары, бер туры буенча хәрәкәт итеп,
бер-берсе белән бәрелешәләр. Бәрелешү алдыннан беренче шарның
X күчәренә тизлек векторы проекциясе 0,2 м/с, ә икенчесенең
0,1 м/с була. Бәрелешкәннән соң беренче шарның тизлек векторы
проекциясе 0,1 м/с ка тигез булып калса, икенче шарның бу вакыт¬
тагы тизлек векторы проекциясен табыгыз.
Ике рәсем ясагыз: беренчесендә бәрелешүгә кадәрге X күчәрен,
шарларны һәм тизлек векторларын, ә икенчесендә — бәрелешүдән
күрсәтегез.
32. Алдагы мәсьәләне түбәндәге очрак өчен чишегез: υ1 = 0,2 м/с,
υ2x= -0,1 м/с, υ'lχ = -0,1 м/с, (биредә vlχ һәм υ2χ — тиңдәшле рәвештә
1 һәм 2 шарларның бәрелешүгә кадәрге тизлек векторлары проек¬
цияләре, ә v'lχ — 1 шарының бәрелешкәннән соңгы тизлек векторы
проекциясе.
33. 32 нче мәсьәләнең шартын һәм чишүнең нәтиҗәсен кулла¬
нып, шарлар бәрелешкән вакытта тулы механик энергия саклану
законының үтәлүен исбатлагыз.
245
Мәсьәләләр
34. 165 нче рәсемдә вакыт узу белән таган утыргычындагы бер
ноктаның тизлек векторы проекциясе ничек үзгәргәне күрсәтелгән.
Бу үзгәреш нинди ешлык белән бара? Тагандагы тирбәнеш ясый
торган теләсә кайсы башка ноктаның тизлек үзгәрешләре ешлыгы
нинди?
35. Арфаның кылы 40 Гц ешлыкта гармоник тирбәнешләр ясый.
Кылның тирбәнешләре амплитудасы 3 мм булган урта ноктасы өчен
X, мм А
0
4 1—0—I 1 1 О—I 1 1—О—< 1 1—О—→-
25 50 75 100 t, mc
Рәс. 166
координатаның вакытка бәйлелеге графигын төзегез. (Графикны төзү
өчен t күчәрен 166 нчы рәсемдәге кебек урнаштыру кулайрак; X
күчәрен мөстәкыйль рәвештә билгеләгез.)
Сез төзегән график шул ук кылның башка нокталары өчен дә
ярыймы? Арфаның башка кылларының урта нокталары өчен? Ни
өчен?
246
Мәсьәләләр
Рәс. 167
36. Резонатор тартмалары булып торучы бер төрле ике камер¬
тонның берсендә, аңа кагылмыйча гына, ничек итеп тавыш булды¬
рырга мөмкин? Бу вакытта тартмаларның ачыклыклары бер-беренә
карата ничек урнаша? Җавапны нигезләгез.
Сез тәкъдим иткән бу тәҗрибәнең нигезендә нинди физик күре¬
неш ята?
37. Таганны периодик рәвештә этеп җибәрәләр, ягъни мәҗбүри
көч куялар. 167 нче рәсемдә тагандагы тотрыклы тирбәнешләр ам¬
плитудасының бу көчнең ешлыгы¬
на бәйлелеге графигы сурәтләнгән.
График буенча билгеләгез:
а) Таганга нинди ешлыкта —
1 Гц яки 2 Гц белән тәэсир иткән¬
дә, аның тотрыклы тирбәнешләр
амплитудасы зуррак булыр?
б) Тотрыклы тирбәнешләр амп¬
литудасы иң зур кыйммәтенә иреш¬
сен өчен, таганны нинди ешлык
белән этәрергә кирәк?
в) таганның үзьешлыгы күп¬
мегә тигез? Сез үзьешлыкны нинди
физик закон нигезендә таптыгыз?
38. 168 нче рәсемдә сурәтләнгән АВ үткәргеченең озынлыгы 10 см,
массасы 2 г һәм ул индукциясе 4∙10^2 Тл булган магнит кырына —
магнит индукциясе сызыкларына перпендикуляр итеп урнаштырыл¬
Рәс. 168
Рәс. 169
ган. Үткәргеч буйлап электр тогы үтә (үткәргечне элеп куйган нәзек
үткәргечләр аша). АВ үткәргеченә тәэсир итүче авырлык көче белә
магнит кырының токка тәэсир итү көче тигезләшсен өчен, токнын
көче нинди булырга тиеш?
247
Мәсьәләләр
39. Бериш магнит кырына урнаштырылган Вильсон камерасы¬
на электрон очып керә һәм әйләнә дугасы буенча хәрәкәт итә (169
нчы рәсемдә ак пунктир сызык). Бу очракта электронның тизлек
векторы юнәлешен үзгәртүче нинди көч үзәккә омтылучы ролен үти?
Электрон камерага кайсы ноктага керә?
40. Магнит индукциясе сызыкларына перпендикуляр рәвештә v
тизлеге белән хәрәкәт итә торган е корылмалы кисәкчеккә индук¬
циясе В булган бериш магнит кыры F көче белән тәэсир итә һәм ул
F = Bev формуласы белән исәпләнә.
Әгәр электрон тизлеге и магнит индукциясе сызыкларына пер¬
пендикуляр юнәлештә һәм 3 ∙ Ю7 м/с ка тигез, корылмасының
модуле е = 1,6∙ Ю-19 Кл, массасы т = 9,1 • Ю-31 кг һәм магнит индук¬
циясе В = 8,5 • 10-3Тл булса, бериш магнит кырындагы электрон нин¬
ди радиуслы әйләнәнең дугасы буйлап хәрәкәтләнер?
41. Нинди радиоактив таркалу вакытында углерод 164C азотка
l*N әверелә?
42. Алюминий 13AI төшләрен нейтроннар белән белдергәндә ха¬
сил булган төштән а-кисәкчек атылып чыга. Бу реакциянең тигез¬
ләмәсен языгыз.
43. Масса һәм корылма саннары саклану законыннан файдала¬
нып, түбәндәге төш реакциясен тулыландырып языгыз: 1θB+...->
→ 37Li+4He
Күнегүләргә җаваплар
Күн. 5. 2. 1,5 м/с2. 3. 0,5 м/с2.
Күн. 6. 1. 1 м/с. 2. 10 с. 5. α1 = 0,5 м/с2; a2 = 1 м/с2.
Күн. 7. 1. 31,25 м. 2. 150 м.
Күн. 8. 1. 0,4 м; 0,8 м/с2. 2. 7 м/с. i
Күн. 9.5*. 248 м/с көнчыгышка һәм 198 м/с көнбатышка таба хәрәкәт иткәндә.
Күн. 11. 2. 36,8 кН. 3. 9,6 Н. 4. 6 м/с2.
Күн. 12. 2. Булмый. 3. a) F2x = 0,3 Н, Flχ = -0,3 Н; б) Flχ = 0,1 Н, F2 =-0,l Н;
г) Fχ = 0,4 Н.
Күн. 13. 1. 19,6 м. 3. 3 с; 4,9 м; 24,5 м.
Күн. 14. 1. 1 с; 4,9 м.
Күн. 15. 4. в) Югарыга таба хәрәкәт иткәндә тизлек һәм тизләнеш векторлары —
капма-каршы якларга, ә түбәнгә таба хәрәкәт иткәндә бер үк якка юнәлә.
Күн. 16. 2. Модуле буенча шундый ук көч белән тартылалар. 6*. h1 =R3; h2 = 27?3.
Күн. 17. 3*. АВ һәм CD бүлемтекләрендә. Әйе.
Күн. 18. 2. 2 ∙ 10^4 м/с2. 4. 3600. Секундлык. 5. a) ≈ 1,9 ∙ Ю20 Н;
б) ≈ 3,17 ∙ 10^5 м/с2; в) ≈ 110,3 м/с. —
Күн. 19. 1. 6,69 км/с. 2. 1,7 • Ю3 км.
Күн. 20. 1. 0,02 кг’м/с; -0,02 kγ∙m∕c. 2. 5∙103 kγ∙m∕c.
Күн. 21. 2. 0,9 м/с.
Күн. 22. 1. 2,25 м/с. 2. ≈ 33 м/с.
Күн. 23. 2. а) Шнурларның эластиклык көче тәэсирендә.
Күн. 24. 4. 10 Гц. 6. 40 см.
Күн. 27. 3. 2 с.
Күн. 28. 1. 20 м/с.
Күн. 30. 2. Түбәнәя. 3. Түбәнәя.
Күн. 32. 4. 20 м/с. 5. Тавыш күзәтүчегә килеп җитсен өчен билгеле бер вакыт
кирәк. Шуңа күрә күзәтүче кыңгырауга сугу тавышын сугуны күргәннән соң
гына ишетә. Әмма кечкенә араларда тавышның соңга калуы гаять дәрәҗәдә
кечкенә һәм күзәтүче аны сизми (мәсәлән, 10 м ераклыктан тавыш нибары
0,03 с ка гына соңара). Күзәтүче ераклашкан саен, тавышның соңаруы арта
бара һәм аны сизеп була башлый (170 м ераклыктан күзәтүче тавышны
күргәннән соң 0,5 с үткәч ишетә). Күзәтүче кыңгыраудан 340 м га ераклаш¬
кач, сугу тавышы 1 с ка соңара һәм икенче сугу белән туры килә.
Күн. 33. 1. Әйе. 2. ЛГ, М.
Күн. 34. 1. a) С һәм D; б) А. 2. Бар.
Күн. 35. 6. Беренчесендә — магнит, икенчесендә — электр көчләре.
Күн. 36. 1. Уңга. 2. А дан В га.
Күн. 37. 1. 0,5 Тл.
Күн. 42. 3. 5*105Гц. 5. Ярамый.
Күн. 43. 3. 6 тапкыр.
Күн. 45. 1. Нуклоннар — 9, протоннар — 4, нейтроннар — 5.
249
Кабатлау һәм атнага 3 сәгать физика укучылар өчен
тәкъдим ителгән мәсьәләләргә җаваплар
1. а) а: (0,5; 5), (0,5; 2); b: (1; 0), (4; 4); б) aμ = -3; Ъу = 4; в) ∣αj= 3; ∣fej = 4;
r)lαl = 3, I Ь|= 5.
2. ах = 0, bχ = Ь.
3. r)*fs∣ = 13*.
4.111 = 13.
6. х = 3 + St.
7. t = 20 с.
8. х = -10 + 2t.
9. t2 = 3 с; s2χ= 6,75 м.
12. ι,ypx≈ 1,4 м/с; vχ≈ 2,9 м/с.
15. υn = 10 м/с; а = 0,5 м/с .
16. υχ = 5 - t.
18. x*= 0,05t2 ; vx= 0,lt.
19. б) υa= 50 км/сәг яки υa = 30 км/сәг, υa ?Тцв,; г) υa =100 км/сәг, υa ТТ ив;
v = 20 км/сәг, и ТJ, v .
Цс.агым уң. . fc,
20. -— = 1-5∙
t^κ.ar.каршы
21. Шар кулдан ычкындырылган урында тикторыш хәлендә кала.
22. Корыч шарның тизләнеш модуле нульгә тигез була алмый. Әгәр корыч
шарның массасы алюминий шарныкыннан зуррак булса, тизләнеше алю¬
миний шарныкыннан кимрәк, ә инде корыч шарның массасы кимрәк бул¬
са, тизләнеше зуррак була.
aγi _
24. — =2;
a∙v9
^-=2.
"γ2 Fγ2
26. v ≈ 6,3 км/с.
28. Δ p1 = 2,94 кг«м/с;Д рп = 2,94 kγ∙m∕c.
30. = pJl ~33
Pal Pa2
31. υ2x = 0>2 м/с.
34. v = 0,5 Гц (таганның тирбәлүче теләсә кайсы ноктасы өчен).
35. Төзелгән график бу кылның башка нокталары өчен дә (аларның тирбәнү
амплитудалары башкача), арфадагы башка кылларның урта нокталары
өчен дә (алар башка ешлыкта тирбәнә) туры килми.
37. a)v = 3 Гц.
38. / =5А. 40. γ=2∙10-2m. 41.1β4C→ 1τ4N+.01e. 42.2jAl + i∏→ JfNa+^He.
250
АТАМАЛАР КҮРСӘТКЕЧЕ
Адроннар 225
Алмаш ток 165, 167
Алмаш электр тогы генераторы
165
Альфа-кисәкчекләр 181, 182
Альфа-таркалу 186, 200
Амплитуда 93
Аннигиляция 224
Антикисәкчек 225
Антиматдә 225
Антинейтрино 201
Антинейтрон 225
Атом 180
Атом төше 185
Атомның протон-нейтронлы
моделе 196
Бәйләнеш энергиясе 204
Бел (тавыш катылыгы дәрәҗәсе
берәмлеге) 121
Берәмлекләр:
— ешлык б. 94
— импульс б. 78
— көч б. 46
— тавыш б. 121
— тавыш дәрәҗәсе 121
— тизләнеш б. 21
Бета-кисәкчек 181
Бета-таркалу 201
Борау кагыйдәсе 145
Бөтендөнья тартылу көче 59
Вектор зурлык 11
Вильсон камерасы 190, 191
Гамма-кисәкчекләр (гамма-квант,
гамма-нурланыш) 181, 182
Гейгер счетчигы 189
Герц (ешлык берәмлеге) 94
Гравитацион даими 59
Грэй (йотылган нурланыш
дозасы берәмлеге) 217
Дейтерий 199
Дефектоскопия 131
Децибел (белның өлешчә
берәмлеге) 121
Доза:
— йотылган нурланыш дозасы
217
— йотылган эквивалент
нурланыш дозасы 218
Дулкын:
— аркылы 110, 111
— буй 110, 111
— йөгерек 109
— озынлыгы 113, 172
Ешлыклар:
— алмаш ток е. 167
— тирбәнешләр е. 94
— төп тирбәнешләр е. 119
— урнашкан тирбәнешләр е. 104
— үз тирбәнешләр е. 94
Җисемнең импульсы 78
Җирнең ясалма иярчене 74
Законнар:
— бөтендөнья тартылу з. 59
— импульс саклану з. 80
— корылма саклану з. 187
— масса саны саклану з. 187
— Ньютонның беренче з. 40, 41
— Ньютонның икенче з. 46
— Ньютонның өченче з. 49, 50
Изотоплар:
— радиоактив 220
— табигый 220
251
Атамалар күрсәткече
— ясалма 220
Интерференция:
— тавыш дулкыннары и. 136
— яктылык дулкыннары и. 175
Ирекле төшү 52, 54, 57, 62, 63
Исәпләү җисеме 7
Йөреш (дулкыннарның)
аермасы 134
Камертон 116
Квант 179
Кварклар 225
Когерент дулкыннар 136
Конденсация төшләре 191
Корылма саны 187, 196
Критик масса 208, 209
Куыклы камера 192
Кыр:
— магнит к. 138
— электромагнитик к. 169
— өермәле к. 169
Күчеш 11, 30, 31, 32
Күчеш кагыйдәсе 200, 201, 202
Лептоннар 225
Магнит агышы (магнит
индукциясе агышы) 158, 160
Магнит индукциясе сызыклары
156
Магнит кыры индукциясе 154,
155
Магнит кыры 138
Масса саны 187, 196
Масса дефекты 205
Математик маятник 100
Материаль нокта 6, 7
Мәҗбүр итүче көч 103
Нейтрино 201
Нейтрон 195
Нуклон 196
Ньютон (көч берәмлеге) 46
Обертон 119
Позитрон 224
Протий 199
Протон 193
Пружиналы маятник 91
Радиоактивлык 180
Ракета 84
Резерфорд тәҗрибәләре 183, 184
Резонанс 106
Резонатор 128, 129
Рентген (нурланыш дозасы
берәмлеге) 217
Ротор 165, 167
Сегнер тәгәрмәче 83
Синусоида 98
Системалар:
— инерциаль с. 41
— инерциаль булмаган с. 41
— йомык с. 80
— исәп с. 8
— тирбәнүләр с. 90
— Халыкара берәмлекләр с. 11
Скаляр зурлыклар 10
Сон (тавыш катылыгының шарт¬
лы шкаласы берәмлеге) 121
Сопло 84
Статор 165, 167
Сул кул кагыйдәсе 150
Сцинтилляцияләр методы 183,
189
Сыйфат (радиоактив нурланыш¬
ның) коэффициенты 218
Тавыш
— югарылыгы 119, 120
— резонансы 128
252
Атамалар күрсәткече
— катылыгы 121
Тамгалы атомнар методы 220
Тембр 119, 120
Термотөш реакциясе 222
Тесла (магнит индукциясе
берәмлеге) 155
Тизлек:
— беренче космик т. 75
— дулкын т. 114
— икенче космик т. 76
— моменталь т. 20
— тавыш т. 124, 125
— турысызыклы тигез хәрәкәт
т. 17
— электромагнитик дулкыннар
т. 170, 171
— яктылык т. 124, 125
Тизләнеш:
— ирекле төшү т. 54
— үзәккә омтылу т. 70
Тикторыш энергиясе 204
Тирбәнешләр:
— гармоник 97, 99
— инфратавыш 117, 130
— ирекле 90
— мәҗбүри 103
— сүнә баручы 103
— тавыш 117
— ультратавыш 117, 130
Тирбәнүләр периоды 88, 94
Төп тон 119
Төш бүленү 206, 207
Төш көчләре 203
Төш реакторы 210
Трек 191
Тритий 199
Үзәккә омтылу көче 72
Фазалар аермасы 95
Фон (тавыш катылыгы дәрәҗәсе
берәмлеге) 121
Фотон 179
Хәрәкәтләр:
— әйләнә буенча х. 69
— йөреш х. 7
— кәкресызыклы х. 67
— периодик х. 88
— реактив х. 83
— тигез х. 20
— тигез булмаган х. 20
— турысызыклы тигез х. 16, 17
— турысызыклы тигез тизләнеш¬
ле 20, 21
— тирбәнү х. 87, 88
Хәрәкәтнең чагыштырмалылы-
гы 36
Чиста тон 119
Чылбыр реакцияләре 222
Эйнштейн формуласы 204
Электр кыры көчәнешлелеге 171
Электромагнитик индукция 163
Электрон 181
Электрон-позитрон пары 224
Электромагнитик кыр 169
Элементар кисәкчекләр 223
Эхолация 131
Юнг тәҗрибәсе 175
Яктылык турында корпускуляр
(һәм дулкын) төшенчәләр 218
Яктылык йөртүче эфир 178
253
ЭЧТӘЛЕК
Кереш 3
I бүлек. Җисемнәрнең үзара тәэсир итешү һәм хәрәкәт
законнары 5
§ 1. Материаль нокта. Исәп системасы 5
§ 2. Күчеш 10
§ 3. Хәрәкәт итүче җисемнең координаталарын билгеләү 12
§ 4. Турысызыклы тигез хәрәкәт вакытында күчеш 16
§ 5. Турысызыклы тигез тизләнешле хәрәкәт. Тизләнеш 20
§ 6. Турысызыклы тигез тизләнешле хәрәкәт вакытында
тизлек. Тизлекнең графигы 24
§ 7. Турысызыклы тигез тизләнешле хәрәкәт вакытында
күчеш 28
§ 8. Башлангыч тизлеге булмаган турысызыклы тигез тизлә¬
нешле хәрәкәт вакытында җисемнең күчеше 31
§ 9. Хәрәкәтнең чагыштырмалыгы 34
§ 10. Инерциаль исәп системалары. Ньютонның беренче
законы 39
§ 11. Ньютонның икенче законы 42
§ 12. Ньютонның өченче законы 48
§ 13. Җисемнәрнең ирекле төшүе 52
§ 14. Вертикаль рәвештә югарыга ыргытылган җисемнең
хәрәкәте 57
§ 15. Бөтендөнья тартылу законы 58
§ 16. Җирдә һәм башка күк җисемнәрендә ирекле төшү
тизләнеше 61
§ 17. Нептун һәм Плутон планеталарының ачылуы 64
§ 18. Турысызыклы һәм кәкресызыклы хәрәкәт 66
§ 19. Җисемнең әйләнә буйлап даими модульле тизлек
белән хәрәкәте 69
§ 20. Җирнең ясалма иярченнәре 73
§ 21. Җисемнең импульсы 78
§ 22. Импульс саклану законы 79
§ 23. Реактив хәрәкәт. Ракеталар 82
254
Эчтәлек
II бүлек. Механик тирбәнешләр һәм дулкыннар. Тавыш 87
§ 24. Тирбәнү хәрәкәте 87
§ 25. Ирекле тирбәнешләр.Тирбәнү системалары. Маятник 89
§ 26. Тирбәнү хәрәкәтен характерлаучы зурлыклар 93
§ 27. Гармоник тирбәнешләр 97
§ 28. Тирбәнү хәрәкәте вакытында энергия әверелеше. Сүнә
баручы тирбәнешләр 101
§ 29. Мәҗбүри тирбәнешләр 103
§ 30. Резонанс 105
§ 31. Тирбәнешләрнең тирәлектә таралуы. Дулкыннар 108
§ 32. Буй һәм аркылы дулкыннар 110
§ 33. Дулкын озынлыгы. Дулкыннарның таралу тизлеге 112
§ 34. Тавыш чыганаклары. Тавыш тирбәнешләре 115
§ 35. Тавышның югарылыгы һәм тембры 118
§ 36. Тавышның катылыгы 120
§ 37. Тавышның таралуы 122
§ 38. Тавыш дулкыннары. Тавышның тизлеге 124
§ 39. Тавыш кайтарылу. Кайтаваз 126
§ 40. Тавыш резонансы 128
§ 41. Ультратавыш һәм инфратавыш (өстәмә уку өчен) 130
§ 42. Тавыш интерференциясе 132
III бүлек. Электромагнитик кыр 138
§ 43. Магнит кыры һәм аның график сурәте 138
§ 44. Бериш булмаган һәм бериш магнит кыры 141
§ 45. Токның юнәлеше һәм аның магнит кыры
сызыкларының юнәлеше 144
§ 46. Магнит кырын аның электр тогына тәэсире
буенча белү. Сул кул кагыйдәсе 148
§ 47. Магнит кырының индукциясе 154
§ 48. Магнит агышы 158
§ 49. Электромагнитик индукция күренеше 161
§ 50. Алмаш электр тогын алу 165
§ 51. Электромагнитик кыр 168
§ 52. Электромагнитик дулкыннар 170
§ 53. Яктылык интерференциясе 174
§ 54. Яктылыкның электромагнитик табигате 178
255
Эчтәлек
IV бүлек. Атом 180
§ 55. Радиоактивлык — атомнарның катлаулы төзелешен
раслаучы факт 180
§ 56. Атом модельләре. Резерфорд тәҗрибәсе 182
§ 57. Атом төшләренең радиоактив әверелешләре 186
§ 58. Кисәкчекләрне тикшерүнең эксперименталь методлары 189
§ 59. Протон ачылу 192
§ 60. Нейтрон ачылу 194
§ 61. Атом төшенең составы. Масса саны. Корылма саны....196
§ 62. Изотоплар 198
§ 63. Альфа- һәм бета-таркалу. Күчеш кагыйдәсе 200
§ 64. Төш көчләре 203
§ 65. Бәйләнеш энергиясе. Масса дефекты 204
§ 66. Уран төшләренең бүленүе 206
§ 67. Чылбырлы реакция 207
§ 68. Төш реакторы. Атом төшләренең эчке энергиясен
электр энергиясенә әверелдерү 210
§ 69. Атом энергетикасы 213
§ 70. Радиациянең биологик тәэсире 216
§ 71. Радиоактив изотопларны табу һәм куллану (өстәмә
уку өчен) 220
§ 72. Термотөш реакциясе 222
§ 73. Элементар кисәкчекләр. Антикисәкчекләр
(өстәмә уку өчен) 223
Лаборатор эшләр 226
Кабатлау һәм атнага 3 сәгать физика укучылар өчен
тәкъдим ителгән мәсьәләләр 240
Күнегүләргә җаваплар 249
Кабатлау һәм атнага 3 сәгать физика укучылар өчен
тәкъдим ителгән мәсьәләләргә җаваплар 250
Атамалар күрсәткече 251
256
ISBN 5-94113-168-2