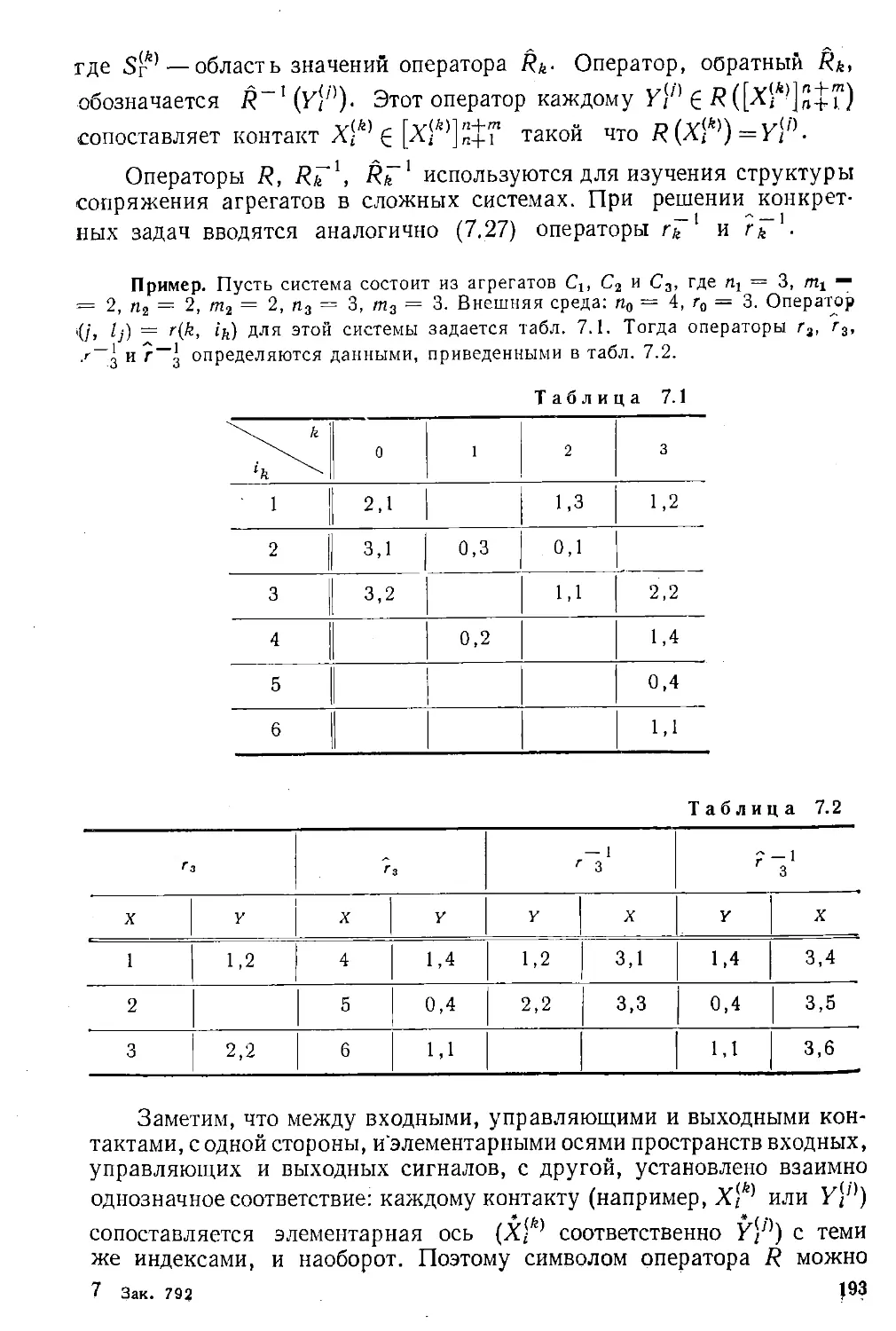
Text
Н. П. БУСЛЕНКО, В. В. КАЛАШНИКОВ,
И. Н. КОВАЛЕНКО
ЛЕКЦИИ
ПО ТЕОРИИ
СЛОЖНЫХ
СИСТЕМ
МОСКВА «СОВЕТСКОЕ РАДИО» 1973
УДК 519.95:621.3
Бусленко Н. П., Калашников В. В., Ковален-
ко И. Н. Лекции по теории сложных систем. М., Изд-во «Со-
ветское радио», 1973, 440 с.
В книге предпринята попытка изложить с единой точки
зрения проблемы построения математических моделей, их
количественного и качественного анализа для класса объектов,
обобщающего наиболее распространенные в технике и на-
родном хозяйстве типы сложных систем.
Вводные главы (1—3) посвящены обсуждению понятия
сложной системы, процесса ее функционирования, а также
функциональных характеристик и показателей, используемых
при проектировании и эксплуатации сложных систем. Главы
4—8 и 16 дают представление о современных схемах мате-
матического описания сложных систем и их моделирования.
В остальных главах книги приводятся некоторые методы ко-
личественного и качественного анализа сложных систем, изу-
чаются переходные и установившиеся режимы функциониро-
вания различных структурных типов систем, а также рассмат-
риваются вопросы устойчивости систем и оценки их характе-
ристик по опытным данным.
Книга предназначена для научных работников, инжене-
ров, аспирантов и студентов старших курсов, работающих в
области системотехники и создания автоматизированных си-
стем управления.
30 рис., 9 табл., библ. 182 назв.
Б -ЗУ^ОО-6-. 92-72
046(01)—73
ПРЕДИСЛОВИЕ
Предлагаемые ниже «Лекции по теории сложных систем» читались
авторами в период 1965—71 гг. главным образом в виде специального
годового курса студентам Московского физико-технического института,
а также в виде отдельных лекций и небольших обзорных курсов —
сотрудникам различных научно-исследовательских учреждений и учеб-
ных заведений. Поскольку как авторы, так и их слушатели интересова-
лись, по преимуществу, вопросами системотехники, в лекциях основ-
ное внимание уделено математическому описанию, моделированию и
анализу так называемых агрегативных систем, само понятие которых
возникло в недрах системотехники.
Введение, гл. 1—3, 7, 8, а также § 17.2 написаны Н. П. Бусленко,
гл. 10, 11, 13, 16, 17 (за исключением §17.2) — И. Н. Коваленко,
гл. 6, 9, 12, 15 — В. В. Калашниковым. Гл. 4 и 5 написаны совместно
Н. П. Бусленко и И. Н. Коваленко, а гл. 14 — совместно И. Н. Ко-
валенко и В. В. Калашниковым.
Единство изложения материала достигнуто, по-видимому, лишь
относительно основных понятий, терминологии и подходов к постанов-
ке и решению задач, возникающих на практике. Что касается матема-
тического аппарата, книгу можно разделить на две отдельные части.
Первая часть (гл. 1—8) является более элементарной и предназначена
для первоначального ознакомления с математическими схемами фор-
мализации сложных систем и общими методами их анализа. Если не
принимать в расчет некоторые математические тонкости, встречающие-
ся в §§ 3.4, 4.6, а также в § 5.4 (которые при первом чтении можно опу-
стить без ущер а для понимания дальнейшего материала), то эта часть
книги оказывается доступной для инженеров и студентов старших
курсов всех технических специальностей. Несколько более специаль-
ная подготовка по теории вероятностей требуется для понимания гл. 17.
Вторая часть книги требует от читателя знания элементов функци-
онального анализа и теории случайных процессов и предназначена для
специалистов, непосредственно связанных с моделированием на ЭВМ
и математическим исследованием сложных систем. Некоторые главы
книги (9,14, 16 и др.) носят обзорный характер. Кроме того, учитывая,
что исследование агрегативных систем достаточно общего вида пред-
ставляет весьма сложную математическую задачу, в гл. 10, 11 и частич-
но 17 изложены имеющиеся в настоящее время результаты более част-
ного характера.
Авторы считают своим приятным долгом выразить благодарность
академику В. М. Глушкову, члену-корреспонденту АН СССР В. С. Се-
менихину, Г. А. Ткачеву, В. С. Манусевичу, беседы и консультации
которых способствовали улучшению отдельных мест книги, а также
рецензентам — профессору Г. А. Фрейману и канд техн, наук В. А. Каш-
танову за исключительно полезные замечания по материалам рукописи.
ВВЕДЕНИЕ
Интенсификация производства и технический прогресс порождают
новые проблемы в сфере управления народным хозяйством. Приобре-
тают существенное значение применение ЭВМ для обработки информа-
ции и создание автоматизированных систем управления (АСУ).
Комплексы задач, решаемых в АСУ, по существу представляют
собой машинные методы анализа и синтеза сложных систем. Для того,
чтобы управлять, необходимо знать поведение объекта управления
под воздействием команд управления, уметь прогнозировать поведение
объекта управления. Такую возможность дают нам математические
модели сложных систем, реализуемые на ЭВМ.
В настоящее время используется большое число математических
моделей различных реальных сложных систем. Эти модели создавались
по мере возникновения соответствующих практических задач примени-
тельно к тем или другим реальным объектам. Поэтому как сами моде-
ли, так и машинные процедуры их анализа представляют собой весьма
пестрое сочетание разнообразных математических схем и методов.
Это обстоятельство в определенной мере затрудняет типизацию задач
анализа систем, увеличивает затраты труда на их программирование
и приводит к нерациональному расходованию сил, средств и времени.
Кроме того, оно вызывает нежелательные явления на этапе эксплуа-
тации АСУ, создавая затруднения при организации обмена информа-
цией между отдельными АСУ и объединении их в единую систе му авто-
матизации.
Одной из важных проблем теории сложных систем является, таким
образом, проблема унификации математических схем, используемых
при моделировании, и методов машинного анализа моделей.
Широко известны математические схемы, общие для некоторых
классов реальных сложных систем (конечные и вероятностные авто-
маты, системы массового обслуживания и др.). Оказывается полезной
и дальнейшая унификация: использование схем, для которых упомя-
нутые выше являются частными случаями. В качестве примеров таких
схем могут быть приведены агрегаты и агрегативные системы. Более
трудная задача — построение унифицированных процедур анализа
и синтеза систем. Тем не менее, определенные достижения имеются
и в этой области. Оказывается, что для унифицированных схем может
быть развит как аналитический, так и алгоритмический аппарат,
позволяющий решать некоторые важные задачи; к ним относятся за-
дачи структурного анализа, анализа функционалов, оценивающих
эффективность и другие свойства систем, решение ряда экстремальных
задач и т. д.
4
По мере усложнения исследуемых систем и углубления их анали-
за значительно возрастает объем информации, выдаваемой ЭВМ в ре-
зультате моделирования. Это обстоятельство лишает результаты моде-
лирования наглядности, затрудняет, а в некоторых случаях практиче-
ски исключает, восприятие и осмысливание их человеком. В связи
с этим появляются специальные методы обработки результатов моде-
лирования, имеющие целью представление их в более удобном для
восприятия и осмысливания виде. Часто приходится при этом доволь-
ствоваться лишь качественной картиной поведения системы. Поэтому
существенное значение приобретает постановка и развитие методов
машинного решения задач качественной теории сложных систем.
Продвижение в этом направлении идет главным образом по пути
обобщения классических постановок задач из области теории диффе-
ренциальных уравнений и теории динамических систем. В частности,
удается сформулировать достаточно общее понятие устойчивости,
выделить в некоторых случаях качественно различные типы движе-
ний сложной системы и использовать для качественной оценки си-
стем ряд результатов теории случайных процессов. Соответствующие
машинные алгоритмы в тех случаях, когда их удается построить, как
правило, представляют собой обобщения классических методов.
Существенное значение для анализа и синтеза сложных систем
имеют методы композиции и декомпозиции унифицированных схем,
а также задачи математической статистики в системной интерпретации.
Однако в этих областях пока сделаны лишь первые шаги. Аналогичное
положение наблюдается и в вопросах оценки качества управления
сложными системами и ряде других проблем. Тем не менее, можно на-
деяться, что по мере роста практического интереса к системным зада-
чам и вовлечения в теоретическую работу новых научных сил дальней-
шие результаты не заставят себя ждать.
ГЛАВА ПЕРВА Я
СЛОЖНЫЕ СИСТЕМЫ
1.1. ПОНЯТИЕ СЛОЖНОЙ СИСТЕМЫ. ПРИМЕРЫ
Увеличивающаяся сложность технических средств, применяемых
в последние годы в народном хозяйстве, повышение быстродействия
технологического оборудования, а также расширяющиеся специализа-
ция и кооперирование предприятий ставят перед инженерной мыслью
новые научно-технические проблемы. Среди них существенное место
занимают вопросы, связанные с более детальным и глубоким изуче-
нием свойств и специфики функционирования отдельных видов аппа-
ратуры и оборудования, особенно если речь идет о средствах, работаю-
щих на новых малоисследованных принципах.
Однако, в отличие от традиционной ситуации, при разработке
крупных автоматизированных технологических, энергетических, гид-
ротехнических, информационных и других сложных комплексов возни-
кают проблемы, относящиеся не только к свойствам отдельных средств
но также и к закономерностям функционирования соответствующей
системы в целом. При рассмотрении «общесистемных» вопросов не
обязательно углубляться в конкретные аспекты функционирования
отдельных элементов. С «общесистемной» точки зрения представляют
интерес лишь те свойства элементов, которые определяют особенности
взаимосвязи их с другими элементами или непосредственно влияют на
свойства системы в целом.
Более того, появился широкий круг проблем, мало связанных
с рассмотрением свойств отдельных элементов: определение общей
структуры системы, организация взаимодействия между ее элемента-
ми, учет влияния внешней среды, определение оптимальных режимов
функционирования и т. д. По мере увеличения сложности систем комп-
лексным, «общесистемным» вопросам отводится все более значитель-
ное место. Они составляют содержание нового направления инженер-
ной мысли, получившего наименование системотехники.
Научной, главным образом, математической базой системотехники
является теория сложных систем*'1.
В настоящее время нет возможности дать общее определение слож-
ной системы, обладающее достаточной четкостью с точки зрения
построения строгой теории. Во избежание бесперспективной и, в зна-
чительной мере, бесплодной дискуссии в настоящей вводной части книги
мы ограничимся рассмотрением типичных примеров сложных систем
*> Наряду с термином «сложная система» в литературе для обозначения
этого же понятия иногда используются термины «большая система» и «система
большого масштаба».
6
и описанием некоторых их отличительных признаков. Во второй части
книги, посвященной математическому описанию процессов функцио-
нирования сложных систем, будут определены некоторые важные
классы сложных систем.
Отнесение той или другой реальной системы к разряду «слож-
ных» или «простых» является в значительной мере условным и свя-
зано, в основном, с тем, насколько существенную роль играют при изу-
чении системы комплексные, «общесистемные» вопросы. Это последнее
обстоятельство зависит как от свойств самой системы, так и от тех
задач, ради решения которых предпринимается исследование.
О задачах исследования систем с точки зрения системотехники
речь будет идти ниже. Относительно свойств системы, наличие которых
позволяет отнести ее к разряду «сложных», целесообразно сказать
следующее. Мы будем считать систему сложной, если она состоит из
большого числа взаимосвязанных и взаимодействующих между собой
элементов. Естественно ожидать, что сложная система способна вы-
полнять сложную функцию.
Конечно, никакой четкой границы, отделяющей простые систе-
мы от сложных, не может существовать. Так же как в математическом
анализе любое фиксированное, хотя бы и сколь угодно большое число
не может рассматриваться как «большое» в абсолютном отношении,
зато можно говорить о «большом» хп, если хп — общий член последо-
вательности, стремящийся к оо, так и в системных исследованиях
можно говорить о тенденции усложнения систем; можно, наконец,
четко определить степень сложности системы, но не имеет реального
смысла противопоставление «сложных» и «простых» систем.
В качестве аналогии рассмотрим пример из теории булевых функ-
ций. Ни у кого не вызовет сомнения, что классификация булевых функ-
ций трех переменных относится к проблематике исследования слож-
ных функций, хотя здесь существует четкое определение сложности
и сложность таких функций имеет заранее известную верхнюю гра-
ницу.
Указанные свойства требуют некоторого пояснения. Однако мы
сначала остановимся на типичных примерах сложных систем.
Система управления полетом самолетов крупного аэродрома (рис. 1.1).
Рассмотрим весьма упрощенную схему одного из возможных вариантов системы
управления полетом самолетов. В нее входит система дальнего обнаружения и
управления, состоящая из радиолокационной станции дальнего обнаружения,
аппаратуры съема данных, вычислительного устройства, аппаратуры отобра-
жения информации (табло, экраны и т. д.), аппаратуры выдачи информации
наземным системам и обмена информацией с бортом самолета [1], [11].
Данные о самолетах, полученные от радиолокатора дальнего обнаружения,
направляются в вычислительное устройство и соответствующим образом об-
рабатываются. При помощи системы многоканальной дальней связи с бортом са-
молета устанавливается двусторонняя радиосвязь. Поступающая информация
позволяет произвести отсев самолетов, следующих в другие аэропорты. Сведения
об этих самолетах дальнейшей обработке не подвергаются; в случае необходи-
мости радиосвязь может служить для передачи на борт метеорологических и то-
пографических данных, сведений о радиомаяках и т. д.
Информация о самолетах, следующих в данный аэропорт, подлежит даль-
нейшей обработке и передаче другим наземным системам.
7
В первую очередь эта информация поступает в систему диспетчеризации и
обрабатывается в центральном вычислительном устройстве. Здесь определяется
порядок посадки каждого самолета, выделяется соответствующая посадочная
полоса и канал многоканальной системы слепой посадки и взлета самолетов.
Последняя имеет радиолокационную станцию аэродромного обзора, вычислитель-
ное устройство с аппаратурой ввода данных и систему передачи команд на борт
самолета. По команде системы диспетчеризации информация об определенном
самолете от системы дальнего обнаружения передается в соответствующий канал
системы слепой посадки. Дальнейшая обработка информации производится в
этой системе. Посадочные характеристики непрерывно передаются на борт само-
Бортовая
аппаратура,
самолета
Система даль^\ [Система много}
у него обнарфке-Х [канальной дальз
'НГ1Я и ипппвлрн\ I вер Связи I
/йтобрах
жение 1
информа\
Ч ции J
Система
диспетчеризации
Радиолока-
ционный
передатчик
Стан-
ция
^''Многоканальная сип}
тема слепой посадки
а взлета самолетов
\Радиолокаци-\
уонный пере-
I датчик I
Радиолокаци-
онный прием-
ник
| Радиопере-
। датчик
Цент-
ральное
вычис-
литель-
ное
устрой-
ство
Комму-,
татар'
Аппаратура
ввода данных
8 вычислит,
устройство
Радиолока-
ционный
передачи
команд приемник
£
Аппара-
тура
выдачи
команд
Аппаратура
съема данных
иввода в вы-
числителен,
устройство
Аппаратура
съема данных
и ввода^в выч.
устройство
Вычисли-
тельное «-
устройство -<
| Радио-
। приемник
Коммута-
тор
Е7
/ЬтобраХ
жение \
унформан
\ ции /
| Аппаратура
обмена ин-
Г формацией
+ с бортом
самолетов
Вычисли-
тельное
устройство
.Аппаратура
выдачи йн-
.форн.назем- ‘
ным системам
Б
I
Рис. 1.1
лета и фиксируются специальными (например, стрелочными) приборами. Совме-
щение в каждый момент времени (при помощи органов управления самолетом)
соответствующих стрелок обеспечивает движение самолета по закону, вырабо-
танному вычислительным устройством, и успешную его посадку. Таким образом,
система слепой посадки вместе с бортовыми стрелочными приборами и пилотом
(или автопилотом) представляют собой замкнутый контур управления с обратной
связью, осуществляемой через радиолокатор аэродромного обзора.
Для того, чтобы получить представление о сложности рассматриваемой
системы управления полетами, обратимся к оценке ее оборудования. В качестве
эталонного устройства (с точки зрения объема оборудования) можно выбрать
центральное вычислительное устройство, так как в системе имеются заведомо
более сложные элементы (например, радиолокационные передатчики и прием-
ники и т. д.) и более простые (например, экраны, коммутаторы и др.). Это устрой-
ство обычно представляет собой электронную цифровую вычислительную машину
средней производительности. Машины такого типа содержат примерно 6000 пер-
вичных элементов (ламп, диодов, транзисторов и т. д.). Таким образом, вся си-
стема может содержать приблизительно 1200000 первичных элементов. Для срав-
нения заметим, что обычный бытовой телевизор имеет около 400 первичных эле-
ментов.
8
Городской транспорт. В качестве следующего примера сложной системы рас-
смотрим городской транспорт. К этой проблеме могут быть различные подходы.
Например, пусть нас интересует городской транспорт как сложная система с
точки зрения интенсивности движения по городским магистралям, пропускной
способности основных перекрестков, оптимального регулирования уличного дви-
жения и распределения его при помощи запрещающих и ограничивающих зна-
ков. Тогда элементами сложной системы будут городские магистрали, перекре-
стки, светофоры (или другие средства сигнализации и управления), а также все
транспортные средства: пассажирские, грузовые и специального назначения
(противопожарные, службы движения, коммунальных служб и т. д.).
При другом подходе бывает целесообразно рассматривать в качестве слож-
ных систем отдельные виды городского транспорта. Например, представляет
большой практический интерес изучение городского пассажирского транспорта
как сложной системы. В эту систему входят транспортные средства (троллей-
бусы, автобусы, трамвай, метрополитен, такси и др.), маршруты движения,
перекрестки и светофоры с учетом их загрузки другими видами транспорта,
а также пассажиропотоки, формирующиеся в различных пунктах города в за-
висимости от времени суток, диспетчерские пункты, средства связи и сбора ин-
формации, органы планирования и управления, средства ремонта и заправки
автомобилей и т. д. В этом случае городской пассажирский транспорт как сложная
система рассматривается с точки зрения качественного обслуживания пассажи-
ров, планирования маршрутов, распределения подвижного состава по маршрутам
определения оптимальных режимов движения (расписаний), планирования те-
кущего и капитального ремонта транспортных средств.
С этой же точки зрения можно рассматривать городской грузовой транс-
порт как сложную систему. Здесь вместо пассажиропотоков должны фигуриро-
вать грузопотоки, формирующиеся из отдельных грузов, поступающих от посто-
янных и временных источников и требующих доставки в постоянные и временные
пункты назначения. При исследовании такой сложной системы возникают анало-
гичные вопросы предварительного и оперативного планирования перевозок,
обеспечивающего своевременную и экономичную доставку грузов, а также про-
блемы, связанные с нормальной эксплуатацией транспортных средств.
Некоторые специфические вопросы, связанные с рассмотрением городского
транспорта как сложной системы, будут затрагиваться в дальнейшем.
Производственный процесс. Часто производственные процессы крупных пред-
приятий целесообразно рассматривать как процессы функционирования сложных
систем. Это тем более оправдано, чем в большей степени предприятие оснащено
средствами механизации трудоемких работ и автоматизации управления отдель-
ными операциями, группами операций и сложными технологическими циклами.
В качестве примера можно привести любой производственный процесс по-
точного выпуска штучных изделий (автомобили, часы, трубы и т. д.). В общем
случае конкретный производственный комплекс (стан, цех, завод и пр.), пред-
назначенный для поточного выпуска штучных изделий, содержит большое ко-
личество станков. Они объединяются в группы, называемые линиями. Каждая
линия обеспечивает выполнение последовательности операций, имеющих единую
цель и предназначенных для осуществления более или менее самостоятельной
части производственного процесса. Так, производственный комплекс может иметь
одну или несколько однотипных или неоднотипных линий сборки изделий, на
которых изделия собираются из отдельных узлов. Каждый узел, поступающий
на сборку, изготовляется либо внутри, либо вне рассматриваемого производст-
венного процесса. В первом случае производственный комплекс должен содер-
жать линии сборки узлов. Здесь узлы собираются из более мелких узлов и дета-
лей. В свою очередь детали, используемые при сборке узлов и изделий, произ-
водятся либо в пределах, либо вне данного производственного процесса. Для
деталей, изготовление которых входит в данный производственный процесс,
необходимо иметь линии, обеспечивающие их производство. Эти линии состоят
из станков, выполняющих такую последовательность операций обработки заго-
товок, которая приводит к изготовлению соответствующих деталей.
Для работы линий обработки или сборки характерны частичная или полная
(конвейер) синхронизация, взаимная связь между отдельными операциями,
зависимость режимов одной группы операций от особенностей протекания дру-
9
гих. Это обстоятельство требует внимания к учету взаимодействия станков в еди-
ном процессе их функционирования.
Производственный комплекс обычно содержит еще ряд элементов, обеспе-
чивающих выполнение других (не технологических) производственных операций;
транспортные средства, средства контроля качества изделий, окраски, упаковки
готовой продукции и т. д.
Существенная роль принадлежит также средствам управления производ-
ством. Их функция состоит в сборе и обработке информации о состояниях произ-
водственного процесса и выработке управляющих команд.
Информационная система. В последние годы все большее внимание уделяется
созданию и внедрению в народное хозяйство сложных информационных систем,
предназначенных для управления объектами в больших масштабах.
Процессы управления всегда связаны с переработкой информации. Однако
наименование «информационных» получили системы управления, которые пред-
назначены для оперирования над особенно интенсивными потоками информации
и структура которых приспособлена к выполнению специальных мероприятии',
направленных на оптимальный сбор, хранение, переработку и выдачу больших
массивов информации.
К информационным системам обычно относятся системы управления
крупными предприятиями, которые решают задачи текущего и перспективного
планирования, а также оперативного управления производством на организацион-
ном уровне. Системы управления предприятием на технологическом уровне и
технологическими процессами, работающие в истинном масштабе времени с ре-
альными объектами (управление станками, металлургическими процессами,
химическими реакторами и т.д.), как правило, перерабатывают незначитель-
ный объем информации и к разряду информационных не относятся.
Системы управления предприятиями представляют собой низший класс
информационных систем. Информационные системы более крупного масштаба
могут быть использованы для управления группой предприятий (например,
в рамках фирм, объединений и т. д.), а также отраслью народного хозяйства или
народным хозяйством страны в целом. Существуют информационные системы и
другого целевого назначения: диагностические (медицинские, технические
и т. д.), библиографические, диспетчерские и другие.
Типичная информационная система имеет следующую структуру.
1) технические средства системы,
2) система внутреннего математического обеспечения,
3) система внешнего математического обеспечения.
В состав технических средств системы включаются ЭВМ с несколькими сту-
пенями запоминающих устройств, развитой системой ввода — вывода информации,
каналами связи, внешними источниками информации.
Система внутреннего математического обеспечения включает программиро-
ванную логику и информационный процесс. Характерным для ЭВМ информацион-
ных систем является перенесение ряда формальных (не связанных с содержатель-
но-смысловой переработкой информации) функций на специальную совокуп-
ность программ, объединенных общим понятием «программированная логика».
Эта часть программ выполняет функции управления потоками информации, дис-
петчерования их, перекодировки, организации взаимообмена информацией с
использованием внутренних и внешних каналов связи и т. д.
Информационный процесс является центральным алгоритмическим элемен-
том информационной системы. Информационный процесс (в отличие от системы
программированной логики) реализует неформальную, а смысловую переработку
информации. Таким образом, речь идет о следующем по степени сложности этапе
переработки информации.
Основные функции информационного процесса:
— ввод в систему информации, формализованной в различной степени
(от «сильно» формализованных позиционных кодограмм до сообщений или запро-
сов на русском языке, обеспечивающих удобство взаимодействия человека с ма-
шиной); с этой целью информационный процесс снабжается системой программ
грамматического анализа и автоматического кодирования;
10
— осуществление эффективных ассоциативных информационных поисков
и выборки информации из полей памяти большой емкости;
— преобразование информации для ее последующего использования: до-
кументирования, отображения на экранах и табло, формирования массивов ин-
формации для расчетных задач и т. д.
В целом, с помощью информационных процессов осуществляется формиро-
вание ответов на запросы, оформление их к выдаче в необходимом виде, а также
обновление основных полей накопления информации; с этой целью в информа-
ционных процессах используется вспомогательная информация: словари, клас-
сификационно-адресные таблицы и т. д.
Кроме того, задачей информационного процесса является подготовка не-
обходимых массивов информации—исходных данных для решения расчетных
задач и оформление полученных результатов. Таким образом, информационный
процесс и комплекс расчетных задач находятся в постоянном взаимодействии:
первый выступает в роли поставщика информации для второго.
Комплекс расчетных задач, составляющих основу внешнего математиче-
ского обеспечения, осуществляет дальнейшую переработку информации,
полученной в ходе реализации информационного процесса. Так же, как
и информационный процесс, комплекс расчетных задач выполняет смысловую,
содержательную переработку информации. Однако условно можно считать, что
этот этап переработки информации связан не только с изменением структуры
информации, как в информационном процессе, но и с преобразованием самих
элементов информации.
Система внешнего математического обеспечения содержит средства для под-
готовки и реализации на ЭВМ комплекса расчетных задач и всего сложного про-
граммного хозяйства информационной системы на основе использования алго-
ритмических языков, трансляторов различных уровней и соответствующих ин-
терпретирующих систем, библиотек стандартных программ и типовых процедур.
Важность этой части математического обеспечения становится очевидной,
если учесть, что, как показывает опыт, объем программ таких информационных
систем может достигать 200—300 и даже 500 тыс. команд.
При решении задач планирования в пределах отдельной отрасли народного
хозяйства обычно учитывается 150—200 тыс. номенклатур материально-техни-
ческих средств. Можно ожидать также, что в этом случае объем постоянной учет-
ной информации (нормативы, цены, данные о производстве и т. д.) составит 10—
12 и более млн. букв, а объем переменной информации (заявки, счета, донесения
наряды и т. д.) — 100—200 млн. букв в год.
Обобщенная схема процесса, приводящая к решению задачи планирования
для упомянутой отрасли, представляется в следующем виде. В отраслевую инфор-
мационную систему поступают заявки, которые отражают потребность в мате-
риально-технических средствах.
Эти данные сортируются по видам запрашиваемых номенклатур, суммиру-
ются и фиксируются в накопителе системы. Одновременно поступают текущие
донесения от потребителей и поставщиков о наличии и движении материально-
технических средств, которые также фиксируются в системе. По имеющимся
в системе данным производится сопоставление потребностей с имеющимися в
наличии материально-техническими средствами на складах, базах, в текущем
производстве и у потребителей. С учетом этого решается задача о рациональном
распределении или перераспределении имеющихся средств, вносятся соответ-
ствующие изменения в учетные данные о наличии и движении материально-
технических средств, составляется план перевозок, выявляется количество недо-
стающих номенклатур.
Исходя из информации о производственных предприятиях, функциониру-
ющих в сфере данной отрасли, данных об их ресурсах, плане выпуска продукции,
снабжении сырьем и т. д., решается задача оптимального распределения заказов
по предприятиям. Решение этой задачи осуществляется по совокупности различ-
ных критериев, учитывающих факторы времени, стоимости, размещения и т. д.
В необходимых случаях рассматривается вопрос о подключении дополнительных
предприятий или строительстве новых. С учетом запросов потребителей, наличия
ресурсов и план-заказов производится оптимальное распределение материально-
технических средств (план снабжения). ♦
11
Информационные задачи, связанные с приемом заявок и донесений, осу-
ществляются в информационной системе непрерывно. Это обеспечивает постоян-
ное обновление информации о состоянии отрасли и правильное периодическое
планирование производства и снабжения.
Мы рассмотрели здесь свойства информационной системы доста-
точно общего вида. Естественно, что на практике могут встречаться
информационные системы, обладающие не полным комплексом пере-
численных свойств, а лишь частью их.
Типичными представителями реальных объектов, которые часто
рассматриваются как сложные системы, являются также телефонные
сети крупных городов и междугородняя телефонная связь, энергетиче-
ские комплексы и гидротехнические узлы, некоторые экономические
и биологические системы. Приведенных примеров, по-видимому, до-
статочно для того, чтобы подчеркнуть некоторые общие свойства и от-
личительные признаки сложных систем.
Выше было отмечено, что характерной особенностью сложной
системы является наличие большого числа взаимно связанных и взаимо-
действующих элементов. Каждая из сторон этой особенности — боль-
шое число элементов и взаимодействие между ними — сама по себе
способна породить соответствующие трудности при изучении системы.
Примеры проектирования и создания современных технологических
комплексов и систем автоматического регулирования являются хоро-
шим подтверждением отмеченного положения. Однако переход к ка-
чественно новой ситуации предопределяется сочетанием этих сторон.
Естественно, что совокупность, состоящая из п изолированных,
не связанных между собой, элементов еще не является системой. Для
изучения такой совокупности достаточно провести не более, чем п
исследований. Когда же речь идет о системе, состоящей из п элемен-
тов, необходимо рассматривать п (п — 1) возможных связей между
ее элементами (в общем случае связь элемента А с элементом В не
эквивалентна связи элемента В с элементом Л). Если характеризовать
состояние каждой связи лишь наличием или отсутствием в данный мо-
мент определенного воздействия (на практике такая характеристика
зачастую оказывается весьма поверхностной и недостаточной для
изучения поведения системы), то общее число состояний будет равно
2ra<n-i). Легко видеть, что для сложной системы это число может
быть фантастическим даже при небольших п. В самом деле, в системе,
состоящей только из 10 элементов, допускается 90 связей и соответст-
венно 290 « 1,3 • 1027 состояний. Поэтому изучение сложных систем
путем непосредственного обследования состояний в некоторых слу-
чаях может оказаться весьма громоздким. Отсюда вытекает важность
использования быстродействующих вычислительных машин для ис-
следования сложных систем и разработки таких методов, которые
позволяют сократить число обследуемых состояний.
1.2. ЭЛЕМЕНТЫ И ПОДСИСТЕМЫ
Расчленение системы на элементы в общем случае может быть
выполнено неоднозначным образом и является в высшей степени
условным,
12
Головной разработчик системы управления полетом самолетов
в качестве элементов этой системы будет рассматривать радиостанции
(дальней связи и передачи команд), коммутаторы, вычислительные
машины, радиолокаторы (дальнего обнаружения и слепой посадки),
аппаратуру съема данных и обмена информацией, устройства отобра-
жения. Разработчики перечисленных средств, наоборот, каждое из
средств будут считать системой, а в качестве элементов рассматривать
составляющие их схемы и узлы. Например, разработчик центрального
вычислительного устройства под системой будет понимать именно это
устройство (вычислительную машину вместе со вспомогательным
оборудованием), а в качестве ее элементов — сумматоры, регистры,
цепи синхронизации, генераторы, коммутаторы операций, матрицы
запоминающих элементов, дешифраторы и другие узлы.
В некоторых случаях целесообразно упомянутые узлы рассма-
тривать как соответствующие системы. Тогда элементами можно
считать триггеры, линии задержки, вентили, переключательные схе-
мы, усилители-формирователи, ячейки индикации и т. д. Наконец,
триггерная ячейка может считаться системой, состоящей из первичных
элементов: транзисторов, сопротивлений, конденсаторов,' ферритов
и других элементов электронных схем.
Аналогично имеется возможность выделить элементы в любой
из рассмотренных выше сложных систем. Так, в случае производст-
венного процесса, связанного с изготовлением штучных изделий, под
системой обычно понимается вся совокупность производственного
оборудования данного предприятия, а элементами этой системы могут
быть отдельные станки и устройства.
Расчленение системы на элементы является одним из первых
шагов при построении формального описания системы. В формализо-
ванной схеме системы элемент выступает как объект, не подлежащий
(при данном рассмотрении системы) дальнейшему разбиению на части.
Внутренняя структура элемента не является предметом исследования.
Имеют значения только те свойства элемента, которые определяют
его взаимодействие с другими элементами системы и оказывают влия-
ние на характер системы в целом.
Формально любая совокупность элементов данной системы вместе
со связями между ними может рассматриваться как ее подсистема.
Однако использование этого понятия оказывается особенно плодотвор-
ным в тех случаях, когда в качестве подсистем фигурируют некоторые
более или менее самостоятельно функционирующие части системы.
Например, в системе управления полетами самолетов можно выделить
следующие подсистемы: 1) систему дальнего обнаружения и управ-
ления, 2) систему многоканальной дальней связи, 3) многоканаль-
ную систему слепой посадки и взлета самолетов, 4) систему диспет-
черизации и 5) бортовую аппаратуру самолета.
Заметим, что подсистемы сложной системы сами могут быть
сложными системами, которые легко расчленить на соответствующие
подсистемы. В самом деле, рассмотрим городской пассажирский транс-
порт как сложную систему. Ее естественно расчленить на подсисте-
мы по видам транспорта: 1) троллейбусное хозяйство, 2) автобусное
13
хозяйство, 3) трамвайное хозяйство, 4) метрополитен, 5) таксомотор-
ное хозяйство и т. п. Однако каждая из перечисленных подсистем
представляет собой сложную систему, состоящую, в свою очередь,
из ряда подсистем. Возьмем для примера таксомоторное хозяйство
крупного города. Оно складывается из ряда самостоятельных хозяйств
(таксомоторных парков), располагающих тысячами автомобилей и соот-
ветствующими средствами технического обслуживания и управления.
Между прочим, парковая структура характерна для организации хо-
зяйства не только в системе такси, но и в других видах городского
пассажирского и грузового транспорта.
Выделение подсистем является важным этапом при построении
формального описания сложной системы. Оно позволяет иногда упро-
стить исследование сложной системы. Действительно, ряд задач, свя-
занных со свойствами отдельных подсистем рассматриваемой системы,
может быть решен при частном изучении соответствующих подсистем,
что во многих случаях существенно упрощает расчеты. Кроме того,
как правило, уменьшается количество связей между элементами си-
стемы, которые подлежат исследованию. Это также сокращает громозд-
кие вычисления.
Поясним упомянутое обстоятельство следующим примером. Пусть
система состоит из п = 20 элементов. Тогда полное количество воз-
можных связей между элементами будет равно п (п—1) = 380. Пред-
положим, что данная система расчленяется на 4 подсистемы по 5
элементов в каждой. Количество возможных связей между элементами
внутри подсистем будет равно 4 X 5 X 4 = 80. Число связей между
подсистемами 4 х 3 = 12. Если связи между элементами различных
подсистем отсутствуют, то общее число связей будет равно только
80 + 12 = 92. Таким образом, в данном случае число связей, подле-
жащих исследованию, сокращается более, чем в четыре раза.
Заметим, что с формальной точки зрения сущность подсистемы
двойственна: с одной стороны она сама является системой, состоящей
из некоторого числа элементов, а с другой — представляет собой эле-
мент сложной системы. Это обстоятельство может быть использовано
при построении процедур структурного анализа сложных систем.
Ниже будут фигурировать и другие соображения, подтвержда-
ющие преимущества представления сложной системы в виде совокуп-
ности подсистем.
1.3. УПРАВЛЕНИЕ И ИНФОРМАЦИЯ
В сложных системах поддержание нужных режимов функциони-
рования обеспечивается за счет управления отдельными элементами
системы и системой в целом. В связи с этим из совокупности элементов
системы наряду с другими могут быть выделены две особые группы
элементов: управляющие устройства и управляемые объекты. Имеются
примеры, когда такое выделение представляется весьма искусствен-
ным и функции управляющих и управляемых элементов тесно перепле-
таются. Тем не менее, мы будем в дальнейшем придерживаться упомя-
14
нутого деления, так как оно окаываестся удобным для исследования
сложных систем.
Управление является процессом переработки информации. От
управляемых элементов системы (рис. 1.2) поступает осведомитель-
ная информация, характеризующая их состояния и режимы работы.
Эта информация по соответствующим каналам передачи информации
(которые также являются элементами системы) поступает к управляю-
щим устройствам. Кроме того, управляющие устройства могут полу-
чать информацию извне, от объектов, не являющихся элементами рас-
сматриваемой системы (от внешней среды). Управляющие устройства
перерабатывают всю поступающую к ним информацию. В результате
переработки информации выясняется необходимость вмешательства
в режим работы упр’авляемых объектов и характер требуемых воз-
действий. Для осуществления упомянутого вмешательства управля-
ющие устройства выдают управляющую информацию, которая по спе-
циальным каналам поступает к управляемым объектам и исполь-
зуется для изменения в нужном направлении режимов их работы.
В реальных сложных системах наряду с упомянутыми элемента-
ми системы в процессе управления принимают участие и другие эле-
менты специального назначения. Совокупность элементов, участвую-
щих в управлении, обычно называют управляющим комплексом слож-
ной системы. Типичный управляющий комплекс содержит: 1) датчики
(на рис. 1.2 обозначены буквами Д), выдающие информацию о состоя-
15
ниях элементов системы и внешней среды (измеряющие параметры
элементов системы и воздействий внешней среды), 2) средства переда-
чи осведомительной информации (обозначены стрелками, идущими от
датчиков к управляющим устройствам), 3) управляющие устройства,
реализующие переработку информации, 4) средства передачи управ-
ляющей информации (обозначены стрелками, идущими от управляю-
щего устройства), 5) различные преобразующие и переходные устрой-
ства Л (кодирование, декодирование, синхронизация и т. д.), 6) органы
управления (обозначены буквой О), осуществляющие изменение режи-
мов функционирования управляемых элементов в соответствии с по-
ступающей к ним управляющей информацией.
В управляющих комплексах сложных систем процесс переработки
информации имеет весьма сложный характер и осуществляется, как
правило, в несколько этапов. Так, осведомительная информация для
передачи ее к управляющим устройствам подвергается различным пре-
образованиям, включающим сглаживание, перекодирование, кванто-
вание и т. д., а по прибытии в управляющие устройства — сортиров-
ке, представлению в новых системах координат и другим видам пред-
варительной обработки. После предварительной обработки осведоми-
тельная информация обычно запоминается в накопителях управляю-
щих устройств. Дальнейшая обработка информации производится с уче-
том сведений, поступивших из внешней срёды, и носит характер под-
готовки исходных данных для принятия решения о необходимости вме-
шательства в режимы работы управляемых элементов системы, а также
выработки, если нужно, самих управляющих команд. Передача по-
следних к управляемым элементам нередко сопровождается перекоди-
рованием, сглаживанием и другими преобразованиями управляю-
щей информации.
Совокупность преобразований, которым подвергается информация,
называют оператором переработки информации. Обычно выделяют
оператор первичной обработки информации, содержащей все этапы ее
преобразования до запоминания в накопителях включительно, опе-
ратор вторичной обработки информации (подготовка исходных данных
для принятия решений), оператор управления (принятие решений и вы-
работка управляющих команд), а также оператор последующей обра-
ботки информации (при передаче к управляемым элементам системы).
В настоящее время в связи с развитием электроники и вычисли-
тельной техники автоматизированные управляющие комплексы слож-
ных систем снабжаются ЭВМ, осуществляющими функции обработки
информации. Выполняя совокупность арифметических и логических
операций, продиктованную заданной программой вычислений, ЭВМ
обеспечивает реализацию алгоритма переработки информации, со-
ответствующего оператору переработки информации управляющего
комплекса сложной системы. Этот алгоритм содержит в качестве со-
ставных частей алгоритмы первичной, вторичной и последующей обра-
ботки информации, а также алгоритм управления (управляющий
алгоритм).
Воздействие управляющей информации на управляемые элементы
системы должно быть таким, чтобы режимы функционирования по-
16
следних обладали заданными свойствами. В связи с этим принятие ре-
шений и выработка управляющих команд оператором управления обыч-
но осуществляется таким образом, чтобы обеспечивался экстремум-
некоторого критерия управления. В этом случае управление называет-
ся экстремальным. Часто также употребляется термин «оптимальное
управление», значение которого будет выяснено ниже.
Совокупность действий управляющего комплекса, связанную
с переработкой данной порции информации и выработкой соответству-
ющих управляющих команд, называют циклом управления. Под дли-
тельностью цикла управления понимают время, прошедшее от момен-
та поступления данной порции информации до момента выдачи управ-
ляющей команды, выработанной с учетом этой порции информации.
В сложных системах, как правило, удается выделить один или несколько
контуров управления, вдоль которых циркулируют потоки информации. На-
пример, в системе управления полетами самолетов легко усмотреть два четко
разграниченных контура управления: 1) самолет—система дальнего обнаруже-
ния-—система многоканальной дальней связи—система диспетчеризации — си-
стема слепой посадки и взлета самолетов и 2) самолет—радиолокатор аэродром-
ного обзора — аппаратура съема данных — вычислительное устройство — ап-
паратура выдачи команд — станция передачи команд — самолет.
Последний из названных здесь контуров является замкнутым контуром
управления или, другими словами, контуром управления с обратной связью.
В самом деле, положение самолета в пространстве, фиксируемое радиолокатором
аэродромного обзора, сравнивается с положением, требуемым программой взлета
(посадки). Наличие отклонения от программы служит основанием для выработки
корректирующих сигналов (управляющей информации). Таким образом устра-
няется опасность грубых ошибок, если только система работает исправно.
В отличие от этого, первый из упомянутых контуров управления может
рассматриваться как разомкнутый. Действительно, информация о самолетах,
поступающая от радиолокатора дальнего обнаружения и системы дальней связи
перерабатывается в системе диспетчеризации и в виде управляющих команд (по-
рядок взлета или посадки, номер посадочной полосы и т. д.) поступает к системе
слепой посадки и взлета самолетов, а также на борт самолета. Однако здесь кон-
тур управления разрывается. История самолета, переданного в ведение системы
слепой посадки и взлета в рассматриваемом контуре управления не фигурирует,
информация о положении его в пространстве дальнейшей обработке не подвер-
гается.
Аналогично могут быть выделены контуры управления и соответствующие
им потоки информации в других сложных системах.
В системе управления полетами самолетов в каждом из отмеченных выше
контуров управления имеюся вычислительные устройства (ЭВМ и вспомогатель-
ное оборудование). Вычислительное устройство системы дальнего обнаружения
и управления реализует алгоритм, обеспечивающий расшифровку пачек радиоло-
кационных сигналов (алгоритм первичной обработки), определение текущих ко-
ординат самолетов, построение и прогнозирование трасс их движения, отсев само-
летов, следующих в другие аэропорты, формирование информации для выдачи
в систему диспетчеризации и многоканальную систему слепой посадки и взлета
самолетов и др. (алгоритм вторичной обработки).
При помошичьлгоритма, реализуемого центральным вычислительным устрой-
ством системы деапетчеризации, ’ решаются задачи, связанные с подготовкой
справок о загрузнеехи состоянии взлетно-посадочных полос и каналов многока-
нальной сиси™ икс лелой посадки, с оптимальным распределением полос п каналов
между самяиетами. олпределенпем порядка и режима взлета и посадки каждого
самолет».-<5'1>равляюшп,м алгоритм), формированием информации для передачи
многомавзллняй снвтеявь с тепой посадки и на борт самолета и т. д. (алгоритм
поел ^нзводеей «вервбо^ктд информации)—Г 1±1.
17
Управление в сложной системе может быть централизованным
и децентрализованным. Централизованное управление предполагает
концентрацию функции управления в одном центре сложной системы.
Децентрализованное — рапределение функции управления по от-
дельным элементам системы. Типичные сложные системы, встречаю-
щиеся на практике, относятся, как правило, к промежуточному типу,
когда степень централизации управления находится между двумя
крайними случаями, упомянутыми выше.
Рассмотрим возможные варианты структуры управления (диспет-
чеоизации) таксомоторным хозяйством крупного города. В случае
высшей степени централизации предполагается наличие единственного
(центрального) диспетчерского пункта, который принимает заказы
на обслуживание перевозок. Водители такси поддерживают связь
с диспетчерским пунктом по радиотелефону или пользуются для этой
цели уличными телефонами-автоматами. В другом варианте диспетчер-
ские пункты распределены по районам города или таксомоторным пар-
кам и связаны с определенным, жестко закрепленным, контингентом
автомобилей. В крайнем случае полной децентрализации можно было
бы предположить возможность приема заказов любым водителем такси
по радиотелефону от любого клиента. Каждый из упомянутых вариан-
тов имеет свои положительные и отрицательные стороны. По-видимо-
му, оптимальным является промежуточный случай, так как он предот-
вращает скопление большого количества заявок на центральном дис-
петчерском пункте. Неприемлемость случая полной децентрализации
очевидна.
Особенно серьезное значение имеет правильный выбор степени
централизации управления для таких сложных систем, где необходима
передача в управляющее устройство и переработка больших массивов
осведомительной информации, и, кроме того, качество управления
существенно зависит от учета состояний всех элементов системы.
Децентрализация управления позволяет сократить объем переда-
ваемой и перерабатываемой информации, однако в ряде случаев это
приводит к снижению качества управления.
Отмеченные трудности в значительной меньшей степени проявля-
ются при использовании систем управления с иерархической структу-
рой. Для управления с иерархической структурой характерно наличие
нескольких уровней управления. Типичным примером системы такого
рода является административное управление. Низший уровень пред
ставляется местным административным органом, следующий, более
высокий, — районной администрацией, еще более высокие уровни —
областной, республиканский и, наконец, высший — центральной ад-
министрацией.
На рис. 13 представлена схема одного из возможных вариантов
управления иерархической структуры с двумя уровнями управления.
На низшем уровне имеется три управляющих устройства (обозначены
номерами 2, 3 и 4). Устройство 2 управляет объектами 5, 6 и 7, уст-
ройство 3 — объектами 8, 9 и 10 и, наконец, устройство 4 — объек-
тами 11,12 и 13. При переходе на высший уровень управления устройст-
ва 2, 3 и 4 оказываются управляемыми объектами, а роль управляю-
18
щего устройства выполняет элемент 1. Существенной особенностью
управления иерархической структуры является то обстоятельство, что
основная масса информации перерабатывается в соответствующих
контурах низшего уровня, а на высшие уровни поступают лишь обоб-
щенные данные, характеризующие не отдельные элементы, а целые
подсистемы сложной системы. Например, в областном центре снабже-
ния концентрируются данные, поступающие от районных центров и со-
держащие обобщенные сведения по районам. Учетная информация,
связанная со снабжением отдельных потребителей (предприятия, хо-
зяйства и т. д.), перерабатывается внутри подсистемы снабжения
каждого района соответственно.
Весьма широкий класс реальных сложных систем имеют иерархи-
ческую структуру управления. Этим объясняется особый интерес
к изучению сложных систем такого типа.
1.4. СЛУЧАЙНЫЕ ФАКТОРЫ
Опыт наблюдения за реальными объектами, которые мы относим
к сложным системам, показывает, что они функционируют в условиях
действия большого количества случайных факторов. Поэтому предска-
зание поведения сложной системы может иметь смысл только в рамках
вероятностных категорий. Другими словами, для ожидаемых событий
могут быть указаны лишь вероятности их наступления, а относитель-
но значений некоторых величин приходится ограничиться законами
их распределения или другими вероятностными характеристиками
(например, средними значениями, дисперсиями и т. д.).
Для изучения процесса функционирования каждой конкретной
сложной системы с учетом случайных факторов необходимо иметь до-
статочно четкое представление об источниках случайных воздействий
и весьма надежные данные об их количественных характеристиках.
Поэтому любому расчету или теоретическому анализу, связанному
с исследованием сложной системы, предшествует экспериментальное
накопление статистического материала, характеризующего поведение
19
отдельных элементов и системы в целом в реальных условиях. Обра-
ботка этого материала позволяет получить исходные данные для рас-
чета или анализа.
Основными источниками случайных воздействий являются факто-
ры внешней среды и отклонения от нормальных режимов функциони-
рования (ошибки, шумы и т. д.), возникающие внутри системы. Слу-
чайные воздействия внешней среды приводят к изменению условий, в ко-
торых функционирует сложная система. Обращаясь к практике, есте-
ственно в первую очередь отметить различные физические условия,
влияющие на работу системы, например непредвиденные случайные
изменения погоды. Очевидно, что туман или гололед оказывают влия-
ние на режимы движения воздушного и наземного транспорта, особен-
но теплая погода ранней весной увеличивает спрос на соответствующие
сезонные товары, осадки и повышенная влажность воздуха, а также
жара в некоторых случаях затрудняют течение различных технологиче-
ских операций и производственных процессов и т. д.
Количество такого рода примеров может быть, при желании,
значительно увеличено. Однако наиболее существенное значение с
точки зрения исследования сложных систем из факторов внешней среды
имеет так называемое случайное колебание нагрузки. Сюда относятся
включение и выключение в случайные моменты времени некоторых
потребителей электроэнергии (сложная система — энергетический ком-
плекс), непредвиденное перераспределение пассажиропотоков или
грузопотоков (городской транспорт), значительное скопление в слу-
чайные моменты времени требований абонентов на телефонные перего-
воры (связь) и др. Случайные колебания нагрузки предъявляют
повышенные требования к пропускным способностям некоторых эле-
ментов системы, а также к оперативности управления ее функциони-
рованием и могут привести к снижению качества работы системы.
Случайные отклонения от нормальных режимов функционирова-
ния, возникающие внутри системы, появляются за счет ошибок (в пре-
делах допуска, определяемого точностью) различных приборов, внут-
ренних шумов аппаратуры, выхода из строя отдельных первичных
элементов системы, ошибок в управляющей информации, объясняе-
мых сбоями вычислительных и управляющих устройств, нарушения
синхронизации в работе некоторых элементов системы, отказов в ра-
боте отдельных агрегатов и т. д. Эти случайные воздействия приводят
к изменению значений некоторых параметров системы, а иногда и к
изменению ее структуры (отказы элементов). Вызванные ими наруше-
ния нормальных режимов функционирования, как правило, сказывают-
ся на качестве работы системы. Например, ошибки аппаратуры, обес-
печивающей заданное течение технологических процессов, снижают
качество продукции, ошибки в координатах самолета, порождаемые
шумами радиолокационного приемника, ухудшают режим слепой по-
садки; выход из строя единиц подвижного состава снижает пропуск-
ную способность транспортных средств; переостывание заготовки при
горячей обработке изделрй, вызванное плохой синхронизацией эле-
ментов прокатного стана, приводит к браку и даже поломке оборудо-
вания.
20
Из сказанного следует, что учету случайных факторов при иссле-
довании сложных систем необходимо уделить весьма серьезное внима-
ние.
Отметим еще одно существенное обстоятельство, связанное с влия-
нием случайных факторов на функционирование сложной системы.
Оно состоит в том, что наличие случайных отклонений в характеристи-
ках элементов сложной системы, интенсивности нагрузки и других
проявлениях внешней среды приводит не только к случайным откло-
нениям от «среднего» поведения системы, которое имело бы место,
если бы случайные факторы отсутствовали, но, в общем случае, и к
изменению самого этого «среднего».
Исследования показывают, что чем больше рассеивание случай-
ных отклонений характеристик системы и внешней среды, тем более
существенным в общем случае оказывается изменение «среднего»
поведения системы. Отсюда следует, что оценка «среднего» поведения
системы, исходя, только из средних значений случайных факторов
(без учета их рассеивания и взаимных влияний), может привести
к грубым ошибкам.
1.5. САМООРГАНИЗАЦИЯ
Рассмотрим некоторую сложную систему (систему I), взаимо-
действующую с внешней средой и выполняющую возложенную на нее
функцию. Пусть, кроме того, существует другая система (система II),
контролирующая качество работы системы I путем оценки тех воздей-
ствий, которые внешняя среда оказывает на систему I. Если воздейст-
вия внешней среды на систему I находятся в допустимых пределах,
зафиксированных в памяти системы II, система II выдает сигнал, под-
тверждающий этот факт. Когда же воздействия внешней среды на
систему I выходят за допустимые пределы, система II вырабатывает
команды, способные изменять свойства системы I. Наиболее распро-
страненными способами изменения свойств системы I являются: изме-
нение значений параметров некоторых элементов, изменение управляю-
щих алгоритмов системы I, а также изменение структуры за счет разры-
ва некоторых связей или подключения новых. Последнее мероприятие
позволяет включать в состав системы I новые (резервные) элементы
или, наоборот, выключать элементы, находящиеся в ее составе. В за-
висимости от вида системы 11 свойства системы I изменяются либо
целенаправленно, либо случайным образом.
Естественно, что после изменения свойств системы I могут изме-
ниться и воздействия на нее внешней среды. Если эти воздействия,
контролируемые системой II, опять не попадают в допустимые преде-
лы, система II снова вырабатывает команды, приводящие к изменению
свойств системы I. В некоторых случаях процесс последовательного
изменения свойств системы I может закончиться попаданием воздейст-
вий внешней среды на нее в допустимые пределы. Это означает, что
качество работы системы I признано удовлетворительным и свойст-
ва ее дальнейшему изменению не подлежат, по крайней мере до тех
21
пор, пока условия внешней среды остаются постоянными и в самой си-
стеме I никаких существенных изменений (например, за счет износа
или поломок ее элементов) не происходит. В случае значительного
изменения условий внешней среды или свойств системы I, обнаруживае-
мых системой II посредством оценки воздействий внешней среды на
систему I, описанный выше процесс начинается сначала.
Легко видеть, что системы I и II могут быть объединены в единую
сложную систему. Если в этой новой системе процессы последователь-
ного изменения свойств приводят за конечное время к тому, что воз-
действия внешней среды попадают в допустимые пределы, то система
называется самоорганизующейся [7].
Таким образом, самоорганизующая система способна на основа-
нии оценки воздействий внешней среды путем последовательного из-
менения своих свойств прийти к некоторому устойчивому процессу
функционирования, при котором воздействия внешней среды находят-
ся в допустимых пределах. Эта же мысль может быть выражена сле-
дующим образом. Самоорганизующимися называются такие системы,
которые за счет изменения своих свойств обладают способностью
устойчиво сохранять характер взаимодействия с внешней средой не-
смотря на возможные изменения внешних и внутренних факторов.
Понятие самоорганизующейся системы включает и тот случай,
когда первоначальная система I представляет собой случайный набор
элементов, связанных друг с другом случайным образом, лишь бы
при этом сохранялись контрольные функции системы II.
Примеры самоорганизующихся систем можно найти в живой при-
роде. Организмы животных и растений способны поддерживать свою
жизнедеятельность в изменяющихся условиях внешней среды за счет-
изменения свойств отдельных органов и] даже перераспределения
функций между ними. Черты самоорганизации носят также некоторые
сложные системы в экономике и технике.
Заметим, что успешному течению процесса самоорганизации в из-
меняющихся условиях внешней среды способствуют возможность опе-
ративного изменения свойств сложной системы и как можно большая
целенаправленность.
ГЛАВА ВТОРАЯ
ФУНКЦИОНАЛЬНЫЕ ХАРАКТЕРИСТИКИ.
РАЗРАБОТКА СЛОЖНЫХ СИСТЕМ
2.1. ЭФФЕКТИВНОСТЬ
Успешное решение задач анализа (определения свойств системы
по ее структуре и значениям параметров) и синтеза (определения
структуры и значений параметров системы по заданным свойствам)
сложных систем, как показывает опыт, не может быть обеспечено од-
ними лишь средствами умозрительной оценки поведения систем в
различных условиях функционирования. Системотехника выдвигает
проблемы, требующие, достаточно глубокой количественной оценки
поведения и свойств сложных систем.
Количественные данные о поведении системы могут быть получе-
ны либо экспериментально, если нам доступны наблюдения и фикса-
ция поведения соответствующих реальных объектов, либо расчетным
путем, если имеется математическое описание системы. Помимо весьма
существенных трудностей как того, так и и другого пути получения
количественных данных о системе существует также проблема нагляд-
ной интерпретации их, позволяющей решать важнейшие теоретические
и практические задачи. Для этой цели массивы информации, описываю-
щие состояния системы в различные моменты времени и при различных
условиях, должны быть сведены к небольшому числу обобщенных
характеристик.
Следуя традиции, установившейся во многих областях науки, будем
оценивать свойства сложных систем при помощи числовых характери-
стик.. Каждая из числовых характеристик, используемых для оценки
свойств сложной системы, должна удовлетворять, по крайней мере,
следующим трем требованиям: 1) представлять собой величину, за-
висящую от процесса функционирования системы, которая по возмож-
ности просто вычисляется, исходя из математического описания систе-
мы; 2) давать наглядное представление об одном из свойств системы
и 3) допускать, в пределах возможного, простую приближенную оцен-
ку по экспериментальным данным.
В качестве примера совокупности числовых характеристик, удовлетворя-
ющих этим требованиям, можно привести рассматриваемые в теории вероят-
ностей моменты случайной величины.
Аналогия, на которую мы хотим обратить внимание читателя, состоит в
следующем. Исчерпывающим математическим описанием случайной величины
является закон ее распределения. Если этот закон задан, могут быть вычислены
моменты а1г р.2, ц3, н4 и т. д. Каждый из них наглядно характеризует важные
свойства случайной величины. Например, оц представляет собой среднее значение
(математическое ожидание) случайной величины, ц2 — дисперсию, описываю-
23
щую рассеивание возможных значений случайной величины относительно сред-
него значения, р,3—ассиметрию распределения случайной величины и т. д.
Очевидно, величины аг, р2. ll.i и т- Д- могут быть оценены по экспериментальным
данным. В самом деле, пусть xlt х.,. хп представляют собой результаты неза-
висимых испытаний над рассматриваемой случайной величиной. Тогда, как из-
вестно, оценками для будет величина
1 V
Х-~2ХГ’ (2Л)
L = 1
для р.2 — величина
1 п
(2.2)
i = 1
и т. д.
Мы убедились, таким образом, что моменты случайной величины как ее
числовые характеристики полностью удовлетворяют упомянутым выше требо-
ваниям. Более того, этот пример подтверждает мысль, что отсутствие исчерпы-
вающего математического описания (в данном случае речь идет о законе распре-
деления) не является препятствием для приближенной оценки свойств объекта
(случайной величины), если имеются экспериментальные данные (например,
xIt х2, ...., хп).
Попытаемся по аналогии с моментами случайной величины вы-
брать такие числовые характеристики, зависящие от процесса функцио-
нирования сложной системы, которые описывали бы основные ее
свойства.
Начнем с показателей эффективности. Любую сложную систему
мы рассматриваем как объект, предназначенный для выполнения не-
которого определенного вида работ или решения достаточно четко
очерченного класса задач. При этом процесс функционирования слож-
ной системы представляется как совокупность действий ее элементов,
подчиненных единой цели. Необходимо обратить внимание на важность
четкого определения задач и целей функционирования системы. Если
они строго определены, можно говорить о качестве работы системы.
Качество работы сложной системы мы будем оценивать при помощи
показателей эффективности. Под показателем эффективности сложной
системы будем понимать такую числовую характеристику системы, ко-
торая оценивает степень приспособленности системы к выполнению
поставленных перед нею задач.
Как было отмечено выше, сложные системы функционируют в усло-
виях действия большого числа случайных факторов. Поэтому и ре-
зультаты работы сложной системы неизбежно носят случайный ха-
рактер.
Если результатом функционирования сложной системы служит
некоторое событие (например, успешная посадка самолета, своевремен-
ная доставка груза или соединение абонентов на телефонной станции),
оно должно рассматриваться как случайное событие.
Иногда результат функционирования сложной системы выражает-
ся количественно в виде некоторой величины (например, число изде-
лий, выпускаемых за смену, число пассажиров, перевезенных за сутки,
время ожидания в очереди, стоимость определенного вида работ
24
и т. д.). Такая величина должна рассматриваться как случайная ве-
личина. Впрочем, и случайные события можно рассматривать, исхо-
дя из случайных величин. Так, каждому случайному событию А взаим-
но однозначно соответствует случайная величина %, равная 1, если А
происходит, и равная 0 в противном случае.
Для того чтобы оценка эффективности системы относилась к не-
которому среднему ее поведению в данных условиях и не зависела от
случайного сочетания действующих на систему факторов, обычно в ка-
честве показателей эффективности выбирают вероятности соответст-
вующих случайных событий или средние значения (математические
ожидания) соответствующих величин. Например, вероятность соеди-
нения абонентов, среднее число пассажиров, перевозимых за сутки,
среднее время ожидания в очереди и т. д.
Поскольку условия функционирования сложной системы носят
не обязательно стационарный характер и могут изменяться с течением
времени, необходимо указывать период времени или условия, к кото-
рым относится рассматриваемое значение показателя эффективности.
Заметим, что от того, какая числовая характеристика системы
выбрана в качестве показателя эффективности, зависит интерпретация
свойств системы и результатов ее исследования.
Для примера рассмотрим некоторый производственный процесс
как сложную систему. Целью функционирования ее является выпуск
определенного вида изделий. Проследим различные варианты выбора
показателя эффективности для этой системы.
Принимаем сначала в качестве показателя эффективности произ-
водительность, измеряемую средним числом изделий, выпускаемых
в течение заданного интервала времени (например, за смену). Исходя
из такого показателя эффективности при проведении мероприятий,
связанных с усовершенствованием производства, мы будем наибольшее
внимание уделять факторам, способствующим увеличению произво-
дительности. При этом неизбежно будут упущены из виду другие
стороны организации производственного процесса, не связанные не-
посредственно с производительностью, такие как качество изделий,
экономия сырья, энергии и фонда зарплаты, предотвращение износа
оборудования и другие.
Предположим теперь, что в качестве показателя эффективности
производственного процесса выбрана средняя величина себестоимости
продукции. В этом случае такие факторы, как экономия сырья, износ
оборудования, расход энергии и фонда зарплаты, будут иметь большой
вес; вместе с тем отойдут на второй план факторы, связанные с произ-
водительностью оборудования и качеством продукции. Это обстоя-
тельство имеет столь существенное значение, что средняя величина
себестоимости продукции редко служит основным показателем эффек-
тивности производственных процессов.
Легко видеть, что характер показателя эффективности определяет
основные направления в поиске свойств системы, которые обеспечивают
ее оптимальность (с точки зрения выбранного показателя эффектив-
ности). Весьма наглядный пример этого положения дает городской
пассажирский транспорт. Здесь удобно рассмотреть две группы пока-
25
зателей эффективности, определяющих цели системы, весьма далекие
по характеру друг от друга: 1) показатели, связанные с экономично-
стью содержания городского транспорта и 2) показатели, обеспечиваю-
щие наилучшее обслуживание населения. Примерами показателей
первой группы могут служить средняя прибыль, получаемая от го-
родского транспорта, средние затраты, необходимые для обеспечения
его работы и т. д., а второй — среднее время, затрачиваемое на поездку,
среднее время ожидания в очереди, средняя стоимость поездки и др.
Для согласования разнородных тенденций в характере работы
системы часто пользуются показателями эффективности, содержащи-
ми ограничительные условия. Например, для производственного про-
цесса такого рода показателями эффективности могут служить: 1) про-
изводительность при условии обеспечения заданного качества изделий
и заданной средней себестоимости продукции; 2) средняя себестоимость
продукции при условии обеспечения заданной производительности
и заданного качества изделий и некоторые другие. В случае городского
пассажирского транспорта: 1) средние затраты на обеспечение работы
городского пассажирского транспорта при условии, что среднее
время поездки не превышает заданной величины, 2) среднее время
поездки при условии, что затраты на обеспечение работы городского
пассажирского транспорта не превышают заданной величины, 3) сред-
няя прибыль, получаемая от городского транспорта при условии, что
среднее время поездки не превышает заданной величины и т. д.
Существенно заметить, что показатели эффективности, содержа-
щие ограничительные условия, имеют свои особые недостатки, су-
жающие сферу их применения. Прежде чем останавливаться на этом,
необходимо установить, что существуют показатели эффективности
сложных систем, позволяющие согласовать разнородные цели их функ-
ционирования. Например, для производственного процесса можно
использовать такие показатели эффективности, которые будут учиты-
вать как себестоимость и качество продукции, так и производитель-
ность оборудования: средняя величина прибыли, средняя рентабель-
ность и т. д. В случае городского пассажирского транспорта это сде-
лать труднее.
В самом деле, для построения показателя эффективности, учиты-
вающего количественно соотношение между экономичностью содержа-
ния городского пассажирского транспорта и качеством обслуживания
населения, необходимо обратиться к рассмотрению сложной системы
более высокого уровня — городского хозяйства в целом. Учет потерь,
связанных с затратами рабочего и личного времени человека на поезд-
ки к месту работы, учебы, в магазины, учреждения бытового и куль-
турного обслуживания, выраженных в количественном измерении,
поможет правильно определить ассигнования на развитие и содержа-
ние транспортных средств при составлении народнохозяйственного
плана.
Возвратимся к показателям эффективности сложной системы,
содержащим ограничительные условия. Пусть, например, для некото-
рого производственного процесса вместо величины прибыли в качест-
ве показателя эффективности выбрана производительность при усло-
?6
вии, что себестоимость продукции не превышает заданной величины.
Легко видеть, что в этом случае ограничение себестоимости продукции
может оказаться тормозом для дальнейшего повышения производитель-
ности, а значит, и величины прибыли. В самом деле, можно предста-
вить себе такой случай, когда небольшое превышение себестоимости
(например, увеличение затрат в связи с введением новой технологии)
позволяет значительно увеличить производительность, валовой вы-
пуск изделий и, в конце концов величину прибыли.
Аналогичные обстоятельства оказываются существенными и для
других сложных систем. Например, пусть эффективность городского
пассажирского транспорта оценивается средним временем поездки при
условии, что затраты на содержание его не превышают заданной ве-
личины. Такой показатель эффективности будет стимулировать опти-
мальное использование выделенных средств для всемерного умень-
шения среднего времени поездки. Однако можно себе представить слу-
чай, когда умеренное превышение затрат (например, для строитель-
ства линий метрополитена) позволяет значительно сократить затраты
времени населения на поездки по городу и, тем самым, получить су-
щественный народнохозяйственный эффект.
Сказанного, по-видимому, достаточно для понимания того, что
пользоваться показателями эффективности с ограничениями нужно
особенно осторожно, отдавая себе отчет в возможных последствиях
этого. Желательно, когда нет непреодолимых препятствий, употреблять
такие показатели эффективности, которые позволяют согласовать
разнородные тенденции в задачах и целях функционирования сложной
системы.
Любой показатель эффективности R зависит от ряда параметров.
Среди них основную роль играют параметры системы ах, а2, .... ап
и параметры, характеризующие воздействия внешней среды 0Х, 02,
IV
Таким образом,
R = R(a1, а2, ..., ап; ₽х, |32, ..., 0т). (2.3)
Помимо параметров системы и внешней среды, явно фигурирую-
щих в математическом описании, показатель эффективности зависит
также от структуры системы, характера связей между элементами,
вида управляющих алгоритмов и закономерностей функционирования,
не поддающихся описанию при помощи параметров. Эти зависимости
учитываются как видом функции R (или видом алгоритма, позволяю-
щего вычислить значения R, если явное выражение для него отсутст-
вует), так и введением дополнительных, так называемых, структур-
ных параметров.
Зависимости вида (2.3) для показателей эффективности сложных
систем с учетом широкого круга действующих факторов, как правило,
получаются весьма громоздкими. Задача расчета показателя эффек-
тивности зачастую требует реализации достаточно сложного алгорит-
ма и переработки большого количества информации. Поэтому вычисле-
ние показателей эффективности сложных систем обычно ведется на
быстродействующих вычислительных машинах. На практике пользу ют-
27
ся также различными приближенными способами, особенно когда речь
идет о предварительных расчетах.
При исследовании сложных систем в связи с решением практиче-
ских задач системотехники показатели эффективности находят широ-
кое применение. Они используются для сравнительной оценки вариан-
тов сложных систем при проектировании, для выбора оптимальных
параметров системы и режимов функционирования, для сравнительной
оценки управляющих алгоритмов и т. д.
2.2. НАДЕЖНОСТЬ
Для современных сложных систем важнейшее значение имеет
надежность функционирования. В самом деле, вспомним пример си-
стемы управления полетами самолетов (§ 1.1). Она выполняет исклю-
чительно ответственные функции, в том числе управляет слепой посад-
кой самолетов в трудных метеорологических условиях. Эта система
содержит около миллиона первичных элементов, тесно взаимодейст-
вующих в процессе ее функционирования. Если не будут приняты спе-
циальные меры обеспечения надежности, то от выхода из строя какого-
нибудь конденсатора или нарушения контакта может зависеть безопас-
ность пассажиров.
В других случаях речь идет не о жизни людей, а об экономиче-
ской стороне вопроса. Массовый выпуск малонадежного оборудования,
которое большую часть времени находится в ремонтных мастерских,
приводит к материальному ущербу по трем причинам: 1) для компенса-
ции количества оборудования, находящегося в ремонте, неизбежно
приходится увеличивать его выпуск, 2) требуются дополнительные
затраты на ремонт и в конце концов, 3) нужды народного хозяйства
не удовлетворяются или удовлетворяются с нарушением сроков и в
ущерб качеству. Поэтому, как правило, затраты на обеспечение надеж-
ности не являются убыточными. Главное — правильно распределить
выделенные средства, чтобы они принесли желаемый результат.
Последнее обстоятельство имеет большое значение, так как пути
обеспечения надежности сложных систем не очевидны и в каждом
отдельном случае обусловлены тонкими особенностями системы. Без
преувеличения можно сказать, что для получения обоснованных реко-
мендаций, связанных с обеспечением требуемой надежности современ-
ной сложной системы с наименьшими затратами, необходимо выпол-
нить серьезное научное исследование, зачастую равное по своим мас-
штабам разработке основной идеи построения системы.
По мере усложнения систем становится более сложной и оценка
их надежности. К сожалению, показатели надежности, хорошо заре-
комендовавшие себя при оценке «простых» систем, и традиционные
методы их определения оказываются практически бесполезными, когда
речь идет о современных сложных системах. Не останавливаясь на этом
подробно, заметим, что такие показатели надежности, как «среднее
время безотказной работы системы» или «вероятность безотказной ра-
боты в течение заданного интервала времени» применительно ко многим
28
Системам лишены практического смысла. Они сосредоточивают слиш-
ком много внимания на самом факте отказа и в то же время не позво-
ляют получить представление о влиянии отказа на конечный эффект
функционирования системы. Очевидно, что многие сложные системы
могут выполнять свои функции при условии, что некоторая часть их
элементов находится в нерабочем состоянии, например, городской
пассажирский транспорт — при выходе из строя нескольких автобу-
сов и троллейбусов; телефонная сеть крупного города — при обрыве
нескольких линий п т. д. В этих случаях речь идет не об отказе системы,
а лишь о возможном снижении качества ее работы. Обращаясь к си-
стеме слепой посадки самолетов, заметим, что отказ даже очень важного
элемента в одном из каналов многоканальной системы может не иметь
значения, если в момент отказа имеются свободные каналы. Если же
каналы заняты — играет роль безотказная работа даже второстепен-
ных деталей.
Эти соображения имеют целью подчеркнуть, что решающим в
оценке надежности сложных систем является правильный учет по-
следствий (с точки зрения конечного эффекта функционирования си-
стемы), к которым приводят отказы тех или других элементов.
Задача оценки надежности сложной системы может быть поставле-
на следующим образом.
Предполагается, что каждый элемент системы состоит из некоторо-
го количества первичных элементов. Все характеристики первичных
элементов и взаимодействия между ними, имеющие отношения к свой-
ствам системы, учитываются параметрами аь оы, ..., ап, входящими
в выражение для показателя эффективности (2.3). Поэтому любые изме-
нения характеристик первичных элементов или взаимодействия между
ними сказываются в той или иной степени на значениях параметров
а1( а2, ..., ап и, в конечном итоге, на величине показателя эффектив-
ности R.
Будем считать, что некоторые первичные элементы в процессе
функционирования системы могут выбывать из строя (отказывать).
Под отказом элемента понимается либо выход его характеристик за
допустимые пределы, либо полное прекращение работы. И в том, и в
другом случае, естественно, происходит изменение значения показателя
эффективности R; в первом случае — из-за изменения характеристик
первичных элементов, а во втором — из-за нарушения нормального
взаимодействия между ними, а также, иногда, из-за изменения перво-
начальной структуры системы.
Надежность первичных элементов (как «простых» систем) можно
описывать различными вероятностными характеристиками, например,
вероятностью безотказной работы в зависимости от времени, параметра-
ми потока отказов и другими. Необходимо теперь установить такие по-
казатели, которые характеризовали бы надежность сложной системы
в целом.
Очевидно, что отказы элементов не могут улучшить эффективность
системы (если исключить из рассмотрения курьезные случаи). Степень
снижения эффективности системы за счет отказов элементов достаточно
хорошо описывает последствия, к которым приводят отказы. На этом
29
пути может быть выбран удобный показатель надежности сложной
системы.
Пусть величина 7? является показателем эффективности некоторой
сложной системы. Предположим, что имеется возможность вычислять
7? по заданным параметрам системы и воздействий внешней среды в со-
ответствии с соотношением (2.3).
Вычислим значение А?°н показателя эффективности 7? в предполо-
жении, что все элементы системы абсолютно надежны (в процессе функ-
ционирования отказы не происходят). Кроме того, вычислим значение
7?*н показателя эффективности 7?, считая, что отказы элементов могут
происходить с интенсивностями, соответствующими заданным вероят-
ностным характеристикам. Тогда величина разности
дкон=к°н-я: (2.4)
может быть принята в качестве показателя надежности сложной си-
стемы.
Величина Д7?“ показывает, насколько снижается эффективность
системы за счет возможных отказов ее элементов по сравнению с эф-
фективностью идеальной системы, элементы которой предполагаются
абсолютно надежными. Легко видеть, что показатель вида (2.4) может
быть с успехом использован для сравнительной оценки различных
вариантов сложной системы. Для этого вместо 7?£ и 7?н достаточно
рассмотреть значения показателя R, относящиеся к этим вариантам.
Если величина Д7?2 мала, значит отказы элементов слабо влияют
на эффективность системы. В этом случае вряд ли имеет практический
смысл тратить средства на повышение надежности элементов. В другом
случае, когда величина Д7?“ не является малой, могут быть предложены
различные подходы к проблеме повышения надежности системы. Среди
них: увеличение надежности элементов, резервирование малонадежных
элементов, использование методов структурной надежности, профилак-
тические мероприятия и т. д.
При решении задач, связанных с оценкой надежности сложных
систем, необходимо учитывать возможность восстановления отказав-
ших элементов. На практике это обстоятельство играет весьма замет-
ную роль. Обычно в сложных системах имеются средства обнаружения
неисправностей и ремонтные средства. Длительность обнаружения
отказа и длительность ремонта задаются соответствующими вероятно-
стными характеристиками как случайные величины.
В заключение заметим, что помимо расчетных методов принци-
пиально возможны и экспериментальные пути оценки надежности
сложных систем. Практически экспериментальные методы широко
используются для получения характеристик надежности элементов,
особенно первичных элементов. Применение экспериментальных мето-
тодов в широком масштабе для оценки надежности сложных систем
в целом наталкивается на ряд существенных трудностей. Среди них —
потребность в больших затратах и длительном времени испытаний,
а также ряд трудностей организационного характера.
30
2.3. КАЧЕСТВО УПРАВЛЕНИЯ
Как было сказано выше, управлению в сложных системах принад-
лежит исключительная роль. Поэтому оценка качества управления
является одной из наиболее важных сторон общей оценки эффек-
тивности системы.
Необходимо отметить, что черты саморегулирования, самоуправле-
ния и даже самоорганизации в той или другой степени присущи не
только подавляющей части наблюдаемых в жизни сложных систем,
но и многим их элементам. Тем не менее, при практическом подходе
в сложных системах выделяются специальные элементы — управляю-
щие устройства — которые обеспечивают переработку информации
для целей управления. Осуществляемые ими функции условно можно
назвать принудительным управлением, в отличие от упомянутых выше
процессов самоуправления. В настоящем параграфе мы затрагиваем
только вопросы, связанные с принудительным управлением.
Качество управления в сложных системах зависит от многочислен-
ных факторов. Наиболее существенные из них для удобства рассмотре-
ния можно свести в следующие четыре группы: 1) факторы, связанные
с качеством критериев управления, 2) факторы, определяющие часто-
ту циклов управления, 3) факторы, характеризующие качество осведо-
мительной информации, и 4) факторы, связанные с качеством опера-
тора (алгоритма) управления. Остановимся кратко на каждой из них.
Воздействие управляющей информации на управляемые элементы
системы можно описать при помощи изменения значений некоторых из
ее параметров а1; а2, .... ап. Параметры системы, посредством которых
производится изменение режимов функционирования управляемых
элементов под воздействием управляющей информации, называются
параметрами управления. В дальнейшем параметры управления будем
обозначать со, а,-, .... со.
1 2 ,
Если_речь идет об экстремальном управлении, то значения atl,
a,-2, ..., aih параметров управления a^, a,-2, ..., aIft выбираются
такими, чтобы критерий управления Ф (aZ1, а,-2 ,..., aife) имел экстре-
мум Ф* при а,- == а(1, а,-2 = а(-2, ..., ath = aih-
Естественно предположить, что целью управления является повы-
шение эффективности функционирования системы. Поэтому в идеале
при a£1 = aZ1, a(-2 = aZ2, ... , aZft = az должен иметь экстремум
не только критерий управления Ф, Ф = Ф*, но и показатель эффек-
тивности системы R, R = R* (при фиксированных значениях других
параметров системы). Очевидно, что это требование автоматически вы-
полняется, когда в качестве критерия управления Ф выбирается
сам показатель эффективности R. Однако в реально существующих
системах далеко не всегда удается это сделать, так как часто показа-
тель эффективности системы (как функция параметров) описывается
весьма сложными соотношениями, затрудняющими решение экстре-
31
мальных задач. Более того, бывают случаи, когда упомянутые соот-
ношения остаются неизвестными.
Существуют и другие соображения практического порядка, вы-
нуждающие принимать в качестве критерия управления величину, от-
личную от показателя эффективности системы. Поэтому в реальных
системах, даже при значениях параметров управления, достаточно
близких к aZ1, аг-2, ..., аг , эффективность функционирования систе-
мы R может более или менее существенно отклоняться от экстремаль-
ной 7?*.
Перейдем теперь к влиянию длительности цикла управления (пере-
работки информации) на качество управления в сложной системе.
Чрезмерное увеличение длительности цикла управления неизбежно
приводит к снижению качества управления. Это объясняется следую-
щими причинами. Во-первых, управляющие команды, выдаваемые
через большой промежуток времени после получения порождающей их
осведомительной информации, строго говоря, уже не соответствуют
изменившемуся состоянию системы (устаревают). Если для снижения
эффекта старения информации применяется прогнозирование состоя-
ний системы (экстраполяция), то большая длительность цикла управле-
ния приводит к накоплению значительной ошибки экстраполяции.
Во-вторых, при большой длительности цикла управления снижается
частота выдачи управляющих команд управляемым элементам систе-
мы, что затрудняет согласование работы управляющего устройства
с динамическими свойствами управляемых элементов с точки зрения
характера переходных процессов.
Вместе с тем, чрезмерное уменьшение длительности циклов управ-
ления может оказать отрицательное воздействие на качество управле-
ния. Очевидно, что уменьшение длительности цикла управления повы-
шает требования к качеству осведомительной информации и быстродей-
ствию управляющих устройств. Действительно, если полнота и точность
осведомительной информации недостаточны, при малой длительности
циклов управления не успевает накопиться необходимое количество
сведений о состояниях системы и внешней среды, это может отрица-
тельно сказаться на точности выработки управляющей информации.
Другими словами, малая длительность циклов управления может при-
вести к принятию ответственных решений без достаточного знания об-
становки. Кроме того, когда длительность цикла управления мала,
управляющее устройство, если оно не имеет очень высокого быстро-
действия, должно реализовать упрощенные управляющие алгоритмы,
соответствующие более грубым методам переработки информации и вы-
работки решений. К этому добавляется перегрузка линий передачи
информации.
Очевидно, что достаточная полнота и точность осведомительной
информации являются необходимыми условиями высокого качества
управления. Чрезмерное увеличение полноты, точности и частоты полу-
чения осведомительной информации сверх минимального объема, выте-
кающего из требований качества управления, как правило, создает
перегрузку средств передачи и хранения информации, средств обра-
32
ботки информации, что приводит к дополнительным затратам
ресурсов.
Качество оператора (алгоритма) управления связано со скоростью
переработки информации, обеспечением высокой точности решения
экстремальных задач, устойчивости его работы при наличии ошибок,
запаздывания или сбоев в осведомительной информации и т. д.
Проблема оценки качества управления в общем виде еще недоста-
точно исследована. Поэтому в настоящее время нет возможности пред-
ложить универсальные методы ее решения. Однако уже имеется неко-
торый опыт, позволяющий рассматривать многие важные задачи, встре-
чающиеся в практике системотехники. Остановимся кратко на этих
вопросах.
В первую очередь рассмотрим задачу сравнительной оценки ка-
чества управления. Пусть считается заданной конкретная сложная
система, эффективность которой характеризуется показателем R.
Предположим, что применительно к этой системе рассматриваются два
варианта комплекса управления: вариант А и вариант В. В общем слу-
чае свойства комплекса управления существенно сказываются на эф-
фективности системы. Поэтому при различных вариантах комплекса
управления показатель эффективности R будет принимать различные
значения. Пусть в случае варианта А его значение будет равно Ra>
в случае варианта В — RB- Тогда, для сравнительной оценки качест-
ва управления сложной системой удобно использовать показатель
= —Rb- (2-5)
При помощи величины Д7?упр можно произвести обследование не-
которого числа вариантов управляющего комплекса сложной системы
и выбрать из них наилучший. Подобный подход нередко используется
при проектировании сложных систем.
Помимо общей задачи сравнительной оценки управляющего ком-
плекса в целом, показатель вида (2.5) можно применять для решения
ряда частных вопросов. Сюда относятся проблемы сравнительной оцен-
ки элементов управляющего комплекса или некоторых его параметров.
Примерами такого рода задач являются: сравнительная оценка крите-
риев управления, сравнительная оценка управляющих алгоритмов,
сравнительная оценка систем передачи информации, сравнительная
оценка точности измерения параметров, сравнительная оценка часто-
ты выдачи управляющей информации и т. д. В результате сравнитель-
ной оценки элементов управляющего комплекса или его параметров
преимущество получает тот вариант, при котором эффективность
сложной системы оказывается более высокой.
Сравнительная оценка качества управления позволяет выбрать
лучший из некоторого числа вариантов управляющего комплекса.
Однако при этом остаются невыясненными весьма принципиальные
вопросы. Например, существуют ли еще лучшие варианты управляю-
щего комплекса? Какими они обладают свойствами? Насколько эффек-
тивность сложной системы в этом случае может оказаться выше, чем
2 Зак. 792 33
при выбранном варианте? Каковы возможности аппаратурной реали-
зации управляющих комплексов очень высокого качества? Является
ли практически целесообразным их использование, или, другими сло-
вами, будет ли ожидаемое повышение эффективности столь существен-
ным, чтоб оправдать неизбежное увеличение затрат?
Ответы на эти вопросы дает абсолютная оценка качества управле-
ния, если она возможна для данного класса сложных систем.
Сделаем (пока необоснованное) предположение, что нам известно
значение 7?уПр показателя эффективности R сложной системы, соот-
ветствующее некоторому «идеальному» комплексу управления, хотя
сам этот «идеальный» комплекс управления может быть неизвестным.
Такое предположение имеет следующий смысл: I) существует, хотя
может оставаться неизвестным, некоторый комплекс управления, при
котором показатель эффективности R системы равен /?уПр и 2) при
любом комплексе управления эффективность системы не может быть
выше, чем 7?упр.
Тогда показателем качества данного варианта комплекса управ-
ления удобно выбрать величину
АЯупр = R°nP~R*, (2.6)
где R* — значение показателя эффективности системы, соответствую-
щее этому варианту комплекса управления.
Величина А/?°пр показывает, насколько снижается эффективность
сложной системы в случае, если вместо «идеального» комплекса управ-
ления принимается данный вариант.
Легко видеть, что показатель вида (2.6) может быть использован
не только для оценки качества управляющего комплекса в целом, но
и его элементов и отдельных параметров, как это было отмечено в свя-
зи с (2.5).
Сделаем несколько замечаний, связанных с оценкой величины
/?упР. Имеются примеры сложных систем, для которых можно опре-
делить (точно или приближенно) как сам «идеальный» комплекс управ-
ления, так и соответствующее ему значение 7?уПр. Сюда относятся слу-
чаи, когда структура и параметры «идеального» комплекса управления
находятся из условия экстремума показателя эффективности R данной
сложной системы. При этом «идеальный» комплекс управления может
быть не принят к реализации по причинам, связанным с трудностями
аппаратурного осуществления или возможностью, с точки зрения прак-
тики, обойтись более простыми (хотя и более грубыми) средствами.
В таких случаях выбирается комплекс управления, который является
по возможности простым и обеспечивает получение R*, достаточно
близкого к /?уПр-
Имеются также примеры сложных систем, для которых упомяну-
тая экстремальная задача не может быть решена (по крайней мере из-
вестными в настоящее время методами). В некоторых случаях, отно-
сящихся к этим примерам, величина 7?уПр может быть найдена точно
34
или приближенно, в то время как сам «идеальный» комплекс управле-
ния определить не представляется возможным.
Когда практически приемлемые способы решения экстремальной
задачи отсутствуют (не разработан метод решения задачи, известные
методы оказываются чрезмерно громоздкими, не построено математиче-
ское описание зависимости показателя эффективности R системы от ее
параметров и т. д.), часто имеется возможность оценить значение /?°Пр
косвенно.
Существуют классы сложных систем, для которых использование
«идеального» комплекса управления, если он существует, неизбежно
проявляется в особых режимах функционирования систем, связанных
с минимальными простоями оборудования, максимальной загрузкой ем-
костей, подвижного состава или каналов обслуживания, минимальными
потерями сырья или готовой продукции, наилучшим качеством изде-
лий или обслуживания и т. д. Во многих случаях для этих систем ве-
личина /?°пр может быть определена как условное значение показателя
эффективности при условии, что выполняется одно из упомянутых здесь
предположений. Например, если показателем эффективности некото-
рого производственного процесса служит производительность, то
в предположении об отсутствии простоев оборудования она может
быть определена как частное от деления длительности работы оборудо-
вания на среднюю длительность изготовления одного изделия. Ана-
логично, если показателем эффективности транспортной системы служит
объем перевозок, то в предположении о максимальном использовании
емкостей он может быть вычислен как сумма емкостей единиц подвиж-
ного состава, участвующего в перевозках, и т. д. Естественно, что мно-
гие практические примеры могут и не быть столь элементарными, тем
не менее косвенная оценка /?упр посредством условных показателей
эффективности широко распространена.
Часто встречаются на практике сложные системы, для которых
эта косвенная оценка позволяет определить лишь завышенное значение
/?°пр, недостижимое в реальных условиях функционирования си-
стемы. Очевидно, что тогда отпадает вопрос о существовании соответст-
вующего «идеального» комплекса управления. Хотя применение завы-
шенного значения А?уПр значительно обедняет наши сведения о ка-
честве просматриваемых вариатов управления, однако на практике
этим иногда пользуются для решения возникающих задач. Характер-
ным примером, когда косвенная оценка дает завышенное значение
показателя эффективности, является загрузка систем массового об-
служивания: максимальная пропускная способность системы прини-
мается равной Т/у, где Т — длительность рабочего интервала, а р —
среднее время обслуживания заявки.
При случайных моментах поступления заявок в систему неиз-
бежны простои, снижающие пропускную способность системы. В дан-
ном случае возможно получить простые поправки к 7?уПр, учитываю-
щие приближенно долю простоев в общей длительности рабочего
интервала системы.
2* 35
Помимо рассмотренных здесь общих показателей качества управ-
ления, позволяющих производить сравнительную и абсолютную оцен-
ку, на практике используются различные частные показатели, не свя-
занные непосредственно с показателями эффективности системы.
2.4. ПОМЕХОЗАЩИЩЕННОСТЬ
Как уже было отмечено выше, процесс функционирования любой
сложной системы подвержен влиянию случайных факторов, связанных
с внутренними состояниями системы и воздействиями внешней среды.
Обеспечение высокой эффективности системы при этих условиях
оказывается весьма серьезной проблемой. Возникающие трудности
усугубляются тем обстоятельством, что мероприятия, необходимые для
компенсации действия различных факторов, часто содержат противо-
положные тенденции и, в общем случае, порождают противоречивые
требования к системе.
Как показывает опыт, создание сложных систем так называемого
«универсального» применения, которые были бы гарантированы от
существенного нарушения режимов функционирования при «наи-
худших» или «наиболее тяжелых» условиях работы, практически не-
возможно. Подобные системы оказались бы чрезвычайно громоздкими,
дорогостоящими и, в то же время, малоэффективными. Поэтому на
практике сложные системы, за несущественными исключениями, созда-
ются для эффективной работы в некоторых типичных условиях, наи-
более характерных для систем данного класса. Эти условия мы в даль-
нейшем будем называть нормальными условиями, а процесс функцио-
нирования системы при нормальных условиях — невозмущенным про-
цессом функционирования системы.
Естественно, что нормальные условия функционирования сложной
системы являются своеобразной идеализацией действительности. В са-
мом деле, реальные условия всегда несколько отличаются от нормаль-
ных. Отклонения реальных условий работы системы от нормальных
порождают отклонения процесса ее функционирования от невозму-
щенного. Эти последние отклонения называются возмущениями, а со-
ответствующий процесс функционирования системы — возмущенным.
Часто оказывается удобным рассматривать отклонения реальных
условий работы сложной системы от нормальных как помехи, снижаю-
щие качество ее функционирования. Внутренние помехи, возникающие
внутри системы, проявляются в виде таких изменений свойств элемен-
тов системы, взаимодействия между ними или структурных характе-
ристик, которые приводят к изменению значений параметров ах, а2,
..., ап сложной системы, фигурирующих в соотношении (2.3). Изменен-
ные (возмущенные) значения а*г параметров а; могут быть представ-
лены в виде
а-+ Даь (2.7)
где а;° — значения параметров системы при нормальных условиях
функционирования, а Да; — изменения параметров, вызванные дей-
ствием помех.
36
Примерами возмущений, вызванных внутренними помехами
в сложных системах, могут служить ошибки в координатах самолетов
из-за собственных шумов радиоприемных устройств и линий передачи
данных в системе слепой посадки, нарушения графиков движения
подвижного состава городского пассажирского транспорта из-за пло-
хого технического состояния дорог и транспортных средств, а также
из-за недостаточной квалификации или дисциплинированности персо-
нала, нарушения технологических режимов и производственных
ритмов предприятия из-за низкого качества инструмента, средств
контроля технологии или плохой организации труда и т. д.
Внешние помехи проявляются в отклонениях от нормы воздейст-
вий на сложную систему со стороны внешней среды. Они приводят
к изменению значений параметров |32, ..., 0т, входящих в соотно-
шение (2.3). Возмущенные значения 0Д параметров также можно
представить в виде
₽; =₽/+А|3;, (2.8)
где 0/ — значения параметров, характеризующих воздействия внеш-
ней среды при нормальных условиях, а Д07- — изменения параметров,
вызванные действием помех.
Распространенными примерами внешних помех, влияющих на
работу сложных систем, являются атмосферные и промышленные
шумы в радиоприемных устройствах системы слепой посадки самоле-
тов, интенсивное движение пешеходов и грузового транспорта/а также
ремонтные работы на магистралях, снижающие скорость движения
в системе городского пассажирского транспорта, нарушения режимов
поставки сырья и комплектующих изделий, а также режимов отгрузки
готовой продукции применительно к производственному процессу и т. д.
В некоторых случаях невозмущенный процесс фукционирования
системы можно считать вполне детерминированным процессом, а все
случайные отклонения — свести к возмущениям. При этом нормаль-
ные условия функционирования будут соответствовать состояниям,
при которых влияние случайных факторов равно нулю.
Однако для многих важных в практическом отношении сложных
систем выбор нормальных условий, при которых влияние случайных
факторов сводится к нулю, оказывается нецелесообразным. В самом
деле, например, в системах массового обслуживания случайные факторы
не являются малыми отклонениями, а отражают собой саму сущность
функционирования. Часто более удобно нормальными считать такие
условия, при которых случайные факторы имеют заданные вероят-
ностные характеристики. Тогда, естественно, невозмущенный процесс
функционирования сложной системы будет случайным. Наличие помех
выражается дополнительными случайными факторами, выходящими
за рамки ограничений, принятых для нормальных условий. Возмущен-
ный процесс функционирования сложной системы в этом случае будет
складываться из двух случайных процессов: невозмущенного процес-
са и возмущений, вызванных действием помех.
Для любой сложной системы существенный интерес вызывает
вопрос о том, как влияют помехи на ее эффективность, или, другими
37
словами, какова помехозащищенность системы (способность эффектив-
но работать в условиях действия помех). Оценку помехозащищенности
системы можно произвести при помощи показателей, аналогичных по-
казателям надежности или качества управления.
Пусть величина 7?, определенная соотношением (2.3), представ-
ляет собой показатель эффективности некоторой сложной системы.
Вычислим значение 7?°орм показателя эффективности 7? для нормаль-
ных условий функционирования системы:
т-)0 ТУ I 0 0 л. 0.£>0л0 л 0 \ /г»
/?норм =-R («1» *^2» Pb Р2» Р/п)* (2*9)
Вычислим, кроме того, значение 7?пом показателя эффективности
R при условии действия на систему внешних и внутренних помех
с заданными характеристиками:
7?пом = Я(аь а*, ..., 0*, 02, .... 0m). (2.10)
Тогда величина разности
А7?пом = 7?2орм — 7?Пом (2.11)
может быть принята в качестве показателя помехозащищенности слож-
ной системы. Величина Д7?пом показывает, насколько снижается эф-
фективность системы при условии действия помех с заданными харак-
теристиками.
Очевидно, что помимо рассмотренной здесь абсолютной оценки
помехозащищенности системы, принятый подход позволяет дать сравни-
тельную оценку действию помех с различными характеристиками.
Для этого достаточно в соотношение (2.11) вместо 7?^орм и 7?„ом под-
ставить значения показателя эффективности R, относящихся к срав-
ниваемыми случаям.
На практике для наглядного отображения значимости той или
другой помехи часто пользуются также относительной оценкой помехо-
защищенности, рассматривая отношения величины АДпом к величи-
не какой-нибудь характеристики самой помехи. Существуют также
различные частные показатели, оценивающие влияние помех с задан-
ными характеристиками на работу сложной системы и ее элементов.
Относительно рассматриваемых показателей возникает вопрос,
нельзя ли ограничиться единственным показателем эффективности R,
хотя бы в тех условиях, когда требуется не синтез системы, а просто
оценка этого показателя? Оказывается, что это не так
Сказанное выше о показателях эффективности можно представить
в виде следующей элементарной схемы. Пусть имеется п факторов xt
(помехозащищенности, надежности и т. д.). Каждому Из этих факторов
можно приписать некоторое идеализированное значение хг° (например,
в случае надежности это означает, что элементы системы абсолютно
38
надежны). Пусть X; — реальные значения факторов. Тогда естествен-
но считать, что возможно приближенное представление
R(xlt х2, .... х°2> .... х°)4-ЛгЯ. (2-12)
где
Л п о ( 0 0 о 0'1 п / о 0\
Д. |х 1, ..., Х[ — 1, X/, Х[-]_ 1Хц)• /\ (х 1, ..., ХцJ,
по крайней мере, если значения Xi близки к идеальным. Расчет зна-
чения R (Х1°, х2°, хп°) обычно можно произвести на основании
сравнительно простой математической модели, а поправки A,R —
на основании специализированных моделей. В современных сложных
системах влияние различных факторов не учитывается одновременно.
Напротив, создаются отдельные модели учета надежности, помехо-
защищенности ит. п., каждая — специалистами соответствующей
области; в результате на основании приближенной формулы (2.12)
оказывается возможным рассчитать значения основного показателя
с учетом всех главных факторов. Разумеется, следует учитывать и эф-
фекты взаимодействия (например, влияние помех на показатель на-
дежности), однако после произведенного расчета AjR пути решения
этой задачи выглядят уже более прозрачно.
2.5. УСТОЙЧИВОСТЬ
Качество функционирования сложной системы, как было отмечено
выше, можно оценивать при помощи набора числовых характеристик,
таких, как показатели эффективности, надежности, помехозащищен-,
ности ит. д., вычисленных для заданных условий функционирования
системы. С этой точки зрения система только тогда обладает требуемы-
ми свойствами, когда выбранные характеристики находятся в задан-
ных пределах или принадлежат некоторым областям.
Однако установление того факта, что характеристики системы
принадлежат заданным областям при упоминавшихся выше нормаль-
ных условиях функционирования, имеет весьма ограниченное значе-
ние. Поскольку в действительности условия функционирования слож-
ных систем в той или другой мере отличаются от нормальных, сущест-
венно знать, сохраняются ли при наличии возмущений требуемые
свойства системы. На этой почве и возникает понятие устойчивости
функционирования сложных систем. Под устойчивостью функциони-
рования сложной системы мы будем понимать способность системы
сохранять требуемые свойства в условиях действия возмущений. Чтобы
сделать это понятие более точным, необходимо определить класс до-
пустимых возмущений, описать рассматриваемые свойства системы,
а также установить, какой смысл придается словам «сохранение тре-
буемых свойств».
Существующие в настоящее время определения устойчивости ис-
ходят из этих понятий и относятся к некоторому классу систем (глав-
ным образом, к динамическим системам, описываемым обыкновенными
39
дифференциальными уравнениями). Например, в определении устой-
чивости по Ляпунову возмущения ограничены любой, быть может,
сколь угодно малой величиной; в определении практической устойчи-
вости возмущения ограничиваются заранее фиксированной величиной;
при рассмотрении стохастической устойчивости возмущения являются
случайными величинами с заранее оговоренными вероятностными ха-
рактеристиками
Строго говоря, понятие устойчивости относится не к системе как
таковой, а к какому-нибудь свойству ее функционирования. Это свой-
ство и является определяющим фактором при выборе способа измере-
ния различия между возмущенным и невозмущенным процессами функ-
ционирования системы.
К строгому определению понятия устойчивости сложной системы
мы вернемся ниже в гл. 9. Здесь целесообразно подчеркнуть, что для
практики важно не только иметь возможность провести анализ устой-
чивости системы (проверить, устойчива ли система в принятом смысле
при заданных значениях ее параметров), но и указать ограничения,
налагаемые на параметры системы, при которых она оказывается
устойчивой. Эти ограничения определяют область устойчивости во
множестве параметров системы. Обычно рассматриваются области
устойчивости во множестве тех параметров, значения которых остают-
ся неизменными при переходе от невозмущенного процесса функцио-
нирования к возмущенному. Построение области устойчивости уже
можно отнести к синтезу системы. В дальнейшем задачи синтеза ре-
шаются с учетом ограничений, налагаемых на допустимые значения
параметров областью устойчивости.
В заключение обрати^ внимание на наглядную интерпретацию
понятия устойчивости. Для системы, устойчивой относительно неко-
торого свойства, можно указать такие ограничения (из заданного
класса ограничений), налагаемые на возмущения, при которых инте-
ресующее нас свойство будет сохраняться в некотором, вообще гово-
ря, вероятностном смысле. В случае неустойчивой системы этого сде-
лать нельзя. Более того, может оказаться, что для выбранного свойст-
ва нельзя подобрать никаких ограничений на возмущения, обеспечи-
вающих сохранение этого свойства, т. е. даже очень малые возмущения
могут привести к существенным срывам, значительно снижающим ка-
чество функционирования системы, вплоть до полной невозможности
ее практического использования.
Заметим, что система, которая является устойчивой в смысле вы-
бранного свойства по отношению к возмущениям заданного уровня,
в общем случае может оказаться неустойчивой, если для рассмотрения
будет взято некоторое другое ее свойство, или допустимый уровень
возмущений увеличивается.
С теоретической и практической точек зрения большой интерес
представляет изучение устойчивости относительно возмущений раз-
личной природы таких свойств систем, как принадлежность показа-
теля эффективности системы заданным пределам (например, средняя
производительность за смену не менее заданной, средний процент
отказов не превышает определенной величины и т. д.).
40
2.6. СЛОЖНОСТЬ
При проектировании сложных систем часто осуществляется выбор
одного из некоторого числа возможных вариантов системы. Естествен-
но, что критерием для такого выбора в первую очередь служит значе-
ние показателя 7? эффективности (с учетом всех остальных, важных
для данного класса систем, свойств: надежности, помехозащищенности
и т. д.). Однако если существуют варианты системы (два или более),
эквивалентные с точки зрения их эффективности, преимущество обыч-
но получает менее сложный из них.
Интуитивное представление о сложности системы связывает это
ее свойство с объемом оборудования (число элементов, их вес, габари-
ты и т. д.), разветвленностью связей между элементами и степенью
их взаимодействия, квалификацией персонала, осуществляющего
изготовление элементов, монтаж, наладку и эксплуатацию системы,
стоимостью изготовления системы и удобством ее практического
применения и т. д.
Однако в современных условиях развития техники одной интуи-
ции оказалось недостаточно. Возникла насущная необходимость в фор-
мальном понятии сложности системы. Это важно с точки зрения исклю-
чения элементов субъективизма и получения по возможности более
объективных оценок. Кроме того, без этого невозможен формальный
(в том числе и машинный) синтез сложных систем, интенсивно разви-
вающийся в последние годы.
Легко видеть, что интуитивное понятие сложности системы учи-
тывает как сложность ее структуры, так и сложность функции, реа-
лизуемой системой. Построение формального понятия сложности си-
стемы, охватывающего эти аспекты, в совокупности, оказалось весьма
трудной научной проблемой, которая в настоящее время находится
лишь в начальной стадии решения.
Наиболее элементарное и (весьма узкое) формальное понятие слож-
ности системы можно построить следующим образом. Пусть в нашем
распоряжении имеется п типов элементов. Для каждого типа интуи-
тивно (с учетом накопленного опыта) устанавливается величина слож-
ности элемента, измеряемая некоторым числом. Обозначим сложность
элемента Его типа через s;. Будем рассматривать системы, состоящие
только из элементов упомянутых п типов.
Сложностью s системы, состоящей из элементов со сложностью
Si, i — 1, 2, ..., п, будем называть величину
s=2 (2.13)
i — 1
где ki — число элементов Его типа, входящих в систему.
Несмотря на примитивность такого подхода с общей точки зре-
ния (величина s никак не учитывает сложности функции системы
и весьма узко, без учета взаимосвязей между элементами, характе-
ризует ее структуру), он оправдывает себя в очень многих практи-
ческих случаях.
41
Для того, чтобы полнее учесть структуру системы, целесообраз-
но выражение (2.13) сделать зависящим от числа связей между элемен-
тами. В частности, для некоторых классов сложных систем можно по-
ступить следующим образом. Легко видеть, что число N элементов
п
системы равно У йг. Как известно, максимальное число связей между
i— 1
элементами будет равно N (N — 1). Пусть фактическое число связей,
реализуемых в системе, обозначается М*. Величина
a = M*l N (N — 1)
(2-14)
характеризует относительное число реализованных связей. Тогда
сложность системы можно оценивать величиной
п
s = (l-(-va) J1 Siki, .(2.15)
i — 1
где v — коэффициент, учитывающий сложность связей по сравнению
со сложностью элементов системы.
Рассмотрим кратко другие возможные подходы к определению
сложности.
Сущность сложности функции проще всего понять на примере дискретных
функций.
Пусть f(xlt х2, ...., хп) — булева функция, т. е. xt, х2, хп и f могут при-
нимать только значения 0 и 1. Известно, что любую булеву функцию можно пред-
ставить в виде суперпозиции элементарных булевых функций. Такое представ-
ление всегда можно изобразить при помощи графа. В этом случае внешние вер-
шины графа будут представлять собой аргументы, а внутренние вершины —
функции. Заметим, что рассматриваемое изображение не является единственным.
Могут быть построены графы с различным числом внутренних вершин.
Очевидно, существует такое представление булевой функции (ре обязатель-
ное единственное), для которого граф содержит наименьшее число внутренних
вершин. Минимальное число внутренних вершин графа называется сложностью
булевой функции.
Заметим, что сложность — внутреннее свойство функции, это сложность
«в себе». Сложность «для нас» может оказаться гораздо более высокой: мы обыч-
но не умеем построить граф с минимальным числом вершин. Впрочем, в случае
дискретных функций минимальный граф в принципе можно построить путем
перебора. Если мы испробовали все графы с числом внутренних вершин, меньшим
чем типи один из них не соответствует заданной функции и если соответствующий
граф с т вершинами найдется, он и будет минимальным графом, а число т —
сложностью функции.
Вопрос о сложности модели, описывающей систему, не дает новых поста-
новок: модель—это тоже сложная система, состоящая из каких-то объектов,
и ей может быть приписана определенная сложность.
Методика оценки сложности систем представляет большой теоре-
тический и практический интерес и заслуживает серьезной научной
разработки.
42
2.7. ПОРЯДОК РАЗРАБОТКИ СЛОЖНОЙ СИСТЕМЫ
Опыт разработки современных сложных систем показывает, что
это мероприятие представляет собой в техническом и организационном
отношениях весьма трудоемкий и многоэтапный процесс, длительность
которого (с момента возникновения идеи создания системы до ввода
в эксплуатацию хотя бы одного экземпляра) колеблется в зависимости
от типа системы и различныхЪбстоятельств от двух до пятнадцати лет.
Основными действующими лицами (точнее юридическими лицами,)
принимающими участие в разработке сложной системы, как правило,
являются: заказчик, головной исполнитель (разработчик), его соиспол-
нители (субподрядчики), опытные и серийные заводы, строительные,
монтажные и испытательные организации, а также организации и уч-
реждения, обслуживающие систему в период эксплуатации.
В качестве заказчика обычно выступает соответствующее мини-
стерство или ведомство. Оно формулирует требования к системе, ут-
верждает проектную, техническую и сметную документацию, произво-
дит финансирование работ и обеспечение ее фондами, организует испы-
тания и эксплуатацию системы.
Головной исполнитель — специальное конструкторское бюро или
проектный институт — является ответственным за разработку всей
системы, создает проекты системы в целом и наиболее существенных
ее частей, координирует работу соисполнителей. Соисполнители —
конструкторское бюро и институты, а также опытные и серийные за-
воды, выполняют исследования, проектирование отдельных элемен-
тов системы и изготовление аппаратуры по заказу головного испол-
нителя. Строительные, монтажные, испытательные и эксплуатацион-
ные организации и учреждения обеспечивают монтаж, наладку, испы-
тания и ввод в эксплуатацию отдельных элементов, системы и системы
в целом.
Для руководства разработкой обычно назначается генеральный
конструктор системы и главные конструкторы основных ее элементов.
На стадии монтажа, наладки и ввода в эксплуатацию руководство ра-
ботами сосредоточивается в руках главного инженера системы.
Весь процесс создания сложной системы можно условно предста-
вить в виде последовательности определенных этапов. Мы в дальнейшем
будем рассматривать следующие основные этапы.
Этап I. Формулирование требований к системе и обоснование
технического задания на проектирование.
Этап II. Разработка эскизного проекта.
Этап III. Разработка технического проекта и создание опытного
образца.
Этап IV. Испытания.
Этап V. Изготовление и ввод в эксплуатацию головного образца
системы.
Этап VI. Опытная эксплуатация головных образцов.
На этом формально процесс создания системы заканчивается.
Однако, по существу, сложные системы отличаются той особенностью,
что усовершенствование и доработки, относящиеся к системе и ее
43
элементам, продолжаются на протяжении всей жизни системы. Поэто-
му целесообразно иметь в виду еще два дополнительных этапа.
Этап VII. Нормальная эксплуатация и развитие системы.
Этап VIII. Модернизация.
Первый этап иногда называют предварительным проектированием
системы. Его результаты служат исходными данными, которые не-
обходимы заказчику для того, чтобы обоснованно поставить вопрос
о разработке системы. Исследования ведутся в двух направлениях:
1) выяснение целей создания системы и задач, которые предполагает-
ся на нее возложить, и 2) изучение особенностей внешней среды,
с которой должна взаимодействовать разрабатываемая система. Это
позволяет получить представление о возможной структуре системы
и технических требованиях к ней. Этап заканчивается представлением
проекта технического задания на проектирование и предложений по
организации разработки.
На втором этапе, при создании эскизного проекта, вступает в строй
разработчик системы. В соответствии с техническим заданием он
разрабатывает проекты основных подсистем и системы в целом. Рас-
четными методами и путем эксперимента устанавливается соответствие
системы заданным техническим требованиям. Рассматриваются вопро-
сы, связанные с созданием опытного образца и испытаниями системы.
Кроме того, производится оценка объема оборудования и стоимости
разработки, выполняются различного рода технологические и эко-
номические расчеты, относящиеся к эксплуатации системы.
После одобрения эскизного проекта заказчиком, разработчик,
главным образом, силами своих соисполнителей, приступает к техни-
ческому проектированию и изготовлению опытного образца (третий
этап), позволяющего провести всесторонние испытания системы. Зада-
ча испытаний (четвертый этап) — подтвердить реализуемость прин-
ципов построения системы, проверить правильность ее функциониро-
вания и соответствие системы заданным техническим требованиям, .
а также получить экспериментальные данные, необходимые для уточ-
нения параметров системы и режимов ее эксплуатации.
Необходимо отметить, что испытания опытного образца связаны
в основном с оценкой технических характеристик системы и, в мень-
шей степени, отвечают на вопросы экономической целесообразности
широкого внедрения системы в народное хозяйство. Это объясняется
обычно двумя обстоятельствами. Во-первых, в целях экономии средств
и времени испытаний, опытный образец исполняется в ограниченном
объеме. С другой стороны, испытания опытного образца обычно прово-
дятся в условиях, которые могут отличаться от реальных условий ис-
пользования системы, например, в лабораторных условиях и т. д.
Поэтому часто перед тем, как начинать серийное производство большого
количества экземпляров системы изготовляется один «головной» обра-
зец или малая серия экземпляров (пятый этап) в целях опытной экс-
плуатации (шестой этап), которая позволяет получить материал для
обоснованного решения вопросов, связанных с серийным производст-
вом.
44
Содержание мероприятий, проводимых в пределах каждого из
перечисленных этапов, легко проследить на примере любой конкретной
сложной системы, в том числе и уже рассмотренных нами. Что касает-
ся седьмого и восьмого этапов, то мы здесь подчеркнем лишь принци-
пиальное различие между развитием сложной системы и ее модерниза-
цией. Развитие системы состоит в наращивании количества типовых
элементов системы и связей между ними, исходя из концепций, прин-
ципов и технических решений, выработанных в процессе ее разработ-
ки (увеличение числа каналов системы слепой посадки самолетов,
наращивание сети трамвайных и троллейбусных линий в системе го-
родского пассажирского транспорта, рост числа абонентских номеров,
а также узлов и подстанций в городской телефонной сети и т. д.). В от-
личие от этого модернизация сложной системы предполагает такие пре-
образования в системе, которые обеспечивают повышение ее эффектив-
ности путем использования новых прогрессивных принципов функцио-
нирования ее элементов, новых концепций в структуре или управлении
системой, а также новых технических решений (переход от элек-
тромеханических счетно-решающих устройств к электронным цифро-
вым машинам в системах диспетчеризации, переход от ручных комму-
таторов к АТС в системе городской телефонной связи, переход на авто-
матические станки и автоматизированные технологические линии в про-
изводственных процессах и т. д.).
В практике разработки сложных систем иногда наблюдаются бо-
лее или менее значительные отклонения от приведенной выше последо-
вательности этапов. Бывают случаи, когда головной разработчик после
получения технических требований к системе и технического задания
на проектирование по каким-либо причинам не желает взять на себя
полную ответственность за основные решения эскизного проекта. Тогда
появляется еще один этап — промежуточный между вторым и третьим—
создание аванпроекта или предэскизного проекта системы. При рассмо-
трении и утверждении аванпроекта заказчик одобряет некоторые основ-
ные концепции, принципы, технические решения. Тем самым, головной
разработчик приобретает большую уверенность в успехе эскизного
проектирования и перекладывает часть ответственности на заказчика,
так как в эскизном проекте получают развитие и дальнейшее обоснова-
ние, как правило, те концепции, которые были одобрены заказчиком
при утверждении аванпроекта.
В некоторых случаях для особенно дорогостоящих сложных си-
стем и при особенно сжатых сроках разработки опускается этап со-
здания опытного образца системы. Роль опытного образца при таких
обстоятельствах возлагается на головной образец и тогда испытания
системы проводятся на головном образце. Как правило, испытания пред-
шествуют опытной эксплуатации системы, но иногда такое разграниче-
ние четко провести не представляется возможным и оба эти этапа в не-
котором смысле совмещаются.
Наконец, в некоторых случаях возникает необходимость прово-
дить испытания не только опытного (или головного) образца системы,
но и всех ее экземпляров, получаемых в результате серийного произ-
водства. Это обычно объясняется либо недостаточно высоким качеством
45
продукции при серийном производстве, либо большим удельным весом
наладочных работ. Испытания серийных образцов, естественно, могут
быть проведены по сокращенной программе (по сравнению с основными
испытаниями опытного или головного образца), так как задачи таких
испытаний всегда являются лишь частью общих задач оценки системы
путем натурных испытаний.
2.8. СИСТЕМОТЕХНИКА
Проектирование сложных систем имеет две достаточно ярко вы-
раженные стадии. Первая относится к функционально-структурным
вопросам и может быть названа макропроектированием, а вторая —
микропроектирование — связана с проектированием элементов систе-
мы как физических единиц оборудования.
Макропроектирование, рассматривающее выбор и организацию
функций и структуры системы в целом, предполагает выяснение целей,
для которых должна служить система, и основных, решаемых ею за-
дач, исследование свойств внешней среды и определение характеристик
воздействия ее на систему, а также обоснование, в результате анализа
этих данных, технических требований к системе и взаимодействию ее
с внешней средой. Иногда эту стадию называют внешним проектирова-
нием системы.
Микропроектирование или, как иногда говорят, внутреннее
проектирование системы, связано с техническими решениями по основ-
ным элементам, их конструкции и параметрам, режимам эксплуатации
и т. д.
Такое разделение проектирования системы на части является
в значительной мере условным и не всегда границы его четко вырисовы-
ваются. Особенно это замечание относится к вопросам, связанным с ор-
ганизацией взаимодействия между элементами системы в процессе ее
функционирования. Естественно, что организация взаимодействия
невозможна без достаточно глубокого проникновения в природу эле-
ментов системы, вместе с тем она является одной из основных обще-
системных проблем.
Системотехника представляет собой совокупность точек зрения,
методов и подходов, связанных с макропроектированием сложных
систем.
Работа по макропроектированию системы начинается с форму-
лировки проблем, которая должна содержать по крайней мере три ос-
новных раздела: 1) четкое определение целей создания системы и круга
решаемых ею задач, 2) перечень и характеристику действующих на
систему факторов, подлежащих обязательному учету при разработке,
и 3) выбор показателя эффективности системы.
Цели и задачи системы определяются исходя из потребностей
практики,тенденций и особенностей развития современной техники,
а также народнохозяйственной (экономической) целесообразности.
В настоящее время пет возможности указать какие-либо формальные
правила для решения этого вопроса, за исключением, быть может,
46
рекомендации рассматривать данную систему как подсистему сложной
системы более высокого уровня. Понимание роли этой подсистемы,
а также опыт применения существующих систем аналогичного типа
и инженерная интуиция, пожалуй, исчерпывают ^арсенал имеющихся
средств.
Для оценки факторов, действующих на систему, помимо предшест-
вующего опыта эксплуатации аналогичных систем, используются ста-
тистические данные, полученные путем специально поставленных экс-
периментальных исследований.
Соображения, связанные с выбором показателей эффективности для
сложных систем, были достаточно полно освещены выше.
После формулировки проблемы обычно приступают к предвари-
тельной наметке одного или нескольких вариантов системы, которые,
по мнению проектировщиков, заслуживают дальнейшего рассмотре-
ния и подробного исследования. Исследования вариантов всегда начи-
нается с оценки их эффективности. Для этого необходимо знать требуе-
мое значение эффективности системы, а также уметь вычислять зна-
чения показателя эффективности, исходя из структуры и параметров
системы. Требуемое значение показателя эффективности определяет-
ся на основе анализа целей создания системы и круга решаемых ею
задач или что то же самое, народнохозяйственной (экономической)
целесообр азности.
Для получения методики расчета показателей эффективности,
а также для исследования различных свойств системы необходимо
построить математическое описание процесса ее функционирования,
или, другими словами, математическую модель. На практике, учиты-
вая специфику сложных систем и особенности задач макропроектиро-
вания, из всевозможных методов физического и математического моде-
лирования обычно отдается предпочтение методу статистического
моделирования. Статистическая модель процесса функционирования
системы представляет собой алгоритм, реализуемый на универсальной
цифровой вычислительной машине, при помощи которого имитируется
работа отдельных элементов системы, их взаимодействие, а также цир-
куляция и переработка информации. Для формирования случайных
воздействий на систему со стороны внешней среды и внутренних источ-
ников помех используются случайные числа с заданными или опре-
деляемыми в процессе моделирования законами распределения. Слу-
чайные числа либо генерируются специальными датчиками (электрон-
ными приставками к вычислительной машине), либо вырабатываются
в самой машине по специальным программам.
Кроме метода статистического моделирования, широкое примене-
ние для математического описания процессов функционирования слож-
ных систем получили и некоторые аналитические методы, основанные
на теории вероятностных процессов. Особенно необходимо отметить
роль так называемых марковских процессов (кусочно-линейные си-
стемы, системы массового обслуживания), а также вероятностных
автоматов и динамических систем со случайными характеристиками.
Во многих случаях применяется также метод динамики средних
(см. [2]). Перечисленные методы уступают статистическому моделиро-
47
ванию в смысле универсальности и применяются, как правило, для
решения частных задач.
Необходимо отметить, что для процессов функционирования слож-
ных систем часто бывают характерными так называемые конфликт-
ные ситуации, связанные с проявлением противоположных тенденций
и противоречивых требований. Такую трактовку можно дать многим
видам взаимодействия сложной системы с внешней средой, а в некоторых
случаях и взаимодействию элементов внутри системы. Для описания
этой стороны функционирования сложных систем могут быть исполь-
зованы методы теории игр и статистических решений, а с учетом того
обстоятельства, что стороны в конфликтных ситуациях стремятся
к оптимальному поведению, также и методы теории оптимального управ-
ления (в том числе линейного, выпуклого, динамического программиро-
вания и др.).
Состояние аппарата теории игр и оптимального управления в на-
стоящее время еще не достигло такого совершенства, чтобы можно
было в полном объеме описывать конфликтные ситуации в сложных
системах. Полученные соотношения оказались бы чрезмерно громозд-
кими. Однако иногда можно обойтись упрощенными моделями кон-
фликтных ситуаций для решения вопросов, возникающих при макро-
проектировании сложных систем. Кроме того, понятия теории игр
и оптимального управления могут быть использованы для включения
состязательных элементов в статистические модели сложных систем.
Математическая модель используется для оценки эффективности
различных вариантов структуры системы и набора ее параметров.
Наряду с математическим анализом сложных систем путем их
моделирования при проектировании проводятся также и эксперимен-
тальные исследования на действующих макетах системы и ее основных
элементов.
Сведения о системе, полученные в результате моделирования и экс-
перимента, дают возможность обосновать оптимальную структуру
системы, определить оптимальные значения ее параметров и убедиться
в том, что выбранный вариант системы соответствует цели ее разра-
ботки и обладает достаточной эффективностью. Таким образом, может
быть решена основная задача макропроектирования системы.
Работа по макропроектированию сложных систем предъявляет
особые требования к специализации инженеров-проектировщиков.
Для этой цели нужны специалисты широкого профиля, инженеры-
системотехники, обладающие достаточным кругозором в наиболее важ-
ных областях современной техники и повышенной математической
подготовкой.
Инженер-системотехник должен иметь серьезную подготовку
широкого диапазона в одной из областей техники, например, машино-
строения, электроники, радиотехники, текстильной или пищевой
промышленности, связи и т. д. Кроме того, он должен знать вопросы
автоматического управления, комплексной механизации и автоматиза-
ции, вычислительной техники, математические методы описания слож-
ных систем и исследования операций, методы математического модели-
рования, должен понимать специфику сложных систем и особенности их
48
проектирования, обладать способностью судить о системе в целом и под-
бирать узких специалистов для более глубокой проработки различных
частных вопросов.
Ниже будут рассмотрены примеры осуществления системного под-
хода на различных стадиях разработки сложных систем.
2.9. ОБОСНОВАНИЕ ТЕХНИЧЕСКОГО ЗАДАНИЯ
Первоначальный этап разработки сложной системы — формули-
рование требований и обоснование технического задания на проек-
тирование проводится по инициативе заказчика и относится почти
целиком к макропроектированию системы.
Министерство или ведомство, несущее ответственность за опреде-
ленную отрасль народного хозяйства, на основании потребностей
практики и возможностей развивающейся техники, ставит вопрос
о необходимости разработки некоторой сложной системы. Например,
Министерство гражданского воздушного флота, убедившись в нецеле-
сообразности или невозможности дальнейшего использования старых
методов управления полетами самолетов, приходит к выводу, что
крупные аэродромы нуждаются в автоматизированных системах управ-
ления полетами, использующих современные достижения радиолока-
ции, радиотехники, автоматики и вычислительной техники.
В зависимости от новизны проблемы и масштабов разработки опре-
деление основных требований к системе поручается ведомственному
научно -исследовательскому институту, одной из центральных отрас-
левых лабораторий или, наконец, группе инженеров из технического
управления министерства (ведомства). Целесообразно также привлечь
к этой работе сотрудников промышленных проектных институтов и кон-
структорских бюро, способных в дальнейшем взять на себя роль го-
ловного разработчика системы или его соисполнителей.
Как было отмечено выше, макропроектирование системы начинает-
ся с формулировки проблемы (цели и задачи системы, характеристика
учитываемых факторов и выбор показателя эффективности). На этапе
определения основных требований к системе и обоснования техниче-
ского задания на проектирование это делается впервые.
Один из возможных вариантов формулировки проблемы для слу-
чая системы управления полетами самолетов может иметь следующий
вид.
Необходимо разработать автоматизированную систему управления
полетами самолетов на базе современных достижений радиолокации,
техники радиосвязи, автоматики и вычислительной техники. Система
предназначается для крупных аэропортов и должна путем повышения
оперативности обработки информации и качества управления обеспе-
чить уверенное и своевременное прибытие самолетов в аэропорты на-
значения, снизить частоту случаев непредвиденного отклонения от
маршрутов и потери ориентировки, обеспечить большую независимость
режимов навигации от климатических условий, времени суток и пого-
ды, увеличение пропускной способности аэропортов путем более ра-
49
ционального использования существующей сети взлетно-посадочных
полос и аэродромного оборудования, а также сокращение времени
непроизводительного пребывания самолетов в воздухе в зоне аэродрома.
В результате создания такой системы ожидается улучшение качества
обслуживания пассажиров и обеспечение большей безопасности полетов
при условии сокращения эксплуатационных расходов.
Структура системы должна предусматривать решение перечисляе-
мых ниже задач [1]:
— обнаружение самолетов в зоне заданного радиуса;
— поддержание связи с бортом самолета и отсев самолетов, сле-
дующих в другие аэропорты;
— выдача самолетам, следующим в другие аэропорты, топографи-
ческих, метеорологических и навигационных данных;
— радиолокационное сопровождение самолетов, следующих в
данный аэропорт, определение их координат и выдача информации
наземным системам;
— обеспечение оптимальной диспетчеризации (определение по-
рядка посадки и взлета каждого самолета, выделение посадочной
полосы и канала системы слепой посадки и т. д.);
— хранение и отображение информации о самолетах, находящих-
ся в зоне аэродрома или следующих в данный аэропорт;
— обеспечение своевременной и качественной посадки каждого
самолета, прибывающего в аэропорт, а также взлета самолетов, от-
правляющихся из него.
При разработке системы необходимо учитывать следующие фак-
торы, противодействующие качественному решению задач: 1) наличие
атмосферных и промышленных помех, затрудняющих работу радио-
локационных систем и каналов радиосвязи, 2) возможность скопления
большого количества самолетов в зоне аэродрома из-за случайных
колебаний моментов прибытия самолетов в аэропорт, 3) отсутствие
в некоторые моменты времени свободных взлетно-посадочных полос
и каналов системы слепой посадки из-за случайных колебаний времени
занятости их, 4) наличие ошибок в перерабатываемой информации,
объясняемых неточностью аппаратуры, которые снижают качество
диспетчеризации и особенно слепой посадки, 5) возможность отказов
аппаратуры в процессе ее работы из-за недостаточной надежности.
В качестве показателя эффективности системы выбирается мак-
симальная интенсивность движения (среднее количество самолетов,
прибывающих в аэропорт за единицу времени), с которой справляется
система при условии, что среднее время ожидания самолета в воздухе
и вероятность потери ориентировки на маршруте не превышают задан-
ных величин.
На этом, собственно, можно было бы закончить краткое описание
рассматриваемого варианта формулировки проблемы. Тем не менее,
представляет интерес следующее замечание. Выбранный показатель
эффективности оказывается сравнительно простым и может быть оце-
нен при изолированном рассмотрении отдельного аэропорта. Отмечен-
ные его преимущества существенно облегчают исследования. Однако
использование такого показателя не позволяет оценить влияние внед-
50
рения автоматизированных систем управления полетами самолетов
на общий уровень качества обслуживания пассажиров и рентабельность
перевозок. Несмотря на это, мы отказываемся от выбора более общего
показателя эффективности, так как для его оценки потребовалось бы
рассмотрение всей сети средств гражданского воздушного флота стра-
ны как единой системы.
Таким образом, для всех исследований, которые необходимо про-
водить в процессе разработки системы, мы будем использовать выбран-
ный показатель эффективности. Оценку качества обслуживания пасса-
жиров и рентабельности в общем масштабе, которая нужна для опре-
деления народнохозяйственной (экономической) целесообразности раз-
работки системы, можно получить косвенно, считая, что внедрение
системы соответствующим образом изменяет пропускную способность
аэропортов.
Четкость и определенность формулировки проблемы имеет боль-
шое значение для успешной работы коллектива, занятого определением
требований к системе и разработкой технического задания на проекти-
рование.
Для дальнейшей работы может оказаться необходимым количест-
венное изучение действующих факторов и определение (в некоторых
случаях предварительное) характеристик воздействия внешней среды.
Применительно к системе управления полетами самолетов это означает
обобщение опыта и анализа статистического материала для определе-
ния интенсивности движения самолетов, характера и параметров помех,
характеристик ошибок, режима загрузки аэродромного оборудования,
частоты отказов различных видов аппаратуры и т. д.
Располагая этими данными и первоначальной наметкой структуры
системы, можно приступить к определению требований к ней. Будем
считать, что в нашем распоряжении имеется требуемое значение пока-
зателя эффективности, определенное, исходя из народнохозяйствен-
ной (экономической) целесообразности создания системы. Располагая
значением показателя эффективности и допустимыми границами сни-
жения уровня эффективности при неблагоприятных условиях функцио-
нирования системы (отказы, помехи и т. д.), можно предъявить обос-
нованные требования к ее надежности, помехозащищенности, устой-
чивости, качеству управления и другим основным свойствам.
На практике для расчетов, связанных с определением требований
к сложным системам, пользуются, как правило, методом статистиче-
ского моделирования.
Вследствие того, что структура системы и свойства ее элементов
на данном этапе могут быть известны только весьма приблизительно,
при моделировании отдельные элементы системы заменяются упрощен-
ными эквивалентными схемами. Так, например, радиолокатор обнару-
жения самолетов (если речь идет об автоматизированной системе управ-
ления полетами) может быть представлен алгоритмом, который в за-
висимости от дальности наблюдения вырабатывает ошибки измерения
координат самолета; система слепой посадки — алгоритмом, выраба-
тывающим сигнал рассогласования в замкнутом контуре и т. д.
51
Построенная таким образом приближенная статистическая модель
процесса функционирования системы используется для определения
эффективности различных вариантов структуры и'набора параметров,
а также для выбора оптимального варианта. На этом пути предприни-
мается первая попытка синтеза системы (в смысле структуры и пара-
метров), хотя решения конструктивного характера еще отсутствуют.
Всесторонний анализ результатов моделирования позволяет полу-
чить материал, необходимый для формирования технического задания
на проектирование системы.
На этом этапе работа выполняется коллективом специально подоб-
ранных сотрудников — группой обоснования требований к системе
и технического задания на проектирование. В группу обоснования в пер-
вую очередь входят специалисты широкого профиля поданной отрасли,
хорошо знающие вопросы системотехники. Их роль заключается в осу-
ществлении комплексного (общесистемного) подхода к оценке вариантов
системы, планирования эксперимента для получения статистического
материала и определения методов его обработки, построения модели-
рующих алгоритмов, а также в анализе результатов моделирования
и определении требований к системе.
Кроме специалистов широкого профиля в группы обоснования
включаются также узкие специалисты,, знающие работу отдельных
элементов системы. Применительно к системе управления полетами
самолетов — это специалисты по радиолокации, электронной вычисли-
тельной технике, средствами связи и передачи данных, навигации,
аэродромному оборудованию и т. д. Оказываются полезными также
экономисты, знающие математическую экономику, специалисты по
инженерной психологии, организации труда, строительству, комму-
нальному хозяйству и другие.
В результате работы группы обоснования выпускается отчет,
содержащий следующие основные разделы: 1) формулировку проблемы
(цели и задачи системы, факторы, подлежащие обязательному учету,
показатель эффективности), 2) краткое описание одного или двух
вариантов построения системы, 3) анализ статистического материала
и результатов моделирования, 4) перечень требований к системе и ос-
новным элементам, 5) экономические расчеты, 6) предложения по
организации разработки и оценки возможных сроков выполнения
работ и 7) проект технического задания на проектирование системы.
Хотя формально первый раздел скорее является исходным мате-
риалом, чем результатом работы группы обоснования, его наличие в от-
чете крайне желательно. Оно помогает любому лицу, рассматривающе-
му отчет, быстрее понять постановку задачи и оценить качество ее
решения. С другой стороны, как показывает опыт разработки ряда
сложных систем, формулировка проблемы нередко подвергается изме-
нениям и уточнениям в процессе работы группы обоснования. Это
касается в какой-то степени всех содержащихся в ней вопросов,
но наиболее существенно обычно пересматриваются (по результатам
анализа статистики и моделирования) действующие факторы и их ха-
рактеристики. Естественно, что уточненная формулировка проблемы
подлежит обязательному согласованию с заказчиком.
52
Варианты системы, предложенные во втором разделе отчета, не
всегда в дальнейшем используются в качестве основы для проектирова-
ния системы. Головной разработчик может найти и другие, более целе-
сообразные, с его точки зрения, варианты. Однако к тому времени они
успевают вполне оправдать свое существование. Помимо исходной базы
для моделирования, эти варианты дают возможность оценить реальность
создания системы при современном развитии техники, удельный вес
использования в системе существующих образцов оборудования и тре-
бования к их модернизации, а также основные направления новых
разработок.
Третий раздел в отчете, содержащий обобщенные данные по ста-
тистике и результатам моделирования, а также их анализ, позволяет
избавиться от многочисленных и громоздких приложений, которые
обычно представляют сырую, необработанную информацию. Вопрос
о разумном объеме обобщенных данных и характере обобщения должен
быть тщательно изучен. При этом желательно соблюсти принцип:
возможная краткость, достаточная полнота материала и наибольшая
наглядность его представления.
Раздел четвертый начинается анализом народнохозяйственной
целесообразности создания системы. На этой основе определяется
требуемое значение показателя эффективности и допустимые пределы
его снижения за счет действия учитываемых факторов. Здесь же фор-
мулируются требования к надежности, помехозащищенности, устойчи-
вости и другим свойствам системы и ее основных элементов, а также
к качеству управления. Каждое требование должно быть подтверждено
ссылками на соответствующие расчеты. Помимо этого, данный раздел
содержит ряд требований конструктивного и эксплуатационного ха-
рактера. Сюда относятся ограничения по габаритам, весу, занимаемым
площадям, потребляемой энергии, составу и квалификации обслужи-
вающего персонала, организации профилактических и ремонтных ра-
бот, использование в системе различных материалов, типовых блоков
и узлов и т. д.
Пятый раздел должен давать представление о стоимости разра-
ботки системы и ее основных элементов на всех этапах (проектирова-
ние, изготовление опытного образца, испытания, изготовление и ввод
в эксплуатацию головных образцов), стоимости и экономического эф-
фекта опытной эксплуатации головных образцов, стоимости серийного
производства и нормальной эксплуатации системы. Здесь же должны
быть даны предложения о возможных путях сокращения затрат и по-
вышения экономического эффекта применения системы.
Очень важное значение имеют предложения по организации раз-
работки, рассматриваемые в шестом разделе. Здесь должны быть реко-
мендованы головной разработчик и его основные соисполнители, опыт-
ные и серийные заводы, монтажные, наладочные и испытательные орга-
низации. Эти предложения желательно предварительно согласовать
или, по крайней мере, обсудить как с самими организациями, так
и с соответствующими ведомственными инстанциями. Кроме того,
должна быть дана оценка сроков выполнения отдельных этапов работы
и увязка их в единый процесс во времени. Необходимо также рассмот-
53
реть вопросы финансирования разработки, материально-технического
снабжения и кооперирования проектных и производственных органи-
заций. Во всех без исключения случаях шестой раздел должен закан-
чиваться подробным сетевым графиком, освещающим организацию
разработки и согласования во времени ее отдельных этапов. Жела-
тельно снабдить этот график примечаниями, связанными со сроками
и размерами капиталовложений и потребностей в соответствующих
фондах и предметах материально-технического снабжения.
Последний, седьмой раздел представляет собой проект официаль-
ного документа — технического задания на проектирование системы.
Он содержит в кратком изложении цели разработки и задачи, возла-
гаемые на систему, круг учитываемых факторов, показатель эффектив-
ности, выводы из анализа статистики и результатов моделирования,
перечень технических и эксплуатационных требований к системе и ее
элементам, сроки разработки системы и ввода ее в эксплуатацию по
этапам, требования к экономике разработки и эксплуатации системы.
Отчет, содержащий обоснование требований к системе, рассматри-
вается заказчиком. Заказчик утверждает после соответствующей кор-
ректировки техническое задание на проектирование системы. Это зада-
ние выдается головному разработчику и служит основным документом,
регламентирующим разработку системы на этапе ее проектирования.
2.10. ЭСКИЗНЫЙ ПРОЕКТ
Эскизное проектирование сложной системы является таким эта-
пом, на котором широко развертываются работы по микропроектиро-
ванию системы, хотя вопросам макропроектирования еще уделяется
весьма много внимания.
Разработка эскизного проекта осуществляется либо по договору
между заказчиком и разработчиком, либо в соответствии с решением
административных органов. В договоре или решении определяется
головной разработчик, задачи и ответственность его соисполнителей,
сроки выполнения работы, а также объем эскизного проекта системы.
Для руководства проектированием назначаются генеральный конст-
руктор системы и главные конструкторы основных ее подсистем. В
ряде случаев для обсуждения наиболее принципиальных вопросов раз-
работки системы создается совет главных конструкторов под предсе-
дательством генерального конструктора.
Важным моментом в организации работ по эскизному проектиро-
ванию системы является создание специальных групп, выполняющих
отдельные разработки, и обеспечение взаимодействия между ними.
В первую очередь должна быть создана общесистемная группа при ге-
неральном конструкторе. Кроме того, такие же группы создаются при
главных конструкторах всех основных подсистем разрабатываемой
сложности системы. В общесистемную группу при генеральном кон-
структоре включаются специалисты широкого профиля по данной от-
расли техники, специалисты по основным подсистемам, сотрудники,
знающие специфику воздействий внешней среды, технологи, специа-
54
листы по организации производства, экономисты, а также специалисты
по строительству, монтажу и наладке системы. Среди специалистов
широкого профиля должны быть лица, владеющие современным арсе-
налом методов системотехники и математического исследования слож-
ных систем.
Системные группы при главных конструкторах подсистем строят-
ся аналогично, с соответствующим сужением профиля: специалисты
широкого профиля по подсистеме, узкие специалисты по основным ее
элементам и т. д.
Характер работы общесистемной группы и системных групп по
подсистемам один и тот же. Проектирование обычно начинается с на-
метки первоначальных вариантов структуры системы и основных ее
элементов. Следующим существенным шагом является оценка вариан-
тов системы и выбор одного из них для детальной разработки. На этом
этапе уже должны вступить в строй группы специалистов, занимаю-
щихся отдельными элементами системы. Получив исходные данные от
общесистемной группы, они приступают к проектированию элементов,
стремясь обеспечить требования, содержащиеся в исходных дан-
ных.
Однако на практике встречаются случаи, когда требования обще-
системной группы, предъявленные к одному или нескольким элемен-
там системы, оказываются невыполнимыми или приводят к невыгодным
техническим или конструктивным решениям. Тогда общесистемная
группа производит соответствующую корректировку структуры и ос-
новных параметров системы. Некоторое количество такого рода кор-
ректировок позволяет, наконец, получить приемлемый вариант си-
стемы, согласованный со всеми группами.
Этот вариант дожен быть подвергнут всестороннему анализу
с целью оценки соответствия его треббйаниям, содержащимся в тех-
ническом задании на проектирование. Для этого проводится оценка
эффективности выбранного варианта системы, а также оценка надеж-
ности, устойчивости, помехозащищенности и других основных ее
свойств. Типичным методом исследования сложных систем на этом
этапе проектирования является метод статистического моделирования.
В отличие от моделей, используемых при обосновании технических
требований к системе, для которых характерна замена элементов си-
стемы соответствующими эквивалентными схемами, модели эскизного
проекта должны быть заведомо более подробными и с достаточной пол-
нотой учитывать специфику функционирования элементов в заданных
условиях внешней среды. Рассматриваемые здесь статистические модели
непременно должны обладать по крайней мере следующими двумя
свойствами: 1) хорошо отражать структуру системы и быть чувстви-
тельными к таким ее изменениям, которые обычно производятся в про-
цессе эскизного проектирования и 2) содержать все параметры систе-
мы, определяемые при разработке эскизного проекта.
В результате моделирования можно получить зависимости, ха-
рактеризующие влияние структуры и параметров системы на ее эф-
фективность, надежность и другие свойства. Эти зависимости исполь-
зуются затем для определения оптимальной структуры и оптимальных
Б5
значений параметров системы с точки зрения выбранных показателей
эффективности. Получение оптимума функционала, заданного стати-
стической моделью, может быть достигнуто либо непосредственно
•(см., например, [1]), либо через приближенное аналитическое выраже-
ние функционала, построенное по результатам моделирования.
Рассмотренные задачи синтеза сложной системы не относятся
целиком к области микропроектирования. Вместе с выбором структуры
системы, значений ее параметров, конструированием отдельных ви-
дов аппаратуры и оборудования и другими вопросами микропроекти-
рования на этапе эскизного проекта с помощью более точных моделей
как самой системы, так и воздействий внешней среды, производится
уточнение требований к системе и дальнейшее исследование ее свойств
и возможностей. Часто с этой целью предпринимается дополнительное
экспериментальное изучение окружения системы и накопление соот-
ветствующего статистического материала, характеризующего взаимо-
действие сложной системы с внешней средой.
Другим характерным отличием работы над эскизным проектом
является создание действующих макетов некоторых видов аппаратуры
и оборудования системы. Это делается для проверки реализуемости
принципов, заложенных в эскизный проект, а также для более глу-
бокого исследования особенностей функционирования элементов си-
стемы. Действующие макеты подвергаются всесторонним испытаниям,
а в некоторых случаях организуется их опытная эксплуатация, поз-
воляющая накопить необходимые статистические данные. Для этой
же цели иногда используется также экспериментальное исследование
серийных образцов аппаратуры и оборудования, намечаемых к приме-
нению в качестве элементов системы, или образцов, близких к элемен-
там системы по своему назначению и основным характеристикам.
Помимо обоснования структуры и значений параметров системы
на этапе эскизного проектирования должны быть рассмотрены важней-
шие эксплуатационные вопросы. Сюда относятся основные технологиче-
ские режимы, функциональный контроль системы и контроль исправ-
ности отдельных элементов, порядок профилактических и текущих
ремонтных работ, правила обслуживания аппаратуры и оборудования
системы и т. д.
Существенное внимание также должно быть обращено на оцен-
ку объема оборудования и экономические расчеты, связанные с раз-
работкой, серийным производством и эксплуатацией системы.
Наконец, необходимы соображения организационного характера,
определяющие порядок дальнейшей разработки системы. Должна
быть предложена кооперация организаций, выполняющих техническое
проектирование и изготовление опытного образца, с указанием распре-
деления обязанностей между исполнителями и сроков производства
элементов, поставки вспомогательного оборудования, строительных,
монтажных и наладочных работ.
В эскизном проекте также разрабатываются вопросы, связанные
с испытаниями опытного образца. Сюда относятся принципы испытаний
системы в целом и основных ее элементов, последовательность и мето-
дики проведения отдельных испытательных мероприятий, предложе-
66
ния по контрольно-регистрирующей аппаратуре и способам обра-
ботки результатов испытаний.
"W Материалы эскизного проекта располагаются в следующем по-
рядке.
В первом разделе определяются цели, для которых создается си-
стема и приводится перечень решаемых ею задач. Эти сведения как
правило, заимствуются из технического задания на проектирование
системы. В ряде случаев результаты эскизного проектирования позво-
ляют внести сюда некоторые уточнения и изменения. Кроме того, для
удобства здесь должны быть помещены технические требования к си-
стеме, утвержденные заказчиком.
Второй раздел посвящается детальному описанию выбранного ва-
рианта (или выбранных вариантов) системы. Это описание содержит
структуру системы, значения ее параметров, соображения, связанные
с обоснованием принятого варианта, а также описание процесса функ-
ционирования системы. Однако в этом разделе излагаются с нужной
степенью детализации только общесистемные вопросы.
Детальное описание подсистем и основных элементов системы,
а также вспомогательного оборудования, выносится в последующие
разделы эскизного проекта.
После описания подсистем и элементов необходимо иметь раздел,
посвященный взаимодействию их в комплексе, в процессе функциони-
рования системы. Здесь должны быть приведены стыковочные парамет-
ры, данные, обосновывающие синхронизацию различных операций,
а также потоки информации в системе.
В заключении излагаются предложения по изготовлению опытного
образца и его испытаниям, экономические и эксплуатационные рас-
четы. Этот материал должен быть иллюстрирован сетевыми графиками
различного характера: по времени, по стоимости, по надежности и т. д.
К эскизному проекту прилагаются обычно проектное задание на
строительство и монтаж опытного образца, проект договора или реше-
ния административных органов о дальнейшей разработке системы,
протоколы испытаний действующих макетов и другие документы.
Выше было отмечено, что в некоторых случаях перед эскизным
проектом разработчик может представить на рассмотрение заказчика
так называемый аванпроект или предэскизный проект. Этот документ
содержит результаты предварительной стадии эскизного проектирова-
ния и отличается меньшей глубиной проработки вопросов. В нем, как
правило, отсутствуют материалы, связанные с созданием и испытания-
ми действующих макетов, а проектные и конструкторские расчеты по
системе в целом и ее элементам имеют ограниченный объем. Основная
задача аваппроекта — довести до сведения заказчика идею построения
выбранного варианта системы и важнейших ее элементов. Поэтому его
содержание часто бывает ограничено первыми двумя разделами: опре-
делением целей и задач системы, а также описанием и оценкой выбран-
ного варианта.
57
2.11. ИСПЫТАНИЯ
Разработка современной сложной системы сопровождается боль-
шим количеством экспериментальных исследований и натурных испы-
таний различных видов аппаратуры и оборудования. Трудно указать
примеры, когда элементы сложных систем и даже отдельные их узлы
и ячейки поступали бы в производство, минуя стадию испытаний лабо-
раторного образца или действующего макета.
Однако, рассматривая лишь общесистемные, комплексные вопросы,
мы не будем останавливаться на различного рода лабораторных, кон-
структорских и даже заводских испытаниях элементов системы. На-
стоящий параграф посвящается некоторым проблемам, связанным с ис-
пытательными мероприятиями, проводимыми на завершающем этапе
разработки, когда уже имеется опытный образец сложной системы.
В совокупности испытательных мероприятий, проводимых на опытном
образце, выделяются обычно две основные стадии: автономные испыта-
ния элементов системы (или ее подсистем) и комплексные испытания
системы в целом.
Формально задачи автономных и комплексных испытаний одина-
ковы, хотя и относятся к различным объектам: элементам системы
(или ее подсистемам) и системе в целом соответственно. Они в общих
чертах сводятся к проверке реализуемости принципов, принятых при
проектировании и правильности функционирования оборудования,
а также к получению экспериментальных данных, необходимых для
оценки параметров аппаратуры и режимов ее эксплуатации. Вместе
с тем, по существу, в идеях автономных и комплексных испытаний
имеются принципиальные особенности.
Автономные испытания в большинстве практически важных слу-
чаев представляют собой необходимую стадию, без которой не могут
быть успешно проведены комплексные испытания системы. Действи-
тельно, не имея уверенности в том, что элементы системы функциони-
руют правильно и обладают параметрами, близкими к требуемым,
вряд ли можно надеяться на успех комплексных испытаний. В такой
обстановке часто вообще не удается добиться сколько-нибудь удовлет-
ворительной работы системы.
Важное значение имеет и то обстоятельство, что подробное обсле-
дование элементов системы на стадии автономных испытаний, позво-
ляет освободить комплексные испытания от ненужных деталей, сде-
лать их в необходимой степени обозримыми и наглядными, а также
сократить объем информации, подлежащей регистрации и обработке.
Часто существенной оказывается и организационная сторона дела:
последовательное проведение автономных испытаний элементов систе-
мы (или ее подсистем) и комплексных испытаний на завершающем этапе
позволяет рационально распределить силы и средства, испытательные
стенды и регистрирующую аппаратуру, обеспечить своевременную об-
работку и анализ информации.
В этой связи приобретают существенное значение вопросы опти-
мального планирования испытательных мероприятий. Сюда относятся
определение последовательности автономных испытаний элементов
58
и этапов комплексных испытаний системы, определение параметров
системы и ее элементов, подлежащих регистрации при испытаниях,
оценка необходимой точности и частоты регистрации информации,
распределение регистрирующей аппаратуры и средств хранения ин-
формации, определение очередности передачи и обработки информа-
ции и т. д. Планирование ведется в соответствии с выбранными пока-
зателями оптимальности испытаний, а результаты его оформляются,
как правило, в виде сетевых графиков по времени и стоимости.
Заметим, что на стадии комплексных испытаний системы обычно
приходится регистрировать не только общесистемные параметры, ха-
рактеризующие взаимодействие элементов, но и основные параметры
самих элементов, несмотря на то, что они уже регистрировались в про-
цессе автономных испытаний. Это объясняется тем обстоятельством
что на стадии автономных испытаний, когда элементы системы функ-
ционируют изолированно друг от друга, в значение их параметров
могут вноситься искажения за счет отличия условий от реальных усло-
вий функционирования в составе системы. Поскольку речь идет о ре-
гистрации только основных параметров элементов, это, как правило,
не приводит к чрезмерному увеличению количества регистрируемой
информации.
Для испытаний сложных систем характерно широкое использова-
ние различных видов имитаций воздействий внешней среды. Сущность
имитации состоит в следующем. Любое воздействие внешней среды на
систему или ее элементы приводит, в конечном счете, к возникновению
информации, которая становится составной частью потоков инфор-
мации, перерабатываемой в системе. В некоторых случаях созда-
ние реальных воздействий внешней среды на систему в процессе
испытаний невозможно или нецелесообразно. Тогда информация, кото-
рая возникла бы в результате реальных воздействий внешней среды,
заменяется искусственной информацией, вырабатываемой при помощи
специальной имитирующей аппаратуры. Характеристики имитацион-
ной информации должны подбираться таким образом, чтобы обеспечить
близость условий функционирования системы к реальным.
В качестве примера рассмотрим испытания системы управления
полетами самолетов (гл. 1), [1]. Натурные испытания с использованием
большого количества самолетов, одновременно находящихся в воздухе,
оказываются дорогостоящими и трудными в организационно-техниче-
ском отношении. Это обстоятельство учитывается при планировании
испытаний. Так, автономные испытания радиолокационных станций
аэродромного обзора и системы слепой посадки в основном проводятся
по одиночным, самолетам. При этом решается большинство вопросов,
связанных с оценкой наземных систем. Когда же речь идет о проверке
влияния посторонних самолетов на процесс сопровождения самолета
радиолокационной станцией аэродромного обзора или на правильность
закрепления самолета за соответствующим каналом слепой посадки,
используются полеты малых групп самолетов.
Более сложная ситуация возникает в случае автономных испытаний
систем дальнего обнаружения и дальней связи. Здесь для проверки
правильности функционирования систем (селекция самолетов, выде-
59
ление трасс полета при перекрещивающихся курсах, стабильность
связи и т. д.) могут потребоваться полеты нескольких малых групп
самолетов.
Наконец, при автономных испытаниях систем обработки информа-
ции и диспетчеризации, при которых требуется достаточно полная
загрузка вычислительных средств поступающей информацией, обой-
тись малым количеством самолетов не представляется возможным.
Вместе с тем, здесь нет необходимости и в натурном эксперименте.
Вместо информации о реальных самолетах, находящихся в воздухе,
в вычислительные средства может быть введена имитационная инфор-
мация, вырабатываемая имитаторами. Для этой цели достаточно моде-
лировать полеты большого количества самолетов с учетом всех необхо-
димых особенностей их трасс на цифровых вычислительных машинах,
не входящих в испытуемые системы. Полученные на модели сведения
о самолетах вводятся в вычислительные средства испытуемых систем.
Для того, чтобы эти сведения позволили исчерпывающим образом
проверить работу систем обработки информации и диспетчеризации,
при моделировании нужно имитировать ошибки и искажения инфор-
мации, свойственные реальной аппаратуре.
При выполнении этих условий результаты переработки имита-
ционной информации в упомянутых системах могут служить исходными
данными для испытаний других элементов системы управления поле-
тами самолетов.
Использование принципа имитации характерно также и для ком-
плексных испытаний. Здесь, как правило, информация о воздействиях
внешней среды представляет собой смесь реальной и имитационной ин-
формации. Например, при комплексных испытаниях системы управле-
ния полетами самолетов представляется целесообразным ограничиться
некоторым количеством малых групп самолетов, находящихся в воз-
духе, а остальную, требуемую для испытаний, информацию синхронно
вырабатывать методом моделирования с учетом особенностей трасс са-
молетов, ошибок радиолокационных станций и помех.
Материалы автономных и комплексных испытаний сложной систе-
мы оформляются в виде протоколов и заключений комиссии, назначае-
мой заказчиком и служат основанием для принятия решений, связан-
ных с дальнейшей разработкой системы.
ГЛАВА ТРЕТЬЯ
ОБЩИЕ СХЕМЫ ФУНКЦИОНИРОВАНИЯ СИСТЕМЫ
3.1. ВВОДНЫЕ ЗАМЕЧАНИЯ
Как уже отмечалось выше, для решения задач, возникающих
при проектировании, создании и эксплуатации сложных систем, тре-
буется проводить многочисленные исследования и расчеты, связанные
с оценкой показателей, характеризующих различные свойства слож-
ной системы, а также с выбором оптимальной структуры системы и оп-
тимальных значений ее параметров. Выполнение таких исследований
возможно лишь в том случае, если мы располагаем математическим
описанием (математической моделью) процесса функционирования
системы.
Сложность реальных систем не позволяет строить для них «аб-
солютно» адекватные математические модели. Математическая модель
описывает некоторый упрощенный процесс, в котором представлены
лишь основные явления, входящие в реальный процесс, и лишь глав-
ные факторы, действующие на реальную систему, причем все они ими-
тируются соответствующими формальными схемами, удобными с ана-
литической точки зрения или в вычислительном отношении.
Какие явления считать основными и какие факторы главными—
существенно зависит от назначения модели, от того, какие исследования
с ее помощью предполагается проводить. Поэтому процесс функцио-
нирования одного и того же реального объекта может получить различ-
ные математические описания в зависимости от поставленной за-
дачи.
Характерным примером является электромагнитное реле
(рис. 3.1). Оно состоит из сердечника с обмоткой (/), якоря (2), кон-
тактов (3) и входного выключателя (4); кроме того, имеются входные
клеммы (х) и выходные клеммы (у). Если входной выключатель разом-
кнут — обмотка обесточена, поэтому контакты разомкнуты. Если вход-
ной выключатель замкнут — в обмотке появляется ток. Когда, прео-
долевая индуктивное и омическое сопротивление обмотки, ток дости-
гает определенной величины, сердечник притягивает якорь и контакты
замыкаются, на выходных клеммах появляется напряжение.
Представим себе, что перед нами стоит задача расчета параметров
реле. Тогда, исходя из характеристик напряжения на входе и усилия
требуемого для притягивания якоря, мы должны определить электри-
ческие параметры обмотки и магнитные параметры сердечника, обеспе-
чивающие нормальную работу реле. Основными явлениями в этом слу-
чае, по-видимому, придется считать процессы нарастания тока в об-
мотке и напряженности магнитного поля, а главными факторами —
61
нагревание обмотки с учетом теплоотдачи во внешнюю среду и силы
противодействующие движению якоря.
При такой постановке задачи математическая модель процесса
функционирования реле должна содержать соотношения, определяю-
щие поведение тока в цепи, включающей обмотку; напряженности маг-
нитного поля сердечника; сил, действующих на якорь, и его движение
под действием этих сил. В электротехнике эти процессы описываются
соответствующими дифференциальными уравнениями (уравнение тока
в цепи, уравнение движения якоря и т. д.).
Электромагнитные реле широко используются в так называемых
контактных схемах, где рассмотренные только что электрические
и магнитные процессы не играют суще-
ственной роли. Основным явлением здесь
оказывается сам факт замыкания или
размыкания соответствующих контак-
тов, или, другими словами, наличие или
отсутствие напряжения на выходе схе-
мы, в зависимости от того, имеется или
не имеется напряжение на входе. Обыч-
ная формализация процессов такого
рода сводится к интерпретации нали-
чия напряжения на входе (сигнал х = 1)
или на выходе (сигнал у = 1) как
Рис. 3.1
истинных высказываний, а отсутствие напряжения на входе (сигнал
х = 0) или на выходе (сигнал у = 0) как ложных высказываний, а
также зависимости у = f (х) как некоторой функции исчисления
высказываний. Таким образом, реле здесь выступает в качестве логи-
ческого элемента. Для описания процессов функционирования кон-
тактных схем используется аппарат математической логики.
Пример электромагнитного реле не исключение. Практика пока-
зывает, что вид математической модели определяется не только физи-
ческим содержанием моделируемых процессов, но и целями моделиро-
вания.
Для построения простой и изящной математической модели, обла-
дающей достаточной степенью адекватности реальному процессу, тре-
буется обычно немалое искусство. Помимо интуиции и понимания
структуры формализуемых явлений, здесь существенную роль играет
знание типичных формальных схем и математических моделей, при-
годных для описания различных процессов. Следующая глава посвя-
щается краткому рассмотрению наиболее распространенных случаев.
В настоящей главе мы остановимся на формализации общей схе-
мы процесса функционирования системы. Желая получить математи-
ческую модель, охватывающую широкий класс реальных объектов,
мы будем исходить из весьма общих предположений о характере функ-
ционирования системы:
1) система функционирует во времени', в каждый момент времени
система находится в одном из возможных состояний',
2) на вход системы могут поступать входные сигналы,
3) система способна выдавать выходные сигналы;
62
4) состояние системы в данный момент времени определяется
предыдущими состояниями и входными сигналами, поступившими
в данный момент времени и ранее;
5) выходной сигнал в данный момент времени определяется со-
стояниями системы и входными сигналами, относящимися к данному
и предшествующим моментам времени.
Первое из перечисленных предположений имеет очевидную цель
отразить динамический характер процесса функционирования системы
в пространстве и времени, подчеркнуть, что процесс функционирования
протекает как последовательная смена состояний системы под дейст-
вием внешних и внутренних причин. Второе и третье — описать взаи-
модействие системы с внешней средой. В четвертом и пятом предполо-
жениях отражаются два важных аспекта, связанных с определением
реакции системы на внутренние факторы и воздействия внешней среды.
С одной стороны, здесь учитывается то обстоятельство, что многим
явлениям и процессам свойственно последействие, вследствие которо-
го тенденции, определяющие поведение системы в будущем, зависят не
только от того, в каком состоянии находится система в настоящий
момент времени, но в той или другой степени от ее поведения в преды-
дущие моменты времени. С другой стороны, отражается принцип
физической реализуемости', система не реагирует в данный момент вре-
мени на «будущие» факторы и воздействия внешней среды.
Для того чтобы придать сформулированным предположениям более
точный смысл и необходимый формальный вид, используем соответст-
вующие математические понятия и символику.
3.2. МНОЖЕСТВА. ОТОБРАЖЕНИЯ. ОПЕРАЦИИ
Будем придерживаться следующих общепринятых обозначений*'.
Множества обозначаются прописными латинскими буквами X, Y, Z, Т
и т. д., а элементы этих множеств — соответствующими строчными буквами:
х, у, z, t и т.д. Запись х Q X или X - х означает: «х является элементом множе-
ства X», «х принадлежит А"» или «множество X содержит х в качестве элемента»,
a Y с X или X => Y — «множество Y является подмножеством множества X».
Объединение X (J множеств X и Y есть множество всех элементов, принадле-
жащих либо множеству Y, либо множеству X. Пересечение X f] Y множеств X
и Y есть множество всех элементов, принадлежащих одновременно и множеству X
и множеству Y. Разность X\Y множеств X и Y есть множество элементов, при-
надлежащих множеству X, но не принадлежащих множеству Y. Пустое мно-
жество обозначается 0.
Операции объединения и пересечения множеств удовлетворяют законам
коммутативности XldY = /(JX; X ("| У = Y П X; ассоциативности
х и (Г U Z) = (X (J Y) J Z; X Q (У ("] Z) — (X ("] Y) ("| Z и идемпотентности X (J X =
X; XQX = X.
Пусть {Zj)n — конечная совокупность множеств Zlt Z2, ...,, Zn и ц — их
элементы, i = 1, 2, ... п. Прямым или декартовым произведением множеств
Zx, Z2, ..., Zn называется множество Z всех упорядоченных последовательностей
z = (г1; г2,..., zn). Прямое произведение обозначается Z = Zt X Z2 X ... X Zn или
Z = n(Z; f {Zj}n/z = 1, 2, ..., n). Например, прямое произведение Z множеств
X и Y есть множество всех упорядоченных пар г = (х, у), где х О X, у f Y.
*' Подробнее см. [3,5 или 6].
63
Прямое произведение U множеств X, Y и 7 есть множество всех упорядоченных
троек и = (х, у, г), где х £ X, у £ У н z Z. Операция прямого произведения
обладает свойством ассоциативности X X (У X Z) = (X X У) X Z = X X
X У X Z, но в общем случае не коммутативна X X У =£ У X X, т. е. (х, у)
не всегда совпадает с (у, х). Прямое произведение X X X обозначается №.
В выражении Z = Zr X Z2 X ... X Zn множества Zj, i = 1, 2, n,
называются осями, прямого произведения Z, а их элементы z2 £ Zj — проекциями
элемента z = (zlt z2.zn) £ Z на оси Z;.
В дальнейшем мы будем пользоваться следующей терминологией: множе-
ство Z будем называть пространством, его элемент z — точкой пространства Z,
а элемент аг £ Z; — проекцией точки z на ось Z;. Нам также потребуются обоб-
щения понятия оси и проекции. Обозначим, например, Z* = Z; X Z2 X Za и
Z = Z6 X Z6 X ... X Zn. Тогда Z = Z* X Z4 X Z. Пространства Z* и Z можно
также рассматривать как оси пространства Z. Проекциями точки z на эти оси
будут соответственно z* = (zj, z2, z3) и z = (z5, z6, ..., zn). В отличие от Z* и Z
исходные множества Zj, которые в условиях данной задачи не являются прямыми
произведениями каких-либо множеств, будем называть элементарными осями
пространства Z.
В трехмерном евклидовом пространстве Z -Zx X Z2 X Z3 множества
Zj, Z2 и Z3 (множества точек числовой прямой) являются элементарными осями
пространства Z; проекции точки z ( Z на эти оси выражаются координатами
(числами) 2Ъ z2 и z3; координатные плоскости Z4 X Z2 и Z2 X Z3 представляют
собой оси пространства Z; проекции точки z £ Z на них описываются парами чи-
сел (Zj, z2) и (z2, z3) соответственно; координатную плоскость Zj X Z3 также бу-
дем считать осью пространства Z, хотя она и не является «сомножителем» в вы-
ражении прямого произведения; проекции точки z £ Z на эту ось описываются
парой чисел (z1, z3).
В общем случае, пусть {Zj}n — совокупность элементарных осей прост-
ранства Z и пусть {Zj}' — какое-нибудь подмножество множества {Zj)n; тогда
прямое произведение
Z=n(Z; aZi}'/z)
элементарных осей, принадлежащих подмножеству {Zj}', взятых в том порядке,
в котором они входят в прямое произведение Z, будем называть осью простран-
ства Z.
Пусть Z— пространство с совокупностью элементарных осей {Zj}n. Рас-
смотрим некоторое подмножество Z* множества точек z = (zlt z2, ..., zn) прост-
ранства Z. Если подмножество Z* само является пространством в том же смысле,
что и пространство Z, то Z* называется подпространством пространства Z .
В частности, пусть Zj о: Zj, i = 1, 2, ..., п, a {Zj)n — совокупность всех мно-
жеств Zi, рассматриваемых как элементарные оси некоторого пространства
Z= Zt X Z2 X .... X Zn; кроме того, пусть {Zj)' — подмножество множества
элементарных осей {Zj)n; тогда пространство
Z*=TI(Z; С {2;}'/z)
представляет собой подпространство пространства Z. Легко видеть, что любая
ось пространства Z является его подпространством, но не наоборот.
Пусть множество А является подмножеством множества точек простран-
ства Zr X Z2. Проекцией множества А на ось Zx называется множество всех гг £
£ Zn для которых существует такое z2, что (Zj, z2) £ А.
Множества, между элементами которых можно установить взаимно одно-
значное соответствие, называются эквивалентными.
64
Рассмотрим два произвольных множества X и V. Если указано правило,
согласно которому каждому элементу хб X ставится в соответствие вполне оп-
ределенный элемент у £ Y, говорят, что задано отображение X Y множества
X в множество Y или задан оператор у = Fix), определенный на множестве X,
с областью значений, принадлежащей множеству Y.
Аналогично можно задать оператору у = F(x), определенный на множестве
X* с. X. Будем называть X* областью определения оператора у = F(x) в мно-
жестве X. Оператор у= F(x) реализует отображение множества X* в множество
Y (или на множество Y* cz Y, где Y* — область значений оператора у =
= Fix') в множестве У).
Пусть оператор у = F(x) определен для всех х £ X и пусть каждый эле-
мент х £ X представляет собой упорядоченную совокупность вида
х = (х1( х2..хп). где x-t Xi, i = 1,2, ..., п. В этом случае оператор у =
= F(x) можно записать в виде
y=F(xlt х2.....хп).
Рассмотрим прямое произведение
Х = Х1хХ2Х ... X хп
как множество всех упорядоченных совокупностей (хх, х2, ...,хп). Очевидно,
что в общем случае множество X является некоторым подмножеством множест-
ва X. Множество X представляет собой область определения оператора у=
= F(xlt х2...хп) в множестве XL X Х2 X ... X Хп. Другими словами, опера-
тор у = F(xlt х2, ..., хп) реализует отображение множества X С X в множест-
во Y. В частном случае, когда множество X совпадает с множеством X, оператор
у = F,(xlt х2...хп) реализует отображение прямого произведения X Х2 X
X ... X Хп в множество Y.
В качестве примера рассмотрим действительную функцию
//=+)/ 1 —х] —х%
двух действительных переменных хг и х2. Здесь множество Y* действительных
чисел у, заключенных в интервале 0 < у < 1, представляет собой область зна-
чений функции в множестве действительных чисел Y. Обозначим множество дей-
ствительных чисел хь содержащихся в интервале — 1 <Xj < 1, через а мно-
жество действительных чисел х2, содержащихся в том же интервале, — через
Х2. Тогда прямое произведение X = Хг X Х2 представляет собой множество то-
чек (х1т х2) плоскости, принадлежащих квадрату с вершинами (—1,—1), (—1, 1),
(1,1), (1, — 1). Легко видеть, что областью определения функции будет множество
точек (xj, х2), принадлежащих кругу (радиуса 1), вписанному в упомянутый
квадрат.
Случай, когда область определения совпадает с множеством X Х2,
можно проиллюстрировать на примере функции у = arcsin хх + arcsinx2.
Говорят, что на множестве М определена бинарная алгебраическая операция,
если указан закон, по которому любой паре элементов a, b £ М, взятых в оп-
ределенном порядке, однозначно ставится в соответствие некоторый элемент
с £ М. В дальнейшем бинарную операцию будем обозначать а ® 6 = с.
Непустое множество Р с бинарной операцией а ® Ь = с, где а, Ь, с £ Р,
удовлетворяющей закону ассоциативности а ® (Ь ® с) = (а ® 6) ® с, назы-
вается полугруппой. Закон ассоциативности' позволяет осуществить операцию
над любым конечным числом элементов полугруппы, заданных в определенном
порядке. Если, кроме того, в Р справедлив закон коммутативности а ® b =
= b ® а, полугруппа называется коммутативной. В коммутативной полугруп-
пе порядок элементов, участвующих в операции, не является существенным.
Полугруппа Р, при дополнительном условии существования решений урав-
нений а ® х = b и у ® а = b для любых 'а, b £ Р, _ называется группой. Из оп-
3 Зак. 792 65,
ределения группы вытекает существование однозначно определенного единич-
ного (нейтрального) элемента е, обладающего свойством
Кроме того, для всякого элемента группы имеется однозначно определенный
обратный элемент, обозначаемый а, удовлетворяющий условию а ® а-1 =
= а-1 ® а = е. Обратным для 'а-1 является элемент а. Полезно также иметь в
виду тождества (ах ® а2)-1 = а2-1 ® а^1 и е-1 = е.
Пусть элементы группы Р однозначно описываются п параметрами:
a = a(at, а2, ...ап). Тогда параметры обратного элемента а~1 = а~1 («х, а2, ап)>
а также параметры результата операции а®6 = с, где b = b (pL, ........ Рп).
с = с(у!, у2, уп), являются функциями от параметров исходных элементов
ai = «i (аь а2, ап),
= *^2- Pi» Ра* • ••» Рп)' i — 1» 2.......п.
Если параметры элементов непрерывно изменяются в некоторой области, а
параметры обратного элемента и элемента с = а®6 являются непрерывно диф-
ференцируемыми функциями от параметров исходных элементов, то группа Р
называется непрерывной п-параметрической группой [9].
Простейшие свойства полугрупп и групп нам понадобятся в дальнейшем
при изучении сложных систем.
3.3. ДИНАМИЧЕСКИЕ СИСТЕМЫ
Прежде чем мы перейдем к формализации процессов функциони-
рования систем общего вида, полезно кратко остановиться на хорошо
изученном частном случае — системах, описываемых обыкновенными
дифференциальными уравнениями. Простейшие примеры таких си-
стем нам доставляют задачи классической механики.
Рассмотрим движение материальной точки А с массой т по пря-
мой ОХ под действием силы F. Положение точки А на прямой ОХ в мо-
мент времени 7 обозначим х (I). Будем считать, что функция х (t)
имеет непрерывные производные до второго порядка включительно.
Производная dxldt = х (t) называется скоростью движения точки А,
a d^xldt'1 = х (t) — ускорением.
В соответствии с законом Ньютона
их- F, (3.1)
где сила F может зависеть от х и х. Например, сила, действующая на
пружинный маятник, определяется расстоянием от положения равно-
весия; для малых колебаний она пропорциональна растяжению пружи-
ны. Соответствующее дифференциальное уравнение имеет вид
тх =—фх, (3.2)
где ф — коэффициент жесткости пружины.
Путем выбора новых масштабов по осям t и х уравнение (3.2)
может быть приведено к виду
66
х = —X. (3.3)
Общее решение этого уравнения
х = сг cos t -фс2 sin./ (3.4)
зависит от двух произвольных постоянных Cj и с2, которые опреде-
ляются начальными условиями. Пусть в момент /0 = 0 имеем х = х°
и х = х°. Тогда
с1 = х°, х =—sin / 4-с2 cos/, с2=х°.
Таким образом, частное решение дифференциального уравнения
(3.3), соответствующее начальным условиям х = х° и х = х° в момент
/ = О, имеет вид
х (/) = х° cos / + х° sin t. (3.5)
Для движения в сопротивляющейся среде сила F (3.1) зависит от
скорости х.
В достаточно общем случае изучение движения системы с одной
степенью свободы приводит к дифференциальному уравнению
х х =f (х, х), (3.6)
где функция f (х, х) удовлетворяет условиям теоремы существования
и единственности решения, [1].
Под числом степеней свободы мы понимаем здесь число перемен-
ных, описывающих положение движущейся материальной точки А.
Поэтому движение материальной точки А (х, у) по евклидовой плос-
кости X X Y, где X — множество значений абсциссы х, a Y — мно-
жество значений ординаты у, можно интерпретировать как систему
с двумя степенями свободы.
В качестве примера системы с Зн степенями свободы рассмотрим
движение п материальных точек A, (xt, yt, Zt) в трехмерном евклидовом
пространстве Е3 = X X Y X Z, где X Э xt, Y Э yi, Z Э z,.
Обычно задачи механики системы п материальных точек сводятся
главным образом, к изучению движения центра инерции системы.
Однако нередки случаи, когда для ответа на поставленный вопрос
важно знать относительное расположение материальных точек Л,
в процессе движения системы (конфигурацию системы) и индивидуаль-
ное поведение каждой точки. Для этой цели удобно использовать
так называемое конфигурационное пространство, размерность кото-
рого совпадает с числом степеней свободы системы. Перейдем к обо-
значениям Xi = x3i_2, yt = x3i_b zt = x3i, где хзг_й t X3i_h,
k = 0, 1, 2.
Под конфигурационным пространством рассматриваемой системы
будем понимать прямое произведение
X = Х2 X Х2х X Х3п, (3.7)
3* 67
1гочки которого представляют собой упорядоченные совокупности вида
(А, х2, ..., х3п).
Уравнения движения системы материальных точек А, в этих
обозначениях можно записать следующим образом:
xi= fj(.xi>x2, хзп> xi> х2< •••. х3п), 1 = 1, 2, .... Зп. (3.8)
Начальные условия: х1=х°, Х2=х°, ..., х3п = x°n; Xi = х°, х2 =
= х2, .... х3п = хз,, в момент t = t0. Любое частное решение системы
дифференциальных уравнений (3.8) представляется совокупностью
функций
х,(/)=хД/, х°1, х°, ..., х°3п; х°, х°, .... х°п), / = 1, 2, .... Зп. (3.9)
Для понимания качественной картины поведения системы су-
щественную роль играет геометрическая интерпретация решений
дифференциальных уравнений. Во многих случаях представляет инте-
рес построение графика движения системы, т. е. кривой в пространст-
ве Т X X, описываемой соотношениями (3.9) при фиксированных
начальных условиях, а также траектории движения системы, которая
является проекцией графика движения на конфигурационное про-
странство.
Для системы с одной степенью свободы (3.6) конфигурационное
пространство есть множество X точек х, характеризующих положение
движущейся точки А на прямой ОХ. График движения представляет
собой кривую на плоскости Т X X. Например, для системы, описывае-
мой дифференциальным уравнением (3.3), график движения определяет-
ся соотношением (3.5). Траектория движения системы — совокупность
точек конфигурационного пространства, соответствующих положени-
ям точки А при ее движении, — является отрезком оси ОХ.
Представление о характере поведения системы в различных си-
туациях можно было бы получить из рассмотрения семейства графиков
движения (или траекторий движения), соответствующих всевозможным
начальным условиям. Однако такая геометрическая картина системы
не обладает желаемой наглядностью даже в случае системы с одной
степенью свободы. В самом деле, частное решение (3.5) дифференци-
ального уравнения (3.3) зависит от начальных условий (х°, х°) в момент-
ов, поэтому через каждую точку (0о, х°) плоскости Т X X проходит
бесконечное множество кривых х = х (f), соответствующих различным
значениям х°. Аналогично для системы с Зп степенями свободы, опи-
сываемой дифференциальными уравнениями (3.8), через каждую точ-
ку (A), Xj0, х2°, ..., хзп°) пространства Т X X проходит бесконечное
множество кривых Xj = Xj (/), / = 1, 2, ..., Зп, соответствующих раз-
личным значениям х/, х2°, •••> ^зп°-
Изложенное позволяет подчеркнуть одну очевидную мысль, пред-
ставляющую интерес для дальнейшего. А именно, знания положения
системы (xj0, х2°, ..., х3п°) в конфигурационном пространстве в некото-
рый момент времени t0 недостаточно для определения ее положения
68
в другие моменты времени. В этом можно убедиться непосредственно
из (3.9).
Заметим, что имеется возможность более наглядного геометриче-
ского представления качественной картины поведения системы. От
системы уравнений (3.8) перейдем к эквивалентной ей нормальной
системе дифференциальных уравнений
X j == Х3п 4- /»
*зп+/ = А,-(-Ч, х2, .... х3п; xi, х2, .... х3п), j = 1, 2, .... Зп, (3.10)
решение которой представляется совокупностью функций
ЛОО 0 ‘0*0 ’0\
х7- = хД/, хь х2, ...» X3n; Х1, х2 ...» х3„),
Xj = Xj (/, х°, х2, .... х°п; х°, х°2. Хзп), / = 1,2.Зп. (3.11)
Пусть Xj — множество значений xjt a Xj — множество значений
Xj, j = 1,2, ..., Зп. Для системы с Зп степенями свободы будем назы-
вать: упорядоченную совокупность (хь х2, ..., х3л; xlt х2, ..., хзл) —
состоянием системы, прямое произведение
X = Xi X Х2 X ... X Х3п хХ, хХ2 X ... X Х3п (3.12)
— пространством состояний, а (6п + 1)-мерное пространство,
Т X X — фазовым пространством системы.
Кривая в фазовом пространстве, определяемая соотношениями
(3.11), называется фазовой траекторией системы, а ее проекция на
пространство состояний — траекторией системы в пространстве со-
стояний.
Легко видеть, что проекция фазовой траектории или траектории
системы в пространстве состояний на конфигурационное пространство
оказывается траекторией движения системы материальных точек Аг
(в конфигурационном пространстве).
В силу теоремы существования и единственности для нормальной
системы дифференциальных уравнений [1], через каждую точку (хх0,
х2°, ..., хзп°; Xi0, х2°, ..., хзп°) би-мерного пространства состояний про-
ходит единственная траектория системы, причем траектории, соот-
ветствующие различным начальным состояниям (xi, х2°, .... х3л°;
xi°, х2°, •••• хзл°), не пересекаются. Это нужно понимать в том смысле,
что любая точка х = (хх, х2, ..., х3п; xlt х2, ...,х3п) пространства состоя-
ний может служить начальной точкой некоторой траектории системы и,
кроме того, все траектории системы, начинающиеся в точках х (/) £ X
и х (/ + с) Е X, при всевозможных с совпадают между собой. В силу
той же теоремы траектории системы в пространстве состояний не имеют
точек самопересечения, в то время как траектории движения системы
материальных точек Аг в конфигурационном пространстве в общем
случае могут иметь точки самопересечения.
Траектории системы разбивают пространство состояний на классы
эквивалентности: если точки лежат на одной траектории, то они при-
69
надлежит одному классу. Такое разбиение называется портретом
системы в пространстве состояний. Например, для дифференциаль-
ного уравнения (3.3) эквивалентная нормальная система уравнений
имеет вид
Х1 = Х2, Х2 =—Xv (3.13)
Пространство состояний представляет собой плоскость*’ X X X,
где X Э х, X Э х. Фазовые траектории задаются выражениями
%(/) = cos t -|- х° sin I, x(t) = —х° sin t + x°cos t (3.14)
и представляют собой семейство винтовых линий в пространстве
Т X X X X, проходящих через точки (1°, х°, х°). Исключив из (3.14)
параметр t, получим уравнение траектории системы
х2 -}-x2 = (xfl)2 +(х0)2. (3.15)
Поэтому траектории системы, описываемой дифференциальным
уравнением (3.3), являются концентрическими окружностями с цент-
ром в точке х° = 0; х° = 0, а портрет этой системы — совокупность
упомянутых окружностей. Изображающая точка (х, х) движется по
окружности в направлении часовой стрелки (при возрастании t) с еди-
ничной угловой скоростью. Функции х (t) их (г) — периодические
функции. Начало координат представляет состояние покоя и являет-
ся траекторией системы, соответствующей нулевым начальным усло-
виям х° = 0, х° = 0.
Портрет системы позволяет дать качественную характеристику
ее поведения. В случае системы, описываемой дифференциальным
уравнением (3.3), он имеет простой механический смысл. В самом деле
(см. [4]), выражение х2 + х2 пропорционально полной энергии мате-
риальной точки (кинетическая энергия есть х'2/2, а потенциальная —
есть х2/2). Таким образом, при движении рассматриваемой системы
сумма кинетической и потенциальной энергии остается постоянной,
равной полной энергии ее в начальный момент времени /0. Когда одно
из слагаемых обращается в нуль (например, кинетическая энергия
при х = 0), другое принимает максимальное значение. Начало коор-
динат (точка покоя) соответствует полной энергии, равной нулю.
Естественно, что с увеличением числа степеней свободы системы,
а вместе с ним и размерности пространства состояний — портрет си-
стемы в пространстве состояний оказывается все более сложным и ме-
нее наглядным. Однако теоремы существования и единственности ре-
шений, а также другие теоремы качественной теории дифференциаль-
ных уравнений дают возможность выработать формальные критерии
для оценки поведения систем, позволяющие решать существенно важ-
*> В физике для обозначения плоскости X X X использовался термин «фа-
зовая плоскость»; отсюда—«фазовая траектория» для обозначения траектории
системы в пространстве состояний, «фазовый портрет» и т.д.
70
ные теоретические и практические задачи. В качестве примера можно
указать на знакомую читателю теорию устойчивости движения и ее
применение на практике.
В результате обобщения разнообразных задач классической ме-
ханики и математической физики возникло понятие динамической си-
стемы как некоторого абстрактного объекта, обладающего важными
в теоретическом и практическом отношениях свойствами.
Пусть задана нормальная система дифференциальных уравнений
Xi = х2, .... хп), i = \,2,...,n, (3.16)
правые части которой не зависят явно от времени t (автономная систе-
ма) и являются непрерывными функциями своих аргументов в некото-
рой замкнутой ограниченной области G н-мерного евклидова простран-
ства. Пусть в G задана произвольная внутренняя точка Л0(Х1°, х2,
..., хп°); существует решение х; (г1) = х; (t, t0, х\п, х2°, .... хп°) системы
(3.16), проходящее через точку Ао в момент tg.
Если правые части системы (3.16) в области G удовлетворяют
условиям Липшица
п
\fi (х'1, х2, ...., x'n)—fi(xt, х"2, ..., Xn)\^L £ К— Х/|,
1= 1
где L — константа, определяющаяся областью G, существует един-
ственное решение, соответствующее заданным начальным условиям,
причем функции xt (f) = Xi (t, t0, x^0, x2°, ..., xn°) являются непрерыв-
ными по всем аргументам. Поскольку правые части (3.16) не зависят
явно от времени, решение системы можно записать в виде
(, , о о 0\
Х; =Xf \t—tg, Х1, Х2, ..., Хп).
Обозначим точку (хь х2, ..., х„) через р, а решение системы
(3.16), проходящее в момент t0 через точку р0,—символом F (р0, t—10).
Тогда
Р (0 = Р (Ро, t ~
Зафиксируем и положим
Pi = Р (^i) = Р (ро, *1 ~ to)- (3-17)
По начальным условиям 1Ъ ръ составим решение
Р (t) = F (Р1, t - у.
Очевидно, что
Р (Pi, t~h) = F (р0, t - i0).
Подставляя в левую часть вместо его значение из (3.17), получаем
FlP(po, h-Q, t~ti) = F(Po, t-to)
71
или, обозначая tr — t0 = t', a t — = t",
F [F (p0, f), П = F (p0, t'+ t"). (3.18)
Функция F (p, i) обладает следующими свойствами: 1) она не-
прерывна по обоим аргументам в области существования решения урав-
нений (3.16); 2) F (р0, 0) = р0\ и 3) F [F (р0, t'), t"\ = F (р0, t' + t").
Если для любой точки р g G функция F (р, f) определена для
— со < t <Z + оо, то она задает однопараметрическое семейство
преобразований области G в себя, называемое динамической системой
(Биркгоф, 1912 г.).
В соответствии с терминологией теории динамических систем
точку р (t) будем называть состоянием системы в момент времени t,
а область G — пространством состояний динамической системы. Пре-
образование F (р1, t) при фиксированном р’ называется движением,
а совокупность точек р (t) при всех t — траекторией динамической
системы.
Во множестве преобразований F (р, t) определим бинарную опе-
рацию, заключающуюся в том, что к результату преобразования
с параметром применяется преобразование с параметром ?2; резуль-
тат операции тоже является преобразованием (с параметром tT + t2).
Операция такого рода над преобразованиями всегда оказывается ас-
социативной. Кроме того, имеет место очевидное равенство, которое
нам пригодится в дальнейшем:
F{F[F(p, /Д h],ts}=F{F(p, t1 + t2),t3} = F{F(p1,t1), t2 + ta}. (3.19)
Рассматриваемое семейство преобразований по отношению к вве-
денной операции является полугруппой.
В полугруппе преобразований F (р, t) существует обратная опера-
ция. Действительно, преобразованием, обратным F (р, t), будет пре-
образование F (р, —I), так как F [F (р, t), —/] = F (р, 0); а нейтраль-
ным элементом — преобразование F (р, 0).
Таким образом, семейство преобразований F (р, t) по отношению
к введенной операции оказывается группой. Учитывая, что параметры
преобразования, являющегося результатом операции, и обратного
преобразования оказываются непрерывно дифференцируемыми функ-
циями t, можно утверждать, что динамическая система есть однопара-
метрическая непрерывная группа преобразований области G в себя.
Рассмотренные выше задачи из классической механики дают при-
меры систем, являющихся частными случаями динамической системы.
Возвратимся к системе с одной степенью свободы (3.3) С помощью тра-
екторий системы (3.15) определяется для каждого t = tQ + т отображе-
ние пространства состояний в себя, переводящее изображающую точ-
ку [х, (4), х (£0)1 в точку [х (i0 + т), х (t0 + т)] на той же траектории
системы. Это отображение является взаимно однозначным и непрерыв-
ным. Кроме того, легко проверить, что оно удовлетворяет условиям
группы. Например, дифференциальное уравнение (3.3) определяет
группу вращений плоскости X X X относительно начала координат,
см. (3.15).
72
Пусть дано произвольное метрическое пространство*’ 2 и семейст-
во его отображений на себя F (z, t), которое любой точке z g Z и любо-
му вещественному числу /, — оо < ^ <; + оо, ставит в соответствие
определенную точку F (z, t) g Z. На функцию F (z, t) наложим следую-
щие ограничения: 1) начальное условие F (г, 0) = z; 2) непрерывности
по совокупности переменных z и t: для заданной точки z0 и числа t0
для любого е > 0 найдется такое 6 >• 0, что если р (z0, г) < <5 и
| t — t0 | <Z 6, то p [F (z, t), F (z0, /0)] < e; 3) условие группы: для
любого z g Z и любых действительных tr и Z2
F[F(z, Zx), Z2]=F(z, /х+/2). (3.20)
Из условий (1) и (3) следует существование обратного преобразо-
вания F (г, —I) к преобразованию F (z, t). В самом деле, F [F (г, —t), /1 =
= г; тождественное преобразование F (г, 0) = z.
Однопараметрическая группа F (г, t), — сю < t < + оо, пре-
образований метрического пространства Z на себя, F (z, t) £ Z, удов-
летворяющая перечисленным условиям, называется динамической
системой (А. А. Марков, 1931 г.). Другими словами, под динамической
системой понимается упорядоченная пара (Z, F) в предположении, что
справедливы условия 1), 2) и и 3).
Из условия 2) следует, что если начальные точки z0 и z'o выбраны
достаточно близкими, р (z0, z0') < 6, то в течение произвольного, но
фиксированного промежутка времени — Т <4 t Т расстояние меж-
ду одновременными положениями движущихся точек будет оставаться
меньше заданного е > 0. Другими словами, для любых е > 0, и Т > 0
существует 6 = 6 (е, Т) такое, что для любых zx, z2, g Z и p (zx,
z2) < б выполняется неравенство p [F (zx, /), F (z2, /)] < e, при лю-
бых t, таких что | 11 T.
В теории динамических систем (см. [8]) существенную роль игра-
ют так называемые инвариантные множества. Пусть F (A, t) — образ
множества ,4 с 2 при преобразованиях группы, соответствующих
данному t. Множество А называется инвариантным по отношению к ди-
намической системе (Z, F), если при всех преобразованиях F (z, t) оно
переходит в себя, т. е.
F(A,t)c.A, —ooctc+oo. (3.21)
Рассмотрим точку z g А; в силу (3.31)
F(z, t)£F(А, 0с:А;
поэтому, если точка г принадлежит инвариантному множеству, то
в это множество входит вся траектория, определяемая точкой z. С дру-
гой стороны, каждая целая траектория является инвариантным мно-
жеством. Объединение и . пересечение инвариантных множеств, а
*> Множество / называется метрическим пространством, если каждой паре
его элементов zx и гг отнесено число p(zx, z2) > 0, называемое расстоянием
и удовлетворяющее условиям: 1) p(zx, z2) = 0 в том и только в том случае,
когда zx = z2 (аксиома тождества), 2) p(zx, z2) = p(z2, zj (аксиома симметрии)
и 3) p(z,, z2) + p(z2, z3) > p(zx, z3) (аксиома треугольника).
73
также замыкание инвариантного множества, представляют собой инва-
риантные множества данной динамической системы.
Для динамической системы характерны три типа движений: покой,
периодическое движение и непериодическое движение. Точка za, для
которой при всех значениях t справедливо F (г0, /) = г0, называется
точкой покоя. Если для какого-нибудь движения существует такое т,
что F (z, t + т) = F (г, t) при любом t, рассматриваемое движение на-
зывается периодическим, а наименьшеет, обладающее этим свойством,—
периодом. Таким образом, имеются три существенно различных топо-
логических типа траекторий динамических систем: 1) точка, 2) зам-
кнутая линия и 3) взаимно однозначный и непрерывный образ откры-
того отрезка.
Можно показать, что ни одна траектория не входит в точку покоя
zQ при конечном значении t, однако если существует lim F (z, t) = z0,
t -> OO
to zQ есть точка покоя.
Изучение упомянутых типов движений и условий, при которых
они осуществляются, составляют основу качественной теории динами-
ческих систем. Особенно большой интерес представляют результаты
(устойчивость, эргодические теоремы и др.) для динамических систем
с инвариантной мерой [8].
В связи с изложенным любопытно поставить следующие два во-
проса: 1) существуют ли динамические системы, выходящие за рамки
систем, описываемых обыкновенными дифференциальными уравнения-
ми и 2) всегда ли система, определяемая обыкновенными дифферен-
циальными уравнениями (3.16), является динамической системой?
На первый вопрос дается утвердительный ответ. Это можно обосно-
вать примерами. Ответ на второй вопрос в общем случае оказывается
отрицательным. Это объясняется тем обстоятельством, что не всегда
все решения уравнений (3.16) могут быть продолжены на— оо < t <Z
<4-оо. Однако для уравнений вида (3.16) всегда можно подобрать
динамическую систему, движения которой совпадают с решениями
уравнений (3.16) в области их существования, см. [8].
Условие группы для динамической системы (Z, F) предопределяет
существование преобразования F (г, —/), обратного преобразованию
F (г, t). Преобразование F (г, —t) соответствует движению системы
в сторону уменьшения значений t. Однако в дальнейшем мы будем часто
встречаться с системами, для которых упомянутое движение, по тем
или другим причинам, не принадлежит множеству допустимых дви-
жений.
Поэтому представляет интерес рассмотрение также систем, для
которых семейство преобразований F (г, t) оказывается полугруппой
по отношению к введенной в нем бинарной операции.
Определение полугрупповой динамической системы можно полу-
чить из определения А. А. Маркова, если вместо области изменения
параметра /(—оо</<-фоо) рассматривать область (0^7< + оо),
и условие 3) понимать как условие полугруппы.
Мы приведем также определение, рассмотренное в [18]. Пусть Т —
множество значений / (0 + оо), Z — метрическое пространст-
74
во, a F — непрерывное отображение топологического произведения*)
Z X Т в пространство Z.
Упорядоченную пару (Z, F) будем называть полугрупповой дина-
мической системой, если выполнены аксиомы:
1) F (z, 0) = z для любой точки z g Z;
2) для любых z 6 Z и tr, t2 £ Т имеет место равенство
F[F(z, tj, t2]=F(z, t. + t,).
(3.22)
Из этого определения как следствие вытекает свойство интеграль-
ной непрерывности: для любых е > 0, F > 0 и z0 £ Z существует
число 6 > 0, такое, что если z f Z и p(z0, z)< 6, то р [F (г0, i),
F (z, /)] < е при всех t, 0 <1 t L.
Полугрупповые динамические системы обладают рядом свойств,
аналогичных свойствам обычных динамических систем. В частности,
на полугрупповые динамические системы переносятся рассмотренные
выше свойства инвариантных множеств (в определении инвариантного
множества нужно (— ею <; t < + оо) заменить на Т). Сохраняются
также некоторые результаты, относящиеся к трем типам движений
системы (покой, периодическое движение и непериодическое движение)
и соответствующим топологическим типам траекторий и т. д.
В качестве примера полугрупповой динамической системы
(см. [18]) можно привести систему, описываемую, дифференциальным
уравнением
^. = Ах1/з х>0,
dt 2
Существуют и некоторые дальнейшие обобщения понятия систе-
мы. Не лишено интереса, например, понятие общей системы, рассмо-
тренное в [11].
Пусть
= Х2, ..., хп,0, 1 = 1,2..п (3.23)
at
— система дифференциальных уравнений, правые части которой опре-
делены при / 0 и х = (лу, х2, ..., хп), принадлежащих «-мерному
евклидову пространству Еп. Предполагается, что выполнены условия,
при которых существует решение системы
х = х (/, /0, х°)
при 0 и х’ £ Еп, определенное при всех t t0 и удовлетво-
ряющее условию х (t, t0,. х°) х° при t t0 + 0.
*> Топологическое произведение двух топологических пространств X и Y
есть топологическое пространство Z, определяемое следующим образом: а) мно-
жество точек пространства Z есть прямое произведение множеств точек X и Y;
б) множество в Z, являющееся прямым произведением двух открытых множеств
в X и в Y соответственно, представляет собой открытое множество (подробнее
75
Через точку (t0, х°) может проходить бесконечное множество ре-
шений системы (3.23). Пусть (х°) — множество точек х £ Еп,
принадлежащих всем упомянутым решениям в фиксированный мо'
мент времени t tQ, причем р\л (х°) —> х° при t 10 + 0. (х)
определяет семейство преобразований, зависящее от двух параметров
t0 и t, и сопоставляющих каждой точке х° С Еп некоторое множество
точек Ft,, (х°) 6 Еп. Это семейство преобразований обладает следую-
щими свойствами.
1. Для любого х° Q Еп множество точек F^ (х°) не пусто
и определено при любом t t0.
2. Ft, (х°)->х° при
3. Если х<'> — некоторая точка множества Fz‘(x°), то при
имеет место Fta (х°) = J Е^(х(1)) по всем х(1) С (х°).
х(1)
Рассмотренное семейство преобразований называется общей си-
стемой в Еп.
Приводится также абстрактное определение общей системы.
В метрическом пространстве R задана общая система, если опре-
делено двупараметрическое семейство преобразований Fta прост-
ранства R на себя, обладающее следующими свойствами.
1. Для любого р£ R и t0>0 определено множество F/0(p) cz R
при t^t0\ Р*1а(р)—не пусто.
2. Г*,(р)-+р при t-+t0 + 0.
3. Для любого элемента gF/0(p) и/определено множество
(р) такое, что (?) = U (Pi) по всем Лб^.(Р)-
₽1 t
При фиксированных tn и р преобразование Ftt(p) называется
движением, а множество всех точек, принадлежащих движению при
f^t0—траекторией этого движения. Траектория движения Fta(p)
обозначается F(/o, р).
Для общих систем вводится понятие инвариантного множества.
Множество А называется инвариантным по отношению к общей систе-
ме, если из р Е А следует, что F (t, р) с А, при любом t 0.
В [11] рассматриваются условия устойчивости и неустойчивости
инвариантных множеств общих систем и некоторые применения ре-
зультатов к нестационарным системам обыкновенных дифференциаль-
ных уравнений.
3.4. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
С ЗАПАЗДЫВАЮЩИМ АРГУМЕНТОМ
Рассмотренные в предыдущем параграфе динамические системы
являются типичным представителем систем без последействия. По-
следние характеризуются тем свойством, что состояние системы в не-
1\
который начальный момент времени /0 полностью определяет состоя-
ния системы в любые моменты времени t > t0.
Обратимся к какой-нибудь конкретной траектории динамической
системы. Она описывается преобразованием (3.17)
р(/)=А(р0, /0)
или частным решением
Х;(/)=Хг(/—t0, X], х°, ..., х„), г = 1, 2, ..., п,
системы дифференциальных уравнений (3.16) при начальных усло-
виях Xj = х/, х2 = х2°, хл = Хп° в момент t0.
Легко видеть, что в рассматриваемом случае начальными данны-
ми, достаточными для определения состояния системы в любой мо-
мент времени t > t0, оказываются координаты состояния системы в мо-
мент t0. Однако отмеченная закономерность отнюдь не является все-
общей. На практике встречаются системы (так называемые системы с
последействием), для которых начальные условия имеют более слож-
ный вид и не могут быть исчерпаны начальным состоянием (хД х2°,
... , хп°) системы в момент t0. Более конкретно: для определения со-
стояний системы с последействием в моменты времени t> t0 необхо-
димо знать не только ее состояние в момент времени t0, но и состояния
системы в некоторые моменты времени t < t0. Другими словами, по-
ведение системы в будущем зависит не только от ее настоящего состоя-
ния, но и от предыстории, т. е. от того, каким образом система пришла
в это состояние.
Важный класс систем с последействием представляют собой си-
стемы, описываемые дифференциальными уравнениями с запаздываю-
щим аргументом. Рассмотрение таких систем начнем с простых прак-
тических примеров.
На молоточек электромагнитного прерывателя (см. [16]) в момент
времени t действуют следующие силы:
kx (t) — восстанавливающая сила пружины, пропорциональная
(для малых отклонений х (/) от положения равновесия) ее растяжению;
gx (t — т) — сила притяжения якоря, зависящая от положения
молоточка и величины тока в цепи обмотки, нарастающей благодаря
самоиндукции с запаздыванием т;
rx (t) — сила трения, пропорциональная скорости движения мо-
лоточка.
Уравнение Ньютона имеет вид
тх(/) =—г x(t)—kx(t) — qx(t—т). (3.24)
Автоколебания генератора с запаздывающей обратной связью
(см. [16]) описываются уравнением
х(/)4-/?С х(/)+х(/) =Л4х(/ — т)я[х(/—т)], (3.25)
где х (t) напряжение в резонансном контуре, ат — запаздывание.
77
Аналогичный вид имеют уравнения для процесса горения жидкого
ракетного топлива, уравнения автоматического регулирования с за-
паздыванием, некоторые уравнения математической экономики и др.
Дифференциальным уравнением n-го порядка с запаздываю-
щим аргументом мы будем называть уравнение вида (подробнее
см. [151)
х(п)(1) = f[t, x(t), x(t), ..., х<га_1,(7),
x(/ —т(/)), X (t—т(/)}, ..., х(п-1)(/ — T (/))],
x(/)>0. (3.26)
Так же как и обычные дифференциальные уравнения, уравнение
(3.26) может быть сведено к «нормальной» системе дифференциальных
уравнений первого порядка
*г(0 = Л [Л *i(0. xn(t),
хД/ —т(/)), х2 (/—т(/)), .... хп (/—т(/))], i = 1, 2, .... п. (3.27)
Практические задачи иногда приводят к уравнениям с несколькими
запаздываниями, например
x(z") =/[/, x(t), x(z" —тДО), ..., x(t—т„(/))]>
x;(/)>0, i=l, 2, ..., n. ’ (3.28)
Рассмотрим простейшее дифференциальное уравнение с запазды-
вающим аргументом вида
x(t)=f [Л х(/), x(t— т)], (3.29)
где т > 0 — постоянная величина.
Чтобы подойти к основной начальной задаче для уравнения (3.29),
перейдем к эквивалентному интегральному уравнению
t
х(7) = х(/0) + § f [Л х(/), x(t — т)] dt. (3.30)
^0
Для решения этого уравнения необходимо помимо начального значе-
ния х (70) задать функцию х (t) в полуинтервале /0 — т Д t < t0.
В самом деле, правая часть (3.30) будет определена для любого
t > t0 только в том случае, если известно значение х (/ — т). Поэтому
начальные условия задаются в виде некоторой функции х (/) = <р (t)
при i0 — т t t0, которая называется начальной функцией.
Основная начальная задача для уравнения (3.29) формулируется
следующим образом: определить непрерывное решение х (/) для
t t0 при условии, что х (/) = <р (t) для t0 — т сС t Д 70.
Если функции f и ф непрерывны и первая из них удовлетворяет
условию Липшица по х (/) и х (1 — т), искомое решение уравнения
(3.29) существует и единственно. Это решение может быть найдено
методом последовательного интегрирования (методом шагов). Сущность
75 '
его заключается В том, что непрерывное решение х (/) находится Из
дифференциальных уравнений без запаздывания:
x(t)=f[t, x(f), ф(/—т)] при tQ < t < iaф-т, х(/0) = ф(г‘о),
x(t)=f [/, x(t), фх(/ — т)1 при /0 + т^/^/0 + 2т, х(/04-т) =
= Ф1 (г'о + 'г).
.............................................. (3-31)
%(/)=)[/, х(г?), фп(Г—т)] при /0 + нт^:г</0 +
+ (п + 1) т, х(/'0+пт) = фп(/0 + /1т),
где ф;(/) — решение уравнений (3.31) на интервале
/0 + (i —1)т^/<Z0 + ir, t = 1, 2, п.
Если функция f достаточное число раз дифференцируема, то
решение х (/) в точках t0 + kx имеет непрерывную производную поряд-
ка не более чем k. В частности, в точке /0 производная х (/) имеет в об-
щем случае разрыв первого рода.
Пусть теперь запаздывание т (t) будет функцией времени. По-преж-
нему рассмотрим простейшее дифференциальное уравнение
*(0 = fl/, x(t —?(/))]• (3.32)
Для решения основной начальной задачи в этом случае начальная
функция х (г) = ф (0 должна быть задана на так называемом начальном
множестве Во значений t, которое состоит из точки t = t0 и из значений
разности t — х (t) при t0 t T, меньших, чем t0 (решение уравне-
ния (3.30) определяется для t0 t < Т).
В случае нескольких запаздываний (3.28) начальная функция
п
х(/) = ф(/) задается на начальном множестве Во = (J В(о‘},
1 = 1
где Bq’ — начальное множество, соответствующее запаздыванию тг(/).
Решение основной начальной задачи для переменного запаздыва-
ния и нескольких запаздываний может быть получено методом после-
довательного интегрирования [15]. Это утверждение справедливо также
для дифференциальных уравнений /г-го порядка с запаздывающим аргу-
ментом.
Существенный интерес с точки зрения моделирования сложных
систем представляют также стохастические дифференциальные урав-
нения с запаздывающим аргументом [20].
В настоящее время имеется значительное число работ, посвящен-
ных методам решения и качественным исследованиям дифференциаль-
ных уравнений с запаздывающим аргументом (см. [12, 16] и указан-
ную там литературу). С точки зрения проблематики настоящей книги
наибольший интерес представляют автономные системы дифференци-
альных уравнений с запаздывающим аргументом, т. е. таких уравнений,
правые части которых не зависят явно от t.
79
Ограничимся рассмотрением простейшего дифференциального
уравнения вида
x(t)=f[x(t — т)], (3.33)
где х — вектор в /i-мерном евклидовом пространстве £п; <
< 4-оо; f—вектор-функция в предположениях, обеспечивающих
существование, единственность и продолжаемость решений на всю
полупрямую ta sC t < 4- оо.
Пусть Ф — множество начальных функций <р (/), заданных на
отрезке S = [/0 — т, f0], со значениями в Еп и непрерывных на этом
отрезке. Заметим, что для любых 0 и <р f Ф функция ф (/) =
=ф (^4- 0 принадлежит Ф. Здесь функция ф (t) — результат сдвига
влево функции <р (t) на t-^ Обозначим
х==х(ф, О (3.34)
решение уравнения (3.33), которое определено для всех t на полупря-
мой Tr = (t0 — т t < 4- оо) и любого <р (Е Ф, причем х (<p, t) =
= ср (0 для t 6 S. Соотношение (3.34) определяет отображение
Ф х Тг-+ Еп прямого произведения множеств Ф и 74 во множество
точек пространства Еп. Это отображение сопоставляет каждой началь-
ной функции <р £ Ф и каждому t (Е Тт точку х пространства Еп.
Можно показать, что решение (3.34) уравнения (3.33) обладает
следующими свойствами:
1) начальное условие х (ф, t)=<p(t) для всех t f S и любого
С ф;
2) непрерывно по совокупности аргументов ф и t\
3) х(ф, ^4-/2) =х([х(ф, 0-Н1))е=ц-т> ^2) Для любых ф^Ф и
/2>0-
Свойство 3 имеет тот смысл, что для перехода от значения х(ф,
к х(ф, /j 4- нужно знать начальную функцию (х(ф, 0)]е=/[-т
на отрезке —т, /х].
Решение (3.34) уравнения^.33) определяет однопараметрическое
семейство преобразований (с параметром f) множества начальных
функций Ф во множество точек пространства Еп. Это обстоятельство
послужило поводом для введения понятия (см. [17]) динамической
системы с последействием.
Пусть R —• метрическое пространство; S — ограниченное замк-
нутое подмножество точек числовой прямой иг — его нижняя грань.
Рассмотрим метрическое пространство Ф, точками которого являются
непрерывные отображения ф множества S в R, с метрикой равномерной
сходимости на S. Кроме того, пусть F (ф, f) — непрерывное отображе-
ние топологического произведения Ф X Тг в R, где Тг — прямая
(г < t < 4- сю ).
Упорядоченную тройку (Ф, Tr, F) будем называть динамической
системой с последействием, если выполнены следующие аксиомы.
1. Для любой ф € Ф и любого s £ S выполняется равенство
F (Ф, s) = ф (s).
80
2. Для любой функции ф £ Ф и любого 0 > О функция Fg (s),
определяемая равенством F$ (s) = F (ср, 0 + s), при любом s(S
принадлежит Ф.
3. Для любых ф£Ф, 0^0 и t£Tr имеет место равенство
F (ф, 0 + t) = F(F?, t).
Заметим, что функция Fg(s) представляет собой сдвиг влево на
0 функции F (ф, 0 + s). При фиксированном ф С Ф функция F (ф, t)
называется движением системы, параметр t — временем, множество
точек F (ф, t) пространства R при t £ Тг— траекторией этого движения.
Решение дифференциального уравнения (3.33) удовлетворяют акси-
омам 1, 2 и 3 и, следовательно, определяют систему, принадлежащую
к классу динамических систем с последействием.
К этому же классу относятся системы, описываемые автономными
дифференциальными уравнениями (без запаздывания) и-го порядка
с краевыми условиями х (aft) = Ah, k = 1, 2, ..., п, системы, описы-
ваемые непрерывными на Тг функциями ф со значениями в метриче-
ском пространстве, если множество этих функций Y ЭФ удовлетворяет
аксиомам 1—3, и т. д.
Для динамических систем с последействием имеются некоторые
результаты, относящиеся к качественным методам. В частности, пока-
зано, что существуют динамические системы с последействием, обла-
дающие стационарными и периодическими движениями, рассмотрены
теоремы об инвариантных множествах, изучены некоторые вопросы
устойчивости и т. д. (см. [17, 18]). Исключительный интерес представ-
ляют также идеи перехода от решений дифференциальных уравнений
с запаздывающим аргументом к траекториям в пространстве начальных
функций и ряд других, [12, 13, 14].
Пусть (Ф, Тг, F) — произвольная динамическая система с после-
действием. Определим отображение % топологического произведения
Ф X Г в Ф, полагая % (ф, t) = Ff. Оказывается, что (Ф, %) — полу-
групповая динамическая система. В самом деле, можно показать, что:
1) Л (ф, 0) = ф, 2) отображение % непрерывно и 3) Z [Л, (ф, ^), /а] =
= X (ср, + /а) для любых ф (Фи ^J2>0. Таким образом, пред-
ставляется возможность переходить от данной динамической си-
стемы с последействием (Ф, Tr, F) к полугрупповой динамической
системе (Ф, X), пространством состояний которой служит множество
Ф начальных функций ф [2]. Этот переход позволяет перенести на
динамические системы с последействием некоторые результаты, отно-
сящиеся к полугрупповым динамическим системам.
Всякую полугрупповую динамическую систему (2, F) можно рас-
сматривать как вырожденный случай динамической системы с после-
действием (Ф, Tr, F), для которой начальное множество состоит из
одной точки t0. В этом случае .пространство Ф перейдет в Z, а система
(Ф, Tr, F) в систему (Z, F).
Динамические системы с последействием представляют самостоя-
тельный интерес для решения некоторых задач системотехники. Кроме
того, они являются примером, опираясь на который легче найти под-
ходы к исследованию систем с последействием более общего характера.
81
3.5. МНОЖЕСТВО МОМЕНТОВ ВРЕМЕНИ. ПРОСТРАНСТВО
СОСТОЯНИЙ СИСТЕМЫ
После рассмотрения характерных примеров возвратимся к общей
схеме формализации сложной системы. Наша конечная цель — дать
формальное определение понятию системы. Она будет достигаться по-
степенно. Опираясь на интуитивные представления о закономерностях
функционирования системы и обобщения понятий, введенных для дина-
мических систем, мы дадим формальную интерпретацию каждому из
пяти упомянутых в §3.1 предположений. Только после этого сможем
перейти к общему определению.
Начнем с первого предположения. Система функционирует во
времени. Множество моментов времени t, в которые рассматривается
функционирование системы, обозначим Т. Множество Т будем считать
подмножеством множества действительных чисел. В частности, оно
может быть конечным или счетным.
С практической точки зрения представляют интерес только такие
счетные множества Т, элементы которых — моменты времени — рас-
полагаются в изолированных точках числовой прямой. В этом случае
будем говорить, что система функционирует в дискретном времени.
К системам, функционирующим в дискретном времени, обычно отно-
сятся контактные схемы, конечные автоматы, вычислительные устройст-
ва ЭВМ и т. д. Часто вместо моментов времени /0, tx, ... пишут просто
ряд неотрицательных целых чисел 0, 1, 2, ..., которые называются
тактами. В другом случае, когда Т представляет собой множество
точек некоторого (конечного или бесконечного) интервала числовой
прямой, будем говорить, что в данном интервале система функциони-
рует в непрерывном времени. К системам, функционирующим в не-
прерывном времени, обычно относят механические и электрические
системы, системы, рассматриваемые в теории колебаний, в теории авто-
матического регулирования и т. д.
В принципе не исключены случаи, когда множество Т имеет сме-
шанный дискретно-непрерывный характер: на одних интервалах
числовой прямой моменты t CZT располагаются в изолированных точ-
ках, а на других — заполняют их целиком.
В каждый момент t ~Т система находится в одном из возможных
состояний z (t). Множество состояний г системы обозначим Z.
Для изучения электромагнитного реле (см. § 3.1) как логического
элемента достаточно рассматривать всего два состояния: zr — контакт
разомкнут и z2 — контакт замкнут. Множество Z в этом случае со-
стоит из двух элементов: и г2.
Заготовка, выходящая из нагревательной печи, при помощи транс-
портера доставляется к станку, осуществляющему горячую штамповку.
Состояние системы, сущность процесса функционирования которой
состоит в транспортировке заготовки, можно характеризовать
расстоянием z (t) между заготовкой и станком и скоростью
перемещения г (/) в момент времени t. Множество Z в данном случае
является множеством векторов с координатами (г, г), принимающими
значения из интервалов на числовой прямой, границы которых зави-
82
сят от параметров системы. С другой стороны, горячая штамповка воз-
можна только при температуре 0 (/) заготовки, не ниже заданной. Изу-
чая процесс остывания заготовки, в характеристику состояния системы
мы будем вынуждены ввести температуру 0 (t) как функцию времени,
а может быть, и ее производную 0 (/). В этом случае множество Z ока-
зывается множеством векторов трехмерного или четырехмерного про-
странства.
Состояние системы однопродуктового производства характеризует-
ся обычно числом изделий z (t), выпущенных к данному моменту
времени t. Множество Z — совокупность целых неотрицательных
чисел 0, 1,2, ...
На практике повседневно приходится встречаться с системами,
состояния которых описываются наборами характеристик. Например,
в системе управления аэродромом (см. гл. 1) положение самолета в дан-
ный момент времени t можно описать тройкой координат (z1( г2, z3),
где zr — наклонная дальность, z2 — азимут, г3 — угол места.
Когда состояние системы z описывается набором числовых ха-
рактеристик (действительных или комплексных), его можно рассматри-
вать как действительный или комплексный вектор соответствующего
числа измерений. Однако для сложных систем, в качестве характери-
стик состояния иногда фигурируют не только числа, но и объекты бо-
лее общей природы. Например, состояние оперативной памяти ЭВМ
в данный момент времени можно описать достаточно полно двумя набо-
рами: Щнабором чисел (представляющих собой исходные данные для
решения задачи, промежуточные результаты решения и т. д.) и 2) на-
бором операций ЭВМ (составляющих программу решения задачи).
Положение луча радиолокатора аэродромного обзора (см. гл. 1)
задается в данный момент времени двумя числами: азимутом и углом
места. Когда радиолокатор рассматривается как система, позволяющая
обнаружить самолет и определить его координаты с некоторой точ-
ностью, упомянутых характеристик недостаточно для описания состоя-
ния системы. Во многих случаях описание состояний этой системы ока-
зывается удовлетворительным, если для данного момента времени задать
еще две «координаты»: вероятность обнаружения самолета как функцию
наклонной дальности и корреляционную матрицу ошибок измерения
координат (элементы корреляционной матрицы являются функциями
наклонной дальности).
В общем случае мы будем предполагать, что состояние z рассма-
триваемой системы описывается некоторым набором объектов z3, z2,
..., zn, таких, nmZifZi, i = 1,2, ,.,n, где Zt — заданные множества.
Рассмотрим прямое произведение
Z-ZfxZ.x ... xZn. (3.35)
Например, если Z, — множества точек числовой прямой, то Z = ZY X
XZ2 можно рассматривать как множество точек z = (г1? z2) плоско-
сти; Z = Zj X Z2 X Z3—как множество точек z = (z1, z2, z3) трехмер-
ного, a (3.35) — как множество точек «-мерного пространства. Когда
элементы z, множеств Z, являются объектами любой природы, а не
83
только числами (например, векторами, матрицами, функциями и т. д.),
будем говорить, что точки z пространства Z имеют координаты zi>
z2, ..., zn. Множество Z (3.35) будем называть пространством со-
стояний системы.
Выше, в начале этого параграфа, мы условились множество со-
стояний системы обозначать Z. Далее, для обозначения пространства
состояний как прямого произведения элементарных осей (3.35) мы
ввели новый символ — Z. Суть дела состоит в том, что множество точек
пространства Z представляет собой множество всех упорядоченных
совокупностей (гх, z2, ..., гп), в том числе, быть может, и таких, которые
не принадлежат множеству Z (по смыслу задачи не являются состоя-
ниями системы). На рис. 3.2 показано
z2| множество Z состояний системы (за-
го ______ ______________ штрихованная область), характери-
2 & зующихся координатами zlt г2. Zj —
множество точек интервала (0, гг°)
J//////у//,-,/////ШТТТттк на оси — множество точек
^^//////////////////mj интервала (0, г2°) на оси 0Z2. Пря-
мое произведение Zt х Z2 есть мно-
z жество точек прямоугольника с вер-
и zf zf шинами (0, 0), (0, z2°), fo0, z2°), (гД 0).
В общем случае множество Z является
ги J i некоторым подмножеством множества
точек пространства Z.
Полезно обращать внимание на аналогию между реальным физиче-
ским пространством, достаточно привычной формализацией которого
является трехмерное евклидово пространство, и пространством состоя-
ний системы Z. Состояние системы z (/) в данный момент времени t
есть «точка» (или «вектор») пространства Z с (обобщенными) коор-
динатами Zj, z2, ..., zn.
В некоторых случаях рассматривается также пространство
Т X Z, точками которого являются упорядоченные пары (/, г). Про-
странство Т х Z иногда называют фазовым пространством системы
(см., например, [19]).
3.6. ВХОДНЫЕ И ВЫХОДНЫЕ СИГНАЛЫ
На вход системы могут поступать входные сигналы х £ X, где X —
множество входных сигналов системы. Входной сигнал, поступающий
в систему в момент t£T, обозначается х (/).
В системе однопродуктового производства, упомянутой выше,
готовность в момент tt i -го изделия можно описать как поступление
очередного сигнала х (/,) = 1. Здесь множество X состоит из одного
элемента х = 1. Если принять, что X = {0, 1 ], т. е. х = 0, когда
очередное изделие не готово, и х = 1, когда оно готово, то можно
считать, что в систему входной сигнал поступает в каждый момент
t £ Т. В случае, когда в моменты оказываются готовыми одновремен-
84
но несколько изделий (например, 0 х < хтах), множество X —
совокупность целых чисел, X = [0, 1, ..., хтах].
В реальных системах зачастую входной сигнал описывается не-
которым набором характеристик. Например, многоразрядное число,
поступающее в арифметическое устройство ЭВМ, можно описать набо-
ром одноразрядных чисел, соответствующих его разрядам; если вход-
ными сигналами системы управления аэродромом считать самолеты,
поступающие в зону аэродрома, то каждый из них может быть описан
координатами точки влета (/ — наклонная дальность, а — азимут и е—
угол места), вектором скорости (/, а, е), признаками, характеризующи-
ми тип самолета (г), вес груза (Р), требования к аэродромному обслу-
живанию (6) и т. д.
В общем случае предполагаем, что входной сигнал х описывается
набором объектов хг £ Xit i = 1, 2, .... т, где Хг — заданные мно-
жества.
Прямое произведение
X = XiXX2X ... хХт (3.36)
будем называть пространством входных сигналов системы. Здесь Хг —
элементарные оси, входной сигнал х представляет собой точку про-
странства X, описываемую координатами х1( х2, ..., хт. Понятия осей,
проекций и подпространств для пространства X оказываются вполне
аналогичными тем, которые были введены выше для пространства со-
стояний системы. Будем также иметь в виду то обстоятельство, что
в общем случае X а X.
Для самолета как входного сигнала системы управления аэро-
дромом можно принять: Хг — множество точек интервала числовой
прямой lmln С I 1тах, Х2 — множество точек интервала 0 а <2л,
Х3 — интервала 0 < в -< л/2, Xt — интервала lmin < I < 1тах,
Х6 — интервала amin < а < атах, Хв — интервала emin < е < Етах,
Х-, — множество целых чисел v = 1, 2, .... vmax, представляющих
собой шифры типа самолета; Х8 •— множество точек интервала число-
вой прямой 0 < Р < Ртах\ Хв — множество целых чисел 6=1,
2, ..., 8тах, представляющих собой шифры типов аэродромного обслу-
живания, установленных заранее, и т. д. Входной сигнал в этом слу-
чае имеет вид
x(t) = (l (0, а-(0, “(О, Е(0> v(Z), Р(0> 6(/))- (3.37)
При исследовании реальных систем нам придется оперировать над
группами входных сигналов, поступающих в моменты времени tr <
< t2 <1 ••• <
Будем предполагать, что множеству X принадлежит и пустой
сигнал xz, означающий отсутствие сигнала в момент t, если х (Z) =
Рассмотрим отображение х = L (/), сопоставляющее каждому
Т некоторый сигнал х £ X (отображение Т -> X). Обозначим через
TL множество моментов времени, TL с Т, такое, что для любого
f £ TL справедливо L (t')^xz. Отображение х = L (/) будем назы-
85
вать входным процессом системы, а совокупность упорядоченных пар
(/', х) для всех t' £ TL, где х = L (t"), — входным сообщением, соот-
ветствующим входному процессу L (/), и обозначать (t, xl)T-
Чтобы задать конкретный входной процесс х = £ (/), достаточно
указать соответствующее ему входное сообщение (/, хг)?, так как ото-
бражение х = L (t) определено на всем Т и для t g (T\TL) имеет место
X (/) = Х0.
Впредь интервал времени tr < t < t2 обозначается (tlt t2), а полу-
интервалы < t t2, i <z t2 — через (tlt t2] и Z2) соответст-
венно.
Сужение*’ отображения x = L (t) на множество T П U
будем называть фрагментом входного процесса, соответствующим
полуинтервалу (tlt /2], а совокупность упорядоченных пар (t', х) для
всех f £Tl П (Ь> где х = L (f),— отрывком входного сообщения
поступающим в систему за полуинтервал (/ь t2] и обозначать (t,
xt]/?. Для конечного множества TL f] (ti, U. например tlt t2, ..., tk,
входное сообщение имеет вид (l1, х2; t2, х2; tk, xk).
Множество всевозможных входных сообщений обозначим
{(/, хл)г}. Оно определяется множеством входных процессов вида
х = L (i), допускаемых условиями функционирования системы.
К множеству {(/, хь)г) будем причислять и пустое входное сообщение
(/, xL)T = 0, для которого TL = 0. Если же (/, Х/.)г ¥= 0, отры-
вок (t, Хь\ц может оказаться пустым за счет того,’что TL (] (/j,
t2] = 0.
Кроме того, множество {(/, х, )г) должно удовлетворять еще одному
требованию, связанному с сочленением входных сообщений. Пусть
(t, xLJT и (t, xL )T — два сообщения из множества {(/, xL)r}. Пусть
далее < t., <; /3; tlr t2, t3 g T. Образуем отрывки сообщений
(t, xLJ'> и (t, xLJ‘>. Совокупность упорядоченных пар (t*, х*), где
t* 6 П (А, М U П (Ь, (3.38)
_/М*) для /*е {т^ п (WJb ,ooQ.
U2(D для /*е \т^ п (/2, Ш
можно рассматривать как отрывок (/, xL,]'« некоторого сообщения
(/, хд,)7-) образовавшийся в результате сочленения отрывков (/, xL Vp
и (z-
Будем предполагать, что для любых двух сообщений (/, хь^т
и (t, xl,)t из множества {(/, xl)t} и любых < t2 < t3, принадле-
жащих Т, существует по крайней мере одно сообщение (t, xl')t 6 ((/,
хС)т} такое, что (/, xl'Ii’ является его отрывком за полуинтервал
(/1( /3]. Принятое предположение позволяет считать, что сочленение
*) Пусть множество X — область определения отображения у = f(x).
Отображение у = g(x) с областью определения X* является сужением отобра-
жения f(x) на множество X* в том и только в том случае, когда X* <— X и
g(x) = f(x) для каждого х X*,
§6
любого числа отрывков различных входных сообщений из множества
[(/, xl)t\ представляет собой отрывок некоторого входного сообщения,
принадлежащего множеству {(/, jqJt}.
Система способна выдавать выходные сигналы у £ Y, где Y —
множество выходных сигналов системы. Выходной сигнал, выдаваемый
системой в момент t £ Т, обозначается у (t).
Если выходной сигнал у описывается набором характеристик
Ут, У к Уть таких, чтоуг Q YI, i = 1,2,..., г; Уг— заданные множе-
ства, то прямое произведение
У = У1ХУ2Х ... \Yr (3.40)
называется пространством выходных сигналов системы. По аналогии
с входным процессом вводится понятие выходного процесса = JV (/),
а также определяется выходное сообщение (/, уы)Т и его отрывок
(Л t/wltj.
На этом можно считать исчерпанной формальную интерпретацию
второго и третьего предположений, сформулированных в §3.1.
3.7. ОПЕРАТОРЫ ПЕРЕХОДОВ И ВЫХОДОВ
Для завершения общей схемы функционирования системы остает-
ся дать формальное описание четвертому и пятому предположениям
§3.1. Другими словами, необходимо ввести соотношения, позволяю-
щие определить состояние системы и ее выходной сигнал в заданный
момент времени t, если известны состояния системы и входные сигналы
в моменты времени, предшествующие t (см. [2]).
В настоящем параграфе мы рассмотрим весьма важный класс
систем, играющий существенную роль в теории и приложениях, —
системы без последействия. Ограничение, при помощи которого они
выделяются из множества систем общего вида, можно сформулировать
следующим образом: будущее поведение системы определяется ее на-
стоящим состоянием и не зависит от прошлого. Иначе, состояние
г (/) системы без последействия в момент времени t > ta определяется
ее состоянием z (t0) и отрывком входного сообщения (t, х^1‘а за полу-
интервал (t0, d, но не зависит от предыстории [от того, каким образом
система пришла в состояние г (4)].
Обобщая понятие динамической системы, рассмотренное выше,
будем предполагать, что состояние системы г (/) для моментов времени
t £Т таких, что t О ^0, определяется оператором
z(t) = H\t, t0, z(t0), (t, (3.41)
удовлетворяющим некоторым ограничениям (см. ниже), который назы-
вается оператором переходов системы (в новое состояние). Состояние
2 (4) будем называть начальным состоянием системы.
Обратимся к отображению, реализуемому оператором переходов
системы. Аргументы в правой части (3.41) являются элементами
множеств: t^T, , z(t0)eZ, (t, xL\\t £ [(/, xJJJ, где ((/, xJ'J —
87
множество всевозможных отрывков входных сообщений, соответ-
ствующих полуинтервалу (/0, /].
Исходя из (3.41) формально можно записать (см., например, [19])
TxTxZ х {(/, (3.42)
Однако соотношение (3.42) не является вполне корректным, так
как не все аргументы правой части (3.41) оказываются независимыми.
Действительно, в силу условия t t0 можно говорить лишь о неза-
висимых упорядоченных парах (t, t0), удовлетворяющих этому усло-
вию. Множество {(/, /0)} всех упорядоченных пар (/, /0), таких, что
является подмножеством множества Т х Т, содержащим
точки плоскости (t, i0), расположенные на биссектрисе координатного
угла и ниже ее. Далее, чтобы определить отрывок входного сообщения
(t, xL\tt при фиксированной паре (/, t0), достаточно выбрать конкрет-
ное входное сообщение (t, xl)t из множества входных сообщений
{(^, xl)t}- Таким образом мы приходим к отображению
|(/, /0)} xZx{(t,xLy->Z. (3.43)
Область определения S отображения, реализуемого оператором Н,
не обязательно должна совпадать со всем множеством {(/, t0)} х Z X
X {(Л xl)t}', она может быть некоторым его собственным подмножест-
вом. В самом деле , существуют примеры реальных систем, для кото-
рых те или другие состояния z(Z или входные сообщения (/, xL)Tf
£{(£, xl)t} сочетаются лишь с определенными интервалами времени
функционирования.
Мы пока рассматриваем детерминистические системы без последей-
ствия, т. е. системы, на которые не действуют случайные факторы.
Стохастические системы, функционирующие в условиях действия
случайных факторов, будут рассмотрены ниже.
В качестве оператора переходов детерминистической системы без
последействия может быть взят не произвольный оператор, реализую-
щий отображение (3.43), а лишь один из тех операторов, которые удов-
летворяют условиям, вытекающим из специфики описания процесса
функционирования системы [19].
1. Начальное условие: для любых t0£Т, z (t0) ^Zu(t, xL}T£ [(t,
при t = t0 имеет место равенство
H\t0, t0,z(t0), (t,xL]^=z(t0). (3.44)
Легко видеть, что здесь (i, xLj^ является пустым отрывком вход-
ного сообщения. Условие требует, чтобы состояние z (t)~ Н(t) при
t = ta совпадало с заданным начальным состоянием z(t0).
2. Для любых входных сообщений (t, xL^T и (t, xL^T из мно-
жества {(/, xL)rj, отрывки которых совпадают на полуинтервале
(/0, t], т. е. (t*L1],0 = имеет место равенство
z(tQ), (ЛхЛ1]^ =
= H[t, t0, Z(/o), (3.45)
88
3. Условие однозначности: для любых t0, 4, t2 из множества Т,
таких, что 4<4<4, имеет место равенство
И [t2, i0, 2(4), (/, = Н (4, 4- z(4), (4 хд]Ь} (3.46)
в предположении, что (4 является результатом сочленения (3.39)
отрывков (4xJ^ и (4 xL]^.
Подставляя в правую часть (3.46) вместо 2(4) его значение
г(4) = /7 {4> 4, г(4)> (4 условие однозначности приведем
к следующему виду:
H{t2, tQ,z(tQY (4xl]';} =
= Н {4, 4. Н {4, 4, z(4), (4 (4 . (3.47)
Заметим, что в правой части (3.47) под Н {4, 4> z(4), (4 xj'1}
имеется в виду не сам оператор, а результат его действия на аргу-
менты 4, 4, (4 хДр, т- е- элемент множества Z.
При фиксированных 4, z (4) и (4 хфт оператор Н реализует ото-
бражение 2 = Н (4 или 2 = 2 (/) множества Т во множество Z, которое
называется движением системы. Множество всевозможных движений
системы обозначается {z (t)}.
Совокупность упорядоченных пар (4 г) для всех t(-T, где 2
определяется заданным движением г = г (4, называется фазовой тра-
екторией системы. Фазовая траектория является подмножеством мно-
жества точек пространства TxZ, которое наглядно можно себе пред-
ставить в виде «кривой» в пространстве Т х Z.
Совокупность точек пространства Z, соответствующих в силу
отображения 2 = 2(4 всем называется траекторией системы
в пространстве состояний. Траектория системы является проекцией
фазовой траектории на пространство Z.
Рассмотрим некоторый полуинтервал времени (4, 41- Сужение
отображения г (4 на множество Т П (4, 4] будем называть фрагмен-
том движения системы на полуинтервале (4, 41- Данному фрагменту
движения соответствуют конечная дуга фазовой траектории, представ-
ляющая собой множество упорядоченных пар (4 г), определяемых ото-
бражением г = г (4 для 14 (Т П (4, 4D, а также конечная дуга тра-
ектории системы в пространстве состояний — множество точек 2,
принадлежащих упомянутым парам.
Для случая конечного входного сообщения (4, ху, t2, х2; ..., tl:,
хА) оператор переходов системы приобретает вид
г (4 = //{4 4, 2(4), 4, xv t2, х2.4, xft). (3.48)
Обратим внимание на аналогию между (3.47) и условием (3.22)
для полугрупповой динамической системы. В самом деле, оператор Н
определяет семейство преобразований, зависящее от трех параметров
4, t и (4 хфт, сопоставляющих в силу (3.43), каждой точке г (4) €Z
89
вполне определенную точку z (t) f Z. При фиксированных /0 и (t, xl)t
выбор точки z (t0) выделяет траекторию системы, которой принадле-
жит точка z (/) при любом t > t0, t 6 T.
Любое преобразование упомянутого семейства удовлетворяет
условию (3.47). По аналогии с (3.22) условие (3.47) иногда называют
условием полугруппы (см., например, [19]).
Кроме того, оператор Н определяет семейство преобразований,
зависящее от параметров tQ и/, сопоставляющее каждой точке z (/0) {^Z
множество точек этого пространства, соответствующих состояниям
системы в момент t при всевозможных входных сообщениях (/, х^)г-
В некоторых отношениях это семейство преобразований напоминает
общую систему [11], рассмотренную кратко в конце § 3.3. В самом деле,
при дополнительных ограничениях (Z — метрическое пространство
Н {t, t0, z (/0), (/, xj* } -> z (t0) при t -> t0 + 0) справедливость усло-
вий аксиомы 3 вытекает из (3.46).
Перейдем к выходным сигналам системы. Будем предполагать,
что выходной сигнал у (/) £ Y для моментов времени t£T, таких, что
t > t0 определяется оператором
y(t)=G{t, t0, z(t0), (/, (3.49)
который называется оператором выходов системы. Обычно предпо-
лагается, что область определения оператора (3.49) в пространстве
{(t, t0)} X Z х {(t, xl)t} совпадает с областью определения S операто-
ра переходов системы (3.41). Поэтому под оператором выходов G
системы будем понимать оператор, реализующий отображение
((/,/„)} xZx\{t,xL}T\ Y. (3.50)
Несмотря на внешнее сходство операторов (3.41) и (3.49), между
ними имеется существенное различие. Отображение, реализуемое опе-
ратором переходов Н, каждому t > tQ из множества Т ставит в соот-
ветствие определенный элемент z £ Z (система в каждый момент време-
ни Т находится в одном из возможных состояний). Из физических
соображений ясно, что существуют системы, которые выдают выход-
ные сигналы не обязательно в каждый момент t g Т. Чтобы устранить
это различие, по крайней мере с формальной точки зрения, можно пред-
положить, что множеству Y принадлежит и пустой сигнал у,%, который
физически интерпретируется как отсутствие выходного сигнала в мо-
мент времени t, если у (t) = у%.
Рассмотрим точку (z, у) пространства Z X Y. Учитывая, что опе-
ратор переходов Н и оператор выходов G имеют одну и ту же область
определения S, можно ввести оператор
(z(/), у(/)) = Л*{/,/0, 2(/0), (Z.xJ'J, (3.51)
который реализует отображение
{(t,toy\xZx\(t,xL)T\^ZxY. (3.52)
90
Оператор Н* не может быть интерпретирован как оператор переходов
системы с «расширенным» состоянием (г, у), так как в левой части
(3.52) множество Y не фигурирует.
Оператор Н*, который иногда обозначается как Н* = Н X G,
будем называть оператором функционирования системы. Тем не менее
точку (г, у) £ Z X Y часто трактуют как «расширенное» состояние
системы (точку г £ Z в связи с этим уместно назвать внутренним со-
стоянием). При фиксированных t0, z (t0) и (t, хфт оператор И* пред-
ставляет собой отображение (z, у)=Н* (I), называемое процессом функ-
ционирования системы. Совокупность точек (г, у) пространства Z X Y,
соответствующих в силу отображения (z, у) = Н (I) всем t£T, яв-
ляется траекторией функционирования системы.
Возвратимся к оператору выходов системы (3.52). Во многих
случаях оператор выходов используется в виде
y(t) — G [t, z(t)]. (3.53)
Подставляя в (3.53) вместо z (t) его значение из (3.48), получаем
y(t) = G(t,H[t, t0, z(ta), (3.54)
Выражение (3.53) соответствует частному случают описания про-
цесса выдачи системой выходных сигналов [по сравнению с (3.49)1.
В самом деле, в случае (3.53) для совпадения выходных сигналов до-
статочно, чтобы система в момент t находилась в состоянии z (/), хотя
не исключена возможность, что это обстоятельство явилось следствием
действия различных входных сообщений на систему, находящуюся
в момент t0 в различных состояниях.
Вместе с тем, случай (3.53) хорошо согласуется с представлением
о системе без последействия, поведение которой не зависит от предысто-
рии, а определяется лишь ее состоянием в данный момент времени t.
Поэтому соотношение (3.53) как более простое весьма часто использует-
ся для описания оператора выходов системы.
Пусть S* с Т X Z, где s* £ S* имеет вид (Zo, z (Zo)), является
проекцией S cz {(t, t0)} X Z X {(t, xl)t} на пространство T x Z,
a S' — областью определения оператора (3.53), реализующего ото-
бражение Т X Z -> Y. В общем случае S* не совпадает с S', так как
с моментами t0 могут сочетаться одни состояния системы, а с t >
другие.
На этом будем считать законченной формализацию всех пяти
предположений, выдвинутых в §3.1. Попутно мы ввели необходимые
понятия и обозначения. Подводя итог сказанному, можно дать формаль-
ное определение детерминистической системы без последействия. Это
определение концентрирует в себе интуитивные предположения о
функционировании реальных систем, изложенные на формальном язы-
ке (§3.5—3.7).
Итак, под детерминистической системой без последействия (или
динамической системой Калмана [19]) мы будем понимать упорядо-
ченную совокупность
(Т, X, Z, Y, {(/, xL)r], Н, G) (3.55)
91
множеств Т, X, Z, Y, {(/, xl)t} и операторов Н и G, обладающих
следующими свойствами:
1) Т является подмножеством множества действительных чисел;
2) {(С хь)г} — множество отображений Т -> X, удовлетворяю-
щее условию сочленения отрывков (3.39);
3) оператор переходов системы
2 (i) = H[t, t0, г (/0),
реализует отображение (3.43) и удовлетворяет условиям (3.44) — (3.46);
4) оператор выходов системы задается соотношением (3.53).
В заключение настоящего параграфа обратим внимание на неко-
торые важные частные случаи.
На практике нередко встречаются системы, режим функциониро-
вания которых не зависит от времени. Другими словами, структура
системы, отношение, определяющее ее реакцию на входные сообщения
и начальное состояние, остаются неизменными, независимыми от того
интервала времени, на котором рассматривается система. В связи с этим
оказывается полезным понятие однородной системы или, как иногда
говорят, системы, инвариантной относительно сдвига времени.
Инвариантность режима функционирования относительно сдвига
времени может быть обеспечена лишь в том случае, когда на множест-
ва и операторы, определяющие систему, будут наложены дополнитель-
ные ограничения. Прежде чем формулировать эти ограничения, сдела-
ем некоторые предварительные замечания.
Сдвиг по времени на величину t' £Т относительно момента t £ Т-
будет иметь смысл, если момент (/+/') £ Т и для t > момент (t —
— t’) £ Т. В противном случае может оказаться, что при сдвиге мы
приходим к моментам времени, для которых система не определена.
Рассмотрим теперь некоторое входное сообщение (/, х£)т 6
6 {(С *ь)т}> реализующее отображение х = L (t). Пусть (Z, xjz’—
его отрывок для tlt t2£T и, кроме того, пусть t' £ Т. Построим сово-
купность упорядоченных пар (t*, х) таких, что t* g (/х + t', t2 + f),
а х (t*) = L (t* — t'). Эта совокупность может рассматриваться как
отрывок (t, + некоторого сообщения (t, Xl>)t, называе-
мого сдвигом на t' входного сообщения (t, Xl)t-
Система без последействия называется однородной или инвариант-
ной относительно сдвига времени, если:
1) для любых t£ Т и f £ Т момент (t + С) £ Т и для t > t'
момент (t — f) £ Т;
2) для любых t'£Т и (t, xl)t € {(/, хь)г} сообщение (/, xL)T,
представляющее собой сдвиг на t' выходного сообщения (t, Xl)t,
принадлежит множеству {(/, xjr},
3) для любых t е Г, t0 е т, Г £ Т, z(t0)=z0 £Z и (/, xL)r £ |(С xL)rj
имеет место соотношение
t0+t', z0,(CxL,]'+_z;,|-
= H{t, ta, z0,(t,xL]t'], (3.56)
92
где в качестве состояния системы в момент t0 + t' принимается то же
самое значение г0 = г (/0);
4) оператор выходов системы имеет вид
у (t) = G [z (t)\. (3.57)
Соотношение (3.56) можно трактовать и таким образом, что опера-
тор переходов Н однородной системы зависит не от t и t0 в отдельности,
а лишь от их разности t — t0 = т:
z(t) = /7 (т, z0, (t, xJJ}. (3.58)
Система без последействия называется автономной*’ (свободной,
изолированной по входу), если множество входных сообщений
{(Л *l)t} состоит из единственного элемента. Автономная система мо-
жет быть интерпретирована как система, в которую не поступают
входные сигналы, так как сигналы, принадлежащие фиксированному
входному сообщению, заранее определены и могут рассматриваться
как известные параметры системы. Несмотря на это, в общем случае,
автономная система способна выдавать выходные сигналы, описывае-
мые оператором выходов. Классическим примером автономной систе-
мы является математическая модель солнечной системы, поведение ко-
торой определяется силами, зависящими только от внутренних факто-
ров: взаимного расположения отдельных планет.
Рассмотрим теперь автономную систему без последействия, инва-
риантную относительно сдвига времени. Легко видеть, что единствен-
ное (в силу автономности) входное сообщение (t, xl)t должно удовлетво-
рять (в силу инвариантности) требованию, в соответствии с которым
(/, xl)t совпадает с собственным сдвигом на любое V £ Т. Этому тре-
бованию удовлетворяют функции L (t) = const и только они.
Оператор переходов рассматриваемой системы имеет вид
z(r) -= Н {т, г0}. (3.59)
Соотношение (3.59) определяет однопараметрическое семейство
преобразований пространства Z в себя, которое переводит точку z0
в точку той же траектории z (т). В силу общих свойств оператора пере-
ходов [см. (3.44)—'(3.46)], преобразование (3.59) удовлетворяет началь-
ному условию z (0) = г0 и условию полугруппы
Н [т2, Н (-q, z0)} =Л(т1+т2, z0). (3.60)
Таким образом, автономная система без последействия, инвариант-
ная относительно сдвига времени, представляет собой однопараметри-
ческую полугруппу преобразований пространства Z в себя. *
При дополнительных предположениях, состоящих в том, что Z —
метрическое пространство, а' Н реализует непрерывное отображение
топологического произведения Т X Z в Z, рассматриваемая система
превращается в полу групповую динамическую систему (см. § 3.3).
*> В теории дифференциальных уравнений под автономной системой пони-
мается система, правые части которой не зависят явно от времени.
93
3.8. ОБОБЩЕНИЯ
Большинство полученных до настоящего времени результатов
в теории систем относится к детерминистическим системам без после-
действия или их частным случаям (однородные системы, системы,
описываемые дифференциальными уравнениями, конечные автоматы
и т. д.), см., например, [19] и др. Однако развитие системотехники и осо-
бенно средств автоматизированного управления сложными системами
настоятельно выдвигает проблемы, изучение которых выходит за рам-
ки детерминистических систем без последействия. Связанное с этим
расширение понятия системы идет по пути учета случайных факторов,
последействия, а также специфики воздействия на систему входных
сообщений различных классов. В настоящем параграфе мы рассмотрим
упомянутые факторы в порядке, диктуемом методическими соображе-
ниями.
В системотехнике и системном анализе встречаются задачи, для
решения которых удобно предполагать, что множество входных сигна-
лов системы X подразделяется на конечное число классов со специфи-
ческим воздействием сигналов каждого класса на процесс функциониро-
вания системы.
Для простоты мы рассмотрим случай двух классов сигналов, ко-
торые условно будем называть «обычными входными сигналами»
и «управляющими сигналами». В дальнейшем упомянутым видам сигна-
лов будет дана соответствующая системная интерпретация.
За обычными входными сигналами мы сохраним все обозначения'
§ 3.6: х (/) g X — входной сигнал, поступающий в систему в момент
Л (t, xl)t — входное сообщение, являющееся элементом множества
((/, лщ)Д, и т. д.
Наряду с этим будем рассматривать также управляющие сигналы
g £ Г, где Г — множество управляющих сигналов системы. Управ-
ляющий сигнал, поступающий в систему в момент времени t £ Т, обоз-
начается g (t). Если сигнал g £ Г описывается набором характеристик
•••> Sm таких, что gs Е Ts, s = 1,2, .... т, то прямое произве-
дение
Г = Г!ХГ2Х ... хгт (3.61)
будем называть пространством управляющих сигналов системы.
Множество Г в общем случае является подмножеством множества точек
(gi, gt, • gm) пространства Г.
Отображение g = M(t), t Т, будем называть управляющим процессом;
совокупность упорядоченных пар (й g), где t Т, a g = M(t), — управляющим
сообщением. Сужение этого отображения на полуинтервал (Щ, /2] — фрагментом
управляющего процесса, а соответствующую ему совокупность упорядоченных
пар (й g) — отрывком управляющего сообщения (t, g^)j-, поступающим в систему
за полуинтервал (Щ, f2] (обозначается (t, Множество всевозможных управ-
ляющих сообщений {(й gM)T^ должно удовлетворять условию сочленения, ана-
логичному (3.39).
94
Когда удобно рассматривать входные и управляющие сигналы
как элементы единого множества, будем считать их точками простран-
ства X = X X Г обобщенных входных сигналов х = (х, g) = (xlt х2,
хп, glt g2, gm)- Обобщенный входной сигнал х содержит полный
набор координат в том случае, если в момент t в систему одновременно
поступают входной сигнал х и управляющий сигнал g. При неодновре-
менном поступлении сигналов х и g обобщенный входной сигнал имеет
вид либо х — (х, g%) — входной сигнал, либо х = (х0, g) — управляю-
щий сигнал (символы х% и g% означают отсутствие сигнала).
Совокупность упорядоченных троек (t, x,g), соответствующих всем
tQT, где х = L (t), a g = М (t) называется обобщенным входным сооб-
щением или (х, ^-сообщением и обозначается (/, xL, gu)r- Очевидно,
что (х, ^-сообщение определяется отображением Т -> X X Г. Су-
жение этого отображения на полуинтервал (^, t2\ определяет отры-
вок обобщенного входного сообщения и обозначается (/, хд, gwlti-
Множество [(t, xl, guh} всех обобщенных входных сообщений удов-
летворяет условию сочленения отрывков, если этому условию удовлет-
воряют множества {(/, хь)т} и {(f, gM)r}-
Если за конечный полуинтервал i2] в систему поступает лишь конечное
число входных и управляющих сигналов, процедура построения (7, xL, gM)f‘ по
заданным (/, х^2 и (/, gM\\2 сводится к упорядочению сигналов по времени их
поступления.
Например, пусть входные сигналы х^1' поступают в моменты времени is,
i= 1,2, s, а управляющие сигналы —в моменты времени t j’,j= 1, 2 s*.
Рассмотрим момент времени = min (^, </) поступления первого обобщенного
сигнала. Если i± < 1г', в момент 1Г* поступил х - (х(1), g%) и t2* = min (i2, it');
если Zj > ii , в момент tY* поступил сигнал х = (х^, g(1') и t2* = min(/1, t2')',
наконец, если tr—, в момент tj* поступил сигнал х= (х^1*, g^) и t2* —
= min (i2, t2'). Далее переходим к t2*. Если t2* = min(i2, i-^') и t2 < Щ, в момент
t2* поступил сигнал х2 = (х^, g®) и i3* = min(/3, t3') и т. д.
Когда в систему поступают как входные, так и управляющие
сигналы, состояния детерминистической системы без последействия
зависят от (t, Xl)t и (t, gMh- С учетом этого обстоятельства оператор
переходов (3.42) приобретает вид \
2(t) = H{t, t0, 2(t0), (t, XL, (3.62)
Нередко также используется другая форма записи оператора пере-
ходов
2(t)=H{t, t0, 2(t0), (t, XL]t', (t, gMVta}, (3.63)
что соответствует отображению {(Mo)) xZ X [(Л xL)r) x {(t, gM)T}^-Z.
Перейдем к детерминистическим системам с последействием.
В теории и приложениях встречаются системы, отличающиеся той
особенностью, что для определения их состояний в моменты времени
t > t0 недостаточно знать состояние z (£0) в момент t0. Для этой цели
95
приходится задавать состояния системы на некотором начальном
множестве моментов времени t £ Т, таких, что t < t0.
Каждому t0 £ Т поставим в соответствие некоторый класс (В}/0
множеств Во а: Т, таких, что для любого t с Во Е (В|;о справедливо
t<.t0. Тогда мы получили параметрическое (с параметром t0 £ Т)
семейство ({£}<„) классов {В}(о множеств Вй, обладающих указан-
ным свойством. На каждом BQ £ ({В)<0) зададим множество (щ(£))в0
отображений B()—rZ, обозначаемых z = w (t), t £ BQ. Совокупность
упорядоченных nap (tBt, zw), где tBa £ Bo, a zw = w (t), для этих
t будем называть предысторией (tBo, zw)t„ системы с последействием,
если существует оператор И, рассматриваемый как оператор переходов
этой системы, такой, что для любых t £ Т и t0 £ Т, t > t0, и лю-
бых z (t0) £ Z и (Z, xl)t 6 {(^ хь)т} состояние г (t) g Z, где
z(t)=H {t, (tB„ zw)tt, t0, z(t0), (i, xJ'J. (3.64)
Оператор переходов (3.64) детерминистической системы с последей-
ствием реализует отображение
{(/, /0)) х {(/в0) zwhj х Z х ((/, xL)r) -э-Z. (3.65)
Здесь [(1В„, zE,)/0} — параметрическое (с параметром tQ Q Т) семейство
множеств всевозможных предысторий системы, идея построения кото-
рого ясна из вышеизложенного.
В случае конечного Во, например (tt, t2, .... ^), предыстория
имеет вид (^, z^), /2, гт(/2), ..., th, z^Q), а оператор переходов
z= t„ zw(t1), t2, zw(t2\ ...
th, t0, z(t0), (/,xJ'J. (3.66)
Оператор переходов (3.64) должен удовлетворять условиям, похо-
жим по смыслу на (3.45)—(3.47). В данном случае, очевидно, законо-
мерна известная аналогия с соответствующими условиями для ди-
намической системы с последействием (см. §3.4).
1. В качестве первого условия рассмотрим начальное условие.
Начальное множество состоит из всех точек tBo Е Во и точки t0.
Поэтому естественно потребовать, чтобы для любых t0 Е Т, tBo Е Вй,
(ts„, zw)tQe{(tB„ zw)t0], z(t0)eZ и (/, хь)г £ {(?, xL)T\ имело место
равенство
H{t, (tBo, 2w)i0, t0, Z{t0), (t, Xj(°) =
__( w(tBo) при t=tB<J, (3 67)
( z(t0) при t = t0.
2. В связи co вторым условием будем предполагать, что при
переходе от значения параметра t0 к его значению > t0 множе-
ство Во из класса {В}^ перейдет в множество В\ из класса
а множество (щ(/))Во—в {w(/))в,-. Сущность второго условия состоит
96
в следующем: если предыстория системы (/Во, zw)lo задана на
множества Во, то для значений t, пробегающих множество В\,
Н {г, (tBo, t0, z(t0), (t, xJ'J как функция t принадлежит мно-
жеству {w(t)}Bl'.
3. Условие однозначности (полугруппы); пусть tQ<itr<. t2,
Во 6 и w(t)e тогда
И {/2. t0, (t, xjpj =
= (tB^, Zw)ta, /о, z(Z0), (t, xJ^'})G, h, (3.68)
H |/1, (tBa-, zw)t„ t0, z(t0), (/, xjy, (t, xj^}.
Заметим, что автономная детерминистическая система с последей-
ствием, инвариантная относительно сдвига времени, при дополнитель-
ных ограничениях может быть представлена как динамическая систе-
ма с последействием (см. §3.4).
Перейдем, наконец, к рассмотрению систем, функционирующих
под воздействием случайных факторов. В отличие от детерминистиче-
ских, эти системы обычно называют стохастическими.
В теории стохастических систем существенную роль играет по-
нятие случайного оператора. Пусть Q Э <о — пространство элемен-
тарных событий с вероятностной мерой Р (А). Пусть, далее, X Э х
и Z Э 2 — заданные множества, а (X —Z) — множество отображений
X в Z. Относительно множества Z и отображений X Z будем счи-
тать выполненными некоторые весьма общие требования измеримо-
сти (см. §4.3).
Случайным оператором Н, переводящим множество X в множество
Z, называется оператор г = И (х, со), реализующий отображение мно-
жества Q в множество {X—<-Z}.
Это означает, что каждому фиксированному со' g Й ставится в со-
ответствие некоторый конкретный неслучайный оператор Н (х, со'), Реа"
лизующий отображение X Z. Таким образом, Н (х, со) определяет
набор отображений X -> Z. зависящих от элементов со £ Й. С другой
стороны, очевидно, что каждому х g X случайный оператор Н (х, ®)
ставит в соответствие не одно определенное г ( Z, а некоторое мно-
жество Z* с Z с распределением вероятностей на нем, зависящим
от Р (А) и вида оператора Н.
С учетом сказанного, операторы переходов и выходов стохастиче-
ской системы без последействия можно представить в виде
?(/) = #{/, t0, z(t0, <о0), (t, xj(o, cd'}, 69)
y(t) = G {/, z(t), ®"}.
где co0, co' и co" независимо выбираются из Й в соответствии с вероят-
ностными мерами Ро (Л), Pz (Л) и Ру (А).
При фиксированных со' и со" стохастическая система называется
системой со случайными начальными состояниями.
Когда фиксированы соо и со", стохастическую систему называют
системой со случайными переходами. В этом случае оператор Н фикси-
4 Зам. 792 97
рованной тройке (/, /0) £ Т X Т, г (/0) £ Z и (/, xl)t £ {(/, xL)r},
см. (3.42), ставит в соответствие некоторое множество состояний
Z* с/с распределением вероятностей на нем, зависящим от Р2 (Л)
и вида оператора Н.
Распространена также следующая интерпретация системы со
случайными переходами. Оператор Н рассматриваем как совокупность
двух операторов Н и Н. Для данных t0, z (tn) и (/, xL]l0 оператор Н
однозначно определяет распределение вероятностей на множестве
Zt* cz Z состояний системы z (t) в момент времени t. Далее, оператор
Н по жребию (в соответствии с этим распределением вероятностей)
выбирает конкретное состояние системы z (/) g Zt*.
При фиксированных и <о' стохастическая система называется
системой со случайными выходами. Распределение вероятностей для
у (/) зависит от Ру (Л) и вида оператора G.
Аналогичный вид имеют операторы переходов и выходов для сто-
хастической системы с последействием, см. (3.64).
Движение стохастической системы можно рассматривать как
некоторый случайный процесс z (t, со), см. §4.3, с областью значений
в множестве состояний системы Z.
Мы не будем подробнее останавливаться на понятии стохастиче-
ской системы общего вида, так как это потребовало бы сложных рас-
суждений, связанных с построением соответствующих вероятностных
пространств. Подобные вопросы мы рассмотрим ниже, применительно
к некоторым важным классам стохастических систем.
ГЛАВА ЧЕТВЕРТАЯ
МАТЕМАТИЧЕСКИЕ СХЕМЫ ДЛЯ ОПИСАНИЯ
ЭЛЕМЕНТОВ СЛОЖНЫХ СИСТЕМ
4.1. БУЛЕВЫ ФУНКЦИИ
Переменные*’ х15 х2, ..., хп, способные принимать лишь два значе-
ния: 0 и 1, называются двоичными или булевыми переменными (цифры
О и 1 как разряды числа в двоичной системе счисления, нижнее и верх-
нее пороговые значения напряжения в электронных схемах, ложное
и истинное высказывание в логике и т. д.). Из п булевых переменных
можно образовать всего 2П не совпадающих между собой наборов вида
(хй, х2, ..., хп), а именно (0, 0, ..., 0), (0, 0, ..., 1), ..., (1,1, ..., 1). Гео-
метрически эти наборы изображаются точками «-мерного евклидова
пространства, которые можно рассматривать как вершины «-мерного
единичного куба; одна из этих вершин находится в начале коор-
динат.
Функции f (xlt х2, ... хп) от любого конечного числа булевых
переменных, способные принимать лишь два значения 0 и 1, называются
булевыми функциями. Имеется точно 22'1 различных булевых функ-
ций от п переменных (включая функции от меньшего числа перемен-
ных).
Существует взаимно однозначное соответствие между булевыми
функциями п переменных и логическими высказываниями с п логиче-
скими переменными.
В случае одного переменного имеется всего четыре различные
булевы функции: функции-константы (х) = 0 и /2 (х) = 1; функ-
ция повторения/ /3 (х) = х;"функция отрицания (инверсия) /4 (х) х
(не «х»), равная единице, когда х = 0, и равная нулю, когда х = 1.
Число булевых функций от двух переменных равно 16.
Эти функции удобно задавать в виде таблиц (табл. 4.1), в которых
для каждого набора переменных х2 и х2 указываются значения функ-
ции'/ (хь х2). Первые шесть функций /х /8 являются вырожденными
(зависят лишь от одной переменной).
Число булевых функций от трех переменных равно 256, а от пяти
переменных превышает 4 млрд.
Значение функций одной и двух переменных состоит в том, что
через них могут быть выражены любые булевы функции произвольного
числа переменных. Это делается при помощи суперпозиции булевых
*> Мы будем придерживаться способа изложения, принятого в [3]; см. так-
же [11 — 13].
4* 99
Таблица 4.1
0 0 1 1 Обозначение и наименование булевой функции
0 1 0 1
fl 0 0 0 0 0, константа
/з 1 1 1 1 1, константа
/З 0 0 1 1 Xj, повторение
fl 0 1 0 1 х2, повторение
fs 1 1 0 0 xlf отрицание
f* 1 0 1 0 х2, отрицание
fl 0 0 0 1 Xj/\x2, коньюнкция, функция совпадения, логическое И
ft 0 1 1 1 %iVx2, дизъюнкция, функция разделения, логическое ИЛИ
N 0 1 1 0 х1-[-х2, mod 2, функция суммы по модулю два (функция неравнозначности)
/10 1 0 0 0 х2, стрелка Пирса, отрицание дизъюнк-
ЦИИ, Xj .! Х2
/11 1 0 0 1 х1~х2, функция равнозначности (эквивалент- ности)
/1-2 1 0 1 1 хг ** xi (
/13 1 1 0 1 х1-^х21 импликация
/14 1 1 1 0 xj/x2, штрих Шеффера, отрицание конъ-
ЮНКЦИИ, Xj h Х2
/15 /16 0 0 0 1 1 0 0 0 А1/ Х2 г функция запрета, отрицание имп- *1ЛД
ликации
функций, т. е. подстановки одних булевых функций вместо аргументов
в другие булевы функции. В табл. 4.1 уже встречались такие примеры:
/10 (-^1> xi) xi) ~ Xj X2,
fii(.xi, Д) =/7 (-*т> х2)=х2/.х2, (4.1)
/15(*1, *2)=/7 [/э(*1> /в(Д- х2)]=х1Лх2
и т. д. Аналогично образуются булевы функции произвольного числа
переменных, например:
/11 {/12 1-^1» /4(^2)], /16 (Xi< Хз)'=(.Х2^Х1) — (Х1Лхз) (4.2)
И т. д.
Можно показать, что для выражения всех булевых функций двух
переменных (а также и любого числа переменных) достаточно иметь
некоторый комплект элементарных булевых функций (так называемую
функционально-полную систему), например:
у1 = 0, у2 = х, у3=х1Лх2, yi = x1\/x2. (4.3)
Этот комплект не является минимально необходимым. Так,
легко видеть, что он может быть сокращен до двух функций (например,
у2 и Уз или у2 и у4, так как х /\ х = 0, а х4 V х2 = Д х2). Более
того, любая булева функция может быть выражена через одну булеву
100
функцию двух переменных, таким свойством обладают (см. табл. 4.1)
/10 — стрелка Пирса и /14 — штрих Шеффера. Однако комплект (4.3)
оказывается весьма удобным с аналитической точки зрения; он поз-
воляет легко записывать булевы функции в виде так называемых
дизъюнктивных нормальных форм, играющих важную роль в теории
булевых функций и ее практических приложениях.
Элементарной конъюнкцией называется булева функция, представ-
ляющая собой конъюнкцию любого конечного числа попарно различных
переменных хь х2, ..., хп, над которыми могут стоять знакиотрицания,
например: у = х1 Д х2 /\ х3 Д xt или У = xi A xi Л хз и т- Д-
Дизъюнктивной нормальной формой называется дизъюнкция
любого конечного множества попарно различных элементарных
конъюнкций, например,
/(х4, х2, х3, х4) = (хг/х2)\/(х1Лх2Лх3Лх4)\/(х1Лх2Лх3) (4.4)
и др. Если элементарные конъюнкции, входящие в дизъюнктивную
нормальную форму, содержат все п переменных, то последняя назы-
вается совершенной дизъюнктивной нормальной формой.
Аналогично вводится понятие конъюнктивной нормальной формы.
Для этого в определении достаточно слово «дизъюнкция» заменить
словом «конъюнкция» и наоборот.
Любая булева функция может быть единственным образом пред-
ставлена в виде совершенной дизъюнктивной (конъюнктивной) нор-
мальной формы. Для приведения булевой функции к дизъюнктивной
(конъюнктивной) нормальной форме (а также и для других преобра-
зований булевых функций) используются соотношения так называемой
булевой алгебры.
Очевидно, что булевы функции могут рассматриваться как опе-
рации над булевыми переменными, а с учетом суперпозиции — и над
булевыми функциями. Так, функция у = х2 Д х2 представляет собой
операцию конъюнкции переменных х± и х2; функция у = хх \/ (х4Д
А хз) — операцию дизъюнкции булевых функций у± = х4 и у2 =
= хх /\ х3 и т. д.
Множество булевых функций по отношению к операциям отрица-
ния, конъюнкции и дизъюнкции обладает тем свойством, что резуль-
тат этих операций над элементами множества сам оказывается элемен-
том данного множества. Обычно множество булевых функций вместе
с упомянутыми операциями называют булевой алгеброй.
Выпишем основные тождества, которые имеют место в булевой
алгебре:
х = х—правило двойного отрицания;
x1Vx2=x2Vx1 ]
. —законы коммутативности;
х1Дх2=х2/х1 J
x1V(x2Vx3) = (х4vx2)vx3 )
.. . . . . .. ? — законы ассоциативности;
xxA(x2Ax3) =(x1Ax2)Ax3 J
101
XiA^Vxg) =(x1Ax2)V(x1Aa:3) ]
x.V^Ax,) = (x,Vx,)A(x, Vx,) J -за,МИЬ' «"«рибутивяости;
xxVx2 = х±Лх21
---- _ _ )— правила де Моргана;
xxAx2 = x1Vx2 J
x1V(x1Ax2) = *i 1
A, .. . —законы поглощения;
V X2J — Xj J
xVx = x]
. _ )— законы идемпотентности.
X/\X — X J
Из этих тождеств можно вывести следующие полезные предложе-
ния:
1) исключая из произвольной дизъюнкции (конъюнкции) дизъюнк-
тивные члены, равные нулю (конъюнктивные члены, равные единице),
мы не изменим величины этой дизъюнкции (конъюнкции);
2) если в дизъюнкции хотя бы один из членов равен единице, то
вся дизъюнкция равна единице;
3) если в конъюнкции хотя бы один из^членов равен нулю, то
вся конъюнкция равна нулю.
Булевы функции находят многочисленные применения на прак-
тике. Использование булевых'функций связано с двумя важными проб-
лемами: техническая реализация булевых функций и описание при
помощи булевых функций процессов функционирования реальных
объектов.
Остановимся кратко на технической реализации булевых функций. Клас-
сической формой реализации булевых функций являются релейно-контактные
схемы (электромеханические, магнитные, электронные, пневматические и т. д.).
В электромеханических реле (см. рис. 3.1) за-
।---------- -0 висимости между состояниями входа и выхода
имеют следующий вид.
0 « о----------+> Если входной выключатель разомкнут
tj (х = 0), то обмотка обесточена, контакты
разомкнуты, и на выходных клеммах напря-
& У жения нет (у = 0). Если входной выключа-
тель замкнут (х = 1), сердечник притягивает
якорь, контакты замыкаются и на выходных
I---гттгп . _ клеммах появляется напряжение (у = 1).
р I иптд Bff g Легко’видеть, что схема (см. рис. 3.1) реали-
зует булеву функцию повторения у = f3(x) = х.
рис [ Если вместо нормально разомкнутых
контактов (см. рис. 3.1) использовать нор-
мально замкнутые контакты (рис. 4.1), можно
реализовать булеву функцию отрицания (инверсию) у = /4(х) = х. В самом
деле, когда входной выключатель разомкнут (х = 0), на выходных клеммах
имеется напряжение (у = 1) и, наоборот, замыкание входного выключателя
(х = 1) приводит к размыканию контактов (у = 0).
Аналогично могут быть реализованы другие булевы функции. Параллель-
ное включение двух схем у = х, т. е. у4 = х4 и у2 = х2 реализует дизъюнкцию
у = х4 V х2', параллельное включение схем у = х4 (см. рис. 3.1) и у = х2
(рис. 4.1) — импликацию у = х2 х4. Последовательное включение схем реа-
лизует суперпозицию соответствующих булевых функций. Например, если ко
102
входу Xj схемы у = ац Л х2 подключить выход схемы уг = xlt а ко входу х2 —
выход схемы у2 = .Д то полученная схема будет реализовать отрицание импли-
кации у = f1& (хъ х2) = хх Д х2.
Булевы функции успешно используются для математического описания
реальных систем. В первую очередь обычно идет речь об электронных схемах
различных автоматических и вычислительных устройств. Однако нельзя забы-
вать, что вид математического описания реального объекта всецело определяется
выбором соответствующей формализации процесса его функционирования.
Если диодная схема рассматривается как электрический контур и исследу-
емым процессом является зависимость выходного напряжения u(t) от времени,
тока на входе и параметров схемы, в предположениях, обычно принимаемых для
электрических контуров, то достаточно точным математическим описанием про-
цесса могут служить соотношения
du . . ( u/m<f \ и
c-— = i-iT{e (4-5)
dt i\ у
Здесь m, (рт, Ry, cz, iT, т — параметры диода.
В другом случае, когда нас интересует лишь наличие или отсутствие сиг-
нала на выходе схемы и состояние выхода можно описать булевыми переменными,
диодные схемы хорошо представляются булевыми функциями.
Практически для построения булевых функций, соответствующих
сложным схемам, используются два принципиально различных под-
хода. Один из них состоит в расчленении схемы на совокупность
простых подсхем, легко поддающихся описанию при помощи булевых
функций, и последующем объединении полученных булевых функций
путем суперпозиций, соответствующих структуре схемы. Сущность его
можно проследить на примерах уже рассмотренных схем. Так, схему,
содержащую параллельно включенные релес нормально разомкнутыми
и нормально замкнутыми контактами, можно расчленить на отдельные
реле, которые описываются функциями повторения и отрицания соот-
ветственно, а затем получить полное описание схемы, подставив полу-
ченные булевы функции вместо аргументов в дизъюнкцию, описываю-
щую параллельную структуру схемы. По мере увеличения сложности
схем, когда приходится иметь дело с большим числом подсхем, исполь-
зование этого подхода затрудняется главным образом из-за усложне-
ния связей между подсхемами. Кроме того, на практике встречаются
случаи, когда исследователь не имеет доступа к структуре схемы или
вынужден пользоваться ограниченной информацией о ней.
Другой подход к описанию схем при помощи булевых функций
основан на использовании так называемой таблицы соответствия, полу-
чаемой путем экспериментального обследования схемы или иными спо-
собами. Таблица соответствия (табл. 4.2) имеет следующий вид. Для
каждого номера k = 0, 1, ..., 2"— 1 в соответствующем столбце
выписаны^наборы (хь х2, ...., хп), выражающие в двоичной системе
счисления число k, а также — значения функции у (последняя строка).
Чтобы записать выражение для булевой функции, заданной
табл. 4.2, поступаем; следующим образом. Для тех столбцов, где
у = 1, записываем конъюнкцию дф Д х2 Д ... Л *п и ставим знак
отрицания над переменными, которые в данном столбце имеют значе-
103
Т а б л и ц а 4.2
0 1 2 3 4 2,г—2 2П- 1
Х1 0 0 0 0 0 1 1
х2 0 0 0 0 1 1 1
хп 0 1 0 1 0 0 1
У 1 1 0 1 0 1 0
ние нуль. Например, для k = 1 рассматриваемая конъюнкция будет
иметь вид Л Л ... Д xn_2 Л xn-t Л хп- Составив упомянутые
конъюнкции для всех столбцов, где у=1, соединим их знаками дизъюн-
кции. При этом мы получим совершенную дизъюнктивную нормаль-
ную форму, представляющую искомую булеву функцию.
Наличие хорошо развитого аналитического аппарата для решения
задач, связанных с анализом и синтезом булевых функций (эквивалент-
ные преобразования, минимизация и т. д.), а также исключительное
удобство реализации его на ЭВМ, привлекают внимание к булевым
функциям как к одной из эффективных математических схем для фор-
мального описания процессов функционирования реальных систем.
Класс абстрактных систем, описывамых булевыми функциями,
может быть выделен из множества абстрактных систем общего вида при
помощи дополнительных ограничений, налагаемых на множества
Т—моментов времени функционирования, Z — состояний системы, X
и Y — входных и выходных сигналов, а также на операторы пере-
ходов Н и выходов G (см. гл. 3).
Пусть Т, X, Z, и Y — конечные множества. Закодируем каждое
из z-Z (а также х£ X и у Y) двоичными числами. Тогда z = (zlt
z2, ..., zn), %=(%!, ..., xm) и у=(ylt y2, ..., yn) будут представлять собой
наборы булевых переменных, соответствующих разрядам двоичных
чисел. Выберем фиксированную пару (t, /0). Не ограничивая общности,
можно вести рассуждения относительно систем без последействия, для
которых операторы переходов Н и выходов G имеют вид (3.42) и (3.49)
соответственно. Пусть теперь для выбранных t и /0 и каждое 2, (/),
i = 1,2, .... п, представляется в виде булевой функции вида zt (t) =
=hi(z1°, z2°, ...,zn°, xlt x2, ...,xm), где набор (z/, z2°, ...,zn°) интерпрети-
руется как двоичное число, соответствующее г0—начальному состоянию
г (t0), а (х1; х2, ..., хт) — отрывку входного сообщения (t, xj/,. Оче-
видно, что рассматриваемая совокупность булевых функций йг,
i = 1, 2, ..., п, реализует отображение прямого произведения Z х {(/,
хл)/-} во множество Z при фиксированных t и t0. Если для всех пар
(t, /0) можно записать аналогичные совокупности булевых функций.
104
мы придем к отображению*’ прямого произведения {(/, /0)} х Z х {(/,
xJt} во множество Z или, другими словами, к оператору переходов Н
некоторой системы (3.42). Аналогично, пусть для выбранных t и /0
каждое у} (t), j = 1, 2, ..., г, представляется в виде булевой функции
вида yj (/) = hj* (z°i,22, ..., zn°, xlt х2, .... хп). Множество совокуп-
ностей булевых функций gi, i = 1, 2, ..., г, соответствующих всем
(/, /0), описывает оператор выходов рассматриваемой системы (3.49).
Таким образом, булевы функции могут быть использованы для
описания систем, функционирующих в дискретном времени и имеющих
конечные множества состояний, входных и выходных Сигналов. Они
находят широкое применение в области анализа и синтеза релейно-
контактных схем, цифровых автоматов, устройств и программ ЭВМ и т. д.
4.2. ВЫСКАЗЫВАТЕЛЬНЫЕ ФУНКЦИИ
В предыдущем параграфе мы имели дело с булевыми переменными,
принимающими только два значения: 0 и 1. Пусть теперь переменные
х1г х2, хп принимают значения, принадлежащие произвольным мно-
жествам: Xi g Xit i = l, 2, ..., п.
Функция у = Q (хх, х2, ..., хп), которая принимает значения 0 и 1,
где xlt ..., хп — элементы произвольных множеств, называется
п-местной высказывательной функцией или двузначным п-местным пре-
дикатом. В отличие от булевых переменных, переменные х1г х2,
..., хп в этом случае называются предметными переменными.
Булевы функции, как известно, описывают высказывания с фик-
сированным логическим значением; высказывательные функции имеют
логическое значение, зависящее от значений предметных переменных,
например: х > 0, х2 < 4, х £ 7? и т. д. Высказывательная функция
превращается в высказывание, если на место предметных переменных
подставить их конкретные значения, например: 8 > О, 9 < 4, х £ R
И Т. д.
В качестве примера рассмотрим высказывательную функцию,
описывающую связи между вершинами ориентированного графа.
Пусть граф G имеет.N вершин, пронумерованных в некотором поряд-
ке: 1, 2, ..., Af, и пусть В (j, k) — функция, принимающая значение 1,
если от вершины графа с номером / к вершине с номером k проходит
дуга (/, k), и равная 0 в противном случае. Функцию В (j, k) будем рас-
сматривать как двухместную высказывательную функцию предметные
переменные которой принимают значения j, k = 1, 2, ..., N.
Над высказывательными функциями можно производить операции
булевой алгебры, а также подставлять их вместо аргументов в булевы
функции. Например, высказывательная функция В (j, k) принимает
значение 1, когда дуга (/, k) отсутствует, и значение 0, когда дуга (/, k)
существует; высказывательная функция
В*(/, k) = B(j, k)VB(k, j) (4.6)
*> Аналогичная идея положена в основу применения так называемых «вре-
менных» булевых функций, см. [13].
105
принимает значение 1 тогда, когда существует хотя бы одна из дуг
(/, k) или (k, j), и значение 0 — в противном случае. По правилу де Мор-
гана
В*(/, k)=B(j, k)AB(k, j). (4.7)
Высказывательная функция В* (j, k) принимает значение 1, когда
не существуют ни дуга (/, k), ни дуга (k, j) и т. д.
Аналогично могут быть образованы высказывательные функции,
зависящие как от предметных, так и от булевых переменных. Напри-
мер, пусть хх, х2 и х3 — предметные переменные высказывательной
функции А (хх, х2, х3), а х4 — булева переменная. Выражение
Q(xlt х2, х3, х4) ^x^Alx^ х2 ха)
следует рассматривать как четырехместную высказывательную функ-
цию.
Если одна из предметных переменных двухместной высказыватель-
ной функции/? (j, k) фиксирована (например, / = 4), то высказыватель-
ная функция В (4, А) будет одноместной (описывающей наличие дуг,
выходящих из вершины № 4 и идущих к другим вершинам графа
k = 1, 2, .... М).
В исчислении предикатов применяются специальные операторы,
называемые кванторами.
Квантор общности — это оператор, который данной одноместной
высказывательной функции у = Q (х) ставит в соответствие булеву
переменную г, принимающую значение 1 тогда и только тогда, когда
у = 1 при всех значениях х. Квантор общности обозначается z =
— (V х) Q (х) и читается «при любом х имеет место Q (х)». Например,
булева переменная
z = (vA)B(4, k) (4.8)
принимает значение 1 тогда и только тогда, когда от вершины № 4 ко
всем вершинам графа проходят дуги (4, k), k = 1, 2, .... N. В данном
примере выражение (4.8) можно заменить эквивалентным выражением
z = B(4, 1)ЛВ(4, 2)Л...ЛВ(4, N). (4.9)
В любом случае, когда предметная переменная, по которой наве_
шивается квантор, имеет конечное множество значений, квантор об-
щности может быть заменен конъюнкцией значений высказывательной
функции, соответствующих всем значениям переменной, и наоборот.
Квантор существования — это оператор, который данной одно-
местной высказывательной функции у = Q (х) ставит в соответствие
булеву переменную г, принимающую значение 0 тогда и только тогда,
когда у = 0 при всех значениях х. Квантор существования обозначает-
ся г = (а х) Q (х) и читается «существует такое х, что имеет место
Q (х)». Например, булева переменная
г = (а k) В (4, k)
(4.Ю)
106
принимает значение 1, если существует хотя бы одна дуга, выходящая
из вершины № 4 данного графа,- В рассматриваемом примере выражение
(4.10) эквивалентно выражению
z = B(4, 1)VB(4, 2)V... V В (4, N). (4.11)
В любом случае, когда предметная переменная, по которой наве-
шивается квантор, имеет конечное множество значений, квантор су-
ществования может быть заменен дизъюнкцией значений высказыва-
тельной функции, соответствующих всем значениям переменной, и на-
оборот.
Навешивание квантора по одной из предметных переменных на
п-местную высказывательную функцию превращает ее в (п— ^-мест-
ную высказывательную функцию, а одноместную высказывательную
функцию — в высказывание. Переменная, по которой навешен квантор,
называется связанной переменной, в отличие от остальных перемен-
ных, называемых свободными переменными. Например,
2= (а/) в (j,k) (4.12)
представляет собой одноместную высказывательную функцию, зави-
сящую от свободной предметной переменной k. В этом легко убедить-
ся, представляя (4.12) в виде дизъюнкции
z = B(l, £)VB(2, £)V ...VB(N, k). (4.13)
Аналогичное замечание относится и к выражению
z* — (yj)B(j, k). (4.14)
В исчислении предикатов используются тождества, аналогичные
тождествам булевой алгебры. Кроме того, существенное значение имеет
ряд тождеств с кванторами.
Если некоторая высказывательная функция U не зависит от пред-
метной переменной х, связанной данным квантором, то
(V х) [U Л Q (х)] = U Л (v х) Q (х),
(Vx)[[/VQ(x)] = l/V(Vx)Q(x),
(а х) [1/ Л Q (х)] =UЛ (ах) Q (х),
(а х) [17 V Q (х)] = U V (а х) Q (х).
Эти тождества носят название эквивалентностей с относительной кон-
стантой.
Эквивалентности с отрицанием включают тождества, аналогичные
правилам де Моргана:
(ax)Q(x) = (v х) Щх),
(Vx)Q(x) = (ax)Q(x).
Из них следуют зависимости:
(ах)Щх) =(vx)Q(x),
(V x)Q(x) = (ax)Q(x).
107
Зависимости для П-операций:
(V х) [Qj (х) Л Q2 (х)] = (V х) Qi (х) A(V х) Q., (х),
(Vx)(vy)Q(x, y)=(V y)(vx)Q(x, у). (4,17)
Эквивалентности для ^-операций:
(я х) [Qx (х) V Qi (х)1 = (а х) Qx (х) V (я х) Q2 (х),
(ях) (я y)Q(x, у) = (яу)(ях)(?(х, у).
Справедливы следующие импликации:
[(V х) Qx (х) V(V х) Q2 (х)] -> (v х) [Qi (х) V Q2 (х)],
(Я х) [Qi (х) Л Qi (х)] -+ [(я х) Qi (х) Л (я х) Q2 (х)], }
(ax)(vy)Q(x, у)-> (V у) (я х) Q (х, у),
(ay)(Vx)Q(x, У)(V х) (я у) Q (х, у).
На примерах можно показать, что ни одну из этих импликаций
нельзя заменить обратной. Кроме того,
(vx)(ay)Q(x, y)^(ax)(vy)Q(x, у).
Заметим, что рассмотренные нами тождества справедливы и в так
называемом расширенном исчислении предикатов, в котором, наряду
с кванторами по предметным переменным, используются кванторы по
предикатным переменным, например:
2 = (Я К) [К (х) Л (V у) И (х, у)].
Здесь Н — свободная предикатная, ах — свободная предметная пере-
менная; F и у — связанные переменные.
Подробнее о высказывательных функциях см. [11, 13].
Высказывательные функции находят весьма разнообразные при-
менения при моделировании сложных систем. Ниже (гл. 8) мы позна-
комимся с использованием высказывательных функций для описа-
ния отношений между элементами и типичных структурных кон-
фигураций элементов в системах (по аналогии с отношениями между
вершинами графа, см., например, (4.6), (4.7) и др.
Класс абстрактных систем, описываемых высказывательными
функциями, оказывается более широким, чем класс систем, описывае-
мых булевыми функциями, и включает последний как частный слу-
чай. Это вытекает из того обстоятельства, что булевы функции можно
рассматривать как частный случай высказывательных функций (ког-
да предметные переменные принимают значения только 0 и 1).
По аналогии со схемой описания абстрактной системы, изложен-
ной в конце предыдущего параграфа, мы в данном случае операторы
переходов и выходов будем представлять в виде совокупностей вы-
сказывательных функций. При этом, очевидно, переменные t £ Т
и (t, xl)t € {(^, xl)t} интерпретируются как предметные переменные
соответствующих высказывательных функций и, значит, могут быть
элементами произвольных множеств. В качестве булевых переменных
108
фигурируют только Zi и tji, являющиеся координатами состояний
z^Z и выходных сигналов у £ Y. Таким образом, для описания
абстрактной системы при помощи высказывательных функций доста-
точно, чтобы конечными множествами были лишь множества Z и Y.
Заметим, что на практике нередко встречаются весьма интересные
применения высказывательных функций для моделирования систем ив
тех случаях, когда множество состояний системы не является конеч-
ным, но для решения поставленных задач достаточно учитывать лишь
конечное число некоторых так называемых особых состояний системы.
4.3. МАРКОВСКИЕ ПРОЦЕССЫ
Рассмотренные в гл. 3 динамические системы являются одним из
наиболее изученных детерминистических представителей систем без
последействия. Однако моделирование сколько-нибудь широкого клас-
са реальных объектов невозможно без рассмотрения вероятностных
схем. Наибольшее распространение в теории систем и ее приложениях
получили марковские процессы, представляющие собой типичную ве-
роятностную модель систем без последействия.
Теория марковских процессов создана за последние десятилетия.
Выдающуюся роль в развитии этой теории сыграли советские ученые —
академик А. Н. Колмогоров и его ученики; теория марковских про-
цессов располагает весьма совершенными аналитическими методами
и многочисленными глубокими качественными результатами. С другой
стороны, важнейшие классы реальных сложных систем допускают до-
статочно адекватное описание в рамках марковских процессов. Это
обстоятельство найдет отражение в дальнейших главах книги.
В нашем изложении принят, в основном, элементарный подход
к заданию марковских процессов.
Случайный процесс мы будем обозначать £ (t), где % принимают
значения из некоторого множества Z, a t — моменты времени, t£T.
Сохраняя системную терминологию, конкретное значение z (t),
z g Z, принимаемое процессом £ (t) в момент t, будем называть состоя-
нием процесса в момент t, множество Z — пространством состояний
процесса, функции z = z (t) для всех t£T — траекториями или
реализациями случайного процесса £ (t).
Будем предполагать, что при любых tr < t существует вероятность
Р (tt, zlt t, D) того, что, находясь в момент tr в состоянии г2, процесс
% (t) в момент t > перейдет в одно из состояний, принадлежащих
множеству D с: Z.
Если для любого конечного набора тх, т2,..., тп, где т;</х,
i = 1, 2,... , п,
P{g(/) еЖ(тх) = z<, £(rn) = z<4
= PO)6£’OiW1}=P{/11 z1( t, D\,
то случайный процесс £ (£) называется марковским.
109
Пусть множества Т и Z — конечные или счетные. В этом случае
процессы | (/) называются процессами дискретными во времени и про-
странстве. Пусть, например, значения случайного процесса | (t) в мо-
менты времени /г = О, 1,2, ... обозначаются £г, а соответствующие
реализации гг. Рассмотрим условную вероятность того, что
%п+1 = Zn+1 при условии = гп, = zn_x, ..., с0 = z0. Обозна-
чим ее
Р 'L+1 — гп+1 /%п — 2n; 1 = 1 i • • • ; = 20}.
Если структура случайного процесса такова, что условное распре-
деление случайной величины £п+1 при заданном £п не зависит от всех
предыдущих значений £г, т. е.
Р {£п+1 = 2«-|-i/Sn = Zn; ^n—1 = 1, ... ; = Zo} =
/?-71 (4.20)
I Sn-{-1 i / cn Zn ],
будем говорить, что случайный процесс £ (/) обладает марковским
свойством.
Дискретные случайные процессы, обладающие марковским свой-
ством, называются цепями Маркова.
В дальнейшем вместо состояния процесса г7- будем писать просто
/. Это не ограничивает общности, поскольку элементы любого конеч-
ного или счетного множества можно закодировать целыми числами.
Обозначим ри (п) = Р (gn+1 = /7gn = i}, i, j = 0, 1, 2, ...
При фиксированных i и j вероятность p;j (n) представляет собой услов-
ную вероятность того, что в момент п + 1 система находится в состоя-
нии /, если известно, что в момент п система была в состоянии i.
Когда ри (п) зависят только от i и / (от состояний) и не зависят-
от времени п, будем рц называть стационарными вероятностями пере-
хода из состояния i в состояние'/. В таком случае цепь Маркова назы-
вается однородной. ,
Для того чтобы задать однородную марковскую цепь, кроме мно-
жеств Т и Z, достаточно определить распределение начальных состоя-
ний р (i) = Р (£0 = 1} и матрицу вероятностей перехода
Poo Poi Ро2
PiO Р11 Р12
Р20 Р21 р22
(4-21)
Наряду с вероятностями перехода рц за один шаг, представляют
интерес вероятности перехода за k шагов Если v — некоторое
«промежуточное» состояние, р^ — вероятность перехода из со-
стояния I в состояние v за пг шагов, а — вероятность перехода
из состояния v в состояние / за k шагов, имеет место следующая форму-
ла:
(m+*> _К1 <т) p(k)
Pi'l —ZJ Plv •
V
(4.22)
110
-SI
Уравнение (4.22) называется уравнением Колмогорова—Чепмена.
В матричной форме это соотношение имеет вид
pm+k==pmpkt (4.23)
где Pk — матрица вероятностей перехода за k шагов, совпадающая
в силу (4.22) с /е-й степенью матрицы Р.
Состояние i называется поглощающим, если рп = 1; рц — О
при i 4= /.
Пусть вероятность того, что в момент t = 0 система находится
в состоянии i, равна р (i); тогда безусловная вероятность того, что в мо-
мент t = п система находится в состоянии /, равна
оо
pw(/)=2 pcopS;’- (4.24)
i—Q
Исследование поведения безусловных вероятностей р(л> (/) при
п -+ оо представляет большой интерес для приложений. Для цепей
Маркова развит весьма эффективный аналитический аппарат. С эле-
ментами теории цепей Маркова можно познакомиться по [14, 16, 4] и др.
Пусть теперь Т — некоторый (конечный или бесконечный) интер-
вал числовой прямой, множество Z совпадает с действительной прямой, а
F(t, zit т, z2)=P (^(T)<z2/g(if)=z1}, т>/, (4.25)
—переходные вероятности процесса £ (/). Функция F (/, zlt т, z2) пред-
ставляет собой условную функцию распределения значения процесса
£ (т) при условии, что I (/) = z2. Условием, выражающим марковское
свойство процесса, является соотношение
+ °°
F(t, z1( т, z2) = § F (s, и, т, z<^duF(t, z, s, и), (4.26)
— оо
которое называется уравнением Колмогорова—Чепмена для веществен-
ных марковских процессов с непрерывным временем.
Если наложить дальнейшие ограничения на вид переходных функ-
ций, которые являются, по существу, ограничениями на характер
траекторий марковского процесса, то можно получить различные
типы марковских процессов — диффузионные (когда траектории про-
цесса непрерывны с вероятностью 1), разрывные (когда каждая траек-
тория является кусочно-постоянной функцией времени) и др. (см. [14]).
В настоящее время успехи в исследованиях случайных процессов
вообще и марковских процессов в частности связаны с аксиоматиче-
скими построениями. В последующих главах нам понадобятся некото-
рые элементы таких построений. Поэтому целесообразно хотя бы
бегло остановиться на некоторых исходных понятиях теории вероят-
ностей и случайных процессов.
В любой задаче теории вероятностей исходят из рассмотрения определенного
опыта (статистического испытания), в результате которого наступает некоторое
алементарное событие о из пространства элементарных событий Q. Так, пусть
опыт состоит в том, что регистрируются космические частицы, попадающие на
111
заданную площадку в течение фиксированного отрезка времени. В этом случае
элементарные события можно отождествлять с целыми неотрицательными числа-
ми, показывающими, сколько частиц зарегистрировано. Пространство Й будет
представлять собой множество всех целых неотрицательных чисел.
На пространстве й задается о-алгебра S его подмножеств, называемых со-
бытиями. Класс S подмножеств пространства Й называется а-алгеброй, если вы-
полнены следующие условия. Требуется, чтобы Й £ S и, кроме того, чтобы опе-
рации объединения, пересечения и взятия дополнения к пространству Й, совер-
шаемые над элементами класса S, не выводили из класса S. При этом указанные
операции можно применять, вообще говоря, счетное число раз. Таким образом,
для любых множеств £ S, fe > 1, справедливы соотношения:
1) fe>l, 2) [J^S, 3)
k k
Отсюда, в частности, следует, что пустое множество 0 £ S, поскольку 0
можно представить в виде 0 =Й \ й, ай 0S. Говорят, что событие А £ S на-
ступает, если исход статистического испытания, т. е. элементарное событие <о,
принадлежит А.
Пример. Рассмотрим опыт, заключающийся в том, что на лист бумаги бро-
сается дробинка, «не имеющая размера». Элементарным событием является воз-
можный исход данного опыта, т. е. точка, в которую попадает дробинка при бро-
сании. Пусть во множество событий S входит любой правильный многоугольник,
лежащий естественно на листе бумаги. Тогда в это множество также должен
войти любой круг, поскольку круг является счетным пересечением множества
описанных правильных прямоугольников. Внутренность круга также является
событием, поскольку она оказывается счетным объединением вписанных пра-
вильных многоугольников за вычетом счетного множества их вершин, которое,
в свою очередь, измеримо как счетное объединение счетных пересечений после-
довательностей квадратов, стягивающихся в точки.
На пространстве элементарных событий Й вводится вероятностная мера
Р(/1): каждому измеримому множеству Л(т. е. .4'5) ставится в соответствие не-
отрицательное число Р(Л) таким образом, что Р(Й) = 1; если А — объединение
последовательности непересекающихся множеств Ап, входящих в S, т. е. А =
= иЛп, то
II
Р(А)=^Р(Ап). (4.27)
п
(Формула сложения вероятностей.)
Тройка (й, S, Р), т. е. пространство элементарных событий Й с заданной
на нем а-алгеброй S и вероятностной мерой Р, определенной на S, называется
вероятностным пространством.
Пусть й(, й2..... Йп, ... — некоторая последовательность измеримых
пространств. Обозначим соответствующие этим пространствам а-алгебры изме-
римых множеств через St, S2, • Sn, ... Тогда можно образовать измеримое про-
странство й, точками которого будут последовательности
ш = (011, ш2, ..., <йп , ...), (4.28)
где wn £ Йп,- п = 1, 2, ...
Класс измеримых множеств пространства й определяется как минимальная
о-алгебра*1, содержащая все множества вида
(w = (w1, ш2, . . .) : < Bk С Sh, k ' N\, ^=l,2, ... (4.29)
Отметим, что множество (4.29) называется цилиндрическим множеством;
оно определяется лишь конечным (но произвольным) числом N множеств Bk.
*’ Минимальной а-алгеброй (подмножеств заданного множества), удовлетво-
ряющей заданному свойству, называется о-алгебра, которая обладает указанным
свойством и является подножеством любой а-алгебры с данным свойством.
112
Определенное таким образом пространство О называется прямым произведением
пространств Q2........
Для нас будет важно определение меры на произведении пространств,
отражающее свойство независимости их элементов.
Допустим, что на пространствах Qn определены вероятностные меры
/>П(АП), n > 1- Тогда на измеримом пространстве Q можно также ввести вероят-
ностную меру Р(А), обладающую следующим свойством. Если множество А
имеет вид
А = {(со1( <о2, ...) С Ль £ Sk, г = 1, 2, ..., N], (4.30)
ТО
P(A) = P1(A1)...PN(AN), (4.31)
каковы бы ни были Л/ > 1, At £ Si, i = 1, 2, ..., TV*’. Определенная таким
образом вероятностная мера Р называется прямым произведением вероятност-
ных мер Pn(An), п > 1.
Все, что сказано относительно счетной последовательности пространств
{йп}, естественно, сохраняется в силе и в случае конечного набора пространств.
Если вероятностная мера Р(А) есть прямое произведение вероятностных
мер Рп(Ап), как было определено выше, то события Л; при различных /, принад-
лежащие различным 3, называются независимыми в совокупности. В этом случае
говорят также, что (сщ, со2, ...)есть последовательность независимых испытаний.
Определим еще два основных понятия теории вероятностей: случайного
элемента и случайного процесса. Пусть задано пространство элементарных со-
бытий Q с определенной на нем вероятностной мерой Р(А). Пусть, кроме того,
задано измеримое пространство X с о-алгеброй измеримых множеств 3* . Слу-
чайным элементом £ = 1(м) пространства X называется произвольная функция
£,(<£»), ш £ й, элементарного события со значениями из X, если выполнено такое
свойство: для любого А* £ S* множество {<£>: £(со) А*} принадлежит 3, где
3—о-алгебра измеримых множеств пространства Й. [со : (со) £ А*} являет-
ся событием и, следовательно, можно определить его вероятность. В частности
если X — числовая прямая, 5* — класс борелевских множеств, т. е. минималь-
ная а-алгебра, включающая все интервалы вида (a, b), a<b, a, b £ X, то слу-
чайный элемент называют случайной величиной.
Пусть I — конечный или бесконечный интервал прямой, которую мы на-
зовем «осью времени». Точки этой прямой будут называться «моментами време-
ни». Если в качестве X выбрать пространство функций времени t, t £ I, со зна-
чениями из некоторого множества Z, случайный элемент называется случайным
процессом. Следовательно, случайный процесс—это функция £(/, со) двух аргу-
ментов: t £ I и со Q И со значениями из некоторого пространства Z. При этом
должно удовлетворяться следующее условие. Заранее задаются «измеримые»
множества А* функций fit), t £ I, образующие а-алгебру, и требуется, чтобы
для каждого такого А* множество тех со, при которых £(/, со) £ А*, имело оп-
ределенную вероятность, т. е. принадлежало 3. При фиксированном со £ Й
функция £(/,со) временного аргумента / называется реализацией рассматриваемого
случайного процесса.
Опишем теперь, с помощью каких дополнительных предположений вы-
деляется класс марковских случайных процессов.
Пусть Z — некоторое множество, на котором задана о-алгебра U его под-
множеств. Каждое подмножество из о-алгебры U называется измеримым. Само
множество Z назовем пространством состояний (значений) рассматриваемого
случайного процесса г(/, со). Для марковского процесса пару (Z, U) иногда на-
зывают фазовым пространством. Пусть (й, 3, Р) — вероятностное пространство
для рассматриваемого случайного процесса. Потребуем, чтобы z(t, со) при любом
фиксированном / £ I, рассматриваемая как функция со, была измерима. Иначе
говоря, для любого множества В £ U
{co :z(/,
*’ Доказательство такой возможности можно найти, например, в [15].
113
Пусть Д — любое числовое множество. Определим совокупность 5Д как
минимальную а-алгебру подмножеств пространства Q, содержащую все подмно-
жества вида {со : z(/, а) £ В £ U\ при любых t £ Af)/, В £ U. Очевидно,
все множества, входящие в 5Д, входят также в S, поскольку S есть о-алгебра,
содержащая все множества вида
{<о :г(/, со) £ В £ U], t £ /.
Возьмем любое фиксированное t £ / и любые два множества
А1 С S(-ac. t) , А2 - S(t, «)•
Короче говоря, — некоторое событие, связанное с поведением процесса г(т)
до момента t, а А2 — событие, связанное с его поведением после момента t.
В теории меры показывается, что при принятых допущениях можно опре-
делить условные вероятности
Р {Аг/г, <} = Р {ш С Л;/г(1) = г}, 1 = 1,2,
(4-32)
Р {Др42/г,1} =Р {св С Ai П Я2/г(/) = г).
Если для случайного процесса г (/, со) для любых Аг £ S(_oo и
£ S(t.
Р{Л1, Adz, И=Р Mi/z, О Р {Л2/г, t}, (4.33)
то случайный процесс z(t, со) называется марковским.
Именно равенство (4.33) выражает независимость будущего течения мар-
ковского процесса от его предыстории. Марковское свойство можно выразить
еще иначе. Для любых Аг £ S(_M t)’ Az С ^(1, со), * €
Р{Л2/ЛЬ г(0=г)=Р{Л2/г(0 = г). (4.34)
В дальнейшем рассматривается применение к исследованию си-
стем частных случаев марковских процессов — цепей Маркова с ди-
скретным и непрерывным временем, диффузионных процессов и марков-
ских процессов с дискретным вмешательством случая.
Отметим, что, как правило, процессы, описывающие поведение
реальных систем, не являются марковскими. Однако возможны прие-
мы, преобразующие процесс к марковскому путем введения дополни-
тельных координат, т. е. путем включения исходного немарковского
процесса в более сложный марковский (т. е. сложный марковский про-
цесс содержит исходный немарковский в качестве компоненты).
Ниже будет приведен ряд примеров, общее назначение которых —
показать, каким образом немарковский процесс превратить в марков-
ский, расширив множество состояний. Мы надеемся охватить достаточ-
но разнообразные примеры, чтобы читатель мог ими руководствоваться
при описании реальных систем.
1. Начнем с простейшего примера. Система может находиться в трех со-
стояниях: исправном (<?), предотказовом (/) и отказовом (2). Начиная с момента
t = 0, исправное состояние длится случайное время £, распределенное по зако-
ну F(x) общего вида. После этого наступает предотказовое состояние, продол-
жающееся время г) с распределением Н(х). Когда происходит отказ, система на-
всегда остается в отказовом состоянии. Предположим, что £ и ц независимы.
Введем случайный процесс z0(t), определив его как состояние системы в
момент t. График траектории процесса 20(1) изображен на рис. 4.2. Этот процесс
в общем случае не является марковским. Пусть zQ(f) — 0. Тогда и при всех
114
Т</будет z0(t) = 0. Следовательно, вероятность любого события при усло-
вии 20(/) = 0 совпадает с вероятностью этого же события при условии фикси-
рования всей траектории процесса до момента t. Далее, при z0(i) = 2 дальнейшая
история также вполне определена: z0(t) = 2 при всех /. А вот при z0(Z) = 1
дополнительная информация о поведении траектории процесса до момента t
(именно, о моменте перехода процесса в предотказовое состояние) может сущест-
венно повлиять на события, связан-
ные с поведением процесса после мо-
мента t.
Покажем, как «марковизиро-
вать» процесс z0(f). Образуем новый 2 - --
процесс
’0, если г0 (О = 0,
(/) = 2, если z0 (0 = 2,
1(1. ? + П—0. если z0 (/) = 1.
(4.35)
Таким образом, множество со-
стояний процесса z(0 состоит из трех О ~---------------------------------
изолированных частей: двух точек — 4 чет
0и2и прямолинейного луча (0, оо),
поскольку каждой точке вида (1, х) Рис. 4.2
можно сопоставить'точку х на полу-
прямой.
Процесс г(0 будет марковским. Действительно, при z(t) = 0 либо z(t) = 2
дальнейшая траектория процесса после момента t, как и в случае процесса г0(0,
не зависит от (г(т), т < t}. Если же z(t) = (1, х), где х — любое положительное
число, то дальнейшее поведение процесса также вполне детерминировано, а
именно:
(4.36)
' Можно сказать, что процесс z(t) вбирает в себя всю информацию о предыду-
щем поведении процесса z0(i), на основании которой можно делать выводы о его
поведении в будущем. . 1
Обратим внимание на то, что процесс z(t) не является однородным, т. е.
переходные вероятности явным образом зависят от t. Так, легко видеть, что
1_р
P(z(< + t)==0/2(0 = 0}=P{£>/ + t/£>/}=—-—(4.37)
1—? (<)
Введя еще одну дополнительную координату, можно построить однородный
марковский процесс. С этой целью введем процесс z*(t) соотношениями
(0, Zi (0) при z0 (0 = 0,
z*(0 = i (1. zi(0) при го(О=1,
(4.38)
при z0 (0 = 2,
где гДО теперь имеет различный смысл в зависимости от того, чему равно z0(f)
а именно;
U + 1!—t при zo(0 = l.
[Можно эти определения и объединить, сказав, что 2х(0 обозначает время до сле-
дующего изменения состояния процесса z0(0-l
115
В начальный момент времени значение процесса z(t) случайно и равно
(О, ^), где, как и выше, £ — время безотказной работы системы. После этого в
течение целого интервала (0, £) траектория процесса детерминирована (рис.4.3).
В момент t = £ вмешивается случай, опре-
деляя, сколько времени процессу надлежит
быть в предотказовом состоянии. Фиксиро-
ванием значения процесса в момент L,, т. е.
(1, Т|), уже вполне определяется все даль-
нейшее течение процесса.
2. Пусть имеется бесконечная сово-
купность элементов, обладающих некото-
рым временем безотказной работы. В мо-
мент t = 0 включается в работу какой-ни-
будь из этих элементов, взятый наудачу;
после его отказа включается второй и т. д.
Обозначим через Лф) число элементов, от-
казавших до момента t. Типичная траекто-
рия процесса Аф) обозначена на рис. 4.4
жирной линией. Если длительности безот-
казной работы различных элементов — не-
зависимые случайные величины £2, ...,
........то поведение процесса Лф) будет опи-
сываться однородным марковским процес-
сом
z(i) = (zo(O> *i (0).
гис’ 4 ,5 гдег0(г‘) = Лф), z^f) — время от момента t
до момента следующего отказа. Траектория
процесса zv(t) показана на рис. 4.4 пунктирной линией. Обратим внимание
на то. что в интервалах постоянства zQ(t) = N(t) траектория процесса zpt) ве-
дет себя детерминированным образом: z1(t) убывает по линейному закону с угло-
вым коэффициентом —1; при обращении z2(t) в нуль вмешивается случай, сооб-
щая значение следующего интервала постоянства N(t).
Процесс вида Лф) в литературе называется процессом восстановления [4],
а множество моментов скачков процесса N(t) — потоком восстановления, а также
рекуррентным потоком, или потоком с ограниченным, последействием. Обычно
предполагают, что g2, £3, ..., £п, ... независимы в совокупности и имеют одно и
то же распределение Е(х), а имеет распределение Е0(х), вообще говоря, отлич-
ное от Е(х); не зависит от {£;, i > 2].
3. Рассмотрим процесс восстановления с положительной длительностью
включения элементов. Пусть элементы отказывают, как и в предыдущем случае,
116
а включаются на протяжении случайного времени г|, равного г|/ для i-ro элемен-
та. Предположим, что все случайные величины независимы в совокупности.
Тогда N(t) можно следующим (не единственным) образом вложить в марковский
процесс
г(<) = (г0(П, г,(0).
Обозначим
'(О, N (t)), если в момент t в работе находится ис-
правный элемент,
2o(O=(Zoi(O, Л^(0)=
(1, N (г)) если в момент t происходит включение
элемента.
Обозначим далее
времени с момента t до момента включения нового элемента, если
г1(0 = Ьо(0 = (1^(0).
1 v 7 времени с момента t до момента отказа, если
I z0 (Z) = (0, М(0).
Короче говоря, зЦ/) — время до следующего изменения состояния процес-
са z0(Z).
Пример траектории процесса zx(Z) показан на рис. 4.5. Вмешательство слу-
чая в данном примере происходит лишь в моменты достижения координатой
Рис. 4.5
нулевого значения. Заметим, что термин «включение» можно было бы заменить
словом «восстановление»: один восстанавливаемый элемент функционирует точ-
но так же. Другие примеры применения марковских процессов для описания
функционирования сложных систем помещены в дальнейших главах книги.
4.4. КОНЕЧНЫЕ АВТОМАТЫ
Из сказанного выше (см. § 4.1 и 4.2) следует, что для описания ди-
скретных детерминистических систем могут быть использованы булевы
и высказывательные функции. Однако существует класс систем (называе-
мых алфавитными преобразователями информации), для описания ко-
торых оказывается весьма полезной специальная математическая схе-
ма— конечные автоматы*
Под алфавитом будем понимать конечное множество объектов,
называемых буквами. В качестве букв можно рассматривать объекты
*> Мы будем придерживаться изложения, принятого в [3].
117
любой природы: буквы алфавита русского или латинского языка, циф-
ры, знаки, рисунки, слова, фразы и т. д.
Словом в данном алфавите называется конечная упорядоченная
совокупность букв. Например, в алфавите (х, у) словами будут хху,
хух, уххух и т. д. Длина слова измеряется числом содержащихся в нем
букв. Употребляется также и пустое слово, не содержащее ни одной
буквы; оно обозначается 0.
В дальнейшем существенную роль играют соответствия между
словами в одном и том же или различных алфавитах. Алфавитным
оператором или алфавитным отображением называется соответствие,
сопоставляющее словам в данном алфавите слова в том же самом или
в некотором другом алфавите. В последнем случае различают вход-
ной и выходной алфавиты оператора и соответственно входные и выход-
ные слова.
Алфавитный оператор является однозначным, если он каждому
входному слову ставит в соответствие не более одного выходного. Если
данному входному слову алфавитный оператор не сопоставляет ника-
кого выходного слова, то он не определен на этом слове. Совокупность
всех слов, на которых алфавитный оператор определен, называется
его областью определения. 0
Два алфавитных оператора считаются равными, если они имеют
одну и ту же область определения и относят любому слову из этой обла-
сти одинаковые выходные слова. Алфавитный оператор может быть
задан при помощи таблицы соответствия, которая для каждого входного
слова содержит определенное выходное слово или правило, следуя
которому для каждого входного слова может быть установлено вы-
ходное слово (если оно существует).
Алфавитные операторы, задаваемые с помощью конечных систем
правил, позволяющих за конечное число шагов для любого входного
слова, входящего в область определения, найти соответствующее
выходное слово, называются алгоритмами. Два алгоритма считаются
равными, если равны реализуемые ими алфавитные операторы,
а также совпадают системы правил, задающие действие этих операто-
ров на входные слова. Алгоритмы, у которых совпадают только реа-
лизуемые ими алфавитные операторы, но, вообще говоря, не совпа-
дают способы задания, будем называть эквивалентными.
Важность для практики алфавитных операторов связана в первую
очередь с тем, что любой реальный преобразователь информации
может рассматриваться (при некоторых весьма общих условиях)
как прибор, реализующий тот или другой алфавитный оператор.
Обратим внимание на алфавитные операторы, осуществляющие по-
буквенное отображение входных слов в выходные слова; они имеют
широкое практическое распространение наряду с другими алфавит-
ными операторами.
Перейдем к определению конечного автомата. Вначале задается
множество моментов времени t0 < tx <_ t2 < ..., в каждый из которых
конечный автомат находится в некотором состоянии. Состояние авто-
мата в момент tn обозначается г (tn) или более кратко, г (п). Множество
состояний автомата будем обозначать Z. Предполагается, что это
118
множество конечно, откуда и название «конечный автомат». В каждый
момент и автоматного времени, начиная с tlt на вход автомата поступает
в качестве входного сигнала одна из букв х входного алфавита X,
т. е. х 6 X. Конечные упорядоченные совокупности входных сигналов
х (1), х (2), ..., х (k) называются входными словами.
Автомат следующим образом реагирует на поступление входных
сигналов. Во-первых, внутреннее состояние автомата изменяется
в соответствии с функцией, переходов (в новое состояние):
г(/) =ф [z(/—1), х(г)]. (4.39)
Во-вторых, в каждый момент автоматного времени на выходе автомата
появляется выходной сигнал у, определяемый функцией выходов:
z/(0=W(^-l), х(0]. (4.40)
Любое допустимое входное слово (из фиксированного множества
допустимых слов) вызывает появление на выходе автомата выходного
слова такой же длины. Получаемое таким образом соответствие между
допустимыми входными и выходными словами называется отображе-
нием, индуцируемым данным автоматом.
Конечный автомат может быть задан при помощи двух таблиц:
таблицы переходов и таблицы выходов. Например, табл. 4.3 и 4.4
описывают автомат с входным алфавитом {хъ х2), множеством внутрен-
них состояний (z0, zlt z2) и выходным алфавитом [уъ у2}. Пусть
в момент t = 0 автомат находится в состоянии z0; если в момент 0
поступает входной сигнал xlt автомат переходит в состояние гг
(табл. 4.3) и выдает выходной сигнал у1 (табл. 4.4); если в момент 4
поступает входной сигнал х2, автомат переходит в состояние г1 и выдает
выходной сигнал у2 и т. д.
Автомат можно задавать при помощи ориентированного графа:
состояниям автомата соответствуют вершины графа, а дуги (t, /) пока-
зывают переход из состояния zt в состояние Zj под влиянием входного
сигнала х. Соответствующие сигналы х и у записываются вдоль дуги
графа.
До сих пор мы изучали так называемый автомат Мили. Для авто-
мата Мура в отличие от автомата Мили функция выходов имеет дру-
гой вид:
y(t) = и [2(01 (4-41)
и называется сдвинутой функцией выходов.
119
Отображение F, индицируемое автоматом, удовлетворяет следую-
щим двум условиям: 1) любому входному слову /вх ставится в соот-
ветствие выходное слово /|1ЫХ = F (1ВХ), имеющее с /вх одинаковую
длину; 2) если /, — начальный отрезок слова /вх, то слово F (/J яв-
ляется начальным отрезком слова /вых = F (1ВХ).
Эти условия называются условиями автоматности отображе-
ния (оператора). Всякое отображение (оператор), удовлетворяющее
этим условиям, будем называть автоматным отображением (операто-
ром). Любое автоматное отображение может быть индуцировано неко-
торым автоматом (не обязательно конечным).
Пример. Для распределения труб, поступающих из нагревательной печи,
между автоматическими линиями обработки служит автомат, называемый де-
лительным устройством. В каждый такт tj работы транспортера к делительному
устройству поступает одна труба, диаметр которой dj равен одному из п возмож-
ных диаметров dx, d.2, dn. Для обработки труб /г-го диаметра имеется группа
из m/j автоматических линий. Автоматические линии занумерованы двойными
номерами: сначала указывается номер группы k (соответствующий трубам дан-
ного диаметра d^), а затем номер автоматической линии в группе (k =
= 1, 2, .... га; vft=l,2, ..., т^). Автоматические линии загружаются в порядке
очереди, т. е. если в момент tj труба была направлена в автоматическую линию
номер k, Vft и в момент /у+1 поступила труба того же диаметра, то она направляет-
ся в линию номер k, Уд+1, когда < т^, или в первую линию данной группы,
если Хд = т.
Функционирование делительного, устройства можно описать в виде конеч-
ного автомата. Примем в качестве входного алфавита совокупность номеров
диаметров труб 1, 2, .... п, а в качестве выходного алфавита — совокупность
номеров автоматических линий /г, Внутренними состояниями автомата бу-
дем считать n-мерные векторы, составляющими которых являются номера
автоматических линий в соответствующих группах, последними получивших
для обработки трубу.
Будем считать, что в момент времени t = 0 трубы еще не поступили и все
автоматические линии свободны. Начальное состояние автомата можно устано-
вить в виде z0 = (0,0, 0), текущее состояние, в виде 2 = (vx, v2, .... vn); вход-
ные сигналы x(j) = kj; выходные сигналы у = k, v^.
Функция переходов в новое состояние <p[z(Z — 1), х(/)] описывается соот-
ношением
vx (/) = vx (/ — 1) + 1 (mod тх) при k = x,
V& (0 = ^А (/ —1) при k^x-,
функция выходов ф[а(/ — 1), х(7)| — соотношением
y(/) = (x(0, vx(/)).
Если предыдущее состояние автомата' z(t — 1) и поступающий входной
сигнал x(t) определяют не состояние z(i), а распределение вероятностей р tj пе-
рехода из состояний 2j = z(t — 1) в одно из состояний Zj £ Zb момент t, то
такой автомат называется автоматом со случайными переходами (вероятностным
автоматом) [9]. Для его задания, помимо элементов (A, Y, Z, ф, 20), вместо
функции ср нужна система матриц вида || pt j(x) ||, определяющая для каждого х
матрицу упомянутых распределений вероятностей
РЦ (х) = Р {г (/) = Zj/z (t—Y)=zh x(t)=x}.
Функционирование автомата со случайными переходами имеет следующий
вид. Пусть в момент t в автомат, находившийся в состоянии z(t — 1) = Zj, по-
ступает входной сигнал x(t) = х. Тогда, из матрицы ||р^(х);| определяются веро-
ятности ptj того, что автомат перейдет в этот момент в состояние 2^; конкрет-
но
ное Zj выбирается по жребию в соответствии с вероятностями ptj{x}. В этот же
момент выдается выходной сигнал
У (t) = г|5 [2 (01-
Описание процесса изменения состояний автомата со случайными перехо-
дами можно свести к виду (4.40)
z(i) = <p*[z(/-l), х (0J,
где под <р* понимается случайный оператор, выполняющий последовательно два
действия: 1) определение вероятностей pij (х) и 2) случайный выбор конкретного
Zj в соответствии с этими вероятностями.
Рассматриваются [9] также вероятностные автоматы более общего вида,
когда начальное состояние z0 является случайным; оно выбирается в соответст-
вии с распределением вероятностей р01, р02, ..., рой, заданным на множестве Z.
Наконец, представляют интерес автоматы, обладающие тем свойством, что
по состоянию z(t) определяется не выходной сигнал y(t), а распределение вероят-
ностей qi (z) на множестве Y. Тогда
р(0=^[2(0], (4.42)
где — случайный оператор, который: 1) определяет по заданному z(Z) вероят-
ности qi(z) и 2) выбирает по жребию конкретное y(t) в соответствии с этими ве-
роятностями.
Конечные детерминистические и вероятностные автоматы широко исполь-
зуются для описания систем, работающих в дискретном времени (устройств ЭВМ,
алгоритмов, программ и т. д.). Методы анализа и синтеза автоматов рассматри-
ваются в [3, 13, 12] и др.
4.5. СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ
Функционирование многих реальных систем носит характер
обслуживания поступающих в систему заявок. Для выполнения сово-
купности действий или операций, подразумеваемых под понятием
«обслуживание», в системе имеются специальные каналы или линии.
Например, в телефонии заявками являются вызовы, возникающие
на АТС в момент снятия абонентом телефонной трубки, а обслужива-
нием — предоставление линии, занимаемой абонентом на время раз-
говора; на бензозаправочной станции в качестве заявок выступают
автомобили, прибывающие на заправку, а каналами являются запра-
вочные колонки. Аналогичные ситуации наблюдаются в системах
посадки самолетов, разгрузки судов, в парикмахерских, магазинах
и т. д.
Изучение обслуживания отдельной заявки сводится, как правило,
к выяснению того, произошло ли событие, понимаемое под словом
«обслуживание», к определению длительности обслуживания (или вре-
мени занятости обслуживающего канала), оценке качества обслужива-
ния и т. д. При обслуживании потока заявок — совокупности заявок
со специальным законом чередования их во времени — возникают до-
полнительные задачи: определение доли обслуженных заявок и доли
заявок, получивших отказ, определение относительного времени заня-
тости и простоя каналов и др.
Если с точки зрения содержания обслуживания все заявки равно-
правны и играет роль лишь сам факт поступления или непоступления
121
заявки в данный момент времени, поток называется потоком однород-
ных событий. Каждая заявка в этом случае характеризуется момен-
том tj поступления ее в систему, а поток последовательностью момен-
тов tx, t2, ..., th, или законом, определяющим чередование момен-
тов tj.
На практике основную роль играют случайные потоки заявок.
Чтобы задать случайный поток, достаточно указать совместный (много-
мерный) закон распределения случайных величин t2, .... th, ...
Для удобства часто вместо величин tj рассматриваются интервалы t,}
между последовательными заявками:
ti = £1>
^2 = ?1 + ^2,
— £1 + Са + • • +
Описание потока при помощи интервалов С; эквивалентно заданию
t}\ в самом деле, зная распределение можно получить распределение
tj, и наоборот.
Закон распределения случайных величин задают в виде сов-
местных функций распределения при всевозможных значениях k 1
К(2!, z2,.... 2Й)=Р^1<21, £2<z2, ....
Обычно рассматриваются только непрерывные случайные величины
t,j, описываемые функциями плотности f (г,, z2, ..., zh).
Известно, что оперирование над многомерными распределениями
отличается исключительной громоздкостью. Математическое описание
оказывается более простым для некоторых важных классов потоков
однородных событий.
Если совместная функция плотности может быть представлена
в виде
/(2Ь г2,..., Zft)=/1(z1)f2(z2) ...fh(zk) (4.43)
(случайные величины t,j независимы), соответствующий поток назы-
вается потоком с ограниченным последействием. Если, кроме того,
£2, $3, ... распределены одинаково, поток называется рекуррентным.
Поток называется ординарным, если Пт[ф(^0, /)//]= 0 при лю-
t-о
бом tQ, где ф(/0, t) — вероятность появления двух или более заявок
в интервале времени (t0, t0 + t).
Пусть k = (klt ... , kn) — любой целочисленный вектор, t =
= (/п t2,... , tn), где 0</1<Д2< <tn. Определим p^(t0,t) как
k
вероятность появления k, событий в интервале (/0, t0 -(-/j),... , kn
событий в интервале (/n-i, tn).
122
Если (/0, t ) не зависит от t0, а определяется только величи-
k
нами t и k, то поток называется стационарным. Для стационарных
потоков справедливо равенство
/2(z)=/3 (z) = ... = Д(з)=/(Л-
Математическое ожидание
оо
Mg,-= z/(z) dz = m (/>1)
'о
(4.44)
(4.45)
представляет собой среднее значение длительности интервала времени
между последовательными заявками. Для ординарного стационарного
потока величина
% = 1/т
(4.46)
называется интенсивностью потока и выражает среднее число заявок,
поступающих в единицу времени.
Для стационарного потока с ограниченным последействием имеет
место формула Пальма
Z1
1 —§ f (2) dz
b
(4.47)
позволяющая найти распределение интервала g,, если известно рас-
пределение интервалов gj при / > 1.
Рассмотрим в качестве примера стационарный ординарный поток
с ограниченным последействием, имеющий равномерное распределение
интервалов времени между заявками
1/6,
О ,
г 6 (0, 6),
г С (0, 6).
(4.48)
Тогда
Mg = 6/2, А = 2/6.
По формуле Пальма
_ 2(й-гх)
62
Таким образом,
Л(д) =
Л 1----------2, ,
\ 2 J
О,
Д € (О, 6),
2ХТ(0, 6).
(4.49)
Легко видеть, что
Mg, = 6/3.
123
Если вероятность pk (t0, t) поступления k заявок в интервале
(t0, tQ + t) не зависит от чередования событий до момента t0, т. е. если
условная вероятность pk (t0, t), вычисленная при любом предположе-
нии о чередовании событий до момента t0, равна безусловной вероятно-
сти того же события, поток называется потоком без последействия.
Можно показать, что единственным стационарным ординарным
потоком без последействия является так называемый простейший
поток или поток Пуассона, для которого
(4-50)
/г!
ИЛИ
/(z) = Xe-^. (4.51)
В соответствии с формулой Пальма можно убедиться, что для про-
стейшего потока
/1(z) = Xe-?-2=/(z).
В общем случае такое соотношение несправедливо [см., например,
(4.49)].
Пусть обслуживающая система состоит из п каналов, одновре-
менно и независимо друг от друга обслуживающих заявки. Канал
может находиться в одном из двух состояний: свободном и занятом.
Заявка, поступившая в систему в момент tj, либо принимается к об-
служиванию (если имеется свободный канал), либо остается в системе
в течение некоторого времени у (если все каналы заняты). Не позднее
чем в момент tj + у заявка должна быть принята к обслуживанию;
в противном случае она получает отказ и покидает систему. Обыч-
но рассматривают три класса систем: системы с отказами (у = 0),
системы с ожиданием (у = оо) и смешанные системы (0 < у < оо).
Для характеристики канала используется величина ц — время
занятости канала (длительность обслуживания). В общем случае у
и ц — случайные величины с заданными законами распределения.
Могут быть сделаны различные предположения относительно порядка
привлечения каналов к обслуживанию заявок (в порядке номеров кана-
лов, в порядке очередности освобождения, в случайном порядке и т. д.),
а также приема заявок на обслуживание (в порядке очереди, по мини-
мальному времени, оставшемуся до получения отказа, в случайном
порядке и т. д.).
Показателями эффективности систем массового обслуживания
служат: 1) для систем с отказами — средняя доля отказов, вероят-
ность обслужить все заявки в течение заданного интервала времени,
2) для систем с ожиданием — среднее время ожидания, средняя длина
очереди и др., 3) для смешанных систем — все перечисленные вели-
чины.
В приводимых ниже примерах рассматриваются и более сложные
системы массового обслуживания.
Исследование систем массового обслуживания может быть выпол-
нено аналитически [4,7] при некоторых (иногда весьма стеснительных
124
с практической точки зрения) предположениях относительного харак-
тера потока заявок и свойств системы обслуживания. В качестве при-
мера приведем наиболее элементарный случай. В n-канальную систему
с отказами поступает простейший поток заявок с интенсивностью л.
Длительность обслуживания — показательно распределенная случай-
ная величина с конечным математическим ожиданием г). Заявки прини-
маются к обслуживанию в порядке очереди, а каналы привлекаются
в порядке их номеров. Тогда, при t -> оо значение средней доли
отказов (в данном случае, в силу стационарности процесса, она также
имеет смысл вероятности отказа для заявки, поступившей в наудачу
выбранный момент времени) будет равно
П (^)" / £ (М)А /4, О Ч
R =—— / V —— (формула Эрланга).
п! / k=o k'-
Заметим, что данная формула, одна из сравнительно немногих,
справедлива и в случае произвольного распределения времени об-
служивания.
Для исследования систем массового обслуживания использует-
ся также метод статистического моделирования (Монте-Карло), реа-
лизуемый на ЭВМ [1].
Ниже мы рассмотрим некоторые типичные примеры математиче-
ского описания процессов функционирования систем массового обслу-
живания. Здесь весьма эффективным оказывается использование ап-
парата марковских процессов.
Пример 1. Пусть имеется и-линейная система массового обслуживания,
т.е. система состоит из п параллельно работающих приборов. В систему поступает
рекуррентный поток требований, т. е. интервалы между последовательно посту-
пающими требованиями являются независимыми одинаково распределенными
случайными величинами [функция распределения Д(х)]. Все приборы работают
независимо. Время обслуживания требования на любом приборе — случайная
величина с заданной функцией распределения В(х). Требование, заставшее все п
приборов занятыми, становится в общую очередь; обслуживание производится
в порядке поступления требований.
Обозначим через w(f) «виртуальное время ожидания» в момент t, опреде-
ляемое следующим образом. Если бы в момент t в систему поступило требование,
постороннее по отношению к входящему потоку, и присоединилось к общей оче-
реди, то его время ожидания составляло бы ta(i). Иначе говоря, w(t) — случайная
величина, равная длительности промежутка времени от момента t до момента
освобождения хотя бы одного из приборов от требований, имевшихся в системе
в момент времени t. Именно, если обозначить через v(t) число требований,
находящихся в системе в момент t, то
[ 0, если v (!) < п,
w (/) = {
(inf{r:T>l, —t, если v (0 > л.
Ясно, что w(t) в общем случае не является марковским процессом (исключение
будет иметь место в случае п = 1, если, к тому же, входящий поток — пуассо-
новский).
Введем следующие случайные величины: z, (<), 1 < i < п, — время с момен-
та t до момента окончания обслуживания i-м прибором требований, поступивших
ранее момента t (если i-й прибор в данный момент времени свободен, полагаем
125
2$) = 0); 2n+i (/) — время с момента t до поступления в систему очередного тре-
бования. (п + 1)-мерный случайный процесс
z(0 = (Zi(0, z2(0. .... zn(<), z„+1 (q)
будет марковским, что непосредственно очевидно. Траектория этого процесса
ведет себя следующим образом: zn + 1(l) убывает с единичной скоростью до того мо-
мента времени, когда она обращается в нуль; в этот момент zn+1 (/) принимает
случайное значение, независимое от течения процесса и равное следующему интер-
валу между поступлением требований, ненова начинается убывание с единичной
скоростью.
Все координаты z^Z), z2(l), ..., zn(l) убывают с единичной скоростью до до-
стижения нулевого значения. Если какая-нибудь из них, скажем Z[(t) = О,
обратилась в нуль, дальнейшее убывание прекращается, и начиная с этого мо-
мента z;(Z) = 0. Так происходит до тех пор, пока zn+1 (t) не обратится в нуль.
В этот момент общая загрузка системы увеличивается на необходимую случай-
ную длительность обслуживания г) с функцией распределения В(х) вновь посту-
пившего требования. Но как изменятся координаты z,(Z)? Очевидно, новое тре-
бование поступит туда, где придется меньше ожидать.
Именно, пусть z( (/)= min z;(l). Тогда
°
zj (i 4-0)=zj (0. /¥=‘o. /<«>
(*+°)=^ (0+n-
В случае, если минимум достигается на двух или нескольких значениях j, можно
условиться, что поступающее требование направляется на прибор, скажем, с
наименьшим номером.
Очевидно, зная значение процесса z(Z), можно найти интересующее нас
значение w(t):
w(t)= min Z;(f).
1 < i < n
Пример 2. Рассмотрим ту же самую систему массового обслуживания, но,
так сказать, более подробно, интересуясь не только загрузкой приборов, но так-
же числом находящихся в очереди требований.
Пусть v(/) — число требований в системе в момент t. При v(t) < п обслу-
живаются все имеющиеся требования; при > п в очереди находится v(t) — п
требований. Введем случайный процесс
z(t) = (z0(/), Z!(0, z|2o (() , (/)),
где zo(0=v(0;
101,1 U + 1 при ;,(()>«.
т. е. |zo(OI —— число занятых приборов в момент /*>; zk(t), k > 2, — время с
момента t до момента окончания обслуживания (k — 1)-м прибором требования
(в случае | z0(/) | = 1 координаты zh, k > 2, не определяются); z^/) — время с мо-
мента t до момента поступления очередного требования.
Введенные функции времени z^t), z2(t), ... убывают с единичной скоростью,
пока какая-нибудь из них не обратится в нуль. Если это была z^t), новым зна-
чением ее будет случайная величина, равная очередному интервалу между по-
ступлением требований; если в нуль обратилась одна из z2(i), z3(/) .... то z0(t)
уменьшается на 1; если до этого было z0(f) > п, обратившаяся в нуль z,(t) заме-
няется случайной величиной, равной длительности обслуживания требования, **
** Величину [z0(0l иногда называют рангом состояния z0(7).
126
взятого из очереди; если же го(О < п, новые значения координат опре-
деляются равенствами
2'(f)=zj(f), j<i; 2'. (i) = г/+ j (f), / > i,
(4.53)
т. е. обратившаяся в нуль координата вектора 2(f) вычеркивается. Интересно,
что при таком подходе необходимость выбора минимальной координаты отпадает;
в то же время вместо процесса фиксированной размерности мы получили процесс
переменной размерности, зависящей от числа занятых приборов. Легко видеть,
что этот процесс является марковским.
Пример 3. Рассмотрим ту же систему, но с учетом возможности выхода из
рабочего состояния и восстановления обслуживающих приборов. В момент
/ = 0 все приборы являются исправными; задается распределение времени безот-
казной работы каждого из них. Если прибор вышел из строя, он поступает в
восстанавливающую систему. Это, в свою очередь, m-линейная система массового
обслуживания с ожиданием (1 < т < и). Рассмотрим вариант, при котором
требование жестко закрепляется за прибором, т. е. в случае отказа последнего
ожидает его восстановления. Если необходимое время обслуживания равно т],
причем до отказа прибора требование обслуживалось на протяжении времени х,
то после восстановления необходимое время обслуживания будет составлять
Г) — X.
Функционирование системы описывается марковским процессом 2(f) =
= (20(f), 2x(f), ..., 2|Zo(ol (f)), где 20(f) = (zoo(f), 201(f), Z02 (f), ..., 2027l(f)) — МНОГО-
мерный дискретный параметр, указывающий состояние всех приборов и число
требований в системе при 1 < i < п;
О, если f-й прибор в момент f исправен,
1, если f-й прибор в момент f восстанавливается,
/4-1, если f-й прибор в момент f находится в состоянии ожидания
ремонта, причем его место в очереди /-е;
г0; (0 =
г0, тц-г (О
О, если f-й прибор свободен от требований в момент f,
1, если f-й прибор обслуживает требование в момент f,
2, если f-й прибор находится в момент t в неисправном состоянии,
причем в момент отказа он обслуживал некоторое требование;
200(f) — число требований в системе в момент f;
zjf) — время до поступления очередного требования;
zi+1(f), 1 < f < и, — время до отказа f-ro прибора, если zoi(f) = 0, время
до окончания восстановления f-ro прибора, если 20i(f) = 1; время, необходимое
для восстановления f-ro прибора, если 20; (f) = 2;
гп+г+1 (0> 1 < f < min {и, 200(f)}, — время до окончания обслуживания
f-ro требования из числа требований, которые либо обслуживаются в момент'f,
либо' обслуживались ранее и в момент f не обслуживаются из-за неисправности
прибора (требованию, обслуживаемому прибором с меньшим номером, приписы-
вается меньший/номер);
| z0 (f) | =/i4-min (п, г00 (f)} 4-1 — число непрерывно меняющихся координат.
До тех пор, пока все 2;(f), f>l, положительны, они изменяются по линей-
ному закону. При этом гг + 1 (f), 1 < f < п, убывают с единичной скоростью при i,
для которых zoj < 1, и остаются неизменными при остальных i;’что'касается
2;(f), i гг + 1, то те из них, которые соответствуют времени до окончания об-
служивания действительно обслуживаемых требований, убывают с единичной
скоростью; остальные же остаются постоянными. ‘ •••*
При обращении 2j(f) в нуль новым значением этой переменной будет время
До поступления следующего требования; z00(t) получает приращение 1. Если все
zo,n+! (f)^ 1, 1 < f < п, остальные координаты останутся неизменными; в
127
противном случае находится I как наименьшее Г, для которого 20гП+1 ,(t) = 0.
Это будет номер того прибора, на который посылается требование, поступившее
в момент t. В этом случае новые значения z'j(Z) координат вектора z(t) опреде-
ляются следующим образом:
гбоЮ=z0o(0 +1;
г0,«-Н =
го/(0 =2о/(0. (4.54)
z-+i(/)=zz+i (0. 1 J
координата (/), 1 <. i < min{«, г00 (/)), образуется так: пусть /' опре-
I- 1
делено равенством Г = У г0 тогда
1 = 2
г;+г+1 (/) = z„ + z+1(0, ККГ; (4.55)
2 2 = т], где т]—длительность обслуживания поступившего требо-
вания ;
<+< + 2 = гп-Н+1 (0, »>/• (4-56)
Предлагаем читателю в качестве упражнения выписать формулы для г;. (/)
в случае обращения в нуль 2; (/), где i > 2.
В следующем примере будет рассматриваться однолинейная система массо-
вого обслуживания; методика рассмотрения многолинейных систем должна быть
ясна из предыдущего.
Пример 4. В систему поступает рекуррентный поток требований. Обслужи-
вание происходит в порядке очереди. С каждым требованием связаны две слу-
чайные величины т] и у, т) — длительность обслуживания; у — характеристика
ограничения, имеющая следующий смысл. Если на протяжении времени у тре-
бование не будет взято на обслуживание, оно покинет систему. В противном слу-
чае, если требование взято на обслуживание через время х после поступления,
оно может ожидать окончания обслуживания не более а(у — х) единиц времени,
где а > 0 — некоторая постоянная (допускается и случай а -= <). Если за это
время требования не обслужат, оно покинет систему.
Как показано в [4], в эту схему включаются в качестве частных случаев
система с неограниченным ожиданием (у = <х), система с ограниченным време-
нем ожидания начала обслуживания (а = '-<), система с ограниченным време-
нем пребывания в ней требований (а = 1).
Пусть z0(t) обозначает число требованийс находящихся в системе в момент t.
Введем (при z0 (t) > 1) следующие переменные; z^t) — время с момента t до мо-
мента поступления следующего требования; zz+1 (t), 1 < i •<, z0(t), —оставшее-
ся время обслуживания i-ro требования (требование, обслуживаемое в данный
момент времени, считается первым); (0> 1 < i < го(О>— оставший-
ся к моменту t запас ожидания.
Начальным запасом ожидания для поступающего требования будет у;
пока требование ожидает в очереди, запас ожидания убывает с единичной ско-
ростью, когда требование будет взято на обслуживание, запас ожидания будет
убывать со скоростью 1/а.
Многомерный случайный процесс
г(О = (го(О, Zj.(O> (0+1 (0)
будет марковским.
128
Пусть в момент t поступает новое требование. Обозначив через z2(f) и г'i{t)
соответственно старые и новые значения координат вектора z(t), получим;
го (О = го(П + 1;
z\(t) = t, (времени до поступления следующего требования);
?-+1 (0 = г2 + 1 (0, 1<г<го(О;
Zza (/)4-2^) = т1 (времени обслуживания вновь поступившего требования)
г2„ (/) + <4-2 (0= 22<| +2+ , (0> 1 < 1 < го (0;
г2 20 (/) 4-3 (0 = У (запасу ожидания вновь поступившего требования).
Если обратится в нуль координата г2_|_ ((Z) , 1 < i < z0 (/), либо (t),
1 z-'Zo (0 то z0(Z) уменьшается на 1, а обе координаты гг-^_ [ (/) игг< (/)
вычеркиваются из записи вектора г (£).
В интервалах времени, когда все z, (/), i>l, положительны, гг (/) и
г2 (/) убывают с единичной скоростью; z3(t), ..., гг (t) остаются постоян-
ными; z2o 2 (0 убывает со скоростью 1/а; z2° j (/), 2<t<zo(O,
убывают с единичной скоростью.
Пример 5. Имеется прибор, способный одновременно обслуживать сколько
угодно требований. Пусть т] — величина работы, которую нужно выполнить для
обслуживания одного требования. Будем считать, что т] — случайная величина,
причем соответствующие величины для различных требований независимы в со-
вокупности и одинаково распределены. При условии, что в системе находятся п
требований (и = 1, 2, 3, ...), темп обслуживания каждого из них составляет ап.
Это означает, что оставшаяся работа убывает со скоростью ап. Входящий поток,
как и ранее, будем считать рекуррентным. Для описания подобной системы вве-
дем случайный процесс
z(0 = (Zo(0- zt (0, z2(0, ..., Z|2o (2) | (0),
где z0(t) — число требований в системе в момент t; zL(l) — время до поступления
очередного требования; z,+i (/)— оставшаяся величина работы по обслуживанию
i-го требования; | z0(6 | = zQ(t) + 1.
Из принятых условий следует, что z2'(6 = —аг„(;)> 1 > 1- При обращении
некоторой из 2;+1(<) в нуль она просто вычеркивается из записи вектора z(t),
a z0(/) уменьшается на 1. При обращении в нуль переменной гх(/), что означает
поступление нового требования, новым значением этой переменной будет случай-
ная величина £, равная времени до поступления следующего требования.
Легко установить, что процесс z(t) является марковским.
Пример 6. Имеется однолинейная система с ожиданием, в которую посту-
пают два независимых рекуррентных потока требований. В момент поступления
требования из первого потока обслуживание требования из второго потока пре-
рывается и при возобновлении предыдущее время обслуживания теряется (вновь
реализуется случайное время обслуживания). Функционирование подобной
системы описывается марковским процессом z(t) = (z0(t), z±(t), ....), где z0(/)=
= (Zoi(0. z02(0); zUi (/)— число находящихся в системе в момент t требований из
i-го потока (Z = 1,2); 2; (/) — время с момента t до поступления в систему очеред-
ного требования i-ro потока (г = 1,2); z3(Z) — время до окончания обслуживания
требования, обслуживаемого прибором в момент t, если таковое имеется.
Рекомендуем читателю выписать формулы для переходных характеристик
данного процесса подобно тому, как это было сделано в предыдущих примерах.
В приложениях иногда пользуются описанием систем массового
обслуживания при помощи высказывательных функций.
Для решения многих задач, связанных с исследованием систем
массового обслуживания, можно обойтись описанием лишь небольшого
5 Зак. 792 129
числа так называемых особых, состояний. К ним обычно относятся
состояния системы в моменты поступления новой заявки, начала и окон-
чания обслуживания очередной заявки, состояние, при котором неко-
торая заявка покидает систему, исчерпав полностою свое время ожида-
ния, и т. д. Достижение системой каждого особого состояния понимает-
ся как наступление одного из заранее предусмотренных событий,
а процесс ее функционирования — как чередование этих событий
во времени.
Для описания события можно использовать высказывательную
функцию, реализующую соотношения между моментами достижения,
системой соответствующих особых состояний (принимающую значение
1, когда данное событие наступает, и значение 0 — в противном случае).
Высказывательные функции, относящиеся к отдельным событиям,
связываются операциями булевой алгебры таким образом, чтобы полу-
ченная высказывательная функция описывала последовательность
событий в процессе функционирования системы. Такое представление
процесса функционирования системы может быть использовано для
формального построения алгоритмов его моделирования на ЭВМ.
4.6. ДИНАМИЧЕСКИЕ СИСТЕМЫ
Функционирование сложной системы можно представить себе как
совокупность двух функций времени: одна из этих функций описывает
внутреннее состояние системы, другая — выходной процесс системы,
т. е. воздействие системы на внешнюю среду. Обе эти функции зависят,
с одной стороны, от воздействия внешней среды на систему, т. е. вход-
ного процесса системы, и, с другой стороны, от воздействия случай-
ных факторов, присущих самой системе. Каким же образом описать
функционирование системы, если не принимать в расчет ни того, ни
другого, т. е. допустить, что состояние системы изменяется в соответ-
ствии с некоторой детерминированной закономерностью, причем слу-
чайные процессы внутри системы и внешние воздействия отсутствуют?
Легко видеть, что таким образом мы приходим к автономной детерми-
нистической системе без последействия (см. гл. 3).
Оператор переходов в новое состояние для такой системы имеет
вид
z(t) t0, z0), (4.57)
а условие однозначности (3.47) — вид
H(t, 4, ta, z0)'j—H(t, t0, ze), (4.58)
Тождество (4.58) можно также интерпретировать в терминах
теории меры. Именно, представим себе, что существует ст-алгебра у
подмножеств множества состояний системы Z с таким свойством. Если
4, € Л 4 < 4 то Для любого А £ у образ множества А состояний си-
стемы в момент t0 при преобразовании оператором Н (t, t0, z0) снова
принадлежит у. Короче, j 7/ (/, 4> 2о). 2о 6 6 У при А £ у.
130
Будем рассматривать меры н (А) на подмножествах А множества Z,
принадлежащих о-алгебре у. Тогда оператору Н (t, t0, z0) будет соот-
ветствовать оператор t0, р0), переводящий одни меры в другие.
Именно, значением ffl(t, t0, р0) является мера р на множествах Л £ у,
определенная тем свойством, что если
В£у, A = [z0 :H(t, t0, z0)£B},
то p(B) = p0(A).
Чтобы избежать тривиальных усложнений, допустим, что опера-
тор Н (t, ta, z0) при фиксированных t0 и г0 можно рассматривать как
функцию z = г (0, t £ /, со значениями во множестве Z. Эту функцию
называют траекторией системы. Для объяснения того, как преобразу-
ются меры оператором Ж, рассмотрим меры, сосредоточенные в конеч-
ном или счетном числе точек. Итак, допустим, что фиксированы две
последовательности точек: г1У z2, ..., zn, ... £Z и р± 0, р2 0, ....
..., рп 0, ..., п и мера р0 определена следующим образом:
НоИ)=2 Рп-
Тогда, если у. — ЖЦ, t0, р0), будем иметь:
= H(t, t0, гп)еВ. (4.59)
Отсюда легко представить себе тот случай, когда меры задаются
плотностями.
Важно заметить, что оператор Ж(1, tQ, |i0) является линейным,
в отличие (в общем случае) от оператора Н (t, t0, г0):
M(t,J0, ацо + PpJ^
= а^(/, /0, р0)+|Ш(/, t0, Hi)- (4.60)
Это обстоятельство является отправной точкой важных методов
исследования свойств системы. Для оператора Ж, действующего во
множестве мер, справедлив следующий аналог тождества (4.58):
W(t, tlt Ж th, to, Ho))=-W. to, Ио). (4.61)
Введенный оператор Ж можно также рассматривать как оператор
переходов в новое состояние, если состояние системы в момент t пред-
ставлять себя как меру pf, определенную на измеримом пространстве
(Z, у). Однако если принять такую точку зрения, то можно охватить
гораздо более общую ситуацию, чем детерминированные движения
Н (t, t0, z0)*’. Именно, представим себе, что состояния системы в момент
t, т. е. z(t), случайны, и описываются распределением вероятностей
или, что то же, вероятностной мерой
Р {z(0 е A] =pt(A), Аеу. (4.62)
*> То есть, не каждому оператору &£ со свойством (4.61) соответствует опе-
ратор Н со свойством (4.58).
5* 131
Тогда оператор р( = Ж(1, 4, р0) будет задавать распределение вероят-
ностей состояний системы в момент t при условии, что в момент
имело место распределение р0.
Рассмотрим вероятностную меру р2а, целиком сосредоточенную
в г0:
11, если 20 £ Л,
Pzo(^) — если 2о—4.
Обозначим
t0, р2„) = р/
Тогда р;л„,2„(Ч) естественно рассматривать как условную вероят-
ность того, что z(t)£A, при условии, что z(t0)=z0. В силу линей-
ности оператора Ж имеем
W- t0, Но)=^Л»,г„Но(^0). (4.63)
Z
Более подробно, значение меры Ж{1, р0) на любом множестве
Л£у равно ^Р/ло,2о(Л)р0(^г0).
z
Допустим теперь, что z (/), I, является марковским процессом.
Любые конечномерные распределения случайных величин z (t) (а при
соответствующих аналитических условиях — и более сложные рас-
пределения — такие, как вероятность нахождения процесса в данной
области в течение заданного времени) однозначно определяются на-
чальным распределением р^0 (Л) = Р [г К0)£Л} и марковской пере-
ходной функцией
^л».2о(^) = Р{г(ПбЛ/2(/0) = го},
представляющей собой при фиксированных /, /0, z0 вероятностную
меру р;, /0,2о в Z. Если теперь задать оператор Ж во множестве
мер соотношением
to, Ио) =$И/Л«,гоРо(^0), (4.64)
z
то этот оператор будет удовлетворять соотношению (4.61). Действитель-
но, по уравнению Колмогорова—Чепмена, при <0 < /
Р (г (/) £ А} = У Р [(г (/„)} е dz0) Р (г (0) С dzjz (/0) = z0] х
X Р [г(0 ЕЛ/г(Ч) = 2!) =
= 5 р {(2Ко) е dzo)p (2(0 6 Л/гК0) =20j. (4.65)
С учетом предыдущего последнее можно переписать так:
МЛ)=П И/о(^о)И^л«.2»(^1)И«.л.2, И)--=
= Jpi„(d2o)pi,/o,2o^). (4.66)
132
Поскольку
Ж (/1, tQ, p,f0) —(d^o) Ц/,, t0,z0,
Ж {t, ti, у/,) — рц (dzi) p<, tt, 21,
ж (I, to, pj = $Рл>(^0)
то мы будем иметь
жа, t0, 1Ч,)=--ЖЦ, tlt Ж(^, t0, р,0))( (4.67)
что соответствует формуле (4.61).
Итак, марковские процессы можно изучать с помощью операторов
перехода, определенных на вероятностных мерах в измеримом про-
странстве (Z, у).
Системы с оператором перехода вида
Н (t, t0, z0)=H(t—t0, z0) (4.68)
называются динамическими системами (см. гл. 3). Обычно динамиче-
ские системы рассматриваются при / = (—оо, оо) либо при I =
= {..., —2, —1, 0, 1, 2, ...}.
Формула (4.58) в случае динамической системы преобразуется
к следующему виду:«
Wr + 4, z0) = H(/2, //(/,, z0)). (4.69)
Это соотношение выражает собой полугрупповое свойство оператора
Н. Оно выглядит более изящно, если использовать обозначение
Htz0=H(t, z0).
Тогда (4.69) запишется так:
#G+G 2o = z0 (4-70)
или еще проще:
(4.71)
Особую роль играют динамические системы с инвариантной ме-
рой. Обозначим
Ж^+t, р0) = ЖЦ, р0). (4.72)
Напомним, что Ж^, р0) — мера. Предположим, что для любых t > 0
и некоторой меры р
ЖЦ, р)=р. (4.73)
Тогда у. называется инвариантной мерой данной динамической си-
стемы. Если мера представляет собой распределение вероятностей
марковского процесса г (/), то инвариантная мера обладает следующим
свойством. Если pZo = р, то р( = р для всех t tQ. Таким образом,
у является стационарным распределением вероятностей состояний
133
марковского процесса. Кстати, динамическими системами Описываются
однородные марковские процессы, т. е. такие, для которых
Л,«о,2.И) = -Р/+тл1>+т,2о И) для любого т>0.
Основой для изучения динамических систем с инвариантной мерой
является построение некоторого множества линейных операторов,
связанных с данной динамической системой.
Рассмотрим класс К комплекснозначных функций f (х), интегри-
руемых с квадратом относительно инвариантной меры ц, и определим
в множестве К оператор Ut [/] соотношением
2)]. (4.74)
Так, если Z — плоскость, задаваемая полярными координатами г,
<р, и динамическая система задается соотношением Gt [(г, <р)1 = (г,
Ф + cf), то любая мера вида
р(Х) =§G(r)drd<f> (4.75)
а
будет инвариантной. Оператор Ut будет иметь такой вид:
(О(г, Ф)=Ж Ф + ^). (4.76)
Оказывается, что Ut — линейный оператор, т. е. Ut (аД + |3/2) =
= aUi?! + |3t/(/2, где f\ и /2 — любые элементы К, а и |3 — любые
комплексные постоянные.
Более того, Ut является унитарным оператором в следующем
смысле. Пусть /, g — функции из К. Определим скалярное произведе-
ние (/, g) формулой
(/. g) = $ f И g(x) dp(х). (4.77)
Тогда
(tU = (Л£)- (4.78)
что означает унитарность оператора Ut. Далее, операторы Ut обра-
зуют однопараметрическую группу: Ut1+t2 = Utl Ut2, где, как обыч-
но, произведение понимается как последовательное применение опе-
раторов. Это позволяет применить к анализу Ut спектральную тео-
рию линейных операторов в гильбертовом пространстве, что, в свою
очередь, приводит к доказательству эргодических теорем о поведении
движений динамической системы.
Современный подход к теории динамических систем состоит в сле-
дующем. Динамической системой называется тройка (Z, ц, G), где Z —
абстрактное множество состояний системы, G — группа операторов,
р — квазиинвариантная относительно G мера. Если элементы группы
определяются числовым параметром t, т. е. G = [Ht, —оо < t < оо},
то элемент Ht этой группы можно интерпретировать как оператор
переходов Н (i, z) рассматриваемого выше типа. В общем случае, если
Н — произвольный элемент G, обозначим через Hz, результат приме-
134
нения оператора Н к элементу z множества Z. Подобным же образом,
для любого множества А £ Z обозначим
H(A) = [Hz, z£A}.
Упомянутое выше определение квазиинвариантности меры р оз-
начает: 1) если А — р-измеримо, т. е. р (Л) определена, то также
Н (Л) р-измеримо при любом Н £ G; 2) р (Л) = 0 в том и только
в том случае, когда р (НА) = 0.
Для определенной таким образом динамической системы можно
ввести семейство унитарных операторов:
(ТнП(г)=У^^1(Нг),
где <Ур (Hz)! du (г) — производная меры р (Hz) по мере р (г); f — любая
комплексная функция, для которой [ /‘Др < оо (см. 15]).
Использование результатов теории динамических систем для изу-
чения моделей реальных объектов представляет большой теоретиче-
ский и практический интерес.
ГЛАВА ПЯТАЯ
АГРЕГАТЫ
5.1. ВВОДНЫЕ ЗАМЕЧАНИЯ
Рассмотренные выше математические схемы (конечные автоматы,
динамические системы, системы массового обслуживания и т. д.)
широко применяются для формального описания элементов при моде-
лировании и исследовании сложных систем. На этом пути получены
многие важные теоретические и практические результаты. Однако
необходимо отметить, что таким образом могут быть решены далеко не
все проблемы, возникающие в теории сложных систем и системотех-
нике. В самом деле, единое математическое описание получают только
те системы, элементы которых в результате формализации либо все
оказываются конечными автоматами, либо все — системами массово-
го обслуживания, либо все динамическими системами и т. д.
Другими словами, мы приходим к весьма узким классам сложных
систем. В наиболее существенном с теоретической и практической
точек зрения случае, когда элементы системы описываются разнород-
ными математическими схемами (некоторые — конечными автоматами,
другие — динамическими системами, третьи — системами массового
обслуживания и т. д.), из-за отсутствия единого формального описа-
ния элементов трудно рассчитывать на создание общих методов иссле-
дования системы в целом, а также единого подхода к классификации
сложных систем, изучению общих свойств важнейших классов систем,
их анализу и синтезу. Даже такой, казалось бы, универсальный метод,
как статистическое моделирование, реализуемое на ЭВМ, для достаточ-
но сложных систем с разнородным описанием элементов оказывается
весьма громоздким.
Введение унифицированной абстрактной схемы, позволяющей
единообразно описывать все элементы системы (дискретные, непрерыв-
ные, детерминистические, стохастические), имеет поэтому существен-
ное значение.
Унифицированной абстрактной схеме нужно придать достаточно
общий вид, с тем чтобы она охватывала разнообразные типы реаль-
ных систем. Очевидно, что она, по крайней мере, должна содержать
перечисленные выше математические схемы как частные случаи. Для
этого необходимо, чтобы унифицированная схема имела динамический
характер, описывала обмен сигналами с внешней средой и учитывала
действие случайных факторов.
Исходя из требований такого рода, в качестве унифицированной
схемы можно было бы взять стохастическую систему общего вида
(см. гл. 3). Однако столь общая абстрактная схема имеет свои отрица-
136
тельные стороны. Ё самом деле, принятые предположения (см. гл. 3)
о характере множеств состояний и сигналов и операторов переходов
и выходов оказываются слишком широкими, не обеспечивающими по-
строения эффективного аналитического аппарата для анализа, экви-
валентных преобразований и синтеза сложных систем. Кроме того,
чрезмерные обобщения неизбежно приводят к обеднению содержания
теории — для систем столь общего вида характерны лишь тривиальные
общие свойства.
Поэтому в дальнейшем на множества состояний, сигналов и сооб-
щений, а также на операторы переходов и выходов мы будем налагать
дополнительные ограничения. В частности, в настоящей главе мы рас-
смотрим унифицированную схему, называемую агрегатом, которая
получается из стохастической системы общего вида конкретизацией
операторов переходов и выходов.
Агрегат оказывается удобной схемой для описания широкого клас-
са реальных объектов. Кроме того, представление реальных систем
в виде агрегатов позволяет изучить некоторые их общие свойства, свя-
занные со структурой и функционированием. Например, реализация
на ЭВМ алгоритмических моделей агрегата дает возможность решать
многие задачи количественного и качественного анализа сложных си-
стем. Еще более привлекательными свойствами обладают частные клас-
сы агрегатов (марковские агрегаты, кусочно-непрерывные агрегаты,
кусочно-линейные агрегаты и т. д.), для исследования которых может
быть использован аналитический аппарат теории марковских случай-
ных процессов.
5.2. ПОНЯТИЕ АГРЕГАТА
Формальное определение агрегата как математической модели
сложных систем дается в § 5.5. В настоящем же параграфе дается опи-
сание агрегата как преобразователя информации. При этом основное
внимание уделяется соотношениям, связанным с путями прохождения
информации в агрегате; поэтому такие понятия, как случайный опера-
тор, объясняются здесь на интуитивном уровне. В § 5.5 этим понятиям
будет придан строгий смысл.
Итак, пусть Т — фиксированное подмножество множества дейст-
вительных чисел (множество рассматриваемых моментов времени),
X, Г, У, Z — множества любой природы. Элементы указанных мно-
жеств будем называть так: t £ Т — моментом времени; х£ X — вход-
ным, g £ Г — управляющим, у £ У — выходным сигналами, z g Z —
состоянием. Ниже состояния, входные, выходные и управляющие
сигналы будут рассматриваться как функции времени; их значения
в момент t будут обозначаться z (Z), х (t), у (t) соответственно.
Под агрегатом будем понимать объект, определяемый множества-
ми Т, X, Г, Y, Z и операторами (вообще говоря, случайными) Н и G.
Операторы Н и G, называемые операторами переходов и выходов, реа-
лизуют функции z (/) и у (t). Их структура, которая собственно и вы-
деляет агрегаты среди прочих систем, описывается ниже.
137
Удобно ввести еще пространство параметров агрегата В. Пусть
элемент этого пространства 0 имеет вид 0 = (0lt 0Г) £ В. Значение
0 фиксировано в рамках каждой конкретной задачи; 0 = (0Х, 0р)
обычно называют конструктивными параметрами. В этой связи значе-
ние управляющего сигнала g можно назвать параметром управления.
Рассмотрим сначала реализацию оператора выходов G. Предста-
вим его в виде совокупности операторов G' и G". Оператор G' вырабаты-
вает очередные моменты выдачи непустых выходных сигналов, а опе-
ратор G" — содержание сигналов. Операторы эти строятся следую-
щим образом.
В пространстве состояний агрегата Z для каждого значения
Р£В и ggГ определим некоторое множество Z^gt^ a: Z, вид кото-
рого, вообще говоря, зависит от (g, 0).
Сказанное имеет целью подчеркнуть, что множество Z^g, в об-
щем случае изменяется при изменении параметров агрегата (когда
мы переходим к условиям другой задачи), а в рамках данной задачи —
в моменты поступления новых управляющих сигналов g (/); в интер-
валах времени между моментами поступления управляющих сигналов
множество Z(g/ не изменяется и остается таким, каким оно оказалось
в момент поступления последнего управляющего сигнала.
Множество Z\g, определяет моменты выдачи выходных сигналов.
Именно, если для данного момента времени t состояние z (0) не при-
надлежит Z\gi р) при t — е < 0 < /, где е > 0 — достаточно малое
число, a z (/) С Z(g, р), то t является моментом выдачи непустого вы-
ходного сигнала
y = G"[ttz(t),g(t),$\. (5.1)
В общем случае оператор G" является случайным оператором.
Это значит, что данным t, г (i), g (t) и 0 ставится в соответствие не
одно определенное у, а некоторое множество значений у с соответствую-
щим распределением вероятностей, задаваемых оператором G".
Работа оператора G' заключается в определении очередного мо-
мента достижения траекторией z (/) подмножества Z^gf p)t который яв-
ляется моментом выдачи выходного сигнала.
Выходной сигнал у зависит от последнего управляющего сигнала
g (t) непосредственно через оператор G", а также через множество
Z\gt р), влияющее на момент выдачи выходного сигнала. Как мы уви-
дим ниже, от g(t) зависит также состояние агрегата z(/), являющееся
аргументом оператора G". В этом состоит сущность одного из возможных
способов управления агрегатом посредством управляющих сигналов,
поступающих из внешней среды.
Обратимся теперь к оператору переходов Н. Наряду с состоянием
агрегата z(t) будем рассматривать также состояние z(Z + 0), в которое
агрегат переходит за «малый» интервал времени. Вид оператора Н за-
висит от того, поступают или не поступают в течение рассматриваемого
интервала времени входные и управляющие сигналы. Поэтому мы
138
будем представлять его в виде совокупности случайных операторов
U, V и V".
Пусть tn' — момент поступления в агрегат входного сигнала
хп', тогда
Z(^4-0)= V \t'n, z(t'n), g(t'n), x'n, 0). (5.2)
Здесь под£ (tn') понимается последний управляющий сигнал, поступив-
ший в момент t <
Если tn” — момент поступления в агрегат управляющего сигнала
ёп, то
z(t"n+ 0) =V"{tn, 2 (5.3)
Далее, если tn — момент одновременного поступления в агрегат
и входного хп и управляющего gn сигналов, то
z(tn + V) = V’{tn,V”{tn,z(tn), gn,0Un,xn,0). (5.4)
В этом выражении под V" [tn, z(tn),gn, 0} понимается не оператор,
а результат его действия на аргументы tn,z(tn), gn, 0, являющий-
ся элементом множества Z. Другими словами, вместо (5.4) можно
записать
z(/n + 0)=I/' (/n,a'(/n+0), gn,xn,$\,
где z' (z“n+ 0) определяется соотношением (5.3) для tn, t(tn), ёп, 0-
Наконец, если полуинтервал (tn, tnVi\ не содержит моментов
поступления входных и управляющих сигналов, за исключением
?n+1, a tn — момент поступления входного или управляющего сиг-
нала, то для t£(tn, ^п+11
2(f) = U (/, /п,2(/п + 0),£(/п), 0}. (5.5)
Здесь, подобно (5.2), под g (tn) понимается последний управляющий
сигнал, поступивший в момент t^tn-
В некоторых случаях удобно рассматривать «расширенное» со-
стояние агрегата г (/) вида z (t) = (z (t), g (t)) (Z X Г. Тогда соот-
ношение (5.1) приобретает вид
y = G"{t,i(f),p]- (5.6)
оператор V' — вид
z(^4-0) = (v' {tn, z( tn),Xn, p{,g(tn))’> (5.7)
оператор V"—вид
z(^+0) = (|/" {С, z (t"n), 0),gn)‘, (5.8)
соотношение (5.4) — вид
z(/n + 0)=(i/'MV''K, z(Q,?)gn), xn,0},gn); (5.91
оператор U—вид
z(t) = (U {t,tn,z(tn + G),$},g(tn)). (5.10)
139
Перейдем к описанию типичного процесса функционирования
агрегата в терминах рассматриваемой выше реализации операторов
Н и G.
Пусть в некоторый начальный момент времени t0 агрегат находит-
ся в состоянии z0 = (z (Zo), g0) и пусть в моменты и // поступают
входные сигналы хг' и х2', а в момент — управляющий сигнал g±
и для определенности Z/ < < t2 .
Рассмотрим сначала полуинтервал (/0, //]. Состояния агрегата
г(/) изменяются с течением времени по закону
2(Z) = H(/Jo,2(/o),go,0}. (5.11)
Предположим, что в момент такой, что t0 < , состоя-
ние г (^*) достигает множества Тогда в момент t* агрегат
выдает выходной сигнал
y^ = G"{ti г(с),£о,₽}- (5.12)
Если состояние z (f) опять достигает множества Zfgo,p) в момент
t2* такой, что t-i* < t2* < , то в момент /2* выдается выходной
сигнал
g(2) = G"\t2, z (£), g0> 0} (5.13)
и т. д. Здесь z (//) и z (t2*) определяются из (5.11).
В момент в агрегат поступает входной сигнал х/. Состояние
агрегата
z (t\ + 0) = V {t'i, z (Л), g0, xi, 0}. (5.14)
Здесь также z (А/) определяется из (5.11).
Далее, в полуинтервале (^', t^'] функционирование агрегата мож-
но описать по аналогии с полуинтервалом (t0, t^]. Состояние z (t)
определяется как
z(t)=U\t, t\,z.(t'\ + 0), g0, 0|. (5.15)
Если в моменты /fe*, такие, что < tk* < t^, состояния z (tk*)
достигают множества Z^0,p), в каждый из моментов th* выдается
выходной сигнал
z/W=G"{/L2(/;),go,01; (5.16)
где z (tk*) определяется из (5.15).
В момент t-/’ в агрегат поступает управляющий сигнал g/. Тогда
состояние агрегата
z(t\ + 0) = П4,г(С(),£н0!- (5.17)
Здесь г (//') также определяется из (5.15).
Далее, в полуинтервале (tj", t2] состояние агрегата изменяется
по закону
Z(O = t/!CC,z(/';+ O),g',',0}. (5.18)
140
Если в моменты /А*+;, такие, что </2)/^1, состоя-
ния достигают множества Z^» в каждый из моментов
t*k+i выдается выходной сигнал
z(fk+l\ g\, ₽). (5.19)
Когда в момент /2' в агрегат поступает входной сигнал х2', со-
стояние агрегата
2(^+ 0) V' !/2,z(/2),^,X2,p}, (5.20)
где z (£2') определяется из (5.18).
Затем состояние агрегата в полуинтервале (t2', F], где t — очеред-
ной момент поступления входного или управляющего сигнала, изме-
няется по закону
z(t) = U\t, t'2, z(t'2 + 0),gi, p} (5.21)
и т. д.
В следующем параграфе мы проследим на примерах использование
агрегата для описания процессов функционирования некоторых си-
стем. В заключение настоящего параграфа остановимся на двух во-
просах, имеющих существенное значение для дальнейшего.
Для решения ряда задач нет необходимости различать виды сигна-
лов (входные, управляющие), поступающих в агрегат; достаточно учи-
тывать факт поступления в агрегат в момент времени t обобщенного
входного сигнала х (/) = (x(t), g (/)) g X хГ (см. гл. 3). В этом слу-
чае реализацию оператора переходов Н можно записать более про-
сто. Именно, оператор переходов Н представляется в виде совокуп-
ности двух операторов
2(U0bnWU*('M (5.22)
z(t)= U 2(Д + 0),Н. (5.23)
Оператор (5.22) реализуется в моменты tn поступления в агрегат
обобщенных входных сигналов хп (/) и принимает вид: (5.2), если
gn gx (5.3), если хп = х0, gn ф g.-, и (5.4), когда хп =£ хг\
gn =+g.. Оператор (5.23) описывает изменение состояний агрегата
г (/) в полуинтервалах (Д, /п+1] между моментами поступления обоб-
щенных входных сигналов [см. (5.10)1. Таким способом представления
оператора переходов Н мы часто будем пользоваться в дальнейшем.
Формальное описание некоторых реальных систем приводит к так
называемым агрегатам с обрывающимся процессом функционирования.
Для этих агрегатов характерно наличие среди координат состояния
Д (0, г2 (0> (^ такой координаты [обычно z± (?)], которая имеет
смысл интервала времени т, оставшегося до момента, когда процесс
функционирования агрегата обрывается, если за это время не поступает
очередной входной или управляющий сигнал.
141
Другими словами, среди координат состояния z (1п + 0), выраба-
тываемых случайным оператором (5.4) в момент tn поступления обоб-
щенного входного сигнала х (/„), имеется координата [пусть это будет
Zi (/)] z1 (i) = тп, где тп — случайное время, оставшееся до обрыва
процесса. Оператор (5.5) описывает изменение состояний агрегата
не в полуинтервале (tn, tn+1), а в полуинтервале (tn, /п+1], где
tn+1 = min (/n+1, tn + тп), причем zx (t) изменяется по закону
г1 (t) = tn + T — t. Когда 2X (/) обращается в нуль (предположим, что
tn + т < tn+1), функционирование агрегата прекращается. В другом
случае, когда tn + т ?п+1, в момент /п+1 поступает очередной
обобщенный входной сигнал х (Д+1) и координаты состояния агрега-
та z (/п+1 + 0), определяемого оператором (5.4), содержат новое зна-
чение тп+1. Оператор (5.5) описывает изменение состояний г (/)
в полуинтервале (/л+1, ^+1], где Тп+1 = min {/п+2, ^+1 + тл+1},
и т. д.
5.3. ПРИМЕРЫ
Рассматриваемые примеры имеют целью проиллюстрировать приемы опи-
сания некоторых формализованных систем в виде агрегатов. Попутно мы также
покажем, что агрегат является достаточно общей схемой и охватывает такие из-
вестные схемы, как: конечный автомат, динамическая система, система массового
обслуживания и т.д.
Пример 1. Рассмотрим одноканальную систему массового обслуживания
следующего вида [8]. В моменты времени tj, образующие случайный поток одно-
родных событий, в систему поступают заявки. Заявка, поступившая в момент tj,
характеризуется случайным параметром oij. Если заявка застала обслуживающий
канал свободным, она немедленно принимается к обслуживанию. В противном
случае заявка направляется в очередь и находится там не более чем yj = 0),
где р — параметр системы. Если до момента времени tj + yj j-я заявка не бу-
дет принята к обслуживанию, она покидает систему. В момент окончания обслу-
живания (освобождения канала) к обслуживанию принимается следующая заяв-
ка в порядке очереди. Длительность обслуживания (занятости канала) r]j =
= ^(ау, ₽)•
Представим рассматриваемую систему' в виде агрегата. Состояния системы
опишем следующими координатами: zx(Z) — время, оставшееся до окончания
обслуживания заявки, находящейся на обслуживании; z2(Z) — число заявок в
системе (в очереди и на обслуживании).
Если z2(Z) = 0 (в системе нет заявок), будем считать, что z,(Z) = 0 для всех
t от момента окончания обслуживания до момента появления новой заявки.
Когда z2(t) > 1, заявки имеются как на обслуживании, так и в очереди. В этом
случае требуются дополнительные координаты состояния z1+2^ (!) = сс^', k =
= 1, 2, ..., z2(t) — 1, где — параметр /г-й заявки в очереди; г2+2^ (?) — остав-
шееся время ожидания в очереди для /г-й заявки.
Входные сигналы (заявки на обслуживание) поступают в агрегат в моменты
tj и принимают значения Xj = a.j. Управляющий сигнал имеет фиксированное
значение (множество состоит из одного элемента).
Рассмотрим операторы переходов и выходов агрегата, описывающего данную
систему массового обслуживания.
Пусть в момент tj поступает новая заявка. Если в этот момент канал
занят (z2 (tj) > 0)—данная заявка поступает в очередь; при этом zx (/) не из-
меняется, z2(t)—увеличивается на единицу, z, _^2k (t) и z2_^2k(t)—не изменяют-
ся;
кроме того,
возникают новые
координаты
г1 +2z2(t.) (0) — и
142
г 2^22 (/ (/у) = ф (aJ> Р) характеризующие Поступившую заявку. Если
же в момент tj канал свободен и заявок в очереди нет (в этом случае
z2(/y) = 0 и координаты и Z2 + 2*W не определяются), поступившая
заявка принимается к обслуживанию. Тогда Zj (/у) = ф (ay, f); z2 (tj) = 1,
остальные координаты не определяются.
Исходя из этого, можно следующим образом записать оператор V:
г1 (z>+0) — 2i (z>)i
z2 (tj + 0) = г2 (tj) + 1,
zi + 2*(Z;+°) = zi-!-2A'(^') )
, । п. .. , « < ^(tj!
г24-24(//+ °) — z2 + 2*(zj) )
Zl+222 (tj) (Zj + °) =ai,
22 + 2z3 (/y)(Zj + 0) = (₽(ar P),
л — J
z2 (tj) > 0,
Zi((j + O) = ip (ay, P),
z2 (0 + 0) = 1,
z 1 -J-2* (0+ 0) I
} не определяются.
Z2 + 2k (h + 0) )
z2 (tj) = 0.
(5.24)
Поскольку управляющий сигнал имеет фиксированное значение, оператор
V" не определяется.
Перейдем к рассмотрению изменения координат состояния в интервалах
между моментами поступления входных сигналов.
Для момента tj + 0 координаты состояния определяются в соответствии с
(5.24). Некоторое время после tj состояния zx(/) и z2+2^ (/) убывают с единичной
скоростью, а г2(/) остается постоянной. Координата zx(/), убывая с единичной
скоростью, обращается в нуль в момент tt окончания обслуживания очередной
заявки, в этот момент заявка покидает систему и принимается к
обслуживанию следующая (i + 1)-я заявка из очереди, если г2(/;') >0; поэтому
zr(t) от нуля скачком возрастает до т];+1 = ф(г3, Р) и далее убывает
с единичной скоростью. В этот же момент координата z2(t) уменьшается
на единицу. Если же заявок в очереди нет, Zj(/) остается равным нулю до поступ-
ления новой заявки и принятия ее к обслуживанию. Координаты г2 + 2Й (/),
убывая с единичной скоростью, обращались бы в нуль в моменты
/у + Tj для соответствующих заявок, если бы заявки не принимались к обслу-
живанию. Для тех заявок, которые принимаются -к обслуживанию в моменты
времени / > соответствующие координаты z2 + 2k (t) не определяются. В мо-
менты времени /у + у у (для заявок, не принятых к обслуживанию) координата
г2(/) уменьшается на единицу (заявка уходит из очереди и покидает систему)..
Поведение координат гх(/), z2(i), z1+2fe(0 и z2+2ft как функций времени для
одного из возможных процессов функционирования системы показано на
рис. 5.1.
Прежде чем записывать соотношения для оператора U, обратимся к мно-
жеству ₽) и опеРатоРУ О- Множество Z^ удобно выбрать в виде
объединения двух подмножеств Zjy> и z!+- Подмножество Z^y' определяется
соотношением z1(t) = O, а подмножество Z^y> — соотношением г2^2<:(0 = °
хотя бы для одного k.
В рамках данного примера под выходным сигналом естественно понимать
совокупность характеристик заявки, покидающей систему. Будем считать, что
у=(у{1\ г/(2)), где—признак (г/11’ = 1, если систему покидает обслуженная за-
143
явка и z/(1> =0—если необслуженная заявка), а у<2)—совокупность сведений о за-
явке, например {/2=(ау, 0, t*) значит, что заявка поступила в систему с харак-
ристикой ay, обслуживалась при значении параметра системы 0, покинула си-
стему в момент t*. В качестве у(2>, в зависимости от конкретной задачи, могут фи-
гурировать и другие величины или функции от них. Таким образом, действие опе-
ратора G сводится к выбору признака у(1)и формированию сведений о заявке
Пусть в момент tr* состояние агрегата достигает подмножества 7± . Зна-
чение определяется из соотношения z1(Z*1) = 0. Это означает, что обслужива-
ние очередной заявки закончилось. В момент агрегат выдает выходной сиг-
нал у =(1, ay, 0, Z*i). Если в момент t*2 состояние агрегата достигает подмно-
жества Z2^y* (значение t*2 определяется из соотношения z2 + 2ft (/*2)=0), значит
время ожидания в очереди одной из заявок истекло п заявка покидает систему
необслуженной. В этом случае у = (0, ay, Р, /*2).
Перейдем к оператору U. Для упрощения записи оператор U удобно пред-
ставить в виде совокупности операторов U, W и W".
Пусть t= (обслуживание очередной заявки закончено). Здесь могут
быть два случая. В первом (когда в системе имеются заявки, г2(Рх) > 0)
к обслуживанию принимается следующая заявка из очереди; время обслужива-
ния т =ф(а1, 0). Во втором (в системе заявок нет, z2(^) = 0) система ждет до мо-
мента поступления новой заявки и ее принимает к обслуживанию . Этот послед-
ний случай мы уже частично рассмотрели выше, когда описывали оператор
V (5.24) при условии, что z2(/y) = 0. Нам осталось определить состояния агре-
гата в полуинтервале от момента окончания обслуживания до момента поступле-
ния новой заявки.
144
Приведенные рассуждения показывают, что состояния агрегата 2(f*j + О
определяются оператором П7':
?1 (/Я 0) = ip (г3, Р)
га(/1 ' о) -:Z2 (/i)— 1
zi+2h (G +°)=г1+2 (*+1) j k 2
г2+2к(^1+°)^22 + 2 (fe-H) (/J J 2 1
21(/;+o)=z1(/d=o
гЖ+0) =0
21+2*(/j+0) 1
} не определяются
22+2и/;+о) I
г2 (/*)= 0.
I
г2(/*) > 0.
(5.25)
В момент /*2, когда истекает время ожидания одной из заявок, например Лй,
число заявок в системе уменьшается на единицу. Состояние агрегата г((*2 + 0)
определяется оператором
zi (i-а + О) = 2а (/г),
2г (/2 +0) = zi(t 2)—
г1+2Л (/2 +0) = 2i+2ft (/2)
г2 + гА (/2 4- о) = 22 + 2Й (/2)
(5.26)
г1 + 2й(^2^0) Z1 -f-2 (й+ I) (Q 1 . ,
, , } I < k < г, U,
Z2+2U^+0) = Z2+2U+1)(/D I
В полуинтервале (tn, /п + 1] между «особыми» моментами tn, tn + 1, к кото-
рым относятся моменты поступления в агрегат, входных сигналов и выдачи агре-
гатом выходных сигналов, состояния агрегата изменяется по закону, определяе-
мому оператором U:
2i (/)=2i (/n4-0) — (t-tn),
гг (/) = 22 (tn +0),
2l + 2fe (t) = 2l + 2fe (tn +0).
22 + 2ft (/) ~ 22 + 2?l (tn 4” 6) (t tn)-
На этом будем считать законченным построение агрегата, описывающего-
рассматриваемую систему массового обслуживания.
Аналогичное описание может быть сделано и для других типов систем мас-
сового обслуживания. В частности, для многоканальной системы необходимо
иметь координаты [вида г^/)], характеризующие время, оставшееся до оконча-
ния обслуживания, для каждого канала.
145
Пример 2. Усложним предыдущий пример таким образом, чтобы полу-
чить систему массового обслуживания с управлением [8]. Пусть в моменты вре-
мени tm, образующие случайный поток однородных событий, в систему поступают
управляющие сигналы g(/m) = Pm. Реакция системы на управляющий сигнал
состоит в том, что в каждый момент tm отменяются назначенные ранее времена
ожидания заявок в очереди у/ и время обслуживания г]/ и независимо от того,
сколько времени заявка ожидала или обслуживалась, реализуются новые, оп-
ределяемые по формулам ?;=ф(а/, Pm). т],/ = Ф(а.7. Pm) при новом значении Pm-
Для заявок, поступающих в систему или принимаемых к обслуживанию в мо-
менты времени tm <t < tm + it времена у7- и т)7- вычисляются по тем же формулам
при Р = Рт-
Состояние агрегата z(t), соответствующего усложненной системе массового
обслуживания, можно описать теми же координатами, которые были введены
в предыдущем примере. Оператор V' будет иметь вид (5.24) с учетом того, что
21 + 2./ (О ”1“ 0) =ф(а/. Pm)-
Поскольку в моменты tm поступают , вообще говоря, различные управляю-
щие сигналы Рт, необходимо ввести оператор V":
г1 РтФЩ — Ф (а/. Рт).
г2 (^т + 0) = г2 (^т).
г14-2А^т + °)=г1 + 2&
22+2И^т + 0)=<Р(«'/г- ₽„Л
(5.28)
определяющий случайный скачок состояния в момент времени tm.
Подмножества Z[y* и Z^v' , а также операторы W, W" и U описываются
теми же соотношениями, что и в предыдущем примере, но при Р = Рт.
Пример 3. Радиолокатор измерения наклонной дальности I и азимута a
в системе управления крупного аэродрома (см. гл. 1) предназначен для опреде-
ления координат самолетов, прибывающих в аэропорт, в секторе, ограничен-
ном азимутами а0 и а*. Угловая скорость вращения луча обзора в горизон-
тальной плоскости равна и. В момент совмещения луча обзора с самолетом
радиолокатор фиксирует азимут луча ал и длительность т интервала времени
между моментами посылки зондирующего импульса и получения сигнала, от-
раженного от самолета. Когда ал(/) достигает значения а* (текущий обзор
закончен), с радиолокатора снимаются- координаты /г, аг всех самолетов,
обнаруженных в секторе (а0, а*). Здесь /, — момент обнаружения /-го само-
лета, ti = t0 ф- (anf — ao)/co; to — момент начала обзора, а Ц = <р(Т;, с),
с—скорость распространения радиоимпульса, а функция <р связывает т; и с с
дальностью Затем луч обзора скачком переходит в положение а0 и начинает-
ся новый обзор. Управление радиолокатором осуществляется путем измене-
ния (сообщения новых) границ сектора обзора а0 и а*, а также значений уг-
ловой скорости <13.
Для представления радиолокатора в виде агрегата введем следующие коор-
динаты состояния:
zr(/) — азимут луча обзора;
z2(/) — число самолетов, обнаруженных в текущем обзоре;
z8j-(/) — момент tj обнаружения /-го самолета, j = 1, 2, ..., z2 (/);
2з/4-1 (t) — азимут а} /-го самолета;
2з;+2 (О—длительность интервала т/, для /-го самолета.
Входной сигнал Xj — самолет, с которым совместился луч обзора, Xj =
= (tj, aj, т?-). Управляющий сигнал g имеет координаты a0, а*, ш.
Множество gj определяется соотношением zx(/) = а* (текущий обзор
закончен). Момент t* выдачи выходного сигнала совпадает с моментом окончания
146
обзора (определяется из уравнения zx(/*) = а*. Выходной сигнал у имеет коор-
динаты yt = tit yi+i = а;, i/;+2 = xit i = 1,2.z2(i*).
Пусть в моменты поступают входные сигналы (луч обзора совмещается
с самолетом). Состояния агрегата z(t^ + 0) определяются оператором V:
zi (Za + °)= г1(<).
0) = Z2(^)+1-
23i(zfe+ °) = z3j(Za)’ /=1-2- •••> т = гМ.
гз/+ 1 0) = гз/+ 1 0а)> (5.29)
г3/+ 2 (^+ 0)|= гЗ/+2 (^а)>
г3 (т + I) ( Ч + °) = *т + 1,
г3 (т+ 1)+ I (**+ °) = am+ 1,
г3 (m-f- 1)4-2 + 0) = T/n4- 1-
Если в момент поступает управляющий сигнал gk = (а'*', а^*, <од), теку-
щий обзор отменяется и начинается обзор в новом секторе; состояние z(/ft +
+ 0) описывается оператором V:
г1 К+ °) = аоА) >
г2(^+°) = °- (5.30)
Остальные координаты не определяются. Новый управляющий сигнал ока-
зывает влияние на множество pj (г1(^) = ал*) и оператор G'.
В полуинтервалах между поступлениями входных и управляющих сигна-
лов состояния агрегата изменяются по закону, описываемому оператором U:
г1 (0 = г1 (^А + 0) + ш (t —
z2 (0 = z2 (Zft + 0),
г3Л0 = г3у(^ + 0), (5.31)
23/4- 1 (0 = гЗ/4- I (^ft+ °).
гЗ/4-2 (/)=гЗ/4-2 (Gi+ °)’
а в момент = + —ао)/Шй — оператором II’:
г10й+°) =“оА)-
z2(^+0) = 0; (5.32)
остальные координаты не определяются.
Пример 4. Конечный автомат. Будем рассматривать следующий вариант
определения конечного автомата [6]. Имеется конечное множество Z состояний
автомата, входной алфавит (множество входных сигналов) X и выходной ал-
фавит (множество выходных сигналов) Y. В начальный момент времени t= 0
состояние автомата есть z0 G Z. В моменты t = 1, 2, .... п на вход автомата по-
ступает последовательность сигналов: соответственно х(1), х (2).. х(п), ...
Состояние автомата в момент t обозначим z(t). Тогда процесс смены состояний ав-
томата определяется рекуррентным соотношением
z(/H-i) = ф(2(0, 2(0). (5.33)
147
В любой момент i = 1, 2, п автомат посылает выходной сигнал y(t),
определяемый соотношением
(5.34)
Функции двух переменных ф и гр называются соответственно функцией пе-
реходов и функцией выходов конечного автомата.
- Покажем, как такой автомат представить в виде агрегата. Для этого в оп-
ределении агрегата выберем в качестве Т множество точек {О, 1, 2, в каче-
стве множеств X, Y, Z — соответствующие множества для рассматриваемого
автомата, т. е. X = X, Y ~ Y, Z = Z, в качестве Г возьмем некоторое одноэле-
ментное множество; примем, что операторы Н и G” определяются функциями ф
и ф соответственно и положим Z^p; = Z. Построенный таким образом аг.
регат будет функционировать в точности так же, как исходный автомат. Правда,
дополнительно следует потребовать, чтобы входные сигналы поступали во все
моменты времени 1, 2, 3,....
В самом деле, если обратиться к описанию агрегата, то в данном случае
получим
z (< + !)=// [г (0, х(/)] = ф[г(0, х (0],
у (0=О’[г(0] = г|;[г (0J.
(5.35)
(5.36)
Выходные сигналы выдаются во все моменты времени t = 1,2,...., посколь-
ку Zjp)g) = Z. В качестве конструктивных параметров |3 можно выбрать неко-
торые параметры, характеризующие функции ф и гр или даже сами эти функции.
Если начальное состояние агрегата, моделирующего конечный автомат, фикси-
ровано, то его функционирование полностью детерминировано.
К этому примеру можно подойти и с другой стороны. Именно, построим
агрегат, работающий в непрерывном времени, выход которого в точности сов-
падает с выходом конечного автомата в моменты времени f = 1, 2, 3, ... . Для
этого рассмотрим агрегат, у которого Г состоит из единственного элемента, X
и Y — конечные множества, совпадающие с соответствующими множествами для
конечного автомата, т. е. X = X, Y = Y, а в качестве пространства состояний
агрегата Z выберем прямое произведение множества Z на отрезок [0, 1],
т. е. Z = Z X [0, 1].
Будем обозначать состояние агрегата через z = (гь г2), где г1 Q Z, a z2
G [0, 1]. Координата г2 имеет смысл времени, оставшегося до очередного изме-
нения состояния автомата, и в момент t > 0 равна
г2(0 = Ш-0
(5.37)
где ]/[ — наименьшее целое число, не меньшее t. Очевидно, г2(0 уменьшается
с единичной скоростью до значения 0, когда i лежит в промежутке между целыми
числами, и совершает единичный скачок в момент достижения нулевого значе-
ния. То есть, если п — 1 < t < п, п — целое положительное число, то
= —1, а z2(0 = п в момент /=п координата z2(0=O; при п < t < п + 1
координата z2(Z) = п + 1 — t и т. д.
Пусть в момент / 0 состояние агрегата z(0) == (z10, 2^0), где z10 — неко-
торая точка из множества Z, a z20 = 1. Зададим множество равенством
Z\g} Р) = !г = (zi. гз); г2= 0|- Тогда оператор перехода V (реакция на поступ-
ив
ление входного сигнала в момент времени п, п— положительное целое число)
задается равенствами:
z1(« + O) = <p[z1(n), х(п)],
г2 (п + 0) = 1.
(5.38)
Оператор перехода U, действующий между моментами поступления входных
сигналов, зададим следующим образом:
z(/) = (zi(/), z2 (t)) = U [г («)] = (?i (п + 0), п+1—О,
(5.39)
где п < t <- п + 1.
Оператор G" имеет вид
i/=G"[z(n)] = ф [гг (п)].
(5.40)
Вспомним, что выходные сигналы выдаются лишь в моменты достижения
координатой z2(l) нулевого значения, т. е. в целочисленные моменты времени.
Если теперь предположить, что Г — произвольное конечное множество,
то получим автомат с переменной структурой, изменяющейся под воздействием
управляющего сигнала. Рассмотрение таких автоматов существенно для теории
надежности вычислительных машин.
Пример 5. Динамическая система. Пусть Z — метрическое пространство,
a F(t, z) — семейство его преобразований, удовлетворяющее условиям гл. 3
Динамическую систему (Z, Е) представим в виде агрегата.
Введем фиктивный входной или управляющий сигнал, поступающий в аг-
регат в момент t0 и имеющий смысл начального состояния динамической систе-
мы z0.
Состояние агрегата z(/0 + 0) определяется оператором V:
2 (^о + О) —z0-
(5-41)
В качестве оператора U используем преобразование динамической системы
z(0 = E {z (Zo + O), t}.
(5-42)
Выходными сигналами можно считать любые функции от состояния дина-
мической системы, моментами выдачи выходных сигналов — любые моменты
времени t Т, определяемые заданными условиями, в том числе и все t £ Т.
В последнем случае множеству Z^ принадлежит каждая точка данной траек-
тории динамической системы.
Пример 6. В n-мерном векторном пространстве рассмотрим систему, описы-
ваемую дифференциальным уравнением
z(0).
at
(5.43)
Предположим, что в некоторые моменты времени в систему поступают
входные сигналы х = (хх, х2.... хп), приводящие к «возмущениям», а именно,
в момент поступления сигнала состояние системы z = (zx, z2, ..., ztl) заменяется
состоянием z* = (zx*, z2*, ..., zn*), где z* = z* (th, z, x).
Описанная система легко сводится к агрегату. Именно множеством состоя-
ний агрегата будет «-мерное пространство векторов z= (zx, z2, ..., zn). Множество
входных сигналов включает фиктивный входной сигнал, задающий в момент t0
начальное состояние системы z0.
Если — момент поступления входного сигнала х, то состояние агрегата
z(.tk “I" 0) определяется детерминистическим оператором V:
г Цй + °)=г*(^’ г- ХУ
(5.44)
149
В полуинтервалах tk, ^+11 состояние агрегата изменяется по закону,
описываемому детерминистическим оператором U:
(5.45)
at
В связи с тем, что решение дифференциального уравнения (5.45) может
иметь конечную область существования при данном начальном условии, рас-
сматриваемый агрегат удобно представлять как агрегат с обрывающимся процес-
сом функционирования. Время т, оставшееся до обрыва процесса, определим как
точную верхнюю грань тех s > t, для каждого из которых в интервале (/, s)
существует решение уравнения (5.45), удовлетворяющее начальному условию
2(^+0)), t'k<t<t'k+x.
Пример 7. Между пунктами А и В шоссейной дороги движутся автомобили
в двух направлениях. Скорость v свободного движения автомобиля зависит от
качества покрытия дороги (коэффициент сцепления /), профиля дороги в верти-
кальной плоскости (угол наклона 0), собственного веса автомобиля т и перево-
зимого груза R, мощности двигателя Н, условий видимости (ночь, туман).
Кроме того, скорость автомобиля снижается за счет интенсивности движения на
дороге, наличия и расположения дорожных знаков, ограничивающих скорость,
запрещающих обгон и пр. (Рх — координата знака, р2 — его содержание, 03 —
протяженность участка действия и т. д.) В процессе движения между автомо-
билями соблюдаются интервалы безопасности /g, зависящие от скорости v.
Интервалы времени между моментами появления новых автомобилей на
дороге в точке А (соответственно точке В) являются независимыми случайными
величинами, имеющими показательное распределение с параметром Хл (соответ-
ственно Хв). Поток прибывающих автомобилей содержит Sx% автомобилей пер-
вого типа, S2%—второго типа, S;%—/-го типа и т. д. Размер перевозимого груза
Ri и скорость автомобиля в момент появления на дороге voi являются незави-
симыми случайными величинами, имеющими заданные распределения вероят-
ностей. Условия движения зависят от погоды (сухо, дождь, гололед и т. д.).
Это обстоятельство учитывается случайными поправками к коэффициенту
сцепления f. Зависимость скорости v автомобиля от условий видимости учиты-
вается случайными поправками Дп,. Поправки и Дп; имеют заданные распре-
деления вероятностей.
Сделанные предположения используются лишь в процессе формирования
входных и управляющих сигналов.
Вследствие наличия на дороге автомобилей, движущихся с различными ско-
ростями, может возникать необходимость обгона. Обгон возможен, когда имеет-
ся интервал между впереди идущими автомобилями не менее 2/g, не мешают ав-
томобили встречного потока (интервал во встречном ряду не менее Lo), нет за-
прета обгона и т. д. Если обгон невозможен, автомобиль снижает скорость и дви-
жется за впереди идущим транспортом, оставаясь претендентом на обгон при бла-
гоприятных обстоятельствах. Автомобили, прибывающие в пункт назначения
(точки А и В), характеризуются (помимо скорости, типа и величины груза) рас-
ходом времени т, затраченного на преодоление участка дороги АВ.
Процесс автомобильного движения рассматривается как агрегат с внутрен-
ними состояниями г, описываемыми координатами; zx = v •— число автомобилей
на участке АВ; = sj — расстояние автомобиля от точки A; zej_3 = Vj —
скорость /-го автомобиля; гв;-_2 = п — номер типа; zey_x = R — величина
груза; zej = т — длительность пребывания автомобиля на участке АВ; z0;-+x =
= р — признак (р = 0, если автомобиль появляется в точке А; р = 1 — в точ-
ке В). Входной сигнал х имеет координаты; хх = р; х2 = т; х3= R; xt = v0.
Управляющий сигнал g описывается координатами: gx = Д/ — поправка к коэф-
фициенту сцепления; g2 = Дц— поправка к скорости. Выходной сигнал у имеет
координаты; у2 — р; у2= v(th), где /й — момент окончания маршрута; у3 =.
= T(/ft); yt = т; уь = R.
150
Перейдем к операторам И и Q. В качестве можно выбрать объединение
множеств, определяемых соотношениями:
z6j-4 (О =SB> 26/+l(Z)=0;
. . (о.4о)
26y —4^) = o> z6/+1 (0 = 1‘
Оператор G' формирует моменты выдачи выходного сигнала (дости-
жения j'-м автомобилем точки В или Д), удовлетворяющие соотношениям (5.46),
а оператор G" формирует сам выходной сигнал
У1 = г6/,+ । (fh),
J/2=Z6/'—з(У >
Уз= z6j, (ih),
Уз=гЬ/.,_1(1к) (5_47)
IF _
Оператор U представим в виде совокупности двух операторов: W и U.
Оператор IK:
zi (*fe + 0) =г1 1> (5 48)
г,(^+0) = г,(/й), / = 6/-4, 6/-3....
а для j = j' координаты zz (ZZ| + 0) не определяются.
Оператор U (1^ —момент поступления последнего входного или управля-
ющего или выдачи последнего выходного сигнала):
ч (0 = 2Д^+0),
t
г6/_4 (0= z6/_4((A+0) + f z6,-_3(0^,
^б/-з(0 = ^(Л 0. ’»> R, Ht pz, bf,bv, t, g),
z6/-2(0=z6/-2(^+0), (5.49)
z6/_i (0=z6y_1(^+ °),
26/W=26/(^+o) + (/-Q,
z6/+ i (0=z6/+1 (^+
Преобразования координат оператором U, описанные (5.49), очевидны, за
исключением, быть может, на котором целесообразно кратко остано-
виться. Скорость автомобиля определяется параметрами, перечисленными в (5.49)
в случае свободного движения (£ = 0), т. е. когда автомобиль не является пре-
тендентом на обгон |s; —зпр|>/б, где зпр —расстояние от точки А до авто-
мобиля, идущего впереди /-го. Если же |sj—snp | = /е и vOj > v (скорость пре-
дыдущего автомобиля), то vj = опр.
Когда появляются условия для обгона: 1) интервал в своем ряду более 2/g,
2) интервал во встречном ряду более L, 3) отсутствует запрет обгона, то ско-
рость V] восстанавливается. Подробное рассмотрение этого вопроса не входит
в нашу задачу.
Если t* — момент поступления входного сигнала х = (р, т, R, v0), состоя-
ния z ((* + 0) описываются оператором V':
z1(/*<E0) = z1(/*) + l, .
zZ ((*4~0) = zz (/*), / = 6/ —4,6/—‘3, 6/4-1; /=1,2, ..., n = Z1(/*),
(0, если ц = 0,
гб (п-Ь1)-4 +°) = L если ц= 1
г6{,1+1)_3(^ + 0)= п0;1, (5.50
z6 (n+i)_2 (/* + 0) = mn,
151
гб (п+ I) — 1 7* + о)~ Rn-
гб(,г+1)^ + °) = 0-
гб (n+i) +1 U*+o)=p.n-
Если в момент t' поступает управляющий сигнал g = (&f, Ло), состояния
агрегата описываются оператором V":
г(Г4-0)=г(Г). (5.51)
Новый управляющий сигнал оказывает влияние на оператор U (в выра-
жение для z0j-_3 подставляются новые значения А/ и Ди).
Данный пример иллюстрирует лишь методику представления автомобиль-
ного движения в виде агрегата. При решении задач исследования автомобильного
движения в конкретных условиях могут быть использованы другие зависимости.
5.4. ОБРЫВАЮЩИЙСЯ СЛУЧАЙНЫЙ ПРОЦЕСС.
СЛУЧАЙНЫЙ ПОТОК
До сих пор мы рассматривали агрегат как некоторый «черный
ящик», способный принимать внешние сигналы х и выдавать выходные
сигналы у. Однако специфика агрегата как математической модели,
пригодной для формального описания реальных сложных систем, глав-
ным образом связана со способами построения операторов движения
и функционирования.
Поскольку процессы функционирования реальных сложных си-
стем, как показано в гл. 1, носят случайный характер по самому своему
существу, независимо от наличия возмущающих факторов, для фор-
мального их описания целесообразно использовать понятия, идеи и ме-
тоды теории случайных процессов.
В § 4.3 были приведены некоторые сведения из теории вероятностей
и теории случайных процессов. В частности, там было сказано, что
случайный процесс является функцией двух переменных: со и t,
где и — элемент вероятностного пространства Q, a t — элемент мно-
жества рассматриваемых моментов времени 1.
Здесь нам, однако, понадобится несколько более общее понятие,
которое назовем обрывающимся случайным процессом. Именно, пусть
каждому со ( Q поставлены в соответствие число оо т = т (со) О
и функция £ (t, со), определенная при любых со для 0 t т (со)*);
определяется ли эта функция на концах интервала (0, т), решают в каж-
дой задаче конкретно по специальному условию. Система функций
(т (со), £ (/, со), 0 < t т (со)) называется обрывающимся случайным
процессом. Иначе говоря, у обрывающегося случайного процесса каж-
дая его реализация £ (7, со) имеет свое собственное время определения
т(со). Понятие обрывающегося случайного процесса играет важную
роль в современной теории случайных процессов.
Наряду со случайным процессом определим понятие случайного
потока. Пусть по-прежнему со — элемент вероятностного пространства
(Q, 5, Р). Случайным потоком назовем пару
{/(ш); УДш), t 6 /(«)),
Разумеется, выбор в качестве начального момента точки 0 не ограничи-
вает общности.
152
где I (<n) — конечное или счетное множество моментов времени, причем
в последнем случае потребуем отсутствия у этого множества конечных
точек накопления; Yt (со) принимают значения у (t) из некоторого
измеримого пространства Y. Таким образом, под случайным потоком
понимается совокупность случайных моментов времени I (со) и слу-
чайных значений некоторой функции Yt (со), принимаемых в моменты,
принадлежащие последовательности I (со). По существу, случайный
поток является специальным случаем случайного элемента.
В данном случае в качестве элемента (со) выбирается пара
[7 (со); Yt {<£>), t Е 1 (со)}. Обозначим множество значений таких пар
через X. Как указывалось выше, это множество должно быть изме-
римым и на нем должна быть задана о-алгебра S*. В качестве S* вы-
берем минимальную о-алгебру, содержащую следующий класс 8\
подмножеств X. Пусть п 1 — произвольное целое число; Aj, Д2,
..., Дп — любые непересекающиеся интервалы на оси времени; Ль
А2, Ап— любые измеримые подмножества пространства У.
Обозначим через х(А/, 7) число точек совокупности I, попадающей
в интервал А;. Тогда класс S*lt порождающий о-алгебру S*, является
совокупностью всевозможных множеств вида
A*=--{(/;K,J 6/):х(Аг,/)=1, У/ПД/еА, /=1,-Д}.
Таким образом, множества вида {со: (7 (со); Yt (ю), t Е 7 (со)) £ В* Е •$*}
являются событиями, т. е. для них определена вероятностная мера Р.
Заметим, что на одном и том же пространстве элементарных со-
бытий Q можно задать сколько угодно случайных процессов, потоков
или тех и других. В дальнейшем нам потребуются параметрические
семейства обрывающихся случайных процессов, и случайных потоков.
Символы, обозначающие параметры, будут записываться как аргу-
менты введенных выше функций перед символом со.
5.5. АГРЕГАТ КАК СЛУЧАЙНЫЙ ПРОЦЕСС
В настоящем параграфе мы остановимся на общем определении
агрегата. Для этой цели будут использованы понятия обрывающегося
случайного процесса и случайного потока, рассмотренные выше.
Исходя из методических соображений сначала определим понятие
автономного агрегата, т. е. агрегата, который не может воспринимать
входных и управляющих сигналов. Другими словами, будем предпола-
гать, что пространство X содержит единственный фиксированный эле-
мент.
Пусть заданы: измеримое пространство элементарных событий
Q с вероятностной мерой Ро (А) и пространства Z — внутренних со-
стояний и У — выходных сигналов агрегата, t0 — фиксированный
начальный момент времени. Кроме того, пусть заданы:
1) параметрическое семейство обрывающихся случайных процес-
сов, зависящих от числового параметра 0:
(то(0,®)Д(0Д,®), О<7<то(0,(о));
£(0Д, <о) QZ, <в Е Й; (5.52)
153
2) параметрическое семейство случайных потоков
(/0 (0, <о); Yt (0, <о), t 6 /0 (9, м)!, (5.53)
где верхняя грань sup [Л t 6 /о(0, со)! т0 (0, со); нижняя грань
inf U : t С /0 (9> И)1 0, а Yt (9> ®) ПРИ 6 1о (9> ю) принимают зна-
чения у (/) из пространства Y, у (Z) £ Y.
Совокупность введенных здесь объектов полностью определяет
автономный агрегат.
При фиксированных 0=fo и <о=со0Е И реализации (t0, t—10, <о0)
случайного процесса С (9. t, ®) в соответствии с введенной выше терми-
нологией представляют собой реализации случайного оператора пере-
хода агрегата z (/), а значения z (Z) Е Z при любом фиксированном
t € [z'o, + Т1 — внутренние состояния агрегата. Реализация случай-
ного потока [/0 (/0, со0), Yt (i0> со0), t—IQ (t0, cd0) } при фиксированных
ta и co0 определяет выходные сообщения [f, У/)ц+т в полуинтер-
вале [/0, t0 + т), а значения Yt 6 Y являются реализациями выходного
сигнала y(t) агрегата.
Автономный агрегат функционирует следующим образом. В мо-
мент t0 выбирается элементарное событие соо из пространства Q в со-
ответствии с распределением вероятностей Ро (А). Вследствие этого
определяется момент времени t0 -j- т0 (£0, и0) — окончание функцио-
нирования агрегата (момент обрыва). При t0 t t0 + т0 (t0, со0)
внутреннее состояние агрегата определяется формулой
?(0 = £о(М~k, ®0). (5.54)
Всякий раз, когда t0 t t0 + то соо) и t — t0 £ /0 (t0, соо) >
в момент t агрегат посылает выходной сигнал
у = (/0, соо). (5.55)
В момент tQ + т0 (f0, со0) функционирование агрегата прекращается.
Заметим, что при фиксированном соо агрегат ведет себя вполне
детерминированным образом; параметр соо как бы вбирает в себя всю
случайность.
Рассмотрев принципы описания процесса функционирования ав-
тономного агрегата, можно перейти к общему случаю — изучению
определения неавтономного агрегата. Будем считать заданными изме-
римое пространство элементарных событий Q с вероятностными мера-
ми Ро (А) и Р (А), а также пространства X —обобщенных входных
сигналов, Z — внутренних состояний и Y — выходных сигналов.
Кроме того, пусть заданы:
1) параметрическое семейство обрывающихся случайных про-
цессов, зависящих от параметра 0 (5.52);
2) параметрическое семейство случайных потоков, зависящих
от того же параметра (5.53);
154
3) параметрическое семейство обрывающихся случайных процес-
сов, зависящих от параметров г, 0, х:
+ {(т (г, 0, х, со); £ (г, 0, хД, со), 0 <(г, 0, х, со)}, (5.56)
где £ (г, 0, х, t,a>) £ 2, со £ Q;
4) параметрическое семейство случайных потоков, зависящих
от тех же параметров:
{/(z, 0,х , со), Yt (z, 0, х, co), t £ I (z, 0, x, co)), (5.57)
где
sup [t: t £ I (z, 0, x, co)] г (z, 0, x, co),
inf \t: t £ / (г, 0, x co,)] 0,
Yt (z, 0, x, co) £ Y.
Пусть t0 — фиксированный начальный момент времени, а
tr < ^2 < ••• < tn < •• моменты поступления в агрегат обобщенных
входных сигналов хх, х2, ..., хп, ... , причем /х. Пусть со0, сох, ...,
соп, ...—последовательность независимых случайных элементов Q и со0
следует распределению Ро (Л), а сох, со2, ... — распределению Р (Л).
Для некоторого п 1 обозначим состояние агрегата в момент tn
символом z (tn) = zn и
1п = min {tn+1 Дп +т (sn, tn, хп, соп)}.
Тогда в полуинтервале (tn, /Д внутренние состояния агрегата за-
даются соотношением
2 (0_= ь (zn,tn, хп, t—tn, соп)._ (5.58)
Если t—tn < т (zn, tn, хп, <оп) и t — tn С 7 (zn, tn, xn, co„), то в момент
t агрегат выдает выходной сигнал
y = Yt~tn{zn, tn, хп, соп). (5.59)
Таким образом полностью определяется функционирование агре-
гата при t > /х. Теперь необходимо рассмотреть отрезок времени
[£0, /х]. В течение этого отрезка агрегат не получает входных сигналов.
Поэтому состояния его можно описать соотношением (5.54), а выход-
ные сигналы определить в соответствии с (5.55).
Функционирование агрегата начинается с того, что в момент /0
реализуется элементарное событие соо в соответствии с распределением
Рй (Л) и определяется значение т0 (£0, со0). В интервале /0 С t +
+ т (t0, cofl) реализуется процесс £ (t0, t, со) и поток {/0 (tQ, со0);
Yf (to, со0), t £ Iо (to, й>о) 1 •
1) определяется неслучайный оператор движения агрегата
z (0 = So (to, t — to, со) как одна из возможных реализаций случайного
процесса t, (t0, t, со), описывающий состояние агрегата в интервале
to t to + т0 (to, СОО);
2) определяется конкретное выходное сообщение (/, У/]/’+т°
как одна из возможных реализаций случайного потока (/0 (t0, <о0);
155
Yt (t0, co0), t £ 70(4, <»o)}, t. e. моменты t выдачи выходных сигналов
(4 sC t t0 + та (tg, coo); t — t0 £ Ig (/0, cou)) и сами сигналы у =
= Yt — ta (4, ®o)-
Функционирование агрегата происходит таким образом до момен-
та 4 = min (4, 4 + то (4, Фо)}, где 4 — момент поступления в агре-
гат входного сигнала х. Если т0 (4, <о0) <4 — 4, то на этом, т. е.
в момент tg + т0 (4, сои), функционирование агрегата заканчивается.
Если же 4^4 + то (4, Фо), то описанный выше закон функцио-
нирования агрегата будет справедлив лишь в интервале 4^7 < 4-
Поступающий в момент t± входной сигнал хг отменяет реализацию
процесса £ (4, t, со) и потока (/0 (4, со0); Yt (4, <о0), t 6 70 (4, со0)}
при 4- В момент 4 реализуется элементарное событие с й
в соответствии с распределением Р (Л), независимое от со0, и определя-
ется значение Tj (гп 4, *i, wi)-
В интервале t t 4 + Л (гс 4, xlt сох) реализуется процесс
£i (z1; 4, xlt t— 4, Ф1) и поток {/ (zx, 4, л'1, Ф1); Yt (zi'< 4, xi, ю1),
t I (г1, 4, xi> Фе)};
1) определяется некоторый неслучайный оператор движения
z (/) = £ (z1; 4, xi, I — 4, ®i) как одна из реализаций случайного про-
цесса £ (zlr tlt xlt t, co), описывающий состояния агрегата в интервале
4 —4 7 4 I 4, Фе),
2) определяется конкретное выходное сообщение (4 Уд4ц+Т1
как одна из возможных реализаций случайного потока {/ (zlr 4, *1,
и1); Yt (z1; 4, xi, ®i), t£I (?!, 4, xi> ©с)}, т- e- моменты t выдачи вы-
ходных сигналов (4^ t 4 + T (zi, 4, *1, ®i), 7— 4 6 I (-4, 4, xi,
Wj)) и сами сигналы у — Yt~tl (4, 4, -4, wi)-
Пусть 4 — момент поступления в агрегат следующего внешнего
сигнала х2. Если 4 > 4 + 4 (4, 4, 4, wi), т0 в момент 4 + 4 (21, 4,
xlr coj) функционирование агрегата прекращается. В противном случае,
когда 4^4+ Ti (2i, 4, xi, Фе), определенный выше закон функцио-
нирования сохранится лишь до момента 4- В этот момент реализуется
элементарное событие со2 в соответствии с распределением Р (Л), не-
зависимое от {со0, cojI, и определяется значение т2 (г2, t2, х2, со2) и т. д.
Таким образом, в моменты поступления входных сигналов проис-
ходит как бы регенерация случайного процесса, описывающего функ-
ционирование агрегата, т. е. развитие этого процесса после таких
моментов не зависит от его предыстории. Если «части» процесса
z (4 ы) между моментами поступления входных сигналов не являются
марковскими, то сделанное предположение, естественно, налагает
неявное ограничение на вид поступающих входных сигналов. Образно
говоря, входной сигнал должен «уметь» переводить процесс г (t, со)
в «марковскую точку», т. е. такое состояние, которым полностью опре-
деляется все дальнейшее течение процесса. Если же агрегат — ку-
сочно-марковский (см. ниже), то для него любое состояние является
«марковской точкой».
156
Поясним сказанное следующим простым примером. Рассмотрим
систему, состоящую из п рабочих элементов. Время безотказной
работы i-го, i п, элемента распределено экспоненциально
с параметром Хг, элемент с номером I имеет nit резервных (резерв нена-
груженный). Как только рабочий элемент выходит из строя, на его
место мгновенно подключается один из резервных, если таковой су-
ществует. Отказавшие элементы поступают в ремонтную бригаду,
состоящую из г, г сС п, ремонтных мест. Дисциплина обслуживания
отказавших элементов не имеет значения. Предположим, что время
ремонта i-го элемента на ремонтном устройстве случайно и имеет функ-
цию распределения (х). К концу ремонта элемент либо бракуется
с вероятностью pt, либо полностью восстанавливается (с вероятностью
qt = 1 — pt). Процесс ремонта каждого элемента не зависит от всех
остальных операций. Восстановленные элементы мгновенно направ-
ляются в резерв или на рабочее место, если оно пустует, а бракованные
элементы далее не используются. Таким образом, число бракованных
элементов в системе не убывает с течением времени.
Если рассмотреть процесс г (/) = (vx (t), ..., vn (/)), где (t) —
число исправных элементов г-го типа, т. е. находящихся в резерве и на
рабочем месте), то данный процесс будет, вообще говоря, немарковским.
Пусть теперь в некоторые моменты времени в системе состояние прину-
дительно изменяется извне, что можно трактовать как поступление
входных сигналов. Именно, пусть в указанные моменты времени систе-
ма приводится в полностью исправное состояние, т. е. резерв элемен-
тов i-го типа пополняется до уровня mt, i = 1, 2, ..., п; на пустующие
рабочие места также ставятся исправные элементы, а все бракованные
и находящиеся на ремонте (или в очереди на ремонт) элементы изыма-
ются из системы. Тогда, как нетрудно видеть, такой входной сигнал
переводит состояние системы z (t) в «марковскую точку» (тх + 1,
m2 + 1, ..., тп + 1).
При решении практических задач часто приходится классифици-
ровать поступающие в агрегат внешние сигналы в зависимости от того
воздействия, которое они оказывают на функционирование агрегата.
В частности, оказываются полезной конструкция, на которую выше
мы уже обращали внимание: х £ X X Г, где X и Г — пространства
входных и управляющих сигналов, или х = (х, g), где х Е X — (орди-
нарный) входной сигнал, a g £ Г — управляющий сигнал. Для учета
специфики воздействия этих сигналов на функционирование агрегата
удобно рассматривать состояние z (/) = (г (Z), g (/)), где z (/) Е Z,
g (/) Е Г и z (t) Е Z, т. е. Z — Z X Г.
В качестве иллюстрации определения агрегата рассмотрим описание си-
стемы подготовки комплектов деталей, предназначенных для сборки некоторых
изделий. Система комплектации и-меет I ячеек для накопления деталей различных
типов. Задания на комплектацию поступают в моменты времени t* и содержат
указания о требуемом составе комплектов $!*, s2*, ..., S;*, где $г* — количество
деталей (-го типа, входящих в комплект (sf* = 0 тогда, когда деталь (-го типа
не нужна для сборки данного вида изделий). Поступившая деталь подвергается
проверке: с вероятностью </, деталь (-го типа может оказаться годной, а с вероят-
ностью 1 — qt — дефектной; в последнем случае она исключается из рассмотре-
157
ния. Детали накапливаются в ячейках до тех пор, пока их количество st st*.
Если Sj = st*, следующая деталь i-ro типа поступает в i-й бункер и ожидает ос-
вобождения ячейки. Объемы бункеров считаем неограниченными. Когда для
всех i = 1, 2, ..., I будет s; = st* (комплект готов), комплект выдается на
сборку. Система функционирует таким образом до получения нового задания па
комплектацию, а затем мгновенно переходит к подготовке комплектов нового
состава. Состояния системы комплектации можно исчерпывающим образом
описать, если указаны для всех i = 1, 2,. I количества s; деталей, имеющих-
ся в каждый момент в ячейке и бункере, с учетом возможного поступления
новых деталей (при поступлении детали i-ro типа = Sj + 1) и выдачи гото-
вых комплектов на сборку (в момент выдачи st' = st —st*, i = 1,2,...,/).
Для представления системы комплектации в виде агрегата будем считать
входными сигналами объекты х = (i, со;), i = 1, 2, ..., I, co; = 0,1; управляю-
щими сигналами — объекты g = (.s\*, s2* ..., s;*); внутренними состояниями —
Объекты z(/) = (Sj, S2, •••, 5/). СОСТОЯНИЯ z(t) = (.S^t), S2(t), ..., S[(t), $!*(/),
s2* (/), •••, s;*(/)). Выходные сигналы у = (sj*, s2*, ..., si*).
Пространство элементарных событий Й состоит из набора независимых
случайных величин (св0, <а1; ..., шг), где св0 принимает единственное значение,
(t>i = 0, 1, i = 1, 2, .... I.
Вероятностная мера Р0(Л) задается соотношением Р(ы0) = 1, а мера
Р(Л) — соотношениями
Р {(£ц — \) = qi, p(ui = 0) = l-qt. (5.60)
Случайный процесс £0 определяется тем, что при t > tQ s, = 0, i =
= 1, 2, ..., I, т0 = оо. Состояния его z(t) = (0,0, ..., 0, 0, 0, .... 0). Случайный
поток (/(/0, Wo) = 0; Yt(t0, w0)[ не определяется. _
Случайный процесс Цг, 0, х, t, св) и случайный поток [/(z, 0, х, со);
Yt(z, 0, х, со), t £ I] определяются следующим образом.
Очевидно, что выходной сигнал может быть выдан либо в момент tn' поступ-
ления очередной детали (входного сигнала), если со; = 1 и
si (О = s*i (?п) Для всех /= 1, 2,...,/, (5.61)
либо в момент /" поступления нового задания на комплектацию (управляю-
щего сигнала), когда
s(- (t"n) > s- (t"n) для всех / = 1, 2,..., /. (5.62)
Поэтому множество /(z, t, х, со) состоит из единственного момента tn; если
выполняется хотя бы одно из условий (5.61) или (5.62) и оказывается пустым в
противном случае.
Пусть для t < tn' состояние z(f) = (s^ s2, ...,_si, st*, ..., si*) = zn и в момент
tn' поступает входной сигнал, хп' = (i, св;), х'п = (х'п, 0). Тогда тп' = оо,
а для t > tn'
С “) =
({$!>•••> s/—i > S,'4-1 ’’ Sl’ s! - •••> S/)> (n’ X7l’ “)>
Выбрав фиксированное значение св; равным 0 или 1 в соответствии с (5.60),
получим z(t) для t^>tn.
158
Пусть теперь в момент поступает управляющий сигнал gn =
sj"), x" = (0,g"). Тогда т" = ос, а для t>i'^
С ~С “) =
j(S1,..,S;,s;v..,s;^<P(^X- ,5 64.
1((S1-S;"),..., (Sr-<),<,..., s;"), Гае1(гп, tn, -*;,<»).
Если в момент tn поступает внешний сигнал хп = (хп, gra), то тп= > ,
а для t > tn
2 (2П, ХП1 t, ш) =
S j ш _,... , S;, Sj j, ^пСНгп> ^n, xn> и)>
- .............(«,+.,-<).................<'•*»
^п(с^(гП, ^n, Xni co)-
Приведенные соотношения полностью характеризуют функционирование
агрегата.
5.6. КУСОЧНО-МАРКОВСКИЙ АГРЕГАТ.
ПОСЛЕДОВАТЕЛЬНОЕ РАСКРЫТИЕ ЭЛЕМЕНТАРНОГО СОБЫТИЯ
Рассмотренное в предыдущем параграфе определение агрегата
наглядно показывает связь этого нового объекта с известными матема-
тическими понятиями и подчеркивает его весьма общий характер.
Последнее обстоятельство, с одной стороны, позволяет надеяться, что
агрегат окажется математической схемой, пригодной для описания
широкого класса реальных сложных систем, а с другой — вселяет
сомнение в возможности построения обозримого аналитического аппа-
рата для расчета и исследования агрегатов в общем случае. В настоящее
время можно опереться только на метод статистического моделирова-
ния агрегата на ЭВМ, имея в виду при этом, что последний еще тре-
бует дальнейшей разработки и приспособления к решению встречаю-
щихся на практике задач.
Вместе с тем, многие реальные сложные системы могут быть описа-
ны математическими схемами, представляющими собой частные слу-
чаи агрегата, соответствующие определенным ограничениям, налагае-
мым на обрывающиеся случайные процессы и случайные потоки. Таким
образом, выделяются классы агрегатов, например: кусочно-марковские
агрегаты, кусочно-непрерывные агрегаты, кусочно-линейные агрегаты
ит. д., для которых надежда разработать обозримый аналитический
аппарат представляется более обоснованной, чем в общем случае.
В настоящем параграфе мы познакомимся с классом кусочно-марков-
ских агрегатов.
Агрегат будем называть кусочно-марковским, если на любом
замкнутом интервале It', t"], принадлежащем интервалу функциони-
рования агрегата и не содержащем моментов поступления внешних
сигналов, при фиксированном состоянии z (t’) Е Z в начальный момент
159
интервала t' процесс t, (z (/'), t', x, t—t', co) оказывается обрывающимся
марковским процессом.
Оперировать с марковскими агрегатами весьма удобно. Однако
следует иметь в виду, что с принципиальной точки зрения любой агре-
гат можно привести к марковскому, достаточно расширив пространство
состояний.
Сделанное замечание наводит на следующий вопрос. Если всякий
процесс можно свести к марковскому, то какая польза от марковского
свойства?
Общее определение случайного процесса, как было отмечено
выше, — это функция двух аргументов £ (С со), где — элемент про-
странства элементарных событий й. Принципиально как будто все
просто, однако в большинстве случаев не удается практически постро-
ить такое й, чтобы по нему можно было определить всю траекторию
процесса. Идут иным путем: путем последовательного раскрытия
элементарного события со. Это можно представить себе следующим
образом.
Пусть при каждом h > 0 задано пространство элементарных собы-
тий ЙЛ с вероятностной мерой Ph (Л). Будем считать также заданным
семейство операторов
fh (т> t, <о), т < t т + h, со g йд, (5.66)
где f и г принимают значения из некоторого множества Z, и началь-
ное распределение L [г (Zo)|. Тогда можно построить процесс zh (t)
следующим образом.
1. Полагаем
гл(/0) = г(и, (5.67)
где г (t0) выбирается по распределению L [г (г'о)!-
2. Производим последовательность независимых испытаний
со0, (Oj, ш2,..., £ йд (5.68)
в соответствии с вероятностной мерой Ph (Л).
3. (7) определяем рекуррентной формулой
?д (0 = f(nh + /0, гд (nA + /0), t, ®п),
nh-}-t0<^i ^(«+ 1)/г + ^0. (5.69)
В пределе, при получим марковский процесс z (t).
Понятно, что описанная конструкция не дает строгого определе-
ния марковского процесса и нуждается в обосновании; однако она
хорошо отражает существо построения подобных процессов и вместе
с тем указывает на способ их моделирования. Более подробно мы
на этом останавливаться не будем.
Самое важное то, что на практике оказывается значительно проще
построить соп при малых h, чем <о, которое сразу определяет всю траек-
торию процесса.
Это обстоятельство широко применяется в теории марковских
процессов, где для нахождения различных вероятностных распределе-
но
ний для процесса используют так называемые инфинитезимальные ха-
рактеристики (локальные по времени). Теория марковских процес-
сов, базирующаяся на изучении свойств полугрупп операторов, также
широко использует локальные характеристики процессов.
В заключение настоящего параграфа сделаем замечание об усло-
вии физической реализуемости процесса t, (t) функционирования агре-
гата: пусть А — любое событие, связанное с поведением процесса
t, (t) в полуинтервале (/0, и пусть /2 > й: тогда вероятность Р (Л)
события А, вычисленная в предположении, что в полуинтервале
(tlt t2\ поступило внешнее сообщение (t, xj^,
Р(А)= P((A)/(/,xl]^, (5.70)
не зависит от (t, xJt" (не зависит от будущего).
Легко видеть, что достаточным условием физической реализуе-
мости процесса £ (/) является независимость в совокупности событий
(5.68).
Понятие системы массового обслуживания точно не определено,
хотя имеется огромная литература, в которой к настоящему времени
исследованы сотни разновидностей систем. Поэтому ограничимся
рассмотрением одного примера системы массового обслуживания,
которую, как будет показано, легко свести к агрегату.
Пусть в систему могут поступать требования, снабженные при-
знаками 0, из некоторого конечного пространства S, которое для
определенности будем считать множеством натуральных чисел от 1
до ЛЕ Каждое требование характеризуется, помимо признака 0, еще
требуемым временем обслуживания л и максимально допустимым вре-
менем ожидания начала обслуживания у. Пара случайных величин
(Л, у) имеет совместное распределение
Е(х1,х2) = Р{т]<х1; у>х2}. (5.71)
Система состоит из п обслуживающих приборов. Если в данный
момент времени свободен хотя бы один прибор, то поступающее тре-
бование посылается на один из свободных приборов.
Если в системе п требований находятся на обслуживании и k
пребывает в состоянии ожидания, причем признаки этих требований
равны соответственно ily i2, ..., in', i'i, Й2, , i'k, то при освобождении
/-го прибора выбирается s-e требование из очереди с вероятностью
й> й, ... ,in’, i'i, 1'2, ,i'k), (5.72)
и не выбирается никаких требований с вероятностью
k
qj(k; ilt, in’, ... ,4) = 1— 3 p;s(...). (5.73)
s= 1
Требования, для которых фактическое время ожидания начала
обслуживания оказывается больше у, теряются. Допустим также,
что теряется любое требование, заставшее в системе М других требо-
ваний.
6 Зак. 792 161
Покажем, как построить соответствующий агрегат. Внутренним
состоянием агрегата будет вектор
(v;0x, 02, ... , 0V; Т]1, т)3. ... , T)v; ft; у2,... , Tv), (5.74)
где v — число требований в системе; 01( 02, 0V—параметры
(признаки) этих требований (первыми перечисляются требования, на-
ходящиеся на обслуживании, а затем требования, ожидающие в оче-
реди); т)1, т]3, ...,T]v — времена до окончания обслуживания требований;
Vi, ft> Tv — времена до моментов, когда требования должны поки-
нуть систему в силу временных ограничений.
Построим пространство элементарных событий. Вспомним, что
случайные факторы определяют время обслуживания требования т),
максимально возможное время ожидания у, а также номер требования,
выбираемого из очереди при освобождении обслуживающего прибора.
Любому набору I = (j; k; ilt ..., in; ..., i'k), где k < M — n,
1 i\, ..., t'h N, поставим в соответствие случайную величину
с возможными значениями 0, 1, ..., k, где
Р f в/ = S | — Pjs • •• Л ni Й , • • , й), 1 Ssgi k, (j. yj.)
Р !£/=0) i2,... , in\
Предположим, что все эти величины £, при различных I независимы
в совокупности.
В качестве элемента выборочного пространства Q возьмем вектор
® = {?/!,--., С/д п, у), (5.76)
где /х, /2, ..., IR— перечисленные каким-либо образом наборы I
распределения — определены выше, а пара (ц, у) не зависит от {С/}
и имеет распределение F (хх, х2).
Покажем, как воспользоваться определенным пространством
элементарных событий для определения функционирования агрегата.
Пусть в некоторый момент t в систему поступает требование с при-
знаком /. При этом реализуется элементарное событие со описанного
выше типа. По вектору со определяем требуемое время обслуживания
т| и максимально допустимое время ожидания у поступившего требо-
вания. Договоримся считать, что если после момента t, но до момента
поступления следующего требования в некоторый момент f освобо-
дится /-й прибор и если до этого в системе имелось k требований с при-
знаками z’j, ..., in (обслуживание) и i\, i' h (ожидание), то на обслу-
живание берется из очереди требование с номером £;, где
/=(/; k; ilt ... , in; i\, ... , Д) (5.77)
Легко видеть, что процесс полностью определен и мы можем ввести
процесс z (0 изменения внутреннего состояния агрегата в интервале
между поступлениями на вход системы требований, полностью опреде-
ляемый реализацией элементарного события и.
Предоставляем читателю определение процесса до момента по-
ступления первого требования, а также выходящего потока агрегата,
моделирующего эту систему массового обслуживания.
162
ГЛАВА ШЕСТАЯ
КУСОЧНО-НЕПРЕРЫВНЫЕ
И КУСОЧНО-ЛИНЕЙНЫЕ АГРЕГАТЫ
6.1. ВВОДНЫЕ ЗАМЕЧАНИЯ
В гл. 5 было введено понятие «агрегат» и дано его определение.
Были также приведены некоторые примеры, показывающие универ-
сальность введенного объекта. В той же главе указывалось на целе-
сообразность выделения схем более частных, нежели агрегат общего
вида, но сохраняющих важную его особенность, такую, как возмож-
ность описания достаточно широкого класса реальных систем. В то же
время эти частные схемы должны допускать возможность постановки
и решения более или менее универсальными аналитическими методами
задач анализа и синтеза сложных систем. Описываемый в настоящей
главе подход является обобщением некоторых методов, применяемых,
в частности, в теории массового обслуживания и теории вероятностных
автоматов.
6.2. КУСОЧНО-НЕПРЕРЫВНЫЕ АГРЕГАТЫ
Обратимся к описанию агрегата как математического объекта
(см. гл. 5). Для поставленных в настоящей главе задач можно считать,
что на агрегат поступают только входные сигналы и не рассматривать
управляющих сигналов. С формальной точки зрения это не ограничи-
вает общности. Итак, предположим, что мы рассматриваем агрегат
как объект, который в каждый момент времени t из заданного интервала
Т характеризуется внутренним состоянием z (/), имеет вход и выход.
На вход агрегата в дискретные моменты времени могут поступать сиг-
налы; считается, что каждый сигнал поступает мгновенно. Аналогично,
с выхода агрегата могут сниматься выходные сигналы. Класс кусочно-
непрерывных агрегатов выделяется с помощью конкретизации струк-
туры множеств Z, X, Y — пространств состояний, входных и выходных
сигналов соответственно, а также операторов переходов Н и выходов
G. Опишем данную конкретизацию. При этом упор будет сделан на со-
держательном, а не формальном описании.
Предположим, что множество внутренних состояний рассматрива-
емого агрегата Z представляется в виде конечного или счетного объе-
динения (J fv, где Tv — замкнутое подмножество многомерного
6*
163
пространства Ev, размерность которого обозначим через | v Тогда
внутреннее состояние имеет следующую структуру: г = (v, zv), где
v — дискретная величина, принимающая значения из конечного или
счетного множества J, которую назовем основным состоянием, a zv —
вектор, имеющий размерность | v |, с компонентами zvi, ..., zV| V|, на-
зовем его вектором дополнительных координат. Неотрицательную ве-
личину | v | назовем рангом основного состояния v. Если | v | = 0, то это
означает, что дополнительные координаты в основном состоянии v
не определяются. Обозначим через границу множества 1\ в про-
странстве Ev, int 1\ == — внутренность множества Tv.
Пусть zv *6 Зададим для каждого v и zv* Eyv следующие ве-
роятности:
Р' {(v, 2v); (v\ £2V')i, QV'CzintrV',
P" {(v, ?C); (v', QC')},
такие, что
3 [P' {(v, zC); (v', int Г<) } +P" {(v, zC); « ?v')l] =
v'
Содержательный смысл введенных вероятностей будет объяснен ниже.
Опишем сначала динамику агрегата (т. е. процесс изменения внут-
ренних состояний во времени) в предположении отсутствия поступле-
ния входных сигналов. Если обратиться к определению агрегата
в гл. 5, то эта динамика задается случайным оператором переходов U,
который в отсутствие входных сигналов совпадает с оператором Н.
Таким образом, нижеследующее описание есть не что иное, как описа-
ние оператора U. Пусть в начальный момент времени t0 z (70) = (v, zv°),
zv° £ int Tv. Тогда в течение некоторого случайного интервала времени,
зависящего от поведения z (t), t > tg, основное состояние v не изменяет-
ся, а процесс zv (f) по предположению является однородным непрерыв-
ным векторным марковским процессом размерности |v|. Упомянутый ин-
тервал времени продолжается до момента /0 + т (z'v0), который является
случайным моментом первого достижения траекторией zv (i),
границы yv. Такиу образом, т (z°) — время первого достижения гра-
ницы yv случайным процессом zv (t), начинающимся в точке zv°. В этот
момент времени состояние процесса г (/) меняется в соответствии со
следующим законом. Если zv* = zv (Zo + т (zv0)) £ yv, to при t > t0 +
4- т (zv°) основное состояние процесса равно v', a zV'(t) является непре-
рывным однородным марковским процессом (рассматриваемым до
момента достижения границы yv<) в области Г<, причем начальное
состояние eroz°-E int 1\" и основное состояние v' являются случайны-
ми величинами с распределением
оо
Р l(nzC);(v', = 2 Р(1г) !(v, zC);(v', Qv,)}, (6.1)
k= 1
*> Обратим внимание на то, что символ | v | здесь не означает операцию взя-
тия модуля. Данное обозначение заимствовано из теории массового обслужива-
ния (см. [1]).
164
где Qv- с: int IV, а
P(A>{(v, z‘); (v', Qv-)}=.3 J P"!(v, 2v); (v",dZv-)} X
v" Yy"
XP(A-I) {(v",2^);(v', QvOh k>\, (6.2)
P{1} {(v, zC); (v', fiV')} = P' {(v, ?*); (v', }. *>
Таким образом,
P{(v, Zv); (v', QV')} = P (z(Z + 0)=(v',2v-), zv- g Qv, cint IV/z(Z) =
= (v,Zv), zv g Yv).
Символом P мы будем обозначать далее вероятность какого-либо со-
бытия, условную или безусловную.
С вероятностью
1 — 3 Р ((v, 4); « int I»}
V '
процесс 2 (Z) для Z > Zo + т (zv°) не определяется, т. е. момент
Zo + т (г°) является точкой обрыва траектории. Можно также условно
считать, что z (Z) = 0 при Z > ta V т (zv°), где 0 — фиктивное
поглощающее состояние.
Соотношения (6.1) и (6.2) имеют следующую наглядную интер-
претацию. При попадании zv (Z) на границу yv агрегат переходит
в основное состояние v' и дополнительные координаты принимают
значения из int IV, причем этот переход может совершиться за ко-
нечное число «мгновенных» скачков, когда при последовательных
скачках значения дополнительных координат агрегата попадают на
границы областей IV. Если агрегат не может перейти в состояние
вида (v', zv<), zv< С int IV за конечное число скачков (вероятность
такого события равна 1 — S P[(v, zv*); (v', int IV))), то считаем
V '
данный момент (накопления скачков) времени моментом обрыва про-
цесса z (Z) или моментом перехода процесса в состояние 0. При этом
ранее введенные функции Р' и Р" являются вероятностными распре-
делениями, задающими состояние агрегата после одного «мгновенного»
скачка. Именно, Р'[(у, zv*); (v', £2V')}, 2v* € Tv. QV'€ int IV есть
вероятность того, что основное состояние после одного «мгновенного»
скачка равно -v', и значение вектора дополнительных координат zv-
принадлежит t-V при условии, что скачок происходит из точки (v,
zv*). Аналогичный смысл имеет и вероятность Р" {(v, zv*); (v', Qv')}>
*> Здесь и далее при написании интегралов мы будем обозначать через
dzv элементарный «объем» того'подмножества Tv, по которому производится ин-
тегрирование. Так, при интегрировании по множеству Tv под dzv подразумевается
элементарный «объем» множества IY. Если же интегрирование идет по границе
7V, то через dzv обозначается элементарная «площадка» этой границы. При напи-
сании интегралов будет ясно, что именно понимается под элементом dzv, посколь-
ку ниже знака интеграла всегда будет указываться область интегрирования.
165
стой лишь разницей, что в этом случае Qt- с: yV', т. е. рассматривает-
ся скачок па границу множества допустимых значений дополнительных
координат. Очевидно, |(v, zv*); (v', QV')}> zv*E Vv. Ov- cz Tv-
есть вероятность того, что переход агрегата из состояния (v, zv*)
совершится за k «мгновенных» переходов, и новое состояние агрегата
имеет вид (v', zv>), zv-gQv<.
Далее, в области для процесса zv-(0 вновь определяется его
момент первого достижения границы и т. д. Из описания ясно,
что процесс z (/) для автономного агрегата (т. е. для такого, на который
не поступают входные сигналы) является однородным марковским про-
цессом. Как уже указывалось, целесообразно этот процесс рассматри-
вать как обрывающийся. Это связано с тем, что на оси времени могут
существовать точки накопления скачков процесса z (f). Кроме того,
может оказаться, что с положительной вероятностью время существо-
вания процесса zv (t) меньше времени его достижения границы yv.
Рассмотрим элементарный пример. Пусть | v | = 2 при некото-
ром v, a Tv = {zv : Zvi > 0, zv2 > 0]. Пусть в этой области век-
тор zv изменяется в соответствии со следующими дифференциальными
уравнениями:
<41 (0 2 ... ,
=zvl(/), = -1
с начальными условиями Zvl(0)=2vi, Zv2(0)=Z°2, Z° = (Zvl>
z°2)- Решение этих уравнений имеет вид
Zvl(0=f~^----, Zv2(0=2v2— t. (6.3)
\zv 1 /
Из (6.3) следует, что при г°г< 1/г°1 траектория zv(t) попадает
через время т(г°)=г“г в граничную точку
zvi (т) =гС1 =(-Q--г°2) , Zv2 (т) = г*2 = о.
\ zvl /
Если z°2 l/z?i, то до момента достижения границы траектория
zv (0 успевает «уйти в бесконечность».
Поэтому будем считать процесс функционирования агрегата опре-
деленным до некоторого случайного момента времени, в качестве кото-
рого можно принять как момент «ухода в бесконечность» траектории,
так и момент накопления скачков. В частном случае в качестве такого
момента может выступать и некоторый детерминированный момент
времени.
Здесь же полезно отметить, что для автономного кусочно-непрерыв-
ного агрегата состояния, имеющие ранг, равный нулю, являются
поглощающими.
Если вновь обратиться к общему определению агрегата, то из
приведенного описания следует, что оператор U перехода из одного
состояния в другое при отсутствии входных сигналов описывается
166
вероятностными закономерностями, определяющими процессы zv (/),
и переходными вероятностями Р {(v, zv*); (vz, Иначе говоря,
для задания оператора U достаточно задать распределения Р'[(у, zv*);
(у', Qv-)}, /’"{(v, zv*); (у', которые определяют P{(v, zv*j;
(vz, Qv-)} [формулы (6.1) и (6.2)1, и характеристики, определяющие
однородные марковские процессы zv (t), v £ J, например векторы
сноса и матрицы диффузии.
Приведенная конструкция определяет автономный кусочно-не-
прерывный агрегат. Еще раз отметим, что процесс изменения состоя-
ния автономного кусочно-непрерывного агрегата является обрываю-
щимся однородным марковским процессом. Аналогично можно было бы
описать работу автономного*) кусочно-непрерывного агрегата неодно-
родным марковским процессом.
Рассмотрим теперь неавтономный кусочно-непрерывный агрегат.
Для такого агрегата пространство входных сигналов X имеет такую же
структуру, что и Z. То есть X = U Gy., где Gy, — некоторое множест-
м>
во в |р|-мерном пространстве, х = (р, хД, хц = (хц1, ..., хц щ|),
координата р может принимать не более счетного числа значений.
В промежутках между поступлениями входных сигналов агрегат
функционирует уже описанным образом. Если же в момент t* z (t*)=
= (v, zv) и поступил входной сигнал х = (р, хД, то основное состояние
агрегата становится равным v', a zV'(t) является непрерывным марков-
ским процессом в области IV при t > t* до момента достижения гра-
ницы уу'(или до момента обрыва траектории) или до момента посту-
пления следующего входного сигнала, если он наступит раньше,
причем начальное состояние этого процесса z°- С int IV и основное
состояние vz являются случайными величинами с распределением
[(v,zv); (v'.CV)] =p{z(^ + 0) = (v',zv.),zv- £fV/z(/*) =
= (v, zv), x = (p, хД], Qv- cz int IV. (6.4)
С вероятностью
1 —2 p(v.. *„) {(v, zv); (vz, int IV)}
V'
процесс z(t) при t>t* не определяется, т. e. момент t* является
моментом обрыва процесса.
Вероятность {(v,zv); (v'.Qv-)},} V'C^intlV, удобноза-
давать с помощью следующей конструкции. Для всех (v, zv) и
(р, хД зададим вероятности
Р{(v> Zv); (vz, Qv')। > tV int Ev,
р(и, *ц) ((v> zv); (v ,£V)}, £2v'CZYv>
такие, что
S {(V, zv); (vz, int IV)) + ЛМ) {(v, zv); (v', yv-)}l =1.
v'
*) По поводу автономности см. гл. 3, стр. 93.
167
Тогда
оо
Лц. {(V, Zv); (v'; Qv-)l = 1; С {(V, Zv); (V', Qv')J,
{(v>2v); (V>^v')i = 2jj P{ii,.«ц){(v>2v); (v ,dzV")\ x
v"
X (« ^); (v',Qv'))>
Р(|1'*ц) ((v, zv); (v , QV')} = Р(ц, Лц) {(v> zv); (v',QV')}.
Вероятности Хц) ((v, zv); (v', QV')} и Рщ,-щ) ((v,zv); (v', Q*-))
имеют интерпретацию, аналогичную приведенной для вероятностей
Р' ((у, г*); (v', QV')}, Р" {(v, z*); (v',Q*')), zv C Yv Именно вероят-
ности Р(ц> х ) и Р{^ х ) задают вероятностное распределение состоя-
ний аргумента после «мгновенного» скачка, происшедшего в резуль-
тате поступления входного сигнала (р., Хц). Всего агрегат при
таком переходе может совершать лишь конечное число скач-
ков. Если совершается бесконечное число скачков, то рассматривае-
мый момент времени считается моментом обрыва процесса.
Особо следует оговорить случай, когда входной сигнал поступает
в момент выхода дополнительных координат на границу области их
изменения. Можно условиться, что при этом, например, сначала со-
вершается преобразование (6.1) состояния вследствие выхода допол-
нительных координат на границу, а затем полученное состояние (если
не произошло обрыва процесса) преобразуется в соответствии с распре-
делением (6.4). Распределения (6.4) и определяют оператор V, управ-
ляющий переходами агрегата при поступлении входных сигналов.
Таким образом, при фиксированных моментах и содержании вход-
ных сигналов функционирование кусочно-непрерывного агрегата опи-
сывается марковским процессом. Данный процесс не является, вооб-
ще говоря, однородным из-за наличия входных сигналов. Все траек-
тории этого процесса в любом интервале до момента обрыва являют-
ся кусочно-непрерывными, причем размерность вектора дополнитель-
ных координат может изменяться со временем от одного основного со-
стояния к другому.
Мы не будем подробно останавливаться здесь на способах зада-
ния и получения выходных сигналов, поскольку сообщения на выходе
агрегата — фунционал от реализации процесса z (/). Заметим только,
что, как правило, интересующие исследователя функционалы можно
получить, считая пространство выходных сигналов Y имеющим струк-
туру, подобную структуре пространств X и Z, полагая моментами вы-
дачи выходных сигналов моменты перехода из одного основного со-
стояния в другое вследствие выхода вектора дополнительных коорди-
нат на границу множества и считая содержание выходного сигна-
ла в момент его выдачи случайной функцией от внутреннего состояния
168
агрегата непосредственно перед этим моментом*). Таким образом, мно-
жеством Z(p) (см. гл. 5, в рассматриваемом случае управляющий сиг-
нал отсутствует, поэтому мы его не пишем в индексе) является сово-
купность границ множеств Tv, т. е. Z(p) = (J yv. Заметим еще, что
V
в качестве (3 можно взять как некоторые числовые параметры, характе-
ризующие распределение Р', Р", Р^.х^у, Р(ц, х^у и непрерывные мар-
ковские процессы zv (t) между моментами изменений основных состоя-
ний, так и сами указанные распределения и, например, векторы сноса
и матрицы диффузии. В число компонент параметра 0 можно вклю-
чить также числовые величины или функции, определяющие границы у v
множеств Tv и число основных состояний, т. е. мощность множества J.
Для практических целей обычно достаточно рассматривать ку-
сочно-непрерывные агрегаты более простой природы, чем было описа-
но здесь. Так, весьма часто встречается случай, когда процессы
zv (t), v е J детерминированы и являются решениями дифференциаль-
ных уравнений
^=fW(2v). (6.5)
Частный случай такого агрегата будет рассмотрен в следующем
параграфе. Области в реальных задачах также имеют довольно
простой, не «вычурный» вид. Случайные переходы, определяемые
функциями' Р[(у, zv*); (v', Qv<)) и Ли. *у.) i(v, zv); (v', Qv<), также
редко имеют произвольный вид и часто достаточно просты.
6.3. КУСОЧНО-ЛИНЕЙНЫЕ АГРЕГАТЫ
Частным случаем описанного в предыдущем параграфе кусочно-
непрерывного агрегата является кусочно-линейный агрегат,* который
получается, если вектор zv описывает равномерное прямолинейное
движение в области Г<.
dzv _
где av =(avi,..., av| v|) — постоянный вектор**).
Сама область Tv является замкнутым многогранником в простран-
стве | v | измерений. Грани этого многогранника обозначим через
Yvj. / = 1Д 2, ... Будем [предполагать, что yVi A у-?; = 0 для
любых i =/= j, т. е. ребра многогранника «приписываются» только
какой-либо одной его грани.
*• Иногда удобно считать, что выходные сигналы выдаются также в моменты
поступления входных сигналов.
**> Вообще говоря, компоненты вектора av могут быть как положительны,
так и отрицательны. Нов большом числе практических задач эти компоненты не-
отрицательны. При этом компоненты вектора дополнительных координат не воз-
растают, а av является вектор-скоростью убывания компонент вектора 2V.
IDA
Выходной сигнал у имеет вид у = (у0, У1, ,У\Уо\), где у0 — дис-
кретная величина, а |у0|—ее ранг. Вероятности P[(v,zv); (v',Qv-)j
и Р(р,,хи) ((v> zv); (v', Qv-)} определяются при помощи следующей
конструкции. Сначала рассмотрим случай выхода zv на границу
множества rv. Пусть zv=zv(t) £ yv/. Тогда в момент т мгновенно
изменяется основное состояние и посылается выходное сообщение
(в частности, пустое). Вероятностные распределения P'{(v, zC); (v',
Qv-)) и P" [(v,zC); задаются с помощью описываемого ниже
случайного механизма. Именно, при фиксированном состоянии
(y,z*) состояние (v',zv<) (соответствующее распределению Р', если
zv- £ intrv-, и распределению Р", если zv- £ yv-) полностью опре-
деляется: 1) значением v, 2) значением zv ^yv/, 3) случайным век-
тором, размерность и закон распределения которого не зависит от
предыстории процесса функционирования и однозначно определяют-
ся указанием v и номера грани /. Обозначим этот случайный вектор
через ц(,. Естественно, для того чтобы знать его, мы должны задать
его вероятностное распределение. Размерность вектора iq(, обозначим
через r'v. Рассмотрим пространство размерности | v | -|-г(. и его раз-
биение на конечное число многогранников D‘vk, & —1,..., не обя-
зательно связных. Каждому многограннику D!vk приписаны вероят-
ностное распределение (Pw-J, S Pvv'= 1 и набор матриц
Размерность матрицы Lvv- равна ]v'|x(|v| + г£), т- е. матрица
содержит | v' | строк и (| v| + r’v) столбцов. Припишем к допол-
нительным координатам zv компоненты случайного вектора т](,. По-
лучившийся вектор (столбец) обозначим через (zvr](). Если
(zv т]() £ D‘vk, то новое основное состояние v' выбирается в соответ-
ствии с распределением^*'), а новые дополнительные координаты
zV' определяются линейным преобразованием вектора (zv т,(,) с мат-
рицей /.у*', т. е.
Zv' ==Evv' X (zv T|v)'
Выходной сигнал у = (уа, уг, ..., у\Уо\) определяется следующим
образом: его основная координата у0 является однозначной функцией
от v, v', /, k, а вектор (у1г у\у„\) — линейным преобразованием
вектора (ZvW) с матрицей, однозначно определяемой величинами v,
v', j, k. В частности, выходной сигнал может быть пустым.
Рассмотрим теперь случай поступления входного сигнала. Пусть
z(Z)=(v, zv) и в момент t поступил входной сигнал (ц, Хр.) . Тогда
вероятностные распределения Р(ц, х ( {(v, zv); (v', QV')} и Рщ, x^j ((v,zv);
(v',Qv'){ задаются описываемым ниже случайным механизмом. Имен-
но, при фиксированном состоянии (v, zv) состояние (v', zv-) (соот-
ветствующее распределению Р(ц,хц), если zv- £ int Tv-, и распреде-
лению Рщ, хц), если zV' £ yV') полностью определяется: 1) состоя-
170
нием z(f), 2) поступившим входным сигналом х, 3) случайным век-
тором ££> размерность и закон распределения которого однознач-
но определяются заданием величин v и р, и не зависят от преды-
стории процесса. Размерность вектора ££ обозначим через Sy. Pac-
смотрим пространство размерности | v | + | р | -f-Sv и его разбиение на
конечное число многогранниковD^k, не обязательно связ-
ных. Каждому многограннику D^k приписаны вероятностное распре-
деление (pvv'}, 2 Pvv- = 1. и набор матриц {А!}*'!-Размерность мат-
V*
рицыГ^ равна | v'I х (Iv I+ 1 И l + sV)-
Припишем к дополнительным координатам zv компоненты век-
торов Хц и |v- Получившийся вектор-столбец обозначим через
(zvXy.^1)- Если (zv-Гц^) £ D^k, то новое состояние v' выбирается в
соответствии с распределением {/?£*'}> а X
Выходной сигнал, который выдается в момент поступления вход-
ного сигнала и который, в частности, может быть пустым, у = (у0, уъ
У\у<>\)> определяется так. Компонента у0 является однозначной
функцией от v, v', р, k, а вектор (ух, ..., г/]Уо|) дается линейным пре-
образованием вектора (zvXp.£v) с матрицей, однозначно определяемой
величинами v, v', р, k.
Из определения следует, что при фиксированных моментах по-
ступления и содержаниях входных сигналов функционирование агре-
гата описывается марковским процессом. Все траектории этого про-
цесса в любом интервале до момента обрыва являются кусочно-линей-
ными, причем размерность вектора дополнительных координат может
изменяться от одного основного состояния к другому. Сообщение же на
выходе агрегата — функционал от процесса z (/).
Кусочно-линейный агрегат полностью определяется заданием
следующих объектов: множества основных состояний J, коэффициен-
тами уравнений, задающих гиперплоскости yv;-, матрицами [М*-],
(Lvv'}, распределениями {pit'} и {р^-}> векторами av, ко-
эффициентами уравнений, задающих многогранники и [£)£*},
распределениями величин {^) и [г](}, а также матрицами и распре-
делениями, участвующими в формировании выходных сигналов. Все
перечисленные объекты можно считать компонентами конструктив-
ного параметра 0, задающего агрегат.
6.4. ПРИМЕРЫ
В виде кусочно-непрерывных и кусочно-линейных агрегатов могут быть
формализованы многие реальные процессы: процессы передачи и обмена данными
в сетях связи, различные процессы обслуживания, процессы автомобильного
движения на участках дороги, разнообразные процессы сборки деталей и т. д.
При этом всюду основные состояния агрегата указывают на качественно различ-
ные состояния исходных объектов. Дополнительные же координаты, как правило,
характеризуют «мелкие» количественные изменения и в качестве их часто при-
171
нимают длительности интервалов времени до какого-либо «существенного» со-
бытия, величины работ, которые необходимо выполнить для завершения неко-
торой элементарной операции, некоторые побочные признаки, которыми могут
характеризоваться элементы систем, и т. д.
Следует отметить, что представление реальных систем в виде агрегатов не-
однозначно, поскольку неоднозначно могут быть выбраны фазовые переменные.
Выбор же фазовых переменных определяется как целями исследования, так и
стремлением уменьшить размерность задачи. При этом всегда приходится идти
на компромисс между точностью описания и полнотой получаемой информации,
с одной стороны, и простотой модели—с другой.
Пример 1. Вероятностный автомат. Рассмотрим конечный асинхронный ве-
роятностный автомат Мура, т. е. такой, который не имеет «жесткой» тактности,
а изменяет свое состояние всякий раз, когда на вход поступает входной сигнал.
Синхронный автомат получается, если потребовать, чтобы входные сигналы по-
ступали в моменты t = 1, 2, ....
Пусть 2а — множество внутренних состояний автомата, Ха — его вход-
ной алфавит. Если в момент t состояние автомата za(i) = 2а, и поступил входной
сигнал xa(f) = ха, то za(V + 0) = za', где za' — случайная величина с распре-
(х )
делением р а Выходной сигнал уа Ya, выдаваемый в этот момент, являет-
ся однозначной функцией состояния га’ : уа = Ф (za'). Определим кусочно-ли-
нейный агрегат, у которого X = Ха, Z = 2а, У = Уа, х = и = ха, z = v =
= Za, у=у0= уа.
Таким образом, и внутреннее состояние агрегата, и его входные и выходные
сигналы состоят из одной дискретной компоненты (дополнительные координаты
не определяются). В соответствии с вышеизложенным, выходные сигналы такого
агрегата могут выдаваться лишь в моменты поступления входных сигналов.
Поскольку дополнительные координаты в данном случае отсутствуют, то гово-
рить о многогранниках D^k и D^ft, матрицах L!^, и L^, и случайных векторах
Г]/ и излишне. Совокупность распределений {pvv'j в Данном случае сво-
дится (при фиксированных и и v) к одному распределению p^v, — р^ха\ .
zaza
Компонента у() = у является однозначной функцией только компоненты га' =
= <, уа = ®(v').
Пример 2. Система массового обслуживания. Обратимся к формализации
систем массового обслуживания (СМО) в виде кусочно-линейных и кусочно-
непрерывных агрегатов. Часто СМО можно представить в виде детерминирован-
ного агрегата, отнеся случайные факторы (случайность в поступлении требований
и их обслуживании) на счет входных сигналов. Однако такое представление мо-
жет привести к потере наглядности при схематизации, которая чрезвычайно
важна, поскольку всякое исследование проводится людьми, связанными с ре-
альным процессом и «чувствующими» его. Ниже дадим два описания одной кон-
кретной СМО — в виде детерминированного и случайного агрегатов.
Рассмотрим СМО с ожиданием, состоящую из двух параллельно работающих
приборов, обслуживающих поступающие однородные требования в порядке об-
щей очереди. Заметим, что никаких дополнительных ограничений на входящий
поток (предположим только для простоты его ординарность) не налагается. За
основное состояние v(i) агрегата, моделирующего СМО, примем число требова-
ний, находящихся в системе. Если v =0, то дополнительных координат не опре-
деляем. Если v = 1, то определяется одна дополнительная переменная zn —
время до окончания обслуживания требования, находящегося на приборе. Если
v > 2, то определяется v дополнительных переменных zvl, ..., zvv, где zvl, zv2 —
времена, оставшиеся до окончания обслуживания требований, находящихся в
рассматриваемый момент на приборе, а координаты zv-, j > 2, — длительности
обслуживания требований, находящихся в очереди. Следовательно, состояние
(5; 1,7; 2,4; 18; 3,2; 1,8) означает, что в системе находится'5 требований, из них 2
находятся на обслуживании и 3 — в очереди; до окончания обслуживания прой-
дет 1,7 и 2,4 единицы времени соответственно, а требования, находящиеся в оче-
реди, нуждаются для своего обслуживания соответственно в 18; 3,2; 1,8 единицах
времени.
172
Очевидно, в рассматриваемом случае |v| = v, а области имеют вид
~ {2v 2V °} 1 ГДе 2V (ZV !>•••> 2vv) , V > 1.
Гиперплоскости, образующие грани yv-, j = 1, ..., v, можно взять в виде
?v/ = {zv :zv/ = °> zvi>0' i=h!}.
Особо следует оговорить, к каким гиперплоскостям относятся граничные
точки, где две и более дополнительных координат обращаются в 0. На практике
эти точки часто не представляют интереса, поскольку при соответствующих ве-
роятностных условиях траектория z(t) может оказаться в них с вероятностью 0.
В частности, для рассматриваемой системы это заведомо будет справедливо,
если вероятностные распределения, «управляющие» СМО, имеют плотности.
В основном состоянии v в силу определения вектора zv имеем: avl = av2 = I,
aV(- =0, i > 2 (время, оставшееся до окончания обслуживания требований,
находящихся на приборе, убывает с единичной скоростью; время, необходимое
для обслуживания требований, находящихся в очереди, остается неизменным).
Входной сигнал х поступает в момент прихода очередного требования. Ди-
скретная компонента этого сигнала принимает единственное значение (скажем, 1)
поскольку требования однородны по отношению к обслуживающему прибору,
а единственная дополнительная координата х1г равна длительности обслуживания
поступающего требования. Поскольку aVj- = 0, j > 2, то дополнительные коор-
динаты не могут достигать j-й грани, / > 2. Поэтому {О',*} и {/.',*,} будем оп-
ределять только для j = 1,2. Случайные векторы г]', в данном случае не опреде-
ляются (имеют размерность 0). /-й грани (/ = 1, 2) множества Tv соответствует
один многогранник О',' = Tv, которому приписано вероятностное распреде-
ление {p'vlv,}, где р^, = 6v, ,v_1,h набор матриц (размерности (v — 1) X v),
который в данном случае состоит из одной матрицы
1 1 0 0 . . 0
0 0 1 0 . . 0
7'1 = '“V, v—1 0 0 0 1 . . 0 , v>2,
_0 0 0 0 ... 1_
^ = [1,1].
Если v — 1, матрица не определяется.
Описанная конструкция соответствует следующим переходам (для v > 2)-.
а) в случае г=(у, 0, zv2, zv3,..., zvv), /=1,
v'=v —1,
2v' 1 = zv2,
Zv'v Zv', V—1 Zvvi
б) в случае z = (v, zvl, 0, zv3,..., zvv), / = 2,
V' = V — 1 ,
2v'l =zvl,
zv'2 “2v3,
zv'v' 2v', v—1 — zvv-
Случай v=l тривиален, поскольку тогда v'=0.
173
Если z(i) = (v, zvl,..., zvv) и в момент t поступил входной сигнал
х (0 = (1, хи), то z(i + 0) = (v+l, zvl,...,zvv, х j j), что соответствует переходу:
v' = v+ 1,
2V' 1 = 2V1>
2V'V 2VV>
2v'v' = zv , v+1 = Ян-
Читателю предоставляется возможность проверить, что такое изменение
состояния укладывается в схему кусочно-линейного агрегата, как это только
что было проделано.
В рассмотренном случае входной сигнал содержал в себе информацию о
том, сколько времени должно обслуживаться поступающее требование. Предпо-
ложим теперь, что входной сигнал содержит в себе только информацию о поступ-
лении требования, и пусть для простоты длительности обслуживания каждого
требования — независимые одинаково распределенные случайные величины с
функцией распределения В(-).
Это соответствует изменению в предыдущей схеме структуры входного сиг-
нала х и переходов, совершающихся при его поступлении. Именно х состоит толь-
ко из дискретной компоненты, принимающей единственное значение 1,
|ц| = 0, т. е. X = {1}. Тогда, если z(/) = (v, zvl, ..., zvv) и в момент t поступил
входной сигнал х = 1, то определяется случайная величина (являющаяся
в данном случае единственной компонентой вектора с^) с функцией распреде-
ления В(-); sfj = s^, = 1. Рассматривается пространство размерности |v|-|-
+ |р,| + s!J = v + 1 и его разбиение, содержащее единственный элемент —
все пространство, которое обозначим через = Dv. Пространству Dv припи-
сано вырожденное распределение {Pvv'J’Pvv' = v-H’ и еДииственная
единичная матрица размерности (v + 1) X (v + 1)
1 о о
О 1 о
О б 1
bv, v+ 1
о'
о
о •
ООО ... 1
Построенная конструкция соответствует следующему переходу при поступ-
лении входного сигнала х:
v' = v+ 1,
V 1 =2V1,
2v'v = 2VV,
2v' V = ZV‘ , V-f- 1
где g —случайная величина с распределением В(-), не зависящая от предысто-
рии процесса.
В качестве дополнительных координат в примере были взяты длительности
обслуживания. Часто более целесообразно рассматривать «энергетическую»
интерпретацию обслуживания, т. е. считать, что для обслуживания некоторого
требования необходимо выполнить определенное (быть может, случайное) ко-
личество работы. Если за дополнительную координату zVj- в примере выбрать
количество работы, которое необходимо затратить для полного обслуживания
174
/-Го требования, находящегося в системе, то av- указывает на интенсивность
выполнения этой работы. При постоянных интенсивностях все конструкции пол-
ностью сохраняются. Однако представляют интерес также случаи, когда указан-
ные интенсивности зависят от значений дополнительных координат, например,
в силу того, что на различных этапах работы по обслуживанию выполняются с
помощью различного оборудования или в силу постепенного изменения свойств
обслуживающих устройств. В этом случае приходим к определению кусочно-
непрерывного агрегата.
В примере ничего не говорилось о выдаче выходных сигналов. Вид их за-
висит от характера решаемой задачи. Если, например, обслуженные рассмотрен-
ной системой требования поступают далее на какой-либо другой прибор, то вы-
ходные сигналы должны выдаваться в моменты окончания обслуживания и со-
держать интересующую следующие обслуживающие устройства информацию
о требовании, такую, как время его нахождения на обслуживании, время ожи-
дания начала обслуживания и т. д. В простейшем случае множество У состоит
из одного символа, который фиксирует факт ухода требования из системы. Ча-
сто количество дополнительных координат увеличивают с тем, чтобы в их число
вошли величины, фиксирующие информацию, необходимую при выдаче выход-
ных сигналов. Так, в рассмотренном примере в число дополнительных координат
можно было бы ввести времена, проведенные различными требованиями в
системе. Это координаты с течением времени (до моментов окончания обслу-
живания соответствующих требований) возрастают с единичными скоростями
Пример 3. Рассмотрим работу одного обслуживающего устройства и пока-
жем, как описать рассматриваемый процесс в виде кусочно-линейного агрегата.
Пусть на обслуживающий прибор поступает ординарный поток требований,
причем i-e по счету требование характеризуется параметром 0,, который пред-
ставляет собой предельное допустимое время ожидания i-м требованием начала
обслуживания. Время обслуживания i-ro требования равно причем {£$} —
последовательность независимых одинаково распределенных случайных величин
с общей функцией распределения В(х). Искомыми являются вероятностные ха-
рактеристики длины очереди и времени ожидания.
Представим данный процесс обслуживания в виде кусочно-линейного аг-
регата. За состояние агрегата выберем вектор 2 = (v, zvl, z ), где v — чис-
ло требований, находящихся в системе, которые дождутся (или дождались) на-
чала обслуживания, 2vl(v >0) — время, оставшееся до окончания обслуживания
требования, находящегося на приборе, a 2VI(1 < i < v) — длительности об-
служивания требований, которые стоят в очереди и будут впоследствии обслу-
жены. Таким образом, в данном случае |v| = v, вектор av скоростей изменения
дополнительных координат имеет следующие компоненты: avl = l,av/ = 0(i>l).
rv = {zv: zv > 0} , yv, = {2V : zv/ = 0} .
В качестве входного сигнала примем пару (1, 0), где символ 1 просто ука-
зывает на факт поступления требования (и, таким образом, компонента р, при-
нимает лишь одно значение 1), а величина 0 равна допустимому времени ожида-
ния рассматриваемого требования (т. е. |р.| = 1).
Рассмотрим теперь возможные переходы данного агрегата. Поскольку
между моментами поступления входных сигналов изменяется лишь первая до-
полнительная координата (если v > 1), тонет необходимости рассматривать слу-
чаи выхода дополнительных координат на гиперплоскости Tvy(/ > 1). Если мо-
мент t* определяется соотношением 2V(/*) £ у, то zvl(Z*) =0. Очевидно, v(t*) >
> 0. Пусть 2(t*) = (v, 0, Zv2, ..., Zvv)- Тогда состояние z(t* + 0) имеет сле-
дующий вид:
Z (Z*4-0) = (v —1, z‘v).
Таким образом, можно принять, что Гу = 0, определяется один много-
гранник Dy1 = fv и вероятность руу' = 6V, v_r
175
В этом случае необходимо определить лишь одну матрицу Lvk- —1> которая
имеет вид
О
О
1 О О
О 1 О
О 0 1
О
О
О
О О О О ... 1
и содержит v столбцов и (v — 1) строк.
Рассмотрим теперь случай поступления входного сигнала (1, 6). Опреде-
лим sv — 1, а функцию распределения случайной величины gv положим рав-
ной В(х). Пространство размерности v + 2 разобьем на два многогранника:
Sv‘={(2v 9- ^):0>pv/)- Bv2 = {(2v е’ ^):0<pv/l-
Если (zv, 6, то определим Pvv' =5v'. v+1 и
L
Г1 О О
О 1 о
О 0 1
ООО-]
ООО
ООО
ООО
ООО
1 О О
О 0 1
Матрица Lv'v+1 содержит v + 1 строк и v + 2 столбцов. Такой переход соот-
ветствует присоединению к очереди поступившего требования. Время его об-
служивания равно
Если (zv, 0, то Pvv'=Sv'v и
О О
О О
1 О
1
О
О
О
1
О
ООО
ООО
ООО
0 0 0 0
1 О О
Матрица Ly?v содержит v строк и v + 2 столбцов. Такой переход соответствует
потере поступившего требования.
Читателю предлагается в качестве упражнения представить в виде авто-
номного кусочно-линейного агрегата описанную выше систему обслуживания
при дополнительном предположении о том, что поступающий поток требований
является рекуррентным, т. е. интервалы между последовательно поступающими
требованиями являются независимыми одинаково распределенными случайными
величинами.
Пример 4. Система передачи данных (СПД) по сети связи. Сеть связи пред-
ставляет собой совокупность узлов и направлений связи. На рис. 6.1 дуги соот-
ветствуют направлениям связи, а вершины — узлам связи. Стрелки показывают
возможные направления передачи данных. На некоторые узлы (на рисунке —
па узлы 1, 4) могут поступать сообщения извне. Узлы связи работают следующим
образом: при поступлении на его вход очередного сообщения узел, в зависимости
от типа сообщения (его адреса, приоритета и т. д.) и состояния (основного), во-
обще говоря, всей сети (на практике учитываются, как правило, лишь локальные
свойства сети), мгновенно в соответствии с заданным алгоритмом работы посы-
лает это сообщение в то или иное направление связи. В силу того, что число на-
правлений связи и возможных основных состояний сети конечно, работу узла
связи можно трактовать как работу конечного (вероятностного) автомата. Выше
в примере 1 такой автомат описывался в виде кусочно-линейного агрегата. Не-
176
обходимость подобной интерпретации в данном случае вызывается потребностью
дать единое математическое описание различным элементам (узлам и направ-
лениям связи) системы. В результате появится возможность (см. гл. 7) описать
всю СПД как кусочно-линейный агрегат.
Предположим, что узел связи абсолютно надежен. Тогда входными сигна-
лами для агрегатов, моделирующих их, являются как необходимая информация
о поступающих на моделируемый узел требованиях, так и информация о состоя-
нии сети, подаваемая в момент изменения этого состояния. Выходным сигналом
является информация о сообщении, выдаваемом этим узлом либо во вне, либо в
некоторое направление.
Опишем теперь работу отдельного направления связи. Обозначим через N
число каналов связи, входящих в данное направление. Одновременно может
работать не более N0(N0 < N) каналов. Следовательно, Л' — No каналов явля-
ются резервными. Резерв — нагружен-
ный. Вообще говоря, характеристики
каналов отличаются друг от друга.
Под характеристиками будем понимать
распределения времен безотказной ра-
боты, ремонта и подключения, о кото-
рых речь будет идти ниже. Заметим
только, что упоминаемые случайные ве-
личины, характеризующие как один
канал, так и различные каналы, незави-
симы. В случае отказа рабочего ка-
нала, он мгновенно поступает на ре-
монтное устройство, а на его место из
резерва (если в нем имеется хотя бы
один исправный канал) подключается
очередной канал. Время подключения
как и в период нахождения в резерве,
моитных мест достаточно для того, чтобы
Если какой-либо канал отремонтировался и
случайно. Во время подключения,
канал может отказать. Число ре-
не создавалось очереди на ремонт,
в это время в рабочем состоянии и в
стадии подключения находится менее Na каналов, он начинает подключаться для
работы. В противном случае — мгновенно поступает в резерв. Если канал отка-
зал, находясь в стадии подключения, то он мгновенно поступает в ремонт, а
вместо него начинает подключаться другой канал, если таковой имеется в резер-
ве. Если канал отказал, находясь в резерве, он мгновенно поступает в ремонтное
устройство.
Все сообщения, передаваемые сетью связи, делятся на несколько типов.
Эти типы имеют различные приоритеты л = 1,2, ..., П. Приоритету с меньшим
номером оказывается предпочтение, т. е. сообщения, имеющие высший приори-
тет (меньший номер), передаются раньше сообщений низшего приоритета. Внут-
ри каждого приоритета сообщения передаются в порядке поступления в направ-
ление связи. Если пришло сообщение и застало все рабочие каналы занятыми,
то оно становится в очередь, не прерывая передачу сообщений низшего приори-
тета. Если в момент передачи сообщения канал отказал, то это сообщение возвра-
щается в очередь и становится первым среди сообщений своего приоритета. Вре-
мя передачи сообщения случайно, не зависит от других характеристик системы
и имеет функцию распределения, определяемую только номером приоритета.
Работу направления связи при данных предположениях можно описать в
виде кусочно-линейного агрегата. Не описывая возможных переходов агрегата,
покажем только, какой вид имеют входные, выходные сигналы и внутренние со-
стояния. Описание динамики агрегата предоставляется читателю в качестве по-
лезного упражнения.
Входной сигнал х(/) поступает в момент передачи в направление связи с
узла очередного сообщения, содержит в себе необходимые данные об этом сооб-
щении и имеет следующую структуру:
х = 7^ист> 7(пол> А^пор, 6),
где л — номер приоритета; /(ИСТ — номер узла, являющегося источником сооб-
щения; Каоя — номер узла-адресата; yVnop — порядковый номер сообщения
177
(необходим для «склейки» из различных сообщений полного текста); б — суммар-
ное время, проведенное сообщением в сети связи.
Вектор (л, Кист> Кпол, A/пор) является дискретной компонентой входного
сигнала, а 0 — единственной дополнительной координатой.
Внутреннее состояние г имеет вид
= (S, Ij,. . ., i’s, Si.Ss* P> /р.’ч /р> £s-H 1 • • • ’ £s+p, ^s+p+1 ’ ’ £s+2p’ cl’
/ П \
S mn )
*1’-» kqi ^+2р+1,..., £s+2p-H, /пП- . ™зан,
»• • •» ^m-jan’ > х2* ^2»•• • । nt3aH> ^тзап)•
Здесь:
s — общее число рабочих и резервных каналов;
1/, 0 < I s,— номера рабочих и резервных каналов (если s > ,V0, то кана-
лы it, I > 7V0, являются резервными);
Si, 0 < / < s,— время, оставшееся до отказа канала ip,
р — число подключаемых каналов;
jl, 0 < I р,— номера подключаемых каналов;
Si, s < I < s + р,— время, оставшееся до отказа подключаемого канала
il — s’
Si, s+p < / ^s + 2p,— время, оставшееся до подключения канала
/1 —p — s'
q — число неисправных каналов;
ki, О С I Ч — номера неисправных каналов;
Si, s + 2р < I < s + 2р + q,— время, оставшееся до окончания ремонта
канала /z;_s_2p;
тл, 1 «С л П,— число сообщений приоритета л в очереди;
П
х<') = (л<о, С’л. <’₽-0(/)).
л=1
— характеристики сообщения, стоящего l-м в очереди;
тзан — число каналов, занятых передачей сообщений (щзап < /Vo);
г;, 0 <1< tn ,—номера каналов, занятых передачей сообщений;
х,= (л К ,, К ,, N 0,), 0<1<т
I 4 I’ ист!’ пол!’ пор! I’ зада
— характеристики /-го передаваемого сообщения;
Si, 0 < I С тзан, — время, оставшееся до окончания передачи сообще-
ния Xl-
Основное состояние образуют величины s, ilt ..., is, р, jlt ..., jp, q, klt ..., kq,
mlt ..., m , m3aH, ri, rm3aH, дискретные компоненты векторов 0 < I С
п
’С 2 тП’ и *i, 0 < / < тзан- Остальные компоненты образуют вектор допол-
л= 1
нительных координат.
Выходные сигналы у (/), выдаваемые агрегатом, моделирующим работу на-
правления связи, имеют вид (/= ((/!, у2). Сигналы y(t) выдаются в моменты изме-
нения его основных состояний. Компонента у2 при этом равна основному состоя-
нию агрегата в момент, непосредственно следующий за его изменением. Компо-
нента t/i определяется только в моменты окончания передачи сообщений и содер-
жит в себе все характеристики переданного сообщения: л, Кист, Кпол, Л'пор , 0-
При этом сигнал уг (/), поступая на агрегаты, моделирующие узлы связи, «инфор-
мирует» его о происшедших с сетью изменениях.
178
6.5. ПРИВЕДЕНИЕ КУСОЧНО-ЛИНЕЙНЫХ
И КУСОЧНО-НЕПРЕРЫВНЫХ АГРЕГАТОВ К КАНОНИЧЕСКОМУ ВИДУ
Путем дальнейшего расширения множества состояний и соот-
ветствующих преобразований координат можно привести кусочно-
линейный агрегат к более простому виду. Рассмотрим этот вопрос
подробнее.
Пусть в момент t состояние кусочно-линейного агрегата г (/) =
= (v, zv). Тогда, если предположить, что, начиная с момента /, внеш-
ние воздействия на агрегат прекратились, можно определить момент
первого выхода вектора дополнительных координат на границу
“14 области 1\, а также ту грань на которую произойдет выход.
Выход на границу произойдет в момент t + т, x=min ту, где величины
/.т/>0
ту = ту (zv) находятся из условия zv — avij g Номер грани j0, на
которую произойдет выход вектора дополнительных координат, опре-
делится равенством ту0 = т.
Из определения кусочно-линейного агрегата следует, что т и /0
находятся из решения конечной системы линейных алгебраических
уравнений, проверки ряда линейных неравенств и взятия минимума.
Заметим также, что номер /0 не меняется вдоль траектории движения
дополнительных координат.
Определим новый агрегат (кусочно-линейный), взяв в качестве
основного состояния пару vk = (v, /0). За первую дополнительную
координату, которую обозначим через zVki, возьмем (в случае |v| > 0)
величину т. По своему смыслу — это неотрицательная переменная,
убывающая с единичной скоростью вплоть до того момента, когда она
обращается в нуль.
Пусть последний переход исходного агрегата из одного основного
состояния в другое имел место в момент t* < t. В этот момент значение
времени до выхода на границу было равно т*. Уже было отмечено, что
номер /0 не изменяется в течение всего времени пребывания агрегата
в некотором основном состоянии. Выберем в качестве второй дополни-
тельной координаты нового агрегата, которую обозначим через г^,
величину т#. Таким образом, zVkz — zVki суть время, прошедшее с мо-
мента последнего изменения основного состояния исходного агрегата.
Выберем в качестве /-й (/ > 2) дополнительной координаты нового
агрегата значение zv, (£*), т. е. zVkii = zv, ,_2 (t*). Отсюда следует,
что все дополнительные координаты нового агрегата (в случае их су-
ществования), начиная со второй, сохраняют свои значения неизменны-
ми вплоть до перехода в другое основное состояние. Очевидно, по-
ступления входного сигнала не нарушают построенной конструкции
и учитываются естественным образом. Построенный агрегат является
кусочно-линейным и его характеристики однозначно определяются
через характеристики исходного агрегата. Легко видеть, что верно
и обратное: зная состояние нового агрегата, который назовем агрега-
том в каноническом виде, можно однозначно восстановить состояния
исходного агрегата.
179
Следовательно, можно вместо кусочно-линейных агрегатов общего
вида рассматривать такие кусочно-линейные агрегаты, у которых пер-
вая из дополнительных координат убывает с единичной скоростью, а
остальные не изменяют своих значений до момента обращения в О
первой координаты. Благодаря этому вид областей чрезвычайно
простой: = [zv: zvi ^0), и отпадает необходимость различать
грани областей Tv. Каждая такая область имеет единственную грань
zvi = 0. При рассмотрении теоретических вопросов часто оказывает-
ся удобным исследовать агрегат в каноническом виде. В то же время
для численных расчетов, моделирования и т. п. это оказывается не
всегда целесообразным. Следует отметить, что для кусочно-линейного
случая нахождение характеристик агрегата в каноническом виде через
характеристики исходного агрегата и обратно не вызывает принципиаль-
ных трудностей.
Укажем, что к такому же (каноническому) виду может быть све-
ден и кусочно-непрерывный агрегат, определяемый в § 6.2. Таким обра-
зом, класс кусочно-линейных агрегатов совпадает, по существу, с клас-
сом кусочно-непрерывных агрегатов. Однако переход от произвольного
кусочно-непрерывного агрегата к каноническому связан с целым рядом
принципиальных трудностей, таких, как нахождение времени т и точ-
ки на границе yv, куда попадает вектор дополнительных координат,
поскольку, в общем случае, эти величины будут случайными, и их
распределения находятся в результате решения достаточно сложных
вероятностных задач.
Если же траектория движения в области является, скажем,
решением системы обыкновенных дифференциальных уравнений, то
для перехода к агрегату в каноническом виде требуется, вообще гово-
ря, произвести интегрирование данной системы.
ГЛАВА СЕДЬМАЯ
АГРЕГАТИВНЫЕ СИСТЕМЫ
7.1. ВВОДНЫЕ ЗАМЕЧАНИЯ
Как было показано выше, в качестве математической схемы для
формального описания сложных систем во многих случаях может быть
использован агрегат. Применение языка агрегатов приводит к унифи-
цированному математическому описанию реальных объектов различ-
ной природы, упрощает построение математических моделей и реали-
зацию их на ЭВМ, позволяет осуществить единый методический под-
ход к количественному и качественному исследованию систем. Однако
как с теоретической, так и с практической точек зрения иредставляет
несомненный интерес рассмотрение и более сложных образований.
В частности, в настоящей главе изучается класс сложных систем, пред-
ставляющих собой некоторые конструкции из агрегатов.
В дальнейшем, говоря о системе S, мы будем иметь в виду сово-
купность конечного числа агрегатов Cj, / = 1, 2, ..., N, вместе со свя-
зями между ними. Таким образом, агрегат рассматривается в каче-
стве элемента системы.
Очевидно, что для описания системы S необходимо иметь описа-
ние как его элементов Cj, так и взаимодействия между элементами. По-
скольку в данном случае элементами системы являются исключительно
агрегаты, вопрос об описании элементов можно считать исчерпанным.
В соответствии с введенным выше определением (см. гл. 5), агрегат
есть объект, задаваемый множествами моментов времени Т, входных
сигналов X, управляющих сигналов Г, внутренних состояний Z, вы-
ходных сигналов У, подмножествами Z<y> и операторами переходов
V', У", U (в новое состояние) и выходов G". Поэтому для построения
формального понятия системы нам остается выбрать достаточно удоб-
ные способы формализации и математического описания взаимодейст-
вия между агрегатами.
Одной из основных особенностей системного подхода к практиче-
ским задачам является то обстоятельство, что поведение системы не
может рассматриваться изолированно от внешней среды. Под внешней
средой (относительно данной системы) мы понимаем совокупность таких
объектов, не являющихся элементами данной системы, взаимодействие
с которыми учитывается при изучении данной системы.
Из методических соображений необходимая степень формализации
достигается постепенно. На протяжении данной главы мы введем ряд
предположений о взаимодействии агрегатов и используем соответствую-
щую символику для описания структуры связей между ними.
181
Предположение 1. Взаимодействие между системой и внешней
средой, а также между агрегатами внутри системы осуществляется
посредством передачи сигналов4, взаимные влияния, имеющие место
вне механизма обмена сигналами, не учитываются.
Это предположение позволяет свести изучение взаимодействия
агрегатов к двум проблемам: 1) рассмотрению сопряжения агрегатов
в системе при помощи каналов связи, обеспечивающих передачу сигна-
лов между агрегатами, и 2) оценке воздействия агрегата, выдающего
сигнал, на агрегат, принимающий этот сигнал. Первая проблема полу-
чит достаточно полное освещение в настоящей главе. Относительно
второй — ограничимся следующими краткими замечаниями.
Пусть выходной сигнал //</>(/) агрегата Cj поступает в качестве
входного (0 или управляющего gW (t) сигнала в агрегат Ch. Мо-
мент выдачи (когда состояние г^"> (I) достигает подмножества Z/V>,
см. гл. 5) и содержание сигнала (формируемое оператором б"(й)
зависят от состояния z('>(£) агрегата Cj. Этот сигнал в агрегате Ch
играет роль параметра случайного оператора V'(i) или К'(А), опреде-
ляющего состояние z(A> (t + 0) агрегата Ck. Мы приходим к схеме
воздействия одного агрегата на другой, при которой распределение
вероятностей для состояний агрегата, принимающего сигнал, зависит
от состояний агрегата, выдающего сигнал. Подбирая соответствующим
образом подмножества Z/y>, операторы , а также операторы
V'(k> или V"(A>, можно, как показывает опыт, сделать упомянутые за-
висимости достаточно близкими к требуемым для весьма широкого
класса реальных сложных систем. Очевидно, что аналогично может
быть описано воздействие агрегата Ck на агрегат Cj.
Прежде чем переходить к сопряжению агрегатов при помощи ка-
налов связи, необходимо договориться о природе сигналов, циркули-
рующих между агрегатами. На этот счет мы будем придерживаться
следующего предположения.
Предположение 2. Для описания сигнала достаточно некоторого
конечного набора характеристик.
Так, входной сигнал х С X может быть описан в виде х = (лу,
х2, ..., хп), где X, £Xt, i = 1, 2, ..., п; Xt — заданные множества
(см. гл. 3). Прямое произведение
Х = Хг хД х ... хХп (7.1)
— пространство входных сигналов агрегата, множества Xt — элемен-
тарные оси пространства X. Аналогично управляющий сигнал
g^T есть £ = (gy,£2, ... ,gm); g3eVs, s = 1, 2, ... ,m; f = f1 x Г2... x
X Tm—пространство управляющих сигналов. Выходной сигнал у Q Y
есть у = (уъу2,... ,yr); y^Yi, I ~ 1,2, ..., г; Y =У21ХУ2... XY —
пространство выходных сигналов. Га и Уг — элементарные оси про-
странств Г и У соответственно.
Для того чтобы сопряжение между системой и внешний средой
можно было описать в той же форме, что и сопряжение между аг-
182
регатами системы, внешнюю среду будем рассматривать как фик-
тивный агрегат С() с пространствами входных сигналов Х(0) = Xi0) х
X Х2 Х...хХ,г, и выходных сигналов У' ’ = Yi XY2 X...xYr,-
Сигналы, выдаваемые агрегатами системы во внешнюю среду, при-
нимаются агрегатом Со как входные сигналы х(0> =(х(10),хУ’, ... ,
х^), i0 = 1,2,..., п0. Сигналы, поступающие в агрега-
ты системы из внешней среды, являются выходными сигналами аг-
регата Со вида t/<°> =(t/i0), У(°\ , Уг°}\, € ^»0), /0 = 1,2,-..Не-
принятые предположения еще не дают возможности построить
достаточно простую математическую модель взаимодействия агрега-
тов. Для этой цели ниже будут сформулированы дополнительные пред-
положения. Однако на имеющейся основе уже можно поставить неко-
торые задачи и выбрать характеристики, описывающие структуру связи
между агрегатами системы.
7.2. ОСИ ПРИЕМА И ВЫДАЧИ СИГНАЛОВ
Общая структура сопряжения агрегатов в системе отображает
совокупность непосредственных связей между отдельными агрегатами.
Поэтому изучение структуры системы целесообразно начать с формаль-
ного описания сопряжения двух агрегатов Cj и Ck системы S; j, k =
= 0, 1, ..., N.
Рассмотрим те выходные сигналы агрегата Cj, которые посту-
пают в агрегат Ck в качестве входных сигналов. Обозначим их
Множество уУ,А) сигналов является некоторым подмно-
жеством множества Уб). Подмножество может быть как пустым,
когда выходные сигналы агрегата Cj не поступают в качестве входных
сигналов в агрегат Сй, так и совпадающим с Уб\ когда любой сигнал
У<Р у(/) оказывается входным сигналом Ck. Очевидно, что t/V’А)
является точкой пространства У(/), поэтому, по крайней мере фор-
мально, его можно представить в виде 1/У,А) = (г/У/А), г/У2'&),..., г/У'*’)»
(М) МЛ
где y*t GYX[ cYYi , 1 = I, 2,..., rj.
Некоторые изУУ;'&) могут оказаться пустыми множествами. Каж-
дому непустому множеству У^'А) поставим в соответствие элементар-
ную ось У/П (с тем же номером /) пространства У(/). Множество та-
ких элементарных осей обозначим [уУ’^]. Рассмотрим прямое про-
изведение элементарных осей Yi х [У J , взятых в том порядке,
в котором они представлены в пространстве У(/\
уУ'А) =П {у/’ 6 [уУ,4)]/У(/>1 (7.2)
Это произведение является осью пространства У(/) (в смысле гл. 3).
183
Например, если пространство выходных сигналов агрегата Cj
р(/) = у(/,ХУ^)хГз;,хГ4/)х^5/)ХУб/)- (7.3)
сигнал
.(/)_ (Ah Ah Ah Ah Ah Ah\
У > »2 » Уз ’ У± » Уз > Уз )
и
Ai.k)_( Ah Ah Ah\
Ух —\У2 ’ у4 » Уз )'
y^^A^A^A^ , (7.4)
а сигнал у^’А как точка пространства Y^ имеет вид
г/У,А) = (0- У(2}’ 0- У(4П’ У(А 0)- (7.5)
Очевидно, что сигнал у^,к} может рассматриваться как проек-
ция t/(/) £ У(/) на осьУУ,<:). Последнюю в дальнейшем будем назы-
вать осью выдачи агрегатом, Cj входных сигналов агрегату Ck-
Аналогичные рассуждения можно провести для выходных сиг-
налов уг,/г) агрегата Q, которые поступают в агрегат Ck в качестве
о л(М)
управляющих сигналов. В результате, вводится осьУг выдачи аг-
регатом Cj управляющих сигналов агрегату Ck,
Yr 'k) =П |у/’ £ [Уг ,k)]/Y(/)}. (7.6)
Например, если
#ft) = (HZ)- <#’> у1А
у(./’А) = У</>хЙ^’хГ^), (7.7)
а сигнал у^,!^ как точка пространства имеет вид
= 0-0- У4}’ у(А 0)- (7.8)
Очевидно, что i//,4) может рассматриваться как проекция у(,) £ У(у)
Л(М)
на осьУг
В реальных системах встречаются случаи, когда выходной сигнал
одного агрегата поступает в другой агрегат и как входной сигнал и как
управляющий (обобщенный входной сигнал х = (х, g) Е X = X х Г).
Такого рода выходной сигнал агрегата Cj, поступающий в агрегат Ch,
будем обозначать уО-^.
Ось выдачи агрегатом Cj сигналов агрегату Ch может быть опи-
сана как
У(М) =П {у/’ е ([Ух',А)] и [Уг ,k>])/A) I • (7.9)
184
В рассматриваемом выше примере
У </•*) = У </) х у!/* X У X У (5;)
Выходной сигнал как точка пространства имеет вид
У(ЛА) = (у</), Уг}' 0> У4}’ У5}> 0)- (7-Ю)
Необходимо обратить внимание на одно обстоятельство, возникаю-
щее в связи с соотношением (7.9). В общем случае множества элементар-
ных осей [Уб’А> ]и могут иметь одну или несколько совпадаю-
щих элементарных осей, т. е.
[Й,Л] П [V0] *0.
Это означает, что выходные сигналы и уг’к} содержат одинако-
вые значения некоторых координат г/р. Однако в силу идемпотент-
ности операции объединения множеств (см. гл. 3), множество
[У* ] U |Хг J содержит каждую из имеющихся элементарных
„ • (/) „ *(/.*)
осей Yt лишь в одном экземпляре. Поэтому ось Y является пря-
* (/)
мым произведением несовпадающих элементарных осей Уг .
Перейдем теперь к пространству входных сигналов агрегата.
Выходной сигнал агрегата Cj поступает в агрегат Ck в каче-
стве входного сигнала x^k’’Y Сигнал х^а) является точкой прост-
ранства Х(А), поэтому
х — 1 > > •••, ) ,
где
е аХ^’схГ’, г = 1,2, ...,nk.
Пусть [Л ]—множество элементарных осей А, , для которых
соответствующие хУ’у) =?^0. Прямое произведение
Х(А’/)=П[Х-й> Q [Х(М)]/Х(А)) (7.11)
является осью пространства Х(*), которую будем называть осью
приема агрегатом Ck входных сигналов от агрегата Cj. Сигнал
можно рассматривать как проекцию С на ось Х<М).
Аналогичные построения можно выполнить для пространства
управляющих сигналов Г(*> агрегата Ch. Если [Г(М>] — множество
элементарных осей, для которых соответствующие =/=0, то
прямое произведение
f(ft,/)=n{fsA) £ [f<*’/>]/f<*)) (7.12)
будем называть осью приема агрегатом Ch управляющих сигналов от
агрегата Cj.
185
V v^-i)
Характеристики Y , л и Г , а также множества элемен-
тарных осей [У ], [л J и [Г ] играют важную роль в структур-
ном анализе сложных систем.
7.3. АГРЕГАТ КАК ЭЛЕМЕНТ СИСТЕМЫ
Обязательной составной частью оценки роли и места агрегата как
элемента данной системы, является изучение его связей с другими агре-
гатами системы и внешней средой. Необходимые сведения об этом
доставляют нам оси приема и и выдачи У(М) сигналов.
Однако с точки зрения решения практических задач большей нагляд-
ностью обладают некоторые частные, производные от них, характери-
стики.
Обратимся к пространству выходных сигналов Уб) агрегата Cj.
Сигналы, выдаваемые агрегатом Cj во внешнюю среду, характеризуют-
ся внешней осью этого пространства У^(/>°>, а сигналы, выдаваемые дру-
гими агрегатами системы, — внутренней осью-.
Ум ==П[у,(/) £ U [Й(',А)]/у(/)} . (7.13)
4=1
Здесь некоторые множества элементарных осей [Уб'.*)]' могут быть
иустыми (если выходные сигналы агрегата Cj не поступают к агрега-
ту Cft).
Когда требуется различать входные и управляющие сигналы, вы-
даваемые агрегатом Cj, удобно пользоваться внутренними осями
у!м = п (у,(/) е и [у!М)]/У(/)}, (7.14)
4=1
Угк = П{У2(/)б и [УгМ)] /У(/)), (7.15)
k= 1
* (/)
которые связаны с Yifl соотношением
Ум =П {У?'1 £ ([Им ] U [HL])/У(/)} • (7.16)
Перейдем к пространствам входных и управляющих сигналов.
Агрегат Ck может принимать входные сигналы от других агрегатов
данной системы и из внешней среды. Сигналы, поступающие от агре-
гатов данной системы, характеризуются внутренней осью пространства
входных сигналов агрегата Ch:
и [х(М)1/х(% (7.17)
/=|
а сигналы, иостуиающие из внешней среды, — внешней осью Х(4’°>.
186
По аналогии с (7.17) можно записать выражение для внутренней
оси пространства управляющих сигналов П*’:
Гм=П[г‘А) е U [f(ft,/)]/r(A)}. (7.18)
/=1
Соответствующая внешняя ось имеет вид
На практике обычно мы встречаемся с двумя подходами к формаль-
ному описанию реальных объектов: «аппаратурным» и «функциональ-
ным». Сущность их состоит в следующем.
При аппаратурном подходе одинаковые физические элементы си-
стемы получают одинаковое математическое описание, независимо от
их функций, роли и места в данной сложной системе. Например, если
вычислительный комплекс, наряду с многочисленными другими эле-
ментами, содержит несколько ЭВМ типа «Минск-32», то при аппаратур-
ном подходе все они описывались бы одинаково — в виде агрегата
с определенными множествами X, Г, Z, У, хотя одна из этих ЭВМ может
быть управляющим элементом вычислительного комплекса, другая —
обыкновенным вычислителем, третья — машиной-сателлитом, обеспе-
чивающей взаимодействие комплекса с источниками информации,
и т. д.
Наоборот, при функциональном подходе элементы системы полу-
чают математическое описание, исходя из их функций, роли и места
в системе, независимо от физической реализации. В упомянутом выше
примере ЭВМ-сателлит будет представлена агрегатом с такими мно-
жествами X, Г, Z, У, которые определяются числом и свойствами ис-
точников информации, порядком поступления ее в вычислительный
комплекс, режимом работы других ЭВМ комплекса и т. д.; множества
входных, управляющих и выходных сигналов агрегата, описывающего
ЭВМ-вычислитель, могут в общем случае иметь совсем другой вид.
При аппаратурном подходе описание Элемента должно быть агрега-
том столь общего вида, чтобы различные агрегаты, соответствующие
отдельным функциональным вариантам этого элемента, были его
частными случаями.
С формальной точки зрения функциональный подход выглядит
предпочтительнее: описание элементов оказывается более компактным,
математическое исследование модели сложной системы упрощается
и т. д. Однако на практике не всегда эти преимущества оказываются
решающими. Дело в том, что построение математического описания
элементов часто требует значительных затрат ручного труда. При
аппаратурном подходе иногда можно получить некоторую экономию:
наиболее трудоемкая работа выполняется один раз, а выделение част-
ных случаев является задачей более простой и к тому же легко под-
дающейся решению на ЭВМ-.
Учитывая эти чисто практические соображения, целесообразно
предусмотреть возможность оперирования над агрегатами, описываю-
щими реальные объекты в общем виде, независимо от их функций,
роли и места в исследуемых системах. Поэтому в дальнейшем, характе-
ризуя агрегаты системы пространствами Х(/'>, Гб'), у(/>, / = 1, 2,
187
..., X, мы будем предполагать, что речь идет о наиболее общих схемах
описания, присущих данному типу реальных объектов. Пространства
Хб), Гб’) и Уб) отражают лишь допустимые возможности обмена сиг-
налами агрегата Су с другими объектами, независимо от того, являет-
ся ли он элементом данной системы или нет. Включение агрегата Cj
в качестве элемента в конкретную систему некоторым конкретным обра-
зом накладывает на агрегат определенные ограничения, которые опре-
деляют истинные пространства входных, управляющих и выходных
сигналов агрегата как подпространства пространств Хб), Гб), Уб).
С формальной точки зрения, для построения истинных пространств
входных, управляющих и выходных сигналов агрегата как элемента
системы, включенного в нее заданным способом, необходимо из мно-
жеств элементарных осей пространств Хб), Гб') и Уб) выделить эле-
ментарные оси, принадлежащие множествам [Хб. *)], [Гб'. *)] и
[Уб> *)], характеризующим связи между агрегатами системы. Выделен-
ные элементарные оси войдут в состав множеств элементарных осей
истинных пространств, а остальные должны быть исключены из рас-
смотрения.
Обозначим истинные пространства входных, управляющих и вы-
ходных сигналов агрегата Cj через Хб), Гб') и Уб), а соответствующие
им множества элементарных осей—через [Хб)], [Гб')] и [Уб>].
Легко видеть, что множество [Уб>] содержит такие элементарные
оси У/7?, которые принадлежат или [Уб'.о>] или [у!^]. Поэтому
истинное пространство выходных сигналов агрегата Cj как элемента
системы имеет вид
у(/) =П {yz(/) £ U [У(М)]/^(/)!- (7-19)
1 k=0
Множество элементарных осей [Хб')] можно получить как объеди-
нение [Хб'.о)] и [Х*„]. Поэтому истинное пространство входных
сигналов агрегата Cj как элемента системы описывается соотношением
Х(/)=П{Х(/’е U [Х(М)]/Х(0}. (7.20)
1 k=0
Аналогичные рассуждения дают возможность записать соотноше-
ния для истинного пространства управляющих сигналов агрегата Cj
как элемента системы
Г(/) = П {г'П е и [г(/,А)]/Г(/)}. (7.21)
J А=0
Приведенные здесь соотношения для истинных пространств вход-
ных, управляющих и выходных сигналов агрегата как элемента, вклю-
ченного заданным образом в некоторую систему, используются при
переходе от аппаратурного описания реальных объектов к соответст-
188
вующему функциональному описанию, а также при других формальных
операциях, совершаемых над агрегатами системы. Когда же речь идет
о наглядной интерпретации истинных пространств Х(;), Гб) и Уб)
и сопоставлении их с пространствами АД), Гб") и Уб), часто пользуются
различного рода «отмеченными» пространствами.
Рассмотрим прямое произведение
ХУ? = П [Х-р б [Х(/)]; е [Х(/)] /Х(/)} (7.22)
всех элементарных осей Х\^ пространства Хб), взятых в том поряд-
ке, в котором они располагаются в пространстве Хб'). Пространство
(7.22) отличается от АД) лишь тем, что элементарные оси Хр?, не
принадлежащие множеству элементарных осей истинного пространст-
ва входных сигналов агрегата Cj, помечены черточкой. Пространство
(7.22) будем называть отмеченным пространством входных сигналов
агрегата С7- как элемента данной системы.
Аналогично описываются также отмеченные пространства управ-
ляющих и выходных сигналов агрегата.
Отмеченные пространства входных, управляющих и выходных
сигналов оказываются весьма удобными для графического представле-
ния сопряжения агрегатов системы при помощи структурных схем.
В этом случае способ включения агрегата в систему отображается
особенно наглядно.
7.4. ОПЕРАТОР СОПРЯЖЕНИЯ АГРЕГАТОВ
Рассмотренные в предыдущих параграфах характеристики сопря-
жения агрегатов системы введены пока чисто формально. Для исполь-
зования их при решении практических задач необходима математиче-
ская модель сопряжения, позволяющая выразить эти характеристики
в зависимости от структуры связей между агрегатами. Построение до-
статочно простой математической модели опирается на дополнитель-
ные предположения о характере сопряжения агрегатов, которые мы
сфомулируем ниже.
Без ограничения общности входной сигнал х (/), поступающий
в агрегат в момент t £Т, можно рассматривать как совокупность
«элементарных сигналов» х± (/), х2 (/), ..., хп (Z); Xi £ Xi, одновременно
возникающих на входе агрегата. Аналогично вводятся элементарные
сигналы gs(t),s = 1,2, ...,т\ gs € Гв, и yt (/), Z = 1, 2, ...,r;z/z € Yt.
Предположение 3. Элементарные сигналы передаются в системе
независимо друг от друга по элементарным каналам', каждый элемен-
тарный канал, подключенный к выходу агрегата Cj, способен переда-
вать элементарные сигналы, принадлежащие одному из множеств
Yi‘], и только эти сигналы.
189
Сформулированному предположению можно дать следующую си-
стемную интерпретацию.
Независимо от физической конструкции реальных объектов,
удобно представлять себе вход агрегата как совокупность п входных,
контактов (клемм)-, контакт предназначается для приема эле-
ментарных сигналов хг-(’(/)£ А*'?, zj=l,2.п,. Аналогично уп-
равляющий вход агрегата содержит т управляющих контактов-, кон-
такт Н'? предназначен для приема элементарных сигналов g(s’l (/) £ Гр?,
в/ = \,2, ..., тр, выход агрегата является набором г выходныхкон-
тактов; контакт Ур? способен выдавать элементарные сигналы
<(0 оу, h = K2,...,r}.
Элементарные сигналы, выдаваемые данным выходным контактом,
передаются некоторому входному или управляющему контакту другого
(или того же) агрегата лишь в том случае, если в системе реализован
элементарный канал, соединяющий упомянутые контакты.
Предположение 4. А каждому входному или управляющему кон-
такту подключается не более чем один элементарный канал-, к каждому
выходному контакту может быть подключено любое конечное число
элементарных каналов при условии, что ко входу и управляющему входу
одного и того же агрегата направляется не более чем по одному из этих
каналов.
Это предположение отражает главное условие сопряжения агре-
гатов: совокупность реализованных элементарных каналов каждому
входному или управляющему контакту ставит в соответствие единст-
венный вполне определенный выходной контакт того же самого или
другого агрегата системы. Выполнение этого условия гарантирует
поступление к входным и управляющим контактам в каждый момент
времени единственного элементарного сигнала. Невыполнение этого
условия повлекло бы за собой возможность одновременного поступле-
ния на вход агрегата сигналов (в общем случае несовпадающих) от
различных источников. Это обстоятельство приводило бы к неопреде-
ленности в функционировании агрегатов системы. Кроме того, пред-
положение 4 предусматривает, что дублирование при передаче
элементарных сигналов исключается.
Очевидно, предлагаемая формализация сопряжения агрегатов
обеспечивает адекватность математической модели и реальной системы
лишь при условии, что структура наборов входных, управляющих
и выходных контактов агрегатов соответствует структуре сигналов,
рассматриваемых как конечные совокупности одновременно поступаю-
щих элементарных сигналов.
В общем случае в реальных системах отмеченного здесь соответст-
вия может и не быть. Иногда причиной этого оказывается неидентич-
ность кодирования элементарных осей пространств входных, управ-
ляющих и выходных сигналов тех или других элементов системы.
Такого рода причины легко устраняются единым кодированием эле-
ментарных осей для всех входящих в систему агрегатов. В некоторых
190
случаях упомянутое выше соответствие входных, управляющих и вы-
ходных сигналов не может быть установлено по существу (требуемый
способ кодирования не существует). Тогда в реальных системах, в слу-
чае необходимости, между соответствующими объектами включаются
специальные устройства сопряжения, которые должны рассматривать-
ся как самостоятельные агрегаты системы. В качестве примера могут
быть названы устройства сопряжения между ЭВМ (параллельный код)
и телеграфной линией связи (последовательный код). В дальнейшем
мы будем считать, что требуемое соответствие элементарных осей тем
или другим способом установлено.
Как показывает опыт, сформулированные предположения не яв-
ляются сколько-нибудь стеснительными, они оказываются справедли-
выми для весьма широкого круга реальных сложных систем.
Пусть система содержит агрегаты Cj, j = 1, 2, ..., N, и взаимодей-
ствует с внешней средой, формализуемой в виде фиктивного агрега-
та Со.
Обозначим rs(? через Xn^s.. Тогда для множеств контактов
будет справедливо соотношение
? и [г^]7М*о’]?+тл (7.23)
где —множество входных контактов агрегата С/, [rs?]7J —
множество управляющих контактов агрегата Cj. Множество выход-
ных контактов агрегата Су обозначим [У^?] р. Для упрощения запи-
си формул будем избегать двойных индексов. Например, вместо
[х/^]"/ используем [хр]"; верхний индекс / указывает на то, что
i = ij, n = nj и т. д.
Пусть
[Хгк= U [хР]?+т, (7.24)
/=о
№=UHn]i- (7.25)
/=о
Рассмотрим отображение [XJw-> [KJw с областью определения
во множестве [XJ^ и областью значений во множестве [У^д,, реализуе-
мое оператором
Ур=7?(Хр), /, k = Q, 1, .... N, (7.26)
которое данному контакту ХР Е (Xfljv ставит в соответствие единствен-
ный контакт Ур Е [yjw, соединенный с ним элементарным каналом.
Если в данной системе некоторый контакт Хр не соединен ни с каким
контактом Ур, оператор (7.26) не определен на этом Х,-А).
Оператор R будем называть оператором сопряжения агрегатов
в системе. В область определения оператора R входят все входные
и управляющие контакты всех агрегатов системы и агрегата Со, к ко-
торым подключаются элементарные каналы (которые не являются
191
свободными в данной системе). Оператор R описывает совокупность
элементарных каналов, соединяющих эти контакты с выходными кон-
тактами соответствующих агрегатов системы и агрегата Со. Введение
оператора R завершает формализацию сопряжения агрегатов в систе-
ме. В связи с этим можно дать следующее определение.
Системой будем называть упорядоченную совокупность агрегатов
С1г С2, ..., Сы, множеств фиктивных контактов и [У<0)]
характеризующих внешнюю среду, и оператора R.
Заметим, что наряду с оператором R используется оператор
(/,/,-) = г (Mft), (7.27)
сопоставляющий каждой паре индексов (k, ih) соответствующую пару
индексов (/, lj) для контактов, соединенных элементарными каналами.
Оператор г (k, ih) удобно задавать в виде таблиц, где на пересечении
столбцов k = 0, 1, ..., N и строк ih = 1, 2, ..., nh + tnh помещается
пара индексов (/, /;).
Рассмотрим некоторую совокупность входных контактов
<= IXjLv. Для каждого Х{к] £ [Х'А)]' найдем соответствующий
ему У/(/) = R (Х;к)), если он существует в силу отображения R. Со-
вокупность полученных контактов Ур обозначим [У/(,)]'. Для обоз-
начения описанной здесь процедуры будем использовать символиче-
ское соотношение
[Ур>]'=Я([*Н')- (7-28)
Например, R ([Ар]?) представляет собой совокупность тех выходных
контактов всех агрегатов системы и агрегата Со, от которых передаются
элементарные сигналы, составляющие входной сигнал агрегата Ck,
a R (1Х!к)]"+?), — от которых передаются элементарные сигналы,
составляющие управляющий сигнал агрегата Ck.
Рассмотрим сужение оператора R (Х/й)) на множество [X*ft)]"cz
cz [Хг]ль Обозначим его Rh(X{k}). В силу предположения 4, при-
нятого в начале настоящего параграфа, этот оператор реализует
взаимно однозначное соответствие между входными контактами
Х[к} 6 Sxl> az [Х/А)]ь где Sxk}— область определения оператора Rk,
и выходными контактами Ур Е с= [Уг]л/, j =0, 1, ..., N, где
S^A)—область значений оператора Rk.
Из изложенного вытекает существование оператора Х^ =
= Rk~1 (Ур), обратного оператору Rk, с областью определения
Оператор R71 сопоставляет каждому УР Е Д ([^А>] i) соответствую-
щий контакт X\k} Е такой, что R (Х/А)) = Ур.
Аналогично сужение оператора R (Хр) на множество |хР]
обозначается Rk(X{k'1'). Этот оператор реализует взаимно однознач-
ное соответствие между
Х<*> Е <= [*Н»+Г и Ур Е Sp az [Уг]„, 7 = 0, 1, ..., N,
192
где Sp0 — область значений оператора Rk- Оператор, обратный Rk,
обозначается R~l(Y{il}). Этот оператор каждому У/(/) £ Я ([Х^]^™)
сопоставляет контакт Х;А) £ [Х^1]^^1 такой что 7? (Хр’) =Y^-
Операторы R, ЯГ1, КГ1 используются для изучения структуры
сопряжения агрегатов в сложных системах. При решении конкрет-
ных задач вводятся аналогично (7.27) операторы гГ* и г*-1.
Пример. Пусть система состоит из агрегатов С1( С2 и С3, где щ = 3, mj-
= 2, и2 = 2, т2 = 2, п3 = 3, т3 = 3. Внешняя среда: и0 = 4, г0 — 3. Оператор
'(/> h) — r№' ik) Для этой системы задается табл. 7.1. Тогда операторы г3, г3,
,г~з и г~з определяются данными, приведенными в табл. 7.2.
Таблица 7.1
Таблица 7.2
Г 3 Г 3 — 1 г 3 'I*
X Y X У У X У X
1 1,2 4 1,4 1,2 3,1 1,4 3,4
2 5 0,4 2,2 3,3 0,4 3,5
3 2,2 6 1,1 1,1 3,6
Заметим, что между входными, управляющими и выходными кон-
тактами, с одной стороны, и элементарными осями пространств входных,
управляющих и выходных сигналов, с другой, установлено взаимно
однозначное соответствие: каждому контакту (например, Х*А) или Уг(/))
сопоставляется элементарная ось (X;-ft) соответственно У|л) с теми
же индексами, и наоборот. Поэтому символом оператора R можно
7 Зак. 792 193
пользоваться и для описания соотношений между элементарными ося-
ми. Так, выражение R определяет множество тех элемен-
тарных осей (пространств выходных сигналов некоторых агрегатов),
контакты которых соединены элементарными каналами с контактами,
принадлежащими множеству [Х<.*)]]+'и.
Через оператор R легко выражаются характеристики сопряжения
агрегатов, рассмотренные в предыдущих параграфах настоящей гла-
вы.
В соответствии с (7.28) R ([X^l?) представляет собой множество
выходных контактов, вообще говоря, различных агрегатов системы,
от которых передаются элементарные сигналы к входным контактам
агрегата Ck, a R ([ХУ’]"+^) — аналогичное множество контактов,
от которых передаются элементарные сигналы к управляющим контак-
там того же агрегата. Чтобы выделить из этих множеств подмножества
выходных контактов агрегата Cj, достаточно рассмотреть их пересече-
ния с множеством [У,'’]'. Поэтому множество элементарных осей
[УЧ.*)] оси УЧ-*) выдачи агрегатом Cj входных сигналов агрегату
Ck (7.2) будет иметь вид
[уУ’*Ч =[у?3]; /, k = 0, 1, ..., N, (7.29)
а сама ось УУ'является прямым произведением элементарных
осей, принадлежащих множеству (7.29), взятых в том порядке, в ко-
тором они располагаются в пространстве УЧ) выходных сигналов
агрегата Cj,
УУ'*’=П ly?’£ {[уУ’П П R([X-"’]i)l/y(/)}- (7.30)
В дальнейшем в случаях, которые не могут привести к недоразу-
мениям, для краткости мы будем выписывать соотношения только
для множеств контактов или элементарных осей, опуская соответствую-
щие прямые произведения вида (7.30).
Для оси Уг 'k} (7.6) выдачи агрегатом Cj управляющих сигналов
агрегату Ck имеем
[Уг’*Ч = [yi;)K АЯОхГЧп + 'Г), /, k = Q, 1, ..., N. (7.31)
Проекция выходного сигнала yW 6 УЧ) на ось УУ’А) состоит
из элементарных сигналов, поступающих от выходных контактов агре-
гата Cj к входным контактам агрегата Ck, а на ось Ур — к управ-
ляющим контактам агрегата Ch.
Подобным же образом могут быть записаны соотношения для оси
уч.*) (7.9) выдачи агрегатом Cj (обобщенных входных) сигналов агре-
гату С\:
fy(M] = [уУ’К п r([xH? + '"), j, k=0, 1, .... N. (7.32)
124
Проекция выходного сигнала //<'> С У</> на ось Y составляет-
ся из элементарных сигналов, выдаваемых агрегатом Q агрегату Ck.
Перейдем к пространству входных сигналов агрегата Cj. Если
к множеству (7.29) применить оператор R^1, мы получим множество
элементарных осей пространства входных сигналов агрегата Ch
контакты которых связаны индивидуальными каналами с выходными
контактами агрегата Cj. Легко видеть, что это множество совпадает
с множеством ] оси приема агрегатом Ck входных сигна-
лов от агрегата Cj (7.11). Поэтому
[л<А,/)] n j, k = 0, N. (7.33)
Аналогичные соотношения имеют место для оси приема агрега-
том Ck управляющих сигналов от агрегата Cj (7.12):
[f(A’/)]=JR~1{[y?')jr1 /, & = 0, 1, N. (7.34)
Проекция входного сигнала агрегата Ск на ось X'k’’^ состоит из
элементарных сигналов, поступающих от агрегата Cj к входным
контактам агрегата Ck, а проекция управляющего сигнала агрегата Ск
на ось Г<М) — из элементарных сигналов, поступающих от агрегата
Cj к управляющим контактам агрегата Ck.
В заключение остановимся на внешних и внутренних осях про-
странств входных, управляющих и выходных сигналов, определяемых
соотношениями (7.13)—(7.18).
Выходные сигналы агрегата Cj, выдаваемые во внешнюю среду,
характеризуются множеством элементарных осей
Г'°’] = [у(/’]; n7?(W0)]?), (7.35)
а выходные сигналы, выдаваемые другим агрегатам системы, — мно-
жеством элементарных осей
т = й ИуПпЖ^+и).|. (7.36)
А= 1
Таким же образом описываются внешние и внутренние оси про-
странств входных и управляющих сигналов:
ИуН^ПШГЧЖ (7.37)
[Г'°ч (7.38)
в = и r:' куП п «жт (7.з9)
/=1
Ki - и к' (7.40)
/= I
7*
195
7.5. ПОДСИСТЕМЫ
С теоретической и практической точек зрения существенное зна-
чение имеет промежуточное между элементом и системой понятие
подсистемы. Выделение подсистем в исследуемой системе и отнесение
каждой из них к одному из известных классов упрощает изучение
структуры системы и заметно повышает наглядность результатов
структурного анализа.
Удобство использования понятия подсистемы объясняется двоякой
сущностью последней: с одной стороны, подсистема как совокупность
элементов сама является своего рода системой, а с другой — пред-
ставляет собой элемент системы. Эти обстоятельства мы будем иметь
в виду при описании и классификации подсистем.
Рассмотрим систему S, содержащую агрегаты С7-, / = 0, 1, ..., N,
связи между которыми заданы в соответствии с § 7.4 оператором сопря-
жения R. Расчленим мысленно эту систему на некоторое число под-
систем, содержащих не менее чем по одному агрегату. При этом будем
придерживаться правила, согласно которому данный агрегат может
быть элементом только одной из выделенных подсистем 3V, v = 0,1,
..., М (нуль соответствует внешней среде).
Для подсистемы Зр с заданным набором агрегатов Cj С Зр внеш-
ней средой являются не только объекты внешней среды относительно
системы 3, но и агрегаты Ch системы 3, не включенные в подсистему
Зц, т. е. Ch £ Sp. В общем случае подсистема Зр может принимать
входные и управляющие сигналы как от внешней среды (подсистемы
30), так и от других подсистем данной системы (точнее, от агрегатов
Ch € Зр). Аналогично подсистема Зр может выдавать выходные сигналы
как во внешнюю среду (подсистеме 30), так и другим подсистемам дан-
ной системы (точнее, агрегатам Ск £ Зр).
Чтобы охарактеризовать подсистему Зр как элемент системы 3
(с точки зрения сопряжения ее с другими подсистемами), достаточно
задать пространства входных Х(ц) управляющих Г^) и выходных
сигналов подсистемы Зр. Соответствующие множества контактов
определяются соотношениями
[Х(ц)]= и Слб5р 0)] и ( и S-ё^р [х<*''•>])!, (7.41)
[г = и СЛ^р {[Г<*’ 0)] и( и CjSS^ [г(А''>])), (7.42)
[к(ц)]= и ([У</. 0)] и( и [К(Л А)])). и (7.43)
Контакты, принадлежащие множествам (7.41)—(7.43), являются
контактами агрегатов, входящих в подсистему Зр и имеют, естествен-
но, поагрегатную нумерацию (поскольку другой нумерации в системе
3 пока нет). Это обстоятельство чрезвычайно усложняет описание со-
196
пряжения подсистем. Поэтому целесообразно ввести фиктивные кон-
такты, соответствующие упомянутым, но пронумерованные по подси-
стемам.
С другой стороны, поскольку подсистема сама является систе-
мой, для описания соответствующей внешней среды требуется ввод
фиктивных контактов, отражающих свойства агрегата С^).
Таким образом, каждому входному и управляющему контакту
Хр’6 ([Х(м)] и [Г'-Ч): / = 2, пУ+1, +
поставим в соответствие пару контактов: фиктивный входной (для
подсистемы Su) контакт Xpl) f [X(-H)]i и фиктивный выходной (для
агрегата Со1*) контакт У/0)ц g |У/О)И]1- Аналогично введем фиктив-
ные входные (для агрегата Ср1’) контакты Ар0)ц Е |Х(-0) Ч i и выход-
ные (для подсистемы SM) контакты У/и) £ [У/ц,]'1 таким образом,
чтобы каждому У/(,) g [У(р)] соответствовала пара: фиктивный контакт
Ар0)|Х и фиктивный контакт У^*.
Легко видеть, что оба контакта любой пары имеют один и тот же
верхний индекс р, (относятся к одной и той же подсистеме S,,). Для удоб-
ства дальнейшего использования нумерацию фиктивных контактов
будем строить таким образом, что бы и нижние индексы i и I также были
равны в пределах данной пары.
В общем случае к контакту Ур' Е [У(ч>] агрегата Cj Е Зц может
подключаться несколько элементарных каналов, передающих сигналы
агрегатам Ck £ Sg. В силу идемпотентности объединения множеств
множество (7.43) содержит только по одному экземпляру контактов
Ур’, входящих в различные [У0’-*>] для Ck Е (все фиктивные
контакты соответствующие данному контакту Ур’, совме-
щаются в один фиктивный контакт). Это согласуется с требованием,
чтобы к каждому входному контакту Xt-O)|x фиктивного агрегата Со,1)
подключался только один элементарный канал. К выходному кон-
такту У/м) подсистемы отвечающему данному Ур\ может быть
уже подключено любое конечное число элементарных каналов, пере-
дающих выходные сигналы другим подсистемам системы S. Таким об-
разом, роль распределителя каналов между подсистемами переклады-
вается на контакт У;ц). В том случае, когда два или более агрегатов,
связанных элементарными каналами с этим контактом, принадлежит
одной и той же подсистеме Sv, сохраняется лишь один элементарный
канал, идущий от выходного контакта Ур11* подсистемы к входному
контакту Xt-V) подсистемы Sv, а роль распределителя каналов (внутри
подсистемы Sv) перекладывается на фиктивный контакт yz(0)v агрегата
Cov\ соответствующий входному контакту X;v> подсистемы Sv.
На рис. 7.1 представлена система с заданным сопряжением агре-
гатов. На рис. 7.2 изображена та же система, расчлененная на три
подсистемы. От выходного контакта 2 агрегата С4 (рис. 7.1) идут
197
Рис. 7.1
Рис. 7.2
198
элементарные каналы к следующим входным контактам: 2 агрегата
С3, 3 агрегата С2, 4 агрегата Со, 2 агрегата Са и 3 агрегата С5. Ког-
да мы расчленили систему на подсистемы Slt S2 и 83 (рис. 7.2), со-
пряжение агрегатов изменилось следующим образом. От выходного
контакта 2 агрегата С4 имеется два канала: к входному контакту 2
агрегата С3 (агрегаты С3 и С4 принадлежат одной и той же подсисте-
ме S2) и к фиктивному контакту 3 агрегата С32). Последнему соответ-
ствует выходной контакт 3 подсистемы S2. От этого контакта идут
каналы к входным контактам: 3 подсистемы 8Ъ 4 подсистемы 80 и 2
подсистемы 83. Таким образом, вместо двух каналов, связавших
агрегат С4 с аргегатами С5 и Са (см. рис. 7.1), остается один канал,
связывающий подсистемы S2 и 83. Входному контакту 2 подсистемы
83 соответствует фиктивный выходной контакт агрегата С<,3>. От этого
контакта идут каналы к входным контактам 3 агрегата С5 и 2 агрегата
Са. Из изложенного следует, что в случае разбиения системы 8 на
подсистемы передача сигналов от контакта 2 агрегата С4 к контактам 2
агрегата С6 и 2 агрегата Са обеспечивается (так же как и по другим
адресам — к контакту 3 агрегата С2 через клемму 3 подсистемы 8Ь
а также к контакту 4 агрегата Со).
Для перехода от поагрегатной нумерации контактов к нумерации
их по подсистемам и обратно используются следующие отображения.
Отображение
([Х(Ц)] j [fU*)])^^)]"
обозначается
(7.44)
а отображение
([Х(ц)] U [Г(ц)])^ [У^0)д;
обозначается
У;(0)ц (7.45)
Аналогично, отображение
обозначается
У|ц)=Сц(Гг(/)), (7.46)
а отображение
обозначается
Х^ = (?;(/!'>). (7.47)
Из правил введения фиктивных контактов вытекает, что отобра-
жения (7.46) и (7.47) взаимно однозначны; поэтому существуют обрат-
ные отображения 1 и Q^-1. В общем случае фиктивный контакт
Xju) (через соответствующий ему У/0)|1) соединен с некоторым числом
199
контактов Х,-^; выберем один из них произвольным образом и обозначим
символом
XF’^VP^’)- (7.48)
Для фиктивной подсистемы So, представляющей внешнюю среду
системы S, нумерацию контактов можно сохранить такой, какой она
была у фиктивного агрегата Со, т. е. Х(-0) и У<0) будем считать те-
перь входными и выходными контактами подсистемы So соответ-
ственно.
Соотношения (7.44) — (7.48), по существу, представляют собой
таблицы индексов для фиктивных контактов, вводимых при расчлене-
нии системы ,8 на подсистемы р. = 0, 1, ..., р. В силу равенства
верхних и нижних индексов у контактов каждой пары эти таблицы
имеют весьма простой вид: паре индексов (/, /_,) сопоставляется пара
индексов (р, для отображений и и паре (/, I/) сопоставляется
пара (р, щ) для отображений Q и Q'. В качестве примера рассмотрим
соответствующие табл. 7.3 и 7.4 для подсистем, представленных на
рис. 7.2 (первая цифра — номер агрегата или подсистемы, вторая —
номер контакта).
Таблица 7.3
Х</) Х(!Р (У*?1)
1 •A (^ )
1,2 1,1
2,1 1,2
2,3 1,3
3,1 2,1
4,1 2,2
4,2 2,3
7,з (-7J 3)
5,1 3,1
5,3 .3,2
6,1 3,3
6,2 3,2
Таблица 7.4
у(/)
Qi (Qi)
1,1 1,1
2,1 1,2
<?2 (Q2)
3,1 2,1
3,2 2,2
4,1 2,4
4,2 2,3
Фз (Q3)
5,2 3,1
6,1 3,2
Обратимся к некоторой подсистеме Slt системы S и будем рассма-
тривать ее как самостоятельную систему. Введем отображение
|fx(0,N?u( и pdy)]i+т)!-!и( и М'1]?)!, (7.49)
С.е5ц С.6 5'ц
200
реализуемое оператором
У?'
(7.50)
Оператор R^ называется внутренним оператором сопряжения под-
системы
Теперь для подсистемы 5ц известны: совокупность входящих
в нее агрегатов, множества контактов [Х;0^]” и [У/0)ц][ агрегата
представляющего внешнюю среду, и оператор R^. Легко видеть,
что подсистема 5ц таким образом оказывается системой с характери-
стиками, не зависящими от характеристик других подсистем. Поэтому
любые задачи структурного анализа внутри подсистемы Хц могут ре-
шаться отдельно от других подсистем системы 5.
Оператор R^ выражается через оператор R. Соответствующая
процедура будет рассмотрена ниже.
Подойдем к подсистемам 5ц, р, — 1, 2, ..., р, как к элементам дан-
ной системы S. Каждая из них характеризуется множествами входных
[Х*ц)]" и выходных контактов. Кроме того, будем учитывать
и «подсистему» So, представляющую внешнюю среду (агрегат Са
системы S), задаваемую множествами контактов [Xz0)]? и [У/0)]1,
эквивалентными соответствующим множествам агрегата Со.
Рассмотрим отображение
и [Х^’П-Л и [кН1 , (7.51)
\ц=0 / \Ц=0 /
реализуемое оператором
Kz(v) =РП(Х^)-
(7.52)
Оператор /?п называется оператором сопряжения подсистем в си-
стеме (или оператором сопряжения второго уровня).
Очевидно, что подсистемы 5ц могут быть объединены в более круп-
ные подсистемы системы 5 и т. д. В этом случае полезно рассматривать
операторы Рш, R\\ и т. д. по соответствующим уровням иерархии.
При решении задач, связанных с изучением особо сложных систем,
в первую очередь задач структурного анализа, часто бывает целесооб-
разно от заданной системы перейти к совокупности ее подсистем. Здесь
возникает следующая задача.
Пусть для данной системы (Cj, / = 1, 2, ..., N\ [Xz0)]" и [У/0)]1, R)
задано разбиение ее на подсистемы: Cj 6 5ц, р = 1, 2, ..., М. По
известным характеристикам системы и спискам подсистем требуется
определить оператор сопряжения подсистем Rn и совокупность внут-
ренних операторов сопряжения RiX для всех подсистем 5Ц.
Чтобы построить оператор R}i., необходимо найти контакты У*А)
и фиктивные контакты yz0)|i для всех и Х;0)ц, относящихся
к подсистеме Хц. Естественно, следует рассматривать только такие
Х\‘\ которые принадлежат множеству (J [Хр*]"4'"1. Выбрав неко-
cj e sfj.
201
торый контакт Хр'1 из этого множества, мы приДем к одному из
трех случаев.
1. Контакт Х\‘} связан с контактом агрегата Ch £ SM. Легко
показать, что в этом случае
U U [Х(/'А>], (7.53)
а соответствующий контакт Ур> = R (Хр*).
2. Контакт Хр’ связан с контактом Ур* агрегата Ch £ Зц.
Тогда
Хр> € U U [Ха k)] (7.54)
c-j е e six
и ему соответствует фиктивный контакт УР)Ц = Дд (Хр^-
3. Контакт Хр* не связан ни с какими контактами в системе S.
Оператор R не определен на данном Хр1. Тогда оператор Rg тоже
не определен на этом Хр*.
Наконец, чтобы найти Ур\ связанные с фиктивными контакта-
ми ХР)|Л, достаточно обратиться к таблице Qp. Легко видеть, что
У<?)=<2ц"1 (х<-0)м).
Подводя итог сказанному, получаем соотношения, определяю-
щие оператор
R(Xp>) для хр> е и и [х<;- й>],
Ур> = ^ц(Хр’) ДЛЯ хР> 6 и и C;6su ckesl) [х(л *>], (7.55)
(хр^) ДЛЯ ^(0)ц е [хР),х]?.
Для построения оператора Rn необходимо указать фиктивные кон-
м
такты УР’, соответствующие фиктивным контактам Х*ц) € J [Х/^]".
, ц=0
Выбрав некоторый фиктивный контакт Хр’, определим один из
контактов Хр-) =3^1 (Хр;). Оператор R всегда определен на таком
Хр\ поэтому существует У/й) = R (Хр1).
Здесь возможны два случая.
1. Контакт У;(А) является фиктивным контактом у)0) агрегата
Со (й = 0). В этом случае в качестве значения оператора Rn берем
фиктивный контакт У*0) подсистемы So.
2. Индекс k ^=0. Тогда по спискам агрегатов, принадлежащих
подсистемам, найдем такую Sv, которая содержит агрегат Ch. Иско-
мый фиктивный контакт Ур* =Qv(yp)).
202
Другими словами, оператор /?ц определяется соотношениями
yz(v)________(<2v (К/ )), если О, Ch£Sv,
„ (7.56)
д'° , если k = Q,
где
у<*» = R [^“'(Х^’)]. (7.57)
Заметим, что, получив в соответствии с (7.55) оператор 7?м для
некоторой подсистемы можно построить операторы, аналогичные
Rk § 7.4, а именно, оператор R^ как сужение R[L на множество
[Xr-fe)]7 и оператор Rllk как сужение на множество [х’*’]”^”1 для
ch е
В силу взаимной однозначности отображений, реализуемых этими
операторами, можно ввести обратные операторы R^ и R^ и ис-
пользовать их для решения задач анализа сопряжения агрегатов в каж-
дой из подсистем S^.
На практике нередки случаи, когда описание сопряжения агрега-
тов по экспериментальным данным (по результатам обследования ре-
альных объектов) строится в пределах отдельных подсистем (опреде-
ляются операторы R^) и, кроме того, описывается сопряжение под-
систем в системе (определяется оператор /?ц). Располагая этими све-
дениями, построим оператор R, характеризующий сопряжение агрега-
тов в системе в целом. Для решения такой задачи необходимо установить
соответствие между каждым X*'1 и отвечающим ему Y^.
Выбрав некоторый входной контакт Х*;) £ [J [Xt-/)]"+m, мы
/=0
приходим к одному из двух возможных случаев.
1. Контакт Хр’ агрегата С? связан с выходным контактом Y^
агрегата Ск, такого, что Cj, Ск £ 5ц,. Тогда, как легко видеть, для
Х*7) выполняется условие (7.53) и искомый Y^ = R^ (Хр).
2. Контакт Xj;) агрегата Cj связан с фиктивным контактом yj0'11
подсистемы В этом случае
е U и [X(/'ft)], ii^=v, (7.58)
cy£?s(lcftesv
нему соответствует Y^ = 7?ц [ЗРДХр’)]. Здесь опять имеются две
возможности: a) v = 0; тогда искомый контакт является фиктивным
контактом У<0); б) v 0; в этом случае фиктивному контакту K;v)
соответствует выходной контакт Y^ = Qv-1 (K/v)) агрегата Ск.
В результате получаем
(/?м(хР), хР е и и [х(Л*>],
[-^иСХ?’)], V = 0|x('V II и [x(/,ft)]
<271 (Яп [^(х^)]), v^of 1 (7.59)
203
Заметим, что построение оператора 7?и и совокупности операто-
ров Rу, по заданному /?, а также оператора /? по заданным 7?ц и сово-
купности для достаточно сложных систем связано с громоздкими
вычислениями. Однако соотношения (7.55)—(7.57), а также (7.59)
позволяют построить эффективные алгоритмы решения этих задач на
ЭВМ.
Выше мы уже отмечали, что при структурном анализе сложных
систем удобно пользоваться подсистемами, рассматриваемыми в каче-
стве элементов данной системы, описанных по тем же правилам, по
которым описывается агрегат как элемент системы. С этой точки зре-
ния представляют интерес характеристики непосредственных связей
между подсистемами.
По аналогии с (7.36), (7.39) и (7.41) вводятся оси y(^-v> выдачи
подсистемой Sy сигналов подсистеме Sv и приема X<V’H) и под-
системой Sv входных и управляющих сигналов от подсистемы SM.
Множества контактов [AT<'V< м.)], [Г<^. ц)] и [y(n.v)] могут быть вы-
ражены через оператор /?ц равенствами, вполне аналогичными (7.33),
(7.34) и (7.32), а также через оператор 7?. В последнем случае оказы-
ваются полезными следующие соотношения:
[X(v. Ю] = и и /)],
Ch &svCj€ ~'ii.
[B(v. Ю]= и и (7.60)
cAesvc_.6Sy
[у(|х. v)]= (J J
ck £ Cj 6
Сделанные замечания относятся, естественно, и к случаю объеди-
нения подсистем в более крупные конструкции, соответствующие не-
скольким уровням иерархии.
7.6. ВЫДЕЛЕНИЕ КЛАССА АГРЕГАТИВНЫХ СИСТЕМ
Модель сопряжения агрегатов, определяемая оператором R, может
быть использована для адекватного описания весьма широкого клас-
са реальных объектов. Однако наряду с системами, изучение которых
имеет существенное практическое значение, в этот класс включаются
также объекты, выходящие за рамки наших представлений о правиль-
ном функционировании системы. Это объясняется главным образом
тем обстоятельством, что взаимодействие элементов реальных систем
даже в рамках механизма обмена сигналами не сводится к одному только
сопряжению. Помимо сопряжения контактов серьезную роль играют
также согласование функционирования агрегатов во времени, согласо-
вание совокупности элементарных сигналов, поступающих в элементар-
ный канал от выходных контактов и воспринимаемых входными и управ-
ляющими контактами, а также влияние реальных средств передачи
204
сигналов на их форму и содержание. Кроме того, оказываются по-
лезными некоторые дополнительные ограничения на структуру сопря-
жения агрегатов с внешней средой. ,.Y'
С этой точки зрени^ представляет интерес понятие агрегативной
системы (или, короче, Л-системы) как математической модели, отра-
жающей наши представления о взаимодействии реальных объектов
в рамках механизма обмена сигналами.
Упорядоченную совокупность конечного числа агрегатов
/ = 1, 2, .... N, множеств элементарных осей [Х*0)]? и [K/0)]'i, ха-
рактеризующих внешнюю среду, и оператора R, реализующего
N . N .
отображение J [Хр]"+т-> (J [У;(;)] [, будем называть агрегатив-
i=o 1=0
ной системой, если выполняются следующие условия.
1. Для любых Х-0) б [х‘0)]? и У/(0) 6 М0)] 1 в данной системе
у<°>^7?(Х<0))-
2. Если = 7?(Хр)), то:
* (&) * (/) * (&) * (/)
1) Yi Xi, > гдеуг и —соответствующие множества эле-
ментарных сигналов;
2) для любого момента /' выдачи непустого элементарного
сигнала y\k} (/') g Y\k) имеет место:
а) /' П ^(/)),
б) № (t') = xf (Г), где х\!} (t) £ х\'}.
Перечисленные условия являются ограничениями на объекты,
которые мы относим к Л-системам. Этим ограничениям можно дать
следующую системную интерпретацию.
Первое ограничение относится к структуре сопряжения агрега-
тов Л-системы с внешней средой. Оно требует, чтобы: а) каждый эле-
ментарный канал, передающий элементарные сигналы во внешнюю
среду, начинался в одном из выходных контактов одного из агрегатов
системы (не являлся бы продолжением элементарного канала, пере-
дающего элементарные сигналы из внешней среды) и б) каждый эле-
ментарный канал, передающий элементарные сигналы из внешней
среды, заканчивался на одном из входных или управляющих контак-
тов одного из агрегатов системы (не являлся бы началом элементарного
канала, передающего элементарные сигналы во внешнюю среду).
Второе ограничение предусматривает, что любой элементарный
сигнал, выдаваемый выходным контактом и поступающий по элементар-
ному каналу к некоторому- входному или управляющему контакту,
обязательно принимается этим контактом (принадлежит множеству
элементарных сигналов, которые данный контакт способен принимать).
Другими словами, передача сигналов в системе происходит непосред-
ственно от агрегата к агрегату, без селектирующих устройств, способ-
ных отсеивать сигналы по каким-нибудь признакам.
205
Заметим, что для многих реальных систем это ограничение оказы-
вается несправедливым, в системах имеются отдельные селектирующие
устройства или их роль выполняют реальные средства связи. Для того
чтобы Л-система была адэкватной модельюАреальных объектов, до-
статочно селектирующие устройства описать как самостоятельные
агрегаты системы, связи между которыми удовлетворяют условию 2.
Третье ограничение относится к согласованию функционирования
агрегатов во времени. Смысл его состоит в том, что момент выдачи
сигнала должен принадлежать не только множеству моментов функцио-
нирования агрегата, выдающего сигнал, но и множеству моментов
функционирования агрегата, принимающего сигнал. Это обстоятельство
является решающим с точки зрения возможности совместного функцио-
нирования объектов, входящих в состав реальной системы.
Наконец, четвертое ограничение, так же как и второе, связано
с режимом передачи элементарных сигналов по индивидуальным кана-
лам. Оно предусматривает, что сигналы между агрегатами системы
передаются мгновенно, без искажений и без перекодирования, изменяю-
щего структуру сигнала как конечной совокупности элементарных
сигналов. Как правило, реальные средства передачи сигналов этим
требованиям не удовлетворяют. Они могут вносить искажения и по-
мехи в передаваемые сигналы, приводить к запаздыванию сигналов
в процессе передачи, требовать подключения кодирующих и декодирую-
щих устройств.
Для того чтобы Х-система оказалась адэкватной моделью реаль-
ного объекта достаточно реальные средства передачи сигналов и все-
возможные вспомогательные устройства описать как самостоятельные
агрегаты системы, связи между которыми удовлетворяют перечислен-
ным ограничениям.
Определенная таким образом Х-система может служить математи-
ческой моделью для очень широкого класса реальных сложных систем.
Как абстрактный объект она обладает интересными общими свойствами,
которые в настоящее время пока еще недостаточно изучены. Некоторые
общие свойства Х-систем будут рассмотрены ниже.
Охарактеризуем сигналы, поступающие в Х-систему из внешней
среды в качестве входных сигналов для ее агрегатов. Очевидно, что
множество контактов [X], описывающее эти сигналы, будет объедине-
нием множеств [Х(*’°>] (7.11) для всех агрегатов системы:
[Х] = U [*<* 0)]. (7.61)
k= I
Рассмотрим прямое произведение элементарных осей, соответст-
вующих контактам Х(-А) £ [X], k = 1,2, ..., N, ik = 1,2, ..., nh, взя-
тых в порядке номеров агрегатов системы по возрастанию индекса iA:
, w ГЛ(*> 0)1 / . \
Х = П X- ’ е и Ж Д . (7.62)
''4=1 >
Пространство X, задаваемое соотношением (7.62), естественно
назвать пространством входных сигналов Х-системы.
206
Аналогично можно охарактеризовать сигналы, поступающие из
Внешней среды в качестве управляющих сигналов агрегатов системы.
Множество [Г] контактов, описывающее эти сигналы, имеет вид
[f] = U [Г(*’0)]. (7.63)
k = 1
Пространство
Г=п(г“’уПг'‘'0Ч/Ъд) (7.64)
естественно назвать пространством управляющих сигналов А-системы.
Наконец, сигналы, выдаваемые агрегатами системы во внешнюю
среду, характеризуются множеством контактов, см. (7.9),
[У]= U [У(/’0)]. (7.65)
i — 1
Прямое произведение элементарных осей
Г = П(у/’б U [у(А 0)]//,/;) (7.66)
R= I
естественно назвать пространством выходных сигналов А-системы.
Пространства X, Г и Y характеризуют обмен сигналами между
A-системой и внешней средой. Однако этим не исчерпывается характе-
ристика A-системы как абстрактного объекта. Представляет также
интерес описание процесса функционирования A-системы во времени.
По аналогии с агрегатом рассмотрим пространство состояний А-си-
стемы, а также операторы переходов и выходов.
Пусть каждый агрегат Cjt j = 1, 2 ..., N, входящий в А-систему,
характеризуется пространством состояний Z(/), подмножеством Z}y),
операторами V'(/), V’^, и G"(') (см. гл. 5).
Для описания внутренних состояний A-системы недостаточно
знать только внутренние состояния z^ (t) Е Z6') входящих в нее агре-
гатов. Кроме того, необходимо учесть также и состояния элементарных
каналов, передающих сигналы между агрегатами. Рассмотрим упоря-
доченные пары
(г('М ^W(Z(/) ХУ/'’) (7.67)
внутренних состояний и выходных сигналов, вьщаваемых агрегатом
Cj в момент t агрегатам A-системы. Прямое произведение
Z=(z"’xy!?)x(z<”xr‘.!’)x... x(ZmxiT) (7.68)
естественно назвать пространством состояний А-системы.
Выделим теперь во множестве Z состояний А-системы г (точнее,
во множестве точек г пространства Z) такое подмножество Z(v>, при
достижении которого состояниями z (t) А-система выдает выходной
сигнал. Очевидно, что любой выходной сигнал любого агрегата А-си-
207
стемы, выдаваемый во внешнюю среду, одновременно является вы-
ходным сигналом Л-системы. Поэтому точка г принадлежит подмноже-
ству Z(y> тогда и только тогда, когда ее проекция на Z(ft> хотя бы для
одного k, такого, что У/А) С [У], принадлежит подмножеству Z1V).
Таким образом,
Z<y> = U Z'y>, (7.69)
/=А
где множества Z,y) имеют вид:
г7’ = {zr> Xг."’)X (z,!>х © х... х (z1"' х у'Э,
ХгГ> =(Z”’хЙм) X(z'2y’ хЙи ) X
/а(3) *(зц /Л")
X (Z хУ/п ) X ... X (Z X Yin ),
(7.70)
Zr=(Z(1)xy'‘>)x(Z(2,xy((:))x...X
х(2(Л/-1,хУ;(Г1))х(У^)хуГ).
В самом деле, когда состояние Л-системы z (/) Е Z достигает под-
множества Z(y), внутренние состояния z(ft) (/) Е Z(*) одного или не-
скольких агрегатов Ck достигают подмножеств Z^'1 и эти агрегаты вы-
дают выходные сигналы, формируемые соответствующими операто-
рами. Остальные агрегаты Ch, внутренние состояния которых в рассма-
триваемый момент времени не достигли подмножеств Z*K}, выдают вы-
ходные сигналы у = уЭлементарные сигналы, принадлежащие не-
пустым выходным сигналам агрегатов С^, по элементарным каналам
направляются во внешнюю среду, если соответствующие им эле-
ментарные оси У/А) Е [У], или к другим агрегатам Л-системы, если
соответствующие им элементарные оси У/А) Е U [У/п].
/=*
Без ограничения общности можно считать, что оператор G"</)
любого агрегата Q является совокупностью операторов
вырабатывающих элементарные сигналы y\i} (t) Е У/(/).
Оператор, представляющий собой совокупность операторов G’iw,
соответствующих элементарным осям У/;) Е 1^1, обозначим G" и
будем называть оператором выходов Л-системы.
Входной сигнал, поступающий в Л-систему в момент времени f,
содержит элементарные сигналы, направляемые по элементарным ка-
налам к тем входным контактам агрегатов С\, которые соответствуют
элементарным осям А**’ Е [А]. Остальные входные контакты агре-
гатов Ck (если в момент f к ним не поступают сигналы от других
агрегатов Л-системы) воспринимают в момент t' элементарный
сигнал х (f) = х2. Внутренние состояния агрегатов Ck в момент t'
208
изменяются в соответствии с операторами в зависимости
от поступивших к ним сигналов х(/г> (/) 6 Внутренние
состояния других агрегатов Л-системы (если к этим агрегатам в момент
/'не поступают никакие сигналы), а также состояния y\n(t) элемен-
, N » .
тарных каналов, соответствующих элементарным осям Y\^ £ LI [V/и ]
, /=1
(если в момент t не выдаются выходные сигналы), остаются в момент t
неизменными.
Оператор, представляющий собой совокупность операторов V'(k>
для всех k таких, что Хг<*) Е [X], и тождественных операторов, остав-
ляющих неизменными внутренние состояния и состояния выходных
элементарных каналов других агрегатов Л-системы, обозначим V.
Рассмотрение управляющего сигнала, поступающего в Л-систе-
му в момент времени /", приводит нас к оператору V", представляющему
собой совокупность операторов для всех Ch таких, что fsA) Е [Г],
и тождественных операторов, оставляющих неизменными внутренние
состояния и состояния выходных элементарных каналов других агре-
гатов Л-системы.
Проследим поведение состояний Л-системы в моменты времени,
располагающиеся между моментами поступления в Л-систему входных
и управляющих сигналов. При этом удобно выделить моменты
в которые выдаются агрегатами Л-системы выходные сигналы, посту-
пающие в качестве входных или управляющих сигналов к другим агре-
гатам Л-системы. В эти моменты изменяются в соответствии с операто-
рами 6"(й состояния элементарных каналов, передающих упомянутые
сигналы, а также в соответствии с операторами У'О’) и — внут-
ренние состояния агрегатов, воспринимающих эти сигналы. В интер-
валах между моментами внутренние состояния всех агрегатов Л-си-
стемы изменяются в соответствии в операторами UW, а состояния
всех элементарных каналов описываются как у,я.
Оператор, представляющий собой совокупность операторов [/</>
для всех агрегатов Л-системы, операторов G,</г) для всех Е
N *
Е U [Км1], операторов и для всех агрегатов, принимаю-
*=1
щих входные или управляющие сигналы от других агрегатов Л-си-
стемы, а также тождественных операторов, сохраняющих неизменными
состояния элементарных выходных каналов в интервалах между мо-
ментами обозначим U.
Множество моментов ввемени t, в которые рассматривается функ-
N
ционирование Л-системы, представляет собой Т = J где
;=1
Тб') — множество моментов времени агрегата Cj.
Приведенные здесь рассуждения показывают, что для Л-системы
может быть построена совокупность множеств Т, X, Г, Z, Z<r>, Y
и операторов V', V", U и G". Другими словами, любая А—система мо-
жет рассматриваться как агрегат, определяемый упомянутыми мно-
жествами и операторами.
209
На этой почве возникают проблемы композиции и декомпозиции
Л-систем. Под композицией Л-системы, заданной входящими в нее
агрегатами Cj, j = 1, 2, X, множествами элементарных осей
[X*0)]V и и оператором сопряжения ??, понимается пред-
ставление Л-системы в виде агрегата, описываемого множествами Т,
X, f, Z, Z(Y\ У и операторами V', V", U и G", выраженными через
соответствующие множества и операторы агрегатов С; и оператор R.
Декомпозиция Л-системы является процедурой в некотором смысле
обратной композиции: по известным множествам Т, X, Г, Z, Z(Y\ У
и операторам V, V", U и G" Л-системы определить составляющие ее
агрегаты Cj, j = 1, 2, .... N, множества элементарных осей [xj0)]"
и [У/0)]Г1 и оператор сопряжения R. Решение задачи декомпозиции
в такой постановке, если оно существует (кроме тривиального:
N = 1), как правило, оказывается не единственным. На практике
играют существенную роль различные модификации этой задачи: опре-
деление совокупности агрегатов при заданном операторе сопряжения
R, определение агрегата, дополняющего данную совокупность агрега-
тов до заданной Л-системы при некоторых предположениях относитель-
но оператора R, ит. д. Существенную роль при этом играют понятия
эквивалентности агрегатов и Л-систем.
ГЛАВА ВОСЬМАЯ
СТРУКТУРА СЛОЖНЫХ СИСТЕМ
8.1. ПОЛЮСЫ И ВНУТРЕННИЕ ЭЛЕМЕНТЫ
Введенные в предыдущей главе характеристики связей между
агрегатами внутри системы и агрегатов с внешней средой могут быть
использованы для изучения некоторых вопросов, связанных со струк-
турой систем. Математическое описание структурных соотношений поз-
воляет четко определить различные структурные образования в си-
стеме и провести классификацию элементов и подсистем. Это дает воз-
можность построить формальные процедуры и машинные алгоритмы
структурного анализа, имеющие особенно существенное значение
применительно к системам большой сложности, для которых исследо-
вание «вручную» практически неосуществимо.
В зависимости от глубины структурного исследования прини-
маются во внимание те или другие группы факторов, определяющих
отношения между агрегатами системы. Так, при первоначальном ана-
лизе структуры системы оказывается достаточным установление самого
факта наличия реализованных каналов передачи сигналов между
теми или другими агрегатами. Более глубокое изучение структуры
системы требует учета направления передачи и вида передаваемых
сигналов (входные, управляющие, внешние, внутренние для системы
и др.). При дальнейшем углублении структурного анализа может быть
принят во внимание перечень и взаимное расположение элементарных
сигналов, образующих передаваемый сигнал, а также их содержание
и т. д.
Конкретные задачи структурного анализа систем рассматриваются
ниже. Прежде необходимо построить формальное описание различных
типов отношений между агрегатами, концентрирующих в себе сведе-
ния о структуре системы.
Следует отметить, что рассматриваемые в настоящей главе соот-
ношения с формальной точки зрения верны и для систем более широко-
го класса, чем агрегативные (например, для систем, элементы которых
являются агрегатами, и др.). Однако практическая интерпретация
упомянутых соотношений в общем случае не всегда оказывается столь
ясной и наглядной, как в случае A-систем, отличающихся особенно
простыми закономерностями функционирования.
Для описания структуры системы только с учетом наличия кана-
лов связи и видов передаваемых сигналов можно обойтись менее пол-
ными характеристиками сопряжения агрегатов, чем оператор R и оси
р(/,4) и у</,л)> введенные в предыдущей главе.
211
Рассмотрим систему, содержащую агрегаты Cj, j = 1, 2, .... N.
С осью Х<М> (7.11) приема агрегатом Cj входных сигналов от агрегата
Ch свяжем двухместный предикат S (j, k), j, k = 0, 1, N (нуль со-
ответствует внешней среде), принимающий значение 1, когда множест-
во элементарных осей 0, и значение0, когда [%</•*)] = 0.
Назовем £ (j, k) компонентой приема агрегатом Cj входных сигналов
от агрегата Ch. Аналогично введем предикаты (j, k) и q (j, /г), связан-
ные с осями f(M) (7.12) и YC-^(7.9). Предикат £ (/, k), равный 1,
когда [Г<'0] 0, и равный 0, когда [Г</-*>] = 0, назовем компо-
нентой приема агрегатом Cj управляющих сигналов от агрегата Ch\
предикат q (/, й), равный 1, когда =0= 0, и равный 0, когда
[/(/.*)] = 0 — компонентой выдачи агрегатом Cj сигналов агрегату
Из соотношений (7.9), (7.11) и (7.12) вытекает, что при любых
/, k = 0, 1, .... N
£(М) V£(/> Ф = П(£. /)• (8.1)
С парой агрегатов Cj и Ck, j, k = 0, 1, .... N, свяжем двухместный
предикат
® (/, &) = £ (/, k)VL (j, k) V q (/, k). (8.2)
Если в предикате со (j, k) мы зафиксируем одну из переменных / или
k, получим одноместный предикат относительно переменной k или /
соответственно. Когда обе переменные фиксированы, со (/, k) представ-
ляет собой высказывание.
Положим k = 0. Одноместный предикат
Ш(/, 0)=U/,0)Vt(/, 0) Vq(/, 0) (8.3)
описывает отношение между некоторым агрегатом Cj, j = 0, 1, ...,
N, и внешней средой Со.
Рассмотрим теперь какой-нибудь фиксированный агрегат С;,
j = I. Если высказывание со (/, 0) истинно, а именно
[g(/, 0)V£(/, 0)Vq(/, 0)] = 1, (8.4)
агрегат Сг принимает входные или управляющие сигналы от внешней
среды или выдает выходные сигналы во внешнюю среду. Такой агрегат
будем называть полюсом системы. Если высказывание ы (/, 0) ложно:
[Е (/, 0)V£(/, °) V q (/, 0)1=0, (8.5)
то агрегат С, будем называть внутренним элементом системы.
Система взаимодействует с внешней средой только через полюсы
Внутренние элементы могут выдавать сигналы лишь агрегатам данной
системы и от них же принимать сигналы. На рис. 8.1 представлена
схема одного из примеров системы. Здесь полюсами являются агрегаты
Clt С3, Cit Cit С7. Агрегаты С2 и С5 — внутренние элементы.
212
Полюсы классифицируются в зависимости от значений компонент
£ (j, 0), £ (/, 0) иг| (/, 0). Если
|(/, 0) = 1, (8.6)
полюс С/ называется входным. Это значит, что входные сигналы агре-
гата Сг полностью или частично поступают из внешней среды, от объек-
тов, не являющихся элементами рассматриваемой системы. На рис. 8.1
входными полюсами оказываются агрегаты Сг и С4. Все входные сигна-
лы поступают к агрегату Сх из внешней среды. Относительно агрегата
(д) (д)
Рис. 8.1
С4 этого сказать нельзя. Некоторая часть входных сигналов поступает
к агрегату С4 от агрегата С5 и представляет собой внутренние сигналы
системы.
Если
S(Z, 0) = 1, (8.7)
полюс С; называется управляющим. Это означает, что управляющие
сигналы, поступают к агрегату С; (полностью или частично) из внеш-
ней среды. В системе, схема которой представлена на рис. 8.1, управ-
ляющими полюсами являются агрегаты Сх, С3, С6. Все управляющие
сигналы поступают к агрегатам Сх и С3 из внешней среды, а к агрегату
С6 — частично из внешней среды и частично от агрегата С2.
Если
П(/, 0) = 1, (8.8)
полюс Cz называется выходным. Это означает, что выходные сигналы,
вьщаваемые агрегатом Сг, поступают полностью или частично во
внешнюю среду к объектам, не являющимся элементами данной систе-
мы. На рис. 8.1 выходными полюсами являются агрегаты С3 и С7.
Все выходные сигналы, выдаваемые агрегатом С7, поступают во внеш-
нюю среду (являются выходными сигналами системы). Выходные сиг-
213
налы, выдаваемые агрегатом С3, лишь частично поступают во внешнюю
среду, некоторые из них поступают к агрегату С7.
Полюс может быть: только входным [£ (Z, 0) Д £ (Z, 0) Д
Д т] (Z, 0)1 = 1 (например, агрегат С4 на рис. 8.1), только управляющим
[£ (I, 0) Д £ (I, 0) Д г] (/, 0)] = 1 (например, агрегат Св), только
выходным [В (/, 0) Д С (Z, 0) Д т] (/, 0)] = 1 (например, агрегат С7),
входными управляющим [£ (Z, 0) Д £ (Z, 0) Д ц (Z, 0)] = 1 (например,
агрегат CJ, выходным и управляющим l£ (Z, 0) Д С (I, 0) Д г) (I, 0)] = 1
(например, агрегат Са), входным и выходным [£ (Z, 0) Д £ (Z, 0) Д
Д т] (Z, 0)1 = 1 и, наконец, входным, выходным и управляющим
[£ (Z, 0) Д £ (Z, 0) Д т] (Л 0)1 = 1.
С агрегатом Cj, j = 1,2, ..., Л\ данной системы свяжем одномест-
ный предикат
<t(/) = (v^)({0<^ C2V}^{co(/, *)=0}). (8.9)
Поскольку в силу тождеств булевой алгебры импликация х± -> х2 =
= х1 V х2> выражение для о (/) можно записать в виде
о (/) = (v&) ({k = 0} V {со (/, k) = 0}). (8.10)
Если для некоторого фиксированного агрегата С; справедливо
о (Г) = 1, то агрегат С; не взаимодействует (не выдает и не принимает
сигналов) с другими агрегатами системы, за исключением, быть может,
Со (внешней среды). Такой агрегат будем называть изолированным
элементом системы.
Изолированный агрегат, как правило, должен быть полюсом си-
стемы, в противном случае его принадлежность системе может оказать-
ся чисто формальной. В реальных сложных системах, встречающихся
на практике, изолированный агрегат чаще всего бывает выходным по-
люсом, выполняющим функцию, не связанную с работой других эле-
ментов системы (например, генератор тактовых импульсов, выдавае-
мых только во внешнюю среду, наряду с выходными сигналами других
элементов системы).
Если в (8.9) вместо со (/, k) подставлять его составляющие, полу-
чаются различные типы частично изолированных элементов: £ (у, k) —
по входу (например, агрегат на рис. 8.1), £ (/, k) — по управлению
(например, агрегаты Съ С3, С4, С5 и С7), ц (/, k) — по выходу (напри-
мер, агрегат С7), £ (j, k) V С (/, &) — по входу и управлению (напри-
мер, агрегат С4), £ (/, k) \/ ц (/, /г) — по выходу и управлению (на-
пример, агрегат С7) и т. д.
8.2. ВИДЫ СВЯЗЕЙ МЕЖДУ АГРЕГАТАМИ СИСТЕМЫ
В настоящем параграфе мы познакомимся с типичными видами
связей, характерных для взаимодействия агрегатов в системе.
Рассмотрим два агрегата Cj и Ck, j, k = 1,2, ..., N, принадлежа-
щих данной системе. Если
М (/, k)Vr\(k, /)] = 1, (8.11)
214
to агрегаты Cj и Ch называются непосредственно связанными в данной
системе. Очевидно, что в силу (8.1) соотношение (8,11) эквивалентно
Ш A)Vg(A,/)V^(/, A0V£(£,/)] = !• (8.12)
Выполнение соотношений (8.11) или (8.12) означает, что хотя бы
одно из множеств и оказывается непус-
тым, т. е. между непосредственно связанными агрегатами, происходит
прямая передача сигналов. В примере системы, схема которой пред-
ставлена на рис. 8.1, агрегат Сх непосредственно связан с агрегатами
С2 и С5, агрегат С6 — с агрегатами С2, С5 и С7 и т. д. Непосредственные
связи агрегатов в системе можно наглядно изобразить в виде неориенти-
рованного графа, вершины которого соответствуют агрегатам системы,
а ребра — каналам передачи сигналов. Граф непосредственных связей
для того же примера системы показан на рис. 8.2.
Иногда существенно различать виды непосредственных связей
между агрегатами. Агрегат Cj можно назвать непосредственным
источником сигналов для агрегата Ck (агрегат Ch — непосредствен-
ным потребителем сигналов агрегата Cj), если
Ш ^) = 1. (8.13)
Это означает, что выходные сигналы агрегата Cj поступают в агрегат
Ch в качестве входных или управляющих сигналов. В самом деле,
в силу (8.1) соотношение (8.13) эквивалентно выражению
/т(М)] = 1- (8.14)
Непосредственная связь этого вида изображается ориентирован-
ными графами (направление дуг совпадает с направлением передачи
сигналов). Для рассматриваемого примера системы граф непосредст-
венной передачи (обобщенных входных) сигналов показан на рис. 8.3.
215
Будем говорить, что агрегат Ск непосредственно следует за
агрегатом Cj (агрегат Cj непосредственно предшествует агрегату Ch),
если
l(k, /) = 1. (8.15)
Это означает, что выходные сигналы, выдаваемые агрегатом Cj другим
агрегатам системы, поступают и к агрегату Ск, причем воспринимаются
последним как входные сигналы (в общем случае наряду с входными
сигналами, поступающими от других агрегатов системы и внешней
среды).
Очевидно, что данный агрегат, если даже он является полюсом
системы, может непосредственно следовать за несколькими (непосредст-
венно предшествовать нескольким) агрегатами системы. Обратимся
к примеру системы, представленному на рис. 8.1. Агрегат Сх непо-
средственно предшествует агрегатам С2 и С5; агрегат С5 непосредствен-
но следует за агрегатами Ct и С4 и в то же время непосредственно
предшествует агрегатам С4 и Св; агрегат Са непосредственно сле-
дует за агрегатом С2 и непосредственно предшествует агрегату С,
и т. д.
Будем говорить, что агрегат Cj непосредственно управляет агре-
гатом Ck (агрегат Ch непосредственно подчинен агрегату С}), если в дан-
ной системе
£(£,/) = 1- (8.16)
Это означает, что выходные сигналы, выдаваемые агрегатом Cj другим
агрегатам системы, поступают и к агрегату Ск; упомянутые сигналы
воспринимаются агрегатом Ck как управляющие сигналы (в общем
случае наряду с управляющими сигналами, поступающими от других
агрегатов системы и внешней среды). Данный агрегат может непосред-
ственно управлять несколькими агрегатами системы и быть непосред-
ственно подчиненным нескольким агрегатам системы. В рассматривае-
мой в качестве примера системе (см. рис. 8.1) агрегат С4 непосредствен-
но управляет агрегатом С2, а агрегат С6 непосредственно подчинен
агрегату С2.
Графы (ориентированные) непосредственного следования и непо-
средственного подчинения для рассматриваемого примера системы
изображены на рис. 8.4 и 8.5 соответственно. Представляет также
интерес граф, образующийся наложением двух последних графов;
такой граф (передача управляющих сигналов изображена прерывисты-
216
ми дугами) будем называть графом передачи входных и управляющих
сигналов. Для того же примера системы упомянутый граф показан на
рис. 8.6.
С точки зрения структуры систем представляют интерес различ-
ные виды посредственной связи между агрегатами Cj и Ch, осуществляе-
мой не напрямую, а через другие агрегаты системы, отличные от Cj
и Ck.
В системе, содержащей агрегаты Cj и Сй, /, k = 1, 2, .... N,
образуем совокупности агрегатов Sr вида Cj, Сщ, Ci2, Ctm, Ск
помещая между Cj и С,, всевозможные размещения из остальных
N — 2 агрегатов по 1, 2, .... N — 2. Пронумеруем полученные сово-
купности Sr числами натурального ряда г = 1, 2, ..., s в некотором
фиксированном для данной системы порядке. Кроме того, введем нуме-
рацию агрегатов Cj в каждой совокупности S,., i = 0, 1, ..., р (г)—1;
под Со будем понимать Cj, а под Cp^-i — Ck. Обозначим через
Рис. 8.6
п (I, г) тот номер i-го агрегата r-й совокупности, который этот агрегат
имеет в системе, п (i, г) = 1, 2, ..., N. Введенные обозначения будут
использованы для описания отношений между элементами системы.
Будем говорить, что агрегаты Cj и Ck слабо связаны в данной си-
стеме если в этой системе существует хотя бы одна совокупность агре-
гатов Sr такая, что любые два ее соседних (i-й и (t + 1)-й, i = О, 1,
..., р (г) — 1) агрегата непосредственно связаны.
Отношение слабой связи между агрегатами системы можно пред-
ставить неориентированным графом, соединив ребрами слабо связан-
ные агрегаты. Однако такой граф часто оказывается недостаточно
наглядным. Обычно отношение слабой связи представляется цепями
217
(цепь — последовательность ребер графа, в которой каждые два
соседних ребра имеют общую концевую точку) на графе непосредствен-
ных связей (см. рис. 8.2). В рассматриваемом примере системы между
агрегатами Сг и С6 существуют три цепи: 1) С1С2Св, 2) С^С^ и 3)
3) С1С2С3С7Св.
Из сопоставления определений можно заключить, что непосред-
ственно связанные агрегаты слабо связаны, т. е. что отношение непо-
средственной связи является частным случаем отношения слабой
связи (когда совокупность 5Г состоит только из двух агрегатов Cj
и Ch).
Определение отношения слабой связи для любых двух агрегатов
Cj и Ск требует, чтобы в системе существовала хотя бы одна совокуп-
ность агрегатов <Sr, обладающая следующими свойствами: 1) агрегат
Cj является первым элементом Sr, агрегат Ck — последним,
2) для любого i из условия 0 i < р (г) вытекает наличие непосред-
ственной связи между Cn(i,r) и C„(i+i,r).
Первое из перечисленных свойств можно описать трехместным
предикатом
т(/, k, г) = ({п(0, г) = /} Л {га [p(r)—1, г]=£}). (8.17)
Второе свойство разобьем на две части: условие и следствие из него.
Условие описывается двухместным предикатом
0(z, г)= [0 < i<p(r) —1], (8.18)
а следствие — предикатом
(r| [п (i, г), п (i + 1, г)] V Л Ь (i + 1» И. п Г)П-
Для учета посылок «существует такая совокупность Sr» и «для
любого is используем кванторы существования (gr) и общности
(yt) соответственно. Таким образом, отношение слабой связи между
агрегатами Cj и Ck данной системы описывается двухместным преди-
катом
а (/. k) = (ПО П (/, k, г) Л (yt) (6 (i, г) -э- {л [п (i, г), п (i + 1, г)] V
Vri[n(i+1, г), n(i, г)]})]. (8.19)
Учитывая упомянутое выше тождество для импликации [см. (8.10)],
выражение (8.19) можно представить в виде
«(/, ^) = (дг)(т(/, k, r)A(yz){0(t, г) Vr][ra(t, г), п (J. Д-1, г)] V
Vt] [га(t + 1, г), n(z,r)]j). (8.20)
Очевидно правомочно определение отношения слабой связи, ис-
ходящее из предиката а (/, k): агрегаты Cj и Ch называются слабо
связанными, если для фиксированных j и k предикат а (/, k) = 1.
Если агрегаты j и k не являются слабо связанными, они называ-
ются несвязанными', тогда для фиксированных/ и k предиката (j,k) =
= 0. С этой точки зрения представляет интерес выражение для пре-
диката а (/, k), которое можно получить последовательным примене-
218
Йием правил де Моргана к кванторам существования и общности, а
также к конъюнкциям и дизъюнкциям, содержащимся в (8.20):
“(/. ^)=(VH <ЧА k, г) V (gi) {0(4, г) -[п (/, г), /г (z +1, г)1 V
V ц [«(/' + 1, г), п(1, г)]) |) (8.21)
или с учетом упомянутого свойства импликации
а (А £) = (Vr) (т (A k, r)V(gz){0(i, г) Л л [«(/, г), zi(i-|-1, г)] Л
Л Ц [n(i + 1, г), n(i, г)]}), (8.22)
Таким образом, если агрегаты С; и Ck являются несвязанными
в любой совокупности Sr, обладающей свойством (8.17), найдется
хотя бы одна пара соседних агрегатов, которые не являются непосред-
ственно связанными.
Будем говорить, что агрегат Cj является источником сигналов
для агрегата Ch (агрегат Сй является потребителем сигналов агрега-
та Cj), если в данной системе существует хотя бы одна совокупность
агрегатов Sr, такая, что любой агрегат из этой совокупности является
непосредственным источником сигналов для последующего агрегата.
На графе непосредственной передачи сигналов (см. рис. 8.3)
существует хотя бы один путь (путь — ориентированная цепь; после-
довательность дуг, начало каждой из них является концом предыду-
щей) от источника сигналов к потребителю. Например, агрегат С2
является источником сигналов для агрегатов С3) Ce, С,, потребителем
сигналов от агрегата Q и лишь слабо связан с агрегатами С4 и С5.
На графе передачи входных и управляющих сигналов (рис. 8.6) путь
от источника к потребителю сигналов может содержать в общем случае
как сплошные, так и прерывистые дуги.
Применение термина «источник сигналов» здесь является весьма
условным. Сигналы, принимаемые агрегатом Ck, могут зависеть от
сигналов, выдаваемых агрегатом Cj, но не являются в общем случае
(если совокупность Sr состоит из более чем двух агрегатов и нет
транзитной передачи сигналов без искажений) сигналами, выдавае-
мыми агрегатом Cj.
Путь CjCk гарантирует одностороннюю «проводимость» (прохожде-
ние сигналов) от агрегата Cj к агрегату Ck. Относительно передачи
сигналов от агрегата Сй к агрегату Cj никаких предположений не
делается.
Легко видеть, что совокупность Sr, существование которой тре-
буется определением отношения источник — потребитель сигналов,
обладает свойством (8.17). Кроме того, должно иметь место условие
(8.18). Следствие, вытекающее из условия (8.18), в данном случае
принимает вид т] [п (/, г), п (/ + 1, г)]. Поэтому отношение источник —
потребитель сигналов описывается двухместным предикатом
₽(А ^)=(дг)[т(/, k, г)л(У‘){0(А г), п (4Ч-1, г)]}] (8.23)
или
0 (A k) = (аг) [т(/, k, г) Л(у0|0 (i. r)vn[n(i. г), n(i + \, г)]]]. (8.24)
219
Очевидно, можно дать определение отношения источник — по-
требитель сигналов, исходя из предиката р (/, /г): агрегат Cj называет-
ся источником сигналов для агрегата Ck (агрегат Ck называется потре-
бителем сигналов агрегата Cj), если для фиксированных j и k предикат
Р (/, k) = 1.
Если агрегат Cj является источником сигналов для агрегата Ck
или потребителем сигналов агрегата Ck, то агрегаты Cj и Ch называют-
ся сильно связанными. Можно показать, что отношение сильной связи
описывается двухместным предикатом
7(/, k)=(^r) (Чь MaUvO Iе G- Н->
г) n(i+ 1, г)]} V(vO ИП [л G’+ h г), n(i, г)]]]). (8.25)
Другими словами, агрегаты С, и Ch (для фиксированных / и k) назы-
ваются сильно связанными, если у (/, k) = 1.
Соотношение (8.25) выражает требование, чтобы в данной системе
существовала хотя бы одна совокупность агрегатов Sr, такая, что каж-
дый агрегат является непосредственным источником сигналов для сле-
дующего за ним агрегата или каждый агрегат есть непосредственный
потребитель сигналов от следующего за ним агрегата.
Отношение сильной связи между агрегатами системы эквивалент-
но наличию хотя бы одного из двух путей CjCh или CkCj на графе
непосредственной передачи сигналов (см. рис. 8.3) или на графе пере-
дачи входных и управляющих сигналов (рис. 8.6); в последнем слу-
чае путь может содержать как сплошные, так и прерывистые дуги.
Целесообразно обратить внимание на различие отношений силь-
ной и слабой связи между агрегатами. Оно вытекает из различия ра-
венств (8.19) и (8.25) — навешивание квантора общности на дизъюнк-
цию предикатов не эквивалентно навешиванию того же квантора на
каждый из дизъюнктивных членов (см. гл. 4). Это различие хорошо
интерпретируется на упомянутых графах. В отличие от сильно свя-
занных агрегатов для слабо связанных агрегатов существование путей
не обязательно, достаточно существование хотя бы одной цепи.
В нашем примере агрегаты С2 и С7 сильно связаны (путь С2С6С7
на графе рис. 8.6), но агрегаты С2 и С5 слабо связаны (цепи на графе
С2С6С5; CaC^Cj); агрегаты С\ и С7, а также Сх и С4 сильно связаны
(пути СГС2С6С7 и С4С5С7); агрегаты С3 и С4 слабо связаны и т. д.
Отношение слабой связи между агрегатами обладает свойством
транзитивности: если агрегаты Сг и Ск слабо связаны, агрегаты Ch
и Cj слабо связаны, то агрегаты С, и Cj также слабо связаны. Это не-
посредственно следует из (8.20). Для отношения сильной связи между
агрегатами свойство транзитивности в общем случае не имеет места.
В упомянутом примере агрегаты С2 и С7 сильно связаны, агрегаты С7
и С4 сильно связаны, но агрегаты С2 и С4 лишь слабо связаны.
Сильно связанные агрегаты всегда являются слабо связанными,
но не наоборот; слабо связанные агрегаты в некоторых случаях могут
не быть сильно связанными.
Возвратимся к отношению источник — потребитель сигналов
между агрегатами Cj и Ch. В зависимости от того, какой сигнал (вход-
220
ной или управляющий) потребляется агрегатом Ск от агрегата Cj,
имеют место частные случаи этого отношения: отношение «предшест-
вует — следует» и отношение «подчинен — управляет». Выражение
(8.23) с учетом (8.1) приобретает вид
Р (/> k) = (аг) [т (/, k, г) д (yi) (0 (i, г) V | [п (i + 1, г),
И (I, И] V S [и (i + 1, г), n (I, г)]}]. (8.26)
Агрегат Cj предшествует агрегату Ск (агрегат Ск следует за
агрегатом С7), если в данной системе существует хотя бы одна сово-
купность агрегатов ST, такая, что любой, принадлежащий ей агрегат,
непосредственно следует за предыдущим. В рассматриваемом примере
системы агрегат С3 следует за агрегатом Съ агрегат С4 предшествует
агрегату С, и т. д. Если агрегат Cj предшествует агрегату Ск, то на
графе непосредственного следования существует путь Cj Ск, например,
пути Cfi^CsC-,, СуС^С^С^, С^С:,С,.С7 и т. д. На рис. 8.4 (на графе
передачи входных и управляющих сигналов существует путь, состав-
ленный из сплошных дуг). Очевидно, что данный агрегат может сле-
довать за несколькими агрегатами и предшествовать нескольким агре-
гатам в системе.
Исходя из выражения (8.26) отношение предшествует — следует
можно описать двухместным предикатом
Р'(/> ^)=(Дг)1т(л k, г) /\(yi) [0(i, r)-^g[n(i + 1, г), n(i,r)]}]- (8.27)
Другими словами, агрегат Cj предшествует агрегату Ск (агрегат Ск
следует за агрегатом Cj,), если 0' (/, k) = 1.
На практике весьма часто встречаются совокупности агрегатов,
связанные отношением предшествования — следования: последова-
тельные операции в технологии и обработке информации, фазы много-
фазного обслуживания и др. Отношение управления — подчинения
не всегда наглядно интерпретируется в структуре систем. Тем не ме-
нее формальное описание различных видов этого отношения представ-
ляет значительный теоретический и практический интерес.
Будем говорить, что агрегат Cj прямо управляет агрегатом Ск
(агрегат Ск прямо подчинен агрегату Cj), если в данной системе сущест-
вует хотя бы одна совокупность агрегатов Sr, такая, что каждый агрегат
непосредственно подчинен предыдущим). Если агрегат Cj прямо управ-
ляет агрегатом Ск, то на графе непосредственного подчинения сущест-
вует путь CjCh; например путь С1С2Св на рис. 8.5 (на графе передачи
входных и управляющих сигналов существует путь, составленный из
прерывистых дуг). Очевидно, что данный агрегат может прямо управ-
лять несколькими агрегатами и быть прямо подчиненным нескольким
агрегатам системы. Исходя из выражения и (8.26), для описания отно-
шения прямого управления (подчинения) можно использовать двух-
местный предикат
₽"(/> k) =(аг)[т(/, k, r)/\(\fi) [0 (i, r)->£[n(t+ 1, r), n(i, г)]}]. (8.28)
Другими словами, агрегат Cj прямо управляет агрегатом Ск (агрегат
Ск прямо подчинен агрегату Cj), если р" (/, k) = 1.
221
Будем говорить, что агрегат Cj управляет агрегатом Ck (агрегат
Ch подчинен агрегату Cj), если в данной системе существует хотя бы
одна совокупность агрегатов STI такая, что каждый агрегат является
непосредственным источником сигналов для последующего и, кроме
того, последний из них непосредственно подчинен предыдущему. Если
агрегат Cj управляет агрегатом Ск, то на графе передачи входных
и управляющих сигналов существует путь CjCh, составленный из
сплошных и прерывистых дуг, причем на последнем этапе обязательно
имеется прерывистая дуга. Данный агрегат может управлять несколь-
кими агрегатами и быть подчиненным нескольким агрегатам системы.
Для описания отношения управления—подчинения может быть
использован двухместный предикат
Р* (J,® = (зИ (т (/, k, г) д (yi) [0 (i, г) ->
-> г), n(i +1, г)]д^ [^, и[р(г) —2, г]])])- (8.29)
Агрегат Cj управляет агрегатом Ск (агрегат Ch подчинен агрегату Cj),
если р* (/, k) = 1.
Определенному таким образом отношению управления (подчине-
ния) агрегатов можно дать простую практическую интерпретацию,
например, агрегат Cj вырабатывает выходные сигналы, предназначен-
ные для управления агрегатом Ch, а все промежуточные агрегаты
представляют собой средства передачи и преобразования этих сигналов
в требуемую форму. Однако такой же формальный вид имеет другое
отношение агрегатов Cj и Ch, удовлетворяющее (8.29), например
агрегат Ck подчинен агрегату СП[Р(Г)_2,г], а остальные агрегаты рас-
сматриваемой совокупности, по существу, не имеют отношения к управ-
лению агрегатом Ch. Можно ввести понятие различных косвенных
видов подчинения агрегатов, аналогичных (8.29). Однако это имеет
смысл сделать не в общем виде, а применительно к конкретным струк-
турам систем. Заметим, что задачи исследования структуры управле-
ния в системах не всегда могут быть решены, исходя лишь из факта
передачи управляющих сигналов между агрегатами. В некоторых слу-
чаях оказываются полезными отношения управления, учитывающие
содержание управляющих сигналов и вид зависимости от них операто-
ров переходов и выходов агрегата. Как правило, такие случаи выходят
за рамки структурного анализа и рассматриваются с учетом функцио-
нирования агрегатов системы.
Предикаты (8.26)—(8.29) и др. могут быть использованы для по-
строения машинных алгоритмов распознавания вида отношения между
элементами системы. Эти алгоритмы являются обязательной составной
частью процедур структурного анализа систем большой сложности.
При решении практических задач важнейшее место занимает изу-
чение отношений между подсистемами данной системы. Как было
показано в гл. 7, для характеристики сопряжения подсистем могут
быть использованы оси АЗю'Д ptn-.v), и y(n.v) [см. (7.60)1. Далее
можно ввести предикаты £ (у, р), £ (v, р) и р (р, v), а также a (v)
и со (v, р) по аналогии с (8.1), (8.2) и (8.9). Оказывается также полез-
222
ним предикат р (k, v), равный единице, когда агрегат Ch принадлежит
подсистеме Sv, и равный нулю в противном случае.
Перечисленные здесь характеристики подсистем вполне анало-
гичны соответствующим характеристикам агрегатов, рассматриваемых
в качестве элементов данной системы. Поэтому и подсистемы в задачах
исследования структуры систем могут рассматриваться как ее элемен-
ты, описываемые соответствующими осями и компонентами. В связи
с этим будем говорить о подсистемах — полюсах: [Е (v, 0) V £ (v, 0) V
V Л (v> 0)] = 1, см. (8.4); изолированных подсистемах: о (v) = 1,
см. (8.9); непосредственно связанных подсистемах ц (v, р.)\/ т; (р, v) --
= 1, см. (8.11) и т. д. По аналогии с определениями §8.2 вводятся
отношения слабой связи, следования, подчинения и др. между различ-
ными подсистемами данной системы.
Очевидно, что подсистемы данной системы в случае надобности
могут быть объединены в более крупные подсистемы (подсистемы более
высокого ранга). Для определения характеристик сопряжения под-
систем следующего ранга пригодны соотношения, рассмотренные
в гл. 7, если вместо характеристик агрегатов подставить соответствую-
щие характеристики подсистем предыдущего ранга.
Учитывая сказанное, мы в дальнейшем при рассмотрении струк-
туры систем будем применять термин элемент, понимая под ним агре-
гаты или подсистемы наименьшего ранга, для которых известны соот-
ветствующие оси или компоненты выдачи и приема сигналов. Термин
подсистема сохраним для обозначения подсистем более высокого
ранга.
Непосредственно из определения отношений между подсистемами
вытекает ряд очевидных следствий, которые оказываются полезными
для структурного анализа систем.
Следствие 1. Два элемента, принадлежащие несвязанным между
собою подсистемам данной системы, являются несвязанными.
Следствие 2. Если элемент С, подсистемы Sp, слабо связан с эле-
ментом Ck подсистемы Sv, то подсистема Зц слабо связана с подсисте-
мой Sv.
Следствие 3. Если элемент Q подсистемы является источни-
ком сигналов для элемента Ck подсистемы Sv, то подсистема Хц яв-
ляется источником сигналов для подсистемы Sv.
Следствие 4. Если элемент Cj подсистемы S|t предшествует эле-
менту Ck подсистемы Xv, то подсистема X|t предшествует подси-
стеме Sv.
Следствие 5. Если элемент Cj подсистемы Хц прямо управляет
элементом Ch подсистемы Xv, то подсистема Хр прямо управляет под-
системой Xv.
Следствие 6. Если элемент С7- подсистемы Хц управляет элементом
Ch подсистемы Xv, то подсистема Хц является источником сигналов
для подсистемы Xv.
Число такого рода следствий может быть при желании увеличено.
Перейдем к рассмотрению частных случаев подсистем, представляю-
щих интерес с точки зрения изучения структуры систем.
223
8.3. ТИПИЧНЫЕ СТРУКТУРНЫЕ КОНФИГУРАЦИИ
В сложных Л-системах весьма часто встречаются некоторые ти-
пичные структурные конфигурации элементов (структурные виды под-
систем), обладающие специфическими свойствами как с формальной
точки зрения, так и по существу их роли в функционировании системы.
Выделение и математическое описание таких конфигураций играет
существенную роль в структурном анализе, так как это позволяет
от трудной задачи распознавания структуры подсистем перейти к бо-
лее простой задаче классификации их (отнесению данной подсисте-
мы к одному из заранее описанных классов). В настоящем параграфе
мы кратко ознакомимся с наиболее распространенными примерами
упомянутых структурных конфигураций.
Интерпретация отношений между элементами системы при помощи
графов приобретает здесь еще большее значение. Некоторые понятия
и свойства графов используются в структурном анализе непосредст-
венно, особенно для случая подсистем, описываемых единственным
видом отношения [например, (8.27) или (8.28)1 и т. д.
Подсистема называется связной, если любой ее элемент слабо
связан с каждым из остальных элементов S^.
Пусть Cj, Ck СЗц, /, k = 1, 2, ..., A7U; тогда в силу (8.19) и опреде-
ления связной подсистемы
(V/) (Vй) tlP (b Н-) Л Р(й. И)1 ->“(/, к)} (8.30)
или
(V/) (Vй) (р(Л И) VP(&, р) V«(b к)\- (8-31)
Очевидно, что для связных подсистем справедливы следствия 1 —6
рассмотренные выше. Кроме того, из определения связной подсистемы
вытекают еще некоторые полезные следствия.
Следствие 7. Любой элемент связной подсистемы непосредствен-
но связан хотя бы с одним элементом этой же подсистемы, т. е.
(V/)(a^) (К/ #= к) л Р (/, P)AP(&, |1)1 -> И (/, к) /)]}. (8.32)
Это следствие можно сформулировать и по-другому: связная подси-
стема не содержит изолированных элементов. Легко показать, что
(8.32) вытекает из (8.30). Обратное утверждение в общем случае невер-
но; подсистема, не содержащая изолированных элементов, не всегда
является связной. В этом легко убедиться на примерах (рис. 8.7).
Следствие 8. Если связная подсистема 5ц. слабо связана со связ-
ной подсистемой Sv, то любой элемент Cj £ слабо связан с любым
элементом Ск £ Sv-
Справедливость его вытекает из транзитивности отношения сла-
бой связи.
Следствие 9. Подсистема, состоящая из слабо связанных между
собой связных подсистем, сама является связной.
Для связной подсистемы граф непосредственных связей (см., на-
пример, рис. 8.2) является, как это следует из соответствующих опре-
224
делений, связным неориентированным графом. С точки зрения изуче-
ния свойств связной подсистемы представляет интерес интерпретация
некоторых известных теорем теории графов. Одна из них утверждает,
что каждый неориентированный граф распадается единственным обра-
зом в прямую сумму своих связных компонент. Применительно к си-
стемам этот факт может быть сформулирован следующим образом.
Следствие 10. Представление системы в виде совокупности не-
связанных между собой связных подсистем единственно.
Аналогично интерпретируются соотношения между числом вершин
и числом ребер связного графа.
Рис. 8.7
Следствие 11. Система из п элементов, имеющая
(п — 1) непосредственных связей, не является связной.
Следствие 12. Система из п элементов, имеющая
менее чем
более чем
г = 1/2(«—1)(п—2)
(8.33)
непосредственных связей, является связной.
Рассмотрим некоторые частные случаи связных подсистем.
Обратимся к совокупностям Sr, введенным для определения отно-
шения слабой связи между элементами Cj и Ck, и соотношениям (8.17)
и (8.18). Любая совокупность Sr, для которой
(V')([t(/, k, r)A0(i,r)]->
-> [г] [п (i, г), п(г’ +1, г)] vr][n(i +1, г), n(i, г)])), (8.34)
называется цепью CjCh. Поскольку в системе может быть несколько
цепей CjCh, обычно они обозначаются перечислением полного набора
содержащихся в них элементов в соответствующем порядке. Например,
цепи C^CgCgC^, С^СзС^С? и С^С^С^С? на рис, 8.1. Цепи CjCk, не со-
держащие общих элементов, кроме Cj и Ch, будем называть непересека-
ющимися (например, цепи С^Сз и С^С^Сз на рис. 8.1).
Сопоставляя (8.34) и (8.30), мы приходим к следствию, которое
может служить также определением связной подсистемы.
Следствие 13. В связной подсистеме для любых двух элементов
Cj и Ck существует цепь CjCk.
8 Зак. 792 225
Цепь CjCh называется каналом CjCk, если элемент Cj является
источником сигналов (8.23) для элемента Ck. Каналу соответствует
путь на графе непосредственной передачи сигналов (например, СгС2СеС7
на рис. 8.3). Очевидно, что каналом оказывается любая совокупность
Sr, если выполняется условие
(yi) ([т (/, k, f) д 0 (i, г)] -> ц [п (i, г), п (i + 1, г)]). (8.35)
Элемент Cj называется начальным элементом канала, а элемент
Сг, — конечным элементом. Если начальный элемент Cj канала являет-
ся входным или управляющим полюсом подсистемы, а конечный эле-
мент Ch — выходным полюсом, такой канал будем называть сквоз-
ным. Иногда оказывается, что все элементы канала — внутренние
элементы подсистемы. В частности, начальный элемент Cj, не являю-
щийся входным или управляющим полюсом и изолированный по входу
и управлению, (у/)([£ (/, /) \/ Щ, Z)] = 0), будем называть родником
данного канала, а конечный элемент Ch, не являющийся выходным
полюсом и изолированный по выходу, (у/) [т] (й, [) = 0], — тупиком
канала.
Каналу соответствует путь на графе непосредственной передачи
сигналов (см., например, СхС2СйС7 на рис. 8.3). На графе передачи
входных и управляющих сигналов этот путь может состоять из сплош-
ных и прерывистых дуг (рис. 8.6).
Если элемент Ch канала CjCh следует за элементом Cj, то CjCh мож-
но назвать каналом следования. В этом случае
(yt) ([т (/, k, г) д 0 (t, г)] g [ft (г + 1, г), п (t, г)]). (8.36)
Каналу следования соответствует путь на графе передачи входных
и управляющих сигналов, составленных из сплошных дуг (например,
С2СъС£7 на рис. 8.6).
Если элемент Cj канала CjCk управляет элементом Ck, то CjCk
можно назвать каналом управления. В таком случае
(v№(/> r)Ad(i, HI-*
Л [n(t, r), «(t’ + l, г)])д 1, p(r) —2]. (8.37)
Каналу управления соответствует путь на графе передачи входных
и управляющих сигналов, составленный из сплошных и прерывистых
дуг, причем последняя дуга обязательно прерывистая.
Наконец, когда элемент Cj прямо управляет элементом Cfe, канал
CjCk можно назвать каналом прямого управления (на графе передачи
входных и управляющих сигналов путь, составленный из прерывистых
дуг, например С1С2С6 на рис. 8.6); совокупность элементов Sr.k
удовлетворяет соотношению
(yi)([т(/, k, г) д 0(i,r)]—> £ [n (г 4-1, г), п (i, г)]). (8.38)
226
Цепь CjCk называется циклом, если элементы С} и Ck непосредст-
венно связаны между собой. Из (8.34) и (8.11) вытекает соотношение,
справедливое для цикла,
(vO (Ц (/. k>г) л0 W Г)1 -*
->Сп [п (i, г), п(И-1> /)] V т] [п (i + 1, г), п (i, r)])A(r][pW —
-l.01vnl0.PW-И))- (8.39)
Канал Cfih называется контуром, если элемент Ch является не-
посредственным источником сигналов для элемента Cj. Тогда из
(8.35) и (8.13) следует, что
(уО(Ц(/, k, г) д 0(i, г)1-»
->t][h(z, г), n (t' +1, г)1 А-г) [р (г) — 1, 0]. (8.40)
В частном случае, когда выходные сигналы элемента Сг_1 вос-
принимаются элементом Сг как входные сигналы, т. е.
(v№(/> k, г) A0(i, г)]->
^g[n(i + l,r), n(t.r)]Al[0, p(r)_lj), (8.41)
контур CjCk можно назвать контуром следования.
Если выходные сигналы хотя бы одного из элементов контура
воспринимаются следующим элементом в качестве управляющих, т. е.
(yi) (Ц (j, k, г) л 0 (i, г)] -> П l« (t. г), n(i-\-l, г)] а
AWW — 1. 0])А(30(0(Ь НлИл(1 + 1. г), n(t, г)]), (8.42)
контур CjCh можно назвать контуром управления.
Наконец, если выходные сигналы любого элемента Сг_1 воспри-
нимаются элементом С, как управляющие сигналы, т. е.
(v0 ([т(/, k, г) A9(t. r)]->
-^[n(i + l,r), n(i.r)])AU0, PW-11, (8.43)
контур CjCh можно назвать контуром прямого управления.
Заметим, что цепи и циклы, а также каналы и контуры перечис-
ленных типов легко интерпретируются на графах и представляют собой
весьма распространенные структурные конфигурации в реальных
сложных системах; выделение их составляет, как правило; одну из
основных задач структурного анализа. Вместе с тем играют существен-
ную роль и более сложные структурные образования.
Подсистема называется сильно связной, если любой ее элемент
сильно связан с каждым из остальных элементов Пусть Cj,Ch 6
€ Зц, j, k = 1, 2, ..., N. Тогда в силу данного определения и (8.25)
(V/) (v^) to) [р (/. И) Л Р р)л т (/> 0 л KvO (0 (h И -*
-> П [п (i. г), n(i + 1, г)]) V (v0 (0 W И ~>
->n[n(i + l, г), n(i, г)])]). (8.44)
8* 227
Граф непосредственных связей для сильно связной подсистемы являет-
ся сильно связным. Сильно связная подсистема является связной, но
не наоборот, т. е. (8.44) оказывается частным случаем (8.40). Сопостав-
ляя (8.44) с (8.35), мы приходим к следствию, которое может также
служить определением сильно связной подсистемы.
Следствие 14. В сильно связной подсистеме для любых двух эле-
ментов Cj и Ch существует по крайней мере один из каналов CjCh
или ChCj.
Следствие 15. Каналы (в том числе и контуры) являются сильно
связными подсистемами.
С точки зрения решения практических задач структурного ана-
лиза сложных систем понятие связной подсистемы оказывается слиш-
ком широким. Оно не позволяет с достаточной глубиной выяснить
структурные особенности типичных конфигураций элементов. Наобо-
рот, понятие сильно связной подсистемы слишком узко. Этот тип под-
систем далеко не всегда охватывает реальные конфигурации элемен-
тов, имеющие четкое функциональное назначение. Поэтому целесооб-
разно ввести еще один, в некотором смысле промежуточный, тип под-
систем.
Связная подсистема 5ц, называется комплексом, если среди ее
входных и управляющих полюсов имеются такие, каждый из которых
является источником сигналов хотя бы для одного выходного полюса.
Очевидно, что для комплекса выполняется соотношение (8.30), описы-
вающее связную подсистему. Кроме того, для некоторых входных
или управляющих полюсов С, (£ (/, 0) \/ £ G, 0) = 1) найдется такая
совокупность элементов S т, начинающаяся элементом Сг и заканчиваю-
щаяся выходным полюсом Ст (ц (т, 0) = 1), что С; является ис-
точником сигналов для Ст (8.18), или, что то же самое, совокупность
Sr представляет собой сквозной канал (8.35).
Ознакомимся с простейшими структурными свойствами комплек-
сов.
Следствие 16. Сквозной канал подсистемы является комплексом.
Следствие 17. Контур, содержащий входной или управляющий
полюс и выходной полюс, является комплексом.
Следствие 18. Любой комплекс содержит по крайней мере один
сквозной канал.
Рассмотрим комплекс 8’ц,. Пусть 1 — множество его входных
и управляющих полюсов, а Т — множество выходных полюсов. Про-
следим возможные сквозные каналы, для которых Cj С / является
начальным элементом. Если такие каналы существуют, они приведут
нас к одному или нескольким конечным элементам, представляющим
собой выходные полюсы. Обозначим множество такого рода выходных
полюсов через Тj, Tj £ Т. Пусть теперь Ch g Т — выходной полюс.
Проследим всевозможные сквозные каналы, для которых Ch является
конечным элементом. Если такие каналы существуют, мы выделим
множество Ih а I входных и управляющих полюсов, представляющих
собой начальные элементы упомянутых каналов.
228
Следствие 19. Если 7'\ U Tj=£0, то комплекс содержит
/
по крайней мере один родник, являющийся источником сигналов
ХОТЯ бы ДЛЯ ОДНОГО ИЗ ВЫХОДНЫХ ПОЛЮСОВ Cfe 6 (J Tj, и слабо связан-
/
ный хотя бы с одним выходным ПОЛЮСОМ Е U Tj .
i
Из сформулированного здесь условия вытекает, что комплекс
имеет хотя бы один несквозной канал, заканчивающийся выходным
полюсом, не принадлежащим ни одному из множеств^;. Ни один эле-
мент этого канала не является потребителем сигналов от элементов,
принадлежащих сквозным каналам.
Если родник несквозного канала при этом не был бы слабо свя-
зан хотя бы с одним из элементов, принадлежащих сквозным каналам,
то несквозной канал оказался бы изолированной подсистемой комплек-
са, что противоречит определению последнего как связной подсистемы.
Следствие 20. Если /\ (J /^#=0,™ комплекс содержит, по
k
крайней мере, один тупик, являющийся потребителем сигналов хотя
бы от одного из входных полюсов Cj Ё U Л и слабо связанный хотя
k
бы с ОДНИМ ИЗ ВХОДНЫХ ПОЛЮСОВ Cj с U Ik-
Доказательство аналогично.
Следствие 21. Если множество Т (или /) данного комплекса мож-
но представить в виде совокупности попарно непересекающихся под-
множеств T'i (соответственно Гг), каждое из которых является объе-
динением подмножеств Ту (соответственно Ih), тогда данный комплекс
представляет собой совокупность лишь слабо связанных между собой
комплексов, число которых равно числу непересекающихся подмно-
жеств Т[ (соответственно Гг), с выходными полюсами, принадлежа-
щими подмножествам T'i, и входными полюсами, являющимися
источниками сигналов для этих выходных полюсов (с входными полю-
сами, принадлежащими подмножествам Гг и выходными полюсами, яв-
ляющимися потребителями сигналов от этих входных полюсов).
В самом деле, существование упомянутых комплексов (являющих-
ся подкомплексами данного комплекса) вытекает из наличия сквозных
каналов, конечные элементы которых принадлежат подмножествам
Т[ (начальные элементы которых принадлежат подмножествам /г).
Эти комплексы слабо связаны, иначе данный комплекс не был бы связ-
ной подсистемой. Они не могут быть сильно связанными, так как это
противоречило бы условию, что подмножества Т[ (соответственно Гг)
не пересекаются.
Очевидно, что следствие 21 справедливо и в том случае, когда
подмножества Tf (соответственно Ih) данного комплекса попарно
не пересекаются.
Можно получить еще некоторые аналогичные следствия, вытекаю-
щие из того, что комплекс представляет собой связную подсистему
со сквозными каналами. Однако на этом останавливаться не будем.
Элемент, являющийся непосредственным источником сигналов
для двух или более элементов, будем называть узлом выдачи сигналов.
229
Элемент, являющийся непосредственным потребителем сигналов от двух
или более элементов, будем называть узлом приема сигналов. Элемент,
представляющий собой одновременно и узел выдачи и узел приема
сигналов, будем называть транзитным узлом.
Узел выдачи сигналов, являющийся источником сигналов для
всех остальных элементов подсистемы, называется центральным
узлом выдачи сигналов данной подсистемы. Узел приема сигналов,
представляющий собой потребитель сигналов от всех остальных
элементов подсистемы, называется центральным узлом приема сигна-
лов данной подсистемы. Транзитный узел, сильно связанный со всеми
остальными элементами подсистемы, называется центральным тран-
зитным узлом данной подсистемы. Наконец, узел, не являющийся
центральным для данной подсистемы, называется местным узлом
(приема, выдачи или транзитным). Возможна и дальнейшая классифи-
кация узлов, основанная на конкретизации отношения источник —
потребитель сигналов: узлы управления, узлы следования и т. д.
На практике существенную роль играют сложные системы с иерар-
хической структурой. Примером простейшей иерархии может служить
структура, при которой некоторый узел выдачи сигналов (например,
центральный) непосредственно управляет некоторым числом местных
узлов выдачи сигналов, а каждый из последних в свою очередь управ-
ляет некоторым числом подчиненных узлов выдачи сигналов и т. д.
Упомянутые управляющие узлы разграничивают соответствующие уров-
ни управления: низший, более высокие и, наконец, высший. Можно
построить аналогичную структуру, отправляясь от узлов приема сиг-
налов, а также от транзитных узлов. В общем случае уровни иерар-
хии могут быть связаны любыми отношениями (предшествует, следует,
управляет, подчинен, прямо управляет и т. д.). Заметим, что исчерпы-
вающий анализ иерархичности структуры системы возможен лишь
с учетом функционирования ее элементов и содержания сигналов, цир-
кулирующих между элементами системы.
В заключение отметим, что наряду с каналами и контурами ком-
плекс является одной из наиболее распространенных структурных
конфигураций для описания частей реальных систем с достаточно четко
выделяемыми функциями (комплекс обработки данных, управляющий
комплекс и т. д.). В общем случае комплекс представляет собой под-
систему с двумя видами отношений между элементами (соответствую-
щий граф содержит как сплошные, так и прерывистые дуги). Методы
формального структурного анализа графов с несколькими видами от-
ношений между вершинами в настоящее время еще недостаточно раз-
виты. Поэтому на практике приходится расчленять комплексы на
составные части, описываемые графами с одним видом отношения,
функциональное назначение которых не всегда оказывается достаточно
наглядным. Это обстоятельство снижает ценность результатов струк-
турного анализа систем.
Сказанное свидетельствует о том, что изучение общих свойств
комплексов как типичных структурных конфигураций, а также раз-
витие методов анализа графов с несколькими видами отношений меж-
ду вершинами имеет существенное значение для системотехники.
230
8.4. СТРУКТУРНЫЙ АНАЛИЗ СЛОЖНЫХ СИСТЕМ
Структурный анализ входит в качестве составной части в исследо-
вание сложных систем при решении многочисленных практических
задач. В результате структурного анализа удается оценить отношения
между элементами и подсистемами сложной системы, проследить по-
токи информации, циркулирующие в системе, выделить элементы
и структурные конфигурации, существенные для функционирования
системы и управления ею.
Задача структурного анализа состоит в том, чтобы исходя из за-
данного описания элементов'системы и непосредственных связей между
ними получить заключения (как правило, качественного характера)
о структурных свойствах системы в целом и основных ее подсистем.
С математической точки зрения смысл этой задачи заключается в пе-
реходе от описания всевозможных непосредственных связей между эле-
ментами системы к описанию структурных конфигураций. Содержание
предыдущих параграфов гл. 8 свидетельствует о том, что преобразова-
ния соотношений, описывающих непосредственные связи, в соотноше-
ния для типичных структурных конфигураций имеют формальный ха-
рактер и поэтому могут быть выполнены при помощи ЭВМ. По мере
усложнения систем это обстоятельство приобретает все большее прак-
тическое значение. Умозрительные и графические методы применитель-
но к системам большой сложности становятся слишком громоздкими
и теряют главные свои преимущества — наглядность и доступность
для непосредственного осмысливания человеком.
При решении практических задач структурного анализа сложных
систем обычно принимаются во внимание три уровня описания связей
между элементами: 1) наличие связи, 2) направление передачи сигна-
лов и 3) виды сигналов (входные или управляющие).
На первом уровне, когда мы исходим лишь из наличия или отсутст-
вия непосредственных связей между элементами системы, анализ
структуры сводится к изучению отношения слабой связи между эле-
ментами. В этом случае изучаемой системе может быть поставлен в со-
ответствие неориентированный граф, вершинами которого изображают-
ся элементы системы, а ребрами — существующие непосредственные
связи между ними (граф непосредственных связей, см., например,
рис. 8.2). На этом уровне граф непосредственных связей исчерпываю-
щим образом описывает все имеющиеся в нашем распоряжении
сведения о связях между элементами, поэтому структурный анализ
системы в данном случае сводится к структурному анализу графа
непосредственных связей.
Методы структурного анализа неориентированных графов доста-
точно широко представлены в специальной литературе (см. [1], [2],
[5] и др.), поэтому мы не будем останавливаться на изложении их
содержания. Ограничимся лишь перечислением основных задач струк-
турного анализа систем, которые решаются этими методами.
Приступая к структурному анализу данной системы, мы в первую
очередь интересуемся, является ли она связной; если же данная си-
стема не является связной, возникает задача представления ее в виде
231
совокупности изолированных связных подсистем. В терминах теории
графов эта задача может быть сформулирована так: проверить, яв-
ляется ли граф непосредственных связей данной системы связным,
а если нет, то представить его в виде совокупности связных подграфов.
Решение задачи можно получить путем построения графа слабых свя-
зей для данной системы (вершинами изображаются элементы системы;
два элемента соединены ребром тогда и только тогда, когда они слабо
связаны), или, что то же самое, матрицы слабых связей по заданному
графу (матрице) непосредственных связей (см., например, [6]).
Как правило, этим и ограничивается структурный анализ систе-
мы на данном'уровне. В некоторых случаях, однако, решаются и дру-
гие задачи: определение минимальных множеств сочленения, выделе-
ние цепей минимальной и максимальной длины, выделение циклов и т. д.
На втором уровне, когда задано направление передачи сигналов
между элементами, анализ структуры системы сводится к изучению
отношения источник — потребитель сигналов. В этом случае каждой
из изолированных связных подсистем, входящих в систему, ставится
в соответствие связный ориентированный граф, направление дуг кото-
рого совпадает с направлением передачи сигналов (граф непосредствен-
ной передачи сигналов, см. рис. 8.3). Методы структурного анализа
связых ориентированных графов также излагаются в упомянутой
специальной литературе. На этом уровне результаты структурного
анализа систем оказываются более содержательными.
В первую очередь целесообразно выделить полюсы системы и клас-
сифицировать их по назначению; обобщенные входные (входные и
управляющие) полюсы и выходные полюсы. Решение этой задачи вы-
текает из рассмотрения предикатов, являющихся компонентами при-
ема и выдачи сигналов, см. (8.4)—(8.10), или крайних столбцов и
строк матрицы непосредственной передачи сигналов.
Следующий шаг связан с выделением сквозных каналов подсистем
и проверкой того, является ли данная подсистема комплексом. Для
этого на графе непосредственной передачи сигналов отыскиваются
пути, начинающиеся в обобщенных входных полюсах и заканчиваю-
щиеся в выходных полюсах. Выделение сквозных каналов в комплек-
сах представляет самостоятельный интерес для анализа структуры
систем. Кроме того, по результатам этой операции могут быть выделены
узлы приема и выдачи сигналов и транзитные узлы, а также построены
множества Tj и lk как подмножества множеств обобщенных входных
и выходных полюсов. Далее, воспользовавшись следствиями 19—22
и другими аналогичными признаками, оцениваем наличие в комплек-
сах тупиков и родников, еще не выявленных при анализе сквозных
каналов. Знание тупиков и родников позволяет продолжить выделение
несквозных каналов комплекса (часть несквозных каналов обнаружи-
вается при поиске сквозных каналов). Аналогично анализируются
подсистемы, не являющиеся комплексами. Наконец, производится
выделение контуров в подсистемах данной сложной системы. Таким
образом, система оказывается представленной в виде совокупности
ряда типичных структурных конфигураций и еще, быть может, неко-
торого числа элементов и подсистем, требующих дополнительного
232
анализа. В последнюю категорию входят главным образом узлы, род-
ники и тупики, не являющиеся множествами сочленения сквозных
и несквозных каналов, а также^некоторые элементы, непосредствен-
но связанные с ними.
Помимо упомянутых основных задач структурного анализа, на
втором уровне иногда решаются и другие задачи. К ним относятся:
выделение совокупностей каналов,ч представляющих собой подком-
плексы данного комплекса, особенно когда речь идет о подкомплек-
сах, начинающихся (оканчивающихся) полюсами, принадлежащими
непересекающимся множествам (Т,); определение множеств сочле-
нения подкомплексов или каналов; оценка каналов и контуров, со-
держащих минимальное или максимальное число элементов (например,
кратчайших сквозных каналов) и ряд других.
На третьем уровне описания связей между элементами системы,
когда учитываются виды сигналов—входные и управляющие—.струк-
турный анализ заключается в изучении отношений предшествования—
следования и управления — подчинения. Множество 7 обобщенных
входных полюсов разбивается на подмножества входных Г и управ-
ляющих 7* полюсов. Аналогично классифицируются все источники
и потребители сигналов, узлы, тупики и родники. По результатам
классификации в общем случае могут быть построены два ориентиро-
ванных графа: граф непосредственного следования (см. рис. 8.4)
и граф непосредственного подчинения (см. рис. 8.5). Для каждого
из этих графов должен быть выполнен весь комплекс исследований,
аналогичных исследованиям второго уровня. Анализ первого графа
позволяет выделить сквозные и несквозные каналы и контуры следо-
вания, а второго — сквозные и несквозные каналы и контуры прямо-
го подчинения.
Необходимо отметить, что раздельное изучение отношений пред-
шествования — следования и управления — подчинения является
лишь промежуточным этапом структурного анализа системы на тре-
тьем уровне. Оно оказывается особенно эффективным для систем боль-
шой сложности. Однако раздельное исследование не дает цельного
представления о структуре системы и потоках информации в ней.
Для рассмотрения структуры системы в целом по данным о видах
передаваемых сигналов может быть построен граф непосредственной
передачи входных и управляющих сигналов (см. рис. 8.6). Этот ориен-
тированный граф отличается от ранее рассмотренных тем, что в общем
случае в нем имеются дуги двух типов: сплошные (для изображения
передачи входных сигналов) и прерывистые (для изображения передачи
управляющих сигналов). Общие методы структурного анализа графов
такого типа еще недостаточно разработаны, хотя в них ощущается оче-
видная практическая потребность. Об этом свидетельствует не только
ряд проблем структурного анализа систем на третьем уровне, не полу-
чивших до настоящего времени удовлетворительного решения. На
практике, в особенности в области исследования структуры управления
в больших системах, встречаются задачи, которые приводят к дальней-
шей классификации входных и управляющих сигналов по видам
содержащейся в них информации или в зависимости от воздействия
233
их на функционирование отдельных элементов и подсистем сложной
системы. В таких случаях может возникнуть необходимость структур-
ного анализа систем на четвертом и более высоких уровнях описания
связей между элементами системы.
Возвратимся, однако, к третьему уровню. Одной из задач второго
этапа структурного анализа, соответствующего графу непосредствен-
ной передачи входных и управляющих сигналов, является изучение
каналов и контуров, выделенных еще на втором уровне, но не попав-
ших в классы каналов и контуров следования и прямого управления.
Легко видеть, что эти каналы и контуры, если они существуют, пред-
ставляют собой различные модификации каналов и контуров управле-
ния. Сущность структурного анализа каналов и контуров управления
обычно заключается в оценке долей элементов, находящихся в отно-
шениях предшествования — следования и управления — подчине-
ния, оценке числа перемен вида отношения, определении длин от-
дельных звеньев прямого управления и следования, входящих в дан-
ный канал или контур управления и т. д.
Однако главная задача этого этапа — использование результатов
всех предыдущих этапов структурного анализа для осмысливания об-
щей структуры системы. На предыдущих этапах мы стремились вы-
делить в системе ее изолированные части, полюсы, неизолированные
типичные структурные конфигурации (комплексы, сквозные и несквоз-
ные каналы, узлы, тупики и родники, контуры), множества сочлене-
ния для них, а также классифицировать полюсы, узлы, тупики, каналы
и контуры по видам отношений между элементами и подсистемами.
Теперь, имея представление системы как совокупности типичных
структурных конфигураций, можно решить некоторые качественные
задачи общего анализа структуры системы, а также описать структуру
в виде, удобном для восприятия и осмысливания человеком.
Окончательные результаты структурного анализа системы обычно
содержат следующие сведения.
1. Указание о том, является ли данная система связной.
2. В случае, когда система не является связной, — перечень
изолированных связных подсистем со списками входящих в них
элементов.
Дальнейшие сведения приводятся для каждой из связных под-
систем в отдельности или для системы в целом, если последняя ока-
зывается связной.
3. Перечень входных, управляющих и выходных полюсов, а так-
же указание о том, является ли данная подсистема комплексом.
4. Перечень центральных и местных узлов приема и выдачи сигна-
лов, а также транзитных узлов.
5. Отношения (предшествования — следования и управления —
подчинения) между узлами, находящимися на минимальных расстоя-
ниях (измеряемых числом промежуточных элементов), а также при-
надлежность узлов предполагаемым уровням иерархии.
6. Перечень сквозных каналов и их классификация (каналы сле-
дования, управления и прямого управления).
234
7 Перечень родников, тупиков, несквозных каналов и классифи-
кация последних; указание множеств сочленения для сквозных кана-
лов.
8. Перечень контуров и их классификация.
9. Представление системы (подсистемы), если в этом ощущается
потребность, в виде совокупности неизолированных подсистем и клас-
сификация последних (комплекс, канал, контур с соответствующей
х ар актер истиой) и указание видов отношений между ними и предпо-
лагаемых уровней иерархии.
10. Представление неизолированных подсистем, если в этом
имеется потребность, в виде совокупностей неизолированных подси-
стем более низкого ранга, классификация последних и указание видов
отношений между ними и предполагаемых уровней иерархии.
Если дальнейшее деление подсистем нецелесообразно, переходят
к более подробному описанию подсистем самого низкого уровня.
11. Тип подсистемы (комплекс, сквозной или несквозной канал,
контур с классификацией отношений между элементами, узел с груп-
пой непосредственно связанных с ним элементов и т. д.).
12. Характеристика долей элементов, находящихся в заданных
отношениях, числа перемен вида отношения, длины звеньев, сохраняю-
щих данное отношение, множеств сочленения и т. д.
Перечисленные сведения представляют существо так называемой
структурной схемы системы. Для непосредственного восприятия и
осмысливания структуры системы целесообразно рассматривать струк-
турную схему с точностью до подсистем наиболее высокого уровня,
затем для каждой из них’(если это требуется) рассматривать структур-
ную схему с точностью до подсистем более низкого уровня и т. д.
ГЛАВА ДЕВЯТАЯ
УСТОЙЧИВОСТЬ функционирования
сложных СИСТЕМ
9.1. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
При проектировании сложных систем возникает вопрос, на-
сколько реальный процесс функционирования системы будет соот-
ветствовать расчетному, так как всегда в действительности при рас-
четах пользуются приближенными моделями, и целый ряд факторов
неизбежно не учитывается. Ответ на этот вопрос дает анализ устойчи-
вости. Таким образом, под устойчивостью функционирования подразу-
мевают сохранение некоторого свойства процесса функционирования
по отношению к возмущению или неопределенности некоторых консти-
туэнт (параметров') системы или ее математической модели. При этом
обязательно должен быть оговорен допустимый класс возмущений. Не-
смотря на выразительность термина «устойчивость», а может быть,
благодаря этому, существует множество определений данного понятия.
Поэтому целесообразно привести некоторые примеры, чтобы выявить
ббщность, присущую всем этим определениям.
Определения устойчивости можно отнести к двум категориям.
К первой относятся определения, которые характеризуют поведение
каждой отдельной траектории. Ко второй относятся определения,
характеризующие поведение траектории в связи с поведением «сосед-
них» траекторий.
Приводимый ниже обзор постановок задач об устойчивости ни-
сколько не претендует на полноту, тем более, что методы решения этих
задач, по существу, не рассматриваются. Читатель может ознакомить-
ся с интересующими его задачами теории устойчивости по целому
ряду прекрасных монографий и обзоров, из которых упомянем лишь
книги А. М. Ляпунова [19], Ж. Ла-Салля и С. Лефщеца [16],
И. Г. Малкина [20], А. Пуанкаре [23], Б. Г. Демидовича [6], Л. Че-
зари [29], содержащую огромную библиографию, и обзор В. В. Ру-
мянцева [25].
Большинство результатов теории устойчивости, полученных на
сегодняшний день, относится к обыкновенным дифференциальным
уравнениям. Кроме того, на примере дифференциальных уравнений
нетрудно проследить различные тенденции в исследованиях устойчи-
вости. Поэтому рассмотрим сначала некоторые постановки задач устой-
чивости для решений обыкновенных дифференциальных уравнений.
236
9.2. УСТОЙЧИВОСТЬ РЕШЕНИИ ОБЫКНОВЕННЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Акцент в приводимых ниже примерах сделан на формулировке
и интерпретации понятий устойчивости с тем, чтобы выявить то об-
щее, что имеется между ними. Даже для обыкновенных дифференци-
альных уравнений имеется множество различных определений устой-
чивости, оттеняющих те или иные особенности поведения траекторий
и требующих различных желаемых свойств решений или целых сово-
купностей решений. Нет возможности перечислить всю литературу,
в которой обсуждаются различные формулировки устойчивости, их
взаимосвязи друг с другом.и индивидуальные особенности. Упомянем
лишь некоторые, на наш взгляд, наиболее полно освещающие данные
вопросы, работы. Это — уже упоминавшиеся книги Ж- Ла-Салля
и С. Лефшеца [16], Л. Чезари [29], обзор В. В. Румянцева [25]. Кроме
них следует перечислить книги Г. Дж. Кушнера [15], Н. Н. Баутина
[2], статью Дж. Дж. Стокера [26].
Основным объектом рассмотрения ниже будет система обыкно-
венных дифференциальных уравнений в евклидовом пространстве Z:
0. (9.1)
at
для которой в некоторой области Q cz Z выполнены условия сущест-
вования и единственности решения. Для простоты будем считать, что
й совпадает со всем пространством Z. Мы интересуемся решениями
системы (9.1), начинающимися в момент /0, который без ограничения
общности положим равным 0. Обозначим метрику пространства Z
через р, а через z (t, z0), t 0, — решение системы (9.1) с начальным
условием z (0) = z0.
Пример 1. В этом примере рассмотрим классическое определе-
ние Ляпунова и некоторые его модификации. Анализ устойчивости по
Ляпунову дает ответ на вопрос о том, насколько отличается возмущен-
ное движение от невозмущенного. При этом под невозмущенным дви-
жением понимается некоторое фиксированное решение системы (9.1),
а под возмущенным — решение этой же системы, полученное при
варьировании начальных условий.
Определение 1. Решение (невозмущенное) z (/, z0) системы (9.1)
устойчиво по Ляпунову, если для всякого 0 > 0 существует такое
6 (0) > 0, что при любом z'o, удовлетворяющем условию р (z0, z'o) < 6,
р [z (t, z0), z (7, z'0)l < 0 при всех i > 0.
Иначе говоря, устойчивость по Ляпунову системы (9.1) есть не
что иное, как равномерно непрерывная зависимость ее решений от
начальных данных на бесконечном интервале времени. Заметим, что
это свойство, рассматриваемое на конечных интервалах времени, вы-
полнено для достаточно широкого класса функций F [22].
Если дополнительно к устойчивости по Ляпунову потребовать,
чтобы lim р [г (t, z0), z (/, z'o)] = 0 для решений, упоминаемых в оп-
t -ЮО
ределении 1, получим определение асимптотической устойчивости,
237
Таким образом, асимптотическая устойчивость, помимо непрерыв-
ности, требует, чтобы «возмущенная» траектория при t оо стреми-
лась к «невозмущенной» в смысле расстояния р.
На практике важное значение имеют не только чисто качествен-
ные выводы о существовании устойчивости, например в смысле Ляпу-
нова, но и, скажем, характер зависимости функции sup А (I) =
t
= sup р [z (t, z0), z (t, z'o)] от б, а для асимптотической устойчивости —
t
порядок убывания функции А (/). Это приводит к необходимости изме-
нения формулировок устойчивости для учета указанных требований.
Определение 2. Решение z (t, z0) устойчиво, если существует такое
число б0 > 0, что для любого б б0 и всякого z'o, такого, что
р (z'o, z0) < б, при всех t 0 выполняется неравенство
р [z(t, Zo), z(t, Zfl)] < 0(6),
где функция 0 (б) принадлежит заданному семейству функций L.
Заметим, что всегда 0 (6)^6.
Если в качестве L выбрать семейство всех таких функций
0 (б), 0 < б б0, что 0 (б) -> 0 при б 0, то получим определение
Ляпунова. В качестве L может быть выбрано семейство функций, имею-
щих видО (б). Другой пример доставляют функции 0 (б), удовлетворяю-
щие условию 0 (б) Дба, где /( О и 0 -< а 1 — некоторые
константы.
Аналогичным образом для асимптотической устойчивости можно
оговорить характер стремления функции А (/) к 0. При этом появляют-
ся такие термины, как экспоненциальная устойчивость, гармониче-
ская устойчивость и т. д.
Некоторые подробности и дальнейшие ссылки можно найти в уже
цитированной книге Л. Чезари [29].
Пример 2. В предыдущем примере рассматривалась устойчивость
по отношению к возмущению начального состояния z0 системы (9.1).
На практике, однако, представляет значительный интерес выявление
вопроса о том, насколько изменится решение системы (9.1) при вариа-
циях ее правой части, поскольку всегда в действительности на описы-
ваемую систему действуют силы, учесть которые при составлении
уравнений попросту невозможно. Эти соображения приводят к сле-
дующему определению, являющемуся расширением определения Ля-
пунова. Наряду с системой (9.1) рассмотрим систему
Я 2
^- = F(z,t)+R(z,t). (9.2)
at
Определение 3. Скажем, что решение z (t, z0) системы (9.1) устой-
чиво при постоянно действующих возмущениях, если для любого
0 > 0 существуют бх (0) >0 и б2 (0) > 0 такие, что при любом на-
чальном состоянии z'o и функции R (z, t), удовлетворяющих условиям
1) Р (z0, zo)<61(0),
2) p[/?(z, t), 0] < б2 (0) при i^O, р [z, z(t, zo)]<0,
238
Имеет место р [z* (t, г'й), г (I, г0)1 < 0 при всех t > 0, где z* (t, г'о) —
решение системы (9.2) с начальным состоянием г'о.
Укажем, что если в определении Ляпунова сравнивались два
решения одной и той же системы уравнений, то в определении 3 срав-
ниваются решения различных систем. Рассматриваемый случай являет-
ся типичным примером действия возмущений на параметры системы,
не являющиеся числовыми. В самом деле, в определении устойчивости
при постоянно действующих возмущениях предполагается, что возму-
щаемыми параметрами являются точки пространства {г0( X [F (г, /)|,
где [F (z, t)} — пространство всевозможных функций переменных
г и t, обеспечивающих существование и единственность решений си-
стемы (9.1), а (г0) — пространство начальных состояний системы (9.1),
совпадающее с фазовым пространством. При этом ограничения на воз-
мущения задаются условиями 1 и 2, приведенными в определении.
Как и определение Ляпунова, данное определение допускает раз-
личные модификации и «усовершенствования», позволяющие учесть
те или иные ранее неучтенные факторы. Так, можно потребовать, чтобы
функция R была не равномерно мала (в некоторых задачах такое пред-
положение нереально), а мала лишь в среднем или еще в каком-либо
другом смысле.
Близкой (по постановке) является задача об устойчивости при
параметрических возмущениях, когда правая часть системы (9.1)
зависит от некоторых числовых параметров и параметров, имеющих
функциональную природу. При этом вид допустимых возмущений, дей-
ствующих на параметры системы, определяет семейство «возмущенных»
функций F.
Пример 3. Вновь рассмотрим систему (9.1). Если все решения этой
системы ограничены при t 0, то говорят об устойчивости по Лаг-
ранжу. Следовательно, устойчивость по Лагранжу можно интерпрети-
ровать как сохранение свойства траекторий находиться в ограниченной
части фазового пространства при действии возмущений произвольной
величины на начальные состояния. Понятие устойчивости по Лагранжу
широко применяется при изучении различных качественных свойств
решений дифференциальных уравнений. При анализе сложных систем
мы неоднократно будем обращаться к понятиям, аналогичным устой-
чивости по Лагранжу. Там же будут даны их различные практические
интерпретации. Иногда бывает необходимо наложить более жесткие
ограничения на поведение траекторий системы (9.1), нежели ограничен-
ность всех решений. Одно из таких ограничений приводит к понятию
предельной ограниченности. Именно, говорят что решения системы
(9.1) предельно ограничены, если существует такое ограниченное мно-
жество Q в фазовом пространстве системы, что для любого начального
состояния г0 существует число Т (г0), для которого справедливо
г (t, z0) £ Q при всех t > Т (г0). Следовательно, при предельной огра-
ниченности все траектории системы (9.1) в конце концов попадают
в множество Q и там остаются.
Пример 4. Предположим, что решения рассматриваемой систе-
мы устойчивы по Ляпунову (или асимптотически, при постоянно дейст-
вующих возмущениях и т. д.). Такого рода устойчивость гарантирует
239
существование достаточно малой области в пространстве возмущае-
мых параметров, такой, что при нахождении в ней значений параметров
выполняется то или иное свойство системы. В практических задачах
часто нельзя обеспечить сколь угодно малую величину возмущения
и поэтому необходимо дополнительное исследование (помимо анали-
за устойчивости), чтобы оценить действительную величину указанной
области. Далее имеются с прикладной точки зрения важные примеры
неустойчивых (по Ляпунову) решений, в достаточно малой окрестности
которых существует устойчивое решение, которое с точки зрения
практики также удовлетворительно*’.
Кроме того, указанные определения, как правило, теряют содер-
жательность, если анализируется поведение систем на конечном ин-
тервале времени. Учитывая все сказанное, перейдем к формулировке
практической устойчивости.
Рассмотрим систему (9.2). В-фазовом пространстве системы выбе-
рем множество Q. Выберем также число Т < <ю и множество Qo
в пространстве начальных состояний системы (совпадающем с фазо-
вым пространством). Зафиксируем некоторое семейство Р функций
R (z, t) (например, Р = {R (z, Z): р [/? (2, t), 01 < 6; t < Т, г £ Z],
где 6 > 0 — фиксированное число).
Определение 4. Система обладает практической устойчивостью
[или устойчивостью относительно (Q, Qo, Р, Т)], если для любого
2о 6 Qo и (2> ^)] € Р имеем г (t, 20) £ Q при t<Z.T.
Из определения 4 ясно, что множество Q является множеством
допустимых состояний системы, множество Qq — множеством допу-
стимых начальных состояний, а семейство Р определяет допустимые
постоянно действующие возмущения. Определение является содержа-
тельным как при конечных, так и при бесконечных значениях Т. В об-
щем случае целесообразно не задавать множеств Qo и Р, и задать одно
подмножество Qo допустимых значений параметров в множестве воз-
мущаемых параметров системы.
Часто множество Q имеет вид Q = {г: р (2, 0) < а], где а > 0 —
фиксированное число. В этом случае практическая устойчивость есть
не что иное, как равномерная ограниченность фиксированным числом
решений системы (9.2), рассматриваемых на полуинтервале [0, Т),
Т С оо, относительно множества Qo начальных значений и семейства
Р постоянно действующих возмущений. Множества Q, Qo, Р должны
задаваться исходя из условий функционирования реальной системы
и требований, налагаемых на характер ее функционирования.
В последнее время интерес к исследованию практической устойчи-
вости возрос. Читатель может обратиться за дальнейшими подробно-
стями к работам Ж. Ла-Салля и С. Лефшеца [16], К. А. Карачарова
и А. Г. Пилютика [12], Э. Инфанта и Л. Вайса [8, 9].
*> Например (см. [20]), уравнение dz/dt = z(a2— z2) допускает решение
z(t) = 0, которое неустойчиво по Ляпунову. Однако можно показать, что
lim z(/) = ±a при любом г0. Если а мало, то неустойчивость решения z(t) — O
t оо
может быть несущественной с практической точки зрения.
240
Пример 5. Рассмотрим систему
= F(z,t) + о (z, (9.3)
где п (/) является векторным случайным процессом, называемым в тех-
нике «белым шумом»*’, а (г, t) — матрица с элементами (z, t).
Обозначим
MI-sup ( 2 t))1/2.
2. t I, j > I
Скажем [27], что решение z (t, z0) системы (9.1) слабо устойчиво отно-
сительно случайных возмущений, если для любых е > 0 и у > О
существуют &, с > 0 такие, что при всех / С [0, оо ), р (z0, z'o) <С 6,
а || < с имеет место
Р {р [z (/, г0), Z (л z'o)] < у} > 1 —е,
где 2* (t, z'o) — решение системы (9.3) с начальным состоянием z'o.
Сформулированное определение является вероятностным анало-
ном устойчивости при постоянно действующих возмущениях. Другие
определения устойчивости для стохастических дифференциальных
уравнений можно найти в работах Г. Дж. Кушнера [15], И. Я. Каца
и Н. Н. Красовского [13], Р. 3. Хасьминского [27] и др.
Выше были сформулированы определения устойчивости для обык-
новенных дифференциальных уравнений. Понятия устойчивости по
Ляпунову, асимптотической устойчивости и другие естественным обра-
зом могут быть обобщены для систем более общего вида. Укажем на
работы В. И. Зубова [7], Е. А. Барбашина [1], изучающие такие
обобщения. Ссылки на другие работы этого направления можно найти,
например, в обзоре В. В. Румянцева [25].
9.3. УСТОЙЧИВОСТЬ сложных СИСТЕМ
Выше рассматривались различные известные постановки задач
об исследовании устойчивости либо применительно к детерминирован-
ным системам, либо к стохастическим, у которых невозмущенное
движение детерминированное. Таким образом, если говорить о прак-
тической применимости этих понятий, то они используются при иссле-
довании систем, в которых либо случайными факторами можно пре-
небречь, либо они носят характер «малой» помехи, как это имеет место,
например, во многих системах автоматического регулирования.
*> Мы записали уравнение (9.3), следуя традиции, установившейся в тех-
нической литературе. Математически правильнее его записать в виде стохасти-
ческого дифференциального уравнения [5]:
dz(0 = F(z, +
где £ (f)—стандартный векторный винеровский процесс, MS?
241
Совершенно иное положение возникает при исследовании сложных
систем. В этих системах, как писал А. Я- Хинчин [28], «элементы слу-
чайности отнюдь не имеют характера небольших «возмущений», на-
рушающих собой плавный и закономерный ход явления; напротив,
они представляют собой основную черту в картине изучаемых процес-
сов». При исследовании устойчивости эта специфика должна учиты-
ваться прежде всего. Вообще, определение и изучение устойчивости
функционирования математических моделей реальных систем возмож-
но лишь после изучения особенностей конкретной модели, после ясно-
го осознания ее назначения. Подобное же положение имеет место и при
изучении устойчивости динамических систем, описываемых обыкно-
венными дифференциальными уравнениями. Так, в зависимости от
решаемой задачи, от назначения системы применяются различные
варианты понятий устойчивости — устойчивость по Ляпунову, устой-
чивость по вероятности, практическая устойчивость, устойчивость
по Лагранжу, орбитальная устойчивость и т. д. Важная особенность
устойчивости состоит в том, что это понятие относится не к рассматри-
ваемому физическому объекту, как таковому, а только к какому-либо
его свойству. Так, система может быть устойчива по отношению к не-
которым возмущениям в смысле одного определения и неустойчива
в смысле другого определения. Точно так же может наблюдаться устой-
чивость по отношению к одним возмущениям и неустойчивость по отно-
шению к другим возмущениям в смысле какого-либо одного определе-
ния устойчивости. Аналогично тому, как в предыдущем параграфе рас-
сматривались возможные постановки задач об устойчивости для диф- ,
ференциальных уравнений, в этом параграфе рассмотрим различные
формулировки устойчивости для сложных систем.
Пример 1. Этот пример стимулирован работами Р. М. Лойнса
[17, 18] об устойчивости систем массового обслуживания (СМО).
Рассмотрим некоторую СМО с ожиданием. Относительно структуры
системы и поступающего потока требований не будем делать никаких
специальных предположений, кроме однородности потока. Заметим,
что это требование также может быть снято. Пусть Wn (t) — функция
распределения времени ожидания n-м требованием начала обслужива-
ния. Следуя Лойнсу, назовем СМО:
а) функционирующей устойчиво, если последовательность функ-
ций распределения [Wn (/)] имеет пределом при и оо собственную
функцию распределения W (/) во всех точках непрерывности IF (/) (на-
помним, что IF (0 называется собственной функцией распределения,
если W (оо) = 1);
б) функционирующей субустойчиво, если для последовательности
[Wn (01 при всех и и / выполняется W (/) Wn (/), где W (t) —
собственная функция распределения;
в) функционирующей неустойчиво, если не выполняется свойст-
во субустойчивости.
Из определения видно, ч-то субустойчивость является более широ-
ким понятием, чем устойчивость. В случае субустойчивости очередь
не может расти бесконечно. Точнее, при этом случайная последова-
тельность [йУн] времен ожидания ограничена по вероятности. Таким
242
образом, этот случай можно трактовать как вероятностный аналог
устойчивости по Лагранжу. При устойчивости в дополнение к ограни-
ченности по вероятности требуется сходимость функций распределе-
ния Wn, т. е. существование стационарного режима. В случае неустой-
чивости длина очереди не ограничена (по вероятности).
Для практических целей может оказаться целесообразнее рассма-
тривать не последовательность функций распределения [Wn (/)}, а по-
следовательность некоторых функционалов от этих функций (f (U7n)|•
в частности, в качестве / могут выступать моменты функций Wn,
значения функций при фиксированной величине аргумента (квантили)
и т. д. При этом под устойчивостью можно понимать, например, огра-
ниченность последовательности (/ (Н^)}.
Для того чтобы вышеприведенные определения были коррект-
ны, необходимо сказать, при каких значениях параметров системы
(при каких возмущениях) выполняются указанные свойства.
Параметрами для рассматриваемой системы могут служить функ-
ция Го (/), параметры, характеризующие входящие потоки требований
и процесс обслуживания, параметры, описывающие структуру СМО.
Пусть а — параметр системы, принимающий значение из некоторо-
го множества Л. Можно считать СМО функционирующей устойчиво по
отношению к Qo, если для каждого а из фиксированного подмножест-
ва Qo с JL выполняется одно из указанных выше свойств. Если
Qo = А, то приведенное определение аналогично устойчивости по
Лагранжу. Физически определение требует ограниченности (либо
в смысле среднего, если рассматривается последовательность
оо
{] tdWn (/)}, либо по вероятности, если рассматривается последова-
о
тельность [№п (/)), либо в каком-нибудь другом смысле) очереди при
любом значении параметра а g Qo. Можно дополнительно потребовать,
чтобы эта ограниченность была равномерной по а С Qo-
Можно, наконец, не фиксировать заранее множества Qo, а потребо-
вать его существование, оговорив, быть может, свойства этого множест-
ва — его форму, объем, местоположение и т. д. (если, конечно, имеет
смысл говорить о них). Такое определение будет требовать возможности
выбора параметров, лежащих в множестве оговоренного типа, при
которых очередь ограничена в некотором смысле.
Пример 2. Рассмотрим систему передачи данных (СПД), состоя-
щую из узлов и каналов связи. Задачей системы является передача
сообщений из одних узлов в другие по каналам связи. При этом, если
из одного узла в другой нет прямого пути или по нему не ведется
передача, то сообщения передаются через промежуточные узлы.
В связи с тем, что передаваемая информация может устаревать,
часто требуется, чтобы с вероятностью 1 — е время передачи сооб-
щения было не более /,(р (если имеются разнотипные сообщения, то
для каждого типа можно задавать свои е и /кр). В общем случае
можно задавать «критическую» функцию распределения GKp (г) време-
ни передачи, т. е. требуется, чтобы функция распределения времени
передачи каждого сообщения была не меньше GKp (I).
243
Функция GKp (t) может быть несобственной, так как часто сооб-
щения, которые провели в системе время, большее некоторой фикси-
рованной величины, дальше не передаются. В связи с этим целесооб-
разны следующие определения устойчивости функционирования СПД,
аналогичные приведенным в предыдущем примере [11].
Определение 1. СПД функционирует устойчиво, если для любого
а из фиксированной области Qo cz Л (Л— множество значений пара-
метров) Gn (/) GKp (/) для всех 1 > 0 и n > 1, где Gn (t) — функ-
ция распределения времени передачи n-го по счету сообщения.
Определение 2. СПД функционирует устойчиво при значении
параметра а0, если существует такая окрестность О (а0) точки а0, что
Gn (0 > GKP (i) при любом a С О (а0) для всех t Q, п > 1.
В определении 2 под окрестностью точки а0 понимается некоторое
множество определенного вида, содержащее точку а0. Слова «определен-
ного вида» означают, что указанное множество не может быть произ-
вольным, а должно удовлетворять ряду условий, касающихся его
размеров, форм и т. д. Под параметрами понимаются любые консти-
туэнты, характеризующие СПД.
Пример 3. Приведем естественный стохастический аналог опре-
деления практической устойчивости (см. пример 4, § 9.2).
Сформулируем сначала определение, а затем дадим примеры си-
стем, для которых такое определение представляет интерес. Пусть
процесс функционирования системы определяется параметром а, яв-
ляющимся элементом множества параметров Л. При фиксированном а
процесс функционирования системы описывается случайной функ-
цией времени z (f, a), t £ I, I — интервал функционирования системы.
В каждый момент времени t функция z (I, а) принимает значение йз
множества Z. Зафиксируем в Z подмножество Q, а в множестве Л—
подмножество Qo. Выберем е > 0 и подмножество Тс/.
Определение. Процесс z (t, а) назовем устойчивым относительно
(е, Т, Qo, Q), если
inf P[z(t, а) £ Q, —е. (9.4)
а 6 Qa
Множество Qo задает допустимые ограничения на возмущение,
a Q является множеством допустимых или приемлемых значений про-
цесса в интересующем исследователя подмножестве моментов Tai.
На практике наиболее часто встречается случай I = [0, оо ).
В качестве Т в этом случае обычно выбирают полуинтервал [0, /),
где t < оо. Однако может потребоваться оценить устойчивость на
интервале вида [t, t), t <Zt, или множестве более сложного вида. Имен-
но в силу этого целесообразно говорить о подмножестве Т.
Говоря о практической целесообразности сформулированного
определения, следует отметить его важность в задачах анализа надеж-
ности. Как известно, в задачах теории надежности фазовое пространст-
во Z исследуемой системы разбивается на множество Q рабочих со-
стояний и множество Z\Q отказовых состояний. Под надежностью по-
нимается вероятность, стоящая в левой части неравенства (9.4). Таким
образом, анализ устойчивости в смысле вышеприведенного определе-
244
ния для моделей, изучаемых в теории надежности, позволяет получить
оценки надежности.
В гл. 15 будут даны примеры оценок надежности с помощью ка-
чественных методов, характерных для теории устойчивости и, следо-
вательно, упомянутая аналогия между исследованиями надежности
и устойчивости получит «подкрепление» в виде общности методов иссле-
дования. Сейчас же приведем еще несколько примеров систем, требую-
щих анализа устойчивости в смысле сформулированного определения.
К таким системам относятся: некоторые радиолокационные станции
слежения, которые могут потерять цель, если ошибка слежения пре-
высит некоторую величину; системы движения транспорта, для кото-
рых интересно знать вероятность образования заторов и пробок (что
можно свести к выходу траектории из некоторой области) на фиксиро-
ванных интервалах времени; энергетические системы, в которых вслед-
ствие случайных колебаний нагрузки при достижении током критиче-
ской величины (выход из области) начинаются необратимые процессы,
приводящие в лучшем случае к срабатыванию элементов защиты гене-
раторов, а в худшем — к выходу из строя целых систем генераторов.
Подобные примеры можно продолжить. Некоторые из них читатель
найдет в книге Г. Дж. Кушнера [15].
Пример 4. Рассмотрим вероятностный автомат с входным алфави-
том X и множеством внутренних состояний Z. Если в момент времени
t — 1 автомат находился в состоянии z(t — 1) =z (Z и в момент t
поступил входной.сигнал х (/) = х g Z, то z (/) = z' £ Z, где состояние
z' выбирается случайно в соответствии с распределением
р<£\ = Р {z(f) = z'/z(t— l)=z, x(t) = x}, 2 P(,x2i = l-
2' £Z
Обозначим через P (x) матрицу с элементами p2z-- Пусть
л (z) = P{z (0) = z} — распределение начальных состояний, л —
вектор-строка, элементами которого являются вероятности л (г). Оче-
видно, что если на вход автомата поступило слово х = Х]Х2...хп
(т. е. х (1) = х1г х (2) = х2, .... х (п) = хп), то в момент п состояние
г(и) случайно с распределением
nP(Xj)P(X2) ... Р(хп) = лР (х),
п
где через Р (х) обозначено произведение П Р(хр.
г = 1
Напомним, что словом называется любая конечная последователь-
ность символов рассматриваемого алфавита. Отметим, что Р (х) яв-
ляется матрицей перехода за п шагов неоднородной цепи Маркова,
описывающей поведение автомата и соответствующей поданному вход-
ному слову х = х1...хп.
В множестве Z выделим подмножество Q и образуем вектор-
столбец %q, элементами которого являются величины Xq(z), где
х<э(2)={о,’
z e q,
z^Q-
245
Очевидно, величина
(х ) = лР (х )
есть вероятность того, что состояние автомата принадлежит Q после
подачи входного слова х при начальном распределении л.
Рассмотрим множество слов 7\, состоящее из тех и только тех
слов, для которых pQ (х) > X, где 0 < % < 1. Таким образом,
Тк = {x:pQ (х) >Ц.
В теории автоматов любое множество (конечное или бесконечное)
слов некоторого алфавита принято называть событием. Скажем, что
рассмотренное выше событие 7\ представимо множеством Q в вероят-
ностном автомате с точкой сечения X. То есть в представимое событие
Тх входят те и только те слова, после подачи которых на вход вероят-
ностного автомата его внутреннее состояние оказывается в множестве
Q с вероятностью, превышающей Л. Точка Л называется изолированной
точкой сечения, если существует такое число б > 0, что \Pq(x)—
— > б для любого слова х. В этом случае ни при каком входном
слове х вероятность pq (х) не может быть ближе к X, чем на величину
б. Вырожденным примером вероятностного автомата с изолированной
точкой сечения является детерминированный автомат, где pQ (х) _
может принимать лишь два значения: 0 и I. В этом случае любая точ-
ка 0 < X < 1 является изолированной точкой сечения.
Ниже в определении речь будет идти о двух автоматах А и А'
с одинаковыми входными алфавитами X, множеством внутренних
состояний Z и фиксированным подмножеством Q с Z. Один из
автоматов определяется распределениями л, Р (х) = ЦдЙ'Н > дру-
гой — распределением л’ и Р’ (х) = ||p'zz- 11-
Определение. Вероятностный автомат А с изолированной точ-
кой сечения X устойчив, если существует такое число е > 0, что для
любого автомата А, удовлетворяющего условиям
sup[ л(г)—л'(г)|<е, sup I р<*> — р'W I< е,
zea x£X-,z,z'GZl 1
X является изолированной точкой сечения и, кроме того, 7\ = Т{.
Устойчивость требует, чтобы при небольшом изменении началь-
ного распределения и переходных вероятностей автомат с изолирован-
ной точкой сечения оставался таковым и событие, представимое в нем,
также не изменилось. Такую постановку задачи можно считать неко-
торым развитием известной задачи синтеза надежных схем из ненадеж-
ных элементов. Подробнее о задачах, рассмотренных в настоящем
примере, говорится в работах М. О. Рабина [24], А. Паза [21],
Б. С. Кочкарева [14] и в обзоре Р. Г. Бухараева [4].
Пример 5. Как и в примере 3, сформулируем сначала определе-
ние устойчивости для случайного процесса г (/, а), г ( Z, а ( а за-
тем дадим его интерпретацию. В множестве Z выделим ограниченные
замкнутые подмножества QY, образующие систему подмножеств
2 = [(?,}.
24fi
Определение. Процесс z (t, а) назовем устойчивым, если для
фиксированного 0 <1 е 1 и каждого а £ So cz Л, где So —
заданное подмножество Л, найдется множество Qv С 2 такое, что
существует случайный момент времени т (а), для которого Р [т (а) <
< оо} 1 — е, z (t, a) g Qy, при всех t > т (а).
Такое определение имеет смысл для систем, способных работать
в различных режимах, характеризуемых множествами Qy. Определе-
ние требует, чтобы с вероятностью, не меньше заданной, траектория
системы попала в один из возможных рабочих пределов (некоторое мно-
жество Qy) и оставалось там.
Рассмотрим один пример — модель приспособления живых орга-
низмов, изучаемую У. Р. Эшби в своей монографии «Конструкция
мозга» [301. Эта модель (в частности, формальное описание гомеостата)
является специальным случаем кусочно-непрерывного агрегата
(см. гл. 6).
Если говорить о физической интерпретации понятий, введенных
в определении кусочно-непрерывного агрегата для рассматриваемого
случая, то области Pv соответствуют областям удовлетворительного
физиологического состояния организма, уравнения (6.5) описывают
эволюцию организма внутри областей rv, а скачки траекторий про-
исходят при достижении переменными zv (которые Эшби называет
существенными) критических состояний, расположенных на грани-
це 1\. Определение, приведенное выше соответствует определению
ультрастабильности, данному Эшби, если положить е = 0, So = Л
и в качестве множеств Qv выбрать множества 1\.
Заметим, что необходимым (но не достаточным) условием устой-
чивости в этом смысле является существование у уравнений (6.5)
хотя бы при одном v в области 1\ либо точки равновесия, либо пре-
дельного }цикла. Заметим также, что системы подобного рода обладают
свойством адаптации, т. е. могут выполнять возложенные на них функ-
ции в случае изменения условий функционирования. Для возможности
адаптации к широкому диапазону внешних условий необходимо, чтобы
число основных состояний агрегата было достаточно большим и, кроме
того, типы движений в областях, задаваемых уравнениями (6.5), также
обладали достаточным разнообразием.
9.4. ОБЩЕЕ ОПРЕДЕЛЕНИЕ УСТОЙЧИВОСТИ
В предыдущих параграфах было дано достаточное количество
примеров, с тем чтобы попытаться проиллюстрировать, что же такое
устойчивость. Легко можно видеть, что различные опеределения порой
весьма далеки друг от друга. То или иное определение принимается
в зависимости от типа исследуемой системы и характера поставленной
задачи. В этом смысле постановка задачи об устойчивости не должна
идти вразрез с целями построения системы, а, напротив, должна быть
согласована с ними. Например, бессмысленно считать генератор рабо-
тающим неустойчиво, если неустойчиво его положение равновесия —
генератор строится не для того, чтобы находиться в равновесном со-
стоянии, а для того, чтобы выдавать колебания некоторой формы.
247
Поэтому для генератора целесообразна поставка задачи об устойчивости
предельного цикла в том или ином смысле, что опять-таки определяет-
ся назначением генератора — служит ли он, например, для отсчета
времени (когда уместна асимптотическая устойчивость) или для модуля-
ции других сигналов (когда имеет смысл говорить об орбитальной устой-
чивости). Вместе с тем, несмотря на все различие и своеобразие поста-
новок задач об устойчивости, между ними существует много общего,
поскольку каждая из постановок характеризует способность системы
сохранять определенное свойство функционирования. Именно эта
общность и позволяет говорить об исследовании устойчивости как об
отдельной специфической задаче, являющейся одной из компонент
системного подхода.
В связи с этим целесообразно попытаться дать определение
устойчивости, охватывающее различные частные случаи и выявляющие
имеющуюся между ними связь. Вряд ли следует ожидать, чтобы такое
определение было рабочим. Тем не менее оно может иметь методологиче-
ское значение и использоваться как база для формулировки новых
частных определений. Однако следует еще раз подчеркнуть, что при
выработке новых определений устойчивости необходимо тщательно
изучать рассматриваемые системы, их особенности и назначение, с тем
чтобы определение было согласно с целями системы и способом ее
функционирования.
Итак, пусть внутреннее состояние г рассматриваемой системы яв-
ляется элементом множества Z (фазового пространства). Процесс функ-
ционирования определяется законом изменения внутреннего состоя-
ния во времени. Будем считать, что функционирование системы опре-
деляется некоторым набором конституэнт или параметров а. Понятию
«параметр» будет придаваться весьма широкий смысл. В соответствии
с этим скажем, что а — элемент множества Л, называемого в даль-
нейшем множеством или пространством параметров. Таким образом,
изменение внутреннего состояния во времени z (/, а) зависит от а.
При этом t £ I, где I — совокупность рассматриваемых моментов
времени (интервал функционирования системы).
В общем случае функция времени z (t, а)является реализацией
некоторого случайного процесса. Качество работы любой системы оце-
нивается с помощью функционалов. Поэтому будем считать, что на
реализациях z (t, а) при любом а g Л задано однопараметрическое
семейство действительных функционалов Fx = Fx (z (t, a), t т,
t, а£Л\. Значение функционала Fx при фиксированном т
оценивает работу системы до этого момента. При фиксированном а
и фиксированной реализации z (t, а) функционал Fx является дейст-
вительной функцией времени т £ Z.
Рассмотрим множество D всевозможных действительных функ-
ций с областью определения 1. Пусть S3 — совокупность некоторых
подмножеств этого множества. Аналогично, для каждого множества
В £ ® определим совокупность 53v (В) некоторых подмножеств В,
определяемую параметром у.
Физический смысл введенных понятий следующий. Если дейст-
вительная функция принадлежит одному из множеств совокупности
248
S3, то это характеризует, так сказать, основное свойство выбранного
определения устойчивости. Принадлежность же одному из подмножеств
совокупности Ду (В) говорит о некоторых дополнительных свойствах,
придающих «окраску» понятию устойчивости. Ниже будут разобраны
примеры, поясняющие сказанное.
Пусть В — некоторое множество функций. Будем обозначать
через В* множество значений всех функций из В, рассматриваемых
в точке t. Для дальнейшего удобно считать, что в интервал I входит
фиктивная точка оо. Тогда, если некоторая реализация {FT, х £ 1}
является элементом заранее выбранного множества В, т. е. [Ft,
т Е /} Е В, то положим по определению Fx Е В°°. Если же {Fx, т Е
Е /) $ В, то Ем $ В°°. Следовательно, можно сказать, что (FT, т Е
Е 1} Е В тогда и только тогда, когда Fx Е В°°.
Аналогично тому, как это делалось для множества D, пусть Л —
совокупность некоторых подмножеств множества параметров Для
каждого множества А Е Л найдем совокупность Л¥ (А) некоторых
его подмножеств, также определяемую параметром у. Условимся
различать два числа: а и а — 0. При этом неравенство b > а — 0
понимается как b а.
Определение. Рассматриваемая система функционирует устой-
чиво относительно (Д, (Ду), Л, (Лу), е0, FT, Т), где —0 е0 < 1 —
некоторое число, FT — выбранное однопараметрическое семейство
функционалов, Т — некоторое подмножество интервала функциони-
рования I, если для любого е > е0 и любого множества ВЕД можно
найти множество Л Е Л такое, что для каждого Аг Е Лв (А) существует
Bi Е (В), удовлетворяющее при всех т Е Т и а Е Ах неравенству
Р {FT[z^, а), / s^x] ЕВл,} > 1 —8. (9.5)
Здесь в качестве параметра для набора совокупностей (Лу) вы-
ступают множества В из Д, а параметрами для {Ду} являются мно-
жества из Лв. Грубо говоря, это определение требует, чтобы некото-
рое свойство системы сохранялось в том или ином вероятностном смысле
на заранее выбранном интервале времени.
Заметим, что если е0 = —0, то, в частности, неравенство (9.5)
должно выполняться при е = 0, т. е. с вероятностью 1. Хотя определе-
ние может показаться громоздким, оно, по существу, содержит не
более понятий, чем различные частные определения.
Мы уже указывали на физическую интерпретацию совокупностей
Д и Ду (В). Аналогично множества из совокупности Л указывают
на характер допустимых возмущений. Если же параметры изменяются
в одном из множеств совокупности Лв (А), то с точки зрения постав-
ленной задачи поведение системы должно изменяться незначительно.
Подмножество Т, характеризующее интервал времени, на котором
исследуется устойчивость, и семейство функционалов Е*. являются
непременными «атрибутами» любого частного определения. Разумеет-
ся, выбор тех или иных объектов, упоминаемых в определении, дик-
туется характером исследуемой задачи.
249
Покажем теперь на нескольких примерах, как интерпретируется данное
определение в различных частных случаях.
Пример 1. Рассмотрим систему обыкновенных дифференциальных уравне-
ний (9.1). Если г — n-мерный вектор, то Z — «-мерное пространство с метри-
кой р. В качестве пространства параметров г/k выберем пространство начальных
состояний системы (9.1), совпадающее с Z. Интервал функционирования систе-
мы I = [0, оо]. Выберем Т = [0, со). Напомним, что мы условились включать
в I фиктивную точку (о:). Зафиксируем в множестве ./£ некоторую точку а0.
В качестве Fx выберем
Fx {z (t, a), t < т, t, T] =p [z (т, a), z (r, a0)].
Пусть совокупность Si состоит из всевозможных множеств В0 неотрицатель-
ных действительных функций [Гт, т £ Т\ вида
Be = {Fx-.Fx<e, хст, е>0].
Очевидно, Z) B0j при 0Х > 62. При этом В0 = [0, 0) для всех t £ Т.
Пусть совокупность 3) А (В) не зависит от Aj и состоит из одного множества В:
^Л,(В)={ВЬ
Примем, что совокупность Л состоит из всевозможных множеств А& вида
{a : p(a, a0) < б]. Совокупность Лв (А) = {А} для всех Вх Посколь-
ку рассматриваемая система—детерминированная, то положим е0=—0. Тогда
из общего определения следует, что система (9.1) устойчива, если для любого
0 > 0 существует такое б = 6(0) > 0, что при любом а, удовлетворяющем ус-
ловию р(а0, а) < б, p[z(£, а0), z(t, а)] <0 при всех t > 0. Получили определение
устойчивости по Ляпунову. Заметим, что можно было взять Т = {со} и получить
тот же результат.
Аналогичным образом можно получить и определения асимптотической
устойчивости и устойчивости при постоянно действующих возмущениях.
Если в условиях примера выбрать в качестве .©^(Sg) совокупность, состоя-
щую из множеств вида Вв^ с: В0, где функция 0(6) принадлежит заданному
семейству В, а остальные конструкции оставить неизменными, то получим опре-
деление 2 из § 9.2. Это же определение можно получить, рассматривая в качест-
ве ЛВ(А6) совокупность множеств {А51}б1,^в.
Пример 2. Вновь рассмотрим систему (9.1); Z, е0, I и Т те же, что и в
примере 1. Пусть ET[z(7, a), t < т; t, x£I] = p[z(7, a), 0]. Пусть совокупность .5?
состоит из одного множества В равномерно ограниченных на Т неотрицательных
функций. Аналогично пусть совокупность Л состоит из одного множества А ~
= 3b. Примем, что ЛВ(А) состоит из всевозможных одноточечных подмножеств
пространства параметров А, т. е. множества At АВ(А) имеют вид Ах = {а},
а А.
Если А1 = {а} и р(а, 0) = 7?, то совокупность Si А (В) состоит из всевоз-
можных подмножеств В вида
{Fx-.Fx'b, хСТ, b>R}.
Тогда из общего определения нетрудно получить определение устойчивости по
Лагранжу.
Если выбрать ЛВ(А)= {А}, совокупность (В), состоящую из подмножеств
В всевозможных неотрицательных функций, ограниченных в пределе некоторым
числом b (т. е. для каждого множества из совокупности свое число b), Т ={оо],
а остальные конструкции оставить без изменения, то получим определение пре-
дельной ограниченности.
Пример 3. Рассмотрим систему '(9.3). Для нее / = [0, оо]. Пусть Т =
= [0, оо), Fx — р[с*(т, cz), z(t, z0)], т £ Т. Выберем a = (z0, a(z, 7)).
250
Пусть совокупности <5& и <5&V(B) выбраны таким же образом, как и в приме-
ре 1. Примем, что совокупность Л состоит из всевозможных множеств Ай с вида
А6,с= {а :Р(го> го) < 11<г (г, 01| < с).
Совокупность ЛВ(А) = {А} для всех В£3}. Выберем е0 = 0. Тогда общее опре-
деление сведется к определению слабой устойчивости решений системы (9.3)
относительно случайных возмущений.
Пример 4. Вернемся к СПД, описанной в примере 2 § 9.3. В качестве Z вы-
берем множество функций распределения (возможно несобственных), заданных
на положительной полуоси. / — множество целых положительных чисел и точка
со, Т — множество целых положительных чисел. Если {С/г}2= i —последова-
тельность функций распределения времен передачи сообщений, то примем Fn—
= 0, если все Git(x) > GKp(x), k «С п, и Fn = 1 в противном случае. Пусть е0=
= — °.
Рассмотрим множество Во в пространстве действительных функций, задан-
ных на Т, состоящее из единственной функции Fn = 0, n > 1. Выберем
= {Во} - Совокупность Л состоит из всевозможных окрестностей точки а0. Напом-
ним, что под окрестностью в примере 2 § 9.3 понималось некоторое множество в
пространстве параметров, содержащее а0, удовлетворяющее ряду условий,
касающихся его размеров, формы и т. д. Положим ЛВо(А)=(А} и 3) А(В0) =
= — {Во) при А £ Л. Тогда общее определение устойчивости сводится к определе-
нию 2, примера 2, §9.3. Аналогичным путем можно получить и остальные опре-
деления, содержащиеся в примерах 1 и 2, § 9.3.
Пример 5. Покажем теперь, как из общего определения можно получить
стохастический аналог практической устойчивости (см. пример 3 § 9.3). Зафик-
сируем в фазовом пространстве системы Z множество Q и в пространстве парамет-
ров at — множество <?0. Выберем подмножество Т £/. Введем следующее семей-
ство функционалов:
( 0, если 2 (t, а) G Q при всех t ст,
Fr{z(t, а), «<т; t, 'с^Т} = {
т (1 в пр отивн см случае .
Пусть Во—мноисество действительных функций, равных 0 на Т.
Определим
г0={Во), A={Q0), ЛВо (Qo)= {Qo}, ^Qo(Bo) = {Bo}.
Выберем е0 = —0. Тогда из общего определения непосредственно следует опре-
деление устойчивости относительно (е0, Т, Qo, Q), данное в примере 3, § 9.3.
Пример 6. Рассмотрим определение устойчивости, приведенное в примере 5
§ 9.3. Положим FT = у, если г(т,а) £ Q? (предполагается, что у — числовой
параметр, у Г, где Г — множество рассматриваемых параметров). Выберем
е0 = — 0. Яз состоит из одного множества В действительных функций, опреде-
ленных на [0, со), которые, начиная с некоторого момента, постоянны и равны
у С- Г. Пусть Л = '<2о} । где Qo — фиксированное подмножество пространства
параметров at, AB(Q0)—совокупность всевозможных одноточечных подмножеств
множества Qo. Пусть для каждого а £ Qo совокупность Зза (В) состоит из мно-
жеств действительных функций вида В0 = (Fx : Fx = const =у, у £ Г, т>0),
где 0 £ [0, оо). Ясно, что Ве ZD В0 при 0Х > 02. Если выбрать Т= {оо),
то определение, данное в примере 5 § 9,3, получается как частный случай общего
определения.
Можно показать, что сформулированное общее определение устой-
чивости действительно включает в себя как частные случаи по меньшей
мере большинство известных определений.
Мы ограничились рассмотрением лишь нескольких примеров.
Заметим также, что одно и то же определение устойчивости можно полу-
чить, используя различные математические конструкции, упоминае-
мые в определении (см. пример 1).
251
9.5. ОПРЕДЕЛЕНИЕ S-ОБЛАСТИ
Исследование устойчивости относится к задачам анализа систем.
В принципе анализ устойчивости должен считаться завершенным, если
на вопрос о том, сохраняет ли система некоторое свойство процесса
функционирования при определенных условиях, получен ответ типа
«да—нет». Однако для практических целей часто такого ответа недо-
статочно, а необходимы еще некоторые количественные характеристи-
ки, относящиеся к устойчивости. Так, при асимптотической устойчиво-
сти (см. пример 1, §9.2) обычно интересуются размерами максимальной
области в пространстве начальных состояний, в которой еще справед-
ливо
limp)[z(/, z0), z(t, 2о)]=О.
t ->00
Такая область называется областью притяжения решения z (/, ze)
или областью асимптотической устойчивости. При практической
стохастической устойчивости (см. пример 3, § 9.3) интересно знать
вероятность, стоящую в левой части неравенства (9.4). Иногда инте-
ресуются тем, при каких значениях невозмущаемых параметров со-
храняется устойчивость в том или ином смысле. Множество таких
значений называют областью устойчивости.
Часто задачу о нахождении указанных количественных оценок
можно сформулировать так — построить такую область S в множестве
некоторых параметров системы аь что если а, 6 S, то система остается
устойчивой в смысле того или иного определения. Если параметры аг
отличны (вернее, независимы)*7 от параметров а, упоминаемых в об-
щем определении § 9.4, то, как уже говорилось, такие области назы-
ваются областями устойчивости. В некоторых случаях рассматривают
множество параметров ab частично или полностью совпадающих
(зависимых) с а, как, например, в случае области асимптотической
устойчивости.
Построение указанных областей необходимо прежде всего для
задач синтеза систем, поскольку при синтезе следует, по возможности,
выбирать значения параметров системы таким образом, чтобы они ле-
жали в построенных областях.
Кроме того, иногда построение области S необходимо для задач
анализа. Так, зная область асимптотической устойчивости, можно сде-
лать вывод о наличии практической устойчивости. Вообще в теории
динамических систем и особенности при проектировании конкретных
систем нередки ситуации, когда одно понятие устойчивости использует-
ся для того, чтобы сделать заключение о наличии устойчивости в дру-
гом смысле. Зто связано с тем, что пока методы анализа устойчивости
развиты недостаточно и отнюдь не для всех использу емых в практике
определений. При этом, конечно, следует помнить о различии в опре-
делениях устойчивости.
*> Независимость понимается в том смысле, что произвольная вариация
параметров не влияет на значения параметров а.
252
В силу того, что области S, о которых говорится в настоящем пара-
графе, не обязательно являются областями устойчивости, будем назы-
вать их для краткости S-областями. Повторим, что если ах g S, то
либо система устойчива в смысле какого-либо определения (если ах —
невозмущаемые параметры), либо система сохраняет некоторое сущест-
венное свойство, присущее устойчивости (если ах хотя бы частично
совпадает с возмущаемыми параметрами). Отметим теперь, что, по
существу, второй случай можно свести к первому. Для простоты рассмо-
трим случай частичного совпадения ах с а, а не случай их зависимости.
Обозначим условно через а — ах параметры, входящие в а, но не
входящие в ах. Тогда указанное сохранение свойства функционирова-
ния системы при ах g S есть не что иное, как устойчивость в некотором
смысле при фиксированном параметре «2и возмущаемом параметре
а — ах. В частном случае, тогда а = ах, все параметры системы ока-
зываются фиксированными. Это лишь означает, что семейство Л
(см. общее определение) состоит из одного одноточечного множества
(а). Конечно, поскольку изменились возмущаемие параметры систе-
мы, то новое определение устойчивости, вообще говоря, не совпадает
с прежним. В силу сделанного замечания можно считать, что пара-
метры ах отличаются от а.
Нахождение S-области можно осуществлять на ЭВМ с помощью
алгоритмов, описанных ниже в § 9.6. При этом в блоке 2 (см. рис. 9.3)
должна осуществляться проверка системы на устойчивость при значе-
нии параметра ах. Такая проверка может осуществляться с помощью
любого метода анализа устойчивости.
К настоящему времени для различных систем и различных опре-
делений разработано достаточно много методов анализа устойчивости.
О них можно прочитать в цитированных выше работах. Мы совсем
коротко остановимся на одном, наиболее распространенном — прямом
методе Ляпунова. Этот метод позволяет анализировать устойчивость
широкого класса систем в различных смыслах. Суть метода заключает-
ся в построении специальных (пробных) функций, называемых функ-
циями Ляпунова, обладающих определенными свойствами. Преиму-
щество метода заключается в том, что для его применения не нужно
знать траекторий системы, а достаточно знать лишь некоторые «ло-
кальные» свойства, и, кроме того, при применении этого метода «бес-
платно» получаются интересующие исследователя количественные ха-
рактеристики. В гл. 15 будетсформулирован ряд теорем этого направле-
ния и будут проиллюстрированы указанные свойства прямого метода
Ляпунова на примере анализа агрегативных систем.
9.6. НЕКОТОРЫЕ АЛГОРИТМЫ ПОСТРОЕНИЯ ОБЛАСТЕЙ
В ПРОСТРАНСТВЕ ПАРАМЕТРОВ
В предыдущем параграфе была показана необходимость построения S-
области в пространстве параметров для разнообразных систем. Аналогичные
задачи (т. е. задачи построения тех или иных областей в пространстве параметров)
возникают достаточно часто при анализе и синтезе систем. Такие задачи, как мы
говорили, возникают в задачах исследования устойчивости, при построении раз-
253
лййных поверхностей уровня и т. д. В силу этого целесообразно привести неко-
торые методы, которые могут применяться для подобных целей. Очевидно, что
при необходимости эти методы могут модифицироваться.
Обозначим искомое множество через R, а пространство параметров систе-
мы— черезМножество R описательно можно характеризовать тем, что если
значение параметров а £ R, то процесс функционирования системы обладает неко-
торым желаемым свойством. Обычно при этом требуется, чтобы искомое множе-
ство R являлось подмножеством некоторой фиксированной области Ro (Rcz Ro CZ
r~ —допустимой области изменений параметров системы. Будем в дальней-
шем предполагать, что если задано значение параметра а, то мы располагаем
критерием, позволяющим судить, принадлежит а множеству R или нет. Так,
если R — множество, где значение некоторого функционала <р(а) превышает
значение <р0, то проверка принадлежности а множеству R состоит в вычислении
(или оценке) конкретного значения функционала и сравнении его с <р0. Если R —
область устойчивости по Ляпунову решений обыкновенных линейных дифферен-
циальных уравнений, то можно, например, проверить условия Гурвица в точ-
ке а и т. д.
При исследовании реальных систем обычно известны некоторые априорные
сведения относительно множества R. Такие сведения имеют, как правило, доста-
точно общий характд^— олносвязность R, гладкость ее границы, максимальная
кривизна поверхности, выпуклость и т. п. Однако и они позволяют создавать
специализированные алгоритмы нахождения множества R, учитывающие специ-
фику имеющейся информации. Рассматриваемые ниже алгоритмы относятся к
этому типу. Всюду будет предполагаться, что граница искомого множества до-
статочно гладкая и сведения об этой гладкости позволяют выбрать конкретное
число точек и максимальное расстояние между ними, с достаточной степенью точ-
ности задающее искомое множество, поэтому на указанных вопросах останав-
ливаться не будем.
Приведем сначала алгоритм нахождения множества R в двумерном ев-
клидовом пространстве, если известно, что множество R односвязно и лежит в
области Ro . Пусть aL и а2 — компоненты вектора а, а = а2). Будем
отмечать символом «+» значения параметров, принадлежащие R, а символом
«—» — не принадлежащие R. Результатом работы алгоритма является фиксиро-
вание точек, лежащих в R и отстоящих от границы R не далее, чем на заданное
число Д > 0. Обозначим i-ю такую точку через а[р (с компонентами и а^Р).
Работа алгоритма складывается из трех, последовательно выполняемых этапов:
1) поиск точек a^J" (с компонентами а‘о^ и а^2) и
2) нахождение точки а,р;
3) обход границы множества R и фиксация граничных точек a^p, i > 2.
Опишем коротко работу алгоритма на этих этапах, а затем приведем пол-
ную’блок-схему алгоритма, которая может быть использована для конкретных
исследований.
На первом этапе ищутся две точки: c/.q~ и Методы поиска могут быть
самые разные. Можно применять детерминированные методы поиска, просмат-
ривая точки области Ro в соответствии с каким-то заранее определенным прави-
лом до тех пор, пока не найдем искомые точки. Разумеется, должна быть преду-
смотрена остановка, если достаточное число проверок не обнаружило точки а^“.
Ниже (см. рис. 9.3) в блок-схеме такая остановка не показана. Можно применять
и случайный поиск, как целенаправленный, так и слепой. Наконец, если априо-
ри известно расположение двух точек, обладающих требуемыми свойствами, то
необходимость в поиске отпадает. Так, например, в качестве точки можно
взять любую точку вне области Ro.
После того как точки и найдены, наступает второй этап—нахожде-
ние точки ajP, лежащей на границе множества R. Здесь можно воспользоваться
алгоритмом, приведенным на рис. 9.1, который, разбивая отрезок прямой, про-
254
ходящей между точками и ад , пополам, проверяет, принадлежит ли точка
разбиения множеству в зависимости от результата проверки записываются
новые значения или а^, затем новый отрезок между и а0 вновь делится
пополам и т, д., до тех пор, пока получающийся отрезок не станет достаточно
мал (< А).
На третьем этапе осуществляется обход границы множества 7?, начиная
с найденной точки ajp. При этом граница «нащупывается» с помощью поисковых
движений. На рис. 9.2, а показан характер обхода границы, зафиксированные
точки обозначены крестиками, а остальные
проверенные точки — кружками. Траектория
поиска показана стрелками. На рис. 9.2, б
с целью пояснения логики поиска границы
показана часть рис. 9.2, а, обведенная пунк-
тиром. Для краткости точку, принадлежа-
щую R, назовем положительной, а не при-
надлежащую R, — отрицательной. Поиск
границы идет следующим образом. Из неко-
торой положительной точки 1, зафиксирован-
ной как граничная точка по «рабочему»
направлению, показанному стрелкой 1
(рис. 9.2, б), переходим в точку 2 и исследуем
ее на «положительность». Пусть эта точка
положительная. Тогда, по «пробному» направ-
лению, образующему прямой угол с «рабо-
чим», и отсчитываемому против часовой стрел-
ки, переходим в точку 3 и исследуем ее на
«положительность». Пусть она «отрицатель-
ная». Тогда фиксируем точку 2 как граничную
и переходим по «рабочему» направлению, сое-
диняющему две последние зафиксированные
граничные точки, в точку 4. В данном слу-
чае это направление совпадает с прежним.
Точка 4 оказалась отрицательной. Поэтому ра-
бочее направление изменяется на 90° по часо-
вой стрелке. Полученная точка 5 является
положительной. Проверяем на «положитель-
ность» точку 6; поскольку и она является
положительной, то 6 и фиксируется в каче-
стве граничной. По новому «рабочему» нап-
равлению переходим в точку 7 и т. д.
Алгоритм заканчивает свою работу, когда граница множества замыкается.
Очевидно, если Ro — ограниченная область, то алгоритм завершит работу че-
рез конечное число шагов. Число шагов зависит от периметра множества R
величины шага А и конфигурации границы. На рис. 9.3 показана блок-схема ал-
горитма для случая, когда Ra имеет вид прямоугольника, Ro = {«• < а, <
< В,, А2 <а2 < В2}.
Точка на 1-м этапе алгоритма ищется методом слепого поиска, когда
испытываемые значения а независимы и равномерно распределены в Ro, а в ка-
честве точки а^" берется ближайшая к aQ^ граничная точка. На показанной блок-
схеме точка ищется в блоках 1—5, точка — в блоках 6—17, точка «]Р _______
в блоках 18—21, а обход границы осуществляется в последующих блоках. При-
знак Пр1 принимает значение 1 после отыскания положительной точки а+, Пр,
принимает значение 1 после того, как найдена точка ajp, признаки Пр2 и /7р4 обес-
печивают должную фиксацию граничных точек. Величины ут и у2 определяют
«рабочее» направление обхода границы, a [Jj и ₽2 — пробное направление.
Величина А определяет величину шага.
Алгоритм может быть использован для нахождения областей в случае,
255
когда размерность вектора а превышает 2. Это осуществляется построением дву-
мерных сечений множества R, когда все компоненты, кроме двух, фиксированы.
Получая указанные сечения при различных значениях фиксированных компо-
нент, можно найти все множество R. Правда, при размерности вектора а уже
более трех возникает проблема (помимо роста числа-граничных точек) обозри-
Рис. 9.2
мости полученной информации коорди-
нат граничных точек. Эта проблема ни-
чем, по существу, не отличается от
проблемы задания многомерных обла-
стей общего вида.
Путем неоднократного применения
описанного алгоритма можно находить
многосвязные и состоящие из несколь-
ких односвязных множеств R, после-
довательно обходя различные границы.
Трудности, возникающие при этом, ана-
логичны трудностям нахождения гло-
бальных экстремумов функций, в част-
ности неизвестно, все ли части границ
уже просмотрены. Однако при ограни-
ченной области Ro эта трудность ско-
рее теоретического характера, нежели
практического.
Рассмотрим еще один алгоритм,
который в принципе пригоден для по-
строения односвязных выпуклых мно-
жеств R в пространстве произвольной конечной размерности. Путем некоторой
модификации алгоритма можно его применять и при построении просто одно-
связных множеств и т. д. Однако принцип работы объясним на примере вы-
пуклого множества R. Работа алгоритма состоит, по существу, из первого этапа
предыдущего алгоритма и многократного повторения его второго этапа. Укруп-
ненная блок-схема алгоритма показана на рис. 9.4. _____
Л m о
Обозначим через аг, i = 1, ..., т, компоненты вектора а, || а || = 1 / 2 а, .
256
О
Зак. 792
22
24
£
N: = //* 7
1 28
29
^о/-=а(м ^,'^аг '=J
Проверка: а.д £ *-
I i
Пр :~-ff
Проверка;
Ч).
И
Выбача Xj а х г как
координат грснаць!
о&ласгпи P:a.r^~lxhx2 ?
Гработа _____
I окончен^
Рис. '9.3
1ррмд: /7р3 - Пр^ 7 |~
*1
j Проверка: Пр
у}: = х/ ; у,: = х2;
f:.x2-npp-P
Ёрверка:тах [
Для простоты в алгоритме принято Ro — [а : Aj a; fi;, i= 1, .... m). Пусть
а(/?0' Выберем некоторым образом (с помощью случайного или детерминиро-
ванного правила) m-мерный вектор -у = (у;, ут), который будем называть на-
правлением и который задает направление поиска граничных точек. Всего рас-
сматривается N направлений. Число N и механизм выбора различных направ-
лений должны удовлетворять, например, следующему условию. Если зафикси-
ровать некоторую величину «телесного угла» <о в m-мериом пространстве,то с
Рис. 9.4
достаточно большой вероятностью в любом телесном угле величины ш с верши-
ной в выбранной точке а+ должен лежать по крайней мере один их N векторов
Пусть
Pii= (Bi-a+i)/Y». Pi2 = (Лг -а+г)/?;,
Pi = min р,;, р2= max ptj.
г=1.....m;/=l;2, г=1.....m;/=l,2;
Pi>>° РИ °
Тогда, очевидно, векторы а+ + PiT и а+ р.,у лежат па границе области _А?0.
Работа блок-схемы совершенно ясна из рис. 9.4. Выбор очередного направления
1 = 1.......... N, происходит в блоке 2. Учитывая, что на каждом направлении
ищутся две граничные точки, должно выполняться очевидное неравенство
N > (т + 1)/2 для того, чтобы построенное множество R не оказалось вырож-
денным (т .е. не имело размерности, меньшей т).
Для выпуклых множеств можно ограничиться выбором сравнительно не-
большого числа N, поскольку, если принять найденные точки за вершины выпук-
лого многогранника, то этот многогранник будет вписан в множество R, т. е.
будет представлять собой часть искомого множества, быть может, вполне доста-
точную для решения поставленных задач.
ГЛАВА ДЕСЯТАЯ
ИСПОЛЬЗОВАНИЕ МАРКОВСКИХ ПРОЦЕССОВ
С КОНЕЧНЫМ ИЛИ СЧЕТНЫМ МНОЖЕСТВОМ СОСТОЯНИЙ
ДЛЯ АНАЛИЗА СЛОЖНЫХ СИСТЕМ
10.1. РАЗЛИЧНЫЕ ПОДХОДЫ К ОПРЕДЕЛЕНИЮ МАРКОВСКОГО
ПРОЦЕССА С КОНЕЧНЫМ ИЛИ СЧЕТНЫМ МНОЖЕСТВОМ СОСТОЯНИЙ
Аппарат процессов, указанных в заглавии, является простейшим
в теории случайных процессов, наряду с аппаратом стационарных
в широком смысле процессов. Марковский процесс может служить
моделью реального явления в случае отсутствия последействия в воз-
можных изменениях состояний системы. Однако в действительности,
как будет показано ниже, возможности применения марковских про-
цессов значительно шире. Что весьма важно, марковское свойство со-
храняется при объединении агрегатов в сложные системы: если агрега-
ты являются «марковскими», то таковой будет и составленная из них
система. Все эти вопросы будут рассмотрены в настоящей главе.
В этом параграфе мы приведем основные определения процессов ука-
занного вида. Следует отметить, что возможности марковских процес-
сов в настоящее время используются в расчетах, связанных со слож-
ными системами, далеко не полно, в противоположность корреляцион-
ной теории стационарных процессов.
Марковский процесс (слова «с конечным или счетным множеством
состояний» внутри данной главы будем опускать там, где это не может
вызвать недоразумения) задается множеством состояний Z, которое
должно быть конечным или счетным, начальным распределением
{рн (4), k £ %] и набором интенсивностей перехода Хг; (/), i £ Z,
j б Z, i =/= j (более полно: интенсивность перехода из i в j в момент t),
представляющих собой любые неотрицательные, интегрируемые по
Лебегу*’ в любом конечном интервале функции.]
Функция
М0=2М) (Ю.1)
/ I
называется интенсивностью выхода из состояния i в момент t.
Примем предположение, состоящее в том, что для некоторой по-
стоянной с и равномерно по i £ Z и t > tQ имеет место неравенство
М)<с- (Ю.2)
*’ Для лиц, нс знакомых с теорией функций действительной переменной,
дадим объяснение, что любая функция, интегрируемая по Риману, интегрируема
также по Лебегу. В частности, интегрируема любая ограниченная кусочно-
непрерывная функция.
9* 259
Условие (10.2) сразу избавит нас от необходимости иметь дело с трудно
интерпретируемыми процессам т. например с процессом, «уходящим
в бесконечность» за конечное время (см. [1]), которые вряд ли могут
встретиться в действительности как модели функционирования слож-
ных систем. (Разумеется, составив модель, следует проверить, выпол-
няется ли данное условие.)
Марковский процесс можно интерпретировать тремя способами;
все они эквивалентны. Приведем все три интерпретации.
1. Инфинитезимальная интерпретация. В момент 4 разыгрывает-
ся случайная ситуация, исходом которой может быть любой элемент
k множества Z с вероятностью pk (4). Это будет состояние процесса
в момент t0. Далее фиксируем некоторое h > 0 так, чтобы ch < 1, и
строим вспомогательный случайный процесс (I) следующим образом.
Определим £h(t) — k при tQ < t < t0-\-h. Предположим, что
данный процесс уже построен в интервале t0 < t <_t0 + mh, при-
чем gn(/) = i при t0 + (m—l)/i + Введем постоянные
(/0 ф-ш/z) = и реализуем случайное испытание,
/о -\-mh
исходом которого может быть любое j g Z, j i, с вероятностью
p!/’ (t0-\-mh). Если реализовался исход j, определяем значение про-
цесса в интервале tQ -\-mh <; t < tQ ф- (m ф-1) h как j. С вероятностью
1—(to + mh) полагаем %h(t) = i при t0 + mh^.t<t0 ф-(тф- 1)/т.
i
Повторяя указанную процедуру, можно определить процесс
£/г (/) при любых t 10.
Пусть теперь взята последовательность [hn), /гп —0, и при лю-
бом h = hn построен процесс вида (/). Тогда стохастический предел
(t) при и —оо и будет марковским процессом с интенсивностями
переходов (t) и начальным распределением \ph Точнее, при
любом гф 1, любых 4 < 4 < t2 < ... tT и произвольных ф, i2
..., iT справедливо равенство
lim Р (40 = 1 = Р(Ш = 4 1 (Ю.З)
п
Более того, если взять конечное число (г) непересекающихся интерва-
лов времени Др Д2, ..., Дг, то
lim Р [Zh = l<j<r} =
= P(U4 = 4- !</</-}• (10.4)
Наглядный вариант только что сформулированного определения
сводится к следующему. Марковский процесс — это такой процесс
£ (4, для которого
РГе(4) = &}=М4), kez, (10.5)
Р(£(/ + Л)=/О) = 4=Ы^Ж /V», (Ю.6)
Р Ш ф- dt) = i/Ui) = i ] = 1 -%2(0 dt,
260
причем последние вероятности не изменятся, если помимо условия
g (t) = i мы добавим любое условие, касающееся поведения процес-
са до момента t.
la. Пожалуй, будет полезна еще одна интерпретация, примыкаю-
щая к предыдущей и отправляющаяся от процесса Пуассона как от из-
вестного статистического объекта. (Определение процесса Пуассона
имеется во всех учебниках по теории вероятностей и поэтому здесь
не приводится.) Нам понадобится еще интуитивно очевидное понятие
процесса с независимыми значениями в каждый момент времени.
Итак, введем два случайных процесса: ц (t) — процесс Пуассо-
на с параметром (интенсивностью) с, где с взято из условия (10.2),
и процесс v (t, i) с независимыми значениями в каждой точке*’. Зна-
чениями процесса v (t, i) являются элементы i множества Z, причем
P(v(MWl=MU h kez-
(10.7)
P[v(/, i)=/)=X/7.(/)/C,
i, j£Z, i^j, t>to, (10.8)
p (v(/, i)=i) = 1—X;(/)/c0, l£Z, t>t0. (10.9)
Марковский процесс g (t) строится следующим образом. Пусть
/0 < И < Ь < — моменты появления событий про-
цесса Пуассона ц (/). Положим £ (t) — v (t0, i) (где i произвольно, но
выбрано заранее) в интервале /0 t < t1# Предположим, что | (0
построен при t0 t < тп, причем |(/) = t Для Tn-i «С t < тп. Тогда
в интервале тп t <Z тп+1 положим
l(0=v(/n, i).
(10.10)
Поскольку, как известно, тп-> со при п-> оо, то подобная кон-
струкция приводит к определению процессов £ (/) при всех t t0.
Данное определение можно записать в виде стохастического дифферен-
циального уравнения
d-W)= [v (/, g(0)~£(0]<М): (Ю-H)
приращение процесса | (0 равно 0 на участках, где приращение
ц (Z) процесса Пуассона равно 0; если г] (/) получает единичное прира-
щение, | (/) получает приращение v (/, % (Z)) — % (/).
Внимательный читатель заметит некоторый пробел в нашем
построении: мы говорим о разности v — %, в то время как Z — произ-
вольное пространство, где не обязана быть определена операция вы-
читания. Однако этот пробел легко устраним, поскольку в самом деле
речь идет не о вычитании, а о замене одних значений другими, т. е.
об операции вида а 4~ (Ь — а) = Ь, которая, конечно, может быть
применена к любым объектам.
*> Имеется в виду, что при любом гг н любых парах (/lt г\), (/2, Ц), ..., (tn, in),
среди которых нет совпадающих, значения процесса ц), v(/2. h)............
v(tn, in) независимы в совокупности.
261
2. Последовательная интерпретация. В соответствии с распределе-
нием ph (t0) выбирается начальное состояние процесса: £ (Zo) = k.
Реализуется случайная величина с функцией распределения
Р{^<х} = 1—exp j— § Xft(£)dH (10.12)
I ^0 J
и полагается
S(0 = £O h<t<t6 + h-
(10.13)
Предположим, что процесс g (t) уже определен в интервале времени
fo<f<Jo + 4 + ••• + tn, причем в интервале t0 4- + ... +
+ Z„-i t < t0 + tA + ... + tn_\ + tn процесс | (t) принимает
постоянное значение i. Тогда производится случайное испытание,
исходом которого может быть любой элемент / множества Z с вероят-
Xi. (tn "Т ti—I— ... -р 171 ) / • , u
ностью ——44-------п-(] ф I), реализуется случайная величи-
лг ЦО “г *1"Г + ‘п)
на с функцией распределения
Р (6г+1 < х} = 1 —ехр
и полагается
/о + G + • + +*
§ X;- (/) dt
о + 1 + . . . -f- f n
(10.14)
£(0 —/> ^o + ^i+ ••• 4- t < 4~ + ••• 4~^п4*^+1- (10.15)
К этому следует добавить, что случайные испытания, о которых
говорилось, при различных п независимы в совокупности.
3. Развернутая последовательная интерпретация. Эта интерпре-
тация отличается от предыдущей только следующим. Вместо £п+] реа-
лизуется последовательность независимых случайных величин i,
где
Р {/^+1 < х) =1 —ехр
И- + *
io + ii -h • +
(10.16)
Затем tn+i определяется как min/^i.
k e z
Пусть kg—то значение k, при котором данный минимум достигает-
ся. В таком случае в момент t0 -j- tr 4~ tapi значение процесса g (Z)
определяется как kg. Таким образом, реализация случайного испыта-
ния для определения значения процесса после изменения его состоя-
ния в данной интерпретации не нужна.
10.2. СВЕДЕНИЕ РЕАЛЬНЫХ ПРОЦЕССОВ
К МАРКОВСКИМ МОДЕЛЯМ. ЗАМЕЧАНИЕ О МОДЕЛИРОВАНИИ
Последняя интерпретация марковского процесса, как нам ка-
жется, наиболее наглядна для целей схематизации функционирования
реальных сложных систем. Опишем физические предпосылки, достаточ-
ные для возможности такой схематизации.
262
Предположим, что физическая система в любой момент t может пре-
бывать в состояних дискретного (конечного или счетного) множества
Z. Пусть в момент t состояние системы есть I. Представим себе, что
существует некоторое число физических факторов, способных вывести
систему из состояния /; воздействие /-го фактора может привести к тому,
что она перейдет в состояние /. Основное предположение состоит в том,
что воздействия различных факторов независимы в совокупности и что
время, которое пройдет с момента t до того, как воздействует /-й фак-
тор, есть случайная величина т] (t, i, j), не зависящая от поведения си-
стемы до момента t. В таком случае от распределений случайных ве-
личин т] (t, i, j) легко перейти к интенсивности перехода из состояния i
в состояние /. Именно при условии, что каждая из функций Ft, t, j (х)
абсолютно непрерывна (т. е. является первообразной от своей произ-
водной), справедливы формулы
Ft, t, j (х) = Р {tj (t, i, j) < х} = 1 —exp
i+x
— $ ^ii (u)
t
(10.17)
W +*) =F't, t,, (?)/(! -Ft, t. i (T)). (10.18)
Однако существуют гораздо более широкие возможности для ис-
пользования марковских процессов с конечным или счетным множест-
вом состояний. Предположим, что время «срабатывания» некоторого
фактора обладает функцией распределения F (х), совпадающей с функ-
цией распределения времени пребывания некоторого марковского
процесса с конечным или счетным множеством состояний в фиксиро-
ванном множестве состояний. Тогда за счет расширения пространства
состояний можно интерпретировать данный факт как «марковский».
В качестве примера рассмотрим известный в теории массового
обслуживания закон распределения Эрланга, характеризующийся
плотностью вида
р п— 1
р(х) = 1}, х>0, « = 1,2, ... (10.19)
Если случайная величина £ имеет распределение Эрланга, спра-
ведливо представление
£ = (Ю.20)
где — независимые случайные величины, распределенные по пока-
зательному закону с параметром %. Следовательно, можно построить
марковский процесс, попадание которого в некоторое состояние будет
интерпретироваться как истечение времени Такой процесс имеет
п + 1 состояний: 0, 1,2, ..., п. В каждом из них, кроме последнего, он
находится показательно распределенное время (это и есть |г). Из со-
стояния i (0 г /I — 1) возможен переход лишь в состояние t 4~ 1.
Из состояния п выход невозможен. Попадание в это состояние проис-
ходит через время | после начала процесса.
263
Можно пойти и дальше, рассмотрев плотности вида
™ rnkxnk~l
х>0, (10.21)
где Сх, С2, Ст — положительные коэффициенты, в сумме рав-
ные 1.
Случайная величина £ с указанным распределением интерпрети-
руется следующим образом. Построим марковский процесс с состояния-
ми вида (k, i), где k — 1, 2, ..., tn, a i при фиксированном k принимает
значения 0, 1, 2, ..., nk. Вначале разыгрывается случайная ситуация,
возможными исходами которой являются числа k с вероятностями Ch.
Процесс попадет в состояние (k, 0), где k — исход данного случайного
испытания. В состоянии (k, i), где 0 сС i nh — 1, процесс находит-
ся показательно распределенное время с параметром Попадание
в состояние (k, nh) означает, что время % истекло.
Описанный метод давно известен в теории массового обслужива-
ния; однако при моделировании он используется, к сожалению, не-
достаточно. Приведем рассуждение, убедительно демонстрирующее его
преимущество перед обычным методом моделирования.
Пусть требуется моделировать сложную систему, состоящую из
Sj агрегатов первого типа, S2 агрегатов второго типа, ..., Sr агрегатов
r-го типа. После каждого «случайного события» в системе нужно
знать, через какое время будет послан сигнал каждым из агрегатов.
Иными словами, в памяти моделирующего устройства нужно хранить
Sj + S2 + ... + Sr вещественных чисел-времен до «срабатывания»
всех агрегатов. Операция выбора минимального из этих времен сво-
дится к Sj + S2 + ... + Sr — 1 бинарным операциям. Предположим
теперь, что состояние каждого агрегата изменяется, как марковский
процесс с т состояниями. Тогда можно запоминать лишь ktj —
число агрегатов i-ro типа (1 i < г), находящихся в состоянии
j (1 < j т). Для этого достаточно хранить
( [ + 1 log2 S2 [ + ... +] log2 Sr [ ) (m — I)*’
двоичных единиц информации; данная оценка даже завышена. Далее,
при изменении состояния одного из агрегатов i-ro типа, на что укажет
переход процессов из одного состояния в другое, нужно определить,
какой из агрегатов «сработал» (в системе они могут использоваться
по-разному). Для этого нужно случайным образом выбрать один из
Si исходов, на что пойдет ]log2 SJ двоичных случайных выборов.
Из сказанного можно сделать вывод: при наличии в системе мно-
гих однородных объектов весьма эффективно построение модели на
основании марковского процесса с конечным числом состояний. Это
позволяет намного сэкономить как память ЭВМ, так и число операций
при моделировании процесса.
*> Символ ]«[ обозначает а, если а — целое число, и наименьшее целое чис-
ло, большее а, если а — дробное.
264
10.3. ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ ГИПЕР-ЭРЛАНГОВСКОЙ
АППРОКСИМАЦИИ
Если случайные величины, участвующие в определении процесса
функционирования системы, обладают плотностями вида (10.21)*’,
указанный выше прием непосредственно приводит к построению
марковской модели. Однако распределения обычно задаются либо
гистограммами, либо аналитическими выражениями, либо графиками.
Возникает вопрос о том, в каком строгом смысле можно говорить
о приближении произвольного распределения смесью эрланговских
распределений. Обозначим через Е класс смесей эрланговских распре-
делений, каждое из которых обладает плотностью вида (10.21), а через
Е* — класс бесконечных смесей эрланговских распределений. Каж-
дое из распределений этого класса записывается в виде (10.21), с тем
лишь отличием, что в сумме может быть бесконечное число слагаемых.
Таким образом, Е с Е*.
Теорема 1. Пусть F (х) — произвольная функия распределения,
подчиненная условию F (0) = 0. Тогда для любых а и е > 0 найдется
такое распределение G (х) 6 £'*, что
§|G(x)—F (х) | еах dx < е. (10.22)
о
Доказательство. Очевидно, достаточно установить тео-
рему для произвольных а > 0. Покажем сначала, что можно выбрать
ступенчатую функцию Н (х) таким образом, чтобы удовлетворить
условию
J |Д(х) — F(x)\eaxdx : (10.23)
__ . о 2
тогда утверждение теоремы будет следовать из того, что для любой
ступенчатой функции распределения Н (х) можно найти такую функ-
цию G (х) С Е*, что
$ |G(x)—H(x)\eaxdx^-, (10.24)
о 2
поскольку из (10.23) и (10.24), очевидно, следует (10.22).
Пусть Xj х2 < ... < хп < ... — некоторая последователь-
ность чисел. Определим Н (х) следующим образом:
[ F(xn), если хп х + i Для какого-нибудь /г^1;
Я(х)= „
' ( 0, если х < Xj.
Н (х) будет ступенчатой функцией.
*> Подобные распределения иногда называют гппер-эрланговскими,
265
Далее,
хп + 1 хп 1
§ \Н(х)—F(x)\eax dx[F(xn+i)—F (xn)] § eax dx =
xn xn
^[e^+i-e-n] [£(x„+,)-£(xn)]; (10.25)
Xt Xt
| H (x)—F(x) | eax dx^F(x1} eaxdx = — [eax> — I] F (Xj). (10.26)
о о a
Положим
1 , пае]
x.=max 0, —In — 1.
( a 2 j
Тогда
°’ еслих1 = °-
a |e/2, если x1>0;
_L [еа*л+1_еа*п] (10.27)
Просуммировав соответственно левые и правые части неравенств
(10.25) при п = 1, 2, 3, ... и добавив к результату соответствующие
части неравенства (10.26), получим
§ | Н (х) —F (х) | е.ах dx<F
о
^~IF(X1)+F (x2)-F(x1)+F(x3)T...1=-|-. (10.28)
2 2,
Итак, остается удовлетворить неравенству (10.24).
Определим функцию Е (х) следующим образом:
( 0 при X С; 0,
£(х)= . Н „ (10.29)
' ' (1 при х>0.
Положим
Рп=Н(хп + 0-)-Н(хп), п^1, (10.30)
Можно записать
оо
Я(х)=£ РпЕ(х-хп). (10.31)
П=1
Предположим, что для любого т>0 можно найти такую функ-
цию Gt (х) 6 Е, что
$|Gt(x)— £(х—r)|ea*dx^— . (10.32)
о 2
Oftft
Тогда, положив
оо
= 2 PnGxn(x),
/1=1 п
(10.33)
придем к следующей оценке:
| G (х) —Н (х) | еах dx =
о 'о
—Е(х—хп)]
2 Pn[Gx (х) —
п=\
оо р
2 Рп М G^n(x) —
п=1 0
ОО
-Е (х-хп) | е« dx < Рп = -|-.
2 п=1 2
(10.34)
Таким образом, доказательство теоремы сводится к выбору
функции GT(x), удовлетворяющей неравенству (10.32).
Положим
(10.35)
где п — пока неопределенное натуральное число, и пусть т] — слу-
чайная величина, функция распределения которой равна Gx (х).
Имеем
| GT (х) —Е (х—т) | еах dx =
о
Т оо
= GT (х) еах dx + [1 —Gx (х)] е“ dx =
о т
Т оо
= Р {ц < х} еах dx Р [т] >xj еах dx.
О т
Можно записать:
n = — (li+^+ ...+U,
п
(10.36)
(10.37)
где ^2,..., — независимые случайные величины с плотностью
е-*(х>0). Поэтому для любого р<«/т
Мерп = (MePTsi/")" = (1—р—V". (10.38)
Поскольку при р > 0
Р e-p-'MeP’i,
267
имеем
Р [Г]
е-рхЬ-РТр
к « 7
Тогда при р >а
Р {л > х} еаЛ' dx (1—~) е—(р—а) х dx =
t ' t
= -J— e-<P-a’*i 1 —!-'Г" — ►-— e« (10.39)
p—a \ nJ n-»oop_ a
Поскольку p произвольно с единственным ограничением р<л/т, то
при достаточно большом п можно выбрать настолько большое р,
чтобы
\ Р (л > х | еах dx < — .
J I । 4
Аналогично, поскольку при р>0
находим, что
т t
Р {л < х] еах dx ( 1 + —^ П е<Р+а> Xdx<j
о \ « / о
e<p+a)Tf 1+ —V"—” —- еат, (10.40)
р + ч п I п^сср+а v
так что при достаточно большом п будет выполняться неравенство
$Р{Л<х) —. (10.41)
о 4
Этим неравенство (10.32) и вместе с ним и теорема полностью доказаны.
Для практических целей интересна, однако, аппроксимация ко-
нечными, а не бесконечными смесями эрланговских распределений.
Сделаем некоторые замечания на этот счет.
Заметим, что если исходная функция распределения F (х) обла-
дает свойством F (Т) = 1 для некоторого конечного Т, или, что то же,
соответствующая этому распределению случайная величина с вероят-
ностью 1 меньше Т, то прием аппроксимации, использованный при
доказательстве теоремы, приводит к конечной смеси эрланговских рас-
пределений.
Остается исследовать случай, когда F (х) < 1 при всех х. В этом
случае необходимо вводить дополнительные условия, касающиеся
поведения F (х) при х -> оо .
Так, предположим, что интеграл
оо
[1 — F (х)] еах dx
о
268
сходится. При таком условии по заданному е > 0 найдем такое Т > О,
что
Положим далее
[ 1 —F] еа* dx < — .
J 2
п , ч (F (х) при х < Т,
F, (*) = I 1
v [1 при х >Т.
Если мы подберем такую конечную смесь Н (х) эрланговских распре-
делений, что
ОО
$ | Н (х) — Fr (х) I eaxd х < -F- ,
о 2
то отсюда будет следовать, что
со
| Н (х) — F (х) I е°-1' dx < s,
о
что и требовалось.
10.4. КОНЕЧНО-МАРКОВСКИЙ И СЧЕТНО-МАРКОВСКИЙ АГРЕГАТЫ
Рассмотрим агрегат следующего вида. Множество состояний агре-
гата Z — конечное (счетное) множество. При отсутствии входных
сигналов состояние агрегата z = z (t) изменяется во времени, как одно-
родный марковский процесс. При поступлении входного сигнала х
агрегат переходит в новое состояние, выбираемое случайным образом,
в зависимости от z и х. При переходе агрегата из состояния i в состоя-
ние /, если этот переход не обусловлен поступлением входного сигнала,
на выход агрегата посылается случайный сигнал, в частности пустой;
распределение содержания сигнала зависит от i и /. Множество входных
и выходных сигналов конечны (счетны). Назовем агрегат описанного
вида конечно-марковским в случае, если множества состояний агрега-
та, а также множества входных и выходных сигналов конечны; в про-
тивном случае будем говорить о счетно-марковском агрегате.
Легко видеть, что оба вновь введенных типа агрегатов являются
частными случаями кусочно-линейного агрегата. Внутренним состоя-
нием кусочно-линейного агрегата, соответствующего конечно-марков-
скому (счетно-марковскому), будет пара (z0, z±), где г0 — состояние
марковского агрегата, — время до перехода агрегата в другое со-
стояние. Переменная zx = zx (/) убывает с единичной скоростью, пока
не обратится в нуль. В этот момент, а также в момент поступления на
вход агрегата сигнала, величина zx «обновляется», принимая значение,
взятое на основании реализации некоторой показательно распределен-
ной случайной величины.
269
Мы не будем останавливаться на технике подобной реализации:
она достаточно тривиальна. Сделаем лишь замечание об объединении
агрегатов подобного рода в сложные системы.
Следующие утверждения почти очевидны.
Лемма 1. Сложная система, состоящая из конечного числа конеч-
но-марковских агрегатов, является конечно-марковским агрегатом.
Лемма 2. Сложная система, состоящая из конечного или счетного
множества конечно-марковских или счетно-марковских агрегатов,
является либо конечно-марковским, либо счетно-марковским агрега-
том.
Таким образом, свойство марковости инвариантно относительно
операции объединения агрегатов в сложные системы. Легко видеть, что
марковский процесс, описывающий изменение состояний системы,
будет тем сложнее, чем большее число агрегатов объединено в систему
(если, конечно, не выявлен эффект однородности агрегатов, позволяю-
щий группировать состояния процесса с сохранением свойств марко-
вости). Если число состояний i-ro агрегата равно тг, то число состояний
системы будет составлять уже П ггц. При моделировании поведения
i
системы подобного затруднения не возникает, поскольку в запоминаю-
щем устройстве нужно хранить не все возможные состояния, а единст-
венное состояние системы в данный момент времени. Для этого доста-
точно иметь
N = ] 2 logs mi I
L
двоичных единиц памяти.
Теперь — о более тонком вопросе — моделировании перехода из
одного состояния в другое.
Без ограничения общности можно считать, что состояния системы
закодированы п двоичными символами и записываются в виде z =
— (zlt z2, ..., zn). Для перехода к следующему состоянию достаточно
задать две вещи: 1) интенсивность выхода из состояния г; 2) случай-
ную ситуацию выбора нового состояния после выхода из состояния г.
Все это можно перевести на язык теории алгоритмов. Именно, интен-
сивность выхода из состояния z есть некоторая функция X (z). Схему
вычисления этой функции можно задать в виде графа, внутренние вер-
шины которого соответствуют производимым элементарным операциям,
а п входных вершин — переменным zx, z2, ..., zn. Определение элемен-
тарной операции можно давать по-разному: либо приспосабливая его
к логике той или иной конкретной машины, либо исходя из определен-
ного набора элементарных операций, скажем отображений (а, |3) -> у,
где а, (3, у — булевы переменные. В таком случае z следует интерпре-
тировать как совокупность некоторого числа двоичных символов,
скажем разрядов двоичного разложения. Далее выбор нового состоя-
ния также можно записать в виде некоторой вычислительной схемы.
Естественно интерпретировать эту схему также в виде графа, вершины
которого соответствуют элементарным операциям. В качестве послед-
них мы предлагаем случайные отображения (а, |3) -> у, где а, р, у —
булевы переменные. Различные операции, входящие в схему как
270
случайные элементы, независимы в совокупности. Условие, которому
должна удовлетворять данная случайная функция (выбора следующего
состояния), состоит в том, чтобы ее значения принимались с вероятно-
стями, согласованными с интенсивностями перехода марковского про-
цесса.
Теперь можно определить сложность моделирования следующими
параметрами:
— числом двоичных разрядов, требующихся для кодирования
состояния процесса;
— сложностью вычисления А2 и выбора следующего состояния при
выходе из состояния г.
Под сложностью можно понимать сложность реализации функции
заданным классом формул начальных элементов, либо, учитывая огра-
ниченный объем запоминающего устройства ЭВМ, сложность в смысле
Б. М. Клосса и В. А. Малышева [4]: сложность автомата, вычисляющего
данную функцию не более чем за N тактов. Это определение в нашем
случае необходимо видоизменить, считая элементарные булевы функ-
ции случайными. В качестве альтернативы можно предложить опре-
деление Б. М. Клосса и В. А. Малышева, считая случайные двоичные
элементы входными переменными, наряду с zlt z2, ..., zn.
В некоторых случаях целесообразен несколько иной подход. Фик-
сируем объем памяти, и обозначим через Т (г) среднее число тактов
работы машины для вычисления Az и следующего состояния при выходе
из состояния z. Пусть приближенно известно распределение вероятно-
стей состояний данного процесса, а моделирование должно лишь уточ-
нить его. Тогда естественно усреднить Т (z) по этому приближенному
распределению и полученную характеристику считать показателем
сложности моделирования.
Таким образом, можно сформулировать задачу построения моде-
лирующего алгоритма как задачу построения минимально сложного
способа вычисления заданных функций Аг и г' (г), где г’ (г) — состоя-
ние, в которое попадет система, выйдя из состояния z. Понятно, что
решать эту задачу каким-либо способом, требующим записи таблицы
значений вычисляемой функции, бессмысленно: если есть возможность
перечислить состояния системы, то в большинстве случаев и модели-
ровать процесс не нужно — основные его характеристики можно найти
аналитическим путем или обычными численными методами. Можно,
как нам кажется, исходить из определенной формальной записи функ-
ции и искать упрощения, используя эквивалентные преобразования
формул.
10.5. АНАЛИТИЧЕСКИЕ МЕТОДЫ
В случаях, когда число состояний марковского процесса невели-
ко, либо когда путем группировки состояний мы привели процесс
к более простому, либо, наконец, при малой насыщенности матри-
цы ||А^ (0|| ненулевыми элементами, практически возможно предпри-
нять аналитическое исследование характеристик марковского про-
цесса.
271
Многочисленные примеры аналитического исследования марков-
ских процессов, отображающих функционирование различных сложных
систем типа систем массового обслуживания, можно найти в моногра-
фии Саати [5] и в других книгах по теории массового обслуживания.
Интересный пример применения марковских процессов к исследованию
эффективности системы защиты сложной автоматизированной системы
предложен в работе П. И. Попова и В. Г. Терентьева [6]. Не останавли-
ваясь на рассмотрении примеров, приведем сводку основных формул,
ио которым можно находить характеристики марковского процесса
с конечным или счетным множеством состояний.
Пусть имеется марковский процесс ё (t), характеризующийся
интенсивностями перехода (t), i 6 X, j Е X, i=/= j. Одной из основ-
ных характеристик является вероятность перехода ptJ (/), опреде-
ляемая как условная вероятность события {£ (t) = j} при условии, что
£ (0) = Л (Легко видеть, что Р {£ (т + /) = j/l (т) = ij равна ptJ (t),
для вычисления которой используются функции кц (t + т) вместо
“кц (t). Поэтому, чтобы не вводить лишнего аргумента в обозначения,
мы будем рассматривать в качестве начального момента 0.)
Для составления уравнений относительнорц (t)*> при большом
числе состояний удобно пользоваться так называемой кинематиче-
ской схемой переходов марковского процесса. Она строится следующим
образом. На листе бумаги точками изображаются все возможные со-
стояния процесса. Затем дугами со стрелочками изображаются воз-
можные переходы из одних состояний в другие; численное значение
или обозначение интенсивности перехода надписывается над соответст-
вующей дугой. При этом мы рекомендуем вначале составить перечень
возможных физических причин, обусловливающих переходы из одних
состояний в другие (отказы элементов системы, появление или оконча-
ние обслуживания требований, уход требования из очереди и т. п.)
и затем для каждой из причин перебирать все состояния и смотреть,
куда изданного состояния может перейти система под действием данной
причины и с какой интенсивностью. После этого уже составление урав-
нений для ри (t) не представляет труда.
Именно, возьмем, какую-либо точку на схеме; пусть она соответст-
вует /-му состоянию системы. Тогда следует подсчитать X, (/) — сумму
по всем стрелочкам, выходящим из этой /-й точки, и затем пере-
брать все состояния (k), из которых в данную точку идет стрелочка.
Получим уравнение
р'ц (0 PiJ (t) (/). (10.42)
Ах/
Подобное уравнение можно составить для любого / £ Z. Получим си-
стему уравнений, которая обладает (в принятых нами предположениях)
единственным решением, удовлетворяющим начальным условиям
( 1 при i = /,
РгД0) = 6/7-= _ (Ю-43)
lJ v 11 (0 при l =/= /, v
означающим стохастическую непрерывность процесса £ (I).
*> Эти уравнения впервые были установлены А. Н. Колмогоровым.
272
Часто представляет интерес определение характеристики рг (/, А) —
вероятности того, что за время t процесс ни разу не выйдет из множест-
ва состояний А при условии, что £ (0) = I. Нахождение этой функции
легко сводится к предыдущему. Действительно,
Pi(t, Л) =2 рМ (10.44)
1GA
где рц (/)— вероятность сложного события (процесс ни разу не выйдет
из множества А и при этом в момент t будет принимать значение / (.
Введем вспомогательный процесс % (t), у которого состояниями являют-
ся все J, принадлежащие множеству А, и еще одно состояние а; интен-
сивности перехода данного процесса задаются формулой
если j£A, i£A,
2^гл.(0> если j = a> i£A. (10.45)
. k£A
Легко видеть, что рц (t) есть обычная вероятность перехода нового
процесса £ (/) за время t из состояния i в состояние /.
Пусть известно, что | (0) = i £ А. Требуется найти среднее вре-
мя Ti (Л) до выхода процесса из множества состояний Л. Для этой
характеристики существует простая формула
Т.(Л) = ^р;(^, Л) dt. (10.46)
о
Особый интерес представляют стационарные распределения вероят-
ностей состояний марковского процесса. Их можно искать в случае,
когда кц (/) -> Кц*}. Стационарное распределение является неот-
/ —► оо
рицательным решением системы уравнений
Pi = S Рй> (10.47)
где = подчиненным условию
I
= (10.48)
/ex
Пусть Xij постоянны. Тогда стационарное распределение будет
истинным распределением вероятностей состояний процессов в любой
момент времени t t0, если только его принять в качестве началь-
ного распределения в момент tg. Если система уравнений (10.47)—
(10.48) обладает единственным неотрицательным решением, приписы-
вающим положительную вероятность любому из состояний, это реше-
*) Строго говоря, стационарный режим может устанавливаться при/->оо
и в более общем случае, например, в случае, если — некоторая осциллиру-
ющая функция с безгранично увеличивающейся при t -> оо частотой колебаний.
Важна не сходимость в обычном смысле, а некоторый средний эффект.
27.3
ние называется эргодическим распределением процесса £ (?). В таком
случае, независимо от начального состояния системы в момент t0,
с течением времени устанавливается один и тот же случайный режим.
Вероятность pj можно интерпретировать как среднюю долю времени,
на протяжении которого процесс пребывает в состоянии /.
Для теории сложных систем представляет интерес также исследо-
вание распределения вероятностей состояний марковского процесса
при периодической интенсивности переходов:
хгд?)=лгд?+т), i, jez, ?>о.
В таком случае естественно ожидать, что в системе установится ста-
ционарный периодический режим:
Рц(пх + Г)— > i, jCZ, Г(10.49)
fl —► оо
где pj (t) — некоторые периодические функции с периодом т. Для на-
хождения последних имеем систему уравнений
Pdt) + Zj(t)Pj^=24Ai)PuV), iez, 0<?<т, (10.50)
с условиями
Pj(O) = Pj(t), (10.51)
2 рД?) = 1, 0<?=^т. (10.52)
/ех
В одном частном случае, когда Хг/ (?) = а (/), где от (?) —
периодическая функция, стационарный режим не зависит от ?. В этом
легко убедиться, заметив, что для некоторой монотонно возрастающей
до оо функции (?) процесс £ (|3 (?)) будет однородным марковским
процессом с интенсивностями перехода Хг;.
10.6. АСИМПТОТИЧЕСКИЙ АНАЛИЗ
Представляет большой практический интерес теория' возмущений
характеристик марковских процессов под влиянием малых отклонений
их интенсивностей перехода. Действительно, очень часто производит-
ся исследование тех или иных характеристик без учета каких-то на
первый взгляд несущественных факторов. Спрашивается: насколько
сказываются эти отброшенные факторы? Поскольку переходные ха-
рактеристики марковских процессов определяются как решение си-
стемы обыкновенных линейных дифференциальных уравнений, теория
возмущений может основываться на методах, разработанных в теории
дифференциальных уравнений (см., например, монографию И. 3. Што-
коло [7]). Однако использование чисто вероятностных методов также
приводит к ряду полезных предельных теорем и асимптотических
оценок. Приведем одну из наиболее простых теорем такого рода,
полезную, однако, во многих приложениях, в частности в теории
надежности.
274
Теорема. Пусть £ (t) — однородный марковский процесс с конеч-
ным множеством состояний Z, состоящим из непересекающихся под-
множеств Zo, Zlt ..., Zr. Обозначим номер множества, которому при-
надлежит состояние I, через р (г). Предположим, что интенсивности
перехода обладают следующими свойствами:
1. Для любых i и j
где k (i, j) = 0, 1, 2, е > О — некоторый параметр; о (1) — бес-
конечно малая при е 0 величина.
2. При р (z) > 0 существует хотя бы одна цепочка состояний
i0, z\, ..., Д со свойствами р (i0) = 0 и k z\) + k (z\, z2) + ... +
+ k (ih, i) = p (z); не существует цепочки j0, jlt ..., jt co свойствами
p (/0) = 0 и k (j0, + k j.) + ... + k (h, i) < p (z).
3. При p(z)>0 существует такая цепочка Й, i2, ... , im, что
p(tm)<P(i) и /г(н, /;.)=&( i', z=Д(Д_1, z,'n)=0.
4. При e = 0 случайный процесс £ (f) обладает эргодическим рас-
пределением, при котором любое состояние множества Zo имеет поло-
жительную вероятность.
Пусть, далее, А—любое множество состояний процесса, имеющее
общие элементы с некоторым Zm, 1 < т <; г, но не пересекающееся
с Zo, Z1( ..., Zm-1. Тогда при е -> 0 поток попаданий процесса Ее (/) =
= | (Z/em) в множество состояний А сходится к стационарному (в об-
щем случае неординарному) потоку без последействия*’.
Приведенная теорема допускает значительное обобщение на
регенерирующие, полумарковские и другие классы случайных процес-
сов. В настоящее время возможности подобных обобщений до конца
не исчерпаны, хотя в этом направлении имеется ряд интересных работ
(см., например, [9]).
Приведем пример применения к теории надежности асимптотиче-
ского разложения характеристик марковского процесса по степеням
малого параметра. Этот пример принадлежит В. А. Ивницкому [9].
Задача ставится следующим образом. Имеется п одинаковых устройств в
основном соединении и т таких же устройств в ненагруженном резерве (т. е.
не выходят из строя). Время безотказной работы распределено по экспоненциаль-
ному закону с параметром к, время восстановления отказавшего устройства —•
аналогично с параметром ц и время переключения ( или регулировки) тоже рас-
пределено по экспоненциальному закону с параметром V. Время поиска отказав-
шего устройства предполагается равным нулю. Отказавшее в процессе работы
устройство начинает немедленно восстанавливаться (т. е. ремонтных бригад и
устройств достаточно), а на его место подключается исправное устройство из не-
нагруженного резерва (если оно есть) и начинает регулироваться. После того как
оно отрегулировалось, продолжается нормальная работа. Каждое устройство
может находиться в четырех состряниях: работе, восстановлении, регулировке
и резерве.
*> Теория потоков подобного рода была развита А. Я. Хннчииым [8]. Кратко
можно сказать, что любой такой поток порождается стационарным потоком Пу-
ассона, в каждый момент скачка которого реализуется случайное число собы-
тий с некоторым распределением.
275
Обозначим через число устройств, которые восстанавливаются в мо-
мент времени I, через K2(tj — число устройств, которые регулируются в момент
времени t\ величины и Т<2(/) полностью характеризуют состояние системы
в момент t. Введем случайный процесс 3(7) = В силу предполо-
жения относительно законов распределения он будет марковским. Обозначим
через рij(t), i -j- j п + т, вероятность того, что в момент t i устройств восста-
навливаются и j устройств регулируются. Тогда для обычным путем со-
ставляется система дифференциальных уравнений:
Poo ^=-п1р00 (О + рр1о (O + vpo. (0;
P'oi </>=-№-'') Л'-Ь iv] poi (0 + цРн (0 +
+ (l’+ 1) vp0, (-+ j (£);
Pki (t) =—[(n — i)^ + kp + iv] ph. (0 +
+ (n —г'+ 1) ^-P k~ 1 , i—1(0 +(^+ 1) PPi-'- 1 ,/(0 +
+ (' + l) vpki j+1 (0, 0<k<m, ] i П-];
p'kn W ~ (^ + nv) Pkn (0 + , n-i (0 +
+ +1) fiP*+1, n (0;
Pmi (0 = — l(n-i) X+w+'v] pmi(0+(i+I)vpOT> г+ ! (/);
P'tnn (0= -(«fl + nv) Pmn (t) + Kpm_ha_l (0 +
+ (пг+1)|лрш+1 (0, k>m,
1 < i < n -J- m — k — 1;
Pki (0 = —[(n-}-m—k—i) X + fep-H'v] pk. (/) +
+ (»+ra-fe — i-Hl) XpA_ j , i (0 +
-U (/г -|-1) р.Р/г тГ i, j _ i (0 + (' T 1) vPk , i— 1 (0 >
Pk, n+m-k (0 = -[^+(« + m-*)vl Pk, n + m-k^ +
+ '^P k— 1, kW i HP&-L1 .гг+т—/г —1 (0 ‘
(10.53)
В установившемся процессе p(- (<) = 0, поэтому для стационарных вероят-
ностей Pij получаем следующую систему линейных алгебраических уравнений:
— ftXpoo + pPiQ-rvptH =0;
— [(га — 0 Х + iv] Poi + M-Pii + (( + О vPq , i + 1 =0;
_[(« — /) X + /гр + Zv] pki + (n — i + l) ХрА_|> _ j +
+ (fe+l)ppA+I,rH^l)vpA,z.|.1=0> 0<k<m,
1 ц i <. п— 1:
— (/гц. + nv) Plin~r^Pk-!, п- 1 + (й+ !) М-РЛ+ 1, п = °’
— [(и— 1) X+mp-Hv] pmi + (ii— i' + l) Xpm_j, г_! +
+ (m~r О PPm+ 1, i — 1 + (* + 1) vPm, i -J-1 " Q’
— (mp + nv) pn, n -1- Xp m _ j , n _ i + (rn + 1) ppm+ j, „ _ , = 0, । q
m < k n -{- in, 1 : i 7 и + m — k — 1; (
276
— [(лг-'-m — k— i) '<kp + iv] Pki + (n+m—k —1'+ l)x
X^PA_lr (-+(fe+l)HPA+1> ;_i + (i+l)vpA, г+,=0;
-ф (я -ф ffl k) v] P/> ( n _|_/n — £ 4“ ^'P k — 1, nj-m— k +
+ (4) PP*-|- 1 , n + m — k — 1 = 0'-
Ввиду того, что Vv в практических задачах является малой величиной,
естественно искать ptj в виде
оо
Pij = 2
k = о
(10.55)
Поскольку pij как решение системы (10.54) является дробно-рациональной
функцией от */v при фиксированных значениях остальных параметров и посколь-
ку, очевидно, эта функция непрерывна при x/v 0, то такое разложение дейст-
вительно справедливо для достаточно малых x/v. Подставляя выражения (10.55)
в систему (10.54) и приравнивая к нулю коэффициенты при одинаковых степе-
нях 1lv, получаем для atjh следующие уравнения:
—пИок+^аюд+ао, 1, k+i —°;
— (яХ-фгр.) aiok -ф(<’+ 1) [W.-.l 1, о, k +ai, 1,4+ 1 =0> z < т’>
-(.nK + mp)am01i + ami ь ft+1=0;
— —‘) ^~г‘Р1 aioil + (п ~гт —ф-ЧЧ — 1, 0, k 1~
+ ai, 1, A+l=°- i>m’
-(n+m)pan + mi о./г + Чг-Нч-ПО, fe = °;
fe-1 k — L 1
iauii=— 2 i(n—о 4ф) ai, i, k~i + (‘+о Iх 2 ai+1, i, k-1+
i—i I=i
k
+ 2(ra —/-1 A-l’ i<m’
l = i
k- 1
iamjh= - 2 Ип-/) И«И] I, A-l +
l = i
k 4-1 k
+(m+i)[i 2 am+1, i, k—i + 2 i)4i— i, i—i,k—i;
/=/-i i=i
k-1
>aiJ!i = •- 2 [(я+яг-i-Z) Х-Нр]ог, I,k~i +
i=i
k k—\
+ (‘ + 1) P 2 al + 1 l-i k-i + l 2 (n + m-l-i + l)X
i=i l=i
iym;
aijk~O, ее™ хотя бы один индекс меньше 0;
(10.57)
277
a.^0, k<j-,
a0MT=Q’ k>°’
i<m’
aitlk = 0, i < min(£, zn);
aikk = cn ai—k, о. о > * 1 > m;
amhh = Cn am — k, 0, 0 + Cm + A V^/nj. k, 0, 0 >
amkk = cm + k I1* am+k, 0, 0’ m<k.
(10.58)
m>k',
I
Подставляя в (10.56) вместо a(. , выражение (10.57) и прибавляя к
каждому уравнению предыдущее, получаем такую систему:
п^аоок + Наюь + со. 1 ,й+1 — °>
0. а + с/, 1,а+1=°;
- (п + т—1) + (z + 1) , 0, й + ч i, * + 1 = °;
-^ап + , о. k + («-г"О + т, о, k = °:
где
k k
Ci, 1,*+1 = — 2 Z) + + W 2ai+l, i,/e- 1 :-m'<
1=1 1 = 1
k k
ci. !,k+l=— >](« + /«—/ —I) A,a -I-(I H-1) p. 1 , ъ i>m.
1=1 i=i
(10.60)
Из (10.59)
(яА.)1' ch 1A + i (n^)1 1 7 /1
aioii=~—“aooft— z,------------:—:-------, t < m;
11 i^0 Пр'-7
nm nl "уч’ cj, l,k+\ nm~i~in! j!
10fe ц1(п~\-т—1)111 юк il — i)l y.‘~7 (10.61)
/, i,fe+illV 1 7 (M Vm-)—1)1
il (n+/n—l)l
i > m.
n±m n
Учитывая условие 2агЛ = 0> k >0, находим а^:
1 = 0 / = о
aooft =
cj, 1, A + 1 1 ' i'
n + m m— 1
i = tn 4-1 / » 0
С/, I,fe+1^ 1 ' п"г 7(л-1)1/1
i! (n+tn—i)l p,1-7
278
n + m k
гу с,, 1,А+1 Л (n + ш —/•—1)1 ~
i = m-f-l j = m 4 '
m 4- 1 , . . m 4- n , . i,
(nX)* 11 n! nm f,k
2d ixA ftf “ k\(n-\-m— ft)! p*
*=1 r fe=m+2 ' 1 .
(10.62)
Таким образом, из формул (10.37) (10.40) — (10.42) получено рекуррент-
ное соотношение через аг у ь—1, 11<‘< /1< /•
Далее заметим, что
т -|- 1;
Ро =
(niy
aioo — , ., Ро
р111
nl пт У
аюо=тг, : Г) i^0’ Z>« + 1;
г! (n-\ m —1)! p1
(nW п^т п\пт№
~ 2d Ц.* ft! + 2d ft! (п + т— k)\р*
*4-1 r fe=m+2 ' 1 г
1
как видно из (10.61).
Используя указанное рекуррентное соотношение, можно последовательно
находить aij^. Например, найдем aij^.
аои = О;
Лг/1 = 0, />1;
а.п = /гЦ._1100, i<m;
aiii = (t’ + 1) P^+i, 0, о- z>m’-
amll = (-nl+m^amOO=fl)M^-i. 0, o + (/n+1)Ham+ 1,0, Ol
m n + m m . .. ,4
" • V i V /, ' _L
laioo — H zaioo+ paioo n_ "Г
i~l i = m+l
i i м m-1
m(tn+1) у
pOjco 2 —a<00
П i = 0
ai01~ai00 [ • • • 1 —aion pl: Г1 + “T-
[ 2n
m (m+1)
aioi = aioo [ • • • 1— aioo p
а001 — Ро И 6
2гг
(10.63)
п-{-т
т\
Таким образом, найдены поправки первого порядка малости к формулам,
соответствующим случаю нулевого времени переключения.
ГЛАВА ОДИННАДЦАТАЯ
ИССЛЕДОВАНИЕ СИСТЕМ, СОСТОЯЩИХ
ИЗ БОЛЬШОГО ЧИСЛА ПАРАЛЛЕЛЬНЫХ АГРЕГАТОВ
11.1. ВОЗМОЖНЫЕ ПОСТАНОВКИ ЗАДАЧ
При проектировании сложных систем типа систем массового об-
служивания часто возникает проблема распределения потока требова-
ний между параллельными агрегатами (обслуживающими приборами).
Если поток, подлежащий обслуживанию, интенсивен, то, естественно,
для того чтобы система с ним справлялась, нужно поставить много
параллельных приборов. Существуют различного рода ограничения,
из-за которых для обслуживания поступающего требования иногда
можно использовать не все, а только часть приборов. Например, в те-
лефонных системах при поступлении вызова могут использоваться
только те линии, которые идут к району, в котором находится вызывае-
мый абонент. Однако системы, в которых число параллельных прибо-
ров, могущих быть использованными для обслуживания, достаточно
велико (50—100 и более), встречаются довольно часто; с ростом
автоматизации производства, созданием современных сложных авто-
матизированных систем подобная ситуация, по-видимому, будет ти-
пичной. В особенности это касается сложных систем обработки ин-
формации, например системы вычислительных центров страны. Дело
в том, что системы обслуживания типа магазинов, столовых, аэропор-
тов иД. п. обслуживают требования, находящиеся в определенном
объеме пространства; в то же время, вычислительные системы могут
обслуживать требования, возникающие где угодно (управление с по-
мощью вычислительной машины полетом космического объекта; ди-
станционное управление технологическим процессом). Обычно ин-
формация, необходимая для задания программы ЭВМ, представляет-
ся в виде, допускающем быструю передачу по каналам связи. Поэтому
систему вычислительных машин иногда можно рассматривать как много-
канальную систему массового обслуживания.
Основные задачи, связанные с расчетом многоканальных си-
стем, формулируются в терминах теории массового обслуживания.
Это — нахождение вероятности отказа в системах с отказами, распре-
деления длительности ожидания в системах с ожиданием, нахожде-
ние того и другого в системах с ограничениями на число требований
в очереди, длительность ожидания и пребывания требования в системе.
При этом важно уметь не только рассчитывать характеристики системы
при фиксированном числе приборов, но также находить асимптотику
280
при числе приборов, стремящемся к бесконечности. Это важно для
решения задач синтеза, когда оптимальная система находится как
решение определенной задачи нелинейного планирования.
В настоящей главе будут рассмотрены некоторые методы расчета
характеристик систем массового обслуживания с большим числом
параллельных приборов; мы укажем также метод расчета числа при-
боров с учетом возможного отказа системы.
Вместе с тем следует подчеркнуть, что приводимые здесь методы
нуждаются в дальнейшей разработке, поскольку к расчету формализо-
ванных сложных систем (типа агрегативных) они могут применяться
только в некоторых частных случаях и то не вполне обоснованно с ма-
тематической точки зрения. В тексте под словом «прибор» понимают-
ся вполне конкретные объекты, обычно рассматриваемые в теории
массового обслуживания. Вместе с тем имеются основания полагать,
что некоторые результаты подобного рода могут быть в дальнейшем
распространены на системы достаточно общего вида, в которых вместо
приборов системы массового обслуживания будут фигурировать агре-
гаты более сложной структуры.
11.2. СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ,
СОСТОЯЩИЕ ИЗ БЕСКОНЕЧНОГО МНОЖЕСТВА ПРИБОРОВ
Рассмотрим известную формулу Эрланга—Севастьянова:
(?-тп 2(н.п
k / 1=0 II
для вероятности занятости ровно k линий в телефонной системе с от-
казами; к обозначает интенсивность входящего потока требований
(предполагается, что этот поток простейший); т — средняя длитель-
ность обслуживания; п — число обслуживающих приборов.
Пусть теперь п устремлено к бесконечности. Тогда для распреде-
ления числа занятых линий получим выражение
= OsC&Coo. (11.2)
Рассмотрим распределение
Pk=Po + Pi + ---+Pk’ 0<£<оо, (11.3)
Qk ~ <7о + <7i + ••• + <?&, 0<&<оо, (И.4)
считая, что Pn-i-i =р„+2 = ••• =0.
Имеем оценку
Ph>Qh, # = 0,1,2,... (11.5)
Действительно, в бесконечнолинейной системе можно выделить п
линий, на которые требования поступают в первую очередь. Для этих
п линий они теряются, для системы же в целом остаются. Этим простым
281
приемом установлено взаимно однозначное соответствие между реали-
зациями процессов (t) и gOT (t) — числа занятых линий в момент t
для системы с п линиями и системы с бесконечным множеством линий;
при этом соответствии всегда gn (/) < (t), причем, очевидно, с по-
ложительной вероятностью при любом k > О возможен случай, когда
A = gn(0<U(/).
(11-6)
Из неравенства (11.6) и следует формула (11.5). Таким образом,
в частности,
Рп < 9?i + Яп +1 + • • •,
(11.7)
так что мы получаем одностороннюю оценку вероятности отказа «-ли-
нейной системы суммой вероятностей соответствующих состояний бес-
конечнолинейной системы.
Посмотрим, намного ли мы ошибемся, заменив левую часть формулы
(11.7) правой. Поскольку при любом п > О
e-u 2 4(%т)‘<1,
i=0 11
из формулы (11.1) непосредственно следует, что
9n = -Y(We“?-t<Pn;
объединив это неравенство с неравенством (11.7), придем к оценке
(И.8)
Очевидно, второе слагаемое в правой части (11.8) может быть оценено
следующим образом:
ОО |
У — Пт)*
НМ-1 fel 1т П (1т)» 1
1 п «+1[ п + 2 (га+2)(«+3) J
—- (It)11
п!
1т у. / 1т V 1т
п -| -1 \ л + 2 / л 4-1 — 1т
А=0
Отсюда
К— < -+1-~ . (11.10)
qn n+i—1т
Таким образом, при 1т < п будет рп ~ Цп, в противном случае qn
можно считать нижней оценкой рп.
282
Приведенные рассуждения наводят на мысль о полезности иссле-
дования бесконечнолинейных систем — систем, в которых невозможны
ни отказы, ни ожидание требований. Подобные системы исследовались
многими авторами. Мы не будем здесь формулировать конкретных ре-
зультатов, а лишь поясним один общий метод, уместный в данной си-
туации.
Пусть имеется система из бесконечного числа приборов; в нее по-
ступает поток требований. В моменты времени, образующие нестацио-
нарный пуассоновский поток однородных событий интенсивности Л (Z),
поступают группы требований случайного объема. Обозначим через
vt случайную величину, распределенную как число требований в груп-
пе, если эта последняя поступает в систему в момент t. Обозначим
%(/) = Р — k = \, 2,..., (И-И)
Длительность обслуживания одного требования предположим
случайной величиной с функцией распределения Н (х); длительности
обслуживания разных требований будем считать независимыми в сово-
купности.
Обозначим через | (t) число требований в системе в момент t.
Для нахождения распределения этой случайной величины применим
следующий прием, облегчающий выводы такого рода. В любом отрез-
ке (О, Т) нестационарный поток Пуассона является пределом при
N оо (в смысле сходимости всех конечномерных распределений)
потоков XN следующего вида. Отметим на интервале (О, Т) случайное
число точек ( < Л/') с помощью следующего механизма. Произведем N
независимых испытаний. При каждом испытании в интервал (О, Т)
может попасть лишь одна точка. С вероятностью X (/) dt/N она попа-
дает в интервал (t, t + dt) С (0. Т), а с вероятностью 1 — J X (if) Лона
yv о
не попадает в (0, Т). Таким образом, суммарное число точек, попавших
в интервал (0, Т), случайно, но не превышает N. Конечно, предпола-
т
гается, что J Л. (/) dt<Z оо. С i-й точкой сопоставим группу требований,
о
поступающих в z-й момент времени. Обозначим теперь через v, (/) число
требований в момент t из числа требований, поступивших в i-й момент
времени tt. Очевидно, (f) = 0 при t < /г; it) = v (/,) при t =
= ti + 0; затем эта функция убывает единичными скачками по мере
того, как требования обслуживаются, пока не обратится в нуль.
Имеем
1(0=2 МОг (11.12)
i= 1
причем слагаемые этой суммы независимы в совокупности и одинаково
распределены.
*> Более точно, левая часть является стохастическим пределом правой.
Чтобы избежать громоздких выкладок, которые могли бы лишь отвлечь внимание
читателя от главного, мы будем писать строгое равенство.
283
Обозначим через a (z, t) производящую функцию случайной вели-
чины % (t):
ОО
a(z, /)=Mz^() = Ц P{%(t) = k}zk, |z|< 1.
k=0
(11.13)
По свойству производящей функции суммы независимых случайных
величин имеем
a(z, t) = \aN(z, ty\\ (11.14)
где ах (s, t) — производящая функция случайной величины Vt (t). Вы-
числим эту последнюю.
Пусть i-я группа требований поступает в момент /г. Как было ука-
зано выше, V; (/) =0 при t<Z ti. Возьмем теперь t > /г. Вероятность
поступления k требований в момент /г- (при условии, что хотя бы одно
требование поступило) равна (/г). Число требований, оставшихся
не обслуженными к моменту/ — биномиально-распределенная случай-
ная величина, соответствующая k независимым испытаниям с вероят-
ностью успеха 1 — Hit — ti) в каждом из них. Остается вспомнить,
что плотность вероятности момента /г составляет X (/) внутри интерва-
ла (0, Т). Отсюда следует формула
*=/ о 'v
х№~Щ-u)[l— H(t — и)]1'du, (11.15)
При / = 0 формула примет несколько иной вид:
. р 0° К , .
Р (у. (/) =0} = 1 —— ^ %(«) du + S ~ Hk(t — и) du.
Отсюда следует, что
1 ? 1 °° с
aN (z, /) = 1----Л, (w) du -j-\ (u) (^ — u) du +
о a=i о
+ — V г/ Ciknk^(u)Hk-i (/ —н)[1— H(t—и)\! du.
N /=1 k=j о
Применив теперь формулу (11.14), найдем с использованием заме-
I а \к
нательного предела 1---------^е-я,
г t
a(z, /) = expj —
[ b
<30 oo
i — У. 2i 2 Ck nkx
i=0 k=i
X Hk~i (t — u) (1—H (/ — «))' du
(11.16)
284
Во многих частных случаях эта формула допускает дальнейшее упро-
щение; мы не будем на этом останавливаться.
Подобным же образом можно составить двумерную производящую
функцию
a(zb г2; tY, A2) = Mzf(MzI(4 (11.17)
трехмерную и т. д. Из производящих функций путем дифференцирова-
ния легко получить
(/) =Л (г, 01г=1> (11-18)
02
ЛП(Ш(4) =
= -^— a(zlf г2; /2)|Z1=Z,=] . (11.19)
02! дг2
Возникает вопрос: насколько полно эти характеристики описывают
случайный процесс % (t)? Б. В. Гнеденко [1] поставил общую проблему
исследования суммарного процесса нарастающих сумм независимых
случайных процессов и нашел, что в широких предпосылках суммар-
ный процесс будет приближаться к гауссовскому случайному процес-
су; данный факт использован Б. В. Гнеденко для обоснования методов
расчета мощности электросетей.
Для наших целей будет достаточна предельная теорема А. М. Ля-
пунова [2]. Предположим, что при некотором 6 > 0 случайные вели-
чины vt обладают абсолютным моментом порядка 2 + 6. Далее допу-
стим, что X (f) пропорциональна некоторому большому параметру N:
Х(О=Л+о(Г). (11.20)
Тогда, как нетрудно показать, из теоремы Ляпунова следует сходимость
последовательности случайных процессов
TW (0 =(^ (0-м {Lv (/)})//О{Ы0} (11-21)
к некоторому гауссовскому процессу ц (/). Но последний, как хорошо
известно [3], полностью характеризуется математическим ожиданием
и корреляционной функцией. Это решает нашу задачу.
Произведем некоторое обобщение, простое с математической точ-
ки зрения, но приводящее к полезным практическим результатам.
Пусть имеется бесконечное множество агрегатов, находящихся
(до поступления сигналов извне) в некотором состоянии, скажем в со-
стоянии 0. Сигналы образуют нестационарный поток без последействия
с параметром X (/). Каждое требование входящего потока посылает-
ся на некоторый, не использовавшийся ранее, агрегат; оно выводит
его из нулевого состояния на конечное случайное время. В любой мо-
мент времени может поступить группа требований случайного объема.
Выделим некоторые подмножества AL, А2, ..., Ап состояний агре-
гата, не включающие состояние 0, и обозначим через h (f), 1< п,
285
число агрегатов, находящихся в момент t в любом состоянии из под-
множества состояний Ai. Будем иметь л-мерный случайный процесс
Ш=(Ы0, ^(0,, МО),
каждая компонента которого может принимать значения 0, 1, 2, ...
Предположим, что в момент и произошло событие входящего потока,
а следовательно, на некоторые агрегаты посланы сигналы. Обозначим
через аи (z1T z2, ..., zn; t) многомерную производящую функцию слу-
чайной величины (vj, (f), v2 (t), ..., vn (t)), где v, (/), 1 < i < n, —
число агрегатов, находящихся в момент t в состояниях множества
Аг, из числа агрегатов, на которые в момент и послан сигнал:
au(z., z2,... , zn; 0 = z? (/) ...z*nnW !u\. (11.22)
Тогда, буквально повторив все рассуждения использованные при вы-
воде формулы (11.16), мы получим для производящей функции
a(zlt z2,, zn- 0=M{zV(Z'42(o ...zSn(')) (11.23)
следующую формулу:
{t )
—[1— au(zlt ... , zn; /)] du . (11.24)
b J
Подобным же образом можно выписать общее выражение для
функци
а^, z2,..., zn; wlt w2, ..., wtl; tlt t2) =
('•) ...a, (G) „Ь (M /119^
— /73(^1 Zv “• ^2 I [11.ZD)
через соответствующую функцию au (z1; z2, .... zn; wlr w2, .... wn
tlt t2). Эта формула будет иметь в точности тот же вид, что и (11.24)-
Отсюда легко найти все корреляционные характеристики многомер'
ного случайного процесса.
Пусть теперь задано некоторое ограниченное число агрегатов,
находящихся в состояниях из подмножеств Аъ А2, , Ап. Именно,
задана некоторая функция L* (лу, х2, ..., хп) и соответствующая по-
верхность L* (лу, ..., х„) = 0 /2-мерного пространства со следующей
интерпретацией. Если L* (£1Т (/), £2 (/), ..., ёга (7))'О, система счи-
тается работоспособной, в противном случае наступает отказ. (На-
пример, L* может иметь вид (t) + s2 g2(0 + ... +. sn t71 (t) = s0,
где Si — некоторые постоянные.)
Можно поставить три задачи:
1. Найти математическое ожидание времени, на протяжении кото-
рого система находится в состоянии отказа.
2. Найти среднее число отказов в заданном интервале времени.
3. Найти вероятность того, что в течение заданного времени
система будет находиться в исправном состоянии.
(Термин «отказ», конечно, в каждом конкретном случае может
интерпретироваться по-своему.)
286
Будем считать, что А, (/) -> оо и выполнены условия сходимости
к гауссовскому процессу. Таким образом, путем центрирования и нор-
мирования можно привести процесс g (I) к некоторому другому про-
цессу
т](/) = (П1 (О, W), . Лп(0)- (11.26)
Предположим, что соответствующий предельный переход совершен,
так что г] (0 является n-мерным гауссовским процессом. В свою оче-
редь, функция L* преобразуется в некоторую функцию L, так что кри-
терием отказа системы будет неравенство
Ь(тц(0. Ъ(0, %(0)>0. (11.27)
Рассмотрим здесь решение лишь первой из этих задач для гауссов-
ского процесса, оставляя в стороне вопрос о сходимости распределений
функционалов от допредельных процессов к распределению соответст-
вующего функционала от предельного процесса. Пусть pt (хь х2, ...,
хп)— многомерная плотность случайного процессат] (/). [Это многомер-
ное нормальное распределение, параметры которого вполне опреде-
ляются совокупностью первых и вторых частных производных функций
a (zlt z2, ..., zn; t) в точке zr = z2 = ... = zn = 1, а также коэффи-
циентами преобразования, переводщяего £ (t) вт] (£).] Тогда математиче-
ское ожидание М (/) суммы длин интервалов, на протяжении которых
система находится в состоянии отказа в течение интервала (О, Г),
имеет следующее выражение:
г
М(Т)=$ di § ... ^/(Xj, х2, ... , xn) dx± dx2... dxn. (11.28)
О b(x,,x2...........JCn)>0
11.3. ПРЕДЕЛЬНОЕ ПОВЕДЕНИЕ СИСТЕМЫ
МАССОВОГО ОБСЛУЖИВАНИЯ С БЕСКОНЕЧНО ВОЗРАСТАЮЩИМ
ЧИСЛОМ ПРИБОРОВ И ЗАГРУЗКОЙ, СТРЕМЯЩЕЙСЯ К КРИТИЧЕСКОЙ
Напомним, что загрузка р системы массового обслуживания определяется
формулой р = Хт/n, где X — интенсивность входящего потока; т — математи-
ческое ожидание длительности обслуживания; п — число приборов. Рассмотрим
следующую постановку задачи. Пусть п -> ос, р -> 1; ищутся условия, при ко-
торых средняя длительность ожидания остается ограниченной. Здесь будет рас-
смотрена простейшая система массового обслуживания, распределения вероят-
ностей состояний которой имеют простое аналитическое выражение. Из этого
выражения непосредственно и будет получена предельная теорема. Отметим, что
выводы, следующие из этой теоремы, по-видимому, будут иметь силу и в более
общих ситуациях.
Теорема. Пусть имеется n-линейпая система массового обслуживания с ожи-
данием; входящий поток — простейший с параметром X; длительность обслужи-
вания распределена по показательному закону с параметром 1. Тогда, если
п -> ? _ и
Х = /г—с, (11.29)
где с > 0 — некоторое фиксированное число, то средняя длительность ожида-
ния требованием начала обслуживания в стационарном режиме сходится к Чс
При П > оо.
287
Доказательство. По формуле А. Н. Колмогорова (см. [4]) вероят-
ность нахождения в системе равна k требований, имеет следующий вид:
1 ( \k
Pk=U ------ Ро. 0 < k < п’
Й! \ fl J
Pk = ^/nii)!‘-n рп, k>n.
Постоянная р0 находится из соотношения
1 / X \ 1 / X Vz 1
kl \ Р / + '1! \ К / V
(11.30)
(11.31)
(11,32)
Оценим правую часть этой формулы при п —> оо, ц = 1 и X, удовлетворя-
ющем равенству (11.29). Пусть у — случайная величина, распределенная по
закону Пуассона с параметром, равным X. Тогда
" 1
2ir^ = e’‘p{v <п}- (н.зз)
й = 0 й'
Вследствие формулы (11.29)
Му = /г — с. (11.34)
Известно, что дисперсия пуассоновской случайной величины равна ее матема-
тическому ожиданию, поэтому среднеквадратическое отклонение
ov= ]/Му ~я|/2
(11.35)
Известно далее, что нормированное пуассоновское распределение при парамет'
ре, стремящемся к бесконечности, сходится к нормальному распределению. Из
этого следует, что
Р (у < п]
(11.36)
Таким образом,
~-5—ех — е'
k\ 2 2
(11.37)
Последнее слагаемое первой части формулы (11.32) оценим с помощью фор-
мулы Стирлинга. Имеем
№ X е,г п—с
-----------------— (п — с\п---------------
п\ п—% Т/2лм пп п
е"
п п-'с
----г с
2л
(11.38)
Ро ’
k= о
При п -> со по сравнению с этим слагаемым можно пренебречь первым слагае-
мым в правой части (11.32), задаваемым формулой (11.37). Кстати, отсюда мож-
но непосредственно усмотреть, что вероятность наличия очереди в системе при
п -> со с точностью до величины более высокого порядка малости составляет
Рп+ 1 + Рп+2^ •
(11.39)
Таким образом, полная занятость системы — явление типичное. Итак,
,г п-с
— е с
2л
(11 .40)
288
Тогда по формуле (11.30) при k = п находим, что
и отсюда, в силу (11.38),
Pk~~ Pft
п
где
р = 1 —с/п.
(П.41)
(11:42)
(Н.43)
При условии, что поступившее в систему требование застанет в системе k
требований, где k > п, ему придется ждать в среднем (k — п + 1)/п единиц вре-
мени (поскольку интенсивность обслуживания составляет п). Таким образом,
среднее время ожидания равно
k = n k =п
с 1 с re2 1
я2 (1 — р)2 я2 с2 с
(11.44)
Теорема доказана.
Замечание. В условиях доказанной теоремы предельное распределение
длительности ожидания w требования при я -> оя существует и имеет вид
Р < х} = 1 —е
х
0.
(11.45)
Это утверждение доказывается следующим образом. При любых X, р и п плотность
р(х) случайной величины w записывается как
р(х) = Р З(х) + Р {w > 0} ое~ах,
(11.46)
где Q — некоторая константа. Записанная формула выражает тот факт, что ус-
ловное распределение времени ожидания при условии, что это время положитель-
но, является показательным.
Из формулы (11.46) следует, что
М ш = Р {w > 0} о *.
(Н-47)
Так как в условиях нашей теоремы и, как мы видели, также Р{ш >
> 0} 1 [см. формулу (11.39)1, то ст -> с. В силу непрерывности показательной
функции их этого следует, что предельное распределение случайной величины
ш существует и описывается формулой (11.45); это и требовалось доказать.
Мы видим, что система, состоящая из большого числа параллельных
приборов, соединяет в себе два, вообще говоря, противоречивых качества: почти
полную загрузку обслуживающих приборов и достаточно малое среднее время
ожидания. Если фиксировать число приборов в системе, то эти требования никак
нельзя совместить: у систем с малой загрузкой прибор почти все время бездей-
ствует, у систем с большой загрузкой длительность ожидания велика: ее мате-
матическое ожидание обратно пропорционально «недогрузке» системы, т. е. ве-
личине 1 — р.
Ю Зак. 792 289
11.4. НАКАПЛИВАЮЩАЯ МОДЕЛЬ ОБСЛУЖИВАНИЯ
В СИСТЕМАХ С БОЛЬШИМ ЧИСЛОМ ПАРАЛЛЕЛЬНЫХ ПРИБОРОВ
Как мы видели в предыдущем параграфе, при интенсивном вхо-
дящем потоке за счет увеличения числа параллельно функционирую-
щих приборов можно добиться того, чтобы средняя длительность
ожидания была достаточно малой и при этом загрузка приборов была
достаточно близка к критическому значению. Этот факт является
весьма общим, он имеет место и для значительно более сложных систем,
чем рассмотренная в § 11.3. Если параметры системы рассчитаны долж-
ным образом и на вход системы поступает эргодический поток требо-
ваний, то действие системы можно представить себе следующим обра-
зом.
Обозначим через X (t) суммарную длительность обслуживания
требований, поступающих в систему в интервале (0, t). (Будем считать
для определенности, что в момент t = 0 загрузка системы составляет
Хо единиц.) X (t) будет ступенчатой функцией, возрастающей в моменты
поступления требований на величины, равные необходимой длитель-
ности их обслуживания. Обозначим также через Y (t) суммарное время,
потраченное приборами на обслуживание требований в интервале
(О, t). Y (t) будет ломаной линией; если в момент t в системе имеется
k требований, то
d [k при
(11.48)
dt (и при k>n.
Нагрузка £ (t) системы в момент t определяется так:
ё(0=Х(0-У(0- (Н.49)
При предположениях типа эргодичности относительно X (t) при соот-
ветствующем подборе постоянной % > 0 будет иметь место равенство
X (f) — M = o(kt)t t^oo. (11.50)
Следовательно, после линейного преобразования координат (сжа-
тия по обеим осям координат) X (/) будет приближенно описываться
линейной функцией времени
X(0=W- (11.51)
Если загрузка близка к критической, то можно показать (в пре-
дыдущем параграфе это показано в простейшем случае), что доля вре-
мени, на протяжении которого заняты все приборы, близка к 1. На
этих участках Y — Y (ZJ = п (t2 — Если изменить масштаб
времени таким сбразсм, чтобы функция X (/) незначительно отлича-
лась от линейной, то угловой коэффициент прямой Y (Z) (на участках,
где заняты все приборы) также примет некоторое значение р > 0:
У^-П^р^-^). (П-52)
В пределе при п -> оо имеет место следующий эффект: g (/) пред-
ставляет собой кусочно-линейный процесс, изменяющийся по закону
(11.53)
ООП
в интервалах, где I (t) > 0, и остающийся на нулевом уровне после
достижения этого уровня. Данная ситуация вполне аналогична про-
цессу наполнения сосуда водой и его опорожнения; в единицу времени
поступает А единиц воды и вытекает р единиц. Это оправдывает назва-
ние настоящего параграфа. Легко видеть, что очередь исчерпывается
через время х0/(р— А) после начала работы системы, если только
р, > А. (Условие ц > А, очевидно, эквивалентно условию р < 1,
где р — загрузка системы.)
Ввиду простоты накапливающая модель, казалось бы, могла при-
нести мало пользы, если бы не одно обстоятельство. Дело в том, что
при проектировании сложных систем приходится учитывать возмож-
ность отказа системы. В интервалы отказов требования по-прежнему
продолжают поступать, однако обслуживания нет. Возможен и такой
случай, когда темп обслуживания снижается (например, при выходе из
строя части обслуживающих приборов). Мы рассмотрим одну полезную
модель, которую во многих случаях можно положить в основу описа-
ния процесса обслуживания при наличии отказов; очевидно, при рас-
смотрении конкретных примеров эту модель необходимо модернизи-
ровать. Тем не менее излагаемый нами метод может быть при этом поле-
зен.
Система может находиться в исправном состоянии (0) и в k раз-
личных состояниях отказа (1, 2, ..., k). Поток требований 'во всех слу-
чаях описывается линейной функцией X (t) = М, где А > 0 — по-
стоянная величина; в состоянии 0 обслуживание происходит с интен-
сивностью ц0, в состояниях 1, 2, ..., k интенсивности обслуживания
составляют соответственно pn р2, ..., рй. Длительность пребывания
системы в исправном состоянии — случайная величина £0 с функцией
распределения Fo (х); длительность пребывания в состоянии отказа
z-го типа (1 i < k) — случайная величина £г- с функцией распре-
деления Ft (х). Будем предполагать, что |г, 0 < i < k, обладают
конечными математическими ожиданиями. По истечении времени £0
система может перейти в состояние i с вероятностью лг, 1 < й;
JTj + л2 4- ... + = 1. После устранения отказа система с вероят-
ностью 1 возвращается в исходное нулевое состояние.
Если даже ц0 > 1, подобная система может не обладать устано-
вившимся режимом: отказы могут быть настолько частыми, что за-
грузка будет возрастать до бесконечности. Достаточным условием эрго-
дичности является неравенство
И = 2 И; Р; > ^. (11.54)
где pt — стационарная вероятность нахождения системы в состоянии
i (0 < z < k)*>.
*> Пусть Tj—средняя длительность пребывания системы в состоянии i.
Тогда
ЗТI ТI
Pi=---------k-----
то + У, Д' Т;
/=1
1 < i < k; ри =-----------
то+ Д Н
/=1
10*
291
Обозначим через § (/) загрузку системы в момент t\ £ (/) — это
величина работы, которую должна выполнить система, чтобы закон-
чить обслуживание требований, поступивших до момента t. Легко
видеть, что £ (/) не является марковским процессом. Введем переменную
v (/) — состояние, в котором система находится в момент t, и еще
г) (t) — время от момента t до следующего изменения состояния про-
цесса v (t). Процесс С (0 = (у (0> £ (0> Л (0) Уже будет марковским;
это кусочно-линейный марковский процесс.
Наибольший интерес представляет стационарное распределение
F (х) случайного процесса £ (t) в предположении, что условие (11.54)
выполнено. Для его нахождения мы используем методы теории инте-
гральных уравнений типа свертки на полуоси (см. М. Г. Крейн [5]).
Рассмотрим возрастающую последовательность моментов времени
(/п), определяемую следующим свойством. В моменты t2n система вос-
станавливается; в моменты tin + 1 она отказывает. Пусть Фо (х)—
стационарное распределение £ (t) в моменты вида /2п, ЙД (х) — то же
для моментов вида tin+ ь Предположим (это имеет физический смысл),
что р, < Z для любого i = 1, 2, ..., k, а р0 > X; условие (11.54) будем
считать выполненным. Тогда справедливы соотношения
Ф0 = Ф1*О, (11.55)
Ф1 = (Ф0*Д)+, (11.56)
где * — символ операции свертки распределений,
6(х)=2лгЛк~’ ' (11.57)
i=l \л Рг J
Д(х) = 1-К0(-^-) , (11.58)
\л—ро/
(. .|..)+ — символ операции усечения, имеющий следующий смысл.
Если К — распределение некоторой случайной величины %, то К+ —
распределение случайной величины шах {0, х). Подставив (11.55) в (11.56), получим (11.59)
Ф1=(Ф1ФС*Н)+
или, что то же, Ф1=(Ф1*К)+, (11.60)
где К = G*H. (И.61)
Уравнение вида (11.60) в литературе решено методом факториза-
ции (см. Линдли [6], Смит [7]). Пусть бД (х) — функция распределе-
ния, удовлетворяющая уравнению (11.60). Тогда стационарное рас-
пределение F (х) случайного процесса £ (I) можно найти из следующих
соображений.
292
Пусть t — некоторый момент времени, относящийся к стационар-
ному режиму системы. Можно записать
k
fw = p{?(0<4= 2piP{l(O<^(O=!'}- (Н.62)
г‘ —О
Примем гипотезу, что v (t) = i. Тогда время, прошедшее с момента
вхождения системы в это состояние до момента t, обладает плотностью
вероятности вида
Qt (х)= —[1-^(х)],
Тг
0 < i < k.
Следовательно,
оо
Р {с (/) < x/v (/) = i} = — [1 —Ft (u)] Li (х/и) du,
Тг о
(11.63)
(11.64)
где Lt (х!и) — условная вероятность событий [£(/)< х) при условии,
что вхождение в состояние I, в котором система находится в момент
t, произошло за и единиц времени до этого момента. Для полного ре-
шения задачи достаточно заметить, что
Lt(xlu) = Ф0(х + (рг — Х)п), 1<1^/г,
Ло (х/н) =ФХ (х + (ц0—X) и).
(11.65)
(11.66)
Подставив последние два соотношения в формулу (11.65), интересующее
нас распределение F (х) найдем по формуле (11.62).
Практический вывод, который следует из произведенного рассмо-
трения — необходимость давать «запас» пропускной способности боль-
ших систем в расчете на возможные отказы. Формулы, подобные
только что приведенным, позволяют оценить необходимый «запас»
такого рода.
ГЛАВА ДВЕНАДЦАТАЯ
АНАЛИЗ УСТАНОВИВШИХСЯ И НЕУСТАНОВИВШИХСЯ
РЕЖИМОВ РАБОТЫ АГРЕГАТОВ
12.1. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
В настоящей главе будут рассматриваться и решаться некоторые
задачи, возникающие при анализе агрегативных систем. Объектом
рассмотрения всюду (если не сказано противное) будет автономный
агрегат, вид которого (кусочно-линейный, кусочно-непрерывный и т. д.)
будет всякий раз специально оговариваться.
Рассматриваемые в главе задачи относятся к двум типам. Решение
задач первого типа характеризует в какой-то степени «неустановив-
шийся» режим работы систем. Именно, в первом случае ищется функция
распределения случайного времени первого выхода траектории про-
цесса из фиксированной области фазового пространства. Решение
таких задач имеет первостепенное значение прежде всего для теории
надежности, когда искомая функция распределения есть не что иное,
как «ненадежность» системы, если указанная область является мно-
жеством рабочих состояний. Если же эта область — множество отказо-
вых (или «нежелательных») состояний, то задача сводится к оценке
в статистическом смысле времени достижения системой «приемлемого»
режима. Отметим аналогию между рассматриваемой задачей и практи-
ческой устойчивостью (см. гл. 9).
Второй тип задач относится к «установившемуся» режиму системы,
когда интересно знать финальное распределение состояний процесса.
Кроме того, в задачах этого же типа обычно выясняются условия су-
ществования установившихся режимов. Постановка этих задач являет-
ся традиционной для теории случайных процессов и имеет практиче-
ское значение для тех случаев, когда исследуемая система работает
в течение достаточно длительного времени и интересуются некоторы-
ми средними показателями ее работы за большой интервал времени.
В гл. 15 будет установлена аналогия между устойчивостью по Лагран-
жу и рассматриваемой задачей. Аналогия эта (как и для случая прак-
тической устойчивости) будет подкреплена в гл. 15 использованием
методов, «типичных» для теории устойчивости, применительно к ука-
занным задачам.
В настоящей главе для решения этих задач будут использованы
методы, более традиционные для теории случайных процессов.
294
12.2. НАХОЖДЕНИЕ СЛУЧАЙНОГО ВРЕМЕНИ ПРЕБЫВАНИЯ
ТРАЕКТОРИИ АГРЕГАТА В ФИКСИРОВАННОЙ ОБЛАСТИ
ФАЗОВОГО ПРОСТРАНСТВА
Рассмотрим кусочно-непрерывный агрегат (см. определение, дан-
ное в § 6.2), у которого внутреннее состояние z имеет вид z = (v, zv),
где v — дискретная компонента (основное состояние), zv— |vj-
мерный вектор дополнительных координат, изменяющийся в замкнутом
множестве | v | -мерного пространства. Внутри областей Tv траек-
тории zv (t) являются реализациями | v | -мерного однородного диффу-
зионного процесса. Пусть т — некоторый (быть может, случайный)
момент времени, такой, что zv (т) g где — граница Fv. Тогда
считаем, что состояние г (т + 0) = (у', zv-) определяется в соответст-
вии с переходной функцией
Р j(v,z*);(v',B'| — Р{2(т0) — (v', zv'), zv' £ В' с Г¥-\Ь'/г(т)^
= (v,?v),
2,^ i(v,^);(v',rv-\Yv')} = h
V cJ
Предположим также, что в течение любого конечного интервала
времени с вероятностью 1 происходит конечное число «скачков» тра-
екторий, вызываемых попаданием дополнительных координат на гра-
ницы областей IV
Кроме того, предположим, что траектория агрегата не может
«уйти в бесконечность» за конечное время (регулярность процесса
z (/), см. также гл. 15).
Зафиксируем в фазовом пространстве системы множество Q. Пред-
положим, что Q = {2 = (v, zv): zv g rv, c J), т. e. множест-
во Q полностью определено заданием некоторого подмножества J {
множества J основных состояний агрегата. Отметим, что в практических
задачах интересующие исследователя области Q либо имеют указанный
вид, либо легко могут быть приведены к такому виду*’.
Пусть 2° g IV Тогда можно в принципе найти случайный момент
I (z“) первого выхода на границу (в частности, может оказаться, что
с положительной вероятностью £ (2V°) = 00). Таким образом,
I (2°) = inf {t: zv (t) c yv/zv (0) = z°)
*> Например, можно определить новый агрегат, у которого основные со-
стояния и дополнительные координаты те же, что и у исходного агрегата, и вво-
дится еще одно фиктивное поглощающее состояние 0, а множества измене-
ния дополнительных координат имеют вид; ~QV. где Qv~[zv: (v, zv)gQj.
Если вектор zv(Z) попадает в точку границы Г^, не лежащую на границе
множества Tv, то новый агрегат переходит в состояние 0. Если же эта точка
(обозначим ее Zv) является точкой границы множества Гу, то с вероятностью
Yp[(v, z *); (v', Гу,—Qv,)] агрегат переходит в состояние 0, а с до-
v'CJ
полнительной вероятностью развивается по тем же законам, что и исходный
агрегат
295
Значение дополнительной координаты zv в момент выхода на гра-
ницу, т. е. величину zv [g (zv0)], будем обозначать ZvP(zv°). подчеркнув
тем самым ее зависимость от исходного значения дополнительных коор-
динат zv°. Очевидно, z;p(?O) g Vv.
Обозначим через Р {(v, zv); Q, t] — вероятность того, что траекто-
рия агрегата выйдет из области Q за время /, если z(0) = (v, zv).
Предположим сначала, что дополнительные координаты изменяют-
ся во времени по детерминированному закону и являются непрерыв-
ными функциями времени в каждом множестве 1\. Тогда Ej (zv°) и
Zv₽(zv°) также являются детерминированными функциями от zv°.
В силу своего определения функция Р {(v, zv); Q, t] обладает следую-
щими свойствами:
Р {(v, z°); Q, t\ = 0 при/<НА (12.1)
р {(v,z“);Q, t} =P {(v,zv(t, z°));Q, t — t},
t<£(z°)</. (12.2)
Здесь через zv (r, zv°) обозначено значение дополнительных координат
в момент т при условии, что zv (0) = zv°.
Из формулы полной вероятности^следует, что
Р {(v, z°); Q, t\ = 3 P[(v,2pp«': «!>)} +
+ 2 J P {(v,ZvP (z“)); (v', dzV’)} P {(v', zv<); Q, t—^(г°)}.
v'e^i rv.
z°crv, (12.3)
Уравнения (12.3) справедливы при
В силу свойства (12.1)
P{(v,z°); Q,Z} = 0, /<£(г°).
Если ввести функцию
[1, х>0,
Н (О, х<0,
то соотношения (12.3) и (12.1) можно объединить в одно:
P{(v, S Р {(v, г? (г?)); (v', Г» 1 +
J
+ S f P{(v, Zvp(z?)); (v',dzv0)x
v'e^i rv,
X P ((V', zv0; Q, t-l (zS) 1), z° 6 rv, V 6 J}.
(12.4)
296
Уравнения (12.4) являются, по существу, специальной формой
формулы полной вероятности и выражают тот факт, что траектория
агрегата может покинуть область Q за время t, либо переходя в «не-
дозволенное» состояние сразу после первого скачка (если время g (2V°)
достижения границы yv меньше /), либо переходя в этот момент водно
из допустимых состояний, а оттуда — за время t — g (zv°) — в «не-
дозволенное».
Вернемся к случаю, когда функции zv (t) являются реализациями
диффузионного процесса. Очевидно, в этом случае уравнения (12.4)
сохраняются, если их усреднить по всевозможным значениям £ (zv°)
и ZvP (zv°). Если обозначить через Х(Л) индикатор случайного собы-
тия*’ А, то после усреднения равенства (12.4) получим
P{(v,z2);Q,/) = M{%[g(z°)<z] [ 3 P[(v,4P(z°); (v',I»} +
+ S f P {(v, z7(z°)); (y',dzV’)\ P ((v',zvJ; Q, t— g(z“)|]},
z°erv, тел. (12.5)
Как и уравнение (12.4), это уравнение является частным случаем
формулы полной вероятности и интерпретируется подобно (12.4).
Для использования уравнений (12.4) и (12.5) необходимо, чтобы
величины g (zv°) и ZvP(zv°) могли эффективно вычисляться для задан-
ной системы. Однако эта задача связана с определенными трудностями
для произвольного кусочно-непрерывного агрегата. Все дальнейшие
результаты будут относиться к агрегатам, у которых дополнительные
координаты zv в области Гг изменяются по закону
где av — постоянный вектор размерности | v|. Очевидно, в этом слу-
чае
гД = z° — ccvg(z°), a zv (/, z°) = г°— avt.
Свойство (12.2) приобретает вид
Р {(v, z°); Q, t} — Р {(v, z° — av т); Q, t—xj, т< g(z“) <Л
Величины | (г°) определяются особенно просто, когда Tv—выпук-
лый многогранник, Tv = [zv: yVk zv-pbvk^ 0, k = 1,2,...}, где yVk—
вектор размерности | v |, yvk zv—скалярное произведение двух век-
торов, a bVk—скаляр. Тогда
g(z°)= min/ь,
где
th= (yvk z^ + M/Yvaccv.
*’ Индикатором случайного события называется случайная величина, при-
нимающая значение 1, если это событие происходит, и 0 —-в противном случае.
297
Уравнения U2.4) в рассматриваемом частном случае примут
вид
2 Р {(v, 4-ca(z°)); (v',rv-)| +
|v'G./\J 1
4- 2 f P ((v, 4 — av£(zv)); (v',dz'V')\x
v'EJi rV'
X H(v',M;Q,/-£(2X Zv6rv, vUi- (12.6)
Уравнениям (12.6) можно придать более простой вид, позволяю-
щий эффективно воспользоваться преобразованием Лапласа—Стиль-
тьеса, если представить агрегат в каноническом виде (см. § 6.5), когда
все компоненты вектора zv, кроме одной, сохраняют в состоянии v
постоянные значения, а оставшаяся компонента убывает с единичной
скоростью до нулевого значения, когда и совершается скачок. В это,м
случае будем обозначать через zv неизменные компоненты вектора
дополнительных координат (и пусть Г\, — множество их значений),
а через х — переменную компоненту вектора дополнительных коор-
динат,
^42=—1, х>0. (12.7)
dt
Тогда Н (х°, 2°) = х°, х° > 0, z°6Tv. Учитывая (12.7), урав-
нения для агрегата, представленного в каноническом виде, непо-
средственно получаются из (12.6):
P{(v,x°,2°);Q,H = W-x°)( 2 P{(v,0,2°); (v', (0, оо), !>)) +
4- з .( f P{(v, 0,2°); (v’,dx',dzv)\ x
v'EJi v-Crv- x‘ =0
XP {(v',x', 2V-); Q, t — x°}, х0> 0,2° 6 rv, v £ Jx. (12.8)
В силу свойства (12.2) для определения вероятности p{(v, х°,
2°)‘> Q, /), t> х°, достаточно знать Р {(v, 0, 2°); Q,/} ,t > 0, поскольку
p((v,x°, 2°.);Q,H =Р {(v,0,2°);Q,/— х0}.
Поэтому, полагая в (12.8) х°=0 и используя свойство (12.2), по-
лучаем
Р ((v, 0. z°); Q, = 2 P{G,0,z°);(v',(0,oo),rvJ) +
4- 2 J (’ P !(у 0, 2°); (v', dx’, c?2V')) x
2v'6rv' x'=0
X P((v',0,zv4;Q, t—x'}, 2° 6 rv, veJj. (12.9)
298
Обозначим
Р* {(v, 0, z"); Q, s} - f° e-st dt P {(v, 0, z°'l; Q, /!,
о
P* ((v, 0, z°); (v',s, rfzv-)} - f e p {(v, 0, z°); (v\ dx', dzv>)\,
о
Считая обе части уравнений (12.9) функциями временного пара-
метра t и преобразуя их по Лапласу — Стильтьесу с аргументом s,
получаем
Р* {(v,0,z°);Q,s} = 3 r P{(v, 0,Zv);(v',(0, oo),rv')} +
+ 3 ,f p* {(v, 0,Zv);(v',s, dzV’)] x
v'CJi £v'^rv'
xP*{(v',0,zv,);Q,s}, zoerv. Vgj,. (12.10)
Обозначим через
Th(v,zv)--=\l!{dtP ((v,O,zv);Q,/J =
6
= (-l)*± p*{(v, 0, zv); Q, s j| s=o»
ds
x,_ [(v, z°); (v', dzv-)] — ) xk P {(v, 0, z°); (v.dx. dzV')} =
b
= ( — i)A — p* {(v, o, Z°); (v'; S, rfzvO} I s=u.
^k,
Тогда, последовательно дифференцируя (12.10) no s и полагая s = 0,
получаем для zv° £ rv, v £ уравнения относительно моментов, кото-
рые могут затем решаться соответствующими методами при различных
предположениях о характере функционирования агрегата (стацио-
нарность, высокая надежность и т. д.):
A(v,^)= S A [(v,z?); (v', Tv')] +
v'e/i
+ 2 J /5{(v,0,zS);(v',(0,oo),dZv0^i(v\Zv^> (12.11)
v'tJ, 2v,erV'
7\(v;Zv)= x2 [(v,z°);(v', Fv-)]
V.'fcJi
+ J Xi[(v, Zv!;(v',cfzv-)] +
v't/i 2V'eiv
+ 3 p {(v> °,г°); «(0, °°). rf-v-)J t.^v',zV'),
V (. .«/ i 2 у ' 11 у '
299
При выводе этих уравнений предполагалось, естественно, сущест-
вование соответствующих моментов и, как следствие этого, то, что
lim Р {(v, 0, zv°); Q, /} = 1 для всех zv° g Г\>, v g Jt. Заметим, что во
/-<-00
многих практических случаях для решения уравнений (12.9), (12.10)
или (12.11) могут быть предложены достаточно простые вычислитель-
ные алгоритмы, учитывающие частные особенности реальных схем,
структуру их переходов из состояния в состояние.
Пример 1. Рассмотрим полумарковский процесс, который определяется
следующим образом (см. работу В. С. Королюка [16]). Процесс имеет конечное
или счетное множество состояний J. В каждом состоянии v g J процесс пребы-
вает случайное время, имеющее функцию распределения Pv(t); qvv, (т) — усло-
вная вероятность того, что совершится переход v -> v', если в состоянии v про-
цесс находился время т. Построим агрегат в каноническом виде с состоянием
2 = (v, х, zj, где первая компонента v описывает исходный полумарковский
процесс, вторая компонента х — время, оставшееся до перехода в следующее
состояние, а третья компонента zv указывает суммарное время, проводимое про-
цессом в состоянии v. Тогда вероятность перехода P((v, 0, zj; (v', dx', dzy,^
имеет вид
р {(v- °’ zv); (v'’ dx'< dzv')} = dPV (*') <lvv’ (zv) dzv. H (ZV —«')
Следовательно, P* {(v, 0, zv); (v', s, dzv,)J = e dPv, (zv,) qvv, (zv).
Подставляя выписанные выражения в (12.10), получаем
Р* {(v, 0, z°); Q, s) = S +
V' 6
+ S fe-S^'dPv,(zv,)i?vv,(z°)P*{(v', 0, zv,); ]Q, s], z°>0, vg/p
v' GA 0
(12.12)
/
Обозначим теперь Pvv, (i) = (qvv, (t)dPv(ty, Pvv, = limPvv, (/). Най-
o l-’00
дем вероятность выхода агрегата (равную вероятности выхода исходного полу-
марковского процесса) из области Q за время t, начиная с момента попадания его
в состояние V, т. е. величину
t
Pv(O = fP{(v, х, х); Q, t} dPv(x) =
о
t
= fP {(v, 0, x); Q, t—x}dPv(x). (12.13)
b
Применив к равенству (12.13) преобразование Лапласа - Стильтьеса, получим
<(s) = f е-“Р* {(V, 0, х); Q, s}dPv(x). (12.14)
О
Учитывая (12.14), уравнения (12.12) можно записать в виде
Р* {(v, 0, z°) ; Q, sj = 3 ?vv'(z°)+ 3 <7vv,(z°)p;.(s). (12.15)
v' e -/\^i v' e Ji
300
Умножая правую и левую части (12-15) на е VdPv(z^) и интегрируя по
г° от 0 до находим
<(«)= и p'vv>&+ з p;v,(S)(s), v(/i, (12.16)
v' £ v' 6 Л
ОО
где -P//(s)=f е —sxdPij(x) Уравнения (12.16) являются линейными алге-
о
браическими относительно преобразований искомых величин /?v*(s). Они
впервые были получены в работе В. С. Королюка (16]. Здесь эти уравнения
следуют из общих уравнений (12.10).
Аналогично можно выписать уравнения для моментов, например
T’i (v, г°) = 2j Qvv' (zv)*v' +
v's6 Ji
oo
+ S Qvv'(2v)Hi(< zv>°- (12.17
v'.e/t о
oo
где xv =«J xdPv (x).
о
Если интересоваться средним временем пребывания процесса в множестве
Q, начиная с момента выхода из состояния v £ Jlt которое равно T^v) =
= (7\(v, х) dPv(x), то из (12.17) следует, что
о
Tx(v)= 2 PW’Xv+ 2j ^vv-7i(O. (12.Щ
v' 6 Ji v' e Ji
Уравнение (12.18) можно также получить, дифференцируя найденное выше соот
ношение (12.16), если заметить, что
ds Pv(s) |s = 0 = ~xv Pl (v)‘
Пример 2. Рассмотрим агрегат, представленный в каноническом виде
с внутренним состоянием z(t) = (v(0, x(t), zv(t)). В настоящем примере будет пред
полагаться, что размерность вектора zv не зависит от v; v(t) принимает, как и ра
нее, целочисленные значения, но в отличие от сказанного выше может изменять
ся не только в те моменты, когда х = 0. Именно, предположим, что в промежут
ках между обращениями x(t) в 0 случайная функция v(/) является разрывньл
марковским процессом:
Р {v(f+A0 = v7v(0=v, х (/) > 0] =lv avv, Д/ + о(Д/),
гДе S“vv' = 1’ а
Р {v(/ + A/)=v/v(0 = v, х(0>0} = 1-^Д< + о(Д0
остальные координаты, т.е. zv и х, в моменты «спонтанных» скачков v(i) не из
меняются). В моменты же, когда х(/)=0, переходы агрегата по-прежнему опре
деляются функцией Р {(v, 0, zv,); (v', dx', dzv,)}. Можно считать, что такое допол
нительное изменение основной координаты соответствует поступлению в агре
гат некоторого входного сигнала. Заметим, что класс входных сигналов полис
стью определяется заданием параметров и avv,.
.30
Агрегат такого вида моделирует так называемые марковские процессы с
дискретным вмешательством случая, широко применяемые для описания слож-
ных систем, в частности систем массового обслуживания. В данном случае оче*
видно
Р {(V, X, zv); Q, /} 4-- р {(V, о, zv); Q, i — Л'},
Из уравнений (12.8), полагая в них — 0, получаем
Р* {(v. О, z«); Q, s}~ 3 P{(v, 0, г°); (v't (0, оо), Гу,)} +
v' е-/\л
+ 3 У J P{(v, о, г°); (v', dx', dzv,)}x
V * 6 >71 tyjt бГу/ х'^0
XP*{(V', х', zv,); Q, s}, z°crv> vCA. (12.19)
Кроме того, из формулы полной вероятности следует, что при х° > О
p((v, х°, z°); Q, /} = Kaw д< +
V е
+ \avv. MP J(v', x° — M, z°); Q, i —Д1!} +
v' 6 Jt
-Ц1-\М)Р {(v, х°-дг, z°); Q, /-дг}+о(Л0,
x° > 0, zjerv, vUp (12.20)
Отсюда
+ 3 M™- mp* !(v'- *° —д^> z°); Q’s} +
V' 6
+ (1-\,Д/) P* |(v, x°-M, z°) ; Q, «)+о(Д0, (12.21)
Предполагая существование производных и корректность совершения пре-
дельного перехода, из (12.21) получаем систему дифференциальных уравнений:
дР* |(v, х°, z°) ; Q, s)
У \ aw' +
+ 2j 4avv'P*{(v'> x°, z°);Q, s)-
V' 6 JI
-(s + Xv)P* |(v, x°, z°); Q, s), x°>0, z° G Ц, v G Л- (12.22)
Полученные дифференциальные уравнения являются линейными и, сле-
довательно, их решение имеет вид
Р* |(v, х°, г®); 0, s} = eDx° [р* {(v, 0, г®) ; Q, s}— p] +P, (12.23)
где D — матрица правой части системы (12.22), a R — постоянное частное ре-
шение этой системы, которое, как нетрудно видеть, существует и может быть най-
дено из решения системы линейных алгебраических уравнений, получаемых из
(12.22) приравниванием нулю правой части. Как D, так и R зависят от s и пара-
метров avv., v С Л. G J-
Подстановка (12.23) в (12.19) дает для определения величин P*{(v, 0, z®);Q,s}
систему интегральных уравнений Фредгольма II рода. Решая ее и подставляя
302
решение в (12.23), находим вероятность Р*{(у, х°, zv°)-, Q, s}. Если координата
2° может принимать лишь конечное или счетное число значений, то упомянутые
уравнения Фредгольма сводятся к системе (конечной или бесконечной) линейных
алгебраических уравнений.
Разумеется, путем введения еще одной дополнительной координаты можно
привести рассматриваемый агрегат к автономному. Такой прием соответствует
созданию еще одного агрегата, вырабатывающего входной сигнал, а затем объе-
динению двух агрегатов в один. Однако при марковском характере входного сиг-
нала такое преобразование, по-видимому, нецелесообразно.
12.3. СУЩЕСТВОВАНИЕ РЕШЕНИЯ ПОЛУЧЕННЫХ УРАВНЕНИЙ
Остановимся на вопросе существования решения уравнений (12.9) и (12.10).
Заметим, что в силу определения вероятности P{(v, 0, 2°v); Q, 1} имеет место ра-
венство
ОО
= S3 I 1
n = o V- 6 j\Ji V,, •• . vn 6 Jt п ,0 ег
2 Vi
i= I
f П p {(v о. 2° ); (vA_j_i, dxk+l , dz° J} у
erv k = o
vn n
xH(v Mn); (v'-[°>-)> (>2-24
где v0 = v. При n = 0 подынтегральное выражение в (12.24) считается равным
P{(v, 0, 2v0); (v', [0, <ю), Tv,)}.
Из равенства (12.24) получаем
ОО
P*((v,0,2°); М=3 3 3 I
n = Q v' в vv . . . , V € Ji 20 с г
Vj Vi
... J П,р*[К,°,гу;(^р^Ч+1)|х
г° ег *=°
vn
х р °' Ч): (v'- f°- М’
f rv, J±. (12.25)
Возникает вопрос, если величины Р и Р* известны, то зачем относительно
них составлять уравнения? Однако, как видно из равенств (12.24) и (12.25), при
вычислении искомых величин могут возникнуть значительные трудности, так
как требуется вычислять многократные интегралы и производить неоднократное
суммирование. Поэтому может оказаться целесообразнее решить известными ме-
тодами уравнения относительно искомых величин. Кроме того, как показывают
приведенные примеры, эти уравнения в некоторых частных случаях можно пре-
образовать в более элементарные, например алгебраические. Конечно, все ска-
занное не исключает случая, когда воспользоваться готовым ответом легче чем
решать уравнения.
Докажем теперь, что выражения (12.24) и (12.25) являются решениями
уравнений (12.9) и (12.10) соответственно и найдем некоторые свойства этих ре-
303
ш ений. Доказательство приведем только для уравнений (12.9). Уравнения
(12.10) рассматриваются аналогично. Для краткости перепишем равенства (12.24)
и (1 2.9) в виде
Р= Рп,
п = 0
Р —Ро~\~РР
(12.24')
(12.9')
В этих равенствах опущены аргументы; выражения для рп ясны из равенства
(12.24), а вид линейного оператора L подробно записан в (12.9). Заметим, что
величины pn{(v, 0, z^); Q, 1} имеют прозрачный физический смысл—это вероят-
ности выхода траекторий агрегата из множества Q за время t равно за п + 1
переход из одного основного состояния в другое.
Наряду с уравнением (12.9') рассмотрим рекуррентное соотношение
Р(п + В = po + LP^l; Р(й> =0.
(12.26)
Из вида оператора L ясно, что последовательность } монотонно возраста-
ющая и, кроме того,
Р(п+*> = ^р..
поэтому
со
lim P(n)=P= Pi.
«-►ОО ; = п
Имеет место соотношение
£р(п)=р(л+1) _р0 <
Следовательно, выполнены условия теоремы о переходе к пределу под знаком ин-
теграла (см. книгу Э. Камке [11], § 9.2) и, совершая в соотношении (12.26) пре-
дельный переход при и->-<, получаем (12.9). При этом решение системы (12.9)
определяется равенством (12.24). Докажем, что это решение является мини-
мальным неотрицательным решением системы уравнений (12.9).
В самом деле, пусть Р >0—какое-либо решение уравнений (12.9) или,
что то же, уравнений (12.9'). Тогда < Р. Предположим теперь, что
pl") < р. Докажем, что Имеем Р^п~^ В =р0_|_др('1) р0-|-£р _
ОО
= Р. Следовательно, Р= У р;= lim Р^ < Р. Тем самым доказана мини-
1=0 п -> со
мальность искомого решения.
Таким образом, искомые решения уравнений (12.9) совпадают с решения-
ми, получаемыми с помощью метода последовательных приближений при р(°>=
= 0. Они являются минимальными неотрицательными решениями системы
(12.9). Из этого следует, что при решении могут оказаться полезными методы
математического программирования. Так, если заменить систему (12.9) прибли-
женной системой линейных алгебраических уравнений, то задача отыскания
нужного решения сведется к задаче линейного программирования.
304
12.4. ПРЕДЕЛЬНАЯ ОГРАНИЧЕННОСТЬ
Как говорилось в гл. 9, иногда представляют интерес события,
состоящие в том, что траектория системы попадает в некоторое множест-
во Q фазового пространства системы и там остается. Вновь рассмотрим
кусочно-непрерывный агрегат, у которого дополнительные координаты
изменяются по закону
Обозначим через ф {(v, zv); Q) вероятность того, что траектория
такого агрегата, начинающаяся в точке (v, zv), попадет в множество
Q и не выйдет из него в дальнейшем. Пусть множество Q вновь имеет
вид Q = {(v, zv): v £ А с J, zv E rv). Можно показать (аналогично
тому, как это делалось в § 12.2), что функция ф удовлетворяет урав-
нению
ip((v,Zv);Q}= 3 f ^{(v',zv0;Q} х
v'ej rv,
xP[(v,z? — av£(z°));(v',dzV')J. z°6rv, vgj. (12.27)
В данном случае искомая функция ф {(v, z°); Q} является мини-
мальным решением среди решений системы (12.27), которые не меньше
чем
1—Р {(v, z°); Q, оо} при v 6 rv.)
Доказательства сформулированных утверждений почти дословно пов-
торяют рассуждения § 12.2 и 12.3. Естественно, что таким же образом
может рассматриваться и агрегат в каноническом виде.
Обратим внимание на то, что если Р {(v, z°); Q, оо) = 1 для любых
г® (Г,, v ( J1( то ф {(v', zV'); Q} = О для всех zV' £ IV, v' £ J.
12.5. СУЩЕСТВОВАНИЕ УСТАНОВИВШЕГОСЯ РЕЖИМА
В КУСОЧНО-ЛИНЕЙНЫХ АГРЕГАТАХ
В прикладных вопросах теории вероятностей и теории случайных
процессов большое значение имеет факт существования установившего-
ся или стационарного режима функционирования исследуемой систе-
мы. Для существования стационарного режима требуется, чтобы при
любом начальном условии с течением времени вероятностное распре-
деление состояний процесса (или некоторой функции от состояний)
стремилось к распределению, не зависящему от выбранного начального
условия.
Что это означает? Пусть мы рассматриваем некоторый случайный
процесса (/), значения которого принадлежат фазовому пространству Z.
Если для каждого (измеримого) множества Г с 2 существует предел
305
lim P (z ([) £ Г/z (0) = z0], не зависящий от z0, то on и называется
t
стационарным или равновесным распределением процесса. Можно
фиксировать не начальное состояние, а начальное распределение со-
стояний.
Вполне понятно, что для существования у процесса функциониро-
вания системы предельного распределения необходимо на этот процесс
наложить те или иные дополнительные условия. Как уже говорилось,
свойство процесса иметь установившийся режим можно трактовать
как своего рода устойчивость; подход к анализу стационарных режи-
мов’с этой точки зрения будет изложен в гл. 15. Здесь же остановимся
на том, как такой анализ для марковских процессов рассматриваемых
типов, может осуществиться чисто «вероятностными» методами. Для
этого потребуется ввести понятие «регенерирующий процесс», широко
используемое в теории массового обслуживания и теории случайных
процессов вообще (см. работы В. Л. Смита [15], В. Феллера [17]).
Вероятностный процесс z (t) называется регенерирующим, если
существуют такие случайные моменты времени {/J, вообще говоря,
определяемые предыдущим течением процесса, что величины 0, =
= ti — ti — i, i 2, взаимно независимы, одинаковы распределены,
а течение процесса z (/) при t > ti не зависит от его предыстории, т. е.
от течения z (t) при t /г. Величина 0Ь независимая от 0г, I 2,
может иметь распределение, отличное от распределений 0г, i 2.
Моменты ti называются точками регенерации исходного процесса. Как
нетрудно видеть, последовательность {0г}г > i образует процесс вос-
становления. Развитие процесса после каждого момента не зависит от
его предыстории и как бы начинается заново. Если с положительной
вероятностью у процесса не наступает момента регенерации, то это
означает, что функция распределения величины 0j или 0г-, i 2,
является несобственной. Более строгое и более общее определение
регенерирующего процесса можно найти в уже упомянутой работе
В. Л. Смита. Если z (t) является однородным, марковским процессом
и если 2*—некоторое фиксированное его состояние, то моменты возвра-
щений процесса в это состояние являются точками регенерации про-
цесса (в силу свойства марковости). Однако отнюдь не всякая точка
обладает таким свойством, что время возвращения в нее конечно с ве-
роятностью 1 и, тем более, среднее время возвращения конечно.
Рассмотрим, например, систему массового обслуживания, состоя-
щую из двух обслуживающих приборов, с отказами, с поступающим
пуассоновским потоком требований. Предположим, что времена об-
служивания требований на приборах — независимые одинаково рас-
пределенные случайные величины с функцией распределения В (х),
причем пусть у этой функции существует плотность b (х). Тогда рас-
сматриваемую систему можно описать однородным марковским про-
цессом, имеющим следующие состояния: 0, (1, zj, (2, z21, z22). Дискрет-
ная компонента указывает на число требований, находящихся в си-
стеме; — время, оставшееся до окончания обслуживания единствен-
ного требования в системе; z21, z22 — времена, оставшиеся до окончания
обслуживания каждого из двух требований, имеющихся в системе.
306
Зафиксируем состояние (2, z21°, z22°). Тогда при принятых предполо-
жениях система с вероятностью 1 никогда не возвратится (или не по-
падет) в это состояние, хотя с той же вероятностью 1 может иметь место
возвращение в любую его окрестность S& вида
Зе ~ {(2, г21, 222): | z2i — 2211 <S, | г23 2221 б}>
Состояние же г ~ О является возвратным.
Если процесс г (0 является регенерирующим, то можно показать,
что в весьма широких предположениях для существования предель-
ного распределения достаточно, чтобы выполнялись свойства:
1) Р{01<оо} = 1, 2)М01<оо, i^2.
Эти условия являются достаточными, если, например, функция
Р{02<х} имеет абсолютно непрерывную компоненту.
Другие предпосылки для применения упомянутого результата
можно найти в работах В. Л. Смита [15] и В. Феллера [17]. Там же при-
ведена соответствующая библиография. Таким образом, если рассмат-
риваемый процесс регенерирующий, то, по существу, для доказатель-
ства существования равновесного распределения достаточно оценить
функцию распределения первого момента регенерации и средний
интервал М9г, i 2. На этом факте основано большинство теорем,
касающихся вопроса существования предельного распределения.
Приведем формулировку одной такой теоремы, доказанной
И. Н. Коваленко [14].
Рассмотрим автономный кусочно-линейный агрегат, описываемый
процессом z (/) = (v(Z), zv (t)), относительно которого выполняются
следующие предположения:
1. | 1 при всех v f J.
2. Tv = [zv : 2V> 0), v g J.
3. av]= 1 при всех v f A
4. Если агрегат из основного состояния v в соответствии
с некоторым вероятностным законом перешел в момент t в основ-
ное состояние v', что происходит в моменты обращения одной из
дополнительных координат в нулевое значение, то образуется слу-
чайный вектор (2V1, zv2,..., 2V|V|, T}YV', T]2V , ••), где СпГ' ,•••) —
случайный вектор, не зависящий от предыстории процесса. Тогда
2v-i = Л1™ , причем предположим, что функция
Ир 1чГ [Р W>m-'
[ dx
существует и равномерно по х ограничена.
5. Если скачок v->v' произошел из-за обращения в нуль ко-
ординаты zvi, то при всех /]>2 компонента zv-j не превосходит по
величине Sj-ю координату вектора (zvl, ... ,zV|v|, TIP', 'r12V’,•••)> причем
s;=^sfe при j^k.
Если скачок v->v' произошел из-за обращения в нуль коорди-
наты /^2, то компоненты zv-/, j > 2, не превосходят по вели-
чине Sj-ю координату вектора (zvi, ..., zV|vi), причемSj =£ sh, j^k.
307
6. S avy>0 при всех v £ J.
i>2
7. Если в некотором основном состоянии v, таком, что | v | = 1
дополнительная (единственная), координата обратилась в нуль, то
множество основных состояний, в которые с положительными вероят-
ностями может перейти процесс, одно и то же для всех v', | v'| = 1.
8. J — конечное множество.
9. Для всех v, v' £ J компоненты случайных векторов t]vv' не
решетчаты и обладают конечными математическими ожиданиями.
Теорема. В сформулированных условиях для кусочно-линейного
марковского процесса, описывающего агрегат, существует равновесное
вероятностное распределение состояний.
Доказательство теоремы основано на вышеприведенном утвержде-
нии относительно регенерирующих процессов. За точки регенерации
выбраны моменты обращения в нуль дополнительной координаты в не-
котором фиксированном основном состоянии v0, таком, что | v0 | = 1.
Некоторые проблемы, относящиеся к тематике настоящей главы,
поставлены и решаются в работах Б. В. Гнеденко и И. Н. Коваленко [1],
И. И. Ежова [2—5], И. С. Житомирского [6], В. В. Калашникова
[7—101, И. Н. Коваленко [12, 13].
ГЛАВА ТРИНАДЦАТАЯ
АНАЛИТИКО-СТАТИСТИЧЕСКИЙ МЕТОД РАСЧЕТА
ВЕРОЯТНОСТНЫХ ХАРАКТЕРИСТИК СЛОЖНЫХ СИСТЕМ
ПРИ МАЛОИНТЕНСИВНЫХ ВНЕШНИХ ВОЗДЕЙСТВИЯХ
13.1. ПОСТАНОВКА ЗАДАЧИ
При математическом анализе сложных систем типичной является
следующая ситуация. Если вероятностный закон функционирования
системы определяется набором распределений F\ (х), F2 (х), Fm (х),
то интересующий нас показатель эффективности системы зависит от
{ Ft (х) } сложным образом, так что аналитическим формулам предпо-
читают метод Монте-Карло; в то же время, если допустить, что функции
Ft (х) зависят от некоторого малого параметра е, то при удачном выборе
этого параметра можно построить асимптотическое разложение показа-
теля эффективности по степеням е, и воспользоваться этим в прибли-
женных расчетах.
Развивая этот метод, мы, однако, замечаем, что построение каж-
дого нового члена асимптотического разложения связано со все более
усложняющимися формулами: так, типична ситуация, когда коэффи-
циент при е" представляет собой n-мерный интеграл Стилтьеса не-
которой функции по заданному n-мерному распределению. Поэтому
возникает задача построения вычислительных методов, которые поз-
волили бы эффективно находить асимптотические разложения. В на-
стоящей главе эта задача решается для агрегатов общего вида, удов-
летворяющих, однако, тому условию, что существуют моменты вре-
мени, когда вся информация о предыдущем поведении агрегата, кото-
рая может повлиять на прогноз его поведения в будущем, сосредотачи-
вается в некотором дискретном параметре. Сформулируем точные пред-
посылки.
Пусть функционирование системы описывается случайным про-
цессом z (/) в фазовом пространстве Z. Предположим, что этот процесс
описывается следующими условиями. Существует конечное множество
Zo a Z состояний системы, Zo = {0, 1,2, ..., т\, с такими свойствами.
1. Если г (t0) = i £ Zo, то дальнейшее течение процесса после
момента t0 зависит только от i и не зависит от поведения z (t) до момен-
та t0.
2. При фиксированном z (t0) = i £ Zo при t > tQ поведение
z (t — t0) не зависит от t0.
3. При условии z (/0) = i С Zo распределение времени от t0 до
следующего момента попадания в множество Za имеет конечный первый
момент.
309
4. Поведение z (f) определяется некоторой внутренней случай-
ностью, свойственной системе, и воздействием внешнего случайного
фактора.
Более точно. Пусть г (4) — i € Zo. Тогда определяется некоторый
процесс г, (t, со) для 0 < t < т; (и), причем г, (т; («)) g Zo; г, (Z) 6 Zo,
t 6 (0, тг (со)), где со — случайный элемент вероятностного пространст-
ва Й, и определяется условный процесс г (/) — г, (/ — /0, со), t0< t <
< i0 + (co).
Смысл этого состоит в следующем. Если от момента i0 до момента
io + П (со) на систему не будет оказано входное воздействие, то при
всех t0 < (й + тг (со) будет
z (/) = ?(/).
Если же в некоторый момент t' g (/0, t0 + т, (со)) поступит воздействие,
тогда только
Z (/) = z (/), t0 < t 5^ t’.
Далее, реализуется случайный элемент со' G Q, независимый от
со, и определяется функция
г2'(/, со'), 0 t с: т2< (со'),
(z2' (tz, (со'), со') 6 Zo),
где z' = z (/') — значение процесса в момент поступления воздейст-
вия. После этого, как и выше, определяется условный процесс
z (t) = zZ' (t— t', co'), /' < / (co'),
и T. Д.
Остается схематизировать поступление входных воздействий. Бу-
дем считать, что они полностью задаются интенсивностью X (г), так
что если в момент t состояние процесса равно г, то вероятность поступ-
ления воздействия в интервале (t, t + dt) составляет A (t) dt.
Этими условиями полностью определяется процесс г (t) как слу-
чайный процесс, если задано его начальное распределение.
Рассмотрим некоторые характеристики системы, описываемой
процессом г (/).
1. Пусть А — некоторое подмножество множества Z. Нас может
интересовать случайный процесс (/), определяемый следующим
образом:
дло=!(,'
еслпг(/) (Л в момент /;
в противном случае.
Процесс Ал (/) имеет вид, изображенный на рис. 13.1.
2. Основные характеристики случайного процесса Ад (/), интере-
сные в практическом отношении:
310
a) Pa (t) — вероятность того, что в момент t процесс z (t) принад-
лежит множеству А, т. с. Ра (t) = Р (Ал (Z) = 1);
б) Qa (t) — вероятность непопадания в множество А за время
от 0 до I;
в) распределение времени пребывания в множестве А процесса
z (/) за время t, т. е. величины
t
IA(t) = \ Ал(и)<1и.
о
Все эти функционалы при конкретизации множества А могут быть
интерпретированы как основные показатели эффективности и надеж-
ности сложных систем.
13.2. ВВЕДЕНИЕ МАЛОГО ПАРАМЕТРА
В ряде работ (см., например,.[1, 21) исследовалась более частная
математическая модель применительно к расчету надежности сложных
систем. В этих работах в качестве малого параметра использовалась
величина, пропорциональная интенсивности отказа А, элемента систе-
мы. Здесь мы обобщим данную постановку задачи, считая, что Л (z) =
= Z.o (z) е, где е > 0 — малый параметр, (z) — множитель про-
порциональности, представляющий собой некоторую ограниченную
функцию. Таким образом, данной схемой, в частности, охватываются
системы теории надежности с произвольно распределенной длитель-
ностью безотказной работы элементов. Конечно, условие ограничен-
ности Хо (г) ограничивает класс рассматриваемых функций распределе-
ния.
Пусть z (0) = i 6 Zo, <_ <Z ... < tn < ..., — моменты сле-
дующих после t = 0 попаданий z (/) в множество состояний Zo. Будем
через Ро(...] обозначать вероятности событий, соответствующие слу-
чаю е — 0.
Примем предположение, согласно которому для любых i =р j
найдется такое п = п (i, j), что P0{z (/„) = j/z (0) = i} > 0. Это обес-
печивает сообщаемость состояний множества Zo.
311
Введем следующие понятия. Назовем рангом г (Л) подмножества
A cz Z\Z0 целое неотрицательное число со следующими свойствами.
1. Найдутся такое состояние i Е Zo и такое е' > 0, а также такие
множества Ао, Аг, ..., Аг<а} = А, что: а) множество тех t, для
которых Zt (t, со) С Ао и 0 < t < 1/е', с вероятностью, большей
имеет меру, большую s', равномерно по 8 > 0; б) для любого т = 0,
1, ..., г (А) — 1 и;любых z' £ Ат множество тех t, для которых
z2' (/, 0)) £ 1 и 0 < / < 1/е' , с вероятностью, большей е , имеет
меру, большую б', равномерно по е > 0.
2. Пусть i Е Zo, m<Zr(A). Определим
2г(^>“о) = а1. z0I (/ъ coj = tz2,
Za2 ^а) — аз> : Zam (tm, (i>m) =ап-^. i.
Тогда с вероятностью 1 относительно независимых элементов <о0, 04,..,
®т вероятностного пространства Q имеем am+i Е А при любых
t2 < М“2), • •
Заметим, что существование ранга налагает некоторые условия на
закон изменения процесса z (/). Если ранг существует, то он имеет
следующий простой смысл. Попадание из некоторого состояния
i Е Zo в множество А имеет положительную вероятность при условии,
что до следующего попадания процесса в множество Zo произойдет
г(А) воздействий; если же число воздействий меньше г (Л), то при
этом условии вероятность попадания в А при любом I равна 0.
Проводимый ниже асимптотический метод позволяет оценивать
описанные характеристики процесса z (t) при малых е > 0 и усло-
вии, что Хо (z) с, z Е Z.
13.3. ВЫРАЖЕНИЕ ХАРАКТЕРИСТИК ПРОЦЕССА z (/)
ЧЕРЕЗ ХАРАКТЕРИСТИКИ ЕГО ПОВЕДЕНИЯ В ИНТЕРВАЛАХ
МЕЖДУ ПОПАДАНИЕМ В НЕКОТОРОЕ СОСТОЯНИЕ ИЗ МНОЖЕСТВА Zo
Индексом 8 будем обозначать вероятность какого-либо события
или распределение какой-либо случайной величины, а также числовые
характеристики этого распределения при фиксированном значении
е > 0.
Нам понадобятся следующие характеристики:
(Л) — вероятность попадания процесса z (/) в множество со-
стояний А между двумя попаданиями в состояние i Е Zo;
Ti (Л) — математическое ожидание времени пребывания процес-
са z (f) в множестве состояний Л в интервале между двумя попаданиями
в состояние i Е Zo;
Тi (Л) — математическое ожидание квадрата времени пребывания
процесса z (/) в Л в интервале между двумя попаданиями в состояние
i Е Zo при условии, что попадание в Л имело место;
Ut — математическое ожидание времени возвращения в состояние
i Е Zo.
312
Если эти характеристики известны хотя бы для одного фиксиро-
ванного i £ Zo, тогда интересующие нас основные характеристики при
е —> 0 будут иметь следующее приближенное выражение:
Рл(/) = ЦИ)+7д(0 + о(1)1 е->0, (13Д)
«г
где
?л(/) = о(-Ц^), /->оо, (13.2)
Сл t ')=e_f + о (1), е->0. (13.3)
Найдем теперь распределение функционала 1д (/).
Случай I: предельная теорема для (Л)/иг -> оо.
Если tnt (A)/ut -> оо и при этом время возвращения в состоя-
ние i имеет конечную дисперсию, а отношение среднеквадратического
отклонения времени пребывания процесса г (I) в множестве состояний
А в интервале между двумя попаданиями в состояние i С Zo к матема-
тическому ожиданию этой же случайной величины (среднеквадратиче-
ское отклонение и математическое ожидание вычисляются при условии,
что попадание в множество А имеет место) ограничено, тогда случайная
величина 1д (/) асимптотически нормальна. Асимптотическое выраже-
ние математического ожидания нормального закона есть tTг (А)/щ;
асимптотическое выражение дисперсии выводится из следующих со-
ображений.
Пусть v — число попаданий в состояние i в интервале (0, t),
за которыми следуют попадания в множество состояний А, и пусть
В; — длительность пребывания z (t) в множестве А за /-м попаданием
1 v). Тогда с точностью до времени порядка ut
(13.4)
1=1
Введем функцию
( 1, если х > О,
£(х) = _ „ (13.5)
v ' [0, если х< 0. '
Формула (13.4) перепишется следующим образом
со
i= 1
Отсюда
М[/д« = М S g;gft£(v-j)£(v-^) =
i. 4=1
= М 2 E^,t£(v-max{/^)). (13.6)
/. 4=1
313
Перепишем это равенство, разбив сумму на подсуммы, где соответст-
венно k = j и k =£= j:
со оо j— 1
М[/Л(/)]2=М з ^?£(v-/)+2 s 3 Mg;^E(v —/) =
/=1 /=2 k=l
ОО оо
= S Р (V > /] + 2 (Mgx)2 2 (/-1) Р (V > i\ =
,=1 /=2
= Mv + (М^)2 Mv(v — 1) = ЛЦХ2 МV + (MSJ2 [Mv2—Mv]. (13.7)
Отсюда
D [1Л (/)] = М£? Мv + (М^)2 [Mv2 — Mv] — (MgJ2 (Mv)2 =
= D^Mv + (M^)2Dv. (13.8)
Имеем, далее, асимптотические формулы:
Mv^^i^, Н3.9)
и l
(13.10)
Ui
Отсюда следует [если подставить (13.10) в (13.8)], что
О[/л(0]^<2^м??=/-^-)т;(Л). (13.11)
Ul lit
(Л)'| . (13.12)
Таким образом, время пребывания в множестве состояний А
асимптотически нормально:
диНаИ)
\ «г
Случай II: предельная теорема для ограниченного /л,(А)/иг.
Если /л, (A)/ui ограничено, тогда Iд (/) будет в пределе иметь
распределение суммы пуассоновского числа случайных величин.
Пусть
f(s)=Me-s% (13.13)
где т]; — время пребывания процесса z (/) в множестве состояний А
между двумя попаданиями в состояние i при условии, что между этими
двумя попаданиями попадание в А имело место. Пусть, далее,
Тогда получим
оо
ф(*)^ 2
г .0 k=0
где и = tn,i (A)lui. При
по s: Re s > 0.
Формула (13.15) дает исчерпывающую характеристику предель-
ного распределения случайной величины /л (/). В частности, ее можно
использовать для расчета моментов этого распределения.
314
<p(s) = Me-s//i(') , (13.14)
е- м./* (s) = е- »S>1, (13.15)
этом имеет место равномерная сходимость
13.4. УПРОЩЕНИЕ ФОРМУЛ
Между двумя попаданиями в фиксированное состояние i Е Zo
процесс z (i) может пройти достаточно длительную эволюцию, поэтому
введенные в предыдущем параграфе характеристики являются до-
вольно сложными. Покажем, однако, что их можно выразить через
более простые характеристики процесса в интервале между двумя по-
паданиями в множество состояний Zo.
Пусть 2 (0) ~ i Е Zo. Если j £ А, обозначим через лг> (Л) вероят-
ность того, что следующим состоянием из Zo, в которое попадает про-
цесс, будет /. Если / Е А, обозначим через (Л) вероятность того,
что первым состоянием из Zo, в которое попадает процесс, будет /,
причем до этого процесс побывает в множестве состояний Л. Тогда,
как легко видеть, справедлива система уравнений
лр’(Л)= 2 тМЬ 2 K,-(Z)-лг;(Л)]л<-*>(Л), i,kezo- (13.16)
iQZ«
л(А (Л) = лДЛ)*’.
Таким образом, по Лц (Л) однозначно определяются лг (Л).
Далее, имеет место система уравнений, аналогичная (13.16), для
Tt (Л). Для ее формулировки понадобится одно определение.
Пусть 2 (0) = i Е Zo. Фиксируем некоторое j Е Zo и обозначим
через v состояние, вхождением в которое процесс z (/) впервые достиг-
нет множества Zo при t > 0. Пусть также t* — момент наступления
этого события. Введем случайную величину, равную t* при v = j и
равную 0 в противном случае. Обозначим через ТД(Л) математи-
ческое ожидание этой случайной величины. Тогда
S k£Z0- (13.17)
(Л) = 'Д(Л).
Затем,
Д = Л(Д; (13.18)
отсюда следует, что tit находятся из системы уравнений (13.17) при
Л = Z.
Характеристику 77 (Л) запишем в таком виде:
Д(Л)==7\ (Л)/д(Л), (13.19)
где Т"i (Л) — безусловное математическое ожидание квадрата вре-
мени пребывания процесса z (f) в множестве состояний Л между двумя
попаданиями в состояние i Zo.
Характеристики 77 (Л) определяются из следующих соображе-
ний.
1’ л(-г)(Л) есть вероятность попадания из состояния i £ Zo в множество со-
стояний А до попадания в состояние k £ Zu
315
Обозначим через Т" и (Л) математическое ожидание квадрата вре-
мени пребывания z (/) в А между моментом пребывания в i и первым
моментом попадания после этого в множество Zo, умноженного на
индикатор события { в указанный момент времени состояние z (/)
равно /gZ0}. Тогда справедлива система уравнений
^’(Л) = 2 Т'^А)+ 2 MZHWH
/г^ег0
+ 2 2 Т„(А)Т^(А), i,keZ0- (13.20)
(А)=-Т-(А).
13.5. АЛГОРИТМ АСИМПТОТИЧЕСКОГО АНАЛИЗА
ВСПОМОГАТЕЛЬНЫХ ХАРАКТЕРИСТИК
Пусть г (Л) = г. Введем еще понятие /-ранга гг (Л) множества со-
стояний Л. Это понятие состоит в следующем. Предположим, что най-
дутся такие е'>0 и множества состояний Ло, Лъ Л2, ..., Аг.(А) = А,
что:
1) множество тех/, для которых z, (/, оз) Е ЛоиО < t <_ 1/е', с веро-
ятностью, большей е', имеет меру, большую е', равномерно по
е > 0;
2) для любого m = 0, г — 1 и любых г' £ Ат множество
тех /, для которых z2- (/, to) £ Лт_|_ i и 0 < / < l/s', с вероятностью,
большей е', имеет меру, большую е', равномерно по е > 0;
3) описанная конструкция невозможна при замене г, (Л) на
п (Л) — 1.
В этих предположениях гг (Л) называется /-рангом множест-
ва А. Легко доказать, что
г (Л) min г,- (Л). (13.21)
‘ezo
Как было показано в предыдущем параграфе, основные характе-
ристики процесса z (/) элементарным образом выражаются через набор
характеристик:
Т^Т^, Т"ц(А). (13.22)
Покажем, как рассчитывать эти характеристики с помощью комбини-
рованного аналитико-статистического метода.
1. Фиксируем определенное i Е Zo (нужно перебрать все возмож-
ные /).
2. Случайно выбираем w, ( Q и моделируем траекторию процесса
г0(/)=2;(/, и0), 0 С t < Ti (<оо).
(13.23)
3. Вычисляем zt (тг(ы0), и0) = С Zo (по определению).
316
4. Вычисляем
тг(а0)
Ло = $ 70(г;(/, ю0)М (13.24)
О
и моделируем случайную величину с плотностью вероятности
рЛ/)= - °^(Л то)) , 0 < / < тг (<в0). (13.25)
Ло
Обозначим
2i (Vl, ®0)=Z1.
5. Случайно выбираем (Dj С Q независимо от ю0 и моделируем
траекторию процесса
= z21- (/, coj, 0</<т2?(®1). (13.26)
6. Вычисляем гх (т21- (о>1), (o1)=i2^Z0.
7. Вычисляем
tZ1' («о
Лх = Хо (гх (/, wj) dt, (13.27)
о
и моделируем случайную величину у2 с плотностью вероятности
р,(р!= ?'°(г1 (/’ Ю1)) , 0</<т21-(И1). (13.28)
Лх
Обозначим
г (т2/ (coj), toj =Z2-
8. Случайно выбираем ю2 С Q независимо от (соо, coi), и модели-
руем траекторию процесса
z2(0 = z2j< (/, ю2), 0<(<т22-(ю2), (13.29)
и т. д. до того, как будет построен гГ(д> (()•
Таким образом, в результате одной статистической пробы мы имеем
набор траекторий:
z0(Z), 0 < t < tz (®0),
Zi((), 0<(<т2/(®1),
г2 (/), 0 < t < тг/ (®2),
ги.4)(/), 0< zt < Т , (Юг (Л)). гг (Л)
(13.30)
317
Имеем такие наборы функционалов:
т; (“о)
Ло = $ л0 (z0 (/)) dt,
о
лх = $ /„ (?! (Z)) dt,
о
(13.31)
Запишем еще
Xz'r (Л) - 1 мл(Л- 1 )
ЛГ(Л)-1= § л0 (^г(А)- 1 (О) dt.
о
*0 (тг(СОо)) = 11,
G21- (СО1)) =12,
(13.32)
Zr (/1) (Tz'r (А) (аг (А))) ~ ir (Л>;
А0(Л) =
если z0 (/) g А для некоторого
t 6 [0, тг (со0)],
в противном случае,
А1И) =
О,
если Zj (/) б А для некоторого
t Е [О, т21- (coj)],
в противном случае,
(13.33)
Аг(Л)(А) =
О,
если zr(A)(t)^A для некоторого
1 е [0, ^г’г (Л) (СОГ (Л))] ,
в противном случае;
Wo (Л) = mes {/ g [0, т; (<о0)] : t g Л},
Wr (Л) (А) = mes {/ С (0, Тг'г (л>) '-i 6 А)
(13.34)
(суммарные времена пребывания в множестве состояний А в соот-
ветствующих интервалах).
Выписанные характеристики, расчет которых при моделировании
не представляет труда, достаточны для нахождения главного члена
асимптотики характеристик (13.22). Это делается следующим образом.
В каждой статистической пробе величины Ло, An Л2, ..., ЛГ(Л) - г,
г\, i2, ..., А0,(А), AX(A), .... АгМ) (А); №0 (А), (А).....
318
Wr(A) И) являются случайными. При этом выполняются такие усло-
вия. Если
niJ-(Z)=n<7)(Z)ep«(<'’/'Z)+0(ePll(‘''/'Z) + 1), е->0, (13.35)
то
М{А0 ... ЛРя(1-,/, z)-i 6(гРя(/,/, z)+i,/)} =
= Л//’(Z)+ 0 (s'), 8->0. (13.36)
л;ДЛ)--= л,^ (Л) 8Ря (г'Л)+ 0 (еРя ЛЛ)+1), 8->0, (13.37)
то
М{А0 ... ЛРл(1-, j, а)- 1 АРял>(Л)6(tpnU./M)> /)} =
= 40)(Л)+О(е), е->0*’. (13.38)
Если
ТгДА) = Т'70)(Л)8Ря(/,/'Л)+О(е,)я</'ЛЛ) + 1)> е->0, (13.39)
то
М{Аи ... АРя (/,/, Л)_1 IFPjt л) 6(iPjt </,/, д)4-1,/)} =
= 71/0)(А)+О(8). (13.40)
В частности, приняв А — Z, найдем Тц} (Z).
Наконец, последняя характеристика 7\/(Л). Если
Т"ц(А) = Т"^ (Л) 8Ря А) +0 (еРя (Л л Л) +1), (13.41)
то
М {Ао ... АРя (г> /, л) — 1 И7рл j. А) 6 (г'ря а, /, Д) + ь /')} =
= т"^} (Л) +0(8). (13.42)
Таким образом, производится серия статистических проб, в ре-
зультате которой статистически определяется ря (г, /, Л) как наи-
меньшее k, для которого хотя бы в одной пробе Ай(Л) 6 (tA+1( j) = 1,
а постоянные л’/1 (Z), л’-Р) (Л), (Л), Тц^А) оцениваются средними
арифметическими соответственно:
6(1ря (/,/.z)+i, /)А0 ... Аря(/, /р г; —1,
Aplt U. /• л) И) (г'рл ((. /. Л)1 /)-^0 Лря (i, /,Л) —I,
И7Ря (i, у, л> 6 (ipjj <z, /, л), /) Ао ... Аря (/, д л)~ 1,
^Рл (‘. /• А) 6 (1рл (i, /, А), /)А0 ... Аря (£;
•'»«. />-[ J;
если i = j,
если i + /.
319
Следовательно, дан асимптотический алгоритм расчета харак-
теристик сложной системы, подверженной редким случайным воз-
действиям.
13.6. ОПЫТ РЕАЛИЗАЦИИ АЛГОРИТМА НА ЭВМ
В данном параграфе будет сделан краткий обзор результатов реализации
алгоритма асимптотического анализа в сочетании с методом Монте-Карло на
ЭВМ. Разработка алгоритма моделирования и реализация его на ЭВМ для ряда
схем теории надежности и теории массового обслуживания осуществлена
В. А. Капыриным.
Программирование алгоритмов анализа вероятностных характеристик
схем надежности и массового обслуживания осуществлялось на языке АЛГОЛ-
60. Общим для рассматриваемых схем являлось то, что все они описываются
кусочно-линейным процессом z(l). Кроме того,
— отказавший элемент системы восстанавливается в течение времени,
распределенного по произвольному закону G(x);
— одновременно может ремонтироваться г элементов;
— интенсивность отказа элемента пропорциональна малому параметру е;
— фиксировано некоторое множество А состояний системы; определяются
вероятностные характеристики, связанные с попаданием случайного процесса
z(l) в множество А;
— при соответствующем выборе г система сводится к схеме массового об-
служивания либо с очередью, либо с неограниченным обслуживанием;
— алгоритмы предусматривают получение двух первых коэффициентов
разложения некоторой вероятностной характеристики Р(А) по степеням е,
Р (Л) = СоеРо’('4) -'pCi ер| (/1’+О(ер‘
— каждая система характеризуется числом S цепочек случайного процес-
са z(0, по которым производится подсчет коэффициентов разложения, неучиты-
ваемые цепочки влияют на члены при е в степени, большей Р1(Л);
— время реализации одной цепочки на ЭВМ (30—40 тыс. опер/с, объем
оперативной памяти 4096 ячеек) составило 0,008—0,02 с для множеств Л таких,
что в разложении учитываются члены при е и в2;
— время программирования готовых алгоритмов схем примерно 2,5—3
месяца;
— объем в оперативной памяти, занимаемый собственно программой, не
зависит от соотношения параметров и чисел, характеризующих систему;
— число используемых случайных чисел 2pj(A)cM (У — количество реа-
лизаций, 1 < с < 2); в моделях, использующих непосредственное моделирова-
ние аналогичных систем методом Монте-Карло, требуется 10е— 109 случайных
чисел.
Время одной реализации (выраженное в секундах) при непосредственном
моделировании и при расчете коэффициентов асимптотического разложения
характеризуется следующей таблицей.
Таблица 13.1
Число элементов Непосредственное мо- делирование Реализация коэффици- ентов только до £2
20 о,1 0,01
1 000 2,25 0,1
8 500 20 2
9 500 ; 20 2,25
70 000 2,5
320
Моделировались следующие системы.
1. Система из п одинаковых зависимых элементов, отказывающая при вы-
ходе из строя т элементов. Скорость восстановления элементов и интенсивность
отказа зависят от состояния системы (например, система энергопитания из п
генераторов).
2. Система из п различных элементов, интенсивность отказа i-го элемента
A,oierf, восстановление по закону G(x, а,). А —множество состояний, связанное
с отказом фиксированных элементов, или множество состояний, при которых не
менее т элементов находятся в состоянии отказа;
3. Резервированная система из п основных и пг резервных элементов, ре-
зерв нагруженный. Время переключения из резервной группы в основную рас-
пределено по закону Gj(x); одновременно может переключаться не более г± эле-
ментов.
4. Резервированная система с облегченным резервом. Интенсивность от-
каза элемента в резерве Хр < Хое. В период переключения Хр = Xp(Z)s, t — вре-
мя от начала переключения — имеет распределение G2(x). Множество А соответ-
ствует tn отказавшим элементам в основной группе.
5. Система с резервом двух типов (например, приемо-передающая группа
из восьми комплектов основных и двух резервных устройств радиорелейной ли-
нии связи).
6. Система из п одинаковых групп элементов с задержкой начала ремонта
после /г-го отказа на величину т, распределенную по закону F(x) (необслужива-
емый усилительный пункт 24-канальной линии связи).
7. Система передачи информации, являющаяся комбинацией систем 3—6.
Компактность программ позволяет использовать их одновременно.
8. n-канальная система передачи информации с периодическим контролем
исправности элементов (во время контроля система неработоспособна).
Системы массового обслуживания. 1. n-линейная система массового обслу-
живания с приборами, подверженными малоинтенсивным отказам. Предпола-
гается, что при е = 0 стационарное распределение вероятностей состояний си-
стемы известно. Интенсивность отказа прибора
(Хде, если прибор свободен,
I Хо (/) е, если с начала занятия прибора прошло время t.
Множество А состояний определяется числом имеющихся в системе требо-
ваний и числом отказавших приборов.
2. п-линейная система массового обслуживания, на вход которой посту-
пают типов простейших потоков, i-й поток характеризуется интенсивностью
Xje, распределением времени обслуживания G(x, i) и весом pt- Приоритет Pt
поступившего в систему требования i-го типа определяется весом pt и состоянием
системы v в момент поступления и в дальнейшем изменяется при каждом осво-
бождении прибора, если обслуживание данного требования еще не начато, и в
зависимости от остатка времени до окончания обслуживания, если оно начато.
Множество А определяется наличием определенного числа требований каж
дого типа.
П Зав. 792
ГЛАВА ЧЕТЫРНАДЦАТАЯ
ИССЛЕДОВАНИЕ СЛОЖНЫХ СИСТЕМ МЕТОДАМИ
ТЕОРИИ ДИФФУЗИОННЫХ ПРОЦЕССОВ
14.1. ВВОДНЫЕ ЗАМЕЧАНИЯ
Выше уже неоднократно говорилось о том, что основной целью
анализа сложных систем вообще и агрегативных в частности является
исследование поведения различных функционалов от процесса функци-
онирования системы. Сами процессы функционирования являются
случайными и имеют весьма сложную природу. Поэтому, по-видимому,
бесполезно надеяться получить необходимую информацию о системе,
рассматривая изучаемый процесс во всей его сложности. К счастью,
для практических целей бывает достаточно изучить поведение указан-
ных функционалов лишь при некоторых «предельных» режимах рабо-
ты системы. Для таких режимов могут быть доказаны предельные тео-
ремы, суть которых заключается в том, что в этих случаях исходные
сложные по структуре случайные процессы можно заменить более
простыми так, что искомые функционалы от исходных процессов бу-
дут близки в каком-либо вероятностном смысле к таким же функцио-
налам от этих простых процессов.
В качестве таких процессов весьма часто выступают хорошо изу-
ченные диффузионные процессы, хотя могут встретиться и другие ва-
рианты. Примером могут служить хорошо известные в теории массово-
го обслуживания предельные теоремы о сходимости последователь-
ности сумм «слабых» потоков общего вида к пуассоновскому, о сходи-
мости редеющих потоков и т. д. Ниже будет рассмотрен лишь случай
сходимости к диффузионным процессам, вернее будет дан беглый обзор
полученных к настоящему времен результатов. Однако перед этим
целесообразно привести простейший пример такого сорта, с тем чтобы
прояснить идею обсуждаемого подхода (см., например, А. Т. Баруча-
Рид [4]).
14.2. ДИФФУЗИОННЫЕ УРАВНЕНИЯ
Рассмотрим процесс случайного блуждания на прямой, которую
обозначим через /?. Пусть в моментыh, 2h, ... частица меняет свое поло-
жение zh. При этом, если z(fl>(t) = z, то z(,l> (t + h) является случай-
ной величиной с распределением P(z\E, t) = P{zfh> (t + h) 6 E a
cz Rlz<h)(t) = z]. Покажем теперь, что при естественных предполо-
жениях при й -> О процесс случайного блуждания сходится к диффу-
зионному процессу. Предположим, что при любом 6 усеченные моменты
322
(сами моменты могут не существовать) распределения P(zh\E, t) име-
ют вид:
$ (у—z) Pzh} {dy, t) = fL(t, z)h+o(h),
\U — z\^6
5 (у—zf Pzh} (dy, t)=f2(t, Z)h + o(h),
|y-z|<6
$ P^(dy, t)=o(h),
I y~ z| > 6
где величины о (Аг)/Л —0 равномерно относительно г.
Обозначим Р(/1> {т, z; t, Е} =^Р [z(A) (f)£Eс R/z{h~> (т) =z\. В силу
уравнения Колмогорова — Чепмена имеем для т</
Р^ [т, z; t, Е\ = ^P(P(dy, t)Pw {r + h, у, t,E} =
= Pz1’ (dy, t) P(h‘ (t Ц-й, y, t, E} +o (Л) =
= $ (dy, t)
l!/-z|<6
P*'0 (r+h, z; t, E] +
+ (У—z)
dPw |r + /t, z; t, E]
dz
+ y [(У — z)2+o(y — z)2]
d2 P(,1) {r + h, z; t, E]
dz2
+ o(h).
Разделим обе части полученного равенства на h и перейдем к пре-
делу при h -> 0. Затем устремим 6 -> 0. В результате получим
дР {т, z; t, Е] = дР {т, z; t, Е) ।
дт дг
+ -/2(4Z)------ ага (14.1)
где Р (т, z; t, £] = Р (z (t) g Elz (т) = z|, a z (t) — процесс, полу-
чающийся из исходного при /г —0. Но (14.1) есть не что иное, как
уравнение Колмогорова для диффузионных процессов. Таким образом,
при сделанных предположениях процесс случайного блуждания схо-
дится к диффузионному (отметим, что хотя в математическом отноше-
нии проделанные переходы не являются безупречными, они обладают
достаточной наглядностью). При этом величина (г, г) характеризует
среднюю тенденцию в эволюции случайного процесса г (т) и называет-
ся коэффициентом сноса. Величина /г (т, г) характеризует среднее
квадратичное отклонение процесса г (т) от его среднего значения и на-
зывается коэффициентом диффузии.
11* 323
В качестве простейшего примера применим полученные резуль-
таты к анализу системы массового обслуживания, состоящей из од-
ного прибора. Пусть wn — время ожидания начала обслуживания
n-го поступившего требования, — разность между временем обслу-
живания n-го требования и интервалом, прошедшим с момента по-
ступления п-го требования до момента поступления (п + 1)-го
требования. Очевидно,
wn+i = max [щп-|-£п, 0].
Если {ёп} является последовательностью независимых одинаково
распределенных случайных величин, то, как показал Д. Линдли [10],
функция распределения случайной величины wn совпадает с распреде-
лением величины max Xk, где случайные величины Хп связаны
соотношением
Хп+1=Х„ + ?Л. (14.2)
Рассмотрим поэтому поведение цепи Маркова, описываемой соот-
ношением (14.2). Если система нагруженная, то это означает, что
М£п = —аге, где 0 < е < 1. Пусть DS„ = о2. Для того чтобы изу-
чить предельное поведение (при е —0) рассматриваемой цепи, положим
уп = е.Хп. Как следует из (14.2),
Уп+1 =Уп+Лп.
где Мг)л=а1е2, Dr]n=o2E2.
Если теперь считать, что изменения состояния цепи происходят
через промежутки времени длительности е2, то процесс в пределе (при
8 -> 0) перейдет в диффузионный с коэффициентом сноса аг и коэффи-
циентом диффузии о2. Анализ этого процесса не сложен. Подобным
образом можно исследовать более сложные системы. Соответствующие
примеры можно найти в работах Д. Баррера [2, 3], С. М. Броди [81,
И. Н. Коваленко [91, Л. Г. Афанасьевой [1] и др.
14.3. НЕСКОЛЬКО ПРЕДЕЛЬНЫХ СООТНОШЕНИЙ
Невозможно упомянуть все имеющиеся к настоящему времени ра-
боты, изучающие предельное поведение различных случайных процес-
сов. Поэтому мы ограничимся обзором лишь тех из них, которые, как
представляется, скорее всего могут использоваться при анализе изу-
чаемых систем. Вместе с тем следует отметить, что в большинстве этих
работ используется весьма сложный математический аппарат, и поэ-
тому изложение применяемых в них методов, а иногда и строгая фор-
мулировка полученных результатов нецелесообразна в рамках дан-
ной книги. Большое количество работ посвящено изучению поведения
систем массового обслуживания в условиях большой загрузки
(см. Э. Г. Самандаров [12], Ю. В. Прохоров [11], А. А. Боровков [5]).
324
При этом, как правило, изучались случаи сходимости случайных про-
цессов, описывающих систему, к винеровскому процессу. Приведем
ряд результатов, следуя работе А. А. Боровкова [5].
Рассмотрим следующий процесс обслуживания. В систему по-
ступает m > 1 потоков требований, причем в /-м потоке (/ = 1, ..., т)
требования поступают группами случайного объема через интерва-
лы %j. Упомянутые случайные величины и образованные ими последо-
вательности независимы. Требования в порядке поступления (с точ-
ностью до произвольного порядка внутри групп) становятся в общую
очередь и ждут обслуживания. Обслуживание происходит на М — т
приборах, которые будут нумероваться от т. + 1 до М, группами слу-
чайного размера. Именно, в /-м приборе (/ = т + 1, ..., М) группа
объема —г]; > 0 (пли меньшего объема, если длина очереди меньше
—т]у) обслуживается время ту, Xj > 0. Случайные величины Xj, т]7-
и образуемые ими последовательности независимы. Кроме этого опре-
делены правила (возможно, рандомизированные), не зависящие от
времени и длины очереди, устанавливающие дисциплину занятия сво-
бодных приборов, если в некоторый момент окажется, что их несколько.
Рассматриваются приборы двух типов. Приборы 1-го типа не на-
чинают обслуживания, если отсутствует очередь; при появлении хотя
бы одного требования мгновенно начинает действовать один из свобод-
ных приборов, выбор которого определяется установленной дисци-
плиной. Приборы 2-го типа начинают процесс обслуживания в моменты
времени, разделенные случайными промежутками Xj, независимо от
наличия требований в очереди. Назовем систему обслуживания систе-
мой z-го (i = 1, 2) типа, если она содержит лишь приборы i-ro типа.
Если в системе есть приборы обоих типов, то назовем ее системой 3-го
типа.
Предположим, что М |т];| < оо, Мту < оо, / = 1, ..., М. Рас-
ти
смотрим величину 6 = —• ^Мл/Мту), характеризующую загрузку
/ = 1
системы. Очевидно, 6 представляет собой разность между средним ко-
личеством требований, которые система может обслуживать за едини-
цу времени при бесконечной очереди и средним количеством требова-
ний, поступающим в систему за единицу времени. Как это обычно де-
лается при изучении предельных случаев, предположим, что рассма-
тривается последовательность систем, «управляемых» случайными ве-
личинами Xj (б) и т], (б), зависимыми от б, и
At
- 2 (Мт1/(б)/МтН6))=6.
/=1
Пусть va (Т) — длина очереди в момент Т при некотором фикси-
рованном начальном значении va (0). Кроме того, начальное состояние
системы будем характеризовать следующими величинами: > О,
j = 1, ..., tn, — моментами поступления первой группы требований
в /-м потоке, iJO>0, j = т + 1, .... 7И, — моментами начала работы
/-го прибора.
325
Теорема. Пусть при 6 —О (безразлично, 6 < 0 или 6 > 0)
2
ВЦ, (Мц,)2 Рт,
Мт, (Мт,)3
—>-о2>0
и при некотором у > 0 моменты
Мт,, М
т,-— Мт,-
Vdt;
2+V
М|гц- —Mn,|2+v
Di],
равномерно по 6 ограничены. Предположим, что для начальных усло-
вий vs (0), /*0, j = 1, .... М, выполняется
/ /в \
(6Т)~1 max (0), ‘° j —>- 0 при 6—>0, если 6 \rT1;
/ t6 \
Т-1''2 max I v. (0),—-— —0 при 6->0, если 6 VТ <Z 1,
/ \ Л ' Мт, (б) / р н г
где -> означает стремление по вероятности (начальные условия могут
р
быть и случайными, но не зависящими от последовательностей |т/},
(Л/})-
Тогда для системы любого из трех типов предельное распределе-
ние V6 (Т) при 6 -> 0, Т -> оо описывается следующими соотноше-
ниями.
А. Если 6 УТ -+ 0, то
__ */<т
lira P{v6(T)<x]T/v8(0), ^о(/ = 1, М)] = ]/ - i e-'V2 dt,
6->0 F л J
0
Б. Если б УТ — оо, to
lim P^tTX-ST’+x/f/VjfO), ^>(/ = 1, ..., M)} =
= —A— i e-'!/2rf/,
V'2n
В. Если 6 УT и
limP{v6(T)<^^v6(0), ^о(/ = 1, .... М)} =
= Р (— , о sign 6, и2~\ ,
\ о 7
где Р (а, Ь, и2) = Р | w (/) + — , 0 t X u2 I — вероятность не-
( Ь ' J
пересечения стандартным винеровским процессом w(t) прямой
a,-\-tjb до момента и2.
326
Аналогичные предельные соотношения справедливы для времени
ожидания. Заметим, что можно не только получить вид предельных
законов для рассматриваемых случаев, но и найти асимптотические
разложения функций распределения, к примеру, величин ve (Т) по
степени параметра 6, где главным членом являются найденные в тео-
реме предельные законы. Соответствующие результаты можно найти
в упомянутых выше работах А. А. Боровкова.
В последнее время получены новые результаты, развивающие
рассматриваемый подход и дающие условия сходимости не только к ви-
неровскому процессу, но и к диффузионным процессам более общего
вида, в том числе и с условиями на границе (см. А. А. Боровков [6, 71).
Рассматриваемые в этих работах случайные процессы имеют достаточно
общую природу и с их помощью можно описать широкий класс реаль-
ных систем. Налагаемые на процессы требования позволяют назвать
их обобщенными регенерирующими процессами. Именно, требуется
существование такого возвратного множества D состояний процесса,
чтобы:
1) время возвращения в D имело равномерно ограниченный мо-
мент порядка 1 + у, у > О,
2) «выбросы» траектории процесса за время возвращения в D
имели равномерно ограниченный момент порядка 2 + у,
3) среднее и дисперсия приращения процесса за «большой» про-
межуток времени после попадания в D мало зависели от истории про-
цесса, предшествовавшей его попаданию в D, именно, требуется, чтобы
указанные величины были ограничены функциями, зависящими толь-
ко от времени, прошедшими с момента последнего попадания в D,
и принадлежащими специальному семейству функций.
Ряд из сформулированных условий, по-видимому, может быть
ослаблен. Следует отметить, что при доказательстве предельных тео-
рем в последнем случае нет необходимости знать конкретные вероят-
ностные законы, от которых зависит рассматриваемый процесс, а нуж-
но проверить лишь ряд условий общего характера.
ГЛАВА ПЯТНАДЦАТАЯ
ПРИМЕНЕНИЕ КАЧЕСТВЕННЫХ МЕТОДОВ
ДЛЯ АНАЛИЗА ПОВЕДЕНИЯ СЛОЖНЫХ СИСТЕМА
15.1. ВВОДНЫЕ ЗАМЕЧАНИЯ
При исследовании динамических (в широком понимании этого
слова) систем возникают задачи как количественного, так и качествен-
ного характера. К задачам первого типа относятся такие, в которых
требуется определить конкретное значение некоторого показателя,
характеризующего систему. Примером могут служить различные зада-
чи оптимизации, когда требуется найти значения параметров системы,
при которых некоторый функционал принимает экстремальное зна-
чение. К задачам этого же типа относятся, скажем, задачи определения
вероятностных распределений (или их моментов) функционалов, за-
данных на траекториях стохастических систем. Если, например, си-
стема описывается цепью Маркова, то часто представляет интерес
найти ее стационарное распределение (в случае существования послед-
него). Рассмотрим вновь пример с цепью Маркова и покажем, какие
качественные задачи могут ставиться при ее исследовании. К таким за-
дачам, которые обычно предваряют количественные исследования,
относятся задачи классификации состояний цепи Маркова, когда ре-
шаются принципиальные вопросы о количестве замкнутых классов,
возвратности и невозвратности состояний, периодичности цепи.
К задачам качественного исследования систем относятся также
задачи анализа устойчивости. Ряд таких задач сформулирован в гл. 9.
При изучении сложных систем удельный вес качественных исследова-
ний возрастает, поскольку применение количественных методов ста-
новится затруднительным ввиду больших объемов вычислений. В то
же время часто при качественных исследованиях удается оценить не-
которые представляющие интерес показатели системы. Это имеет место,
например, при использовании для качественных исследований анало-
гов прямого метода Ляпунова.
В данной главе будут рассмотрены лишь три задачи** ’, относящие-
*> Содержание данной главы базируется на работах [7—11].
**> В работах: —В. В. Калашников, Г. Ш. Цициашвили. Об
устойчивости систем массового обслуживания относительно возмущений опре-
деляющих их функций распределения. «Известия АН СССР», Техническая ки-
бернетика, 1972, № 2; Г. Ш. Цициашвили. Устойчивость многолинейных
систем обслуживания относительно возмущений определяющих их функций
распределения. «Известия АН СССР». Техническая кибернетика, 1972, №2 —
начато изучение еще одного типа задач качественного анализа систем не рассмат-
риваемого в настоящей главе. Именно, предметом изучения является чувстви-
тельность характеристик рассматриваемых систем (например, функций распре-
деления времени ожидания, длины очереди и т. п.) по отношению к вариациям
функций распределения времени обслуживания и интервалов между поступающи-
ми требованиями.
328
ся к качественному исследованию систем, описывающихся с помощью
марковских процессов специального вида. Заметим, что с помощью
подобных процессов могут, в частности, быть описаны кусочно-ли-
нейные и кусочно-непрерывные автономные агрегаты (см. гл. 6).
Вопросы, изучаемые в данной главе, во многом пересекаются с во-
просами, рассматриваемыми в гл. 12. Методы же их решения отличают-
ся принципиально. Ниже будут решаться задачи о вероятности нахож-
дения случайного процесса, описывающего функционирование слож-
ной системы, в фиксированной области фазового пространства, о ре-
гулярности и об ограниченности по вероятности этого процесса методом,
аналогичным второму или прямому методу Ляпунова, который широ-
ко используется в теории устойчивости. j
Данные задачи представляют значительный интерес на практике.
Например, если в системе массового обслуживания с ожиданием длина
очереди (или очередей) ограничена в некотором вероятностном смысле,
то это означает, в частности, что при реализации данной системы
можно в принципе выбрать бункер (или систему бункеров) конечного
объема для хранения требований, и при этом доля потерянных требо-
ваний может быть сделана сколь угодно малой. Если же ограниченно-
сти нет, то такой выбор принципиально невозможен. Задача о нахож-
дении траектории процесса в фиксированной области фазового про-
странства чаще всего возникает при рассмотрении процесса функцио-
нирования систем на конечных интервалах времени. При этом, как
правило, рассматриваемая область интерпретируется как множество
«допустимых» с той или иной точки зрения состояний системы. Задачи
этого типа имеют особое значение при рассмотрении энергетических
систем (например, систем автономно работающих синхронных преоб-
разователей частоты), систем, изучаемых в теории надежности, тео-
рии запасов и т. д.
В гл. 9 упоминался ряд особенностей метода Ляпунова. Здесь эти
особенности будут проиллюстрированы на примерах. Поскольку у чи-
тателя не предполагается предварительных знаний второго метода
Ляпунова, то изложение материала будет сопровождаться достаточно
большим количеством примеров, в том числе и элементарных, позво-
ляющих, как нам кажется, понять суть метода, его основную идею.
Кроме того, изложение ведется «в два этапа». На «первом этапе» со-
ответствующие результаты доказываются для марковских процессов
с дискретным параметром, когда доказательства могут быть проведены
методами, «традиционными» для теории цепей Маркова. На «втором
этапе» рассматриваются марковские процессы с дискретным вмешатель-
ством случая. При этом доказательства несколько усложняются и тре-
буют привлечения некоторых сравнительно недавно появившихся по-
нятий и результатов теории марковских процессов. Необходимый ми-
нимум сведений приводится в § 15.4.
Цель настоящей главы — показать, что, трактуя некоторые
известные задачи как задачи анализа устойчивости функционирова-
ния (в том или ином смысле), можно получить их достаточно эффек-
тивное решение (по сравнению, например, с решениями, приведенными
в гл. 12) с помощью методов, «присущих» теории устойчивости.
329
Следует отметить, что всюду ниже будут рассматриваться одно-
родные марковские процессы. Неоднородный случай может быть рас-
смотрен аналогично. Кроме того, расширяя множество состояний про-
цесса, можно привести неоднородный процесс к однородному.
15.2. ОСНОВНЫЕ РЕЗУЛЬТАТЫ (ДИСКРЕТНЫЙ СЛУЧАЙ)
Рассмотрим марковский процесс с дискретным временем. Пусть
гп — случайное значение процесса в момент п, Z — его пространство
состояний. Обозначим через' Р (z; £} переходную вероятность этого
процесса, т. е. Р [г; £) = Р \гп + ] g Е cz Z/zn = z]. Будем считать,
что время жизни процесса равно оо. Если бы это было не так (на
пример, процесс может быть определен лишь до некоторого случайного
момента времени), то путем введения фиктивного поглощающего со-
стояния, в которое переходит процесс в «последний» момент его жизни,
процесс становится определенным при всех п. Зафиксируем в Z не-
которое множество Q, Q с Z. Обозначим через tq (2), 2 £ Q, случайный
момент первого выхода рассматриваемого процесса с начальным со-
стоянием 2 из множества Q, т. е.
tq (z) = inf {п : zn Q/z0 = 2}.
Естественно считать, что те (г) = 0 для z Q. Фактически те (z)
является функционалом, заданным на реализациях рассматриваемого
процесса, и принимающим значением момента первого выхода траек-
тории из множества Q. Если некоторая реализация не выходит из
Q, то полагаем время выхода равным оо.
Пусть N оо — некоторый фиксированный момент времени.
Введем обозначение
т (2) = Af П Tq (2) = min (jV, tq (2)).
Заметим, что т (2) является, вообще говоря, случайным моментом вре-
мени. Полезно отметить, что если положить N = оо, то т (2) = (г);
если же выбрать в качестве Q все пространство Z, то т (2) = N*\
Ниже будет рассмотрен случай, когда Р (т (г) < 00} = 1, т. е.
с вероятностью 1 рассматриваемый случайный момент времени коне-
чен. Это свойство заведомо выполняется, когда N <Z 00. Если же
N = оо, то требуется, чтобы Р [tq (2) < 00} = 1. Предположим
*> Последнее равенство, вообще говоря, не выполняется в случае непрерыв-
ного времени. Это связано со свойством регулярности рассматриваемых про-
цессов.
я.чп
сначала, что N < оо. Пусть / (г) — некоторая (измеримая) функция,
заданная на Z. Введем следующие обозначения:
MJ- $ P{z;dy}f(y),
ufz
g(z)=Mzf—f(z),
M2{f(zx))= $ P {zT£dy/z0=z}f(y).
y'ez
Теорема 1. Для рассматриваемого процесса имеет место равен-
ство (при N < оо)
р (г) — 1
м2 {Ж (2)]}=f(z) + Mz X £(zft)
I k=0
(15.1)
(при условии существования написанных выражений).
Доказательство. По определению математического ожи-
дания имеем
Мг!Ж(г)1}=2 S ₽ е гА_2 6 <Э. !
k= 1 гь— i е<2
edzk_Jz0 = z} dzk}W +
^kaz\Q
~Ь § Р {^1 Е Q, • • • > Е Q> z] £ dzN_ j[Zq = z} x
2v-i 6 Q
X $ P {zN^l-dzN\f(zN').
(15.2)
Последнее слагаемое в (15.2) отличается от предыдущих, так как в мо-
мент N процесс может находиться в любом из состояний Z, в момент
жету<; N он может находиться лишь вне Q.
Обозначим для краткости k-й член суммы в (15.2) через Sk, а по-
следнее слагаемое — через Sjv. Таким образом, соотношение (15.2)
переписывается в виде
N— 1
М2 {/ [zx (z)]} = S sft4-Sw.
k= 1
(15.2)'
331
Пользуясь марковостью процесса и введенными обозначениями,
получаем
P{Zi£Q, zN_2e.Q, z^^dzN-i Jz0—z}X
e<?
X [f(2iV_1)+^(Z1V_l)]^
S P € Q’ • • • > 3 € Q> 2Л'—2 € d-ZZq =- Z } X
x $ p(2.v-2; dzN_l}f(zN_j+
ZN-\eQ '
+ M2{x[4z)>^-l]gr(z^1)}, (15.3)
где % (Л) — индикатор'события A.
Из (15.3)
S.v^s,v-i = Sv-i +M2{x[t(z)>?V— (15.4)
Подставляя (15.4) в (15.2'), получаем
Mz{/[zT (г)]} = *2 sa + Sa_1+Mz(%[t(z)>jV—
Продолжая эту процедуру N раз, находим
M2{f[zt (2)]-/(z)+ 2 М2 {х h (г) > k] g (гй)}. (15.5)
k= о
Поскольку
2 M2{x[r(z)>Z:]^(zfe)} = М2| f g(zk) 2 Xh (г) = r]! =
А= 0 1а= о r=k+ 1 )
-М2 | 2 х(т=г) 2 g(zfe)! = M2! 2 £(гь)|. (15-6)
I, г= 1 о ) и = о )
то из (15.5) и (15.6) следует утверждение теоремы.
Следствие 1. Если Р {tqС оо} = 1, то
| х<?<г) ~1 1
M2{f[zT (Z)]}=/(z) + M2 £(гь) • <15-7)
у I *=о j
Доказательство получается непосредственно из утверждения
теоремы, поскольку в рассматриваемом случае
Мг {/12% (г)]} = Нт М2 {/ [гх (2)]}
Q jV->00
и
X lTo (г) = И = Нт X [Т (г) = г].
332
Следствие 2. Пусть / (z) = 1 — Xq (2)> где Xq (2) — характе-
ристическая функция множества Q, т. е. принимающая значение 1 в
точках z £ Q и 0 в противном случае. Тогда из равенства (15.1) сле-
дует, что при z g Q
Р{т (z)<A/} = M Г £ g(zh)
4 I Л = 0
[Т(2)-1 1
= Mj 2 P{zfe;Z\Q),
Н=о )
(15.8)
поскольку
мг {1 -XQ [гх (г)]} = р {т0 (г) <7}, g (г) = Р {г; Z \ Q).
Рассмотрим задачу о времени пребывания процесса (zn) в фикси-
рованном множестве состояний Q пространства состояний Z. Как не-
однократно говорилось (см., например, гл. 9), эта задача является
вероятностным аналогом задачи практической устойчивости. Естест-
венно поэтому попытаться сформулировать теоремы, позволяющие ре-
шить указанную задачу, аналогичные в некотором смысле теоремам,
эффективно используемым в теории устойчивости. Следующая теоре-
ма является «представителем» теорем такого рода.
Теорема 2. Пусть в пространстве Z зафиксировано некоторое под-
множество Q и задана функция V (z), такая, что V (z) 1 — х<г(2)-
Пусть функция A (z) удовлетворяет неравенству
A(z)>M, V — V (z). (15.9)
Тогда
Р{т (z)<A/}<E(z) + M Г 2 ^(zJ. (15.10)
4 1 А = 0 )
Доказательство. Полагая в (15.1) / (z) = V (г) и учи-
тывая (15.9), получаем
Mz{V[zt (г)]}<К(г) + Мг {Х(у ‘ A (zj! .
I k = Q J
(15.11)
Неравенство (15.10) непосредственно следует из (15.11) и того факта,
что
Р {тс (г) < А} = Мг {1 -Х(? (2t (г)» < Мг {V [zT (г)]}.
Следствие 1. Если А (z) 0 при всех zgQ и доопределить
Д(г) = 0 при z^Q, то из (15.10) следует, что
P{tq(z)<A/}<V'(z) + 721MzA(z)1).
v k = 0
В частности, если А(г) <А, А>0, то
P{tq (z)<V}<|/(z) + WA.
(15.12)
(15.13)
333
Следствие 2. Пусть А (г) 0 при всех z g Q. Тогда, как следует
из неравенства (15.13),
P{rQ(z)<N} <V(z)
при любом N. Отсюда
Р{т0(г)<оо}<И(г). (15.14)
Следствие 3. Если можно выбрать функцию А (г) в виде А (г) =
= RV (г), то имеет место оценка
Р{\>(г) < V(z)(l +7?)". (15.15)
Примеры применения полученных результатов будут даны в сле-
дующем параграфе.
Сейчас же обратимся к другой задаче, также существенной как
с теоретической точки зрения, так и с точки зрения приложений.
Именно, рассмотрим вопрос об ограниченности по вероятности изучае-
мого процесса, которая есть не что иное, как вероятностный аналог
устойчивости по Лагранжу (см. гл. 9). Напомним, что процесс [гп]
ограничен по вероятности, если для любого е > 0 существует такое
ограниченное множество ЕЁ cr Z, что Р [гп £ Ее] > 1 — е при
каждом м > 0.
Обратимся к изучаемому процессу и предположим, что в множе-
стве Z существует единственное подмножество С, обладающее следую-
щими свойствами:
1) P{z; Z\C} = 0, zEC;
2) если C'aZ— такое подмножество Z, что Р {z; Z\C'} = 0,
г g С, то С Щ) С.
Чтобы пояснить смысл введенного предположения, дадим не-
сколько примеров цепей Маркова с конечным и счетным числом со-
стояний и найдем для них множество С.
Пример 1. Пусть матрица переходных вероятностей цепи Маркова
имеет вид
-1/з 2/3 0 0 -
’А 0 0
0 Ч2 Ча 0
_ 0 0 3/4 1/4 _
Для такой цепи множество С состоит из двух состояний: 0 и 1. Множества
С' = {0, 1, 2} и С" = {0, 1, 2, 3), последнее из которых совпадает с Z, также об-
ладают тем свойством, что P(z; Z\C') = 0, z£C', и P{z; Z\C"}=0, z^C". Ясно,
что C'ZDC и C"zdC. Нетрудно видеть, что для такой цепи процесс «в конце кон-
цов» попадает в множество С и там остается.
Пример 2.
1/3 2/3
1/4 3/4
0 1/2
0 0
*- о о
О О 0
ООО
1/2 0 0
1/3 1/3 1/3
0 О 1 -
334
Для цепи Маркова, определяемой такой матрицей, указанное свойство не
выполняется, поскольку для каждого из непересекающихся множеств: С\ •=
= (0, 1} и С2=(4} справедливо Р{г; 2\Ср = 0, z^Q, и P(z; Z\C2} = 0, z £ С2.
Предельное распределение состояний цепи в данном случае существенно
зависит от начального состояния. Так, если г0 £ С1( то предельное распреде-
ление сосредоточено в подмножестве Сх, а если z0 £ С2, то в С2.
Пример 3.
ГО 1 О О О ..."
О О 1 о о ...
Р= О О 0 1 о ... •
Для каждого из множеств Ck вида Ck = {k, k + 1, ...} справедливо
P{z; Z\Cfe} = 0,z £ Ck- В этом случае указанное множество С = Игл С
ь- оо k
= 0, где 0 —пустое множество. Предельная вероятность нахождения цепи
в любом из ограниченных множеств равна 0.
Если для процесса выполняется сделанное предположение, то
говорят, что С — единственное минимальное инвариантное множество.
Дополнительно потребуем, чтобы множество Z\C (в случае С#=0)
было несущественным множеством состояний, т. е. таким, для ко-
торого P[z„ £ Z\C7z0} -> О при любом z0 £ Z. Тогда, если С=# 0,
М—>оо
то lim P(zn £ C/z}= 1 при любом z0 £ Z. Если же С = 0, то по-
/г-*- оо
требуем, чтобы для любого ограниченного замкнутого множества
Kc.Z выполнялось равенство lim P(zn £ Л} = 0.
п->0
Рассмотрим еще один пример, поясняющий смысл введенного дополнитель-
ного требования.
Пример 4. У цепи, задаваемой матрицей
“10 0 0 0 . . . '
р О 1 — р 0 0 ...
pk О О О
существует единственное минимальное инвариантное множество С = {0[. Однако
с вероятностью, большей чем 1—(р + р2+...)=(1—2р)\(1—р), цепь не поки-
нет множества Z\C={0 1,2,...), т. е. в этом случае множество Z\C не яв-
л яется несущественным.
Таким образом, мы ограничиваемся рассмотрением лишь таких це-
пей Маркова, которые имеют одно минимальное инвариантное множе-
ство, а дополнения к нему есть несущественное множество состояний*’.
*>При рассмотрении процессов с непрерывным временем (см. ниже) будут
сделаны предположения, несколько отличающиеся от данных. Аналог этих пред-
положений может быть с очевидностью использован и для «дискретного» случая,
и наоборот. Заметим, что в «непрерывном» случае доказательства являются бо-
лее замкнутыми в том смысле, что требуют привлечения меньшего количестве
дополнительных сведений о поведении рассматриваемого марковского процесса.
331
Если С у= 0, то возможно три типа поведения цепи:
1. В множестве С цепь является эргодической, т. е. у нее сущест-
вует единственное стационарное распределение lim Р{ zn С Е с С],
п —> оо
не зависящее от начального состояния цепи.
2. Множество С состоит из d непересекающихся подмножеств
(циклическихподклассов) Clt Cd,Ci f] Cj = 0,t'#= j, (J С, = C,
L
таких, что Р{г;Сг} = 1 при всех z£C;_i, i = 2, ..., d, P{z;C1) = l
при всех z £ Cd, и для всех i, j d и z £ Ct существуют предель-
ные вероятностные распределения
lim Р {znd+i-i eE<^Cj/z0 = z£ CJ,
n->oo
ие зависящие от z. В перечисленных случаях, естественно, процесс
ограничен по вероятности.
3. Для любого ограниченного замкнутого множества К из Z спра-
ведливо lim Р [zn £ Ё) = 0, в частности для любого /(с С выпол-
П-*-ао
няется равенство lim Р [zn £ Л) = 0.
П-*ОО
Докажем теперь теорему для процессов Маркова с дискретным
параметром, дающую достаточные условия ограниченности по вероят-
ности. Предполагаются выполненными указанные ограничения.
Теорема 3. Пусть в пространстве состояний Z рассматриваемого
однородного марковского процесса с дискретным параметром сущест-
вует единственное минимальное инвариантное множество. Пусть
{G>)^Li — последовательность замкнутых ограниченных измеримых
подмножеств фазового пространства процесса такая, что
Gr+1=iGr, lim GT = Z.
r->oo
Если в Z задана функция V (г) такая, что выполняются условия:
1. 0< V(z)<Z оо, z g Z.
2. Существует функция A (z), для которой:
a) Mz V — V(z)< A (z), z£Z,
б) sup А (г) = А+ < оо, А+0-0,
26Z
в) —АД = sup A(z)< 0 начиная с некоторого г0^ 1 (очевидно,
2 е z \ ог
А* при г Д k), то при любом г £ Z последовательность [гп\ ог-
раничена по вероятности*’.
Доказательство. Зафиксируем z0 С Z. Положим в ра-
венстве (15.1) Q = Z, Т = п (тогда т (z) = п) и f (z) = V (г). Выберем
*> Если множество состояний цепи счетно, то из данной теоремы можно по-
лучить известный критерий Мустафы [13]. Заметим, что ниже при этом получает-
ся еще и оценка предельного распределения.
336
г таким, чтобы выполнялось условие 2в. Воспользовавшись условиями
2а и 26 настоящей теоремы, получим из (15.1)
{V (?„)}-V (г0) < Мг. ("S A (2ft)) =
1*= о J
л—1 . п—i(
= 2 J P{zk(dy/z0}A(y) = 2 $ P{zk€dy/z0}A(y) +
*= о z fc= 0 I О
C n— i
+ \ P {2ft € dylzQ} A (y)} {P {2ft £ GTlzQ} A+—
Z \ Gr k = Q
n — 1
-P{2jl£Z\Gr/2o}Ar} = 2 {(A+ + Ar")P{zh€Gr/2o}-A7). (15.16)
4 = 0
Предположим, что процесс не ограничен по вероятности. В силу
сделанных предположений это возможно лишь в случае, когда для
всякого замкнутого ограниченного множества К
lim P{ze е К} =0,
s -*оо
в частности, когда
lim P{2ft g Gr/z0} =0 (15.17)
Поскольку A+ < oo, Ar > 0, V (г0) < oo, то из (15.16) и (15.17)
получаем, что существует такое (достаточно большое) число N, для
которого
Мг.{И(2„)}<0.
(15.18)
что невозможно в силу неотрицательности функции V. Теорема до-
казана.
Из соотношения (15.16) можно получить оценку нормированной
<V — 1
суммы — У Р {2fe £ Gr/z0}, которая в рассматриваемом случае
N 4 = 0
не зависит от г0. Из (15.16) имеем
infI/(2)CM2oV(2jv)<V(2o) +
г 6 Z jv j
+ (д+-АГ) 2 P{2n€Gr/2o}-tfA7. (15.19)
п = 0
Отсюда
Л' - 1
4- 1 P{zntGr/z0} > —--Гдг—J-(V(2o) —inf V(2))l (15.20)
n=о Д+ + ДГ L N гег J
Устремляя в (15.20) оо, получаем
w-1 д_
lim 4 2 Р{гпеад>—(15.21)
N п^*0 Д+4-Д7
337
Если величина Л 7 -> оо при г -> оо, то правая часть неравенст-
ва (15.21) стремится при этом к 1. Неравенство (15.21) может служить
односторонней оценкой стационарного распределения (в случае его
существования).
Теорема 3 дает достаточные условия ограниченности по вероят-
ности рассматриваемых процессов. Однако аналоги прямого метода
Ляпунова можно использовать и для доказательства отсутствия такой
ограниченности. В частности, для этой цели можно использовать след-
ствие 2 теоремы 2.
Теорема 4. Пусть процесс [гп] и множества Gr те же, что и в
теореме 3. Пусть следствие 2 теоремы 2 выполнено для каждого множе-
ства Qr = Z\GT и соответствующая пробная функция VT (z) удовлет-
воряет условию sup Vr (z) = Vr-< оо. Пусть V = sup Vr< 1.
2 r
Тогда процесс (zn) не является ограниченным по вероятности.
Доказательство. Утверждение теоремы следует из не-
равенства (15.14), поскольку для процессов рассматриваемого типа
в случае их ограниченности по вероятности при каждом г, начиная
с некоторого должно выполняться равенство
Р<Тг\ог(г)< °о} = 1.
Из формулировок приведенных теорем следует, что они могут
применяться, если известна или построена некоторая пробная функция
V, удовлетворяющая определенным условиям. Поэтому одна из основ-
ных проблем состоит в выделении класса систем, для которых эта функ-
ция является, например, представителем выбранного семейства функ-
ций. Проблема эта достаточно сложна и не получила.полного решения
даже для классических задач устойчивости.
Вместе с тем следует подчеркнуть такие особенности излагае-
мого метода, как общность методики исследования задач разного ха-
рактера, достаточная простота в применении метода, а также возмож-
ность получения необходимых количественных оценок наряду с чисто
качественными выводами.
15.3. ПРИМЕРЫ
Пример 1. Вероятностный автомат с двумя состояниями. Рассмотрим авто-
номный вероятностный автомат, имеющий два внутренних состояния {1, 2}.
Его вероятности перехода следующие:
рн=1—а, Р12 = а, р21 = 0, р22 = 1. 0<а<1.
Таким образом, состояние 2 является поглощающим.
Пусть при совершении перехода 1 -> 1 автомат «приносит доход» с± > О,
при совершении перехода 1^-2 — убыток с2 > 0, а при совершении перехода
2 -»2 — доход с3 = 0. Пусть в момент 0 автомат находится в состоянии 1. Зада-
чей является определение функции распределения суммарного дохода, «прино-
симого» автоматом. Пусть т — может первого попадания автоматом в состояние 2,
т. е. z(t) = 1 при i < т, г(т) = 2. Очевидно, суммарный доход равен с^т — 1) —
с2. Таким образом, задача свелась к нахождению функции распределения момента
выхода автомата из множества состояний Q = {1). Прежде чем решать ее, ука-
338
жем, что подобная задача возникает, скажем, при рассмотрении работы переда-
ющего устройства, расположенного на космическом объекте. При этом состояние
1 соответствует исправной работе этого устройства, а состояние 2 — отказу,
наступившему, например, из-за столкновения с метеоритом. Тогда доход су соот-
ветствует ценности той информации, которая передается с борта объекта, а с2 —
затратам на установление связи с неисправным передатчиком.
Выберем функцию V’(z) =1 — (2). Найдем Д(г)
2
Д(1)= 2 PizV(z)-V(l) = p12V(2)=ce, Д(2) = 0.
2 = I
Применим следствие 1 теоремы 2 [в частности, оценку (15.15)] для нахождения
функции распределения величины т = т^(1):
Р [т < М] < Ма. (15.22)
Отметим, что точное решение задачи следующее:
Р (тс. Л/} = 1— (1—ce)v
Приведенное решение можно использовать также для решения следующей
задачи. Рассмотрим распространенную схему, изучаемую в теории надежности.
Имеется система, состоящая из двух элементов. Один из элементов являет-
ся рабочим, а другой находится в ненагруженном резерве. В момент отказа
рабочего элемента на его место становится резервный, отказавший элемент посту-
пает на ремонтное устройство. Считается, что система отказывает, если в момент
выхода из строя рабочего элемента второй элемент находится в ремонте. Пусть
время безотказной работы элемента является сл-учайной величиной, имеющей
функцию распределения F(x), а время ремонта элемента'—случайной величиной
с функцией распределения G(x). Указанные случайные величины предполагаются
независимыми. Пусть в начальный момент времени оба элемента исправны и один
из них только что начал работать. Рассмотрим систему в момент, непосредствен-
но следующий за отказами рабочего элемента, и примем за ее состояние в эти мо-
менты — число отказавших элементов.
Смена состояний системы происходит, очевидно, в соответствии с цепью
Маркова, имеющей следующие переходные вероятности (положим, для опреде-
ленности, отказовое состояние поглощающим):
Роа = Роа= Рю = 0;
Р<,1= 1;
ОО
Ри = $G(x)dF(x)-,
о
Pi2= f [1 —G (х)] dF (х) = се;
0
Раа=И
p2i = 0, 1 = 0,1.
В данном случае Q = {0, 1}. Поскольку состояние 0 невозвратно, то
M°)=tq(1) + i-
Следовательно,
Р{то(0) <M+1} = P{tq(1) <Л/}_
Оценка величины Р{т^(1) N} дается неравенством (15.22).
Ниже будет показано, как можно воспользоваться полученными оценками
для оценки надежности рассматриваемой системы, которая работает в «непре-
рывном» времени.
339
Пример 2. Резервированная система с постоянным временем восстановле-
ния. Рассмотрим систему, состоящую из одного рабочего элемента, имеющего
случайное время безотказной работы с функцией распределения F(x), п резерв-
ных элементов (резерв ненагруженный), п ремонтных мест. Характеристики всех
элементов идентичные. Предположим, что время ремонта вышедшего из строя
элемента постоянно и равно Vp..
Вновь рассмотрим систему в моменты, непосредственно следующие за вы-
ходом из строя работающего элемента. Скажем, что в этот момент система нахо-
дится в основном состоянии v, если имеется v неисправных элементов. Будем
характеризовать систему в основном состоянии v > 1 дополнительными перемен-
ными Г)1( т]2, ..., r]v, являющимися временами до окончания ремонта вышедших
из строя элементов. Удобно в каждом основном состоянии v так пронумеровать
дополнительные переменные, чтобы они были упорядочены по принимаемым зна-
чениям: т)1 < 1)2 ... < t]v. В силу сделанного предположения 0
1/ц, j v. Очевидно, что в рассматриваемые моменты времени процесс с
состояниями z = (v, th, ..., r]v) является однородным марковским с дискретным
параметром. Поскольку состояние v = 0 является невозвратным, ниже будут
рассматриваться лишь значения v > 1.
Будем считать, что система находится в «отказовом» состоянии, когда все
элементы неисправны. Это соответствует следующему выбору множества Q:
Q = {z = (v, Лщ • • •> nv):v <«}.
В качестве функции V(z) возьмем следующую:
V[(1,t)1)]=0,
п— 1
V [(« — /, V Пп-/)1= S (п*_—
*=/ + 1
- F\ (ПА_/ _ 1)] > 0</<п—2,
V (n —1) = 1.
Здесь принято, что т|0 = 0, Fk — fe-кратная свертка функции F. По ин-
дукции несложно показать, что
v (z) > Р {tq(z) <ге- 1}.
Найдем теперь функцию Д(г). Пусть z = (v, т],.r]v). Тогда, очевидно,
v ’'а Г ] \т
М2У —У(г)=» f dF(x) V (v-fe + 2, T]fe, .... Tlv) — +
* = > L P /J
+ [ rfF(x) У Г( 1, — Yl-V(z).
Нетрудно показать (например, воспользовавшись индукцией), что при
2= (П-/, Т)1..... Пл_/)
v - V (г) < F" (Т)„ _ (!)„_,._ 0.
Следовательно, если выбрать Д = /г" (1/р,), то
МУ —У(г)<Д, z С Q-
Применив следствие 1 теоремы 2, получим
Р {т^ (г) < N} < V (г)Н-(1/р). (15.23)
340
Заметим, что если обозначить l/X=»JxdF (х), то Fn (1 /р.)->• 0 ири
о
Х/р, -> 0. Кроме того, Е"(1/р) -+ 0 при фиксированных X и р. В частности,
* п-*оо
, XV'
если F (х) =е— тКх —-— (распределение Эрланга), то
j=m !'
rj(l/p)=e-m*/.u -у(тХ/р)/.
/ = пт
Если Х/р мало, то
Р" (1/р) =-^Г M/p)'lm [ 1 + е (Х/Р)], (15.24)
где е (Х/р) 0 при Х/р -> 0.
Если п велико, то
Fn (1 /р) = е ~тК/“ —Ц- (шХ/р)"т [ 1 + —1— e0mX^ mX/pl =
* (пт)! |_ тп+1 J
= е-/пХ/м._!_ (тХ/и)""1(1+е„), (15.25)
(пт)!
где 0 < 0 < 1, а е„^0 при п ->• оо.
При т= 1 выражения (15.24) и (15.25) дают соответствующую асимптоти-
ку для экспоненциальных распределений.
Пример 3. Система массового обслуживания с отказами. Рассмотрим си-
стему обслуживания с одним прибором, рекуррентным входящим потоком, оп-
ределяемым функцией распределения F(x), и функцией распределения времени
обслуживания G(x). В случае занятости прибора требование ожидает окончания
обслуживания лишь в том случае, если нет больше ожидающих требований.
Иначе говоря, количество мест для ожидания равно 1.
Пусть мы интересуемся долей потерянных требований. Более точно, нас
будет интересовать функция распределения числа требований, поступивших в
систему до первой потери требования. Для этого рассмотрим систему в моменты,
непосредственно следующие за моментами поступления. Тогда работу системы до
момента потери требования можно описать вложенной цепью Маркова со следу-
ющими состояниями:
z-= 1 — в системе имеется одно требование (следовательно, оно только
что поступило на обслуживание);
z = (2, t]) — в системе имеется два требования, из которых одно только
что поступило на обслуживание, а другому осталось ждать время г] до оконча-
ния обслуживания;
2=3 — вновь поступившее требование получило отказ (поглощающее
состояние).
Поскольку состояние 2=0 (система пуста) является невозвратным, его
можно не рассматривать.
Переходные вероятности процесса имеют вид;
ОО 00
Р{1; 1} = [ G(x)dF(x); Р {1; (2, <й])} = f dF (х) G (х+т));
О х = 0
оо
Р {(2, П); 1} =f dG (х) [1-F (х+n)];
о
341
Р [2. -и; (2,<ф) = j' dF(x)^G(x + £-i]);
Р ((2, л); 3)=F(T]); Р{3;3} = 1.
Остальные переходы совершаются с вероятностью 0.
Выберем в качестве V(z) функцию P(z; 3}, т. е. 7(1) = 0, V(2, i]) = F(q),
(V3) = 1. Тогда имеем
A (1) = M,V — V (1) = f dF(x) J F^^Gfx + r)),
x = 0 T] = 0
Д(2,т]) = М(2 )V-V(2,t])= f dxF(x + n) J F(g)^G(x + £).
x=0 g=0
Очевидно, A(2, 0) = A(l).
Легко проверить, что в данном случае А(2,1]) -» 0 при т] . Это дает
возможность воспользоваться неравенством (15.13), полученным в следствии I
теоремы 2. Для этого .достаточно взять
A=max(A(2), A (I)), (1э.26)
где А (2) = max А (2, т]) .
Рассмотрим более подробно случай, когда функции F и G являются эрлан-
говскими распределениями:
k = m
F(x)=e nU V
k =п
Обозначим р = Л/ц. Несложно проверить (предоставляем эту проверку читателю),
что
v]) = (пР/тУг "V' сг у (г + /г)! (/?t —1—г + 'г —1)! =
(т — 1)! (п — 1)! k\ (1+ iip/tn)k^ т+п
= (пр/т)2п С|"+ ,п_ j До (р2'1)-
Несколько более громоздкое выражение получается для Д(2, т]). Рассмот-
рим частные случаи.
1. n = m = i F (х) = 1 —е—?л, G (х) = 1 -е“»“.
Тогда легко проверить, например, непосредственно вычисляя выражение для
А(2, 1]), что
Д(2)=Д(2, 0) = Д (1) = Д=р2 + о (р2).
2. « = 1, т = эо, F (х) = 1 - е ~ G(x)=|°’ Х < И ’
(1, х > р,-1.
В этом случае
Д(2) = А(2, 0) = А (1) =A = F2 (1/ц) = р2/2 ф- о(р2).
342
В этом случае
А (2) = А (2,1/X) = 1 - G (1/1), А = Д (2) = 1—0(1/1).
В частности, если G (х) = 1—е~,1Х, то Л = е~1/,р.
В примерах величины А выписывалось с точностью до о(р2). Можно было
найти и их точные выражения. Из полученных оценок следует, что вероятность
потери требования уменьшается при уменьшении коэффициента вариации одно-
го из законов (F или G), причем большее влияние оказывает изменение коэффи-
циента вариации закона F.
Пример 4. Резервированная система с одним рабочим элементом, двумя
элементами, находящимися в ненагруженном резерве, и двумя ремонтным иустрой-
ствами. Рассмотрим эту систему в моменты времени, непосредственно следующие
за моментами отказов работающего элемента. Состояния системы следующие:
2=0 — все элементы исправны;
2=1 — один элемент находится в ремонте и, следовательно, он только
что отказал;
2 = (2, т|) — в ремонте находится два элемента, из которых один только
что отказал, а другому осталось ждать время г] до окончания ремонта;
2 = 3 — все элементы неисправны (поглощающее состояние).
Вновь состояние 2=0 является невозвратным и мы его рассматривать не
будем.
Заметим, что пример 3 можно интерпретировать в «надежностных» тер-
минах как систему с одним рабочим элементом, двумя, находящимися в ненагру-
женном резерве, и одним ремонтным устройством. Переходные вероятности вло-
женной цепи Маркова, построенной по моментам отказов, имеют вид:
Р {1; l)=f G (х) dF(x);
О
оо
Р{1; (2, dn)}= f dF(x)d^G(x + rfr
х — 0
оо
Р{(2, tj); 1) = J G (х) dF (х);
и
Р{(2, п); (2, dg)} = -G(n-g)d6F(n-g)4-
ОО
+ J dF{x)diG(x + l);
Х = Т]
П
р f(2, Т)); 3} =pF (X) [1-G (х)];
О
Р{3;3)=1.
Остальные переходные вероятности равны нулю.
Снова выберем
V (г) = Р {г; 3); V(l)=0;
V(2, n)=JdF(x)[l-G(x)]sa(T1); V(3) = l.
0
343
Функция а(т]) является неубывающей. Обозначим а = lim a(t]). Заметим, что
л
для высоконадежных элементов а является малым параметром. Найдем Д(а) =
= М2 V — У(г):
Д(1)= f dF (х) f a(T)dTG(x+T);
х=0 Т=0
Л
Д (2, т]) = J dF (х) G (х) а (т]— х) +
о
+ f dF (x)f a(T)dtG(x+T).
л о
Воспользуемся неравенством (15.12). Для этого нужно оценить величину
МД(гА) = Р (2ft= 1} Д (1) +
+ 1 Р {гй = (2, g), g е (Г], T) + dr|)} А (2, П) •
о
Задача свелась к нахождению или оценке вероятностей Р(2^ £ Е с: 2),
что представляет собой достаточно трудоемкую и не всегда выполнимую работу.
Тем не менее покажем, как для рассматриваемой задачи при некоторых предпо-
ложениях относительно вида закона G(x) эта трудность может быть преодолена.
Рассмотрим такие законы, для которых при всех неотрицательных х, t
G(x+0—б(х) >_G(/)[1 — G(x)].
Если это неравенство переписать в виде
>G(0.
1— G(x)
то ему можно придать следующий вероятностный смысл: вероятность того, что
влемент, который уже ремонтируется время х, будет исправен через время t,
не меньше вероятности того, что время ремонта элемента не превышает t. Тогда
функцию распределения и «остатка» времени ремонта в основном состоянии
2 (обозначим ее Р2(х)) можно ограничить снизу функцией G(x). Поэтому,
если /(т]) — монотонно возрастающая функция т], то
J f.(x)dP2 (х) <p(x)dG(x).
о о
Отсюда следует, что
Мг Д (zft) < max | Д (1), J 6 (2, х) dG (х)|, (15.27)
I о J
где в качестве 6(2, т|) взята любая неубывающая функция т), такая, что 6(2, т]) >
> Д (2, т]). Ниже преимущественно будет использована следующая неубываю-
щая функция:
Л’
6 (2, т|) = J G (х) а'(г)—х) dF (х) + Д (1) > max (Д (1), Д (2, т])).
о
Из соотношения (15.27) имеем
М Д (zA) < J </G(x) [Д (1)+ J dF (х) G (т) а (х—т)] = Д.
о о
344
Выпишем значение V(2, t]) = а(г]) и Д для различных частных видов G(x),
когда F(x) -= 1 — е—UJC, не приводя промежуточных достаточно утомительных
вычислений.
1. G (х)= 1 — е—р = Х/ц;
a(D=^[i-e-<*+|l”1l;
3
Д = —р2 + ° (Ра)-
4
В этом случае элементарно находится точное выражение для МгД(2д).
В самом ' "
скольку
деле, пусть — число неисправных
Р2(х) = 1 — е“1ХЛ:, то
в момент
по-
Mz Д(гА) = P(vft= 1}Д(1) + Р {vft = 2) [ Д (2, х) ne~^dx.
'о
Так как
f" Д (2, х) [ie цх^х = Д (1) = -^- +о (р2),
0 2
то
Ра
MzA(zft) = A(l) = -!|- + o(p2),
2.
(0, х < и, *,
йМ-{|.х>Д '
If (и ), Л > р."
Р2
Д = Д(1)=^ + о(р2).
p =
Заметим, что такая же оценка была получена в примере 2.
3. G(x)=e~m'1* 2 (mpx)ft; р = Х/р;
k — m
а(П) = -^ Ё -----ЦгГг(1-е_<Х+тЦ)’1 3 — [(Ь + 'пЮЧ2
/пй = о (1+р/т)*+* I r = o rl
Л = Р2(у+ Рт]+о(р2), (15.28)
где
+ "S' i C^+r_12-r(fe-r+l) +
2 т2 ( 4=о г-о
т—1 k 4-1 2 т—2 Л4-1
+ 3 (*+1) 3 ^ + г_,2-г+ 2 (2т—1 —fe) 2 Crm+r_,2-r
k =0 r=0 k = tn r = 0
(15.29)
345
Вычисления величины pm при различных значениях т показали, что зависи-
мость Д от т достаточно хорошо аппроксимируется следующей зависимостью:
— [1 +------------------
2 L 2 (5 + 6С2)
+ о(р3),
где С — коэффициент вариации закона G(x)*\
О, х < у,
4. G(x) =
е v) У -L [тр. (х — у)]А, х > у;
k = m kl
р* = к/р, р = р* + +у, у > 0;
a (t]) = F(ti) при г, < у,
m—1
a(n) = F(y)+e-Xv Р*
а = о
[1—ехр (—(% + »гр) (т]—у)} X
х ij — l(^+mP) (n-v)lr] при Г| > у;
r = 0 И
р2
Д = у + ЗтР*2-| О (р2),
где коэффициент 0т определен формулой (15.29).
Уточнение полученных оценок может вестись несколькими путями. Одним
из возможных путей является более точная оценка условного распределения ве-
личины т] в состоянии v = 2. Другой путь применительно к рассматриваемому
классу распределений G, который, естественно, может сочетаться с первым,
состоит в нахождении наименьшей неубывающей функции 6(2, г]) > Д(2, т]). В ка-
честве простой иллюстрации сказанного улучшим оценку для случая G(x) =
= 1 —е—с помощью нахождения минимальной неубывающей функции 6(2, т|) >
> Д(2, г]). Для рассматриваемого случая
Д (2, т1) = —Д-е-^ (1 +р)+е - (Х+^)Т’ [гГТ + Р+п]} +
1 + p U + P U+P JJ
______В!_____g(x+юп
(2 + P) (1 + Р)
Можно показать, что Д(2, 1]) < Д(1) при 1] < 1/ц, а при г) > 1/р. функция
Д(2, т]) монотонно возрастает. Несложно найти точку т]* такую, что т)* > 1/р. и
Д(2, т]*) = Д(1). В данном случае т]* = с/р, где с ж 1,77. Таким образом, ми-
нимальной функцией 6(2, т|) является следующая:
6(2, ri) =
( Д (1) .
(д (2, п).
г] <: г)* ж 1,77 р 1,
П > г)*-
В этом случае
Д = [ 6 (2, х) dG (х) = Д (1) + р2 е~с [— 1,5 + с + е-е (1,5 + 0,5с)] +
о
+ о (р2)^0,615р2 + о(р2).
*> Если гп и а2 соответственно среднее и дисперсия некоторой функции рас-
пределения, то ее коэффициентом вариации называется отношение а]т.
346
Отсюда видно, что с помощью более точной мажорации функции Д(2, г|) удалось
улучшить оценку приблизительно на 20% по сравнению с ранее полученной
(0,75 р2 + о(р2)).
Ниже для простоты изложение будет вестись в «надежностных»
терминах, хотя сами результаты имеют более общий характер.
Основную трудность при практическом использовании теоремы
r-v(z)— 1 1
2 составляет вычисление величины Mz j 2 Д (zft)?. На примерах
было показано, как в некоторых случаях эту трудность можно прео-
долеть. Вместе с тем не было предложено способа, пригодного для до-
статочно широкого класса, позволяющего избежать указанной труд-
ности. Ниже предлагается один из возможных способов.
Обычно на практике приходится иметь дело с высоконадежными
системами. Это означает, что имеется некоторый параметр а, принимаю-
щий значения из пространства .А и характеризующий рассматривае-
мую систему (число резервных элементов, надежность отдельного
элемента и т. д.), такой, что если а а0, то надежность системы воз-
растает до 1. При а = а0 система считается абсолютно надежной. В со-
ответствии с этим рассмотрим цепь Маркова, определяемую некоторым
параметром а, и предположим, что при a g О (а0), где О (а0) — неко-
торая окрестность точки а0, у цепи существует стационарное распре-
деление, быть может зависящее от начального условия. Тогда, если
Д (г) — функция, для которой написанные ниже выражения имеют
смысл, то при a g О (а0) существует
N
Д(2)= lim 4 2 Мг{Д(гд)}. (15.30)
Фактически нам потребуется существование в (15.30) лишь верхнего
предела.
Пусть Д (z) 0. Если при каждом a £ О (а0) существует число
ka i> 0, такое, что для всех N 1
(15.31)
то как следствие получаем
Мг( 2 A(zfe)!<A/A(z) + &a.
(4=1 J
(15.32)
Заметим, что условие (15.31) выполняется для эргодических
процессов Маркова во многих практически важных случаях.
Покажем, что предположение об эргодичности процесса не нару-
шает общности для рассматриваемых задач. Предположим, что Mtq(z) <
< оо. Обозначим
Д(2)
М2
т<2
2 А(гй)
4 = 1
(15.33)
1
М та (г)
347
Рассмотрим марковский процессе возвращением {zfe}, который при
fe = 1, tq (г) совпадает с исходным, а в момент tq (z) + 1 вновь
попадает в точку z и начинает развиваться заново. Полученный про-
цесс {zft} является регенерирующим*’. Время между моментами ре-
генерации (моментами попадания в точку z из множества Q) распреде-
лено по закону
А(х) = Р{tq (z)<х — 1}, х^2; Л(1)=0.
Для простоты предположим, что А (х) не является арифметическим рас-
пределением с шагом, отличным от 1. Очевидно, что поведение исход-
ного процесса {zft} до момента tq (z) полностью совпадает с поведением
Ы •
Пусть ф (п, Е) = Р |tq (z) п, zn £ Е a Z/z0 = г}. Тогда, как
известно из теории восстановления, существует вероятностное рас-
пределение
Р {z; Е} =? lim {z; Е} =------?--- У ф (k, Е) =
n->-oo М Tq (г) k__ j
= » 1 z ч 2 Р {т<2 & >k' £/го = г},
м(г) 4=1 V
где Р<п> {г; Е} = Р {zn £ E/z0 = z\, и, следовательно, процесс {гп}
является эргодическим. Тогда существует
N
Iim т 2М‘ <*У}Д(У)^Д(4
W ->оо п k= , z
Покажем, что A(z) = A(z), где А (г) определяется соотноше-
нием (15.33). В самом деле,
TQ (г)
СО k
— 1 / С 2 2 $P{tq(z) = 6, z^dy/z0 = z}A(y) =
М XQ (г> k= 1 j= 1 Z
ОО
= ТГ 1 /Т~ 2 $ Р{то (г) >/> zi € dy/zo = z) А (У) =
м Tq (г) 1 z
ОО
= Д 1 / С 2 $ (/’ rfy)д (у) = S р {z; dy} А (у) = д (2)-
м т<? (г) ~ z z
*> Краткие сведения о регенерирующих процессах содержатся в § 12.5.
Подробности читатель может найти, например, в книгах Д. Р. Кокса и
В. Л. Смита [14] и В. Феллера [20].
348
Тем самым изучение исходного процесса, быть может, не обладающе-
го эргодическим распределением, сведено к изучению эргодического
процесса. Зависимость величины А от 2 отражает тот факт, что 2 —
точка возвращения процесса.
Если {гп} — цепь Маркова, имеющая стационарное распределе-
ние Р [г; Е}; А (г) —функция, определенная в теореме 2,
A(z) = 0. z^Q,
А(г)= J Р{г; dy}b(y) = $ Р {z; dy}A(y),
z Q
и выполняется условие (15.31), то из теоремы 2 и оценки (15.32) сле-
дует, что
Р{т0(г)<М}<1/(2) +MA(z) + ^. (15.34)
Сформулируем условие А, которое будет использовано ниже при
анализе высоконадежных систем.
Условие А.
1. Существует точка z£Q, такая, что при каждом а£О(а0),
а=Н=а0 A(z)>0;
2. lim А (г) = 0;
ОС ССо
3. lim&a = 0.
а->а0
Физический смысл условия А очевиден: первое из введенных
ограничений исключает тривиальный случай Р {V (zft) = const,
k гС (z)/z0 = г] = 1 (т. е. случай постоянства функции V на каж-
дой траектории) и случай абсолютно надежной системы; второе
ограничение требует, чтобы при а—> а0 надежность системы повышалась;
третье ограничение условия А непосредственным образом связано
со вторым и утверждает, что при а -> а0 характер сходимости к ста-
ционарному режиму цепи Маркова не изменяется. Для большинства
практически важных случаев это ограничение выполняется. Так, оно
заведомо справедливо при часто встречающемся экспоненциальном
характере сходимости к предельному распределению.
Если выполнено условие А, то из неравенства (15.34) можно
получить следующее асимптотическое соотношение (при нормирующем
множителе А (г)/а, а > 0):
Ншр|т (z)<^-|<l/(z) + JVa. (15.35)
( А (?) 1
Заметим, что при V (z) = 1 — х<? (г)> A (z) = Р {z; Z\Q) из формулы
(15.35) следует
lim Р | т (z)< _^а | Na. (15.36)
tx-»a0 ( Л (?) J
349
Полученные результаты показывают, в частности, как можно оценить
надежность системы, зная эргодическое распределение описывающего
ее случайного процесса.
Выше было получено неравенство для вероятности Р {tq (z) < jV}.
Однако реальные системы работают, как правило, в непрерывном вре-
мени. Поэтому покажем, как можно, используя найденные формулы,
оценить функцию Р [z; Q, t\ — вероятность выхода из множества Q
на время t. Вероятность 1 — Р (z; Q, t\ в теории надежности называет-
ся надежностью системы.
Рассмотрим только наиболее простой случай, когда изучаемая
цепь Маркова вложена в процесс функционирования системы, причем
моменты рассмотрения образуют процесс восстановления с функцией
распределения интервалов между моментами восстановления F (х).
Пусть при каждом а £ О (а0) существуют
4г= S xdF(x^
Если Л л/[z; Q}—событие, заключающееся в том, что траектория
системы, начинающаяся в точке z, покинет множество Q не более чем
за N переходов вложенной цепи; BN (t) — событие, заключающееся
в том, что за время t произойдет ровно N отказов, то
P{z\ (?./}= 2 Р{Лг(г; Q) П В, (/)} = 2 Р{Лг(г; Q) (] Bt (t)} +
i>1 х=1
+ /=2 + 1Р{Лг(г; С)П5г(О}<
<Р{Лм(г;(2)} + Р{ U
t i>Nt
(15.37)
где Nt — фиксированное число, быть, может, зависящее от t.
Зададимся е > 0 и определим число Rs соотношением
е-^!/2 dx — г
У 2л
(15.38)
Выберем Nt = ] V + Re, У Kt [. Тогда, как известно из теории
восстановления, Р{ (J В;(/)}<8 при достаточно больших Nt; точнее,
для каждого е>0 существует число Nt такое, что Р{ (J #,(0}<е-
Вероятность Р{Лд^(г; Q)} оценивается с помощью неравенства (15.34).
Из соотношений (15.37) и (15.34) получаем
Р {г; Q, t} <V(z) + ] V+7?eXo/U [A(z) + ^+e.
(15.39)
350
Оценка (15.38) будет выполнена для всех t, если вместо (15.38)
использовать равенство е = fl Х(+ЛеХст (/), т е
Р{г; Q, У(г)4-]Х/ + 7?е_Х<у/Г/[Д(г) +
+ A!a + FjW + «e Хо 1/171 (О-
Из (15.39) найдем
р !г; «У <17 +] та +R- /та р «+*«+’
Воспользуемся условием А и перейдем к пределу при а->а0.
Дополнительно введем естественные предположения, касающиеся
функции/7^): limXA(z)=0, lim X2 о2 А (г) = 0; первое предположение
а^а0 а -аа
говорит о высоконадежное™ системы, работающей в непрерывном вре-
мени, при а —а0; второе предположение выполняется, например, для
таких функций F (х), коэффициент вариации которых равномерно
ограничен в некоторой окрестности точки а0. Получим
limp(2; Q, V(г) + /+е.
GC-XXq I АД (г))
В силу произвольности е
limP/;Q, -^-| <!/(?) +А (15.40)
а->а0 I лД (г))
Рассмотренные примеры, в частности, найденные в них значения
[см. формулы (15.22)—(15.27)], которые в данном случае играют роль
малого параметра, показывают, что асимптотическая оценка (15.40)
хорошо согласуется с известными асимптотическими результатами
теории надежности (см. монографию Б. В. Гнеденко, Ю. К. Беляева,
А. Д. Соловьева [2]).
Пример 5. Для иллюстрации полученных выше результатов рассмотрим
марковскую схему резервирования с восстановлением с одним работающим эле-
ментом, п резервными элементами и п ремонтными местами, поскольку для такой
системы весьма просто находится эргодическое распределение.
Пусть F(x)= 1 — е—''х, G(x) = 1 — с~ yj = .—— количество
/И + Д
неисправных элементов в момент t. Рассмотрим систему в моменты, непосредст-
венно следующие за отказами работавшего элемента и будем считать в соответ-
ствии с изложенными выше соображениями, что из состояния п + 1 цепь возвра-
щается в состояние 1 (т. е. начальным состоянием системы является 1). Состоя-
ния 2=1, ..., п + 1 образуют замкнутое множество; Q = {г : 2=1, ..., пу. Мат-
рица переходов Р — (ptj), i, j = 1, .... п + 1, имеет вид
0 0 ...
1— 7г о ...
Тз(1— Тг) 1— Уз
Тп Уп- • -Т2(1— Т1) Ттг - • Тз(1 —Тг) •1—Тп
1 0 0 • • • 0 -
г- Ti 1 —Т1-
7г 71 72(1—71)
7з 71 71 7з7г(1—71)
351
Эргодическое распределение
имеет вид
(определяемое точкой возвращения 2=1)
п
П Ъ
Pk=Pn+i
i^k -f1 -Yj)
где p= X/p., a
рЛ—1
=Pn+1 (fe —1)1
=*-l p'
k= 1, ... , n+ 1,
из условия нормировки:
п ,, ft j "| —1
_k=0 р 1=0 /I
V(z)=l— Xq (г). Тогда Д (г) =рп (1 — ?„) = pn+i-
Pn+i находится
Pn+i =
Выберем
Рассмотрим два частных случая:
n
1. а = р0, рп+1 = Р1 + о( р«)
Я I ' ' ’
2. а = п^оо, рп+1 = £1 е р(1 + еп),
где еп - 0 ,
П-*оо
( п!ерМ
lim Р |z; Q,----1 < t.
( Хр™ )
Пример 6. Покажем, как можно воспользоваться неравенством, данным в
следствии 3 теоремы 2, для оценки надежности на начальных участках работы.
В качестве примера рассмотрим систему, описанную в примере 5.
Выберем V (г) = 1—z, г=1, ... , л-|-1,0<ti< 1. Легко проверить, что при
1 —v
этом удовлетворяются условия указанного следствия, причем R =----- (1 —yj.
Таким образом,
Р (tq(2) < N] < v,!+1-z(l + /?)'v.
Переходя к непрерывному времени путем, аналогичным показанному
выше, несложно получить оценку
lim Р II; Q, ) <ипе(1-^‘^.
р-> о ( 'ф )
В силу произвольности v
lim Р 11; Q, —inf vn e(l~v}t/v = Р (t) <
p-* О I J 0<y< 1
’ /п 4.П ____
— еп~1 x;—l/2nne~l,
1, t > n.
Таким образом, при малых р, оценка вероятности выхода из области Q имеет
вид (kpt)n~[/2rin что значительно лучше оценки, полученной в при
мере 5 для t ~ 1/А.р.
352
Рассмотрим теперь ряд примеров, иллюстрирующих применение
теоремы 3, которая дает достаточные условия для ограниченности по
вероятности рассматриваемых процессов, и теоремы 4.
Пример 7. Случайное блуждание по целочисленным точкам на полупрямой.
Предположим, что блуждающая частота из точки п, п > 1, с вероятностью р
совершает скачок в точку п 1, а с вероятностью q = 1 — р —в точку п — 1.
Пусть из точки п = 0 частица совершает скачок в точку п = 1 с вероятностью 1.
Заметим, что такое граничное условие является необязательным. Можно было бы,
например, рассмотреть скачок в случайную точку, имеющий конечную среднюю
величи ну.
Функция Ляпунова V задана в данном случае только в целочисленных не-
отрицательных точках. Выберем V(n) = п, а в качестве множеств Gr, упоминае-
емых в теореме 3, выберем GT = {п:п <1 г). Тогда, очевидно, функция V удов-
летворяет первым двум требованиям теоремы 3. В данном случае
( р — q, п > 1,
A(n) = MnV-V(n)= я = 0
Если р < 1/2, то, очевидно, выполнены и остальные требования теоремы, причем
Д7 = q — р, г > 0, а &+ = 1.
Таким образом, если р < 1/2 (или, что то же, р < <?), цепь Маркова, опи-
сывающая случайное блуждание, ограничена по вероятности. Нетрудно понять,
что в данном примере, как и в последующих, где это не будет специально ого-
вариваться, выполнены все предпосылки применения указанной теоремы.
В рассматриваемом случае из ограниченности по вероятности вытекает су-
ществование стационарного распределения. Оценим это распределение с помощью
неравенства (15.21). Заметим, что для выбранной выше функции Е(га) величина
Дг = const и, следовательно, оценка (15.21) не может быть эффективной.
Выберем V(n) = vn, v > 1, тогда
( v — 1, п = О,
A (n) = ! ,
I V"-1 (V—1) [р («+1)—1]. « >1-
Если р < q и выбрать 1 < v < q/p, то функция V(n) = vn будет удовлетворять
всем условиям теоремы 3. Кроме того, А (п) -> —со.
Из (15.21) имеем
N-1
lim Р {г(<V) < г} = lim — Y Р {z (k) > г) >
N->x ‘ N N £ = 0
vr (v — 1) [p (г> + 1) —1]
> ----------- ------------J— = 1— il+t/[ 1— Plv+l)] -1.
(u-1) (v' [p(v + l) - 11+1}
Следовательно,
lim P (z(M) < r) > sup {1 —[1 H-f'' (1 —P («+ I))]-1} =
1- (-?[(-/+ , ‘ =1 —A-
\ q / L\ <7 ) («+ 1) e J
12 Зак. 792
353
Для сравнения приведем точный вид решения
lim P{z(N) <r} > l_(p/9)^(l+?)-: = l-Pr.
Легко видеть, что
lim (in Рг/1п Pr)= 1.
г -oo
Пример 8. Система массового обслуживания с интервалами недоступности*'
Система обслуживания состоит из п параллельно работающих приборов, на ко-
торые поступает квазипуассоновский поток требований (т. е. моменты поступле-
ния требований образуют пуассоновский поток с параметром X, а в каждый та-
кой момент поступает группа требований случайного размера, не зависящего от
предыстории процесса обслуживания; cp^, fe > 1, — вероятность того, что в
группе имеется k требований (D(s) = Sq^s*). Время обслуживания требования
на каждом из приборов распределено экспоненциально с параметром р.. Система
«открыта» для поступления требований из очереди только в случайные моменты
времени {/;}. Каждый промежуток 0, = /;+1 — ft складывается из двух неза-
висимых случайных интервалов с функциями распределения соответственно
R(x) и Н(х), на которых первый является интервалом работы системы — когда
требования, находящиеся на приборах, обслуживаются, а второй — интервалом
простоя, когда процесс обслуживания «заморожен».
Описанная система массового обслуживания используется с помощью ме-
тода вложенных цепей Маркова, за состояние которой гй принимается число тре-
бований в системе в момент Ц + 0. Цепь является неприводимой и непериоди-
ческой. Очевидно,
Zft+i = zA — т (2й) + 1й>
где т (г^) — число требований, обслуженных за время 0^, а —число требо-
ваний, поступивших за это время. Вновь выберем V (z)=z (z принимает цело-
численные неотрицательные значения). Тогда
MZftV-V(zA) = M[^-m (zft)].
Нетрудно найти, что при 2\ > п величины и т(з,г) имеют следующее
совместное распределение:
Р(Ь=Л m(zft)=r} =
ОО оо
= f [ Рг(Х,ФЛ + т)С^[1-е-1ХТ]ге-^<'1-г> dR (т) dH (/),
о с
где РДХ, Ф, t + т) — вероятность того, что за время / + т поступит ровно I
требований квазипуассоновского потока, определяемого интенсивностью X и
производящей функцией Ф(з). Отсюда
М (zft)] = — If е-W[1 ~ ф(5)] dt Г(1 —е-м-т) £ +
ds to о L s
+ е-^
Здесь
= ХФх (йх + гЦ + п [г(р)-1],
ф1= 3 ЬрА=-^-Ф (s) г
А>1 ds 1
ОО ОО
г(ц)=[ е-^ dR (t), ht = ftdff(t),
о b
CO
rx = f tdR(t).
b
*> Подробный анализ системы дан в работах В. В. Калашникова [5, 6].
354
Из теоремы 3 вытекает, что если
ХФх (Й1+ гх) < п[1 — г (р.)],
то рассматриваемая цепь Маркова является эргодической. Чтобы не загромож-
дать изложение утомительными выкладками, при оценке эргодического рас-
пределения рассмотрим следующие два частных случая.
1. Система М|Л1|л| со (пуассоновский входящий поток, экспоненциальное
обслуживание, п параллельно работающих приборов, система с ожиданием), ко-
торая получится, если положить
(О, I < О,
7? (/) = //(/) =J ] Ф (s) = s (т. е. <рх= 1).
2. Групповое обслуживание с постоянным временем обслуживания:
Я(0 =
t < о,
t > 0;
(0>
t < \/Г1,
t > 1/гх;
Ф (s) = s;
Ц = оо.
Для того чтобы рассмотреть первый случай, выберем
( о.
t > 1/Г1,
t > \/rlt
и устремим затем гхк 0. Выберем V (?) =---vz. Тогда
Г1
lim [М2У — V (z)] = t)2~1 (о—1) [Хц —ц min («, г)].
Если % < и(ц), то существует число 1 < v < гер/%, для которого выполнены ус-
ловия теоремы 3;
А+ = тах1)г— 1 (u — 1) [Хц —р.г].
Если воспользоваться оценкой (15.21), то получим при г > п
lim Р (г(N) > г] < А+ (А+ + Дг_)-1 =
= max У-1 I а—Г max У — —or-1 ( v— — 'Я * .
2<П \ A J \_2<п \ А / \ % / I
Пц / 1 \ / пи, I 1 \
Положим V = — 1 — — —— 1—— > 1 при достаточно большом т
А\ Г / \ а \ Г )
Тогда получим
lim Р {г (N) > г}
N оо
/ 1 у / , 1 \Г
а+ — I 1 —— I
\ Р / \ г J
1
г— 1
= Рг,
< а
где a —max
z<n
а р = %/лр,.
12*
1 ‘'/"‘Г1'', И г1
— 1 —— — |1 —— — — —ограниченная величина,
Р ) \ г ) LP \ r ) P«J
355
Точное решение, которое можно в этом случае найти, имеет вид (при г > п)
lim Р {г (N) > гJ = Ро рг
N -*оо ’
где
Ро=Р" + (1-Р)4 3
Очевидно, lim (in Pr/ln Ро pr) = 1.
Г-*оо
В случае группового обслуживания и V(z)=o2, о >1,
Г / 1 \ min(n, 2) , , “1
M2V — V(z) = o2 I— j 1 I
Условия теоремы 3 выполнены при l<v< v, где величина и определяется
из уравнения
eV1 (о-1) =~п.
Заметим, что если zz/= 1-Н, е< 1, то и ~ 1 + е, v > 1 + 8.
Аналогично тому, как было проделано ранее, можно показать, что
lim (— In Рг/г In v)= 1,
Г-fOO
где Pr — верхняя оценка предельной вероятности
lim Р{z (N) > г}.
7V -> оо
Проиллюстрируем теперь применение теоремы 4 к анализу системы, рас-
сматриваемой в настоящем примере. Напомним, что состоянием является число
требований в системе в момент + 0. Докажем, что при ЛФД/ц + rj >
> n[l — г(ц)] изучаемая вложенная цепь не является эргодической. Из
доказательства теоремы 4 следует, что при этом цепь невозвратна. Множество
Qr --^Z/GT = (z:z > г}. Выберем для каждого Qr функцию Vr(z) в виде
Vr(z)=cr(l—е)2, 0 < е < 1, а постоянные е и ст будут определены ниже.
При z > п
Mz Vr-Vr (z) = сг (1 - g)2 j° e“1 ~ф <1 ~£)] dH (!) X
VO
X “ е-Хг[1-Ф(1-е)] Г) —!— + е-мт Г dR (т)_ I j .
0 L 1 е J J
Нетрудно проверить, что при ХФД/ц + гД > п[1 — г(6)] и достаточно малом е
выражение в фигурных скобках отрицательно. Выберем cr = (1 —е)~г. Тогда
Vr(z) > cr (1 — e)r — 1 при z Qr и Vr (z) < сг(1 — 8)г+* = 1 — е при z £ Qr
Условия теоремы 4 выполнены и, следовательно, цепь является невозвратной.
15.4. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
МАРКОВСКИХ ПРОЦЕССОВ
В дальнейшем нам понадобится ряд определений и фактов, имею-
щихся в теории марковских процессов. Сводка их дается в настоящем
параграфе. Изложение не претендует на достаточную полноту и стро-
гость.
356
Читатель, интересующийся затрагиваемыми здесь вопросами,
может обратиться, например, к монографии [4]. Ниже предполагает-
ся, что марковский процесс определен до некоторого случайного мо-
мента £ и что все рассматриваемые моменты времени меньше £.
Как известно, марковский процесс обладает свойством отсутст-
вия последействия, т. е. его течение после некоторого момента t за-
висит от состояния процесса лишь в момент времени t. При этом под-
разумевается, что t является хотя и произвольным, но фиксированным
моментом времени. Естественно было бы ожидать, что это свойство
марковских процессов сохраняется и для случайных моментов вре-
мени, зависящих, вообще говоря, от предыстории процесса. Такими
моментами являются, в частности, момент выхода процесса из некоторой
области Q фазового пространства, tq, момент т = min (т0, t) == f) t,
где t — фиксированный момент времени. Марковские процессы, обла-
дающие указанным свойством, называются строго марковскими про-
цессами, а рассматриваемые случайные моменты времени — марков-
скими моментами. Следует отметить, что произвольный марковский
процесс не является, вообще говоря, строго марковским. Тем не ме-
нее класс строго марковских процессов черзвычайно широк. Во вся-
ком случае многие встречающиеся в прикладных задачах процессы
являются строго марковскими.
Пусть Р [z0; t,E\ = Р [zt g Е a Z/za—z\ — переходная функция
рассматриваемого марковского процесса (напомним, что мы условились
рассматривать лишь однородные процессы). Пусть f (z) — некоторая
функция, заданная в фазовом пространстве процесса Z. Назовем инфи-
нитезимальным оператором функции Р (z; t, Е} функцию
Af (z) = lim -j- [J Р {г; t, dy} f(y) — f (z)]=s g (z). (15.41)
Область определения инфинитезимального оператора состоит
из всех функций f (г), для которых предел в правой части (15.41) су-
ществует равномерно по г g Z. Можно определить расширение инфини-
тезимального оператора — слабый инфинитезимальный оператор, кото-
рый определяется также формулой (15.41), но имеет более широкую
область определения, состоящую из всех функций / (г), для которых
предел в правой части существует при каждом г £ Z и дробь в (15.41)
ограничена при всех г С Z, и t из некоторой окрестности нуля. Инфини-
тезимальный оператор является прямым вероятностным аналогом
производной по времени.
В самом деле, пусть z ft) является решением следующего диффе-
ренциального уравнения
at
Тогда, как нетрудно видеть,
Af (г) = lim А / (Zj) |z=0 = (' A, f(2)y
no t at \ dz J
357
Для данной системы имеем очевидное равенство
f(2x)=/(2)+ f
J at
о
f (Z) + J Af (zf) dt =
0
т
= f(z) + $ g(2z) dt.
0
Оказывается, данная формула интегрирования также имеет ве-
роятностный аналог. Именно, для любого марковского момента т,
М2 т <С оо, строго марковского процесса и функции f (г) из области
определения инфинитезимального оператора справедливо
т
M2{f(zT)} = /(2) + Mz$ g(zt)dt.
о
(15.42)
Здесь Mz — символ условного математического ожидания при усло-
вии zQ = z.
Равенство (15.42) остается в силе при замене инфинитезимального
оператора на слабый инфинитезимальный оператор. В последующих
параграфах будут рассматриваться только строго марковские процес-
сы. Заметим также, что формула (15.1), полученная в § 15.2, является
дискретным аналогом формулы (15.42).
15.5. ОСНОВНЫЕ РЕЗУЛЬТАТЫ (НЕПРЕРЫВНОЕ ВРЕМЯ)
Рассмотрим однородные марковские процессы с дискретным вме-
шательством случая zt (со), широко используемые в теории сложных
систем. В частности, процессами рассматриваемого типа описывается
функционирование автономных кусочно-непрерывных агрегатов. Опи-
шем структуру процесса. Пусть (Z, ст) — фазовое пространство про-
цесса zt (со), о — сигма-алгебра в Z. Пусть t, (со) — время жизни
процесса. Ниже на £ (со) будут наложены некоторые ограничения.
Предположим, что Z — Ц 1\, где Г\, — замкнутое множество | v |-
V
мерного пространства Ev, — граница множества 1\, v — дискрет-
ная величина, принимающая значения из конечного или счетного мно-
жества J. Обозначим через [т<га) (со)}л^1 последовательность мо-
ментов времени таких, что zх(п)(ш)(<о) 6 U Tv, т. e. моментов выхода
процесса на границу областей Tv. Предположим, что: 1) время жизни
процесса £ (со) не меньше любого момента выхода из произвольной
ограниченной замкнутой области, 2) точка накопления моментов т</г)
не меньше t, (со).
Заметим, что любое ограниченное множество G в Z имеет вид
G = (J Ку, где Ку — ограниченное подмножество Ev, a J' — конеч-
V GJ'
ное подмножество J.
358
Второе из введенных предположений говорит о том, что до любо-
го момента 0 (со) < £ (<о) процесс zt (со) имеет лишь конечное число
точек «дискретного вмешательства случая» т<л). Первое же предполо-
жение гарантирует, что время жизни процесса не меньше времени
«ухода в бесконечность». В дальнейшем будем полагать £ (со) равным
времени «ухода в бесконечность» рассматриваемого процесса, т. е.
(со) = sup (со), (15.43)
а
где £а (со) — время выхода из ограниченного замкнутого множества
Ga, a (Ga} — набор всевозможных ограниченных замкнутых мно-
жеств.
В интервалах (т</г~0, ["] £) процесс г((со) развивается в об-
ласти (J int 1\.. Через z(tn} (со) обозначим однородный марковский
V
процесс, определенный при t > т(л) и совпадающий при t g (т^-О,
т<л) f) £] с процессом zt (со). В момент т<п> (со) процесс z(tn} (со) оста-
навливается, т. е. z!n) = zfy} при />т<л>. Процессы ztn} (со) могут
иметь «спонтанные» скачки, которые иногда называют непрерывным
вмешательством случая. Предположим, что единственной точкой на-
копления моментов этих скачков может быть £ (со), т. е. момент «ухода
в бесконечность».
Пусть Ап — слабый инфинитезимальный оператор процесса г}п).
Чтобы формулируемые ниже утверждения не носили чисто абстрактного
характера, нужно чтобы области определений операторов Ап были
достаточно велики. В прикладных задачах (например, при анализе
кусочно-непрерывных агрегатов) часто можно считать, что траектории
процессов ztn> являются реализациями диффузионных или даже де-
терминированных процессов. Иногда, например при учете поступления
входных сигналов в агрегат, бывает удобно предположить, что в неко-
торые случайные моменты, зависящие, вообще говоря, от состояния
процесса, процесс совершает «спонтанные» скачки из внутренних то-
чек областей 1\. Области ГЛ,, как правило, являются объедине-
нием конечного числа выпуклых множеств или даже выпуклых много-
гранников.
Зададим теперь характер изменения состояния процесса при «ди-
скретном вмешательстве случая». Пусть z* = zx(„) £ yv. Тогда при
t > т<л) (до момента т<п+*) П £) процесс zt (<о) является однородным
марковским процессом, развивающимся в области (J int 1\, распре-
V
деление начального состояния которого равно
Р {?*', fi} = P{zT GQczU int rv/zT(n) =z*},
4 / ~ у
P(z*; U intrv} = 1.
V
Область определения инфинитезимального оператора процессов
рассмотренного типа может быть чрезвычайно узкой, например со-
стоять лишь из постоянных функций. В то же время области определе-
359
ния операторов Ап достаточно широки. Поэтому целесообразно выра-
жать искомые распределения для процесса z( (со) через операторы Ап
и характеристики скачков процесса в моменты т<п>, что, по существу,
эквивалентно введению «обобщенного» инфинитезимального оператора.
Теорема 1. Пусть т (со) — марковский момент времени для zt (со),
Мт (со) < оо , для которого
Р{П [т<А> (со)< т (со)]} =0, (15.44)
а функция f (z) принадлежит области определения каждого Ап.
Тогда
{/(Zt}=/(z) + M2
k : < т Z
т "j
$ g (zt) dt +
. о J
dy]f(y)—f(zT(*))]j,
(15.45)
где g(zt) = Af (zt) = An f (zin}) при t 6 (t(n ”, t(n) (] ?)•
Доказательство. Заметим, что последовательность {z(rt> (co)}n>0,
где z(n> (co) = z [т(п> (co) (] r (co)], t(0>(co) = 0, связана в однородную
цепь Маркова. Из дискретного аналога формулы (15.42) и условия
(15.44) следует
MJ(zT)=/(z)+M2( (15.46)
k : nW <с т
Поскольку
/ X(k)
Mzr(A-i)f (Zt(*))=/(ZT(A-1)) + Mzt(ft_1) j j Ak f (z(tA)) dt +
' т(й— 1)
+ Jjp [zT(A); dy]f(y) — f [zT(A)]l, x(k) = tW Д t. (15.47)
z 1
то из (15.46) и (15.47) следует (15.45).
Зафиксируем в фазовом пространстве Z множество Q. Пусть
tq (z, со), z С Q, — случайный момент первого выхода процесса zt (со)
из множества Q при условии, что в начальный момент состояние про-
цесса было равно г*’. Множество Q в ряде задач может трактоваться
как множество «допустимых» состояний системы, выход из которого
приводит к некоторому нежелательному событию, например к отказу
*> Если область Q неограниченная и процесс «ушел в бесконечность»,
не выходя из Q, то момент «ухода в бесконечность» будем считать за момент пер-
вого выхода из Q. В этом случае фазовое пространство процесса нужно пополнить
одной фиктивной поглощающей точкой со, в которую переходит процесс в момент
«ухода в бесконечность». При этом считается, что со (р Q. Таким образом, новый
процесс уже становится определенным на бесконечном интервале времени. За-
метим, что эта конструкция является излишней для регулярных (см. ниже) про-
цессов.
360
системы. Нашей задачей является оценка распределения величины
TQ (г, со). Отметим, что в теории обыкновенных дифференциальных
уравнений данная задача приводит к понятию «практической устой-
чивости» [161.
Теорема 2. Пусть Q £ о — измеримое подмножество Z, и задана
измеримая функция V (г) (для которой написанные ниже выражения
имеют смысл), такая, что V (г) 1 — Xq (г). Тогда
Р {tq (z, ш) <7 t} <7 V (z) + M2 AV (ze) d6 -|-
o
dy\V (y) — V
I k : t^) < t Г) tq Z
(15.48)
Доказательство следует непосредственно из равенства
(15.47), если положить т (gj) = tq (г, со) f| t, f (z)=V (z) и учесть, что
P{tq(z, со)</} = М2{1 — %q(zt)}.
Пусть функция Д (z) удовлетворяет неравенствам:
а) Д (z) > AV (z), г g J int Tv,
V
б) Д (z) > 5 Р <z; V — V <z)> z 6 U Tv.
z "J
Следствие 1. Если Д (г) <7 Д^ г( (J intrv и Д(г)<Д2,
V
z e и Tv, д1; Д2 > °. TO
V
P{Tq(z, co)< t} < V (z) + Дх t + Д2 Ht (z), (15.49)
где Ht (z) — среднее число моментов «дискретного вмешательства
случая» в процесс zf (со), начинающийся в точке z, за время t.
Следствие 2. Пусть Д2 = Д2 = 0 (см. следствие 1). Тогда
Р {tq (z, со) < оо) V (г).
(15.50)
Перейдем теперь к формулировке теорем, позволяющих судить
об ограниченности по вероятности процесса zt (со), являющейся ана-
логом устойчивости по Лагранжу динамических систем [161. Предва-
рительно нам потребуется один результат, касающийся регулярности
процесса.
Определение. Назовем процесс zt (со) регулярным, если величина
£ (со), определяемая равенством (15.43), удовлетворяет условию
Р{?(со) = оо} = 1.
(15.51)
361
Таким образом, процесс называется регулярным, если он может
«уйти в бесконечность» лишь за бесконечное время. Иначе говоря,
регулярный процесс определен на бесконечном интервале времени,
а понятие регулярности является аналогом понятия неограниченной
продолжаемости решений, известного в качественной теории динамиче-
ских систем [16]. Ясно, что ограниченный по вероятности процесс
с необходимостью регулярен. Заметим, что «уход в бесконечность»
за конечное время может наблюдаться не только у случайных процес-
сов, но и у процессов, определяемых, скажем, обыкновенными диффе-
ренциальными уравнениями, Например, решение дифференциального
уравнения
с начальным условием z0 > 0 выражается формулой 2 (/) = -----t]
и определено лишь до момента —, lim z (t) = оо.
z0
Вернемся к исходному процессу. Обозначим через по-
следовательность ограниченных замкнутых измеримых подмножеств
фазового пространства процесса. Предположим, что Gr-..i^>Gr,
lim GT = Z.
ff oo
Теорема 3. Пусть существует измеримая неотрицательная функ-
ция V (z), 2 £ Z, такая, что выполняются следующие условия:
1) V,. = sup V (г) < оо, г =1,2....;
vT— infV(z)->oo, гоо, Gr = Z\Gr.
2 е о;.
2) ЛУ(г)^0, z£Gro (г0— некоторое число),
Р {z; dy}V — V (z) <0, г 6 U yv, z £ Gro
7 V
(величина AV (г) определена в теореме 1).
3) Существует функция РГ1 (Gr)r^x~^ 0 (rx —фиксированное чис-
ло) такая, что
Р{2[тГ1(х)1 6Gr!<P(Gr)
для всех х 6 Gr„, где тГ1 (х) — момент первого выхода из множества
Gri траектории процесса, начинающейся в точке х С Gro.
382
4) Существует число г* и функция распределения F (/) такая, что
P{Tr*(xX/}<F(Z),
О < J tdF = < оо*1.
о
Тогда процесс Zt регулярен.
Доказательство. Без ограничения общности можно по-
ложить г0 = 0. Выберем число R > 0 и оценим вероятность того, что
траектория процесса, начинающаяся в точке z g GR\G0, выйдет из
множества G# раньше, чем попадает в Go. Для этого рассмотрим новый
процесс zt (и), получающийся из исходного остановкой в множестве
Go.
Пусть тк (г) — время выхода остановленного процесса из множест-
ва Gr. Применим теорему 2 к процессу zt (<в) и множеству Q = GR. Для
этого рассмотрим пробную функцию V (?) = V (z)/vR. Данная функция
удовлетворяет теореме 2, т. е.
<2)
V(z)+M2 ^V(z0)d9 +
b
Но для остановленного процесса стоящие в правой части величины
AV (ze) и Р (ZXW, dy) V (у) — V (zx(k)} неположительны. Следова-
z
тельно,
Р {т« (?)</} < V(z)/vR.
*> Заметим, что это условие заведомо выполняется, если существуют чис-
ла /0* > 0 и 8* < 1 такие, что Р{тг(г) с t0*} < е* для всех z £ Gra. В этом
случае в качестве F(t) можно взять ступенчатую функцию
F («) =
0,
е*,
1,
t <0,
0 <4q ,
Условие fx < ос не является стеснительным, поскольку если существует мажо-
рирующая функция F, pdF(^) = oo, то существует и мажорирующая функция
о
с конечным средним. В качестве такой функции можно взять, например, следую-
щую:
F(0 =
F(0.
1,
t<
t >
где Zj* — некоторое достаточно большое число.
363
Заметим, что если z € GT az GR, to
P < VrlvR. (15.52)
Отсюда следует, что при фиксированном z
Р {^(zX/JiZS 0.
Таким образом, с вероятностью 1 перед моментом ухода в бесконеч-
ность процесс, по крайней мере, один раз попадет в множество Go.
Найдем теперь Р [тЛ (г) /}, где xR (z) — момент первого вы-
хода траектории исходного процесса, начинающейся в точке г, из
множества Gr (при достаточно больших R). Пусть Gr, и Gr, —два
множества такие, что Go с: Gr, cz Gr, az Gr. Конкретные значения
г\ и г2 будут выбраны ниже.
Рассмотрим следующие моменты времени, определяемые рекур-
рентным образом:
т<0’> — момент первого попадания траектории процесса в множест-
во Go (если г0 (со) С Go, то положим xj,1) = 0);
х^> — момент первого (после т</>) выхода траектории процесса
из множества Gri, i 1;
х<‘> (i ^2) — момент первого (после т^~'>) попадания траекто-
рии процесса в множество Go.
Следует отметить, что подобные разбиения траекторий процессов
применялись ранее Р. 3. Хасьминским [21] и рядом других авторов.
Зафиксируем t > 0 и z £ Go. Пусть z £ Gr. Выберем так, чтобы
«мгновенный» переход процесса из множества Gf, (дополнение Gr,)
в множество Go был бы возможен лишь в результате скачка («спонтан-
ного» или при «дискретном вмешательстве случая»). Тогда, поскольку
по предположению единственной точкой накопления таких скачков
может быть £ (со), число моментов х</> < £ не более чем счетно. Сле-
довательно,
{тщ (г) < /} = {т/? (г) С (г) 4° (г)} U
U
U {тЛ(г)</, (г) <xR (г) <х(ог + ° (г)}
Заметим, что
|x«(z)^Z, тя(г)<^’(г)| = {Пг(г)<Ф
Далее,
U {гЛ(г)СЛ 4‘\г)<М2) <4‘+‘’(г)} с
U {x₽(z)^Z, xV* (г)<т/<(2)<т'1 н> (г)} U
= 1
и {тог)(2ХО •
(15.53)
(15.54)
(15.55)
U
Величина п будет выбрана ниже.
364
Поскольку Tq ° (2) sC to’ (2), TO
hoZ-1>(2)<d => H’(2)</}.
Следовательно, используя (15.55), получаем
U 4i)(z)<t«(zXt(0‘+I) (г)} С=
1 = 1
п —
и
{т« (г) < t, (г) < т« (?) < 4i+ ° (?)}
и
и Wn)(Z)<z).
(15.56)
В силу (15.52) —(15.54), (15.56) получаем
P{Mz)</}<~Vr-J-PM'',(z)<H +
VR
+ 2* Р Ь (z) < т° ’ (г) С VR (г) < Т</+ ” (г)} =
i = 1
=J_]/r + p{T<")(z)<0 +
VR
+ П2Р{т«(г)^/, т);) (z)< тНг) < тУ+‘> (?)}. (15.57)
/ = 1
Обозначим через Rt (х) функцию распределения величины
т(1‘)(г), R,(x) = P {т4/’(z) х}. Пусть
Р(/) {г, А} = Р (г(г'/’) 6 A/?iZ) = г}.
Тогда
Р{тНг)^С т)г) (z) <Mz)<r(o'+1’(?)}==
= $t/Ri(T) $ P{rK(y)^t-t}P^{r-dy} +
0 У e ar2
+ J dRi (г) P {xR (y)^ t - t} P(/) {t; dy}
°
< f dR, (t) + f dRi (г) P<‘) {t;
J Vn j
0 K 0
^^-Ri(t) 4- p(Gr,)Ri(t}^^ +P(GJ. (15.58)
VR VR
365
Таким образом, из (15.57) и (15.58) следует, что
р{^(2)</}< A+p{t<")(2)c/ji +
VR
Г V _ _ “I
+ («-!) + Ш,) •
vr
(15.59)
Зададимся произвольными е > 0 и t > 0. Выберем число п таким,
чтобы Р (т(оя>(г) гС < е. Это заведомо можно сделать, если
г2 > г* (в силу условия 4 доказываемой теоремы). Выберем, кроме
того, г2 таким, чтобы Р (GrJ (п — 1) < е. Тогда из (15.59) следует,
что
Р (тя (2) < /} J- (+ V„) + 2е -> 28.
VR R^-ao
В силу произвольности 8 получаем
lim Р {т^ (z) t} = 0,
7? -* оо
(15.60)
что и доказывает регулярность процесса.
Определение. Процесс zt (со) ограничен по вероятности, если для
любого 8 > 0 существует такое число г = г (е), что
P{z((0))C6,}>l-8.
при всех t.
Теорема 4. Пусть существует измеримая неотрицательная функ-
ция V (г), г £ Z, такая, что выполняются следующие условия:
1) Vr = sup V(г) < оо, г = 1,2, ...;
2 6 ог
vr = inf V (г) -> оо, г —> оо.
2 есг
2) AV(z)^ — Аь Аху> О, г g Gr„ (г0— некоторое число);
$Р{г; ^}V(//)-V(2)<-A2, А2>0,
2
zGUVv, z£Gro.
V
3) J_ P{?Tr(x) edy}V(y)<oo
у eor
равномерно пох£ф0иг ^0. Заметим, что из данного условия сле-
дует условие 3 теоремы 3.
4) Существует число г* и функция распределения F (t) такая, что
p{tr*w^o<m
оо (15.61)
0< j‘/dF(/)=/1<oo.
о
3S6
5) Найдется область S cz Gr. такая, что в ней существует плот-
ность рх (у) случайной величины z [тг* (х) + 0], х £ Gra, удовлетво-
ряющая условиям
inf px(y)>0, inf <\px(y)dy>0.
xe\Gro. yes xEGr0 S
Тогда процесс zt (co) ограничен по вероятности при любом z0.
Доказательство. Вновь без ограничения общности поло-
жим г0 = 0. Зафиксируем начальное состояние z0. Оценим вероятность
pt (z0> Дд = р \zt е GRlz0\. Прежде всего заметим, что в силу усло-
вий 1—4 теоремы 4 процесс г( (со) является регулярным (см. теорему
3) и, следовательно, время его жизни равно оо. Вновь рассмотрим
«циклы» процесса, введенные в теореме 3. То есть пусть т</>, i = 2,3,
..., — моменты первого попадания (после Д/-1)) траектории процесса
в множество Go, а т^>, 1=1,2,..., — моменты первого выхода (после
т<‘>) траектории процесса из множества Gr„ тф1) — момент первого
попадания траектории процесса в множество Go,
Пусть 0г = х\‘} — т(1‘-1). Обозначим через функцию рас-
пределения величины 0;. Если zx„ (/) = z* £ Go, то, очевидно,
0г^тГ1(г*). Следовательно, Р {0г <./}^Р {тГ1 (z*) t}. Выберем
настолько большим, чтобы выполнялось условие (15.61). Тогда
Р{9г^/}^т (15.62)
Определим новый немарковский процесс zt следующим образом:
?0= ze, OCTf)1’,
2(0 , „ = z(i),
т0 4-е т0 ’
o<0«U1F
2Т(1) , s Д’кп = 2Т<2»’
т0 +Ч + (т0 —TI ) + 9 т0
О<0<?2,
+ е =гг<.2)+е’
О^-0<Гт(3) Д2)
V << и <5- Tq -Т1 ,
где [£jj — совокупность независимых случайных величин с общей
функцией распределения F (t). Таким образом, построенный процесс
zt развивается от момента выхода из области Gr, до момента попадания
в Go как исходный марковский процесс, а в множестве Go проводит
время сохраняя постоянное значение, а затем мгновенно переходит
в одно из состояний множества Gr,.
367
Оценим для построенного немарковского процесса функцию
Pt [г; GR\ = Р {г( £ GR/z0 = г0 = г). В силу построения процесса z
очевидно, что для любого Т
{г; dt {г; G«| dt. (15.63)
о о
Прежде чем оценивать величину Pt [г; G>|, получим два вспомога-
тельных соотношения.
1. Введем обозначение
Р* {t, у} = Р НГ °- т</> > tlz.i} = У\, y^G0.
Т I Н-0
Тогда
J Р* {Ру} dt = Мт<1 ’(//)< р V (у). (15.64)
О
В самом деле, полагая в формуле (15.45) т = т(0' ’ (у) () t, а
I (z) = V (г), получаем
0<My{V(ZT)}<V((/)-ДМ.т;
отсюда при 00 получаем (15.64)
2. Р{тя(х)<Л Tq1’(х) > г7х £ Gr\G0, /-<P)sg
<min(Vr/L^, Р* {/, х}) = Р*к* {/, х). (15.65)
Из (15.64) и (15.65) следует, что
р«(х) = f PR{t, x}dt-+O. (15.66)
о
Соотношение (15.65) следует из (15.52) и очевидного неравенства
Р {тЛ (х) sg/, Tq” (х) >//х 6 Gr\G0, г<7?}^
Р [то0 (х) > Их € Gr\G0, г < 7?) = Р* {/, х}.
Оценим теперь величину Pt (z; G^j. Выберем r1<r2<7?. Тог-
да, очевидно,
Pt k; G«} 2 \dFW (т) $ PR{t-x,y}P[z (i) fdy} +
t = i о yGGTi 1
+ 2 $ P*{t—т, у}Р{гт(1-) edy}. (15.67)
0 u<z ar2
где —i-кратная свертка функции F.
368
Пусть сначала х является случайной величиной со следующим
распределением:
Р°0(Г) = Нт У Р (г (/) С Г)
V II I r'l \zo) + 0 - I ’
L = 1
где x0 — фиксированное состояние, x0 C Go. Пусть
р° U; cj = J < (dy) pt(y- g*).
(j q
T or да
OO t
Pt ix0; Gr} < 2 S^(Z)(0; j PrU-x-, y}Pl(dy) +
,=l 0 nr.2/aa
co t
-h 2 \ЛРЩХ) $ P*{t-x- y} Px„(dy). (15.68)
Используя (15.64), (15.66) и узловую теорему восстановления
[17], из (15.67) получаем, что первое слагаемое в правой части(15.68)
ограничено величиной
7" f Pr (У) Р°„ (dy) -> 0,
/ 1 J /? -> оо
0„
а второе — величиной
у- \ ±-V(y)P0x,(dy)->0.
/1 _J A r2->oo
Отсюда следует, что величина Р° [х0> Gr} равномерно (по /) стре-
мится к 0 при R -> оо . Для завершения доказательства достаточно
показать, что величина Pt [х; Gr] также равномерно (по t) стремится
к 0 при R -> оо . Заметим сначала, что в силу возвратности множест-
ва Go для исходного процесса распределение РХа (Г) в области
S с G,. обладает плотностью, удовлетворяющей условию 5 теоремы 5.
Следовательно, почти для всех начальных условий х0 £ S процесс zt
ограничен по вероятности. Кроме того, в силу (15.64) и того, что
inf ) рх (у) dy > 0, любая траектория процесса zt с произволь-
х£Са S
ным начальным условием г0 с вероятностью 1 попадет в множество
S за конечное время. Теорема доказана.
Прежде чем переходить к примерам, иллюстрирующим доказанные
теоремы, обсудим некоторые трудности, возникающие при их приме-
нении. Основной трудностью, конечно, является подбор пробной функ-
369
ции, удовлетворяющей условиям теоремы. Эта трудность является
органической для метода Ляпунова и его аналогов, и мы не будем на
ней подробно останавливаться. Остановимся лишь на таком ее аспек-
те. В условиях теорем 3 и 4 требуется, чтобы функция V была из об-
ласти определения оператора А. Однако для процессов описываемого
типа нахождение области определения оператора А является, как пра-
вило, достаточно трудоемкой задачей. Иногда эта область не очень
широка. В то же время бывает относительно несложно определить
принадлежность функции гораздо более широкой области определения
инфинитезимального оператора Ат процесса zm (t, ы), который полу-
чается из исходного процесса zt (<о) остановкой в момент выхода из
множества Gm. В связи с этим представляет интерес следующее утвер-
ждение, доказательство которого повторяют, по существу, доказатель-
ство теоремы 4.
Теорема 5. Утверждение теоремы 4 остается в силе, если ее усло-
вия выполняются для всех (кроме, быть может, конечного числа)
процессов zm (t, со), т — 1,2, ... При рассмотрении процесса гт (/, со)
повсюду в условиях теоремы 4 следует вместо Ga писать G\mGa.
Ниже в примерах мы будем писать A V(z) вместо AmV (z). Следует,
также отметить, что теоремы, аналогичные доказанным, можно при-
менять для анализа поведения лишь некоторых компонент процесса
z. (<а). Кроме того, из теоремы 1 или 2 можно получить оценки стацио-
нарного распределения. Здесь мы не будем касаться этих вопросов.
Для случая дискретного времени они затронуты в § 15.3.
Приведем еще одну теорему, которая может оказаться полезной
при доказательстве отсутствия ограниченности по вероятности.
Теорема 6. Пусть процесс zt (<а) и множества GT те же, что и в те-
ореме 4. Пусть, кроме того,
1) при любом z С Z
inf Р {тг (z) < оо} > 0;
Г
2) для любого Gr (кроме, быть может, конечного их числа) су-
ществует функция Vr (z), удовлетворяющая условиям:
a) Vr (z) > 1 — х<5;. (г),
б) ДКг(г)<0, z С (U int rvj П Qr,
Jp{z;dz/}V(z/)-V(z)<0, ze(UYv)UQr,
в) lim sup Vr (z) < 1,
r->-oo zg Qr
где Qr=Z\Gr, %q (z)— характеристическая функция множества Qr.
Тогда процесс zt (со) не является ограниченным по вероятности.
Доказательство следует непосредственно из следствия 2
теоремы 2 и предоставляется читателю.
370
15.6. ПРИМЕРЫ
Примеры 1—6 посвящены вопросу пребывания процесса в фиксированном
множестве фазового пространства*1.
Пример 1. Процесс рождения и гибели. Рассмотрим марковский процесс
с конечным числом состояний Z = {0, 1, ..., п}, развивающийся следую-
щим образом. Из состояния / за время А/процесс с вероятностью Х;-А1 + о(Д1)
переходит в состояние j + 1, ас вероятностью pjAl + о(А/) — в состояние
/—1, = р,п = 0 (« — поглощающее состояние), р0 = 0. С помощью такого
процесса описывается широкий класс систем, изучаемых, в частности, в тео-
рии надежности при экспоненциальных законах распределения, «управляю-
щих» работой системы.
Пусть Q = {0, .... п — 1}. Поскольку в данном случае отсутствует дискрет-
ное вмешательство случая, то воспользуемся следствием 1 теоремы 2, в котором
положим А2 = 0. Если V(J) — функция, заданная на Z, то, очевидно, ее инфи-
нитезимальный оператор имеет вид
4V(/) = lim (АО’1 {[MZ + ° (АО] V (У+1) + [|1,^ + о(Л01П/-1) +
Af-0
+ [1 -(^+ Ь.) A/+o(A0] V (j)-V(/)} =
= ^[V(/+l)-V(/)] + p> [V (j-l)-V (/)].
Функцию V (j) найдем из следующих условий:
AV(/)=const, V(0)=0, 1/(п)=1, (15.69)
которые возникли из стремления минимизировать получаемую оценку. Система
(15.69) легко решается:
/ / , *—1 \
V(/) = Ai V J-+ У Hfe-i P-fe-r I ( (15.70)
Г— 1 ^й-l--Afe-r-1/
(15.79.
Следовательно , из (15.49) получаем
В частности,
P{tq(j) <t} +
Р (rQ (0) < t] <. Дх i.
Пример 2. Полумарковский процесс. Рассмотрим случайный процесс с
конечным множеством состояний Zo = {0, 1, ..., п}, который пребывает в
состоянии j случайное время с функцией распределения Fj(x). Пз состояния /
процесс переходит в состояние k с вероятностью руд. Сведем процесс к марко-
вскому путем введения дополнительных переменных. Именно, за состояние
системы в момент i будем считать пару z = (i, т]$), z £ Z, где i — состояние
исходного процесса в текущий момент времени, а т],— время нахождения про-
цесса в этом состоянии. Множество Za разбито на два подмножества <9;, и Qa,
которые соответствуют «рабочим» и «отказовым» состояниям. Этим подмножест-
вам в расширенном множестве состояний Z соответствуют подмножества
Q={z=(i, г];) : ieQ0}> Q=2\Q-
Построим функцию V(z) следующего
жим, что функции Fi(x) имеют плотности
вида: V(z) = 1 — %q(z). Предполо-
fi(x) и величины Хг(х) = /г(х)/[1—
*> Примеры 1—3 рассмотрены в работе В. И. Луткова [17].
371
— fj(x)] равномерно по х ограничены. Это условие необходимо только для су-
ществования инфинитезимального оператора функции V, и от него можно отка-
заться, вводя в рассмотрение остановленные процессы zm (t, <л)(см. § 15.5). Тогда
при z = (i, T]j) £ Q
XV(?)=S = А (г). (15.72)
HQ
Дискретное вмешательство случая в рассматриваемом примере отсутствует.
Положим Л(г) = 0 при г (j- Q. Тогда из теоремы 2 следует
t
P{TQ(z)< t}< f Mz А (ге) <40.
о
(15.73)
Предположим теперь, что рассматриваемая система находится в стацио-
нарном режиме, P(dz) —ее стационарное распределение, А = fP(dz)A(z). Усред-
z
няя обе части неравенства (15.73), получаем
jP(dz) Р (г) < i } с /А/-К,
Q
где К = P(ff) — коэффициент готовности системы. В данном случае для P(dz)
можно найти явное выражение через характеристики исходного процесса.
Обозначим:
Pi — стационарная вероятность пребывания исходного процесса в состоя-
нии /, К = ^Pi,
ie.Q _
С. Qa — подмножество состояний Qa, из которых можно попасть в Qo
за один переход,
Tij — среднее время пребывания процесса в состоянии I при условии пе-
рехода в состояние j.
Используя результаты теории восстановления [17], можно показать, что
в стационарном режиме
Р (Z=(‘, T|i), Т)г < х} =
PijTij'] ' ] [1-Fi(y)]dy
(15.74)
Из (15.72) — (15.74) следует, что
Р ' (г) < / / 2 С Q !• — 3 Pi 3 Pij (
К ‘е<7+ i£Qo \Aezo '
Отметим, что данная система рассматривалась в работе И. А. Ушакова
[19] с целью определения среднего времени выхода процесса из множества Qo
в стационарном режиме.
Пример 3. Рассмотрим систему, состоящую из п одинаковых элементов,
т из которых работают в режиме нагруженного резерва, остальные находятся
в ненагруженном резерве. Для ремонта отказавших элементов имеется г ремонт-
ных мест. Пусть время безотказной работы и время ремонта элемента—незави-
симые случайные величины с функциями распределения Р(х), G(x), плотностями
Дх), g(x) и средними X-1, р.-1 соответственно. В общем случае процесс, описыва-
ющий систему, немарковский. Сведение процесса к марковскому осуществляется
за счет введения дополнительных координат.
Скажем, что процесс находится в состоянии z= (j, ....
gi, .... ^(yj), если j элементов неисправно, из них r(j) ремонтируются (r(j) =
= min(r, /')); т]А, < г(/)> — времена, прошедшие с начала ремонта элементов;
k w(j), — времена, прошедшие с начала работы работающих элементов,
w(/) = min (т, п — j).
372
Предположим, что множество рабочих состояний Q имеет вид
Q = (г=(/, Ъ......Лг(/). 51, . Sw(/)): / < п~1]-
Обозначим Х(х) = f(x)/(l — F(x)), ц(х) = g(x)/(l — G(x)) и предположим,
что Х(х) и ц(х) равномерно по х ограничены. Выберем функцию 1/(2), зависящей
только от первой компоненты j, V(z) = V(/). Тогда при z = (j, nlt .... т)г(/),
51, •••, ^t»(/))
“’(/)
XV(z) = A(z) = 2 Л.(^г)(^(/+1) —V(J)) +
i = 1
<(/)
+ s и (Л0 (V (J—1)—V(/))-
i= 1
В данном случае вновь отсутствует дискретное вмешательство случая.
Пусть у процесса z(/) существует стационарное распределение и оно равно P(dz).
Обозначим через Pj стационарную вероятность того, что в системе имеется /
отказавших элементов; через i = 1, ..., w(j), — стационарное распре-
деление времени в основном состоянии /, а через Pj(dr\t), i = 1, ..., г(/),—
стационарное распределение времени т]г в основном состоянии /. Пусть
_ w(i} Сна
1 = 1 о
= 2 f Pj №) и (ш).
1 = 10
&j = h [V (/+ П-V (/)] +Й; [V (J-I)-V (j)}.
Выбирая функцию !/(/), как и в примере 1 (беря вместо /.j и Ц; соответствен-
но Xj и цг), получаем из теоремы 2 следующую оценку надежности рассматрива-
емой системы в стационарном режиме
_ 1 Г"-1
J P(dz)P (xQ(z) < /} < — ^Pj V (j) + Дх /J ,
где V(j) и Дх определяются формулами (15.70) и (15.71) с заменой Л; и ц; на Л;
р,г. В некоторых случаях величины Z; и несложно найти. Например, если
= т = г (нагруженный резерв с достаточным числом ремонтных мест), то
Pj №) = Х [1 -F О dgi,
/’j- (<^Пг) = Н [! —
Ъ=(«—/)
pj = ip-
[ j ц \п "1—1
L \ л* / J
Пример 4. Схема резервирования с конечным временем переключения эле-
ментов. Рассмотрим следующую систему (рис. 15.1), состоящую из л идентичных
элементов. В полностью исправном состоянии в системе имеется т элементов,
находящихся на рабочих местах («рабочих элементов»), п — т элементов, нахо-
дящихся в нагруженном резерве («резервных элементов»). При выходе какого-
либо рабочего элемента из строя он мгновенно поступает на одно из г ремонтных
мест, г п, если имеется свободное, либо становится в очередь на ремонт. За-
373
мена отказавших элементов происходит следующим образом. Если в наличии есть
хотя бы один резервный элемент, а общее количество работающих и подключае-
мых элементов меньше т, то этот резервный элемент немедленно начинает пере-
ключаться с резервного места на рабочее. Время переключения каждого отдель-
ного элемента— случайная величина с функцией распределения Н(х) = 1 — е—vx.
Дополнительно предположим, что число одновременно переключаемых элемен-
тов не может превышать некоторого числа s (имеется s каналов переключения).
Элементы системы являются ненадежными и могут отказывать как на ра-
бочих местах, так и в резерве и в состоянии переключения. Будем называть эле-
мент исправным, если он находится в одном из этих трех состояний—рабочем,
Рис. 15.1 Рис. 15.2
резервном и переключения. Время пребывания элемента в исправном состоянии
является по предположению случайной величиной с функцией распределения
Е(х) =1 — е ''х. Время ремонта отдельного элемента также случайно и имеет
функцию распределения G(x) = 1 — е~цг.
Если за состояние системы выбрать пару z(i) = (Е1(0, 52(О), где —
число рабочих элементов, a £2(1) — число неисправных элементов в момент t,
то. очевидно, z(t) — однородный марковский процесс с конечным числом состоя-
ний. Множество возможных состояний Z системы определяется неравенствами-.
° < < т, 0 < 5i+52 < п (см. рис. 15.2).
Будем считать, что отказ системы наступает, когда нет ни одного работаю-
щего элемента, т. е. в качестве множества «рабочих» состояний Q выберем мно-
жество {z = (£i, g2) : gj =/= 0}. Процесс z(Z) характеризуется следующими интен-
сивностями переходов (показаны справа, см. также рис. 15.2)
(g±, 53) (51-1, 52+1),
(51, 52)-(5i, gz+l),
(&1, 52) > (51, g2-l),
(5i, 52) - (5i+>, u
374
5i > o,
52<«-5i, -
52 >o,
£i<min(/T?, n — 5a)> —
^5i,
5i—5г),
pmin(r, g2),
— v min (s,m—|i, n-5i—g2).
Воспользуемся для оценки вероятности Р{т^ t) формулой (15.49)
при Д2 = 0, поскольку дискретное вмешательство случая в данном примере от-
сутствует. Вид инфинитезимального оператора, действующего на функцию
V(z) = V(glt g2), следующий:
g2) = 4i 1, &+1)-g2)] +
+ X(n-g1-g2)[V(g1, ga+l)-V(g1, g2)J +
+ fxmin(r, g2) [V (L, b-1)-V (L, Ы1 +
4-vmin(s, m—gj, n — h— g2) [V <gi +1, g2) —V (gi, g2)[.
Как уже неоднократно указывалось, качество получаемой оценки вероят-
ности выхода существенно зависит от вида пробной функции К. Приведем неко-
торые соображения эвристического порядка, помогающие построить пробную
функцию в данном случае. Заметим, что в двух предельных случаях р -> оо и
v —> оо процесс z(t) сводится к процессу рождения и гибели. Это обстоятельство
было принято во внимание, поскольку случай X р, v на практике чрезвычай-
но важен (случай высоконадежной системы). В этих двух предельных случаях
надежность системы можно исследовать с помощью следующих пробных функций
соответственно (см. пример 1): и 02\g2), где
r , т(т— l)...(m-fe+l) /X у
Ч=(« - ч ч = —-k------------------)
П min (s, i)
i = 1
k
v<2)(0) = 0, v(24i) = У A- 2 0;
Ab Ob
k=Q R H1 = 0
/ — 1 k
2 tv 2
V, 0/1 1 = 0
, . . „ n(n-l). ..(n-fe+1) M V
Xft = X (n—£), 0ft =---------------- — ,
* \ в /
П min (r, i)
Пробная функция l/^, g2) искалась в виде IZ^, g2) = I/(1)(D + K(2)(g2) —
— HTD И2Ч£2), который отражает предельную независимость двух причин от-
казов системы: конечности времени ремонта и времени переключения.
Пользуясь видом функций И1’ и V<2> и видом инфинитезимального опе-
ратора, можно показать, что при достаточно малых величинах X/v и Х/р
AV(g1; g2) <4V(/n, 0).
Обозначим AV(m, O)=Aj и воспользуемся для оценки надежности форму-
лой (15.49). Для завершения анализа приведем выражение для Лх:
Д1 = ДУ(/я, 0)=%/n[V(1) (/«—1)-|-V<2) (1)-У(|> (т — 1) У<2> (]) —
— V(1> (m)-V<2’ (0) + V(l> (m) V(2) (О)]ф-Х (n — m) [V<’> (m) + V(2) (1)-
— V(l) (m) V(2> (1)— V(1> (m)—V(2) (0) + V(1) (fft) V(2) (0)] =
= XnV(2) (l)4-XmV(1) (m—1) —{tn — 1) V(2) (l) = ai + a2—«i«2,
Л /I
375
где
a2 =
tn— 1
ГТ 2'
°* 1—0
mt
m — i
П min (s, г)
nl
_k =
%
П min (г, i)
X \n~ 1
* = 0
k
= o
Полученные оценки сравнивались с точными значениями надежности для
некоторых конкретных систем, найденных с помощью решения соответствующих
систем дифференциальных уравнений на ЭВМ. Сравнение показало эффектив-
ность предлагаемых оценок. Расчеты были проведены В. И. Лутковым.,
Рассмотрим теперь два примера, когда необходимо учитывать ди-
скретное вмешательство случая.
Пример 5. Дублирование с восстановлением. Рассмотрим систему, состоя-
щую из одного ремонтного устройства и двух рабочих элементов, один элемент
находится в ненагруженном резерве, а другой работает. Время безотказной ра-
боты случайно с функцией распределения F(x). Время ремонта имеет функцию
распределения 0(х). Состояния системы выберем следующим образом:
z = (0, g), g > 0, — все элементы исправны, до отказа работающего эле-
мента осталось время g;
z = (1, ё, *1), £ > 0, т] > 0, — один элемент работает и до его отказа оста-
лось время g, второй элемент ремонтируется, г]—время, оставшееся до окончания
ремонта;
2 = 2 (поглощающее состояние) — оба элемента неисправны.
Если в основном состоянии 0 координата g обратилась в 0, то система пере-
ходит в состояние z = (1, g, г]), где g, ц — независимые случайные величины с
функциями распределения F(x) и G(x) соответственно. Если в основном состоя-
нии 1 координата g обратилась в 0, то система переходит в состояние 2, если же
г] = 0, а g = g* > 0, то новым состоянием системы будет (0, g*). Выберем
0,
2 = (0, |)
или z=(l, g, T|), g > rj;
V(z)= l/(l+a), z=(I, I,
1,
2 = 2.
Тогда, очевидно,
(0,
M2)=U,
z=(0, |), g>0, или г=(1, g, г;
г=(0, 0) или z=(l, 0, rj), г|>0.
0, или z = 2J
a = J F (tj)dG (п).
о
следствием 1 теоремы 2. Получим
P{rc(z, <о) < /} < V(z) + AW((z).
где Hf(z) — среднее число переходов системы из-за отказов работающих эле-
ментов за время t при начальном состоянии г. В частности, если т^(0) — случай-
ное время выхода из строя при полностью исправном начальном состоянии, то
Здесь Ht (0) = 2 Р» (0> —А-кратная свертка функции F.
где & = a/(l + a),
Воспользуемся
376
Пример 6. Резервирование с восстановлением. Рассмотрим ту же систему,
что и в предыдущем примере, но с двумя резервными элементами. Состояния
системы имеют вид:
z = (0, 5), | > 0, — все элементы исправны, до отказа работающего эле-
мента осталось время
z = (к, £, г]), £ > 0, т| > 0, k = 1, 2—k элементов неисправно и до оконча-
ния ремонта осталось время т), до отказа работающего элемента осталось время
2 = 3 — отказовое состояние, когда все элементы неисправны.
Выберем У(г) в следующем виде:
У(0Л) = 0, g > 0;
(a, F (ti—£), 0 < av < 1, т] > g,
а2(0 < а2 < 1), т] > g,
V (2 ё nl = 00
1 ’ 61 17 at f dG(y)F(y-l + ^, т) < g;
S-Tl
V(3) = l.
Тогда Д (г) отлична от 0 только в следующих граничных точках:
Д(0,0) = а1а, где а= J dG Ку) F? (у),
° оо оо
А (1, О, Т]) = (а2 — ai)F(T]) + ai f dF (х) J dG (у) F [у — (х — т))],
Ч Х-П
Д (2, 0, т]) = 1 — а2.
Выберем а1=1/(1 + 2а), а2 = (1 +а)/(1 +2а), так что 1—а2 = а1а = а/(1+
+ 2а). Тогда а2— а1 = а1а и Д(1, 0, т]) можно преобразовать к виду
Д (1, 0, T]) = a1pG (t/)J dF (х) [F (у — х + ц) + F (у— х) F(т])— F (п)]•
о о
Заметим, что Д (1, О, т]) -> О, Д (1, 0, 0) = а.а2.
П-оо
Обозначим через Д! = шах Д(1, 0, т]). Очевидно, Дт > aaT. Тогда из след-
fl
ствия 1 теоремы 2 получаем оценку
Р {Д (г) < 0 < V (г) + Д1 fit (г) •
Эта оценка может быть уточнена, если знать оценку распределения величины 7]
в основном состоянии 1.
Следует отметить, что если известно вероятностное распределение
состояний рассматриваемой системы во времени либо его оценка, то
можно оценить вероятность выхода траектории процесса из фиксиро-
ванной области фазового пространства за заданное время с помощью
хорошо известного свойства полуаддитивности вероятностной меры.
На это обстоятельство неоднократно указывал А. Д. Соловьев. В свя-
зи с этим следует отметить, что не во всех приведенных примерах ис-
пользовалась информация о вероятностном распределении состояний
процесса. Заметим также, что с помощью предлагаемого метода можно
получать нелинейные (по 0 асимптотические оценки функции Р (tq /}
и нетривиальные оценки при малых t.
Рассмотрим теперь примеры, относящиеся к вопросу об ограничен-
ности по вероятности.
377
Пример 7. Процесс рождения и гибели. В этом случае фазовое пространст-
во Z состоит из неотрицательных целочисленных точек. Кроме того,
Р {г(/ + Д/) = 1 + 1/г(0 = 1’}=ХгД/ + о(Д0, > 0, i > О,
Р {z (/ +Д<) = i— \jz (t) = i} =p.j Д/4-0 (Д/), [io = O, Ji; > 0, i>l,
P (z (/ 4- Д/) = i/z (t) = i} = 1 — (X; 4- р.г) M -f- о (kt),
P {z(i + M) = j/z (t) = i}=c (M), | j-i | > 1.
С. Карлин и Дж. Мак-Грегор с помощью достаточно сложных рассуждений
показали [12], что при выполнении условий
1) 2 0ft < ~ и 2) 2 Г = ’ где efe= 1 , 0О=1, про-
k = 0 й = 0 Ц1---МА
цесс z(0 эргодичен.
Покажем с помощью теоремы 5, что при условиях Карлина и Мак-Грегора
процесс z(Z) ограничен по вероятности. Выберем пробную функцию в виде
п
V(n) = 2
k= 1
Pi • • — i
Н1 ••Иг
V-A'-i
Р > О,
где считается, что при k = I
_ 0 Их--- 1____1
щ... цг
Данная пробная функция
В силу условия 1
- j
предложена Г. Ш. Цициашвили.
Выберем величину Р такой,
что
Отсюда следует положительность функции V. Кроме того, в силу условия
2 К(п)-> оо при п -> то. Найдем величину AV:
АV (п) = Xn [V (п + 1)- V (n)] + цп [V (п-1) -V (п)].
Несложно показать, что ДУ(п) = — р. Построенная функция V принадлежит,
очевидно, области определения инфинитезимального оператора любого процесса
zm(t, со), получаемого из исходного остановкой в момент выхода из множества
Gm = {0, ..., т}, и удовлетворяет всем условиям теоремы 5. Таким образом, при
выполнении условий 1 и 2 процесс рождения и гибели ограничен по вероятности.
Заметим, что применение теоремы 4 в данном случае затруднительно, по-
скольку проверка принадлежности пробной функции области определения инфи-
нитезимального оператора процесса представляет известные трудности.
Пример 8. Кусочно-линейный процесс. Определение кусочно-линейных про-
цессов, описывающих функционирование кусочно-линейных агрегатов, дано в
гл. 6. В данном примере рассмотрим кусочно-линейный процесс специального
вида [3], служащий моделью разнообразных многолинейных схем массового
обслуживания. Опишем структуру его состояний и переходов. Состояния данного
378
Процесса имеют вида = (v, zv). Размерность вектора дополнительных координат
zv в основном состоянии v обозначим через | v |. Величину |v| назовем рангом ос-
новного состояния v; предполагается, что v — целочисленные величины, v > 0.
Будем считать, что | 0 | — 0 и для v > 0 | v | > 0. Динамика развития процесса
описывается следующими закономерностями.
d
В основном состоянии v=£0, — zv (t) =—vv, где vv — постоянный век-
тор размерности |v|, t>v = (ovl>..., nV|V|). Области Tv изменения дополнитель-
ных координат имеет вид rv = |zv = (2vI,..., zv (v|) : zv > 0}. Обозначим Rk —
x={v:|v|=fe)—множество основных состояний, имеющих одинаковый ранг,
равный k. Если 2(f) = (v, zvl,..., ?v /_], zv/ = 0, zv/+I,..., zv(v|), то
z(/ + O) = (p., zy. /+!,•• zv|v|)> где P- выбирается случайно
с условным распределением , /=!,..., |v|, p<^|v| —1- Кроме указан-
ны? изменений могут происходить «спонтанные» скачки процесса z(t). Именно
за малое время Л/ процесс, находящийся в основном состоянии v, с вероят-
ностью L.4f-|-o(4/) переходит в основное состояние ц, u. £ U R^. Если та-
кой переход произошел в момент t и z(t) = (y, zvl. 2v|v|), то z(f + O) =
= (Ц, zvl,..., zv|v|, |V|), где случайные величины
— |v|, распределены по закону Hvtl(xv..., Х|ц1_|Л!)) = Р
t = l,... , | ц| —Ml-
Потребуем дополнительно, чтобы число элементов в каждом Rk было ко-
нечным, и все перечисленные параметры процесса скорости изменения допол-
нительных координат и интенсивности переходов были конечными, хотя в ряде
случаев некоторые из этих требований излишни. Описываемый кусочно-линей-
ный процесс, очевидно, принадлежит к классу исследуемых процессов. Применим
для анализа его ограниченности по вероятности теорему 5. Рассмотрим ряд ча-
стных случаев.
Случай 1. Пусть М =sup|v| < оо. Чтобы избежать в примере чрезмерно
V
громоздких построений, сделаем предположение, что inf t>vl = v > 0, которое
v
не является стеснительным и во многих задачах, представляющих практический"
интерес, выполняется. Вместо исходного процесса z(f) будем рассматривать спе-
циально построенный z(t), «мажорирующий» исходный. Если будет доказана ог-
раниченность по вероятности процесса z(f), то из этого факта будет следовать и
ограниченность по вероятности исходного процесса г(/). Заметим, что принцип
«мажорации» успешно используется в теории массового обслуживания для ре-
шения разнообразных задач [3]. Будем отмечать все относящиеся к процессу
2(f) величины черточками сверху. Динамика z(f) полностью аналогична динами-
ке z(f):
z(/) = (v, zv);
£v={v}, |v| = v;
= й-. = о, />1, при v > 1;
Чц = 2 2 Чц, 4=Sочевидно, = 0;
H—(x,,...,x- -)= inf (x.,..., x- _), u>v.
v
Поскольку ниже рассматривается только процесс z(f), то черточки будут опу-
скаться.
379
Предполагается рассмотреть функцию У(г) следующей конструкций.1
У(0) = О,
а при 1 иг =- (v, xv .... xv)
[iv + Vv(Xi,..., xv) при Vv(xr..., xv)>H,
V (2) = <
[Lv при Vv (xp..., xv) <//,
где H>h>0, а значения постоянных L, H и h будут определены ниже. Функ-
ции Vv (•*!,•••, xv) зададим следующим образом:
{(xi... xv) :Vv(xr..., xv) <К} = {(х1,..., xv) :FV(K, xv) < K},
а функции Fv определяются рекуррентным соотношением
f / h\
Fv+i(K> xv-’ xv+1) = ™x{Fv(K, xr..., xv); jFv(K, x1,..., xv)+
S I-1 j’ (15.75)
Fi(K, x1) = x1.
Из (15.75) следует, что при любом v>l и /С > /г:
!) fv+l(^’ xv-> xv+ 1) |^+ [ = 0 = Fv (^> xv)>
2) Fv + I (^> xi’ • •’ xv+ 1) = Q = Fv (X’ x2 ‘xv+l),
3) если K = FV(K, x xv) = Fv+1(K, x xv, xv+1)| ,
I v-f I —u
toFv+i(K, xr..., xv+1)=X = Fv+1 (K, x1,..„ xv+1)|^+i = o при xv+i<A.
Положим Gr— {2 : V (г} < г, г £ Z]. Нетрудно найти, используя свойство 3
функции Fv, что при z = (v, Xj,-.., xv) в области Z\GH
(н—v)-
|1>V
Если при всех ц, v и /=1,..., ц—v
ОО
l^ = ^Xjdx.HvtL («,..., 00, х., ск)<с», (15.76)
о
то, выбрав достаточно большие Л, Н > h и достаточно малую постоянную L 0.
можно добиться того, что при всех г Z\GH
AV(z) < — Д-, Д->0.
-Далее, из свойств 1 и 2 функций Fv следует, что в области Z\GH
j Р (2; dy} V (y) — V (2)= — L, z£ UYV.
UfzZ v
Тем самым выполнены условия теоремы 5 и, следовательно, рассматриваемый
процесс ограничен по вероятности*’.
*’Для выполнения условия 5 (см. теорему 4), конечно, следует дополнитель-
но потребовать от функций Hvil достаточной гладкости. Условия 3 и 4 выполнены
с очевидностью.
380
Случай 2. Рассмотрим еще один случай. Не будем Требовать конечности
Л1 = sup|v|. Зато предположим, что inf vv, = v > 0. Выбрав при 2 =
v v. I
= (v, 2П .... z(v|)
V(z) = sup Zj+L\v\, (15.77)
v|
легко показать, что в рассматриваемом случае при
sup 2 М) 2 Чц<о°
v k> I vl
имеет место ограниченность по вероятности. Пользуясь функцией вида (15.77),
можно рассмотреть и более сложные случаи, встречающиеся на практике, на-
пример случай одновременного убывания величин inf vv- и с ростом | v |.
Случай 3. Рассмотрим общий случай. Ограничимся лишь приведением окон-
чательного результата. Достаточным условием ограниченности по вероятности
является существование такого числа М, для которого равномерно по v и k,
v £ Rk, выполняются соотношения
ОО
2 2 <15-78)
k
k<M, (15.79)
i = 1
oo I— k
‘2 2 Чц2 1Г) <э - k<M< (15-8°)
l = /=1
k oo I — k
2yv/- 2 2 4 2 i?g)>°-
/=1 i = *+in6Rz /=1
k>M.
(15.81)
Из (15.78)—(15.81), в частности, следует, что если общее число основных состоя-
ний конечно, то при sup X1 < оо процесс ограничен по вероятности.
/. v. ц '
Условия (15.78) — (15.81) имеют ясный физический смысл — они требуют
конечности средних величин скачков, а (15.81) является обобщением известных
в теории массового обслуживания условий существования стационарного режи-
ма для распространенных схем. Для этих схем, как правило, условия (15.78)—
15.80) выполнены с очевидностью. Следует, однако, отметить, что полученные
условия заведомо не являются необходимыми, как в том убеждает пример про-
цесса рождения и гибели.
Итак, в данной главе было показано, что, трактуя пребывание
траектории в фиксированной области фазового пространства, регуляр-
ность и ограниченность по вероятности как различные типы устойчи-
вости можно взглянуть на эти различные стороны функционирования
систем с единой точки зрения. Более того, анализ указанных свойств
может проводиться с помощью разновидностей одного и того же ме-
тода—аналога прямого метода Ляпунова. В последнее время аналоги
381
прямого метода Ляпунова стали широко использоваться для анализа
стохастических систем [15, 21]. Это, в первую очередь, объясняется
их эффективностью. Действительно, проверить, удовлетворяет ли та
или иная функция условиям теорем «ляпуновского типа», как правило,
несложно. Таким образом, единственной, но существенной трудностью
является подбор пробной функции. Эта трудность является органиче-
ской для прямого метода Ляпунова, и пока пробные функции строят-
ся, в основном, с помощью эвристических рассуждений, что естествен-
но, не гарантирует успеха [1]. Тем не менее имеются более или менее
удачные попытки возложить построение пробной функций на ЭВМ при
исследовании поведения систем, описывающихся дифференциальными
уравнениями [18]. Во всяком случае, данное направление исследовано
далеко не полностью.
ГЛАВА ШЕСТНАДЦАТАЯ
МОДЕЛИРОВАНИЕ АГРЕГАТИВНЫХ СИСТЕМ
16.1. МОДЕЛИРОВАНИЕ АГРЕГАТОВ ОБЩЕГО ВИДА
Методы моделирования агрегатов и агрегативных систем на ЭВМ
представляют существенный практический интерес с точки зрения ре-
шения многих задач проектирования и эксплуатации сложных систем.
Элементарные приемы моделирования систем на Э ВМ, способы фор-
мирования случайных чисел и их использование для имитации случай-
ных факторов будем считать известными (см., например, [1]). В на-
стоящей главе мы рассмотрим некоторые более специальные соображе-
ния, связанные с моделированием агрегатов и агрегативных систем.
Начнем с принципов моделирования марковского агрегата, не выдаю-
щего выходных сигналов. Основой модели агрегата являются два слу-
чайных генератора: № 1 и 2. Генератор № 1 вырабатывает опе-
ратор Ufyz], т. е. значение вектора внутреннего состояния агрега-
та в момент при заданном его состоянии z в момент Таким
образом, этот оператор определяется для всех возможных /, из напе-
ред фиксированного интервала времени и всех z £ (г}. При реализа-
ции модели придется обращаться к генератору № 1 много раз. Сущест-
венно (и вносит упрощение) то, что всякий раз значения оператора
оказываются независимыми. Более точно это можно объяснить сле-
дующим образом.
Пусть генератор № 1, в свою очередь, зависит от выхода датчика
случайных чисел (ДСЧ) со, так что
= (16.1)
где функция в правой части (16.1) является уже детерминированной
(всю случайность вобрало в себя со). Тогда, если придется вычислять
значения оператора
t^[2(1)], Ult\ [г<2)], .... и^[г{т+ *>],
где /0 < Ч <... < tm < tm+1, то это будет эквивалентно вычислению
детерминированной функции при значениях переменных
^[2(,\ coj, [г(2>, <о2]....U%+1[z(m+1)’ “-+1].
где «!, <о2, ..., сот+1 — независимые случайные величины с фиксиро-
ванным распределением. Таким образом, не нужно заботиться о взаим-
ной связи случайных величин.
383
Генератор №2 вырабатывает значения оператора Vt,x[z], т. е.
значение внутреннего состояния агрегата в момент t по заданному со-
стоянию z в момент t — 0 и значению х сигнала, поступившего в агре-
гат в момент t. Подобно предыдущему,
Vi. x[A=Vt. x[z, со], (16.2)
где со, соответствующие разным t, независимы в совокупности и не
зависят также от со, участвующих в вычислении значений оператора
и{\ ы.
По поводу операторов t//J[z] заметим следующее. Пусть нужно
вычислить его значение для момента при заданном состоянии z в мо-
мент t0. Тогда это все равно, что задаться некоторым набором промежу-
точных точек /0<т1 < т2<... < ts < и последовательно вычислять:
z^ = Vxt\[z, coj.
z^ = Ux} [z{’W
z(') = t/TT.i_i[z(Z-|), co;], (16.3)
= [z(s),cos+1],
где co, — независимые случайные величины. Отсюда следует, что
можно задать лишь программу для вычисления оператора t7z‘[z]
при tr — t0 h, где h > 0 — некоторое фиксированное число, а на
больших интервалах применять итераций согласно формуле (16.3).
В применении к оператору Vt, х[г] этот вопрос, понятно, не возни-
кает.
Мы будем рассматривать циклическое моделирование действия
агрегата. Оно, как обычно, состоит в том, что воспроизводится его
поведение в некоторые дискретные (но, возможно, неизвестные зара-
нее) моменты времени. Эти моменты назовем узловыми и обозначим
/о</1</2<...</п<..., (16.4)
считая 10 фиксированным. (Выбор /0 по случайному закону дополни-
тельных трудностей не вызывает.)
Моделирование, собственно говоря, состоит из двух процессов:
— вычисления следующего узлового момента времени,
— вычисления состояния агрегата и посылаемых им выходных
сигналов в узловые моменты.
Эти процессы чередуются: задается /0; вычисляется z (t0); вычис-
ляется ti, вычисляется z (Zt); ... Под z (t) мы в данном случае понимаем
совокупность двух векторов: z (t— 0) и z (t + 0), если их значения
не совпадают.
Нам понадобится особый блок модели, который можно назвать
блоком потенциальных сигналов (БПС). Это ячейка памяти, которая
в любой момент t либо пуста, либо содержит запись вектора (т, х),
384
интерпретируемого следующим образом. Через время т после данного
момента времени на вход рассматриваемого агрегата может поступить
сигнал х. Если сам этот агрегат за время т не выдаст выходного сигна-
лу, этот сигнал обязательно поступит; в противном случае он мо-
жет быть отменен или заменен другим. Но, поскольку мы сейчас
занимаемся моделированием действия отдельного агрегата, формирова-
ние заполнения БПС нас не должно интересовать; к этому блоку всегда
можно обращаться за справкой о потенциальных входных сигналах,
но в процессе действия модели обстановка может меняться. Если БПС
пуст — это означает, что потенциальных сигналов в данный момент
нет.
На БПС, не усложняя его структуры, можно возложить еще одну
функцию: контролирование шага моделирования. Дело в том, что
обычно бывает целесообразно воспроизвести поведение процесса в ка-
кие-либо, наперед фиксированные либо возникающие в зависимости от
обстановки, моменты времени. Далее, как было указано выше, иногда
целесообразно случайный оператор моделировать на малых интерва-
лах. Во всех этих случаях можно поступить очень просто: наделить
БПС возможностью содержать векторы вида (т, 0) (на втором месте
пустой сигнал) или просто т. Это будет означать, что в случае, если не
существует других ограничений, согласно которым значение процесса
нужно вычислять для более раннего момента времени, его нужно
вычислить через время т. В дальнейшем мы опишем процесс модели-
рования без дифференциации заполнения БПС на элементы вида
(т, л-) и вида т; действительно, второе — частный случай первого. При
составлении программы в соответствующем месте нужно поставить опе-
ратор логического перехода, чтобы исключить излишние обращения
к вычислению Vt, х[г\ там, где х — пустой сигнал. Мы позволим себе
также не останавливаться на введении оператора останова; это можно
сделать, исходя из различных критериев окончания реализации про-
цесса.
Итак, мы имеем генераторы № 1 и 2 и блок потенциальных сигна-
лов. Теперь моделирование происходит следующим образом.
Пусть в начале некоторого цикла (скажем так: в момент tn + 0)
состояние агрегата есть г (это состояние хранится в памяти ЭВМ).
Обращаемся к БПС (там содержится длительность очередного
цикла С+1 — Ci). Обращаемся к генератору № 1 и вычисляем
z {tn+\ —0) -= U‘n + '[г]. Если в момент t,l+i поступает входной
71
сигнал х, обращаемся к генератору № 2 для вычисления z (Z„+i + 0) =
= Vi , xtz (Ci+i —0)]. Если необходимо, значение процесса вы-
дается на печать. После этого мы оказались в той же ситуации, что
и вначале, т. е. процесс циклически повторяется.
Перейдем теперь к случаю агрегата, способного выдавать выход-
ные сигналы. Почти вся процедура остается подобной предыдущей, за
исключением генератора № 1. Определим теперь его следующим обра-
зом. На вход генератора № 1 подаются:
— моменты времени t0 и (t0 < /J;
— значение процесса z в момент t0 + 0.
13 Зак. 792 385
На выходе генератора № 1 получается либо г (/г—0), если за
время от 4до ^данный агрегат не выдавал сигналов, либо (т, г (т—0)),
где т — момент первого выходного сигнала данного агрегата в интер-
вале (/0, /г), если хотя бы один такой сигнал имеется.
Моделирование происходит следующим образом. В начале неко-
торого цикла tn + 0 состояние агрегата есть г. Обращаемся к БПС.
Момент времени, записанный там, равен s>0. Теперь обращаемся к ге-
нератору № 1, задавая на его вход tn, snz. Если он выдастz (/л4~з — 0),
поступаем, как и в случае моделирования агрегата, лишенного выхода.
Если генератор № 1 выдаст (т, г'), tn<x < tn+s, полагаем tn+i = т,
z — 0) = z (in+i + 0) = z и реализуем посылку вовне вы-
ходного сигнала, являющегося согласно определению агрегата одно-
значной функцией т и г'.
Пусть теперь имеется система, состоящая из конечного числа
агрегатов. Для каждого из них согласно предыдущему можно построить
модель с генераторами № I и 2 и БПС. Функционирование модели про-
исходит циклически; в начале п-ro цикла, т. е. в момент tn + 0, со-
стояния агрегатов характеризуются векторами г, (г — номер агрегата).
Для всех I по очереди обращаются к (БПС)г, где может содержаться
указание о потенциальных сигналах в моменты^ 4-Si>/n. Выбираются
s == min Si и обращаются к генераторам № 1; для вычисления следую-
i
щих состояний, задавая в качестве входных данных tn, s, гг.
Если все генераторы выдали состояния агрегатов в момент tn +s—0
(ни один агрегат не выдал сигналов), то обращаемся к очередным гене-
раторам № 2 для вычисления zt (tn + s, +0). Если же некоторые агре-
гаты выдали результат, соответствующий появлению сигналов (ть z't),
где z’t — возможное состояние i-го агрегата в момент т, — 0, то вы-
числяем tn+x — min Tj и поступаем как в предыдущем случае. При
t
этом оказывается, что один из выходных сигналов (именно тот, для
которого Т; оказалось минимальным) в действительности реализован;
остальные же остались потенциальными сигналами. Их мы заносим
в БПС тех агрегатов, для которых они предназначаются, стирая пре-
дыдущую информацую. Таким образом, и формирование состояния агре-
гатов, и формирование заполнения БПС определены как циклический
процесс.
Если имеются модели отдельных агрегатов, то моделирование
системы удобно осуществлять при помощи особого регистра, в котором
хранятся моменты (или время до) следующих сигналов. Над регистром
производятся следующие операции:
— сдвиг по времени (определяется минимальное время до воздейст-
вия некоторого сигнала и вся информация преобразуется к этому мо-
менту) ;
— введение новых моментов времени (выдаваемых генераторами
№ 1г);
— вычеркивание «подошедших» моментов времени.
В функцию регистра входит также указание направлений (откуда
и йуда) посылки сигналов и узловые моменты времени.
386
' Возвратимся к реализации генератора № 1. Основная трудность
при машинной реализации генератора № 1 состоит в вычислении
момента следующего сигнала. По определению агрегата этот момент
наступает при выходе г (t) на границу некоторой области. Можно ре-
шить эту задачу приближенно: следя за состоянием агрегата в дискрет-
ные моменты времени и считая, что между ними мы не можем пропу-
стить сигнал. Очевидно, для оценки степени приближения необходимо
учитывать аналитические свойства траекторий процесса г (t). Для ку-
сочно-линейных агрегатов этот вопрос решается тривиально.
Действительно, пусть состояние агрегата есть
г(/) = (г0, гь гг, ..., г|го|).
Тогда вплоть до момента поступления следующего сигнала, при на-
хождении процесса г (t) внутри области Z)2|, поведение этого процес-
са детерминированно. Значит, следует решить систему уравнений
равномерного прямолинейного движения для определения момента
попадания на границу области DZlt. Таким образом, непрерывного
слежения за траекторией здесь производить не нужно: следующий
узловой момент всегда легко определяется по состоянию процесса.
16.2. СВЕДЕНИЕ КУСОЧНО-ЛИНЕЙНОГО АГРЕГАТА К СИСТЕМЕ,
СОСТОЯЩЕЙ ИЗ ЭЛЕМЕНТАРНЫХ АГРЕГАТОВ
В различных математических системах, используемых в киберне-
тике, одним из желательных свойств является представимость произ-
вольной системы из заданного класса в виде некоторой структуры,
состоящей из фиксированных элементарных объектов, которые можно
сочетать посредством применения конечного числа правил или опре-
деляющих соотношений.
В качестве примера приведем теорию булевых функций многих
переменных, где, как известно, любую функцию можно представить
в виде суперпозиции элементарных функций двух переменных.
Второй пример относится к теории линейных систем автоматического
управления, где известен метод замены любой системы эквивалентной
ей, состоящей из элементарных звеньев. Подобных примеров, имеющих
далеко идущие последствия, можно было бы привести очень много.
Нашей ближайшей целью будет указание способа представления любого
кусочно-линейного агрегата в виде системы, состоящей из конечного
числа элементарных агрегатов.
Будем называть элементарными агрегатами агрегаты следующих
типов.
1. Элемент памяти. Такой агрегат способен хранить информацию
в виде некоторого вещественного числа или элемента не более чем
счетного множества х. Еслй на вход этого агрегата поступает сигнал
(1, х), то с этого момента до момента поступления следующего вход-
ного сигнала состоянием агрегата будет х независимо от предыдущих
состояний агрегата. Если на вход агрегата поступает сигнал 0 и
если в этот момент состояние агрегата есть х, на выход агрегата не-
13* 387
медленно посылается сигнал вида х, а внутреннее состояние агрегата
остается неизменным.
2. Элемент задержки. Такой агрегат в любой момент / обладает
некоторым состоянием х (t) в виде неотрицательного числа. Если в ин-
тервале (Tj, т2) на вход агрегата не поступают сигналы, то внутри это-
го интервала х (t) убывает с единичной скоростью, пока не достигнет
нулевого значения. В этот момент на выход подается сигнал с фиксиро-
ванным значением, не являющимся неотрицательным числом, после
чего агрегат остается в нулевом состоянии до следующего входного
сигнала.
Агрегат подобного типа может воспринимать входные сигналы
двух видов: (1, х) и 0. В первом случае сразу же после поступления
сигнала х (I) принимает значение х независимо от предыстории. Во
втором случае на выход агрегата посылается сигнал х, где х = х (/)
(t—момент поступления входного сигнала).
3. Мгновенный кусочно-линейный случайный преобразователь
(в дальнейшем для краткости будем говорить просто преобразователь).
Преобразователь имеет конечное число входов и выходов. Входы обоз-
начим /1( /2, ..., /т, выходы — О1( О2, ..., Оп. Часть входов и выходов
(соответственно Jlt /2, ..., 1т' и Ох, О2, ..., Ол-) приспособлены для
восприятия и посылки дискретных сигналов, число возможных зна-
чений которых конечно; остальные входы и выходы (/т-+], /т-+2> •••,
/т; Ол-4-1, ОИ'+2, ..., Оп) связаны с передачей информации в виде ве-
щественных чисел. Если в некоторый момент на входы /х, /2, ..., 1т
поступают сигналы хх, х2, ..., хт соответственно, то на выходы в тот
же момент времени подаются сигналы ylt у2, ..., уп. При этом ylt у2,
..., Уп — результат преобразования х1г х2, хт, выполненного в со-
ответствии со следующими правилами.
Реализуется случайный вектор у = (ft, у2, ..., уг) с размерностью
и распределением, зависящим только от хх, х2, ..., хт<. Составляется
вектор
(ху)= (xm- + i, хт- + 2, ..., хт. ft, ft, .... ft).
Проверяется конечное число линейных неравенств относительно коор-
динат вектора (ху). (Вид неравенств может зависеть от хх> х2, х3, ...,
хт-.) Пусть е; — результат проверки Pro из этих неравенств, т. е.
е, = 1, если неравенство имеет место, и е, = 0 в противном случае.
Тогда мы имеем булев вектор е = (ех, е2, ..., es). В зависимости от е
реализуется случайное испытание, результат которого есть некоторый
вектор (ylt у2, ..., уП'). (Некоторые из его компонент могут быть пусты-
ми.). Этот вектор и составляет содержание первых п' выходов. По
Xj.Xa, ..., хт', е, ylt у2, ...,у,,- определяются сигналы yt. n'<Zi^n
как линейные функции от компонент вектора (х, у) с параметрами хх,
Х2, хт', 8, У1, Уз. Уп'.
Теорема. Пусть множества J -= {-v}, |ц| и {у0} (см. определение ку-
сочнолинейного агрегата) конечны. Тогда данный агрегат представим
в виде сложной системы, состоящей из агрегатов трех перечисленных
388
выше типов, т. е. элементов памяти, элементов задержки и мгновен-
ных кусочно-линейных случайных преобразователей.
Доказательство. Прежде всего, достаточно ограничить-
ся случаем, когда агрегат задан в каноническом виде. Кроме того,
чтобы не вводить лишней буквы будем вместо v и р, писать соответ-
ственно z0 и х0. Поскольку (z0) конечно, то .¥ = max |z0| также ко-
го
нечно. Возьмем N элементов памяти, в которых будут записываться
соответственно z0 (t), z2 (Z),..., г| z0(f) I (Z) (при | z0 \<ZN некоторое число
элементов будет не использовано). Легко видеть, однако, что можно
определить гг (Z) = 0, | z0 (Z) | < i N; это не нарушит свойства
кусочной линейности агрегата. Поэтому без ограничения общности
можно считать, что всегда | z0 (Z) [ = N. Нам понадобится далее один
элемент задержки для записи в нем гх (Z).
Далее построим два преобразователя: преобразователь № 1 и пре-
образователь № 2. Первый из них предназначается для преобразова-
ния состояния агрегата в моменты, когда zx (Z) = 0, и выработки вы-
ходных сигналов, второй — для преобразования состояния агрегата
в моменты поступления входных сигналов. Схема сочетания всех этих
элементов изображена на рис. 16.1. Для краткости будем называть
элементы, в которых записываются z, (Z), просто zf. Выход z, развет-
вляется и идет к элементам z0, z9j .... zN. В момент, когда zx (Z) = 0,
на выход Zj посылается сигнал 0. По этому сигналу от элементов z0,
z2, ..., zN на входы преобразователя № 1 поступают сигналы, воспро-
изводящие.внутренние состояния этих элементов, т. е. z0 (Z), z2 (Z), ...,
zn (t). После мгновенного кусочно-линейного преобразования, описан-
ного в определении агрегата, от преобразователя № 1 на входы z0,
z1; z2, ..., zN поступают новые состояния этих элементов: z'o, (Z), z\ (Z),
..., zA' (Z). В этот же момент преобразователь № 1 посылает на выход
агрегата сигнал у.
13В Зак. 792 389
Преобразователь № 2 имеет вход, по которому на него поступает
входной сигнал агрегата х. Далее, имеются входы 0, 1, 2, ..., N, свя-
зывающие этот преобразователь соответственно с элементами z0, гъ
г2, ...,z,v. Преобразователь № 2 имеет JV + 1 выходов: 0, 1,2,..., Л', свя-
занных со входами соответственно г0, zlt z2, ..., zw. Если поступает
входной сигнал х, преобразователь № 2 посылает на все свои выходы
сигнал 0, по которому на входы 0, 1, 2, ..., N поступают сигналы соот-
ветственно z0 (7), zx (t), ..., Zn (t). По правилам, описанным в определе-
нии агрегата, преобразователь № 2 осуществляет некоторые преобразо-
вания переменных х, z0 (Z), zr (t), z2 (t), zN (0> в результате чего на-
ходятся новые значения г'й (/), z\ (/), ... состояний агрегата. Эти зна-
чения и посылаются на соответствующие выходы в виде (1, z'o (t), ...),
достаточном для соответствующего изменения состояний z0, zlt z2,
..., Zn.
Описанная конструкция и доказывает сформулированную теоре-
му. Проверку того, что преобразователи № 1 и 2, удовлетворяющие
определению кусочно-линейного агрегата, действительно являются
мгновенными кусочно-линейными случайными преобразователями,
предоставляем читателю.
Данная теорема раскрывает логическую структуру кусочно-ли-
нейного агрегата как преобразователя информации. Мы видим, что
все преобразования осуществляются мгновенно. Исключение состав-
ляет лишь элемент задержки, срабатывающий через заданное время
после введения в него соответствующей информации.
Выясним теперь структуру мгновенного кусочно-линейного слу-
чайного преобразователя. Поскольку множество возможных значений
дискретных сигналов, посылаемых в данном направлении в любой
момент времени, конечно, мы можем без потери общности предполагать,
что на входы Ilt /2, ..., 1т’ и выходы О1( 02, ..., 0П' посылаются лишь
двоичные сигналы: 0 или 1.
Рассмотрим элементы следующих типов.
1. Линейный преобразователь. Этот элемент имеет два входа
и один выход. Если на входы в некоторый момент поступают сигналы
в виде вещественных чисел хТ и х2, на выход мгновенно посылается
число вида у = ах/+ рх2, где а 11 Р — постоянные для данного эле-
мента.
2. Условный линейный преобразователь. Этот элемент имеет три
входа. Если на вход № 3 подается сигнал, данный элемент как пре-
образователь входов № 1 и 2 выполняет функцию линейного преобра-
зователя; в противном случае на выход не подается никакого
сигнала.
3. Датчик случайных чисел. По входному сигналу это устройство
вырабатывает и посылает на свой выход реализацию случайного век-
тора с фиксированными размерностью и распределением.
4. ' Пороговое устройство, вычисляющее функцию
( 1, если х > О,
У~ 1
I 0, если х < 0.
390
5. Инвертер, вычисляющий по двоичному входу х функцию
( 1, если х = О,
У = I
(О, если х = 1.
6. Элемент логического умножения. Такой элемент имеет два
входа и один выход. Если на оба входа подается сигнал 1, на выходе
также появляется 1. Если хотя бы на один вход поступает сигнал О
либо вообще сигнал отсутствует, то на выходе сигнал не появляется.
Для последующего рассмотрения существенны не сами элементы типов
5 и 6, а более сложный элемент — дешифратор, который можно из них
построить. Дешифратор имеет k входов и 2* выходов. Если на входы
подаются двоичные сигналы xit 1 i k, выходной сигнал образуется
только на выходе с номером хт + 2х2 + ... + 2*-1 Один из спосо-
бов синтеза дешифратора — непосредственная реализация на элемен-
тах типа 5 и 6 2*функций вида (^©zj (x2©z2) ...(хй©гй), гдегг —
двоичные числа, © — символ сложения по модулю 2.
Опишем, каким образом синтезировать преобразователь интересу-
ющего нас вида с помощью определенных выше элементов (рис. 16.2).
Двоичные сигналы xlt х2, ..., хт- поступают на дешифратор, име-
ющий 2т' выходов; каждый выход соответствует определенному соче-
13В* 391
танию входных сигналов. В любом случае выходной сигнал дешифра-
тора посылается только на один из этих выходов. Каждый из выходов
дешифратора соединен со входом датчика случайных чисел, который
вырабатывает случайный вектор у = у2, ..., уг), размерность и за-
кон распределения которого могут зависеть от номера датчика*’. С по-
мощью линейных преобразователей составляются линейные комбина-
ции компонент вектора (х, у). Эти числа подаются на входы пороговых
элементов, вырабатывающих дискретные сигналы gj, е2, ..., ss. Пос-
ледние вместе с Xj, х2, ...,л'ш- подаются на вход еще одого дешифратора,
имеющего 2s+"!' выходов. Каждый выход подается на систему ли-
нейных и условных лиейных преобразователей, в результате действия
которых образуются выходы агрегата.
Замечание. Свободные члены линейных комбинаций могут быть
реализованы с помощью элементов памяти без входов.
16.3. ОПЕРАЦИИ НАД АГРЕГАТАМИ В СЛОЖНЫХ СИСТЕМАХ
Наиболее важный вопрос, связанный с операциями над агрегатами,
состоит в следующем.
Пусть имеется конечный набор агрегатов, входы и выходы кото-
рых некоторым образом соединены между собой. Спрашивается: ка-
кому агрегату эквивалентна такая сложная система? Другими сло-
вами, речь идет о формальном описании системы на основании формаль-
ного описания составляющих ее подсистем и связей между ними.
Именно эта задача, существенная в связи с моделированием слож-
ных систем, будет решена в данном параграфе.
Имеется и другой важный аспект рассматриваемой задачи: управ-
ление данными агрегатами с помощью других агрегатов. Введение
алгоритма управления можно в некотором смысле рассматривать как
операцию над агрегатами. Поскольку обычно рассматриваемые
алгоритмы управления представимы как кусочно-линейные агре-
гаты, формальное описание таких сложных систем может быть произ-
ведено в полном соответствии с предлагаемыми в настоящем параграфе
способами.
Пусть имеются два агрегата, описываемые векторами внутрен-
них состояний z(l> = (г*,1*, г*/), ...) и z<2) = (z{,2), z[2\ ...). (Индекс/
для краткости будем опускать.) Оба агрегата имеют входы и выходы,
причем вход и выход каждого из агрегатов соединены как с внешней
средой, так и с другим агрегатом.
Данной системе эквивалентен кусочно-линейный агрегат с внут-
ренним состоянием г == (г0, z), где
z0 = (z<‘>, ?<2’), 2 = (г(1), г<2’),
где, в свою очередь, z(I)=(z<il>, zV’, ...), z<2) = (z(|2’,
*> На практике можно обойтись одним датчиком случайных чисел, получая
различные законы распределения с помощью функциональных преобразований
его выхода.
392
Область D2o определяется следующим образом:
!?2’}) и х dz(2}].
О 1 х о '
Здесь {z(,)}, i =-- 1,2, обозначает пространство векторов г(,) =
= (г<|,), zV*,---), а «X» — символ декартова произведения: Ах В—
множество пар (а, Ь), таких, что а£А, Ь^В. Короче говоря, усло-
вие, определяющее область DZa, представляет собой объединение
условий, определяющих области D(i; и D (2). Движение точки z
го го
внутри области Dzv определяется следующим простым условием:
координаты г/1’, г = 1, 2, />1, совершают равномерное прямолиней-
ное движение в соответствии с уравнениями
Теперь нужно определить поведение агрегата в моменты достиже-
ния точкой z границы области DZo. Если точка z = (z<’), z(2>) такова,
что z(1> лежит на границе D <i), a z<2) — внутри области D (2), преобра-
го
зование вектора z(l> осуществляется по правилам, имеющим место для
агрегата № 1. По этим же правилам вырабатывается выходной сигнал
агрегата № 1. Данный сигнал поступает к агрегату № 2 или на выход
системы. Состояние агрегата № 2 под воздействием этого сигнала пре-
образуется в соответствии с правилами, принятыми для данного агре-
гата.
Таким образом, правила преобразования полностью определены
в случае, когда точка z(I> лежит на границе области D <t), а точка
_ 2°
z(2> — внутри области D (2). Совершенно аналогично поступаем и в
_ го _
случае, когда точки z(2> оказываются на границе, a z(|) — внутри со-
ответствующей области. Остается неопределенным случай, тогда z(1
и z(2> в один и тот же момент времени оказываются на границе обла-
стей D ([) и, следовательно, (2). Если такой случай имеет ненуле-
го 2о
вую вероятность, для полной определенности следует осуществить
разнесение времени. Это может быть осуществлено, например, следую-
щим образом. Каждому возможному событию (появление сигнала извне
системы, выход z(‘> на границу области, посылка сигнала от одного
агрегата к другому) ставится в соответствие некоторый дискретный
параметр (1 (индекс предпочтения). Если одновременно может быть
осуществлено несколько событий, которым соответствуют индексы
предпочтения рх, |32, .., ph, из них предпочтение отдается р; с ве-
роятностью pt (pj, р2, ..., pk), 1 А.
Столь же элементарно решается и вопрос о преобразовании слож-
ной системы из двух агрегатов под действием входных сигналов. Мы
не будем на этом останавливаться.
393
В двух случаях определение алгоритма предпочтения при одновре-
менном поступлении нескольких сигналов излишне: при условии ком-
мутативности и условии асинхронности. Сформулируем эти условия.
Условие коммутативности состоит в независимости результата пре-
образований состояния агрегата и содержания выходных сигналов от
Pi (Pi> Ра. Рл)- Условие асинхронности состоит в том, что совпаде-
ние моментов посылки двух сигналов или моментов поступления сиг-
нала и выхода точки г на границу области DZa возможно лишь с ну-
левой вероятностью.
Оба сформулированных условия являются довольно типичными
для сложных систем. Так, в системах массового обслуживания обычно
совпадение моментов поступления требования и окончания обслужи-
вания другого требования не вносит никакой неопределенности; в этом
смысле большинство систем массового обслуживания обладают свой-
ством коммутативности. Как коммутативность, так и асинхронность
системы обычно следуют из выполнения соответствующего свойства
для произвольного агрегата, входящего в систему. Заметим, что асин-
хронность системы, состоящей из агрегатов, заданных в каноническом
виде, следует из такого свойства. При любых преобразованиях (свя-
занных с поступлением входного сигнала или с попаданием z на гра-
ницу области D2o) новое значение координаты есть случайная ве-
личина с непрерывной функцией распределения, т. е. вероятность ра-
венства zv = и равна 0 при любом и.
16.4. МОДЕЛИРОВАНИЕ КУСОЧНО-ЛИНЕЙНЫХ АГРЕГАТОВ
Понятие моделирования имеет следующий строгий смысл. Пусть
имеется случайный процесс £ (/), заданный на множестве элементарных
событий Q = ! со} с введенной на некотором борелевском поле S3 его
подмножеств вероятностной мерой Р (Л). Таким образом,
= <->),
где при любом о функция £ (/, <а) представляет собой детерминирован-
ную функцию t.
Допустим, что имеется случайный датчик, вырабатывающий после-
довательность {со„} независимых реализаций со, а также вычислитель-
ное устройство, способное вычислять функцию f (t, oj) при почти любом
(о. Тогда под моделированием понимается процесс воспроизведения
независимых реализаций
£(/, од), £(/, од). £(/, юД...
и вычисление некоторых характеристик вида
Фге[€(/, «J, о)2),..., £(/, (оп)]
для оценки вероятностей различных событий и математических ожида-
ний случайных величин, связанных с процессом £ (/).
394
В соответствии с этим определением конструкция, описанная в
§16.1, может интерпретироваться как модель для получения одной
реализации процесса £ (/). Ее следует дополнить лишь устройством,
вычисляющим характеристики реализации, входящие в выражение
для <рп Таким образом, задача построения модели кусочно-линей-
ного агрегата, а следовательно, и любой системы, построенной из таких
агрегатов, формально решается путем логического анализа агрегата
и построения моделей элементарных агрегатов.
Рассмотрим теперь некоторые принципиальные вопросы, связан-
ные с реализацией моделей на ЭВМ. Напомним, что в интервалах
между узловыми моментами (т. е. моментами, когда либо поступает
входной сигнал, либо состояние агрегата достигает предельных зна-
чений) многомерный процесс, описывающий функционирование агре-
гата, изменяется по детерминированному линейному закону. Поэтому
в принципе нам достаточно построить модель, имеющую последователь-
ный характер: каждый ее шаг соответствует переходу к следующему
узловому моменту.
Если имеется система из некоторого числа агрегатов, то узловые
моменты каждого из них, вообще говоря, различны. В любой момент
времени нужно производить пересчет состояний только тех агрега-
тов, для которых этот момент является узловым. Чтобы избежать
излишних пересчетов состояний, предлагается следующий регистро-
вый метод моделирования сложных систем. Понятие регистра нами
используется в смысле В. М. Глушкова [2]. (Будем считать, что моде-
лируемая система автономна, т. е. входа не имеет.)
В памяти цифровой машины для каждого агрегата выделяется
некоторая совокупность ячеек; в этих ячейках записывается пара
(z<‘>, /(*)), где i — номер агрегата (1 i n), — последний узловой
момент для данного агрегата, z(,’> — состояние г-го агрегата в мо-
мент -|- о.
В некоторой ячейке ведется отсчет текущего времени. Далее,
имеется специальный регистр, имеющий п ячеек памяти, в г-й из
которых записывается время тг от текущего момента t до момента,
когда состояние r-го агрегата вышло бы на границу допустимой
области, если бы с момента t поступление входных сигналов на
этот агрегат прекратилось. (Если агрегат задан в каноническом виде,
т( есть его координата 2Г (/).)
Над регистром могут производиться следующие операции.
1. Вычисление min (т/} = т и посылка на выход сигнала вида
(т, г0), где i0 — номер агрегата, для которого тго = min (тг).
2. Сдвиг всех т; влево на т.
3. Замена одного из т, по сигналу извне.
Для t-ro агрегата имеются две подпрограммы /7*1* и /7,-2), пер-
вая из которых реализует алгоритм преобразования его внутреннего
состояния и выработки выходного сигнала при выходе на границу
области DZa, а вторая — алгоритм преобразования внутреннего со-
стояния при поступлении входного сигнала.
Алгоритм моделирования работает циклически. По сигналу, по-
сылаемому регистром, управление передается подпрограмме
395
в результате выполнения которой преобразуется внутреннее состоя-
ние некоторого агрегата и вырабатывается выходной сигнал этого
агрегата. Данным сигналом, в частности, определяются номера Д, /2,
..., Д тех агрегатов, на входы которых он должен быть послан. Тогда
включаются подпрограммы П^}, П/2а>, , Л/2), в результате вы-
полнения которых преобразуется внутреннее состояние агрегатов с но-
мерами Д, /2, ..., Д. Это состояние записывается в соответствующих
ячейках памяти с моментом времени, когда произошло преобразова-
ние. После выполнения указанных операций в регистр посылаются
сигналы, по которым времена т/о, Т/,, т;-2, ..., ту заменяются их новыми
значениями. Затем над регистром производятся операции № 1 и 2
(см. выше), после чего цикл повторяется.
Естественно, что описанный алгоритм должен быть дополнен пра-
вилом останова и правилом вывода вовне информации о поведении
агрегата.
Пусть в некоторый момент t необходимо иметь информацию о те-
кущем внутреннем состоянии некоторого агрегата. В соответствующих
ячейках хранится информация вида
(z(i>, Д')),
что дзначает равенство
?(') (/(О +0) = z(0
для некоторого момента Д‘> <; д где Д') (0 — вектор, описывающий
состояние данного агрегата.
Имеем
(ДО) = (z0, 2Ь Z2, ...).
Поскольку, в силу принятого алгоритма моделирования, от момента
Д') до момента t на i-й агрегат не поступило ни одного сигнала и про-
цессом z (/) ни разу не была достигнута граница области DZo, полу-
чаем
?(г> (() = (z0, г2 —а2о]Х, z2—а2о 2 х, ...),
где х =Л—
Представляет интерес решение следующей математической зада-
чи. При заданной структуре связей между агрегатами требуется найти
алгоритм моделирования, обладающий наименьшей сложностью
в смысле одного из общепринятых определений сложности. Данная
задача, насколько нам известно, в настоящее время не решена. Описан-
ный выше регистровый метод моделирования оценивается с точки зре-
ния его сложности следующим образом.
Во-первых, данный алгоритм требует выполнения преобразова-
ний с агрегатами в узловые моменты времени. Эти операции можно
считать неизбежными, коль скоро мы хотим воспроизвести процесс
функционирования системы во всех подробностях. Кроме того, произ-
водится некоторое число вспомогательных операций, связанных с пре-
образованиями состояния регистра. Как легко видеть из изложенного
396
выше, в каждый узловой момент времени приходится производить
порядка п арифметических операций (выбор минимального из двух
чисел, вычисление, замена одного числа другим). Для того чтобы на-
глядно представить себе эту сложность, предположим, что агрегаты,
входящие в систему, сходны по своей структуре и что для каждого из
них узловые моменты встречаются с частотой X в единицу времени.
Тогда в единицу времени понадобится порядка скп2 вспомогательных
операций, где с 1 — некоторая константа. При малых /г, учитывая
сложность моделирования отдельных агрегатов, составляющая вида
cZ/i2 не будет вносить существенного усложнения. Однако при больших
п эта составляющая получит перевес над линейным относительно п
членом, соответствующим основным операциям. Поэтому представляет
важность исследование возможности снижения оценки ckn2 за счет
усовершенствования регистра как в общем, так и в частных случаях
моделируемых систем. К настоящему времени решение этой задачи не
получено.
16.5. УПРОЩЕНИЕ АЛГОРИТМА МОДЕЛИРОВАНИЯ
ЗА СЧЕТ ИСПОЛЬЗОВАНИЯ СТАЦИОНАРНОГО РАСПРЕДЕЛЕНИЯ
Описанный в § 16.3 алгоритм моделирования может оказаться не-
удобным в вычислительном отношении при моделировании системы,
состоящей из большого числа агрегатов, поскольку этот алгоритм пред-
полагает, что моделирование функционирования системы в заданном
интервале Т, по существу, сводится к воспроизведению функциониро-
вания в этом интервале всех агрегатов системы. Возможен, однако,
прием, позволяющий намного понизить сложность моделирования.
Сущность этого приема состоит в замене распределений состояний агре-
гата и его выходного процесса их предельными распределениями.
Пусть имеется некоторый (не обязательно кусочно-линейный) агре-
гат, на вход которого поступают сигналы х1( х2, ..., хп,... в моменты
si < s2 < ••• < sn < , где Sj > 0. Пусть известно начальное состоя-
ние агрегата г (0). Распределение состояния агрегата в момент t обоз-
начим Pt (А) = Р (г (0 6 Л}. Пусть р (Р, Q)— расстояние распре-
делений по вариации:
р(Р, Q) = sup | Р (Л) —Q (Л) |.
А
Предположим, что состояние агрегата преобразуется по закону
z(t} = z(t — sn, zn, хп, а>п), sn<^s„+b
где гп = z (sn), {<ап} — независимые элементы вероятностного про-
странства (Q, S3, Р).
Пусть Px,zn,xn(A) = P{z(t, zn, хп, шп)-Л}, и пусть известно
семейство вероятностных мер Qx,!n,xn(A) со свойством
где е > 0 — фиксированное число.
397
Предполагается, что мера PXt 2n, х — «трудно вычислимая»,
a Qx, zn, хп — «легко вычислимая», т. е. моделировать случайную
величину с распределением, соответствующим этой мере, значительно
легче.
Алгоритм приближенного моделирования поведения агрегата
состоит в следующем. Если sn — 8п_\<_Тг >х , тогда определяем
z(sn) = 2(sn—sn-i, zn_i, (On-J, если же sn —sn_i > модели-
руемУг(sn) в соответствии с вероятностной мерой Qsn-s„_], zn_{>xn_x
Пусть состояние агрегата в момент t = 0 фиксировано и в течение
времени Т было п замен меры Р мерой Q. Тогда можно вывести оценку
расхождения по вариации между распределениями, соответствующими
точному и приближенному алгоритму моделирования процесса г (О
в любой момент t Т. С этой целью обозначим через и
вероятностные меры, задающие распределение zk при точном и прибли-
женном алгоритмах моделирования. Пусть р (Р(А>, Q(ft)) = Тогда
можно записать
Q(fe) =Р^+6кР^—6кР^\
где P\k\ Р1^— некоторые взаимно сингулярные вероятностные меры.
Можно, далее, записать при k 2:
P^+')(A)=$PSft+1_Sft,Zfe.Xft(A)PW(d2fe),
Q^+ »(А) = $QSk+ }-Sh.zk,xh (A) Q(^ (dzh).
Отсюда
P(4+D (Д)—Q(ft+i) (A) = J PPW (dzk) — $ QQ^ (dzh) =
= $(?-(?) PW {dzh) + $ QPW (dzk) - $ QQW (dzk) =
= S (P—Q) Pw (dzh) + \Q [PW (dzh)-QM (dzh)],
где обозначено сокращенно P=Ps ft+I_Sft, (A), Q=QSft+1_Sft ,Zft,(A).
Имеем, далее,
$ (P-Q) Р^ (dzh) e, $ Q [PW (dzk)-QW (dz*)] < 6ft.
Отсюда
6A+i^6fe + c, t. e. 6n<ne,
где можно положить бо = 0.
Таким образом, при п заменах PSft+1_sft на QSft+I_sA приближенное
распределение z(sn) отличается от истинного не более чем на пе по
вариации. Отсюда можно найти допустимое число таких замен.
398
ГЛАВА СЕМНАДЦАТАЯ
СТАТИСТИЧЕСКИЕ ЗАДАЧИ
ТЕОРИИ СЛОЖНЫХ СИСТЕМ
17.1. ВВОДНЫЕ ЗАМЕЧАНИЯ
В связи с исследованием сложных систем возникают многочислен-
ные статистические задачи. Это обстоятельство объясняется главным
образом тем, что основным источником сведений о характеристиках
сложных систем и особенно их элементов является наблюдение над
реально функционирующей системой.
Среди возможных постановок статистических задач мы выделяем
две наиболее распространенные: 1) проверка статистических гипотез
о соответствии характеристик системы некоторым заранее сформулиро-
ванным требованиям и 2) оценка количественных характеристик си-
стемы по результатам наблюдения. Вместе с тем, часто встречаются
и комбинированные постановки задачи.
Относительно условий получения экспериментальных данных
обычно могут быть сделаны следующие предположения: 1) наблюде-
ния ведутся в естественных условиях функционирования системы,
2) наблюдения находятся в ведении экспериментатора, т. е. возможна
постановка специальных экспериментов.
Общая схема статистической оценки сложной системы, состоящей
из некоторого числа подсистем, выглядит следующим образом.
Во-первых, мы задаемся математическими моделями подсистем
как некоторых агрегатов. Первой возникающей при этом задачей яв-
ляется задача проверки статистической гипотезы о том, что та или иная
подсистема может быть описана соответствующим агрегатом. Одним
из вопросов при решении этой задачи является вопрос об отсутствии
взаимного влияния подсистем иначе, чем посредством передачи сигна-
лов, предусмотренной моделью функционирования агрегатов.
Коль скоро гипотеза принята, мы можем пойти дальше — оце-
нивать параметры и распределения, характеризующие агрегат. Пусть
параметры или функции распределения, характеризующие i-й агре-
гат, представляются точкой х; некоторого пространства Xt. Тогда,
на основании аналитических расчетов или статистического моделиро-
вания, мы назначаем такие.области Dt с: Xit что если все xt £Dt, то
система считается удовлетворяющей заданным требованиям. Таким
образом, задача статистической проверки системы сводится к проверке
совокупности гипотез Hi = (х, ££);}.
Пусть имеется агрегат со входом и выходом. Ставится задача:
по наблюдениям над тем и другим найти показатели, которые ха-
рактеризуют этот агрегат в некотором классе агрегатов (например,
399
в классе кусочно-линейных агрегатов). В зависимости от условий можно
различать следующие постановки задачи:
1. На вход агрегата можно посылать произвольные сигналы в про-
извольные моменты времени; наблюдается как вход, так и выход.
2. Вход не управляем, но наблюдаем. Выход наблюдаем.
3. Вход не управляем и не наблюдаем; однако известно, какому
классу процессов принадлежит входной процесс. Наблюдается только
выход. В некоторых случаях можно считать наблюдаемыми внутрен-
ние состояния исследуемой системы.
Легко видеть, что дальнейшее усложнение ситуации не имеет
особого смысла: если мы откажемся от использования информации о
классе случайного процесса на входе, то задача всегда будет обладать
тривиальным решением: можно всегда представить себе агрегат, на
выход которого поступают входные сигналы с постоянной задержкой т.
Если о входном процессе ничего не известно, то любой выходной про-
цесс может быть совместим с гипотезой о том, что агрегат принадлежит
только что описанному типу. Однако утверждение, что в этом случае
выходной процесс несет в себе нулевую информацию об устройстве
агрегата, было бы неверным. В самом деле, для данного агрегата су-
ществуют недопустимые или маловероятные выходы при любом входе.
Например, какой бы поток ни посылать на вход системы массо-
вого обслуживания, выходящий поток всегда будет обладать интенсив-
ностью, не превосходящей n/т, где п — число обслуживающих при-
боров, т — средняя длительность обслуживания одного требования.
Поэтому наблюдение выходящего потока позволяет ограничить мно-
жество допустимых агрегатов и иногда выбирать между несколькими
гипотезами; однако всегда будет сохраняться многозначность.
Ниже мы рассмотрим некоторые статистические задачи, связан-
ные с оценкой сложных систем по экспериментальным данным.
17.2. ОЦЕНКА ПАРАМЕТРОВ СЛОЖНОЙ СИСТЕМЫ
Предположим, что испытывается сложная система, причем целью
испытаний является оценка некоторого параметра а = (а1, а2, .... afe),
где «!, а2, ..., ай — числовые параметры. Эти параметры непосредст-
венно измерить невозможно, зато можно наблюдать некоторый слу-
чайный процесс
y(t) +Ар(/), (17.1)
где у (/) — среднее значение процесса, зависящее от параметра а;
Др (/) — ошибка измерения, имеющая известный закон распределения.
Процесс у (/) может быть векторным: у (t) = (рх (/), .... уг (/)), где
Спрашивается: как оценить параметр а по наблюдению у (/)?
Если известна зависимость у (t) от а, тогда задача может быть
решена аналитически, например методом максимального правдоподо-
400
бия. Так, пусть а принимает значения из множества А. Тогда для
любого а £ А можно определить р (х; а), где р (х; а) — многомерная
плотность вероятности случайного вектора наблюдений (у (/J, у (/2),
..., У (U) в предположении, что процесс наблюдался в моменты tly
t2, .... ts. Теперь ищется а0, обращающее в максимум выражение
Р (а) р (у, а), где
У = (уЦ1), y(h)... y(ts))’
р (а) — априорная весовая функция, часто приравниваемая 1 для всех
а £ А.
Специфика испытаний сложных систем состоит в том, что, как
правило, явной зависимости у (/) от а, которая была бы доступна в вы-
числительном отношении, не существует. Вместо этого, однако, су-
ществует математическая модель, реализованная на ЭВМ, позволяю-
щая для любого а £ А вычислить у (t) с некоторой погрешностью,
так что наблюдается
y<t)=y^A-by(t), (17.2)
где у (t) = (ут (t), у2 (I), ..., уг (/)). При этом имеется возможность
в принципе неограниченное число раз воспроизводить процесс моде-
лирования при произвольных значениях а. Возникает вопрос об опти-
мальной оценке параметра по результатам моделирования.
Исходя из конкретного вида множества А, множества моментов
наблюдения процесса у (t), а также законов распределения ошибок
Ду (/) и заданной функции убытка от ошибки в определении а, во
многих случаях можно выбрать такой функционал р [у, у\, что мини-
мизация этого функционала означает (точно или с допустимой степенью
приближения) минимизацию среднего убытка от неточности оценки а.
Для иллюстрации этого принципа рассмотрим следующий эле-
ментарный пример. Допустим, что параметр а является числом и мо-
жет принимать N возможных значений а(|>, а(2>, ..., а(Л/> с равными
априорными вероятностями. Предположим также, что имеется един-
ственное наблюдение у = у (ZJ, г = 1, и как ошибки измерений на
системе, так и ошибки модели являются нормальными с нулевыми ма-
тематическими ожиданиями. Итак,
У = УА-^У, У = У + &У, (17.3)
где случайные величины Ду и 8у имеют распределения N (0, Oj2)
и N (0, о22) соответственно. При этом у = у (а). Обозначим также
yt = У (а(/)), 1 < 1 < N.
Пусть на модели получено N независимых реализаций, по одной
для каждой точки а(‘>. Итак, имеем
= + ..., yN=yN+&yN.
В качестве функции убытка И7 (а, 0) возьмем U7 (а, 0) = с > О
при а =/= 0, И7 (а, а) = 0. Очевидно, в качестве наилучшей оценки
401
нужно взять а(<>, для которого \у, — у\ минимально. Итак, в данном
случае расстояние р есть обычное евклидово расстояние двух точек.
Важно подчеркнуть, что минимизируется на самом деле математиче-
ское ожидание убытка W (а, а), где а — истинное значение параметра,
а — его оценка; однако оказывается, что минимум этого математиче-
ского ожидания соответствует минимуму расстояния между у и у.
В зависимости от конкретных условий задачи, от того, каким
образом выбрана функция убытка, а следовательно, и определяемое
ею расстояние р, задача оценки параметра а приобретает тот или дру-
гой конкретный вид, а сама оценка — тот или иной статистический
смысл (например, эффективные оценки, оценки максимального правдо-
подобия и др.). Мы не будем останавливаться на случаях, когда
сформулированная задача сводится к известным задачам математиче-
ской статистики случайных величин или случайных процессов. В рав-
ной мере мы не готовы дать достаточно общую и строгую формулиров-
ку этой задачи и тем более предложить общие методы ее решения. Цель
настоящего параграфа — познакомить читателя с некоторыми част-
ными случаями, важными с практической точки зрения.
Рассмотрим случай, когда параметры системы а1( а2, •••» аь пред-
ставляют собой числовые константы; характеристики yi(t) измеряют-
ся в фиксированные моменты времени I = 1, 2, ..., L, результаты
этих измерений обозначим yt (tj); в нашем распоряжении находятся
результаты измерений рг (/) по каждой из конечного числа реализа-
ций процесса у, (t) = ^in (t,), п = 1, 2, ..., N. Будем считать, что
интервалы t!+i — времени достаточно велики, а корреляционные
функции случайных процессов yL (t) быстро убывают с ростом ^+1 — th
поэтому корреляцией между yi (//+i) и yt (tt) можно пренебречь для
всех I = 1, 2, ..., L. Результаты моделирования находятся в нашем
распоряжении, поэтому есть возможность вывести их на печать для
тех же моментов времени и для нужного числа реализаций 7V. Ошиб-
ки измерений Дг/г (/) представляют собой независимые случайные ве-
личины с математическими ожиданиями, равными нулю, и дисперси-
ям О?/.
Для рассматриваемого случая в качестве расстояний можно при-
нять функционалы г, R и р, квадраты которых имеют вид
Г2 [уп ^-Уп &)] =2 , (17.4)
>=i а‘‘
L г - 12
(П.5)
а-.
i=\ i=i ‘‘
р- Ю1. И = 2 2i . (17.6)
П=1 / = 1 i=l 11
402
Оценки alf a2, .... an, полученные из условия минимума (17.6),
имеют ясный статистический смысл, так как р2 в выражении (17.6)
пропорционально среднему квадрату нормированной разности между
соответствующими опытными характеристиками и характеристиками,
полученными по результатам моделирования. Кроме того, выражение
(17.6) обладает известными аналитическими преимуществами. Тем не
менее на практике встречаются случаи, когда вместо квадратов разно-
стей используются абсолютные величины разностей (с соответствую-
щей заменой нормирующего множителя).
Для других условий, когда опытные данные представляют собой
записи уin (t) для всех /, принадлежащих некоторому интервалу (О, Т),
в качестве R2 часто используется функционал вида
т г
R2 [уп (t)-yn (/)] = $ 2 —— [уin V)-Уin (0]2 dt, (17.7)
о i=i a2 (0
где интеграл (17.7) конечен; здесь о2 (/) — обобщеннаяДдисперсион-
ная функция, вычисленная с учетом корреляционных характеристик
случайных процессов уг (/). Тогда
N т г
Р2 [{£}, Ы] = 2S2 -^—[yin^-yin^dt. (17.8)
n=i о i=i а2 (/)
В выражениях (17.7) и (17.8) обычно в качестве Ут (0 используется
кусочно-постоянная функция, которая при t = tL равна yin (ti).
На практике встречаются и другие случаи, на которых мы за
недостатком места останавливаться не можем.
При любом конкретном р [|у[, {у)] задачу оценки параметров,
как это следует из (17.8), можно сформулировать как задачу выпукло-
го программирования относительно искомых параметров а1( а2, ..., ак,
при которых функционал р имеет минимум при некоторых весьма об-
щих ограничениях.
Рассмотрим кратко методы решения задачи оценки параметров
ах, а2...ак. Во многих случаях оказывается удобным метод после-
довательных приближений в следующем виде. Представим пара-
метры aj в виде сумм
а,-= а° + Да,, (17.9)
где а/ — так называемое нулевое приближёние параметра а,-, опре-
деляемое грубо по непосредственным измерениям или каким-нибудь
косвенным данным, а Да,- — поправка. В этом случае функционал р
будет функцией k переменных:
р = р(Дах, Да2.... Дай), (17.10)
а результаты моделирования yln (ti), а также и (t/) будут зависеть
от а°.
403
Итак, первоначально в нашем распоряжении находятся: опытные
данные {у}, математическая модель системы вместе со средствами ее
реализации на ЭВМ, и параметры нулевого приближения а0 = (аД
а2°, ..., аА°). Реализуя модель при а = а0, мы получаем совокупность
результатов моделирования [у (а0)}, соответствующую совокупности
опытных данных [у]. Затем, располагая этими результатами, решаем
задачу на минимум р [{z/(, [у (а0)}] и определяем так называемые по-
правки первого приближения Д(1>а/. Наконец, вычисляем первые при-
ближения параметров а*1* = а° + Да*1*; а(1) = (а*1*, «V\ ,
а*1*). На этом первая итерация заканчивается.
Переходя ко второй итерации, мы должны реализовать модель
при а = а(1' и получить совокупность \у (а(1))}, соответствующую
тем же опытным данным {//}, решить задачу на минимум р [ {у], [у (а(1>)}]
и определить поправки второго приближения Д(2> а/ вычислить
а(/2)= а/!) + Д(2>а7- и т. д.
В настоящее время имеются примеры, когда процесс последователь-
ных приближений быстро сходится и для достижения точности, выте-
кающей из требований практики, можно ограничиться двумя-тремя
приближениями. Для широкого круга практических задач сходимость
можно оценить, исходя из принципа сжатых соображений.
Заметим, что поправки Да/ (особенно второго и последующих
приближений), как правило, оказываются достаточно малыми. Это
обстоятельство может быть использовано для упрощения процедуры
последовательных приближений, а в некоторых случаях и самой моде-
ли системы. В частности, хорошие результаты дает линеаризация соот-
ношений yi (/) = yt (/, а0, Да) — приближенное представление их
в виде линейной части степенного ряда по Да:
- -41 dth (/, а,) ,
yt(t)^yi(t, а°)+2^4--------(17.11)
£1 да t
Значения частных производных (если таковые существуют) при-
ближенно вычисляются по результатам моделирования на каждой ста-
дии последовательных приближений.
Как показывают расчеты, удовлетворительные с практической
точки зрения оценки могут быть получены даже в случае весьма гру-
бых способов измерения yin (/,), если число опытных данных достаточ-
но велико.
17.3. ОБЪЕДИНЕНИЕ РАЗНОРОДНОЙ ИНФОРМАЦИИ
ПРИ ПОСТРОЕНИИ ТОЛЕРАНТНЫХ ПРЕДЕЛОВ
ДЛЯ ХАРАКТЕРИСТИК СЛОЖНЫХ СИСТЕМ
Одной из главных задач статистики сложных систем является объединение
разнородной информации для выводов относительно данной системы. Известно,
что современные сложные системы состоят из многих элементов. Элементы про-
ходят стадии разработки, лабораторных испытаний, доработки, заводских ис-
404
пытаний, далее испытаний в собранном виде и т п На каждой из этих стадий
собирается определенная статистика относительно характеристик элементов
Общий объем статистического материала оказывается весьма впечатляющим;
в то же время, поскольку при переходе от стадии к стадии элементы претерпевают
изменение, нельзя непосредственно объединять результаты наблюдений над ха-
рактеристиками элементов на различных стадиях создания системы. С другой
стороны, возможности экспериментирования с готовой системой зачастую весьма
ограниченны. Путь преодоления указанной трудности состоит в том, чтобы из-
влекать информацию о характеристиках системы даже в условиях, когда законы
распределения этих характеристик изменяются в процессе ее создания.
В настоящем параграфе будет дана простая процедура построения толерант-
ных пределов для случайных величин на основании разнородной информации
Предположим, что имеется случайная выборка (£,, ..., £.п) независимых
наблюдений над случайной величиной £ с неизвестной функцией распределения
F(x); требуется построить толерантный интервал, т. е. статистику <р =
= <Р(=1, £п) со свойством
Р &„)} <е,
(17.12)
где е > 0 — заданное число*1. Весьма часто мы находимся в ситуации, когда
объем рассматриваемой выборки мал, так что либо построение толерантного
интервала по одной этой выборке вообще невозможно либо получается недопу-
стимо широкий интервал. В этом случае можно привлечь дополнительные наблю-
дения над интересующей нас характеристикой, произведенные в других условиях,
и, следовательно, при ином виде закона распределения
Пусть, помимо fcj, ..., £п, можно построить т независимых выборок:
£ц >•• > £1п’ £1 , « + 11
1 &2п ’ ^2, п-f- 1 >
(17.13)
’ml’"’’ гчГ Sm, п+1 >
где обладает функцией распределения F(x, 0,); 9г- — неизвестный параметр
произвольной природы, принадлежащий множеству 0
Допустим, что существует семейство функций
<р(х1,..., хп; р), —оо<Х;<с», 1</<п, —оо<р<оо,
со следующими свойствами
1. <р (Xi... хп; р) не убывает по р и q>(xlt..., хп; р) -* оо при р->оо.
2. Если — независимые случайные величины с функцией распределе-
ния F(x, 0), то вероятность Ф(р) = P{gn+, > <р(^, ..., £п; р)} определена и не
зависит от 0 £
Приведем пример. Пусть 0 = (а, о), где —оо <а < оо , а > 0, и
F (xt Q) = F(x; a, a) = F
(17.14)
Положим
Ц У (Xi— х)2,
(17.15)
<р(х1,..., хп\ p) = x-|-ps.
(17.16)
*> Толерантный интервал подобного рода называется верхним односторон-
ним. Аналогичным образом определяются нижний односторонний и двусторон-
ний толерантные интервалы.
405
Тогда свойства 1 и 2, очевидно, выполняются, если В(х) — непрерывная функ-
ция.
Поставленная задача в общем случае решается следующим образом. Обо-
значим Vi(p) = P’ если л+1>Ф^г, >•••> ^п. Р)> (17.17) (0 в противном случае
и, далее, 1 П(Р)=—Tv;(p). (17.18) til
Зададимся некоторым е' > 0 и найдем максимальное 6 > О, для которого вы-
полняется неравенство
Р{Вт е <т6} < е', (17.19,
где Вп е — случайная величина, имеющая биномиальное распределение с па-
раметрами т, в. Далее обозначим через р„ наименьшее значение р, для которого
т) (р) < 8. (17.20;
Справедливо следующее утверждение
Теорема. Соотношение (17.12) выполняется с вероятностью, не мвньшей
1 — s', если положить
р £„) = <р (h..... In, р0). (17.21)
Доказательство. Обозначим
А = {р : Л/т] (р) > в}. (17.22)
Возможны два случая; 1) А = ( — с-о, р*], 2) А = (—оо, р*), где р* — неко-
торое конечное число. В первом случае
Р (р0^Д) < Р [т] (р*) с 6} < Р [Вт>£ < тб} < е'. (17.23,
Во втором случае возьмем последовательность pn f р*. Имеем:
Р(РоСЛ}=р| U (П(Рп)<6) • (17.24)
(л=1 J
Ввиду того, что
)Т|(рп) < 6} С {т|(Р,!+1) <6}, М>1, (17.25;
Р |роС'4)= Ит Р {п (Рп)<6). (17.26)
Г7->ОО
Однако вследствие того, что рп £ А при любом и>1,
Р {В (Р„) < 6) < Р{Вт,е < тб} < е'’
отсюда находим, что неравенство
р {роб Л} < е' (17.27)
выполняется также во втором случае.
Далее,
p{p0(M} = P{,Vl(p0; < s} = P {Р h>q> (£,,..., g„)} < в), (17.28)
откуда
₽{₽{£><№........ gn)}<e}>l-s', (17.29)
что и требовалось доказать.
406
17.4. ОБ ОПТИМАЛЬНОМ ПЛАНИРОВАНИИ ИСПЫТАНИЙ
ДЛЯ ОЦЕНКИ ПАРАМЕТРОВ СЛОЖНОЙ СИСТЕМЫ
(17.30)
В настоящем параграфе будет описана одна математическая схема,
связанная с оптимизацией оценки параметров сложной системы.
Пусть система характеризуется некоторым набором числовых пара-
метров xlt х2, ... хп, подлежащих статистической оценке, и задан набор
показателей эффективности системы уг, у2, .... ут, известным образом
зависящих от этих параметров
У1 =Ф1 (Xj, х2,... , хп),
Z/2=<P2(*1. Х-2. Хп),
Ут=Фт(х1> *2......хп).
Обозначим через xilt ..., xin некоторые статистические оценки
xlt х2, Хп соответственно, и предположим, что в качестве оценок по-
казателей эффективности системы используются значения функций
Ф, при подстановке в них х^ вместо х}:
У,(хп, х!2,..., xjn), (17.31)
Допустив, что функции ср, достаточно гладки, а ошибки статистиче^
ских оценок могут рассматриваться как малые величины, найдем:
й. ~ У1 + 2 -,хл) (17.32)
/= I °xj
где обозначено
У;, lu^x^ — Xi. (17.33)
Будем считать, что приближенные значения хп известны на
основании предварительного эксперимента или расчетов. Поэтому
значения производных можно приближенно заменить некоторыми из-
вестными константами
0'<Pi ....Хп) _
dXj
и тогда получим
i=\
d, (17.34)
1 <3 n. (17.35)
Для дисперсий оценок у, имеем следующие приближенные фор-
мулы:
п
5 a^a^cov^j, gih),
i. k= i
(17.36)
где, в частности, соу(|г,, £гу) = Щг;.
407
Пусть, далее, имеется N типов испытаний. В результате проведе-
ния испытаний r-го типа, 1 N, получаем несмещенные оценки xrj
параметров Xj, 1 j п, причем
cov(xr/, xrk)=brjlt, 1 <; i n, 1 < j n. (17.37)
Числа brjh мы считаем заданными. При различных г оценки указан-
ного вида считаем некоррелированными.
Решим вначале задачу построения по совокупности (xrJ} линей-
ных несмещенных оценок Хц параметров xj, при которых линейный
член (17.35) обладает наименьшей дисперсией. Оценки Xj будем искать
в виде
N N
•И ~ 2 Pjr Xri> 2 Pir ~ 1 •
r= I Г= I
(17.38)
(В действительности pjr зависят также от i, однако этот индекс мы
будем считать фиксированным; поэтому для упрощения обозначений
будем писать pjr вместо рцг.) Итак, по формуле (17.35)
2 ан 2 Р}Л;, (17.39)
i= I r= 1
где
lrj=xrj-xj. (17.40)
Отсюда
n n NN
Oyi-^i ^аиаш 2 2 PjrPfe8cov(xr?, xsk) =
/=J jfe=I r=I S=1
n n N
= 2^ 2 aih 2 PjrPhrbrih. (17.41)
/= I 4=1 r= I
Теперь нужно найти минимум квадратической формы [обозна-
.V
чим ее Л ({р>г})1 при условии 2р?г=1> 1 1п- Для этого
г= I
введем функцию Лагранжа
ф({Ы) =л ({Ы)-2 2 Nj 2 Pir. (17.42)
/=1 г=1
Использовав формулу (17.41), найдем:
п п N п N
ф = 2 2 ^«^2 pirPhrbrjh— 2 2 Pjr- (17.43)
/=1 4=] /=1 ,'=1 г=1
Уравнение экстремума имеет следующий вид:
nN п
ап 2 aih 2 brjh phr = 2 Pir = 1,
4=1 r=l Z=1
l^rs^Af, 1 < j n. (17.44)
408
Решив эти уравн ения, найдем выражения Dt/£ через {brih}:
D^=Gi({W)- (17.45)
Предположим теперь, что с r-м типом испытаний, 15g: г Af, свя-
зывается некоторая стоимость tr (зависящая, например, от продол-
жительности испытаний), причем известны зависимости
brik = brik (7), icjs^n, 1 (17.46)
В таком случае можно поставить задачу об оптимизации плана испыта-
ний при удовлетворении заданных требований к точности оценки пока-
зателей системы. Эта задача формулируется следующим образом.
Требуется определить /1( Л2, .... Av при условии минимума суммы
+ /3 4- ... + tN и ограничениях
-(17-47)
если Dz/j определяются правой частью формулы (17.41), где pjT нахо-
дится вместе с постоянными кц из системы уравнений (17.44), причем
brjh связаны с tr уравнениями (17.46).
Решение задачи в случае некоррелированных оценок. Предполо-
жим, что
. (Brj при j = k,
6,Л=«Щхг,. xj = ( 0 прв/>(, (17.4»)
Тогда уравнения экстремума (17.44) примут следующий вид:
аЧ Brj Pjr =
" (17.49)
2 Pjr = 1, 1 г < Af, 1 j "С п.
Г=1
Мы видим, что эти уравнения решаются непосредственно, а именно:
(17-5о>
Приближенное выражение дисперсии z/;- примет вид
2 al-(Я В-1} . (17.51)
/=1 \г=1 /
Предположим, что дисперсии оценок xrj обратно пропорциональны
стоимости наблюдений. Тогда можно записать:
Вг7’=1М,- (17.52)
где рг2 — некоторые константы, и формула (17.51) примет вид
= 2 й/( 2 ’• (17.53)
/= 1 \ г= 1 /
14 Зак. 732
409
Таким образом, задача формулируется как задача минимизации суммы
/1 + ... + tn при условиях
2
i N
I <; i <; m,
(17.54)
и дополнительных условиях
tT > 0, 1
N.
(17.55)
Отметим случай, когда эта задача является задачей линейного
программирования. Пусть
2 1 сг при i = j,
ац = { „
( 0 при i=£j.
вид
(17.56)
Тогда условия (17.54) будут иметь
/ tt
Ci
A,
1 tn,
(17.57)
или, что то же,
N
Cj
At’
.Все же остальные условия и в общем случае явлются линейными. Ус-
ловие (17.57) выполняется, если задаются ограничения не на Dyit
а непосредственно на Dx,.
m.
(17.58)
1 < t
17.5 ОЦЕНКА ВИДА АГРЕГАТА ПО НАБЛЮДЕНИЮ
ВХОДА И ВЫХОДА
В настоящем параграфе мы кратко наметим возможные подходы
к решению задач оценки вида агрегата по наблюдению входа и выхода,
если, к тому же, на вход можно подавать любой (допустимый) процесс.
Через X = X (t) мы будем обозначать входной процесс, через
Y = Y (t) — выходной процесс агрегата. Тогда полная характеристи-
ка агрегата как «черного ящика» заключается в указании соответствия
каждому входу распределения выхода, т. е. совокупности [Z-х (У)} при
всех допустимых входных процессах X, где {Lx (У)) обозначает сово-
купность всех конечномерных распределений выходного процесса Y
при фиксированном входном процессе X.
Пусть имеется некоторое множество гипотез 0 = {0} относитель-
но вида агрегата. Например, 0 может состоять из двух точек: 0! —
гипотеза о том, что агрегат является однолинейной системой массового
обслуживания с показательно распределительной длительностью об-
служивания, заданной средней длительностью обслуживания и с по-
терями; 02 — то же с тем отличием, что допускается ожидание требо-
ваний.
410
Под тестом для выбора среди гипотез множества 0 мы будем по-
нимать фиксирование конечного числа входов Хъ Х2, Хп. Тест
интерпретируется таким образом, что на вход агрегата подаются про-
цессы = Хъ (/), А"2 =» Х2 (t), , Хп = Хп (t), и статистическим
путем, посредством многократного повторения эксперимента, находят-
ся £х,(Е), £х2(У), Lxn (У). Под разделяющим тестом в соответст-
вии с общепринятой терминологией мы будем понимать тест (Х1; Х2,
..., Хп) со следующим свойством. Для любых двух 0! £ 0, 02 £ 0,
61 ¥= 02> найдется такое i, 1 i п, что при гипотезах 0Х и 02
распределения Lxi (У) будут различны.
Введем также полезное понятие е-разделяющего теста. Предпо-
ложим, что в пространстве 0 введено расстояние р (0, 0') между лю-
быми двумя агрегатами 0, 0' так, что выполняются естественные усло-
вия р (0, 0') = р (0', 0); р (0, 0") sC р (0, 0') + р (0', 0")*’. Тогда
е-разделяющим тестом мы будем называть тест (Xlt Х2, ..., Хп), обла-
дающий следующим свойством. Если £хг (У), 1 i п, совпадают
при каких-либо 0х £ 0, 02 Е то р (01; 02) е.
О полезности данного определения говорит следующий пример.
Представим себе, что выходной процесс данного агрегата поступает
в качестве входа на другой агрегат, причем последний принимает сиг-
налы лишь в дискретные моменты времени: t = а, а + h, а + 2h, ....
а + kh, ...; сигналы, поступающие в перерывах между этими дискрет-
ными моментами времени, задерживаются до наступления очередного
момента вида а + kh. Естественно, что любые два агрегата, различаю-
щиеся распределением времени посылки сигналов в пределах дискрета
h, будут играть одинаковую роль; это порождает естественное поня-
тие неразличимости (нулевого расстояния) между агрегатами. Испыты-
вая подобный агрегат, естественно ограничиться О-разделяющими те-
стами (е = 0).
Перейдем к рассмотрению конкретных статистических задач ста-
тистики сложных систем типа сформулированных в§ 17.1 на примерах,
сформулированных в терминах теории массового обслуживания.
1. Имеется однолинейная система массового обслуживания с потерями
Время обслуживания г; распределено по неизвестному закону Щх) = РЩ < х}
Требуется, задавая соответствующий входящий поток, восстановить Н(х).
Будем различать две разновидности постановки задачи: а) в любом случае
можно наблюдать момент окончания обслуживания; б) наблюдаются только мо-
менты потери требований.
В случае а) задача решается очень просто: входящий поток состоит из един-
ственного требования; время подачи его в систему не существенно. Мы непосред-
ственно наблюдаем момент окончания обслуживания: вычтя из него момент
подачи требования, получим реализацию случайной величины щ повторяя этот
процесс достаточное число раз, мы можем с любой достоверностью и любой точ-
ностью оценить распределение. Н(х), скажем, пользуясь критерием Колмого-
рова—Смирнова.
В случае б) поступаем следующим образом. Входящий поток строится из
двух требований, отстоящих во времени на некоторое х. Пусть п±(х) — число от-
*> От условия, что р(0, 0') = 0 лишь при 0 = 0', в нашем случае можно
отказаться.
14* 411
казов, происшедишх при п реализациях обслуживания таких пар требований.
Тогда при п -» оо
п— п-t (х)
-----—->Н(х), х>0. (17.59)
п
Варьируя х, мы оценим Н(х) при всех х > 0.
Можно поступить и несколько иначе: посылать требования через случай-
ное время распределенное по показательному закону с параметром X. То-
гда, если V — число отказов при п испытаниях, то при п -> оо
п—v ir
-------- f e“u dH(x). (17.60)
п о
Таким образом мы получаем возможность непосредственно оценивать преобра-
зование Лапласа - Стилтьеса случайной величины т].
2. Имеется многолинейная система массового обслуживания с потерями.
Число приборов равно п. Время обслуживания распределено по закону Н(х).
Требуется восстановить п и Я(х). Данная задача — обобщение предыдущей.
Образуем входящий поток следующим образом. Пошлем в систему одно-
временно N требований. Если М п, отказов не будет; если М > п, будет
наблюдено ровно N — п отказов. Таким образом, выбрав достаточно большое М,
мы однозначно восстановим число обслуживающих приборов. После этого будем
посылать в систему потоки, состоящие из п требований, поступающих одновре-
менно. Тогда, наблюдая выходящий поток, мы получим п независимых реализа-
ций случайной величины ц; дальнейшее очевидно.
3. Имеется многолинейная система массового обслуживания с ограниче-
нием на время ожидания. Число приборов равно п. Время обслуживания рас-
пределено по закону Я(х). Время ожидания требованием обслуживания ограни-
чено сверху случайной величиной с функцией распределения G(x). Предположим,
что, наблюдая выходящий поток, мы можем видеть, обслужено ли требование,
или же оно покинуло систему, не дождавшись начала обслуживания. Будем счи-
тать, что п, Н(х) и G(x) неизвестны; укажем способ, как их найти.
Сначала будем посылать в систему поток из единственного требования.
Поскольку отказов не будет, то, подобно случаю 1, можно непосредственно
определить Н(х). Число приборов находится следующим образом. На протяжении
достаточно большого интервала времени Т будем посылать в систему требования
через каждые h единиц времени. Если h достаточно мало, все приборы почти все
время будут заняты; стало быть, за время Т будет обслужено примерно пТ!х
требований, где т = f xdH(x). Выбрав надлежащим образом Т и h, с достаточной
б
надежностью восстановим п. Осталось найти функцию распределения G(x) мак-
симальной длительности ожидания требования. Мы покажем, как это сделать
в случае, когда Н(х) < 1 при любом конечном х. Для этого будем посылать в си-
стему поток из п + 1 одновременно поступающих требований (п нам уже изве-
стно!). Мы можем наблюдать время s, через которое первое из требований будет
обслужено. Пусть имеется k реализаций, в которых х < s < х + Ах, и пусть сре-
ди этих k реализаций было m отказов. Тогда при k -> оо будет выполняться
асимптотическая оценка
пг — m
G (х) lim — ; lim — : G (хф-Ах). (17.61)
Разбив ось времени на надлежащее число отрезков Ах, можно оценить -О(х)
в соответствующем наборе точек, а в пределе при числе испытании, возрастаю-
щем до бесконечности, — во всех точках х.
4. Имеется однолинейная система массового обслуживания. Время обслу-
живания г) распределено по закону Я(х). Время пребывания требования в системе
ограничено сверху случайной величиной у с функцией распределения G(x). Тре-
буется восстановить оба эти распределения.
412
Будем посылать в систему поток из единственного требования. Следующие
характеристики непосредственно восстанавливаются по последовательности не-
зависимых реализаций обслуживания таких единичных потоков: К(х) — доля
требований, обслуженных полностью и пребывающих в системе меньше х
единиц времени; L(x) — доля требований, обслуживание которых прервано
меньше чем через х единиц времени после поступления каждого из них.
Имеем следующие уравнения:
К (х) = Р {г) < у, r)<x)=f[l-G(U)]d/f(U),
О
L (х)=Р (у< т), Y<x}=J[l —Н (и)] dG(u).
о
(17.62)
Эта система уравнений обладает единственным решением. Действительно из нее
легко следует, что
[1 - Н (х)] [1 —G (х)] = 1 —/< (х) —L (х), (17.63)
а отсюда
р 1 /м) (и)
I 1-GM ‘«М-ИЧ. (17.64)
О
Продифференцировав обе части этого равенства по х, найдем:
dG(x) = dL (х)
1— G(x) 1—K(x)—L(x)’ ' ‘ }
откуда
( р dL (и) ]
1—G(x)=exp — -————— ; (17.66)
J 1 — д (и) — L \ U) J
аналогично,
[ р dK (u) 1
1-Я(х) = ехр - - J . (17.67)
VI Д у U ) Li \ J
17.6. ВОССТАНОВЛЕНИЕ АГРЕГАТА ПО НАБЛЮДЕНИЮ
НАД ВЫХОДНЫМ ПРОЦЕССОМ ПРИ УСЛОВИИ,
ЧТО ИЗВЕСТЕН КЛАСС, К КОТОРОМУ ПРИНАДЛЕЖИТ
РАСПРЕДЕЛЕНИЕ ВХОДНОГО ПРОЦЕССА
Мы опускаем рассмотрение второй задачи из сформулированных в § 17.1
(она сводится к постановкам § 17.5) и переходим к наиболее сложной постановке
задачи о восстановлении агрегата в условиях, когда входящий поток не наблю-
дается. Первый пример решения задачи такого рода был дан в [1]. Именно, была
исследована однолинейная система массового обслуживания с ожиданием, пуас-
соновским (простейшим) входящим потоком интенсивности А и произвольным рас-
пределением Н(х) длительности обслуживания требования. По наблюдению
выходящего потока (моментов окончания обслуживания требований) надлежит
восстановить А и Н(х). В одном частном случае задача не имеет единственного
решения: при Я(х) = 1 — е—^х, х > 0. В этом случае выходящий поток, подоб-
но входящему, будет простейшим; его интенсивность будет составлять min{A, р},
так что восстановить А и р не представляется возможным.
413
Покажем, что данный случай является исключительным: если только за-
грузка системы меньше критической и длительность обслуживания имеет закон
распределения, отличный от показательного, то этот закон однозначно восстанав-
ливается по совместному распределению двух- последовательных интервалов
между окончанием обслуживания требований.
Рассмотрим однолинейную систему массового обслуживания с ожиданием,
простейшим входящим потоком интенсивности X и длительностями обслуживания,
представляющими независимые в совокупности случайные величины г]/ с общей
функцией распределения Я(х). Обозначим Mr); = т. Пусть, далее, £п — длитель-
ность интервала между выходом из системы n-го и (п + 1)-го требований;
Ф (х) = lim Р {£п<х}; р = Хт; a (s) = f е — “d® (х);
" о
ОО 00
©i (х, = Р{£п<х, ; |<У}', «1 (s, 0=j f е-“~/у d®! (х, у); (17.68)
" о о
ф(з) =Je~s*dH (х).
о
Введенные пределы существуют, поскольку при р 1 число требований
в системе в любой момент времени t является регенерирующим случайным про-
цессом, функционалами от которого и являются величины £п; если же р 1,
то в силу известного результата Д. Линдли [2] вероятность равенства ]
стремится к единице при п -> оо .
Теорема. При р < 1 справедлива формула
Хф- s
Ф(«) =г—------«(«)•
X + ps
(17.69)
Величина р определяется как единственная отличная от 1 постоянная,
при которой при всех s, f 0 справедливо равенство
Hi Г
*) = а(Огп—: «(«)—0— р)«(«Ч-Мх
л ~г Р* L
+ $ / Н-Р s \ t 1
^ + ^p + ps \ 2а (X) s + M + d
Постоянная X находится из условия
Z-1= —а' (0).
При р > 1 имеем
«1(5, 0 = <P(s)1’(0;
(17.70)
(17.71)
(17.72)
в этом случае тождество (17.70) справедливо лишь при замене р единицей.
Доказательство. Пусть сначала р X 1. Будем считать, что рас-
пределение случайной величины совпадает с Ф(х) (для этого достаточно задать
соответствующее начальное распределение). Тогда с вероятностью, равной
р, £п = т]rtн х (данное равенство будет справедливо в том случае, если (п+1)-е
требование застанет обслуживающий прибор занятым); с вероятностью, равной
1 — р, будет состоять из двух независимых интервалов: т]п-п и показательно
распределенного интервала между выходом из системы п-го и поступлением
(п + 1)-го требования. Формула полной вероятности приводит к равенству
Ф(х) = рН(х) + (1 — р) j’ [l-e-1^-^] dH (р), (17.73)
о
последнее, очевидно, эквивалентно (1/ .69). Отсюда же непосредственно следует
и (17.71).
414
Введем вспомогательные случайные величины: vn — число требований,
остающихся в системе после окончания обслуживания n-го требования; рп —
число требований, поступающих в систему за время обслуживания л-го требо-
вания; tn — время от момента окончания обслуживания n-го требования до мо-
мента поступления следующего требования; /{А) — индикатор события А:
. . __ I 1, если А произошло;
~ | 0, если А не произошло.
Рассуждение, использованное при выводе равенства (17.73), можно сим-
волически записать следующим образом:
Sn=nn+14-^/{v« = 0}. (17.74)
Далее, т>п+1 = 0 в том и только в том случае, когда vcl и р„+1 = 0;
отсюда
Cn+i = rln+2 + £n+i 7 (vn < 1 > p.n+i = 0p (17.75)
В равенствах (17.74) и (17.75) случайная величина vn имеет распределение,
совпадающее со стационарным распределением числа требований в системе
М | G | 1; последнее задается известной формулой Полячека — Хинчина.Из этой
формулы находим
P{vn = 0}=l-p, P{v„ < 1} = (1 —р)/а(Х). (17.76)
Затем, г|я+1 и т]п+2 независимы; gnu и gn+2 не зависят от случайного
вектора {vn, t]n+1, tln+a)- Наконец, prt+1 зависит только от цп+1; при т)п+1 = х
условная вероятность равенства ря+1 = 0 составляет Использовав указан-
ные свойства и применив к обеим частям равенства
ехр { —s?„— /£л+1}=ехр {—з Глп+1 + In 1 {vn = о}] —
-<[iln+2 44n+i/{v„ < 1, рл+1 = о}]} (17.77)
оператор математического ожидания, найдем
ГХ 4- ps /1 s \ i 1
«1(5, 0 = ^(0 T2T^(5)-(1-P) —77,-7— + M . (17.78)
Чтобы из (17.78) получить (17.70), достаточно заменить ф(з) на
Допустим, что тождество (17.70) выполняется при замене р некоторой от-
личной от нее постоянной г =/= 1. Тогда будем иметь тождество
(Л + ri) (% +t) a (s) -(1 -р) ta (s + X) (2Л 7 s) х
. , [ 1 + р
xa + Xp + ps)’1 -^77
\ 2а (Л.)
з \1
. Л I = (^ + Р0
S + X/J
(% + 0«(5)~
I 1 4- г s \ 1
-(1-г) ta (S L >-) (2H-S) (Х +V + rs)-i —I— .
\ 2а(Х) s+ X (J
(17.79)
Приравняв коэффициенты обеих частей при t и /2, получим, что 2а(Х) = 1, и
функция a(s) должна удовлетворять функциональному уравнению
a(s) (X + s) = a(s + %)(2X + s). (17.80)
Заметим, что a(s) в силу (17.80) аналитически продолжается во всю левую
полуплоскость, причем вследствие периодичности функции X(s)(X + s) и нера-
венства |a(s)| 7 1. Res 7 0, a(s) всюду ограничена вне окрестности точки s =
= —Л. Применение обобщенной теоремы Лиувилля приводит нас к выводу, что
a(s) = Х/(Х + s), т. е. что длительность обслуживания распределена по показа-
тельному закону. Та часть теоремы, которая относится к случаю р 7 1, триви-
альна и не требует специального доказательства.
415
Из приведенной теоремы следует, что при фиксированной a(s) существует
линейный функционал от распределения Ф1(х, у), по которому однозначно вос-
станавливается р. Однако статистика, связанная с функционалом, пригодным
для любых a(s), по-видимому, имеет довольно сложный вид. Для практических
целей можно рекомендовать уравнения, получающиеся при сравнении производ-
ных обеих частей равенства (17.70) при s = t = 0. Так, простейшее из этих урав-
нений имеет вид
(2А,«1 —а0) ра + 2а0 [X2 т-|-2а0—2] р + 2Х2 а0 т — 2)м1—4ао2 + ао = О,
где
а0 = а(Х), ai=—a'(2v),
d2 aj (s, f)
m= ds di
s = t = O
Ряд задач подобного рода решен В. А. Ивницким. Приведем один из его
результатов. Этот пример интересен тем, что по статистике выходящего потока
восстанавливается структура системы.
Пусть по-прежнему имеется однолинейная система с простейшим входящим
потоком требований, длительностью обслуживания, распределенной по закону
Н(х), но в отличие от предыдущей постановки задачи общее число находящихся
в системе требований ограничено сверху постоянной величиной т > 1. Требуется
найти Л, Н(х) и /и по наблюдениям над выходящим потоком требований. Считается,
что, наблюдая выходящее требование, мы фиксируем, к какому типу — обслу-
женных или потерянных требований—оно принадлежит. Покажем, что стати-
стика выходящего потока позволяет однозначно восстановить все эти характе-
ристики.
Параметр X восстанавливается однозначно как интенсивность выходящего
потока, которая при т <С 00 равна интенсивности входящего. Чтобы найти Н(х),
будем набирать статистику интервалов между выходом из системы двух обслу-
женных требований при условии, что последнее требование, вышедшее из си-
стемы перед первым из этих двух, было потеряно. Условное распределение таких
интервалов и будет, как нетрудно видеть, совпадать с безусловным распреде-
лением длительности обслуживания.
Остается определить параметр т. С этой целью рассмотрим интервал £
между моментами выхода из системы обслуженных требований. Пусть г] — дли-
тельность обслуживания требования, £ — время между поступлением в систему
последовательных требований. Можно записать:
Mg=Mn + p0Mg, (17.81)
где ро — вероятность того, что в момент выхода из системы обслуженного требо-
вания прибор остается свободным. Таким образом, для р0 получаем формулу
р0=А. (М£—Мт]), (17.82)
в правую часть которой согласно вышеизложенному входят лишь параметры»
доступные статистической оценке.
Зададимся целью найти связь р0 с т. Рассматривая в качестве вложенной
цепи Маркова количества требований в моменты окончания обслуживания, по-
лучим для финальных вероятностей такой цепы систему уравнений:
k+ 1
Рд= 2 Рг^_;+1 + Рос&, 1 <k<m-2-,
L — 1
Рщ-1= 2 Pi 2 Ck+Po 2 СЛ; (17.83)
i— 1 k~m — i k=m— I
Po + Pl + • • • + Pm-1 — 1 »
oo
V p •
где Cj = —j x'dH(x), i = 0, 1, 2,...
о
416
Это и будет искомой системой уравнений: для любого т из этой системы получает-
ся свое значение ра = р0(т).
Легко видеть, что р0(т) является монотонно убывающей функцией (чем
больше т, тем больше в среднем требований обслуживается в единицу времени).
Поэтому из уравнения рд(т) = Х(М£ — Mt]) значение т находится однозначно.
Восстановление характеристик бесконечнолинейной системы по статистике
выходящего потока. В качестве последнего примера рассмотрим задачу, решен-
ную Кендаллом и Льюисом [3].
В бесконечнолинейную систему массового обслуживания поступает поток
восстановления с функцией распределения F(x) интервала £ между прибытием
требований. Длительность обслуживания г] имеет функцию распределения Н(х).
Предположим, что наблюдаются моменты in окончания обслуживания требова-
ний. Допустим также, что для всех обслуженных требований известны их но-
мера во входящем потоке. Оказывается, что такая статистика достаточна
для восстановления обеих функций распределения: F(x) и Н(х\
Очевидно, по указанной статистике однозначно восстанавливается двумер-
ное распределение случайного вектора (а, 0), где а — интервал между оконча-
нием обслуживания n-го и (п + 1)-го требований, 0 — то же для (п + 1)-го и
(п + 2)-го требований.
Пусть
/(0=Ме;/5, й(0 = Ме“т'. (17.84)
Тогда
Me““ = f(0|/i(0|2, Ме,7а+,ч0 = /(/)/(?)/г (-/)й (/-т)й(т). (17.85)
Согласно предыдущему функции, входящие в левые части этих уравнений,
восстанавливаются по статистическим данным. В указанной статье доказывается,
что эти два уравнения позволяют однозначно определить /(/), a h(t) восстанав-
ливается с точностью до множителя вида exp (i/u), и = const. Неоднозначность
легко объяснить: если увеличить длительность обслуживания всех требований
на постоянную к, стационарные свойства выходящего потока не изменятся.
17.7. ИСПОЛЬЗОВАНИЕ НЕРАВНОПРАВНЫХ НАБЛЮДЕНИЙ
В статистике сложных систем часто имеют дело с неравноправными
измерениями не в смысле точности, а по самой их физической приро-
де. Так, при совместном использовании результатов испытаний реаль-
ной системы и результатов ее статистического моделирования в пер-
вом случае реализуются все влияющие на функционирование системы
факторы, а во втором — только некоторые из них. Ниже будет рассмо-
трено решение задачи о совместном использовании разнотипных изме-
рений в довольно простой постановке; однако эта постановка поз
воляет проиллюстрировать отмеченную важную особенность статисти-
ки сложных систем.
Пусть работоспособность некоторой системы зависит от парамет-
ра £, причем известно, что при £ х0 система работоспособна, при
£ > х0 — не работоспособна, где х0 — некоторое неизвестное число-
вое значение [4], g является случайной величиной с неизвестной
функцией распределения F (х). Таким образом, вероятность безот-
казной работы системы есть
р = F (х0), (17.86)
417
При испытаниях системы мы получаем независимые реализации
случайной величины 5: ^2, .... 5м, причем в каждой реализации
известно, работоспособна ли система при реализовавшемся значении
5. Таким образом, если
f 1 при X < х0,
/ W = л
[О при х >х0,
(17.87)
то результаты N независимых испытаний системы можно представить
таблицей:
51 5з 5м
/(51) /(5з) /(5м)
Допустим далее, что имеется статистическая модель, раскрываю-
щая механизм образования случайной величины 5, но не позволяющая
судить о работоспособности системы при тех или иных значениях 5.
Следовательно, в результате т реализаций модели мы получаем т зна-
чений т)!, т]2, ..., г]т, где щ— независимые случайные величины с
функцией распределения F (х).
Задача состоит в том, чтобы на основании наблюдений
Si. Kit), и ri(, l<i<m,
построить точечную оценку и доверительный интервал для показателя
р, а также выбрать оптимальное соотношение между Num при задан-
ной стоимости испытаний. Более точная постановка задачи оптими-
зации будет сформулирована ниже.
Пусть 5и> <15(2) < ... С 5<м>— вариационный ряд, составленный
по выборке (£1( 5г, •••, 5м). Обозначим для единообразия 5(0) = —оо,
5(м-н) =°°. Тогда для некоторого г, 0 < г < IV, будут выполняться
соотношения
/(5(0)) = ...=И5о)) = 1,
f (5(r+i)) = =Н5(м+1>) = о.
(17.88)
Обозначим v = г + число тех г|7-, которые меньше 5(г), или, иначе,
tn
V = r+ 2 (5(r) — Л1),
1=1
где
( 0 при х < 0,
£(*)=, н
' (1 при х > 0.
(17.89)
(17.90)
Доверительный интервал для р будем строить на основании
статистики v. Прежде всего, имеет место неравенство
Б(5(г)-х)</(х) (17.91)
418
для всех х, что легко проверить в силу (17.87), (17.90) и неравенства
?(/•) < А'о- Поэтому в силу (17.89)
т N т
Ш+УЖЛ (17.92)
/= 1 >= 1 i = I
Однако правая часть (17.92) есть число успехов в п = N + т неза-
висимых испытаниях с вероятностью успеха, равной р = F (х0) в
каждом из них. Отсюда следует, что если
Л< т
>=1 /=I
и мы построим для р доверительный интервал вида (р*, 1), где р* —
неубывающая функция v*, то при замене v* величиной v получим до-
верительный интервал для р с не меньшим доверительным уровнем.
Теперь остается применить стандартную процедуру. Зададим некото-
рое е, 0 < е < 1, и определим k (р) из условия
*'<₽) —1 ь (р)
2 С^А(1-р)п“/г<1-е< £ C*pk(\~p),l-k. (17.93)
fe=0 4 = 0
Затем положим
р* = р* (й) = min {р : k(p}^ А}.
Это и будет искомым р* при условии, что v = k. Важнейшими харак-
теристиками р* являются: доверительный уровень (равный согласно
предыдущему 1 — е) и математическое ожидание отклонения р* от р
А=М{р—р*}. (17.94)
Произведем асимптотический анализ А при больших п. Заметим,
что в формуле (17.93) фигурируют вероятности попадания в интервал
случайной величины с биномиальным законом распределения. Отсю-
да следует, что k (р) при больших п приближенно выражается следую-
щим образом:
k(p) = np + 2e Vnpq, (17.95)
гдеД? = 1— р, Зачесть корень уравнения
е = —— f е~х^2 dx.
У 2л J
ze
Доверительный интервал определяется решением р* уравнения
k — пр = 2е]Упр (1—р), (17.96)
р*= —-z£-]/(17.97)
г п I/ Л П \ nJ’
419
с точностью до величин порядка о (1//г). Можно записать:
Мр*=-^р + ^-Р{Л;<тахО-ге1 / Pl + of-LV (17.98)
п п ‘ 1 у п \ п )
или
Мр*=:р_^_р{п.>тахО Нпг) = 1}~
—zz I Л^ + о (—V (17.99)
Если обозначить р = х0 — max {£fj, случайная величина р бу-
1 < I
дет распределена следующим образом:
Р{р>х} =[Р{£г <х0-х/Ъ < х0}У (17.100)
при условии, что г приняло некоторое фиксированное значение.
По теореме Муавра—Лапласа,
r=--Np + O(i ~N} (17.101)
с вероятностью, сколь угодно близкой к 1. Предположим, что в точке
х0 функция F (х) имеет производную b > 0. Тогда
nf . Г. ь , . ,-|Wp+o(/w)
Р{р>х} =| 1-----х + о(х)| ; (17.102)
отсюда при любом фиксированном х>0
Р(р>— J -Г1 — — +о ( J_'|]A,p+0(/A,)__ е-Ч (17.103)
V n I L w \ д' Л
Следовательно, случайный интервал Мр имеет асимптотически пока-
зательное распределение с параметром Ь. Кроме того, поскольку фор-
мула (17.103) выполняется при любом нормальном отклонении г,
Np асимптотически независима от г. Далее, так как т|7- не зависит
от (£{},
P{ri,>max{BJ, f(i]7) = l} =
= 5 Pii(x)tP—F (xo—x)]dx~Nb^ e~Nbx bx dx = — , (17.104)
b b
где рц, (x) — плотность вероятности случайной величины р. Под-
ставив (17.104) в (17.99), получим
— • (17.105)
nN V п
420
Искомое математическое ожидание отклонения левой границы
доверительного интервала от истинного значения параметра р со-
ставляет
A~M(p-p*)=4+zel(17.106)
nN |/ п
Положим, что стоимость одного испытания системы равна 1, стои-
мость одного эксперимента с моделью составляет с, где 0 < с < 1.
Тогда можно решить задачу о минимизации А при условии, что общая
стоимость испытаний ограничена:
N -\-ст < а.
(17.107)
Для этого нужно найти минимум функции
А = А(Д\ т) =---------(17.108)
' 7 У(У + т) у N + m v
при условии
N -\-ст^.а, (17.109)
подставив вместо р некоторое ориентировочное его значение.
Данную задачу проще всего можно решать методом перебора.
Однако можно также использовать непрерывную интерпретацию,
рассматривая N=x, т = у как непрерывные переменные; при этом
условие экстремума сводится к некоторому алгебраическому уравнен
нию пятой степени.
Решим теперь задачу о точечной оценке параметра р. Предлагает-
ся следующая процедура оценивания. Рассмотрим величины £(Г)
и ^(r+i). (Напомним, что f (g(r>) = 1, / (£(/•+!)) = 0.) Возьмем среднюю
точку t = [^(г) + £(г+1)1/2 и образуем оценку
1 / m \
Р = — \г + £ б; ,
п \ /=1 /
где
при T]j
При Т];
(17.110)
(17.111)
Ниже будут исследованы математические ожидания и дисперсия
оценки р. Имеем:
Мр=—Мг + —М0Х.
п п
Поскольку, очевидно,
Mr = Np,
то
Мр= — р + — М0Х.
п п
(17.112)
(17.113)
(17.114)
421
Можно записать:
(17.115)
где pt _ л-0 (х) — плотность вероятности случайной величины t — х0
MJ0J — условное математическое ожидание 0! при условии, что
t — х0 = х. Понятно, что при N -+ оо случайная величина t — х0
будет бесконечно малой. При малых х
Мх {01} = Р Oh < tit = хй + =
= Р + Рж (г) dz = р + Ьх + о (х),
х.
(17.116)
где, как выше было обозначено, b = F' (х0).
Найдем плотность вероятности случайной величины t — х0.
Можно записать
Pt-xa (x) = £prp(_^.r(x),
Г
(17.117)
где рт — вероятности частных значений случайной величины г
pt-x0,r(x) — условная плотность\ t — х0 при частном значении г
Заметим, что при фиксированном г случайные величины £(г) и
независимы. Если г = Np + где и — ограниченная величина,;
то соответствующие условные плотности можно вычислить так:
Р{М>—?(г) >*} =[Г(х0 — х)/Е.(х0)Г,
Pxa-i{r}. r{x)=r[F (х0—x)/F(x0)]r~ 1 F' (x0—x)/F(x0) =
где bx = F" (О’), О — некоторая точка интервала (х0 — х, х0), в
предположении, что F (х) дважды непрерывно дифференцируема.
Далее,
Рх.-^,.г(^)=у(^р + «ГЛ/)р + о(^]х
X Р-у- Y =A7e^U + о(1)]. (17.119)
Точно так же,
^Е(г+1)-х.,г(х)=Ме-^[1 +о(1)]. (17.120)
422
Поскольку при нормальных уклонениях правые части (17.119) и
(17.120) асимптотически не зависят от г, то подобные же формулы спра-
ведливы и для безусловных плотностей. Отсюда при х > 0
pf_Xo(x)=p! (х) =
•у [£ р-н )+s(n
= р 1 I (х) ~
y[S(r+i)-4-y (г)Г
~2№62jj e~Nbu-Nb(u+2x-)dx== NbQ-2Nbx. (17.121)
о
Аналогично вычисляется pt-Xa (х) и при х<0; в результате находим:
pt-Xll (х) ~ Nbe.~2Nb Iх ।, —оо<х<;оо. (17.122)
Мы видим, что величина (t — х0) асимптотически независима от г.
Следовательно, р асимптотически представима в виде суммы двух
случайных величин: асимптотически нормальной с математическим
ожиданием р и дисперсией Npqlti? и асимптотически нормальной
со случайным математическим ожиданием р + 0 и дисперсией mpqln\
где, в свою очередь, 0 — бесконечно малая случайная величина
с плотностью
ре(х) =Ае-2Л'1-,;1, —оо<х<оо. (17.123)
(0 при t > х0 есть вероятность попадания случайной величины с рас-
пределением Р (х) в интервал (х0, /); при t < х0 — вероятность попа-
дания такой же случайной величины в интервал (t, х0). Поскольку t —
случайная величина, то и 0 случайна.)
Теперь можно вычислить М {Qj}:
M{9i}=P+§P;-x»(x)xdx~p, (17.124)
т. е. оценка р — асимптотически несмещенная.
Для дисперсии р легко найти такое выражение:
<17л25)
Это показывает, что в данной частной постановке можно почти все
испытания производить на модели, не теряя в точности по сравнению
со случаем, когда испытывается сама система.
Рассмотрим численный пример. Пусть ориентировочное значение
р = 0,96; требуется оценка р со среднеквадратическим отклонением
не более 0,005. Тогда, если бы все испытания производились с систе-
мой, понадобилось бы их N = 160. Этот же результат может быть по-
лучен, если взять N = 50, /п = 750, т. е. если 50 испытаний произвести
с системой, а 750 испытаний — на модели.
Л ИТЕРАТУРА
К главе 1
1. Г у д Г. X., Макол Р. Э. Системотехника. Пер. с англ. Изд-во
«Советское радио», 1962.
2. О п т н е р С. Л. Системный анализ для решения деловых и промышлен-
ных проблем. Пер. с англ. Изд-во «Советское радио», 1969.
3. В е н т ц е л ь Е. С. Введение в исследование операций. Изд-во «Со-
ветское радио», 1964.
4. «Наука — техника — управление». Сб. статей. Пер. с англ. Изд-во
«Советское радио», 1966.
5. Хедли Дж., У айтин Т. Анализ систем управления запасами.
Пер. с англ. Изд-во «Наука», 1969.
6. «Принципы самоорганизации». Сб. статей. Пер. с англ. Изд-во «Мир»,
1966.
7. Ляпунов А. А., Яблонский С. В. Теоретические проблемы
кибернетики. В сб. «Проблемы кибернетики», вып. 9. Физматгиз, 1963.
8. Пляцидевский И. А. Информационные системы в технике и
экономике. Изд-во «Московский рабочий», 1966.
9. «Справочник по системотехнике». Пер. с англ. Изд-во «Советское радио» ,
1970.
10. Б у с л е н к о Н. П. Моделирование сложных систем. Изд-во
«Наука», 1968.
11. Бусленко Н. П. Сложные системы и машинная математика.
«Вестник АН СССР.» 1967, № 4.
К главе 2
1. Бусленко Н. П. Моделирование сложных систем. Изд-во «Наука»
1968.
2. В е н т ц е л ь Е. С. Введение в исследование операций. Изд-во «Со-
ветское радио», 1964.
3. К о ф м а н А. Методы и модели исследования операций. Пер. с франц.
Изд-во «Мир», 1966.
4. Понтрягин Л. С. и др. Математическая теория оптимальных про-
цессов. Физматгиз, 1961.
5. 3 у б о в В. И. Теория оптимального управления. Изд-во «Судо-
строение», 1966.
6. Ш и ш о н о к Н. А. и др. Основы теории надежности.Изд-во «Советское
радио», 1964.
7. Гнеденко Б. В. и др. Математические методы в теории надежно-
сти, Изд-во «Наука», 1965.
8. Г у д Г. X., Макол Р. Э. Системотехника. Пер. с англ. Изд-во
«Советское радио», 1962.
9. О п т н е р С. Л. Системный анализ для решения деловых и промыш-
ленных проблем. Пер. с англ. Изд-во «Советское радио», 1969.
10. «Справочник по системотехнике». Пер. с англ. Изд-во «Советское р а-
дио», 1970.
424
К главе 3
1. Понтрягин Л. С. Обыкновенные дифференциальные уравнения.
Изд-во «Наука», 1970.
2. Красовский Н. Н. Некоторые задачи теории устойчивости дви-
жения. Физматгиз, 1959.
3. Колмогоров А. Н., Фомин С. В. Элементы теории функций
и функционального анализа. Изд-во «Наука», 1968.
4. Арнольд. В. И. Лекции ио классической механике. Изд-во МГУ,
1966.
5. Куратовский К., Мостовский А. Теория множеств.
Изд-во «Мир», 1970.
6. Ф о р Р., К о ф м а н А., Ден и-П а и е н М. Современная мате-
матика. Изд-во «Мир», 1966.
7. А н д р о н о в А. А., Витт А. А., X а й к и н С. Э. Теория
колебаний. Физматгиз, 1959.
8. Немыцкий В. В., Степанов В. В. Качественная теория
дифференциальных уравнений. Гостехиздат, 1949.
9. К У р о ш А. Г. Курс вышей алгебры. Изд-во «Наука», 1968.
10. Бесекерский В. А., Ионов Е. П. Теория систем авто-
матизированного регулирования. Изд-во «Наука», 1966.
11. Зубов В. И. Методы А. М. Ляпунова и их применение. Изд-во
ЛГУ, 1957.
12. Н о р к и н С. Б. Дифференциальные уравнения второго порядка с
запаздывающим аргументом. Изд-во «Наука», 1956.
13. К р а с о в с к и й Н. Н. Теория управления движением. Изд-во
«Наука», 1968.
14. Красовский Н. Н. Игровые задачи о встрече движений. Изд-
во «Наука», 1970.
15. Э л ь с г о л ь ц Л. Э. Качественные методы в математическом ана-
лизе. Гостехиздат, 1955.
16. Р у б а н и к В. П. Колебания квазилинейных систем с запазды-
ванием. Изд-во «Наука», 1969.
17. Д у б о л а р ь В. К- Динамические системы с запаздыванием.
ДАН СССР, 1968, т. 183, № 5.
18. Д у б о л а р ь В. К- К теории дифференциальных уравнений
с последействием. Диссертация. Кишинев, 1970.
19. К а л м а н Р., Фалб П., Арбиб М. Очерки ио математиче-
ской теории систем. Изд-во «Мир», 1971.
20. Э л ь с г о л ь ц Л. Э., Н о р к и н С. Б. Введение в теорию диффе-
ренциальных уравнений с отклоняющимся аргументом. Изд-во «Наука», 1971.
К главе 4
1. Бусленко Н. П. Моделирование сложных систем. Изд-во «Наука»
1968.
2. В е н т ц е л ь Е. С. Введение в исследование операций. Изд-во
«Советское радио», 1964.
3. Глушков В. М. Синтез цифровых автоматов. Физматгиз, 1962.
4. Гнеденко Б. В., Коваленко И. Н. Введение в теорию мас-
сового обслуживания. Изд-во «Наука», 1966.
5. Канторович Л. В., Акилов Г. П. Функциональный ана-
лиз в нормированных пространствах. Физматгиз, 1959.
6. Карлин С. Математические методы в теории игр, программирова-
нии и экономике. Изд-во «Мир», 1964.
7. Коваленко И. Н. Некоторые задачи массового обслуживания с
ограничением. «Теория вероятностей и ее применение», 1961, т. 6, №2.
425
8. Рабин М. О. Вероятностные автоматы. «Кибернетический сборник»,
вып . 4, 1962.
9. Яровицкий Н. В. О вероятностно-автоматном моделировании.
«Кибернетика», 1965, № 5. i
10. К а л м а н Р., Ф а л б П., А р б и б М. Очерки по математической
теории систем. Изд-во «Мир», 1971.
11. Куратовский К-, Мостовский А. Теория множеств.
Изд-во «Мир», 1970.
12. А й з е р м а н М. А., Гусев Л. А., Р о з о н о э р Л. И.,
Смирнова И. М., Таль А. А. Логика. Автоматы. Алгоритмы. Физмат-
гиз, 1963.
13. К о б р и н с к и й Н. Е., Т рахтенброт Б. А. Введение в те-
орию конечных автоматов. Физматгиз, 1962.
14. Б а р у ч а-Р ид А. Т. Элементы теории марковских процессов и их
приложения. Изд-во «Наука», 1969.
15. Г и х м а н И. И., Скороход А. В. Введение в теорию случай-
ных процессов. Изд-во «Наука», 1965.
16. Ф е л л е р В. Введение в теорию вероятностей и ее приложения,
т. I. Изд-во «Мир», 1964.
К главе 5
1. Б а р у ч а - Р и д А. Т. Элементы теории марковских процессов и их
приложения. Изд-во «Наука», 1969.
2. Г и х м а и И. И., Скороход А. В. Введение в теорию случай-
ных процессов. Изд-во «Наука», 1965.
3. Д ы н к и н Е. Б. Марковские процессы. Физматгиз, 1963.
4. Л о э в М. Теория вероятностей. Изд-во иностранной литературы,
1962.
5. Неве Ж. Математические основы теории вероятностей. Изд-во «Мир»,
1969.
6. Г л у ш к о в В. М. Синтез цифровых автоматов. Физматгиз, 1962.
7. Гнеденко Б. В., Коваленко И. Н. Введение в теорию-мас-
сового обслуживания. Изд-во «Наука», 1966.
8. Б у с л е н к о Н.П. Моделирование сложных систем. Изд-во
«Наука», 1968.
К главе 6
1. Гнеденко
сового обслуживания.
Б. В., К о в а л е и к о И.
Изд-во «Наука», 1966.
Н.
Введение в теорию мас-
К главе 7
fl. Б у с л е н к о Н. И. Моделирование сложных систем. Изд-во «Наука»
1968.
2. Бусленко Н.П. Об одном классе сложных систем. Сб. «Пробле-
мы прикладной математики и механики». Изд-во «Наука», 1971.
3. Куратовский К., Мостовский А. Теория множеств.
Изд-во «Мир», 1970.
4. Г л у ш к о в В. М. Синтез цифровых автоматов. Физматгиз, 1962.
К главе 8
1. Б е р ж К- Теория конечных графов и ее применение. Изд-во иност-
ранной литературы, 1962.
2. 3 ы к о в А. Теория конечных графов. Изд-во «Наука», Новосибирск,
1969.
426
3. Куратовский К- Топология, т. 1. Изд-во «Мир», 1966.
4. Н е ч и п о р е и к о В. И. Структурный анализ и методы построения
надежных систем. Изд-во «Советское радио», 1968.
5. О р е О. Теория графов. Изд-во «Наука», 1968.
6. П о в а р о в Г. Н. О матричном анализе связей в частично-ориен-
тированных графах. УМН, 1956, т. 11, выи. 5.
К главе 9
1. Б а р б а ш и н Е. А. Введение в теорию устойчивости. Изд-ов
«Наука», 1967.
2. Баутин Н.Н. О поведении динамических систем вблизи границ
области устойчивости. Гостехиздат, 1949.
3. Бусленко Н. П., Калашников В. В. Об устойчивости
функционирования сложных систем. «Кибернетика», 1967, № 2.
4. Б у х а р а е в Р. Г. Теория вероятностных автоматов. «Кибернетика»,
1968, №2.
5. Г и х м а н И. И., СкороходА. В. Введение в теорию случайных
процессов. Изд-во «Наука», 1965.
6. Д е м и д о в и ч Б. Г. Лекции по математической теории устойчиво-
сти. Изд-во «Наука», 1967.
7. 3 у б о в В. И. Методы А. М. Ляпунова и их применение. Изд-во ЛГУ,
1957.
8. I п f а п t е Е. F., W е i s s L. On the stability of systems defined
over a finite time interval. Proc, of the National Academy of Sciences, 1965,
v. 54, № 1.
9. 1 n f a n t e E. F., Weiss L. Finite Time Stability under Pertur-
bing Forces and on Product Spaces. IEEE Trans, on Automatic Control, 1967,
AC-12, № 1.
10. К а л а ш н и к о в В. В. О затаче исследования устойчивости функ-
ционирования сложных систем. ДАН СССР, 1967, т. 177, № 6.
И. Калашников В. В. О понятии устойчивости функционирова-
ния сложных систем. В сб. «Большие информационно-управляющие системы».
Изд-во МДНТП им. Ф. Э. Дзержинского, 1969.
12. К а р а ч а р о в К. А., П и л ю т и к А. Г. Введение в техниче-
скую теорию устойчивости движения. Физматгиз, 1962.
13. Кац И. Я., Красовский Н. Н. Об устойчивости движения,
со случайными параметрами. «Прикладная математика и механика», 1960,
т. 24, № 5.
14. К о ч к а р е в Б. С. Об устойчивости вероятностных автоматов.
«Кибернетика», 1968, № 2.
15. К у ш и е р Г. Дж. Стохастическая устойчивость и управление.
Изд-во «Мир», 1969.
16. Л а-С алль Ж., Лефшец С. Исследование устойчивости прямым
методом Ляпунова. Изд-во «Мир», 1964.
17. L о у п е s R. М. The stability of a queue with non-independent in-
ter-arrival and service times. Proc, of the Cambridge Phil. Soc., 1962, v. 58, №.3 .
18. L о у n e s R. M. The stability of a system of queues in series. Proc,
of the Cambridge Phil. Soc., 1964, v. 60, № 3.
19. Л я п у н о в A. M. Общая задача об устойчивости движения. Гостех-
издат, 1950.
20. М а л к и н И. Г. Теория устойчивости движения. ГИТТЛ, 1952.
21. Р a z A. Some aspects -of probabilstics automata. Information and
Control, 1966, v. 9, № 1.
22. П о н т p я г и н Л. С. Обыкновенные дифференциальные уравне-
ния. Физматгиз, 1961.
23. П у а н к а р е А. О кривых, определяемых дифференциальными урав-
нениями. Гостехиздат, 1947.
24. Рабин М. О. Вероятностные автоматы. «Кибернетический сбор-
ник», № 9, 1964.
427
25. Р у м я н ц е в В. В. Метод функций Ляпунова в теории устойчи-
вости движения. В сб. «Механика в СССР за 50 лет». Изд-во «Наука», 1968.
26. S t о k е г J. J. On the stability of mechanical system. Comm. Pure
Appl. Math. 1955, № 8, p. 133—141.
27. X а с ь м и и с к и й Р. 3. Устойчивость систем дифференциальных
уравнений при случайных возмущениях их параметров. Изд-во «Наука», 1969.
28. X и и ч и н А. Я. Лекции по математической теории массового обслу-
живания. Физматгиз, 1963.
29. Чезари Л. Асипмтотическое поведение и устойчивость решений
обыкновенных дифференциальных уравнений. Изд-во «Мир», 1964.
30. Э ш б и У. Р. Конструкция мозга. Изд-во иностранной литературы,
1962.
К главе 10
1. Ч ж у н К а й-л а й. Однородные цепи Маркова. Изд-во «Мир», 1964.
2. Б е р ж К. Теория графов и ее применение. Изд-во иностранной лите-
ратуры, 1962.
3. Л у п а и о в О. Б. О сложности реализации функций алгебры логики
формулами. В сб. «Проблемы кибернетики», вып. 3, 1960.
4. Кл осс Б. М., Малышев В. А. Оценки сложности некоторых
классов функций. «Вестник МГУ», Математика и механика, 1965, № 4.
5. С а а т и Т. Элементы теории массового обслуживания и ее прило-
жения. Изд-во «Советское радио», 1965.
6. Попов П. И., Терентьев В. Г. Надежность систем автома-
тики. Изд. МИФИ, 1966.
7. Ш т о к а л о И. 3. Линейные дифференциальные уравнения с пере-
менными коэффициентами. Изд-во АН УССР, Киев, 1960.
8. X и н ч и н А. Л. Работы по математической теории массового обслу-
живания. Физматгиз, 1963.
9. Ивницкий В. А. Об одной задаче теории резервирования с пере-
ключением. В сб. «Кибернетику—на службу коммунизму», т. 2. Изд-во «Энер-
гия», 1964.
К главе 11
1. Гнеденко Б. В. Об одной задаче массового обслуживания. «Докла-
ды АН УССР», 1958, № 5.
2. Г н е д е и к о Б. В. Курс теории вероятностей. Изд-во «Наука»,
1965.
3. Г и х м а и И. И., Скороход А. В. Введение в теорию случай-
ных процессов. Изд-во «Наука», 1965.
4. Гнеденко Б. В., Коваленко И. Н. Введение в теорию мас-
сового обслуживания. Изд-во «Наука», 1966.
5. К р е й н М. Г. Интегральные уравнения на полуоси. УМН, 1961,
т. 13, № 5.
6. L i п d 1 е у D. The theory of queues with a single server. Proc. Camb-
ridge Phil. Soc. 1952,48.
7. К о к с Д. P., С м и т В. Теория восстановления. Изд-во «Советское
радио», 1967.
К главе 12
1. Гнеденко Б. В., Коваленко И. Н. Введение в теорию мас-
сового обслуживания. Изд-во «Наука», 1966.
2. Е ж о в И. И. Цепи Маркова с дискретным вмешательством случая,
образующим полумарковский процесс. Украинский математический журнал,
1966, № 1.
423
3. G ж о в I. I. Ергодичш теореми для марковських процещв з дис-
кретним втручанням випадку. Доповш АН УРСР, 1966, № 5.
4. Ежов И. И. Эргодическая теорема для марковских процессов, опи-
сывающих общие системы массового обслуживания. «Кибернетика», 1966, № 5.
5. 6 ж о в I. I. Про час досягненняя задано! облает! у випадку ланцю-
га Маркова з дисретним втручанням випадку. Допов!д! АН УРСР, 1966, № 7.
6. Ж и т о м и р с к и й И. С. Некоторые вопросы теории скачкообраз-
ных процессов с детерминированным сносом. «Теория функций, функциональ-
ный анализ и их приложения». Республиканский научный сборник, вып. 2,
1966.
7. Калашников В. В. О задаче исследования устойчивости функ-
ционирования сложных систем. ДАН СССР, 1967, т. 177, № 6.
8. Калашников В. В. Об устойчивости кусочно-линейных агрега-
тов. «Кибернетика», 1968, № 4.
9. Калашников В. В. Об устойчивости функционирования агре-
гативных систем. «Кибернетика», 1968, № 5.
10. Калашников В. В. Применение метода Ляпунова для решения
некоторых задач теории массового обслуживания. «Известия АН СССР», Техни-
ческая кибернетика, 1968, № 5.
11. Камке Э. Интеграл Лебега—Стилтьеса. Физматгиз, 1959.
12. Коваленко И. Н. Некоторые аналитические методы в теории
массового обслуживания. В сб. «Кибернетику — на службу коммунизму», т. 2.
Изд-во «Энергия», 1964.
13. Коваленко И. Н. Некоторые вопросы теории надежности слож-
ных систем. В сб. «Кибернетику—на службу коммунизму», т. 2, Изд-во «Энергия»,
1964.
14. К о в а л е н к о И. Н. О некоторых классах сложных систем. «Из-
вестия АН СССР», Техническая кибернетика, 1964, № 6; 1965, №1и№3.
15. Кокс Д. Р., Смит В. Л. Теория восстановления. Изд-во «Со-
ветское радио», 1967.
16. К о р о л ю к В. С. Время пребывания полумарковского процес-
са в фиксированном множестве состояний. «Украинский математический жур-
нал», 1965, № 3.
17. Ф е л л е р В. Введение в теорию вероятностей и ее приложения,
т. 2, Изд-во «Мир», 1967.
К главе 13
1. Коваленко И. Н. Некоторые вопросы надежности сложных
систем. В сб. «Кибернетику — на службу коммунизму», т. 2. Изд-во «Энергия»,
1964.
2. Коваленко И. Н. Асимптотический метод анализа надежности
сложных систем. В сб. «О надежности сложных технических систем». Изд-во
Советское радио», 1967.
К г лаве 14
1. Афанасьева Л. Г. О существовании предельного распределения
в системах массового обслуживания с ограниченным временем пребывания.
«Теория вероятностей и ее применение», 1965, 10, № 3.
2. В а г г е г D. Y. Queueing with impatient customers and indifferent
clerks. Oper. Res. 1957, v. 5, № 5..
3. BarrerJD. Y. Queueing with impatient customers and ordered
service. Oper. Res., 1957, v. 5, № 5.
4. Б a p у ч’а-Р и д А. Т. Элементы теории марковских процессов и их
приложения. Изд-во «Наука», 1969.
5. Б о р о в к о в А. А. Некоторые предельные теоремы теории массо-
вого обслуживания. «Теория вероятностей и ее применение», 1964, т. 9, № 4;
1965, т. 10, № 3.
429
6. Боровков А. А. О сходимости слабозависимых процессов к вине-
ровскому. «Теория вероятностей и ее применение», 1967, т. 12, № 2.
7. Боровков А. А. О сходимости к диффузионным процессам. «Те-
ория вероятностей и ее применение», 1967, т. 12, № 3.
8. Б р о д и С. М. Об одной задаче массового обслуживания. Труды
V Всесоюзного совещания по теории вероятностей и математической статистике.
Ереван, Изд-во АН АрмССР, 1960.
9. Коваленко И. Н. Некоторые задачи массового обслуживания
с ограничениями. «Теория вероятностей и ее применение», 1961 т. 6, № 1.
10. L i п d 1 е у D. V. The theory of queues with a single server. Proc, of
the Cambridge Phil. Soc., 1952, v. 48, p. 277—289.
И. Прохоров Ю. В. Переходные явления в процессах массового
обслуживания. «Литовский математический сборник», 1963, т. 3, № 1.
12. С а м а н д а р о в Э. Г. Системы обслуживания в условиях большой
загрузки. «Теория вероятностей и ее применение», 1963, т. 8, № 3.
К главе 15
1. Б а р б а ш и н Е. А. Функции А. М. Ляпунова. Изд-во «Наука»,
1970.
2. Гнеденко Б. В., Беляев Ю. К-, Соловьев А. Д. Ма-
тематические методы в теории надежности. Изд-во «Наука», 1965.
3. Гнеденко Б. В., Коваленко И. Н. Введение в теорию мас-
сового обслуживания. Изд-во «Наука», 1966.
4. Д ы н к и н Е. Б. Марковские процессы. Физматгиз, 1963.
5. Калашников В. В. Система массового обслуживания с интер-
валами недоступности. «Известия АН СССР», Техническая кибернетика , 1966 ,
№ 6.
6. Калашников В. В. Об одной модели обслуживания. «Известия
АН СССР», Техническая кибернетика, 1968, № 1.
7. Калашников В. В. Применение метода Ляпунова для решения
некоторых задач теории массового обслуживания. «Известия АН СССР», Тех-
ническая кибернетика, 1968, № 5.
8. Калашников В. В. Оценка надежности резервированных систем
с постоянным временем восстановления с помощью прямого метода Ляпунова.
«Известия АН СССР», Техническая кибернетика» 1969, № 3.
9. К а л а ш н и к о в В. В. Анализ надежности с помощью метода
Ляпунова. «Известия АН СССР», Техническая кибернетика, 1970, № 2.
10. Калашников В. В. Анализ эргодичности систем массового об-
служивания с помощью прямого метода А. М. Ляпунова. «Автоматика и теле-
механика», 1971, № 4.
11. Калашников В. В. Анализ процессов функционирования слож-
ных систем с помощью качественных методов. В сб. «Вопросы конкретных систем-
ных исследований». Изд-во МДНТП, 1970.
12. Karlin S., Mc-G г е g о г J. L. The Classificatiori of birth-and-
death processes. Trans. Am. Math. Soc., 1957, v. 86, p. 366—400.
13. К л и м о в Г. П. Стохастические системы обслуживания. Изд-во
«Наука», 1966.
14. Кокс Д., Смит В. Теория восстановления. Изд-во «Совет-
ское радио»,‘ 1967.
15. К У ш н е р Г. Дж. Стохастическая устойчивость и управление.
Изд-во «Мир», 1969.
16. Л а-С а л л ь Ж-> Л е ф ш е ц С. Исследование устойчивости пря-
мым методом А. М. Ляпунова. Изд-во «Мир», 1964.
17. Л у т к о в В. И. О методе анализа надежности, основанном на ис-
пользовании стохастических функций Ляпунова. «Известия АН СССР», Техни-
ческая кибернетика, 1970, № 6.
18. «Современная теория систем управления». Под ред. Леондеса К. Т.
Изд-во «Наука», 1970.
430
19. У ш а к о в И. А. О вычислении среднего стационарного времени
пребывания полумарковского процесса в подмножестве состояний. «Известия
АН СССР», Техническая кибернетика, 1969, № 4.
20. Ф е л л е р В. Введение в теорию вероятностей и ее приложение,
т. 2. Изд-во «Мир», 1967.
21. Хасьминский Р. 3. Устойчивость систем дифференциальных
уравнений при случайных возмущениях их параметров. Изд-во «Наука», 1969.
К главе 16
1. Бусленко Н. И., Шрейдер Ю. А. Метод статистических
испытаний (метод Монте-Карло) и его реализация на ЭВМ. Изд-во «Наука»,
1969.
2. Глушков В. М. Теория автоматов и вопросы проектирования струк-
тур цифровых машин. «Кибернетика», 1965. № 1.
К главе 17
1 Коваленко И. Н. О восстановлении характеристик системы по
наблюдениям над выходящим потоком. ДАН СССР, 1965, т. 164, № 5.
2. Гнеденко Б. В., Коваленко И. Н. Введение в теорию
массового обслуживания. Изд-во «Наука», 1966.
3. К е и d а 1 1 D. G., Lewis Т. On the structural information con-
tained in the output of GUG/oo. «Z. Wahrscheinlichkeitstheor. ur.d verw. Geb.»
1965, 4, № 2.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЕ
Автомат вероятностный 338, 339
— конечный 117, 118, 119
— Мили (см. автомат конечный)
— Мура 119, 172
— со случайными переходами 120,
121
Автоматное отображение 120
Агрегат 4, 137, 138, 142—145, 152,
153, 162, 163, 181, 182, 212, 214,
410
— автономный 154
— конечно-марковский 269
— , конструктивные параметры 138
— кусочно-линейный 169—171
179, 269
— — автономный 307, 308
— кусочно-марковский 156, 157,
159, 160
— кусочно-непрерывный 163—167,
180, 295, 305
— — автономный 164—166
— — неавтономный 167
— , классы 159
— неавтономный 154, 155
— с обрывающимся процессом функ-
ционирования 141
— , параметр управления 138
— счетно-марковский 269
Агрегативная система (А-система)
3, 4, 181, 192, 205-207, 209
— —, режимы работы 294
Агрегаты непосредственно связан-
ные 215, 216, 218, 219
— несвязанные 218, 219
— связанные сильно 220, 221
---слабо 215, 217, 218, 220
Алгоритм 118
— переработки информации 16
Алфавит 117
— , буквы 117, 118
— , слово 118
— , — пустое 118
Алфавитные преобразователи ин-
формации 117
Алфавитный оператор 118
Бинарная алгебраическая опера-
ция 65, 72
432
Блок потенциальных сигналов
(БПС) 384
Булева алгебра 101
Булевы переменные 99
Булевы функции 99, 101 — 104, 108
— —, дизъюнктивная нормальная
форма 101
— —, конъюктивная нормальная
форма 101, 102
— — элементарные 100, 101
Вероятностная мера 113
Вероятностный автомат 172
— — с двумя состояниями 338, 339
Вероятность безотказной работы
системы 417
— — — —, доверительный интер-
вал 418—421
— — — —, точечная оценка 418
421, 423
Внешняя среда 181, 183, 201
Время жизни процесса 358, 359
Входное сообщение системы 86
— — — обобщенное 95
— — —, отрывок 86
Входной процесс системы 86
— — —, фрагмент 86
Высказывание 212
Высказывательная функция 105,
106, 108
Граф непосредственного подчине-
ния 217
— — следования 216
— непосредственной передачи сиг-
налов 215, 219, 232
— непосредственных связей 231
— передачи входных и управляю-
щих сигналов 217, 219, 221
График движения системы 68
Группа 65, 66, 72
Декомпозиция А-системы 210
Де Моргана правило 106, 107
Двоичные переменные (см. Булевы
переменные)
Динамические системы 71—75, 133,
134, 149
— —, инвариантная мера 133, 134
— — полугрупповые 74, 75, 81
— — с последействием 80, 81, 97
Диффузионные процессы 322, 323,
327
Доверительный интервал 418, 419
— уровень 419
Закон ассоциативности 63
— идемпотентности 63
— коммутативности 63
Инвариантные множества 73, 74,
76
Интеграл Стильтьеса 309
Интенсивность выхода 259
— перехода 272, 273, 275
— потока заявок 123, 281
Инфинитезимальный оператор 357,
360
— — слабый 357—359
Канал 226, 228, 230
— передачи информации 15
— следования 226
— управления 226
---прямого 226
Квантор общности 106
— существования 106
Колмогорова—Чепмена уравнение
323
Комплекс 228, 229, 230
Композиция А-системы 210
Конечные автоматы 117—119, 147
Контакты 190, 193, 196, 197
— входные 190
— выходные 190
— управляющие 190
— фиктивные 197
Контур 227, 230
— следования 227
— управления 17, 227
— — прямого 227
Конфигурационное пространство
67, 68
Коэффициент диффузии 323
Кусочно-линейный мгновенный пре-
образователь 388, 390
Лагранжа функция 408
Липшица условие 71, 78
Ляпунова метод прямой (второй)
253, 328, 329, 338
— теорема 285
Макропроектирование 46, 49
Малый параметр 309, 311, 351
Маркова цепь ПО, 111, 324, 329,
334—336, 347, 349, 555
— — вложенная 350, 354
— — однородная ПО, 360
Марковская модель 264, 265
Марковские моменты времени 357,
358, 360
Марковский процесс 109, 114
— — с возвращением 348
— — с дискретным вмешательст-
вом случая 358, 376—377
— — — параметром 336, 337, 357
— — с конечным или счетным мно-
жеством состояний ПО, 257, 259,
263
— — ..., инфитезимальная интер-
претация 260, 261
— —4..., последовательная интер-
претация 262
— — ..., развернутая интерпрета-
ция 262
— — ..., характеристики 272—274
Математическая модель системы 47,
61—63
Метод Ляпунова 253, 328, 329
— максимального правдоподобия
400
- последовательного приближе-
ния 403, 404
— статистического моделирования
47, 48, 55
Микропроектирование 46, 48, 56
Минимальная о-алгебра 112, 153
Множества 63
—, объединение 63
— , пересечение 63
—, прямое произведение 63, 64
—, разность 63
— эквивалентные 64
Моделирование агрегатов 4, 5
— — кусочно-линейных 394
— — регистровое 395—397
— — циклическое 384, 386
— системы 270, 271
— —, сложность 271
Мустафы критерий 336
Накапливающая модель обслужи
вания 291
Надежность системы 350
Общие системы 76
Оператор 65
— алфавитный 118
— выходов А-системы 208
— — агрегата 137, 138
— — детерминированной системы
90, 91
— — стохастической системы 97
— переработки информации 16
— переходов автономной системы
93
— — агрегата 138, 139, 141
— — детерминированной системы
87—90, 95, 96
433
— — однородной системы 93
— — стохастической системы 97
— случайный 97
— сопряжения агрегатов 191 —194,
196, 203, 204
— — подсистем 201, 202
— — подсистемы внутренний 201 —
204
— функционирования системы 91
Отображения 65
Отрывок входного сообщения 86
Ось внешняя сигналов входных 186,
195
— — — выходных 187
— — — управляющих 187
— внутренняя сигналов входных
186, 195
— — — выходных 187, 195
— — — управляющих 187, 195
— выдачи сигналов входных 184,
194
— — — управляющих 184, 194,
204
— приема сигналов входных 185,
195
— — — управляющих 185, 195
— пространства элементарная 64
Пальма формула 123
Параметры управления 31
Подмножества 63, 64
Подсистема 13, 14, 196, 198—201,
203, 204, 22, 223
— связная 224, 225
— — сильно 227, 228
Показатель эффективности 24—27,
29, 38, 30—35, 38, 309—311
Полугруппа 65, 72
— коммутативная 65
Полумарковский процесс 300, 301,
371
Полюса системы 212
— — входные 213, 214
— — выходные 213, 214
— — управляющие 213, 214
Помехи 36, 37
Портрет системы 70
Поток восстановления 116, 117
— заявок 121, 122
— — с ограниченным последейст-
вием 122
— — ординарный 122
— — без последействия 124
— — Пуассона 124
— — рекуррентный 122
— — стационарный 123
Предметные переменные 105
Принцип физической реализуемости
63
Проектирование систем внешнее 46
— — внутреннее 46
Пространство сигналов входных 85,
187—189, 195, 196, 206
— — выходных 87, 187—189, 196,
207
— — управляющих 187—189, 196.
207
— состояний 64, 69, 70, 84, 207
Процесс восстановления 116
— диффузионный 322, 323, 327
— Пуассона 261
— регенерирующий 306, 307, 348
— регулярный 361—363, 366
— случайный 113, 114, 152, 153
— —, характеристики 310—315
— стационарный 305, 306
Разделяющий тест 411
Ранг 312, 316
— основного состояния 164
Регенерирующий процесс 306, 307,
348
Регулярный процесс 361—363, 366
Рекуррентный поток (см. поток вос-
становления )
Связанная переменная 107
Свободная переменная 107
Системотехника 6
Системы бесконечнолинейные 281 —
289
— информационные 10—12
— массового обслуживания (СМО)
121, 124—129, 142, 161 , 172, 287 ,
306, 307
— — —, загрузка 287, 289, 290,
292, 325, 326
— — — с интервалом недоступ-
ности 354—356
— — — с одним прибором 324
— — —, особые состояния 130
— — — с отказами 341, 343
— — —, показатели эффективно-
сти 124
— — — с управлением 146
— общие 76
— с последействием 77
— — детерминистические 95
— — — автономные 97
— — динамические 30, 81, 97
— —, предыстория 96
— — стохастические
— — — со случайными выходами
98
— — — — начальными состояния-
ми 97
— — — — переходами 97, 98
— без последействия 87
— — детерминистические 88, 91,
92, 130
— — — автономные 93
— — однородные 92
434
— — стохастические 88
— самоорганизующиеся 22
— устойчивые 40
Сложность системы 41, 42
Сложные системы 6, 7, 12, 82, 181,
192, 213, 270, 309, 310, 322, 399,
400, 404
— —, аппаратурное описание 187—
189
— — высоконадежные 347—351
— — с иерархической структурой
230
— —, примеры 8—12
— —, статистическая оценка 399,
400
— —, условие асинхронности 394
— —, — коммутативности 394
— —. функциональное описание
187
Случайный процесс 152
— — обрывающийся 152
Сопряжение агрегатов 183, 199, 204
— подсистем 222
Состояние системы 69
Стационарный режим 305, 306
Строго марковский процесс 357,
358
Структурные конфигурации 224
Толерантный интервал 405
— предел 405
Траектория системы 69, 89, 91
— — фазовая 69
Узел выдачи сигналов 229
— — — местный 230
— — — центральный 230
— приема сигналов 229
— — — местный 230
— — — центральный 230
— транзитивный 230
— — местный 230
— — центральный 230
Унифицированные схемы 4, 5
Управление 14, 15
— , децентрализованное 18
— с иерархической структурой 18,
19
— , качество 31, 33, 34
— , контуры 17
— , критерий 15, 17, 18, 31
— , параметры 31
— , уровни 230
— централизованное 18
— , цикл 17, 32
— экстремальное 17
Управляющая информация 15
Управляющие сигналы 94, 181
— устройства 14, 31
Управляющий комплекс 15, 16, 33
Уравнение Колмогорова— Чепмена
111, 323
Устойчивость асимптотическая 237
238, 241, 252
— вероятностного автомата 245
246
— по Лагранжу 239, 250
— —, вероятностный аналог 334,
361
— по Ляпунову 40, 237—239', 241,
250
—, общее определение 248, 251
— практическая 240, 244, 245, 252,
361
— —, вероятностный аналог 333
Устойчивость системы массового
обслуживания 242, 243
— — передачи данных 243, 244,
251
— — сложной 39, 40, 236, 242, 306
— — —, области 252, 253
Устройство сопряжения 191
Фазовая траектория системы 69, 89
Фазовое пространство системы 19
Фрагмент движения системы 89
Функция высказывательная 105,
106, 108
— выходов автомата 119
— — — сдвинутая 119
— Лагранжа 408
— Ляпунова (пробная) 253,338, 361 ,
362, 370
— переходная агрегата 295—299,
303, 304
— переходов автомата 119
Цепь 225
Цикл 227
— управления 32
— —, длительность 17, 32, 34
Числовые характеристики системы
23, 39
Элемент задержки 338
— памяти 387
— системы 7, 12, 13, 223
— — внутренний 212
— — изолированный 214
— — неуправляемый 14
— —, отказ 29
— — управляемый 14
Элементарные агрегаты 337, 338
— оси 64, 194
Эрланга закон распределения 263,
341
— формула 125, 281
435
СОДЕРЖАНИЕ
Предисловие...................................................... 3
Введение......................................................... 4
ГЛАВА ПЕРВАЯ
СЛОЖНЫЕ СИСТЕМЫ
1.1. Понятие сложной системы. Примеры....................... 6
1.2. Элементы и подсистемы..................................12
1.3. Управление и информация................................14
1.4. Случайные факторы......................................19
1.5. Самоорганизация .......................................21
ГЛАВА ВТОРАЯ
ФУНКЦИОНАЛЬНЫЕ ХАРАКТЕРИСТИКИ. РАЗРАБОТКА СЛОЖНЫХ СИСТЕМ
2.1. Эффективность..........................................23
2.2. Надежность.......~.....................................28
2.3. Качество управления....................................31
2.4. Помехозащищенность.....................................36
2.5. Устойчивость...........................................39
2.6. Сложность............................................. 41
2.7. Порядок разработки сложной системы.....................43
2.8. Системотехника . . .:..................................46
2.9. Обоснование технического задания.......................49
2.10. Эскизный проект.......................................54
2.11. Испытания.............................................58
ГЛАВА ТРЕТЬЯ
ОБЩИЕ СХЕМЫ ФУНКЦИОНИРОВАНИЯ СИСТЕМЫ
3.1. Вводные замечания.............................................61
3.2. Множества. Отображения. Операции .....................63
3.3. Динамические системы..........................................66
3.4. Дифференциальные уравнения с запаздывающим аргументом 76
3.5. Множество моментов времени. Пространство состояний си-
стемы 82
3.6. Входные и выходные сигналы....................................84
3.7. Операторы переходов и выходов.................................87
3.8. Обобщения......................................................94
ГЛАВА ЧЕТВЕРТАЯ
МАТЕМАТИЧЕСКИЕ СХЕМЫ ДЛЯ ОПИСАНИЯ ЭЛЕМЕНТОВ СЛОЖНЫХ СИСТЕМ
4.1. Булевы функции.........................................99
4.2. Высказывательные функции..............................105
4.3. Марковские процессы...................................109
4.4. Конечные автоматы.....................................117
4.5. Системы массового обслуживания........................121
4.6. Динамические системы..................................130
436
ГЛАВА ПЯТАЯ
АГРЕГАТЫ
5.1. Вводные замечания.....................................136
5.2. Понятие агрегата......................................137
5.3. Примеры...............................................142
5.4. Обрывающийся случайный процесс. Случайный иоток .... 152
5.5. Агрегат как случайный процесс .............................153
5.6. Кусочно-марковский агрегат. Последовательное раскрытие
элементарного события .................................... 159
ГЛАВА ШЕСТАЯ
Кусочно-непрерывные и кусочно-линейные агрегаты
6.1. Вводные замечания..........................................163
6.2. Кусочно-непрерывные агрегаты...............................163
6.3. Кусочно-линейные агрегаты..................................169
6.4. Примеры....................................................171
6.5. Приведение кусочно-линейных и кусочно-непрерывных агре-
гатов к каноническому виду 179
ГЛАВА СЕДЬМАЯ
АГРЕГАТИВНЫЕ СИСТЕМЫ
7.1. Вводные замечания..........................................181
7.2. Оси приема и выдачи сигналов...............................183
7.3. Агрегат как элемент системы................................186
7.4. Оператор сопряжения агрегатов..............................189
7.5. Подсистемы.................-...............................196
7.6. Выделение класса агрегативных систем.......................204
ГЛАВА ВОСЬМАЯ
СТРУКТУРА СЛОЖНЫХ СИСТЕМ
8.1. Полюсы и внутренние элементы...............................211
8.2. Виды связей между агрегатами системы.......................214
8.3. Типичные структурные конфигурации..........................224
8.4. Структурный анализ сложных систем..........................231
ГЛАВА ДЕВЯТАЯ
УСТОЙЧИВОСТЬ ФУНКЦИОНИРОВАНИЯ СЛОЖНЫХ СИСТЕМ
9.1. Предварительные замечания.......................236
9.2. Устойчивость решений обыкновенных дифференциальных
уравнений.......................................237
9.3. Устойчивость сложных систем.....................241
9.4. Общее определение устойчивости..................247
9.5. Определение S-области...........................252
9.6. Некоторые алгоритмы построения областей в иространстве
параметров ................................................253
ГЛАВА ДЕСЯТАЯ
ИСПОЛЬЗОВАНИЕ МАРКОВСКИХ ПРОЦЕССОВ С КОНЕЧНЫМ ИЛИ СЧЕТНЫМ
МНОЖЕСТВОМ СОСТОЯНИИ ДЛЯ АНАЛИЗА СЛОЖНЫХ СИСТЕМ
10.1. Различные подходы к определению марковскго процесса
с конечным или счетным множеством состояний................259
10.2. Сведение реальных процессов к марковским моделям. За-
мечание о моделировании....................................262
10.3. Теоретическое обоснование гипер-эрланговской аппрок-
симации ...................................................265
10.4. Конечно-марковский и счетно-марковский агрегаты . . . . 269
10.5. Аналитические методы......................................271
10.6. Асимптотический анализ....................................274
437
ГЛАВА ОДИННАДЦАТАЯ
ИССЛЕДОВАНИЕ СИСТЕМ, СОСТОЯЩИХ ИЗ БОЛЬШОГО ЧИСЛА
ПАРАЛЛЕЛЬНЫХ АГРЕГАТОВ
11.1. Возможные постановки задач.........................280
11.2. Системы массового обслуживания, состоящие из бесконеч-
ного множества приборов.................................281
11.3. Предельное поведение системы массового обслуживания
с бесконечно возрастающим числом приборов и загрузкой,
стремящейся к критической...............................287
11.4. Накапливающая модель обслуживания в системах с боль-
шим числом параллельных приборов ...................... 290
ГЛАВА ДВЕНАДЦАТАЯ
АНАЛИЗ УСТАНОВИВШИХСЯ И Н ЕУСТАНОВИВШИХСЯ РЕЖИМОВ
РАБОТЫ АГРЕГАТОВ
12.1. Предварительные замечания..........................294
12.2. Нахождение случайного времени пребывания траектории аг-
регата в фиксированной области фазового пространства . . 295
12.3. Существование решения полученных уравнений.........303
12.4. Предельная ограниченность..........................305
12.5. Существование установившегося режима в кусочно-линей-
ных агрегатах...........................................305
ГЛАВА ТРИНАДЦАТАЯ
АНАЛИТИКО-СТАТИСТИЧЕСКИЙ МЕТОД РАСЧЕТА ВЕРОЯТНОСТНЫХ
ХАРАКТЕРИСТИК СЛОЖНЫХ СИСТЕМ ПРИ МАЛОИНТЕНСИВНЫХ
ВНЕШНИХ ВОЗДЕЙСТВИЯХ
13.1 Постановка задач....................................309
13.2. Введение малого параметра..........................311
13.3. Выражение характеристик процесса z(l) через характери-
стики его поведения в интервалах между попаданием
в некоторое состояние из множества Z°..............312
13.4. Упрощение формул...................................315
13.5. Алгоритм асимптотического анализа вспомогательных харак-
теристик ................................................316
13.6. Опыт реализации алгоритма на ЭВМ...................320
ГЛАВА ЧЕТЫРНАДЦАТАЯ
ИССЛЕДОВАНИЕ СЛОЖНЫХ СИСТЕМ МЕТОДАМИ ТЕОРИИ
ДИФФУЗИОННЫХ ПРОЦЕССОВ
14.1. Вводные замечания..................................322
14.2. Диффузионные уравнения.............................322
14.3. Несколько предельных соотношений...................324
ГЛАВА ПЯТНАДЦАТАЯ
ПРИМЕНЕНИЕ КАЧЕСТВЕННЫХ МЕТОДОВ ДЛЯ АНАЛИЗА ПОВЕДЕНИЯ
СЛОЖНЫХ СИСТЕМ
15.1. Вводные замечания..................................328
15.2. Основные результаты (дискретный случай)..........330
15.3. Примеры............................................338
15.4. Некоторые сведения из теории марковских процессов .... 356
15.5. Основные результаты (непрерывное время)...........358
15.6. Примеры. 371
438
ГЛАВА ШЕСТНАДЦАТАЯ
МОДЕЛИРОВАНИЕ АГРЕГАТИВНЫХ СИСТЕМ
16.1. Моделирование агрегатов общего вида...............383
16.2. Сведение кусочно-линейного агрегата к системе, состоящие из
элементарных агрегатов............................387
16.3. Операции над агрегатами в сложных системах.......392
16.4. Моделирование кусочно-линейных агрегатов.........394
16.5. Упрощение алгоритма моделирования за счет использования
стационарного распределения.......................397
ГЛАВА СЕМНАДЦАТАЯ
СТАТИСТИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ СЛОЖНЫХ СИСТЕМ
17.1. Вводные замечания.................................399
17.2. Оценка параметров сложной системы.................400
17.3. Объединение разнородной информации при построении толе-
рантных пределов для характеристик сложных систем . . . 404
17.4. О б оптимальном планировании испытаний для оценки па-
раметров сложной системы...............................407
17.5. Оценка вида агрегата по наблюдению входа и выхода .... 410
17.6. Восстановление агрегата по наблюдению над выходным про-
цессом при условии, что известен класс, к которому принадле-
жит распределение входного процесса .................. 413
17.7. Использование неравноправных наблюдений...........417
Литература............................................ . . . 424
Предметный указатель.........................................432
Николай Пантелеймонович, Бусленко
Владимир Вячеславович Калашников
Игорь Николаевич Коваленко
ЛЕКЦИИ ПО ТЕОРИИ СЛОЖНЫХ СИСТЕМ
Редактор Н. Г. Давыдова
Художественный редактор В. Т. Сидоренко
Художник Б. К. Николаев
Технический редактор А. А. Белоус
Корректоры: Е. П. Озерецкая, Л. Л. Максимова
Сдано в набор 2 5/11 1972 г.
Подписано в печать 7/XII 1972 г. Т 16764
Формат 60X90/16 Бумага типографская № 2
Объем 27,5 усл. п. л. 30,566 уч.-изд. л.
Тираж 18 000 экз. Зак. 792 Цена 2 р. 07 к.
Издательство «Советское радио», Москва, Главпочтамт,
и/я 693.
Московская типография № 4 «Союзполиграфпрома»
при Государственном комитете Совета Министров СССР по делам
издательств, полиграфии и книжной торговли
Г>. Переяславская, 46