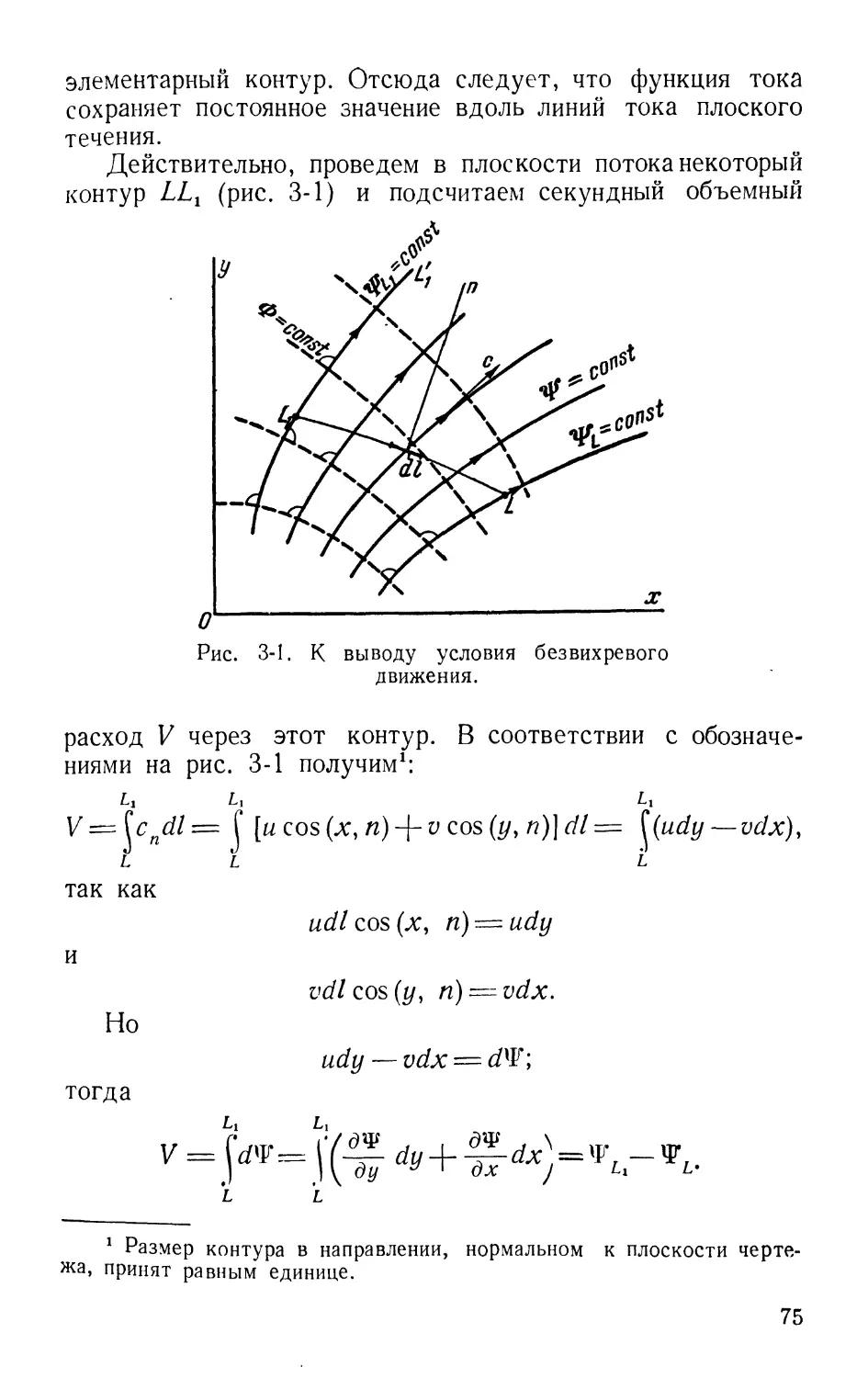
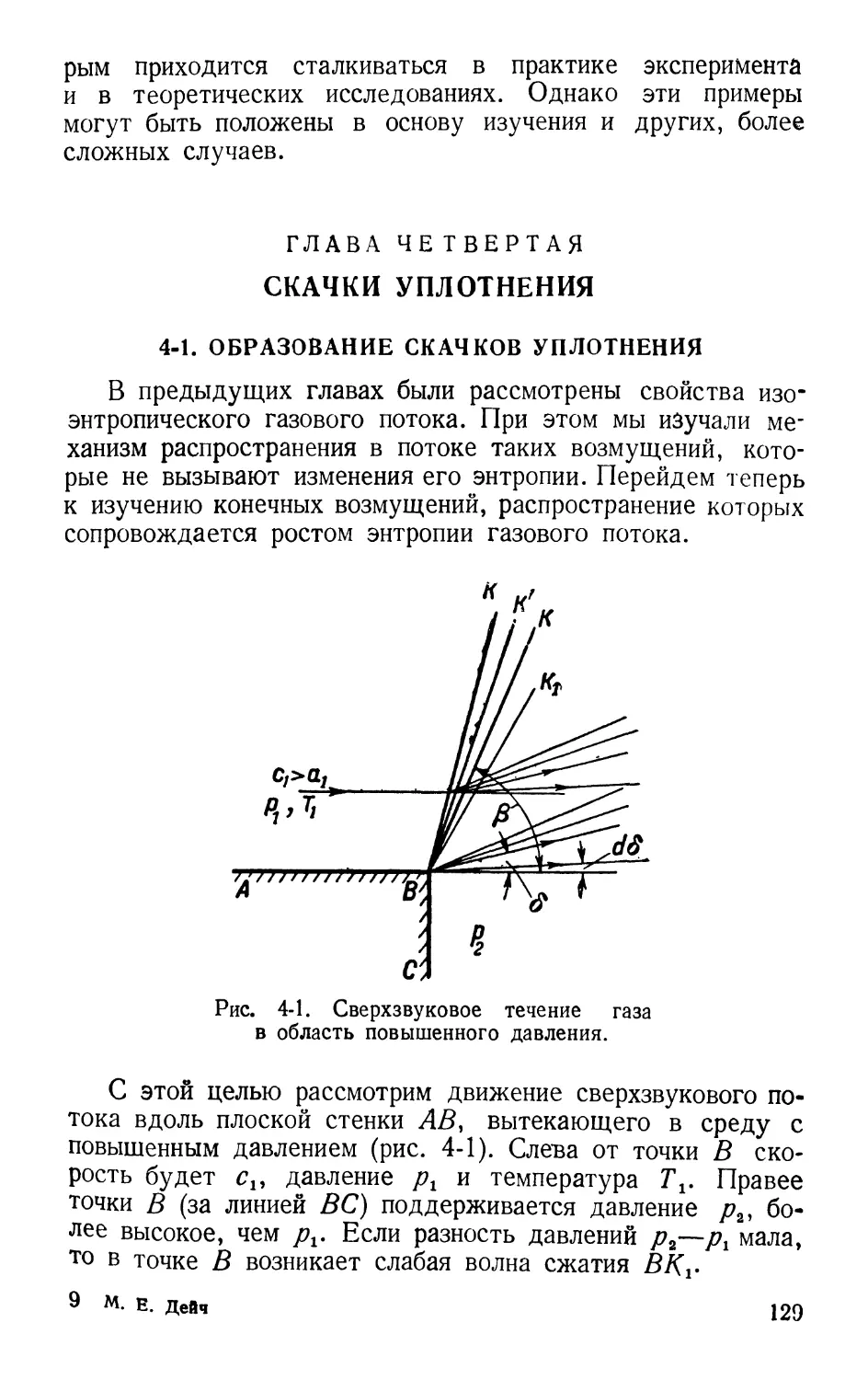
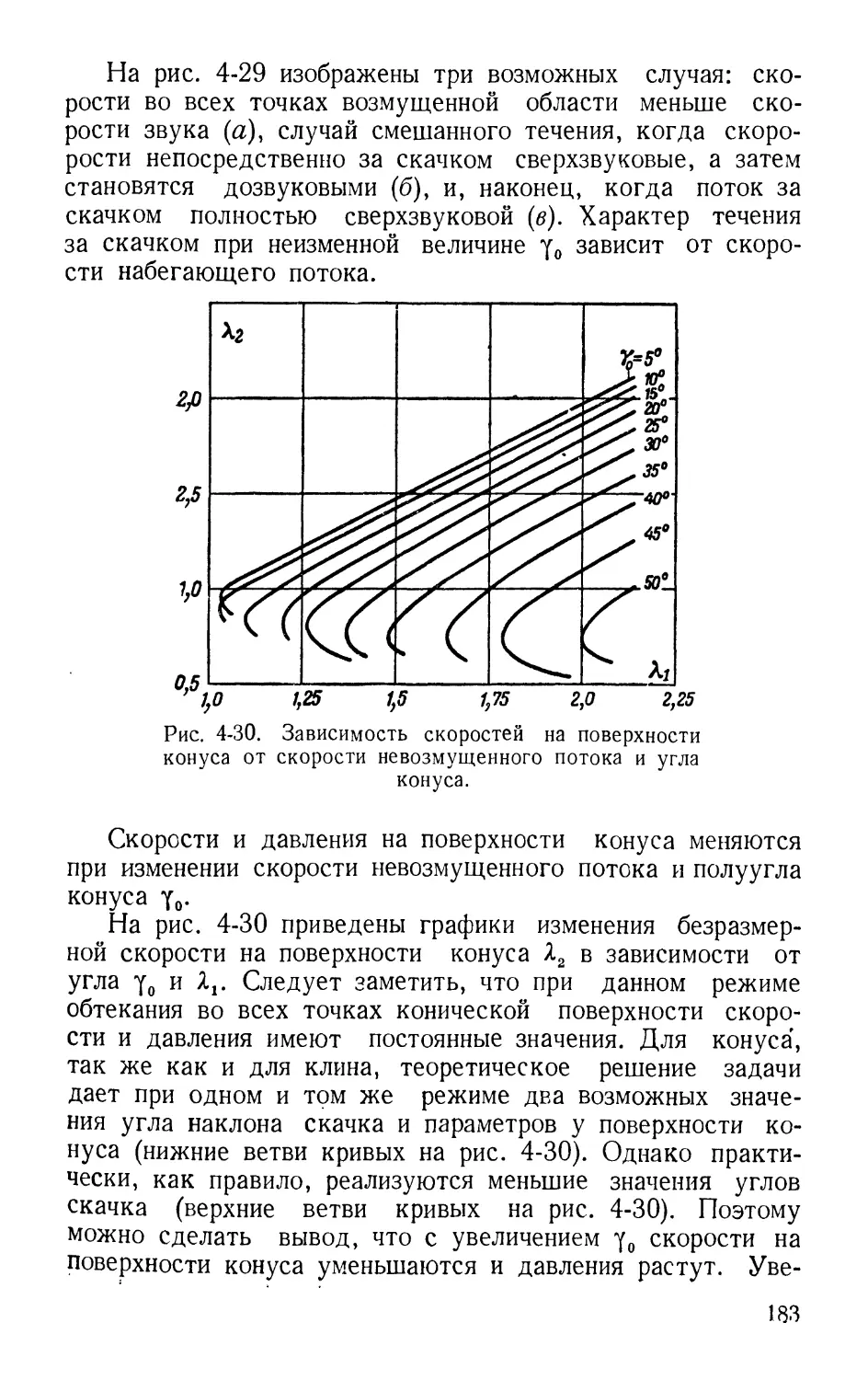
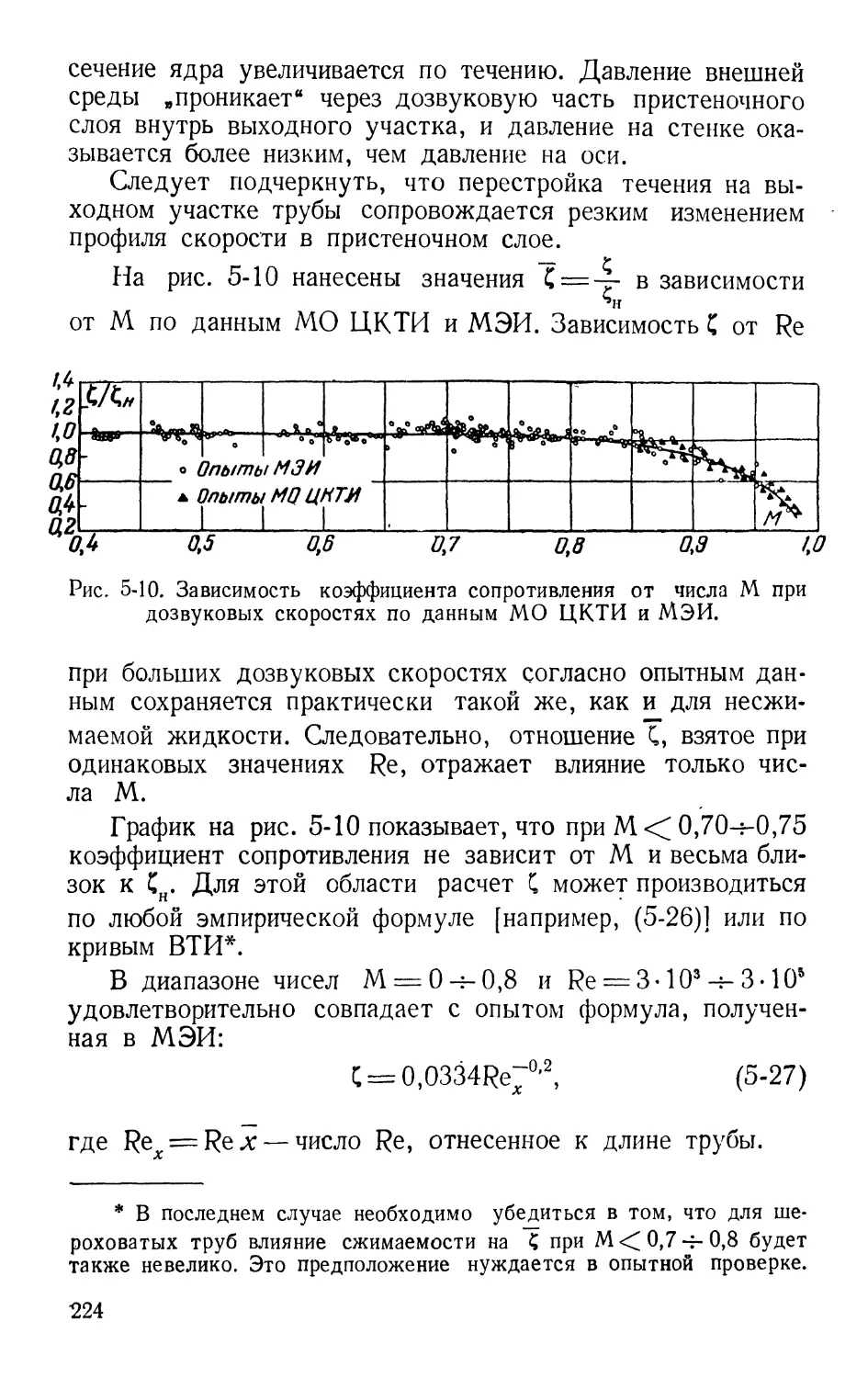
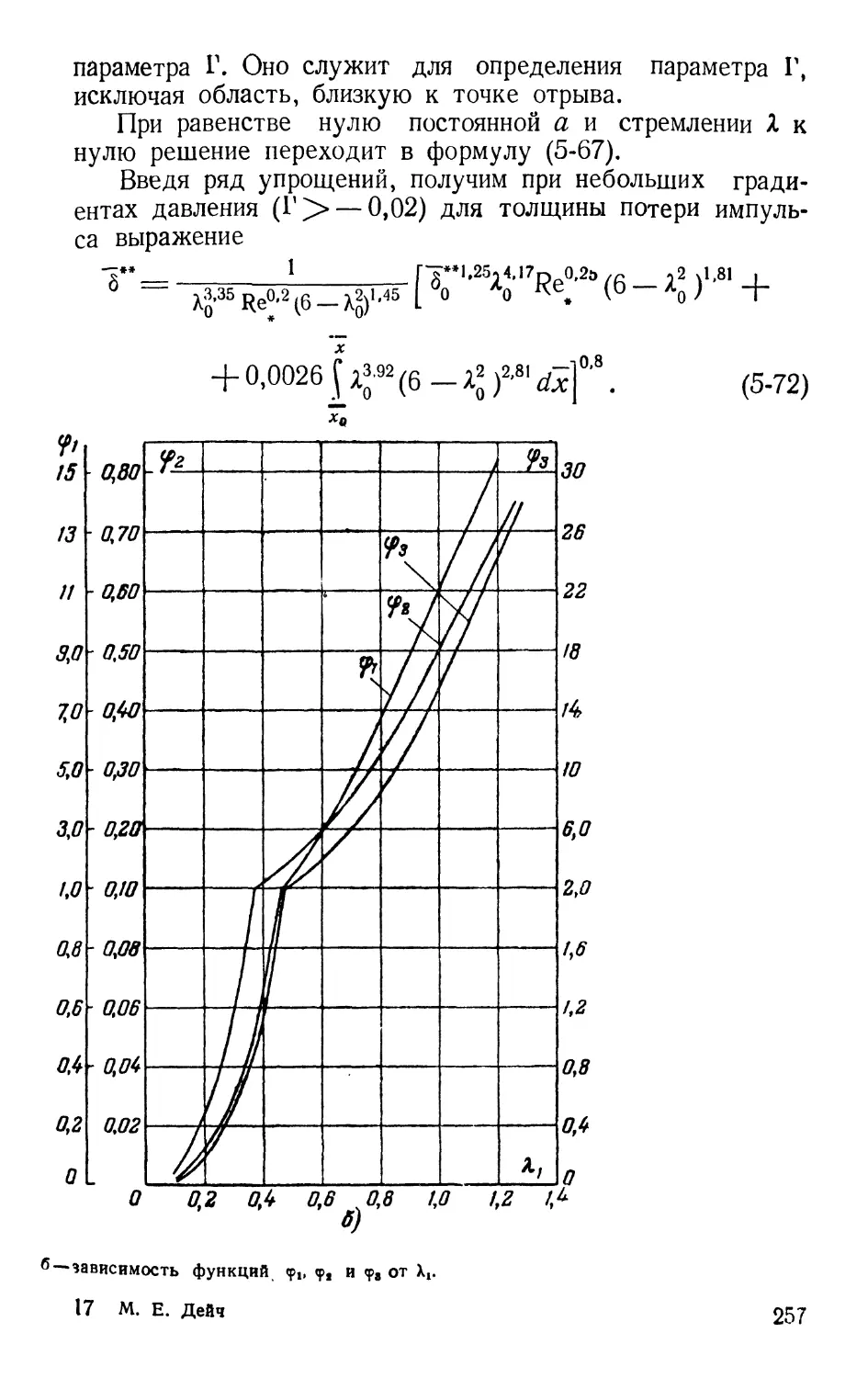
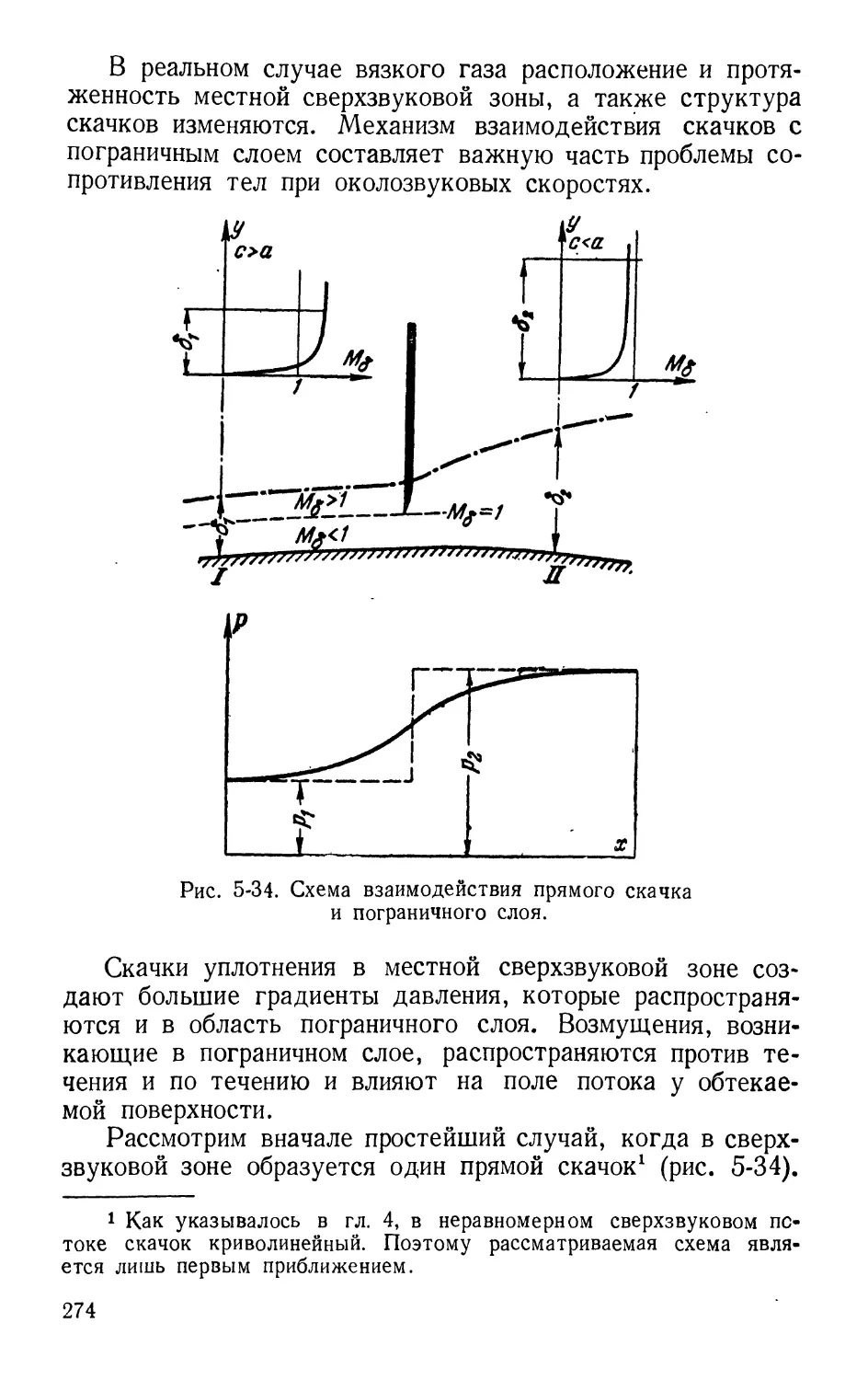
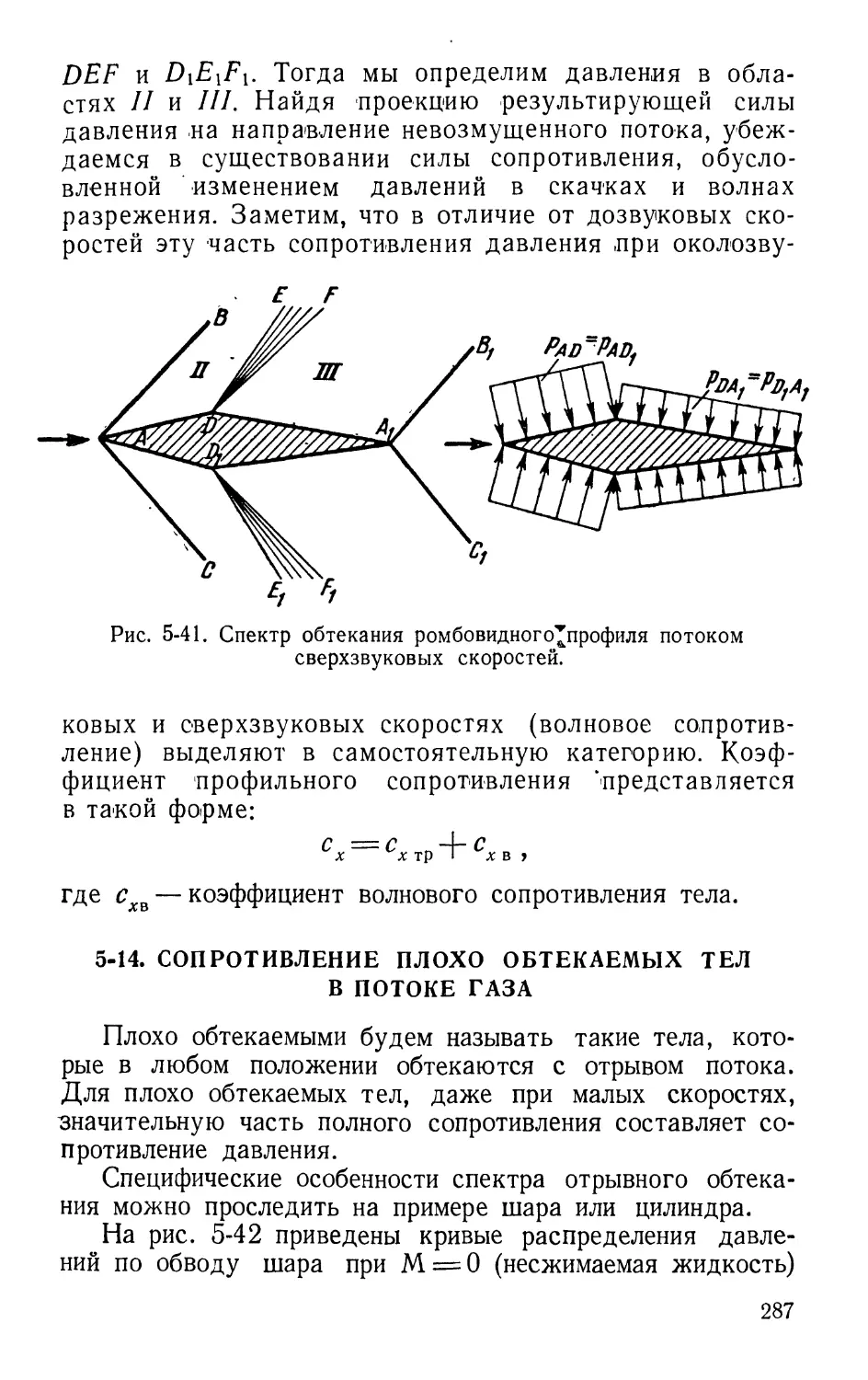
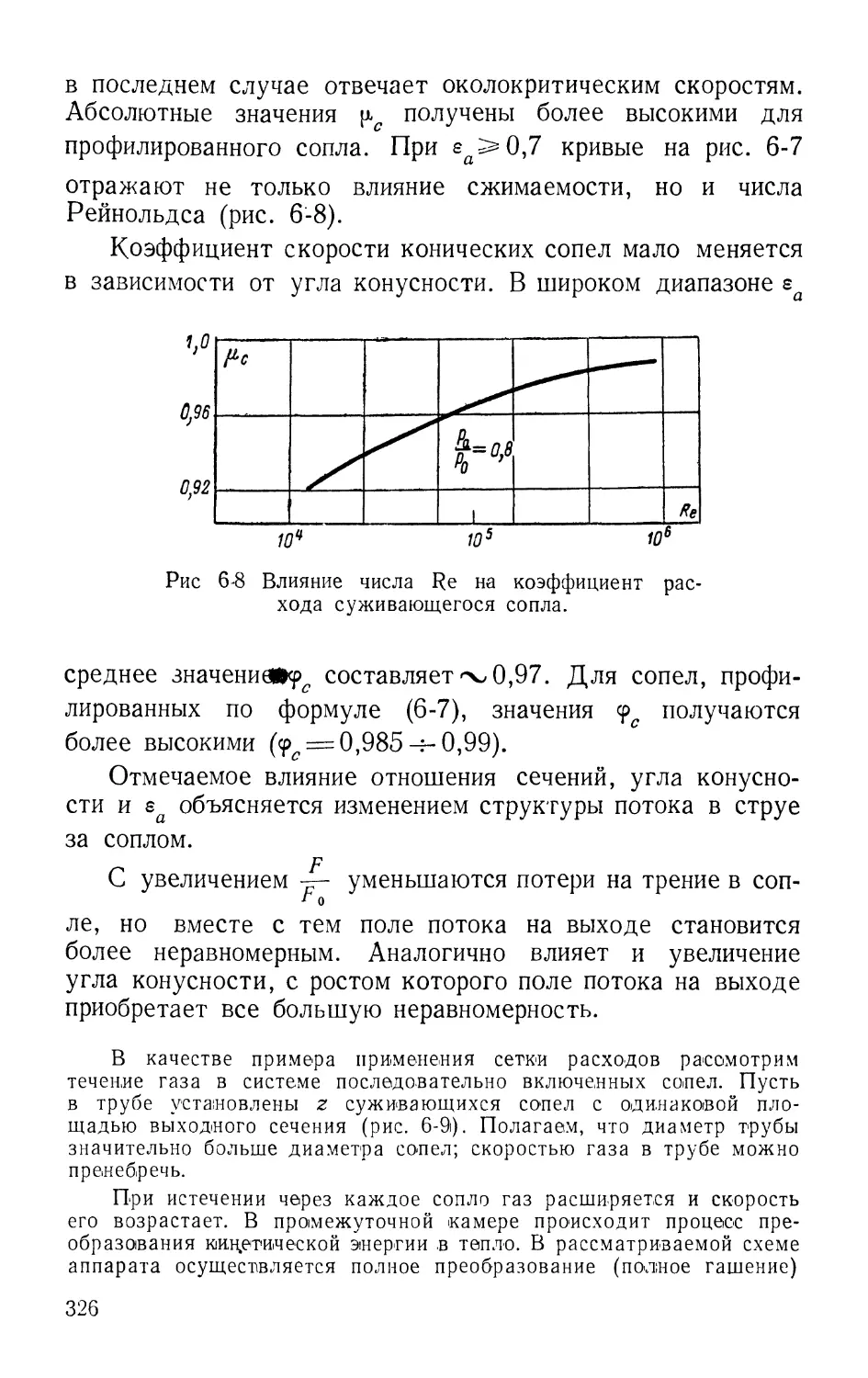
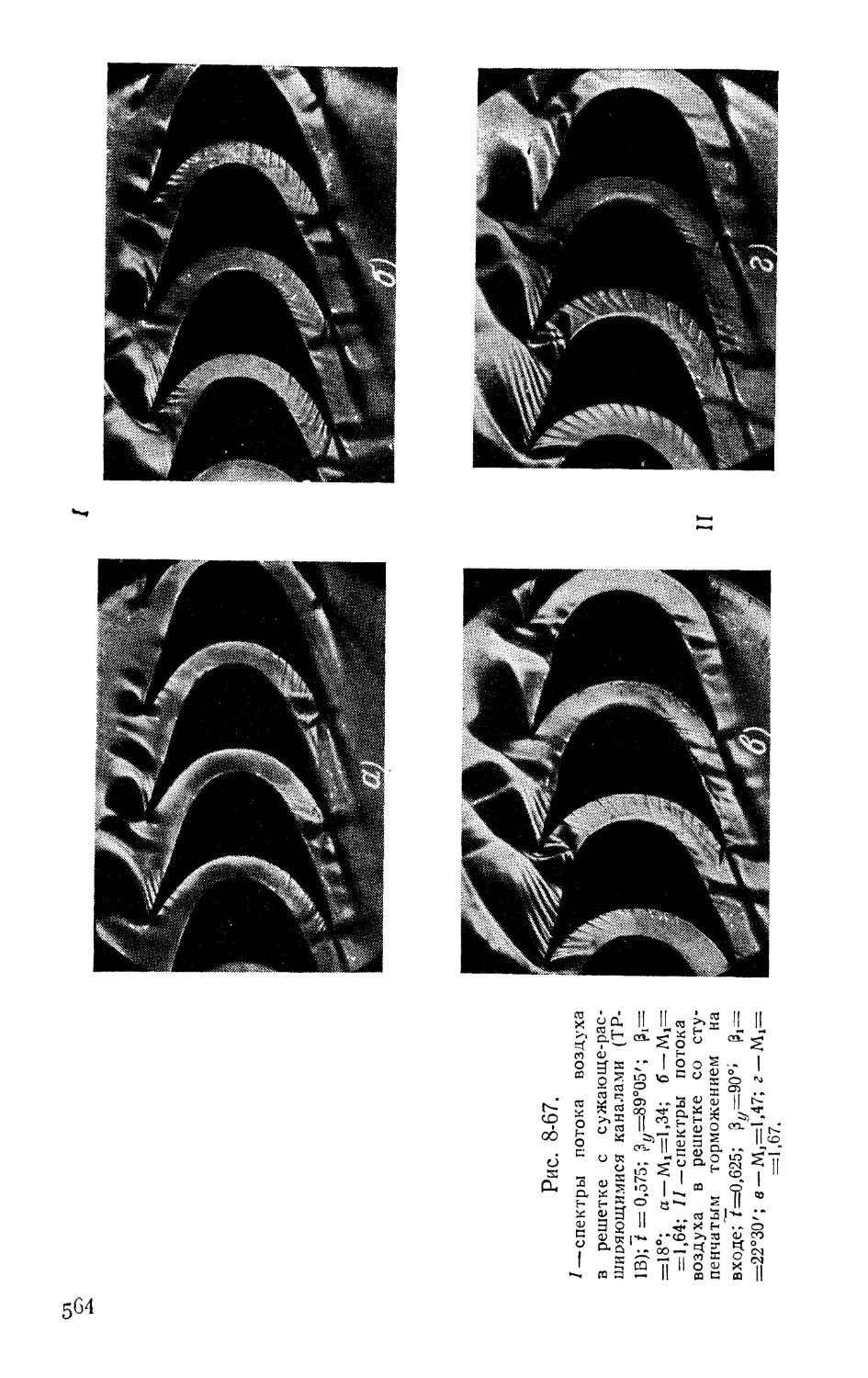
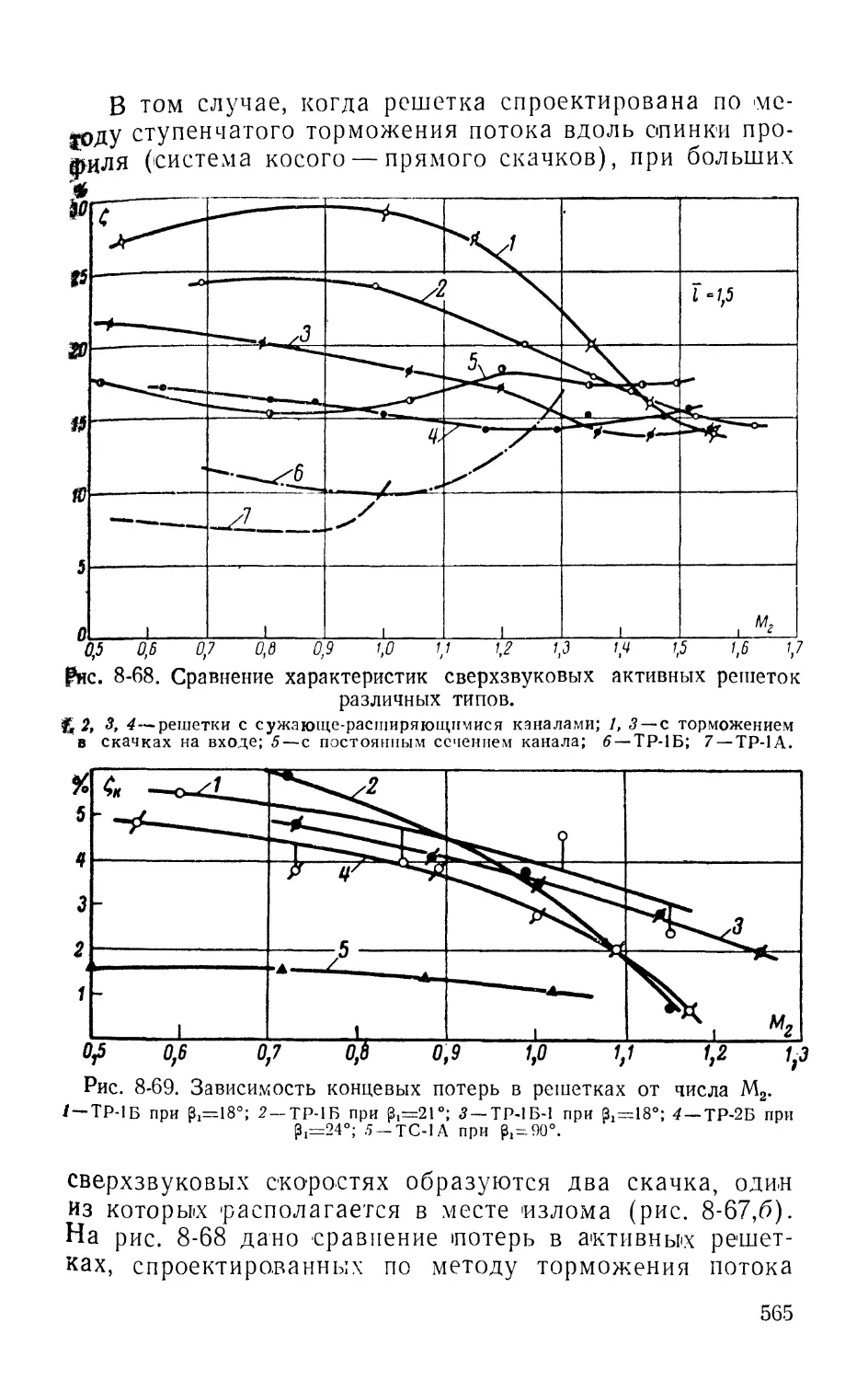
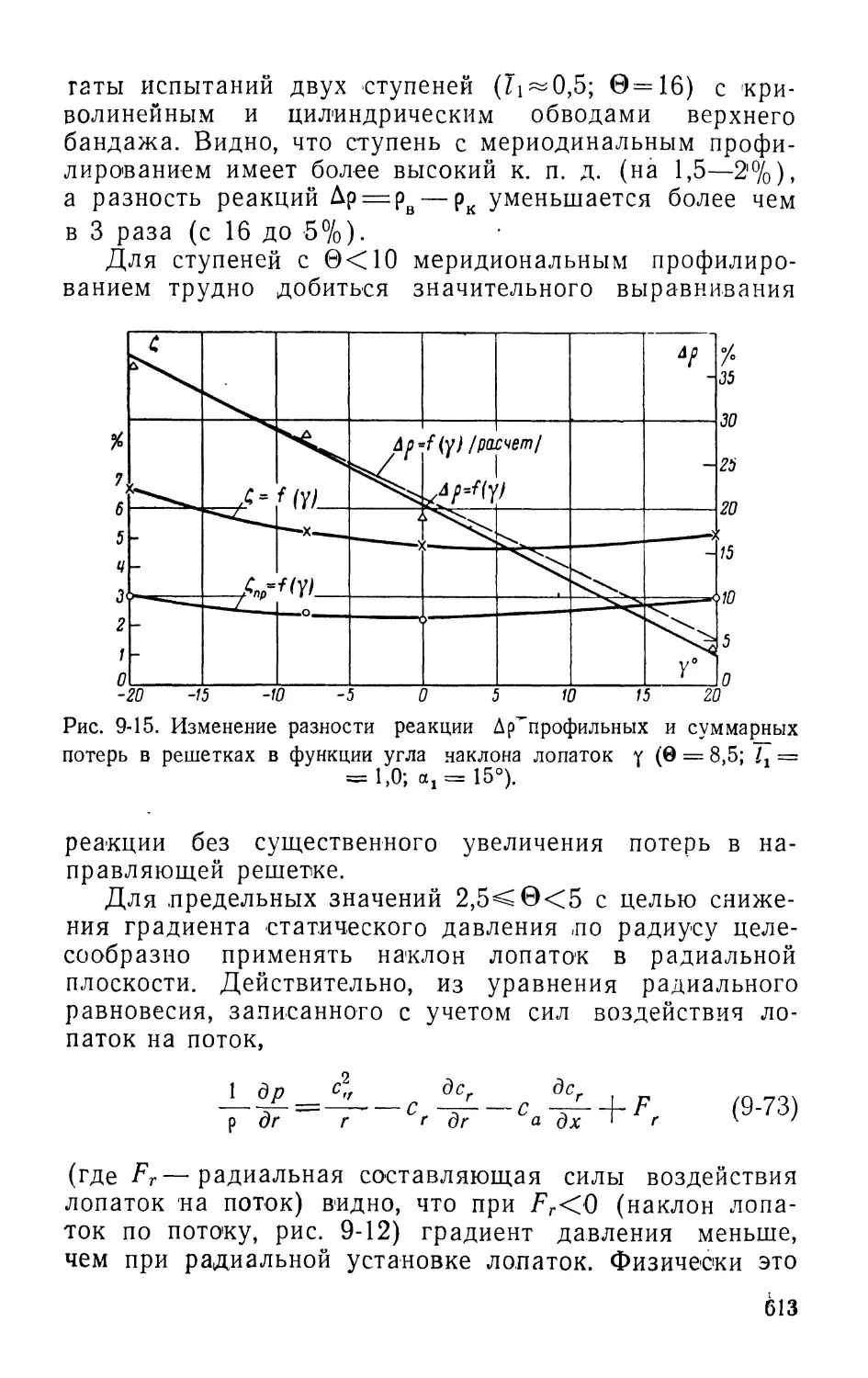
Text
М. Е. ДЕЙЧ
ТЕХНИЧЕСКАЯ
ГАЗОДИНАМИКА
ИЗДАНИЕ ВТОРОЕ, ПЕРЕРАБОТАННОЕ
ГОСУДАРСТВЕННОЕ ЭНЕРГЕТИЧЕСКОЕ ИЗДАТЕЛЬСТВО
МОСКВА 1961 ЛЕНИНГРАД
ЭТ-5-2
Ёо втором, переработанном издании книги
рассматриваются основные задачи движения газов с большими
скоростями. В первой части книги, состоящей из пяти
глав, излагается общая теория одномерных и плоских
течений. Материалы последующих глав являются
прикладными. В них последовательно рассматривается
движение газа в соплах, диффузорах, эжекторах,
решетках и ступенях турбомашин.
Книга представляет собой учебное пособие пф
курсу основ газовой динамики для теплотехнические
специальностей энергетических и политехнических
институтов.
Книга может быть полезной для инженерных и
научных работников лабораторий и конструкторских
бюро заводов.
6П2.2 Дейя Михаил Ефимович,
Д 27 Техническая газодинамика. Изд. 2-е, переработ. М.—Л.
Госэнергоиздат, 1961
с черт, и илл. 6П2.2
Редактор Б. Я» Шумяцкпй Техн. редактор А. М. Фридкин
Сдано в набор 21/VHI 1931 г. Подписано к печати 12/ХП 19GI г.
Т-12151 Бумага 84Х103732 34,44 печ. л. + 2 вклейки. Уч.-изд. л. 35,4
Тираж 12 000 экз. Заказ 525
Цена в переплете № 7—1 р. 92 к. в переплете № 5 — 1 р. 87 к.
Типография Госэнергоиздата. Москва, Шлюзовая наб., 10.
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
За 8 лет, прошедшие с момента первого издания
настоящей книги, различные разделы газовой динамики
развивались весьма интенсивно. Значительные успехи достигнуты
в решении ряда важнейших газодинамических задач в
области ракетной техники, авиации, внутренней и внешней
баллистики, промышленной аэродинамики. Прочное место
методы газовой динамики заняли в теплоэнергетике.
В связи с необходимостью повышения экономичности
паровых и газовых турбин и компрессоров широким
фронтом развернуты работы в области газодинамики проточной
части турбомашин.
Вместе с тем за истекший период накоплен
дополнительный опыт преподавания ряда разделов газодинамики
в энергетических и политехнических вузах.
Указанные обстоятельства послужили основанием для
существенной переработки книги. Все главы книги, за
исключением гл. 4, подверглись методической переработке,
в их содержание внесены существенные изменения,
некоторые главы написаны заново.
Теория одномерного изоэнтропического движения
выделена в самостоятельную главу и дополнена (гл. 2). Гл. 3
(теория плоского течения идеальной сжимаемой жидкости),
дополнена более подробным изложением приближенных
методов учета влияния сжимаемости в дозвуковых
течениях. В нее включен метод расчета криволинейных каналов.
Гл. 5—10 написаны практически заново.
В связи с большой практической важностью методов
расчета потерь на трение в различных аппаратах в гл. 5
даны новое изложение теории пограничного слоя при
градиентном течении и результаты опытного исследования
ламинарного и турбулентного слоев при больших скоростях.
В этой главе добавлены также параграфы, посвященные
вопросам газодинамического подобия, сопротивлению плохо
обтекаемых тел, движению в трубах и криволинейных ка*
налах.
3
Гл. 6 дает представление о расчете конфузорных
потоков в соплах. В связи с изданием нами специализированной
книги, а также с целью сокращения теория лабиринтовых
уплотнений во втором издании не излагается. Методика
расчета сопел на переменных режимах уточнена и развита.
Теория и методы расчета диффузоров и эжекторов
выделены в самостоятельную главу — гл. 7. Все параграфы
этой главы составлены по данным исследований,
проведенных в МЭИ и других институтах в последние годы.
В гл. 7 особое внимание уделено выхлопным патрубкам
турбомашин.
Гл. 8 написана по результатам теоретических и
экспериментальных исследований решеток, полученным в период
1954—1959 гг. Все опытные данные в этой главе
обновлены.
В гл. 9 во втором издании выделены вопросы
движения газа в ступени турбомашины. Здесь изложены новые
методы расчета пространственного потока газа в ступени
и некоторые результаты экспериментов, полученные в
последнее время. Вопросы переменного режима ступени,
широко освещенные в специальной литературе, опущены
в настоящем издании.
В гл. 10 отражены некоторые новые результаты,
достигнутые в области методов экспериментального
исследования проточной части турбомашин. Однако в связи с
ограниченным объемом книги эта глава представлена в
сокращенном виде.
В отличие от первого издания сделана попытка анализа
течений реального газа (гл. 2—4).
При переработке книги были учтены замечания,
изложенные в опубликованных рецензиях на книгу, а также
сообщенные автору лицами, пользовавшимися первым
изданием в своей работе. Все содержание книги,
предназначенной в качестве учебного пособия по курсу
гидрогазодинамики, пересмотрено в соответствии с изменениями в
учебных планах по теплоэнергетическим специальностям, а
также с учетом личного опыта преподавания курса.
Изложение отдельных вопросов упрощено и уточнено, исправлены
допущенные в первом издании ошибки и опечатки.
В книге излагаются результаты исследований,
полученные в СССР и за рубежом. Значительную часть
приводимых материалоз составляют результаты работ, выполнен-
4
ных сотрудниками кафедры паровых и газовых турбин МЭИ
и, в частности, автором.
При подготовке второго издания автор стремился
сохранить общую направленность книги, ориентированной на
изучение основных проблем аэродинамики проточной части
турбомашин.
В работе над вторым изданием автору была оказана
существенная помощь сотрудниками кафедры паровых и
газовых турбин МЭИ. Гл. 5 написана совместно с А. Е. За-
рянкиным, гл. 8 составлена при участии А. В. Губарева,
гл. 10 написана совместно с Ф. В. Казинцевым.
Автору была оказана помощь сотрудниками кафедры
паровых и газовых турбин МЭИ, инженерами Г. А.
Филипповым, А. В. Робожевым, В. Г. Филипповой и доц.
А. Н. Шерстюком.
При рецензировании и редактировании книги важные
замечания были сделаны докт. техн. наук, прсф. С. Ф.
Абрамовичем и канд. техн. наук, доц. Б. Я. Шумяцким.
Указанным лицам, а также коллективу кафедры и
лаборатории паровых и газовых турбин МЭИ автор
выражает глубокую благодарность.
СОДЕРЖАНИЕ
Предисловие ко второму изданию - 3
Глава первая
Основные понятия и уравнения газовой динамики
1-1. Параметры течения 9
1-2. Некоторые основные понятия аэрогидромеханики 12
1-3. Уравнение неразрывности 23
1-4. Уравнения количества движения 29
1-5. Уравнения движения в гидромеханической форме. Уравнения
И. С. Громеко 32
Глава вторая
Одномерное движение газа
2-1. Основные уравнения одномерного течения. Скорость звука 38
2-2. Различные формы уравнения энергии 44
2-3. Параметры течения в произвольном сечении трубки тока . . 47
2-4. Изменение скорости вдоль трубки тока. Приведенный расход
газа 54
2-5. Некоторые газодинамические функции одномерного
адиабатического потока 60
2-6. Особенности расчета одномерного потока реального газа . . 67
Глава третья
Плоское движение газа при постоянной энтропии
3-1. Потенциальное движение жидкости 69
3-2. Коэффициенты давления. Критическое число М 77
3-3. Учет влияния сжимаемости по методу малых возмущений . . 81
3-4. Теорема Н. Е. Жуковского 94
3-5. Плоское дозвуковое потенциальное течение газа в
криволинейных каналах 98
3-6. Плоский сверхзвуковой поток 104
3-7. Диаграмма характеристик 116
3-8. Пересечение и отражение волн разрежения 122
Глава четвертая
Скачки уплотнения
4-1. Образование скачков уплотнения 129
4-2. Уравнения косого скачка 132
4-3. Ударная поляра 145
4-4. Изменение энтропии в скачке 151
4-5. Потери в скачках уплотнения. Построение процесса в
диаграмме is. Скачки уплотнения в реальном газе 154
4-6. Пересечение скачков . . t . f . , , . , f t , , , . . . 162
б
4-7. Ступенчатое торможение Потока ...»..«.. 4 ., . 16?
4-8 Отражение скачков 175
4-9. Взаимодействие скачка и волны разрежения 178
4-10. Конические скачки уплотнения 181
4-11. Скачки конденсации (тепловые скачки) 187
Глава пятая
Движение газа при наличии трения
5-1. Температура торможения в вязкой жидкости 197
5-2. Условия газодинамического подобия 203
5-3. Одномерное течение газа при наличии трения. Основные
уравнения 208
5-4. Движение газа в цилиндрической трубе 211
5-5. Потери на трение в цилиндрической трубе (опытные данные) 217
5-6. Пограничный слой. Основные понятия и уравнения .... 229
5-7. Условные толщины и интегральное соотношение для
пограничного слоя 235
5-8. Общее выражение для коэффициента сопротивления трения
в пограничном слое при наличии градиента давления . . . 240
5-9. Расчет ламинарного пограничного слоя при наличии
градиента давления 244
5-10. Переход ламинарного пограничного слоя в турбулентный . . 247
5-11. Расчет турбулентного пограничного слоя 253
5-12. Пограничный слой при больших скоростях.
Экспериментальные данные 262
5-13. Сопротивление тел при дозвуковых и сверхзвуковых
скоростях 279
5-14. Сопротивление плохо обтекаемых тел в потоке газа . . . 287
5-15. Движение газа в криволинейных каналах 298
5-16. Вращающиеся потоки вязкого газа 303
Глава шестая
Истечение газа из суживающихся сопел и отверстий.
Сопла Лава»ля
6-1. Суживающиеся сопла 312
6-2. Суживающееся сопло при переменном режиме 316
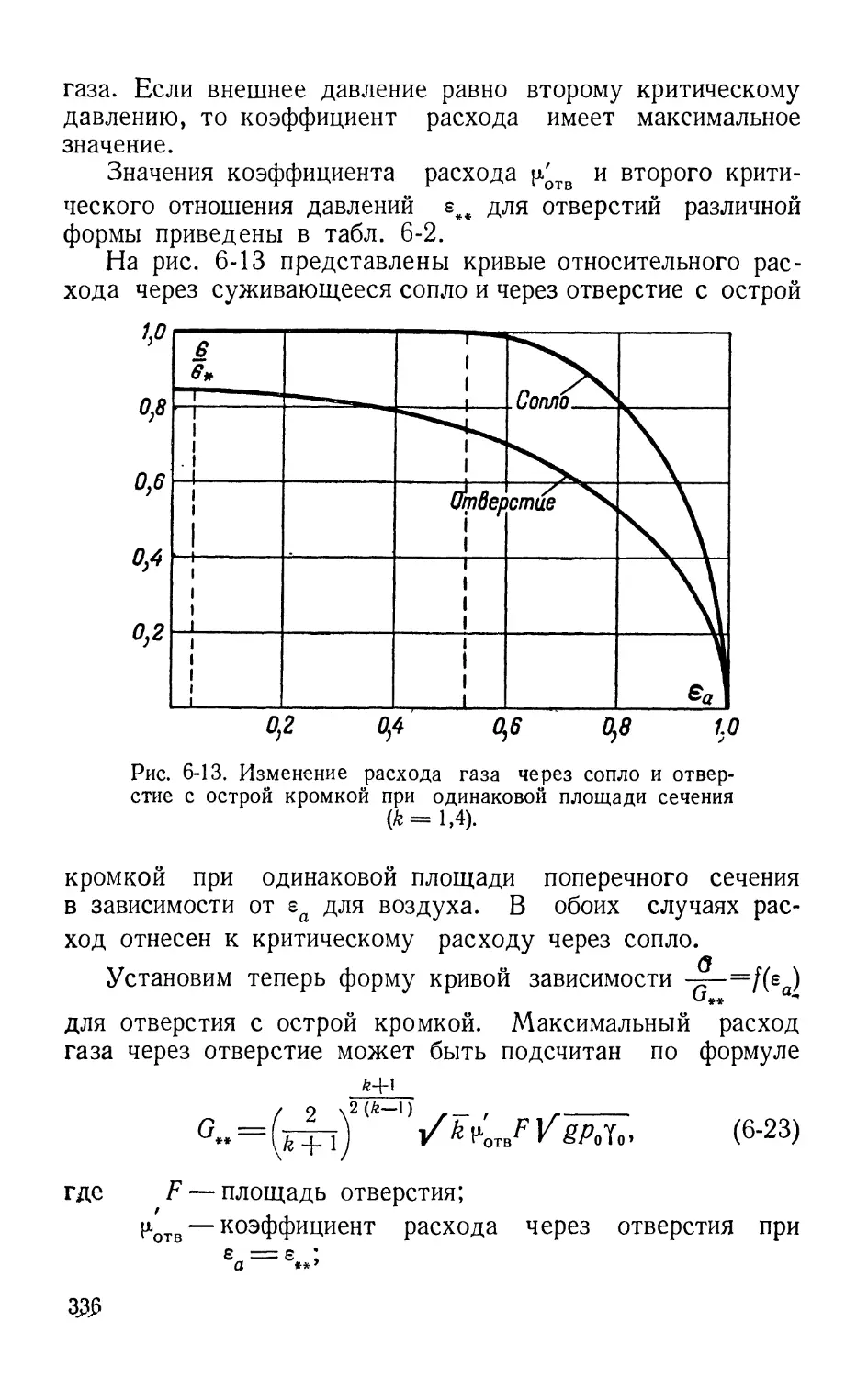
6-3. Истечение газа из отверстия с острой кромкой. Второе
критическое отношение давлений 330
6-4. Расчет сверхзвукового сопла 339
6-5. Плоское сопло Лаваля при нерасчетных условиях 347
6-6. Конические сопла Лаваля в нерасчетных условиях.
Реактивная сила 367
6-7. Сверхзвуковое сопло с косым срезом ' . 378
Глава седьмая
Движение газа в диффузорах. Ступень эжектора
7-1. Основные характеристики и расчет диффузоров 382
7-2. Дозвуковые диффузоры 392
7-3. Выхлопные патрубки турбомашин 401
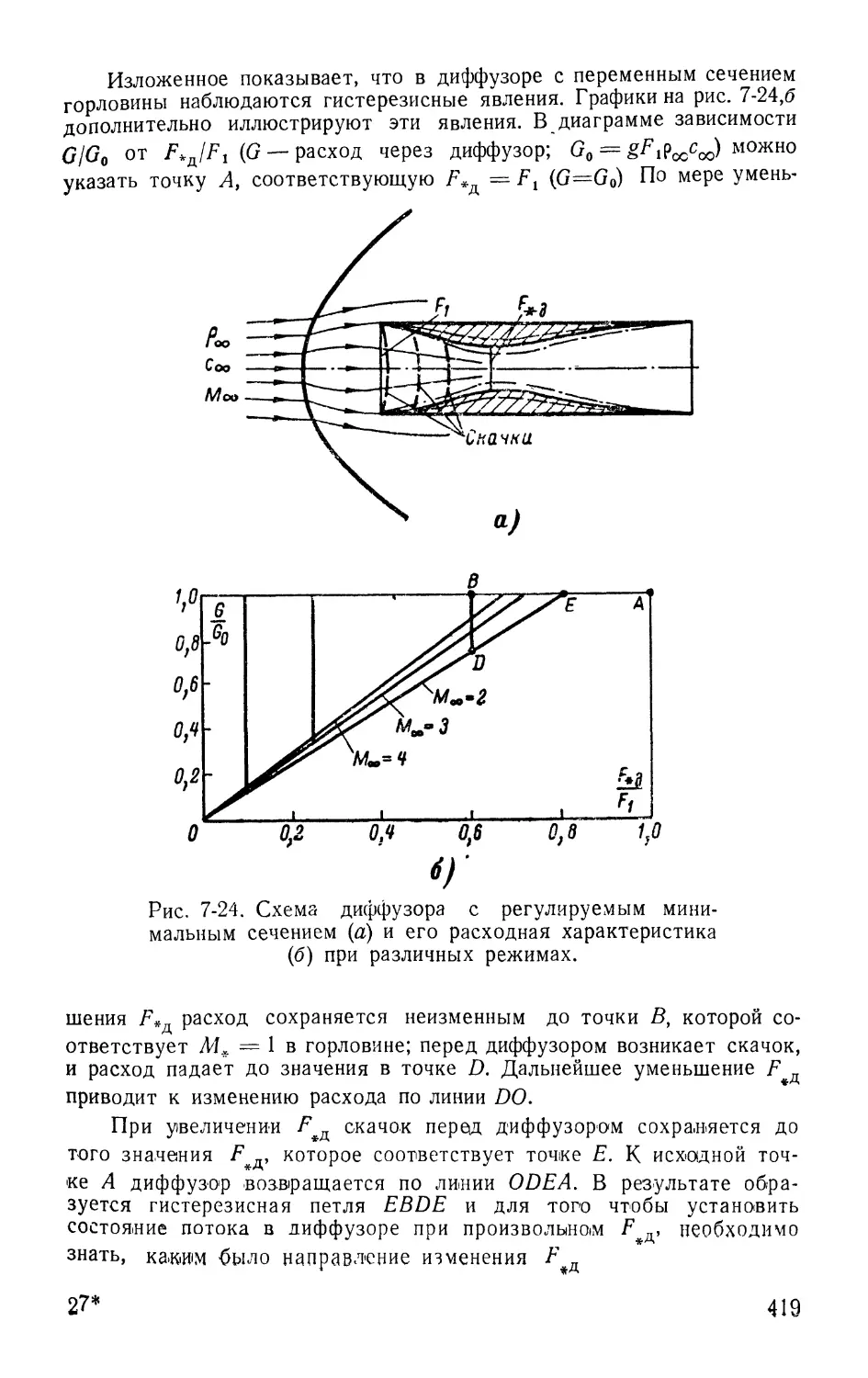
7-4. Сверхзвуковые диффузоры 409
7-5 Ступень эжектора 421
7-6 Ступень эжектора при переменных режимах; предельный
режим 430
7-7. Выбор геометрических параметров ступени эжектора .... 443
7
Глава восьмая
Течение газа через решетки турбомашин
8-1. Геометрические и газодинамические параметры решеток.
Особенности потока в решетках . . 449
8-2. Расчет потенциального потока в решетках по теории канала 460
8-3. Силы, действующие на профиль в решетке. Теорема Н. Е.
Жуковского для решетки 464
8-4. Классификация потерь и основные характеристики решеток 470
8-5. Пограничный слой и потери на трение в решетках .... 476
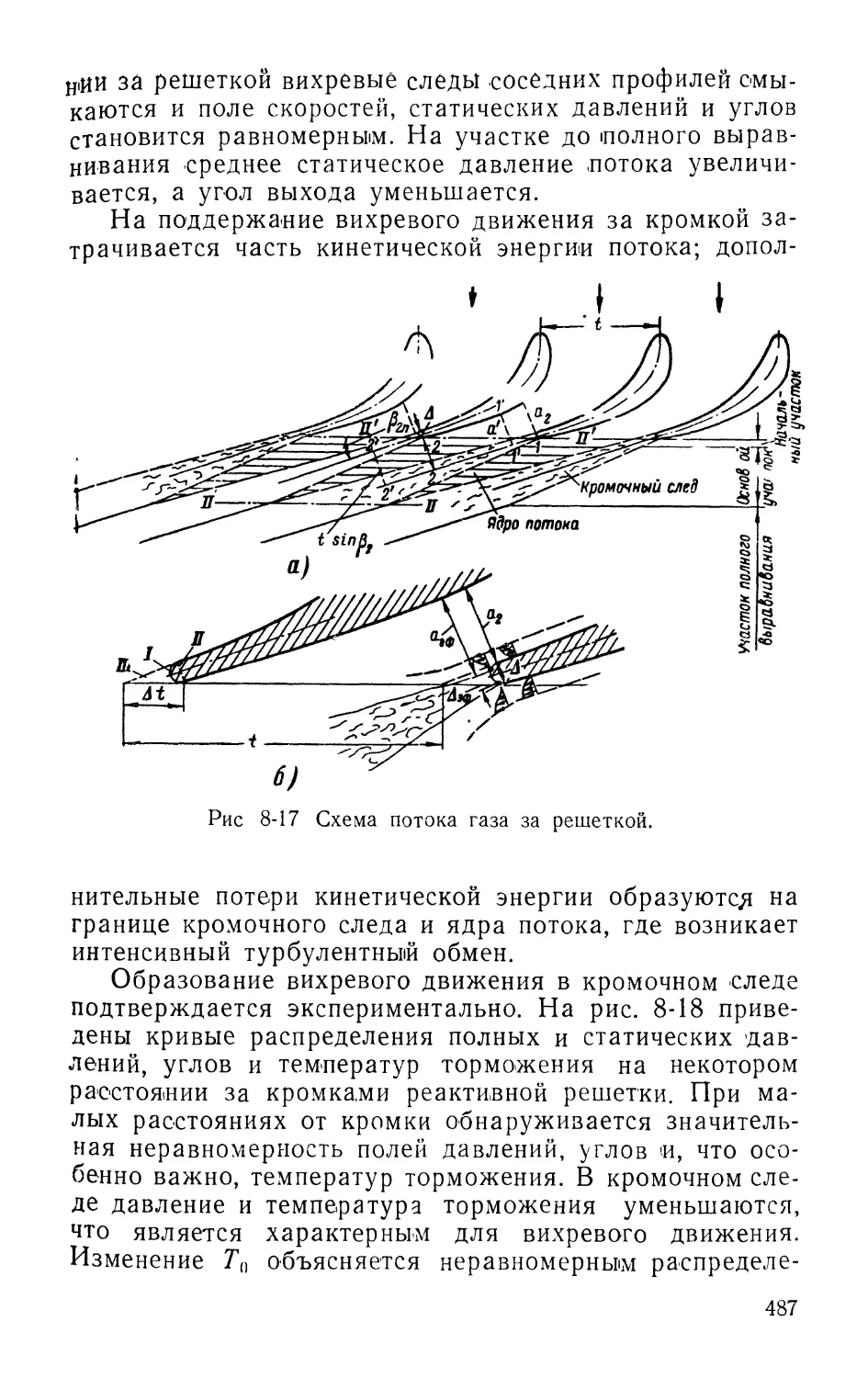
8-6. Кромочные потери в решетках 486
8-7. Некоторые результаты экспериментального исследования
плоских решеток при дозвуковых скоростях . . . 497
8-8. Пространственный поток газа в решетках. Концевые потери
и способы их уменьшения 506
8-9. Методика расчета концевых потерь в решетках 519
8-10. Структура потока и потери в реактивных решетках при
околозвуковых и сверхзвуковых скоростях 523
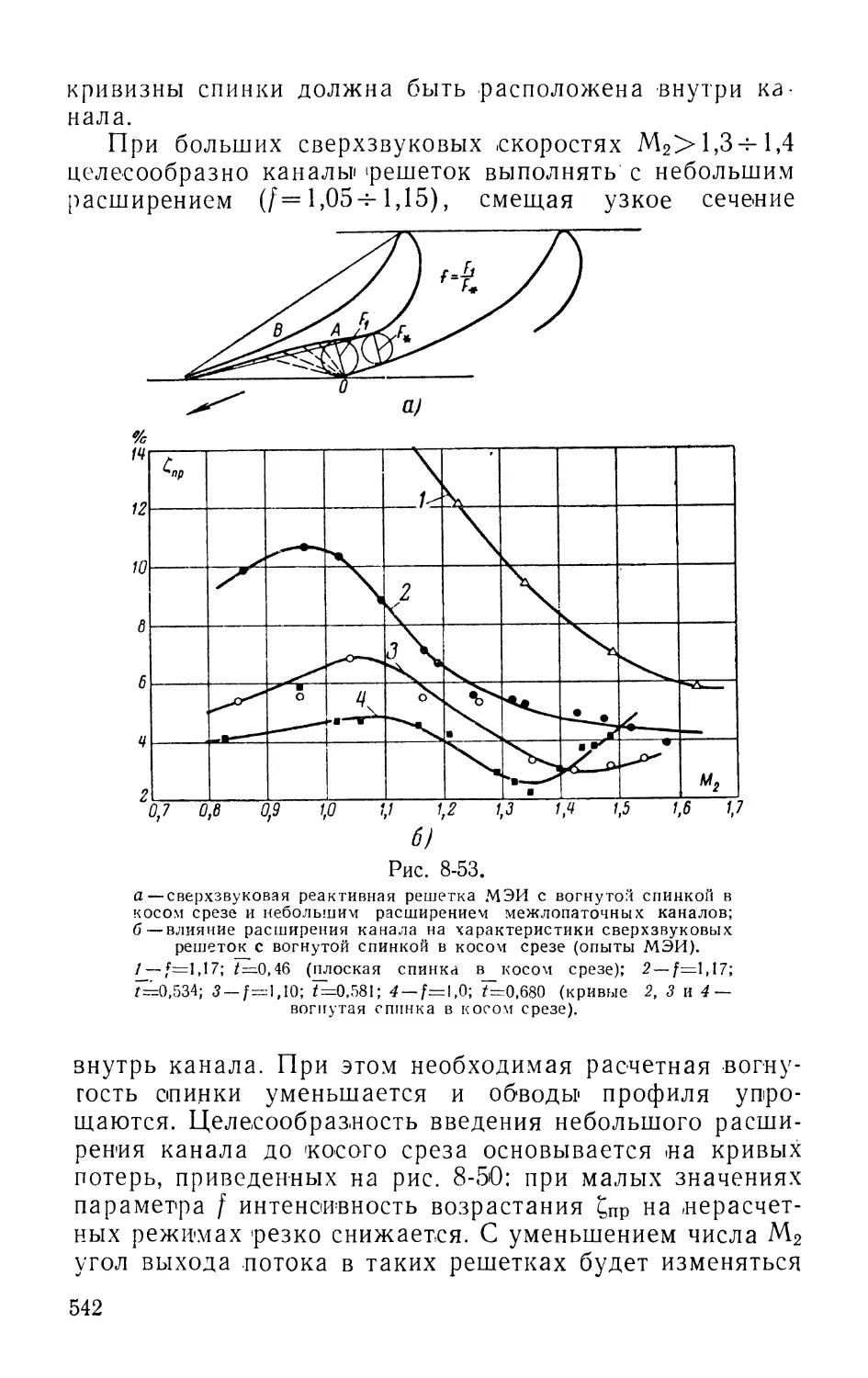
8-11. Расчет угла отклонения потока в косом срепе и
профилирование реактивных решеток при околозвуковых и
сверхзвуковых скоростях 536
8-12. Структура потока в активных решетках при околозвуковых
и сверхзвуковых скоростях 543
8-13. Приведенный расход газа через решетку. Особый режим
активной решетки в сверхзвуковом потоке 547
8-14. Профилирование и результаты экспериментального
исследования активных решеток jipn больших скоростях 557
Глава девятая
Течение газа в ступени турбомашины
9-к Основные уравнения 566
9-2. Параметры потока в абсолютном-и относительном движении.
Одномерная схема потока 577
9-3. Уравнения для расчета распределения параметров потока по
радиусу в рамках струйной теории . . 591
9-4. Расчет потока в ступени с длинными лопатками постоянного
профиля 598
9-5. Некоторые способы профилирования длинных лопаток
ступеней с осевым потоком газа 603
9-6. Осевая ступень с малым изменением реакции по радиусу. . 611
Глаза десятая'
Методы экспериментального исследования газовых
потоков и проточной части турбомашин
10-1. Экспериментальные стенды для исследования проточных
частей турбомашин 619
10-2. Методы измерения параметров рабочего тела при
исследовании газовых потоков 624
10-3. Оптические методы исследования газовых потоков 638
10-4. Установки для исследования решеток в статических условиях 644
10-5. Экспериментальные турбины 650
Приложения 654
Литература 664
ГЛАВА ПЕРВАЯ
ОСНОВНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
ГАЗОВОЙ ДИНАМИКИ
Ы. ПАРАМЕТРЫ ТЕЧЕНИЯ
Состояние неподвижного газа, как известно,
характеризуется давлением, плотностью и температурой —
параметрами состояния. Связь между параметрами состояния
устанавливается в термодинамике. Для совершенного газа
эта связь выражается в простой форме уравнением
состояния:
Z^gRT, (1-1)
где g — ускорение силы тяжести, м/сек*\
R — газовая постоянная1, имеющая в технической
системе единиц размерность кГм/кГ-град.
Для воздуха газовая постоянная
R = 29,27 кГм\кГ-град,
Для перегретого водяного пара (приближенно)
# = 47,1 кГм/кГ'-град.
Вместо плотности р в уравнение состояния может быть
введен удельный вес или удельный объем газа.
1 В ряде случаев оказывается удобным объединить постоянные
величины в уравнении состояния (1-1) и записывать его в таком виде:
■j = RT, (1-1 а)
где R — о% в технической системе единиц имеет размерность
м2/сек2-град. Здесь р в кГ/м2, р в кГ-сек21м* и Г в °К.
9
Между плотностью, удельным весом и удельным
объемом существует очевидная зависимость
где y~ удельный вес; v — удельный объем.
При движении газа параметры состояния являются не
только физическими, но и динамическими характеристиками
потока. В общем случае они меняются при переходе от
одной точки пространства к другой, от одного момента
времени к другому. Следовательно, /?, р и Т зависят от
положения точки и от времени и должны быть определены
как точечные параметры.
В каждой точке движущегося совершенного газа
параметры состояния связаны между собой уравнением
состояния (1-1). Во многих практически важных случаях
связь между параметрами р, р и Т выражается в более
сложной форме. При рассмотрении физических свойств
реальных газов иногда нельзя пренебрегать собственным
объемом молекул и силами взаимодействия между ними. Эти
факторы сказываются особенно существенно, если
давления газа велики и, следовательно, концентрация молекул в
определенном объеме велика.
Таким образом, в общем случае неустановившегося
течения газа параметры состояния зависят от координат и
времени:
р = р(х, у, г, t)\ Л
р = Р(х, у, z, /); (1-2)
Т = Т(х, у, г, t), J
где х, у, z — координаты точки; t — время.
Для решения задачи о течении сжимаемой жидкости,
которая в конечном счете сводится к установлению
силового взаимодействия между обтекаемым телом и жидкостью
(внешнее обтекание) или — в случае внутреннего течения
(трубы и каналы) — к установлению энергетического
баланса потока, необходимо определить кинематическую
картину течения, т. е. найти скоростное поле потока. Это
значит, что наряду с зависимостями (1-2) должны быть
найдены составляющие скорости частицы как функции
координат и времени. Скорость газовой частицы меняется при
переходе от точки к точке и с течением времени. Сдедо-
10
ва'гельно, проекции скорости на оси координат могут быть
представлены уравнениями:
и = и{х, у, г, t)\ Л
v = v(x, у, 2, /); ) (1-3)
w = w (х, у, г, t), )
где и — проекция вектора скорости с на ось х, а г;, w—
соответственно на оси у и z.
К числу параметров течения реальной (вязкой) жидкости
относится также вязкость, которую необходимо
определять как параметр в точке.
Известно, что коэффициентом вязкости называют
отношение
дп
где z — сила трения, отнесенная к выделенной
поверхности, кГ/м2;
дс
j— —градиент скорости по нормали к выделенной по-
0п ( 1 \
верхности трения в данной точке — .
V СвК I
Коэффициент вязкости имеет размерность в технической
системе единиц кГ-сек/м2.
В общем случае для реального газа коэффициент
вязкости зависит от температуры и давления. Однако
зависимость от давления в широком диапазоне изменений
давления оказывается весьма слабой и ею можно пренебречь.
Таким образом, коэффициент вязкости может быть выражен
в зависимости только от температуры. Соответствующие
формулы для различных газов устанавливаются
экспериментально.
Отметим, что закон трения в газах, выражаемый
формулой (1-4), принадлежит Ньютону и справедлив только
для ламинарных течений. При турбулентных режимах
течения коэффициент трения приобретает совершенно новое
содержание в соответствии с другим, значительно более
сложным механизмом внутреннего трения.
Для решения указанной выше основной задачи
необходимо определить и, v и w, а также /?, р и Т как функции
координат и времени. В дальнейшем будут рассмотрены
только установившиеся течения газа и перечисленные пара-
11
^етры течения должны быть определены только в
зависимости от координат х, у и г.
Для этой цели мы располагаем шестью основными
уравнениями: уравнениями количества движения в проекциях на
оси координат, уравнением сохранения массы, уравнением
сохранения энергии и уравнением состояния.
1-2. НЕКОТОРЫЕ ОСНОВНЫЕ ПОНЯТИЯ
АЭРОГИДРОМЕХАНИКИ i
Прежде чем перейти к выводу основных уравнений
движения, остановимся на некоторых понятиях
аэрогидромеханики, необходимых для дальнейшего.
Рассмотрим в движущейся жидкости ряд точек,
каждая из которых лежит в направлении вектора скорости
Рис. 1-1. К определению линий тока.
предыдущей точки. Уменьшая расстояние между
соседними точками до нуля и проведя через эти точки линию,
получим линию тока. В каждый момент времени
векторы скорости будут касательными к этой линии.
Следовательно, движение жидких частиц в данный момент
времени происходит вдоль линии тока.
Если движение неустановившееся, то, очевидно,
скорость в точке А в следующий момент времени будет
отличной от сх по величине и направлению (рис. 1-1). В
результате линия тока займет новое положение в
пространстве. Отсюда следует, что при неустановившемся движении
линии тока меняют форму и положение в пространстве.
Для установившегося движения величина и направление
вектора скорости не меняются во времени; в этом случае
линии тока сохраняют, неизменное положение в пространстве
и форму.
1 В § 1-2 весьма кратко излагаются некоторые основные понятия
аэрогидромеханики, встречающиеся в специальных главах книги
12
На линии тока 5- (рис. 1-2) выделим элементарный
отрезок ds и спроектируем его на координатные оси (отрезки
dx, dy, dz) Найдем углы между элементом ds и вектором
скорости
Отсюда
с с осями
получим:
координат:
cos (xs) =
cos (ys) =
cos(zs)-
dx dy
и v
a
с
_ V
с
w
с
_dz
w
dx
~~ds~'
_dy .
"ds '
dz
''ds'
__ds
с
Следовательно, дифференциальное уравнение линий тока
имеет вид:
dx dy dz
и v w
(1-5)
Выделим в движущейся жидкости некоторый бесконечно
малый замкнутый контур, через каждую точку которого
проходит линия тока (рис. 1-3). Совокупность всех линий
тока образует некоторую замкнутую поверхность—т рубку
тока. Жидкость, движущаяся внутри трубки тока,
называется элементарной струйкой.
С,'
'У
Рис 1-2
К выведу дифференциального
уравнения линий тока.
13
Возвращаясь к понятию линии тока, отметим, что в
установившемся движении, она совпадает с траекторией частицы.
Траектория представляет собой линию,
изображающую путь, пройденный в пространстве частицей за
некоторый отрезок времени. Линия же тока является мгновенной
линией, вдоль которой в данный момент движется
совокупность частиц. Очевидно, что только при установившемся
движении эти понятия могут совпадать, так как в этом
случае траектории всех частиц, проходящих через какую-
либо определенную точку пространства, будут одинаковыми
Рис 1-3 К определению трубки тока и
элементарной струйки.
и, следовательно, в каждый момент времени все частицы,
которые лежат на траектории, будут образовывать и линию
тока.
В общем случае движение жидкой частицы является
сложным. Наряду с поступательным движением вдоль
некоторой траектории частица может вращаться относительно
собственных осей и в процессе этого движения
деформироваться.
Благодаря неодинаковым скоростям на различных гранях
частица испытывает линейную деформацию и деформацию
скашивания или сдвига. Если в первоначальный момент
движения частица имела форму параллелепипеда, то с
течением времени вследствие деформации форма ее изменяется.
В случае сжимаемой жидкости меняется также и объем
частицы.
14
Обращаясь к рис. 1-4, проанализируем вращение и
деформацию одной из граней параллелепипеда, показанного
на рис. 1-2. Если в точке D (рис. 1-4) проекция скорости
на ось х будет «, то в точке А она будет ti]-\-^-dy. Под
Г¥^
Рис. 1-4. Деформация грани частицы жидкости
в процессе движения.
действием разности скоростей в этих точках, равной -g-dy,
ребро DA повернется на некоторый угол йги
переместившись относительно точки D за элемент времени dt в
положение DAt. Величина отрезка АА1 определяется по
формуле
За рассматриваемый элемент времени точка U сместится
по оси у на величину
При этом ребра DA и DD' повернутся на малые углы
dex и de2, которые определяются по очевидным уравнениям:
dex % tg det
АА1
,pdt
ду
15
и
1 i 1 D'D* dv ,.
Рассматриваемые перемещения ребер DA и DU вызваны
как вращением плоского жидкого элемента (грани
параллелепипеда), так и его деформацией. Заметим, что если бы
грань только деформировалась, без вращения, то ребра DA
и DD' поворачивались бы на одинаковый угол навстречу друг
другу или в противоположных направлениях. Наоборот,
если бы грань совершила только вращательное движение
(как абсолютно твердое тело), то ребра DA и DD'
поворачивались бы на одинаковый угол в одном направлении.
Движение элемента в общем случае можно
рассматривать как сумму деформационного и вращательного
движений и таким путем определить углы dex и de2. Принимая,
что в результате вращения (против часовой стрелки) ребра
DA и DD' повернулись на угол dy, а в результате
деформации—дополнительно на угол яф, найдем:
del = d$ — dy,
Из этих двух уравнений получим:
2dY — de2 — de1.
Угловая скорость вращений грани будет равна:
d-j __\ /de2_del\
dt ~~2 [dt dt y
Подставив значения производных -j. и ■— , находим
угловую скорость вращения грани в таком виде:
dt 1 /dv ди\
®z—Tt^\Jx Ту у
где о) — составляющая вектора угловой скорости
вращения, параллельная оси z (индекс z указывает направление
оси, относительно которой происходит вращение). Заметим,
что со является угловой скоростью вращения биссектрисы
угла в точке D. Аналогичные рассуждения приводят нас
к заключению, что угловые скорости вращения двух дру:
16
гих граней, расположенных в плоскостях хог и yoz,
выражаются через соответствующие значения частных произ-
ди dw dv dw
водных у, у-, -р -g-, причем вращение каждой грани
параллелепипеда определено двумя угловыми скоростями.
Таким образом, уравнения для всех трех составляющих
вектора угловой скорости вращения будут иметь вид:
1/dw dv\
1 /да dw ^
1 , dv да t
тг~1Г\дх dyf }
Уравнения (1-6) выражают компоненты вектора угловой
скорости вращения жидкой частицы со, величина которого
определяется как геометрическая сумма ш^, со и со2:
w = K0)* + % + cV С1"7)
Формулы (1-6) определяют в дифференциальной форме
связь между составляющими угловой скорости вращения
и составляющими скорости поступательного движения.
Вращательное движение частицы вокруг осей,
проходящих, через частицу, называют вихревым движением.
Опыт показывает, что во всех случаях движения реальной
(вязкой) жидкости все поле потока или часть его являются
вихревыми. В тех областях течения, где вихревое
движение частиц отсутствует, угловая скорость вращения равна
нулю (о) = 0). В этих областях частицы жидкости могут
двигаться по траекториям любой формы, деформируясь при
этом, но не вращаясь относительно своих осей.
Если в частном случае при а> = 0 траектории частиц
являются замкнутыми кривыми, то такое движение будет
частным случаем циркуляционного движения. Следует
подчеркнуть, что при таком движении частицы совершают
вращение вокруг некоторой оси, расположенной вне
траектории, но не вращаются относительно собственных осей.
Понятия вихревого и циркуляционного движений
жидкости играют большую роль в гидромеханике. В этой связи
остановимся на одной весьма важной характеристике по-
тока —цирку л я ци и скорости. Рассмотрим еще один
(1-е)
2 М. Е. Дейч
17
пример циркуляционного течения. При обтекании
несимметричного профиля крыла (рис. 1-5) плоскопараллельным
потоком линии тока в области потока у крыла искривлены,.
Циркуляционное
2 течение у
""^^-^крыла
так как крыло возмущает
поток. Характер
возмущения, вносимого крылом в
поток, можно выяснить,
определяя скорости в
различных точках поля у
крыла.^: Сравнивая локальные
значения скоростей со
скоростью набегающего
потока, нетрудно установить,
что течение у крыла можно
представить как сумму
поступательного
невозмущенного потока и течения по замкнутым траекториям.
Интенсивность потока у крыла можно характеризовать величиной
циркуляции скорости, которая определяется по уравнению
Рис. 1-5. Схема обтекания
крылового профиля.
i
(1-8)
где с
/ проекция вектора скорости на направление
элемента контура Л
В общем случае произвольно выбранный контур / может
не совпадать с линией тока циркуляционного течения.
Формулу (1-8) можно записать в таком виде:
Г =§с cos (cTl)dl.
(1-9)
Таким образом, циркуляционным движением можно
назвать такое движение, при котором циркуляция скорости
отлична от нуля. Если Г = 0, то движение называется
бесциркуляционным1.
При вычислении циркуляции скорости по формуле (1-9)
необходимо условиться о направлении обхода контура
интегрирования. Положительным направлением обхода, как пра-
1 Обращаясь к формуле (1-9), мы видим, что выражение для
циркуляции скорости напоминает известное уравнение работы вектора
силы. Эта внешняя аналогия позволяет понять механический смысл
циркуляции (произведение скорости на путь) и дает основание
условно называть величину Г работой вектора скорости.
18
вило, считают такое направление, при котором заключен*
ная внутри контура область потока остается справа (рис. 1-5).
Понятие циркуляции весьма широко используется при
исследовании вихревых движений газа. В теории вихревого
движения доказывается ряд фундаментальных теорем,
связывающих циркуляцию скорости с основными
характеристиками вихря. Остановимся прежде всего на основных
понятиях вихревого движения: вихревой линии, вихревой трубки
и вихревого шнура.
Эти понятия близко совпадают с приведенными выше
понятиями линии тока, трубки тока и элементарной струйки.
Рис. 1-6 Вихревая^трубка и вихревая нить.
Вихревой линией называют такую линию в потоке,
в каждой точке которой направление вектора угловой
скорости совпадает с направлением касательной к этой линии.
Напомним, что вектор угловой скорости направлен
перпендикулярно плоскости вращения. Следовательно, вихревая
линия представляет собой мгновенную ось вращения частиц
жидкости, которые располагаются на этой линии.
Вихревой трубкой называют замкнутую
поверхность, состоящую из вихревых линий, построенную на
элементарном контуре (рис. 1-6,а). Жидкость, заполняющая
вихревую трубку, образует вихревую нить. Если
вихревая трубка имеет сечение конечных размеров, то частицы,
заполняющие ее и находящиеся во вращательном движении,
образуют вихревой шнур.
Рассмотрим вихревую нить (рис. 1-6,6). Проведем
сечение, нормальное к оси нити. Интенсивность или
напряжение вихревой нити характеризуется удвоенным произведе-
2*
19
нием вектора угловой скорости вращения со на площадь
сечения нити dF:
dJ = 2<»dF.
В общем случае рассматриваемое сечение нити может
быть проведено произвольно под некоторым углом к ее оси
(рис. 1-6,6); тогда интенсивность dJ определяется по
формуле
dJ = 2vndFl ,
где и>п — проекция вектора угловой скорости на
направление оси вихревой нити:
О) = a) COS Ф.
п г
Таким образом, напряжение вихревой нити определяется
как удвоенное произведение площади произвольного
сечения нити на проекцию вектора со на направление нормали
к выбранному сечению.
В теории вихревого движения доказывается, что
циркуляция скорости по замкнутому контуру, охватывающему
вихревую нить, равна интенсивности вихревой нити, т. е.
dV = dJ =2ш dF.
п
Для контура, охватывающего вихревой шнур конечного
сечения, состоящий из бесчисленного множества вихревых
нитей, циркуляция скорости определяется криволинейным
интегралом
Г=2$о) dF.
J п
I
Это выражение, полученное Стоксом, позволяет
сформулировать одну из основных теорем вихревого движения:
циркуляция скорости по любому замкнутому
контуру, проведенному в жидкости, равна сумме интен-
сивностей вихрей, охватываемых контуром, если
этот контур путем непрерывной деформации можно
стянуть в точку, не выходя за пределы жидкости.
Если контур охватывает твердое тело (например, профиль
лопатки), то непосредственно применить рассматриваемую
теорему в этом случае нельзя, так как контур невозможно
стянуть в точку, не выходя за пределы жидкости. Однако
20
если замкнутый контур провести так, как это показано на
рис. 1-7 (контур ABCDA), то согласно уравнению Стокса
получим:
VABCDA= VAB + !V + VCD + VDA = ^^
так как VK = - Тм и Г,в = 2$шя dF + VCD.
Рис 1-7. К определению
циркуляции скорости по
замкнутому контуру,
охватывающему профиль.
Формула Стокса приводит к заключению, что ядро
прямолинейного вихря постоянного сечения вращается, как
твердое тело, с постоянной угловой скоростью.
Действительно, на основании указанной теоремы для
прямолинейного бесконечно длинного вихря можно записать, что
циркуляция по контуру, охватывающему вихрь,
Г = 2а)/7 = const.
При F = const в произвольной точке ядра вихря
со = const. Линейная скорость в ядре будет:
где г — радиус рассматриваемой точки.
Следовательно, распределение скоростей в поле вихря
будет линейным. На внешней поверхности ядра скорость
имеет максимальное значение:
С«макс=а,Го
(г0 -- радиус вихря).
21
В гидромеханике доказывается также теореМа о
неизменности циркуляции во времени в идеальной невязкой
жидкости (теорема Томсона).
Согласно теореме Томсона для идеальной жидкости вне
вихря циркуляция сохраняет постоянное значение по любому
контуру, охватывающему вихрь. Циркуляционное течение
около бесконечно длинного прямолинейного вихря (вне его)
имеет гиперболическое поле скоростей (рис. 1-8), так как
Г = 2тог2 = 2^ г
и
q и макс о Г
"~~ } ~ЪГг'
Легко видеть, что в соответствии с теоремой Томсона
в идеальной жидкости вращательное вихревое движение
частиц возникнуть или исчезнуть не может. Это и физи-
Рис. 1-8. Поле скоростей в ядре вихря
и во внешнем потоке.
чески понятно, так как в такой жидкости отсутствует
механизм передачи вращательного движения и торможения.
Наблюдая течения реальной вязкой жидкости, можно
указать большое число примеров возникновения и
затухания вихрей. При этом условие постоянства циркуляции,
которое является важнейшим свойством движения
идеальной жидкости, не сохраняется.
Различия в свойствах идеальной и реальной жидкостей
можно проследить при рассмотрении спектра
несимметричного обтекания тела. Если задняя кромка тела выполнена
острой (тело крылового профиля), то безотрывное обтека-
22
ние такой кромки идеальной жидкостью должно привести
к тангенциальному разрыву скоростей за профилем
(рис. 1-9)/ В реальной вязкой жидкости наличие такого
разрыва приводит к тому, что при сходе с задней кромки
поток завихривается (рис. 1-9,6).
Таким образом, возникновение вихрей, а следовательно,
и циркуляции вокруг профиля объясняется влиянием вязко-
Рис 1-9 Образование вихрей при сходе потока с крылового профиля.
сти. В начальный момент времени поток у крыла
бесциркуляционный. В точке схода в силу свойства вязкости
зарождается начальный вихрь (рис. 1-9,6), который
создает циркуляцию. Опыт показывает, что при не очень
большой несимметрии этот вихрь возникает у задней
кромки. Соответствующее условие в потоке идеальной
жидкости, согласно которому точка схода должна
находиться на задней кромке, носит название постулата
Жуковского—Чаплыгина: при безотрывном
несимметричном обтекании идеальной жидкостью профиля
вокруг него образуется такая циркуляция Г, которая
обеспечивает сход потока с задней кромки.
Это условие, сформулированное Н. Е. Жуковским и
С. А. Чаплыгиным, позволяет вычислять циркуляцию Г и
вместе с тем подъемную силу крыла.
1-3. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ
Выделим в движущемся газе элементарный объем в
форме параллелепипеда (рис. 1-10) и запишем условие
неизменяемости массы во времени для этого элемента. Это
условие будет выражать закон сохранения массы;
оно может быть представлено в таком виде:
^=0, (1-10)
dt
где AV — объем элемента;
р — средняя плотность элемента.
23
Дифференцируем, имея в виду, что р и AV —
переменные величины:
ду^ + Р —=0.
dt
dt
Разделим это уравнение на pAV. Получим
уравнение неразрывности в виде:
1 ?[?4-— —=п
р dt*AV dt
(1-10а)
А2
(p + jjj-(k)dxdy
pdyfe I » Up
^—t
1 *в'У'
dx^
(p+ ^dxjdydz
&L,
r-^+m**
pdxdy
Рис. 1-10. К выводу уравнений Эйлера.
dLV
Здесь производная —гг выражает скорость
изменения
объема или, следовательно, скорость объемной деформа-
ции жидкой частицы. Член -^ —-• представляет собой
скорость относительной объемной деформации.
В частном случае несжимаемой жидкости, когда р =
=const, последнее уравнение принимает весьма простую
форму:
dLV
at
"=0,
выражающую условие постоянства объема
элемента: скорость объемной деформации элемента
равна нулю. Отсюда следует, что частица несжимаемой
24
жидкости деформируется в процессе движения так, что
объем ее сохраняется неизменным.
Определим величину скорости относительной объемной
деформации частицы, выразив ее через соответствующие
проекции скорости и, v и w.
Подсчитаем линейную деформацию частицы в
направлении оси х (рис. 1-10). Эта деформация будет происходить
в связи с тем, что скорости граней ABCD и A BCD'
неодинаковы. Если скорость левой грани равна и, то
скорость правой будет и -\- -т- dx.
Предположим, что в пределах каждой из
рассматриваемых граней параллелепипеда скорости постоянны. За элемент
времени dt левая грань ABCD переместится на расстояние
udl вправо. За тот же отрезок времени грань А'В'С'П
переместится в том же направлении на расстояние (w-f-
dt. Следовательно, объем элемента изменится,
+?.«*)
так как скорости этих двух граней различны. Подсчитав
абсолютное изменение объема частицы по направлению
оси х, получим:
[uJrj~ dx\ dy dz dt — udy dz dt= ~dxdy dz dt.
Рассуждая аналогично, для других двух пар граней
можно получить приращения объема частицы по осям у и
2 в следующем виде:
■р dxdydzdt',
-г- dxdydzdt.
Полное изменение объема частицы определяется как
сумма этих приращений.
Следовательно, скорость относительной объемной де
формации определяется весьма просто:
1 dAV ди, dv , dw /I 1 n
так как объем элемента AV = dxdydz.
25
Подставив (i-li) в уравнение неразрывности (1 - 10а),
получим:
Н (й+S+S)-»- с-1»»)
Заметим здесь, что входящие в уравнение (1-11)
пряди dv dw
мые частные производные ^- , -г-, ^— имеют конкретный
механический смысл. Из предыдущих рассуждений
очевидно, что эти производные определяют величины
скоростей относительных линейных деформаций граней
параллелепипеда. Рассмотрим, например, линейную деформацию
грани DCCD' в направлении оси х. Так как скорость
ребра CD равна и, а ребра CD u-\- ^dx, то удлинение
грани по х будет:
(и-\- -^ dx\dt — udt = ~ dxdt.
Относительное удлинение составляет -=- dt, а скорость
ди
относительного удлинения -г- .
Преобразуем теперь уравнение (1-106). Так как р =
= p(x,y,z,t), то полная производная плотности равна:
dp dp dx_td$ dy,d? dz . dp
Tt~dxdt~*dy li*~dz dt~^"di'
T;r dx dy dz
Имея в виду, что — = w, -£=v\ -ji—1®, получим:
dt dx ' dy l dz ' d/
Подставив -^ в уравнение (1-106) и преобразовав, будем
иметь:
МГЧ-тГ+^-О. 0-12)
Если движение является установившимся, то 37=0.
Для несжимаемой жидкости (р = const) легко получить
из уравнения (1-12):
г,+%+ш=°- (•■»)
26
Уравнение (1-12) является уравнением
неразрывности газового потока в дифференциальной форме. Это
уравнение было впервые получено Эйлером в 1659 г. Мы
видим, что оно связывает изменения плотности с
ниями составляющих скорости и, v и w. Имея
ди
dv
ду
т- и
измене-
в виду
dw
дг'
k
Рис.
точки в
. Положение
прямоугольной и цилиндрической
системах координат.
механический смысл частных производных ^—
выражающих скорости
относительной линейной
деформации жидкой частицы в
направлении осей х, у и г, можно
на основании уравнения
неразрывности заключить, что
деформация такой частицы
подчиняется определенной
закономерности и не может быть
произвольной. Для несжимаемой
жидкости уравнение (1-13)
показывает, что частица
несжимаемой жидкости в
процессе движения
деформируется с сохранением объема.
Для сжимаемой жидкости
деформация частицы происходит с изменением объема. В
этом случае уравнение неразрывности связывает изменения
объема и плотности частицы.
Уравнение (1-12) записано в прямоугольной системе
координат. Во многих случаях, в особенности при изучении
процессов, протекающих в турбомашинах, удобно
пользоваться цилиндрической системой координат.
Положение некоторой точки А в цилиндрических
координатах определяется радиусом-вектором г, полярным
углом б и аппликатой г (рис. 1-11). Давая указанным
координатам бесконечно малые приращения dr, db и dz,
выделим в массе жидкости частицу ABCDAB'C'U (рис. 1-12).
Движение точки в рассматриваемых координатах задано,
если известны составляющие скорости:
dr
с =
dt
dti
-радиальная составляющая;
С6 = г -^ — тангенциальная составляющая (нормальная к
радиусу-вектору);
27
dz
w=-77— осевая составляющая скорости.
Составим уравнение неразрывности в цилиндрических
координатах. Подсчитаем скорость относительной объемной
деформации движущейся жидкой частицы, показанной на
рис. 1-12. Изменение объема этой частицы за элемент
времени dt в направлении радиуса-вектора можно выразить
так:
[(Cr + Trdr)lr + dr)d9-Cr
или, оставляя члены одного порядка,
(с дс \
-L^^ydrdzdUt.
rdb
dzdt
Рис 1-12 К выводу уравнений Эйлера
в цилиндрической системе координат.
Изменение объема в направлении, нормальном к
радиусу-вектору, будет:
дсЙ \ 1 1 дсЙ
с, + -ш <*в 1 — сa dzdrdt = -~ dzdrdbdt.
По оси z объем меняется на величину
(w-\-~dz\ -w
rd\drdt= —rdzdrdhdt.
dz
28
Суммарное изменение объема за рассматриваемый
отрезок времени составляет:
"»v.=(f'+£44£+s)"'*ww-
Тогда скорость относительной объемной деформации
будет:
Iv ~~иГ 7"~т"а7~т"7"?е" « dz *
Подставив это выражение в уравнение неразрывности
(1-10а) и выразив полную производную плотности в
цилиндрических координатах, после преобразований окончательно
получим:
д? , d(pw) 1 д(?гсг) , 1 ^(Рсб)
dt ' dz ■ г дг * г дб
- = 0. (1-14)
1-4. УРАВНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ
Ниже рассматривается движение газа без внутреннего
теплообмена при отсутствии теплопроводности и трения.
Такое движение является, конечно, идеализированной
моделью действительного движения, в котором
проявляются силы трения, возникают градиенты температуры и
совершается внутренний теплообмен между соседними
частицами.
Принимаемая упрощенная схема потока сжимаемой
жидкости, однако, играет весьма важную роль в газовой
динамике, так как она служит известным эталоном при
анализе действительных процессов течения. Многие
практически важные реальные случаи течения газа весьма
близки по своим свойствам к рассматриваемому
идеализированному течению, закономерности которого в этих
случаях могут быть использованы для расчетов. Получаемые
при. указанных упрощениях зависимости широко
используются для анализа физических свойств потока,
энергетически изолированного от окружающей среды.
Установим основные закономерности, которым
подчиняется такая схематизированная модель течения..
Выделим в потоке жидкости элементарный
параллелепипед. Внутри замкнутой Поверхности параллелепипеда
заключена масса жидкости. Применим к рассматриваемому
элементу теорему количеств движения.
29
Изменение количества движения массы газа,
сосредоточенной внутри поверхности, происходит в общем случае
вследствие того, что каждая частица, перемещаясь,
занимает с течением времени новое положение и приобретает
новую скорость, а также потому, что в каждой точке
пространства скорость изменяется во времени. При
установившемся движении количество движения меняется
только в связи с изменением положения частиц.
В соответствии с известной теоремой механики
изменение количества движения массы, заключенной в выделенном
элементе, равно импульсу внешних сил. Составим
уравнения импульсов в проекциях на координатные оси
(рис. 1-10).
На грань ABCD в направлении оси х действует сила
давления pdydz, импульс которой будет:
pdydzdt.
Импульс сил давления, действующих на грань AB'C'D',
равен:
— (p + dfxdx\dydzdt.
Заметим, что, кроме сил давления, на элемент могут
действовать массовые силы (гравитационные, магнитные и
электростатические). Из них чаще всего необходимо
учитывать гравитационную силу — силу тяжести. Для газов
вследствие относительно малой их плотности сила тяжести
по сравнению с силами давления оказывается малой и ею
обычно можно пренебречь.
Однако в некоторых задачах влияние массовых сил
должно быть учтено. Обозначим через X, Y и Z проекции
единичной массовой силы (отнесенной к массе жидкости)
на оси координат jc, у и • г. Тогда проекции полной
массовой силы на координатные оси будут:
Xpdxdydz, Ypdxdydz'n Zpdxdydt.
Введем импульс массовых сил в проекции на ось х,
равный Xpdxdydzdt. Тогда суммарный импульс равен
изменению количества движения:
Xpdxdydzdt — ^ dxdtydzdt = ydxdydzdu}
где pdxdydz — масса элемента,
30
Следовательно,
Аналогичные
У и 2:
du у 1 др
dt $ вх '
уравнения получим в
dv у 1 дрш
~di~' 7' <V
dw 7 1 dp
проекции
(l-15a)
на оси
(1-156)
(1-15в)
Имея в виду, что приращения скорости равны:
du-
ди , , да 1 , да , , du #,
' дх
dz
dt
i dv , х dv i x dv , , dv ,,
dv=6-xdx+dydy+Tzdz+Ttdt>
, dw i , dw * \ dw * , dw ,,
dw ^dx dx+d^ dy+d7 dz+*Tdt>
dz
dt
для проекции ускорения на координатные оси получим
из (1-15):
du du i du . du г du v 1 dp
= *7+U^, + V?-j+W-r = X--- '
Л d/
dx
^
dy _
It''
p d;c'
du . dv , dy , dy T/ 1
Л/ ' ^y. ' d# ' dz p dz/
d/
day
= dT
dx
, дм/ , dw x dw rj
+ Udx-+Vdj + W^ = Z~
dz
1 0Л.
p d*
(i-i6)
Производные •£, -^ и -^ выражают проекции полного
ускорения движущейся частицы. Уравнения (1-16)
показывают, что ускорение жидкого элемента вызывается
соответствующими изменениями сил давления, действующих
на этот элемент, и массовыми силами. Уравнения (1-16)
были также получены Эйлером.
Составим теперь уравнения импульсов в
цилиндрических координатах. С этой целью найдем составляющие
ускорения в новой системе координат. Полное ускорение
вдоль радиуса-вектора выражается как сумма относитель-
31
dc,
ного ускорения — и центростремительного ускорения-
—Л Следовательно, радиальное ускорение равно:
dt i '
Полное ускорение в направлении, нормальном к
радиусу-вектору, складывается из тангенциального ускорения
/720 fjr jfl
г -тр и кориолисова ускорения 2 —
dt dt '
tdr dft 1 d(rc^ dcQ
T. e.
dF* l* ~di Tt=T~~dT=dt
Тогда уравнения импульсов (1-15) можно записать в
такой форме:
dt r K
dc~ сгс^
dw у 1 dp
~dF~L "~7 dz '
_1_ dp .
P
dp . I
rrifl' I
(1-17)
;
где /?, 0 и Z — проекции единичной массовой силы на
оси координат г, 0 и г.
т-т &СГ
Подставив в (1-17) значения полных производных
^св dw
dF и Ж чеРез частные, окончательно находим:
dt
дс,
дс„
дс„
дст
Ж + сгдГ+т Ж+Шд7-Т ~/< —7 ^ '
дсв dcQ cQ dcQ dcQ crc{
dF + CrdF+T db+Wd!+-
= 0-
p roe'
| (Ы7а)
day , d£# , c9 dw . dw rj 1 dp
dF + crd7+FM+wdF = Z-J di>
)
1-5. УРАВНЕНИЯ ДВИЖЕНИЯ В ГИДРОМЕХАНИЧЕСКОЙ
ФОРМЕ. УРАВНЕНИЯ И. С. ГРОМЕКО
Уравнения движения в форме Эйлера являются общими
уравнениями механики. Особенности движения жидкой
среды могут быть отражены введением специфических
32
элементов движения — компонентов вихря, кинетической
и потенциальной энергии — в уравнения Эйлера.
Компоненты угловой скорости вращения о^, юу и «»2
могут быть непосредственно введены в уравнения
движения (1-16) и (1-17а). Если к левой части первого из
уравнений (1-16) добавить, а затем отнять v^ и ш —, то после
несложных преобразований получаем:
да
, да i dv . dw /dv да \ , (да dw \
X
р дх
Имея в виду, что
да , dv t dw д ( с2\
и учитывая формулы (1-6), представим первое из
уравнений движения (1-16) в такой форме:
да
dt
ma>
др
dt +cU [YJ 2 ('vwz ""V —" p dx
^j = Z-_f ^-. (l-18a)
Аналогично можно преобразовать и два других
уравнения движения. В результате получим:
dv
dt
+i(4)-2<~*-»-",>=1'-Tt; <'-ш>
£+£(4)-*<».—j=*-t &■ <Ы8в>
Аналогично можно преобразовать уравнения (1-17а) в
цилиндрической системе координат. Компоненты угловой скорости врящения
в этой системе координат выражаются уравнениями:
1 (dw d(y) у
dz У
\
1 /дсг dw
°0~ 2 \dz Or
1. (<>(cbr) dcr
2r \ Or
(Mi)
(90
3 M E. Дейч
33
Пользуясь известными формулами перехода от прямоугольных
к цилиндрическим координатам, нетрудно выразить компоненты
угловых скоростей соЛ, со и со2 через ь>г со0 и со2. Угловая скорость
вращения w может быть выражена через составляющие ыг со0 и <*>г по
уравнениям (149), так как
0)2:
:^+^ + (0z^wr + (0e + ^-
Смысл величин о>г, cog и со2 поясняется на рис. 1-13.
Составляющая со определяет такое вращение частиц, осью которого является
радиус-вектор (радиальный вихрь); компонента со0 характеризует
вращение частиц относительно оси, имеющей форму окружности
(кольцевой вихрь); со2 представляет собой угловую скорость вращения вокруг
оси z.
dw
Введем в левую часть первого уравнения (1-17а) члены: ±_w^r ,
dw
±ct
Вдгу тогда
- + -
dt ^ дг
д-
2 (с*>.
Гг
.^ = R-±-dP;
0 р дг
(1-20)
аналогично преобразуются второе и третье уравнения (1-17а).
Преимущества уравнений количества движения (1-18)—
(1-20) очевидны. В отличие от уравнений Эйлера они
содержат в явной форме величины, характеризующие
особенности движения жидкости — легко деформируемой среды.
Эти уравнения включают компоненты угловой скорости
вращения частиц, т. е. члены, характеризующие вихревое
движение жидкости, кинетическую энергию и
потенциальную энергию давления, а также потенциальную энергию
массовых сил.
Введение этих величин
существенно упрощает
анализ многих сложных видов
движения жидкости и, в
частности,облегчает
исследование некоторых свойств
потока в проточной части
турбомашин.
В некоторых частных
случаях уравнения (1-18)
или (1-20) легко
интегрируются. Для этой цели
уравнениям движения мож-
Vr„je
Рис. 1-13. К определению
компонентов вихря в цилиндрической
системе координат.
34
но придать еще более простую и наглядную форму, вводя
некоторую "функцию давления
Р =
\Н-
(1-21)
Кроме того, влияние массовых сил учитывается путем
введения потенциальной функции £/, частные производные
от которой по координатам выражают проекции ускорения
массовых сил на оси координат:
dU. т, _dU, 7__dU
ду' дг '
Х=-Ш> Y-
(1-22)
Тогда уравнения (1-18) принимают вид:
dw i д
+5г(-Г + £, + Яу = 2К-0Ш> J
(1-23)
Уравнения (1-23) были получены профессором
Казанского университета И. С. Громеко в 1881 г.
Для установившегося движения (^=^=-7ff — Q)
после умножения обеих частей уравнения (1-23)
соответственно на dxy dy и dz и суммирования нетрудно получить:
-d(^- + U + P^=2
dx dy
и v
(О О)
х у
dz
W
2
(1-24)
Определитель (1-24) равен нулю в следующих частных
случаях:
а) при отсутствии вихрей в жидкости, т. е. когда
б) при условии
аз =ш = ш = 0;
х у z '
dx dy dz t
a v w !
35
в) при условии
dx dу dz .
условия „б" и „в" являются дифференциальными
уравнениями линий тока и соответственно вихревых линий [см.
уравнение (1-5)]; следовательно, согласно условиям „б"
и „в* определитель (1-24) равен нулю для линий тока и
вихревых линий;
г) при
via =wsi ; way = #'j> ; им =v<» ,
или
и v w
°>x % "г
(1-25)
Во всех перечисленных случаях из (1-24) получаем:
или после интегрирования
-£- + [/+ P = const. (1-26)
Интеграл (1 -26) является уравнением энергии
для струйки, т. е. выражает баланс энергии
жидкой частицы: сумма кинетической и потенциальной
энергии, т. е. полная энергия частицы является величиной
постоянной. Следует вспомнить, что функция U выражает
потенциальную энергию массовых сил, а Р —
потенциальную энергию сил давления. Первый член (1-26) дает
величину кинетической энергии жидкой частицы. Все
указанные составляющие полной энергии отнесены к секундной
массе протекающей жидкости.
Несмотря на то, что интеграл (1-26) имеет одинаковую
форму для всех рассмотренных случаев, смысл его и
область применения различны в зависимости от условий, для
которых интеграл был получен.
Для безвихревого установившегося движения жидкости
(случай „а") интеграл (1-26) справедлив для всех точек
потока.
При выполнений условий „б" или „в" полная энергия
частицы сохраняется постоянной только вдоль линии тока
36
или соответственно вдоль вихревой линии. При переходе
от одной линии тока к другой или от одной вихревой
линии к соседней величина постоянной в правой части (1-26)
может меняться.
Условие „г" пропорциональности линейных и угловых
скоростей (1-25) приводит к интегралу (1-26), т. е. к
постоянству полной энергии жидкой частицы, справедливому
для всех точек потока. Следовательно, в рассматриваемом
частном случае вихревого движения полная энергия
сохраняется неизменной для всех вихревых линий. Особенность
этого вида движения состоит в том, что каждая частица
вращается вокруг оси, вдоль которой она движется.
Действительно, условие (1-25) означает, что направления
векторов линейной и угловой скоростей совпадают, так как
пропорциональность этих векторов указывает на то, что эти
векторы ориентированы под одинаковыми углами к осям
координат. В рассматриваемом движении линии тока и
вихревые линии совпадают. Заметим, что во всех изучаемых
случаях при адиабатическом течении в точках, связанных
между собой интегралом (1-26), энтропия остается
постоянной.
Интеграл (1-26) можно преобразовать для практически
важного случая, когда из массовых сил действует только
сила тяжести; при этом
(ось z направлена вертикально вверх).
Следовательно,
После подстановки [этих величин уравнение (1-26)
приобретает вид:
4+^+JT=const- (1_27)
Для несжимаемой жидкости (р = const) находим:
l| + * + f-const. (1-28)
Последнее уравнение получено Д. Бернулли. Величина z
в этом уравнении характеризует потенциальную энергию
37
положения, обусловленную движением в однородном поле
земного тяготения жидкой частицы, и называется
нивелирной высотой. Величина —представляет собой потенциаль-
с2
ную энергию давления (пьезометрическая высота), а ^
кинетическую энергию; все члены уравнения (1-26)
отнесены к секундному весу протекающей жидкости.
ГЛАВА ВТОРАЯ
ОДНОМЕРНОЕ ДВИЖЕНИЕ ГАЗА
Значительное число технических задач газовой динамики
можно решать, предполагая движение одномерным, т. е.
таким, в котором все параметры течения меняются только
в одном направлении. Этим условиям отвечает течение газа
вдоль слабо искривленных линий тока или в трубках тока.
Одномерным можно считать течение газа в трубе с мало
изменяющимся поперечным сечением и малой кривизной оси.
В ряде случаев результаты исследования одномерного
течения могут быть применены и к потокам с неравномерным
распределением параметров по сечению.
2-1. ОСНОВНЫЕ УРАВНЕНИЯ ОДНОМЕРНОГО
ТЕЧЕНИЯ. СКОРОСТЬ ЗВУКА
Для получения основных уравнений одномерного
движения рассмотрим течение газа в трубке тока. Направление
оси выберем так, чтобы оно совпадало с осью трубки (рис.
2-1). Воспользуемся первым уравнением системы (1-16).
Пренебрегая для газа влиянием массовых сил, полагаем
Имея в виду, что для рассматриваемого одномерного
течения и=с, у = ш = 0 и перейдя в уравнении (1-16)
к полным производным, получим:
cdc+±dp==0
dx ■ р ах
или
cdc + lf = Q. (2-1)
38
Уравнение изменения количества движения (уравнение
импульсов) (2-1) справедливо только для таких течений,
в которых отсутствуют силы трения, т. е. для обратимых
течений. Легко показать, что в этом случае если
система адиабатична, изменение параметров состояния
совершенного газа подчиняется изоэнтропическому закону:
4 —const. (2-2)
Следует заметить, что формулируя обстановку процесса
течения, считая, что поток непрерывен, энергетически
изолирован и трение отсутствует, мы тем самым определили
его изоэнтропичность, так как в таком потоке отсутствуют
необратимые преобразования механической энергии в тепло
и, следовательно, энтропия потока не меняется. Поэтому
мы можем непосредственно проинтегрировать уравнение
(2-1), предполагая очевидной связь (2-2).
Действительно, проинтегрировав уравнение (2-1) и имея
в виду (2-2), получим:
f^-f-f~ = T- + consU [ ?к~% =
= ^+k^lf = const' (2-3)
Это уравнение, известное под названием уравнения
Бернулли для сжимаемой жидкости, выражает
закон сохранения энергии для адиабатического
течения. После простой подстановки
оно преобразуется к виду:
i'4-y- — const. (2-4)
Здесь энтальпия газа i и теплоемкость газа при
постоянном давлении с отнесены к единице массы и
измеряются в механических единицах1.
1 В технической термодинамике внутреннюю энергию, энтальпию
и теплоемкости принято выражать в тепловых единицах. При этом
А
1{ккал1кГ) = — i (м2/сек2) и т.д., где А— тепловой эквивалент
механической работы.
39
Уравнению энергии (2-4) можно дать простое газокине-
с2
тическое толкование. Член -^- в этом уравнении выражает
энергию направленного движения частиц, а энтальпия /,
пропорциональная температуре, определяет энергию
движения молекул. Следовательно, уравнение (2-4) выражает
факт взаимного превращения энергии направленного
движения частиц и тепловой энергии.
Таким образом, мы установили, что при изоэнтропи-
ческом течении газа интеграл уравнения изменения
количества движения совпадает с уравнением энергии1.
Следует отметить, что уравнения (2-3) и (2-4) можно
непосредственно получить и из интеграла (1-26),
записанного для, сжимаемой жидкости (газа). Пренебрегая
влиянием массовых сил, т. е. полагая [/ = 0, из (1-26) легко
получаем уравнение (2-3), принимая связь между р и р по
формуле (2-2)*.
Уравнение неразрывности для одномерного
установившегося потока можно получить, рассматривая
движение газа в трубке тока переменного сечения (рис. 2-1).
Предполагая, что по сечению струйки параметры течения
не меняются, рассмотрим часть потока, заключенную между
сечениями /-/ и 2-2. По определению трубка тока
представляет собой замкнутую поверхность, образованную ли-
1 Уравнение энергии легко может быть получено из первого
начала термодинамики, записанного для потока жидкости:
dQ=di + d'/J~'j + dLT,
где dQ — удельное количество тепла, сообщаемое газу (или отводимое
от газа) в элементарном процессе;
dLT — удельная работа, совершаемая газом.
Для энергетически изолированного течения (dQ — dLT — 0) после
интегрирования получаем (2-4).
* Уравнение (2-4) справедливо и для адиабатических течений (при
наличии трения), сопровождающихся возрастанием энтропии. В этом
случае баланс энергии частицы должен быть дополнен двумя членами:
одним, учитывающим работу сил сопротивления, и другим,
выражающим приращение теплоты в газовом потоке. Эти два члена одинаковы
по величине, но имеют различные знаки и поэтому взаимно
уничтожаются. Это означает, что в такой изолированной системе работа сил
трения не меняет полной энергии частицы; меняется только
соотношение между энергией направленного движения и тепловой энергией.
Течение газа является необратимым часть механической энергии
необратимо превращается в тепло.
40
пиями тока. Через ее боковую поверхность частицы газа
не проникают, так как векторы скорости касательны к этой
поверхности. За 1 сек через сечение 1-1 внутрь
рассматриваемой части трубки втекает масса газа, равная p^/V,
вытекающая через сечение 2-2 масса газа равна p2c2F2.
По условию неразрывности течения эти количества должны
быть одинаковыми, т. е.
или
m = pcF — const, (2-5a)
где^ т ~ секундная масса газа.
Рис. 2-1. Трубка тока.
Уравнение неразрывности можно получить в
дифференциальной форме. После логарифмирования и
дифференцирования под знаком логарифма формула (2-5а) принимает вид:
Заметим, что для струйки постоянного сечения
уравнение неразрывности (2-5) дает:
рс = ~ = const. (2-7)
Произведение рс = -у- определяет удельный
расход массы газа в данном сечении (расход массы
через единицу площади сечения).
Выражение (2-7) для удельного расхода можно было
также получить непосредственно из дифференциального
уравнения неразрывности (1-12) для пространственного
потока, полагая #—с и у = ш = 0. Тогда, полагая движение
установившимся и перейдя к полным производным,
получим:
d (?с) _ Q
dx
41
Отсюда, интегрируя, получаем (2-7). Очевидно, что по
смыслу вывода уравнение неразрывности (1-12) при
переходе к одномерному потоку может дать только условие
рс = const.
Для одномерного течения несжимаемой жидкости (р =
= const) уравнение неразрывности (2-5) принимает такой
вид:
clFl = ctFt, (2-8)
или
cF = const.
Формула (2-8) выражает условие постоянства секундного
объемного расхода жидкости, протекающей через сечения
трубки Ft и F2. Эта формула применима к газовым
потокам только в тех случаях, когда на рассматриваемом
участке трубки 1-2 изменением плотности можно пренебречь.
Для газов это условие выполняется, если скорость
движения мала по сравнению со скоростью звука.
Скоростью звука, как известно, называют скорость
распространения малых возмущений в физической среде.
Скорость звука имеет особенно большое значение при анализе
процессов течения сжимаемой жидкости. Многие свойства
потока, в том числе и характер изменения параметров
течения вдоль трубки заданной формы, при различных
условиях взаимодействия с окружающей средой
существенно зависят от того, в каких пределах лежит отношение
скорости к скорости звука.
Влияние сжимаемости в газовом потоке становится
ощутимым в том случае, когда в результате изменения
давления объемная деформация частицы и изменение
скорости течения соизмеримы.
Воспользуемся уравнением неразрывности одномерного
потока, записав его в таком виде:
dAV . dp г.
AV "+~~7" '
где -дуг — относительное изменение объема элемента 1—2
(рис. 2-1), переместившегося в новое
положение Г — 2\
Умножив это равенство на dp, после преобразований
получим:
, dp dAV
42
Из уравнения импульсов (2-1) следует:
d/? = — pcdc.
Сопоставляя два последних выражения, получаем:
dAV с2 dc
Д1/ idp\
(Индекс 5 свидетельствует об h
Обозначим
тогда
\d4s~
dAV _ с2
с
[зоэнтропичности
■ а\
dc
процесса.)
(2-9)
AV а*
Таким образом, мы видим, что если с и а величины
одного порядка, то относительная объемная деформация
элемента будет такого же порядка, как и изменение
скорости. При —<^ 1 даже значительные изменения скорости
не приводят к большим изменениям объема частиц.
Из курса физики известно, что величина а,
определяемая по формуле (2-9), является скоростью распространения
волн малых возмущений. Характерным примером таких
волн могут служить звуковые волны.
Для совершенного газа скорость звука равна:
а = У k -?-=]/rkgRT. (2-9a)
Для воздуха (&=1,4) скорость распространения звука
а = 20,\УТ. (2-96)
Следовательно, скорость звука в совершенном
газе зависит только от физических свойств и
абсолютной температуры газа. Этот вывод находится
в полном соответствии с газокинетическими
представлениями о процессе распространения малых возмущений в
среде, состоящей из движущихся молекул. Скорость
распространения возмущения должна зависеть от скорости
43
движения молекул, которая определяется температурой.
Хорошо известно, что средняя скорость движения
молекул газа близка к скорости звука.
В этой связи необходимо подчеркнуть, что отношение
о / С2 \
квадратов скоростей ( — ] является мерой отношения
средней кинетической энергии направленного движения к
средней кинетической энергии беспорядочного движения частиц.
2-2. РАЗЛИЧНЫЕ ФОРМЫ УРАВНЕНИЯ ЭНЕРГИИ
Уравнение Бернулли устанавливает баланс энергии
адиабатического течения газа в трубке тока. Выше мы
познакомились с двумя формами этого уравнения: (2-3) и
(2-4).
Постоянная в правой части уравнения энергии может
быть выражена различным образом. Применяя это уравнение
к двум сечениям трубки тока, в одном из которых
скорость уменьшается до нуля и, следовательно, поток
тормозится, можно уравнения (2-3) и (2-4) записать в
следующем виде:
X + ' = '.i <2-10>
где i0 = c T0 — энтальпия заторможенного потока;
'Ро> Ро> ^о — параметры заторможенного потока или
параметры торможения.
В результате полного торможения потока вся
кинетическая энергия направленного движения переходит в
тепловую энергию. Заметим, что при полном торможении потока
совершенного газа температура торможения Г0, так же
как и энтальпия, может иметь только одно вполне
определенное значение, в то время как давление торможения
р0 и плотность р0 могут принимать любые значения, но
такие, при которых отношение — остается постоянным.
Параметры торможения имеют весьма большое значение
при рассмотрении как теоретических, так и
экспериментальных задач газовой динамики.
Таким .образом, мы видим, что правая часть уравнения
энергии, выражающая полную энергию частицы, может
быть представлена через параметры торможения.
44
Рассмотрим другие возможные формы уравнения
энергии.
Вспомним, что
р
Тогда уравнение (2-11) приобретает вид:
4+CT = ,4l=const, (2-12)
где а0 — скорость распространения звука в полностью
заторможенной среде.
Если применить уравнение энергии к двум сечениям
трубки тока, в одном из которых давление р
уменьшается до нуля, то скорость течения с будет стремиться
к некоторой максимальной величине смакс, которую будем
называть максимальной скоростью. В
соответствии с рассмотренными условиями эта скорость отвечает
истечению газа в пустоту (/ = 0; /?;=0; 7 = 0).
Следовательно, правая часть уравнения (2-12) может быть
выражена через максимальную скорость:
2
С2 i а2 смакс (с> |Q4
При максимальной скорости течения, равной £макс, вся
тепловая энергия молекул преобразуется в энергию
направленного движения. Практически максимальная
скорость течения недостижима и является известным
теоретическим пределом для скорости газа.
Следует иметь в виду, что с приближением скорости
течения к максимальной разрежение газа становится
весьма большим и поэтому к рассматриваемому потоку
нельзя применять уравнения состояния совершенных газов
и уравнение энергии в известной нам форме (2-10) или
(2-П).
Из формулы (2-12) может быть получено еще одно
выражение для постоянной в правой части уравнения
энергии.
Согласно (2-12) вдоль оси трубки тока с увеличением
скорости с скорость звука а падает. Совершенно
очевидны при этом пределы возможных изменений с и а:
45
Скорость течения может изменяться of нуЛя до д
а скорость звука — от а0 до нуля. В одном из сечений
трубки тока скорость движения газа с может стать
равной местной скорости звука, т. е.
В этом случае уравнение (2-12) запишется таким образом:
2 2 2
а* а* £ _(_ J а%
k—l k — l 2
Следовательно, постоянная в правой части уравнения
энергии может быть выражена через скорость а# и
уравнение энергии примет тогда вид:
г2 . a2 k -4- 1 #*
с 1 а _Л+1 (2И)
2 i k — 1 k—l 2 *
Скорость течения, равную местной скорости звука а,
называют критической скоростью.
Из уравнения энергии, записанного в различных
формах, следует, что между характерными скоростями и
параметрами торможения существует определенная связь.
Приравнивая правые части уравнений (2-10) — (2-14),
можем получить такое соотношение:
2 2 2
; k Л, __ „ Т Ч Смакс а* k+ 1 /0 , q.
0 " ^ — 1 p0 P °^~ k — 1 2 2/5—1
Отсюда получаем выражения для характерных
скоростей потока через параметры торможения.
Так, максимальная скорость будет равна:
^aKc=/2i0 = V2cpT0 = Y-^^- . (2-16)
Критическая скорость
Кроме того,
макс
--аУт^
(2-16а)
46
а*=аоу^Лг[' (2"17а)
Из формул (2-16) и (2-17) следует:
смакс "1 /
Л* — V
ёт • (2-18)
Таким образом, мы видим, что максимальная и
критическая скорости зависят от физических свойств газа
(показателя изоэнтропы k) и температуры торможения.
Для воздуха при k = 1,4 и R = 287,1 м2/сек2-град
я# = 18,ЗК7о м/сек.
Для перегретого водяного пара при k = 1,3 и R =^=
^462,0 м2/сек2-град
а#« 22,8 /77.
По формуле (2-18) можем получить:
для воздуха -f^- = 2',45;
для перегретого водяного пара =2,77.
2-3. ПАРАМЕТРЫ ТЕЧЕНИЯ В ПРОИЗВОЛЬНОМ СЕЧЕНИИ
ТРУБКИ ТОКА
Пользуясь уравнением энергии, выразим параметры
течения в некотором сечении трубки тока через параметры
торможения и скорость в этом сечении.
С этой целью, преобразовав формулу (2-14), получим:
г&+1 & 4акс
2 ' £—1 £—12
Деля все члены на с2, получим:
1
2
1 аг_ k + i а\ _\ 4акс
1 £_1 С2 2(fe— 1) с2 2 с2
(2-14а)
(2-146)
47
Введем следующие обозначения для безразмерных
скоростей:
с
а"'
с
"а?
X:
? = ■
(2-19)
тогда уравнение (2-146) будет иметь вид:
1,1 1 _k + \ 1 _ 1 1
1 М2 2(£—1) X2 2 £2*
(2-20)
Уравнение (2-20) устанавливает связь между
безразмерными скоростями. После простых преобразований
получаем:
2 X2 2
М2 =
k+ 1
£+1 Л
1 1 — £2
(2-21)
Воспользуемся теперь формулой (2-10). Выразим
температуру торможения в таком виде:
2с.
(2-10а)
Разделим левую и правую части на Т0 и определим
отношение температур:
Т_
То
так как
то
СР7 ° ^ — 1 2 S
— = i — -^=4-я2=г1—$2.
(2-22)
Кроме того, определив из (2-10а) отношение
— = 1 4- —
т * 2срт
48
и заменив в правой части
rp a2 d
kR ср№- О '
получим:
I? = l-f^M2. (2-23)
Для изоэнтропического течения
!_=(Р_\ k = (1\к"1 (2-24)
^о \Ро) [?.) '
Пользуясь формулами (2-22) и (2-23) можно
представить относительные давление и плотность газа в
произвольном сечении трубки тока в зависимости от
безразмерных скоростей М, Я и £ (табл. 2-1).
Таким образом, зная параметры полного торможения
потока и одну из безразмерных скоростей, по уравнениям
(2-22) и (2-23) можно определить температуру, а по
формулам, представленным в табл. 2-1, — плотность и
давление газа в данном сечении трубки тока.
Из основных уравнений легко получить связь между
параметрами в двух произвольно выбранных сечениях
трубки тока.
Из формул (2-22) и (2-23) выразим температуру
торможения в таком виде:
То=т(\ + к-^м*у
k + \
Для двух сечений изоэнтропического потока (/-/ и 2-2)
можем записать уравнение энергии для совершенного газа
в такой форме:
* 01 ==' ' 02'
тогда
k — 1 ,,2 k— 1 -, 2
И—5-*' '-ГнЧ '-в
т- н-ц^ <-Ш1' '"*'
(2-25)
В предположении изоэнтропического течения, используя
соотношения (2-24), получим формулы для отношений
давлений и плотностей (табл. 2-1).
4 М. Е. Дейч 49
Таблица 21
Отношение плотностей
Отношение давлений
А-(,+Ц»~
*-(-fcW
■(■+t^-)'
.А., Л . А—1.._\*-«
Р* \
=П_^1ХЛ-'
£+1
Ро
= (1 — S2)^-1
(■Р-Р)*-1
^м?^"1
Pi
2 "Ai
£—1 о
J2_
Pi
■1 ^Zli>2\^-1
Л-l 2
_P2_,_
p. I i-e?
Pi
k — \ .
2\*-l
,1 + -2~М2У
Pl
1^нГТЛ2
1-^=4л?
/г +1 1
50
Легко также получить отношение абсолютных
скоростей в этих сечениях:
\ М2а2 _ AU |/ Т*
или после подстановки Т2/Тг из (2-25):
••у .+
Л*, 1/ -.Л-1^2
(2-26)
Так как при Г0 = const скорости а*, а0 и смакс
постоянны, то
^2 ^2_ J?2
Заметим, что уравнения (2-22) — (2-26) и формулы,
представленные в табл. 2-1, являются модификациями
уравнения энергии, полученные путем преобразования
уравнения (2-10) и введения безразмерных скоростей.
В практических расчетах газовых течений может быть
использована любая форма уравнения энергии и параметры
/?, р и Т могут быть выражены через любую из
безразмерных скоростей М, Я, (■.
Однако в зависимости от рассматриваемой задачи
оказывается целесообразным применять ту безразмерную
скорость, которая обеспечивает максимальную простоту
окончательных уравнений.
Если в рассматриваемой области скорости меньше
критической, т. е. если
то
0<М<1;
0<Я<1;
0<£<j/
k+i
Если скорости течения больше критической, т. е.
4*
51
то
1<М<сс;
/ k + \_
1
/
В первом случае течение называется дозвуковым
или докритическим, а во втором —
сверхзвуковым или сверхкритическим. Следовательно,
значение безразмерных скоростей
М=А=1
разделяет области течений с дозвуковыми (докритиче-
скими) скоростями и со сверхзвуковыми
(сверхкритическими) скоростями. Можно видеть, что безразмерные
скорости Я и Е имеют конечные предельные значения, причем
скорость Я=1 при с —а*, в некоторых случаях более
удобна для пользования.
Следует подчеркнуть, что безразмерные скорости имеют
определенный физический смысл.
В § 2-2 было установлено, что в зависимости от
соотношения спав большей или меньшей степени
проявляется сжимаемость потока и, следовательно, М=—в
каждой точке течения определяет степень влияния сжимаемости.
Кроме того, физическое значение числа М выявляется при
рассмотрении величины
М2'
/так как j —^—Л откуда следует, что квадрат числа М
пропорционален отношению кинетической энергии потока
к его потенциальной энергии в данной точке.
Зная, что квадрат критической скорости может быть
выражен через энтальпию торможения:
2 _pk—\ .
a* — zk + \l°'
52
можно представить Я2 в следующем виде:
£1
Л — jfezrri;-
Таким образом, квадраты безразмерной скорости Я,
а также £ пропорциональны отношению кинетической
энергии потока к его полной энергии /0.
При течениях газа без энергетического обмена с
окружающей средой полная энергия потока /0 является в
каждой точке величиной постоянной. Соответственно
постоянными являются и скорости а,, а0 и смакс, зависящие
только от /0 (при k = const). В этом случае 2 и Е дают
нам скорость течения, отнесенную к различным, но
постоянным для всего потока масштабам.
В энергетически неизолированном течении, когда имеет
место теплообмен с окружающей средой (dQ=£0) или
обмен механической работой (с1Ьт=^=0), полная энергия
меняется от точки к точке. В соответствии с изменениями
/0 меняются скорости а*, а0 и смакс.
Следует подчеркнуть, что формулы (2-23), (2-24) и др.,
связывающие параметры торможения с параметрами потока
(табл. 2-1), справедливы и для течений с энергетическим
обменом, но, однако, в этом случае связь между
параметрами торможения, статическими параметрами и
безразмерными скоростями является локальной, т. е. относится
только к данной точке или данному сечению трубки тока,
причем под р0 и р0 понимаются параметры изоэнтропи-
ческого торможения в данной точке. Эти уравнения не
могут быть применены к двум различным сечениям трубки,
так как на участке между сечениями меняется полная
энергия потока. Следовательно, формулы для статических
параметров, указанные в табл. 2-1, и формулы (2-25) и
(2-26) для таких течений неприменимы.
Отметим, что безразмерная скорость М является одним
из основных критериев в теории подобия при рассмотрении
процессов движения с большими скоростями1, так как
коэффициент сопротивления в основном зависит от
отношения —.
а
См. гл. 5.
53
2-4. ИЗМЕНЕНИЕ СКОРОСТИ ВДОЛЬ ТРУБКИ ТОКА.
ПРИВЕДЕННЫЙ РАСХОД ГАЗА
Подвергнем более подробному исследованию характер
изменения скорости вдоль трубки тока. Для этой цели
воспользуемся уравнениями одномерного течения:
cdc + ^ = 0;
г
^ I -р4-— = 0
F ' р ' с
Простые преобразования позволяют получить:
отсюда
(с2-а2)^-=а2^. (2-27)
Разделив обе части уравнения на a2dx и выразив
логарифмическую производную скорости, получим:
1 dF
1 dc =F'dx • (2"28)
с ' dx М2— 1
Выразив с помощью (2-21) М2 через Я2, получим:
6—1
\ dk _l k+lX2 \dF
I dx X2—1 F dx-
(2-29)
Уравнения (2-28) и (2-29) являются
дифференциальными уравнениями распределения скоростей вдоль оси
трубки тока. Они могут быть проинтегрированы, если
известен вид функции F (х). Вместе с тем эти уравнения
весьма удобны для качественного анализа изменения
скорости потока в трубках тока различной формы.
Из уравнения (2-29) следует, что ;г~ = 0 ПРИ
а) Я = 0; j
б) X = Vk+l = X ;
/ V k — 1 макс' \
(2-30)
-о I
dx
\ dF A I
54
Случай „а" отвечает неподвижному газу и поэтому
интереса не представляет. Случай „6е соответствует
максимальной скорости течения и вполне очевиден: при Л =
= Ямакс дальнейшее возрастание скорости невозможно.
Наконец, случай „в" приводит к :т—= 0 только при А^1.
Легко видеть, что при этом в рассматриваемой точке
х = х„ функция F(x) имеет максимум, минимум или точку
перегиба. Следовательно, в таких сечениях трубки тока
скорости также имеют экстремальные значения.
По уравнению (2-29) можно заключить, что
производная скорости —-=оо при Х = \ и -г-=^=0. Однако такое
решение, означающее наличие разрыва скорости, физически
невозможно (мы рассматриваем непрерывно изменяющееся
движение газа).
Рассмотрим качественную картину течения газа в трубке
тока, имеющей в х = х„ максимум или минимум сечения
(рис. 2-2). Пусть функция F (х) имеет в этой точке ма-
Рис. 2-2. Изменение скорости вдоль трубки тока.
55
ксимум (рис. 2-2,а). Допустим, что слева от F(x) = FMaKc
скорость Я<;1. Тогда из (2-29) следует, что так как
-^г>0, то -т- <0, т. е. скорость в трубке тока к ^макс
убывает-. Справа -г- < О и -т— >> О — скорость течения
возрастает.
Аналогично при Я > 1 будем иметь слева -г— > 0 и
d\ . п
справа -т— << 0.
Если функция ^(л;) имеет минимум в рассматриваемой
dF
dx
dF
точке, то слева от F(x) = F при Я<1 и -т— <0
скорость будет возрастать, так как — > 0 (рис. 2-2,6). При
Я>1 будет слева j-<0, справа -г->0.
Таким образом, мы показали, что в максимальном
сечении трубки тока дозвуковой поток приобретает
минимальную скорость, а сверхзвуковой — максимальную. В
расширяющейся части трубки тока скорость дозвукового течения
падает, а в суживающейся — растет. Сверхзвуковой поток
в расширяющейся части ускоряется, а в суживающейся —
тормозится. При любых значениях Я на входе кривая
скорости в этом случае (F (х) == Fыакс) имеет экстремум.
Отсюда следует весьма важный вывод: характер
изменения скорости вдоль трубки тока принципиально
различен для дозвуковых и сверхзвуковых течений.
В первом случае поток газа с качественной стороны ведет
себя так же, как и поток несжимаемой жидкости, а во
втором случае кривая скорости Х{х) имеет характер,
аналогичный кривой сечений F{x). Очевидно, что в трубке
тока, имеющий максимум сечения, невозможен переход из
области дозвуковых в область сверхзвуковых скоростей и
наоборот.
В трубке тока с минимумом сечения скорость как
дозвукового, так и сверхзвукового течения приближается к
значению Я = 1 в минимальном сечении. Если скорость
течения в минимальном сечении будет Я=1 и dX^=0, то
переход через критическую скорость, очевидно,
осуществляется.
56
Рассмотрим теперь изменения давления, температуры и
плотности газа в трубке тока. Непосредственно из
формулы (2-13) и др. следует, что, там, где скорость
увеличивается, температура, плотность и давление при изоэн-
тропическом течении газа падают, и наоборот.
Таким образом, в суживающейся струйке при
дозвуковом течении температура, давление и плотность
уменьшаются, а при сверхзвуковом — растут. В расширяющейся
струйке картина будет обратной.
Параметры, отвечающие сечению трубки тока, в
котором Я = 1, будем называть критическими
параметрами. Они легко определяются по формуле (2-22) и
формулам для — и —, представленным в табл. 2-1, после
Ро Ро
подстановки Х = 1:
Т =
k + \
т -
1 0>
(2-31)
/V
Ро-
(2-32)
(2-33)
Мы видим, что критические параметры зависят от
физических свойств газа (показатель k) и параметров полного
торможения.
В табл. 2-2 приведены значения относительных
критических параметров (отнесенных к соответствующим
параметрам торможения) для различных показателей k.
Таблица 2-2
Критические отношения параметров для различных газов
_?*
Ро
Р*
Ро
1,67
0,7491
0,6498
0,4867
1,4
0,8333
0,6339
0,5282
1,33
0,8584
0,6296
0,5404
1,30
0,8696
0,6276
0,5457
1,25
0,889
0,624
0,555
1,20
0,9091
0,0209
0,5645
1,15
0,9292
0,6173
0,5746
1,1
0,9524
0,6139
0,5847
57
Полученные выше основное закономерности,
определяющие изменения параметров течения в трубке тока,
физически могут быть понятны из рассмотрения уравнения
постоянства расхода в трубке тока [формула (2-7)]. С
помощью уравнения
1
(табл. 2-1) определим удельный расход газа:
1
т=у- = P^ = PoM(l-^ri1)*"1. (2-34)
Секундный массовый расход т для каждого сечения
трубки тока будет одним и тем же. Интенсивность
изменения плотности р и скорости с будет различной в
дозвуковой и сверхзвуковой областях. В дозвуковой области
с ростом с плотность р падает медленее, чем растет
скорость, поэтому трубка тока должна суживаться, сечение
F — уменьшаться. При сверхзвуковых скоростях, наоборот,
падение плотности будет более интенсивным, чем
возрастание скорости, и трубка тока будет расширяться.
Как видно из формулы (2-34), функция /тг (Я) = 0 при
Я = 0 иЯ=1/г^т и, следовательно, при некотором Я
имеет экстремальное значение. Для определения этого зна-
иения Я продифференцируем (2-34):
dm d(?c)
2—k
-M.(l-fcH"0-*>
Отсюда следует, что максимальное значение удельного
расхода соответствует Я = 1, т. е. критическому значению
скорости, так как ~zr- обращается в нуль при Я=1.
Следовательно,
1
^макс = РоД* \^fi) = P*<**- (2-35)
58
Приведенным расходом назовем отношение
ч=—
РЛ—V 2 У Ч к + \ )
\
(2-36)
На рис. 2-3 представлены зависимости параметров те-
Р 9 Т
чения —; —; — и приведенного расхода q от безраз-
Ро Ро * о
мерной скорости (для различных k).
Здесь приведена соответствующая схема • изменений
сечений трубки тока, вдоль оси которой скорость
непрерывно возрастает. Нетрудно видеть, что при максимальной
скорости Я = Я
■■/&
у приведенный расход ^ =
= -jr=0, т. е. F = oo. Физически это понятно, так
как при Я = Ямакс /? = О (истечение в абсолютную пустоту)
и р = 0.
0,2 Oft 0,6 Ofi 1,0 1,2 1ft 1,6 1/3 2,0 2,2
Рис. 2-3. Газодинамические функции одномерного изоэнтропического
потока qx pjpv Т/Т,, Р/Р? , /, (* = |,1; 1,3; 1,4),
59
Таким образом, мы установили, что в трубке тока,
имеющей минимальное сечение, может происходить переход
через критическую скорость. Необходимыми и достаточными
условиями для такого перехода являются условия 2 = 1 и
dl/dx^O в минимальном сечении. Приведенный расход
газа при этом приобретает максимальное значение.
Если скорость в минимальном сечении достигает
критического значения, а второе условие I — =^(л не
выполняется, тб перехода через критическую скорость не
произойдет. Этот случай соответствует появлению критических
скоростей в трубке тока и является важным как в теории
сопла Лаваля, так и в задачах внешнего обтекания тел.
2-5. НЕКОТОРЫЕ ГАЗОДИНАМИЧЕСКИЕ ФУНКЦИИ
ОДНОМЕРНОГО АДИАБАТИЧЕСКОГО ПОТОКА
Выше (§ 2-3 и 2-4) мы познакомились с некоторыми
важными безразмерными характеристиками одномерного
потока газа, которые выражаются в виде простых функций
безразмерных скоростей М, Я или S. Эти газодинамические
функции играют важную роль при выполнении различных
газодинамических расчетов, а также при обработке
результатов эксперимента.
Кроме уже известных, нетрудно получить и другие
газодинамические функции, встречающиеся в преобразованиях
уравнений сохранения расхода, количества движения и
энергии.
С помощью приведенного расхода q легко определяется
полный весовой расход газа через заданное сечение:
G = gF9c = gFqaj„ (2-37)
или после подстановки
1 _j
/ 2 \k~l ( 2 \k~l р0 ш [ 2ks> n~
р* = (л+т) р° = (г+т) W7 *a*=VT+iRT*
и преобразований находим:
G = KF -&L, (2-38)
У Tq
где
К =
60
jA
kg ( 2 n k~x
k+ 1
Расход можно выразить и через статическое давление
потока в данном сечении. С этой целью разделим и
умножим правую часть формулы (2-38) на р\
G = KF-^L = KF-£=-3, (2-39)
где
— новая функция безразмерной скорости Я, зависящая также
только от k и Я.
Уравнения расхода в форме (2-38) и (2-39) могут быть
использованы для расчета адиабатического потока в
изолированной системе (без энергетического обмена с внешней
средой) при наличии трения. Действительно, условие
постоянства расхода (2-38) для двух произвольно выбранных
сечений канала можно записать в такой форме:
р Ро\Я\ р
1 1 ч/*^— А 2
РъЯ%
VrQi~ 2Vt02'
Так как для изолированной системы Т01 = Т02 = Т0, то
Po2_=F± Я±.
Poi F2 ' Яг '
(2-41)
для каналов постоянного сечения
Рог _ Яг
Р%\ Яъ
(2-41а)
Формулы (2-41) и (2-41а) позволяют найти изменение
давления торможения, обусловленное необратимыми
изменениями состояния движущегося газа и, в частности,
потерями, вызванными внутренними силами трения.
Аналогично с помощью (2-39) можно получить (Т01 =
1 02 л О/*
откуда
^=£-°-Ч (2-42)
или для цилиндрического канала
7Г=!г- (2-42а)
61
Соотношения (2-42) можно использовать для
определения статического давления в одном из сечений потока, если
известны скорости в двух сечениях (Ях и Я2) и статическое
давление в одном из них.
Введем еще одну функцию, которая характеризует
импульс потока, равный
J=-YC + pF. (2-43)
Учитывая, что
F=G
перепишем (2-43а) в виде:
/=f(c+f-)- (2"43a>
Из (2-17) и (2-22) имеем:
f=«W= MRT. (1 - fcji')-'-^ (1 - £■ *■)
и с = Ха^\ тогда уравнение (2-43) можно записать в виде:
J=±c + pF=±±!..±aJ, (2-44)
где
Ф = * + Х (2-45)
—некоторая новая функция безразмерной скорости Я.
Уравнение для импульса газового* потока (2-44) было
впервые получено Б. М. Киселевым. Оно широко
используется в различных задачах и, в частности, для расчета
энергетически неизолированных потоков (расчет течений
с подводом или отводом тепла при наличии сил трения,
расчет внезапного расширения канала, процесса смешения
и др.).
Исходное уравнение импульса (2-43а)
J О 0,(1+-^
нетрудно преобразовать к другому виду, используя новую
важную функцию безразмерного статического давления
— Р -Р * = -£' (2-46)
№* ?с ?а:
62
Заменив здесь — = gRT и а\ по формуле (2-17) полу-
Р
k + 1 1 л k — \
2k A
(1-J=ir). (2-46a)
Следовательно, импульс потока выражается через
функцию тс по формуле
/=-§-<* (Я+ *). (2-47)
а связь между ф и те. устанавливается соотношением
Воспользуемся теперь формулами (2-38) и (2-39) и
заменим величину расхода G в уравнениях (2-44) и (2-47).
После несложных преобразований находим:
/= kB.FpQq (Я + «) =1//?0<7ф (2_49>
и
У = ke.Fpa (Я -f те) = р>/?аф. (2-50)
Здесь s* = ( ь ■ i) —критическое отношение
давлений;
1
*- / 2 \*-1
Р я==(^4-1) —критическое отношение
плотностей.
С помощью формул (2-40) и (2-50) легко
устанавливается связь между газодинамическими функциями q, a,
фите.
В некоторых расчетах удобно ввести также функции
Т = Р.^ = Ав.<7(Я + «) = (Л»+ 1)^1 — |=4л»)* ' (2-51)
1 Функция п впервые была предложена А. Ф. Гандельсманом и
использована в работах А. А. Гухмана 'и А. Ф. Гандельсмана по
исследованию сопротивления труб при адиабатическом течении газа.
63
A = P *!> = ke.3 (Я + v) = X'+' . (2-52)
Тогда
J=lFpu = LFp. (2-53)
Функция безразмерного статического давления тс
встречается также при использовании уравнения энергии.
Выразим из (2-14) скорость звука:
, ft + 1 2 /j 1 2
2 ~* 2 " *
Разделив это уравнение на а\ получим:
Ш=Ч1{1-Ш»)=ы* (2-54)
Если воспользоваться уравнением энергии в форме (2-11),
то нетрудно найти отношение скоростного напора ~-
к статическому давлению р\
: _ Р^2 _ * /_Al J i
/ 2/? ft - 1 ^ p0 ■
После подстановки значений — и — получим:
к л «> /i к — 1 о «Л-1 ^
■fe+i
i'(1-lrii,)",=^- (2"55)
Скоростной напор, отнесенный к давлению торможения,
можно найти по формуле
/0 = ^^^=^^=^rfl^^r;"(2-56)
Таким образом,- ряд характеристик одномерного
газового потока выражается в виде функций безразмерной
скорости Я и показателя изоэнтропического процесса к.
Наиболее важные из функций сведены в таблицы
газодинамических функций, построенные для различных постоянных
значений k (приложение 1). Пользование такими таблицами
существенно упрощает газодинамические расчеты, что и
определило широкое распространение таблиц.
64
Вместе с тем анализ изменения некоторых
газодинамических функций позволяет сделать важные выводы о
свойствах газового потока. Так, например, на рис. 2-4,
дополняющим рис. 2-3, приведены функции те, з, Д, у и j(k =
= 1,4). Функция /0 показана на рис. 2-4.
Функция тс монотонно убывает с ростом скорости Я
и при Я=1 принимает критическое значение, равное
[формула (2-46а)]:
Вспоминая выражение для критического отношения дав
лений, легко находим:
Обращаясь к рис. 2-4, можно отметить, что функция у
слабо меняется в широком диапазоне скоростей 0<Я<1,5.
Имея в виду смысл этой функции [формула (2-51)], нетрудно
прийти к выводу, что при постоянном давлении торможе
ния импульс потока слабо зависит от безразмерной
скорости при Я < 1,5. При постоянном статическом давлении
Рис. 2-4. Газодинамические функции я, у, а, Д, /, у одномерного
потока газа для k = 1,4.
5 М. Е. Дейч 65
импульс в данном сечении интенсивно возрастает с
ростом Я, так как функция А резко увеличивается от
единицы при Я —0 до бесконечности при Я -+ Ямакс.
Расход газа через заданное сечение F меняется весьма
интенсивно при изменении Я, если статическое давление
1-775
Po/
1 / т
(о OjLJ^T
iao
725 /
700/{
А
)
/i
/t
/ t
rlD~jrfi
t/
/ i
/ /
<*>
,A*^
y
) '
/
/
x
кпал/кг
800x
775}
750
725\
кг/м -cen
3500
3000
2500
7001 I I III Г c'u 12000
200 300 Ш 500 600 700 м/сек ~
Рис. 2-5 Изоэнтропический процесс расширения
в тепловой диаграмме (а) и определение
критических параметров для реального газа (б).
66
сохраняется постоянным, что характеризуется поведением
функции а (рис. 2-4).
В выведенные выше формулы входят постоянные,
зависящие только от k. Значения некоторых постоянных
приведены в табл. 2-3.
Таблица 2-3
k
I k+1
У*(4гГ
*(^гГ
1,67
0,72-38
0,8128
1,6
0,7164
0,7947
1.5
0,7011
0,7680
1,4
0,685
0,7395
1,35
0,676
0,725
1,3
0,667
0,7095
1,25
0.658
0,6938
1,2
0,6486
0,6895
1,1
0,6285
0,6432
2-6. ОСОБЕННОСТИ РАСЧЕТА ОДНОМЕРНОГО ПОТОКА
РЕАЛЬНОГО ГАЗА
Уравнение энергии (2-10) позволяет широко
использовать диаграммы состояния для расчета газовых течений,
что особенно важно при исследовании потоков реальных
газов, изменение состояния которых не подчиняется
уравнению (1-1), а теплоемкость является функцией давления
и температуры.
В практике расчетов тепловых двигателей (паровых
и газовых турбин, компрессоров и др.) наибольшее
распространение находят тепловые диаграммы, в которых по осям
координат отложены либо температура и энтропия, либо
энтальпия и энтропия (диаграммы Ts и is). Такие
диаграммы строятся по экспериментальным данным и
позволяют с достаточной точностью рассчитывать различные
процессы изменения состояния газов, в том числе в области
влажного пара и вблизи линии насыщения.
Диаграммы состояния Ts и is могут быть широко
использованы и при исследовании газовых течений.
Действительно, выразим из уравнения энергии (2-10)
скорость течения:
c=V2{it-i).
После подстановки / {ккал\кг) получим:
5*
67
Подставляя значения постоянных g и Л, находим:
с = 91,53 ^(«о — i). (2-106)
Формула (2-106) показывает, что для определения
скорости течения необходимо знать разность энтальпий /0 — /,
которая легко определяется по диаграмме is, если
известны параметры полного торможения газа (/?0, Т0) и
статические параметры течения (р, Г).
На рис. 2-5,а представлена часть диаграммы is для
водяного пара. Если нам известны два любых параметра
полного торможения (р0 и 70), то на диаграмме is легко
находится точка О, определяющая состояние
заторможенного потока. Эта точка может быть найдена и по другим
параметрам состояния (например, /0 и s0). Проведя
вертикальную линию до точки пересечения с изобарой статиче-.
ского давления р, изотермой Т или изохорой v, определим
состояние движущегося газа (точка 1) и прежде всего его
энтальпию /; тогда скорость течения легко может быть
определена по уравнению (2-106).
Входящую в это уравнение разность энтальпий Н0 =
= /0 — / называют изоэнтропическим перепадом
энтальпий.
Тепловые диаграммы могут быть использованы и для
расчетов необратимых течений (см. ниже). В этом случае,
однако, для определения скорости течения трех
параметров состояния недостаточно.
Рассматривая изоэнтропическое движение вдоль трубки
тока переменного сечения в диаграмме / — s, нетрудно
найти удельный расход газа в различных сечениях — и
построить эту величину, а также и другие параметры в
зависимости от скорости с (рис. 2-5,6). Максимум удельного
расхода соответствует критическому сечению трубки,
определяемому по уравнению расхода:
и
Параметры в критическом сечении находятся из
условия с—а^ С этой целью можно построить кривые изме-
63
нений скорости звука а (/) и скорости потока с (/) в
зависимости от энтальпии; точка пересечения указанных
кривых дает значения а и / в критическом сечении. Перенеся
эту точку в диаграмму i—s, можно найти и другие
параметры в этом сечении (рис. 2-5,6).
ГЛАВА ТРЕТЬЯ
ПЛОСКОЕ ДВИЖЕНИЕ ГАЗА ПРИ ПОСТОЯННОЙ
ЭНТРОПИИ
3-1. ПОТЕНЦИАЛЬНОЕ ДВИЖЕНИЕ ЖИДКОСТИ
Условие безвихревого движения можно получить из
уравнении (1-6). Для пространственного безвихревого
потока ((Ох = (Dy = 0)2
(3-1)
Имея в виду механический смысл частных
производных в уравнениях (1-6), можем заключить, что формулы
(3-1) действительно выражают условие отсутствия
вращательного движения жидкой частицы. С другой стороны,
равенства (3-1) математически выражают тот факт, что
существует некоторая функция координат Ф(х, у, г),
частные производные от которой по координатам равны
проекциям скорости на соответствующие оси координат,
т. е.
0) из (1-6) следует:
dw dv t \
~dH~Jz~ ;
du dw
dz дх '
dv да
дх ду
.
и =
w-
дф
~дх~
дф
дф
dz~
)
(3-2)
Действительно, подстановка (3-2) в (3-1) приводит
к тождествам.
69
Функция Ф(х, у, г) называется потенциалом
скоро сти.
Понятие потенциала скорости в аэрогидромеханике
тождественно понятию потенциала сил в механике твердого
тела. Из механики известно, что производная потенциала
сил по какому-либо направлению дает проекцию
потенциальной силы, действующей в этом направлении. По
аналогии интенсивность изменения потенциала скорости в
направлении координатных осей определяет проекции
скорости на соответствующие оси [формулы (3-2)].
Изложенное выше показывает, что потенциальное
движение газа в изолированной системе является изоэнтро-
пическим, т. е. если поток безвихревой и адиабатический,
то изменение энтропии по любому направлению в потоке
равно нулю и течение газа описывается некоторой
функцией координат Ф(х, уу г).
Ограничиваясь в этой главе рассмотрением только
плоских потенциальных течений газа, мы можем получить
уравнение потенциала скоростей с помощью уравнений
Эйлера.
Для плоского установившегося потока в
предположении X = Y — 0 уравнения (1-12) и (1-16) дают:
да , да 1 dp \
дх
dv
дх
, да 1 др
1 ду р
, dv
1 ду
дх
1 др
Р ду
д(рц) I d(pv)
"*" ду
дх
:0.
(3-3)
г, др др
Градиенты давления j- и ~^- можно выразить
следующим образом:
д?_
дх
д^=(д-£-\ ^ = а>
дх \ dp Js дх
HlL=(dP\ dP _д2 dp
ду \ dp '5 ду ду
(3-4)
Из третьего уравнения (3-3) после дифференцирования
получаем:
д?_
дх
+'%+'(&+%)=°- <з-5>
70
После подстановки (3-4) в (3-3) будем иметь:
dp р / <^_ \ ди \
5Г— 1Г\идх"^и~ду)9
dp р / dv , dy \
Подставляя производные плотности в (3-5), получаем:
Имея в виду (3-2), перепишем (3-6) в виде:
^ a2 J дх2 ' ^ а2 у д#2 а2 длгдг/ v ;
Уравнение (3-7) является нелинейным
дифференциальным уравнением потенциала скоростей
в частных производных второго порядка.
Введение потенциала скорости позволило систему трех
уравнений (3-3) свести к одному (3-7), уменьшить число
неизвестных с шести до пяти и оставить в уравнении
только кинематические параметры.
Если в исследуемом поле потока известен потенциал
скорости Ф (х, у), то при заданных граничных условиях
могут быть определены все параметры течения. Потенциал
скорости позволяет определить скорости потока (и, v) по
формулам (3-2). С помощью уравнения энергии совместно
с уравнением изоэнтропического процесса легко
определяются давление /?, плотность р и температура газа Т.
Таким образом, при исследовании потенциальных
движений газа основная задача сводится к определению
потенциала скоростей Ф(х, у) для данного вида движения,
т. е. к нахождению решения уравнения (3-7). Если
потенциальная функция Ф(лг, у) определена, то кинематическая
часть задачи решена. Далее без особых затруднений
решается и динамическая часть задачи. Однако уравнение
(3-7) в общем виде не интегрируется.
Заметим, что потенциальная функция должна
удовлетворять определенным начальным и граничным условиям
данной конкретной задачи. В качестве кинематических
начальных условий должно быть задано распределение
параметров течения в определенной—начальной—области по-
71
тока, а также должны быть известны условия на границе
обтекаемого тела. При решении конкретных задач
обтекания тел чаще всего задаются параметры течения
невозмущенного потока на бесконечном удалении от тела
(начальные условия) и условия непротекаемости — нормальная
составляющая скорость у поверхности тела равна нулю
(граничные условия).
Так, например, если плоский поток в бесконечности
параллелен оси х, то потенциал скорости должен отвечать
следующим условиям:
/дФ\
При этом известными должны быть также и остальные
параметры:
Poo* Poo' ' оо"
На границе обтекаемого тела физические условия
обтекания диктуют распределение скоростей. Предполагая
безотрывное обтекание, мы можем записать, что нормальная
составляющая скорости на поверхности обтекаемого тела
должна быть равна нулю и, следовательно,
Рассматривая идеальную жидкость (при отсутствии сил
вязкости), мы должны допустить, что частицы жидкости
скользят вдоль обтекаемой поверхности тела и,
следовательно, касательные составляющие скорости
/' дФ \
(при этом рассматривается подвижная система координат,
расположенная таким образом, что направление оси х в
каждой точке совпадает с направлением касательной к
поверхности тела; ось у нормальна к поверхности тела и,
следовательно, к линиям тока).
Более подробное рассмотрение уравнения (3-7), по
которому определяется потенциальная функция Ф(лг, у),
однако, показывает, что оно обладает различными свой-
72
ствами в зависимости от соотношения между
составляющими скорости и и v и скоростью звука а. Действительно,
a v
допустим, что величины — и — весьма малы и ими
можно пренебречь, т. е. допустим, что скорость газового
потока мала по сравнению со скоростью звука. Тогда из
(3-7) следует:
д2Ф д2Ф
-з^+т?=°- (И)
Уравнение (3-8) характеризует потенциальное течение
идеальной несжимаемой жидкости.
При больших- дозвуковых скоростях, когда влиянием
сжимаемости пренебречь нельзя, нелинейное
дифференциальное уравнение (3-7) значительно упрощается в случае, если
поток можно считать слабо возмущенным (§ 3-3).
Изучение установившихся плоских и некоторых осесим-
метричных течений газа можно также упростить введением
другой функции координат — функции тока ЧГ.
Обращаясь к третьему уравнению системы (3-3), видим, что оно
удовлетворяется, если положить
дЧГ дЧ*'
или
1 6W
р ду
i_ а*г_
р ' дх
Для того чтобы функция тока и потенциал скорости
имели одинаковую размерность, коэффициент при
производных целесообразно привести к безразмерному виду. Тогда
в случае потенциального потока уравнения для а и v
запишутся в следующем виде:
(3-9)
^ЧГ = РоЧг.
_ Ро дФ ___ д^ . \
р ■ ду дх '
?о md4f =дФ
р " дх ду * \
73
В простейшем случае движения несжимаемой жидкости
в уравнениях (3-9) величину относительной плотности
_i
можно положить равной, единице.
При этом уравнения (3-9) принимают вид:
v = — _
дх '
Нетрудно заметить, что в случае безвихревого потока
[условия (3-1)] функция *Fn удовлетворяет уравнению
дх2 = ду2 '
Если во всей области течения газа скорости
изменяются незначительно и можно принять — — const, то
переход к уравнениям (3-11) достигается подстановкой ^1ГН =
=— ЧГ. При такой подстановке скорость газа просто
равна скорости несжимаемости жидкости:
Таким образом, указанные простейшие случаи перехода
от дозвуковых течений газа к течениям несжимаемой
жидкости являются по существу просто пренебрежением
влиянием сжимаемости. Возможности такого
пренебрежения, обусловленные зависимостью плотности от числа М,
являются весьма ограниченными. В самом деле, если
потребовать, чтобы величина — отличалась от единицы не более
Р
чем на 2°/0, то в соответствии с (3-10) число М должно
быть не больше 0,20.
Физическое значение функции тока W выясняется при
определении расхода газа через элементарный незамкнутый
контур в плоском потоке. Можно показать, что функция
тока численно равна объемному расходу газа через такой
74
(3-11)
элементарный контур. Отсюда следует, что функция тока
сохраняет постоянное значение вдоль линий тока плоского
течения.
Действительно, проведем в плоскости потока некоторый
контур LLX (рис. 3-1) и подсчитаем секундный объемный
Рис. 3-1. К выводу условия безвихревого
движения.
расход V через этот контур. В соответствии с
обозначениями на рис. 3-1 получим1:
и и I,
V=[cndl = Г [a cos (л;, /г)-|-а cos (#, n)\dl= Uudy-—vdx),
так как
и
Но
тогда
udlcos (x, n) = udy
vdl cos Q/, п) = vdx.
udy — vdx = dW;
и
v=.fdM(^+^*r^-*i
1 Размер контура в направлении, нормальном к плоскости
чертежа, принят равным единице.
75
Область потока, ограниченная линиями тока 4'^ = const
и Wr = const, является трубкой тока. Следовательно,
разность значений функции тока WL—WL равна объемному
расходу жидкости через сечение трубки тока,
ограниченной линиями тока, прохо-
Результируюшй дящими через точки L и L,.
"птп" Из уравнений (3-11)
следует, что для несжимаемой
жидкости
поток
Z-й лотон
Рис. 3-2. Сложение плоских
поступательных потоков.
дх
ду
дх
(3-12)
Придавая функции Ф
различные постоянные значения,
мы получим семейство изопотенциальных линий. Пользуясь
условиями (3-12), можно показать, что линии тока (линии
*Гн = const) и изопотенциальные линии (линии Фн = const)
взаимно ортогональны, т. е. пересекаются под прямым
углом (рис. 3-1).
Рис. 3-3. Вихреисточник (вихресток).
Уравнение потенциала скоростей плоского потока
несжимаемой жидкости (3-8) позволяет развить широко
применяемый метод наложения потенциальных потоков. Из
теории дифференциальных уравнений эллиптического типа
известно, что если функции Ф р Фн2, ... Фнп являются
решениями такого уравнения, то и сумма Фн = Фн1-(-
76
-j- Фи2 -f- . . . + Ф|1/? является также решением этого
уравнения. Отсюда следует, что, складывая потенциалы
скорости Ф и функции тока lF простейших потоков, можно
получить характеристики более сложного движения. При
этом потенциалы скоростей и функции тока складываются
алгебраически, а векторы скоростей — геометрически.
Метод наложения потенциальных потоков при
некоторых условиях может быть использован также для
построения сложных течений сжимаемой жидкости.
На рис. 3-2 приведен простейший случай сложения
двух плоских поступательных потоков, понятный без
пояснений.
Другой пример сложения потенциальных потоков
показан на рис. 3-3. Сложение плоского- источника (стока) и
циркуляционного течения дает более сложное движение,
называемое вихреисточником (вихрестоком), линии тока
которого имеют форму спиралей.
3-2. КОЭФФИЦИЕНТЫ ДАВЛЕНИЯ. КРИТИЧЕСКОЕ
ЧИСЛО М
Остановимся на некоторых простых понятиях, имеющих
существенное значение при рассмотрении конкретных
теоретических и экспериментальных задач газовой динамики
и используемых нами в дальнейшем.
Поместим в газовой поток дозвуковой скорости
некоторый криволинейный профиль и рассмотрим изменение
параметров элементарной струйки, охватывающей такой
профиль (рис. 3-4).
Создаваемые профилем возмущения потока при
дозвуковых скоростях будут распространяться во всех
направлениях, в том числе и против течения. Под влиянием
этих возмущений элементарные струйки, движущиеся
к профилю, будут деформироваться. У носика профиля
центральная струйка расширяется; скорость течения При
этом падает и в точке разветвления А обращается в нуль.
В этой точке параметры будут равны параметрам
полного торможения потока. На передней части профиля
сечение струйки уменьшается, вследствие чего скорость
увеличивается, а давление падает. На верхней и нижней
поверхностях профиля продолжается поджатие струйки
с соответствующим, нарастанием скорости. В некоторой
точке сечение струйки минимально. В этом месте скорость
77
будет максимальной. Далее, на задних поверхностях
профиля струйка вновь расширяется, скорость ее падает,
а давление растет.
Таким образом, в результате деформации струек,
характер которой определяется формой обтекаемого тела,
вдоль поверхности профиля давление меняется.
Распределение давлений обусловливает возникновение аЭрОДИНаМИ-
Рис. 3-4. Распределение коэффициентов давления по
профилю.
ческих сил, действующих на профиль: подъемной силы,
вызванной разностью давлений на верхней и нижней
поверхностях профиля, и силы лобового сопротивления,
вызванной разностью давлений на переднюю и заднюю части
профиля и силами трения1.
Распределение давлений вдоль обтекаемой
поверхности характеризуется безразмерной величиной —
коэффициентом давления, который определяется как
отношение разности давлений в данной точке на поверхности
1 Если пренебречь влиянием вязкости и рассматривать
дозвуковое и безотрывное обтекание профиля, как это делается в
настоящей главе, то сила лобового сопротивления будет отсутствовать.
78
и статического в бесконечности к скоростному напору
невозмущенного потока:
p^Lzpi. (3-13)
Роосоо
2
Скоростной напор можно выразить через безразмерную
скорость Мю или Я воспользовавшись формулами (2-21)
и (2-55).
Тогда
p-TJ%[l£- 1)-«^(^- ^O-STTV
(3-14)
В некоторых случаях распределение давлений вдоль
поверхности характеризуется безразмерным давлением /?,
которое представляет собой отношение давления в данной
точке к давлению торможения невозмущенного потока:
Очевидно, что связь между коэффициентом давления р
и относительным давлением р выражается формулой
При малых скоростях набегающего потока более удобно
для подсчета коэффициента давления пользоваться
формулой (3-13).
На рис. 3-4 показано примерное распределение р
вдоль поверхности профиля. До тех пор, пока скорость
с^ значительно меньше скорости звука, характер
деформации струек, а вместе с тем и картина распределения
коэффициентов давления по профилю при изменении
скорости невозмущенного потока сохраняются практически
неизменными. Однако по мере увеличения М^ влияние
сжимаемости сказывается все более ощутимо;
распределение р по профилю начинает меняться особенно сильно
79
там, где местные скорости в струйке (на поверхности
профиля) велики. В минимальном сечении струйки скорость
наибольшая. Найдем зависимость между безразмерной
скоростью М^ и скоростью в некоторой точке на
профиле М..
С этой целью воспользуемся формулой (3-14), заменив
в ней отношение давлений через соответствующие
числа М:
Р
Ро
Роо
Ро
k —
k
Ml
k— 1 „
получим
kMi
k
а—l
l+-
Ml
Mi
(3-16)
При некотором значении Mg=M# в минимальном
сечении трубки тока устанавливается критическая скорость
М|.= 1. Соответствующая величина коэффициента
давления будет:
k k
Р*=
kMi
k—\
k + \
о+^
V)
ft—i
1
(3-17)
Величина M* называется критическим числом М
набегающего потока; оно определяет то значение
безразмерной скорости набегающего потока, при котором
максимальная местная скорость на контуре тела становится
равной местной скорости звука. Из определения
критического числа М# следует, что эта величина разграничивает
дозвуковые режимы обтекания тела на две группы.
Первая группа докритических режимов (М^^М*)
характеризуется тем, что во всех точках поля потока местные
скорости дозвуковые (M^l). Ко второй группе (М^^М*)
относятся режимы обтекания с местными сверхзвуковыми
скоростями.
80
При исследовании плоских движений сжимаемой
жидкости, относящихся как к первой, так и в особенности ко
второй группе режимов, необходимо учитывать влияние
сжимаемости. Эта задача решена в работах ряда
советских ученых. Еще в 1902 г. С. А. Чаплыгин в своей
работе „О газовых струях" опубликовал метод учета
сжимаемости для плоского потока. Эта работа приобрела
особенно большое значение в настоящее время и явилась
отправной для большинства современных исследований по
определению влияния сжимаемости при обтекании тел
потоком газа. Советские ученые С. А. Христианович,
Л. И. Седов и др., плодотворно развивая идеи С. А.
Чаплыгина, разработали надежные методы учета влияния
сжимаемости. Эти методы находят широкое распространение
и при решении задач, связанных с течением газа в
проточной части турбомашин.
Наряду с относительно сложными методами учета
влияния сжимаемости рядом авторов предложены
приближенные методы, позволяющие ценой тех или иных
допущений упростить задачу и путем сравнительно простых
вычислений оценить влияние сжимаемости на обтекание
тела. К числу таких методов относятся методы Л. Пран-
дтля, С. Г. Нужина, Г. Ф. Бураго, А. Н. Шерстюка
и др.
3-3. УЧЕТ ВЛИЯНИЯ СЖИМАЕМОСТИ ПО МЕТОДУ МАЛЫХ
ВОЗМУЩЕНИЙ
Рассматриваемый ниже простейший метод оценки
влияния сжимаемости в плоском дозвуковом течении применим
в тех случаях, когда возмущение потока можно считать
слабым.
Выберем систему координатных осей так, чтобы ось х
была направлена по скорости невозмущенного потока,
а ось у — нормально к скорости.
Обозначив через с' и соответственно и' и v' добавочные
скорости, вызванные тем или иным возмущением потока
(так, например, влиянием обтекаемого тела), представим
скорость в некоторой точке возмущенного течения в
таком виде:
c = cQO-\-cr, или \x = u,OQ-\-v!\ v = vf.
При этом мы считаем, что v = 0, так как поток на
бесконечности параллелен оси х(соо = и ). Полагая далее,
6 М Е. Дейч
81
что ii и v' являются малыми величинами порядка Д,
приходим к заключению, что производные
да да'. да да' т dv . dv
длГ дх ' ду ду ' дх ' ду
имеют тот же порядок Д. Оценив члены, входящие в
уравнение (3-6), найдем:
i-^-i-i+Д+Д'; l-f=l-S-i5-_5,
аоо
Г2
где Д и Д — малые величины, имеющие порядок Д или Д2.
Оценка членов, входящих в уравнение (3-6),
позволяет упростить это уравнение, если пренебречь членами,
порядок малости которых выше Л. После указанных
упрощений получим:
0-<>ё+£ = 0, (3-18)
или для потенциального течения
Таким образом, излагаемый метод, предложенный
Л. Прандтлем, основывается на предположении, что
отклонение скорости возмущенного течения от скорости
невозмущенного потока с00 = и настолько мало, что
степенями указанного отклонения выше первой можно
пренебречь. Уравнение для потенциала скорости (3-19) в
отличие от (3-7) является линейным дифференциальным
уравнением, поэтому метод малых возмущений вызывается
также методом линеаризации. Рассматриваемый
метод может дать удовлетворительные результаты при
расчете обтекания тонких слабо изогнутых профилей,
расположенных под небольшими углами к направлению
скорости невозмущенного течения, а также при исследовании
потока в каналах с малой кривизной ограничивающих
стенок. Отметим, что вблизи точек разветвления потока
(критические точки на поверхности обтекаемого тела) основное
допущение метода не оправдывается, так как в этих
областях поток тормозится и величина изменения скорости
соизмерима со скоростью на бесконечности.
82
Уравнение (3-19) при дозвуковых скоростях можно
привести к уравнению (3-8), определяющему потенциал
скорости потока несжимаемой жидкости. Действительно,
сравним рассматриваемый дозвуковой поток газа с потоком
несжимаемой жидкости, полагая, что скорость и плотность
обоих потоков на бесконечности будут одинаковыми.
Допустим, что потенциалы скоростей сравниваемых потоков
связаны соотношением
Ф = оФи. (3-20)
Обозначим координаты точек потока несжимаемой
жидкости хн и ун. Предположим далее, что между
координатами х, у и х , ун существует зависимость
следующего вида:
у х
Для упрощения моя-но принять х = хп\ тогда
УН = *У- (3-21)
Подставим теперь соотношения (3-20) и (3-21) в
уравнение (3-19):
о д2Ф д2Ф
Отсюда следует, что если принять
yJL=*=</\-Ml, (3-22)
у_
У
то уравнение (3-19) преобразуется к виду:
д2Фи дФн
-т^+Т^ = °- (3-8а)
дхн °Ун
Уравнение (3-8а) в новых переменных совпадает
с уравнением (3-8). Используя полученные соотношения,
нетрудно найти связь между параметрами двух
сравниваемых потоков.
Рассмотрим обтекание одного и того же тела потоком
несжимаемой жидкости и потоком газа. Обозначим через
а и а углы наклона малых отрезков линий тока
6*
83
(рис. 3-5). Имея в виду, что в соответствии с основным
допущением метода эти углы малы, найдем:
tg«*«^;tgeH« «„*£;. (3-23)
В идеальной жидкости одна из линий тока совпадает
с контуром тела. На граничной линии тока должно
выполняться условие
tga=tgaH,
или согласно (3-23)
dx dx
Рис. 3-5 Линии тока при обтекании профиля потоком газа (пунктир)
и несжимаемой жидкостью.
Учитывая, что скорости на бесконечности одинаковы,
находим, что указанное условие соблюдается, если v =v
дф дФ
или у=—-; на основании соотношений (3-20) и (3-22)
устанавливаем, что в рассматриваемом случае о& = 1, или
1 1
0
/1-<
Отношение продольных составляющих скорости в двух
сравниваемых потоках равно:
Л-=дФ.д± = а= * , (3.24)
ии дх <ЭФН Kl-M^
Для сравнения распределения давлений достаточно
сопоставить градиенты давления в обоих потоках, так как
ранее принято было, что х = хн и, следовательно, отно-
84
шение конечных разностей давлений равно отношению
градиентов
dp dx A/?
Jx"dp^~ Ар^'
На основании уравнения импульсов (2-1) градиенты
давления в сжимаемой и несжимаемой жидкости будут:
df]L — _ ^л- d^_ — __ dc_*
dx ^C»dx dx ^с ax '
тогда
А/7 р£ fife
или с учетом формулы (3-14)
~Р с dc coo + с' <Ис<х> + <?)
где с\ с'п — как и ранее, добавочные скорости (малые
величины), вызванные возмущением, вносимым обтекаемым
телом.
После соответствующих преобразований окончательно
получаем:
~Р 1
Рп У\-м*ш
(3-25)
Из формул (3-24) и (3-25) следует, что при обтекании
одного и того же тела газом скорость и разность
давлений больше, чем в случае обтекания несжимаемой
жидкостью.
Это различие между течениями газа и несжимаемой
жидкости можно объяснить зависимостью плотности газа
от скорости (§ 2-4). На рис. 3-5 показаны линии тока при
обтекании тела сжимаемой и несжимаемой жидкостью при
одинаковых параметрах и скорости с^ невозмущенного
потока.
Другое упрощение исходных уравнений, основанное
также на предположении о слабом возмущении потока,
дано А. Н. Шерстюком, развившим упрощенный, но
более точный метод учета влияния сжимаемости.
Для оценки влияния сжимаемости в слабо
возмущенном плоском потоке с докритическими скоростями
85
(М00<М#) воспользуемся уравнением неразрывности (1-12),
записав его для плоского установившегося движения газа:
дх
а») ч (!»)=»• <з-2б>
а также условием отсутствия вихрей (3-1) для плоского
течения.
В этом случае из формул (1-6) получаем:
•.=4-(&-£)=* <3-1а>
Рассмотрим обтекание плоским потоком газа крылового
профиля, показанного на рис. 3-5.
Следуя за А. Н. Шецстюком, перейдем в уравнениях
(3-26) и (3-1а) от скоростей и, v потока сжимаемой
жидкости к скоростям в потоке несжимаемой жидкости
ин, vH, положив
с„ = с
(£)'■ (3-27)
Здесь показатель степени 8 определяется на основании
упрощенных связей, соответствующих предположению
о малой возмущенности потока; р — плотность потока
в данной точке; р^ — плотность невозмущенного потока.
Как уже отмечалось выше, в соответствии с методом
малых возмущений можно принять:
и = соо + и'> Т~<1> (3"28)
v = xf\ — < 1. (3-28а)
Для несжимаемой жидкости справедливы аналогичные
упрощения:
и
"-='«,+«»; г^1 (3-29)
v =0 ; — <1.
н н ' с ^
86
Используя эти соотношения, подставляя (3-28) в
уравнения (3-27) и (3-5а) и отбрасывая члены второго порядка
малости, нетрудно получить:
1-ML
1 __ 62М^ дх
1 дии
ди„ dv
= 0;
(3-30)
1 — ем* ду дх
:0.
Для того чтобы уравнения (3-30) привести к
уравнениям неразрывности и отсутствия вихрей для несжимаемой
жидкости, достаточно принять, как и ранее, связь между
координатами в сжимаемой и несжимаемой жидкости (3-22):
х-
н « Г о
и, кроме того, положить:
я 1-1/1-М2
Действительно, после подстановки
в уравнения (3-30) находим:
да,, ди
дх
(3-22)
дин t dv
"_L —-=0* -
г -Гдун ' дун
дх
^ = 0.
(3-31)
(3-31)
(3-32)
Отсюда следует, что скорости ин и vR действительно
являются местными скоростями в потоке несжимаемой
жидкости при обтекании того же тела при том же угле
атаки.
Для определения скоростей при обтекании тела
сжимаемой жидкостью необходимо вначале рассчитать поле
скоростей в потоке несжимаемой жидкости при той же
величине и том же направлении скорости невозмущенного
потоки (сноо=с00). При этом местная безразмерная скорость Я в
произвольной точке потока будет:
А = Я
р
,^)
= л
Г 1
1
1.
k —
-" k +
k — \
k + \
'я2
>2
Ar—1
(3-27a)
87
Зависимость 6 = /(Яоо) представлена на рис. 3-6. Из
этого графика следует, что коэффициент 8 можно
приближенно считать постоянным при числах Я^ < 0,7 -ь- 0,8.
Резкое возрастание 6 при больших Я^ обусловливает
непригодность рассматриваемого метода в этой области.
100
ОМ
от
ом
от
ojs\
о jo
0,65\-
ощ
0,55
0,50\
о oj ot2 о,з 0,4 Q5 as oj о,е аз /,о
Рис. 3-6. Зависимость показателя степени 0 от
безразмерной скорости Л^.
Связь между скоростями в сжимаемой и несжимаемой
жидкостях по формуле (3-27а) для различных скоростей
набегающего потока показана на рис. 3-7. С увеличением
Я скорость в потоке сжимаемой жидкости в данной точке
обтекаемого тела интенсивно возрастает по сравнению со
скоростью в несжимаемой жидкости.
Установим теперь связь между коэффициентами
давления в несжимаемой и сжимаемой жидкостях.
Из уравнения Бернулли для несжимаемой жидкости
в
Y
\
Цл 1
__.! ..„,
. ,. . • L
А-
/'oo + P-f =/'„ + Р-Г
86
находим коэффициент давления в следующем виде:
Для сжимаемой жидкости коэффициент давления
определяется по формуле (3-16). Выражая р через
безразмерные скорости Я и Я находим (табл. 2-1):
- k +
k+ 1
]я2
-X2
£-1
/г—1
(3-34)
Пользуясь формулами (3-27а), (3-33) и (3-34), можно
получить связь между коэффициентами давления в
сжимаемой и несжимаемой жидкостях р и рн. Эта связь
представлена на рис. 3-8 и 3-9. Здесь показана зависимость
0,8
0J
од
0,5
оА
0,3
0,2
Ан
J?
J0ys
•Syr у»"*
У
s ** (
)л
^^.
\
A«e---J
я
0,3
OA
as
06
OJ
0,8
0,3
/tO
Рис. 3-7. Зависимость между безразмерными скоростями в сжимаемой
и несжимаемой жидкостях по А. Н. Шерстюку.
89
между р и рн для различных значений А^. Кривые на
рис. 3-8 пригодны для пересчета положительных
значений рн. В этом случае давление в рассматриваемых точках
на поверхности тела выше давления набегающего потока.
Для пересчета отрицательных значений рн служит график
на рис. 3-9. Пунктирная линия, ограничивающая диаграмму
p=.f(p{) сверху, соответствует значениям /?*, при
которых Л=1. Другими словами, эта линия определяет
критические значения безразмерной скорости набегающего
потока М =М# в зависимости от р или от рн и тем са-
90
мым ограничивает ту область величин Моо<М# = /(/?н),
для которой может быть произведен учет влияния
сжимаемости рассматриваемым методом.
На рис. 3-10 приведена кривая по данным развитой
теории, устанавливающая зависимость между минимальным
коэффициентом давления в точке обвода тела при
обтекании его несжимаемой жидкостью ря мнн и критическим
числом Я, набегающего потока. Кривая на рис. 3-10
О 0,5 1,0 1,5 ' 2,0
Рис. 3-9. Зависимость между отрицательными
коэффициентами давления для сжимаемой р и несжимаемой рн
жидкостей при различных Х^.
91
в координатах (рн , Я ) воспроизводит граничную линию
Л = 1 на рис. 3-10.
Формула для расчета этой кривой может быть
получена из (3-33) с помощью (3-27а). Действительно, из этих
соотношений имеем:
(К Ч2
/>„=*
Заменив отношение
/V
Положив Я — 1 и Я = Я#
(3-35)
k + 1
находим:
20
/V
/г + 1
' k + l
(3-36)
Таким образом, если известно распределение давлений
по обводу тела при малых скоростях, когда влиянием
сжимаемости можно пренебречь (распределение ^н), то,
пользуясь кривыми на рис. 3-8 и
3-9, легко можно найти
распределение давлений и при
больших дозвуковых скоростях
с учетом сжимаемости. Как
видно из графиков, влияние
сжимаемости сказывается в
том, что в области
положительных значений р
коэффициенты давления для
сжимаемой жидкости будут выше,
а в области отрицательных
значений—ниже, чем для
несжимаемой жидкости.
Следовательно, благодаря
сжимаемости увеличиваются абсолют-
о,и
-15
-ко
-0,5
О
- _ ' ■ -т - -
Рнмин
1
\
\
^4*
Ц5 0,6 0,7 Ц8 0,3 КО
Рис. 3-10. Зависимость между
коэффициентами давления /?н.мшг
и безразмерной.критической
скоростью Х#
92
ные значения коэффициента давления. При этом области
минимальных давлений становятся более крутыми и
вытягиваются (рис. 3-4)*. Из рассмотрения рис. 3-4 видно, что
с ростом М увеличивается площадь, заключенная между
кривыми давлений для верхней и нижней поверхностей
Рис. 3-11. Сравнение опытных и расчетных
коэффициентов давления.
/ — по Л. Прандтлю; 2 — по С. А. Христиановичу;
3 — по формуле Кармана — Цзяна (3-37); 4— по
А. Н Шерстюку, 5 —опыт
профиля. При этом, очевидно, подъемная сила с
увеличением М^ возрастает.
Все выводы рассматриваемого метода хорошо
подтверждаются опытными данными.
Сопоставление опытных и расчетных значений р в точке
верхней поверхности крылового профиля, расположенного
в потоке под небольшим углом атаки, показано на рис. 3-11.
Профиль имеет относительно большие толщину и
кривизну.
Для сравнения на рис. 3-11 приведены также расчет-
* Соответствующие графики изменения коэффициентов давления
по профилю крыла и лопатки приводятся в гл. 5 и 8. •
9а
ные кривые, соответствующие формуле (3-25) Л. Прандтля
и по более точной формуле Кармана — Цзяна:
Г*
-< +
р,К
(3-37)
2(1+1/1-^)
Совпадение расчета по формулам (3-27а)—(3-34) и по
формуле (3-37) с опытом является вполне
удовлетворительным. Значительно худшие результаты получены при
использовании формулы (3-25).
3-4. ТЕОРЕМА Н. Е. ЖУКОВСКОГО
Теория силового воздействия потока идеальной
жидкости на обтекаемые тела основывается на известной теореме
Н. Е. Жуковского. Н. Е. Жуковский установил вихревое
происхождение силы взаимодействия и нашел простую связь
между этой силой и интенсивностью циркуляционного те-
Ъ-А
/Sf/ffS/tttS/tt/tt/fMt'ttt/t/rtt/.
СГС<*1_
/s////s//////(//// ,р
Рв
PfPoo
|g?sgoc
\Р2=Роа
\pfp«
, cjoPh_ t_ ,
Рис. 3-12. К доказательству теоремы Н. Е. Жуковского.
чения,. возникающего при обтекании тела. Эта задача была
решена Н. Е. Жуковским в 1906 г.
Для доказательства1 теоремы Жуковского
воспользуемся схемой, показанной на рис. 3-12. Расположим
крыловой профиль в плоском потоке между двумя непрони-
1 Приведенное ниже доказательство теоремы Н. Е. Жуковского,
предложено Г.* Ф. Бураго.
94
цаемыми плоскими контрольными поверхностями,
ориентированными по потоку и удаленными друг от друга на
расстояние h. Систему координат хОу разместим так, чтобы
направление оси х совпадало с направлением вектора
скорости невозмущенного потока с^. На бесконечном
удалении от профиля проведем сечения аЬ и cd, нормальные
к направлению потока.
Предполагая, что профиль обтекается безотрывно, и
применяя теорему об изменении количества движения к
массе жидкости, заключенной внутри объема abed, найдем,
что сила, направленная против течения и называемая
лобовым сопротивлением профиля, определяется формулой1
Рх = { (А — A) dy — [ р.с, (с, — с2) dy.
(A) (А)
Так как скорости и давления в сечениях ab и cd
одинаковы, то
Р =0.
X
Приведенный результат был получен впервые Л.
Эйлером в 1745 г. и независимо от него в более общем виде
Даламбером. Он может показаться парадоксальным, так как
противоречит опыту. Однако следует иметь в виду, что
этот результат получен в предположении отсутствия
вязкости и отрыва потока от поверхности обтекаемого контура.
В действительности всегда в какой-то степени оба эти
фактора имеют место.
В практическом отношении можно сделать вывод, что
следует стремиться добиваться таких форм контура, при
которых обеспечивались бы безотрывное обтекание и
наименьшие воздействия сил вязкости; в этом случае,
по-видимому, сила сопротивления будет наименьшей.
Найдем теперь величину силы Р , нормальной к
вектору скорости с . Эту силу называют подъемной силой.
Обозначив через ри давление на нижней контрольной
поверхности и через рв давление на верхней контрольной
поверхности, получим:
-Ру+](Рп-Рв)*х = 0>
—00
1 Рассматриваемые силы относим к единице длины крыла
95
так как проекция скоростей у непроницаемых
контрольных поверхностей на ось у равняется нулю. Следовательно,
Рв= \(P«-PB)dx- (3-38)
—оо
Увеличивая расстояние между стенками /г, в
предельном случае (при h -> оо) получим обтекание тела
безграничным потоком. При этом поток у стенок будет слабо
возмущенным. Скорости такого течения, как известно,
можно представить в виде [формулы (3-28)]:
Сн = Соо + 0 ]
(3-286)
с —с А-с ,
В 00 » В' I
где сн, св—малые добавочные скорости у стенки,
вызванные влиянием обтекаемого тела.
Давление в произвольной точке возмущенного потока
связано с давлением на бесконечности уравнением
Бернулли:
Р Роо , k — 1
Р~ Роо^ 2k
■(С-О.
которое при принятом допущении (слабо возмущенный
поток) на основании (3-286) преобразуется к виду:
Р Роо к °°
г\ Р гоь Роо k
Отсюда, имея в виду, что -^=—г и — = -тг> после
Р* Роо Р"> 4>
несложных преобразований находим:
1-Ш^, (3-39)
ИЛИ
P = Pao — ta0CooC'- (3"39a)
Уравнение (3-39) или (3-39а) справедливо для
линеаризованного течения и называется линеаризованным
уравнением Бернулли. Уравнение (3-39а) можно
96
записать для сечении на верхней и нижней контрольных
поверхностях:
/7 = /7 — р С С
*Н ^00 гОО 00 Н
и
р =. р — р с с '.
'В ^00 "00 ОО В
Подставляя рн и рв в уравнение (3-38), находим:
+00
Л, = Роо^оо J (*в-0**-
—00
+оо
Нетрудно видеть, что интеграл Г (с'в — сн) dx
-8
можно выразить через циркуляцию скорости по замкнутому
контуру (рис. 3-12). Действительно,
abcda ab \ be I cd I da1
так как
+ oo +oo
Г = Г (с 4- <?') dx; \\ = — [ (с -\-с) dx; Г . = — Г .
be J \ оо I в/ ' da J \ оо I н/ ' ab cdt
ТО
+00
1\ ^ = \ (с — с ) dx.
abed J V в н / *^
—оо
Следовательно,
^=рЛ.- (3-4°)
Формула (3-40) выражает теорему Н. Е. Жуковского,
являющуюся основной теоремой аэродинамики. Теорему
Жуковского можно сформулировать так: при обтекании
тела плоскопараллельным безграничным потоком
идеальной сжимаемой жидкости на тело единичного
размаха действует сила, равная произведению
циркуляции скорости Г на скорость с^ и на плотность
р^ невозмущенного потока. Направление этой силы
нормально к направлению скорости невозмущенного
потока с^. При этом, как следует из вывода, если
циркуляция скорости, вычисленная при обходе по часовой
стрелке, окажется положительной, то и Pv будет
положительной. Подъемную силу Р часто называют силой Жуков-
7 М. Е. Дейч 97
ского. Для определения Р необходимо знать величину
циркуляции скорости, которая вычисляется на основании
постулата Жуковского—Чаплыгина (§ 1-2).
3-5. ПЛОСКОЕ ДОЗВУКОВОЕ ПОТЕНЦИАЛЬНОЕ ТЕЧЕНИЕ
ГАЗА В КРИВОЛИНЕЙНЫХ КАНАЛАХ
Рассматривая плоское или осесимметричное
потенциальное движение газа по криволинейным траекториям, выберем
в качестве независимых переменных расстояние вдоль линий
тока (S) и вдоль эквипотенциальных линий (п) (рис. 3-13).
Рис. 3-13. К выводу уравнений движения
в криволинейном канале.
Преобразуем уравнения неразрывности (1-14) и
отсутствия вихрей [третье уравнение системы (3-1)] в новых
координатах. Для элементарного объема, ограниченного в
плоскости чертежа отрезками линий тока AS и Д5', и
эквипотенциальных линий An и An' условие неразрывности
запишется в такой форме:
±(РсгАп) = 0,
98
или
din (per) , J_ дкп ^
as "• лл' as ~~~ '
где г — радиус центра тяжести сечения An (рис. 3-13,а).
Далее, так как
адп ay A
(у —угол наклона линии тока), представим уравнение
неразрывности в такой форме:
а'У+г=0- С3"41)
dS ' дп ч '
Условие отсутствия вихрей будет (рис. 3-13):
После дифференцирования получим:
a in с , 1 aAs
=-0.
дп ' AS дп
Так как (рис. 3-13,а)
aAS___aYA9
~дп~— dS^'
то окончательно находим:
d\n_c_dj_ ^ (3.42)
дп OS v '
Уравнения (3-41) и (3-42) справедливы для осесиммет-
ричных течений сжимаемой жидкости. Для плоских задач эти
уравнения упрощаются и приводятся к следующему виду:
dln(pg) I dy п.
dS *дп '
a in с ay
art ds'
:0.
(3-41a)
Полученные уравнения позволяют наиболее простыми
способами рассчитать течение газа в плоских или осесим-
метричных криволинейных каналах1. С этой целью
необходимо найти распределение скоростей вдоль
эквипотенциальных линий в канале.
1 Излагаемая методика расчета потока в каналах разработана
Г. С- Самсщловичем и А. Н. Шерстюком.
7*
99
Для приближенного определения длины
эквипотенциальных линий в канал вписываются окружности (рис. 3-13,6),
касающиеся стенок в точках А и В. Через точки касания
проводится дуга окружности, нормальная к стенкам канала,
которая приближенно дает длину эквипотенциальной
линии.
Такой способ определения линий Ф = const справедлив
только при малой их кривизне.
Уравнения неразрывности (3-41) и (3-41а) показывают
характер изменения угла наклона вектора скорости в
поперечном сечении канала, а уравнение отсутствия вихрей
позволяет сформулировать условие, которому должна
удовлетворять эпюра скоростей на любой линии тока, в том
числе и на стенках канала:
1 дс ду гг
Для нахождения распределения скоростей вдоль линий
Ф = const воспользуемся уравнением (3-42), заменив
ду__ 1_
1
где -~ кривизна линии тока.
*s
Тогда
дс с
дп Rs'
Умножим обе части этого выражения на трехчлен Rsl-{-
-j-n-\-Kn2 и прибавим к ним величину с ^-(Rsx-\-n-\-Kn2).
После несложных преобразований найдем:
д / R^+n + Кп2 \
£№,+ » + **')! =-'(-*^ 1-2/сЛ
Левая часть этого выражения обращается в нуль при
я = 0; постоянную К можно выбрать таким образом, чтобы
производная
100
была равна нулю и при RS{ = RS2 (Рис- 3-13,6). В этом
случае она мало отличается от нуля и во всех точках
линий Ф = const. Это условие означает, что закон
изменения скоростей вдоль линии Ф = const будет:
или
с (RS{ -j- n -f- Kn2) = const,
с 1
ci \ +п — Кхпг
(3-43)
где
Л52~" пВ
\S1
Изменение скоростей вдоль границ канала
устанавливается с помощью формулы (3-43), справедливой и для
сжимаемой жидкости. Исходным служит условие
постоянства расхода, через канал.
При малых числах М«<0,4, когда влиянием
сжимаемости можно пренебречь, объемный расход жидкости через
плоский канал будет:
Q— Г cdn.
о
С помощью формулы (3-43) после интегрирования
получим:
с,пв с,
пвУ\+4Кг 1-2*1Лд/(1 + К1+4/С,) '
Здесь ст — средняя скорость в сечении канала; сх —
скорость в точке на выпуклой стенке.
Для удобства расчетов на рис. 3-14 представлен
график зависимости b = f(nB, x), выражаемой формулой (3-44).
В случае осесимметричного канала объемный
расход жидкости определяется по формуле
Q = 2* ^Rscdn.
101
''"к] ' I 1 Т 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
rl tx
Л\\
JijK I
Жк
Pwl
1 1 1 тд\к 1 1 1 1 1 1 I 1 1 1 1 1 1 1 1
M%H M ' M
%N 1 Jtc=oo
/7 7 №44 I 4—Г 1 1 1 1 1 -1 1 1 1
' гамчп
1 1 1 1 1 I^KS 1 1 1 1 И 1 1 1 1 1
rcMS
wN
шк
\>vnm M
Р¥^МЧ Ы
«ж^ИШ'т
Ш1л
м ЖчкуШ
' M\S>>n
M токкж
и №>>>>к
1 / hw>>nS
Г M^WsH
It^ tvN
IvRkK
fws
fw
П 7 ' ' L/M-1
U,' 1 1 A M\
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 '}^\ 1 1
П f!\ -
' Mi t 1 1 1
п. я 1.11, J 1 1 1 1 11 1 1 1 1 1 1 1 1 1 1
M M M \ \ 1 V\ \ 1
Ml
. U I 1 I 1 1 1 1 1 I I 1 1 1 1 j 1 1 1
4 r
чЧ 1
№W4111111111111111
чЖШ
тШчИ
Т^^Й>Й>1 з\ 1 1 MM
|1^Ш^1$№Ч
II ^Ш^^^^Й^Н] Mil
Kp*>Nn >Bj4
'j■ ^4>NS4>t>is>L
\fS 1 г>mKrflwi
lK>N >T rSNJ
KjS>±Нчгч i
Тгчт^Н п
M HJ>Kj4
°1 1 N Л-ТЧ
M Mn
i 1 i i i i 1 i i i 1 i i i i i ij i i
r*
1 1 1 1 1 1 1 M M 1 ,1 1 1 M I 1 1
0,5 КО 15
Рис. 3-14. График зависимости д от пв и х.
гд
Упрощая решение задачи, можно принять линейную
связь между Rs и п:
в
По аналогии с формулой (3-44) можно получить1:
К =
Q
2KRSl Cllg
= b-K,Z.
(3-45)
1 Формулы (3-44) и (3-45) справедливы в том случае, когда вну?
тренняя и наружная стенки канала имеют кривизну одного знака.
}02
Расчет осесимметричных каналов существенно
упрощается применением графиков, представленных на рис. 3-15.
Приведенные выше формулы (3-44) и (3-45) справедливы
для малых чисел М (несжимаемой жидкости). Однако
закон распределения скоростей, выражаемый формулой
(3-43), может быть принят и для сжимаемой жидкости
в такой же форме:
Слабое влияние сжимаемости на эпюру скоростей в
поперечном сечении объясняется тем, что условие
безвихревого движения, использованное для получения (3-43), не
содержит плотности.
Заметное изменение кривизны линий тока и закона
распределения скоростей в поперечном сечении отмечается
только при больших безразмерных скоростях и значитель-
?П I II Ml Ml II II II II MJ II II II I». I
О 0,5 /,0 1,5 2,0
Рис. 3-15. График зависимости z от пв и х.
103
ных градиентах скоростей вдоль канала. В широком
диапазоне дозвуковых скоростей (M<MJ расчет канала с
учетом сжимаемости может быть произведен путем
введения средней плотности в данном сечении. На основании
метода малых возмущений А. Н. Шерстюком было
показано, что средний приведенный расход в сечении, равный:
где G — весовой и G# — критический расходы газа через
данное сечение, связан со средними скоростью и
плотностью соотношением
(рш, %т — средние для сечения плотность и безразмерная
скорость). Средняя плотность Pm = <7mP*x~ легко может
быть определена по qm с помощью таблиц
газодинамических функций. Скорости с учетом сжимаемости могут
определяться по простой формуле: -т-=— (с и ст — ско-
рости, определенные без учета сжимаемости).
Метод, изложенный выше, пригоден для расчета
различных каналов, например, каналов решеток1 турбомашин.
3-6. ПЛОСКИЙ СВЕРХЗВУКОВОЙ ПОТОК
Перейдем к изучению основных свойств плоского
сверхзвукового течения. С этой целью рассмотрим простейший
случай установившегося равномерного сверхзвукового
потока, движущегося с постоянной скоростью вдоль стенки
В А (рис. 3-16). Допустим, что по нормали к стенке В А
скорости также не меняются. В точке А этой стенки
возникает возмущение потока, обусловленное.поворотом стенки
на малый угол. Вследствие малости угла db возмущение
в точке Л, выражающееся в изменении параметров потока
(давление и температура уменьшаются, скорость
возрастает), можно считать слабым.
Легко видеть, что в сверхзвуковом потоке возмущение
может распространяться только в направлении течения,
так как скорость движения частиц газа больше скорости
1 См. § 8-2.
104
Mf>1
в
Рис. 3-16. Обтекание
сверхзвуковым потоком угловой точки.
распространения слабых возмущений (с1^>а1).
Возмущение, возникшее в точке Л, сносится по потоку, причем
некоторая линия Am служит границей между двумя
различными областями потока; слева от линии Am
расположена невозмущенная область течения, а справа от этой
линии поток возмущен поворотом в точке А. Таким
образом, линия Am является границей, отделяющей
невозмущенную часть потока от возмущенной. Так как в
рассматриваемом случае речь идет о слабом возмущении, то эту
линию называют гр а н и ц е й
слабых или звуковых
возмущений, слабой
волной,
характеристикой или линией Маха.
При этом имеется в виду, что
любые слабые возмущения
потока распространяются со
скоростью звука (гл. 2).
Механизм распространения
слабых возмущений можно
проанализировать более
подробно, рассматривая другой
непрерывно действующий источник возмущения в плоском
безграничном сверхзвуковом потоке. Таким источником
слабых возмущений может служить остроконечное тонкое
тело бесконечного размаха с весьма малым углом
раствора переднего клина (рис. 3-17). Создаваемые телом
небольшие изменения параметров потока распространяются
со скоростью звука <zn тогда как скорость набегающего
на тело потока сх >ах.
Волны возмущения представляют собой круговые
бесконечные цилиндры, радиус которых легко определяется
как a^t, где At — отрезок времени, исчисляемый от
момента зарождения рассматриваемой волны в точке А.
За этот же отрезок времени частицы проходят путь,
равный cxbt. Следовательно, центр наблюдаемой волны
перемещается в новое положение Аг. При непрерывном
обтекании тела в точке А последовательно образуется
бесконечное количество волн, движущихся по направлению
потока. Так как скорость течения сх^>аи то позднее
образовавшиеся волны отстают от предыдущих, причем все
семейство волн имеет две общие касательные: Am и Апг^
исходящие из точки Л.
105
В этом легко убедиться, найдя соотношение между
радиусами волны и перемещениями ее центра:
где ат — угол наклона касательной к направлению вектора
скорости с1.
Появление линий Am, Aml можно рассматривать как
результат непрерывных слабых (звуковых) возмущений
потока; они стационарно связаны с источником возмущений
(носиком тела).
Рис. 3-17. Обтекание тонкого остроконечного
тела сверхзвуковым потоком.
При пересечении такой волны частицы газа
испытывают изменения всех параметров: давления, плотности,
температуры и скорости. Однако в связи с малостью
возмущения эти изменения бесконечно малы. В
рассматриваемом случае обтекания острого носика тела происходит
незначительное уплотнение потока и давление за волнами
Am, Amx увеличивается на малую величину dp, а скорость
соответственно падает на dc. Поэтому волны Am, Amx
называют слабыми волнами .уплотнения.
В тех случаях, когда переход через волну
сопровождается расширением потока и, следовательно, уменьше-
106
нием давления на dp, волну называют слабой волной
разрежения. Звуковые волны разрежения возникают,
например, при обтекании сверхзвуковым потоком внешнего
тупого угла (рис. 3-16).
Из рассмотрения обтекания тонкого клина можно
заключить, что в сверхзвуковом течении образуются
характеристики двух семейств, расположенные под углом ;±: а
к вектору скорости в данной точке.
Из формулы
aw = H-arcsin^
следует, что в ускоряющемся сверхзвуковом потоке углы
характеристик в направлении течения уменьшаются, а
^7777;
Ф б)
Рис. 3-18. Слабые волны в плоском потоке с неравномер
ным полем скорости.
в диффузорном потоке — увеличиваются. Отсюда можно
также заключить, что при изменении скоростей в
поперечном направлении к потоку характеристики приобретают
криволинейную форму.
Так, если по нормали к линиям тока скорости
увеличиваются, характеристика обращена выпуклостью к
невозмущенной области течения (рис. 3-18). Если, наоборот,
скорости в направлении нормали к стенке падают, то
характеристика обращена выпуклостью к возмущенной
области потока. При сложном неравномерном
распределении скоростей в потоке характеристики могут приобретать
и более сложную форму.
Перейдем теперь к изучению конечных возмущений
сверхзвукового потока. При этом рассмотрим вначале
только такие возмущения, которые вызывают
непрерывное изменение параметров течения.
107
Предположим, что вдоль стенки ВА движется
равномерный сверхзвуковой поток (рис. 3-19). За точкой А газ
попадает в область с пониженным давлением (p2<iPi)-
При этом поток отклоняется от направления стенки В А,
поворачиваясь на некоторый угол относительно точки А
в сторону[пониженного давления. Возмущение, создавае-
М,Р,
~?1
-Г7Т77777Т777777777
В А\
\
в/
/т'
г\т?А^
"><4?™>
^^-^><^
v
^^\^
7П2
Рис. 3-19. К образованию волны разрежения при
обтекании угла сверхзвуковым потоком.
мое точкой Л, распространяется в сверхзвуковом течении
вдоль характеристик Атх, Am.,..., Ат2, образующих
стационарную волну разрежения тхАт2. Возмущение
сверхзвукового потока начинается на характеристике Атх\
угол наклона волны Атх к направлению невозмущенного
течения определяется по формуле ат =arcsin^-.
Возмущение заканчивается на линии Ат2\
рактеристики может быть определено,
рость возмущенного потока:
a =arcsin
положение этой ха-
если известна ско-
1
м2 •
Между характеристиками Атх и Ат2 происходит
расширение газа от рх до р2. При пересечении волны
разрежения линии тока соответственно искривляются, так как
при обтекании точки А поток расширяется: скорость
потока увеличивается, а температура и плотность падают.
Промежуточным точкам линии тока в пределах волны
разрежения отвечают характеристики Атр Атп и т. д.;
вдоль каждой характеристики параметры течения оста-
108
ются неизменными. Углы между характеристиками и
касательными к линиям тока в направлении течения
уменьшаются:
а *> а ^> а *
Рассматривая постепенный переход к параметрам
возмущенного потока М2 и р2 с бесконечно малыми
интервалами AM и А/7 в пределах между Ат1 и Ат2У можно
провести бесчисленное множество характеристик,
составляющих стационарную волну разрежения конечной
интенсивности. Интенсивность волны тхАт2 меняется при
изменении давления р2. При этом, если параметры
невозмущенного потока остаются неизменными, характеристика Ат1
сохраняет прежнее положение, а характеристика Ат2
перемещается в зависимости от изменения р2. С ростом
р2 характеристика Ат2 приближается к Ат1 и при /72=/?i
обе характеристики совпадают (слабое возмущение потока).
Установим зависимости между параметрами потока
на границах волны разрежения. С этой целью
воспользуемся основными уравнениями плоского изоэнтропического
течения — уравнениями Эйлера. Имея в виду, что
параметры потока вдоль характеристик не меняются,
указанные уравнения используем в цилиндрических координатах.
Для плоского установившегося движения газа
уравнения (1-17а) и (1-14) в координатах (г, 6) принимают вид1:
с ^1-—-—=---•
г дг * г дЪ г р дг '
С
дсв cQ дсв сг св ^ 1 др
г дг ' г ае |~ г ~ р гс/е
д(?гсг) д(9св) _
дг i дЬ —и*
(3-46)
Рассматривая простейший случай, когда
невозмущенный поток перед волной разрежения имеет равномерное
поле скоростей и характеристики, образующие волну
разрежения, прямолинейны, можно считать, что параметры
потока сохраняют постоянные значения вдоль любого ра-
радиуса в пределах волны.
1 Влиянием массовых сил пренебрегаем.
109
Математически это условие можно записать так:
др дс dp р.
дг дг дг
Тогда в уравнениях (3-46) можно перейти к полным
производным. После упрощений получаем:
dcr
(3-46а)
Уравнение (3-46в) выражает в полярных координатах
условие плоского безвихревого течения.
Действительно, из третьего уравнения (1-19), полагая
(о2 —0, легко получить формулу (3-46в).
Отсюда приходим к заключению, что при обтекании
угловой точки А поток остается потенциальным и
безвихревым, а следовательно, и энтропия потока,
пересекающего волну разрежения, сохраняется неизменной.
Совместное решение уравнений (3-466) и (3-46в)
позволяет установить еще одно важное свойство сверхзвукового
потока.
Подставим в (3-466) производную плотности:
d§ \dp)s dti ~~ /U d§ '
Исключая из (3-466) и (3-46в) —^ , получаем:
Последнее означает, что отклонение потока в волне
разрежения происходит таким образом, что составляющая
скорости, нормальная к радиусу-вектору, равна скорости
звука в данной точке.
Этот вывод можно получить также из анализа картины
распространения слабых возмущений в сверхзвуковом
потоке (рис. 3-19). Отсюда следует, что принятое
допущение о постоянстве параметров течения вдоль радиуса
позволяет рассматривать возникновение волны разрежения
110
конечной интенсивности как результат последовательного
расширения потока в системе бесконечного множества
слабых (звуковых) волн разрежения.
Установим теперь, как меняются скорость и давление
вдоль линии тока, пересекающей волну разрежения. Для
этой цели воспользуемся уравнением энергии:
£+12 к —1 2
яг = —£— а^ ^~ с ;
имея в виду, что
<:* = с)-\-с\\ св = а,
получим:
k+ 1 2 __£+ 1 2 k— 1 2
2 Св 2 а* 2 Сг '
dc
Подставим в это уравнение сб= —«-; тогда получим
дифференциальное уравнение для определения радиальной
составляющей сг:
Интегрируя последнее выражение, приходим к
уравнению
Q
arc sin m — = яг (0 + Я),
где
Постоянная интегрирования /( определяется из
граничного условия. Примем, что при 0 = 0 радиальная
составляющая скорости сг = 0; это значит, что мы
рассматриваем расширение невозмущенного потока, имеющего
скорость, равную скорости звука (Я} =1); отсюда /С=0.
Окончательно получаем:
Я = —= —sin(m6).
111
Составляющая скорости св определяются по уравнению
»,«-£-£=<»(««>.
Безразмерная скорость X в произвольной точке волны
разрежения
Я2 = х) + X) = ± sin2 (/иО) + cos2 (mO),
или
Я2 = 1 + ^ sin2 (/юв). (3-47)
Для определения давления-в той же точке
воспользуемся уравнением
Отсюда после подстановки Я из (3-47) получим:
k
р Г1 +cos(2m9) |*-i /3.48)
A L Л+! J '
Пользуясь формулой (3-47) или (3-48) и имея в виду,
что в волне разрежения процесс изоэнтропическии, можно
также подсчитать изменение плотности и температуры
Р Т
в волне разрежения: — и -=-.
Ро ^о
Формула (3-47) показывает, что максимальной скорости
о ,/мЛ 1 л
макс = У ь __ \ = — отвечает предельное значение угла (к
8!п2Ммакс)=1'
или
В этом случае при обтекании угла поток приобретает
давление /?2 = 0 (истечение в пустоту). Заметим, что при
таком режиме направление граничной характеристики Ат
совпадает с направлением линии тока отклонившегося
течения, так как
а = arcsin тт— = arcsin — = 0.
т2 М2 С2
112
Необходимо подчеркнуть, что рассматриваемый режим
течения (* = *макс) является теоретическим — предельным—
режимом:
Второй предельный . режим обтекания угловой точки
отвечает значению скорости Я = 1. При этом 0 = 0
(звуковой поток с бесконечно малым изменением давления
у точки Л).
Уравнения (3-47) и (3-48) применимы и для других
сверхзвуковых значений скорости перед волной разрежения,
больших единицы, но при этом начальный угол отсчета
определяется по формуле
1 /аГ^Л
6, = — arcsin у ~2~ (Я* — 1)
и линия отсчета располагается не перпендикулярно
направлению невозмущенного потока, а под углом 8i-j-am K немУ-
Большой практический интерес представляет
возможность определения формы линии тока в пределах волны
разрежения. Для решения этой задачи можно
воспользоваться дифференциальным уравнением линий тока Плоского
течения в полярных координатах
dr _ rd§
сг~~ св '
Используя формулы для Яг и Я0, получаем:
d[nr = ~^- tg(m0)d8.
После интегрирования приходим к выражению
-i/EL
r = r0[cos(mO)] *+1 , (3-50)
где r0 — радиус-вектор линии тока при 6 = 0.
Из уравнения (3-50) следует, что все линии тока
в пределах волны разрежения представляют собой систему
подобных кривых; расстояние между соседними линиями
тока в соответствии с основными свойствами
сверхзвукового потока увеличивается в направлении течения.
Как уже указывалось, обтекание угловой точки,
сверхзвуковым потоком является потенциальным. Составляющие
8 М. Е. Дейч
ИЗ
скорости cr, cQ можно выразить через потенциал скорости:
дФ . __дФ
Отсюда после подстановки сг или cQ и интегрирования
получаем:
Ф = а„— rsin(m9).
(3-51)
Рис 3-20. К определению угла
отклонения в волне разрежения.
Остановимся в заключение на способе расчета угла
отклонения потока 8. Из рис. 3-20 следует, что при
известном положении граничной характеристики Ат2 угол
отклонения определяется по формуле
8 = °» + а,и. '?-
т2
(3-52)
Имея в виду, что
a =arcsm
m2
■/
(Л+ !)-(*-1)Х|
и согласно (3-47)
02 = |/ |i^ arcsin ( у
(к—\)Ц — (к—\)\
2 J
получим:
»=/
/г+11
Т
arcsin
/£
D^-(fe-l)
+
4-arcsin _
j/cm^:
|АП
(3-53)
ill
Применяя известные тригонометрические преобразования,
из (3-53) найдем:
6=)/Шагс5т[Ь-(^-1)Я22]+
-f- arccos
Л0
(3-53a)
Величину о можно представить в зависимости от М2
или р2/р0. Соответствующие значения 8 для трех.-различ-
ных показателей £=1,135; 1,3 и 1,4 приведены на рис. 3-21
и в таблице функций изоэнтропического потока (см.
приложение).
ш°\ ^
0,1 0,2 0J ОА 0,5 0,6
Рис. 3-21. Изменение углов 6' и 9 в зависимости
от отношения давлений.
115
Максимальный угол отклонения 8макс отвечает
максимальной скорости течения Лмакс (или р2/р0 = 0)- В этом
случае, как уже указывалось, ат2 = 0 и, следовательно,
g _q ^_
макс макс 2 '
или с учетом (3-49) получим:
»_=-K/S-0- <3-54>
3-7. ДИАГРАММА ХАРАКТЕРИСТИК
Пользуясь уравнением (3-53), рассмотрим изменение
скорости вдоль некоторой линии тока EFH (рис. 3-22).
Допустим, что скорость невозмущенного течения перед
угловой точкой А Я1=1. За угловой точкой давление
/?2 = 0. Таким образом, вдоль линии тока EFH происходит
непрерывное расширение потока от рх = р* до /?2 = 0;
Рис. 3-22. Годограф вектора скорости при обтекании угла
сверхзвуковым потоком.
при этом скорость потока увеличивается от Х1 = \ до
Я2 = Ямакс. В каждой точке линии тока можно определить
величину и направление вектора скорости Я. Отложим эти
векторы из некоторого центра 0. Тогда концы векторов
опишут кривую—годограф скорости для данной линии тока.
Заметим, что точки годографа скорости E'F'H'
соответствуют точкам EFH линии тока. Отсюда следует, что
отрезок ОЕ'=\, а отрезок OLr=y rzrp Уравнение (3-53),
116
выражающее функцию 5 (Я), является уравнением годографа
скорости в полярных координатах. Согласно (3-53)
годограф скорости представляет собой эпициклоиду.
Остановимся более подробно на некоторых свойствах
годографа скорости. Проведем в плоскости потока
характеристику AF, пересекающую линию тока EFH в точке F
(рис. 3-22), и найдем в плоскости годографа
соответствующую ей точку F\ Это можно сделать, проведя из
точки О линию вектора скорости Хр под углом S^ к
направлению потока ОЕ'. Направление вектора Хр совпадает
с направлением касательной к линии тока в точке F. При
перемещении в бесконечно близко расположенную точку F"
скорость потока меняется на dXf (угол отклонения
изменился на db). Угол между касательной к годографу
в точке F.ii вектором скорости можно найти по уравнению
lF do
Величину ~y~ определяем дифференцированием
уравнения (3-53); получим:
Л= |/'
Следовательно,
d\F
d\
1 k+\K
х" Vm2f-\
Очевидно, что
tg?F=/MT=rr-
Угол между нормалью к годографу F'A' и
направлением невозмущенного потока OF' равен:
1 ]
"mF **р Vm%-\ '
или
sina- =
mF— MF
117
Следовательно, нормаль к годографу скорости F'Af
является характеристикой в плоскости потока, так как угол
этой нормали с направлением вектора скорости равен углу
наклона характеристики amF. Отсюда следует очевидный
вывод о взаимной ортогональности характеристик и
касательных к годографу скорости (рис. 3-22). Линию
годографа скорости E'F'H'U называют характеристикой
течения в плоскости г од ографа (плоскость и, v).
Следует подчеркнуть, что все линии тока имеют общий
годограф скорости, т. е. форма характеристики в плоскости
годографа не зависит от характера течения и одинакова
для всех плоских сверхзвуковых потоков газа с данными
физическими свойствами.
Так же как и в поле потока, в плоскости годографа
можно построить две характеристики, симметричные
относительно оси, которые относятся к двум различным
семействам. Для решения ряда практических задач удобно
использовать сетку характеристик первого и второго семейств.
Совокупность характеристик двух семейств в плоскости
годографа называется диаграммой характеристик.
Диаграмма характеристик может быть построена по
уравнению (3-53) или графическим способом.
Графический способ основывается на следующих соображениях.
Установим характер зависимости между вектором скорости X и углом
наклона характеристики а . Заметим, что в плоскости годографа
сверхзвуковая область заключена в кольцевой области между двумя
окружностями (рис. 3-23). Радиус внутренней окружности равен X = 1.
v\+]
Внешняя окружность имеет радиус, равный I/ , i . Как уже ука-
, j угол на-
клона характеристики меняется в пределах от <хт = -у до ат = 0.
Учитывая, что
sm2 am = 2\2
\2
и К2 = Xr -f- Xj, где Xe = Xsinotm, приходим к уравнению
k + lK + h^1'
118
Таким образом, зависимость ат (к) в полярных координатах
(К ат) выражается уравнением эллипса. Длина малой полуоси эллипса
Расположим эллипс в плоскости годографа (рис. 3-23).
Отрезок, соединяющий центр О с некоторой точкой на дуге
эллипса F, определяет в масштабе построения вектор скорости X. Угол
между вектором \ и большой
полуосью эллипса равен ат.
Очевидно, что большая
полуось ON при этом дает направление
характеристики в поле потока, а
малая полуось OL — направление
характеристики в плоскости
годографа. Следовательно, отрезок FH',
параллельный OL, является
касательной к характеристике в
плоскости годографа в точке F.
Проведя в нескольких точках
эллипса отрезки, параллельные
малой оси, и поворачивая эллипс вокруг
центра О, мы можем построить
группу характеристик первого
семейства в плоскости годографа
PFJ, P'FT и т. д.
Так как при повороте эллипс
проходит через каждую точку
кольцевой области дважды, то
легко нанести и другую группу
эпициклоид, составляющих второе семейство характеристик (пунктирные
кривые на рис. 3-23). Характеристики второго семейства являются
зеркальным отображением характеристик первого семейства.
Годограф скорости можно также получить путем качения без
Рис. 3-23. К построению
характеристик в плоскости годографа.
скольжения окружности радиусом —^
(vm-
по внутренней
окружности кольцевой области (штрих-пунктирная окружность на
рис 3-23)
Диаграмма характеристик в плоскости годографа
используется для приближенных расчетов плоских
сверхзвуковых течений. С этой целью в плоскости годографа
наносят отрезки характеристик двух семейств на одинаковом
и достаточно малом расстоянии друг от друга. Для
практического использования достаточна часть кольцевой области,
расположенная в секторе с углом 70°. Каждой эпициклоиде
присваивается определенный номер.
Заметим, что любая окружность в плоскости годографа
представляет собой линию постоянного модуля скорости,
а любой луч, идущий из центра О, определяет направление
119
вектора скорости в данной точке (рис. 3-24). Внутренняя
окружность разбивается на градусы; отсчет угла ведется
от горизонтальной оси плоскости годографа (положительные
углы откладываются вверх, а отрицательные — вниз).
Каждой эпициклоиде приписывается номер,
показывающий угол луча, продолжением которого служит рассматри-
Рис. 3-24. Обозначения характеристик и окружностей
(линий X = const) в диаграмме характеристик.
ваемая эпициклоида (рис. 3-24). Эпициклоиды первого
семейства, идущие вверх, имеют индекс 1 (10г\ 20^ 30г и т. д.),
идущие вниз обозначены соответственно индексом 2(102,
202, 302 и т. д.).
Окружности (линии Я = const) также обозначены
определенным номером. При ускорении от Я=1 до
заданного значения Я поток отклоняется на определенный угол 8,
который можно найти наложением двух лучей,
пересекающих характеристику на окружности радиуса Я = 1 и на
окружности радиуса Я (рис. 3-24). Вдоль окружности угол
отклонения 8 сохраняет постоянное значение; он равен
полусумме номеров эпициклоид двух семейств,
пересекающихся на Аанной окружности. Если номера эпициклоид
120
обоих семейств уменьшаются или увеличиваются на одну
и ту же величину, то соответствующая им точка в
плоскости годографа перемещается вдоль окружности.
Каждая окружность в диаграмме характеристик
обозначена номером, показывающим сумму номеров эпициклоид
[имеющих разный знак (it)] или разность номеров
эпициклоид [имеющих одинаковый знак (-J- или —)], пересекаю-
Рис. 3-25. Пример расчета
сверхзвукового потока вдоль криволинейной
стенки методом характеристик.
а и в — плоскость потока; б — плоскость
годографа скорости.
"" 26 "'
щихся на данной окружности, и равным удвоенному углу
отклонения потока при расширении от А"= 1 до Я,
отвечающему рассматриваемой окружности.
Ниже приводятся примеры, иллюстрирующие методику
пользования диаграммой характеристик.
Так, на рис. 3-25,а показано обтекание выпуклой
криволинейной стенки плоским сверхзвуковым потоком. Для
приближенного расчета потока заменим плавную линию
стенки ABCD ломаной линией; каждый отрезок этой линии
(АВ, ВС, CD) поворачивается на одинаковый угол, равный,
например, 5°. Перед характеристикой Атг известны
скорость потока Х1 = 1,227 и соответствующий угол ат] =
= 50°37't В плоскости годографа (рис. 3-25,6; этой харак-
121
теристике отвечает точка А', которая в диаграмме
характеристик может быть выбрана произвольно на окружности
10, соответствующей скорости Х1 = 1,227. Возьмем эту
точку на пересечении характеристик _ J .
При переходе в область // поток отклоняется на угол 5°.
Следуя вдоль характеристики -\-52 в плоскости годографа,
находим окружность, проходящую через точку В' (номер
окружности равен 15—сум-ме 5 и 10), и соответствующие
скорость в области /7Я2= 1,344 и угол &т = 42э54'.
Переходя в область /// и далее в область IV,
последовательно находим в диаграмме характеристик точки С и D'
и соответствующие скорости потока Я3 и Я4, а также <хт
и °W
Совершенно аналогично может быть произведен расчет
течения около вогнутой стенки (рис. 3-25,в). Если скорость
перед Dml равна Я1 = 1,539, а углы поворота отрезков
DC, С В, В А одинаковы и, как и в случае «а», приняты
равными 5°, то изменения скорости и направления потока
в областях /, ТУ, /// и IV находим по диаграмме
характеристик, переходя вдоль эпициклоиды-)- 52 от точки П
к точке Аг.
3-8. ПЕРЕСЕЧЕНИЕ И ОТРАЖЕНИЕ ВОЛН РАЗРЕЖЕНИЯ
На рис. 3-26 представлена схема пересечения двух волн
разрежения, образующихся благодаря поворотам стенок
канала на углы Ьг и соответственно 82.
Так как угол b2<Z^i> T0 волна BCD имеет меньшую
интенсивность по сравнению с волной АСЕ. Если принять,
что во всех точках области / скорости одинаковы, то
первые характеристики АС и ВС имеют одинаковый угол
наклона к линиям тока невозмущенного течения. В области
II устанавливается давление, которое может быть
определено по формулам § 3-6. Правее характеристики АЕ
давление /?3 будет меньше, чем р2, так как поток проходит
более интенсивную волну разрежения АСЕ. В зонах /7 и
/// линии тока принимают направление, параллельное
стенкам ААг и ВВг. Вслед за тем линии тока еще раз
пересекают участки волн разрежения DIKF и EFGH, которые
являются продолжением волн АСЕ и BCD. При этом
давление потока снижается до /?4, а скорость
соответственно увеличивается (Я]у > Яш > Яп > Х{).
122
При пересечении волн DIKF и EFGH линии тока
отклоняются в противоположных направлениях, при этом
линия тока а—а поворачивается на больший угол, чем
линия тока b—b. Правее KFG линии тока имеют
одинаковое направление и отклонены на угол Д8 = 5Х — 82 от
первоначального направления, так как пересекающиеся волны
Рис. 3-26. Взаимодействие двух волн разрежения.
имеют различную интенсивность. Результативное отклонение
потока происходит в том направлении, которое диктуется
более мощной волной, в данном случае волной AJKA.
Параметры потока за системой пересекающихся волн
(область IV) могут быть определены по формулам,
приведенным в предыдущих параграфах. Построение спектра
течения и определение параметров в зоне пересекающихся
волн можно осуществить с помощью диаграммы
характеристик.
123
Рассмотрим пересечение двух пар характеристик
(рис. 3-26,6), причем параметры и направление потока
в области / будем считать заданными. Величина и
направление скорости в этой области определяются в той точке
плоскости годографа, в которой пересекаются эпициклоиды
двух семейств. Пусть для рассматриваемого примера число
Я в области / равно 1,522 и соответствующие эпициклоиды
имеют номера -\-202 и — 20 х (_ 2Q2 \ (номер окружности 40).
Направление потока в области / совпадает с направлением
луча О (см. диаграмму характеристик). При переходе
в область // поток пересекает характеристику Ь1У причем
мы предполагаем, что при переходе через эту
характеристику угол отклонения потока составляет 1°. Тогда,
перемещаясь вдоль эпициклоиды 20, находим в плоскости
годографа точку, отвечающую состоянию потока в области //
f^~ 2 ^ Аналогично находим величину, и направление ско-
(+222 \
\-20j-
рости в зоне 77/ после пересечения характеристики аг.
Соответствующие эпициклоиды имеют номера -[- 22 2 и
/4-22 \
— ^i Ьг • При переходе в область IV отклонение
потока происходит в противоположном направлении на ту же
величину (1°). В этом случае, перемещаясь вдоль
эпициклоиды — 22г, находим величину скорости в зоне /V,
которая определяется суммой номеров эпициклоид -\-242
и —22t. Переход в область V из области IV связан с
поворотом потока на угол 1° в противоположном
направлении. Одновременно происходит дальнейшее расширение
потока и сумма номеров эпициклоид увеличивается. Этой
+ 242 п
зоне отвечают эпициклоиды 9 . Скорость потока здесь
составляет Ау —1,558. Последовательный переход через
характеристики разрежения в диаграмме характеристик
показан на рис. 3-26,#. Здесь точки /', П\ ИГ и т. д.
соответствуют областям /, //, III... на рис. 3-26,6.
Рассмотренный метод построения потока в зоне
пересекающихся звуковых волн является приближенным. В основу
метода положено допущение, что при пересечении каждой
характеристики поток поворачивается и расширяется на
одинаковые величины, т. е. все волны имеют одинаковую
интенсивность. В пределах между соседними
характеристиками параметры потока считаются неизменными,
124
Указанным способом можно рассчитать поток в
четырехугольнике CDFE (рис. 3-26,а), в пределах которого
происходят интенсивное расширение газа и деформация линий
тока. В этой области характеристики криволинейны. Если
обе взаимодействующие волны разрежения обладают
одинаковой интенсивностью, то четырехугольник CDFE
является симметричным и отклонения нейтральной линии тока
в зоне IV не происходит.
Таким образом, мы видим, что в результате
взаимодействия волн разрежения происходят расширение и ускорение
потока.
Практический интерес представляют случаи отражения
волн разрежения от стенки или свободной границы струи.
Первый случай показан на рис. 3-27,а. При пересечении
Рис. 3-27 Отражение волны
разрежения от плоской
твердой стенки.
125
первичной волны разрежения ABC линии тока,
деформируясь, поворачиваются на угол 8. Первая характеристика
АВ отражается от стенки, причем элемент отраженной
волны BD пересекает первичную волну разрежения.
Следовательно, вдоль BD давление должно падать, а скорость—
увеличиваться. К такому же выводу мы приходим,
рассматривая поведение линий тока непосредственно у стенки:
здесь при безотрывном обтекании линии тока параллельны
стенке и, следовательно, повернуты на угол 8 к линиям
тока, расположенным за характеристикой AD. Такой
поворот означает разрежение сверхзвукового потока. Отсюда
заключаем, что волна разрежения отражается от плоской
стенки в форме волны разрежения, т. е. сохраняет знак
воздействия на поток.
Легко видеть, что отраженные характеристики
составляют с направлением стенки угол, меньший угла
соответствующих первичных характеристик, так как скорость за
точкой падения увеличивается.
С удалением от стенки угол отраженной
характеристики уменьшается в связи с тем, что характеристика
пересекает область разрежения (на участке BD) и вдоль
характеристики скорость увеличивается. Отсюда следует,
что отрезки характеристик, лежащие в пределах первичной
волны разрежения, будут криволинейными. Лишь за
последней характеристикой DC отраженные характеристики
становятся прямолинейными. Аналогичный вывод можно сделать
и для участков первичных характеристик AU и др.
При переходе через первичную и отраженную волны
разрежения поток расширяется: давление падает, а
скорость соответственно увеличивается. Параметры потока
в зоне // определяются по известным значениям Х1У рх,
#!, 8. Параметры зоны III можно найти, учитывая, что
угол поворота потока в отраженной волне EBCF равен 8.
Тогда после определения Я2, /?2, а2 по тем же формулам
находим Я3, /?3, а3.
Построение отраженной волны можно выполнить,
пользуясь методом характеристик. Так, например, допустим,
что при переходе через характеристику АВ, падающую на
стенку в точке В (рис. 3-27,6), направление скорости
изменилось на 1°. Если скорость перед А В составляет Я1==
= 1,522 (эпициклоиды ^W" » то э зоне АВСА} номера
126
соответствующих характеристик в плоскости годографа
i 20
равны _ 2 (Яи = 1,535). При пересечении отраженной
волны ВС поток возвращается к первоначальному
направлению и, следовательно, в этой области величина и
направление скорости определяются в точке диаграммы
характеристик _ 2 (Я = 1,558).
22!
а)
Рш=РгР*
Рис. 3-28. Отражение волны
разрежения от свободной
границы струи.
Переход из зоны // в зону IV приводит к новому
изменению величины и направления скорости, отвечающих
4- 20
характеристикам _ 2 (Я1у = 1,558).
В результате пересечения отраженной волны BD поток
отклоняется в противоположном направлении (волна разре-
-4- 22
жения) и его характеристики будут ^-^-2-(Яу=1,575).
Наконец, за второй отраженной волной BlDl величина и на-
j_ 24
правление скорости отвечают характеристикам _ 2 (^VI =
127
= 1,595). Положение соответствующих точек в диаграмме
характеристик можно видеть на рис. 3-27 ,#.
Аналогично можно рассмотреть отражение от свободной
границы струи волны разрежения ABE, образующейся при
обтекании внешнего угла (рис. 3-28). Характеристики, не
проникая во внешнюю среду, отражаются от границы,
причем линии тока и граница струи искривляются. Вдоль
первой волны АВ давление равно давлению внешней
среды ра\ за последней волной ри<1ра- Однако
непосредственно на границе струи с внешней стороны давление,
температура и скорость не меняются. Следовательно, если
вдоль отрезка характеристики BF давление падает, то
вдоль FE оно растет. Но отрезок FE пересекает
отраженную волну. Это означает, что при переходе через
отраженную волну давление повышается до значения р
Отсюда заключаем, что волна разрежения от свободной
границы струи отражается, как волна сжатия.
Характеристики отраженной волны сходятся. Это очевидно, так как
угол между отраженными характеристиками и границей
остается одинаковым (в точках В, С, D, Е давление,
скорость и температура одинаковы).
В отраженной волне сжатие газа происходит постепенно
(не скачкообразно) и изменение состояния является изоэн-
тропическим.
Построение процесса в волнах разрежения и сжатия
в диаграмме характеристик показано на рис. 3-28,6. Точки
1\ 1\ 2Г и т. д. позволяют определить величину и
направление скорости в областях потока 1,1,2 и т. д. (рис. 3-28,а).
Пересекая обе волны, поток поворачивается на угол,
равный 28.
Таким образом, мы видим, что отражение волн
разрежения от свободной границы происходит с изменением
знака воздействия на поток. В результате взаимодействия
волны разрежения с границей происходит отклонение
струи.
Принципиальное различие между свойствами отраженных
волн от стенки и свободной границы объясняется в
конечном итоге тем, что вдоль обтекаемой стенки распределение
параметров потока диктуется самим потоком, тогда как на
свободной границе оно задано внешней средой.
Рассмотренные примеры взаимодействия волн отнюдь
не исчерпывают того круга задач в этой области, с кото-
128
рым приходится сталкиваться в практике эксперимента
и в теоретических исследованиях. Однако эти примеры
могут быть положены в основу изучения и других, более
сложных случаев.
ГЛАВА ЧЕ ТВЕРТАЯ
СКАЧКИ УПЛОТНЕНИЯ
4-1. ОБРАЗОВАНИЕ СКАЧКОВ УПЛОТНЕНИЯ
В предыдущих главах были рассмотрены свойства изо-
энтропического газового потока. При этом мы изучали
механизм распространения в потоке таких возмущений,
которые не вызывают изменения его энтропии. Перейдем теперь
к изучению конечных возмущений, распространение которых
сопровождается ростом энтропии газового потока.
с,>а
Рис. 4-1. Сверхзвуковое течение газа
в область повышенного давления.
С этой целью рассмотрим движение сверхзвукового
потока вдоль плоской стенки АВ, вытекающего в среду с
повышенным давлением (рис. 4-1). Слева от точки В
скорость будет с19 давление рг и температура 7\. Правее
точки В (за линией ВС) поддерживается давление /?2,
более высокое, чем рг. Если разность давлений p2~Pi мала,
то в точке В возникает слабая волна сжатия BKV
9 М. Е. Дейч 129
Если изменение давления в точке В станет конечным,
то, как показывает эксперимент, волна переместится в
положение ВК и будет обладать не бесконечно малой, а
конечной интенсивностью. По мере увеличения давления р2
линия ВК будет поворачиваться относительно точки В
влево {ВК\ ВК" и т. д.). При переходе через волну ВК
газ сжимается и поток отклоняется на некоторый угол о
вверх от направления невозмущенного потока АВ. С ростом
с, (М,)
Р, Ъ
А
п
1 I
I
1
'///
III
1,
'в
г/ /
t
а;
' ^ -'
"Л* <Л
<%Тг
V
Рис. 4-2. Обтекание сверхзвуковым потоком
внутреннего угла.
/?2 сжатие газа в волне ЯК и угол отклонения 8
увеличиваются.
Волна В К называется плоским косым скачком
уплотнения или плоской ударной волной. При
переходе через такую ударную волну поток испытывает
скачкообразные изменения давления, скорости и других
параметров. Положение скачка определяется углом р между
плоскостью скачка ВК и первоначальным направлением
потока АВ (рис. 4-1).
Образование косых скачков уплотнения можно
проследить также на простейшем примере обтекания стенки ABC,
повернутой в точке В на некоторый конечный угол 6
навстречу потоку (рис.4-2).
Благодаря такому повороту стенки сечение струйки
уменьшается и она суживается. В сверхзвуковом потоке
это приведет к повышению давления (р2^>рг). Причем
повышение давления происходит скачкообразно при
переходе через поверхность ВК, являющуюся поверхностью
130
скачка. Можно показать, что при обтекании
рассматриваемой Стенки непрерывный переход от параметров в области
АВК к параметрам в области КВС физически невозможен.
Действительно, границей возмущения для области АВКг
должна быть звуковая волна ВКХ, угол наклона которой
к вектору скорости сх будет <zml = arc sin — . Вторая
граница возмущения ВК2 имеет угол наклона а = arc sin —.
Так как с2<^с1 и а2">аи то <*m2>aml. Характеристика
ВК2 оказывается в невозмущенной области АВКг и линии
тока должны были бы иметь форму, показанную
пунктиром, что физически совершенно нереально.
Можно предположить, что косой скачок занимает
среднее положение между волнами ВКХ и ВК2\ тогда угол
косого скачка (3 связан простым приближенным
соотношением с углами aml, am2 и 8:
Мы рассмотрели стационарный случай образования косого скачка
уплотнения, неподвижного относительно очага возмущения.
Такой случай соответствует набеганию плоского сверхзвукового
потока постоянной скорости на бесконечный клин или движению
плоского клина в среде с постоянной сверхзвуковой скоростью. При
нестационарном движении скачки уплотнения могут возникать и при
дозвуковых скоростях движения. В общем случае нестационарного
движения ударная волна, являющаяся результатом конечного
уплотнения или разрежения потока, может перемещаться относительно
твердого тела, которое вызвало ударную волну.
Проанализируем условия образования таких движущихся ударных
волн. Пусть в трубе постоянного сечения находится поршень (рис. 4-3).
Толчок поршня вызывает слева слабую волну разрежения т' — /г', а
справа слабую волну уплотнения т — п. Продолжая увеличивать
скорость поршня толчками, мы создадим ряд слабых волн возмущений
(т{ — п]9 mi — пх и т. д.), перемещающихся в потоке газа в
противоположных направлениях от поршня, каждая со своей скоростью,
соответствующей скорости звука в данной области.
Нетрудно видеть, что справа каждый толчок повышает давление
газа на малую величину, а слева — снижает его. Следовательно, в
области /// давление и температура будут выше, чем в областях // и /,
а следовательно, и скорость звука CLniy an^> av Наоборот, в
областях //', ///' скорости звука будут меньше, чем в области /' (аш <
<С #п <[ aj). Следовательно, справа от поршня слабые волны уплотне.
ния нагоняют друг друга, слева волны разрежения отстают друг от
9*
131
Через некоторый промежуток времени волны справа сольются в
одну волну, фронт которой будет границей между невозмущенной и
возмущенной областями.
Рис. 4-3. Распространение слабых возмущений
в трубе.
4-2. УРАВНЕНИЯ КОСОГО СКАЧКА
Как и ранее, будем рассматривать установившееся
течение газа без теплообмена с окружающей средой и без
трения. Предположим, что в некоторой точке
сверхзвукового потока возник косой скачок уплотнения (рис. 4-4).
Параметры газа до скачка обозначены индексом 1, а за
скачком — соответственно индексом 2.
Рассмотрим движение газа по линии тока ABC,
пересекающей плоскость косого скачка в точке В. Как указывав
лось, при переходе через косой скачок линия тока
деформируется, отклоняясь, на некоторый угол б. Скорость до и
после косого скачка можно представить составляющими,
132
нормальными к плоскости скачка (сп1 и сп2) и касательными
к ней (сп и ct2) и, таким образом, построить треугольники
скоростей до и после скачка.
Очевидно, что
с2=с2 4-с2
И
с2—с2 -4-с2
Для решения основной задачи о косом скачке, которая
сводится к установлению связи между параметрами до и
после скачка и к
определению потерь,
возникающих при переходе через
скачок, используем
основные законы механики.
Закон сохранения
массы — уравнение
неразрывное и—для двух
сечений трубки тока до и
после скачка может быть
записано в следующем
виде:
Закон сохранения импульсов — уравнение
изменения количества движения — в проекции на нормаль
к плоскости косого скачка дает:
Pi-P2 = ?iCnl(cn2~cnl),
или
A+Piu=A + P.4- (4-2)
В проекции на плоскость скачка получим:
так как давление вдоль всех поверхностей,
параллельных поверхности скачка,остается постоянным. Следовательно,
cti = ct2 = cr (4"3)
Рис. 4-4. К выводу основных
уравнений косого скачка.
133
Таким образом, касательные составляющие скоростей
до и после плоского косого скачка уплотнения одинаковы.
Закон сохранения энергии — уравнение Бернул-
ли — может быть использовано в любой известной нам
форме. Рассматриваемое течение происходит без
теплообмена с окружающей средой и, следовательно, полная
энергия потока сохраняется неизменной:
! gl _, k J?* __ <£ k + 1
9 I h — 1 п.
ИЛИ
с\
2
1 k
1 k-\
сп\ ,
2 ~\h
Pi
Pi
k
' — 1
2 k-
& — 1 pi 2 ' & — 1 p2
2 2
°* £ + 1 C±_
~~" 2 k — \ 2 *
(4-4)
Найдем связь между скоростями до и после скачка.
Преобразуем уравнение (4-2); с учетом формулы (4-1)
получим:
А rV^-W^+ЛУ (4-2а)
Из уравнения энергии (4-4) выразим отношение
давления к плотности:
и
/?2 & — 1 / ^2 & + 1 „2 „2
р2 2/г
■(<г:-±т-4-«!)- ("•«)
Подставив (4-4а) и (4-46) в уравнение (4-2а), получим:
2 1 Z /С 1 Z / Z I „Z n /П /Zl Z
После простых преобразований приходим к уравнению
2 & — 1 2 /л г\
CnlCn2 = a*-~k+-\Ct' ^
Формула (4-5) устанавливает связь между нормальными
составляющими скоростей при переходе через косой скачок
134
и является исходной для получения зависимостей между
другими параметрами течения до и после скачка.
Заменим в формуле (4-5) al по уравнению
2 k — l/2i 2ч| 2 2
«• =)ЙЛ (*»i+C< )+ft+"l Л1 =
k—l,2 | 2 ч | 2 2.
тогда
^=^(4+^W («)
>% — 1 / С/м2 | 2 \ 2 /у1 ~ v
C»lCn2=k + T \^- + k=l) "I ' (4"63)
или, выражая скорость звука через давление и плотность
а2 — k — , получим:
AfiL+J_LWA+J.^ (4-7)
Pi ^ a? ^-lj Ра^Л| -Г/5-lJ- ^
Воспользуемся уравнением неразрывности (4-1); возведя
в квадрат обе части этого уравнения:
Л2 Л2 2 Л2
Pi ^1 = Р2 Сп2
и заменив
получим:
t. Р\ и Рг
Л1 a2
„2
С/г1
■iPi —
а\
=АРа
9
6/7?
2
а2
(4-8)
Исключая последовательно из уравнения (4-7) с помощью
уравнения (4-8) рх и р2 или рх и /?а, приходим к
выражениям
с1\ , 2 \ <£, 2 / 4 2 \ 4 2 п m
^+,—]^Л=^Т+,—!]Т^ (4-9)
135
1 +
*-» 4 ) рг
Из уравнений (4-6) и (4-ба) можно получить:
п2
сл2 _
а-2
Сп\
«1
26
, 2
'*-1
* ,
(4-10)
(4-11)
Из треугольников скоростей на скачке следуют
очевидные соотношения:
^2 = ^2 sin у;
^ = ^ cos (3 = £2 cos y,
(4-12)
где
Тогда из уравнения (4-11) совместно с формулами (4-12)
можно получить:
М? +
yKJ2 26
1 vk — \
М\ cos2 ■
| у 1
kZT\ /Vjf sin2 ^ — 1 —g— A^?sin2p+1
или
k — 1
a;=a; cos8
l-jqrrMcos^
X? Sin2 $
, (4-1 la)
(4-116)
Уравнения (4-9) и (4-10) совместно с уравнениями (4-11)
и (4-12) после несложных преобразований дают искомые
зависимости:
p2_k—\ I 2k
(£-jA«;si!i'p-i)=
k— 1
26
(4-13)
136
k+ 1
Ц2С,„8 ft
(4-14)
P2 _
Pi
2
&— 1
k—l
i "
1 1
M?sin2B ~r
X? sin2 §
1 1-^ nr>c2 ft
J—^+1 Al^-P
Из уравнения состояния легко найти отношение
абсолютных температур до и после скачка:
После подстановки — и — получаем:
(4-15)
Формулы (4-5), (4-11) — (4-15) выражают изменения
параметров газа при переходе через косой скачок
уплотнения в зависимости от показателя k, скорости потока до
скачка Мг и угла косого скачка (3. Эти формулы вместе
с тем вскрывают основные физические свойства косого
скачка. Так, из формулы (4-13) можно заключить, что
нормальная составляющая скорости до скачка больше
критической скорости. Действительно, так как —>1 и
М\ sin2 р = -^- , заключаем, что
а\
и, следовательно,
cn\ -^
«1
Нормальная составляющая скорости за скачком меньше
критической скорости:
Из формулы (4-13) следует, кроме того; что угол
косого скачка больще угла характеристики amlf
137
При
P=ami = arcsini;
Pt Pi Tt
В этом случае косой скачок вырождается в слабую
(звуковую) волну уплотнения (слабый скачок) и угол
отклонения потока стремится к нулю.
Связь между углами |3 и Ь устанавливается по
уравнению (4-6), которое можно преобразовать к виду:
f*L — k—L±(] 1 . 2 а* \
Но на основании формул (4-12)
сп2 сп2 ct tg y tg (ft — 8)
cn\ ~ ct ' cn\ ~ t&P _ 4*
(4-16)
Следовательно,
tg(P — a) _*-i/i i
te 8 Л + l "f" ,
;+H I /5 1 Aff Sin* P
Вспоминая, что
получим:
tg(R_8)—JgP-te*
»' = , Л*"'! , • (4-«4
sin2M + 1
tg
На рис. 4-5 представлены графики 8ф) при различных
значениях Ях для А = 1,3. Отметим, что с увеличением
скорости невозмущенного течения увеличивается
максимальный угол отклонения потока 8 . Следует подчеркнуть, что
в соответствии с двойственным решением уравнения (4-17)
одному значению угла -отклонения потока 8 соответствуют
два различных значения р. Опыт показывает, что плоскому
косому скачку отвечает только меньшее значение р.
13§
Выше в предположении, что скачок занимает среднее
положение между характеристиками невозмущенного и
возмущенного потоков, была дана формула
~-rKl+am2 + b)-
(4-17а)
Сравнение этой формулы с точным выражением (4-17)
для нескольких значений Х1 приведено также на рис. 4-5.
Кривые показывают, что с увеличением скорости перед
скачком Хх расхождение между результатами расчета по
60 j 70 80 SO
Рис. 4-5. Зависимость между углом отклонения потока
и углом скачка при различных скоростях
невозмущенного потока (для k = 1,3).
точная формула (4-17); приближенная формула
(4 17а).
точной и приближенной формулам увеличивается. Величина
погрешности зависит также от 6.
Из уравнения (4-17) следует, что В = 0 при р = а
ml
при р = -£-. Таким образом, кривая 8 = 8(р) имеет макси-
139
мум, положение которого определяется обычным способом.
Продифференцировав уравнение (4-17) и приравняв
производную нулю, после преобразования получим:
sina« =-
km
k+ l
АГ
1 +
+ |A+l)(l+~
М
k+ 1
16 К
(4-18)
где рт— угол косого скачка, соответствующий
максимальному углу отклонения потока 8
Отсюда следует, что при Мх-=\ угол p^=-|-} а при
Мх = оо угол Pm = arcsin ( у ~^ъ~) * ^ля пРомежУточных
значений угол Рш с ростом Мх вначале уменьшается,
а затем несколько возрастает.
Уравнение (4-11а) позволяет проследить изменение
скорости потока за косым скачком М2 в зависимости от Мг
и р. С увеличением р (при постоянном Мг) М2 уменьшается:
перепад скоростей в скачке увеличивается.
При некотором значении р = [5* скорость за скачком
становится звуковой (М2=1). При дальнейшем увеличении р
течение за скачком будет дозвуковым.
Величину р^ можно определить по уравнению (4-11а),
подставляя /И2=1. Тогда после преобразований получим:
sin2p* =
kMi
+ |/(*+1)(!
9 + k
16
fe + 1
16
м
')
(4-19)
Заметим, что при М1=1 угол р^ = рт = _; при Мх=
= оо угол p^ = pw = arcsin(|/^J.
Последнему значению р* отвечает максимальный
угол 8 , определяемый из (4-17):
8 =ъгс\<у( 1 V
140
Для значений Mx<ioo угол рт>р* и, сЛедовагелыф,
М2т<М- Это означает, что при максимальном угле
отклонения потока скорость за скачком будет дозвуковой. Так
как, однако, для всех Мх углы (Зт и [$# весьма близки, то
в первом приближении можно считать, что максимальный
угол отклонения для каждого значения скорости
невозмущенного потока достигается при звуковой скорости за
скачком (М2 ^ 1).
Мы установили, что параметры течения за косым
скачком зависят от угла косого скачка (3. При увеличении (3
давление, температура и плотность газа за скачком
увеличиваются (параметры потока до скачвд предполагаются
неизменными), а безразмерная скорость уменьшается. Угол
отклонения потока, как было показано, вначале
увеличивается (при (3<рт), а затем уменьшается (при Р>Рт).
В частном случае р = -|- изменения параметров в скачке
оказываются максимальными, а угол отклонения 8 = 0.
Такой скачок расположен нормально к направлению
скорости невозмущенного потока и называется прямым
скачком.
Прямой скачок является частным случаем косого скачка;
основные уравнения прямого скачка получаются из формул
(4-11) — (4-15) после подстановки (3 = -|-.
Изменения давлений и плотностей в прямом скачке
найдем из формул (4-13) и (4-14):
ь=т^(гЧК- 0= ' /V ; (4-20)
рх k+l\k — \ I J ^12' v ;
17= *-, , = Ъ (4-21)
отношение температур — из формулы (4-15):
H&)'(&«-%^-k+1)- <4-22>
141
Безразмерная скорость за прямым
получена по формуле (4-11а):
9 2
M2=-2k ~
или по формуле (4-116)
А1Я2 = 1 ,
т. е.
схс2 — а .
Мы видим, что произведение скоростей до и
после прямого скачка равно квадрату
критической скорости. Отсюда прежде всего следует, что
скорость газа за прямым скачком всегда меньше
критической скорости (c2<aj.
Формулы (4-20) — (4-23) показывают, что интенсивность
прямого скачка увеличивается с ростом скорости
невозмущенного потока Мх (или Ях). Отношение плотностей при
максимальной скорости стремится к конечному пределу
11111 Pl k — v
а отношения давлений и температур возрастают
безгранично.
Необходимо иметь в виду, однако, что при больших
сверхзвуковых скоростях, когда в результате скачков
температура и давление газа повышаются весьма сильно,
полученные формулы являются приближенными, так как они
не учитывают развивающейся зависимости теплоемкости от
температуры, диссоциации молекул и отклонения свойств
реальных газов от свойств совершенного газа, состояние
которого описывается уравнением (1-1).
Формулы косого скачка могут быть преобразованы к виду,
удобному для анализа влияния физических свойств газа (показателя k).
с
С этой целью введем безразмерную скорость £ = и выразим
^макс
142
скачком может быть
(4-23)
(4-24)
(4-24а)
показатель изоэнтропического процесса через максимальную скорость
\макс & — 1 •
Хмакс + 1
k = :
макс
Заменив k в уравнениях (4-13) и (4-14) его значением, получим:
Р-2 \чакс~"~ 1 Sin1
\макс — l Sin2 В 1
X2 1 X2
дмакс —jr- — 1 макс
(4-1 За
i2
.макс
Й
(4-14а
1 + ~9~
g I sin2 p
Скорость за скачком выражается уравнением [формула (4-116)]
л2 £2
л1 ?i
где
-« cos2?
__ J? 1
"макс
Как видно, каждая из приведенных формул содержит два
сомножителя, один из которых зависит только от ?j и g и не зависит от /г,
а второй является функцией только к.
Такая структура формул скачка позволяет приближенно оценить
влияние изменения физических свойств газа и производить расчет
параметров косого скачка при различных постоянных значениях k*.
Для определения других параметров скачка можно пользоваться
очевидными соотношениями. Отношение температур
г, 1-й
Тг 1-Й
Угол скачка
1-е'
2
tg?= П + -р—il^tg(p-e)^
макс
Формулы даны М. В. Поликовским.
143
т—i—I—i—I—I—i—I—I—i—i—I—i—i—I—i—i—I—i—r
«I ....
«ST
oo
144
Для расчета скачков при различных k могут быть построены
графики p2IPi в зависимости от £,, р (или д) и k (рис. 4-6). Влияние k
можно оценить при одинаковых р или д. Сравнение при одинаковых р
показывает, что с уменьшением k интенсивность скачка возрастает.
4-3. УДАРНАЯ ПОЛЯРА
можно
С этой
скачке
Зависимость между параметрами на скачке
в весьма удобной форме представить графически,
целью рассмотрим треугольники скоростей на
(рис. 4-7).
Расположим вектор скорости до скачка сх по оси х
(отрезок OD). Отрезки OF и FD представляют собой
соответственно касательную ct и нормальную спХ
составляющие скорости до скачка. Зная угол отклонения потока 8,
Рис 4-7. Треугольники скоростей на скачке.
проведем линию вектора скорости за скачком с2 до
пересечения с отрезком FD. Точка пересечения (точка
Е)определяет величину вектора с2, а отрезок EF выражает
нормальную составляющую скорости за скачком.
Вектор скорости с2 можно представить двумя другими
составляющими: и2 и v2. Компоненты и2 и v2 являются
проекциями с2 на направление скорости потока перед, скачком
и на нормаль к этому направлению.
Найдем уравнение кривой, описываемой концом вектора
скорости за скачком е2, при постоянном значении вектора
скорости перед скачком сх и переменных значениях угла
поворота потока за скачком 6.
Выражая это уравнение в форме связи между и2 и и2У
мы получим кривую скорости за скачком в плоскости
годографа скорости.
№ ME. Дейч
145
Для получения искомой зависимости используем
основное уравнение косого скачка (4-5). Подставив в это
уравнение значения сп] и ct из формул (4-12), получим:
c1sinp(Clsinp--E^F)=a;-^|C;cos»p, (4-25)
так как (рис. 4-5)
v2
Сп2—Сп\~~^Ц '
Преобразуем уравнение (4-25) к следующему виду:
с^ cos2 р tg2 р — ^лу2 tg р = а; — |^i^j cos2 p.
Отсюда, имея в виду, что
получим:
с] (сх — и2)2 — сх (с, — и2) [vl + (ct — u2)2]=z
2 Г 2 I / \21 ^ 12 2
==а ^[v2 + (cl—u2)2]—rpiclvr
Окончательно
а\
vl = (Cl-uuy 9 "2~ Cl . (4-26)
77 + F+\ Cl ~~щ
Кривая, отвечающая уравнению (4-26), представленная
на рис. 4-8, называется ударной полярой. Кривая при
надлежит к классу гипоциссоид. Ударная поляра может
быть широко использована для расчета косых скачков
графоаналитическим методом и для выяснения некоторых
особенностей таких скачков.
Обратимся прежде всего к предельным значениям v2,
даваемым уравнением (4-26).
Легко видеть, что v2 = 0 при
и2 — с j
и
и2с1 =а .
т
Первый случай (и2 — с^) отвечает бесскачковому
процессу; косой скачок уплотнения переходит в волну
слабого возмущения (характеристику). Касательные к гипо-
циссоиде в точке D расположены под углом aml = arcsin -тт-
Рис. 4-8. Ударная поляра в плоскости
годографа.
к вектору сх. Заметим, что эта точка является
одновременно точкой диаграммы характеристик и ударная поляра
здесь переходит к эпициклоиду.
Второй случай (и2с1=а) характеризует переход косого
скачка в прямой скачок, угол которого ^ = ~. Этому
случаю на гипоциссоиде отвечает точка А.
Из уравнения (4-26) следует, что v2 может обратиться
в бесконечность при
Очевидно, что ветви гипоциссоиды асимптотически
приближаются к прямой, проведенной параллельно оси v на
расстоянии ОЯ = -
\-. . сх от начала координат. Эти
ветви не имеют физического смысла, так как они дают
значения скорости за скачком {точка Е3 на рис. 4-8),
большие, чем до скачка. Таким условиям отвечал бы скачок
10* 147
разрежения, но скачков разрежения существовать не моЖе!\
Отбрасывая внешние ветви гипоциссоиды как физически
нереальные (см. ниже), мы замечаем, что ударная поляра
в пределах между крайними точками А и D дает два
значения для вектора скорости за скачком.
Обычно плоские скачки реализуются при значениях
вектора скорости потока за скачком, отвечающим точкам Е2
(рис. 4-9,а). Второе значение скорости с2, соответствующее
Рис 4-9 Отрыв и искривление скачка
уплотнения
точкам £\, в плоском скачке может быть реализовано лишь
при специальных условиях.
Рассмотрим сверхзвуковое течение газа ёдоль стенки
LBC (рис. 4-9,а), постепенно увеличивая угол отклонения
потока 8 (угол поворота стенки в точке В), При малых
значениях 8, близких к нулю, возмущение потока невелико
и скорость за скачком с2 близка к скорости до скачка сг.
По мере увеличения 8 точка Е2 (рис. 4-9,6) перемещается
вдоль ударной поляры от D к г, где точка г дает скорость
за скачком М2 = 1. Дальнейшее весьма небольшое
увеличение 8 приводит поток за скачком к состоянию,
определяемому точкой /С. Здесь течение за скачком уже
дозвуковое (М2<^\) и S достигает максимального значения 8т.
На рис. 4-10 представлено обтекание клина
сверхзвуковым потоком. Если половинный угол раствора клина 8
меньше 8^ для данной скорости Ми то на носике клина
возникают два прямолинейных косых скачка: АВ и Л5П
образующих так называемую головную ударную
волну клина.
При дальнейшем увеличении угла 8>8т скачок
отходит от передней точки и искривляется (рис. 4-9,в). Это
148
объясняется тем, что скорости распространения
возмущений становятся больше скорости потока. Действительно,
увеличивая угол поворота стенки 8, мы тем самым
увеличиваем поджатие потока, т. е. его давление, плотность
и температуру. Вместе с тем растет и скорость
распространения возмущений, равная скорости звука
возмущенного потока a2=\fkgRT2. При S>^m эта скорость
становится больше скорости потока и поэтому возмущения
проникают вперед по потоку. Однако при удалении от
стенки ВС (рис. 4-9,в) давление, плотность и температура
Рис. 4-10. Обтекание клина сверхзвуковым потоком.
будут уменьшаться; вместе с тем будет падать и скорость
распространения возмущений. На некотором расстоянии от
стенки возникнет геометрическое место точек PQ (рис. 4-9,#),
в которых скорость распространения возмущений снизилась
до скорости потока. Очевидно, за пределы этой
поверхности возмущения, вызванные стенкой, не смогут
проникнуть, так как они будут сноситься потоком назад.
Поверхность PQ отделяет зону невозмущенного потока от
зоны возмущенного потока и представляет собой
отошедший скачок уплотнения.
Следовательно, если 8 > 8^, то плоский косой скачок
сменяется криволинейным скачком (рис. 4-10), который
располагается не на носике клина, а на некотором расстоянии
перед ним. Это расстояние зависит от скорости
невозмущенного потока М! и 5. С ростом Мг скачок приближается
к носику тела. С увеличением угла отклонения при 8>8т
скачок удаляется от тела. Обтекание скругленного
носика тела сверхзвуковым потоком всегда будет
происходить с образованием криволинейной головной волны, отор-
149
вавшейся от носика, а расстояние межДу волной и носиком
для центральной линии тока будет зависеть от скорости
Мх и от формы носика.
Заметим, что при 5 = 8^ поток за скачком дозвуковой
и М2 несколько меньше 1 (точка К на рис. 4-9,6). Так как
для нейтральной линии тока, разветвляющейся в точке А
(рис. 4-10), Р = -7г и 5 = 0, то элемент скачка,
пересекающий эту линию, должен быть прямым. Скорость потока
за элементом прямого скачка определится точкой А на
ударной поляре (рис. 4-96,). Поток за скачком на этой линии
тока всегда дозвуковой.
Все участки скачка, кроме центрального, расположены
под различными углами к вектору скорости
невозмущенного потока $i<C~2' •
Рассматривая такую искривленную головную волну,
состоящую из большого числа малых прямолинейных
элементов, можно убедиться, что по мере удаления от
центральной линии тока уменьшается и угол наклона
элементов скачка р/# При этом можно воспользоваться ударной
полярой для расчета потока за скачком для каждой линии
тока в отдельности. Участку головной волны KL отвечают
точки ударной поляры от Л до г, в которой скорость
М2 = \. На этом участке поток за криволинейным скачком,
будет дозвуковым. Следовательно, если головная волна
отрывается от тела, то в некоторой области, прилегающей
к носику тела, течение будет дозвуковым (эта область на
рис. 4-10,6 заштрихована), а линии тока здесь будут иметь
разную кривизну. В различных точках за скачком давления
будут различными.
По мере удаления от точки К уменьшается наклон
элементов скачка и вместе с тем уменьшается интенсивность
скачка. В некоторой точке L скорости за скачком
становятся звуковыми. Выше этой точки состояние за скачком
определяется отрезком ударной поляры от г до D. На
бесконечном удалении от тела криволинейный скачок
вырождается в слабую волну уплотнения, которой отвечает точка
D на ударной поляре.
Таким образом, если происходят искривление и отрыв
скачка от носика тела, то каждая точка ударной поляры
характеризует состояние за скачком только для одной
150
линии тока, а не для всей области течения, как это имеет
место в случае плоского скачка. Следовательно,
криволинейному скачку в целом соответствует не одна точка ги-
поциссоиды, а вся ее ветвь AD.
В табл. 4-1 приведены значения 8т для двух значений
^=1,4 и 1,3. Значения Ът зависят от числа М1(Х1) и
физических свойств газа (k) и могут быть определены по
уравнению (4-17) при условии подстановки в него р —рт
из уравнения (4-18).
Таблица 4-1
Значения максимальных углов отклонения потока в плоском
косом скачке уплотнения
>ч
1
1,2
1,3
1,4
1,5
1,6
к = 1,4
ьт
0
5°25'
9°41'
13°55'
18°00'
2Г41'
k= 1.3
ьт
0
5°14'
9°30'
13°24'
17°30'
2Г15'
К
1,7
1,8
1,9
2,0
2,2
2,4
k = 1,4
ът
25° 15'
28°55'
32°00'
35° 00'
40° 15'
45°00'
k= 1,3
ьт
24°42'
28°18'
ЗГЗО'
34° 18'
39°40'
43°50'
4-4. ИЗМЕНЕНИЕ ЭНТРОПИИ В СКАЧКЕ
Как известно из термодинамики, для элементарного
процесса без теплообмена с окружающей средой,
происходящего в совершенном газе, изменение энтропии
определяется уравнением
так как
т — р р '
то
х р ' р р р k — \\p ру
Интегрируя это уравнение, получим
k — i V Pi н )
хь\
или
^=^?AV- <4-27>
Для обратимого (изоэптропического) процесса Д$ = 0 и
Посмотрим, как изменяется энтропия при переходе через
скачок уплотнения. Исключив из уравнений (4-13) и (4-14)
Afj sin2 p, получим:
!_*+!. Ра.
р2 — k — Г р,
pi *-i
Произведя расчет, легко убедиться, что для скачка
уплотнения, для которого — >1, всегда
Pi
Pl[?l)
и, следовательно, согласно (4-27) при переходе через
скачок энтропия газа возрастает.
Увеличение энтропии при переходе через скачок
объясняется необратимым характером изменения состояния газа
в скачке, „ударным* характером процесса. В результате
такого процесса часть кинетической энергии газа
необратимо переходит в тепло; при отсутствии энергетического
обмена с внешней средой внутренняя энергия потока-
необратимо возрастает. Кривую, характеризующую процесс,
протекающий по уравнению (4-28), называют ударной
адиабатой.
Для скачка разрежения — <Ч и — ( —)<1 получаем
As<0, что невозможно при отсутствии энергетического
обмена с внешней средой, так как противоречит второму
закону термодинамики. Отсюда следует, что скачки
разрежения в энергетически изолированном течении не могут
возникнуть, так как это противоречило бы второму началу
термодинамики. Однако, как показано в гл. 3, в
сверхзвуковом течении волна разрежения с непрерывным паде-
152
As = -t ; 111
X<'
нием давления представляет собой вполне устойчивое
явление; энтропия при переходе через такую волну сохраняется
неизменной.
Изменение энтропии в скачке уплотнения может быть
выражено через параметры Мг и р путем замены в
уравнении (4-27) ^ и — по формулам (4-13) и (4-14); тогда
(^Г(А«;--р-.)х
v-.i^-1)*]- (4-29>
Уравнение (4-29) позволяет заключить, что изменение
энтропии в косом скачке зависит от скорости
невозмущенного потока Мх и угла косого скачка р. При
неизменной скорости Мг энтропия при переходе через скачок
меняется в соответствии с изменением угла р. Если скачок
прямолинейный и, следовательно, вдоль скачка р сохраняет
постоянное значение, то для всех линий тока,
пересекающих скачок, изменение энтропии будет одинаковым. Если
же скачок криволинейный, то увеличение энтропии для
каждой линии тока будет различным, так как вдоль скачка
угол р меняется. Это означает, что за криволинейным
скачком поток будет вихревым; за прямолинейным скачком
течение остается потенциальным.
Пользуясь уравнением (4-28), можно рассмотреть
изменение состояния газа при переходе через слабый скачок.
Полагая рг==р, р2 = р и считая, что давление и плотность
в скачке изменяются на бесконечно малую величину, т. е.
p2 = p + dp; р2 = р + ф;
из (4-28) получим:
P + dP= р^гг(р + ^р)
Р l ллч k+X '
(p + tfp) — jzri р
Отсюда, пренебрегая бесконечно малыми второго
порядка, приходим к уравнению изоэнтропического процесса:
Р Р
153
Таким образом, изменение состояния ё скачке бесконечно
малой интенсивности (слабый скачок) является изоэнтропи-
ческим.
4-5. ПОТЕРИ В СКАЧКАХ УПЛОТНЕНИЯ. ПОСТРОЕНИЕ
ПРОЦЕССА В ДИАГРАММЕ i-s. СКАЧКИ УПЛОТНЕНИЯ
В РЕАЛЬНОМ ГАЗЕ
Рассмотрим более подробно энергетические
преобразования в скачках. Предполагая энергетически изолированное
течение, заключаем, что полная энергия потока при
переходе через скачок не меняется. Это значит, что
С\ I k А = с2 | k р2
2 ^к— 1 рх 2 *k — 1 р2 '
или, пользуясь параметрами полного торможения,
£*! = ***. (4-30)
РОЖ Р02 Ч
Условие (4-30) можно заменить эквивалентным условием
постоянства энтальпии торможения при переходе через
скачок:
Л,- = *о1 = *о> (4"30а)
или при
с„ = const; )
т ' = т -т (4"30б)
1 01 л 02 1 0* /
Имея в виду эти условия, рассмотрим процесс скачка
в диаграмме is (рис. 4-11). Зная давление торможения до
скачка р01 и энтальпию торможения /0, найдем в
диаграмме is точку Ох, характеризующую состояние изоэнтропи-
чески заторможенного газа до скачка. По известной
скорости потока до скачка сг или давлению рх находим
точку D, которая определяет состояние движущегося газа
перед скачком. В скачке статическое давление потока
увеличивается до р2. Если известен угол отклонения потока 8 и,
следовательно, (3, то состояние газа за скачком
определено (точка Е2 на рис. 4-11), так как по формуле (4-29)
можно найти приращение энтропии As*. Заметим, что
линия, соединяющая точки D и Е% на рис. 4-11, не
характеризует изменения состояния газа в скачке, так как в диаг-
* Рассматривается совершенный газ.
154
Ji* №
Рис. 4-11. Скачок уплотнения
в тепловой диаграмме.
Сс
0,15
0,1
Q/B
1 П
ljU
°fl
Of—
-0,4—
-0,2
V
ч
\
\
\
\
J
So
4
\
\
\
k4
N
4
\/
JLV^
/ ?
/\
4>ч,/
~1
***>£
f v
V
s/1
*s^
\ \\ к 1 \i
20 30
40
SO 60 Ю 00
90
Рис. 4-12. Коэффициенты потерь и отношение давлений
торможения на скачке в зависимости от угла р и
скорости невозмущенного потока.
155
рамме is неквазистатические процессы могут быть
представлены только начальной и конечной точками процесса.
Если поток за скачком изоэнтропически затормозить, то
состояние полного торможения характеризуется точкой 02,
в которой легко находится значение/?02. Если предоставить
теперь потоку возможность изоэнтропически расшириться
до давления перед скачком, то его состояние будет
определено точкой Ё2 . Скорость газа при этом может быть
вычислена по уравнению энергии:
~2f = io — '2 = //о2 ккал/кг,
где #02— изоэнтропический перепад энтальпий за скачком.
Величину #02 можно рассматривать как сумму
где #0к — кинетическая энергия потока за скачком:
и -ii-
#0п — изменение потенциальной энергии потока в скачке:
Очевидно, что
_ А(с'22-4)
Л0п 2g
Ас\
^02 \ " 01»
где #01=:—^ изоэнтропический перепад энтальпий до
скачка.
Потери кинетической энергии в скачке будут:
где Д/г легко определяется по диаграмме is как разность
энтальпий i2 — ix.
Потерю энергии нетрудно связать с основными
параметрами скачка. Выразим
"•--.ЗД'-ЙЛ-
156
k~\
"~=^t,v- mk ]=>--'>■
k-\
k-\
Следовательно,
так как
P0L=1P02
Yoi Y02
Введем понятие коэффициента потерь энергии в скачке:
тогда после подстановки Я01 и Яоа получим:
2 1
le— k-\ M2
или с помощью (2-21)
4 + 1 1
/W
— 1
(4-32)
(4-33)
С =
U?
1
КйГ-1]- <4-33а>*
Отношение -^ = г0 характеризует изменение давления
Рог
полного торможения в скачке. Эту величину можно
представить в зависимости от параметров скачка Мх и р.
Так как
Рог Рг Ро2
Pi ~ Px Рг"
то из (4-13) и табл. 2-1 получаем:
5Н£{ (Лф^ i)(«+4-^«sf' («♦)
* Из формулы (4-ЗЗа) следует, что коэффициент потерь £в = О
при Х1==1. Если >i=XlMaKC = l/^ii, то формула (4-ЗЗа) дает
неопределенность, которая легко раскрывается.
157
Отсюда с помощью (4-11а) получаем:
fk+\\k-\ 2 Л-1
х (Л*? sin2 g)
(•
Е ]_. (4-35)
Af"f sin» P + ^^TTJ (^ГТ Mi sin2 §- *)
Представим в зависимости от тех же параметров скачка
коэффициент потерь в скачке Сс, используя формулы (4-33)
и (4-35):
<.=ч^г [(£!)* (!§!*>■?-i)Tx
х^ + ^т^)-1]- (4-36)
Заменив число Мх через Ях по формуле (2-21), получим
зависимость в виде:
C,=?(*i, Р).
На рис. 4-12 представлен график е0 и Сс в косом скачке
в зависимости от угла (3 и безразмерной скорости
невозмущенного потока Яй для'£=1,3. Из графика видно, что
коэффициент потерь интенсивно возрастает с увеличением
угла косого скачка и с ростом скорости Я1? достигая
максимальных значений при [J = -|- (прямой скачок).
При обтекании тела сверхзвуковым потоком перед телом
возникает ударная волна (скачок уплотнения); при переходе
через эту волну энтропия газа растет, а скорость
уменьшается.
Таким образом, в сверхзвуковом потоке идеальной
жидкости появляется особый вид сопротивления —
волновое сопротивление, зависящее от потерь в скачках,
а следовательно, от формы и интенсивности скачков. Как
мы видели, форма скачка и его интенсивность зависят от
формы тела и скорости обтекания. Учитывая, что при
уменьшении угла отклонения 8 (а, следовательно, и (3) потери
в скачке уменьшаются, можно заключить, что
остроконечные тела в сверхзвуковом потоке должны обладать меньшим
сопротивлением, чем тела, имеющие скругленную форму.
Изменение потерь в скачках в зависимости от их
интенсивности МРЖно проследить в тепловой диаграмме. Построе-
158
йие „ударной поляры* в тепловой диаграмме удобно
выполнить следующим образом1.
По параметрам до скачка р1 и Т1 находим точку D
(рис. 4-13) и при известной скорости с1 точку Ог Задаемся
рядом значений р в пределах от p = aml = arcsin-rr- до
В = -£-. Для каждого значения р определяем -- и ^,на-
носим в диаграмме /s точки Е'2 , Z^' и т- Д- Д° точки Л,
которая соответствует прямому скачку. Геометрическое
место этих точек дает состояние газа в координатах is,
соответствующее ударной поляре. Заметим, что полученная
кривая должна быть
касательной к линии изоэнтро-
пического изменения
состояния ОД), так как при
бесконечно малых возмущениях
потока энтропия газа
остается постоянной,
Для каждой точки
кривой (например, Е[') легко
определяются;
кинетическая энергия за скачком
Ас\
Я0к = -g— , изменение по-
Рис. 4-13. Построение в
тепловой диаграмме линии
изменения состояния газа,
соответствующей ударной поляре.
1 Соответствующая кривая в диаграмме is может быть названа
«ударной полярой" лишь условно, т. к. она не является векторной
кривой. Приводимое построение справедливо для идеального газа.
159
тенциальной энергии в скачке #оп и потери
кинетической энергии ДА. Вместе с тем здесь можно определить
и все параметры скачка: /?2, Т^ р2, /?02, As и тем самым
существенно дополнить ударную поляру, построенную в
плоскости годографа. В плоскости годографа ударная поляра
дает кинематическую картину течения (поле скоростей);
в тепловой диаграмме мы получаем характеристики
энергетических преобразований на скачке и изменения параметров
потока. На линии DA легко найти также точку г,
соответствующую М2 = Я2=1. Для этой цели подсчитываем
критический перепад энтальпий:
Ас? ь — \
и откладываем его от линии /0= const.
Характер полученной кривой, обращенной выпуклостью
к оси /, отчетливо показывает, насколько интенсивно
увеличиваются потери с ростом (3 и приближением к прямому
скачку.
Для расчета скачков оказывается весьма удобным
пользоваться специальными диаграммами. Такие диаграммы
позволяют легко определить характеристики скачка по двум
заданным параметрам. В приложении даны диаграммы косых
скачков для & = 1,3 и £ = 1,4*.
Способ пользования диаграммой косых скачков поясняется на
рис. 4-14. В правом верхнем квадранте диаграммы нанесены графики
о
д = д (Р) и —— == р ф, отвечающие различным, но постоянным значе*
ниям скорости перед скачком \v На каждой кривой надписано
значение Xj*, в скобках указывается та величина, которую изображает
данная кривая. В левом верхнем квадранте представлены графики 5 =
= #(Х2)и ~r~=/J(X2) Для различных, но постоянных значений X,.
Pi
В левом нижнем квадранте дана зависимость отношения температур
Т
на скачке от скорости за скачком у~ = Т (Х2). В правом нижнем
квадранте нанесены кривые коэффициентов потерь энергии в скачке Кс =
= Кс (?) и коэффициентов восстановления давлений е0 = е0 (£). Таким
образом, в качестве параметра для всех кривых диаграммы выбрана
скорость потока до скачка X,.
* Расчет диаграмм скачков выполнен А. Е. Зарянкиным.
160
Поясним на примере способ пользования диаграммой. Допустим,
что нам известны угол отклонения линии тока д и скорость потока
до скачка X,. На кривой S — д (jl), соответствующей заданному
значению Xv находим точку А. Проектируя эту точку на горизонтальную
ось, найдем в точке Аг угол косого скачка $v На кривой — = р(Р)»
Pi
отвечающей тому же значению X,, получим точку Л2, которая
определяет отношение плотностей р2/р,. Зная X, и S, на кривой д = д1 (Х2)
7Х
1
J*
\Рг
. П
\
с
Bt
i
'
\
<?°
*-№\J/
1/
\
\е° \.
Г Х- 1 |
\|
1
Л 1
1
WX '
-So-So(P) 4^-1
I
J»
k
Рис. 4-14. Способ пользования диаграммой косых
скачков.
в левом квадранте находим точку Bv которая определяет безразмерную
скорость за скачком Х2. Перейдя при том же значении Х2 на кривую
■—■ = р (Х2), получим в точке В2 отношение давлений на скачке — .
Pi px
Т2 —
В точке С на кривой у- = Т (Х2) определяем отношение темпера-
Т
тур -—- . Проектируя точку Лг на линии Сг = С (?) и е0 = е0(р) в
точках Dj и D2, найдем значения коэффициента потерь энергии и
коэффициента восстановления давления. Рассматриваемая диаграмма
позволяет, производить расчет скачков по любым двум параметрам. Так,
р2
например, заданными могут быть: X, и р; -— и S; В и р и т. д.
11 м. е. Дейч
161
Тепловая диаграмма удобна для расчета скачков уплотнения
в реальном газе и, в частности, во влажном паре и диссоциирующем
воздухе Параметры потока перед скачком и угол отклонения на скачке
обычно известны. Задаваясь рядом значений угла скачка ^-, нетрудно
найти соответствующие значения нормальных составляющих скорости:
сг cos ^
cnU =сг sin p.; cn2i = ctg ^ _ S) .
По основным уравнениям (4-1)—(4-4) определяются параметры за
скачком i2i, Рц и удельный объем v2i, отвечающие текущему
значению рх- Искомое решение можно найти в диаграмме is в точке
пересечения двух кривых, одна из которых построена по параметрам /2.
р21, а вторая—по i2i, v9i (рис. 4-13,а). С диаграммы снимаются
значения /2, р2, v2\ действительный угол наклона скачка определяется по
формуле ■
*Р 2tg$ - у \2tgdJ
- vi
где v = — .
Эта же задача решается с помощью вспомогательного графика, на
котором наносятся кривые v2i (^) и v2i (^-) (рис. 4-13,(5). Для
построения второй кривой необходимо по диаграмме is перейти от значений
р2 и /2 к значениям v2. Решение получается в точке пересечения этих
кривых, где определяются d2 и | и соответственно все остальные
параметры за скачком. В частности, скорость за скачком
сх sin £
c»=lTsin(p-*)-
4-6. ПЕРЕСЕЧЕНИЕ СКАЧКОВ
Рассмотрим некоторые практически важные случаи
взаимодействия скачков.
Два последовательных поворота стенки ABCD
(рис. 4-15,а) на угол 8 приводят к образованию двух
косых скачков: ВК и С/С. Угол второго скачка pa>Pi> так
как после первого скачка поток имеет скорость Яя<Я1в
В результате скачки пересекаются в точке А". За точкой
пересечения оба скачка сливаются в один скачок KF.
Линия тока, пересекающая систему двух скачков,
деформируется, поворачиваясь в точках b и d на угол 8; при
пересечении скачков скорости потока падают, а давления
растут скачкообразно.
Рассматривая линию тока КН и предполагая, что rfpo-
никновения частиц газа из области 4 в области 3' и, на-
162
оборот, из области 3' в область 4 не происходит, можно
заключить, что в указанных областях давления и
направления скоростей должны быть одинаковыми (поперечный
градиент давления отсутствует). Но если предположить
направление линии тока за скачком KF таким же, как и
за вторым скачком С/С, т. е. что суммарное отклонение
линии тока составляет 28, то давления в областях 3 и 3'
будут различными, так как линия тока bd прошла че-
Рис 4-15. Взаимодействие двух последовательно
расположенных косых скачков
рез два скачка, а линия тока КН — только через один
скачок; следовательно, потери в первом случае будут
меньше, чем во втором (при сжатии с бесконечным числом
скачков бесконечно малой интенсивности процесс будет
изоэнтропическим—без потерь), причем р3 может быть
меньше или больше р3. Отсюда можно заключить, что
области течения 3 и 3' разделены слабой волной
разрежения или слабым скачком уплотнения /CL, при
пересечении которого поток приобретает давление /?4 = ръ.
Интенсивность волны KL в этом предположении легко
определяется. Действительно, зная угол S и 21( находим
давление /?4 за скачком KF. Давление р3 нам известно в ре-
зультате расчета скачков ВК и СК. Отношение — дает
Рг
интенсивность отраженной волны KL.
В общем случае углы отклонения потока в точках
В и С могут быть неодинаковыми. При этом в
зависимости от соотношения углов 8Х и Ь2 (Sx — отклонение в
первом скачке ВК и 62 — отклонение во втором скачке С К)
и суммарного угла отклонения 8Х -|— S2 меняются
интенсивность отраженной волны /CL, а также суммарные потери
в рассматриваемой системе скачков. Расчеты показывают,
что интенсивность отраженной волны KL, как правило,
невелика и поэтому поворот потока на этой волне
пренебрежимо мал, что и делает обоснованным
предположение о повороте потока на волне KF на угол Вх —{— В2.
В зависимости от скорости невозмущенного потока
и суммарного угла отклонения Sx -j— S2 меняется и знак
волны /CL.
Характерно, что скорость за скачком KF всегда
меньше скорости за скачком СК (Я4<С^3)» отсюда следует,
что линия КН является линией тангенциального разрыва
скорости. В вязкой жидкости вдоль КН развивается
вихревое движение.
Изменение состояния газа вдоль линии тока при
переходе через рассматриваемую систему скачков может быть
представлено в тепловой диаграмме (рис. 4-15,6). В
точке 2 определяется состояние газа после первого скачка,-
а в точке 3 — после второго скачка, так как углы ^ и (32
известны. Легко определяются также все параметры
за скачками: р3. Т3, Я3 и параметры торможения /?03, р03.
Точка 3' на изобаре р3 дает состояние газа за
скачком /С/71. В точке 03' находим давление торможения за
скачком KF р03<СРоз- Потери энергии в скачке KF
выше суммарных потерь в скачках ВК и С/С, т. е. &s'^>
^>As. Таким образом, при заданных пределах изменений
давлений торможение потока одним скачком
обусловливает большую потерю энергии, чем в случае
последовательного торможения двумя скачками.
Предельным случаем является торможение потока
вдоль плавной вогнутой стенки, в каждой точке которой
поток испытывает отклонение на малый угол db (рис. 4-16).
1 При построении процесса в диаграмме is принимаем р3 =^ /?3.
164
При этом у стенки образуется волна сжатия, состоящая
из бесчисленного множества характеристик уплотнения.
Движение газа через такую волну сжатия совершается
при постоянной энтропии. Однако плавное изоэнтропиче-
ское торможение здесь может происходить только в слое
газа, прилегающем к стенке. В результате пересечения
характеристик уплотнения на некотором расстоянии от
стенки, зависящем от скорости набегающего потока,
возникает криволинейный скачок переменной интенсивности.
Рис. 4-16. Сжатие потока при обтекании
плавной вогнутой стенки.
Поток за скачком вихревой, так как скорости в разных
точках за линией ВК различны.
Взаимодействие волны сжатия со скачком уплотнения
качественно происходит так же, как это было указано
при рассмотрении взаимодействия двух косых скачков
(рис. 4-15). В точках пересечения слабых волн и скачка
возникают отраженные слабые волны (рис. 4-16), так как
изменения давления и направления потока при переходе
через волну сжатия и скачок будут различными.
В зависимости от скорости набегающего потока
повышение давления в скачке может быть более интенсивным
или менее интенсивным, чем в волне сжатия.
Следовательно, отраженные волны могут быть либо волнами
сжатия, либо волнами разрежения.
165
Отличный от рассмотренного случай пересечения двух
косых скачков-показан на рис. 4-17. Косые скачки
возникают в результате поворота двух противоположных
стенок канала на разные углы 8Х и 82. Направления потока
в. зонах // и /// будут неодинаковыми*, в зоне ///
отклонение будет больше на угол 82 — 81# Параметры течения
за косыми скачками АВ и АХВ легко могут быть
определены по известным параметрам до скачков Х19 рх, Тх
и углам St и о2, если эти углы меньше соответствующего
максимального значения Ьт для данного вектора скорости Я1в
Рис. 4-17. Схема пересечения двух косых скачков,
а —нормальное пересечение; б-—процесс в скачках в тепловой диаграмме.
Параметры потока в области IV можно найти, исходя
из граничных условий для линии тока, проходящей через
точку В. Примем, что направления скоростей и давления
во всех точках области IV будут одинаковыми. Отсюда
определяется угол между вектором скорости в зоне IV
и вектором Ях. Действительно, если результативное
отклонение потока в зоне IV обозначить 84, то из
рассмотрения рис. 4-17 легко установить, что отклонение потока
при пересечении скачка ВСХ равно 81-(-84, а при
пересечении ВС оно равно 82 — 84. Задаваясь различными
значениями давления в зоне IV (/?IV) по формулам (4-13) и (4-17)
или по диаграммам косых скачков, находим углы наклона
скачков ВС и ВСХ и углы отклонения потока 81-|- 84 и
82 — 84. Значение /?lv, при котором величины 84,
определенные по параметрам зон // и ///, будут одинаковыми,
166
можно найти, построив зависимости ^4BCi и %4ВС от /?]у.
Точка пересечения этих кривых даст искомое значение 84.
Зная величину 84, находим углы косых скачков р и рБС.
Изменение состояния газа вдоль двух линий тока,
пересекающих зоны // и ///, в тепловой диаграмме
показано на рис. 4-17,6.
Суммарное приращение энтропии для '///////////^
этих линий тока будет
одинаковым только в тех случаях, йОГ^АШ
когда 81 = 82. Если
интенсивность скачков АВ и АгВ
различна, то приращение
энтропии вдоль рассматриваемых
линий тока будет различным '////////////&
(ТОЧКИ 4 И 4' на рис. 4-17,6). Рис. 4-18. Мостообразный
При этом, если во всех точ- скачок.
ках зоны IV давления
одинаковы, скорости, температуры и плотности за скачками
ВСХ и ВС будут различными. Вдоль линии тока,
проходящей через точку 5, образуется тангенциальный разрыв
скоростей, в результате чего в вязком газе возникает
вихрь.
Устойчивое существование системы двух
пересекающих косых скачков возможно не при всех условиях. Если
углы вторых скачков рБС и рвс будут больше
соответствующих значений р характер течения меняется. Вблизи
нейтральной линии тока, проходящей через точку В,
образуется криволинейный скачок. Система пересекающихся
прямолинейных косых скачков переходит в мостообразный
скачок (рис. 4-18). Потери энергии в потоке при этом
увеличиваются.
4-7. СТУПЕНЧАТОЕ ТОРМОЖЕНИЕ ПОТОКА
Ступенчатое торможение потока можно получить,
применяя различные системы косых скачков. В предыдущем
параграфе было показано, что если при заданных
пределах изменений статического давления увеличивать число
косых скачков путем увеличения последовательных
поворотов стенки, то торможение потока будет более плавным,
а суммарные относительные потери будут уменьшаться.
167
Обычно за последним косым скачком располагают прямой
скачок, на котором происходит переход к дозвуковой
скорости.
Торможение потока в различных системах скачков было
подробно исследовано Г. И. Петровым и Е. П. Уховым.
Следуя основным выводам этой работы, рассмотрим
частный случай торможения потока в двух скачках — косом
и прямом.
Рассматриваемая задача формулируется так:
определить угол наклона первого — косого — скачка, при
котором переход от заданной сверхзвуковой скорости к
дозвуковой происходит с минимальными потерями (рис. 4-19).
Расчет такой системы можно осуществить последовательно,
применяя диаграммы косых скачков (см. приложение).
При заданной скорости невозмущенного потока Хх и
выбранном значении угла 6 (или (3J легко определяются
скорость Я2 и давление р2 за косым скачком.
Соответствующая потеря энергии Сс или изменение давления полного
торможения е01 также определяется по диаграмме косых
скачков (или по формулам § 4-5).
Аналогично можно найти скорость и статическое
давление за прямым скачком (Я3 и р3) и коэффициент потери
энергии Сс (или е02).
В качестве примера на рис. 4-19 показано изменение
скорости потока и коэффициентов потерь в системе
косого и прямого скачков в зависимости от угла (^ для Ях =
= 2,0 (£ = 1,3). Кривые показывают, что для данной
скорости Х1 имеется такое наивыгоднейшее сочетание
косого и прямого скачков, при котором суммарные потери
будут наименьшими.
Действительно, с увеличением угла косого скачка рх
растет коэффициент потерь Сс1 в косом скачке и уменьшается
скорость за косым скачком Я2. Очевидно, что при 8 = 0
и (31=ат1=22°45'(дляЯ1=2,0) косой скачок переходит в
характеристику. В этом случае Сс1.= 0. Предельное значение
угла р1э при котором еще возможно существование
плоского косого скачка, составляет (^г^^г^бб^О'. При
этом значении рх поток за косым скачком имеет
дозвуковую скорость. В указанных пределах изменений угла ^
(22°45' — 65°40') за косым скачком может существовать
прямой скачок. При ^ = 22°45' существует только
прямой скачок, а при р2 = 65°40'— только косой.
168
Меняя в этих пределах угол косого скачка и
подсчитывая Я2 и /?2 (параметры перед прямым скачком), можно
найти параметры газа за прямым скачком. Скорость за
Рис. 4-19. Изменение скоростей и потерь в системе двух
скачков (косой + прямой) в зависимости от угла косого
скачка рх при Х1 = 2,0; ^ = 1,3.
прямым скачком Я8 = -г- увеличивается с ростом Вх в пре-
делах от Я3 = 0,5 при В1 = 22°45' до Я3 = Я2 = 1 при $х=
= 65°4(У.
При определении коэффициента потерь в прямом скачке
необходимо величину потерь относить к кинетической
169
энергии невозмущенного потока, т. е. подсчитывать
где £с2 определяется по диаграмме косых скачков для Я2.
На рис. 4-19 нанесены значения KcY Можно видеть, что
t!c2 уменьшается с ростом рх. При pi = 22°45' C^2 = Cc2 =
=-0,227, а при р1 = 65°40' ^2 = 0.
Коэффициент суммарных потерь в системе двух
скачков, очевидно, будет равен:
Кривая суммарных потерь в системе двух скачков
имеет минимум при р1 = 45°. Очевидно, что значение рх
является оптимальным в отношении потерь энергии в
системе скачков.
Аналогичные расчеты можно выполнить для различных
скоростей Х19 определяя наивыгоднейшее значение рх.
Результаты таких расчетов даны на рис. 4-20, где
суммарный коэффициент потерь Сс представлен в зависимости
от угла рх для различных значений Хх. Жирными линиями
проведены кривые Сс в диапазоне углов р1э при которых
возможно существование системы косого и прямого
скачков. Пунктирная линия ABCD соединяет точки,
отвечающие [J1 = aml. Для этих точек косой скачок имеет
бесконечно малую интенсивность и, следовательно, торможение
потока осуществляется только в одном прямом скачке.
Точки FGHJ отвечают углу ^ = [5^, при котором поток
за плоским скачком имеет звуковую скорость. Для ^х^>
>Р1# кривые Ъс проведены тонкими линиями. В этом
случае расчет может быть приведен в предположении
существования скачка, скорость за которым дозвуковая.
При Pj = 90° он становится прямым. Легко видеть, что
при р! = аот1 и (^ = 90° коэффициент потерь Сс имеет
одинаковое значение.
Сопоставление кривых на рис. 4-20 показывает, что
оптимальные значения р]опт зависят от скорости
невозмущенного потока Хг. С ростом Хг до некоторых пределов
значения Р1опт уменьшаются. Для Я1 = 1,6 коэффициент
1/0
потерь йрй оптимальном значении £1опт = 52° составляеФ
С =0,035. В этом случае один прямой скачок дает
(точка А на рис. 4-20) Сс2 = 0,ПЗ, а один косой при
скорости за скачком, равной скорости звука (точка J на
рис. 4-20), С„ =0,073. Следовательно, переход от одного
1 -zZ
\ Прямой
скачан
Г
D X
с
Л^ Прямолинейный косой + >i КриболинейныйА
+ прямой
Wk
А
л\
Хг2£
^р2£
г >^ /
\£j2^
скачок " 1
i
У
\И/
i^>
.^А
L*
0,3
0,25
0,2
0,15
0,1
0,05
10 20 30 40 50 60 70 80 90
Рис. 4-20. Кривые коэффициентов потерь в системе двух скачков
(косой -f- прямой) в зависимости от угла косого скачка j, и скорости
X,; Л=1,3
скачка к системе двух скачков (косой -f- прямой)
позволяет уменьшить коэффициент потерь более чем вдвое.
При больших значениях Хх двухступенчатое торможение
оказывается еще более эффективным.
Следует заметить, что с ростом Ях минимум кривых £>с
становится более пологим. Это обстоятельство позволяет
выбирать оптимальные значения ^ таким образом, чтобы
и статическое давление за вторым прямым скачком было
наибольшим. Отношение статического давления за систе-
171
мои скачков pz к полному давлению перед скачком pQl
можно представить в следующем виде:
Рг.
Ли'
_Р* Ръ Pi
'PiPzPoi
Рг
здесь — характеризует повышение статического давления
Рг
на косом, а -—3 — на прямом скачке.
Изменение этих величин, а также е01=^-2 и е02 = ^3
Pol Po2
в зависимости от угла косого скачка (^ для Я2 = 2,0
представлено на рис. 4-21. С ростом ^ отношение давлений
на косом скачке — увеличивается, а на прямом — умень-
Р\ Рг
шается. График показывает, что относительное
статическое давление за системой скачков для Ях = 2,0 имеет
максимальное значение при ^ = 40°, тогда как
минимальная величина Ъс была получена при рх == 45°.
Учитывая, что кривые Сс в области минимума протекают
полого, оптимальные значения рг можно выбирать по
данным расчета восстановления статического давления в си-
Рдг.Рдз Д?
Poi'Poz Poi
Рис. 4-21. Изменение статического давления и давления торможения
в системе двух скачков (косой + прямой) в зависимости от угла
косого скачка ^ для А, = 2,0; /г =1,3.
172
стеме скачков, т. е. принимать значения р1опт несколько
меньшими, чем это диктуется кривыми С..
Такое решение целесообразно в том случае, когда
основная задача сводится к максимальному восстановлению
статического давления в системе скачков, как, например,
это имеет место для сверхзвуковых диффузоров.
Рис. 4-22. Процесс торможения в системе двух
скачков (косой + прямой) в тепловой диаграмме.
173
Последовательное торможение потока в системе
скачков можно наглядно представить в тепловой диаграмме.
На рис. 4-22 показан этот процесс для двух скачков. При
р1==а существует только один прямой скачок (точка Л).
При р! = Р, скорость за плоским косым скачком звуковая
и торможение происходит только в одном косом скачке
(точка К). В пределах ат1<^<р1# может существовать
система двух скачков. Задаваясь различными значениями
Рл (точки Е1 — Е^), можно построить линию предельных
состояний газа за системой двух скачков при различной
интенсивности косого и прямого скачков (линия АВХ.. .5Д).
Малым углам ^ косого скачка отвечает верхняя ветвь
кривой предельных состояний ABXB2BZ. Нижняя ветвь
соответствует большим углам скачка Pi^Pv Характер
кривой состояний АВХ... ВАК отчетливо указывает на
существование оптимальной комбинации двух скачков. При
некотором значении угла р, опт потери энергии в системе
скачков оказываются минимальными (точка В3). При другом,
близком значении угла $г потери несколько выше (Д/*к+п>
>ДД- ), но статическое давление достигает максимально
возможного значения /?3макс (точка В2). Линия предельных
состояний может быть построена путем последовательных
расчетов системы скачков.
Рис. 4-23. Изменение потерь в скачках при
ступенчатом торможении (цифры указывают число скачков).
174
Для совершенного газа можно получить уравнение этой
линии в форме связи между изменением энтропии и
изменением энтальпии в системе скачков.
При больших сверхзвуковых скоростях для перехода к
дозвуковым скоростям целесообразно применять более
сложные системы скачков, состоящие из нескольких косых
и одного завершающего прямого скачка. С ростом числа
косых скачков потери энергии будут уменьшаться. Для
каждой скорости потока Хг при заданном числе косых
скачков существует оптимальная схема расположения
скачков, которую можно найти последовательным расчетом.
Графики, приведенные на рис. 4-23, отчетливо
показывают преимущество более сложных систем скачков при
больших сверхзвуковых скоростях. Кривые ^с==С(Я1)
позволяют выбрать наиболее рациональную схему ступенчатого
торможения для заданной скорости.
4-8. ОТРАЖЕНИЕ СКАЧКОВ
а) Отражение от твердой стенки
Рассмотрим отражение косого скачка от прямой твердой
стенки, расположенной параллельно направлению скорости
невозмущенного потока (рис. 4-24). Скачок образуется в
Рис. 4-24. Схема нормального отражения плоского
косого скачка от твердой стенки.
точке Л, где стенка поворачивается на угол 8. При
переходе через первичный скачок АВ линия тока отклоняется
к прямой стенке на угол 8. Очевидно, что в точке В этот
поворот неосуществим и граничная линия тока сохраняет
направление стенки. Это означает, что в точке В стенка
принудительно отклоняет линию тока в обратном направ-
175
лении на угол о. В результате возникает отраженный
косой скачок ВС. Заметим, что углы падающего и
отраженного скачков неодинаковы, так как перед скачком ВС
безразмерная скорость A2<Aj при том же угле
отклонения 8. Из графика р = /(8, AJ (рис. 4-5) видно, что угол
Расчет отраженного скачка не встречает затруднений.
Зная параметры ^невозмущенного течения Я1Э рх и угол
Рис. 4-25. Анализ отражения £качка в диаграмме ударных
поляр.
а —определение углов и скоростей при неправильном отражении; б —
Х-образный скачок при отражении.
отклонения 8, с помощью диаграммы скачков легко
определяем параметры потока за первичным скачком: Я2, р2 и (За.
При том же значении В находим состояние газа за
отраженным скачком: Я3, рь и f53- Изложенным выше способом
находим потери энергии в первичном и отраженном
скачках. Следует иметь в виду, что такое отражение косого
скачка возможно не всегда. Если угол отклонения б
больше максимального значения для скорости Я2, то
картина отражения меняется. Допустим, что в диаграмме
ударных поляр (рис. 4-25,а) отрезок OD изображает
скорость потока до скачка Ях. Если угол отклонения стенки
176
8<5m2, то гипоциссоида, отвечающая скорости за скачком
Я2 (отрезок 02), пересекает линию вектора Хг (точки 3 и 4).
При 8 = 8от2 линия OD касательна к ударной поляре
Х2 (точка <?'). Картина течения при этом остается прежней
(рис. 4-24). Вектор скорости за вторым скачком 03' (Х3)
будет меньше единицы (скорость дозвуковая).
Если &>Sm2, то ударная поляра, построенная для
скорости 1г, не имеет общих точек с вектором OD и
отраженный скачок не может обеспечить выравнивание потока.
Часть потока, прилегающая непосредственно к стенке,
становится дозвуковой. Отраженный скачок CD
искривляется и сдвигается против течения. При этом
деформируется и первичный скачок АВ. Элемент СВ этого скачка
становится нормальным к стенке, система скачков
приобретает Я-образную форму. За участком прямого скачка
поток дозвуковой. За криволинейной частью отраженного
скачка поток может быть сверхзвуковым. В результате
образуется линия тангенциального разрыва СЕ, по обе
стороны которой давления одинаковы, а температура и
плотности различны, так как изменения энтропии при
переходе через ВС и АС — CD будут различными. В области 3
за А-образным скачком поток вихревой.
Отражение скачка, показанное на рис. 4-25,6 может
возникнуть при значительных углах отклонения 8 и малых
сверхзвуковых скоростях Ах. Подчеркнем, что механизм
возникновения Я-образного и мостообразного скачков
одинаков.
б) Отражение от свободной границы струи
Такое отражение рассмотрено на рис. 4-26. Во всех
точках на границе FBE давление одинаково и равно
давлению внешней среды ра. В струе это же давление имеет
место только до скачка АВ. При переходе через скачок
АВ давление изменяется от р1 = ра до р2*>ра.
Следовательно, точке В свойственны одновременно два давления:
ра со стороны среды и р2 со стороны струи. Такая точка
является очагом возмущения сверхзвукового течения,
создающим стационарную волну разрежения. При обтекании
точки В давление потока должно упасть от р2 до ра, что
и приводит при сверхзвуковых скоростях к образованию
волны BCD.
12 М. Е. Дейч
177
Первая характеристика BD составляет с направлением
вектора М2 угол ат2 = arcsin -tj- , где М2 — скорость
потока за скачком AB(Mz<^Ml). Угол последней
характеристики аш3 = arcsin-Г7-. Здесь скорость за отраженной
Рис. 4-26. Отражение косого скачка
от свободной границы струи.
волной разрежения М3 определяется по отношению
Р02
где р02 — давление торможения за косым скачком.
Отражение скачка приводит к деформации границы
струи, которая в точке В отклоняется на угол 82>8,.Это
отклонение вызывается расширением струи. Таким образом,
при отражении от свободной границы струи, вдоль, которой
давление сохраняется постоянным или падает, скачок
уплотнения преобразуется в волну разрежения. Если давление
вдоль границы возрастает, то в зависимости от
интенсивности изменения давления отражение может быть погашено
или оно происходит с сохранением знака (как и от
твердой стенки).
4-9. ВЗАИМОДЕЙСТВИЕ СКАЧКА И ВОЛНЫ РАЗРЕЖЕНИЯ
При обтекании тел конечных размеров сверхзвуковым
потоком совершенного газа интенсивность скачков на
различных расстояниях от тела будет различной. Благодаря
взаимодействию с волнами разрежения по мере удаления
от тела интенсивность скачков уменьшается и на
бесконечном удалении становится бесконечно малой.
Щ
Рассмотрим в качестве примера обтекание заостренной
пластинки (рис. 4-27). На переднем остром (S<&OT) носике
пластинки возникает плоский косой скачок АВ. При
обтекании точки D образуется стационарная волна
разрежения, причем характеристика, на которой начинается
отклонение потока, расположена под углом
am2 = arcsin —
где М2 — скорость за скачком.
Рис. 4-27. Схема взаимодействия скачка
и волны разрежения.
12*
179
Так кай
то характеристика пересечет скачок уплотнения в
Некоторой точке В. Второй границей волны разрежения является
. 1
характеристика, расположенная под углом <zm3 = arcsin —.
На участке правее точки В волна разрежения
взаимодействует с косым скачком. В области ABD скорость
постоянна и равна М2\ линии тока параллельны образующей
клина AD. Проведем через точку В характеристику не-
. 1
возмущенного потока под углом aml =arcsin-rr- к
направлению вектора скорости сг. Так как косой скачок
располагается под углом Р/~-2"(а/„1 + а/я/4'^)> a Угол
ближайшей к DB волны DE меньше ат2, то на участке BE
косой скачок отклоняется на малый угол так, что р.<р»
с уменьшением угла наклона скачка р, уменьшается и
угол отклонения потока 6.. Соответствующие отклонения
скачка и изменения угла поворота потока 8 имеют место
и на участках EF, FG и т. д.
Следовательно, скачок, начиная от точки 5,
искривляется и отклоняется в направлении потока; угол скачка
уменьшается, приближаясь к <хот1.
В соответствии с основными формулами скачка можно
заключить, что при взаимодействии с волной разрежения
интенсивность скачка уменьшается и, следовательно,
уменьшаются потери в скачке. Изменение энтропии, как
показывает анализ, становится равным нулю на
бесконечности.
Аналогичные результаты получаются, если волна
разрежения расположена перед скачком (рис. 4-27,6). В точке
Dx возникает волна разрежения, а в точке Аг — скачок
уплотнения. Взаимодействуя с волной разрежения, скачок
искривляется. Так как после пересечения с последней
характеристикой волны разрежения DlB1 скачок АгВг
попадает в зону меньших скоростей, угол его рх. увеличивается.
Заметим, что в реальной (вязкой) жидкости затуханию
скачков способствует также внутреннее трение.
180
4-10. КОНИЧЕСКИЕ СКАЧКИ УПЛОТНЕНИЙ
В предыдущих параграфах настоящей главы были
рассмотрены скачки уплотнения в плоском течении. При
обтекании осесимметричных тел поверхности разрыва имеют
осесимметричную форму. Рассмотрим особенности осесим-
метричного скачка на примере обтекания кругового конуса
(рис. 4-28). Перед конусом образуется конический скачок,
вершина которого совпадает с вершиной конуса, если
угол раствора конуса меньше максимального значения для
данной скорости набегающего потока.
Рис. 4-28. Форма линий тока в возмущенной
области за коническим скачком при обтекании
конуса.
Основные соотношения при переходе через поверхность
конического скачка, как легко видеть, будут теми же,
что и для плоского скачка [уравнения (4-13), (4-14) и др.].
При одинаковых углах раствора клина и конуса скачок
на конусе будет иметь меньший угол наклона, чем на
клине, так как конус вызывает меньшие стеснения потока,
чем клин бесконечного размаха того же угла раствора.
При переходе через конический скачок линии тока, так
же как и в случае плоского скачка, претерпевают излом.
Однако так как скачок на конусе слабее, чем на клине,
непосредственно за скачком линии тока будут наклонены
к вектору скорости невозмущенного потока под углом,
меньшим угла раствора конуса у0. Расчеты показывают,
что в возмущенной области линии тока не являются пря-
181
мымйг как при обтекании клина, а кривыми, причем
кривизна их различна и зависит от расстояния от поверхности
конуса. Кривизна линий тока, ближайших к поверхности
конуса, весьма мала.
Из рис. 4-28 следует, что с удалением от скачка угол
наклона линий тока к оси конуса увеличивается и линии тока ~
асимптотически приближаются к направлению, заданному
образующей конуса. Здесь можно видеть, что кольцевая
трубка тока, образованная двумя смежными линиями тока,
а) б) в)
Рис. 4-29. Схемы спектров обтекания конуса при различных
скоростях невозмущенного потока.
имеет плавно суживающуюся форму. Линии тока обращены
выпуклостью к поверхности конуса. При сверхзвуковых
скоростях такая форма означает уменьшение скоростей и рост
давлений вдоль линий тока, т. е. торможение потока.
Отсюда следует, что за коническим скачком продолжается
сжатие газа. Однако если в пределах скачка повышение
давлений сопровождается ростом энтропии, то сжатие
газа в возмущенной области за скачком происходит изоэн-
тропическим путем, без потерь. На этом основании можно
заключить, что при одинаковом отношении давлении —
Р\
(р2—давление на поверхности обтекаемого клина или конуса)
сжатие газа при обтекании конуса происходит с меньшими
потерями, чем при обтекании клина, так как для конуса
полное повышение давления является суммой изоэнтропи-
ческого сжатия и сжатия по ударной адиабате.
В сверхзвуковой части возмущенной области благодаря
кривизне линий тока характеристики криволинейны.
182
На рис. 4-29 изображены три возможных случая:
скорости во всех точках возмущенной области меньше
скорости звука (а), случай смешанного течения, когда скоро-
рости непосредственно за скачком сверхзвуковые, а затем
становятся дозвуковыми (б), и, наконец, когда поток за
скачком полностью сверхзвуковой (в). Характер течения
за скачком при неизменной величине у0 зависит от
скорости набегающего потока.
~Ц0 1,25 1,5 1,75 2,0 2,25
Рис. 4-30. Зависимость скоростей на поверхности
конуса от скорости невозмущенного потока и угла
конуса.
Скорости и давления на поверхности конуса меняются
при изменении скорости невозмущенного потока и полуугла
конуса y0.
На рис. 4-30 приведены графики изменения
безразмерной скорости на поверхности конуса Я2 в зависимости от
угла у0 и Хг. Следует заметить, что при данном режиме
обтекания во всех точках конической поверхности
скорости и давления имеют постоянные значения. Для конуса,
так же как и для клина, теоретическое решение задачи
дает при одном и том же режиме два возможных
значения угла наклона скачка и параметров у поверхности
конуса (нижние ветви кривых на рис. 4-30). Однако
практически, как правило, реализуются меньшие значения углов
скачка (верхние ветви кривых на рис. 4-30). Поэтому
можно сделать вывод, что с увеличением у0 скорости на
поверхности конуса уменьшаются и давления растут. Уве-
183
личение скорости невозмущенного потока приводит к
противоположным результатам.
Такой характер изменения параметров потока на
поверхности конуса имеет место до тех пор, пока угол
конуса не достигнет пре-
£0'
ЯГ
«0°
30°\
гсг
10'
о*
\^туУот
1
Конус
ь
1
У
тот
*т
1—
ч
1 1,2 1,4 1,6 18 2,0 2t2 2£ 2,6
Рис. 4-31. Зависимость
максимальных углов клина и конуса от
скорости невозмущенного потока
(Л =1,4).
дельного значения, при
котором происходят отход
и деформация скачка, так
же как и в случае клина.
При этом конический
скачок преобразуется в осе-
симметричную поверхность
разрыва с криволинейной
образующей. Однако
максимальные полууглы конуса
Тот, ПРИ которых для
данного Aj происходит
преобразование конического
скачка в осесимметричный
с криволинейной
образующей, будут больше
соответствующих значений 8щ для клина. На рис. 4-31
приведены зависимости максимальных углов отклонения 8 и
Тот 0Т числа К Для клина и конуса.
Для конического скачка можно построить в плоскости годографа
и, v и в тепловой диаграмме ударную поляру (рис. 4-32).
В плоскости годографа изменение скорости непосредственно в
коническом скачке изображается линией DEA, причем вектор скорости
за скачком определяется отрезком ОЕ- (скорость невозмущенного
потока OD). Угол скачка 0 можно найти, проведя нормаль в точке Е к
отрезку DE. Изменение скорости в возмущенной области за скачком
описывается кривой EEV Эта линия отвечает изоэнтропическому
изменению скорости (сжатию) за скачком.
Яблоковидная кривая DEXA определяет годограф скорости на
поверхности конуса; ее можно назвать ударной полярой конуса. Наклон
отрезка ОЕг определяет полуугол конуса у о- Область, заключенная
между кривыми DEA и /)£,Л, характеризует поток в возмущенной
области. В любой точке N отрезок ON определяет величину и
направление скорости. Нормаль, проведенная к годографу скорости в точке N,
дает полуугол конической поверхности, проходящей через эту точку
в плоскости потока.
Каждая промежуточная кривая DNAt соответствует постоянному
значению разности углов Ь— Y. Так как в возмущенной области
давление полного торможения не меняется, то годографу скорости ЕЕг
184
отвечает Постоянное значение ^-2. Нанося эти значения дЛя различи
Ли
ных точек Е, можно при пользовании ударной полярой определить
изменение давления торможения. В плоскости годографа можно
провести дугу окружности радиусом а#, которая выделяет группу режи-
Рис. 4-32. Ударная поляра
для конического скачка в
плоскости годографа и в
тепловой диаграмме для
k = 1,4 (яблоковидные
кривые).
мов обтекания конуса с дозвуковыми скоростями за скачком. При
этом легко устанавливаются точки возмущенного потока, в которых
скорость течения равна критической. Для данного угла скачка (1 эти
точки получаются пересечением дуги а* с годографом скорости Е'Е±
(точка К).
В тепловой диаграмме ударная поляра строится уже известным
нам способом (рис. 4-32,6). Линия DEtA соответствует изменению состоя-
при изменении ро в пределах от
ния газа за
коническом скачком
К = ао (точка D) до {J0 = 9~ (прямой скачок). При определенном зна-
скачком характеризуется точкой Ev определяющей изменение
энтропии (потери Ah) и изменение потенциальной энергии газа в скачке (//п1).
185
Отрезок ЁХЕ отвечает изоэнтропическому сжатию за скачком, и в
точке Е можно найти параметры газа на поверхности конуса.
Соответствующее изменение потенциальной энергии равно //Il2. При
одинаковых углах плоского и конического скачков (р = Р0) изменения
параметров получаются близкими, так как изоэнтропическое сжатие
в возмущенной области значительно менее интенсивно, чем ударное
сжатие в скачке.
В системе конических скачков можно осуществить
последовательное торможение сверхзвукового потока, так же
как и в системе плоских скачков.
В заключение необходимо сделать следующее замечение.
До сих пор мы предполагали, что любой скачок
представляет собой геометрическую линию (или поверхность).
мм
хЮ6
125
100
75
50
25
[д1 Г
<л
-Jl.
Рг\
Р,\
10
20 25 30 35 АО 45
Рис. 4-33. Толщина скачка в зависимости от его
интенсивности.
Это означает, что переход от параметров невозмущенного
потока к параметрам за скачком совершается в бесконечно
тонком слое. Существование двух смежных областей
потока с различными температурами и скоростями в
реальном—вязком—газе возможно только при наличии
некоторого переходного слоя конечной толщины, в пределах
которого и происходит весьма интенсивное, но все же
постепенное изменение параметров.
186
Привлекая методы кинетической теории газов и
основные уравнения газодинамики с учетом теплопроводности и
вязкости, можно получить приближенную оценку толщины
прямого скачка.
Расчеты показывают, что толщина скачка имеет
порядок удвоенной длины свободного пробега молекулы и
поэтому уменьшается с ростом его интенсивности.
Соответствующий график изменения толщины скачка в зависимости
от — при не слишком малых давлениях представлен4 на
рис. 4-33. Мы видим, что толщина скачка в обычных
условиях весьма мала. Опыты подтверждают, что принятая
выше упрощенная схема бесконечно тонкого скачка и
выведенные в этом предположении формулы в обычных
условиях весьма точно отражают действительную картину.
Следует иметь в Еиду, что в разреженных газах при больших
длинах свободного пробега толщина переходной области
может оказаться весьма существенной; очевидно, в этом
случае полученные соотношения для скачка могут давать
существенные погрешности.
4-11. СКАЧКИ КОНДЕНСАЦИИ (ТЕПЛОВЫЕ СКАЧКИ)
Скачки могут возникнуть не только в адиабатических потоках»
но и в тех случаях, когда на малой длине потока происходит
интенсивный подвод или отвод энергии (например, тепла) При этом
образуются скачки, называемые тепловыми Наибольший интерес
представляют два вида тепловых скачков* распространение детонации и
горения и скачки конденсации, связанные с движением двухфазной
жидкости и, в частности, влажного пара или воздуха
Первый тип тепловых скачков подробно изучен и освещен в
специальной литературе Второй тип — скачки конденсации, широко»
встречающиеся, в практике аэродинамического эксперимента, в соплах
Лаваля, в проточных частях турбомашин, изучен менее подробно.
Анализ свойств скачков конденсации основывается на некоторых
допущениях: а) конденсация происходит мгновенно, так что образуется
резкая граница, отделяющая газ с несконденсировавшимися водяными
парами, от газа, содержащего конденсат; б) эффект конденсации
сводится к освобождению скрытой теплоты парообразования; в) этот
процесс сопровождается изменением физических свойств газовой
составляющей и уменьшением ее весовой доли в смеси; изменение
физических свойств газа и его параметров происходит только в пределах
скачка; г) влиянием вязкости, теплопроводности, диффузии можно пре_
р
небречь; д) газовая фаза подчиняется уравнению состояния —=gRT
и k меняется только при переходе через скачок; е) после скачка
жидкая фаза имеет ту же скорость, что и газообразная.
187
Основными уравнениями скачка, конденсации * являются общие
уравнения, выведенные в § 4-2.
С учетом обозначений, принятых на рис. 4-34, уравнение
неразрывности запишем в следующем виде:
Picn\ = P2U +Псп2 = Ра 0 + Л ("2 sin PK—y2cos у, (4-37)
где Рк — Угол косого скачка конденсации;
Р 7
/= ——- отношение массы жидкости к массе газа за скачком;
Р2 (1 X)
1 — степень влажности за скачком;
рн — плотность жидкости.
^/,2 = "* sin Рк— y2C0S?K-
Рис. 4-34. К выводу уравнений косого
скачка конденсации.
Уравнения количества движения в проекциях на нормаль к скачку
и на плоскость скачка будут:
Рг — Рх = Pi^i - Р2 (1 + У) fe sin pK- v2 cos pK)2; (4-38)
?lCn\Ct=Z?*(l +DCn2Ct =
= Р2 U + Л ("2 sin pK— v2 cos рк) (u2 cos pK+ v2 sin PK)=0, (4-39)
где ct= cx cos рк = u2 cos fK + u2 sin PK.
Уравнение энергии запишем в такой форме:
с2 с2
1 См. список литературы. Теоретическое исследование
конденсационных скачков впервые было произведено С. 3. Беленьким. В работе
Р. Германа дано решение для прямого скачка конденсации. В работе
В. А. Андреева и С. 3. Беленького рассмотрен более общий случай
косого скачка. Ф. Росс решил задачу о косом скачке конденсациц
с учетом изменений физических свойств газа.
188
где Д/0 = l02 — i0\ — изменение энтальпии торможения вследствие
выделения теплоты при конденсации.
Так как энтальпия торможения при пересечении скачка меняется,
то критические скорости до и после скачка будут неодинаковыми:
a-=V*i^\^ *^V*
1
kt + \
Здесь kv k2 — показатели изоэнтропического процесса до и после
конденсационного скачка.
Соотношение между критическими скоростями выражается
формулой
*1 __
где
<2 * + А'о
— М0 kx — \ k2 + 1
(4-41)
Левую часть уравнения энергии (4-40) можно представить в
следующей форме
kx рх
*• + * alv
а правую часть
4 + А , k,
2 ' kx-\ Pl 2(^-1)
(4-40а)
2 ' Л, — 1 Р. (1 -Н Л 2(*,_1)
Учитывая, что
сх— и2 ^ v,
k2+-~al2=i01(\+Ai0) (4-406)
(4-42)
где дк—угол отклонения линии тока при пересечении скачка
конденсации, с помощью выражений (4-37), (4-38), (4-40), (4-41) и (4-42)
получим уравнение ударной поляры для скачка конденсации в таком
виде:
X,
v\ = (К1 — U2y
Xj — щ
и2(Хх — и2)—
kx + 1 Ai
А — М2 +
■ AL — к
(fea — 1)и| — (^ж + !)(!+ д/0)
{kx-k)(k\-\)
{kx-k)(kx + \) ^
— 1
(4-43)
* Под / понимается энтальпия газовой фазы без учета теплоты
конденсации.
189
Здесь приняты следующие обозначения:
Aj == —— ; и2= ~ ; я2=
а*,
: ^1 ^2-
Уравнение (4-43) при Д/0 = k = 0 переходит в формулу (4-26) для
адиабатического скачка.
С помощью (4-43) по формулам (4-42) определяются угол косого
скачка конденсации рк и угол отклонения потока &к#
Из уравнения энергии (4-406) можно получить формулу для
определения числа М2 за скачком:
М,
V
g2p2
РгЬ>2,
(1+/) =
_ _ / k, + 1 1 + Д«, 1
Отношение давлений на скачке находим по формуле
Л = 1 +^iAff singK
v< (kx —~k) (i + ml - л -
-2 I2 ^ 2 ("2 sin pK- vt cos рк)»
(4-44)
(4-45)
1 +
U0 + V2
Аналогично тому, как это сделано при выводе формулы (4-35),
получаем формулу для отношения давлений торможения на скачке
конденсации:
Pa Pi'
l+(*i-l-*)^.
Л4-1- к
Ь
(4-46)
М\
1 + №1 — 1)-J-
*i-i
Отношение плотностей на скачке
Р2 _Р*[М2\* *'
Pi
(4-47)
Полученная система шести уравнений (4-42) — (4-47) позволяет
найти параметры за скачком у2, и2, М2, Аг» А и *g PK ПРИ заданных
параметрах до скачка cv /?„ р1? ап и известных Д/0, /, k.
С помощью общих соотношений нетрудно рассмотреть отдельные
частные случаи.
190
Во многих практически важных случаях можно полагать, что
физические свойства газа сохраняются неизменными (kt = k2; k = 0) и
что масса конденсированной фазы за скачком пренебрежимо мала по
сравнению с газообразной (/ = 0). В этом случае уравнение (4-43)
упростится и примет вид:
a, (s,--£=)-i
■% = (Л, --игу -Л hZ^L (4-48)
Совместное решение исходных уравнений после соответствующих
упрощений позволяет получить связь между нормальными
составляющими скорости на скачке конденсации в следующей форме:
2сп\ f \ 2сп\
где
J; Ц=-|/^-^1^со52рк;
Ь*2 = у а\
^,-г-Т-ПСТ • (4"50)
*2 —
^■-А+ТХ1С08'Рк
Величина ## определяется по формуле (4-41). Для отношения
давлений на скачке находим:
Это уравнение переходит в формулу (4-13) при Т# = 1 (адиабати-
сп\
ческии скачок) после подстановки-— из уравнений (4-5) и (4-11).
сп2
Из уравнения (4-48) следует, что вертикальная составляющая
скорости за скачком обращается в нуль при трех значениях вектора иг.
191
Первое соответствует вырождению скачка в слабую волну [и2 ■■
= \х(к2 = аД,)]. Второе и третье значения получаются из условия
М "2-т^= )-i=o,
или
■4-^г + т;^^^
Два корня этого уравнения будут:
("2)1,2 = '
*? + !
(Х2),,2 = ( ^ ) =-1- «4tJl ± / Ж+О' _ J. ( 4-51)
Полученное соотношение выражает связь между скоростями для
прямого скачка конденсации. В этом легко убедиться, под
ставив в уравнение (4-49) условия прямого скачка: рк=9" и 6* = д# .
Из уравнения (4-51) вытекает, что скорость за прямым скачком
зависит от \ и Ai0 — теплоты, выделяемой при конденсации, которая
в свою очередь определяется количеством конденсирующегося газа.
Из уравнений (4-49) и (4-50) следует, что величины Ь* и а# не
могут быть меньше некоторого предельного значения для заданного
спХ или \у так как в противном случае сп2 и Х2 будут мнимыми
величинами. Из (4-51) для прямого скачка
"*мин-Л2 + Г
В согласии с формулой (4-41) при kx = k2 минимальному
значению а# соответствует максимальное изменение энтальпии торможения
в скачке:
/X2 —Л2
AWc=(Vj- (4-52>
В общем случае для косого скачка из уравнения (4-49) получим:
OtuuH
мин -2 /
сп\ + !
192
соответственно из (4-50) будем иметь:
2(4 + 1)
/ [ft+l+A»(2fesin'PK + l-fe)]'
X? sin2 jJK
■f 4(i»—1)Х?со8Чв
(4-53)
Д(,
~~2
Омакс —о
Как указывалось, относительное изменение энтальпии торможения
в скачке конденсации М0 характеризует количество конденсирующейся
жидкости Полученные соотношения показывают, что скачки
конденсации могут возникать только при определенных количествах
конденсирующейся жидкости. Предел конденсации в скачке зависит от
скорости перед скачком и от угла скачка.
Возвращаясь к анализу уравнения ударной поляры (4-48), отметим,
что у2— °° ПРИ
YAk + i
\\' + 1 или
#*2 ^l \k + *
x? + i
Зависимость (4-48) графически представлена на рис. 4-35 для раз
личных значений а*. Для плоского косого конденсационного скачка
-«*ь
ащ=1,052
Рлс. 4-35. Ударные поляры конденсиционных скачков для различных
значений Д/^ (различной относительной влажности); X, = 1,5'.
k = 1,4.
13—М. Е. Дейч
193
при данном а*(М0) на ударной поляре находим две точки: Е21 и Е22,
отвечающие двум различным углам скачка. Причем точка £21
соответствует криволинейному конденсационному скачку. Точки Е3
отвечают скачку разряжения.
Ударной поляре адиабатического скачка соответствует значение
а* = 1. По мере уменьшения я* (увеличения М0) угол скачка
конденсации при данном дк возрастает. Прямому конденсационному скачку
в соответствии с формулой (4-51) отвечают два значения вектора и2
(точки Z)j и D2). Отрицательный знак перед корнем в (4-51) дает точку
D,, а положительный — D2.
Таким образом, уравнения (4-43) и (4-48) и ударная поляра на
рис. 4-35 показывают, что теоретически возможно существование
четырех типов прямых и косых конденсационных скачков, отвечающих
различным скоростям перед скачком и величинам а*(Ы0).
Соответствующая классификация указана в табл. 4-2.
Таблица 4-2
Возможные типы конденсационных скачков
Р1ормальная
составляющая скорости
перед скачком
сп\ <Л1
cn\>ai
Отношение
критических скоростей
1 >а. >в# мин
1 > а. >"а# шт
Нормальная
составляющая скорости
за скачком
1. сп2>а2
2 сп2 < а2
3- сп2 > а2
4 сп2 < а*
Тип
скачка
Скачок
разрежения
Скачок
уплотнения
Однако если учесть некоторые дополнительные условия, то
возможными оказываются скачки всего двух типов: 1) сверхзвуковые
скачки, в которых cnl^av сп2<^а2 и конденсация сопровождается
сжатием газа (р2 > р^)\ 2) дозвуковые скачки, отвечающие условиям
cn\<^av cn2^ia2 ив которых конденсация сопровождается разрежением
газа (/?2 < А)- Скачки, отвечающие соотношениям сп^> ах и сп2 ^> я2,
не могут реально осуществиться, так как такой скачок перемещался
бы относительно находящегося перед ним газа со сверхзвуковой
скоростью и его возникновение не должно было бы отразиться на
состоянии этого газа.
Скачки конденсации в дозвуковом потоке не могут перевести газ
в область сверхзвуковых скоростей (спХ<^ах\ сп£> #2)> так как в этом
случае необходимо отводить от газа теплоту, что не соответствует
условиям конденсации.
194
Определим изменение энтропии в конденсационных скачках.
В частном случае к — 0 получим
(4-54)
В формулу (4-54) входит отношение —-1, которое можно найти по
Ро2
- /?2
уравнению (4-46), подставляя k = 0; при этом М2 и — определяются
по формулам (4-44) и (4-45).
Исследуя уравнение (4-54), можно убедиться в том, что для
скачков первых трех типов (табл. 4-2) As > 0. Однако, привлекая
дополнительное условие (термодинамическое состояние перед скачком
должно соответствовать началу быстрой конденсации) и учитывая
влияние теплообмена, можно показать, что скачок первого типа, как
и четвертого, невозможен
225
60"
50'
40'
30°
и,ои\
0J55
0,50
0,45
0,40
0,35
- 0,30
- 0,25
~ 0,20
l а/5
\PilPoi
\ |
\ i
А \
\ \
- \ \
"***/^
1 i
JPm .
Vм'
^ч
1
Pmfr
Pt/Pot
1^. ^
^^=::^сг
Ън I
А
* 1
н
■*J
200-
175 -
/50 -
/25 ~
100-
75 J
50 -
М,
1,8
/,7
UB
U5
*А
из
\иг
25
/О 12 г/нг
й Л 1,0
U
Рис. 4-36 Зависимость относительного давления и числа М,
от абсолютной влажности х в соплах Лаваля.
13*
195
Опыт подтверждает возможность образования скачков второго и
третьего типов.
На положение скачка, его форму и интенсивность решающее
влияние оказывают влажность воздуха и скорость потока. На рис. 4-36
приведены кривые относительного давления и числа Мх перед
скачком конденсации в зависимости от абсолютной влажности воздуха i
по опытам А. А. Степчкова, проведенным в соплах Лаваля. С
увеличением влажности скачок конденсации перемещается в область
меньших чисел Мх.
0,9
0,6
OJ
0,6
ол
0,3
0,2
' О ТО 2CT3LТ"~60 50 60 70 80 90%
а)
Рис 4-37
а —изменение положения конденсационных скачков
в сопле Лаваля в зависимости от скорости X! и
относительной влажности х, б — схема скачка
в сопле.
С увеличением влажности уменьшается пересыщение потока
воздуха парами воды, определяемое отношением парциального давления
Pl«
пара к давлению насыщения —— , а также переохлаждение ДГ =
Р\н
= Гн1—Тх (рис. 4-36), где тн1— температура насыщения, a
Тх—температура перед скачком По мере возрастания влажности величины
пересыщения и переохлаждения уменьшаются.
Перемещение скачка конденсации в зависимости от влажности
объясняется, по-видимому, тем, что с уменьшением количества паров
воды конденсация их происходит при более низкой температуре,
соответствующей большому числу Мх При перемещении меняется и
196
.27 =
X
\\
V
\
м
у/
■1,72
.1,30
Ч
г
^
\Ч
\
*
форма скачка: при большой влажности скачок становится мостообраз-
ным и приближается к прямому; с уменьшением влажности
наблюдается, как правило, система двух пересекающихся скачков.
В заключение отметим, что изложенная теория конденсационных
скачков оставляет в стороне вопросы механизма конденсации,
зарождения и развития ядер конденсации.
ГЛАВА ПЯТАЯ
ДВИЖЕНИЕ ГАЗА ПРИ НАЛИЧИИ ТРЕНИЯ
5-1. ТЕМПЕРАТУРА ТОРМОЖЕНИЯ В ВЯЗКОЙ ЖИДКОСТИ
При рассмотрении движения реальной (вязкой)
жидкости необходимо учитывать диссипацию (рассеяние)
энергии, вызываемую внутренним трением и теплопроводностью,
т. е. термодинамической необратимостью процесса.
Движение вязкой жидкости описывается системой
уравнений сохранения: расхода, количества движения и энергии.
Уравнение неразрывности (1-12), как уже указывалось,
справедливо и для вязкой жидкости. Уравнения
количества движения в форме Эйлера (1-16) должны быть
дополнены членами, учитывающими влияние вязкости.
Следует подчеркнуть, что для необратимых процессов
движения интегралы уравнений движения и энергии
несовпадают. При выводе уравнения энергии для струйки
(§ 2-1) указывалось, что' оно справедливо и для
адиабатических (необратимых) течений. Однако это замечание
вполне справедливо только в частном случае, когда
работа сил трения полностью преобразуется в тепло. Такой
процесс соответствует простейшей схеме одномерного
потока или движению газа с равномерным полем скоростей.
При рассмотрении движения вязкой жидкости с
неравномерным распределением скоростей в потоке условие
эквивалентности теплоты трения и работы трения не
выполняется. В таком потоке только часть работы трения
превращается в теплоту, а другая часть вызывает чисто
механический эффект: перестройку поля скоростей, в
процессе которой происходит перераспределение кинетической
энергии между частицами жидкости. Отсюда вытекает,
что различные частицы приобретают разное количество
теплоты трения и имеют разный запас полной энергии.
Следовательно, условие i0 = const в общем случае не
является интегралом уравнения энергии для всей массы
197
жидкости, так как в потоке образуется местное
перераспределение энергии.
В качестве примера рассмотрим движение вязкой
сжимаемой жидкости ме > ду двумя плоскими стенками
*У
:0.
Рис 5-1. К выводу уравнения энергии для потока сжимаемой вязкой
жидкости между двумя плоскими стенками (безградиентное течение).
(рис. 5-1). Верхняя стенка движется в направлении оси х
с постоянной скоростью, равной скорости газа с . На
нижней стенке скорость равна нулю, так как эта стенка
неподвижна1. Полагаем, что давление сохраняется
постоянным вдоль осей х и у, т. е.
dp dp
dx dy
Если скорость движения верхней стенки мала, для
адиабатического потока можно считать, что температура
постоянна и одинакова для всех точек потока. Если же
величина с^ достаточно велика, то необходимо учитывать,
что температура Т является функцией у. В таком течении
эффект сжимаемости проявляется только в связи с
изменением температуры газа; плотность газа меняется в
соответствии с формулой (для идеального газа)
р const
W(y)~~TW
р(«) =
1 Рассматриваемый частный случай движения газа называют
течением Куэтта.
198
Так как в рассматриваемой задаче скорости по оси xs
не меняются, а давление сохраняется постоянным как
по у, так и по х, то закон сохранения энергии
формулируется весьма просто: количество теплоты, подведенное
к элементу, плюс работа сил трения равны нулю.
Обозначим: Q — количество тепла, переданное элементу
в единицу времени от соседних частиц; т— напряжение
трения, Количество тепла, полученное элементом,
определяется как разность (рис. 5-1):
Qdx- (Q+«Ldyyx = _Wdydx*m
Разность секундных работ сил трения находим по
уравнению
Тогда уравнение энергии будет:
dx = -т- {tc)dydx.
£(-Q+«)=0.
ИЛИ
— Q + хс = const.
Постоянная в правой части уравнения энергии
определяется из граничных условий. Так, при г/ = 0, £ = 0 и
Q = QQ1 где Q0 — удельное количество тепла,
передаваемое потоку газа от внешнего источника.
Следовательно,
-Q + w = -Q0.
Для ламинарного движения % определяется по формуле (1-4).
Вспомним, что
dy
где Я — коэффициент теплопроводности.
После несложных преобразований получаем:
Q dT , dc d fcPT . с* \
dy ' r dy { dy \ Pr ~ 2 )
Размер элемента в направлении оси г принят за единицу.
199
Величину
Pr=-f-
называют числом Прандтля. Отметим, что входящие в
выражение для Рг коэффициенты теплопроводности и
вязкости зависят от температуры:
Я = А(Г) и !А = |1(Г).
Интеграл уравнения энергии для случая ^ = const
позволяет связать статическую энтальпию в потоке с
энтальпией у неподвижной стенки следующим образом:
/_,; + Рг4=-Рг<г.]^.
о
// у
Cdu (da и
где при линейном распределении скорости \—=1 — = ^-;
* ° °
т0—-напряжение трения на стенке; i*0 = cpT0 —энтальпия
торможения на стенке.
Следовательно,
/-/•+Рг^-=-Рг^л (5-1)
Для верхней стенки, движущейся вместе с потоком со
скоростью с^ нетрудно получить:
ioo-/; + PrC-f. = -Pr-^^. (6-la)
С помощью (5-1) и (5-1а) после несложных
преобразований находим:
' + РГ(^Н-^^) = ^+РГ(^ + ^Соо). (5-16)
или
'оо J оо \ °° J
+ Рг-§М*-1)(1-^-)лС (5-1в)
200
Найдем для случая адиабатического течения (Qo = 0)
отношение температур торможения на движущейся стенке
и в произвольном сечении потока (на расстоянии у),
учитывая, что температура торможения и термодинамическая
температура связаны соотношением
Имея в виду, что рассматривается случай с = const,
следовательно i — c T, а для адиабатического течения и
Qo = 0, из (5-1) и (5-1г) получим:
г;=<+о-рг)£.
р
Для движущейся стенки с помощью уравнений (5-1а)
и (5-1 г) будем иметь:
7,. = 7'оЧ(1-РО^;-
Следовательно,
^= 1 _ (1 _ Рг)%^1= 1 -0 -Рг)(£-Р), (5-2)
где
» соо . р С
Формула (5-2) показывает, что для Рг ф 1 в вязком
газе температура торможения, т. е. полная энергия
не сохраняется постоянной по сечению. При
Рг = 1 температура торможения Т,{у=Т0 = const для всех
точек потока.
Число Рг характеризует соотношение между теплом,
выделившимся вследствие трения, и теплом, отведенным
от элемента теплопроводностью. При Рг<1, что имеет
место для всех газов, отвод тепла совершается более
интенсивно, чем его выделение. В этом случае Т*0 <То- При
Рг>1 выделение теплоты трения происходит более
интенсивно, чем ее отвод, и Г*>Г0.
201
Для совершенного газа число Рг является физической
константой, не зависимой от состояния газа.
Для более общего случая плоского потока газа, когда скорости
зависят от х и у, дифференциальное уравнение энергии может быть
(d2T (l +Pr—ft- М2 j д2Т И + Рг
PF \ ~dx~2 I ду'
аг(1+^т^М2) дт(] +
да да да 1 др
-дГ + идх-+ид^==Х-Т'дх~ + "
1 д /да dv V
~]~~~3~' dx [дх +ду )
dv dv dv 1 dp
Tf + u'd7 + vdi==Y ~~?~'W
Г /d2u d2a
[\dx2~jrdy2
>
2
dx +v~ Ту -• (5"3>
Уравнения количества движения с добавлением членов,
учитывающих влияние вязкости (уравнения Навье — Стокса), записываются
в следующей форме:
(5-4)
+ v {\dx~'>-dy2)~^ 3 ' dy {дх"~*ду)у
Эти уравнения дополняются уравнением неразрывности (1-12) для
плоского потока*
уравнением состояния (1-1) и уравнением трения, например для
ламинарного течения законом Ньютона (1-4).
При исследовании движения газа в трубах и каналах с учетом
вязкости, а также при изучении обтекания тел газовым потоком
задача сводится к определению потерь энергии и аэродинамических
сил, действующих на обтекаемую поверхность С этой целью
необходимо решить совместно замкнутую систему шести уравнений (5-3),
(5-4), (5-4а), (1-1), (1-4), определяя неизвестные функции координат:
/?, р, и, vy T и 1 (для установившегося потока).
1 Вывод дифференциальных уравнений энергии и количества
движения можно найти в книге Л Г Лойцянского и др (см список
литературы).
202
5-2. УСЛОВИЯ ГАЗОДИНАМИЧЕСКОГО ПОДОБИЯ
В связи с весьма большими трудностями решения
системы уравнений движения в общем случае (такие
решения удается получить только для простейших частных
случаев) в практике коэффициенты сопротивления и
коэффициенты потерь энергии часто определяются
экспериментально путем испытания моделей в лабораторных
условиях. При этом необходимо соблюдать такие условия
испытания моделей, которые обеспечивают надежность
получаемых результатов и позволяют распространить эти
результаты на натурные объекты.
/ Я
Рис. 5-2 Схема подобных потоков
Широко применяемый в механике метод подобия
позволяет сформулировать указанные условия модельных
испытаний и устанавливает приемы переноса результатов
лабораторных исследований на натурные объекты.
Аэродинамические силы, действующие на обтекаемое
тело или на стенки канала (в том числе и силы
сопротивления), выражаются через безразмерные коэффициенты.
Установим, от каких параметров в общем случае зависят
коэффициенты сопротивления.
С этой целью рассмотрим обтекание жидкостью двух
геометрически подобных тел (рис. 5-2).
В случае кинематического и динамического подобия
двух рассматриваемых явлений поля скоростей и сил
в двух потоках должны быть взаимно пропорциональными.
Тогда, вводя масштабы длин L, времени Т и массы М,
можно представить связь между длинами, временами и
массами двух подобных потоков следующим образом:
/' = !/; f = 77; т' = Жт.
Масштабы всех других величин, входящих в уравнения
(5-4), легко выражаются с помощью указанных масштабов.
Допустим, что уравнения (5-4) выражают связь между
параметрами течения первого потока. Имея в виду размер-
203
ности величин, входящих в эти уравнения, отраженные в
единицах измерения: длины х, у[м], скорости и, и[м/сек]у
плотности р [кг • сек2/м*], кинематической вязкости v [м2/сек\,
массы т\кг*сек2\м\ и давления р [кГ/м2], легко связать
параметры первого и второго потоков с помощью
масштабных коэффициентов:
х у г г _с_ и v L
х' ~~~y — с~~"с7"~л?~~v~T;
h — -L — — • h — JL—^L-
P~~ p' "~L3 > «v— у — Г '
kP=zY=T4?' (5~5)
Здесь и выше штрихом обозначены параметры течения
второго потока. Соотношения между параметрами (5-5)
являются очевидным следствием пропорциональности
линейных размеров, времен и масс двух подобных потоков.
Располагая оси координат в обоих потоках одинаковым
образом, путем подстановки соотношений (5-5) в первое
уравнение (5-4) можно записать для второго потока:
Уравнение (5-6) выражает уравнение количества
движения в дифференциальной форме для второго потока,
записанное через параметры первого потока.
Все члены уравнений (5-4) и (5-6) имеют, естественно,
одинаковую размерность ^ \м\сек% в чем легко
убедиться с помощью соотношений (5-5). Чтобы потоки были
динамически подобными, необходимо, чтобы они
удовлетворяли одним и тем же дифференциальным уравнениям
движения. Отсюда следует, что комплексные множители
перед членами уравнения (5-6) одинаковы, т. е.
kC К_ %ж ^р К^С
или
Т k±
bj k2 kk2~~ М-
С кс КрКс
204
Заменяя здесь масштабные коэффициенты из (5-5),
окончательно получаем с учетом уравнения энергии (5-3)
следующие условия подобия:
lc__l'c'm ct_c't'u gl __gT.
v" I '
p __ p' .
pc2 pV 2 '
V ' с* c'2
№p ^Cp
\ ~ V '
(5-7)
Таким образом, два потока являются динамически
подобными, если выполняются соотношения (5-7) между
параметрами этих потоков. Соотношения (5-7) называются
критериями подобия. Первое соотношение (5-7)
устанавливает равенство чисел Рейнольдса в двух
потоках:
Re = ^- = Re'.
Критерий Рейнольдса выражает соотношение между
силами вязкости и силами инерции в потоке.
Второе условие является единственным, куда входят
сходственные отрезки времени t и f, и оно получилось как
следствие подобия членов, содержащих локальные
ускорения (~jr и -^-) в уравнениях движения. Локальные
ускорения характеризуют только неустановившиеся, в том
числе и периодические, процессы движения газа.
Следовательно, второе равенство является условием подобия для
неустановившихся потоков.
Отношение
носит название числа Струхаля; для периодического
движения
nl
где п = — частота периодически нестационарного
процесса.
Третье уравнение дает равенство критериев подобия,
учитывающих влияние массовых сил в потоке. Если
ускорение в поле земного притяжения можно считать постоян-
205
ным (g — g), то этот критерий, называемый критерием
Фруда, легко представить в таком виде:
Fr = -^ = IV.
с2
В газовых потоках влияние массовых сил, как правило,
невелико и поэтому критерий Fr при моделировании
газовых потоков не принимается во внимание.
Четвертое уравнение (5-5) выражает связь между
статическими давлениями и скоростными напорами в
сходственных точках подобных потоков. Величину
можно рассматривать как характеристику, учитывающую
влияние сжимаемости. В этом легко убедиться, заменяя
р через скорость звука:
т2
Р--Т-
Тогда для двух потоков получаем:
r2 rf 2
k — k9 —
R а2 —Я а!2"
или
Ш2 = £'М'2.
Следовательно, одинаковость чисел р имеет своим
следствием равенство чисел kN[ в сходственных точках
потоков. Отсюда следует, что число М, известное нам из
предыдущего, выступает как критерий подобия,
отражающий свойства сжимаемости. В такой же мере и показатель
изоэнтропы k в совершенном газе следует рассматривать
как критерий подобия.
Рассматривая дифференциальное уравнение энергии
(5-3) для сжимаемой вязкой жидкости, можно получить
дополнительный, уже знакомый из предыдущего критерий
подобия Прандтля:
Рг = -/.
Из этого же уравнения вытекает также одинаковость
критериев k и М для газовых потоков.
206
При турбулентном течении вводится важная характери
стика — степень турбулентности:
где с2 = -£f \ (с — ст)2 dt — средняя квадратичная скорость
пульсации; с — мгновенное значение скорости; ст —
средняя скорость турбулентного течения:
п
Резюмируя, отметим, что необходимые условия подобия
двух потоков сводятся к равенству определяющих
критериев в сходственных точках натуры и моделей и
тождественности начальных и граничных условий.
Анализ уравнений движения и размерностей величин,
определяющих сопротивление обтекаемого тела или потери
энергии в потоке газа, показал, что соответствующие
безразмерные характеристики сопротивления являются
функциями основных критериев подобия1:
^ = ^(Re,M, Pr, Sh, E)\
C = C(Re, M, Pr, Sh, £), (5-7а)
где сх — коэффициент сопротивления (см. § 5-13);
£— коэффициент .потерь энергии (см. §§ 4-5; 5-14;
8-5 и др.).
При исследовании различных явлений не все критерии
имеют одинаковое физическое значение. В зависимости от
конкретной задачи один или несколько критериев могут
иметь преобладающее значение, в то время как другая
группа критериев не оказывает заметного влияния на
характеристики движения.
Так, например, для установившегося движения
несжимаемой жидкости критерии М и Sh теряют смысл и
зависимость (5-7а) упрощается.
С учетом сжимаемости при установившемся движении
1В соотношения (5-7а) критерий k не входит, так как согласно
молекулярно-кинетической теории газов условие Pr = Pr' эквивалентно
условию k = k'.
207
для газов с одинаковыми физическими свойствами сх =
= сх(Яеу М).
Обеспечить равенство всех критериев подобия возможно
только в натурном эксперименте, который связан с
большими трудностями.
Обычно осуществляется приближенное подобие
(частичное моделирование) по одному или двум наиболее
важным критериям. Результаты эксперимента нетрудно
скорректировать и на другие критерии, если известны
значения этих критериев в. опыте и зависимость изучаемых
характеристик от этих критериев.
При исследовании потоков, в которых определяющими
являются два или три критерия (например, Re и М или
Re, M и Sh), необходимо осуществлять принципы
раздельного моделирования, т. е. обеспечивать возможность
независимого изменения каждого из критериев в определенном
диапазоне его значений.
В заключение отметим, что рассмотренный выше прием
анализа размерностей может оказаться весьма
эффективным, если известны физические параметры, определяющие
исследуемый процесс, но не удается решить или даже
записать систему дифференциальных уравнений задачи.
В этих случаях метод размерностей в сочетании с
экспериментальными данными позволяет получить решение для
целого класса механически подобных явлений.
5-3. ОДНОМЕРНОЕ ТЕЧЕНИЕ ГАЗА ПРИ НАЛИЧИИ ТРЕНИЯ.
ОСНОВНЫЕ УРАВНЕНИЯ
Основными уравнениями установившегося
адиабатического движения вязкого газа являются уже известные нам
уравнения неразрывности, количества движения и энергии.
Уравнение импульсов одномерного установившегося
потока без энергетического обмена с внешней средой при
наличии трения можно записать в таком виде:
cdc+df + dXTp = 0, (5-8)
где dXtp — единичный импульс сил трения.
Величина dX может быть выражена по гидравлической
формуле:
d*TP = cT"lT' (5-9)
208
где С — коэффициент сопротивления; D — внутренний
диаметр трубы.
Решая совместно уравнения (5-8), (5-9), (2-14) и (2-6),
можно получить дифференциальное уравнение
распределения скоростей вдоль трубы переменного сечения с учетом
влияния вязкости. Очевидно, что это уравнение аналогично
(2-29), но должно содержать еще один член, учитывающий
влияние вязкости. Простые выкладки приводят к такому
выражению:
(Я'-1)^=(1-^Я*)^-С^№, (5-10)
где х=-£-.
Формулу, определяющую изменение давления потока
вдоль трубки переменного сечения, следуя уже известному
методу, изложенному в гл. 2, можно получить в
следующем виде:
I_i сах . (5-п)
Из уравнений (5-10) и (5-11) можно заключить, что
изменение параметров течения в трубке переменного сечения
происходит под воздействием двух факторов: деформации
потока (изменение сечения трубки) и сил трения.
Уравнения показывают, что влияние трения всегда является
односторонним. Так, например, при дозвуковых скоростях (*<1)
в суживающейся трубке (dF<^0) трение способствует
ускорению течения (dl^>0 и d/?<0). При сверхзвуковых
скоростях в такой же трубке (dF < 0) трение приводит к
замедленному падению скорости и соответственно к более
медленному возрастанию давления по сравнению с
идеальным процессом без потерь.
Из уравнений (5-10) и (5-11) следует, что в
простейшем случае трубки постоянного сечения (dF = 0) при А<1
имеем-у-> 0 и— <0 и, следовательно, поток
ускоряется. Нетрудно видеть, что в этом случае при
сверхзвуковой скорости (Я>1)—<0: поток тормозится.
dp_
Р
2k
Л2
dF
k + l X2
14 М. Е. Дейч
209
Сопоставляя влияние изменения сечения трубки
(деформации трубки тока) и влияние трения, можно заключить,
что в дозвуковом и сверхзвуковом потоках трение
приводит с качественной стороны к такому же изменению
скорости течения, как и уменьшение сечения трубки.
Следовательно, воздействие сил трения в потоке можно
заменить эквивалентной деформацией струи — уменьшением
ее сечения в направлении движения.
Правомочность такой замены вытекает из следующих
рассуждений. Движение газа в трубе без энергетического обмена, но при
наличии сил трения является необратимым адиабатическим процессом.
Такой процесс, как нам уже известно, сопровождается ростом
энтропии. Приращение энтропии можно выразить по уравнению (4-27)
Для энергетически изолированной системы I имен в виду, что
Г01 = Г02 и что уравнение состояния дает —— — -^М получим.
Poi Poi /
bs=~R\n~=:R\n —. (5-12)
Ро2 £0
Так как энтропия в направлении потока возрастает, давление
торможения р02 должно уменьшаться.
По уравнению неразрывности (2-41) для двух сечений трубы
заметим, что при одинаковых в обоих случаях величинах Fv Xt и Х2
сечение F2 при наличии сил трения должно быть больше, чем для
изоэнтропического потока.
Величину eQF можно рассматривать как живое сечение струи.
Для трубы постоянного сечения (F = const) очевидно, что живое
сечение eQF при наличии трения уменьшается, так как уменьшается
величина е0.
Уравнение (5-10) может быть использовано для
некоторых заключений о положении сечения, отвечающего
экстремальным значениям скорости. Выразим из уравнения (5-10)
логарифмическую производную сечения:
d\ k , -
1 k + \A
отсюда следует, что при dX = 0 и Я ^= 1
k
£ , , t k2dx
210
Следовательно, сечение, соответствующее максимальной
скорости при Я<4 и минимальной скорости при Я>1, не
совпадает с минимальным сечением, а смещается в
расширяющуюся часть трубки. Соответственно критическим
условиям (Яг=1) также отвечает сечение в расходящейся части
трубки. Это означает, что минимальное и критическое
сечения трубки при наличии трения не совпадают. В этом
случае, полагая в (5-10) Я = 1, получим:
dF k
5-4. ДВИЖЕНИЕ ГАЗА В ЦИЛИНДРИЧЕСКОЙ ТРУБЕ
Из уравнения (5-10) для цилиндрической трубы
(-у =0 j получим:
1 0^=rtrU*. (5-14)
К [) X /г + 1
Из предыдущих рассуждений, а также непосредственно
из анализа уравнения (5-14) легко прийти к выводу, что
критическая скорость течения может возникнуть только в
выходном сечении цилиндрической трубы. Действительно,
согласно уравнению (5-14) при Я<М и <й>0 поток в
трубе ускоряется, а при 2>1 и й<(0 он замедляется.
Случай Я = 1 в промежуточном сечении трубы противоречит
уравнению (5-14) и физически нереален.
Допустим, что коэффициент сопротивления является
величиной постоянной1. Тогда уравнение (5-14) можно
проинтегрировать.
Интеграл уравнения (5-14) запишем в такой форме:
Af-"xr-ln^-=ifeTTu' (5"14a)
где Хх-—безразмерная скорость в начальном сечении
трубы;
Я — безразмерная скорость в некотором сечении на
расстоянии х от начального.
1 Такое допущение оправдывается только в первом приближении.
В действительности $ зависит от чисел Re и М.
14* 211
Введем безразмерную координату, которую называют
приведенной длиной трубы:
Х =
2k r-
k+ 1
Тогда уравнение (5-14а) можно записать так:
in
X2
_ J 1 t
(5-15)
Зависимость между X и х при постоянном значении Ях
приведена на рис. 5-3. Величина х имеет максимум при
Я = Я1 = 1.
Максимальное значение приведенной длины трубы
выражается формулой
= -L_l+lni
(5-16)
Кривые xW состоят из двух ветвей, отвечающих
дозвуковому (Я<4) и сверхзвуковому (Я>1) потокам в
трубе постоянного сечения (рис. 5-3).
Кривые наглядно иллюстрируют невозможность
перехода в цилиндрической трубе из одной области скоростей
0
ос
6,0
о
с
/1С
и,а
Л
If
с
N
£=
W>
7*
У
^
\
г
#"
х 1
Рис. 5-3. Зависимость безразмерной
скорости на выходе из трубы от скорости
на входе и приведенной длины трубы.
в другую. В такой трубе, как было показано выше, при
определенной скорости на входе Хх и соответствующей
длине на выходе достигается критическая скорость (Я2=1).
Дозвуковым потокам на входе* трубу (Ях <С 1)
отвечает участок кривой А В (рис. 5-3), а сверхзвуковым
(*i>l) — участок СВ. Точка В определяет максимальную
величину функции х Аля данного значения Я1#
212
Из формулы (5-16) следует, что при Ях = 1 умакс = 0.
Графически зависимость (5-16) представлена на рис. 5-4.
Кривая также имеет две ветви. Нижняя ветвь отвечает
дозвуковым скоростям на
3
2
1,5\
1
о
F>
\
\/
]/
Г
£мщ\
в
10
входе в трубу, а верхняя —
сверхзвуковым.
Таким образом,
уравнение (5-16) показывает,
что для цилиндрической
трубы заданных размеров
/ и D при скорости на
выходе из трубы Я2 = 1 и для
определенных значений k и
С безразмерная скорость на
входе в трубу Ях, а вместе
с тем и приведенный расход
газа qx имеют строго
определенные значения.
При дозвуковой скорости на входе в цилиндрическую
трубу длиной /, характеризуемую коэффициентом
сопротивления С, при установившемся движении может пройти
максимальное количество газа, если Ла = 1.
Абсолютный расход газа через трубу предельной длины
будет равен:
Рис. 5-4. Максимальная
приведенная длина трубы в зависимости от
скорости на входе.
:^(Р,^)макс = ^<71максР,
а =
Вспоминая, что
k — \ Я2
k -\-\ 1 макс
k—\
Р. А = Р
2k - __
k + 1«'о~
i
/ 2 ч*-' |/ 2k />„,
V* + V ^(ft + i^VTT,'
получим:
макс р
-Я.
О
(& + 1)/? "1макс \^ £ + 1 1ма
экс I
1
/г—1
Кг. "
(5-17)
213
Таким образом, для увеличения абсолютного расхода
газа через цилиндрическую трубу определенных размеров
необходимо увеличивать давление полного торможения на
входе в трубу или — при постоянном значении /?01 —
уменьшать температуру торможения Т0. При этом в выходном
сечении трубы будет по-прежнему критическая скорость,
абсолютное значение которой уменьшается по мере
снижения температуры торможения. Однако расход будет
увеличиваться за счет увеличения плотности.
При сверхзвуковых скоростях на входе в трубу, как
показывает опыт, обнаруживаются некоторые новые
свойства потока, которые не описываются уравнением (5-15).
Заметим, что согласно уравнению (5-15) приЯх>1
скорость в трубе должна непрерывно падать к выходному
сечению по кривой СВ на рис. 5-3, а давление —
соответственно непрерывно возрастать. Однако в действительности
изменение скоростей и давлений в трубе в ряде случаев
происходит скачкообразно.
Прежде чем подробнее разобрать этот случай
движения газа, найдем зависимости, определяющие изменение
параметров потока между двумя произвольными сечениями.
Так как в изолированной Чрубе /0 = const, то для
любых двух сечений можно написать Г01 = Г02 = const. Из
этого условия получаем уравнение для Т/Т0 в форме
уравнения (2-22).
Для отношений давлений можно воспользоваться
формулами (2-41а) и (2-42). После несложных преобразований
получим связь между статическим и полным давлениями
в следующем виде:
jf-(i+T) «■—т— • <5-'8>
Отсюда при Я = Я2 = 1 определяется критическое
отношение давлений:
k
\=(*-ТтГ* = '^- (5"19)
Формула (5-19) показывает, что критическое отношение
давлений — для необратимых течений будет меньше чем
214
для изоэнтропических, для которых
k
k + l
Уравнения (5-18) и (5-15) позволяют построить графики
изменения давлений вдоль трубы для заданных значений
Ях и
неподобный график приведен на рис. 5-5 для случая
сверхзвуковой скорости на входе в трубу Л1 = 1,76 и ql-=-
= 0,453. Здесь кривая АВ характеризует повышение
давления в трубе до критического значения в точке В,
равного:
е' = 0,528- 0,453 = 0,239.
Если известно распределение скоростей по трубе, а оно
легко подсчитывается по уравнению (5-14а), то можно по
формулам (4-20) и (4-24) определить скорости и давления
за прямым скачком уплотнения в каждом данном сечении
(линия СВ).
За прямым скачком поток — дозвуковой и,
следовательно, давление в нем под влиянием сил трения должно
падать. Так, если прямой скачок возникает
непосредственно во входном сечении, то дальнейшее изменение
давления протекает по кривой CD. Характер изменения
давлений в дозвуковом участке трубы при различных промежу-
ч
ОА
0,3
0,2
0,1
п
F
1 ■
jw^>/
s
е
>
^^Нг
JB Q N ^
"""""""--£
м
X
1 1
0,1 ОЛ 0,3 ОЛ 0.5 0,6 0,7 Oft
Рис. 5-5. Распределение давлений по трубе постоянного
сечения.
215
точных положениях скачка представлен соответственно
кривыми FM, HN и т. д. Диаграмма давлений позволяет
проанализировать различные режимы течения в трубе.
При указанной скорости на входе Ях и приведенном
расходе газа qx режимы в трубе без скачков возможны в
тех случаях, когда Х<Умакс, причем максимальное
значение приведенной длины отвечает точке В. При условии
Х<ХМакс скачки в трубе возникают только тогда, когда
давление на выходе из трубы больше соответствующего
давления, показываемого кривой АВ.
Допустим, что труба имеет длину, определяемую
точкой / (х = 0,35), а давление за выходным сечением задано
точкой L, которая лежит на кривой СВ. В этом случае
прямой скачок располагается в выходном сечении трубы IL.
Если давление среды, куда вытекает газ из трубы,
определяется точкой /С, то прямой скачок перемещается внутрь
трубы и располагается в сечении EF, причем отрезок FK
соответствует понижению давления в дозвуковом участке
трубы. Последующее повышение давления среды приводит
к дальнейшему перемещению скачка внутрь трубы (к
входному сечению).
Если давление среды определяется точкой 5, то в трубе
скачков не возникает, а в струе, выходящей из трубы,
образуется конический скачок (или система плоских косых
скачков, если труба прямоугольного сечения). При
уменьшении давления до величины давления в точке /
интенсивность конического скачка уменьшается. В точке /
конический скачок вырождается в слабую коническую волну, при
пересечении которой энтропия не меняется1.
Если, наконец, давление среды меньше, чем давление
в точке /, то за выходным сечением образуется коническая
стационарная волна разрежения и поток газа расширяется
за пределами трубы.
Кривые давлений в трубе (рис. 5-5) показывают, что
при постоянной длине х и давлении на выходе р2 с
увеличением скорости на входе 1г прямой скачок смещается к
выходному сечению. При увеличении сопротивления трубы
(путем, например, подключения дополнительного участка
трубы) перемещение скачка происходит в обратном
направлении (ко входу в трубу).
1 Различные системы скачков, образующихся в струе на выходе
из трубы, подробно рассмотрены в гл. 6.
216
5-5. ПОТЕРИ НА ТРЕНИЕ В ЦИЛИНДРИЧЕСКОЙ ТРУБЕ
(ОПЫТНЫЕ ДАННЫЕ)
Выше рассматривалось движение вязкого газа в трубе в
предположении, что коэффициент сопротивления С постоянен.
В действительности коэффициент сопротивления зависит
от числа Рейнольдса и—в общем случае — от безразмерной
скорости М. Такая зависимость устанавливается
экспериментально.
Число Рейнольдса для произвольного сечения
цилиндрической трубы определяется по формуле
Для цилиндрической трубы
следовательно,
■H^r/jr^^- <5-2о>
Из формулы (5-20) видно, что число Re меняется вдоль
трубы только вследствие изменения коэффициента вязкости
р., который зависит от температуры. Можно показать,
однако, что в теплоизолированной трубе изменения
температуры невелики. Так, при изменении "скорости водяного
пара в трубе от Я1 = 0,2 доЯ2 = 1 температура изменяется
на 11%, в то время как давление уменьшается в 4,5 раза,
а плотность — в 5 раз.
Изменение коэффициента вязкости воздуха в
зависимости от температуры можно оценить по приближенной
формуле
^о (яз)". (5-21)
где а — постоянная величина; ц0 — коэффициент вязкости
при температуре Т = 273°.
По опытным данным для воздуха
а = 0,76; у0=1,76.10-в.
217
Более простая зависимость для ц выражается формулой
р. Ю6 = 1,757 + 0,00483/° С.
Основная задача опытного исследования адиабатических
потоков газа в трубах сводится к определению
коэффициентов сопротивления С и, следовательно, к нахождению
потерь энергии. Методика опытного определения местных
значений коэффициентов сопротивления в различных
сечениях трубы основывается на уравнении (5-8), которое после
деления всех членов на а2 принимает вид:
d* + rTT + C-fd* = 0. (5-22)
Замечая, что для цилиндрической трубы произведение
рХа = qp а2 = qs kp0
является постоянной величиной, имея в виду (2-46),
запишем уравнение (5-22) в такой форме:
dx + dic + t \dx = 0.
Здесь функция к зависит только от Я по формуле
(2-46а).
После подстановки этой функции получим:
*+*а1«[-гО-:-?т»,)]+ст<*=°-
Отсюда можно выразить коэффициент сопротивления:
<«'4Ч*-4;&- (5'23)
Уравнение (5-23) является исходным для
экспериментального определения местных значений С. Перейдя в этом
уравнении к конечным разностям, будем иметь:
'-'4Ч*-4-)£- ^
Если известны расход газа G, температура, торможения
Т0 и распределение давлений вдоль трубы [р = р(х)]> то
по формуле (5-24) можно найти средний коэффициент со-
218
противления для некоторого небольшого участка трубы
длиной Длс Если участки Дл; выбираются небольшими, то
определенное таким путем значение £ не сильно отличается
от его местного значения.
Для нахождения связи между р и Я можно
воспользоваться формулой (5-18).
Заменив здесь из уравнения неразрывности величину q,
получим:
_P__k + l Ga^ f k-l Л -„
Рассмотрим вначале некоторые результаты опытного
исследования потоков в цилиндрических трубах при
небольших скоростях.
На рис. 5-6 показано изменение профиля скоростей
в трубе в зависимости от числа Re для турбулентного
режима. Здесь же нанесена эпюра скоростей для
ламинарного потока в трубе. Сравнение кривых показывает, что
профиль скоростей при турбулентном режиме значительно
более „полный", чем при ламинарном, причем с ростом
числа Re наполнение профиля увеличивается.
0,1 02 OJ O.U 0J 0,0 0,7 OJS 0J9 W
Рис. 5-6. Распределение скоростей при
ламинарном и турбулентном режимах в трубе.
219
Как известно, при турбулентном двил ении,
возникающем в трубах при Re > 3 000, имеют место перемещения
макрочастиц1 в поперечном направлении. При этом частицы
внешнего потока, обладающие большой кинетической
энергией, перемещаясь к поверхности, увеличивают
кинетическую энергию частиц у стенки, движущихся с малыми
скоростями, и наоборот, частицы, переместившиеся от
стенки в ядро потока, тормозят здесь движение, жидкости.
В соответствии с изменением профиля скорости в
зависимости от числа Re коэффициент сопротивления трубы
должен также меняться в функции этого параметра.
Для оценки коэффициента сопротивления
цилиндрических труб при небольших скоростях можно .пользоваться
кривыми Всесоюзного теплотехнического института,
построенными Г. А. Муриным (рис. 5-7). Здесь коэффициент С
представлен в зависимости от числа Re и величины, обратно
пропорциональной относительной шероховатости D/k9, где
кэ — средняя высота бугорков шероховатости. Заметим, что
при больших значениях Djk3 (малая шероховатость)
значения С по кривым ВТИ удовлетворительно совпадают с
формулой Никурадзе:
_L = _0,8 + 21g(ReKC). (5-26)
Кривые ВТИ и формула (5-26) отчетливо показывают,
что влияние числа Рейнольдса на коэффициент
сопротивления в гладкой трубе простирается до весьма больших
значений Re^ 106. По мере увеличения шероховатости влияние
Re (при Re>2-105) на увеличение шероховатости
ослабевает. На рис. 5-7 пунктирной линией соединены точки,
соответствующие тем значениям Re, выше которых влияние
этого параметра практически не обнаруживается. Справа
от этой линии расположена область, которую принято
называть автомодельной2.
Перейдем теперь к рассмотрению влияния второго
основного критерия подобия — числа М — на коэффициент
сопротивления в трубах. Соответствующие опытные данные
1 Под макрочастицами понимаются частицы жидкости (газа),
содержащие достаточно большое число молекул-микрочастиц, —для
возможности применения к ним законов статистики.
2 Область независимости коэффициента сопротивления от числа
Рейнольдса.
220
0,035
0.030
0,025
0,020
0,015
0,010
2000
2500
\3000
Рис. 5-7. Зависимость коэффициента сопротивления $ стальных труб
от числа Re и относительной шероховатости по данным ВТИ.
получены в МО ЦКТИ1, в МЭИ2 и ряде других
организаций.
1 А. А. Гухман, Н. В. Илюхин, А Ф. Гандельсман,
Л. Н. Мауриц, ЖТФ, вып. 12, 1954.
2 Б. С. Петухов, А. С. Сукомел, В С Протопопов,
Исследование сопротивления трения и коэффициента восстановления
температуры стенки при движении газа в круглой трубе с высокой
дозвуковой скоростью, „Теплоэнергетика", 1957, № 3.
221
На рис. 5-8 показано распределение статических
давлений по длине гладкой трубы при дозвуковых- скоростях,
отвечающее различным числам Rex и Мх на входе в трубу.
В соответствии с методикой проведения опытов кривые на
рис. 5-8 показывают совместное влияние числа Rex и
отношения давлений (числа MJ, так как раздельное
моделирование по Re и М не осуществлялось. По мере снижения s
О W 20 30 40 50 60 7Q 8U
Рис. 5-8. Распределение давлений, температур и скоростей по длине
трубы для дозвуковых скоростей.
(увеличения ReJ характер кривых давлений меняется и
особенно интенсивно на выходном участке (х^> 60-—70).
Переход к большим значениям Re и Мх сопровождается
увеличением градиентов давления: наклон линий р
возрастает. Для группы режимов, отвечающих
сверхкритическому перепаду давлений в трубе, статическое давление
в выходном сечении превышает давление внешней среды,
но оказывается ниже той величины е' , которая, соответ-
*
ствует критическому истечению. Значение е можно найти
по формулам (5-19) или (5-25), подставив Я=1.
Величина е отмечена на рис. 5-8 пунктиром. Отсюда
следует, что критическое сечение не совпадает с выходным
222
сечением трубы и располагается внутри на некотором
небольшом расстоянии от выходного сечения. С увеличением
перепада давлений критическое сечение смещается
навстречу потоку.
Специальные исследования выходного участка за
критическим сечением показывают, что в этой области поток
обладает сверхзвуковыми скоростями. Результаты исследо-
Я*/
A=/J jAV
ы
Граница
пограничного
слоя
1\ Д\
0,01
t~t--
Api=
Pi-Ра
Ро
да выходе
ным
сечением
»^И
Aki
а.8
ко
иг
Рис. 5-9. Изменение статических давлений и скоростей по диаметру
трубы вблизи выходного сечения.
вания поля скоростей и давлений на выходном участке
приведены на рис. 5-9. Здесь отчетливо видна
неравномерность в распределении статических давлений по
диаметру трубы, причем давление на оси во всех сечениях за
критическим выше, чем у стенки.
Эпюры скоростей (рис. 5-9) позволяют заключить, что
толщина дозвукового пристеночного слоя на выходном
участке уменьшается в направлении потока. Можно
предполагать, что такая структура потока объясняется
взаимодействием вытекающей струи с внешней средой.
Благодаря интенсивному отсосу пристеночного слоя во внешнюю
среду происходит его утонение на выходном участке
(рис. 5-9). При этом в ядре потока создаются условия,
необходимые для перехода к сверхзвуковым скоростям:
223
сечение ядра увеличивается по течению. Давление внешней
среды „проникает" через дозвуковую часть пристеночного
слоя внутрь выходного участка, и давление на стенке
оказывается более низким, чем давление на оси.
Следует подчеркнуть, что перестройка течения на
выходном участке трубы сопровождается резким изменением
профиля скорости в пристеночном слое.
На рис. 5-10 нанесены значения С = -£- в зависимости
от М по данным МО ЦКТИ и МЭИ. Зависимость С от Re
«4
1.2
Щ
щ
щ
\
\
-Цяр-Ч
о t
* 1
1
y°<b
■.лЛа-J
1пыты МЭИ
1пыты
1 1
MQW
ЧТИ
1
U&*
0
^4W
•в^
j^AJv
^£к
м*
ОА
0,5
0,5
OJ
0,в
0,3
КО
Рис. 5-10. Зависимость коэффициента сопротивления от числа М при
дозвуковых скоростях по данным МО ЦКТИ и МЭИ.
при больших дозвуковых скоростях согласно опытным
данным сохраняется практически такой же, как и для
несжимаемой жидкости. Следовательно, отношение С, взятое при
одинаковых значениях Re, отражает влияние только
числа М.
График на рис. 5-10 показывает, что при М<< 0,70-7-0,75
коэффициент сопротивления не зависит от М и весьма
близок к Сн. Для этой области расчет С может производиться
по любой эмпирической формуле [например, (5-26)] или по
кривым ВТИ*.
В диапазоне чисел М = 0-*-0,8 и Re = 3-103 -ч- 3• 105
удовлетворительно совпадает с опытом формула,
полученная в МЭИ:
C = 0,0334Re"
-0,2
(5-27)
где Re = Re x — число Re, отнесенное к длине трубы.
* В последнем случае необходимо убедиться в том, что для
шероховатых труб влияние сжимаемости на $ при М<0,7~-0,8 будет
также невелико. Это предположение нуждается в опытной проверке.
224
При М > 0,7 ~- 0,75 коэффициент сопротивления трубы
уменьшается с ростом М; особенно интенсивное снижение С
наблюдается при скоростях М>0,85.
Напомним, что изменение давления на элементарном
участке трубы dx выражается известной гидравлической
формулой:
dp = yJ4j-dx.
Разность сил давления, действующих на выделенный
элемент жидкости, при равномерном движении в трубе
равна силе трения на стенке трубы, т. е.
Отсюда можно получить формулу, связывающую
напряжение трения на стенке и С:
С=^°. (5-28)
В соответствии с формулой (5-28) результаты
изложенного выше опытного исследования можно выразить так:
влияние сжимаемости, заметно проявляющееся при УИ>0,75,
приводит к некоторому уменьшению силы трения,
отнесенной к кинетической энергии потока в данном сечении.
\ Физически этот результат объясняется тем, что с ростом
числа М увеличиваются градиенты давления в трубе
(рис. 5-8). Возрастание градиентов давления в конфузорном
течении вызывает деформацию профиля скорости у стенки;
наполнение профиля скорости увеличивается. Кроме того,
пристеночный слой при этом утоняется.
Околозвуковой поток особенно чувствителен к
изменению сечения, что видно из уравнения (5-8). Поэтому на
концевом участке трубы, где М> 0,9, наблюдаются весьма
большие отрицательные градиенты давления и соответственно
резкое снижение С.
Резкое уменьшение С при М > 0,9 связано также с тем,
что область скоростей М = 0,9-5-1,0 расположена вблизи
концевого участка трубы, где пристеночный слой
нарушается. При расчете по формуле (5-28) значительная
деформация профиля скоростей на выходном участке трубы
не 'учитывается.
15 М. Е. Дейч
225
Оценивая влияние сжимаемости на коэффициент
сопротивления трубы при сверхзвуковых скоростях, необходимо
различать три основных режима течения в трубе. Первый
режим отвечает бесскачковому движению потока, скорости
которого в каждом сечении трубы сверхзвуковые. Как уже
было показано, такой режим возможен, если длина
цилиндрической трубы меньше предельного значения (^<Схмакс)-
Если же в трубе имеется соответствующий источник
возмущения, то при Х<СХмакс сверхзвуковой поток может
быть насыщен скачками уплотнения. Возмущение потока
в трубе может быть вызвано угловым поворотом стенки,
который образуется в сечении стыка сопла Лаваля с
трубой. В простейшем случае расширяющаяся часть сопла
выполняется конической с различными углами раствора.
Чем больше угол раствора сопла, тем больше угол
отклонения потока при входе в трубу и тем интенсивнее скачок,
образующийся в точке поворота стенки. Такие режимы
течения с коническими скачками, когда поток вплоть до
выходного сечения остается сверхзвуковым, составляют
вторую группу режимов. Наконец, если Х>ХМакс'Т0
внутри трубы возникает сложная система скачков, за
которой поток будет дозвуковым; это — третья группа
режимов течения. Распределение параметров течения по
длине трубы в тех указанных случаях оказывается
существенно различным.
Для третьей группы режимов, когда в результате
скачков поток становится дозвуковым, характер распределения
давления по данным Неймана и Лустверка показан на
рис. 5-11 (для Я1 = 2,2). По мере повышения давления в
выходном сечении трубы система скачков перемещается
к соплу. Интенсивность скачков при этом повышается.
Отметим, что протяженность системы скачков оказывается
значительной. За системой скачков поток дозвуковой, и
давление вдоль трубы падает.
В соответствии с различным характером распределения
давлений по цилиндрической трубе при сверхзвуковых
скоростях будут различными и коэффициенты сопротивления.
При равномерном сверхзвуковом потоке в трубе (без
скачков) коэффициент сопротивления имеет наименьшее
значение.
На рис. 5-12 нанесены значения коэффициента
сопротивления в зависимости от М по данным МО ЦКТИ
226
для интервала чисел М = 0-^-1,65. Здесь воспроизведены
опытные точки С для дозвуковых скоростей, частично
представленные на рис. 5-8, и добавлены результаты более
поздних исследований для М > 1. Характерным для области
небольших сверхзвуковых скоростей следует считать
заметное возрастание С: здесь коэффициент сопротивления
меняется от 0,007 до 0,018.
о,от
\р
\Рщ f
г/ / А*
(h
/
«о 1
-о
£J
о.озо\
омо\
ощ
0,№\
10 20 30 'W 50
Рис. 5-11. Распределение давлений по длине трубы при
сверхзвуковых скоростях на входе; Aj = 2,2 (воздух).
Можно предположить, что на этом участке происходит
турбулизация пристеночного слоя в трубе, т. е. переход
его из ламинарного режима в турбулентный1. В
предыдущей области М = 0,95-т-1,03, где градиенты давления
достигают максимальных значений, по-видимому,
происходит ламинаризация пристеночного слоя, так как при
больших отрицательных градиентах давления интенсивность
турбулентных пульсаций снижается.
1 Аналогичный характер изменения £ отмечается в начальном
участке трубы, где происходит переход ламинарного режима в
турбулентный.
15*
227
0,02fr
0,0201
0,016
0,012
aooel
0,004
и
I С
1 •
н
/** 2
*
1 * *,
V
v;
л 1Л
/
•
•» Q 1 Ч» I
*••*.** ^
м
as
0,6
0,7 0,8
0,3
1,0
U
1.2
КЗ
1А
1.5
1,6
а
1/8
Рис 5-12. Зависимость коэффициента $ от числа М для цилиндрической трубы по данным'
МО ЦКТИ.
На участке М = 1,25 -гЛ,6 С снижается и при М = 1,65
достигает минимального значения С^ 0,01. Это снижение
объясняется наполнением профиля скорости в области
сверхзвукового течения с отрицательными градиентами
давления.
При М>1,3 влияние числа Рейнольдса на С невелико.
5-6. ПОГРАНИЧНЫЙ СЛОЙ. ОСНОВНЫЕ ПОНЯТИЯ
И УРАВНЕНИЯ1
Современные представления о механизме сопротивления
тел, обтекаемых потоком газа, и методы расчета
сопротивления основываются на теории пограничного слоя2.
Как показывает опыт, при больших числах Re влияние
вязкости сосредоточивается в области потока,
непосредственно прилегающей к поверхности тела. Эта область
имеет малую по сравнению с длиной протяженность в
направлении нормали к поверхности тела и называется
пограничным слоем. Вне пограничного слоя поток имеет
пренебрежимо малую завихренность и на этом основании
рассматривается как потенциальный. В пограничном слое
скорости меняются от нуля на поверхности тела до
скорости потенциального потока на внешней границе. Так как
толщина слоя невелика, то градиенты скоростей в этой
области достигают больших значений и, следовательно, поток
здесь обладает большой завихренностью.
Характер распределения скоростей в пограничном слое
на плоской стенке показан на рис. 5-13. Непосредственно
на стенке жидкость „прилипает" к поверхности (Я6 = 0).
В тонком пограничном слое с удалением от поверхности
тела скорости меняются весьма интенсивно и на небольшом
расстоянии от поверхности достигают скорости внешнего
потока.
Сопротивление обтекаемых тел существенно зависит от
режима течения в пограничном слое. Движение жидкости
в пограничном слое может быть ламинарным или
турбулентным.»
Законы изменения скорости по нормали к поверхности
для ламинарного и турбулентного режимов должны быть
различными.
1 §§ 5-6-Г-5-12 составлены совместно с А. Е Зарянкиным.
2 Теория и методы расчета пограничного слоя подробно
изложены в монографии Л. Г. Лойцянского (см. список литературы).
229
Так как скорости в пограничном слое меняются от нуля
на стенке, то естественно предположить, что некоторый
участок пограничного слоя, прилегающий к стенке, всегда
находится в ламинарном режиме. Это предположение
подтверждается распределением скоростей у стенки в
пограничном слое.
Рассмотрим более подробно условия образования
пограничного слоя на поверхности крылового профиля (рис. 5-13).
В направлении потока вдоль поверхности толщина
пограничного слоя 6 увеличивается. Заметим, что понятия
внешней границы и толщины пограничного слоя
не.являются определенными, так как изменение продольных
скоростей при переходе из пограничного слоя во внешний
поток происходит плавно. Приближенно внешняя граница слоя
определяется в тех точках, где продольная скорость
отличается от скорости внешнего потока на малую величину
порядка 1°/0.
Внешняя граница пограничного слоя не совпадает с
линией тока, так как частицы внешнего потока непрерывно
проникают в пограничный слой (рис. 5-13).
Передний участок слоя, расположенный вблизи носика
профиля, обычно является ламинарным. На небольшом
расстоянии от носика (сечение 77 на рис. 5-13,а и б)
обнаруживается ламинарный профиль скоростей. В некотором
сечении /// начинается переход ламинарного упорядоченного
движения в турбулентное, которое носит пульсационный
характер.
В переходной зоне течение в пограничном слое
смешанное: значительная часть слоя, ближайшего к поверхности,
находится в ламинарном режиме.
За переходной областью развивается устойчивый
турбулентный слой. Здесь область ламинарного подслоя
настолько мала, что экспериментально ее трудно обнаружить.
Как видно из рис. 5-13,6, турбулентный слой имеет более
полный профиль скоростей.
Схема образования пограничного сл€я на рис. 5-13
изображена не в одинаковом масштабе по осям х и у.
Толщина слоя 6 весьма невелика по сравнению с размерами
тела и составляет сотые и тысячные доли хорды профиля.
Расчет ламинарного пограничного слоя основывается на
дифференциальных уравнениях энергии (5-3) и движения вязкой
жидкости (5-4). Используя отмеченные выше физические
230
особенности движения в слое, уравнение (5-4) можно
существенно упростить.
С этой целью перейдем в уравнениях (5-4) к
безразмерным величинам. Для простоты рассмотрим
установившееся движение несжимаемой жидкости. В качестве мас-
Рис. 5-13. Схема образования пограничного слоя на поверхности
крылового профиля.
а —изменение толщины и структуры слоя вдоль поверхности: / — ламинарный
участок слоя; 2 — переходная область; 3 — турбулентный участок слоя;
4—ламинарный подслой; 5 —переходный слой; б —распределение скоростей в различных
сечениях слоя.
штабов продольных скоростей и координат выберем
некоторую характерную скорость и0 и характерный линейный
размер L0. Масштабы поперечных скоростей и координат
обозначим соответственно vQ и 8. Обозначим масштабы для
давления и плотности р0 и р0. Тогда после преобразований,
аналогичных преобразованиям § 5-2, получим следующую
систему уравнений:
ди , L^ ди =_?оР(>д£_\ L_^!ff_L-^- — • )
дх ' Ьи0 ду рй2 dx*L0u0dx2~r'd2uu ду*'
и du4-Louo7,dv—^JoPoLo дР\ L-^_I_—°~- \ (Ъ 9Qt
дх~ Ьи0 и ду ?duQv0 ду ■ L0uQ дх^Ьи, ду2' [ к z }
ди i ^Л^__о I
дх* ди0 ду ' )
Масштабы величин, входящих в систему уравнений
(5-29), можно выбрать на основании следующих
соображений. Если масштабы и0 и LQ выражают характерную
скорость и линейный размер обтекаемого тела, то величины
231
voi 8» pQ и p0 пока остались неопределенными. Пользуясь
этим произволом, уравнения (5-29) нетрудно привести к
каноническому виду.
Действительно, полагая /?0=p/j~ ^ р0=1 полуЧИМ РоА>_ j ^ a
поперечные масштабы vQ и 8 выберем таким образом, чтобы
А.
L v
коэффициенты ~^- и
от числа Re.
Положим
$2ип
были постоянными и не зависели
0W0 д2И0
\>L0
1.
Принципиально эти комплексы можно приравнять любой
постоянной, но в данном случае выражения для
поперечных масштабов получаются наиболее простыми.
Решая написанную систему относительно vQ и Ь для
масштабов поперечных скоростей и линейных размеров,
получаем следующие значения
VRe ' ° VT& '
При этом уравнения (5-29) примут вид:
др
да , да
дх ' ду
дх 'Re дх2
д2а , д2и,
~^ду^
Re
^i dv\ др, 1 d2v , 1 д'р.
U dx^V ду)~ ду ""Re2 dT2 ' Re (fy2'
(5-30)
(5-31)
Если допустить, что неизвестные величины и, v, p и их
производные с увеличением числа Рейнольдса стремятся
к определенным пределам в фиксированных точках, то при
больших Re в уравнениях (5-31) можно отбросить все чле-
1 1
ны, имеющие множители ~- и -гг-9, как малые величины
Re Re**
по сравнению с другими членами.
232
В результате перехода вновь к размерным величинам
получим дифференциальные уравнения ламинарного
пограничного слоя в форме Л. Прандтля:
ди , ди
1 dp
дх
ду
р дх
+
д*и.
д_£
ду
= 0;
(5-32)
ди ■ ди
дх*ду
= 0.
Система (5-32) должча быть решена при следующих
граничных условиях:
у = 0; ц = 0; а = 0;
у-+со\ и—т(х).
Последнее условие означает, что скорость в
пограничном слое переходит асимптотически к скорости внешнего
потока. В действительности этот переход, как уже
отмечалось, происходит при значении у, соизмеримом с
поперечным масштабом 8.
Полученное условие ~-
:0 означает, что распреде-
Условие
:0 позволило объяснить весьма важное
ление давлении на внешней границе слоя и
на поверхности обтекаемого Tejja совпадает.
Отсюда следует, что во всех точках поперечного сечения
слоя давления одинаковы, т. е. давление внешнего потока
передается через пограничный слой к поверхности тела без
изменения.
др_
ду~
явление отрыва пограничного слоя. Рассмотрим обтекание
некоторой криволинейной поверхности АВ (рис. 5-14),
предполагая, что давление внешнего потока вдоль этой
поверхности вначале уменьшается, достигает минимального
значения в точке М и затем увеличивается. Участок внешнего
потока, в котором градиенты давления отрицательны
(^<0 , называется конфузорным участком.
Область течения за точкой М, характеризуемая
положительными градиентами давления (^ >> 0], называют диф-
233
фузорным участком. На конфузорном участке
внешний поток ускоряется, а на диффузорном — тормозится.
Учитывая, что в пограничном слое -р = 0, заключаем, что
совершенно аналогичное распределение давлений имеет
место и вдоль поверхности АВ на любом расстоянии у<С%
в пограничном слое.
Рис. 5-14. Схема образования отрыва пограничного слоя
В пределах пограничного слоя скорости перед точкой М
увеличиваются, а за нею — уменьшаются (см. эпюры
скоростей на рис. 5-14). Частицы жидкости вблизи стенки
обладают малой кинетической энергией, причем в диффу-
зорной области вдоль поверхности АВ запас кинетической
энергии частиц уменьшается. В результате в некотором
сечении 5 частицы у стенки не могут преодолеть
тормозящего влияния внешнего потока и останавливаются. Эпюра
скоростей принимает характерную остроконечную форму.
На стенке кривая скоростей удовлетворает условию
(tL=a (5-32a)
Дальше за точкой S под воздействием перепада
давлений, направленного против течения, начинается возвратное
движение частиц у стенки. Встречаясь с основным
потоком, возвратно движущиеся частицы оттесняются от стенки,
234
tjTO и приводит к отрыву пограничного слоя и к резкому
увеличению его толщины. За точкой отрыва 5 эпюра
скоростей имеет также весьма характерную петлеобразную
форму, причем непосредственно у стенки
Изложенное показывает, что отрыв пограничного
слоя при обтекании плавной стенки может происходить
только в диффузорной области.
Используя уравнения (5-32), легко показать, что
положение точки отрыва ламинарного пограничного слоя не
зависит от числа Re. Действительно, решение системы
(5-32), дает:
u = f(x,y), (5-326)
где х и у — безразмерные координаты.
Тогда, продифференцировав по у и используя в точке
отрыва условие (5-32а), получим:
f'(xs,0) = 0.
Поскольку масштаб по оси х от числа Re не зависит,
приходим к выводу, что координата точки отрыва
ламинарного слоя также не зависит от числа Рейнольдса.
5-7. УСЛОВНЫЕ ТОЛЩИНЫ И ИНТЕГРАЛЬНОЕ
СООТНОШЕНИЕ ДЛЯ ПОГРАНИЧНОГО СЛОЯ
Выше указывалось, что понятие толщины пограничного
слоя не имеет точного количественного смысла.
Действительно, скорость в пограничном слое и с ростом у
асимптотически приближается к значению скорости внешнего
потока и0. Величина 8 зависит от того, где выбрана точка,
условно показывающая границу слоя.
Поэтому в расчетах пограничного слоя вводятся другие
интегральные толщины, зависящие от 6: толщина
вытеснения 8*, толщина потери импульса 8** и толщина потери
энергии 8***.
Для выяснения физического смысла указанных толщин
сравним течение идеальной и вязкой жидкостей около
твердой стенки (рис. 5-15).
При отсутствии трения за единицу времени через
поперечное сечение потока высотой dy и шириной, равной еди-
235
нице, протечет масса pQuQdy. В пограничном слое за то же
время через сечение dy протечет масса pudy.
Разность этих количеств составит:
о
7^ччччччч^СчччччччЧччч,1ччччччч^
$ Ъ*\
и
\ГчТ
4
Рис. 5-15 К определению условных толщин пограничного слоя (а).
К выводу уравнения импульсов для пограничного слоя (б).
Второй интеграл правой части мал по сравнению с
первым. Поэтому интегрирование достаточно проводить только
в пределах физической толщины слоя 6.
Разделив найденный излишек массы на р0и0, получим:
5
(5-33)
••-К'-й)*-
236
Величина 8* показывает смещение линии тока в
направлении внешней нормали к контуру обтекаемого тела.
Вместе с тем 6* характеризует уменьшение расхода
жидкости через сечение слоя, „нормальное" к стенке,
обусловленное „вытеснением" жидкости пограничным слоем,
и поэтому носит название толщины вытеснения.
Толщина потери импульса 6** равна такой толщине
слоя жидкости, движущейся со скоростью и0 вне
пограничного слоя, количество движения которой равно импульсу
сил трения в пограничном слое. Это количество движения,
„потерянное" в пограничном слое, будет равно:
ь ь
Г pu (uQ — u)dy=[ рии0 (\ — ±\ dy.
6 о
Разделим полученное выражение на р0и^ . Тогда
получим:
(Г
Масса жидкости pudy теряет в пограничном слое
кинетическую энергию, равную ри(и0—u2)dy. Для всего слоя
эта потеря составит:
ь
Тогда толщина потери энергии
^-j&O"?)* (5'35)
представляет собой толщину движущейся вне слоя
жидкости, обладающей кинетической энергией, потерянной в
пограничном слое.
Для решения задач о течении сжимаемой жидкости в
ряде случаев целесообразно иметь одинаковую структуру
формул, определяющих интегральные толщины. Поэтому
237
наряду с формулой (5-33) толщину вытеснения Ь* часто
подсчитывают по формуле
о
При этом, естественно, нарушается приведенный ранее
физический смысл толщины вытеснения. Для несжимаемой
жидкости уравнения (5-33) и (5-36) оказываются
тождественными.
Решение задачи о сопротивлении тела в потоке вязкой
жидкости при безотрывном обтекании сводится к
установлению распределения сил трения вдоль обтекаемых
поверхностей тела, а следовательно, к расчету пограничного
слоя.
Широко распространенный приближенный метод расчета
основывается на оценке изменения количества движения
в пограничном слое. Произведем такую оценку.
Из определения толщины вытеснения следует, что всю
массу жидкости, протекающей в пограничном слое, можно
условно заменить массой, расположенной между линией ab
и стенкой cd (рис. 5-15), скорость которой равна нулю
(„вытесняемая" масса), и массой, протекающей выше ab
со скоростью и*.
Со стороны стенки на вытесняемую массу действуют
силы трения, а в направлении течения будут приложены
силы давления. Скорости выше линии вытеснения ab равны
и0 = и0(х) и в пределах рассматриваемого объема на
основании дифференциальных уравнений пограничного слоя
(5-32) -^- = 0. Применяя уравнение импульсов, можно найти
величину потери количества движения на участке dx:
d/=,z0dx + dpb\ (5-37)
где z0dx и dpo* — секундные импульсы сил трения и сил
давления, действующих на
„вытесняемую" массу жидкости.
* Изложенный ниже вывод интегрального соотношения дан
А. П. Мельниковым.
238
Количество движения / на основании уравнения (5-34)
можно выразить через толщину потери импульса:
/ = Ро«о8**
Поскольку на внешней границе пограничного слоя
течение считается потенциальным, продольный градиент
давления -~ легко выражается на основании уравнения Бернулли
через скорости и0 и плотность р0:
dp du0 '
Подставляя эту величину в (5-37), находим:
«о8** 41 + Ро6**2гг0;/ + Ро^о Ж = то — Ро«о^8*- (5-37а)
Заменим далее
dp0 dp0 dp 1 '
~dx"~~dp"Tx~ ^9°U°llo
и разделим (5-37а) на р0д*. В результате получим для
сжимаемой жидкости следующее уравнение:
4т+/-(2 + Я-М0) = -\-. (5-38)
Здесь
# = £ и М0 = -^.
Уравнение (5-38) носит название интегрального
соотношения, так как величины S** и &* выражаются
интегралами (5-33) и (5-34).
Интегральное соотношение (5-38) для пограничного слоя
можно получить, не прибегая к понятию толщины
вытеснения. С этой целью уравнение импульсов применяется
к объему жидкости, заключенному между двумя
бесконечно близкими поперечными сечениями пограничного слоя
239
(рис. 5-15,6). Подставляя в (5-38) выражения для условных
dp
dx
толщин 8*, 8** и заменяя и через —-, после
преобразовании находим:
г
f pu2dy — u^[ pudy = — *о — 5 % • (5"39)
_d_
dx
б о
Для несжимаемой жидкости получим:
s г
d f „iAtt „ d [* tAtt т0 Ь dp
dx
о о
■J«^-«.£f*&=-f-f-£. (5-39a)
Интегральное соотношение для пограничного слоя
пригодно для расчета как ламинарного, так и турбулентного
пограничных слоев, так как при его выводе не делалось
никаких предположений относительно касательного
напряжения х0. Эта величина определяется различно в
зависимости от режима течения жидкости в пограничном слое,
что и является отражением различной природы трения при
ламинарном и турбулентном движениях.
При возникновении отрыва уравнение импульсов может
служить для определения положения точки отрыва, в кото-
5-8. ОБЩЕЕ ВЫРАЖЕНИЕ ДЛЯ КОЭФФИЦИЕНТА
СОПРОТИВЛЕНИЯ ТРЕНИЯ В ПОГРАНИЧНОМ СЛОЕ
ПРИ НАЛИЧИИ ГРАДИЕНТА ДАВЛЕНИЯ
В уравнении импульсов содержатся две искомые
переменные величины: толщина слоя 5 (или взаимосвязанные
условные толщины 8* и 8**) и напряжение трения на
стенке т0.
В общем случае %0 определяется скоростью на внешней
границе пограничного слоя, ее производными и , и , и0 и
т. д., характерным размером, например толщиной потери
импульса 8**, плотностью р, температурой Т и
коэффициентом кинематической вязкости v.
240
Следовательно,
*o = cP(«o; ii\ и|',...; Т; р; 5**; v). (5-40)
Используя основные положения теории размерности,
из функциональной зависимости (5-40) нетрудно получить
структурную формулу для коэффициента сопротивления.
Примем в качестве основных размерности скорости и0,
плотности р, длины 5** и температуры Г. Простой
проверкой легко убедиться, что, комбинируя указанные
величины, можно получить размерности всех остальных
параметров. Действительно, т0 имеет размерность кг/м2. Ту
же размерность будет иметь и комплекс щ\:
[кг • сек2[м*• м?\сек2\. Следовательно, отношение t0/p0#o>
представляющее собой местный коэффициент трения с,
окажется безразмерным. Переходя в выражении (5-40) от
размерных величин к безразмерным, получим
*о ( ипд** и'д**2 \
с,=£ = 9[Ъ».П V! J^"} (5"41)
и $**
Здесь Re**= —^ число Рейнольдса, подсчитанное
по толщине потери импульса.
Число безразмерных параметров в выражении (5-41)
можно сократить, если принять, что напряжение трения
определяется так же, как и в случае ламинарного течения
только первой производной скорости и .
Это предположение подтверждается для конфузорных
течений и течений при небольших положительных
градиентах давления. Вблизи точки отрыва роль старших
производных возрастает, и здесь сохранение только первой
производной уже недостаточно.
Далее, можно показать, что при отнесении физических
постоянных v и р к температурным условиям на стенке
число М исключается из зависимости (5-41). Таким
образом, с учетом принятых допущений
''-а-'(*-": %■)■ (542)
sfc^c // Й * *
где 1^=-^—, v^—кинематическая вязкость, подсчитан-
Voy ная по температуре стенки.
16 М. Е. Дейч 241
Разложим (5-42) в ряд по параметру
и0д**
+
/ Uq5**
+ t.(Re.)v B
+ ■
(5-43)
Здесь cf—местный коэффициент трения, подсчитанный по
плотности у стенки pw.
Выражение (5-43) является общим как для ламинарного,
так и для турбулентного режимов течения в пограничном
слое. В зависимости от режима течения коэффициенты ф0,
ф1? ф2 и т. д. будут принимать различные значения.
Найдем конкретный вид выражения (5-43) для
ламинарного течения. С этой целью запишем (5-43) в таком виде:
ci =
Рши0
= Ф.
!+v
Ф, иоь*
ф2 "0°
Фо
(5-44)
При и—О формула (5-44) должна совпадать с
соответствующей формулой для коэффициента сопротивления
плоской пластинки при безградиентном ее обтекании.
В этом случае задача решается достаточно точно путем
численного интегрирования системы (5-32) и независимо от
метода решения для безградиентного течения коэффициент
сопротивления cfQ выражается формулой
п — и» — —»—
ТО Ра** '
"f0"
Re*
где а0 — постоянная величина.
Следовательно,
ф1 w'5**2
Re*
i +
*2 "^**4
+••■
В точке отрыва ^0 = 0; в этом случае выражение в
квадратных скобках должно обращаться в нуль. Учитывая, что
положение точки отрыва не зависит от числа Re**,
получим: ф1 = const; ф2 = const; ф3 = СОП8* и т- Д- Отсюда
1 Г //Л**2 l/2fi**4 1
cf=^-[a. + al4^-+a^- + ...\. (5-45)
242
Коэффициенты а0, а19 а2 и т. д. в общем случае
определяются экспериментально. Однако для ламинарного
пограничного слоя их можно определить и теоретически.
Так, например, А. М. Басин получил а0 = 0,22; а1=1,85;
а2 = — 7,35.
Обозначим
а0$**2
= / (5-46)
t(f) = [a0 + aj + atr + ...]; (5-47)
тогда
<7=^<(/)- (5-48)
Параметр / часто называют формпараметром; как будет
показано ниже, он определяет форму профиля скорости
в ламинарном пограничном слое. Следует отметить, что
структура формпараметра, содержащего производную
-г-5, отражает влияние продольного градиента давления
внешнего потока.
Для турбулентного слоя многочисленные
экспериментальные данные дают при и = 0:
с/0 = <]>„ = С Re**-m, (5-49)
и для коэффициента сопротивления получается из (5-44)
следующая формула:
c, = Re;*-mlC + ar+...]. (5-50)
Здесь
Г = ^-Ъ:т- (5-51)
Параметр Г (параметр Бури), так же как и формпара-
метр /, отражает влияние продольного градиента давления
и числа Рейнольдса на профиль скоростей в турбулентном
слое.
Зная зависимость для cf и закон изменения величины
л*
Н = — в зависимости от продольного градиента давле-
16* 243
ния, нетрудно получить из интегрального соотношения (5-38)
дифференциальное уравнение для определения толщин
пограничного слоя.
Рассмотрим отдельно решение уравнения (5-38) для
ламинарного и турбулентного слоев.
5-9. РАСЧЕТ ЛАМИНАРНОГО ПОГРАНИЧНОГО СЛОЯ
ПРИ НАЛИЧИИ ГРАДИЕНТА ДАВЛЕНИЯ
Расчет пограничного слоя сводится к решению
интегрального соотношения (5-38) [или (5-39)], которое
содержит три неизвестные величины: толщину потери
импульса 5**, коэффициент сопротивления с. — ^г и вели-
' Р"о
чину # = #(M;g-).
Следовательно, для решения задачи необходимо иметь
еще два дополнительных соотношения, связывающих
указанные величины. Используя общее выражение (5-48) для
коэффициента сопротивления и рассматривая для простоты
случаи несжимаемой жидкости, получим уравнение с двумя
неизвестными: 6** и Я, связь между которыми нетрудно
получить, если известен профиль скорости в пограничном
слое.
В общем случае скорость в поперечном сечении слоя
зависит от местного градиента давления и расстояния от
стенки у. Влияние градиента давления учитывается форм-
параметром /. Следовательно, относительную скорость
в точке слоя можно представить в таком виде:
и
— =(Р
и0 т
Тогда
4o-i)<4[
_У_
***
О
Проинтегрировав полученное
пределах, найдем:
5* = 8**//(/),
"9 ( §**> / )
./)]*(&)•
выражение
dy-
в
=
указанных
244
или
?, = *(!£). (5-52)
Далее, подставив в уравнение (5-38) зависимости (5-48)
и (5-52), получим после несложных преобразований
дифференциальное уравнение первого порядка относительно форм-
параметра /:
£ = ^-f+!TF- (5-53)
ах Uq u0
Здесь
F = 2{C(/)-2/[2 + tf(fl]}.
Конкретный вид функции F (f) зависит от формы
профиля скорости в пограничном слое. Вычисления
показывают, что F(f) очень мало отличается от линейной
функции, т. е.
F(f) = a-bf.
При этом уравнение (5-53) переходит в линейное
относительно параметра / уравнение
интеграл которого имеет, вид:
t аи'о С ь-\. , „ Ч
"о J ио
Если при х = 0 и0 = 0, то из условия конечности /
следует положить постоянную интегрирования с = 0.
В практике удобнее вести "расчеты, пользуясь
безразмерными величинами.
Положив и0 = — и x=-j-> где и^ — скорость
набегающего потока, a L — длина обтекаемой поверхности,
получим:
-/ х
f{x) = ^-\ub-x{x)dx. (5-54)
«о J
245
Постоянные а й b могут быть приняты соответственно
равными 0,45 и 5,35.
Для толщины потери импульса получим:
*"=%=]/ щЦ*"**' (5-55)
Далее, по формуле (5-48) нетрудно определить местный
коэффициент сопротивления с. и по выражению 8* =
-0,06 -0,04-0,02 О 0,02 0,04 0,06 0,08 0,Ш
Рис. 5-16. Зависимость величин ?, F и И
от параметра /.
= Н (/) 8** — толщину вытеснения. Значения функций С (/)
и //(/) приведены на рис. 5-16.
Рассмотренный метод расчета может быть распространен
и на случай течения сжимаемой жидкости, если перейти
к новым переменным, предложенным А. А. Дородницыным
х у
о о
246
Тогда для сжимаемой >. идкости получим:
Расчет по формулам (5-48), (5-54), (5-55) и (5-56)
оказывается относительно простым и обеспечивает вполне
удовлетворительную точность.
Для примера рассчитаем ламинарный пограничный слой на плоской
пластинке. Здесь и0 = const; uQ = 0; f = 0 и т ■= 1.
Тогда из (5-55), (5-47) и (5-48) получим:
т/6^57
d** = b**L=L у __. ? (/) = 0,22;
1 0,22v
^ = 0,22 „
= 0,332 У ~ !
*п = С
/0,45v.
5-10. ПЕРЕХОД ЛАМИНАРНОГО ПОГРАНИЧНОГО СЛОЯ
В ТУРБУЛЕНТНЫЙ
При определенных условиях ламинарный пограничный
слой теряет устойчивость и переходит в турбулентный.
Ориентировочно границу потери устойчивости ламинарного
течения можно установить по критическому числу Рей-
нольдса ReKp. Пользуясь аналогией между явлениями
перехода ламинарного режима в турбулентный в цилиндрической
трубе и в пограничном слое, можно, как это уже
указывалось, ввести характерные для слоя числа Рейнольдса,
отнесенные к толщинам1 б, 8* и 5**:
Re5=^i; Re* = i^; Re** = ^ .
Опытные данные показывают, что критические значения
числа Re6 пограничного слоя имеют тот же порядок, что
1 Величина Re** введена была ранее при выводе уравнения (5-41)
и др.
247
и для труб, но могут колебаться в более широких
пределах (Re. = 2 000 -г- 5 000). Согласно многочисленным
х йкр
исследованиям критическое число ReKp зависит в основном
от состояния поверхности обтекаемого тела, степени
турбулентности (возмущенности) внешнего потока и градиента
скорости, т. е. параметра /.
Теоретические и экспериментальные исследования
устойчивости ламинарного пограничного слоя показали, что
„потеря устойчивости" происходит либо в результате
наложения возмущений, вызванных срывом с бугорков
шероховатости на поверхности обтекаемого тела, либо
вследствие конечных возмущений, вносимых в пограничный слой
внешним потоком. Первая причина оказывается
существенной только при малой турбулентности набегающего
потока (порядка 0,1°/0) и большой шероховатости.
Используя общие положения теории размерности и
опытные данные, нетрудно получить соответствующую
зависимость в явном виде. Опуская вывод, запишем
формулу для определения Re**, полученную А. П.
Мельниковым:
Re;;=^(l-!;f+225, (5-58,
где Е0 — начальная степень турбулентности;
/ — формпараметр;
fs — значение формпараметра в точке отрыва; для
ламинарного слоя можно принять fs = — 0,085.
Таким образом, для определения точки потери
устойчивости ламинарного пограничного слоя нужно найти по
уравнению (5-55) изменение толщины потери импульса
вдоль поверхности рассматриваемого тела и построить
кривые Re**p = <р (*) [уравнение (5-58)] и Re** = <p1(^:) =
V
Точка пересечения указанных кривых будет
представлять собой искомую- координату хкр*
Результаты экспериментального исследования
показывают, что переход ламинарного пограничного слоя в
турбулентный происходит в некоторой области, размеры
которой зависят от местного градиента давления, чисел М и
248
Re, степени турбулентности и некоторых других
факторов.
Определение положения и протяженности переходной
зоны, а также характера изменения 6** в этой зоне
составляет важную часть задачи по расчету смешанного слоя
и, в частности, последующего турбулентного участка1.
Переходная область может быть определена
экспериментально путем измерения профилей скорости в
различных сечениях по длине поверхности. Характер изменения
профиля скорости в переходной области можно проследить
на рис. 5-17, а. На расстоянии х = ЪЪ мм от передней
кромки пластины слой — ламинарный; все точки образуют
кривую, соответствующую уравнению —=2~ — 2(|-] -|-
При переходе в сечение х ^ 50 мм профили
+(*г
скорости резко деформируются и приобретают форму,
типичную для турбулентного пограничного слоя.
Профили скорости в пограничном слое позволяют
вычислить толщину потери импульса Ь** (х) и по характеру
изменения этой величины установить протяженность
переходной зоны (рис. 5-17,6).
Длину переходной области 5 принято определять в
долях общей длины обтекаемой поверхности.
Изменения &**в этой области характеризуются величиной
Re**
ReH
где Re**, 5**— число Re и толщина потери импульса в
**
конце и Re** = -^ — число Re и 6* в начале
переходной области. При безградиентном течении величина г* —
В общем случае г зависит от профиля скорости в
начале переходной зоны, чисел Re и М, степени
турбулентности. С увеличением чисел Re и М величина г**
несколько возрастает (рис. 5-18). По опытам МЭИ измене-
1 Исследованию переходной области посвящены работы Л. М. Зы-
синой-Моложен и др.
249
6,U
1,6
1,2
0,k
r*>
w3
i i
К
V^
X
0 OJ 0,2 0,3 0,4 0,5 0,6 0,7 0,3 0,3 1,0
5)
Рис. 5-17.
а —изменение профиля скорости в пограничном слое вдоль плоской стенки; б-
изменение толщины потери импульса вдоль плоской стенки.
ние Е0 в пределах 0,5—1,5°/0 не приводит к заметным
изменениям величины г . Дальнейшее увеличение Е0 вызывает
резкое уменьшение г*\
Для характеристики влияния профиля скорости на
рис. 5-19 показан график г**=?1(/0)|Где /0—формпараметр
в начале переходной зоны. Как следует из кривой,
с ростом формпараметра г** возрастает. Аналогично в
зависимости от формпараметра /0 изменяется и
протяженность переходной зоны 5 (рис. 5-19). Такое поведение
кривых г** = 9i (/о) и 5 = ср2 (/0) можно объяснить следую-
0 О J 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,3 КО
Рис. 5-18. Зависимость величины г** от числа М.
щим образом. В переходной зоне вследствие поперечного
перемещения частиц толщина пограничного слоя 8
увеличивается, а профиль скорости становится более полным.
Если в результате роста толщины 8 происходит увеличе-
**
ние 5 , то увеличение полноты профиля скорости
вызывает падение интегральной толщины 8**. В конфузорной
области основное значение имеет возрастание толщины
пограничного слоя 8, ибо здесь профиль скорости
достаточно полный и в результате перехода его полнота
изменяется незначительно1. Наоборот, в диффузорной области
в результате перехода ламинарного течения в
турбулентное происходит значительная деформация профиля
скорости, причем эта деформация оказывается тем большей,
чем больше положительный градиент давления в месте,
где происходит переход.
При некотором значении параметра / в диффузорной
области оба фактора, влияющие на величину 8**, взаимно
1 Следует отметить, что в конфузорной области с большими
градиентами давления возможен переход турбулентного слоя в
ламинарный (стр. 227). Такой переход весьма вероятен при M^sl.
251
компенсируются и величина г оказывается равной 1.
Протяженность переходной зоны при этом также оказывается
незначительной. По опытам МЭИ г** = 1 при /0=—0,06-*-
— 0,07.
Если же по какой-либо причине переход начнется
ПрИ ^<^_о,07, то, по-видимому, процесс турбулизации
слоя и перестройка профиля скорости будут происходить
против течения, пока профиль ламинарного слоя не
окажется достаточно устойчивым.
1 у*
А
А
•
5
%
О
- ■ 5
•
ч
п
и
■ 6 -
Г**
/ 9
1%г
ft
V
^8
а]
• Г** 1
▲ S
1
' 2\
fo*'°\
-5Ш0 ~*,0 -dfi -2,0 "1,0 О 1,0 2%0 J,0 4,0 5,0
Рис. 5-19. Зависимость величин г и 5 от формпараметра f0.
Отсюда, между прочим, следует, что отрыв
пограничного слоя может произойти только в области либо
ламинарного, либо турбулентного движения, так как переход
ламинарного слоя в турбулентный в диффузорной области
происходит при значении параметра /, меньшем, чем его
значение в точке отрыва.
На основании обработки опытных данных для расчета
переходной области получены следующие эмпирические
формулы:
F^(^6)0,,5(3J + 5j5/o)0/o; (5_59)
r*V-(7 + 100/0)°',2f2 + 0,12 М.
(5-60)
Зная величины 5 и г*\ легко найти координаты
сечения, от которого следует вести расчет турбулентного
слоя, и значение в нем толщины потери импульса.
252
5-11. РАСЧЕТ ТУРБУЛЕНТНОГО ПОГРАНИЧНОГО СЛОЯ
Расчет турбулентного пограничного слоя строится на
экспериментальных данных, позволяющих приближенно
выразить напряжение трения в слое.
Во многих случаях удобно пользоваться приближенным
степенным законом распределения скоростей в слое,
выражаемым формулой
и ( у \п
. йГ\-т) ■ (5-61)
Формула (5-61) построена на основании сравнения
профилей скорости в турбулентном слое и в цилиндрической
трубе. Как было показано, профиль скоростей в трубе
меняется при изменении числа Re (рис. 5-6).
Следовательно, показатель п в формуле (5-61) является функцией
числа Рейнольдса. Так, по опытам Н. Никурадзё показа-
1 1
тель степени п меняется в пределах -g—г- у^ при изменении
Re от 4-Ю3 до 3- 10е. Однако в первом приближении
показатель степени п может быть принят постоянным в
определенном диапазоне чисел Рейнольдса. В расчетах часто
принимают п = у и профиль скорости задают формулой
jf. /J/.Y
"о V5/
(5-62)
Напряжение трения на стенке при турбулентном
движении можно представить также упрощенной опытной
зависимостью
Подставив опытные коэффициенты С = 0,00655 и т =
= — 0,166 в формулу (5-63) и рассматривая частный
случай безградиентного течения, из уравнения (5-38) найдем:
с, =^=0,00655 Re**"0'166. (5-64)
/о иХ
Введем в это уравнение число Re^ = -^-. Заметим, что
(5-65)
253
d$"
dx
__d\~t~)_dR<r
/хиЛ d Re
Тогда дифференциальное уравнение для толщины
потери импульса запишется в таком виде:
^^==0,00655 Re**"0'166. (5-66)
Предполагая, что на стенке образуется только
турбулентный слой, проинтегрируем уравнение (5-66). Тогда
получим:
б_
Re" = 0,0153 Re^ .
Отсюда, заменяя Re и Re^., находим уравнение для
толщины потери импульса:
8" = 0,0153 (£Л х , (5-67)
или, выразив 8** в функции числа Re^., найдем:
8** = 0,0153 jcRe^ 7 . (5-68)
Полученное простое решение для толщины потери
импульса в турбулентном слое не учитывает влияния
сжимаемости и продольного градиента давления. Оно
справедливо при М^0,5 и -р=0.
Как уже отмечалось, уравнение импульсов (5-38)
связывает три неизвестные величины: 8*, 8** и т0.
Дополнительные связи, необходимые для решения задачи,
устанавливаются опытным путем.
На рис. 5-20 приведена экспериментальная зависимость
Н0 = Н (М) для плоской пластины при нулевом градиенте
давления. Величина Н0 существенно зависит от числа М;
приближенно эту зависимость можно представить
следующей формулой:
Я0 = Я00(1+аМ°)==Я00(1+0,ЗМ2), (5-69)
где для несжимаемой жидкости при нулевом градиенте
давления можно принять И00 = 1,3 -г- 1,4, причем меньшее
254
значение И00 соответствует большим числам Re: С
увеличением числа М несколько уменьшается относительная
толщина потери импульса (рис. 5-26)
Влияние градиента давления на параметр Н можно
видеть на рис. 5-21, где дана зависимость Н=Н/Н0 от
параметра Бури Г.
Отсюда следует, что в зоне умеренных значений
параметра Г(—0,015<Г«<0,02)/7 изменяется на 7°/0. Поэтому
при построении решения в отмеченном диапазоне
будем учитывать только изменение //0 —//(М).
Для коэффициента сопротивления в турбулентном слое
для общего случая была получена формула (5-50). Если
отнести х0 к плотности на внешней границе пограничного
слоя ри то формула (5-50) может быть представлена в
форме:
Pi"0 Pl
Е(г;+аг) =
= (С + аГ)Ре:-(1+^М02|
(5-70)
'"О OJ 0,2 0,3 0,4 0,5 0.6 0,7 0,8 0,9 to V 1,2
Рис. 5-20. Злияние числа М на параметр HQ.
1,3
1,2
и
1,0
oja
и
•
•V •
Sij
•
^r*tcrz
-3,0 -2,5 -2,0 -1,5 4,0 -0,5 О 0,5 1,0 1,5 2.0 2,5
Рис. 5-21. Изменение величины И в зависимости от параметра
Бури Г.
3.0
255
Подставим (5-69) и (5-70) в интегральное соотношение
(5-38). После несложных, но кропотливых преобразований
^можно получить дифференциальное уравнение относительно
параметра Г в следующем виде:
V' + P(x)r + Q(x) = 09
(5-71)
где х — безразмерная длина обтекаемой поверхности.
Уравнение (5-71) относится к типу линейных и может
быть приведено к квадратурам и решено относительно
15.6
ЦБ
16
3,6
3,2
2,8
2Л
2,0
/,6
12
оА
О
\огр
-0,16
~оА
-0,10
-0,08
-0,07
-0,06
-0,05
-ОМ
-0,03
-0,02
-0,01
h
/,
//
4L
f's
h\
f*.
1
//
//
/
//
/
1 /
/
/
/
/
/
7
/
/
//
//
и
/
/
y h
/
/
ta\
AJ
Г
\26
\l8
\l6
Г
\l2
I/O
\8
6
\4
\z
\0
0,2 OA 0,6 0,8 1,0 1,2
a)
Рис. 5-22.
а —зависимость функций flt fa и ft от bil
256
параметра Г. Оно служит для определения параметра Г,
исключая область, близкую к точке отрыва.
При равенстве нулю постоянной а и стремлении Я к
нулю решение переходит в формулу (5-67).
Введя ряд упрощений, получим при небольших
градиентах давления (Г> —0,02) для толщины потери
импульса выражение
-;** 1
i3,35Da0,2,
+ 0,0026 [я^2(6 -Xlf^dx
[T,^o,74°'2i>(6-;io)1'81 +
(5-72)
-10,8
15
13
11
6,0
ю
5,0
3,0
ио
0,8
0,6
ОЛ
0,2
0
060
0,70
-0,60
-0,50
-0,40
- 0,60
-0,20
- o,w
-0,06
- 0,06
-0,04
ом
0
?*
J
£
о.
1
/
1
II
1
Iff
2 0,
f
* о,
fl
f/
в .о,
\
bl
///
у
/
8 t.
0 U
ГЦ
//
/
*■>
2 1,
30
26
22
18
Л
10
6,0
2,0
1,6
1,2
0,8
0,4
в)
б —зависимость функций q>1( <p, и <ра от Х^
17 М. Е. Дейч
257
Здесь о** и Я0 — значения толщины потери импульса
и безразмерной скорости в начале турбулентного участка;
^ a L v
Re =-^ число Реинольдса, определенное по критической
скорости а и кинематической вязкости на стенке.
Вводя обозначения:
/лЗ,35 /п л2 \1,45.
1=Я0 (6~ Яо) >
/а = 0,0026 Я^92 (6 - Я2, )2,81; (5-73)
преобразуем (5-72) к виду:
"?** J Г ***1.25 n 0,25с | Г с Г"!0'8 /с- 7/1\
=/^ч ° Re. f* + y*dx\ • <5'74)
Функции /15 /2 и /з от Я0 представлены на рис. 5-22,а.
Расчет по формуле (5-74) с использованием расчетных
графиков оказывается относительно простым и дает
хорошее совпадение с опытными данными.
При больших градиентах давления для толщины потери
импульса получим:
T* = rior2IC'-25RerV3+lW8. (5-75)
Здесь
?i = Ao (6~Яо) * '
О 31x2
?2 = 0,0078 Я2'69 (6-Я2)262*' °;
?! = Я0 (6 — Я0 ) в
(5-76)
Соответствующие значения <Pi ?2 и ?з приведены на
рис. 5-22,6.
В заключение остановимся на существенном различии
в свойствах ламинарного и турбулентного слоев. С этой
целью в табл. 5-1 приведены основные расчетные формулы
258
для простейшего случая обтекания плоской стенки (без"
градиентное течение) несжимаемой жидкостью.
Сопоставление показывает: 1) профиль скоростей в
турбулентном слое более полный, чем в ламинарном; 2)
толщина турбулентного слоя растет вдоль стенки значительно
быстрее, чем ламинарного, так как в первом случае 8 уве-
6/7
личивается пропорционально х , а во втором —
пропорционально х1 ; 3) сравнение местных коэффициентов со-
Таблица 5-1
Основные
характеристики
пограничного слоя
Закон
распределения скоростей
по сечению слоя
Толщина слоя
Толщина
вытеснения
Толщина
потери импульса
Напряжение
трения
Местный
коэффициент трения
Коэффициент
сопротивления
трения
Режим пограничного слоя
ламинарный
i
8-5'8зЫ =
1
= 5,83л: Re^ 2
1
<Г = \J2xRex 2 ^0,35
1
Г* = 0,664л; Re^ 2 ^
=^ 0,11753
1
| T0 = 0,332p^Re7r
1
cf = 0,664 Re^ Г
l
Cf= 1,328 Re^ 2
турбулентный
1
5^0,211 (i;)**
xzO,2\\xRe~T
l
5* ^ 0,02x Re^ 7 =^0,095д
l
5**^r0,015xRe77 ^=
^0,0715
l
T:e = 0,0132pi£gReJC 7
l
cf == 0,0263 Re^ 7
l
Cf = 0,0307 Re,, 7
17*
259
противления трения
показывает, что при одинаковых
значениях Re^
сопротивление трения в
турбулентном
пограничном слое
значительно выше, чем в
ламинарном.
Этот весьма важный
вывод хорошо
подтверждается опытными данными.
На рис. 5-23 приведены
экспериментальные и
расчетные зависимости
коэффициентов £., полученные
для турбулентного режима
с помощью различных
полуэмпирических формул.
Кривые показывают
достаточно высокую точность
формулы, приведенной в
табл. 5-1.
Сравнение с, для
ламинарного и турбулентного
слоев показывает, что при
одинаковом значении Reje=
4 • 104 коэффициент cfTyp6
в 2 раза превосходит с,лам
(W =0>0054; cfMH =
= 0,0022). С ростом Re^
разность CfTyV6-cfjiaM
резко увеличивается.
Отсюда следует, что
при безотрывном обтекании
тела необходимо
стремиться к „затягиванию*
ламинарного участка слоя, т. е.
к сдвигу области перехода
в направлении потока.
Обнаруженная разница в
сопротивлениях трению при
260
ламинарном и турбулентном режимах объясняется
различным механизмом трения в том и другом случаях. Если
при ламинарном режиме сопротивление обусловлено
поверхностным трением между слоями жидкости
(перемешиванием макрочастиц—молекул), то при турбулентном
режиме имеют место интенсивные поперечные
перемещения микрочастиц. Очевидно, что перемешивание этих
частиц связано с потерей значительного количества
движения, т. е. с появлением существенных сил трения в
потоке.
Многочисленные опыты в соответствии с выводами
полуэмпирической теории указывают на еще одно
существенное различие в свойствах ламинарного и
турбулентного пограничных слоев. Точка отрыва ламинарного слоя
при больших числах Re занимает фиксированное положение
на обтекаемой поверхности. Точка отрыва турбулентного
слоя при одинаковом распределении параметров внешнего
потока располагается дальше точки отрыва ламинарного
слоя. Другими словами, турбулентный слой
отрывается позднее ламинарного. Это становится
понятным из рассмотрения профилей скорости при одном
и другом режимах слоя: кинетическая энергия частиц,
движущихся вблизи стенки, при турбулентном режиме
значительно больше, чем при ламинарном.
В тех случаях, когда на обтекаемой поверхности
существует смешанный пограничный слой, необходимо
суммировать сопротивление на ламинарном и турбулентном
участках.
Изложенная методика расчета не учитывает влияния начальной
турбулентности потока. Для небольших степеней турбулентности
уравнение импульсов пограничного слоя для несжимаемой жидкости
получено В. А. Врублевской в таком виде:
(1 + hEl) ж + -L- (2 + Н) = -^ + Е\. (5-77)
Здесь А = 4,;;Г0-осреднение* значение скорости внешнего
потока; о —толщина потери импульса, подсчитываемая по осред-
ненным скоростям.
Графическое решение уравнения (5-77) для безградиентного
течения в логарифмических координатах показано на рис. 5-24. Здесь же
нанесены опытные точки, относящиеся к эксперименту на плоской
261
стенке, проведенному в МЭИ. Графики на рис. 5-24 отчетливо
показывают влияние Е0 на потери в пограничном слое; так, при Re^ =
= 2• 106 увеличение Е0 от 0 до 5% повышает число Re**, а
следовательно, и величину потерь на трение в слое на 70%.
Рис. 5-24. Влияние степени турбулентности на толщину потери
импульса в турбулентном пограничном слое.
5-12. ПОГРАНИЧНЫЙ СЛОЙ ПРИ БОЛЬШИХ СКОРОСТЯХ.
ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ
Рассмотрим некоторые результаты опытного
исследования турбулентного пограничного слоя при больших
дозвуковых скоростях при безградиентном течении и докрити-
ческих скоростях (М<^М).
На рис. 5-25 приведены шесть профилей скорости,
полученные, при постоянном числе Re, равном 2,5-10е, и
переменном числе М. Все экспериментальные точки в
интервале М = 0,31 -г- 0,98 образуют одну кривую, которую
можно представить зависимостью вида:
£=/(-$-)• (5"78)
262
Следовательно, при нулевом градиенте давления с
изменением числа М профили скорости в координатах у, Я
изменяются подобным образом. Кроме того, в указанном
диапазоне изменений числа М толщина пограничного слоя
при постоянном числе Re изменяется незначительно; поэтому
можно говорить не толь- ; 0
0,3
0,8
у/*
М=0,3!0
0,5Ub
0,610
0,734
0,300
М=0,380
\
ко о подобии, но и о
тождественности
профилей скорости. Отсюда
можно заключить, что
непосредственно на
профиль скорости в
пограничном слое влияние
сжимаемости при М < 1
сказывается
незначительно. Таким образом, в
первом приближении
профиль скорости при М > О
можно представить
обычной степенной
формулой (5-62).
Формула (5-62) не
является, конечно,
единственной. Любая
зависимость,
удовлетворительно аппроксимирующая
профиль скорости в
пограничном слое
несжимаемой жидкости, может
быть распространена и на
течение сжимаемой
жидкости. Пределы такой
экстраполяции не
ограничиваются , по-видимому,
звуковой скоростью и
могут быть распространены и на сверхзвуковые скорости.
Дальнейшая обработка профилей скорости дает
возможность вычислить значения интегральных толщин 8#,
8 и построить кривые их изменения в зависимости от
числа М (рис. 5-26). Разброс экспериментальных точек
в области околозвуковых скоростей объясняется
возникновением конфузорного течения. Кривые для околозвуко-
0,5 0,6 0,7 0,3 0,3 ко
Рис. 5-25. Влияние числа М на
профиль скорости в турбулентном
пограничном слое.
263
вых скоростей проведены через точки, полученные при
минимальном градиенте давления; поэтому в области
звуковых и сверхзвуковых скоростей основная масса точек
располагается под кривыми. Разброс точек,
обнаруживаемый в области дозвуковых скоростей, объясняется тем,
что здесь нанесены точки, относящиеся к различным
числам Re.
Полученная картина находится в полном соответствии
с теоретическими результатами. Увеличение числа М
прилил*
о,зь
о,зо\
0,26\
0,22
о,/з
О,/4
0,10
8**
А
• .
r-2-o-
>
С
•
о
О
0° "
•
К У*оо
1
L
"V**"
о
•
LA°A
о о j t oF
Re=(2+4)-W6
о
п
°0
>
• ***■
в
^1
/"00П
Н
• j.
м
/,/
г,о
0,3
0,8
0,7
О О,/ 0,2 0,3 0,4 0,5 0,6 0,7 0,3 0,3 /,0 /,/ 1,2
Рис. 5-26. Влияние числа М на толщину потери импульса.
водит к падению толщины потери импульса и к росту
толщины вытеснения 5*. Такое поведение кривых при
одинаковых профилях скорости обусловлено изменением
плотности поперек пограничного слоя, причем противоположное
влияние этого изменения на толщины 6 и 5 объясняется
тем, что подынтегральные функции, через которые
выражаются толщины 5*, 6**, по-разному реагируют на
изменение плотности.
Для приближенной количественной оценки влияния
сжимаемости на толщину потери импульса 5 на рис. 5-26
приведено изменение относительной толщины
иоо
зависимости от М при нулевом градиенте давления. С
приближением к звуковой скорости уменьшение толщины
потери импульса составляет около 15°/0.
Независимость профиля скорости от числа М дает
основание считать число Re основным параметром, опре-
264
деляющим профиль скорости при отсутствии градиента
давления,, и распространить результаты многочисленных
экспериментов по определению его влияния в несжимаемой
жидкости на течение сжимаемой жидкости.
КО
0,9
оА
0,7\
0,6
0,51
оЛ
0,3
Оу2\
О
0,5 0,6 0,7 0,8 ОМ 1,0
Рис. 5-27. Влияние числа Re на профиль
скорости в турбулентном пограничном
слое.
\у/е
1 Г
• Re=Q,61W6
о
Л
1,08 Ю6
2,00-10 6
* 3,50W6
в ч,3310 ■
* Re^SJZIO6
M=0,L
в Л
15
•
«
1
т
А
^_
8
б
в
о
«V
а»
~1^Г~~
0
•о
7&
1
"/ио\
На рис. 5-27 приведены шесть профилей скорости,
полученные при изменении числа Re и постоянном числе М.
Увеличение числа Re от 0,6Ы06 до 1,08.10е приводит
к характерному изменению профиля скорости. Дальнейшее
увеличение числа Re не вызывает заметного изменения
профиля скорости. Другими словами, начиная с величины
265
Re^lO6, профили скорости могут быть выражены общей
зависимостью.
Исследование влияния числа Re на интегральные
толщины 6* и б** показало, что с ростом Re, как и в случае
несжимаемой жидкости, эти величины уменьшаются. В
области малых значений Re изменение 5 * оказывается
довольно заметным. С увеличением числа Re уменьшение
толщины 6** происходит менее интенсивно. Аналогичным
образом меняются и толщины вытеснения.
Таким образом, влияние числа Re при больших
скоростях на турбулентный пограничный слой с качественной
стороны оказывается того же порядка, что и в потоках
несжимаемой жидкости.
Для исследования вопроса о влиянии числа М при
наличии градиента давления были сняты профили скорости
в диффузорной области (рис. 5-28,#) и при конфузорном
течении (рис. 5-28,6). Как видно из приведенных кривых,
все экспериментальные точки независимо от числа М
образуют практически одну кривую. Этот факт еще раз
подтверждает сделанный ранее вывод о том, что при
дозвуковых скоростях изменение числа М не приводит
к заметным изменениям профилей скорости. Следовательно,
основным фактором, определяющим течение в
пограничном слое сжимаемой жидкости, является продольный
градиент давления.
Результаты исследования показывают, что влияние
сжимаемости на структуру турбулентного пограничного
слоя является косвенным. При изменении числа М меняется
распределение давлений вдоль обтекаемой поверхности.
С ростом числа М абсолютные значения градиентов
давления возрастают. В соответствии с этим меняются
основные характеристики слоя. В конфузорном течении 8**
уменьшается, а в диффузорном—возрастает.
Изменение продольного градиента давления от
положительного до отрицательного значения приводит к
существенной деформации профилей скорости. Это отчетливо
видно из рис. 5-29, где изображены профили скоростей,
полученные в диффузорном канале при различных
градиентах давления.
На рис. 5-30 приведена кривая изменения толщины
потери импульса в функции параметра Г, полученная из
эксперимента. Чтобы исключить влияние сжимаемости, тол-
265
-о,/
-0,2
■6,3
-6,4
0,5
г>
9
^-5
L (
"~~~
£Й
~\Zi
^
ГЧП
—
/ 234 5 6 7 В 8 10 II 12 13 14 15 16 17 18 /3
№ точен
U0
0,6
0,8
0,7
р,6
0,5\
0,4
0,3
0,2
0,1
О
У16
—г 1
о А/= 0,256
а 0,670
0,280
* 6,5 6 Ь
•М=0,63
><
о а
о V
&
/
Л
JSJ
-Ж
?
Фо
сГз 0^4 05 06 0J Хз Ш W
о)
Рис. 5-28. Влияние числа М на профиль скорости в турбулентном
пограничном слое.
а—профиль скорости в диффузор ной области, Re=l,5»105:
267
W rr
0,9
0,8
oj\
0,6
0,5\
0,4
0,3
0,2\
0,1
0
—f~"
n
i
e-i
'.—.
p
K—>
<—.:
Css.
.._.
Л
к
N
|»
^
. ._|
4
^
•I
1
l 1 >i
1 234 5 6 7 8 9 JO 11 12 13 14 15 16 17 18 19
№ точек
0,9
0,8
0,7
0,6
0,5
0Л
0,3
0,2
0,1
Ш*
x /
•
A
4=0,4
0,6
0,8
60
80
46
\Ll^J/////// ///?,, , ,,,,,,.,«
p
•
*~
*****
'•*"
>
<•
•
X
«
A
H
Щ
•j
X
A
5
a|
5
a|
A
*
A
A
i\
r
U/Ug
0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
*)
Рис. 5-28.
б —профиль скорости в кон})узорной области, Re=2«10.
ЩйнЯ 3** была1 6fнесена К Соответствующей толщине 5*
для безградиентного течения при той же скорости
внешнего потока. Все точки группируются вокруг одной
кривой.
Из кривой следует, что в данном случае 8** является
функцией одного параметра Г. Следовательно, когда
распределение скорости на внешней границе пограничного
мм
/,и\
№
5Л
*.о
3,0
2,0
ко
У 1
\ i ■
Ъ/ г/ f////////// ///,/.' t V///////J 1
.—>_
/-
/
x'lLr^^*-*
"rvrnfrrb
X
\ J
/
V2
Ytj
yJ/
L. i
ll
1
J /
/11
-nil
* IIP)
1 -> ■
о oj o,2 аз o,u as oj nj as o,s wo
Рис. 5-29. Профили скорости в диффузоре
при различных градиентах давления.
/—&**=0,61 мм; 8*= 1,095 мм; М=0,960; Я=2,4; Я0=1.65; 2~5**=0,552 мм; Ь*=
=0,765 мм; М=0,548; #=1,57; Я0=1,4; 3 — Ь**=0,384 мм; S*=0,52 мм; М=0,54; Н-
=1,52; Я0=1,4; 4-5**=0,37 мм; 5*=0.638 мм; М=0.985; Я=2,2; Яв=1,7.
269
слоя близко к линейному, расчет по однопараметрическому
методу физически обоснован. Отсутствие
экспериментальных данных, относящихся к другим значениям второй
производной, не позволяет сделать более общего вывода.
Опытные данные, характеризующие влияние начальной
турбулентности на структуру пограничного слоя, показаны
на рис. 5-31. С увеличением Е0 возрастает полнота
профиля скорости. Однако наполнение профиля существенно
3.001
гщ
ш
о
-300
1 О/0
**/s0
** "1
о^
Чч^
\
о
°\
'
W
1
с
1 ~^ -4
Г/0
J J
-200
-/00
/00
200
300
Рис. 5-30. Зависимость относительной толщины потери импульса
от параметра Г.
зависит от знака и величины градиента скорости
внешнего потока. Наибольшее влияние Е0 оказывает в диффу-
зорном течении, что подтверждают графики изменения 6**
вдоль плоской стенки при различных градиентах давления
(рис. 5-32). Наименее чувствительным к изменению Е0
является конфузорный поток | -~~ << 0 j.
С возрастанием числа Рейнольдса влияние Е0
уменьшается (рис. 5-32). Аналогичный результат получен и при
различных числах М; с увеличением М расхождение
кривых уменьшается, в особенности при М, близких к
единице.
Отметим, что в связи с увеличивающейся полнотой
профиля скорости в слое параметр Н = ^г заметно сни-
270
/,0
0,9
0,8
0,7
w\
0%5
0Л
0,3
0,2
OJ
0
[^
Е<ГО№
0,075^
£0=6,Q8
Lfcr
</
s //
y/
a/"o\
0,5 o,6 oj o,e as w
2Лг^
2,0\-~i
6) U
U2
0.8
#•••/0*
•r^**^^
--«^•^
1
1* t».
0,015
0,01
■ "4
i
Re-W'5
8Л6
/а в
4,3 6,5
Рис. 5-31. Влияние начальной турбулентности.
а — на профили скорости в турбулентном пограничном слое; б — на
толщину потери импульса при различных градиентах давления.
271
жается с ростом степени турбулентности; в зависимости
от знака продольного градиента давления это снижение
составляет 15 — 20%.
Особенно велико влияние начальной турбулентности
при отрывном обтекании поверхности. В этом случае
увеличение £"0 приводит к резкому смещению точки отрыва
по потоку и к улучшению обтекания поверхности.
пй\ 1 I 1 1 1 I I I g I
аг аз оЛ о.5 о.б 0.7 о,в ао ко /,/
Рис. 5-32. Влияние начальной турбулентности на
толщину потери импульса при градиентном течении.
Приведенные данные показывают, что при расчете
турбулентного пограничного слоя необходимо учитывать
влияние начальной турбулентности. Заметные расхождения
между опытными и расчетными [по формуле (5-70)]
значениями б** отмечаются при Е0^3°/0.
Рассмотрим некоторые свойства пограничного слоя при
околозвуковых скоростях1.
Если скорость набегающего потока М^ будет больше
критического значения М#, то у поверхности обтекаемого
тела образуется область сверхзвуковых скоростей.
1 Рассматриваемые здесь вопросы обтекания тел при
околозвуковых скоростях частично затронуты в гл. 3,
272
Область сверхзвуковых скоростей имеет ограниченную
протяженность в направлении, нормальном к обтекаемой
поверхности. В направлении течения (вдоль обтекаемой
поверхности) область сверхзвуковых скоростей также
ограничена. К этому]"заключению легко прийти, вспоминая, что
на некотором удалении за телом скорость должна быть
дозвуковой, так как скорость невозмущенного потока
(перед телом) — дозвуковая.
Таким образом, зоны сверхзвуковых скоростей,
появляющиеся при Моо>М#, имеют местный характер. В
местной сверхзвуковой области течение газа вначале
ускоряется, а затем тормозится. Однако торможение сверхзвуко-
Рис 5-33. Схема образования скачка
уплотнения в местной сверхзвуковой
зоне.
вого потока, как правило, происходит с образованием
скачков. Благодаря большим ускорениям в зоне
сверхзвуковых скоростей газ оказывается значительно
перерасширенным, т. е. его давление падает значительно ниже
давления внешней среды. Это перерасширение сверхзвукового
течения погашается скачком уплотнения.
Как выше уже отмечалось, скорости при удалении от
тела меняются по величине и направлению (возмущение
потока в направлении от тела уменьшается). Благодаря
этому образующиеся скачки уплотнения будут
криволинейными с переменной вдоль линии скачка интенсивностью:
за скачком поток становится вихревым. Образующиеся
скачки уплотнения замыкают область сверхзвуковых
скоростей. Передней ее границей является линия перехода
(линия М; = 1). Для идеальной жидкости замыкающей
поверхностью служит поверхность обтекаемого тела (рис. 5-33).
18 М. Е. Дейч
273
В реальном случае вязкого газа расположение и
протяженность местной сверхзвуковой зоны, а также структура
скачков изменяются. Механизм взаимодействия скачков с
пограничным слоем составляет важную часть проблемы
сопротивления тел при околозвуковых скоростях.
у
dr:r^i--Jl^=, f
—Я&»
—^ м*<1
I Л
'7771ЧГЪ777>.
Рис. 5-34. Схема взаимодействия прямого скачка
и пограничного слоя.
Скачки уплотнения в местной сверхзвуковой зоне
создают большие градиенты давления, которые
распространяются и в область пограничного слоя. Возмущения,
возникающие в пограничном слое, распространяются против
течения и по течению и влияют на поле потока у
обтекаемой поверхности.
Рассмотрим вначале простейший случай, когда в
сверхзвуковой зоне образуется один прямой скачок1 (рис. 5-34).
1 Как указывалось в гл. 4, в неравномерном сверхзвуковом
потоке скачок криволинейный. Поэтому рассматриваемая схема
является лишь первым приближением.
274
В пограничном слое скорости меняются от нуля на стенке
до сверхзвукового значения во внешнем потоке.
Следовательно, в пределах слоя располагается линия перехода
(М = 1), которая делит область пограничного слоя на
дозвуковую и сверхзвуковую части. Заметим, что в
турбулентном пограничном слое дозвуковая часть имеет
относительно меньшую толщину, чем в ламинарном. Очевидно,
что повышение давлений распространяется через
дозвуковую часть слоя навстречу течению.
Возрастание давлений в зоне скачка может привести
к появлению отрыва. При турбулентном режиме
интенсивность скачка, вызывающего отрыв, должна быть более
высокой, ибо, как было показано выше, турбулентный
слой всегда отрывается позднее. Заметим, что так как в
дозвуковой части слоя повышение давления
распространяется против течения, то точка отрыва, как правило,
располагается перед скачком.
Так как интенсивность скачка в направлении от стенки
меняется (в соответствии с изменением скоростей), то в
пограничном слое образуется поперечный градиент
давления и основное условие, принятое в расчетах слоя
(-^ = 0), в области скачка не соблюдается.
Возмущение, распространяющееся в дозвуковой части слоя,
приводит к нарушению этого условия и перед скачком.
Отсюда заключаем, что режим течения в
пограничном слое должен оказывать существенное влияние на
положение скачка в местной сверхзвуковой зоне, на
структуру и интенсивность скачка. Это влияние
объясняется различием в профиле скоростей ламинарного
и турбулентного слоев. Следует, однако, учитывать, что
распределение скоростей в пограничном слое зависит не
только от режима течения, но и от характера изменения
скорости внешнего потока и, следовательно, от
кривизны обтекаемой поверхности.
Опытные исследования .подтверждают возникновение
различных по структуре скачков в ламинарном и
турбулентном пограничных слоях (рис. 5-35).
При ламинарном слое местные скачки имеют, как
правило, Я-образную форму; такой скачок состоит из
наклонного криволинейного скачка, сливающегося с
более мощным и более протяженным окачком небольшой
кривизны, замыкающим сверхзвуковую зону. Появление
275
криволинейного скачка можно объяснить следующим
образом. Повышение давления, распространяясь в
дозвуковой части .слоя, вызывает заметное увеличение его
толщины перед .скачком. Линии тока в пограничном слое
отклоняются -от поверхности тела; в результате
возникает система слабых волн уплотнения, (которые и обра-
Ламинарнь/й
слой
Тур5улвмтный
слой
'/>/S?SSS>J/JS///>
Рис. 5-35. Схемы скачков (а)
и спектр течения (б) в местной
сверхзвуковой зоне при
ламинарном и турбулентном режимах
пограничного слоя.
зуют наклонный скачок. С увеличением числа Re (при
M1==.const) по мере выравнивания поля скоростей в
пограничном слое кривизна линий тока перед скачком
уменьшается и при развившемся турбулентном профиле
скоростей первый скачок исчезает; остается один, но
более мощный скачок небольшой кривизны.
Отрыв потока в местной сверхзвуковой зоне
происходит не во всех случаях. Иногда в зависимости от
распределения скорости во внешнем течении отрыв имеет
локальный характер и на некотором расстоянии за
276
скачками -восстанавливается нормальное обтекание
поверхности дозвуковым потоком. В диффузорном течении
за скачками отрьгв обычно развивается и переходит
в кормовую область за телом.
На рис. 5-36 .приведена схема образования отрыва
в сверхзвуковой области. Точка перехода ламинарного
слоя в турбулентный (точка Т)у -как правило,
располагается вблизи точки отрыва 5.
Перейдем теперь ,к краткому рассмотрению схемы
взаимодействия .пограничного слоя при сверхзвуковых
скоростях с волнами
разрежения и скачка-ми уплот- I
нения. Так как в реаль- 1
ном сверхзвуковом тече- м >j \ м <1
нии всегда образуются \ 2
скачки уплотнения и вол- /jk
ны разрежения, то одной /v//\ ///^-^
из важных задач теории _ у^/^-\^^^м^
пограничного слоя при г^Т\Га^^.-7 ^~~L_
/Woo>l является изучение ^^З^^т^^^^^^^Ш
взаимодействия скачков и ^^%*
ВОЛН с-пограничным слоем. Рис. 5-36. Схема отрыва погранич-
Опытные данные позволя- ного слоя перед скачком уплотне-
ют заключить, что уело- ния*
вия взаимодействия
скачка с пограничным слоем могут быть различными в
зависимости от интенсивности скачка, распределения
скоростей внешнего потока и режима течения в слое.
Принципиальные схемы взаимодействия скачков
и волн разрежения с пограничным слоем приведены на
рис. 5-37. При небольшой интенсивности скачка
(рис. 5-37,а) перед ним вблизи точки его падения
происходит «разбухание» слоя.
В результате перед скачком образуется система
слабых волн уплотнения, создающих отраженный
скачок CD. Обтекание утолщенной дозвуковой части слоя
сопровождается образованием слабой волны
разрежения и второго отраженного скачка FE. При
значительной интенсивности падающего окачка (рис. 5-37,6)
повышение давлений перед скачком вблизи точки падения
может привести тс 'местному отрыву потока.
При падении на стенку волны разрежения толщина
пограничного слоя перед волной может убывать.
277
Таким образом, мы видим, что действительные схемы
отражения скачков и волн разрежения от стенки,
обтекаемой вязкой жидкостью, существенно отличаются от
схем, рассмотренных в гл. 3 и 4, для идеальной
жидкости. Основное отличие заключается в том, что скачки
(волны разрежения) через дозвуковую часть слоя
изменяют поле потока перед точкой падения, а
деформируемый при этом пограничный слой создает новые
волновые образования. Однако основное свойство твердой
стенки, отражающей скачки (волны) с тем же знаком,
сохраняется и в вязком потоке.
Рис. 5-37. Схемы взаимодействия скачков с
пограничным слоем при сверхзвуковых скоростях.
278
5-13. СОПРОТИВЛЕНИЕ ТЕЛ ПРИ ДОЗВУКОВЫХ
И СВЕРХЗВУКОВЫХ СКОРОСТЯХ
На тело, обтекаемое потоком газа, действуют силы
давления и касательные силы трения. Результирующая
этих сил является полной аэродинамической силой. При
изучении ^плоского обтекания аэродинамическую силу
принято -представлять двумя составляющими: Рх и Ру
(рис. 5-38). Как известно1, составляющую Рх,
направление которой совпадает с направлением скорости
набегающего потока, называют силой лобового
сопротивления, а составляющую Ру, нормальную
Рис. 5-38. Силы, действующие на обтекаемое тело.
к вектору скорости набегающего .потока, принято
называть 'подъемной силой или силой Жуковского.
Имея в виду происхождение силы Рх, лобозое
сопротивление подразделяют на сопротивление
трения и сопротивление давления. Такое разделение,
несмотря на некоторую условность, практически весьма
удобно при расчете сопротивления.
Тело, помещенное в поток, создает возмущение,
в результате которого в области, прилегающей к телу,
меняются параметры течения. Распределение давлений
у поверхности тела зависит от его формы и
ориентировки в потоке, а также от скорости невозмущенного
потока. Распределение сил трения на поверхности тела
также зависит от этих факторов.
Распределение давлений по поверхности тела
характеризуется коэффициентом давления. Рассмотрим
распределение давлений по крыловым профилям различной
формы при различных небольших углах атаки (рис. 5-39)
1 См. гл. 3 и 5.
279
для небольших скоростей1. На верхней и нижней
поверхностях вблизи носика профиля происходит интенсивное
ускорение потока с соответствующим снижением
давления. Эти участки профиля являются конфузорными.
Снижение давления на верхней поверхности профиля
60 80 100%
-0/71 II
C'U\ 1 1 1 1 1 1 II 1
Л
III
-f n\ W 1 1 1 1 1 1 1 j
• ГгШ M/
J г ml f
4 Гт гт4
TI11 1 ГТ
£0| 1111ILLLL
1гтттпТг
т /П
/|
+1 пМ 1 1 1 1 1 1 1 1 1
'*ио 2й w
1 I 1 1 I I г- —Пйп\
1 \Си UgDUX
1 п6'°
lepx \\\\\\\\
\\ 1 1 г 1 1 1 f 1 11
L
ImJsJJ 11
ГПтт И 1
ЛТП 71
№7
ГI '-
1 1 1 1 1 1 1 1 1 х\
60 80 tOO
40 60 80 100% ~1>°
ро
*1,0\
1 1 -1—1—h4J 1 1 1 J 1 I 1 Лгч-П W\
лТП tWjPwx № u>™\
И г пч1 k*^
/1 Г psL Mil
/ГПТ111111 ^чТТтгн]
М \Низ\ N IN
11111111 111 1 1 1 1 II 1 х\
о
20 U0 60 60 100%
\
'I
т
20
Щерх
Шиз
\си=0,60\
l*W
ОТ
jd
М 60 60 100%
Рис. 5-39. "Распределение давлений по двум профилям различной
толщины при разных углах атаки для небольших дозвуковых скоростей.
а —угол атаки; ^—-коэффициент подъемной силы.
происходит более интенсивно, чем на нижней. За
точками минимума <на нижней и верхней поверхностях поток
замедляется. Эта область течения у крыла является
диффузорной. Заметим, что диффузорныи участок на
1 Обычно принято картину распределения давлений строить по
хорде профиля, причем отрицательные значения коэффициента
давления (разрежения) откладываются вверх, а положительные — вниз.
280
верхней поверхности характеризуется более высокими
значениями градиента давления. На задней кромке
профиля, где происходит слияние струй, сбегающих с
верхней и нижней поверхностей профиля, .полное давление
не восстанавливается, так как в пограничном слое
имеют место необратимые потери (рис. 5-38).
При увеличена угла атаки картина давлений на
профиле существенно меняется. Значительные диффузор-
ные участки появляются на нижней поверхности
у носика.
Как мы видели, лри сходе с задней кромки профиля
образуется вихревой след, насыщенный вихрями,
зарождающимися в пограничном слое. Структура вихревого
следа меняется с удалением от профиля. Вихри,
зарождающиеся в -пограничном слое, развиваются при срыве
с профиля и затем на значительном расстоянии за телом
затухают в результате взаимодействия с внешним лото-
ком. При этом энергия вихрей преобразуется в тегую.
Образование вихрей приводит к снижению давления
в области задней кромки и за 'Профилем в следе.
При известном распределении давления по контуру
крыла можно найти проекцию сил давления на
направление вектора скорости с .
Легко видеть, что
Р'х = j P. cos {хг п) ds,
s
где ds — элемент поверхности профиля.
Сила Рх, обусловленная разностью давлений в точках
обтекаемого тела и направленная против его движения,
является силой сопротивления давлений. Кроме силы Р' , на
профиль действует результирующая касательных сил
трения Р'х'.
Таким образом, полное лобовое
сопротивление тела в плоском потоке является суммой
сопротивления давления и сопротивления трения:
Р =р>Л-Р".
X X I X
Необходимо особо подчеркнуть, что сопротивление
давления и сопротивление трения имеют одну и ту же при-
281
чину — вязкость жидкости. Профильным
сопротивлением называют сопротивление
цилиндрического крыла при его безотрывном
обтекании безграничным плоским потоком.
Для оценки силового взаимодействия между потоком
и обтекаемым телом вводятся безразмерные коэффициенты
сил, которые называются аэродинамическими
коэффициентами.
Так, сопротивление тела характеризуется
коэффициентом лобового сопротивления
2РХ 2РХ
Poo гоо *iV1oo г°°
где F — характерная площадь1 тела;
р— статическое давление невозмущенного потока.
Коэффициентом подъемной силы по
аналогий называют величину
_ 2Ру _ 2Ру
Как уже указывалось, силы, действующие на
обтекаемое тело, а следовательно, и аэродинамические
коэффициенты сх и су зависят от формы тела, режима его
обтекания и ориентировки тела ib потоке. При малых
скоростях, когда сжимаемость практически не
сказывается, основное влияние на коэффициент
сопротивления оказывают форма тела, угол атаки и число Re.
Существование такой зависимости, подтверждаемое
многочисленными опытами, вытекает из физической
природы сопротивления давления и сопротивления трения.
Действительно, в зависимости от формы тела
меняется характер возмущения, создаваемого телом в потоке.
При этом изменяются распределение параметров
течения по обводу тела и, следовательно, обе составляющие
силы Рх. Сопротивление трения меняется в связи с
изменением структуры пограничного слоя и режима течения
в нем.
Аналогичная перестройка спектра обтекания про-
1 В формулы для сх и с крыловых профилей вводится площадь
крыла, равная произведению хорды профиля на длину крыла.
282
исходит при изменении ориентировки тела в потоке.
В этом случае точно так же меняются полное
сопротивление тела и его составляющие. Отсюда также
следует, что в полном 'балансе сопротивлений тела
удельный вес сопротивления давления и сопротивления
трения может быть различным в зависимости от указанных
.параметров. Так, профили хорошо обтекаемой формы
при малых скоростях имеют сравнительно небольшое
профильное сопротивление, причем основным является
сопротивление трения. При увеличении относительной
толщины профиля и угла атаки роль сопротивления
давления увеличивается. Сопротивление трения вначале
меняется мало, а затем снижается. Так же как и полная
сила лобового сопротивления, коэффициент
сопротивления может быть представлен в виде двух слагаемых:
с =с -Х-с ,
X ХД I АГТр'
где сХА — коэффициент сопротивления давления;
с— коэффициент сопротивления трения.
С увеличением толщины профиля положительные
градиенты давления на кормовой части профиля
увеличиваются и точка отрыва смещается против потока. По этой
причине увеличивается сопротивление давления. Так как
при этом величина поверхности трения сокращается, то
с снижается.
С ростом числа Re^ для хорошо обтекаемого профиля
схл незначительно убывает, так как уменьшаются толщина
пограничного слоя и зона срыва. Вместе с тем при
возрастании Re^ уменьшается и коэффициент трения (см.
предыдущие параграфы). При оценке влияния формы тела и
числа Re^ иногда следует учитывать, что пограничный
слой оказывает влияние на внешний поток: линии тока
внешнего течения вытесняются пограничным слоем.
Подробное исследование позволяет установить, что
распределение давлений по контуру профиля в потоке вязкой
жидкости совпадает с распределением давлений по обводу
некоторого фиктивного тела (полученного из профиля путем
утолщения его на величину толщины вытеснения 6*),
обтекаемого идеальной жидкостью. Отсюда следует, что
структура пограничного слоя определяется внешним потоком, а
с другой стороны, пограничный слой может оказывать
283
обратное влияние на внешний поток. Заметим, что
обратное влияние слоя оказывается особенно существенным у
задней кромки профиля, где толщина слоя имеет
наибольшее значение. Толщина и распределение скоростей в
пограничном слое у задней кромки в значительной степени
влияют на профильное сопротивление.
Число Re^ влияет на отрыв потока. Отрыв потока
может появиться при больших углах атаки, когда
положительные градиенты давления в диффузорных областях
достигают больших значений. Увеличение числа Re^,
приводящее к турбулизации слоя, может резко уменьшить
коэффициент профильного сопротивления при больших углах
атаки, так как отрыв перемещается к задней кромке
профиля и сопротивление давления снижается. Увеличение
числа Re^ при смешанном безотрывном обтекании смещает
область перехода против потока и может привести к
возрастанию сопротивления трения.
При больших значениях М^ набегающего потока на
профильное сопротивление влияет сжимаемость. При
безотрывном обтекании тонких тел хорошо обтекаемой формы
точка перехода смещается по потоку и коэффициент
сопротивления несколько уменьшается. При появлении на
контуре тела отрыва увеличение М^ смещает точку
отрыва против потока, чем ухудшает обтекаемость тела.
Следует заметить, что, помимо этого, с ростом М^ возрастает
интенсивность вихревого движения в кормовомследе тела.
Заметное увеличение коэффициента сопротивления
обнаруживается при околозвуковых скоростях. В этом
случае коэффициент сопротивления в функции числа Моо
резко возрастает и в зависимости от формы тела может
в несколько раз превысить значение сх при Моо<М##.
Ранее было показано, что скачки часто (Приводят к
отрыву потока, что вызывает еще более резкое
возрастание сопротивления.
Характер распределения давлений по профилю при
околозвуковых скоростях можно видеть на рис. 5-40,а
(зона сверхзвуковых скоростей заштрихована). Здесь
отчетливо заметны .место расположения скачков и
.повышение давлений в скачках. На рис. 5-40,6 приведена
кривая коэффициентов профильного сопротивления
в этой зоне скоростей для крылового профиля.
284
-1*1
-1,2
-ол
-т
о
о,"
Oft
1,2
0J 0,4 0,8 Qfl 1,0 1'2 0,2. ОА 0,6 0J 1,0
Сверхзвуковые скорости
Скачки
ОЛ AS 0,8 1,0
"Скачки
0,2 ОМ JJi„0>8 W
Скачка
Сверхзвуковые
Скорости-"
Рис. 5-40 а.
285
Рис. 5-40. Распределение
давлений по профилю при
околозвуковых скоростях (а) и
коэффициенты сопротивления профиля
в зависимости от числа Мю (б).
0,7 0,8 0,9 ^ 1,0 1,1 tj
б)
Отмеченные выше особенности обтекания тел при
околозвуковых скоростях характеризуют специфическое
влияние сжимаемости. Изложенное показывает, что
возрастание коэффициента профильного сопротивления
при Моо>М объясняется увеличением сопротивления
давления. При развитой системе скачков на профиле и
отрыве потока доля сопротивления трения невелика и
его изменение не может объяснить столь значительное
возрастание сх. Заметим, что при Моо>Л1# может
происходить резкое уменьшение коэффициента подъемной
силы су] изменение су также обусловлено
перераспределением давлений на профиле и наступает обычно при
больших числах M^, чем те, при которых отмечается
возрастание сх.
Появление звуковых скоростей в точках профиля
можно установить по 'картине распределения давлений.
Коэффициент давления -в этих точках принимает
значение, определяемое ino формуле (3-17).
Из предыдущего следует, что значение М зависит
не только от формы тела, но и от ориентировки тела
в потоке, т. е. от угла атаки.
При сверхзвуковых скоростях набегающего потока
сопротивление давления в основном определяется
волновым сопротивлением. Расположение и интенсивность
скачков и волн разрежения зависят от формы
обтекаемого тела, расположения тела в потоке и числа Моо.
Рассмотрим обтекание ромбовидного профиля при
Моо>1 (рис. 5-41). Зная геометрические размеры
профиля, используя формулы, приведенные в гл. 3 и 4,
можно расчетным путем .построить картину обтекания
такого профиля: найти углы и интенсивность головного
и хвостового скачков ABC и А\ВХСХ и волн разрежения
и,ич
о,оз\
ом
щ
\с*
ш
286
DEF и D\EXF\. Тогда мы определим давления в
областях // и ///. Найдя проекцию результирующей силы
давления на направление невозмущенного потока,
убеждаемся в существовании силы сопротивления,
обусловленной изменением давлений в скачках и волнах
разрежения. Заметим, что в отличие от дозвуковых
скоростей эту часть сопротивления давления при околозву-
Рис. 5-41. Спектр обтекания ромбовидного^профиля потоком
сверхзвуковых скоростей.
ковых и сверхзвуковых скоростях (волновое
сопротивление) выделяют в самостоятельную категорию.
Коэффициент профильного сопротивления 'представляется
в такой форме:
с =с пА-с
X JCTp I X В >
где схъ — коэффициент волнового сопротивления тела.
5-14. СОПРОТИВЛЕНИЕ ПЛОХО ОБТЕКАЕМЫХ ТЕЛ
В ПОТОКЕ ГАЗА
Плохо обтекаемыми будем называть такие тела,
которые в любом положении обтекаются с отрывом потока.
Для плохо обтекаемых тел, даже при малых скоростях,
значительную часть полного сопротивления составляет
сопротивление давления.
Специфические особенности спектра отрывного
обтекания можно проследить на примере шара или цилиндра.
На рис. 5-42 приведены кривые распределения
давлений по обводу шара при М = 0 (несжимаемая жидкость)
287
для различных чисел Рейнольдса. На участке от передней
критической ' точки до точки М давление вдоль обвода
шара резко снижается (конфузорная область), а затем за
миделевым сечением наблюдается рост давления (диффу-
зорная область). В некоторой точке 5 происходит отрыв
слоя; за линией отрыва давление меняется слабо.
Рис. 5-42. Распределение давлений по обводу шара при
разных числах Рейнольдса.
/-Re=157200; ^=0,471; // — Re=251<300, ^=0,313; ///—Re=
=298 500; ^=0,151; IV — Re=»424 500; ^—0,143.
При рассматриваемых скоростях (М^^ 0) значительное
влияние на распределение давлений оказывает число
Рейнольдса. Можно отметить, что с ростом Re^ давление в
точке М уменьшается, а в точке 5 — растет. Характерно
также смещение точек М и 5 по потоку.
Многочисленные опыты подтверждают существование
зависимости коэффициента сопротивления шара (цилиндра)
288
от числа Re^. На рис. 5-43 приведены соответствующие
графики. Здесь могут быть отмечены пять характерных
областей изменения сх. При Reoo< 2-103 —- 3-103 сх
уменьшается1 с ростом Re^ и особенно интенсивно в зоне
малых Reoo<100. На участке Reoo = 2-103--2.104
коэффициент сопротивления несколько возрастает (область ///),
а затем в интервале Reoo = 2-104-r-2-105 сх сохраняется
постоянным (область /V). Вслед за тем в узком
диапазоне изменений Reoo=2-105-т-4-105(4,5-105)с^ кризисным
образом уменьшается (область V). При Reoo>4,5-105
отмечается некоторое увеличение сх, после чего сх
принимает практически постоянное значение.
Опыты показывают, что переход из одной области в
другую сопровождается изменением спектра обтекания
шара (рис. 5-43). При малых Re^^lOO основную роль
играет сопротивление трения, причем резкое уменьшение
сх с ростом числа Рейнольдса в этой области
подтверждает отсутствие «квадратичной" зависимости между
силой сопротивления и скоростью с^. Образование отрыва в
кормовой части вызывает далее медленное падение сх с
ростом Re^. Область /// характеризуется слабым
возрастанием сх, что объясняется интенсификацией вихревого
движения в кормовой, области. В этой области
сопротивление трения в пограничном слое невелико. Основную роль
играет сопротивление давления.
Здесь, как и в области IV, на линии отрыва слой
ламинарный. Как известно, положение точки отрыва
ламинарного слоя не зависит от числа Рейнольдса.
Следовательно, при некотором значении Re^^ 108 -г-2-104 линия
отрыва занимает фиксированное положение на поверхности
шара (цилиндра) и дальнейшее возрастание Re^ не
приводит к изменению положения линии 5.
Область IVу соответствующую постоянному значению
сх, называют областью „автомодельное™* по числу
Рейнольдса. Однако и в этом интервале изменений Re^.
происходит перестройка спектра обтекания шара. Отрываю*
1 Верхняя граница Re < 3-103 соответствует шару, а нижняя
Re < 2 • 103 — цилиндру.
19 М. Е. Дейч 289
V2 * V
Рис. 5-43. Схемы обтекания и коэффициенты сопротивления шара и цилиндра в зависимости от числа Рейнольдса.
1 — для цилиндра; 2— для шара.
щийся в точке S ламинарный слой турбулизируется в
некоторой точке Т на границе зоны отрыва. С ростом числа
Re линия перехода Т перемещается в направлении к
линии отрыва S, так как при этом увеличивается
турбулентность в кормовой вихревой области.
При достижении некоторого критического числа
Рейнольд са ReK ^ 3-105-н4-105 точка перехода совпадает
с точкой отрыва. Следовательно, в точке отрыва слой —
X
з
2
1
О Г 2 ~" " 3 4
Рис. 5-44. Изменение критического числа
Рейнольдса ReKp в зависимости от степени
турбулентности EQ для М =^ 0.
турбулентный, обладающий большей сопротивляемостью
отрыву. В результате изменения режима движения в слое
вблизи отрыва точка S резко перемещается по потоку и
обтекание шара улучшается кризисным образом:
коэффициент сопротивления уменьшается в 2 — 4 раза (область V
на рис. 5-43). Уменьшение сх происходит за счет
снижения сопротивления давления, так как сопротивление
трения в турбулентном слое больше, чем в ламинарном. Это
явление называют „кризисом сопротивления" плохо
обтекаемых тел.
Положение линии перехода Т при Re^^ ReKp зависит
от степени турбулентности набегающего потока. Поэтому
и критическое число Re существенно меняется в
зависимости от Е0. Соответствующая экспериментальная кривая
приведена на рис. 5-44. При увеличении турбулентности
до Е0 ж 3 % критическое число Re уменьшается почти
в 3,5 раза.
19* 291
Кривая на рис. 5-44 может быть использована для
определения степени турбулентности набегающего потока
по критическому числу Re . При этом критическим
числом Re считают значение Re^, соответствующее
коэффициенту сопротивления шара £^ = 0,3 (рис. 5-43).
Следует отметить, что при Re >> Re (область VI на
рис. 5-43) коэффициент сопротивления вначале несколько
возрастает, а затем практически не зависит от Re: эта зона
является второй областью автомодельности, соответствующей
фиксированному положению точки отрыва турбулентного слоя.
Таким образом, на поверхности шара имеются три
характерные точки: минимума давления (М), отрыва (S) и
перехода (71), в которой происходит турбулизация слоя.
Взаимное расположение точек М, S и Г оказывает
решающее влияние на механизм обтекания и сопротивление шара
при малых скоростях.
Изучение влияния сжимаемости на расположение
указанных точек позволяет оценить изменение спектра
обтекания и сопротивления шара при переходе к большим
числам JV1
00*
Опыты показывают, что по мере увеличения числа М^
картина распределения давлений по обводу шара меняется
(рис. 5-45). Важным является тот факт, что при М >
>Моо>0,3 с увеличением М^ давление в кормовой
области за шаром снижается.
При М^^М на поверхности шара образуются
кольцевые зоны сверхзвуковых скоростей, которые замыкаются
скачками уплотнения. Соответствующие спектры
обтекания показаны на рис. 5-46. Влияние числа Re^ на этих
режимах снижается, однако остается значительным. Только
при М^Х)^ влияния Re^ практически не наблюдается.
В интервале М^^М давление в кормовой области
продолжает снижаться и достигает минимальных значений при
1,1 >М^ 0,8 (рис. 5-45).
Для больших дозвуковых скоростей характерны резкое
сокращение диффузорной области и уменьшение
градиентов давления в ней. При этих скоростях отрыв происходит
в зоне расположения местных скачков уплотнения
(рис. 5-46) независимо от того, каков режим течения в
пограничном слое — ламинарный или турбулентный.
292
-0,2
-ОЛ
~0t6\
-0,8
-uo
-кг
40\\ 6Д° 8Д° ЮЦ° 120° //40° 160° W0K
Рис. 545. Распределение давлений по обводу шара при различных
числах М^.
293
Рис. 5-46. Спектры обтекания шара при околозвуковых
и сверхзвуковых скоростях.
= 3.0.
294
При больших сверхзвуковых скоростях (М^ > 1,5)
кривые давления имеют иной характер: давление в точках
минимума продолжает увеличиваться, диффузорный участок
смещается по потоку. Давление в кормовой части шара
с ростом сверхзвуковой скорости увеличивается.
Графики давлений можно использовать дл
ориентировочного определения положения характерных линий на по-
грав _
0.2 0.4 06 0,8 /.О /}2 .1,4 1,6 1,8 2,0 2,2 2,4 2,6 2,8 .3,0
Рис. 5-47. Изменения положения линий минимума давления и отрыва
в зависимости от числа М^ для шара. Изменение давления в
кормовой части шара в зависимости от М^ (опыты автора).
верхности шара. Соответствующие кривые 6Ж и §s
приведены на рис. 5-47. Здесь можно видеть, что в диапазоне
скоростей М =0,3-г- 1,1 имеет место значительное
перемещение линии отрыва, причем независимо от характера
обтекания шара при ^№^ = 0,2 значения 6Ж и 85
уменьшаются, т. е. линия отрыва перемещается против потока
и обтекание шара ухудшается.
Следовательно, как для Re^^Re^, так и для Re^^*
> ReKp влияние сжимаемости при М^ < 1 оказывается
качественно одинаковым. С ростом М^ обтекание шара
приближается к тем условиям, которые отвечают отрыву
ламинарного слоя. В области сверхзвуковых скоростей угол
отрыва б5 возрастает с ростом числа М^ и обтекание
шара улучшается (рис. 5-47). Интенсивность смещения линии
295
отрыва снижается при Моо>2. В таких режимах перед
шаром образуется криволинейный скачок уплотнения
(рис. 5-46); в точках отрыва возникают слабые конические
скачки.
Таким образом, в дозвуковой области с ростом числа
М^ линия отрыва перемещается к передней критической
точке и при 1^ = 0,95-н 1,0 занимает наиболее близкое
к ней положение, а при сверхзвуковых скоростях отрыв
смещается в направлении к кормовой части. Отсюда можно
заключить, что при дозвуковых скоростях с увеличением
Mw обтекаемость шара ухудшается, а при сверхзвуковых
скоростях — улучшается.
Изложенное показывает, что при скоростях М^^М,
положение линий отрыва на шаре существенно зависит от
режима течения в пограничном слое и, следовательно, от
Re. Влияние сжимаемости здесь сказывается в том, что
с увеличением М^ возрастает критическое число ReKp
(рис. 5-47), Это означает, что турбулизация слоя в точке
отрыва происходит при больших числах Re и линия
перехода Т медленнее сближается с линией отрыва 5.
Другими словами, сжимаемость затягивает переход ламинарного
режима в турбулентный.
При 1 >> М >> М в исследованном диапазоне чисел
Re^ кризисное изменение картины обтекания, связанное с
турбулизацией слоя, вообще не обнаруживается и вне
зависимости от Re^ обтекаемость шара резко ухудшается.
Отсюда можно заключить, что при околозвуковых
скоростях скачки приводят к отрыву ламинарного слоя примерно
в одном и том же сечении.
Влияние числа Мто на коэффициент сопротивления шара
сх можно оценить по кривым на рис. 5-48. С увеличением
М <М сх возрастает, причем при докризисном обтекании
(Re^^Re^, кривая /) коэффициенты сопротивления
возрастают менее интенсивно, чем при закризисном (Re^^*
> ReKp, кривая 2), При М^ > М# влияние Re^ на сх
ослабевает и для Л1^0,8 кривые сх для различных Re^
практически совпадают.
Полный коэффициент сопротивления шара можно
представить в виде: ,
с — с •■ с
х хт I х кор>
296
где с —коэффициент головного • сопротивления;
с —коэффициент кормового (донного) сопротивления.
На рис. 5-48 дополнительно представлены кривые
схкор — сх{Жоо). Сопоставление кривых сх и схкор
показывает, что коэффициент головного сопротивление шара сх =
Ю
0Ч3\
о,в\
oj\
0,6
0,5\
оА
0,3
о А
о J
о о.г ол о,б as /,o h2 /A /,o t%8 2,0 г,г гчь г,о 2.8 з,о з,2 з,4
Рис. 5-48. Коэффициенты сопротивления шара в зависимости от числа
Mqq по данным испытаний в аэродинамической трубе и в натурных
условиях.
кг
1 1\
\~~*
Г ?
хГ''
I i
У
• J
\ \°/а/
Ж
1
°/
/
//
//s
Г
о
'Ss&st
^2
1.
/
' Л-
г о
^х
~Схкор'
1
ы
~_—
,1 — 1
р^
\/
+
U <■».
> Испытании о труоаз:
\ Натурные испытания
- По фо/
^А^1
1мулеЗй\
а
-ь 1
1 1
пера
fc~
м\
= сх — сх при дозвуковых скоростях возрастает
незначительно. Следовательно, „волновой кризис" сопротивления
шара в зоне околозвуковых скоростей, выражающийся
в весьма резком увеличении сх (от 0,15 — 0,35 до 0,9 —
— 0,95), происходит главным образом за счет роста
кормового сопротивления.
При сверхзвуковых скоростях сх продолжает
достигает максимального значения при М^'^Ьб.
мум кривой сх в этой зоне весьма пологий. При
схкор интенсивно уменьшается.
На рис. 5-48 приведены также результаты других
исследований. Характерно, что при околозвуковых и сверх-
расти и
Макси-
297
звуковых скоростях все опытные данные хорошо
совпадают1.
При М > 1 сопротивление плохо обтекаемого тела
практически не зависит от Re.
5-15. ДВИЖЕНИЕ ГАЗА В КРИВОЛИНЕЙНЫХ КАНАЛАХ
При движении газа в криволинейных каналах
возникают специфические явления. Действительно,
рассмотрим течение газа по каналу постоянного сечения, в
котором поток совершает поворот на 90° (рис. 5-49).
Скорости движения в канале малы по сравнению со
скоростью звука, так что влиянием сжимаемости можно
пренебречь. В связи с тем, что частицы газа движутся
по криволинейным траекториям, давление на внешней
(вогнутой) и внутренней (выпуклой) стенках канала
оказывается разным и различно меняется в
направлении движения. Так как частицы ядра потока под
действием центробежных сил оттесняются к внешней стенке,
то давление вдоль АВ возрастает по сравнению с
давлением входящего потока ри а вдоль A{Bi — уменьшается
(рис. 5-49,а). За поворотом давление на вогнутой стенке
снижается, а на выпуклой возрастает; на значительном
расстоянии за поворотом давления выравниваются.
Таким образом, -в сечениях криволинейного канала
устанавливается неравномерное распределение
скоростей и давлений; здесь 'возникает поперечный градиент
давления. Частицы жидкости, движущиеся в
пограничном слое вдоль плоских стенок, находятся под
воздействием разности давлений и, обладая малой скоростью
в направлении основного движения, перетекают к
внутренней стенке, испытывая большее отклонение, чем
частицы, более удаленные от стенок. По условию
сплошности в ядре потока должны возникать компенсирующие
течения, направленные к внешней стенке. В результате
1 На рис. 5-48 нанесена также кривая сх, построенная по
формуле Эйлера:
Любопытно отметить, что формула Эйлера, полученная около
200 лет назад, дает близкие к опытным значения сх при M^^l.
298
в канале образуется вторичное вихревое движение,
которое налагается на основной поток. Линии тока
вторичного течения являются замкнутыми в поперечном
сечении канала (рис. 5-49,6).
. Вторичное течение состоит из двух потоков, которые
около плоских стенок направлены к (выпуклой поверх-
Рис. 5-49. Схема потока в криволинейных каналах с различной формой
поперечного сечения.
ности, а в центре канала—к вогнутой .поверхности
канала. Вторичные потоки имеют симметрично-винтовой
характер. Линии тока вторичного течения на плоских
стенках показаны пунктиром (рис. 5-49,а).
Вдоль участка вогнутой стенки АВ и вдоль участка
выпуклой стенки BiDx течение диффузорное. В
зависимости от формы криволинейного канала здесь могут
возникнуть отрывы (зоны / и // на рис. 5-49,а). Отрыв
на вогнутой стенке АВ может быть локализован
последующим конфузорным течением на участке BD. Отрыв
299
на участке BXDX имеет более значительную
протяженность по потоку.
Структура вторичного течения в криволинейном
канале и вызываемая им дополнительная потеря
энергии существенно зависят от геометрической формы
канала >и режима потока (чисел Re и М).
^Опыты .показывают, что структура вторичных
течений меняется при изменении формы сечения канала
Рис. 5-50 Влияние радиусов кривизны вогнутой и выпуклой стенок
ния проходных сечений канала с углом поворота
(рис. 5-49,6). Наибольшие отличия от рассмотренной
выше схемы обнаруживаются в каналах с
прямоугольной формой сечения (/>аи/<а). В случае />а
вторичное движение газа по вогнутой и выпуклой стенкам
затруднено, так 'как частицы должны проделать
длинный путь, на протяжении которого сказывается трение.
Такое перетекание оказывается возможным только
в пограничном слое вдоль плоских стенок; оно
начинается на вогнутой поверхности (у плоских стенок)
300
и продолжается на .плоских стенках в направлении
к выпуклой поверхности, где пограничный слой,
участвующий в периферийном движении, сливается с
пограничным слоем основного потока и интенсивно набухает.
Вместе с тем благодаря движению в пограничном слое
от вогнутой поверхности к .выпуклой в ядре потока
у плоских стенок образуются компенсирующие течения,
направленные к вогнутой стенке. Эти течения совместно
криволинейного канала с углом поворота 90° (а) и~влияние соотноше-
180° на потери по данным X. Нипперта (l/at = 4).
с пограничным слоем, движущимся вдоль плоских
стенок в противоположном направлении, образуют
замкнутые вихревые абласти, охватывающие не все сечение
потока, а только часть его вблизи выпуклой и плоских
стенок. В рассматриваемом канале прямоугольного
сечения вторичное течение вырождается в лару вихрей,
вращающихся в противоположных направлениях.
На образование вторичного течения затрачивается
часть кинетической энергии потока. Потери энергии,
301
обусловленные кривизной канала, можно рассматривать
как сумму: а) дополнительных потерь на трение
вследствие вторичного движения; б) вихревых потерь в зонах
отрыва; в) шотерь, вызванные вихревыми
компенсирующими течениями. Наибольшую часть потерь составляют
вихревые потери вследствие отрыва.
На рис. 5-50,а приведены данные X. Нипперта,
характеризующие влияние некоторых геометрических
характеристик канала на потери. Здесь коэффициент Спов
определен как разность полных энергий на входе и выходе,
отнесенная к скоростному напору на входе в канал.
Как видно из рис. 5-50,а Спов существенно зависит
от внутреннего г. и наружного га радиусов кривизны и
геометрической конфузорности канала, определяемой
отношением # = -*-. Еслиа>1, то канал конфузорный,
а если а < 1, то канал диффузорный. При заданном
отношении а изменение г. или га приводит к изменению отно-
шения #т=—и, следовательно, площади сечения вдоль
оси потока. Точки минимума кривых Спов соответствуют
различным г =—- в зависимости от г. =— . Оптимальные
U U-l CI}
значения г. несколько меньше г . При данном г.
увеличение ^а>^аопт приводит к особенно резкому возрастанию
потерь. В этом случае криволинейный канал приобретает
суживающе-расширяющуюся форму; скорости потока на
повороте и потери возрастают.
Кривые на рис. 5-50,а отражают также влияние
параметра а. В диффузорных каналах (а<1) потери выше,
чем в каналах постоянного сечения (а=1) и конфузорных
Ja>l).
Во всем диапазоне значений г. и га огибающая кривых
^пов (г*> О лежит выше для диффузорного канала (а —
= 0,787). Промежуточное положение занимает канал
постоянного сечения (а=1).
Аналогичное влияние геометрического параметра а
обнаруживается и для канала с углом поворота 180°
(рис. 5-50,6). Минимум потерь в таких каналах отвечает
302
а) б)
Рис. 5-51. Оптимальные соотношения геометрических параметров криволинейного канала с углом
поворота 90°, обеспечивающего минимальные потери от вторичных течений, по X. Нипперту.
2,25\
значениям ат > 1, причем оптимальное поджатие в
выходной части канала уменьшается с переходом к диффузор-
ным каналам (а<М).
На рис. 5-51 даны значения радиусов кривизны и
соотношения характерных сечений канала, обеспечивающие
минимальную интенсивность вторичных течений в
криволинейном канале. Из графиков следует, что в диффузорных
и слабо конфузорных каналах
целесообразно среднее сечение
канала ат выполнять
увеличенным (ат> 1), а затем
обеспечить конфузорное течение
соответствующим поджатием
( — > 1). В этом случае
уменьшается разность давлений
между вогнутой и выпуклой
поверхностями в сечениях, где
кривизна канала максимальна,
и, следовательно, снижается
интенсивность вторичных
течений. Кроме того, поджатие
выходной части канала
сокращает область отрыва на
выпуклой стенке Л1В1 (рис.
5-49,а), а в некоторых случаях
и предотвращает отрыв.
Опыты X. Нипперта показали, что
в зависимости от угла
поворота, радиусов кривизны вогнутой и выпуклой стенок
оптимальные соотношения величин ат и ах меняются.
Эти соотношения зависят также от геометрической
конфузорности канала, т. е. от а. Опыты показывают, что
с увеличением радиусов кривизны спинки и вогнутой
поверхности потери от вторичных течений уменьшаются.
Вместе_с тем (рис. 5-51,а) с увеличением радиуса
кривизны г. возрастает оптимальное значение ат при данных
угле поворота^потока и степени конфузорности (а).
Зависимость ат от а, соответствующая минимальным потерям
в криволинейном канале с углом поворота 180°, показана
на рис. 5-52.
0J5 /,0 Ш
5-52. Оптимальные
IJS
Рис. ь-Ъ2. иптимальные
значения ат в зависимости от
геометрической конфузорности
криволинейного канала ал по
данным X.
Нипперта. Угол
рота 180°
пово-
304
Следует также отметить влияние относительной вы-
/ -
соты канала — на оптимальное значение параметра а
Как видно из рис. 5-51,6, зависимость am=f (—) имеет
О 0J 0,2 0,3 0,4- 0,5 0,6 0,7 0,8 0,3
Рис. 5-53. Изменение коэффициентов потерь в криволинейных каналах
в зависимости от числа М2 на выходе (опыты В. И. Никитина).
максимум, положение которого определяется общей кон-
фузорностью канала а.
Влияние двух важнейших режимных параметров —
чисел Re и М — на потери и структуру потока в
криволинейных каналах можно оценить по кривым на рис. 5-53.
С увеличением Re потери в канале уменьшаются. Турбули-
зация слоя вблизи отрыва приводит к смещению линии
отрыва по потоку, что и вызывает резкое снижение потерь.
Влияние сжимаемости при докритических скоростях
сказывается в том, что интенсивность вторичных течений
снижается. Анализ кривых распределения давлений
(рис. 5-54) показывает, что с ростом М уменьшаются
поперечные градиенты давления в канале, так как
коэффициенты давления возрастают более интенсивно на
выпуклой поверхности, чем на вогнутой. При М>М# на вы-
20 М. Е. Дейч
305
Рис. 5-54. Распределение давлений по контуру криволинейного^ канала.
конфузорный канал, 77=2,4; диф ^узорный канал, /2=1,875.
пуклой стенке возникают местные зоны сверхзвуковых
скоростей и замыкающие их скачки. Отрыв потока,
вызываемый скачками, приводит к росту коэффициентов потерь
(рис. 5-53). При сверхзвуковых скоростях отмечается
снижение потерь от вторичных течений.
5-16. ВРАЩАЮЩИЕСЯ ПОТОКИ ВЯЗКОГО ГАЗА
В §1 5-1 отмечалось, что энтальпия торможения в потоке
вязкого газа с неравномерным распределением скоростей является
переменной величиной и условие /0=const не может служить
характеристикой течения и интегралом уравнения энергии
адиабатического потока.
Наиболее отчетливо этот эффект обнаруживается во
вращающихся потоках газа и, в частности, в вихревой трубе Ранка
(рис. 5-55).
306
to
о
ШЕ I j£ PooJoo
граи
20
Ьо
60
в\
700 7*0
<z
Тоо~~~то
У^У^
У
У
V
У У
K^yr
7,
и
\У\ \/
У /
^'''
Х^\>У
<УЪ
N
г/г0\
200
150.
то
150
со
о
^1
Z7,2 0,U 0,6
б)
0,8 /,0
ОМ
0,6
nh
и*'
0,2
Ро/Роо
; р/Роо
Ро/Роо^
_,—":
~*£^*\*'
п
ш
J&s^S
Jv
>£г ^~N
^^
"*"-vT^*^*5"
P/Poo
\""^J
^^r*""?
r/ro\
0 0,2 «4 0,£ 0,<? /,0
Рис. 5-55. Принципиальная схема вихревой трубы (а)
и распределение параметров по радиусу в
различных сечениях (б и в).
В вихревую трубу газ подводится соплами тангенциально под
давлением (сечение 00 на рис. 5-55,ai) и образует внутри трубы
вращающийся поток. С одной стороны (в сечении ЛЛ) поток
выходит через отверстие, расположенное на оси трубы. На
противоположном конце трубы (выходное отверстие выполняется в виде
кольцевой щели, расположенной у периферии (сечение ББ). Как
показывает опыт, газ, вытекающий через центральное отверстие (в
сечении АД), имеет значительно более низкую температуру торможения,
чем на периферии в сечении ББ (рис. 5-55,6). Так, например, по
данным И. Гаршетта и Б. Эккер та максимальная разность
температур торможения соответствует сечению /—/ и достигает величины
7\ю—Го = 75ч-800 С. По мере удаления от сечения 00 профиль
температур торможения выравнивается и в сечени,и /// указанная
разность достигает только 40° С. Характерно, что температура
торможения на периферии Г0о меняется вдоль трубы менее
интенсивно, чем температура на оси трубы, резко возрастающая к
сечению ББ. Наиболее низкая температура торможения на оси
соответствует сечению /—/. Следовательно, в такой трубе
происходит температурное разделение газового потока, причем через
центральное отверстие выходит сильно охлажденный газ.
Профили скоростей в различных сечениях показывают
(рис. 5-55,6), что в трубе происходит интенсивная перестройка
потока: скорости к периферии интенсивно снижаются к сечению ///—///,
а в ядре на оси несколько возрастают.
Неравномерное распределение скоростей по радиусу объясняет
интенсивную диссипацию механической энергии, внутреннее
тепловыделение и неравномерное распределение температуры торможения.
О весьма интенсивной диссипации энергии .можно судить на
основании опытных графиков распределения давления торможения и
статического давления (рис. 5-55,el).
■Приближенное теоретическое решение рассматриваемой задачи
можно получить для простейшего случая одномерного кругового
движения газа. При этом полагаем, что поле осевых составляющих
скорости в трубе равномерно. Поверхности тока такого
вращательного движения газа будут цилиндрическими: радиальные
составляющие скорости и их производные обращаются в нуль.
Пренебрегая влиянием» массовых сил и считая движение установившимся,
можно воспользоваться уравнением сохранения энергии (5-3) в
цилиндрической системе координат:
d f Г d ( i . с\\ cl
l[FYrldi\pr + Y)~—
Здесь св — окружная (тангенциальная) составляющая скорости.
Принимая, кроме того, р. = const и Pr — const, уравнение (5-79)
можно проинтегрировать. Общий интеграл (5-79) для
рассматриваемого случая получен Л А Вулисом в таком виде:
i + Рг -у = Pr J с\ — + const. (5-80)
> = 0
(5-79)
308
Для получения искомой связи в конечном виде необходимо знать
закон изменения cQ(r). Целесообразно рассмотреть два предельных
случая: а) в предположении циркуляционного (квазипотенциального)
течения, распределение скоростей в котором подчиняется условию
с г = const, (§ 1-2), и б) для линейного распределения скоростей
cJr = const, соответствующего вихревому ядру (квазитвердое
течение) (§ 1-2).
В первом случае после подстановки в (5-80)
2 2
2 Ч го
св — г2 '
где с9 — тангенциальная составляющая скорости в периферийном
0 сечении, вне пограничного слоя;
г<> — радиус трубы,
можно получить:
с2 с2
i. = * + -f = (l-2Pr)-t. + const, (5-81)
г
где г=— — относительный радиус;
i0 — текущее значение энтальпии торможения.
Постоянную в правой части находим, записывая (5-81) для
сечения г = г0, г = 1. Тогда
const = /00 — (1 — 2Pr) y •
Здесь /00 — энтальпия торможения в сечении г = 1 (в
периферийном сечении трубы).
После подстановки значения постоянной в (5-81) окончательно
находим
is=l_(I_2Pr)(l-4t)-^-. (5-82)
Так как смакс = V2iQ0 — максимальная скорость в
периферийном сечении, то
с2о c2cos2*0
Yi 12 = 6ocosf ao»
v °макс
где а0 — угол между вектором скорости с0 и плоскостью вращения
газа.
Следовательно,
£=l_(l_2Pr)(l-^-)&os««..
(5-82а)
Из уравнения (5-82а) следует, что при условии c^r = const
энтальпия торможения возрастает с приближением к стенкам трубы,
309
если число Рг>0,5. При Рг =0,5 энтальпия торможения сохраняется
постоянной по радиусу, а при Рг <^ 0,5 — возрастает к оси трубы.
Для закрутки потока но закону —- == const из (5-80) нетрудно
получить следующую формулу.
-it = 1 __ (1 - ГТ) JiL = ! _ (1 _72) § C0S24 (5_83)
too -^оо
В этом случае вне зависимости от значения числа Прандтля
энтальпия торможения уменьшается к оси трубы.
Очевидно, что если для двух различных законов распределения
скоростей по радиусу энтальпия торможения уменьшается к оси
трубы, то и для любого промежуточного закона будет иметь место
аналогичное изменение i0*.
Представляет интерес оценить изменение энтальпии торможения
по радиусу в долях кинетической энергии — ш
Обозначим:
•т-г ^ voo 'о) *оо *о
Д*п= о ; ;—'
где i1Q — энтальпия движущегося газа в сечении г = г0.
Использовав формулы (5-82а) и (5-83), получим для двух
различных законов распределения скоростей:
AT0=(l-2Pr)(l-i)cos2a0;
1Г0 =(1 — 72)cos2a0.
Л. А. Вулисом рассмотрен более общий случай распределения
скоростей, отвечающий уравнению
■~ч ('"+-=)■
При этом интеграл (5-80) после обычных преобразований
принимает вид:
= 1+Рг[(т^г2)+2(21п"
$ cos2 cc0. (5-84)
— *о
* Формула (5-82а) в точке г=0 дает -т~" = — °°- Этот резуль-
*00
тат легко объяснить, если вспомнить, что на оси циркуляционного
течения скорость принимает бесконечное значение (cQr = const). Здесь
расположен точечный вихрь, распределение скоростей в котором —
линейное.
3.10
Отсюда следует, что при таком круговом движении при Рг ^> 0
энтальпия торможения меняется вдоль радиуса.
Для плоскопараллельного течения с неравномерным
распределением скоростей энтальпия торможения определяется формулой (5-2).
Распределение статической температуры по сечению
вращающегося потока газа устанавливается с помощью уравнения энергии
(5-80). Рассматривая частные случаи закрутки по законам су = const
сВ
и — — const и вспоминая, что
9
'о = * + у .
из формул (5-82а) и (5-83) находим:
v^k=l~[l+2(^-1) рфо-2ао
(5-85)
для cQr = const
и
i T — су
г ^^ = 1 _(l_ri)«^ cos2 «, (5-86)
100 1 00
для — = const
Изменение статического давления по радиусу можно найти,
пользуясь уравнениями движения в цилиндрических координатах
С учетом основных допущений (радиальные составляющие скорости
и продольные градиенты давления малы, поле осевых скоростей
равномерно) первое уравнение системы (1-17) приобретает
следующий вид
±9--. (5-87
р dr r v
Смысл уравнения (5-87) состоит в том, что оно выражает
условие радиального равновесия частицы газа, совершающей
вращательное движение.
Учитывая, что
Р _ *Р
9~~ gRT (A —1)/'
представим (5-87) в новой форме:
р k-T i r ' (5"88)
Подставив сюда / из формул (5-85) и (5-86), после
интегрирования можно получить приближенные зависимости р(г).
Полученные выше формулы изменения параметров по сечению
вихревой трубы могут быть использованы, если известна скорость
на периферии трубы cQ . Для расчета потока в различных
сечениях по длине трубы необходимо располагать опытными зависимостями
Сд {х) и а0 (х) (х — расстояние по оси трубы).
311
В соответствии с изменением св по длине трубы меняется и
распределение всех параметров по радиусу1. В некоторых сечениях
происходит выравнивание поля статических давлений и температур и
температур торможения, причем эти сечения (/? = const; Т = const
и TQ = const) не являются совпадающими.
М. Г. Дубинским теоретически доказано, что в сечении с
постоянной статической температурой по радиусу достигается
максимум энтропии вращающегося потока газа. Следовательно,
закрученный поток в вихревой трубе стремится к равновесному состоянию,
которое и достигается в сечении с Г= const.
Вьирашшвание потека в вихревой трубе иллюстрируется
графиками на рис. 5-55.
Таким образам, в вихревой трубе обнаруживается эффект
температурного .разделения газа, который может быть .использован для
целей охлаждения различных тел и, в частности, в холодильных
установках кратковременного действия и пр. Вместе с тем этот
эффект заслуживает дальнейшего подробного теоретического и
экспериментального изучения, так как он проявляется во всех
случаях, когда возникает вращательное движение газа (ступень турбо-
машины, вихревой насос и др.).
Необходимо (подчеркнуть, что неравномерное распределение
температур торможения в адиабатическом потоке вязкого газа,
связанное с неравномерным распределением скоростей, обнаруживается
и при внешнем обтекании тел (в попранич'ном слое и в кормовом
следе). Во всех случаях, когда выделяющаяся теплота трения2 не
равна количеству тепла, отводимому тепло-проводностью, имеет
место неравномерное распределение полной энергии.
Значительный интерес представляет движение закрученного
потока в цилиндрической кольцевой трубе3. В этом случае исходное
уравнение энергии (5-79) необходимо проинтегрировать для
кольцевого вращающегося потока.
ГЛАВА ШЕСТАЯ
ИСТЕЧЕНИЕ ГАЗА ИЗ СУЖИВАЮЩИХСЯ СОПЕЛ
И ОТВЕРСТИЙ. СОПЛА ЛАВАЛЯ
6-1. СУЖИВАЮЩИЕСЯ СОПЛА
Суживающиеся сопла широко применяются для
создания потоков дозвуковых и околозвуковых скоростей.
Гидравлический расчет таких сопел весьма прост и сво-
1 Напомним, что весь расчет выполнен без учета пограничного
слоя: скорость с$ берется на внешней границе слоя.
2 Выделение теплоты трения происходит только в тех областях
потока, где устанавливается неравномерное распределение скоростей,
связанное с действием вязкости.
3 Такая задача возникает при исследовании закрученного потока
в ступени турбомашины (турбины или компрессора).
312
дится к определению размеров выходного сечения пс
заданному расходу газа и заданной скорости
истечения. При расчете считают, что течение газа в сопле
адиабатическое, так как за короткое время протекания
газовых частиц через сопло теплообмен с окружающей
средой практически не устанавливается. Следовательно,
для расчета сопла могут быть использованы уравнения
адиабатического течения. Если пренебречь влиянием
трения, то течение в сопле можно считать изоэнтроличе-
ским. Как показывает опыт, потери на трение в
коротких соплах невелики.
Обозначив, как и раньше, параметры полного
торможения ро, Т0 и р0 (в рассматриваемом случае — это
параметры газа в резервуаре), а параметры среды за
соплом ра, Ta и ра, можем определить скорость в
выходном сечении F сопла по уравнению (2-10):
Ра
где еа = отношение давления за соплом к давлению
р" в резервуаре;
По уравнению неразрывности можно найти весовой
расход газа;
G = gFpc = F-{c = ~ .
Подставив сюда значение скорости из формулы (6-1),
получим:
G^fY^P^&V'^:. (6-2)
Формула (6-2) дает расход газа в зависимости от
давления и плотности газа в резервуаре и давления среды.
Эта формула справедлива в предположении равномерного
распределения скоростей в выходном сечении сопла F.
Расход газа G в зависимости от еа меняется так же, как
приведенный расход q.
313
Действительно, так как G = gFqp*a„ то после
подстановки значений р, и а получаем:
Gs=
k+ l
k-\
V k + \
+ 1
РоЧьЯ--
JL
^awo-^r- <M)
Из сопоставления уравнений (6-2) и (6-3) следует:
цф/VS-^
1
(6-4)
Формулы (6-2) и (6-3) показывают, что
максимальное значение расхода отвечает критической
скорости Х = \ и соответственно критическому
отношению давлении еа = е*
Максимальный или критический расход получаем после
подстановки еа = е* в уравнение (6-2) или 1^=\ в
уравнение (6-3):
Формула (6-5) легко получается подстановкой Я = 1
в уравнение (2-38).
Для
£ = 1,4 G# = 2,145F//7oTo = 0,396F-^;
Для
£ = 1,3 G# = 2,09VaTo«0>305F-^=.
г Т 0
(6-6)
Уравнение расхода (6-2) показывает, что при заданном
выходном сечении сопла с уменьшением еа при еа > ё*# рас*
ход газа увеличивается, а при еа<е, согласно уравнению
(5-2) расход газа должен уменьшаться. Однако последнее
314
не соответствует действительности. Следовательно,
уравнение (6-2) неправильно описывает процесс истечения газа
при га<е#, если в него подставлять отношение давления
среды ра к давлению в резервуаре р0.
Рассмотрим истечение из суживающегося сопла при
фиксированных значениях давления и температуры в
резервуаре и переменном давлении среды ра.
До тех пор, пока давление среды больше критического
давления, подсчитанного по параметрам газа в резервуаре,
любые изменения ра распространяются и внутрь сопла.
В этом случае расход газа изменяется в соответствии
с формулой (6-2). Когда уменьшающееся давление ра
достигает критического значения /?*, в выходном сечении
суживающегося сопла устанавливается критическая скорость
и дальнейшие изменения давления окружающей среды не
могут проникнуть внутрь сопла. Следовательно,
фактический перепад давлений, создающий расход газа через сопло
при ра<Ср*, вне зависимости от величины давления
внешней среды будет критическим, а расход газа —
максимальным и постоянным. Отсюда следует, что формула (6-2)
при ра<Ср* только в этом случае дает правильные
значения расхода, если в нее подставляется критическое
давление, которое устанавливается в выходном сечении
суживающегося сопла, вне зависимости от величины ра. В
момент, когдя в выходном сечении достигаются критические
параметры, происходит своеобразное явление „запирания"
сопла1, в результате которого сопло и резервуар
оказываются изолированными от внешней среды.
Таким образом, при ед<е# в формулу (6-2) необходимо
подставлять е,. Расход газа при этом остается постоянным
и определяется по формуле (6-6).
На характер зависимости G от га оказывает влияние
распределение скоростей в выходном сечении сопла.
Полученные выше формулы хорошо подтверждаются
экспериментом только в том случае, когда профиль
сопла выполнен плавным. Плавно суживающаяся форма
сопла приближает распределение скоростей в выходном
сечении к равномерному. С этой целью стенки сопла
должны быть особым образом рассчитаны
Так же как и в случае истечения из трубы (гл. 5).
315
Профиль суживающегося сопла может быть
рассчитан по формуле Витошинского:
г»
у -i-<44
(6-7)
Величины, входящие в формулу (6-7), пояснены на. рис.
-f=L. Такой профиль пригоден для сопел, соеди-
6-1; V
няющих две трубы различных диаметров, когда поток при
Г
la
L.
г 1 г
■*—х—»-|
1 Н
Рис 6-1. К построению суживающегося
сопла
переходе в трубу меньшего диаметра должен быть
ускорен, а скорости в каждой точке выходного сечения сопла
должны быть одинаковыми. Сопла такого профиля
применяются для аэродинамических труб дозвуковых скоростей.
Опыт показывает, что в широком диапазоне скоростей
до Я = 0,90-г-0,95 поле скоростей за соплом достаточно
равномерно.
При подключении сопла непосредственно к резервуару
его профиль может быть очерчен дугами окружности.
Иногда профиль сопла очерчивается лемнискатами.
6-2. СУЖИВАЮЩЕЕСЯ СОПЛО ПРИ ПЕРЕМЕННОМ РЕЖИМЕ
При изменении параметров газа в резервуаре и за
соплом меняются расход газа и спектр вытекающей струи.
Пользуясь соотношениями (6-2) и (6-5), можно проанализи-
316
ровать изменение расхода при одновременном изменении
давления в резервуаре р0 и давления среды ра.
Обозначим:
/?0макс — максимальное давление в резервуаре;
G#MaKC — соответствующий этому давлению максимальный
критический расход;
/70, G* — текущие значения давления в резервуаре и
критического расхода.
На основании формулы (6-5) можно выразить
отношение критических расходов:
и* макс Pq макс У J о
Предполагая, что при изменении давления р0
температура газа в резервуаре Г0 сохраняется постоянной, получим:
°* D" . (6-9)
G* макс А)
макс
При TQ = const и неизменном давлении в резервуаре
изменение расхода в зависимости от давления за соплом ра
выражается уже известным над уравнением (6-2).
Легко заметить, что отношение расхода при данном
противодавлении к критическому расходу равно:
£=я. (6-ю)
Из выражения (6-9) следует:
л> г* Ро г* g
* * макс пп * макс 0*
^0 макс
Подставив G* в уравнение (6-10), получим:
yj* макс
:e0q-.
-C-^ry^vj/i-T1- «и»
317
Отсюда следует, что при изменении начального
давления все точки кривой приведенного расхода сдвигаются
пропорционально е0, т. е. пропорционально изменению
давления перед соплом.
Следовательно, отношение расхода G к максимальному
критическому расходу G*MaKC можно представить в зависи-
Рис. 6-2. Коническая поверхность приведенного расхода.
мости от еа и е0. Эта зависимость наглядно изображается
в трехосной системе координат (рис. 6-2), где по трем
осям отложены
Ра Ро
а Рп Рп м
/'о /^0 макс
В результате мы '.получаем некоторую коническую
поверхность, каждая точка которой определяет расход
газа через сужизающееся сопло в зависимости от
давлений перед соплом и за ним. Продолжением конической
поверхности ОАВ (рис. 6-2) служит плоский
треугольник ОЕВ, точки которого отвечают области критических
расходов газа.
Уравнение (6-11) можно представить и в двухосной
системе координат, построив кривые qM = f(ea) для
различных, но -постоянных значений е0- Тогда мы получаем
сетку относительных расходов газа, которая
представляет собой проекцию конической поверхности на
плоскость (#, е). Сетка расходов (рис. 6-3) весьма удобна
31$
для графического расчета сопла при изменениях
режима
Многочисленные опыты показали, что уравнение
поверхности расходов (6-11) можно упростить, заменяя
точную формулу приведенного расхода q приближенным
выражением. При докритичеоких перепадах давлений
Go-J,0 В
0}1 0,2 0,3 0,4 0,5 0,6 £0,7 £0,8 ^0,9^ 1,0
Рис 6-3 Сетка приведенных расходов газа.
(£a>BJ зависимость q = q(sa) может быть
.представлена дугой эллипса, уравнение -которого имеет вид:
*f£$+ *■ = !■ (6-12)
Во всем диапазоне дозвуковых скоростей эта формула
весьма точно аппроксимирует зависимость между q и ед.
Заменив в уравнении (6-12)
<7м
получим:
K~**Y
Обозначим:
Ра Рс
О
(6-13)
Ро макс Ро Р$ макс
1 А. В. Щегляев, Паровые турбины, Госэнергоиздат, 1947.
319
Тогда (6-13) преобразуется к виду:
(в' — s*e0)2 2 2 <а \Л\
(!_«.). +^м-£0> С6"14)
откуда
^м = Г=^-И(«о—«') К — «о (2в, — 1)]. (6-15)
*
При е0 = const уравнение (6-15) дает зависимость #м =
= <7(е'), так как для плавно суживающегося сопла е#
зависит только от физических свойств газа и является при
k = const величиной постоянной.
При изучении переменного режима сопла большой
практический интерес представляет характер изменения спектра
струи за соплом. Для докритических режимов истечения
изменения параметров на входе в сопло и выходе из него
слабо влияют на форму струи за соплом.
При сверхкритических перепадах давлений переход от
критической скорости в выходном сечении к сверхзвуковой
скорости происходит в свободной струе за соплом.
В этом случае кромка выходного сечения AAt (рис. 6-4,а)
является источником возмущения звукового потока. За
выходным сечением струя встречает давление среды ра (ра
меньше критического) и, следовательно, в точках А и Лх
(рис. 6-4,а) давление меняется от /?* до ра. В результате
от кромок сопла распространяются две волны разрежения:
АА1В1 и АХАВУ крайними границами которых являются
характеристики. Первая граница ААХ представляет собой
характеристику, угол которой ат] = -у ; вторая граница АВх
должна проходить в свободной струе под углом
aw2 = arcsinl/ ^ *а ; w = —• (6-16)
f l ~~еа
Между двумя этими границами располагаются
характеристики, углы которых меняются в пределах
320
В действительности, однако, все характеристики,
включая АВХ и А\В, имеют переменный угол наклона и,
следовательно, являются криволинейными, так как
волны разрежения из точек А и А\ в пределах струи
пересекаются. Пересечение волн происходит .в
треугольнике ААф. Кроме того, характеристики, попадая на
Рис. 6-4, Схемы спектров струи за сужк»
вающимся соплом при нерасчетных ре
Жимах (еа;> е,).
свободную границу АВ и АхВи отражаются от нее
с обратным знаком и волны разрежения переходят
в волны сжатия.
В результате пересечения в струе образуется клин
разрежения ADAU основание которого расположено
в выходном сечении сопла. В пределах клина
происходит значительное уменьшение давления, которое в этой
зоне становится ниже давления среды ра.
Так как отраженные от свободной границы волны
пересекаются в пределах второго клина DBBU то здесь
давление повышается до значения р в сечении ВВ{;
клин разрежения переходит в клин уплотнения.
Следовательно, точки В и Ви давление в которых меняется
от /?# до ра, также являются источниками волн
разрежения и спектр струи повторяется. Нетрудно заметить,
что отрезки АА\ и ВВХ равны. При пересечении клина
21 М. Е. Дейч
321
разрежения линии тока деформируются, отклоняясь от
оси сопла: сечения струи увеличиваются, и струя
«разбухает». В пределах отраженных волн поток
уплотняется и его сечения уменьшаются. Границы струи,
симметричные относительно оси, приобретают волнистую
форму.
На основании изложенного можно предвидеть
характер изменения давления по оси струи. В .пределах клина
разрежения давление падает от /?# до некоторого
значения Pd<Pcl, а в пределах клина уплотнение возрастает
до р ; дальше процесс повторяется. Давление в струе
меняется по некоторому периодическому закону,
близкому к синусоидальному. Соответствующим будет и
характер изменения скоростей вдоль оси струи. В
сечениях ААХ и ВВХ скорости критические. Между этими
сечениями скорости сверхкритические, причем в точке D
скорость будет максимальной. Следовательно, вся
область струи АВВХАХ является сверхзвуковой.
Спектры струи при рассматриваемых режимах
сохраняются качественно одинаковыми для плоских и осе-
симметричных сопел, однако в последнем случае волны
разрежения и уплотнения имеют коническую форму.
В осесимметричной струе поэтому образуются конусы
(а не клинья) разрежения и уплотнения. По мере
повышения давления в резервуаре или снижения давления
за соплом спектр течения постепенно перестраивается
(рис. 6-4,6). Углы волн АВХ и АХВ уменьшаются, высота
клиньев ADA\ и DBBX увеличивается и углы при
вершине клиньев (конусов) уменьшаются. Расстояния
между сечениями ААХ и ВВ{ увеличиваются.
Для осесимметричного сопла такая постепенная
перестройка происходит до определенных пределов. При
достижении некоторого отношения давлений ei картина
течения за соплом меняется кризисным образом.
Благодаря интенсивному уменьшению давления газа
в пределах конуса разрежения его образующие AD и
AiD переходят в криволинейные скачки AD и AXD\
(рис. 6-5,а), а в ядре струи образуется прямой
скачок DDX, замыкающий криволинейные скачки. Во
внешнем потоке возникают криволинейные скачки DB и DXBX.
Таким образом, в струе за соплом возникает мостооб-
разный скачок ADBBXDXAX. Скачки DB и DXBX выходят
322
за свободную границу .струи и отражаются от нее в виде
волн разрежения. Волны разрежения также замыкаются
криволинейными скачками.
При пересечении прямого скачка DDX скорости
центральной части струи становятся дозвуковыми, а
давление интенсивно возрастает (//>ра). При переходе через
скачки DB и D\BX скорости остаются сверхзвуковыми.
Следовательно, линии DE и
D\E\ являются линиями
тангенциального разрыва скоростей.
В результате взаимодействия
с внешним сверхзвуковым
течением дозвуковое ядро потока
ускоряется, а сечение его
уменьшается до минимального
ЕЕи в котором достигается v
звуковая скорость (М=1). За N^
сечением ЕЕХ скорости во всех
точках струи сверхзвуковые
По мере дальнейшего
увеличения перепада давлений
система скачков постепенно
'перестраивается (рис. 6-5,6).
Увеличивается протяженность
прямого скачка, изменяется форма
криволинейного скачка,
ограничивающего лерерасширен'ное
сверхзвуковое ядро. Необходимо подчеркнуть, что
внешние части струи ABFEDA и соответственно A\BxF\E\DxAu
так же как и ядро ADDXAX, при любом значении еа<£
остаются сверхзвуковыми. Дозвуковые скорости
обнаруживаются только на небольшом участке внутри струи
за скачком DDX. Следует иметь в виду, что все
вышеприведенные рассуждения не учитывают влияния
вязкости и, в частности, взаимодействия струи с окружающей
средой.
Спектры истечения из суживающегося осесимметрич-
ного сопла даны на рис. 6-6. Здесь отчетливо видны все
стадии развития спектра струи при £а<е#. Заметим, что
сверхзвуковые участки спектра для плоского сопла
могут быть рассчитаны методом характеристик.
Для оценки качества сопла служат коэффициент
21 * 323
Рис. 6-5. Схемы спектров за
суживающимся соплом при
ea<eV
Рис. 6-6. Истечение воздуха из суживающегося сопла при
сверхкритических перепадах давлений.
а—8а=0,51; б —еаг=0,412; в — еа=0,267; г— еа=0,05.
324
расхода fic, 'коэффициент скорости срс и коэффициент
потерь £с.
Коэффициент расхода определяется по
формуле
где G — действительный расход газа через сопло;
Gt — теоретический расход (при изоэнтропическом
процессе).
Коэффициент скорости представляет собой
отношение скоростей в действительном и теоретическом
процессах:
9с = ~
(6-18)
На рис. 6-7 и 6-8 приведены коэффициенты рс и <р для
суживающихся профилированных и конических сопел в за-
Рис. 67. Коэффициенты расхода рс и
коэффициенты скорости ус для конических и
профилированных сопел.
висимости от га и Re. Кривые показывают, что при
увеличении перепада давлений и уменьшении угла конусности
коэффициент расхода возрастает. Аналогичный результат
получен и для профилированного сопла. Однако максимум и
325
в последнем случае отвечает околокритическим скоростям.
Абсолютные значения рс получены более высокими для
профилированного сопла. При еа^0,7 кривые на рис. 6-7
отражают не только влияние сжимаемости, но и числа
Рейнольдса (рис. 6-8).
Коэффициент скорости конических сопел мало меняется
в зависимости от угла конусности. В широком диапазоне е
1,0
0,96
0,92
\Fc
t°>8
I J
Re
10ч
10*
10°
Рис 6^8 Влияние числа Re на коэффициент
расхода суживающегося сопла.
среднее значение*^ составляет ^ 0,97. Для сопел,
профилированных по формуле (6-7), значения <рс получаются
более высокими (<рс = 0,985 -г- 0,99).
Отмечаемое влияние отношения сечений, угла
конусности и еа объясняется изменением структуры потока в струе
за соплом.
п F
С увеличением — уменьшаются потери на трение в соп-
ле, но вместе с тем поле потока на выходе становится
более неравномерным. Аналогично влияет и увеличение
угла конусности, с ростом которого поле потока на выходе
приобретает все большую неравномерность.
В качестве примера применения сетки расходов рассмотрим
течение газа в системе последовательно включенных солел. Пусть
в трубе установлены z суживающихся сопел с одинаковой
площадью выходного сечения (рис. 6-9). Полагаем, что диаметр трубы
значительно больше диаметра сопел; скоростью газа в трубе можно
пренебречь.
При истечении через каждое сопло газ расширяется и скорость
его возрастает. В промежуточной камере происходит процесс
преобразования кинетической анергии .в тепло. В рассматриваемой схеме
аппарата осуществляется полное преобразование (полное гашение)
326
кинетической энергии. Струя газа теряет скорость благодаря
взаимодействию с частицами в камере, а также удару о стенку
следующего сопла.
Процесс гашения кинетической энергии в аппарате является
изобарическим. При этом состояние газа на входе в сопла
характеризуется условием /01 = const или To^const (рис. 6-10).
**v
Ли -Е
Рис. 6-9. Схема соплового
аппарата с полным гашением
скорости в промежуточных
камерах.
Рис. 6-10. Изображение процесса
в тепловой диаграмме для
соплового аппарата.
Характерной особенностью процесса в сопловом аппарате
является увеличение энтропии в промежуточных камерах.
Расчет соплового аппарата осуществляется с помощью
уравнений (6-3) и (6-12). Учитывая, что расход для всех сопел будет
одинаковым, из указанных уравнений легко получаем:
с0я
(/.-(^Мг/Ч^)'
(6-19)
Здесь q1 — приведенный расход через первое сопло;
Р02
Ли
&0/2
Poi
__Р0к
е0к~ р » Ли> Ро2> Роп
Рок-
- давления торможения соответственно перед и за первым
соплом, за соплом (п — 1) и за аппаратом;
Ро(п + \) Рог
~~ ' е* = ~7,—'— отношение давлении на сопле
2 Рок
Р0п
п и z.
Значение гп определяется по формуле (6-19):
+"-■/'-Ш"
(6-20)
327
Отсюда заключаем, что Так как ё0п <^ e0(/2_j^, ТО &п <С s^—i 4
Для каждого последующего сопла отношения давлений будут меньше,
чем для предыдущего. В соответствии с этим безразмерные скорости
вдоль соплового аппарата будут возрастать (кп > ХЛ__1) и,
следовательно, критическая скорость (?^=1) появится в последнем сопле
(вне зависимости от того, происходит ли полное или частичное
гашение кинетической энергии в промежуточных камерах), если eQk ^ е0 ,
где е0 — критическое отношение давлений для соплового аппарата.
К этому же выводу можно прийти из простых физических
соображений. Действительно, с падением давления падает и плотность газа.
Но так как выходные сечения сопел одинаковы, то для того чтобы
расход газа оставался постоянным, необходимо, чтобы в каждом
последующем сопле скорость возрастала. Очевидно, наибольшая скорость
установится в последнем сопле
Из уравнения (6-19) для последнего сопла можно получить, что
при е2 = —— = е# = I £ _[_ 1 } критическое отношение давлении
для соплового аппарата будет:
•^-(-£) = ••*.• (6-2,)
где ql — приведенный расход через первое сопло при критическом
истечении из последнего.
Для каждого сопла при е0п = const можно нанести кривые
q = q(e) (рис. 6-3). Линия критических расходов определена
уравнением (6-21) (линия О В на рис. 6-3).
Следует подчеркнуть, что формула (6-21) полностью эквивалентна
формуле (5-19), полученной для трубы постоянного сечения. Отсюда
можно заключить, что вне зависимости от физических особенностей
движения газа (без энергетического обмена с окружающей средой),
но сопровождающегося ростом энтропии предельный режим этого
движения, рассматриваемого в рамках одномерной схемы, описывается
одинаковыми уравнениями.
С помощью диаграммы на рис. 6-3 можно решать следующие
задачи:
1. Если заданы приведенный расход газа и «число сопел в
аппарате 2, то можно определить еод,, а также eQn и е^, т. е. установить
распределение давлений в соплах.
2. Можно найти число сопел, если известны расход qx и
относительное давление за последним соплом eok .
3. Для известного значения qx можно определить критическое
отношение давлений еп и число сопел 2.
и*
Рассмотрим соответствующие примеры.
1. Допустим, что число сопел 2 = 4, а приведенный расход
^ = 0,5.* На пересечении линии ^ = 0,5 с кривой q = q (e) для
первого сопла найдем точку blf которая определяет е,. Кривая b\ b2
даст ту же зависимость для второго сопла. Следовательно, в точке
328
b\ получим е02 = e^a. Повторив' это построение до точки 64 ,
определим относительное давление eok = е1е2езе^
2. Пусть заданы расход qx == 0,5 и отношение давлений е0А,=0,69.
Тогда исходной точкой в сетке расходов будет точка Ьь на
пересечении линии qx = 0,5 дуги эллипса eQk == 0,69. Перемещаясь по этой
линии до оси е и затем по вертикали до линии qx = 0,5,
последова0,50
0}45\
0,40
0,35
0,30
0,25
0,20f
\*°*
к-
/
?
/[-1,4
\
1 |
ю
Рис. 6-11. Критическое отношение давлений для
соплового аппарата в зависимости от числа сопел z для различных
значений /г.
тельно находим точки ЬА, 64, 63, Ьъ и т. д. до точки bv Число
вертикальных линий 64, 64, 63, Ь3 и т. д. равно числу сопел аппарата z.
3. Найдем теперь число сопел при qx = 0,5, отвечающее
критическому режиму соплового аппарата eQft = е0 . Определив на линии
ОВ точку Ьт , соответствующую критической скорости в последнем
сопле, находим линию q = q(e), проходящую через эту точку,
и далее последовательно определяем распределение давлений и число
сопел z так же, как и в предыдущем случае.
Задаваясь различными значениями qx по (6-21), находим
соответствующие значения е0 и, решив задачу 3 описанным выше методом,
рпределяем число сопел при критическом режиме соплового аппарата.
329
Результаты таких расчетов представлены на рис. 6-11, где
нанесены значения еп в зависимости от г.
Большой практический интерес представляет также возможность
определения расхода газа через сопловой аппарат при заданных
eok и z. Такая задача, однако, решается просто только в том случае,
когда сопловой аптрат работает в критическом режиме (£q^^£o*)
с полным гашением кинетической энергии в промежуточных камерах.
В этом случае из графика на рис. 6-11 находим критическое
отношение давлений е0 для заданного числа сопел. Величину приведенного
расхода q{ можно определить по формуле (6-21) или по рис. 6-3
(прямая ЛВ).
Отметим, что кривые на рис. 6-11 подчиняются уравнению
so = г £* (б-22)
6-3. ИСТЕЧЕНИЕ ГАЗА ИЗ ОТВЕРСТИЯ С ОСТРОЙ КРОМКОЙ.
ВТОРОЕ КРИТИЧЕСКОЕ ОТНОШЕНИЕ ДАВЛЕНИЙ
Теоретические исследования и эксперимент
обнаруживают некоторые новые свойства потока газа,
вытекающего из отверстия с острой кромкой.
Теоретические решения этой задачи были даны
в классических работах Н. Е. Жуковского и С. А.
Чаплыгина как для небольших скоростей, так и для
скоростей, соизмеримых со скоростью звука. Дальнейшее
развитие метода С. А. Чаплыгина применительно к
истечению из отверстия с острой кромкой было
осуществлено Ф. И. Франклем для области звуковых и
сверхзвуковых скоростей.
При истечении из суживающегося сопла плавный
профиль стенок обеспечивает постепенное расширение
потока и определяет форму линий тока. Возникающие
на входе радиальные составляющие скоростей
уменьшаются при течении по соплу и к выходному сечению
обращаются в нуль. Поток в выходном сечении имеет
равномерное поле скоростей. При сверхкритических
перепадах давлений выходное сечение сопла совпадает
с критическим.
Истечение из отверстия с острой кромкой происходит
иначе (рис. 6-12). В сосуде на достаточно большом
удалении от отверстия скорость газа равна нулю, а
давление— р0. За отверстием поддерживается давление ра<Ро-
Вблизи отверстия слева скорости газа интенсивно
нарастают, струйки газа суживаются и искривляются.
§30
*
(О
4-
izAiias*
(О"
и
^S4
о
ли
331
Поток газа срывается с острых кромок отверстий и
дальше движется, как свободная струя.
Спектр струи в отверстии показывает, что кривизна
разных линий тока оказывается различной. Наиболее
искривленными являются линии тока у границы струи,
а наименее искривленными — линии тока вблизи оси.
Поэтому скорости .на 'внешних линиях тока будут
больше, чем скорости в ядре струи. На выходе из
отверстия устанавливается неравномерное распределение
скоростей и давлений. Неравномерность потока усугубляется
влиянием вязкости. Нетрудно видеть, что струя будет
увлекать за собой газ окружающей среды и
тормозиться. Средняя скорость струи будет уменьшаться, а
поперечное сечение ее — увеличиваться. Размывание струи
начинается непосредственно от кромок отверстия.
Однако происходит оно достаточно медленно. На этом
основании можно воспользоваться следующей
идеализированной схемой истечения через отверстие. Предполагаем
газ совершенным, а движение — безвихревым.
На острых кромках Л и В будет происходить отрыв. Так
как мы предполагаем, что трение отсутствует, то
подмешивания окружающего газа к струе не будет.
Следовательно, справа от отверстия образуются две области:
свободная струя и неподвижный газ с давлением ра. Так как
давление на границе струи является постоянным, то
очевидно, что скорость на границе также постоянна.
Задача по определению формы такой струи и расхода
газа через отверстие была решена в классической работе
С. А. Чаплыгина „О газовых струях". С. А. Чаплыгин
рассмотрел случай плоской струи, когда отношение
давлений еа = —- больше критического или близко к нему.
В этом случае струя имеет форму, изображенную
на рис. 6-12,а. Струя непрерывно суживается, причем
максимальное сужение имеет место на бесконечном
удалении от отверстия. Если еа = е* , то на границе струи
скорость течения равна критической. Внутри струи скорости
меньше критической. С удалением от отверстия эпюры
скоростей выравниваются и на некотором конечном
расстоянии от отверстия скорости в струе становятся
равными скорости на границе, причем выравнивание поля
скоростей происходит вследствие поджатия струи и ускоре-
332
Ния ядра. Образующееся при этом сужение струи
характеризуется коэффициентом сужения, который определяется
как отношение минимальной ширины струи к ширине
отверстия (плоская задача).
Таким образом, при sa = £* критическая скорость
обнаруживается на границе струи и в поперечном сечении
на конечном удалении от отверстия. Линия критических ско*
ростей для такого режима показана на рис. 6-12,6. При
дальнейшем понижении противодавления (еа<е#) струя
становится сверхзвуковой.
Переход через скорость звука совершается на линии
звуковых скоростей AN В, которая идет от кромок
отверстия и вдается в струю в виде „язычка" (рис. 6-12,в).
Следовательно, при £a<Cs* спектр струи
перестраивается. Линия звуковых скоростей (линия перехода),
совпадавшая при еа=е#с границей струи и минимальным
сечением, по мере уменьшения еа деформируется и
приближается к выходному сечению отверстия. Справа от
переходной линии течение сверхзвуковое. Деформация линии
перехода объясняется перестройкой поля скоростей в
выходном сечении АВ* и в последующих сечениях, связанной
с изменением кривизны граничных линий тока.
Внутри „язычка" скорости дозвуковые. Характер
деформации линии перехода свидетельствует о том, что
сверхзвуковые скорости достигаются вначале во внешней части
струи (на границе и вблизи нее), а затем в ядре, что
полностью соответствует распределению скоростей в
поперечном сечении струи. Граница струи расширяется.
Деформация „язычка" при изменении еа будет происходить
до тех пор, пока линии слабых возмущений
(характеристики), отходящие от границ АЕ и ВЕХ, будут попадать
на линию перехода AN В. Углы характеристик ат с
уменьшением еа уменьшаются (рис. 6-12,в).
Следовательно, деформация линии перехода при
уменьшении еа не будет беспредельной. Существует такое
значение внешнего давления р9#, при котором
линия перехода занимает стабильное
положение; дальнейшее снижение давления
внешней среды уже не приводит к ее. деформации.
Этот режим соответствует такому углу ат^ первых
характеристик, исходящих из точек А и В, при котором они
333
касаются линии перехода, но не пересекая ее (рис. 6-12,г).
Давление р^ было названо Ф. И. Франклем вторым
критическим давлением. Соответствующее отношение
будем называть вторым критическим
отношением давлений.
Характерными особенностями стабилизировавшейся
линии перехода являются участки, лежащие внутри сопла
около точек А и В (рис. 6-12,г) которые показывают, что
у краев отверстия со стороны резервуара скорости уже
сверхзвуковые. Кроме того, при ед = е## линия перехода
в струе занимает ближайшее к отверстию положение.
В соответствии с перестраивающейся (в зависимости
от &а) картиной течения изменяется расход газа через
отверстие Назовем коэффициентом расхода отверстия ротв
отношение действительного расхода через отверстие
к расходу газа через суживающееся сопло, имеющее
ту же площадь поперечного сечения на в#ыходе при одном
и том же перепаде давлений.
Значения коэффициента расхода при еа>£* ,
подсчитанные С. А. Чаплыгиным для воздуха, приведены в
первых пяти графах табл. 6-1. Для несжимаемой жидкости
ц =0,63. '
Выше указывалось, что максимальный расход для сопла
имеет место при критическом противодавлении и
дальнейшее снижение противодавления не влияет на расход.
При истечении из отверстия благодаря изменению формы
линии перехода при еа<Се* расход газа будет
увеличиваться до тех пор, пока е >е^.
Таблица 6-1
а Р.
f^OTB
0,676
0,680
0,641
0,700
0,606
0,710
0,559
0,730
0,529
0,740
0,037
0,850
При еа<е^ уменьшение противодавления не влияет
на форму линии перехода и, следовательно, на расход
334
Таблица 6-2
Форма отверстия
АЪ
М
ж
м-\^=аз
1*г*
1
4L
£
и
1Г*
1*4*^='
СО
СО
ел
Второе критическое отношение
давлений £##
Коэффициент расхода ^тв
Воздух
Водяной пар (перегретый)
Воздух
Водяной пар перегретый)
0,037
0,13
0,85
0,18
0,27
0,88
—
—
—
0,90
—
0,47
—
0,92
—
0,528
0,546
0,99
0,985
газа. Если внешнее давление равно второму критическому
давлению, то коэффициент расхода имеет максимальное
значение.
Значения коэффициента расхода ji/tb и второго
критического отношения давлений е^ для отверстий различной
формы приведены в табл. 6-2.
На рис. 6-13 представлены кривые относительного
расхода через суживающееся сопло и через отверстие с острой
Of
0,6
0,4
0,2
i
i
_~—\ -
i
Отвер
i
l
»
i
i
i
!
1
.1
Ппппп ^
стие >
ej
0,2
¥
0,6
¥
10
Рис. 6-13. Изменение расхода газа через сопло и
отверстие с острой кромкой при одинаковой площади сечения
№=1,4).
кромкой при одинаковой площади поперечного сечения
в зависимости от еа для воздуха. В обоих случаях
расход отнесен к критическому расходу через сопло.
Установим теперь форму кривой зависимости -^—=f(sa)
для отверстия с острой кромкой. Максимальный расход
газа через отверстие может быть подсчитан по формуле
отв
G =
где
F — площадь отверстия;
2(4-1) ,
(6-23)
У'отв — коэффициент расхода через отверстия при
330
/?0, y0 — параметры газа в резервуаре на значительном
удалении от отверстия (параметры
торможения).
Расход газа через отверстие при произвольном sfl
можно найти по уравнению
G = ?отв F /Ш* /j/_^_ (!_.«). (6-24)
Обозначим приведенный расход через отверстие с острой
кромкой
Тогда расход через отверстие
G = д0О„ = (—)' {k~X) V TwmM VAV (6-24a)
Формула для приведенного расхода газа qQ на
основании уравнений (6-23) и (6-24) принимает такой вид:
*.= (*±! #Ws^(/ А4т0—D- С6-25)
Значения коэффициентов расхода ротв и ji/tb могут
быть приняты по табл. 6-1 и 6-2.
Можно получить простое приближенное выражение
для q0, предположив, что зависимость д0 от еа при ед^е##
описывается уравнением эллипса:
^о+£=££= 1, (6-26)
или
(1 - К J 4 = 1- 2«„ (1 —в) - «J. • (6-27)
Сопоставление точного и приближенного решений
показывает, что уравнение эллипса с большой степенью
точности описывает зависимость приведенного расхода д0
от ег для отверстия с острой кромкой, так же как и для
J22 М. Е.^ДеАч 337
суживающегося сопла. Различие состоит только в том,
что в случае сопла максимальный расход достигается
при первом критическом отношении давлений е# , а в
случае отверстия — при втором критическом отношении
давлений е^.
Отсюда следует, что влияние формы
отверстия на расход может быть учтено
соответствующим выбором второго критического
отношения давлений, так как следует ожидать, что
эллиптическая зависимость будет точной для любого
очертания стенок, если она точна для двух крайних случаев:
сопла и отверстия с острыми кромками.
Опыты, поставленные с целью определения расхода
воздуха и перегретого пара через отверстия различной формы,
подтверждают эллиптическую зависимость q0 от sfl. Для
перегретого водяного пара второе критическое отношение
давлений по опытным данным составляете^^0,13 (табл. 6-2).
Следовательно, с уменьшением k (показатели изоэнтропы)
е##, так же как и е^ , увеличиваются. Отсюда можно
заключить, что изменение физических констант газа
влияет на е^ в том же направлении, что и на е# . Этот
вывод отчетливо подтверждается данными, приведенными
в табл. 6-2.
Таким образом, мы видим, что свойства струи,
вытекающей из резервуара, существенно меняются в
зависимости от характера распределения параметров в
поперечном сечении струи. При неравномерном распределении
параметров течения (истечение из отверстия или из щели)
в потоке обнаруживаются новые свойства и уравнения,
описывающие истечение равномерной струи, оказываются
неприменимыми.
Заметим, что на спектр струи за отверстием и на
коэффициент сужения струи оказывают некоторое влияние
размеры камеры, из которой струя вытекает.
Теоретическая зависимость коэффициента сужения плоской струи
от размеров камеры и скорости в минимальном сечении М2
по Г. А. Домбровскому приведена на рис. 6-14. Кривые
показывают, что с ростом — (с увеличением относительно
а0
размера отверстия) и М2 коэффициент сужения возрастает.
Влияние — сказывается ощутимо только при— >0,3.
clq aQ
338
Для расчета отверстия или щели при различных
начальных и конечных давлениях можно использовать метод,
описанный выше для сопла. Исходя из условия
неизменной температуры в резервуаре, строят сетку
относительных расходов газа через отверстие, каждая кривая кото-
/fit
0,91
0,8
0,7
0,6
1 1—- г
т
1 * <Л
Мг
г
И-тЙ
\ м?\
к 9Н
| тпа
а
0,2 0,4 0,6 0,8
1,0
Рис. 6-14. [Зависимость коэффициента
сужения плоской струи от размеров камеры и
скорости в минимальном сечении по
Г. А. Домбровскому.
рой <70==:/(ва) соответствует постоянному начальному
относительному давлению е(
Р0п
0/2 "
6-4. РАСЧЕТ СВЕРХЗВУКОВОГО СОПЛА
Сверхзвуковые сопла (.оапла Лаваля) применяются
для создания потошв газа со сверхзвуковыми
скоростями. Эти сопла используются в качестве одного
из основных элементов реактивных двигателей, а также
в паровых турбинах, эжекторах и других аппаратах.
Анализ одномерного течения показал, что поток со
сверхзвуковой скоростью может быть получен в трубе
с минимальным сечением, если в этом сечении будет
достигнута критическая скорость ]. В соответствии с этим
1 Рассматривается частный случай адиабатического движения
газа в трубе без энергетического обмена с окружающей средой.
В общем случае условие минимума сеченчя не является
необходимым для перехода в область сверхзвуковых скоростей.
22*
339
сопло Лаваля представляет собой трубу переменного
сечения, состоящую из двух частей. Скорость газа,
протекающего через нормально работающее сопло Лаваля,
непрерывно увеличивается, причем в суживающейся
части сопла скорость дозвуковая, а в расширяющейся —
сверхзвуковая (рис. 6-16).
Элементарный расчет сверхзвуковых сопел
производится по уравнению неразрывности, причем должны
Рис. 6-15. Сопло Лаваля.
быть заданы параметры газа перед соплом, расход газа
и скорость потока в выходном сечении.
Пренебрегая влиянием трения, можно считать, что
критическая скорость устанавливается в минимальном
сечении сопла. Размеры этого сечения определяются по
уравнению (6-5):
F =
_ /fc + l\2(*"!)i/X G.VT0
v 2 / У & Ро
Выходное сечение рассчитывается по формуле
р F* __ G*
1 !
<7i
(6-28)
g*
./.
2k
1
k + 1 1
Промежуточные' сечения сопла могут быть определены
в зависимости от скорости или отношения давлений
из формулы для приведенного расхода:
1 _ 1
Я =
F*
k+ 1
Г'/ffiV'
(6-29)
340
где Р — промежуточное сечение;
Я И е — соответствующие этому сечению скорость й
относительное давление ( е = —).
Если задано распределение скоростей или давлений
по оси сопла, то формула (6-29) определяет профиль
сопла. Однако такой расчет промежуточных сечений,
а тем самым и профиля (формы) сопла является
приближенным и может не обеспечить заданного
распределения давлений, так как скорость в сечении непостоянна
ни по величине, ни по направлению >и, следовательно,
поток не является одномерным.
В случаях, когда важно .получить лишь заданную
среднюю скорость на выходе из сопла, а характер
распределения скоростей по сечению не имеет большого
значения, .промежуточные сечения сопла не
рассчитывают, а для простоты изготовления как суживающуюся,
так и /расширяющуюся части выполняют коническими.
При этом в узком сечении и тем более на выходе июле
скоростей получается неравномерным.
В некоторых случаях для уменьшения
неравномерности поля скоростей суживающуюся часть сопла
рассчитывают по формуле Витошинского (6-7), а угол
раствора конической расширяющейся части выбирают
малым (до 12°). Опыт показывает, однако, что эти меры
не всегда достаточны для .получения нужного поля
скоростей.
Лучшие результаты можно получить? применяя
профилированные сопла, расширяющаяся часть которых
рассчитана методом характеристик. Рассматривая
плоское сопло и пренебрегая влиянием трения,
предположим, что все параметры течения остаются неизменными
вдоль линий, нормальных к плоским стенкам. Допустим,
что в узком сечении сопла АА' поток имеет .равномерное
поле скоростей М=1 (рис. 6-16).
Для ускорения потока, имеющего в сечении АА'
критическую скорость, (необходимо увеличивать сечение
сопла. С этой целью повернем участки стенки АА{ и
соответственно А'А\ на малый угол от оси сопла бо.
Тогда в точках А и А' возникнут слабые волны
разрежения. При пересечении этих волн поток ускоряется и
приобретает скорость Xj,2, которую можно определить
34)
С помощью диаграммы характеристик (рис 6-16,6) или
с помощью таблиц.
Состояние потока в критическом сечении АА! в
диаграмме характеристик изобразится точкой (Av А[) на
окружности Я=1. Скорость потока в области 1 определяется
в точке Г на эпициклоиде А[Г, если провести луч из
начала координат под углом о0 к направлению оси сопла х.
Симметрично расположена точка 2\ которая соответствует
области 2 потока. Через точки /' и 2' проходит
окружность, отвечающая скорости Х{ 2.
Непрерывное расширение газа в стационарных волнах
разрежения, возникающих в точках А и Л', можно
заменить, проводя из этих точек звуковые волны АЕ и АГЕ
под углом aml-f--^- к направлению оси сопла (aml — угол
звуковой волны, соответствующей скорости потока в
области 1).
В диаграмме характеристик найдем точку Е\ соответст-
вующую отклонению потока на угол ~-, и определим
величины скорости ^АЕ(ЛА>£)у отвечающей направлению
звуковой волны АЕ1.
При переходе из областей / и 2 в область 3 линии
тока пересекают волны ЕЕг и ЕЕ2 (поток ускоряется)
и поворачиваются на угол 50 к оси сопла. Следовательно,
в областях 3 скорости потока имеют направление,
параллельное оси. В диаграмме характеристик легко
определяется точка 3', отвечающая этой области течения.
В точках Аг и А\ (рис. 6-16,а) стенки сопла вновь
поворачиваются на угол 80. При переходе в области 4 и 5
поток ускоряется и приобретает скорость Л4Ь=Л3.
Аналогично можно найти величину и направление скорости
в областях 6, 7, 8 и т. д., а также направления звуковых
волн, которые являются границами этих областей.
В результате последовательного поворота стенок
сопла образуются две стационарные волны разрежения
конечной интенсивности, .при переходе через которые
поток расширяется и достигает заданного значения
скорости.
Скорость ^i(Mj) будет достигнута в пределах зоны
342
пересечения волн разрежения на участке HL. За
последней характеристикой LQ, угол наклона которой равен
поток должен иметь равномерное поле скоростей, в
каждой точке которой скорость равна Мь Все линии тока
правее LQ должны быть параллельными оси сопла.
Отсюда следует, что каждую звуковую волну от
противоположной стенки, выходящую за пределы AnL,
необходимо погасить соответствующим поворотом стенки на
угол, равный углу отклонения потока в такой волне.
343
Начиная от точки Ап, стенка сопла поворачивается так,
чтобы падающие на нее 'волны NS, PF и т. д. не
отражались.
Таким образом, на первом участке стенки сопла
поворачиваются от оси сопла, а на втором участке, где
волны от противоположной стенки гасятся, наклон
стенки постепенно уменьшается и в точке Q бо = 0. В пределе
при уменьшении б0 ломаная стенка AAnQ переходит
в плавно искривленную стенку. *
Вблизи узкого сечения, где скорость течения
незначительно превосходит критическую скорость, точность
расчета 'методом характеристик первого участка сопла
недостаточна, в особенности если расчетное значение к\
невелико.
Подбор профиля стенки поэтому производят, начиная
с некоторого начального сечения, где течение уже
обладает сверхзвуковой скоростью. Распределение скоростей
■в начальном сечении должно быть известным.
В некоторых случаях начальный участок сопла
выполняют коническим. Угол конусности Yo выбирается
в зависимости от заданного значения Х\ и составляет
половину максимального угла поворота потока при
увеличении скорости от Х=\ до Х\.
Широкое применение находят также аналитические
методы расчета сверхзвуковых сопел, разработанные
С. А. Христиановичем « др.
Методы расчета и .профилирования сверхзвуковых
сопел не учитывают влияния вязкости. На стенке сопла
образуется пограничный слой, толщина которого
нарастает по длине сопла. Отметим, что в соответствии с
выводами гл. 5 влияние трения приводит <к смещению
критического сечения, которое сдвигается в
расширяющуюся часть сопла.
Пограничный слой на стенках вызывает некоторое
перераспределение скоростей и давлений потока у
стенок и смещение характеристических линий.
Действительные скорости .и давления в различных сечениях и на
выходе из сопла будут отличаться от расчетных
значений.
Для получения заданного распределения скорости и
расчетного значения Х\ необходимо увеличивать
площадь поперечных сечений сопла, полученную при
условии изоэнтропического течения. Точное решение такой
Щ
задачи требует расчета пограничного слоя на стенках
сопла (гл. 5).
Приближенное решение можно найти, если известно
распределение коэффициентов сопротивления по оси сопла.
Удельную работу сил трения для трубы переменного сечения
(сопла) можно представить в следующей форме:
с2 dx
dLjp = Z2g * g »
_ d* - D
где dx — jr-; D = jr- ; D* — диаметр горлового сечения сопла.
Приращение энтропии, обусловленное влиянием сил трения, равно:
dS dLTp C2 JTX
- S
где 5 = —= — приведенная энтропия.
Л г\
На основании (6-30) после несложных преобразований находим
такое выражение для коэффициента сопротивления:
к \* \ к + 1 У dx
Учитывая, что согласно формуле (5-12)
di 1 dz0
dx eo dx'
где е =^- — отношение давлений торможения на входе в сопло
Ро ив данном сечении, можем получить:
х
k Г &Чх
1» •• = *+! 17 k=T\- (6'31)
Если известен вид функции ? (х), то с помощью (6-31) нетрудно
найти изменение е0 по длине сопла. Значения *£(лг) можно принять
по графику на рис. 5-12. В соответствии с уравнением неразрывности
(2-41) связь между сечениями в действительном (F) и изоэнтропи-
ческом (F0) потоках можно представить так:
f = fo-y«o. (6-32)
где t = -б- ; fо = J-'» Qt= 0 п \ Я = Г-^- '» Я и qt — приведенные
1 * 1 * г^и* г* и*
расходы для теоретического и действительного процессов.
345
Исследования, проведенные йод руководством А. А. Г^ухмана,
теоретически и экспериментально показали возможность линейной
аппроксимации закона изменения энтропии по длине сопла.
Следовательно, если принять
dS d In с
UL = —== =r— — COnSt,
dx dx
то, положив в критическом сечении х = О, с помощью (6-32) найдем
(/•?/ = !):
In б0 = 1п(/^)= рГл;,
или
f=-je**. (6-33)
Опыты показывают, что для сопел с полированной внутренней
поверхностью можно принять \ъ =^= 0,011 -4- 0,018.
Уравнение (6-33) используется для решения прямой и обратной
задач. В первом случае заданными являются f (x) и ц; по формуле
(б-ЗЗ) устанавливается приведенный расход q(x); распределение
параметров потока по длине канала (к, /?, р, Т) устанавливается по
таблицам газодинамических функций. При решении обратной задачи
по известному распределению q (x) или X (х) устанавливаются те
сечения, в которых достигаются заданные значения X(f(x)). Значения
0 (х) в обоих случаях можно найти по формуле (6-32) (при этом
<7/ = <7).
Влияние трения на скорость и другие параметры в
выходном сечении сопла оценивается с помощью коэффициента
скорости, который выражается по формуле
j/l-F^T^^-1)' (6-34)
— 1 ] — коэффициент потерь энергии
/ в сопле;
=——отношение давлений тормо-
Ро1 жения на выходе и на входе
в сопло;
Ми — теоретическое значение
числа М в выходном сечении.
Из формулы (6-34) следует, что величина е0
неоднозначно связана с коэффициентами ус и (^. При одинаковых
yi-e.
. 2 1
346
значениях в0 коэффициенты <рс и Сс меняются в зависимости
от величины располагаемой энергии, пропорциональной М1Г
На рис. 6-17 приведены графики, устанавливающие связь
между <рс, е0 и М1Г
1,0——
0,9
0,8
0,7
0,6
0,5 0,6 0,7 0,8 0,9 КО
Рис. 6-17. Зависимость коэффициента ско*
рости сопла ус от е0 и Ми.
6-5. ПЛОСКОЕ СОПЛО ЛАВАЛЯ ПРИ НЕРАСЧЕТНЫХ
УСЛОВИЯХ
В условиях эксплуатации параметры, а также расход
газа через сопло могут изменяться. Существенно при этом,
Ра
что меняется отношении давлении еа=—, где р —по-
прежнему давление окружающей среды.
Рассмотрим работу сопла при переменных режимах
в первом приближении, пренебрегая трением и
теплопроводностью. На рис. 6-18 показано распределение давлений
в сопле Лаваля при различных давлениях внешней среды р
Кривая АОВ, построенная по уравнению (6-29),
соответствует расчетному режиму течения в сопле, при котором
а Х Ро
Предположим, что при постоянном значении р0 давление
внешней среды меняется в пределах рх^ра^р0, и
проследим изменение структуры потока как внутри сопла, так
347
и за ним. При этом можно выделить четыре характерные
группы режимов; в пределах каждой группы режимов
картина течения качественно сохраняется неизменной.
Первая группа режимов характеризуется пониженными-
давлениями среды -^-<С~:
В этом случае в выходном
сечении сопла устанавливается расчетное давление рх% так
Рис 6-18. Диаграмма распределения давлений
в сопле Л а валя при различных режимах.
как параметры газа в резервуаре, а следовательно, и
расход газа через сопло не меняются. Это очевидно также и
потому, что в сверхзвуковой струе возмущение против
течения не распространяется и, следовательно, падение
давления среды не скажется в выходном сечении сопла. Во
всех промежуточных сечениях сопла поэтому давления
также остаются расчетными. Параметры течения
изменяются только за соплом, в свободной сверхзвуковой струе.
На рис. 6-19,а представлены схемы спектров струи на
выходе из плоского сопла при пониженном противодавлении.
В угловых точках А и Ах давление меняется от значения
А Д° Ра. Линии тока в точках А и Аг отклоняются на
некоторый угол 8 в связи с возникновением в этих точках
волн разрежения, вызывающих изоэнтропическое расширение
газа от рх до ра. Вдоль характеристик АС, АгС и АВ,
АХВХ в соответствии со свойствами прямолинейных харак-
348
Рис. 6-19. Схемы спектров струи за плоским соплом при различных
режимах
теристик давление не меняется. Следовательно, в областях 2
устанавливаются постоянная скорость и давление ра, равное
давлению окружающей среды. Волны разрежения AD^^A
и AXDEAX выходят на свободную границу струи, вдоль
349
которой давление остается неизменным и равным ра%
В зоне СВСХВХ пересечения этих волн, как уже известно,
происходит искривление характеристик. В результате угол
звуковой волны BD становится меньше угла волны АХС и
а <С а ; соответственно а <^ а ; а <Г а
"^Di тАС' тСгН ^ "W mdH^ m BlDl
От свободной границы волна разрежения отражается,
как волна сжатия, при прохождении через*которую линии
тока деформируются, отклоняясь на угол 8 к оси струи.
В точках L иЬх волны сжатия выходят на свободную
границу.
За пересекающимися волнами разрежения (в области 3)
устанавливается давление, меньшее давления окружающей
среды (струя перерасширена). В области 4 после
пересечения волн сжатия давление повышается до давления рх
в выходном сечении сопла ААХ. К сечению LLX струя
суживается и ширина ее равна ширине выходного сечения ААХ.
В областях У, 3 и 4 линии тока прямолинейны и
параллельны оси сопла. В областях 2 линии тока также
прямолинейны и параллельны, но расположены под углом 6 к оси
сопла. Для рассматриваемой первой группы режимов при
принятых допущениях потерь энергии в струе нет.
По мере повышения давления среды ра
характеристики АВ, BD, АХВХ, *BXDX, СХЕ и С1Е1 меняют свое
положение в струе. Так как разность давлений в областях /
и 2 при этом уменьшается, то углы указанных
характеристик увеличиваются, интенсивность волн разрежения ADXEXA
и AlDEA1 уменьшается. Углы отклонения линий тока
в области 2 также уменьшаются. В пределе, при расчетном
режиме (ра=:рл), характеристики АЕХ и АХЕ сливаются
с волнами ADX и AXD. Струя приобретает формулу,
приведенную на рис. 6-19,6.
Вторая группа режимов характеризует истечение из сопла
Лавйля при повышенном противодавлении среды или при
пониженном начальном давлении (еа >> ех). Зная расчетную
скорость в выходном сечении сопла Я,, легко определить
то значение давление среды, при котором в выходном
сечении образуется прямой скачок уплотнения [рис, 6-18 и
формула (4-20)]:
К
2
k — \
/>,»=А VI' • (6'35)
1 >2
350
Рассматриваемая вторая группа режимов характеризуется
следующим соотношением давлений среды: Pi^Pa^ P]k.
В этом случае в сечении ААХ (рис. 6-19,#) также
устанавливается расчетное давление рх. Если давление среды ра
сравнительно немного превышает давление р19 то в
точках ААХ образуются два косых скачка: АС и АХС,
пересекающихся в точке С. Косые скачки выходят на свободную
границу струи (после пересечения в точке С углы косых
скачков увеличиваются). При прохождении через скачки
АС и АХС линии тока отклоняются на угол 8, который
легко подсчитать. В областях 2 давление равно давлению
окружающей среды, линии тока параллельны друг другу
и свободной границе струи А В и АХВХ.
Из условия симметрии за скачками СВ и СВ\
скорость должна стать параллельной оси потока, т. е.
линии тока должны повернуться в обратном направлении
на угол б. В этой области устанавливается давление,
повышенное по сравнению с давлением среды.
Следовательно, в точках В и В{ со стороны -струи давление
более высокое и из этих точек распространяются волны
разрежения. При переходе через волны разрежения
давление падает до давления окружающей среды и
линии тока отклоняются от оси — струя расширяется.
После пересечения волн разрежения давление разно р\.
В точках выхода волн разрежения на свободную
границу струя имеет ширину, равную ААХ. Рассматриваемая
группа режимов характеризуется .потерями энергии
в струе, обусловленными возрастанием энтропии в
системе косых скачков уплотнения. Поле давлений по оси
и в поперечных сечениях приобретает значительную
неравномерность.
Описанная схема истечения 'возможна лишь при
небольшом превышении давления ра над ри когда угол б
невелик. При некотором давлении среды Pik^p^ р'
спектр струи на выходе из сопла меняется.
Существование системы двух косых скачков уплотнения со
сверхзвуковой скоростью за точкой их пересечения
становится невозможным. При ра^Р\н угол косых скачков,
отходящих от кромок А и Ль достигает значения, .при
котором в некоторой области за скачком скорости будут
дозвуковыми и спектр истечения резко изменится
Трис. 6-19,2 и д).
351
, Для плоского сопла угол отклонений линии тока 6mi
(или угол скачка pmi), при котором изменится картина
истечения, легко определяется с помощью диаграммы
ударных поляр.
Ударная поляра АК1 (рис. 6-20) соответствует
расчетной скорости %\ потока в выходном сечении сопла
Рис. 6-20. Определение режима течения за скачками, образующимися
при нерасчетных условиях в сопле Лаваля, с помощью диаграммы
ударных поляр.
(отрезок 01) и, следовательно, во всей области 1
(рис. 6-19,в). При некотором давлении среды pa = p'ik
скорость за скачком измеряется отрезком 02 (скорость
в области 2 на рис. 6-19,в); предельная скорость за
косыми скачками СВ и СВХ в области <?, где линии тока
параллельны оси струи, определяется отрезком 03
(рис. 6-20).
Величина давления р\к может быть определена по
формуле (4-13):
2k _ / 2 ^?sin2pml k-.\\
'\k-
l" M-T
'k+ l
2k
(6-36)
В эгом случае в струе за скачками СВ и СВ\
(рис. 6-19,в) скорости будут дозвуковыми.
Если pa>p'\h, то при пересечении скачков СВ и СВ\
поток уже не сможет no-вернуться на угол 6i>6mi
(пунктирная линия на рис. 6-20), на который он
повернулся при переходе через АС и А\С. Схема истечения
при этом качественно изменится. На выходе из сопла
образуется мостообразный скачок.
От угловых точек А и А\ (рис. 6-19,г) распростра-^
няются косые скачки АС и A{Dt ^переходящие в прямой"
352
(или —при неравномерном распределении скоростей —
криволинейный) скачок, за -которым скорости будут
дозвуковыми. За косыми скачками СВ и DBX скорости
остаются сверхзвуковыми, а давление оказывается бо-
. лее высоким, чем давление <среды ра-
За прямым скачком CD давление значительно более
, высокое, чем за скачками СВ и DB\. Следовательно,
в струе создается сложное распределение давлений по
сечению: выравнивание давлений приводит к резкому
уменьшению р в ядре струи, т. е. к ускорению ядра, что
сопровождается уменьшением его сечения. Линии
раздела СЕ и DF образуют суживающийся участок ядра,
вдоль которого скорости растут и в сечении EF
достигают звуковых значений. Кроме того, внутренний поток
дозвуковых скоростей непосредственно за скачком CD
. ускоряется внешним сверхзвуковым потоком. Косые
скачки СВ и DBi отражаются от свободной границы
в форме волн разрежения, которые также ускоряют
ядро струи. В результате скорость внутреннего потока
становится сверхзвуковой. Интенсивность изменения
давления в прямом скачке CD и за ним по данным
А. А. Гухмана и А. Ф. Гандельсмана для двух режимов
иллюстрируется кривыми на рис. 6-21. Опыты
подтверждают, что на весьма коротком участке за скачком поток
достигает расчетного давления р\ и соответственно
сверхзвуковой скорости.
Итак, при давлении внешней среды pa>p'\k система
пересекающихся косых скачков разрушается и переходит
в мостообразный скачок. Это явление аналогично
рассмотренным в гл. 4 случаям неправильного отражения
косого скачка от твердой стенки и пересечения скачков.
При дальнейшем повышении давления среды
внутренняя дозвуковая область течения расширяется,
а внешняя сверхзвуковая — суживается. Существует
такое давление среды p"lft, при котором криволинейный
скачок распространяется почти на все сечение; в этом,
случае за скачком АА\ скорости становятся
дозвуковыми (рис. 6-19,д), за исключением узкой периферийной
области. Этот 'криволинейный скачок располагается
вблизи выходного сечения сопла.
Давление p"lk будет соответствовать такому режиму,
при котором угол .поворота б на скачках АС и AXD
(рис. 6-19,2) становится равным максимальному углу 6т
23 М. Е. Дейч
353
(штрихпуиктирная линия на рис. 6-20). Определив^ с
помощью ударной поляры угол j3m, соответствующий углу
(поворота бщ, можно, пользуясь формулой (4-13) или
(6-36) для косого скачка, подсчитать давление р"\к'.
Ц sin2 g„
k— Г
Л+1^1 k+\
мм рт.ст.
2k
' к + гч
20 -30мм
Рис. 6-21. Изменение давления вдоль оси
сопла и в струе за соплом на режимах
с мостообразным скачком в выходном
сечении; М, = 1,5. Опыты МО ЦКТИ.
(6-37)
При давлениях среды pa>p"\k скачок
выпрямляется и при Pa^Pik [формула (6-35)] скачок должен стать
прямым, располагаясь в выходном сечении сопла.
Фактически вследствие неравномерного распределения
скоростей в конических соплах и влияния пограничного
слоя (вязкости) скачок входит внутрь сопла несколько
•искривленным (рис. 6-19,е).
354
Если давление за соплом pa>p"\hi то в выходном
сечении сопла давление будет меняться. Дальнейшее
повышение давления среды (pa>P\k) вызывает
перемещение системы скачков внутрь сопла, как показано на
рис. 6-19,е.
Из формулы (6-36) для отношения давлений на
границах скачка следует, что данной скорости Х\
сверхзвукового потока перед скачком соответствует вполне
определенное повышение давления в скачке. Если давление
средьи превысит величину р1й, то, очевидно, условия
равновесия на прямом скачке нарушатся и он .переместится
в такое место в потоке, которое соответствует
равновесному положению скачка при новых параметрах среды.
Следует иметь в виду, что перемещение скачка внутрь
сопла сопровождается новыми качественными
изменениями потока (третья группа режимов). Давление
за скачком в этом случае уже не равно давлению среды;
оно оказывается меньше ра. Поэтому за скачком
давление продолжает возрастать. Распределение давлений
в потоке .при промежуточных положениях прямого
скачка показано на рис. 6-18 линиями K\L{EU K2L2E2 и т. д.
С ростом давления среды скачок продолжает
перемещаться внутрь сопла к минимальному сечению. При
этом изменяется соотношение между степенью
восстановления давления на скачке и степенью изоэнтропиче-
ского восстановления давлений за скачком. В
соответствии с последовательным смещением скачка в область
меньших скоростей отношение давлений на границах
скачка уменьшается, а степень восстановления давления
в расширяющейся части сопла за скачком
увеличивается 1 (см. кривые LXEU L2E2 и т. д. на рис. 6-18).
При некотором давлении среды р{т скачок входит
в минимальное сечение сопла и здесь исчезает. В
минимальном сечении сопла параметры .потока при этом
критические, но перехода в сверхзвуковую область не
происходит. Линия ОЕ является границей между
дозвуковыми и сверхзвуковыми режимами сопла. При ра>р\т
скорости во всех точках сопла дозвуковые и мы
получаем четвертую группу режимов сопла. Для этой группы
характерны последовательное расширение потока в
суживающейся части и сжатие в расширяющейся части
1 Рассматривается случай безотрывного течения за скачком.
23* 355
солла. Минимум давления достигается в узком сечении.
Известно, что таков характер распределения давлений
в трубах Вентури, применяемых для измерения расхода
газа.
До тех пор, пока ,ра<Р\т, расход газа через сопло
при различных противодавлениях сохраняется
неизменным (в минимальном сечении сопла параметры газа
критические, а начальные параметры остаются
неизменными). Изменение расхода начинается только при
противодавлениях, больших, чем pim,*T. е. в пределах
четвертой груплы режимов. На рис. 6-18 справа показано
изменение расхода газа через сопло в зависимости от
противодавления ра.
Величина давления рХт может быть определена, если
известны геометрические характеристики сопла -и
параметры потока перед соплом. Пренебрегая потерями
в расширяющейся части сопла, 'можно с помощью
уравнения неразрывности получить:
где qlm = 1ш ш-—приведенный расход в выходном сече-
р*а* нии сопла для рассматриваемого режима.
С другой стороны, qlm можно выразить через отношение
давлений —- по формуле (6-4); тогда, имея в виду, что
?1ш=
_2_
k
г
ч&г-
приходим к следующему уравнению для еш:
2 k-\ 2
i
•,i(i-«,:)=^4'.'4-. №
где fx = -=L
Нетрудно видеть, что уравнение (6-38) при fx = 1 (су-
k
ч / 2 \Л=1
живающееся сопло) имеет корень е{т = е^ = ) , а при
f1==oo (сопло, рассчитанное на максимальную
скорость Я1макс)—два корня: е1/п = 1 и eIm = 0. Второе значе-
356
ние (slm = 0) соответствует. расчетному режиму сопла при
f^oo и поэтому не рассматривается.
Зависимость е1ш от -=- по формуле (6-38) представлена
на рис. 6-22.
Для е]т можно получить более простую формулу, если
воспользоваться эллиптической зависимостью между qlm
И е1ш«
0,8 10
Рис. 6-22. Предельное отношение
давлений на сопле е1ш в зависимости от /,.
Согласно уравнению (6-12) можно записать:
(«Im-'.)'
С - е. Y
отсюда
\т
= *. + (!-О
^
а
(6-39)
В уравнение (6-39) можно ввести поправку,
учитывающую потери в расширяющейся части сопла. В этом случае
е. =s
+ (l-Oj/l-^-.
(6-39а)
где
Pq*
357
Из уравнения (6-39а) следует, что с возрастанием
потерь в сопле величина предельного
противодавления pim уменьшается.
При определении г\т с учетом потерь можно
пользоваться графиком на рис. 6-22, откладывая по горизон-
1
тальнои оси величину —.
Вернемся к рассмотрению некоторых особенностей
третьей группы режимов со скачками уплотнения
внутри сопла. Необходимо учитывать, что в
действительности в сопле создается не прямой скачок, а сложная
система криволинейных скачков. Большое значение при
этом имеет форма расширяющейся части сопла. При
небольших углах раствора расширяющейся части в сопле
возникают скачки, близкие по форме к прямым. Около
стенок сопла происходит разветвление криволинейного
скачка, принимающего . форму мостообразного скачка
(рис. 6-19,е).
Третья группа режимов характеризуется
значительными потерями энергии. Наряду с волновыми потерями
в скачках возникают потери вследствие отрыва потока
от стенок сопла. Отрыв сопровождается образованием
вихрей и характерным подсосом газа из окружающей
среды.
В ряде случаев практический интерес представляет
определение положения скачка внутри сопла и потерь
в сопле при заданном отношении давлений. Так как
структура скачков зависит от формы расширяющейся
части сопла, то такая задача не может быть точно
решена. Приближенное решение можно получить для
простейшего случая, принимая скачок прямым и поток
в сопле безотрывным..
Задача решается следующим образом. До скачка
расширение газа следует по кривой АОВ (рис. 6-18),
соответствующей расчетному режиму. Параметры газа
на входе и в сечениях К связаны уравнениями изоэнтро-
пического течения. Изменение состояния в сечении К
определяется по формулам прямого скачка (линии
процесса /С, L и т. д.). Наконец, за скач-ком можно
использовать данные, характеризующие потери в диффузоре
(гл. 7).
Допустим, что прямой скачок возникает в некотором
358
Сечении сопла FCK. Из уравнения неразрывности можно
получить известное соотношение:
?ск
где qCK — приведенный расход перед скачком.
Из формулы (6-40) можно выразить /ск через Яск или
с помощью уравнения (6-4) через отношение давлений
е^=_^1. Приведенный расход в этом же сечении за скач-
Ро
ком равен:
^ск=^7 = ^-- (641)
Ро £о
Здесь р'0 — давление торможения за скачком.
Из уравнения неразрывности для сечений FcK и Fx
получим:
FcK Яа Роа=^%п, (6-42)
tl ?ск Ро ?ск А
где q'CK и qa — приведенные расходы за скачком и в
выходном сечении при заданном давлении /? ;
е0д = -^г — изменение давления торможения в расширяю-
Ро щейся части сопла за скачком1.
Тогда с помощью уравнения (6-40) получим:
/ск=/Л*0с,Лд. (6"43)
"с к
Ро
где s0ck = —т изменение давления торможения в скачке.
Подставляя в уравнение (6-43) значения q'cK и qa,
находим:
' k ЛГ л 'mm k-^-X
£а V 1 — еа £0ск ,_ СГ .
' 1f 1 'т
/ск=л а ;,^Ч£ w*v (6-44)
1 Значения е0 могут быть приняты по экспериментальным
данным, приведенным в гл. 7.
359
Здесь е'а = —^ — относительное давление за соплом;
Ро
k— 1
Если пренебречь потерями в сопле до скачка, то
Ра
а Ро
Отношение давлений полного торможения на скачке
определяется по уравнению (4-35). Формула (6-44) при
подстановке — из (4-35) становится весьма громоздкой;
Ро
значительно удобнее пользоваться уравнением (6-43),
которое содержит табличные функции изоэнтропического потока
и прямого скачка. Задаваясь величиной qCK в пределах от
?ск = 1 до #с'к = #а' находим /ск по формуле (6-43).
Определив по таблицам соответствующие значения —, найдем
Ро
" ' Ро
величину qcK ±= qCK~ • Оценка коэффициента е0д
производи
дится после расчета дск (Яск) и -~- . Затем определяется
величина ?a = <7"KV Зная 6од и sa = ~/"> нах°Дим:
^Оа
" Роа
S =8 .
а р0
Таким образом, можно построить зависимости /ск от ед
для различных, но постоянных значений /Х = -А. При
■**
sa = slw скачок располагается в горле сопла и /ск = 1. При
sa~e\k скачок находится в выходном сечении сопла.
Анализ формулы (6-43) показывает, что в интервале
изменений /ск от 1 до 2 зависимость /ск от sa может быть
выражена приближенной формулой
/«^(..„.-.J+l, (6-45)
где А — безразмерный коэффициент, зависящий от ft.
360
Подсчитав f по формуле (6-45), можно определить
q ' и Яс'к (или eJK) и найти -S-; тогда коэффициент потерь
энергии в скачке определяется по формуле (4-33) или по
таблицам. Коэффициент потерь в расширяющейся части за
скачком определяется по формуле
S k— i м"2
ск
?~1
60д
Коэффициент полных потерь в сопле в режимах третьей
группы равен:
м' 2 м" 2
а- V СК _| >г ' СК
Ч Чж ~^Г 7Г '^д М2 '
1 а а
где М —безразмерная скорость, соответствующая отно-
- Ра
шению давлении —.
Ро
С учетом отрыва потока потери и положение скачка
будут отличаться от рассчитанных указанным способом.
Отрыв потока за скачком .приводит к резкому
возрастанию потерь К
Результаты опытного исследования подтверждают
указанные особенности потока в сопле при нерасчетных
режимах.
Так, на рис. 6-23 приведено распределение давлений
вдоль сопла при различных режимах. Штрихпунктирны-
ми линиями показаны результаты расчета,
выполненного указанным выше способом. С уменьшением угла
раствора расчетные кривые сближаются с опытными.
Однако совпадение расчета с опытом не является
вполне удовлетворительным. Повышение давления
в месте расположения скачка происходит хотя и весьма
интенсивно, но не скачкообразно. Следовательно, только
при весьма малых углах раствора скачки,
соответствующие третьей группе режимов, близки к прямым.
Заслуживает внимания также тот опытный факт, что
положение скачка в сопле зависит от того, каким путем
меняется режим сопла: изменением начального давле-
1 Влияние отрыва на положение скачка может быть учтено
опытным путем в уравнение (6-45) можио ввести опытные значения
коэффициента Л.
361
ния ро или противодавления ра- Этот результат
объясняется влиянием числа Рейнольдса при взаимодействии
скачка уплотнения с пограничным слоем.
Графики 'на рис. 6-24,а доказывают 1, что положение
системы скачков сопла зависит от основного геометри-
Рис. 6-23. Распределение давлений в сопле Лаваля при
различных режимах и угле раствора ус = 18°.
ческого параметра ft—у и угла раствора ус. С увеличе-
*
нием ус система скачков при том же отношении
давлений еа смещается к минимальному сечению.
Относительное давление за скачком s{k не зависит
от yc (кривая 1 на рис. 6-24,#) (точки при разных ус
ложатся на одну кривую).
'Изменение положения скачка в зависимости от
расчетного перепада давлений в сопле е1 (или, что то же, от /,)
и отношения давлений в выходном сечении (/?,) и
окружающей среде (ра) подтверждают графики на рис. 6-24,6.
Вместе с тем опыты подтвердили, что на режимах,
соответствующих расположению скачков в выходном сечении
1 По данным Асвуда и Кросса,
362
со
со
Рис. 6-24. Характеристики плоских
сопел Лаваля в третьей группе режимов
со скачками уплотнения в расширя
ющейся части.
а — безразмерное расстояние системы
скачков в зависимости от отношения давления
га = Ра/Ро и геометрических параметров fi=F1/F#n ~с, б—положение скачка в зависимости от
отношения давлений на срезе сопла и в среде при различных расчетных отношениях давлений;
в—действительные отношения давлений st и ej£ в зависимости от теоретического отношения давлений е^; / — скачки
Ро 1
внутри сопла, = ; 2 —скачки в выходном сечении Po/Pi= I/£i-
P\k г\к
a)
б)
в)
Рис. 6-25. Спектры потока в плоском сверхзвуковом сопле при
нерасчетных условиях. Параметры расчетного режима: £^=0,052;
М
и
2,57; угол раствора сопла 1С= 19°40'.
-ед =0,683; б —ea = 0,R18; с — еа = 0,362; г-ва = 0,068.
364
ебпла, давление в этом сечеыии (и скорость перед скачком
не зависит от угла раствора V (кривая 2 на рис. 6-24,я)
Отношение давлений e1 = J-±- отличается от расчетного
только на величину,, характеризующую потери на трение.
Последовательное развитие спектра в плоском сопле
с углом раствора расширяющейся часта ус = 19°40'
показано на рис. 6-25. При давлении в среде Рш^> Pa^>Pi
(третья и вторая группы режимов) внутри сопла возникает
Рис. 6-26. Диаграмма нерасчетных режимов
сопла Лаваля (по Б. Я- Шумяцкому).
система скачков. Замыкающим эту систему является скачок
малой кривизны (рис. 6-25,а), за которым скорость
дозвуковая. На некоторых режимах обнаруживаются
колебательные движения струи за точкой отрыва (рис. 6-25,6).
С понижением давления среды ра скачки продвигаются
от критического к выходному сечению; при некотором
давлении внутри сопла образуется система пересекающихся
косых скачков (рис. 6-25,#), которая с понижением давления
среды перемещается к выходному сечению сопла и выходит
в струю (рис. 6-25,?).
Режим работы плоского сверхзвукового сопла без учета
влияния пограничного слоя можно определить с помощью
365
диаграммы, построенной Б. Я. Шумяцким (рис. 6-26). Т\о
вертикальной оси здесь отложено относительное давление,
а по горизонтальной—расчётное число М2 для сопла. Если
Ра
известны отношение давлении £а =— и расчетное
числа Мп то, пользуясь диаграммой, можно установить, на
каком режиме будет работать данное сопло.
Кривая А соответствует расчетным значениям — . Точки,
Ро
лежащие ниже этой кривой, относятся к ^режимам первой
группы, когда на срезе сопла образуются волны
разрежения. Кривая Б соответствует предельному случаю двух
пересекающихся скачков [формула (6-36)]. Между кривыми
А и Б располагается область режимов с косыми скачками
на срезе сопла. Кривая В отвечает случаю предельного
отношения давлений за первым косым скачком [формула (6-37)].
Области между кривыми Б и В соответствуют режимы
с мостообразным скачком на срезе. Кривая Г соответствует
прямому скачку в выходном сечении сопла [формула (6-35)].
Режимы с криволинейным скачком располагаются в области
между кривыми В'к Г. Выше кривой Г находится область
прямых скачков внутри сопла. Верхней границей этой
области служит кривая Д, а нижней—кривая Г. Значе-
Ра « тт
ния —, соответствующие кривой Д, определяют режимы,
Ро
при которых скачки в сопле исчезают (прямой скачок
перемещается в минимальное сечение сопла, где М=1).
Диаграмма на рис. 6-26 построена в предположении,
что поток в сопле и струе плоский и симметричный и
течение безотрывное.
Результаты- опытов, приведенные на рис. 6-24,0,
показывают, что отношение давлений, соответствующее
положению скачка в выходном сечении сопла, с
удовлетворительной точностью можно определить по формуле
Потери энергии в .плоских соплах Лаваля при
различных режимах можно оценить по рис. 6-27. Здесь
пунктиром нанесены коэффициенты волновых потерь
в скачках уплотнения 'и коэффициенты потерь на
расширяющемся участке сопла. Кривые показывают, что на
366
Рис. 6-27. Потери энергии в плоском сопле Лавалл при различных
режимах.
опытные кривые; волновые потери (расчет) и потери в
расширяющейся части
режимах третьей группы, когда скачки располагаются
вблизи минимального сечения, основное значение
приобретают потери в диффузоре за скачком (потери трения
и вследствие отрыва).
6-6. КОНИЧЕСКИЕ СОПЛА ЛАВАЛЯ
В НЕРАСЧЕТНЫХ УСЛОВИЯХ. РЕАКТИВНАЯ СИЛА
Истечение из осесимметричного сопла при расчетном
и нерасчетном режимах обладает рядом особенностей К
Рассмотрим вначале результаты опытного изучения
спектра потока за соплом при истечении в среду с
пониженным давлением (первая группа режимов).
На кромке выходного сечения АА\ (рис. 6-28,а)
образуется коническая волна разрежения, и давление падает
от р\ до ра. В ядре струи давление снижается до
меньшего значения. В результате возникает поперечный
градиент давления, натравленный внутрь струи.
Расширение потока в конической волне разрежения приводит
к отклонению линии тока от оси и вызывает
соответствующую деформацию внешней границы на участке AD.
На участке DC граница струи -под .влиянием разности
Частично эти вопросы— затронуты в § 6-2.
367
Рис. 6-28. Схемы спектров струи за коническим соплом при
различных режимах,
давлений (давление среды'более высокое)
деформируется в противоположном направлении — струя сжимается
(рис. 6-28,а). Все слабые волны, отходящие от
границы, образуют с ней одинаковый угол (давления,
скорости и "температуры! во всех точках границы
одинаковы). При этом характеристики сходятся к оси струи.
Как известно, сходящиеся характеристики образуют
36§
криволинейный скачо-к. В случае осесимметричной
струи такой скачок имеет форму 'поверхности вращения
с криволинейной образующей.
Скачок ABBxAi (рис. 6-28,а) может зарождаться не
у выходной кромки сопла, а в ядре струи, на некотором
расстоянии от ее границы.
При значительном отклонении режима от расчетного
(pa^Pi) скачок отходит непосредственно от кромки
сопла. На оси струи возникает лрямой скачок ВВи
за которым скорость потока становится дозвуковой.
Следовательно, при пониженном давлении за соплом
в этом случае возникает мостообразный скачок.
Криволинейный скачок СВВХСХ во внешней
сверхзвуковой области является продолжением скачка АВВХА\.
Струя суживается до того сечения, где скачок СВВХС\
выходит на поверхность струи, и отражается в форме
волны разрежения. Далее струя вновь разбухает. От ее
границы отходят звуковые волны, пересекающиеся
в ядре струи. В результате здесь образуется 'конический
скачок EExFFXy замыкающий волну разрежения СЕЕХСЛ
и выходящий на поверхность струи в точках F и Fx.
По мере повышения давления среды система скачков .на
выходе из сопла меняется мало и при расчетном режиме
за выходным сечением сохраняются два осесимметрич-
ных криволинейных скачка (рис. 6-28,6). При
дальнейшем возрастании давления среды (вторая группа
режимов) форма границы струи меняется. За лервым
скачком линии тока отклоняются от оси струи (рис. 6-28,в).
Таким образом, для конического сопла первая группа
режимов непрерывно переходит во вторую без
существенных качественных изменений спектра течения
внутри струи. В отличие от плоского сопла в коническом
сопле при всех режимах в струе возникают скачки.
Если угол раствора сопла невелик, то в расчетном
режиме отсутствуют внутренний прямой окачок и
дозвуковое ядро. При повышенном противодавлении среды
система скачков вновь перестраивается: два конических
скачка соединяются прямым скачком, и внутренняя
часть струи становится дозвуковой. Повышение проти-
йода.вления приводит к расширению дозвуковой области
и соответственно к сужению внешнего сверхзвукового
течения (рис. 6-28,г). В этой группе режимов осесим-
метриччая струя также имеет ряд особенностей. Криво-
£4 М. Е. Дейч
369
линейные скачки АВ и А\В\ разветвляются в точках В
и В\, образуя уже известную мостообразную систему.
В области 3 устанавливается повышенное давление и
в сечении ССХ скачок ВСВХСХ отражается в виде волны
разрежения. Однако в этом случае отраженные
характеристики являются криволинейными.
Характеристики, отходящие от свободных границ CF
>и CiFh пересекаются. В результате, как и в случае,
показанном на рис. 6-28,а, волна разрежения из точек С
и Сх замыкается скачком CD (C\D{), На участке
правее второго прямого скачка, расположенного на оси,
поток ускоряется и становится сверхзвуковым. Далее
процесс повторяется.
Дозвуковое ядро струи обнаруживается при всех
режимах, отличных от расчетного. Однако, как и во всех
разобранных выше случаях, протяженность дозвукового
ядра невелика. Внешняя сверхзвуковая часть струи
ускоряет внутреннюю часть так, что уже на небольшом
расстоянии за скачком ВВг (рис. 6-28,а и г) поток на
оси достигает сверхзвуковых скоростей. На оси
образуется как бы сопло Лаваля, границами которого
служат линии раздела BQ и SiQi.
Для всех рассмотренных режимов характерной
особенностью осесимметричной струи является различная
кривизна ее границы, внутренних линий тока, скачков
и волн разрежения. Действительно, как уже
указывалось в гл. 4, при переходе через конический скачок
линии тока непосредственно за скачком искривляются,
причем их кривизна переменна вдоль скачка. Если осе-
симметричный скачок имеет криволинейную
образующую, то кривизна линий тока увеличивается. Линии
тока искривляются и при переходе через -коническую
волну разрежения.
Форма расширяющейся части сопла оказывает
значительное влияние на спектр струи за соплом. Опыт
показывает, что в правильно профилированном осесим-
метричном сопле скачки уплотнения за выходным
сечением возникают только при больших отклонениях
режима от расчетного (pa^Pi)- На расчетном режиме и при
незначительных отклонениях от него (pa<pi) сопло
работает без скачков уплотнения на выходе.
В конических соплах скачки в струе обнаруживаются
при всех режимах. С увеличением угла раствора расши-
370
рющейся части интенсивность скачков и их кривизна
увеличиваются. При больших углах раствора на выходе
из сопла на расчетном режиме возникает мостообраз-
ный скачок (рис. 6-29).
Расширяющаяся часть непрофилированных сопел
Лаваля выполняется, как правило, конической с неболь-
Рис. 6-29. Спектры потока в струе за осе-
симметричным соплом Лаваля. Расчетные
характеристики сопла: / = 1,52; еи = 0,066;
Ми = 1,8.
а — еа = 0,546; б — га —0,04; в —ва = 0,16.
шим углом раствора, равным 8+12°. На расчетных
режимах течение газа в сопле может быть безотрывным и
при значительно больших углах раствора.
Величину предельного угла раствора плоского сопла,
отвечающего безотрывному течению, на расчетном
режиме можно легко определить по диаграмме
характеристик (гл. 3) или с помощью таблиц (ом. приложение),
если задано расчетное значение Хь Угол сопла должен
24*
371
быть не больше угла отклонения в волне разрежения
при ускорении потока от Я.= 1 до Х\.
Вместе с тем увеличение угла раствора оказывает
значительное влияние на структуру потока в сопле при
расчетном и нерасчетных режимах. По мере увеличения угла
раствора растет величина отрицательного градиента давле-
Рис 6-30 Схема расположения скачков
в сопле Лаваля с большим углом раствора.
ления в расширяющейся части; возрастает неравномерность
потока по оси струи и в выходном сечении.
Выше были приведены спектры потока в плоском сопле
Лаваля с большим углом раствора. Опыт показывает, что
и в конических соплах с большими углами раствора
обнаруживаются аналогичные качественные изменения спектра.
Схема перемещения системы скачков внутри конических
сопел при различных режимах £a>£Ife приведена на
рис. 6-30.
Таким образом, характерные релимы сверхзвукового
сопла с большим углом раствора нельзя определять по
формулам, приведенным в предыдущем параграфе. Для
такого сопла значения pxk, pxk и plk ниже, чем для сопла
с малым углом ус, и следовательно, переход в третью
группу режимов происходит при меньших изменениях
начального или конечного давления.
На рис. 6-31 приведены коэффициенты потерь £с для
нескольких осесимметричных сопел.
Отсюда можно заключить, что минимальные потери
соответствуют режиму истечения, близкому к
расчетному. При возрастании еа потери в сопле резко
увеличиваются и достигают максимальной величины вблизи кри-
372
тйческого значения еа ж 0,55 -=- 0,65. При еще больших
значениях еа потери уменьшаются. Такой характер кривых Сс
объясняется изменением волновых и вихревых потерь в сопле
для второй и третьей групп режимов. Теоретически изме-
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7
Рис 6-31. Кривые коэффициентов потерь $с в зависимости
от еа и fv
нение потерь должно происходить только при ea>s]k.
Однако, как показывает опыт, увеличение потерь с
возрастанием еа происходит при меньших значениях sa.
Повышение давления в системе скачков, возникающих в точках
А и AY при еаО,£, распространяется через дозвуковую
часть пограничного слоя внутрь сопла и приводит к
перераспределению параметров в выходном сечении..
Максимальные волновые потери соответствуют режиму 6^ = 8^. По
мере перемещения скачков внутрь сопла (sa^>£]k) волновые
потери уменьшаются, а вихревые—увеличиваются. В соплах
с небольшим углом раствора, когда скачок приближается
К критическому сечению, отрыв потока имеет локальный
характер. На небольшом расстоянии за скачком поток вновь
подходит к стенкам сопла и вихревые потери уменьшаются.
Поэтому коэффициент потерь начинает уменьшаться. На
режимах sa^s,m волновые и вихревые потери в сопле
373
отсутствуют (режимы трубы Вентури); потери энергии ёоз-
никают только из-за трения. Как видно из рис. 6-27 и 6-31,
с увеличением [^т1 потери на режимах третьей группы
> г *
увеличиваются и область максимальных значений Сс несколько
смещается в сторону больших еа. Следует подчеркнуть,
что суммарные потери в сопле значительно выше волновых
Рис. 6-32. К выводу формулы для расчета реактивной силы R.
потерь при данном режиме ea^elk. Заметим, что характер
кривых Сс = Сс (е ) остается одинаковым для плоских и
осесимметричных сопел, однако абсолютные значения Сс
несколько отличаются.
На рис. 6-31 указаны также значения коэффициентов
расхода цс.
Сопла Лаваля весьма широко применяются в реактивных
двигателях. В этой связи остановимся кратко на
характеристиках сопел, необходимых для расчета реактивной силы.
Для определения реактивной силы, под действием
которой осуществляется полет реактивного аппарата,
воспользуемся уравнением импульсов. Для этого
опишем около аппарата замкнутую цилиндрическую
поверхность abed, все элементы которой удалены на достаточно
большое расстояние (рис. 6-32). Возмущения,
создаваемые аппаратом на выделенной замкнутой поверхности,
будут бесконечно слабыми. Запишем уравнение
количества движения в проекции на ось х (уравнение Эйлера):
374
00 OO CO "Г
0 0 О О
(6-46)
Здесь ра — давление набегающего потока в сечении
а — Ь\ /?2, с2 — давление и скорость потока за аппаратом
в сечении с — d\ F — площадь сечений а — Ь и с — d\
GJg— секундная масса воздуха, втекающая в контур;
GJg— секундная масса горючего, подаваемого в
двигатель; R — реактивная сила.
Так как сечения а — b и с—d расположены на
большом удалении от аппарата, то ра = р2. В этом случае
силы давления в указанных сечениях уравновешиваются
всюду, за исключением участка, равного площади
выходного сечения сопла Fr. Скорости отдельных струек, охва-
* тывающих аппарат, также мало различаются. Обозначив
са — скорость истечения из сопла; рх — давление в
выходном сечении сопла F19 из (6-46) получим:
GB Gr Л
R = Y\(ca-c1)dGB-^^-^cadGr-{-l(pl-pa)dFl.
О О
(6-47)
Для неподвижного аппарата, не использующего
атмосферный воздух, из формулы (6-47) находим:
G Fx
R—^l^dG^^p.-p^dF^ (6-48)
О
где G — секундный расход рабочего тела.
В средних величинах формулу (6-48) можно записать
так:
Заменив здесь
k
f са =9 A Fx = kPlfA\ Fx =k (^у-1р&Р„
окончательно получим:
Я = k (^)*~ W. + (A - Ра) Л- (6-49)
375
Заметим, что добавочный член в уравнении (6-49)
вводится только для первой и второй групп режимов
работы сопла, т. е. при сверхзвуковых скоростях
истечения.
При повышенных противодавлениях {р\>р2)
реактивная сила уменьшается, так как разность р2—р\
отрицательна. Наоборот, при расширении струи за соплом
разность (р2—р\) положительна и R увеличивается.
Если скачки расположены внутри сопла, то
истечение происходит с дозвуковыми скоростями (Р2 = Р\)
и второй член отпадает. Изменение реактивной силы
в этом случае обусловливается уменьшением скорости
истечения, которая должна быть определена с учетом
потерь в системе скачков и в расширяющейся части
сопла.
Реактивную силу удобно представить в безразмерном
виде. С этой целью разделим (6-49) >на величину p\F\.
После несложных преобразований получим:
1
R = tf+l)(l-k-=\x*y-lfa-l. (6-50)
Для оценки эффективности сопла реактивного аппарата
иногда вводится понятие коэффициента тяги
**=-%-• (6-51)
где R , Rt — реактивные силы в действительном и
теоретическом (без потери в сопле) процессах.
Связь между /?д и Rt можно найти в таком виде:
эквивалентная скорость:
8
действительный и теоретический расходы через
сопло;
теоретическая скорость истечения из сопла.
где сэ —
G и Gt —
376
Следовательно^
Vr
:Wc
(6-52)
т. е. коэффициент тяги является произведением
коэффициентов расхода и скорости.
Рис. 6-33. Изменения коэффициента <?R = ix^c в зависимости
от режима (еа), отношения f{ и угла раствора сопла ?
Характеристики <?R по опытам В. Ф. Степанчука
приведены на рис. 6-33 для сопел с различным параметром f и
для разных углов раствора.
В режимах первой группы (еа<е1) величина yR
практически не меняется. В третьей группе режимов, когда
система скачков входит в расширяющуюся часть сопла,
величина fR падает в связи с появлением значительных
волновых и вихревых потерь. Минимальное значение ?
резко уменьшается с ростом /х. Этот результат объясняется
большей интенсивностью скачков и увеличением потерь в
диффузоре за скачками в соплах с большим /1#
377
Для углов yc=126-t-24° характеристики сопел
совпадают. Дальнейшее увеличение ус ведет к резкому
снижению <pR для третьей группы режимов.
При ус = 48° на кривой ср^ появляются два максимума,
первый из которых соответствует расчетному режиму, а
второй — режиму работы сопла, как обычного
суживающегося (рис. 6-33). Это означает, что при больших ус
отрыв потока на режимах, соответствующих третьей группе,
происходит вблизи критического сечения. Опыты
подтвердили, что значение sfl, при котором в расширяющейся части
образуется отрыв, существенно зависит от угла раствора
и растет с увеличением ус.
Таким образом, в соплах с углами раствора ^{с^> 5-^-8°
на режимах третьей группы возникает сложная система
скачков. В соответствии с данными опыта чаще всего эта
система может быть аппроксимирована двумя
пересекающимися на оси косыми или коническими скачками. В этом
случае для расчета третьей группы режимов работы сопла
необходимо знать угол косого скачка в зависимости от
sm<sa<si£* ПРИ больших углах раствора, когда поток
за скачком отрывается, можно принять, что Рск~Ра- По
известным значениям М1ск и —г нетрудно найти угол
скачке к
ков (3. Если отрыва за скачком не образуется, то задача
может быть решена только подбором.
6-7. СВЕРХЗВУКОВОЕ СОПЛО С КОСЫМ СРЕЗОМ
При расчетном режиме истечение из сверхзвукового
сопла с косым срезом происходит с небольшими
изменениями спектра потока. Эти изменения обусловлены
влиянием пограничного слоя на стенке косого среза КА
(рис. 6-34).
При нерасчетном режиме, когда давление среды ра
меньше расчетного (режим 1), дополнительное
расширение струи происходит в косом срезе или за его
пределами. Если угол первой характеристики меньше, угла
косого среза ф, то расширение потока происходит за
пределами косого среза (рис. 6-34,а). В этом случае кромки
сопла А и А\ создают стационарные волны разрежения.
378
пересекающиеся не на оси струи, а в области, лежащей
ближе к кром-ке А. По этой причине нарушается
симметричность спектра истечения и струя отклоняется от
оси сопла. Волны разрежения отражаются от границы
Рис. 6-34. Схемы спектров струи за соплом с косым срезом.
струи, как волны сжатия (BCDX и B\CXD),
пересекающиеся вблизи противоположной границы. В зонах
струи 2, примыкающих к границе, давление равно
внешнему давлению ра, в зоне 3 (за пересечением волн
разрежения) давление пониженное, а в зоне 4 —
повышенное, равное давлению в косом срезе сопла р\.
При пересечении несимметрично расположенной
системы волн углы отклонения линий тока меняются от
379
сечения к сечению. Соответственно меняется и средний
угол отклонения струи.
Если первая волна разрежения из точки А частично
или полностью лежит в пределах косого среза, то
характер течения меняется (рис. 6-34,6). Отраженная от
стенки косого среза (частично или полностью) волна
разрежения приводит к понижению давления, и у кромки А
давление оказывается меньшим, чем /V В результате
в точке А образуется косой скачок уплотнения; система
волн изменяется и углы отклонения будут уже другими,
по сравнению с первым случаем. В косом скачке AD
линии тока отклоняются по часовой стрелке, поэтому
средний угол отклонения струи несколько увеличивается.
Такой характер истечения будет иметь место в том случае,
когда угол косого среза
<p<arcsinM-.
Для второй группы режимов (давление среды выше
расчетного) на кромках А и А\ возникают косые скачки
(рис. 6-34,в), пересекающиеся за косым срезом, если
угол Pi скачка из точки А\ меньше угла косого среза ф.
Точка пересечения скачков В лежит у верхней границы
струи. Поток отклоняется от оси струи, проходя
несимметричную систему скачков и отраженных волн
разрежения, причем поворот потока происходит в
противоположном первому случаю направлении. Заметим, что для
первой группы режимов (ра<Р\), поворот струи
происходит относительно точки Л, а при ра>Р\ (вторая
группа режимов) струя поворачивается относительно
точки А\. Углы отклонения линий тока, а следовательно,
и всей струи меняются вдоль потока, так же как и в
первом случае, благодаря влиянию отраженных волн.
Если cp<Pi (рис. 6-34,г), то первый косой скачок
лежит в пределах косого среза. В отраженном скачке НВ{
давление увеличивается до значения, большего, чем ра.
В результате на участке НА и в области LAKB{ давление
повышенное. Из точек А и Вх распространяются волны
разрежения AC\DX и В{ВС. В зо.нах 2 устанавливается
давление ра. В зоне 4 давление равно р\9 а в зоне 5 (за
пересечением отраженных волн сжатия) давление вновь
повышается. Далее процесс повторяется. Легко
заметить, что средний угол отклонения струи в этом случае
380
может увеличиться. При дальнейшем повышении
противодавления скачок А\Н будет поворачиваться к
сечению А{К, При «некотором значении pa = P/\k нормальное
отражение скачка А\Н становится невозможным, так
как скорость за первичным скачком близка к скорости
звука. Скачок принимает форму Я-образного скачка
Рис 6=33. Спекгр потока за соплом Лаваля с косым срезом
(волна разрежения в пределах косого среза).
А\НВ{ (рис. 6-34,(9), и в косом срезе у стенки НА
образуется отрыв струи.
Если ра — Pik, то мостообраз-ный скачок
располагается в сечении сопла А\НХ и спектр струи почти не
отличается от рассмотренного выше для сопла с прямым
срезом.
Расчет спектра и определение, среднего угла
отклонения на выходе из сопла с косым срезом могут быть
произведены методом характеристик (режимы /) в
комбинации 'с методом ударных поляр, если ра>Р\
(режимы //).
Приближенную оценку углов отклонения можно
осуществить и более простыми способами, изложенными
в гл. 8, с помощью уравнений нераврывности
-количества движения и энергии.
Опыты подтверждают рассмотренные выше спектры
истечения из сопла Лаваля с косым срезом. На рис. 6-35
отчетливо виден волновой спектр струи за косым срезом.
Заметим, что отклонение струи в косом срезе
вызывает изменение реактивной силы, расчет которой
должен быть произведен ,по измененной формуле с учетом
отклонения потока.
381
ГЛАВА СЕДЬМАЯ
ДВИЖЕНИЕ ГАЗА В ДИФФУЗОРАХ.
СТУПЕНЬ ЭЖЕКТОРА
7-1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ И РАСЧЕТ ДИФФУЗОРОВ
В диффузорах происходит преобразование
кинетической энергии потока в энергию давления. Уравнения
одномерного течения (гл. 2) показывают, что такой
процесс при дозвуковых скоростях можно осуществить
в трубе с увеличивающимся вдоль потока сечением.
Течение газа в диффузоре характеризуется
положительными градиентами давления, наличие которых
создает условия для интенсивного -нарастания
пограничного слоя и- 'в ряде случаев отрыва потока от стенок.
Влияние положительного градиента давления на
структуру пограничного слоя было подробно
рассмотрено в § 5-11. Графики на рис. 5-29 и 5-30 показывают,
что с увеличением положительного градиента давления
(параметр Г<0) резко возрастает толщина потери
импульса б** и уменьшается наполнение профиля
скорости у стенки.
При значительных градиентах давления в диффузоре
может возникнуть отрыв (гл. 5). В этом случае потери
энергии резко возрастают и диффузор не обеспечивает
заданного повышения давления.
Основная задача расчета сводится -к установлению
оптимальной формы диффузора, соответствующей
безотрывному течению и минимуму потерь энергии при
заданных режимных параметрах (числах Re и М) и
условиях на -входе 1.
С этой целью выбирается такая эпюра распределения
давлений по диффузору, который дает наименее
интенсивный рост толщины потери импульса к выходному
сечению и не приводит к отрыву слоя или смещает отрыв
к выходному сечению. Подобная задача может быть
решена путем вариантных расчетов пограничного слоя
методами, изложенными -в гл. 5.
Выбрав рациональное распределение давлений,
нетрудно рассчитать проходные сечения, установить фор-
1 Имеются в виду длина, ферма и шероховатость стенок вход-
лого участка диффузора, начальная степень турбулентности потока,
распределение скоростей по сечению и пр.
382
My диффузора и определить величину потерь й нем.
В случае, когда форма диффузора является заданной,
распределение давлений по оси рассчитывается по
методу канала (§ 3-5).
В практике расчетов принято потери энергии в
диффузорах рассматривать как сумму двух составляющих:
потерь на трение в пограничном слое £тр и потерь
расширения £р. По смыслу величина £р характеризует
потери, вызванные вихревым
характером движения в
зонах отрыва.
При этом
предполагается, что рассматриваемые
потери аналогичны потерям
при внезапном расширении
потока, когда при 'переходе
из узкой части трубы в более
широкую граница струи распадается и свертывается
в вихри. На поддержание вихревого движения
затрачивается часть энергии потока. В результате внезапное
расширение сопровождается потерей давления, причем
коэффициент потерь для несжимаемой жидкости при
внезапном расширении (потери на удар) мож^т быть
определен по формуле
Рис. 7-1. Схема диффузора.
С.
уд
(7-1)
где ! = у—степень расширения диффузора [Fl—сечение
входа и F2— сечение выхода диффузора (рис. 7-1)].
Соответствующая потеря давления выражается
формулой
Ч. = *-А = -£с = ^--т('-Й)'. (7-2)
где p2t—давление за внезапным расширением при отсутствии
потерь; сг и с2 — скорости в сечениях Fx и F2.
В диффузоре (рис. 7-1) потери энергии и давления,
обусловленные расширением сечений, будут меньше, так
как сечения меняются постепенно.
Отношение
уд
(7-3)
383
где Ар —потеря давления в диффузоре, называют
коэффициентом смягчения удара. Следовательно, коэффициент ф
представляет собой отношение потерь давления в
диффузоре к потерям давления при внезапном расширении.
f>°
Ofi
0.6
V
0.2
\t
/
1
1
1
1
1 J
/ /
/
t
jP*
*r=2J5
--4,0
9
»..
10°
20°
30°
W°
Рис. 7-2. Коэффициент смягчения удара в
зависимости от угла раствора и параметра f для
диффузоров ( — круглого сечения;
квадратного сечения).
Как видно из рис, 7-2, коэффициент ф слабо зависит
Р
от отношения f = -^ и формы сечения и в основном опре-
деляется углом раствора диффузора уд.
Использование коэффициента ф для расчета диффузоров
является формальным и может быть оправдано только тем,
что обнаруживаемые потери в диффузорах оказываются
большими, чем потери на трение, определяемые для
безградиентного течения.
Действительно, при вычислении потерь на трение, как
правило, используют известную формулу (гл. 5):
иг рР^о dx
(7-4)
с коэффициентом 5, определяемым по одной из известных
формул для безградиентного течения, например по
формуле Блаузиуса:
384
S=0,3164Re 4. (7-5)
Здесь c0 — скорость на оси диффузора; dx — элемент
длины; D — диаметр поперечного сечения рассматриваемого
участка и
Re = ^ (7-6)
— число Рейнольдса.
Величина абсолютных потерь на трение,
вычисленная таким способом, оказывается значительно меньше
экспериментальных значений, даже при безотрывном
течении, так как формула (7-5) не учитывает влияния
градиента давления.
Потери в диффузорах любой формы при безотрывном
течении -могут быть вычислены с использованием теории
пограничного слоя, например по методу А. Е. Зарянки-
на, основанному на применении понятия толщины» потери
энергии.
Для конических диффузоров путем некоторых
упрощений им получена формула для коэффициента потерь
в следующем виде:
^=М2£± (, i). (7.7,
Re0'2 sin 1*K ' >
2
Используя этот коэффициент, можно вычислить потери
давления в диффузоре:
ЬРя = Ри-Р* = 1л94- (7"8>
Сравним результаты- расчетов по формуле (7-7)
с данными эксперимента.
Из кривых потерь на рис. 7-3 следует, что потери
в изоградиентном диффузоре1 значительно больше, чем
в коническом. Все диффузоры имели одну и ту же
степень расширения / = 2,25. Изменение потерь в
зависимости от числа Mi<0,8 показывает, что с ростом скорости
1 Изоградиентными диффузорами называются диффузоры с
постоянным значением градиента давления dp/dx вдоль оси.
25 м. е. Дейч
385
Потери несколько снижаются Однако всюду величине
потерь в ,изоградиентном диффузоре примерно в 3 раза
больше, чем в 'коническом, что указывает на отрывный
характер течения в нем.
Оценка потерь по формуле (7-7) для конических
диффузоров при Mi = 0,7 дает 5,5°/0 для уд=10° и 5°/0 для
Рис. 7-3. Изменение потерь в различных диффузорах в
зависимости от числа М,.
/ —изоградиентный диффузор; 2 — конический дирфузор (y„ = 6°);
3 — конический диф рузор (уд —• П°).
уд = 6°. Эти значения Сд практически совпадают с
данными эксперимента.
Для расчета распределения скоростей по оси
диффузора проинтегрируем уравнение (5-10):
d\t
-(i._l)_ M-J-j *.)!£
k — \~2\dF , 2k gdL
k + l
яг
£ = 0, (7-9)
где элементарная работа трения dL может быть выражена
через коэффициент потерь в диффузоре.
В результате интегрирования получим:
Л.
k—l , у
(7-Ю)
386
где
(7-12)
* у у /v — 1 у
Следуя методу, изложенному в работе [Л. 4], введем
по аналогии с приведенным расходом в данном сечении
q(%) функцию
1 k
1 k — l
1 k+ 1
1
1-F
-П
Ч~2~У
"Ч1-^*2/- (7"13)
При отсутствии потерь ^ (Я) = ^(Я), поэтому функцию
^(Я) можно назвать обобщенным приведенным расходом.
Зная распределение скорости вдоль оси диффузора, по
уравнению неразрывности с помощью этой формулы можно
найти отношение давлений полного торможения в
произвольном сечении диффузора [см. формулу (2-41)]:
. — Р*.— х ^ (7-14)
0 Рог f ?*№
и соответствующее отношение статических давлений:
a-7W (7"15)
Здесьа(Я) = ^?(Я) (см. гл. 2).
Расчет распределения параметров потока вдоль оси
диффузора с учетом вязкости показывает, что скорость
потока в произвольном сечении больше, а статическое
и полное давления меньше, чем соответствующие
значения этих величин, полученные без учета влияния
вязкости. Кривые р показывают, что восстановление
статического давления в коническом диффузоре происходит
наиболее интенсивно в начальном участке. Далее
возрастание р резко замедляется, а, начиная с некоторого
■предельного значения /пред, давление начинает
снижаться.
25*
387
Формула (7-15) отражает также влияние
сжимаемости: с увеличением скорости на входе положительные
градиенты давления возрастают особенно интенсивно
на начальном участке.
Для оценки точности расчета по формуле (7-14) на
рис. 7-4 приведены значения ео по данным К. С. Сцил-
ларда для диффузора с / = 4,92 и уд = 4 и 8°. Совпадение
расчетных и опытных данных следует пригнать
удовлетворительным во всем диапазоне чисел M\<Mi:
Ь°
0,96
0,92
0;8д
ОМ
' 0
Год "
Г^г^
Га
°»xJo^
шЧ°
4^^v
*•*
• *
• X
М1 |
0,2
0,4
0,6
с,д 1,о
1,0
0,96
0,92
0,8в
0,84
*>ГЧц
(
:
4>ч
«
хх"Ч.
х**Ч
в хх
•
1
1
1
х ^Ч.
XX {
х
оо
X
д Ml
0,2
0,f
0,6
0,8
],°
Рис. 7-4. Сравнение расчетных и
экспериментальных значений е0 для конических диффузоров
с различными углами раствора (опыты
К. С. Сцилларда),
388
Остановимся теперь на характеристиках диффузоров,
получаемых .при экспериментальном исследовании.
Рассмотрим в тепловой диаграмме изменение
состояния газа в дозвуковом диффузоре. Параметры полного
торможения потока на входе в диффузор определяются
ioj т> ш
Рис 7-5 Процесс изменения состояния газа
в дозвуковом диффузоре в тепловой
диаграмме.
точкой 0\ (ри'с. 7-5), а параметры движущегося газа до
диффузора — точкой 1.
Сжатие в диффузоре происходит с .возрастанием
энтропии. Этот процесс изобразится линией /—2, причем
точка 2 соответствует параметрам газа за диффузором.
Точка 02 соответствует состоянию полностью
заторможенного за диффузором потока. В тепловой диаграмме
легко найти соответствующие энергетические
характеристики: потерю кинетической энергии ДА, изменение
потенциальной энергии Н0п и кинетическую энергию
потока в выходном .сечении Я0к. Коэффициент потерь
энергии в диффузоре, как и в случае скачка, определяется
по формуле (4-ЗЗа):
— ( £=ГГ-Т2 ~1 И 8од — 1 Ь (7~16)
С
%н
\
389
где е0д=г^ — коэффициент восстановления давления тор-
Ро1 можения в диффузоре.
Эффективность диффузора можно характеризовать
также энергетическим к. п. д.
^=Й7 = 1-Сд- (7"16а)
В некоторых случаях для оценки диффузора пользуются
другим понятием к. п. д., определяя эту величину по
формуле
п Ок
где Н0п — изменение потенциальной энергии потока в
диффузоре;
Hqk — разность кинетических энергий потока во
входном и выходном сечениях диффузора.
После подстановки HQn и Н0к можно получить к. п. д.
диффузора в виде:
-!■*« *=!
Энергетический к. л. д. зависит только от потерь
энергии в диффузоре, в то время >как г]д' меняется при
изменении степени сжатия. Легко видеть, что т]д>г]д/.
Выбор оптимального эпюра скоростей (или
давлений) вдоль диффузора осуществляется на основании
вариантных расчетов.
Величины 6** и dp/dx, определяющие состояние
потока в диффузоре, зависят от степени расширения
(отношения f = F2/Fi) и угла раствора диффузора уд- Отсюда
вытекает, что форма оптимального эпюра давлений
зависит от этих геометрических .параметров.
В диффузорах с плавным .изменением .сечения (с
малыми углами раствора) при безотрывном течении
целесообразно выбирать эпюры с большими градиентами на
входных участках (эпюры 2 или 5 на рис. 7-6,а)
и с уменьшающимися значениями dp/dx в среднем и
выходным участках; удовлетворительные результаты
могут быть получены в диффузоре с прямолинейными
стенками (эпюр 3 на ри'с. 7-6,а).
390
В диффузорах с большими углами раствора отрыв
возникает в сечениях входного участка. Для того чтобы
сместить отрыв к выходному сечению, необходимо
Рис. 7-6. Эпюры давлений и проходных
сечений диффузоров различной формы.
уменьшить градиенты давления на входе, т. е. перейти
к кривой dp/dx = const (эпюр 4 ,на ржа. 7-6,а и др.).
Изменение проходных сечений диффузоров,
обеспечивающих эпюры указанных давлений, представлены на
рис. 7-7,6.
£91
?-2. ДбЗВУКОВЫЕ ДИФФУЗОРЫ
.Рассмотрим влияние основных геометрических и
режимных параметров на эффективность .плоских и
конических диффузоров. Как указывалось, важнейшими
геометрическими параметрами являются угол раствора уд
и степень расширения f.
Из приведенных формул (§ 7-1) следует, что при
заданном распределении скоростей значение .параметра Г
не зависит от уд и эт^ величина может быть выбрана
произвольно. На основании формулы (7-11) можно
заключить, что при больших углах уд потери в диффузоре
уменьшаются.
Однако, как показывают опыты, при уд^8-М2° в
конических диффузорах возникает отрыв; потери энергии
при этом резко возрастают.
Можно полагать, что образование отрыва при
больших углах раствора 'связано с неравномерным
распределением скоростей на входе. В большинстве случаев
переход от конфузорной части к коническому диффузору
осуществляется с резким изменением кривизны стенок,
причем скачок кривизны возрастает с увеличением уд
Такое местное нарушение граничных условий является
причиной раннего отрыва пограничного 'слоя при
увеличении угла уд- Влияние указанного нарушения особенно
велико в тех случаях, когда пограничный слой на
значительном расстоянии от входа ламинарный.
Отметим, что характер неравномерности поля
скоростей на входе существенно влияет на потери в
диффузоре. Особенно неблагоприятным является эпюр
скоростей 1У вытянутый в средней части (рис. 7-7); менее
существенно влияние неравномерности, если «поток
характеризуется повышенными скоростями у-стенок (эпюра 2).
В этом случае потери могут оказаться меньшими по
сравнению с равномерным полем -скоростей (эпюра 3).
Неравномерность, характеризуемая эпюрой 2 на рис. 7-7,
благоприятна потому, что в этом случае пограничный
слой в диффузоре становится тоньше, а точка отрыва
смещается по потоку.
При правильной организации потока на входе в
диффузор угол раствора уд можно принимать увеличенным.
При определении оптимального угла раствора уд. опт,
т. е. такого максимального угла, при котором еще не
392
произошел отрыв потока, можно для круглых
диффузоров при 'малых скоростях пользоваться формулой
И. Ё. Идельчи'ка:
Тл
=°-«'деГ
\ч»
где <рн — опытный коэффициент, учитывающий влияние
неравномерности поля скоростей на входе в
диффузор.
Следует подчеркнуть, что формулы для Тд опт
представляют эту величину в зависимости от числа Рейнольдса,
&///////////£.
\777777777,
О,"
0,3
о, г
0,1
\сз
1 "^
л
*s—^
jl .
Уз
10°
12°
16°
1д°
Рис. 7-7. Влияние характера неравномерности поля
скоростей во входном сечении диффузора на потери; Re! =
= 3.105; Mi = 0,5.
функцией которого является коэффициент сопротивления ?.
Расчеты показывают, что с ростом Rex удопт
увеличивается.
По опытным данным К. С. Сцилларда с ростом
числа Mj преимущество малых углов возрастает.
Следовательно, с увеличением Mt оптимальный угол раствора
должен уменьшаться (рис. 7-4). Этот результат
представляется очевидным, так как влияние сжимаемости прояв-
393
ляется в том, что увеличиваются продольные градиенты
давления. Так, при увеличении числа Mi от 0 до 0,8удопт
уменьшается на 0,7 — 0,9° (Rex = 106). Эта зависимость
Тдопт от числа ^i оказывается менее интенсивной, чем
от Re1#
Опыты показывают, что для круглых конических
диффузоров оптимальные значения Тдопт можно принимать в
пределах удопт = 6-г-15°. Наиболее употребительны
средние значения 10—12°.
Важной геометрической характеристикой диффузора
является отношение сечений /. При заданной скорости на
входе повышение давления происходит только до
определенных пределов, причем в коническом диффузоре и в
диффузоре оптимальной формы наиболее бурный рост давления
соответствует начальному участку.
Значение параметра f, отвечающее максимальной
степени сжатия в диффузоре, называется предельным.
Выполнение диффузора с большим отношением / нецелесообразно,
так как при этом на выходном участке обнаруживается
снижение давления.
Результаты расчета показывают, что / зависит от
угла раствора диффузора уд, безразмерной скорости
потока Ях и числа Rex на входе. С увеличением уд и Ях
величина / уменьшается. Физически этот результат
объясняется тем, что с ростом уд и *i увеличиваются градиенты
давления. Возрастание числа Рейнольдса приводит к
увеличению f , так как при этом уменьшаются потери на
трение в диффузоре.
Следует отметить, что практически принимаемые
значения /пред должны быть меньше расчетных. Действительно,
наиболее интенсивное сжатие газа происходит во входном
участке диффузора, так что в сечениях / = 2,5-г-3,5
повышение давления составляет около 90°/0 максимального,
соответствующего /пред (для диффузоров с углами
раствора уд = 8 н-15°). При окончательном выборе / следует
производить детальный расчет пограничного слоя и
оценивать вероятность образования отрыва по параметру
Г<Г5-
Результаты соответствующих расчетов для конических
диффузоров показаны на рис. 7-8. Видно, что предельные
394
значения f д , определенные по условиям безотрывного
течения (Г << Г5) и максимального повышения давлений в
диффузоре рг/рх = 0,9 (p2/Pi)M3KC, существенно ниже
теоретических /п ед, изображенных сплошными линиями.
Для диффузоров, построенных по рациональному
распределению давлений, значения / могут быть выбраны
in\ i i I u±J
1 0° 10° 20° 30° 40°
Рис. 7-8. Предельные степени расширения
диффузора в зависимости от угла
раствора и безразмерной скорости на входе.
большими, так как в этом случае течение в диффузоре
безотрывное.
Влияние формы диффузора на его основные
характеристики частично рассматривалось в § 7-1. Как указывалось,
решение этого вопроса не является универсальным;
оптимальный эпюр давлений меняется в зависимости от двух
основных геометрических параметров — отношения
сечений / и длины диффузора. При малой длине и больших /,
когда градиенты давления на входе весьма резко
возрастают, возможно образование отрыва уже во входных
сечениях.
В этих случаях необходимо уменьшать dp/dx на входе,
причем диффузоры с постоянным ] градиентом давления
оказываются более эффективными для больших углов рас-
395
твора, т. е. при малой длине и больших f. Этот факт
отчетливо подтверждается опытами И. Е. Идельчика с
плоскими диффузорами (рис. 7-9).
Так как в изоградиентных диффузорах потери на
трение больше (в связи с тем, что Ь** возрастает на выходе
интенсивнее), то применение таких диффузоров следует
считать целесообразным только при больших углах рас-
Рис 7-9 Изменение коэффициента потерь в плоских
диффузорах в зависимости от относительной длины /
твора уд^18°. В интервале уд=12~-18° лучшие
результаты дают диффузоры с прямолинейными стенками
(Тд = const). При малых углах уд<12° следует переходить
к диффузорам с криволинейными выпуклыми стенками
(кривые 2 на рис. 7-6).
Возможно также применение комбинированных
диффузоров, принципиальные схемы которых приведены на
рис. 7-10. Особый интерес представляет ступенчатый
диффузор. Повышение давления здесь происходит вначале в
обычном плавно расширяющемся канале, а затем давление
растет при внезапном расширении сечения. Такие
диффузоры следует применять при малой длине и больших
отношениях /. Для каждого значения f существует
определенная оптимальная длина /д, соответствующая минимальным
потерям. При выбранных оптимальном угле раствора у опт
396
й / однозначно определяется площадь выходного сечений
плавной части диффузора F2 .
Ступенчатые диффузоры имеют существенные
преимущества в тех случаях, когда необходимо сократить
длину диффузора. При малых уд применение
ступенчатого диффузора нецелесообразно, так как суммарные
потери при внезапном расширении возрастают.
Рис. 7-10 Схемы комбинированных диффузоров.
а, б и а —ступенчатые диффузоры, в —диффузоры с малыми (/) и
большими (2) градиентами давления на входе; г —диффузор с разделительными
стенками, е —изоградиентный диффузор.
Опыты показывают также, что на эффективность
диффузора влияет форма его поперечных сечений.
В круглых и плоских диффузорах потери энергии
оказываются минимальными. В диффузорах квадратного или
прямоугольного сечения с расширением в двух
плоскостях потери выше. Это объясняется различным
изменением давлений вдоль потока: градиенты давлений в
круглых и плоских диффузорах при одинаковых Fx и F2
будут меньше, чем .в квадратных. В некруглых
диффузорах потери .повышаются вследствие интерференция
пограничных слоев в углах.
397
Опыты подтверждает значительное влияние
Начальной турбулентности на характеристики диффузора в
полном соответствии с тем, что было получено при
исследовании пограничного слоя (гл. 5). Коэффициенты
потерь интенсивно 'возрастают с увеличением начальной
турбулентности.
Остановимся на оценке влияли я основных режимных
параметров, чисел Rei и Mi на характеристики диффу-
Рис 7-11. Влияние чисел Rex и Mt на коэффициент
потерь в конических диффузорах.
зоров. Опыты показывают, что характер кривых ^(Rei)
зависит от геометрических характеристик диффузора:
Уд и /. Соответствующие кривые по данным различных
исследований приведены на рис. 7-11. Как видно,
влияние Rei ощутимо лри Rei^3-105 в зависимости от уд, f2
и формы диффузора. Отметим, что характеристики
gA(Rei) при больших углах раствора и f>4 протекают
более полого. Здесь наблюдается'аналогия с влиянием
начальной турбулентности: при больших уд влияние Е0
ослабевает.
Возрастание числа Mi приводит к увеличению
градиентов давления; в соответствии с этим потери на
трение в диффузоре с ростом Mi начиная с Mi>0,7
увеличиваются. Сжимаемость приводит к росту вихревых
потерь в диффузоре; при отрывном обтекании с
увеличением Mi точка отрыва потока перемещается -к входному
сечению.
При околозвуковых скоростях на входе (при Mi<l)
потери в диффузоре возрастают особенно интенсивно,
так как градиенты давления во входном участке резко
393
увеличиваются, чтб приводит к раннему отрыву даже
при .небольших углах раствора (рис. 7-4). Следует
подчеркнуть, что кривые на рис. 7-3 отражают влияние не
только сжимаемости, но и числа Рейнольдса.
Уменьшение £д 'с ростом Mi при 0,КМ1<0,5 обусловлено
изменением Reb так как в этом диапазоне чисел Mi влияние
сжимаемости еще не сказывается.
Рассмотрим в заключение некоторые результаты
опытов, проведенных <с целью снижения потерь в
диффузорах с 'большими углами раствора. По данным
И. Е. Идельчика, наряду с применением изоградиентных
диффузоров понижение потерь в диффузоре может быть
достигнуто установкой сеток, разделительных сгенок
и организацией отсоса или сдува пограничного слоя,
а также применением ступенчатых диффузоров.
О.пыты В. Кмоничка показали, что установка
проволочного пучка приводит к заметному уменьшению
потерь в плоском диффузоре с большими углами раствора
(рис. 7-12,а, бив). Аналогичные.результаты были
получены для круглых диффузоров при радиальном
расположении проволок (рис. 7-12,г).
Обнаруживаемый эффект объясняется тем, что
вводимое в диффузор сопротивление выравнивает поле
скоростей на выходе из диффузора. Выравнивание
скоростей приводит к смещению точки отрыва по потоку, так
как .профиль скорости у стенок становится более
полным (рис. 7-7).
Оптимальное положение и форма проволочных
решеток, вводимых в диффузор, существенно зависят от
формы и угла раствора диффузора, а также от режима
потока (чисел Mi и Rei).
Исследования В. Кмоничка проведены были с
сопротивлениями, введенными внутрь диффузора. При этом
оказалось, что для плоского диффузора с углом
раствора уд= 15° оптимальным является вариант нарис 7-12,а,
для уд = 30° лучшие результаты показали варианты б и е.
Улучшение течения газа в диффузоре с большими
углами раствора можно обеспечить также с помощью
глубоких канавок, вытачиваемых на некотором расстоянии от
входного сечения (рис. 7-12,(9). Создаваемый канавками
otcoic -слоя смещает отрыв по потоку, как это показа™
опытами В. К. Мигая,
399
4^
О
О
_>^
**%^ ч
Рис. 7-12. Влияние местных сопротивлений на потери в плоских диффузорах при небольших скоростях*
7-3. ВЫХЛОПНЫЕ ПАТРУБКИ ТУРБОМАШИН
Отвод газа из турбомашины осуществляется по оси
вращения либо по конструктивным условиям под
прямым углом к ней. Частичное преобразование
кинетической энергии выхлопа в потенциальную дозволяет
повысить к. п. д. турбомашины. Такое преобразование осу-
Рис. 7-13 Рациональные схемы выхлопных патрубков
турбомашин.
ществимо в диффузорных выхлолных патрубках,
различные схемы которых приведены на рис. 7-13.
Первые две схемы (а и б) показывают наиболее
простые криволинейные «кольцевые диффузоры F2>FX с
осевым или диагональным потоком газа.
Три других патрубка должны обеспечить поворот
потока на угол 90° к оси вращения. В схеме патрубка
на рис. 7-13,6 применен развитый кольцевой диффузоре
с диагональным или осевым направлением потока. В
таком диффузоре в основном и происходит лреобразова-
ние кинетической энергии в потенциальную; поворот
потока на угол порядка 90° осуществляется уже при
малых скоростях в улитке 2. Выходная часть патрубка
(радиальный диффузор) ,имеет относительно -малую длину.
26 М. Е. Дейч
401
Другая схема (рис. 7-13,г) обеспечивает
восстановление давления по'сле поворота в радиальном
диффузоре. В таком патрубке поворот желательно осуществлять
в конфузорном потоке или в 'крайнем случае ,при
постоянной скорости.
Как видно' из сравнения схем в >и г, первая схема
имеет значительно большие осевые размеры, а вторая —
радиальные.
Третья схема (рис. 7-13,(5) является
комбинированной. Здесь выполняются относительно короткие осевой
(или диагональный) и радиальный диффузоры.
Следовательно, восстановление давления в таком патрубке
осуществляется частично до поворота >и частично после
него. Такая же задача решается в схеме е,
выполненной со ступенчатым диагональным диффузором.
Эффективность каждой схемы существенно зависит от
организации поворота потока в улитке (при переходе из
осевого в радиальный диффузор). Эта задача решается
соответствующим выбором рациональной системы
кольцевых поворотных направляющих лолаток и ребер,
устанавливаемых на повороте.
Как указывалось в § 5-15, в криволинейные каналах
возникают вторичные движения жидкости, связанные
с неравномерным распределением давлений на повороте.
В кольцевых криволинейных каналах структура
вторичных течений в зависимости от отношений диаметров
d2/dx может существенно отличаться от обычной для
простого поворота. При больших значениях d2/d\ опыт
подтверждает существование двух вихрей в поперечном
сечении кольцевого канала. Если отношение диаметров
близко к единице, то в поперечном сечении возникают
четыре вихря, расположенных в сечении кольцевого
канала (два внутренних ,и два наружных).
Имея в виду сказанное выше о влиянии формы
сечения канала, можно заключить, что неизбежное
переформирование сечения лотока в патрубках турбомашин
должно быть организовано с учетом дополнительных
потерь, которые могут при этом возникнуть.
Конструктивно неизбежными в патрубках являются
ребра жесткости. Выбор рациональной схемы
расположения ребер и их формы, обеспечивающей
минимальные потери, составляет важную задачу при
конструировании патрубков.
402
Особенно сложными конструктивно являются
выхлопные патрубки мощных паровых турбин. Большие
объемные расходы .пара в конденсатор при конструктивно
ограниченных осевых и радиальных размерах приводят
к сложной схеме патрубка с большим .количеством
ребер жесткости. Пример рационального размещения
ребер на 'повороте показан на рис. 7-13 и 7-17.
При исследовании .выхлопных патрубков
экспериментально определяются основные характеристики,
Рис. 7-14 Процесс в выхлопном патрубке
в тепловой диаграмме.
к числу которых относятся а) коэффициент,
оценивающий энергетические потери патрубка; б) коэффициент
восстановления давления, показывающий изменение
статического давления; в) коэффициент неравномерности
поля скоростей в выходном сечении.
Процесс в патрубке удобно рассмотреть в тепловой
диаграмме (рис. 7-14). Обозначив через Poi и ро2
давления торможения на входе >и на .выходе из .патрубка,
Рх и р2 — статические давления .в этих же сечениях,
находим коэффициент потерь энергии по формуле (7-16).
Получив после коэффициентов .потерь в выходном
сечении патрубка, можно найти его среднее значение по
уравнению энергии.
На р.ис. 7-14 рассмотрены два возможных случая:
а) выхлопной патрубок турбомашины работает как
диффузор (процесс 1—2)] б) в выхлопном патрубке проис-
26*
403
ходит снижение давления вследствие больших потерь
(процесс 1—2'). Здесь же можно указать величину
кинетической энергии за .патрубком (/ы), изменение
потенциальной энергии в .патрубке (h2n) и потери (Ah или
соответственно Д/i').
В практике лабораторных исследований выхлопных
патрубков находят применение и другие оценочные
коэффициенты. Так, например, лаборатория турбин ЛМЗ
использует для оценки патрубка величину
где //02 — изоэнтропический перепад, соответствующий
расширению от давления торможения на входе
р01 до статического давления на выходе /?2.
Связь между коэффициентом потерь энергии С и Сп
устанавливается следующими очевидными соотношениями
(рис. 7-14):
"02 ~ Иог - h2n = Я01 - (Я02 - h2k) = СдЯ01 + А2Л,
поэтому
С = С _)_ — =С +А
Отсюда следует, что Сп включает кинетическую
энергию на выходе из патрубка h2k = h2k/H01. Нетрудно
видеть, что если Сп>1 (Я^2>Я01), то p2<CPi (выхлопной
патрубок не является диффузором); если Сп<1, то p2^>Pi-
Для несжимаемой жидкости коэффициент патрубка
определяется по формуле
С„
, Pol — /*1
п Pox — Pi
С учетом сжимаемости Сп можно получить в таком
виде:
404
Коэффициент Сп позволяет вычислить потерю мощности
з выхлопном патрубке:
где Gn — расход газа через выхлопной патрубок.
Вторая характеристика выхлопного патрубка —
коэффициент восстановления — определяется по формуле
с p2—p1__k + \Poi Pox п 1Q
~~2 Р°*
Из формулы (7-19) видно, что для определения
величины 1Р необходимо измерение статических давлений
на входе в патрубок. Такой опыт оказывается
трудоемким. Используя расходную характеристику Gn=/(poi)
и таблицу газодинамических функций, давление pi
можно получить расчетным-путем.
Тре1ья характеристика патрубка позволяет оценить
неравномерность поля статических давлений и скоростей
в выходном сечении.
Как указывалось, важным элементом выхлопного
патрубка является криволинейный кольцевой диффузор.
Опыты М. Хибша показали, что коэффициент потерь для
такого диффузора зависит от следующих геометрических
параметров (рис. 7-15,а):
Р
отношения площадей сечений / = —; относительной вы-
соты кольца на входе сьх\гту относительной кривизны
средней линии —^-; относительной длины средней линии
и закона изменения площади f (x).
Примеры соответствующих зависимостей приведены на
рис. 7-15,6. Кривые показывают, что оптимальное значение
-£- лежит в пределах 0,25 — 0,4, причем с ростом / эта
величина увеличивается.
При расчете криволинейных диффузоров используют
понятие эквивалентного конического диффузора, длина ко-
405
торого, а также площади Fl и F2 совпадают с
соответствующими геометрическими параметрами исходного
диффузора. В соответствии с этим вводится понятие
эквивалентного угла раствора.
Аналогичная характеристика может быть использована
и для кольцевых криволинейных диффузоров.
Потери в кольцевом криволинейном диффузоре
возрастают с увеличением / и с уменьшением aJrmV
Рис. 7-15. Схема (а) и коэффициенты потерь в криволинейном
кольцевом диффузоре в зависимости от основных геометрических
параметров (б, в и г).
Значительное влияние на потери оказывает форма
диффузора в продольном разрезе. Вид функции / (х)
определяет изменение давлений по диффузору, т. е. структуру
пограничного слоя и 8*#(лг).
Выбор рациональной функции f (х) можно осуществить,
например, путем оценки изменения 6** при различных
эпюрах давления. При этом необходимо учитывать
конструктивные особенности проектируемой машины.
406
Схемы часто применяемых кольцевых выхлопных
патрубков приведены на рис. 7-16. Следует подчеркнуть, что
потери в таких диффузорах, как правило, невелики, если
указанные геометрические параметры близки к оптимальным.
Вариант диффузора 4 (рис. 7-16) с максимальной кривизной
образующих дает максимальные потери, а вариант
диффузора 2 — минимальные.
Результаты исследования кольцевых диффузоров были
положены в основу разработки выхлопного патрубка тур-
Рис 7-16 Схемы применяемых кольцевых выхлопных патрубков (а)
и зависимость коэффициентов потерь от числа Rex (б).
бины, схема которого приведена на рис. 7-17,а. Патрубок
состоит из криволинейного кольцевого диффузора / и
улитки 2 (выхлопной части), в которой происходит поворот
потока на 90°. На входе в улитку при повороте поток
раздваивается центральным ребром 3 и растекается по
криволинейным каналам, образованным ребрами 4,4', 5,5' и
т. д. Профилировка межреберных каналов осуществляется
таким образом, чтобы потери от вторичных течений были
минимальными. Это'достигается выполнением канала вначале
(ат ат \
— > 1 и —' > 1 )•
а1 аг J
Представленные на рис. 7-17,6 результаты исследования
такого патрубка показывают, что его эффективность
существенно зависит от соотношения площадей кольцевого
Р
диффузора и улитки /=р? и f1 = FJF2. Наибольшие зна-
чения коэффициентов Сп получены для вариантов / = 2,5 и
fх = 1Д6. С увеличением / до 3,32 и при соответствующем
уменьшении fx до 1,1 Сп уменьшился до 0,75. Близкий к
407
оптимальному вариант соответствовал отношениям сечений
/ = 3,04 и ^ = 1,2.
Полученные при этом значения коэффициентов £п
и их изменение в зависимости от числа Rei отчетливо
показывают, что при правильном выборе соотношения
Рис. 7-17. Схема выхлопного патрубка турбины (а) и его
характеристики (б).
проходных сечений выхлопной патрубок менее резко
реагирует на изменение этого режимного параметра.
Вариант комбинированного патрубка с коротким
осевым и радиальным диффузорами при условии
правильного выбора соотношений проходных сечений дает
результаты, 'близкие к тем, которые получены для первого
варианта.
Влияние сжимаемости на характеристики выхлопного
патрубка можно оценить по кривым на рис. 7-18. С ро-
408
-Ctoim Mi отмечается возрастание йотерь (£п
увеличивается), особенно интенсивное при Mi>0,8. Характерно» что
патрубки 'с развитым 'кольцевым диффузором менее
чувствительны -к изменению Mi (кривые 1 и 2 на рис. 7-18).
Патрубок без диффузора практически не реагирует на
изменение Mi (кривая 4) и имеет £П>1.
Таким образом, проведенные опыты показали, что
введение осевого 'И радиального диффузоров в схему
выхлопного патрубка позво- ^
ляет существенно улучшить * г
его характеристики и
обеспечить частичное
восстановление давления за турбома-
шиной.
Правильным выбором
формы' и трО'Ходных сечений
диффузоров и улитки, а
также рациональным
расположением ребер жесткости
можно повысить
эффективность патрубка.
Опыты показывают, что
в некоторых случаях
заметные преимущества имеет выхлопной патрубок с
лопаточными решетками диффузорного типа,
устанавливаемыми на повороте (рис. 7-13).
Практический интерес представляет «вопрос о
влиянии неравномерности (закрутки) потока на входе в
патрубок. Соответствующие опыты показали, что
отклонение от осевого входа в пределах ±15° не приводят к
заметному .изменению характеристик патрубка.
7-4. СВЕРХЗВУКОВЫЕ ДИФФУЗОРЫ
Из основного уравнения одномерного течения
следует, что торможение сверхзвукового потока можно
осуществить в трубе переменного сечения, входная часть
которой выполнена суживающейся, а выходная —
расширяющейся. В первой части скорость уменьшается и
достигает критического значения в минимальном сечении.
Тогда в расширяющейся части продолжается процесс
сжатия дозвукового потока.
Отсюда следует, что принципиально в 'качестве
«идеального» диффузора можно использовать сверхзву-
Рис. 7-18. Характеристики вы*
хлопного патрубка с
диффузором (У, 2 и 3) и без
диффузора (4).
409
Ковоё сопло с профилированными стенками,
предполагая течение в нем обращенным (рис. 7-19). Благодаря
плавности профилированных стенок, в каждой точке
которых поток совершает поворот на малый угол, <во
входной части диффузора должна возникнуть система
слабых волн сжатия (характеристик). Проходя эту систему,
Рис. 7-19. Схемы сверхзвукового (а) и около-
- звукового (б) диффузора с прямым скачком
уплотнения на входе.
поток тормозится изоэнтропически. Система слабых волн
сжатия при этом полностью совпадает с системой
слабых волн разрежения (характеристик) в
расширяющейся части сопла.
В горлов-ине поток приобретает критическую скорость
>„=1. В расширяющейся части диффузора скорости
дозвуковые, уменьшающиеся в направлении потока.
В действительности, однако, такой диффузор
осуществить не удается, так как течение в нем оказывается
неустойчивым: .малые возмущения потока на входе
приводят к конечным возмущениям на выходе. Это
объясняется тем, что при малом уменьшении числа М на входе
в горловине не установится критическая скорость^ в
результате чего леред диффузором возникнет отошедшая
'волна. Фактически поле потока, .поступающего в
диффузор из сопла Лаваля, как правило, неравномерно и
насыщенно скачками. Кроме того, вследствие
возникновения потерь во входной части и образования погранич-
410
ного слоя характер изменения проходных .сечении не
будет соответствовать расчетному. В результате во
входной части возникает система скачков.
Процесс движения газа в диффузоре в тепловой
диаграмме строится известным способом (рис. 7-20).
Точка 1 соответствует состоянию потока на входе в
диффузор. Линия 1—2 условно
изображает процесс сжатия
газа в системе скачков в
сверхзвуковой части
диффузора. Соответствующее шри-
ращение энтропии Asi
характеризует в основном
волновые потери во входной
части диффузора. За
скачками устанавливается
давление p2s. . ЕСЛИ P2s/P02<&^
то (после скачков поток еще
сверхзвуковой и в
суживающейся части диффузора
продолжается сжатие газа.
ЕСЛИ p2slp02>&*> TO ПОТОК
за скачками дозвуковой. Это
означает, что в
суживающейся части до
минимального сечения лоток будет __
ускоряться и давление его h '*!■ *1
будет падать. Если в мини- рис. 7-20. Процесс изменения
мальном сечении скорость состояния в сверхзвуковом диф-
ПОТОКа достигает критиче- Фузоре в тепловой диаграмме,
ского значения, то в
расширяющейся части Я>1. В этом случае торможение
потока будет происходить в системе скачков за узким
сечением. Увеличение энтропии As2 обусловлено потерями
в дозвуковой части диффузора.
Заметим, что полное .изменение потенциальной
энергии в сверхзвуковом диффузоре Я0п можно
рассматривать как сумму изменения потенциальной энергии в
системе скачкоБ h0s и :в дозвуковой части /г0д. •
При небольших сверхзвуковых скоростях на входе
(M^ljS) можно применять обычные расширяющиеся
дозвуковые диффузоры (рис. 7-19,6). В этом случае пе-
411
ред расширяющейся частью возникает прямой скачок
уплотнения, в котором поток переходит к дозвуковым
скоростям. В расширяющейся части продолжается
сжатие дозвукового потока. Потери в таком диффузоре
могут быть умеренными, так как при Mi < 1,5 волновые
потери в скачках невелики.
Гидравлический расчет сверхзвукового диффузора
основан на уравнениях одномерного течения. С помощью
уравнения энергии определяется энергетический к. п. д.
диффузора по формулам (7-16) и (7-16а).
Сечения диффузора рассчитываются по уравнению
неразрывности, которое (для суживающейся части) можно
записать в виде:
PiVi = P#' *Хд'
где р и Я —плотность и скорость в минимальном
сечении диффузора.
После преобразования получим:
Г, -М'-\/ Р>1_?>о. (7-^0)
f д —AI, V flp, —qt Л, { "">
Если в узком сечении устанавливается критическая
скорость М [ = 1, то
^-м^У "7^7" ~л7' (1 г1)
или
J_ \—к~х х2
где Сд1 — коэффициент потерь в суживающейся части
диффузора.
Формула (7-22) показывает, что с увеличением потерь
в суживающейся части отношение сечений FJF
увеличивается. Отсюда также следует, что при фиксированном
значении Л/^д изменение параметров на входе приводит
к изменению потерь в суживающейся части. Сравнивая
412
два режима течения при одинаковых начальных условиях
с различными потерями, из выражения (7-22) можно
получить формулу, показывающую, что минимальное сечение
диффузора должно увеличиться пропорционально изменению
давления торможения в сечении F :
или
Jj_ F, p'q*
F
Р%
(7-23)
Здесь pQ —давление торможения в критическом
сечении при данном режиме; /?0' — то же при другом режиме.
3,5^ 4,0 4<3
Рис. 7-21. Коэффициенты полезного действия
сверхзвукового диффузора в зависимости от Mv
/ — с прямым скачком в горловине; 2 — с прямым
скачком на входе.
Для расчета входной части диффузора необходимо
знать величину коэффициента потерь Сд1, а следовательно,
структуру и положение скачков уплотнения на этом участке.
В простейшем случае можно принять, что во входной части
расположен только один прямой скачок. Величина Сд1 при
этом зависит от положения прямого скачка. Если скачок
возникнет в сечении F1, потери энергии будут
максимальными; если скачок расположится в узком сечении, потери
значительно снизятся.
Для иллюстрации на рис. 7-21 приведены
соответствующие к. п. д. диффузора т^д и ц' для двух предельных
413
случаев (/ — с прямым скачком в горловине и 2 — с
прямым скачком во входном сечении), а также опытные
значения к. п. д. Сравнение показывает удовлетворительное
совпадение расчетных и опытных величин.
Выходное сечение диффузора определяется по
уравнению неразрывности. Коэффициент потерь в расширяющейся
части диффузора Сд2 в первом приближении можно принять
по данным испытаний дозвуковых диффузоров. Скоростью
на выходе из диффузора задаются.
Полный коэффициент потерь в диффузоре можно найти
по формуле (при Я' = 1)
Давление торможения за диффузором определяется по
уравнению
Ы^-^+Л" <7-24>
Волновые потери на входе можно уменьшить, вводя
ступенчатое торможение потока во входном
участке (гл. 4).
Торможение в системе скачков осуществляется
различными способами. Один из способов заключается
в том, что стенки входного участка выполняют с
изломами (рис. 7-22,а). Лучший результат можно получить
с помощью профилированной иглы (рис. 7-22,6). В
диффузорах реактивных двигателей применяется
аналогичная система ступенчатого торможения (рис. 7-22,в).
Для уменьшения волновых потерь на входе
используется также система отраженных скачков (рис. 7-<22,г
и д).
Расчет сверхзвукового диффузора со ступенчатым
торможением состоит из нескольких этапов. Вначале
устанавливается система скачков на входе и
определяются восстановление полного давления и коэффициент
волновых .потерь в системе скачков. Затем по заданному
расходу рассчитывается критическое сечение:
414
где в0д =
Скачки
Pq
—- — коэффициент Boccfановления полного дав*
Pqi ления в системе скачков.
Начальный участок расширяющейся части диффузора
целесообразно выполнять коническим. Выходная часть
диффузора рассчитывается по
выбранному рациональному
распределению давлений (§ 7-1).
По результатам расчета
пограничного слоя определяются
потери энергии в дозвуковой
части диффузора Сд2 и при
выбранной площади выходного
сечения F% скорость на
выходе из диффузора Я2
Рассмотрим некоторые
особенности работы
сверхзвукового диффузора при
нерасчетных условиях. Режим в
диффузоре может измениться в
результате изменения параметров
потока на входе (Я1Э р1Л р01 и,
следовательно, расхода газа G)
и давления на выходе р2.
Допустим вначале, что
параметры потока на входе и
расход через диффузор
остаются неизменными, и проследим
влияние меняющегося
противодавления р2. Предположим,
что в сечении F, скорость
равна критической, а давление
среды значительно ниже
расчетного (ра < р2). В этом
случае расширяющаяся часть диффузора работает как
сверхзвуковое сопло. На срезе выходной части в зависимости от
ра возникают волны разрежения или косые скачки. По мере
повышения ра система скачков перестраивается; при
давлении pa — p2k в выходном сечении располагается мостообраз-
ный скачок; при дальнейшем увеличении р скачок
перемещается внутрь расширяющейся части и движется к
минимальному сечению. При некотором предельном противо
Рис. 7-22. Схемы сверхзвуковых
диффузоров со ступенчатым
торможением потока в системе
скачков уплотнения.
415
давлений Ра — Р2т скачок располагается в горловине
диффузора (узкое сечение); при этом поток в
расширяющейся части полностью дозвуковой. Такому режиму со
скачком в горловине соответствует максимальная степень
сжатия в диффузоре.
Соответствующие графики распределения давлений по
диффузору при ра <р2т показаны на рис. 7-23,а (кривые
О AC, OADE и др.). Эта часть диаграммы давлений
полностью соответствует диаграмме давлений в сопле для
второй и третьей групп режимов.
Дальнейшее повышение противодавления приводит к
изменению параметров потока (давления и плотности) в узком
сечении и во входной части.
Рассмотрим теперь влияние изменения параметров потока
на. входе в диффузор. .Допустим, что давление за
диффузором поддерживается постоянным {ра<^Р2гг)\ Скорость на
входе Я1 увеличивается. При дозвуковых скоростях на входе
(l[<^\) в суживающейся части поток ускоряется и
максимальная скорость достигается в узком сечении /%д. По мере
увеличения %[ растут расход газа и скорость в узком
сечении Я*.
При некотором значении 1{'<^\ скорость в сечении 7%
равна критической (ЯЛ = 1). Дальнейшее увеличение
расхода при неизменном статическом давлении перед
диффузором становится невозможным. В соответствии с этим
увеличение скорости Я1 >Я^ повлечет за собой увеличение
давления во входном сечении диффузора и во всех других
сечениях суживающейся части; в результате при l[ > 1
перед диффузором возникнет скачок. С увеличением Я[,
скачок приближается к диффузору и при некотором
значении Я} располагается во входном сечении Fx. Если скачок
на входе прямой, то в суживающейся части поток
дозвуковой и ускоряющийся к минимальному сечению. Для того
.чтобы прямой скачок (или система скачков) проник в
суживающуюся часть диффузора, необходимо дальнейшее
увеличение скорости Х'х {Х[^>1^).
Так как при движении скачка к горловине потери энергии
уменьшаются, то в минимальном сечении может вновь воз-
416
Рис 7-23. Распределение давлений в сверхзвуковом
диффузоре при различных режимах
никнуть критическая скорость. В некоторых случаях при
ра — Р2т ПРИ пеРех°де в расширяющуюся часть поток
продолжает ускоряться и становится сверхзвуковым. Тогда и
в расширяющейся части диффузора возникают скачки.
27 М. Е. Дейч
417
На таких режимах notepn в диффузоре резко возрастают *.
Рассмотренные режимы иллюстрируются графиками
распределения давлений на рис. 7-23,6. При одновременном
появлении скачков в суживающейся и расширяющейся
частях диффузора кривые распределения давлений
приобретают характерную петлеобразную форму.
Рассмотрение условий работы сверхзвукового диффузора
при нерасчетных режимах показывает, что отношение
сечений F* jFx должно изменяться при изменении параметров
потока на входе или на выходе. В период пуска
отношение F* jFx должно быть максимальным. В эксплуатации
любое нарушение режима может быть частично
компенсировано соответствующим изменением отношения F* jFx.
Проанализируем более подробно переменные режимы диффузора
с меняющимся в процессе эксплуатации минимальным сечением. Если
постепенно уменьшается минимальное сечение от Т7* = F\ до того
значения, при котором скорость М„ = 1, то расход газа через
диффузор будет сохраняться неизменным (G = gF^^^. Однако если
площадь горловины будет и далее уменьшаться, то расход через
диффузор снизится. При этом вблизи узкого сечения возникнет скачок
уплотнения, так как обуженная горловина представляет собой
дополнительное сопротивление. Благодаря повышению энтропии в скачке
давление в минимальном сечении падает, а скорость и температура
сохраняются постоянными. Вследствие уменьшения плотности расход
уменьшается в еще большей степени и скачок переместится против
потока. При этом интенсивность скачка возрастет. Движение скачка
в направлении против потока будет продолжаться до тех пор, пока
он не выйдет за пределы входного сечения Fx; скачок займет такое
положение относительно Fv при котором часть газа будет выходить
во внешний поток, минуя диффузор (рис. 7-24,а).
При дальнейшем уменьшении F*A скачок будет перемещаться
против потока, обеспечивая необходимое уменьшение расхода через
диффузор; интенсивность скачка будет сохраняться практически
неизменной.
Рассматривая теперь обратный процесс — увеличение F*„, можно
заключить, что если F+ достигнет того значения, при котором
впервые появился скачок, то скачок не исчезнет, так как уменьшенная
плотность в горловине обусловливает частичное вытеснение массы
газа во внешний поток. Следовательно, У7* необходимо увеличить до
таких пределов, чтобы компенсировать уменьшение плотности в
горловине. Последующее увеличение У7* приведет к перемещению скачка
внутрь диффузора и обеспечит постоянный максимальный расход через
диффузор.
1 Рассматриваемый случай показан штрихпунхтирной линией на
диаграмме / — s на рис. 7-20.
418
Изложенное показывает, что в диффузоре с переменным сечением
горловины наблюдаются гистерезисные явления. Графики на рис. 7-24,6
дополнительно иллюстрируют эти явления. В диаграмме зависимости
G/G0 от F.JF, (G — расход через диффузор; G0 = gFtf^c^ можно
указать точку Л, соответствующую F* = Fx (G~G0) По мере умень-
О 0,2 0,4 0,6 0,8 1,0
Рис. 7-24. Схема диффузора с регулируемым
минимальным сечением (а) и его расходная характеристика
(б) при различных режимах.
шения F»A расход сохраняется неизменным до точки В, которой
соответствует AL = 1 в горловине; перед диффузором возникает скачок,
и расход падает до значения в точке D. Дальнейшее уменьшение F
приводит к изменению расхода по линии DO.
При увеличении /^д скачок перед диффузором сохраняется до
того значения 7^д, которое соответствует точке Е. К исходной
точке Л диффузор возвращается по линии ODEA. В результате
образуется гистерезисная петля EBDE и для того чтобы установить
состояние потока в диффузоре при произвольном F д, необходимо
знать, каким было направление изменения F
27* 419
Необходимо подчеркнуть, что режимы со скачками уплотнения
перед диффузорам характеризуются резким возрастанием
сопротивления Размер гистерезисной петли зависит от числа Mi, с
возрастанием которого отрезок BD перемещается влево (рис 7-24,6)
Следует отметить, что область между кривыми / и 2 на рис 7-24
Рис 7-25 Схемы спектров в диффузорах со
ступенчатым торможением на входе при
различных режимах.
характеризует неустойчивые режимы работы диффузора, при
которых скачок может появиться и может исчезнуть
Как указывалось, в практике применяются регулируемые
сверхзвуковые диффузоры Ч[рис. 7-23) со ступенчатым торможением на
входе
В тех случаях, когда внутренний конус имеет возможность
осевых перемещений, можно не только улучшить условия пуска и
эксплуатации сверхзвукового диффузора, но и обеспечить более
высокий кпд диффузора при расчетном и нерасчетном режимах.
Изменение скорости потока на входе в такие диффузоры
приводит к изменению углов наклона скачков: при Mi>MiP углы
скачков уменьшаются, а при Mi<MiP — увеличиваются.
В первом случае (рис. 7-25,0,) взаимодействие скачков с
противоположной стенкой будет происходить внутри горловины или
в расширяющейся части Возможно также искривление скачков
вблизи наружной поверхности диффузора. При обтекании кромки
420
возникает волна разрежения ЛВС; в результате поток на В/ходе
в диффузор становится неравномерным
Во втором случае, когда Mi<MiPi скачки не попадают на
входную .кромку диффузора (рис 7-25,6) По этой причине уменьшается
расход газа через диффузор и возрастают волчовые потери в
скачках (гл 4). На входной кромке диффузора возникает волна
разрежения ЛВС
При уменьшении Mi скорость потока перед вторым поворотом
(точка D) может стать меньше того значения, при котором еще
0,6,
о,ч\
£м
Ъ
%
ч
ч
X
Чч
^Ч
1
Рис. 7-26. Коэффициенты восстановления
давления торможения в сверхзвуковых
диффузорах при переменных режимах. Цифры на
пунктирных кривых указывают число
скачков (по расчету). Опытные точки нанесены
для четырехскачкового диффузора.
возможно существование прямолинейного скачка (угол 6з>б3т).
В этом случае происходят искривление и отход скачка.от угловой
точки; потери на входе в диффузор заметно возрастают.
Характеристики регулируемого диффузора при переменных
скоростях на входе представлены на рис. 7-26.
Положение замыкающего систему прямого скачка зависит от
выходного сечения диффузора. Если выходное сечение становится
больше расчетного, то прямой скачок в горловине не возникает —
течение остается сверхзвуковым в расширяющейся части/ где, как
указывалось выше, возникает система скачков, в которой поток
переходит к дозвуковым скоростям.
Лри уменьшении выходного сечения прямой скачок
перемещается из горловины в направлении против потока. В обоих
случаях возрастают волновые потери в диффузоре.
7-5 СТУПЕНЬ ЭЖЕКТОРА 1
Газовые эжекторы находят широкое и разнообразное
применение в технике. В таких аппаратах 'происходит
1 § 7-5 составлен при участии М В Поликовского; § 7-6 и 7-7
написаны совместно с А. В Робожевым,
42!
смешение газовых потоков (в простейшем и наиболее
распространенном случае — двух). В результате
смешения изменяются .параметры торможения и статические
параметры смешиваемые потоков Основная
особенность физического процесса в эжекторе заключается
в том, что смешение потоков происходит при больших
скоростях эжектирующего (активного) газа.
Принцип действия (ступени эжектора можно уяснить
из рассмотрения схемы, представленной на рис. 7-27.
Рис. 7-27 Схема ступени эжектора.
Основными элементами ступени являются сопло Л,
камера смешения Б и диффузор В *. Эжектирующий газ
под давлением подается к соплу А. Расширяясь в сопле,
поток газа .приобретает в сечении / сверхзвуковую
скорость В камере смешения Б струя активного газа
взаимодействует с эжектируемой (-пассивной) средой и
увлекает ее в диффузор, где и происходит сжатие
образовавшейся смеси.
Ошытное изучение механизма эжекции в камере
смешения показывает, что наиболее существенное влияние
на процесс смешения оказывают турбулентность
потоков и волновая структура сверхзвуковой эжектирующей
струи.
* Диффузор сверхзвукового эжектора обычно состоит из
конического входного участка, цилиивдр'Ической горловины И расигирякз*
щегося выходного участка,
422
Изучение спектров осесимметричной сверхзвуковой
струи (рис. 6-28 и 6-29) позволяет установить, что по
мере удаления от сопла на 'периферии струи образуется
пограничный слой. В кольцевом пограничном слое
скорости меняются от малых дозвуковых на периферии до
сверхзвуковые на участке, примыкающем к ядру струи.
Заметим, что в соответствии с волновым спектром
струи статическое давление по оси ядра Струи
-периодически меняется. По диаметру струи давления
распределяются также неравномерно: в струе образуются
'поперечные градиентьп давления. В сечениях за скачками
градиенты давления направлены к периферии струи,
а в сечениях за волнами разрежения — к оси струи.
В дозвуковом участке пограничного слоя статическое
давление близко к давлению среды. На некотором
расстоянии от сопла вся струя становится дозвуковой:
в этой области статическое давление распределяется 'по
оси и по сечению практически равномерно.
Эти особенности поля осесимметричной
сверхзвуковой затопленной струи позволяют заключить, что между
внешней средой и струей .происходит непрерывный обмен
частицами. Поперечные перемещения частиц из
пограничного слоя в ядро и из ядра в пограничный слой
осуществляются с интенсивностью, переменной вдоль оси.
Вернемся к рассмотрению процесса в ступени
эжектора («рис. 7-27). В сечении 2 смешанный поток с
неравномерным профилем скоростей заполняет входную
часть диффузора. На участке 2—3 в горловине
диффузора происходит дальнейшее перемешивание потока К
На участке 1—2 процесс смешения можно приближенно
считать изобарическим. На участке 2—3 смешение и
выравнивание потока сопровождаются повышением
среднего по сечению давления В выходной части
диффузора (участок 3—4) происходит дальнейшее
повышение давления.
В литературе иногда рассматривается иная схема
процесса смешения, когда расстояние между выходной
кромкой сопла и входным сечением горловины
диффузора х = 0. Такие эжекторы (компрессоры) называют
эжекторами с цилиндрической камерой смешения или
с постоянной площадью смешения.
1 Входную часть и горловину диффузора иногда называют
камерой смешения.
423
Однако указанное деление не имеет особого смысла,
так как рассмотренная схема (рис. 7-27) 'переходит
в другую путем непрерывного уменьшения' величины х
до нуля.
Для определения параметров смешанного потока
в выходном сечении горловинь» (сечение 3)
воспользуемся уравнениями количества движения, сохранения
энергии и неразрывности. В первом приближении будем
считать, что поля давлений и скоростей в сечениях 1 к 3
равномерны; силовое воздействие стенки на поток
отсутствует; сильи давления, действующие на поток от стенки
горловины, не дают осевых составляющих; силами
трения в первом приближении также можно пренебречь.
Поэтому изменение количества движения между
сечениями 1 и 3 равно разности импульсов сил давления
в этих сечениях. Следовательно, уравнение количества
- движения для сечений /—3 можно записать в виде:
=q±±^-c3 + p3F^ (7-25)
где G — расход эжектирующего (активного) газа;
си> А— скорость и давление в выходном сечении сопла при
изоэнтропическом истечении;
с2, G2 — расход и скорость эжектируемого (пассивного)
газа;
сг> А— скорость и давление смешанного потока в
выходном сечении горловины диффузора;
^*д» Л —площади сечения горловины диффузора и
выходного сечения сопла.
В общем случае сумма количества движения и силы
давления, т. е. импульс потока, выражается формулой
Б. М. Киселева [(2-44) и (2-45)].
Подставив выражение (2-44) в уравнение (7-25), получим
после несложных преобразований:
Ч/Г! <•■.(*..+ »У+Г JA* + Р„ (Г.А - F.) =
=ttia,j2^,+J_), (7.26)
424
Где х = GJGj^ — коэффициент эжекции;
аПу #*2 и я*3 — критические скорости активного,
пассивного и смешанного потоков;
Хи — безразмерная скорость на выходе из сопла
при изоэнтропическом истечении.
Расход активного газа можно выразить формулой
где р*— плотность в критическом сечении сопла:
И^ГИ^П^: (7-27)
имея в виду, что а,{=-у -f—rjRT01, и вводя функцию <J>
[формула (2-45)], представим уравнение (7-26) в виде:
<ш ^-i-i*_xi/S?i | А + 'У^У^д А
<К*„)+й + 1*|/ г,/*+^ 2 J Л^ч-лс
= 0+*) ]/"•£-; Ж), (7-28)
где Г03 — температура торможения смешанного потока.
Отношения температур торможения Т02/Т01 и Т03/Т01
можно выразить с помощью уравнения энергии:
Gi'oi + G2*o2 = (^i + Ga) *03.
Отсюда, считая теплоемкости смешиваемых потоков
одинаковыми, приходим к выражению
где тх — относительная температура торможения пассивного
тока:
_ *02 __ J_02
*03 ■* 03
Заметим, что критические скорости а*, и а„„, а и я#„
потоков связаны очевидными соотношениями:
0..-J/ г.,-^1 и^-|/ 17.-Kv
425
Подставив выражение (7-29) в уравнение (7-28),
получим:
i_
= V (1+*)(1+«,)«!»(A J. (7-30)
Уравнение (7-30) устанавливает связь между
безразмерными газодинамическими параметрами pjp0, *, хх и Я3 и
геометрическими характеристиками эжектора F*JF*C и FJF^.
Следует иметь в виду, что отношение -тг- также представ-
ляет собой функцию Х{Г Скорость Я2 обычно мала, и в
практических расчетах вторым членом уравнения можно
пренебречь.
Анализ уравнения (7-30) показывает, что при заданных
значениях %, Я2, pjp0 и тх скорость в выходном сечении
горловины Я3 определяется неоднозначно; уравнению (7-30)
удовлетворяют два значения Я3, связанные зависимостью
я3я3 = 1.
Физический смысл неоднозначности определения Я3
очевиден, если учесть, что в прямом скачке уплотнения
скорости перед скачком и за ним связаны таким же
соотношением. Поскольку в скачке импульс, расход газа и
температура торможения не изменяются, основное уравнение
ступени эжектора (7-30) остается справедливым независимо от
того, .возникает ли или не возникает скачок в горловине.
При достаточно длинной горловине, обеспечивающей
выравнивание смешанного потока, обычно осуществляется
дозвуковое решение уравнения (7-30). Переход к дозвуковому
течению происходит при этом в системе скачков в горловине.
Уравнение (7-30) служит для определения основной
геометрической характеристики" ступени эжектора F*JFtQ или,
если эта величина известна, уравнение (7-30) может быть
использовано для определения газодинамических параметров
х и pJPo или * и pjp0 в условиях переменного режима.
В последнем случае необходимо использовать еще одно
уравнение — неразрывности, которые позволяет определить
давление торможения в сечении <?,
426
Уравнение неразрывности для выходного сечения
горловины представим в виде:
Gl + G2 = F.Ap,cig.
После деления на GY находим:
Так как
то
(1 -4-х) =а. -=А.—.— .
Замечая, что
*Ч = Ро* ± = Роз 1 + * д+3 /— = /1 +х^
Р* Ро ■*! /^0 " 1+«1 ЛМ К 2 [/ 1+Х '
окончательно получаем:
^,=r4rV'(1+*)(1+"i)- (7-31)
-ГО Г*д 7 3
Из уравнения (7-31) следует, что давление торможения
в выходном сечении горловины зависит от скорости Я3(^3),
Статическое давление /?4 за диффузором связано с
давлением полного торможения /?04 и безразмерной скоростью
Я4 на выходе из диффузора очевидным соотношением:
Обычно скорость Я4 невелика и в первом приближении
можно считать, что /?4 ^ /704. Если в расширяющейся части
диффузора потери невелики, то давление торможения в
сечениях 3 и 4 приближенно можно принять одинаковыми,
т. е. считать
Таким образом, предполагая, что скорость ^4 мала и
потери в расширяющейся части отсутствуют, мы можем
427
■Определить давление за диффузором Ра — Роъ -по формуле
(7-31). Если скорость Ха не может рассматриваться как
величина пренебрежимо малая, то р4 определяется по
формуле (7-32).
Полученные в .предположении простейшего
одномерного характера процесса в эжекторе уравнения (7-30)
и (7-31) оценивают только потери смешения, которые
являются в рассматриваемой задаче основными. Однако
наряду с потерями смешения необходимо учитывать и
другие потери в отдельных элементах эжектора: потери
в сопле, во входной части диффузора и в горловине1,
а также потери в расширяющейся части. Кроме того,
процесс во входной части диффузора в действительности
может отклоняться от изобарического процесса,
принятого при выводе уравнения (7-30). Изменение давления
в общем случае начинается не точно во входном
сечении горловиньп 2, а выше или ниже по потоку в
начальном участке диффузора. Далее, основное уравнение
количества движения необходимо дополнить членом,
выражающим воздействие сил давления от стенки входного
участка диффузора. Вместе с тем, даже при
значительной длине горловины, следует учитывать
неравномерность поля потока в сечении 5, которая существенно
сказывается на эффективности диффузора.
Учет всех перечисленных факторов,
характеризующих действительный процесс в ступени эжектора,
осуществляется на основании следующих соображений.
Потери в сопле учитываются коэффициентом
скорости фс. Действительная скорость истечения из сопла
равна:
Коэффициент <pc~Kl—£с определяется с помощью
кривых, представленных на рис. 6-31.
Потери в.расширяющейся части диффузора, >читы-
ваемые коэффициентом еод, можно принимать по
графику на рис. 7-4 в зависимости от скорости Яз в выходном
сечении горловины.
Силовое воздействие стенки входной части диффузора
на поток учитывается введением в уравнение количества
1 Во входной части и в горловине, кроме основных потерь
смешения, возникают потери, вызываемые трением, и волновые (потери
428
движений импульса от стенок /ст. При этом подсчитываема
удельный импульс от стенок начального участка диффузора,
равный:
1
^аь °(ФГ'эт:- (7-33)
2k ' g a^
Абсолютное значение ?в зависит от режима работы и
геометрических параметров ступени, прежде всего от
коэффициента эжекции х, отношения pk/p0, угла конусности
входной части диффузора, расстояния от выходной кромки
сопла до начала горловины диффузора и отношения F*JF*C.
Опытное исследование влияния неравномерности потока
в выходном сечении горловины показывает, что и этот
фактор должен быть учтен при расчете ступени.
При этом установлено, что неполное выравнивание потока
в горловине приводит к перераспределению работы сжатия
между горловиной и расширяющейся частью диффузора.
С увеличением неравномерности в сечении 3 работа сжатия
и потери в горловине уменьшаются, а в расширяющейся
части растут. Детальный анализ показывает, что в
основные уравнения эжектора должны быть введены
коэффициенты, учитывающие влияние неравномерности.
С учетом' всех потерь и неравномерности поля в
сечении 3 уравнения ступени эжектора принимают вид:
«к*.)
где
+я«*+(ч±Г%%-
-^вУ=|/0+-)(1+^Ж(Яз);
f*-'frFr0+*)(l+«1);
ф(А.) = 9Я„4 ~ .
Ых»)=?нх» + -^'.
с _ Л. .
°* А.'
(7-34)
(7-35)
(7-36)
429
9H — коэффициент, учитывающий неравномерность поля
в выходном сечении горловины; он может быть подсчитан»
если известен профиль скорости.
Опытом установлено, что в предельном режиме (см. ниже)
при определенной (оптимальной) длине горловины средняя
скорость смешанного потока в выходном сечении горловины
диффузора достигает критического значения, а профиль
скоростей приближается к квадратичной параболе. Это
позволяет для частного случая подсчитать этот коэффициент
и принять 9Н = 1,22 -г-1,26. По опытным данным значения
коэффициента <рн на переменных режимах колеблются в
среднем в пределах срн = 1,0 -^- 1,3. Меньшие значения <рн
соответствуют более равномерному полю скоростей. Все
коэффициенты: е0 =—, 9с, ср„ и £ву меняются при
изменении режима работы ступени и профиля проточной части
ступени (формы сопла и диффузора) и пока могут быть
получены только опытным путем.
Расчет ступени для х —0 производится по
аналогичным уравнениям. Уравнение импульсов для этого случая
имеет вид:
ф(А1) + *Угт1ф(*,)=ф,(*»)»'г (1 +*)(! +Х-Ч), (7-37)
где
w=?ca,+ ~; (7-38)
9с2—коэффициент скорости сопла пассивного газа.
Уравнение (7-37) не содержит основного
геометрического параметра ступени F*JF*C- Связь между F*JF*C и
коэффициентом эжекции по-прежнему выражается
уравнением (7-35).
7-6. СТУПЕНЬ ЭЖЕКТОРА ПРИ ПЕРЕМЕННЫХ РЕЖИМАХ;
ПРЕДЕЛЬНЫЙ РЕЖИМ
В условиях эксплуатации ступень эжектора часто
работает на режимах, отличающихся от расчетного. Причинами
отклонений от расчетного режима могут быть изменения
начальных параметров (следовательно, и расхода) эжекти-
рующего газа, параметров и расхода эжектируемого газа
и давления смешанного потока за диффузором.
430
Количество независимых параметров, определяющих
режим ступени, и связь между этими параметрами
устанавливаются уравнениями (7-34) и (7-35), которые при
F*JF#C = const являются основными уравнениями
переменного режима ступени.
Согласно уравнениям (7-34) и (7-35) к числу
определяющих безразмерных параметров режима ступени относятся:
а) коэффициент эжекции х = -2;
б) степень сжатия (повышения давления) в ступени ед =
= PjPk>
в) располагаемый перепад давлений pk/p0\
г) отношение температур торможения смешиваемых
потоков Х1 = -=г1.
* 01
При изменении режима ступени меняются условия
работьп отдельных ее элементов: сошла, камеры
смешения и диффузора. При этом происходит
перераспределение потерь в указанных элементах ступени. В условиях
эксплуатации возможно одновременное изменение всех
четырех параметров. При этом все элементы ступени
работают в нерасчетных условиях.
Проанализируем поведение ступени при отклонениях
режима, вызванных изменением давления за
диффузором р4 или изменением давления в камере смешения ри,
предполагая, что давление эжектирующего газа перед
соплом ро и отношение ti остаются неизменными.
При .постоянном давлении «перед соплом изменение
давления в камере смешения рк или давления за
ступенью р4 приводит к изменению количества эжектируе-
мого газа. Очевидно, что при этом изменяется и степень
сжатия в диффузоре ед=р4//?&-
По уравнениям (7-34) -и (7-35) между
коэффициентом эжекции х и степенью сжатия ед существует
определенная зависимость, которую называют
характеристикой ступени или диаграммой -режимов. Вид
этой характеристики определяется тем, какой из двух
основных параметров (ри или р*) изменяется при
изменении режима.
1. Работа ступени при постоянном
давлении всасывания. Проследим характер
изменения основных параметров режима при увеличе-
431
нии коэффициента эжекции от х = 0 (холостой ход) до
максимального значения х = хПр* при ри — const.
При х = 0 задвижка на линии всасывания закрыта
полностью и давление за диффузором достигает
(максимального значения р4 = рт при данном рн- Для
увеличения х необходимо уменьшать противодавление р4, т. е.
led
Рис. 7-28. Характеристики ступени эжектора.
сопротивление проточной части, сохраняя ри
неизменные; при этом степень сжатия в ступени снижается.
На участке СВ рассматриваемой характеристики
(рис. 7-28) скорости в сечениях 2 и 3 (Х2 и Аз),
показанных на рис. 7-27, увеличиваются (из условия
неразрывности).
При некотором значении коэффициента эжекции
х^Хпр скорость в начальном участке горловины
диффузора достигает максимального значения, а скорость
в выходном сечении горловины близка к "критической
* хПр — предельный коэффициент эжекции.
432
(Аз— 1) Отношение давлений Рз/Роа в расширяющейся
, части диффузора также близко к критическому.
Дальнейшее уменьшение противодавления не приводит к
изменению коэффициента эжекции. На этом участке
характеристика ступени ед = /(х) располагается
параллельно оси 8Д (отрезок АВ). Это означает, что ,на
рассматриваемом режиме производительность ступени не
зависит от степени сжатия и коэффициент эжекции
равен предельному (х=хпр).
Предельным называется
максимальный для данного значения рн/ро
коэффициент эжекции; соответствующее
противодавление называется предельным <п<р от и в о д а в л е-
•н и е м. Этот режим, отвечающий на диаграмме
точке В, называется предельным. Механизм наступления
предельного режима представляется следующим. По
мере увеличения х в некотором сечении входного
участка диффузора средняя скорость потока становится
сверхзвуковой. Пристеночный дозвуковой слой в этом
сечении имеет минимальную поперечную
протяженность и не способен передавать возмущение «против
потока. Поэтому снижение оротиводавления (Р4<р4пр) не
влияет на условия в камере смешения и коэффициент
эжекции сохраняется .постоянным. Он может быть
увеличен только за счет повышения плотности потока, т. е.
давления в камере смешения ph. Поэтому на участке ВА
характеристика pk= const параллельна оси ординат.
Процесс в ступени эжектора на этом участке
характеристики принципиально отличается, как видно из
дальнейшего, от процесса на участке СВ\ вслед за зоной
максимальной скорости, расположенной в начальном участке
горловины диффузора, смешанный поток тормозится
в горловине, .пересекая сложную систему скачков
уплотнения, до дозвуковой скорости во входном сечении (если
длина горловины соответствует оптимальной)/после чего
осуществляется дальнейшее (уже плавное) торможение
в расширяющемся участке. Описанная картина
иллюстрируется графиков распределения давлений вдоль
контура диффузора на рис. 7-29. Если длина горловины
меньше той, при которой обеспечивается торможение
Потока до дозвуковой скорости, то в расширяющейся
Части диффузора поток разгоняется, а затем в системе
скачков, переходит в дозвуковой (расширяющаяся
28 м. е. Дейч
43?
часть диффузора работает, как сопло Лаваля в
нерасчетных условиях). По мере снижения рА система
скачков смещается к выходному сечению диффузора.
Возвращаясь к кривым изменения давления то
контуру диффузора (рис. 7-29) на предельном (р4/Р4пр=1)
и запредельном (р4/р4пр<1) режимах, видим, что
возмущения от снижения р4 не передаются выше определен-
f**«——————п
1,50
(.0
0,75
0,50
0,25
Рис. 7-29. Распределение давлений по контуру диффузора при
различных режимах работы ступени эжектора; U = 4; х — 6. Опыты МЭИ.
ного сечения, расположенного в начальном участке
диффузора. Это сечение (точнее, зона, прилегающая к
нему), как указывалось выше, является запирающим. На
рис. 7-30 можно видеть, что при переходе от предельного
режима к запредельному профиль скорости в начальном
участке диффузора и коэффициент эжекции х
практически не. изменяются. В то же время в выходном сече-
кии горловины при неизменном коэффициенте эжекции
средняя скорость увеличивается. Опыты показали, что
на предельном режиме профиль скоростей в выходном
сечении горловины приобретает форму, близкую к
параболической, что характерно для течения в трубе, когда
средняя скорость близка к критической (гл. 5).
434
A,i
О
х=0у25-7Сф
Предельный режим -
Запредельный режима
Рис. 7-30 Распределение безразмерных скоростей Л£. во входном и выходном сечениях горловины длиной /*д =-. 4
при различных режимах. Расстояние между соплом и диффузором х = 6. Опыты МЭИ.
На рис. 7-31 показан «универсальный профиль»
относительных-средних скоростей А,зАо (А,о — скорость на оси
диффузора), полученный в результате наложения
скоростных полей в выходных сечениях горловин
различных диффузоров на предельных режимах1. Как видно,
1г2
V
Qfl
0,6
0,4
~'~1fi 0,8 0,6 0,4 0,2 0 0,2 Ofl Ofi 0,6 1fi
A Pf 0,107, x~0,25\
opK-0,067; * = 0,109 \T Ra
opH--0,042,K~0,083\l*r«,X~V
§pK-Q,042', x=0 J
ы pf 0,037; x-0, Ьд*Ч, X -7,9
+ pf0fl67; x~QJ29 l+f12;S = 6fi
Рис. 7-31. Универсальный профиль скорости
в выходном сечении горловины на режимах,
близких к предельным.
Есе кривые практически совпадают и мало отличаются
от квадратичной параболы независимо от относительной
длины горловины ^д = ^д/^д. Такая перестройка
профиля скорости при околозвуковых скоростях
объясняется влиянием вязкости в околозвуковом потоке, весьма
чувствительном к любому 'Внешнему воздействию.
1 Опыты проводились при различных безразмерных давлениях
в камере смешения рк=Рк1ро и оптимальных безразмерных
расстояниях менаду срезом сопла и входом в горловину x=x/di (d\ —
диаметр сопла на выходе).
436
1
1 t
*?
ji>
1 / *
j /
/
/
г '
+л
A i
./
/
/
/
'
i
j
t
1$
ii * *
yfr*
i
П^
\
1
%
*
I L...
i
Ч
\
\
1 . .
tl
Л
\
! т
Расчет харамеристик эжектора pjp0 = const произво*
дится по уравнениям (7-34) и (7-35). Для предельного
режима (* = *пр и ед = едл1р) после подстановки Я3 = 1 и
^3 = 1 эти уравнения принимают вид (скорость Я2 ^ 0):
1
=«+ i)/(i+%)(i+*„P^i); (7-39)
где ^(Я^ср'яu+-rf-;
9c ; <pH'; SB'y— коэффициенты, характеризующие
рассматриваемые предельные режимы, причем срс сохраняет
постоянное значение для всех точек данной кривой /?^//70= const.
По уравнению (7-39) при заданном значении рк/р0
определяется предельный коэффициент эжекции х , а по
формуле (7-40) — предельное противодавление р. . С помощью
этих зависимостей могут быть построены кривые
■ хп?=Ц%) и %.np=^(e)-
Значения е =f3(pk/p0) для холостого хода легко могут
быть получены из выражений (7-34) и (7-35) после
подстановки х = 0.
Характеристики ед(х) при pjp0 = const, как правило,
весьма пологи и поэтому с достаточной для практики
точностью могут быть построены по двум точкам: х = 0 и
* = х . Отметим, что с уменьшением pjp0 диапазон
регулируемой производительности ступени снижается [участок
характеристики, соответствующий допредельным режимам,
/?4>/?4пр, сокращается (рис. 7-28)]. При этом предельный
коэффициент эжекции уменьшается, а предельная степень
сжатия возрастает. При х = 0 и ед = е п участок
характеристики рк/р0 = const, соединяющий точки х = 0 и
х = х превращается в точку.
437
Линия DBK на диаграмме режимов ступени,
соответствующая предельным значениям ед = едпр и * = *п для
различных pjp0, называется предельной линией. Во всех
точках этой линии при правильном выборе длины горловины
скорость Я3^ 1.
2. Характеристики ступени при постоянном
давлении за эжектором pjp0 — const. Так же как
и на режимах pk = const, характеристики /?4 = const имеют
две ветви: допредельную и запредельную, отвечающие
соответственно условиям Pt^Pinp и /?4^/?4пр. Проследим
протекание процессов в эжекторе при изменении давления
всасывания pk.
Пусть в точке F (рис. 7-28) /74>/?4пр; здесь едОдпр,
Pk^Pkw Чтобы увеличить коэффициент эжекции при
заданном противодавлении, необходимо увеличить давление
перед диффузором, т. е. в камере смешения рк. Степень
сжатия ед при этом уменьшится, а средняя скорость
смешанного потока возрастет. Так будет продолжаться по
мере увеличения *, пока средняя скорость потока в
запирающем сечении не достигнет максимального значения Я*=1.
При дальнейшем возрастании х процесс в эжекторе
меняется. Увеличение коэффициента эжекции по-прежнему
достигается за счет повышения давления перед диффузором
pk, но скорости в запирающем и выходном сечениях
увеличиться не могут и производительность аппарата
возрастает только за счет повышения плотности потока.
Статическое давление и давление полного торможения
в сечении 3 р3 и р03 также увеличиваются. В
расширяющейся части диффузора поток приобретает сверхзвуковые
скорости. В результате здесь возникает скачок-(или система
скачков), положение которого зависит от
противодавления /?4. При снижении /?4 скачок смещается к выходному
сечению диффузора.
Точки рассматриваемого участка характеристик pjp0=
= const со скачками в расширяющейся части лежат на
вертикальных участках соответствующих характеристик
pjp0=const. На режимах со скачками уплотнения потери
в расширяющейся части диффузора возрастают вследствие
уменьшения давления торможения в скачках и отрыва по-
438
тока. Рассматриваемые режимы сопровождаются
возрастанием pk, и степень сжатия ед продолжает снижаться.
Таким образом, характеристики ступени,
соответствующие условию pjp0 = const, изображаются линиями, форма
которых показана пунктиром на рис. 7-28 (линия FBL),
причем на участке FB противодавление /?4> рА , а на
участке BL противодавление /?4</?4пр.
Расчет характеристик pjp0 = const осуществляется
с помощью уравнений (7-34) и (7-35), если известны гео-
-^
/
/
С
£в.у
0,ч
п ?
П 9
П1
1
/А
^
•
!
1
-*«
0.4
0,7 0,05 0 0,1 0,2 0,3
Рис 7-32. Изменение коэффициента входного участка
диффузора в зависимости от pk/p0 и х.
метрические параметры эжектора (/7#д//7»с, FJF*C) и Ава
параметра режима (например, pjpk и х). В этом случае по
формуле (7-35) определяется величина х (в
предположении
что ^-3,
Ро
, а по уравнению (7-34) — значение pjp0.
Ро/
Графики распределения давлений на рис. 7-29 позволяют
установить характер изменения удельного импульса £ в
зависимости от х и pjp0. На рис. 7-32 приведена такая
зависимость для входной части с углом конусности 20°.
Отсюда можно заключить, что при больших значениях х,
отвечающих условиям заполнения свободной струей
входного сечения горловины, величина Е близка к нулю.
С уменьшением х возрастает давление за диффузором и во
входном сечении горловины (на стенке входного участка).
Повышение давления от pk до давления во входном сечении
горловины (рассматриваются режимы pjp0 = const)
осуществляется во входном участке диффузора.
430
При уменьшенных * во входном сечении горловины
возникают обратные токи: излишек газа, вошедшего в
активную струю, выбрасывается вблизи входного сечения
горловины. Часть струек при этом притормаживается и затем
ускоряется в направлении, обратном движению основного
потока. Торможение и поворот отдельных струек не могут,
очевидно, произойти без повышения давления в направлении
движения основного потока. Отсюда вытекает, что
независимо от формы профиля проточной части эжектора
уменьшение х всегда приводит к интенсификации сжатия в
начальном участке смешения.
Давление в камере рк влияет на величину £в лишь при .
существенных отклонениях режима от расчетного.
Уменьшение давления приводит к возрастанию £ц . Эгот факт
объясняется увеличением подсоса в струю и
соответствующей интенсификацией обратных токов.
3. Режимы с переменным
противодавлением при неизменном положении задвижки на
линии всасывания1 (т. е. npft одновременном
изменении pk и /?4). Очевидно, что при р±<СрАпр такая характе-
„ Pk ,
ристика ступени совпадает с характеристикой — = const.
Ро
При /?4> р4пр с увеличением /?4 коэффициент эжекции
уменьшается, так как pk резко возрастает (кривая ABE на
рис. 7-29). При этом одновременно падает и степень
сжатия. Чем больше открыта задвижка на линии всасывания,
тем менее интенсивным оказывается изменение степени
сжатия. Все линии ?= const сходятся в точке х = 0 (точка £),
где давление pk равно давлению внешней среды 2.
Область, заключенную между предельной линией и
осью х, будем называть диаграммой режимов
ступени. Диаграмма режимов, полученная опытным путем,
показана на рис. 7-33. Следует подчеркнуть, что расчет,
произведенный с помощью опытных (переменных)
коэффициентов <рс » ?н', ?' ' удовлетворительно совпадает с
данными эксперимента.
1 Рассматриваемые режимы иногда называют режимами с
постоянным дросселированием на линии всасывания
2 Буквой g условно обозначена величина открытия задвижки на
линии всасывания.
440
До сих пор мы предполагали, что давление активного
газа перед соплом сохраняется постоянным По опытным
данным изменение р0 оказывает весьма большое влияние
на эффективность ступени, так как при этом меняются
расход и располагаемая энергия активного газа.
В ступени заданных размеров расход активного газа
прямо пропорционален ро. Если давление за ступенью р\
О 0,05 Of 0,15 0,2 0,25 0,3 0,35'
Рис. 7-33. Экспериментальная диаграмма режимов ступени
эжектора.
и положение задвижки на линии всасывания
сохраняются неизменными, то с ростом vp0 давление в камере
смешения рк уменьшается, а расход эжектируемого газа
увеличивается. При достижении некоторой оптимальной
величины! ро давление рк 'приобретает минимальное
значение.
Дальнейшее увеличение ро приводит к
возрастанию рк и уменьшению расхода эжектируемого газа.
Распределение давлений по диффузору позволяет
объяснить влияние р0 (рис. 7-34). При р0>р'о заметно
резкое увеличение давления во входной части
диффузора, которое вызывается появлением системы скачков.
Поток в суживающейся 'части за скачками становится
дозвуковым и ускоряется, приобретая критическую
скорость в горловине. В расширяющейся части диффузора
441
Продолжается ускорение потока, заканчивающееся
системой скачков.
Предельное противодавление пропорционально
начальному давлению [уравнение (7-39)]. При заданном
открытии задвижки и p4 = const по мере увеличения ро
эжектор от допредельного режима (р4>Р4пр)
приближается к предельному (р4 = Р4пр). Поэтому степень сжа-
Рис. 7-34. Распределение давления по контуру диффузора
при различных начальных давлениях активного газа.
тия возрастает, а рк уменьшается. При дальнейшем
увеличении ро(р4пр>Р4) Рк увеличивается, т. е. эжектор
«переходит на запредельный режим.
Визуальные исследования потока в ступени эжектора
отчетливо показывают, что на всех режимах с
завышенным начальным давлением (р0 > р) в расширяющейся
части возникают скачки (рис. 7-35,а). Аналогичная картина,
как мы видели, наблюдается и на режимах * = *пр при
/?4<</?4пр- Скачки приводят к отрыву вихреобразованию
в расширяющей части диффузора (рис. 7-35,6).
В ступени с малым расстоянием между соплом и
диффузором (х = 0), кроме рассмотренного первого предель-
442
Рис. 7-35. Спектры потока в ступени эжектора,
а—скачок уплотнения в расширяющейся части дифф\зора; р0 =
= 5,02 ата; р^ =0,81 ата; б —отрыв потока в диффузоре"
(визуализация потока парами нашатыря, опыты МЭИ).
ного режима (критическая скорость достигается в
выходном сечении горловины: А3 = 1), может возникнуть и
второй предельный режим, соответствующий критической
скорости пассивного газа в сечении 2 (А2=1).
7-7. ВЫБОР ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ СТУПЕНИ
ЭЖЕКТОРА
При расчете ступени эжектора заданными, как правило,
являются: параметры и расход активного газа (/?0, Г01, G,)-,
параметры и расход пассивного газа (pok, pk, Т02, х) и
необходимая степень сжатия в . Тогда по уравнениям (7-34)
и (7-35) определяется основной геометрический параметр
ступени F JF с (при условии Я3=1). Как нетрудно
заметить, увеличение расчетных коэффициентов эжекции
приводит к росту параметра /\д//\с, возрастание расчетных
«еденей сжатия — к уменьшению зтого параметра.
443
Перед определением F*JF*C необходимо рассчитать
сопло. При заданных значениях /70, pk, ?с расчет сопла
элементарно производится по таблицам газодинамических
функций. При этом давление в выходном сечении на
расчетном режиме следует выбирать несколько большим рк.
Для низконапорных эжекторов можно применять
суживающиеся сопла.
Влияние всех основных геометрических параметров
эжектора, не поддающихся расчету, можно оценить по
опытным данным. Различные варианты ступени
сопоставляют при наивыгоднейших условиях: при оптимальном
расходе эжектирующего газа (оптимальном начальном
давлении) и при оптимальном расстоянии между соплом и
диффузором. Сравнение исследуемых вариантов целесообразно
производить по предельным характеристикам ступени е =
Характер зависимости давления в камере смешения от
х при постоянном давлении /?4 показывает, что pjp0
меняется периодически при изменении x — xjd^ {dl—диаметр
выходного сечения сопла), если поток на входе в
диффузор сверхзвуковой (рис. 7-36). При больших значениях х
давление рк непрерывно увеличивается с ростом х (в этом
случае скорость на входе в диффузор дозвуковая).
Периодический характер зависимости рк от х при М2>> 1
объясняется волновой структурой потока. Если при перемещении
сопла относительно диффузора на стенку входной части
попадают скачки, импульс от стенки уменьшается
(снижается £в ) и давление в камере увеличивается. Наоборот,
если на входе в диффузор расположены волны
разрежения, давление в камере смешения возрастает. Изменение
коэффициента эжекции при этом происходит по
характеристике ступени, соответствующей постоянному давлению
за диффузором (pjp0 — const).
Как показывают опыты, л:опт соответствует такое
положение сопла, когда смешанная струя приблизительно
вписывается в горловину диффузора; однако при этом
должно быть удовлетворено основное требование:
поверхность смешения активной струи должна быть достаточной
для присоединения заданного количества пассиЕного газа,
444
Можно приближенно рассчитать расстояние между соплом
и горловиной диффузора1 по эмпирической формуле
и затем для контроля определить диаметр струи на
расстоянии х от выходного сечения сопла d ^ 1 + 0,35х.
в 6 i 2 О -2 J -k -5
Рис. 7-36. Зависимость давления в
камере смешения Р^/Ро = Рк от Рас"
стояния между соплом и диффузором
х = xjdx.
/ —М1= 1; 2— Mj= 1,59; 3 — М,= 1,94; 4—М,=
■ = 2,31; 5 —Mj= 2,95.
При проектировании эжектора для заданного
коэффициента эжекции диаметр струи должен несколько
превышать (примерно на 10°/0) диаметр горловины диффузора.
Представленные на рис. 7-37 кривые иллюстрируют
влияние основного геометрического параметра F9 /F4 (при
F*A = const). По мере увеличения F#c (или G2) при прочих
1 Отрицательные значения х соответствуют такому
расположению сопла, когда его выходное сечение находится правее входного
сечения горловины.
445
6 t 2 0 -2 -t -5 О
a) d)
Рис. 7-37. Влияние параметра F*JF*A на давление в камере смешения эжектора (а) и параметра FJF. на
предельную характеристику эжектора (б).
' *С ^*С ^*С ^*С F F F F F
я:/——=1,8; 2- — =2,2; <?-—= 3,5; 4- — = 4'8>' б: 1~ мГ~= ^ 2 — ^-= 1,27; 5-^-= 1,67; 4—^- = 1,78; 5- -р- = 5,0.
h*A
*Д
^*Д
*д
Лг
равных условиях кривые pk(x) снижаются. Объяснение
этого факта дает анализ уравнения неразрывности (7-40).
Так как на предельном режиме при оптимальной длине
горловины скорость Я3-^1, а следовательно, и <78ж1, то
для х1 = 1 имеем (полагая, что /?03 = /?4):
*д
С увеличением расхода активного газа Gn т. е.
отношения FJF^, растет и /?4пр (при /?0 и х постоянных).
Следовательно, при постоянном противодавлении р4
разность /?4 — р4п? будет уменьшаться, пока /74 не станет
равным /74пр. При дальнейшем увеличении отношения
-Д /74 — р4п становится меньше нуля, т. е. аппарат пере-
/'*д
ходит на запредельные режимы, что должно
сопровождаться уменьшением £д и ростом pk (/?4 = const).
Влияние отношения -^ (или MJ на величину давления
в камере смешения можно проследить по рис. 7-37,6.
С ростом числа Мх минимальное давление в камере
смешения уменьшается и при М1 = Ммакс = 2,95 достигает
наименьшей величины. При этом давление в камере
смешения и давление на срезе сопла сближаются, потери
в струе уменьшаются.
Характерно, что с увеличением х влияние параметра
Л/^*с резко снижается и при значениях х = 0,1 почти не
обнаруживается; кривые е (х) на этом участке практически
сливаются.
Опыты показали также, что оптимальные значения углов
раствора сопла составляют ус = 12-^-24°.
На эффективность ступени эжектора большое влияние
оказывает длина горловины. При всех расходах эжекти-
руемого газа увеличение длины горловины от /* =0 до
/*д=4 приводит к резкому повышению предельной степени
сжатия (рис. 7-38). Дальнейшее удлинение горловины не
вызывает заметного изменения предельной характеристики
при заданном значении F*JF^. Величина /~*допт меняется
при изменении основного геометрического параметра сту-
447
пени Лд/Лс. Для условий, в которых работают обычно
эжекторы с изобарическим участком смешения, длину
горловины следует выбирать в пределах 4—8 диаметров
горловины. Для ступеней с х^О L опт увеличивается до
10—12.
Диффузоры эжекторов с короткой горловиной плохо
работают на переменных режимах. В этом случае поток
Рис. 7-38. Влияние длины горловины диффузора на предельную
характеристику эжектора.
на входе в расширяющуюся часть может быть
сверхзвуковым, что приводит к образованию скачков и резкому
возрастанию потерь в расширяющейся части.
При взаимодействии струи со стенкой входного участка
последняя воспринимает часть скоростного напора, которая
тем больше, чем больше угол конусности входного участка.
Поэтому желательно выполнение входного участка с
небольшим, около 20°, углом сужения. Однако при этом
длина входного участка увеличивается.
В тех случаях, когда эжектор стабильно работает на
режимах, близких к расчетным, можно допускать угол у }
до 50°, обеспечивая плавное сочленение входного участка
с горловиной.
При нормальной горловине (/ =4d ) лучшая
характеристика получена с коротким входным участком и углом
YAl = 19°. При /*д = 0 хорошие результаты показал у дли-.
ненный входной участок.
Результаты исследования различных выходных участков
диффузора показали, что лучшими оказались выходные
участки с углами раствора 5 и 8°. Меньшие углы конус-
448
ности уД1 и ТД2 Целесообразно выбирать при малой длине
горловины; в этом случае во входной и выходной частях
диффузора происходит частичное выравнивание смешанного
потока.
ГЛАВА ВОСЬМАЯ
ТЕЧЕНИЕ ГАЗА ЧЕРЕЗ РЕШЕТКИ ТУРБОМАШИН
8-1. ГЕОМЕТРИЧЕСКИЕ
И ГАЗОДИНАМИЧЕСКИЕ ПАРАМЕТРЫ РЕШЕТОК.
ОСОБЕННОСТИ ПОТОКА В РЕШЕТКАХi
Преобразование энергии в ступени турбомашины
.происходит в результате взаимодействия потока газа
с неподвижными и вращающимися лопатками, которые
образуют направляющую и рабочую решетки.
Решетки турбомашин в общем случае представляют
сабой систему лопаток одинаковой формы, равномерно
размещенных на некоторой поверхности вращения.
Частным случаем пространственной решетки является
кольцевая (решетка с радиально установленными
лопатками, расположенными между соосными
цилиндрическими поверхностями вращения.
Протекая через решетку, лоток газа изменяет
скорость и направление своего движения. При этом на
решетку действует сила реакции. На вращающихся
решетках турбины эта сила совершает работу;
вращающиеся решетки компрессоров, наоборот, увеличивают
энергию протекающего газа. В неподвижных решетках
энергетического обмена с окружающей средой не
происходит; здесь осуществляются необходимые
.преобразования энергии для получения требуемой скорости и
поворот потока.
Классификация решеток может быть произведена по
различным параметрам.
В зависимости от расчетных условий обтекания и
соответствующих им геометрических параметров профиля
и канала различают три основных типа решеток:
а) конф узорные — используются в турбинах
в качестве как сопловых или направляющих
('неподвижных), так и реактивньих рабочих (вращающихся);
§ 8-1 написан для первого издания Г. Ю. Степановым.
29 М. Е. Дейч
449
б) а к т и в н ы е —используются в турбинах в
качестве рабочих (вращающихся);
в) Д1иффузорные решетки — используются в
компрессорах в качестве как направляющих
(неподвижных), так и рабочих (вращающихся).
В зависимости от общего направления движения газа
по отношению к оси вращения решетки подразделяются
Рис. 8-1 Геометрические параметры решетки
а —кольцевая (цилиндрическая) решетка; б-прямолинейная решетка, в —
плоская решетка.
на осевые и радиальные. В некоторых конструкциях
машин поток газа движется под углом к оси вращения
(диагональные решетки).
К числу важнейших геометрических параметров
кольцевой (цилиндрической) решетки относятся:
средний диаметр d, длина ((высота) лопатки /, ширина
решетки В, шаг профилей на среднем диаметре t,
хорда 6, угол установки |5У и другие параметры профиля и
канала (рис. 8-1), а также форма меридиональных
обводов решетки.
Существуют различные способы задания формы»
профилей лопаток. Наибольшее распространение нашли
координатный способ (рис. 8-2,а), а также способ по-
450
строения профиля сопряженными дугами окружностей
(рис. 8-2,6).
Если отношение среднего диаметра решетки d к
высоте лопатки / велико, то для упрощения задачи можно
считать решетку прямолинейной. При этом форма
межлопаточного канала по высоте сохраняется постоянной.
В простейшем случае, предполагая, что диаметр
решетки, количество и длина лопаток неограниченно
возрастают, получим плоскую
бесконечную решетку (рис.
8-1,в).
Переход от цилиндриче-
toftm^
а)
Рис 8-2 Различные способы задания профиля лопатки,
а —координатный, б —дугами окружности
ской к плоской решетке осуществляется следующим
способом. Проведем два соосных цилиндрических
сечения кольцевой решетки по средне'му диаметру d и по
диаметру d+Ad. Полагая, что Ad мало, развернем на
плоскость полученную кольцевую решетку весьма малой
высоты. Увеличивая количество лопаток до
бесконечности, получим плоскую бесконечную решетку, шоказа.н-
ную на рис. 8-1,в.
Гипотеза плоских сечений, положенная в основу
исследований и .расчетов современных турбомашин, была
впервые плодотворно применена Н. Е. Жуковским
в 1890 г. Ценность этой гипотезы подтверждена
многочисленными экспериментами.
Геометрические характеристики решеток задаются,
как правило, в безразмерном виде. Например,
относительный шаг профилей определяется по формуле
т t T t
t^T или *в = ~в •
Относительная высота (или длина) лопатки
7 / т /
/ = -г ИЛИ / = —
Ь а а,
а
29*
451
где а2 — ширина минимального (узкого) сечения канала
(рис. 8-1).
Прямолинейную (решетку располагают <в системе
координат ху у, z, причем направление х называют осью
решетки (рис. 8-1,6). Все профили должны совпадать
при поступательном перемещении вдоль оси решетки.
Шаг t решетки равен расстоянию между любыми двумя
соответственными точками.
При заданном .профиле форма межлолаточного
канала решетки зависит от относительного шага и угла
установки профиля ру, который определяется как угол между
осью решетки и «ордой профиля (рис. 8-1,в).
Процесс течения газа через решетки лопаточной
машины является весьма сложным. Теоретическое решение
задачи нестационарного пространственного движения
вязкой сжимаемой жидкости в решетке представляет
большие трудности. Правильный подход к решению этой
задачи заключается в исследовании упрощенных
моделей действительного процесса, сохраняющих его
наиболее существенные черты, с учетом и последующим
анализом влияния второстепенных факторов.
В настоящее время наиболее разработана теория
•плоского стационарного периодического 'потока через
решетку идеальной жидкости -при докритических
скоростях. Такое течение можно рассматривать как
.предельный случай действительного течения в решетке с малым
влиянием вязкости (при 'больших числах Re).
Эта упрощенная схема позволяет установить
основные характеристики потенциального потока в решетке.
Однако .получаемые решения нуждаются в существенной
корректировке. Наибольшие погрешности возникают за
счет .неучета вязкости. Поэтому важной задачей является
экспериментальная и теоретическая оценка влияния
вязкости.
Рассмотрим некоторые особенности плоского
потенциального течения идеальной несжимаемой жидкости на
примере обтекания реактивной решетки (рис. 8-3).
Вследствие «периодичности потока достаточно изучить
течение в одном межло-паточном канале или обтекание
одного .профиля. На рис. 8-3,а сплошными кривыми
изображены линии тока Чг = const; пунктирными кривыми
показаны изопотенциальные линии Ф = const,
нормальные к линиям тока. Достаточно густая сеть этих линий
452
Рис. 8-3. Течение идеальной несжимаемой жидкости через
направляющую решетку.
а-изопотенциальные линии и линии тока в Решеткечб-г0^Ж*
скорости- в-распределение относительных скоростей и
коэффициентов давления по профилю.
хорошо характеризует течение Скорость с в любой
точке потока равна:
0 dS dn '
453
где vS и п — криволинейные координаты соответственно
вдоль линий тока и изопотенциальных линий.
Дифференциалы приближенно можно заменить
конечными приращениями и получить:
_ АФ _ L4?
С ^ IS ~ An '
При АФ = ДЧГ ~*= const в каждой точке AS =5г Дя. В этом
случае отдельные ячейки ортогональной сети линий Ф =
= const и ЧГ = const в пределе (при AS->0 и Aaz->0)
становятся квадратами, поэтому сеть течения идеальной
несжимаемой жидкости называют квадратной.
Другой важной характеристикой течения является
план скоростей, или годограф скорости (рис. 8-3,6).
Каждой линии тока и изопотенциальной линии
соответствует в плоскости годографа геометрическое место
концов векторов скорости на этой линии. Соответствующие
геометрические места в плоскости годографа также
образуют ортогональную сеть, которую можно считать
сетью некоторого течения в плоскости годографа,
ограниченного геометрическим местом концов векторов
скорости на поверхности профиля и вызванного так назьи-
ваемым вихреисточником в конце вектора скорости сх
на бесконечности до решетки и -вихрестоком в конце
вектора скорости с2 за решеткой. Точки Оь сх и с2 образуют
треугольник скоростей решетки. На основании равенства
расходов жидкости до и за решеткой
сх/ sin рх = с2/ sin p2
следует, что .проекции скоростей с\ и с2 на нормаль
к фронту (оси) решетки равны или что прямая,
-проходящая через концы векторов С\ и с2 в плоскости
годографа, параллельна фронту решетки. Рассматривая
годограф скорости решетки, можно прийти к заключению,
что в точках спинки профиля, касательные к которым
параллельны! управлениям скоростей на бесконечности
до и за решеткой, скорости должны быть больше, чем
соответственно с\ и с2.
Большой интерес представляет распределение
скорости или давления на поверхности профиля. На рис.8-3,в
показано примерное распределение относительных ско-
454
ростеи с = —и относительных давлении р=—j—— =
== I-1— с2 в функции длины дуги профиля S Если известны
величина С\ и направление |3i скорости на бесконечности
до решетки, а также положение точки схода потока 02
(на вьиходной кромке), то течение через заданную
решетку является определенным. В потоке идеальной
несжимаемой жидкости при изменении величины скорости с\
форма линий тока.и изопотенциальных линий, а также
величины относительных скоростей или давлений не
изменяются.
На конечном расстоянии от решетки поле скоростей
и давлений неравномерно. Линии тока ('при |3i^90°)
И'Меют волнообразную форму, периодически отклоняясь
от своего направления в бесконечности. В соответствии
■с условиями неразрывности и при отсутствии ' вихрей
средняя скорость вдоль любой линии ab (рис. 8-3,а)
между двумя точками, отстоящими на целое число
периодов t решетки, постоянна и равна скорости на
бесконечности. Одна из линий тока разветвляется на входной
кромке профиля, подходя к ,ней по нормали. В точке 0\
(называемой иначе точкой входа) скорость становится
равной нулю, а давление максимально. Начиная от
точки разветвления, в которой S = 0 (рис. 8-3,в), скорость
•на профиле резко возрастает. В зависимости от формы
входной кромки, а также от направления скорости на
входе (угла входа |3i) скорость -вблизи точки
разветвления может иметь один или два максимума. На спинке
профиля скорость в среднем больше, а давление ниже,
чем на вогнутой поверхности. Общий характер
распределения скорости по профилю можно оценить,
рассматривая ширину межлопаточного канала и кривизну
контура профиля. В частности, сужение канала,
характерное для турбинной решетки реактивного типа, приводит
к ускорению потока; на участке канала между
профилями турбинной решетки активного типа с
приблизительно постоянными шириной и кривизной средние
значения скорости и давления мало изменяются (рис. 8-4);
•в компрессорной решетке межлопаточный канал
расширяется и скорость соответственно уменьшается
(рис. 8-5).
Распределение локальных скоростей в точках обвода
455
*вог Q) Sen
Рис. 8-4. Течение идеальной несжимаемой жидкости через
активную решетку.
а —профиль активной решетки; б—годограф скорости; в —
распределение относительных скоростей по профилю.
профиля существенно зависит от формы вогнутой и
выпуклой поверхностей и степени сужения канала, а также
геометрических и режимньих параметров решетки.
Увеличение кривизны на выпуклых участках профиля
■приводит к увеличению скорости, и обратно. При
скачкообразном изменении кривизны, например в точках
сопряжения дуг окружностей, теоретические кривые рас-
155
Рис. 8-5. Течение идеальной несжимаемой жидкости через
компрессорную решетку.
а —профиль решетки, б —годограф скорости, в —распределение
относительных скоростей по профилю
пределения давлений и скоростей претерпевают разрыв.
На выступающих углах профиля скорость теоретически
возрастает до бесконечности. Вследствие этого обводы
профиля современных решеток выполняют с плавно
изменяющейся кривизной.
У выходной кромки конечной толщины 1, как и на вход-
1 Случай бесконечно тонкой кромки не рассматривается, как не
имеющий практического значения.
457
ной, скорость имеет один или два максимума и она
теоретически падает до нуля в точке схода, которая
располагается на выходной кромке в области наибольшей
кривизны. На большом .расстоянии за решеткой
направление потока определяется углом р2-
Выше рассматривалось течение идеальной
несжимаемой жидкости через решетку. В действительности с
учетом влияния вязкости картина течения в решетке может
существенно отличаться от рассмотренной.
При течении реальной вязкой жидкости на
(поверхности профиля образуется пограничный слой, .в котором
концентрируются потери энергии, обусловленные
трением.
На участках канала с увеличением давления (диффу-
зорных участках) может .происходить отрыв потока.
Диффузорные участки в зависимости от формы профиля
могут возникнуть внутри канала; появление диффузор-
ных областей неизбежно на входньих и выходных
кромках профиля. На выходной кромке всегда происходит
отрыв потока; в образующейся закромочной зоне
движение вихревое. На границах закромочных зон
происходит скачкообразное изменение скорости. В
действительном потоке вязкой жидкости такое изменение
скорости привело бы к появлению бесконечно больших сил
трения; поэтому границы! отрывных зон распадаются на
отдельные вихри, уносимые потоком.
В результате отрыва давление за выходными
кромками оказывается пониженным. На некотором
небольшом расстоянии за кромками происходит выравнивание
потока, сопровождающееся изменением статического
давления, угла выхода потока и скорости.
При выравнивании потока за решеткой возникают
потери кинетической энергии, составляющие вторую
часть профильных потерь в решетках (кромочные
потери).
В случае больших скоростей (,М>0,5) распределение
скоростей в решетке претерпевает изменение
(проявляется эффект сжимаемости). При этом обычно
увеличиваются градиенты скоростей вдоль линий тока,
изменяется форма линий тока, а также смещаются области
максимальных и минимальных скоростей. При
определенных значениях М<1на некоторый частях поверхности
профиля появляются сверхзвуковые скорости. Характер
458
обтекания решетки в этом случае резко изменяется; при
сверхзвуковых скоростях возникают дополнительные
потери в скачках.
Профильные .потери характеризуют плоскую решетку.
В прямой и кольцевой решетках образуются
дополнительные потери, обусловленные конечной длиной лопаток
((концевые .потери) и веерностью решетки.
Потери энергии в решетках, обусловленные при
малых скоростях влиянием вязкости и периодической
нестационарностью, а также высокой турбулентностью
потока, а при околозвуковых и сверхзвуковых скоростях —
еще и необратимыми процессами изменения энергии
в .скачках, в значительной степени определяют к. п. д.
лопаточной машины.
При проектировании лопаточных решеток
необходимо обеспечить заданное .преобразование энергии потока
с минимальными потерями. Отсюда вытекает
необходимость детального изучения процесса обтекания решеток
,и установления влияния формы профиля и других
геометрических параметров решетки на её к. п. д. и угол
выхода «потока в широком диапазоне режимов,
определяемых углом входа потока, числами М и Re и пр.
Выше частично была дана классификация решеток
в зависимости от характера изменения .параметров
потока в межлопаточных каналах и налравления
движения газа относительно оси турбомашины.
Классификация применяемых решеток может быть
существенно расширена. Так, в зависимости от скорости
(числа М) все решетки следует разделить на три группы:
дозвуковые, околозвуковьие и сверхзвуковые. В пределах
каждой группы .решетки различаются углом поворота
потока (т. е. углами входа |3д и выхода Рг).
Кроме того, применяемые решетки различают то
относительной высоте, характеризуемой отношением 1 =
= ^-: решетки малой высоты (/"< 1,0-5-1,5 ) и решетки
большой высоты (Г> 1,5-г-2,0).
Вместе с тем разньпе решетки различаются
веерностью 0=т~> ПРИ малых в (в< 10) лопатки
выполняются с переменным по высоте профилем (закрученные
лопатки).
Учитывая, что характеристики решеток в определен-
459
ном диапазоне изменений режимных и геометрические
параметров меняются незначительно, число профилей,
удовлетворяющих потребностям турбостроения, можно
свести к необходимому минимуму.
8-2. РАСЧЕТ ПОТЕНЦИАЛЬНОГО ПОТОКА В РЕШЕТКАХ
ПО ТЕОРИИ КАНАЛА
В теории <решеток и при их экспериментальном
исследовании возникают две основные задачи. Одна из них,
называемая прямой задачей, состоит в определении поля
скоростей тотенц'иального течения через решетку,
состоящую из профилей заданной формы, и в
последующей оценке потерь энергии при различных режимных
(угол входа, числа М и Re) и геометрических (шаг, угол
установки профиля, высота решетки и ,пр.) .параметрах.
Следовательно, прямая задача имеет большое значение
при изучении переменного режима решеток и построении
кх аэродинамических характеристик.
Обратная задача заключается в построении решетки,
отвечающей выбранному или заданному потоку в
решетке 1. В этой постановке практически важной
является задача построения решетки с рациональным
распределением скоростей (давлений) по поверхности профиля,
обеспечивающим минимальные .потери энергии.
В настоящее время разработаны методы расчета
потенциального потока в решетках, иапользующие атшарат
функций комплексного переменного. Однако эти методы
оказываются громоздкими. Они подробно изложены
в специальной литературе2.
Значительно более простые способы расчета,
позволяющие с достаточной точностью решать прямую и
обратную задачи, основаны на теории канала 3. К
настоящему времени известно несколько методов расчета
решеток по теории канала. Одним из .первых быш предложен
метод Г. Флюгеля, развитый позднее Г. Ю. Степановым.
Задача обтекания решеток может бьпть успешно
сведена к расчету потока в канале только при умеренных
1 Легко видеть, что прямая и обратная задачи /взаимосвязаны.
2 См., например, монографию М. Е. Дейча и Г. С. Самойловича
«Основы аэродинамики осевых турбомашин» (Машгиз, 1959), а
также М. И. Жуковского [Л. И].
3 См. § 3-5.
460
Зйй^ениях относительного шага. Кроме того, теория
канала дает возможность расчета потока только в
межлопаточном канале; в области входного участка спинки и
в косом срезе необходимо использовать дополнительные
«приемьи, и точность расчета на этих участках .снижается.
При расчете потока на входе и в косом срезе решетки
необходимо -с известным приближением определить гра-
Рис 8-6. К расчету обтекания решетки по методу канала
ничные линии тока. В простейшем случае граничные
линии тока леред и за решеткой могут быть выбраны в
виде отрезков прямых линий (рис. 8-6). Направление этих
линий на входе в решетку задано (угол pi), а на выходе
оно может быть определено одним из и^вестньих методов.
В действительности выделенные граничные линии
тока до и после решетки искривляются вблизи входных и
выходных кромок, причем это искривление тем
значительнее, чем больше относительный шаг лопаток и
циркуляция скорости. Некоторое влияние оказывает режим
патока: угол входа, числа М и Re. По предложению
ЛМЗ три расчете потока на входе рассматривается
некоторый фиктивный входной участок EDFL (рис. 8-6),
служащий непосредственным продолжением межлопа-
точного канала. Одна граничная линия участка проходит
461
под углом Pi и является линией невозмущенного потока,
а вторая — спинкой профиля Отрезок DN можно
принять равным (l,5-f-2)/.
На выходе из канала граничные линии тока KS
(рис. 8-6) строятся в предположении, что изопотенциа-
лами являются лучи, ортогональные к опинке профиля.
Линии тока KS в этом случае служат продолжением
вогнутой поверхности соседнего профиля. На некотором
расстоянии за решеткой (от точки 5) линия тока
переходит в прямую, .проведенную под углом р2*.
Распределение скоростей по сечению канала решетки
в соответствии с § 3-5 выражается формулой (3-43).
При малых числах М (М<0,4) расчет распределения
скоростей может быть произведен с помощью графиков,
приведенных на рис. 3-14. Для сжимаемой жидкости
необходимо учитывать изменение плотности. В этом
случае можно воспользоваться методом, указанным в § 3-5.
Методика расчета скоростей сводится к следующему:
1. В канал вписываются окружности (рис. 8-6).
Через точки касания этих окружностей со стенками
канала А и В проводятся эквипотенциальные линии (в
виде дуг окружности). Определяются длины этих
эквипотенциальных линий а и радиусов кривизны граничньих
линий в точках А и В (гх и г2).
2. Для каждой эквипотенциальной линии вычисляются
безразмерные геометрические параметры: а=— ; г2 = —;
г2 — 1 у х — 1
а 2г2 — а
3. Определяются параметры газа на входе в решетку:
безразмерная скорость Я1= —-; приведенный расход q =
#
= q(X) и отношение плотностей — =/(Я1) по таблицам
Ро
газодинамических функций.
4. Средний приведенный расход удается определить по
приведенному расходу на входе:
G p.cJ sin В, / . Q /о 1 \
* Угол р2 вычисляется' по опытным формулам, например, по
формуле (8-36) (§ 8-6).
462
5. Отношение плотностей— определяется по вычис-
Ро
ленному среднему приведенному расходу qm с помощью
таблиц газодинамических функций.
6. Объемный расход Q через рассматриваемое сечение
а определяется по 'формуле
Q = Q>-±-> (8-2)
Ро
где Ql = c1tlsm$l представляет собой объемный расход
на входе в канал.
7. По формуле (3-44), которая в наших обозначениях
имеет вид:
2/С,д
8=4г
1 1 _ 1— У\+4КХ
а } 1 +4К, 2/С,а
1 + V\ +4Ki
(или по графику на рис. 3-14) находим 6.
8. Скорость газа в точке А определяется
соотношением
а по ней определяется величина Ха.
9. Скорость (безразмерная, а по ней — размерная)
в точке В определяется по формуле
h _ 1
(8-3)
О точности определения скоростей в решетке по
методу канала можно судить по рис. 8-7, на котором
приведено сравнение расчетных и опытных данных для
активной решетки. Как следует из рис. 8-7, заметное
расхождение расчета и опыта наблюдается только вблизи
входных и выходных кромок, что вполне закономерно.
463
Рис 8-7. Сравнение расчета потенциального "потока в решетке по
методу канала с экспериментом ( опытные кривые,
расчетные кривые)
8-3. СИЛЫ, ДЕЙСТВУЮЩИЕ НА ПРОФИЛЬ В РЕШЕТКЕ.
ТЕОРЕМА Н. Е. ЖУКОВСКОГО ДЛЯ РЕШЕТКИ
Для определения сил, действующих на профиль,
выделим часть потока, как это показано на рис. 8-8 и 8-9.
Внешними границами выделенной области служат
отрезки ab и dc, параллельные оси решетки и равные шагу г,
Рис. 8-8. Силы, действующие на профиль в турбинной (конфузорнои)
решетке.
464
и линии тока ad и be. Линии ab и dcf строго говоря,
должны находиться на бесконечно большом расстоянии
от решетки, так как параметры -потока вдоль этих
линий предполагаются постоянными. Внутренней границей
области служит контур профиля.
Проекции силы, с которой поток действует на
профиль единичной длины, обозначим
Рис. 8-9. Силы, действующие на профиль в компрессорной (диффузор-
ной) решетке.
Величины этих сил можно определить по уравнению
импульсов. Так как линии тока ad и be эвидистантны то
результирующие силы., действующие на выделенную
этими линиями часть потока, равны по величине и
противоположны по знаку. В проекция на направление,
нормальное к оси решетки, изменение количества движения
равно:
где Ра — составляющая силы Я в направлении,
нормальном к оси решетки.
30 М. Е. Дейч
465
Секундная масса газа определяется по формуле
поэтому
Ра = t [(р/а2 - P^L) + Л - А]- (8-4)
Проекция силы Я на ось решетки может быть
выражена уравнением
Ри = ^са1{сих-си2). (8-5)
Уравнения (8-4) и (8-5) можно представить в другой
форме, выразив силы Ри и Ра через циркуляцию скорости Г
и параметры потока на входе и выходе из решетки.
Согласно уравнению неразрывности
где р — средняя плотность газа.
Скорость са, входящую в это выражение, определим
как среднюю арифметическую скоростей на входе и
выходе:
р са\ + са2
Са — g *
Легко показать, что при этом
2PlP2
(8-6)
Г Pi + Р2 '
Циркуляция скорости вокруг профиля равна:
r = t(cul-cu2), (8-7)
так как циркуляции по эквидистантным линиям ad и be
одинаковы по величине и противоположны по знаку.
После простых преобразований из (8-4) и (8-5)
получим:
Ра = < [А - А - Р^„ {cal - cj\, (8-8)
466
Воспользуемся уравнением энергий (2-11). Так как
2 2,2 2 2 | 2
С1=С«.+ С01 И С2=Са2+Си2>
g> CU\ + Си2
то, обозначив £w— о > получим:
са (са1 - с J = ^ (^--^ ] - си (cul - cj. (8-10)
Подставив это выражение в уравнение (8-8) и
учитывая формулу (8-7), получим:
Силу Ра удобно представить в виде суммы двух сил:
где
= рГси
АРв = /[А-А-44тР(^-^)|
(8-12)
Результирующую сил Ра и Рц обозначим через Р ,
а общую результирующую силу — через Р (рис. 8-9).
Силу Р определим по формуле
Но
Р =]/р2Л-Р2 .
у У ul^aV
Подставив сюда значения Ри и Ра], получим:
< + с2а = с\
где с — средняя векторная скорость.
30*
467
Следовательно, выражение для Р у при обтекании
решетки имеет такой же вид, как и в случае одиночного
профиля (§ 3-4):
Ру = ?Тс. (8-13)
Направление силы Ру перпендикулярно направлению
средней векторной скорости с. Это следует из очевидного
равенства
си ^а\
Итак, сила Жуковского, действующая на
профиль в решетке, равна произведению
средней плотности газа на циркуляцию скорости
вокруг профиля и на среднюю векторную
скорость. Направление силы ру определяется поворотом
вектора скорости с на 90° в сторону, противоположную
направлению циркуляции.
Напомним, что плотность р соответствует среднему
удельному объему, т. е.
Таким образом, мы установили, что в отличие от
одиночного профиля результирующая сила, действующая на
профиль в решетке, равна сумме силы Жуковского Ру
и добавочной силы ДЯа, перпендикулярной оси решетки:
P = Pv + APa.
Важно отметить, что природа сил Ру и АРа различна
В то время как сила Ру зависит от циркуляции потока
и обращается в нуль при Г = 0, сила АРа от циркуляции
непосредственно не зависит.
Сила, действующая на профиль, определена для
общего случая движения газа. С помощью полученных
общих соотношений нетрудно получить величину
аэродинамической силы, действующей на профиль, для
некоторых частных случаев. Так, например, переходя от
решетки к одиночному профилю, увеличивая шаг
решетки до бесконечности, шолучим р2 = р\ и р2 = рх; тогда
АРа = Ри = 0 и, следовательно, в случае изоэнтропическо-
468
Го обтека.йий изолированного профили результирующая
сила, действующая на профиль, равна силе Жуковского:
Р = Рв = 9Гс,
где рис — плотность и скорость набегающего потока.
Направление силы перпендикулярно налравлению
скорости набегающего потока.
Переходя к случаю обтекания решетки несжимаемой
жидкостью, прежде всего следует обратить внимание на
то, что в уравнении (8-12) второй член правой части
пропорционален изменению потенциальной энергии шотока
(с учетом гидравлических потерь), т. е.
*. г2 г2
Для несжимаемой жидкости (р1 = р2 = р) из уравнения
энергии находим:
ci - 4 Pit - А
где p2t — теоретическое давление при отсутствии потерь.
Следовательно,
ьРа=-*(р«-Р1=-*Рп-
Разность давлений Д/7п = /72,— р2 равна потере
давления в решетке. Итак, в случае обтекания решетки
потоком несжимаемой жидкости добавочная сила отрицательна
и определяется потерей давления в решетке (не следует
смешивать потерю давления А/?п с разностью давлений
А —А)-
При отсутствии потерь Арп = 0 и ДРа = 0. В этом
случае результирующая сила для несжимаемой жидкости равна
силе Жуковского1:
Р = Р =рГс.
1 Возможность обобщения теоремы Жуковского на случай
течения несжимаемой жидкости через решетку была указана впервые
Б. С. Стечкиным в 1944 г. Точное решение было получено Л И
Седовым в 1948 г. Обоснование приближенной теоремы Жуковского
для решетки в потоке сжимаемой жидкости было предложено
Л. Г. Лойцянским в 1949 г. Изложенное в настоящем параграфе
обобщение теоремы Жуковского для решетки в адиабатическом
потоке газа дано А. Н Шерстюком.
469
8-4. КЛАССИФИКАЦИЯ ПОТЕРЬ
И ОСНОВНЫЕ ХАРАКТЕРИСТИКИ РЕШЕТОК
При движении газа через решетки турбомашин
возникают потери энергии: часть кинетической энергии
потока вследствие вязкости необратимо преобразуется
в тепло.
Рассмотренные в настоящей главе некоторые
результаты теоретических и экспериментальных исследований
потока газа в решетках позволяют классифицировать
потери энергии по следующей схеме:
A. Профильные потери (в плоской решетке, т. е. при
бесконечно большой высоте), включающие: 1) потери
на трение в пограничном слое; 2) вихревые потери три
отрьивах потока на профиле; 3) вихревые потери за
выходной кро-мкой (кромочные потери).
Б. Концевые потери в прямой пространственной ре1
шетке (дополнительно"к группе «А»).
B. Волновые потери (дополнительно к группам «А» и
«Б» при околозвуковых и сверхзвуковых скоростях)
в скачках уплотнения.
Г. Потери, вызванные нестационарностью и высокой
турбулентностью потока.
Д. Веерные потери в кольцевой решетке,
обусловленные отклонениями геометрических -параметров решетки
от оптимальных значений и радиальными -перетеканиями
газа.
Следует подчеркнуть, что профильные потери в
решетке аналогичны (профильному сопротивлению при
обтекании одиночного крылового профиля (гл. 5).
Различие состоит только в том, что при исследовании решеток
устанавливаются относительные -потере энергии, а
профильное сопротивление характеризуется силой
сопротивления, отнесенной к скоростному напору набегающего
.потока. Физическая природа профильных потерь и
профильного сопротивления тождественна. Вихревые
потери при отрыве тотока на профиле и за вьиходной
кромкой эквивалентны сопротивлению давлений.
Следовательно, профильные потери можно также рассматривать
как сумму потерь трения и «потерь давления».
Потери, отнесенные к группам «Б», «Г» и «Д»,
являются специфическими для решеток. Волновые потери
(группа «В») проявляются в решетках в специфической
форме. Однако эта группа потерь, обусловленная необ-
470
ратимыми процессами в скачках, аналогична волновому
сопротивлению при обтекании одиночного профиля.
При расчете ступени турбомашины необходимо знать
направление потока на выходе из
решетки (угол выхода потока) и энергетические или
силовые характеристики решеток. Ниже
рассмотрены отдельные составляющие потерь и указаны
методьи расчета основных аэродинамических
характеристик решеток.
Для оценки турбинной решетки в отличие от
одиночного профиля вводятся главным образом энергетические
характеристики. Компрессорные решетки
характеризуются в основном силовыми коэффициентами.
Энергетической характеристикой решетки является
коэффициент .потерь, определяемый как отношение части
кинетической энергии, необратимо перешедшей в тепло,
к располагаемой кинетической энергии:
с=]2 -VFf—^-О. с8-14)
где /701, p02 — давления полного торможения перед и за
решеткой;
М2/ — число М за решеткой в случае изоэнтропи-
ческого течения.
Учитывая, что числитель выражения (8-14)
представляет собой квадрат некоторого фиктивного числа М,,
подсчитываемого по параметрам торможения:
М2= —Г(^~-11
формулу для коэффициента потерь можно представить
в виде:
е=ж- <8-i5>
Коэффициент полезного действия решетки определяется
очевидным выражением
4=1— С. . (8-15а)
471
При экспериментальном исследовании решеток
определяется поле давлений торможения перед и за решеткой
Рои и Ро?л и статических давлений ри и р2Г По этим
данным с помощью формулы (8-14) подсчитываются точечные
значения С,.
Реальный поток на входе и на выходе из решетки
является неравномерным: скорости, углы потока и
статические давления меняются по шагу, поэтому значения
местных коэффициентов потерь энергии, а также другие
характеристики решетки приходится осреднять по шагу.
Для определения осредненных характеристик следует
сформулировать понятие идеального (теоретического)
процесса в решетке при неравномерном потоке.
Идеальным .процессом можно считать такой изоэнтропический
процесс, при котором в исследуемом сечении
сохраняются неизменными по сравнению с реальным процессом
поля статических давлений и направления скоростей 1.
Коэффициент полезного действия .решетки в
неравномерном потоке подсчитьивается по формуле
t
■n=-t , (8-16)
б
где с2 — действительная скорость;
р2 — плотность газа в действительном потоке.
Введя в это выражение приведенный расход q, после
элементарных преобразований получим:
t
\fy2t 7TsinM'
j xttbt j^sin №
0
1 При другом определении идеального процесса считают, чго
углы на входе и выходе из решетки равны средним углам Pi и р2>
определяемым ло уравнению импульсов.
°- . (8-17)
472
Последнее выражение получено в предположении Я2/—
^ const. Величина т}.= -^-; Я2Р q2t — теоретическая ско-
рость и приведенный расход в точке за решеткой.
Для расчетов по формуле (8-17) удобно пользоваться
диаграммой, предложенной А. В. Губаревым (рис. 8-10).
Диаграмма строится для раздельного определения
величин
Л „ Л Ро2 „ D - А)2
Порядок построения и пользования диаграммой легко
понять с помощью рис. 8-10. По значениям/702.//?01 и/?2///?01
в точке исследуемого потока определяются соответственно
А{ и В.. Затем производится раздельное суммирование
величин А^'т^2. и 5.sinp2/. Окончательное выражение для
к. п. д. решетки имеет вид:
X Aisinh
1i= — >
.где п — число выбранных участков в пределах шага
решетки.
Кроме коэффициента потерь (к. п. д.) решетки, в
расчетах ступени применяют коэффициент расхода, равный
отношению действительного расхода к расходу в
идеальном процессе. Так как расход газа [через один и тот же
канал
t t
Gi=gj?iCi sin $ldt = g^?2c2 sin pa dt, (8-18)
о о
то, используя формулу (2-38), найдем коэффициент расхода
в таком виде:
t
~t • (8-19)
\ q2t sin $2dt
о
473
I'
Рис. 8-10. Диаграмма для определения потерь в адиабатических
потоках (k— 1,4).
С помощью формулы (8-18) и (2-38) количество
движения за решеткой может быть представлено в виде:
,-c2 = ksAp02qiX2sin%dt.
474
Тогда коэффициент использования импульсов1
И^"аГ81П?2
t
Г Р™ • а а*
W2/T~Sin^
(8-20)
где 9i = r~ '
Легко показать, что диаграмма, построенная для
определения i\ (рис. 8-10), позволяет также найти ц и <р в
неравномерном потоке. Для определения |х достаточно на
диаграмме В найти значение B.t= qm -^- (на пересечении
экспериментальных значений P02i/p0i и P2JP01) и ^/ = #2/
(на пересечении кривых p2ifpol и р^Ро1 = 1)> т°гда
i=\
* п
У Bisin hi
£fi,sin?2
/=i
Для определения ср необходимо построить
дополнительную диаграмму зависимости yt=f (-^- ; — j .
Так как
ъ~У\=Ух-ь
1 Коэффициент <р часто называют коэффициентом скорости
Формулы (8-19) и (8-20) получены с помощью уравнений неразрывности
и количества движения в предположении, что в идеальном процессе
поле углов и давлений сохраняется таким же, как и в
действительном процессе.
475
то
Осредненное значение угла выхода потока определяется
по уравнению количества движения. Средние значения
проекций скорости за решеткой равны:
t
(£2cos|32)ka = -^ s# jV02?Acos|32sin|32d/;
о
t
fo s}n Ря)к д = ^ s* jVo2<72*2 sin2 parf/.
0
Тогда средний угол
t
2 1^02^2 sin2j*2fltf
Р2кд = а^е-Л • (8-21)
8-5 ПОГРАНИЧНЫЙ СЛОЙ
И ПОТЕРИ НА ТРЕНИЕ В РЕШЕТКАХ
Определение структуры пограничного слоя,
образующегося на профиле, установление точек перехода и
отрыва слоя являются ^важной частью задачи о
«профильных .потерях в решетках. Схема образования
пограничного слоя на профиле в плоской решетке показана на
рис. 8-11,а.
Пользуясь графиком распределения скоростей по
обводу профиля, проследим характер изменения слоя на
вогнутой и выпуклой поверхностях лопаток.
На вогнутой поверхности за точкой торможения
(критической точкой) толщина слоя вначале нарастает
незначительно. В местах увеличивающейся кривизны, где
476
скорость внешнего потока либо не меняется, либо
падает, толщина (пограничного слоя возрастает. В этих
точках может возникнуть переход ламинарного слоя
в турбулентный, а .при некоторых режимах— даже
местный отрыв слоя. На конфузорном участке вблизи
узкого сечения, где давление интенсивно падает, а скорость
Рис 8-11. Схема образования пограничного слоя на профиле в
решетке,
а —без отрыва, б —отрыв на спинке лопатки
возрастает, толщина пограничного слоя уменьшается и
достигает минимальных значений на сходе с профиля.
На спинке в направлении к узкому сечению толщина
слоя также уменьшается. Вдоль спинки в косом срезе
заметно интенсивное нарастание толщины слоя,
достигающей у выходной кромки максимальных значений.
Некоторая часть спинки в косом срезе обтекается, как
правило, с положительным градиентом давления (диффузор-
ный участок спинки), что иногда может привести к
отрыву (рис 8-11,6).
477
При проектировании решетки практически
существенным является определение положения области .перехода
ламинарного слоя в турбулентный и условий
безотрывного обтекания профиля. Как показывают расчеты и опы-
ТЫ1, точка перехода чаще всего совпадает с точкой
минимума давлений на спинке или несколько смещается
в диффузорную область. В тех случаях, когда поток
сильно ту.рбулизирован, точка перехода может
существенно смещаться против течения (в конфузорную
область).
Рассмотрим 'Некоторые результаты опытного
исследования пограничного слоя в активной и реактивной
турбинных решетках.
На рис. 8-12 приведены! результаты измерений в
пограничном слое на спинке профиля ТС-2А. Значительная
конфузорность каналов этой решетки (.рис. 8-12,а)
создает благоприятные условия для сохранения
ламинарного режима в слое. Однако при выходе в косой срез
(жсп = 0,5) ламинарный слой теряет устойчивость и
переходит в турбулентный. Зона перехода вполне
удовлетворительно определяется описанным в гл. 5 способом и
занимает около 4% общего обвода профиля. Далее
течение в пограничном слое носит яв*ш выраженный
турбулентный характер (рис. 8-12,6). За областью перехода
в косом срезе на спинке отмечается интенсивное
нарастание толщины потери импульса.
Пограничный слой на вогнутой поверхности до
выходной кромки ламинарный. Отсюда можно заключить,
что точки отрыва на выходной кромке расположены
несимметрично относительно средней линии профиля.
Результаты исследования пограничного слоя в
активной решетке, составленной из профилей МЭИ ТР-ОА,
показали, что и здесь при расчетном угле входа
существуют три зоны течения в слое, которые располагаются
таким же образом, как и в каналах реактивных решеток.
При оптимальном угле входа Pi = 23° (рис. 8-13)
распределение скоростей вдоль спинки является конфузор-
ны-м. Переходная зона при всех значениях М2
располагается за минимальным -сечением канала при входе в
косой срез и изменение режима по М и Re не приводит
к заметному перераспределению протяженности
ламинарные и турбулентных участков слоя.
478
Рис. 8-12.
Распределение скоростей
в пограничном слое
на спинке профиля
(а) и распределение
толщин потери
импульса вдоль
спинки (б) для
реактивно -L _1 ной решетки ТС-2А.
о.)
Jf*
°сп
td3-ili
V
>,о
0,8
0,6
0,4
0,2
0-
r Kl
■ 0,6
■ 0,7
■ 0,6
- 0,5
■ о,ч
■ 0,3
■ 0,2
■ 0,1
0
Vх.
/
l-"'
,/
A
t
• -Результаты расчетов
^-Результаты опытов
{
._ —
*-■"
-—-
г-*-*
±^4С
•*с—
^
f
*/
--*
лЧ-К-
t,<?
S*
■-**-—
~s
Г
-V*
-Л
Ъ
хсп
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0;9
Ч
479
При малых углах входа (^ЦМ3) весь пограничный
слой на спинке оказывается турбулентным и толщина
потери импульса у выходных кромок на спинке возрастает
в 2 — 2,5 раза по сравнению с р1==23° (рис. 8-14).
Существенные изменения в распределении толщины 8**
отмечаются и на вогнутой поверхности (рис. 8-15). Если
Рис. 8-13. Изменение толщины потери импульса на спинке профиля
активной решетки ТР-ОА при различных числах М2 (опыты МЭИ).
при р1 = 23° (М, = 0,52)бв"г оказалось порядка 0,7.10~3,
то с переходом к р1=14° толщина ~&в*г уменьшилась до
0,27• 10 "3. Суммарная толщина потери импульса при
уменьшении угла входа потока увеличивается на 60 — 70°/0.
С увеличением ^ возрастает Т* на вогнутой
поверхности и уменьшается на спинке. Однако суммарная
толщина потери импульса растет менее интенсивно, чем при
уменьшении угла входа потока. Отсюда непосредственно
следует, что при некотором оптимальном угле входа ES**
является минимальным. Зависимость толщины Т* у
выходных кромок от р, для реактивной решетки показана на
480
MM
',5
',«
0,5
0
71
с
d
%
—-J
n
► -xcn-Of905
ь-хсл=0,795
*-XarO,S50
4 Xa-?
r—~^
мг*0,7
r^
---*"
7°5Я'
1
Л
Ai
0,3 0,1 0,5 0,6 0,7 0,8 0,9 1,0
«Г h
Ю**3,2\
ч
',e
№~це
0,! 0,2 0,3 0,4 0,5 0,5 0,7 0,8 0,9 1,0
*)
Рис. 8-14. Профили скорости (а) и изменение толщины потери
импульса вдоль спинки (б) для активной решетки при р, = 14°.
31 М. Е. Дейч
481
Ц2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2
Рис. 8-15. Зависимость $** от угла входа потока ?, для
активной и реактивной решеток (опыты МЭИ).
4S2
рис. 8-15, б. Чем меньше конфузорность потока в
решетке, тем более интенсивным является изменение 2S в
зависимости от рх.
Влияние двух других режимных параметров (Re2 и М2)
на структуру слоя в решетках можно проследить по
графикам на рис. 8-13 и 8-15, в. С ростом Re2 и М2
толщина "§** заметно уменьшается.
Интенсивное уменьшение 6СП с ростом М2 объясняется
в значительной степени изменением градиентов скорости
в межлопаточном канале. Из приведенного на рис. 8-13
распределения скоростей отчетливо видно увеличение
конфузорности на спинке с ростом М2.
С переходом к сверхзвуковым скоростям величина 6
заметно возрастает в результате взаимодействия скачка
уплотнения с пограничным слоем. В месте падения скачка
на спинку в косом срезе может наблюдаться отрыв слоя.
Весьма существенное влияние на структуру
пограничного слоя оказывает степень турбулентности потока,
величина которой в ступенях турбомашин может достигать
больших значений.
Влияние степени турбулентности на структуру погранич:
ного слоя1 на спинке реактивного и активного профилей
можно оценить по рис. 8-16, а и б. С увеличением
турбулентности происходит перестройка профилей скорости
в слое: увеличивается наполнение профилей скорости
(гл. 5). Увеличение степени турбулентности приводит к
сокращению участка ламинарного слоя и к возрастанию
толщины турбулентного слоя.
Характер изменения профильных потерь и потерь на
трение в зависимости от степени турбулентности для двух
типов решеток можно оценить по кривым на рис. 8-16, б.
В реактивной решетке ТС-1А увеличение Е0 с 1 до 9°/0
приводит к возрастанию Стр с 2,6 до 4°/0. Для активной
решетки ТР-ОА кривая С имеет минимум при Е0 = 3°/0.
На участке 1°/0 < f0 ^ 3°/0 происходит турбулизация слоя
в точке отрыва на спинке и потери снижаются. Прц £0>
>3°/0 с ростом Е0 потери на трение возрастают более
интенсивно, чем в конфузорной реактивной решетке.
Расчет пограничного слоя в решетках производится
1 Опыты проведены В. А. Врублевской.
31*
483
с помощью методики, изложенной в гл. 5. При этом
предварительно должно быть рассчитано или определено
опытным путем распределение скоростей по обводу профиля.
Рис. 8-16. Влияние степени турбулентности на распределение толщин
§** вдоль спинки (а) и на профильные потери и потери трения в
реактивной и активной решетках TC-1A и ТР-ОЛ (б) (опыты МЭИ).
По нему производится расчет толщины потери импульса.
Предварительно необходимо правильно определить
положение переходной области на спинке и вогнутой
поверхности.
484
"При отсутствии опытных данных о в зоне перехода
можно определить по формулам, приведенным в § 5-10.
При высоких степенях турбулентности переход
совершается вблизи входной кромки; в этом случае отпадает
необходимость учитывать ламинарный участок.
Потеря кинетической энергии в пограничном слое
(потеря на трение) определяется по уравнению энергии,
записанному для выходного сечения решетки:
А£,тР=4" | К?и ("i ~ и2У>dy
Ч о
• оо
I pu (и* — и2) dy
+
(8-21)
где и — скорость в данной точке слоя;
иг — скорость на внешней границе слоя;
у— координата, нормальная к профилю в данной
точке.
При отсутствии потерь кинетическая энергия за
решеткой будет:
(8-22)
тде G — действительный расход через один канал,
определяемый по формуле
G=Gt~g
, (8-23)
\ (pi«i — ?'An dy + f (pi«i — p")Bor dy
LO 0 -
где Gt, ut — теоретические расход и скорость на выходе
из решетки.
Коэффициент потерь на трение равен:
ДЯ,
С
^тр
тр
Выразив АЕтр и Et по формулам (8-21), (8-22) и (8-23)
после некоторых преобразований можно получить:
С
Y>{kxk2H Ь )
гр
f sinp2—S^^Z/V*)
(8-24)
485
где
^= Ul ; S<7 =— безразмерные скорости за решеткой
смакс смакс для действительного и теоретиче-
ского процессов. Знак Е указывает
на суммирование по спинке и
вогнутой поверхности.
Результаты проверки точности расчета слоя для
нескольких решеток можно видеть на рис. 8-13 и 8-14.
Сравнение показывает удовлетворительную сходимость
опытных и расчетных значений Ь во всей области
дозвуковых скоростей (до М2 = 0,955).
После расчета толщины 8** определение потерь на
трение не представляет труда, если известна величина //* =
***
=—^г • Для расчета турбинных (конфузорных) решеток
можно принимать // = 1,8.
В диффузорных (компрессорных) решетках величина
//* несколько повышается. Таким образом, потери на
трение в первом приближении можно считать
пропорциональными толщине потери импульса на выходной кромке
профиля и по ее величине судить об относительной
эффективности решеток.
8-6. КРОМОЧНЫЕ ПОТЕРИ В РЕШЕТКАХ
При сходе с выходных кромок профиля происходит
отрыв пограничного слоя. В результате отрыва и
взаимодействия слоев, стекающих с вогнутой и выпуклой
поверхностей, с внешним потоком за выходной кромкой
возникают вихри, которые образуют начальный участок
кромочного следа (рис. 8-17).
В пределах начального участка и в том месте за ним,
где образуется вихревая дорожка, взаимодействие
между кромочным следом и ядром потока приводит к
выравниванию поля потока за решеткой. В некотором сече-
486
ими за решеткой вихревые следы соседних профилей
смыкаются и поле скоростей, статических давлений и углов
становится равномерным. На участке до «полного
выравнивания среднее статическое давление .потока
увеличивается, а угол выхода уменьшается.
На поддержание вихревого движения за кромкой
затрачивается часть кинетической энергии потока; допол-
Рис 8-17 Схема потока газа за решеткой.
нительные потери кинетической энергии образуются на
границе кромочного следа и ядра потока, где возникает
интенсивный турбулентный обмен.
Образование вихревого движения в кромочном следе
подтверждается экспериментально. На рис. 8-18
приведены кривые распределения полных и статических
давлений, углов и температур торможения на некотором
расстоянии за кромками реактивной решетки. При
малых расстояниях от кромки обнаруживается
значительная неравномерность полей давлений, углов и, что
особенно важно, температур торможения. В кромочном
следе давление и температура торможения уменьшаются,
что является характерным для вихревого движения.
Изменение Т() объясняется неравномерным распределе-
487
нием скоростей и вихревым эффектом за кромкой (§ 5-1
и 5-16). Быстрое выравнивание Т0 свидетельствует об
интенсивном обмене между ядром (потока и кромочным
следом.
При небольшой толщине кромки на структуру
кромочного следа и кромочные потери решающее влияние
оказывают толщина пограничного слоя и распределение
-t-
ви мм
Рис. 8-18. Распределение параметров потока за выходными
кромками реактивной решетки.
скоростей вблизи точек отрыва потока, а также
разность давлений в этих точках.
По мере увеличения толщины кромки заметное
влияние приобретают потери, связанные с внезапным
расширением потока.
На рис. 8-19 показаны результаты дренирования
выходной кромки. Как видно, давление вдоль кромки
резко меняется- Со стороны вогнутой поверхности поток
конфузорный, а со стороны спинки — диффузорньнй.
Следовательно, точки отрыва смещены ik спинке лопатки.
При изменении толщины выходной кромки Л
(рис. 8-17) меняется распределение скоростей по обводу
профиля и, следовательно, происходит некоторая пере-
488
стройка пограничного слоя вблизи выходной кромки.
Потери на трение три этом изменяются в соответствии
с изменением толщины потери энергии на выходной
кромке. Опыгьи В. С. Елизарова (рис. 8-20) отчетливо
о,Зг
0,2
0,1
-0J
*1
fM2-0,65
-о,г\ £__]
5 Номера точен'
а)
Рис. 8-19. Распределение давлений по выходной кромке реактивной
решетки при различных режимах.
подтвердили, что с увеличением А сумма 6 4-5 =:
** си * вог
= //*£6** изменяется.
Значительное влияние на структуру потока за
кромкой оказывает шаг лопаток. При малом шаге (рис. 8-19)
мм
Ц
о
\dm
- А
S \
JZ-
Т-В
1 t
$2
» *
J
t
A J
мм
мм
3
2
1
Онр
£&Л
х~Ъх
^^о
а
ч /
/°
X
а)
25
50 П 100 125
б)
Рис. 8-20. Изменение толщин потери энергии на профиле и за
решеткой (а) и д*** в зависимости от параметра ^ (б) по В. С.
Елизарову.
489
за кромкой обнаруживается разрежение, несколько
увеличивающееся с ростом М2. По мере увеличения шага
среднее давление за кромкой возрастает и при
некотором шаге достигает значений, больших, чем давление за
решеткой, Следовательно, с увеличением шага должны
уменьшаться не только относительные, но и абсолютные
значения кромочных потерь, что и подтверждается
экспериментом.
Некоторое влияние >на кромочные потери оказывает
форма кромки, определяющая при известных условиях
положение точек отрыва. Опыты показывают, что в
случае скругленной кромки при дозвукоъьих скоростях
начальный участок следа более узкий (точки отрыва
смещены то .потоку), чем у плоско срезанной кромки.
Теоретический расчет кромочных потерь весьма
сложен, и эта задача до сих пор еще не решена.
Имеющиеся полуэмпирические методьи позволяют оценить
кромочные .потери и угол выхода из решетки на основании
опытных данных, полученных для определенных
классов профилей.
Параметры выровнявшегося потока за решеткой мо-
Рут быть найдены путем совместного решения уравнений
неразрывности, импульсов и энергии. Для жидкости,
заключенной между контрольными поверхностями
(рис. 8-17), расположенными «параллельно друг другу на
расстоянии, равном участку выравнивания, указанные
уравнения могут быть записаны при следующих
допущениях: а) плотность потока мало меняется в процессе
смешения (между сечениями //—// и //'—//'); б) поля
скоростей и давлений между кромками и в сечении
//—// являются однородными; в) спинка профиля в
косом срезе выполнена прямолинейной.
В этом случае уравнение неразрывности можно
представить в виде:
?сЛ* — ДО sin Р2п = C2*>P'sin i3»'
или
с 2 (1 — -с) sin 32п = с2ос sin p2, (8-25)
At
где ^=yi
At — толщина кромки в плоскости выходного сечения
(рис. 8-17).
490
Уравнение импульсов в направлении оси решетки дает:
с\ cos $2n?(t — M)sm$2n = c22oocos$2?ts'm$2. (8-26)
Уравнение импульсов в направлении, перпендикулярном
оси решетки, можно написать в виде:
cLp sin2 Р2п (t - Д<) + А (' - ДО + Рквы =
= 4osm*?.J + p2J. (8-27)
Из уравнений (8-25) и (8-26) легко получить:
P, = arctg[(l-x)tgp20]. (8-28)
Уравнения (8-25) и (8-27) позволяют найти повышение
давления за решеткой:
ДА = %^ = [2 (1 - *) sin2 Р2/2 + ^кр] х. (8-29)
"2?С2
Для определения теоретической скорости на
бесконечности за решеткой воспользуемся уравнением энергии,
которое при принятом допущении р2 = р2оо = р можно
представить в виде:
Р '
(8-30)
где с2оо — теоретическая скорость в сечении // — //.
С помощью уравнений (8-27), (8-28) и (8-30) получаем
коэффициент кромочных потерь
= * sin* М-р j
КР l-A/^200
Входящее в уравнения (8-29) и (8-31) безразмерное
давление за кромками рщ> должно бьить определено по
опытным данным.
Согласно (8-31) при увеличении толщины выходных
кромок А/ целесообразно одновременно увеличивать от-
491
носительный шаг t и уменьшать угол установки с тёк
чтобы сохранить заданный угол выхода потока и
обеспечить умеренные потери.
Приведенные выше формулы, полученные Г. Ю.
Степановым, удовлетворительно согласуются с опытньими
данными, однако практическое использование уравнения
(8-31) затруднено, так как величина /?кр может меняться
в весьма широких пределах в зависимости от режимных
и геометрических параметров решетки.
В. С. Елизаровым предложен приближенный метод
определения кромочных потерь как разности потерь на
определенном расстоянии за решеткой ('.профильных
потерь) и потерь трения. Коэффициенты профильньих
потерь и потерь ,на трение могут быть выражены через
соответствующие условные толщины потери энергии
[формула (8-24)].
В соответствии с рассматриваемым методом толщина
потери энергии в кромочном следе выражается
формулой
*** *** *****
Ь =8,, и Ь ,
кр 2 Л1 тр '
***
где о2 — толщина потери энергии в сечении кромочного
следа на выбранном расстоянии за решеткой.
Относительная толщина потери энергии в следе
"кр
кр Н Ь д
11 тр тр
зависит в основном от комплекса
Д£5*** Д£5*
*сп 8вог Н *сп»вог
(8-32)
(8-33)
Соответствующая зависимость, полученная
экспериментально для безотрывно обтекаемых профилей, приведена
на рис. 8-20,6. Формула, аппроксимирующая эту
зависимость, имеет вид:
~СР = (0,21 Х2 +12,4/ +220)-10"3. (8-34)
Следовательно,
2 тр\ кр I /
492
Коэффициент профильных потерь определяется по
формуле
Спп =—Д=. (8"35)
где а2 — ширина узкого сечения канала;
Ст — коэффициент потерь на трение, определяемый по
формуле (8-24).
Таким образом, рассматриваемый способ расчета
профильных потерь основан на установлении связи между
кромочными потерями и потерями на трение \ причем эти
потери определяются раздельно.
Очевидное преимущество метода состоит в том, что
он позволяет учесть влияние различных геометрических и
режимных параметров решетки на кромочные и
профильные потери. При изменении этих параметров меняются
условные толщины пограничного слоя, через которые
выражаются коэффициенты £Пр и £Кр-
Однако фактически вид функции &кр*(х) может
меняться в зависимости не только от типа решеток, но и от
режима обтекания, что является недостатком метода.
Для решеток с толстыми кромками, толщина которых
существенно больше толщины слоя (А = Д/я2>0,3), метод решения
предложен А. Н. Шерстюком. Рассматривается течение в одном
межлопаточном канале, границами которого за пределами выходных кромок
служат прямые, проведенные под углом выхода потока р2 к фронту
решетки (рис. 8-17)
Приближенно угол выхода потока определяется по эмпирической
формуле
?2эф = агс^п(тт), (8'36)
где т — опытный коэффициент.
При большой толщине выходных кромок можно считать, что
переходы от сечения 1 — 1 к сечению )' — Г и от сечения 2—2
к 2'— 2' (рис. 8-17) вызывают такие же потери энергии, как и при
1 Для решеток с острыми кромками метод расчета профильных
потерь разработан Л. Г. Лойцянским. Решение В. С. Елизарова
является распространением метода Л. Г. Лоицянского на решетки с
кромками конечной толщины.
493
внезапном расширении потока. Определив величину этих Потерь,
можно получить приближенную формулу
^кр = То
I» ^(1+0,7Дэф)2 ' (2т
-W
0,25т2 , 1
д .V J I
(8-37)
2 2 / 0,25m2 1 \
+ ^эф(д1+0,7Аэф)2+ (2т-Аэф)2;]
Аэ»
Здесь (рис. 8-17) Д . = —— > Д . —эффективная „толщина"
выходной кромки, определяемая как расстояние между точками отрыва
Д
ДЭф =£: 0,7 Д; аЭф = а2 + -?г — эффективная „ширина" узкого сечения;
<р0 — коэффициент скорости для бесконечно тонкой кромки.
Наиболее простая эмпирическая формула для
определения кромочных потерь предложена Г. Флюгелем:
кр а
где К = 0,2. Однако опыты показывают, что коэффициент
К может меняться в весьма широких пределах в
зависимости от геометрических и режимных параметров решетки
(рис. 8-21).
Сопоставление различных приемов расчета кромочных
потерь показывает, что лучшие результаты дает формула
(8-34), учитывающая влияние чисел Re2 и М2 и основных
геометрических параметров.
Влияние чисел Re2 и М2 (рис. 8-21,6 и в) объясняется
главным образом перемещением точек перехода и отрыва
по кромке, а также изменением потерь на трение (гл. 5).
Особенно характерной является кривая Скр(М2) для Д =
= 0,42. Первый максимум кривой объясняется смещением
точек отрыва против потока (ламинарный отрыв). Турбу-
лизация слоя в зоне отрыва приводит к перемещению
точек отрыва по потоку („кризис сопротивления"). Второй
максимум связан с образованием местных сверхзвуковых
зон на кромке и перемещением отрыва против потока
(Аэф возрастает). Переход к сверхзвуковым скоростям
сопровождается улучшением обтекания кромки. Таким
образом, обтекание толстой кромки при различных Re2 и М2
494
Рис. 8-21. Изменение кромочных потерь в зависимости от толщины
кромки и относительного шага (я), чисел М2 (б).
качественно напоминает спектр обтекания плохо
обтекаемого тела (§ 5-14).
Влияние толщины кромки на угол выхода потока
(рис. 8-22) оказывается различным в зависимости от
способа образования кромки. При подрезке кромки по способу
/ угол (32 уменьшается с уменьшением А. Подрезка
вогнутой поверхности (по способу //) приводит к увеличению р2
по мере уменьшения А. Следует подчеркнуть, что
эффективный угол, определяемый по формуле (8-36), как пра-
495
',°
0,9
j m
1—9
_A
Re2>6-10
<
5
; *^
**I
0,4 0,5 0,6 0,7
6)
0,8
0,9
Рис 8-22. Зависимость угла выхода потока от
относительного шага и толщины кромки {а)> чисел Re (б) и чисел
М2 (в).
вило, не совпадает с действительным углом j$2, причем
0 $р2 (рис. 8-22,6). Поправочный коэффициентов
формуле (8-36) позволяет перейти от р к р2. В соответствии
49Q
с физической природой явлений за кромками коэффициент
т зависит от чисел Re2 и М2, а также от толщины
кромки А (рис. 8-22) и формы спинки в косом срезе. Опыты
показывают, что для профилей с прямолинейной спинкой
в косом срезе угол Р2^Р29ф(/гг^1). Для выпуклой спинки |32
несколько меньше [32 .
8-7. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ
ЭКСПЕРИМЕНТАЛЬНОГО ИССЛЕДОВАНИЯ ПЛОСКИХ
РЕШЕТОК ПРИ ДОЗВУКОВЫХ СКОРОСТЯХ
Рассмотрим результаты опытного (исследования
профильных потерь и углов выхода потока -в зависимости
от геометрических и режимных параметров и формьи
профиля для некоторых реактивных и активных решеток.
Рис. 8-23. Влияние шага на распределение давлений по профилю в
решетке реактивного типа (а)\ профильные потери и угол выхода
потока (б).
Влияние шага и угла установки профилей.
Распределение давлений по профилю реактивной решетки (рис. 8-23)
показывает, что при 1=0,7^0,8 течение конфузорное по
всему обводу профиля, за исключением коротких
участков вблизи входной и выходной кромок. По мере уве-
32 М. Е. Дейч
497
личения шага точка минимума давлений на спинке
смещается против потока, сокращаются области конфузор-
ного течения в косом срезе; градиенты! давлений в кон-
фузорных и диф'фузорных областях возрастают.
Следовательно, область перехода смещается против потока и
несколько увеличиваются потери на трение в косом
срезе. Обтекание .вогнутой поверхности при увеличении шага
"/ П\ lTj/j
3d 40 42 44 46
б)
Рис. 8-24. Влияние угла установки профиля в решетке реактивного
типа на распределение давлений (я), профильные потери и угол
выхода потока (б).
становится благоприятным, так как конфузорность
течения вблизи выходной кромки увеличивается. При
малых шагах течение вдоль спинки в косом срезе более
конфузорно, однако градиенты давлений уменьшаются.
Следовательно, с увеличением шага при
безотрывном обтекании- профиля потери на трение и кромочные
потери меняются различно: £тр вначале уменьшается,
так как снижается относительное значение толщины по-
тери импульса ——, а при больших шагах возрастает
вследствие увеличения толщины! (потери импульса;
кромочные потери с ростом t уменьшаются непрерывно.
В результате профильные потери вначале уменьшаются,
а затем увеличиваются. Диапазон относительных щагов4
498
соответствующий минимуму профильных потерь,
называется оптимальным (рис. 8-23,6). Опыты
отчетливо показывают, что диапазон оптимальных шагов
зависит от формы -профиля.
Изменение угла установки профиля |3У вызывает
изменение распределения давлений то профилю (рис. 8-24).
В соответствии -с этим изменяются градиенты давления
в диффузорных и конфузорных участках на профиле и
структура пограничного юлоя. В результате профильные
потери при увеличении |3У вначале уменьшаются, а
затем возрастают (рис. 8-24,6), т. е. имеется определенный
диапазон оптимальных углов установки. Необходимо
отметить, >что этот диапазон зависит от шага решетки.
Угол выхода потока из решетки увеличивается при
увеличении шага и угла установки. В интервале
значений £0пт и Ру.опт угол выхода лри изменении шага
меняется примерно пропорционально arcsina2//.
Слабое изменение £Пр в широком диапазоне
изменений шага и ру является важной особенностью
реактивные решеток, составленных из хорошо обтекаемых
профилей К Абсолютное значение £Пр не превосходит 2—3%.
Аналогично меняются профильные потери и угол
выхода потока в зависимости от_£ и |3У для решеток
активного типа, однако диапазон t0m и |3У опт для активных
решеток оказывается более узким, так как
геометрическая и аэродинамическая конфузорность каналов таких
решеток будет меньшей
Отметим, 'Что наличие диффузорных участков на
спинке -в косом срезе с небольшими градиентами давле-
ления не приводит к резкому возрастанию потерь, так
как при малых степенях турбулентности (переход в
пограничном слое происходит быстрее и отрыв .на
выходных 'кромках смещается по «потоку.
Влияние режимных параметров на профильные потери.
В .предыдущем параграфе было показано, что в
зависимости от угла входа .потока |3i меняется распределение
толщин 6** на вогнутой и выпуклой поверхностях, так
как меняется распределение давлений по профилю
(•рис. 8-25,а). Наиболее неблагоприятными являются
режимы с малыми углами входа (|3i<45°), когда на вход-
1 Реактивные и активные рабочие решетки с малыми
профильными потерями разработаны в МЭИ, ЦКТИ, ЛМЗ и ЦНИИ им.
Крылова.
32*
499
йом участке спийки пойвляе^й заметный диффузорный
участок. При этом резко утолщается 'пограничный слой
на обводе спинки, ухудшается распределение скоростей
в слое и даже при умеренных градиентах в диффузорной
Рис. 8-25. Распределение давлений по профилю реактивной решетки
(а), профильные потери и угол выхода потока (б) в зависимости от
угла выхода fo М2 = 0,5; Re =* 3,46-105
области в косом срезе возникает отрыв; иногда отрыв
может «возникнуть и на входном участке спинки. При Рь
больших расчетного, диффузорная область
обнаруживается на вогнутой поверхности. Однако в связи с ггем, что
на сходе с этой поверхности течение конфузорное, отрыв,
500
ofl
0,05
0,04
пР *Ч,
j
1 ±fi
15 20 25
Рис 8-26 Распределение давлений по профилю решетки активного типа (а); профильные потери ь зависимости
от Мб); Ма = 0,7; Re2 = 4.10*.
ка'К правило, до выходной кромки не распространяется.
Аналогичная, но более резкая картина
обнаруживается в решетках активного типа (рис. 8-26).
Следовательно, три малых углах входа отмечается значительно
более резкое возрастание потерь, чем при больших (ом.
также рис. 8-15). Сравнение реактивньих и активных
решеток при различных Pi отчетливо показывает, что
решетки с меньшей геометрической конфузорностью —-
более чувствительны к изменению (Зь
При небольших дозвуковых скоростях, когда влиянием
сжимаемости можно пренебречь, профильные потери
зависят от числа Рейнольдса. Влияние Re2 особенно велико
при отрывном обтекании спинки профиля, когда отрыв
происходит до точки перехода ламинарного слоя в
турбулентный. В этом случае при увеличении Re2 точка отрыва
смещается по потоку. При этом потери в зависимости от
числа Re2 меняются резко (рис. 8-27).
Влияние Re2 на профильные потери следует
рассматривать при различных углах входа ^ и степенях
турбулентности набегающего потока. Геометрическая конфузор-
ность также влияет на характер зависимости Cnp(Re2).
При малых степенях турбулентности и расчетных
углах входа отчетливо видно существенное влияние Re2
на Спр при Re2<(6-r-8). 105. С ростом Е0 (рис. 8-27,6)
область практической автомодельности смещается в
сторону меньших Re2 (§ 5-14). Уменьшение ReaBT отмечается
также при малых pt < ${ расч и для решеток с небольшой
конфузорностью каналов. Таким образом, значения чисел
Re2, определяющих области автомодельного течения в
решетках, могут изменяться в широких пределах в
зависимости от формы профиля, геометрических параметров
решетки, степени турбулентности и угла входа.
Влияние сжимаемости (числа М2) на характеристики
решеток при докритических скоростях обнаруживается,
начиная примерно с М2>0,5 (рис. 8-28). С увеличением
М2 Спр уменьшается и достигает минимального значения
М2^ 0,75 ч-0,95 в зависимости от типа решетки и формы
профиля.
Изменение Спр в зависимости от М2 в докритической
области при безотрывном обтекании легко объяснить тем, что
502
bj A. ~ fv, i^> ш
н « лХ a.
x ca ^ ■=; <u л
О) О tt £ ?
ал i) \o (-
oj «,fr _ о
д ш д ° j_ со
н (-£2 s 2 о
^ ° " О * ^
<-> и <l> л aS vo
к go ч с * о
a; s cx-e-S X о
^c°ms x
КЯ SC<y e;
1=5 С 2 д t-r
ш О W £ H О
| и «5Г л в s
Q x m^ о Ч н
£
1 •**
"1
1 it
я
ар
/
/
\"Э»
sfe
иГ
градиенты давления в сжимаемой жидкости увеличиваются
с ростом М2 (гл. 3).
При конфузорном обтекании профиля толщина потери
импульса В** уменьшается, а при диффузорном —
соответственно возрастает (§ 8-5).
Рис. 8-28. Влияние числа М2 на распределение давлений, профильные
потери и угол выхода потока для . решеток реактивного и активного
типов.
По мере увеличения М2 точка минимума давлений в
косом срезе несколько смещается по потоку и значение ~р
снижается. В результате увеличивается протяженность
конфузорного участка на спинке. По этим причинам по-
504
0,5 0,55 0,6 0,65 0,7 0,75 0,8 0,85
a)
W 18 22 26 30 34 3d 42 46 50 54 58 50
с)
Рис. 8-29. Профильные характеристики реактивных (а и б) и активных (в)
решеток (А—О, А—/, А—2иА—3—решетки старого типа).
505
Тёрй снижаются. Аналогичные результаты получены и для
активных решеток.
При больших дозвуковых скоростях (начиная с М2 =
= М2* и при больших М2) в косом срезе канала и на
кромках профиля появляются сверхзвуковые области,
которые замыкаются скачками уплотнения. По этой причине
появляются дополнительные волновые потери и Спр
увеличивается.
Угол выхода потока в зависимости от М2 изменяется
незначительно (рис. 8-28,6). С увеличением М2 угол |В2
несколько уменьшается, а при М2>М2* он возрастает,
что объясняется увеличением потерь в местной
сверхзвуковой области.
Профильные характеристики решеток. Результаты
измерений Спр и р2 в решетках различных типов
показывают, что профильные характеристики являются сложными
функциями большого числа параметров: С= C(V> Py>Re2>
М2,А, форма профиля) и могут быть установлены только
опытным путем.
Примеры построения таких характеристик для решеток
МЭИ реактивного и активного типов можно видеть на
рис. 8-29. Как видно из рис. 8-29,6, профильные потери
в реактивных решетках при ^ = 99° слабо зависят от
угла (32 в интервале fi2 — 12-ь-18°.
Профильные потери в активных решетках невелики
(3,0 —7°/0) и для каждой решетки в широком диапазоне (^
меняются незначительно (рис. 8-29,я). Кривые Спр = / (Pi)
для этой группы решеток имеют пологую огибающую.
На рис. 8-29 приведены также кривые потерь в решетках
старого типа, образованных дугами окружностей и
отрезками прямых. Легко видеть, что новые решетки,
разработанные аэродинамическими методами, имеют значительно
лучшие характеристики. Этот результат подтверждается
также графиками распределения давлений для
сравниваемых форм профилей при одинаковом угле входа потока.
8-8. ПРОСТРАНСТВЕННЫЙ ПОТОК ГАЗА В РЕШЕТКАХ.
КОНЦЕВЫЕ ПОТЕРИ И СПОСОБЫ ИХ УМЕНЬШЕНИЯ
В межлопаточных каналах решетки конечной высоты,
как и в одиночном криволинейном канале !, возникают
1 Анализ вторичных те ;ений в криволинейных каналах дан в § 5-15.
506
вторичные течения: под влиянием поперечного градиента
давления (происходит перетекание газа но плоским (или
цилиндрическим) стенкам [ от вогнутой / .поверхности
к спинке (рис. 8-30).
На спинке, на некотором удалении от концов
лопаток, пограничный слой, притекающий с плоских стенок,
сливается ic основным пограничным слоем, движущимся
Рис. 8-30 Схема образования вторичных течений в
межлопаточном канале решетки.
а —линии тока на плоскси стенке и на спинке; б —периферийные
течения в пограничном слое у концоз лопатки.
по траекториям, 'параллельным плоским стенкам; в
результате здесь происходит интенсивное набухание
пограничного слоя и появляются составляющие скорости,
направленные в ядро потока. В ядре у концов лопатки
возникает течение, направленное от спинки к вогнутой
поверхности, образующее ©месте с периферийным
течением вдоль торцовых стенок вихревые области. Таким
образом, у-спинки профиля на концах лопатки возникает
парный вихрь, состоящий из двух вихревые областей.
Вихри имеют противоположные направления вращения.
На фотографии следов потока (рис. 8-31) отчетливо
видно перетекание пограничного слоя на плоских
стенках и на спинке. Так как за областью возникновения
вихрей продолжается 'притекание газа с торцовых
1 В дальнейшем рассматриваются вторичные течения только
в обандаженной решетке.
507
стенок, то вихревое «движение развивается к выходному
сечению канала; область -взбухания пограничного слоя,
а также ядро парного вихря смещаются к среднему
сечению. При малых высотах вихревые области
распространяются -по всему сечению канала, образуя парный
Рис. 8-31. Следы периферийных
перетеканий в межлопаточном канале.
вихрь, характерный для криволинейных каналов
квадратного сечения (§ 5-15).
Представленное на рис. 8-Э2 распределение потерь
и углов выхода по высоте решетки показывает
характерное для вихревых областей изменение этих величин.
При удалении от торцовьих стенок потери вначале
уменьшается (рис. 8-32,а), затем резко возрастают и -потом
вновь уменьшаются к среднему сечению (потери в
среднем сечении при достаточной высоте решетки равны
профильным). Максимальные потери соответствуют
области утолщенного пограничного -слоя на спинке. Минц-
508
,мальное значение £ у олоских стенок можегг быть
больше или «меньше £Пр в зависимости от интенсивности
вторичных течений; для реактивной решетки (минимум
потерь, как правило, не обнаруживается (.рис. 8-32,6).
0,12\
0,08
ОМ
О
с
и
5
1-QJBI
1 1
<2
5 2
J
zJ
г
0 мм
6)
Рис. 8-32. Влияние вторичных перетеканий на
распределение потерь и углов выхода
потока по высоте активной (а) и реактивной (б)
решеток при различных высотах.
В золе вторичньих течений в соответствии с изменением £
угль» -выхода вначале увеличиваются, а затем к
среднему сечению уменьшаются.
Концевые потери определяются как разюость между
суммарными и профильными потерями. Оценка 'здвдния
509
■на концевые потери высоты, шага, угла установки,
формы .профиля и канала, а также угла входа, чисел Re2 и
М2 можегг быть произведена на основа мши опытных
данных.
Опьиты показывают, что, как и в -случае одиночного
криволинейного канала, любые изменения
геометрических и .режимных параметров, вызывающие увеличение
поперечны* градиентов давления в решетке, утолщение
Рис. 8-33. Изменение концевых потерь в зависимости от высоты,
углов входа потока, углов установки и шага в активных (кривые /)
и реактивных (кривые 2) решетках.
погра-ничного слоя и появление диффузорлых участков
на выходе, приводят к росту концевых потерь.
С уменьшением высоты решетки до известных
пределов 'сокращается плоский участок потока в средних
сечениях канала; область ловьишенных потерь
в золе вихрей практически не меняется.
Следовательно, коэффициенты! концевых
потерь линейно изменяются в зависимо-
сти от — ——.При некоторой минимальной высоте
происходит смыкание вторичных течений; область увеличен-
,ных потерь занимает всю среднюю часть калала
(рис. 8-32,а).
Характер зависимости концевых лотерь от I
существенно меняется для решеток различных типов. Наклон
510
линий £ft = /(y) уменьшается с уменьшением угла
поворота потока в решетке Ар=-180-—(pi + p2) (рис. 8-33).
Минимальные значения ^ соответствуют реактивным
решеткам, которые характеризуются большой конфузор-
ностью каналов и 'малым углом поворота потока.
При увеличении шага реактивной решетки концевые
потери вначале уменьшаются, так как возрастает конфу-
зорность потока, достигают минимума, а затем
увеличиваются в связи с ростом поперечного градиента
давлений. Увеличение угла установки дрофиля при
оптимальном шаге приводит к снижению концевьих .потерь, так
как уменьшаются угол «поворота потока и поперечный
градиент давлений, а при мальих шагах с ростом ру
концевые потери увеличиваются. Влияние шага особенно
велико для активных решеток, причем минимальные
концевые потери соответствуют такому шагу, при котором
межлопаточный канал вначале расширяется (на входе),
а затем сужается.
Интенсивное влияние угла входа потока Pi на £ь
(рис. 8-33) объясняется изменением, поперечных
градиентов давления в канале, .появлением диффузорньих
участков на входе и в косом срезе и в некоторых случаях
образо1ванием отрывов. Концевые потери заметно
возрастают при уменьшении Pi (увеличении Ар). При
постоянном значении pi £& возрастает с уменьшением угла
выхода Р2 (при малых р2< 11-5-12°), так как при этом
увеличивается кривизна канала (рис. 8-33).
Изменение концевых потерь в зависимости от числа
Рейнольдса можно оценить по кривым на рис. 8-34.
С увеличением Re2 концевые потери уменьшаются.
Влияние числа Re2 на £& велико при Re2<5- 105. Это
объясняется тем, что с ростом Re2 пограничный слой
утоняется.
Влияние' сжимаемости при докритических скоростях
сказывается в уменьшении концевых потерь с ростом
числа М2 (рис. 8-34) в связи с тем, что поперечные
градиенты давления в канале уменьшаются (§ 5-15) (см.
также рис. 8-69).
Структура пространственного потока »в кольцевых
неподвижных решетках обладает некоторыми
особенностями. Важ,нейш'им следует считать .наличие
радиального градиента давления; давление у периферии выше, чем
511
у корневого сечения'1. Вследствие этого развиваются
радиальные «перетекания вдоль лопаток, направленные от
периферии к корневому сечению. Эти радиальные
перетекания .накладываются на поперечные (рис. 8-35).
Кроме того, в кольцевой решетке форма канала изменяется
по -высоте (из-за изменения шага и цилиндричности тор-
Рис. 8-34. Влияние числел Re2 и М2 на концевые потери
в решетке.
цовых -стенок) и поэтому интенсивность периферийных
перетеканий у торцовых стенок различна. Как правило,
потери энергии вблизи корневых сечений, где радиальные
перетекания совпадают с поперечными, в кольцевой
решетке, выше, чем на «периферии. Отмеченное влияние
веерноети существенно зависит от параметра d/l,
с уменьшением которого возрастает разность скоростей
и давлений в корневом и периферийном сечениях.
Большой практический интерес представляет
разработка способов уменьшения концевых потерь. Сниже-
*яе t>h можно обеспечить, увеличивая относительную
высоту лопатки, что при заданной абсолютной высоте
достигается уменьшением хордьи (ширины) профиля.
Однако в связи с тем, что при изменении хорды
меняются не только концевые, но и профильные потери, воз.ни-
1 См. § 9-3 и 94.
512
кает задача об установлении оптимальной хорды
решетки.
Уменьшения концевых шотерь можно также добиться
соответствующим выбором геометрических параметров
решетки и формы профиля (межлопаточного канала).
а) 6)
Рис. 8-35. Структура вторичных течений в кольцевой решетке
Результаты исследования потока в криволинейных
каналах показывают, что минимальная интенсивность
вторичных течений в каналах активного типа
обнаруживается в тех случаях, когда входная часть канала
выполняется диффузорной. Аналогичные данньне получены
и для решеток активного типа К
На рис. 8-36 приведены 'результаты исследования
двух решеток, имеющих одинаковые относительную
высоту, t и ру, а также форму спинки. Вогнутые
поверхности сравниваемых профилей различаются радиусом
кривизны: решетка ТР-1А имеет плавно суживающийся,
а решетка ТР-1Ак— диффузорно-конфузор-ный канал.
Распределение потерь по высоте для различных
режимов показывает, что в решетке ТР-1Ак уровень потерь
существенно ниже. Суммарные потери в сравниваемьих
решетках в зависимости от угла входа Pi и числа М2
1 Диффузорно-конфузорные каналы активных решеток впервые
предложены ВТИ.
33 М. Е. ДеПч 513
TP-1AH TP-1A ду>^^А
\c__
0 к
/z~~
f '
\
-0,6
IP-
кЛ _
IVL*
/ *
■/'-//I
f
1АнУ\
ЛЯ7*Ч
I
? /
p
0 U
-21°
^
г «
f
2 i
/5
Рис. 8-36. Влияние
формы канала на
потери в активной
решетке,
а —изменение С в
зависимости от pi для
двух типов решеток;
б —влияние числа Ма
на потери в решетках
двух типов;
е-—распределение потерь по
высоте решетки.
514
меняются аналогично (рис. 8-36,а и б). Особенно
существенны преимущества ,решетки ТР-1Ак при небольших
скоростях и малых углах входа.
Эффективность диффузорно-конфузорных решеток и
(ат «1
оптимальные геометрические соотношения у~^Г> "J"
и др.) зависят от угла поворота потока в решетке и
Рис 8-37. Оптимальные значения ат в зависимости от
относительной высоты /.
относительной высоты I (рис. 8-37). С увеличением угла
поворота потока и уменьшением относительной высоты
ат
решетки оптимальное соотношение — «вначале возра-
стает, а затем уменьшается. Результаты опытов
показывают, что решетки с диффузорно-конфузорньими
каналами целесообразно применять «при ГПр< 1,2 ч-1,8 в
зависимости от угла поворота потока; при больших Ар
'возрастает предельное значение /пр.
В реактивные (конфузорных) решетках
существенного снижения концевых потерь можно добиться
профилированием каналов по высоте (профилирование в мери-
33* 515
Рис. 8-38. Влияние меридионального профилирования на потери в направляющей решетке,
а —формы верхнего бандажа исследованных решеток и распределение потерь по высоте для различных форм верхнего обвода и
высот; б—влияние числа М2 на потери в решетках с различной формой верхнего обвода; в —влияние относительной высоты на
потери в решетках с двумя вариантами бандажа. Цифры на кривых указывают вариант обвода. Профиль ТС-2А; М2 = 0,87;
t =0,724; ру = 34°.
диональной плоскости). Этот способ приобретает
особенно большое значение для кольцевых решеток, в
корневом «сечении которых обычно обнаруживаются
повышенные потери.
На рис. 8-38,а показаны схемы вариантов
направляющей решетки с различными формами верхнего
бандажа, а на рис. 8-38,6 и в — соответствующие
результаты испытаний прямой решетки в статических условиях
Здесь же приведена кривая потерь «в кольцевой решетке
с цилиндрическими бандажами той же высотьи.
Опыты показывают значительное снижение потерь
в решетке с профилированным 'верхним бандажом.
Существенным является также перераспределение потерь
по высоте решетки: у нижнего бандажа потери резко
уменьшаются.
Профилирование верхнего бандажа позволяет также
уменьшить разность реакций в корневом и лериферий-
ном сечениях, что повышает к. п. д. ступени турбины.
Кривые на рис. 8-39 позволяют объяснить
преимущество решеток с профилированным бандажом: в таких
решетках обеспечивается более конфузорное течение на
спинке в косом срезе и точка минимума давления
смещается к выходной кромке; кроме того, скорость потока
перед основным поворотом потока в канале
уменьшается, что приводит к снижению поперечного градиента на
участке максимальной кривизны и, следовательно,
интенсивности вторичных течений. Задаваясь
рациональным распределением давления по 'каналу, можно найти
оптимальную форму бандажа.
Приведенные на рис. 8-38,в потери в зависимости
от I показывают, что описываемый способ
профилирования особенно эффективен при малых относительных
высотах.
Следует отметить, что несимметричное поджатие
верхнего обвода решетки расширяет диапазон
оптимальных шагов и углов установки.
Оптимальная величина поджатия, определяемая
h — h
отношением —,—-, меняется в зависимости от высоты
п
решетки (рис. 8-39,6).
Необходимо подчеркнуть, что указанные способьи
уменьшения концевых потерь в активных (диффузорно-
конфузорные каналы) и реактивный (несимметричное
517
поджатие) решетках физически тождественны. В обоих
случаях достигаются уменьшение скоростей .на повороте
потока в канале и увеличенная конфузорность на
выходе из решетки.
Условия на входе в решетку и, в частности,
неравномерность поля скоростей по высоте и высокая турбу-
5 6 7
Спинка профиля
в 9 idll 12 13 14 15 16 17 1д д
Вогнутая поверхность профит
Рис. 8-39.
а —влияние меридионального
профилирования решеток на
. распределение давлений по
профилю; б— уменьшение
потерь в зависимости от I, и от
степени поджатия /0 — IJlj.
лентность потока оказывают большое влияние на
концевые потери. Увеличение неравномерности по данным
ВТИ .вызывает рост ко-нцевых потерь (рис. 8-34).
Повышение начальной турбулентности приводит «
уменьшению угла наклона прямых £/* = /(—), но суммарные
«потери в реактивной решетке возрастают. Физически
этот результат объясняется тем, что при увеличении не-
518
равномерности и турбулентности растут толщина
пограничного 'слоя на торцовых стенках и масса газа,
участвующая в периферийном движении.
8-9. МЕТОДИКА РАСЧЕТА КОНЦЕВЫХ ПОТЕРЬ В РЕШЕТКАХ
Строгое решение за-дачи о концевых потерях в решетках должно
основываться на уравнениях пространственного движения вязкой
сжимаемой жидкости. В связи с очевидными трудностями такого
решения можно использовать другой путь: на основании теории
размерности .построить, исходя из соображений о физической
природе вторич.ных течений, структурную формулу и ввести опытные
коррективы [Л. 5].
В общем случае концевые потери энергии могут быть
представлены как сумма:
AEk = Д£, + АЕ2 + А£3>
где AEY — часть концевых потерь, обусловленная взаимодействием
пограничных слоев и периферийным движением;
АЕ2— потери на трение у торцовых стенок канала;
АЕ3— дополнительные вихревые потери, включающие потери
от компенсирующих движений у концов.
Легко видеть, что вихревые потери SEX и АЕ3 зависят от
циркуляции скорости Г, а АЕ2 не зависит от Г.
Анализ опытных данных показывает, что величина АЕ^ может
быть выражена следующей функциональной зависимостью:
AEk = f(T,hy са2, Ь, Тл, va, pa). (8-38)
Запишем (8-38) в безразмерном виде:
— f*\cab > sin p2, Re2, M2j-
(8-39)
Г
Разлагая выражение (8-39) в ряд по параметрам Г=- ,
са2Ь
и sin g2, можно получить зависимость (8-39) в явном виде. Учитывая,
что функция (8-39) четна относительно аргументов Г и sin (12 и при
Г = 0 не зависит от f2, получим:
АД* . ._ ( ^._
Ргса26
Фо (Re„ М,) I 1 + фГ Г« sin2 р* J. (8-40)
)•
Если предположить, что коэффициенты ф, и ф0 с изменением
чисел М и Re изменяются пропорционально, т. е. ф,/ф0 = В, где В —
некоторая экспериментальная константа, то нетрудно получить
выражение для коэффициента ф0.
519
(8-41)
При нулевой циркуляции (Г = 0)
AEk
Величину Д£2 можно выразить через толщину потери энергии д***
по уравнению
AE2 = ?24d***t sin $2= а2 .
Lsin2p2J
тогда
а***; Т"7
*в=="5«81п57Г= sin2p2"
Для определения коэффициента концевых потерь £k найдем
кинетическую энергию потока за решеткой:
Здесь G = gfac^F — действительный расход через канал
решетки; F— эффективная площадь канала, которую легко определить,
если воспользоваться толщиной вытеснения:
где дтор, 5СП, 8В0Г — толщины вытеснения на торцовой стенке, на
спинке й на вогнутой поверхности профиля
Следовательно,
?2C3a2t
Е = 2sin2 pt" L l ■" 2^тор — T (5сп + Сг) J -
^[^2Ср-14в], (8-42)
_Р*4'
2sin2
где С + С = С
СП I ВОГ ЭКВ •
Величину Г sin (i2 представим в таком виде:
- л t (сп\ + с<г2) -( са\ \
Г sin ра = —г sin ра = * — ctg р, + ctg р2 sin р2 =
са2у \ са2 /
са\ Ctgf,\- л Г ^ ctg?,
где
520
t cos p2, (8-43)
,(X)=^' = f (8-44)
са2 Pi
Для несжимаемой жидкости при турбулентном режиме течения
в пограничном слое с достаточным основанием можно положить:
тор
Н*
** 0,036
3;* =W'
,4;
С помощью формул, (8-40) — (8-43) и пренебрегая величиной
/
Л21
0,1 ——1 ] по сравнению с членом Re^' /, получим для несжимае
мои жидкости:
?*=
0,13
[1+5(1+^ItO'2cos2?2] (845)
В общем случае для сжимаемой жидкости коэффициент концевых
потерь определяется по формуле
фт{1 + Б[1 + ^Ш\^0"2Ч
^■С08'Ь}.
(8-46)
Здесь k\ — поправочный множитель, учитывающий влияние
сжимаемости. Его зависимость от безразмерной скорости М2
приведена iHa рис. 8-40.
Для определения числовых значений коэффициентов Ли В на
рис 8-41 нанесены экспериментальные данные по концевым поте-
Рис. 8-40. Зависимость поправочного
множителя kx от безразмерной скорости.
рям, полученные как для активных, так и для реактивных решеток
при различных шагах, высотах, углах входа и выхода потока.
Здесь в качестве аргумента принят комплекс
[,+?w^f;P,costp..
521
а по оси ординат отложена функция т . В принятой системе
координат формула (8-46) изображается прямой, отсекающей на оси
ординат отрезок, равный А, наклоненный к оси абсцисс под углом
b = arctgAB.
Результаты указанной обработки i экспериментальных данных
позволяют заключить, что коэффициенты А и В существенно
зависят от .режима течения в пограничном слое и типа решетки. Для
у\ *-Профили лмз
Рис. 8-41. Сопоставление расчетных и опытных значений
концевых потерь для реактивных (прямые 1,2 ц 3) и активных (прямые
4, 5 и 6) решеток.
реактивных решеток с плоскими торцовыми стенками
экспериментальные точки довольно хорошо группируются в зависимости от
режима течения в пограничном слое около прямых / и 2. Для
реактивных решеток с несимметричным поджатием наклон линии
меняется (прямая 3).
Прямые 4 и 5 характеризуют активные решетки с плавно
суживающимися каналами, а прямая 6 — с диффузорпо-конфузорными
каналами.
Значения коэффициентов, полученных на основании обработки
опытных данных, приведены в табл. 8-1.
Интересно отметить, что для активных и реактивных решеток
при наличии диффузорного участка на .входе в решетку
коэффициент А = 0,13, что соответствует турбулентному режиму течения
в пограничном слое. При переходе ог одного режима течения
к другому происходит параллельное смещение прямой,
соответствующей данному типу решетки. Влияние формы межлопаточных
каналов характеризуется коэффициентом, значения которого резко
различны для разных типов решеток.
Формула (8-4G) позволяет установить влияние некоторых
геометрических и режимных параметров на концевые потери.
Коэффициент ^ь. меняется обратно_ пропорционально относительной
высоте I. С увеличением шага t коэффициент £* вначале уменьшается,
а затем возрастает. Уменьшение угла выхода р2 и увеличение угла
поворота потока в решетке приводят к росту £*• При возрастании
1 Изложенная методика разработана совместно с А. Е. Зарян-
киным.
522
Таблица 8-1
Активные решетки без диффузор-
ного участка на входе
Ламинарный
пограничный слой
А
0,45
В
5,5
Турбулентный
пограничный слой
А В
0,13 1,90
Активные решетки с диффузорно-
конфузорными каналами
—
—
0,13 1.0
Реактивные решетки без поджа-
тия по высоте
Ламинарный
пограничный слой
А
В
0,45 2,0
Турбулентный
noi раничный
слой
А В
0,13 0,7
Реактивные решетки с
несимметричным поджатием в косом
срезе
—
—
0,13 0,3
чисел Re2 и Мг концевые потери снижаются. Эти результаты хорошо
согласуются с опытными данными \ приведенными в § 8-8.
8-10. СТРУКТУРА ПОТОКА
И ПОТЕРИ В РЕАКТИВНЫХ РЕШЕТКАХ
ПРИ ОКОЛОЗВУКОВЫХ И СВЕРХЗВУКОВЫХ СКОРОСТЯХ
В реактивных решетках скорости на входе
дозвуковые; переход к сверхзвуковым .скоростям происходит
в межлопаточном 'канале. В зависимости от положения
минимального (переходного) сечения в канале
реактивные решетки делятся на два типа: с суживающимися
и 'расширяющимися межлопаточными каналами.
а) Решетки с суживающимися
каналами. В таких решетках переход к сверхзвуковым
скоростям происходит в косом срезе.
Во многих случаях переход в околозвуковую область
сопровождается значительным изменением
характеристик решеток. В этой связи необходимо знать
критическое число М2#? три котором в решетке появляются
местные области сверхзвуковые* скоростей.
На рис. 8-42,а даны кривые максимальных скоростей
на спинке профиля .направляющей решетки в зависимо-
1 Формула (8-46) не учитывает влияния неравномерности и
высокой турбулентности потока. Соответствующие коррективы
могут быть введены после .накопления необходимых опытных данных.
523
сти от М2 и относительного шага. За линией M;=l
образуются замкнутые области сверхзвуковых
скоростей. Местные сверхзвуковые скорости могут также
возникать в области потока, примыкающей к выходной
кромке.
Критические числа М2* в зависимости от шага для
реактивной решетки представлены на рис. 8-42,6. Отсюда
К5
'
1,25
W
0,75
0,
-ml
—
5
'"Г
мак
с
|
I
I
h
0,75
| |
I |
I
I
i I
Г
\mi
U t
!
г,
~ г~
/L
=0,860
=0,707
= 0,614-
'= 0,5U3
J Щ
9
1,25
Рис. 8-42. Местные максимальные скорости на спинке профиля
в зависимости от М2 (а); критические значения М2* в
зависимости от шага для реактивной решетки (б).
следует, что для решеток существует такой шаг Т„ при
котором звуковые скорости достигаются одновременно
у спинки и в области кромки. Этому шагу соответствует
максимальное значение числа М2#.
Значения М2# для решетки, характер изменения М2# =
==/('»Py)i a также положение и протяженность
сверхзвуковой области зависят от формы профиля (кривизны выходного
участка спинки, толщины и формы выходной кромки).
С увеличением Af2>M2# сверхзвуковая область
увеличивается и граница ее смещается внутрь канала.
При числе М2« 1 линия перехода приближенно
совпадает с узким сечением канала1 и сверхзвуковая область
1 При большей кривизне спинки эта линия смещена внутрь канала.
524
на спинке профиля соединяется с областью сверхзвуковых
скоростей за выходной кромкой.
Наиболее характерной особенностью обтекания решеток
потоком околозвуковых скоростей является возрастание
',о " — "
0,95
0,90
0,85
OfiO
0,75
О JO
V,* 1/,-г u,U U,U ,}и
Рис. 8-43. Распределение давлений
торможения по шагу в реактивной решетке при
различных М2.
градиентов давления в конфузорной и диффузорной
областях и смещение точек рмин по потоку.
Показанные на рис. 8-43 графики распределения
давлений торможения по шагу направляющей решетки позволяют
заключить, что с увеличением М2 возрастает
неравномерность потока: увеличивается глубина кромочных следов
при переходе к околозвуковым скоростям, кромочный след
расширяется.
Анализ кривых профильных потерь, представленных на
рис. 8-44, показывает, что характер изменения С в зави-
525
10
- ^np
j-
I '"^
h
\
■- (
J
У
s
О—^
(
•"^^
'tC-2A
/
TC-26
»\
/
/
TC-2B
X
TC-2P
*-4k
M2
)l
^5 p £17 ^fl 49 $ V P P ^ ГГ5-
6)
0 Tl OfiOfi Ofi Ifl p 1/
6}
Рлс. 8-44. Влияние числа М2 на профильные потери в реактивной
решетке,
а —при изменении относительного шлга /; б — при изменении формы спинки
профиля в косом срезе; в —при изменении толщины и формы выходноЛ кромри.
симости от М2 определяется формой профиля (главным
образом), кривизной спинки в косом срезе, формой и
толщиной кромки и геометрическими параметрами решетки. При
этом следует различать две основные зоны изменения: до-
критическую (М2<М2#) и закритическую (M2>M2J.
В докритической области с увеличением М2 коэффициент
потерь для большинства решеток несколько уменьшается.
При отрывном обтекании спинки профиля увеличение М2
обычно приводит к возрастанию Спр.
При уменьшении шага интенсивность возрастания С
в околозвуковой зоне уменьшается, а значение М2*, после
которого происходит рост потерь, увеличивается.
Важным следует считать обнаруженное в опытах
Н. А. Скнаря влияние числа Рейнольдса, с возрастанием
которого интенсивность увеличения С в околозвуковой зоне
снижается. Эти данные относятся к малой степени
турбулентности потока1. При искусственной турбулизации потока
также наблюдается уменьшение степени возрастания
потерь (М2>М2/).
Влияние формы спинки в косом срезе на потери ъ
решетке показано на рис. 8-44,6. Потери в решетке ТС-2А
интенсивно возрастают при М2>0,85, что обусловлено
большой кривизной спи.нки. Для решетки ТС-2Б,
профили которой имеют в косом срезе 'меньшую кривизну,
рост потерь наблюдается только при М2> 1,05-5-1,1-
Вьпполнение спинки профиля вогнутой в косом срезе
позволяет область (кризисного возрастания потерь
сместить в зону еще больших чисел М2.
При изучении влияния сжимаемости -на
характеристики решеток следует учитывать толщину и форму 'вьг-
ходной кромки. Показанные на рис. 8-44,в результаты
опытов подтверждают влияние этих параметров на
зависимость £пр(М2).
1 Влияние степени турбулентности на характеристики реактивных
решеток при околозвуковых скоростях объясняет несовпадение кри
вых 5 = / (М2), получаемых на разных трубах, имеющих различную
турбулентность. При низкой турбулентности переход через скорость
звука сопровождается резким возрастанием профильных потерь, так
как скачки в местной сверхзвуковой зоне на спинке приводят к
отрыву ламинарного пограничного слоя. При высокой турбулентности
пограничный слой в сверхзвуковой зоне турбулентный и отрыва, как
правило, не возникает или он смещается по потоку.
527
При сверхкритических перепадах давлений в решетке
в зоне узкого сечения межлопаточного канала 1
устанавливается критическая скорость. За выходной кромкой
давление -ниже критического; поэтому при обтекании
кромки (точки Л, «рис. 8-45) давление падает — в косом
срезе канала распространяется волна разрежемия ABC.
Необходимо подчеркнуть, что интенсивность волны
ABC определяется закромочньш давлением, а не
давлением на бесконечности за решеткой. В первичной и
отраженных от спинки профиля волнах разрежения поток
перерасширяется: статическое давление на спинке
профиля за волной ABC будет более низким, чем на
бесконечности за решеткой.
Дальнейшее развитие спектра зависит от структуры
потока за выходной кромкой и степени перерасширения
потока в волне ABC. Граничные струйки газа, сходящие
с вогнутой и -выпуклой поверхностей «профиля,
сближаются и «а некотором расстоянии за кромкой резко
поворачиваются. На границах начального участка
кромочного следа возникает система скачков и волн
уплотнения, сливающихся в косьие скачки FC и FH.
Перерасширение потока в первичной и отраженные
волнах разрежения частично «исправляется» первичным
скачком FC. Скачок, взаимодействуя с пограничным
слоем на спинке профиля -в косом срезе, отражается и
вновь попадает на кромочный след. В зависимости от
среднего значения числа М в этом сечении кромочного
следа отраженный скачок FC либо пересекает
кромочный след (Мкр>1), либо отражается от его границы.
Таким образом, «поток, движущийся в косом срезе,
последовательно проходит через первичную и отраженные
волны разрежения, первичный и отраженный скачки2.
Поведение граничных линий тока при сходе с кромки
(со стороны спинки профиля) существенно зависит от
соотношения давлений в точке D и за 'выходной кромкой.
Если давление в точке D более высокое, чем за кром-
1 Поверхность перехода приближенно совладает с узким сече-,
нием капала. В действительности вследствие неравномерности
потока в канале и влияния вязкости поверхность перехода имеет
некоторую кривизну и смещается против потока.
2 Интенсивность первичного и отраженного скачков переменна
вдоль фронта, так как они распространяются в неравномерном
потоке и взаимодействуют с волнами разрежения.
528
■*/***
Рис. 8-45. Схемы истечения газа из направляющей решетки
при сверхзвуковых скоростях.
34 м Е. Дейч 5
кой, то в точке D образуется волна разрежения и
обтекание кромки улучшается. Линия тока сходит с
профиля не в точке Ь, а в точке Е. Волна разрежения DLKD
замьикается системой -слабых скачков уплотнения,
сливающихся в криволинейный скачок FH. Система
скачков FC и FH образует хвостовую ударную волну
профиля.
Если давление вблизи точки D будет ниже давления
за кромкой, то скачок образуется в точке D. В этом
случае кромочный след оказывается более размытым.
В некоторых случаях скачок располагается выше по
потоку относительно точки D.
Перерасширение потока в волнах разрежения,
интенсивность кромочных скачков FC и FH, а также их
положение определяются кривизной спинки профиля в косом
срезе и толщиной и формой -выходной кромки. Так, при
уменьшении кривизны спилки перерасширение потока
уменьшается и, следовательно, снижается интенсивность
скачков. Заданием спинке профиля в косом срезе
обратной кривизны можно перерасширение потока свести
к «минимуму; кромочные скачки в этом случае будут
ослаблены.
При пересечении системы- волн разрежения и косых
скачков отдельные линии тока многократно и различно
деформируются, причем при е*<е2 средний угол выхода
потока увеличивается по 'сравнению с дозвуковым
режимом: поток отклоняется в косом срезе.
С увеличением перепада давлений меняется спектр
потока в косом срезе канала и за решеткой; изменяются
интенсивность и характер расположения волн
разрежения и скачков уплотнения. Увеличиваются
протяженность и интенсивность первичной -волны разрежения.
Углы первичного, отраженного и кромочного скачков
уменьшаются, и точка падения косого скачка FC на
спинку профиля (точка С) смещается по потоку. В
соответствии с этим «меняется и характер деформации
отдельных линий тока. Однако интенсивность скачков
возрастает только до определенного значения числа М2,
зависящего от геометрических параметров решетки.
Расширение потока в косом срезе решетки
заканчивается «при отношении давлений 82 = е*. Точное
определение значения es затруднительно, однако можно считать
предельным такой режим, при котором первичный ска-
530
Рис. 8-46. Спектры течения воздуха через реактивную
решетку с суживающимися каналами при околозвуковых
и сверхзвуковых скоростях Относительный шаг ^=0,543;
выходной угол профиля 15°52';
а - е2 = 0,528; б — е2 = 0.4Г.0; в — е2 = 0,379; г - е2 = 0,261.
34*
531
чок попадает в точку D (рис. 8-45,в). В этом случае
вместо трех скачков образуются только два:
отраженный скачок СР сливается с кромочным FH.
Если e2<es, то
расширение потока
частично происходит за
пределами решетки (рис.
8-45,г). Система
скачков на выходной
кромке остается в основном
прежней, но структура
кромочного следа
изменяется. Левая ветвь
кромочного скачка FC
попадает на
дозвуковую часть кромочного
следа и резко
деформирует его. Давление за
кромкой в этом случае
определяется скачком,
а следовательно, и
противодавлением. При
значительном
уменьшении е2<85
первичный скачок попадает в
сверхзвуковую часть
кромочного следа (рис.
8-45,5). При этом
обтекание выходной
кромки профиля и
кромочное давление
определяются только
геометрическими
параметрами решетки и не
зависят от
противодавления. Это значение 82
соответствует второму
предельному режиму
течения в решетке.
Рассмотренные схе-
решетки подтверждаются
с помощью оптического
Рис. 8-47. Распределение давлений вдоль
спинки профиля в косом срезе
реактивной решетки с суживающимися
каналами при сверхкритическом истечении.
мы истечения из реактивной
визуальными наблюдениями
прибора (рис. 8-46).
532
На рис. 8-47 дано распределение .давлений на
участке спинки профиля в косом срезе решетки при
различных отношениях е2 = р2/ро. За узким сечением
(точки 2—6) можно отметить значительное »перерасширение
потока, которое заканчивается резким увеличением
давления, что вызвано взаимодействием первичного и отра-
Рис. 8-48. Распределение давлений по профилю в решетках
с расширяющимися межлопаточными каналами.
женного скачков с пограничным слоем. После скачков
давление .вдоль спинки «падает. С уменьшением е2 зона
максимального разрежения смещается по потоку к
выходной кромке. На режиме предельного расширения
(е2^0,205) давление вдоль спинки профиля непрерывно
падает.
б) Реактивные решетки с
расширяющимися межло «паточными каналами.
Рассмотрим некоторые результаты опытного исследования
таких решеток. На рис. 8-48 показано распределение
давлений по профилю для четырех решеток. Отсюда
видно, что на определенных режимах в межлопаточном
канале, как и в одиночном сопле Лаваля, возникают
скачки уплотнения (диффузорный участок), причем их
533
Рис. 8-49. Спектры потока в решетках
с расширяющимися каналами, а — е2 = 0,4; б — г2 = 0,3; в — е2 = 0,2.
положение и интенсивность зависят от режима 82 и гео-
метрического параметра /== -*=—?- (рИС 8-53). По мере
уменьшения 82 скачки перемещаются к выходному
сечению канала. На расчетном режиме, определяемом по
отношению f, образуются только кромочные скачки.
Характер 'изменения спектров течения в
межлопаточных каналах решетки можно проследить по
фотографиям на рис. 8-49.
534
Кривые коэффициентов потерь (рис. 8-50) показы
взю1, что течение в решетках с расширяющимися
каналами сопровождается резким увеличением потерь при
* -,
<;
£^d
l^^- ч
— с
^=4
1 *
fulfil
i 1/ tM
Г ~7'
г У
V-7,5;
6
$-0,487
,т I
£г
0,1
0,2
0,3 0,4
0,5 0,6
6)
0,7
0,8 Ifl
Рис. 8-50 Характеристики решеток с расширяющимися
каналами.
а - из icnemie CIip в зависимости от е2 и f; б— зависимость угла выхода
потока о г е2 и /.
отклонениях режима от расчетного. Изменение
коэффициента потерь оказывается тем значительнее, чем боль*
ше геометрический параметр /, т. е. чем выше расчетное
значение М2р (см. гл. 6).
Наибольшее изменение потерь происходит при
увеличении е2 от расчетного до 0,5—0,6. При больших 82
скачки располагаются вблизи минимального сечения;
интенсивность скачков уменьшается, и £Пр снижается.
На режимах е2<е2Расч потери возрастают, так как
535
происходит расширение потока в косом срезе решетки.
На режимах, близких к расчетным, потери для всех
решеток невелики, причем профилирование
расширяющейся части методом характеристик позволяет лишь
незначительно снизить -потери на таких .режимах.
На рис. 8-50,а приведена кривая коэффициента
волновых потерь £в для решетки с /=1,6, построенная по
кривым распределения давлений (рис. 8-48) в
предположении, что скачки прямые. Отсюда вадно, что волновьпе
потери -невелики; основные потери на нерасчетном
режиме обусловлены отрьгвом потока. На рис. 8-50,а
.нанесена также кривая £Пр для решетки с суживающимися
каналами. Точки пересечения кривой £Пр для этой решетки
с кривыми для решеток с расширяющимися каналами
позволяет установить области рационального
использования сравниваемых решеток.
Изменение среднего угла потока за 'решеткой в
зависимости от е2 .показано -на рис. 8-50,6. Для решеток
с />1 средний угол потока слабо меняется во 'всем
диапазоне изменений е2. Для решетки с /=1,0 характерно
увеличение 02 п:ри сверхзвуковых скоростях,
обусловленное отклонением потока в 'косом срезе.
8-U. РАСЧЕТ УГЛА ОТКЛОНЕНИЯ ПОТОКА В КОСОМ СРЕЗЕ
И ПРОФИЛИРОВАНИЕ РЕАКТИВНЫХ РЕШЕТОК
ПРИ ОКОЛОЗВУКОВЫХ И СВЕРХЗВУКОВЫХ СКОРОСТЯХ1
Существует несколько методов расчета угла
отклонения потока в косом срезе решетки. Наиболее
распространенными и простыми являются методы, основанньне
на уравнениях одномерного потока.
Предполагая, что поле потока в сечениях АА
(рис. 8-51) и EF (выбранном на большом расстоянии
за решеткой) равномерно, можно записать уравнение
неразрывности следующим образом:
~АА
р2с2 sinр2 = Р2оо^2ооsinp2oo, где sinp2==.
Разделим обе части этого выражения на рм а*, тогда
получим:
<72sinp2 = <72oosinp2oo.
1 Параграфы 8-11-J-8-14 написаны А. В. Губаревым.
536
• Учитывая, что при е2<!в* ^2 = 1 и р2оо == ра —{— в,
где 6 — угол отклонения потока в косом срезе, приходим
к формуле Бэра:
6 = arcsin (— sin рЛ— р2. (8-47)
1,0 J/ ^ 1,3 1,4 1,5 1,6 1,7 1,8 1,9 йр
6)
Рис. 8-51.
а —к определению угла отклонения потока в косом
срезе решетки; б — расчетная зависимость угла
выхода потока из решетки от скорости Х2 и fan-
С учетом потерь между сечениями АА и EF формула
Бэра принимает вид:
8 = arcsin (± .^-sinp2)-p2. (8-48)
Отсюда следует, что с ростом потерь угол отклонения
увеличивается. Существенным также является тот факт,
что угол отклонения б зависит не только от скорости
истечения и потерь, но и от расчетного угла выхода р2
(рис. 8-51,6).
537
Формула Бэра справедлива только при е
тех пор, пока первичная волна разрежения находится в
пределах косого среза. Угол отклонения, соответствующий
предельному расширению в косом срезе, приближенно
определяется по соотношению
о =а —89,
s ms г2>
где a s — угол характеристики, совпадающей с выходным
сечением.
Отсюда с помощью (8-47) получаем очевидное равенство
sin(p2 + §s) = sinams = ^=s-^. (8-49)
Выражая q0s через е5, находим отношение давлений для
рассматриваемого режима:
,(sin pa)
2/г
/г + 1
Из уравнения (8-49) легко определяется предельный
угол отклонения bs%
С по'мощью уравнений неразрывности, импульсов и
энергии, можно получить точное решение для угла
отклонения потока в косом срезе решетки с кромками
конечной толщины.
Полагая, что в сечениях АА и EF (.рис. 8-51,а)
лоток равномерный, воспользуемся уравнениями
сохранения, приведенными в § 8-6. Решая эти уравнения
совместно, можно получить расчетную формулу,
предложенную А. С. Наталевичем:
tg8=
/ik- \2 -( - 2k - k\k
-1
k+\ — Np
k -
~"kZT\ Pn ct£ P2
=—. (8-50)
k + 1 — Np
При 8 <c^ 10° целесообразно пользоваться приближенным
выражением
k (k + I) k — \
tgs
538
2np
— 1
tgpt. (8-51)
Здесь и выше ооозначено: п=у—^, Т=Т'
pz=z—^~; N = j ( 1 —т-^-];/7—закромочноедавление
А !~^\ />2:
Для случая бесконечно тонкой кромки формулы
(8-50) и (8-51) были впервые даны Г. Ю. Степановым.
Решение системы трех уравнений дает возможность
также определить волновые потери в косом срезе. Для
случая бесконечно тонких кромок волновые потери
определяются формулой Г. Ю. Степанова:
Г 1
i+ir,
-/>)-!
к
2
1
cos 5
1
CD = 1 - i ^ ^nr • (8"52)
i±Jl
Необходимо отметить, что коэффициент вол-новых
потерь учитывает только потери, связанные с поворотом
потока в косом срезе.
Потери, обусловленные взаимодействием скачков
уплотнения с пограничным слоем, потери трения и
потери на выравнивание потока обычно значительно превьи-
шают волновые потери, подсчитанные для идеальной
жидкости. Поэтому угол отклонения как по формуле
(8-47), так и то формулам Г. Ю. Степанова и А. С. На-
талевича оказывается меньше действительного.
Формула Бэра с учетом потерь в косом срезе ('8-48) дает
близкое совпадение с экспериментом, но применение ее
ограничено, так как необходимо предварительно
определить потере.
В § 8-10 было показано, что угол выхода потока из
решеток с расширяющимися каналами остается
практически неизменным в широком диапазоне режимов
М2<М2р. Используя такой характер
зависимости 02 (М2), можно расчетным путем определить потери
в решетке на шеременньих режимах.
Запишем уравнение неразрывности для критического
сечения F = amm и сечения на бесконечности за решеткой
в таком виде:
aMnnPA = p*^sinP»'
где р2с2 — действительные параметры потока.
539
Разделим и умножим правую часть на p2tc2t и после
преобразований получим:
t sin p.
. ? 2t P.
_P2/ _pa_
Po P2/
где
Решив это уравнение относительно <р, найдем:
F
~р _t sin p2
г-
1 A+l
U*"
Y
(8-53)
(8-54)
(8-55)
Знак минус в уравнении (8-54) не имеет физического
смысла, так как <р]>0.
В том случае, когда ра = const, <sinpa = aa и
fat 1--ЪГ
1 ^+2
1
Д2/
(8-55а)
На рис. 8-52 представлены расчетные кривые
зависимости <р от е2 и параметра / =
при (32 = const.
Предлагаемая методика дает возможность с достаточной точ-
1,0г
Рис. 8-52. Расчетная зависимость <р от е2 для
решетки с расширяющимися каналами (&=1,4).
ностью определять дополнительные потери на нерасчетном
режиме, если известна зависимость [58 от еа.
Легко видеть, что для уменьшения потерь в широком
диапазоне режимов s2>e необходимо, чтобы угол
выхода ра был переменным.
540
Идеальной в этом смысле является такая решетка, для
которой изменение (32 соответствовало бы уравнению (8-54)
при <р=1. Отсюда после ряда преобразований можно
получить следующий оптимальный закон изменения угла
потока:
Следовательно, при М2/ = 1 (<72, = 1) угол выхода
потока должен быть минимальным, а при М2/ > 1 —
увеличиваться. Однако опыты показали, что для решеток с
расширяющимися каналами такой характер изменения. $2
невозможен.
Для решетки с суживающимися каналами #MHH/f = sinp2 .
При этом условии получаем обычное уравнение Бэра для
угла выхода потока (8-47).
Таким образом, для решеток с суживающимися
каналами закон изменения %(М2) совпадает с теоретическим.
Однако, как известно, в таких решетках на
нерасчетных режимах (е2 < е) потери интенсивно возрастают
(рис. 8-44).
Это обусловлено появлением волновых потерь и
взаимодействием скачков с пограничным слоем на
спинке в косом срезе.
Как уже указывалось, интенсивность скачков в косом
срезе .п,ри М2>1 зависит от кривизны спинки, причем
минимальные волновые потери могут быть получены при
выполнении спинки с обратной вогнутостью в косом
срезе.
Исследования, проведенные в МЭИ, показали
возможность создания -реактивных решеток с (малыми
«потерями при М2>1 на расчетный и нерасчетных
режимах. В таких решетках рационально сочетаются
положительные свойства решеток с расширяющимися и
суживающимися каналами. При умеренных сверхзвуковых
скоростях М2< 1,3-=-1,4 'Межлопаточные каналы
выполняются суживающимися, а спинка в косом срезе
рассчитывается методом характеристик таким образом,
чтобы вдоль спинки не происходило лерерасширения
потока. Метод характеристик может быть (использован
только для оценки стрелы прогиба спинки. Точка изменения
541
кривизны спинки должна быть расположена внутри
канала.
При больших сверхзвуковых .скоростях М2> 1,3ч-1,4
целесообразно каналы' решеток выполнять с небольшим
расширением (/= 1,05 ч-1,15), смещая узкое сечение
^ а)
Рис. 8-53.
а— сверхзвуковая реактивная решетка МЭИ с вогнутой спинкой в
косом срезе и небольшим расширением межлопаточных каналов;
б —влияние расширения канала на характеристики сверхзвуковых
решето^ с вогнутой спинкой в косом срезе (опыты МЭИ).
/_— f=l,17; /=0,46 (плоская спинка в косом срезе); 2~/=1,17;
/=0,534; 3 —7=1,10; /=0,581; 4 — /= 1,0; /=0,680 (кривые 2, 3 и 4 —
вогнутая спинка в косом срезе).
внутрь канала. При этом необходимая расчетная
вогнутость опинки уменьшается и обводы- профиля
упрощаются. Целесообразность введения небольшого
расширения канала до 'косого среза основывается «а кривых
потерь, приведенных на рис. 8-50: при малых значениях
параметра / интенсивность возрастания £Пр на
-нерасчетных режимах резко снижается. С уменьшением числа М2
угол выхода потока в таких решетках будет изменяться
542
более интенсивно, чем в решетках с расширяющимися
каналами.
На рис. 8-53 представлены некоторые результаты
исследования решеток, спрофилированных указанным методом.
Сравнение кривых показывает, что такие решетки имеют
значительные преимущества не только на переменных, но
и на расчетных режимах по сравнению с решетками,
имеющими большое расширение канала (/^>1,2). Опыты
показывают также, что для околозвуковых скоростей (М2<4,2)
удовлетворительные результаты могут быть получены путем
выполнения прямолинейной спинки в косом срезе; при этом
точка разрыва кривизны на спинке располагается внутри
канала.
е-12. СТРУКТУРА ПОТОКА В АКТИВНЫХ РЕШЕТКАХ ПРИ
ОКОЛОЗВУКОВЫХ И СВЕРХЗВУКОВЫХ СКОРОСТЯХ
Обтекание активных решеток потоком околозвуковых
скоростей характеризуется наличием сверхзвуковых зон как
на спинке в косом срезе, так и на входном участке спинки.
Поэтому наряду с М2 —критическим числом М2, при
котором возникают звуковые скорости в косом срезе, имеет
смысл введение понятия второго критического числа М2 ,
определяющего такой режим обтекания, при котором
звуковые скорости возникают на входной кромке. Так же
как и М2 , величина М2 зависит от шага и угла
установки. Кроме того, второе критическое число М2
решающим образом зависит от угла входа потока.
На рис. 8-54 представлены значения М2 и М2 в
зависимости от t, §y и угла входа потока рх. Как видно,
при малых pj и больших t М2 <М2, т. е. звуковые
скорости в активной решетке возникают вначале на входных
кромках лопаток. С увеличением шага М2 увеличивается.
Характер изменения М2 и М2 в значительной степени
определяется также фермой профиля: кривизной спинки в
косом срезе и на входном участке и толщиной кромок.
На режимах М2 > М2 на входном участке спинки
каждого профиля решетки образуется Я-образный скачок. При
увеличении скорости этот скачок развивается в головной
скачок для соседнего профиля (рис. 8-55). Непосредственно
за каждым головным скачком поток дозвуковой, однако
543
такая схема обтекания, очевидно, имеет место только в том
случае, когда после каждого скачка поток ускоряется и
перед следующим скачком скорость М > 1. По мере
увеличения скорости набегающего потока головные скачки
приближаются к входным кромкам и искривляются. При этом
поток за скачком вихревой и вдоль фронта ([решетки
скорости меняются по величине и направлению.
При некотором значении Мх
sin
когда осевая
составляющая скорости сверхзвуковая, скачки, возникающие
ож
Рис. 8-54. Влияние относительного шага ty угла
установки (L и угла входа потока ^ на
критические значения М2 для активной решетки.
перед каждым профилем, сливаются в единый
волнообразный скачок (рис, 8-55,6). Левые ветви головных скачков
поворачиваются в направлении к вогнутой поверхности
профиля. При дальнейшем увеличении N[1 скачки входят
в межлопаточный канал. Следовательно, на режимах
М^-т-т- соседние профили не оказывают влияния на по-
sin Pi
ток перед входными кромками и поэтому обтекание
входных участков таким сверхзвуковым потоком можно
рассматривать изолированно.
Однако в большинстве встречающихся случаев скорости
на входе в решетку недостаточно велики и осевая
скорость потока значительно меньше звуковой. В этом случае
влияние профилей распространяется в направлении против
потока.
544
Рассмотрим обтекание сверхзвуковым потоком
идеальной жидкости решетки с конечным числом профилей при
условии, что осевая скорость меньше звуковой.
Предположим, что толщина входной кромки равна нулю,
конструктивный угол кромки весьма мал и спинка профиля до
входного сечения канала образована прямой, угол наклона
которой к фронту решетки равен рс.
Если вектор скорости на входе в решетку направлен
под углом рс, со стороны спинки на входной кромке
возникает слабый разрыв — характеристика. Вдоль прямолиней-
Рис. 8-55. Схемы течения сверхзвуковог о потока в активной решетке.
ного участка спинки скорость сохраняется постоянной и,
следовательно, перед кромками следующих профилей
скорость потока равна скорости перед первым профилем
(рис. 8-56,а). Таким образом, в этом случае поток перед
решеткой с бесконечным числом профилей не отличается
от потока на бесконечности.
В том случае, если вектор скорости на входе в
решетку направлен под углом, меньшим рс, на входной
кромке первого профиля (со стороны спинки) образуется
волна разрежения, в которой поток ускоряется и
поворачивается на угол & = рс — р! (рис. 8-56,6).
Вдоль прямолинейного участка спинки профиля скорость
сохраняется большей, чем скорость на бесконечности перед
решеткой, и вектор ее направлен под углом (51=Рс>р1.
Поэтому на кромке следующего профиля возникает волна
уплотнения и все ниже расположенные профили обтекаются
потоком большей скорости, чем первый.
При pj > pc на входной кромке первого профиля
возникает скачок уплотнения, в котором происходят уменьшение
35 М. Е. Дейч
545
скорости и поворот потока на угол 8 = ^ — рс.
Дальнейшие рассуждения аналогичны случаю, когда ^ <C$C-
Если при §хф$с рассмотреть решетку с бесконечным
числом профилей, то необходимо допустить, что на
бесконечности перед решеткой должны существовать или волна
разрежения (при р!<<Рс), в которой поток поворачивается
на угол 5 = рс — (Зп или скачок уплотнения (при (3i>pJ.
Это противоречит условию (3,т^Рс- Следовательно, при
Рис. 8-56. Структура сверхзвукового потока
на входе в активную решетку.
сверхзвуковой скорости перед решеткой поток на
бесконечности может быть направлен только под углом р2 = (3 .
В реальных условиях рабочая решетка обтекается
совместно с направляющей. В этом случае все изменения
структуры потока на входных кромках первого профиля
локализуются в косом срезе направляющего канала, причем
в такой системе можно обеспечить обтекание решетки
546
сверхзвуковым потоком при любом угле входа (3, ф §с (до
наступления режимов „запирания", § 8-13). При этом
обтекание ниже расположенных профилей в значительной
степени определяется системой скачков и волн разрежения,
отраженных от стенки косого среза сопла. Структура
потока перед решеткой усложняется, и нарушается
однообразное обтекание всех профилей. Периодичность потока на
входе в рабочую решетку при сверхзвуковых скоростях
будет наблюдаться в интервале, кратном шагу
направляющей решетки.
К. Осватичем было обнаружено, что даже в случае
ножевой входной кромки при расчетных углах входа
потока в решетке может возникать сложная система
скачков. Анализ этих результатов показывает, что головные
скачки, возникающие перед решеткой, формально можно
разделить на три основные группы: скачки, обусловленные
толщиной и формой входной кромки, скачки, зависящие
от формы межлопаточного канала (скачки „запирания"
межлопаточного канала), и скачки (или волны разрежения),
обусловленные нерасчетным углом входа потока в решетку
(j31=7£=j3J. В реальных условиях эти скачки разделить
практически невозможно, так как они образуют единую
сложную систему.
8-13. ПРИВЕДЕННЫЙ РАСХОД ГАЗА ЧЕРЕЗ РЕШЕТКУ.
ОСОБЫЙ РЕЖИМ АКТИВНОЙ РЕШЕТКИ
В СВЕРХЗВУКОВОМ ПОТОКЕ
Запишем уравнение неразрывности для сечений входа
и выхода из решетки (рис. 8-57) в следующей известной
нам форме (см. § 8-11):
4r1sinp1 = i7,e0sinpai; s0 = ^r- (8-56)
Fax
Это уравнение может быть использовано для
графического расчета параметров потока в решетке.
Заметим, что осевая проекция qx равна:
ЯХа = Ях sin h = q^osin P2 = <72ee0. (8-57)
С другой стороны,
Отсюда следует, что постоянному значению qa могут
соответствовать различные значения Я и р. Следовательно,
при qa = const конец вектора Я описывает в полярной си-
Рис. 8-57 К выводу уравнения
годографа
стеме координат (Я, р) некоторую трансцендентную
кривую. Эту кривую будем называть годографом
вектора Я.
Задаваясь различными, но постоянными qa в пределах
от q = 0 до <7а = 1 и рх от 0 до тс, в плоскости
годографа можно построить группу кривых, позволяющих
графически рассчитывать поток в рабочих решетках.
Форма годографа Я для некоторого qa показана на
рис. 8-58. Окружность, соответствующая Я = 1, разделяет
плоскость годографа на две области [дозвуковую (Я<1)
и сверхзвуковую (Я>1)].
При дозвуковых скоростях на входе использование
графического метода не вызывает особых затруднений.
Действительно, при б0 = 1 (идеальная жидкость) <72а = <7,,,
и вектор Я2 при заданном р2 находится на той же кривой
(q = const), что и вектор Я,. Следовательно, по известным
Я,*и Pj находим точку Л, определяющую кривую qXa =
548
= const, a no pa в точках В и В' находим вектор Я2 (или
l[ , если скорость на выходе сверхзвуковая).
Метод годографа можно распространить и на случай
течения с потерями. С этой целью построим кривую
(пунктир на рис. 8-58) по уравнению
_j
Рис 8-58. Графическое определение параметров потока
в решетке.
На этой кривой находим точки Е и Е\
соответствующие скорости потока за решеткой с учетом потерь. Отсюда
видно, что при Я2"<^ 1 скорость выхода потока из той же
решетки при наличии потерь будет больше, чем в случае
е0 = 1, а при Я2>1—меньше (при условии сохранения
того же угла выхода потока).
Большой интерес представляет определение условий,
при которых на входе или на выходе из решетки скорости
549
достигают критических значений. Из (8-5.6) можно
получить, что при Х1 =■ 1
р* = arcsin (?2e0 sin pa) = arcsin (<72fle0). (8-60)
При отсутствии потерь
**
р, = arcsin <72u.
Легко видеть, что при
q2a = const ир;<р;#. (8-60а)
Критическая скорость на выходе из решетки
устанавливается в том случае, когда
P^arcsin^-^). (8-61)
При отсутствии потерь
р**= arcsin qla. (8-6la)
Отсюда следует, что при
qla = const и р2#>р2*.
Значения PJ , р* , р**, а также f* можно определить
с помощью годографа (рис. 8-58).
При сверхзвуковых скоростях .на входе не все
режимы, отвечающие годографу скорости, реально
достижимы. Опыты показывают, что в некоторые случаях при
к\>1 на входе в решетку возникают системьи скачков,
не связанные с обтеканием профилей; при пересечении
этой системы скачков поток .становится дозвуковым.
Такие режимы обтекания активных .решеток называют
режимами «запирания».
Вместе с тем тю условию непрерывности движения
оказывается недостижимой некоторая другая группа ре'
жимов с доз!вуковь»ми и сверхзвуковыми скоростями на
входе. Установим вначале диапазон недостижимых
значений 1\. Рассмотрим движение газа в системе
подводящее сопло — решетка (рис. 8-59,а). Проходные сечения
550
в этой системе определяются очевидными
соотношениями:
F^ = al; Fl = lHtsin^; F2 = lUsm%. (8-62)
Запишем уравнение неразрывности с учетом потерь:
*Л = ^. = *^,. (8-63)
j,
If
Рис. 8 59 К анализу режимов „запирания" рабочей решетки.
55
Отсюда видно, что критическая скорость в сечении /\, и,
следовательно, сверхзвуковой поток на входе в решетку (в
сечении jFj) могут возникнуть только при условиях Fl <^F2 и
F <F2. При F ^>F2 поток перед решеткой будет
дозвуковым, а следовательно, не могут наблюдаться режимы
„запирания".
Подставив (8-62) в (8-63) и учтя, что ^ sin ^ = #^ ,
а максимальный расход через систему соответствует <72=1,
получим:
Отсюда следует, что режимы, отвечающие условию
(r.w=(,ia>s'mi'l^ (8-64)
неосуществимы.
В плоскости годографа (рис. 8-58) область,
соответствующая недостижимым на входе в решетку
значениям Ки заштрихована. Таким образом, перед решеткой
не могут быть осуществлены как некоторые
сверхзвуковые скарасти (область 0—2—3), так и некоторые
дозвуковые (0—1—2). Следует еще раз подчеркнуть, что
область невозможных режимов на входе в решетку не
совпадает с областью режимов «запирания». В
последнем случае перед решеткой возникают скачки и,
следовательно, режимы «запирания» могут образоваться
только в том случае, когда в -направляющем аппарате
достигается сверхзвуковая скорость.
Для решения этой задачи удобно использовать
упрощенную схему подводящее сопло — канал, в которой
решетка заменена суживающимся каналом (рис. 8-59,6).
В такой трубе переменного сечения при е>е скорости
всюду дозвуковые (е — предельное отношение давления;
при котором в критическом сечении Я^=1). В случае
е<С£т в начальном участке после сечения F^ появляется
сверхзвуковая зона, которая замыкается скачком
уплотнения. Режимы е<Сет> гДе вт — отношение давлений, при
котором скачок располагается в сечении F = F2,
теоретически могут осуществляться тремя путями: со
скачком в выходном сечении и в промежуточных сечениях
552
сопла Fп и канала Fn. Однако первый и третий пути
достижения е<Сеш не могут быть реализованы, так как
даже слабые возмущения выше по потоку приводят к срыву
режима. Таким образом, на режимах sm>e>e' при
уменьшении противодавления сверхзвуковая область в
начальном участке сверхзвукового сопла увеличивается —
скачок уплотнения перемещается к выходному сечению F\.
При s^=*s'm сверхзвуковая зона остается постоянной и
скачок располагается в сечении Fn, которое может быть
определено из условия, при котором в сечении F2
устанавливается критическая скорость.
Дальнейшее снижение противодавления не изменяет
режима течения в системе. При определенном
соотношении F2/F.x. и FJF.x сечение Fп совпадает с F1( В этом
случае перед каналом и в канале возможно существование
сверхзвуковых скоростей.
Следовательно, в системе сопло —канат сверхзвуковые
скорости могут быть достигнуты только при /72>/7.х.. При
определенном соотношении F2jFx и FJF^ на режимах
£<Csm на входе в канал возможно существование
сверхзвуковых скоростей.
Возвращаясь к схеме сопло — решетка (рис. 8-59,а),
отметим, что отношение -^- — — определяет расчет-
ное значение 11 для расширяющегося сопла, а ~]Г =
sira Раэ^
sin pj
Как было показано выше, сверхзвуковые скорости перед
решеткой возможны только в том случае, когда
удовлетворяется уравнение неразрывности с учетом потерь:
<7, sink = ,7,^-^-sinp,.
Здесь р02/р01 — изменение давления торможения в
прямом скачке, зависящее только от Ях; р02/р02ь—изменение
давления торможения в решетке.
553
р Щ Щ 076 0,6 1,0 1,2 1,4 1,6 1,6 2,0 2,2 2,4
Щ
0,4
0,6
1,0\ -£
Рис. 8-60. Диаграмма годографа X.
554
При р02/р02 =1 и Я2 = 1 из уравнения неразрывности
получим:
1 1
(ФГ' vO-J-rJ ij~l sinp'=sin|w (8-65)
Формула (8-65) определяет в плоскости годографа
кривую, ограничивающую область режимов, при которых
сверхзвуковые скорости на входе в решетку недостижимы.
При 11 = \ р1 = Р2эф' т- е* кРивые> описываемые
формулой (8-65), совпадают с кривыми, построенными по
формуле (8-59).
Для практического пользования целесообразно построить,
диаграмму годографов, соответствующих различным, но
постоянным значениям qal (рис. 8-60).
Диаграмма строится следующим образом. Задаваясь
постоянной величиной qa и рядом значений q2, определяем
по (8-59) соответствующие значения [3. В области Я>1
строим также семейство кривых по формуле (8-65), причем
в этом случае sin[B93(J) = #a. Эти кривые используются для
определения зоны возможных сверхзвуковых скоростей на
входе в решетку.
Для удобства построения и пользования диаграммой
внизу нанесены функции одномерного изоэнтропического
потока:
ах\ —; —; -=- и т. п., а также 92 = -i-2L-01.
Рассмотрим на частном примерз использование этой диаграммы.
Будем считать заданными значения qa = 0,5 и ql = 0,7.
0,5
Тогда sin pj = ttj = 0,714 и Ji = 45°30' На горизонтальной оси
находим два значения: Х1 и Х[. Проведя из точки О радиусами А.,
и Х{ двз окружности, получим на пересечении с лучом (^ = 45°30'
точки А и В, соответствующие годографу qa = 0,5. Определив
указанным способом входной и выходной треугольники скоростей, мы
можем найти параметры потока. Предварительно необходимо
произвести проверку возможности достижения скорости Х{ на входе в
решетку.
Для такой оценки необходимо знать ?2эЬ* Примем р?эк =36°50'.
Тогда при сверхзвуковой скорости на выходе из решетки q2a —
5Г)5
= sin (12эф == Qfi. Следовательно, перед решеткой сверхзвуковая
скорость недостижима, так как точка В находится в области,
ограниченной пунктирной кривой р2 э, = 36°50'.
Годограф Я можно использовать также для
приближенного расчета углов отклонения потока в косом срезе как
направляющей, так и рабочей решеток.
Для этого предварительно из уравнения неразрывности
(8-56) при отсутствии потерь (е0 = 1) получим:
• sin р,
откуда
s == Р2 — Р2эФ = arcsin ^sin p^ — р2эф.
Учитывая, что при р2 = рг и q2 = qx угол отклонения
потока равен 6 = ^ —13 , приходим к заключению, что
При ^! = [В2 — 8 = 0 и, следовательно, при любой
сверхзвуковой скорости набегающего потока отклонения в косом
срезе не происходит. В случае, когда [^ < ?2,^ < 0, т. е.
в косом срезе, происходит не расширение, а поджатие
потока. К аналогичному выводу можно прийти и при
анализе потока в плоскости годографа.
Такое поведение сверхзвукового потока в активных
решетках связано с тем, что при сверхзвуковых скоростях
возмущения не распространяются навстречу потоку и
давление перед решеткой рх может быть выбрано произвольно.
Это условие нарушается только на режимах „запирания",
т. е. в том случае, если вектор Я лежит в области,
ограниченной пунктирной кривой g2a = sin[32.
Таким образом, до наступления режимов „запирания"
угол выхода потока из решетки можно определить по
значению Я2 = /(/?2//?01) на основном семействе кривых #а =
= const, причем р2 не зависит от геометрических
параметров решетки и числа М. На режимах „запирания" вектор Я'
находится внутри области, ограниченной пунктирной кривой
#а = const; угол выхода определяется по Я2 на кривой
<7a = sinp23. , т. е. зависит от геометрических параметров
решетки.
5 56
На рис. 8-61 представлены расчетные кривые
зависимости угла выхода потока из решетки от рх и М2/ при
18°20' и М1/? = М2,,
где М.
^ - —\р 2п *—1/, расчетное значение
числа М для подводящего сопла. На график нанесены
гч
22
20
18
16
р;
—
_^
/
hvi
У-*
S
X"'
1
I
•А
i
i
9
r^—
кспе(.
2
Рас
^
шме!
0
чет^
i^""
-—
,
(
У/77 При М2 —
2
2
2
!&lMA
—1
►
-Мц
1,62
Ч
1JL
1,б\
/ ч
•
'Ж
26
——•*"
А'
28
Рис. 8-61. Зависимость угла выхода потока р2 из активной решетки
от р, при Ми=М2/, и ?2э4э = 18°20'.
также экспериментальные точки, полученные при М2,=
= 1,62. Можно отметить удовлетворительное совпадение
расчета с опытом.
8-14. ПРОФИЛИРОВАНИЕ
И РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТАЛЬНОГО ИССЛЕДОВАНИЯ
АКТИВНЫХ РЕШЕТОК ПРИ БОЛЬШИХ СКОРОСТЯХ
Проектирование и отработка «профилей решеток для
около- и сверхзвуковых скоростей осуществляются
экспериментально.
Опыгг показывает, что сверхзвуковые активные
решетки имеют -малые .потери только в том случае, когда
на входе в решетку поток затормаживается до малых
сверхзвуковых скоростей. Рассмотрим два возможных
метода профилирования сверхзвуковых' активных
решеток с торможением потока на входе.
Первый метод заключается в том, что торможение
организуется на входном участке спинки профиля.
557
С этой целью входной участок спинки выполняется
вогнутым для плавного торможения .сверхзвукового
потока (с возможным образованием отсоединенного
криволинейного .скачка) или с угловыми изломами для
ступенчатого торможения ! ib системе косых скачков.
Второй метод основывается на торможении потока
в криволинейном или косом скачках, организуемьих во
входном участке канала. При этом входной участок
опинки вьшолняется прямолинейным или очень малой
кривизны, а конструктивный угол входной кромки
выбирается таким, чтобы торможение потока происходило
в скачке, возникающем со стороны вогнутой
поверхности.
При небольших сверхзвуковых скоростях (Mi<< 1,25)
1 См. гл. 4.
558
потери в прямом скачке невелики (1 —1,5%). Потери
при расширении потока в косом срезе также могут быть
сведены к минимуму. Поэтому межлопаточный канал
решетки, работающей при небольших сверхзвуковые
скоростях, можно проектировать суживающимся так,
чтобы перед нею возникал прямой ,скачок «запирания».
При больших сверхзвуковые скоростях целесообразно
межлопаточный канал делать сужающе-расширяю-
щимся.
Возможные формы «профилей и каналов активных
сверхзвуковых решеток приведены на рис. 8-62.
Как показывает теоретический анализ, даже в
межлопаточном ка.нале относительно большой кривизны
можно избежать образования скачков уплотнения. Этот
вывод подтверждается также данньгми эксперимента.
На рис. 8-63 представлены схема и фотографии
спектров обтекания сверхзвуковым потоком активной
решетки ТР-2А1. Перед толстой входной кромкой
возникает скачок уплотнения а. На входной кромке и на
спинке профиля поток ускоряется в волнах разрежения.
Волны разрежения замыкаются скачком б, который
вместе со скачком а образует головной Я-образный
скачок. В точке А наблюдается отрыв пограничного слоя.
А-образный головной скачок 'вызывает излом границы
вихревой зоны в точке В. Однако отрыв пограничного
слоя сохраняется до выходного сечения межлопаточного
канала, причем граница вихревой зоны и вогнутая
'поверхность профиля образуют фиктивный канал
практически (Постоянной ширины. В месте падения кромочного
скачка на спинку возникает локальный отрыв
пограничного слоя вследствие кривизны спинки; за скачком
(точка С) поток ускоряется. На подход*е к выходной
кромке образуется отсоединенный скачок уплотнения в.
За кромкой возникает второй, кромочный, скачок е. Оба
скачка сливаются в один А-образный скачок.
В решетках группы А при сверхзвуковых скоростях
'появляются дополнительные .потери: в скачках
уплотнения на входе, в вихревой зоне, образующейся вследствие
отрыва пограничного слоя за скачком б, в кро'моч-ном и
отраженном скачках d и в А-образном скачке. С
увеличением скорости эти потери интенсивно увеличиваются.
1 Решетки группы А рассчитаны на обтекание потоком
дозвуковых скоростей.
559
СЛ
О)
о
Рис. 8-63.
а—схема и б, в, г—фотог-
ра рии спектров течения
воздуха в активной
решетке ТР-2А; б — Mi=l,205;
в—М1=1,395; г—М1=1,1б35.
Решетки группы Б, разработанные в МЭИ для
околозвуковых -скоростей, характеризуются меньшими
толщиной входной кромки и кривизной спинки на входном
участке и в 'косом срезе. В этих решетках перед
входной кромкой возникает криволинейный скачок а
(р»ис. 8-64) меньшей интенсивности. На криволинейной
поверхности спинки (за точкой А) происходит интенсив-
Рис. 8-G4. Схема сверхзвукового
потока в решетках группы Б.
ное ускорение потока. Замыкающий зону расширения
скачок расположен внутри канала (канал № 1 на
рис. 8-64). В том случае, когда перерасширение
небольшое, торможение «происходит только в головном скачке
(в точке В, канал № 2 на рис. 8-64).
При большой конфузорности канала .перед ним (не
перед кромкой) возникает скачок уплотнения (режим
«запирания», канал № 3 на рис. 8-64). Такое положение
скачка обеспечивает устойчивое дозвуковое течение
в межлопаточном канале. Если профилированием
выгодного участка спинки добиться малых потерь при
расширении потока ib косом срезе, то такая решетка может
оказаться высокоэкономичной до чисел Mi— 1,25.
На рис. 8-65 приведены кривые потерь в решетках
групп А и Б. При М2< 0,95 потери в решетке ТР-1А
ниже, чем в решетках группы Б. Однако при М2>1
потери в решетке ТР-1А резко возрастают; в решетках
группы Б при Ms^ 0,95—1,25 потери ниже.
Значение критического числа М2^ для решетки
группы Б во всех случаях выше, чем для решетки типа А.
В решетке ТР-2Б уменьшение потерь происходит до
М2=1,0. Однако при М2>1,1 наблюдается более интен-
еив-ны'й рост потерь, чем в решетке ТР-1Б. Это обуслов-
36 М. Е. Дейч
561
лено большей кривизной спинки профиля ТР-2Б в косом
срезе.
На рис. 8-66 представлены! кривые распределения
давлений «по профилю решетки ТР-1В, спроектированной
в МЭИ для сверхзвуковых скоростей по методу
торможения потока в косом скачке, возникающем внутри
канала со стороны вогнутой поверхности. Межлопаточный
Рис 8-65. Зависимость профильных потерь в решетках групп А и Б
от числа М2.
капал решетки сужающе-расширяющийся. Минимальное
сечение расположено на входном участке (точки 8 и 7
и 13—14).
Торможение потока происходит перед входным
сечением канала (точки 10—12). При Mi>l,0 перед каналом
возникает прямой скачок, который с увеличением
числа Mi приближается к входному сечению.
При Mi>l,5 головные скачки входят в
межлопаточный канал и торможение происходит в системе 'косых
скачков; в канале поток ускоряется, причем в зоне
минимального сечения на спинке профиля обнаруживается
глубокое разрежение. При увеличении М} минимальное
давление уменьшается, а начало диффузорного участка
смещается по потоку.
На рис. 8-67 показаны .спектры обтекания решеток
группы В. Характерно, что при достаточно больших
числах Mi скорости в межлопаточных каналах
сверхзвуковые, но скачки уплотнения отсутствуют, несмотря на
большую кривизну каналов. На входном участке
профиля, перед кромкой, образуется система головных-
скачков.
562
Рис 8-66. Распределение давлений по профилю ТР-1В (сужающе-расширяющиеся каналы] в решетке.
7^тП575; (3,у=89°05'; 0,-20°.
Рис. 8-67.
J — спектры потока воздуха
з решетке с сужающе-рас-
шиояющимися каналами (ТР-
1В);7 = 0,575; ^=89°05'; р1==
=18°; a — Mi=l,34; б — М1=
= 1,64; //—спектры потока
воздуха в решетке со
ступенчатым торможением на
входе; *=0,625; ^=90°» р,=:
=22°30'; в — М,=Г,47; г —М1==
=1,67.
II
В том случае, когда решетка спроектирована по <ме-
1©ду ступенчатого торможения потока вдоль опинки про-
тнля (система косого — прямого скачков), при больших
'0,5 0,6 0,7 0,8 0,9 ~Щ 11 1,2 1,3 1,4 1,5 1,6 1,7
Рис. 8-68. Сравнение характеристик сверхзвуковых активных решеток
различных типов.
% 2f 3, 4—решетки с сужающе-расширяющимися каналами; /, 3 — с торможением
в скачках на входе; 5 — с постоянным сечением канала; 6 — ТР-1Б; 7 — ТР-1А.
V
0,5 Ofi ~0? 0$ 0,9 1,0 1,1 1,2
Рис. 8-69. Зависимость концевых потерь в решетках от числа М2.
I — ТР-1Б при р!=18°; 2 — ТР-1Б при р,=21°; 3~ТР-1Б-1 при B^ie0; 4 — ТР-2Б при
р,=24°; 5-ТС-1А при р,=-.90°.
сверхзвуковых скоростях образуются два скачка, один
из которые располагается в месте излома (рис. 8-67,6).
На рис. 8-68 дано сравнение шотерь в активыьих
решетках, спроектированных по методу торможения потока
565
вдоль спинки профиля и по -методу торможения в косом
скачке на вогнутой -поверхности. Можно отметить, что
первый метод позволяет добиться несколько лучших
характеристик решетки при М2>1,3 (на 1—2,5%). Однако
этот вывод сделай на основании ограниченного
количества экспериментальных данных.
Опыты показывают, что при околозвуковых и
сверхзвуковых скоростях концевые потери для всех решеток
значительно уменьшаются (рис 8-69). Уменьшается
также неравномерность углов вьихода потока по высоте
решеток.
ГЛАВА ДЕВЯТАЯ
ТЕЧЕНИЕ ГАЗА
В СТУПЕНИ ТУРБОМАШИНЫ
9-1. ОСНОВНЫЕ УРАВНЕНИЯ
В ступени турбомашиньи происходит преобразование
потенциальной энергии газа в механическую работу
(турбина) или механической работы в потенциальную
энергию газа (компрессор). В обо'их случаях поток газа
совершает энергетический обмен с окружающей средой.
Рассмотрим принципиальную схему ступени турбины
с осевым потоком газа. На рис. 9-1 показаны основные
элементы такой ступени. По входному патрубку / газ
подводится к неподвижной направляющей решетке 2,
где часть его потенциальной энергии преобразуется
в кинетическую энергию. Приобретая в направляющей
решетке значительные скорости, поток газа проходит
через зазор 3 и попадает на рабочие лопатки 4,
укрепленные на колесе 5. Здесь происходит перенос энергии к
ротору турбины.
Радиусами г и r + dr проведем два цилиндрических
сечения, ось которых будет совпадать с осью турбины.
Этими сечениями выделим элементарную ступень турби-
ньи; развертывая ее на плоскость (рис. 9-2,а), можно
проследить характер изменения скоростей в проточной
части ступени К
1 Проточной частью будем называть .направляющую и рабочую
решетки ступени.
566
Введем в отличие от
предыдущего следующие
обозначения скоростей:
с — скорость
абсолютного
движения газа;
w — скорость газа в
относительном
движении;
и — скорость
переносного
движения (окружная
скорость);
сч и wu — проекции
скоростей
абсолютного и
относительного
потоков на
направление скорости
и\
W
проекции
скоростей
абсолютного и
относительного
потоков на
направление оси
вращения;
wr — радиальные
составляющие
скоростей
абсолютного и
относительного
потоков.
Рис. 9-1. Схема ступени турбины
в осевом потоке газа (а) и
распределение параметров торможения,
статических давлений и скоростей
в проточной чзсти (б).
Индексом 1 обозначим
скорости, относящиеся ко
входу, а индексом 2— к выходу из рабочих лопаток.
Рабочий процесс ступени турбины можно «проследить
по рис. 9-1 и 9-2. В межлопаточных каналах
направляющей решетки поток газа ускоряется и одновременно
поворачивается, покидая ее со скоростью си направленной
под угло'М си к оси решетки (рис. 9-2,а). При этом ,по-
567
re-нциальная энергия газа преобразуется в кинетическою
энергию потока.
На рабочие лопатки поток входит с относительной
скоростью Wi, которую легко получить, построив
входной треугольник скоростей.
В межлопаточных каналах рабочей решетки
происходит поворот потока в относительном движении; при
Рис. 9-2. Развертка проточной части (а) и треугольники
скоростей осевой ступени {б).
этом силы давления газа производят работу вращения
ротора турбины. Поток выходит из рабочих лопаток
с относительной скоростью w2 под углом (Зг к оси
решетки. Зная окружную скорость и, легко .построить
выходной треугольник скоростей и определить скорость
абсолютного потока на выходе из ступени с2 (рис. 9-2,а).
Часто входной и выходной треугольники скоростей
изображают из одного полюса, как показано на рис. 9-2,6.
Таким образом, энергия газа передается к ротору
турбины благодаря тому, что силы давления три
повороте потока на лопатках производят работу вращения ро-
568
fopa. В результате температура и давление торможения
абсолютного потока уменьшаются так, что
Т ">Т
1 ос\ ^ 1 ос2
И
Рос\ ^ Рос2»
Характерной особенностью рассмотренного процесса
является его ступенчатый характер: потенциальная
энергия вначале преобразуется ^ кинетическую энергию
движущегося газа, а затем на рабочем колесе
кинетическая энергия преобразуется в механическую работу.
Такой процесс в чистом виде имеет место в активной
Ътупенм: статические давления на входе и выходе из
рабочей решетки примерно одинаковы, а скорости W\
р W2 различаются только за счет потерь в рабочей ре-
1иетке.
В чисто реактивной ступени оба составляющих
процесса протекают одновременно ;на рабочем колесе.
Поток газа в рабочих каналах в относительном движении
ускоряется и одновременно совершает работу вращения
ротора. Широкое применение находят промежуточные
типы ступеней, в которых рационально сочетаются оба
принципа — активный и реактивный В этом случае
преобразование потенциальной энергии газа в кинетическую
осуществляется частично в неподвижной решетке и
частично в рабочих каналах.
Изменение статических параметров потока и
параметров торможения в проточной части такой ступени
показано на рис. 9-1,6.
Ступень может быть выполнена также с радиальным
дотоком газа. В такой ступени газ движется в
радиальных плоскостях от оси вращения к периферии или,
Наоборот, к оси вращения. Радиальная ступень может
•быть активного, реактивного или промежуточного типа.
Схемы проточных частей ступеней турбины с
радиальным потоком газа показаны на рис. 9-3. В
радиальном сечении видны формы профилей
направляющей и рабочей решеток ступени и треугольники
скоростей на входе и выходе из рабочих каналов. Заметим,
£то в радиальной ступени окружная скорость меняется
От входного к выходному сечению решетки.
569
В некоторых ступенях поток газа направлен под
углом к оси вращения. При этом радиальные
составляющие скорости сг не равны нулю и при анализе
свойств -потока должны учитываться (рис. 9-4).
В ступени компрессора (осевого или центробежного)
происходит преобразование механической работы в по-
Рис. 9-3. Схемы центробежной (а) и
центростремительной (б) радиальных
ступеней турбины.
тенциальную энергию газа. Каналы рабочей решетки /
осевого компрессора — расширяющиеся (рис. 9-5).
Давление газа в относительном движении возрастает, а
скорость уменьшается. Этот процесс -продолжается в
направляющем аппарате 2. Э.нтальпия полного
торможения в абсолютном движении возрастает.
В ступени центробежного компрессора движение газп
осуществляется от центра к периферии (рис. 9-6), рабо
570
чие лопатки колеса / образуют расширяющиеся каналы,
в которьих происходит торможение относительного поти-
ка< Сжатие газа может продолжаться в лопаточном
диффузоре 2.
В точной постановке задачи течение газа в ступени
турбомашины описывается дифференциальными
уравнениями пространственного потока вязкой сжимаемой
Рис. 9-5. Схема и развертка
проточной части ступени осевого
компрессора.
Рис. 9-4. Схема
диагональной ступени,
жидкости. Приближенные
решения основываются на
уравнениях идеальной
сжимаемой жидкости,
выведенных в гл. 1.
Исходные уравнения
(сохранения количества движения, неразрывности и
энергии) целесообразно записать в цилиндрической
системе координат. В качестве независимых
переменных, как и ранее, выбираются: радиус-вектор г
полярный угол 0 и аппликата г. Направление оси
* совпадает с осью вращения турбины. Тогда
система уравнений сохранения в абсолютном
установившемся движении
(6 p/dt = dcjdt = дсе/д t = dcjdt — 0)
при /? = 9 = Z = 0 сводится к уравнениям (1-14) и (1-17а).
Для исследования потока в рабочей решетке основные
Уравнения идеальной жидкости целесообразно записать для
571
относительного движения. При этом используются
очевидные соотношения (рис. 9-2):
wa = ca; wr = cr кхв)и = си — и = с„ — <йг,
где со — угловая скорость вращения рабочей решетки.
F^
Рис. 9-6. Схема ступени центробежного
компрессора.
После подстановки этих соотношений в уравнения (1-17а)
для установившегося относительного движения получим:
W
dwr wudwr
/-1Г + ТЖ
-W
dwr
°> dz
w
о , 0 I dp
■ gov 4- 2аш = f-;
» и р дг
dwu wu dwu dwu
r
dwn
■2о)ш
1 др.
w„ dwn
pr d0
dw„
W
r dr
-W
d6 ~wa dz
J_dp_
p dz
)
(9-1)
Дифференциальное уравнение неразрывности для
установившегося относительного потока имеет вид:
dr г г дЪ • dz
= 0.
(9-2)
572
Система уравнений движения (1 - 17а) и (1-14) или
(9-1) и (9-2) дополняется уравнениями сохранения
энергии 'И изоэнтропического процесса. При этом
система уравнений, определяющая пространственное
установившееся движение идеальной сжимаемой жидкости
в ступени турбомашины, является замкнутой.
Перейдем тетерь к выводу уравнения энергии для
струйки газа в проточной части ступени. Уравнение
энергии может быть записано в параметрах абсолютного
или относительного движения. В первом случае в
уравнение энергии вводятся члены, учитывающие
энергетический обмен между потоком и окружающей средой.
Во втором случае (для относительного потока)
необходимо учитывать дополнительные силы, введение которых
позволяет рассматривать относительное движение, так,
как если бьи оно было абсолютным. Такими
дополнительными сила-ми являются кориолисова сила инерции и
центробежная сила.
Уравнение энергии для абсолютного потока напишем
в форме первого начала термодинамики. С учетом
сделанных допущений получим:
di + cdc—gdLT = 0. (9-3)
Здесь LT — работа, совершаемая газом.
Величина LT может быть определена с помощью
уравнения моментов количества движения. Момент сил,
действующих на рабочие лопатки при установившемся движении,
будет:
Ми = — (с2 cos а2г2 — сх cos ахгх),
где G — секундный расход газа через решетку.
Умножив Ми на угловую скорость вращения решетки а>,
найдем секундную работу или мощность, которой
обмениваются лопатки с газовым потоком:
Mw«> = — (c2#2cosa2 — clul cosax).
Следовательно, работа, отнесенная к весу
протекающего газа, равна:
Lt =i~(cu2u2 — c«M (9"4)
573
Уравнение (9-4) получено Эйлером. В
дифференциальной форме уравнение Эйлера имеет вид:
dLT=-j-d(cuu). (9-5)
Так как в турбине газ совершает работу, то вдоль
струйки абсолютного течения d(cuu)<^0. Для ступени
компрессора выражение внешней работы аналогично, но в этом
случае d(cuu)^>0. Использовав выражения (9-3) и (9-5),
получим дифференциальное уравнение энергии для потока
в абсолютном движении:
di + cdc — d (cji) = 0. (9-6)
В соответствии с законом сохранения энергии
изменение кинетической и внутренней энергии газа в
относительном движении .равно количеству 1Подведенного ('или
отведенного) тепла и .работе действительных и
дополнительных сил. Так как кориолисова сила инерции
натравлена нормально к О'си струйки ,в относительном
движении (к вектору w), то работа этой силы равна
нулю.
Таким образом, из числа дополнительных сил в
уравнение энергии для потока газа в относительном
движении необходимо ввести центробежную силу,
направленную вдоль радиуса нормально к оси вращения. В
частном случае аксиальной ступени вектор центробежной
силы нормален к линиям тока и работа центробежные
сил также равна нулю.
Уравнение энергии для потока в относительном
движении получаем :на основании первого начала
термодинамики (9-3).
Учитывая, что с2 = с -\- с2 -\- с2 и используя связь
между абсолютными и относительными скоростями,
преобразуем выражение (9-6). Получим:
di + wdw — udu = 0. (9-7)
Интегрирование уравнения энергии (9-6) для потока
в абсолютном движении дает:
с2
i -f- ~2 сии = const. (9-8)
574
Интеграл уравнения энергии потока в относительном
движении (9-7) равен:
f-|- w2~u2 = const. (9-9)
Переход от уравнения (9-8) к уравнению (9-9),
очевидно, совершается с помощью формулы (рис. 9-2,6)
w2 = c2 + u2 — 2c uu. (9-10)
Полученные уравнения для относительного движения
могут быть использованы для расчета ступени не только
турбины, но и других турбомашин (компрессор,
вентилятор). Направление энергетического обмена (отвод или
•подвод механической работы) при этом не имеет
значения. Это замечание вполне справедливо только в
предположении изоэнтропического течения в ступени турбо-
машиньи. В реальных условиях движение газа
сопровождается потерями. При этом направление энергетического
обмена существенно влияет на структуру потока (.на
характер распределения параметров в проточной части),
а следовательно, и на к. п. д. ступени.
При отсутствии шотерь изменение состояния газа
в абсолютном и относительном движении подчиняется
изоэнтропическому закону, который для идеального газа
может быть представлен формулой pl$K = const.
В этом случае интегралы уравнений количества
движения и энергии совпадают. Действительно, для
одномерного потока в абсолютном движении уравнение
импульсов имеет вид:
cdc + ^- — d(cun) = 0. (9-11)
Считая относительное движение газа в ступени
установившимся, запишем уравнение импульсов в такой форме:
wdw -|- — — ra>2 cos (r,x) dx = 0,
где га)2 cos (r x) dx — импульс центробежных сил.
Так как т = и, то
wdw-\-d-p- — iidit = 0. (9-12)
575
Интегральг уравнений (9-11) и (9-12) совпадают
с уравнениями (9-8) и (9-9), если di = dp/p, что
соответствует изоэнтро-пическому процессу.
Уравнения импульсов для абсолютного и
относительного движений с учетом потерь можно получить, введя
в (9-11) и (9-12) импульс сил трения; в этом случае
/, с и w и являются параметрами действительного
течения.
При исследовании ступени в рамках упрощенной
одномерной схемы! потока используется уравнение
неразрывности:
m=-Foc = Fow — Fqo a -=F п о а
где Fc — площадь сечения, нормального к вектору
скорости С)
Fw — площадь сечения, нормального к вектору
относительной скорости w\ qc и qw — приведенные
расходы при абсолютном и относительном
движениях.
Из уравнения неразрывности находим:
Рс w Qw ?*w a*w
где р с, р ш, а с, aw — критические плотности и скорости
для абсолютного и относительного
потоков.
Очевидно, статические параметры р, р, Т как в
абсолютном, так и в относительном движении одинаковы.
Действительный процесс движения газа в проточной
части ступени отличается рядом особенностей, не
учитываемых выведенными выше уравнениями. Так, поток
газа в зазоре между направляющей и рабочей
решетками обладает неравномерностью. В рабочих каналах,
воспринимающих поток из зазора, течение газа оказывается
периодически нестационарным, с непрерывной
пульсацией скоростей и давлений.
Кроме того, поток совершает теплообмен с внешней
средой в связи с непроизводительными потерями тепла
и вследствие организуемого искусственного охлаждения
лопаток, подверженных высоким нагрузкам. В
уравнении энергии эта особенность может быть учтена •введс-
576
нием соответствующего члена, учитывающего внешний
теплообмен.
При движении в .проточной части основной поток
разветвляется; при этом некоторое количество газа,
минуя рабочую -решетку, протекает в зазоры между
статором и ротором. В зависимости от распределения
давлений в проточной части может происходить подсос газа
через зазоры в основной поток.
Таким образом, в общем случае поток газа в
ступени подвергается различным внешним воздействиям,
влияющим на процесс преобразования энергии. Оценка
этих воздействий производится на основании данных
эксперимента.
9-2. ПАРАМЕТРЫ ПОТОКА В АБСОЛЮТНОМ
И ОТНОСИТЕЛЬНОМ ДВИЖЕНИИ. ОДНОМЕРНАЯ СХЕМА
ПОТОКА
Величину постоянной в правых частях уравнений
энергии (9-8) и (9-9)
С2 | . W2 — U2 , . , /п 1 оч
-2 cuu-\-i = g И = const (9-13)
можно определить из граничных условий.
При расчете ступени турбины обычно известны
параметры течения на входе в рабочее колесо. Для входа
имеем:
2 2
с\ w\ — и1
~2" ~ С*\Ul + il = 2 Ь il = COtlSt-
Обозначив, как и раньше,
где ioc — энтальпия полного изоэнтропического торможения
в произвольном сечении потока в абсолютном
движении,
запишем (9-13) в такой форме:
iL _ саи + i = iocX - cuXux% (9-15)
или для совершенного газа:
(9-15а)
577
2с.
г. I
37 М. Е. Дейч
где iocV TocX—энтальпия й температура изоэнтропи^еског^б
торможения на входе в рабочее колесо
в абсолютном движении.
С другой стороны, при полном изоэнтропическом
торможении потока в относительном движении его кинетическая
энергия обратимо переходит в тепло. Энтальпия
торможения определяется очевидным уравнением
£ + '■ = <«.■ (9-16)
Следовательно, уравнение энергии принимает вид:
2 ' + t = towl 2"' (9_17)
где / ы —энтальпия полного торможения относительного
потока на входе в рабочее колесо.
Заметим, что если поток на входе не закручен и си1=
= 0, то из (9-15) следует
^-cuu + i = ioc-cuti=iocV
Такой случай может иметь место только для чисто
реактивной ступени или для ступени центробежного
компрессора.
С учетом выражений (9-14) и (9-16) уравнение (9-13)
можно записать так:
loe~ouu = iow-^. (9-18)
Связь между iocV iowi, ioc и iow можно представить
в виде:
с, —в»,
owl ocl
OW ОС
2
с2 — w2
2
(9-19)
(9-19а)
578
Соответственно получаем зависимость между
температурами торможения в абсолютном и относительном
потоках:
с„и сп]и, /72 и,
т ^- = 7 £1_1 = т — ^т L Г9-2СП
1 ос с ос\ с ow 2с owl 2с ' \ '
Р Р LP °р
Уравнение (9-20) показывает, что температура
торможения в общем случае является переменной вдоль струйки
величиной не только для абсолютного, но и для
относительного движения. Представим (9-20) в несколько иной
форме:
Г~ - 1 - £=£ ; (9.20а)
Т 9r T
1 owl ^ р1 owl
* ОС - С п\^Л С,М
_2£_ = 1 _ JHLL !L_ . (9-206)
1 ос\ ср* ос\
Разность температур торможения
m г2 — 7W2 (2С„ U) U
Т т — с w v а } /Р-9П
1 ос J ow— 2cp — 2ср ' ^Z1>
Из уравнения (9-20а) следует, что температура
торможения относительного потока меняется соответственно
изменению окружной скорости вдоль трубки тока. При
и = const температура Tow постоянна. На этом основании
можно заключить, что температура торможения Tow
постоянна в ступени с осевым потоком газа. В радиальной
ступени Tow вдоль трубки тока меняется. Если в такой
ступени поток направляется от оси вращения к периферии, то
Tow увеличивается. В случае, когда поток движется к оси
вращения, Tow убывает.
Полученный результат имеет простое физическое
объяснение.
Полная энергия относительного потока,
пропорциональная Tow, изменяется вследствие работы
центробежных сил, в поле которых движется газ. Если радиальные
составляющие скорости не равны нулю (сг=дог#0)
и струйка газа движется не только вдоль оси вращения,
но и радиально, то центробежные силы совершают ра-
37*
579
боту перемещения частиц в радиальном направлении
и увеличивают или уменьшают полную энергию частицы
в зависимости от направления потока. Если направление
относительного потока совпадает с направлением
центробежных сил (радиальная ступень с.потоком газа к
периферии), то Tow увеличивается. В противном случае
(радиальная ступень с потоком газа к оси вращения)
полная энергия уменьшается.
Формула (9-206) показывает, что температура тор-
можен-ия в абсолютном движении во всех случаях
убывает. Из рассмотрения принципа работы турбинной
ступени следует, что в произвольном сечении трубки тока
cvu<cuiUi и убывает по направлению течения, так как
газ совершает работу вращения колеса.
В ступени компрессора, наоборот, сии>сиХих и
возрастает в направлении потока, так как работа к газу
подводится.
Вернемся <к уравнению энергии (9-13). Заметим, что
величина постоянной в правой части уравнения (9-13)
различна для разных струек, так как cu\U\ может
изменяться .при переходе от одной струйки к другой. Отсюда
заключаем, что, строго говоря, уравнение энергии
следует применять для каждой струйки в отдельности. Для
•канала в целом уравнение (9-13) может быть
использовано, если все величины, входящие в это уравнение,
подсчитывать как средние по сечению канала.
Уравнению энергии в относительном движении можно
придать известную форму, заменяя t по формуле
.__& р _ а2 .
£ Л— 1 р ~k—V
тогда согласно уравнению (9-16)
w2 . k р k Pqw
2 T^iJ-A-i ?ow
или
w2 i a2 alw
2 \ k — 1 ~~ k — 1 '
где pow, pow, aow — давление, плотность и скорость звука
в изоэнтропически заторможенном
относительном потоке.
(9-22)
(9-22а)
880
Подчеркнем еще раз, что скорость звука и
статические параметры течения /?, р и Т для абсолютного и
относительного движений имеют одну и ту же величину.
Скорость звука заторможенного относительного потока
меняется вдоль струйки в соответствии с изменением
энтальпии i0Wm При любых изменениях iow вдоль струйки
сумма кинетической и потенциальной энергии
относительного потока в данном сечении по уравнению (9-16) равна
/ . В частном случае скорость относительного потока в
некотором сечении может достигнуть местной скорости
звука; тогда
Из уравнений (9-16) можно получить значение правой
части уравнения энергии в виде:
«■ , а» _ < _ k+l (9_22б)
2 ~ k—l ~ 2 k—l '
Приравняв правые части уравнений (9-22), (9-22а) и
(9-226), получим:
2 2 п
. т aow a*w k+l k Pow __
low Cp1ow k—\ ~~ 2 k—l *~~ k— 1 ?ow
w2
макс =;„..,-^K-«2)-
— 2 owl
Аналогичные преобразования для потока в абсолютном
движении приводят к соотношению
. _ т _ alc = a\ k+l _ k Рос _
ос "р ос k—l 2 k—l k—l poff
С помощью этих соотношений нетрудно получить
выражение для характерных скоростей а#с, £макс, d*w и т. д.
Так, например, для относительного потока находим:
^=]f
2k Po
*+1 Ро
■/'
2-fcrf'с-?■(«?-«')]• (9-23)
581
Для абсолютного потока
/
2k Рос
*+1 ' ?ос
= |/ ^[ioe-(cul »i-cuu)\ (9-24)
Из уравнения (9-24) следует, что характеристики
абсолютного потока, зависящие от величины полной энергии
ioc (от параметров торможения), меняются вдоль трубки
тока. Следовательно, а*с, смакс и аос являются
переменными величинами для струйки газа в абсолютном
движении.
В относительном движении критическая и
максимальная скорости могут меняться или оставаться постоянными
в зависимости от того, меняется ли или не меняется вдоль
струйки окружная скорость и. Если вдоль струйки и =
= const (ступень с осевым потоком), то iow = const и
соответственно а#ю = const и эдмакс = const. При переменной
вдоль струйки окружной скорости эти основные
характеристики потока газа изменяются соответственно
изменению и.
Уравнение (9-21) позволяет установить связь между
температурами торможения в относительном и абсолютном
потоках в следующей форме:
Tow (2cu-u)u
= 1
ЪсрТ0С
Заменив
получим:
2си11 = с2-}-и2 — w2,
1 ос °pJ ос '
После замены (см., например, треугольники скоростей
на рис. 9-2,6)
=Ж4 -2v"4=3St (9-26)
с* ' \ с ] се sirr
682
уравнение (9-25) преобразуется "к виду:
■* Q7D1 _ О / ~ ^11
"Т
= 1 -a (*4"-')=I -#£№$-' • <9-25а>
где я0 = .
смакс
Уравнение (9-25а) показывает, что вдоль струйки
отношение температур торможения меняется. При и = 0 ки =
=z2cu отношение T0JT0C^=\. Первый случай
соответствует неподвижному колесу (# = 0), когда механическая
работа газом не совершается (cuii = 0). Второе значение и
определяет то сечение струйки, в котором температура
торможения в абсолютном и относительном движениях
одинакова.
Безразмерные скорости Мс, Mw, У-с и Xw связаны с
температурой торможения в данном сечении известными
соотношениями (гл. 2):
для относительного потока
^==1+^lLa£=_L_; (9.27)
k+ l
для абсолютного потока
% ==1+^=^1= * (9.28)
' k + \
4
Отсюда по известным формулам изоэнтропического
процесса:
k k
,fe—1 р /т \k-\
\ г ос I * ос \
Pow / ow\
И Т. Д.
Р
Pow „ л РоС
^018) л roc л
можно получить связи между —- и Я^, —- и %с иг т. д.
С помощью уравнений (9-27) и (9-28) можно также
получить зависимость между параметрами изоэнтропического
торможения в абсолютном и относительном потоках:
Го* + 2 Mw_l~k+i К
Тос ^*=1М2 ^^я.
(9-29)
2 m* /j _|_ 1
583
row I a ow \
Рос ~~ ^ Toc
(9-30)
P / T \k-\
"ow ow \
Учитывая выражение (9-25а) представим отношение
в виде:
l_tt^2-"-l
0 V U
k
k-l
(9-32)
С помощью уравнения (9-20) легко получить
зависимость между параметрами полного торможения на входе и
на выходе из колеса.
Для относительного потока получим [см. формулу
(9-20а)]
r°w2 i-^-Uji
' owl
к + 1 *wl
u\) ow] \
где
и.
owl '
Vii
owl ^AiaKcl
(9-33)
(9-34)
(9-35)
Соответственно для абсолютного потока [см. формулу
(9-206)]
-=—= 1 = i— 2j(cuu), (9-36)
где
Z(CUU):
си\ ы1 — си2 "г
Выразим iocl через сшкс1; тогда
f!=1-2"o.sM
1 ocl
(9-37)
(9-38)
584
и
k
^=[1-2<S(^J1*-'. (9-39)
В формулы (9-27) — (9-39) входят безразмерные
скорости абсолютного и относительного потоков. Связь между
М и М выражается так:
Из уравнения
находим*.
X2--
W
где и# = ~ .
Мш since
Мс sin f *
w2=c2 + и2 — 2с ии
(9-40)
(9-41)
(9-42)
Последнее уравнение показывает, что отношение
температур торможения T0JT0C служит переходным
коэффициентом от абсолютного потока к относительному. Эта
величина меняется вдоль струйки. На входе и на выходе
Т
из рабочего колеса ~^- для данного режима приобретает
* ос
определенные значения.
Основные газодинамические зависимости, приведенные
выше, справедливы как для аксиальной, так и для
радиальной ступеней турбомашины.
Практические расчеты показывают, что влияние
центробежного эффекта в осевой ступени невелико1. К этому
выводу легко также прийти с помощью уравнения (9-33),
из которого следует, что если отношение и2/иг мало
отличается от единицы, то изменение температуры торможения
относительного потока пренебрежимо мало. Только при
1 Здесь не рассматриваются влияние центробежных сил на
пограничный слой в межлопаточных каналах, а также и другие
особенности пространственного потока вязкой жидкости в ступени при
наличии радиальных составляющих скоростей,
585
значительном изменении окружной скорости вдоль трубки
тока, как это, например, имеет место в ступени
центробежного компрессора или радиальной турбины, влияние
указанного эффекта будет^существенным.
Для обычных турбинных радиальных ступеней
отношение окружных скоростей и2/иг колеблется в пределах
и%0 1,02 1.04 1,06 1,08 1,10 1,12 W
Рис. 9-7. Изменение температуры торможения относительного потока
в зависимости от u2lul и и wl.
1,02—1,10. На основании рис. 9-7 заключаем, что для
^/^ = 1,10 относительное изменение температуры
торможения Tow при #*ш1 —0,3-f~0,5 составляет 0,25 — 0,70°/о>
т. е. невелико.
Изобразим изменение состояния газа вдоль струйки в
тепловой диаграмме с учетом потерь энергии в элементах
ступени турбины. Параметры полного торможения на входе
в направляющую решетку находим в точке О (рис. 9-8):
Рос и *ос\- Соответствующие статические параметры
определены точкой 0[. Если обозначить статическое давление
за направляющей решеткой рх, то точка Г фиксирует
состояние газа при изоэнтропическом расширении, а точка 1
показывает действительное состояние потока (с учетом
потерь). Потеря энергии выражается отрезком 1 — Г.
Давление торможения абсолютного потока за
направляющей решеткой будет р0(,{ (энтальпия торможения остается
586
неизменной). Разность pQc — р0с[ эквивалентна потерям
энергии Ahc.
Коэффициент потерь в направляющей решетке равен:
г — Л/*с — (k + 1 1
1
\
Рос2
— 1
где Я0
- безразмерная скорость, эквивалентная изоэнтропи-
ческому перепаду тепла в ступени И0.
Разность энтальпий торможения абсолютного и
относительного потоков определяется по уравнению (9-19).
Откладывая величину iQcl — i0wl от точки О' на линии
iQcl = const, находим точку 2, которая определяет
состояние заторможенного относительного потока на входе в
рабочее колесо.
В рабочих каналах в результате потерь часть
кинетической энергии необратимо переходит в тепло. В
результате давление торможения в относительном движении
падает. Если вдоль струйки газа окружная скорость не
меняется, то соответствующий процесс изображается
линией 2—3 (iQwl = const). При увеличении и вдоль струйки
(радиальный поток от оси вращения к периферии) iQw
возрастает (пунктирная линия 2—<?'). Если и уменьшается,
то i0w снижается (линия 2—3").
Статические параметры на выходе из рабочей решетки
определяются в точке 4, причем отрезок 3—4! (или соот-
Aw\t
ветственно З1 — 4' и 3" — 4') равен -х— .
Коэффициент потерь кинетической энергии в рабочей
решетке будет:
АЛ.
^2
A(w22t-
-4)
Яо
2*tf.
k + \
k — \
w\
Pqw\
Pqw2
k-l
k
T0cl "Ag"
Поток покидает ступень с некоторой абсолютной
скоростью с2. Часть кинетической энергии, эквивалентная
скорости с2, является потерей (ДА ).
587
Коэффициент потерь с выходной скоростью
Ah»
Т I2
1 0с2 Ас2
О Ut-4 G.£
и
'o*i А*
Ррс2
Рос J
hc2
I2 '■
к0
где р0с2 — давление тормон ения абсолютного потока за
ступенью;
р ■—фиктивное давление торможения за ступенью
(рис. 9-8).
Как видно из формул', коэффициенты потерь С2 и С3
зависят в неявной форме от -1 , так как от этой
величине
Рис. 9-8. Процесс в тепловой диаграмме для турбинной ступени.
588
f f
Owl Oc2 гл
rtbi зависят отношения температур у— и -^— . Величй-
J Ocl J Ocl
на Cx, характеризующая потери в неподвил ной решетке,
также зависит от —; при изменении — меняются числа М
и Re на выходе из направляющей решетки.
В тепловой диаграмме отложим от точки 4' вверх
величину А/гв; тогда получим точку 4, характеризующую
состояние заторможенного абсолютного потока за ступенью-
Предположим, что вся кинетическая энергия абсолютного
потока за ступенью необратимо переходит в тепло; тогда
на изобаре р2 в точке 5 определяется состояние газа за
ступенью (процесс торможения за ступенью принят
изобарическим).
Введем теперь понятие степени реакции. Степенью
реакции называют отношение
располагаемого теплового перепада на рабочей
решетке к полному располагаемому перепаду
тепла в ступени. Следовательно, степень реакции
указывает ту часть располагаемой потенциальной энергии
газа (тепла), которая Преобразуется в механическую работу
непосредственно в рабочей решетке (на колесе).
По определению (рис. 9-8)
/?02_ *1 ~~l2t __ i l0cl —Н ^
11 о lQc\ ~~L2t L0cl ~~ L2t
где h02 — изоэнтропический располагаемый перепад тепла
в рабочей решетке.
Формулу для степени реакции можно преобразовать к
виду:
1 / л 2 T0w2 02 "\ T0wl
?=^2 К
х% \ ^ тм wij т0с1
Отсюда следует, что для аксиальной ступени [у^— =1
Т,
Т,
Owl
степень реакции обращается в нуль при X } = Х Для
радиальной ступени р = 0 при
т^~ V •
*w\ I / л 0w2 I / 1 *2 ( 1 и2
кг2^у т^-у 1_И°Чх-^\
589
Из этой формулы следует, что степень реакции може^
быть равна нулю при движении газа в радиальной ступени
от оси вращения к периферии {uz^>ux) при Xw{ >Яш2. При
движении газа к оси вращения р = 0, если Xwl<^Xw2.
Действительная удельная работа, развиваемая в
ступени при любой степени реакции р, может быть
подсчитана по формуле
= 'ос,
(-
ALj *0cl 10с2
=
Т0с2\ Ak DT
1 —
*—i
/ Poc2\ k ]
\ Рос J J
Отсюда с помощью уравнения (9-36) находим:
ALT = 2i0elu2Qficuu.
Тогда к. п. д. ступени на ободе можно найти по
формуле tiu=—£~. Подставив сюда значения ALT и //0, по-
лучим:
Из формулы видно, что даже в случае, когда потери
энергии в направляющей и рабочей решетках отсутствуют
(Сх =^ С2 = 0), к. п. д. ступени на ободе равен нулю при
Формула (9-37) показывает, что такое условие
выполняется, если
Cu\Ul — Cu2U2-
Очевидно, что в этом случае поток газа в ступени
работы не совершает. Величина 2<уг = 0 и для
неподвижного колеса (г/х = г/2 = 0). Максимальное значение -ци
соответствует (Щ^)макс = си1и1.
Легко видеть, что в рассматриваемом случае
си2и2 = 0, или си2 = 0 (йат^О)-
По треугольникам скоростей можно заключить, что при
этом выходные потери минимальны, так как при си2 = 0
Ся = С2 мин'
590
9-3. УРАВНЕНИЯ ДЛЯ РАСЧЕТА
РАСПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ПОТОКА
ПО РАДИУСУ В РАМКАХ СТРУЙНОЙ ТЕОРИИ'
Рассмотрим поток газа через ступень осевой турбо-
машины (рис. 9-9). Выберем три контрольных сечения:
О—0—перед направляющей решеткой, 1—1 — между
направляющей и
рабочей решетками и 2—2—
за рабочей решеткой.
Найдем
распределение параметров «потока
по радиусу в двух
контрольных сечениях (1—
1 и 2—2), если
известные распределение
параметров в сечении
О—0, давление газа на
корневом или среднем
радиусе сечения 2-2, ЛЛ);;у;/жА\\
геометрические
размеры ступени, число
оборотов ротора турбины Рис- 9"9- Схема проточной части
и аэродинамические ха- стУпени с Длинными лопатками.
рактеристики решеток.
Имея в -виду трудности, связанные с исследованием
пространственного течения сжимаемой жидкости, можно
в первом приближении рассмотреть упрощенную осе-
симметричную схему .потока в ступени турбомашины.
Так, если принять, что течение в ступени является
установившемся и осесимметричным (д/дб —0), а
радиальные составляющие скорости (cr = wr), а также их
производные
dz
дг
dwr
~dz~
dwf
весьма малы, то
уравнения (1-17а) и (9-1) упрощаются и принимают вид (/?=6=z=0):
\_dp_
р dr
C*dz
a dz
:0;
\_d£
р dz '
(9-43)
1 Вопросы, изложенные в этом параграфе, разработаны
совместно с Г. С. Самойловичем.
591
1 dp, dw»
r ' v "; p dr ' a dz
dwa l ^
^ — #
a dz о dz
(9-44)
Первое уравнение (9-43) выражает условие
радиального равновесия частицы газа, при котором
центробежные силы на любой из соосных цилиндрических
поверхностей уравновешиваются силами статического давления
газа. Так, согласно обозначениям на рис. 9-9 для
единицы длины зазора (сечение /—/) можно записать:
2Ttrdpi = 2jtrdr p\C2u\/r и получить из него первое
уравнение (9-43).
Второе уравнение (9-43) выражает условие
неизменяемости си по оси ступени. Из третьего уравнения
нетрудно получить dcjdz = 0 три dp/dz=0, т. е. если
давление по оси не меняется, то осевые составляющие
скорости также сохраняются неизменными.
Принятым допущениям в наибольшей степени
отвечает поток в контрольных сечениях 1—1 и 2—2\
движение в межлопаточных каналах не лодчиняется таким
упрощенным закономерностям.
Введем дополнительно ряд упрощений.
Пренебрегаем периодической •нестационарностью потока,
вызванной вращением рабочего коле-csi, или, точнее, считаем,
что рассмотрение осредненных по времени скоростей
также не вносит существенной ошибки. Предполагаем
также, что после перестройки поток в контрольных
сечениях движется по цилиндрическим поверхностям (т. е.
радиусы кривизны меридионального сечения
поверхности тока R на рис. 9-9 достаточно велики). Считаем, что
внешний и внутренний теплообмен отсутствует, а
решетки ступени обтекаются безотрывно.
Рассмотрим поток за направляющей решеткой.
Воспользуемся упрощенным уравнением радиального
равновесия (9-43), записав его в следующей форме:
для сечения 0—0
hw=-±r-11 (9-43а)
592
для сечения 1—/
I£=if£i. «9.43,,
где /?0, р0, /?х, р19 с0, а0, сх, а1 — давления, плотности,
скорости и углы потока перед
и за направляющей
решеткой.
Предполагаем, что функция ai = ai(r) известна. Вид
этой функции определяется принятым законом закрутки
направляющих лопаток. Очевидно, что поток газа
должен удовлетворять уравнениям энергии и
неразрывности. Для каждой элементарной кольцевой струйки,
протекающей через направляющую решетку, уравнение
энергии можно записать в такой форме:
h=U+4==iu+£rl=i*+fir' (9"45)
где iQ — энтальпия торможения в зазоре;
си, си iir ix — скорости и энтальпии газа в конце изоэн-
тропического и действительного процессов
расширения в направляющей решетке;
т]1 — к. п. д. направляющей решетки
(приближенно определяемый как тзх = ср2).
Продифференцируем уравнение (9-45) по радиусу г:
■5Г=-5Г+1Л <dr у (9-46)
Производная характеризует изменение энтальпии
потока в зазоре за направляющей решеткой по радиусу
и, как известно, может быть записана таким образом:
dhl=JLiEi = h. LdJb (9-47)
dr Ри dr p„ Pl dr ' y '
Здесь pu — плотность газа в конце изоэнтропического
расширения в направляющей решетке; р1 — плотность газа
в конце действительного расширения (при наличии потерь).
38 М. Е. Дейч
593
Отношение плотностей можно выразить формулой
1
^ V '-* + ! W
где Ли — си/а с1 —теоретическая безразмерная скорость
за направляющей решеткой.
Следовательно, производная
dr ^pj dr '
или с учетом (9-436)
Подставляя (9-49) в уравнение энергии (9-46), получаем
дифференциальное уравнение распределения абсолютных
скоростей по радиусу в зазоре:
4-fy т, cos2ai--L^li !_^Л <* —о (9-50)
^\ЪЪ г 2^xdr 2hot dr) ci —u' ^0UJ
2
где /*ol = Cj /2т)х — располагаемый теплоперепад в
направляющей решетке в данном сечении по
радиусу.
Интегрируя уравнение (9-50), находим:
где Кх — постоянная, отвечающая исходному (среднему
или корневому) сечению.
Уравнение (9-51) в рамках рассматриваемой струйной
задачи является наиболее общим.
594
Из (9-48) следует, что при До^ЁукоЁыХ скоростях
и умеренных потерях в направляющей решетке отношение
плотностей ?iJ9\t близко к единице. Расчеты позволяют
установить ту область значений ^ и %, в которой можно
принять ic = 1. Без большой погрешности такое
упрощение допускается при Яи<;1.
При сверхзвуковых скоростях функция ус должна быть
сохранена в уравнении (9-50). Однако в некоторых случаях
можно использовать упрощенные зависимости xc(\t, ?ь),
а при слабом изменении Я,^ и ^t по радиусу хс
принимается для каждого участка постоянной. Имея в виду, что
1с зависит от Хи и т^, следует заключить, что при
точном расчете ступени на сверхзвуковых скоростях метод
последовательных приближений становится неизбежным.
Следует подчеркнуть также, что влияние сжимаемости
косвенно учитывается в уравнении (9-51) функциями
ах и т)!. В зависимости от числа М2 меняются потери
и угол выхода из направляющей решетки. Следовательно,
вид функций iq1 (r) и а1(г) зависит от Мх; согласно (9-51)
при изменении этих функций меняется и характер
распределения абсолютных скоростей сх (г) в зазоре.
Необходимо также отметить, что уравнения (9-50) и
(9-51) справедливы для любого закона закрутки.
Перейдем теперь к расчету потока за рабочей
решеткой. При сделанных выше допущениях условие
радиального равновесия в сечении 2 — 2 выражается первым
уравнением (9-44):
1 dp2_ w\i — 2uwn2 + и2 _ (w2 cos g2 - uf _ 4 cos2 *2
p2 dr r r r '
(9-52)
где р2 и p2 — давление и плотность, а с2 и <х2 — скорость
и угол потока за рабочими лопатками в абсолютном
движении; и — окружная скорость на текущем радиусе г;
Рг = Р2 (г) — Угол выхода в относительном движении,
являющийся заданной функцией радиуса; w2 — относительная
скорость за рабочей решеткой.
Предполагаем далее, что радиальное смещение струек
при переходе из контрольного сечения 1 — 1 в контрольное
38*
595
сечение 2 — 2 будет малым (uL^u2). Тогда уравнение
энергии для относительного потока можно представить
в известной форме:
2 2
где wx — относительная скорость на входе в рабочую
решетку;
ix — энтальпия газа перед рабочей решеткой;
т|2 — к. п. д. рабочей решетки (тд2^ф2);
i2t — энтальпия газа за рабочей решеткой в изоэн-
тропическом процессе.
Теоретическая и действительная скорости за решеткой
связаны соотношением
Очевидно, что i2t = i2t(r) и w2 = w2(r) являются
искомыми функциями, а 7,2 = т)2(г)и w1 = w1(r) могут
рассматриваться как заданные функции радиуса г.
Энтальпия потока за направляющей решеткой
определяется по уравнению энергии:
После подстановки ix в (9-53) находим:
2 2 9
10 — l2t Т 2^2 Т 2
Продифференцировав уравнение энергии, получим
(полагаем dtQ /dr = 0):
Заменим в уравнении (9-54)
с\ — хв?х = 2ис1 cos a2 — а2. (9-55)
596
Используем уравнение радиального равновесия
^ = Л±4Л=у (и>, COS ?,-£*)» ,Q-fi.
dr p2 p2/ dr . ****> } 9 (У-ОЪ)
где
—А
*»— р2/"
Уравнения (9-54), (9-55) и (9-56) решаем совместно.
После некоторых упрощений получаем искомое
дифференциальное уравнение:
dw2 , / xJ^cos2p2 i ^ \ 2
^"rfT + l г WJW2~
- 2Zwvd cos р2ш2 + y)2 1^ = 0. (9-57)
Уравнение (9-57) является нелинейным. Оно
линеаризуется только в частном случае, когда d(cul r)/dr = 0.
Интегрируя (9-57) в этом случае, т. е. с учетом
d(c,i r)
—-—=0, находим:
Г If/ Хи>Ъ C0S2 Р2 1 df]2 0 0 w
^2 = ^2ехр И ^ _._!!_2^^шcosp,)rfr
(9-58)
где /С2 — постоянная, определяемая для исходного
(среднего или корневого) сечения.
Условие d(cuir)/dr = 0 выполняется строго при
закрутке ступени по методу постоянной циркуляции1.
Однако, как. показывает опыт, это условие приближенно
осуществляется и в ряде других практически важных
случаев.
Постоянные К\ и /Сг в уравнениях (9-51) и (9-58)
определены, если известны скорости С\ и w2 в каком-
либо сечении по высоте лопаток. Эта задача решается
применением уравнения неразрывности для сечений 1-1
и 2-2:
1 См. § 9-5.
597
t
г*
G = 2irg-a#clp cl \ qxsm a^dr, (9-59)
ГК
r
J^asinpadr. (9-60)
'к
Входящая в уравнение (9-58) функция %w при
упрощенных решениях может быть принята равной %w = const
для .всей ступени или отдельные кольцевых струек 1.
Следует также отметить, что дифференциальное
уравнение (9-57) для неподвижного рабочего колеса (со=0)
переходит в уравнение (9-50).
9-4. РАСЧЕТ ПОТОКА В СТУПЕНИ
С ДЛИННЫМИ ЛОПАТКАМИ ПОСТОЯННОГО ПРОФИЛЯ
Рассмотрим ступень с осевым потоком газа, полагая,
что поток на входе в направляющую решетку имеет
равномерное ,поле скоростей. Поставим следующую задачу:
установить распределение параметров в зазоре и за
рабочей решеткой по радиусу, есл'И лопатки имеют
постоянный профиль по высоте. Решение этой задачи
позволяет дополнительно получить исходные данные для
расчета ступени с лопатками .постоянного профиля .по
аэродинамическим характеристикам решеток и может
быть использовано для определения той предельной
веерности решеток, при которой можно применять
лопатки постоянного профиля.
Расчет ступеней с лопатками .постоянного профиля
можно выполнить, полагая постоянными углы по
радиусу ai и р2. Более точный прием расчета, излагаемый
ниже, состоит в том, что углы си и р2 задаются в виде
функций радиуса г. Этот способ 'целесообразно
применять в тех случаях, когда веерность ступени
оказывается значительной.
Многочисленные опыты показывают, что угол ccj можно
выразить в зависимости от относительного шага или радиуса формулой
tg«1-tgalK + ^|^(0-l)(7-l), (9-61)
1 Поток газа в ступени за направляющей и рабочей решетками
является закрученным, т. е. имеет неравномерное .поле скоростей как
при абсолютном, так и в относительном движении. Как показано
в § 5-16, в таком потоке поле полной энергии будет неравномерным.
598
где
Д tgor1 = tgalB —tgaiK;
alB, alK — углы выхода потока у вершины и соответственно в
корневом сечении; г = r/rk\ rk — радиус корневого сечения; г — радиус
текущего сечения;
d__
I —" I
Подставив (9-61) в уравнение (9-50) и проинтегрировав последнее,
получим:
- с, F(r)
b\k
(9-62)
Здесь
FjF) =
1+_J-L(e-l)(r-l)+ lV 2; (г-\у
l+/if
i+zif
*- 1+[«,-Мв-1)]« '
1
(9-63)
Для определения скорости с, необходимо знать величину с1к
в корневом сечении. С этой целью преобразуем уравнение
неразрывности (9-59), записав его для сечений 0 — 0 и 1 — 1:
^!-»=
9ica\ridrv
(9-64)
где £fl0, са{ — осевые составляющие скорости в сечениях 0—0
и 1—1\
р, = pj/po — относительная плотность в зазоре.
Функция саХ в уравнении (9-64) может быть определена по
формуле
или приближенно
cal=clsina1
ьа\
с
' ГТ
=°rlk
ltg«I
+ tg2o
— >
<1
sin
clkc1sinal=^r{k-^r-S'm «j, (9-65)
где ctt принимается по формуле (9-61 /f
Приведенные выше зависимости справедливы, если поток в
зазоре дозвуковой. При смешанных течениях в зазоре, когда в нижней
599
части ступени (у корневых сечений) сх^а^\у формула (9-62)
неприменима. В этом случае необходимо учитывать отклонение потока
в косом срезе направляющей решетки.
Перейдем теперь к расчету потока за ступенью. Воспользуемся
основным уравнением (9 57) и проинтегрируем его при т]2 = const и
d(ct(lu) — 6 для принятого закона изменения углов по радиусу
A sin B2 —
sin р, = sin р2Л + 2~^- (0 - l) f~ ')'
В результате интегрирования находим приближенное выражение
2 W2k V '
Здесь w2k — значение w2 в корневом сечении;
!*2£ — Угол вектора w2il\
<1 = {1— К — b2(B— l)]2}; rtj^sin^;
1 1
&2 = — д sin р2= ~y (sin р2в — sin р2Л).
При известных значениях ш2 легко определяется располагаемый
теплоперепад в ступени.
С помощью выведенных уравнений можно рассчитать
распределение параметров по радиусу в зазоре и за ступенью с лопатками
постоянного профиля.
Располагаемый теплоперепад в направляющей решетке согласно
(9-62) будет:
oi==^;=Ci=="7^' (9*67)
Найдем изменение степени реакции по радиусу:
*01
Р = 1-7Г =1-H-fto>=l-ft.1
/-/ — /У 01 01 А/ А/ '
/70 /70 /7qk/70
где рк — степень реакции в корневом сечении.
Использовав (9-67), получим:
\FU)Y
77 Я°
где Я0 = Т7~~ •
Q00
Отсюда можно получить Приближенную формулу для
определения реакции на среднем диаметре ступени с незакрученными
лопатками, исходя из заданной величины рк в исходном — корневом —
сечении. Замечая, что гт = 0/0 — 1 и полагая Ьх ^ 0, из формулы
(9-68) получаем:
1 — Рк /в — 1 \2*
'*=l-lf^(—)- <9-б9>
Формула (9-69) имеет ограниченную область применения.
Очевидно, что она справедлива для относительно больших 0, так как
только в этом случае разность ах у вершины и у корня мала и
МОЖНО ПРИНЯТЬ Ъх ^: 0.
Минимальную степень реакции в среднем сечении можно
определить, полагая, что в корневом сечении р^ ^ 0. Тогда из (9-69)
получим:
1 / 2/1,6! \ /0—1 2х
"о 1Ч 1 + '
А) \—) •
или приближенно {Ьх ^г 0)
С* (-5-) •
Изменение работы на венце по радиусу можно найти по формуле:
__ Lrg _ сиХ + си2
L„= —т— = г
Luk cn\k + cu2k
где са2 = w2k w2 cos [l2 — и.
Функция са1 (г) также известна. Следовательно, величина Lu (r)
определена.
Поле осевых составляющих скоростей за ступенью
рассчитывается по формулам.
Са2 = си2 Ч «2 = Wtt2 Ч h = (с„2 + U) tg ?2
В заключение отметим, что исходная формула для степени
реакции (9-68) позволяет определить разность р у вершины и у корня
лопатки Так как
- 0 + 1
/"в ='
0—1
тб после подстановки в (9-68) получим:
Х— Рв Л 4я
1 +
где рв —степень реакции у вершины.
601
Для прикидочных расчетов можно рекомендовать формулу
1-Рв [в-1\2
Т^^^ь + Т) (9-70)
Используя полученные соотношения, можно
проанализировать изменения параметров ,по радиусу в зазоре
и за ступенью и оценить дополнительные потери,
возникающие в ступени с лопатками .постоянного профиля.
Рис. 9-10. Сравнение опытных и расчетных значений степени реакции
в различных сечениях по радиусу ступени с лопатками постоянного
профиля; 0 = 7,73; М0 = 0,65.
Результаты соответствующих расчетов показывают,
что дополнительные потери в ступени с незакрученными
лопатками обусловливаются увеличением выходных
потерь, изменением угла входа лотока на рабочую
решетку, а также изменением отдаваемой работы по радиусу.
За ступенью поток вихревой; выравнивание поля
скоростей сопровождается .потерями кинетической энергии,
которые должны быть включены в общий баланс потерь
ступени.
Результаты расчетов по предлагаемой методике
удовлетворительно совпадают с экспериментальными
данными.
602
Подробное экспериментальное исследование потока
в зазоре и за ступенью с цилиндрическими лопатками
было выполнено в МЭИ при 6 = d// = 7,73. Был
произведен расчет испытанных ступеней по приближенному
методу, изложенному выше. Соответствующие 'кривые
изменения реакции по радиусу приведены на рис. 9-10.
Сравнение показывает удовлетворительную сходимость
опытных и расчетных значений реакции. Опытные и
расчетные значения углов, давлений и скоростей также
удовлетворительно совпадают.
В заключение отметим, что при больших в
изменение углов ел и р2 «по радиусу невелико.
Расчет . скоростей с\ и w2 в таких ступенях можно
производить по формулам, которые легко получить из
основных уравнений (9-50) и (9-57) лри следующих
допущениях-: г)1 = const; 1)2 = const; cti = const и f}2 = const.
9-5. НЕКОТОРЫЕ СПОСОБЫ ПРОФИЛИРОВАНИЯ
ДЛИННЫХ ЛОПАТОК СТУПЕНЕЙ
С ОСЕВЫМ ПОТОКОМ ГАЗА
Изложенная выше методика расчета ступеней с
лопатками постоянного профиля позволяет оценить
дополнительные потери в ступени, обусловленные изменением
параметров и углов потока по радиусу <в зазоре, а также
возрастанием выходных потерь.
Результаты такого расчета приведены на рис. 9-11.
Здесь даны кривые, устанавливающие дополнительные
потери в .ступени с лопатками постоянного профиля в за-
висимости от Q=d/L Кроме того, на график нанесены
опытные значения дополнительных потерь Дг)и. При
0<1О дополнительные потери превосходят 1%.
Следовательно, в таких ступенях необходимо специальным
образом организовать поток, обеспечивая минимальные
потери энергии. С этой целью лопатки направляющей
и рабочей решеток выполняют закрученными
(винтовыми) с переменным .профилем по высоте.
Закрутка лопаток может быть осуществлена
различными методами. Исходное дифференциальное уравнение
распределения скоростей в зазоре (9-50) имеет
бесчисленное множество решений. В соответствии с этим число
методов закрутки лопаток теоретически может быть
бесконечно большим. Однако только незначительная часть
603
этих методов отвечает условиям рациональной
организации потока в ступени турбины. По этой причине, а
также имея в виду, что уравнение (9-60) является
приближенным, следует развивать те методы профилирования,
которые строятся на четких физических предпосылках.
В практике турбостроения наибольшее
распространение получили следующие методы организации потока
в зазоре: а) постоянной циркуляции скорости при ра.в-
т
j-H
'
^V
^
*
По опытам
д.Г./Тырышкин
а
• A.M. Завадовсиого
А и.и. Кириллова
Ъ^г-
"••
д
10 11 12 13
Рис. 9-11. Уменьшение к. п. д. ступени
от незакрутки лопаток в зависимости от
8 = d/l; сравнение расчетных и опытных
значений Дт)/Г
номерном поле осевых скоростей (си\г=^const); б)
постоянного по радиусу направления абсолютного потока
(ai = const); в) специального выбранного закона
изменения направления абсолютного потока [ai = /(r)],
включая направляющие лопатки постоянного профиля.
Организация потока за рабочими лопатками
осуществляется в предположении: а) равномерного поля
абсолютных скоростей; б) постоянства работы, развиваемой
потоком в различных сечениях по радиусу; в)
постоянства располагаемого теплаперепада по радиусу.
Количество сочетаний любых перечисленных
способов организации потока в зазоре и за ступенью
ограничивается условием неразрывности, связывающим поток
в этих сечевиях.
Рассмотрим в качестве примера изоэнтропиче-
ское течение га за -в ступени ;при
равномерном поле осевых скоростей в зазоре
604
и за ступенью (метод постоянной циркуляции
скорости),
В этом случае коэффициенты г) = %=1, di0 = 0 и
уравнение (9-50) приобретает простой вид:
^ + cosS44lr = 0- (9-50a)
Так как
Cidcl=caldcttX+caldc
а\
и согласно принятому допущению cal = const, то
уравнение (9-50а) преобразуется к виду:
dcu\ , dr
= 0.
btt\ Г
Интегрируя это уравнение, получаем:
си\ f = const.
Последнее условие выражает постоянство циркуляции
скорости вокруг направляющей решетки. Действительно,
в простейшем случае осевого входа в направляющую
решетку (сп0 = 0) циркуляция скорости равна:
v = t(cttl—ctfQ) = tcttl=^cal=coust9
где z — число лопаток в решетке.
Основоположником рассматриваемого метода
является Н. Е Жуковский. Еще в 1912 г. при исследовании
воздушных винтов Н. Е. Жуковский показал, что
осевые скорости постоянны в радиальном направлении,
если изменение окружных составляющих скоростей
соответствует закону постоянства циркуляци-и. Хорошо
известно, что воздушные ви>нты, а затем и вентиляторы,
построенные согласно вихревой теории Н. Е.
Жуковского, отличались высокой экономичностью. Для
расчета длинных лопаток паровых и газовых турбин этот
метод был впервые .применен В. В. Уваровым.
С помощью уравнения (9-50а) нетрудно найти
распределение абсолютных скоростей в зазоре:
где
с, = — с. = = const.
Изменение реакции по радиусу устанавливается с
помощью очевидных соотношений
Р=1_*&=1
Л2 Л2
Я0 2gHQ
ИЛИ
p=l_L_?*[l+(r«-l)sm»au]. (9-71)
В соответствии с условием cal r = const можно найти
изменение углов абсолютной скорости по радиусу в таком
виде:
■°а\
Закрутку лопаток по условию постоянства
циркуляции скорости можно осуществить с учетом потерь в
решетках.
Для адиабатического течения (с учетом потерь)
расчетные зависимости, полученные путем
интегрирования исходных дифференциальных уравнений, даны
в табл. 9-1.
Для течения с потерями, как это видно из формул,
«приведенных в табл. 9-1, условия car = const и
cai='Const являются несовместимыми. При условии
равномерного поля осевых скоростей в зазоре циркуляции
скорости вокруг направляющей лопатки должны
увеличиваться к ее вершине. Если в основу профилирования
ступени .положено условие постоянства циркуляции
скорости, то осевые скорости в зазоре также несколько
увеличиваются к вершине.
Адиабатическое течение в зазоре при ai=const и
T]i = const подчиняется уравнению, получаемому
интегрированием (9-50), в следующем виде:
Ci = —L = r
1 'С in
606
Таблица 94
Величина
Расчетная формула
сх\ спХ
са\=са\1°а\к
COS (Xi
tg?l
V \ — Yilcos2a|K(! - г2); г"1
У К -cos2 alKhl + (1-^7]"-^
cos ajK
7j/l -irjlCos2alK(l -72)
1 —tj! cos2alK (1— r)
*к^
j/l-T]lcos2aiK(i —Т'2)
7j/l -cos2 olK [r]2 + (1 -г],)?-2]
cos a|K — xKr'2
1 — yj, cos2aiK(l —72)
l-d-Рк)
c2
1 — ——(1 — r
#0к
V"i["b-^]-'i^"-)
Следовательно, располагаемый теплоперепад в
направляющей решетке будет:
-— ~о « 2t]j COS2 OCj
Отношение скоростей меняется по радиусу в
соответствии с формулой
U "~l+^i cos2 a,
где Хк = ик1сХк — отношение скоростей для корневого
сечения.
Угол относительного потока
sin a,
igpi=-
COS Ctl— X Г
—■1+1)! COS2 a,
go?
Следует подчеркнуть, что осуществление метода
закрутки при ai = const приводит к направляющим
лопаткам переменного профиля по высоте, та!к как пр.и
малых Э значительно меняются шаг лопаток и
скорость С\ вдоль радиуса. Следовательно, чтобы осуществить
условие си = const, необходимо менять установочный угол
профиля (ху, т. е. выполнять лопатку закрученной. При
больших скоростях необходимо также учитывать
влияние сжимаемости на средний угол за решеткой, что
также приводит к необходимости закручивать
направляющие лопатки.
Для большого числа ступеней представляется
возможным направляющие лопатки выполнять без
закрутки. Расчет направляющих решеток производится по
формулам, приведенным в § 9-4. С помощью этих
соотношений рассчитываются параметры потока в зазоре.
Расчет рабочих лопаток как при cti = const, так и при
ai=/(r) производится, -исходя из принятых условий за
ступенью. Как указывалось, могут быть приняты
условия отсутствия закрутки потока на выходе (си2 = 0),
постоянства работы по радиусу (Lu = const) и др.
Расчет ступени при течении, близком к
цилиндрическому, можно осуществить, разбив поток на ряд
элементарных кольцевых струек. В пределах каждой струйки
можно считать задачу одномерной и применять
обычную методику расчета. Закрутка направляющей
решетки, вообще говоря, может быть выбрана любой:
(Xi = const; cuir = const; a\=f(r). При этом, естественно,
для определения параметров в зазоре можно
воспользоваться одним из частных решений (9-50). Определив
параметры в зазоре, записываем уравнения
неразрывности для каждой струйки в контрольных сечениях 1—1
и 2—2:
AG ,
— ^g^cj,;
AG t
где AG — расход пара через элементарную струйку;
ри и р2, — плотности в конце изоэнтропического
расширения в направляющей и рабочей
решетках;
608
cu, w2t — теоретические скорости выхода потока;
/i и /а — площади выходных сечений в пределах
одной элементарной струйки;
Рч, ц2 — коэффициенты расхода в данном
кольцевом сечении направляющей и рабочей
решеток.
Из уравнения неразрывности и треугольников
скоростей определяем параметры, необходимые для
проектирования рабочей решетки. Полный расход газа через
ступень G равен сумме расходов ло всем элементарным
струйкам. Общий к. п. д. ступени находится по к. п. д.
элементарных струек как усредненный по расходу.
При подобном методе расчета коэффициенты расхода
1*! и [х2 и коэффициенты скорости <р и ф следует
принимать переменными, зависящими от геометрических и
режимных параметров в рассматриваемых сечениях решеток.
Описанный метод расчета весьма прост и дает надежные
результаты.
Построение направляющей и рабочей лопаток
осуществляется по данным расчета закрутки. По вычисленным
значениям М^, (г) и ах (г) подбираются профили в
корневых, средних и верхних сечениях направляющей решетки.
При больших теплоперепадах в ступени в корневых
сечениях Мс1>1, а в периферийных Мс1<1. Соответственно
корневые сечения образуют профили группы В (с обратной
вогнутостью в косом срезе и небольшим расширением
канала), средние сечения — профили группы Б (прямолинейные
участки спинки в косом срезе), а верхние — профили
группы А (выпуклая спинка в косом срезе). Аналогично
строится рабочая лопатка, для которой исходными служат
параметры: $х (г), Mwl(r), Mw2(r) и ff2(r). При построении
желательно выбирать шаги и установочные углы профилей
в диапазоне оптимальных значений.
Рассмотренные выше способы профилирования дают
практически совпадающий характер изменения реакции
по радиусу, что непосредственно вытекает из
приближенного уравнения (9-50).
Некоторые различия обнаруживаются в
распределении углов абсолютного и относительного потоков си и |3ь
а также осевых составляющих скорости.
39 М. Е. Дейч
609
Сравнение трех методов закрутки (cMir=-const,
ai = const и для цилиндрического течения pxcal^const)
приведено на рис. 9-12. Несколько большую закрутку
рабочей решетки дает метод си = const. При этом
направляющие лопатки оказываются наименее
закрученными. Для метода профилирования cuir = const закрутка
рабочих лопаток уменьшается, а направляющих —
возрастает. Промежуточные результаты получены для
цилиндрического течения, отвечающего закономерностям
потока, организованного .по методу cu\r = const при
pb=const.
Опыты показывают, что ступени, спрофилированные
указанными методами, имеют практически одинаковую
эффективность. Дальнейшее повышение к. п. д.
ступеней можно, ло-в'идимому, обеспечить путем выбора
рационального распределения реакции по радиусу. Такому
условию отвечает закон р(г), при котором радиальные
градиенты давления в корневых сечениях будут
минимальными.
9-6. ОСЕВАЯ СТУПЕНЬ
С МАЛЫМ ИЗМЕНЕНИЕМ РЕАКЦИИ ПО РАДИУСУ
Возможность осуществления ступени турбомашины
с уменьшенным изменением реакции по радиусу
представляет большой .практический интерес. В турбинной
ступени выравнивание реакции приводит к 'более
равномерному полю скоростей в зазоре, к уменьшению разно-
2J0
ho
1,в
'»*
1,2
г
1
/'/
'■■■(■
cc^const
WW
1
/
//
//
'J
//л
у
i
/
f
' 1
/
7
у
/
[л
'
/
/
/
■/
Pi°aC
Wf ,,
JoMo
4
/
/
И
/
/
т
25/
0,C
/
CUf
com
"7
f
/
• r=
t
~
/
con
tg
?
st
<*1
tga1f<
2JJ
1,8
№
1,2
r
/)
fy
Y
Л
Y
^
'#*
ош-г
1
=const-^
fio^const^
Ot^L
w
Ы
ionst
^
^p
L—Jk
L ««и
A
r
W
2,0
ЗД 9,0 5,0 frjpu
1,0 1,2 1,4- 1,6 tf 2J0 0.1 0,2 О J 0,6 0,8 p
Рис. 9-12. Сопоставление некоторых методов закрутки лопаток.
610
сти углов входа потока |3i в верхнем и корневом сече-
ния\, к снижению ,потерь от утечек, уменьшению
осевых усилий и т. п. Для компрессорной ступени с
реакцией р =0,5 за счет выравнивания поля скоростей по
высоте может быть отодвинута предельная граница по
числу М, повышены окружные скорости и,
следовательно, увеличен коэффициент напора при сохранении
высокой экономичности ступени.
Рис. 9-13. Схема кольцевой решетки направляющих
профилей с наклонными кромками и меридиональным
профилированием.
Для ступеней турбин с небольшими высотами
лопаток (К 0,8 и 0^13) выравнивание реакции может
быть осуществлено применением меридионального
профилирования каналов направляющей решетки по
высоте.
Условие равенства центробежных сил, действующих
внутри канала на элемент массы от окружной ,и осевой
составляющих скорости, т. е. условие постоянства ста-
39*
611
тического давления по высоте канала, можно
представить в таком виде:
PC
rf
(9-72)
Здесь R — радиус кривизны верхнего обвода в
меридиональной плоскости; гк — радиус корневого сечения
(рис. 9-13).
Из (9-72) находим:
Как указывалось (§ 8-8), (Применение
меридионального профилирования в ступенях с небольшими вы-со-
Рис. 9-14. Зависимость к. п. д. t\oi и реакции от
и/с0 для ступени с меридиональным
профилированием (КД-2-2Ам) и ступени с цилиндрическими
обводами (КД-2-2А); 0=16; /7=0,5.
тами лопаток* позволяет не только уменьшить разность
реакций, но -и значительно уменьшить потери -в
направляющих решетках. На рис. 9-14 представлены резуль-
612
гаты испытаний двух ступеней (Zi~0,5; 0=16) с
'криволинейным и цилиндрическим обводами верхнего
бандажа. Видно, что ступень с мериодинальным
профилированием имеет более высокий к. п. д. (на 1,5—2%),
а разность реакций Ар = рв — рк уменьшается более чем
в 3 раза (с 16 до 5%).
Для ступеней с в<10 меридиональным
профилированием трудно добиться значительного выравнивания
-20 -15 -Ю -5 0 5 Ю 15 20
Рис. 9-15. Изменение разности реакции Др^профильных и суммарных
потерь в решетках в функции угла наклона лопаток у (® = 8,5; /2 =
= 1,0; 04 = 15°).
реакции без существенного увеличения потерь в
направляющей решетке.
Для .предельных значений 2,5<в<5 с целью
снижения градиента статического давления ,по радиусу
целесообразно применять наклон лопаток в радиальной
плоскости. Действительно, из уравнения радиального
равновесия, записанного с учетом сил воздействия
лопаток на поток,
др
дс
дс.
or г г дг а дх ' г
(9-73)
(где Fr—радиальная составляющая силы воздействия
лопаток на поток) видно, что при Fr<0 (наклон
лопаток по потоку, рис. 9-12) градиент давления меньше,
чем при радиальной установке лопаток. Физически это
613
означает, что на элемент газа действует сила, налра-
вление которой противоположно направлению
центробежной силы. Следовательно, в этом случае
уменьшается разность статических давлений, обеспечивающих
равновесие элемента газа К
Таким образом, наклоном направляющих лопаток
в плоскости вращения можно изменить распределение
статического давления в зазоре и распределение
реакции по радиусу.
На рис. 9-15 представлены результаты испытаний
четырех кольцевых решеток с различными углами
наклона y^O; 0; —8; —20°, проведенных в МЭИ. Как
видно из графика, с увеличением угла наклона лопаток
по потоку разность реакций в периферийном и
'корневом сечениях значительно уменьшается; для 0 — 8,
Др~0 может быть достигнуто при y~25°. На этом же
графике нанесены профильные и суммарные потери
в решетках.
В пределах изменений угла наклона у от —8 до +8°
профильные потери практически не меняются и
составляют 2—2,5%. При у—+20° и у — —20° профильные
потере возрастают до 3%. Этот результат объясняется
искажением формы межлопаточных каналов при
большом наклоне лопаток.
Суммарные потери в решетках остаются практически
постоянными в пределах изменения угла у от —8
до +20°. Интенсивный рост потерь наблюдается при
углах наклона —8°>у>+20°. Графики изменения
потерь по высоте решеток (рис. 9-16) показывают, что для
отрицательных углов наклона потери возрастают в
корневых сечениях, где возникает отрыв потока. Для
решеток с наклоном лопаток по потоку, когда
осуществляется поджатие потока в корневых сечениях, .потери
увеличиваются в периферийных сечениях.
Опыты показали, что одновременным введением
меридионального профилирования верхнего обвода
решетки и наклоном лопаток можно уменьшить потери
в верхних сечениях (y>0)- При этом оба фактора —
наклон лопаток по потоку и профилирование верхнего
1 Исследование ступеней с наклонными лопатками проведены
Ю. И. Митюшкиным (ЛМЗ) и Г. А. Филипповым (МЭИ),
614
обвода—позволяют более резко снизить разность
реакций Ар = рв — рк.
Приближенная формула для определения реакции
в ступени с различными углами наклона лопаток у
может быть получена путем совместного решения уравне-
^корневое сечение \ L
О Ю 20 30 40 мм
Рис. 9-16. Характер изменения потерь по
высоте решетки при различных углах наклона
лопаток (0 = 8,5; 7^ = 1,0; а, = 15°).
ний количества движения и радиального равновесия
цилиндрического потока (9-73). Сила воздействия
лопаток на поток определяется через окружную
составляющую по уравнению (сг~0):
F = ?п — °а dc"
г tg (90—Y) tg (90—Y) dx '
где Ри — окружная составляющая силы воздействия
лопаток на поток.
615
Приняв линейный закон изменений са Но Ширине
решетки для средней линии канала cn=^xcaJB, получим:
сх cosotj
г * г jbtg (90 —у)
Подставляя Fr в уравнение (9-73), находим:
Р
С, COS^ a.
dr
с\ sin 04 cos a,
tftg(90-YT
■dr.
Из последнего уравнения совместно с уравнением
энергии получим:
dc1
sin a,cos a1
tf tg(90-Y)
rfr
2 ^r
COS2^ ,
1 r
Проинтегрировав это уравнение для случая ax = const
получим распределение скоростей по высоте лопаток:
г ai Г sino^ cos a, (rt — rR)
eXP| /3tg(90-Y)
(9-74)
Реакция в произвольном сечении зазора рассчитывается
по формуле
'-«'-^■T-lt
Разность реакций при
профиля)
2 cos2 a.
ехр
2sin al cos а2 (г2 — гк)
^tg(90 —Y)
(9-75)
р. =0 и 6 яг 1,55 (6 —хорда
Др=1 —
Ve+i У р 2tg(90-Y) Л
2 A cos2,"a, •/!,
-^-. (9-76)
Полученные формулы дают несколько завышенные
значения разности реакций, что связано в основном
с отклонением потока в зазоре ступени от
коаксиального, наличием радиальных перетеканий газа в
пограничном слое лопаток, утечками в ступени, влиянием
рабочего колеса. Погрешность расчета объясняется также
принятым приближенным законом изменения си по оси
канала и пр.
G16
Влияние перечисленных факторов учитывается по
опытным данным введением коэффициента А = 0,65
в формулу (9-76).
Расчет реакции в ступени с наклоном лопаток по
потоку и меридиональным профилированием верхнего
обвода осуществляется по формуле
п 1 п n\ril« f, , /iSin4\71V,3cos,e,v
p = l_(l_pK)_^l + __J (y) X
[1,3 sin a, cos at (r, — rj) 1
—*tg(9o-; J. (g-77)
полученной с учетом влияния кривизны верхнего
обвода на распределение скоростей по радиусу в зазоре.
Опыт подтверждает удовлетворительную точность
формулы (9-77) при 6 > 6.
Для ступеней с малыми 6 < 5 и сверхкритическими
теплоперепадами применение наклона лопаток также
целесообразно. Действительно, при большой веерности
проточной части (рис. 9-17) поджатие потока лопатками
позволяет улучшить обтекание корневых сечений; обтекание
верхних сечений практически не изменится, так как угол
наклона ув у периферии значительно меньше, чем у корня.
(Так, например, для ступени с 6 = 2,6 и ^т = 9° наклон
у вершины ув = 5°40', а у корня ук= 14°.) Уменьшение
реакции в верхних сечениях и соответственно уменьшение
угла входа потока на рабочие лопатки рх приведет
к уменьшению закрутки рабочей лопатки.
Перераспределение теплоперепада между
направляющей и рабочей решетками и уменьшение угла (^ в
периферийных сечениях, обусловленное наклоном лопаток по
потоку, облегчают профилирование верхних сечений
рабочей решетки при Сверхзвуковых скоростях.
Влияние наклона направляющих лопаток в ступени
0 = 2,6 и е2 = 0,27 на распределение параметров по
радиусу показано на рис. 9-17. При наклоне в среднем
сечении Ym = + 3° реакция в верхнем сечении снизилась
с 75 до 56°/0, угол входа потока рх уменьшился со 155°
до 127°. Число МсХ возросло у вершины лопатки до 0,9,
а число Nlw2 уменьшилось до Мвд2=1,08.
617
Последние ступени турбин часто приходится
выполнять с коническими обводами (рис. 9-12). Наличие
конусности приводит к уменьшению реакции в ступени.
О 10 20 30 40 50 60 70 f % 80
Рис. 9-17. Изменение параметров по высоте лопатки
(0 = 2,6; е2 = 0,27).
с наклоном кромок; кромки радиальные.
Для конусной направляющей решетки изменение
реакции по радиусу можно приближенно определить по
формуле
/ 1 \2cos2a, yj
где /Ci=l+sin2a^g2SB — коэффициент, учитывающий
влияние конусности; 8в — угол конусности у вершины.
613
ГЛАВА ДЕСЯТАЯ
МЕТОДЫ
ЭКСПЕРИМЕНТАЛЬНОГО ИССЛЕДОВАНИЯ
ГАЗОВЫХ ПОТОКОВ
И ПРОТОЧНОЙ ЧАСТИ ТУРБОМАШИН
10-1. ЭКСПЕРИМЕНТАЛЬНЫЕ СТЕНДЫ
ДЛЯ ИССЛЕДОВАНИЯ ПРОТОЧНЫХ ЧАСТЕЙ ТУРБОМАШИН
Задачи опытного исследования проточной части турбомашин
можно разбить на три группы. В первую группу включаются
вопросы, связанные с исследованием структуры потока в отдельных,
рассматриваемых изолированно элементах ступени и в первую
очередь ,в направляющей и рабочей решетках.
Вторая группа задач заключается в дифференцированном
изучении физических явлений, происходящих в ступени.
Третья группа задач сводится к определению опытных
коэффициентов, необходимых для теплового расчета турбомашины, и к
выяснению зависимости этих коэффициентов от основных
конструктивных, геометрических и режимных параметров ступени.
Основные требования к эксперименту в лабораторных условиях
формулируются теорией -подобия. Практически не все эти
требования могут быть реализованы с одинаковой степенью точности, так
как действительные процессы в турбомашине отличаются большой
сложностью. Поэтому при постановке эксперимента в каждом
отдельном случае следует установить наиболее существенные
особенности процесса, пренебрегая его второстепенными признаками.
Правильное решение этого вопроса определяет направление и методику
экспр'имента, а также теоретическую и практическую ценность
результатов исследования. Если основной целью эксперимента является
получение интегральных характеристик ступени, то очевидно, что
в модельных условиях должны быть воспроизведены все наиболее
существенные признаки процесса. Поэтому опытное исследование
характеристик ступени необходимо проводить на специальных
экспериментальной турбине или
экспериментальном компрессоре, позволяющих установить надежные
значения характеристик и изучить основные особенности потока в
решетках.
Последняя задача, однако, решается в экспериментальной
машине нелегко, так как требует применения сложной специальней
измерительной аппаратуры. Поэтому при детальном изучении
обтекания решеток, при изучении механизма образования и развития
потерь в изолированно рассматриваемых решетках необходимо
прибегать и к другим, более простым методам эксперимента,
поступаясь некоторыми требованиями теории подобия. Отсюда следует,
что наряду с использованием экспериментальной турбомашины
в качестве основного метода исследования необходимо применять
и более простые и поэтому широко распространенные методы
испытания неподвижных решеток.
Исследования элементов проточной части паровых и газовых
турбин могут производиться на водяном паре или на воздухе, при-
619
чем схема испытательного стенда существенно зависит от
применяемого рабочего тела. Исследования элементов компрессора
производятся, естественно, на воздухе.
Рис. 10-1. Принципиальная схема воздушного
экспериментального стенда.
1 — двигатель; 2 — компрессор; 3— ресивер; 4 — фильтр; 5 —
подогреватель; 6 и 7 — статические установки; 8, 9 —
экспериментальная турбина, Ю — установка для взвешивания реактивных
усилий; 11 — аэродинамическая труба; 12 — оптическая
установка; 13 — холодильник, 14 — дополнительный компрессор;
/5-—фильтр; /£ —глушитель; 17 — стенд испытания клапанов,
эжекторов и т п , 18 — эжекюр, 19 — баллоны; 20 и 21 — фильтр
и влагоотделитель.
Принципиальная схема воздушного экспериментального стенда
для исследования проточных частей турбин и компрессоров
представлена на рис. 10-1.
620
Воздух сжимается компрессором 2 и, проходя через ресивер 3,
очищается в фильтре 4. В случае необходимости температура
воздуха может быть поднята в воздухоподогревателе 5. Это особенно
важно при достижении в исследуемой решетке больших скоростей,
когда температура воздуха резко падает, что вызывает
конденсацию водяных паров, всегда находящихся в воздухе.
Очищенным .и подогретым воздухом питаются:
экспериментальные установки для исследования плоских неподвижных решето-к 6
'и для исследования кольцевых неподвижных решеток 7, воздушная
экспериментальная турбина #, установка, работающая на принципе
взвешивания реактивных усилий 10, аэродинамическая труба //
с оптическими приборами 12 и блок 17 для испытаний эжекторов,
патрубков, ислапанов и т. п.
Кольцевая аэродинамическая труба 7 спроектирована так, что,
помимо пневмометрических измерений, позволяет измерять
крутящий момент и осевое усилие на исследуемой решетке. Аналогично
спроектирована и воздушная экспериментальная турбина 8 с
гидравлическим или индукционным тормозом 9.
Аэродинамическая труба является необходимым элементом
стенда и предназначается для тарирово-чных испытаний различных
измерительных приборов и необходимых методических работ. На
плоской установке 6 или аэродинамической трубе 11 проводятся
эксперименты с применением оптической аппаратуры 12. Стенд может
работать как по открытой, так и по замкнутой схеме. Замкнутая
схема, являясь более сложной, дает, однако, возможность
независимого изменения чисел М и Re, т. е. позволяет раздельно
исследовать4 влияния сжимаемости и вязкости. Для постановки ряда
экспериментов это требование является основным.
При использовании открытой схемы воздух выбрасывается
в атмосферу через глушитель 16. При работе по замкнутой схеме
воздух через охладитель 13 подается во всасывающую линию
компрессора.
Для создания в замкнутом контуре стенда повышенного
давления и возмещения утечек через неплотности и уплотнения
необходим дополнительный компрессор 14 с давлением, превышающим
максимальное давление во всасывающем патрубке основного
компрессора. Если компрессор 14 имеет достаточные степень сжатия и
производительность, то для ряда режимов вместо основного
компрессора 2 могут быть использованы компрессор 14 и эжектор 18,
питающие экспериментальные установки воздухом пониженного
давления.
В случае необходимости проведения эксперимента, требующего
больших секундных расходов и высоких скоростей, может быть
применена баллонная схема, состоящая из компрессора 14 и группы
баллонов 19. В течение определенного времени баллоны 19
наполняются компрессором 14 через фильтр 20 и влагоотделитель 21.
Затем воздух из .баллонов через регулирующие вентили
направляется в экспериментальную установку. Так как при работе
давление в баллонах будет падать, то для поддержания постоянного
режима экспериментальной установки необходимо использование
автоматически управляемых вентилей. Кратковременность действия—
основной недостаток баллонной схемы.
Методика эксперимента на воздухе при температурах порядка
621
50—100° С значительно проще, чем -на паре при температурах
250—350° С. Это определило широкое применение воздуха в
лабораторных .исследованиях проточных частей турбомашин.
Однако ряд задач, связанных с длительной работой
экспериментальных установок с большими секундными расходами и при
больших скоростях, требует чрезвычайно мощных и громоздких
компрессорных установок. Работы, связанные с исследованием
последних ступеней конденсационных паровых турбин, мопут проводиться
на воздухе только частично, а ряд вопросов вообще не может быть
решен на воздушном стенде.
Оптимальным решением, дающим наибольшую возможность
ведения различных исследований проточных частей турбин с
минимальной затратой времени и средств, является использование
комбинированного паровоздушного стенда, принципиальная схема
которого приведена на рис. 10-2.
Большинство установок такого стенда может работать как на
паре, так и на воздухе, что позволяет выбирать оптимальный для
данного эксперимента вид рабочего тела. Воздушный контур стенда
не отличается от приведенного на рис. 10-1. Использование шара
позволяет легко получать большие секундные расходы, большие
скорости, независимо менять числа М и Re, обеспечивает
проведение всех исследований, связанных с влажностью. Пар через редук-
ционно-охладительную установку 29 подается к экспериментальным
установкам стенда, проходит через них и направляется в основной
конденсатор 21. Конденсат конденсатным насосом 24 подается
в мерный бак 25, а затем в линию возврата конденсата ТЭЦ.
Паровоздушный стенд состоит из установки для исследования
кольцевых неподвижных решеток 7, высокооборотной
одноступенчатой экспериментальной осевой турбины 8, двухвальной
экспериментальной турбины 14, предназначенной в основном для
исследования последних ступеней, экспериментальной турбины для
исследования радиально-осевых ступеней 20, осевого 26 и центробежного 27
экспериментальных компрессоров с паротурбинным приводом 28
и установки для испытания плоских решеток 6.
При необходимости в паровоздушном стенде могут быть
использованы эжекторные аэродинамические трубы 18 и 19, воздушный
поток в которых создается паровым эжектором, засасывающим
воздух из атмосферы.
В схему стенда включен блок 17, позволяющий устанавливать
для периодических испытаний различные вспомогательные детали
турбин.
Для отсоса пара из уплотнений экспериментальных турбин
используется вспомогательный конденсатор 23. Вакуум в
конденсаторам поддерживается паровыми эжекторами 22.
Выхлопные патрубки турбин желательно снабжать
дроссельными устройствами, позволяющими поднимать противодавление за
рабочим колесом до 3—5 ата. Для подавляющего большинства
экспериментов достаточно давление свежего пара 5—7 ата при
температуре 250—350° С.
Редукционно-охладительная установка должна допускать
питание стендов не только перегретым паром пониженных параметров,
но и влажным паром.
622
ы
V If
<3
mnunurji ini ij
16
-оэ
28
v\26
17
Рис. 10-2. Принципиальная схема паровоздушного стенда МЭИ.
/ и 2 —двигатель и компрессор; 3 — ресивер; 4 —фильтр; о —подогреватель; 6, 7, Ю, 11, 18 и 19 — аэродинамические трубы; 9 —
нагрузочные устройства; 8, 14 и 20—экспериментальные турбины; 21 и 23 — конденсаторы; 22 — эжекторы; 24 — насос; 25 — мерный бак; 26
и 27 — экспериментальные компрессоры; 28 — приводные турбины; 29 — РОУ.
10-2. МЕТОДЫ ИЗМЕРЕНИЯ ПАРАМЕТРОВ РАБОЧЕГО ТЕЛА
ПРИ ИССЛЕДОВАНИИ ГАЗОВЫХ ПОТОКОВ
Осно1вны1ми параметрами рабочего тела, непосредственно
измеряемыми ,в процессе эксперимента, являются: давление и
температура .полного торможения, статическое давление, а также
направление и величина вектора скорости. При исследовании
.нестационарных явлений измеряются частота, амплитуда и форма изменения
тех же .параметров во .времени.
Для измерения давлений в газовых потоках применяются
различные насадки.
Размеры исследуемых решеток обычно невелики, особенно при
испытаниях на больших скоростях. Следовательно, размеры
насадка должны быть минимальными, чтобы не .происходило ощутимого
искажения исследуемого поля. Значительная неравномерность
потока за решеткой также заставляет предельно уменьшать размеры
приемника и менять его конструкцию в отличие от широко
известных насадков, применяемых для измерения в относительно
равномерных потоках.
Рассмотрим некоторые конструкции насадков.
Давление полного торможения измеряется насадками,
схематически изображенными на рис. 10-3. Совершенство насадка
характеризуется безразмерными коэффициентами:
_ Ро ~~ Р* . _ Р^1
Р*~ 1 ; "Ч ~ р0 '
где К —коэффициент, характеризующий чувствительность
насадка к изменению угла атаки; v p^—коэффициент, характеризующий
качество приемника; ро— действительное давление полного
торможения при угле атаки 6 = 0; /^ — измеряемое давление торможения
при данном § ф 0; рои — измеряемое давление торможения при
6 = 0.
Экспериментально установлено, что при 6 = 0 коэффициент v
примерно одинаков для всех приведенных на рис. 10-3 форм носика
насадка и близок к единице. Величина Кр существенно зависит
от формы носика, что иллюстрируется характеристиками на
рис. 10-3.
Для измерения давления торможения вблизи стенок, где имеются
значительные градиенты р0, применяются микронасадки. Для
измерений в ограниченных областях, например в зазорах между
направляющими и рабочим аппаратами, применяются насадки типов д
и е. Насадок д более пригоден при малых скоростях и отличается
от насадка е только меньшей жесткостью.
Для измерения статического давления применяются насадки,
схемы и характеристики которых приведены на рис. 10-4.
Измерение статического давления представляет трудности из-за
необходимости более строгой ориентировки оси насадка по направлению
вектора скорости потока.
Чувствительность насадка к изменению угла атаки потока и ка-
624
чество приемника статического давления характеризуются
следующими безразмерными коэффициентами:
РЬ-Р Р-Рч
урс2
где рь — давление, показываемое прибором при данном угле атаки;
р — статическое давление невозмущенного потока;
ри—измеряемое давление при 5 = 0.
Рис. 10-3. Насадки для измерения давления торможения.
а — з — формы приемников и результаты тарировки.
Для измерения статического давления в потоках дозвуковой
скорости удовлетворительные результаты дает насадок типа б
Насадок состоит из трубки со сферическим носиком, диаметром d =
— 0,9-1-1,2 мм с двумя приемными отверстиями диаметром d1 =
= 0,2 ~ 0,3 мм. Измерения в зазорах и других труднодоступных
40 М. Е. Дейч
625
C^Zb
\tZ2^_
(6H0/d
I! (M=1,3J
j= [0,12+0,10)
*10)d
<*=**
jpw
a) (3*5) d
6)
1Г~|
Ml
;£ 0,025-
д (M=0,3f"
0,050 \
a w»w
$(M*0,3)
J.oh
0,8\
4
0,2
0.4
0.6
0,8
•)
0,050л
ESS
S£S
e)
0,025
12 8 4
4 8 12 8°
Рис. 10-4. Насадки для измерения статического давления в потоке
а — е — формы приемников и результаты тарировки.
626
местах иногда требуют применения насадков типов в, г и д,
отличающихся большей жесткостью, меньшими линейными размерами, но
и худшими характеристиками.
Для измерений статического давления при сверхзвуковых
скоростях применяется насадок а, имеющий благоприятную
характеристику. Независимо от конструкции насадка приемные отверстия его
удобно располагать на оси вращения.
При обтекании насадка полного торможения сверхзвуковым
потоком перед носиком образуется криволинейный скачок. Предполагая,
что нейтральная линил тока пересекает элемент прямого скачка,
fit
Pf
Х
4W А^^^^^^^и
Рис 10-5 Криволинейный скачок перед
носиком насадка полного давления.
можно использовать уже известные уравнения для определения
давления полного торможения, еслл известны безразмерная скорость
набегающего потока Мх и статическое давление рх (рис. 10-5).
В условиях эксперимента обы-шо удается измерить р1 и
давление торможения за скачком р02- С помощью уравнений прямого
скачка нетрудно найти связь между р021р2 и р2\рх и окончательно
Pi__ Рг Pi
получить зависимость для — — ,
Ро2 Ро2 Pi
М, (или Xj):
позволяющую определить
1±,
Р02
/
k— 1 1
"*+1 X?
k
'±±±_±
~~ k+ 1
=2-
[4/feMf — 2(k—\)]
k—\
2k
{k-l
Вместо непосредственных расчетов по этой формуле удобно
пользоваться таблицами функций прямого скачка или диаграммой
скачко-в.
Для измерения .направления вектора скорости в газовом потоке
применяются разнообразные конструкции угломерных насадков:
сферические, цилиндрические, трубчатые и клинозые. Наиболее
удобными являются трубчатый и клиновой угломерные насадки
(рис. 10-6). Сферические и цилиндрические насадки не могут быть
40*
627
рекомендованы .из-за .сложности изготовления, тарировки и значи*
тельных погрешностей при измерениях в неравномерном потоке.
С помощью трубчатого или клинового .насадка направление
скорости олределяется л о .разности давлений, измеряемых на
поверхности клина на одинаковом расстоянии от кромки.
В потоках больших дозвуковых и сверхзвуковых скоростей
насадки типов а я б имеют примерно одинаковую характеристику.
Рис. 10-6. Насадки для измерения направления вектора скорости
в точке; г — результат тарировки.
Насадок типа а имеет большие линейные размеры, менее
виброустойчив, но более точен и в меньшей степени нарушает поток
вблизи точки измерения. Насадок типа б более жесткий и компактный,
но не допускает измерений вблизи ограничивающих поток стенок.
Если клин ABC (рис. 10-6,в) расположен под углом атаки 6
к линии тока, то головная волна, возникающая в точке В, при
М\>\ будет несимметрична относительно оси клина BE.
Следовательно, давление в точке К будет более высоким, чем в точке К\-
При 6>6л вместо юкачка BG может .возникнуть вол:на разрежения.
Разность давлений рк—Рк\ при этом еще больше увеличивается.
Так как первоначальная ориентировка оси насадка известна, то,
поворачивая насадок до наступления равенства давлений рк и рК1 по
лимбу, устанавливают направление скорости потока. Желательно,
чтобы угол заострения насадка был меньше предельного угла, при
котором образуется криволинейный скачок, существенно снижающий
чувствительность насадка.
628
Измерение статической температуры Движущегося газа вызывает
значительные трудности. Сравнительно просто может быть измерена
температура торможения, методы измерения ее рассматриваются
ниже.
Существует большое количество конструкций термонасадков для
измерения температуры торможения, основанных на одном и том же
принципе: струя исследуемого газа тем или иным способом
затормаживается, и термочувствительный элемент помещается в зону
заторможенного потока.
Температура торможения То связана со скоростью потока и
статической температурой Т известным соотношением:
/ k — 1 \ Ас*
Термоприемник, введенный в область заторможенного потока,
из-за теплообмена с. внешней средой и неполного торможения будет
иметь некоторую температуру 7\, ограниченную пределами Т < 7\ <С
Ас2
<С Г0 и определяемую уравнением Тх ■= Т + г ^— ' где г <
1—коэффициент восстановления термоприемника. хИзмерив температуру Tt
и зная из тарировочных испытаний величину г, нетрудно подсчитать
истинную температуру торможения Г0 по формуле
Ас2
Основные требования, предъявляемые к термонасадку, сводятся
к следующему: 1) величина г должна быть 'возможно 'ближе -к
единице, так как при г=\ Т\ = Т0\ 2) величина г должна оставаться
неизменной в возможно более широком диапазоне чисел М и Re;
3) габаритные размеры термонасадков должны быть минимальными.
Как правило, чувствительным элементом термонасадка служит
термопара. В последнее время получают распространение
полупроводниковые термоэлементы (термисторы), обладающие более
высокой чувствительностью.
На рис. 10-7 и 10-8 приведены некоторые схемы и характеристики
термонасадков, наиболее подходящих к условиям
экспериментального исследования проточных частей турбомашин. Для исследования
температурных полей за ступенью можно рекомендовать тер.мона-
садки типа г, обладающие весьма стабильными характеристиками.
Такие насадки нечувствительны к углу скоса потока в пределах
±(10-=-12)°. Для измерений в зазорах ступеней турбомашмн
.наиболее подходящим является термонасадок типа б.
Несколько улучшенная модификация поперечно обтекаемого
малоинерционного насадка, допускающего измерения при
повышенных давлениях с полной герметизацией, приведена на рис. 10-7,в.
Один электрод этого насадка выполнен в виде тонкостенной, надри-
мер медной, трубки размером 1,1X0,8 мм, внутри которой ib
фарфоровой соломке вставлен второй электрод.
'.После установки внутреннего электрода торец трубки
зашлифовывается и покрывается тонким слоем электролитической меди.
«Спай» такой термопары при диаметре внутреннего электрода по-
629
%2 p Щ Й5 Ofi ^
1,0
u,y
0,8
L
r
12
0,3
0.1 0.5
1
0,6
0.7
И 6) |
лЗ
л"\
£f
, м
0,8 0,9 1,0
и 6)
t,0\
0,9\
C,8
1 r
i 1
_ 1 ..
,
и г)
=±Ls2
\j
, "
Na
В
г'
d
d,
I
I,
\h
\d„
1
6
4,5
V
0,75
22
15,7
8
0,7
2
10
8
5
7,5
31,7
25
10JS
1.2
3
15
12
7,5
2/5
47,3
37,5
15,7
1,2
HZ)
№
tD
h
d
di
d„
1
6
9
8
3
0,7
2
8
13
12
4,5
0,7
3
10
n
16
6
1>2
OJ 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
Рис. 10-7. Термонасадки для измерения температуры торможения и результаты их
тарировки.
0,99^0,002
Рис. 10-8. Продольно обтекаемые термонасадки и результаты их тарировки.
рядка 0,05 мм облапает .ничтожной инерцией, а сам термоприемник
весьма легко уплотняется. На рис. 10-8 приведены конструкции и
характеристики насадков, применяющихся при больших
сверхзвуковых скоростях и значительных температурах. Хорошие
результаты показал насадок типа а.
Корпус экрана и чувствительного элемента этого насадка
выполнен из кварца, покрытого слоем платины, что значительно
уменьшает конвективный и лучистый теплообмен при высоких
значениях Т0.
Для измерения температуры торможения в погра.ничном слое
и в потоках с малым живым сечением может с успехом
применяться термонасадок в, однако изготовление насадка столь малых
размеров представляет определенные трудности.
При исследованиях в области повышенных температур, где
приходится считаться с лучистым теплообменом, может быть
использован термонасадок г, нечувствительный к скосу потока в пределах
±12* и экранированный двойным экраном.
При сравнительно больших размерах исследуемого поля удобно
применять комбинированные насадки, дающие одновременно
значения дв.ух и более параметров. Некоторые конструкции таких
насадков приведены на рис. 10-9. Насадок а применяется для
одновременного измерения давления полного торможения и направления
плоского дозвукового потока.
Насадок б широко применяется в МЭИ при одновременном
измерении давления полного торможения и направления плоского
дозвукового и сверхзвукового потоков и является наиболее
совершенным из насадков подобного типа.
Гребенчатый насадок удобен при 'измерении давлений полного
торможения в потоках с малым изменением углов по сечению.
Дисковый насадок может применяться для одновременного
измерения статического давления и направления плоского
потока. Насадки а и б на рис. 10-10 применяются для одновременного
измерения давления полного торможения и статического давления.
Насадок в, состоящий из трубок полного торможения и трубки
Вентури, нечувствителен к углам сксса потока вплоть до 40—45°,
что делает его весьма удобным в ряде экспериментов, где поворот
насадка для ориентации его оси затруднителен.
На рис. 10-10,г представлен комбинированный насадок для
измерения давления и температуры полного торможения,
предложенный И. Цубером.
Процессы, протекающие в ступенях турбомашин, являются
периодически нестационарными. Поэтому значительный интерес
представляют методы измерений параметров неустановившихся газовых
потоков 1.
Так как при исследовании нестационарных процессов приходится
иметь дело с частотами, достигающими тысяч герц,
непосредственное измерение параметров обычными приборами становится
невозможным.
1 Ниже рассмотрены только некоторые из числа разработанных
способов измерений в неустановившихся потоках. Электрические
схемы измерительных устройств, описанные в прилагаемой
специальной литературе, выходят за рамки книги и не рассматриваются.
632
Рис. 10-9. Комбинированные насадки для измерения
давления торможения, статического давления и
направления вектора скорости.
11
c§
з)
+ -
-50 -40-30-20-10
д)
-0,02Ь '
0 ^*
-0,025 ff
10 20 30 40 50
Рис. 10-10. Комбинированные насадки для измерения давления торможения и статического
давления.
В этом' случае пользуются специальными малоинерционнымй
«асадками, однозначно преобразующими из.ме|ряемый параметр в ток
или э. д. 1С. 'некоторой величины. По изменению -во времени тока или
э. д. с. судят об изменении .измеряемого параметра.
В основу проектирования малоинарционного насадка с
электрическим преобразователем могут быть положены разные физические
принципы (изменение сопротивления, емкости и т. п. в функции,
например, давления^.
Желательно, чтобы -выбранный принцип обеспечивал измерение
возможно большего числа параметров нестационарного потока.
Для возможно более точной регистрации формы .исследуемого
процесса собственная частота преобразователя должна по меньшей
маре на порядок превосходить максимальную частоту изменения
исследуемого параметра. Усилительная аппаратура, обычно
применяемая совместно с датчиками, должна иметь линейную частотную
характеристику.
Осуществление усилительной и регистрирующей частей
измерительной установки с подобными требованиями не представляет
особенных трудностей, но высокая собственная частота
воспринимающей системы преобразователя достигается нелегко.
Насадок должен обладать возможно большей
чувствительностью, линейностью характеристик в области измерения,
стабильностью во времени, допускать температурную компенсацию -и .иметь
минимальные габариты. В целом измерительная система должна
допускать одновременные измерение и фиксацию различных
параметров в нескольких точках для выявления временной связи между
ними, быть по возможности простой в эксплуатации и
нечувствительной к механическим, тепловым и электрическим внешним
воздействиям.
Основная трудность в создание подобной аппаратуры
заключается в удовлетворении всех или во всяком случае большинства
этих требований. Для измерения в ядре потока быстропеременных
давлений (полного торможения, статических давлений и углов в МЭИ
разработана серия малоинерционных насадков с танзометрическими
преобразователями; один из них изюбр а жен на рис. 10-11.
Собственно насадком такого прибора а является короткая
трубка полного торможения. Преобразователь давления в э. д. с.
расположен в малогабаритной коробке / обтекаемой формы,
укрепленной на линзовой державке. Пульсирующее измеряемое давление
подводится под мембрану 2, на обратной стороне которой намотан
спиральный тензометрический датчик сопротивления 3.
Диаметр слюдяной мембраны — около 5 мм, толщина 0,012—
0,050 мм. Спиральный тензометрический датчик диаметром 3 мм
намотан из константановой '.проволоки 0 0,03 мм и имеет
сопротивление —-100 ом. Тензодатчик включен в мостовую входную
схему измерительного устройства, состоящего из стабилизированного
блока питания, электронного многоканального усилителя и
осциллографа.
Описываемые насадки с тензопреобразователями имеют вполме
удовлетворительные характеристики. Это иллюстрируется
приведенной на рис. 10-11,6 осциллограммой, полученной на специальной та-
риршочиой установке, дающей трапецеидальные импульсы давления
разных величины и частоты.
635
Ка.к указывалось выше, одной из важнейших характеристик
насадка с преобразователем является собственная частота
колебаний упругой системы.
Повышения собственной частоты преобразователя и
увеличения его относительной чувствительности можно достигнуть,
заменив тензометрический
принцип измерения
деформации мембраны
емкостным, не требующим
расположения на мембране какой-
либо дополнительной массы.
В МЭИ разработаны
образцы малоинерционных
насадков с емкостными
преобразователями
Принципиальная схема
преобразователя ясна из рис 10-12.
Подвижным электродом
преобразователя служит
слюдяная мембрана /,
покрытая тонким слоем
алюминия. Неподвижный
электрод 2 тщательно изолирован
от корпуса. Рабочий диаметр
мембраны 5 мм.
Усилительную электронную схему
удобно располагать
непосредственно на державке
насадка, так как это
избавляет ют погрешностей,
возникающих из-за переменной
емкости ■ соединительных
проводов.
ДЛЛЛЛЛЛЛ/
6)
Рис. 10-11. Тензометрический
насадок длят" измерения давления
торможения и результаты_ тарировки.
Рис. 10-12. Насадок с емкостным
преобразователем.
Для измерения переменных давлений на поверхностях
обтекаемых тел весьма широко применяются индуктивные преобразователи.
Несмотря на относительную сложность их конструкции, они
удобны тем, что при соблюдении определенных условий могут ра-
636
богать .непосредственно на шлейф осциллографа без электронных
усилителей.
Индуктивные преобразователи позволяют измерять как
постоянную, так и переменную составляющие давления и особенно
удобны в случае необходимости многоточечных дистанционных
измерений.
, У
гп
£
pi
ъ
а)
Рис 10-13. Насадок электротермоанемометра (я),
его принципиальная электросхема (б) и
осциллограмма пульсаций скорости (в).
637
В настоящее время наиболее разработанным методом
исследования нестационарных газовых течений является термоапемомет-
рия. Современная термоанемометрическая установка, позволяющая
определять пульсацию скорости, величину и направление
скорости и температуру исследуемого потока, является довольно
сложным комплексом, состоящим из нескольких насадков,
измерительного моста, специального электронного усилителя и осциллографов.
Насадок термоа1немометра (рис. 10-13,а1) состоит из тонкой
(0 0,01^-0,02 мм) платиновой или вольфрамовой проволоки /,
приваренной к двум никелевым держателям 2, являющимся токопро-
в одам и.
Существуют две основные принципиальные схемы
измерительной системы терм о анемометров. В обоих случаях насадок Rn
(рис. 10-13,6i) включается в одно из плеч моста, остальные плечи
которого выполнены из сопротивлений, не зависящих от
температуры.
Сбалансированный при с = 0 -мост разбалансируется при
введении насадка в поток с некоторой скоростью с. Бал awe моста можно
восстановить либо увеличением тока при помощи реостата R$, либо
компенсацией изменения сопротивления RH при помощи R2.
Первый метод — «постоянного сопротивления». Более
распространен второй метод — постоянного тока.
При измерениях в нестационарных потоках в измерительную
диагональ включается электронный усилитель со специально
подбираемой характеристикой, позволяющей в определенных предел ад
компенсировать тепловую инерцию нити.
Термоанемометры допускают проведение экспериментов в
широком диапазоне скоростей и частот пульсаций газовых потоков.
10-3. ОПТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ГАЗОВЫХ
потоков
При больших скоростях в поле газового потока возникают
значительные градиенты плотности. Неоднородность потока при этом
позволяет широко применять оптические методы исследования.
В некоторых случаях неоднородности поля создаются в потоке
искусственно путем местного нагрева. При таком способе
визуализации оптические .методы могут быть применены и для
дозвуковых потоков небольших скоростей.
Оптические .приборы основаны на использовании известных
свойств световых лучей, отклоняющихся от первоначального
направления при пересечении среды переменной плотности и,
следовательно, .переменной преломляющей способности.
Если п — показатель преломления световых лучей в данной
точке поля, то значение плотности потока в точке определяется
по соотношению
1 п2 — 1
которое может быть заменено приближенным выражением:
п — 1 п. — 1
—y-=-L^- = const, (10-1)
638
где nv p, — показатель преломления и плотность в некоторой
начальной точке; обычно эти величины относятся к
нормальным атмосферным условиям (^=0°С и рх =
= 760 мм рт. ст.).
Из формулы (10-1) следует, что поле плотностей потока
будет определено, если опытным путем найти .поле показателей
преломления световых лучей в исследуемой области. Давления и
температуры могут быть определены, если -известны еще два
уравнения, связывающие параметры течения р, р и Г. Для этой цели
служат уравнение состояния и уравнение изоантропического
процесса.
Дифференцирование уравнения (10-1) приводит к очевидным
соотношениям:
дп dp дп dp
~ду = КЪу ' ~дг = Kdz~
и
dbi д2^ дЬг д2?
ду2==КдуГ' ~dz2=lK~dz2'
где К — постоянная величина.
Отсюда заключаем, что в зависимости от принципа действия и
схемы оптические приборы могут быть использованы для
непосредственного измерения плотности или первой или второй производной р.
Для качественного изучения потока пригодны все приборы вне
зависимости от того, каким методом определяется поле плотностей
при количественном исследовании. Однако четкость и наглядность
получаемой качественной картины потока, а также точность и
трудоемкость обработки результатов качественного анализа существенно
зависят от схемы и конструкции прибора.
Наиболее простыми являются оптические системы, в которых
используется теневой метод определения плотностей. Схема такого
устройства приведена на рис. 10-14,а. Расходящийся пучок света
от источника 5 проходит через линзу L и становится параллельным.
Параллельный пучок лучей пересекает воздушный поток, в котором
находится модель А, и падает на экран или фотопластинку /. При об -
текании модели возникают градиенты плотности. Так, например, если
линия тока 1—2 пересекает головной скачок у модели, то плотность
в зоне пересечения изменяется скачкообразно (рис. 10-14,6). При
dp д2р
этом ^Ф0и^2ф0.
д2р
В тех точках поля, где ~г~!>>0, лучи параллельного пучка рас*
д2Р
ходятся и на экране образуется темная область. Там, где ri<0,
лучи сходятся и освещенность на экране увеличивается. В точке 1
рис. 10-14,0) d2p/dz2 > 0, а в точке 2 d2p[dz2 4i 0. Отсюди следует,
что изображение головной волны у модели будет состоять из двух
расположенных рядом линий: черной и белой. В простейшем случае
теневой метод может быть осуществлен в расходящемся пучке
639
света (без линзы). Этот Метод, наиболее простой и дешевый,
находит применение при изучении скачков в потоке.
Другой, более чувствительный и точный оптический прибор,
позволяющий измерять первые производные плотности, основан
также на теневом методе. В этом приборе лучи, прежде чем
попасть ,на экран, фокусируются в точку, к которой подводится нож.
При наличии неоднородности в потоке точка фокусировки части
лучей сместится и попадет на нож, который не препятствует их
I*
а)
<0
Рис. 10-14. Схема теневого метода.
дальнейшему распространению. В результате картина,
образующаяся на экране, будет иметь большую контрастность, чем в простом
приборе (рис. 10-14).
Широкое распространение получили зеркальные системы
теневых оптических приборов. Наиболее совершенным является
прибор с зеркально-менисковой системой, предложенной
проф. Д. Д. Максутовым (рис. 10-15). От источника пучок света
проходит через конденсор К и щель D. Плоское диагональное
зеркало S\ изменяет направление хода лучей. Лучи попадают на
вогнутое сферическое зеркало 52, преобразующее расходящийся
пучок света в параллельный. Сферическое зеркало S2 вместе с
рассеивающей менисковой линзой L\ образует зеркально-менисковую
систему.
Эта часть прибора, состоящая из осветительного узла,
зеркала S2 и линзы Lu создает параллельный пучок света и называется
коллиматором.
Приемную часть прибора составляют- менисковая линза L3,
сферическое зеркало S3, плоское диагональное зеркало 54, нож Я,
поворотное зеркало 55, экран / и фотоприставка Ф Поворотное
зеркало S0 в осветительном узле служит для контроля фокусировки
щели.
Для того чтобы источник света, который должен находиться
на оптической оси системы, не закрывал центра поля изображе-
640
ния, оптическая ось системы смещена к ее краю. Поэтому система
несимметрична относительно геометрической оси, что хорошо видно
на р.ис. 10-15.
Основное достоинство зеркально-менисковой системы
заключается в том, что при одинаковой светосиле она имеет
значительно меньшие сферические и хроматические аберрации по сравнению
с линзовой системой.
Таким образом, в рассматриваемой схеме основными узлами
являются: крупная оптика прибора (зеркально-менисковая), осве-
Рис. 10-15. Схема зеркально-менискового прибора Д. Д. Максутова.
тительный узел, включающий механизм перемещения и изменения
щели и фокусировки источника света и механизм перемещения
ножа с фотоприставкой.
В процессе эксперимента работа с прибором сводится к
воздействию на осветительный узел, на механизм перемещения щели,
на фотоприставку и на механизм перемещения ножа.
В качестве -источника света могут быть применены различные
осветители, в том числе ртутная лампа, кинопроекционная лампа,
искровой разрядник и пр. В ряде случаев оказывается
целесообразным последовательное использование двух осветителей.
При качественном исследовании потока основная задача
заключается в правильном выборе степени освещенности поля,
которая зависит от размеров щели, положения ножа и типа осветителя.
Наибольшая освещенность подучается при максимальной щели и
выведенном ноже.
Необходимо, однако, учитывать, что с увеличением
освещенности чувствительность прибора уменьшается. Поэтому область потока
с небольшими градиентами плотности следует фотографировать при
небольших размерах щели и введенном в пучок света ноже. Если
основной интерес представляет исследование системы скачков, то
размеры щели увеличиваются.
Существенное значение имеет также (расположение ножа
относительно изучаемого объекта. В зависимости от положения ножа
(горизонтальное, вертикальное или диагональное) лучи, прошедшие
неоднородное поле .и отклонившиеся, могут быть задержаны ножом
41 М. Е. Дейч
641
или, наоборот, проходят к экрану. В первом .случае неоднородность
получается на экране темной, а во втором — светлой. Четкость
изображения при этом сохраняется одинаковой. Лучшие результаты
получаются тогда, когда кромка ножа расположена (Нормально
к направлению максимального градиента плотностей.
Таким образом, тип оозетителя, размер щели и /положение
ножа необходимо в каждом отдельном 'Случае находить подбором
в зависимости от режима по-
fS
Й
ш
тока, объекта и задачи
исследования.
При количественном
исследования потока нож
оказывается непригодным, так как
он задерживает лучи и не
позволяет измерить углы
отклонения, необходимые для
определения поля коэффициента
преломления. В этом случае
диафрагмирование пучка света
производится тонкой нитью.
Такой метод количественного
исследования с помощью
оптического прибора получил
название метода нити и щели.
Для непосредственного
измерения поля плотностей
потока применяется оптический
прибор, известный под названием
интерферометра. Принцип
действия интерферометра можно
уяснить из рассмотрения схемы,
приведенной на рис. 10-16.
Прибор состоит из двух
отражательных зеркал Si и S2
и двух полупрозрачных зеркал
П{ и Я2, расположенных в
углах прямоугольника под углом
45°. Рассмотрим вначале
случай, когда поверхности зеркал
строго параллельны.
Расходящийся пучок света от источника 5 проходит через линзу L и
становится параллельным. Лучи параллельного пучка раздваиваются
при прохождении полупрозрачного зеркала П\. Часть лучей АСЕ'
проходит через полупрозрачное зеркало Я! и, отражаясь от зеркал S{
и Я2, попадает на экран Э в точке /. Другая часть лучей
отражается от Пх и S2 и, пройдя зеркало Я2, попадает в ту же точку экрана /
(траектория этого луча — АЕА'С'1). Отражение лучей будет
происходить также в точках С и В (лучи СВ и BD) и С и В' (лучи С В' и
B'D') полупрозрачных зеркал. Эти лучи приходят на экран -в
точке К. Следовательно, часть лучей, идущих в точку /, пересекает
полупрозрачные зеркала (Яь Я2) один раз, а та часть, которая
попадает в точку К, пересекает Пх или Я2 дважды. При этом в
точке К сила света будет меньшей.
Так как все четыре зеркала имеют параллельные поверхности,
Т I И
Рис. 10-16. К пояснению принципа
действия интерферометра.
642
то длина оптического .пути (произведение траектории луча на
показатель преломления) обоих пучков, идущих в точку /, будет
одинаковой. В это1М случае экран будет освещен равномерно.
Характер освещенности экрана резко меняется, если зеркала
(Si или S2) повернуты на некоторый небольшой угол относительно
оси, перпендикулярной плоскости чертежа. При
этом изменяется длина оптического пути
одного из пучков лучей, отраженных
соответствующим зеркалом S\ или S2 и идущих в
точку /. В результате происходит интерференция
лучей, встречающихся в точке /,
заключающаяся в том, что часть лучей гасит друг
друга и на экране образуются перемежающиеся
темные и светлые полосы !, расположенные на
некотором одинаковом расстоянии Q одна от
другой (рис. 10-17,а).
Если между зеркалами Пх и S\ будет
помещено исследуемое поле R, плотность в
котором р отличается от плотности среды
между Я2 и S2, то благодаря изменению
оптического пути луча СЕ' разность хода лучей СЕ'
и ЕЛ' изменится. При этом полосы
'интерференции сместятся на некоторое расстояние
параллельно самим себе (рис. 10-17,6).
Величина смещения полос .интерференции
определяется по уравнению
l(nf — 1) р —р'
где / и /' — длины оптического пути луча
в средах с плотностями
соответственно р и р'.
Отсюда получаем разность плотностей:
Рис. 10-17
Схематическое
изображение
интерференционного спектра.
р — р':
е
где т -■
Р'/'
// / п —величина, зависящая от условии эксперимента:
угла поворота зеркал, плотности р' и коэффициента преломления
среды п'
Величины т, £ и Q определяются в ходе эксперимента.
В тех случаях, когда исследуемое тюле характеризуется
неравномерным распределением плотностей, смещение полос
интерференции будет различным ча разных участках экрана; в результате
полосы будут искривлены. При этом линии одинаковых смещений
полос интерференции (g/Q = const) отвечают линиям постоянной
плотности (р— p/=const) в исследуемой области. Таким образом,
1 Лучи, идущие в точку К, также интерферируют друг с
другом, однако, как указывалось, вследствие значительно меньшей силы
света в точке К интерференция здесь будет более слабой;
небольшим дополнением схемы прибора ее можно исключить.
41*
643
принцип действия интерферометра основан и а измерении разностей
длин оптических путей света. Интерференционный метод позволяет
детально (Последовать структуру потока в межлопаточных каналах
решеток и с достаточно высокой точностью определять
количественные характеристики во всех точках толя потока.
С помощью интерферометра легко установить изменение
толщины пограничного слоя вдоль профиля, а также положение точек
отрыва слоя. Этот прибор позволяет раздельно определять потери
трения, кромочные и волновые потери в плоских решетках.
В качестве примера .на рис. 10-18 приведен интерференционный
Рис. 10-18. Интерференционный снимок течения
газа в турбинной решетке (опыты ЦКТИ).
снимок потока в турбинной решетке. Сравнение картин
распределения давлений по профилю, полученных пневмометрическим и
интерференционным методами, показывает хорошее совпадение
результатов оптических измерений с данными непосредственных
намерений.
Схема интерферометра путем небольшого дополнения позволяет
одновременно получать интерференционные .и теневые фотографии
спектров потока. С этой целью в схему прибора *можно ввести еще
одно полупрозрачное зеркало Я3 (рис. 10-16). Тогда часть лучей,
отраженных зеркалом Я3, даст на экране в точке Т теневое
изображение спектра. Другая часть лучей, пройдя через зеркало Я3,
отразится зеркалом Я2 так же, как и в обычной схеме прибора.
10-4. УСТАНОВКИ ДЛЯ ИССЛЕДОВАНИЯ РЕШЕТОК
В СТАТИЧЕСКИХ УСЛОВИЯХ
Испытания неподвижных решеток выполняются на установках
различных типов, схема и конструкция которых определяются
задачами исследования и принятой методикой эксперимента.
644
Испытания в статических условиях, как уже указывалось,
производятся с целью сравнительной оценки решеток и для изучения
особенностей физического процесса обтекания различных решеток.
Получаемые опытные характеристики в некоторых случаях могут
быть использованы и для теплового расчета ступени.
Для определения характеристик и для 'исследования структуры
потока .в решетке используются [различные «методы
аэродинамического эксперимента. К ним относятся*
A. Методы изучения спектра .потока, включающие:
1|) измерения поля потока .в характерных сечениях решетки
насадками, а также различными электрическими приборами,
фиксирующими полное и статическое давление, температуру полного
торможения, направление скорости в точке; 2) изучение поля плотности
оптическими методами (теневыми и интерференционными); 3)
визуализацию потока путем подмешивания инородных частиц.
Б. Методы изучения потока у границ .профиля,
в том числе: 1) измерение температур и давлений на
поверхности профиля лопатки путем дренирования; 2) изучение профиля
скоростей в .пограничном слое с помощью микротрубки или
электрических приборов; 3) .визуальное исследование структуры
пограничного слоя на профиле путем окрашивания поверхности лопатки.
B. Методы взвешивания, включающие: 1|)
определение "суммарного импульса потока за решеткой; ' 2) определение
сил, действующих на решетку в целом и на отдельную лопатку
в бесконечной решетке, с помощью специальных весов.
Г. Методы изучения нестационарных
процессов, связанных с обтеканием отдельной лопатки или решетки.
Исследуются колебания обтекаемого профиля, а также пульсации
скоростей, давлений и температур обтекающего потока.
Не останавливаясь на сравнительной оценке различных
'методов исследования, отметим, что одновременное их использование
в одной установке представляется нерациональным. Осуществление
такого требования делает установку хотя и универсальной, но
конструктивно слишком сложной, дорогой и неудобной в эксплуатации.
Следует учитывать, что к схеме и конструктивному оформлению
установки предъявляются дополнительные требования,
обусловленные конструктивными параметрами исследуемых решеток и
газодинамическими параметрами потока перед решеткой и за нею. Так,
в исследуемой решетке могут изменяться: форма профиля, шаг и
высота лопаток, угол их установки.
Важнейшими газодинамическими параметрами, являются: ' угол
входа потока на решетку, изменение которрго [дблжнд
'предусматриваться в любой установке, скоростьдотока за решеткой М2 (или
на входе в решетку Mi) число #Re„ При этом в ряде случаев
представляется необходимым обеспечить раздельное изучение влияния
сжимаемости и вязкостд. на характеристики решетки путем
независимого изменения чисел М и Re. Диапазон изменения режимов
диктуется в конечном итоге заданными условиями эксперимента и
требованиями практического моделирования.
К числу последних, кроме очевидных условий M = idem и
Re = idem, относятся специальные требования к организации потока
перед решеткой. В некоторых случаях оказывается необходимым
вводить искусственную турбулизацию потока, в других — тщатель-
645
но выравнивать поток на входе, а также обеспечивать условия
обтекания бесконечной -решетки.
Изложенное выше .показывает, что принципиальные схемы -и
конструктивною формы установок для статических испытаний
решеток можно .классифицировать in о объектам исследования
(установки для испытания плоских или цилиндрических решеток), то
условиям испытания решеток (установки с открытой рабочей частью
или с камерой противодавления для испытания в равномерном или
Рис. 10-19. Принципиальная схема аэродинамической трубы для
статического исследования плоских и кольцевых решеток.
/ — подвот. воздуха; 2—кольцевая камера; 3— сетка; 4 — измеритель Ра; 5 —
измеритель Мкр; 6 — тарировочное устройство; 7 —подшипник; 8 и 13 — обечайка;
9 — // — уплотнение; 10 — исследуемая решетка; 12 — координатник; 14 и 20 — вьг
хлопная камера; /5 —съемный фланец; /6—сопло плоского пакета; /7 —плоский
пакет; /5 —поле координатника; 19 — диффузор; 21 — вал; 22— упорный
подшипник.
турбулиз/ировавном дозвуковом или сверхвузковом потоке на
входе) и ino принятой .методике исследования (установки для
детального изучения аэродинамических полей, для определения усилий,
действующих на профиль в решетке, для исследования решеток
оптическими методами и т. in.).
Установки можно классифицировать также в зависимости от
применяемого рабочего тела (пароьые, воздушные,
паровоздушные и др.) и способа организации рабочего потока (установки
с избыточным или атмосферным давлением на входе, эжекторные
установки, паровые установки, работающие на 'конденсатор).
Лабораторные стенды должны, как правило, включать
несколько экспериментальных установок. При этом круг задач, решаемых
на каждой установке, ограничен ее конструкцией, принятой
методикой исследования и -предельными значениями параметров рабочего
тела.
Рассмотрим принципиальные схемы некоторых испытательных
установок. На рис. '10-19 приведена схема аардинамической трубы,
646
в которой предусмотрена возможность простой смены рабочих
частей. Воздух от компрессора .подается .в трубу через .патрубок / и
попадает в кольцевую камеру 2. Пройдя через конус 3, имеющий
большое число отверстий, воздух 'попадает в ресивер и обтекает
исследуемую кольцевую решетку 10. Нужное направление потока на
входе IB исследуемую решетку создается обечайкой с
направляющей решеткой 8.
Исследуемый кольцевой пакет крепится к фланцу вала 21,
установленного в шариковых опорном подшипнике 7 и
опорно-упорном 22. Осевое усилие через подшипник 22 передается на упругий
элемент 4, а крутящий (момент с вала на корпус передается через
симметричные упругие элементы 5. На .упругие элементы наклеены
проволочные тензодатчики, при помощи которых с достаточной
точностью определяются крутящий момент и осевое усилие.
Решетка 10 снабжена уплотнением 9, в камеру // которого
подается воздух под давлением, равным давлению в ресивере. Таким
образом, перетекание из ресивера в выхлопную камеру устраняется
и расход, прошедший через решетку 10, равен намеренному
расходу через патрубок /. Такое определение расхода необходимо при
применении метода взвешивания. Для повышения точности
измерения Мкр и Ра предусмотрено специальное тарировочное
устройство 6.
Для исследования поля потока перед решеткой и за нею
используются насадки, перемещаемые автоматизированным коорди-
натником 12.
При исследовании кольцевой решетки фланец 15 отсутствует и
воздух сбрасывается в выхлопную коробку 20.
При необходимости исследований решеток в плоском пакете
кольцевой пакет 10, обечайки 8, 13 и уплотнение 9 удаляются.
Устанавливается фланец 15, а на него — плоская рабочая часть
нужной конструкции с «соплом 16, исследуемой решеткой 17, коор-
динатником 18 и диффузором 19.
Рабочие части для исследования плоских пакетов имеют
различное конструктивное оформление. На рис. 10-20 приведен общий
вид одной из рабочих частей для плоских решеток.
Здесь верхняя стенка сопла 5 болтами 6 неподвижно крепится
к корпусу 3 так, что ее выходная кромка совпадает с общей осью
двух дисков 8, 0. Диски 8 с помощью сухарей 7 неподвижно и со-
осно скреплены между собой. Нижняя стенка сопла 4 скользящими
шпонками 10 и винтами // крепится к вертикальному ползуну Л
скрепленному с корпусом 3 винтом 2.
Перемещая стенку 4 относительно ползуна / и ползун —
относительно корпуса 3, можно изменять расстояние ОС в пределах ОБ
при заданном угле входа в зависимости от длины исследуемого
пакета. Изменение угла входа производится поворотом дисков 8
относительно корпуса 3.
Координатник за решеткой, жестко скрепленный с дисками 8,
обеспечивает четыре независимых перемещения насадка: линейные
перемещения в направлениях осей xyz и поворот вокруг оси г.
Три из этих перемещений (в направлениях х и z и поворот
вокруг оси z), осуществляются электродвигателями, дистанционно
управляемыми оператором по заданной программе.
На установках -рассмотренного типа решетки могут быть
испытаны в равномерном или турбулизированном потоке. С целью
647
искусственной турбулизации .потока в «параллельном участке перед
решеткой можно расположить турбулизирующие сетки. В
зависимости от густоты сетки (размеров ячеек) и диаметра 'проволоки
при неизменной скорости потока может быть (получена различная
степень турбулентности 'перед решеткой.
Наряду с рассмотренными схемами установок, работающих
с избыточным давлением, находят применение схемы с атмосфер-
Рис. 10-20. Плоская рабочая часть с
переменной длиной пакета и автоматическим коор-
динатником (продольный разрез).
/ — ползун; 2, 6 и //—-винт; 3— корпус; 4 и 5
—сопло; 7 —сухари; 8 — диск; 9 — крепление пакета; 10 —
шпонка.
пым давлением в форкамере, в том числе установки эжекторного
типа. В таких установках воздух засасывается в форкамеру из
атмосферы, ускоряется в сопле и направляется к ре летке. Поток
в решетке индуцируется эжектором. Такая установка работает
с (Незамкнутым потоком >и позволяет -получить низкие давления за
решеткой (и соответственно низкие числа Re).
Приведенный краткий обзор показывает, что количество
возможных схем установок для статических испытаний решеток
достаточно велико. Выбор той или иной схемы определяется задачами
эксперимента, .причем в основу сравнения различных схем должны
быть положены соображения экономичности и требования теории
моделирования.
Имея в виду принятые ранее обозначения, можно записать
выражения для чисел М и Re в известном виде:
с 1 с ?cL __Vf _P^_
643
где L — характерный линейный размер; р, Т, с — параметры потока
в рабочей части установки (за решеткой).
Из выражений для М и Re исключим скорость с; тогда
L-\ ti^j-k^Kljw (10-5)
Обозначим Ку коэффициент качества установки, определяемый
как отношение мощности потока к потребной мощности компрессора
в рабочем сечении установки. Потребная мощность компрессора
определяется по формуле
1 г2,5
Nk==I^N1^ — MRe2. (10-6)
В уравнениях (10-5) и (10-6) KL и KN являются постоянными
величинами.
Из формулы (10-6) следует, что при одинаковых параметрах
газа (р <и Т) габариты установки в рабочем сечении увеличиваются
пропорционально отношению Re/M. С увеличением давления
размеры (установки сокращаются. Мощность установки пропорциональна
MRe2.
Повышение коэффициента качества установки Ку достигается
путем введения диффузора, снижения потерь в установке и
использования компрессора с высоким к. п. д. в пределах рабочих
режимов.
С помощью формул (10-5) и (10-6) 'можно сравнить две
принципиально различные схемы установок: с избыточным и
атмосферным давлением в форкамере.
При соблюдении подобия одновременно по М и Re мощность
установки с атмосферным давлением получается значительно
больше (мощности установки -с избыточным давлением. Вместе с тем
в первом случае размеры исследуемых .моделей также возрастают,
что особенно важно при исследовании пограничного слоя в
решетке. Установки «с избыточным давлением .могут работать с камерой
противодавления и с открытой рабочей частью. В последнем
случае техника эксперимента значительно упрощается.
Следовательно, в установках с избыточным давлением можно
осуществить раздельное исследование влияния сжимаемости и
вязкости, в то время как в установках с атмосферным давлением
в форкамере раздельное моделирование неосуществимо. При малых
значениях М экономичность обеих схем одинакова.
Таким образом, мы видим, что установки с избыточным
давлением в форкамере в общем случае (подобие по М и Re)) обладают
большей экономичностью и более универсальны. Они имеют
поэтому более широкое распространение. В некоторых случаях, однако,
установки с атмосферным давлением более экономичны (если
исследуется влияние только сжимаемости) и являются единственно
возможным решением. Только по такой схеме может, например,
работать паровоздушная установка с паровым эжектором.
649
10-5. ЭКСПЕРИМЕНТАЛЬНЫЕ ТУРБИНЫ
Опытное исследование характеристик турбинной или
компрессорной ступени производится на специальных экспериментальных
турбинах или компрессорах.
Стенд экспериментальной турбины состоит из турбины,
электрического или гидравлического нагрузочного устройства,
воздушной, паровой 'Или паровоздушной тепловой схемы и специальной
системы измерительных устройств.
В некоторых случаях турбина и нагрузочное устройство
конструктивно объединяются. В установках большой мощности
турбина и нагрузочное устройство обычно выполнены отдельно и
соединяются муфтой.
Общим >и весьма важным требованием, 'предъявляемым к
.нагрузочным устройствам экспериментальны* турбин, является
возможность максимально точного измерения крутящего момента на
валу турбины. Желательной является возможность измерения
осевого усилия ротора.
Экспериментальная турбина должна обеспечивать возможность
испытания ступеней с различными геометрическими размера-ми,
надежную работу в широком диапазоне чисел оборотов, удобную и
правильную расстановку измерительной аппаратуры и простоту
монтажных работ.
Принципиально можно спроектировать универсальную
экспериментальную турбину, обеспечивающую испытания как отдельных
ступеней, так и групп их, работу с различными оборотами,
позволяющую испытывать модели регулирующих, промежуточных и
последних ступеней. Однако конструкция и эксплуатация такой
машины будут весьма сложными и создание ее едва ли
целесообразно. Очевидно, рациональнее иметь несколько экспериментальных
машин, каждая из которых ориентирована на исследование
определенных типов ступеней.
На рис. 10-21 в качестве примера приведен продольный разрез
быстроходной экспериментальной воздушной турбины,
предназначенной для детального исследования ступеней с относительно
длинными лопатками (® = d/l= 2,8ч-4,51). Турбина рассчитана на
максимальный расход воздуха G = 4,5 кг/сек; Г0 = 200СС при
максимальном давлении ро = 3 ата и АгМакс = 20 000 об/мин.
Ресиверная часть турбины 1 сварная, без горизонтального
разъема. Воздух через патрубок 2 подается в кольцевую камеру 3,
откуда он через сверления 18 равномерно подводится в воздушную
коробку 19. Для организации потока перед направляющей
решеткой 22 служат обтекатели 20 и решетка пластин 21, позволяющая
изменять угол входа в направляющую решетку. Корпус
турбины 25 сварной с горизонтальным разъемом. Воздух, прошедший
через рабочую часть, выбрасывается через выхлопной патрубок 37.
Конструкцией предусмотрена работа машины в качестве
экспериментальной турбины или аэродинамической трубы для исследования
кольцевых решеток.
Конструкция позволяет взвешивать крутящий момент и осевое
усилие как на рабочем колесе, так и на направляющем аппарате.
650
Рис. 10-21. Быстроходная воздушная экспериментальная турбина МЭИ с взвешиванием М и Ра на диафрагме
и роторе.
/ и 25 — корпус; 2 — подводящий патрубок; 3— кольцевая камера; 4 — привод поворота соплового аппарата; 5—игольчатый
подшипник; 5 — упругий луч весов Мкр; 7 —зубчатое колесо; 8 — шпонка; 9 — измерительная му фта; 10 — жесткий луч измерительной муфты
мкр; /^ — эксцентрик; /2 —кольцо; 13 — подшипник; 14 — срерическая вставка; 15 — упругий эчгмент весов; 16 —уплотнение; 17—вал
диафрагмы; 18 — решетка; 19 — ресивер; 20 — обтекатели; 21 —направляющая решетка пластин; 22 — сопловой аппарат; 23 — рабочее
g{ колесо; 24 —люк координатника; 26 — плавающая втулка; 27 — втулка; -28 и 36 — камеры; 29 — кольцевая камера; 30 — диск тормоза;
~ 31 и 32 — корпус тормоза; 53 —питательный канал; 34 — индукционный датчик; 35 — слив; 37 — выхлопной патрубок.
Последний укреплен на полом валу 17. Передний ша.риковый
подшипник вала .не воспринимает осевой нагруз.ки. Осевая нагрузка
воспринимается задним упорно-опорным «подшипником 13 и через
сферическую вставку 14 передается на упругий элемент 15.
Крутящий момент через шпанку 8 .передается на трехлучевую
измерительную муфту 9, два упругих симметричных луча которой
6 (Предназначены для измерений крутящего момента и один
жесткий 10— для тарировки измерительной муфты.
Для TOiro чтобы трение в контактах упругих лучей
'измерительной муфты не вносило погрешности в измерение осевого усилия,
контакт осуществлен через игольчатый подшипник в -сферическом
корпусе 5. Крутящий момент передается через кольцо 12 на
червячную .пару 4. Для измерения крутящего момента и осевого
усилия ,на диафрагме применяются электрические тензометры
сопротивления, пакленные на гибкие элементы 6 и 15.
Весовое устройство описываемой машины -позволяет легко
проводить тарировки в процессе эксперимента, а три .необходимости —
перед каждым измерением.
При /необходимости 'параллельно с электротензометрами для
измерения Мкр и Ра могут применяться высокоточные механические
или оптико-механические индикаторы.
Рабочее колесо 23 экспериментальной турбины выполнено
с фланцевым креплением. Вал — гибкий, вращающийся в
'Специальные .прецизионных 'подшипниках качения. Нагрузочное
устройство— о:днодисковый гидротормоз консольной конструкции.
Специфическим для экспериментальных турбин является вопрос
об измерении момента трения в подшипниках. В ряде
существующих машин момент в подшипниках вообще не измеряется и в расчет
вводится поправка, полученная .на основании тарировки. Однако
для точных экспериментальных турбин такой метод является
недопустимым, так как момент в упорном подшипнике зависит от осевой
нагрузки, а следовательно, и от режима работы турбины.
В экспериментальной турбине (рис. 10-21) корпуса опорного
и опорно-упорного подшипников размещены в разъемной
«плавающей» втулке 26. В неразъемной и неподвижно связанной с
корпусом втулке 27 в сечениях АЛ и ББ выполнено по четыре
симметричные камеры 28, питаемые через дроссельные шайбы сжатым
воздухом с давлением^6 ата из кольцевой камеры 29. В рабочих
условиях из-за разности зазоров между втулками 26 и 27 вверху
и внизу давление в верхних камерах 28 будет меньше давления
в нижних камерах. 36. Разность давлений, направленная вверх, при
определенных условиях уравновесит силу веса конструкции,
заключенной во втулке 26, и заставит ее «всплыть»
Основной нагрузочный момент с диска гидротормоза 30
передается на корпус гидротормоза 32, жестко связанного с
«плавающей» втулкой 26. Поэтому моменты подшипников и нагрузочный
момент диска тормоза суммируются и уравновешиваются моментом
весовото устройства, приложенным к корпусу 32. Таким образом,
весовое устройство измеряет сумму трех моментов: момента
опорного подшипника, момента опорно-упорного подшипника :и
момента на диске гидротормоза. Момент, развивающийся в результате
трения диска 23 о воздух, весами не учитывается, но с
необходимой точностью может быть определен путем тарировки.
652
Осевое усилие рабочего колеса, передаваемое На «плавающую»
втулку через опорно-упорный подшипник, измеряется специальной
весовой головкой.
Вода в гидротормоз подается открытой 'Струей в питательный
капал 33 и удаляется через сливной вентиль 35. Счетчик оборотов,
тахометр и автомат безопасности в описываемой машине —
электрические, работающие от общего индукционного датчика 34.
Для измерения аэродинамических полей за колесом или
направляющим аппаратом при работе без колеса применяется специальный
координатник с автоматическим электроприводом,
устанавливаемый в люке 24.
га
о о о
4^ 4^ СО
to о оо
О О О
о о о о о о
со со со со to to
<J5 *- tO О 00 О)
о о о о о о
о о о о о о
to to to — — •—
tMOOOOOJ^
о о о оо о
о о о о о о
— — о о о о
tO О 00 05 *- tO
оо о о о о
CD CO CD
О О —
О СО 00
00 -д СО
СО СО СО СО СО СО
to со 4=- 4^ сп о)
CD 4=- *— 00 СП —
4^ ~ СП СП О ►—
со со со со со со
CD -<1 -<1 00 00 00
05 tO 05 — СП 00
00 О 00 tO — CD
СО СО СО СО СО СО
со со со со со со
— 4^ CD -<1 СО СО
CD >— СО СО О 00
О О О ОО О
оооооо оооооо
СО СО СО
tO CO rf>
00 4^ О
— CD СО
СО СО СО СО СО СО
4^ 4^ СП О) 05 -Ч
CD tO -4 tO CD tO
СО СП СО СО ^4 >—
СО СО СО СО СО СО
-д --J 00 00 00 СО
CD CO CO CD СО —
tO CD rf> СП СО СО
со со со со со со
со со со со со со
4^ СП -4 00 СО СО
О 00 4^ СП СО 00
ООО ОООООО ОООООО ОООООО
sh»
СО СО СО
^1 ^1 ^1
О СО СП
CD СО СО
СО СО СО СО СО СО
^4 00 00 00 00 00
00 О tO СП CD 00
^ЧСО ОСОЧ
со со со со со со
со со со со со со
О —' СО 4> СП CD
4> СО СО О) -<1 »>1
со со со со со со
со со со со со со
-х| 00 СО СО СО СО
О) СО СО 4> -J СО
ОООООО ОООООО
оооооо
CD СП СП
— 00 О)
4^ СО 4*.
СО ^1 О
СП СП 4^ 4^ 4^ СО
СО ~ 00 СП tO СО
--J о Со сп -q оо
-<1 СО СП ~«4 4^ ~«4
со со со to to to
CD 4^ —' 00 4^ —
CD О О О CD CD
05 — tO — -vj О
~ — — О О О
00 СП tO CD 05 СО
00 ^v) СП 4^ СО —
tO — СО СП >— СП
ООО
■vj 00 00
со о to
tO ^4 tO
ОООООО
00 00 00 00 00 00
СО 4^ CD "Ч 00 СО
СП 00 ~ Ю СО СО
ОООООО
со со со со со со
О — — tO СО СО
tO О 00 СП — 05
ОООООО
со со со со со со
4^ 4^ 4* СП СП СП
— СД СО — СО 4^
ОООООО ОООООО
ОООООО
-<1 О) СП
— СО СП
СП СО ~
4^ СО СО tO — О
-vj 00 О tO 4^ CD
О 00 О) СП СО —
ОООООО
СО 00 00 -<| О) СП
00 СО — СО СП -д
О 00 CD СП СО >—
ОООООО
4^ 4=- СО Ю — О
СО О tO 4^ О) 00
О 00 ^Д СП СО —
ОООООО ОООООО ОООООО
ООО
СО 00 ^v)
СИ ^v) СО
сп to со
ОООООО
-Ч CD СП СП 4^ СО
CD tO tO СД tO CO
оооооо
со to to — — ~
tO -О tO 00 4=- —
00 --J CD О) 00 CO
ОООООО
ОООООО
00 СП СО tO О О
со оо -ч — со to
to to со
00 СО О
ОО —
— to
СО СО СО СО СО 4^
— tO 4^ CD 00 ~
СО 00 4^ СО СП О
00 — СП СО — CD
4^ 4^ СП СП CD "Ч
4^ ^v) tO ^v) 4^ tO
00)000-00
Ч0100)ОЮ
— >— — to сп
00 О tO О) СП О
СП О 00 tO 4^ tO
СО
ООО ОООООО ОООООО ОООООО
Jatf
у*
•-I
Т1
СО
£
S
гг
о
я
о\
fc4
S
с
Е
-(
СО
СО
о
fcl
° 2
сососо со со to to сп to
оо --j ел со — со -J -о со
COO— tO СО 4^ СП СО 00
Ю .— >— to 4^ CD CO -4
to to — — — —
Ю О 00 О) 4^ tO
О — CO 4^ О) 00
— CD tO 00 4*. О
— О О О О О
О СО "<1 СП tO —
CD •—' СО 4^ О) 00
-<| 4^ — 00 СП tO
>
о
я
я
>
я
m
Г)
я
•е-
я
я
я
о я
1!
—
СО
ДЛЯ
*г
II
II
—
4=-
К
<&»
II
я
43
Я
о
и
з:
я
CO LO CO CM 00 -* —< О CD О СО CD
O0NCOCOЮЮ LO LO ^ LO Ю Ю
OM^CDOOO (M^CDOOOO
•^^^^^Ю LO LO lO LO CD CO
-н 00 Ю CD 00 —•
CD CD N~ 00 CD —■
^f CD CO О CM Ю
CDCDcDN N N
CM ~* CD ОО О СО
N- О —i CO CD 00
N-. N CO CO CO 00
CM CM CD
CO CD CM
OtMlO
СГ;О5С0
oooooo oooooo oooooo
oooooo-ooo
MINI МММ I M M I МММ I
I I
CO ^f CO О CO CM
—« CO CD О ^f CD
N- CD LO Ю ^ CO
см см см см см см
CD •* Г- CO CM LO
t^OCDCOON
CO CO CM CM CM —<
см см см см см см
r— CD CD — CD CM
lO CM О CD N- 00
— — —< О О О
см см см см см см
О CD О CO CD —
ю со со см —i —i
oooooo
см см см см см см
N rf CM
ooo
ooo
CM CM CM
О CO CD — Ю CM
Tf CM —« —< О О
о —> см со •* ю
CD CD CD О СМ Ю
CD CD CD О О О
LO CD N- CD О —«
—< —. ~-« —. CM CM
О ~ —> —■ <—' —
CM CO "f LO CO N-
см см см см см см
CD rf —■ LO 00 00
—< — —« О CD 00
00 CD О — — CM
CM CM CO CO CO CO
CD ^ CO
N- CD ^f
CO -Ф LO
со со со
oooooo
oooooo
oooooo
oooooo
CD 00 О —' CO Tf
CD N- CO ^P CM О
N- 00 CD О •—> CM
—' —« —■ CM О) CM
CD 00 CD —« CO "*•
00 CD -* CO —< CD
CM CO ^ LO CD CD
CM CM CM CM CM CM
CD 00 CO — CO ^
N- Ю CO CM О OO
NOOCOO^-
см см см со со со
CD 00 CD —h CO ^f
CD ^h CM —' CD N
CM CO ^ LO LO CD
со со со со со со
CD N- CD
LO CO —i
N 00 CD
со со со
OOOOOO OOOOOO
OOOOOO
oooooo
CD О CM ^ Ю LO
N Ю 't WO 0O
N- N- N- N- N- CD
OOOOOO
^ со
CD ^ CM О N Ю
CD CD CD CD Ю LO
OOOOOO
(NON^-<00
oooooo
LO CM CD CD CM CD
со со см см см -ч
oooooo
LO — 00
—. — о
ooo
rf CO lO —' CD —<
CD CO CD CD О CM
CO CD 00 О CO Ю
CD CD CD NN N
-* О 00 00 О CO
CM CM О СО CD CM
N- CD —< CM ^ CD
NN0O0O0OOO
00 ^ CM CD CO 00
N- CM LO CO О —•
NCDO^COi4
00 00 CD CD CD CD
00 О CM ^ CD О
— —с CD CD CM 00
LO CD CD N- 00 OO
CD CD CD CD CD CD
CO CD —
CM LO 00
CD CD CD
CD CD CD
OOOOOO OOOOOO OOOOOO
OOOOOO
N- N- CD CO CD ^f
N- ^t- —■ CO rf —■
CD CD CD LO LO LO
CD CD CD CD CD CD
N- CD О CD N- -Ф
N- CO О LO —> N-
M< ^Г "*f CO CO CM
CD CD CD CD CD CD
CD CO CD N- N CD •
CM CO CO 00 CO 00
CM — — О О CD
CD CD CD CD CD 00
CO CD Tf N- CD О
CO N- CM CD О LO
CD CO 00 N- N- CO
00 00 00 00 00 00
OOOOOO
OOOOOO
OOOOOO
oooooo
CD N- -*
CO CM CD
LO LO ^T
00 00 00
CO CM l4 1 — CD
—' ^f CD CD —. CM
CM — О CD CD 00
CD CD CD 00 00 00
^f N- N- rt< CD CO
rf Ю CD N- N- 00
N- CD LO ^ CO CM
CO 00 00 00 00 00
•CO CM CO CM -Ф LO
00 00 N N- CD LO
— О CD 00 N- CO
00 00NNNN
CO CD -rf N- CD CD
CD CM — CD N- Ю
LO ^f CO —' О CD
N- N- N- N- N CD
N LO —•
CO —'CD
CO N- LO
CD CD CD
OOOOOO OOOOOO
oooooo
oooooo
1-* CD CD CD CD О
—' ~ -ч -^ О О
CD 00 N- CD LO •*
00 00 00 00 00 00
N- — CO —i OO —■
00 b- LO CO О O0
CM —' О CD 00 CD
00 00 00NNN
CO CM CD CO N- CD
LO CM CO LO —ч N-
LO rf CM —< О CO
N- N N N- N- CD
00 N- ^f О LO О
CO CD LO —' CD CM
N LO -rf CO — О
CD CD CD CD CD CD
oooooo oooooo oooooo
oooooo
CO CD CD
N- CM N-
00 N LO
LO LO LO
OOOOOO
rf CD 00 О CM •*
rf ^ ^ LO LO LO
oooooo
CD CO О CM "Ф CD
LO LO CD CD CD CD
OOOOOO
00 О CM ■* CD CO
OOOOOO
О CM ^f CD 00 О
00 00 00 00 00 CD
OOO
CM rj« CD
CD CD CD
655
9§9
4^^^CO WW
О О OO О О
wwtotowto
tO О С» CD Ф> tO
о о о оо о
ооо cd ^ to о
о о о о о о
о о о о о со
00 CD 4*- tO О 00
ОО О ОО О
to to to to to to
tO CO СЛ CD ~«4 CO
cd оо о to сл oo
scnooowo
CO CO CO СО CO СО
о — to 4^ ел О)
ь- 4^ -q ~ 4^ 00
о-слоооч
CO CO 4^ 4^ 4s» 4^
оо со — to 4^ ел
to CD — ел о 4^
-о оо — сл о cd
4^ Ф' 4^ сл ел ел
CD 00 CD — tO Ф-
CD ф. 00 СО 00 СО
со о -ч сл со о
о оо о оо
оооооо оооооо оооооо
со со со со со 4^
Ф- СЛ ^4 СО CD —
CD CD tO 4^ 00 ■—
^ЮОСООО
to со ел cd -ч cd
— СО СЛ 00 О СО
сл сл сл сл ел сл
О — СО Ф> СЛ CD
СО CD О СО О CD
сл оо о to со 4^
СЛ СЛ CD CD CD CD
00 CD О tO CO 4^
tO СЛ 00 —* CO CD
СЛ СЛ Ф- tO CD СЛ
оооооо оооооо
оооооо оооооо
CD CD CD CD CD "4
СЛСПЧООСОО
Ф- CO CO tO — О
4^ CD CO CD ~«4 -4
-4 -О -4 -4 -4 ^4
о *— cd со фь ел
CD 00 CD СЛ CO •—
CD CO CD Ф- -O CD
^4 ~4 -4 -<| -4 -4
CD ^4 -4 00 CD CD
О — СЛ СО О 00
о оо -ч ф» cd eo
00 00 00 00 00 00
о — — to со со
СЛ tO CD CD CO CD
CD -О -О CD CO CD
ОООООО
ОООООО ОООООО О О О О ~ О
-ч оо оо оо оо оо
оо о to со ел cd
CD 4^ — 00 СО 00
CD СЛ CD О 00 00
00 00 CD CD CD CD
00 CD О Ю СО 4^
со cd cd —* eo со
to oo ^1 оо — ел
CD CD CD CD CD CD
СЛ CD CD ^4 00 CO
CO ^- CD CD tO 00
— CD 00 00 CD —
CD CD CD CD О CD
CD CD CD CD CD
tO СЛ 00 CD CD
4^ -Ч — СЛ СЛ
ОООООО
ОООООО
оооооо
о о о о — —
00 00 00 CD CD CD
00 CD CD О •— >—
CD tO 00 СЛ ►— -4
— CD CD О — О
CD CD CD CD CD CD
tO tO CO CO фк 4^
ЮОО^СО^СО
OO^O^SCD
CD CD CD CD CD CD
СЛ CD CD CD ^4 -4
СЛ О 4^ CD Ф- 00
О О 00 О tO 00
CD CD CD CD О О
00 00 CD CD О
CO ^4 ►— CD 4s»
tO CD 00 О
ОООООО ОООООО ОООООО ОООООО
ел сл сл cd ел ел
оо ^4 ^4 ел ел 4^
^4 CD — СО СЛ -Ч
cd -ч ел 4^ to о
сл сл сл ел ел 4^
СО СО to — О CD
00 О tO 4^ CD 00
CD "4 CD 4*> tO —
4s» 4s» 4s» 4s» 4s» 4s»
CO 00 ^4 CD СЛ Ф-
CD ^ CO СЛ ^1 CD
CO ^4 CD 4s» tO —
4s* 4s» 4s» 4s». 4s» 4s».
4^ CO tO — О CD
О tO 4** CD 00 О
CD -4 CD 4^ tO —
ОООООО
ОООООО ОООООО ОООООО
4*. 4^ 4^ 4^ 4s» 4^
— Ю tO tO tO СО
CD tO СЛ ^vj CD О
О СЛ CO CD 4^ СЛ
4s» 4s* 4s* 4s» 4s* 4s»
CO CO CO tO tO tO
•— >— CD СЛ CD "4
4s» 4s» 4s» 4s» 4s* 4s»
tO ~ — — О О
tO CD CD — -4 ~
CD4O00h-cd
CO CO CO CO CO CO
CD CD 00 -4 CD CD
CD О CO ^4 CD tO
CO CO 00 О 00 CD
totototototo to to to to to to totototototo totototototo
-*>— — >— О О
CO to — О CD CO
4s» 4s» 4s» СЛ СЛ CD
ОООООО
"Ч CD CD СЛ 4s» 4^
00 CD ►— 4». CD О
ОООООО
со to to —* — о
СО -Ч tO -Ч СО CD
ОООООО
оооооо
CD СО и— о ОО
4s* СЛ 4* 4^
СО СО СО 4s* 4^ 4^ 4s» 4s». 4s* 4-* 4^ СЛ Сл Сл СЛ СЛ CD CD CD CD "Ч ~Ч СО
*Ч 00 СО О tO CO 4-^ СЛ CD 00 СО -— tO 4^ CD 00 О tO СлООЮОО,
оооооо оооооо оооооо о о о о о I
СЛ СЛ СЛ СЛ О — tO СО СЛ — СО О 4s* tO — — tO СЛ COtOCOCO '
CD"4COCD4^H— _- сл ,— tO 00 00 ^ Я? Ч? 4? Q? ""С CO tO CD CO
СЛ 4s- CO tO — О CO 00 *Ч "Ч CD СЛ 4^ 4s* CO tO tO ►— — О О О .
оооооо оооооо оооооо о о о о О
— *— — tO СО СО СО 4sx СЛ СЛ — СО СЛ — СО СЛ tO СЛ Ю СЛ СО —' '
ел о ел ел о о сл ел ел о ел сл о о о сл ел ел ел сл о о
— к— — — — и- _- — >— — к- и- — — к- — — — — — — — ~ О
cd ел сл сл 4s* 4s» 4s* 4* со со со to to to to —i — *— ooooocd
tO CO СЛ tO CO CD COO-44^ — 00 СЛЮОЧСЛЮ СО Ч ^ Ю О ^J
СЛ — ЧСЛ W- OOO^W^ "4 CO tO CD О 4s* 00 CO CO 4^ CD
Si
О Ю CM CD ОС N N CD —- LO —' N ЮЮС^ОЮСО ^ "* S £^ °2 £3 — CO О
CD CD CO CO О ^ (X)(MS-<tDO ЮОЮ —' CD CM 00 ^ О N ^t C^ OCON
CD CO NN 00 00 00 CD CD О О —ч —< CM CM CO CO rf ^ЮССЮЬОО CDCDO
—Г _Г —Г _ _Г .—Г ,-, _Г ~-Г csTcsT см" см" см см см см см см см см см см см см см со
ЮОЮОЮСМ ~ СМ N 00 ^-< О О О OO CD CD N 00 О CM rf rf N СО Ю CD
— CM CM rf LO О — (N CO ^ О CM CO LO rf CM rf CO СООСОО^^ rf CM rf
oooooo oooooo oooooo oooooo ooo
CD N QO CD О CM СО^ЮСОООСО О^М^ЮСО 00 О —- CO rf Ю N CD —н
^, _____ CS, CM CMCMCMCMCMCM COCOCOCOCOCO CO ^ ^ rf ^f rf rfCMLO
00 00 00 CD —« CO
CO Ю —> CO О CM
N CD СО Ю Ю ^
см см см см см см
LO CD CM CD О Ю
oooooo
CO CO CM *— — О
см см см см см см
LO CD N 00 CD —
^ЮСОЬООО
CO LO Ь- О CM LO
— CD CO LO CD N
CM CM CM CM CM CM
CO — LO 00 CM LO
CO О — CM ^ LO
см со со со со со
CD CO 00 rf CD —■
CD 00 CD —« CM ^f
CO CO CO rf rf rf
LO О LO
LO N- 00
rf rf ^f
CMCMCMCMCMCM CMCMCMCMCMCM CMCMCMCMCMCM CMCMCMCMCMCM CMCMCM
—' rf CO CD -rf N
Ю О Ю CD CO CD
—■ — О CD CD 00
rf ^f rf CO CO CO
^N^NCDO
CD —< CO rf Ю CD
NN CD LO rf cO
CO CO CO CO CO CO
—• N —. О 00 CM
CD LO LO rf CM *-н
CM —' О CD CO N
CO CO CO CM CM CM
LO LO rf CM CD LO
CD N LO CO О 00
LO rf CO CM —ч CD
CM CM CM CM CM —«
oooooo oooooo
oooooo
oooooo
CM CD N
CD CO —'
OONCD
О CM rf LO N- CD
CD ^ CM О 00 CO
CD О — CM CM CO
Ю CD CD CD CD CD
О CM rf Ю N- CD
ЮсО-нСПМО
rf LO CO CD N 00
CD CD CD CD CD CO
О CM CO LO N 00
rf CM О 00 CD rf
coo —« —' см со
CD N N NN N
О CM CO LO N 00
CO '—« CD N Ю CO
rf LO Ю CD N 00
N NN NN N
OOOOOO OOOOOO OOOOOO
OOOOOO
о см со
CM О 00
CDO О
N 00 00
CO CD О О CD CO
CD CM CO CD —■ rf
N N CO LO LO rf
CO 00 00 00 00 00
—н rf CD N LO CM
N CD —« CO LO h-
CO CM CM — О CD
00 CO 00 00 00 N
N CD О CD LO О
00 CD — — CM CO
00 NN CD LO rf
N NN NN N
—. —« со см со см
CO CO CM CM —■ О
CO CM —« О CD 00
NN NN CD CD
CO О CD
00 N rf
CD LO rf
CD CD CO
oooooo oooooo oooooo oooooo
N CD N О 00 CO
OOOIO-hOO
CO rf со *-> CD N
NN NN CO CO
rf CM N CD О CD
CD 00 CO rf CO О
rf CM О 00 CD rf
CD CO CO LO LO LO
N rf ^ CO COCO
00 CO rf __ CD N
—« CD N LO CM О
LO rf rf ^f Tf rf
LO N CO О *— CO
Ю CO CM t-h О CD
CO CO rf CM О N
CO CO CO CO CO CM
LO О CD
CD О О
Ю rf CM
CM CM CM
oooooo-
oooooo oooooo oooooo
N CD О CD N rf
rf rf LO rf rf rf
rf CO CM — О CD
CD CO CD CO CD LO
CD CO CD NN CO
CO CO CM —< О CD
00 N COLO rf CM
LO LO Ю LO Ю LO
CO CD rf N CD О
00 CO LO CO — О
-- О CD 00 N CO
LO LO rf rf Tf rf
CD N rf CD CO CO
N LO CO О 00 LO
rf CO CM —■ CD 00
rf rf Tf rf CO CO
OOOOOO OOOOOO
oooooo
oooooo
NN CO
CM CD CD
N Ю rf
со со со
CO CM 00 Ю rf rf
CO — 00 CO rf CM
CO CM О CD 00 N
CO CO CO CM CM CM
CO CD rf —. о *-<
О 00 N CO LO rf
CD rf CO CM — О
CM CM CM CM CM CM
rf О NN О LO
со со см см со со
CD 00 N CO LO rf
CM CO CO CM —i CO
rf LO CD СО О CM
CO CM — О О CD
CO CO N
rf N О
00 N N
OOO
OOOOOO OOOOOO OOOOOO OOOOOO OOO
CM О О СО О CD — N LO CD CM —«
LO rf CO CM CM —« CMCMCOrfCOOO
— О CD 00 N CO Ю rf CO CM —« О
CM CM —' —' '— —' —* —,_____-, _
CMNCONCMO —" CO rf LO CD CO COCDlO
OCMLOOOCMCO OrfCDrfCDlO —« N rf
О CD 00 NN CO CO LO rf ^ CO CO CO CM CM
—■ О ОООО OOOOOO OOO
OOOOOO
CD CO О CM rf CO
rf rf lO LO LO LO
oooooo
00 О CM rf CO CO
LO CO CO CO CO CD
OOOOOO
О CM rf CD 00 О
N NN NN 00
OOOOOO
CM rf CO CO О CM
00 00 00 00 CD CD
OOO
rf CO 00
CD CD CD
42 M. E. Дейч
657
<
*o
#
5
■э-
, о
ULT
CN О ^f СО Ю "*
СО -О СО Г- О) СМ
! — СМ СО *Ф Ю С--
со со со со со со
CO Ю —■ -Ф -«f СО
CO О 00 CD Ю CD
GO — — CO CD h-
CO rf -34 Tf rf "^
ю ю о> о о см
о со со —< со см
Ю Ю Ю СО CD N
LO 00
CD 00 CD CD t--
О — CD CM СО О
00 CD О ^f Ю
— ~- CN
CD —. h- СО СМ СО
t СО - О О Ю
о о о о о о
M^CDOOO^
Ю Ю Ю Ю СО СО
Ь CD N 00 Ю N
Ю Ю О « CO LO
о о о о о о
СО Ю 00 О CM rf
СО CD CD t-- l— Ь-
Ю —• СО СМ СО 00
CMOCO^'tO
о о о о о о
^ О CM LO 00 СМ
Ь. 00 00 00 00 О»
00 ^ CN CM 00 —
rf LO ^f CO О CM
о о о о о о
юо^осло
О О О —« —< СО
CD —• 00 ^ CD Ю
С^Ю — ^ОСО
о о о о о о
00 t-- О- СО СО Ю
CD\Jb О Ю ~ СО
О —н СО rf СО t-^
LTD Ю Ю Ю Ю Ю
СМ СМ СМ СМ СМ СМ
f- 00 —< 00 t"*- О
CD t-- СО *Ф СО СО
^ СО СМ —| О О)
оо оо о о
lONOOOC^CO
CD -«f CM — CD t--
—i CM CO -rf ^f Ю
00 00 00 00 00 00
О СО — Ю CD СМ
О СМ Ю —' СО О
о о о о о о
Ю "Ф СО СО СМ СМ
(М N СО 05 ^ О
О) О С1 СО Ю N
Ю СО СО CD CO CD
СМ СМ СМ СМ СМ СМ
N00LC Ю^ N
СМ СМ СО ^Г СО 00
00 t-- СО Ю т}« СО
О О О О ОО
О О О О О О
Ю CD 00 О — СО
LO СО —' О О СО
CDN00O1QO
00 00 00 00 00 О»
Ю NSCDCON
см -^ о см -rf ю
о о о о о о
— — — О О» 00
CD CM CD Ю — f-
00 О —' СО LO CD
CD h~ Ь- t-- h- t^
см см см см см см
00 ^f 00 CD l^ CM
- Ю CD ^ О N
CO CM —■ —< — О
О ОО О О О
о о о о о о
Ю СО 00 О О СО
—1 О) СО СО rf Ю
CD О О О О Oi
00 t-- ^ — Ю
о о о о о w
00 h~ СО -Ф СМ
^ONCOOOO
ОО О —< СО Ю Ю
N 00 00 00 00 00
СМ СМ СМ СМ СМ СМ
см
ЮЮ-нСОО
о о о о о
о о о оо о
о о о о о
юсоооо-н
СО —. CD 00 СО
СО l^ t-- 00 CD
CD CD O CD CD О
oooooo oooooo oooooo ooooo*—
CM CD CO CM 00 CO
CO — О CD t^- CD
CD CO CD LO LO LO
h- О СО Ю CO CD
00 CO CO O) — CM
•^ CO —< CD OO CO
LTD LO LO ^f -Ф ^
CM ^f ^f 00 Tf 00
CO CM О CO — CO
•^ CM О С"- LO CM
rf -rf ^T CO CO CO
CO О О Tf CM
CO CD О CD CO
CD LO — CO CD
CM CM CM — О О
oooooo oooooo oooooo ooooo
CO Ю CM CD 00 00
CM т1 t-- О ^ CD
О 00 CO LO CO —-
CM ——-—'—' —«
LO О LO 00 О CM
LO CM CD h- t>- t--
О CD N CO Ю f
-*0 О ОО О
CO ^ LO LO Tf CO
CO О CO t^ CN 00
COCOM^-hO
oooooo
CM Ю
*-< CD CM CO О
LO CM — О О
ooooo
oooooo
оооооо oooooo oooooo ooooo
COCD^NCDO
CO CD CO CM 00 Ю
CO —• О CD b. CD
со со со см см см
CDN^CDCOCD
OCOWNCOOO
LO CO CN О CD h-
CM CM CM CM —* —«
t^ t^ CD CO CD ^f
COOCOOOOCNN
CO^CO-^000
N05005N
—« Ю О CO О
oooooo
oooooo oooooo
oooooo ooooo
—« CD О ^ — —«
^ t*- CM CD —' СО
ЮЮЮ^^СО
oooooo
ЮСОСОЬ^Ю
— t-- CO CD CD CO
CO CM CM —• *-< *—
oooooo
ооююсо^со
О 00 CO ^ CO CN
— о о о о о
oooooo
ю
CM CD О
^ CD СО О О
— О ОО О
о о о о о
oooooo
oooooo
oooooo
oooooo ooooo
^f Ю CD CO LO CD
^00LOCO«CD
CM —< *-, —, —, О
oooooo
CD LO CN — CN Tf
ЬСОЮ^СО CN
OOOOOO
OOOOOO
00 CO CD CD Tf CN
—« —« О О О О
OOOOOO
oooooo
см
^ — о
— о о о
о о о о
о оо о
oooooo
oooooo oooooo
oooooo
о о оо
О СМ 'Ф CD 00 О
о о о о о —
^ СО 00 О СМ 'Ф
см см см со со со
CD
CD 00 О CM Tf ^f
СО СО Tt* ^ rj« Tt*
CN CM CM CN CN CN CN CM CN CM CM CM CM CM CN CM CM CN CM CN CN CM CM CM
658
OCOOOCOO N- ^ CM О 00 О Ю ^ ^ -^< Ю О NCn^OOin О к~ ^-й
OONl^^rOtN OOlOOMCt CO CM — О О 00 Ь- О О LO *Ф ^f< ^сосл
— СО Ю Ь- О — СО ^ О 00 О СМ ^ О 00 О — СО ЮЬО-^Ю N- О ~
О О О О О — —■ — —^- СМ СМ СМ СМ СМ СО СО СО СО СО СО ^ -* -=f •^•^'Ю
oooooo oooooo ooo о~о ooo о'о" о" о" о~о~о~
МММ МММ I М I I I ММ
I I
СО О СО — СО О 00 — О СМ О Ю О СМ —' СО —' — ООО
СМ О О О О О O^COOlNNN — 00 О ^ — СМ О СО СМ Ю О О ЮОСО
О О CM CO LO 00 О -* 00 СМ О — N СМ 00 Ю СМ О CD Tf W О 00 N О Ю ^
OOOOOO — — —< CM CM CO CO<t^LOCDt£> t-- 00 О О О — CMCO^
oooooo oooooo oooooo ooo — —^ — — — —
о o~o~o~o o~ о о о о о о" о~о о о~о~о oooooo о о" о"
СМ^Ь-О — С0О00 —'CMLOh- — COtOOlO CN^N05-< COOCOO
S^-нООСОсО О t-- Ю CM О О CO —'00Ю NO N^-nOOtDcO О N Ю
О —< CM CM CO ^ Ю LO О N t-- OO О О О — CM CO rO'tlOLOCDN OOOOO
OOOOOO OOOOOO О — — — — — — — — —^ — — — —^ —
oooooo о oooooo oooooo о о ооо~о ooo
СМ СМ СМ СМ СМ — *-- — О О О 00 OONCDlO^CO W^OONtO LO CO CM
nnnnni^ n-nnnoo oooooo о о о ю lo lo loiolo
oooooo oooooo oooooo oooooo ooo
N О О
00(£)Tt-^O CM —' 00 О CM О CM —■ О LO О О CO — CO 00 h- О CO — —
— CO LO N- 00 О — CM CM N CO CM CM — О b- LO CM 00 Co Q CO N О СО СО О
СОООСМЮО (МЮОО-^h OCOLOOO — -=f О ^ — *Ф О О — Ю LO
OOO——— CM CM CM CO CO CO -* ^f -^ ^ LO Ю ЮЮОООО h-NN
о^о^о^сГо^о"" о о o~o o~o" ooo o~o~o oooooo' o~o o"
О 00 Ю CM N — ^NOOOONIO CMOOCOOO— CM— ON^O -* N- О
OOOOOOOO t-- О LO ^ CO CM — О 00 О ^ СО —• О h- -3< CM О h-^CM
OOOOOO OOOOOO 00000000000 00NN-h-t--O OOO
oooooo oooooo oooooo oooooo ooo
о o*o ooo o~o oooo oooooo о o~o ooo ooo
00 CO LO W Ь N LO 00 О Ь- — CM ОСО^СМООО О — CO CO О CO "^ CM 00
О О 00 N- Ю CO — 00 О CM О LO О О — О О ^ ООСМЮОООСО ION00
OOOOOO C0 00 0OOONN h- О О Ю LO -*f CO CO CM — —' O OOON
OOOOOO OOOOOO OOOOOO OOOOOO OOOOOO
o~ o~o~ o~ o~o oooooo oooooo oooooo ooo
«4 5
00 —' О ^ ^ О ОЮ00ООО CO -* — ^ CO 00 О N О — — —« СМОСО
OOOOOO— ОЮ- h-СМЬ- СМООСООСО ОСМ^ЮЮО OlOLO
OOOOOO OOOOCXINNCD О LO Ю ^ CO CM CM — OCDOON О Ю *Ф
oooooo oooooo oooooo ooooooooo oooooo
oo~o~o'oo oooooo oooooo о oooooo ooo
CMrhOOOOCM ^OOOOCM^f О 00 О CM ^ О 00 О CM ^ О 00 О CM ^
OOOO — — — — — CM CM CM CMCMCOCOCOCO CO ^ M< -* ^ ^ lOLOLO
oooooo" o~o о о о о о о о о~о~о о' о~о~о о о о а<^>
42*
659
£
♦о
о
JUL/
Us
°"
кк
О- О
н*
<<
СМ —i — CM rf Ь-
СО СО СО СО СО СО
СО Ю N CD —' СО
oooooo
МММ
1 1 1 1 М
СМ N СО О 00 CD
rf СО СО СО О) СМ
Ю CD N 00 CD О
oooooo"
CM CD CD СО —< 00
О О *— СМ СО СО
СМ CM СМ СМ СМ СМ
OOOOOO
ОСОЬЮСО-н
Ю ^f rf 'ф ^h 'ф
oooooo
СО 00 Ю CM CO CO
СО Ю ^ СМ CD LO
N CD —« СО ^t4 CD
NN 00 00 00 00
OOOOOO
— — О CD CD CM
CD CD CO CD CO CO
LO Ю Ю ^ ^ -*f
CD CD CD CD CD CD
OOOOOO
О О CD rf 00 CD
О — — CM CM CM
N CD Ю rt< CO CM
00 00 00 00 00 00
oooooo
^ CO CD CM CO О
-* CO — О 00 CD
CO CM —- О 00 N
0O0O0O0ONN
OOOOOO
CO 00 О CM -<f CO
LO LO CD CO CO CD
oooooo
"^ rf LO CD N OO
LO N О —■ Ю Ю
CD CDCDN N N
OOOOOO
МММ
МММ
^(N000^0
CM CM CM — — —
— CM CO -^ LO CD
CM CM CM CM CM CM
oooooo
CD 00 О CM Ю N
LO CM О N -^ —
'ф LO CO CD N 00
CM CM CM CM CM CM
oooooo
CD 00 LO CO —■ CD
со со со со со см
CDOlC-iMO
О Ю OO '—■ CM CO
00 CD О CM CO ^
00 00 CD CD CD CD
OOOOOO
Г- ' rf CD N CD
CD CD CM 00 -* О
со со со см см см
CD CD CD CD CD CD
OOOOOO
t^. rf CD —' CM —н
CM CM —- —< CD CD
«OCOOOSlO
00 00NNN N
CD CD CDCDCD CD
l> ' ^ CO CM CD
CO — 00 Ю CM 00
CD Ю CO CM — CD
Г-. r-. t- N N CO
oooooo
00 О CM rj« CD 00
CD N N N N N
OOOOOO
CM CO О N LO rf*
CD О CM CO Ю N
N OO CM ^ CD 00
N0O0O0O0O0O
О CDCD CDCD О
II 1 M 1
МММ
LO CD —■ —■ О Ю
О CD CD 00 N Ю
NN00QO-
CM CM CM CM CO CO
OOOOOO
CD —« ^ CD 00 О
00 CD CO О N LO
00 CD О — — CM
см см со со со со
oooooo
CM CM CM •—■ •—■ —
oooooo
CO CM CM — CO -^
со см о n со со
LO CD N N 00 CO
CD CD CD CD CD CD
OOOOOO
to со о со о со
CD CM 00 LO CD 'ф
««ООФО)
CD CD CD CD 00 00
OOOOOO
00 'Ф 00 О CM CM
N CD ^f CO — CD
^ CO CM — О CO
t^ t^ t^. t^. t^- CD
oooooo
"«f 00 '—■ CO ^ т^
OONlO^ CO —
CD CO CD CD CD CO
oooooo
О CM -*f CD 00 О
00 00 00 00 00 CD
CD CD CD CD CD CD
CO CD ^ —н О —<
CD —i^NOCO
О СО Ю N О CM
CD CD CD CD О О
1М1°г
О
1 ' l '*ь
CD О CD Ю N CD
CO CM CD N "* —'
CM CO CO -^ Ю CD
со со со со со со
CDCD CDCD CDCD
CO LO N CD CM rf
CM CD CD CO —< 00
CO CO ^ LO CD CD
со со со со со со
OOOOOO
О
— CD CD CO О N
— О О О О CD
CD CD CD CD CD СП
LO 00 CM CD О Ю
CM Ю 00 CD О CD
CD CD CD CD О CD
CD CD CD CD О CD
CD CD CD CD ~ CD
CD N OO N CD CO
CD -^ CD 'ф CD -^
OO OO N N CD ^D
00 00 00 00 00 00
oooooo
—< CD Ю —i CD О
N -*f CM О N LO
N CD LO -^ CM —
CD CO CD CD CD CD
OOOOOO
CO CM О CD N LO
CM 00 ^ CD LO —н
О 00 N Ю -*f CO
CO Ю LO LO LO Ю
oooooo
CM 'Ф CO 00 О CM
CD CD CD CD О О
CD CD ^
^t4 CO CD
OOO
О LO LO
CO LO CM
OOO
О О —
CM CD CO
LO О О
OOO
CM CD CO
N CD CO
CO LO CO
00 "xT О
CD N 00
со со со
OOO
CD 00 О
to см о
N 00 CD
со со со
OOO
CD N rf
COON
CD CD 00
CD CD CD
OOO
CM О 00
00 CO CM
CD CD CD
CD CD CD
OOO
CD ^ CD
00 CO N
Ю LO ^
OO 00 00
CD CD CD
^Ф N CD
CM CD CD
COON
CD LO Ю
OOO
-tf1 CM •—■
N CO CD
— О CO
LO LO ^f
CD CD CD
•*? CD ОС
OOO
660
199
440)0)0)0)0)01 Ol Ol Ol Ol 4^ ►£>. 4^ 4^ 4^ СО СО СО СО СО to tO tO tO tO '— '— — — >—
tOOGOO)^lOOOO ОЗ 4^ЮС00СП 4^ tO О 00 О) 4^ ЮОООСП^Ю О00О)^ЮО
CDCDCDCDCDCDCDCD OOOOOO OOOOOO CD CD CD CD CD CD OOOOOO
— — — >— — "-* ~ — — Ю Ю tO tO tO tOtOtOtOOOOO O0 CO CO CO O0 "bo 4^ 4^ 4^ 4^ 4^ 4^
ts2t0^^OlO400 (DO- tO 00 4^ UlOiNjCDO^ Ю СОСЛО) Ч UD О — CO 4^ О) 4
O000)0lC0t0 — — — — — — tO O0 Ol O) 00 О tO 4^ 4 CD Ю СЛ СО Ю СЛ CO GO 4 ^- СЛ
CD400t0004C04^ — — 4^ CD 4 GO О OHO — CO 4 tO CO 00 CD — Ol О O) CO — — О
OOOOOOOO CD CD О О О О OOOOOO OOOOOO OOOOOO
— tOtOtOtOtOtOlO tOtOOOOOOOOO О0О0О0О0О0Ф- 4^^4^4^4^4^ ^ СЛ СЛ СП СП СЛ
COO'— tO CO 4^ СЛ О) 00 CD О — tO CO 4^ O) 4 CD CO »—' tO CO 4^ O) 4 00 CO'— tO CO Ol O)
0)0)0)0)0)4 00 10 О — tO 4^ Ol 4 CO1— 000)000 CO O) 00 — 4^ 4 CO tO O) 00 — 4^
СО0)О1О)СО^-С OtOO)tO00O) СЛО)0004^СО 4^ О S ^ Ю О 00 4 OO 4^ W ь-
OOOOOOOO OOOOOO CD CD CD CD CD CD CD CD CD CD CD CD CD CD CD CD CD CD
CJ)CJ)CJ)CJ)CJ)CJ)CJ)CJ) О) О) О) 4 4 4 4 4 4 4 4 4 4 4 4 4 4 00 000000000000
>-ЮОЗ^^СЛО)4 00 CO CO О — tO tO CO 4^ Ol Ol O) 4 S 00 CO CO О — — tO CO CO 4^
4^ CO — О CO 4 O) 4^ tOOOOO)4^tO CO 4 4^ —* 00 СЛ tO CO O) tO CO СЛ tO 00 4^ О О) Ю
— — CO O) tO 4 — 4^ 0)40)01000 Ol О 4^ O) 00 GO 4 O) W CO 4^ CO tO 4^ Ol Ol 4^ tO
OOOOOOOO OOOOOO CD CDCD CD CD CD CD CD CD CD CD CD OOOOOO
СЛСЛСЛСЛО)0)0)0) 0)44444 ОООООООООООО GO CO CO ^D CO CO CO CD CO CO CO CO
О0СП4СО1— СОСД4 CD — CO Ol O) 00 О — CO 4^ О) 4 CO О — Ю СО 4^ СПО)440000
CO CD CD CO CD 00 00 4 O) 4^ tO — 00 Ol t0000000004 О00СЛО)4О) Ol 4^ CO GO CO GO
0)0)СЛ4^ — 40t0 — O) CD О CO 4^ О tO 00 CO 4^ CO 00tOtO4^O4 00040004
OOOOOOOO OOOOOO OOOOOO OOOOOO OOOOOO
OOOOOOOOOOOOOOOO OOOOOOCDCOCD СОСОСОСОСОСО СОСОСОСОСОСО СОСОСОСОСОСО
4^4^01010)0)400 OOCOCOOO— - Ю Ю Ю CO CO 4^ 4^ Ol Ol Ol O) 0)4440000
OO)t0004^C00lO CF> ~ 0~) <—> <J~> ~* 01001(0 4^00 tO О) О 4^ GO tO 0)ОСОЧ04^
4^0l4^COOtOtOO) О tO CO 4^ CO tO CO O) tO 4 — 4^ 400COC0004 4^ ' ^W4-
OOOOOOOO OOOOOO CD CD CD CD CDCD OOOOOO OOOOOO
0)0)0)0101010101 OlOlOlOlOlOl Ol Ol Ol 4*- 4^ 4^ 4^4^4^4^4^4^ 4^4^4^4^4^O0'
tO—' О CD CO 00 4 4 0)Ol4^4^00tO Ю — О CD CD 00 40)0)014^4^ CO tO — — О CO
— 4^0)CDtOOl40 COCDCO — 4^ 4 О tO Ol 00 — CO O) CD tO Ol 4 О CO O) GO — 4^ 4
Ю04СЛСО-00 0) 4^t0040lCO — 00 O) 4^ tO CO 4 Ol CO — 00 O) 4^ tO CD 4 Ol CO
OOOOOOOO CD CD CD CD CD CD CD CD CD CD CD CD CD CD CD CD CD CD OOOOOO
WCO COCOCO 00 COW CO CO CO CO 4^ 4^
^C4?'^CJ]l<53^"^'^ 00 CO CO CO О О О ►
4^4^4^4>4^4^ 4^4^4^Ф^4^4^ 4^4^4^000000
.. _. „ , о — — — — —— — — — — OOO4^CDCD00
CO40ltOO400C0 OlOOlCDCOO) CD tO 4^ Ol O) 4 4 O) Ol 4^ Ю CO 0)00001001
tOOl4^CDtOOOlOl tO4^tOO)4^00 4— — OlOlO О Ol Ol О ' vj GO СЛ О) СЛ CO 00
tO Ю CO CO CO CO CO W ОООООООООООО O04^4^4^4^4^ 4^4^4^4^0101 OlOlOlOlOiO)
COCQO — — tOCOCO 4^010)0)400 CO О — tO CO 4^ OlO)4CDOtO CO Ol 4 CD — CO
OOOOOOOO OOOOOO OOOOOO OOOOOO OOOOOO
— OlC004^tO- Ol 00000014^00 COtOiOtOtOtO CO hp* Ol — CO О CO — OOOtO
Cnt0000400000 CO OO GO О) О) 4 О О 4^ 00 CO 4 СЛ Ol CO О» 00 СХ> СОСОСЛО^О)
COtOtOtOtOtOtOtOtOtO'— '— — "—' н— н— н— _*н— н-
O004O)Ol4^00tO —000000)01 4^4^COtO — О CD00440)01 4^ 4^ CO to tO ~
OOOOOOOO OOOOOO OOOOOO OOOOOO OOOOOO
OOl4^COtOtO-О ООСП0 0101 Ol О — О — — CO 4^ СЛ О tO CO Ol — tO Ol tO Ol
4O1400CD — OlOO 0)СП4^ОС0С0 Ю 4^ 4 ^ GO O) tO 4^ tO CO О 4 tO CD CO ^ СЛ СЛ
ЮЮ--Н-Н--,- ^_ _- — h— H— — ~ h— — — h— — — к- — — h— — ^- — _- _* _- ►—
О О CO CO GO ОоЪо~4 VjVlOiVo) O) o/oi 014^4^4^ 4^ CO OO CO tO tO tO tO — — — —
4^O400CDO)tOCD 0)tOCDO)000 4 4^» — 00 Ol tO О 4 4^ — CO O) 4^-CDO)^1—
400 — 4^0000004^ — OO O) 4> OO tO tO Ю OO 4J* O) 00 О CO O) CO CO 4 tO O) — CO tO 00
CD CD t-- Oi CN CD
00 CN CD ОЮ СП
О —н —i CM CN CN
— 00 CDiO Ю N-
•^ 00 CO 00 CO 00
CO CO rf rf LO LO
^ СП LO —« t-- CO
CD CD b- 00 00 05
rf CO LO Oi N- 00
QO«(M(Nco
CN CN CN ON CN CN CN CN CN CN CN CN CN CN CN CN CN CN CO CO CO CO CO CO
CO CN CO CD rf CD
Ю CN CO О *— CO
I
. °
AXf
« J CS
o»
1 °
e.| 5
r<
t^- CO СП LO CN СП
CO О CM LO CN rj«
о о о о о о
00 00 Г»- CD CD LO
CN CN CN CN CN 00
t-- СП 00 CD — -^
О -' (N CO t rf
CN-OCnoON
CO CO CO CN CN CN
О О О О О О
т^ CD СП —н СО Ю
ООЮСМОЬ^
CN СО ^ Ю LO CD
CD CD CD CD CD CD
О О О О О О
CN 05 rf СП CN ^f
^ Г-- —< "«f 00 —
CO CN CN — О О
00 00 00 00 00 00
о о о о о о
CD CD CD 00 О ^
СП СП СП 05 О О
—< СП t^- Ю ^t< CN
LO Tf ^f -^ ^ "«f
О ОО О О О
LO CD CD t-- 00 00
О СП 00 t- CD LO
CD LO LO LO LO Ю
О О О О О О
rf —н —н СО t^- -^
ЬООСПО'-'СО
00 t^- CD CD LO ^
О О О О О О
CN CD 00 b-
-* CN CN Ю —« О
СО CD СП CN Ь- О
— О СП СП 00 00
~ — О О О О
О О ОО О О
^CDOO OCN 't
Ь- t^- t^- 00 00 00
t^- 05 rf rf 00 "«f
—- -* —■ rf —' тр
о о о о о о
Ю ^ "*Р СО СО CN
CN CN CN CN CN CN
ЮЮЮ'Ф —'СП
•^^^^^со
CD LO -^ CO CN —<
CN CN CN CN CN CN
О О О О О О
1^- О CN -* CD СП
— СП CD СО О t>~
NN00 05OO
CD CD CD CD t-- h-
O О О О О О
^t4 CO ~ t-- CNIO
-хТ t>~ О CN Ю Г--
05 00 00 l>- CD Ю
t— t— l>— t— t— t^-
О О О О О О
OOOOO^NN
—■ —• CN "*Р LO Г-
О 00 CD 'Ф CN О
^ со со со со со
ОО О О О О
00 О ~* CN -н СП
00 СП СП 05 О 00
-* СО CN —н О СП
ЮСОЮЮЮ^
о о о о о о
СО ^Р 00 LO rj« Ю
Ю t— 05 CN LO 00
CO CN —. —< О СП
О О О О О О
rf О —' О rj« Ю
CN t-- -Ф ^Р CD —«
rf 00 СО 00 СО СП
t^- CD CD LO LO тр
О О О О О О
о оо о о о
CD00O(Mrt(D
00 00 СП СП СП СП
СП CD Ь- СП —< rf
о о о о о о
(М-н-ООО)
CN CN CN CN CN *—
t>~ *Ф СО CN CN СО
со со со со со со
О СП 00 t- CD LO
О О О О О О
—■ СО Ю 00 О CN
LO CN СП CD ^f *—
—н CN CN СО -Ф Ю
t— Г-- t— t— t— t—
<CO <C0 СС0 CZT> <СО СС0
CD CD ^ —н CD СП
СП —и СО LO CD t--
^ ^ CO CN ^ О
ь-1*- ь- ь-1--t>~
cd cd cd cd cd cd
о t-- ю со со оо
О CN СП СП СО t>~
СП t-- LO CO CN О
CN CN CN CN CN CN
О О О О О О
ьсооомю^
ОО 00 Г»- Г»- CD LO
оо t-- cd ю -*f со
•rp -rp "^ •ф тр "'Jf
О О О О О О
—< CD CD CO ^f —■
С5Ю ^CDON
— LO 05 CO 00 CN
05 00 t— l>- CD CD
О О О О О О
о о о о о о
—< CN t>~ CD 00 CN
СП СП —■ CD СО СО
i'ONCOON
'Ф тр СО СО СО CN
cd cd cd cd cd cd
о о о оо о
00 О CN -Ф CD 00
СП CD CD CD CD CD
—' CN CN CN CN CN
CD СП CN CD СП СО
CN LO CO О CO T-<
О О О О О О
05 00 00 00 Ь- t^
LO
О ^ 00 Ь- 05 СО
СО ^t4 "st4 LO CD 00
rf CO CN —• О 05
О О О О О О
rf CD СП — СО Ю
OOIOCNON^
LO CD N 00 00 СП
ь-1--t^- ь-1--1^.
О О О О О О
СП 00 LO О CN CN
00 050 — ^ —
О О0 ОО l>- CD LO
CD CD CD CD CD CD
О О О О О О
00 rj« тр —< CN О
CN ОО тр *— О0 CD
05 Ь- CD Ю СО CN
О О О О О О
00 ОО i>- LO — t>~
-* СО CN — О 00
CN — О СП 00 CD
rf rf -^ со со со
О О О О О О
CN О CN СП 05 LO
CD 00 CN 00 1^ 05
Ь- CN 00 СО 05 Ю
•^ LO "* ^ СО СО
CD CD CD CD CD CD
CD CD CD CD CD CD
00 LO CN 00 CO LO
^ OO •*? — — CN
^-OiNlOCO
CN CN -и -и — —
о о о о о o
о о оо о о
О CN Th CD 00 О
CN CN CN CN CN CN
^f CO N- N- О) CO
ЮЮ^ ^lOCD
^Г Ю СО N- 30 СП
— 00 СО N- -^ СО
00 О тГ ОО •*? —'
О О) СО "* CD ОО
О
00 О СО — СП ^
СЛОС0 N^t Ю
СП СЧ -^ СО СП СМ
h^ СП —■ СЧ — —■
СЧ -^ Ю CD СО -^
СО О Ю *—■ СП СП
со со со со со со
^^^^"t^
-ФЮЮЮЮСО CD N- N- 00 00 СП
—• СО N. СМ
О *— CO CD -^ о
О СП —н СЧ —н —■
СО СЧ СО Ю СО LO
о о о о о о
CD 00 О СЧ -^ CD
N- t^ 00 00 00 00
rf -^ ОО OA •*? N
О СЧ тГ СЧ Ю CO
СП —' CO CD ОО —■
00 СП СП СП СП О
СЧ СЧ СО СЧ СО ^
о о о о о о
00 Ю N- СП СЧ
О СЧ т}< —. —,
о о о о о
СО —« N 1ч. СП
СЧ СО СО -^ Ю
СОСОЮЮЮ'Ф
—i LO СП СЧ СО СП
— Tt —■ Ю СЧ LQ
о о о о о о
-^ СО СО СЧ СЧ '—«
СЧ Ю t-- СП О —>
СО О СО О •* —
— — О О СП СП
— СП СО СЧ Ю СО
^ о со о сч ^
о о о о о о
00 00 t>- N- СО Ю
СО -* СО СО
О —- — тГ ,
Ю -^ СО —i
00 О 00 СО — СО
О — Tf СЧ СО N-
СП 00 N- CD CD LO
О О О О О О
О -* N- г^ О0
со оо •*? сч сп n
ь- — со ю со сч
^ rf СО — СЧ СЧ
cdcd cdcocd cd
LO 00 00 00 СО
о со сч о оо сп
_ __ сч —н о о
о о —« о о о
cd cd cd •*& cd ~
^ —• — со оо -«f
^ СО СЧ —< О О
о о о о о о
о о о о о о
о о о о о о
cd cd cd cd cd cd
О т}« —
СЧ О О
оо о
о оо
о о о оо
CD CD CD CDCD CD CD CD CD CD CD CD CD CD CD
ОООСЧ-^NQ
— СП СО СО О N-
o о — сч со со
оо оо оо оо оо оо
—^ со со оо осч
Ю СЧ СП СО tF —н
'ФЮЮСОЬОО
оо оо оо оо оо оо
•*? N- СП —- СО СО
00 СП О — *— СМ
00 00 СП СП СП СП
CX)O(NVDSC0
-CncDCOON
СО СО -^ Ю СО CD
СП СП СП СП СП СП
— СО СО 00
1^ ОА СП (£)
N- ОО ОО СП
СП СП СП СП О
оооооо оооооо о оо cdcd о оооооо
о о о о -н
СП rf СО Ю — rf
ООСЛоОЬЮ
^ со —■ о сп оо
СО СО СО СО Ю Ю
СО СП —< ОО —н СП
СО О 00 ^ —1 СО
N- CD rf СО СЧ О
Ю LO LO LO LO Ю
СЧ СП О -* О СО
СЧ СО — Tf N- 00
СП N- CD ^ СЧ О
СО 00 О "«f О0 00
СП 00 ^ СО N- СП
00 СО N- СЧ СП CD
СО СО СО СО СЧ СЧ
СО СП
OONCDON
N- О -<f СО СО
СООЮООО
СЧ СЧ —н О О
ОООООО ОООООО
оооооо
оооооо
О О CDCD CD
—> со сч —-
•^f СО СП —> СП СО
-* со сч со со ю
~ О СП 00 N- СО
— — оо о о
LO N- О СЧ СП СЧ
СО СП СЧ О СО СО
N- СП СО N- ~ СО
ю ^ ^f со со сч
CD CD CD CD CD CD
CO«^OOIOCD
ООООСОСМЬЮ
—■ N- ^f —> CO tD
СЧ — -и — О О
CD CD CD CD CD CD
«CDlOCO^CO
^ CO СЧ —1 О О
ОООООО
оооооо
00
сч ю о
см о о
о о о
о о о
CD CD CD CD CD
OOOOOO CD CD CD CD CD CD OOOOOO OOOOOO
О О О
сч ю оо о о о
Г»- LO СО СЧ О ОО
LO ^f СО СЧ —' СП
со со со со со сч
00 СО СЧ N- —н Ю
Ю СО 1—1 00 СО СО
оо N со -^ со сч
сч сч сч сч сч сч
N- 00 00 N- Ю СЧ
— СП 00 N- LO -*
СО СО О
00 СО N- СП —н СЧ
-hOO^CNCO
СО —* CD СП Ь- CD
— — — О О О
N- СО 00 ^f ^
—> О N- ^ О
СП LO О СО О
t CO (M О О
о о о о о
оооооо
ОООООО CD CD CD CD CD CD
OOOOOO
CD CD CDCD CD
CO СП 00 00 '— CO
сч оо ю сч о n-
co см сч сч сч —
CD CD CD CD CDCD
00 СП СП CO rf N-
CO CM CO CO —. N-
Ю CO — СП 00 CO
— —< -н CD CD CD
OOOOOO
N- — О — CO —i
LO LO CO 00 — CO
ю ^f со сч сч —«
OOOOOO
CD CD CD CD CD CD
— 00 LO CO СЧ —н
~ CD CD CD CD CD
CD CD CD CD CD CD
CD CD CD CD CD CD
CM
LO —< О
О О О
CD CD CD
CD CD CD
CD CD CD CD CD
CD CD CD CD CD CD OOOOOO OOOOOO OOOOOO
ОО О
ЮО-OlON
LO LO CO t-- CM CM
— О 00 N- CO LO
—« ~ О О О О
ОООООО
О ^f 00 —« СЧ —
^f СО СП rf СП Ю
Tf СО СЧ СЧ —н —(
ОООООО
ОООООО
N- СП СО 00 "<f -=f
г-н 00 СО rf СО СМ
^ CD CD CD CD CD
CD CD CDCD CD CD
CD CDCD CD CD CD
CO
LO О CO CO СЧ О
-и — О О О О
ОООООО
ОООООО
CD CD CD CD CD CD
СЧ
о
о
о
о
о о о о о
оооооо оооооо
оооооо оооооо
CM rf СО 00 О СМ
СМ СМ СМ СМ СО СО
СО 00 О CM rf СО
rf rf LO LO LO Ю
00
О CM rf CO CO
N- t^ N- N- N-
см см см см см см см см см см см см см см см см см см см см см см см см см см см см см
663
ЛИТЕРАТУРА
1. Н. Е.'Ж У к о в с к и й, Видоизменение метода Кирхгофа,
Полное собрание сочинений, т. III, ОНТИ, 1936.
2. Н. Е. Жуковский, О присоединенных вихрях, Полное
собрание сочинений, т. V, ОНТИ, 1936.
3. Н. Е. Жуковский, Вихревая теория гребного винта,
Полное собрание сочинений, т. VI, ОНТИ, 1936.
4. С. А. Чаплыгин, Теория решетчатого крыла, Собрание
сочинений, т. II, Гидродинамика, Аэродинамика, Гостехиздат, 1948.
5. С. А. Чаплыгин, О газовых струях, Собрание сочинений,
т. II, ГИТТЛ, 1948.
6. Л. Г. Л о й ц я н с к и й, Механика жидкости и газа,
Гостехиздат, 1957.
7. Л. И. Седов, Плоские задачи гидродинамики и
аэродинамики, Гостехиздат, 1954.
8. Н. С. Аржаников и В. Н. Мальцев, Аэродинамика,
Оборонгиз, 1957.
9. Г. Н. Абрамович, Прикладная газовая динамика,
Гостехиздат, 1953.
10. Л. И. Седов, Методы подобия и размерности в механике,
Гостехиздат, 1950.
11. В. С. Жуковский, Техническая термодинамика,
Гостехиздат, 1952.
12. Л. А. Вулис, Термодинамика газовых потоков, Госэнер-
гоиздат, 1950.
13. Л. Прандтль, Гидроаэромеханика, Изд. иностранной
литературы, 1949.
14. Современное состояние гидроаэродинамики вязкой
жидкости, Сборник под редакцией С. Гольдштейна, Изд. иностранной
литературы, 1948.
15. Современное состояние аэродинамики больших скоростей,
Сборник под 'редакцией Р. Хоуэрта, Изд. иностранной литературы,
1955.
16. Н. Е. К о ч и н, Гидродинамическая теория решеток, ГИТТЛ,
1949.
17. Т. Карман, Сверхзвуковая аэродинамика, Изд.
иностранной литературы, 1948.
К гл. 1
1. Н. Я. Фабрикант, Аэродинамика, Гостехиздат, 1955.
2. А. П. Мельников, Основы теоретической аэродинамики,
Изд. ЛКВВИА, 1953.
К гл. 2
1. Ф. И. Ф р а н к л ь, С. А. X р и ст и а н о в и ч, Р. Н.
Алексеева, Основы газовой динамики, Труды ЦАГИ, вып. 364, 1938.
664
2. С. А. Хр и с т и а н о в и ч, В. Г. Гальперин, М. Д.
Миллионщиков, Л. А. Симонов, Прикладная газовая динамика
Изд. ЦАГИ, 1948.
3. Б. М. Киселев, Расчет одномерных газовых течении,
«Прикладная математика и механика», 1947, № 1.
К гл. 3
1. С. А. X р и с т и а н о в и ч, Обтекание тел газом при больших
дозвуковых скоростях, Труды ЦАГИ, вып. 481, 1940.
2. С. А. Христианович, О сверхзвуковых течениях газа,
Труды ЦАГИ, вып. 543, 1941.
3. А. Н. Ш е р с т ю к, Расчет крыловых .профилей при больших
дозвуковых скоростях, Известия АН СССР, ОТН, 1956, № 8.
4. Г. Ф. Б у р а г о, Теория крыловых профилей с учетом
влияния сжимаемости воздуха, Изд. ВВИА им. Н. Е. Жуковского, 1949.
5. Л. И. Седов, Плоские задачи гидродинамики и
аэродинамики, Гостехиздат, 1950.
6. Н. Я. Фабрикант, Аэродинамика, Гостехиздат, 1949.
7. Г. Ф. Б у р а г о, Б. Я. Шумяцкий, Основы теоретической
аэрогидромеханики, ч. I, Изд. ВВИА им. Н. Е. Жуковского, 1951.
8. В. С. П о л я д с к и й, Расчет распределения давления при
больших скоростях полета, Изд. Бюро новой техники, 1943.
9. Г. В. Л и п м а н, А. Е. Пакет, Введение в аэродинамику
сжимаемой жидкости, Изд. иностранной литературы, 1949.
10. Проблемы полета с большими скоростями, Сборник статей,
Изд. иностранной литературы, 1960.
К гл. 4
1. Я. И. Л е в и н с о н, Аэродинамика больших скоростей,
Оборонгиз, 1950.
2. А. Ф е р р и, Аэродинамика сверхзвуковых скоростей,
Гостехиздат, 1952.
3. Р. Зауэр, Течения сжимаемой жидкости, Изд.
иностранной литературы, 1954.
4. ,В. А. Андреев, С. 3. Беленький, Влияние
конденсации паров воды на сверхзвуковые течения, труды ЦАГИ, № 579,
БИТ, 1946.
5. F. W. Ross, The propagation in a compressible fluid of finite
oblique distrurbances with energy exchange and change of state,
Journal of Applied Physics, 1951, v. 22, № 12.
К гл. 5
1. Г. М. Бам-Зеликович, Расчет отрыва пограничного слоя,
Известия АН СССР, ОТН, 1954, № 12.
2. А. А. Гухман, А. Ф. Гандельсман, Н. В. Илюхин,
Исследование изменения коэффициента сопротивления при течении
газа со сверхзвуковой скоростью, «Теплоэнергетика», 1955, № 1.
3. А. А. Гухман, А. Ф. Гандельсман, Л. Н. Н а у р и ц,
О гидродинамическом сопротивлении в трансзвуковой области
течения ,«Теплоэнергетика», 1957, № 7.
4. М. Е. Дейч, А. Е. Зарянки н, Экспериментальное
исследование турбулентного пограничного слоя при больших дозвуковых
скоростях, «Теплоэнергетика», 1958, № 3.
665
5. М. Е.Дейч, А. Е. Зарянки н, Приближенный метод
расчета турбулентного пограничного слоя при больших скоростях,
Труды МЭИ, вып. XXX, 1958.
6. А. А. Дородницын, Пограничный слой в сжимаемом
газе, «Прикладная математика и механика», 1942, т. VI, № 6.
7. А. Е. 3 а р я н к и н, Исследование пограничного слоя в
турбинных решетках при больших скоростях, Диссертация, МЭИ, 1956.
8. Л. М. 3 ы с и н а - М о л о ж е н, О характере перехода от
ламинарного к турбулентному режиму течения в пограничном слое,
Журнал технической физики, 1955, т. XXV, вып. 7.
9. Л. Е. Калихман, Газодинамическая теория
теплопередачи, «Прикладная математика и механика», 1956, т. X.
10. Л. Е. К а л и х м а н, Турбулентный пограничный слой на
плоской пластинке, обтекаемой газом, Оборонгиз, 1954.
11. Л. Г. Л о й ц я н с к и й, Аэродинамика пограничного слоя,
Гостехиздат, 1941.
12. Е. М. Минский, Влияние турбулентности набегающего
потока на переход, Труды ЦАГИ, вып. 415, 1939.
13. А. П. Мельников, Основы теоретической аэродинамики,
Изд. ЛКВВИА, 1953.
14. Б. С. Петухов, А. С. С у к о м е л, В. С. Протопопов,
Исследование сопротивления трения и коэффициента
восстановления температуры стенки при движении газа в круглой трубе с
высокой дозвуковой скоростью, «Теплоэнергетика», 1957, № 3.
15. Г. Шлихт-инг, Теория пограничного слоя, Изд.
иностранной литературы, 1956.
16. Н: N i p p e r t, Uber den Strommungsverlust in gekrummten
Kanalen, Forschungsarbeiten auf d. Geb. (d. Ing. Wes, 1929, H. 320
17. J. P. Hartnett, E. R. Eckert., Experimental study of
the velocity and temperature distribution in a high-velocity vortex-
type flow, Transaction of the ASME, 1957, v. 79, № 4.
18. А. П. Алексеев, В. С. Мартыновский, Исследование
эффекта вихревого температурного разделения газов и паров,
Известия АН СССР, ОТН, 1956, т. 26, № 10.
19. Л. А. Вулис, Об эффекте Ранка, Известия АН СССР,
ОТН, 1956, № 10
20. М. Г. Д у б и н с к и й, О вращающихся потоках газа,
Известия АН СССР, ОТН, 1954, № 8
К гл. 6
1. В. И. А с т р о в, Е. А. Левин, Л. Д. Павлов, С. А. X р -и-
стианович, О расчете сопел Лаваля, «Прикладная математика
п механика», вып. 1, т. II, 1943.
2. А. В. Болгарский, В. К. Щукин, Рабочие процессы
в жидкостно-реактивных двигателях, Оборонгиз, 1958.
3. Н. Д. Доброхотов, Газодинамические схемы истечения
из сопла ракетного двигателя при нерасчетном давлении, 1947.
4. М. С. К и с е н к о, Сравнительные испытания нескольких
вариантов сопел, Труды ЦАГИ, вып. 478, 1940.
5. J. E. Beckwith., J. А. М о о t e 1., An accurate and rapid
method for the design of supersonic nozzles, NACA, TN, 1956,
№ 3322.
6. A. S t о d о 1 a, Dampf-und Gasturbinen, 1924.
666
К гл. 7
1. Аэродинамика, Под общей редакцией В. Ф. Дюренда,
т. III, Оборонгиз, 1940.
2. Л. П. Волкова, М. Я- Ю д е л о в и ч, Потери на ->дар
в ступенчатых трубках при сверхзвуковых отношениях давления,
Изв. АН СССР, ОТН, 1958, № 4.
3. И. Д. В и н н и к, М. П. У м а н с к и и, В. А. Черников,
Некоторые результаты аэрдинамического исследования выхлопного
патрубка транспортного газотурбинного двигателя, ,
«Энергомашиностроение», № 4, 1959.
4. А. Ш. Д о р ф м а н, М. М. Н а з а р ч у к, Н. И, Польский,
М. И. Сайковский, Аэродинамика диффузоров и выхлопных
патрубков трубо'машин, Изд. АН УССР, 1960.
5. М. Е. Дейч, А. В. Р о б о ж е в, Ф. В. Степанчук,
А. А: Ко х, Исследование структуры потока в ступени эжектора
с изобарическим начальным участком смешения,
«Теплоэнергетика», 1954, № 12.
6. М. Е. Дейч, А. В. Р о б о ж е в, А. А. Кох, Влияние
некоторых геометрических и газодинамических параметров ступени
эжектора на эффективность ее работы, Труды МЭИ, вып. XXIII,
1955.
7. М. А. Дементьев, А. К. Чертков, Гидромеханическое
исследование . вариантов выхлопного патрубка паровой турбины,
«Котлотурбостроение», 1948, № 1.
8. И. Е. И д е л ь ч и к, Гидравлические сопротивления, Госэнер-
гоиздат, 1954.
9. О. Н. Овчинников, Влияние входного профиля скорости
на работу диффузора, «Вестник машиностроения», 1954, № 6.
10. И. И. Орлов, Продувка моделей входного патрубка
осевого компрессора, «Вестник машиностроения», 1954, № 6.
11. Р. П э н к х е р с т, Д. X о л л е р, Техника эксперимента
в аэродинамических трубах, Изд. иностранной литературы, 1955.
12. Е. Я. Соколов и Н. М. Зингер, Струйные аппараты,
Госэнергоиздат, 1960.
13. Л. П. Соколовский, Исследование аэродинамики
выходных патрубков турбин и компрессоров, «Энергомашиностроение»,
1952, № 9.
14. К. С. С ц и л л а р д, Исследование диффузоров
аэродинамических труб больших скоростей, Технические заметки ЦАГИ,
№ 160, 1938.
15. Г. А. X а н и н, Некоторые вопросы аэродинамического
исследования вспомогательных элементов проточной части турбома-
шин, «Теплоэнергетика», 1955, № 1.
16. Б. Н. Юрьев, Экспериментальная аэродинамика,
Оборонгиз, 1939.
17. Ф. Клауз ер, Работа диффузоров прямоточных
реактивных двигателей при сверхзвуковых скоростях полета, «Вопросы
ракетной техники», 1954, № 2; 1955, № 1.
18. Е. Нейман, Ф. Люстверк, Сверхзвуковые диффузоры
высокой эффективности, «Вопросы ракетной техники», 1951, № 6;
1953, № 1,
667
20. С. А. X р и с т и а >н о в .и ч, О расчете эжектора,
«Промышленная аэродинамика», 1944, № 3.
21. С. А. Христ<ианович, М. Д. Миллионщиков,
Г. М. Р я б и н к о в, Ф. А. Т р е б и н, Применение эжекторов в
газосборных -сетях, Известия АН СССР, ОТН, 1946, № 3.
22 М. Н i b s, Mezikruhove difuzory, Proudeni v lopatkovych stro-
jich, Sbornik ustavu pro vyzkum stroju, 1958.
23. V. Kmonice k, Zlepseni cinnosti difusoru jednoduchymi
zasahy, Strojnicky sbornik, 1956, 13.
К гл. 8
1. E. Ax. Гукаеова, Исследование концевых потерь в
решетках турбинных профилей, Труды ЦКТИ, Аэрогидродинамика,
кн. 27, 1954.
2. М. Е. Дейч, К вопросу о концевых потерях в
направляющих каналах паровых турбин, «Советское котлотурбостроение»,
1945, № 6.
3. М. Е. Дейч, А. В. Губарев, К вопросу о «запирании»
подводящего сопла и рабочей решетки профилей в сверхзвуковом
потоке, «Теплоэнергетика, 1960, № 12.
4. М. Е. Дейч, А. В. Губарев, Исследование активных
рабочих решеток при больших скоростях», «Теплоэнергетика», 1958,
№ 12.
5. М. Е. Дейч, А. Е. 3 а р я н к и н, Г. А. Филиппов,
М. Ф. Зацепин, Повышение эффективности турбинных активных
решеток малой высоты, «Теплоэнергетика», 1960, № 9.
6. М. Е. Дейч, А. Е. 3 а р я н к и н, Приближенный метод
расчета концевых потерь, «Теплоэнергетика», 1958, № 9.
7. М. Е. Дейч, Г. С. С а м о й л о в и ч, Основы аэродинамики
осевых турбо'машин, Машгиз, 1959.
8. М. Е. Дейч, В. В. Фролов, А. В. Губарев,
Исследование новых профилей решеток регулирующих ступеней и ступеней
давления турбин, «Теплоэнергетика», 1956, № 5.
9. М. Е. Дейч, К- А. Розанов, В. В. Фролов,
Исследование и улучшение профилей двухвенечной регулирующей ступени,
Труды МЭИ, вып. 23, 1955.
10. М. Е. Дейч, А. Е. 3 а р я н к и н, Исследование и улучше- '
ние сопловых «решеток регулирующих ступеней, «Теплоэнергетика»,
1955, № 10.
11. М. И .Жуковский, Расчет обтекания решеток профилей
турбомашин, Машгиз, 1960.
12. М. И. Жуковский, Н. А. С к н а р ь, К вопросу о
применении утолщенных кромок 'направляющих лопаток,
«Энергомашиностроение», 1957, № 2.
13. М. И. Жуковский, Н. А. Скнарь, Новые решетки
турбинных профилей, «Теплоэнергетика», 1955, № Г.
14. В. И. Кирсанов, Об улучшении турбинных реактивных
решеток профилей на основе исследования характера их
обтекания при изменении режима работы по числу М и числу Re,
Известия АН СССР ОТН, 1954, № 7.
15. Г. С. С а м о й л о в и ч, Расчет потенциального потока
в криволинейном канале, «Теплоэнергетика», 1954, № 7,
668
16. Г. Ю. Степанов, Гидродинамические исследования
турбинных решеток, «Обзорный бюллетень авиамоторостроения», 1949,
№ 4 и 5.
17. Г. Ю. Степанов, Основы теории лопаточных машин,
комбинированных и газотурбинных двигателей, Машгиз, L958.
18. Н. М. Марков, Расчет аэродинамических характеристик
лопаточного аппарата турбомашин, Машгиз, 1955.
19. И. Д. Л я х о в и ц к и и, Турбулентность потока в турбинной
ступени и профильные потери активных лопаток, «Известия ВТИ»,
1950, № 5.
20. Н. Г. Родин, О концевых потерях энергии в решетках
турбинных лопаток, Труды Л ПИ, 1951, № 1.
21. О. Н. Е м и н, Вторичное течение и потери при движении
жидкости на повороте, Труды МАИ, вып. 68, 1956.
22. А. Н. Ш е р с т ю к, К определению потерь в турбинных
решетках с утолщенньпми выходными кромками, «Теплоэнерретика»,
1959, № 6.
23. А. Н. Ш е р с т ю к, Приближенный метод расчета
криволинейных каналов, «Теплоэнергетика», 1955, № 8.
24. Г. Ф л юг ель, Паровые турбины, ГОНТИ, 1939.
25. Л. Велик, Применение теоретических и
экспериментальных методов при проектировании турбинных решеток активного
типа, «Теплоэнергетика», 1958, № 8.
26. Я. Буковский, Методы экспериментального исследования
потока в решетках профилей турбомашин при больших скоростях,
«Теплоэнергетика», 1958, № 9.
27. A. D., С о г t e r, E. M. Cohen, Preliminary investigation
into the three-dimensional flow through a cascade of aerofoils, ARC,
1946, № 2339.
28. H. B. Squire, K. G. Winter, The secondary flow in a
cascade of aerofoils in a non-uniform stream, J. Aeron. Sc, 1951,
v. 18, № 4.
29. J. M. Stephenson, Secondary flow in cascades, J. Aeron.
Sc, 1951, v. 18, Nb 18.
30. P. H. Алексеева, И. Д. Л я х о в и ц к и й, Ю. В. Р ж е з-
ников, «Теплоэнергетика», 1956, № 6.
К гл. 9
1. М. Е. Дейч, Экспериментальные исследования и основы
аэродинамического расчета ступеней паровых и газовых турбин,
Диссертация, 1956.
2. М. Е. Дейч, Г. С. С а м о й л о в и ч, Основы аэродинамики
осевых турбомашин, Машгиз, 1959.
3. М. Е. Дейч, Ф. В. К аз и нц ев, Л. Е. Киселев,
В. Г. Ф и л л и п о в а, Исследование переменного режима ступеней
с длинными лопатками постоянного профиля, «Теплоэнергетика»,
1959, № 6.
4. В. Е. Ершов, К вопросу о движении газа через ступень
осевой турбомашины, Сборник трудов лаборатории быстроходных
машин и механизмов, вып. 5, 1955.
5. Г. С. Ж и р и ц к и й, Авиационные газовые турби,ны, Оборон-
гиз, 1950.
$69
6. И. И. Кириллов, Метод проектирования проточной части
паровых турбин с закрученными лопатками, Сборник трудов,
БИТМ, вып. 15, 1955.
7. И. И. Кириллов, Газовые турбины и газотурбинные
установки, Машгиз, 1956.
8. Б. С. С т е ч к и н, П. К. К а з а н д ж а н, Л. П. Алексеев,
А. Н. Говоров, Ю. Н. Нечаев, Р. М. Федоров, Теория
реактивных двигателей (лопаточные машины), Оборонгиз, 1956.
9. Г. С. С а м о й л о в и ч, Б. М. Трояновский,
Переменный режим работы паровых турбин, Госэнергоиздат, 1955.
10. В. Г. Тырыш-кин, К вопросу о рациональном
проектировании лопаток турбинной ступени с учетом сжимаемости, «Котло-
турбостроение», 1949, № 3.
11. А. Н. Ш ер с тюк, Осевые компрессоры (аэродинамический
расчет), Госэнергоиздат, 1955.
12. Я. И. Ш н е е, Теория газовых турбин, Машгиз, 1950.
13. А. В. Щ е г л я е в, Паровые турбины, Госэнергоиздат,
1955.
14. В. В. Уваров, Профилирование длинных лопаток газовых
и паровых турбин, Оборонгиз, 1945.
15. J. Bile k, J. С а те к, P. Vesely, Soustavny vyzkum
lopalkove ucinnosti na modelovych turbinach, Proudeni v lopatkovych
strojich, Sbornik ustavu pro vyzkum stroju, 1958.
16. Wu Chung-Hua, The aerodynamic problem of radially
long blades in turbomachines, Chinese Journal of Mechanics, 1957,
v. 1, № 1.
17. A. Stodola, Die Dampf-und Gasturbinen, 1924.
К гл. 10
1. M. E. Дейч, Ф. В. К а з и н ц е в, В. А. Г о л о в и н,
Счетно-решающее устройство для определения коэффициента потерь
энергии, «Энергомашиностроение», 1959, № 3.
2. Н. А. 3 а к с, Основы экспериментальной аэродинамики,
Оборонгиз, 1953.
3. Г. С. Самойлович, Е. В. Майорский, И. Неруда,
А. В. Стекольщиков, Малоинерционные тензометрические
зонды для исследования неустановившихся процессов в турбома-
шинах, «Теплоэнергетика», 1959, № 1.
4. И. Л. П о в х, Аэродинамический эксперимент в
машиностроении, Машгиз, 1959.
5. С. Г. Попов, Некоторые задачи и методы
экспериментальной аэромеханики, Гостехиздат, 1952.
6. А. Н. П р я д и л о в, Пьезоэлектрический индикатор давления
для исследования частоты и характера пульсаций воздуха в тур-
бомашине, «Энергомашиностроение», 1956, № 12.
7. Р. П э к х е р с т, Д. X о л д е р, Техника эксперимента в
аэродинамических трубах, Изд. иностранной литературы, 1955.
8. В. П. Преображенский, Теплотехнические изменения
и приборы, Госэнергоиздат, 1953.
9. А. И. Т у р и г и н, П. В. Новицкий, Проволочные
преобразователи и их технические применения, Госэнергоиздат, 1957
10. А. М. Т у р и ч и н, Электрические измерения неэлектрических
величин, Госэнергоиздат, 1954,
G70
11. "М. М. Фетисов, Использование индуктивных
преобразователей для изменения нестационарных давлений, Труды ЛПИ,
1955, № 17.
12. Физические измерения в газовой динамике и при горении,
Изд. иностранной литературы, 1957,
13. У. Ф. Хилтон, Аэродинамика больших скоростей, Изд.
иностранной литературы, 1955.
14. Электрические измерения, Под редакцией А. В. Френке,
Госэнергоиздат, 1954.
15. А. Уорант, И. Г е ф ф н е р, Методы обработки
экспериментальных данных, Изд. иностранной литературы, 1953.
ОПЕЧАТКИ
Страница
26
27
38
65
32
87
144
153
193
207
226
241
243
261
261
289
371
391
398
403
Строка
Формула (1-106)
3 сверху
5 сверху
5 сверху
12 снизу
4 сверху
Рис. 4-6,
обозначение
горизонтальной оси
4 снизу
Формула (4-53)
4 сверху
19 снизу
18 снизу
Формула (5-46)
5 сверху
7 сверху
10 снизу
Рис. 6-29
1 снизу
14 снизу
6 снизу
Напечатано ,
1 dp/
9'dt[
в 1659 г.
уравнения. (1-26)
на рис. 2-4.
вызывается
1-М2
00
1—0*М2
00
а,
р£зт<р. + *р>
<P+rfP>~|~lP '
Под знак корня вне
и
в тех
и0Ь**
«'5***
0
vo
макрочастиц
микрочастиц
Re^ ~ 10»-г-2-10*
а — 9а = 0,546; б — «а = 0,04,
в — еа = 0,16.
рис 7-7,6.
/>4
после •
Должно быть
Р dt^\
в 1755 г.
уравнения (1-28)
на рис. 2-3.
называется
1-М2
00
1 —вМ2
00
S,
p-jf~f(p+rfp)
(p+dp)_*±jp '
сти весь знаменатель
т = 1/ 1й\1с-с**м
¥ 1
в трех
и0Ь**
и'0Ъ**»
микрочастиц
макрочастиц
Reoo ~ 10*-5-2-10»
а-8а = 0,04; 6-ea=:0,t6;
в —«Л =0,546
рис. 7-6,6.
f <4
поле
М. Е. Д е й ч—Техническая газодинамика
to. E. Дейч.
Диаграмма для расчета с<ачков уплотнения (/г=1,3).
Диаграмма для расчету скачков уплотнения (&=1,4).