V
V
«¦
\ >'

Е. И. Игнлтьевъ.
ВЪ ЦАРСТВЪ СМЕКАЛКИ
ИЛИ
АРИ0МЕТИКА ДЛЯ ВСВХЪ.
КНИГА ДЛЯ СЕМЬИ И ШКОЛЫ.
ОПЫТЪ МАТЕМАТИЧЕСКОЙ ХРЕСТ0Ш1И.
Книга 2-я.
С.-ИЕТЕРБУРГЪ
1909

) Tmorpaoifl А» С. Суворина. Эртелевъ, 13

Заставка изъ знаыенитаго сочинсн!я Эйлера «Introdtictio in analysin
iufiiiitorura». Издано въ Лованн'Ь въ 1748 г.
ПРЕДИСЛОВ1Е.
То несомненное вниман1е, которымъ встречена наша
попытка составлен! я русской математической хрестома-
т1и, позволяетъ намъ, спустя всего годъ, предложить вни-
внимание) читателя эту вторую книгу. ЦЬль ея, въ общемъ,
та же, что и первой: въ доступной, легкой и по воз-
ложности занимательной формЬ вводить читателя въ
область математическихъ знанш,—въ необъятное «цар-
«царство смекалки». Какъ первая книга, такъ и эта, на-
надеемся, можетъ послужить недурнымъ пособ!емъ для
математическаго саморазвит1я, само деятельности и
уяснен1я- весьма важныхъ дисциплинъ. Для чтен1я и
усвоетя содержатя всей почти этой книги не требуется
никакой особой специальной математической подготовки.
Это—Аривметика для вегьхъ, чувствующихъ желаше и
склонность къ работе ума. Здесь нетъ ничего или по-
почти ничего, чего не осилилъ бы не только взрослый че-
ловЬкъ, но любой нзъ юныхъ читателей, знакомый съ

IV
т?ми элементами математики, которые преподаются въ
начальныхъ и среднихъ школахъ. Многое, если не все,
можетъ зд'Ьсь служить предметомъ бесЬдъ, развлече-
нш и завдтШ съ дътьми.
Но если по общимъ ц'Ьлямъ эта книга есть про-
должеше Д"Ьла, начатаго въ первой, то она значительно
разнится отъ предыдущей выполнешемъ. Такъ какъ
предпринятый трудъ является у насъ чуть ли не един-
ственнымъ, то въ первой части составитель не особенно
заботился о «свежести», если можно такъ выразиться,
и оригинальности, во что бы то ни стало, содержашя. Та
книга им'Ьла прежде всего въ виду ознакомить русскую
СеМЬЮ И ШКОЛу СЪ ТТэМЪ ТОЛЬКО СаМЫМЪ H3BiCTHbB№
и распространеннымъ матерхаломъ, что имъ-етъ уже
давно въ своемъ расиоряженш западная школа и семья.
Вотъ почему въ первую часть вошло довольно много
такихъ задачъ и вопросовъ, которые иному знатоку
могутъ показаться известными и шаблонными. Впро-
чемъ, много ли у насъ такихъ знаток овъ?
Въ этой книгЬ, какъ читатель можетъ убедиться,
мы поднимаемся на следующую, высшую ступень. Съ
одной стороны, значительно расширяется математи-
математически кругозоръ, съ другой, бол"Ье тщательно и строго
подбирается матерьялъ. На ряду съ легкостью, до-
доступностью и возможной занимательностью изложешя
составитель старается, гд? возможно, побудить чита-
читателя и къ научному, теоретическому взгляду на пред-
метъ. Выясняются основы понявд о числ-Ь, о свойствахъ
и характер^ алгебраическихъ и геометрическихъ аксюмъ,
объ Евклидовской и не-Евклидовской геометрш, о «чет-
вертомъ изм-Ьреши», о н'Ькоторыхъ главнМшихъ ре-
зультатахъ, достигнутыхъ математикой вообще, Д'Ь-
лаются всюду, гд-Ь возможно, неболышя историческ1Я
справки... И читатель, конечно, не посЬтуетъ на
насъ, если въ настоящей книг-fe мы, помимо общихъ

Iutroductio in analysiu infinitorum. Лозанна. 1748.

V/
указашй на значеше и сущность трудовъ II. И. Лоба-
чевскаго, приводимъ даже его небольшую бюграфшэ.
Великш свъ-точъ русской математической мысли умеръ,
непонятый современниками, но им?етъ всЬ права на
то, чтобы въ иопытк'Ь первой русской математической
хрестоматш отнеслись къ нему съ должной данью ува-
жешя.
Быть можетъ, ничто такъ не изощряетъ и не от-
тачиваетъ въ изв?стномъ отношенш математической
смекалки, какъ умЬнье разбираться въ такъ называс-
мыхъ «математическихъ софизмахъ» и парадоксахъ.
Жаль только, что въ имЬющихся у насъ книжках!:,
съ попытками подобнаго сорта предлагаются просто
самыя задачи безъ общаго, хотя бы, разъяснешя сущ-
сущности софизма. Вотъ почему этому предмету, помимо
задачъ, посвящены и главы общаго содержашя. Ду-
маемъ, что даже для знатоковъ софизмовъ онъ1 не бу-
дутъ лишними. Не безъ интереса также, полагаемъ,
отнесется читатель къ попыткамъ беллетристической
обработки чисто математическихъ темъ. Помимо Э. По
и Г. Уэльса, читатель найдетъ зц-Ьсь главу «Въстран'Ь
чудесъ математики», составленную по мало извъетной
у насъ книгё Abbott, E. A.: «Flatland; a Romance of
Many Dimensions by a Square».
Иному, пожалуй, покажется страннымъ найти въ
конц"Ь книги несколько страницъ, посвященныхъ из-
в-Ьстнаго рода «математическимъ фокусамъ». На это за-
м'Ьтимъ, что въ область смекалки входитъ также ум'Ьнье
разбираться, продЪлываютъ ли предъ вами просто фо-
кусъ, или же действительную математическую комби-
нацю.
Въ зaключeнie считаю долгомъ поблагодарить уче-
наго л-Ьсовода Я. И. Перельмана за ту готовность, съ
которой онъ делился со мной своими задачами, зна-
щями и опытомъ при cocтaвлeнiи этой книги. Ему же

VII
здЬсь принадлежим обработка главы «Математика въ
природ-Ь» и «Новый родъ задачъ». Давнишнему своему
пр1ятелю и товарищу по факультету, Н. П. Соколову,
тоже приношу здЪсь свою благодарность за ту готов-
готовность, съ которой онъ сд-Ьлалъ пересмотръ и допол-
нешя главы «Новыя начала Геометрш». Единственная
попытка изложить кратко и популярно замечательный
мемуаръ Н. И. Лобачевскаго принадлежнтъ ему. Съ
гЬмъ большимъ удовольсгаемъ беремъ изъ его бро-
брошюры эту главу въ его собственной переработка для
настоящей книги.
Августъ. 1909 г.
С.-Петербургъ.
Introductio in analysin infinitorum. Lausannae. 1748.

Задача 1-я,
ГдЪ начинается новый годъ?
Обыкновенно спрашпваютъ, когда начинается новый годъ, и
мало кто задается вопросомъ: гдй онъ начинается? Вопросъ
этотъ, пожалуй, можетъ даже показаться нел-Ьпымъ, какой-то
задачей-шуткой, въ роде вопросовъ: почему (по чему) птица ле-
таетъ, или отчего (отъ чего) утка плаваетъ? Кажется яс-
нымъ, что новый годъ начинается тамъ, где онъ начинается,
и спрашивать тутъ собственно не о чемъ.
Однако, Д"Ьло не такъ-то просто, какъ кажется, и вопросъ—
где, въ какомъ пункте земного шара впервые наступаетъ но-
'вый годъ, им-Ьетъ вполне определенный смыслъ.
Допустимъ, что вы встречаете новый годъ въ Москве. Вотъ
бьетъ двенадцать часовъ: въ этотъ моментъ въ Москве насту-
пилъ новый годъ. Но мы знаемъ, что наши нижегородце зна-
знакомые уже полчаса какъ встретили новый годъ, такъ какъ въ
Нижнеыъ часы показываютъ половину перваго, когда въ Мо-
Москве дв'Ьпадцать. Въ Омске новый годъ встретили еще 21/2 ч.
тому назадъ, въ Красноярске—целыхъ 4 часа тому назадъ, а
въ Петропавловске — даже на целыхъ Я часовъ paiiee. Следо-
Следовательно, вы сейчасъ встретили въ Москве вовсе ужъ не но-
новый годъ: ведь ему уже, по меньшей мере, девять часовъ,
этому новому году1
Итакъ, новый годъ начался где-то далеко на востоке и от-
оттуда пригаелъ къ намъ. Но где, въ какомъ месте земного шара
онъ впервые явился? Такой вопросъ, какъ впдимъ, пм'Ьетъ вполне
определенный смыслъ. И на него надо уметь ответить.
ВЪ ЦАРСТВЬ СМВЕАЛЕИ.	¦	1

Мы знаемъ уже, что въ Потропавловск'Ь (иа Камчатки) но-
новый годъ наступилъ на 8 часовъ раньше, чтшъ въ Москве. По-
пробуемъ подвигаться далее на востокъ и попытаемся отыскать,
где онъ начался всего ранее. Въ Ворпнговолъ проливт. онъ
наступилъ на 11 час. раньше, ч'Ьыъ въ Москве. Въ Санъ-Фран-
циско—на 14 часовъ раньше, въ Чикаго—на 16 час, въ Фи-
Филадельфии—на 17 час, въ Лондоне—на 20 час, въ Париже—
почти на 22 часа, въ Bini—на 23 часа и, наконецъ, въ Мо-
Москве—на 24 часа!
Мы пришлп къ абсурдному выводу, что въ Москве новый
годъ наступаетъ на 24 часа раньше, чгьмъ въ той же Москве!
Недоумътае наше еще более возрастаетъ, если мы будемъ
двигаться отъ Москвы на западъ. Въ тотъ моментъ, когда въ
Москве только что наступилъ новый годъ, въ Петербурге всего
половина двенадцатая), т. е. тамъ еще старый годъ. Идя все
далее и далее на западъ, мы, наконецъ, прпбудемъ снова въ
Москву,—и окажется, что танъ одновременно долженъ быть и
старый и новый годъ. Получается опять нелепость, — что въ
Москве новый годъ наступаетъ и въ дапный моментъ, и на 24
часа ран'Ье, и на 24 поздние.
Очевидно, все это происходить вследствие того, что земля—
шаръ. Однако же мы знаемъ, что въ Москвт. новый годъ на-
наступаетъ въ вполнт, определенный моментъ, и следовательно
наше разеуждеше чт.мъ-нибудь да грешить, разъ мы при-
пришлп къ выводу, что на однолъ и томъ же пунктЪ новый годъ
наступаетъ три дня кряду.
Не трудно догадаться, въ чемъ тутъ промахъ. Разъ въ дан-
данный момента къ востоку отъ Москвы новый годъ, а къ западу
отъ нея пока еще старый годъ, то, вслгЬдств1е шарообраз-
шарообразности земли, должна существовать гдт>-то пограничная лишя,
разделяющая область съ старьтмъ годомъ отъ области съ но-
выыъ годомъ.
Такая пограничная ливпя на самомъ дйлгЬ п существуетъ;
положеше ея определяется не какими-нибудь аст1)ономическплгп
услов1ями, а просто практикой мореплавашя.
Дело въ томъ, что затруднетя, съ которыми мы сейчасъ
встретились, возникаютъ не только въ этомъ случае, но и тогда,

когда ищутъ начала счета любого дня недели. Разсуждешямп,
вполнт, сходными съ только что приведенными, легко убедиться,
что гд'1;-то на земномъ шарЬ должна существовать лншя, по
одну сторону которой оудетъ определенный день педали,—на-
пршгЪръ среда, а по другую слЪдуюицй, четвергъ.
Практическая же надобность въ установлены подобной гра-
границы, плц такт, называемой демаркащонной лиши, возникла
пзъ необходимости регулировать ведеше календаря во время
плаватй. Известно, что при кругосвгЬтныхъ путешеств1яхъ съ
запада на востокъ одипъ день какъ пы выигрываотся, н путе-
шественннкъ, нрпоывъ въ исходный пунктъ, считаетъ на день
бол'];е, чгЬмъ слЬдуетъ; при путешествш jkc съ востока на за-
падъ наблюдается обратное: путешественникъ въ счегЬ дней
ототаетъ отъ истиннаго н какъ бы теряетъ одн'Ь суткп. При-
Причину этого на первый взглядъ непонятнаго явлетя легко рас-
раскрыть, ослп принять во внпмаше, что кругосв-Ьтный путепте-
ственникъ дг1иаетъ одинъ лпшшй оборотъ вокругъ земной оси—
при [.виженш па востокъ п, напротпвъ, Д'Ьлаетъ однимъ обо-
ротомъ менъ'е — при двпж(Ч11и на западъ г). Другими словами,
путешественникъ въ первомъ случай увидптъ восходъ солнца
однимъ разомъ oojrfee, во второиъ—мен'Ье, нежелп проч1е люди,
остагонцеся па мт,сггЬ. А если онъ увпдитъ однимъ восходомъ
солнца болЬе или мен'Ье, то, следовательно, оудетъ насчитывать
въ протекгнемъ времени одними сутками бол'Ье пли же менЪе.
Мы знаемъ, что только благодаря этому Фплеасъ Фоггъ, герой
романа Жюля Верна «80 дней вокругъ свгЬта», выитрадъ свое
оригинальное пари.
Виервые указанная особенность въ счегв дней при круго-
св'Ьтпыхъ путешеств1яхъ стала изв-Ьстна послй перваго круго-
св'Ьтнаго плаван1я Магеллана. Спутипкъ погпбшаго Магеллана,
Себасиапъ-дель-Кано, прп возвращены въ Европу «прпвезъ
съ собой» четвергъ, въ то время какъ зд'Ьсь была уже пятница
(онъ т,халъ съ востока на западъ).
') Напомнпыъ, что тавъ вакъ кажущееся суточное движен!е солнца со-
совершается съ востока на западъ, то истинное вращеше зешли вокругъ своей
оси происходить въ обратномъ паправлсши, то-есть съ запада на востокъ.
1*

Съ этого времени мореплаватели начали постепенно уста-
устанавливать демаркацюнную лишю, положеше которой и теперь
еще определено но во веЬхъ пунктахъ. Лишя эта, ограничи-
ограничивающая области съ различными днями нед'Ьлн, гл'Ьдуотъ по
западной части Великаго океана. Она проходить черезъ Берин-
говъ проливъ, затЬмъ направляется къ берегамъ Японш, оги-
баетъ съ запада острова MapiancKie и Каролинсые и идетъ да-
лЬе къ югу, огибая съ востока Филиппины, Новую Гвинею, Ав-
стралШсшй матерпкъ, Новую Каледотю п Новую Зеландш
(см. карту фиг. 1).
Такимъ образомъ, когда на Филипппнскихъ островахъ, ска-
жемъ, четвергъ, тогда на соевднихъ съ ними Каролинскихъ,
всего въ полусотни веретъ, тотъ же день называется средой.
Произошло это просто потому, что Филиппины были открыты
голландскими мореплавателями, прибывшими съ востока, а Ка-
ролинсте о-ва открыты испанцами, отправлявшимися въ путь
изъ Европы на западъ, черезъ Атлантически океанъ, мпмо
Южной Америки и черезъ весь Велишй океанъ.
Рассматривая карту, мы видимъ также, что подобная же
разница въ счете дней недели наблюдается и между Камчат-
Камчаткой и Аляской: когда на Камчатки понедт>льникъ, на Аляск'Ь
воскресенье.
Понятно, что это вносило бы невероятную путаницу въ
календарь и вызвало бы значительные неудобства, если бы де-
демаркацюнная лишя проходила не черезъ водныя пустыни Тихаго
океана, а черезъ ыатерикъ Европы и С'Ьверной Америки.
Но какимъ же образомъ эта демаркацюнная лишя помогаетъ
мореплавателямъ регулировать календарь? Вотъ какпмъ. Когда
судно переевкаетъ эту лпшю съ запада на востокъ, то слЪду-
ЮЩ1Й день и число месяца счптаютъ за предыдущее, т. е. дважды
считаютъ одинъ и тотъ же день недели и чпело месяца. Если,
наприм^ръ, демаркацюнная лишя была пересечена въ среду
14 мая, то и следующей день считаютъ за среду 14 мая. Въ
судовой книги, такимъ образомъ. на этой неделе будутъ две
среды и два раза подрядъ 14 мая. Благодаря этому уничто-
уничтожается лишшй день, который «выигрывается» при путешествш
съ запада на востокъ. Наоборотъ, когда судно пересекаетъ де-

Отъ Ферро
30
40
240
Фиг. 1. Гд-Ь начинается новый годъ?—IIo.TOKCHie домарвацгопной липпг.

маркацюнную лпшю съ востока на западъ, то после nepcce-
чешя пропускаютъ ц^злыя сутки, другими словами, счптають
уже сл'Ьдующхй день п число. Налрпмеръ, если лишя пересе-
пересечена въ воскресенье 3 августа въ 7 часовъ вечера, то счита-
ютъ 8-й часъ уже не воскресенья, а понедельника 4 августа.
Такъ навёрстывается день, который былъ бы «потерянъ» при
кругосветномъ плаванш.
Само собою разумеется, что все это было проделано капи-
таноыъ и того судна, па которомъ плылъ герой романа Филеась
Фоггъ. Если бы педантичный аиглпчанинъ не былъ такъ погло-
щенъ своиыъ пари п обращалъ BiimraHie на окружающее, а
наивный Паспарту пе впображалъ, что часы его идутъ «вернее
солнца»,—то, конечно, они не могли бы проглядеть того, что у
нихъ пятница, когда кругомъ всего еще только четвергъ.
Теперь мы уже знаеыъ, гд* начинается новый годъ, гд4 за-
зарождаются дни, недели, месяцы. Таиъ, далеко, на островахъ
Тихаго океана они впервые отделяются отъ вечности и без-
беззвучно опускаются на, нашъ земной шаръ. А оттуда быстро-
быстро, со скоростью пятнадцати градусовъ въ часъ, они бегутъ
легкою тенью по земле, одинъ за другпмъ, посещая все пункты
нашей планеты. И обежавъ кругомъ земной шаръ, опять воз-
возвращаются къ этой границе, чтобы здесь покинуть землю п
снова уйти въ вечность—увы!., навсегда.
Если вы теперь въ состоянш правпльно решить задачу, где
начинается новый годъ, то, вероятно, разберетесь п въ слйду-
ющемъ вопросе.
Задача 2.
Три воскресенья на одной недЪлЪ.
Можетъ лп на одной неделе быть три воскресенья? Мы
знаемъ, что у некоторыхъ людей бываетъ «семь пятиицъ па
одной неделе». По бываетъ лп три воскресенья?
Вместо ответа предлагаемъ читателю прочесть следующш
небольшой остроумный разсказъ знамеиитаго амерпканскаго ши-а-
теля Эдгара По, — разсказъ, который мало кому пзвестенъ п
который такъ п называется:

«Три воскресенья па одной недплп».
«Ахъ ты, упрямый старикашка!»—мысленно обратился я
однажды къ дяд'Ь Ремгеджеру, гневно сжавъ кулакъ (тоже, впро-
челгь, лишь въ мысляхъ).
Да, только мысленно. На самомъ дъмгЬ то, что я думалъ,
нисколько отличалось отъ того, что я действительно исполнилъ.
Когда я открылъ дверь въ комнату дяди, старикъ сид'Ьлъ, вы-
тяиувъ нош къ камину, держа кружку съ ппвомъ въ рукахъ,
и добросовт.стнъ'йшимъ образомъ псполнялъ совт,тъ старой п'Ьсни:
Наполняй пустой бокалъ,
Полный—выпивай до дна!
—	Дорогой дядя, — началъ я, тихо притворивъ дверь его
комнаты и подходя къ нему съ сладкой миной, — вы всегда
были ко мн'Ь такъ расположены и столько разъ доказали свою
доброту, что я не сомневаюсь въ вашей полощи и на этотъ разъ.
—	Продолжай, мальчикъ, продолжай!—процедилъ дядя.
—	Я убеждонъ, дорогой дядя (чтобъ тебя, стараго скрягу!),
что вы не станете серьезно противиться моей женитьбе на Кэтъ.
Вы ведь только шутплп, не правда ли? О, вы такой шутникъ,
дядюшка, ха-ха-ха!
—	Ха-ха-ха! — подхватилъ дядя.—Вотъ это правда, чортъ
побери!
—	Ну, вотъ, я такъ н зналъ! А теперь, дорогой дядя, я и
Кэтъ жделъ отъ васъ только указатя... относительно срока...
Словомъ сказать, дорогой дядюшка, на когда, по вашему мн4-
хпю, всего удобнее будетъ назначить нашу свадьбу?
—	Свадьбу? Какую? Вотъ еще повости! II думать не смей
объ этомъ!
—	Ха-ха-ха! Хо-хо-хо!.. Хп-хп-хи-хи... Это славно! Милый
дядюшка, какой вы весельчакъ! Теперь остается только точно
назначить день...
—	А? Точно назначить?
—	Да, дядюшка, если будете такъ добры...
—	Ты хочешь точно знать срокъ? Хорошо, Воббп, такъ и
быть, убла1Ч)творю тебя.

—	Ахъ, ыилый дядюшка!..
—	Погоди. Итакъ, я изъявляю полное соглайе. Сегодня вос-
воскресенье, да? Хорошо-съ. Такъ слушай же: можешь венчаться
съ Кэтъ, ну, когда бы?.. Когда будетъ три воскресенья сряду
на одной цед'Ьлъ'! Чего ты глаза вьшучплъ? Говорю же теб'Ь:
свадьба твоя будетъ, когда три воскресенья придутъ сряду на
одной недъ'лт,. Ни однимъ днемъ раньше! Ты знаешь меня, слово
мое неизменно. А теперь проваливай!
И онъ снова принялся за свое пиво. Я же въ отчаянш вы-
б'Ьжалъ пзъ комнаты.
Дядя мой, Ремгеджеръ, былъ, что называется, очень милый
старнчокъ, но имъ-лъ свои странности. Будучи добродушенъ по
натур'Ь, оиъ, благодаря страсти противоречить, прюбр'Ьлъ среди
многихъ, не знавшихъ его близко, репутащю скряги. Въ него
словно вселился б'Ьсъ отрицашя, и на каждый вопросъ онъ
спъ-шилъ ответить «нътъ!» Но въ концт, концовъ, нослт, долгихъ
переговоровъ, никогда почти не случалось, чтобы просьба оста-
оставалась неисполненной. Мало кто дъмилъ столько добра, сколько
дтлалъ онъ—и въ то же время такъ неохотно, какъ онъ.
Оставшись сиротой послт, смертп моихъ родителей, я все
время воспитывался и жплъ у старика дяди. Можетъ быть, по-
своему чудакъ и любилъ меня, хотя не такъ, какъ свою внучку
Кэтъ. Съ перваго же года онъ частенько дралъ меня, съ пяти
лъть до пятнадцати — стращалъ исправительнымъ домомъ; съ
пятнадцати до двадцати—ежедневно грозилъ выгнать меня безъ
копейки денегъ. Зато я гайль въ-рнаго друга въ Кэтъ. Она
была прелестная девушка п премило заявила мн"Ь, что стаиеть
моей, со веЬмъ своимъ приданымъ, какъ только я уговорю
ея дедушку Ремгедзкера. Бедняжки было всего шестнадцать
лъть, п до совершеннолъ"г1я она не въ правт, была распоря-
распоряжаться свопмъ капиталомъ безъ соглас1я дгЬда. Но дедушка оста-
оставался непоколебимъ, несмотря на всЬ наши мольбы. Саыъ би-
блейсхой 1овъ возропталъ бы при впдй того, какъ онъ изда-
издавался надъ нами, словно котъ надъ мышами. Въ глубин^ душн
дедушка былъ доволенъ нашимъ рт,шен!емъ и охотно выложилъ
бы десять тысячъ фунтовъ изъ собственныхъ средствъ, если бы
Кэтъ не шила прпданаго. Но ему нуженъ быль благовидный

предлогъ, чтобы уступить наппшъ мольбамъ. Наша ошпбка со-
состояла въ томъ, что мы вздумали сами хлопотать о своей свадьба,
а при такихъ обстоятельствахъ дедушка положительно не въ
силяхъ былъ не оказать намъ противодт>йств1я.
Дядя считалъ безчестаеыъ отступать отъ разъ данпаго слова,
но за то готовъ былъ толковать смыслъ вкривь и вкось, лишь
бы остаться в'Ьрнымъ буквгЬ. Вотъ этой чертой и воспользова-
воспользовалась лукавая Еэтъ вскор'Ь послт. моего знаменательнаго разго-
разговора съ дядей.
Разскажу вкратц'в, какъ это произошло. Судьба угодно было,
чтобы среди знакомыхъ моей невесты были два моряка, по-
подавно возвративнлеся въ Англ1ю послт. кругосвт/гпаго плава-
шя. Недели черезъ три посл'Ь памятнаго разговора, въ воскре-
воскресенье послт. обт>да я вм^стт, съ этими моряками зашелъ къ
дяди въ гости. Около получаса мы говорили о разныхъ без-
различныхъ вещахъ, пока разговоръ нашъ не принялъ такое
направлеше:
капитанъ пратъ. Цтлый годъ пробылъ я въ плаваши.
Ей-Богу, сегодня какъ разъ годовщина моего отъезда. По-
Помните, м-ръ Ремгеджеръ, какъ я пришелъ къ вамъ прощаться
ровнехонько годъ тому назадъ? И замечательно, что тутъ же
сидитъ нашъ пр1ятель Смисертонъ, который тоже въ'дь пропла-
валъ цт^тый годъ.
капитанъ смисертонъ. Да, годъ безъ малаго. Помните,
м-ръ Ремгеджоръ, какъ я зашелъ къ вамъ проститься?
дядя. Еще бы! Въ самомъ дтлгЬ поразительно—оба вы про-
пропадали ровно годъ. Замечательное совпадете.
кэтъ. ТгЬмъ болт,е, что капитанъ Пратъ и капитанъ Смп-
сертонъ 4хали совс^змъ разными путями: первых"! обогиулъ мысъ
Доброй Надежды, а второй—мысъ Горнъ.
дядя. Вотъ именно. Одинъ держалъ путь на востокъ, дру-
другой—на западъ, и оба 4хали кругомъ веыного шара.
я [быстро]. Не зайдете ли, господа, завтра посидъть съ
нами вечерокъ? Поговорили бы о вашихъ странствовашяхъ,
сыграли бы въ вистъ и...
капитанъ пратъ. Въ впстъ? Вы вг1;рпо забыли, что завтра
воскресенье. Въ другой день я готовъ...

кэтъ. Да что вы? Робертъ не такой узкъ гръ'пшпкъ. Вт,дь,
воскресенье-то сегодня!
дядя. Ну, конечно.
капптапъ смпсертонъ. О чемъ тутъ спорить, господа.
Да, в'Ьдь, вчера же было воскресенье!
дядя. Воскресенье сегодня. Не понимаю, какъ можно этого
не знать!
капитанъ пратъ. Ничуть не бывало! Воскресенье завтра!
капптапъ смисертонъ. Да вы, господа, съ ума сошлп,
право! Воскресенье было вчера,—я такъ же увйренъ въ этомъ,
какъ и въ томъ, что сижу здт,сь передъ вами!
кэтъ [громко]. Ну, дедушка, теперь вы попались! Капитанъ
Смисертонъ утверждаете, что воскресенье было вчера—и онъ
правъ. Кузепъ Бобби, вы и я утверждаемъ, что воскресенье
сегодня—и мы правы. Капптанъ Пратт. заявляетъ, что воскре-
воскресенье .завтра—и онъ тоже правъ. Мы веЬ правы, и вотъ вамъ
три воскресенья на одной недйл'Ь!
канитанъ смпсертонъ [ппсл* паузы]. Кэтъ разсудыла пра-
правильно. KaKie мы съ тобою дураки, Пратъ! ДгЬло, видите ли,
вотъ въ чемъ, м-ръ Ремгеджеръ. Земля имйетъ въ окружпо-
сти, какъ вы знаете, 24 тыс. миль и обращается вокругъ оси,
съ запада на востокъ, дйлая полный оборота въ 24 часа. На
одпнъ часъ приходится, следовательно, тысяча миль. Такъ видь?
дядя. Разумеется, такъ.
капитанъ смисертонъ. Теперь вообразите, что я отплы-
отплываю на тысячу миль къ востоку отсюда. Легко понять, что я
долженъ буду увидать восходъ солнца ровно на часъ раньше,
нежели вы зд'Ьсь, въ Лондонт,. Если я въ томъ же направле-
нш пройду еще тысячу пиль, то увижу солнце на два часа
раньше васъ; еще черезъ тысячу миль—на три часа и т. д.,
пока не объеду кругомъ всего земного шара и снова не вер-
вернусь сюда. И здт,сь, пройхавъ 24 тысячи миль, я увижу вос-
восходъ солнца на цтлыя сутки раньше, нежели вы; другими сло-
словами—я буду считать на одни сутки меньше, нежели вы. Дру-
Другое дтло капитанъ Пратъ: пройхавъ тысячу миль къ западу,
онъ внд'Ьлъ восходъ солнца часомъ поздние васъ; а проъ-хавъ
всЬ 24 тысячи миль, отсталъ ото Лондона въ счет! времени

11
на ц'Ьлыя суткп. II вотъ почему для меня воскресенье было
вчера, для васъ—сегодня, а для м-ра Прата—будетъ завтра.
Очевидно, мы всгЬ правы, н нътъ основашй считать, что кто
нпбудь изъ насъ болйе правъ, нежели друйе.
дядя. II то правда! Ну, Еэтъ п Бобби, торжествуйте, я
попался. Но я никогда не пзы'Ьшш своему слову. II если трп
воскресенья случились на одной недели, то знай, мальчуганъ,
что можешь получить приданое и все прочее, когда хочешь.
Д'Ьло въ шляп'Ь, чорть побери!
На этомъ разсказъ По кончается. Выходить, стало быть,
что па одной недели возможны три воскресенья кряду. На са-
момъ же д'влЪ моряки провели упрямаго дядю, который, ве-
вероятно, не слишкомъ силенъ былъ въ астрономш. Объяснешя
капитана Смисертона совершенно правпльпы, по онъ умолчалъ
объ одномъ важномъ обстоятельств'!;: о поправки календаря при
пересЬченш демаркационной лиши. ПересЬкая ее на своихъ
судахъ во время плавашя, капптанъ Прать должеиъ былъ
одппъ день считать дважды, а капптанъ Смисертопъ—одинъ
день пропустить; вслъ-дспис этого возстановилось бы единство
времянечпелешя. какъ мы это уже знасмъ изъ предшествую-
предшествующей главы.
Такъ что, въ концгБ концовъ, бол1е одного воскресенья па
одной недЪл'Ь быть не можетъ.
Задача 3-я.
ОпредЪлете направлешя съ помощью нарманныхъ часовъ.
Съ помощью карманныхъ часовъ въ солнечный день можно
определить всегда съ достаточной для житейской практики точ-
постью Bci четыре «страны свита», т. е. точки сЬвера, юга, во-
востока и запада горизонта. Способъ этотъ настолько проетъ п
легко объяснимъ, что остается только удивляться, какъ опъ не
получилъ еще всеобщаго распрострапен!я. Опредйлеше папра-
влешя заключается въ сл'вдующемъ.

12
Повернуть циферблатъ карманныхт> часовъ, держа
ихъ горизонтально такъ, чтобы часовая стрЬлка была
направлена въ сторону солнца. Тогч,а точка на окруж-
окружности циферблата, лежащая посредине между показа-
шемъ часовой стрЬлкп въ этотъ моментъ и чпсломъ XII,
покажетъ вамъ иаправлеше къ югу.
Такъ, наприлъ-ръ, еслп часовая стрълка показывает*, I часа,
то, направивъ ее къ солнцу, найдемъ, что средняя точка между
ноказашемъ часовъ D) и Х1Г-ю будетъ совпадать съ точкой
циферблата, указывающей два часа. Эта точка и опредъ-лить
югъ горизонта, противоположная ей по наираклешю дастъ cf,-
всръ, иалъш), следовательно, будетъ востокъ, а направо —¦
западъ.
Предыдущее правило можно свести и на такое:
Найти на окружности циферблата среднюю точку
межцу показан1ел!ъ часовой стрЪлки и точкой ХП-ти
часовъ; направить эту среднюю точку къ солнцу,—
тогда точка циферблата съ отдгьткой двенадцати ча-
часовъ и укажетъ южное направлен1е.
Если часы, нанр., указываютъ 4 часа, то направить точку
циферблата съ ноказатемъ II часа на солнце. Тогда лншя,
проведенная изъ центра часовъ къ ХП-тп, п будетъ полуден-
полуденной лпш'еи, т. е. направленной къ югу.
Доказательство.
Для доказательства стоить только вспомнить, что въ 12 ча-
часовъ (полдень) солнце, часовая стрелка и точка на циферблат^,
отм'Ьченпая цифрой XII,— вев они лежатъ въ одной лиши, на-
направленной къ югу («на полдень»). Бслт.дъ загЬмъ и солнце,
и часовая стр-Ьлка двигаются въ одпнаковомъ направлешя. Но
стр'Ьлка часовъ совершаетъ свой полный оборотъ въ 12 ча-
часовъ, а солнце въ 24 часа, т. е. въ вдвое болышй иромежу-
токъ времени. Отсюда и вытекаютъ данпыя выше правила.
3aMt4aHie. Само собою разумеется, что полученное указап-
нымъ путемъ опредгЬлсн1С иаправлен1я не будетъ вполн-Ь точно.

13
Ошибка получается потому, что мы помйщаеыъ часы въ пло-
плоскости горизонта, вместо плоскости эклиптики, и кромй того не
принимается во внпмаше разница между истиннымъ солпеч-
нымъ временемъ и такъ называемымъ среднпмъ временемъ. Но
для т$хъ чисто практическихъ ц4лей, Еоторыя преследуются
при примйнеши указаннаго выше правила, получаемые резуль-
результаты совершенно достаточны.
Еслп бы вместо сйвернаго мы находились на южномъ полу-
шарш земли, то указанное выше правило соответственно ви-
видоизменилось бы,—а именно въ этомъ случай:
Если точку, обозначенную на циферблат^ часовъ числомъ
XII, поверпуть къ солнцу, то равнодйлящая угла между пока-
зан1емъ часовой стрелки и точкой съ числомъ 12 покажетъ
направлеше къ сЬверу.

Задача 4-я.
Сколько воды въ бочкЪ?
Двое засп*°Рили о содержимомъ бочки. Одинъ спор-
щикъ говори.71Ъ> чТО воды въ бочкЬ бол-fee, чЬмъ на
половину, а Другой утверждалъ, что меньше. Какъ
убедиться, ктГ° правъ, не употребляя ни палки, ни ве-
веревки, ни вообще какого-либо приспособлешя для изм'Ь-
ренш?
Фиг. 2.

Решете.
Это не задача-шутка, а настоящая геометрическая задача,
хотя и р-Ьшается до сметного просто. Рйшешя подобнаго рода
задачъ заслужпваютъ всегда того, чтобы надъ ними подумать.
Воть ръчнеше этой задачи. Если бы вода въ бочки была
налита ровно до половины, то, наклонив! бочку такъ, чтобы
уровень воды пришелся какъ разъ у края бочки, мы увидЬин
"бы, что высшая точка дна находится также на уровни воды.
Это ясно изъ того, что плоскость, проведенная черезъ д1аме-
трально противоположныя точки верхней и нижней окружно-
окружностей бочки, делить ее на двЪ равныя части. Если вода налита
Meiiie ч$мъ до половины, то при такомъ же наклоненш бочки
должепъ выступить изъ воды болышй пли ыенышй сегментъ
дна. Наконецъ, если воды въ бочки болЪе ч$мъ половпна, то
при наклопеши верхняя часть дна окажется -нодъ водо!т.
Такимъ образомъ вопросъ решается правильно безъ вся-
кпхъ изм^решй.
Задача 5-я.
Нрестъ обратить въ квадратъ.
Крестъ, составленный изъ пяти квадратовъ, тре-
требуется разр-Ьзать на так!я части, изъ которыхъ можно
было бы составить одинъ равновелик!й кресту по
площади квадратъ?
Р4шете.
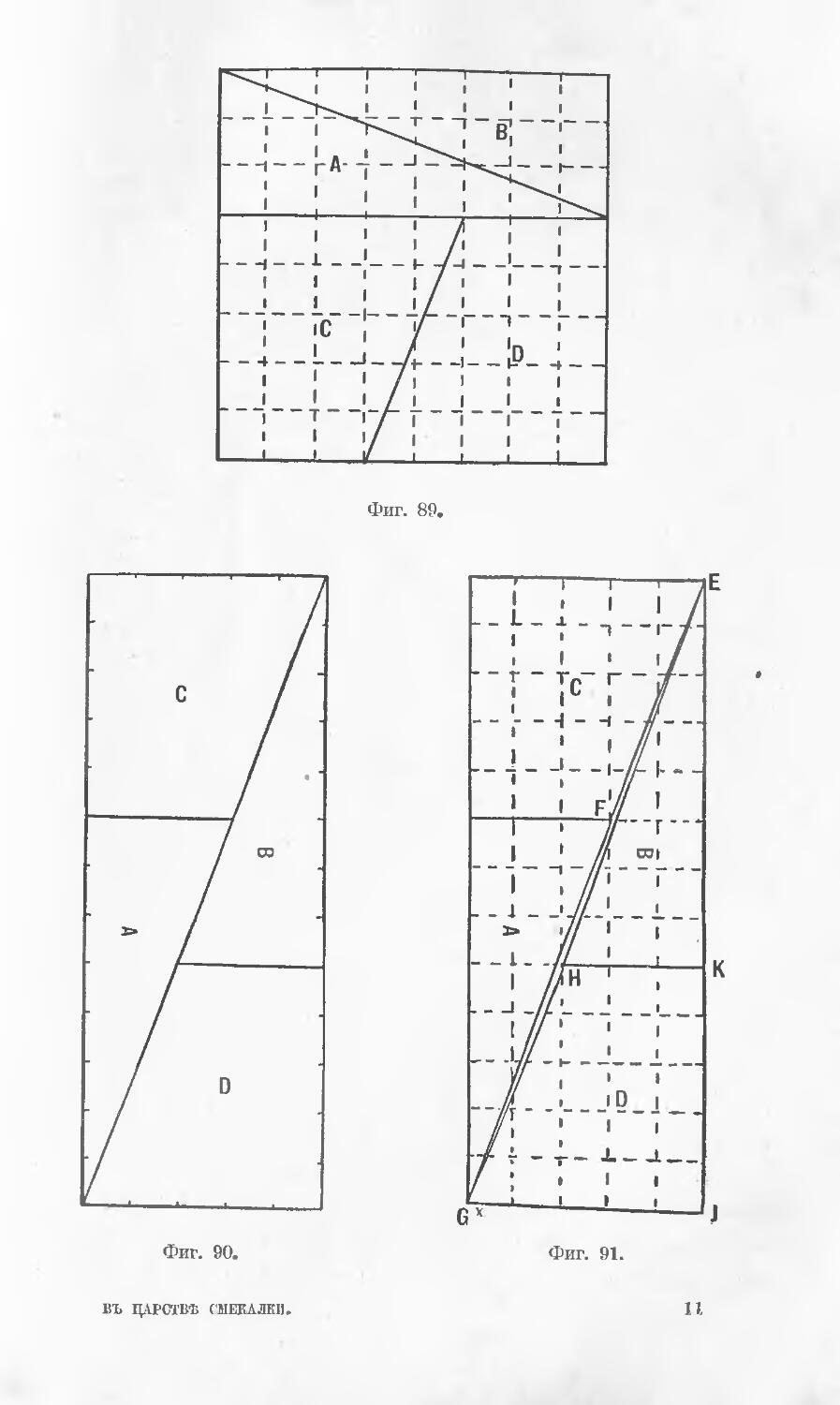
На прплагаемыхъ чертежахъ читатель найдетъ два р^шен1я
этой задачи: одно старое х) (фиг. В) и одно, предложенное въ
новейшее время (фпг. 4). Второе ръчпеше столь же просто,
сколь п остроумно: задача решается проведетемт. всего двухъ
ПряМЫХЪ ЛИН1Й.
Ср. задачу 64-ую 1-ой части этой книги

16
3
А
9
V
Фиг. 3.
Фпг. 4.
Задача 6-я.
Коврикъ.
У одной дамы былъ прямоугольный коврикъ раз-
размерами збХ27 дюймовъ. Два противоположныхъ угла
его истрепались,—пришлось ихъ отрезать въ видъ
треугольныхъ лоскутковъ, зату-
шеванныхъ на нашемъ чертежъ-
(фиг. 5)- Но дам-в, все же, хо-
т-Ьлось имЬть коврикъ въ форм-в
прямоугольника. Она поручила
обойщику разрезать его на тагая
дв-б части, чтобы изъ нихъ можно
было сшить прямоугольникъ, не
теряя, конечно, ни кусочка матерш. Обойщикъ испол-
нилъ желан1е дамы.
Спрашивается, какъ ему удалось это едъ-дать?
Pliiueme.
PimeHie задачи впдно изъ прила-
гаемаго чертежа (фиг. 6). Если зубча-
зубчатую часть А вынуть ивъ части В и
зат^мъ снова вдвинуть ее между
зубьевъ части В, перем^стивъ на
одинъ зубъ вправо, то получится без-
укоризненный прямоугольникъ.
Фиг. 6.

17
Задача 7-я.
Оригинальное доказательство.
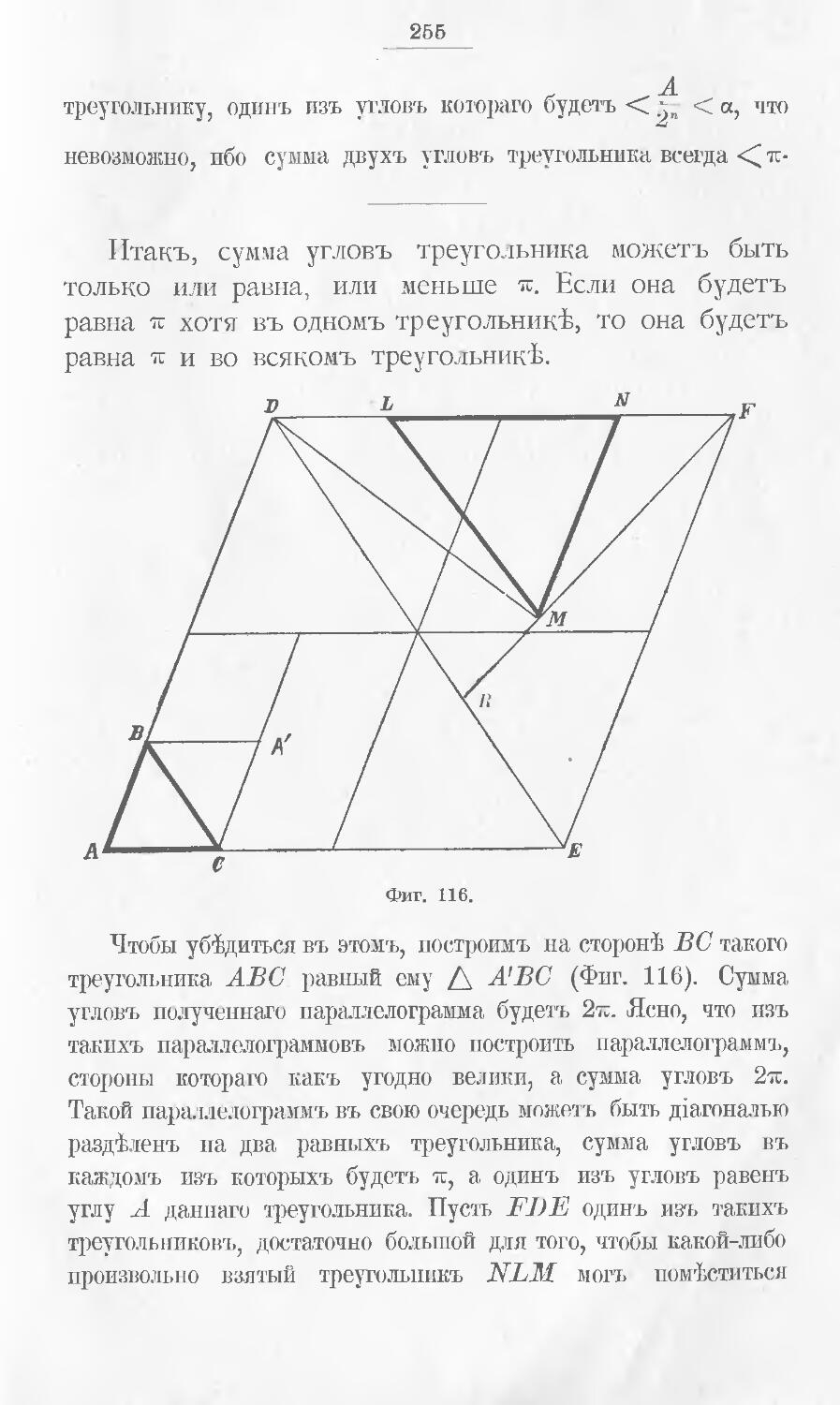
Всяшй, проходивппй геометрш, внаетъ, что сумма утловъ
треугольника равна двумъ прямымъ утламъ.
Но мало кому известно, что эта основная теорема, на кото-
которой зиждется все стройное Евклидово здаше, можетъ быть «до-
«доказана» съ помощью простого лоскутка бумаги.
• Мы ставпмъ слово «доказана» въ кавычкахъ, потому что,
собственно говоря, это не доказательство въ строгомъ смысл1!
слова, а скор'Ье лишь наглядная демонстрация. Но, все же, этотъ
остроумный пр1емъ, приду-
придуманный Томомъ Титомъ,
очень любопытепъ и поучи-
тсленъ.
ВырЪаютъ изъ бумаги
любой формы треуголышкъ
и перегибаютъ его сначала
по лиши АВ (фиг. 7). За-
тгЬмъ, снова разогнувь бу-
бумагу, перегибаютъ тре-
угольникъ по лиши CD
такъ, чтобы вершпна Л по-
попала въ точку В. Пере-
гпувъ затймъ треугольника
по лишямъ DII и CG и получивъ прямоугольникъ С GUI),
мы наглядно убеждаемся, что Bci три угла треугольника A, 2, 3)
составляютъ въ сумм4 два прялыхъ.
Необычайная наглядность и простота этого npieua позво-
ляетъ познакомить даже д4тей, не пзучающихъ геометрш, съ
одной изъ ея важнййшихъ теоремъ. Для знающихъ же геоме-
геометрш онъ прсдставляетъ интересную задачу—объяснить, почему
такое сгибай ie бумажнаго треугольника всегда даетъ желаемый
результатъ. Объяснить это не трудно, и мы не хотели бы ли-
лишить читателя удоволъсттая самому подыскать геометрическое
основаше этого своеобразного доказательства.
ВЪ ЦАРСТВА СШСКАЛКИ.	2
Фпг. 7.

18
Задача 8-я.
Вычерчиваше циркулемъ овальныхъ линш.
Решете.
Для вычерчивашя по плоскости замкнутыхъ овальныхъ
кривыхъ, извйстныхъ подъ именемъ эллипсисовъ (или эллип-
совъ) существуетъ спещальный приборъ, такъ называемый
эллипсографа. Но можно получать овалы правильной формы
и безъ этого сложнаго и дорогого прибора—просто съ помощью
циркуля, если только прибегнуть къ небольшому ухшцренш,
о которомъ даетъ поняие настояшДй рисунокъ (фиг. 8).
Обверните цилиндръ бумажкой и начертите циркулемъ
замкнутую кривую на этой цилиндрической поверхности. Раз-
вернувъ затймъ бумажку, вы убедитесь, что начертилп пе
кругъ, а овалъ, Т'1;мъ бол'Ье вытянутый, чЪмъ мепыпе рад]"усъ
цилиндра по сравнепш съ растворешемъ циркуля.
Такимъ практическимъ способомъ вычерчиванья оваловъ
часто пользуются въ разлпчныхъ мастерскихъ, хотя среди чер-
тежниковъ и рисовалыциковъ онъ сравнительно мало пзв^стенъ.

19
Слйдуетъ имйть въ виду, однако, что получаемый таквмъ
пршмомъ овалъ не есть, вообще говоря, эллипсъ въ собствен-
номъ смысл Ь этого слова, какъ бы велпко ни казалось сход-
сходство. Получаемый овалъ есть кривая ыересЪчешя шара и ци-
цилиндра, т. е., говоря математически,—кривая 4-го порядка.
Не трудно убедиться также въ томъ, что вычертить сплош-
сплошной овалъ указаннымъ нами путешъ возможно только въ томъ
случай, если радгусъ взятаго нами цилиндра больше половины
растворешя циркуля.
Задача 9-я.
Теорема Пиеагора.
Посредствомъ плитокъ домино доказать Пиеаго-
рову теорему1).
Решете.
Сложите плитки домино такъ, какъ показано на нашемъ
рисунки (фиг. 9). Вы убедитесь, что квадратъ, построенный
на гипотенуз^, состоитъ изъ 25-ти мелкихъ квадратовъ, а ква-
Фиг. 9.
г) Т. г. что площадь квадрата, построеннаго на гипотенуз!; прямоугольного
треугольника,равна сумм!; площадей киадратот>,1гостроснБыхъ на его катетахъ.
2*

20
драты, построенные на катетахъ,—соответственно пзъ 9 и 16-тп
такихъ же мелкихъ квадратовъ. А такъ какъ 25 = 9 -|- 1С, то
теорема «доказана» (прямоуголыюсть треугольника поверяется
прямымъ угломъ какой-нибудь костяшки плп группы пхъ).
Само собою разумеется, что это не доказательство, а лишь
наглядная иллюстращя, да и то пригодная лишь для тт,хъ
случаевъ, когда вст> три стороны прямоугольнаго треугольника
выражаются целыми числами. Въ данномъ случай для сторонъ
треугольника имт>емъ числа 3, 4 и 5. Такихъ чиселъ, впро-
чемъ, есть сколько угодно, какъ читатель можетъ убедиться
изъ поясненШ къ следующей задаче.
Задача 10-я.
Египетская задача.
Съ помощью веревки въ 12 единицъ длины по-
построить прямоугольный треугольникъ.
Р^шеше.
Задача эта известна издревле также подъ назвашемъ «пра-
«правила веревки».
На веревке отмеривались три последовательныхъ отрезка
длиною въ 3, 4 и б единицъ длины. Если, теперь, соединить
концы этой веревки п натянуть ее
на третьемъ и седьмомъ дйленш, то
получиться прямоугольный треуголь-
треугольникъ (фиг. 10).
Пр1емомъ этимъ пользовались еще
древше египтяне при постройке пм-
рампдъ. Быть можетъ, поэтому еги-
_ ?/.	петское слово для назвашя землеме-
Фпг. 10.	"
ровъ въ дословномъ переводе значить
«вытягиватель веревки». Нынъчпше землемеры для получешя
прямого угла также прибегаютъ къ подобному npieMy, отмечая
ца своихъ землемерныхъ цепяхъ такую комбипацш изъ трехъ

21
ц-Ьлыхъ чиселъ, которая выражала бы длины сторонъ прямо-
угольнаго треугольника съ соизмеримыми сторонами.
Числа эти должны удовлетворять условш Пиеагоровой тео-
теоремы, т. е. сумма квадратовъ двухъ изъ нихъ должна быть
равна квадрату третьяго числа. Взятыя выше н/Ьлыя, числа 3,
4, 5 удовлетворяюсь этому условно: 32 + 42 = 52. Но легко
влдъть, что подобныхъ чиселъ можно найти, сколько угодно.
Bci эти такъ называемый Пиеагоровы числа заключаются
въ тождествснномъ равенств!, которое каждый легко можетъ
проверить:
= a2b*A
. а2-Ъ2	а2 + Ъ2
од'Ьсь, значить, ab и —-— даютъ катеты, а —~— со-
отв4тствуюш,ую имъ гипотенузу.
Если вместо а и Ъ подставлять два любыхъ нечетныхъ и
первыхъ между собой числа, то и будемъ получать различные
требуемые треугольники и при томъ тате, что стороны одного
не будутъ кратными сторонами другого какого-либо треугольника.
Ташя же Пиеагоровы числа можно получать и на осно-
ванш тождества
(w2 — п2у + B т пJ = (т2 + да2J,
подставляя сюда вмъчуго т и п кашя угодно ц'Ьлыя числа.
Если же мы желаемъ избежать кратныхъ группъ или повто-
рен1я вида треугольниковъ, то числа надо брать первыя между
собой и одно четное, а другое нечетное.
Вотъ небольшая табличка части Пиеагоровыхъ чиселъ, pi-
шающихъ египетскую задачу:
3,	4,	5
5,	12,	13
7,	24,	25
9,	40,	41

22
11,
13,
15,
15,
17,
19,
21,
27,
33,
35,
39,
45,
45,
51,
55,
57,
63,
.65,
75,
77,
85,
91,
95,
99,
60,
84,
8,
112,
144,
180,
20,
36,
56,
12,
80,
28,
108,
140,
48,
176,
16,
72,
100,
36,
132,
60,
168,
20,
и т. д.
61
85
17
ИЗ
145
181
29
45
65
37
89
53
117
149
73
185
65
97
125
85
157
109
193
101
Начатки математики на НилЪ.
Упоминаше о египетскомъ треугольники, сделанное въ пре-
предыдущей задачи, заставляетъ насъ сделать маленькую экскурсш
въ область исторш. Можно считать несомненно установленнымъ,
что древше египтяне обладали знашемъ многихъ математи-
ческихъ фактовъ и умйньемъ производить н4которыя матема-
тичесшя дййсттая настолько давно, насколько только мы мо-
жемъ проникнуть въ глубину вйковъ этой древнт>ишей цивили-
защи на землъ\ Пиоагорова теорема въ пршюженш къ равно-
бедреннылъ прямоугольнымъ треуголышкамъ (оба катета равны)

23
была известна имъ съ незааамятныхъ временъ. Треуголышкомъ
со сторонами 3, 4 и 5 пользовались строители древнййшихъ
пирамидъ и храмовъ для получешя прямого угла. Одпнъ изъ
дошедшихъ до насъ египетскихъ папирусовъ писанъ за 1700 лгетъ
до Р. X. на основанш египетскихъ же писашй за 3000 л"Ьтъ
и более до Р. X. Въ немъ уже содержатся некоторый ариуме-
тичесшя задачи, таблица дробей и рЪшеше прост'Мшихъ урав-
неы1й, где неизвестное обозначается знакомъ хау (хииъ). Суще-
ствуетъ ын'Ьше, будто ариеметика (особенно — начатки ея) есть
самый стар'Ьйнпй изъ членовъ великой семьи математическихъ
наукъ. Но трудно какъ-либо убедительно доказать эту мысль.
Начало алгебры и геометрш также скрываются въ таинствен-
помъ мраке допстирическихъ судебъ человечества.
Всюду, где только мы въ состоянш приподнять завесу падъ
драмой чатовеческой исторш отдаленнейшихъ вековъ, мы ви-~
димъ, что люди уже считаютъ, решаютъ уравнения 1-ой степени
и прилагаютъ простейшие случаи Пиеагоровой теоремы.
Задача 11-я.
Численный кругъ пиеагорейцевъ.
Этотъ «Circulus Pythagoricus» находится въ сочинен1п одного
изъ учениковъ Пиеагороиой школы Ямвлика, жившаго въ IV-иъ
веке после Р. X.г). Вотъ въ чемъ состоить этотъ кругъ.
Будемъ писать по кругу рядъ посл'Ьдовательныхъ
чиселъ отъ I до какого-либо числа, т. е. рядъ чиселъ
I, 2, з, 4>- п- Дойдя до этого напередъ заданнаго
себЬ числа п, продолжаемъ писать по кругу rfe же
числа, но въ обратноыъ уменьшающемся порядк"Ь, пока
не напишемъ опять единицу, — т. е. пишемъ: п—I,
2) Jamldicus Chalcideusis ex Coele-Syria in Nicomachi Gerasini Arithmeticam
introdnctionem et de Pato. Nunc primum editus, in latinnm sermonem conversiw,
notis perpetuis illustratus a Samnele TeBnulio. Acceilit Joachimi Campraiii.
Kxplicatio in duos libros Nicomachi, cum iudice rerum et verboruiu locupletis-
simo, Amhemiae. Postaut apud Jali. Frideriaiu Hagium. Daventrae typis dis-
cripsit AVilhelmus \J.'ici CICICCLXV1II A668).

	24 _
п— 2,.... 2, I. Тогда сумма всЬхъ чиселъ, написанныхъ
въ круг-Ь, даетъ квадратъ числа п (т. е. число л умно-
умноженное само на себя).
Такъ, напр., если желаеыъ найти квадратъ 7, пишемъ (фиг. 11):
3 4 5	3 4 5 6
2	6	2	7
1
2	6 2	7
3 4 5	3 4 5 6
Фиг. 11.	Фиг. 12.
Сложивъ всЬ числа этого круга, действительно, получимъ:
49 = 72.
Для числа, напр., 9 будемъ нмъть кругъ (фпг. 12), судша
чиселъ котораго равна 9^ = 81 и т. д.
Доказательство.
Для какого бы то ни было числа п этотъ ппоагорейсшй
кругъ можно представить такъ
12 3 4 5	..п—1
12 3 4 5..	„и —1
Т. е. получается два одинаковыхъ ряда посл-Ьдовательныхт,
чиселъ отъ 1 до п — 1 и къ сумм4 обонхъ этихъ рядовъ надо
прибавить еще число п.
Но сумма п — 1 последовательных* чиселъ, начиная съ
п(п — 1) _, Y
единицы, какъ знаемъ, равна 	^—-. Следовательно, для
суммы двухъ такихъ рядовъ да еще числа п цм'Ьемъ
п (п — 1)-{-п = п2,
что и доказываетъ задачу о пиоагорейскомъ tpyri.

25
Обобщеше задачи.
Для желающнхъ несколько иол-Ье углубиться въ сущность
шшагорейскаги круга сд'Ьлаелгь еще несколько дополнешй. Обо-
значимъ черезъ 8п сумму носл'Ьдователышхъ чиселъ отъ 1 до п.
Тогда доказанное выше прсдложеше Ямблика выразится фор-
формулой.
У	2Sn^ + n = n*	A).
Разсматривая рядъ цъигыхъ чиселъ, мы находпмъ, что для
числа 2, &п_1<.щ для числа 3, 8я _ у = п, а для вс-Ьхъ осталь-
ныхъ чиселъ 8п1~> п. Итакъ, можно высказать такое предло-
жеше:
Если квадратъ ц-Ьлаго числа (кром-Ь 2 и з) разд-Ь-
лимъ на сумму всЬхъ послЬдовательныхъ чиселъ до
этого числа, то въ частномъ будетъ 2, а въ остаткъ-
само число.
Подобно формул'Ь A) можно написать еще рядъ равепствъ:
2 = 22
Складывая вс4 эти равенства съ A) и означая для краткости
I2 + 22 + З2 +.-..+ (я — IJ + ns = S?,
яолучаемъ:
Что тоже можно написать въ вид4 пиеагорейскаго круга:
& S, 8'	S .
тд4 сумма в&хъ членовъ даетъ Sf\

26
Задача 12-я.
Земля и апельсинъ.
Въ перелагаемой ниже интересной задачи мы впервые
встречаемся съ числомъ, выражающиыъ отношеше длины окруж-
окружности къ д1аметру. Это знаменитое, такъ называемое, «иррацю-
пальное» число пзгЬетъ свой особый спыволъ. Оно изображается
греческой буксой т: (пи). Приблизительно
тс = 3,141 692E...
Въ пастоящей книге наыъ не разъ еще придется говорпть объ
этомъ числи.
Вообразимъ, что земной шаръ обтянуть по экватору
обручемъ и что подобнымъ же образомъ обтянутъ и
апельсинъ по его большому кругу. Далъ-е вообразимъ,
что окружность каждаго обруча удлинилась на I са-
сажень. Тогда, разумеется обручи отстанутъ отъ поверх-
поверхности тЬлъ, который они раньше стягивали, — оста-
останется некоторый прозоръ (промежутокъ). Спраши-
Спрашивается, въ какомъ случай этотъ прозоръ будстъ
больше,—у земного шара или апельсина?
Решете.
Обыкновенно на этотъ вопросъ отв'Ьчаютъ такъ: «Конечно,
у апельсина останется болышй прозоръ, нежели у земли! В'Ьдь
по сравненш съ окружностью земного шара—38.000 верстъ—
какая-нибудь одна сажень есть столь ничтожная величина, что
прибавка ея останется совершенно незаметной. Другое дгЬло
апельсинъ: по сравненш съ его окружностью сажень—огромная
величина, и прибавка ея къ длпнт, окружности должна быть
весьма ощутительна».
Такой отвгЬтъ естественно навязывается уму всякаго—и
математика и ие-ыатеыатика. Математшп. еще иодкрЬцигь его
геометрическими соображенЬшн, въ родгЬ сл'Ьдующаго: «Такъ

27
какъ oTiiouieuie длины окружности къ Д1аметру есть величина
постоянная, то прпращеше pafliyca земли (т. е. прозоръ) дол-
женъ быть во столько разъ меньше приращсшя рад1уса апель-
апельсина, во сколько разъ рад!усъ земного шара больше рад1уса
апельсина» п т. д...
Но всЬ эти разсуждешя—одно только лукавое мудрствова-
ше. Простымъ вычислешемъ легко доказать, что — именно въ
виду постоянства отношешя окружности къ fliasieTpy—прозоръ
совершенно не зависитъ отъ pafliyca окружности и должснъ
быть одинаковъ у земли и апельсина.
Въ самоиъ д4л4, пусть окружность экватора равна С саже-
С
нямъ, а окружность апельсина с. Тогда рад1усъ земли _R=^-,
а рад!усъ апельсина г = тг- Послт, прибавки къ обручамъ од-
ной саженп, окружности ихъ будутъ равны земли С-\-1, апель-
апельсина с + 1; pafliycbi же ихъ будутъ: земли —^—, апель-
сина —^—. Если изъ новыхъ рад1усовъ вычтемъ прежн1е, то
получимъ въ обоихъч случаяхъ одно и то же приращеше:
С+1 С 1
с 1
к~ = 7г~ Для апельсина.
Итакъ, у земли и у апельсина получится одинъ и тотъ
же прозоръ въ ^— саж., т. е. примерно въ полъ-аршина.
Этотъ результатъ кажется до такой степени неожиданнымъ
и неправдоподобнымъ, что намъ случалось видгвть людей, ко-
которые, сами получивъ его, все же въ него не в'Ьрили: они
проделывали съ помощью бечевки рядъ обм4ровъ и опытовъ
съ монетами, тарелками и др. круглыми предметами,—и лишь
тогда успокаивались, когда воочш убеждались, что опытъ под-
тверждаетъ пхъ вычпслен1е. А одинъ математикъ такъ даже

28
формулировать намъ свой отв-Ьтъ на вопросъ буквально въ
агьдующихъ выражешяхъ:
«Прозоръ для земли долженъ, конечно, быгь меньше, чгьмъ
для апельсина, хотя геометрически, казалось бы (!), они должны
быть одинаковы». Чудакъ больше в'Ърилъ «здравому смыслу»,
чгЬмъ ыатематическимъ выкладкамъ,—которыя, къ слову сказать,
онъ прод1;лалъ безукоризненно. Оно, пожалуй, и понятно: трудно
найти бол'Ье разительный прим'Ьръ геолетрическаго парадокса
(не софизма, а именно парадокса, т. е. неправдоподобной съ
виду истины), ч'Ьмъ эта задачка о земл'Ь и апельснн'Ь.

Обманы зрйшя.
Кажущееся вращеше.
Лвлеше, о которомъ мы сейчасъ будемъ говорить, было впер-
впервые лодм'Ьчено Спльванусомъ Томпсономъ, ирофессоромъ уни-
университетской коллегш въ Бристшть. Почтенный ученый нола-
галъ, что это именно явлеше не можетъ быть объяснено спо-
способностью человъческаго глаза сохранять воспринятая зрптель-
ныя впечатлгьшя. Онъ думалъ, что изучеше подобныхъ явлешй
можетъ повести къ открътю новыхъ свойствъ глаза. Между
т4мъ въ «Журнал^ Элементарной Математики» за 1885 г. есть
весьма удачное объяснеше этого явлешя С. Шостака, въ основ4
котораго лежитъ именно способность глаза сохранять зритель-
ныя впечатлгЬн1я.
Приводимъ onncanie явлен!я и его объясиеше г. Шоста-
комъ для прим'Ьра читателю, какъ можно (и даже по возмож-
возможности всегда нужно) пользоваться математическпмъ аналпзомъ
при pascMOTpiniii разлпчпыхъ встречающихся намъ явлевпй.
Возьмемъ прилагаемую зд^сь фигуру 13-ю, которую каждый
желающш можетъ нарисовать п самъ, для удобства наблюден1й,
на отдъигьпомъ листк-Ь.
Если листку бумаги (или книгЬ) съ предложенной
фигурой сообщить незначительное круговое движете
въ плоскости фигуры, то каждый изъ шести кружковъ
будетъ казаться вращающимся «около своего центра въ
сторону движешя фигуры и съ такою же скоростью,

30
т. е. будетъ казаться, что каждый кругъ описываетъ
полный оборотъ въ то же время и въ томъ же направле-
ши, какъ и бумага или книга, гдЬ онъ нарисоваыъ.
ЗамЪтимъ здт,сь же, что то же самое явлеше можно наблю-
наблюдать и въ томъ случай, если вместо шести кружковъ, какъ на
Фиг. 13.
фиг. 13, возьмемъ только одпнъ, составленный изъ концентри-
ческихъ окружностей.
Объяснеше явлешя. Если взять чертежъ, данный на сле-
следующей фиг. 14-й, п сообщить ему быстрое движете взадъ и
впередъ, какъ покавываетъ стрелка а, читатель замгьтитъ, что
Фиг. 14.
рпсунокъ потеряетъ свою отчетливость и сделается какъ бы
туманньшъ. Это заг.пситъ оттого, что черныя полосы запп-
маютъ мйсто бйлыхъ и б'Ьлыя—черныхъ, такъ что получается
какъ бы смъчпеше чернаго цвгЬта съ бтлымъ, всл4дств!е чего
является сирый тонъ. Если тому же рисунку сообщить движе-
движете взадъ и впередъ по направлетю стръ'локъ Ь, то черный

цвъ'тъ не будетъ занимать мъ'ста б-Ьлаго и б'Ьлый—чернаго, по-
поэтому рнсунокъ не долженъ будетъ потерять свою отчетливость,
что п подтверждается опытомъ. Еслп мы дадимъ рисунку дви- .
жеше по направленш среднему между двумя названными, то
фигура также потеряетъ свою отчетливость, и тъчяъ болгЬе, ч-Ьмъ
направлеше движешя будетъ ближе подходить къ направлетю,
указанному стрелками а. Изъ этого заключаемъ, что бйлый
цвйтъ остается чисто бйлымъ только въ томъ случай, когда
движете происходитъ параллельно направлетю полосокъ.
Вообразимъ теперь, что мы сообщаемъ фигурй пе круговое
движете, а по направлетю сторонъ
шестиугольника 123456 (фиг. 15), такъ
что каждый кружокъ движется сначала
по направлетю отъ 1 къ 2, потомъ отъ
2 къ 3, отъ 3 къ 4 и т. д. Разсмотрпмъ
тотъ перюдъ, когда движете происхо-
происходить параллельно лиши 1 —2, п прове-
демъ Д1"аметръ ЛВ, перпендикулярный
къ 1—2. Части концентрпческпхъ кру-
говъ, заключающаяся въ узкой полоски
вдоль ЛВ} можно считать перпендику-
перпендикулярными къ ЛВ и, следовательно, па-
параллельными къ 1—2, т. е. параллель-
параллельными къ лиши движетя, а всл4дств1е
этого, на основанш сказаниаго выше,
б'Ьлыя части этой полоски останутся 6i-
лыми, а па кружкЬ обозначится поэтому светлый д1аметръ но
направленно ЛВ (д1аметръ будетъ казаться узкпмъ по середпнт.
п широкпмъ по концамъ). Остальная часть кружка будетъ бо-
лйе пли менъ-e туманною, такъ какъ друпя части концентрп-
чеокихъ круговъ будутъ двигаться по направлепш непараллель-
непараллельному лптп двпжен1я 1—2, а подъ угломъ къ-ней. Обратимся
ко второму перюду. т. е. къ тому времени, когда двп-
происходптъ параллельно линш 2—3. Проведемъ д1а-
метръ CI) перпендикулярно къ направлента лип1п движе1пя,
т. е. перпендикулярно къ линш 2—3. Мы доказали, что въ
первый перюдъ движешя на кружк'Ь долженъ обозначиться
Фиг. 16.

32
светлый дхаметръ по направлешю АВ. Подобно же можно до-
доказать, что во второй перюдъ движетя этимъ свъ"глымъ д1а-
ыетромъ будетъ уже не АВ, a CD. Въ трепи перюдъ светлый
д1аметръ будетъ направленъ по EF (предполагая, что EF
перпендикулярна къ лпнш 3—4. Въ четвертый перюдъ опять
по АВ (такъ какъ 4—5 параллельна 1—2) и т. д., т. е. свъ'Т-
лый д1аметръ, по ыгЬр4 изменешя направлешя двпжетя, будетъ,
такъ сказать, перескакивать изъ АВ въ CD, изъ CD въ EF
п т. д. Если мы вместо того, чтобы заставлять двигаться фп-
гуру по направлетямъ сторопъ шестиугольника, ваставимъ ее
двигаться по сторонамъ двенадцатиугольника, то получиыъ не
три, а шесть св^тлыхъ д1аметровъ п т. д.; словомъ съ увели-
чешемъ числа сторонъ и, следовательно, съ приближешемъ къ
окружности, число свйтлыхъ дхаыетровъ будетъ увеличиваться,
скачки будутъ становиться все меньше п меньше, п когда
центръ, вместо многоугольника, станетъ описывать окружность,
намъ будетъ казаться, что светлый д1аметръ плавно вращается
вокругъ центра кружка. Следовательно, при нашемъ опыте
действительно существуешь вращен1е, но не кружка, а свет-
лаго д1аметра; и это вращеше глазомъ приписывается кружку.
Все сказанное выше объ одномъ кружке относится и къ
остальнымъ. А потому намъ будетъ качаться, что каждый изъ
нихъ самостоятельно вращается около своего центра.
Ниже следуетъ еще несколько интересныхъ примеровъ ил-
люз1Й spenifl, толковаш'е которыхъ ыы предлагачп бы дать
читателю самому.
Задача 13-я.
Какая лишя длиннее?
Взглянувъ на прилагаемый зд-Ьсь чсртежъ (фиг. i6),
скажите, какая лишя длинн-Ье АХ или AY?
л	В
Фиг. 16.

33
Разъяснеше.
Можно утверждать наверняка, что каждый, взглянувъ на
чертежъ, скажетъ, что диагональ ЛХ несомн-Ьнно, молъ, длин-
длиннее AY. Но стоитъ вамъ смерить ихъ хотя бумажкой,—и вы,
къ пзумленго, убедитесь, что они равны! Сообравивъ, можно
ото сказать и бевъ прим-Ьрки: если изъ точки Л провести пер-
перпендикулярную лпнш къ XY, то станетъ ясно, что перпендп-
куляръ раздали тъ ее пополамъ, а вслтдоттае равенства про-
екцш, наклонныя ЛХ и ЛY должны равняться.
ЧгЬмъ же объяснить такой странный обманъ врътя? Воз-
Возможно равсуждать такъ: если бы наше сознаше воспринимало
вещи такими, каковы они на самомъ д-бл-Ь, ничего къ нимъ не
присочиняя,—то подобныхъ иллюзШ не могло бы быть. Но въ
томъ-то и дъ-ло, что мы незаметно для самихъ себя разсужда-
емъ, воспринимая впечатлтлпя внФшняго Mipa. Эти-то «под-
«подсознательный» разсуждешя и являются причиной подобныхъ опти-
ческихъ обмановъ.
Такъ какъ этотъ процессъ разсуждешя совершается без-
сознательно для насъ, то довольно трудно бываетъ съ досто-
достоверностью его возстановить: приходится строить лишь болйе
или менФе правдоподобныя догадки. Въ данномъ случай, на-
прим'Ьръ, мы безсозпательно, плп, лучше сказать, «подсозна-
«подсознательно», разсуждаемъ, по всей вероятности, такъ: «Передъ 1гами
два параллелограмма — длинный и коротмй. Ясное дъмго, что
у длипнаго параллелограмма д1агонали должны быть длиннее,
ч'Ьыъ у короткаго».
Впрочемъ, предлагаемъ желающему дать бол'Ье удачное
объяснен1е.	р	д
Вотъ еще подобный же
прпмфръ.
Не правда ли, что
на фигур'Ь 17-й лишя
АВ кажется намъ длин-
лиши АС?	. ,„
Фиг. 17.
ВЪ ЦАРСТВ Ь СМЕКАЛКИ.

34
Въ действительности же он-Ь строго равны между собой.
Точно такъ же:
Кажется совершенно невЪроятньшъ, чтобы точки
А и С (фиг. i8-ft) одинаково отстояли отъ точки В.
Фнг. 18.
А между т-Ьмъ это такъ! Разстояше скрадывается вд-Ьсь
наклономъ лиши и ихъ толщиной.
Задача 14-я.
ДвЪ пары дугъ.
На фиг. 19-й изобра-
изображены двЪ пары круго-
выхъ дугъ. Если продол-
продолжить лЪвыя дуги, то встр"Ь-
тятъ ли он-Ь оконечности
правыхъ?
На ввглядъ это кажется
невозможныыъ; а между гЬмъ
возьмите въ руки циркуль и
рад1усами окружностей, ко-
которые на фигурЬ указаны,
продолжите эти дуги. Вы
убедитесь, что продолжешя
Л'Ьвыхъ дугъ точно встр'Ьтятъ
концы правыхъ. Это тоже
весьма интересный обыанъ
врйшя, отъ котораго мы ппкакъ не можемъ отделаться, cmotjm
ua рысунокъ.
А/
/ В/
1 г~
IA/1/V
¦—-—.
С
D >v
\\
Фиг. 19.

36
Задача 15-я.
Какъ написано слово?
Прилагаемая и следующая фигуры (фиг. 20 и 21) даютъ
едва ли не самые интересные образчики врительныхъ ил-
люз1Й. На фиг. 20-й вы видите написанное англшское слово
LIFE (жизнь), при чемъ вамъ до очевидности ясно, что
буквы рйзко наклонены
въ разныя стороны. Но
приложивъ линейку, вы
можете убедиться, что
эти буквы поставле-
поставлены совершенно прямо и
только начерчены мел-
мелкими наклонными штри-
штрихами.	Фиг- 2°-
Задача 16-я.
Какая кривая?
На фигуръ1 21-й изображены концентричесшя окруж-
окружности, а вовсе не спираль, или рядъ спиралей, какъ ка-
кажется на взглядъ.
Фиг. 21.

36
Въ этомъ легко убедиться. Поставьте карандашъ на одну
изъ дугъ и ведите его по ней. Противъ ожндашя, вы будете
кружиться въ замкнутшъ круг-Ь, а вовсе не приближаться къ
центру или удаляться по перпферш, какъ должно быть, если бы
на чертежи была изображена спираль. ОЬтчатый фонъ, на ко-
торомъ начерчены об'Ь посл-Ьдшя фигуры, много способствуетъ
усплешю этихъ эффектныхъ иллюзШ.

Задачи и развлечешя со спичками.
Въ первой части настоящаго опыта математической хресто-
матш мы уже указали на нъ-которыя прост-Ьйшхя математпче-
ciua задачи и игры со спичками. Приводимъ зд'Ьсь еще не-
несколько простыхъ и интересныхъ вадачъ и развлечетпй этого
рода, при чемъ считаемъ нужнымъ обратить внимаше читателя
ла небольшую книжечку Софуса Тромгольда «Игры со спич-
спичками», довольно полно и всесторонне исчерпывающую предметъ.
Книжечка эта есть въ русскомъ перевод^, въ прекрасномъ из-
данш одесскаго книгоиздательства «Mathesis», и стоить всего
полтинникъ. Обыкновенная коробка шведскихъ спичекъ есть
незаменимое по своей доступности и дешевизн^ noco6ie, кото-
которое д^тямъ, учащимся и вврослымъ можетъ помочь провести
досуги не только весело, но и съ пользой. Объ этомъ следо-
следовало бы постоянно помнить. Начнемъ съ незамысловатыхъ за-
дачъ на переложеше спичекъ.
Задача 17-я.
Этотъ домъ составленъ изъ ю спичекъ.
Требуется повернуть его къ намъ другой I
стороной, передвинувъ только 2 спички.	фИг. 22.
Р-Ьшеше.
(—(\	Отвить ясенъ изъ фиг. 23-й, которая получается
'—'—' изъ предыдущей, если въ «крыш!» дома (ф»г. 22)
Фиг. 23. прюпустпть одну спичку и приподнять другую.

Задача 18-я.
Въ-сы составлены изъ 9 спичекъ и не находятся въ
состоянш равновЪая (фиг. 24). Требуется переложить въ
нихъ 5 спичекъ такъ, чтобы въсы были въ равнов-Ьсш.
Pimeme.
Дается фиг. 25-ой.
Задача 19-я.
Этотъ греческш храмъ (фиг. 26) построенъ изъ
11 спичекъ. Требуется переложить 4 спички такъ,
чтобы получилось II квадратовъ.
Pimeme.
См. фиг. 27-ю.
Задача 20-я.
Въ памятник^, составленномъ изъ 12-ти спичекъ
(фиг. 28) требуется переложить 5 спичекъ такъ, чтобы
получилось з квадрата.
Ясно изъ фиг. 29.
Задача 21-я.
ДвЪ рюмки (фиг. зо) составлены изъ десяти спи-
спичекъ. Переложить въ нихъ б спичекъ такъ, чтобы по-
получился домъ.
Р'Ьшеше.
См. фиг. 31.
Задача 22-я.
Флюгеръ (фиг. 32) составленъ изъ ю спичекъ. Пе-
Переложить 4 спички такъ, чтобы получился домъ.

39
Фиг. 24.
_|_
_|_
I 1
ЛА
Фиг. 25.
Фиг. 26.
Фиг. 27.
Ln \7 \/
у у
I	i U 1 1
Фиг. 28. Фиг. 29. Фиг. 30.
Фиг. 31.
Фиг. 32.
См. фиг. 33.
Pimeirie.
Задача 23-я.
Вотъ фонарь (фиг. 34) и вотъ топоръ (фиг. 35)-
Каждый изъ нихъ составленъ изъ 9 спичекъ. Перело-
Переложить въ фонарЪ б спичекъ и получить четыре рав-
ныхъ треугольника, составляющихъ въ свою очередь
четыреугольникъ. Переложить въ топоръ" 4 спички
такъ, чтобы получилось з равныхъ треугольника.
А
1>
О
д
Фиг. 37.
Фиг. 38.
Фиг. 33. Фиг. 34. Фиг. 35. Фиг. 36.
Р-Ьшеше.
Ивъ фонаря получается фиг. 36-я.
Изъ топора получается фиг. 37-я.
Задача 24-я.
Въ этой лампЪ, составленной изъ 12 спичекъ (фиг.
переложить з спички такъ, чтобы получить 5 равныхъ
треугольниковъ.

40
См. фиг. 39.
Р'Ьшеше.
Задача 25-я.
Изъ ю спичекъ сдЬланъ ключъ (фиг. 40). Перело-
Переложить въ немъ 4 спички такъ, чтобы получилось з ква-
квадрата.
P-fcmeHie.
См. фиг. -±1.
\
V
л
Фаг. 39:
о
I
О
Фиг. 40.
Н
Фиг. 41.
Фиг. 42.
Задача 26-я.
У звезды, составленной изъ 12-ти спичекъ (фиг. 42):
а) переложить 4 спички такъ, чтобы получился 4-ко-
нечный крестъ. Ь) Въ полученномъ крестЬ переложить
8 спичекъ такъ, чтобы получить крестъ, состояний
изъ 4 крестовъ. с) Въ этомъ послЬднемъ крестъ- пе-
переложить 8 спичекъ такъ, чтобы получилось \ ква-
квадрата, d) Наконецъ, переложить 8 спичекъ такъ, чтобы
получилась мельница.
Фиг. 43.

41
PimeHie.
ВсЬ требуемыя р4шешя означены соответствующими бу-
буквами а, Ъ с, и d на фиг. 43-ей.
Задача 27-я.
Д-Ьлежъ сада.
Изгородь квадратнаго сада составлена i6 спичками
(фиг. 44)- Въ ней находится домъ, представленный ква-
дратомъ изъ 4~хъ спичекъ. Требуется разделить садъ
(безъ дома) между 5~ю наследниками, при помощк
ю-ти спичекъ, такъ, чтобы каждый получилъ части
одинаковыя по величинъ- и по форм-fe.
1 1
П 1 м
1 1 1
1 1 1 °
J ' 1 |0
__| 1 1
о с |
со,
о -J
1 о " 1
Г~1:1°
Фиг. 44.	Фиг. 46.	Фиг. 46.	Фиг. 47.
Р-Ьшеше.
См. фиг. 45-ю.
Предложенную задачу можно видоизменить и такт.:
4 брата получили отъ дяди въ наследство садъ
(обнесенный i6 спичками), въ которомъ находится
12 шгодовыхъ деревьевъ (монеты или пуговицы), распо-
ложенныхъ, какъ указано на рисункъ\ Требуется 12 спич-
спичками разделить садъ на 4 равныя части одинаковой
формы, содержания ио равному числу деревьевъ.
Pisineme ея дается фиг. 47-ой.
Задача 28-я.
Сообразите-ка!
123456789	Кладутъ произвольное,
I I I I I I II II I М I I 11 I I не очень малое количество
спичекъ въ рядъ, надписываютъ надъ 9 спичками, сл'Ь-

42
дующими другъ за другомъ, числа отъ i до 9 и про-
сятъ кого-нибудь изъ присутствующихъ заметить одно
изъ этихъ 9 чиселъ. Въ ум-fe выбираютъ какое нибудь,
не особенно малое число (напримЬръ, 23) и считаютъ
отъ 9 дал-Ье вправо ю, и, г2 и т. д. до 23; если
рядъ оканчивается, продолжаютъ счетъ, переходя 1съ
началу ряда (у насъ придется считать до спички, поме-
помеченной 4)- Теперь просятъ считать подобнымъ образомъ
другого отъ замЪченнаго имъ числа вправо до 23, въ
то же время сообщите ему, что когда онъ назоветъ
число 23, то укажетъ на спичку № 4-
Подумайте немного, и вы убедитесь, что такъ, оно и должно
быть! Это очень легкая и простая задача. Но какъ она ни
проста, а иныхъ она на первыхъ порахъ удивляетъ.
Задача 29-я.
Разстановка часовыхъ.
Вдоль стЪнъ квадратнаго бастюна требовалось по-
поставить 12 часовыхъ. Полковникъ разм-Ьстилъ ихъ,
какъ указано на рисунк^ (фиг. 48) по 4 съ каждой
стороны. ЗатЬмъ пришелъ комендантъ и, недовольный
| | | | размЪщешемъ часовыхъ, распорядился разста-
|| || вить солдатъ такъ, чтобы съ каждой сто-
| | | | роны было по 5- Всл-Ьдъ за комендантомъ
Фиг. 48. пришелъ генералъ, разсердился на коменданта
за его распоряжеше и размъхтилъ солдатъ по 6 чело-
в^къ съ каждой стороны. Каково было разм'Ьщеше въ
двухъ послъдаихъ случаяхъ?
Pimeme.
даются разм-Ьщетямп а и Ъ на фиг. 49.
Mill	МММ
I I
Mill, III 111
Фиг. 49.

43
Задача 30-я.
Хитрецы.
Въ корчдгЬ стояло четыре стола, образуя четыре-
угольникъ. Проголодавииеся, возвращавпиеся съ манев-
ровъ солдаты остановились тамъ въ числ^з 21 чело-
человека пообедать и пригласили къ объ-ду и хозяина. Раз-
склись всЬ такъ: за тремя изъ столов!^ сели солдаты—
по 7 за каждый столь (фиг. $о), а за __ |
чствертымъ столомъ сЬлъ хозяинъ. Сол- —	~
даты уговорились съ хозяиноыъ, что Z	~
платить по счету будетъ тотъ, кто оста- —	Z
нется поел Ьднимъ при елвдующемъ усло-
Bin: считая въ круговую (по часовой
стръ'лк'Ь) всЬхъ, въ томъ числ'Ь и хозяина, освобождать
каждаго седьмого. Каждый освобожденный уходилъ
изъ корчмы и послЪднимъ остался самъ хозяинъ. Съ
кого начали счетъ?
Съ кого нужно было бы начать, если бы солдатъ
было только по 4 за каждымъ изъ трехъ столовъ?
Pimeme.
Надо начинать счетъ съ 6-го солдата, епдящаго по лйвую
руку отъ хозяина. Во второмъ же случай съ 5-го изъ голдатъ
направо отъ хозяина.
Задача 31-я.
Предложите кому-либо взять въ каждую руку по
равному какому угодно числу спичекъ (или какихъ-
либо иныхъ предметовъ). Это число вамъ неизвестно.
Предложите партнеру переложить изъ правой руки въ
л-ввую то число предметовъ, которое вы ему скажете,
(напр, число а). Затъмъ, ничего не показывая и не го-

44
воря вамъ, пусть онъ отложитъ изъ л бвой руки столько
спичекъ, ci лько у него осталось въ правой; и нако-
нецъ, опять-таки ничего вамъ не показывая, пусть от-
отложитъ въ сторону всъ1 спички изъ правой руки. Те-
Теперь вы можете см'Ьло утверждать, что у вашего парт-
партнера осталось въ лЬвой рукЬ всего la спичекъ.
НаприагЬръ: Пусть партперъ возьметъ по 15 спичекъ въ
каждую руку. Вы требуете, чтобы въ лъ-вую руку изъ правой
онъ переложилъ, наир., 10 сппчекъ (Значить, у него въ пра-
правой осталось б сп., а въ лъ"вой 26). Затъчиъ по вашему требо-
ватю онъ изъ лйвой перекладывает* въ правую столько спп-
сппчекъ, сколько гамъ есть (т. е. въ правой у него станетъ
5 -|— 5 = 10 спич.), и все эти спички откладываетъ. Вы и «уга-
«угадываете», что въ лъчвой рук/Ь у него должно остаться 2Х1^ =
20 спичекъ.
PinieHie.
Общее piineme и доказательство этой задачи можегь найти
каждый. Пусть только онъ проследить, что въ сущности де-
делается при последовательномъ переложенш и откладыванш
спичекъ. Пусть у партнера въ рукахъ по п спичекъ, и вы го-
говорите ему переложить изъ правой руки въ лт>вую а спичекъ.
Получается:
I. Въ обеихъ рукахъ по п спичекъ.
П. въ лт>вой п -(- а, въ правой п — а спичекъ.
III. Въ л^вой (п-\- а) — (п — а) = 2а спич., изъ правой
веЬ спички откладываются. Итакъ, всегда въ лйвой руки полу-
получится въ конп/Ь концовъ удвоенное число тЬхъ спичек ь, кото-
рыя вы сказали переложить въ первый разъ.
Задача 32-я.
В%рная отгадка.
Иванъ беретъ въ одну руку четное, а въ другую
нечетное число спичекъ. Петръ предлагаетъ ему по-
помножить число спичекъ въ правой рук'Ь на нечетное

46
число, а число спичекъ въ л-Ьвой рук? на четное и
сказать ему сумму полученныхъ произведен^. ВслЬдъ
заттзмъ онъ угадываетъ, въ какой рукъ~ у Ивана чет-
четное и въ какой нечетное число спичекъ. Какъ это онъ
дЬлаетъ?
Pinieme.
Если названная сумма—число четное, то у Ивана въ пра-
правой рук/Ь четное число спичекъ и въ лъвой —• нечетное. Если
же эта сумма -— нечетная, то въ правой рукт> нечетное число
спичекъ.
Доказательство относптельно подобнаго рода задачъ см. въ
первой части этой книги—задача 94-я.
Задача 33-я.
Собрать въ группы по 2.
123456789 10
I I I I I II I I 1
ю спичекъ положены въ одинъ рядъ. Требуется
распределить ихъ попарно, всего въ 5 паръ, перекла-
перекладывая по одной спичк-fe черезъ двв (напридгЬръ, № г
переложить къ Js« 4 и т. д.).
PiineHie.
Можно перекладывать такъ:	пли:
4	къ 1	7 къ 10
7	» 3	4 » 8
5	» 9	6 » 2
6	» 2	1 » 3
8	» 10	5 » 9

46
Задача 34-я.
Собрать въ группы по 3.
15 сгшчекъ лежать въ рядъ:
1 2 3 4 5 в 7 8 9 10 11 12 13 14 15
I I I I I I I I I I I I I I I
Требуется собрать ихъ въ 5 группъ (или кучекъ)
по з спички въ каждой, при чемъ перекладывать спички
по одной и каждый разъ перескакивать черезъ з спички.
Pimeirie.
Обозначимъ положенный въ рядъ сппздга соответственно
числами 1, 2, 3	, 15. Тогда задача решается путемъ слгЬду-
ющихъ 12-ти переложешй:
2 на 6	4 между 5 и 6
1 » 6	3 » 5 » 6
8	» 12	11 » 5 » 6
7 » 12	13 на 11
9	» 5 14 » И
10 » б 15 » 11
Задача 35-я.
Переп/гЬщеше лошадей.
12345678	9
FT l~l N R П Fl Fl R Й
Въ конюшнЪ устроено 9 стойлъ въ рядъ. 5-ый но-
меръ не занятъ: въ ноыерахъ I, 2, з и 4 находятся
черныя лошади (копейки), а въ 6, 7» 8 и 9 бЪлыя ло-
лошади (гривенники или иные предметы). Требуется пе-
перевести бъ-лыхъ лошадей въ I, 2, з и 4 номера, а чер-
ныхъ въ 6, 7^ 8 и 9 на сл'Ьдующихъ услов1яхъ: каждая

47
лошадь можетъ перескакивать въ ближайшее стойло
или соседнее съ нимъ, но не дальше; никакая лошадь
не должна возвращаться на прежнее мъсто, и въ ка-
ждомъ стойлЬ не можетъ быть больше одной лошади.
Начинать съ б'Ьлой лошади.
Р^шеше.
Задача решается въ 24 хода следующими перемещешямн:
в въ 5 2 въ 4 4 въ 6
4 » G 1 » 2 2 » 4
3	» 4 3 » 1 3 » 2
6	»	3	5	»	3	5	»	3
7	»	5	7	»	5	7	»	5
8	»	7	9	»	7	6	»	7
6	»	8	8	»	9	4	»	6
4	»	6	6	»	8	5	»	4
Задача 36-я.
Поднять одной спичкой 15 спичекъ.,
Pimeiiie.
Эта на первый взглядъ трудная задача решается, однако,
легко. Положиыъ на столъ спичку А (фиг. 61), а поперекъ этой
спички положимъ затъчиъ вплотную одну около другой, попере-
попеременно вправо и вл^во, 14 спичекъ, и именно такъ, чтобы ихъ
головки выдавались на 1—l'/a сантиметра надъ -А,.въ то время
какъ концы безъ головокъ опирались бы на столъ. Сверху, въ
углублете, образуемое верхними частями спичекъ, кладутъ за-
теыъ 16-ю спичку параллельно А. Если поднять теперь по-
последнюю за конецъ, то къ нашему удпвленго вместе съ нею
поднимутся п остальныя 15 спичекъ (фиг. 52). Для этого опыта
удобнее брать болышя, толстыя четыреугольныя спички.

48
Фиг. 61.
Фиг. 52.
Задача 37-я.
Спичечный телеграфъ.
Спичечный телеграфъ строится, какъ указано на рпсупк-Ь
(фиг. 53). Можно, конечно, удлинить или укоротить его по же-
желанно. Если нажать въ В, то А подпрыгнетъ.
Фиг. 63.
Фиг. 64.
Задача 38-я.
Легно или н%тъ?
Въ заключеше этого небольшого отдела задачъ со спичками
предлагаешь вамъ проделать уже не задачу, а маленькое физи-
физическое, что ли, упражнеше.
Вотъ положено на стол'Ь 5 спичекъ, которыя пред-
лагаемъ вамъ поднять двумя руками такъ: сперва спичку
№ г двумя большими пальцами; оставивъ ее между
этими пальцами, поднять затъмъ двумя указательными
пьльцами спичку № 2; оставляя эти двъ- спички между

49
пальцами, поднимите зат-Ьмъ спички № з средними
пальцами, спичку 4—безыменными и спичку 5- мизин-
мизинцами. У васъ должна получиться фиг. 54-
Интересно знать, удастся ли это ваыъ? Скоро ли и легко
лп? А если не легко, то почему? Но если, въ концй концовъ,
это вамъ удалось бы сделать, то попробуйте точно такъ же
соответствующими пальцами об'Ьихъ рукъ поднять по 2, по
3 спички.
JB'L ЦМ'СТВЬ CI4EL:.V.4IjII.

Лабиринты.
Вотъ задача, происхождете которой относится еъ глубокой
древности и теряется во мрак/в легендарныхъ сказашй. Древ-
ще,—да, пожалуй, мнопе и теперь,—задачу о лабиринтахъ счи-
считали вообще неразрешимой. Челов'Ькъ, попавппй въ лабиринтъ,
не могъ уже изъ него выйти, если только какое-либо чудо или
случай не приходили ему на помощь.
Изъ настоящей главы мы, наоборотъ, увидимъ, что безвы-
ходныхъ лабиринтовъ н^тъ, что разобраться и найти выходъ
изъ самаго запутаннаго лабиринта не составляетъ особаго труда.
Рътаенш задачи мы предпосылаемъ никоторый историчесшя
справки о лабиринтахъ. Эти справки, помимо общаго ихъ инте-
интереса, докажуть намъ, съ одной стороны, насколько интересова-
интересовались этой задачей, а съ другой,—дадутъ намъ наглядное пред-
ставлеше посредствомъ рисунковъ о существовавшихъ и суще-
ствующихъ лабиринтахъ.
Слово «-лабиринтъ»—греческое и въ переводи означаетъ
ходы въ подземельяхъ. Существуетъ, действительно, очень боль-
большое количество природныхъ подземныхъ пещеръ съ такимъ
огромнымъ количествомъ по веЬмъ направлешямъ перекрещи-
перекрещивающихся коридоровъ, закоулковъ и тупиковъ, что нетрудно
въ нихъ заблудиться, потеряться и, не найдя выхода, умереть
отъ голода и жажды.
Примеры такого же рода, но уже пскусственныхъ лабирин-
лабиринтовъ могутъ представить шахты пныхъ рудниковъ пли такъ на-
называемые катакомбы.

61
ВгЬроятнгЬе всего, что подобный подземелья возбудили у строи-
строителей еще древнъ'йшихъ временъ охоту подражать имъ искус-
искусственными сооружетяыи. И у древнихъ писателей мы встрй-
чаемъ указаше на существоваше искусственныхъ лабпринтовъ,
напр., у египтянъ. Въ концт> концовъ, словомъ лабиринтъ чаще
всего обозначали именно искусственное чрезвычайно сложное
сооружеше, составленное изъ очень большого числа аллей или
галлерей, безчисленныя развйтвлетя, перекрестки и тупики кото-
рыхъ заставляли попавшаго туда безконечно блуждать въ лаби-
ринт^ въ тщетныхъ поискахъ выхода. Объ устройств^ такихъ
лабиринтовъ слагались ц'Ьлыя легенды.
Извйстнйе всего разсказъ о лабиринтъ1, построенноиъ миеи-
ческимъ Дедаломъ на островй КритЬ для миоическаго же царя
Миноса. Въ центрт, лабиринта жило чудовище Минотавръ, и
никто изъ попавшихъ туда не могъ выйти обратно, делаясь, въ
конц'Ь концовъ, жертвой чудовища. Семь юношей и семь дт>ву-
шекъ приносили аеиняне въ дань ежегодно чудовищу, которое пре-
исправно ихъ пожирало. Наконецъ, Тсзей не только убплъ Мп-
нотарва, но п вышелъ изъ лабиринта, не заблудившись въ немъ,
при помощи, впрочемъ, нити клубка царевны Ар1адны. Съ той
поры слова «нить Ар1адны» гш'Ьютъ символическое значеше,
какъ способъ, даннщй выходъ изъ самаго затруднительнаго по-
ложен!я.
Лабиринты бываютъ самой разнообразной формы и устрой-
устройства. До нашихъ дней сохранились еще и запутанно-сложные
галлерей, и ходы пещеръ, и архитектурные лабиринты надъ мо-
могилами, и извилистые планы на стйнахъ пли полахъ, обозна-
обозначенные цв^тнымъ мраыоромъ или черепицей, и извивакящяся
тропинки на почв'Ь, и релъефныя извилины въ скалахъ.
Рисунками лабиринтовъ украшались одйяшя хрисйапскихъ
императоровъ до девятаго стол^щя, и остатки такихъ же укра-
meHifl сохранились до сихъ иоръ на стт>нахъ церквей и собо-
ровъ того времени. Вероятно, эти украшен1я служили символомъ
сложности жизненнаго пути и челов^ческихъ заблуждешй. Осо-
Особенно употребительны были лабиринты въ первой половин^ двЬ-
падцаго стол'Ьйя.
4*

52
Иа фиг. 55-й зд'Ьсь приведено изображеше одного изъ лаби-
ринтовъ того времени во Францш, въ церкви святого Квентина.
Лабирпнтъ этотъ выложенъ изъ камня на полу посреди церкви,
и Д1аиетръ его равняется тридцати четыремъ съ половиной фу-
тамъ. Путь къ центру зд'Ьсь есть сама лишя. Если вести каран-
дапгсмъ по линш отъ точки А (не обращая вшшавая на внтлпнюю
окружающую лабиринтъ линш), то вн придете къ центру по длин-
длинной извилистой дорой черезъ всю внутреннюю площадь, но сомнт.-
шя относитачьно выбора пути у васъ быть не можетъ. Въ подоб-
ныхъ случахъ этп древше духо вные лабирпнты отличаются во-
Фиг. 66.
ооще но головоломпьшъ, а просто продолжительнымъ извплистымъ
нутемь, который держптъ васъ все время внутри лабпринта.
Въ церкви аббатства св. Вертина во Францш есть еще бо-
лЬе любопытное изображеи!е подобнаго рода на полу, предста-
представляющее въ центр-Ь 1ерусалимсий храмъ, съ остановкалш для
пилпгримовъ. Этотъ лабиринтъ действительно посещался пили-
пилигримами взам'Ьнъ путегаеств1я по объту въ Святыя Ьйста.
Пройти ползкомъ весь путь лабпрпнта назначалось также вме-
вместо эпитпм1и.
Лабпринтъ въ Шартрскомъ соборй, изображенге котораго
здхст. дано (фиг. 56),' сорока футовъ въ поперечнпкт,, также
посещался кающимися, и они совершали весь его сложный и
длинный путь, выполняя наложенную на нихъ эпптимш пли обт>тъ.

63
Подобпаго же рода лабп-
рпнтъ, но гораздо ыеньшихъ
разыт,ровъ, пом'Ьщающйся
Фиг. 67.
Фиг. 68.
всего на одной плитЬ пола, есть въ каоедральномъ соборй въ
Луккт, (фиг. 57). Въ натуральную величину онъ имйетъ 19х/2
дюйзювъ въ поперечники.
Друйе подобные лабиринты были и, можетъ быть, существу-
ютъ до сихъ поръ въ аббатствгв Туссарта въ ШалонЬ на Мары!,
во многихъ древнихъ соборахъ и церквахъ въ Ахеий, въ Римй,
въ РавенцТ) и во многихъ другихъ м'Ьстахъ. Лабиринты въ
церквахъ большею частш
назывались «путп въ Iepy-
саливхъ» и служили симво-
лолъ труднаго земного пу-
тешеств1я въ Святыя М'Ьста,
наградой за которое яв-
является небесная благодать,
поэтому центръ лабиринта
часто называли «Небомъ».
Въ Англш не встреча-
встречаются лабиранты на церков-
помъ полу, но за то было
очень много лабпрпнтовъ,
сдт.лапцыхгь изъ дерна ан	ФлГ. 69.

64
лужапкахъ. Опп носплп
различный цазвашя: «Го-
родъ Троя», «блйды па-
пастуха» и т. п." Большин-
Большинство изъ нихъ находится
вблизи церквей или на
кладбищахъ, что указы-
ваетъ тоже на пхъ ду-
духовное пропехождете. О
такихъ лабирпнтахъупо-
иинаетъ Шекспиръ въ
свопхъ пьесахъ «Сонъвъ
Л'Ьтнюю ночь» и «Буря».
Образцы подобпыхъ
«дерновыхъ» лабирин-
товъ приведены зд4сь на
фиг. 58 и фиг. 59. Изъ нихъ первый (фиг. 58) въ графствЬ
Эссексъ им&лъ 110 футовъ въ лгаис-трй, а второй (фиг. 59)
въ Ноттипгеймширъ" 51 футь въ д1аметр4 съ лин!ей пути въ
535 ярдовъ длины (Лпнш извилистыхъ путей обоихъ этихъ
Фиг. 60.
Фиг. 61.
лаоирннтовъ ясно видны, на чертежи). Оба этп лабиринта были
взрыты плугоыъ и уничтожены въ 1797 году. Для полноты п
разнообраз1я возьмемъ еще образецъ итальянскаго лабиринта 16
столг1шя (фиг. 60), лабирпнтъ взятый изъ книги англШскаго

бб
Фиг. 62.
писателя 1706 года (фиг. G1),
п, наконецъ, датсшй лабирннтъ
т-Ьхъ же времеиъ (фнг. 62).
Все вышепреведенные лаби-
лабиринты пм^ютъ бол'Ье псторпче-
сгйй, чймъ математпческш ин-
тересъ. Распутать пхъ не трудно.
Но посл4 Рсформацш фигуры
эти потеряли свое символическое
значеше и сделались мало-по-
мало-помалу предметомъ развлечешя.
Лабиринты переходятъ въ сады,
цветники и парки, гд^ путемъ проведешя прихотливо извиваю-
извивающихся, то пересекающихся, то внезапно прегражденных!., или
заканчивающихся тупикоыъ, дорожокъ получались самыя запу-
танныя н головоломный фигуры, въ которыхъ, действительно,
нелегко было найти дорогу отъ края къ центру, и гд4 трудно
было не заблудиться. Изъ такпхъ затейливыхъ садовъ если не
самый головоломный для решешя, то наиболее известный былъ
лабиринтъ одного изъ дворцовыхъ садовъ англйскаго короля
Вильгельма III. Вотъ что можно прочесть о немъ въ Ency-
Encyclopaedia Britannica подъ словомъ «Labyrinth» съ соответствую-
щимъ рисункомъ (фиг. 63):
"* I
Фиг. 63.
«Лабиринтъ въ садахъ дворца Хэмптонъ - коуртъ считается
однимъ изъ самыхъ красивыхъ въ Англш. Онъ былъ устроенъ
въ первую половину царствовашя Вильгельма III, хотя суще-
ствуетъ предноложете, что онъ существовалъ тамъ со времени
Генриха VIII. Въ саду переплетается целая система аллей и

56
изгородей, и опъ былъ, какъ говорятъ, обсаженъ грабаып, кото-
которые потомъ были уничтожены и заменены остролистами, тисами
и др. растешями. Аллеи были около полмили длиной, а весь
онъ занималъ пространство около четверти акра. Въ центр-в
находились два болыпихъ дерева со скамейками около пихъ».
Фиг. 64.
Способъ пройти къ этому центру и выйти изъ сада состоялъ
въ томъ, чтобы, вступивъ въ лабиринтъ, съ перваго же шага
и до конца касаться изгороди правой рукой. Пройденный такимъ
образомъ путь обозначенъ у насъ лишей, состоящей изъ точекъ,
на фиг. 64.
СлйдующШ лабиринтъ (фиг. 65) во
владйшяхъ маркиза Солсбери (Hatzfield
1
Фиг. 65.
Фиг. 66.
House) хоть и сложнее предыдущаго, но довольно легко решается
на бумаги. Другое д4ло получится, если мы вздумалп бы обойти
его въ действительности, не пм^я плана, или не руководствуясь
известной системой. Лабпрпнтъ, представленный зд-Ьсь на фиг.
66, былъ устроенъ королевскимъ обществомъ садоводства, въ

57
Фиг. 67.
южномъ Кессннгтонт, и нынт, не существуетъ. Онъ очень простъ,
хотя и имт>етъ три входа, изъ которыхъ обозначенный бу-
буквой Л ведетъ почти прямо къ центру.
Вотъ еще образецъ (фиг. 67) нт,мецкаго лабиринта—изящ-
наго, но, въ сущности, незамысловатаго, и, наконецъ, па фиг.
С 8 представленъ интересный
образчикъ лабиринта въ граф-
ствт, Дорсетъ. Онъ состоялъ изъ
грядъ холмиковъ (около фута вы-
высоты) и зашшалъ около акра пло-
щадп земли. Въ 1730 году ла-
биринтъ этоть былъ запахань,
и земля, очевидно, была обра-
обращена на болйе производитель-
производительный предметъ.
Приведенныхъ образцовъ лабиринтовъ и псторическихъ спра,-
вокъ, полагаемъ, достататочно, чтобы доказать, насколько старъ
вопросъ о лабиринтахъ и вмгЬстгЬ съ тт.мъ насколько многихъ
онъ интересовалъ въ
свое время. Люди изо-
изощрялись въ изобрт/генш
самыхъ [замысловатыхъ
и «безвыходныхъ» лаби-
лабиринтовъ. Но, въ самомъ
дъ"лт>, возможно ли по-
построить или даже начер-
начертить безвыходный ла-
биринтъ?—т. е. такой, въ
которомъ найти путь къ
его «центру» и найти
отсюда обратный выходъ
было бы только дт>ломъ
удачи, случая, счастья,
а не совершенно опредт,леннаго и правильнаго математическаго
•расчета? Съ этой последней точки зр'Ьшя вопросъ прюбрт>таетъ
но только теоретически, но и большой практически иптересъ.
Въ сущности, устройство пашпхъ городовъ, с^тей жел'Ьзныхъ
Фиг. 68.

68
дорогъ, каналовъ ргвкъ, телеграфовъ и т. д.—все это болЪе пли
мспЬе сложные лабиринты. И если взглянуть на Д'Ьло съ этой
стороны, то задача о распутываши любого лабиринта можетъ
считаться не однимъ только «развлечешемъ»...
Итакъ, представляется вопросъ: есть ли безвыходные лаби-
лабиринты, или въ каждомъ лабиринт^, руководясь общими извест-
известными правилами, можно разобраться, свободно войти въ него,
посетить любую данную въ немъ точку (если она, конечно, не
вполнт, изолирована отъ всей системы непроходимой стеной) и
яатЬмъ выйти обратно?
Разръчпеше этого вопроса принадлежитъ сравнительно позд-
позднейшему времени, и начало ему положено знаменитьтмъ Эй-
леромъ. Результаты произведенныхъ въ этомъ отнотенш пзы-
скатй привели къ заключенш, что
Шзтъ безвыходныхъ лабиринтовъ.
Разръчпеше каждаго лабиринта можетъ быть найдено и прп
томъ сравнительно простымъ путемъ. Внимательный читатель,
преодолевши нижеслЬдуюшш главы, самъ сейчасъ убедится
въ этомъ.
Геометрическая постановка задачи о лабиринтахъ.
Аллеи, дорожки, коридоры, галлереи, шахты и т. п. ла-
лабиринта, какъ знаемъ, тянутся, изгибаясь во вст. стороны, пе-
перекрещиваются, расходятся по всевозможнымъ направлешямъ,
ответвляются, образуюсь тупики и т. д. Но мы, для большей
ясности разсмотрйтя вопроса, веЬ перекрестки обозначимъ про-
просто точками, а вст, эти аллеи, дорожки, коридоры и т. д.
будемъ принимать просто за линш, прямыя, или кривыя, пло-
плоская или нить—все равно, но эти линш соединяютъ наши точки
(перекрестки) двт. по двъ1.
Вслъ-дъ зат^мъ мы говоримъ, что эти точки и эти линш
вмйстъ1 составляютъ геометрическую с4ть, или лабиринтъ, если
какая либо точка, движущаяся по лишямъ этой сЬти, можетъ
придти къ любой другой точк'Ь, не покидая лиши нашей си-
системы (или ст/ги).

69
Прппявъ это, мы докажемъ, что
подобная движущаяся точка (представляющая, напр.,
человека) ыожетъ последовательно описать всЬ лиши
сети безъ всякихъ скачковъ и перерывовъ, и при этомъ
по каждой лиши сети она пройдетъ не бол^Ье двухъ
разъ.
Другими словами,—лабиринтъ всегда можетъ быть разрт,-
шенъ.
Но еще раньше, чъчиъ приступить къ этому доказательству,
можно доставить себъ- довольно интересное математическое раз-
развлечете, которое поможетъ уяснить все предыдущее и весьма
полезно будетъ для усвоешя самаго доказательства. На лпстт,
бъ-лой бумаги возьмите произвольно несколько точекъ и соеди-
соедините ихъ двт, по двт> столько разъ, сколько хотпте пропз-
вольнымъ "числомъ прямыхъ или кривыхъ лин1й, но такъ, чтобы
ни одна точка системы не осталась совершенно изолированной.
Итакъ, вы получите то, что мы назвали геометрической съ-тью.
Или нарисуйте, напримъ-ръ, съ-ть трамваевъ или конокъ города,
ст>ть желт.зныхъ дорогъ страны, ^ть ръчкъ и каналовъ и т. д.,
прибавьте къ нимъ, если хотите, границы страны, — вы опять
получите геометрическую стлъ, или лабиринтъ (Для начала,
конечно, лучше брать не особенно сложную стяъ).
Теперь на куски непросвъ-чивающей бумаги, или картона,
вырежьте небольшое отверсие, черезъ которое была бы видна
только небольшая часть составленной вами решетки, или лаби-
лабиринта. Безъ такого приспособлешя въ глазахъ рябитъ, и легко
запутаться въ с?ти. Затймъ направьте окуляръ (отверсйе для
глаза) вашего «экрана» на какой либо перекрестокъ (точку)
вашей ст,ти, — наприм., точку, которую назовемъ А, — и сде-
сделайте себт. такое задаше: обижать этпмъ окуляромъ непре-
непрерывно вс4 лин1и с^тп два раза (пройти каждый путь впередъ
и назадъ) и возвратиться въ точку Л. Чтобы помнить уже
пройденныя окуляромъ лпнш, примите за правило на каждой
проходимой лиши ставить поперечную черточку при вход'Ь въ
перекрестокъ п при выходгЬ изъ него. Отсюда слйдуетъ, что двгЬ
оконечности каждаго пути отъ перекрестка до перекрестка (отъ

GO
точки до точки) послгЬ выполнегпя задан1я (пройти каждую
сЬтъ лиши 2 раза) должны быть обозначены 2-ыя поперечными
черточками, но не болйе.
Если мы имгЬемъ дъ\ю съ дгЬйетвительньшъ лабярйнтомъ,
пли галлереями подземныхъ шахтъ, съ разв'Ьтвлешямп пещеръ
и т. д., то блуждающему въ этихъ шахтахъ вместо черточекъ
на бумагЬ придется Д'Ьлать уже иной знакъ, чтобы ор1ентиро-
ваться, и класть, напршгЬръ, камень при входи и выходЬ изъ
каждаго перекрестка,—въ галлерет,, которую онъ покидаетъ, и
въ той, въ которую онъ входитъ.
Но обратимся къ намгЬчешюыу раньше доказательству, что
всяшй лабнринтъ разр'Ьшимъ, что н'Ьтъ «безвыходнаго» лаби-
лабиринта. Другими словами: рйштгь общую задачу о лабприитахъ.
РЪшеше задачи.
Правило I.—Отправляемся отъ начальнаго пункта
(перваго перекрестка) и идемъ по какой угодно дорогЬ,
пока не приходимъ или въ тупикъ, или къ новому пе-
перекрестку. Тогда:
1Э. Если окажется, что мы попали въ тупикъ, то
возвращаемая назадъ и пройденный путь долженъ быть
уже отброшенъ, такъ какъ
мы его прошли два раза
(впередъ и обратно).
2°' Если же мы прихо-
приходимъ къ новому перекрестку,
то направляемся по новому
произвольному пути, не за-
забывая только всякш разъ
отметить поперечной чер-
черточкой путь, по которому мы прибыли, и путь, по ко-
которому отправились дальше.
Какъ это показано иа фиг. 09-ой, гдгЬ мы движемся въ
налравленш, показанномъ стрелкой /, приходимъ къ пересх-
ченш путей п береыъ паправлеше, обозначенное стр-Ълкой #,
Фиг. С9.

но тотъ п другой путь ыы обозначает, черточкой, нлп крести-
коыъ (При чеыъ крестикъ обыкновенно ставится, чтобы обо-
обозначить второй, позднъ'йнпй, путь).
Мы глъ-дуеыъ указанному выше первому правилу всякШ
разъ, когда приходимъ на такой перекрестокъ, на которомъ мы
еще не были. Но, въ конц-Ь концовъ, ыы необходимо должны
придти къ перекрестку, на которомъ ыы уже были, и здъ'сь
ыожетъ представиться два случая. На извъ-стный уже намъ
пунктъ мы проходпмъ по дорогЬ, уже разъ пройденной нами,
или же по пути новому, не отмеченному еще черточкой. Въ
такомъ случай слт>дуетъ придерживаться такихъ правилъ:
Правило II. — Прибывъ на
известный уже намъ перекре-
перекрестокъ по новой дорогъ- мы
должны сейчась же повернуть
обратно, предварительно отмъ--
тивъ этотъ путь двумя чер-
черточками (прибьте и обратное
отправлеше),
какъ это указано на фиг. 70-ой.
Правило III.—Если мы приходимъ на известный намъ
перекрестокъ такимъ путемъ, которымъ мы уже разъ про-
прошли раньше, то отмЬтивъ этотъ путь второй черточкой
(или крестикомъ), отправляемся
дальше путемъ, которымъ мы
еще не шли, если только та-
такой путь существуетъ.
Этотъ случай пзображенъ на
фиг. 71-ой.
Но если такого пути нъ-тъ,
то выбираемъ дорогу, по кото-
которой прошли только одннъ разъ.
Случай этотъ изображенъ на
фиг. 72-ой.
Придерживаясь точно указанныхъ правилъ, мы необходимо
обойдемъ 2 раза всЬ лиши сЬти и придемъ въ точку отпра-
Фиг. 70.
Фиг. 71.

62
влешя. Это можно доказать, сдтлавъ
и уяснивъ себт> предварительно так1я
замтлашя:
1 . Выходя изъ точки отправле-
отправлешя, скажемъ А, ыы сташшъ началь-
начальный знакъ (поперечную черточку или
крестпкъ).
2°. Прохождение черезъ перекре-
фиг_ 72	стокъ по одному изъ предыдущихъ
3-хъ правилъ каждый разъ добавлястъ
два знака (двгЬ поперечныя черточки) на лишяхъ, которыя схо-
сходятся въ этой точки.
3°. Въ любой моментъ прохождешя лабирпнта, передъ при-
бьшемъ на какой либо перекрестокъ, или послй отправлешя
изъ него, начальный перекрестокъ (пункта отправлешя) имйетъ
нечетное число знаковъ (черточекъ и крестиковъ), а всякш
другой перекрестокъ имйетъ ихъ четное число.
4°. Въ любой иоментъ, до или послй прохода черезъ пере-
перекрестокъ, начальный перекрестокъ иы4етъ только одинъ путь,
обозначенный только одной черточкой. Всяий же иной изъ по-
съчценныхъ уже перекрестковъ можетъ нйАть только два пути,
обозначенныхъ одной черточкой.
5°. Посл^ нолпаго обхода лабирпнта у вс^хъ перекрестковъ
всЬ пути должны им^ть по дв'Ь черточки. Это^ впрочемъ, вхо-
дптъ прямо въ ycjiOBie задашя.
Принявъ во внимаше все вышеизложенное, мы легко уб'Ь-
дпмся, что если кто-либо отправляется изъ начальнаго пере-
перекрестка, скажеиъ Л, и прибываетъ въ какой-либо иной пере-
перекрестокъ М, то онъ не можетъ встретить таких1> трудностей
задачи, которыя могли бы остановить его дальнейшее путе-
шеств1С. Въ самомъ д'Ьлт., въ это м'Ьсто М онъ нрпходитъ пли
новымъ путемъ, или путемъ, который уже одинъ разъ ирой-
денъ. Въ первомъ случай прилагается 1-е или 11-е изъ данныхъ
выше правплъ. Во второмъ—вступлете на перекрестокъ М. и
остановка зд?сь дала бы нечетное чпсло знаковъ около него,
следовательно, за нешгЬшемъ новаго пути иадо пойти по уже
пройденному одршъ разъ пути, и около перекрестка будетъ четное
число знаковъ (если онъ не начальный), по замЪчанш 3°.

G3
Пусть, наконецъ, мы будемъ вынуждены закончить нашъ
путь и возвратиться въ начальный перекрестокъ А. Назовенъ
эту последнюю линш ZA, т. е. она ведетъ пзъ перекрестка Z
въ начальный А. Этотъ путь долженъ быть необходимо т'Ьмъ
самьшъ, кото])ыыъ мы отправились первый разъ пзъ А, иначе
путь можно было бы продолжать. И если теперь мы прину-
принуждены имъ же возвратиться въ точку исхода, то это значитъ,
что въ перекрестки Z нгЬтъ уже никакого другого пути, кото-
который бы не былъ уже 2 раза пройденъ. Пначе это значило бы,
что забыли приложить первую часть правила Ш-го,—бол'Ье
того, это значило бы, что въ Z есть какой-то путь YZ, прой-
пройденный только одинъ разъ по замйчашю 4'. Итакъ, при по-
сл'Ьднемъ возвращении въ А вст> пути въ Z должны быть от-
м'Ьчены 2-мя черточками. Точно также это можно доказать для
предшествующаго перекрестка Y, и для всЬхъ остальныхъ. Дру-
иши словами,—наше предложеше доказано, и задача р'Ьшена.
Этотъ изящный способъ ртлпешя задачи данъ французскпмъ
инженеромъ М. Тремо. Какъ видпмъ, онъ виолнй доказываетъ,
что н'Ьтъ безвыходныхъ лабпринтовъ.
Филадельфшскш лабиринтъ.
Объ одномъ пзъ нов'Ьйшихъ, не построенныхъ, впрочемъ,
а только начерченныхъ лаоиринтовъ поучительную пстор1ю раз-
сказываетъ Н. Е. Dudeney въ журнал^ «The Strand Magazine»
за 1908 г.
«Несколько л^тъ тому назадъ,—сообщаетъ упомянутый ав-
торъ,—одинъ странствующ!й торговецъ, живя въ Филадельф1и,
въ Соединенныхъ Штатахъ Америки, увлекся головоломными
лабиринтами такъ, что забросилъ Bci свои д?ла. Дни и ночи
проводилъ онъ за разртлпешеыъ и составлешемъ головоломныхъ
лабиринтовъ. Приводимый зд^сь лабиринтъ (фиг. 73) довелъ
его до пьянства. Въ концй концовъ онъ помешался. Разу-
Разумеется, мозга его и раньше были не въ порядк'Ь, если такой
незначительной причины было достаточно, чтобы окончательно
разстроить ихъ».

64
Во всякомъ случай, отсюда слйдуетъ вывести такую мораль,
что лабирипты совсЬмъ ужъ не такая важная вещь, чтобы изъ
за нихъ стоило голову терять. Приводимъ этотъ (фиг. 73), въ
буквальномъ смысли слова, «головоломный» лабиринтъ уже съ
Фиг. 73.
готовымъ и упрощеннымъ рЪгаешемъ его: всЬ тупики (сл'Ьпые
проходы) въ нсмъ уже заштрихованы и главн'Мнле пути ука-
указаны точечными или штриховыми лпшями. И по р'Ьшешю, дан-
данному на этой фигур'Ь, видно, что отъ А надо сначала идти
къ G, и потомъ отъ Е къ В.
в
	"	Но, когда мы придсмъ къ
С, у насъ являются три до-
дороги, обозначенныя 1, 2, 3,
чтобы дойти до JD. Точно также, когда мы дойдемъ до Е, тоже
видны три дороги, обозначенныя 4, 5, 6, чтобы дойти до F, У
насъ есть такимъ образомъ обозначенная точками дорога отъ С
до -Ь', другая—обозначенная точками дорога отъ D до F и про-
ходъ отъ D до Е, указанный звездами. Мы можемъ. слЪдова-
Фиг. 74.

	66
тельно, выразить шложете д'Ьла маленькой упрощенной Д1а-
граммой на фиг. 74-ой. Зд?сь Bci услов1я пути соотвйтствуютъ
путямъ кругообразнаго лабиринта, но только болйе доступны
глазу. И вотъ при такихъ-то ушшяхъ, при условш также, ко-
которое здйсь можно выполнить, не проходи ть дважды черезъ
одинъ и тотъ же проходъ, окажется 640 путей отъ Л до В.
Для головоломнаго лабиринта,—это, не правда ли, довольно
хорошо.
Задача 39-я.
Хижина Розамунды.
Фиг. 76.
А теперь, почтенный читатель, послт> изложеннаго уже и,
думаемъ, усвоеннаго вами ртлнешя задачи о лабиринтахъ для
васъ будетъ не трудно найти путь къ хижинЬ прекрасной Роза-
Розамунды, поселившейся въ парки, изображеннонъ на фиг. 76. Если
ВЪ ЦАРСТВ* СМЕКАЛКИ.	б

6в
до спхъ порь вамъ не приходилось еще слышать о прекрасной
РозамущгЬ, то, кстати, достаньте книгу и прочтите эту исторш...
Быть можетъ, для сокращешя времени вамъ не безполезенъ
будетъ сов^тъ начать поиски отъ хижины^ и найти лучше
выходъ пзъ этого коварнаго парка, ч'Ьмъ начинать со входа.
Впрочемъ, прп наличности свободнаго времени это безразлично.
Зацача 40-я.
Еще лабирйнтъ.
Фиг. 7A.
Вотъ еще любопытный образчикъ лабиринта, въ которомъ
надо пробраться по кратчайшей дорогт. къ центру (фиг. 76).
Обиця замЪчажя.
Задача о лабпрпнтахъ находится въ непосредственной связп
съ задачей Эйлера о мостахъ и островахъ, а также съ вопро-
сомъ о вычерчиваи1п однпмъ почеркомъ различннхъ фигуръ
(унпкурсальныя фигуры). На стран. 162 —168 первой части
папгей- книги этп задачи разобраим довольно подробно. Зд4сь

67
не лишнимъ будетъ привести тгЬ обшдя теоремы, которыя ле-
жатъ въ основ! подобпыхъ задачъ. Условимся прежде всего на-
называть точкой четнаго порядка такую точку, изъ которой вы-
выходить четное число лиши, и точкой нечетнаго порядка такую,
въ которой встречается нечетное число лиши. Тогда:
1°. Въ замкнутой фигур* можетъ быть только четное
число нечетныхъ точекъ,—все равно, уникурсальная эта фи-
фигура, или н*тъ.
2°. Замкнутая фигура, вс* точки которой суть четнаго по-
порядка, всегда можетъ быть вычерчена однимъ почеркомъ, на-
начиная съ любой изъ ея точекъ; т. е. такая фигура всегда
уникурсальна.
3°. Если въ замкнутой фигур* не бол*е 2-хъ нечетныхъ
точекъ, то она можетъ быть вычерчена однимъ почеркомъ,
начиная только съ одной изъ этихъ точекъ.
4°. Замкнутая фигура съ числомъ нечетныхъ точекъ бо-
л*е двухъ не вычерчиваетя однимъ почеркомъ.
5°. Пусть въ замкнутой фигур* есть 2 и нечетныхъ то-
точекъ, тогда необходимо и достаточно п пр1еэтовъ, чтобы
вычертить фигуру.
Доказательство этихъ теоремъ можно найти частью въ 1-й
части пашей книги, частью у Lucas, «Theorie des Nombres»,
глава VII.
Изъ этихъ теоремъ вытекаетъ и рйшеше задачи о лабирин-
тахъ Тремо,—рйшеше, сводящее лабиринтъ къ такой замкну-
замкнутой кривой, которая вычерчивается двойпымъ непрерывнымъ
движешемъ, если каждую линш пройти дважды: впередъ и
назадъ.
Такимъ общимъ путемъ, какъ мы уже указали, можетъ быть
рйшенъ всякШ лабиринтъ. Если же на практики рйшеше можно
упростить, то, конечно, слйдуетъ это д-Ьлать.

68
Задача 41-я.
Картографически вопросъ
или
теорема о четырехъ краскахъ.
Вопросъ, на который мы сейчасъ желаемъ обратить внима-
ше читателя, извъчзтенъ уже давно вавмъ, специально занимаю-
занимающимся черчешемъ и раскрашивашемъ географическихъ картъ
и плановъ. Состоитъ онъ въ слйдующеыъ:
Для всякой карты достаточно четырехъ различ-
ныхъ красокъ, чтобы любыя двЪ области, им-Ьюпп'я
общую пограничную линю, не были окрашены въ одннъ
и тотъ же цвътъ; при чемъ все равно, сколько бы ни
было областей, какъ бы прихотливы ни были ихъ по-
граничныя очерташя и какъ бы сложно ни было ихъ
расположеше.
Выяснеме задачи.
Изъ прилагаемой фиг. 77 можно убедиться, что четыре раз-
личныхъ краски действительно необходимы. Н4сколькихъ попы-
токъ, предпринятыхъ въ этомъ направленш,
достаточно для большинства, чтобы убедиться
въ невозможности составить карту съ такимъ
расположешемъ областей, или участковъ, гд"Ь
потребовалось бы для выполнешя условШ за-
Фпг. 77.	дачи бол^е четырехъ различныхъ красокъ.
Но дать этому последнему положенш мате-
математическое доказательство — составляем, уже совершенно иное
д4ло.
Спещалистамъ картографическаго д4ла этотъ вопросъ, какъ
упомянуто выше, известенъ уже давно. Но какъ математиче-
математическую теорему, или задачу для ръчпешя, впервые выдвинули его
Мёб1усъ въ 1840 году и Гютри, а затЬмъ еще болйе популя-
ризовалъ его Морганъ. Вопросъ получилъ известность и былъ
объявленъ, какъ одинъ изъ нерътпенныхъ, или даже, быть мо-
жетъ, неразр^шимыхъ съ помощью математики. Начиная съ

69
1878 года, талантливый математикъ Кэли (Kayley) обнародо-
валъ несколько доказательств!, этой теоремы, но вс4 они ока-
оказались несостоятельными. Профес. Кемпе и проф. Тэтъ также
тщетно пытались решить вопросъ. Итакъ, задача остается до
сихъ поръ открытой и ждетъ еще овоихъ победителей.
Если бы разсматриваемое нами предположеше было неверно,
то это можно было бы обнаружить хотя однимъ какимъ-либо
примйромь,—наприм., составлешемъ такой «карты» съ пятью
или болйе, областями, гд^ четырехъ разлвчныхъ красокъ для
выполнешя заданнаго услов1я недостаточно. Мноп'е и попыта-
попытались это сделать, но... вопросъ такъи остается открытымъ.
Пока что, доказано только, что существуютъ поверхности,
для которыхъ данная теорема не иьгветъ мъчуга. Теорема мо-
жетъ емъ"гь м^сто на плоскости, или на поверхности шара.
Выть можетъ, кто либо пзъ нашихъ читателей займется
этимъ вопросомъ и будетъ настолько настойчивъ и счастливь,
что разрешить erol Аналойя этой задачи съ Эйлеровой задачей
о мостахъ, съ задачей объ уникурсальныхъ кривыхъ и съ пре-
предыдущей задачей о лабиринтахъ напрашивается какъ-то сама
собой. Но аналопя въ математик'Ь, увы. ничего не доказываетъ.

О весьма болыпихъ и весьма малыхъ числахъ.
Что такое биллюнъ?
Въ Англш, Германш и въ нйкоторыхъ иыыхъ странахъ
северной Европы часто въ основу счета кладутъ группы изъ
шести знаковъ:
КN = 1 000 000 = миллюнъ; 1012=1 000 000 000 000 бил-
биллюнъ, 1018=^триллюнъ и т. д.
Въ Америки и въ южно-европейскихъ странахъ въ основу
счета кладется группа изъ трехъ цифръ:
106 = мпллшнъ; 109~ биллюнъ; 1012 = трпллюнъ и т. д.
Вопроса о томъ, какая изъ этихъ системъ правильнее, быть,
конечно, не можетъ. Вйрно и то, и другое. Все дъ-ло въ разъ
навсегда принятомъ услов1и о значеши того или или иного
слова. Англичане, впрочеыъ, указываюсь на филологичеекш,
такъ сказать, преимущества ихъ счислешя: биллншъ, т. е.
вторая степень миллюна; триллншъ, т. е. третья степень мпл-
люна, и т. д...
Впрочеыъ, разница въ наиыеноваши касается, какъ видимъ,
такихъ большихъ чиселъ, которыя лучше всего определять
просто количествоыъ входящихъ въ нихъ знаковъ (цифръ), а
потому на практики изъ такого различна™ употреблешя въ
разныхъ странахъ одного и того же слова не создается затруд-
затруднений; и это обыкновенно не отмечается даже въ учебникахъ
ариеыетики. Но о словй биллюнъ следовало бы упоминать.
Слово это приходится слышать часто, а потому надо имйть въ
виду, что оно означаетъ тысячу миллюновъ въ устахъ обита-
обитателей однихъ странъ и мпллюнъ миллюновъ въ устахъ обита-

71
телей другихъ. Разсказываютъ по этому поводу о безпокойств!,
а затъчиъ о «радости» французовъ, когда они заключали тяже-
тяжелый миръ съ победителями, немцами. Р!чь шла объ огромной
контрибуцш въ пять «биллюновъ» франковъ, которую затребо-
затребовали нъ"мцы. Такъ какъ «биллюнъ» у нъ"мцевъ есть миллюнъ
миллюновъ (т. е. Ю12), а у французовъ онъ равенъ тысяч!
миллюновъ (Юа), то французы, говорятъ, переживали дни тяже-
лыхъ недоум-Ьшй, пока отъ нъ-мцевъ не была получена бумага,
гдъ- цифрами (б 000 000 000), а не словами, была указана
требуемая сумма. И оказалось, что победители на этотъ разъ
слово «бшшонъ» приняли такъ, какъ понимается оно побе-
побежденными ими французами. Вотъ почему, пожалуй, было бы по-
полезно разъ навсегда условиться принять вм'Ьсто слова «бил-
«биллюнъ» французское слово милл1ардъ, какъ назваше тысячи
миллюновъ.
Въ наше время различнаго рода «милл1ардёровъ» слово «мил-
л1ардъ» или «биллюнъ» сделалось привычнымъ и нисколько,
вообще говоря, не поражаетъ обывательскаго ума. Нисколько
иначе къ этому слову отнесется бол!е развитой математически
умъ. Онъ скажетъ вамъ, напримъ"ръ, что отъ начала нашей
эры, т. е. отъ Рождества Христова и до 10 час. 40 м. 29 апреля
1902 г. протекъ только биллюнъ (мшшардъ) минутъ.
Пытаясь сосчитать биллюнъ (мшшардъ = 109) спичекъ,
считая по одной и предполагая, что надо употребить по секунд!
на спичку, занимаясь такимъ счетомъ по десяти часовъ въ сутки,
окажется, что на этотъ процессъ счета придется употребить
76 лъ"тъ!
Если взять биллюнъ въ анппйскомъ значенш этого слова,
т. е. миллюнъ миллюновъ— 1012, то можно привести еще бол^е
разительный приы4ръ, который данъ однимъ аншйскимъ про-
фессоромъ:
Если, говоритъ этотъ профессоръ,—Адамъ былъ сотворенъ
за 4004 года до Р. X. (библейская хронолоия) и если бы онъ
могъ считать непрерывно вс! 24 часа въ сутки, и въ ка-
каждую секунду называть три посл'Ьдовательныхъ числа, то, доживя
до нашихъ дней, онъ сосчиталъ бы только немногимъ бол!е
половины биллюна въ анпнйскомъ смысл! этого слова...

72
Въ повседневномъ обиходе намт, приходится обыкновенно
встречаться со сравнительно неболыпимъ числомъ какихъ-либо
предметовъ или съ неболыпимъ числомъ пхъ частей. Но въ
науке, вообще говоря, мы можемъ встретиться съ числомъ какой
угодно величины,—чрезвычайно большой и чрезвычайно малой.
Разстояшя неподвижныхъ звъздъ, скорость света, возрастъ
вселенной и т. п. представляютъ примеры весьма большихъ
чиселъ, а размеры атомовъ, продолжительность ихъ удара
одного о другой суть [гримеры величинъ другого, чрезвычайно
малаго порядка. Но если написано число, ст. болыпимъ коли-
чествомъ знаковъ, — скажемъ 1б-ти-значное, 20-ти-значное
и т. д. число, то нашъ умъ отказывается соединять съ такимъ
числомъ какое-либо представлеше; и чтобы «объяснить», такъ
сказать, это число, мы должны прибегать или къ какимъ либо
такимъ новымъ единицамъ сравнешя, какъ световой годъ, или
къ инымъ какимъ либо npieMaira. иллюстращи. Такъ, напр., если
мы скажемъ, что въ капле жидкости, висящей на конце остр1Я
булавки, заключается несколько милл!ардовъ атомовъ, то это, ко-
конечно, дастъ намъ более ясное представлеше о величине атома,
чемъ если бы мы написали дробь съ единицей въ числителе, а въ
знаменателе ея—огромное многозначное число.
Для пояснешя величины некоторыхъ чиселъ существуютъ
целые разсказы и даже легенды. Двадцатизначному числу, пред-
представляющему 64-ю степень 2 безъ единицы, особенно повезло
въ этомъ отношенш. Помимо легенды о брамине Сессе и повели-
повелителе Индщ Шеране, разсказанной нами въ 1-й части этой
книги, есть и такая иллюстращя этого числа, предлагаемая Оли-
веромъ Лоджемъ въ его «Легкой математике».
«Страна, величиной съ Англш, была осаждена непр!ятель-
скимъ флотомъ, и ея обитателямъ грозила опасность умереть
съ голоду, такъ какъ они не выращивали собственнаго зерна.
При этихъ обстоятельствахъ капитанъ одного коммерческаго судна
настойчивыми просьбами добился отъ непр1ятеля пропуска чрезъ
блокаду, причемъ ему разрешено было провести шахматную
доску, покрытую пшеницей, для его умирающей съ голоду жены
и семьи: на первомъ квадрате должно было находиться одно
зерно, на второмъ—два, на следующемъ—четыре и т. д.

78
«Но ^когда непр1ятельсшй адмиралъ сдтлалъ необходимыя
вычислешя при помощи одного японскаго моряка, случайно на-
ходившагося на борту, то оказалось, что зерна, которое онт,
долженъ былъ пропустить, хватптъ не только, чтобы накормить,
но чтобы задушить всЬхъ обитателей страны (Оказалось, что
число зеренъ равни IS 44C 744 073 709 661 616). Такимъ коли-
чествомъ зерна можно было бы покрыть всю землю слоемъ толщи-
толщиной въ 4 метра.
«Тогда адмиралъ разртлпилъ пропускъ лишь при томъ условш,
чтобы весь запасъ былъ провезенъ съ одного раза».
Сл4дуетъ заметить, впрочемъ, что въ очень многихъ слу-
чаяхъ при весьма болыпихъ числахъ не такъ важно точное
численное впредь1 леше величины, какъ порядокъ этой величины.
«Порядокъ же величины» определяется просто числомъ цифръ,
потребныхъ для ея обозначешя.
Задача 42-я.
Довольно большое число!
Съ помощью трехъ девятокъ написать возможно
большое число?
Р^шеше.
Очень часто въ отвита на предложенный выше вопросъ пи-
гаутъ число 999, но это неверно. Точное pimeHie вопроса пред-
ставитъ число:
9'*
Другими словами, 9 нужно помножить само на себя столько
разъ сколько единицъ заключается въ числт, 98. Но
99 = 387 420 489.
Итакъ, нужно произвести 387 420 489 умножешй девятки
самой на себя, чтобы получить искомое число! Получится «до-
дольно большое число». Но въ остроумной л талантливой кни-
жечкй «Initiation mathematique» г. Лэзанъ (Laisant) реши-
решительно не сов4туетъ тратить время на отыскаше этою числа.

74
«Нъ"гь, решительно не советую вамъ,— оворптъ г. Лэзанъ,—
приниматься за эту задачу. Позвольте мн4 вамъ сказать и по-
повторите свипыъ ученпкамъ, которые позже фактически убедятся
въ этомъ, что число, 9У, если бы его написать по десятичной
систем!1, им'Ьло бы
369 692 128 цпфръ.
«Чтобы написать его на бумажной лент!, аредполагая, что
каждая цифра заиметь 4 миллиметра въ длину, нужно было
бы, чтобы эта лента им^ла
1478 километровъ, 772 метровъ, 40 сантпметровъ.
«Это немножко больше удвоеныаго разстояшя отъ Парижа
въ Авиньонъ и обратно по железной joporb.
«Необходимое время, чтобы написать это число, полагая ао
секунд! на цифру и работая по 10 часовъ въдень, не превы-
превысило бы '28 лить и 48 дней, съ услсшемъ включить сюда всЬ
воск])есенья и вей праздники, т. е. не пм'Ьть ни дня отдыха.
«Для болыпаго освгЬдомлешя могу вамъ сообщить, что первая
цифра искомаго чпела 2, а последняя 9. Намъ остается, значитъ,
найти не бол!с 369 692 126 цифръ. Вы подумаете, ложетъ
быть, что облегчеше довольно слабое, я то же думаю. Зато,
надеюсь, согласитесь, что заглав1е «Довольно бильшое число»
поистпн'Г. оправдало себя...».
Задача 43-я.
Лавины.
Не такъ давно часто бывало (да п теперь это бываетъ), что
русекгй обыватель неожиданно получалъ письмо отъ неизв-Ьст-
наго даже ему лтща съ просьбой переапсать присланное письмо
въ 5, наприм., кошяхъ и разослать эти пять itonifl пяти раз-
лпчньшъ лицамъ съ такой же просьбой, т. е. чтобы получивпйе
•въ свою очередь сделали съ письма но 5 когай, разослали ихъ
и т. д... Чаще всего подобнымъ образомъ распространяли раз-
наго сорта «молитвы»,— особенно приписываемыя покойному
популярному npoi'oiepero 1оанну CeprieBy (Кронштадтскому). Въ

76
провингцп обыватели на письма такого сорта откликались до-
довольно охотно, пока не надо'Ьло.
Бе особенно давно также, быть можетъ, читателю приходи-
приходилось встречаться или слышать о ловкой решшгЬ какого-то про-
продавца часовъ. Этотъ господинъ предлагалъ каждому желаю-
желающему имъ-ть «даромъ» часы на слЪдующпхъ услов!яхъ: Прода-
вецъ высылаетъ желающему талонъ съ 6-го отр-Ьзнымн купо-
купонами. Пусть получатель убЬдитъ шестерыхъ своихъ знакомыхъ
взять по одному купону въ рубль. Деньги эти пересылаются
продавцу, а тотъ немедленно за это получателю высылаетъ
«даромъ» часы. Но въ свою очередь каждый куппвшш за
1 рубль купонъ получаетъ отъ продавца талонъ съ шестью
купонами: пусть опъ уб'Ьдитъ 6 своихъ знакомыхъ взять 6 ку-
поновъ по 1 рублю, и тогда онъ получитъ тоже часы «даромъ».
Въ свою очередь каждый изъ куппвшихъ купонъ получаетъ
книжку съ 6-ю купонами, «уб4ждаетъ» шесть своихъ знако-
лыхъ купитъ по купону въ 1 рубль, получаетъ часы п т. д...
Своеобразная реклама эта даетъ поводъ къ постановка и
ръчпенпо следующей интересной задачи, въ которой для боль-
большей разительности возьмемъ даже неболышя числа.
Пусть кто-либо пошлетъ три письма, обозначивъ
каждое номеромъ i; каждый получивши такое письмо
въ свою очередь пусть пошлетъ по з копш съ него,
обозначая эти копш номеромъ 2; каждый получивши
эти копш № 2-й въ свою очередь тоже пошлетъ по
3 копш съ письма, обозначивъ ихъ номеромъ з и т. д...
до тЬхъ поръ, пока номеръ разсылаемой копш не до-
стигнетъ какого либо опредъ'леннаго числа, напр., 50.
Предположимъ теперь, что каждый, кого просятъ, сд-Ь-
лаетъ это и пошлетъ по з копш, предположимъ также,
что письма всегда будутъ получать разныя лица,
такъ что никто не получитъ письма дважды Спраши-
Спрашивается, при какомъ номер!- копш каждый мужчина,
женщина и ребенокъ на всей землЪ получитъ подобное
письмо?

76
Р^шеше.
Пусть искомый номеръ кошй будетъ л. Примемъ населеше
земного шара круглымъ счртомъ въ полтора милл!арда, т. е.
въ 1 600 000 000 челов-Бкъ. По условно задачи, эти число должно
получиться, какъ сумма членовъ ряда чиселъ
3, З2, З3,	3х.
Рядь этотъ есть геометрическая прогреаля изъ х членовъ
съ знаыенателеыъ прогрессш 3. Какъ известно, сумма членовъ
такой прогрессш, S, выражается формулой
Значитъ, для нашей задачи им-Ьеыъ:
^— 1 боо ооо ооо.
Или
З3— 1 == ] 000 000 000 = 109.
Полученное yp-ie 3х—1 = 109 принадлежитъ къ виду такъ
называемыхъ показательныхъ уравнонга и решается съ помощью
логариемировашя об^ихъ его частей. Для нашей цъ\пи, оче-
очевидно, будетъ совершенно безразлично, если мы пренебрежем?,
входящей сюда единицей. Тогда логариемироваше даетъ:
ж = -г-^= 18.86.
Ig3
Полученное решете доказываетъ, что если лавину писемъ
указаннымъ въ задачт, способомъ довести только до копи за
№ 19, то число писемъ уже превысить весь живущдй на зем-
номъ mapi человеческий родъ!
Часовщикъ, о которомъ мы говорили выше, очевидно, имъмгь
понятие о геометрическихъ прогрессгяхъ. Другой вопросъ, однако,

77 .
насколько осуществимъ подобный способъ распространена сво-
ихъ товаровъ и даже,—насколько опъ добрисив'Ьстенъ!
Насколько быстро увеличиваются числа въ геометрическихъ
прогрешяхъ, вы поймете также изъ следующей главы.
Прогрессия размножения.
Думали ли вы когда нибудь, что представлялъ бы собой
нашъ м1ръ, если бы въ неыъ не было смерти, и вст, живыя
существа размножались бы безпрепятственно? Легко показать,
что законъ геометрической прогрессш размножешя привелъ бы
такой м1ръ къ самому прискорбному состояшю, какое только
можно себт, виобразить. Въ какихъ-нибудь два-три десятилтдая
вся поверхность суши сплошь заростетъ непроходимыми дебрями
растеши, въ которыхъ будутъ буквально кишеть милл!арды
всевозможныхъ животныхъ, яристно пожирая другъ друга въ
борьба за м-всто. Океанъ, вместо воды, наполнится рыбой до
того, что никакое судоходство не будетъ возможно, а воздухъ
сделается непрозраченъ отъ птицъ и насвкомыхъ. Все это бу-
будетъ теснить другъ друга, безжалостно пожирая и уничтожая,
такъ какъ для новыхъ пришельцевъ буквально не будетъ м-вста.
Зд4сь будетъ непрерывный вопль и зубовный скрежетъ, и все
ужасы Дантова ада по6лт,днгбютъ предъ такой картиной.
Цифры и вычислешя показываютъ, что въ такихъ мрачныхъ
пророчествахъ н^тъ ни т'Ьни преувеличешя. Если бы даже на
земномъ inapi было первоначально одно растете, занимающее
не бол-Ье квадратнаги фута почвы, то и для него вскоре не
хватило бы м^ста, если бы смерть не уничтожала его потом-
потомства. Вообразимъ, что оно даетъ ежегодно всего 60 сЬмянъ —
цифра небилыная, такъ какъ мноия растешя (макъ, белейа и
друг.) даютъ ихъ тысячи и десятки тысячъ. Н^тъ ничего легче,
какъ разсчитать, что уже черезъ 9 л^тъ такое растете сплошь
покроетъ вс4 60 милл!оновъ квадратныхъ миль поверхности
суши. Вотъ ходъ вычислетй, который каждый можетъ про-
проверить:

78
Число рсастешй.
Черезъ	1 годъ	 1X^0= 60
»	2 года	 50X60= 2,500
»	3 » 	2,600X60 = 125 000
»	4 » 	 6 260 000
»	5 » 	.\ ... 312 600 000
»	6 » 	16 626 000 000
»	7 » 	781 250 000 000
»	8 » 	39 062 500 000 000
»	9 » 	 1 953 125 000 000 000
Число квадратныхъ футовъ поверхности твердой землп меньше
и равно всего 1 421 798 400 000 000. Другимл словами, ыенФ>е
чъ"мъ въ девять лЪтъ растеше сплошь покроетъ всю землю, и
для дальн-Ьйшаго разыножешя физически не будетъ ы'Ьста. Но
ьшоия живыя существа размножаются гораздо быстр'Ье, нежели
взятое выше для примера растеше. Обыкновенная муха въ те-
чеше одного лита дала бы — не будь въ nipi смерти—потом-
смерти—потомство ни мало ни много, какъ въ двадцать миллюновъ! А въ
пять л-втъ потомство ея выразилось бы умопомрачительнымъ
числомъ, состоящилъ изъ 37 цифръ C2 XIО35)- Пауки не
уступаютъ ыухамъ въ этоыъ отношенш: каждый кладетъ сотни
яицъ, и въ несколько л-Ьтъ пара пауковъ населила бы землю
не мепыпиыъ числомъ потомковъ, нежели муха,—если бы смерть
не уничтожала 99°/о всвхъ яичекъ. Еще быстрее размножаются
тли (Aphis), которыя даютъ около 25 особей въ сутки. Въ какихъ-
нибудь 10 дней эти легчайипя. эеирныя создашя составили бы
колоссальную гору т?лъ, равную по Bicy биллюну людей!
Смерть уничтожаетъ ежегодно не мен4е трехъ четвертей
всвхъ рождающихся птицъ. Не будь этого, каждая пара птицъ
въ 15—20 лъть превратилась бы въ тысячи миллюновъ экзем-
пляровъ; пара голубей уже въ 7 л&тъ дала бы почти 10 мил-
лпшовъ птицъ. Рыбы размножаются не ыен^е быстро, нежели
обитатели воздушной стихш. Треска на третьемъ году жизни
мечетъ 9 000 000 икринокъ; легко разсчитать, что если бы Bci
икринки развивались безпрепятственно, то въ несколько л^тъ
треска наполнила бы сплошь моря и сделала бы невозможнымъ
ыореплаван1е.

79
I \
Фиг. 78. Иргпрессгя размножения. Потомство одной трески посл'Л; трсхъ л*тъ
бизпрепятстиепнаго размножеп1я: 40 милл]оновъ ocoOeii.
И,ть наземпыхъ существъ всего медленнее размножается
слонъ, но и онъ въ 500 л"Ьтъ припесъ бы потомство въ
15 000 000 слоновъ. По если бы всЬ зв'Ьри беспрепятственно
размножались, то ужасныя послгЬдств1я такого положешя вещей
сказались бы, конечно, гораздо ран-Ье, нежели черезъ столЗте:
Фиг. 79. Прогрсссш размиоженш. Потомство пары голубей посл-Ь селиг л-Ьтх
бозпрепятствоннаго ра8мпожон1я: 10 мнлл1оновъ особой.

въ какихъ-нибудь два-три десятил-Ыя крокодилы зааолнилп бы
все р4кн, медвъущ, тигры, волки стаями ходили бы по нашимъ
городамъ и деревням ь, и никакая культура не была бы
возможна.
На прилагаемыхъ рисуикахъ читатели нандутъ наглядное
изображеше тЬхъ фантастаческихъ ландшафтовъ, которые по-
появились бы на нашемъ земном ь niapi, если бы смерть хотя бы
на время остановила регулирующую работу своей страшной
косы. При всей фантастичности, рисунки эти им-Ьютъ, какъ мы
вид-вли, некоторое реальное ocuoBaiiie въ геометрической про-
rpeccin размножешя.
А человйкъ? Въ настоящее время па всемъ земномъ шаръ1
круглымь счетоль 1 */2 мшшарда людей; число же квадратныхъ
футовъ твердой земли — въ миллюнъ разъ болт,е. Полагая по
футу на человека, мы имЬемъ, что если населеше земного
шара увеличится въ мнллюцъ разъ, то оно сплошь покроетъ
всю сушу, какъ колосья въ полъ\ Какъ скоро наступило бы
это, если бы не было естественной смерти? Статистика пока-
зываетъ, что средшй процет^ь рождаемости населешя равенъ
З'/г. Капиталь, положенный въ банкъ по 3V2% (сложныхъ),
удваивается, какъ известно, каждые 20 л^тъ; тоже буде1"ь и
съ населешемъ. Сколько же такпхъ удвоенги нужно, чтобы на-
населеше увеличилось въ миллюнъ разъ? Ръ'шивъ уравнеше
2Х= 1 000 000,
найдемъ, что х равно
]? 1 000 ООП	 6 	 „
~~ lgT ~~ 0,30103 1У-
Другими словами, черезъ 20X19 = 380 лъть люди сплошь
покрыли бы все материки и острова земного шара, не будь
естественной смерти. А въ 2400-мъ году по Р.Х. вновь рожда-
юпп'еся должны были бы уже помещаться на головахъ стар-
шаго поколтлпя.
Такъ было бы, если бы люди были безсмертны. Но даже и
при настоящихъ услов1яхъ возросташе населен1я внушаетъ
серьезныя опасен!я за будущее. Естественный приростъ насе-

81
t
i
.1
- m
'.*'
Фиг. 80. Ilpoipeccin размножения. Чергзъ 60 л'Ьтъ безпропятственнаго раз-
чножетя крокодилы заполнили бы всЬ р^ки земного шара. Даже въ Лон-
дон-Ь, у набережной Темзы, толпились бы тысячи крокодиловъ.
лешя въ европейскяхъ странахъ колеблется отъ 1,8% (въ
Porrin) до 0.36°/о (во Франщи). Прпнявъ за среднее 1%, легко
вычислить, что насачен1е будетъ удваиваться каждые 70 л-Ьтъ
Aо^2 : logl,01). Если норма прироста останется неизменной,
то послЪ 19 удвостпй, т. и. мен'Ъе, ч^ыъ черезъ 1400 л^тъ, иа-
селен1е увеличится въ 1 000 000 разъ, — и на нагаеп шганетъ-
не будетъ буквально ни одной пяди свободной земли.
Такова безпощадная прогресая размножешя!
Задача 44-я.
Загадочная автобтграф1я.
Въ бумагахъ одного чудака-математика найдена была его
автоб1огра({ця. Вотъ ея начало:
«Я окончмлъ курсъ университета 44~хъ л"Ьтъ отъ
роду. Спустя годъ, юо-л-Ьтшшъ люлодымъ челов'Ьком-ь,
я женился на 34~л"Ьтнеп дЬвушк"Ь. Незначительная раз-
разница въ нашихъ лъчгахъ,—всего II лъ^гь,—способство-
ПЪ ЦАРСТВИ ГМЕКАЖИ.	1;

82
вала тому, что мы жили общими интересами и мечтами.
Черезъ небольшое число лъ-тъ у меня была уже и ма-
маленькая семья въ ю челов-Ькъ дъ-тей. Жалованье я
получалъ, положимъ, слишкомъ скромное,—всего 2ОО
рублей въ мъ-сяцъ. Изъ этого жалованья г/ю прихо-
приходилось отдавать cecrpi, такъ что мы со своей семьей
жили на 130 р.» и-т. д.
Предлагается объяснить: что за .странныя и явныя
противорЬч!я получаются въ числахъ?
Разгадка заключается въ томъ, что математику пришла
фантаз!я написать BCi числа не но привычной и обычной для
насъ систем!; счислешя, а по систем'Ь пятеричной, т. е. по
такой систем^, гдЪ въ ocuoBauie положено число пять. Дру-
гиш1 словами, — въ такой снстемт, есть только цифры: 0, 1,
2, 3, 4, а число 5 изобразится уже цифрами 10. Вступая
«въ царство смекалки», сл'Ьдуетъ разъ навсегда усвоить ceoi
уы&нье нисать числа не только по нашей десятичной системъ'
съ десятью цифрами, но и по любой другой. Въ первой части
этой книги, въ главъ1 о двоичной систем^, объ этомъ сказан"
вполнъ' достаточно, чтобы не повторяться. Впрочелъ, сейчасъ
ниже мы даемъ указашя, какъ отъ десятичной системы счи-
слен!я переходить къ другой. Теперь же переведемъ языкъ за-
загадочной автоо1ограф1и на нашъ обыкновенный «десятичный^-
языкъ и тогда увидимъ, что дт>ло объясняется нросто:
Число, обозначенное въ автоб1ографш черезъ 44, равно по
десятичной систем-Ь: 4 • 5 + 4 = 24; другими словами,—матема-
тикъ окончилъ курсъ университета по нашему счету въ 24 года.
Точно такъ же:
100 соотв-Ьтствуетъ десятичному числу 25
35	»	3-5 + 4 19
11	»	1-5 + 1^= 6
200	»	2 ¦ 52 = 50
i_	1
ю	*	б
130	»	5L' + 3-5-=40

	83
Послй этого перевода на нашу десятичную систему всЬ
видимыя противоргЬч1я загадочной автобюграфш исчезают?,. Те-
Теперь ясно, что автобюграфш чудака сл'Ьдуетъ «по нашему»
читать такъ: «я оконталъ курсъ университета 24 мътъ отъ
роду. Спустя годъ, 25-лптшмъ молодымъ человйкомъ, я женился
на 19-лгьтней дйвушк-Ь. Незначительная разница въ 6 лгьтъ
и т. д.
Для облегчешя чтешя следующей главы сд'Ьлаемъ зд^сь
кстати указашя, какъ числа, написанныя по десятичной систем-Ь
счислешя, писать въ иной
Предположить, вы желаете число 25 написать по восьми-
восьмиричной систем^. Д'Ьлите 25 па 8— получаете въ частноыъ 3,
въ остатки 1. Это значитъ, что число ваше состоитъ изъ трехъ
восьлерокъ и одной единицы; следовательно начерташе его по
восьмеречной cncTebii будетъ 31.
Еще прим^ръ: написать 267 по четверичной систем-Ь. Д'Ь-
Д'Ьлите 267 на 4, частное—снова на 4 и т. д., запоминая каждый
разъ остатки.
267
3
4
66
"8
4
Тб
~о
4
т
т
Итакъ:
267 —44+ 2-4 + 3.
Мы узнали, что наше число содержитъ три единицы, дв-Ь
четверки (т. е. двй единицы второго разряда) и одну единицу
пятаго разряда. Следовательно, начерташе его будетъ 10023.

Новый родъ задачъ.
Задача 45-я.
Написать единицу тремя пятерками.
РЗшгеше.
Задача состоитъ въ томъ, чтобы, пользуясь тремя б-ками
и какими угодно знаками шатематическихъ дМствШ, написать
выражете, равное единицй.
Если вы никогда не пробовали решать подобныхъ задачъ,
то вамъ не мало придется подумать, прежде чймъ вы нападете
на одно изъ правильныхъ р^Ьшешй. Вотъ н^которня изъ рт>-
шешй предлагаемой задачи:
т)=1. ибо 4 = 1, а15=1-
у
~ = ], ибо -§- = 1, а |/Т=1.
= 1, иоо б — 5 = 0, а о =1.
(Ig55M = 1, ибо Ig56 = l, а 15,= 1.
^1^5 = 1, ибо Ig66=l, a f Г=1.
Можно пытаться найти и друпя решетя, кромй этихъ
пяти. Ниже мы укажешь систематически npieMb, пользуясь
которымъ можно отыскивать вс& р^шешя этого типа.

85
Задача 46-я.
Написать нуль тремя пятерками.
Решете.
Задача одного порядка съ предыдущей. Теперь уже чита-
читатель безъ труда сможетъ дать отвить
E—5M = 0, пбо 5 — 6 = 0, а 05 = 0.
Вотъ еще рЪшешя этой же задачи:
5ХE-б); ^; i>5^ lgB|, lg5lg56
Задача 47-я.
Написать 2 тремя пятерками.
Piiireirie.
^ = 2 и lgBFX6) = 2.
Задача 48-я.
Написать 5 тремя пятерками.
Р"Ьшеше.
Задача имйетъ не менЪе десяти р1;шешй:
б+б-б; 5x1; 55> ?; 51^5; 51ёз5; ^ ig/;
5 1 5 г-
w lgV65-
Задача 49-я.
Написать 31 пятью тройками.
Решете.
Эта задача гораздо сложнее предыдущихъ. Она не нова, п
обыкновенно считаютъ, что она шгЬетъ всего три р^шешя:

86
3
31 = 3
31 = 33
31 = 33- i±>-
Однако, ръчпешй зд^сь гораздо больше. Мы остановимся
подробнее на разсмотр^шн этой задачи, попутно изложивъ ме-
тодъ, съ которымъ сл'Ьдуетъ приступать ко встжъ подобнымъ
задачамъ.
Общее рЪшеше.
Выразить какое-либо число посредствомъ пяти троекъ можно
трояко. Во-первыхъ, соединяя тройки знаками математическихъ
д-бйствш; во-вторыхъ, пользуясь, наряду съ знаками д'Ьйствш,
еще приписывашемъ троекъ одна къ другой; либо же, нако-
иецъ,. пользуясь, наряду съ упомянутыми npieMaira. различными
математическими символами.
А. Разсмотримъ первый щяемъ. Прежде всего найдемъ вс*
числа, которыя могутъ получиться, какъ результата математи-
математическихъ дМствш надъ пятью тройками,—считая семь дъ'йствШ:
сложеше, вычпташе, умножеше, д'влеше, возвышеше въ сте-
степень, извлечете корня и логариемировате.
Произведемъ сначала последовательно семь дМствш надъ
двумя тройками; получимъ рядъ изъ семи выражешй: 3 -\- 3;
3—3; 3X3; -у-; 3 ' 1 / 3 и Ig33- Для удобства обозначимъ
этотъ рядъ римской цифрой I.
Сочетая по очереди каждое изъ выражешй этого ряда опять съ
тройкой посредствомъ веЪхъ знаковъ дт>иств1й, получимъ но-
новый рядъ чиселъ. Этотъ 11-ой рядъ будетъ заключать въ себт»
вс* числа, которыя можно написать посредствомъ трехъ тро-
троекъ по разсматриваемому способу.
Наконецъ, сочетая такимъ же образомъ каждое изъ выражешй
I ряда съ каждымъ шъ выражешй II ряда, получимъ Bci числа,
кашя могутъ быть написаны пятью тройками съ помощью зна-
знаковъ Д'ЬЙСТВШ.

87
Въ этой посл'ЬднеГг таблицт, мы ищемъ число 31, и находимъ
его всего два раза:
- и 31 =
Но такъ какъ число 31 можеть быть написано и не по
десятичной систем^ счислешя, то въ таблиц^ III мы ищемъ
вообще число, равное За-]-1, гд4 а — любое ц'Ьлое число, мо-
могущее быть основашемъ системы счислешя (но больше, чт>мъ 3,
ибо въ троичной системт, уже н4тъ цифры 3). Другими сло-
словами, мы будемъ искать т-Ь числа, которыя безъ единицы де-
делятся на три. Такимъ путемъ найдемъ, что число 31 посред-
ствоыъ пяти троекъ можетъ быть выражено следующими спосо-
способами.
По четверичной систем* счислешя — два р*шешя:
31 = 3 + (ЗХЗ)+-3Г п 31 =
По 6-еричной систем* — два р*шешя:
31
По 8-ричной систем*—два р*шешя:
31 = 33— 3 + 4" и 31 = 33 —3 + lg33.
По 9-ричной систем*:
31 = 3X3X3 + ^; 31 = 3) 3X3 + lg33;
3 8~3; 31 = 33 + (lg33K
По 27-ричной систем*—два р*шешя:

88
По 72-рвчвой систем*—два рЗштешя:
По 243-ричной систем* — четыре р-Ьшешя:
4	, и т. д.
Словомъ, пользуясь объясненныыъ выше методомъ, можно
получить вс-Ь р-Ьшешя этого типа. Между прочимъ. весьма инте-
интересно р-кпеше такого вида:
31=33Vf (т. е. ЗХ326+1),
гд-Ь число 31 написано по систем-Ь счислен1я съ основан1"емъ 32С.
На этомъ прым'Ьр-Ь отчетливо выступаетъ преимущество изло-
женнаго метода: едва ли кому-нибудь пришло бы въ голову это
р^шеше, если бы онъ не улавливалъ его сетями систематиче-
скаго метода.
Намъ остается разсмотр^ть остальные два npieMa.
В. Прииисыван1е троекъ одна къ другой даетъ сл-Ьдуюиця
р^шешя:
31 = 33 — 3+|; 31 = 33 —
31 = 33— Ш И 31 = 33 — lg3 CX3).
Эти решетя в^рны при всякой систем^ счислешя.
Изъ другихъ р^шешй этого типа весьма интересны
юпдя—по 4-ричной систем-Ь:
31 = ЗХЗ,C) + | и 31 = 3X3,C)+ lg33-
Зд-Ьсь выражен!е 3,C) означаетъ «три ц-Ьлыхъ и три въ
з
перюдй» и равно, по 4-ричной систем^, З^-, т. е. 4.
С. Этотъ способъ, т. е. пользовал1е всевозможными математиче-
математическими символами—знаками факультета (I), знаками тригонометри-

89
ческихъ функщй п круговыхъ (sin., arcsec. и т. д.), знакомъ ти,
производной ('), дифференщала (d), интеграла (Г), символами
теорш соединешй (А — число разм-Ьщетй, P — перестановок^.,
С—сочеташй) и т. п.—открываетъ безпред'Ьльное поле изобре-
изобретательности рт>шающаго. Приводить эти р&шешя мы не станемъ,
такъ какъ въ сочетан!и съ предыдущими двумя этотъ щлемъ даетъ
задачи неопределенное множество ргЬшен1й. Отдельные же при-
примеры подыскать очень легко, и мы на нихъ останавливаться
не удемъ.

Сто тысячъ за доказательство теоремы,
Осенью 1907 года въ Даршптадтъ1 скончался математика.
Пауль Вольфскель (Wolfskehl), оставивнпй не совсЬиъ обычное
зав-Ьщате: капиталъ въ 100,000 марокъ онъ завъчцалъ тому,
кто докажетъ одну теорему изъ Teopin чиселъ,—теорему, извест-
известную подъ назвашеыъ «великой теоремы (или великаго предло-
жешя) Ферма».
Теорема, за доказательство которой предлагается такой ог-
огромный гонораръ, очень проста и можетъ быть изложена въ
немно^гихъ словахъ: сумма одинаковыхъ степеней двухъ ц4лыхъ
чиселъ не можетъ быть тою же степенью третьяго цъмаго числа,
если степень больше двухъ. Другими словами, уравнеше:
П 1	П	П
х -\-у =е
неразрешимо въ цъмыхъ числахъ, если и> .
Для случая, когда п = 2, такое уравнеше разрешимо (это
такъ называемая задача о Пиеагоровыхъ треугольникахъ, раз-
сыотр-Ьнныхъ нами при р'Ьшенш задачи 10-ой).
Но вамъ никогда не удастся подобрать ташя два числа,
чтобы сумма ихъ кубовъ была бы тоже кубоыъ, или сумма
4-тыхъ степеней была бы сама 4-ой степенью, и т. д.
Въ этомъ и состоитъ теорема, именуемая «великимъ пред-
ложешемъ Ферма». Какъ ни проста она съ виду, но строгаго
доказательства ея въ математик^ еще не существуете
Не мало великихъ математиковъ въ свое время трудилось
надъ доказательствомъ этой неподатливой теоремы, высказанной
Ферма болйе двухъ съ половиной вйковъ тому назадъ,- и ни-

91
кому еще не удалось найти общее, строгое ея доказательство
для всЬхъ степеней выше второй. TI если теперь искомое дока-
доказательство оц'Ьнено такой огромной суммой, то оно вполнт. за-
заслужило это за свою упорную неуловимость для самыхъ силь-
ныхъ математическихъ умовъ.
Нельзя сказать, чтобы это доказательство было очень ужъ
важно для науки. Гауссъ, одинъ изъ величайшихъ мате-
матиковъ всЬхъ временъ, относился къ теоремт, Форма довольно
пренебрежительно. «Признаюсь— ппсалъ онъ своему щпятслю—
что Ферматова теорема, какъ изолированно*} предложеше, для
меня большого интереса не нредставляетъ, ибо легко можно
придумать множество подобныхъ предложешй, которыхъ нельзя
пи доказать, ни опровергнуть».
II, тЪмъ не мепт.е, лучппе математики (да' и самъ Гауссъ)
бились надъ ея доказательством'!.. Конечно, дЗифлось это не-
неспроста: Ферматока теоречашгЪетъ свою крайне любопытную исто-
рш. Опа, можно 1-казать, прямо заинтриговала математиковъ.
Ея авторъ, Пьеръ Ферма (Fermat, 1001—1665), юристъ по
по профессш, совт.тнпкъ Тулузскаго парламента по положен™,
поэтъ п ученый въ дуигЬ—занимался математикой лишь между
прочимъ, для развлечешя. Это не мтлиало, однако, ему сделать
цълый рядъ огромной важности открьтй, справедливо окружпв-
шпхъ его славой гешальнаго математика. Онъ почти не печа-
талъ своихъ трудовъ, а сообщалъ ихъ въ ппсьмахъ къ своимъ
друзьямъ, среди которыхъ были таше ученые, какъ оба Па-
Паскаля, 1'оберваль, Декартъ, Гюйгенсъ и др. Ц-Ьлый рядъ тео-
ремъ пзъ области теорги чиселъ ралбросанъ этимъ ген1алытымъ
диллетантомъ... на поляхъ одной греческой книги! Бпрочемъ,
автором!. сочинен1я, которому посчастливилось служить запис-
записной книжкой для Ферма, бьтлъ никто иной, какъ не менгЬе
знаменитый александр1йск1Й математнкъ Дюфаптъ, так^ке запп-
мавш1йся Teopiefi чиселъ J). Т\1ног1я изъ георемъ, пайдеппыхъ
]) О жшщи атои загадочной личности памт. пявЬстно очень мало. Невоз-
Невозможно дала; съ точностью установить в1жъ, когда онт. я:цлъ;съуверенностью
можно указать лишь на ироыежутокъ времени отъ 180 г. до Р. X. до 370 г.
поел* Р. Хр.

	92_
Ферма, записывались имъ белъ доказательства Отп доказатель-
доказательства такъ до насъи недошли. Но нпосл-Ьдсткш веЬ его теоремы
были строго доказаны позднейшими математиками, всЬ, кроыгЬ
одной,—той самой, о которой у насъ ссйчасъ идетъ р^чь.
Упомянутая заметка на поляхъ книги Дюфанта наппсана
прогивъ того листа текста, где алексаидрШсшй математпкъ
трактуетъ о разложенш полнаго квадрата на сумму двухъ ква-
дратовъ. Вотъ буквальный переводъ того, что Ферма записалъ
сбоку, на поляхъ:
«Между тЬмъ, совершенно невозможно разложить
полный кубъ на сумму двухъ кубовъ, четвертую сте-
степень на сумму двухъ четвертыхъ степеней, вообще ка-
какую либо степень на сумму двухъ степеней съ тЬмъ
же показателемъ. Я нашелъ поистинЪ удивительное
доказательство этого предложенш, но здЬсь слишкомъ
мало мъхта, чтобы его помЬстить».
Въ чемъ состояло это «поистине удивительное» доказатель-
доказательство,—никто теперь не знаетъ. Но въ то же время ни одпнъ
математнкъ не сомневается, что такое доказательство действи-
действительно бнло найдено Ферма, и что оно было вгЬрно. Не таковъ
былъ челов^къ Пьеръ Ферма, чтобы покривить дутой, и не
гаковъ онъ былъ математикъ, чтобы ошибаться. ВгЬдь ксЬ дру-
ия теоремы, высказанныя пмъ безъ доказательства, были до-
доказаны поздн'Ьишимп математиками. Такова, напрпмъ'ръ, теорема:
«каждое простое число впда 4» 4 1 есть сумма двухъ квадра-
товъ». Она дана была Ферма безъ доказательства, но сто .гЬть
спустя. Эйлсръ нашелъ—довольно сложное п грудное—дока-
грудное—доказательство ея.
Кажущееся исключеше, бросающее, повнднмому, тйнь ira
репутац1Ю Ферма, какъ ноногрЪшпчаго теоретика чиселъ, со-
ставляегь гл^здующШ случай. Ферма высказалъ теорему, что
всякое число вида:
2П
22+1
есть простое число. Въ течете ц-Ьлаго столгЬт1я пе возни-
возникало сомнйшй въ ея правильности. Но вотъ "другой гешй тео-

93
pin чиселъ, Эйлеръ, доказалъ, что теорема в'Ьрпа лишь для
«<32, п что уже прп « = 32 получается число:
4 294 967 297,
которое не простое, а составное, ибо делится безъ остатка на 641.
Однако это не только не подрываетъ в4ры въ добросовест-
добросовестность Ферма, но, напротлвъ, скорее даже утверждаетъ ее. Дело
въ томъ, что и самъ Ферма сомневался въ абсолютной вер-
верности этой теоремы и откровенно заявлялъ, что ему еще не
удалось дать исчерпывающее доказательство ея. «Доказательство
очень кропотливо—говоритъ онъ—и должент. признаться, что я
еще не довелъ его до удовлетворительна^) завершешя».
Посл'Ь этого едва ли можно еще сомневаться въ томъ, что
Ферма действительно доказалъ свое «великое предложеше». А
если такъ, то вполне возможно, что кому-нибудь посчастливится
подыскать доказательство этой теоремы и сделаться обладате-
лемъ кругленькой суммы въ 100,001) марокъ.
Маленькая историческая справка покажетъ, впрочемъ, что
эти 100,000 едва ли попадутъ въ руки зауряднаго математика.
Вотъ краткш перечень того, что уже сделано въ этомъ напра-
вленш.
Прежде всего легко доказать, что если теорема справедлива
для показателя п, то она справедлива также и для всякаго
другого показателя, кратнаго п. Значитъ, все Д'Ьло въ томь,
чтобы доказать справедливость теоремы для всякого простого
показателя. Для суммы кубовъ теорема доказана была еще древ-
древними арабами. Для п = 4 ее доказалъ Эйлеръ. Для % —5—до-
—5—доказали Гауссъ и Дирихле. Для п = 7—доказалъ Ламе. Нако-
нецъ Куммеръ доказалъ ее для всякаго показателя, меньшаго 100.
Такимъ образомъ, для многихъ частныхъ случаевъ теорема
Ферма доказана. Но у Ферма было общее доказательство ея,
для всякаго %, и это-то общее доказательство требуется найти.
При этомъ достойно быть отмечено, что мнопе позднейнпе ма-
математики (Эйлеръ, Куммеръ), доказывая частныя случаи Ферма-
товой теоремы, пользуются такими пр1емами, которые далеко
выходятъ за пределы элементарной математики и которые са-
самому Ферма не могли быть известны. Очевидно, гешальный

94
французски математикъ шелъ какямъ-то совершенно особымъ
путемъ, ускользнувшимъ изъ поля зрйшя позднМшихъ мате-
матиковъ.
Прежде чймъ кончить эту главу, ечитаемъ не лишнимъ
сказать несколько словъ по поводу слуховъ о томъ, будто «ве-
«великое предложеше Ферма» доказано недавно русскимъ реали-
стомъ. Въ ноябре 1908-го года всЬ руссюя газеты облетало
телеграфное извъ'сйе, что «юному б^лостокскому реалисту Ч. по-
посчастливилось доказать такъ наз. великое предложеше Ферма» J).
Газеты прибавляли даже, что доказательство это одобрено
специальной конференцией Петербургской Акадеыш Наукъ.
Опровержешй со стороны Академш Наукъ не последовало, и
такъ какъ слухъ зат^мъ заглохъ, то у широкихъ круговъ об-
общества такъ и осталось убйждете, что наследство Вольфскеля
перешло къ бъмюстокскому реалисту.
Ученый л^соводъ Я. И. Перельманъ любезно сообщилъ
намъ по этому поводу сведешя изъ первыхъ рукъ. Вскоре
после опубликовашя въ иностранной печати завъчцашя Вольфс-
Вольфскеля—осенью 1907 года—г. Перельманъ пом^стши. небольшую
статью о Ферматовой теореме и стотысячной премш въ журнал'Ь
«Природа и Люди». Наружная простота самой теоремы и пер-
перспектива получетя цгЬлаго капитала сделали то, что теорема
сразу же стала известна въ большой публики, и мнопе ты-
тысячи любителей засели за отыскаше неуловимаго доказатель-
доказательства. Въ редакцш журнала полетали запросы объ адресЬ того
н^мецкаго научнаго общества, которое присуждаетъ премш
(Gottinger Gesellschaft der Wissenschaften). Сотни людей утвер-
ждали^ что они уже нашли требуемое доказательство и боятся
лишь, какъ бы друйе ихъ не упредили и не перехватили при-
причитающаяся имъ сто тысячъ марокъ.
И вотъ, въ разгар^ всей этой «математической лихорадки»
появляется въ газетахъ слухъ обь упомянутомъ выше белосток-
скомъ реалисте Ч. и объ одобренш его доказательства Акаде1Йей
Наукъ. Редакщя названнаго журнала наводитъ справку въ Ака-
демш Наукъ и получаетъ ответъ, что «сообщен1е о г. Ч. предста-
1) «Русское Слово» 26. XI. 1908.

95
вляется явпьшъ недоразум^ьпемъ». Д-Ьло обстояло такъ. Г. Ч.
изъ Б'Ьлостока, действительно, послалъ въ Академш Наукъ свое
«доказательство» Ферматовой теоремы п, действительно, полу-
получи лъ отъ неирсм'Ьнцаго секретаря Академш отвЬтъ, который
юный математпкъ прпнялъ, по наивности, за одобреше его до-
доказательства. Вотъ текстъ этого ответа:
«Имею честь, по лоручешю Конференцш I Операторской
Академш Наукъ, сообщить Вамъ, что присланное Вами руко-
рукописное доказательство теоремы Фермата передано въ I Отдт,-
jienie Бнблютеки Академш.
«Пересылка сего доказательства въ Геттингеиъ не предста-
представляется возможною, ибо на преыш, о которой Вы упоминаете,
работы не могутъ быть представляемы авторами, а отмечаются
самою КомпсКею, присуждающею цремго. Примите и проч.».
Не зпая, что Акададпя по уставу обязана хранить въ своей
бпблютекъ1 всякую поступившую въ нее книгу или рукопись,
молодой математикъ п окружающее его поняли бумагу, вероятно,
въ томъ смысл!;, что Академ 1я, очевидно, одобрпла доказатель-
доказательство, разъ опа постановила хранить его въ библЬтек! (Между
т'Ьмъ, Академ1я даже не разсматривала его по существу). От-
Отсюда и иошелъ упомянутый сенсацшнный слухъ.
Думаемъ, что еще не мало лт,тъ пройдетъ, прежде чъ-ыъ
прндсяся тронуть капиталъ, завещанный н'Ьмецкимъ математп-
комъ, а впрочемъ,—кто зпаетъ!.. Во всякомъ случай читатель
не потеряетъ времени даромъ, въ смысле расширешя своихъ
математическихъ нознан1п н навыковъ, если внимательно зай-
займется знаменитой задачей Ферма.

облаети изучешя чиеелъ.
Задача 50-я.
Быстрое возвышеше въ квадратъ.
Существуетъ оченъ простой npieirb для устнаго быстраго
возвьппешя въ квадратъ двузначпыхъ чпселъ, оканчивающихся
на 5:
Нужно цифры десятковъ умножить на ближайшее
высшее число и къ произведешю приписать 25.
Такъ, напр., 352 = 1225, т. е. 25 приписано къ произве-
произведешю 3X4; 852 ~ 7225. т. е. 25 приписано къ пронзведешю
8X9, и т. п.
Доказательство.
Нетрудно объяснить, на челъ основанъ этотъ npieM'b. Вся-
Всякое число, оканчивающееся на 5, ложно выразить черезъ
10«-)-5, гдЪ а—число десятковъ. Квадратъ этого чиста выра-
выразится черезъ
A0а + бJ = 100а2 + 2 ¦ 5 " 10« + 25 = 100а2 + 100а + 25.
Вынеся 100а за скобки, иийемъ
100а (а+ 1) + 2б,
или
а (а+1). 100 + 25.
Отсюда ясно, что нужно число десятковъ а умножить па
ближайшее высшее число (а+ О, и къ результату пргтжатъ 25.
Т'Ьмъ же пр1слтмъ ложно пользоваться п не для однихъ
двузначныхъ чиеелъ, —но, конечно, въ этоыъ случа'Ь не всегда
легко производить нужное неремножеше въ ум4. Но и при
улшоженш на бумага пользоваше этиыъ пр1емомъ создаетъ эко-

97
позпю во времени. Такъ 1052 = 11025 (т. е. 25 приписано къ
произведешю 10 Х^)-
1252= 15625;
335 =112225 и т. п.
Особенные случаи умножешя.
Н'Ькоторыя особенности чиселъ находятся въ прямой зави-
стюстн отъ принятой нами десятичной системы ихъ обозначе-
Н1я. ОнгЬ легко запоминаются, интересны п могутъ пригодиться
для црактическихъ п теоретическихъ приложений. Къ числу
важн'Ьшихъ пзъ иихъ относится сумма цифръ всъ'хъ чиселъ,
но.тучаемыхъ въ таблицЪ умножешя на 9.
9X1 = 9
9X2 = 18; 1-|-8 = 9
9X3 = 27; 2 + 7 = 9
9X4 = 36; 3 + 6 = 9
9X5 = 45; 4 + 5 = 9
9X9 = 81; 8 + 1=9
9ХЮ = 90; 9 + 0 = 9
9ХП = 99; 9 + 9 = 18; 1 + 8 = 9
9X12 = 108; 1 + 0+8 = 9
9X13 = 117; 1 + 1 + 7 = 9
и т. д.
Вотъ несколько интересныхъ образчнковъ ушножещй, кото-
которые легко удерживаются въ памяти, благодаря своему внеш-
внешнему виду.
1X9 + 2 = 11
12X9 + 3 = 111
123X9+4 = 1111
1234/S9 + 5 = 11 111
12345X9 + 6 = 111 111
123456X9 + 7 = 1111111
1234567X9 + 8 = 11111 111
12345 678X9 + 9 = 111 111111
ВЪ ЦАРСТВ» СМЕКАЛКИ.	7

98
9X9 + 7 = 88
98X9 + 6 = 888
987X9 + 5 = 8888
9876X9 + 4 = 88 888
98 765X9+3 = 888 888
987 654 X 9 +2 = 8 888 888
9 876 543 X 9 +1 = 88 888 888
98 765 432 X 9 + 0 + 888 888 888
1X8+1=9
12X8 + 2 = 98
123X8 + 3 = 987
1234X8 + 4 = 9876
12345X8 + 5 = 98765
123456X8 + 6 = 987 654
1 234 567 X 8 + 7 = 9 876 543
12 345 678 X 8 + 8 = 98 765 432
123 456 789 X 8 + 9 = 987 654 321
Число, состоящее изъ встжъ значащихъ цифръ кромт; 8,
написанныхъ въ послтдовательномъ порядки при умноженш на
8, а также на 9 и числа кратныя 9 A8, 27, 36 п т.) даетъ
нижеслйдунлще интересные и легко запоминаемые результаты:
12 345 679 X 8 = 98 765 432
12345 679X 9 = 111111111
12 345 679 X 18 = 222 222 222
12 345 679 X 27 = 333 333 333
12 345 679 X 36 = 444 444 444
12 345 679 X 45 = 555 555 555
12 345 679 X 64 = 666 666 666
12 345 679 X 63 = 777 777 777
12 345 679 X 72 = 888 888 888
12 345 679 X 81 = 999 999 99!)

99
Девять.
Интересныя свойства числа 9 часто применятся въ ариеме-
тик'Ь какъ для теоретпческихъ изыскатй п практнческпхъ %Ш-
ствШ, такъ и для составлешя разлпчныхъ занимательныхъ за-
дачъ. плп такъ называемыхъ «головоломокъ». Въ отделе «Уга-
«Угадыванье чиселъ» въ первой части настоящей книги мы уже
широки пользовались девяткой. Распространено также практи-
практическое примкнете девятки для поверки умножешя и д'Ьлешя.
Основано оно на томъ свойстве всякаго числа, что остатокъ,
получаемый отъ делешя числа на девять, всегда равенъ остатку
отъ дйлетя на 9 суммы цпфръ этого числа. Укажемъ здесь
еще несколько интересныхъ применешй этого числа.
Прежде всего нетрудно убедиться, что если згы наппшемъ
произвольное двузначное число, а затемъ напишеыъ цифры
этого же числа въ обратноиъ порядке и возьмемъ разность по-
полу ченныхъ чпселъ, то эта разность всегда разделится на 9.
Напрпм. 72 — 27 = 45; 92 — 29 = 63, 63 — 36 = 27 и т. д.
Вообще ясно, что A0а-\-Ъ) — A0Ъ-}-а) = 9(а—6), т. е. по-
получается число, делящееся на 9 (Кром-Ь того разность эта
равна произведешю 9 на разность цифръ даннаго двузначнаго
числа).
Знате этой особенности можетъ принести практическую
пользу, напр., многиыъ бухгалтерами Въ двойной бухгалтерш
случаются иногда опшбки, происходящгя отъ перестановки цифръ
въ числахъ. Такъ, напр., бухгалтеръ можетъ вписать въ сто-
сторону, скажемъ, «дебета»: 4 р. 38 к., а въ «кредите» по ошибке
поставить 4 р. 83 к., т. е. чпсло, состоящее изъ техъ же цифръ,
но две изъ нихъ переставлены. Если другихъ ошибокъ нЬть,
то при подведешп баланса между дебетомъ и кредитомъ всегда
будетъ выходить такая разница, которая делится на 9. Обра-
тивъ на это вшшаше, бухгалтеръ тотчасъ долженъ справиться,
не перепутаны ли где цифры.

100
Задача 51-я.
Попросите кого-либо написать какое угодно число
изъ трехъ цифръ, но только такое, чтобы крайтя
цифры были различны. Пусть потомъ онъ возьметъ это
число наоборотъ, т. е. переставить въ немъ крайшя
цифры, и вычтетъ одно число изъ другого. Полученная
разность всегда д-Ьлится на 9, и вы можете всегда ска-
сказать впередъ, каково будетъ частное.
,	Р^шеше.
Паприм'Ьръ, если взято сначала число 845, то 845—548=
= 297; 297:9=33, т. е. разницп между первой и послпдней
цифрой взятаго числа, умноженной на 11.
Чтобы доказать это правило для всякого трехзначнаго числа,
въ которомъ первая и последняя цифра различны, обозначимъ
черезъ а, Ъ и с соответственно цифры сотенъ, десятковъ и
единицъ числа. Тогда взятое число есть
а написанное наоборотъ:
Вычитая одно изъ другого и дт;ля на 9, иыъ-емъ:
с—A00с+Ш+«)_99 (а—с)
9	9
= 11 (а—с).
Итакъ, какое бы трехзначное число ни написалъ кто-либо,
вы, взявъ разность между крайними цифрами и поыноживъ ее
на 11, тотчасъ говорите частное, которое получится отъ дъчтге-
шя на 9 разности между взятымъ числомъ и тъ-мъ же числомъ,
написаннымъ наоборотъ.
Предыдущую задачу можно предложить въ еще бол^е зани-
яательноыъ, въ особенности для дт;тей,

101
Напишите на бумажкъ- число 1089, вложите бумажку
вь конвертъ и запечатайте его. ЗатЬмъ скажите кому-
либо, давъ ему этотъ конвертъ, написать на немъ
въ рядъ три любыя цифры, но таюя, чтобы крайшя изъ
нихъ были различны и разнились бы между собой
болъе, ч'Ьыъ на единицу. Пусть затъ-мъ это число онъ
напишетъ наоборотъ и вычтетъ изъ большаго меньшее.
Получится некоторое число. Пусть подъ этимъ числомъ
онъ подпишетъ его же, но наоборотъ, т. е. переста-
вивъ крайшя цифры, и сложитъ оба числа. Когда онъ
получить сумму, предложите ему вскрыть конвертъ.
Тамъ онъ найдетъ бумажку съ числомъ 1089, кото-
которое, къ его удивленно, и есть точь-въ-точь получен-
полученное имъ число.
Напримйръ: Пусть онъ напишетъ 713; взявъ наоборотъ,
получаемъ 317; 713—317 = 396; 396 + 693 = 1089. Тотъ же
результатъ получится, какъ легко видеть, и для всякаго такого
3-значнаго числа, .въ которомъ первая и последняя цифры раз-
различны, и разность этихъ цифръ больше единицы.
Болъ-е распространены слъугуюшш три «головоломки» съ
числомъ 9. ВсгЬ они основаны на томъ, что остатокъ, получае-
получаемый при дйлеши числа на 9, всегда равенъ остатку, получае-
получаемому отъ дъигешя на 9 суммы цпфръ этого числа.
Задача 52-я.
Возьмите, не говоря mh? ничего, любое двузнач-
двузначное число, переставьте въ немъ цифры и вычтите большее
число изъ меньшаго. Скажите теперь мнъ4 только одну
цифру полученной разности, и я скажу вамъ тотчасъ
другую.
PiineHie.
Если кто скажетъ вамъ любую одну цифру, то другая бу-
детъ дополнительная сказанной до 9-ти. Такъ что, если кто-
либо скажетъ вамъ послЪ того, какъ вычтетъ одно число изъ

102
другого, что одна цифра разности 6, то вы тотчасъ ему гово-
говорите, что другая есть 3 и т. д... Доказательство этого настолько
легко, что читатель справится съ нимъ самъ безъ затруднений.
Задача 53-я.
Возьмите, не говоря ничего мн"б, число изъ трехъ
или бол-Ье цифръ, разделите его на 9 и скажите мн"Ь
только остатокъ, который получится отъ такого д'Ь-
лешя. Зачеркните теперь во взятомъ вами числъ1 какую-
либо цифру (но не нуль) и опять скажите мнъ1 оста-
остатокъ отъ д-Ьлешя на 9 числа, полученнаго посл'Ь за-
черкиванья цифры, и я тотчасъ назову зачеркнутую
вами цифру.
Pimeirie.
Изъ перваго остатка надо вычесть второй остатокъ, если же
онъ больше, то къ первому остатку надо прибавить девять п
изъ полученной суммы вычесть 2-й остатокъ, тогда всегда и
получится зачеркнутая цифра. Читатель легко можетъ доказать
это самъ.
Задача 54-я.
Напишите число съ пропущенной цифрой, и я
тотчасъ вставлю туда такую цифру что число точно
разделится на 9-
Р^шеше.
Пусть, напримйръ, кто либо нашппетъ съ пропускомъ рядъ
цифръ 728 57. Тогда, отбрасывая отъ суммы цпфръ всЬ девятки,
катя возможно, получаемъ въ остатки 2, но 9 —2 = 7. Зна-
читъ на пустое мйсто надо поставить цифру 7. Доказательство
очевидно.
Задачу эту, какъ и предыдущая, можно всячески разнообразить.

103
Некоторые числовые курьезы,
Въ главт, о нйкоторыхъ особенныхъ случаяхъ умножешя
мы уже показали, что легко получить и запомнить результаты
н'Ькоторыхъ перемноженш. Очень легко также запомнить квадраты
такихъ чиселъ, какъ 11, 111, 1111 и т. д. А именно:
112=121; Ш2=12 321; 1 1112=1 234 321; и т. д.
Нетрудно убедиться, что эти полученныя отъ возвышешя въ
квадратъ числа: 121, 12 321, 1234 321, 123 454 321 и т. д. въ
въ свою очередь отличаются любопытными свойствами. Такъ,
разематривая сумму ихъ цифръ, замйчаемъ прежде всего, что
1+2+1=4=22
1+2 + 3+2+1=9=32
1+2+3+4+3+2+1 = 16=42
1+2+3+4+6+4+3-1-24-1=26—б2
и т. д. (Ср. задачу о ииеагорейскомъ круги, стр. 23).
Кромй того каждое изъ этихъ чиселъ можно представить въ
видй нижеслъ'дующихъ интересныхъ по форлъ1 неправильныхъ
дробей:
22X22.	333X333 .
1234!
123 454421 =
1 + 2 + 3+4+3+2+1
55 555X55 555
1 + 2+3+4+5+4+3+2 + 1
и т. д.
О числахъ 37 и 41.
Число 37 обладаетъ многими любопытными свойствами.
Такъ, умноженное на 3 и на числа кратныя 3 (до 27 вклю-
включительно), оно даетъ произведешя, изображаемый одной какой-
либо цифрой:
37ХЗ = Ш; 37X6=222; 37X9 = 333; 37X12 = 444;
37X15=655; 37X18=666; 37X21=777; 37X24=888;
37X27=999.

104
Произведете отъ умножешя 37 на сумму его цифръ рав-
равняется суммъ1 кубовъ т'Ьхъ же цифръ, т. е.:
37ХC+7) =33+73=370.
Если въ числ4 37 взять сумму квадратовъ его цифръ л
вычесть изъ этой суммы произведете т4хъ же цпфръ, то опять
получимъ 37:
C2-1-72)—3 • 7=37.
Но едва ли не самымъ интереснымъ свойствомъ числа 37
является то, что н'Ькоторыя кратныя ему числа при круговой
перестановки входящихъ въ нихъ цпфръ даютъ опять-таки
числа кратныя 37. Наирпм.:
259= 7X37
592 = 16X37
925 = 25X37.
То же самое вйрно относительно чиселъ 185, 518, 851 и
чиселъ 296, 629, 962. ВсЬ эти числа состоятъ изъ т'Ьхъ же
цифръ, только переставляемыхъ въ круговомъ порядка, и все
они кратны 37.
Подобнымъ же свойствомъ отличаются и н'Ькоторыя числа
кратныя 41. Такъ, числа:
17 589; 75 891; 58 917; 89 175 и 91 758,
какъ легко проверить, всЬ кратны 41 и каждое получается
изъ предыдущаго путеиъ только одной круговой перестановки
входящихъ въ число цифръ.
Числа 1375, 1376 и 1377.
Написаниыя выше трп послтьдователъпыхъ числа, кажется,
суть напмснышя изъ такпхъ, что каждое д'Ьлится на кубъ нгЬ-
котораго числа, отличнаго отъ единицы: 1 375 делится па 53
1 376—на 23 и 1 377—на З3.

105
Степени чиселъ, состоящ1я изъ одн%хъ и тЪхъ же цифръ.
Вотъ несколько посл'вдовательныхъ чиселъ, квадраты ко-
торыхъ пишутся тгЬмп же цифрами, но только въ изийненномъ
порядки:
132 —169: 1572 = 24 649; 913-= 838 569.
142=196; 15Н2 = 24 904; 9143 = 83б396.
Изъ однихъ и т4хъ же цифръ, написаниьтхъ въ разномъ
порядки, состоять кубы слйдующихъ чиселъ:
3453 = 41 063 625; 3313 = 36 264 691;
= 56 623 104; 4О63 = 66 923 416.
4;
Следующая пара чиселъ представляетъ ту огобенность, что и
квадраты ихъ квадратовъ также состоятъ изъ однихъ и тгЬхъ же
цифръ, только написшшыхъ въ иномъ порядк'Ь:
322 = iQ24 324= 1048 576
492 =С 401 494 = 5 764 801.
Квадраты чиселъ, не содержание однЪхъ и тЪхъ же цифръ.
1 .—Квадраты чиселъ, состояице изъ девяти различпыхъ
цифръ:
~', 118262=139 854 276	23 4392 = 549 386 721
/ 12 3632 = 152 84-3 769	24 2372 = 587 432 169
12 5432 = 157 326 849	24 2762 = 589 324 176
14	676^ = 215 384 976	24 4412 = 597 362 481
15	6812 = 245 893 761	24 8072 = 615 387 249
15 9632 = 254 817 369	26 0592 = 627 953 481
18	0722 = 326 597 184	25 5722 = 653 927 184
19	0232 = 361 874 529	25 9412 = 672 935 481
19- 3772 = 375 468 129	26 4092 = 697 435 281
19 5692 —382 945 761	26 7332 = 714 653 289
19	6292 = 385 297 641 27 1293 = 73б 982 641
20	3162 = 412 739 856 27 2732 = 743 816 529
22	8872 = 523 814 769 29 0342 = 842 973 156
23	0192 = 529 874 361 29 1062 = 847 159 236
23 1782 = 537 219 684 30 3842 = 923 187 456

106
2°.— Квадраты чпселъ, состоящее изъ десятп разпыхъ цифръ:
32 0432 = 1 U26 753 849	45 6242 — 2 081 549 376
32	2862 = 1 042 385 796	55 4462 = 3 074 258 916
33	1442 — 1 098 524 736	68 7632 = 4 728 350 169
35 1722=1 237 069 584	83 9192 = 7 042 398 561
39 1472 = 1 532 487 609	90 О66а = 9 814 072 356.
Все разныя цифры.
Если число 123456789 умножить на всякое п/Ьлое чпсло
меньшее, ч?мъ 9, и первое съ ипмъ, т. е. па числа 2, 4, 5. 7
8, то каждое полученное произведете будетъ состоять ызъ 9-тп
различпыхъ цифръ.
Въ слЗздующемъ вычиташи:
_987 6,кА 321
123 456 789
864197 532
Уменьшаемое, вычитаемое и разность каждое состоитъ изъ
девяти разлпчныхъ цпфръ.
Числа, отличаюицяся отъ своихъ логариемовъ только п/гЬстомъ
запятой, отд%ляющей десятичные знаки.
Изсл'Бдовашями объ отыскапш подобнаго рода чиселъ зани-
занимались въ особенности знаменитый Эйлеръ и анппйсгай иро-
фессоръ Тэтъ. 'Ниже мы даемъ только три примера подобныхъ
чпеелъ, обращая внимаше на то, что рядъ ихъ можетъ быть
продолжеиъ псопред4ленно далеко.
t
log 1,3 712 885 742 = 0, 13 712 885 742
log 237,5 812 087 593 = 2, 375 812 087 593
log 3550,2 601 815 865 = 3,5 502 601 815 865

107
Круговыя числа.
Число 142 857 отличается многими замечательными свой-
свойствами. Если его умножать на последовательный числа 2, 3,
4, 5 и 6, то иолучениыя произведешя бу-
дутъ состоять изъ ¦ тгЬхъ же цифръ, что п само	1
число, только псреставленныхъ въ круговомъ 7
порядки. Другими словами: все эти произ-
ведетя можно получить пзъ представленнаго
зд'Ьсь круга, читая все числа подрядъ, въ на-
иравлеши движсшя часовой стрелки, но ка-	"
ЖДЫЙ раЗЪ Начиная СЪ ДРУГОЙ Цифры:	Фиг. 81.
2X142 857=	285 714
ЗХ	»	=	428 571
4Х	»	=	571428
5Х	»	=	714 285
6 X	»	=	857 142
7Х	»	=	999 999
8Х	»	=1142 856.
При умноженш числа на 7 получается, какъ видимъ, шесть
девятокъ, при умножепш же на 8 получается уже семизначное
число 1 142 856. Это последнее замечательно темъ, что, прп-
ложнвъ его первую цифру A) къ последней (E), получпмъ опять
данное число 142 857. Вследъ за этнмъ уыножешя на даль-
HefiHiia числа даютъ тотъ же результатъ, т. е. мы получаемъ
опять числа, написаниыя цифрами 1, 4, 2, 8, 5, 7 п въ ука-
занпоыъ круговомъ порядки, если въ получаемыхъ семизнач-
иыхъ числахъ будемъ первую цифруй переносить пазадъ и при-
прибавлять къ послгьдней. Вь самомъ деле:
9 X 142 857 = 1 285 713 B85 714)
Ю X » = 1428 570D28 571)
ИХ » = 1571427 E71428)
23 X » = 3 285 711B85 714)
89 X » =12 714 273.

108
Зд-Iicb опять слтдуетъ отметить, что, улпожая на 89, мы
получаемъ уже 8-ми-значпое число, но если въ пеыъ двгЬ пер-
выя цифры A2) придать къ двуиъ посд-Ьднимъ G3), то опять
получгогь число, состоящее изъ т'Ьхъ же цпфръ, что и взятое
начальное, но написанное къ пномъ порядки, а именно: 714 285.
Точно также:
356 X142 857 = 50 857 092 (получаемъ число
857 142, если прпложимъ 50 къ 092).
Что же за «особенное» такое число 142 857, и въ чемъ
секретъ его особенности?
Ключъ къ уразум'Ьшю веЬхъ особенностей этого числа даетъ
то именно, якобы, «исключеше», которое нарушаетъ приведенный
выше круговой порядокъ, а именно, произведете 7X142 857 =
= 999 999.
Число 142 857 есть, какъ оказывается, перюдъ дроби —, если
ее представить въ видй десятичной дроби.
Совершено т4ми же свойствами будетъ отличаться всякш
другой «полный» или «совершенный перюдъ», т. е. перюдъ,
получаемый отъ обращешя въ десятичную простой дроби вида
- (гд$ р есть первоначальное число), и при томъ такой перюдъ.
что число его цифръ ровно на единицу меньше, ч'вмъ показы-
ваетъ число знаменателя данной простой дроби.
Такимъ образомъ свойствами числа 142 857 будетъ обла-
обладать Ту = О, @ 588 236 294 117 647). Въ самомъ дйл&
2X0 588 235	=1 176 470 588 235 294
т. е. получаемъ число, написанное тйми же цифрами, но въ
иномъ круговомъ порядки. И точно также:
7X0 588 235	=4 117 647 058 823 529
Въ то время, какъ
17X0 588 235	=9 999 999 999 999 999.

109
Точно такимп же свойствами будетъ отличаться перюдъ дроби
— = 0,@ 344 827 586 206 896 551 724 137 931), въкоторомъ
28 цифръ.	_^__^
Нетрудно доказать, что каждая обыкновенная дробь вида
-, гдгЬ р есть первоначальное число, при обращенш въ деся-
десятичную дастъ перюдъ, въ которомъ должно быть меньше, чъчмъ
2>, десятичныхъ знаковъ.
Въ самомъ дъмт., при долети остатокъ всегда долженъ быть
меньше делителя. Отсюда сл'вдуетъ, что въ остаткахъ при дгЬле-
нш 1 на р для обращешя въ десятичную дробь можетъ полу-
получиться только р — 1 различныхъ чиселъ, а зат4мъ процессъ
начистъ опять повторяться.
Такъ, напр,, для известной уже намъ дроби -- им^емъ:
^ = 0,1 | = 0,14 у= 0,142 ^ = 0,1428 | = о,14285|==
= 0,142857-- = . . . (дальше, очевидно, начнется повтореше
т4хъ же цифръ).
Отсюда ясно, что если мы будемъ помножать число 142 857
на 3, 2, 6, 4, 5, то мы будемъ получать перюдъ, начинающиеся
соотвт/гствеио послгъ 1-й, 2-й, 3-й, 4-й п 5-й цифры.
Отм^тимъ также еще и сл^дуют^я положешя:
Если перюдъ, получаюип'йся отъ обращешя дроби вида
(гдъ р есть простое число) въ десятичную, содержитъ —-—
цифръ, то при умноженш этого перюда на всЬ множители отъ
р—1
1 до р — 1 всегда будемъ получать числа изъ	ЦПФРЪ)
при чемъ всв эти числа можно разбить на два ряда такихъ, что
каждое чисто каждаго ряда ыожетъ получаться пзъ предыду-
щаго путеыъ только круговой перестановки цифръ.

110
Для примера будемъ обращать въ десятичную дробь ... .
Получается, jo = 0,@76923). Помножая число перюда на мно-
множители 1, 2, 3, . . . 11, 12, находимъ:
2X076 923 = 153 846
5Х	=384 615
6	X » = 461 538
7	X » = 538 461
8Х » =615 384
ИХ » =846 153
1X076 923 = 076
3 X » = 23° 769
4Х » =307 692
9 X » = 692 307
Ю X » =769 230
12 X » =923 076
Возьыемъ снова уже известное намъ число, представляющее
перюдъ дроби , т. е. чисто 142 857. Помимо извйстныхъ уже
намъ свойствъ оно обладаетъ и такимъ: разобьемъ его на двъ1
половины по три цифры въ каждой и сложиыъ эти части, найдемъ
число, кратное 9-ти, т. е.
142 + 857 = 999.
Подобныыъ же свойствомъ отличается и число, представля-
представляющее перюдъ у= (см. выше) и т. п... То же относится и къ
1
числамъ, полученнымъ нами выше изъ перюда утг.
Т4мъ не мен4е, если мы найдеыъ такой перюдъ дроби -,
р—1	р—1
который содержитъ—„—цифръ) и это последнее число —^—
будетъ само вида 4и-}-3, то такой иерюдъ нельзя, следова-
следовательно, разделить на 2 равныя половины, гд-Ь каждая цифра
дополнила бы соответствующую до 9. Но въ такомъ случай
число	(дополняющее - до единицы) даетъ перюдъ тоже изъ
Р1 *	• х
ЦИФРЪ? дополнительный перюду—.
¦	р
7)ЦИФРЪ? дополнительный перюду

Ill
НапримЪръ:
i = 0.@32 258 064 616 129)
40
— = 0,(967 741 936 483 870)
О J
О J.
Сумма — 0,(999999999990999)
Полезное примЪнеше.
Изъ указанныхъ выше особенностей извйстнаго рода чиселъ
можно извлечь н^которня поле,чныя практичест'я примт>нешя.
И прежде всего можно ввести значительныя упрощешя и сокра-
щешя въ вычислешя, когда мы обращаемъ - (р = первоначаль-
первоначальному числу) въ десятичную дробь.
Въ такомъ случай, нашедпш никоторое число десятичныхъ
знаковъ, мы еще бол'Ье значительную часть ихъ можемъ найти,
умножая полученную уже часть частнаго на остатокъ. Для
удобства вычислешя процессъ дйлешя слЬдуетъ продолжать до
тт>хъ пор7>, пока остатокъ получится сравнительно небольшой.
Будемъ, наприм., обращать въ десятичную дробь-=-.Начавъ
дйлеше числителя на знаменатель, ли, положимъ, получимъ въ
частномъ 0,01 030 927 836 и въ остатки 5. Остатокъ невеликъ,
поэтому разсуждаемъ такъ: начиная съ последней полученной
цифры частнаго, дальн'Ьйппя цифры должны быть татая, как!я
получатся отъ обращешя въ десятичную дроби —, умноженной
на 5. Итакъ, умножая на 5 получешшя цифры частнаго (или
прибавя нуль справа и д-Ьля на 2), мы сразу получаеыъ еще
11 цифръ частнаго.
Задача 55-я.
Мгновенное умножение.
Если вы въ достаточной степени внимательно отнеслись къ
предыдущей глав'Ь и усвоили свойства повторяемости однихъ и
тт>хъ же цифръ, которыми обладаютъ нъкоторыя числа, то это

112
доставитъ вамъ возможность производить надъ числами пзвестныя
flificTBifl, которыя для непосвященнаго покажутся прямо пора-
поразительными. Такъ, напр., вы можете кому-либо предложить сле-
следующее:
Я пишу множимое, а вы подписываете подъ нимъ
какой хотите множитель изъ двухъ или трехъ цифръ,
и я тотчасъ же напишу вамъ произведете этихъ чиселъ,
начиная отъ „тьвой руки къ правой.
Р-Ьшеше.
Въ самоыъ дта-Ь, вы напишете, какъ множимое, першдъ
дроби - , т. е. число 142 867, о которомъ мы говорили въ пре-
предыдущей главе. Предположимъ, что другой потребует!,, чтобы
вы это число умножили, напр., на 493.
Дело, въ сущности, сводится къ тому, что вы это число 493
мысленно умножаете на -, а зат'Ьиъ мысленно же обращаете
въ перюднческую дробь, что при свотЭствахъ извЬстнаго вамъ
перюда A42 857) совсЬмъ не трудно. Поэтому, глядя на число
,„„ , 493
493, вы мысленно делите его на сень и получаете 	=
= 70-. Следовательно, вы пишете 70, какъ две первыя цифры
пскомаго произведешя (пишете слева направо).
3 /	1\
Теперь остается - т. е, 3 X ), иначе говоря,— 3, умно-
умноженное на перюдъ 142 857, и вся задача заключается только
въ тоыъ, чтобы определить первую цифру, съ которой надо
начинать писать этотъ перюдъ въ круговомъ порядке. Раз-
суждаемъ такъ:
Единицы мпожпмаго, 7, на множитель, 3, даютъ въ произведе-
нш 21. Значитъ последняя цифра въ пскомомъ пропзведен1и
должна быть 1, а следовательно, первой въ перюде придется
ближайшая следующая, т. е. 4 (или находимъ 4, деля 3 на 7).
Итакъ, пишемъ (после 70) еще цифры 4 286, а отъ 71, которыя

113
должны бы стоять на конце, надо отнять т-б 70, что написаны
въ начали (сравните съ умножешемъ 89 X 142 867 въ предыду-
предыдущей главе). Это дастъ две посл'Ъдшя цпфры искомаго произ-
произведения: 01. Итакъ, искомое произведете есть 70428501.
Все это можно (при усвоенш сущности задачи) проделать
весьма быстро. II когда вашъ собесЬдникъ, непосредственнымъ
умножешемъ привЬрпвъ верность вашего ответа, предложить
опять взятое вами число A42 857) умножить сразу, напрнмеръ,
на 825, вы опять разсуждаете точно также:
825 iif_6	„,
—- = 117- и пггшете 117.
Такъ какъ 6 X 7 = 42, то последняя цифра искоыаго про-
изведен1я будетъ 2; значптъ, круговую последовательность чи-
селъ иер1ода надо начинать съ непосредственно за 2 следую-
следующей цифрой, т. е. съ 8, и вы пишете (за 117) 857J дальше
должны идти цифры перюда 142, изънпхъ надо отнять 117, и
вы пишете еще три цифры 025. Получаете:
142 857 X 825 = 117 857 025.
И слава ваша; какъ «необыкновеннаго счетчика», пожалуй,
упрочится!
Вотъ еще пршгЬръ: 142 857 надо умножить на Н78.
378	- .	г-п'	т
	= 54 = 5о—, пишемъ од.
7	7'
7 X на псршдъ даетъ 6 девятокъ. Вычитаемъ мысленно 53
пзъ 999 999 и результата, приппсываемъ за 5В; получаемъ
53999946.
ЗамЪчаше. При некоторой практпкъ' это «умножеше» де-
делается чрезвычайно быстро и действительно поражаетъ незнаю-
щаго, въ чемъ дтло. Надо, однако, — если желать сохранить
секретъ п занимательность,— всячески разнообразить это мате-
математическое развлечете. Можно, иапртгйръ, партнеру сказать
такъ:
ВЪ ЦАРСТВТ, СМВЕАДКИ.	8

114
Вотъ я пишу некоторое число; подпишите подъ
нимъ какого угодно множителя изъ 2-хъ, или 3"хъ
цифръ, умножьте и полученное произведете разделите
на 13- То частное, которое вы постЬ этого получите,
я вамъ напишу сейчасъ же, какъ только вы напишете
множитель.
Въ этоыъ случай, конечно, вы пишете въ качеств^ мно-
жимаго не 142 857, а 13 X 142 857 = 1 867 141. Такъ какъ 13
въ данномъ случай, въ сущности, сокращается, то частное вы по-
получите совершенно такъ же, какъ получали произведете въ пре-
дыдущпхъ прпмЬрахъ. Вместо числа 13 можно взять всякое
иное число.
Нисколько замйчашй о числахъ вообще.
Теорема Ферма, за доказательство которой, какъ мы уже
говорили въ одной изъ предшествующихъ главъ, можно полу-
получить 100 000 марокъ, кромъ1 титула «великой», носить еще на-
зваше его посмертной теоремы. Вопросы подобнаго рода изу-
изучаются въ той части математики, которая носитъ общее назва-
Hie meopiu чиселъ. Въ этой области сравнительно мало кто ра-
ботаетъ, хотя, по выраженго шногихъ, она исполнена «волшеб-
наго очаровашя». «Математика—царица наукъ, но ариометпка,
(т. е. теор1я чиселъ) есть царица математики»,— говорилъ «пер-
«первый изъ математиковъ (princeps matheuiaticorum)» Гауссъ, а ужъ
онъ-то въ этомъ вопрост. можетъ считаться вполн^ компетент-
нымъ судьей. Но, быть можетт., ни одна изъ областей матема-
тическихъ наукъ не требуетъ такой силы и строгости мышле-
шя, остроум1я пргемовъ и глубокаго про1шкиовен1я въ природу
числа, какъ именно эта теорш чпселъ, пли «высшая арпеме-
тика», какъ ее иногда называютъ. Читатель FiaB'bpnoe не посЬ-
туетъ на насъ, если мы сд'Ьлаемъ небольшую историческую
экскурсш въ эту область. Начнемъ опять съ упомянутой уже
знаменитой посмертной теоремы Ферма. Теорема состоитъ въ
томъ; что

115
Невозможно найти ц-Ьлыя числа для х, у, ^, который
удовлетворяли бы уравнешю
если п есть ц-Ьлое число большее, ч-бмъ 2.
Теорема Вильсона состоптъ въ сл-Ьдующемъ:
Если р есть первоначальное число, то число
I + I-2-3-4	(р — I)
делится безъ остатка на р.
Эта знаменитая теорема была высказана Джономъ Вильсо-
номъ A741—1793), воспиташшкомъ Кэмбриджскаго универси-
университета. Какъ и Ферма, онъ не занимался специально математикой.
Теорему свою онъ предложилъ ученьшъ безъ доказательства.
Впервые опублпковалъ ее Уорингъ (Waring) въ своихъ «Mecli-
tationes Algebraicae», а общее доказательство ея далъ Лагранжъ
въ 1771 году.
Формулы для пахождетя первоначальпыхъ чиселъ. Общей
формулы для получетя ряда посл'Ьдивательныхъ первоначаль-
ныхъ чиселъ въ любыхъ пред'Ьлахъ пе найдено. Лежандръ
предложилъ формулу 2х2 + 29, которая даетъ иервоначальпыя
числа для всЬхъ посл'Ьдователт.ныхъ значешй х отъ х = 0 до
х = 28, т. е. для 29 значешй х. Эйлеръ далъ формулу:
ж2+ж + 41, которая даетъ первоначальныя числа для зпаче-
нш х отъ 0 до 39, т. е. для 40 значешй х. Американски ма-
тематикъ Эскоттъ (Escott) нашатъ, что если въ формулъ- Эйлера
заменить х черезъ х—40, то найдемъ формулу х2 — 79 х + 1601,
которая даетъ первоначальныя числа для 80 посл'Ьдовательныхъ
значешй х. Въ особенности замечательны въ этомъ отношенш
труды русскаго академика Чебышева.
Можетъ ли быть больше оОной группы жрвонпчальиыхъ
множителей числа? ВсЬ почти наши учебники ариеметпки на
этотъ вопросъ отв'Ьчаютъ: тьтъ. Число, моль, разлагается только
на одну группу нервоначалышхъ множителей. II этотъ отв'Ьтъ
а*

НС
совершенно вт.ренъ, пока мы держимся только т^снаго чисто
«ариеметическаго», такъ сказать,— прпвычнаго понятая о еди-
ниц'е, о числи. Но если взглядъ на число мы расширишь до
поняия о комплексномъ числи (см. дал-Ье главу «Наглядное
изображеше комплексныхъ чиселъ»), то положеше, что всякое
число можетъ быть разложено на первоначальныхъ производи-
производителей только единственнымъ путемъ, лишается математической
достоверности. Такъ, наприм^ръ:
Развитге понятгя о чиелгь. Начиная съ учешя о ц'Ьлыхъ
числахъ древнихъ грековъ, переходя черезъ рацюнальныя дроби
Дюфанта, такъ называемыя «ращопальности» и «иррацюналь-
ности» разематриваются, какъ числа, только въ шестнадцатомъ
вЬсЬ. Отрицательныя числа, какъ обратным положительнымъ,
были выдвинуты Жираромъ и Декартомъ. «Мнимыя» и ком-
плексныя числа ввшги въ MaTeMaTH4ecKift_ обиходъ Арганъ, Вес-
сель, Эйлеръ и Гауссъ.
Такимъ образомъ въ последнее время создалось новое, общее,
понят1е о чиелт, и, говоря кратко, математики приняли за пра-
правило, что оправдате для введетя въ аривметику числа осно-
основывается только па опредгьленги этого числа. Исходя изъ
этой точки зр^шя, и развивается вся современная теоретическая
ариеметика.

Графики.
Какъ-то прсЬздомъ черезъ уЬздный городъ западнаго края
пишущему эти строки случилось разговориться съ мЬстныыъ
обывателемъ и узнать, что у нихъ въ городт, есть своего рода
чудо-математпкъ. Этотъ математикъ мало того, что ръчпалъ
«всякую» и «какую угодно» предложенную ему задачу, но pi-
шаль чрезвычайно быстро, почти не думая, при помощи всего-
на-всего обыкновенной шахматной доски. Кусочкомъ мтла онъ
нзв'Ьстнымъ ему образомъ разставлялъ на ютЪткахъ доски числа
задачи и затЬмъ, не производя никакихъ письменныхъ вычи-
слешй, говорилъ тотчасъ отвить.
—	И это каждую предложенную задачу онъ ръчпаетъ та-
кимъ образомъ? — заинтересовался я.
—	Какую угодно! Можете, если угодно, убедиться въ этомъ
сами. И главное, необразованный... а самъ дошелъ...
Къ сожал'Ънш, ни время, ни обстоятельства не позволили
мнт, познакомиться съ этпмъ еще однимъ скрывающимся въ
нашей глуши самородкомъ. Но не разъ, признаться, задумы-
задумывался я надъ тъчмъ, какъ это «простой и необразованный» 6ГЬ-
лоруссъ ръчпаетъ всгь задачи съ помощью шахматной доски, не
прибегая къ выкладкамъ п вычпслешямъ. Арпеметика или ал-
алгебра безъ вычислешй!.. На первый взглядъ это удивительно,
но это только на первый взглядъ.
Быть можетъ, «секреть» уроженца бйлорусскаго городка
окажется не столь ужъ загадочнымъ, если сообразить, что шахмат-
шахматная доска есть не что иное, какъ площадь, разграфленная вер-

118
тикальнымп и горизонтальными лишямп на квадратньш клтьтки.
Листъ же бумаги, разграфленной на шгЬточкп, какъ сейчасъ
увидимъ, можетъ оказаться пезамт>нпмымъ подспорьемъ для
быстраго р'Ъшешя весьма мпогпхъ п вссыга сложныхъ задачъ.
Таги, какъ клетчатую бумагу можно теперь встретить въ про-
продажи почти всюду, то п мы здФсь со своей стороны повторяема,
совт,тъ почтеннаго профессора Джона Перри, который въ своей
«Практической Математики1» говорить: «очень важно, чтобы
ученикъ извелъ много листовъ бумаги (клгьтчатои) на своп
упражнения, расточительпо пользуясь этимъ матерт.яломъ». До-
бавимъ къ этимъ словаыъ почтеннаго ученаго, что «изводить»
клт/гчатую бумагу слйдуетъ и не «ученику» въ точномъ зна-
ченш этого слова, а всякому любителю точпыхъ знанШ. При
помощи такого рода бумаги весьма легко вычерчивать графики
п приытлять ихъ къ рйшенш различныхъ задачъ.
Эти графики въ наше время вы можете найти во многихъ
газетахъ и журналахъ. Чаще всего пми пользуются для нагляд-
наго представлешя хода изм'Ьнешй температуры и давлетя ба-
барометра за известный перюдъ времени. Примйръ такого гра-
графика дань на фиг. 81.
Лонед-Ёльнккъ Вторникъ Среда	Четвергъ Пятница Суббота Воскресенье
790 гй
780
770
760
750
740
730
6 12 6 it 6 12 fj \k 6 I? 6 k 6 12 6 1'2 6 \l Б ife 6 12 6 1I2 6 12 6 k
—•
...
...
¦-
¦*¦¦
¦¦•
-..
s
-v.
-¦..
f
N
Фиг. 81.
На этой фигурт, изображены даже не одинъ, а два графика:
сплошная черная лншя изображаетъ колебашя за нед-Ьлю въ
показашяхъ барометра, а лпшя колебан1й температуры обозна-
обозначена пунктиромъ. Разобраться въ подобномъ график^ очень легко.

119
По горизонтальному направленно означено время: семь дней
недели и для каждаго дня главнМгше часы наблюдешй—12
часовъ ночи. 6 час. утра, 12 час. дня и 6 час. пополудни.
Такъ что сторона каждаго квадратика въ горпзонтальномъ на-
правлеши соответствуешь промежутку времени въ 6 часовъ,
1	i
а — стороны — 1 часу и т. д...
По вертикальному направленпо слива помещены дйлетя
въ мпллпметрахъ шкалы барометра, а справа шкала термо-
термометра.
Пусть теперь, скажемъ, каждый часъ въ сутки или черезъ
каждые 2, 4, E п т. д. часа опред'Ьляютъ высоту барометра п
показаше термометра. Каждое такое показаше на югЬткахъ гра-
графика легко отметить соответствующей точкой. Положимъ, на-
примйръ, что во вторникъ въ шесть часовъ утра высота баро-
барометра была 780 миллиметровъ, а термометръ показывалъ 0°.
Тогда на пересЬченш вертикальной лиши, проходящей черезъ.
noKasame «Вторникъ 6 час. утра», съ горизонталью, проходя-
проходящей черезъ д^леше барометра 780, мы ставимъ точку, обозна-
обозначающую показаше барометра. Точно также на той же вертикали,
но въ перес^ченш ея съ лишен, противъ которой поставлено
пулевое показаше термометра, мы ставимъ точку. Это будетъ
пок'азаше термометра. Соединяя все послт.довательныя показашя
барометра сплошной лшпей, а показашя термометра пункти-
ромъ, получаемъ графики недъ'льныхъ температуръ и барометри-
ческаго давлешя, даюпд'е полную картину измФнешя погоды за
недтлю. Никакой путаницы и неясности здЬсь быть не можетъ.
Если вы хотите проследить лишю барометра, справляйтесь съ
цифрами налЬво; желаете проследить температуру, смотрите
цифры направо. Точно также каждая точка горизонтали соот-
вт/гствуетъ известному часу и дню недели.
Но графики находятъ себ4 примкнете не въ одномъ только
ученш о погоде (метеоролопи). Можно сказать, что ч!мъ дальше,
тЬмъ область ихъ примт.нешя становится шире. Въ высшей
степени плодотворно пользоваше графиками, напримЬръ, въ
статистик^. Въ железнодорожномъ д-Ьл^ они представляютъ чуть
ли не единственное средство для обозначения движешя по^здобъ,

120
п графики послйдняго рода вы, вероятно, встречали на ст'Ьнахъ
иныхъ станщй ж&тЬзныхъ дорогъ. Графиками же часто поль-
пользуются на биржахъ для обозначешя колебашй курса. Графики—
необходимое nocodie въ области практической механики, строи-
строительства и т. д., п т. д.
Вообще когда одна величина, Y, завесить отъ другой, X,
такъ, что съ измйнешемъ X изменяется Y, и если эти вели-
величины и измйнетя ихъ конечны, то съ помощью графика можно
представить какое угодно изы'Ьнеше величины Y въ зависимости
отъ измйнешл X.
Величина Y въ такоыъ случай называется функцией отъ
величины X. Пояснимъ нисколько подробнее это весьма упо-
употребительное въ математики слово.
Если мы будемъ чертить рядъ окружностей, все более и бо-
более увеличивая радгусъ, то и самыя окружности будутъ все
длиннее и длиннее. Следовательно, длина окружности есть функ-
цгя ея радгуса. Если къ резиновой нити подвесить -тяжестъ,
то она вытянется,—и вытянется больше или меньше въ зави-
зависимости отъ того, большую или меньшую тяжесть мы подв4спмъ.
Длина резиновой нити есть, следовательно, функщя подвешенной
къ ней тяжести. Если подогревать въ котле паръ, то давлеше его
увеличится — и те>мъ больше, че>мъ выше будетъ температура.
Давлеше пара есть, следовательно, функщя температуры и
т. д. Читатель можетъ теперь самъ подобрать сколько угодно
примеровъ величинъ, находящихся между собой въ функцио-
функциональной зависимости.
Посредствомъ графика можно всегда наглядно представить
функщю съ помощью чертежа. И для этого прибътаютъ всегда
къ одному и тому же нижеследующему npieMy.
На клетчатой бумаге берутъ две взаимно-перпендикуляр-
ныя лиши ОХ и OF, называемыя осями коордгтатъ и пересе-
пересекающаяся въ точке О (Фиг. 82). Условимся, теперь, направлешя
вправо и вверхъ по осямъ считать положительными (съ зна-
комъ +), а направлешя влево и внизъ — отрицательными (съ
знакомъ —).
Какъ же намъ теперь графически п?образить некоторую фупк-
• цш у, зависящую отъ х?

121
X'
Y
Фиг. 82.
Условимся въ единиц! м'Ьры, прииявъ, скажемъ, каждую
сторону клетки за 1. Заттдгь беремъ известное значете для х
п откладываемъ его по оси
О х вправо, если х положи-	у
тельно, и влй-во, если х—
отрицательно.
Пусть, напр., въ дан-
номъ случай х изобрази-
изобразилось у насъ длиной Ор. Для
взятаго значешя х опред'Ь-
лимъ соответствующее зна-
4eHie у; пусть оно выра-
выразится числомъ, которое
можно представить длиной
Oq. Эту длину мы откла-
дываемъ по оси ОЗ^вверхъ,
если она го знакомъ +, и
внизъ, если она со знакомъ.—Изъ точекъ^ и q проведемъ те-
теперь лпнш, параллельныя осямъ OY и ОХ. Лиши эти пере-
пересекутся въ точкъл Р. Вотъ эта точка и представляетъ совокуп-
совокупность двухъ соотвЬтствующихъ значен ш хну. Построивъ рядъ
такихъ точекъ и соединивъ ихъ непрерывной лпшей, получаемъ
графикъ, изображающий наглядно пзмЬнегпя функщп у въ зави-
зависимости отъ измйнешй ос.
Способъ этотъ, какъ мы уже видФли, былъ примгЬненъ для
получешя предыдущаго графика (Фиг. 81) температуръ и ба-
рометрическаго давлен!я. Онъ, — повторяемъ, —¦ общи для по-
строенья всЬхъ графиковъ вообще.
PtiueHie уравнен!й.
При пользовании графиками н4тъ. вообще говоря, неразрт;-
шнмыхъ уравнехпй. Для образца, какъ для решетя yp-ifl можно
пользоваться графиками, возьмемъ простой прим^ръ изъ «Практи-
«Практической математики» проф. Джона Перри. Пусть требуется графп-
ческимъ путемъ решить yp-ie:
'ж2 —б,11ж +5,709 = 0.

122
ПОЛОЖ
и сдйлаемъ графикъ функщи у.
Возьыеыъ н'Ькоторыя значила х отъ нуля до б и вычислпмъ
соответствующая значила х. Получаеыъ два ряда:
для ж: 0 1 1,5 2,0 2,5 3,0 3,5 4,0 5,0
для у. 5,709 1,599 0,294 -0,511 -0,816 -0,621 -0,074 1,269 5,159
Нанося эти значешя па тгЬточиую бумагу, получаемъ гра-
фпкъ, iisoopaHieHHbifr на фиг. 83.
Кривая графика перееЬкастъ ось ОХ въ двухъ точкахъ Р и
Q, следовательно, существуетъ два корня уравнешя х2 —
О
Фиг. 83.

123
— 5, Нж-j-5,709 = 0. Вычисляя эти корпи по графику, нахо-
дпмъ пхъ приблизительную величину: 1,65 и 3,46.
Вотъ зд'Ъсь-то и сл'Ьдуетъ отм'Ьтить, что вст> почти резуль-
результаты, получаемые помощью графиковъ, лишь приблизительны,
а не вполн'Ь точны. Ото всегда сл'Ьдуетъ пм'Ьть въ впду; когда
пользуемся графиками. Но сл-Ьдуетъ также знать и то, что при
тщательномъ составлены графпковъ получаемые результаты
вполп/Ь удовлетворяютъ требован1ялъ практики.
Итакъ, если мы не умт>емъ даже ръчпать алгебраически
yp-iS 2-й, 3-й и 4-й степени, то намъ помогут!, графики. Они
же могутъ помочь найти корень и всякаго иного уравнешя.
въ томъ чпслт, даже неразръ-шилаго алгебраически yp-ifl выше
четвертой степени, и разръ-шать ихъ съ желательной степенью
точности. Теперь вамъ, вероятно, понятно значеше графпковъ,
хотя врядъ ли можно согласиться съ уважаемымъ проф. Перри,
который всякого защитника чисто алгебраическихъ «точныхъ»
способовъ р^зшешя задачъ обзываетъ «самоувт,рениымъ, какъ
пгЬтухъ, академическимъ ученымъ съ деревянной головой».
Хорошо именно то, что для даннаго случая нужно!—можно
на это сказать.
Къ числу преимуществъ графиковъ предъ иными способами
ръчиешя задачъ принадлежитъ еще наглядность,—возможность
действовать на умъ посредствомъ глаза. Это, въ частности, для
педагога—великая вещь!
Но перейдемъ къ нтзкоторымъ другимъ задачамъ, рЬшае-
мымъ съ помощью графиковъ. Задачи эти, вероятно, болъ-е
всего объяснять намъ тотъ секретъ pimeHifl задачъ на шах-
шахматной доски, о которомъ мы упоминали въ начали этой главы.
Задача 56-я.
Знаменитая задача Люка.
Вотъ задача, предложенная извъ-стнымъ (ныпъ- покойпымъ)
математикомъ Эдуардомъ Люка, о возншшоветпи которой та-
талантливый математикъ г. Лазаиъ разсказываетъ следующую псто-
piro, ручаясь за ея полную достоверность:

124
На одномъ паучпомъ конгресс^, въ кошгЬ завтрака, на
которомъ находилось много пзв^стиыхъ математиковъ, и между
ними было нисколько, знаменитостей разныхъ национальностей,
Эдуардъ Люка вдругъ объявплъ, что онъ хочетъ задать пмъ
одинъ изъ самыхъ трудныхъ вопросовъ:
«Я полагаю, что каждый день, въ полдень, отпра-
отправляется пароходъ изъ Гавра въ Ныо-1оркъ и въ то же
самое время пароходъ той же компанш отправляется
изъ Нью-Горка въ Гавръ. ПереЪздъ совершается ровно
въ 7 дней въ томъ и другомъ направлеши. Сколько
судовъ своей кампанш, идущихъ въ противоположномъ
направленш, встръ-титъ пароходъ, отправляющейся сего-
сегодня въ полдень изъ Гавра?»
Ptnieme.
Некоторые изъ п|жсутствовавшихъ знаменитостей,—говоритъ
по этому поводу Лэзанъ,—опрометчиво ответили «семь!» Боль-
Большинство же хранило молчаше. Ни одипъ не далъ вйрнаго
отвита, но если бы для рътиешя этой задачи призвать на по-
помощь графикъ, представленный на фиг. 84, то pinieme выри-
вырисовалось бы тотчасъ
со всей ясностью. Слу-
шавппе Люка, оче-
очевидно, думали только
о пароходахъ, кото-
которые должны еще от-
отправиться въ путь,
забывая о тйхъ, кото-
которые уже въ дорой.
Вйрно же то, что па-
пароходъ, графикъ котораго на фиг. 84-й изображенъ лишен АБ,
встръ-тятъ на Mopi 13 судовъ, да еще тотъ, который входитъ
въ Гавръ въ моментъ его отъезда, и еще тотъ который отпра-
отправляется изъ Нью-1орка въ ыоментъ его прибыря, или всего 15
судовъ. Графикъ доказываете, кромй того, что встречи будутъ
происходить ежедневно въ полдень и въ полночь.
Гаесъ
О 1 2 3 <• 5 6 7 ,8 9 10
Нью-lopm,
0 1 ? 3
Фиг. 84.

12Б
Если бы кто сомневался еще до сихъ поръ въ огромной
пользе графиковъ, то настоящая задача, думаемъ, должна раз-
сЬять подобиыя сомн'Ьн1я. Тоншй и сложный вопросъ получаетъ
въ данномъ случай быстрое, простое п наглядное решете.
Задача 57-я.
Курьеры.
Въ общераспространенныхъ задачникахъ въ ряду иныхъ
часто встречаются «задачи о курьерахъ», или путникахъ, пли
по^здахъ, идущихъ съ различной скоростью отъ язв4стнаго
пункта, вдогонку другъ за другомъ или же навстречу одинъ
другому. При этомъ спрашивается обыкновевно время нхъ
встречи и разстояше места встречи отъ точки отправления.
Задачи эти слишкомъ общеизвестны, чтобы о нихъ стоило
много здесь говорить. Въ школахъ они относятся обыкновенно
къ числу «трудныхъ». Укажемъ поэтому зд'Ьсь, что задачи п
этого рода могутъ решаться съ помощью графиковъ. Для этого,
взявъ разграфленную въ кл-Ьткп бумагу и построивъ две вза-
взаимно перпендикуляриыя оси, мы на оси ОХ откладываемъ
время, а на оси OY соответствующая разстояшя, и стропмъ
затймъ по прежнему графики для каждаго «курьера», «путни-
«путника», «поезда» и т. д... Точка пересЬчешя графиковъ съ совер-
совершенно достачиой точностью опред^литъ время и место встречи:
для этого нужно только изъ этой точки опустить перпендику-
перпендикуляры на оси ОХ м ОГ. Пересечете перпендикуляра съ первой
осью дастъ точку, по которой определяется время встречи, а
пересечете другого перпендикуляра съ осью 0Y дастъ точку,
которая позволить намъ определить разстояте места встречи
отъ точки отправлетя.
Взявъ изъ любого задачника подобную задачу п постропвъ
соответствующая графики, читатель легко убедится въ простоте
и пригодности этого метода для приложения къ подобнымъ за-
дачамъ. Здесъ же ыы предложимъ внимашю читателя следую-
следующую более сложную задачу о собаке и двухъ путешествешш-
кахъ, решить которую безъ помощи графиковъ не такъ-то
легко.

Задача 58-я.
Собака и два путешественника.
Два пешехода идутъ по одной и той же дорогЬ,
въ одномъ и томъ же направленна. Первый, А, нахо-
находится на 8 кил. впереди другого и д-Ьлаетъ 4 кил- въ
часъ; второй, В, дЬлаетъ по 6 кил. въ часъ. У одного
изъ путешественниковъ есть собака, которая, именно
въ тотъ моментъ, когда мы говоримъ, б-Ьжитъ къ дру-
другому путешественнику, со скоростью 15 кил. въ часъ,
потомъ сейчасъ же возвращается къ своему хозяину;
прибтжавъ къ нему, она снова б'Ьжитъ къ другому
путешественнику, и такъ до т4хъ поръ, перебегая
отъ одного къ другому, пока оба путешественника
встретятся. Нужно узнать, какой путь иробъжитъ
собака.
Р^шеше.
На оси ОХ отклады-
ваемъ время, а на оси О Y
разстояшя. Вопросъ можно
разсматривать двояко, смо-
смотря по тому, кому изъ пу-
путешественниковъ принад-
принадлежишь собака. На фиг. 85
считается время съ того
момента, когда собака вы-
выпущена.
Графики двухъ путеше-
путешественниковъ суть ОМ и
х 8Ж, н точка Ж, т. е. встреч-
встречный пункта, какъ видно
пзъ фиг. 85-ой, соотвЪт-
ствуетъ разстояшю въ 24
километра и 4 часамъ ходьбы. Если собака прпнадлежитъ пут-
нпку, который сзади, то графикъ ея пути есть Оаа...., ломан-
5 Г
Фнг. 85.

127
ная лишя между графиками хода двухъ птлпеходовъ. Если она
прпнадлежптъ путешественнику, идущему впереди, то графпкъ
ея пути есть Sbb...., такая же по происхожденго ломанная ли-
лишя, но отличная отъ первой. Въ обоихъ случаяхъ, ттдгъ не ме-
нъ-е, животное не перестаетъ бежать въ продолженье 4 часовъ
и, дъ-лая по 16 километровъ въ часъ, пробътаетъ 80 киломе-
тровъ. Очевидно, въ томъ и въ другоыъ случай результата одинъ
и тотъ же.
Можно предположить, что путешественники идутъ другъ
другу навстречу, п, вообще,—всячески видоизменять условия
задачи. Въ зависимости отъ этого изменятся нисколько и гра-
графики, но способъ ръ-шешя остается тотъ же.
На этомъ мы п закончимъ главу о графикахъ, предлагал
читателю разрабатывать дальше этотъ вопросъ самому. Вт, во-
просахъ пзъ области физики и механики найдется въ особен-
особенности много задачъ, ръчнаемыхъ графически. Рекомендуемъ также
внимашю читателя книгу Джона Перри: «Практическая мате-
математика» (есть въ русскомъ переводи). Въ этой книжки вопросъ
о графикахъ разобранъ съ надлежащей полнотой и ясностью.
Не совъ-туемъ лишь увлекаться тйми полемическими выпадами
противъ «теоретиковъ», которыми почтенный авторъ безъ вп-
димой нужды уснастилъ кое-гдт> свою въ общемъ полезную
книгу.
Возвращаясь къ тому, съ чего началась эта глава, т. е. къ
оставшемуся въ неизвестности «чудо-математику», решавшему
задачи съ помощью шахматной доски, мы должны признать,
что это возможно. Рйчь пдетъ, очевидно, о графикахъ. При на-
навыки, итькоторыя задачи съ помощью ихъ, какъ вндпмъ, можно
решать удпвптельно быстро. «НЪкоторыя»,—говорпмъ,—по не
вегь! Вотъ почему наыъ кажется, вопреки увт.решямъ почтен-
наго захолустнаго обывателя, что пе всякую задачу могъ «мо-
«моментально» решать 64aopyccitifl «чудо-математикъ».

Объ акиомахъ элементарной алгебры.
При изучеши элементарной алгебры къ ргЬшешю уравне-
иш приступаютъ обыкновенно съ такими аксюмами:
1.—Величины, равным порознь одной и той оке величиюъ
или равнымъ величинамъ: равны между собой.
2.—Если къ равнымъ величинамъ прибавить равныя же,
то и суммы получатся равныя.
3.—Если отъ равпыхъ величинъ отнять поровну, то и
остатки получатся равныя.
4.—Если равныя величины умножать на равныя, то и
произведетя получатся равныя.
5.—Если равпыя величины раздгьлитъ на равныя, то и
частныя получатся равныя.
6.—Цгьлое больше, чгъмъ каждая изъ ею частей.
7.— Одинаковыя степени или одинаковые корни отъ рав-
равныхъ величинъ равны.
Эти освященный временемъ «обпдя понятая» соотавляютъ
основу теоретической ариеяетики. На нихъ же обосновываютъ
точно также и алгебраичесшя разсуждешя.
Но въ высшей степени необходимо относительно этихъ
акс1омъ сделать соответствующая пояснешя и оговорки, когда мы
распространяемъ ихъ и па область алгебраическихъ количествъ.
Обобщеше свойственно математик^. Когда мы обобщаемъ, мы
отбрасываемъ всЬ ограничения, которыя были раньше устано-
установлены, пли подразумевались. Предположеше, в'Ьриоо съ прежде
бывшими ограиичешями, безъ нихъ можетъ быть върно и

129
неверно. Пояонимъ прпм^ромъ: при переходи отъ геометрш
двухъ измйренШ (планиметр1я) къ геометрш трехъ изм^ре-
шй (стереометр1я) приходится отбросить то ограничение, кото-
которое необходимо подразумевалось въ геометрш на плоскости,—
а именно, что вс4 разсматриваемыя фигуры лежать въ пло-
плоскости нашего чертежа, или доски, на которой фигуры изобра-
изображены (за исключешемъ, конечно, того случая, когда мы мы-
мысленно переворачиваемъ фигуры для иаложешя ихъ одну на
другую). Ьйкоторыя изъ теоремъ, вЪрпыя для геометрш на
плоскости, безъ всякихъ изм^нвшй переходятъ и въ стереомет-
piio, а друпя—н^тъ. Сравните въ этомъ отношеши, хотя бы,
две такихъ теоремы планиметрш: 1) черезъ точку, данную
енгъ взятой прямой, можно на эту прямую опустить только
одинъ перпендикуляръ п 2) изъ точки, взятой на данной пря-
прямой, можно къ этой прямой возставить только одинъ перпенди-
перпендикуляръ. Первая изъ этихъ теоремъ безо всякихъ оговорокъ
нриложима и къ геометр1и въ пространстве, а вторая - нъ"гъ.
Для второго, еще более яркаго, примера обратимся къ во-
вопросу (см. стр. 116): можетъ ли быть число |>азложено на более
«гЬмъ одну группу первоначальныхъ множителей?
Нгьтъ!—ответятъ вамъ,—если подъ множителями подразу-
подразумевать обыкновенныя ариеметичесшя числа.
Да!—съ неменьшимъ правомъ ответитъ другой,—если въ
понятае о числе включить и комплексныя (такъ называемыя
«мнимыя») количества.
Въ первомъ случае число 26, напримеръ, разлагается
на первоначальные множители только единственнымъ путемъ:
26 = 2 X 13; а во второмъ:
26 = 2Х13 = (б+ 1/:=Т) (б—/=Г).
Такихъ примеровъ, впрочемъ, моншо привести очень много,
и въ настоящей книге намъ приходилось и придется съ ними
встречаться не разъ.
Такимъ образолъ, мы можемъ всегда ожидать, что аксюмы
ариеметики могутъ нуждаться въ некоторыхъ видоизменешяхъ
или дополнен1яхъ, если попробовать ихъ распространить на
ВЪ ЦАРОТВЪ СМЕКАЛКИ.	9

130
область алгебраическихъ количествъ. И это мы находимъ на
самомъ д'Ьлй. Къ сожалоипю, мы не всегда замечаема., что бы
авторы учебниковъ обращали внимаше своихъ читателей на
подобныя видоизм^нешя иныхъ ажяомъ, или даже, чтобы они
сами применяли эти аксюмы съ надлежащей осторожностью.
Между т-Ьмъ мы прежде всего должны требовать отъ научной
аксюмы, чтобы она была совершенно верна и вполне соответ-
соответствовала смыслу, въ которомъ извгьстныя выражетя употре-
употребляются въ этой науюъ.
Пятая, напримйръ, изъ вышеприведенныхъ аксюмъ, или
«аксюма д-влетя», должна быть сопровождаема необходимой,
но т?мъ не менее редко встречающейся оговоркой: ...«разде-
...«разделить на равныя, исключая нуль-».
Безъ такого ограничешя высказываемое положеше далеко
отъ аксюмы.
Въ иномъ учебник^ гд4 приведена шестая изъ вышеука-
занныхъ «аксюмъ», читатель на следующей страница; можетъ
найти такое, наприм'Ьръ, выражен1е.
_]_2 —6 + 7 —1= + 3,
гр$ «+3 есть «цЬюе» или сумма». Видя, что одна изъ частей
этого «цЬрго» есть +7, иной читатель можетъ искренне по-
подивиться, какъ же это совмещается съ «аксюмой», что «ц-влое
больше каждой своей части».
Въ седьмой акс1ом4 одинаковыя степени и корни изъ рав-
ныхъ количествъ равны только щивметичсски. Иначе говоря,—
одинаковые действительные корни изъ равныхъ количествъ
равны при условш одинаковыхъ знаковъ.
Употребляя въ аксюмй слово «равный», не принимаемъ ли
мы его какъ бы въ смысле «тотъ самый»? Напримо^ръ, если
два числа те же самыя, что и третье число, то и первое есть
то же число, что и второе, и т. д...

131
О приложенш аксшмъ къ рйшенш уравнешй.
Иногда въ элементарныхъ руководствахъ, а тт>мъ болт>е въ
объяснешяхъ иныхъ репетиторовъ и даже преподавателей,
д-бло ставится такъ, что какъ будто при дт,йств1яхъ надъ урав-
нешями возможно прямое, непосредственное приложеше аксншъ.
Возьмемъ для примера постоянно встречающееся и въ учебни-
кахъ и въ учебной практики такое разсуждеше:
Дано уравнеше
Вычитая взъ каждой части по 4, получимъ
Зж = 15 	(аксюма 3).
Д'Ьля обт> части на 3, получаемъ
х = 5 	(аксюма 5).
И уравнеше считается р'Ьшеннымъ безо всякихъ оговорокъ
пепосредственнымъ приложешемъ акс1омъ. Но это доказываете
только, насколько распространены на этотъ счетъ совершенно
ошибочные или непродуманные взгляды.
Хотя въ выполненныхъ выше алгебраическихъ д^йств1яхъ
и н^тъ ошибки, но ссылка для пояснешя этихъ дМствш просто
на аксюмы можетъ толкнуть ученика на ложный путь. «Со
спокойнымъ сердцемъ», какъ говорится, нри такомъ способ^
разсужденШ онъ под-блетъ об^ части уравнешя на неизвестное,
если это возможно, и не замт.титъ. что при этомъ уже теряется
одно ртлпеше (корень) уравнешя. Точно также приложешемъ
той или иной «аксюмы» онъ можетъ ввести въ вопросъ совер-
совершенно постороннее ръчиеше.
Слйдуетъ разъ и навсегда освоиться съ мыслью, что прямое,
непосредственное примкнете аксюмъ къ р'Ьшешю уравненш
неприложимо,—и вотъ почему:
А.—Можно, следуя акс1оыамъ и не сд^лавъ ника-
никакой ошибки въ дМств1яхъ, получить, все же, неверный
результатъ.

132
В.- - Можно нарушать аксюмы, т. е. поступать во-
вопреки ихъ прямымъ указашямъ, и, все же, получить
верный результатъ.
С.—Аксюмы по самой внутренней сущности не мо-
гутъ прямо и непосредственно применяться къ уравне-
шямъ.
Разсмотримъ теперь каждое изъ высказанныхъ выше положе-
шй отдельно.
А.—Примпнете аксгомь и получете огщбки.
Пусть дано
х —1=2	 A)
Умножаемъ o6i части уравнешя на х— 5, получаемъ
х2 — 6х-\-5 = 2х—10 	 акс. 4.
Вычитаемъ изъ обйихъ частей уравнешя по х—7:
ж2—7ж+12=ж—3 	акс. 3.
Д'Ьлимъ об'Ь части yp-ia на х — 3:
х — 4=1	акс. 5.
Прибавляя къ об'Бныъ частямъ по 4, находимъ
ж=5	акс. 2.
Но найденное рйшеше не удовлетворяете данному уравне-
шю A). Единственный корень его, какъ легко убедиться, есть
х = 3. Итакъ, совершенно съ виду правильно разсуждая н не
сдЬиавь нн одной ошибки въ дМств!яхъ, мы пришли къ не-
в^рниму рт>шен!ю. Въ чемъ же дЬю?
НедоразумЬпя на этотъ счетъ (осибенни при выясненщ
такъ называемых!, «математическнхъ софизмовъ») настолько
обыкиовенны, что остановимся на вопрос^ подробнъ-е, рискуя
даже несколько наскучить читателю. ПрослФдпмъ пройденный
нами путь:
Умножеше на х — 5 ввело новое ртлиеше: ж =5, а депе-
депеше на х — 3 исключило корень ж=3. Аксншы, прпведенныя

133
въ предыдущей главе и надлежаще понятия, игключаютъ д4-
леше на нуль. Въ этомъ мы убеждаемся и на данпомъ при-
примере, такъ какъ делеше yp-ifl на ж — 3 есть въ сущности де-
делеше на нуль, ибо числи 3 удовлетворяете yp-iro (есть его ко-
корень). Говоря точнее, все ото показываетъ, что при дМств!яхъ
надъ уравнешемъ существо вопроса состоптъ въ томъ, чтобы
значеше входящаго въ него неизвълстнаго оставалось вернымъ
и неизменнымъ. Необходимость квалифицировать аксюмы при-
применительно къ этому требовашю выдвигаетъ важное начало
эквивалентности уравнешй, или равнозначности ихъ, говоря
по-русски. Необходимо, чтобы посл'Ь всякихъ преобразовашй
уравнешя всякое новое по виду получаемое уравнеше было
эквивалентно (или равнозначно) данному; т. е., чтобы можно
было съ уверенностью сказать, что вст> произведенныя надъ
уравнешемъ дейсттая не изменили значешя входящихъ въ него
неизвестныхъ, не ввели новыхъ ргЪшешй, или не лишили его
прежнихъ.
Не входя въ излшпнш зд^сь теоретическ!я подробности,
приведемъ, для ясности, по этому поводу нисколько простей-
шихъ примъ'ровъ.
Если къ обеимъ частямъ даннаго уравненш прибавить или
отъ обт>ихъ частей вычесть одно и то же выражеше (хотя бы
даже содержащее неизвестное), то это не изменитъ значен!^ х
въ уравненш (вновь полученное yp-ie, значитъ, будетъ экви-
эквивалентно, илн равнозначно, данному).
Точно также значеше х не изменится, если данное yp-ie умно-
умножить или разделить на какое либо известное число, кроме нуля.
Но если обе части уравнетя умножить или разделить на
количество, содержащее неизвестное, то вновь полученное yp-ie
будетъ, вообще говоря, we-эквивалентно данному.
Если бы после высказанныхъ здесь замйчшпи у читателя
остались еще кашя-либо сомнетя и возражешя, то мы про-
просили бы его внимательно заняться началомъ эквивалентности
по лучпшмъ учебпикамъ п руководствам^ съ идной стороны, и
действ1ямп надъ уравнен!ями съ другой. Тогда онъ быстро
убедится, что къ вопросу объ уравнешяхъ нельзя подходить
прямо съ однЬмп аксюмами.

134
Необходимо оговориться также, что все предыдущее ни-
нисколько не посягаетъ на правильность и незыблемость аксюмъ,—
оно возражаешь только протпвъ ихъ примйнешя таыъ, где он-Ь
прямо неприменимы.
Иной можетъ возразить, что мы искусственно нагромоздили
прямое примкнете аксюмъ къ решент уравнешя A) въ слу-
случае А, и что никто не сталъ бы решать такъ это простое
уравиеше. Въ этомъ ур-ш (I) piinenie, действительно, само
бросается въ глаза, и каждый, пожалуй, окажетъ его, просто
взгляпувъ на yp-ie. Но станетъ ли кто возражать, что въ гро-
мадномъ большинства случаевъ сложныя ур-1я учениками ре-
решаются именно такг, какъ мы ото привели выше съ урчешъ
A). Простой же и наглядный примеръ выбранъ здесь для того,
чтобы убедительнее привести къ нелепости (reductio ad ab-
surdum) ложь основного положешя.
В. — Парушете аксюмъ и вгьрный результатг.
Чтобы избежать возражетя, что нарушешемъ одновременно
двухъ или бол^е аксюмъ мы какъ-либо уравниваем ъ допущен-
допущенную ошибку, возьмемъ примеръ, где поступимъ вопреки пря-
мымъ указашямъ только одной аксшмы.
ж—1 = 2	A)
Прибавимъ 10 только къ первой части этого yp-ifl. Ta-
кимъ образомъ, мы самымъ грубымъ образомъ нарушаемъ
предписаше «аксгомы сложешя» и получаемъ
ж + 9 = 2	B)
Помножаемъ обе части yp-ifl на х — 3:
ж2 + 6ж —27 = 2ж—6 ... C) акс 4.
Вычитаемъ изъ обеихъ частей yp-ifl по 2ж — 6:
ж2 + 4ж — 21 — 0	D) акс. 3.
Делимъ обе части на ж ^\-7:
х — 3 = 0	E) акс. б.

135
Прибавляя къ об'Ьимъ частямъ по 3, вм-Ьемъ
акс. 2.
Полученное решеше 3 есть втрный корень даннаго ур4я
A), несмотря на то, что нами допущено единственное грубое
противор4ч1е противъ аксшмы 2-й, которое не могло быть
уравновешено неправильнымъ приложешенъ какой-либо другой
аксюмы, ибо въ остальномъ мы прямо и точно прилагали «ак-
«аксюмы». Изъ предыдущаго (А) уже ясно, что невт>рньшъ нони-
машемъ приложешя аксюмъ мы получили загЬмъ здесь ур-1я
C) и (б) неэквивалентныя данному, а потому и получили та-
такой «неожиданный» результат!..
С. — Аксюмы по самой своей сущности не имгьютъ прямого
отношенгя къ уравненгямъ.
Аксюма говорить: если къ равнымъ величинамъ прибавить
равныя и т. д., то и результаты будутъ равны. Вопросъ же,
преследуемый разрешешемъ уравнешя, состоитъ въ томъ: для
какого значенгя х обп части ур-гя будутъ равны. Такимъ об-
разомъ, если къ одной части уравнешя придать никоторую ве-
величину, не придавая ея къ другой; то, все же, для нгькото-
раго значены х, хотя бы и новаго, въ результат^ получится
равенство.
Ариеметика, им^я д-вло съ обыкновенными числами, стре-
стремится только узнать, что известное получаемое въ результат^
число равно известному другому. Но алгебра, имъ\я дйло съ
уравнешями (условными равенствами) желаетъ знать, при ка-
кихъ условъяхъ данныя выражешя представляютъ одни и те
же числа,—другими словами, для какихъ значешй неизвестнаго
данное уравнеше верно.
Въ отделе В настоящей главы возражете противъ уравне-
уравнешя B) состоитъ не въ томъ, что первая часть его не равна
второй (оне «равны» настолько же, насколько и обе части пер-
ваго даннаго ур-1я), но въ томъ, что обе его части не равны
для того оке значенгя х, какъ и въ ур-ш A). Словомъ, yp-ie
A) неэквивалентно B).

136
Вообще, пзучеше и пыводъ принципа эквивалентности мо-
жетъ многое дать въ смысли математическаго развитая каждому
желающему поработать въ области математики. Прежде всего
какъ впдиыъ, это натолкнетъ его на надлежащее приложеше ак-
сюмъ. Въ примйненш къ уравнешямъ, напр., аксюмы пграютъ
роль только при выводахъ п доказательствахъ начала эквива-
эквивалентности. Прямое же приложеше ихъ къ ръчнешю уравнешй
есть заблуждеше, котораго слтдуетъ всячески избегать.
Проверка р-Ьшешя уравнетя.
Весьма часто учапдеся «доказывают^» правильность ръчпешя
какого-либо уравнешя такпмъ путемъ. Найденную величину для
неизвъстнаго подетавляютъ въ обт, части даннаго уравпен1я, за-
ймъ надъ обеими частями полученнаго выражен!я продтлываютъ
указанныя знаками дййстгая и, получпвъ числовое тождество,
смт,ло говорятъ: «что и требовалось доказать», хотя... непри-
непригодность подобнаго «доказательства» можно въ свою очередь
доказать на прим'Ьрахъ, гд^ получаемая нелепость прямо бьетъ
въ глаза.
Возьмемъ такой прим-Ьръ:
1+УжТ2 = 1— 1/12 — х	A)
И, ртшгая его такъ, какъ обыкновенно это делается, по-
лучаемъ:
= — 1/12— ж;	B)
12 —ж;	C)
2ж=10;
х=Ь.
Найденное значеше для х лодставимъ въ данное уравне-
A) и «докажемъ» правильность р-Ьшешя:
Т2 = 1 —1/12 -5;
: = —1/12 — 5;
2=12 — 5;
;
7 = 7.

137
Казалось бы, все обстоптъ благополучно, хотя на самомъ
не трудно видеть, чти если мы въ уравнеше A) подста-
вимъ вместо х число 5 и прпведемъ обе части къ простейшему
виду, то получается для первой части 1 -f- ]/7, а для второй:
1 — j/ 7, — числа явно неравныя другъ другу, а потому, сле-
следовательно, б не есть корень даннаго уравнешя, чтобы нп утвер-
утверждала приведенная нами выше «проверка».
Корень 5 былъ незаметно введенъ въ уравнеше, когда обе
его части возвышались въ квадратъ. Другими словами,—корень 5
удовлетворяешь уравненго C), но никакъ не A) и не B). Но
если бы въ какомъ либо изъ уравненШ A), или B) изменить
знакъ, то получилось бы уравнеше, удовлетворяющееся р'Ьшешемъ
х = 5; а именно:
Итакъ, необходимо всегда помнить, что если ращональное
уравнеше получается изъ прращональнаго путемъ возвышешя въ
степень, то существуетъ всегда другое иррацюнальное уравнеше,
отличающееся отъ даннаго только знакомъ какого-либо члена
или членовъ, и изъ котораго также можно получить то же са-
самое ращональное уравнеше.
Софистическая каррикатура.
Разобранный нами выше неправильный методъ «доказа-
«доказательства» верности решешя уравнешя можно свести къ довольно
известному, хотя и грубому логическому софизму, стремяще-
стремящемуся «доказать», что всякое математическое действ1е можно
свести на что угодно.
Доказать, что 5 = 1.
Вычитая изъ каждой части по 3, находимъ: 2 = -—2.
Возвышая въ квадратъ обе части: 4 = 4.
Итакъ 5 = 1!..

138
Неправильные отвЪты.
Въ учебникахъ и задачникахъ по алгебр^ нередко можно
встретить уравнеше такого вида:
и въ «отвт>тахъ», щт, приведены piineiiifl задачъ, кратко со-
сообщается, что корни этого уравнешя суть «4, или—1». Это не-
неверно. Рйшеше даннаго уравнен1я есть 4, а — 1 не есть pi-
шеше. Къ несчастью, подобнаго рода задачи безъ надлежащихъ
разъясненШ встречаются чаще, чймъ сл-Ьдуетъ.

Алгебраические софизмы.
Какой-то острякъ ув'Ьрялъ, что во всей литературт, суще-
ствуетъ на самомъ д4лгЬ только небольшое число осиовныхъ
острить или анекдотовъ, но со многими видовзмтлешями. Онъ
пытался даже дать классификацию остроумныхъ изречешй, сводя
ихъ къ небольшой таблиц-Ь типичныхъ прим'Ьровъ. Другой остро-
умецъ уменьшалъ и это число типовъ, сведя ихъ, если не оши-
ошибаемся, всего къ тремъ. Въ свою очередь нашелся еще и трети,
который сд'Блалъ посл^дшй шагъ и заявилъ, что ничего подоб-
яаго нъ-тъ, что остротъ, или шутокъ, вообще говоря, не суще-
ствуетъ. Усп-Ьдъ ли этотъ послъ'дшй действительно исключить
понят1е объ остроумш, какъ такивимъ, или же къ огромному
запасу старыхъ остротъ онъ прибавилъ еще одну,—это, конечно,
зависитъ отъ взгляда на предметъ.
Въ настоящей главт, мы, все же, сд'Ьлаемъ попытку если
не классифицировать, то до некоторой степени осветить хотя
бы некоторые изъ наиболее роспространенныхъ алгебраическихъ,
такъ называемыхъ, «софизмовъ» или парадоксовъ. При этомъ
мы им'Ьемъ въ виду не хитроумное запутываше вопросовъ, но
скорее наоборо'гъ,—разборъ изв^стныхъ типовъ этого рода за-
дачъ подъ рискомъ даже въ значительной степени лишить ихъ
присущей имъ «таинственности»... Софизмы подобны привидъ1-
шямъ,—они не выносятъ свита. Анализъ гибеленъ для извгЬст-
наго рода вопросовъ.

140
О т-Ьхъ классахъ, илп подклассахъ, общихъ логическихъ
ошибокъ, которые приводить въ своей «Логике» Аристотель и
которыя зависятъ отъ неправильныхъ построешй силлогизмовъ,—
въ случаяхъ .математическихъ софизмовъ приходится говорить
мало. Наиболее часто въ софизмахъ, разшатрпваемыхъ нами,
изъ этихъ ошибокъ встречается та, которая зависитъ отъ не-
правильнаго построешя или употреблешя такъ называемой ма-
малой посылки. Въ математике подобное логическое противорт,ч1е
прикрывается незам'Ьтнымъ для новичка допущешемъ н-Ькото-
раго обратнаго, съ виду очевиднаго, предложешя, или же при-
мЬнешемъ процесса математическихъ дМств1й, который кажется
неоспоримымъ, каково бы ни было его приложеше по существу.
Возьмемъ хотя бы такой примерь:
Пусть с будетъ среднее ариеметическое между двумя не-
равными числами ало, т. е. с = —-—, и, следовательно:
2с	A)
Отсюда
(а+ 6) (а — Ь) = 2с(а—Ъ);
Перенеся члены, имЬемъ:
а2 — 2ас=--Ъ2 — 2Ъс.
Придавая къ об-Ьимъ частямъ равенства по с2;
а2 — 2ас-\-с2 = Ъ2 — 26с + с2	B)
Отсюда
(а —с)8 = F — сJ;
или
п — с~Ъ — с	C)
Следовательно,
а = Ъ.
А между т'Ьмъ было дано, что а и Ъ неравны' Въ чемъ же
дтло?
Конечно, обе части равенства C) ариеметически равны, по
знаки-то этихъ чиселъ противоположны; такъ что равны только
ихъ квадраты B). Допускаемая здесь ошибка настолько оче-

141
видна, что, казалось бы, не стоило объ ней и говорить, если
бы въ томъ или дномъ вид^ на ней не строились весьма мно-
rie такъ называемые математичеаае «софизмы».
Указывая въ предыдущей главй на ошибочные npienbi про-
проверки правильности решетя уравнений, мы привели тамъ дру-
другой прим^ръ получаемаго, якобы математически, абсурда. По-'
ставимъ теперь вопросъ на обще-логическую почву, и мы тот-
часъ найдемъ источникъ веЬхъ нашихъ ложиыхъ выводовъ.
Въ сущности, мы строимъ неправильные силлогизмы, подобные
нижесл'Ьдующииъ, которые нарочно приводимъ параллельно въ
рядомъ стоящихъ колоннахъ:
тт	Два равныхъ числа им^готъ
Птица — животное.
равные квадраты.
Эти два числа имъчотъ рав-
Лошадь - животное.	нЫе квадраты.
Сл^д.: Лошадь есть птица.	Сл'Ьд.: Эти два числа равны.
По поводу каждаго изъ этихъ неправильныхъ логическихъ
построенШ ст. полнымъ правомъ можно привести и два такихъ
параллельныхъ зам'Ьчашя:
Даже малоразвитой челов'Ькъ	Каждый«первокурсникъ»выс-
будетъ издаваться надъ такимъ	шей школы посмеется всягай
заключешемъ, ибо оно нелЬпо;	разъ, какъ получается нелепое
но тотъ же челов'Ькъ не за-	заключеше; и онъ же съ лег-
мЬтптъ иногда подобной же	кимъ сердцемъ готовъ прими-
ошибки въ устахъ, наприм^ръ,	риться съ ошибочными методами
политическаго оратора, — осо-	njjoBipKH pimemfi, указанными
бенно своей парии.	въ предыдущей главъ\
Въ случаяхъ, когда приходится им'Ьть д^ло съ квадратными
корнями, подмЬтить ошибку иногда не такъ-то легко. По об-
общему соглашение о знакахъ, если н^тъ особой оговорки,—
передъ у подразумевается знакъ +. Сообразно съ этиыъ для
положительныхъ четныхъ или д'Ьйствительныхъ нечетныхъ

142
корней вйрно, что «одинаковые корни изъ равныхъ количествъ
равны»; п отсюда
Но если а и Ъ отрицательны, а п—четно, то этого тождества
уже не существуетъ, и, принимая его, ыы приходимъ къ абсурду:
1) = 1/^11/- 1;
VI- (V- If;
Или же, принимая, что 1 / - = -^ для всякихъ значенш
буквъ, мы, казалось бы, можемъ написать следующее тождество
(ибо каждая часть его = ]/— 1):
— 1 .
Отсюда
1/1 _V-1
V- i *^i
Освобождая отъ дробей:
или
Эти «обманы по несчастью», гд^, отправляясь отъ общаго
правила, ириходятъ къ такому шещальному случаю, когда н^ко-
торыя особыя обстоятельства д^лаготъ это правило неприложи-
мымъ, а также софизмы, получаемые обратньшъ путемъ, извест-
известный математикъ Морганъ предлагалъ разделить на три разряда,
относя ихъ всЬ въ область «псевдо-алгебры». По общему правилу,
напрпм'Ьръ, равныя величины, раздйленныя на равныя, даютъ
и равныя частныя. Но это правило теряетъ свою силу, если
равные делители являются въ вид^ нуля. Приложеше общаго

143
правила къ этому специальному случаю даетъ весьма большое
число весьма распространенныхъ математическихъ софшмовъ.
Такъ, имйемъ тождество:
х2— ж2=ж2— х2.
Первую часть его представимъ какъ произведете суммы на
разность, а во второй вынесемъ общаго множителя; получимъ
(х-\-х)(х — х) = х(х— х)	A)
Сокращая на х — х, получимъ:
х-\-х = х	B)
или
2х = х,
т. е.
2=1	C)
Абсурдъ получился потому, что, д'Ьдя на 0 тождество A),
мы обратили его въ yp-ie B), которое удовлетворяется только
корнемъ х = 0. Д-Ьля же B) на ж, мы и получаемъ нелпмостъ C).
«
Вотъ еще прим4ръ:
Пусть
х=1.
Тогда
Х2 = Х.
И
ж2 —1 = а—1.
Д4ля на х— 1:
а+1 = 1.
Но такт, какъ по положешю ж=1,
то, подставляя, получаемъ 2 = 1.
Употреблен1е расходящихся Сезконечиыхъ рядовъ даетъ
друйе многочисленные образцы математическихъ софизмовъ,
секретъ которыхъ состоитъ въ томъ, что молчаливо принимается
за верное для всЬхъ рядовъ н^то такое, что на самомъ

144
в^рно только для сходящагося ряда. Такъ называемый «гармо-
«гармонически рядъ» употребляется съ этой ц'Ьлью особенно часто.
1+Ы+1+Ъ+ ¦ ¦ ¦
Разобьемъ этотъ рядъ на группы членовъ такъ:
+ ("о + • • . всего 8 член.) -f- (тц ~\~ ¦ • • всего 16 член.)-)-...
Каждая заключенная въ скобки группа членовъ больше -~.
Следовательно, сумма п первыхъ членовъ ряда возрастаетъ
безгранично при безграничномъ возрастанш п. Итакъ, сумма
членовъ ряда безконечна. Рядъ есть расходящШся. Но если въ
этомъ ряду знаки -\- а —¦ попеременно чередуются, то, какъ
известно, рядъ
2^3 4^5 6^' ' ' *
есть сходяпцйся и сумма его равна log 2. Запомнивъ это, не
трудно будетъ разобраться въ такомъ «софизм^», гд4 отпра-
отправляются отъ этого ряда, выражающаго log 2.
Но logl также — 0, значитъ k»g2 = logl = 0.

146
Вместо двухъ посл'Ьднихъ скобокъ мы могли бы написать
знаки безконечности оо и вычесть: оо — оо = 0.
Безконечность и 0 для творца математическихъ софизмовъ,
видь, тоже «количества»!..
Молчаливо допуская, что всякое действительное число им^етъ
логариемъ, и что онъ подчиняется тЪмъ же законамъ, что и
логариемы ариеметическихъ чиселъ, можно создать новый типъ
софизмовъ:
(-1K=1.
Такъ какъ логариемы равныхъ величинъ равны, то:
21og(— l)r=logl = 0.
Итакъ log(— 1) = 0.
А также log(—l) = logl.
Значить— 1 = 1!..
Идея о софизлгахъ этого послйдняго типа была посЬяна
знаменитымъ Иваномъ Бернулли.
Дадимъ еще и такой образепъ софизма:
Если взять дробь —, то она, какъ известно, возрастаетъ съ
уменьшен1енъ знаменателя.
Поэтому, такъ какъ рядъ 5, 3. 1, — 1,-—3, — 5 есть рядъ
убывакищй, то рядъ вида
111	1 1
х = ь> з»1»-1,-з,-бит-Д-
есть возрастающ1й рядъ. Но въ возрастающемъ ряду каждый
посл'ЬдующШ членъ больше предыцущаго,—значитъ:
3>g, 1>д, —1>1, и т. д...
Вотъ noncTHHi нежиданный результатъ! Выходитъ, что мы
«доказали» будто
ВЪ"^АРОТВЬ СМЕКАЛКИ.	10

146
Закончимъ настоящую главу общимъ зам'Ьчашенъ, что здравое
и правильное разсуждеше, все же, не въ силахъ совершенно
• убить ни чисто формальныхъ, логическихъ, ни математическихъ
софизмовъ. Таково ужъ свойство челов'Ьческаго ума. Но что же
изъ этого? Если существуетъ, наприм^ръ, поддельная монета,
то это в^дь не значить, что подлинная не им^етъ никакой
ценности. Изучеше подделки, наоборотъ. можетъ научить насъ въ
будущемъ различать всякую фальшь, какъ бы тонко и хитро
намъ ее ни преподносили. Разборъ всякаго рода фальши и логи-
логическихъ подтасовокъ можетъ въ такомъ случай быть предметомъ
не только пр1ятныхъ, но и полезныхъ развлечешй.
Задача 59-я.
Опровергнуть софизмъ:
Возьмемъ тождество
которое можно представить въ
Извлекая изъ об^ихъ частей квадратный корень, им^ежъ
5
Прибавляя къ об'Ьимъ частямъ по ^, им^емъ:
2 = 3.
Задача 60-я.
Опровергнутъ софизмъ:
Очевидно, что
'-)а>(-У
9 / \ 9 /
Логариемируя об"Б части, получаемъ

147
Д'Ьля o6i части на одно и то же количество lg^, получаемъ:
2>3.
Задача 61-я.
Д'Ьлежъ верблюдовъ.
Старикъ арабъ, имЪвшш трехъ сыновей, распоря-
распорядился, чтобы они посл'Б его смерти поделили принадле-
принадлежащее ему стадо верблюдовъ такъ, чтобы старийй взялъ
половину всбхъ верблюдовъ, среднш—треть и младшш—
девятую часть всЬхъ верблюдовъ. Старикъ умеръ и оста-
вилъ 17 верблюдовъ. Сыновья начали дъ\лежъ, но ока-
оказалось, что число 17 не д-Ьлится ни на 2, ни на з, ни
на 9- Въ недоум^ши, какъ быть, братья обратились къ
шейху (старшина племени). Тотъ прйхалъ къ нимъ на
собственномъ верблюд^ иразд'Ьлилъ позавътцашю. Какъ
онъ это сд-Ьлалъ?
Шейхъ пустился на уловку. Онъ прибавилъ къ стаду на
время своего верблюда, тогда стало 18 верблюдовъ. РаздФливъ
это число, какъ сказано въ завъчцаши, птейхъ взялъ своего вер-
верблюда обратно; и получилось:
у старшего брата у	 9 верблюд.,
у средняго брата у • • . . 6 »
у младшаго брата -г-	 2 »
Всего... 17 верблюд.
Залмчате. Задача представляетъ родъ математическаго со-
софизма. СлЬдуетъ заметить, что сумма ~2"~~~Ь~з~~Н~9~ —"is"' T" е#
не равна единиц^. Но отношен1е ц'Ьлыхъ чиселъ 9, 6 и 2 равно
отяошент дробей -g-, -g- и -g-.

'" Положительный и отрицательныя числа.
Говорить объ ариеметическомъ чжугб, какъ о положитель-
номъ,— до сихъ поръ еще составляешь такое распространенное
и общее заблуждеше, что всегда полезно вносить на этотъ ечетъ
соответствующая поправки. Числа, съ которыми мы оперируемъ
въ ариеметикъ1, нельзя назвать ни положительными, ни отрица-
отрицательными. Это числа, если ложно такъ выразиться, не имтощш
знака. Отрицательныя числа появились не позднее положитель-
ныхъ, какъ иные ошибочно говорятъ, смешивая двъ* разныхъ
вещи; и й и друия числа въ одно и то же время одинаково
лежатъ въ понятш какъ отдельной личности, такъ и народа
вообще. На какомъ основашп мы моженъ утверждать, говоря
о двухъ прямо противоположным вещахъ, что идея объ одной
сделалась принадлежностью человтлескаго ума раньше, чгЬмъ
идея о другой; или же говорить, что первое яснйе, чъчиъ вто-
второе? Выражения «положительный» и «отрицательный» соотно-
соотносительны (коррелятивны), и ни одного изъ нихъ нельзя упо-
употребить, не вспомнивъ о другомъ.
Хорошимъ упражнешемъ для развиия яснаго пониман1я т^хъ
соотношен1й. которыя существуютъ между положительными, отри-
отрицательными и ариеметическпыи числами, служитъ разслотр^те
cooTBfecTBifl между положительнымъ и отрицательнымъ р-Ьше-
н1емъ уравнешя и ариеметическимъ р^шен1емъ задачи, давшей
начало уравненш, въ связи съ вопросомъ, благодаря какимъ
начальнымъ предположешямъ получится это

149
Для нагляднаго выяснешя соотиогдешй, существующихъ
между положительнымъ, отрицательнымъ и ариометиче,скимъ
числомъ, быть можетъ, нътъ лучше прибора, чъ-мъ вйсы. Этотъ
приборъ прежде всего наилучше выясняетъ ту прямую проти-
противоположность, которая существуетъ между положительЕымъ и
отрицательньшъ числомъ. Такъ, тяжесть, находящаяся, скажемъ,
на положительной чашки в'Ьсовъ, уравнов^шивае™ то напря-
напряжете притяжешя, которое оказываетъ равная по массЬ тяжесть,
положенная на другую чашку в'Ьсовъ. Двъ1 тяжести на противо-
положныхъ чашкахъ в^совъ имъчотъ равныя массы, равно какъ
и два числа, выражаюпця эти тяжести, им^ють одинаковое
ариометическое значеше.
Несчастливое выражеше «меньше, ч'Ьмъ ничто» (пущенное
въ оборотъ Штифелемъ), попытка разематривать отрицательныя
числа отдельно отъ положительныхъ, «изучеше» отрицательныхъ
чиселъ позднее положительныхъ, а также назваше «фиктив-
ныхъ», придаваемое прежде отрицательньшъ числамъ,—все это
кажется теперь довольно страннымъ. Но только теперь, поели
того, какъ ясно усвоено истинное значеше положительныхъ и
отрицательныхъ чиселъ, какъ величинъ прямо противоположныхъ
по значеню. Ташя пояснешя, какъ числа дебета и кредита въ
бухгалтерш, или же показашя термометра выше и ниже нуля,
также могутъ до некоторой степени способствовать полнотъ*
пониман1я о противоположности положительныхъ и отрицатель-
отрицательныхъ чиселъ.
Объ иллюстрацш положительныхъ и отрицательныхъ чиселъ
съ помощью прямой лиши см. главу «Наглядное представлеше
комплексныхъ чиселъ».
Зд^сь, пожалуй, кстати будетъ привести и небольшую исто-
историческую справку изъ Кайорп (History of Elementary Mathe-
Mathematics) объ отрицательныхъ чпелахъ: «Отрицательныя числа
казались «абсурдомъ» или «фикщей» такъ долго, что математики
не наталкивалпсь даже на ихъ наглядное или графическое пред-
ставлеше... Впрочемъ, если изгнать всякое наглядное представле-
nie посредствомъ линШ, или термометра, то отрицательныя числа
и HbrniniHeMy учащемуся могли бы показаться такимъ же аб-
абсурдомъ, какимъ они казались прежнимъ алгебраистамъ».

160
Задача 62-я.
Два общихъ наибольшихъ д%лителя.
Допустимъ, что дано два количества
х*—а3 и а2—л:2;
и затЬмъ на вопросъ объ ихъ О. IT. Д. (общемъ наи-
болынсмъ д'кштел'Ь)одинъ отв-втилъ, что О. Н. Д. этнхъ
количествъ есть х— а, а другой, что такой чЬлитель
есть а—х. Спрашивается: кто правъ?
PiiueHie.
Оба ответа правильны. Сл^дуотъ только, чтобы отвЪчающШ
правильно понялъ п обсудилъ вопросъ, такъ какъ въ налич-
наличности Овухъ О. Н. Д. нЬтъ ничего страннаго. Если бы коли-
количества были предложены въ формъ1 х3— а3 и х2— а2, то отвъ1-
чающШ, естественно, сказалъ бы, что U. Н. Д. ихъ есть х—а,
и, пожалуй, ипой настаивалъ бы, что существуетъ только онъ
одинъ. Но не трудно видеть, что а —х есть тоже общ1й дЪли-
тель и такого же порядка, какъ и х—а.
Быть можетъ,—зам'Ьтпмъ здЪсь кстати,—следовало бы при
изучеши элементарной алгебры обращать почаще внпмаше па
то, что всяшй рядъ алгебрапческихъ выражешй можетъ им^ть
два общихъ наиболъшихъ дтьлимеля, равныхъ по величин'!;, но
противоположныхъ по знаку.
Такъ какъ слово «наиболытй» обозначаетъ превосходную
степень, то математику въ данномъ случа'Ь приходится изви-
извиняться предъ филологомъ за nperpimeHie противъ синтаксиса
языка.
Въ самомъ дъчгб, какой солецизмъ!.. Два наибольшихъ...
Лримтьчате. 13се сказанное объ О. Н. Д. можно, очевидпо,
съ такимъ же основашемъ отнести и къ общему наименьшему
кратному. Такъ что съ алгебраической точки зрЪшя совершенно
естественно говорить о двухъ О. Н. Е.

Наглядное изображете комплексныхъ чиселъ.
и
Возьмемъ отр^зокъ прямой OR длиной въ одну единицу,
направленный вправо отъ О (фиг. 86) и прпмемъ.его за -f-'l;
тогда — 1 изображается отр-Ьзкомъ OL той же прямой, равнымъ
OR, по направленнымъ вл-Ьво отъ О. Вообще говоря, -f-o изо-
изобразится лишен въ а едшшцъ длины и направленной вправо
Отъ С, и — а лишей же въ о единпцъ длпны, но направлен-
направленной влт>во отъ О. Таково простейшее а наиболее известное
приложете пряной лпши, которое
даетъ намъ геометрическое изобра-
изображеше такъ называемыхъ дгьйстви-
тельныхъ (положптелъпнхъ и отри-
цательныхъ) чиселъ. Подобное при-
ложеше прямой для геометрпче-
скаго пзоб1)аже1пя чпселъ разпаго
знака было, какъ оказывается, пз-
вЪстно еще древнпмъ индусамъ,
но намъ неизвестны случаи иодоб-
наго примЪиен!я въ Европ^ до
1629, когда въ сочпнеши «Invention Nouvelle en l'Algebre>
далъ его Альбертъ Жпраръ.
Представимъ теперь себт., что направленная въ положитель-
положительную сторону въ единицу длины лпшя OR вращается около О,
какъ центра, въ направлены, прпнятомъ за положительное
(противоложыо движен1Ю часовой стрелки) и изъ положен1Я
OR (+1) приходптъ въ положеше OL (— 1), оппсавъ при этом г
два прямыхъ угла. Такиыъ образомъ круговому вращенш поло-
D
Фиг. 86.

1Б2
жнтслмюп единицы 1,.ишы OR на два прямыхъ угла, когда
она пршгпмаетъ прямо противоположное направлеше OL, соответ-
соответствует*. ii3iii[ieirie при единиц!1 знака: отъ -f" 1 ыы нерехочпмъ
къ — 1. Но тотъ же результата получится, если ыы положи-
положительную единицу уыножиыъ дважды на множитель -\- у — 1
(какъ язв'Ьстпо, ]/— 1 • ]/— 1 = — 1). Итакъ, круговому пере-
м'Ьщенш прямой на каждый прямой уголъ соотвътствуетъ въ
данномъ случат, множитель У— 1. Следовательно, когда лишя
OR приметь наиравлеше OU (вверхъ и перпендикулярно къ
OR), то она изобразится числомъ -\- ]/— 1. Подобнымъ же
образомъ, продолжая вращете прямой въ томъ же направленш,
мы впдпмъ, что изъ положегпя OL (— 1), она черезъ положе-
Hie 01) приходить опять въ положеше OR (+1), описавъ еще
два прямыхъ угла. Аналитически то же получится, еслп мы
—	1 дважды умножпыъ на — V— 1; такъ что множитель
—	у— 1 соотвъ'тствуетъ вращен1ю OL на прямой уголъ къ
положенно 01), и эту последнюю лпшю (перпендикуляръ кь
OL, направленный впизъ), мы и должны обозначить чпслолъ
Итакъ, если раастояшя, отсчитываемыя вправо, мы будемъ
брать съ знакомь -(-, то разстоян1я вл^во должны быть со зна-
знакомь —, количество же Ъ ]/— 1 обозначить лпнш вь Ъ еди-
нпцъ длпны, направленную вверхъ, а количество —Ъ \/—1
означаетъ лпн1ю въ Ъ едннпць длины и направленную внизъ.
Количества, въ которыя входить множптатемъ |/— 1, но-
сять назван1е мнимыхъ, а только что указанное геометрическое
изображеше мншшхъ величинъ было впервые предложено Кю-
номь въ Актахъ С.-Петербургской Акадеыш Наукь за 1750 г.
Для графическаго пзображен!я комплекснаго числа, т. е.
числа вида а+ 6]/—1, отъ точки О (фиг. 87) откладываемь
въ положптельномъ направленш линю О А, равную а единицамъ
длины; пзъ А возставляеыъ перпендпкуляръ АВ, равный Ъ
единицамъ длины и въ направленш, указываемоыъ множителемъ

163
V—1; наконецъ, проводит, прямую ОВ. Эта последняя лпшя
по велпчшгЬ и направленш и есть геометрическое изобразите
комплекснаго количества а-\-Ь}/^Л. Длина ОД равная Уи2-{-Ь2,
носить назваше модуля взятаго нами комплекснаго числа.
о
Фиг. 87.
Только что указанная геометрическая пнторпретащя ком-
плексныхъ количествъ была впервые предложена Жаномъ Ро-
бертомъ Арганомъ (Argand) пзъ Женевы въ 1806 году. Ояъ
же первый въ 1814 г. употребплъ и терминъ «модуль> въ ука-
занпомъ выше смысл^.
Работы Кюна, Аргана п въ особенности датскаго ученаго
Весселя (въ 1797 г. Академ1я Наукъ въ Копенгаген!.), распро-
•странившаго представлен!е комплексныхъ количествъ на гео-
Meipiro въ пространств1!!, представляютъ т-к подготовптельныя
ступени, основываясь на которыхъ въ настоящее время выросъ
новый важный методъ: «тгор1я всжторовъ > (вектор1альный ана-
лизъ). Во всей полнотт. п гаирот^ вопросъ этотъ впервые охва-
ченъ и обработанъ проф. Вильямоыъ Гамильтономъ въ 1852 и
1866 годахъ подъ именемъ «Еватериюновъ».
Вместо символа "j/— 1 обыкновенно употребляется буква' г.
Обозначен1е это впервые было предложено Эйлеромъ. Популя-
ризацш же среди математиковъ какъ этого символа, такъ и

164
работъ Кюна и Аргана слФдуетъ приписать «первому изъ ма-
тематиковъ» К. Ф. Гауссу.
Столь противоположный по смыслу назвашя, какъ «действи-
«действительный и «мнимый» были впервые употреблены Декартомъ при
изсл^доваши корней уравнешй. Съ т4хъ поръ это слово мнимый
такъ и осталось въ математическомъ язык'Ь, несмотря на все
его несоотв4тств1е, какъ видимъ, съ д-Ьйствительнымъ характе-
ромъ количествъ вида а |/— 1 и несмотря на попытки вве-
ввести другое болФе соответствующее наименоваше. ЗдФсь, быть
можетъ, кстати будетъ указать на тотъ огромный авторитета,
которымъ пользовался Декартъ въ математическомъ Mipi даже
въ обозначешяхъ и выработки1 алгебраическаго языка. Первыя
буквы азбуки для обозначения извФстныхъ величинъ п послФд-
шя—для обозначешя неизвъ'стныхъ, нынешнее употреблеше пока-
показателей степени, точка — для обозначешя умножешя— все это
получило начало или окончательно утвердилось авторнтетомъ
Декарта.
Истор1я науки и въ данномъ случай подверждаетъ правило,
что каждое новое обобщвнге вопроса заключаетъ въ себ4, какъ
частные случаи, все то, что прежде было известно объ этомъ
предмет^. Общая форма комплекснаго количества
а-\-Ы
заключаетъ въ себФ, какъ частные случаи, и «действительный!»,
и «мнимыя» количества. При й = 0 комплексъ а-\-Ы даетъ дей-
действительную величину, при а = 0 получается мнимая. Общая
форма комплекснаго числа есть сумма дМствительнаго и мнимаго.
Въ 1799 году Гауссъ обнародовалъ первое изъ своихъ 3-хъ
доказательству что всякое алгебраическое уравнеше имФетъ
корень вида а-\-Ы.
Уравнешя первой степени (линейныя) даютъ намъ возмож-
возможность разсматривать только дМствительныя количества противо-
положныхъ знаковъ: х-\-а = 0 и х — а=0 удовлетворяются
соответственно значешями —а и -\~а. Неполное квадратное
yp-ie вида ос2-{-а2=0 и ос2—а2=0 уже вводить въ разсмотрФ-

155
Hie и чисто мнимыя количества, такъ какъ корни этихъ урав-
нешй суть ± аг и =? а. Наконецъ, полное квадратное уравнете
даетъ для корней уравнешя пару сопряженныхъ коыплексныхъ
корней (т. е. два количества вида: аг-\- Ъхг и ах— Ъхг) при усло-
вш, что Ъ не равно нулю, и что выражение Ъ2—Аас отрица-
отрицательно. Последнее выражеше, составленное изъ коэффищентовъ
даннаго уравнешя, (Ъ2—4ас) носитъ спещальное пазвате
дгмжримипанта yp-ifl.
Какъ видимъ, знакомство съ мнимыми и комплексными ко-
количествами является непосредственнъшъ результатомъ простого
алгебраическаго анализа. Но полное пониыаше и надлежащая
оценка этихъ количествъ невозможны до тт^хъ поръ, пока не
сделается возможнымъ наглядное и, такъ сказать, ощутимое
изучеше ихъ. Истор1я вопроса и показываетъ памъ, какъ въ
изучеше алгебры вводилось постепенно графическое изображе-
Hie положительныхъ, отрицательныхъ, мниыыхъ и комплексныхъ
чиселъ.
Подобно тому, какъ раньше съ помощью вФсовъ мы вы-
выясняли понятие о положительномъ и отрицательном^ количе-
ствФ, можно найти много практическихъ примФровъ, уясняющихъ
комплексное и мнимое число. Такъ, напр., возьмемъ игру въ
ножной мячъ (футболь). Если силы ударовъ, толкающихъ
мячъ по направленно ОН (см. фиг. 86), обозначить положитель-
положительными, действительными числами, то силы, двигающш мячъ
въ прямо противоположномъ направленна, выразятся отрицатель-
отрицательными числами. При этомъ силы, заставляющая мячъ двигаться
въ направленш OU или OZ>, изобразятся мнимымъ числомъ,
а всякая иная спла, двигающая мячъ въ любую иную сторону
площади игры, изобразится комплекснымъ числомъ.
ф>

>>
^
Правила знаковъ при алгебраическомъ умножен1и.
Геометрическое о6ъяснен1е.
Разстояше направо и вверхъ отъ О (фиг. 88) условимся
брать со знакомъ -)-, а разстояше налево и внизъ условимся
брать со знакомъ —. Выполниыъ прилагаемый зд^сь чертежъ
(фиг. 88) и разсмотримъ полученные прямоугольники.
R
S'
+
-
Т
У
О
b
R
S
Фиг. 88.
Прялоугольнпкъ ОН им^етъ а-Ь единицъ площади. Примемъ,
что это произведете тгЬетъ знакъ -J-.
Предположиыъ теперь, что SR, оставаясь параллельной самой
себ'Ь, передвигается вл'Ьво и, переходя черезъ положеше 01,
передвиЕгется еще л'Ьв^е па а единицъ и приыетъ положеЕЙе 8'М'.
Основаше прямоугольника при этомъ будетъ все уменьшаться,
обратится въ нуль и, перейдя черезъ это значеше, станетъ
отрицательнымъ. Точно также сделается отрицательнымъ и

167
прямоугольнпкъ. Значптъ произведете — а на -\-Ь станетъ
отрпцательнъшъ, оно = — аЪ.
Предположимъ далФе, что ТВ1 передвигается внизъ, оста-
оставаясь параллельной самой ce6f>, и опустится на Ь единпцъ ниже
лиши SS'. Прямоугольникъ, раньше отрицательный (со зна-
комъ—), перейдетъ черезъ значеше 0 и станетъ теперь поло-
жительнъшъ. Итакъ, произведете — а на — Ъ даетъ -\- ab.
Путемъ подобнаго же разсуждетя не трудно видтлъ, что
) {Ъ)	Ъ
На основаши опредЪлешя умножен1я.
Умножеше есть д'Ьйств1е, при которомъ изъ одного изъ
двухъ данныхъ чиселъ (множимое) мы получаемъ новое число
(произведете) такъ, какъ другое число (множитель) получается
изъ единицы, принятой за основную.
Предположим?., что даны 2 множителя: -|- 4 и -\-Ъ. При-
Принимая за основную единицу +1, мы видимъ, что множитель
составленъ повторешемъ три раза этой основной единицы:
(+ 1) + (+ 1) + (+1) = 4~ 3. По опред^ленш умножешя, то же
самое надо произвести и съ множпмымъ: (-\- 4) -\- (-\- 4) -f- (-\- 4) =
= +12, т. е. произведете получится положительное. Разсу-
ждая совершенно подобнымъ же образомъ, найдемъ, что произ-
произведете — 4 на +3 = (—4) + (—4) + (—4) = —12.
Возьмемъ теперь множители -)-4 и —3. Множитель —3
получается опять-таки троекратнымъ сложетемъ основной едп-
ницы, но съ излиьненнымъ знакомь. Поэтому, чтобы получить
произведете +4 на —3, мы должны также взять множимое
-(-4 съ шмпменнымъ знакомь и сложить его 3 раза. Получится
Точно также при умножеши —4 на —3, мы во множи-
момъ должны переменить знакъ на обратный и сложить его
3 раза, т. е. (_4)Х(-3)= (+4) + (+4) + (+4) = +12.
Такимъ образомъ для вс^хъ четырехъ случаевъ мы геоме-
геометрически и аналитически вывели то известное правило знаковъ,
которое часто для краткости выражаютъ такъ: «одинаковые
знаки даютъ -)-, а разные' —».

158
Обобщеше правила знаковъ.
Выводя предыдущее правило знаковъ при умноженш, мы
приняли за основную единицу -\-1. Посмотримъ, что произой-
детъ, если за основную единицу примемъ — 1. Исходя изъ
опред-Ьлешя умножешя и разсуждая совершенно такъ же, какъ
въ предыдущей главй, найдемъ, что въ этомъ случай получается:
(-4)Х(+3)=
Разсыатривая эти четыре случая, мы видпмъ, что при
основной единиц'!; - -1 правило знаковъ будетъ уже не то, что
при основной единиц^ -\-1, а именно: въ этомъ случай при
одинаковыхъ знакахъ множителей получается —, я при раз-
ныхъ знакахъ множителей получается +•
То же самое мы могли бы получить и геометрически, но
только тогда на фиг. 88-ой прямоугольникъ (-f- a) X (~Ь Ь) надо
принять отрицательнымъ, т. е. равнымъ —аЪ.
Но примемъ ли мы за основную единицу +1, или —1,
оба правила знаковъ, выведенныя выше, можно объединить въ
одно следующее: Если два множителя имгьютъ одинаковые
знаки, то знакъ ихь произведетя одинаковъ со знакомь основ-
основной единицы; если оке оба мноэюителя имгьютъ разные знаки,
то знакъ ихъ произведетя противополоэюенъ знаку основной
единицы. Или, выражаясь кратко, одинаковые знаки даютъ
знакъ одинаковый (съ основной единицей), а разные—противо-
разные—противоположный (основной единиц^).
Если принять за основную еще какую либо иную единицу,
то получимъ и друпе законы для знаковъ — другую алгебру,
иначе говоря.
Умножеше, какъ пропорц'ш.
По опредйлетю умножетя, произведете находится въ та-
комъ же отношенш къ множимому, въ какомъ множитель на-
находится къ основной единиц1}}. Это равенство отношешй можно
представить пропорцюй:

159
произведете : множимое = множитель : основная единица.
Или:
основная единица : множитель = множимое : произведете.
Постепенное обобщеше умножешя.
Съ т4хъ поръ, какъ Лука Пачюли (въ XV и въ начал4
XVI стол'Ьия) находилъ, что необходимо (и при тоыъ трудно)
объяснять, почему это при перемноженш правильныхъ дробей
(въ ариеметикф) получается произведете меньшее, ч4мъ мно-
множимое, и до нашихъ дней съ современнымъ употреблетемъ
термина «умнооюете» въ высшей математик^, какъ видимъ,
произошла большая перемена. И этотъ математически терминъ
«умножеше» служитъ однимъ изъ лучшихъ примйровъ обоб-
щешя и употреблешя слова совсЬмъ уже не въ томъ этимоло-
гическомъ смыслФ, которое оно им4ло вначал'Ь.

Геометрические софизмы.
Задача 63-я.
Искусная починка.
На дн'Ь деревяннаго судна во время плавашя слу-
случилась прямоугольная пробоина въ 13 дюймовъ длины
и 5 дюймовъ ширины, т. е. площадь пробоины оказа-
оказалась равной 13X5 = 65 квадратныхъ дюймовъ. У су-
судового же плотника для починки нашлась только одна
квадратная доска со стороной квадрата въ 8 дюймовъ,
т. е. вся площадь кваЯрата равнялась 8 X 8 = 64 квадр.
дюймамъ (фиг. 89). Плотникъ ухитрился, однако, раз-
разрезать квадратъ на части и сложить эти части такъ,
что получился какъ разъ прямоугольникъ, соотв-Ьт-
ствуюшдй пробоин^, которую онъ и задътгалъ. Вышло
такиыъ образомъ, что плотникъ влад"Блъ секретомъ
квадратъ въ 64 квадратныхъ единицъ мъ-ры обращать
въ прямоугольникъ съ площадью въ 65 такихъ же
квадратныхъ единицъ. Какъ это могло случиться?
Р^шеше.
Квадратъ площадью въ 64 квадратныхъ дюйма разръ-жемъ
на четыре частв Л, В, С и I) такъ, какъ это указано сплош-
нымв лишями на фиг. 89. Т. е., сначала разрЬкемъ квадратъ

1
1
	1-
1
1
1
1
1
— ч -
1
1
1
1
1
1
1
-I-A-
I
I
_ L
1
1
iC
_ L _
i
i
T
i
i
i
i
i
1 ~
i
i
i
i
i
i
i ,
i /
i г
i/
/
i
i
i
i
\
i /
/
¦Д- -
h
i
i
i
l
! ¦ i
i ¦ i
/' ¦' .'
i i i
¦ ¦ i
~i ~\ —, ~~
_i	(P	t
¦ i i
i i i
i i i
i i •
i i i
Фиг. 89.
Фиг. 90.
Фиг. 91.
ВЪ ЦАРСТВЬ СНЕБАЛКИ.
11

162
на два прямоугольника съ одинаковыми основашями, равными
сторонт> квадрата, но высота одного прямоугольника 3, а дру-
другого б дюйм. Затъ-мъ меныши прямоугольникъ раздтлимъ на
два равныхъ треугольника, А и В, д1агоналыо, а болышй
на двт. равныя трапецш, С и D. Сложимъ вслъ-дъ за этимъ
полученныя части такъ, какъ это указано на фиг. 90, и мы
получимъ прямоугольникъ со сторонами въ 13 и б дюймовъ и
съ площадью въ 66 квадратныхъ дюймовъ!
Выходитъ такимъ образомъ, что мы какъ бы и въ самомъ
дт>лт. геометрически показали, что 64 = 66. Но допущенный
въ нашихъ разсуждешяхъ и построешяхъ софизмъ легко по-
поясняется фиг. 91-й. Сложивъ полученныя части квадрата, какъ
указано рисунками, мы получаемъ, что ЕЕ и HG, каждая
въ отдельности, прямыя лиши, но он4 не составляютъ про-
продолжения одна другой, т. е. одной прямой, а даютъ ломаную
лишю. Точно также и лишя EFG есть тоже ломаная лишя:
и это легко доказать. Въ самомъ дт,лт.:
Пусть X обозначаетъ точку, гдъ1 прямая ЕН встречается съ
прямой GJ. Посмотримъ теперь, совпадетъ ли X съ G или нъ-тъ?
Изъ подобныхъ треугольниковъ ЕНК и EXJ
XJ:HK=EJ:EK
или
Я 1Я
т. е.	XJ=^g—= 4,875
въ то' время какъ GJ= 5.
Площадь полученнаго прямоугольника действительно равна
65 кв. дюйм., но въ ней есть ромбоидальная щель EFGH,
площадь которой равна какъ разъ 1 квадр. дюйму.
Такюгь образомъ хитрому плотнику, все равно, пришлось
замазывать при починки небольшую щель. Иллюзш же сплош-
сплошного прямоугольника получается вслЬдстте весьма незначитель-
незначительной разницы наклонешя д1агонали прямоугольника со сторонами

163
13 и о къ большей сторонЬ и наклонешя къ большей сторон^
Д1агонали прямоугольника со сторонами 3 н 8. Въ самомъ Д'ЬлФ,
X	6	3
наклоненш выражаются соответственно числами —^ и ^-, разность
которыхъ есть:
б 3
ЗамЬтимъ кстати, что встречаемый здъ-сь числа 3, б, 8, 13
принадлежать къ ряду
О, 1, 1, 2, 3, 5, 8, 13, 21, 34, бб, 89,	,
въ котороыъ каждый членъ получается сложешемъ двухъ непо-
непосредственно предыдущихъ членовъ. Этотъ весьма замечательный
рядъ былъ впервые указанъ въ XIII вйкй матеыатикомъ Лео-
нардомъ Фибоначчи изъ Пизы.
Воспользуемся даниымъ геометрическимъ парадоксомъ также
и для того общаго замФчашя, что при разр'Ьзыванш и перело-
женш фигуръ (см. также 1-ю часть «Въ царствй смекалки»
стр. 108—116) не сл'Ьдуетъ доверять исключительно глазу, но
необходимо подкреплять свои дМствщ и математическими дока-
доказательствами.
Задача 64-я.
Обобщеше того же софизма.
На прилагаемой зд^сь фиг. 92-й указано, какъ т4 же четыре
фигуры (два равныхъ треугольника и двЬ равныхъ трапецш),
что и въ предыдущей задач'Ь, сложить 3-мя различньпш способами
и получпть фиг. Л, Б и С.
Если теперь обозначпмъ х = 5 и у = 3, то будемъ лм'Ьть
для площадей полученныхъ фыгуръ: J^=;G3, 2?= 64, С =66,
т. е. С—В=1 в В — А=1.
Словомъ, теперь уже выходить, что будто бы одни и тъ- же
известной формы куски, скажемъ, бумаги даютъ три площади
различной величины, въ зависимости отъ одного только перело-
жешя!
п*

164
х+у
х+у
в
\ у
X
У
X
h
х+у ^—"'
X
Фиг. 92.
ИзслЬдуемт. полученныя три фпгуры алгебралческп:
площадь А = 2ху -\- 2ху -\- у Bу — х) = Ъху -(- 2у2;
» В =( + Y 2\
» С -х(у)	\
» С—В = х2—ху — у2;
» -В — А = х2—ху — у2

166
Итакъ, всЬ эти три фигуры будутъ равны, если
х1 — ху— у2 = 0, т. е., пначе говоря, если
У~ 2
Следовательно, взятыя нами 3 фигуры не могутъ быть
равны, если х и у выражены оба въ рацюнальныхъ числахъ.
Фиг. А и С кажутся намъ сплошными, опять таки, всл4дств1е
зрительной иллюзш.
Попытаемся теперь найти гЬ рацюнальныя значешя х и ?/,
которыя разницу между А п Б, или между В и С дЬтаютъ рав-
равной 1. Иначе говоря, надо решить yp-ie
х2—ху — у2 = ± 1.
Пскомыя намп решетя, какъ оказывается, заключается въ
упоыянутоыъ уже пами въ предыдущей главь- рядъ' Фибоначчи
О, 1, 1, 2, 3, б, 8, 13, 21, 34, бб, . . . . ,
если для у и х соответственно брать въ этоыъ ряду два послЬ-
довательныхъ члена.
Значешя ^ = 3, х = Ь суть т4, которыя обыкновенно даются,
какъ и въ настоящелъ случай; для нихъ мы и иыЪемъ, какъ
указано выше, А<^В<^С
Если взять следующую пару рЪшешй у=б и х = 8, 'то
получится А^>В^> С, ибо въ этоыъ случай ^.= 170, В = 169,
С=168.
Рядъ Фибоначчи.
Какъ видимъ изъ двухъ предшествующихъ задачъ, рядъ Фи-
Фибоначчи
0, 1, 1, 2, 3, б, 8, 13, 21, 34, бб, 89,	,
гдъ1 каждый послйдупцй членъ получается путеыъ сложен!я двухъ
непосредственно предыдущпхъ, пграетъ значительную роль въ
1шслт>дованш геометритескихъ софпзмовъ разслатриваемаго рода.
Укажеыъ еще на нйкоторыя свойства этого замйчательнаго ряда.

166
Прежде всего обратит, внимате на то, что квадратъ ка-
зкдаго члена этого ряда, уменьшенный на произведете двухъ ря-
доыъ обокъ (справа и слива) стоящихъ возл'Ь него членовъ даетъ
попеременно то +1) то ¦—1, т. е.
2а—1.3 = +1,
За —2.б = —1,
б2 — 3.8 = 4-1,
8а—6.13 = — 1.
ВыдЬляя члены, даншде — 1, начиная съ
82— б. 13 = — 1,
212—13.34 = —1,
бб2—34.89 = —1,
мы видимъ, что парадоксы, приведенные нами выше, можно разно-
разнообразить сколько угодно. Такъ, выъ-сто квадрата на стр въ 8 еди-
ницъ длины можно брать квадраты со сторонами 21, 56 л т. д.
единицъ длины п получать изъ нихъ парадоксальный фигуры
съ еще болышшъ видимымъ прнближетемъ.
Точно также, если взять въ ряду Фибоначчи таме члены, что
132—8.21 = 4-1,
34я —21.65=4-1,
то ложно брать квадраты съ сторонами въ 13, 34 п т. д. еди-
нпцъ длины. Но здт>сь для достижешя трэбуемой иллюзш лучше
взять сначала прямоугольникъ (напр., со сторонами 8 и 21), а
затъчиъ разрезать его такъ, чтобы скрываемая нами щель полу-
получалась внутри квадрата A3X13).
Замътпмъ также, что если взять простМшую непрерывную
дробь
'+ТТГ..

167
п начать вычислять ея послъ-довательныя подходящая, то опять
получимъ рядъ Фибоначчи.
Птакъ, разр'Ьзываше п переложеше фигуръ, подобныя ука-
занныиъ выше, можно разсматривать, какъ геометрическое пред-
ставлеше величины прпближешя, даваемаго этой непрерывной
дробью.
Задача 65-я.
Похоже, но не то.
Софизыъ, похожи съ виду на данный раньше (задача 63),
получится, если построить прямоугольникъ со сторонами въ 13
и 11 едпнпцъ длины (фиг. 93), разсЬчь его дгагоналыо и сдви-
1
" " Т "
1
1
р
- -L -1
1
1
1 _
1
1
1
1 I
J,
1
1
1
1
- J _-
1
1
1
1
X
/ •
1
, 1
| i ; ¦-.
1 t - | - Ч - -
1 , ! , у
t +	1 г У-
-г-ЬК-
^ ' :
, / III'
/:¦¦¦¦
, i ¦ ¦ i
* - + 1 1- ~ ¦
• • :
I . , и -1 - -
i *,/
- J - X-
У'
/:
" Г
- т -
1
~ 1
1 J
— 1— — 1— — *- — — - - 1
j . 1 • . .
1 1 ¦ 1 I I
Фиг. 93.
нуть зат4мъ полученные треугольники по ихъ общей гипоте-
нуз4 въ положен1е, указанное па фиг. 94-ой. Эта последняя
фигура по виду состоптъ пзъ квадрата VliXS со сторонами
въ 12 едшшцъ длины, т. е. площадью въ 122 = 144 квадр.
единицъ. Кром4 того къ этой площадп надо прибавить площадп
треугодышчковъ PQ В п ST U, каждая величиной въ 0,6 квадр.
едшшцъ. Сл'Ьдовататьно, площадь всей фиг. 94 равна 115 квадр.
единпцамъ. Но какъ же это получилось, если площадь прямоуголь-
прямоугольника на фиг. 93 равна только 13 X 11 = 143 квадр. единидамъ?

168
Разсмотрйше фигуръ, особенно если обратимъ внимате на
то, какъ Д1агональ на фиг. 93-ой пересЬкаетъ лянш, докажетъ
намъ, что VBXS не есть квадратъ. VS равна 12 единицамъ
длины, но SX<^12; TX (меньшая сторона на фиг. 94) равна
11 един., по ЯТ< 1 (си. ST на фиг. 94). Съ другой стороны,
разбирая то же аналитически, пмйемъ:
у к
или
т. е.
Значитъ, прямоугольникъ
VBXS= 12 X
Фиг. 94.
ST: VP=SU:VU
ST: 11 = 1: 13,
11
Тз"
,11
|4§
Следовательно:
Фигура 94-я = прямоугольнику -\~ 2 треугольника
=144+т1=148-

169
Если бы мы треугольники по той яге д1агопалп сдвинулп
(до первой перекрестной лпнш) съ мЪста въ панравлепш, про-
тпвоположыомъ тому, какое указано фпг. 94, то получили бы съ
виду пряыоугольипкъ 14 „ 10 и два треугольника съ площадью
въ - каждый, т. е. выходило бы, что полученная фигура шгЬетъ
будто бы площадь 141 квадр. един., т. е. меньшую, чъ-мъ
площадь прямоугольника, изображённаго фиг. 93. Разобрать и
доказать ошибочность этого заключешя такъ же легко, какъ и
въ предыдущемъ случай.
Задача 66-я.
Еще парадоксъ.
Фиг. 95а.
Фиг. 966.
Вотъ еще одинъ «фокусъ», который можно сделать съ ква-
дратомъ.
Возьмемъ квадратъ со стороной въ 8 единицъ длины п,
следовательно, съ площадью въ 64 квадр. един. РазрЪжемъ
его, какъ указано на фиг. 95а, и переложить части такъ, какъ
указано па фиг. 956. Получается, невидимому, прямоугольникъ
съ площадью 7 X 9 = 63. и это ничего не отбрасывая отъ
площади квадрата, равной 64 квадр. единицамъ.

Три знаменитыхъ задачи древности.
Эти задачи сл'Ъдуюшдя:
1.	— Трисекщя угла или дуги.
2.	— Удвоеше куба.
3.	— Квадратура круга.
Трнсекшя угла, или разд'Ьлеше (съ помощью только цир-
циркуля и линейки) угла или дуги на три равныя части есть не-
несомненно весьма древняя задача, хотя съ ней не связано ни-
какихъ поэтическихъ вьшысловъ или любопытныхъ преданШ,
на что древте и средневековые писатели были тате охотники
и мастера. Задачу <> квадратуре круга, т. е. о построенш ква-
квадрата, равновеликаго площади даннаго круга, говорятъ, пытался
решить впервые гречесюй философъ Анаксагоръ (въ V в. до
Р. X). Задача объ удвоенш куба носитъ иначе вазваше «Де-
л!йской задачи», такъ какъ съ ней связана легенда о томъ,
какъ древше советовались относительно решетя съ просла-
вленнымъ Шатинолъ.
Предан1е, передаваемое н4клилъ Филопопомъ, говоритъ, что
въ 430 году до Р. X. въ Аеинахъ разразилась моровая язва.
Аеиняне послали къ оракулу на остров^ ДелосЬ вопросить,
какъ остановить это б4дств1е. Аполлонъ ответил!., будто бы,
что они должны удвоить величину его жертвенника, который
шгЪлъ форму куба. Иевежествешшмъ просптатямъ д'Ьло каза-
казалось очень легкииъ, и новый алтарь былъ воздвигнут^., — или
такъ, что каждая его сторона была вдвое больше стороны преж-
ияго куба (т. е. объемъ прежняго куба увеличили въ 8 разъ),
пли же еще проще,— пом-Ьстивъ на старый алтарь еще новый

171
такой же величины. Эшщезйя, однако, не прекращалась, п къ
оракулу было снаряжено новое посольство, которое п узнало,
что предппсаше Аполлона не было выполнено. Требовалось,
чтобы новый алтарь пмтлъ также форму куба и 1шт>лъ ровно
вдвое большш объемъ, чт>лъ старый жертвепнпкъ. Подозревая
тайну, Аоиняно обратились за разгадкой ея къ Платону, кото-
который отослалъ пхъ къ геометрамъ н въ частности—къ Евклпду,
который, будто бы, специально занимался этой задачей. Несмотря
на всю заманчивость и некоторое правдоподоб1е этой ncTopin
(оракулы любили говорить загадками), приходится ц4ликомъ
отбросить ее, хотя бы потому, что Платонъ до 429 г. до Р. X.
еще п не родился, а знаменитый Евклидъ появляется не менее
вика спустя.
Во всякомъ случай мы имт>емъ несошгЬнныя свидетельства,
что древн1е_ весьма упорно и настойчиво работали надъ ргЬше-
шемъ указанныхъ выше 3-хъ задачъ. Гпшпй элпдеюй нашелъ
даже специальную кривую «квадратриксу», решающую вопросъ
о трисекцш угла, которой можно пользоваться и для pinie-
шя вопроса о квадратур^ круга. Найдены были и шгопя дру-
пя кривыя, решаются задачу о трисекцш угла и квадратуре
круга. Эратосоенъ и Никомедъ изобрели даже механические
приборы для черчешя такихъ кривыхъ. Но... ни одна изъ этихъ
кривыхъ не можетъ быть построена только съ помощью цир-
циркуля п линейки, а это какъ разъ и было главнымъ требова-
нгемъ при ръ-шенш задачи.
Древность такъ и завъ-щала рт>шеше вс4хъ этихъ трехъ за-
задачъ нашгшъ врененаыъ. НынЬште математики, вооруженные
болт.е могущественными методами изслъ'дован1я, доказали, что
всЬ три задачп невозможно р'Ьшить построен1емъ съ помощью
только циркуля и линейки, какъ эти приборы употребляются
и понимаются въ элементарной геометрш (см. по этому по-
поводу следующую главу). Подобное разръщеше вопроса даже
самые сильные математические умы древности могли только по-
подозревать, такъ какъ доказать невозможность регаешя прп то-
гдашнпхъ средствахъ математики они не могли. Но, доказавъ
невозможность решен!я этихъ задачъ съ помощью только цир-
циркуля и линейки, математики нашихъ временъ далл новые спо-

172
собы и проложили новые пути къ р'Ьшенш этихт, задачъ, если
отбросить ограничеше о циркуле п дгшейк'Ь. Былъ также изо-
бр4тенъ и прпм4ненъ методъ приближешй, который и ргьшилъ
задачу, если можно здесь применить' это слово.
Что касается въ частности числа тг (выражающаго отно-
шеше окружности къ д1аметру), то только въ 1882 году Лин-
деманну удалось окончательно установить его трансценден-
трансцендентальный характеръ, т. е., что это число не можетъ быть кор-
немъ алгебраическаго уравнешя. Заи4тиыъ здесь кстати, что
это знакомое каждому ученику старшихъ классовъ число тг
играетъ большую роль и въ областяхъ математики, довольно
удаленныхъ отъ такъ называемой «Элементарной геометрш»,
напр., -к довольно часто встречается въ формулахъ теорш
вероятностей.
Приближенное значеше для к (=3,1415 926...) было
между прочимъ вычислено съ 707 десятичными знаками матема-
тикомъ В. Шенксомъ. Этотъ результатъ вмгЬст4 съ формулой
вычислений: онъ обнародовалъ въ 1873 г. Ни одна еще задача
подобнаго рода не решалась съ такпмъ огромнымъ приблпже-
н^емъ и съ точностью, далеко превышающей отношеше микро-
скопическпхъ разстоянШ къ телескопическимъ.
Шенксъ вычислялъ. Следовательно, онъ стоялъ въ противо-
pfein съ требовашями задачи о квадратуре круга, где требуется
найтиргьшете построешемъ. Работа, сделанная Шенксомъ, въ сущ-
сущности, безполезна, или — почти безполезна. Но, съ другой сто-
стороны, она можетъ служить довольно убедительнымъ доказатель-
ствоиъ противнаго тому, кто, не убедившись доказательствами
Лицдеманна и др. или не зная о нпхъ, до сихъ поръ еще на-
надеется, что можно найти точное отношение окружности къ
диаметру.
Квадратура круга была въ прежшя времена самой заман-
заманчивой и соблазнительной задачей. Арапя «квадратурщиковъ»
неустанно пополнялась каждымъ новымъ пoкoлeнieмъ матема-
тиковъ. Все усшпя были тщетны, но число ихъ не уменьша-
уменьшалось. Въ некоторыхъ умахъ доказательство, что решеше не
можетъ быть найдено, зажигало еще большее рвеше къ изы-
ска!пямъ. Что эта задача еще до сихъ поръ не потеряла своего

173
интереса, лучишмъ доказательством^, служптъ появлеше до спхъ
поръ попытокъ ее р'Ьшпть.
Итакъ. все гтарзшя решить три знаменитая задачи при
изв4стныхъ ограничивающихъ услов!яхъ (циркуль п линейка)
привели только къ доказательству, что подобное рЪшеше невоз-
невозможно. Иной, пожалуй, по этому поводу скажетъ, что, следо-
следовательно, работа сотенъ умовъ, пытавшихся въ течеше стшгЬтШ
решить задачу, свелась, следовательно, ни къ чему... Но это
будетъ неверно. При попыткахъ решить эти задачи было сде-
сделано огромное число открьтй, им4ющихъ гораздо болышй инте-
ресъ и значеше, ч^мъ сами поставленныя задачи. Попытка Ко-
Колумба открыть новый путь въ Индш, плывя все на западъ,
окончилась, какъ известно, неудачей. II теперь мы зпаемъ, что
такъ необходимо и должно было случиться. Но гешальная по-
попытка великаго человека привела къ «попутному» открытш
целой новой части свФта, прсдъ богатствомъ и умствспньшъ
развипемъ котораго бл4дн4ютъ нынче вс^ сокровища Индш.
Задача 67-я.
Линейка и циркуль. Трисекфя угла.
Для построений въ элементарной теоретической геометрш
допускаются только два прибора: циркуль и линейка. Говорятъ,
что такое ограничите вспомогательных^ прпборовъ сделано
знамоиитымъ греческимъ философоиъ Платономъ.
При этомъ само собой подразумевается, что циркуль, о ко-
торомъ идетъ ргЬчь, им^етъ неограниченное раствореше. Бслп бы
циркуль не обладалъ какимъ угодно нуяшымъ намъ растворе-
н!емъ, то его нельзя было бы прим'Ьпять для выполнешя Т2№-
бусмаго Эвклидоиъ, ст» иервыхъ же шаговъ, построен1я окруж-
окружности изъ пропзвольнато центра и какого угодно рад1уса C-й по-
стулатъ Евклида). Точно также подразумевается, что геометри-
геометрическая линейка неогранпчена по длине B-й ностулатъ).
Вместе съ темъ необходимо подразумевается, что геоме-
геометрическая линейка не имштъ дтлепш. Еслп бы на ея ребре
было хотя всего два знака, п если бы позволено было ими поль-
пользоваться и вдобавокъ передвигать линейку, приноровляясь къ

174
фигур4, то задача о разд4ленш угла на три равныя части (не-
(неразрешимая въ элементарной геометрш) тотчасъ можетъ быть
решена. Въ самомъ д^лт,:
Пусть данъ какой-либо уголъ ЛВС (фиг. 96); л пусть на
лезвш нашей линейки обозначены 2 точки Р я Q (см. ту же
фиг. внизу).
Р	Q
Фиг. 96.
Построеше.
На одной изъ сторонъ угла откладываемъ отъ вершины В
прямую BA = PQ. Д4лимъ В А лополамъ въ точки М; изъ
точки Ж ироводимъ линш МК || ВС и ML _LBC.
Возьмемъ теперь нашу линейку п приспособим!» ее къ по-
полученной уже фнгур-I; такъ, чтобы точка Р лпнейкп лежала па
прямой КМ; точка Q лежала бы на прямой LM, п въ то же
время продолжеше PQ линейки проходило бы черезъ вершину
даннаго угла В. Тогда прямая ВР п есть искомая, отсекаю-
отсекающая третью часть угла В.
Доказательство. JPJ5C= J ВРМ, какъ накреетъ-лежапуе.
Разд'Ьлимъ PQ пополамъ и середину N соединиыъ съ М пря-

176
мой NM. Точка i\ есть середина гипотенузы пряиоугольнаго
¦ треугольника PQM, а потому PK=NM, а следовательно
/\PNM равнобедренный, и значить
Z ВРМ= Z PMN.
Вн4шшй же Z BNM= Z J3PM+ / PMN= 2 Z ВРИ.
Вместе съ т^мъ:
Значить,
Z MBN= Z
Итакъ:
. Т. Д.)
Приведенное выше рЪшеше задачи принадлежитъ Кемпе,
который при этомъ поднялъ вопросъ, почему Евклидъ пе вос-
воспользовался делеп1емъ липейки п процессомъ ея приспособлешя
для доказательства 4-й теоремы своей первой книги, гд4 вместо
этого онъ накладываетъ стороны одного треугольника на сто-
стороны другого (первое приложеше способа наложешя, известное
каждому ученику). На это можно ответить только, что въ задачу
Евклида и не входило отыскаше некоторой точки посредствомъ
изьйрстя п процесса приспособлетя линейки (какъ это мы
делали выше въ задач4 для отыскашя точки Р). Въ своихъ раз-
сужден1яхъ и доказательствахъ онъ просто накладываетъ фигуру
на фигуру,—п только.
Принимаемая памп геометрическая линейка не должна счи-
считаться разделенной, такъ какъ это слишкомъ раздвинуло бы пре-
пределы «элементарности». Но она должна необходимо быть неогра-
неограниченно длинной,— лначе эти пределы слишкомъ бы сузились.
ВсЬ вышеприведенныя залйчашя сл'Ьдуетъ имйть въ виду,
когда говорятъ о цпркул'Ь п линейки, какъ гооиетрическпхъ
приборахъ.

Два отрицательныхъ вывода XIX в^ка.
I. Общее уравнете выше четвертой степени неразре-
неразрешимо чисто алгебраическимъ путемъ (иначе говоря —
въ радикалахъ).
Piineme уравнений 3-й и 4-й степени было известно, на-
начиная съ 1545 года. Два съ половиной столйтя спустя, моло-
молодой 22-лт.ттй Гауссъ въ своей докторской диссертацш дока-
валъ, что всякое алгебраическое yp-ie пвгЬетъ корень, «действи-
«действительный» или «мнимый». Всл'Ьдъ ваттшъ онъ же далъ еще два до-
доказательства той же теоремы. Въ 1801 году тотъ же Гауссъ
замйтплъ въ однолъ пзъ своихъ сочинен1й, что, быть можетъ,
невозможно разрешить съ помощью радпкаловъ общее yp-ie
степени высшей, ч'Ьмъ четвертая. Это предположенге было до-
доказано зпаменитымъ норвежскиыъ математикоыъ Абелеыъ и было
обнародовано къ 1824 году, когда автору его было всего 22
года отъ роду. Два года спустя то же доказательство было имъ
напечатано въ бо.тЬе пространной п понятной форыт, съ внясне-
шемъ миогихъ деталей. Съ этихъ поръ изыскан1я мателати-
ковъ, силившихся раньше найти общее алгебраическое pimeme
всякого уравпен1я, приняли иное направление.

177
IT. Знаменитый «постулатъ о параллельныхъ» Евклида
не можетъ быть 1,оказанъ съ помощью какихъ-либо
иныхъ его аксюмъ.
Въ виду важности вопроса, остановимся на исторш этого
знаменптаго «постулата» несколько подробнее.
Несмотря на то, что св^д4н1я древпихъ по геометр]"и были
весьма обширны, вст. они до 3-го втжа до Рождества Христова
являлись разрозненными, отдельными научными фактами, не
имеющими между собой связи. Творцомъ геометрш, какъ науки
въ настоящемъ значенш этого слова, былъ Еввлидъ. Въ 3-мъ
вгЬкгЬ до Р. X. (около 270 г.) этоть гречесый философъ за-
задался н/Ьлью собрать веЬ найденныя до его времени свойства
фигуръ на идеальной плоскости и въ пространств^ и опреде-
определить, кашя изъ нихъ существенны, т. е. зависятъ непосред-
непосредственно отъ свойствъ самой плоскостп и пространства, и
кашя, съ другой стороны, могутъ быть выведены, какъ сл4дств!я
первыхъ. Евклидъ выполнплъ свою задачу и создалъ стройную
дедуктивную геометрическую систему, которая явилась первымъ
примт.ромъ строго научныхъ спстемъ. Онъ показалъ, что всгь
свойства пространственныхъ формъ могутъ быть выведены пу-
темъ однпхъ только строго логпческихъ разсуждешй изъ трехъ
основныхъ положешй, или аксюмъ, характеризующих!, идеаль-
идеальную плоскость и идеальное пространство древнихъ геометровъ,
а именно:
1) фигуры на плоскости и въ пространства могутъ быть
перемещаемы безъ складокъ и разрыва, 2) прямая литя
впоянгь определяется какими угодно двумя ея точками и
3) если изъ какой либо точки прямой линги будетъ прове-
проведено къ ней перпендикуляръ, а изъ другой точки той оюе
прямой приведена будетъ какая-либо наклонная литя, то
перпендикуляръ и наклонная необходимо встргьтятся.
Посл1;днее положеше C) и есть знаменитый постулатъ
Евклида (называемый также 11-ой аксюмой Евклида). Въ наше
время его очень часто предпочитаютъ выражать въ такой болйе
краткой, такъ называемой—Плэйферовской формт.: День персаъ-
ВЪ ЦАРСТВ* СМЕКАЛКИ.	12

178
кающгяся прямыя лиши не могутъ быть обгь разомъ парал-
параллельны одной и топ же прямой. Самъ же Евклпдъ этотъ по-
постулатъ (или 11-ю аксшму) дословно выражалъ такъ: «Если
две прямыя встречаются третьей такъ, что сумма внутреннпхъ
угловъ, лежащихъ по одну сторону третьей, меньше двухъ пря-
мыхъ, то две первыя прямыя по достаточномъ продолжены,
встретятся по ту сторону третьей прямой, на которой сумма
внутреннпхъ угловъ меньше двухъ прямыхъ».
Два первыя изъ прпведенныхъ выше положенШ суть
аксюыы настолько очевпдныя и безспорныя, что не возбуждали
никогда никакпхъ coMiitaifl. Не то было съ третышъ положе-
шелъ. Оно уже не было столь очевидно, а требовало необхо-
необходимости убедиться, что какъ бы наклонная ни была близка къ
перпендикулярности, она необходимо пересечется съ перпенди-
куляромъ, можетъ быть на разстоянш очень далекомъ отъ пря-
прямой и для насъ недоступномъ. Такъ какъ непосредственная
проверка по недоступности для нашихъ чувствъ весьма дале-
кпхъ разстояшй была невозможна, то Евклидъ и далъ это по-
ложете, какъ необходимое допущеше, какъ постулатъ.
Последующее геометры, однако, не вполне доверяя генш
Евклида, пытались установить связь между первыми двумя
аксюмами и третьей, т. е. доказать, что это третье допущенге
(постулатъ) Евклида, принятое имъ ва аксшму, можетъ быть до-
доказано на основанш первыхъ двухъ аксюмъ и помещено въ
ряду теоремъ. И вотъ, съ Птоломея (во 2-мъ веке по Р. X.)
вплоть до первой четверти XIX столейя начинается длинный
рядъ попытокъ доказать этотъ постулатъ. Были предложены
сотни « доказательствъ ».
Въ 1826 году знаменитый руссюй геометръ, профессоръ и
ректоръ Казанскаш университета Ник. Нв. Либачевсшй дока-
залъ всю безуспешность подобныхъ попытокъ п обнародовала,
свое доказательство въ 1829 году. Лобачевскш построплъ но-
новую, совершенно самостоятельную геометрго, где, .принимая за
аксюмы первыя два изъ указанпыхъ выше евклидовскихъ ио-
ложешй, онъ вместо третьяго положен1я (постулата Евклида)
принялъ обратное ему. Получилась стройная и логическая гео-
геометрическая система, безъ всякихъ ошибокъ и противоре'пй, и

179
такпмъ образомъ само собой доказывалась независимость пер-
выхъ двухъ аксюмъ отъ постулата, а следовательно, онъ не
можетъ быть доказать посредствомъ ихъ; п остается, значитъ,
принять его за аксюму или строить новую геометрш.
Изайдоватя Лобачевскаго оставались долгое время непо-
непонятыми и неизвестными. Русскими учеными они были встре-
встречены даже недоброжелательно. Первые благопр1ятные отзывы
о нихъ (Гаусса) сделались известными въ Гермаши только въ
184С г. пзъ переписки Гаусса. Но только начиная съ 60-хъ
годовъ XIX столепя труды Лобачевскаго нашли себе достой-
достойную оценку и положили пачало ряду другихъ замечательныхъ
работъ различныхъ математиковъ.
Успл1я, употребляемыя раньше для доказательства невоз-
можпаго, обратились теперь къ развитш, такъ называемой, не-
Евклидовской геометрш, къ изученш геометрш м-изиерешй,
п^ш донущен1яхъ, обратныхъ или несогласныхъ съ общеприня-
общепринятыми аксюмамп геометрш Евклида. И, какъ всегда бываетъ въ
подобныхъ случаяхъ, новое завоеваше человеческаго ума, новая
побежденная трудность открыли новыя области для изследова-
Н1я, новое направлен1в мысли и методовъ изыскашя; и такимъ
образомъ на очередь выдвинулись новыя еще более трудныя
задачи для решешя. Поле деятельности, открывающееся пыт-
пытливому уму,—безгранично.
12*

\
/t^XCc^Aer,
Николай У[ваиовкчъ /[овачевскш.
A793—1856).
Начиная съ Евклида Александр1Г]скаго геомет])ы всего ьйра
въ продолжен1е бол^е чЬчъ двадцати в'Ьковъ работали надъ вы-
яснешемъ истинной связи между основными аксюыаин геоле-
трш. Завидная честь завершить эту многовековую работу и от-
открыть огромные, новые горизонты для дальнЪишпхъ нзсл'Ьдо-
ван1й принадлежптъ, какъ упомянуто въ предыдущей глав-Ь,
нашему великому гоотечептвеинпку, Н. П. Лобачевскому. Имя
этого гешалъпаго математика нынЪ изв'ьттпо всему образован-
образованному, я во всякомъ случай—всему математическому Jiipy, хотя
улеръ онъ непонятый и неоцененный по достоинству. Совре-
Современники, кроме великаго Гаусса, были не въ силахъ его понять.

181
Жизнь и деятельность пныхъ велпкихъ людей, помимо по-
поучительности, всегда еще полна заманчивой таинственности.
Что даетъ силу этилъ рыцарямъ духа иодъ градомъ нагагЬ-
шекъ п общаго непрпзнашя творить и созидать? Где тотъ
псточнпкъ святого безиокойства, который не лаетъ гешю ио-
чить ни на служебныхъ, ни на семейныхъ, ни на всякихъ
пныхъ лаврахъ, а напранляетъ его въ сторону, казалось бы,
однихъ нещнятностей и огорчешй? Ученая деятельность и
жизнь Лобачевскаго весьма замечательны съ этой последней
стороны и могутъ служить ободряющимъ принеромъ для т4хъ,
кто, п|>еследуя ведшая цЬли, иногда пзнемогаетъ п отчаиваемся
цредъ равнодуилемъ, неионимашемъ, а иногда даже и вра-
враждебностью средней обывательщины. Не задаваясь целью дать
зд'Ьсь связную, хотя бы и сжатую, бюграфш Н. И. Лобачев-
Лобачевскаго, постараемся, однако, осветить те важиМпне факты
его жизни, которые имеютъ связь съ его математическпмъ раз-
витаемъ и на которые есть неоспоримые документальные и
архивные документы. О студенчества и иервыхъ ученыхъ
шагахъ Лобачевскаго мы беремъ драгон/Ьнныя данныя въ
«разсказахъ по архивнымъ документамъ» проф. Н. Вулича:
Изъ первыхъ лшпъ Еазанскаго университета. Книга эта мало
кому знакома по ея сиещальному характеру, хотя она и со-
держитъ въ ceoi весьма много ннтереснаго.
Н. И. Лобачевскш былъ сынъ б^днаго чиновника, уЬзднаго
землеи'Ьра изъ Макарьева, Нижегородской губ. Въ оффищаль-
ныхъ бумагахъ оиъ иоказанъ изъ разночинцевъ, что означаете,
неиринадлежность къ оослов1ю дворянъ. Подобно многимъ дру-
гимъ знаменитымъ математикамъ, юноша Лобачеваай въ пер-
первые годы студенчества fie предполагалъ даже избрать предме-
томъ своихъ постоянныхъ занят!й математику. «Онъ приметно
предуготовляетъ себя для медицпнскаго факультета», — пи-
салъ о ыемъ къ попечителю Яковкииъ, заигЬтпвги1й его даро-
ван!я. Ноявлен1е въ Казааскомъ университете профессора ма-
математики Бартельса, вызваннаго нзъ Гермаши,—светлой и уче-
ученой личности,—побудило Лобачевскаго избрать предметомъ за-
няпй математику. Вскоре онъ делается однимъ пзъ самыхъ
усиевающихъ учениковъ Бартельса. Въ свою очередь, ирофес-

182
соръ полюбилъ Лобачевскаго, и его заступничество не разъ по-
помогало молодому и нисколько вйтрепному студенту при столк-
новешяхъ съ университетской полищей. Инспекторсып жур-
налъ,—разсказываетъ Н. Булнчъ въ названной нами книги,—
за годы нребывашя Лобачевскаго въ студентахъ даетъ нгЬ-
сколько свид'Ьтельствъ объ этихъ столкновешяхъ, причина ко-
торыхъ лежала въ жнвомъ характер^ молодого студента, въ
естественномъ чувств^ свободы, которое проявлялось, какъ свое-
BOflie, въ желаши отстоять свою самостоятельность, что счита-
считалось дерзостью. Самыя шалости характеризуюсь тогдашнихъ
студентовъ. ЛобачевскШ, какъ и мнопе изъ его товарищей,
казенныхъ студентовъ, жпвшихъ въ университет!;, любилъ зани-
заниматься пиротехникою. Разъ Лобачевсшй сд'Ьлалъ ракету7 п
вм'Ьстт, съ другими пустилъ ее въ одиннадцать часовъ вечера на
университетскомъ дворй. За это и за то, «что учинилъ непри-
знаше, упорствуя въ немъ, подвергъ наказашю многихъ, совер-
совершенно селу не. причастпыхъ»,—былъ посаженъ въ карцеръ по
определенно совета. Въ другой разъ, будучи уже правящимъ
должность камерного студента («камерный студента есть по-
мощникъ помощника инспектора казенныхъ студентовъ» —по
опредйлетю правилъ того ьреыени), Лобачевмай былъ замт>-
ченъ «въ участвовашм п потачки проступкамъ студентовъ, гру-
грубости и ослушаши». За эти проступки онъ наказанъ былъ пу-
бличнымъ выговоромъ отъ инспектора студентовъ, лишенъ зва-
шя правящаго должность камерного студента, 60 рублей па
книги и учебныя пособ1я, которые только что были ему назна-
назначены «за особенные усп'Ьхи въ наукахъ и благоповеден1е» и
отпуска до разр&пешя начальства. Все это происходило на
святкахъ 1810 года. Лобачевскому шелъ 18-й годъ, онъ былъ
на посл'Ьднемъ курсЬ, молодость требовала удовлетворетя, а
потому совершенно естественно п простительно, что по словамъ
инспекторская) журнала: «въ генварй мъчупгЬ ЛобачевскШ пер-
первый оказался самаго худого поведешя. Несмотря на приказа-
Hie начальства не отлучаться изъ университета, онъ въ новый
годъ, а потомъ еще разъ, ходилъ въ маскарадъ и многократно
въ гости, за что опять наказанъ написашемъ имени на черной
доски и выставлешемъ оной въ студентскихъ комнатахъ на не-

183
делю. Несмотря на cie, онъ после снова еще былъ въ маска-
маскараде».
Студенческая жизнь Лобачевскаго отличалась вообще не-
несколько буриыыъ характеромъ, но изъ среды гвоихъ сверстни-
ковъ онъ выдавался далеко впередъ, какъ по уклонешямъ отъ
тогдашннхъ нравплъ благоповедешя, вызыпавшиыъ каратель-
ныя мъ-ры нротивъ него, такъ и но своиыъ даровашямъ и
уснйхамъ въ математике. Вотъ почему только о немъ одномъ
дошло до насъ историческое изображена поведетя его; про-
проступки Лобачевокаго называются достопримпчателъными, ха-
рактеръ—упрямымъ, нераскаяннымъ, «весьма много мечтатель-
иымъ о самоыъ себ'Ь», его мнете «получило мног1я ложпыя
понятая» (такъ въ журнал^ инспектора, помощнпкомъ его Еон-
дыревымъ, было записано, что Лобачевсшй «въ значительной
степени явилъ признаки безбожгя» (!) — обвинеше, которое
им'Ьло бы во время Магницкаго весьма печальныя последствия).
Требовались инспекцию противъ Лобачевскаго решительныя
мгЬры, «самыя побудительныя средства со стороны мшгосерд1я
или строгости, каковыя найдетъ благоразум1е начальства». Во-
просъ о судьбе Лобачевскаго перенесенъ былъ въ совета. Только
настоян1я Бартельса и гЬхъ профессоровъ, у которыхъ Лобачев-
скй занимался, доставили ему возможность получить степень
кандидата, а вскоре затемъ магистра, наравне съ прочими
его товарищами.
Бартельсъ считалъ Лобачевскаго лучшимъ изъ учениковъ
своихъ. Вотъ что писалъ онъ къ попечителю объ успехахъ
своихъ слушателей и въ особенности о Лобачевскомъ около
того времени (прпводимъ слова его въ современномъ переводе,
сделанномъ саыимъ Руловскилъ и представленномъ илъ ми-
министру):
«ПослгЬдте два (Спмоновъ и Лобачевсшй), особливо же Ло-
бачевсшй оказали столько успеховъ, что они даже на всяеомъ
немецкомъ университете были бы отличными, и я льщусь на-
надеждою, что если они продолжать будутъ упражняться въ усо-
усовершенствованы своемъ, то займутъ значущш места въ мате-
матическимъ кругу. О искусстве последняго предложу хотя
одинъ прнлеръ. Лекдгп свои располагаю я такъ, что студенты

184
мои въ одно и то же время бываютъ слушателями и препода-
преподавателями. По сему правилу поручилъ я прсдъ окончашемъ курса
старшему Лобачевскому предложить подъ мопмъ руководствомъ
пространную и трудную задачу о кругообращеиш (Rotation),
которая мною для себя уже была но Лаграижу въ удобопонят-
номъ внд'ь обработана. Въ то же время Симонову приказано
было записывать течеше преподавашя, которое я въ четыре
npiena кончилъ, дабы сообщить его прочпыъ слушателямъ. Но
Лобачевскш. не пользовавшись сею запискою, ири окончанш
последней лекцш подалъ мн4 р&шеше сей столь запутанной
задачи, на нЗзсколькихъ лпсточкахъ въ четвертку написанное.
Г. акадеыикъ Вишневскш, бывпнй тогда зд^сь, неожиданно вос-
хищенъ былъ симъ иебольшпмъ оиытомъ зпанш нашихъ сту-
дентовъ».
Эти усийхи въ математик^, за которые ЛобачевскШ полу-
чилъ вмйстт, съ другими благодарность отъ министра народнаго
просв'Ьщешя, и были причиною снисходительности къ нему со-
совета, возведшаго его вмести съ прочими въ степень магистра,
т. е. оставившаго его при университет^ (въ педагогпческомъ
пнститут'Ь) съ цт,лью приготовлешя къ профессорскому звашю.
Внрочемъ Лобачевсшй созналъ свое положете. «Вчера по поз-
волен1ю явившись въ сов&тъ, ппшетъ Яковкинъ, оказалъ со-
совершенное нризнан1е и раскаяше въ прежпихъ своихъ постуи-
кахъ, публично об'Ьщавши совершенно исправиться, а по сему
сов^тъ и решился его иом^стать въ число представляемыхъ
къ удостоен!ю зван1я магистровъ, дабы излишнею строгостью
не привести его, какъ весьма лестную надежду даровашямп
и успехами подающаго для университета, въ отчаяше и не
убить духъ его» A2 голя 1811 года). Защитниками Лобачев-
скмго въ coBfei были профессоры Бартельсъ, Германъ, Лит-
тровъ и Броннеръ.
Попечитель Казанскаго учебнаго округа Румовск1Й утвердплъ
представлен1е совета, но далъ съ своей стороны предостереже-
предостережете Лобачевскому: «А студенту Николаю Лобачевскому, — ни-
салъ онъ въ своемъ иредложенш сов-Ьту G августа 1811 г.,
№ 787),—занимающему первое мгЬсто по худому поведенш, объ-
явпть мое сожалгЬн1е о томъ, что онъ отлпчныя свои способ-

186
ностп номрачаетъ несоотвгЬтственньшъ поведегйемъ, и для того,
чтобы онъ постарался переменить п исправить оное,—въ про-
тпвноыъ случат,, если онъ совъ-толъ моимъ не захочетъ восполь-
воспользоваться, п опять принесена будетъ жалоба на него, тогда я
прппужденъ буду довести о томъ до свЪдъ-шя г. министра про-
св'Ьщешя».
Зваше магистра возлагало на него, по тогдашнимъ прави-
ламъ, «спосп'Ьшествоваше профессору или адъюнкту въ разсу-
ждеше большнхъ усп^ховъ ихъ слушателей». Магпстры должны
были заниматься съ студентами повторешемъ пройденнаго (не
въ часы, однако, назначенные для лекцШ) п объяснешемъ слу-
шателямъ того, что они не ионнмаютъ, такъ какъ Miioric пзъ
гг. профессировъ преподаюсь п объясняюсь лекцш на пностраи-
ныхъ языкахъ, слушатели же пхъ, преимущественно же вновь
поступление, часто, особенно въ начали курса, по прпчшгЬ
объяспешя на иностранномъ язык'Ь для матерш совс-Ьмъ повой,
не могутъ иногда всего понимать предлагаемаго профессором'!,
ясно». За это магистры получали жалованье. Лобачевстй какъ,
магпстръ, стоялъ въ самыхъ близкихъ отиошешяхъ къ Бар-
тельсу. Онъ занимался у него на дому по четыре часа въ не-
неделю, и у насъ есть свй-дйтя, что на первыхъ порахъ маги-
магистерства предметами пзучешя Лобачевскаго, подъ руководствомъ
Вартельса, были арпеметпка Гаусса и первый томъ Лапласовой
«¦Небесной механики».
Въ 1814 году Лобачевскш былъ повышенъ въ зван1е адъ-
адъюнкта чистой математики п началъ читать своп лекцш. Съ
1819 года, въ отсутств!е профессора астрономш Спмопова, на-
ходпвшагося въ кругосв^тномъ плаванш, ЛобачевскШ въ тече-
nie двухъ лгЬтъ чпталъ сверхъ того астронол1Ю п зав^дывач^ъ
обсерватор1ей.
Съ изсл^дован1ямп, которыя создаютъ новую эпоху въ
области геометрической науки, ЛобаческШ впервые выступплъ
въ зас4дан1п факультета 12 февраля 1826 года, гд4 онъ чп-
чпталъ свое «Exposition succincte des principes de la Geometrie»,
(«Краткое изложете началъ геометр1п»), которое, къ сожалгЬшю,
и до сихъ поръ напечатано не было. Статья «О Началахъ
Геометрш» была напечатана въ «Казансколъ BicrHUKi» за 1829

186
и 1830 годъ, и представляетъ только весьма сжатое, п потому
трудное для чтешя, изложете нолученныхъ пмъ результатовъ
ностроешя «Геометрщ въ болгЬе обширнолъ слшсл'Ь, нежели,
какъ намъ представплъ ее первый Евклидъ».
Въ сл'Ьдующемъ сочпнсш'п: «Воображаемая Геомет^'я», пе-
реведенномъ такл;е Fia французами: языкъ, Лобачевскгй, «оста-
«оставляя геометричесшя построешя п выбирая краткой обратный
путь», показываетъ, что ; главный уравнешя, которыя онъ па-
шелъ для зависимости сторонъ и угловъ треугольника въ во-
воображаемой Геометрш, могутъ быть приняты с,ъ пользою въ
Аналптпк-Ь и никогда ие приведутъ къ заклочешялгь ложнылъ,
въ какомъ бы то ни было отношенш».
Такимъ образомъ сд'Ьланное допущеше о повозлгожпостп до-
доказать ностулать Евклида было разобрано и изслъдовано какъ
геометрическимъ, такъ и аналитпческпмъ путелъ и ни къ ка-
кимъ протпвор'Мямъ не повело. Вопросъ о возможности не-
неверности одиннадцатой аксюмы Евклида былъ р^шенъ и ргЬ-
шенъ утвердительно. Но, съ одной стороны пршмъ, оказанный
первому сочинешю Лобачевскаго, загтавнлъ его «подозревать,
что его сочинете, казавшись съ перваго взгляда теипымъ, пре-
предупреждало охоту заняться ииъ съ н4которымъ внпмашелъ и
даже могло подать поводъ усуыниться въ строгости его сужде-
н1я и въ верности выведенныхъ заключенШ»; съ другой сто-
стороны косвенная аналитическая поверка не могла заменить стро-
гаго прямого доказательства. Поэтому ЛобачевскШ снова прпни-
мается ва изложеню того же вопроса и въ 1835—1838 годахъ
печатаетъ сочинен1е: «Новыя Начала Геометрш съ полной тео-
piefl параллельныхъ».
Пзъ двухъ остальныхъ его сочинешй по Геометрш первое:
«Beitriige zu den Parallellinien» представляетъ нисколько со-
сокращенное пзложеше «Новыхъ Началъ Геолетрги», а второе:
«Пангеометр1я», записанная подъ дпктовку уже слепого Лоба-
Лобачевскаго его учениками и изданная одновременно на русскомъ
и французскомъ языкахъ незадолго до его смертц, представляетъ
снова конспективное изложеше всЬхъ его шсл'Ьдовашй но Гео-
метрш. Это посл'Ь шее сочинен!?, несколько устунаетъ его ЛТо-
вымъ Началамъ Геометр1и», которыя можно считать лучгппмъ

187
изъ всЬхъ его произведете. По сшгЬ и изяществу пзложетя
«Новыя Начала Геометрш» мало ч4мъ уступаютъ «Началамъ»
Евклида, п по-истиие ыогутъ служить для Лобачевскаго «то-
nutnentum aere perennius, regalique situ pyramidum altius».
Тому, кто хочетъ поянакомиться съ работами Лобачевскаго, не-
необходимо начинать съ изучешя именно этого сочинешя.
Наряду съ ученой и преподавательской деятельностью шла
и высокоплодотворная административная деятельность Н. II. Ло-
Лобачевскаго. Онъ былъ деканомъ и 19 лт,тъ ректоромъ универ-
университета, несъ друпя разнообразный и сложныя обязанности по
управлешю. Вотъ какъ проф. Н. Н. Буличъ отзывается вообще
о деятельности и характере Лобачевскаго: «-Его независимый и
самостоятельный характеръ выдержалъ такую нравственную
ломку, какъ тяжелое время реакцш въ последше годы царство-
ван1я Александра I и попечительство въ Казани Магшщкаго,
не поступившись свошш убеждешями, не пзменивъ имъ и
унеся въ старость молодое стремлеше къ науке, укажете къ
ней и восторги духовнаго наслаждешя. Если специалисты гово-
рятъ о его «по-истипе глубокомысленныхъ лекп,1яхъ», доступ-
ныхъ однако только избранной аудиторш, въ последн1е годы
его жизни, то мы прибавнмъ къ этому личное воспоминаше о
его публичныхъ лекщяхъ по физике, где ему удавалось изла-
излагать науку популярно и где раскрывалъ онъ массу самыхъ
разнообрашыхъ сведен!й. Въ старые rayxie и спящ!е годы про-
вини,1и, когда все было такъ смирно, гладко и довольно кру-
голъ, когда одпообразныя явлен1я жизни только скользили по
дугае, не задевая и не возбуждая ее, таюя лекцш, какъ Ло-
Лобачевскаго, были отраднымъ явлешемъ. Лобачевск1й читалъ
просто, безъ желашя придать внЪшнюю красоту своей речи,
безъ реторической эмфазы и крика, но въ словахъ его слышался
и его логически улъ и широкое образоваше. Спокойнымъ, ров-
нымъ голосомъ онъ д'Ьлалъ своп широк1я обобщен1я, вызывалъ
увлекательные образы и возбуждалъ мысль»...
«Всего интереснее было бы проследить.—замечаетъ тотъ же
проф. Булпчъ, — какпмъ образомъ развилось его глубокое аб-
абстрактное мышлеше. Лобачевсшй не бывалъ въ Европе- две-
три иоездки въ руссшя столицы были кратковременны; онъ

188
почти не осташгалъ Казани. Къ сожалЬнш, и внутреннее раз-
витае и интимная жизнь Любачевскаго мало известны, несмотря
на то, что живы еще некоторые, бывипе съ иимъ въ блпзкнхъ
отношешяхъ. Принадлежа ио женъ- къ тому, что называлось
въ то время казансюшъ обществомъ, Лобачевапй появлялся и
въ немъ, но нредотавлялъ 1шъ себя скор-Ье задумчивую, чгЬмъ
д-Ьятсльную фигуру, особенно вь послъ'дше годы своей жизни.
Сколько намъ известно, даже блпзйе къ нему люди смотрели
на него съ точки зр'Ьшя, раскрывающейся въ обыденной мо-
морали Хемницеровой басни <Метафизикъ».
Какъ же относились современники къ научной деятельности
Лобачевскаго, главное—къ его геомстрическилъ пзсл'вдовашямъ,
составляющпмъ ньпгЬ славу и гордость русской математической
науки? На этотъ счетъ сохранились также весьма любопытный
свидетельства. Въ Poccin работы его были встречены... глу-
млешемъ. Въ № 41 распространеннаго тогда журнала «Сынъ
Отечества» за 1834 годъ появилась статья, оскорбительная для
Лобачевскаго. Но отвъ-тъ его на яту статью, по сообщешю са-
самого Лобачевскаго, наиечатанъ не былъ.
Статья въ «Сын'Ь Отечества» носить заглавп*: «О начертатель-
начертательной Геометрш соч. Г. Лобачевскаго» и содержптъ критичесый
отзывъ о сочнненш Лобачевскаго: «О Началахъ Геометрш». Для
лучшей характеристики впечатлгЬи1я, ироизведеннаго сочинен1емъ
Лобачевскаго на совроменныхъ ему русскнхъ математиковъ сл4-
дуетъ привести здгЬсь nuTepecHifiinia мътта названной статьи
въ подлшшомъ вид!;. Вотъ они:
«Есть люди, которые, прочитавъ иногда книгу, говорятъ:
опа слишкомъ проста, слншкомъ обыкновенна, въ ней не о чемъ
и подумать. Такпмъ любителялъ думанья совйтую прочесть Гео-
метр1ю Г. Лобачевскаго. Вотъ ужъ подлинно есть о чемъ поду-
подумать! Mnorie пзъ иервоклассныхъ нашпхъ мателатпковъ читали
ее, думали и ничего не понялп. ПослгЬ сего уже не считаю
нужныиъ упоминать, что и я, продумавъ надъ сею книгою нгЬ-
сколько времени, ничего не придумалъ, т. е. не поиялъ почти
ни одной мысли. Даже трудно было бы понять и то, какимъ
образомъ г. Лобачевсшп пзъ самой легкой и самой ясной въ
математики науки, какова Геометр1я, могъ сделать такое тяже-

189
лое. такое темное и непроницаемое учете, если бы самъ онъ
отчасти не надоумнлъ насъ, сказавъ, что его Геометр1я отлична
отъ употребительной, которой вс/Ь мы учились, и которой, ве-
вероятно, ужъ разучиться не ыожемъ, и есть только воображае-
воображаемая. Да, теперь все очень понятно. Чего не ыожеть представить
воображеше, особлшю жпвое и вм'ЬстЬ уродливое? Почему не
вообразить, напр., черное бйльыъ, круглое четыреугольиымъ, сумму
вс'Ьхъ утловъ въ нрямолпнейномъ треугольнике меньше двухъ
прямыхъ п одинъ и тотъ же определенный интегралъ равнымъ
то —, то со У Очень, очень можно, хотя для разума все это п
непонятно. Но спросятъ: для чего же писать, да еще и печа-
печатать талия натЬпыя фантазш? Признаюсь, на этотъ вопросъ
отвечать трудно. Авторъ нигде не наыекнулъ на то, съ какою
ц'Ьлью онъ напечаталъ cie сочпнеше, и мы должны, следова-
следовательно, прибегнуть къ догадкамъ. Правда, въ одномъ месте
онъ ясно говорить, что будто бы недостатки, замеченные пмъ
въ употребляемой доселе Геометрш. заставили его сочинить и
издать эту новую Геометрш; но это, очевидно, несправедливо,
п по всей вероятности сказано для того, чтобы еще более скрыть
настоящую цель его гочпнетя. Бо-нервыхъ, это противоречить
тому, что сказалъ самъ же авторъ о своей Геометрш, т. е. что
она въ природе вовсе не существует^ а могла существовать
только бъ его воображенш, я для изм$решй на самомъ деле
остается совершенно безъ употреблешя; во-вторыхъ, это действи-
действительно противоречить всему тому, что въ ней содержится, н
судя по чему скорее можно согласиться на то, что новая Гео-
Геометрия выдумана для опровержешя прежней, нежели для попол-
иешя оной. При томъ же, да позволено намъ будегь несколько
коснуться личности. Какъ можно подучать, чтобы г. Лобачев-
ск1Й, ординарный ирофессоръ математики, наппсалъ съ какою
нибудь серьезною ц!шю книгу, которая пе много бы принесла
чести и последнему приходскому учителю. Если up ученость, то по
крайней мере здравый смыслъ долженъ иметь каждый учитель, а
въ новой Геометрш нередко недостаетъ и сего нослйдняго».
«Соображая все cie, съ большою вероятностью заключаю,
что истинная цель, для которой г. Лобачевскш сочпнплъ п нздалъ.

190
свою Геометрш, есть просто шутка, или, лучше, сатпра на уче-
ныхъ математиковъ, а можетъ быть и вообще на ученыхъ со-
сочинителей настоящаго времени. За спмъ и уже не съ вФроятно-
стш только, а съ совершенною увйренноспю полагаю, что бе-
безумная страсть писать какимъ-то странньшъ и неразумитель-
ньшъ опразомъ. весьма заметная съ н^котораго времени во мно-
гпхъ пзъ иашихъ писателей, и безразсудное желает е открывать
новое при талантахъ, едва достаточныхъ для того, чтобы надле-
жащимъ обраяомъ постигать старое, суть два недостатка, кото-
которые авторъ въ своемъ сочиненш нам'Ьренъ быль изобразить и
изобразить какъ нельзя лучше.
«Во-первыхъ, новая Геометр1я, какъ я уже упомянулъ о томъ
выше, написана такъ, что никто изъ читавшихъ ее почти ни-
чего не понялъ. Желая покороче познакомить васъ съ нею, я
собпралъ въ одну точку все мое вшшате, приковывалъ его къ
каждому перюду, къ каждому слову п даже къ х;аждой букв'Ь,
и при всемъ томъ такъ мало успЬлъ прояснить мракъ, кругомъ
облегающш это сочинеше, что едва въ состоянш разсказать вамъ
то, о чемъ въ немъ говорится, не говоря ни слова о томъ, что
говорится. Авторъ говоритъ, кажется, что-то о треугольникахъ,
о зависимости въ нихъ угловъ отъ сторонъ, ч'Ьмъ гдавнъ-йшимъ
образомъ и отличается его Геометр1я отъ нашей; потомъ пред-
лагаетъ новую теорш параллельныхъ, которая, по собственному
его лризнаню, находится или н4тъ въ прпрод'Ь, никто доказать
не въ состоянш; наконецъ, слФдуетъ разсмотргЬп1е того, какимъ
опразомъ въ этой воображаемой геометрш определяется величина
кривыхъ лиши, площадей, крпвыхъ поверхностей п объемовъ
тъ\иъ,—и все это, еще разъ повторяю, написано такъ, что ни-
ничего и понять невозможно».
«Во-вторыхъ, въ конце книги г. Лобачевсшй помъстплъ два
определенные интеграла, которые онъ открылъ мимоходомъ,
идя прямо къ своей цзьли дать общгя правила для тмгъреигя
ваьхъ геометрическихъ величинъ и дозволивши себгь только
нгькоторыя прим?ънетя. Открьше весьма замечательное! Ибо
одинъ изъ сихъ новкхъ пнтеграловъ уже давно известенъ, и
находится гораздо легчайшимъ образомъ; другой совершенно не-
веренъ, потому что ведеть къ той нелепости, которую мы уже

191
заметили выше, т. е. что одинъ и тотъ же определенный инте-
гралъ равенъ то -г, то оо. Но не таковы лп и въ саыомъ д'ЬгЬ
большею частш бываютъ прославляеыыя у насъ новооткрытая?
Не часто ли случается, что старое, представленное только въ
какоыъ нибудь странномъ образй, выдаютъ намъ за новое, или
п новое, но ложное за чрезвычайно важное открьше? Хвала
г. Лобачевскому, принявшему на себя трудъ обличить съ одной
стороны наглость и безстыдство ложныхъ изобретателей, съ дру-
другой простодушное нев'Ьжество почитателей ихъ новоизобр'Ьтешй».
«Но, сознавая всю цйну сочппетйя г. Лобачевскаго, я не могу
однакожъ не попенять ему за то, что онъ, не давъ своей книги
надлежащего заглавш, заставилъ насъ долго дргать понапрасну.
Почему бы вместо заглав1я: «О началахъ Геометрш», не напп-
сать иаприл'Ьръ — Сатира на Геолетрш, Карикатура на Гео-
Геометрш или что иибудь подобное? Тогда бы всякш съ перваго взгляда
видЪлъ, что это за книга, и авторъ изб'Ьжалъ бы множества
невыгодныхъ для него толковъ я суждешй. Хорошо, что мн'Ь
удалось проникнуть настоящую цъмь, съ которою наппсапа эта
книга,—а то, Богъ знаетъ, что бы и я о ней и ея авторй ду-
ма№. Теперь же думаю и даже ув4ренъ, что почтенный авторъ
почтетъ себя весьма мн4 обязаннымъ за то, что я показалъ
истинную точку зрФшя. съ которой должно смотреть на его со-
чпнеше»...
Такими глумлешяыи встречали руссме современники плоды
глубокихъ изыскан1п великаго ума. И есть весьма вгЬсмя осно-
вап1я думать, что приведенная выше въ отрывкахъ статья въ
«Сын'Ь Отечества» прннадлежитъ не какому либо диллетанту, а
«глубокоученоиу» российскому того времени академику. Известно
также, напр., что талантливый русски математикъ того времени,
Остроградсмй, открыто насмъ-хался надъ изыскан1ями казанскаго
профессора. Заграницей работы Лобаческаго были большпнствомъ
ученыхъ просто не замечены. Только отъ орлпнаго взора великаго
Гаусса не укрылась вся важность изыскашй скромнаго русскаго
провиннтльнаго профессора. Но Гауссъ сообщплъ объ этомъ
только въ частномъ письмй къ Шумахеру въ 1846 году. Вотъ
это историческое письмо:

192
«Въ последнее время я тш'Ьлъ случай перечитать неболь-
небольшое сочинеше Лобачевскаго подъ заикшеяъ: Geometrische Unter-
sucliungen zur Teorie der Parallellinieii. Это сочпнеше содержитъ
въ ce6i основашя геометрш, которая должна бы была суще-
существовать, п строгое развит которой представляло бы непрерыв-
непрерывную цтль, если бы Евклидова геометрия не была истинною. Никто
Швсйкартъ далъ этой геолетр1п гаш «geoinetrie australe», a
Лобачевсмй—геометрш воображаемой.
«Вы знаете, что уже пятьдесятъ четыре года (съ 1792), какъ
я разделяю т4 же взгляды, не говоря здъть о нътюторыхъ раз-
вийяхъ, который получили мои идеи объ этомъ предмет'! впо-
слйдгтвш. Следовательно, я собственно не нашелъ въ сочиненш
Лобачевскаго ни одного новаго для меня факта; но изложешс
весьма различно отъ того, какое я •нрет.полагалъ сделать, и
авторъ трактуетъ о предмет!;, какъ зпатокъ. въ истгтно-гео-
метрическомъ dyxib. Я считалъ себя обязаннымъ обратить ваше
внимате па эту книгу, чтеихе которой не ирешшетъ вамъ до-
доставить живМшее удовольств!е».
Гетингенъ, 28 ноября 1846 года.
Зналъ ли что-либо объ этомъ писыгЬ Гаусса ЛобачевскШ,
уже вступивши въ последнее десятштЬтае своей жизни? Трудно
дать утвердительный ответь. Переписка Гаусса съ Шумахеромъ
была опубликована много позже смерти Лобачевскаго. Нашъ же
«Коперникъ Геометрш», по выражешю англ1йскаго ученаго
Клиффорда, уыеръ въ 1850 году 12 февраля. Пргоиаше и
оц'Ьнка его заслугъ прпнадлежитъ послФдиимъ 2—3 дссяттгё-
тямъ, когда понпыашю и уясненхю его ген1а.1ьныхъ мыслей
бьыа посвящена ц4лая литература.
Понпыашю Лобачевскаго въ особенности содействовали
своими трудами таше выдающ1еся ученые, какъ Бельтрамп,
Риманнъ, Гельмгольцъ, Кули, Гуэль, Клейнъ, Клиффордъ, Ли,
Пуанкаре, Киллингъ и проч...
22 октября 1н!K года Россия, или, Bipn'be,—вс4 русск!я
(|)п31гко-мателатпче<Ж1я общества торжественно справляли 100-
лЬтяш поминки дня рождеи1я Лобачевскаго. Незадолго до этого
времени Казансшй университетъ издалъ «Полное собраше со-

193
чииешй по геометрш Н. II. Лобачевскаго» въ 2-хъ томахъ
A883 п 1886 гг.), но въ самомъ д4л4 «Полнаго собранья»
всЬхъ безъ псключешя сочинешй великаго русскаго «Копер-
«Коперника Геометрш» нт/гъ,—да и будетъ ли скоро?.. Въ оощемъ,
надо сознаться, что Лобачевскому па Руси «везетъ» гораздо
ыен'Ье, чъ-мъ заграницей. ПроявпвшШся было къ юбилею 1893
года интересъ къ Лобачевскому въ широкихъ кругахъ скоро
ослабъ. Были собранш различныхъ обществъ, были дйльныя,
красивыя р'Ьчи, но... «облетали цвФты, догорали огни» и... все
почти остается по старому,—и это въ то время, какъ изыска-
шя Лобачевскаго о параллелышхъ лшпяхъ приняты, напр.,
въ японскихъ школахъ въ качеств^ пособ1я при преиодаванш
геометрш. Слйдуетъ, положимъ, сознаться, что чтете многихъ
ироизведенш Лобачевскаго въ подлинник^ требуетъ довольно
значительной подготовки. Ллбачевсмй, вообще, кратокъ и сжатъ.
Но, съ другой стороны, ничего иочти не сд'Ьлано до сихъ поръ
у насъ къ поиуляризацш работъ Лобачевскаго въ смысли пе-
реложешя ихъ на бол'Ье понятный современный математически
языкъ. Единственную достойную внимашя попытку въ этомъ
отношеиш мы нашли въ работф Н. П. Соколова: ъЗиачете
изелгьдовангп Н. И. Лобачевскаго въ Геомвтрт и ихъ влгяте
на ея дальнейшее развитге».
Талантливый авторъ въ этой книг1}; Д'Ьлаетъ попытку изло-
изложить по возможности кратко и популярно содержаше главнаго
сочинешя Лобачевскаго «Новыя Начала Геомотр1я». Нельзя не
ирив'втствовать такой попытки, какъ нельзя не пожалеть и о
томъ, что г. Соколовъ не продолжалъ своихъ трудовъ къ даль-
дальнейшей и еще большей популяризации трудовъ Лобачевскаго.
Во всякомъ случай ближе къ концу этой книги читатель пай-
детъ содержшие «Новыхъ Началъ Геометр1и» Лобачевскаго въ
пзложенш Н. П. Соколова. Быть можетъ, чтен1е этой главы
заинтересуетъ кого-либо настолько, что направитъ его на путь
изучешя подлинпыхъ трудовъ Лобачевскаго для широкой попу-
ляризап^п его идей.
ВЪ ЦАРСТВВ СМЕКАЛКИ.	13

194
Два письма о постулатЪ Евклида.
Какъ разъ въ то время, когда въ старой губернской назап-
ской глуши Н. П. Лобачевсшй уже рФшилъ п обнародовалъ
свое р'Ьшеше относптельио места и значешя въ геометрш 11-ой
аксшмы (постулата) Евклида, известные европейоше ученые
все еще д4лалп тщательныя попытки «доказать» это Евкли-
довское допущеше. Авторитетъ Евклида былъ еще настолько
велпкъ, что никто не осмеливался подозревать о возможности
геометр1и п пространства, отличныхъ отъ Евклидовскихъ. Все
д'Ьло заключалось только, по ын'Ьшю тогдапшпхъ ученыхъ, въ
возможномъ упрощети < Началъ» александрпкжаго геометра. —
въ стремлешп изложить теорш параллелышхъ лшнй безъ зна-
меиитаго постулата. Нижеприводимое письмо (отъ 1831 г.)
проф. Шумахера къ Гауссу даетъ настолько типичный образ-
чпкъ подобиыхъ попытокъ, что приводимъ его въ подлпнномъ
персвод'Ь:
Шумахеръ къ Гауссу.
Я беру на себя смелость представить вамъ попытку, кото-
которую я сдйлалъ, чтобы доказать, безъ помощи теорш паралле-
параллелей, нредложеше, по которому сумма трехъ угловъ треугольника
равна 180°, — откуда вы-
-Н	текало бы само собою до-
доказательство Евклидовой
аксюыы. Едпнственныя тоо-
ремы, которыя я предпо-
предполагаю доказанными, суть:
что сумма всЬхъ угловъ,
образуемыхъ около одной
ч	N точки, равна 360° пли че-
тыремъ пряиымъ угламъ,
п еще, что углы, противоположные въ вергапн-Ь, равны.
Продолжпиъ неопределенно стороны прямолннейнаго тре-
треугольника ЛВС (черт. А), плп, другими словами, разгаготршгь
систему трехъ прямыхъ въ одной плоскости, которыя своими

196
пересеченьями образуютъ треугольникъ ABC. При трехъ вер-
ппшахъ изгЬеыъ уравнешя:
откуда
Такъ какъ эти соотношешя существуютъ, какъ бы ни были
расположены точки А, В и С, или, что все равно, какъ бы
ни были проведены три прямыя въ плоскости, оставпмъ непо-
неподвижными лиши DG, ЕН и
заставиыъ лишю IF проходить
черезъ точку А (черт. В) такъ,
чтобы она составляла съ ЕН
тотъ же самый уголъ, какъ и
въ первоиачальноыъ своеыъ по-
ложенш, пли вообще,— такъ какъ
этотъ уголъ произволенъ,—такъ,
чтобы лншя IF всегда шла вну-
внутри угла. Мы будеыъ иметь тогда
п -f- Ъ -j- С == 4:d.	Черт. В.
Следовательно
Можетъ быть, возразятъ на это, что хотя и пмееыъ по
предположение)
Ъ (черт. А) = 6 (черт. В),
но что равенство:
с (черт. А) = с (черт. В)
должно быть доказано.
Мн-Ь кажется однако, что. вслйдгтгае произвольной величины
угловъ, въ этоыъ доказательств^ н4тъ необходимости.
Таковы начала доказательства, о котороыъ я жду вашего
отзыва. Я прибавлю только въ оправдаше моего разеуждешя,
что, хотя второе д'Ьйствхе и уничтожаетъ треугольникъ АВС}
13*

196
но оно не уничтожаетъ угловъ треугольника. Какъ бы ни были
расположены лиши, всегда имЪемъ:
1ВН=$, GCF=f, DAE=a,
какъ въ конечиомъ треугольники, такъ и въ исчезающем.;
гумна:
IAH+GAF+DAE
всегда равна, следовательно, суммъ1 угловъ пряыолииейпаго
треугольника.
Такимъ образомъ докажемъ нредложеше для произволь-
наго треугольника (котораго углы суть А, В, С), проводя ли-
лиши DG, ЕН такъ, чтобы было а = А, и дъ-лая крпы'Ь того
1АН=В и GAF= С. Если бы тогда IAF оказалась не пря-
прямою, но ломаною лишею IAF\ то уголь с сдтдася бы меньше
на dc; но уголъ Ъ сталъ бы на ту же величину больше, такъ
что сумма этихъ угловъ осталась бы безъ перемены, и мы
им4ли бы,—что намъ и требуется для доказательства,—равен-
Ъ-\-с (черт. А) = & + с (терт. В).
Копенгагенъ, 3-го мая 1831 года.
Гауссъ къ Шумахеру.
Разсматривая внимательно то, что вы мнй пишете о теорш
параллелей, я замечаю, что вы употребили въ вашихъ разеу-
ждешяхъ, не выразивъ его явно, следующее предложеше:
Если двЪ пересЪкающ!яся прямыя, (i) и B), обра-
зуютъ съ третьего прямою (з), ихъ встречающею, со-
соответственно углы А' а А", и если четвертая прямая
D), лежащая въ той же плоскости, будетъ пересе-
пересекать (i) подъ угломъ А', то та же прямая D) будетъ
пересекать B) подъ угломъ А".
Это предложеше не только требуетъ доказательства, но
можно сказать, что оно-то, въ сущности, и составляете ту тео-
теорему, о доказательств^ которой пдетъ р^чь.
Вотъ уже нисколько недель, какъ я началъ излагать пись-
письменно некоторые результаты моихъ собственныхъ размышленШ

197
объ этоыъ предмет^, занимавшихъ меня сорокъ лить тому на-
задъ и никогда мною не записалныхъ, волгЬдств1е чего я дол-
женъ былъ три или четыре раза возобновлять весь трудъ въ
моей головъч Мн4 не хотелось бы иднако, чтобы это погибло
вм'Ьстъ- со мною.
Гетингенъ, 17 мая 1831 года.
Отв4тъ Гаусса типиченъ въ томъ отношенш, что указы-
ваетъ на тотъ обыкновенный недостаток!., которымъ страдали
всгь безъ исключешя попытки доказать постулатъ Евклида, или
обойти его въ теорш параллельныхъ литй. Вместо этого по-
постулата авторы вводили незамгътно для самихъ себя какое-
нибудь новое, нуждающееся въ доказательств^, И1)едложеше.
Такъ было п съ Шумахеромъ.
Еъ крайнему сожалт.нш, до сихъ поръ ничего неизвестно
о томъ, остались ли, въ самомъ дгЬл4, въ бумагахъ Гаусса
хоть каше-либо наброски по этому поводу, какъ онъ пишетъ
въ своемъ письм'Ь.
Суть ошибки Шумахера еще лучше выяснится изъ даль-
нМшаго, гд4 о суммъ1 угловъ треугольника будетъ также при-
веденъ пзвФстнаго рода «софизнъ».

Выяснеше трехъ постулатовъ о параллелвныхъ
лин1яхъ.
Въ противоположность постулату Евклида, о которомъ мы
говорили въ глав'Ь «Два отрицательныхъ вывода XIX в'Ъка»,
Лобачевсий ставитъ иной, а именно:
Черезъ данную точку на плоскости можно провести
неопределенно большое число лиши, изъ которыхъ ни
одна не пересЬчетъ данной въ той же плоскости лиши.
Въ то же время еще одинъ постулатъ нъчмецкаго геометра
Риманна говоритъ, что
черезъ точку на плоскости нельзя провести такой
лиши, которая не пересекала бы данной линш въ этой
плоскости.
Отправляясь отъ каждаго изъ этихъ допущенш въ отдель-
отдельности, мы получишь три различныхъ системы геометрш на
плоскости. Раз-вгае этихъ геометрШ лучше всего выясняется
на слъ-дующемъ npiiM'bpi:
Фиг. 97.
Пусть АВ п PC (см. фиг. 97) будутъ дв'Ь прямыя липш.
лежа!щя въ одной л той же плоскости и неограниченно про-

199
должакящяся по обопмъ противоположпымъ направлешямъ. АБ
примемъ неподвижной п занимающей определенное положеше,
a PC пусть вращается въ плоскости около точки Р, напр.. въ
направление, принимаемомъ за положительное, т. е. обратно дви-
женш часовой стрелки, и пусть PC сначала пересЬкаетъ АБ,
какъ указано па фиг. 97. При дальпъ'йшеыъ вращепш лиши PC,
точка псресЬчешя уходитъ все далее и далее вправо и здесь
логически возможны три случая:
1) Вращающаяся лишя перестаетъ пересекать неподвижную
прямую АБ съ одной стороны (напр., справа) п тотчасъ же
непосредственно при продолженш вращешя пересЬкаетъ эту ли-
нш съ противоположной стороны (слива); 2) и.ш же литя PC,
переставъ пересекать АБ и продолжая вращаться въ некоторой
части плоскости до новаго пересечешя, совсемъ не встречается
съ лишей АБ; 3) или, наконецъ, наступптъ такой промежутокъ
времени, въ продолжсше котораго обе лиши будутъ одновременно
пересекаться въ двухъ иротпвоположныхъ паправлетяхъ.
Первая пзъ этихъ возможностей даетъ геометрш Евклида,
вторая—геометрш Лобачевскаго, а третья— геометрш Рпманна.
Иявестнымъ образомъ развиваемые п пршбретаемые нами
умственные навыки прпводятъ къ тому, что все три предыду-
Щ1я допущения мы последовательно пллюстрпруемъ довольно
своеобразнымъ путемъ, а именно съ помощью того опыт-
паю понятая о прямой линш, какое мы уже нмеемъ о ней.
Логически каждое изъ этихъ трехъ допущешй, повторяемъ, такъ
же допустимо, какъ и другое. Съ этой точки зрешя, строго
говоря, нетъ никакого основашя одно донущеше (постулата)
предпочитать другому. Психологически, однако же, выходить
такъ, что гипотеза Риманна представляется начпнающему совер-
совершенно недопустимою, п даже допущеше Евклида менее понятно,
чемъ допущеше Лобачевскаго.
Интересный опытъ въ этомъ отношеши былъ сделанъ амери-
канскимъ ыатематикомъ Уайтомъ (White) со своими начинаю-
начинающими курсъ «нормальной школы» учениками. Онъ начертплъ
на доске рпсунокъ, подобный фиг. 97. изложилъ простыли и не-
немногими словами все три допущешя и попросплъ каждаго изъ
учепиковъ высказать свое мнЗзше по поводу каждаго изъ посту-

200
латовъ, заппсавъ свой отзывъ на клочке бумажки. И вотъ ока-
оказалось, что 46 учениковъ (пзъ общаго числа 54) высказались
за верность второго дощ щешя, т. е. постулата Лобачевскаго.
Голоса этпхъ 46 поделились такъ: 2 заявили, что они «дога-
«догадываются», что должно быть такъ, а не иначе; 21, — что они
«думаютъ» такъ, 13 -въ этомъ «вполне уверены», 10—«зна-
ютъ» это. Что касается постулата Евклида, то за него выска-
высказались только остальные 8 пзъ 54 учениковъ и при томъ такъ,
что 6 изъ пихъ «думали», что ато допущете правильно, а два
были въ этомъ «вполне уверены». Интересно отметить обсто-
обстоятельство, что среди зтихъ не искусившихся еще ни въ какихъ
софистическихъ изворотахъ умовъ не нашлось ни одного, кото-
который бы высказался за щлемлемость допущешя Ряманна. Пони-
иате его, очевидно, требуетъ нисколько более повышепнаго
математпческаго развипя. Въ свою очередь, большая часть сто-
ропниковъ большинства, нодавгааго голоса за 2-е предиоложеше
(Лобачевскаго), обнаружили склонность переменить свое мнете,
какъ только они узнали, что это предположеше сводится къ
тому, что дв4 пересекающаяся прямыя могуть быть одновременно
параллельны одной п той же прямой. Во всякомъ случае выше-
вышеизложенное свидетельствуешь о томъ. что постулата Евклида не
гогЬетъ по форме характера убедительности даже для неиску-
шеннаго ума.
Обращаясь къ тригонометрт, возьмемъ лпнш, дающую
значешя тангенсовъ центральнаго угла при возрастанш это1ло
угла отъ 0 до 90°. При величине угла въ 90° тангепсъ его,
какъ известно, равенъ оо (безконечности). Но какъ только вра-
щающался сторона угла перейдетъ хотя бы безкопечно мало за
(левее) значеше 90°, мы прингшаемъ, что она тотчасъ же пере-
пересекается съ лишей тангенсовъ на безконечно далекоыъ раз-
стоян1и, но въ противоположное направлешп (внизу), че>гъ
раньше. Это именно допущен1е п обопювываетъ, следовательно,
нашу тригонометр!ю на началахъ Евклида, а не шгахъ.
Знаменитый астрономъ Кеплеръ ввелъ определен1е парал-
лельныхъ, какъ лтт, встречающихся въ безкоиечности.

201
Такпмъ определешслъ можно пользоваться, пожалуй, даже въ
элементарной геометрш; необходимо только правильно понимать
его п съ этой целью перевести на языкъ такъ называемой
meopiu предпловъ.
Пусть лишя (фиг. 98) РР1 будетъ перпендикулярна къ SQ
и иусть точка Q движется все далее п далее вправо въ то
время, какъ точка Р остается неподвижной, и пусть, наконецъ.
утшъ Р'РВ будетъ предать, къ которому приближается уголъ
P'PQ при безпредт,льномъ возрастали! разстояшя Q отъ Р'. Въ
р
Фиг. 98.
такомъ случай PR есть лпшя, параллельная SQ. То есть парал-
параллельность приписывается предельному положенш пересЬкаю-
щихся лпн1Й, когда точка переоъчешя уходить въ безконечность.
Это попяйе мы п выражаемъ коротко известными словами, что
«параллельный прямыя встречаются въ безконечности».
Возвращаясь къ нашимъ тремъ постулатамъ, предположпмъ
(см. фиг. 98), что точка Р неподвижна, a PS передвигается
такъ, что точка S уходитъ безпредйльно влгЬво, при чемъ, при
безпределыюмъ возрасташл P'S уголъ 1РР1 будетъ пред'Ьломъ
для угла SPP. Въ такомъ случа-Ь ТР есть лишя, параллельная
SQ. Птакъ:
Согласно съ постулатомъ Евклида РТ и PR составляют,
одну прямую линго:
Согласно Лобачевскому, обе эти нрямыя могутъ предста-
представлять п некоторую ломаную линю.
Наконецъ, по допущенш Рпманна, Q и 8 не могутъ уда-
удалиться на безконечное пространство (но Q переходитъ, такъ
сказать, чрезъ значен1е S опять къ Р'), а это, по понят1ямъ
Teopin пределовъ, не есть предельное положеше и. следова-
следовательно, но параллельная лпшя въ Евклидовскомъ смысле этого
слова.

202
Сумма угловъ треугольника.
Изв-Ьстная теорема о суммъ- угловъ треугольника во веЬхъ
учебникахъ геометрии доказывается па огнованш теореиъ о парал-
лельныхъ литяхъ. Но мы зиаомъ уже (си. предыдущую главу),
что въ теорш параллельныхъ есть одно не могущее быть дока-
занньшъ допущеше—знаменитый Евклидовъ постулатъ. Следо-
Следовательно, строго говоря, и теорема о суши угловъ треугольника
оказывается недоказанной.
Но вотъ другое «очепь простое» доказательство этой важней-
важнейшей теоремы,—доказательство, которое, казалось бы, должно по-
положить конецъ всЬмъ сомнгЬшямъ и спорамъ.
Пусть сумма угловъ треугольника равна не двумъ прямымъ,
а какой-нибудь еще неизвестной пока величине, которую обо-
значимъ черезъ х. Проведемъ въ треугольнике ABC линш СЛ,
соединяющую вершпну С съ
произвольной точкой основашя.
Имеемъ два новыхъ треуголь-
треугольника ADC и ВВС. Сумма уг-
угловъ каждаго изъ нпхъ равна х,
а сумма этихъ суммъ = 2х. Ясно,
что если отъ этой суммы отнять
углы 1 и 2 (т. е. 2fZ), то получится сумма угловъ треугольника
ABC. Следовательно, мы въ праве написать уравнеше
2ж — Id = х,
откуда х = 2d, другими словами: сумма угловъ треугольника
равна двумъ прямымъ.
Правильно ли это доказательство? Конечно, нетъ. Это не
болгЬе, какъ софизмъ, и мы сейчасъ укажемъ, где зд^сь кроется
ошибка.
Ходъ доказательства совершенно въ-ренъ, по съ самаго же
начала сделано было бездоказательное допущеше. Вспомнпмъ.
что мы приравняли сумму угловъ всякаго треугольника неиз-
неизвестной величине х. Хотя, казалось бы, мы ничего этпыъ не
предрешаемъ, но на самомъ дг1;ле мы утверждаемъ заранее, что

203
сумма угловъ одинакова у встхъ треугольником, — другими
словами, что она есть величина постоянная. Между тгЬмъ въ
этомъ-то и заключается весь вопросъ. Если бы было доказано,
что у всЬхъ треугольниковъ, разной формы и размйровъ, сумма
угловъ остается постоянной,, то ужъ не трудно было бы, какъ
мы видели, доказать, что постоянная эта есть именно 2d, а не
какая-либо другая.
Итакъ, выше мы доказали не ту теорему, которую брались
доказать, а иную:
если сумма угловъ треугольника есть величина постоян-
постоянная, то она равна 3d.
Эта новая теорема, которую мы случайно и неожиданно для са-
михъ себя доказали, не совсЬмъ, однако, безполезна: она поможетъ
намъ кое-что уяснить въ области не-Евклидовыхъ геометр1й.
Для этого мы'сначала иерефразируемъ эту теорему,— вы-
скажемъ то, что въ геометрш называется теоремой «обратной
противоположной». Получимъ:
если сумма угловъ треугольника не равна 2d, то она не
есть постоянная величина.
Какъ и все «обратныя противоположной», теорема эта
должна быть вйрна, разъ вйрна прямая теорема. Да и въ са-
момъ д^л'в, если бы сумма угловъ Д-ка была величиной по-.
стояшюй, то, согласно прямой теоремф, она равнялась бы 2d,—
что противоречите ус,гов1ю.
Отсюда сразу получается очень важный выводъ. Мы знаемъ,
что въ геометрш Лобачевскаго сумма угловъ треугольника меньше
2d, а въ геометрш Риманна больше 2d,—т. е. и въ томъ п дру-
гомъ случай она не равна 2d. Пользуясь нашей теоремой, мы
заранее уже, не зная деталей этихъ не-Евклидовыхъ геометрш,
можемъ утверждать, что въ этихъ геометр1яхъ сумма угловъ
треугольника есть величина переменная. Въ этомъ-то непо-
стоянствгЬ суммы угловъ треугольника и заключается характер-
характерное отливе упомянутыхъ не-Евклидовыхъ геометрШ. Не то важно,
что сумма угловъ Д-ка больше пли меньше 2d, а то, что она
вообще не есть величина постоянная.
Итакъ, вотъ чему научило насъ разсмотр4ше приведенная)
выше софизма:

204'
1)	Въ Евклидовой геометрш сумма угловъ треугольника есть
величина постоянная и равня Id.
2)	Въ геометрш Лобачевскаго и Рлианпа сумма угловъ тре-
треугольника не есть величина постоянная.
Задача 68-я.
№сколько «коварныхъ» вопросовъ.
Какое число делится на всякое другое число безъ
остатка?
* *
*
Можетъ ли дробь, въ которой числитель меньше
знаменателя, быть равна дроби, въ которой числитель
больше знаменателя? Если н-втъ, то какъ же
*
Бъ пропорщи:
+ 6 : —з = —ю:+5
каждый изъ крайнихъ членовъ не больше ли, чъ-мъ-
каждый изъ среднихъ? Что же сделалось съ извЪст-
нымъ намъ «правиломъ», что въ пропорщи «бблышй
членъ такъ относится къ меньшему, какъ болышй же
къ меньшему»?
* *
*
Можно ли написать равенство, что
полуполный стаканъ = полупустому стакану?
Есть ли на свътЪ люди съ одинаковымъ числомъ
волосъ на голове?

206
О четвертомъ измЪренш по аналогш.
Аморпкаисшй математикъ W. F. White разсказываетъ объ
пнтересномъ вопросЬ, который предложить ему одпнъ нзъ его
слушателей въ нормальной школ'Ь, п передаетъ свой отв'Ьтъ
на него.
Вопросъ. Если сл'Ьдъ движущейся точки (не имеющей изм4-
ренШ) есть лишя (одно изм^рете), а сл'Ьдъ движетя лиши
есть поверхность (два изм^ретя), наконецъ, сл'Ьдъ двнжешя
поверхности есть гЬло (три измйретя),— то почему же не за-
заключить, что сл'Ьдъ движетя тгЬла есть величина четвертаго
измйретя?
Отвгътъ. Если бы ваши нредположетя были вфрны и со-
совершенно точны, то по аналогш могло бы быть вфрнымъ заклю-
чен1е. Путь движущейся въ пространств^ точки есть, действи-
действительно, лпн!я. Слтдъ движешя лин1и даетъ поверхность, но за
исключетемъ случая, когда лишя движется въ своемъ собствен-
номъ изм'Ьренш,—скользитъ, такъ сказать, по своииъ собствен-
нылъ елтдаиъ. Сл'Ьдъ движетя поверхности даетъ тйло, но
только въ тоыъ случай, когда поверхность движется не въ сво-
пхъ двухъ, а въ новомъ, третьемъ, измгЬрен1и. Образованге ве-
величины четвертаго измйретя движенгелъ т^ла предполагает^
следовательно, наличность этого самаго четвертаго измйретя, по
которому т'Ьло могло бы двигаться.

Въ странй чудесъ математики.
Во время своего пребывашя на курсахъ Елена полюбила
математику и делала въ ней болыше ycnfen. Одну изъ лекш'п
профессоръ какъ-то посвятилъ выяснен! ю понятая о простран-
ствт, п - измйрешй, а незадолго передъ этимъ дона Елена
прочла, по его совъ-ту, очень интересную небольшую книжечку
«.Страна плоскости. Разсказъ изъ области многихъ измгърент».
Вернувшись съ зацяйй въ жаркое майское утро, молодая
девушка сила въ легкое кресло-качалку п съ удовольств!емъ
отдыхала. Тихое покачпванье качалки навивало на нее легкое
полузабытье, а въ головгЬ мелъкшш одна за другой геометри-
чесшя фигуры: прямыя, кривыя линш, круги... Въ последнее
время среди студентовъ предметомъ упражнетй и оживленныхъ
обсужден1й были кривыя лиши, носивипя поэтическое назван!е
«irbnefi маргаритокъ».
—¦ Какая она длинная, эта лшпя!—думала Елена. — По-
Пожалуй, что ей нъ-тъ конца... Въ д4тствф я читала книжку «Въ
странф чудесъ» п помню, что- послФ того я несколько ночей
видФла во снф, какъ путешествую но этой странй. Вотъ, если бы
сделаться опять маленькой девочкой, попасть въ страну чудесъ
п тамъ найти концы «маргариткпныхъ цгЬпей». Но возможно лп
это? У круга, напрпм'Ьръ, и4тъ конца, какъ известно. Можетъ
быть, я щ)ишла бы къ безконечнымъ вфтвямъ кривой,..

207
Вдругъ Елена очутилась па узенькой тропинки, почти за-
закрытой большими деревьями. Она пошла по этой тропинки и
пришла въ большую тронную залу, гд! спд'Ьла прелестпая жен-
щина, похожая на фею или «богиню». Приблизясь къ трону,
Елена в'Ъжлшю поклонилась.
—	Здравствуй, Елена! — прпвъ-тлпво сказала фея.
ЕленгЬ не показалось странныш,, что прекрасной незнакомки
известно ея имя.
—	Теб'Ь хочется побывать вт> стран^ чудесъ?
—	О да! — съ жаромъ ответила Елена.
—	Я дамъ теб4 въ провожатые одного изъ ыопхъ прп-
дворпыхъ,—сказала фея, махнувъ палочкой.
Тотчасъ же появился юноша въ костюмъ1 пажа. Онъ прекло-
нидъ колгЬно передъ феей, затймъ приветливо поклонился Елен'Ь.
—	Вотъ, Роландъ, — сказала фея, — эта девушка желаетъ
пдтп въ страну чудесъ,—поручаю ее твоимъ заботаыъ. Покажи
ей все, чФмъ она будетъ интересоваться.
Съ этими словами она передала свой волшебный жезлъ пажу
и сама исчезла.
—	Идемъ!—сказалъ пажъ, подавая руку Елен4 и махнувъ
жезломъ.
Въ ту же минуту они очутились въ совершенно новой свое-
своеобразной и удивительной местности.
Все, что зд^сь существовало, тянулось только въ длину, но
не плйло ни толщины ни ширины. Измйретя въ этихъ двухъ
послъ'днихъ направлешяхъ были совершенно невозможны: на-
настолько предметы были тонки и узки. Жпвыя существа въ этой
странъ- могли двигаться только по одной какой-либо лиши.
—	01 я понимаю!—воскликнула Елена.—Это страна лиши.
Я читала о ней.
—	Да, — сказалъ пажъ, — я только то л могу валъ пока-
показать, о чемъ вы читали или думали.
Елена вопросительно посмотрйла на его жезлъ.
—	II это, въ самомъ д4лъл, великое чудо! — подтвердилъ
пажъ. — Показывать вамъ такпмъ нагляднымъ образомъ все, о

208
чемъ вы только думали, видь и это волшебство! Но показы-
показывать вамъ то, о чеыъ вы никогда и не думали даже, это
было бы...
Елена не разслышшга посл'Ьдняго слова, и нажъ опять
махнулъ. жезлоыъ.
Онп находились теперь въ м4стгЬ, откуда статна лпнш
была видна яснгЬе. Елена протянула ладонь поперекъ лиши
прямо противъ одного изъ движущихся по лиши странныхъ
жителей. Онъ внезапно остановился. Она отняла руку. Но оби-
обитатель страны лпшй остолбен'Ьлъ отъ изуылешя: какое-то таин-
таинственное т'Ьго, или, по его поняиямъ, точка внезапно появилась
въ его пространств^ и такъ же внезапно исчезла!
ЕленФ странно было видфть, какъ вся жизнь обитателя
страны лптй заключена между двумя точками.
—	Они никогда не обходятъ препятствШ!—заметила она.
—	Лишя—это ихъ м1ръ... М1ръ одного пзмт>решя...—ска-
пзмт>решя...—сказать пажъ.—Какъ это кто-либо выйдетъ изъ своего Mipa, чтобы
обойти вокругъ препятств1я?..
—	Не' могла ли бы я поговорить съ ними и разсказать о
второыъ изм'Ьренш?
—	Эти существа не шйютъ второго пзмйрешя!—лакони-
пзмйрешя!—лаконически сказалъ пажъ.
—	Хорошо!—смеясь продолжала Елена.—Действительно,
это такъ. Ну, а если они случайно выйдутъ изъ предгЬловъ
своего узкаго Mipa?
—	Случайно?—съ изумлешемъ повторилъ пажъ.—Я думалъ,
что вы бшгёе философъ!
—	Нфтъ,—скромно возразила Елена,—я еще только школь-
школьная ученица.
—	Но вы ищете зншш п истины и любите ихъ. Развй это
не значптъ быть философомъ?
—	Правда,—согласилась Елена,- -пожалуй, я могу считать
себя философомъ. Но скажите, все-таки, какъ подобное существо
можетъ получить точное поняле о пространств^, отличномъ отъ
того, въ которомъ заключено оно.
—	Оно можетъ, вероятно, обратиться къ существу н^сколь-
кихъ

209
Елена на минуту црпшла въ замешательство, думая, что ея
проводникъ шутить. Но тотъ совершенно серьезно продолжалъ.
—	Существа одного пзмЪрешя могутъ почувствовать другое
1шгЬреше только при возд'Ьйствш иныхъ существъ не пзъ пхъ
пространства. Но обратимся къ другому Mipy.
Пажъ снова махнулъ жезломъ, б они увндалп новую область,
всЬ обитатели которой им'Ьли длину и ширину, но не шгЬли
толщины.
—• Это страна плоскостей!—весело сказала Елена, а чрезъ
минуту прибавила:—но только я думала, что плоскостныя суще-
существа всЬ представляютъ собой правильный геометрпчесыя фигуры,
а зд4сь я вижу очень разообразныя.
Пажъ расхохотался такъ громко и заразительно, что Елена
стала вторить ему, не зная еще причины его смгЬха. Онъ объ-
объяснился.
—	Вы представляли себ$, значить, такую страну плоскостей,
гд-Ti государственные мужи похожи на однообразные правильные
квадраты, и гдф остроумге формъ есть принадлежность низшихъ,
а однообразге считается отлишемъ знатности. Да, есть и такая
страна плоскостей, только пишется она съ прописной, а не съ
маленькой буквы...
Елена стала щжсматриваться къ жизни существъ съ двумя
измъ-решями п размышлять о ихъ сферт, представлений. Она
соображала, что многоугольники, круги и всяшя друпя плосия
фигуры всегда видны имъ только, какъ отрезки лиши; что они
не могутъ вид'Ьть угла, но могутъ вывести заключеше о его
существованш; что они могутъ быть заключены внутри четыре-
угольппка или другой плоской фигуры, если она шгЪетъ за-
замкнутый периметрь, который они не могутъ пересечь; и если
существо трехъ измйрешй пересекло бы пхъ пространство (по-
(поверхность), оно могло бы понять только сЬчеше на поверхности,
сдЬгапное этпмъ трехм^рннмь тФломъ, такъ что тЗуго предста-
представлялось бы имъ существомъ также двухъ изм'Ьрешй, но обла-
дающпмъ чудесными свойствами и могуществомъ движеи!я.
Елена заинтересовывалась все больше и больше.
—	Покажпте мнф пространства еще и другихъ изм^решй!—
просила она спутника.
ВЪ ЦАРСТВЪ СМЕКАЛКИ.	14

210
—	Хорошо! Пространство трехъ пзьгёреши вы можете видеть
во всякое время,—сказалъ пажъ, махнувъ жезломъ и изменяя
картину.—Но, если вы возьмете мой жезлъ п съ его помощью
покажете мнт> пространство четырехъ пзы'Ърешй, то я буду вамъ
очень благодарить!
—	О, этого я не могу!—воскликнула Елена.
¦— И я тоже.
¦— А можетъ кто-нибудь это сделать?
—	Гово2жгъ, что въ пространстве четырехъ пзм^енш можно
впд'Ьть внутренность нашего закрытаго ящика, смотря вт, него
пзъ четвертаго пзмгЬрешя такъ, какъ вы могли видъ-ть внутрен-
внутренность прямоугольника въ стране плоскостей, смотря на него
извн^ сверху внизъ. Говорятъ также, что въ четырехм'Ьрномъ
пространстве не можетъ быть завязанъ узелъ. Существо этого
четырехмйрнаго пространства, переходя въ наше, должно ка-
казаться намъ существомъ трехъ пзм'Ьренгй, такъ какъ все, что
мы можемъ впд'Ьть отъ такого существа, есть только сЬчеше,
сделанное пмъ въ нашемъ пространств'Ь, и это сочило есть то,
что мы называемъ ттдомъ. Это существо можетъ представиться
намъ, скажемъ, какъ человекоподобное. II оно можетъ быть,
действительно, не менее чсловъ'комъ, ч'Ьмъ мы, и не меп'Ье
реалышмъ, а даже болт>е реалышмъ, если только слово «реаль-
«реальный» здгЬсь нриложпмо. Существа страны плоскостей (двухъ
измерили), пересЬкающ1я страну лиши (пространство перваго
пзмт.рен1я) кажутся обптателямъ лпнейнаго пространства суще-
существами одного пзмйрешя, только обладаюициш чудсснымъ могу-
ществомъ. Точно также наше трехмерное т4ло въ плоскомъ
(двухмъ-рномъ) П150странствгЬ. Пересечете наше съ поверхностью—
это и все, что видимо и понятпо для существа плоскостного
пространства, п только это пересечете, только одна фаза нашего
тела доступна существу двухъ пзмерешй. Отсюда следуетъ
заключить, что существа бол'Ье чемъ трехъ пзмерешй пмеютъ
чудесную для насъ способность появляться п исчезать, входить
и уходить пзъ кочнаты, где заперты все двери; отш могутъ
казаться намъ «духами», хотя вместе съ тъ'мъ оне могутъ
быть на самомъ деле существами более реальнылп, чемъ мы
сами.

211
Онъ замолчалъ, а Елена заметила:
—	Все, что вы сказали, есть только результатъ изв4стнаго
рода логическпхъ соображешй. Я хотела бы видтьтъ четырех-
четырехмерное пространство.
Спохватившись, она сообразила, что такая настойчивость мо-
жетъ быть неделикатной по отношенш къ спутнику, и она
прибавила:
—	Но я знаю, что шезлъ не можета показывать намъ все,
что мы захотели бы видеть. Тогда не было бы пред^ловъ на-
нашему познашю.
—	Ыожетъ быть, беспредельное познаше есть то же, что и
безконечное познаше?— спросшгь пажъ.
—	Это похоже на каламбуръ,— ответила Елена.— Не есть
ли это простая игра словъ?
—	А вотъ идетъ господинъ Вычпслителевъ. Спросимъ его
шйшя.—Эй! Господинъ Вычислителевъ!
Елена увидела почтеннаго пожилого господина съ разве-
развевающейся б^лой бородой. Онъ обернулся, когда услыхалъ
свое гош.
Пока онъ приближался, пажъ сказалъ тихо Елене:
—	Онъ будетъ въ восторге отъ такой ревностной ученицы,
какъ вы. Это для него праздникъ.
Вычпслптелевъ съ болыпимъ достоинствомъ раскланялся еь
Еленой п ея спутнпкомъ и, ознакомившись съ темой разговора,
началъ такъ энергично высказывать свои мнйшя, что нажъ
остановилъ его:
—	Осторожнее, это не спещалпстъ по математике.
Елене неособенно понравилось это зазгёчаше, такъ какъ
она вообще не соглашалась, когда девушекъ считали зюн'Ье спо-
способными къ математике, чймь другпхъ людей. «Ну, да это
шутка!»—подумала, она про себя и продолжала слушать.
Вычпслптелевъ иродолжалъ начатое пояснеше.
—	Если вы хотите спросить, одно ли и то же безпред'Ьлыю
увеличивающееся переменное п абсолютная безконечность. то
я отвечу—игътъ! Безгранично, пли безпредельно, увеличиваю-
и*

212
щееся переменное всегда ближе къ нулю, ч4мъ къ абсолютной
безконечгюсти. Для простоты пояснешя сравнпмъ такое пере-
переменное съ другимъ однообразно изменяющимся перем'Ьннымъ,—
со временемъ. Предположпмъ, что разшатриваемое нами пере-
переменное удваивается каждую секунду. Въ такомъ случа'Ь все
равно, — какъ бы долго ни продолжалось подобное увеличеше
переменнаго, оно все - таки будетъ ближе къ нулю, чгЬыъ къ
безконечностп.
—	Поясните, пожалуйста,—попросила Елена.
—	Хорошо! — продолжалъ Вычислителевъ. — Разсмотримъ
значешя переигЬтшаго въ некоторый моментъ. Въ этотъ моыентъ
значен1е переменнаго равно только половине того, которое оно
прюбр-Ьтетъ черезъ секунду, и равно четверти того значешя,
которое получится черезъ 2 секунды, если оно будетъ все воз-
возрастать. Такпмъ образоыъ теперь, въ данный моментъ, оно го-
гораздо ближе къ нулю, чемъ къ безконечности. Но то. что вгЬрно
относительно переменнаго въ данный моментъ, будетъ верно
и въ следующй и, вообще, въ каждый моментъ. II какъ бы
переменное пи возрастало, опо всегда будетъ ближе къ нулю,
чемъ къ безконечностп.
—	Значить, — сказала Елена,— правильнее говорить «без-
предельно увеличивается», вместо «приближается къ безконеч-
безконечности, какъ къ пределу».
—	Разумеется! Переменное не можетъ приближаться къ
безконечностп, какъ къ пределу. Учащимся часто напомпнаютъ
объ этомъ.
—	Я думаю,—заметила Елена,—что знаше можно увеличи-
увеличивать всегда, хотя это и кажется чудеснымъ.
—	Что вы называете чудеснымъ?
—	Потому что...—начала Елена и остановилась.
—	Когда начпнаютъ съ «потому что», редко даютъ ответь!—
сказалъ па;къ.
—	Боюсь, что я действительно не отвечу, — произнесла
Елена. — Обыкновенно называютъ чудеснымъ то, что является
отступлешемъ отт, естсствениыхъ законовъ.
—	Мы должны показать барышне пачерташе кривой,—ска-
кривой,—сказалъ Вычислителевъ пажу.

213
—	Конечно, — отв'Ьтплъ тотъ.— Любите вы фейерверки? —
спросилъ онъ Елену.
—	Благодарю васъ,—ответила Елена,—но я не могу остаться
зд'Ьсь до вечера.
—	Хорошо, мы иокажемъ вамъ ихъ очень скоро.
—	Фейерверки при диевномъ освйщенш?—спросила Елена.
Но въ ту же минуту пажъ ыахнулъ жезломъ п наступила
ночь, светлая ночь, хотя безъ луны и зв'Ьзд'ь.
Такъ какъ эта перемена была сделана при помощи магпче-
скаго жезла, то Елена не очень была изумлена.
—	Теперь вы мн4 покажете начерташе кривой?—спро-
кривой?—спросила она.
—	Да,— сказалъ пажъ.
Разговаривая такимъ образомъ, все трое шли дальше, пока
не подошли къ м'Ьсту, гдЪ находилось ничто въ родт, элек-
электрической станщп подъ наблюдетемъ прелестной молодой жен-
женщины.
—	Это Ана-Литика,—сказалъ Вычислителевъ Елен-Ь,—вы,
вероятно, съ ней знакомы.
—	Знакомое имя, сказала Елена, но я не припоминаю, чтобы
видела гдй-нибудь эту госпожу. Мни хотелось бы познакомиться
съ ней.
Познакомившись, Елена назвала женщину «госпожа Литика».
Но та улыбнулась и сказала:
—	Меня никогда такъ не зовутъ. Вст, зовутъ меня обыкно-
обыкновенно «Ана-Литика».
—	Эта барышня хотела бы познакомиться съ некоторыми
изъ вашихъ работъ,—сказалъ Вычислптелевъ.
—	Пиротехническое начерташе кривой,—пояснплъ словоохот-
словоохотливый иажъ.
—	Пожалуйста, покажите намъ алгебраическую кривую съ
особенной точкой,—прибавилъ Вычислптелевъ.
Ана-Лптика тронула одну рзъ кнопокъ и сквозь темноту
прорезалась полоса яркаго св-Ьта, образовавшая въ пространств*
блестящую плоскость. Зат'Ьмъ она поблекла, но остались два
луча, перпендикулярныхъ одинъ къ Д11угому. Пзображеше было
слабое, но непзм'Ьняющееся.

214
— Это оси координатъ,—объяснила Лна-Лптпка.
Она нажала вторую кнопку, и Елена увпд-Ьла ничто, по-
похожее на шетеоръ. Онъ явился изъ огромнаго отдалетя, пересЬкъ
лучъ свита, который быль названъ одной «пзъ осей», п понесся
по другую сторону этой осп такъ же быстро, какъ появился, все
время двигаясь въ плоскости, показанной первоначальной исчез-
исчезнувшей полосой свт/га. Елена невольно подумала о кометт,. Но
вместо кометнаго блестящаго хвоста пронесппйся «метеоръ» оста-
Фиг. 100.
вилъ за собой неизменяемый путь свита въ видт, кривой линш.
Ана-Литика близко подошла къ Елене, и обе девушки смотр'Ьли
на блестящую кривую, которая тянулась сквозь темноту на все
пространство, которое только было доступно зрешю.
— Какъ это красиво!—воскликнула Елена.
Попытка изобразить на бумаге то, что видела Елена, даетъ
объ этомъ не столь сильное и эффектное представлеше. На фиг.
100-ой даны оси координатъ и самая кривая.
Вдругъ Елена воскликнула:

216
Это, видь, отдгыьная точка септа?—При этомъ она по-
показали на точку, обозначенную па флгурт. буквой Р.
—	Это точка кривой,—сказала Лиа-Лптпка.
—	Но она такъ отдалена отъ всей остальной кривой! — за-
заметила Елена.
Отойдя къ аппарату и д'Ьлая что-то, чего Елена не могла
разсмотр'Ьть, Ана-Литика начала писать въ темноть1, словно
на аспидной доски. Знаки выходили блестлшде и ртжо выд'Ьля-
лпсь на темноыъ фонт, ночи. Ботъ что она иаписала:
Оступя назадъ, она сказала:
—	Это уравнеше кривой.
Елена любовалась горящплгъ въ темнот'Ъ уравнешемъ.
—	Я никогда не представляла себ'Ь геометрическая коорди-
координаты столь красивыми,—сказала она.
—	Точка, о которой вы спрашивали, сказала Ана-Лптпка,
есть точка B, 0). Вы видите, что она удовлетворяете, уравненш.
Это точка изображена.
Елена теперь запятила, что единицы длины были нам'Ьчепы
на слабо видныхъ осяхъ легкими болйе блестящими точками
свита.
—	Да, сказала она, я вижу ее, но странно все-таки, что
она отдалена отъ остальной кривой.
—	Да,—сказалъ Вычпслит&тевъ, который все время внима-
внимательно слушалъ,—вы ожидали, что кривая будетъ непрерывна.
Непрерывность—вотъ постоянная предпосылка нын'Ьшней научной
мысли. Эта точка кажется нарушающей этотъ законъ; она, сле-
следовательно, есть то, что вы назвали нисколько минуть тому на-
назадъ «чудомъ». Если бы bc? наблюдаемыя явлешя, крозгЬ одного,
имйли некоторую видимую связь, мы были бы склонны назвать
это одно «чудеснымъ», а все остальное естествепнымъ. Если
только то кажется удивптельньшъ, что необычно, то п «чудомъ»
въ математик^ следовало бы называть всяшй отдельный случай.
—	Благодарю васъ,— сказала Елена,— я очень хотела бы
согласиться съ этпмъ. Но исключительность смущаетъ меня. Я
хотела бы думать, что зд4сь есть общее царство закона.

216
—	Очевидно,—сказалъ пан;ъ,—здъ-сь исключение! Ясно, что
зд4сь есть разныя альтернативы, какъ, напргшеръ, что точки
н4т7. па чертежи, что чертежъ шгёетъ единственную точку и
такъ далпе...
Вычислнтелевъ, Ана-Лптика п нажъ смеялись. Па вопросъ
Елены пажъ пояснилъ:
—	Мы часто говорпмъ «очевидно» пли «ясно», когда не
можемъ дать объяспешя, п часто говорилъ «и такъ дал'Ье»,
когда не зиаеьи,, какъ продолжать.
Елена сначала думала, что эта насьгЬшка относится къ ней,
но потомъ вспомнила, что она пи одпоги такого выражения не
употребила. Вообще, видь, все это прпключеше съ ней была только
шутка, а потому она успокоилась и стала спрашивать обт. пнте-
ресующихъ ее предметахъ.
—	Разскажите мпгЬ объ этой изолированной, особенной
точки,—обратилась она къ Вычислитатеву.
Этотъ послътщШ обо всемъ говорилъ въ поучптельноыъ тонгЬ,
который былъ ему свойственъ.
Вычислителевъ. Если въ написанномъ выше уравнеши
кривой х=2, то, какъ впдите, «/=-0. Но для всякаго другого
значешя ж, меньшаго, ч4мъ 3, какое получится значен1е для у?
Елена. Такъ называемое мнимое.
Вычислителевъ. А какъ изображаются мпшиыя числа гео-
геометрически?
Елена. Лишей, длина которой дается абсолютнымъ (или
ариометическимъ) числомъ мнимаго количества, и направлеше
которой перпендикулярно къ той, по которой отсчитываются
положительныя и отрицательныя направлен1я.
Выуислителевъ. Хорошо. Въ такомъ случат,...
Елена (съ восторгомъ). 01 Теперь я понимаю, я вижу.
Здъ-сь должны быть еще точкн кривой внъч плоскости.
Вычислителевъ. Вотъ именно. Зд4сь имеются еще такъ
называемыя мнимыя вт^тви кривой, и, можетъ быть, Ана-Литика
будетъ настолько добра, что покажетъ ихъ памъ теперь.
Аиа-Литпка тронула еще кнопку своего аппарата, и другая
блестящая кривая прорезалась на фонъ- ночного неба. Плоскость,
определяемая этой кривой, была перпендикулярна къ преды-

217
дущей плоскости (Обозначеппая точками литя на фиг. 101 вос-
воспроизводить обыдешшмъ образомъ то, что видела Елена) *).
— О, я вижу!—повторила Елена.—Точка Р не есть изо-
изолированная, отдельная, точка отъ кривой. Это точка, въ которой
наша «-мнимая» вътвь (на самомъ дЪлт; столь же дчъиствителъ-
V
-А"
Л
q/
\ 1
\
\ \ /
\ \s /
\ \ /
\ \ /
\ \R /
\\ .' --,/
//¦ "¦" \
/ !R \
i \
•- 4 \
/ \
/ \
/ \
/ \
Фиг. 101.
"пая, какъ и всякая другая) пересЬкастъ плоскость двухъ осей
координатъ..
— Теперь,—сказалъ Вычпслителевъ,—вместо того, чтобы
подставлять ' д'Ьйствительныя значешя для х п находить со-
отвътственныя значен!я */, вы можете придавать дйгствитель-
г) На этой фиг?р1; пунктирная литя QPQ'-, если ее повернуть на 90
около жк', какъ оси, такъ, чтобы она была въ плоскости, перпендикурной къ
плоскости чертежа, и изобразитъ «мнимую часть» чертежа.
Вычерченная точками и черточками лишя SRPBS представляетъ проекцго
на плоскость бумаги двухъ «комплексных?, частей» кривой. Въ.точк* Р каждая
в-Ьтвь находится въ плоскости бумаге, для каждой точки В соотв-Ьтствующ1я
точки на самой в^Ьтби кривой находятся на разстоянш 0,7 отъ плоскости по
ту и другую сторону плоскости, для точки S оютв-Ътствуюпуя точки будутт.
па каждой вЪтви въ разстоянш 1,6 отъ плоскости и т. д...

218
пыя значешя у и решать уравнение относительно х. II тогда,
вообще, для каждаго значешя у вы подучите 3 значешя х:
одно действительное п 2 комплексныхъ сопряженныхъ числа.
Кривая, проходящая чрезъ вст> точки съ комплексными абсцис-
абсциссами, никоимъ образомъ не лежптъ въ плоскости осей, но въ
плоскости, имъ перпендикулярной. Впрочемъ, вы знаете это.
(Лишя SBPBS на черт. 101 представляетъ этп въ'тви).
Ана-Лптика опять обратилась къ аппарату; п эти вт/тви
кривой появились также въ видгЬ светящихся лншй.
Елена была очень возбуждена. Глубочайшее удовлетвореше
звучало въ ея голоси, когда она сказала:
—	Точка, которая смущала меня своей непонятной обосо-
обособленностью, есть, какъ оказывается, общая точка н'Ьсколькпхъ
ветвей одной и той же кривой.
—	Сверхестественное бол'Ье естественно, ч'Ьмъ что-либо
ипие,—сказалъ пажъ.
«Чудесное, размышляла Елена, есть только особенный слу-
случай высшаго закона. Мы не понимаемъ фактовъ, потому что
связь ихъ иногда находится вн4 плоскости нашихъ наблюденШ
плп размышленШ». Заттжъ она прибавила вслухъ:
—	Это я могла бы назвать чудесной кривой.
—	Нтл*ь ничего исключительнаго въ этой кривой,—сказалъ
Вычислителевъ. Каждая алгебраическая кривая съ сопряженной
точкой им4етъ додобныя особенности.
Вычислителевъ сказалъ что-то Ана-Литик-Ь и она прикос-
прикоснулась къ аппарату. Послышался сильный ударъ грома. Елена
очутилась въ своей комнатт, и, действительно, проснулась отъ
сильнаго удара грома. Она приподнялась и старалась припо-
припомнить все, что съ ней было. Зат4мъ она сказала сама себт>:
—	Нт/гъ никакихъ кривыхъ изъ евт/га, пересЬкающпхъ
небеса. И прос^эапства одного пли двухъ измфрешй суще-
ствуютъ только въ нашемъ ум4. Они—абстракнш, какъ п про-
пространство 4-хъ изм4рен1й. Но все-таки они ыыслпмы. Я рада,
что видела такой сонъ. Воображен!е есть волшебный жезлъ.
Предстоящая мн^ жизнь будетъ настоящая страна чудесъ и...
Въ это время бой часовъ прервалъ ея мысли и напомнплъ,
что пора идти на вечершя занятая.

219
Случай съ Пляттнеромъ.
Оппсанныя въ предыдущей главе сопныя грезы молодой
курсистки, въ частности о возможности пространства, отличнаго
отъ нашего, уместно будетъ дополнить здесь еще некоторыми,
соображсшямп о «пространстве четырехъ изыгЬрешй». Чита-
Читатель, надеемся, нрочтетъ эту главу съ ттдп, болыппмъ интере-
созгь, что въ ней излагаются взгляды на четырехмерное про-
пространство Гепри Уэльса,— этого оригпнальнъ'йшаго и пнтерес-
п'Ьйшаго писателя научныхъ роиановъ-утопш. Произведешя Г.
Уэльса норажаютъ какъ полетомъ фантазш, такъ глубиной п
логическпмъ развит1емъ положенныхъ въ основаше научныхъ
мыслей или выводовъ.
Въ небольшоыъ и почти неизвестномъ русскому читателю
раяоказе «Случай съ Пляттнероыъ» авторъ сквозь призму своего
богатаго воображетя и тонкаго диецнилинированпаго ума осв'Ь-
щаетъ «пространство четырехъ измерешй» такъ, какъ оно ему
представляется на основаши последняго слова математической
науки. Утопщ такихъ писателей, какъ Г. Уэльсъ, заслуживаютъ
конечно, самаго серьезнаго вниыан1я: он4—результатъ серьезной
работы мысли.
Суть разсказа «Случай съ Пляттнеромъ» состоитъ въ томъ,
что н4шй школьный учитель, Пляттнеръ, неожиданно для са-
самого себя попалъ въ пространство 4-хъ пзмеренШ, пробылъ тамъ
9 дней и, наконецъ, такъ же неожиданно возвратился въ род-
родное ему и намъ 3-мгЬрное пространство. Не им4я возможности,
въ впдахъ эконоыш м^ста, привести весь разсказъ цфликоыъ,
передаемъ но возможности связно его существенные моменты.
О томъ, какъ Пляттнеръ неожиданно попалъ въ простран-
пространство четырехъ измйрешй, повествуется следующее. Учитель
Пляттнеръ любплъ, между прочпыъ, заниматься химпчеекплъ
анализоиъ различныхъ веществъ. Одппъ взъ его ученпковъ,
Уиббль, интересовался xiiMiefl и постоянно прпносилъ учителю
различный вещества для изеледоватя. Разъ онъ прпнесъ ему
где-то случайно найденную аптечную стклянку съ какимъ-то
зеленымъ порошкомъ.

220
«Это было вечером?.. Пляттнеръ сид'Ьпъ въ классЬ, надзирая
за четырьмя учениками, оставленными для приготовлешя уро-
-ковъ. Въ углу того же класса находился и маленъкШ шкап-
чикъ, содержавши всЬ принадлежности для преподавашя хп-
мшг всю лабораторш школы, такт, сказать. Пляттнеръ, кото-
которому надоило сидеть безъ д-Ьла, очень оо1)адовался зеленому
порошку и тотчасъ же занялся его аналпзомъ; а Упббль иа-
блюдалъ за этимъ процессомъ,—къ счастью,— издали. Четверо
другихъ учениковъ, дъмгая видъ, что прилежно занимаются уро-
уроками, тоже исподтишка сл'Ьдилп за т-Ьмъ, что творилось у шкапа.
«ВсгЬ они единогласно показываютъ, что Пляттнеръ отсы-
палъ сначала немного порошка въ пробирный цилиндрикъ и
попробовалъ растворить его последовательно въ водъ-, хлористо-
хлористоводородной, азотной и сЬрной кислотахъ. Ее получивъ никакого
результата, онъ высыпалъ почти половину всего порошка на
металлическую пластинку и, держа стклянку въ лъ-вой рук'Ь,
попробовалъ поджечь его спичкой. Порошокъ затлелся, сталь
плавиться... и вдругъ вспыхнулъ со страшнымъ язрывомъ!..
«ВсЬ пятеро мальчиковъ, ожидавние съ замирашемъ сердца
какой-нибудь катастрофы, какъ по команд^ спрятались за парты
и никто пзъ нихъ не пострадал.. Окно разлеталось вдребезги,
классная доска упала; пластинка, на которой лежалъ порошокъ,
превратилась, должно быть, въ пыль,—облолковъ ея нигдгЬ не
не нашли, — штукатурка посыпалась съ потолка, но другнхъ,
бол-Ье важныхъ, поврежденШ не оказалось. Когда прошла пер-
первая минута страха, мальчики поднялись изъ-за партъ и, не
видя Пляттнера, думали, что онъ сбить съ ногъ и лежитъ на
полу. ВсЬ, конечно, поспъчпили къ нему на помощь, по были
очень удивлены, когда не нашли его на полу. Оставалось щэед-
положить, что онъ, въ минуту общаго смятешя, выскочилъ пзъ
комнаты. Согласно такому предположенш, мальчики тоже но-
бъжали вонъ изъ класса, но передшй пзъ пнхъ, Карсонъ, чуть
не столкнулся въ дверяхъ съ хозяиномъ школы, мистеромъ
Лпджетолъ.
«Мпстеръ Лпджетъ—кривой, толстый и страшно раздражи-
раздражительный человЪкъ. Мальчики говорятъ, что онъ во21вался въ
комнату, красный, растрепанный, съ ц/Ьльшъ потокомъ свонхъ

221
обычныхъ ругательствъ. «Балбесы», «сонлякп», «паршивые
щепки»—такъ и сыпалось изъ его устъ до тйхъ поръ, пока буря
не кончилась вопросомъ: «Гд-Ь мистеръ Пляттнеръ?»
«Куда давался ыистеръ Пляттнеръ? Этотъ вопросъ былъ
всЬш безпрестанно повторяемъ въ течете нФсколышхъ сл!;-
дующихъ дней, но ответить на него никто не могъ. Мпстеръ
Пляттнеръ исчезъ, не оставивъ за собою никакого глгЬда: нп
капли крови, ни пуговицы отъ своего костюма! Точно будто
'онъ въ самомъ дтлФ разлетался на атомы...»
Черезъ девять дней, однако, Пляттнеръ возвратился въ школу,
но возвращете его было не менйе странно, чтшъ псчезновеше:
«Въ среду вечеромъ, закончивъ дневные труды, мистеръ
Лиджетъ собиралъ въ саду свою любимую ягоду, малину. Толь-
ко-что онъ подошелъ къ особенно усыпанному ягодами кусту,
какъ вдругъ сзади него послышался сильный трескъ, сопрово-
сопровождаемый какъ бы вспышкой лолнш, и какое-то тяжелое ттш)-
такъ сильно толкнуло мистера Лиджета въ спину, что онъ упалъ
на-корячкп, малина рассылалась, а шелковый картузъ съ'Ьхалъ
ему на глаза.
«Сильно разсержешшй, мистеръ Лиджетъ, еще не уетгёвъ
подняться на ноги, выпустплъ цгЬлую тучу ругательствъ по ад-
адресу непзв'Ьстнаго тйла. Каково же было его изумлеше, когда,
обернувшись назадъ, онъ увидалъ мистера Пляттнера, спдящаго
среди куста малины, въ самомъ растрепанномъ вид-Ь, безъ шашш,
безъ галстуха, въ грязной рубашки п съ окровавленными ру-
камп!..»
Съ возвратившимся изъ неожиданнаго «путешеств1я» Гот-
фридомъ Пляттнеромъ произошли, однако, весьма удпвительныя
перемены.
«Начать съ того, что, по изслйдованш, произведенному опыт-
нымъ врачомъ, всЬ внутренн1е органы Готфрпда Пляттнера ока-
оказались перемещенными: сердце перешло на правую сторону
груди, печень сместилась кт. левому боку, а доли легкпхъ по-
м'Ьнялись местами. ПмгЬя въ виду, что такое расположеше вну-
внутренностей, хотя и не часто, но все же встречается, нпч^мъ
до поры до времени не проявляясь, я не придаю ему особен-
наго значешя, такъ какъ оно могло существовать у Пляттнера

222
и раньше случпвшагося съ шшъ прпключешя. Но вотъ что
важно и чего у Готфрвда раньше этого прпключешя положи-
положительно не было: онъ сталъ лгЬвшой, и при томъ до такой сте-
степени, что правая его рука едва держала перо, а л'Ьвая могла
писать только съ правой стороны къ лйвой. Есть еще одно
обстоятельство, указывающее на перемтлу, которая произошла
въ организм! Готфрида Пляттнера, Раньше прпключешя лицо
его, какт. у большей части людей, было не совсвмъ симметрично:
правый глазъ быль немножко больше лйваго н правая щека
массивнее лйвой. Между тгЬмъ теперь, послъ1 прпключетя, у
Пляттнера лъ-вый глазъ и лъвая щека больше правыхъ, какъ
я въ этоыъ уб'Ьдился пзъ сравнетя фотографш...»
Словоыъ, — новое состояше Пляттнера представляло собой
какъ бы зеркальное изображаете нормалънаго человека. Не
мен'Ье интересно п то, что, по увтфешямъ Г. Уэльса, Пляттнеръ
разсказывалъ о собственныхъ свопхъ субъективныхъ ощущешяхъ.
«Пляттперъ говорить, что посл'Ь взрыва почувствовалъ себя
убитымъ наповалъ. Ноги его отделились отъ пола, и все ттдо
было отброшено куда-то назадъ, прп чемъ онъ упалъ на спину.
На ыпнутку nafleHie его ошеломило; зат^лъ онъ ясно ощутнлъ
запахъ жженыхъ волосъ и услышалъ голосъ мистера Лпджета,—-
однако, какт» сквозь сонъ.
«Все кругомъ казалось ему какъ бы въ туманФ. Это онъ
тотчасъ же прпписалъ дыму, выд^лившелуся во время взрыва.
Фигуры Лнджета и учениковъ двигались въ этомъ тулант. без-
птумно. какъ т^нп, но все же онъ ясно ихъ вид^лъ, видтэлъ
обстановку класса п потому сообразилъ, что живъ и даже не
особенно пострадалъ; только лицо саднило отъ ожога, да слухъ
и зр4те несколько притупились, вслгЬдств1е взрыва, какъ онъ
думалъ.
«Мало-по-малу Пляттнеръ приходплъ въ себя и собпрался
встать, какъ вдругь былъ иоражент, иеожиданнымъ и въ выс-
высшей степени странным!, обстоятельствкмъ: два ученика, одипъ
за другимъ, прошли сквозь его тпло, какъ черезъ какой-нибудь
туманъ или дымъ! Ни одпнъ изъ нихъ даже не чувствовалъ
его присутств1я. Трудно описать ощущеше, испытанное Плятт-
неромъ. Онъ вскрикнулъ отъ неожиданности.

223
«Попробовавъ протянуть руку, Пляттнеръ замт,тилъ, что
она свободно прошля сквозь стгЬну дома.
«Стараясь обратить на себя вшшате, Пляттнеръ громко
звалъ Лиджета, ловилъ проходящихъ ыпмо мальчиковъ, но всЬ
они, очевидно, совсЬмъ его не замечали. Онъ чувствовалъ себя
какъ бы отр'Ьзаннымъ отъ jiipa, хотя и не переставалъ быть
его частью. ВсЬ попытки сообщаться съ этимъ м1ромъ остава-
оставались безплодньшп.
«Тогда Пляттнеръ сталт. внимательно осматривать вое окру-
окружающее и съ удпвлешемъ заыгЬтилъ, что онъ находится не въ
класст,. а подъ открытымъ небомт, и сидитъ на камни, который
обросъ бархатистымъ мохомъ. Склянка ст» остаткомъ зеленаго
порошка находилась еще у него въ рукахъ. Совершенно безео-
знательно онъ сунулъ ее въ карыанъ. Кругомъ было почти
совсЬмъ темно.
«Тишина была абсолютная, несмотря на сильный въ'теръ,
который долженъ бы, казалось, сопровождаться пгумомъ деревьев?,
и травы. ВсЬ окрестности казались скалистыми п пустынными.
«Попробовавъ спуститься по склону холма, Пляттнеръ сво-
свободно црошелъ сквозь стгЬну школы и очутился въ залй верх-
няго этажа, гдгЬ панеюнеры приготовляли свои уроки. Плятт-
иеръ замт/гплъ, что некоторые пзъ нпхъ иголками царапаютъ
на таблицахъ геометрпчеекпхъ чертежей полный ходъ доказа-
доказательства соответствующей теоремы, о чемъ онъ прежде никогда
не догадывался.
«Чъ'мъ свъ'тлъ-е становилось, т4мъ Пляттнеръ хуже вид'Ьлъ
земные п]зедметы. Наконецъ, они совсъчмъ скрылись у него изъ
глаз?.. Судя по времени, надо думать, что это случилось какъ
разъ тогда, когда зашло солнце. ВзамЪнъ того передъ его нзу-
мленнымъ взглядомъ р-Ьзко обрисовался скалпстый и пустынный
пеизажъ, надъ которымъ поднялся съ горизонта какой-то огром-
огромный зеленый дпекъ, свйтприпй, однако же, гораздо слабее
земного солнца. Пляттнеръ стоялт. па высокомъ холмъ1. У ногт.
его разстилалась глубокая долина, усеянная камнями.
«Псчезповен1е яемныхъ предметовъ при восход^ зеленаго
солнца въ пространствахъ четвертаго изм-Ьротя есть странный
и въ то же самое время самый интересный пунктъ въ показа-

224
шяхъ Пляттнера. Онъ положительно говорить, что депь въ
этпхъ пространствахъ соответствуем, нашей ночи н, наоборотъ,
ночь соответствуем, дню, при чемъ самое сильное дневное
освещете не достигаешь силы нашего луннаго. Поэтоыу-то, шо-
жетъ быть, днемъ мы и не видимъ того, что происходить въ
четвертомъ измйренш: у насъ въ это время сильный свъть, а
тамошше пейзажи совсЬмъ не освещены.
«Когда зеленое солнце осветило окрестности, то Пляттнеръ
увидалъ на дне долины ц'Ьлую улицу, составленную изъ какихъ-то
черныхъ здашй, похожихъ на гробницы и мавзолеи. Съ боль-
шпыъ трудомъ спустившись по крутому каменистому и скольз-
скому склону горы, Пляттнеръ встръ-тшгь ц'Ьлую толпу какихъ-то
существъ, расходившихся пзъ одного большого здашя, какъ у
насъ народъ расходится изъ церкви. Существа эти издали по-
похожи были на шары, освещенные бл'Ьдно-зеленымъ свъ'томъ.
Одпи изъ нихъ исчезали въ проходахъ, окружающихъ здаше,
друия входили въ дома, а н'Ькоторыя стали подниматься на
гору, навстречу Пляттнеру. При виде ихъ последшй остано-
остановился въ изумлеши, хотя ув^ряетъ, что нисколько не испу-
испугался. Впрочемъ, въ самомъ д^лЪ, пугаться было иечего. Суще-
Существа эти, которыхъ какъ бы несло вЪтромъ, представляли собой
что-то въ родт, головастиковъ: коротеиькое, безрукое и безногое
туловище и большая голова съ лицомъ совершенно человеческой
формы. Только глаза были, пожалуй, нисколько больше человъ--
ческпхъ и выражали, въ большинстве случаевъ, такую скорбь,
такое страдаше, которыхъ человекъ трехъ излгЬрен1н не могъ
бы вынести. Приблизившись къ этнмъ сушестваыъ, Пляттнеръ
заметилт., что они сыотрятъ совсемъ не на пего, а на каше-то
движущ1еся предметы.
«Каждое пзъ нихъ какъ бы приставлено къ кому-нибудь
изъ жпвущихъ въ трехъ измерешяхъ п внимательно следить
за всякимъ его шагомъ. Сначала эти существа не обращали на
Пляттнера никакого внпмашя, но потоыъ дна пзъ нихъ, имЪв-
шпхъ большое сходство съ его покойными отцомъ п матерью,
стали следить за нимъ по пятамъ. Онъ нисколько разъ пробо-
валъ заговорить съ матерью, но она только смотрела иа него
грустно, пристально и какъ бы съ какимъ-то упрекомъ. Впо-

сл'Ьдствш опъ сталъ встречать и еще лица, ианомишшшля ему
людей, которыхъ онъ знавалъ въ д-Ьтств'Б и съ которыми вхо-
дилъ въ как!я-нибудь сношс-шя. ВсЬ они тоже грустно смотрЪлп
на пего, впдшю узнавая и какъ бы упрекая въ чемъ-то.
«... День за днемъ, усталый, излученный, бридилъ Плят-
перъ, такъ сказать, на порог'Ь между двумя паразит, нп къ
одному ira, нпхъ всец'Ьло не принадлежа.
«Въ конц'Ь-концовъ, это ему очень надо'Ьло, п онъ гталъ
сильно желать возвращсиш въ нашъ трехмерный м1ръ.
«На девятый день, вечеромъ, Пляттнеръ, ходя по улицалъ
Суссекгвпля, споткнулся о камень и упалъ на тогь бокъ, гд1;
въ кармангЬ его брюкъ лежала гткляночка съ зеленымъ по-
рошколъ. Раздался страшный взрывъ, — и Пляттнеръ ст. нзу-
млешемъ увпдалъ себя въ старомъ саду школы, лнцомъ къ
лицу съ мистеромъ Лиджетомъ!..»
Зам%чан1я къ «Случаю съ Пляттнеромъ».
Разсказъ Уэльса не есть продуктъ «безночвенной фантаз1и»,
а скорее образчнкъ живого разсуждетя по аналогги.
Мы, конечно, неспособны представить себ4 пространство
четырехъ нзмгЬрен1й. Такъ что олисаше, такъ сказать, внъчпняго
вида этого пространства и его обитателей всецело оставляемъ
на ответственности мистера Пляттнера и его вдохновителя
Генри Уэльса. Но мыслить о пространствахъ, отличныхъ отъ
нашего, мы можомъ, каш. можемъ делать бол^е или менгЬе вЬ-
роятныя заключешя о такихъ пространствахъ — по аналогш.
Аналоия, конечно, не доказательство, но иногда она можетъ
привести къ любопытныыъ п даже полезнымъ соображен1ямъ.
Ост|)Оумный почпнъ въ этомъ отношен1и сдгЬланъ такпми глу-
глубокомысленными учеными, какъ Гельмгольцъ и Рпманнъ, кото-
которые для примера взяли болгЬе понятное п простое для насъ
идеально плоское пространство—«пространство двухъ измърешй»,
въ которомъ живутъ, движутся и мыслятъ существа тоже,
конечно, двухъ измйрешй. Такое пространство можно (прибли-
(приблизительно, впрочезгь) мыслить, какъ огромный листъ не ии-Ью-
щей толщины бузтаги, покрытый мпожествомъ «живыхъ» линШ,
ВЪ ЦАРСТВ* СМЕКАЛКИ.	16

226
треугольниковъ, квадратовъ и другпхъ фигуръ, движущихся въ
плоскости листа. Движете это ыожетъ происходить, понятно,
только въ самой одной этой плоскости, такъ какъ третьяго
изм-вретя нить, и потому фигуры зд^сь не логутъ ни поды-
подыматься, ни опускаться внФ плоскости. Обитатели такого пло-
скаго Mipa, поэтому, не могутъ гагЬть ни малМшаго предста-
влешя о двнженш еще въ одномъ—перпеиднкулярномъ напра-
влеши и такъ же прикованы тйломъ и мыслью къ своему двухмер-
двухмерному пространству, какъ ыы — къ нашему трехмерному Mipy.
Самая идея третьяго изм-врешл была бы пмъ столь же чужда,
какъ многимъ пзъ насъ идея пространства 4-хъ пзмЬренШ.
Каковы, наприыгЬръ, жилища обитателей такого плоскаго
Mipa? Это не что иное, какъ замкнутыя лпнш, открытыя сверху
и снизу. Но будемъ помнить, что <.верхъ» и «пизъ» понятны
только для насъ, существъ трехъ измйретй; обитателямъ же
двухм'Ьрнаго Mipa эти понятая чужды, и они счптаютъ свои
жилища прекрасно защищенными со всЬхъ сторонъ. Чтобы за-
заключить обитателя плоскаго Mipa въ тюрьму, достаточно было
бы начертить вокругъ него замкнутую лишю. Будучи самъ пло-
плоскостью, лишею пли точкой и не щгЬя возможности выйти изт>
плоскости, онъ не можетъ пи перешагнуть черезъ сттшы своей
тюрьмы, ни подлезть подъ нихъ, и они были бы для него не-
непроницаемы, какъ для насъ каменныя или желЬзныя ст-Ьны съ
поломъ и потолкомъ.
Предположимъ, что этотъ Miprb о двухъ пагЬрешяхъ noMi-
щенъ въ самой середингЬ нашего Mipa о трехъ измтфешяхъ.
Обитатели плоскаго Mipa, все же, не нмйли бы ни мал^йшаго
понятая о трехмгЬрномъ пространг.твгЪ, ихъ окружающемъ. Они
просто не замечали бы всего нашего Mipa и даже склонны
были бы отрицать самое его существоваше. Если бы кто-нибудь
изъ нашего Mipa попалъ въ нхъ плоскость, они могли бы узнать,
пожалуй, о сущеотвованш другого Mipa. По, конечно, такой
пршпелецъ казался бы пмъ существомъ сверхъестествеинымъ.
Въ самомъ д^лф, попробуемъ представить себ'Ь ощущен1я
обитателя «плоскаго» Mipa, когда онъ вдругъ замтлаетъ у себя
въ спальн'Ь, скажемъ, человека изъ нашего Mipa. Онъ, ложась
спать, убедился, въ прочности запоровъ на случай ночного

227
вторженья грабителя. И, вдругъ. ого изумленому взору предста-
представляется чудесная фигура, непохожая ни на что виденное пмъ
до сихъ поръ. Наше трехмерное тело не было бы видимо
шюскшгь существамъ въ обычнолъ своемъ образ'Ь, и при ма-
Л'Ьйшемъ движенш вверхъ оно совгЬгь исчезало бы изъ виду -
кт> великому изумленно «двухм'Ьрца»,— тат, мы будемъ назы-
называть это существо двухъ шмгЬрешй. По все время, пока чело-
человека, находился бы въ пересМеши съ плоскпыъ шромъ, онъ
былъ бы впдимъ для ^двухы'Ьрца» въ видгЬ плоской фигуры,
обладающей непостижимой способностью изменять свой видъ п
чудесном силой движешя.
Самый способъ, какпмъ неожиданный гость проникъ въ его
домъ, составлялъ бы для «двухм'Ьрца непостижимую задачу,
настоящее чудо. Не подозревая, что его долъ и спальня, будучи
плоскими фигурами, открыты сверху, онъ не могъ бы додуматься
до того, что чаювтЛгу достаточно было просто перешагнуть че-
резъ лпнпо, чтобы очутиться въ его домФ>.
Его удивлР1пе не им-Ьло бы грашщъ, когда таинственный
иришелецт. сталт> бы перочислять содержимое его кармановъ,
шкафовъ, бюро, кассы, описывать впут[»енн1е (фганы тЬла двух-
м'Ьрца п даже доставать изъ наглухо запортыхъ ящпковъ (на-
(наглухо для двухм'Ьрца, конечно) любую вещь. Двухмт/рецъ
вообразнлъ бы, что пршпелецъ ум'Ьетъ проникать че])е:п» ст'Ьны,
что для него недействителен'!, законъ непроницаемости ыатерш.
Мало того,—«трехмерному» гостю ничего не стоило бы, глядя
поверхъ двухм'Брныхъ ст'Ьнъ, описать самымъ подробиымъ обра-
зомъ, что творится въ сосЬднихъ, также наглухо запертыхъ
домахъ, и даже далеко за горами и морями плоскаго iiipa.
Двухы'Ьрецт. при этомъ р'Ь'ишлъ бы, конечно, что его гость
одарепъ даромъ ясновпдеп1я и т. д...
Итакъ, разг.улгдая логически, нгЬтт. ничего ст]1аннаго въ до-
пущегпи пространства со свойствами, отличными отъ нашего,
<Евклидовскаго», пространства. Ничего нъть страннаго въ
мыслгтости пространства четы]>ехъ изм^ешй, если только
разсу;кден1я о немъ не гаагаютъ за пределы .югпкп п дал;е
здраваго смысла.

_228
Упомянелъ еще о такнхъ весьма интересных* ирпмерахъ,
к акт. cnjuiPTpifl п выворачнваше на шпанку. Еще веяний фи-
лософъ и математикъ Еантъ обратплъ внимаше на некоторую,
словно, бы, «тайну», связанную ст. ташшъ, казалось бы,
простымъ предметомъ, какъ сшшетр1я. Сравните вашу правую
и левую руку. — он4 совершенно сходны во всЬхъ подробно-
стяхъ. А между тЬлъ всяшй хорошо пнаетъ, что эти, казалось
бы, тождественный тгЬла, несовместимы, п правая перчатка не
можетъ быи. надета на левую руку. Запозшивъ это, пойдемъ
далее и разсыотримъ свойства спмметрнчныхъ илоскпхъ фп-
гуръ. Вотъ передъ нами два сшгметрпчныхъ четырехугольника
А и В (фиг. 102). Про пихт, нельзя сказать, что они не-
несовместимы. Правда, если нросто
надвигать В на А, то никакъ не
удастся ихъ совместить, но стоить
Фпг ю2.	перевернуть В, такъ ска;!ать, на лгЬ-
вую сторону, на, изнанку,— п тогда
обт. фигуры не трудно будетъ нривестн къ совмт)щен1ю. Про-
сл'Ьдпмъ, что, собственно, мы сделали. Для того, чтобы пре-
превратить фигуру В въ А. паыъ необходимо было на время ото-
оторвать ее отъ плоскости, перенести въ ш'ръ трехъ измгЬреиш м
снова вернуть ее на плоскость.
Ни сколько бы мы пи поворачивали правую руку, мы ни-
никогда не превраттшъ ее въ лтшую. Отчего это? Да оттого, что
для этого намъ нужно вывести р\ку за пределы трехмъ'рнаго
пространства, — совершенно такт, же, какъ мы только что вы-
иеслп нашъ четырехугольпнкъ пзъ двухлгЬрной плоскости въ
Mipb трехъ H3MTipeuin. Пе покидая же нашего nipa, мы такъ
же не можемъ совместить спмметричцыя тг1;ла. кякъ «двухмт,рцы»
не въ состоян1п совзсЬщать илоскпхъ снмметричиыхъ фпгуръ.
Отсюда замечательный выводъ: еслп бы челов'Ькъ былъ спо-
сооенъ хотя на мгновен1е покинуть нашъ трехмерный м1ръ,
онъ могъ бы вернуться намъ въ виде, снмметрпчномъ самому
себт;: его правая рука сделалась бы левой, сердце п желудокт.
переместились бы на правую сторону, а печень — на, левую.
Словомъ, каждая частица его тела была бы не] (вмещена,—п все

229
это произошло бы чпето геометрически, бенъ малтшшаго расстрой-
расстройства организма—какъ у м-ра Пляттпера въ разсказй Уэльса.
То же самое произошло бы со всякпмъ предметомъ о трехъ
пзл'Ьрешяхъ, даже съ очень масспвнымъ. Наибольшая ппрампда,
пол авт. бъ ьпръ четырехъ изм'вреши, можетъ быть перевернута,
очень легко. КромгЬ того, веЬ пуотыя внутри вещи, какъ рези-
резиновые мячи н пр., ыогутъ быть вывернуты наизнанку безъ вся-
каго ущерба для матер1ала, пхъ составляющаго; наприм'Ьръ,
перчатка правой руки, послт, лутетегтвья въ четвертомъ измй-
peHin, возвратилась он перчаткой л&ой руки, н наоборотъ.
Таковы нтжиторыя логпчесгая заключен1я, «но аналогш», о
прортранств^ 4-хъ пзлгкрепШ.
И читатель теперь, надеемся, вполнф убедится, насколько
уже не фантастически, а, аналого-логпческн, если можно такъ
выразтъся, правъ Генри Уэльсъ во многпхъ существенныхъ
частяхъ своего разсказа.
Взрывъ заюнаго порошка понадобился автору потому, что
только посторонней силой можно существо какого-либо про-
пространства неренестп въ другое пространство. Дъ-лается также
понятнымъ, почему оргаипзмъ Пляттнера посл-Ь «путешеств1я»
сделался собствеппымъ свопмъ «зеркальньпгь изображетемъ».
«Понятно», почему Пляттне2)ъ получплъ способность проходить
сквозь ciiiibi нагапхъ доловъ. «Понятно», пожалуй, даже п то,
что сквозь его т^ло проходили его ученики. Словомъ, теперь
понятны мнойя остроулныя детали разсказа. ЕГепоиятно, по-
пожалуй, какъ ото такъ, все же, у Шяттнера сохранилась сна-
сначала въ рукахъ (а не прошла черезъ т'Ьло) бутылочка съ остат-
остатками зеленаго порошка? Какъ потомъ oua могла удержаться въ
его кармянахъ.. Ну. да это, какъ и «onucauie» вргЬшпостп ш'ра
4-хъ измт,решй, уже всецело остакшется на ответственности
ост1>оумнаго автора. Во всякомъ случай разсказъ его—замоз-
чатсльный п единственный въ своемъ родгЬ разсказъ.

Математика въ природ^.
«Золотое
Подъ назвашемъ «золотого дйлетя», «золотого с'Ьчешя»
пли даже «божественнаго дйлетя» у древнпхъ геометровъ било
известно д'Ьлеше «въ крайпемъ и среднем?, отпошепш», во-
вошедшее теперь во все наши школьные учебники. Напомнпмъ,
въ чемъ оно состоитъ.
Разд'Ьлить данную величину «ег крайнемъ и среднемъ отно-
шенш», значптъ разделить ее па тамя дв-Ь неравныя части,
чтобы большая относилась къ меньшей, какъ вся величина отно-
относится къ большей части. Въ алгебранческпхъ спмволахъ это
выразится такъ. Если а есть величина, подлежащая дтленш,
а х и а — х искомыя части (большая и меньшая), то между
величинами а, х и а — х должна существовать следующая
] фопорщопальная зависимость:
а	 х
х а — ж
т. е. х есть среднее геометрическое между «по — х. Нзъ этой
пропорщп легко олрсд'Ьлить и значоше х. По свойству про-
порцт им4рмъ:
х2 = а (а -— ж),
откуда
ж2 ~Ь ах — а2 = 0.

231
Р'Ьшпвъ это квадратное уравяете, получаемъ, что
1/5 — 1
1/5+1
а g
Условт задачи непосредственно удовлетворяете лишь пер-
первый корень. Отрицательный корень также им'Ьетъ изв'Ьст-
ное значеше, но мы его зд'Ьсь рассматривать не будемъ.
Итакъ, запомним!., что большая часть величины а, разд'Ь-
ленной въ крайиемъ и среднемъ отиошенш, равна иррадюналь-
ному выраженш а
Отношеше этой части къ ц/Ьлому, т. е. а -—-—•: а =
—-—. 1аково же, согласно пропорцш, должно быть и отно-
меньшей части къ большей. Если мы пожелаемъ вычис-
вычислить это выражеше, то полупить безконечпую неперюдическую
дробь:
^^ = 0,61804
И вотъ оказывается, что эта на первый взглядъ столь искус-
искусственная пропорцш, которую нельзя даже выразить рационально,
тгёетъ широкое прим'Ьнен1е въ природт,. Прпведемъ тому два
примера — одинъ изъ anaTOJiin челов^ческаго тгЬиа, другой —
изъ морфологш 1) растен1й..
Что части красиво сложеннаго человт^ческаго тЬла отвт,чаютъ
известной пропорцш—это всяшй знаетъ: недаромъ мы говоримъ
о «пропорцюнально» сложенной фпгуръ'. Но далеко не всв знаютъ,
что здгЬсь нм-Ьетъ мъ'сто именно та нропорщя, которую древхпе
называли золотьшъ дъмешемъ. Антпчныя статуи—лучшее дока-
доказательство того, что древше ваятели хорошо знали о цриыъ'не-
ти золотого д^летя къ расчленетю человъ'ческаго тъла.
х) Отд^лъ ботаники, носящШ назван1е «ыорфолопи* изучаетъ строен1е
органовъ растепШ и, сл4д., соотв15тствуетъ анатомш животныхъ.

232
Идеально сложенное человеческое тйло, можно сказать, вес-
цело построено на принцип!; золотого дъмешя. Еслн высоту
хорошо сложенной фигуры раздълпть въ крайнелъ и среднемъ
отношенш, то лшпя раздела придется какъ разъ на высот!;
талш или, точнее, пупка. Особенно хорошо удовлетворяет^ этой
пропорции мужская фигура,—и художники давно знаютъ, что,
вопреки общему мнгЬшю, мужчины красивее сложены, нежели,
женщины.
На любой антпчпой ста-
статуе можно проверить этотъ
1 своеобразный законъ. Но
дъ;ло этимъ не ограничи-
ограничивается. Если каждую- изъ
нолученныхъ частей въ
свою очередь разделить въ
крайнеиъ и среднемъ от-
ношеши, то лишя раздала
нройдетъ оиять таки въ
вполне онределенныхъ
(анатомически) пунктахъ:
на высоте такъ паз. Ада-
Адамова яблока п надколен-
ныхъ чашекъ. На фигуре
103 обозначено расчленеше
статуи Аполлона Бельведер-
скаго: I дйлитт, всю высоту
AU фигуры въ кр. и ср.
отношенш; лпшя Е дъмитъ
точно такъ же верхнюю часть туловища (короткая часть вверху),
а лишя О—нижнюю часть (короткая часть внизу)"
Но и это еще не все. Каждая отдельная часть тела—голова,
рука, кисть и т. д. также расчленяется на естественныя ча""и
по закону золотого д'Ьлетя. Разделивъ въ крайнелъ п среднемъ
отиошенш самую верхнюю пзъ полученныхъ прежде частей (см.
фиг. 104), мы убедимся, что разде.ть придется на лпн1п бровей
(Ь); при дальнейшимъ делен!и образовавшихся частей получюгь
последовательно: кончикъ носа (с), кончикъ подбородка (d) и т. д.
Фиг. 103.

233
Рука (фиг. 105) при расчлененш согласно принципу золотого дъ-ле-
1пя распадается на своп анатомпчесыя
части—плечо, предплечье, кисть. Послал- д
Фиг. 104.
Фиг. 106.
няя въ своему расчлененш также отвйчаетъ этому принципу
(фиг. 1U6)—и т. д.
Если бы съ саиаго начала мы раздътшли тъмго человека въ
крайнемъ и среднемъ отношенш такъ, чтобы меньшая часть
была не вверху, а внизу, то оказалось бы, иг
что дитя раздала проходитъ черезъ концы
свободно свнсающпхъ рукъ 1). Словомъ, рас-
членеше наружпыхъ формъ правильно сло-
женнаго человъ'ческаго тЪла подчиняется до
мельчайпшхъ частей принципу золотого д'кте-
шя. Этотъ завАчатацьный законъ былъ хорошо
нзвгЬстеигь древнпчъ, по честь воскрсшешя
его прпнадлежитъ немецкому ученому Цей-
зннгу, который шестьдесятъ лгЬтъ тому на-
задъ выпустнлъ книгу, специально посвященную лрпмгБнен1ю
золотого flfeenifl въ прпродЪ и эстетик'Ь,—ибо оказывается, что
15
9
15
24
36
ЮЗ
п
1
"V ¦
1
/О'
-
О \
V,
Фиг. 106.
Ранке, «Чедов1къ«; Проф. Брандтъ, ^Антропологическ1е очерки*

234
тотъ же закоиъ въ шпрокпхъ рамкахъ щшм'Ьпимъ и въ пзопра-
зителышхъ пскусствахъ, и въ архитектур!', п музыке и даже стц-
хосложенш. Останавливаться на этой интересной теме не входптъ
въ нашу задачу, н ыы можемъ отвести ей лишь немного места.
Золотое дЪлеше въ эстетикЪ.
Существует!., какъ известно-, определенный геонетрпчеошй
способъ дт>лешя даннаго отрезка въ крайнемъ и среднемъ отно-
шенш,-—сиособъ хотя и не сложный, однако же и не слишкомъ
простой. Изъ лк>дей, проходпвшпхъ геоме-Tpiio, добрыхъ девять
десятыхъ его забываютъ. Но оказывается, что мы часто совер-
совершенно безеозпательно выполняемъ это дтлеше, при чемъ люди,
никогда не изучавипе reojieipin, Д'Ьлаттъ это нисколько не хуже,
чЪмъ записные математики. Для
А
этого достаточно ооладать лишь раа-
витымъ художественныыъ вкусомъ.
Прнм'Ьровъ такого безеознатель-
IV)	наго прпмгЬнетя принципа золотого
дгЬлен1я можно принести сколько
угодно. Возьмемъ хотя бы обыкно-
обыкновенный креетъ. ВсЬ заметили, ве-
вероятно, что фигура, эта гораздо гоящ-
н4е, если меньшая перекладина
помещается не ровно но середин!
большей, а немного повыше.
Если бы вамъ предложили са-
сами мъ устроить креетъ изъ двухъ
планокъ, то вы, поелт, н'Ьсколькихъ пробъ, придали бы пхъ дли-
намъ определенное отношиие и расположили бы вполнт, опре-
дъ-леннымъ образомъ. Окажется при этомъ, что меньшая пере-
перекладина будеть делить большую въ крапнемъ и среднемъ отно-
шеши. Другими словами, вы совершенно безеознательно приме-
применили здесь пропорцш золотого делешя: отрезки AM, MB и АВ
(см. фиг. 1U7) будутъ удовлетворять пропорщи:
В
Фиг. 107.
AM: MB = MB: AB.

236
Любопытно однако, что части меньшей перекладины- должны
быть равны, чтобы удовлетворять чувству пзящнаго. 1Га этоыъ
npmrbpe очень ясно обнаруживается свойственная наыъ склон-
склонность предпочитать симметрию въ горизонтальномъ направленш
и золотое делеше въ вертнкальномъ. Не потому ли, что и
человеческое тело построено по этому принципу?
Вотъ еще одинъ примерь той -жо категорш. Въ 60-хъ годахъ
истекшаго стол'Ьия члены Рнжскаго общества естествоиспыта-
естествоиспытателей предприняли следующее любопытное изеледоваше: онп
собрали несколько тыгячъ вшитныхъ карточекъ различный,
лицъ и определили criioiueHie длинъ нхъ неравныхъ сторонъ.
Изъ многочисленныхъ цифръ вывели среди юю и оказалось, что
она довольно точно подходитъ къ «крайнему и среднему отно-
отношение». Принципъ золотого дтлешя сказался, следовательно, и
здесь. Очевидно, выбирая форму карточки по своему вкусу, мы
безеознателыю руководимся
этимъ принципомъ. Намъ
представляются одпнаково
некрасивыми и квадратная
и елншкомъ удлиненная
прямоугольная форма — и
та и другая грубо нару-
нарушаете пропорцш ЗОЛОТОГО "	Ф„г. 108. Пареенонъ.
То же наблюдается и во многихъ другихъ случаяхъ, где
прямоугольная форма предмета не зависим, отъ нритязашй
практики п можетъ свободно подчиняться требовашямъ вкуса.
Прямоугольная форма книгъ, бумажнпковъ, фотографпчогкнхъ
карточекъ, рамокъ для картпнъ —более или менее точно удо-
удовлетворяет!, пропорцш золотого д'Ьлепш. Даже такш предметы,
какъ столы, шкафы, ящики, окна, двери — не г< >стаставляютъ
псключешя: въ этомъ легко убедиться, взявъ среднее пзъ ыио-
шхъ иззгЪренш.
Въ а1>хитектуре мы нмеемъ де.'Ю уже от. более пли менее
сознательнымъ прпмт.нетеыъ того же принципа. Для примера
раземотримъ одно пзъ знаменитейшпхъ произведен^ древне-гре-
древне-греческой архитектуры—Пареенонъ (фиг. 108). Длина его архитрава
J-LJ U Ц.|_!.ЬШ-Ц-
—
UUUUUU L

236
. 107 футовъ, высота же всего здашя отъ ссновашя до вер-
верхушки — 65 «рут. г)ти две цифры, ширины и вышины, ияолн'Ь
удовяетворяютъ пропорцш золотого д'Ьлетя: если взять 0,618
отъ 107, получпмъ 65,27 — т. е., пренебрегая дробью, высоту
здатя. Если высот)' Пароенона разбить на части но пропорцш
золотого дъ-лешя, то окажется, что все получаюпцяся при этомъ
точки обозначены характерными выступами фасада.
Пропзведешя. готической архитектуры также часто удовле-
творяетъ тому же математическому принципу.
После этого отступлешя въ область эстетики, вернемся снова
къ нашей основной теме— математика въ природ^.
Законъ листорасположешя.
Листья на стебли могутъ располагаться двояко: либо къ пз-
в'Ьстному пункту стебля прикрепляется всего одицъ .тпстъ, либо
сразу нисколько. Въ томъ и другоыъ случай расположеше ихъ
не случайно и подчиняется опред'Ьлеиньшъ математическпмъ за-
конамъ. Мы разсмотримъ здесь только первый случай, более
общи и интересный.
Если кы внплательно разсмотрите веточку съ одиноко сидя-
сидящими листьями, то заметите, что основашя черешковъ распо-
располагаются но винтовой лпнш: каждый сл4дующ)й листъ при-
прикрепляется повыше и въ стор<1ну отъ предыдущаго. 9то выступптъ
отчетливее, если соедшшть поетъ^овательно основа.1пя листьевъ
ниткой—она будетъ обвиваться вокругъ стебля въ фо])М'Ь пра-
правильной винтовой или спиральной лиши.
Сл'Ьдя за расположен1елъ лпстьевъ на этой спирали1), мы
непременно наткнемся на тате листья, которые сидятъ одинъ
надъ другимъ,— по образующей цилиндрической поверхности
стебля. Часть спирали, заключающаяся между двумя такими
листьями, называется въ ботанике цикломъ; въ пределахъ одного
цикла спираль можетъ несколько разъ огибать стебель, въ зави-
зависимости отъ ея крутизны.
>) Строго говоря, тормипъ «винтовая лшпя» зд'Ьсь ум^стн^р, нежели «спи-
«спираль», ни въ ботаник-Ь установилось употреилеше второго термина, котораго
мы и держимся.

237
Въ Потанпк'Ь листорасположеше характеризуют!, чнсломъ ofio-
ротовъ сппралп и чнсломъ листьевъ—въ предЪлахъ одного цикла.
Для краткости и удобства обозначаюсь листорасположеше въ
вид'Ь дроби: въ числите:!* ппшутъ число оооротовъ одного цикла
спирали, а въ знаменатели число листьевъ въ отомъ цпкл'Ь. Такъ,
3
дробь показывотъ, что одниъ циклъ спирали трижды обходить
о
кругомъ стебля, и что въ этомъ цикл* 8 листьевъ. Легко понять,
что та же самая дробь выражаетъ и уголъ расхождешя двухъ
сосЬднпхъ листьевъ — въ данномъ случай ^ окружности, т. е.
В 5
135°. Отсюда слъ'дуетъ также, что дроби — и о выражаютъ,
о о
въ сущности, одно и то же лпсторапюложеше, ибо уголъ въ <г
окружшсти дополияетъ до 3(>0' уголъ въ -' окружности; разлпчныя
цифры получаются въ зависимости отъ того, что въ одномъ слу-
случай спираль вели, напр., справа налево, въ другомъ — слЪва
направо.
Каждый видъ pacTeiiifi пм^етъ свое листорасположеи1е, пли,
Btpirbe,— свой уголъ расхождегня листьевъ, который выдержи-
выдерживается съ большей или меньшой строгостью во ъсЬхъ его частяхъ
и распространяется не только на листья, но и на расположите
в'Ьтокъ, почекъ, цв'Ьтовъ. четуекъ внутри почекъ. Но этотъ
уголъ, варьируя отъ растешя къ растеи1ю, однако иепропзво-
ленъ: во всемъ растительнолъ iiiprb наблюдается сравнительно
небольшое число тпповъ листорасположешя, выражающихся ие-
многгаш дробями. Вотъ табличка Hauooflie распрострапенныхъ
листорасположешй:
112 3 5 8
2' 3' 5' R' 13' 2Т ' ' '
Ботаники давно заметили, что рядъ этотъ отличается одной
любопытной и довольно неожиданной особенностью, а именно,
что каждая изъ этихъ дробей (начиная съ третьей) получается
пзъ двухъ иредыдущпхъ черезъ сложете пхъ числителей и
знаменателей.

238
Такт.
8 _ 3+5
2Т~8+Тз П Т" Л"
Поэтому достаточно запомнить только дв-fc первыя дроби,
чтопы удержать въ памяти всю табличку.
Однако, въ чемъ разгадка этого страннаго свойства дробей
лнетораоположенш? г)тпмъ ыы еейчасъ п займемся. Прежде
2 3
всего замйнимъ въ табличк! дроби _ , ^ и т. д. равнозначу-
3 б
щими пмъ дрооями —, ц и т. д. -мы въдь знаелъ уже, что
О О
такая замена вполнъ1 допустила, ибо эти дроби выражаютъ одно
и то же листорасположеше. Получилъ рядъ
1 2 3 5 _8_ 13
2' 3' б' 8' 13' 2l"" '
гдт> числители и знаменатели посл'Ьдовательныхъ дробей даютъ
уже известный намъ рядъ Фибоначчи (см. стр. 165). Разгадка
раскрывается довольно просто и находится въ гЬси'Ьйшен связи
опять такп съ принципом* золотого д'Ьлен^я.
Въ самомъ д-Ьл1!), не трудно убедиться, что дроби только
что ириведеннаго ряда суть простгЬйш1я нрпближешя величины
- —„	, найденныя путемъ разложешя ея въ бесконечную не-
прерывную дробь:
J/5 1 1
1+1

1+1
1+
Заинтересовавшее насъ выше правило гиставдошя ряда
(черезъ (уюжен!Р числителей и знаменателей) еегь просто стЬд-
CTBie закона составлешя нодходящихь дробей при знаменатели,
равномъ единиц'Ь:

239
1
1
1
2
1
2
3
1
3
5
1
1 1 1
5 [ 8 | 13
8
13 | 21
Птакъ, къ чему же мы пришли? Къ правилу, что листья
па стаблп, стремятся расположиться такимъ образомъ,
чтобы раздплить окружность стебля въ крайпемъ и среднемъ
отпогиети,—избирая при томъ простпйшгя приблиоюепгя
этой пропорцги.
Простгьпшгя,—ибо въ теорзп непрерывпыхъ дробей дока-
доказывается, что подходящ! я дробп, при данной степени прпблпже-
шя, отличаются наименьшими числителемъ и зиаыенателемъ: не
существуете никакой иной дроби, которая, пм-Ья меньппе члены,
нежели взятая подходящая, выражала бы искомую величину
точнее.
Замечательная связь, существующая между листорасположе-
шемъ и нронорщей золотого д'Ьлешя, бы.ча открыта более
би-тп л'Ьтъ тому назадъ уже упомянутымъ выше Цейзпнголъ
и опубликована въ его труд'Ь гЭететпчеошя пзыскашя; (Aestlie-
tische Forchungen. Frankfurt a. M. 1855). Но его открьте
почему-то забыто п при томъ такъ основательно, что когда
пшпущш эти строки, въ свои студенчесше годы, самостоятельно
noflMiTiLUb эту законосообразноетъ л обратился за разъяснешемъ
къ профессору — выдающемуся авторитету въ ботанической
науке,—то спып'алпетъ откровенно сознался, что ему ничего не-
неизвестно о связи лпеторасположешя съ золотымъ дЗзлешемъ...
Труды Цейзинга (откуда заимствованы некоторые изъ прп-
лагаемыхъ рпсунковъ) стапп теперь редкостью. На русскомъ
языкгЬ въ 1875 г. была издана анонимная брошюра «Золотое деле-
Hie, какъ основной лорфологпчешй законъ въ прпрод^ п искус-
искусстве- (Москва). Но п ее можно достать только у букпнпстовъ. Зна-
Знаменитый художипкъ п ученый Леонардо-да-Впнчи хо]>ошо понн-
малъ и ц'Ьиплъ эстетическое значеше золотого сЪчешя; подъ его
вл1я1пслъ и при его сотрудничестве было написано въ 1609
году сочпнеше Луки Начюло < Божественное целеше» (Dhiua
proportio), где эта тема трактуется съ большой обстоятельностью.

240
Математичесш инстинктъ пчелъ.
Задолго, быть можетъ, до ноявлешя человека на земномъ
шщ>% пчелы разрешили задачу, представляющую не малыя
геометрпчесшя трудности. Хотя она разрешается средствами
элементарной математики, но не думаемъ, чтобы ученпкп вы-
выпускного класса были довольны, еслп бъ пмъ на экзамен^
предложили эту «пчелиную задачу».
Архитектура сотъ съ jix'j. шестигранными ячейками известна
всякому. Однако далеко не веЬ знаютъ, съ какимъ попстпнгЬ
поразительпымъ расчетомъ онт, сооружаются. Стремясь возможно
экономн-Ье использовать мйсто въ тйсномъ уль-Ь п возможно
меньше затратить драгоцъчшаго воска, пчелы показали себя не
только трудолюбивыми архитекторами, но п отменными мате-
математиками.
Остановимся прежде всего на шестиугольной формт, ячеекъ
и разберемъ, почему пчелы отдали предпочтете этому много-
многоугольнику. Передъ ними стояла задача—заполнигь данную
плоскость правильными многоугольниками сплошь бсзъ просвгъ-
товъ, - ибо улей гвсенъ и надо использовать каждоо м-ьстечко.
Каше многоугольники годятся для этой и,гЬли? Воть первый
вопросъ, и мы займемся его разсмотр-Ьшемъ.
Суима угловъ всякаго многоугольника = 2d (п—2), слт,д.
каждый уголъ правильнаго миогоугодьника о п сторопахъ =
2A (п—2) ^
= -	-. Ьели таые многотголышки сплошь иалолняють
п
какую-либо плоскость, то вокругт, каждой вершины тгхъ должно
быть расположено цъмое число такнхъ угловъ. Другплп словами,
правильный многоугольнпкъ только тогда годится для сплошного
заполнешя плоскости, когда уголъ его, повторенной к разъ,
составить Ad. Поэтому мы можемъ составить сл4д. уравнение:
4A
п
Сокративъ па d а сдгЬлавъ унрощен1я, получим*:
rili — 2ii—2n = i)	A)

241
гдт. п—число угловъ (или сторонъ) многоугольника, а к—число
многоугольнпковъ, имт.ющихъ общую вершину. След., п и к
должны быть числа. цт.лыя и положптельпыя. Намъ остается
найги всЬ цълыя и положителышя ртлиешя этого неопределен-
неопределенная уравнешя 2-й степени.
Для этого придется сделать рядъ преобразовашй. Опреде-
Определив^, п пзъ уравнешя A), пм4еыгь:
2к 2А--4+4 о . 4
7- 9
IV- Л
Разсматривая равенство
к—2
-— 2"
мы видимъ, что п будетъ ц'Ьлымъ чпсломъ лишь тогда, когда
4
частное 7 будетъ число цъ'лое; другими словами — когда
к—2
к—2 будетъ однимъ шъ делителей числа 4. Такихъ делителей
немного, и ихъ легко найти Bci: 4, 2 и 1. ДальнМидй ходъ
ii ясенъ.
/с—2 =
4
IV 	?i
4
к —
1
3
6
2
2
1
4
4 fi
4 1 3
Итакъ, только три p'buieilia удовлетворяют!, иаппшъ усло-
вьямъ н, следовательно, только три правильных'!, многоуголь-
ппка могутъ занолнпть плоскость сплошь, безъ просв^товъ. Это—
треугольникъ, квадратъ п шестиугольникъ. Въ иервомъ <\ту-
чагЬ. къ каждой вершин'Ь будутъ сходиться G лшогоугольниковъ,
во второль—4. въ третьемъ—3.
Какому же пзъ ныхъ надо отдать продпочтеше? При устрой-
ствт. торцовыхъ мостовыхъ шашкяыъ прцдаютъ шестиугольную
форму,—но делается это просто потолу, что тупые углы A20°)
БЪ ЦАРСТВ» ОМЕКАЛЕИ.	16

242
мен^е скалываются, нежели прямые углы квадрата или острые—
треугольника (замътимъ, къ тому же, что дерево колется вдоль
годичныхъ слоевъ, пмтлощнхъ форлу концентрическпхъ кру-
говъ). Пчелаыъ съ этпмъ особенно считаться не приходится,
зато имъ крайне важно экономить воскъ для сттлокъ ячеекъ.
Значить, надо определить, какой лзъ этпхъ многоугольниковъ,
при равныхъ площадяхъ, им'Ьетъ наименышй контуръ. Это вто-
второй ыатематпческш воиросъ, также правильно разрешенный
пчелаып, ибо изъ трехъ упомянутыхъ фигуръ шестиуголышкъ
какъ разъ шгЬетъ наименьилй контуръ.
Въ самомъ д4лгЬ. Бообразимъ треугольнпкъ, квадратъ и
шестиугольникъ, пмт,юпце одну и ту же илощадь S, и сравнишь
ихъ периметры.
Для Д-ка изъ равенства
находимъ сначала сторону а, а затЬмъ и перпметръ Рг = 3 а
Для квадрата илг^емь, что сторона его Ъ = VS, а следов,
периметръ
Для правильная) шестиугольника со стороной с им4емъ:
о_зсуз
2 '
откупа иерпметръ
2S
3]/3
Отнотоше:
= 1 : 0,905 : 0.816,
откуда ясно, что щ^шистрь шестиугольника (Р3) напменьшш.

243
Но и это еще не вст, математические вопросы, разрешенные
пчелами. Самую трудную задачу намъ еще предстоптъ раз-
смотр'Ьть. Она-то собственно п есть та «задача о пчелиныхъ
ячейкахъ». которою занима.шсь ученые XVIII вгЬка. Пол-
Полное pimeme ея принадлежите известному математику Макло-
реню, который занялся ею по совету натуралиста Реомюра.
Ниже мы иом'Ьщаемъ задачу и ея ръ-шеше въ томъ вид'Ь, какъ
они приведены въ куреЬ алгебры П. Н. Маракуева,
Задача 69-я.
О пчелиныхъ ячейкахъ.
На продолженш оси 00' правильной шестиуголь-
шестиугольной призмы возьмемъ точку S; черезъ эту точку и чрезъ
каждую изъ сторонъ равносторонняго треугольника
АСЕ, полученнаго соединешемъ
чрезъ одну вершинъ верхняго осно-
вашя призмы, проведемъ три пло-
плоскости, по которымъ отрЬжемъ
отъ призмы три тетраэдра BACK,
DCEH и FEAL и зам'Ьнимъ ихъ
однимъ тетраэдромъ SACE, по-
ставленнымъ надъ призмой. Но-
Новый многогранникъ будетъ ограни-
ченъ сверху тремя ромбами SAKC,
SCEH, SEAL; объемъ его всегда
равенъ объему взятой призмы, гд^
бы ни взять точку S на оси, ибо
пирамида SACE составлена изъ
трехъ пирамид ъ SO AC, SO СЕ и
SOEA, соответственно равныхъ
тремъ отрЬзаннымъ пирамидамъ;
такъ пирамида SO АС = пир. К ABC, ибо он? имътотъ
равныя основан!я (АО^С= 1\АВС, какъ половины
16*

244
ромба АВСО) и равныя высоты SO и KB (по равенству
прямоугольныхъ треугольниковъ SOI и КЫ).
Им?я равные объемы, многогранники имЪютъ, од-
однако, различный поверхности, и задача состоитъ въ
опредгъленш точки S такъ, чтобы поверхность новаго де-
десятигранника имгьм нагтенъгиую величину.
Р'Ъшеше задачи.
Пусть АВ = а, ВВ'=ОО' = Ь, ВК=80 = х; въ та-
комъ случай: АС=а\/3; SI = \/802 + ОТ- =у х2 + ~ =
= ty4x2 + а2; сл'Ьд. SK=\/'Ax2 + a2;
площадь ромба SAKC, равная полупроизведенпо Д1агоиалей
АС и SK, выразится формулою - а |/3 а2 +12 ж2; площадь тра-
пещи СКВ'С—формулою - а B 6 ¦—¦»). Слъдоват., поверхность
многогранника, не считая ооновашя, выражается формулою
3 —г—?	¦
ai / Q ft —1— "I О />*^ ,1 _ Q л /9 л	. 'У \
ИЛИ
— Л.
Постоянный множитель За не вл!яетъ на услов!я max. и
min., и потому вопросъ приводится къ оирецъ'лешю miniinuin'a
скобочнаго выражешя. Положивъ
1
-|/Зй2 + 12ж2 -f 26 — х = т
и освободпвъ это уравнеше отъ радикала, найделъ
8х2— 8 (да — 26)ж + Зй2 — 4(»и — 26J = О,
откуда

246
Чтобы х было действительно, необходимо, чтобы
— 2lf — «3^0, плп (т~2ЪJ^~ или «и —2
Отсюда minim, (да) — 2 i -f- ——. Помноживъ па 3 а, найдемъ,
У 2
что искомая минимальная поверхность равна
V2
1 /—
а соответствующая величина ж=-яу2.
Формула для я; показываетъ, что разпость двух!, смежныхъ
боковыхъ реберъ должна быть равна четверти fliaroHsum квад-
квадрата, построеннаго на стороп'Ь шестиугольника, служащаго
осиован1емъ призмы.
Поверхпость призмы, не считая основашя, былабы 6«6-|— ——;
сл^д. поверхность многогранника минимальнойповерхности меньше
о
на ^а2(\/Ъ — У2) поверхности шестиугольной призмы, имеющей
то же основаше п тотъ же объемъ.
Легко видт,ть, что для треугольника KBI им^етъ м4сто
нропорщя
BK:BI:IK=1 :
откуда (при помощи тригонометр1и) найдемъ, что уголъ ШК =
= 35°15'62".
Остается прибавить, что ячейки пчать суть именно TaKie
десятигранники съ наименьшей поверхностью, т. е. шестигран-
ныя призмы, ограниченныя съ одной стороны гаестиугольникомъ
(входъ въ ячейку), съ другой тремя ромбами подъ указанньшъ
угломъ (дно). Два слоя ячеекъ вплотную входятъ другъ въ друга
острыми выступами своихъ доньевъ и обращены открытыми
шестиугольниками въ противоположныя стороны. Каждая пара
такихъ слоевъ и составляетъ сотъ.

246
Столь совершенная архитектура пчелпныхъ сотъ, съ мате-
ыатнчссшшъ разсчетомъ и экономией использующая пом'Ьщеше
улья и строительный матер1*а.лъ (воскъ), уже давно приводить
въ изумлеше наблюдателей. Еще Патшусъ, ыатематикъ IV вика
по Р. Хр., обратилъ выплате на строго геометрическую форму
ячеекъ. Дарвинъ пытался объяснить возникновете этого слож-
наго инстинкта пчелъ своей Teopifl естественнаго отбора, а именно,
онъ допускаетъ, что предки напшхъ пчелъ сооружали ячейки
цилиндрической формы, и что эти цилиндры, тисня другъ друга,
постепенно превратились въ шестигранники. Однако его теоргя
далеко не объясняетъ всЬхъ особенностей структуры сотъ (напр.
того, что ячейки при данномъ объели им'Ьютъ наименьшую по-
поверхность). Н4тъ сомнътая, что мы стоитъ здгЬсь иредъ одной
изъ глубочайшцхъ загадокъ природы.
Жукъ геометръ.
Если пчелы разрешили задачу изъ курса элементарной ма-
математики, то небольшой зкучекъ семейства слониковъ разр?-
шилъ еще болъ-е трудную задачу—изъ курса высшей математики.
Зоологическое назваше этого жука-мате-
- ЯгH^-	матика Bhyncliites behilae, а народное—
[¦"' N	березовый слоникъ. Этотъ маленькш (-1 ми-
лиметра) черный, блестящи жучокъ съ
1 •	длиниымъ хоботкомъ пмгЬетъ привычку
ыеТ^ъ въ увеЙеншмъ свертывать въ трубки листья березы, ольхи,
вид*. Черточка внизу бука, чтобы положить въ нихъ свои яички.
даетъ поняйе о его на- ^
туральшй величин*. Ьолыпого удовольствия садоводамъ и лъсо-
водамъ березовый слоникъ, конечно, не
доставляете, но зато онъ способенъ привести въ восхищен1е
математика, если иослйдшй обратитъ вниман!е на сиособъ, какпмъ
жучекъ свертываетъ листья. Въ общихъ чертахъ эта манера
такова. Предварительно слоникъ прогрызаетъ блпзъ основатя
листа дв4 кривыя лишя, которыя идутъ отъ средней жилки къ
краямъ (см. фпг. 111, цифра 3). ДошгЬ этого онъ свертываетъ
въ трубку сначала одну половину листа, а зат4мъ обвертываетъ
эту трубку другой половиной. Получается нгбчто въ род4 сигары,

247
которая и остается виеЪть на чсрешк'Ь (фиг. 111, цифры 4 и б),
укрывая положенныя въ нпхъ яйца. Все это длптся около полу-
получаса.
Математичесшй ипстинктъ березоваго слоника проявляется въ
выбора формы кривого npopfea, который опъ дъччаетъ на пла-
Фиг. 111. Жукъ-геомстръ. 1 и 2—Березовый слонпкъ. 3—листъ, на которомъ
показаны форма и положете прор4аовъ. 4 и б—свернутые листья. 6—личинка
7—слоникъ въ увеличенномъ вид4.
листа. Эта кривая выбирается далеко не случайно и
находится въ некоторой, довольно сложной, — однако вполнт,
определенной—связи съ формой самаго края листа. Вы можете
убедиться въ этомъ на опыт'Б. Вырежьте пзъ бумаги фигуру
листа (фиг. 112) и попробуйте свертывать ея половины въ

248
Фиг. 112.
трубку, какъ это д'влаетъ слоникъ, прорйзавъ предварительно
листъ у его основашя. Окажется, что если црор'Ьаъ сд'Ьланъ по
прямой od п.тп по дугаыъ obd и oed,
свертываше удается далеко не такъ
легко и удобно, какъ въ томъ случа'Ь,
когда надрезу придана форма 8- образ-
образной лиши оса или oed. Для полнаго
же усп'Ьха д'Ьла важно, чтобы эта S- об-
образная кривая шгЬла вполн-Ь определен-
определенную форму и занимала определенное
шложеше по отношешю къ краю ли-
листа. Въ термипахъ такъ называемой
высшей математики эта взаимная связь
можетъ быть выражена такъ: лишя про-
pfea должна быть «эволютой» краевой лиши листа; или, что
то же самое, краевая лишя лпста должна быть «эвольвентой?
лиши прорФза.
Эволюта и эвольвента.
Постараемся объяснить кратко и наглядно, что такое «эво-
«эволюта» и «эвольвента». Обратите внимаше иа фигуру 113.
Здъ-сь изображены двгЬ кривыя—окружность О и кривая АВСВЕ.
Зависимость между ними
та, что каждая касатель-
касательная къ кривой О перпен-
перпендикулярна еъ кривой
АВСВЕ. Если дв4 кри-
кривыя находятся между со-
собой въ такой зависимо- D|
сти, то ту, которая пер-
перпендикулярна къ каса-
тельнымъ первой кривой,
называютъ эвольвентой
плп развертывающей, а
первую — эволютой или разверткой. Въ нашемъ npmrbpT, кругь
О будетъ эволютой, а кривая АВСВЕ—эвольвентой.
Если вы желаете по данной эволют^ построить ея эволь-
эвольвенту, то можете поступить сл^дующимъ образомъ. Начертите
Фиг. 113.

249
эту эволюту на толстомъ картонъ- или деревй ir вырежьте ее
по краю. Положите вашу картонную пволюту налистъ бумаги,
запретите нить Аа въ точк-в а (см. фиг. 113); на. другом* же
кошгЬ нити сделайте петельку и вставьте въ нее карандашъ.
Теперь наматывайте нить на эво-
эволюту, гл-Ьдя за т!шъ, чтобы нить все
время оставалась натянутой. Тогда
конецъ А начертить вамъ эволь-
эвольвенту взятой кривой. Это строго до-
доказывается въ курсахъ аналитической
геометрш.
Вы могли поступить п иначе —
а именно, предварительно обмотать
нить кругомъ эволюты и, держа въ
патяпутомъ видй, разматывать ее.
Въ ятомъ случай вы получите ту же
самую эвольвенту, что и ранйе.
Отсюда сл'Ьдуетъ, между прочшгъ,
что касательныя эволюты (онт. же п
рад1усы кривизны эвольвенты) равны
длинъ1 той части эволюты, ст. которой
опЬ смотались. Другими словами: если
мы начали сматывать съ точки х
(фпг. 113), то длина прямой еЕ равна
длинй дуги еж, dU = dex, cO=
cdex и т. д.
Обратно, если по данной эволь-
вептт, надобно начертить ея эволюту,
то проводятъ къ эвольвент^ рядъ нормалей (периендикулярныхъ
лин1й), которыя пересекаясь одна съ другой, образуютъ неко-
некоторую ломаную лин1ю. Вписавъ въ эту ломаную лииш кривую,
касательную къ ея элементаыъ, вы получите искомую эволюту.
Фпг. 114.

260
Задача 70-я.
Построеше жука-геометра.
Вотъ такого-то рода задачу—постройки эволюты по данной
эвольвент^— п рт>шаетъ березовый слоппкъ. На той половши
листа, которая потомъ послужитъ внутренней трубкой, онъ вы-
грызаетъ эволюту краевой Jiunin листа. Если для лннш надр'Ъза
Abcdegildm (см. фиг. L14) построить ея эвольвенту, то эта
последняя будетъ шить форму кривой ABCDEGIKLxy,
весьма близко подходящую къ краевой линш листа.
Ilpopfeb другой половины листа, которая облекаетъ пер-
первую, не отличается такой математической правильностью. Этого
и нельзя ожидать, такъ какъ вторая половина не свертывается
свободно, какъ первая, а навивается на первую.
На жук4-геометргв мы и закончимъ нашу бесЬду о «мате-
матикф въ природ^».

«Новыя начала геометрш».
Знаменитый мемуаръ Лобачевскаю еъ краткот изложены И. П. Соколова.
Тому, кто желаетъ ознакомиться съ работами Лобачевскаго,
лучше всего начинать съ изучешя его сочпнешя «Новыя на-
начала геометрш». Вотъ почему, желая ознакомить читателя съ
характеромъ пзсл'Ъдовашй нашего великаго геометра, мы и дасмъ
ниже разборъ содержашя этого сочинетя. Если читатель,
въ силу малой подготовки, не осилить сразу всей этой главы,
то достаточно внимательно прочесть на первый разъ первую ея
половину,—особенно начала новой теорш цараллельныхъ—до
введешя въ изложеше тригонометрическихъ и пшерболическихъ
фуншцй. Это не составить особаго труда.
Разсматриваемое сочинеше Лобачевскаго состоитъ изъ введе-
шя и тринадцати главъ.
Во введенш, которое Лобачевскш начпиаетъ «разборомъ
прежнихъ теорш», онъ указываетъ недостатки главн'Ьйшихъ
пзъ изв'Ьстныхъ ему доказатедьствъ одиннадцатой аксшмы Ев-
Евклида и старается выяснить пхъ прпчпны. Вопреки MHiHiR)
Леи;андра, онъ находптъ, что эти причины коренятся вовсе не
въ недостаточно точномъ определены прямой и дал;е «нисколько
не завпслтъ отъ т^хъ недостатковъ, которые скрывались въ
первыхъ поня'пяхъ». Т'Ьмъ не мент,е эти недостатки весьма
важны сами по себ'Ь, и, къ чести Лобачевскаго надо сказать,

252
онъ одипъ изъ первыхъ обратилъ вшшаше па эти недостатки,
заьгЬтивъ, что эти первыя поняздя: «пространство, протяжеше,
м'всто, тг1;ло, поверхность, дишя, точка, направлете, уголъ
слова, которыми начинаютъ Геометрш, но съ которыми никогда
не соединяюсь яснаго поняпя».
Онъ первый сд'Ьлалъ попытку устранить эти недостатки,
перестроивъ съизнова начала Геометрш, начала, къ которымъ
со времени Евклида не см'Ьлъ прикасаться ни одинъ смертный.
Только блестящш усп4хъ первыхъ нзслъ'дованш, правда, не
признанныхъ и даже осмъ\янныхъ современниками, могъ внушить
такую см'Ьлую, скажемъ даже, дерзкую мысль.
Уже доказанная предыдущими изсл'Бдовашями необходи-
необходимость опыта для доказательства одиннадцатой акс1омы Евклида,
приводить Лобачевскаго къ заключетю, ныне уже, можно
сказать, ходячему, что «первыми данными будутъ всегда тгЬ
поняия, которыя мы прюбретаемъ въ природе посредством!»
нашихъ чувствъ» и что темноту въ ошовныхъ понятаяхъ Гео-
Геометрш производить именно «отвлеченность, которая въ прим'Ь-
нети къ дМствительнымъ измгЬрен1ямъ д'Ьлается лишней, а
следовательно въ самую -reopiro введена напрасно». Мнопя
опредгЬлеи1я онъ счптаетъ недостаточными уже и потому, что
эти опред^летя «не только не указываютъ на происхожден!е
геометрической величины, которую хотятъ определить, но даже
не доказываютъ, что татя величины существовать могутъ».
Посему онъ «вместо того, чтобы начинать Геометр1ю прямой
лишею и плоскостью, какъ это делается обыкновенно, пред-
почелъ начать сферой и кругомъ, которыхъ опред^лете не
подлежитъ упреку въ неполноте, потому что въ этихъ опред'Ь-
лен1яхъ заключается способъ, какимъ образомъ эти величины
происходятъ».
Плоскость онъ после этого определяетъ, какъ геометриче-
геометрическое место круговъ пересечен1я равныхъ сферъ, оппсанныхъ
около двухъ неподвижныхъ точекъ—иолюсовъ. Изъ этого опре-
делен1я онъ выводить уже все основные свойства плоскости.
Соответственно этому, прямая определяется, какъ геометриче-
геометрическое м'Ьсто точекъ пересЬчешя равныхъ круговъ, описанныхъ
около двухъ данныхъ точекъ на плоскости, хотя это опреде-

263
леше выражено у Лобачевскаго недостаточно ясно н начинается
собственно такимъ опредйлешемъ: «Прямой называется та лишя,
которая между двухъ точекъ иокрываетъ сама себя во вевхъ
положешяхъ». а затЬмъ уже выводятся вг,4 осталышя свойства
прямой п устанавливаются ея отпошешя къ кругу и плоскости.
Этпмъ опред^лешямъ осповныхъ элементовъ геометрш п устано-
вленго ихъ основныхъ соотношешй посвящены об1!1, первыя главы
сочинетя.
Третья глава посвящена изученш мйровыхъ cooTHomeuifl
отръ\зковъ и угловъ. Зд'Ьсь, кажется, въ первый разъ дается
поняие объ углгЬ, какъ числи отвлеченномъ, показывающемъ
только отношеше двухъ дугъ одного круга, изъ которыхъ одна
принята за единицу миры; опред-влеше, которое надо, uwk
кажется, считать единственно правильнымъ, но которое, къ со-
жалгЬшю, во всъ-хъ папшхъ учебникахъ заменяется бол4е или
мен^е неудачными альтернативами опред^лешй Евклида или
Берт]оана изъ Женевы. Ботъ подлинное опредйлеше Лобачев-
Лобачевскаго.
«Величина дут или части сферы, выраженная въ граду-
сахъ и доляхъ градуса, даже вообще по сравнетю съ тчьмъ
оке круюмъ или съ mvw оке сферой, называется уголъ, кото-
который бываетъ прямой, когда равенъ — те, острый, когда <С « ^
тупой, когда^^тс и < тс».
Это опредъ-леше дополняется еще двумя теоремами: 40. Ли-
Линейный уголъ не завпситъ отъ величины полупонеречнпка въ
круггЬ, но служптъ только къ определен iio взатшаго положешя
двухъ прямыхъ; и 42. Плоскостной уголъ не зависитъ отъ
полупоперечника сферы, ни отъ мгЬста для центра на линш
перееЬченгя двухъ плоскостей.
Опредйливъ такимъ образомъ уголъ и указавъ вмести съ
,тгЬмъ способъ его измйретя, Лобачевскш переходить въ следу-
следующей четвертой глав-Ь къ изучен!ю взаимнаго положешя пря-
прямыхъ на плоскости, плоскостей и прямыхъ въ пространств^,
при челъ находитъ основныя зависимости между сторонами и
углами треугольниковъ какъ плоскихъ, такъ и сфсрическихъ.

264
Пятая глава, посвященная изм^ренш тйлесныхъ угловъ, пред-
ставляетъ весьма лзящное нзложеше осиовныхъ теоремъ сфе-
сферической Геомотрш съ приложешемъ ея къ теорш правилышхъ
тъ'лъ. Глава шестая разсматриваетъ услов!я равенства треуголь-
нпковъ л зависимость свойствъ треугольника отъ гипотезы о
сумзгй его угловъ. Наконецъ въ главахъ VII, VIII, X и отчасти
XI Лобачевскш излагаетъ свою новую теорш параллельныхъ
лиши, не зависящую отъ справедливости одиннадцатой аксншы
Евклида. Главы IX, XII и XIII посвящены пзложенш тригоно-
метрш какъ плоской, такъ п сферической, и для насъ особаго
значешя уже не шйютъ; поэтому, не останавливаясь на нихъ,
ограничимся только пзложешемъ новой теорш параллельныхъ.
При этомъ, простоты ради, позволимъ себъ1 отступать иногда
отъ подлиннаго изложен]'я, пользуясь труда^ги другихъ геоие-
тровъ, какъ предшествовавшпхъ, такъ и сл'Ьдовавшпхъ за Лоба-
чевскимъ.
Начиемъ съ доказательства трехъ посл'Ьднпхъ теоремъ главы
шестой.
Сумма угловъ прямолинейнаго треугольника ABC
не можетъ быть больше двухъ прямыхъ.
Пусть эта сумма тс-|-с<, гд4 а какъ угодно малый уголъ,
и пусть А напменышй уголъ А ЛВС (Фиг. 115). Чрезъ сере-
в	дину Ж стороны ВС
ироведеыъ прямую
АЖ и на продолжили
ея отложимъ отр^зок-ь
А ^^	Ъ*?	МХ= AM. Тогда А
Ф„г. пб.	AMB = NMC, ибо
имъ'ютъ равные верти-
вертикальные при вершин^ М углы, заключенные между равными по
построешю сторонами. Значить, сумма угловъ треугольника ANC
должна быть равна суммъ1 угловъ Д-ка ABC, т. е. равна
ти -\- а, причемъ хотя одпнъ пзъ угловъ его будетъ < -А.
Продолжая подобное иостроеше, мы прпдемъ накоиецъ къ такому

266
треугольнику, одпнъ изъ угловъ котораго будетъ < ~п < ос, что
невозможно, пбо сумма двухъ угловъ треугольника всегда < тс-
Итакъ, сумма угловъ треугольника можетъ быть
только или равна, или меньше тс. Если она будетъ
равна тс хотя въ одномъ треугольник^, то она будетъ
равна тс и во всякомъ треугольник^.
Фиг. 116.
Чтобы убедиться въ этоиъ, построимъ на сторонъ1 ВС такого
треугольника ABC равный ему Д А'ВС (Фиг. 116). Сумма
угловъ шлученнаго параллелограмма будетъ 2тс. Ясно, что пзъ
такихъ параллелограммовъ можно построить параллелограымъ,
стороны котораго какъ угодно велики, а сумма угловъ 2тс.
Такой параллелограммъ въ свою оче!)едь можетъ быть д!агональю
разд^ленъ на два равныхъ треугольника, сумма угловъ въ
каждомъ изъ которыхъ будетъ тс, а одинъ изъ угловъ равенъ
углу А даннаго треугольника. Пусть FJ)E одинъ изъ такихъ
треуголышковъ, достаточно большой для того, чтобы какой-либо
произвольно взятый треуголышкъ NLM ыогъ поместиться

26R
внутри его. Поы^стиыъ его такъ, чтобы У a L лежали на FD,
а М гдЪ либо внутри FDE. Прямая FM, иерестжая DE въ
точки 22, разделить FDE иа два треугольника DFB п FEE.
Согласно опред'Ьяенш смежныхъ угловъ, сумма ихъ равна 2d,
т. е. DBF-\- FIXE=к. Следовательно, сумма угловъ этихъ
двухъ треугольниковъ, очевидно, равная суммЬ угловъ Д-ка
DEF, сложенной съ суммой двухъ названпыхъ сиежныхъ
угловъ при точк'Ь В, будетъ равна 2тс. Но, согласно доказан-
доказанному выше,—сумма угловъ треугольника не можетъ быть больше те,
значить, необходимо сумма угловъ каждаго пзъ треугольниковъ
DFB и FBE должна быть равна тт. То же будетъ п для пря-
мыхъ DM, ML и MN. Посему сумма угловъ /\NLM также
равна тт.
Если сумма угловъ треугольника меньше те, то
двухъ неравпыхъ треуюльникивъ, импяощихъ данные углы, быть
не можетъ.
Фиг. 117.
Пусть ABC и А1 В'С1—два треугольника (фиг. 117), такъ
что Л—А1, В = В' и С—С; АС^А'О. Налоалгаъ А'В10
на ABC такъ, чтобы углы А и А' совместились; пусть при
этомъ точка С упадетъ на точку D, точка В' можетъ упасть
либо въ точку Е на сторон!" АВ, либо въ точку F на ея про-
долженш. Въ первомъ случай гумма угловъ четыреугольнпка
BCDE будетъ равна 2тг,—а именно: сумма смоашыхъ угловъ
Z AFD + L BED—т:. Но уголь AED = Z В, поэтому
/_В-\-ZBED =ъ. То а;е, очевидно, им^егь мътто и для
остальной пары угловъ, такъ что Z C-\-L CDE=iz Четыро-
угольникъ BCDE, сумма угловъ котораго равна 2тг, любой изъ

267
fliaronajefr дътттся на 2 треугольника, въ каждомъ изъ кото-
рьшъ сумма угловъ должна быть равна тс, что, согласно выше-
доказанпому, невозможно. Во второшъ случай прямыя ВС п
DF, пересекаясь, образуюсь два треугольника DCH и FBH,
въ каждомъ изъ которыхъ гумма двухъ угловъ тс, а следова-
следовательно сумма исЬхъ четырехъ угловъ больше тс, что невозможно.
И такъ необходимо А'В' = АВ, а потому и А'В'С' = АВС.
Разсмотртлшыя предложешя даютъ возможность уже вполн'Ь
строго изложить новую тсорш парал.гелышхъ Лобачевскаго,
пзложеше коси начнемъ со слгЬду]Ощаго п]»едложен1я.
Чрезъ любую данную точку можно провести пря-
прямую, составляющую съ данной прямой какой угодно
малый уголъ.
Пусть прямая АС, проходящая чрезъ данную точку А
(фиг. 118), составляете, съ данной прямой ВС уголъ а; отло-
жпмъ DC —АО, въ ибйихъ гппотезахъ уголъ ABB будетъ не
больше -г- Повторяя то же построен ie, ыожемъ сд'Ьлать его мень-
меньшее т^, т. е. меньше всякой данной величины. Посему, если
сумма угловъ треугольника равна тс, есть только одпа прямая,
проходящая чрозъ данную точку А параллельно ВС (фиг. 118);
ибо пусть АВ перпенднкуляръ къ ВС, п ATI цсрпондпкулярь
къ АВ, прямая АН не псресЬкаетт. ВС. Проведемъ прямую
АС, составляющую съ ВС уголъ <7<сс, уголъ НАС будетъ
также, следовательно, <а, п потому какъ угодно малъ вм4ст4
съ а, такъ что, какъ бы мало мы ни отклонили АН отъ ея
ВЪ ЦАРОТВЪ СМЕКАЛКИ.	17

258
положешя, она уже будетъ пересекать ВС. Не трудно впд'Ьть,
что п обратное предложение также пдгЬетъ мгЬсто.
Если сумма угловъ треугольника <тс, то прямых!,,
не перес'Бкающихъ данной и проходящихъ чрезъ дан-
данную точку, можно провести безконечно много. Лоба-
чевскш называетъ параллельными данной прямой ВС
дв-fe тагая прямыя AD и АЕ, которыя отд-бляютъ пря-
мыя, перес-вкаюггдя ВС отъ непересъкающихъ. Острый
уголъ, который эти прямыя составляютъ съ перпен-
дикуляромъ АВ изъ А на ВС, онъ называетъ угломъ
параллельности относительно длины А В, и, если АВ=р,
обозначаетъ его символомъ Щр). Ту сторону, съ ко-
которой параллельныя прямыя приближаются другъ къ
другу, онъ называетъ стороною параллельности.
Двъ- параллельныя прямыя параллельны другъ другу
во всбхъ своихъ точкахъ.
Фиг. 119.
Пусть AD параллельна ВС (фиг. 119); па продолжены АВ
въ сторону параллельностп возьлелъ точку А1 и проведемъ пря-
прямую A'F внутри полосы между AD и ВС; прямая AF непре-
непременно пересекаете ВС где либо въ точке И, прямая A'F,
входящая въ треугольникъ АВН, можетъ выйти изъ него, только
пересекая сторону ВС, посему параллельной къ ВС въ точке А'
можетъ быть только прямая АВ. То же можно доказать п для
любой точки прямой АВ.
Прямая ВС также параллельна прямой АВ. Для сего до-
достаточно показать, что всякая прямая BZ между ВС и АВ
пересекаетъ АВ. Опусишъ перпендикуляръ изъ А на BZ'

2Ь9
Фиг. 120.
(фиг. 120), и поверпемъ всю полученную фигуру, кроме пря-
прямой ВС, около точки А такъ, чтобы этотъ перпендикуляръ A О
совместился съ АН,—прямая BZ займетъ тогда положеше IIZ
между AD и ВС, прямая AD положеше AZ u будетъ пере-
пересекать T1Z, пбо въ этомъ иоложенш она должна пересекать
прямую ВС. Следовательно, и въ начальномъ положеши AD
пересекала ВО, что и требовалось доказать.
Дв-fe прямыя, параллельныя третьей, параллельны
между собою.
Пусть изъ трехъ непересекающихся прямыхъ АВ парал-
параллельна CD и EF. Положпмъ, что CD лежитъ между АВ и
EF, тогда любая прямая EF', направленная въ сторону CD,
пересечетъ АВ, а потому и CD, лежащую ближе ея. На до-
доказательстве этой теоремы для случая, когда АВ лежитъ между
CD и EF, или когда АВ, CD и EF не лежать въ одной
плоскости, я останавливаться не буду, и перейду прямо къ вы-
выводу важнейшихъ следствш самой теоремы.
Эта теорема даетъ намъ прежде всего возможность судить
о характергь функцш Щх). Такъ, мы уже можемъ утвер-
утверждать, что эта функщя однозначна и всегда конечна; не трудно
также показать, что она убываем, съ возрасташемъ перемен-
иаго х. Действительно П(а) = П(й) певозможно, пбо иначе
два перпендикуляра къ одной прямой были бы параллельны,
тг
н П(ж) = -fr всегда; въ. то же время П(а) > И(#) при а >> Ъ
17*

260
также невозможно, ибо иначе прямая, проходящая чрезъ конецъ
перпендикуляра а подъ угломъ ЩЬ) къ нему, не нересЬкаетъ
уже п прямой, параллельной къ данной въ концт, перпенди-
перпендикуляра Ь; следовательно, всегда П(я)<П(й), или а>6.
Покажемъ еще, что функцгя 11\х) можетъ принимать
ваь значетя отъ нуля до -• Пусть ВА С (фиг. 121)—данный
А
Фиг. 121.
уголъ. Изъ точки Ъг на стороне АВ опускаемъ перпендпку-
ляръ Ъ1а1 на сторону АС и откладываемъ на АС отргЬзокъ
а1а2 = Аа1. Пусть перпендпкуляръ изъ а2 къ АС пересекаетъ
сторону АВ въ точке Ь2. Если сумма угловъ треугольника
Аа1Ъ1 будетъ тс— а, то въ треугольнике АЬха2 она будетъ
тс— 2а, а въ треугольнике Аа2Ъ2<С.ъ— 2а. Повторяя подоб-
подобное построеше, мы будемъ получать все TaKie треугольники съ
общгшъ угломъ А, гумма угловъ которыхъ будетъ меньше
тс — 4а, тс — бос п вообще после п построенгй меньше тс — 2па.
Но такъ какъ она не можетъ быть меньше А, то такое по-
строеше можетъ быть повторено лишь конечпое число разъ
п ^ - » ' • Дальнейшее перпендикуляры нерестанутъ уже пе-
пересекать АВ, начиная съ нгЬкотораго конечнаго 1)азстоян1я х
отъ точкп А, для котораш Щх) = А. Отсюда заключаемъ, что
функщя П(ж) убываетъ непрерывно, начиная отъ значения

261
П@) = ~ до зпачешя П(оо)=:0. Последнее обстоятельство
позволяем, намъ предполагать, что эта функцш П(гг) будетъ
показательнаго характера.
Всякую показательную фупкцш мояшо выразить съ помощью
простМшпхъ показательныхъ функщй, къ которымъ прпнадле-
жатъ функщй тригонометрическая н гпперболпчесгая. Основнымъ
своиствомъ яхъ является пхъ однозначность. Это свойство утра-
утрачивается при обращенш; функцш обратпыя показательнымъ—
логариош1ческ1я п круговыя оказываются уже безконечно мпо-
го:шач1шми. Т'Ьмъ пе менее он'Ь обладаютъ всеми свойствами
однозначныхъ функщй, если только мы будемъ принимать во
вшшате одну какую либо определенную ветвь такой функцш,
напр, если мы за значение в, соответствующее u = ez будемъ
принимать г = lgp 4" ^' гд% lgp — действительный логариеыъ
модуля го, а & аргумента, и, не превосходящей тс. Воспользовав-
Воспользовавшись этими соображешяын, попробуемъ разыскать аналитиче-
аналитическое выражеше функцш П(ж).
Пусть ВС—данная прямая (фиг. 118), Л — точка вне ея,
АВ = у — перпендикуляръ изъ А на ВС. Пусть AD — какая
либо прямая, проходящая чрезъ точку А, отрезокъ BD = %,
уголъ BAD = Q. Такъ какъ две прямыя пересекаются только
въ одной точке, то каждому знатенш G будетъ тогда соответ-
соответствовать одно и только одно значеше ж, а потому, согласно
вышесказанному, каждому значешю tgG будетъ соответствовать
одно п только одно значеше tghx и обратно. Посему tg6 и tghx
доляшы быть связаны между собою лпнейнымъ соотношешемъ,
А1ф-\-В тт	.
т. е. соотношен1емъ вида tghx = р. ,, .-г Но при о = 0 п
х = 0, а потому tgO и tghx обращаются въ нуль одновременно;
сверхъ того обе функцш прп переходе чрезъ нуль леняютъ
знакъ; посему необходимо В=0, G=0, и искомая зависи-
зависимость принпмаеть впдъ tghx — tgAQ. Пусть теперь 0о — уголъ
параллельности для у, такъ что 0о ^ П(?/), тогда х0 = со,
откуда ^

262
Возьмемъ теперь какой либо треуголышкъ ЛВС прямо-
прямоугольный при точки С, такъ что гипотенуза его будетъ с, ка-
катеты а и Ь. Изъ посл'Ьдпяго соотношешя лаходилъ (rotglia =
d(h)cotgA. cotglil = d(a)cotgB, откуда, згигЬчая, что cos/r = х \ =
~smh2x, находпмъ:
sin7m
ср2 (b) -|- smh'-a-{- cp2 (b) sinh2a
sinhh
sinB —
(a) + sin/*2Z» + <p8 (a) s
Такъ какъ sin^l долженъ обращаться въ единицу при а = г
и въ siiiB при а^=Ь, то выражешя полученный необходимо
Да)
должны оыть вода -т^ и
с) /\с)
= siuh (а). Посему вообще доляшо быть
или послЬ небольшихъ иреобразовашй:
что возможно только прп ъ (а) =
= cotg Щу) = smhy,
1	»
cotg 2 1%) = е
Это выражеше дано Лобачевскпмъ, послт; продолжительныхъ
весьма сдожиыхъ, хотя и болт,е прямыхъ геометрнческпхъ со-
ображешй.
Перейдет, теперь къ пзученш зависимостей между сторо-
сторонами п углами треугольника.
Пусть ЛВС ни'Ьетъ углы Л =
= Ща), В = Щ$) и С' = П(Т). На
гторонт, ВС (фиг. 122) отложпмъ
отр'Ьзокъ CI) :=у и па сторонгЬ АВ
отрЬзокъ ЛЕ = а; изъ точекъ I) и
в Е возставпыъ перпендикуляры DD'
и ЕЕ' къ соотвгЬтственныиъ сто-
ронамъ и проведемъ прямую ВВ',
параллельную прямой DD', а по-
потому и ЕЕ'. Такимъ образолъ у
насъ получаются углы
= Ща — у) п
Е

2G3
связанный между собою соотноннхпемъ Пф) =: П(а — у) —
—П(с — зс). Отр-Ьзкп а и у должны быть взяты съ обратными
зпакомъ, если соответствующее нмъ углы будутъ тупые.
Съ помощью этого соотиошешя могутъ быть найдены вст>
остальныя иавпспмотг между сторонами п углами треугольника.
Если стороны какого либо угла ВАС (фиг. i2i)
пересЬчемъ двумя прямыми, перпендикулярными къ АВ,
то отношеше меньшаго отрезка къ большему на этой
сторон-fc будетъ больше отношешя соотвЬтствующихъ
отр-Ьзковъ на другой сторонЪ.
Чтобы убедиться въ этомъ, отложиыъ на АС произвольное
число равныхъ отръ'зковъ Аал ^= ^а^ ^ й2а3 = ... =ап_1С и
изъ полученныхъ точекъ возставшгь перпендикуляры къ АС,
которые пусть пересЬкутъ АС въ точкахъ b1} b2,.. .bn—v С.
Разсмотримъ два какпхъ либо смежныхъ изъ полученныхъ че-
тыреугольниковъ: а1,_1а„Ь11_лЬр и арар+1&р&р+1 • Перегнеыъ по-
полученную фигуру по прямой арЪр; тогда точки ар+1 и ар_±
совпадутъ, а потому совпадутъ и прямыя ар^1Ьр_1п а]1+1Ьр+1-
Въ полученномъ такпмъ образомъ треугольники bvhv__^v^
очевидно, уголъ Ьр+1 будетъ меньше угла ЬР_1У а потому и
сторона bj_xbv меньше стороны ЬрЬ'р+1 Ьр Ър+1, такъ что отръ-зки
эти возрастаютъ по мгЬръ" удален1я отъ точки А, откуда п слъ1-
дуетъ высказанное предложеше.
ПримЬняя эту Teopeiry къ прямоугольному треугольнику,
найдемъ, что квадратъ гипотенузы больше суммы квадратовъ
катетовъ. Изъ той же теоремы заключаемъ, что разстояте
между двумя перпендикулярами къ одной прямой возрастаешь
по мгьргь удаленья ихъ отъ нея до безконечности. Разстояте
меэюду двумя параллельными прямыми возрастаетъ въ одну
сторону до безконечиости, а въ другую убываетъ до нуля.
Не останавливаясь на доказательствахъ этпхъ предложешп,
перейдемъ къ последнему предложение седьмой главы:

2в4
Перпендикуляры, возставленные изъ средииъ сторонъ
треугольника, могутъ пересекаться въ одной точкъ-,
или вовсе не пересекаться, или быть параллельными.
Если два изъ этихъ перпендикуляровъ переськаются,
то необходимо и третш пропдетъ чрезъ точку ихъ пе-
рес?чегая; это очевидно. Если эти перпендикуляры не
пересЬкаются, то параллельность двухъ изъ нихъ вле-
четъ за собою и параллельность имъ третьяго.
Приведемъ доказательство этого предложешя только для
одного случая, именно, когда углы А и С треугольника ЛВС
(фиг. 123) острые и перпендикуляры изъ срсдшгь сторонъ его
А В п ВС параллельны. Эти перпендикуляры необходимо пере-
с-Ькаютъ сторону АС треугольника въ точкахъ Ж и N, лежа-
щпхъ съ разныхъ сторонъ средины ея Н, такъ что перпендп-
куляръ, возставленный къ АС въ
точк'Ь Н долженъ лежать между
с ниип, а такъ какъ онъ пересЬ-
каться ни съ однимъ изъ нпхъ не
ыожетъ, то онъ пыъ долженъ быть
параллеленъ.
Последнее обстоятельство пока-
зываетъ, что чрезъ три данныя
точки не всегда можно провести
кругъ, и что круъъ съ возрастангемъ радгуса не моэюетъ стре-
стремиться къ прямой, ибо нначе перпендикуляры къ одной пря-
прямой были бы параллельны.
Предъльнымъ положешемъ круга должна, следовательно,
служить какая-то другая лпшя, обладающая тгЬмъ свойствоыъ,
что перпендикуляры изъ срединъ хордт, ея век параллельны
другъ другу. Эту кривую Лобачевсый называетъ предельною
кривою, перпендикуляры изъ средины хордъ ея—осями предель-
предельной кривой, поверхность, происшедшую отъ вращешя предельной
кривой около одной пзъ ея осей,—предельной поверхностью.
Бея восьмая глава посвящена именно изучению свойства,
этпхъ пред'Ьльныхъ лшпй п поверхностей.

265
Въ саыомъ опред-Ълепш предельной кривой уже указывается
и способъ построешя. Именно, на данной прямой .47? стропыъ
уголъ П(а) нрп точки А и на полученной прямой отклады-
ваемъ отргЬзокъ. АС= 2а; точка С будетъ лежать на предель-
предельной кривой. Такпмъ образимъ по точкамъ можеыъ построить н
всю предельную кривую. Изъ самаго способа поетроешя ея
видно, что дугп ея нокрываютъ сами себя во всйхъ частяхъ, и
что кругъ не можетъ пересечь ее более, чЬмъ въ двухъ точкахъ.
Подобными же свойствами должна обладать, конечно, п пре-
предельная поверхность. Плоскость, проходящая по осп поверх-
поверхности, перестяетъ ее по предельной кривой, всякая другая пло-
плоскость—по кругу. Предтзльныя лпшп
на предельной поверхности играютъ
ту же роль, какъ прямыя па плоско-
плоскости п, такъ какъ сумма двугранныхъ
угловъ, происходящпхъ отъ пересече-
шя трехъ плоскостей по пряыымъ, па-
раллельнымъ другъ другу, равна тс, то
сумма угловъ предельнаго треуголь-
треугольника равна %, такъ что на этой поверх-
поверхности геояетр1я Евклида применима
вполне и безъ всякпхъ ограничешй.
Въ заключеше укажемъ eni,e
одно метрическое свойство предельной
кривой.
Пусть АВ и А'?'—дуги предельныхъ крпвыхъ (фиг. 124),
нересеченныя парою параллельныхъ прямыхъ АА' и ВВ'; по-
кажелъ сначала, что отношете этихъ дугъ не завпснтъ отъ
пхъ длины. Для сего разделнмъ дугу АВ па п равныхъ частей
и чрезъ точки деления А1} А2,.. .А„_г проведемъ прямыя
АХА^, А2А2'... А„_1Ап_11, нараллельныя нрямымъ АА'ъ ВВ'.
Эти прямыя разделять дугу А'В' также на п равныхъ частей,
пбо по свойство предельной кривой полоса ААХА^А] можетъ
быть совмещена съ полосою А1А2А'2А'1 п съ каждою сле-
следующею, при чемъ, следовательно, будуиъ совмещаться также
ц дуги А'А^, А\А'2 и т. д. Отношете дугъ двухъ предель-
пыхъ крпвыхъ между двумя параллельнымп прямыми завнсптъ,

266
следовательно, только отъ разстояшя этнхъ крпвыхъ другъ отъ
друга. Если это разстояше будеть х п еслп отношеше двухъ
дугъ, разстояше между которыми равно едишпгБ, примелъ за С,
то это отношегпе будетъ выражаться числомъ Ст, при чемъ С
должно быть необходимо больше единицы. Полагая С — е, гд-Ь е -
основаше Неперовыхъ логарпомовъ, можемъ предстаыш, это
отношеше въ вид1!;
8 АВ Г
S'~A4J< ~e '
На этомъ п закончпмъ пзлоя;ен1е геометрическпхъ пзсл4до-
Лобачевсх;аго.
Результатоыъ втихъ изсл4доваи1й явилась новая, вполне строй-
стройная и строго логическая система Геометрш, которая должна
была бы заменить Геометр1Ю Евклида, если бы его одиннадцатая
aKciojia оказалась ложной. Но непосредственный пзмтзрешя, на-
прим'Ьръ пзм^рен1я суммы угловъ треугольниковъ, вершинами
которыхъ служатъ весьма отдаленныя отъ насъ и другъ отъ
друга пеподвпжныя звезды, не обнаруживают замЬтныхъ откло-
nenifi отъ этой аксюмы; посему Геометр1я Евклида вообще для
любыхъ разстоянШ или по крайней siipi для разстоятй, съ
которыми памъ приходится пмъ-ть д4ло, доляша имт^ть м4сто
безусловно.
Вопросъ о реальномъ существованш Геометрш Лобачевскаго
и о значенш одиннадцатой акглоыы въ Геометр1п Евклида оста-
оставался, следовательно, открытымъ. Решен1елъ этого вопроса пер-
первый началъ заниматься одпнъ изъ наиболее выдающихся со-1
вреыенныхъ геометровъ, птальянск1й ученый, професгоръ Bel-
trami, работы котораго и открываюсь собственно, иынгЬ уже
й&ьыа обширную, область изсл4довап1й по геолетрш Лобачев-
Лобачевскаго. Въ своеыъ «Saggio di Interpretazione della Geoinetria поп
Euclidea»,ii3aTrib№Bb«J1eoria fondamedtale degli Spazii di Curva-
tura coustante» въ 1868 году онъ показываетъ, что FeoMeTpifl
Лобачевскаго для двухъ пзмЬрепШ, т. е. соответствующая Ге-

267
ометрш Евклпда на плоскости, вполпЪ пртгЬшша па. поверх-
ностяхъ, тгЬющпхъ постоянную отрицательную кривизну, ко-
тирыя онъ называетъ псевдосферическими поверхностями.
Такиыъ образоыъ, реальное представлеше для си-
системы Лобачевскаго, по крайней ьгЬр-Ь для двухъ изы Ь-
peHifl, было найдено, а вм-ЬстЬ съ тЪмъ былъ рЬшенъ
вопросъ о значенш одиннадцатой аксюмы Евклида. Эта
аксюма отличаетъ плоскость отъ псевдосферы.

Некоторые фокусы.
Еъ области здраваго развит смекаткп слЬдуеть отнести
ум'Ьнъе пайтись не только нрп pbmeiiin какого-либо хитро-
умнаго вопроса, пли при выяснен ш математпчеекаго парадокса
и софизма. Необходимо, кром-Ь того, развивать въ себт, навыкъ.
чтобы различать истинно математическую задачу отъ простого
фокуса, основаннаго на отвода глазъ или попросту иногда—
обланъ1. Нисколько образцовъ распространенныхъ фокусовъ по-
добнаго рода мы н разъясняемъ въ этомъ отд'Ьл'Ь, начиная съ
простМшаго изъ нихъ.
Странная истор|'я.
На столФ лежитъ б спичекъ (пли иныхъ какихъ предме-
19 3 4 5
товъ) | | | | | и въ каждой руки держатъ по одной. Теперь
разсказываютъ такую исторпо:
Пять овецъ E сппчекъ) паслись на лугу, а въ л icy нахо-
находились 2 разбойника (показываютъ ooi спички въ рукахъ).
Разбойники укралп овецъ одну за другой (берутъ Л? 1 л'Ьвой
рукой, № 5 правой, № 2 лг1;вой, № ± правой, № 3 л'Ьвой).
Въ это время прпшелъ пастухъ, и разбойники отпустили овецъ
обратно (кладутъ обратно на столъ 1 спичку пзъ правой руки,
1 изъ лЬвой, 1 изъ правой, 1 изъ лт.вой, 1 пзъ правой (Те-
(Теперь въ лЪвой рукт; находятся 2 спички, въ то время, какъ
зрители счптаютъ, что въ каждой руки — по одной).
Пастухъ удалился, п разбойники опять забрали одну за дру-
другой всЬхъ овецъ (пачпнаютъ брать .тгЬвой рукой). Но въ это

209
время пришли солдаты, и разбойники убъ-жали, оставивъ оведъ
въ л-Ьсу. Открываютъ руки, п въ самомъ д^лЪ: въ одной рукгЬ
5 овецъ, въ другой 2 разбойника.
Эта веселенькая, хотя нисколько и странная, ncropifiKa
основана, очевидно, только на быстрот^ разсказа п постоян-
номъ подсовыванш внЬ очереди лйвой руки вместо правой.
Какъ ни проста этотъ «отводъ глазъ», но сначала оиъ уди-
вляетъ.
Феноменальная память.
Знаменитый «счетчнкъ» Жакт. Иноди—пропзнодивгшй въ
умъ1 математически дг1зйств1я надъ миогознаннымп числами,
обладалъ, прежде всего, поистлнъ1 феноменальпой памятью чи-
селъ—онъ запомпналъ сразу длишгЬйнпе ряды цпфръ и повто-
рялъ ихъ безъ ошпбки, Словно читалъ по писанному. Здйсь мы
им'Ьемъ дъ'ло съ ръ-дкпмъ прпроднымъ даромъ. Совс^мъ другое
дЪло, когда такую же способность демонстрируют нредъ пу-
блпкой провинц^альныхъ городовъ за4зж1е фокусники. Вдъ'сь д-Ьло
вовсе не въ памяти, а въ прим^непш остроумнаго н крайне
простого мнемонпческаго прхема. Полагаеыъ, что читателю небе-
небезынтересно будетъ съ нпмъ ознакомиться, чтобы ум^ть, при
случай, отличить истпнпую, природную способность отъ про-
простой уловкп.
Вотъ прпмъ'ръ. Фокуснпкъ дпктуетъ вамъ несколько длин-
п^Пшихъ рядовъ цпфръ и загЬмъ безъ зашшкп повторяетъ ихъ
сколько угодно разъ, не смъшпвая одного ряда съ другнмъ и
пе пропуская пп одной цифры.
Весь секретъ въ томъ, что фокусникъ твердо выучплъ не-
небольшую табличку, 1'ДГЬ каждой пзъ 10-тп цпфръ отв-Ъчаютъ
опред'Ьленныя согласныя буквы. Для тйхъ, кто пожелалъ бы
самъ позабавить своихъ гостей рядомъ эффектиыхъ фокусовъ,
мы нрпводимъ нпже такую табличку. Въ ней стоящимъ на-
наверху цнфрамъ отв'ячаютъ по двй согласныхъ буквы.
0.
II
м
1.
г
ж
2.
Д
т
3.
к
X
4.
ч
Щ
б.
п
б
6.
ш
л
7.
с
3
8.
в
ф
9.
Р
Ц

270
Для облегчеш'я небезполезнът будут, кое-каьчя мнемонпче-
ciiifl указашя. Что нулю соотвйтствуетъ буква н легко запо-
запомнить, м же похоже на н, стоптъ ст> ннмъ рядомъ вт> алфавит^.
Г похоже на единицу по начертанш. и часто при смягчепш
переходить въ ж. Буква д выбрана для двойки, какъ началь-
начальная и часто произносится, какъ т. Буква к вашшннаегь три,
потому что состоять пзъ трехъ черточекъ; съ х она родственна,
какъ гортанная. Ч—первая буква слова «четыре» и напоминает,
щ. П—первая буква пяти и родственна б. Точно также ш
напоминаетъ шестерку (л приходится просто запомнить), п с —
семерку; з—родственна с. В—первая буква слова восемь, ф -
родственна в. Наконецъ, р выбрана для девятки, такъ какъ
наноминаетъ ее, если перевернуть ее набокъ; ц —приходится
выучить.
Какъ ни смешны могутъ показаться эти мнемоничесшя
сблнжешя, они все же прппосятъ огромное облегчеше: зная
ихъ, вы въ одну-двй минуты твердо выучите приведенную
табличку и наверно провозитесь надъ ней цйлый часъ, если
пренебрежете ими.
.Затвердивъ табличку, вы можете уже изумлять 1плятелей ва-
вашей феноменальной памятью не хуже упомянутаго выше фо-
фокусника. Передъ тймъ, какъ продиктовать рядъ цпфръ, вы
вспоминаете какое-нибудь хорошо знаковое стихотвореше п мы-
мысленно заменяете въ немъ вей согласные звуки соотвйтстнеп-
ными цифрами. Пусть вами выбраны слгЬдуюиця четыре строки
изъ Пушкина:
Поэтъ, ые дорожи любонш народной,
Восторжепныхъ похвапъ лройдотъ мцыутный шуыъ,
Услышишь судъ глупца и см4хъ толпы холодной,
Но ты останься твердъ, спокооыъ и угрншъ.
Подставляя въ ум-Ь, вместо согласныхъ, отв'Ьчаюп^'я нмъ
цифры, вы диктуете сл'Ьдуюпце ряды чпеелъ:
520291G58O920
8729100353865922002060
766C7216597U32653620
2720728927530190

271
Если васъ, спустя сколько угодно времени, попросятъ по-
повторить продиктованные вами ряды цпфръ, то зная, какими
стихами вы пользовались, вы безошибочно воспроизведете вей
четыре ряда. Если васъ попросятъ сразу сказать, напрпмг1;ръ,
трети рядъ, то вы вспомнит; третью строчку («услышишь
судъ глупца...») и тотчасъ же назовете вей цифры ряда.
«Математическое ясновидЪше >.
Заговоривъ о фокусахъ, разоблачимъ тайну еще одного
весьма эффектнаго фокуса, которымъ ловше «прсстпдижаторы»
часто морочатъ провинциальную публику. Мы говоримъ о такъ
наз. «математическомъ ясновид^ши», «мантевизмй», «чтенш
мыслей» п т. п. «нулгерахъ», которые пересчпеляются въ цро-
граммахъ подобныхъ сеансовъ. Обыкновенно дъ-ло происходить
такъ. Фокусникъ выводитъ на эстраду свою «ясновидящую»,
усаживаетъ ее въ кресло и, для вящшей благонадежности, за-
вязываетъ ей глаза. Затъ'мъ онъ съ аспидной доской спу-
спускается въ зрительный залъ, ходить между креселъ и предла-
гаетъ зрителямъ самимъ написать какое-нибудъ число, меньшее
1000. Когда число написано, фокусникъ, оставаясь нопрежнему
среди зрителей, въ нартерт;, обращается къ ясновидящей съ
просьбой назвать это число—п та тотчасъ же выкрикиваетъ съ
эстрады это число, словно читая его на аспидной доски.
Озадаченные зрители пишутъ второе, третье число, въ оба
глаза слъущтъ за фокусникомъ и «ясновидящей», но ничего
подозрительнаго не открываютъ: фокусникъ спрагаиваетъ, —
«ясновидящая» отвйчаетъ.
Ни ясновидйтя, ни внушешя, ни чтешя мыслей вдйсь
однако никакого нт,тъ. Просто-на-просто фокусникъ и его по-
помощница твердо выучили уже приведенную выше табличку:
обращаясь къ «ясновидящей» съ просьбой отгадать число, онъ
ловко составляем, фразу какъ равъ изъ такихъ словъ, пе})выя
согласныя которыхъ означаютъ написанное зрителемъ число.
Вотъ и вся тайна этого эффектнаго фокуса.
Теперь вы и сами сможете произвести его, разъ Колумбово
яйцо уже поставлено. Вамъ необходимо только изощриться въ

272
составлен!ц соотвйтствующпхъ фразъ, въ быстромъ и ловкомъ
подыскнванш подходящнхъ словъ, начинающихся съ нужной
согласной. Но прежде всего вы должны какъ-нпбудь дать знать
вашей «ясновидящей», сколько цпфръ въ угаднваемоыъ чпсл'Ь:
одна, двгЬ или три. Д'Ьло въ томъ, что въ расчета принимаются
всегда только первыя слова фразы, и «ясновидящая» должна
знать, гд'Ь остановиться.
Для этого фокуснпкъ обыкновенно пользуется опять-таки
разъ навсегда условленными словами. Если задумано однознач-
однозначное число, то онъ начинаем, свое обращеше къ помощшщт,
всегда съ односложныхъ словечекъ: «А» или: «Вогь». Если на-
написано двузначное число, то вопросъ начинается двусложнымъ
обращешемъ: «Ну-ка» или: «Еще». Наконецъ, при трехзначпомъ
числи никакихъ условныхъ обращенШ не употребляютъ, такъ
что OTCyTCTBie въ началъ1 вопроса иеречисленныхъ чстырехъ
словъ указываетъ, что число трехзначное.
Теперь продйлаемь несколько опытовъ. Пусть написано
число 34; фокуснпкъ спрашиваетъ ясновидящую: «Ну-ка, какое
число написалъ этотъ господинъ?» Слово «ну-ка» указываетъ,
что число двузначное; какое = 3, а число = 4.
Пусть написано 92. Фокуснпкъ спраиншаетъ: «Еще разъ,
дружокъ, отгадай-ка!» Еще—дв? цифры; разъ = 9; дружокъ=2.
Написано 4. Фраза: «А что напнсалъ теперь этотъ госпо-
дпнъ? (А—одна цифра, что = 4).
Написано 207. Обращена: «Ты не устала? Какое же число
ссйчась паппсано?» (Отсутгапе условныхъ обращешй указы-
указываетъ на то, что число трехзначное; ты = 2, не = 0; устала = 7).
Какъ впдпгь читатель изъ этихъ нрпм'провъ, составлешс
подходящихъ обращснШ—Д'Ьло не Богь в'Ьсть какое трудное;
навыкъ npioopiTaeTCfl легко.
Часто фокусники нисколько видопзм'Ьняютъ онытъ: просятъ
зрителя обозначить какос-лпбо дгЬйств1е между двумя числами,
и мнимая ясновидящая сразу произпосптъ результата (если
только опъ не больше тысячи). Зритель шипеть, иапрньгЬръ,
11X14. И ясновидящая сразу отв'Ьчаетъ 154. Зная секреть
«мантевпзма», легко догадаться, что при этомъ фокусникъ сна-
сначала мысленно производить въ тм-Ь нужныя flificxBifl и ватъчяъ,

273
извгЬстцымъ уже способомъ, сообщаетъ помощниц^ результатъ.
Въ нашемъ npimip'b онъ можетъ обратиться къ ней такъ:
«Голубушка, прикинь, что составляется изъ этихъ чиселъ?»
(г=1; п = 5; ч = 4).
Можно еще бол'Ье изумить публику, если заставить «ясно-
«ясновидящую» сообщать не только конечный результатъ, по и ука-
указать, отъ какого д'Ьйешя онъ полученъ—сложешя, вычиташя,
умножен ]'я или д'Ьлешя. Для этого опять-таки приб'Ьгаютъ къ
условнымъ обозначешямъ. Именно, связываютъ съ гЬыъ или
пнымъ дгЬйств1емъ определенный буквы, на этотъ разъ—глас-
ныя: о обозначаетъ сложеше, ы или и—вычиташе, т или е—
дгьлеше, и, наконецъ у—?/множеше.
Подобнымъ же образомъ «ясновидящая» можетъ угадывать,
напр., день или годъ рождения. Кто-нибудь пзъ публпкп ии-
шетъ эту дату на доски, фокусникъ проситъ помощнику про-
прочесть написанное и получаетъ вио.тн'Ь точный отвить. Зд^сь
число месяца н годъ рожден1я сообщаются ей, какъ и всяк1я
другая числа, а лъсяцъ—условной цифрой. Напр. 25 марта =
= 25 и 3, такъ какъ мартъ треий вгЬсяцъ.
Хотя гг. фокусники будутъ на насъ въ большой претензш
за то, что мы разоблачаеыъ ихъ незамысловатыя IIpoфeccioнaль-
ныя тайны, мы все же разсыотрпмъ еще одинъ фокусъ. Разъ
ыы забрели въ этотъ уголокъ «царства смекалки», то ужъ осмо-
трпмъ его иовнпмательн'Ье.
Отгадыван1е камней домино.
Этотъ салонный фокусъ обычно также выдаютъ за «чтен1е
мыслей». Но «чтете мыслой» здгЬсь такого сорта-, что вы сами
можете осуществить его, пе обладая никакими сверхъестествен-
сверхъестественными способностями.
Вы заявляете свопмъ гостямъ, что беретесь отгадать заду-
задуманный пмп камень домпно, находясь съ завязанными глазами
въ дальнемъ углу залы пли даже въ сосЬдней комнатъ1. И дей-
действительно, когда гости, выбравъ пзъ груды камней любую ко-
костяшку, спрашпваютъ васъ, какой это камень,—вы сразу же
отвечаете, хотя не можете вид'Ьть пе только камни, но даже гостей.
ВЪ ЦАРСТИ* СМЕКАЛКИ.	18

274
Объяснеше фокуса.
У васъ долженъ быть сообщникъ среди гостей, съ которыыъ
вы предварительно условились, что лпчныя и притяжательныя
ы4стоимешя будутъ означать опред'Ьленныя числа, именно:
я, мой—1
ты, твой—2
онъ, его—3
мы. нашъ—4
вы, вашъ—5
они, ихъ—6
Пусть гостп выбрали камень 4/з. Тогда вашъ сообщнпкъ
обращается къ ваиъ съ такой фразой: «Мы задумали камень,
отгадайте-ка его!» Если нужно «протелеграфировать», напр., 1/ъ,
то вашъ сообщнпкъ, улучикъ моментъ, вставляетъ такую фразу:
«Л я думаю, что вы на этотъ разъ не угадаете». Фраза: «Ну,
теперь у насъ татае камни, что теой ихъ не угадать»—озна-
чаетъ 4/2 и т. п.
Само собой понятно, что им'Ьютъ значеше лпшь первыя
два мъ'стоимешя. Для обозначения бйлаго поля также выбп-
раютъ какое-нпбудь слово, напр. сударь: «отгадайте-ка, сударь,
что мы тутъ задумали» будетъ означать %.
Какъ ни просты секреты этихъ фокусовъ,—ихъ, все же,
трудно рачгадать. Нужно обладать большой смёткой, чтобы до-
догадаться, къ какой уловк'Ь прпб'Ьгъ фокуснпкъ.
Хитрая механика!
Вотъ еще два фокуса, при ловкомъ исполненш которыхъ
иной иожетъ подумать, что вд-Ьсь и въ самомъ д^л-Ь таится ка-
какая либо «хитрая
механика».
Между указа-
тельнымъ и боль-
шпмъ пальцамп
каждой руки я
по спички,—спичку въ лтшой рук-Ь горизонтально, въ
правой вертикально; я приближаю руки другъ къ другу такъ,
чтобы снички скрестились (фиг. 125). Теперь я д-влаю быстрое
Фиг. 125.
Фиг. 126.

276
Фпг. 127.
движете руками... и спички опять образуютъ креетъ, но теперь
горизонтальная спичка находится по другу10 сторону вертикаль-
вертикальной (фиг. 126). Снова дФлаю движете рукамп, п спички снова
находятся въ первоначальномъ ноложеши. Можно повторить этотъ
фокуеь нисколько разъ, но никто не ыожетъ попять, какъ это
делается.
Этотъ фокусъ, требуюнцй предварительнаго небольшого упраж-
упражнения, производится следующим?, образомъ. Вертикальная спичка
помещается головкой внивъ, такъ что последняя покоится на.
большомъ иальцъ1, въ то вреля какъ указательный падецъ опи-
опирается о другой ея конецъ. При не-
болыномъ сдавливанш этихъ пальцевъ
спичка иристаетъ къ указательному
пальцу. Теперь стоить только слегка
раздвинуть пальцы, и спичка удержи-
удерживается однпмъ указательнымъ паль-
цемъ—какъ бы виситъ на немъ (фиг. 127). Черезъ получен-
полученное такиыъ образомъ маленьщй нрозорь между еппчкой и боль-
шимъ пальцемъ вы быстро н незаметно для другихъ вводите
и выводите горизонтальную сничку, веяюй разъ тотчасъ же за-
закрывая отверсие.
По середин'Ь двухъ спичекъ проводятъ поперечную черту.
Вольшпмъ и указательньшъ пальцами правой руки берутъ спички
такъ, чтобы объ- черты были видны сверху (фиг. 128), вслъугь
ватъчяъ tumii же пальцами л'Ьвой
руки поворачиваютъ эти спички
на полъ-оборота вокругъ ихъ ко-
короткой оси (т. е., принимая черту
за ось вращешя) такъ, что пальцы
правой руки будутъ уже касаться
противоположные концовъ спичекъ (фиг. 129). Теперь спраиш-
ваютъ: «черточки- -сверху или снизу?* Всяшй отвъчитъ: «снизу»,
п ошибется, если, поворачивая спички вокругъ ихъ короткой оси,
вы въ то же время, въ пальцахь л^вой руки, незаметно повернете
ихъ вокругъ длппиой оси (т. е. осп, параллельной длинт; спичекъ).
18*
Фиг. 128.
Фиг. 129.

27fi
Математика, какъ упражнеше въ искусствЪ хорошо говорить.
Ценность перевода съ иностраннаго языка заключается въ
умъ'нш проникать въ тайники мысли, изложенной на чужомъ
языкгЬ. Ценность рисовашя состоитъ въ наглядпомъ изображе-
нш точны хъ cooTHonieHift частей п персиектпвы. Ценность есте-
естествознания—въ развитш независимости мысли. Bci эти иоложе-
шя известны прпступающпмъ къ пзученш щлемовъ краснор^-
ч1я; къ выработк'Ь въ себЬ ум'Ьнья говорить плавно, убедительно
и красиво. Начинающее свою жизненную карьеру часто говорить
о польз'Ь пзучешя перечпеленныхъ наукъ. Но р'Ьдко слышно о
математическихъ чтешяхъ и упражнешяхъ, какъ объ образцахъ
красиоргЬч1я. А между тгЬмъ математика пмъ'етъ въ этомъ отпо-
шешп свои несомн'Ьпныя преимущества иередъ вс^ми назван-
названными пауками и искусствами.
Ц'Ьль, къ которой долженъ стремиться говорящ1й, состоптъ
въ томъ, чтобы заставить другихъ сосредоточить все свое шш-
маше на мысли и убтжденш оратора, заставить ихъ отвлечься
отъ ихгь собственной личности. И ни въ одной аудиторш, мо-
жетъ быть, не достигается эта цгЬль легче, чт;мъ въ аудиторш
математика.
Сжатое разсужде1пе, точное доказательство, изображеше не-
обходимыхъ выводовъ пзъ данпыхъ предположешй ириковываютъ
и сосредоточиваю™ всЬ умственныя силы какъ объясняющаго,
такъ и слушающаго.
Въ какихъ иныхт, случаяхъ, пзучающ1й инстинктивно наидетъ
легчайшую возможность въ немногахъ словахъ изложить многое?
Въ какпхъ иныхъ обстоятельствахъ, следовательно, простая,
не бьющая на эффекта, но легкая и красивая форма изложешя
будетъ такъ уместна и плодотворна, какъ здъеь? Вычурность
и аффектап,1я, какъ результаты дурной привычки рисоваться, не
нм^ють вд1сь ы4ста п потому быстро исчезаютъ! Между т'Ьмъ
всЬ друия особенности уменья говорить находять вд-Ьсь при-
мгЬнен1е п постепенно развиваются при общемъ и связномъ тече-
пш мыслей объясняющаго и слушателей.
Одинъ наблюдатель, самъ математикъ, говорнтъ, что oiiy
удалось отметить не более двухъ прпм'Ьровъ вычурности въ

277
чтешя и изложенш лекцш по математики. И въ обоихъ слу-
чаяхъ эта манера исчезла сама собой и незаметно. Въ одномъ
случай жешщша-лекторъ сд'Ьлала введете въ курсъ очень ма-
манерно и вычурно, но тотчасъ же невольно перешла на совершенно
другой топъ, такъ какъ слушатели обратили ея внпыаше нгЪ-
которымп вопросами на сущность предмета и заставили ее со-
собрать всЬ сплы, чтобы объяснить все понятно.
Постоянная необходимость объясиительныхъ чертежей npi-
учаетъ лектора п слушателя также къ шшострацш свопхъ мыслей.
Эффектъ математпческаго краснорг1шя долженъ заключаться
Вт. яснолъ, сжатомъ и точпомъ выводъ1 изъ нзвЬстныхъ фактовъ.
Къ такимъ щломамъ л къ такому образу мышлешя должеиъ
npi учаться матеыатцкъ-ораторъ.
Было бы, пожалуй, хорошо, еслпбы во вейхъ пашпхъ шко-
лахъ не только такъ называемыхъ «точныхъ» наукъ, но п въ
школахъ пли обществахъ, обучающпхъ красноргЬч1ш, было бы
написано пзвЬстное изречехйе Платона: -Пусть не входить сюда
никто не знакомый съ геомег[леи!»
Рисунокъ изъ «Margarita Philosophical
A503 г.). ITpejKHift абакъ и повыя цифры.

0ГЛАВЛЕН1Е.
		Ill
Задача 1. Гд^ начинается новый годъ		1
з> 2. Три воскресенья на одной нед'Ъл'Ь		6
» 3. ОпредЬтеше направлетя съ помощью карманныхъ
часовъ		11
Задача 4. Сколько воды въ бочкъ1		14
» 5. Крестъ обратить въ квадратъ		15
» 6. Коврикъ		16
» 7. Оригинальное доказательство		17
» 8. Вычерчиванье циркулемъ овальныхъ лин!й		18
» 9. Теорема Пиеагора		19
» 10. Египетская задача		20
Начатки математики на НилЪ		22
Задача 11. Численный кругъ пиеагорейцевъ		23
» 12. Земля и апельсинъ		26
Обманы зрЪшя. Кажущееся вращеше		29
Задача 13. Какая лишя длиннее?		32
» 14. Двъ1 пары дугъ	• . .	34
» 15. Какъ написано слово?	:		35
16. Какая кривая?		—
Задачи и развлечеьпя со спичками		37
Задача 17	• . 		—
18		38
» 19	 		—
30.		—
» 21		—
» 22		—
23		39
» 24	 . .'		—
25		40
26.		—
27. Дкпежъ сада ... 		41
-> 28. Сообразите-ка!		—
» 29. Разстановка часовыхъ		42

280
Задача 30. Хитрецы 	 . 		43
» 31		—
» 33. Верная отгадка		44
» 33. Собрать въ группы по 2	 		45
» 34. Собрать въ группы по 3 .... 		46
» 35. ПереагЪщеше лошадей 		—
» 3E. Поднять одной спичкой 15 сппчекъ		47
» 37. Спичечный телеграфъ		48
» 38. Легко или н-Ьтъ		—
Лабиринты 	 		50
Геометрическая постановка задачи о лабирннтахъ		5S
РЪшеше задачи		60
Филадельф1нсгай лабпринтъ		63
Задача 39. Хижина Розамунды		65
» 40. Еще лабиринтъ	 		6С
Общ1я замЪчашя		—
Задача 41. Картографически"! вопросъ		68
О весьма большихъ и весьма малыхъ числахъ		70
Задача 42. Довольно большое число		73
» 43. Лавины		74
» > Прогрессия размножешя		77
> 44. Загадочная автобюграфя	 ...	81
Новый родъ задачъ		84
Задача 45. Написать единицу 3-мя пятеркамЕ		—
» 46. » нуль 3-мя пятерками	¦ .	85
» 47. » два 3-ыя пятерками		—
» 48. » пять 3-мя пятерками		—
» 19. » 31 пятью тройками		—
Общее рЪшеше		8G
Сто тысячъ за доказательство теоремы	 • . .	90
Изъ области изучешя^чиселъ	 . . . .	96
Задача 50. Быстрое возвышеше въ квадратъ		—
Особенные случаи умножешя	-	97
Девять	 		99
Задача 51	•		100
» 62		101
» 53		102
54		—
Некоторые числовые курьезы		103
О числахъ 37 и 41 ¦....• • • • •	—
Числа 1375, 137G и 1377		104
Степени чиселъ, состояшш изъ одн-ьхъ и гЬхъ же цнфръ ....	105
Квадраты чиселъ, не содержащая одн-Ьхъ и т'Ьхъ же цифръ . .	—
Все разныя цифры		106
Числа, отличающаяся отъ своихъ логаривмовъ только агЬстомъ
запятой, отд-Ьляющей десятичные знаки	• . . .	—
Круговыя числа		107

281
СТГАН.
Полезное прим-Ьнеше		111
Задача 55. Мгновенное умножете	•		—
Несколько зам4чанш о числахъ вообще .... 		114
Графики	 		116
Решете уравнешй		121
Задача 56. Знаменитая задача Люка		123
з> 57. Курьеры		125
» 5S. Собака и два путешественника		126
Объ аксюмахъ элементарной алгебры		128
О приложены! аксюмы къ р-Ьшенпо уравненШ 		131
ПровЬрка р-Ьшетя уравнения	¦ . - .	136
Софистическая карикатура 		137
Неправильные отв-Ьты	 		138
Алгебраические софизмы		139
Задача 59		140
» 60.		—
» 61. Д-Ьлежъ верблюцовъ		147
Положительныя и отрицательныя числа		148
Задача 62. Два общих ь напбольшихъ делителя		150
Наглядное изображеые комплексныхъ чиселъ		151
Правила знаковъ при алгебраическомъ умножена		156
Геометрические софизмы		160
Задача 63. Искусная починка		—
» 64. Обобщете того же софизма		163
Рядъ Фиооначчи	••....	1E5
Задача Со. Похоже, но не то		167
у- 66. Еще парадоксъ	•		1G9
Три знаменитыхъ задачи древности 		170
Задача 67. Линейка и циркуль. Трисекцш угла		173
Дв? отрицательныхъ вывода XIX вЪка		17с
Николай Ивановичъ Лобачевскш	 . .	180
Два письма о постулат-Ь Евклида		194
Выяснен1е трехъ постулатовъ о параллельныхъ лин!яхъ . . .	1!'8
Сумма угловъ треугольника		202
Задача 68. Несколько «коварныхъ» вопросовъ		204
О четвертомъ шм^ренга по аналог1и	•		205
Въ стран* чудесъ математики 		206
Случай съ Пляттнеромъ	 		219
Зам%чанш кь «Случаю съ Пляттнеромъ»		225
Математика въ природ*	 		230
«Золотое дЪлеше»		—
Золотое дЬлеше въ эстетикЬ		234
Законъ листорасположен!я		236
Математнчесюй инстинктъ пчелъ	,. . . .	240
Задача 69. О пчрлины ячейки		243
Жукъ-геометръ		24G
Эволюта и эвольвента		248

282
СТРАН.
Задача 70. Построеше жука геометра		250
"Новыя начала геометрт»		251
Некоторые фокусы		268
Странная истор!я		—
Феноменальная память		209
«Математическое ясновид'Ьте»	 .... .	271
Отгадывате камней домино		273
Объяснете фокуса		274
Хитрая механика		275
Математика, какъ искусство хорошо говорить-	 . .	276